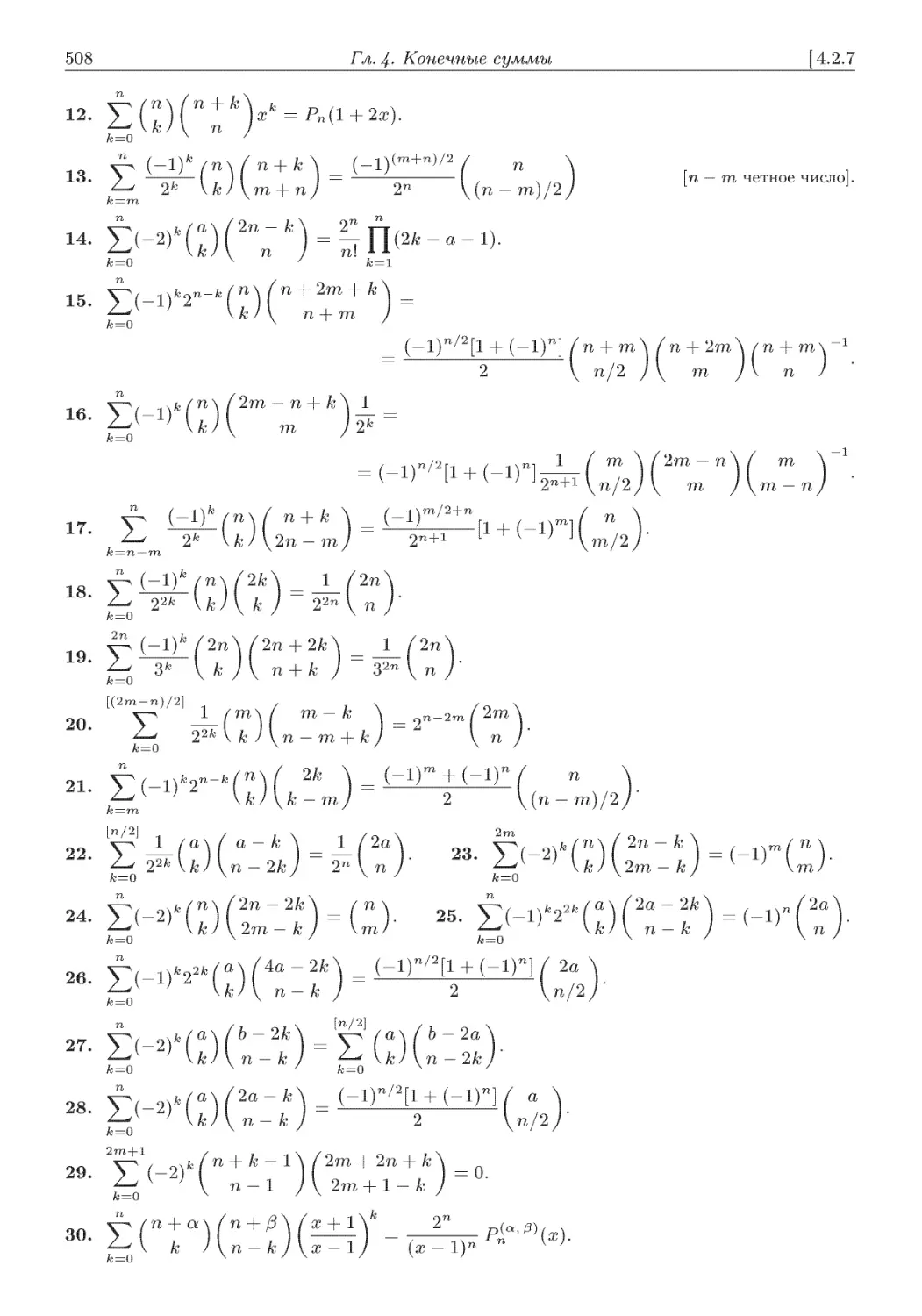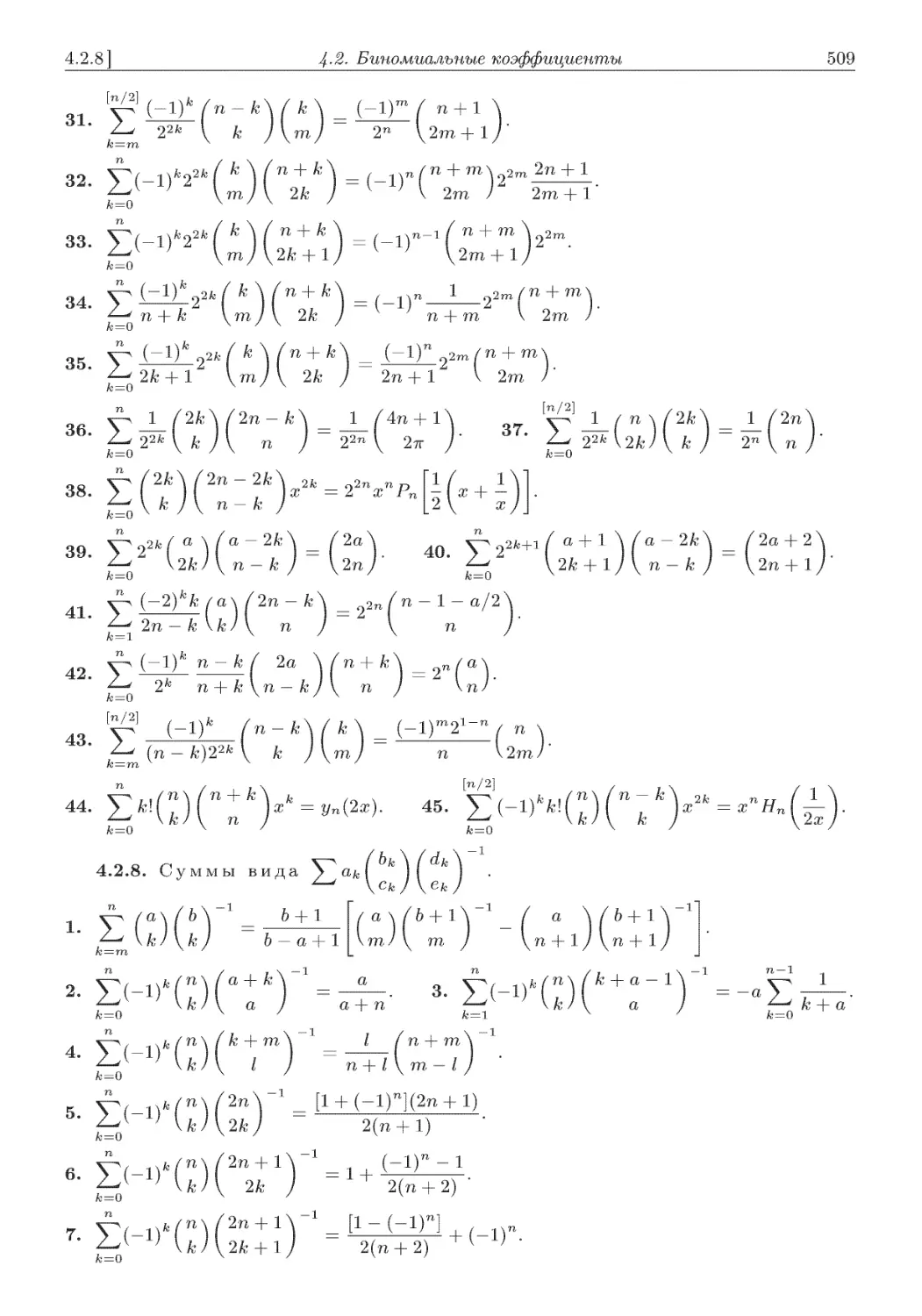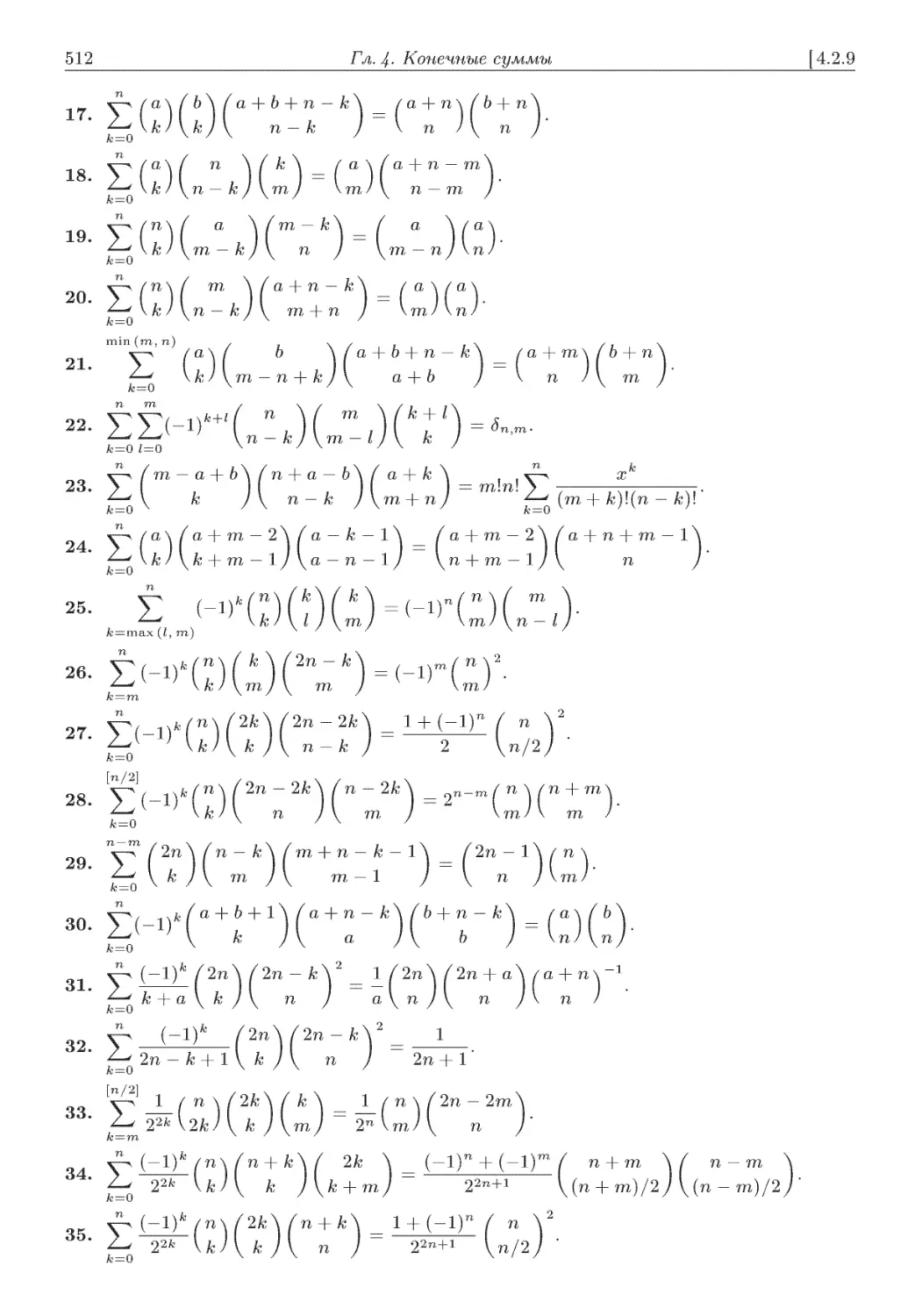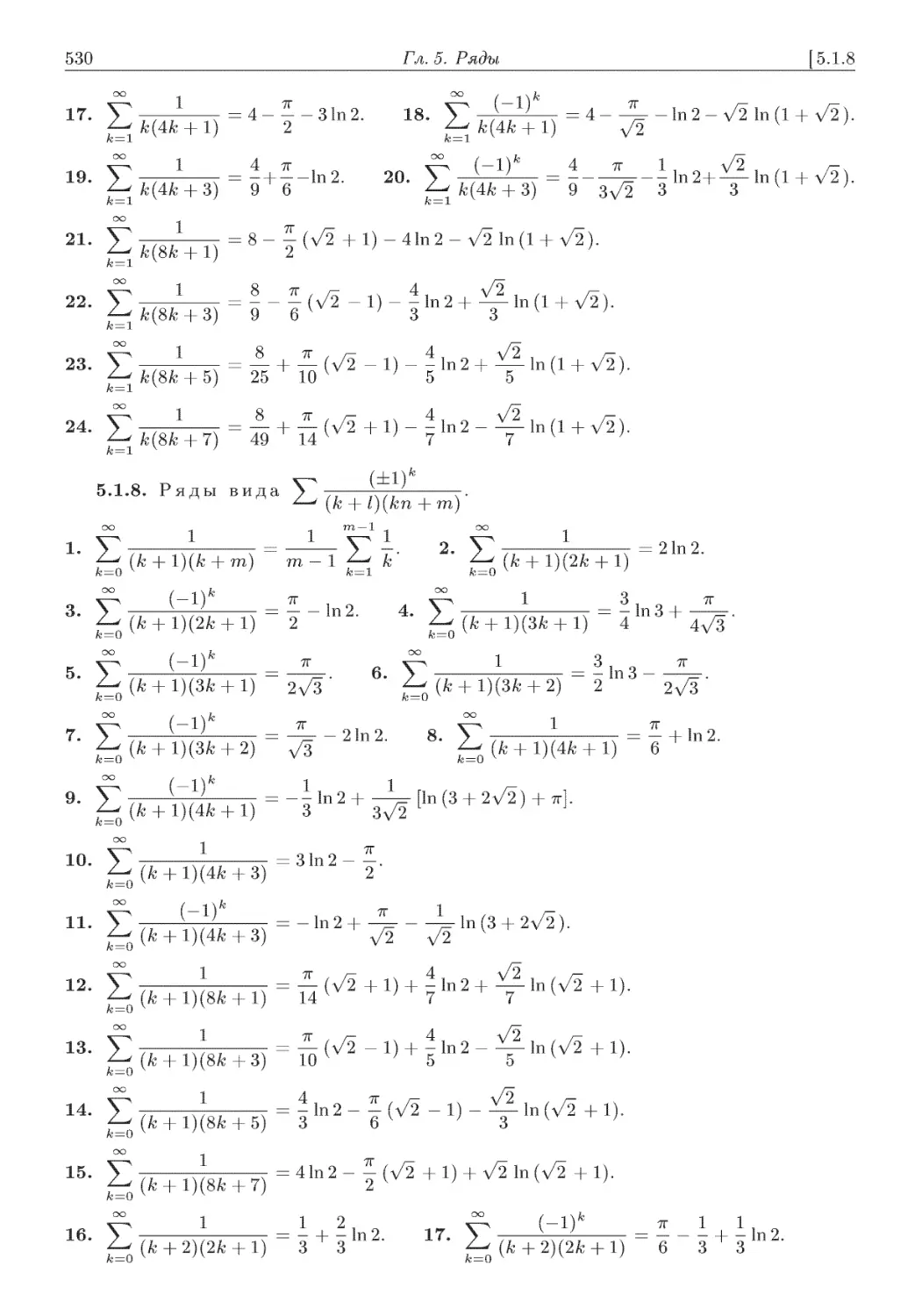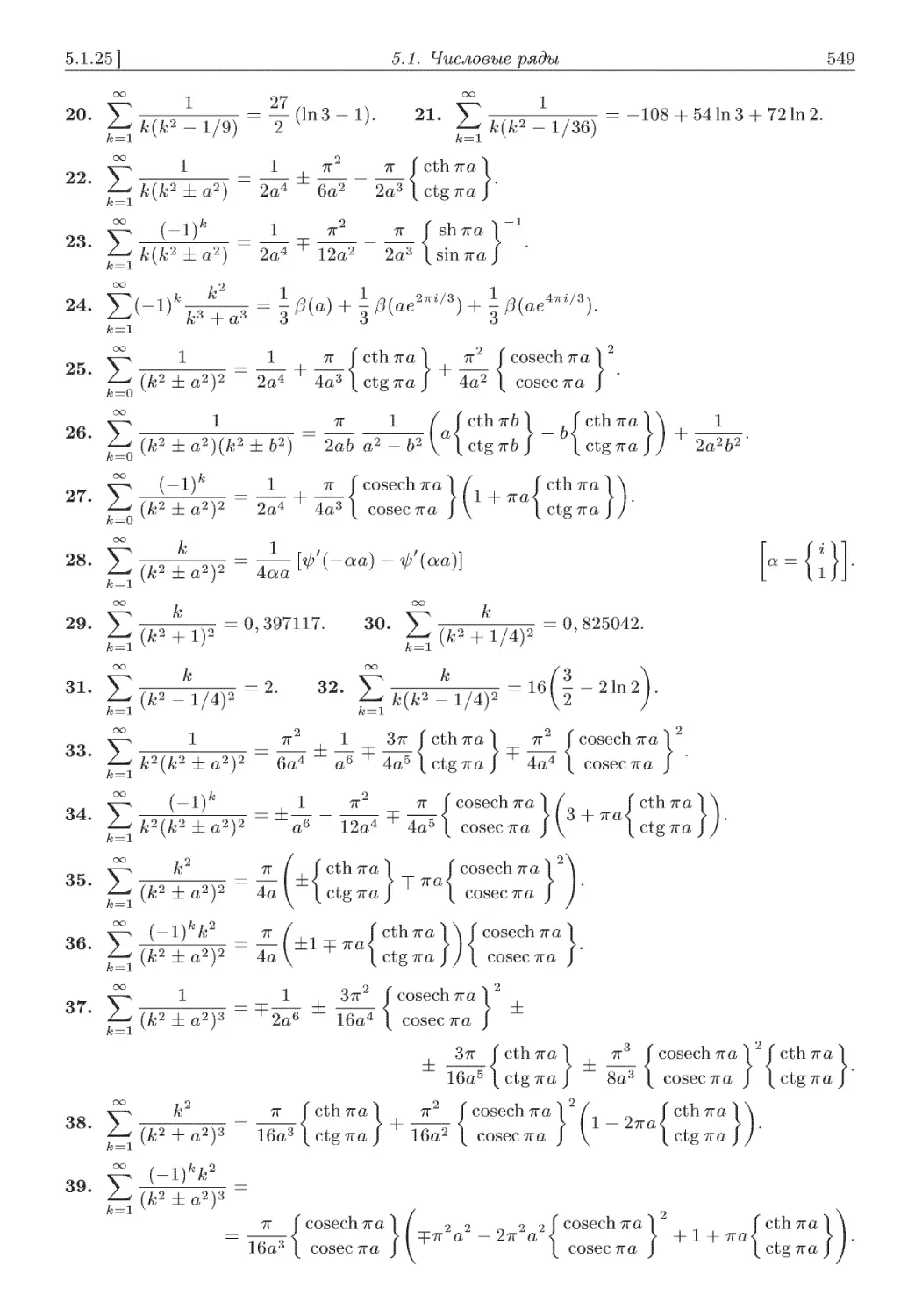УДК 519.6
ББК 22.194
П85
Прудников А. П., Брычков Ю. А., Маричев О. И. Интегралы и ря-
ряды. В 3 т. Т. 1. Элементарные функции. — 2-е изд., исправ. — М.: ФИЗМАТЛИТ,
2002. - 632 с. - ISBN 5-9221-0323-7.
Книга содержит неопределенные и определенные (в том числе кратные) интегралы,
конечные суммы, ряды и произведения с элементарными функциями. Она является наибо-
наиболее полным справочным руководством, включает результаты, изложенные в аналогичных
изданиях, а также в научной литературе.
Книга предназначена для широкого круга специалистов в различных областях знаний,
а также для студентов вузов.
Первое издание — 1981 г.
Библиогр. 37 назв.
ISBN 5-9221-0323-7 (Т. 1)
ISBN 5-9221-0322-9	© ФИЗМАТЛИТ, 2002

ОГЛАВЛЕНИЕ
Предисловие ................................................... 20
Глава 1. НЕОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ ....................... 21
1.1.	Введение. ................................................. 21
1.1.1.	Предварительные сведения ...................................... 21
1.1.2.	Основные интегралы .......................................... 21
1.1.3.	Общие формулы ............................................ 22
1.2.	Степенная и алгебраические функции ............................ 22
1.2.1.	Введение ................................................. 22
1.2.2.	Интегралы вида J хр(ахг + ЬL dx ................................. 24
Г хт dx
1.2.3.	Интегралы вида 	 ..................................... 25
) хп ±ап
f xp dx
1.2.4.	Интегралы вида 	 ..................................... 26
Г dx
1.2.5.	Интегралы вида 	 .................................... 27
Г	( х + а\ч
1.2.6.	Интегралы вида (ж + с)р I 	 J dx .............................. 28
f	xp dx
1.2.7.	Интегралы вида 	 ................................. 30
J (ж + ар(х + by
1.2.8.	Интегралы вида J Я(ж, ах2 + Ьх + с) da; ............................. 31
1.2.9.	Интегралы вида J R(x + d, ax2 + bx + с) da; .......................... 33
f xm dx
1.2.10.	Интегралы вида —	— ................................... 35
J (x2 ± aA)n
f	dx
1.2.11.	Интегралы вида	—— .................................. 37
f x±m dx
1.2.12.	Интегралы вида -—	—- ................................... 38
f x±m dx	f	x±m dx
1.2.13.	Интегралы вида —	—,	 ..................... 39
1.2.14.	Интегралы вида J Я(ж, аж2^ + bxk + с) da; ...........................	41
1.2.15.	Интегралы вида J R(x1'2, ах + b) dx ..............................	41
1.2.16.	Интегралы вида J Я(ж1/2, ж2 ± a2) dx ..............................	43
1.2.17.	Интегралы вида J ж±т(аж + 6)п+1/2 с!ж .............................	43
Г хт dx
1.2.18.	Интегралы вида 		................................. 44
Г	dx
1.2.19.	Интегралы вида 	гу^- ............................... 45
1.2.20.	Интегралы вида J Я(ж, л/ах + b , л/сх + d) da; ........................ 45
1.2.21.	Интегралы вида Я(ж, у/ах + b ) da; ............................... 47

Оглавление
Интегралы вида R[x, (ax + b)p'n] dx .............................. 47
Интегралы вида \ R\ ж, П	 1 dx .............................. 48
J \ V сх + d '
Интегралы вида J R{x1'n, ж2 ± а2) da; .............................. 49
Ж
Интегралы вида J R(y/x — а , л/ж — 6 , у/х — с) dx ....................... 49
а
со
Интегралы вида j R(y/x — а , л/ж — 6 , \/ж — с) dx ...................... 51
ж
а
Интегралы вида J R(y/a — ж , л/ж — 6 , у/х — с) dx ....................... 52
ж
Ж
Интегралы вида J R(y/a — ж , у/х — 6 , у/х — с) dx ....................... 54
Ь
ъ
Интегралы вида J R(y/a — х , \/fe — ж , л/ж — с ) rfa; ....................... 55
X
X
Интегралы вида J R(y/a — х , у/Ь — х , л/ж — с ) rfa; ....................... 56
с
с
Интегралы вида J R(y/a — ж , л/б — ж , л/с — ж ) rfcc ....................... 58
аз
ж
Интегралы вида j R(\/a — х , -\/Ь — ж , i/c — ж ) da; ..................... 59
X
Интегралы вида J R(y/x — а , л/ж — 6 , л/х — с , л/х -— d) dx ................. 61
а
а
Интегралы вида J R(y/a ¦— ж , л/ж — 6 , л/х — с , л/ж -— d) dx ................. 62
аз
ж
Интегралы вида J R(y/a ¦— ж , л/х -— Ъ , \/ж — с , \/ж -— d) dx ................. 64
Ь
ь
Интегралы вида J R(y/a —¦ х , л/6 — ж , л/ж — с , л/ж — d) dx ................. 65
ж
33
Интегралы вида J R(y/a —¦ х , л/b — х , \/ж — с , д/ж — d) da; ................. 67
с
с
Интегралы вида J R(y/a —¦ х , \/6 — ж , \/с — ж , д/ж — d) da; ................. 69
ж
33
Интегралы вида J R(y/a —¦ х , \/6 — ж , у/с —¦ х , л/х —¦ d) dx ................. 70
d
d
Интегралы вида J R{\/a — ж , л/b — ж , у/с — ж , Vd — ж ) da; ................. 72
аз
Интегралы вида /жт(ж2 ± a2)n+1/2 da; ............................. 74
Г (ж2±а2)-+1/2
Интегралы вида 	da; ............................... 75
J	хт
Г	жт die
Интегралы вида	................................. 76
J (ж2 ± ai)n+1/2
Г	da;
Интегралы вида 	—ттг ............................... 77
F	J жто(ж2±а2)те+1/2
Г	dx	Г	с!ж
Интегралы вида 	,	, 	,	................. 78
J (ж + 6)тел/ж2±а2 J (ж2±62)у/ж2±а2
Интегралы вида /жт(а2 - ж2)те+1/2 dx ............................. 79
1.2.22.
1.2.23.
1.2.24.
1.2.25.
1.2.26.
1.2.27.
1.2.28.
1.2.29.
1.2.30.
1.2.31.
1.2.32.
1.2.33.
1.2.34.
1.2.35.
1.2.36.
1.2.37.
1.2.38.
1.2.39.
1.2.40.
1.2.41.
1.2.42.
1.2.43.
1.2.44.
1.2.45.
1.2.46.

Оглавление	5
Г (а2~ж2)п+1/2
Интегралы вида 	da; ............................... 80
J	хт
Г	жт с!ж
Интегралы вида —	2 +1/2 ................................. 81
Г	с^ж
Интегралы вида		2\п+1/2 ••••••••••••••••••••••••••••••• 82
Г	с^ж
Интегралы вида	, , ,п ......................... 82
J (хт ±Ьт)п(аа - ж2)п+1/2
Интегралы вида J х±т(ах2 + 6ж + c)n+1/2 do; ......................... 83
Интегралы вида	^——¦— ; ............................. 85
J (ах2 + 6ж + с)п+1/2
Интегралы вида J R(x + р, «ж2 + 6ж + с) dx .......................... 86
Интегралы вида J /(ж, уж2 — ж + 1) dx ............................. 88
ж
Интегралы вида J Я(ж, ух2 + «2 , V ж2 -{- b2 ) dx ....................... 89
о
со
Интегралы вида j Я(ж, у ж2 + а2 , уж2 + б2 ) с!ж ....................... 90
ж
X
Интегралы вида J Я(ж, ух2 + а2 , уж2 ~~ b2 ) dx ....................... 91
ь
о©
Интегралы вида j R(x, ух2 + а2 , уж2 — Ь2 ) с!ж ....................... 92
ж
ж		 ^
Интегралы вида J R(x, ух2 + а2 , V б2 — ж2 ) с!ж ....................... 93
о
Ь
Интегралы вида J Я(ж, уж2 + а2 , \/б2 — ж2 ) dx ....................... 94
ж
X
Интегралы вида J Я(ж, ух2 — а2 , уж2 ¦— b2 ) dx ....................... 95
а
оо
Интегралы вида j R(x, ух2 — а2 , уж2 — b2 ) dec ....................... 96
ж
а
Интегралы вида J Я(ж, у а2 — ж2 , уж2 -— Ь2) dx ....................... 97
ж
ж
Интегралы вида J Я(ж, у а2 — ж2 , уж2 — b2 ) dx ....................... 98
ъ
ж
Интегралы вида J Я(ж, у а2 — ж2 , у б2 — ж2 ) dx ....................... 99
о
ь
Интегралы вида J Я(ж, у а2 — ж2 , у б2 — ж2 ) dx ....................... 100
X
Интегралы вида J Я| ж, у(ж2 + р2)(ж2 + р2) j dx ...................... 101
Интегралы вида J Я(ж, уж3 + 1) dx 1) .............................	102
Интегралы вида J Я(ж, уж3 — 1) dx ) .............................	103
Интегралы вида J Я(ж, у 1 — ж3 ) dx 3) .............................	104
Интегралы вида J Я(ж, уж4 + 1) dx ...............................	105
Интегралы вида J Я(ж, у ±ж4 =р 1) dx ..............................	106
Интегралы вида j /(ж, уж + ж4 ) dx ...............................	107
Интегралы вида J Я(ж, уж — ж4 ) dx ...............................	107
Интегралы вида J Я(ж, \/хА + 262ж2 + а4 ) dx .........................	108
1.2.47.
1.2.48.
1.2.49.
1.2.50.
1.2.51.
1.2.52.
1.2.53.
1.2.54.
1.2.55.
1.2.56.
1.2.57.
1.2.58.
1.2.59.
1.2.60.
1.2.61.
1.2.62.
1.2.63.
1.2.64.
1.2.65.
1.2.66.
1.2.67.
1.2.68.
1.2.69.
1.2.70.
1.2.71.
1.2.72.
1.2.73.
1.2.74.
1.2.75.

6	Оглавление
1.2.76.	Интегралы вида J Я(ж, \Дс6 + 1) dx ...............................	109
1.2.77.	Интегралы вида J Я(ж, y/l - ж6 ) da; ...............................	109
1.2.78.	Интегралы вида J Я(ж, уж2 dz I) dx ...............................	110
1.2.79.	Интегралы вида Я(ж, \/ж2 ± l)da;, /я(ж, \/l - х2 ) йж ..................	110
1.2.80.	Интегралы вида J Я( ^±(ж - а) , у/(х -b))dx ........................	Ill
1.2.81.	Интегралы вида J Я( \J xA + 1) daj .................................	112
1.3.	Показательная функция ......................................	112
1.3.1.	Интегралы вида J f{eax) dx .....................................	112
1.3.2.	Интегралы вида J/(ж, еаш)с1ж ...................................	112
1.3.3.	Интегралы вида J /(ж, е~а ж ) dx .................................	114
1.4.	Гиперболические функции. ....................................	115
1.4.1.	Введение .................................................	115
1.4.2.	Интегралы вида shp xdx^J chp x dx ...............................	115
1.4.3.	Интегралы вида J shp x chg ж da; ...................................	116
Г shp x Г ch9 ж
1.4.4.	Интегралы вида 	б?ж, 	dx ...............................	117
J ch^ x J shp ж
Г с!ж
1.4.5.	Интегралы вида 	 ....................................	119
J shp x chg ж
1.4.6.	Интегралы вида Шржйж,] cthp ж йж ...............................	120
1.4.7.	Интегралы вида J R(sh ж, ch ж, th ж, cth ж) dx ..........................	120
1.4.8.	Интегралы вида J R(sh (аж + 6), ch (еж -f d)) с!ж .........................	124
1.4.9.	Интегралы вида shp ж<	> dxA chp ж<	У dx ....................	124
J [ ch ax J J	[ ch аж J
1.4.10.	Интегралы вида J R(sh2ax1ch2ax1ysh2ax)dx .......................	125
1.4.11.	Интегралы вида J R(sh 2аж, ch 2аж, Vch 2аж ) dx .......................	126
1.4.12.	Интегралы вида J R(sh x, ch ж, \/« + 6 sh ж ) dx .........................	126
1.4.13.	Интегралы вида J R(sh x, ch ж, л/Ь ch ж — a ) с?ж .........................	127
1.4.14.	Интегралы вида J jR(sh ж, ch ж, л/Ь ch ж — a ) dx .........................	127
1.4.15.	Интегралы вида J R(sh ж, ch ж, у/а — b ch ж ) cfж .........................	128
1.4.16.	Интегралы вида J jR(sh ж, ch ж, л/« + b ch ж ) dx .........................	129
1.4.17.	Интегралы вида j K(sh ж, ch ж, у a2 sh2 ж dz fe2 , у b2 — a2 sh2 ж ,
л/a2 ch2 ж ± б2 , y/b2 - a2 ch2 ж ) с!ж .....................	130
1.4.18.	Интегралы вида J jR(sh ж, ch ж, %/« sh ж + 6 ch ж ) dx ......................	130
1.4.19.	Интегралы вида Vth ж с!ж, J л/cth ж с!ж .............................	131
Г f sh ж 1ч
1.4.20.	Интегралы вида жр<	> dx .................................	131
J I ch ж j
Г 1 f sh ж 1 g
1.4.21.	Интегралы вида —<	> dx .................................	132
J xP { ch ж j
Г f th ж 1 m
1.4.22.	Интегралы вида жр^	> dx ................................	133
J [ cth ж J
1.4.23.	Интегралы вида J xr shp ж chg ж с!ж ................................	133
Г жр	Г жр
1.4.24.	Интегралы вида 	dx, 	dx ..............................	134
J sh9 ж J chg ж

Оглавление	7
1.4.25. Интегралы вида \ Щ хр Л^ Ж >, а + 6< S \) dx ...................... 135
J V I h J	[ h J /
>, а + 6<
ch ж J	[ ch x
1.4.26.	Интегралы вида \(Ьх + c)±ni S	> dx ............................	135
J	[ ch аж J
1.4.27.	Интегралы вида J Я(ж, eax, shbx, chbx) dx ...........................	136
1.5. Тригонометрические функции ..................................	137
1.5.1.	Введение .................................................	137
1.5.2.	Интегралы вида J slnp ж da; ......................................	138
1.5.3.	Интегралы вида J cosp ж с?ж ......................................	139
1.5.4.	Интегралы вида J slnp x cosg x dx ..................................	140
Г sinp x
1.5.5.	Интегралы вида 	dx ..................................... 141
J cos*? x
Г cosg ж
1.5.6.	Интегралы вида 	йж ..................................... 143
J sinp x
Г	о*ж
1.5.7.	Интегралы вида 	 ................................... 144
J sinp x cos*? x
1.5.8.	Интегралы вида tgp xdx,j ctgp x dx ...............................	145
1.5.9.	Интегралы вида J R(sin x, cos ж, tgx, ctga;) о*ж ..........................	145
Я sin (ож + Ь) sin (еж + d) 1	f ,	.	,	.
> йж, sin (аж + 6) х х cos (ex + d) dx .	149
cos (аж + b) cos (еж + d) J J
1.5.11.	Интегралы вида j sinp ж sin аж с!ж .................................	150
1.5.12.	Интегралы вида] Бтржсо8ажа|ж .................................	150
1.5.13.	Интегралы вида j cosp ж sin аж dx .................................	151
1.5.14.	Интегралы вида] cosp ж cos аж dx .................................	151
1.5.15.	Интегралы вида <	> <	> dx ..........................	152
J [ cos ж J [ cos пж J
1.5.16.	Интегралы вида J Ji!(sin аж, cos аж, л/sin 2аж ) а*ж ........................	153
1.5.17.	Интегралы вида J R(sin ах, cos ах, ycos2ax ) dx .......................	154
1.5.18.	Интегралы вида j Ji!(sin аж, cos аж, у/— cos 2аж ) а*ж ......................	156
1.5.19.	Интегралы вида j K(sin ж, cos ж, у/a dz 6 sin x) dx .......................	157
1.5.20.	Интегралы вида j K(sin ж, cos ж, у/a dz 6 cos x) dx .......................	158
1.5.21.	Интегралы вида j K(sin ж, cos ж, л/а + b sin ж + с cos x) dx ..................	160
1.5.22.	Интегралы вида J R(yl — к2 sin2 x) dx .............................	161
1.5.23.	Интегралы вида J Я(8тж, yl — le2 sin2 ж ) о*ж .........................	161
1.5.24.	Интегралы вида J Я(со8ж, у 1 — к2 sin2 x) dx .........................	162
1.5.25.	Интегралы вида J sinm x cosn ж у A — 1г2 sin2 x)p dx .....................	164
Г sinm ж /
1.5.26.	Интегралы вида 	у 1 — 1г2 sin2 ж а*ж ...........................	165
J cosn ж
Г sinp ж cos"? ж
1.5.27.	Интегралы вида —,	dж .............................	166
J д/A - ^2 sin2 ж)^
Г sinp ж	с!ж	Г cosp ж	о*ж
1.5.28.	Интегралы вида		г,		г .........	168
J cos*? ж ^/A _ к2 sin2 ж)*- J sin^ ж y/(i - к2 sin2 х)г
VI1 — k sm •
si
1.5.30. Интегралы вида 		- ....................... 170
1.5.29. Интегралы вида ^^		^; с!ж ............................. 169
J sinm ж cosn ж
ж cosn ж ^

8	Оглавление
1.5.31.	Интегралы вида J R(sin х, cos ж, yl — р2 sin2 ж , yl — q2 sin2 ж ) dx ............ 170
г (а + sin ж)р
1.5.32.	Интегралы вида /	dx ............................... 171
(а + sin ж)
V 1 — fc2 sin2 ж
г A _|_ a sin2 ж)р
1.5.33. Интегралы вида \	=^=- Aж ............................... 172
J \Д - к2 sin2 ж
1.5.34. Интегралы вида	f dx ............................... 173
J у 1 — к2 sin2 ж
1.5.35.	Интегралы вида —	с?ж ............................... 174
J л/l - fc2 sin2 ж
1.5.36.	Интегралы вида j K(sin ж, cos ж, yl — р2 sin2 ж ) с!ж ......................	176
1.5.37.	Интегралы вида J R(sm ж, cos ж, yl + p2 sin2 ж ) dx ......................	176
1.5.38.	Интегралы вида J R(sm ж, cos ж, \/a2 sin2 ж — 1) dx ......................	177
1.5.39.	Интегралы вида /(tg аз) da;,J /(ctgаз) da; ............................	178
Г	Гвтж!9
1.5.40.	Интегралы вида жр<	> da; ................................. 179
J [ cos ж J
Г 1 f sin ж 1 q
1.5.41.	Интегралы вида —<	> da; ................................. 180
J xP {cos ж J
1.5.42.	Интегралы вида \ xp I	\ dx ................................. 182
J I ctg ж J
1.5.43.	Интегралы вида J xr sinp ж cos*7 ж с!ж ............................... 182
f жр с^ж
1.5.44.	Интегралы вида —	 ....................................... 183
J sing ж
Г жр о!ж
1.5.45.	Интегралы вида 	 ....................................... 184
J cos*? ж
1.5.46.	Интегралы вида J Я(жр, sin ж, cos ж, а + 6 sin ж + с cos ж) dx ................. 185
Г ж sin ж cosn ж
1.5.47.	Интегралы вида —,	dx ............................. 185
J V(l - к2 sin2 ж)^
1.5.48.	Интегралы вида (ж + 6)±ni SmaX \dx ............................ 185
J	[ cos ax J
1.5.49.	Интегралы вида J eax sinp ж cos*1 a; da; ............................... 186
1.5.50.	Интегралы вида \eax\ gX \ dx ................................ 188
J Ictg ж J
1.5.51.	Интегралы вида J R(x, eax, sin bx, cos баз) dx .......................... 188
Hsh (аж + b) } m f sin (еж + d) 1 n
)	A < )	A dx .................... 189
ch (ax + b) j [ cos (еж + d) J
f _ f в!пж2 1
\ xp { 0 }
J у cos ж^ J
1.5.53. Интегралы вида жр<	2 > dx ................................. 192
1.6. Логарифмическая: функция .................................... 193
1.6.1.	Интегралы вида J xp In*1 ж dx .................................... 193
Г жр dx
1.6.2.	Интегралы вида 	 ....................................... 194
J In*3'
1 ж
1.6.3.	Интегралы вида J (ж + aL In ж с!ж .................................. 194
Г жта1пж
1.6.4.	Интегралы вида —	j- dx ................................. 195
J (а2 ± ж2)п/2
1.6.5.	Интегралы вида J xp In (аж + 6) da; ................................. 195
1.6.6.	Интегралы вида ж т In	dx ................................
J	ж — а
196

Оглавление
209
1.6.7.	Интегралы вида J ж In (ж2 db a2) dx ............................... 196
1.6.8.	Интегралы вида J х±т In (ж + \/х2 ± а2 ) с!ж .......................... 198
1.6.9.	Интегралы вида	^ - In (ж + \/ж2 ib 1) dx, f 1пр(ж + \J x1 ±\)dx .......... 199
1.6.10.	Интегралы вида J /(ж, In ж, еаж, sin ж, cos ж, ...) о*ж ...................... 199
Г 1п(аж + b) In (еж + d)
1.6.11.	Интегралы вида —	 da; ........................... 201
J	fx + g
1.7.	Обратные тригонометрические функции .......................... 202
1.7.1.	Введение ................................................. 202
1.7.2.	Интегралы вида < arcsm\x/a) I dx ............................... 203
J [ arccos (ж/а) j
1.7.3.	Интегралы вида f Ж±"{ аГС8'П {х/п) ) dx	 203
J	[ arccos (x/a) J
1.7.4.	Интегралы вида f(l ± ж)±«+1/2 ( arcsm ж 1 dx ......................... 204
J	[ arccos x J
1.7.5.	Интегралы вида f x^(l - ж2}д+1/2 f arcsin ж lr ^ ....................... 205
J	[ arccos x J
1.7.6.	Интегралы вида xp\ arcsecWa) 1 da, ............................ 207
J [ arccosec (ж/а) J
1.7.7.	Интегралы вида \{х ± 1)±п+1/2( агсзесж ) ^ ........................ 209
J	I arccosec ж J
1.7.8.	Интегралы вида L™^2 - l)±n+1^{ Ж€5есх X dx ....................
J	^ arccosec ж J
1.7.9.	Интегралы вида f xp\ агс^(ж/а) I ^ .............................. 211
J [arcctg(x/a) J
1.7.10.	Интегралы вида [>(ж2 + a2L arctS (ж/«) Г da, ...................... 212
J	[arcctg^/a) J
1.8.	Обратные гиперболические функции ............................. 214
Глава 2. ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ .......................... 215
2.1.	Введение. ................................................. 215
2.1.1.	Предварительные сведения ...................................... 215
2.1.2.	Общие формулы ............................................ 216
2.2.	Степенная ж алгебраическая: функции ............................ 222
2.2.1.	Введение .................................................	222
2.2.2.	Интегралы общего вида ........................................	222
2.2.3.	Интегралы от (ж*4 Т «м)р и (а** - х^)р ..............................	237
2.2.4.	Интегралы от ха(а^ ± х^)р .....................................	237
2.2.5.	Интегралы от (aM ± жм)рF1/ =р ж17) ................................	239
з
2.2.6.	Интегралы от Y\ (ak ± ^)pfe ..................................... 241
fe=i
з
2.2.7.	Интегралы от f\ (а^к ± х^к)Рк .................................. 244
k=i
п
2.2.8.	Интегралы от f\ (а^к ± х^к)Рк , п ^ 4 .............................. 245
fe=i
2.2.9.	Интегралы от жа(аж2 + Ьх + с)рЛ(ж) ............................... 247
2.2.10.	Интегралы от жа(аж4 + 26ж2 + с)рА(х) ............................. 251
2.2.11.	Интегралы, содержащие А{\/ах2 + баз + с) ........................... 252
2.2.12.	Интегралы, содержащие разности алгебраических функций ................ 255

10	Оглавление
2.3.	Показательная функция ......................................	256
2.3.1.	Введение .................................................	256
2.3.2.	Интегралы общего вида ........................................	256
2.3.3.	Интегралы от хае~рх .........................................	259
2.3.4.	Интегралы от (ж ± а)ре~рх .....................................	260
2.3.5.	Интегралы от (хп ± ап)ре^рх ....................................	260
2.3.6.	Интегралы от ха(х ± а)ре^рх ....................................	261
2.3.7.	Интегралы от жа(ж2 ± а2)ре^рх и ха(а2 - х2)е^рх ......................	262
2.3.8.	Интегралы от ха Y\(a^k ± х^к)Рке^рх ..............................	264
к
2.3.9.	Интегралы от ха(л/х7Т^ + ахр + hz^)pe^px ..........................	265
2.3.10.	Интегралы от ха(\/х2 + z2 + ах + 6^)ре^рж .........................	265
2.3.11.	Интегралы от жа[(л/аж^ + 6 ± -\/сж^ + rf)^ ± (у/ах» + 6 =F л/сж17 + с!)р]е^рж .....	266
2.3.12.	Интегралы от xa(eqx + z)Ae^pa; ..................................	269
2.3.13.	Интегралы от xa(eqx - z)xe^px ..................................	271
2.3.14.	Интегралы от (ae^qx + beqx + c)/^) .............................	274
2.3.15.	Интегралы от Л(ж)е"рж2т<|Ж ....................................	276
2.3.16.	Интегралы от A(x)e^px^q/x ....................................	277
2.3.17.	Интегралы от Л(ж)е~ь^2±«2 -рх ................................	278
2.3.18.	Интегралы от eg^f(x) .......................................	279
2.3.19.	Интегралы, содерж:ащие разности алгебраической и показательной функций .....	279
2.4.	Гиперболические функции. ....................................	281
2.4.1.	Введение .................................................	281
2.4.2.	Интегралы общего вида ........................................	282
Г sh bx I a
2.4.3.	Интегралы от А(х)<	> ....................................	283
П( sh b^x I
<	>...................................... 284
Ich6fcxj
2.4.5.	Интегралы от А(х) flfshbkX\ .................................. 286
11 [ сЬб^ж J
2.4.6.	Интегралы от (а + 6 chn 6ж + с shnbx)pTJ\ B11Cfcii; L ..................... 287
Y [сЬс^-ж j
2.4.7.	Интегралы от Л(ж)(а + 6chn 6ж + cshn 6ж)р FT I S С|гЖ I .................. 290
2.4.8. Интегралы от A(x)chbx I	,	 > ............................ 291
2.4.9.	Интегралы, содержащие Шаж^Ьаж и разности гиперболических и алгебраических
функций .....................................................	291
2.4.10.	Интегралы от хае~рх\Ьх 1 ..................................	292
{ ch bx j
2.4.11.	Интегралы от е~~~рх и гиперболических функций .......................	293
2.4.12.	Интегралы от А (ж), е^рх и гиперболических функций ....................	294
2.4.13. Интегралы от ха(ех + а)ре~рх{ShbX\ ............................. 295
[ ch bx J
{b 4- sh ax 1 °"
} ............................... 296
6 + ch ax j
2.4.15. Интегралы от жае^аж2"сж(811бЖ1 ................................ 296
[ ch bx J
iI So СХЖ I
2.4.16. Интегралы от А(ж) ехр (-р\/ж2 + z2 )	\ ........................ 298
I ch ax J

Оглавление	11
2.4.17.	Интегралы от жае/(ж)(8Ь6Ж1 ................................... 298
1 ch 6ж J
f sh bx I
2.4.18.	Интегралы от /(ж)ехр <	> .................................. 298
[ ch bx j
I 2"
2.4.19.	Интегралы от А(х)е~рх { "Л ?Х	} ......................... 299
+ bx + с 1
+ 6ж + с J
1
2.4.20.	Интегралы от Л(ж)е/(ж) { ""Г"' ^ " п ^ .......................... 301
ch [cx/(a — ж )]
2.4.21.	Интегралы, содерж:ащие Л(ж), е^*^ж% 8Ь^(ж), сЬ^(ж) ..................... 302
2.4.22.	Интегралы, содерж:ащие разности Л(ж),е~~рж, I	> ................... 303
[ ch 6ж J
2.5. Тригонометрические функции .................................. 305
2.5.1.	Введение ................................................. 305
2.5.2.	Интегралы общего вида ........................................ 306
2.5.3.	Интегралы от ха \ ШП \ ..................................... 312
[ cos bx j
2.5.4.	Интегралы от хт\ ШПХ \ ..................................... 314
[ cos ж j
2.5.5.	Интегралы от (ж + z)^ <	> .................................. 315
[cos bxJ
2.5.6. Интегралыот(ж2±а2)^(81п6ЖГ,(а2^Ж2)^(81п6ЖГ .................. 315
[ cos bx J	[ cos bx J
2.5.7. Интегралы от ж«(ж±а)^(81п6Ж },ж«(а^ж)^(8Ы 6Ж1 ................... 316
[cos bxJ	[cos bxJ
2.5.8.	Интегралы от жа(ж2^а2)^(81п6Ж1,Ж«(а2^ж2)^(81п6Ж1 ................ 318
[ cos bx J	[ cos bx J
2.5.9.	Интегралы от —-^—-— I	X \ ................................ 319
(ж2 + z2)P [соБбж j
xm	( slnbx 1 l
2.5.10.	Интегралы от 	—	\	\ .................... 320
апжп + an-ixn г + . . . + ао [ cos bx J
2.5.11.	Интегралы от жа(\/ж2 ± z2 + аж + 6^I/Л(ж)^	I ................... 323
[	J
2.5.12.	Интегралы от П ( Sin а*Ж Г* ( sin ^ж Г" ? ГТ sinMfe а&ж cos-fe 6fca. ........... 324
AfcA [ cos akx J [ cos bkx J AfcA
2.5.13.	Интегралы от xa sin^ а ж cos17 6ж .................................. 327
xa
2.5.14.	Интегралы от —	 sin'" a ж cos17 Ьж ............................... 331
x1 db z1
2.5.15.	Интегралы от ха О sin'" а^ж cos17 b^x .............................. 333
к
sin еж
p
2.5.16.	Интегралы, содержащие I a + b{	> I .......................... 334
V	I cos ex J/
2.5.17.	Интегралы, содержащие (a cos ж + b sin ж + с)р ......................... 340
2.5.18.	Интегралы, содержащие (acos2 ж + 6sin2 ж + c)^n ...................... 342
2.5.19.	Интегралы, содержащие (acos2 ж + bsin2 ж + сI'2 ...................... 344
. ч f sin ax 1 M f sin (Ьж + с) 1 v , . f sin аж 1 M f cos Fж + с) ) "
2.5.20.	Интегралы от Л (ж) <^	\ { ,	А ,Л(х)<	\ { )	{).... 348
[ cos ax J [ cos (bx + с) J	[ cos аж J [ sin Fж + с) J
Г з1п(ажр + 6жд + с) ]
2.5.21.	Интегралы от < х	; ^ ............................... 349
1соз(ажр + bxq + c) J
_, Г sin ажр sin 6ж 1 _, Г sin ажр cos bx I
2.5.22.	Интегралы отжа	Ь ж 1	.	^ ................... 349
I cos axp cos 6ж I	I cos axp sin 6ж I

12	Оглавление
2.5.23.	Интегралы от А(х){ 8Ш ^Х + &^ I ............................... 351
[ cos (ах + Ь/х) J
_, f sin (а/ж) sin bx I _, f sin (а/ж) cos 6ж 1
2.5.24.	Интегралы отжа	)' {	>, % { , ' \	\ ................. 352
[ cos (а/ж) cos bx J	[ cos (а/ж) sin bx J
Г sin (су а2 ± ж2 ) sin Ьх\	\ sin (су а2 ± ж2 ) cos bx ]
2.5.25.	Интегралы от А (ж) I V ,	;	М(ЖН	,		}..... 352
\/|	/ / 9 I 9 \	L I	^ ' I	/ / 9 I 9 \ • L I
^ cos (с v «¦ ± xz ) cos ож J	^ cos (су az ± xz ) sin ож j
Г tg аж 1
2.5.26.	Интегралы, содержащие <	> ................................ 354
{ ctg аж J
2.5.27.	Интегралы, содержащие тригонометрические функции от тригонометрических функ-
функций ......................................................... 356
2.5.28.	Интегралы, содержащие ха и тригонометрические функции от тригонометрических
функций ..................................................... 357
2.5.29.	Интегралы, содержащие разности тригонометрических и алгебраических функций . 358
Г sin bx I n
2.5.30.	Интегралы от е^рх {	\ ................................... 361
[cos ож J
2.5.31.	Интегралы от хае^рх\ smbx\ .................................. 362
[cos bxJ
2.5.32.	Интегралы от А(х)е^рх{ ШП Ы 1 ................................. 363
[cos bx j
Sin ОТ I r* Г GiTi hk 'T* 1
cos аж
{Sin ОТ
i J	\ 1xaepxmn^axcos1Jbx ............. 364
cos аж J [cos bx J
2.5.34.	Интегралы от хаR(eax){ smbx\ ................................. 365
[cos bxJ
2.5.35.	Интегралы от /(ж, еаж, sin bx, cos баз) ............................... 366
2.5.36.	Интегралы, содержащие е~аа;2™сж J	X 1 .......................... 367
[ cos bx J
_ _ / Г sin bx 1
2.5.37.	Интегралы от хае рх q/x<	} ............................... 368
[cos bxJ
2.5.38.	Интегралы, содержащие е~а^х , ea^, I	I ....................... 368
[ cos 6ж J
2.5.39.	Интегралы, содержащие ел(х' ml	> ........................... 370
[ cos Ьж J
2.5.40.	Интегралы, содержащие показательную функцию от показательной и тригонометри-
f sin bx I
ческих функций и<	> ......................................... 370
[ cos bx J
2.5.41.	Интегралы, содержащие А(х),е^х\1	9	,-,	>................ 371
I cos (аж + bx + с) J
2.5.42.	Интегралы от Л(ж)е^раЧ Sm >^	 } ......................... 373
1 cos \/аж2 + 6ж + с
2.5.43.	Интегралы от А(х)е^хЧ	7/2 2	......................... 375
cos [сх/(х ±. а )\
2.5.44.	Интегралы, содерж;ащие показательную и тригонометрические функции от тригоно-
тригонометрических функций ............................................. 376
2.5.45.	Интегралы, содержащие разности функций А(х), е^рх,<	> ............. 378
[ cos bx J
е ( sin bkX \ Vk j~j Г sh a^x \ ^k f cos b^x \ Vk
* l<
|-r f shafcxlMfe f sin6fea; 1 fe n f sh а^-ж l f cos bkx \
2.5.46. Интегралы от	> <	} , Ц<	} < . , } ........ 380
^[chai^J [соэб^ж] у [hJ {bj
о c лп тл	а П f shafc« 1 Mfe f sinbkx 1 ^ !-| f shafea? 1 Mfe f cos6fc« 1
2.5.47. Интегралы от ж	> <	> ,ж	<	> <	> .... 381
LkL [chakX) [созб^ж]	жкж {chakX) [ sin б^ж j
{sin еж 1
> ..................... 382
_ cos ex J

Оглавление	13
2.5.49.	Интегралы, содержащие А(х)(а + bch2 x)vI	> ..................... 384
[cos еж J
2.5.50.	Интегралы, содержащие A(x)(ch ах ± cos bx)"'11	> .................. 384
[cos ex J
2 2 —1 f ^ ^*^ 1 f ^^ ^
2.5.51.	Интегралы, содержащие (ж -f z ) {	> <	/,
I ch аж J I cos 6ж I
}()		385
[ ch ax J [ sin bx J
2.5.52.	Интегралы, содержащие А(х), зпбж, сЬбж, sin ax , cos bx .................	387
[ sh (v a2 — ж2 ) sin 6ж 1	[ sh (\fa2 ¦— x2 ) cos 6ж ]
2.5.53.	Интегралы от А (ж) {	;		М(ЖМ	,		> .......	388
У ch (v a2 — ж2 ) cos bx J	[ ch (ya2 — ж2 ) sin 6ж J
2.5.54.	Интегралы, содержащие тригонометрические функции от гиперболических функций	389
2.5.55.	Интегралы, содержащие гиперболические функции от тригонометрических функций	390
2.5.56.	Интегралы, содержащие е^рж, эЬаж, сЬаж, sinbx, cosbx ..................	391
2.5.57.	Интегралы, содержащие е*^х\ яЬаж, сЬаж, sinte, cos bx ..................	392
2.6. Логарифмическая функция ....................................	393
2.6.1.	Введение .................................................	393
2.6.2.	Интегралы общего вида ........................................	393
2.6.3.	Интегралы от ха \па ж .........................................	397
ха
2.6.4.	Интегралы от 	1пст ж ...................................	398
(х^^а^)Р
ха
2.6.5.	Интегралы от 	\па ж ...................................	399
(а^-х^)Р
ха In*7 ж
2.6.6.	Интегралы от	 .....................................	402
ах1 + bx + с
2.6.7.	Интегралы от ха(а2 - ж2) Inn ж ...................................	404
2.6.8.	Интегралы от А(х) 1пте ж .......................................	404
2.6.9.	Интегралы от ха 1пп(аж + Ь) .....................................	406
2.6.10.	Интегралы от жа(аж + 6)^ 1пп (еж + d) ..............................	408
2.6.11.	Интегралы от жа(аж2 + Ъ)& In (еж + d) ..............................	413
2.6.12.	Интегралы от жа(а1Ж + 6i)/3(a2aj + 62O 1пте(сж + d) .....................	414
2.6.13.	Интегралы от ха \пп	 ....................................	416
еж + d
2.6.14.	Интегралы от А(х) In (аж2 + bx + с) ...............................	418
Р(х)
2.6.15.	Интегралы от А(х) In	 .....................................	420
Q(x)
2.6.16.	Интегралы от А(х)\па(л/ах^ + bz^ + cxv) ...........................	420
2.6.17.	Интегралы, содержащие А(х) и 	 ..............................	424
1пп ж
А(х~) 1пте ж
2.6.18.	Интегралы от —^	 ......................................	428
lnm ж + a
2.6.19.	Интегралы от произведений логарифмов ............................	429
2.6.20.	Интегралы, содержащие In In ж ...................................	430
2.6.21.	Интегралы от хае^рх^ \пп х ....................................	431
2.6.22.	Интегралы от xaeax2+bx±1 lnn x .................................	431
2.6.23.	Интегралы от хае^рх In B + bx) .................................	432
2.6.24.	Интегралы от А(х)е~рх In (ах2 + bx + с) ............................	433
2.6.25.	Интегралы от е~рх \п А(х) .....................................	434
2.6.26.	Интегралы от R(ex) In ж .......................................	434
2.6.27.	Интегралы, содержащие жа,е~~рж и 	 .........................	435
1пп(ж + а)
2.6.28.	Интегралы от ха In (a + be~px) ..................................	435
2.6.29.	Интегралы от ха R(sh ж, ch ж) In ж .................................	435

14	Оглавление
2.6.30.	Интегралы от A(x)R(shx, сЬж) In А(х) ............................. 436
2.6.31.	Интегралы, содержащие логарифмическую функцию от гиперболических функций . 437
N f sin bx
[ cos bx
2.6.32. Интегралы от Л (ж К t } lnn x ................................. 438
2.6.33.	Интегралы от А(х)<	> In A(x) ............................... 439
[cos bxJ
Г sin bx 1
2.6.34.	Интегралы, содержащие In <	> ............................... 440
[ cos bx j
Г cifi fjnr* I
2.6.35.	Интегралы, содержащие Inn <	> .............................. 444
[cos bxJ
2.6.36.	Интегралы от A(x, sin ж, cos ж) In (a cos ж + 6 sin ж + с) .................... 444
a\ cos ж + 6i sin ж + ci
2.6.37.	Интегралы, содержащие In	 ....................... 446
«2 cos ж + 62 sin ж + C2
2.6.38.	Интегралы, содержащие In (a cos2 ж + b sin2 ж + с) .......................	447
2.6.39.	Интегралы, содержащие In A{igx) ................................	448
2.6.40.	Интегралы, содержащие показательную, логарифмическую, гиперболические и триго-
тригонометрические функции ...........................................	450
2.7. Обратные тригонометрические функции .......................... 451
2.7.1.	Введение ................................................. 451
2.7.2.	Интегралы общего вида ........................................ 451
Г arcsin bx I
2.7.3.	Интегралы, содержащие <	> ............................... 455
[ arccos bx J
2.7.4.	Интегралы от А (ж), <	> .................................. 455
[ arcctg ж J
arctg 6a
\ arcctg bx ,
2.7.5. Интегралы от А(х), е~^х, ( arctg 6ж 1 .............................. 457
[ arcctg bx J
w ч f sin ax 1 I arctff bx I
2.7.6.	Интегралы от Л(ж), <^	>, <	+1 ? .........................	458
[ cos ax J I arcctg 6ж J
2.7.7.	Интегралы, содержащие arctg ax и логарифмическую функцию ..............	459
Г arctg fix) 1
2.7.8.	Интегралы, содерж:ащие <	>..............................	459
[arcctg/(ж)]
/ Г arctg ж 1 \
2.7.9.	Интегралы, содержащие /<	> I .............................	460
V [ arcctg ж J /
2.8. Обратные гиперболические функции .............................	461
Глава 3. КРАТНЫЕ ИНТЕГРАЛЫ ................................	462
3.1.	Двойные интегралы .........................................	462
3.1.1.	Введение .................................................	462
3.1.2.	Общие формулы; интегралы от алгебраических функций ...................	463
3.1.3.	Интегралы, содержащие показательную функцию .......................	464
3.1.4.	Интегралы, содержащие гиперболические функции ......................	468
3.1.5.	Интегралы, содержащие тригонометрические функции ....................	469
3.1.6.	Интегралы, содержащие логарифмическую функцию .....................	474
3.1.7.	Интегралы, содержащие обратные тригонометрические и обратные гиперболические
функции .....................................................	474
3.2.	Тройные интегралы ..........................................	475
3.2.1.	Введение .................................................	475
3.2.2.	Общие формулы; интегралы от алгебраических функций ...................	477
3.2.3.	Интегралы, содержащие показательную, гиперболические и тригонометрические функ-
функции .........................................................	478
3.3.	Многомерные интегралы ......................................	479
3.3.1.	Введение .................................................	479
3.3.2.	Интегралы по области х\ + х\ + . . . + х\ ^ г2 .........................	479

Оглавление	15
a 2
3.3.3.	Интегралы по области —	1	Ь • • • Н	— ^ 1 ...................... 481
«1	«2	On
3.3.4.	Интегралы по области xi ^ О, Х2 ^ 0, . . . , хп ^ 0,Ж1 + Ж2 + • . • + жп ^ а ........ 483
ь ъ
3.3.5.	Интегралы вида J*. . . J /(x) dx ................................... 485
Глава 4. КОНЕЧНЫЕ СУММЫ
4.1. Введение. ...............
4.1.1. Суммы вида ^(±1)кР{к) . . . .
Ef±l)fe
	— ......................................... 490
ks
f±l)
4.1.3. Суммы вида V -^	^-— ....................................... 490
^ (к + а)
f±l)
4.1.4. Суммы вида \"^	 ................................... 491
^^ (к + а)(к + Ь)
(il)
4.1.5. Суммы вида \"^	 ............................... 491
У	^ (к + а)(к + Ь)(к + с)
р( L\
4.1.6. Суммы вида ^J —т~т и ДРУгие ................................... 492
4.1.7.	Суммы вида ^J akx	...................................... 493
4.1.8.	Суммы вида ]T(±l)fc - ...................................... 494
Ln J
4.2. Биномиальные коэффициенты .................................. 495
4.2.1.	Суммы вида V(±l)fe | fe ) ..................................... 495
\Ьк/
4.2.2.	Суммы вида \^ ак[ 1 ....................................... 496
\Cfe/
4.2.3.	Суммы вида V ак ( к )хк ...................................... 499
^ Чел/
4.2.4.	Суммы вида \J ад. ( J ...................................... 500
4.2.5.	Суммы вида y(±l)fefafe)fCfe ) ................................. 501
'bk\fdk
/bk\fdk ^fc
4.2.6. Суммы вида V ак ( Ьк ) ( dk ) ................................... 506
4.2.7. Суммы вида / a^ I I I J ж
^ \ckj\ekj
Ьк
.................................. 507
-i
4.2.8. Суммы вида VaJ M M .................................. 509
bk\fdk\ffk
4.2.9.	Суммы вида У" аМ ) ( ) ( ) ............................... 511
^^ \ckj\ek)\gk)
4.2.10.	Суммы вида VoJ fc J ( fe ] ( fc J ............................. 513
^^ \Ck/ \ek/ \gk/
4.3. Гиперболические функции. ....................................	514
4.3.1.	Суммы вида / од, я	> .................................	514
^^ { ch (А;ж + a) j
4.3.2.	Суммы, содержащие sech ж и th ж .................................	515

16	Оглавление
4.4. Тригонометрические функции ..................................	515
лл 1 гл V^ \ s'm(kx + a) 1	С1С
4.4.1. Суммы вида > ск^< > .................................	515
^^ [ cos (кх + a) J
^ fsinfcx1
4.4.2.	Суммы вида Л a^<f	> ....................................	517
z—' [ cos кх J
4.4.3.	Суммы вида /а^<	> ...................................	518
^-^ [ cos ЬкХ )
v^ Г sinkx )l ( sin ку)т
4.4.4.	Суммы вида > ад.<	><	> .............................	519
z-^ [ cos Дгж J [ cos ky J
4.4.5.	Разные суммы, содержащие sin ж, cos ж ..............................	520
4.4.6.	Суммы, содержащие sec ж, cosecx .................................	521
4.4.7.	Суммы, содержащие tga&, ctga^ ..................................	522
4.4.8.	Суммы, содержащие логарифмы ..................................	523
4.4.9.	Суммы, содержащие арктангенсы ..................................	524
Глава 5. РЯДЫ. ..............................................	525
5.1. Числовые ряды .............................................	525
5.1.1. Введение .................................................	525
5.1.2. Ряды вида V -	}— .......................................... 526
^^ ks
E(±l)fc
-±	Ч— ........................................ 526
(к + a)s
5.1.4. Ряды вида \"^	 ........................................ 527
Е( — ~\_\к
	 ......................................... 528
кп + те
5.1.6. Ряды вида V (i }^}\ t i4 ..................................... 528
5.1.7. Ряды вида > —-^	 ....................................... 529
^^ к(кп + те)
	 ................................... 530
Ь те)
(±1)к
5.1.9. Ряды вида V		¦	 ................................... 531
^^ Bк + 1)(^п + те)
5.1.8. Ряды вида Т,,кА(к'п
5.1.10.	Ряды вида V	^	 .................................. 532
^ (Зк + /)(Лп + т)
5.1.11.	Ряды вида 5] ^.^t^ ^ ч .................................. 532
^^ Dfe + /)(А;п + те)
5.1.12. Ряды вида ^ ,к, , ^ ,	г .................................. 533
^^ EА; + 1)(кп + те)
5.1.13. Ряды вида V	^	 .................................. 533
Z^ (пк + 1)(к + )
5.1.14. Ряды вида ? ,,, ^^ ^ ч .................................. 534
^^ (8А; + 1)(кп + те)
5.1.15. Ряды вида V	^	 ............................. 534
^ (ка + Ъ)(ка + с)(ка + d)
5.1.16. Ряды вида Y, ТУТ	Т^Щг	"	7 ............................. 535
?—J к{кть\ + mi)(«Ti2 + шч)
5.1.17. Ряды вида ? ,, , iU,	^^ w,	г .......................... 536
/^ (к + \)(кп\ + )(k + )

Оглавление	17
fdzl)^
5.1.18. Ряды вида V	-	-	 ........................ 538
Z^ Bk + т)(кт + т1)(кп2 + ш2)
5.1.19.	Ряды вида V	-	-	 .......................... 540
Z^ Ck + m)Ck + mi)Cife + m2)
/ii \fc
5.1.20.	Ряды вида У^	 .......................... 540
^ Dfc + )Dfc + )Djfe + )
5.1.21. Ряды вида V	Ц^	 ............... 541
/-^1 [кп\ + m\)(kni + m2)(kn% + тз)(/еп4 + 7714)
fdzl)^
5.1.22. Ряды вида V	-	-	 .................... 543
/-^1 (kni + т\)(кП2 + ГП2) • • • (kns + ТЛ5)
5.1.23.	Ряды вида ^ ^^		^^ 	т——	-, г = 6, 7, 8, 9 ............ 545
5.1.24.	Ряды вида V	^	}-	 ........................... 546
^ (k + ai)(k + a2) . . . (k + an)
5.1.25. Ряды вида E (fc2 ± a2), 	 548
5.1.26.	Ряды вида }^	 2—^- ..................................	550
fdbl)^
5.1.27.	Ряды вида Л —	™	 ......................................	552
5.1.28.	Ряды вида ^	 ..................................	552
5.1.29.	Ряды вида V 6П ——— .......................................	553
^^ 1 ± а1п
5.1.30.	Ряды вида ^ ^| ...........................................	553
5.1.31.	Ряды вида \J — ...........................................	554
N(k)
5.1.32.	Ряды вида \J a^ I /J &m J ....................................	554
5.2. Степенные ряды ............................................	554
5.2.1.	Введение .................................................	554
5.2.2.	Ряды вида ^ Р(к)хк .........................................	555
хк
5.2.3.	Ряды вида \J	 ........................................	555
(к + a)s
5.2.4.	Ряды вида V -^	— хк ....................................... 556
^-^ пк + т
хк
5.2.5.	Ряды вида > 	 ................................... 557
5.2.6. Ряды вида V у-	¦	 V /	¦	-, j > 2 ................. 559
z-^ (kni + mi)(kn2 + ГП2) . • . («%' + wij)
5.2.7.	Ряды вида V ^'^ V ^'^ ..............................	560
5.2.8.	Ряды вида V	^	xfe ................................	561
5.2.9.	Ряды вида V	 хк ......................................	562
^^ (к + m)!
5.2.10.	Ряды вида ? ___^__ я*		563
5.2.11.	Ряды вида Е^?^^ 		564
2 А. П. Прудников и др., т. 1

18	Оглавление
5.2.12. Ряды вида V —	ч , Qfc	—	 хк ........................ 565
^ Г(ка + Ь)Г(кс + d)T(ke + /)
5.2.14. Ряды вида ^g/(fca + fe)r(fcC + rf)x^ 	 567
ГAее + /)
5.2.15.	Ряды вида > afc^	—	 ж1" .............................	567
^ kF(ke + f)F(kg + h)
5.2.16.	Ряды вида > аи	ж ........................	568
5.2.17.	Ряды вида V afc j V ^"^ )a;fc .................................	568
5.2.18.	Разные ряды вида \^а^жй ........... 	 .......................	569
5.3.	Ряды с показательной ж гиперболическими функциями ...............	570
5.3.1.	Ряды вида > оь—:	 ......................................	570
' -J	рПКТТ -Х- 1
5.3.2.	Ряды вида ^afcg(fca+6J .......................................	571
5.3.3.	Ряды, содержащие sha^a? и сЬа^ж ................................	571
5.3.4.	Ряды вида ^J an cosech bnx .....................................	572
5.3.5.	Ряды вида ^J ak cosech ктт ......................................	572
5.3.6.	Ряды вида \^ «те sech 6na; .......................................	573
5.3.7.	Ряды вида \J a^ sech 6д.тг .......................................	573
5.3.8.	Ряды вида \J a^ th b^ .........................................	574
5.3.9.	Ряды вида \J a^ cth кж ........................................	574
5.4.	Тригонометрические ряды .....................................	575
5.4.1. Введение .................................................	575
(±l)k ( sinkx 1
^1	}	575
E(±l)k ( sinkx
	^1
ks {coskx
^ (±l)fe ( sin(kx + b))
5.4.3. Ряды вида V-^	^l )	{} .............................. 576
^-^ (k + a)s { cos (Агж -'
5.4.4. Ряды вида V	^	{¦"***} 	 577
Z-^ («ni + ГП1)(КП2 + Wl2j [ COS kx J
5.4.5. Ряды вида V ^ \ s'm kx X ................................ 578
5.4.6. Ряды вида V ак{Ш^ ^'l ' 'Г } .................................. 579
sin (
^cosBfc + 1)ж ,
5.4.7.	Ряды вида V — I Sm Ж I ...................................... 581
^-^ Аи! [ cos kx J
х—ч 1 f sin (А;ж + a) 1
5.4.8.	Ряды вида Y^jzl )t , \\ .................................. 582
^^ k\ { cos (А;ж + a) J
r	f sin kx
(A; + a)s ( coskx
Er	f sin kx 1
~	^<	} .................................. 583
(A; + a)s ( k J
x-^ rk ( sin (Лж + a) 1
5.4.10. Ряды вида У2тт\ ,,	M ................................. 584
^^ k\ { cos(kx + a) J
\ J sin kx
\ cos kx
5.4.12.РядывидаУо^е~ьГтЬ I .................................. 585
/-^1	I cos ^ж J
5.4.11. Ряды вида V afcga(fc)	.................................. 585
Z—J	{ cos /гж J
, f sin i

Оглавление	19
5.4.13. Ряды вида \^ akrk I sm ж I .................................. 586
zJ { cos кх J
5.4.14.	Ряды вида > 	<	> .................................	586
L^ \±qmn {cosnx j
5.4.15.	Ряды вида \J a^ О sin kxj Т\СОБ^У1 ..............................	587
5.4.16.	Разные ряды, содержащие тригонометрические функции ..................	589
5.5.	Ряды с логарифмической и обратными тригонометрическими функциями .	590
5.5.1.	Ряды вида \J a^ In 6^ .........................................	590
5.5.2.	Ряды вида ^J ak arctg b^ .......................................	592
5.6.	Кратные ряды ..............................................	592
Глава 6. ПРОИЗВЕДЕНИЯ .....................................	594
6.1.	Конечные произведения ......................................	594
6.1.1.	Степенная и алгебраические функции ...............................	594
6.1.2.	Тригонометрические функции ....................................	594
6.2.	Бесконечные произведения ....................................	595
6.2.1.	Степенная и алгебраические функции ...............................	595
6.2.2.	Произведения, содержащие A ± хп)т ...............................	596
6.2.3.	Показательная функция ........................................	597
6.2.4.	Тригонометрические функции ....................................	597
Приложение I. НЕКОТОРЫЕ ЭЛЕМЕНТАРНЫЕ
ФУНКЦИИ И ИХ СВОЙСТВА ....................................	598
1.1.	Тригонометрические функции ..................................	598
1.2.	Гиперболические функции .....................................	604
1.3.	Обратные тригонометрические функции ..........................	606
1.4.	Обратные гиперболические функции .............................	608
1.5.	Биномиальные коэффициенты ..................................	609
1.6.	Символ Похгаммера (а)& ......................................	610
Приложение II. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ
ФУНКЦИИ И ИХ СВОЙСТВА ....................................	611
11.1.	Гамма-функция T(z) .........................................	611
11.2.	Функция ф{г) ..............................................	611
П.З. Функция /3(z) ..............................................	612
11.4.	Дзета-функция Римана C(z) .•...••...•••..•••...•....•••...•..	613
11.5.	Многочлены Бернулли Вп(х) ..................................	613
11.6.	Числа Бернулли Вп .........................................	613
11.7.	Многочлены Эйлера Еп(х) ....................................	614
П.8. Числа Эйлера Еп ...........................................	614
Приложение III. ТАБЛИЦА ФУНКЦИЙ Vi И V± .....................	615
Список литературы ...............................................	618
Указатель обозначений функций и постоянных .............................	621
"Указатель обозначений символов ......................................	627
Указатель разложения некоторых функций в ряды...........................	628
Указатель интегральных представлений некоторых специальных функций через элементар-
элементарные .........................................................	631
2*

ПРЕДИСЛОВИЕ
Книга содержит неопределенные и определенные (в том числе кратные) интегралы,
конечные суммы, ряды и произведения с элементарными функциями. Она написана с
целью удовлетворения запросов широкого круга специалистов в различных областях знаний
и включает результаты, изложенные в аналогичных изданиях, а также в научной и периоди-
периодической литературе, опубликованной в последнее время. Ряд результатов публикуется впер-
впервые. Отметим, что, интерпретируя некоторые интегралы и ряды как обобщенные функции,
интегральные преобразования обобщенных функций или рассматривая их регуляризации,
молено придать им смысл в более широкой области изменения параметров.
Достаточно подробное оглавление позволяет ознакомиться с содержанием книги и отра-
отражает ее отличие от ранее выпущенных справочных руководств в этой области математиче-
математического анализа.
Найти вполне оптимальную систему упорядочения материала книги вряд ли представ-
представляется возможным, но мы надеемся, что с помощью оглавления читатель сумеет отыскать
нужные формулы.
Применяемые обозначения, как правило, общеприняты в математической литературе
и приводятся в указателях в конце книги. При ссылках запись вида 5.1.4.3 обозначает
формулу 3 из пункта 5.1.4; к, I, т, п = 0, 1, 2, . . . , если не указаны другие условия.
Для компактности изложения в ряде формул используется сокращенная запись. Напри-
Например, формула
1
а_1 J Ш-CSIII X I ^ _ 7Г / j 1 I _ 1 ^ ] (« + l)/2l
^	1	f ""^ — 9 I 1 П Г "r /— ж I 1 4- /9 I
0
представляет собой сокращенную запись двух формул:
hraarcsina;da; = — A--=Г	I	[Rea > -1]
J	la \ а/ж I 1 + a/2 J /
V V L a/2
(берется только верхний знак и верхнее выражение в фигурных скобках) и
"-1 arccos х dx = ^- Г [(° + Ч^]	№ « > 0]
(берется только нижний знак и нижнее выражение в фигурных скобках).
Следует также отметить, что для некоторых интегралов имеется несколько различных
представлений, которые записываются под разными номерами, но без повторения левой
части.
Книга содержит три приложения, которые могут быть использованы при вычислении
рядов и интегралов, а также при приведении их к виду, содержащемуся в книге.
При составлении настоящего справочного руководства использованы литературные ис-
источники, список которых приводится в конце книги.
Мы будем весьма признательны всем читателям, которые обратят наше внимание на
неизбежные в работе такого объема недосмотры.

Глава 1. НЕОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
1.1. ВВЕДЕНИЕ
1.1.1. Предварительные сведения.
В этой главе содержатся неопределенные интегралы от элементарных функций; постоя-
постоянная интегрирования для краткости опущена. Например, вместо
sin х dx = — cos x + С
sin ж dx = — cos ж.
В ряде формул, где при интегрировании возникает логарифм абсолютной величины,
знак абсолютной величины для простоты опущен.
Некоторые формулы при определенных значениях параметров теряют смысл. Если эти
значения следуют из структуры формулы, то соответствующие разъяснения опускаются.
Выражения для интеграла при этих значениях параметров, как правило, даются в после-
последующих формулах.
Ниже используются следующие обозначения:
х, t, з, и, v — независимые переменные;
f,g — функции;
Р, Q, Pi, Qi — многочлены;
Р
R = — — рациональная функция;
Q
а, 6, с, d — действительные числа;
р, q, r, a, A, jn, и — комплексные числа;
к, 1,т,п = О, 1, 2, 3, ...
В случаях, когда имеются ограничения на значения параметров, делаются специальные
оговорки.
1.1.2. Основные интегралы.
1.
2.
{
ж dx =
А + 1
dx
= In |ж|.
sir
4. | ax dx =
5.
8.
11
14.
15.
In a
sin x dx = — cos ж.
dx
= tgx.
9.
ex dx = ex.
6. cos ж dx = sin x.
sin x
[a > 0, a^ 1].
cosz ж
¦ dx = secx.
7.
10.
= — CtgiE.
¦ dx = — соэесж.
. tg ж <^ж = —
In
12. ctgx dx =
In
13.
da;
= ln
dx
cos ж
dx
= ln
= — arctg —
a	a
[а^О].

22
Гл. 1. Неопределенные интегралы
[1.1.3
16.
17.
18.
19.
dx
х^
\fa
л/х
— а
dx
2°ТГ
dx
^+
dx
2
ГШ	1
. - = — In
а 2а
[а^О].
. х
= arcsin —
а
= Arsh — = In |ж + л/х2 + а2
_ = Arch — = In
2	а
21.
22.}
dx
sh2 ж
= — cth ж.
23.
26.
ch2 ж
dx
= thsc. 24. Шж йж = In ch ж. 25. cth ж dx = In | япж
27. [— =2 arctge".
J сЬж
1.1.3. Общие формулы.
. [(а/(ж) + %(ж))с!ж = а \f{x)dx + b \g{x)da
2.
dx
dx
[интегрирование по частям].
4.
[интегрирование подстановкой; х = g(y)].
1.2. СТЕПЕННАЯ И АЛГЕБРАИЧЕСКИЕ ФУНКЦИИ
1.2.1. Введение.
В этом пункте кратко изложены некоторые сведения общего характера, которые могут
быть использованы при вычислении неопределенных интегралов.
1. Если Pi (ж) и Qi(x) — произвольные многочлены, то их отношение может быть
представлено в виде
где Р2(х), Р(х), Q(x) — многочлены, причем степень Р{х) меньше степени Q(x). Пусть а*,
г = 1, . . . , т, — корни многочлена Q(x), n% — соответствующие кратности корней. Тогда
Р(х)
А
?
А
?
Ajm)
где
к (щ - k)l
P(x)
Q(x)
(х - аг)п'
Если гц = 1 для всех г, то
Q(x)
где
При объединении пар слагаемых, соответствующих комплексно сопряженным корням,
*	ЛХ + В	2 , , ,
получаются дроби вида 2 | и—j—, где трехчлен ж + ох + с имеет действительные
ж2 + 6ж + с
коэффициенты. Поэтому вычисление интеграла
^ „ Г dx Г Аж + В
рациональных дробей: т	^7 ^^	;	г
• dx сводится к интегрированию
¦ dx.

1.2.1]	1.2. Степенная и алгебраические функции	23
2. Интегралы вида xp(axr + b)q dx (р, g, r — рациональные числа) выражаются в виде
конечной комбинации элементарных функций только в следующих случаях:
а)	q — целое число;
б)	(р + 1)/г — целое число; тогда
f xp(axr + b)q dx = ^ hip+1)/r^(at + b)q dt	[t = xr];
в)	h q — целое число; тогда
г
Жи (л т -\- п\ пт — 	 I 	 \ t	fit	\т — т \
г I V t J
I /	/ CLX ~~\~ О \ / (XX "T~ О \	\
3.	Интегралы вида ЯI ж, I 	— J , I 	— J , . . . j dx, где p, q . . . — рациональные
,	„	„ ax + b m
числа, приводятся к интегралам от рациональных функции подстановкой	 = t , где
сх + а
m — общий знаменатель дробей р, q, ...
Г Ri(x) + _Я2(ж)-\/Р(ж)
4.	Интегралы вида / = 		dx, где Ri, R2, R3, R4 — рациональные
функции, а Р(х) — многочлен 3-й или 4-й степени с действительными коэффициентами
и простыми корнями, приводятся к виду
г	I г> / \ J 1	V / j
1 — I J1L5\^/ CJ/X ~t™ I	(JjJb j
где
l, R(x)=(-^^
'^J~	Rl(x)-Rl(x)P(x)
Эллиптический интеграл —	dx при помощи замен переменных, которые указаны
J у/Р(х)
ниже, может быть приведен к форме, содержащей рациональные функции от эллиптических
функций Якоби. Интегралы от эллиптических функций Якоби см. в [24].
1) Пусть Р(х) = <2о(ж2±а2)(ж2±62). Тогда интеграл	dx может быть представ-
—	'
\/Р(х) J
dx f	dx
Выраж:ение уР(ж) мож:но записать (после вынесения множителя у|ао|) одним из
следующих шести способов:
- ж2)
где а2, Ъ2 — действительные числа, р2 и р2 — комплексно сопряженные числа.
2 Аг + А2 sn2 и .	ч
В первых пяти случаях подстановка ж =	— и ^ м ^ К , где sn и — эл-
В\ + i?2 sn2 и
липтический синус Якоби и А\, А2, В\, В2 — некоторые постоянные, приводит интегралы
к виду Re(snu)du, где R§ — рациональная функция.
В шестом случае следует использовать замену х = 	 @ ^ и ^ 2К). где
Вг + В2 сп и
спи — эллиптический косинус Якоби и А\, Ai^ B±, B2 — некоторые постоянные.

24
Гл. 1. Неопределенные интегралы
[1.2.2
2) Пусть Р(х) = ао(ж + a\){x + аг)(ж + аз), где все а« различны. Интеграл
может быть представлен в виде линейной комбинации трех интегралов:
dx	Г х dx	Г	dx
¦ dx
/Р(х) J у/Р{х)
Выражение y/P(x) можно записать (после вынесения множителя \/|ао|) одним из
следующих пяти способов:
\/{х — а)(х — Ь)(х — с) , \/(а — х)(х ~~ Ь)(х — с) , \/(а — ж)F — ж)(ж — с) ,
где а, 6, с, 6i, 62 действительны и а > b > с. В первых трех случаях к интегралам от
эллиптических функций Якоби приводит подстановка
Ь А2 sn2 и	//Л ^	г^ч
ж =
sn2 и
(*)
где /ti, A2, ^1, ?»2 — некоторые постоянные. Если два корня многочлена Р(х) комплекс-
комплексны, то следует сделать замену
- А2 спи ,_
X =
сп
2К).
(**)
3) Пусть Р(х) = ао(х + а\)(х + аг)(ж + аз)(ж + «4), где все пг различны. Интеграл
- dx может быть представлен в виде линейной комбинации четырех интегралов:
/Р(х)
dx
P(x)
х dx
х dx
dx
Выраж:ение уР(х) можно записать (после вынесения множ:ителя у|ао|) одним из
следующих шести способов:
у (ж — а)(ж — Ь){х — с){х — d) , у (а — ж)(ж — Ь)(х — с)(х — d) ,
(а - х)(Ъ - х)(х - с)(х - d) , ^{х - а){х - Ь)[(х - ЬгJ
где а, 6, с, d, 61, 62, 6з5 ^4 действительны иа>6>с>A.
В первых трех случаях следует сделать замену (*), а в остальных — замену (**).
1.2.2. Интегралы вида \хр{ахг + ЪL dx .
t Г р/ г , u\q j xp+1{axr + b)q qrb Г V( r u^q-i ,
1. x (ax + о) аж =	1	 x (ax + 0) ax.
x (ax +b) , gr + r + p+lf p r ,+1^
)rb J
2.
3.
4.
5.
6.
l)rb
¦l)rb
p+1
(ax
p +
+ 6)g gra f p+r/
1	^nj-p («
dx.
(g + l)ra	(g + l)ra ,
	— 	 ^ (
(a/ + 6)g+1 (gr + r + p + l)a
L с/ж.
7. / аж + b) dx =
J

1.2.3]
1.2. Степенная и алгебраические функции
25
8.
9.
10.
12.
13.
14.
хр dx
(ахг + Ь
(g - l)r -р-
(q - l)rb(axr
(g - l)ra(axr
-1
xr~1dx
(axr + by ~ (q - l)ra(axr +
da;	1
^г	(g - l)rb J (axr
p — r + 1 Г xp^r dx
)ra J (axr + bL^1
xr^dx 1
(g - l)ra J (аж
(g -
ажг + b ra
p + (g — l)r — 1
= — In \axr + 6|.
xP(axrjrb)	I
с!ж	1 .
ж(ажг + 6) rfe '
rfa;
xP~r(axr + 6)"
axr + 6
1.
1.2.8. Интегралы вида
dx
2.
xmdx
xn ±an
i / 2 о
7Г In ( ж — 2аж cos
тг + а ) +
-^—г /^ sin	тг arctg
2ife + l
ж — a cos	тг
	2n
fc=0
2n
In
dx
2n+l
In ж + а
/ 2
тг In ( x — 2ax cos
тг + a +
. 2/s + 1
ж-acos
2 ra + 1
. 2k+ 1
asm	тг
3.
4.
dx
¦In
H
¦In
cos — In 1 ж — 2аж cos	ha ) —
'	П	V	71
. кж
sin — arctg
ж — a cos (ктт/п)
a sin (кж/п)
2k-
тг In ж + 2аж cos
тг + а | —
.ST
2k + 1
sin	 тг arctg ¦
ж + a cos ¦

26	Гл. 1. Неопределенные интегралы	[1.2.4
к
о. 2
в [
т2
жт
Хт€
Bп
г
1
п + 1
2
1ж
а2п+1 (
1
+ 1)а2п^ш
,2n^m^l ^
1 \^
па2""*71 ^-^
fc=O
2п + 1)а2п-т
V^ лл„ (т +
> (т + 1)B
о 2пЛ
1
^^^ (т 4
In ж + а
1)BА; + 1
2п + 1
* + 1К
¦1
)BА; +
- 1)BА;
2п
^ In
ш
2
arc g
2ife + l
lj X асоо ^^ тг
тг arc g ^ 2fe + 1
2n
2Jfe + 1
a sin	тг
— 7Г
+
+
n -
•')
"I)]-
7- J J^
1 in |* + a|]
os	In I ж — 2ax cos
у	П
H	7 > cos	In I ж — 2ax cos	ha I —
22nml Z^	у	J
^
от 7 sin	aretg,, ,
na2"- ^	n	asin(for/n
Г жтс1ж	1
" J 2п+1 2n+i - B + lJ«w П
x - acos(kw/n)
aretg	,, , \	1 ^ m ^ 2(n - 1) .
asin(for/n)
1 / 2^о	2fc + l	2\
In ж + 2ax cos	тг + a +
V	2 + l	/
1.2.4. Интегралы вида
xpdx	xp
(q - l)(x + a)*-1 + g — 1 J (ж - a)''
2. [ Ж fe =1жлф(^^, 1, Л)	[ЕеЛ>0;Ж<а].
} х+а а	\ а	J
о
3-
о
л^1dx x	(	a\

1.2.5]
1.2. Степенная и алгебраические функции
27
5.
xmdx
^
m\ (-a)k(x + a)m
к J m — q — к ¦
если к = m — q -\- 1, то вместо соответствующего члена в сумме следует взять
6. \^^: = -±(Пк
(ж + а)^	^ \ к J (q - к - 1)(ж + а)**-*-1'
если к = q — 1, то вместо соответствующего члена в сумме следует взять
7.
9.
10.
11.
12.
13.
15.
16.
17.
19.
21.
22.
1.
2.
dx
(ж + а)п	(п - 1)(ж + а)п^г'
х dx	1
ж2 dx	1
8.
х + а
а
= 1п
(п -
2а
а)п	(п ^
(п - 2)(х + а)п~2 (п -
1
(ж + а)п ~~ (п - 4)(ж + а)
¦ +
За
За2
ж + а ^ m — к
к=0
(п — 3)(ж + а)п 3 (п — !
	Ь (-а)т1п|ж + а .
(п -
х dx
= ж —а1п|ж
ж + а
ж3 а*ж ж3 аж2
ж + а ~~ 3	2
14.
ж + а
=	аж + а 1п
а ж^а In |ж + а|.
(ж + аJ
(ж + аJ ж + а
ж3 dx х2
fe=l
а
fcfcafc~^m~fc
m — к
i 1п |
(ж + аJ 2
ж2 а*ж
2а
ж + а
2
(ж + аK ~ ж + а 2(ж + аJ
ж б?ж	За	а
18.
- In |ж
Л 1	Л
х dx a	.	.
= ж	;	2а In ж + а .
(ж + аJ
20.
ж + а
ж dx
(ж + аK ~ ж + а ' 2(ж + аJ"
1	а
(ж + аK
ж + а 2(ж + аJ
— За In ж + а
1.2.5. Интегралы вида
dx
(р -
1(ж + а)^^1 (р - 1)а
а)? *
(q - 1)а
dx

28
Гл. 1. Неопределенные интегралы
[1.2.6
3.
dx
то+п-2
т + п — 2Л
к ) (га — к —
если к = га — 1, то вместо соответствующего члена в сумме следует взять
ж + а
1 In
га — 1
4.
5.
6.
7.
8.
9.
11.
12.
13.
14.
15.
16.
17.
dx
dx
А; V &
1
аТ1
ж
x + a
ж + ау
п —1
а
	In
n
•In
х + а
dx
2а2 J ж(ж + а)п'
(-1)т , х + а
dx
х(х + а) а
dx
ж + а
1	1
10.
dx
1
а2ж 2аж2 а3
ж2(ж + а)
х + а
2
ж + а
ж
	In
ж + а
ж(ж + аJ а\ж + а а
da _ 1 / 1
а2 \ ж + а " ж а
ж2(ж + аJ
dx
1 2.
	In
г(гт
1
ж 2ж2 а
ж + а
1	1
ж(ж + аK а2(ж + а) 2а(ж + аJ а3
dx	12
ж
ж + а
ж2(ж + аK	2а2(ж + а)
/1т»	1 Г Ч
ж3(ж + а)
4
а 6
¦а 2(ж + аJ ж 2ж2 а
1.2.6. Интегралы вида (ж + с)
ж + a
ж + Ъ
2. ж
ж + a
ж + 6
q(b — а) + р(Ь + а)
Т
а)"
»-1
ж + а
ж + b
ж + 6
dx.
_ (ж + а)9+1 дF - а) + а + b Г /ж + аY

1.2.6]
1.2. Степенная и алгебраические функции
29
4.
5.
6.
7.
(ж
¦ о*ж = — -
\р-1
g^lj (ж + 6)9-1
dx.
о'ж =
ж + а
(ж + с)р \х + 6
(ж-
(* + <*
(ж-
Ж + а\р+1
(р
dx =
2)F - аJ(ж
-| (а. + с)р-х Z + bl-i
ж + а
(ж + с)? \х + 6
+ (Р - 3)
8.
9.
10.
11.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
ж + с V ж + b
ж + а
ж + 6
с/ж =
п-к\\Ь- с
- 1
(ж +
— 1 In |ж + 6| +
ж + а
ж + 6
ж + b
In ж + с
^ (п- к)(п - к - 1) (ж + 6)
^_fc_1 + п(ж + а) — ггF — a) In
(a^6)fe+1
4
ж+о
;—h ж + гг(а — b) In |ж + 6|.
12.
ж+o
(а - 6)(ж - bin |ж + 61)
Ж "у" О
ж+а
—р——гг
ж(ж + 6)
= — + (а - 6) (— - bx + b2 In |ж + Ь\
О	V
а
= - In
6
а-Ъ
In ж + Ъ .
ж + а\2	(а - бJ .	ч ,	.
dx = ж —	—г	h 2(а — 6) In |ж + 6|.
ж + 6
ж + 6
= —±2(a^ Ь)х + (а - 6) Р f
2	| ж + о
(а - 36) In |ж + 6| I.
2( Х-
ж+
1 /ж + а
ж \ ж + 6
Х + ^
ж + о
ж +¦ о
dx =
3
(а - ЬJ
6(ж + 6)
(а - 6 ж
2 6(а — 6J
2 + l I
ж + 6
+ (а - 6)[(а - 36)(ж + 6) - 26(а - 26) In \x + 6|].
2
¦In
а
б2"
-1) 1п|ж
Bа - Ь)х + (а - бJ In \x + 61.
= ^- + Bа - 6)^- + (а - 6J(ж - 6In \x + 6|).
ж2 ( + а) da; = — + Bа^6)— + (а ^ бJ f — ^ 6ж + б2 In |ж + 6| ).
Ж +¦ 0	4	о	V ^
(ж + аJ
ж(ж + 6)
dx = ж + — (а In |ж| — (а — 6) In |ж + 6|).

80
Гл. 1. Неопределенные интегралы
[1.2.7
i ж + a	a — b „	,.
23. I	— dx =	h In \x + b\.
с + bI	x + о
24.	ж
25.	\x
ж + a	6(a — b)
(x + bJ ~	x + 6
2 ж + а	ж2 ,
26.
ж + а
а — b a .
	 	 	 In
{ + b) b2
(а- 26Iп
b2(a~b)
x + b
x + b
— 6Bа — 36) In
1.
2.
1.2.7. Интегралы вида
х
хр dx
1	I	x*
- [(p^r)a + (p^gN]
жfc йж
р^г dx
(ж + аУ(х
- (p- l)ab
dx
(ж + а)
m"~1 / ixm + p+fc + l r-m — k — l	/	j	,
\~-л (-—I)	v-^ (p\ I m -\- n — к — I — 1
- >	;!:		>	III
/ -j b(<r -\- n\k	' ^	\ 1 / \ n 	 1
fe=l V 7	L 1=0 x
w — 1 / - \ m.
F- a)
fc=0
m + n~k~l — 2
I
##i» — i	/I" — "•/
nQ 	 L 	 2
+ (-1
3.
4.
5.
6.
rfa;
7.
(*-
(ж-
(Ж-
Ьа)^(ж
dx
rn
2-
О*Ж
Ь а)(ж -
(r-
-l)(a
ffe)
1
(-l)m
(b-a)
n+k fm +
{
1 In
ш
a — 6
X
+?
n
1
ж
X
1
+
l-
+
+
a)
(x
k-
n
m
a
tin-'*
-k-2\
-1 J
1
- A;
+
a)m
+
*
- 1
С
a)
(b
q
(r-
/
I
{
П + 1
n -
1
(-1)
-a)
_l_ r _
A;
i-2
- 1
1
m + l
2 1
-6)J
f
J (x +
-At
)(b-
a)
(m
A
(t 4- a'
dx
f v A- aX
-i \m —1
a)m
+ n - 1
dx
я(х + Ь
' + fe)r"
n —fe —1
In
Ж
Ж
),„
Ж
ж
+
+
+
+
а
0
а
b

1.2.8]
1.2. Степенная и алгебраические функции
31
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
ж dx
(а In
(ж + а)(х + b) a — b
х2 dx	1
(ж + а)(х + 6)	а — b
dx
F21п|ж
dx
= —In ж + —	—
ab	a (a — b)
1 а + b ,
dx
абж
-1
— a In | ж
In | ж + а •
1
b(a - b)
7Y In ж + а
1п|ж
¦ In x
х dx
ж а*ж
—6
(a - b)*
a
(a — bJ
a2
(a - bY
x -
x -
x -
x -
- a
b&
- a
In
In
In \x + a\
b — lab
In
dx
ж(ж + а)(ж + ЬJ
аЪ2
1
In
1
(а - ЬK
In ж + а +
¦In
21)-
In
ж + b
х dx
¦аJ(ж-
ж2 dx
(а-
a + b
(a - 6K
In
ж + 6
b) (а-Ь)*
In
ж + 6
1.2.8. Интегралы вида Я(ж, ах2 + 6ж + с) dx.
[Г
Bаж + Ъ)(ах2 + Ъх + с)п - пF2 - 4ас) (
1
)" dx .
2.
3.
4.
5.
6.
(аж2 + bx + c)n da _ (аж2 + &ж + с)
n + l
+
xmdx
(vn 	 1 1СЖ'пг — "^
- m + 2) Г (аж2 + bx + с)те а*ж аBп - ш + 3) Г (аж2 + Ьх + с)"
Г(аж + &ж +
с(т — 1)
¦ а|ж.
(ах2 + 6ж + с)п	Bп -т- 1)а(аж2 + Ьх + сO1
(п — т)Ь
1 dx
Bп — т — 1)а J (аж2 + Ьх + с)те Bгг — m — 1)а J (аж2 + Ьх + с)п *
23	ж2пс1ж	6 Г ж2пс1ж
(ах2 + 6ж + с)п а j (аж2 + Ьх + с)*1™1 а J (аж2 + Ьх + с)те а J (аж2 + Ьх + с)п *
ж а*ж	1	& f	dx
(ах2 +
- с)п	2(п — 1)а(аж2 + Ьх + с)та^1 2а J (аж2 + 6ж + с)п *

32
Гл. 1. Неопределенные интегралы
[1.2.8
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
Ьх + 2е
Bга - 3N
(га - 1)F2 - 4ас)(ах2 + 6ж + с)" (га - 1)F2 - Aac) J (ах2 + 6ж + с)"'
da;
х dx
(b2 ~~ 2ас)Bах + b) ~~ b(b2 - Aac)
(ax2 + bx + с)те	2(ra - I)a2F2 - 4ac)(ax2 + Ьж + с)*1
2Bn - 3)F2 - 2ac) - 2(ra - 1)F2 - 4ac)
rfa;
2(n-l)a(b2 -4ac)
1
жга(
с)те	(ш -
(т + га — 2N
(т — 1)е
с!ж
dx
(т + 2п — 3)а
Ьх + с)п	(ш —
Ъх + с)п'
х(ах2 + Ьх + с)п
1
" 2(п - 1)с(ах2
dx
2с J (ах2
1
- с)п с
(ах2
dx
(п - 1)F2 - 4ас)(аж2 + Ьх + с)"-1 (п - 1)F2 - 4ас) J (аж2 + Ьх + с)"-1"
6 v^	2fcBw - l)Bn - 3) . . . Bп - 2k - 1)ак
2n -
- 2) . . . (n - A; - 1)Dас -
(га — 1)!Dас — 62)п~
2аж + b — \/b2 — 4ас
da
2ах +
1
а(р - q)
arctg -
2аж + b
[b2 - 4ac > 0].
[b2 - Aac < 0].
\b2 = 4acl.
In
x — p
x ~~ q
где р, q — действительные корни многочлена аж + Ьх + с.
da;	2аж + 6	2а
17.
18.
19.
(ax2 + bx + cJ Dac — 62)(аж2 +
dx	2ax + 6
dx
с) 4ac — b2 J аж2 + 6ж + с
(аж2 + Ьх + сK 2Dас — 62)(аж2 + Ьх + сJ
ЗаBаж + 6)
¦ +
6a2
Dас - b2
ж da;
аж2 + bx + с 2а
1	2
= — In lax + 6ж + с
-In
arctg
20.
ж2 dx
ax2 + &ж + с a 2a2
In lax + 6ж + с +
2 + 6ж + с
[Ъ2 >4ас],
[4ас> б2].
2а2
+ bx + с

1.2.9]
1.2. Степенная и алгебраические функции
33
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
х3 dx
ах2 + ож + с
2а2 " 2а
6ж + 2с
Ь2 - ас Л 2 _	, bib2 - Зас)
Н	т-;— In аж + Ьх + с - l	;
2а3
dx
dx
ах2 + Ьх + с
(аж2 + Ьх + сJ (Ь2 — 4ас)(аж2 + Ьх + с) Ь2 — 4ас J аж2 + Ьх + с *
ж2 с/ж
^ 62)ж -
2с
(аж2 + Ьх + сJ аE2 — 4ае)(аж2 + 6ж + с) &2 — 4ас J аж2 + Ьх + с
с/ж
ж с/ж
(аж2 + 6ж + сJ
^Ь2)
= —In
ж(аж2 + 6ж + с) 2с |аж2 + Ьх + с
2 2аж + b + V62 ^ 4ас
arctg -
[б2 > 4ас]5
[б2 < 4ас].
dx
dx
ж(аж2
еж 2с2 |аж2 + Ьх + с
2с2ж2	2с3	|аж2 + Ьх + с
¦ сJ 2с(аж2 + 6ж + с)
2с2
In
2с2 V б2 - 4ас У j аж2 + Ьх + с *
с + 6ж
х2(ах2 + 6ж + сJ с2Dас — 62)(аж2 + Ьх + с) с2ж(аж2 + 6ж + с)
с3 |аж2 + Ьх + с б2 — 4ас V с3
'
dx
с У j аж2 + 6ж-
dx
ж3(аж2
+ сJ
Збж — с
362 - 2ас
dx
9ab
dx
2с2ж2(аж2 + Ьх + с) с2	J ж(аж2 + Ьх + сJ 2с2 J (аж2 + Ьх + сJ *
1.2.9. Интегралы вида Я(ж + d,	аж2 + 6ж + с) dж.
г 1	Г
L (ж + d)m^2 + bx + с)те dж = ^	^ I (ж + d)m(аж2 + Ьх + с)те+1 +
7
(rn + 2п
(m + n)Bad - Ъ) Ux
¦ 6ж + с)п dж —
f	1
- (m - l)(ad2 - 6d + с) (ж + d)TO~2^2 + bx + c)n dж .
J	J
2.
(аж2
2n(ad2 -
(т — 2п — 1)(ж
(аж2 + bx + i
га — 2п — 1
3 А. П. Прудников и др., т. 1
(ж + d)r
п(Ь - 2ad) Г (аж2 + bx + сO1^1
аж	- —	; ¦ т—— - аж.
m — 2п — 1
(ж + d)r

34	Гл. 1. Неопределенные интегралы	[1.2.9
~ (m-l)(ad2 ~
. ow. o JX {(ах + Ъх + с) J Цах + Ьх + с) J )
(m - n - 2)(b — 2ad) ^—,	-	-^— dx + (m — 2n - S)a ^—,	^	^- dx .
1	A	}] (x + d)m^	K	) J (ж + d)^2	J
_ (аж2 + bx + с)п
n(b — 2ad) Г (ах2 + bx + c)n 1	o f (аж2 + bx + c)r
ra — 1 J (ж + dO71™1
¦ / 2.1 , \n
упХ -\- OX -j- CJ	, 2 iii \n i i i л i
5.	dx = (ad — bd + c) In ж + a +
'
(аж + & — ad) 2,(a<^ ~ bd + С)П (аж + Ьж ¦
L fe=o
(OnИ -— h\(Onv Л- h\ A~ (Ann — Л2>1	fi» 4- Л>|т+1
(аж2 + 6ж + c)n 2(n — l)Dac — b2)(ad2 — bd + с) (аж2 + 5ж + c)n х
2(m^2fi + 4)a	(ж + d)m+1
+ (n - l)(n - 2)Dac - b2)(ad2 - bd + с) (ажЧЬ + с)™-2 "
4Bra-3)a	2(m - n + 2) 1 Г (ж + d)m dx
(n - l)Dac - &2) (n - l)(ad2 - bd + c) J J (аж2 + kc + e)^1
(ж + d)m dж
(n - l)(n - 2)Dae - b2)(ad2 - bd + c) J (аж2 •
1	Г
7.
8.
9.
(га — 2n + l)a [(аж2 + 6ж + с)те 1
+ (га — n)Bad — 6) -™—-——	—^ — (га. — l)(ad2 — bd + с)
Bах + 6)(ж + d)m
(п - 1)Dас - fe2) L (аж2 + 6ж + с)^^1
- 2(ш-2п + 3)а 7—^—г^	^—r^(fe^2ad)ml/ о ,	ч
J (ах2 + bx + с)Пм1	J (аж2 + ож + с)п"
dж	—1
(ж + d)m(o^2 + 6ж + c)n (m - l)(ad2 - bd + c)
x 7	г	tz—7:	г	™ + (m + n - 2)F - 2ad) x
L(ж + d)w^1(aж2 + feж + c)n^1 l	A	;
dж	,	ч Г	dж
-;	2	Г	\	h (w + 2п — 3)а
ю.	-	х
11.
2(ad2 - bd + c) [(n - l)(x + d)m(aж2 + bx + сO1™
,	. Г	dж	?тг + 2n — 3 Г	dж
^	^J	J
(ж+ d)m(ax2+ 6ж + с)п	n-1 J (ж + d)то(aж2
1
(ra + ra - l)Bad- fe)
1	Г	dж
[1
(ж + d)m^2 + 6ж + с)" ^W ^^ ^a
[ad2 - bd + с = 0].

1.2.10]
1.2. Степенная и алгебраические функции
35
12.
13.
f
J (x
I
J (x
+
+
dx
d){ax2 + bx
d)(ax2 + bx
1
2(ad2 -
2ac
bd +
ad2
1
2(acf2
l-b
1
- 6d + с
->Ь
1
— 6cf +
— Aac\
\ г
[2(?г-1)(аж2 +
dx
2a
In
(ж + аJ
аж2 + bx +
2аж +
2аж + 6 - V
2аж + & + л/
bx -Ь
Г
J (ж
с
6
кгс|
1
\ 1 1
dx
+ с!)(аж2 +
Aac
Aac
bx +
[62 4
[62 4
ас <
ас >
1
0],
0].
14.
dx
(ж + dJ(ax2
1
1
¦In
: - bd + с [ж + d 2(ad2 - bd + с) |аж2 + 6ж + c|
" -6rf + c) - Bad-62) f	^ж
1.2.10. Интегралы вида
тт (It
1. [ / f i d^ =±
xmdx
m - 2n + 3 Г жт dx
(ж2 ± a2)^	2(n - 1)а2(ж2 ± a2)n~
(ж2 ± a2)^^1'
2.
3.
4.
5.
(m-l)a2
(га - 2n + 1)(ж2 ± a2)^-1 ^ ra - In + 1 J (ж2 ± a2)" '
1	xm~2dx
1 dx	x2n
(x2 + a2)n 2(n-l)a2 [{x2 + a2)^1
Y^ Bn - 2m - 3)Bn - 2ra - 5) . . . Bn - 2ra - 2A; - 1) 	1
+ ^	2fc(n-2)(n-3)...(fi-ife-l)	a2fc(x2 + a2)""fc
xm 2m-2n+i Bn - 2ra - 3)Bn - 2ra - 5) . . . C - 2ra)(l - 2m)
6.
(ж2 - a2)n	2{n - l)a2 [(ж2 - а2)^1
^ k Bn - 2m - 3)Bn - 2m - 5) . . . Bn - 2m - 2k -
7.
,/ пчп+1
-T\iJC2
ж2т+1сгж
2m^2n+i Bn - 2m - 3)Bn - 2m - 5) ... C - 2ra)(l - 2m)
2^^1(n-l)!
x
^2k-l\aJ	2
а
2k
(п - га + А; - 1)(ж2 ± a2)^
з*

86
8.
9.
10.
11.
Гл. 1. Неопределенные интегралы
[1.2.10
2(±а2
x2mdx T1	-2fc»2m-2*-1
п-т-2
ж2±а2
Х2±а2 L^y^> 2m-2k-l
k=0
ж
arctg ~~
ж — а
[п ^ т -
ж + а
2что , _2 , 2
т-к	2
I (Та2)™ In jar2 ± а
х2т dx	х
2т+1
12.
13.
(ж2±а2J	2а2(ж2±а2) 2
с!ж
- A - 2те)а2т~3 х
arctg —
а
х + а
dx
(ж2 ± а2)^	2(п - 1)а2(ж2 ± а2)^1 2(п - 1)а2 J (ж2 ± а2У
к	Bга-1)Bп-3) ...Bп-2к-
{х2±а2)п
. - 2) . . . (n - fe)a^
+ (±1) 9П-1ГИ_
ж — а
¦ +
arctg
п
ж
ж
ж
а
+
—
а
а
14.
15.
16.
17.
19.
21.
dx
ж2 ± a2 all
1	arCtga
(ж2±а2J 2а2(а2±ж2) 2a3
(ж2 ± а2K	4а2(ж2 ± а2J + 8а4(ж2 ± а2) + 8а5
arctg -
1{
ж — а
ж + а
ж2 ± а2 2
1	2,2
= - In ж ± а
2
ж
arctg —
а
ж + а
ж — а
2 2
ж с/ж
(ж2±а2J	2(ж2±а2
20.
а arctg —
а
ж2 ± а2 3
— In
ж + а
ж — а
22.
ж2 с/ж
1	ж
— arctg -
la	a
(ж2±а2J	2(ж2±а2) ' | J_
4а
In
ж — а
ж + а

1.2.11]
1.2. Степенная и алгебраические функции
37
23.
24.
ж3 dx
= ±-
-\п ж2±а2|.
(ж2±а2J	2(ж2±а2) 2
ж dж
(ж2±а2J = Х 2(х2 ± а2) ] За ^
За	ж
— arctg -
А	(Л
х + а
ж — а
1.
2.
1.2.11. Интегралы вида
dж
3.
4.
5.
6.
7.
8.
9.
dx
(ж2 ±
= Т
хт(х2±а2J'
1
-3
Bт- 1)а2ж
±1
Bт - 1)а2
dx
Bт + 2п - 1)(ж2 ± а2O1
Л (=pl)fcBm + 2п - 1)Bт + 2п - 3) . . . Bт + 2п - 2k -
^	Bт - 1)Bт - 3) . . . Bт - 2k + l)a2fc
т Bп - 1)Bп + 1) . . . Bп + 2т - 3)
[см. 1.2.10].
1
т + п — 1
:±а2)^
1
± а2)^
та2 J x2m^1(x2±a2)n°
ч^b/m + n-l^ 1 /ж'гЬа2^1
А; ) к — п + 1 V ж
±1
ж(ж2±а2)те
п —1
~" 2 ^ "
: а2)п -1 а2 J
(±1)к
2а2п \х2±а2\'
dx
ж2т(ж2 ±а2)
с/ж
dx
х2т{х2±а2J
«* /	Bfe + l)a2(w^
(Tl)
т arctg-
k=0
,
- 1
X + С
(Tl)
fe+1
k=Q
п-1
\х2±а2\'
2а2т+3
1
2
arctg
In
ill
Ж
Ж
ж
а
а
а
10.
11.
12.

38
Гл. 1. Неопределенные интегралы
[1.2.12
13.
14.
15.
16.
17.
18.
19.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
dx
ж4(ж2±а2)
1	11
а4ж а5
arctg -
-In
х — а
ж + а
1
П
ж(ж2 ± а2J ~ 2а2(а2 ± ж2) + 2а4 П |ж2 ± а2\'
dx
х
arctg —
а
х2(х2±а2J	а4х 2а4(ж2±а2) 2а5
х + а
ж3(ж2±а2J	2а4ж2 2а4(ж2 ± а2) ^ а6
1 -±-?-±
ж4(ж2±а2J	За4ж3 а6ж 2а6(ж2±а2) 2а7
ж
arctg —
а
х + а
х — а
,w 9 ,—^Т = 9 , L9 In |ж + 6| - - In (ж + а ) + - arctg - I.
¦6)(ж2 + а2) а2 + Ь2 I	2	а	а1
а2-
1п|ж + Ь\
¦In
2а(а - Ь)
In |
1.2.12. Интегралы вида
т j	m + 1
(ж3 + а3)^ 3(п - 1)а3(ж3 + а3)" 3(п - 1)а3
тт^2	(т - 2Ь;
xmdx
3
(га - 3n + l)(a
m j_	«,wi —2
dj	Ubdj	Jb	3
ж3 + a3 ra — 2
с!ж
ж3 + а
х
з '
m - Зп + 1 J (ж3 + а3)п '
Зтг-4
ж с!ж
3a2(n- 1) J (ж3 + а3)'
ж а'ж
fT3 _|_ a3)n~l '
dx
х dx
ufl ж аж ~т~ t
= — ln-
6a
1 2ж - а
w^ arctS	/=-•
1 2ж - а
—— arete	=—.
х2 dx 1 з,з
^^—- = - In ж + а
хЛ + аЛ 3
х3 dx	а . х2 — ах + а2
= ж + - In
ж3 + а3
dx
1
ж(ж3 + а3) За3
dx
In
(ж + аJ
ж3
1 2ж - а
— arctg	—.
ж3 + а3
6а4
1	2ж - а
—=¦ arete	=—.
dx
— ах + az
1 ln (ж + аJ
ж3(ж3 + а3)	2а3ж2 6а5 ж2 — ах + а2 а
1	2ж - а
—^ arctg ¦
а^З

1.2.18]
1.2. Степенная и алгебраические функции
39
13.
14.
15.
17.
18.
dx
1
(ж3 + а3J За3(ж3 + а3
х dx	ж2
In-
{x + af
2ж — а
9а5 ж2 — аж + а2
1
(ж3 + а3J За3(ж3 + а3
ж с/ж	1
+ а3J
dx
18а4
16.
In
ж2 — ах + а2
(ж + аJ
dx
arctg ¦
1	2ж - а
а^З
За3ж(ж3
(ж3 + а3J За3(ж3Н
4	2	(ж + аJ
За6ж 9а7 ж2 — аж + а2
За6
In
с/ж
ж3(ж3 + а3J
1.
2.
3.
4.
5.
6.
7.
8.
9.
11.
12.
13.
За3ж2(ж3 + а3)
1.2.13. Интегралы вида
хт dx	,	xm+[
ln
6а6ж2 18а8 ж2 - ах + а
x±mdx
(ж4 ± a4)n ' J (аж4 -
, An — т — 5
+ с)п '
xmdx
(ж4 ± а4)те	4(га - 1)а4(ж4 ± а4)" А(п - 1)а4 J (ж4 ± а4)п~г'
(ж4 ± а4)п (т - An + 1)(ж4 ± а4)^1 т - An + 1 J (ж4 ± а4)п '
xmdx хт^л
ж4 ± а4
dx
.-3
ж4 ± а4
— 5
жто(ж4 ±а4)п
, 1
(т - 1)а4
а4 жт(ж4
dx
И\п-
In-
arctg
ж4 ±а4
ж с/ж
ж4±а4
xz dx I
4а3
4а2 ж2 + а2
1 . Ж2^1
In
In
+ а2
аГС §
^—In
4а
ж4 ± а4 4
а*ж
ж2(ж4±а4
= - In ж4 ± а4
+ —- arctg -
2а	а
dx
1	ж4
In ¦
ж(ж4±а4)	4а4 |ж4 ± а4
1	1 Г x2dx
J
ж4 ± а4
In
ж3(ж4±а4)
хш dx _
(ж4±а4J ~ 4а4(а4±ж4) ± Аа4
З-m
\ xmdx
J х4 ±а4
ж3 + а3
2ж — а
arctg :
5 2ж — а
—-=¦ arctg	—.
а4)п "

40
Гл. 1. Неопределенные интегралы
[1.2.13
14.
15.
16.
17.
19.
20.
21.
22.
23.
24.
25.
dx
3 , ж2 + аж^2 + а2
¦ In ¦
3	ах\
arctg -
16а7^2 ж2 - аж^2 + а2 8а7^2	а2 - х
(х4±а4J 4а4(а4±ж4)
х dx
16а7
In
х + а
ж — а
^т arctg -
8а7	а
(х4±а4J 4а4(а4±ж4)
х dx
¦ In ¦
1 л х2 - ахл/2 + а2
— In	—
arctg —
(ж4±а4J 4а4(ж4±а4)
26.
(ж4±а4J	4(ж4±а4)
dx
18.
16а5
dx
¦In
ж — а
ж + а
arctg —
а
In -
4а4(а4±ж4) 4а8 |ж4 ± а'
ж2(ж4±а4J	а8х 4а8(ж4±а4
(ах4 + 6ж2 + с)п (т - An + 1)а(аж4 + Ьх2 + с)п
\ III — ОIС I	JL	UJL
la J
dx
(т - An + 1)а J (аж4 + &ж2 + c)n (m - An + l)a J (аж4 + ож2 + с)п "
1 Г	xm^4dx	с Г xm^4dx	b	2
а J (аж4 + Ьх2 + сO1 а J (аж4 + Ьх2 + с)п а } (ах4 + 6ж2 + с)п '
dx	_	abx3 + (б2 - 2ас)ж	(An - 7)ab
2(n- l)cF2 -
(аж4
2(п ~~ 1)(Ь2 ~~ Аас) + 2ас - Ь2
2(п-1)с(Ь2-
2(п — 1)еF2 — 4ас)
dx
(аж4
с/ж
xm(ax4 + bx2 + c)n (m -
bx2
dx
m + An — 5
(т - 1)с J жт™2(аж4 •
dx	2a
c)n	(m - l)c J жт~4(аж
с/ж
dx
dx
1
2ax2 + b - л/b2 - Aac J 2аж2 + b + л/Ь2 - Aac
а х2 + 2ж У с/ a cos (а/2) + \/ с/ а
sin — In ¦
Л	[62>4ac].
4 v а3с sin а L 2 ж2 — 2ж у/с/a cos (а/2) + у/с/а
a	x2 - y/c/a
¦ 2 cos — arctg	.
2	2x^fc/asin(a
b < 4ac; cos a = —
а'ж
abx3 + (б2 — 2ае)ж
(аж4 + 6ж2 + сJ ~ 2сF2 - 4ас)(аж4 + ож2 + с)
б2 — бас Г	dx
ab
2c(b2 - Aac) J аж4 + 6ж2 + с 2еF2 - 4ас) J аж4 + Ьх2 + с'
х dx

1.2.15]
1.2. Степенная и алгебраические функции
41
27.
28.
29.
30.
ж dx
ах4 + 6ж2 + с 2л/Ь2 - Аас
In
2аж2 + 6 - V62 ~~ 4ас
2аж2 + 6 + V62 - 4ас
1	2аж2 + 6
arctg -
/Аас - Ь2
/Аас - Ь2
х dx
6 + V62 — Аас
dx
2аж2 + b + V62 - 4ac
6 — V62 — 4ac Г	с!ж
б2 — Аас J 2аж2 + 6 — \/Ь2 - Аас
х dx
\b2 > 4acl.
\b2 < 4acl.
[b2 > 4ac].
ia) - 6/Da))V2 у] Х2 _ 2(^/c/(Aa) - Ь/Dа)I/2ж
ж dx
la) - 6/Dа)I/2ж + 2%/с/Dа)
4acl.
1.2.14. Интегралы вида
аж21г + bxk + с)
(m
2.
3.
4.
5.
6.
6^ Г
п + 1 J
+к{ах2к
O1-1 dx -
c)
т-2к/ 2k
x f хт~2к(ах2к
c)n dx -
(т + nfe — к + 1N
(га + 2пк ¦
^ [ xm~k(ax2k
a J
c)n da;.
хт+1{ах1к + Ъхк + с)п
т + 2пк + 1
x [ xm(ax2k + bxk + c)"^1 dx +	—,	 [ xm+k(ax2k + bxk + c)" da;.
J	m + 2nk + 1 J
(аж2|г + bxk + c)n (m - 2nk + 1)а(
(га- — 2nfe + 1)а
с!ж
(т - nfe - А; + 1N
с)те (т -
—1
1N Г	ж
а J (ах2к
; с!ж
(т + гг!г — к — 1N
жт(аж2|г + Ьхк + с)п (т -
+ Ьхк + с)п^х
2пк — 2^ — I
(т -
1.2.15. Интегралы вида /^(ж1 , аж + 6) с^ж.
1. [ж"
dx
akbn~kxk

42
Гл. 1. Неопределенные интегралы
[1.2.15
2. i^±^dx = 2
xrn^l/2
к=0
n-k к
3.
4.
5.
6.
dx
- 2m + 1"
2m+ 1
(ax±b)n	(n- 1)а(аж±.
2 f t2m+2dt
vTT +
2(n - l)a J (ax ± Ъ)п^г'
an J
dx
(t2 ± b/a)n
ax±b
dx
b_
^ Bт^2к + 1)ак+г \ aj J x1/2(ax±b)'
dx
хт+г/2(ах ± b)n ^ Bm - l)bxm^/2(ax ±
Bm + 2 га — 3)a
dx
7.
8.
9.
10.
11.
12.
13.
14.
=
ax db b	a
1/2
Bm- 1N J xri
/axx1/2
2arctg(T)
61/2 - (axI/2
± 6)n ате
In
ax±6
x1/2dx
За2
3\1/2
In
1/2
61/2 - (axI/2
dx 2аж3/2 ±
(аж ± bJ	а2(аж±6)
1/2
6V2 + (axI/2
ax \i/2
i-
6V2 _ (axI/2
dx
= ±-
x1/2(ax±b)	(abI/2
In
аж у/2
61/2 + (ажI/2
dx
x3/2(ax±b)
с!ж
(ПТ + 1,42
'ТЫ
,1/2
- (axI/2
In
1/2
б1/2 - (ахI/2
Ь1/2 + (ажI/2
V2
±6) (a
с!ж	—Заж =р 26
ж3/2(аж±6J = 62ж1/2(аж±б)
21"
/аж л1/2
arctg(Tj
. Ь1'2 - {ахI'2
6V2
CM.1.2.10].
dt

1.2.17]
1.2. Степенная и алгебраические функции
43
1.2.16. Интегралы вида R(x ' , ж ± a )dx.
Условие: а > 0.
ж
m+l/2
¦ dx =
ж2±а2
¦ а*ж =
2m-
ж2 ± а2
2m + 3/2
^^ 4т - 4к + 1
к=0
1 . х -\- а — \/2ах
¦ In ¦
x2 + a2 2V2a ж + a + у2аж V2a	ж - a
ж2 + а2
In
1.
2.
3.
4.
5.
6.
7.
8.
1.	I xm(ax + b)n^4'zdx = ^
J
2.	[(^ + 6)»+^=^
3.
х
m+3/2
4n - 2т - 7
x
m + l/2
2(п^1)а2(ж2±а2)" 4(п^1)а2 J (ж2 ± а2)п~
2 т_1/2 2 1 ж"
¦ с!ж.
-1
ж2±а2
¦ da;.
р1/2
2m-2fc+l/2
arctg
ж + а —
1	/а
Ja	Ух
ж + а + \f2ax
\/х — у/а
г-	Га
у a arctg 4 / — .
V х
1.2.17. Интегралы вида ж т(ах + Ь)п+ ' dx.
k=0
2mb
Bт + 3)
Г т-1
Ж	{
a J
, .' (аж + 6)п+1/2 , (ах-
4.	dx = ^т
к=0
)а Пах-
2(т-1)Ь
¦ dx.
5.
6.
7.
8.
10. I ж^(аж-
6)
п+1/2
Bп
Bп -
чп^1/2
¦ dx =
(аж
(ax
dx = — ¦
2
(аж + 6K/2 E^2т)а
т-1Nжто™1 + 2(т-1)Ь
¦ dx.
UX.
9. I x(ax + b) ' dx = —
i/2 л„ - А ^+
21 5
11. ж (аж
^|(аж + 6K/2.
ах + Ъ) Ь3
3/2
Ь)л'\

44
Гл. 1. Неопределенные интегралы
[1.2.18
12.
13.
14.
15.
16.
17.
18
19.
in
21.
i
•>
3.
4.
5
7
8.
9.
11.
12.
Г
(аж -
fbK/2<
[ж(аж + 6K/
!¦'<•
!*¦<•
j
Г (
J
J
1* (аж
J
(* (аж
J
J
1.2.18.
Г т
f
J (ax Л
[ ж™
( 4
* + *>•
ж
+ *)*"
ж2
+ 6I/2
+ бK/2
ж
+ бK/2
ж2
+ 6K/2
ж3
iaj =
dx =
/^
о*ж —
dx —
dx
2
5a
с
(аж
+ 6M/2
2 Гаж + 6
2 Г
а3 [
2 I
а4 [
2(ax-
2
3
(аж
26 4
46
(аж
(аж
(
\2Ъ
7
(аж + 6
9
(аж + 6
11
^bf^~
+ 6I/Я
ж
- аж
+ 6K/2
+ Ь)Б/2
6ж
L
Г
Интегралы вида -
J
dx
-6)n+1/
dx
2(ax
a
J (ажЧ
f T2
J (аж 4
Г ж3
J (аж4
Г d
J (аж 4
Г т
J (аж
г *
J (аж
- 6I/2
dx
-ьу/2
dx
- 6I/2
ж
- 6K/2
2с1ж
+ бK/2
3dx
+ бK/2
2 6
2
Bn
+ 6I
m + l
2
a ^
a3
a4
a
2
a3
2
a4
E
2
г4
/2
(с
In-
- 1)а
то
Е
16^
IX +
5
(аж +
Г
L
Г
7
2
>ж-
^аж -
2
2
1)а(аж
-ж-(аж
2т - 2
1/2
бJ 2
5j(t
K
¦1"
{
+ 26(
I За
1 26
а \
, ,\5/2
IX + 6) 7 .
26(аж + 6) 6
7 ' 5
36(аж + бJ
9 '
/21п
(аж + 6I
(аж + 6I
1/2
Г dx
ж(аж + 6I/2"
2 Р
/2 а Г
86 J ж(ая
_L l^^^"/2 _i_ l2
f (ах + бK/2
J X
xmdx
(ах +
+ 6)п
в Г
6, J
6(аж
3
бK 36(аж
f бJ
f6K
5
10.
ЩаХ
Ь(ах
lj\ Ti-f-1/2
—"^ (— 1) "
^ 2т - 2п - '<
-1/2-
/2 2т6
Bт + 1)а
G)(а, + 6Г
ЖAЖ
(ах + Ъу/2
+ 6) 21
j(ax
-f 6J
+ 62(аж -
(* ж а*ж
J (аж + 6K/2
+ бJ
Ь\(аХ
+ 362(аж
- (аж + 6) .
362(аж + 6) 631 ( .5/2
7 5 J 1аж
/2 _ 51/2
/2 + fel/2
[Ь>0],
(аж + бI/2
с!ж
J _l_ 6I/2 *
[ б?Ж
J ж(аж + 6)!/2'
12 1 (аЖ + ЬK/2 Jx
,9 ал.
Ь2 J ж
гк + Лк)ах
Г жт^1а1ж
J (аж + бI/2 *
"\
2(аж - 26) 1/2
За2 (аж 1 ) •
1/2
1
J ^
2(аж + 26)
а2(аж + 6)!/2'
1
+ 6)V2*
+ 6) + б3
1
(аж + 6)!/2-

1.2.20]
1.2. Степенная и алгебраические функции
45
1.
1.2.19. Интегралы вида
dx
dx
хт(ах + 6)п+1/2*
Bга
хт(ах + 6)п+!/2 (т _ 1)хт^1(ах + Ь)п+г/2 2(га - 1)
2.	= 7=	„ ^2	—- 2™ Г
тЫ
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
Bп-
= 2ат
dx
b; см. 1.2.ю1.
ж(аж
dx
ж(аж
dx
(ах + 6I/2 Bт - 3)а
жт(аж + 6I/2	(т-
1
2(га - 1N J хт^г(ах + ЬI/2 "
In
(аж
-бI/2 а
ж	26
dx
dx
Заж - 26
462ж2
2
6)
1/2
За^ Г
862 J
ж(аж + бK/2 6(аж
+ -
^6
х(ах
За
ж2(аж + бK/2 62ж(аж + ЬI/2 262 J ж(аж + ЬI/2 "
dx
5а
463 у (аж
dx
6)
1/2
c-d\,	.1
2	\(ах + 6)
а L
..I
J
1.2.20. Интегралы вида Я(ж, ^аж + 6 , Vex + d) dx.
(т + п + 2)с
Bm + l)(ad- 6c)
2.
= (ex + a1)
п + З/2 '
2(m + n + 2)c Jv™ ' 6j	(сж + ^
h l)Bra - 1) ... Bт - 2k + 3)(ad - .
(m + n + 2)(m
2)cfe
fe+i
m!!
Bn + l)Bn- 1) . . . Bn-
x (еж + d)n"fc+1/2 +
+ n + 1) . . . (n - k + l)
m\\n\\(ad - bc)m+n+2
— f"
6)(сж

46
Гл. 1. Неопределенные интегралы
[1.2.20
4.
5.
(аж + 6)т+1/2 Bm + l)(ad^6c) f (аж + 6)"
(ra-ra + l)c ^ + d)n~1/2	2(m-ra + l)c J (еж + d)n'
2	(аж + 6)m+3/2 2(n - m - 2)a f (аж + 6)m+1/2
dx.
Bn-l)(ad-bc)
Bn - l)(ad - 6c) J (еж + d)»-V2
-( | h\m+%/2 П\^2 (n-m- 2)(n -m-S)...(n-m-k- 1Jк+1ак
™1аЖ+ j	^ Bn^l)Bn^3)...Bn^2Jfe^l)(ad^'
1
[n ^ m + 2].
6.
7.
dx
(аж
Bm - l)(ad -
2c(m + n — 1)
Bm - l)(ad - 6c) J (аж + 6)т™1/2(сж + djn+1/2 •
(m + n - l)(m + n - 2) . . . (m + n - k)(^2)k+1ck
x
- Ьс)к+г
(еж + d)n™1/2 Z_^ Bm - l)Bm - 3) ... Bm -2k- l)(ad - 6c)fe
ж + Ь)™-*^ (m-1)!!
(m + n - l)(m + n - 2) . . . (n - ^)
1
8.
9.
10.
11.
^ Bn - l)Bn - 3) . . . Bn - 2k - l)(ad - 6c)n+fc+1 (еж + d)n^k^
dx	2
y/[ax + 6) (еж + d)
2
ln
6)
In л/-
6)
1	е(аж + 6) + а(сж + d)
^^ arcsm ^	р^	-^	'-
i—ас	\ad — bc\
dx
[ac > 0; ж >max(-6/a, -d/c)].
[ac > 0; ж < max(-6/a, —d/c)}.
[ac < 0].
(ж — p) <у/(аж + b)(cx + d)
¦In
(cp + d)(ax + b) -
ж -p|
[(ap + 6)(cp + d) > 0; (cp + с!)(аж + 6) > 0; (ар + Ь)(сж + d) > 0].
12.
13.
¦In
ж -p|
0? (CP + d)(ax + 6) < 0, (ар + 6)(сж + d) < 0].
. (cp + d)(ax + 6) + (ap + 6) (еж + d)
,,	,
— bc\\x — p\
0].

1.2.22]
1.2. Степенная и алгебраические функции
47
14.
Ал/ах + Ъ + By/ сх + d
А
¦ dx =
аА2 - сВ2
В ( „ Г у/сх + d
п Г у/ах + Ь	v^ n^fc Г fe_i i	—=- \
р 	dx + > р	ж v аж + 6 с?ж )
I х — р	/-^	I	у
J	F	fe=i	J	7
аА2 - сВА X J ж ~~ ;
15.
.,„ I У ах + 6	у	—
1о. 	ах = Ау/ах + о
6Л2 - dB2
/ах + 6 +
In
/аж ¦
2 arctg и
Р =
п^сж + d dж [аЛ2 - сБ2
[ар + b > 0],
[ар + b < 0].
0].
аж + b
17.
¦ dx =
0:7a
¦ х —
aS —
I
III
¦2а _|_ §2С V \""^ '
+ b + 8 у/сх + d
dx
у/(ax + 6) (еж + d)
1.2.21. Интегралы вида Я(ж, \/аж + b ) с?ж.
t=
. [
- п + 1)а"
(пр + п + 1)а
3.
4.
5.
6.
7.
8.
9.
ж + bI/n dx =
bI/ndx=
f	ч (
(ra + l)a
(га — :
(m-l)nb J хт~г
dt
(ax
1
ax.
(аж + бI/" (win + n — 1)а
1 /	. ч 1 —1 /эт Ч ""'
(тп + п — 1)а J (аж
m+1
т - к
dж
-(аж + 6)
l-1/n
" (п-1)а
1.2.22. Интегралы ви д а [ R[x, (ax + b)p/n]
dx.
(ran + п + р)а"
7ч
(mn + п + р)а

48
Гл. 1. Неопределенные интегралы
[1.2.23
2.	= -(ая + ЬI+р/пх
га(га — 1) . . . (га — А; + 1)
у
~ (гпп + р + п)(тп + р) . . . (ran + п + р — fe
3.
4. | (аж ¦
(аж -
7т+1
(ax + 6I+"/" V -Ak-L——Ux + 6Г"*.
5.
6.
(ж -
¦ dx =
(аж + ЬI+р/п [(га-2)п-р]а Г (аж + b)p/n
(т - 1)(аа + 6) (ж - а)т~г (т - 1)п(аа + b) J (ж -
J
7.
8.
"V i\fe G?г "~ P "" ^п) (mfl ~ P — 3n) ... (ran — p — fife) afc 1	1
-^ '	(m - l)(ra- 2) . . . (ra- fe)nfc™1(aa + 6)	(ж _ а)
T%( T} ^L 1 I	G) ^L TTi _ 1 ) /| m ~ С (П Hf* -4- h)
JL/ I ij \^ J_ j * e * I JL/ f^ # # ?/	J_ I CJ/	I 1 \Jj el/ jp U I
~ n"l-1(m-l)!(aa + 6)m J ж-а
_ m —1
_ 	M	 (аж + 6jl-m+P/n
р/п
(га — 1)п — р
(аж
f-1
dy
аа + Ь
[аа + 6 = 0].
1
= ±1, ±2, ...; см. 1.2.3 .
/ ax ~4~ fe
1.2.23. Интегралы вида I Rl ж, Xl	:—; \ dx.
1.
ж,
еж + d
ex + d
n(ad^bc) { J~adtn + Ъс п[а~
dx = —^	 R\	т	г- ?/ —
J
ac(tn - 1) Vе J (^п - 1)
а(сх
/ i i \ р/та	i i / i i \ p/n
. . ax + 6 \ , аж + b ( ax + о \
2. I ( 	— I dж = 	 ( 	—; ) +
а \ еж + d
3. | ж
аж =
1 (ах + Ъ
; J t»-i
а(сж + а)
; см. 1.2.3.
(ra + l)ac
(ad - bc)p + mn(ad + 6c) г	/~™ ' ^xp/n
р/п
(ra + l)nac
l^
сж + «
(ra- + l)ac
. Г
4. ж
J
\сх
n	(aж + 6)(cж + d) /аж-
2ас	\сж
р/те
(ad - 6с)р + (ad
p/n

1.2.25]
1.2. Степенная и алгебраические функции
49
5.
(ж — а)т+1 \сх
ах + b
р/п ,	Аах + 6)(еж + d) /аж + 6\р/те
«ж = л		 +
(ж — а)т \сх + а/
1 /«ж^6\р/п	„Г	1	(ах + Ъ^р/п
Л =
-1
т(аа + 6)(са + d)'
(ж — а)т \сх + d)	J (ж — а)т^1 \сх + d
~п(т — l)(ad + 6с + 2аса) + p(ad — 6с)
тп(аа + 6)(са + d)
— (гм — 2)ас
dx,
В =
D =
6.
dx = n I
т(аа + 1?)(са + d) *
'п Г t13^1	(а\р^п Г s13™1
	d? — ш — 1
Jt"-1	\с/ Je"-1
п
„lc(ax + b)
а(сх + d)
; см. 1.2.3 .
1.
2.
3.
4.
5.
1.2.24. Интегралы вида f Я(ж1/п, ж2 ± a2) da;.
Bm - S)n - р Г жр/п da;
(ж2 ± а2)т ~ 2(т - 1)а2(ж2 ± а2
2(т - 1)а2п J (ж2 ± а2
Bтп — Зп — р)Bтп — 5гг — р) . . . Bтп — 2пк + п — р)
(in — 1)(га — 2) . . . (т — fe)n.fc™1(±2a2)fc
1	^ (n-p)Cn-p)...Bmn-3n-p) f жр/п
(?тг — 1)!(±2а2п)т^1
i-fe
Г жр^п с!ж
j ж2 ± а2 '
р/п — 1
(ж2 ± а2) р — п
с!ж	_ ±пж1тр/п 1
жР/п(ж2±а2) (п — р)а2 а2
ж2±а2
dx
1±а2)'
1 ^/ . 4Л + 1
fe=O
sin	ртг In 4/ж2/п — 2(ажI/п cos	тг + а2/п
1/п	1/п
х ' — а ' cos
¦ рж arctg
2п
2п
[р = 1, 2, . . . , п- 1; а > 0].
6.
^p/n-l f ^n+p-l	wnp/n-l
J tn + 1
tn-l	2
\t = (x/aI/n; p = ±1, ±2, . . . ; а >0; см. 1.2.з].
X
1.2.25. Интегралы вида R{s/x — а , у/х — b , \/ х — с) dx.
а
Условие: х > а > Ъ > с.
„г . /х - а	\Ь- с
Обозначения: (р = arcsin \j	 , к =
1.
2.
dx
х — b
2
— а){х — Ъ){х — с)
х dx
у/(х — а)(х — Ь)(х — с) by/a — с
4 А. П. Прудников и др., т. 1
¦F(V)fc).
[а(а-Ь)П(^, 1,
, к)].

50
Гл. 1. Неопределенные интегралы
[1.2.25
dx
,*)-
(Ь — с) у/а — с
4.
5.
dx
[Ь-с)у/а-с
dx
(х — р)у{х — а)(х — Ь)(х — с)
2
6.
(Ь — р)(о> — р)л/а — с
dx
F-а)П U,
\
Ъ — р
а — су (ж — Ь)(х — с)
\рфа].
— а)(х — ЪK(х — сK
2
¦ [Bа -Ь- с)Е(<р, к) - 2(а - b)F(<p, к) +
2
7.
8.
9.
ю.
11.
[ /
JV(*-
а
f /
JV(*-
а
X
\ 1
JV(«-
а
X
1 1
JV(*
а
X
Г /
х - а
Ь)(х-
а)(х —
х - с
«к*-
ж - а
-ЬK(х
х —- а
И-
с)
ч d
с)
Ь)
- с)
2(а —
(ж — а)(х — с)
, A;)
(х — а)(х — с)
^	^
х-Ъ
(ж 7Гс)
b — с
, к) - Е(<р, к)}.
(ж — Ъ)(х — сK
dx =
6-с
, к) -
, *)] - 2
(х — Ъ)(х — с)
12.
13.
14.
\\
X
г
а
ж
Г.
/
/(х
/
1 (х
ж — 6
— а)(ж —
ж — с
— а)(ж —
-а)(ж-
с)з
бK
da; = 2 ^(^/ ife) -2-
а — с у (х — Ъ)(х — с)
dx =	— Е((р, к).
, ife) - (а - b)F(y?, k)]
(ж - а)(х - с)

1.2.26]
1.2. Степенная и алгебраические функции
51
15.
п){Х С)
[(а + с - 2b)E((pJ k) - (а - b)F(<p, к)] +
(а-с)
(Ь-с)
[х — а)(х — с)
х — b
16.
, A;)]
1.
2.
со
Г		 ,
1.2.26. Интегралы вида Я(уж — а , л/х — b , уж — с) dx.
Условие: ж ^ а > b > с.
_	. 1а- с	Ib- с
Обозначения: (р = arcsin \ 	, к = \ 	.
\ х — с	У а — с
со
dx	2
— а)(х — Ъ){х — с) Va — с
dx	2
, к).
х — b
а — 6 у (ж — а)(ж — с)
[х > а].
3.
dx
%/(ж-а)(ж-&K(ж-с) (а-Ь)(Ь-с)
2 2
ч /	 F(y, fc)
(ж — 6)(ж — с)
4.
dx
5.
dx
x [(a - b)F((p, ife) - (a + 6 - 2c)E((p, к)] +
2x - a-
(a -
\x > a .
6.
, к) ^ (a ^ b)F(tp, к)}
x — b
(а — Ь)(а — с) у (ж — а)(ж — с)
[ж > о].
7.
х [Bа - b - с)Е((р, к) - 2(а - b)F((^, A;)] -
(а-6)(Ь-с) у (ж-
[ж > а].
4*

52
Гл. 1. Неопределенные интегралы
[1.2.27
8.
dx
х [(a - b)Ba -Ъ- c)F(<p, к) - 2(a2 + б2 + с2 - ab - ас - Ьс)Е(<р, к)} ¦
2[х(а + 6 - 2с) - a(a - с) - 6F - с)]
9.
10.
dx
(а - bJ(a - с)(ft - с)у/(х - а)(х - Ь)(х - с)
2
[х > а].
(ж - р)у/(х - а)(х - 6)(ж - с) (р - с)у/а - с [ \ а - с'
11.
12.
13.
14.
15.
ж — с
(ж — аK(ж
2
(ж — аK(ж
ж — с
(ж — а)(ж -
ж — а
(ж^6K(ж
ж — 6
(ж — а)(х -
х ~~ а
-Ъ)
тр
С
-с)
-бK
-с)
dx =
2\Ja — с
а — 6
, Л)-
2(а — с)
а — 6 у (ж — а)(х — с)
dx =
а — с
- с
, k)-E(<p,
х — b
(х — а)(х — с)
[х > а],
[х > а].
dx= v	E(y, ife)-2-
dx =
а — 6
2\/а — с
а — 6 у (ж — 6)(ж — с)
с!ж = ,
2V'а ~~ с
[F(<p, k)-E(<p, k)] + 2^j
2(a-ft)
ж — 6)(ж — с)
Е(<р, к) -
(х - Ь)(х - сK ^	 b - с ^v" "' (b - с)^а
х
а
1.2.27. Интегралы вида R(y/a — х , \/х — b , \/х — с) dx.
F(<p, к).
Условие: a > ж J^ b > с.
^г . I а — х	I a — b
Обозначения: (р = arcsin \l	г , л =
1.
2.
3.
dx
а-Ь '
2
\/(а — х)(х — Ъ)(х — с) л/а —
ж dx	2c
F(^, ife) + 2-л/а-сЕ((р1 к).
dx
у/(а — ж)(ж — 6K(ж — с) (а — 6)Va — «
" (а^6)F^с)
{a-b)(b-c)\ x-b
{а-х)(х-с)
[ж > ft].

1.2.27]
1.2. Степенная и алгебраические функции
53
4.
5.
dx
dx
(b — с) у/а — с
2
,*)"
» — с)(а — с) V ж — с
(а — ж)(ж — Ь)
(ж-р)у(а - ж)(ж - &)(ж - с) (a-pJVfl-
_ / а — & .
П [ ^>, 	, А;
6.
(а - х)(х - ЬK(х - сK
2
(а -Ь)(Ь- сJ1/^^
[(& - c)F(y?, ife) - 2Bа - & - с)Е((р, к)] +
^ 6^ с + х)
(а ~ Ъ)(Ь ~ с)(а ~ с) У (х ~ Ь)(х - с)
[х > Ь].
7.
(ж — Ъ)(х — с)
dx = Чу/a- c[F((p, к) - Е(<р, к)].
8.
9.
Ю.
11.
12.
13.
14.
(а — ж)(ж — Ь)
(а — ж)(ж — с)
dx = Чу/а — с Е((р, к).
den. =
i к) -
t h)
2\/а — с
а-ж	2y/a - с
dx =
(ж — Ь)(х — сK	6 — с
ж — 6
(а — ж)(ж — сK
ж — с	2\/а —
аж = 	г-
(а — ж)(ж — бK
^—^ dx = -у/а=
х — с	3
2 /(а —ж)(ж —с)
	J±	J\	J-
[x > b].
, A;)-
, A;)--
2 (a - x)(x - b)
2 (а-х)(х-с)
х — b
, k)^2(b^c)F(ip, к)}^
2 п	п
[х > 6].
15.
16.
Щ
х — о
—— dx = -V^cKfl + с - ЧЬ)Е(<р, k) + (b^ c)F(<p, к)] -
о
2а-b- c)E(<p, k)-(b- c)F(<p, к)] +
2
3

54
Гл. 1. Неопределенные интегралы
[1.2.28
X
1.2.28. Интегралы вида R(\fa — ж , V' х — Ь , \/х — с) dx.
ъ
Условие: а ^ х > b > с.
„r	. (a-c)(x-b) . la-b
Обозначения: 99 = arcsin 4 / -7	тт^	г , к =
1.
(а — ж)(ж — Ъ)(х — с) л/а — с
ПЧ>, к).
2.
х dx
у/(а — х)(х — Ь)(х — с)
[(Ь-с)Щ<р,
, к)].
3.
dx
(а - жK(ж - 6)(ж - с) (а - 6)^а -
ж — 6
а — 6 у (а — ж)(ж — с)
ж < а .
4.
dx
5.
х [{Ь - c)F(<p, к)-Bb-а- с)Е(ц>, к)} +
2
ж — b
(а — Ь)(а — с) у (а — ж)(ж — с)
[ж < а].
6.
dx
(ж — р)у/(а — ж)(ж — Ь)(х — с)

(с — p)(b — р)уа — с
(с -
» к + {b~p)F(Lp, к)\	[рф Ь]
7.
(ж — Ь)(х — с)
8.
(а — ж)(ж — с)
dx =
ч 2F - с) . ч	(а-х)(х
, к)	v 7 F(<p, А;) — 2- ' v	/v
-ь)
9.
(а — х)(х — Ь)
- 2
(а-х)(х-Ь)
10.
х — b
(а — жK(ж — с)
dx = —
¦Е(<р, к)+ 2
х — b
(а — х)(х — с)
[ж < а].
11.
dx =
- с)
(а — Ь)^/а — с
2хПГ^Ъ
х — Ъ
а — Ъ у (а — х)(х — с)
[х < а].

1.2.29]
1.2. Степенная и алгебраические функции
55
12.
13.
(а — ж)(ж — сK
[F(<p,k)-E(<p,k)].
(х — Ъ)(х ~~ сK
dx = —^	Е((р, к)		F((p, к).
Ь-с
14#
15.
16.
х — о
ЧМ	СА dx = t^3^ра -ь- c)E(<p, k)-(b- c)F((p, k)]
о. ж	о
Па
V
*)] +
/(ft
*)] +
— х)(х
- х)(х
-ъ)
-ь)
(а - x)(x - b)
0
1.2.29. Интегралы вида R(y/a — x , V& — ж , V^ — с) dx.
X
Условие: a > b > x ^ с
n«	¦ l(a-c)(b-x) ,
Обозначения: 9? = arcsin 4/ -^	^7^	™ , A; =
1.
dx
(Ь — с) (а — ж)
2
\J(cl — x)(b — x){x — c)
, k).
2.
ж dx
y/(a - x)(b - x)(x - с) у/а- с
[{Ь-с)П{<р, к\
3.
4.
5.
dx
¦sf(a - жK(& - ж)(ж - с) (ft - b)s/a - с
dx
(a — x)(b — x){x — cK (b — c)y/a —
, k).
, k)-E{V,
dx
y/(a-xf(b-x)(x-cf (Ь-с)(а-Ь)у/(а-сK
x [(ft - b)F(tp, к) + B6 - a - c)E((p, к)]	2
b — x
b ~ cy (a — x)(x — c)
[x > c].
b — x
(b — c)(a — с) у (a — ж)(ж — с)
[х > с].
6.
dx
(p - x)yf(a - x)(b - x)(x - c)

56
Гл. 1. Неопределенные интегралы
[1.2.30
n
7.
8.
9.
10.
11.
12.
a-x	f	 ( л	(b-x)(x-c)
—	-	 dx = 2л/а - с Е((р, к) - 2\ ~	'-
(Ь — х)(х — с)	V	а — х
(а — ж)(ж — с)
dx =
J к)
, fc) ^
(Ь-х)(х-с)
ж-с	, 2V« - с . N	2
da; = —	^- E(y?, A;)		F(y?, A;).
(a — xK(b — x)
(b — x)(x —
dx =
dx =
а — b
2
/а — с
, k) -
(Ь — с) у/а — с
F(tp, к) - \а С Е{<р, к) + 2°-^
13.
14.
(а — ж)(ж — сK
dx =
b — х
(а — х)(х — с)
(а — ж)(ж — с)
[х > с].
5 A;)]
(Ь-х)(х-с)
а — х
15.
и — ж
, к)] ¦
16.
dx = ±y/^—
2a^b^ c)E(<p, k)]
1.
1.2.30. Интегралы вида R(y/a — х , yb — x, у/х — с) dx.
с
Условие: а > Ъ ^ ж > с.
Обозначения: ip = arcsln \j ^	^ , к =
X
dx
b — с	V о, — с
2
у/(а — х){Ъ — х){х — с) л/а — с

1.2.30]
1.2. Степенная и алгебраические функции
57
2.
3.
4.
ж dx
2а
у/(а — x)(b — ж)(ж — с) Va — с
dx
у/(а - хK(Ъ - ж)(ж - с) (а - Ь)у/а - с
dx	2
, k) - 2у/а - сЕ(<р, к).
E(ip,k)-
(а — Ь)(а — с)
(Ь — х)(х — с)
5.
у/(а - х)(Ь - жK(ж - с) (Ь - с)у/а - с
2\/а — с
Е{<р, к)
dx
(а — ж)(ж — с)
b — х
у/(а — хK(Ь — хK(х — с)
2
== [(а - b)F(<p, k)^(a + b^ 2c)E(<p, к)] ¦
(а — оI^ — с)уа — с
2[а2 + б2 - ас - be - х(а + Ъ - 2с)] I x - с
(а — х)(Ь — ж)
6.
7.
8.
9.
10.
11.
12.
dx
(р-х)у/(а-x)(b-х)(х-с) (р-с)у/а-с \ р-с
» — х)(х — с]
dx = 2у/а — с Е((р, к).
(а — х)(х — с)
(а — х)(Ь — х)
dx =
(а — хK(Ъ — х)
(а — хN(х — с)
1 к) - Е((р, к)}.
2у/а - с р/ п	2
Е(, к)
[х < Ь].
[х < 6].
\рфс].
а — b
2
2 (Ь - х)(х - с)
[F(<p, k)-E(<p, k)] +
a — b V a — x
2 Hb-x){x-c)
2 (а - х)(х - с)
	V
13.
14.
(а — ж)(Ь — жK
2\/а — с
= 2^—— + ь _
о
2 (a-x)(x-c)
[х < 6].

58
Гл. 1. Неопределенные интегралы
[1.2.31
15.
16.
^—^ dx = ^V^^[Bb ^а^ с)Е(<р, к) + (а - b)F(<p, к)} -
о — х	«5
- ^V(a - х)(Ь- х)(х - с).
dx = -Va^c[Ba -b- c)E(<p, k) - 2{a - b)F(tp, к)] -
- с).
1.2.31. Интегралы вида R(y/a — ж , у/ b — ж , у/с —¦ ж ) dx.
X
Условие: а > b > с > х.
_	. 1с- х . la-b
Уоозначения: ш = arcsin \\	, к =
1.
2.
3.
4.
5.
b — х
2
ж dx
> — х)(с — ж) v а ~ с
, к).
, Aj) + (а — .
- 2
о — х
•^(а — жK(& — ж)(с — ж)
(а — Ъ)\/а — с
[F(<p, k)-E((p,k)] +
dx
da;
- с)
2
(а — b)y/a — i
а — с у (а — х)(Ь — х)
, к).
6.
х [(а + 6 - 2c)?J(^, А;) - 2F - e)F(<^, A;)] +
dx	2(c — 6)
(р -
- х)(с - х) (р- Ь)(р- с)л/а -
(р — 6)i/a — с
{а-х)(Ь-х) '
F(<p, к)	[рфс].
7.
8.
9.
[ /
ж
f /
jV(a
С
Г /
а — ж
-Ж)(с-
6 — ж
- х)(с-
с — х
х)
х)
dx =
, к) - E{<fi, к)]
b — х
(a — x)(b — x)
b — x

1.2.32]
1.2. Степенная и алгебраические функции
59
10.
il
11.
12.
13.
14#
15.
16.
(а — жK(с — х)
а — с у (а — х)(Ъ — х)
dx = 	г— Е(<р, к) -
а Ь
2(Ь-С) F(V,k)-2' C-X
(a — b)y/a — с
(а — х){Ь — х)
(а — х)(Ь — жK	а — Ъ
а - х	j 2V« - с ( ч
ах = —;	^(^5 к).
(Ь — жK(с — ж)
Ь-с
¦ Bс - а - Ь)Е(<р, к)] + - (а + 26 - 2с -
«5
о — ж
и Ж
- a - c)E((p, к) - (b- c)F((p, к)]
2 ,
(а-х)(с-х)
\a-b- c)E((p, k)-(b- c)F((p, к)] +
1.2.32. Интегралы вида Щл/а — ж , л/Ь — х , л/с — х ) dx.
— сю
Условие: а > Ъ > с ^ х.
^г	. Iа - с t /a-b
Обозначения: (р = arcsin \ 	, к =
1.
2.
3.
4.
dx
(а - х)(Ь - х)(с- х) у/а- с
dx	2
F(<p, к).
dx
2\/a — с
¦[F(<p, к)-Е(ч>, к)].
2	2
F(tp, к) -
(а — Ь)у/а — с
b — су (а — х)(Ь — ж)
dx
у/{а — х){Ъ — х)(с — жK
(с — b)y/a — с
Ъ — х
b — су (а — ж)(с — ж)
[ж < с].

60
Гл. 1. Неопределенные интегралы
[1.2.32
5.
6.
dx
а - х)(Ь - х)(с - х)
dx
nU ^, * ) - F(<p, к) I.
у' а-с' '	п
х [(а + b - 2с)Е(<р, к) - 2F - c)F{(p, к)] -
а-Ь)(Ь-с)\ (а^
7.
dx
8.
х [F - c)Ff>, А;) - (а + b - 2с)Е(<р, к)} +
dx
2F + с -2х)
F -
9.
х [B6 - а - с)Е((р, k)-(b- c)F((p, к)] +
с
dx
6 — х
F — с)(а — с) у (а — х)(с — х)
2
х [F - с)(а + 6 - 2c)F((p, к) - 2(с2 + а2 + б2 - аЪ - ас - Ьс)Е((р, к)] ¦
2[с(а - с) + Ь(а - 6) - жBа - с - 6)]
10.
11.
12.
(а
(а
6^
с —
-жK
а —
X
(с-
X
(ь-
X
х)
х)
dx =
dx =
(а — 6)(а — с)F — сJу(а^:
2
а ~ b
(Ь — х)(с — жK
9 k) _
, к) -
13.
14.
15.
(а
а —
— жK1
Ь-
— ж)(|
с —
ж
(с-ж)
ж
с-х)*
X
dx = ±v^—^(^, А;)_
(а — Ь)у/а — с
о - с
2(а — с)	6 — ж
6 — с у (а — ж)(с — ж)
а — 6
Ъ-с
2
/а — с
6 — с у (а — ж)F — ж)
, k)-E{<p, к)]+ 2,
6 — Ж
(а — ж)F — жK
dx =
[ж < с].
[ж < с].
[ж < с].
[х < с].
(а — ж)(е — ж)
(а — ж)F — ж)
[х < с].

1.2.38]
1.2. Степенная и алгебраические функции
61
X
1.2.33. Интегралы вида R(y/x — а , V' х — Ь , \/х — с , ^ж — d) dx.
Условие: x>a>b>c>d.
Обозначения: ш = arcsln a
(b^c)(a^d)
1.
2.
— a)(x — b)(x — c)(x — d) \/ia —
x dx
— с) (ж — d)
2
F(<P, *)¦
\J(x — a)(x — b)(x — c)(x — d)
3.
dx
ж у (ж — а)(х — Ь)(х — с)(х ~~ d)
aby/(a — c)(b — d)
(а-Ь)Щ<р, j-Z, k) +bF(V, k)\.
aF(<fi, к) \.
4.
dx
(p — x)^/(x — a)(x — b)(x — c)(x — d) (p — a)(p — b)^/(a — c)(b — d)
5.
6.
7.
8.
Г
л
а
X
г
X
г
а
ж
Г.
/
/ fr
/
/(Ж
/
/ (х
1
X
-b)(x
X
— а)(х
X
— а)(х
X
— а
^с)(ж^
~Ь
^с)(ж^
— с
- Ь)(х -
-d
d)
d)
d)
j	2(Q - b)
dx = —	—^—
dx =
dx =
if
a — d
' b^d
, k
(ж — а)(ж — b)(x — с)
V(o-c)(b-d)
<^Ж =
(a -
- c)F(<p, k) I
9.
10.
(ж — b)(x — с)'л(х — d)
(b-c)(c-d)
2(a - b)
(b-c)y/(a-c)(b-d)
F(<p, k) -
2 (x-a)(x-d)
с — dy (x — b)(x — c)

62
Гл. 1. Неопределенные интегралы
[1.2.34
11.
12.
dx =
2 /(ж — а)(ж — с)
(х - Ь){х - с)(х - df	c-d\ b-d K*' ' c-dV (x-b)(x-d)'
х — b
(х — а)(х — с)(х — dK	(a — d)(c — d) у (ж — b)(x — d)
2(а - Ь)
13.
14.
15.
16.
17.
x — b
(x — a)(x — cK(x — d)
dx =
2 b-d	_ 2(b - c)	(x-a)(x-d)
c-d\l a-c W' ' (a-c)(c-d)\j {x - b){x - c) '
(х — а)(х — ЬK(х — d)	а — i
(ж — а)(ж — 6)(ж — dK
ж — d
{x — a)(x — bK(x — c)
dx =
a — dy (x — b)(x — d)
= 2y/(a-c)(b-d)	2(c - d)
(a-b)(b-c) yv'	(b-c)y/(a-c)(b-d)
, к).
(x — a)(x — b)(x — cK
dx =
2 lb-
b — с V а — с
[F(V,k)-E{V,k)]+
a — с у (ж — &)(ж — с)
a
1.2.84. Интегралы вида R(ya — x , ух — b , ух-~~с , уж — d) с!ж.
1.
2.
Условие: a>x^6>c>d.
Обозначения: (р = arcsln ,
а
х dx
/(а-ж)(ж-Ь)(ж-с)(ж-<0
dx
7 к =
(a-b)(c-d)
(cb — ж)(ж — b)(x — c)(x — d) \f(a — c)(b — d)
dx
F(<p, k).
(a — ж)(ж — b)(x — c)(x — d)
ad'\J{a — c)(b — d)
(d-a)n\<p,
, k)

1.2.34]
1.2. Степенная и алгебраические функции
63
4.
dx
(р — х)у/(а — х)(х — Ъ)(х — с){х — d) (р — а)(р — d)^J{a — c)(b — d)
\рфа].
5.
6.
7.
8.
9.
ж — 6
(a — ж)(ж — с)(ж — d)
dx =
г
л
ж
а
г
Ь
а
Г
/
/ («
/
/(а
/
Ж
— ж)(ж
ж
— ж)(ж
а
— с
-Ь)(х
-d
-Ь)(х
— X
-d)
-с)'
^/(a^c)(b^d)
dx =
' b^d"
- c)F{<p,
dx =
/ 6^ a .
П ш,	:,k].
V'bd' f
b-cV (x-b)(x-d)
[х > Ь].
10.
11.
12.
da; =
(ж — Ь)(х — с)(ж — dK	с ~ dy b —
k) - E(V, A)].
(a — ж)(ж — сK(ж — d)
13.
х — b
(а — ж)(ж — е)(ж —
с — dy а ~~ с
dx =
2 (a-x)(x-b)
	1/ /	w	j\
a-сУ ж-с ж-d
2F - с)
, к).
14.
(а — ж)(ж — bK(x — d)
a-b\b-d
a-bV (x-b)(x-d)

64
Гл. 1. Неопределенные интегралы
[1.2.35
15.
16.
{а - ж)(ж - Ъ){х -
(a - x)(x -
dx =
a-d]/ b-d
2(а - d)
(a-b)y/(a-c){b-d)
, k) -
17.
2yf(a~c)(b~d)	2F -d) l(a-x)(x-c)
—r— E{<p, k) + j-	7V77	"T4 7-	VV7Z	^	Iх > 4-
dx =
\a-b){b-c)\ (x-b)(x-d)
ж — d
(a — x)(x — b)(x — cK
b — с V a — с
4c ~d) l(a-x)(x-b)
J (a^c)(b^c) у (ж-с)(ж-<0 "
1.2.85. Интегралы вида R{\/a — х , V^ — 6 , V^ — с , Va; — d) dx.
Условие: a^x>b>c~:
Обозначения: ш = arcsln
(а-Ь)(ж-с)
, А; =
1.
2.
3.
4.
у (а — ж)(ж — b)(x — с)(ж — d)
Ж б?Ж
\/(a — ж)(ж — 6)(ж — с) (ж — d)
ж у (а — ж)(ж — Ь)(х — с)(ж — i
(a-b)(c-d)
, A).
у (а - с)F -
, fc)|-
(ж - р)у/(а - ж)(ж - Ь)(ж - с)(ж - d) F - р)(р - с)^/(а - с)(Ь - rf)
5.
6.
7.
(ж — b)(x — с) (ж —
ж — 6
(о - ж)(ж - 6)(ж - d)
,f(a~c)(b~d)
„_	2F-с)
(С_Ь)П(^^-4,Л
П(^, 5—^, ife) -F{<p,k)\.
, ife) I
о?ж = —	, ,	П( ср, 	, А; .

1.2.36]
1.2. Степенная и алгебраические функции
65
8.
9.
10.
li.
х — d
(а-х)(х-Ъ)(х-с)
dx =
(a — жK(ж — Ь)(х ~~ с)
y/{a-c)(b-d)
dx =
b-c)nl<p,
\
> k)\.
О у Gj С
, k) - E{V, k)]
2 (x-b)(x-d)
dж =
'
a — by (a — ж)(ж — с)
2(a - rf)
dx =
, , x-b f 2 b-d^, J4 2 (x-b)(x-d)
12. L/y	^t	w	-p-dx = -	J	E(<p,k) +	-J)	^	{.
(a — х)л{х — с)(ж — d)	a — а у а — с	a — d у (а — ж)(ж — с)
6
13.
14.
(a — ж)(ж — сK(ж — d)	c^dVtt^<
к) - E(<p, k)].
(a - ж)(ж - с)(ж -
dж =
15.
(a — d)(c — d)^(a — c)F — d)
x [(a — c)(b — d)E((p1 к) — (a — d)(b —
2F - c)
dж =
(a - xK{x - 6)(ж - d)	(a-b)y/(a-c)(b-d)
F(<p,k)-
2(a-c) \(x-b)(x-d)
16.
2V(a-c)(b-ri)
(a - b)(a - d) ^l^' 'v/ ' (a - b)(a - d) V (a - ж)(ж - с)
2
[x < a].
17.
_
а - с	_ с - d / (а - ж)(ж - 6)
6d? (ж ^ с)(ж ^ d) J"
1.
(a — ж)(ж — b)(x — сK
ь
1.2.36. Интегралы вида R(y/a ~~ x , V& — ж , V^ — с , ^/х — d) dx.
X
Условие: a>6>ж^:c>d.
Обозначения: (р = arcsln (
ь
dж
(а-с)F-ж) ,	(b-c)(a-d)
F — с)(а — ж)	у (а — с)F — d)
'(а — х)(Ь — ж)(ж — с) (ж — d)
5 А. П. Прудников и др., т. 1

66
Гл. 1. Неопределенные интегралы
[1.2.36
2.
3.
4.
х dx
\J(cl — x)(b — х)(х — с) (ж — d)
(Ь-а)П(<р, -—-, к
, к)\.
dx
(а — х)(Ь — ж)(ж — с)(х — d)
ab\J (ci — c)(l? — d)
,к)\.
dx
(р — х)у/(а — х)(Ь — х){х — с)(х — d) (р — сь)(р — b)-\/(a — c)(b — d)
¦ L x/P lm k\ +{p-b)F{^1 к)
5.
6.
7.
8.
9.
Г
ж
Ь
f
ь
г
X
ъ
Г.
/
/ F-
/
/
/ (а-
/
а
х)(х
ж)(ж
ж
ж)F
ж
— х
-с)(х
-с)(х
— с
— х)(х
-d
-d)
-d)
-d)
2{a-b)	( b- с х
П Ш, 	, к .
ip, 	, к — F((p, к)
dx =
(b-a)n(<p, -—-, к) +(a-c)F(<p, k)\.
(а — x)(b — ж)(ж — с)
(b ~ a)U L, ^^, к ) + (a -
V a-c §
dx =
- х)(х - сK(ж - d)	(Ъ- с)у/(а- c)(b- d)
y/(a-c)(b-d)	2{a - c) I (b - x){x - d)
10.
11.
12.
• — ж)(ж — с) (ж — dy
b — х
dx =
2 fa-с , .	2(a - d)	(b - x)(x - c)
{^J } (b-d)(c-d)V (a-x)(x-d)'
dx =
(a — xK(x — c)(x — d)	a — d V cl —
b — x
(a — x)(x — cK(x — d)
dx =
2 b-d _, 1Ч 2 Hb-x){x-d)
~j	V 	^(^j ^) H	ji 7	V7	V
a^cvti^c	c^dy(a™ ж)(ж — с)

1.2.37]
1.2. Степенная и алгебраические функции
67
13.
b — х
dx =
(а - х)(х - с){х - d)s	(а - d)(c - d)y/(a - с)(Ь - d)
х [(а - с)(Ь - d)E(tp, k)- (a- b)(c - d)F(cpJ к)] -
2 (Ь-х)(х-с)
с — dy (а — х)(х — d)
14.
(а — хK(Ъ — х)(х ~~ d)
dx =
15.
16.
17.
(а — x)(b — х)(х —
x — d
(а ~~ b)(a — d)
dx =
¦E{y,k)-
2(c - d)
(a-d)v/{a-c){b-d)
F{tp, к).
2 I'a — с
2 / (b — x)(x — c)
dx = 	7i/	E(cp, k).
{a — xK(b — x)(x — c)	a — by a — с
dx =
(a — x)(b — x){x — cK	b — с V a —
2 (b-x)(x-d)
b — с у (a — x)(x — c)
x
1.2.37. Интегралы вида R{\/a ~~ x , л/b — x , ^/x — с , л/х — d) dx.
Условие: a>b^x>c>d.
1.
2.
3.
4.
Обозначения: ip = arcsln
X
dx
\/(a — x)(b — x){x — c)(x — d)
x dx
y/(a — x)(b ~~ x)(x — c){x ~~ d)
dx
x^{a — x)(b — x)(x — c)(x — d)
— d)
F(<p, к).
(a - c){b - d)
(c-d)U(<p,
V
cdy/(a-c)(b-d)
dx
(p — x)y/(a — x)(b — x)(x — c)(x — d) (p — c)(p — d)y/(a — c)(b — d)
(b-c)(p-d)
' (b-d)(p-c)
,k\+(p-c)F(<p,k)\	\рфс\
[x > c].
, k)\
5*

68
Гл. 1. Неопределенные интегралы
[1.2.37
X
5-Iv
с
Чу
с
X
- и
9-lv
с
as
4
с
с
ж
с
ж
с
ж
-1
с
-I-
с
/ а^
(Ь — ж)(ж —
/ ь-
(а — ж)(ж —
1
(а — х)(Ь ~~
1 о-
/
V (Ь-х)(х-
1 ь
у (а~жK(ж
/ ь-
у (а — ж)(ж -
/
/
/
V(a-x)(b-
/
У (а~жK(&
ж
с) (ж™
ж
с)(х-
с
х)(х-
d
ж)(ж —
ж
— ж
-с)(ж-
— ж
-с) (ж
— ж
- с)(х -
~~ с
— с
^жK(ж
— с
- ж)(ж -
^d
— х){х
d)
d)
d)
с)
-d
-d
- п
—
—
- о
dx —
ч/(«
dx —
dx
\
\
;j3 dx
d) dX
2
dx
d) x
(a
dx
2
~c)(b~
2
~c)(b~
2(c~
2 fa
2 /
c-d)j
jb^d
l\a-c
d)
d)
d)
[ь-
'b-
', —
b-
Г/7
[i
(a-d)(c
x [(a-
. 2\/(a -
2 l
2
a-dV
2 ПГ-
- с
-
6
6
-[(d-c)I
г [(d - C)]
-d) L v
TTi (/
— 111 ^
с , ,
— f»
2
-c)F-<
)(b-d) .
i)
c)(b-d)
~ c Fi..
-d
	 ?
—- d
П | ip C к ) I (b t
ю Ь~С k\ F(m k)
/
k)-E(<p,k)] +
2 j(a-x)(x-c)
fe-cy (b-x)(x-d)
к).
E(- !¦)} 1 2 f^1
^''"N ' a-cY(a-
X
I)E((p, к) - (a^b)(c^
¦ FW, к) а/;
a — о у (а —
2 l(a-x)(x
' 'a-6VF-*)(*
2(o-rf) /F-
i)F((p
[
[x
¦ x)(x -
¦ ж)(ж -
¦ x)(x -
~ C)
ж)(ж-
1
* J'
k)]
Arj.
<6].
-c)
-d)'
, fc)].
—
-c)
a — b V а —
(a — b)(a — с) у (а — ж)(ж — d)

1.2.38]
1.2. Степенная и алгебраические функции
69
17.
х — d
dx =
(а - x)(b - x)s(x -с)	F - c)^(a^
¦E(<p, к)'
2F -d)	(a-x)(x-c)
(a - b)(b - c) v^' ; (a - b)(b - c) у (Ь - ж)(ж - d)
с
1.2.88. Интегралы вида R{-\/a — х , Vb — ж , Vc — ж , V^ — d) dx.
Условие: аУЪУсУх^
Обозначения: ю = arcsln
(с ^0F^ ж
(a-b)(c-d)
1.
2.
— х)(с — х)(х — d)
х dx
F{<p, к).
у/(а — х)(Ь — х)(с — х)(х — d) \J/(а — c)(b — d)
3.
dx
ху{а — x)(b ~~ ж)(с — х)(х ~~ d)
4.
dx
5.
(b — x)(c — x)(x — d)
dx =
y/(a-c)(b-d)
[x < b].
, к) у
(р — ж)у (а — х)(Ь — х)(с — х)(х — d) (р — Ь)(р — с)у{а — с){Ъ — d)
b) 1
х <(с-Ь)П\<р, т,	^	(, A; +{p^c)F{(p, k)\	\рфс].
(a- b)F{<p, к) |.
6.
7.
8.
9.
Ъ-х	2F^ с)	.
dx = —	. ,	П ср,
(a - ж)(с - ж)(ж - d)
(а — х)(Ъ — х){х — d)
ж — d
(а — х)(Ь — х)(с — ж)
.-d)
2F - с)
' ft-d'
, к] — F(<p, k)\.
(с -
(fe -
, 2 /а^с
«ж =	1/-	; Е((р, к).

70
Гл. 1. Неопределенные интегралы
[1.2.39
10.
11.
dx =
» — х)(с — х){х — dK	с — dy b — d
, к) - E(<p, к)]
2 (a-x)(c-x)
b — x
12.
(a — xK(c — x)(x — d)
b — x
dx =
dx =
¦E(<p,k)-
2
c-d^ (b-x){x-d)
2(a - b)
[x > d].
(a ~ х)(Ъ ~ x) '
(a - x)(c - x)(x - d)s	(a - d)(c - d)y/(a - c)(b - d)
x[(b-c)(a-d)F(<p, k)-(a-c)(b-d)E(<p,
2F -d)	(a-x)(c-x)
a-d)(c-d)V (b-x)(x-d)
[x > d\.
13.
(a — xK(b — ж)(ж — d)
14.
15.
(a - x)(b - х)'л(х -d)	a-by b-d
ЧЬ -с)	2 \(c-x)(x-d)
(a-b)y/(a-c)(b-d)	a - d\J (a - x)(b - x) '
dx =
16.
17.
(a — x)(b — x){x —
(a — xK(b — x)(c — x)
dx =
(a — x)(c — x)
\b-x)(x-d)
dx =
2 lb->
ж — d
(а — x)(b — хK(с — х)
—by а —с
dx =
2 (c-x)(x-d)
a-сУ а-ж fe-ж
2у/(а - c)(b - d)
(a-b)(b-c)
2(o - d)
, к).
1.2.39. Интегралы вида R(y/a — x , V& — ж , Vc — ж , ^ж — d) dx.
Условие: a>b>c^x>d.
_	. (a-c)(x-d) ,	(a-b)(c-d)
Обозначения: <p = arcsin ^/ ^	-(™	™ , к = W )	^7	-( .
!/ (c — d)(a - x)	у (a — c)F — d)
1.
у/(a — x)(b — x)(c — ж)(ж — d) \/(a ~
) к).

1.2.39]
1.2. Степенная и алгебраические функции
71
2.
3.
4.
х dx
у/(а, — х)(Ь — х){с — х){х — d)
y/(a-c)(b-d)
d~c
1 k)\.
dx
x\f(a — x)(b — х)(с — х)(х — d)
2
ad\J (a — c)F — d)
dx
(p — x)y/[a — x)(b — x)(c — x)(x — d) (p — a)(p —
(d — c)(p — a)
5.
6.
7.
8.
9.
10.
(b — x)(c — x)(x — d)
b — x
(a — x)(c — x)(x — d)
(a — ж)F — x)(x — d)
x — d
dx =
<" (a_c)(p_d)'
2(a-d)
<p,
, к .
dx =
y/(a-c)(b-d)
dx =
2
~ у/{а-с){Ь-Щ
(a -
_ 2 ia-c	2(a-b) \(x-d)(c-x)
dx — - \ i - ; hi(ip, k)
dx =
b-cMb-d
2(a - d)
(b - x)(c - xf(x -d)	(c - d)y/{a-c)[b-d)
{b-c){b-d)\ (a-x)(b-x) '
F(<p, k) -
y/(a-c)(b-d)
а-с	\(b-x)(x-
(b-c)(c-d)V (a-x)(c-x)
\x < c].
11.
12.
13.
b — x
(a — xK(c — x)(x — d)	a — d\/ a —
b — x
(a — x)(c — xK(x — d)
dx =
dx =
с — a V a —- с
k) _ E{V, к)]
2 (b-x)(x-d)
(a — b)(a — d)
E(<p, k)-
c — dV (a — x)(c — x)
2F-c)
(a-b)y/(a-c)(b-d)
[x < c].
F{<p, к).

72
Гл. 1. Неопределенные интегралы
[1.2.40
14.
(а — х)(Ь — жK(ж — d)
15.
16.
dx =
2
a-b\b-d
2 Ib-
(а-х){Ь-х) '
dx =
(a — xK(b — x)(c — x)	a — by a — с
(а — х)(Ъ — жK(с — ж)
dx =
, к) -
2(а - d)
F(<p,k)-
2 (c-x)(x-d)
b — с у (а — x)(b — x)
17.
х — d
dx =
-2 b-d
2 \(b-x)(x-d)
(a^x)(b^x)(c^xf	b^cM a^c l^' ; b ^ cV (a - x)(c - x) '
1.
2.
1.2.40. Интегралы вида R(ya — x , v b — ж , у/с — ж , yd — х ) dsc.
ж
Условие: a>b>c>d>x.
. \(a-c)(d-x)	l(b-c)(a-d)
Обозначения: (р = arcsin л ™	-~~~z	™ , к = д / ™	™ут	-г™ .
F(<p, к).
> — ж)(с — x)(d — ж)
ж dx
— d)
{а — х)(Ъ — х){с — x){d — х)
(a-c)(b-d)
3.
dx
х^/(а — x)(b — ж)(с — x)(d — ж)
cdy/(a-c)(b-d)
,*) ¦
4.
dx
(р — х)у/(а — х){Ъ — х)(с — x)(d — ж) (р — с)(р — d)yj(a — c)(b — d)
5.
F — ж)(е — ж)(с? — ж)
dx =
	^_^
(a - c)(b - d)

1.2.40]
1.2. Степенная и алгебраические функции
73
6.
7.
8.
9.
b — ж
(а — х)(с — x)(d — х)
dx =
c-d)Tl(<p,
V
, k)\.
г
h
X
d
Г
i\
X
d
f
/
/ (a
/
/
С
-x)(b
d
~X){b
a
— x
— x)(d — x)
~~ X
-X)(c-x)-
— x
2(c — d)
2(c-d)
„/ ad .
II \ (р. 	, к
\ а, - с
a-d
, к — Flip, к) \.
жK(с — x){d — х)
dx =
2 (a-x)(d-x)
10.
v^'
b- с
11.
12.
13.
b — x
(a — x)(c — x)(d — x)
b — x
dx =
a — dy a —
' ,	2 Ib-d
dx =
(a — ж)(с — xK(d — x)	с — dy a —
2(c-d)
dx =
(a - х)ЦЬ - x)(d -x)	(a -
.-d)
(b~x)(d~x)
(a — b)(a — d) У (a — x)(c — ж)
14.
15.
16.
dx =
l^' j
2F - c)	(a-x)(d-x)
d-ж
2 b-d
(a — ж)^(Ь — x)(c — x)	b — a
2 (b-x)(d-x)
	74/7	W	(•
a - H (a - ж)(с — ж)
d — x
(a — x)(b — жK(с — ж)
2y/(a-c)(b-d)
dx = —,	tvj-,	;— E(ip, к) -
(a-b)(b-c)
2(c - d)
F(<p,k)-
2 (a-x)(d-x)
a — by (b — x)(c — x)

74
Гл. 1. Неопределенные интегралы
[1.2.41
17.
d — ж
(а — х)(Ь — х)(с — жK	Ь^
1.2.41. Интегралы вида [ жт(ж2 ± a2)n+1/2 dx.
dx =
2п + 2т + 2
х ж +
- 3) . . . Bш - 2fe
22кх2т~2к~1
¦ (Tl)"
а2таBт-1)И	Г 2 2 +1/2
v, I i\/« I ^\ /^ I o\ vA ^а /
2m(n + m + l)(n + m) . . . (n + 2)
т\(т
A;/
5	1' <г>
I Ж
6.
2(п + 1)	2(п-
x \{x
•l)Bn-l)...Bn-2fc + 3)
n-l)...(n-ife + 1)
а2те+2Bп
а (ж ± а )п
ж + (ж2 ± аА
7.
2(w + 1)
feB77i-l)Bm-3)...Bm-2ife + l) 2fc 2m-
2кт(т -1) . . .(т- k + 1)
, ^ixwa2-Bm^l)??
1	2
о I / 2 i 2\l/2 i	J- / 2 i 2\l/2 i а i
8. I (ж ± а ) ' dx = - x(x ± a ) f ± — 1п
2 i 2\l/2
zbaO
9.
10.
! ± а2I/2 dx = - ж(ж2 ± а2K/2 Т — х(х2 ± а2I/2 - - Ы |ж + (ж2 ± а2I/2
4	8	8
11. х3(х2 ± а2I/2 dx = - (х2 ± а2M/2 Т — (х2 ± а2K/2.
5	3
12.
± a2K/2 dx = - x(x2 ± a2K/2 ± - а2Ж(Ж2 ± a2I/2 + - a4 In \x + (x2 ± a2I'2
2±a2f/2dx=-{x2±a2f'2
13. \x{x2±a2f/2dx=-{x2±a
5

1.2.42]
1.2. Степенная и алгебраические функции
75
14. f x2(x2 ± a2f/2 dx = ^ x(x2 ± a2f/2 T fj х(х2 ± а
2 ± а2K/2
«- / 2 i 2\1/2 " 1	, / 2 | 2\1
^—х{х ±a)f :f—1п|ж + (ж ±а)
15. [ ж3(ж2 ± а2K/2 dx = ± (х2 ± а2O/2 Т у О*2 ± «2M
1 (ж2 ± а2)п+1/2
1.2.42. Интегралы вида 1	^	dx.
¦ dx.
(т —
|
\n-l/2
т — 1
i 2хп+3/2
ж2-	---т Bт^1)а2
1	^ (zpl)fc2fe(m - п - 2)(т ^n^3)...(m^n^Jfe^l)	1
fc=i
+
Bт - 3)Bт - 5) ... Bт - 2k - 1)а2к	Х2т^2к-
'2т(т — п — 2)(т — га — 3) . . . (—ге)(—п - 1) Г, 2 , 2чп+1/2
a2mf2m^l)!!	nx ±a )	<
V J
х2±а2\к
[т > п + 2].
^0 [Bп -
'' ±aI/2dx.
± a2)n+3/2 ^ fc Bn - 2m + l)Bn - 2m + 3) . . . Bn - 2m + 2A; - 1)
'
- 1) . . . (m - A; + 1)а2*ж2т-2*+2	+
Bn - 2m + 3)Bn - 2m + 5) . . . Bn + 1) Г (ж2 ± a2)n+1/2
dx.
¦ dx =
( .n2
1,
/ж2 + а2 — а
/ж2 + а2 + а
а
8.
9.

76
Гл. 1. Неопределенные интегралы
[1.2.43
10.
(х2±а2I'2
2ж2	+ 2а'
In
I (ж itt )	1 / 2 | 2\3/2 | 2/ 2 , 2\1/2	3
11. I	dx = - (х ± а ) ' ± а (х ± а ) ' q= a -
Ж	О
In
Ж
arccos
12.
13.
14.
15.
dx = —
(Ж2±а2K/2 , 3
± 2 а 1п
о I In
x + (ж ± а
2 ,2x1/2
ж
arccos
к=0
¦In
х + уж2 ± а2
т2п+4
¦ с!ж = =р-
1.
2.
3.
4.
1.2.43. Интегралы вида
= ±-
/О/п 	 iUa>2 4~ Л2\п —1/2	О-п 	 1 ^2 ~L Л2\п™1/2 '
Жт'	*?Т1	ТП	*? Г	гп'ГП Arm
/ 2 _j_ 2\n	1/2 ~~^ /*l 1 \ 2 I / 2 _J_ 2,\n-
1-1/2*
(ш-2п)(ж2±а2)«-1/2 ^
ж2тос1ж	ж2т+11/ж2±а2
(х2±а2)п+1/2	Bп- 1)а2
Bn - 3)Bга - 5) . . . Bn - 2А; - 1)	(ж2 ± а2)п~
(±l)n2n(n -т- 1)(п - т - 2) . . . (-т + 1)(-т) Г ж2т dx
а2пBп-1)П	J y/x* ± а2
5.
6.
— {±1) а
к
[n ^ m + 1].
/ж2 ± a2
/ж2 ± a2	2m
m —1
(Tl)fcBm - 1)Bт - 3) . . . Bт - 2к -
7.
(ж2 ± а2
_ 1)а2

1.2.44]
1.2. Степенная и алгебраические функции
77
8.
9.
10.
x2m+1dx
(ж2 ±а2)п+1/2
k=0
dx
(ж2 ± а2)п'
= ±
Bra -2k- l)(x2 ± а2)п^к^/2 '
2n - 2 Г	dx
¦± ¦
— f-
1)«2J
Bn _ 1)а2(ж2 ± a2)^1/2 Bn - l)a2 J (ж2 ± a2)n
±x{x2±a2I'2
X
(x2±a2)n+1/2
11.
12.
13.
15.
16.
17.
19.
20.
Ж2±.
(±1)^ \
,
Bn - 3)Bn - 5) . . . Bn - 2A; - 1) а2*(ж2 ± a2)r'
n-1
ж dx
(x2 ± a2)^
= ln
ж + (ж ±а )
2ч1/2
14.
(ж2±а2I/2
= (ж2±а2I/2.
a
Y
ж + (ж ±а
ж3с1ж
(ж2±а2K/2
ж с/ж
(ж2±а2K/2
ж3 б?ж
= - (ж ± а
ж
2 , 2x3/2	2/ 2 , 2x1/2
=
18.
(ж2±а2K/2
1п
х2 ± 2а2
/^.2 4- л2\3/2	/«.2 4- /,2^1/2
1.2.44. Интегралы вида
ж + (ж ±a
dx
1.
2.
3.
4.
5.
хт(х2±а2)п+1/2
= ±
1
2п - 2
Bп - 1)а2хт~1(х2 ± а2)
— 1	т +
Bп -
=Ь a2
Bп - 1)а2
с!ж
2п - 1
(ттг —
dx
2jfe - 2m
(ж2 d= a2)n
771 + 72 — 1
ж2 ± a2
dx
ж(ж2 ± а2)те
(±1)
fc+1
Bn - 2k - I)a2k+2{x2 ± a2)*-*-i
(±1)
n + l
In

78
Гл. 1. Неопределенные интегралы
[1.2.45
6.
8.
9.
10.
11.
dx
In
х(х2±а2I/2 а
7.
dx	_ (x2±a2)^2
пХ	I Ж it U I	JL
xs(x2±a2I/2 = T ^2^2 + ^з
In
In
а2I'2
ж(ж2±а2K/2 ±a2(x2±a2I/2 аз
dx
x
a
*os —
ж
p2 _|_ п2\г/2
X
ж2(ж2 ± а2K/2	а4ж(ж2 ± а2I/2 '
dx
ж3(ж2±а2K/2 =
3	± 3
In
'2а2ж2(ж2±а2I/2 2а4(ж2 ± a2)V2 2a5
1.
1.2.45. Интегралы вида
dx	-
(ж + b)n\/x2±a2 J (ж2 ±
± а2
-Bп-3)б[-	-4
J (ж + bO1^1
(ж + b)n~Wx2±a2 + ^ J (ж + Ь)п~2л/х2±а2
dx
2.
3.
4.
5.
6.
8.
dx
(х + b)Vx2 + а2
da:	I
¦In
¦In
а2 - 6ж -
ж + 6
а2 + Ъх + ^F2 -а2)(ж2 -а2
ж + 6
[Ь2>а2
/а2 - б2
1
arctg -
а2 + 6ж
с!ж
1 / ж — а
(х + a)V^2 - а2 а
da;
7.
1 х + а
(ж - a)V^2 - а2	И
ж
(r»1 _|_ |i2\m/^,2 i n2\n+l/2	9(<т -— "\\(n% -—
I dU	\ U I I «JU	| 1* I	?	Z«l|##l/	ill LI/
Bm - 3)a2 - Bn + 4m - 6I'
m + n — 2
9.
(m — 1)(«2 — 62N2 J (ж
(ж2 + 62)(ж2 + a2)n+1/2 BП _ i)(a2 - 62)а2(ж2 + a2)n^

1.2.46]
1.2. Степенная и алгебраические функции
79
Dга - 3)а2 - Bга - 2)Ъ2
dx
Bп - 1)(а2 - 62)а2 J (ж2 + 62)(ж2 + а2)»^
10.
11.
12.
13.
14.
15.
16.
dx
(ж2
(ж2
(ж2
(ж2
+ 62)V
Ъх/
dx
dx
dx
^Ь2)л/
bx/
1
Ж2 +
ж2-
w^
1
^^
1
а2
а2
а2
"а2"
б2
¦In
Bга - 1)(а2 - 62)а2 J (ж2 + &2)(ж2 + а2)п
х\/Ъ2 — а2 + 6V^2 + а2 I
arctg ¦
— b2
1
26V^
1
-In
/ж2 + б2
ж^а2 + b2 ~~ b\Jх2 + а2
[б2>а2]
Га2>621
¦In
¦In
xxja2 + b2 + bxjx2 — a2 I
x\/b2 — a2 — b\/x2 — a2
arctg -
bx/x2 — a2
' а^ж2 - b2
bx/x2 — a2
bx/a2 — b2	xx/a2 — b2
1.2.46. Интегралы вида [жт(а2~ж2)те
[a2>62]
Га2>621
+1/2
dx.
xn+l/2 »
m + 2n + 2
m + 2n + :
(a2 - ж2)п+1/2
dx.
m/ 2	2\n —1/2 i
ж (a — x ) ' dx.
2n + 2m + 2
^ Bm - l)Bm - 3) ... Bm — 2Aj + 1)
^ 2fc(m + n)(m + ra - 1) . . . (rra + ra - A; + 1)
2m(m + n + l)(m + n) . . . (n + 2)
l)	a
/2
(a — ж
2
22 _ж2чп+Л + 3/2>
5.
6.
7.
/ 2	2\n+l/2 i	1/2	2\n4
x(a — x ) ' dx =	(a — ж )
in + Л
(a2 - ХГ
?*f J(a2
x (а2-ж2)п-
Bn
- ife
!!a2n+2
l)!!a
/ 2 2\l/2 i ж / 2 2\l/2 , a
(a — ж ) 7 аж = ^ (a — ж ) 7 H	arcsin ¦
2	2 a\

80
9.
10.
11.
12.
13.
14.
15.
1.
2.
Гл. 1. Неопределенные интегралы
[1.2.47
2/ 2	2\l/2 i	х /г» 2	2\/ 2	2\1/2
ж (а — ж ) ; ах = — Bж — а )(а — ж ) ' ¦
8
жЗ(а2_ж2^1/2^_
dx = - (а2 - х2M/2 - - (а2 - *
5	о
а
~8~
2x3/2
'а2^ж2K/2«*ж=^
dx = - J (8ж4 -
/ 2	2\1/2 , ^а	• ж
¦ (а — ж ) 7 Н	arcsin —г.
8	п\
За4)(а2 -
(а2 - Ж2K/2 dx = \ (а2 - Ж2O/2 - - (а2 - х2M/2.
7	5
1 (а2 - ж2)п+1/2
1.2.47. Интегралы вида |	-^	dx.
(а2 - Ж2)п+1/2	(а2 - Ж2)та
-	(lj
(а2 - Ж2)те
с2т^ ^	Bm-3)Bm-5)...Bm-2fe-:
2m(m ^n^ 2)(m - n - 3) . . . (-n){-n - 1) ff 2 _ 2
2mBl)!!	J1
¦ /Л2 ^2\n + l/2	n	2fc
5.
6.
Ж
(а2 _ ж2)^'
/ 2	2\п-
I ft	Ж I
+
(а2 - ж2
Г fa2 _____ ж2I/2
7. ^	^	с/ж = (а2 -
(а -х2I/2 -а 1п
8.
9.
Ю. | (^ ~ ж2^/2 da- = I (а2 - ж2K/2 + а2(а2 - ж2I/2 - а3 1п
ж	о
11. |^	^	с!ж = ^^(а2^ж
X2	X
2\3/2 "Ж / 2	^\1/2 О1Л
• ;	(а — ж ) ;	arcsin
2	2	а
,

1.2.48]
1.2. Степенная и алгебраические функции
81
(а2 -х2K/2
12- '	х»	dX~~ 2x*
(a2 -x2f'2 3 , 2 _ 2,1/2 . За
1.
1.2.48. Интегралы вида
xmdx
(а2 -
?п —
г-2
с/ж
(а2 - х2)п+г/2 Bп - 1)(а2 - х2)п~
хт+1	2п — т — 2 Г хт dx
тт~г	(
3.
2n-l J (а2 ™ж2)те/2-
^Т/2-
(ш- 1)а2 Г хт~2 dx
[т~2п){а2 -х2)^1/2 т ~ 2п J (а2 - х2)п+г^
(п2 г»2\п-\-1/2 ~ / j о« 9°^ 1~~ I fc / 7^2 ^2\n-fc-l/2 "
4.
x2mdx _ x2m+1Va2 -x2
- т - 1)(га - т - 2) . . . (п - т - к) а
:a2 - ж2)те ^ Bn - 3)Bn - 5) . . . Bn - 2ife - 1)	(a2 - ж2)^
2n(n — m — l)(n — rn — 2) . . . f^m + 1)(—rr;
6.
7.
8.
x2mdx
(а2 - ж2)
2m-
n — m —
к
771 + 1].
2to i	/ 2 _____ 2\l/2
(а2 ^
X Ж
2w
г —1
9.
[а2 -
Bm - l)Bra - 3) ... Bm - 2ife +
^ 2fc(m-l)(m-2),..(m^)
ж(а2^ж2I/2
In- 1
2
+ а
2тт\
10.
11.
12.
14.
15.
(a2 - ж2)теа2 ^ Bn - 3)Bn - 5) . . . Bn - 2A; - 1) (a2
1 ^ 1 /п-1л
a2n ^ 2k
x dx
x
к /la^a;2
1
(а2 - ж2)те+!/2 Bп - 1)(а2 - ж2)те
ж dx
ж2 с!ж
= arcsin -—. 13.
а
J- / 2	2\3/2	2/ 2	2\l/2
= - (а -жO -а (а -жO.
6 А. П. Прудников и др., т. 1

82
Гл. 1. Неопределенные интегралы
[1.2.49
16.
18.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
dx
(а2 ^ж2K/2 а2(а2-х2у/2'
ж2 dx	х
(а2-х2у/2'
(«2^ж2K/2 (а2 ^ж2)!/2
1.2.49. Интегралы вида
dx	1
Г х dx
¦ • J (a* - х*)*>
ж	f x3 dx	ca
lR"	J (а2 - ж2K/2 = (а
2oa -
_ж2I/2-
Bra-l)
¦ + ¦
- 2
- 1)а2
(т -
— Г
)«2 J
2n -
— f-
-ij
dx
с/ж
Ь2 _ ж2\п + 1/2	а2п+2т 21^ 2ш - 2k - 1
;	fc=O
dx
i	-i \ / 2	2 \ "г — fe —1/2
m + n —l\/a—ж4	7
^ Bn -2k- I)a2k+2(a2 -
In
dx
x(a2 - x2I/2	а 1П
dx	1
a + tf-x2I'2
x
2	2\l/2
a - ж ) 7
(А	Л\1
(а -х )
2а2ж2
1
2x1/2	1_ |
}	2a3
a + (о2 -
а2(а2-ж2)!/2 аз
2ж2 - а2
a + (a2 - ж2I/2
ж2(а2 ^ж2
2а4(а2 - ж2I^ 2а5
In
1.2.50. Интегралы вида
(хт±Ьт)п(аа -х2)п
1.
2.
3.
4.
(х + b)nVa2 - ж2 (га - 1)F2 - а2) [(ж + б)-^1
с/ж	/ Лч Г
с!ж
Bга- 1)а
dx
-(п-1)
J (ж-
dx
(х + 6)V«2 - ж2 V«2 - б2
1
¦In
Ъх + а2 +
-ж2)
/Ь2 - а2
arcctg
а2 + Ъх
[6=-а].
[а2>Ь2].
Га3<Ьа1.

1.2.51]
1.2. Степенная и алгебраические функции
83
5.
6.
7.
8.
1	. а2 + bx
¦ arcsin ¦
л/b2 - а2	а|ж + 6|
dx	1 I a — x
(x + a)\/a2 — x2
dx
dx
a \j a + x
1 la + x
[a2<62].
[a > 0].
[a > 0].
- x2)m(a2 - ж2)^+!/2 2(m - l)(a2 -
Bm - 3)a2 - 2Bm + n - 3N2
+	2(m-l)(a2 -
dx
(б2 - ж2)
т + п — 2
(ш - 1)(а2 -
9.
О2 - ж2)(а2 - ж2)^+!/2 Bп - 1)(а2 - 62)а2(а2 - ж2)"
Dп - 3)а2 - 2(п - 1N2 f	dx
+ ¦
Bп - 1)(а2 - 62)а2 J (б2 - х2)(а2 - х2)"
10.
11.
12.
13.
dx
¦In
Bп - 1)(а2 - 62)а2 J (б2 - ж2)(а2 -
\x\fa2 — Ь2 + б^л2 — х2
(b2 - x2)Va2 -x2 Ъл/а2 - b2
1	x\/b2 — a2
¦ arctg -
/ж2 - Ь2
Ьл/а2 — x2
1	. xVb2 - a2
¦ arcsin ¦
dx
a\fb2 — x2
1	ж^«2 + b2
¦ arctg ¦
a2 + б2
[a2>62].
[а2<621.
1.2.51. Интегралы вида ж±ГГ1(аж2 + bx + c)n+1/2 da;.
1.
2.
3.
4.
5.
6.
6*
Обозначение: X = ax + bx + c.
xm^lXn+3/2
dx =
2(ш + 2п + 2)а
2а
dx.
4(п + 1)а
(т + 2п + 2)а
rn-1/2
4(п + 1)а
п
2n + l)Bn-l)...Bn-2fc
/ 4ac — b \ ^rn-k-i\ Bn + l) ( 4ac — о \	dx
2)a
(m + 2)a
«3/2
¦In
X1/2'
[a > 0].

84	Гл.1. Неопределенные интегралы	[1.2.51
2ах + 6 1/2 Ь2 — 4ас . 2аж + 6	г	2	п
7.	= 	X ' Л	==- arcsin ,	\а < 0; Ъ2 > 4ас .
4a	8/H	V62 4	L	J
8.	[ЖХ1/2^=—Х3/2^—
J	За	2а
о Г 2vi/2 i баж - 56 з/2 , 562 - 4ас Г 1/2 ,
9.	ж X 7 da; =	— X 7 Н	—^— \Х ' dx.
J	24а2	16а2 J
10 I г3 X^2.ir - 48aV ~ 42аЬх + 35&2 ~ 32аС X3/2
10. [ ж A dz -	24(J	X
• уп+1/2	-,
d	\
11.
Bп -2то + 5N [ Хп	Bпт + 4)а Г Х
2(rn-l)c J ж-^1	' (m-l)c
yn|l/2	i p	p yn-1/2
12. |^	-dx=^	'-+b\xn-1'*dx + clZ	-dx.
2 + 12J	J
13.
h Г ^п+1/2
J ж^2
2(m^2fi^3)a Г (аж2 + 6ж)п+1/2
B2 + 3Nj	тг
da;
,K ," X1/2 ,	X1/2	f da; 6 f da;
15.	^	h
•Г
XV2 ' 2 J a;XV2-
16.	—	dx =	h a
fXdx	/ 1	6 \ 1/2 /а 62\ Г dx
J 3	V22 47
,A f (аж2 + 6жI/2 л	2	2
18. ^	—'-	dx = -777—^ (аж
J x3	Збж3
20.
vl/2 A2ac - 62N
X' + 16a
4
3Dac + 62) Г о'ж 36c
36 , 2 , u/2 62 f dx
T (aX + ЬХ) + J
J^ dX	2X
22. [4!	(Л
23. | v""" ^; с!ж= (a- — (аж^ + бжI^ + ^^
X J	A
3(а6ж + 2ас + 62) 1/2 Заб f da; 3Dac + 62) f dx
Tc	+^JXI^ +
2&\, 2 . , ,i/2 . Заб

1.2.52]
1.2. Степенная и алгебраические функции
85
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
14.
15.
17.
18.
19.
20.
21.
1.2.52. Интегралы вида
Обозначение: X = ах2 + Ъх + с.
xmdx	xm^
x±mdx
(ах2 + 6ж + е
Bт ^2п^ 1N Г хт^г dx (m -
(m - 2n)aXn-V2	2(m-2n)a J Xn+V2 (m - 2n)a
2Bn - m - 1) f хт~г dx 2c f хт~г dx
f n-l/2	5
' dx
1 f/
Bn- 1N
то~2с1ж 6
x dx
dx
l Ж	С 1 Ж
з^"	Af:
Bn — l)aXn™1/2 2a J
2Bаж + 6)
2n-l)Dac-
2Bаж + 6)
^^2
^n^l/2 *
)a	 Г da;
c- 52) J X—V2-
Bn - l)Dac -
X
n-1
dx
¦In
Arsh ¦
+ X1/2
2аж + 6
= ^^ In Bаж + b)
\/a
XV2 - а
dx
2a I X1/2'
13.
62 - 16ac
Bп-1)Dас-.
8fc(n-l)(n-2)...(n-Jfe)	afcXfc 1
2n - 3)Bn - 5) . . . Bn - 2ife - 1) ' Dac - 62)fcJ*
[a > 0].
[a < 0; 62 > 4ac].
[a < 0; b2 > 4ac].
[a > 0; b2 = 4ac].
362 — 4ac
XV2
Dас -
24a3
16.
ж - 26c 1
2аж — 36
4a2
563 - 12a6c
16a3
_ 2Fж + 2с)
8a2
XV2-
1/2
A
XV2-
X3/2
aDac - 62)ж2 + 6A0ac - 362)ж + c(8ac - 362) 36
dx
2(ш-1)с
1	6
dx
2а2 I XV2-
Bп + т - 2)а
(in — l)c
dx
dx
dx
2с)Хп+1/2
2
1
dx
хт(ах2
Bт
Bm + 2n^ 1N

86
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
Гл. 1. Неопределенные интегралы
[1.2.53
dx
хХ1/2
¦In
1 . , 2с + hx
—j= Arsh —	-
Vе	жу 4ае — б2
¦In
2с
1	2c
¦ arctg
/ — с
1
2\/bx + аж2
bx
dx
\
dx
dx
ex 2c J xX1/2'
2( 1 . 2a\
Ъх2 + Ь2х)
(ах
ч1/2
) '
dx
1
x^X1/2 \ 2cx2
dx	_ 2
~ 5
а
2с
dx
4а
dx _ 2(abx - 2ac + 62) If dx
|(аж2 + 6жI
cF2 -4ac)XV2
dx	_ 2 ( 1 4a 8а2ж
ж(аж2 + 6жK/2 3 \ bx b2 b3
1
СЖ
c2Dac-62) J XV2 2c2
1 2a 8a2
bx2 b2x 63
1
[с > 0].
[с > 0].
[с > 0; б2 < 4ас].
[с > 0; Ь2 = 4ас].
[с < 0].
[с < 0; б2 > 4ас].
[с = 0; 6^0].
56
2с2ж
- 52ас)ж
2 -4ас)
1562 - 12ас f dx
8с3
dx
8a 16a2 64a3 128а4ж
562ж2
1
1.2.53. Интегралы вида \ R(x + p, аж + 6ж + с) а*ж.
1.
Обозначение: X = ах + Ьж + с.
Г	dx
(X
(m _ l)(ap2 - 6р + С)(Ж
Bт + 2п ~~ 3)(Ь - 2ар) Г
2(m-
с) J (ж
(m + 2n - 2)a
(w — l)(ap2 — bp + c) J (ж +

1.2.58]
1.2. Степенная и алгебраические функции
87
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
-2
Bт + 2n — 1)F — 2ар)(ж -
+
dx
(ж
Bгс - 1)(ар2 - 6р + с)Хп-]
i	f_
- bp + с J (ж -
¦ +
а*ж
- 2ар)
[ар2 - 6р + с = 0; 6 - 2ар ^ 0].
- Ъ
-1
ар-
Ь- 2ар
[ар2 - Ьр + с = О].
¦ dx =
(ж + р)т	(га — 1)(ар2 — 6р + с)(ж + р)г
2(т-1)(ар2 -Ър + с)
J (ж +р)т х
Bn — m + 4)a
c) J (ж
Bn -
- 2ар)J (ж ¦
? ~~ Ьр + с = 0; b ~~ 2ар ф 0]
vn+l/2	vn+1/2 Li	P
х	а„-Х	b^2ap [ vn^
ж + р
- dx =
2п + 1
Н
, / 9 » ч
dx + (ар - Ьр + с)
F + 2аж)с1ж
ж + р
dx.
(ж + р)п	(п - 1)(ж + р)п^г 2(п - 1) J (ж + р)п
X1/2 ^ж Г ах + 6 — ар
ж + р
(ж + р)п
(n — 1)(ар2 — 6р + с) (ж +
dx
х "
Bn^3)(fe^2ap)
~ 2(п - 1)(ар2 -Ьр + с)
(п — 2) а	Г	dx
(ж + р)"™1^1/2 (п — 1)(ар2 — Ьр + с) J (ж + р)п™2
2(п- 1)а
^ l)Bap-6)
Г dt
[ар2 - Ьр + с = 0; 2ар - 6 ф 0]
1 1
dx
[а + F - 2ap)t + (ар2 - bp + c)t2]x/2
1
t =
х In
Ь- 2ар
ж + р
2(ар2 ^
2(ар2 ^
¦In
[ар2 - 6р + с > 0].
» — 2ар
(Ьр^ар2 -сI/2
ж + р
» — 2ар)х — Ьр + 2с
[ар2 - 6р + с > 0].
[ар2 - 6р + с < 0; б2 > 4ас]
[ар2 - 6р + с = 0].

88
Гл. 1. Неопределенные интегралы
[1.2.54
17.
dx
dx
dx
18.
¦Iwn?
)t2 + {p2 + p2)][(aa2 + 6a + c)t2 + a/32 + 6/3 + c]1/2
It = 	; а и C определяются из системы уравнений 6(a + /3) + 2с — 2ap2 = 0, a/5 + р2 = О
L a - ж	J
(аж + /3) dx _ а Г dn	2/3a - aft Г A - аи2)" rfv
19.
э + гл2)"-	2а J (р + с — 62/4а — apv2)n
[	2а)
1.2.54. Интегралы вида /(ж, ^ж2 — ж + 1) dx.
Условие: ж > 1.
Обозначение: у? = arcsln ¦
1.
2.
3.
4.
5.
6.
7.
/ж2 - ж + 1
dx
= -\f( —}-e( —\\
[х 2 1].
ж(ж — 1)
2ж - 1 V ж2 - ж + 1
dx
Bж -
9Bж - IK
' 2
2ж- 1

1.2.55]
1.2. Степенная и алгебраические функции
10.
11.
dx =
' 2 ) 2Bж - 1)
ж(ж — 1)
1)ж]
ж2 — ж + 1
12.
ж(ж
,	1 _/
dx = ..	 Е arccos
^27 V
Fa
27 I
2B
¦A-л/3)ж / жA + ж)"
1.2.55. Интегралы вида Я(ж, ^ж2 + а2 , л/х2 + Ь2 ) dx.
Условия: х > О, а > b > 0.
Обозначения: у? = aretg —, к =
1.
2.
3.
4.
ж2с1ж
/ж2 + а2
dx
а2(а2 -
5.
6.
7.
8.
dx
х dx
1	2	2
	тгт- [а Е((р7 к) — b F[(p, к)} —
,, k) - Е(<р, к)].
[ж > 0].
[х > 0].

90
Гл. 1. Неопределенные интегралы
[1.2.56
9.
10.
11.
12.
13.
14.
15.
Ж2 + 62
dx = a[F((p, к) - E((p, к)] + xa
jx2 + b2
ж2 + а2
dx = — [F((p, к) - аЕ((р, к)] + ж
ж2 + b2 '
/ж2 + а2
Ж2 + 62
т2 + b2	1	а2 —
, 9 ,—трг^ ах = — Ь((р, к)
[х2 + аА)л	а	а1

+ а*)(х2 + Ь2)
dx = ^ [2b2F(if, к) - (а2 + Ь2)Е(^, к)]
5
dx
		- F arccos -—	ч5/
2Ja(a + 1) L V	(ж +V«J + (а + 1)ж 2(а ¦
+§(.¦+.¦+^1^.
=Ь FI arccos
dx
1 Ж д/CL ) {0L ~~т~ JL JЖ
(ж^-^аJ + (а + 1)ж' 2(а + 1)
х, а > 0;
0 ^ х ^ \/а
i/а С х < оо
Ft arccos
ЕJ + (а + 1)ж ' 2(а
16.
17.
18.
=F FI arccos ¦
dx
(ж- у^J^(а
(а + 1)ж' 2(а
с, а > 0; < ^ ^
[ Va ^ ж < оо
ж > 0; с= \/а2 + б2 ].
1 FBarctg / дЖ
р(ж + а) ' 2
[Ж>0; р2 = 62 + с2; д2 = F + аJ +
dx
2 arctg
(а — ж)
оо
1.2.56. Интегралы вида R(x,
Условия: ж ^ 0, а > b > 0.
ж
Обозначения: ^> = arctg — k =
а
рж ' 21
[а > ж > 0; р2 = F - аJ + с2; д2 = б2 + с2].
~b2)dx.
1.
2.
¦E(<p,k)
[х > 0].

1.2.57]
1.2. Степенная и алгебраические функции
91
dx
(р -
4.
5.
6.
7.
8.
9.
10.
11-
12.
dx
dx
а62(а2 -
ab2(a2 ^
х2 dx
^w[(a2
[а2Е((р, k) -b2F(Vl к)].
х dx
ж2 + а2
ж2 + б2
ж2 + Ъ2 ж2 а
dx
, А;).
[F{<p,k)-E{<p,k]\-
(a2 - 62)ж
а	а2
, А;) - т^ Е(<^, А;) + т^-х
б2	Ь2ж
ж2 + а2
= - [F((p, к) - Е(<р, к)] + -4
ж
1.2.57. Интегралы вида R(x, Vx2 + a2 , 1/ж2 — Ь2 ) dx.
ь
Условие: ж > 6 > 0.
Обозначения: ю = arccos —. k = —,
ж'	V«2 + b2
1.
2.
3.
dx
/a2 + i
, к) -
, к) + ^
, A;)].
[х > 0].
[ж > 0].

92
Гл. 1. Неопределенные интегралы
[1.2.58
4.
5.
6.
7.
8.
9.
dx
(р -
р(р - Ъ2)л/а2 + Ъ2
dx	1
x dx
, fe) - B(v> fc)]
¦b2
[а2-
¦x^b2
dx =
- b2
b2
, к) - Е(ц>, к)] + -у/(ж2 + а2)(ж2 - б2).
, k).
1
х
11.
12.
- б2
1.
2.
3.
Условие: х ^ b > 0.
Обозначения: <р = arcsln *
СХЭ
с!ж
da;
¦, А; =
¦[(а2
dx
E(<p, k).
M 1
ж V x2 +
, к) - b2F(tp, к)} +
х2 + а2-Ь2 г^г-
Зж
oo
1.2.58. Интегралы вида R(x, л/х2 + a2 , Va?2 — b2 ) с!ж.
-b'Fi^k)]--^,

1.2.59]
1.2. Степенная и алгебраические функции
93
4.
5.
6.
7.
8.
I
X
со
I
X
со
J
X
CO
г
ж
CO
Г —
аж
Е2+а2K(а
ж2 dx
Е2+а2K(а
с!ж
ж dx
dx
.2 _ 62)
,2 _ Ь2)
г _ 62)з
! _ 62K
a2 + b2
я(р, л).
.[F(^5^)^?;(^5^)]
a2){x2 -b2)
9.
, к)
, fe)-
2 + a2)(x2 - b2)
/а2 + Ь2
[ж > 6].
[x > 6].
:2 V X2 — Ь2
1 /Т2 _ К2
11. I —4/ —т——- dx =
х2 V х1 + а2
12.
ж2 + а2
2 +
Ь2
а2
р
"F
F
ж2 + а2 '
_ 1,2
a? Jo? + fe2
F(<p,k).
X
1.2.59. Интегралы вида Я(ж, ^ж2 + а2 , л/b2 — ж2 ) <ia
Условие: 6 > ж > 0.
Обозначения: ср = arcsln —... _ _
b V ж2 + а2
, А; =
/а2 + б2
1.
dx
F(<p, к).
2.
3.
dx
(р -
pF{<p, к)

94
Гл. 1. Неопределенные интегралы
[1.2.60
4.
dx
5.
6.
7.
1
х dx
/а2 + б2
1
,k)-E(<p,k)] +
E(<p, к)
[ж < b].
8.
2 + 62K L V ; V	; V Л
Ъ2(а2
[ж < Ь].
9.
E(<p, к) - Xi
ж2 + а2 '
10.
(b2 - ж2K
0 f	Л2
(а2 + Ь2)х
[х < Ь].
11.
dx = л/а2 + b2 [F((p, к) - E{ip, к)] + Ж4
12.
- ж2
+
/а2 +
F(<p, к).
13.
1
Ъ2 -х2) dx = "Va
, к) - (а2 - Ь2)Е((р, к)] +
о
1.2.60. Интегралы вида Я(ж, ^ж2 + а2 , \/b2 — ж2 ) dx.
X
Условие: b > х ^ 0.
ж	b
Обозначения: (р = arccos —, к =
о
1.
b	y«
1
, к).
2.
, к) -

1.2.61]
1.2. Степенная и алгебраические функции
95
3.
4.
5.
6.
7.
8.
dx
[a2F{tp, k) ~ {a2
dx
(р -
-, к
dx
-ж2) {р^Ь2)л/а2 + b2 \ b2-pJ
1	„, ,ч	х	[Ь2-х2
1
б2 ^ж2
/а2 + б2
]Е(^,к).
ж /б2 — ж2
а2 + б2 V ж2 + а2
ж2 V б2 - х2
, A;) - ?J(^, A;)]
Ь2х
, Ь2-х2 ,
ж2 + а2
i[F{<p,k)-E(<p,k)].
Ю. 4т
1 /б2^
ж2 V х2 + а2
с!ж =
, к)
11.
12.
dx =
/а2 + б2
62~;
ж / oz — ж
dx = -
3
Va2 + Ь2
[a2F((^, А;) + 2F2 - a2)E(ip, к)} ¦
ж
1.2.61. Интегралы вида R(x, Vx2 — а2 , ^ж2 — b2 ) dx.
1.
2.
3.
Условие: ж > а > 6 > 0.
Обозначение: ш = arcsln >
х dx
dx
/ж2 -а2
х2 ~~ Ь2 '
- +Ж1
/ж2^а2
ж2 - Ь2 '
1 /^2 - а2
х2л/(х2 -а2)(х2 -Ъ2) аЬ2[ \ а)	\ aj\ a^x V ж
2^62 "
[х > 0].
[ж > 0].

96
Гл. 1. Неопределенные интегралы
[1.2.62
4.
5.
6.
dx
(р -
7
dx
х2 dx
а	( Ь
9.
10.
12.
13.
14.
а2)(ж2 - б2) da?= | [(а
=F F arcsin
OG
1.2.62. Интегралы вида Я(ж,
Условие: ж ^ a > b > 0.
Обозначение: у? = arcsin а/ж.
1.

1.2.68]
1.2. Степенная и алгебраические функции
97
2.
F ш, — \ — Е\ (х>. — 1 .
V а	V «
4.
5.
6.
7.
8.
с!ж
-а2K(ж2 -
а2K(ж
a(b2 -a2) \ \ a/ x V x1 - a?
'' a/ + ж(о2-
9. 4,1
& = ^v, -
10.
dx = T2\
Ь2
11. | -г
2
12.
ж2-62
1.2.63. Интегралы вида Я(ж, va^
Условие: а > х ^ b > 0.
Обозначения: (р = arcsln
¦, А; =
1.
3.
2.
\х > а .
ж > а .
= аЕ((р, к).
dx
= 47^(^л)- х
7 А. П. Прудников и др., т. 1

98
Гл. 1. Неопределенные интегралы
[1.2.64
4.
5.
6.
7.
8.
dx
(x2^p)y/(a2^x2)(x2^b2) a{a2~p) \ ^ ~ V
a2^62
аЬ2(а2 - Ь2)
, к) - а2Е(^, к)
х2 dx
а2 - Ь2
aF((p, к) - аЕ(<р, к) + a^
а2 — х2 . х а2 — х2 а
б2
' JV(-2^2)
^b2
12 V 2i^
б2 V х2 — Ь2
10.
11.
dx = aE(ip, k)	F(<^, A;).
az-a;z	a
ж2Ь2- ж2
, A;) - E((p, k)] + ¦
{а2 -х2){х2 -b2)
1J*. \/yo, — x )\X — о ) dx = — [{а ~т
J	3
ж
ж
1.2.64. Интегралы вида R(x, л/а2 — х2 , ^ж2 — б2 ) dx.
Условие: а ^ ж > b > 0.
Q< IX 	 I/
Обозначения: <z? = arcsln ^4/^	г- ,
ж V a — b2
ft 	 &
1.
2.
ж dx

у (a2 - ж2)(ж2 - б2)
dx
4.
(p - ж2)^(«2-ж2)(ж2-62)
- b2)
-']+<>-»¦)''(«•
. *)}
[ж > 6].
[ж > 6].
[х > 6].

1.2.65]
1.2. Степенная и алгебраические функции
99
5.
6.
dx
x dx
а(а2 - b2)
1
(9 L9 \
[x < a].
a
x
Ix2 -b2
\x < a .
7.
dx = a[F{<p, k) - Е(^р, к)] + -vV^
8. ^
хл V x* - <
9. — 1
J a
10.
x2
^ ^ ^ ^ ^ ^	^ 1у/(а2^ж2
а	ж
11-
(a2 — ж2K
x \ a2 — x2 a
[x < a].
12. I ^/(a2 -ж2)(ж2 -b2) dx = - [(a2 + Ь2)Е((р, к) - 2b2F((p, k)] +
x2 - a2 - b2
X
1.2.65. Интегралы вида R(x, л/а2 — x2 , \/b2 — x2 ) dx.
Условие: a > b ^ ж > 0.
x
Обозначение: Lp = arcsln —.
b
1.
1
= — F
2.
Г / 6\
	 = a\F\ ш. — — E
2)	L V aJ
3.
ар V^' p ' а
[рфЪ].
.
/ 6\ _
62-a;2
5.
x dx

{a2 -x2)s(b2 -x2)
±^LeL,±)-x\
1
a

100
Гл. 1. Неопределенные интегралы
[1.2.66
6.
7.
dx
I \	/9
ab2' V" a) b2(a2~b2)\aE{ip"a)^X\lw^2
x2 dx
1 Г /а2^ж2	/ b
~~2	ЙП 12	2 -flE^ ~
[ж < 6].
[ж < b].
8.
[а4 + б4 - (а2 + Ь2)х2]х
aj a2b2(a2->
6].
9.
yr	 с!ж = aEl <p, -).
b2 — x2	\ a
10.
11.
(б2 — ж2K
Ib2^:
b2 I \' ' aj	\" ' a
b\ a2~b2
[ж < 6].
12.
Г2Ш
(а2 — ж2K
= -\F[<p, -)-
а[ \ а)
Ь\ х Ib2 ^х2
) +
) \ г2
aJ а V а — ж2
13.
dx =
= - (а +6 )?7(у?, - 1 -(а -
3	\ а
ж /7 о 94/L9 «м
-\/{а2 - х2){Ь2 - ж2).
а I \ 6
о
1.2.66. Интегралы вида R(x, \/а2 — ж2 , \/b2 ~~ х2 ) dx.
Условие: a > b > x ^ 0.
Обозначение: ш = arcsln —
ЬУ a2 -x2
1.
dx
2.
=a\F[<p, -)-Е\(р, -
2)	V о.)	V «
б2 ^
3.
dx
1 lF^b4^/l ' ^b2-,2
1 b2-x2
4.
(р -

1.2.67]
1.2. Степенная и алгебраические функции
101
5.
dx
-x2)
6.
х2 dx
f Ь\ 1 / b\
[х > 0].
10.
7^*dx = l\FL!L)-EL!L)l
(а2 — ж2K	а\_ \ а)	\ а11
11.
dx = —a
[x > 0].
12.
a2 - x2){b2 - x2) dx = ^ \(a2 + Ь2)е(<р, -) -
3 L	\ aj
f
1.2.67. Интегралы вида Я1ж,
х2 — рр 1 / (р — рJ	_
Обозначения: ш = arccos —	—, к = —\	—— , рир — комплексно сопряженные
х2 + рр	2 У	рр
1.
2.
х dx
= E(<p,k).
3.
р2)(х2 + р2)
4.
x2dx
1
- рJл/р~Р
2х(х2 — р~р)
рр

102
Гл. 1. Неопределенные интегралы
[1.2.68
5.
(ж — рр) dx
, к) - Е((р, к)] +
2х(х2 — рр)
6.
7.
Л
8.
(ж2 — ррJ dx
(р-;
[(ж2
+ р2)(ж2 + р2)
1
,к).
1.2.68. Интегралы вида R(x, л/х3 + 1) dx г).
Условие: ж ^ — 1.
Уоозначения: ср =
-, к = sin — =
12
12	2
1.
2.
3.
4.
5.
я"		2 „
^^^^ «ж =	 ж
с!ж
2п-
1
ГТ л/з -1
, к).
¦ dx = -уж3 + 1.
3
dx
cos ж с/ж
=
A + pi sin2 ж)-\/1 - ib2 sin2 ж J
_ ^з см. 1.5.33.12-14] .
6.
7.
8.
— /ч	/ч
= 	F(w, к) Н	— arcsln (A; sin ш).
dx
4 ж2 + 2 -
х)См. также 1.2.73.

1.2.69]
1.2. Степенная и алгебраические функции
103
1.2.69. Интегралы вида Я(ж, Уж3 — 1) dx ).
У
Условие: х > 1.
Обозначения: <р = arccos
ж ^ 1 ~ Уз f . 7г
= arccos	—, « = sin — =
ж^1 + Уз	12
1.
/ж3-1
2-
гЗ _
4.
dx
{x - l)Vx3 - 1
[х > 1].
5.
2(УЗ -2)
л/З -
6.
(g-l)rfa;	_ 2B-л/3) Уж3 -1	2 -
к
с2 - 2ж - 2 У27
, А;).
7.
(ж -
8.
(x-l)dx	2 + •
(ж - 1 + л/3Jл/ж3 -
9.
(ж2 + ж + 1)с1ж _ 1
(ж- 1 + УЗJУж3 - 1 ~ УЗ
10.
(ж2 + ж
11.
(ж — 1) dx
2 +УЗ F	2^ УЗ 2(ж-1)(>/3
У27 l<^' j УЗ (УЗ ^1 + ж)
12.
[(ж - 1 + УЗJ - 4УЗр2(ж - 1)]Уж3 -1
13.
[(ж - 1 + УЗJ - 4УЗр2(ж - 1)]Уж3 -Т
х)См. также 1.2.73.

104
Гл. 1. Неопределенные интегралы
[1.2.70
1.2.70. Интегралы вида Я(ж, \fl — ж3 ) dx ).
Условие: ж ^ 1.
_	ж - 1 + л/3 ,	л/3 - 1 + ж . . 5тг У 2
Обозначения: ш = arccos	=-, ф = arccos —=	, к = sin — =
ж^1^Уз	у^ + 1^ж	12	2
жтс1ж _ -2хт~2л/1-х3 2(т-2)
1.
2.
4.
5.
6.
+
7.
8.
9.
10.
11.
12.
13.
14.
15.
2т- 1
dx
2т - 1
1
3.
dx
— оо
1
ж2
/1-ж3
dx
-1
pi,
cos ж dx
A + pi sin2 х)л/\ — к2 sin2 ж
Pi =
(p-1-
4л/3(р-1) '
-l) Lp-i-v:
1, 1 + л/З; см. 1.5.33.12-14 .
(ж - 1 - л/3)л/1 - ж3
dx
5 A;) + — arcsln (A; sin ф).
¦ж + 1
^ 1-
-^=-[F(y>, *) - 2Я(?, *)]
dx
ж л/1 - ж3
I"
J (
--oo
X
r
J (
— oo
1
r
1 (x
X
X
I
J (
— oo
1
f
>-
>-
_ 1
I
>-
(x
1
1
(Ж
(x
. -
(Ж-
(Ж
1
2
2 +
- — ¦
+ Ж
—
1)
X
+
1)
1)
^ж
^yr^^
^ж
dx
2v
+
i;
/^ _ xs
l)dx
\dx
E(ip,k)-
6 ~'kl ' 4'
с2 - 2ж - 2
-2
^27
-2
, *) " E(V, к)}.
,k)-
1
Е(ф,к).
[(ж - 1 - УЗJ + 4УЗр2(ж -
х)См. также 1.2.74.

1.2.71]
1.2. Степенная и алгебраические функции
105
16.
(ж - 1 - лДJ dx
— ос
1
[(ж - 1 - УзJ + 4УЗр2(ж - 1)]У1-ж3
р	I
17. Vl-ж3 с/ж = -
5
- 2жл/1-ж3].
18.
х dx
F I arccos¦
¦y/S)x
-\
- ж)
[ж < 1].
1.2.71. Интегралы вида R(x, Уж4 + 1) dx.
Обозначения: ip = arccos —	, ф = arctg (I + л/2)	 , к =
X т J-	I	J- т Ж J
-1)-
1.
xndx xn
/ж4 + 1 п - 1
/ж4 + 1 -
п-3
^ 1 J Уж4 + 1
¦ dx.
i dx	1 _ /
2. I ,	= — F[ arccos
3.
4.
2 * у— 1 + ж2' 2
1 „/ У2~
rfa;
, к)
[х <: 1].
[я > 1].
ж< 1].
i x dx	1, / 2 r^i	\
5. I / 4	=2 ^ + ^ + ^"
6.
7.
8.
10.
11.
12.
7 .	= 	5——	h-F arccos -—¦—-, ^^ - К arccos -—¦—-, -—
/ж4 + 1	ж2 + 1	2 \	1 + ж2 2 /	\	1 + ж2 2 /
1].
ж dx жУж4 +1 1
Ж2^1
- - F ( arccos	— + ?J arccos	— ) [ж ^ 1].
Ж -|- 1 ^ /	\	X -\- L Z
ж2 - 1 У2
= 2^Ж4
9.
1 2 Уж4 + 1 + 1
dx
(ж2 -жУ2 +1)Уж4
(ж2 - хл/2 + 1)
У2
ЗУ2 +4
ж(ж2 ¦
3^2 -¦
, к)
[« ? 1].
1].
1].

106
Гл. 1. Неопределенные интегралы
[1.2.72
13.
14.
15.
16.
(rr.2	Vs./9 I '
x2 dx
х2 dx
: + l
1
' 2
у/2\ 1
] " 4
х\/х4 + 1 1
^4
2(ж4 -
\/2\	ж(ж2-1)
2(ж2
л/2
[0 ^С х < 1].
[x > 1].
1].
1].
17.
'
[« > У-
18.
ж4 + 1 dx 1
2 \ 2
г/2\	/ л/2
J4y
+ 1
ж4 -1
1.2.72. Интегралы вида R(x, \/±ж4 =р 1) ^ж-
Обозначения: у? = arccosl/ж, t/> = агссозж.
1.
2.
3.
4.
5.
6.
J
1
ж
f
J
1
as
r
J
1
1
J
ж
1
r
J
X
1
f
x2dx
s/xA -1
ж4^
Уж^Т
ж2йж
xUx
V2 ' Г' 2
' 2
2
, лД\ 1 „( , ^2
ф,	— Fi ф,
2 / /2 V 2
3^2 Г' 2
1].
1].
[ж > 1].
[х > 1].
[х > 1].
1].
< 1].
[х < 1].
< 1].

1.2.74]
1.2. Степенная и алгебраические функции
107
1.2.73. Интегралы вида /(ж, Уж + ж4 ) dx.
У
Условие: ж ^ 0 или х ^ — 1.
Обозначения: ш = arccos
, k = sin — =
'	12	2
1.
ж4
, xdx 1, 2ж2 + 1 + 2Уж4 + ж
2. I	— = — In
3.
4.
2^УЗ / 3 + 2УЗ .
• П ф,	, А; .
, /г) - V3 ?J(y?, к).
da;
-1 -
cos ж dx
J A + pi sin2 ж) у 1 — к2 sin2 ж J
-; р^О, -1, *~ ; см. 1.5.33.12-14 .
5.
6.
7.
(x + 1)^ж4 + ж л/3 (ж
dx
Уз Г	2 + Уз .... .
= 	 F(^>, A;) H	arcsin (A; sin ip) |.
1.2.74. Интегралы вида R(x, \/х — ж4 ) dx.
У
Условие: 0 ^ ж ^ 1.
Обозначения: у? = arccos
1.
2. I ,	= - arctg ,
2 1 + V3
3.
4.
/ж — ж4
2 i
/ж-ж4
A- УЗ)Уж^ж4 1
¦ - ж4 УЗ ж - ж ¦
5 А;).
-л/3 +1
F(y), Л)-
5.
6.
2Уж - ж4
A + pi sin2 ж) у 1 — ^2 sin2 ж J
3, 1,	+ ; см. 1.5.33.12-14 .
(ж - 1)Уж - ж4 УЗ (ж - 1)(УЗж - ж + 1)
dx
^3 Г_, 2^УЗ	.
= 	 F(<p, А;) Н	arcsin (A; sin ш)\.
6 L	^	'

108
Гл. 1. Неопределенные интегралы
[1.2.75
7.
dx
1.2.75. Интегралы вида Л(ж, л/х4 + 2Ь2х2 + а4 ) dx.
Условия: а > Ъ > 0, х ^ 0.
Обозначения: (р = arccos
1.
2.
dx
dx
а2ж(ж2 + а2)
ж с!ж
(ж2 + а2J^ж4 + 262ж2 + а4 4а(а2 - б2)
4.
5.
6.
7.
8.
9.
ж с!ж
(ж2 - а2
2ж2 + а4 2(а2
- а4
а4) 4а(а2 + б2)
(ж2 + а2
а2 -
2а(а2 - Ъ2)
(ж2 + а2J dx
[(ж2 + а2J-
ж2 dx
1
2а
2(а4^64) v^? ; 4а(а2^62)
(ж2 + а2Jс1ж
12.
(а2
[х > 0].
Е(<р, к) [х > а].
2(а
2 _
Ь62)
(а2
(ж2
-6
ж
+
2)
(ж
о5
2
!)
ж
V
2
¦а2)
'(X* + 262Ж2 + а4)
-а2)
2(а2 - б2)
х(х2 — а2)
(ж2 + а2
х F arctg
а].

1.2.77]
1.2. Степенная и алгебраические функции
109
1.2.76. Интегралы вида Я(ж, Vx6 + 1) d.
A-
Обозначения: <р = arecos
V3
, -0 = arccos
1-л/3
А; = sin— =
1.
3.
4.
5.
6.
7.
dx
1 2 V3	J
/ж^П).
k.)
dx = -In (ж3
¦ dx =
¦1 + л/З
З-л/3
6
, к)
,*)-^-Я(у>,
Ж5	2
{?ж = -уж6 + 1.
/ж6 + 1
dx
(х-
р2 + 1 -
— 1 — л/3
pi,
2(Р2
¦ 1(ф, pi, A;)
¦ПО, -pi, A;) -
2p2(p2
?5 Р2, А;) >
>, p, A;)= [
cos (p d(p
dx
4^3
A + psin2 if)y/l - lc2sin
2™ V3
=^; ж > 0; рт^О; pi =
-; см. 1.2.50 .
1, ж4 + 2
--In
1 — 9-%/V6 4- 1
1.2.77. Интегралы вида R(x, \/l — ж6 ) dsc.
У
Условие: 0 ^ ж ^ 1.
Обозначения: <р = arccos
. тг
, A;i = sin — =
12
1.
3.
4.
5,
ф
I:
I-
[¦
Г
= arccos
с!ж
^1 _ же
ж2
х3
А _ Ж6
ж4
V3
-1
5тг V 2 +
''C2 = SmT2=	2"
, fa).
аж = — arcsin (ж ).
— 1 — л/3
, fa)+ ^3^(^, fa).
, Л0 --^-?(?>, М-

110
Гл. 1. Неопределенные интегралы
[1.2.78
6.
7.
8.
^=^=- С?Ж = 	VI — Ж6 .
dx
(х - Р)у/1 - х6 2
dx
di
dt
x\/l —
6
\t = x1; см. 1.2.70 и 1.2.741.
1 ж4 + 2 - 2V1 - ж6
8 П х4 + 2 + 2л/1 - ж6
1.2.78. Интегралы вида Я(ж, vж2 ± 1J
1 R(r \/т2 + 1 ) dr —
A — COS (fJ
^TT-iI/2
— 1) cos (p + \/3 + 1
1 — cos (p
2 + cos (p — 2k2 sin2 <
A — cos (pJ-\fl — k2 sin2 (p
dtp
! + l + лД -1
,|,
— 1) с!ж =
! + l + лД -
cos (p + •
— cos (p
; k =
X
2 + cos ш — 2k2 sin2 cz?
sin y? = —5
A — cos <^J у 1 — й;2 sin2 <^
|/ж2 - 1 + 1 - \/3 f л/2 + л/З
: cos w = э ш	—-; к =
V ж -1+1 + V 3	*
1.2.79. Интегралы вида Д(ж, ^ж2 ± 1) dx, Д(ж, \/l — ж2 ) <
Обозначения: (р = arccos ni	w = arccos
1 + V^2 - 1
Л = arccos vl-ж2.
1
2.
4.
5.
J Л
0
ж
1<
ж
[
4
0 ^
Ж
f
ь
ж
г
с!ж
dx
У(х* +
х2 dx
1/{х* +
dx
1K
1)8
1)8
[x > 0].
[ж > О].
[ж > 0].
[ж > 0].
> 1].

1.2.80]
1.2. Степенная и алгебраические функции
111
6.
7.
8.
9.
dx
4// 2 I \3
V \х ~ 1)
dx
ж2 Ьх2 - 1
= Е[ф
bVi-lrUVi-h
л/2/ 2 V л/2/ 1 + V^2— 1
х2 dx
-е(ф —
K	V V2
11.
12.
13.
14.
15.
dx
/ 1 \ 2
F(Л, ^^
3 V V^/ 3
а
[ж > 1].
[ж > 1].
[ж > 1].
[ж > 1].
[О < ж ^ 1].
[О < х ^ 1].
[О < х ^ 1].
[О < х ^ 1].
[О < х ^ 1].
- л/1 - х2
dx
л/2
[О < ж ^ 1].
1.2.80. Интегралы вида R( \/it(x — а) , ^(ж — 6)) dx.
^	а-Ъ-2у/(х-а)(х-Ъ)	4/4(а
Обозначения: 9? = arccos	;	 ;/	¦	;	¦	•, ф = arccos ¦ '
2у/{х-а){х-Ь)
- 6)
1.
dx
2.
3.
(ж~а)(ж~&)
dx
dx
2Bх ~a~
[х > а > Ь].
[ж > а > Ь].
;'7f
[а ^ х > Ь].

112
Гл. 1. Неопределенные интегралы
[1.2.81
4.
dx
а - х)(х - b)f
1.2.81. Интегралы вида R(Vx4 + 1) dx.
1.
dx
1,
= - In
/ж4 + 1 4 ^ж4 + 1 - ж 2
1
	 arctg
2. ж л/ж4 + 1 dx = - ж2 л/ж4 + 1 Н	— F ( arccos ..
J	3	3^2 V	^ж4
1.3. ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ
1.3.1. Интегралы вида \f(eax)dx.
2.
3.	I eaxdx= ^eax.
а
4.	1Г dx = ^у
1 6
5.
6.
7.
8.
1	/	b
= —7^arcts(e V:
¦In-
dx
/b + ceax
2
с — еаху/—Ьс
1 , \/b + ceax — л/b
—— In ¦
arctg ¦
/b + ceax
1.3.2. Интегралы вида /(ж, eax)
dx.
xxeaxdx=^xxeax -^
a	a
1	eax
1
Г(Л,
л/2
[а ^ ж > Ь].
[Ь> 0;
[6> 0;
[6с >	0].
[fee <	0].
[6 >	0].
[Ь <	0].
[Re Л > 0].
[Re a > 0].

1.3.2]	1.3. Показательная функция	113
( Л\п П^1
к	A-n-1 -as , _ 	l^1/ a		А-1 ^<хх j
о. ж	е ах —	г-тт	г	гт	jz	гт ж е ах -\-
J	(Л)(Л 1)A Л) J
(п-Л)(п-Л- 1)...A- Л)
X
(-1)л(аж)*
Ai)(lAfc)	[Rea>0]"
6. [ Ж-в- <te = в- [^ + V (-1)»
j	l a f^
7. \xea* dx = ea* [ - - ЛУ 8. fasV" dx = eax (— - Щ + 4r ].
а or or
9. | P(x)eax dx = -— V^ -—^— ™^™^ P(x)i гДе Р(ж) — многочлен степени т.
k=0
10. [Жп/2е"аж da: = Bп - 1)!!у^2^па^п/2 er
аХ	G ^ Bп^2к^1)\1[
1	;
ax	n^1 k — 1 n — 1
i i I S j	ax V^ fl fl T-1- / \
11. 	 CtX =	—e >	-:	Г7	:	;	:	:	h -;	r" -^1 [ax).
1 гпП	/ -J	I rn 	 Inn 	 9l 1П 	 h\r»n — K I ггъ 	 1\| x 7
tJL/	lit/	J- I I I D	j?™i I * » » Iff/	Д; I e-C/	I # ?/	_1_ I *
12.	'e"
Ж
со	/ ч
,	i v^	(аж)
^^ к\к '
k=i
14. I	dx = - El (-аж)	[а > 0].
eax	/тг
15.	I ^^ dx = w— erfl (^/аж)	[а > 0].
/ж	V ct
16.	—=- <^ж = д/— erf (y/ax)	[a > 0].
v ж	V a
, е^аж	2 _	,		>
17.	I —^— с!ж =	—e - 2фш erf (y/ax)	[a > 0].
Ж '	\/ Ж
T -n-i/2 -ax , _ (-2)пап^1/27тг — e^ax ^ Bn - 2k - 3)l\(-2ax)k
(t2f} 	1 \If	лг.п—1/2 / .v	Г2т7 	1V
[a > 0].
CO	^_
p --ax	r~~
19.	—=r- с!ж = л/— erfc (у^аж)	[а > 0].
J у x	у а
X
Г еаж еаж	Г еаж еаж аеах а2
20.	—— ^ж =	h a EI (аж). 21. —— с?ж =	1	EI (аж).
22.
24.	^ =	6е^а6Е1 (ax + ab).
J х + 6 а
8 А. П. Прудников и др., т. 1

114	Гл. 1. Неопределенные интегралы	[1.3.3
t2eax dx ax — ab —
х + b	а2
25. 	— =	е + be Ei (ax + ab).
еах (JT	еах	,
е	^ e~ab
26.	е ™	= ^^ + ae~ab Ei (аж + ab).
J (ж + бJ ж + b
Г reax dr beax
27.	j
+ Aа6)вЕ(аЯ! + а6).
)х + (а&2Ь^аЬEi
29. е. 9 = — [еа EI (-а + ix) - е^а EI (а + ix)].
J х2 + а2 2а
30.	—	 = - [e а Ei(a + ix) + ea EI (-a + гж)].
J ж -\- а Л
31.	I I dXo = - lm[eia Ei (x-ia)]. 32. | X? ^ = Re [eia Ei (ж - га)].
Г еж _ 1
33. 	dx = EI (ж) - С - In х	[х > 0].
J ^
о
1.3.3. Интегралы вида /(ж, е а х )dx.
X			X
. L~a2x2dx= ^ erf (ах). 2. f е^ ^ж = ^ erfi (аж).
1
о	о
3 1 —ax i	v	r / \
. I e	dx = —— еггс(аж).
f 2n -a2x2	Ж2П^"
ZiC*	Zi \?itb — Zilb — IJlIICiitl/ J
i,	n \	/ \ /
^rr erf (аж).
e	ж -	— 2^'
7
Г -аж2	1 -аж2	Г 2 -а2ж2	1	-а2ж2 V^
• J	2а	'	J	~ 2а2	+ 4а3 l j"
е"~аш	2а
(р- 1)хР^г ^ р- 1
2а2Г(п-
Г о 2 ОТ +12 Г р™аЖ
.же	йж =	—j—е • 10- 	йж = -7	гт	т	г|	 с?ж.
J	2а2	J хр	(р - 1)ж^
-а2ж2	П	/	1 \
11 | :	л^.	±	Р~а2х2 Х^( 1\кг п k + 1\п2к™2к~2п~
2Г(га-
+ ~™7Г7—Гч^— EI

1.4.2]	Ц. Гиперболические функции	115
2 2	„2,^2
13. 1 e	dx = ^ Ei(-aV). 14. ^6
X	Л
JL О •	ill s^~/ I щ-^	\Jj dU 		,
\t = VZ(x + — ),*>o\.
18. (ж^а)пе c {x b) ^ж = ХлГ)	Ш	 \tke f dt	[t = c(x - 6), с ф 0].
f n -а2Ж2 + ЬЖ	1	Ъ2/Dа2)\^ (П\ ( Ь \П~к Г fc _t2	Г	6 1
JL cf # X С	CieL ^^ ______ ?	m * * I ___ -	I I/ с СХб	L — CXsl/ "™" ——
J	an+1	^\к/\2а/ J	L	2«J
ш	/~ Г	/	A\	/	h\	1
20. е~~а ж "" /ж ^|ж = 	 e a erf I дж H	I + e"~ a erf I аж	\ — e a + e~~
[Re 62 > 0].
1.4. ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
1.4.1.	Введение.
Интегралы вида Л^Ьж, сЬж, 1Ьж, сШж^ж, где R — рациональная функция своих
аргументов, приводятся к интегралам от рациональных функций при помощи следующих
формул:
fn/1 , ,	, ч, Г„/^2^1 t2 + l t2 - 1 t2 + l\dt
1.	Я(зЬж5 сеж, th ж, с!Ьж) ах = Я| —	, —	, —	-, —	 I —	[t = е ].
j \	"^	/
2.	R(sh ж, ch2 ж) ch ж с/ж = Я(?, 1 + t2) dt	[t = sh ж].
Г	2	Г	2
3.	R(sh ж, ch ж) sh ж dx = ^(t — 1, ?) d?	[t = ch ж].
J	J
4J?ff Ъ 'г r»f Ь тЛ /7'г — I /? i ¦/• i		\f •
J l '	)	J V */ !^^2
1.4.2.	Интегралы вида 8пржс1ж, сЬржс1ж.
8пж]р, \ { <ehx\v^ Г ch ж I р^1ГГ8Ьж]р™ .
I
char/	^
J	fc=o
2m^2fe + l\ A; / [ sh Bm - 2k -
эпж] _,__ [спж]	„ ffshжl2J^ 1
4'
5. N	}dx = {	k 6. J
M ch ж Г	I sh ж Г	1 ch ж
8*

116
Гл. 1. Неопределенные интегралы
[1АЗ
7.
8.
9.
10.
11.
sh ж
1 _ 3 f ch ж 1 1 f ch Зж 1	f ch ж
" Т4{ h j + ЩЪЗ j~T
1 f спЗж!3
1	I О rl Of"8 I	~C I O g% -С ^Y9 I
J	^ oil X J	О ^ oil OX J
sh Ж 1	3	1 u о . 1 u и	"	" u u
> аж = - ж =p -- sh 2ж Н	sh 4ж = ™ ж ^ - sh ж eh ж + ™ <
ch ж J	8 4	62	8 8
I чп т I
1 Г sh ж 1 Г ch ж 1
ch,
shx
ch ж
{sh ж
сЬж
p-1
dx.
1 ГсЬж!
dx = 	< , > x
2m — 1 [ вЬж J
впж] m ,	1ГсЬж1ГГзЬж1
ch x
dx =
2m 1 shx
{
сЬж J
fc_i Bm - l)Bm - 3) ... Bm - 2^ + 1) J sh ж
2fc(m - l)(m - 2) ... (m - /г) \ ch ж
ln
th2
Bm)!! I arctg sh ж f'
12.
13.
14.
ch ж
A ch ж — 1
2 П ch ж + 1
2 arctg еж
1
ch ж j
fcthxl
tha; J
ch ж
da; = =Fx
Ksh ж 1 .	if cth ж 1 f cth ж 1
^ dx = --i , >	+ < , >.
сЬж] 3[шж] [ th ж J
1.4.8. Интегралы вида	shp ж ch*1 ж с!ж.
,.|,
1. | shp ж ch*7 x dx =
2.
3.
4.
5.
6.
7.
shp ж ch9 2 x dx.
a ^a
	 sh^^ ж ch?
p+1	p+1
hp+1 x chq+1
p + 1
shp+1
Р + д + 2[8Ьр+2жс^жс1ж.
P + 1 J
ap ж chg+2 x dx.
shnxch^1 ,	1 ГзЬж1п+1
> dx =:: 	\	/
chn жзЬж]	n + 1 1 ch ж J

1.4.4]	Ц. Гиперболические функции	117
chp ж sh n х j	2n + p\chxj \\s\\x \
, - 3) . . . Bп - 2А; + 1) Г сЬж"
E
-^ Bп + р - 2)Bп + р - 4) . . . Bп + р - 2k) \ sh ж _
eta	[р^ ™2, -4, ..., -2п].
Bгс + р)Bп + р - 2) . . . (р + 2) J \ ch ж J
, ,' shp ж ch2n+1 ж],	1	f sh ж 1 р Г f ch ж 1 п
^ Bп + р - 1)Bп + р - 3) . . . Bп + р - 2^ + 1) \ sh ж j
[р ^ -1, -з, . . . , -Bп-
1П Г,	, , i сЬ(а + Ь)ж сЬ(а~6)ж	.. Г,	. .	I . _
10. зЬажсЬожаж= —	-*¦	1	Т\- -Ч* l^hax chax dx = — сЬ2аж.
J	2(а + о)	2{а — о)	J	4а
Г Г sh ж chp ж 1 ,	1 Г ch ж 1 р+1	г2 l2 ,	ж 1
12.	, lV }dx = 	1	}	13. \shxchxdx =	1
J \ ch ж shp ж j	p + 1 \ sh ж J	J	8 32
Ksh2 ж ch3 ж 1 f If ch2 ж sh3 ж 1 2 f sh3 ж 1
ch ж sh ж J	5 [ sh ж ch ж J 15 [ ch ж J
ЯзЬ2жсЬ4ж1 , ж 1 , , 1 , 1
2 , } dx = =p	sh2x±—зЬ4жН	g
ch2 ж sh4 ж j ^16 64 64 192
16. sh3 ж ch3 ж dx = — sh6 ж Н— sh4 x = — ch6 ж	ch4 ж.
J	6	4	6	4
Г f sh3 x ch4 ж 1 _ 1 J sh x \2 ^ 2 J sh2 x ch5 ж
_
ch3 ж sh4 ж J Ж ~ 7 f ch ж J T 35 \ ch2 ж sh5 ж
1 Я
-л i ! ill j сЬ(а + 6 + с)ж ch(—a + b + c)x
19. sh аж sh ож sh еж ож =
20. sh ax sh 6ж ch еж dx =
4(а + b + с)	4(-а + 6 + е)
ch (а — & + с)х ch (а + b — с)х
4(а — 6 + с)	4(а + b — с)
sh (а + b + с)ж sh (—а + b + с)ж
4(а + 6 + с)	4(-а + 6 + е)
sh (а — b + е)ж sh (а + b — с)х
4(а — 6 + с)	4(а + 6 — с)
21. sh аж ch bx ch еж о?ж = ^"^ ! Г I ^ч^ ~ ™™тт—"IT! ^ч*^ +
ч
22. ch аж ch 6ж ch еж da; =
4(а + 6 + е)	4(-а + 6 + с)
ch (а — & + с)х ch (а + b — с)х
4(а — 6 + с)	4(а + b — с)
sh (а + Ъ + с)ж sh (—а + Ъ + с)ж
sh (a — b + с)ж sh (a + b — c)x
1 л л тл-	Г shp ж	Г chg ж
1.4.4. Интегралы вида ———аж, —г-=—ах.
J ch9 x J shp ж
Г shp ж .	1 sh13^1 x p — 1 Г shp^2 ж
1. —r-z— dx =
J h9
rzdx =31гт;
ch9 ж	р — g ch11 ж p — g J ch9 ж

118
2.
3.
5.
6.
7.
Гл. 1. Неопределенные интегралы
[1.4.4
1 shp+1 ж p-g
9-1
8Ьрж
dx.
1 shp 1 ж р — 1 Г !
^Т ch^1 ж + g- I J \
'сЬ?ж ,	1 eh*7™1 ж q-1
¦dx =	1 ч
shp ж	q — р shp г ж ' g — р ,
^Т shP ж + р - 1 J shp a
8.
9.
10.
11.
12.
13.
14.
15.
p -
1
ch" х
р - 1 sh"-1 х р - 1 J shp~2 ж
dx.
shp
dx = ±
2п-1\сЬж/ [\ sh ж /
К
(±l)fcBw - р - 2)Bп - р - 4) . . . Bп - р - 2к) ( ch ж
Bп - 3)Bп - 5) . . . Bп - 2А; - 1)	\
,пB^^р^2)Bп^р^4)...(^
¦ (±l)r
ch ж f
dx.
chp ж sh
,-2те-1_
^2п^1
' Ж
ch ж
-2п
shx j
п Х ' ' ^)fcBn-p- l)Bn-p-3)...Bn-p-2ife + l) f сЬж
fe=i
•(±1)
n Bn - р - l)Bn - р - 3) . . . C - p)(l - p) f / shp ж ch^1 ж
chp ж sh™1 ж
sh2m ж ch 1 ж
ch m x sh™ x
sh m+ ж ch ж
сЬ2т+1ж8Ь^ж
(Tl)
m+k
2Aj — 1 I ch ж
2nn\
2fc-l
dx.
(Ti)r
arctg sh ж
fe = l
I сЬж I
m+fc /m\ ГсЬж rfe , ЧШ1 f сЬж 1
€ V к / | sh ж |	[|shx|J
sh2m+4ch™2n;
ch2m+1 x sh™2n ;
sh2m+1xch-2rl-
ch2m+1xsh-2n-
n + k
;-2n + l\k
n\2fe-2n+l
m+k
to
кфп
m\ 1 ch x 1
chx 1
fc=O
зЬж ch~p x
ch ж sh^p ж
shp x ch™p™2
chp ж sh^p^2
с!ж = —
[n ^ ra].
[n > m].
p — 1 [
1
ж ,
dx = ^.	л
x I	p + 1 [ cth ж

1.4.5]
. Гиперболические функции
119
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
30.
31.
1.
2.
3.
4.
-1
зпж ch
ch x sh
sh ж ch"
ch2 ж sh"
sh3 ж ch"
ch ж sh"
sh4 ж ch"
ch4 ж sh"
зпж ch™"
ch ж sh™"
sh2 ж ch"
ch2 ж sh"
sh ж ch"
ch3 ж sh"
sh4 ж ch"
ch4 ж sh
впж ch
ch x sh
-3 /
-3
sh2 ж ch
ch ж sh"
sh3 ж ch"
ch3 ж sh"
sh4 ж ch"
ch ж sh
sh ж ch™
ch x sh
sh3 ж ch
ch ж sh
sh4 ж ch"
ch ж sh"
ж
-3
-4
с!ж = In
dx
dx
hub —
dx
dx
dx =
dx
dx ¦
arctg sh x
ln|th(a;/2)|
{ch x 1
J
спж 1
бпж| J
fshsl
[ eh ж J
- ch2 ж =F In
1 J япж
3 I ch ж _
J СПЖ 1
\ sh ж J
f tha; 1
\ cth ж j
\ sh ж j \ sh ж J
3 1
= =F— Ж H	вЬ2ж :
^2 4
If tha; I2
2 1 cth ж J "
arctg sh ж 1
ln|th(x/2)|J-
ch x sh™ ж
с/ж = ± —
1	f sh ж ch
~2 x
f	Л 2
.IJ thX I
2	\ cth ж j
1 f sh ж ch™
f tha; 1
\ cth ж J
1 J arctg sh ж 1
+ 2\ln|th(a;/2)| J"
-In
ch ж 1
j *
dx
dx
dx
2 [ ch x sh
1 |спж1 ™3
I ch т I
^= I h 1
tha;
cth ж
J
\
29.
3[8Пж|
thж
cth ж
1 3 J arctg sh ж 1
iT2\ln\th(x/2)\j-
ch2 ж sh 4 ж
cth ж I
1.4.5. Интегралы вида
Г dx
dx
_ sh^ch9x'
1	p
shp ж chg ж
(p- l)shp™^<
1
(g-l)shp™^chg™^
" ж
+ g-2f	da;
p- 1 J shpa;c
q-2
- 1
dx
зЬржсЬ9™2ж"
dx
sh2m ж ch2n ж
2m - 2k - 1
- n —
к
2m^2k\ k
I th	ж + ( —1)	In th ж .
J	v ; V m J	'
кфт
sh 2m ж ch 1 ;
fc f | shin
-2m+2fe-l
2w - 2k + 1 I спж j
arctg sh ж

120
Гл. 1. Неопределенные интегралы
[1А6
6.
7.
9.
10.
11.
12.
13.
14.
15.
16.
sh m ж ch ;
^ 2m ~~ 2k + 2 \ ch ж J
! . , i i	о I ish ж ch ж 1	f ch ж 1
= In tha; . 8. < , _i , _2 } dx = ±< , > ± < • ',''}•
sh ж ch ж	J I ch ж sh ж J	I sh ж J	I arctg sh ж J
sh™1 x ch™3 ж 1 _ lfth-ж!2
ch a;sh~3 a; /	2 [cthж/
J tha; 1
1 cth ж Г
f ch ж 1 . 1 f ch a; I
-1	-4 f "ж :=: 1	Г ^1 — <	>
ch ж sh ж J	[ sh ж J	3 [ sh ж J
In I th(x/2)| 1
arctg sh ж J *
sh2 ж ch2 ж
8п™2жсп™3ж] ,	(sha;l~ 1[8ЬжсЬ™2ж1 3f arctg sh ж 1
. О	. Q	> С|Ж = ^ < .	>	<_	.О	>	<_	.....>.
x sh^3 ж
I U1 J' J
sh™2 ж ch™4 ж
. 1 Г sh ж ch ж
. _2 , -4 г dx = ^z—\ _i . _з
ch ж sh ж J	3 I ch ж sh ж
-2
2 | ch ж sh™ ж
8
3
J
2\ln|th(a?/2)| J
dx
	cth2 x - 21n|tha;|.
2	' '
sh ж ch ж
ch ж sh ж
dx
с!ж =
}"'
1 f сг!ж] 3_ 1 f сЬж зЬ™2ж] _ 5 f In th(a;/2)|
J
3 1
2\зЬжсЬ 2ж/ 2 \ arctg sh ж J *
sh ж ch ж
1.4.6. Интегралы вида thp a; da;, cthpж<iж.
> dx =	\	(
cth ж J	p — \\ cth ж J
tha;
cth ж ^
tha; l2n+1
dx = -Y	-,
tha; V
cth ж J
tha;
cth ж
cth ж j
fe=i
th ж 1	f ch ж 1
> dx = In < 1 >.
cth ж I	I sh ж J
ch ж 1	J ch ж 1
sh ж j	\ sh ж J
3. <
J [
cth ж
f сЬж 1
/tha;\
< , >.
[ cth ж J
1.4.7. Интегралы вида Д(вЬж, спж, th ж, cth a;) dx.
В chx + Cshx
dx =
(а + b ch ж + с sh ж)п
Be - Cb + (Ac - Co) ch ж + (АЬ - Bo) sh ж
(n- 1)(Ла-
1
-1 (n^l)(a2^62 + c2)
- (n - 2)(АЬ - Ба) ch ж - (п - 2)(Ас - Со) sh ж
(a + b ch x + с sh
dx

1.4.7]
. Гиперболические функции
121
2.
(ВЪ-
4
Be — Cb — С a ch x — Ba sh ж
(n — l)a(a + bch x + cshx)n ' [a ' (n — l)a:
(га - 1)!
-fc-l)!afe (a
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
Bchx + Cshx
dx = —	-
b2 — c2
Bb-Cc
In (tt + О СП Ж + С SO X) +
b2 -с2
x + I A ~~ a-
A + Bchx + Cshx
а + 6сЬж±6эЬж
"A (B-
a	2a2
dx
2a
С±В МА
b2 -.
(сЬж =р sh ж) Н-
dx
±
a
2а2
In (a + 6ch ж zb bshx)	[ab Ф 0].
F — a) th — + с
— ^^^^^^^^^ aretg —
b2 > a2 + c2; a^ 6].
Vа2 - б2
¦In-
(а - 6) th - - с + V«2 - б2 + с2
с2 (а _ ft) th - - с - V«2 - б2 + с2
1 /	ж
= — 1п( а + cth —
с V	2
(ach ж
(a- 6)th(x/2) + c
dx	_	1	Г
? + 6sh^)TC ~ (а2 - б2)"/2 J Т^
dx
chn I ж + Arth -
а
dx
shn ( ж + Arth ^
0
[62 = a2 + c2]
a>
aft.
A+B chx
a ch x + 6 sh ж
+
/а2 - б2
aretg
sh ж + Arth —
а
a2 -b
A
/b2 - a2
-In
2 (Ca - Б6) In ch ж + Arth - J + (Ba - Cb)x
\	a
x + Arth —
th-
2 Х 2 (С6 - Ва)ж + (БЬ - Ca) In sh (ж + Arth -
1 ГБ + С B~C ^2x
a I 2
1 \B^C
a 2
- Ae"
[a =
¦ e2x + Леж
с!ж
ath	b + Va2 + b2
a + 6 sh x
¦In-
ath- - 6^ ¦
ж
л	a th — — о
t	Arth 2
Va2 + I?2	V«2 + 62

Гл. 1. Неопределенные интегралы
[1А7
где
23.
где
24.
25.
b + a ch x
[b2 > a2; x < 0].
[б2 > a2; ж > 0].
[a2>62].
+ b2 ch x + c2 sh x
J «i + 61
dx = Ло In
61 ch ж + a sh ж
«2 + &2 ch ж + C2 sh ж
д Г	dx
+ A
ch ж
: ЭЬЖ
+ 62 ch x + C2 sh x '
ai
61
В
a2
Cl
С
b
Cl
С
b
1
ai
Л
2
Cl
ai
Л
c2
bi
В
at
a2
bi
62
2
61
62
Cl
C2
2
Cl
c2
at
a2
at 61
tt2 62
2
61 ci
62 C2
2
«2
C2
ai
«2
В
b2
с
c2
bt
62
л
a2
В
62
Cl
c2
Л
a2
at bt
a2 b2
+
61	ci
62	c2
ci at
c2 a2
«1 61
CX 2 ^2
2
+
bi ci
62 C2
2
Ф
ct at
C2 «2
Ach2 x+ 2Bshxchx + Csh2 x
dx =
• {[4Bb - (A + C)(a + c)]x
a ch2 ж + 26 sh ж ch ж + с sh2 ж	462 ~~ (a + cJ
+ [(Л + GN - B(a + c)] In (a ch2 ж + 26 sh x ch ж + с sh2 ж) +
~ f 2Bb(a - c) + (Ca -
1
¦In-
2V62 — ac с th ж + 6 + V62 — ac
1	cth ж + 6
¦ arctg -
+ 6
В chx + Cshx
x (а +
(а + 6ch ж)
dx = - L4 In
dx =
th-
¦6 In
а + 6 sh ж
¦ (Са - ЛЬ)
> ас],
[Ь2 <ас],
dx
а + bshx

1.4.7]
. Гиперболические функции
123
а + ВЬ)\п
th-
(АЬ- Ва) In
а + & ch ж
sh ж
а + Ь ch ж
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
В ch ж + С sh ж
(I ± ch ж)
		. . .		 Ш(ж/2) I2
2 Ш|\сШ(ж/2)||+ 4 \cth(<c/2)J
¦In
с
+ Вспж
ch ж (а +
(Аа + С&) arctg sh ж + (АЪ - С a) In
а + 6 sh ж
Вспж
ch ж (а + 6ch ж)
dx
а + b sh ж y/a(b — а)
= —\А arctg sh ж — G In
а [_
arctg li/	1 thsc I
а + b ch ж
спж
сЬж
- (ЛЬ - Ва)
dx
а + 6 sh ж
с!ж 1
а + 6 ch ж J *
[6/а > 1].
^^=^=- Arth H/l	th ж )	[0 < 6/а < 1] или [6/а < 0; sh2 ж < -a/b].
[6/а < 0; sh2 ж > -а/б].
[а = Ь].
[а = —6; sh2 ж ^ ll.
/	Arcth Wl	thx
/а(а - Ь)	IV а
= — th ж
а
_ 1 Г Arth (л/2 th ж) 1
~ ал/2 \ Arcth (л/2 th ж) J
1	/ / / 6 , .
arctg 4 / — I 1 Н— cth ж
\V V a
[6/а < -1].
t	Arth ( 4/1 + - cth ж
/а(а + 6)	\V а
Arcth ( i/l H— cth ж
= —— Arcth (л/2 cth ж)
ал/2
= — cth ж
[-1 < 6/а < 0; ch2 ж > -а/b].
[6/а > 0] или [-1 < 6/а < 0; ch2 ж < -a/b].
[а = 6].
[а = —6].
+ H	Г I "Ж =
[ сЬж J
1
Та)[
1
(а + Ы	\
V	1 ch ж J
f 1
I СП "Т*
а + 6^ ,
[ ch ж
а + 6 th2 ж
ж + 4/ — arctg I 4/ — th ж
V а	V у а
1 I	b
X -\	;
/^аб — 6 th ж]
/^аб + 6 th ж]
[ab > 0; a + 6^0].
[ab < 0; a + 6^ 0].
= — ж H
2a 4a
[a + 6 =

124	Гл. 1. Неопределенные интегралы	[1.4.8
1.4.8.	Интегралы вида LR(sh (аж + 6), ch (еж + d)) dж.
sh (аж + b) sh (еж + d) 1
ch (аж + b) ch (еж + d) j
= —(	г sh [(a + c)x + b + d] =p ~~7	г sh [(a — с)ж -\- b — d].
z(a "}~ c)	2(a — c)
2. sh (аж + b) ch (еж + d) dx =
= —;	г ch [(a + c)x + b + d] + —;	r- ch [(a - с)ж + 6 - d].
Ksh(ax + бЬЬГаж + d) 1 ,	ж , /f I4 1 , ,	,
ch (аж + b) ch (аж + d) j	2	4a
Г ж 1
4. sh (аж + 6) ch (аж + d) dж = — sh (b — d) -\	ch Bаж + b + d).
. . Л тж	Г . p f sh аж 1	Г р (sh аж 1
1.4.9.	Интегралы вида sir ж<	> аж, сЬ^ж<	> аж.
J [ ch аж J J [ ch аж J
p ГсЬаж]	Г , p-i f ch (a — 1)ж 1 . 1
x<	-p sr ж<	> аж .
I shaa; I	I	I shfa^ 1)ж
o I 1P ГзЬаж)	1 Г р ГсЬаж)
2. I chp x{	~
I сЬаж
1 1 Г p f ch аж 1	f i P-i Г sh (a - l)x 1 , 1
> а^ж =	 сЬрж< , >+p chp ж< 1 ; ; S йж .
]	р + а[	[яЬаж] J	[сЬ(а^1)ж] J
f
\
3 i , « . — . , . 2^ 1 Г 1 f sh ж
[P*-2,-4,...,-2n].
4. | ch2nx\	> dж = (±l)n J "Ait" J> ?|ж .
[ ch ж J	J [ ch ж ^
k4n2Dn2 - 22) . . . [4n2 - Bfc - 2J] ^ j shx)
ix)
5.
a; =	sha;
p+1	\ch(p + l)x
}
+ 1)ж
, h [Bn + IJ - I2][Bn + IJ - 32].. . [Bn + IJ - Bfc - lJ] Г f sha;l2*+>>+1 1
'( }	BЛ + 1)!	Jlchx/	И'
\" Г ok r» 1 P+1
Г f sh^chBn + lbl , (±1)пГ8Ьж1?
'" ' "У 4-1) I	= 	TTl h I
.n+k \{2n + IJ - I2][Bn + IJ - 32] . . . [Bn + IJ - Bk - IJ] (Shx\2k+p+1
k = l
9.	I / «h Bn + 1)» sh-1 Ж 1	^	к sh Bn - 2Й)Ж "
i I ^j| с277, -f- 1)ж ch~~ ж I	^ 2?2	2ife
/	fc=O
i , oxi Bn + 1)жсЬ ж I	\-^/	\fc ch Bn — 2k)x , чте1 Г спж 1
10.	N v	;	л \dx = 2j (=р1Г—	-^—+ (zpl) b\{ , . .
1 л сЬBп + 1)ж8Ьм1ж I	P	' 2n-2k x^ J \\shx\j

1.4.10]
Ц. Гиперболические функции
125
11. \sh2nx
J
12. \ch2nx
13.
15.
16.
chx
sh ж
спж
l. OV? (=bl)fc fshBn-2fc-l)s)
> da; = 2 >	< )	{ У
j	^ 2n-2k- l\chBn-2fc- l)x j
(±l)h
l j
14.
!1
ch x J
arcsin th ж J
21n^	У
СПЖ J
f sh ж 1 ~
in th
\ сЬж j
dx = —
18.
19.
20.
21.
эпж 1
eh ж j
— i
^3
17. |сп2ж<ГГ^ dx = -^ir"r-2"} + {
J cth ж 1
1	tha; j
f ch ж si
2	1 shx ch™2 ж
1 f ch ж sh 2 ж '
In | th(?c/2)| 1
arcsin th ж J*
x
сЬЗж ch™1 ж
ch Зж ch 2 ж
ЛсЬаП ±Jln|th(a:/2)n
\ sh ж J X arcsin th ж J
_
J cth ж
\ tha;
4 fcha;\3
}¦
— n\shx
23.
ch ж
Г f sh Зж ch 1 ж 1 .	. 2 , f ch ж 1
22.	, , _! > с!ж = 2sh ж T In , , У
J [спЗжзп x)	{ 8пж|]
_ If thx I2
~ ^2 | cth ж} +
1.4.10. Интегралы вида \ R(sh2axJ ch2ax, ysh2ax) dx.
Условие: а ж > 0.
Обозначение: ш = arccos ¦
— sh.2ax
1.
2.
4.
5.
6.
da; = —
a
-2~7
^)}+1a
/sh 2аж da;
X
/sh2ax 2a
' V2 J'
ch ax dx
1 / 1 \
~ 2a V ' л/2 У
^K"'7f)-F(?'w)]-
[A + sh 2ажJ - 4р2 sh 2ax]Vsh2ax ~ 2а V ' Р ' V2 ) '

126
Гл. 1. Неопределенные интегралы
[1.4.11
1.4.11. Интегралы вида R(sh2ax7 ch2ax, Vch2ax) dx.
Условие: ах > 0.
Обозначение: <р = arcsln
1. vch2ax dx =
ал/2
2.
4.
5.
6.
7.
/ch 2ax dx
сЬ2аж — 1
ch2ax
3'7f)-2?(^7f
TTf 2 —
V' F ' ^2
3.
/ch2аж
-W.,4
/ch 2аж
1 r AT^— -.1
= — [УсЬ2аж — 1].
sh2 2аж dx
л/ch 2аж
th 2аж dx
Vch 2аж
F{ (f,
За'
1.4.12. Интегралы вида R(sh ж, спж, л/а + bshx ) о'ж.
Условия: а, 6 > 0, ж > Ж1.
/а2 + б2 — а — 6 sh ж .
Обозначения: (р = arccos
/а2 + Ь2 + а + 6 sh ж '
а + \/а2 + б2	. . а
, xi = — Arsh —.
+ 62	6
1.
2.
3.
4.
5.
6.
ch2 ж
с!ж = ^а2 + b2 [F((p, к) - 2Е(ср, к)] +
E{(p, k)-
26 ch xy/a + 6sh x
. _ /aq — bp , . I q(a + b sh ж)
dx = 2\ / ^!	 Arcth ¦ ' v	7
a + л/a2 + 62 V«2 + 62 — a — b sh ж V« + b sh ж
6	V«2 + 62 + а + b sh ж ch ж
[bshx > 0; (ag - bp)/q > 0].
ag — bp
bp — aq
[bshx < 0; (aq - bp)jq > 0].
[(aq-bp)/q < 0].
л/а + 6 sh ж а*ж
/a2 + b2 (л/a2 + 62 - a;
¦E(<p,k)-
chx\/a -^ bshx
/a2 + b2 ^a a2 + b2 -(a + bshxJ'

1.4.14]
1.4- Гиперболические функции
127
7.
dx
fa2jrb2
, A;). 8.
ch ж dx
Zi /	1	1
= -л/a + osha:.
9.
ch2
E(<p, k).
Г cth ж ^ж	2 . . /. b
10.	— = ^^ Arcthi/l + -
J л/a + bshx л/а	V a
11.
12.
9	I	h
=¦ ArthJl + -
fa	V a
arctgi/^| 1+ -shx
V V a
[bshx > 0; a > 0].
[bshx < 0; a > 0].
[a < 0].
1.4.13. Интегралы вида Д (sh ж, ch ж, Vb ch ж — a) dx.
Условия: b > a > 0, ж > 0.
la + b
„	• /Ь(сЬж-1) ,
Обозначения: Lp = arcsin \ -1	 , k =
-а dx = (b-
bchx - a
, k) - 2
26
, k)
_
Voch ж — а
2.
- a dx
ch ж <
sh ж
oil л Сал	Zi r /7	;		/z	-,
6. 		= - [ybchx ^ a — vb — a j
J у о ch ж — а	о
о
7.
л/F ch ж - аK
- (b - a)F(y, fe)].
Ь KTl J
1.4.14. Интегралы вида R (sh ж, ch ж, Vb ch ж — a ) d ж.
Условия: a > о > 0, ж > жь
_	. bchx - а . I 2b	a
Уоозначения: ср = arcsin 4 / —7	г ? ^ = 1/	? ^i = Arch —.
у 6(сЬж — 1)	V а + b	b
— а с!ж = ^2
2 cth — л/bchx — а .
А

128
Гл. 1. Неопределенные интегралы
[1А15
2.
dx
\/b ch ж — а л/а + 6
3.
V6 ch ж — а	а — b
4.
5.
dx
(ch ж + 1)-^6спж — a \J a + 6
dx
(ch ж — 1)-^6спж — a a — b
, А;) - #(<р, А;)
2^6 ch ж - а
6.
7.
dx
(ch x
¦ [(a + 2b)F(<p, k)-(a + ЗЬ)Е(<р, к)]
л/bсЬж-а / a + 36
\ + 6
1
(ch ж — '
-а 3(a - 6JV/«
+ Ca - 6)(a
1.4.15. Интегралы вида R(sh x, ch ж, V« — 6 ch ж ) dx.
Условия: a>6>0, 0<ж<Ж1.
„ . . / a — b ch x . fa — b	A . a
Обозначения: cz? = arcsin \	— , к = \	 , x\ = Arch —.
V a — b	V a + b	b
1. Va-bchx dx = 2Va
,k)-E(<p,k)\.
th f '•
2.
dx
Va — 6 ch ж V« + 6
, A;). 3.
« — b ch ж
= ™vtt — бспж .
4.
\/a — b ch x
сп2жс1ж
36у a
, к) -
F(<p, к).
« + 6
6.
7.
8.
dx
26
¦П
a — 6 ch ж ay a + 6
da	1
A +
— 6ch ж
dx
к ).
th — Va — 6 ch x .
2
, k)-bF(ip, k)]-
th — л/a — 6 ch ж
¦ [2a + 46 + (a ¦

1.4.16]
Ц. Гиперболические функции
129
9.
dx
(а — b — ар2 + bp2 chx)\fa — bchx (a — b)y/a + b
Щ<Р, Р2, *)•
1.4.16. Интегралы вида R(sh ж, ch ж, У'a + bchx) dx.
Условия: a > b > 0, ж > 0.
Обозначения: Lp = arcsln I th — 1, к =
V 2 /
1.
dx = 2VaTb[F((p, к) - Е(<р, к)] + 2th -\/a + bchx .
2. I 	dx = va + b Е(ш. к).
ch x + 1
3.
4.
5.
p + g ch x
. Л I aq ~ bp д .
dx = 2а 	 Arcth
ag —
Arth
dx
\/a + b ch
g(a + bchx)
bp — aq
, A;). 6.
[(aq-bp)/q>0].
/а + 6 ch ж
= — (л/а + 6ch x — \/a + b ).
7.
ch ж
F((p, к)
2 . ж
th
, Л;) Ч— th -Va
8.
ch ж — 1
V а +
2[, ж
dx = - th —¦ vo-
о 2
, А;) .
9.
10.
¦\/а + 6 ch ж
th
362
Iftch - -
_ ^- А х1 L b .
= 2у« Arcth 4/1 Ч— ch ж .
6 ch ж	V а
th ^
2
11-
л/а + Ъ ch ж
[F((p, к) - Е((р, к)].
12.
13.
¦ l)i/a + бсЬж a ^ ft
с/ж	1
Я(р, k)-
а — b)\/a + b
F(<p, k).
¦[b{bb-a)F{<p, к)-
S(a-bJy/a
+ (a^36)(a + fe)?J(^, k)] +
6(а-Ь)
/a + b ch ж .
9 А. П. Прудников и др., т. 1

130
Гл. 1. Неопределенные интегралы
[1А17
14.
A + ch ж) dx
bchx
, р\к).
1.4.17. Интегралы вида
R(sh ж, ch ж, у a2 sh2 ж ± б2 , v б2 — a2 sh2 ж , у a2 ch2 ж ± б2 , уб2 — а2 ch2 ж ) с!ж.
1.
2.
J вЬж
г
= \n
спж]
sh ж J
V sh2 ж — а2
1
Г	1	Г sh ж 1 ,
3.		<	} dx =
J у а2 ^ sh2 ж I c" ж J
Г sh ж 1 , I arcsln [(ch х)/л/а2 + 1
<	} dx = <	г/ , ч / i
arcsin [{shx)/a\
4.
5.
6.
7.
1	f sh ж 1
Vch2 ж + a2 I ch ж J
sh ж
yW х-а2 1 ch ж J
1
= In [<	+ Vch ж - a2
V I sh x J
- ch2 ж
Г sh ж 1 f Г
\cha:J	\
arcsln [(sh ж)/
О/а] 1
- = F(arcsln th ж, vl — 1г2 )
¦ ife2 sh2 ж
[sh2 ж < a2].
[сЬ2ж > a2].
[ж > 0; к2 < 1].
8.
= = F(arcsln tha;, k)
h2x
[ж > 0; к2 < ll.
9.
10.
11.
x
= F [ arcsln •
thaj
2ж^^2
dx
= F(arcsln эесЬж, к)
%/sh2 ж + к2
= F (arcsln
\ — к2
Обозначения: ср = arccos
- а2
1.4.18. Интегралы вида i?(sh ж, спж, ^<18Ьж + 6ch ж ) с!ж.
Условия: b > а > 0, ж > жь
Va sh ж + 6 ch ж
, Ж1 = — Arsh •
/b2 - a2
1. Vashx -
dx =
M
J
-\
); к2 < l].
[ж > 0; к2 < 1].
ж > 0; к1 < 1 .
2.
— а2) F ш. —^ — 2Е\ ш. —^ -\	\	.
L V л/2/	V V2/J Vashx + bchx
7f)-

1.4.20]
Ц. Гиперболические функции
131
dx
\/{а sh ж + Ь ch жK
I (л/b2 — a2 + a sh ж + b ch ж) dx
4/ 4	/ _?_
_ (аэЬж + бсЬжK	У62^а2 V 'л/2
1.4.19. Интегралы вида Vths с/ж, Vcthlr с!ж.
1.	л/tha; с/ж = Arth лЛЬж — arctg Ушж .
2.	усйГж с/ж = Arcth Vcth ж — arctg Vcth ж .
Г ( бЬж 1 9
1.4.20. Интегралы вида \ xpI , > с/ж.
J i ch ж J
\ ch ж J
g 1 ж sh ж j g2	\ ch ж J
\ ch ж /
1 9-2
ch ж J
2. ж
2ra\ жт+1
n
. f sh x X
4. I ж< . > dx =
[ сЬж J
- 2k
fc Bn + l)Bn - 1) . . . Bn - 2A;
dx.
fc=O
-1 ГвЬж!2
2k+1n(n - 1) . . . (n - k)
2n — 2k X chx j
f !	Ч2П+1	-	П	«fey	i4	/	I , i\
5* lX\chx]	= ^TT ^	Bn + l)Bn - 1) . . . Bn - 2k + 1)
.BП-1)!! ж2
6
ю Г sh ж 1 .	„ГсЬж]
2n-2ife
_ 1J ch ж
dx.
г^ ж2/г ГсЬж] ^c^ ж
1сЬЖГЖ = ^+^BА
{ch ж 1 f sh ж 1
sh ж J [ ch ж J
shx
9*

132	Гл. 1. Неопределенные интегралы	[1.4.21
Г
11. ж
J
/¦ ! л 2	т,	2
12. ж<	}- dic=-sh2x	сЬ2ж=р—
J |_ ch ж J	4	8	4
4
' 4
14. \х2Г Х\
1 dax j
15 hci	i rfx^!!:
} \chxj	4
fchxil п!\Д ж"^2^1 Г 1 fsh3^] (shxY\
T \shxf\~ T ^ (n - 2A; - 1)! [3^+2 \ ch Зж J T \ ch x j J'
Г fshxl3 _ 3 fshxl _ Jfsh3a;l 3 ГсЬж! ^
]Ж\Ь/	4\Ь/ 3	ТЖ+
f* Г \chaj аЖ"
±з Jsh*\__< >
2 \сЬж/ 18\сЬЗж/'
Г 1 Г sh ж 1 9
1.4.21. Интегралы вида —<	> dx.
J xp { ch ж J
1 ГзЬж1д _	1	fshx!g	g	fsh^^cha;!
* ^|Ь} Ж™ ^A)Р1|Ь/ ~ ( 1)( 2)^2 \ h^1 ж sh ж J
[ 1 fshail _
^2 BA; 4
жBп-1)!
1 J chi ж 1
Bn- l)!\shia; J
' shl ж 1
fc=O
Bп)\\сЫх)°
, 2n
_,_ I вП 1» Г
4. I — <
ж I сЬж

1.4.23]	1.4- Гиперболические функции	133
ж2 1 ch ж J	22пж \ п
п-1
k /2n\ [ch Bn — 2k) x .	. ч ..
(j [—^—- - Bn -2fc)shi
k=0
х1 1 ch ж I	21п
1 J	k=o
Х 1ж\сЬBп^2^ + 1)ж/ BП 2к + 1\вЫBп^2к +
J ж [ ch ж J	[ chi ж J
о
^л Г ch ж - 1 .	. . .	_	^^ Г 1 Г sh ж 1 .	1 Г sh ж I f chi ж
10. 	ах = chi ж — In ж — С.	11. —^-s , } dx =	< 1 У + \ ,
Jж	Jж^[chжJ	ж^сЬж]^ shi ж
о
1.4.22. Интегралы вида жр<	> dx.
I cth ж I
2
2. |жр<	^
k=0
In	.,	n — 1	n f i \ 2fc —2n
p+1	IS	^^ \shx
2n+1	Г
с!ж = \ xp { Л }
[cth ж]
. Г J Шж l2n+1	Г Л Шж 1
4. жр< , > с!ж = \ xp { Л } dx
J \1Ь]	J [th ]
л 2fc —2n	n	/ , n 2fc —2п
aO	f p_ijcha;l
^	ife/ L \sha;J	J	\shx j
1.4.28. Интегралы вида жг shp ж chg ж dsc.
. f жг shp ж ch^ ж da; = 7—^7 [(p + д)жг shp+1 ж eh9 ж -
J	(p + gJL
— гжг"х shp ж chg ж + r(r + 1) жг™2 shp ж ch9 ж dx +
+ rp f жг sh13^1 ж eh9™1 ж Aж + (q - l)(p + g) f жг shp ж chg ж dx].
= j^^ [(p + д)жг sh^1 ж ch^+1 ж -
shp ж chg x + r(r — 1) жг™ shp ж chg ж dx —
\xr^ shp^ жсЬ9^ ж da? — (p — l)(p + g) xr shp^ ж chg ж dx].
2.	j^^ [(
— гжг
rq
k=0
4. l:B^ch2m+la,sh-na,
J	k=0

134
Гл. 1. Неопределенные интегралы
[1.4.24
5. хр{
J [ ch ж s.
, fsha^ch^2'
~те
гг — 1 \ sh ж J
р Г р_1 (chxl~n
— lj	\hj
\sha:j
Г ch ж 1	J arctg sh x
J arctg sh x 1
\lnth(as/2)J-
Г x	f x
1.4.24. Интегралы вида -г-—dx, —--—dx.
J sh9 x J ch9 x
гdx,
sh9 x J ch9 x
_
р fcha;sh~g+1
±
(q-l)(q-2)
5
ch2»
2n - 2k\ сЬж J
1
j
dx.
I
chx
2nBn - 2) . . . Bn - 2fc + 2)
1/"" 1	*\ ^j aJ ^ #1 X ™|	/ ^ь	-i \ f I Г*	f 1	*\ -*-
I oil X I	I . / -.чпЛ^1" -1/11	J oil л I
xp I ch ж J
9.
(shx\
-q+2
1 Г
(q- 1)(д-2)жР+1\сЬж/	^ (q-l)xP{
• I ch ж J
' xj
- 1 J a;p
1 fsha!]-9+2
(qr - l)(qr - 2) J х?+2 \ chx J
кфп/2
\x\ < тг; те ^ 1].
10
1 г.. / i\n1
2[ l" j J
1
< тг/2].
da;	ctha;
2nn
In |ж —

1.4.26]
. Гиперболические функции
135
?j Bк)\Bк -п-
Bх)
12.
dx
tha;
хп ch2 ж
(п + 1)!
1п
13.
14.
х dx
x dx
= V-
2fe + l
E
15. I ж
16.
17.
f sh ж 1
f cth ж
(^ th ж
f I sh ж I
1
Г sh ж 1 .	ж f ch ж sh 2 ж 1 1 f sh ж ^
ft Т — ШС	<	> ^С 	<
2 1 sh ж ch™ х I 2 1 ch ж
X chx
Г sh ж 1 ~
т~^х{Тх} ¦
ж[сЬжзЬ3ж] 1 Г sh ж 1	2 f cth ж
Т6[сЬж/ +3Ж'
1.
2.
3.
4.
Г / Г sh ж
1.4.25. Интегралы вида R\ хр' <
J \
жр ch ж dx
1	I sh ж I \
>, а + 6<	> 1 а*ж.
хр sh ж с!ж
(qr — 1N J (а + бзЬж)^
р Г ж13" с!ж
х dx
1 ± ch ж
ж sh ж d;
(q-
t\i(x/2)
(q - 1)Ъ } (а
KcthtS}
ж	f th (ж/2) ]
chxil \cth(a;/2)/'
Г	/¦ -1	"ч
1.4.26. Интегралы вида \(Ьх + с) п< , >(
J	[ ch аж J
„f sh*
ch*
(bx + c) i	}dx= ——- ch— \t I
} X ch ax J	ате+! \ b } \
^n f ch*
I sh*
dt
Ж| < 7Г].
<7Г].
< тг/2].
[- t =
La
bx + cl
2.
3.
4.
(bx-
(bx-
(bx-
. J зЬаж
\ сЬаж
v2 Г зЬаж 1
\ ch аж J
1 ch аж j
<
1 ,
-(
а
l
а
ч f ch аж 1 6 f sh аж 1
[ sh аж J а [ ch аж J
,2 , 262] f сЬаж 1 2&(&ж + с) f
с) Н	-N	>	^—	L\	У.
а J Is"аж J	a	[ ch аж J
bx
(bx + cJ +
662]ГсЬаж1 36
(bx + cJ + ¦
ch аж
(ож + с)п

136	Гл. 1. Неопределенные интегралы	[1.4.27
ап~г ( Л ас Г 1 f shtl , , ас Г 1 Г chtl , \	г с	i
= —	 ch — —< % }dt-sh—\ —< , > dt	\ — t = bx + c\.
bn \ b]tn\cht)	b)tn\shtj J	U	J
Г 1 ( shax] . 1 . ac f shi (аж + ac/b) 1 1 . ac f chi (аж + ac/b)
6.	< ,	da; = -ch-- ,	t1{ } ~ t ^^r\ , )	,,[
Joж + c[chажJ	о о [ chi (аж + ac/b) J о о { shi (аж + ac/b)
= \ e~ac/b EI (аж + ac/b) т Л еас/Ь EI f ^аж -
2b	2b	\
¦ 1 J sh аж 1	1 Jshaxl at 1 (chax .
Fж + сJ \ ch аж J	ЬFж + с) \ ch аж j b } bx -\- c\shax
. ^ ,' sh аж 1 .	1	(shax}
	:—~ *	= ^^foffo 4- J I
а	ГсЬаж] а2 Г 1 ГэЬаж , .
1. [e
2.
1.4.27. Интегралы вида й(ж, еах, shbx, chbx) dx.
ax / sh (bx + c) \ _ eax Г (sh(bx + c)\_ f ch Fx + c)\
— 2 L2 ^ I I-» /I»	\ I	I U /1^	\ i
о Г ^аж Г яЬ(аж + с)
3. е < ,	;
J	\ ch (аж + с)
+ с) j
1	1 с . 1
> dx = - же =Ь —«
J	2	4а
4. [ жреаж | ^ ^ | ^ = И жре(а+Ь^ dx T | f ЖРе(^Ь)ж dx	[ см. 1.3.2].
5. [ж^1е^аж(8^Ж1а1ж = i [(а - ЬГа1(а, ах - bx) =F (а + byaj(a, ax + bx)]
J	I ch bx J	2
0	Г	Г l
Re а > -6, 8 = i
6. [ xa^1e^axl^b1X\dx = ^[(а^ЬуаГ(а, ах - bx) T (« + ЬуаГ(а, ах + bx)]
J	[ ch bx J	2
7
, sh bx
2a(a2 + 362)l ( shbx'
(a2 -b2J \\ chbx ^
2 4a6 . 26Ca2 + 62I f ch bx '
8. ж e
J
2 axfshbx\,	e Г 2
e <	Ыж	аж
a2 -
2
аж
az — oz
6ж^-
е	2	a6	6Ca + 6)l f c 6ж 1
a2 - b2 [ X ^a2-b2X+ (a2-b2J \{shbxj'
2
1	1Ь]	4 V	22	6
11. I -^eaa4 ,° Ыж= ^ [EI (аж + Ьж) =F EI (аж ^
ж [ ch ож J	2
12. I -е^ах\ \ , \dx =	[Е1Fж^аж)тЕ1(^аж^6жI	[а
х	I ch ox I	2

1.5.1]	1.5. Тригонометрические функции	137
X
13. [ - е^ах sh bx dx = - In ^-Ь^ + - [El Fж - аж) - El (-аж - bx)]	[a > \b\].
x	2 a-b 2
о
* J ж \ ch ax J	2
as
15. [ i е±ж sh ж dx = ±i [El (±2x) - С - In Bx)].
J ж	2
о
I _L		лд. I Oil Ubie I ,	JL
ift I 	б л	V dx :=z
ж	\ ch ax j	2
-.o i - -аж Г shax 1
18.	I —5" e <	> «,«, —	^|
ж^	[ сЬаж J	2ж [2ж
I Жб!ж	Ж	1	,
19.	—р	 = ^ th аж	-In ch ax\.
1 ch аж а	аг
1
20. liJ^l
ж [ ch ax J	^
i х dx	2
21.
cost — спаж а2 sin
о
[	/ ах t\	1
6» = arctg I th — ctg - j; Ьф 2жк; к = 0, ±1, ±2, . . . .
22. ""^/^ с!ж =
cost^chаж	a2 sin (t/2)
Г	{ ах t\	( ах t\	1
0 = 4arctg I th — ctg - J; ф = 4arctg cth — ctg - I; t Ф 2жк: к = 0, ±1, ±2, ....
L	V 4 4/	V 4 4/	J
1.5. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
1.5.1. Введение.
Интегралы вида R(sinx, cos ж, tgж5 ctgж)dж, где R — рациональная функция своих
аргументов, приводятся к интегралам от рациональных функций при помощи следующих
формул:
I	I гъ ( G1T1 ОТ31 f*f\C /Т* 4" СТ ПГ* Г*4" СУ 'Т9 1 /I 'Т* "~~" 1 r™i I ™-™-™_________. ________________________ „______________________. _________________________ I „______________________.
i.^n(Bmx,cosx,tgx,agx)ax-^ni1 + t2,1 + t3,1_t3 ^ \ x + ^
Если i?(sinaj, cos ж) = ^Я(^з1пж5 cos ж), то
2.	^(sin ж, cos ж) а*ж = — Д(\/1 — t2 , t)	[t = cosa;].
J J V1 ~~ t2
Если i?(sinaj, cos ж) = —R(sinx, —cos ж), то
3.	.Rfsln ж, cos ж) а*ж = R(t, v 1 — t2 ) —,	ft = sin ж].

138
Гл. 1. Неопределенные интегралы
[1.5.2
Если R(sinx, cos ж) = Я(—sina;, ^совж), то
4. R(sin ж, cos x) dx = RI	,
1.5.2. Интегралы вида sinpa;da;.
Г . р ,	1 . p-i	, р — 1 Г . р--
sin^ х ах =	smK ж cos ж Н	smF
J	p	p J
. Jsln2n:
dt
If
1.	siir x ax =	smK
J	p
Г 2n ,	COS Ж Г 2та 1
2.	sin2" ж da; = - —— | sin2 ж
' х dx.
2п
(n^ l)(n-2)...(n-A;)
2nn\
3.
1 /2n
1 n
k=0
2n\ sinBn -
2n-2k
I. [sin2n+
COS Ж . 2n
" ж аж =	sin ж -
5.
6.
Г. jsi
1. {si
}. fsi
L. ("si
2. [sin6
= > 	 I
Bn - l)Bn - 3) . . . Bn - 2k - 1)
cos Bn — 2Дг + 1)ж
cob2*+1 x.
7. I sin x dx = ^ cos ж. 8.1 sin2 ж da; = — — sin 2ж -\— ж =	sin ж cos ж -\— ж.
1	4	1
9.	| sin x dx = — cos Зж — — cos x = - cos ж — cos x.
10.	| sin x dx =	— sin 2ж Н	sin 4ж = — sin ж cos ж — — sin ж cos ж Н— ж.
8 4	o2	8	4	8
11.	I sin x dx = — — cos ж + — cos Зж — -— cos 5ж = — — sin ж cos ж + -— cos ж — — cos x.
48
80
15
12. | sln° ж da; = — ж	sin 2ж Н	sin 4ж	sin бж =
1.5	5.3	5 .	5
=	sin ж cos ж	sin ж cos ж	sin ж cos ж H	ж.
13.
14.
15.
16.
17.
da;	со:
slnp x	(p — 1) i
dx
P —
dx
COS Ж

2ra — 1
cos ж
^ Bra - 3)Bn - 5) . . . Bn - 2A; -
2n
cosec ж¦
dx
sin ж
dx
= ln
n-l
k = l
X
g2
¦In
t -
S 2
= ln
1 — cos ж
= ln
1 + COS X
= -In
1 — cos ж
= -ctgx.
18.
1 COS Ж	1
2 sin2 ж 2 '
1 + COS X
X
'~2

1.5.3]
1.5. Тригонометрические функции
139
19.
20.
21.
1.
2.
dx
sin4 x
dx
sin5 ж
dx
sin6 x
COS Ж
COS Ж
4 sin4 ж
cos ж
5 sin5 ж
2
3
3 cos ж
8 sin2 ж
4 з
15C S
1
3ct
4
5 €
з
X
^ 2
gx
1.5.8. Интегралы вида \cospxdx.
cosp x dx = — sin ж cospMl ж Н	cosp~2 ж dx.
J	P	P J
fcos2n;
Sin Ж I 2n-l
' x dx = —— I cos ж +
3.
2n
2n
Bn- l)Bra-3)...Bra-2fc-
2n\ sinBn - 2k)x
2«n!
JcoS2"+1
x dx =
SHIS I 2я
	— cos
2fe+1ra(ra - 1) . . . (та - к)
Bга - l)Bn - 3) . . . Bn - 2A; - 1)
cos2"**
5.
6.
7.
9.
10.
11.
12.
13.
14.
15.
16.
2n
sin Bn -
cos x dx = sin x. 8. cos2 x dx = - sin 2ж Н	= — sin ж cos ж Н— ж.
J	J	4	z> Л	Л
з ,	1 .	3 .	.	1.з
cos ж аж = — sin ож Н— sin ж = sin ж	sin ж.
JlZi	4	о
cos x dx = - x + — sin 2ж Н	sin 4ж = — ж Н— sin ж cos ж + — sin ж cos ж.
8 4	32	8 8	4
,5 5 1 4 4314
cos ж аж = - sin ж + — sin Зж Н	sin 5ж = — sin ж	sin ж Н— cos ж sin ж.
48'
80'
15
6,	5	15 . п 3.,	1 . „
cos х dx = — ж Н	sin 2ж -\	sin 4ж -\	sin 6ж =
16 64	64	192
5,5.	5.	з,1.	5
= — ж Н	sin ж cos ж Н	sin ж cos х Л— sin ж cos ж.
16 16	24	6
dx	sin x
cosp ж (р — 1) cosp'
dx	sin ж
p-2f dx
~г x p — 1 J cosp™2 ж
9fcf<n 1U« O^ f« L\
Zl I ft» 	 \-l\ll 	 Zil . . . 1 ft. 	 Hi I
: +
dx
cos2n+i x
n-l
2ra
V^ Bra-l)^
n - 5) . . . Bn - 2ife -
x\ +
2n—2k—l
- sec	ж .
^ln
dx
= ln
7Г X
I+ 2"
= ln
1 + sin x
1 — sin ж

140	Гл.1. Неопределенные интегралы	[1.5.4
dx	Г dx I sin x 1
^ 18	+
cos2 ж	J cos3 ж 2 cos2 ж ' 2
dx	sin ж
1 .
о 1п
7Г	Ж
4 + 2
Г ^ж	sin ж 3 sin ж 3
J ^s^ = 4cos4 ж + 8 ^s^ + 8
х тг
+
(х тг
g\2 + I/ |*
Г dx	sin ж 43 4	1 5 23
21. 	— =	— + -- tg3 ж + - tg ж = - tg5 ж + - tg3 х + tg ж.
J cos6 ж 5 cos5 ж 15	5	5	3
1.5.4. Интегралы вида sinp ж cosg ж dx.
Л Г • р	д »	Sin13™1 ЖСО8д+1 Ж р-1 Г . р_2	д+2 ,
1.	siir ж cos х dx =	sirr ж cos ж dx.
J	q+1	p+1J
sin15 scos9+1 ж 0-lf . p_2	q ,
2.	=	1	sirr ж cos ж ож.
+	+J
1 f •
— sir
¦ g j
P + i " p+T^lsir
slnp+1 ж cosg+1 ж p+g + 2. . №	q ,
4.	=	1	sin ж cos ж ож.
Sill* ' Ж COS' Ж	g-1 f . „+2	g^2 »
4.	=	sirr ж cos жаж.
+1	P+1J
P+1
slnp+1 ж cos9™1 ж g — 1
5.	=	1
+
sir
> + g	p + <
> + g + 2 f . p	g+2
g + 1 J
sinp+1 x cos9+1 ж|р + д + 2,.р	g+z
1	' "'^F ж cos ж аж.
g + i
;lsir
3. [sir
Slnp iCCOS9 х/ . 2	9-1 \ .	(P-1)(9-1) Г • p-2	<j-2 ,
7.	= 	 sin ж	 + ¦r^?—w 	^ sirr жсоэ^ xdx.
p + q V	P + g- 2/ (p + g)(p + g2) J
- 1)Bп - 3) . . . Bп -
^ Bn + p - 2)Bn + p - 4) . . . Bn + p - 2A;)
'ln-l)\\	f ю
	Ц:	т	г- smF ж аж	\р Ф —2, —4, . . . , —2nl.
+ р — 2) . . . (р + 2) J
9. sinp ж cos2n+1 x dx =
2те
соч т*
[р^-1, -3, ..., -Bп + 1)].
10. cosp ж sln2n х dx =
1 - 1)Bп - 3) . . . Bп -
^ Bп + р - 2)Bп + р - 4) . . . Bп + р - 2ife)
^ 	^	;	г cosp xdx	\рф -2. -А. .... -2п].
n + p2)(p + 2) J	iP^ ' '	J
11. [
J
12. sin ж cosp ж с!ж =	cosp+ x
J	+ 1
p + 1

1.5.5]	1.5. Тригонометрические функции	141
г	1
13. sinp ж cos x dx = 	sinp+1 x	\p Ф —1]-
J	p + 1
Г 2	3	1/1	1	\
15. sin ж cos x dx =	I — sin 5ж -\— sin Зж — 2 sin ж J =
sin3 x ( 2 2\ sin3 ж /5 . 2
cos ж H— =	sin ж 1.
5 V	3/	5 V3
cos3 ж.
16.	sin x cos x dx =	1	sin 2x	sin 4ж	sin 6ж.
J	16 64	64	192
17.	sin3 ж cos2 x dx = — I — cos 5ж	cos Зж — 2 cos ж J = ~~ cos5 ж
18.	sin3 ж cos3 x dx = — ( — cos 6ж	cos 2ж ).
J	32 \6	2 /
Г	1	f *? 4	\
19.	sin3 x cos4 x dx = — cos3 ж I	sin2 x + sin4 x j.
20.	sin4 ж cos2 x dx = — x	sin 2ж	sin 4ж -\	sin 6ж.
J	16 64	64	192
Г	¦	1	/2 3	\
21.	sin4 ж cos3 x dx = ~~ sin3 xl —I— cos2 ж — cos4 ж 1.
Г	4	11
22.	sin x cos x dx = 	ж	sin 4ж -\	 sin Sx.
J	Iz8	128	1024
23.	sin ax sin bx sin еж dx =
1 [cos (a — b + с)ж cos F + с — а)ж cos (a + b — c)x cos (a + b + с)ж]
24. sin аж cos bx cos еж <ia? =
1 [cos (a + b + с)ж cos F + с — а)ж cos (a + 6 — с)ж cos (a + с — b)x~\
4[ a + 6 + с
25. I cos ax sin 6ж sin ex dx =
4-
sin (a + 6 — с)ж sin (a + с — 6)ж sin (a + b + с)ж sin F + с — a)
26. cos аж cos bx cos еж <ix =
[sin (a + b + с)ж
sin(a + c6)a?
4 [ a + 6 + e	6 + c^a	a + c^6	a + b — с
Г sln x
1.5.5. Интегралы вида 	dx.
J cos^ x
Г sinp ж , sin13™1 ж p-1 f slnp™2 ж .
1. 	dx =	г	— +	 	dx.
cos*? ж	(p — q) cos*?^1 x p — q J cosg ж
sin x	pg + 2 f sinp x
(q — 1) 91	1 J ^2
sin13™1 ж	p-1 f
3.	= 7	?
[q — 1) cos9 l x q — 1 j
x .
	— dx.
— 1 j cos*? A x

142
Гл. 1. Неопределенные интегралы
[1.5.5
. sinpai
4. 	=—п— dx =
, 2п
х sec ж
5.
2п
Bп - р - 1)Bп - р - 3) . . . C - р)A - р) (* sin*
sinF ж
cos2n ж
X
dx =
2га - 1
п-1
Bп - р - 2)Bп - р - 4) . . . Bп - р -
2m+l	1
I hill	Л	1
6. 	г—^— da = -
fc=O
Bга - p - 2)Bra - p - 4) . . . (-p + 2)(-p) f .
slnp x dx.
[n ^ m].
k) n-k
[n > m].
8.
cosin ж
" x	I sin ж
У»
cosg ж	(g — 1) cos9 ж *
10.
— с!ж =
ж	p +
11.
— In I cos x
12.
cos2fc ж — In I cos x .
13.
14.
16.
17.
18.
20.
22.
24.
26.
27.
COS Ж
sin ж .
	d
cos ж
fe=l
= — In I cos ж
- 1
ln
15.
/тг ж
tgU+2
sin2 ж
COS Ж
dx = — sin ж + In
7Г X
4 + 2
sin3 ж . sin2 ж . ,	1 2 i
	аж =	In I cos x = — cos ж — In
COS Ж
sin4 x 1.3	• , ,
аж =	sin ж — sin x + In
о
COS Ж
sir ж
dx =
— (p — 1) sinp ж dx.
tg ( ^ + ^
к i 2 -г 4
19.
sin ж , 1
	— dx =
• dx = ter ж — ж.
21.
cosz ж
X
dx = cos x -\
sin ж	1	3
	— аж = tg ж Н— sin ж cos ж	ж.
cos2 ж	2	2
23.
COS Ж
sin ж
dx =
sin2 ж .	sin ж
	— dx =
2
2 cos2 ж 2
7Г Ж
4 + 2
25.
1	1 2
	r— = - tg ж.
2 cos2 ж 2
ln
2 cos2 ж
sin x	1 sin ж
	— аж = —
, sin ж - - In
2 cos2 ж	2
, X
tgB
• dx =
3 cos3
28.
sin ж	1
	— dx = — tg
cos4 ж	3

1.5.6]
1.5. Тригонометрические функции
143
29.
1.
2.
3.
4.
sin3 ж , 1	1
dx =	Ь
cos ж 3 cos3 ж
1.5.6. Интегралы вида
5.
6.
30.
dx.
1 з
= - tg х - tg ж + ж.
3
¦ dx =
sin^ ж
o-l f eosg™2 ж
slnp ж	(я ~ P) s'mP 1 x 4 — P
g-p + 2
«9+1.
(p — 1) sinp 1 ж	p — 1 J slnp 2 ж
cos9™1 ж	g-1 [ cosg~2 ж
dx.
dx.
¦ dx = —-
In
cosec2n ж +
^ - P ^ 1) B^ - P - 3) • ¦ ¦ BП - P - 2k
Bn^p^ l)Brc - p - 3) . . . C - p)(l - p) f cosp ж
Г cos
J sir
dx = -
SP+1
ж +
2n^ 1
Bra - p - 2)Bra - p - 4) . . . Bn - p - :
Bn - 3)Bn - 5) . . . Bn - 2ife - 1)
2n-2fc-i
C
1) + ( , )
ш/п\
l)m( J
in
| cosp ж da;.
[m ^C n].
7.
8.
10.
11.
12.
13.
15.
17.
18.
m — к
ln
к \к
fe=l
2ife-l
• 2k i
sin ж In
ln
J sir
[m > n].
(p-
. . . COS Ж	...
14. 	dx = In sin x
¦ dx = cos ж + In
, cos3 ж . cos2 ж
16. 	dx =	h In
cos4 x	1 з
—	ож = - cos ж + cos ж + In
— (p — 1) cosp 2 ж с!ж.

144
Гл. 1. Неопределенные интегралы
[1.5.7
19.
21.
23.
25.
27.
29.
1.
2.
3.
4.
5.
6.
7.
8.
9.
11.
13.
15.
16.
18.
COS Ж _	1
ах =
sin2
cos3
sin2
X
X
X
cos ж
sin3
cos3
sin3
X
X
X
cos ж
• 4
sin
cos3
X
X
20.
¦ dx = — ctg ж — ж.
. . 1
аж = — sin ж
, cos ж .	1 .	3
22. I 	~— dx = — ctg ж	sin ж cos ж	ж.
sin x	2	2
аж = — -
1
2 sin х
24.
cos ж I
" 2 sin2 ж ~ 2
.	1
dx =	о	In
dx = —
.	1
dx =
2 sin2 x
1
28.
sin ж Зз1п3ж
1.5.7. Интегралы вида
-1
30.
, cos ж , 1 cos ж 3 .
26. I 	5— dx =	к	cos ж	In
\пл ж	2 sin'2 ж	2
_ г з
3
cos4 ж .	1 з
	7— аж =	ctg ж + ctg ж + ж.
sin ж	3
sinp ж cos*1 ж
sinp ж cos^ ж (р — 1) sinp * ж cos9 ж	р—1 J slnp 2 ж cos*? ж"
д-2 f	dx
(q - ljsin*
— 1 J slnp ж cos*?™2 ж
[см. также 1.5.4].
n-l
2k-2m
dx
n-\-n
2n+l x	Z-, \ k
k=0
кфт
dx
Jm+l
ж cos ж	^ Bт -2к + 2) sin2
~2то
= -?¦
1
sin""* ж cos ж	^ Bт - 2/г + 1) sin2
j	m	-I
«Ж	v~^	1
ln
sin ж cos2m+1 ж ^ Bт — 2ife -f- 2) cos2
dx	x~^	1
sin ж cos2m ж ^^ Bm — :
fe=i l
с!ж
sin ж cos ж
= In I tga:|. 10
•ь
dx
ln
-In
sin ж cosz ж cos ж
t -
g 2
sin ж cos3 ж 2 cos2 ж
с!ж
¦1п^ж|. 12.
1	1
= ln
sin ж cos ж
, 7Г Ж , .
*в1 4 + 2 'I-
3\ 1
sin ж cos4 ж cos ж 3 cos3 ж
dx
-In
14.
sin2 ж cos3 ж \ 2 cos2 ж 2 у sin ж ' 2
3.
^ In
sin ж cosz ж
7Г Х^
с/ж
8
1	8 + _
о:= 	5	ctg2ж. 17.
sin ж cos4 ж 3 sin ж cos*5 ж 3
sin3 ж cos ж	2 sin2 ж
+ In | tg ж .
dx
1
1
sin3 ж cos2 ж
3\ 3.
со8ж\281п2ж 2 у 2

1.5.9]
1.5. Тригонометрические функции
145
19.
20.
21.
22.
23.
24.
dx
2 cos 2ж
sin ж cos*3 ж
sin3 ж cos4 ж
sin4 x cos ж
sin4 ж cos2 ж
sin4 x cos3 ж
Ь 2 In | tg ж .
1	COS Ж
sin ж
¦In
¦I"
ж ж
2 + 4
3 cos ж sin3 ж 3
2	1	sin ж
sin ж Зз!п3ж 2 cos2 ж 2
«in
Ж 7Г
2 + 4
. 4 Ж 4 = ^8 CtS 2Ж - о Ctg3 2Ж-
sin ж cos4 ж	о
1.5.8. Интегралы вида tgpж<iж, \ctgpxdx.
ctg ж J
tga;l ^
ctgxj
.	\2n+l
ctgx)
- 1 [ ctg ж
?t IЬ	?л?ъ "у
1Л*	!
tga: 1P'
ctg ж/
I [ ctg ж J
f tga;
dx.
{| cos ж 1
I sin ж J
\n+fc
2k
\ k / I si
}¦
5.
7.
8.
9.
ctg ж
}f	PAG O*	1	f I +ГУ О* 1	f \ €J гш
^Ж = =р1п^	.	L	6. N 5 \	dx = ^s
I	gi?i лр	I	1 I г*4"it o^ 1	I /^4"it o^
I	olll Jy	J	J I Llg Jy J	I LLg X
"" ^2
с?ж = -j=r [In (sin ж + cos x — Vsin 2ж ) + arcsin (sin ж — cos ж)].
= —=- — In	,	h 2 arcter	 .
y/2 L2 l + ^2tg^+tgж	&l^tgжJ
1.5.9. Интегралы вида Я(зтж, совж, tgж, ctgж) с?ж.
А + В cos ж + С sin ж .
7	:	г— dx =
(а ~\~ о cos ж + с sin х)п
(Вс - СЬ) + (Ас - С a) cos ж - (АЬ - Во) sin x	1
(?г^1)(а2 ^62 ^<
(п - 1)(а2 - Ь2 - с2)
(га - 1)(Ла - ВЬ- Сс) - (га - 2)[(ЛЬ -
- (Лс - Са) sin ж]
(а + Ъ cos ж + с sin ж)"^1
[п;
2, а2
dx
21
2.
G6 — Вс + С a cos ж — Ва sin ж
(га — 1)а(а + & cos ж + с sin ж)п
х (—с cos х + Ъ sin ж)
А
а (п — 1)а2
Bга — 1)!! ~ (п — к — \)\ак (а + 6cos ж + csina;)n~fe
10 А. П. Прудников и др., т. 1

146
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
Гл. 1. Неопределенные интегралы
[1.5.9
А + В cos ж + С sin ж . Вс — СЬ , , .	ч
da; = —	— In (а + о cos ж + с sin ж) ¦
а + Ъ cos ж + с sin ж
— а)
f 4 В6 + Gс
+ [А- ,о , о а
dx
с!ж
(а + 6 cos ж + с sin ж)п J [а + г cos (ж — а)]п
dx	2
b2 + с2 у J а + 6 cos ж + с sin ж "
[6 = г cos а, с = г sin а].
а + b cos ж + с sin ж ^/а2 — Ъ2 — с
W arctg
a-b)tg-+c
Va2 - b2 - Ж
¦In-
(а - 6) tg - + с - V62 + с2 ^ а2
_ 6) tg ^ + с
= ilnfa
с V
с + (а - b) tg -
(a cos x + 6 sin X)n
A + В cos ж + С sin ж
sinn ^ + arctg а
[а = 6].
[см. 1.5.2].
dx =
а cos ж+ 6 sin ж """ а2 + б2
—	In sin ж + arctg - +
sin ж |	1
аж = ——
а cos ж + b sin ж [ cos ж
^ж	1а sin ж — 6 cos ж
(а cos ж + 6 sin жJ	а2 + б2 acoss + fesinaj'
dx	2
a + bsinx Ja2 - b2
arctg
ж
a ^ 2" +
/a2 - 62
7==lntg^^ + arctgi)|.
In (a cos x + b sin ж)
[a2>62].
-i	a tg	h 6 — V&2 — a2
	-In-	^
^ж
а + 6 cos ж ^а2 _ ^2
ж
2	V«2 - b2 tg -
arctg -
а + b
/b2 - a2 tg - + a + b
¦In-
/fe2 - «2 "" V^2 - a2 tg | - a - b
[a2>62].
[a2<62].
A + В cos ж + С sin ж
A ±з!пж)п
dx = —
2n^l
-2'n-2^tg
,2fc + l
^E
4T2
2k+ 1
±
T2fc + 1
П - 1
A;
4T2
2Jfe + 1
В
П — 1 A ± 81ПЖ)П
18.
= ±Cx + (Л т C) tg ( - =F - ) ± В In A ± sin ж)

1.5.9]
1.5. Тригонометрические функции
147
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
32.
33.
А + В cos ж + С sin ж .	1
	;	аж =
±
у±Bк + 1) ?
= ±Вж ± (А =р В) tg±:L ^ т С In (I ± cos ж)
±
С
1
n — 1 A ± cosa;)"
бвтж С a — Ah
1
А + В cos ж + G sin ж . Л . ж В .
	— ах = — In tg	In
sin ж (а + о sin ж)	а	2 а	sin ж
А + В cos ж + С sin ж
sin ж (а + b cos ж)
= ^[(Да-В6Iп48| + (Д6-ВаIп: ^ j
Л + В cos ж + С sin ж	Л ± В
sin ж A ± cos ж)	2
А + В cos ж + С sin ж
cos ж (а + 6 sin ж)
= д2^&2 \(Аа - СЪ) In tg Cj + |^ - (Л6 - Са) In ¦
A + В cos ж + С sin ж
cos ж A ± sin ж)
osmx
С
а + 6 cos ж *
±i
a + b sin ж
A + В cos ж + С sin ж
cos ж (а + b cos ж)
& cos ж
А л (ж х , *_, .
= — In tg - + - + — In
a	\ 4 2 / a	cos ж
± sign a
. f sin ж 1
a + b{	}
{ cos ж J
а / J а + 6 cos ж *
->4
a	J
sign а
Arth
а + 6 f tg ж
a I cte ж
= ±-
sign а
'—а(а -|- о)
Arcth
a + b ( tgж 1 \
а \ctgжJy
cos ж J	6
b	( sin ж 1 2	о
- < -1; ^	\ > —r\
a	I cos ж J	6
{sin ж 1
COS Ж J
1 +
dx
1-
sin ж I 2	I ctg ж
tgx
¦ Jsi
ice
sin ж
COS Ж
2а(а
Bа + 6)
cos ж
b sin ж cos ж
а*ж	6 sin ж cos ж
, f sin ж 1	. f sin ж 1
a + b{ }	a + bl } .
{ cos ж J	[ cos ж J
а*ж
1 +
{sin ж V
COS Ж J
-^arctgf^*^
ctg ж
sin ж cos ж
1 +
{sin ж 1
COS Ж J
10*

148
34.
35.
Гл. 1. Неопределенные интегралы
[1.5.9
dx
(а + 6 sin2 жK Spa
11/ 2 3
3+ ~2 + ~4 ) arctg(ptga)
3+4-4
36.
37.
38.
где
39.
40.
р2 р4 у 1 + р2 tg2 ж
рл рч
1	 tg2 ж
р2 р2
2ptgж
*>ol.
а I
з 2 3
2qtgx
[q2 = —1 — b/a > 0; sin2 ж < — a/b; при sin2 ж > —a/b
следует Arth (q tg ж) заменить на Arcth (q tg ж)].
(а + b cos2 жK	8ра3
pctgж
1 Г/	2	3 \
3 + -г- + -т arctg (p ctg ж)
p2 p4y
р2 р4 у 1 + р2 ctg2 ж \ р2 р-
2	1	2
1	 ctg x
pi pi
2p ctg ж
A + p2 ctg2 ж)
= l+_ >0 .
8да3
i	2 Н	J ) Arth (</ C^g Ж) "
с/ctg ж
2q ctg ж
A + В cos ж + С sin ж
b\ cos ж + a sin ж) (a2 + &2 cos ж + C2 sin ж
Г	с/ж
(l-^ctg2*)*]
= —1 — 6/а > 0; cos2 ж < —а/Ь; при cos2 ж > —а/Ь
следует Arth (q ctg ж) заменить на Arcth (q ctg ж)].
л 1 ai + &i cos ж + ci sin ж
¦ dx = Aq In 	—	;	;	h
«2 + b2 cos ж + C2 sin ж
dx
b\ cos ж + ci sin ж	J fl2 + 62 cos ж + С2 sin ж '
ЛВС
at 61 ci
Я-2 62 C2
в
bi
a2
G
Cl
A
аг
bi
b2
с
Cl
В
bi
Cl
c2
A
ai
Oi
a2
61
62
2
61
b2
Cl
c2
2
ci ai
c2 a2
CLl bl
d2 b2
2
61 ci
62 C2
2
С
C2
at
a2
В
b2
с
c2
bi
b2
A
a2
A
a2
Cl
C2
В
b2
bi
a2
bi ci
b2 c2
dx
Ci CL\
C2 «22
«1
«2
6l
62
2
ci ai
C2 Cl2
2
6l
62
Cl
C2
; см. 1.5.9.5 .
a cos2 ж + b sin ж cos ж + с sin2 ж
2	2^ж-
¦ arctg ¦ Б
[b2 >4ac].
[62 < 4ac].

1.5.10]
1.5. Тригонометрические функции
149
41.
42.
где
= 4acl.
1
2ctgж + b
A cos2 ж + 2 В sin ж cos ж + С sin2 ж
a cos2 ж + 26 sin ж cos ж + с sin2 ж	462 + (а — сJ
+ [(А — С)Ь — В (а — с)] In (а cos2 ж + 2b sin ж cos ж + е sin2 ж) +
+ [2(А + С)Ъ2 - 2ВЬ(а + с) + (аС - Ас)(а - c)]f(x)},
с tg ж + b — л/b2 — ас
¦In
2\fb2 — ас ctgж + 6 +
- arctg
[Ь2 > ас],
<ас ,
ctgж + Ъ
43.
(a cos2 ж + b sin ж cos ж + с sin2 жJ
b cos 2ж + (с — а) sin 2ж
Dас — б2)(а cos2 x + b sin ж cos ж + с sin2 ж)
2(а + с) Г	dж
4ас — б2 J a cos2 ж + b sin ж cos ж + с sin2 ж
44.
45.
46.
47.
48.
49.
= 16а
За2}
tgxdx
+ а а2 + 1
- dx =
Bа cos ж + b sin жL
i
[ж — a In (a cos ж + sin ж)].
[Ь2 ф 4ас].
[б2 = 4ас1.
1 + а2
ж
tg ж + а
а*ж
а2 + tg2 ж ~ а2 ~~ 1 ~ (а2 - 1)а
1 + а2
1
In sin (ж + arctg а),
arctg ^^.
dx
1
а2 - tg2 ж а2 + 1 2(а2 + 1)а
In
tgsc — а
dx
ж 1
= - + -sin2aj. 50.
-Ы2х 2 ' 4
tga; + a
tg
In (a2 cos2 ж + sin2 ж)
2A- а2)
1.
2.
3
1.5.10. Интегралы вида
х cos (еж + d) dsc.
sin (аж +
cos (аж + 6) j """ "^ а \ sin (аж + 6)
sin (аж + 6) sin (еж + d) 1	1
sin (аж + 6) sin (еж + d)
.	1 f cos (аж + b)
dx = =p — { ;
cos (аж + b) cos (еж ¦
}
+ d) 1	г
> аж, sin (аж + oj
Н™ ct) J J
sin [(a + c)x + 6 + <
cos (аж + 6) cos (еж + d) J
sin (аж + b) cos (еж + d) dж = —
4.
sin (аж + b) sin (аж + d)
; ; ) J
cos (аж + о) cos (аж + d)
1
" 2(a-c) LV ; '	J^	2(a4
cos [(a — c)x + 6 — d] cos [(a + с)ж + 6 + d]
2(a - c)	2(a + c)	'
_ x ^tu j\^- sin Bаж + 6 + d)
5. I sin (аж + b) cos (аж + d) dж = — sin (b — d) —
d)TA
4a
cos Bаж + b + d)
4a	'

150	Гл. 1. Неопределенные интегралы	[1.5.11
1.5.11. Интегралы вида sinp ж sin ax dx.
1 Г . р • j -в^жсоваж	р Г . р_1	( .
1. smF ж sin аж аж =	1	smF ж cos (a — 1)ж dx.
J	р + а	P + ttJ
з!пржсо8аж psinpml ж sin (а — 1)ж
— -,	г-т	г sinp ж sin (а — 2)ж dx.
3. sinp ж sin 2nx dx =
b^-2,-4, ...,-2n].
4. sinp a; sin Bn + 1)ж da; = Bn + 1) <^ sinp+1 x dx +
f 2fc
J
Г
Г -i	1
5. sinp ж sin (p + 1)ж dx = — sinp ж slnpx.
J	P
!-.)<•-;"--'(?-'•
Г -1 Г
6.	sinp ж sin (p +
J	L
Г sin аж .	f cos (а — t)x . Г sin (а — 2)x .
7. 	dx = 2 	^—^—— аж +	— dx.
J sinp ж	J sinp ж	J sinp ж
г • о	n • /«mi	i\	p • /o i
8. 	dx = 2 > 	^-	^. 9.	— dx = 2 >	h ж.
sin ж	^^ 2fe — 1	I sin ж	^^ 2k
fe=i	fe=i
,'sin2ic	2	Гз1п2ж	, .
10. I —-— ax = ^t	^yi—• 11- —ц— dx = 2 in sin ж
smn ж	(n — 1) sinn ^ ж	J sin2 ж
12. | ^^^ = ж + 81п2ж. 13. Г 51ПЗж da? = з ln
J i
sin ж
14. 1 —5— dx = ^3cter ж — Ax.
ж
- 4 cos ж.
1.5.12. Интегралы вида sinp ж cosaa; dx.
Л Г . p	, 81пржз1паж	р Г . p-i . / 1X ,
1. smF ж cos ax dx =	smF ж sin (a — 1)ж dx.
J	p+a	P+aJ	l	;
sinp ж sin аж psinp
p(p — 1)	Г . „^2	/ ox ,
— -.	™-7	г smF ж cos (а — 2)ж dx.
Г	Г
3.	sinp ж cos 2тгж dx = sinp ж dx +
\4 1)fc4^2Dn2^22)...[4n2^Bfc^2J] fcin2fc+Pxdx
k=i
Г . ©	/	\	sinp+1 ж
4.	smF ж cos Bra + 1)ж аж =	h
J	P + l
, ^, 1,fc[Bn + lJ^l2][Bn + lJ^32]...[Bn + lJ^Bfc^lJ] . 2k+p+1
2k + p + l)
[p ф -1, -3, -5, . . . , -Bn + 1)].

1.5.14]
1.5. Тригонометрические функции
151
Г -l	1
5. sinp ж cos (p + 1)ж dx = — sinp ж соэрж.
6. sinp 1 ж cos (р + 1) (	ж J dx =	sinp ж sin p (	ж 1.
J	L	V2 /J	Р	V2 У
7.
8.
dx = 2
sm^ ж
cos BA; -
9. \C°s{2n + 1)xdx = '
2/г - 1
. cos 2 А; ж
¦In
ж
tg2
¦In
dx = 2 cos ж + In
ж
tg-
11.
13.
, , _ . cos 2ж cos ж 3
dx = — ctg ж — 2ж. 12. 	^— dx =	«	In
1 ~т^ж	2sin^ ж 2
. - 3) sinn~3 ж (n - 1) sin" ж "
14.
¦ dx = ^2 sin ж + In I sin ж
15.
dx = —-
2 sin ж
— 4 In I sin ж
1.5.13. Интегралы вида cosp ж этаж с/ж.
cosp ж cos аж	р Г „__i
	 cos ж sin (а — 1)ж dx.
1. cosp ж sin ax dx = — -
+ a
2. cosp ж зт2пж с/ж = (—1)
П-1	,. 9,	п0.\
п f COSp+2 ;
I P + 2
2k+p+2
fe=l
[рф-2, -4, ..., -2n].
3. cosp ж sin Bn + 1)ж dx = (^1)та^
p+i
k iBn + IJ - I2][Bn + 1)^- 32] . . . [Bn + IJ - Bfe - IJ]
Bk)lBk + p + 1)
Г -l	1
4. cosp ж sin (p + 1)ж с/ж =	соз^жсоэрж.
[рф -1, -3, -5, ..., -Bn + l)].
5.
sin ax
cosp ж
_ Г sin (a - 1)ж Г sin (a - 2)ж
= 2	rJ— dx —	— dx.
cosp ж
6. ¦' sin B« + 1)« rfa. =
7.
9.	— dx = —2 In I cos ж
1 cos^ ж
(^l)^+i In | СО8Ж
dx =
10.
,' sin Зж .	2 i i
11. 	dx = 2 sin ж + In cos ж
cosTi ж
12.
dx =
cosn ж
4
(n — 2)
1
(n — 3) cosn™3 ж (n — 1) cos"™1 ж
COS Ж .
2 cos2 ж
1.5.14. Интегралы вида cosp ж соэаж с/ж.
1. cosp ж cos аж dx =
p + a
cosp ж cos (а — 1)ж dx.

152
Гл. 1. Неопределенные интегралы
[1.5.15
г
J
г
2. cosp
Г г
dx = (™1)та< cosp x dx +
- 2^) .[4n2 - Bk - 2J]
LoS2k+pxdx\
f
J
f
3. cosp
f Г
)xdx = (~1)теBв + 1I cosp+1
«L J
[Bn + IJ - I2][Bn + IJ - 32] . . . [Bn + IJ - Bk - IJ]
BAj + 1)!
f -l	i
4. cosp ж cos (р + 1)ж dx = — cosp ж slnpx.
J	P
X COS'
,2fe+p+l
5»
6.
7.
8.
10.
12.
cos аж
COSp X
uX ^= zl
cos (a — 1)ж	Г cos (a — 2)ж
-l)x . Г
i 7 dx —
~гх	J
cosp ж
n^k sin BA; — 1)ж
}	2k^l +(^
dx.
cos Bn + 1)ж
cos ж
cos2x
1 Ж — In
tg
sin x
2 cos2 ж
in ж — 3 In
/тг
3
2ln
-(
(ж
tg \4 +
ж x\
4 + 2 )
9.
13.
7Г Ж
4 + 2
с!ж = 2ж — tgж.
11. | 	dx = я!п2ж — ж.
cos ж
dx = 4ж — Stgx.
COS*5 Ж
— 1
1.
2.
i с ic тл-	| ¦ sinai	sinna; ,
1.5.15. Интегралы вида <	> <	> dx.
cos ж I cos nx
slnm ж dx
¦ dx =
2n-
(-1Г
2n
2Bn
(A; — n)n x
. [A; + n + 1 ж
sin
In
2m+l
I hill	X
3. 	dx =
In
fe=l
Ж X
cos2 ж — sin2
~2n
tg
n + к	x
n — к
An
4.
(^1)*и
In
кж
¦In
tg
4Bn
4Bn
n2m+1
J cos Bn -
In
|^(-1) cos"
кж
¦In
cos ж —sin
[то ^ 2n].
[to ^ n].
[?71 < 7l].
[to ^ n].
2 ^7Г
[га ^ тг].

1.5.16]
1.5. Тригонометрические функции
153
6.
7.
sinTO ж dx 1
2n
An
ж I In
2n + l x
	Ж
8n	2
[m < 2n].
cos2m+1 x dx
2n
.2	.2
sm ж — sm
, cos m x dx	1 , .
8. -r—т-—~—~ = -——-< In
ж	кж \ (x	кж
+	)t(
[m <C n].
[m ^ n].
9.
10.
11.
2m+l
s
i
In
x kir
+
2 4r
I	f
—<
II	^
In I sin ж| + yj(—1)
¦In
• 2	-2
sm ж — sm
dx= ^y(^l)fccosm^tl7rm
cos nx	n
2n
An
к + i ж
[m ^ n].
[m ^ n].
1.5.16. Интегралы вида R(smax, cosax, Vsin2ax) dx.
Обозначение: ip = arcsln -
2 sin ax
1 + sin ax + cos ax
{ CO!
1. | sin ; 2ж<!	} dx =
cos ж
2n+l
¦ rft
_ 2
t =
t =
2. sin
cosec x
n —m —1
tg ж
1/2
E
n-m-l
ctgx
3. 81пт+1/ж
к J 2m - An + Ak + 1 [ tg ж
sin ж J
Г r^—— f sin ж 1 .	If cos x 1 /—.—-—
4. vsinis <	> ax = =F —"S	Wsinzsc
J	[ cos ж J	2 1 sin ж J
m--2n+2fe
cos ж J I sm ж
t =
f tgx 11/2'
\ ctg x J
I tgc
[n ^ m + 1].
'} •
+ — [In (sin x + cos ж ± vsln2a?) + arcsin (sin x — cos ж)].
5.
^ж = лД / ^\
/sin 2аж а V ' V^/'

154
Гл. 1. Неопределенные интегралы
[1.5.17
1	sin,
J 81ПП + 1/22ж\сО8ж/
2то+1
4т -
}3/2 п — то — 1
^ V ^
^	ГА-.« 1 2m-n + 2fc
Ctg Ж
[n ^ m + 1].
Г	1	f Sin ж] .	1 г, /	/	ч	/	чп
7.	,	<	> ах = — In (sinж + cosж =F v sin2ж ) + arcsin (sinx — cosж) .
J л/sin 2ж [cos ж j	2
ft Г	1	f SeC Ж l2m+l
8. 	-rjr	<	>	dx =
J 8шп+1/22ж lcosec« J
f ,	л 1/2 то+п	r
= ±2i/2-nf tga; 1 y^ fm + n\	1	j t
\ ctg x J ^ V A; / 4m + 2n - 4k + 1 \ c
ga;
ctg ж
2m+n-2fe
9.
10.
'
cos ж . ±2ro
sin x ax =
8т2т+1ж8тп+1/22ж
12. 1 , tg±lxdX,ln =2-+1/2
m-\-n
fc >/ 4m + In T 21 - 4k + Г
tg
13.
14.
15.
1fi
16.
17.
18.
COS2-+1 ж sfnn+1/2 2ж
	sinaxdx
A
. i/2 v^ /m + n\
g	^ V к ) 4k ± 21 - In + Г
( 1\
F[ ip,
= \F[ ip, = ) E[ <p, = )\
+ cosax)\/sm2ax aL\ v 2 /	V v2/J
1\	( 1 \\
) — E[ <p, —= )\.
sinaxdx
л/2
A — з!паж + cosax)\/sin2ax
9,
1 \
у 2 /
г/2].
v^ p/ 1 \
= 	л 1 99, —^- J.
v 2 /
A -si
A-
1\
v 2 /	\ л/2/
— E
=ЩгЕ( 1) _ F( 1
a L V л/2/	V \/2
r,
/tgаж
7Г/2].
A + sin аж + cos аж) dx
[1 — ссшаж + A — 2r2) sin ax]ysm2ax
л/2 „ / 2 I \
= 	U[(p, r , ^^ 1.
o	/2
^ 1.
л/2/
1.5.17. Интегралы вида Л^таж, соваж, Vcos2ax) dx.
Условие: 0 < аж ^ тг/4.
Обозначение: ^ = arcsin (л/2 sinaa;).
f			1 Г
1. i?(sin аж, соэаж, л/cos 2аж ) а1ж = — i?(sin t, cost, л/l — 2 sin2 t) dt
[t = ax; см. 1.5.36].

1.5.17]
1.5. Тригонометрические функции
155
2. v cos 2ax dx =
J
О
Е
Г п+1/2 f sin ж 1 .	Vcos 2ж fees ж]
3. cos + ' 2х{	\dx = ^^7	-\	\
J	[cos ж]	2(п + 1) I sinsc J
x cos" 2ж
-2fc
2k+1n(n - 1)... (n - к)
.„ Bn + l)!!
(-1Г
f
arcsin(v^sina!)
coe2x
4.
K
5.
6.
f sin ж 1 ,	1 /	r cos ж ] 1
<	> dx = =F^vcos2a: <	>H
I cos ж]	2	I sin ж] 2^
2^2
In cos ж -
dx = 	\F[ <p, —^ — E[ <p, —^ -\— tgажуcos2ax .
со82аж	« L V л/2/	\ л/2/J «
da?
/cos 2аж
Bn _ 3)Bn - 5) . . . Bn - 2k - 3)
^2
dx = 	E \(p, - ,	_ , , ^, _
а \ л/2 / ал/2 \ л/2
14.
fc+1

156	Гл. 1. Неопределенные интегралы	[1.5.18
15.
dx	1 / 2 1 \
A - 2r2 sin2 ax)y/cos2ax алД \	лД J
о
16. ¦ dx
cos4 axycos2ax
о
у/2 J 3a V л/2/	ЗасоБ3аж
cos2as.
17.	f_^= = J-FL 1 j-H^L 1 , 	.
J у cos3 2аж ay 2 \ у 2 у a \ V2 J ay cos 2аж
о
X
f sin2 ax .	зш2аж
18.	— dж = 	^=^= -
J у cos3 2аж	2ау cos 2аж
о
1.5.18. Интегралы вида Я(з1паж5 соваж, у/— cos 2аж ) dx.
Условие: тг/4 ^ ах < тг/2.
Обозначение: у? = arcsln (y2 соэаж).
1.	R(sln аж, cos аж, у/— со8 2аж ) dж = — i?(sln t, cos t, у 2 sin2 t — 1) dt
[t = ax; см. 1.5.38].
тг/Bа)
2.	у/- cos2аж dж = —^ 2E| у?, -^ ) - F
J	ал/2 L V л/Г
L V y/2
тг/Bо)
J V^ cos 2аж ал/2 \ лД)'
X
тг/Bа
f si
- j
sin ax dx	1 / 1
™ cos 2аж а^2 \ л/2 / '
/Ba)
cos26^d^	1 Г / J_
[	)
/Ba)
5- J ^^=^fK^^'-s^'^ii-
Г ctg2
6
Г ctg2aжdж	1 Г ^Z 1\ ^/ 1\] 1
.	,	- = —— \2E [ер, —= \- F [ер, —=)\
J y/-co8 2ax алД[ \ лД)	\ y/2 J \ a
it/Ba)
Г cos4 аж dж	1 [5 _./ 1 \ _./ 1 M 1 .	/
Г.	t	= 	=¦ - El cp, —^ -3Fl<p, —= Л	з1п2аж^со8 2аж.
J xf- cos 2аж Зау2 L2 V л/2/	V v2/J 12а
X
тг/Bа)
f	^Ж	v^J П i	/	«—
В.	—^		=з- = 	?/ <р, —=г 1	ctg ажу — cos 2аж .
J sin ажу —cos 2аж а \ у 2 / а
ж
т/B<
тг/Bа)
A - 2r2 cos2 аж)л/^ cos 2аж а

1.5.19]
1.5. Тригонометрические функции
157
10
тг/Bа)
J sir
dx
-2
1
у/2
cos ax	. 2
За sin3 ax
F sin аж + 1)\/— cos 2ax .
т/Bо)
• J
тг/Bо)
12
- cos3 2аж ал/2
cos2 аж а*ж
1 12e(<p, -^1 -Flip, ->)| -
у/2 j \ ay/-cos2ax '
г 	^^=_	^ ^?
J V^ cos3 2ах ал/2 \ ' ^2 / 2ал/— cos 2аж
X
1.5.19. Интегралы вида 7?(sin ж, cos ж, \/а ± 6 sin x ) с/ж.
Обозначения: 99 = arcsln
тт/2
1 — sin ж
5 -0 = arcsln
. t /6A-sina;)
. Va
b sin ж с?ж = 2\/a
, A;)
2.
T/2
dx
\/a + 6 sin x y/a + 6
4.
5.
6»
7.
8.
9.
, А; =
a>&>0; -J
0 < \a\ < 6; — arcsin — < x < — .
а > 6 > 0;	< ж < - .
2	2J
0 < Iа < b] — arcsin — < x < — .
sin ж а*ж
i/а + 6 sin ж
E((p,k)-
2а
¦Ffo»,*)
a>6>0; --
" fe
fo < |a| < 6; - arcsin - < ж < —1.
tt/2
sin2 ж dx
y/a + 6 sin ж
E((p, k)
2Bа2
362 -^'"' ¦ ЗЬ2у^
1 \ 4а„/,1\] 2
^r- cos ж-^а + 6 sin ж
а > b > 0; -— < ж < —1.
2	2J
36
тг/2
tg2ж<
-1
л/а + 6 sin ж ^а + 6
F(<p,k)-
(а — 6)i/a + Ъ
6 — a sin ж
|0 < |а| < Ь; - arcsin - < ж < —I.
L	о	2 J
Е(<р, k) +
(а2 — 62) cos ж
/	J—:		Г	ъ	^Л
V а + о sin ж	0 < 6 < а;	< ж < — .
10.
6 — а sin ж
о — а sin ж /	.	г	а	тг]
^^	-гт	Vfl + о sin ж	0 < а < 6; -arcsin - < ж < — .
(а2 — б2) cos ж	L	b	2 J

158
Гл. 1. Неопределенные интегралы
[1.5.20
тг/2
B — р2 + р2 sin х)\/а + 6 sin ж V« +
тг/2
(а + 6 —
т/2
1 — sin х	dx
1 + sin ж у/а + Ъ sin ж
11.
12.
13.
14.
15.
16. [A ± sinахГ
J
dx
ТГ	ТГ]
О < b < щ	^ х < —\.
2	2J
6 sin ж
\	/	а
О < |а| < 6; — arcsin — < ж < — I.
—^-г\-у/а + ЬЕ(<р, A;)+tg( j-|)Va + 6sinaj}
fl"° I	\4Г/	ТГ
тг/2
—2b cos ж
\/(а + b sin жK (а2 — &2)Va- + 6 sin ж (а — Ь)\/а +
¦Е{<р,к)
0<6<о; --
ft — o, \f a + ft sin ж
[о < |а| < 6; - arcsin - < ж < —1.
17.
sin a^)fe+
Bn - l)Bn - 3) . . . Bn - 2fe - 1)
2n _ 2)Bn - 4) . . . Bn - 2A; - 2)
- VI T sin аж
1.5.20. Интегралы вида 7?(sin ж, cos ж, s/a ± 6 cos ж ) dx.
^r	. b(l- cos ж) .	.
Обозначения: (р = arcsin \j —^— L—- , -0 = arcsin
¦, k =
x
1. Va + 6 cos ж dsc = 2\/a -\- b EI —, A;
J	M
0
3. V«- — b cos ж с?ж = 2ya^b Е(ф, к) —
2&81ПЖ
« — ^ cos ж
о
. Г /а- & cos ж 2(а - 6) „/, 2ар
4. д/	 с^ж =		ГТ W?	^^
JVl + Pcosx	(l + )V^T5 V	(а + 6)A
о
5.
dx
\/a + b cos ж ^л + b V 2 '
[a > 6 > 0; 0 ^ x ^ тг].
> 0; 0 ^ ж < arccos	I .
b,
[a > 6 > 0; 0 ^ ж ^ тг].
[a > 6 > 0; 0 ^ x ^ тг].

1.5.20]
1.5. Тригонометрические функции
159
6.
7.
8.
9.
10.
11.
13.
dx
\/ а — 6 cos x x/a + 6
cos x dx
ft + ocoss
arccos (
b
[a > b > 0; 0 ^ ж ^ тг].
[a > b > 0; 0 ^ ж ^ тг].
6>|а|>0;0^ж< arccos j	1 .
cos x dx
л/a — b cos x Ьл/а + b
cos ж dx
{(b - а)Щф, k2, k) + uFO), k)}	[a > b > 0; 0 ^ x ^ тг].
\/ a + 6 cos x 3b2 ya-
2
— sin хл/а + b cos ж	[а > 6 > 0; 0 ^ ж ^ тг].
Зо
-\	 sin ж л/а + 6 cos ж	6^|а|>0;0^ж< arccos (	J .
oo	I	V b,
¦ {Ba2 + b2)F{tj), k) - 2a(a + Ь)Е(ф, к)}
2
36	\/a — b cos x
2 . a + 6 cos x
sinx^z	[a > 6 > 0; 0 ^ ж < тг].
л	П
14. (l±cosax)n+1/2d^ = ±Vl T cos аж V(^l)n f ^Ъ^
15.
16.
17.
18.
19.
dx
B — p2 + p2 cos ж) V<i + 6 cos ж i/a + 6 \2'
[a > 6 > 0; 0 < ж < тг].
dx
(a + b — p2b + p26cos x)y/a + 6 cos ж (a
^( 2 1
П \<p, p , —
V	^
. arccos |
6
1 — cos ж
2 ж
a, /	:		A\f CL + 0 -. ( X .
	 —	tg — v a + 6 cos ж	i? I —, к
1 + cos ж s/a + 6 cos ж«^о2	а — b \2
(а - 6)Va
[o > 6 > 0; 0 < ж < тг].
26	sin ж
2 ' '7 " ^^ ^а + 6со8ж
[а > 6 > 0; 0 ^ ж ^ тг].
a2 - 62
26	sin ж	Г	/ а \ ,
ТЗ	о /	=¦	6 ^> а > 0; 0 ^ ж < arccos -- .
б2 - а2 V« + 6 cos ж	L	V b; '

160
Гл. 1. Неопределенные интегралы
[1.5.21
20.
21.
dx
(а — b cos жK (а — b)y/a + b
Е(ф, к)
dx
= ±-
A ± cos аж)п+!/2	па2пA + cos ах)п+г/2
п — 2 ,п
;?jBn-2)Bn-4)...Bn-2A:-:
[а > b > 0; 0 ^ х ^ тг].
,п + 1 ±
Bгс-1)!! I	V2 + Vl T cos аж
Bп)!!
T cos аж
1.5.21. Интегралы вида i?(sln ж, cos ж, V« + b sin ж + с cos ж ) dx.
_^ . i УЬ2 + с2 — 6 sin ж — с cos ж
Обозначения: ш = arcsin4/	1		, к =
2л/Ь2 + с2
г^2 '
/W
. Va
6 sin ж + с cos ж da; = 2у а + л/b2 + с2
у а
[о<
с2 < а; Ж1 - тг ^ ж <
2.
3.
4.
0 < |а| < v б2 + с2 ; Ж1 — arccos
/б2 + с2
Ж <
dx	_	2
Va + & sin ж + с cos ж ^/а _|_ Vfe2 + с2
, к)
0 < у б2
с2 < а; Ж1 — тг ^ ж <
=- F(K(p1 к)	0 < |а| < V^2 + с2 ; Ж1 — arccos I		- 1 ^ х < х\ .
5.
sin ж с!ж
Va + Ь sin ж + с cos ж
2с
+ с2
б2
о V/а + Ь sin ж + с cos ж	0 < а < уР + с2 ; Ж1 — arccos ( —
2	[	х
Ж < Ж1 .
Г F cos ж — с sin ж) dx _ у	:—:
6. ~^^^^^=^^^^== = 2у a + о sin ж + с cos ж .
J у а + 6 sin ж + с cos ж
7.
/б2 + с2 + Ъ sin ж + с cos ж	/ ' / 9 9 . ч
	 t 	о?ж = 2у а + л/b2 + с2 F(y>, к) -
у а + 6 sin ж + с cos ж
¦а*ж = 2^
2(а - V&2 + с2 ;
\/а + V&2 + с2
8.
/б2 + с2 + 6 sin ж + с cos ж
Va + Ь sin ж + с cos ж
, А;)	[о < Vb2 + с2 < а; жх - тг ^С х < хг].
L	J
с2 #(<р, А;)
Ж < Ж1 .
0 < \а\ < у б2 + с2 ; Ж1 — arccos ( —

1.5.23]	1.5. Тригонометрические функции	161
1.5.22. Интегралы вида Я(у 1 — k2 sin2 ж ) dx.
Условие: 0 < к2 < 1.
Обозначение: А = у 1 — к2 sin2 ж .
1. \Andx = —-B-k2) iAn-2dAk2) \An-4d +
n	J	п	J	п
9 Г dx	к2 sin ж cos ж	(га — 2)B —
J An+1	(га — 1)A — ^2)АП (г,
Г	Г	2
3. A dx = ?/(ж, А;). 4. A3 dx = — B^^2)?/(ж, к) —	— Fix, к)-\- — Дягажсояж.
J	J	3	3	3
Г dx r-i/ i\	Г с^ж	1 ,-./ , ч	^2 sin ж cos ж
5. — = F(x, Л). в. — = —-— Е(х, к) -
A v ' r	J Д3 1-fc2 v ' ' 1-fe2 L
1.5.23. Интегралы вида LR(sin ж, у 1 — 1г2 sin2 ж ) с!ж.
Условие: 0 < /с2 < 1.
1.
Обозначение: А = у 1 — 1г2 sin2 ж .
sin х dx	— cos x	p — 3
(р - 2)A -
' sin ж dx	v^	2l(n — 1)(га — 2) . . . (га — I — 1)
¦1	1 _________________ — ___ ЛАП /М Ж,	_шшшшш„	Х	/ Х	/	\	/
^»	* о., i 1 — — COS Ж > _ -jz
о.
'
21 '
' ж с!ж
(p
2(р^1Iг2^р + 2 Г slnp 2 х dx	р^З	(* sinp 4 ж dx
Г a	i	A cos ж 1 — Аг . ,.	А ч
5.	A sin х dx =	г-™— In (A; cos ж + А).
J	?	Ак
Г	А	1 — к2	2к2 -— 1
6.	A sin2 х dx =	sin ж cos ж -\	—^— F(ж, к) -\	г^— Е(х, к).
J	о	ok	ok
т Гл .з ,	2Jb2 sin2 ж + 3ife2 - 1 А	3Jfe4 -— 2jfe2 -— 1
7.	Asm x dx =	—	A cos ж +
A cos ж Н
Hk2	Hks
Г A . 4 ,	3ife2 sin2 ж + 4ifc2 - 1 A .
8. Asm x dx =	A sin ж cos ж —
J	15A;2
4 k2 1)
Глз. i 2k<2 sin2 x + 3Jfe2 - 5 .	3A — ife2J , /f
9.	A sin x dx = 	A cos ж	—— In (k cos ж + A).
J	8	ok
Г A3 . 2 , 3ife2 sin2 ж + 4Jb2 -6 A .
10.	A sin x dx = 	A sin ж cos ж +
J	15
^ fA3.3 , 8ife4sm^ + 2Jc2EJfe2 ^ 7) sin2 ж + 15ife4 — 22jfe2 + 3 A
11. A sin x dx =	L-T%	A cos ж -
J	48J2
11 А. П. Прудников и др., т. 1
1 n	лх
In (fe cos ж + A).

16.
20.
162	Гл. 1. Неопределенные интегралы	[1.5.24
„л fslnnxdx sinn~3x А	п^2 1 + к2 Г stnn~2 ж ,	п^З Г sinn~4 ж ,
1 2 I 	 — 	/\ ГТ1Ч т -4- 	 	 I 	 п т 	 	 I 	 п т
"* J Д " (п-1)^Асо8Ж+п_1 у J Д dx (n-l)H Д dX-
ГsInжdж 1 . А — к cos ж	1. ,.	АХ	1. ,.
13.	 = —In-	 = -т\п(ксоЕХ + А) = ^т1п(А -
J А	2к А + к cos x	A;	A; v
fsln2xdx 1 , ч 1 ( х
Г sin3 ж dx A cos ж 1 + А;2. ,.	АЧ
15. 	г	 = 	—	~^~~ 1° (я cos ж + А).
I /\	oi?^	*??•«
f sin ж dж
А3	A-
sin2 x dx	1	„, , ч 1 „, , ч	1 sin ж cos ж
, Adx	1, A + cos x . . /f	A4
21. 	 = ^-ln™rJ	h ^1п(^созж +A).
1 sin x	2 Д ^ cos ж
22.	I ^^ = A - k2)F(x, к) - Е(х, к) - Actga.
1 sin ж
,—«,«,	A cos ж 1 — к2 . А + cos ж
23.	^^ = -о ¦ 2 +—л—1п^	•
sir ж	2 smz ж	4	А — cos ж
sin4 ж 3
24. I ^^ = - [-Actg3 ж + (к2 - 3)Actgx + 2A - k2)F(x, к) + (к2 - 2)Е(х, к)}.
25.
Asinnx	А	/	ч/
A cos ж	(n-2)(l + i
dx	(n-3)ife2 Г dx
Asinn^2x	n-1 J Asinn"
27- л 2 =	л& da = F(a, A;) - Е(х, к) - Actgx.
(п — 1) sinn 1 ж	п — 1
, dx	1 . А + cos ж . А + cos ж
26. I -—;	 =	In	 = In	;	.
A sin ж	2 А — cos х	sin x
dx	г1 « ~^2 ¦
A sin2 ж
Г dж	A cos ж 1 + к2 А + cos ж
28. 	о— =	о— — 	In —	.
J A sin*5 ж	2 sin2 x	4	А — cos ж
29.	f —^j— = i [-A ctg3 x - АBк2 + 3) ctg ж + (Jfe2 + 2)F(x, A;) - 2(к2 + 1)^(ж, А;)].
J A sin4 ж 3
1.5.24. Интегралы вида Д(созж, у 1 — ^2 sin2 ж ) dx.
Условие: 0 < к2 < 1.
Обозначение: А = у 1 — Is2 sin2 ж .
Г cos ж dx	sin ж	р — 3 [* cos ж dж
(р-2)АР^2 р-2
cos ж dж	. v-v	2Z(^

1.5.24]
1.5. Тригонометрические функции
163
f a	i
4. A cos x dx =
J
k21 8ш
2|+1
21
A sin x
2k
arcsin (k sin ж).
5.	A cos2 x dx = — sin ж cos ж	—~ ^(ж, A;) -\	—^— E(x, k).
J	О	OK,	OK
fA з , 2Jfe2 cos2 ж + 2k2 +1 A .	4k2-1 . /f . ч
6.	A cos x ax = 	—	A sin ж Н	——arcsin («sin ж).
J	Oft	Oft
7. I A cos x ax =
A .
A sin ж cos ж +
8. A cos ж dx =
О I дЗ 2 ,
9. I A cos x dx =
JL о
Asm ж Н	arcsin (A; sin ж).
О ft
л .
Asm ж cos ж™
10. I A3 cos3 ж dx =
(' j
15Jfe2
13.
14.
16.
20.
21.
22.
A
A sin ж
=	48fc2
f cosn ж dx cosn ж л .	n - 2 2Jb2 - 1 f cosn~2 ж ,
11.	 = 7	rrrrAsin ж H	 ———	dx +
J A	( l)k2	1 k2 J A
16fc3
arcsin (A; sin ж).
7rrrr
(n — l)k2
— 1 k2
n-31-ife2 f cosn~4 ж ,
H	 —r^—	dx.
n — 1 ^2 J A
Г cos x dx 1 . /, . \ 1	A; sin ж
12. 	—	 = — arcsin (A; sin ж) = — arctg ———.
cos2 x dx 1
1 ,-./ ,x 1
= — E(x, k) - -^
dx A sin ж 2/c2 — 1
F(x, k).
15.
совж^ж sin ж
.
1 .	1 . . sin ж cos ж
= ^ F(x, fc) - -^ E(x, k) +	.
^^ ( cos3 x dx 1 —A;2 sin ж 1 . /, . \
17. J 	—	 =	p^	+ — arcsin (A; sin ж)
ж dx 2 — k2
2A — k2
Adx
+ ^E(a!)jk) +
- k2 л A + у/1 - k2 sin ж ,	/t	ч
In	,	h к arcsin (A; sin ж).
Д /k2 sin ж	l	;
Д _
cosz ж
A dx A sin ж
cos3 x 2 cos2 ж 4-/L -
¦In-
/1 — k2 sin ж
д _ ^i _ Jfe2 sin
11*

164	Гл. 1. Неопределенные интегралы	[1.5.25
Adx
23.
1ж 3
, k) + ^—^ E(x,
. cf ж	1 . A — л/l — ^2 sin x
24. I 	 =	^=^=- In	^=^=	.
A cos ж	2л/1-к2 A + VI ^ k2 sin ж
г/т	1	1
I с!ж	A sin ж	2fe2 — 1	A — Vl — ^2 sin ж
A cos3 ж 2A ^F) cos2 ж 4A — ife2K/2 A + Vl - P sin ж'
dx
27.
28.
A cos4 ж
о (-L	) L	J
daj	A sin ж
/\ рлсП /тр	i /ins 	 1 1 I 1 	 йл s /^i^G^"""""-^ Or1
~ - 1) Г
Jfe2)
1.5.25. Интегралы вида sinm ж cosn xy A — ^2 sin2 x)p dx.
Условие: 0 < к2 < 1.
Обозначение: А = у 1 — Is2 sin2 ж .
	r— (
m^2 ж cosn ж da - (m - 3) f Ap sinm^4 ж cosn ж d»}.
1. f Ap sinm ж cosn ж dx = 7	r— (Ap+2 sinm^3 ж cosn+1 ж
J	(m + + )fe2 I
2.
(га + и + \
г
+ [(п + р _ l)jfc2 _ (m + n _ 2)A - к2)] Ар sinm ж cosn^2 х dx +
J
+ (n - 3)A - Jfe2) Ap sinm ж cosn^4 ж dx У	[т + п + рфЪ].
3. I Ар sin ж cosn ж dx = ^^		 п \ Ар cosn^2 ж sir
f l)fe2 (п + р + 1^
п ж	га — 1
4.	Ар sinm
5.	|*Apsin3;
— —	-7-^-	 	^^м	 ^Р cosn™2 ж sin ж с^ж.
л Гдр • т	з , (т + р + l)fc2 sin2 ж - [(р - ш + l)fc2 + т + 1] р+2 . т_х
6.	AF sin ж cos ж аж =	^	rj1	г^	^Д^^ sin ж +
+ ——z	—г^	 —- Ар sinm^2 ж cos ж {?ж.
Г	А3
7.	A sin ж cos х dx =	—^.
J	ЗР
Г	2ife2 cos2 ж + 1 — Jb2	A — Jb2J
8.	A sin ж cos2 x dx =	—	A cos ж +		In (k cos ж + A).
J	Oft	OK

1.5.26]
1.5. Тригонометрические функции
165
, А .	з ,
9. I A sin ж cos ж ах =
15 А;4
Д.
10. (Asm ж cos x ax =
л
A cos ж™
A -
16fc5
Mfccoss
11. Asm ж cos ж аж =
1
A .	1	. /, . ч
A sin ж Н	 arcsin bin ж).
8k2	Sk6
- o , л . -z	2 ,	3fe2 cos2 ж - 2fe2 + 1 .
12. I Asm ж cos x ax =	—	A sin ж cos ж —
15Ar
13.
14.
15.
16.
17.
18.
19.
A sin2 ж cos3 x dx =
Asina;
2k2 - 1
J-D tb
arcsin (k sin ж).
* . з , 3fe4 sin4 ж — к2 sin2 x — 2
Asm ж cos ж б(ж = 	^ -. ,	A.
л .3	2 ,
Asm ж cos x ax =
A sin4 x cos x dx =
^
A
A cos ж +
- 3
A . 1	. /, . ч
A sin ж Н	— arcsin (A; sin ж).
Лил
A sin ж cos ж йж =
A3 sin ж cos2 x dx =
A sin ж cos x dx =
A
A cos x +
; In (k cos ж + A).
ж - 3
A sin ж
1.5.26. Интегралы вида
Условие: 0 < А; < 1.
48k2
	у 1 — к2 sin2 ж dx.
cosn ж
16kd
16fc3
arcsin («sin ж).
Обозначение: А = у 1 — ,fc2 sin2 ж .
1.
2.
3.
5.
6.
cos ж
8ШЖ
cos3 ж
sin ж
ГЛ , л VI- к2 , А
= Atgжdж =-А+	In-
A dx =	A; In (A; cos ж + А).
cos ж
cos ж
А
А;2
А -
I -
2 cos2 ж 4V1 - к2
А ах =
3A-fc»
A sin ж 2jfe2 ^
1
cos ж
• 2
1
2A;
arcsin (A; sin ж) -\
In ¦
- A:2 sir
,
A - Vl - к2 sir
p
= Atg2xdx =
I

166
Гл. 1. Неопределенные интегралы
[1.5.27
к arcsin (к sin ж).
13.
16.
17.
18.
20.
^,ь — 4k — 1 . /, . ч Vl — к2 . А + \J\ — к2 sin ж
Н	7з	arcsin (A; sin ж) -\	In ¦
ой	Л
f*f\Q Пр*	I	11 — /\
11.	| 	Ас?ж = A ctg ж йж = А + - In	-.
sin ж	J	2 1 + А
,' cos2 ж . . A cos ж
12. 	Ас1ж =
2k
1/}	A ч 1 . A + cos x
In (A; cos ж + A) + - In	.
K	' 2 A-cosa;
Adx =
ife2 sin2 ж-
Sk2
л 1,
A+ -In
2
1 - A
In.
2 1 + A
^ . , cos ж А . ^2fe sin x + 5fe + 1 .
14. I 	A dx = 	—	A cos ж -
iin ж	8k2
2 A — cos x
ln (k cos ж
f cos ж A .	A	. /1 . \
15. —«—A ax =	A; arcsin (A; sin ж).
J in ж	sin ж
Adx =
= -Actgx + A - k2)F(x, к) ^
к).
sin ж
A dx =
2 sin ж
A
2 sin2 ж
In
2к
1 + A
arcsin (A; sin ж).
cos ж
Ас1ж =
cos ж
	5—
2 sin x
A
1-A'
In
19.
sin4 ж
A + cos ж

A — cos ж
— A; ln (A; cos x + A).
dx.
*
1.5.27. Интегралы вида
Условие: 0 < к2 < 1.
Обозначение: А = у 1 — к2 sin2 ж .
sinp ж cos9 ж б?ж ^,fc2 slnp+1 ж cosg+1 ж р — q — B — к2)(р — г + 3)
4.
6.
slnp ж cosg ж
sinp ж cosg ж
1 Г
= J-2 J
1 Г sln
p™2
А;2 — 1 Г sinp ж cosg^2 ж dx I fsln^cos^2
1
sin ж cos ж dx
А^	= (r-2)ife2Ar-2'
sin ж cos2 x dx	cos ж A 1 — A;2
4-
sin ж cos x dx
A_
"A;2*

1.5.27]	1.5. Тригонометрические функции	167
smxcos3xdx=_ I {k2coa,x_2 + 2k2)^
ok
fslnxcos^^ 3 - 51г2 + 2fe2 sin2 ж . 3^-6^+3, ,.	лч
8. J	 = 	—	cos xA	—	In (k cos x + A).
.' sin x cos x dx	A sin x arcsln (k sin x
10-
sin2 ж cos2 ж с^ж	A sin ж cos ж 2 — к2„, , ч 2А;2 — 2
Д
Г sin ж cos ж dx	2к cos ж + 21с ™ 3 л .	4Jfe — 3 . ,, . ч
11.	 =	7^	A sin ж Н	т^—arcsin («sin ж).
J	Za	o«J	o«J
f sin2 ж cos4 ж dx	3k2 cos2 ж + 31г2 — 4 . .
12. 	—	 =	—	Asm ж cos ж +
9J^4-m2+8	3jfe4 ^ 13Jfe2 + 8
+	15fce	^Ж' >	I5jfe6
13.
14.	 =	A cos х	=	In (к cos x + А).
1	А	8к4	8к5	v	;
sin3 х cos3 ж dx _ Зк4 sin4 ж - Eк4 - Ак2) sin2 x - Шк2 +8
А	~~	15Jb6
sin3 ж cos4 ж dж _ 8fe4 sin4 ж - 2jfe2 Gife2 - 5) sin2 ж + 3fe4 - 22Jfe2 + 15
g +
17. 	 =	A sin ж Н	 arcsin (k sin ж).
1	A	8k4	8k5	K	}
.' sin4 x cos2 ж dx $k2 cos2 ж — 21c2 — 4 .
18.	I 	—	 = 	—	A sin x cos x +
k4 + 7Jb2 - 8 „, , ч 2ife4 + 3Jb2 - 8
, sin4 ж cos3
JL«J •
. .	6k2 ~~ 5 . /f . ч
A sin ж + wk7 arcsin (A; sin ж).
slnm ж cosn
— 1 Г sinm 2 ж cosn ж с!ж n-1 f sinm ж cosn 2 x dx
Jb2 J	A	k2 J
Г sin ж cos ж da? 1 Г sin x cos2 ж dx cos ж 1 . / _
21. 	—	 = —г-. 22. 	—	 = —— - — In гг
J	A3	k2A	J	A3	k2A к3 v
sin ж cos3 x dx к2 sin2 ж + к2 — 2
sin x cos4 x dx к2 sin2 x + 2k2 - 3	3A -
Г sin2 x cos x dx sin ж 1	. .. . ч
25. 	—	 = —г—	— arcsin bin ж).
J	А3	к2А к3
f sin2 x cos2 ж dж 2 — к2^, 1Ч 2 _.. I4 sin ж cos ж
26-	F{k)E(k) +

168
Гл. 1. Неопределенные интегралы
[1.5.28
27.
28.
29.
30.
A3
к2 sin2 ж + 2k2 - 3 .
	sin ж —
- 3
A3
k4A
sin ж cos ж dx —к sin ж + 3
2k4A
2кБ
arcsin (« sin ж).
¦ In (к cos ж + A).
A3
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
1.5.28. Интегралы вида
Условие: 0 < к2 < 1.
Обозначение: А = у 1 — 1г2 sin2 ж .
smp ж с!ж	sinp+1 ж
¦ sin ж	— arcsin (A; sin ж).
ip ж	с!ж
cos* ж x/(l^ k2sm2x)r
cos*? ж Ar
- к2)
Ъ)к
жДг~2
2 Г sinp
Г sir
J COS*5
cos9 ж dx
sinp ж Ar (p- 1) sl
p^ q - 2 + (p
x
cos*1 ж с!ж (р — g + r — '
з1пр^2 ж Ar	p - 1
cos ж dж
sln2m ж
sin ж с!ж
(m + n-l-1)
COS Ж
sin ж dx
~ J
dx
A
¦In
2n - 2/ - 1 V A
COS2 Ж А
sin ж dx Г .
—= |tga:(l
cos3 ж А
sin ж dx
cos4 ж А
Jfe2
- A;2 si
(g- 1)A —
Г sinp ж с!ж
J cos*?™4 ж Ar"
cos9 ж dx
с Аг"
sin-
/COS Ж\2
A 2A ~k2) cos2 ж 4A
cos2 ж - 1 + к2
In-
A^ Vl^7!2
¦A.
1
. A + \/l — к2 sin ж 1 . /, . ч
. 	 .	 In	.	— arcsin (A; sin ж).
cos ж А 2л/1 - ^2 A - Vl^2 sin ж к
sin2 ж с!ж
cos2 ж А
¦ dx =
A """	 1 - к2
A sin ж
^ж —
1
cos3 ж А 2A-^2)со82ж 4A —
In
A + i/l — к2 sin ж
A — \/l — Aj2 sin ж
sin3 х dx A
cos ж А 1с2 2л/1 —
sin3 ж с!ж	А
¦In-
/l^fe2
A - x/1 - к2
cos2 ж А A^Р)со8ж А;
cos ж + А).

1.5.29]
1.5. Тригонометрические функции
169
14.
15.
16.
18.
19.
21.
23.
25.
26.
sin4 x dx
cos ж А
cos x dx
sin ж А
cos2 x dx
sin ж А
cos4 ж dx
sin ж А
cos ж dx
sin ж А
cos3 ж с!ж
sin2 x A
A sin ж
2k2 Ч
dx 1 . 1 - A
ctg ж — = - In	.
Б А 2 1+A
1	. A — cos x 1 .
-In-	Ьт]
2	A + cos ж /г
A cos ж 1 A + cos ж
2k2 + 2 П A - cos ж +
2k2
¦1
17.
arcsln (k sin ж).
cos3 ж с!ж А 1 1 1 + A
	— = —	In	-.
sin ж А к2 2 1 - A
— 1
2к3
In (A; cos ж + A).
20.
ctg2 ж
dx = —A ctg ж — ?7(ж, к).
1
sin ж
A cos ж
sin3 ж А
n dx
dx

л
А
— — arcsin (k sin ж). 22.
1 — к2 А + cos x
4	A — cos ж *
cos ж dx
sin3 ж А
2 sin2 x 4 1 - A '
2 sin2 ж
tffn~3 ж
24. fi?
J si
cos x dx
sin ж
A
¦ dx —
' X
n — 1 cos2 ж га — 1
Tb JL
1.
1.5.29. Интегралы вида
Условие: 0 < к2 < 1.
значение: А = V
A dx	1 , 1 - А
А
sin ж cosn ж

Обозначение: А = у 1 — ,fc2 sin2 ж .
¦In-
sin ж cos ж
Adx
- cos ж
sin ж cosz ж
Ас!ж
3.
4
5.
6.
7.
8.
9.
10.
) sin ж cos3 ж
Г Adz
) sin ж cos4 ж
¦
) sin2 ж cos ж
• 2 2
| sin ж cos2 ж
Г A dx
] sin2 ж cos3 ж
Г Adz
) sin3 ж cos ж
f Adx
) sin3 ж cos2 ж
sin4 х cos ж
COS Ж
A
1,
~ In	.
2 A — cos ж
	1 1
2 cos2 ж ~ 2 П 1 - A
1Д+^—¦
2 А — cos ж
2 sin3 ж
-A.
3sln3 х

170
Гл. 1. Неопределенные интегралы
[1.5.30
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
1.5.30. Интегралы вида
"Условие: 0 < к < 1.
Обозначение: А = у 1 — «fc2 sin2 ж .
dx
dx
slnm ж cosn xy/(l - к2 sin2 x)r
A sin ж cos ж
dx
A sin ж cos2 ж
^ж
,,	ч dx 1. 1-Д
= (tga + ctga;) — = -In-
•In
А + л/1 - к2
A
1 А — cos ж
— ^2)созж 2 А + cos ж
dx
= (ctgж + 2tgж + tg х, —
A sin ж cos3 ж I	д	А
J А 1 1 +А	2-
- - In з	 +
dx
2A ^P) cos2 ж 2 1-Д ' 4A -
- 3)з1п2ж - %k2 + 4	1 A + cos ж
In-
/т^
¦ А- л/l^W
A sin ж cos4 x
dx
-A- -In-
1
¦In
2 А — cos ж
А — \/1 — к2 sin ж
Asm ж cos ж	sin ж 2 л/1 — ^2 А + л/1 — ^2 sin ж
с/ж
A sin2 ж cos2 ж
"ctg Ж
Jfe2^2
A sin2 ж cos3 ж	2A — fc2) sin ж cos2 ж
^А-
4A-
In-
I Ж
A sin3 ж cos ж	2 sin2 ж 2л/1 — ^2 А — л/1 — ^2
А — у 1 — ^2 sin ж
1„1 + А
1-A
dx
jfe2
A sin3 ж cos2 ж 2A — к2) sin2 ж cos ж
A sin4 ж cos ж
Зз!п3ж
А — cos ж
А + cos ж *
А — л/1 — «fc2 sin ж
2^1 — к2 А + y/l — k2 sin ж
1.5.31. Интегралы вида i?(sln ж, cos ж, у 1 — р2 sin2 ж , yl — д2 sin2 ж ) с!ж.
- < ж ^ тг/2.
1 — р2 sin ж
Условия: 0 < р2 < д2 < 1, 0 < ж ^ тг/2.
Обозначение: ш = arcsln ¦
у 1 — р2 sin2 ж
1.
2.
— р2 sin2 ж)A — д2 sin2 ж) \/l — р2
te2 ж с?ж
— р2 sin2 ж)A — q2 sin2 ж)
y 1 — q2 sin2 ;
3.
sin2 ж dx
/Г^2
- р2 sin2 ж)A - q2 sin2 жK A ~~ Ч2){Ч2 - V
1
A - g2)i/(l - р2 sin2 ж)A - q2 sin2 ж)

1.5.32]
1.5. Тригонометрические функции
171
— р2 sin2 жKA — q2 sin2 ж)
1 — о2 sin ж у 1 — рл sin ж
1 + (р2г2 — р2 ~~ г2) sin2 ж у 1 — q2 sin2 ж
Г j /J, —I— sin Ж )
1.5.82. Интегралы вида	dx
J у 1 — k2 sin2 ж
Условие: 0 < А; < 1.
Обозначение: А = у 1 — к2 sin2 ж .
а + f Ж) d	L \(а + sin ЖГ3 cos ЖА + 2BР -
2.
3.
4.
f dx = t—L—
+ (p - 2)A + к2 - 6а2к2)
dx
dx - aBp - 5)A + к2 - 2a2k2) x
- (p - 3)A - a2)(l - a2k2)
l,To прир = -1, -2, ...
kz
dx = aF(x. к) -\	In ——
dx =
A
(a + sin жJ
A
dx	_ 	1
(a + sina?)nA ~ (n - 1)A - a2)(l - a2k2)
a A — к cos ж
cos ж А
(a + sins)n-2A
dx
da;
~(п~3)Г
(a + sin ж) А
dx
a \ a2
1
¦In-
A cos ж
(a + smsJA~(l-a2)(l-a2fc2)[ a + sin ж
(a + sin ж) А
2 f (fl + sin ж) dx „2 f (a + sin жJ
I 	—	 "г" n5

172	Гл. 1. Неопределенные интегралы	[1.5.33
i	dx	1	Г A cos х
2A - а2)A - а2к2) [ (а
- ЗаA + к2 - 2а2к2) [	dx Ч9Л - (па2к2 - к2 - 1) f 7	^—- + 2ak2F(x, к)}.
1	;J (а + sin жJ A v	;J (а + sin ж) A	v ;J
A
А " J J A±8тЖ)«-2А (П 2JA J
9-
Г	rfa;	_	1 Г A-A:2) A cos ж
/-1 I	•	\O Л	о /-1	I О \O ~Г	/-I i	•	\ о	I
(lib sin жJ A 3A -- Дг2J [^ (lib sin жJ	(lib sin ж)
+ A - 3Jfe2)(l - k2)F(Xj k)-(l- 5k2)E(Xl к)].
i	dx	1	Г	fe A COS Ж	,	..	2x
I (l±jfesina;)nA = Bn - 1)A - A;2) [ (lihina;)n + (n - l)(b - к ) x
dx	/	ч Г	<^ж	/	ч
2B 3)	+ (" - 2)
Г	с!ж	fe A cos ж	1
J (lib A; sin ж) A = A	+
f	с/ж	_	1 Г k{l-k2)Acosx
' J (lib A; sin жJ A ~ 3A - fe2J [ A±^1J
± М5ГЛ)АСШЖ - 2A - k*)F(x, к) + E - ^2)?;(Ж, ife)l.
J it К Sill Ж	J
Г A + аз1пж) ,
1.5.33. Интегралы вида	ах
J VI - ife2 sin2 ж
Условие: 0 < к < 1.
Обозначение: А = у 1 — ^2 sin2 ж .
Г A + a sin2 х)р 1	Г 2/1 , .2 чР-2Л .
1.	— ах = ~	гт^7 а A + а sm ж) A sin ж cos ж
J	А	Bр^ 1)к2 I
Bр - 2)C^2 + ife2a + a) f С1 + а™ ^ dx - Bр - 3)Cfe2 + 2aife2 + 2а + а2) х
х ^	}-	dx + 2(р - 2)(а + 1)(А; + а) ^	'-	dx .
_ fl + asin ж, л , а \ . ч a , ч
2.	с!ж = A + j^)F(x, к) - — Е(х, к).
J	A	V к /	к
п Г A +a sin2 жJ ,	а2 л .
3.	I	—	— dx = —Asm ж cos ж +
2а . B + ^2)а21 л/	[2а
с, А;) — — '
,	rfж	1	Г A sin ж cos ж
4.
2(п - 1)A + а){а + fe2) [(I + asm2 х)п
Bп - 3)(а2 + 2а + 2afc2 + ЗГ)
- Bп - 4)(к2а + а + Зк2) \	.***	+ Bп -
J A + asin ж ПД
A + asin2 ж)п~1А
2 f	dx

1.5.34]
1.5. Тригонометрические функции
173
5.
6
7.
8.
9.
10.
JL JL m
dx
= П(ж, —а, к).
а2 А sin ж cos ж
asin2a;
2)F{x к) + а#(ж А;) + (а2 + 2а + 2ак2 + 31Ь2)
- (a + kA)F{x, к) + aE(x, к) + (a2 + 2a + 2аАГ + ЗАГ )П(ж, -a, A;) .
sin ж dx	1	.	\/l + йА- \/к2 + a cos ж
а - л/к2 + а
[a>-*'j.
¦2a + ife2l
1 - Jfe2 J
hl< a < -A;2!.
¦In-
^(k2 + а)cosx ~~ V^(
[а < -1; 0 ^ sin2 ж < -1/а].
sin ж ds	A
. — sin2 ж)A A — ^2)созж
sin ж dx
COS Ж	1
+ z	;
cos ж dx
a sin2 ж) А
13.
14.
1 A + \/—{k2 + a) sin ж
In	V; l	L
B ) A /B )
r 9	9	# n
[a < -k2; 0 ^C sin2 ж < -I/a 1.
L	J
cos ж с!ж
А '
1.5.84. Интегралы вида
Условие: 0 < к2 < 1
Обозначение: А = у 1 — к2 sin2 ж .
¦ rfaj = -—
у 1 ~
пег.-
2Bр -

A sin ж
dx-(p-
— dx + Bp - 5)a(l - 2fc2 + a2ife2)
- (p — 3)A — «2)A — k2a2)	——	dx
аж +
[p ^ 1; a2 ^ 1, -A -
2.
аж = аг(ж, А;) + — arcsin (A; sin ж).
o i1 (а + сояжJ
3. I	— ax =
+ A;2 - 1
К
, A;) + — E(x, k) -\—— arcsin (A; sin ж).
К	К

174	Гл. 1. Неопределенные интегралы	[1.5.35
i	dx	I	[A sin ж
4.
(а + cosх)пА (п - 1)A - а2)A - к2 + а2к2) [(а + cosж)
- Bп - 3)A - 2к2 + 2а2к2)а
1	А	;
- (п - 2)Bк2 - 1 - 6а2*2)
- Dп -
.\ 1Л
(a + cosa;)n-1A
1	[ sin ж А
5.
Bга - 1)аA - 2Jb2 + 2a2ife2) [(а
(п ^ 1)A ^ 2^2 + 6а2^2) f 7^Ж	2B 3)ife2 f	d X
v	A	;J (аН-
¦ созж)п^1А
dx
1 A±созж)А	sin ж	v ; v ;
dx
A ± cos ж Ы/л/1 - к2) А
к2 sin х cos ж A =р cos kifx^fl — k2)	ki
A	л/1-А:2
=F	Л «in rr _|_ ?;(ж, А;).
JL
8. 7—:	rx = -г	-П(ж, -~2	-, A;
(a + cos ж) A a2 — 1 \	1 !
. v 1 — а2 А + k\fl + А;2а2 — fe2 sin ж
¦ In ¦
— а2 А — A;v 1 + к2а2 — к2 sin x
[	dx	1	Г sin ж А
* J (a + cos жJ А ~ A^а2)A^ к2 + а2к2) [а + cos x ~
J (а + cos ж) A	J A
Г	/7о™	1	Г Л «in о™
10.
(а + cos жKА 2A - а2)A - к2 + а2Jfe2) [ (а + cos ж)
о /ч о?2 , л» 2»2\ [	"Ж	/о#2 1 л 2»2\
— оаA — 2к + za « ) 7	^ТТ" ~~ (^^ — 1 — Ьа к )
J (а + cos жJ А
1.5.85. Интегралы вида —	dx.
7чл
(a + cos ж) A
Условие: 0 < A;2 < 1.
Обозначение: А = yl — fe2 sin2 ж .
л/l ^ ^2 sin2 ж
/	о\ /о , /1 2 ,2 /1 2;2\ (О- "f" tg Ж!
— (р — 2) B + 6а — к — 6а к ) I	^-^
f Bр — 5)аB + 2а2 — к2 — 6а2к
- (p - 3)A + a2)(l + a2 - fcV)

1.5.35]
1.5. Тригонометрические функции
175
2.
3.
4.
А
(a + tgxJ
А
dx
= aF(x, к) + — г In Л '
2уТ^Р
A
(п ~~ 1)A + а2)A + а2 - к2а2)
А	+ Bп - 3)аB + 2а2 - к2 ~~ 2к2а2) х
(a + tg x)n~1 cos2 ж
7	—— (n — 2)B + 6a —A; — 6A; a ) -r-
+ Dn- 10)a(l-Jfe
da;
(а +
l, aV-1, -1/A-
5.
6.
7.
¦F(a, A;)-
П ж,
¦In-
+
а2 ~ k2a2 - Vl + a2 A"
а	/	а"
—^П ж,
¦In-
a2 A cos ж + a Va2 + 1 - ^2
- к2 )y/l + a2 - A;2 sin2 ж
[a > 1].
da;
8.
(а + tgжJA A + а2)A + а2 - к2а2) [(а + tga) cos2 ж
2^2^ Г	^	Wi^i^ Г « + tg я?
(а + 1ёж)А
1
(а + tgжJ
dx .
(a + tgжKA 2A + а2)A + а2 - к2а2) [(а + tgжJ cos2 ж
+ ЗаB + 2а2 — 1г2 — 2к2а2
(а + tgжJA
- B +6a2 -к2 -6k2a2)
dx
(a
, A;) .
9.
¦ dx = -;	г-;
+ Bр - 2)B - За - к2 + 3^2а) ^^1
- Bр - 3)[1 - 4а + За2 + Bа - I
tg»)
p-i
¦ dx -
10.
11.
dx
- 2(р - 2)аA - а)A - а + А;2а)
:, А;) -	т^^(ж, А;).
¦ da; .
(a + tg2x)A o-l v ' ' o(l-o)

176
Гл. 1. Неопределенные интегралы
[1.5.36
1.5.36. Интегралы вида LR(sIn ж, cos ж, у 1 — р2 sin2 ж ) dx.
Условие: р > 1.
Обозначение: (р = arcsln (ps'mx).
1. 1 \/l ~~ р2 sin2 ж dx = рЕ [ <р, ~~ ) - Р	Flip, - I.
2.
3.
с/ж	1
у^1 - р2 sin2 ж Р
{?ж
(l-r2sin2a;)\/l-p2sin2a; P
Для вычисления интегралов вида Я (sin ж, cos ж, у 1 — р2 sin2 ж ) dx при р > 1 можно
пользоваться формулами пп. 1.5.22—1.5.30, произведя в них следующие замены [5]:
,±y, 3) к
¦ р.
1.5.37. Интегралы вида LR(sin ж, соэж, у 1 + р2 sin2 ж ) с!ж.
Обозначение: (р = arcsln
р2 sin ж
1.
2.
3.
4.
5.
6.
7.
8.
9.
\/l + p2 sin2 х
1 + р2 sin2 x dx =
1 + (р2 — г2р2 — г2) sin2 х
dx	I
у 1 + р2 sin2 ж
sin ж dx
V1 + р2 sin2 ж	Р
= — In ( о sin ж + \ 1 + р2 sin ж .
+ р2 sin2 ж — cos ж
sin ж у 1 + р2 sin ж
dx
cos a;\/l + p2 sin2 ж 2-y/l + p2 i/l + p2 sin2 ж —
tga; с/
yl + p2 sin2 ж —
ctg ж dx
p2 sin2 ж
1	1 — yl + p2 sin2 x
2	]_ _|_ ^/l + p2 sin2 ж
Для вычисления интегралов вида Л (sin ж, cos ж, у 1 + р2 sin2 ж ) с!ж мож:но также поль-
пользоваться формулами пп. 1.5.22—1.5.30, произведя в них следующие замены [5]:
1) к2 -+ -р2; 2) F(ж, А;) -^
3) Е(х, к)
е(<р, -
р2 sin2 ж

1.5.38]
1.5. Тригонометрические функции
177
4) — In (k cos ж + А) —^ — arcsin
k	} p
PCOS X
5) — aresln (A; sin ж) —>• — In (psin ж + l/l + р2 sin2 ж ).
/с	р	v
1.5.38. Интегралы вида Lft(sin ж, cos ж, у a2 sin2 ж — 1) dx.
Условие: а > 1.
Обозначение: <р = arcsin ¦
1. \/a2 sin2 ж — 1 с!ж = — F
V	a J
2.
4.
5.
6.
7.
8.
9.
dx
7а2 sin2 ж -
cos ж с/ж
=
у a2 sin2 ж — 1 а
1 / у'а2 — 1 \ о Г 8™ж ^ж У
=- = — У* I у?, 	 ). *>¦ —f11^^^	=	•
1	а \	a J	J Ja2 sin2 x_1	a
1 . ,	/ о . 9	\
= — In (asm ж + у а sin ж — 1).
а
sin ж у a2 sin2 ж — 1
= - arctg
1
V о? sin2 ж — 1
¦In-
/а2 — 1 sin ж + у а2 sin2 ж — 1
cos ж у a2 sin2 ж — 1 2y «2 — 1 -^a2 — 1 sin ж — ya2 sin2 ж — 1
dx	1
/а? — 1 + у а2 sin2 ж — 1
= — arcsin -
¦ 1 -\/a2 — 1 — ya2 sir
1
у a2 sin2 ж — 1
ctg ж ^ж
у a2 sin2 ж — 1
Для вычисления интегралов вида Д^шж, cos ж, у a2 sin2 ж — 1) dx (а2 > 1) мож-
asin ж
но также воспользоваться формулами пп. 1.5.22-1.5.30. Для этого надо произвести в них
следующие замены [5]:
Fix, к) -+
ia
2)	Я(ж, A;) -+-(p,	(V,
а \ a	J \ а
3)	— In (A; cos ж + А) —^ — -т-;	4) — arcsin (A; sin ж) —^ -^—\п(а sin ж + у a2 sin2 ж — 1);
/С %Qj	К "
^ч 1, А — cos ж 1	cos ж
5) — In —	у	arctg	—.
;2 А + созж г	Ja2 sin2 ж - 1
6)
1
¦In
1
А + у/1 — к2 sin ж
' А - л/1 - к2 sin ж 2iVa2 - 1
¦In-
/а2 — 1 sin ж + у а2 sin2 ж — 1
- 1 sin ж -
sin2 ж - 1
- In	^	arcsin	;
2 1 + А	г	a sin ж
2л/1 -
¦In
А + i/l - к2
¦In-
/a2 - 1 + \/a2 sin2 ж - 1
/a2 - 1 - л/a2 sin2 ж - 1 '
9) оставшиеся А —у iya2 sin2 ж — 1; 10) к —у а;
11) умножить полученные равенства на г.
12 А. П. Прудников и др., т. 1

178
Гл. 1. Неопределенные интегралы
[1.5.39
1.5.39. Интегралы вида \f(tgx)dx, \f(dgx)dx.
{tg х 1
>.
ctgaj
1. R(sm2 ж, cos2 ж, tgsc, ctga;, ya2 db b2 tg2 x) dx =
2. i?(sln2 ж, cos2 ж, tgsc, ctga;, \/a2 =b ^2 c^g2 ж ) с!ж =
= \R
г, -, г, Va2±b2r'2
г
. [a2
dx =
(а2 - b2)k^a 	—	Ь
arctg
arcctg
4. [a2 - b2t2{x)]n+1/2t{x) dx = ±Va2^
- 2k + 1
5.
t(x) dx
' 2 ч
n-l
In ¦
/a2 + b2 ^ ^fa2 ^ЬЧ2(х
= ±-
- 2(a2 -
(b2 ^а2)п+г/2
arctg
b2 -
arcctg
6.
7.
8.
9.
t(x) dx
= ±-
1	n-l
L2+2 /«,\ ¦/ ¦-'
l)(a2
±
2(a2
In-
/a2 + б2 ^ у/а2^
dx
1	V^2 - «2 t(x) ± у^а2
= arctg
- aA
'a2 - b2 t(x)
a2 ^b2	^a2 + b42{x)
[a2 < b2]
\a2 > b2]
dx
/a2 + b2
л/a2 + b2 t(x)
arctg	-^-
arcctg -
a2 + b2 t(x)

1.5.40]
1.5. Тригонометрические функции
179
10.
11.
12.
13.
14.
15.
dx
¦In-
/а2 + b2 t(x) ± ^b2
2л/а2 + б2 л/а2 + б2 t{x) T
у/а2 4- 62f2i
arctg -
1
/b2 - a2
arcctg ¦
2л/a2 - b2
¦In-
/a2 ~~ b2
¦In-
/a2 + 62
/a2 + 62
arctg
arcctg
/a2 + 62
1
1.5.40. Интегралы вида
J
Я
I
PiSmXY dx.
{ cos ж J
p\ sin ж 1	xp J sin ж 1
. ж <	> dx = - <	> x
J [ cos ж J	4 1 cos x J
f COS Ж 1 1 O-l f
qx\ . N	a
I sin ж J J	q ]
9-2
2.
3. x
4. xn
5.
6.
7.
12*
COS Ж
sin ж
cos ж
г+fc
fc=O	x
¦ 1Л Г m f sinBn- 2^-
\ cos Bn — 2A;
sin (ж
[a2<62l.
;}dx.
n 1
cos ж
= Bn
f cos ж l ^( ,k x2n 2k (sinxY]
y.Xsinxi +^^ ^ Bn-2ife)!\cosarjJ'
Bn + l)Bn - 1) . . . Bn - 2k + 1)
Bn)!! 2
-	r .	л 2n-2k	f .	\ 2n-2k-l	-\
1 j sin ж 1	J sin ж 1	j cos ж 1
—	2A; \ cos ж J	X cos ж J	1 sin ж /J

180
Гл. 1. Неопределенные интегралы
[1.5.41
о
fiT =
, , Sin Ж .	Sin Ж
9. I x{	> dx = <
COS Ж I	I COS X
10.
11
[1	f sin ж 1
	i	г	=F •
2n - 2k + 1 [cosж j
}J COS Ж 1
1 sin ж J
, 2n-2fc
sin ж	r cos ж
j co
Isi
cos ж J	{ cos ж
2
Г о f sin ж 1 „ /9 x f sin ж 1 , о ч f cos ж I
. ж3<^ }dx = (Зж2 -6)^ 1Т(ж3^6ж)^ L
J [ cos ж J	[ cos ж J	I sin ж J
12. U» 81ПЖ1. dx =
2(n + 1)
±
13. [^8ШЖ\2ЙЖ = ^Т^ ¦
cos ж I	4 4
I
— сов2ж.
8
= тт1т-^)81п2жт1СО82ж-
14.	ж2^	} dx
J [ cos ж J
,r Г з[в1пж12 ж4 /ж3 Зж\ о /Зж2 3\
15.	ж <	> с!ж = — =F	sin 2х =р	cos 2ж.
J [совж/	8^V4 8/	V8 16/
|	ГС
/ Т I si
_ п!
4
СО8Ж
sin ж
^ _ I I "'ПЖ	.	d Sin Ж
17. I ж<»	^с?ж = -jl
cos ж I	4 1 cos ж
18.
Г u_i ( этаж 1 , 1 f г 1 Г/
19. жр <	>аж=-< > (гс
J \ cos аж j	2 \ 1 J LV
Г gin Зж 1
\со83ж/Т
if sin Зж 1 3 J cos ж 1 ж J cos Зж 1
Зб\созЗж/ 4 1 sin ж / 1
, iax) T (^*
. 0 J'
, iax)]
[Re// < 1;
ж > 0].
С(ж,
1.5.41. Интегралы
Г 1 Гв1п
J xp X co
Г 1 Гв1пж1
J p X cos ж J	(p —
вида —<	> dx.
J Xp (COS Ж J
1	Jslnir1g	q
1)жр^1 \ cos ж J (p — l)(p — 2)жр^2
J sin ж I9™ r cos ж 1
\ cos ж J 1 sin ж J

1.5.41]	1.5. Тригонометрические функции	181
g(g-l) Г 1 fsin^r-2^	g^	 [W^sl'
(p- l)(p- 2) J жР~2 [cos ж/	(p- l)(p- 2) J жр-2 \cos ж/
f 1 f sin ж 1 _ 1 f sin ж 1 . 1 f 1 f cos ж 1 .
2. —<	>dx = —-/	г	7<	>±	 	-<	> dx.
J xp [ cos ж J	(p — ljxP^1 [ cos ж J p — 1 J ж?3™1 I sin ж J
1	J sin x 1	1	j cos ж 1
(p — 1)жр^1 \ cos ж J (p — l)(p — 2)жр^2 I sin ж /
1	f 1 I sin ж ,
dx.
(p - l)(p - 2) J жР [cosж
\n+l
f 1 [sins]	(-l)w+1 [ ^(-l^Hl)!^^
]ж2п[со8ж/	жBп-1)![ ^	ж2|й+1 I sin x)
k=0
(-1У
fe=O
x2k	[созж/] Bn-l)!\si(a;)/'
f 1 fsinajl , (^l)n+1 Г ^4 (^l)k+1Bk)\ fcosx}
J ж2п+1 [cos ж]	жBп)! |_ ^^	ж	I sin ж J
. (-!)"["(»)
Bn)!
ж \ cos ж J	\ m } 22m 22m+1 ^v ' \ к ) l	' J
7. I I/ sin x \2m+1 ds = A. V^/^i n-+^2^ + 1M si Bm - 2Л + 1)
ж 1
xf°
ж2 [ cos ж J	I m / 22'
/ ж
^) (Т) [C0SBT2fc)a:
f 1 f sin ж] , ,1 v^
9. —<	>	йж = ±	 >
J ж2 [cosж J	22та ^
2m+ 1
k
x M f sinBm-2A; + l)a;l f2 _ 2fe ^ Г d Bm - 2fe + 1)ж 11
[x \ cos Bm - 2k + l)x J T Ш	[si Bm - 2A? + 1)ж J J *
OG
з1(ж) 1	f 1 f sin ж I .	Г в1(ж) 1
v 7 V	11	I 	 J	V И rp ----- 	 J	>
с1(ж)/*	* J ж [cosx)	[с1(ж)/*
fsmж , _. , ч	^совж . _	. . ч
12. 	da; = Si (ж).	13. 	dx = С + In ж - ci (ж).
J ж	J ж
о	о
ж2 [cos ж)	ж [cos ж) [ si (ж)
f 1 J sin ж 1	1 J sin ж 1 1 r cos ж l 1 J si (ж)
J ж3 [cos ж/	2ж2 [cos ж/ 2ж I sin ж / 2 \ ci (ж)
16. I i{ 8ШЖ 1 dx = ^1п|ж|т^ с!Bж).
J ж [ cos ж j	2	2
17 Г llslnx\dx^ 3 f 81(ж) 1 1|
J ж [cos ж/	4 [с1(ж)/ 4 \ ci (Зж) /

182	Гл. 1. Неопределенные интегралы	[1.5.42
Г t-ж V
С <	>
I ctg ж j
B2fe~1 - 1)
| ч
1.5.42. Интегралы вида I хрI "ь*~ > dx.
. x'tgxdx =
2. j^t^ g(i)"
[cm. 1.5.44, 1.5.45].
4. \4^Jп+\ у±^(пугх}2к-2п r\
\ctgx/	^Q2n-2k\kJ I sin ж/	l ; J \ctgx
-2ndx	[c. 1.5.44, 1.5.45].
Г Г tg Ж 1	Г tgiC 1	( COS Ж 1	Ж2
5. \x< G > с!ж = ±ж< & f+ln< . > - —.
J [ctg ж]	I ctg ж]	( sins j 2
1.5.48. Интегралы вида \ xr s'mp x cos4 x dx.
Г	1
1.	xr slnp ж cosg ж dx = у	г^- [(р + д)жг sinp+1 ж cos9™1 ж +
+ гж smF ж cos ж — r(r — 1) \ x smF ж cos ж аж —
— rp ж7*™1 sin33™1 ж cos9™1 ж dsc + (g — l)(p + g) жг slnp ж cos9™2 ж dx].
2.	=t	— [—(p + q)xr slnp™ ж cosg+ ж +
(p + gJ L
1) xr
ж7"^1 sin13^1 ж cos9^1 x dx + (p — l)(p + g) жг sl
( )	sinp ж cosg x dx
rg 7"^1 i13^1	9^1 d +
i
о	• P	q i	Г	Р+1	9 — 1
3. ж smK ж cos x ax = 	 ж sirr ж cos ж —
J	+ L
— sinp+ ж cosg™ ж rf~ + (g — 1) ж slnp ж cos9™
1	Г
4.	= 	Г—ж sin13™1 ж cosg+1 ж + sin13™1 ж cosg+1 x dx +
Р + Ч1	J
+ (p — 1) ж slnp™ ж cos9
Г „sin ж . жг^/ \kfm>\ I xp dx
5.	жр	Aж=> (-l)fc( , 	^т^	см. 1.5.45.
J созпж	^	\ k J I cosn^2k x
k=0
Г „81п2т+1ж , v^, xfc/m\ Г жр sin ж
6.	жр	с*ж = > (-1I, 	™г™™^ж	см. 1.5.46.
J	cos^ ж	^l ; V к J J cos«^2fc ж	L	J
w Г „ sin ж .	жр	Р Г ж15
7.	жр	dx = т	ч	i	?-— 	i— dx	см. 1.5.45 .
J cosn ж	(га — 1) cos71^1 ж п, — 1 j cos"^1 ж
л	2тт)	''7г	л-	п
„COS Ж .	v^/ \к(ш\\х,
8.	жр	с?ж = > (-1I, I 	от—^~	см. 1.5.44.
J slnn ж	f^nK } \ к ) ] slnnfe х	[	J

1.5.44]
1.5. Тригонометрические функции
183
dx =
fe=O
-l)k(m) f XPCOSX
4 \k)\ sln^2fe :
с?ж
„
COS X
11.
sin ж
ж cos ж .
sin ж
(n — 1) slnn * ж n — 1 J slnn г x
,p-i
In
Г ж sin ж
12.	— dx
J cos2 ж
-In
[см. 1.5.46].
[ см. 1.5.44].
ж жл
1.5.44. Интегралы вида
Г жр ^ж	хр~г[рБт ж + (q — 2)ж cos ж] д —2 Г хр dx	р(р — 1) ( хр~2 dx
¦ - 2) J sin9 ж
3.
4.
5.
x dx
ж cos ж	1	9^2
(g - I)sin9~^ (g - l)(g - 2) sin9 ж g-1
> - 2) . . . Bn- 2A; + 2)[sina; + Bn-
^ Bn - l)Bn - 3) . . . Bn - 2A; + 3)Bn - 2k + l)Bn - 2ife) sin2n"
6.
- 1) . . . Bn-
Bn - 2ife - 1)жсозж]
^ 2nBn - 2) ... Bn - 2k + 2)Bn - 2ife)Bn - 2& - 1) sln2nfc ж
Bn- 1)!! Г xdx
+
2теп! sin ж
7.
xp sing ж
g-2 f dx	p(p + 1)
c,:nq — 2 „ "¦"
q-l) xp sin9 ж (q - l)(q - 2) J xp+2 sin9 ж
BA;)!BA;-n)
кфп/2
ctgs
^ + (n
!Bfc -n-1)
io.

184
Гл. 1. Неопределенные интегралы
[1.5.45
X2 (JX
k=l
, x dx . . . ^ n ( x dx sin ж + ж cos ж 1 ( x dx
12. 1^-5— = — #ctga; + ln sin ж. 13. ^^— =	r^i	1—
2 sin ж
2 sin ж *
14.
x dx	x cos ж
1.5.45. Интегралы вида
- - ж ctg ж + - In
хр dx
1.
2.
4.
5.
6.
7.
х-
p dx
— (q — 2)x sin ж] q^2
COS*? Ж
(9-
2Г^
1 J COSg"
p(p -1)
da;
cosz ж
x dx
cos2n ж
[|ж| < тг/2; р > 0].
[p > 1; |ж| < тг/2].
- 2Jn. . . Bn -
^ Bn - l)Bn - 3) . . . Bn - 2A; + l)Bn - 2fe + l)Bn ¦
(ж tg# + In
ж dx
cos2n+i ж
1
l)Bn - 1) . . . Bn -
- 2fe - 1)ж81пж ^
2n + 1 ^ 2wBn - 2) . . . Bra - 2ife + 2)Bn -
)S^n^/lc Ж
Bn-l)!!
- 2)жр+1 cos^™2 ж
dx
dx
dx
J(n^l)!
In ж +
- 1 J xp cos*?™2 x (qr - l)(g - 2) J жр+2 cos*?^2 ж '
^2fc^n+l
[|Ж|<тг/2]„
8.
da;	tga;
жта cosz ж
(n
<7г/2].
9.
11.
12.
ж da;
^2fc
cos ж ^ Bк + 2)BкI	J соэ^ж
ж cf ж ж sin ж — cos ж 1 Г ж cf ж
ж^ж	,
—-— = ж tg ж + in | cos ж
COS Ж
2 cos2 ж
2 cos ж *
ж dж ж sin ж
12	2 .	,
	— =	1— ж tg ж Н— In cos ж .
cos4 ж 3 cos*5 ж 6 cos^ ж 3	3

1.5.48]
1.5. Тригонометрические функции
185
1.
2.
3.
5.
6.
8.
9.
1.5.46. Интегралы вида Я(жр, sin ж, созж, а + bsinx + ссовж) dx.
xpcosxdx	xp	v f хр~г dx
(а + bs\nx)q
хр sin х dx
(a + bco®x)q (</ —1N(а +
(q - l)b(a + ftsi
xp
(q — 1N J (а + бзтж)^
p f хр~г dx
_xdx_
lisins
+
(tg[(ir-
\ctg[Gr^
licosx
ж cos x dx
-2x)/4] 1
-2*)/4]J
2 In
(q — l)b ] (а
fcos[Gr-2*)/4n
\sin[Gr-2aO/4] J
sin (ж/2)/'
tg [Bж — тг)/4] 1
(lisina:J ~ T 1 ± sin ж + \ctg[B» - тг)/4] /'
ж sin ж с?ж
—^-1
(x/2)
x dx
a2 +
tgж — а
(a2 + 1)A + а
ж sin ж + cos ж
[(аж — 6) sin ж + (а + 6ж) cos ж]2 Ь[(ах — b) sin ж + (а + bx) cos ж] *
cos2 х dx	tg ж
[a cos ж + (аж + 6) sin ж]2 а[а + (аж + Ъ) tg ж]
Ж8ШтЖСО8ПЖ
1.5.47. Интегралы вида
Условие: 0 < А; < 1.
Обозначение: А = у 1 — k2 sin2 ж .
ж sin ж cos ж .	ж А 1 _.
	<Ь = -_ + _я(ж
3.
ж sin ж cos3 ж
1 — ife2
2 — 5
9k4
ж sin ж 1
[3(A2 -
ж sin ж cos ж
- A;2 sin ж cos x].
ж	1
_ Г ж sin3 ж cos ж . 2 — fe2 sin2 ж 1 ,._. 1Ч _. . Ч1
7. j 	^	da; = ж	^	-^ [Е(Ж, fc) + F(x, к)].
Г ж sin ж cos3 ж . к2 sin2 ж + к2 — 2 1 — к2^, . ч 1 _, . ч
	аз	 = ж	1И™л	'	м— ^(ж' ^) + Т4 ^(ж? ^)-
1.5.48. Интегралы вида (ж + 6) п\	> dx.
J	I cos аж j
>/2]	/-,\2fc
1. (ж + .
Гятаж! ж=п!Г ^ fc/l\ (ж + fe)-2fc r cos а
[cosaxj	a [ ^	\«y (^ — 2A;)! lsina
(n-2ife-l)!

186	Гл. 1. Неопределенные интегралы	[1.5.49
Г/ . ч f sin аж 1 .	1 , . ч г cos аж ] if sin аж 1
2 (т + Ьк	> /7 т —- 1С— (т 4- h)i	1-4	I	>
J	[ cos аж J	а	I sin аж J a1 { cos аж J
IV .^Jsinaa;]	1 Г	.2 2 1 r cos аж 1 2 .	.f sin аж 1
J	\ cos аж J	a \_	а2_|1зтаж/ a2	\ cos аж J
. Г/ , ,,3(smax\	ж + 6 Г/ Lx2 бТгсоэаж! 3 Г/ ч2 2] [sina
4.	(ж+ 6) <	Иж = т	 (ж + 6)	-N . ^ + — (ж + Ь)	-N
J	[ cos аж J	a [	a2 J I sin аж J a2 [	a J I cos a
Г 1 fsmaжl	n(	Г 1 fsintl	Г 1 fcostl \
5.	7	-—— <	> аж = a cos ao — <	> at =F sin ao — < . > dt
I (x + b)n \cosax)	\	Jtn{cost)	J tn {sint J /
[t = а(ж 4
f if з!паж 1	ir^ (A; — 1)! . h\~k( \n-k-if cos [тг(^ — A;)/2 — аж] 1
6- J (ж + 6)п\СО8аж Jto = Ъ (n-1)! (Ж+ j (^aj	\8т[тг(п-А;)/2-аж]/
cos (ab + Tin/2) 1 . . / .	ч Г sin (об + nn/2)
;	> ± si (a6 + ax){ )	;
С1(ао + аж)< '	. ч > ± si (ao + аж)
- i 1 Г sin аж 1 .	. f si (аж + ab) 1 , . _ f ci (аж + ab)
7. 	r<	>d^ = cosa6< . ,	,{ >±sma6J v	;
ж + 6 \ cos аж J	\ ci (аж + ab) j	\ si (аж + aft) J
Г 1 fsinaжl .	1 f sin аж 1 . Г 1 f cos аж l .
8. 7	7T^\	> dx =	7<	f±« 	ri	f dx.
J (ж + оJ [ cos аж J	x + ft [ cos аж J J ж + ft I sin аж J
Г 1 ^таж!	1 ^таж!	a r cos аж l
J (ж + bK X cos аж j	2(ж + bJ \ созаж j 2(ж + b) 1 sin аж J
Г sin (об + nn/2) 11
[ cos (ab + ?m/2) J J
1 I sin аж ,
* ax.
2 J ж + b 1 cos аж
1	1
-sinaaj rfa; = 7 [cosabsi (аб + аж) — sinabci (аб + аж) — si (аж)].
о
7гтsinaaj rfa; = 7
ж(ж + о)	о
ж
1.5.49. Интегралы вида еаж sinp ж cosg ж а'ж.
Г	if
1.	еах sinp ж cosg х dx = —	-;	г^- < еах sinp ж cos9™1 ж [a cos ж + (р + a) sin ж] —
j	а -г ^р -г Q) ^
— ра еаж sin33™1 ж cos9™1 ж dx + (а — 1)(р + q) eax sinp ж cos9™2 ж а*ж >.
2.	= —	т	— < еах sin13^1 ж cosg ж [a sin ж — (р + a) cos ж] +
а2 + (р + gJ [
еах sin13™1 ж cos9™1 ж а*ж + (р — 1)(р + q) eax sinp™2 ж cos9 x dx\.
+ да
3.	= ^r	T77<eaa;sinp™ ж cos9™ ж fa sin ж cos ж + gsin ж~рео82ж1 +
a2 + (p + gJ '
- q(q — 1) еаж sinp ж cosg ж а*ж + р(р — 1) еах sinp ж cos9 ж а*ж >.
4.	= —т	г	^~<eaaJsinp ж cos9 ж(ав!пж cos ж + gsin ж^рсоэ ж)+
а2 + (р + qJ {
+ д(д — 1) еах sinp™2 ж cos9™2 ж а*ж — (д — р)(р + а — 1) еаж sinp™2 ж cos9 ж а*ж >.
5.	= -^	гтг < еах sin13™1 ж cos9™1 ж(а sin ж cos ж + a sin2 ж — р cos2 ж) +
а2 + (р + дJ [
+ ~(~ ~ 1) е<1Х sinp™2 ж cos*1™2 ж а*ж + (д — р)(р + д — 1) еах
sinp ж cos*1™2

1.5.49]	1.5. Тригонометрические функции	187
Р	f • 1 Л Р	I	f	I \ f • 1 \ р—1
, пт i —"-«- I	a	nv sm ож	ро	„^ cos ож sin ож
3- е \ к } dx=	еах{	\ Т 2 , 2,2 еаж^ .	Н	> +
J [ cos ож J	а2+р2сИ [ cos ож J а2+р2о2 [ sm ож J [eostej
_l_ J v*	'	I л	У
а2+р262 J \ cos 6ж ^
^	Bn)!62fee^
^ Bn - 2k)\[a2 + BnJ62][a2 + Bn - 2J62] . . . [a2 + Bn -
cos 6ж X / sin ^ж
sin 6ж j \ cos 6ж
f . i ч 2n-2fc	/¦	, ч /¦ . j ч 2n —2fe —1
sm ож	,	,4,1 cos ож sm ox
x \a{	\	T 2п-2Ш	l J	l
[ cos 6ж J	[si
Bп)!62пеаж
[a2 + BnJ62][a2 + Bn - 2J62] . . . [a2 + 462]a"
8.	BП)^ ^y]fcf
9. fe(f
I cos bx
t Bn - 2k + l)![a2 + Bn + lJ62][a2 + Bn - 1J62] . . . [a2 + Bn - 2k + 1J62]
{sin 6ж 1	f cos 6ж 1 f sin 6ж 1
и f	T (^n- 2k + l)b< , ><	>
cos 6ж J	[ sm bx ) { cos ож J
x a
io.	=e-l^—+ 2k + l42,n_k
k=0
. ax . „„. ^^ . .	eax Г f sin 6ж 1 . f cos 6ж 11
sin bx | ^ = ^_ Г f sin Ьж |	cos Ьж 11
cos bx J	a2 + b1 l l cos ож J { sin ож J J
. еаш si
J [совбж]	2a a2+462\2	)
13. I еаш sin 6ж cos еж dx =
eax [asin F + c)x — F + c) cos F + c)x asm F — с)ж — (b — с) cos F — е)ж!
a2 + F + eJ	+	a2 + F^cJ	j
* A [ ax . 2 ,	j еаж Г
14. e sin ож cos еж а ж = —— 2
J	4 [
a cos B6 + c)x + B6 + c) sin B6 + с)ж a cos B6 - с)ж + B6 - с) sin B6 - с)ж]
a2 + B6 + сJ	а2 + B6 - сJ	j
2 , eax Г asin 6ж — 6cos 6ж
P	ax Г
15. eax sin 6ж cos2 еж dx = 	 2
J	4 |_
a2 + 62
asin F + 2с)ж — F + 2c) cos F + 2с)ж asm F — 2с)ж — F — 2c) cos F — 2е)ж1
+	a2 + F +2cJ	+	a2 + F-2eJ	J
ax (slnbx X^P j	e<lx	\	Г8т6ж1^р
\ cos 6ж j	(p — l)(p — 2N2 [	\соз6ж/
cos 6ж I I sin 6ж I	a + (p - 2) 6 I ax I sin 6ж I
. , H l f	+ 7	7T7	^\I2 e 1 и (	dx
sm ож J [ cos ож J	J (p — l)(p — 2)o2 J [ cos 6ж J

188	Гл. 1. Неопределенные интегралы	[1.5.50
_ Г _а.2( sin аа;1 , %/ж _а2 /4 Г Im erf (ж — га/2) 1
' J	[созаж]	2	[Re erf (ж - га/2) J "
г ( +¦ 1 ^
1.5.50. Интегралы вида еаж<	> da;.
J [ ctg г f
ж
I ctg с
2. fe(	\dX=\	}T
J [ ctg ж J	a [ ctg ж J a
3. \е\\\х	±е1
J I ctg ж J	a	I ctg ж
1.5.51. Интегралы вида Я(ж, еаж5 sin &ж, cos bx) dx.
b
Обозначения: sin if =		¦, cos <p =
/a2 + b2
[ p ax(s'mbx^ j	xpeax Г J sin bx 1 J cos bxY\
J	[ cos bx J	a2 + b2 \_ \cosbx j \mnbx)\
- P \хр^геах \a(SlnbX X zpb(COSbxX]
a2 + b2 J	[ \cosbx) [slnte/J
_ xpeax ( sin (bx + <p) 1	p Г p_i аж f sin (bx + <p) 1
~ л/а2 + Ъ2\ cos Fж + <p))~ л/a^TW J ^ 6 [ cos Fж + у?) J
dx.
ibx J J
da;.
3. ж е аж<^	>с!ж=-< >[(а + г'6) 7(А, аж + гбж) =р (а ~ *^) т(^> аж ~ *^ж)]
J	[cos Ьж J	2 [1J
о	l~ , I —1
\ dx = -[ l \[(a + i6)^AF(A, аж + *6ж) =F (a - ^ГЛГ(А, ах - ibx)].
J	2 [1J
4. I xel1
J	[cos bx
Г nax(smbx\ = ^ ()	f ( ) |
JX e [&/ Ж	6 ^ (^ + l)!B + 62)fc/2t(te + Jb)J
Г asBfsin6a;l ,	еаж Г/ а2 - 62 \ f sin 6ж 1 / lab \ (cos 6ж 11
6. жеаж i dx =	ая- 2 2 W T Ь--—^ И.
J [ b J	2 + 62 2 + 62 [ b J 2 + b2 J { 6 j J
i dx =	ая- 2 2 W	T Ь--—^	И.
[ cos bx J	a2 + 62 [ \	a2 + 62 / [ cos bx J \	a2 + b2 J { sin 6ж j J
„, f 2 aJsinkl ,	e Г 2 2(a2~62)	2a(a2 - 362I f sin bx 1
J	\6J	2 + fe2f	2 + Ь2	B + Ь2) Л/
4ab	26Ca2-62I f cosbx
2 + fe2	J\
(a2 + 62J J\sin6a;J'
8. \4S^X + c)\
cos Fж + с)
v k-i (n + 1)п . . . (п — к + 2) п-к+i Г sin (^ж + с + /гу?) 1
. I же < \, _ { У dx =
cos (bx + c)
}1 аж J sin (bx
a2 + 62 e \ cos Fж + с + 2y?) J "

1.5.52]
1.5. Тригонометрические функции
189
10. [ - eix sin xdx = Si Bж) + г [С + In Bж) - d Bx)].
sh (ax + 6) I I sin (еж + a) I
i )	/ } i	}
ch (аж +
Г . /
1. sh аж
J
N f si
[ co
sin (еж + d) 1 ,
v ]" ; > dx=
cos (еж + d) J	a2 + c2
f !
2. ch
J
1
J
sin (еж + d) 1 .
cos (ex + d) J	a2 + e2
ch(ax + b)
sh
cos (ex + d)
sin (еж + d)
ax.
cos (еж + d)
-5——~ sh(a
a2 + c2
sin (еж + d)
cos (еж + d)
Г . f sin ж 1 . 1 . f sin x 1 1 . f cos ж ]
3. sha;<	>аж = -сЬж<	>=F^si^<	f.
J	[ cos ж J	2	[ cos ж J 2 I sin ж J
sin ж 1 1 . f cos ж l
>=р-сЬж<	>.
cos ж J 2 I sin ж J
Г .
4. спж
J
5.
/2m
fc=O
cos (еж + d)
sin (еж + d)
cos (еж + d)
sin (еж + d)
22m+2n-2 Z_j Z_^ Bm ~~ 2jJa2 + Bn - 2JcJe2
x {Bm - 2j)ash[Bm - 2j)(ax + 6)] cos [Bra - 2ife)(ca; + d)] +
+ Bn- 2ife)cch[Bm^ 2j)(a» + 6)] sin [Bra -
d)]}.
6. f sh2m (аж + 6) sin2n+1 (еж + d) dx = ( /^J ( 2W ) V 7—
J	22m+in \ m J ^ Bn
x
- 2k + l)c
)j+kBm\Bn
22m+2n-l ^ ^ Bm _ 2iJa2 + Bn _ 2Jb + l)^2 ^
^ 2j)(aa; + 6)] sin [Bn - 2k + l)(ca; + d)] -
- Bra - 2fe + l)cch [Bm - 2^)(аж + 6)] cos [Bn ~~ 2k + 1)(еж + d)]}.
7.
12т+1(аж + 6) sin2'
x ch [Bm — 2j + 1)(
x {Bm - 2j ¦
d) dx =
i=o
g g Bm _ 2i + xVJ + Bn -
^ 2j + l)(ax + 6)] cos [Bn - 2k)(cx + d)]
Bn- 2ife)csh[Bw^ 2j + l)(ax + 6)] sin [Bra -
d)]}.

190	Гл. 1. Неопределенные интегралы	[1.5.52
J
" " (-ir+fcBm.+ 1)Bn +
22m+2n Z^ Z^ Bm _ 2j + lJa2 + Bra - 2ife + lJc2 ~
x {Bm - 2j + l)ach[Bm - 2j + l)(ax + 6)] sin [Bn - 2fc + l)(ca; + d)] -
- Bra - 2fe + l)csh [Bm - 2j + 1)(аж + b)} cos [Bra - 2k + 1)(сж + d)]}.
q
9 1 ahzm (' n t 4- h\ rc\Q.zn (n'v 4- A\ rl t — v ^f \ """ If *"" \ r» _\_ X '" 7	\ ' 	\ J / Y
x sh [Bm - 2j)(ax + b)]
^ Bm-2j)a
2n"
к
m — l n — 1
i	 V V.
, + 2n^2 Z^ Z^
i=o fe=o
x cospn- 2k)(cx + d)] + Bn- 2fe)ech[Bm~ 2j)(ax + b)] sin [Bn - 2k)(cx + d)]}.
/2m\
10. J 8Ь2т(аж + b) со82п+1(сж + d)dx = 	^^ J У ,Л fe, /^ x
(-1)
Bn-
/	2 \ i
x sin [Bn - 2fe + 1)(сж + d)]	— —
2m+2«~1 Z-j Z^ Bm _ 2jJa2 + Bn - 2ife + lJc2
x {Bm- 2j)ash[Bm^ 2j)(a» + 6)] cos [Bra - 2^ + l)(cx + d)] +
+ Bn -2k + l)cch [Bm - 2j)(aa + 6)] sin [Bn - 2k + 1)(еж + d)]}.
11. I зЬ^ТГ1^А(аж + b) coszn(cx + d) dx = x '" 7 У	\ ^ / x
J	22m+2n ^ Bm — 2j + l)o
m n — 1
v rh \(e)m 	 9i* -J- 1 V/rr 4- Л^1 4-
'v™ ' »n - 22m+2n-i ^^ Bm - 2j + lJa2 + Bn - 2^Jc2
x {Bm- 2j + l)ach[Bm- 2j + 1)(аж + 6)] cos [Bn - 2A;)(ca; + d)] +
+ Bn - 2fe)csh [Bm - 2j + 1)(аж + b)\ sin [Bn - :
12. f sh2m+1 (ax + b) cos2n+1 (еж + d) dx =
22m+2n z_j Z_^ Bm - 2j + lJa2 + Bra - 2ife + lJc2
x {Bm- 2j + l)ach[Bm- 2j + l)(ax + &)] cos [Bn - 2^ + l)(cx + d)] +
+ Bra - 2fe + l)csh [Bm - 2j + 1)(аж + 6)] sin [Bn - 2k + l)(cx + d)]}.

1.5.52]	1.5. Тригонометрические функции	191
Bт\ Bпл
/2п\	Bтл
1 т-1
х sin [Bn - 2ft) (ex + d)] + ^U X) f2 ' J о'-ь sh К2™ - 2j)(ax + 6)] +
3=0 v	J;
(_l)n —1^1	^)\ .
x cos[Bn^ 2A;)(c» + d)] + Bra - 2fe)cch[Bm^ 2j)(a<c + 6)] sin [Bra - 2А;)(сж + d)]}.
'2m + Г
b) sin (еж + dj to _ o2m+2n ^ B _ 2 . 1)a x
i=o v	J ;
i J\k, x
x {Bto- 2j + l)ash[Bm - 2j + l)(ax + 6)] cos [Bn - 2Jc)(cx + d)] +
+ Bn - 2k)cch [Bm - 2j + l)(ax + 6)] sin [Bra - 2^)(сж + d)]}.
1 / \^ _
{_l)k/2m\/2n + l\
xro-Jf2n 2fr I \)(rr I rfli I (~1^" V'V	Vi/V fc /
M	/J г2^2" ^ ^ Bm^2iJa2 + Bn^2fe + lJc2
1 \?illL ?ij 1A oil llZiiib ZjJ llUiJb T^ "/I olil lIZill» Zift/ T^ 1 II СЛ n^ /I
- Bn - 2ife + l)ech [Bm - 2j)(ax + b)} cos [Bn - 2k + 1)(еж + d)]}.
16. f ch2m+1 (аж + b) sin2n+1 (еж
v-"- - 2i + !Ja2 + Bn ~ 2k + !Jc2
x {Bm- 2j + l)ash[Bm- 2j + 1)(аж + 6)] sin [Bn - 2ife + l)(cx + d)] -
- Bn - 2A: + l)cch [Bm - 2j + 1)(аж + b)] cos [Bn - 2ife + 1)(сж + d)]}.
Bm\ Bn\	Bm\
Г	I / I /	V / n^1
17. сЬ2т(аЖ + Ь) COS2" (СЖ + d) dx = Ш2т+2тГ Ж + 2m+2n-l E
^	fc=o
/2n\	Bm\
I / m^1 I ' /
x sin [Bn - 2k){cx + d)] + ?п+2„_1 ^ V J 7 sh
i=o
'2m
^	III	 i 74	 X
^ e E
Bm2;)y+Bn2fc)c
x cos[Bn- 2A;)(ca; + d)] + Bn - 2fe)cch[Bm- 2j)(ax + b)] sin [Bn - 2А;)(сж + d)]}.

192	Гл. 1. Неопределенные интегралы	[1.5.53
'2га\	/2m + l\
^ ~ Bт - 2i + !)а Х
'2т + 1\/2га
т п — 1	1	.	| 1 ,
х sh [Bт - 2j + 1)(ах + 6)] + , „ _ ^^	V J У V
j ^ Bm - 2j + 1Jа2 + Bп - 2кJс2
х {Bт- 2j + l)ash[Bm - 2j + 1)(аж + 6)] cos [Bга - 2^)(сж + d)] +
+ Bn - 2fc)cch [Bm - 2j + 1)(аж + b)] sin [Bn - 2k){cx + d)]}.
2m\	/2ra + l
19. |сп2тта(аж + 6) cos2n+1 (cs + d) dx = ^? ^
2m\ /	\
+^^t e e Bm _ 2;)/a/+ Bn
x cos [Bn - 2^ + 1)(сж + d)] + Bn -2k + l)cch [Bm - 2j)(aa? + 6)] sin [Bn - 2fc + 1)(сж + d)]}.
20. f ch2m+1 (аж + b) cos2n+1 (еж + d) dx =
2m +
Mi
k
22m+2n Z^ zL^ Bm - 2j + lJa2 + Bn - 2ife + lJc2
x {Bm- 2j + l)ash[Bm- 2j + 1)(аж + 6)] cos [Bn - 2Jfe + l)(cx + d)] +
+ Bra - 2^ + l)cch [Bm - 2j + 1)(аж + b)] sin [Bra - 2fc + 1)(сж + d)]}.
1.5.58. Интегралы вида жр<	2
J [cosж
<
[co
2 {sin ж
i , Sin Ж
cos ж"
	 xn	<
\ .	/^/8(ж2)]	Г |шЖ2)	1/со8ж21
\ dx = \ — < о >• 4. ж<	о > da; = q=-<	2/-
J	У2[С(ж2)]	J [созж2/	^2[81пж2/
2 1 1
J
sin ж2 1	х ( cos ж2 1 Гтг \ С(ж )
cos ж J	2 [ sin ж / V 2 ] 8(ж2)
si sin ж2 1 .	ж2 f cos ж2] 1Г8тж21	Г 1 [шж2] , if si (ж2)
2 Мж = Т	{	2 М	<	2 Г-	7. — <	2Г^Ж=™\	2
cos ж J	2 [ sin ж j 2 [ cos ж j	J ж [ cos ж J	2 1 ci (ж )
l/sina;2
1 J sin ж2 1
ж [ cos ж J
8. I — <	2}dx = --<	2f±v27T^ 2
xl [cosж J	ж [cosж J	I S(x )
9- I <	'2,^,4 МЖ = 1/^: СШ 	Z^	1 ^.r/o_ , «Л2 ..-¦ - >±
&J/Da)]
cos (аж2 + bx + c) I """ V 2a | w" 4a | С[Bаж + bf/{4a)]
4ac — 62 j С[Bаж

1.6.1]	1.6. Логарифмическая функция	193
1.6. ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ
1.6.1. Интегралы вида \xp\nqxdx.
g(a;)ria; = a;lng(a0- f Ж^(^ ds.
J g(x)
. f /(ж) 1пте ж& = F(aj) lnn x - n [ ^^ In*1 ж йж	Lf(^) = f f(x) dx).
J	J ж	L	J	J
1пдж^ж = ^!^!^^^±1 |>ln*+1*da;.
g+1	g+lJ
5.
p + 1	F +
в. Жр In" a, dx = ^— ^(-l)*(n + l)n(n - 1) . . . (n - fc + 1)	'	[P Ф -1].
J	n -h i fc=Q	^p -t- ij
8.	| ^ d« = li (xp+1)	[P/-1].
9.	=ln|Ing| + V (P+1J In*».
^^ A;! A;
fe=i
9
f lng ж ,	lng ж	g f In91 ж ,
10. 	daj = -7	:	7 H	— 	dx	p, -g / 1 .
J жр	(p-l)ajP-1 p-lj ж?7	LF' ?7^ J
Г1пдж , 1пд+1ж
11. 	dx = 	.
J ж	g + 1
пж	-1	^ (n + l)n...(n-A; + lI n^fc
	dx = 7	7>	7	Vm	-In ж	m^l.
то	( + 1)т1^	(l)fc+1	L ^ J
. ilnq xdx = xlnq x - ql In9 ж da;	[g^ -1].
n
. ПппжAж = ж^(-1Iг(^)^!1пте"/гж. 15. П
13. ilnq xdx = xlnq x
14
J	k=o
16. In2 x dx = x In2 ж — 2ж In ж + 2ж. 17. In3 x dx = x In3 ж — Зж In2 ж + 6ж In ж — 6ж.
J
18. \xp\nxdx =
J
19.
20.
p + 1 (p + 1J (p + 1K (p + lLJ
Г In ж , In2 ж	Г In ж .	In ж 1
21. 	dx = 	.	22. \—T-dx =	.
J ж	2	J xA	xx
f In ж ,	In ж	1	f In2 ж , In3 ж
23.	^	24	d
ж3	2x2 Ax2	J ж	3
^ Г In2 ж , In2 ж 2 In ж 2	П?Ъ Г In2 ж ,	In2 ж In ж 1
25. —— dx =	. 26. —— с!ж = —-
J ж3
ж2	ж	ж ж	J ж3	2ж2 2ж2 4ж2
13 А. П. Прудников и др., т. 1

194	Гл. 1. Неопределенные интегралы	[1.6.2
Г хр dx
1.6.2. Интегралы вида —-—.
fxpdx _ ^xp+1	р+1 Г хр dx
' ] \nq х (q-l)\nq~x x q-ljli^^x'
^_	1 «ду %Jb елу	&JL/	^к л	I f # €/ | JL I	I f f с/ | JL I	| » / TTJj ~T~ X \
^9 1 ri	/ , ~,	_ ч /	ГТ	/	. ч , "Z T. i	7	., \ i П I Ж	I.
' J I	l ;"
In ж	J жр In9 ж (g — 1)жР In9™1 ж ^ — 1
-' 1пте ж ~ пжт~1 ]~ (n - l)(n - 2) ... (n - A;) Inn^fc ж +
6.
с!ж	Г dx
l|I| 8 \
1.6.8. Интегралы вида \{x + aL\nxdx.
. \{x + a)m\nxdx= ^—{x + a)m+1\nx
ж
m — k fe+1
Г	1	ж2
3.	(ж + a) In ж da; = — (ж + 2ах) In ж — ах	—.
4.	(ж + аJ In ж da; = - (ж3 + Заж2 + За2ж) In ж	а2ж.
J	о	У Л
5.	(ж + а) In ж аж = — [(ж + а) ^а]1пж
За^ж^ з
	а ж.
, lnn ж с!ж	ж lnn ж
(ж + а)т (т — 1)а(ж + аO71^1 (т — 1)а J (ж + а)^1
m - 2 f 1пте
1пжс1ж	(m-l)aj (ж + a
(ж + аJ	ж + а а ж + а
In ж dx	In ж	1	1
+	+
(ж + аK	2(ж + аJ 2а(ж + а) 2а2 ж + а"
	In ж	1	Г ж . ^: (-l)fe /n-2\ / ж xfc
«я \ / . \ ^„ -I 	1	 /	^\ „ ^ j 111
п-
In т3 Нnf*	т* —I— л?	/ т
I JL JL JL еду \Л qJLj	«	« еду	L4/	™~	I	еду i
8. 	 = In ж • In	h Li2	.
ж + а	а	\ а {
, In ж da;	In ж
у»
12.	=2[Aпж-2)(ж + аI/2+2(^аI/2агс1ё(^^) 1	[а < 0].

1.6.5]
1.6. Логарифмическая функция
195
хт In ж
1.6.4. Интегралы вида I ^^~—^ ,п dx.
Условие: а > 0.
(а2±х2)п/2
1.
In ж . 1,	ж 1 _ _ / гж .
ах = — In ж • arctg	Im L12 ( — I.
х2 + а
а
Гж1пж . 1 т . / ж
2- ^5	о «Ж — 7 Ll2	of	¦ о"
J ж2 + а2 4 V а >	2
о
ж In х а /	ж \ а / ж \ ж
3. | —	 dx =	СЬ I 2 arctg — 1	СЬ 1 тг — 2 arctg — I + ж In а — a In a • arctg —.
ж2 + а2 2 V	а У 2 V а I а
4.
5.
6.
7.
^2 + а2
In ж
ж2-а2
ж In ж
2а
In ж • In
ж — а
ж + а
т . I Ж \ т • / *^
¦Li2 - I - Li2 I --
V а I	\ а
j	л.	I	и; \ ±	1/2	2\ 1 2
аж = — — Li2 II	21^— in а • In (а — ж ) — In а -
24"
In ж	а . х 1 /	.ж
- аж = In — arcsin	— СЬ ( 2 arcsin —
а 2
In ж	а	ж 1 /	ж
¦ dx = In — • arccos	1— СЬ ( тг — 2 arccos —
1пЖ	л	1Т. Г, 1 /	Г^П	9\2l ,1,2
,	аж = — Li2 =Ь^7 (ж — Vж^ ± а2 ) Н— In ¦
/ж2 ± а2	2 I а2 1	М ^ 2
4
1.6.5. Интегралы вида \ xp In (ax + 6) с/ж.
. [/(жIпте(
J
2a
^
[t = ах + 6].
Г _i	ха	аха+1	(	-ах\
2.	ж In (аж + о) dx = — In (аж + b) -\	7	— 2Ft I 1, а; а + 1; ^^ .
J	а	а (а + 1N \	6 у
3.	[жт1п(аж + 6)а1ж = —^— (хт+1 + (-1)т^хт) Ш (аж + Ъ) +
J	w +1 V	am+1 У
T,fe —1 •
Г	1
4.	In (аж + b) dx = — (аж + b) In (аж + b) — x.
J	a
f 1 /	i4i	1 Z' 2 Ь2\ , ,	I4 1 /Ж2	6ж\
5.	ж In (аж + о) аж = - I ж	 I In (аж + о)	I	I.
J	? \	о, J	А у z а у
6.	[ ж2 In (аж + Ъ) dx = - ( ж3 + — ) In (аж + Ь)
J	3 \	а у
1/ж3 6ж2 Гж
• •
1п(аж
In (аж + 6)	а
3 V 3 2а а2
dx
8. |'п(аа; + 6)^ =
(р — 1)жр^1 р — 1 J (аж +
— 1 In (аж + 6)	1
9.
10.
13*
ж"
In (аж + 6)
ж
772—1	Хт^г
dx = In |6| • In |ж| — Lb
m — 1
—ax
In
l /_
^^ k\ax
= In \x\ - In (аж + b) ~~ a
6
In |ж| с/ж
аж + 6
[аб^О].

196
Гл. 1. Неопределенные интегралы
[1.6.6
11.
12.
13.
= 1п|Ь|1п|ж
In2 lax
Е-
fe=i
1п(аж
—^—
fe2
¦ dx = — In x ~~ I	1— 1 In (аж + b).
b	\x b '
\ах\
,'1п(аж + 6)	,	. /ж + с\	Га(ж + с)
14. I —-—;	 dx = In F — ас) In ( 	 J — L12 '
15.
X + С
In (ж + а)
а'ж = — arctg ¦
с
еж
ас — b
(ж + bJ + с2	2с
1
2c
2с
о + 2<р) - ^- С12(тг -
2с
х + 6
0	t
+ ^- С12(тг - 2^0)
2с
6	а — 61
= -, tgcp= 	 .
С	С
1.6.6. Интегралы вида \х т In	с!ж.
м ж + а	1
In	аж =
ж — а
2а Г хр
2.
¦ +
ж — а р + 1 J ж2 - а:
In
(ж - а) + ^— V
3.	1 In	с!ж = (ж + a) In (ж + а) — (ж — а) In (ж — а) = ж In	Ь a In (ж2 — а2).
'ж — а	ж — а
4.	I ж In	ах = — (х — а ) In	Ь аж.
ж — а	2	ж — а
е ,21ж + а	131
5. |ж In	dx = - х In
ж — а	3
13,/2 2ч,
-a In (ж ^а)Н
З
6.	\x*in?L^Ldx =
х — а	4
_ , 1 ж + а
7. 	In	dx =
ж4™ а4, ж + а аж3 а3ж
In	1	h -r—.
жт ж — а
(m — 1)жт™1 х — а
1
ж — а y^ I ~~ (~1)
k=i
m-fc-l
ж
о , 1 . а + ж , т./ж\	( х
8. I — In	dx = L12 I — ^ L12
\а
9.
10. |-^ln
1 . ж + а
dx = — In
xz x — a	x
1 . ж — а 1
	In
а
1.6.7. Интегралы вида ж т In (ж2 ± а2) с!ж.
. f x2n In |x2 ± а2| dx = —^
j ' ' 2n
x2n+1 In |х2 ± а2\ - 2
2k+1
¦х2к+1\+

1.6.7]
1.6. Логарифмическая функция
197
{	Oil	T
-1) 2a arctg-
-¦-	I	П.
2. lx2n+1ln\x2±a2\dx =
Г
г 2п
[ж
2п-
3. I In ж2 ± a2 dx = x ln |ж2 ± a21 - 2ж ¦
2n-
2 . 2i
±а|-
ж
2a arctg —
а In
4.	fa;ln|a:2±a2|da; = - [(ж2 ± a2) ln |ж2 ± a2
к Г 2 i i 2 i 2 i	1 3 i i 2 i 2	2
5.	ж 1п|ж ±a dx = — ж In |ж ±a — — ?
J	о	У
-i 2a arctg —
3la3ln
6. | х3 In |ж2 ± a2\dx = i L4 - а4) In |ж2 ± а2| - ^ ± а2ж21.
7. |^4^dx =
Bт -
Bm - 1)а2
2k
Bm - l)a21
8.
9.
10.
п|ж2±а2|
2тх2
2ma2
\п
J2
k=i
In ж2 ± а2
dx = In ж + — Lb ( =F
= ln a • ln ж	Li2 I T^7
2 V a1
лл . ln\x2 ±a2\	1 2 , 2,
11.	L dx =	In ж ± a
ln
ж
ж + a
ж — a
12.
13.
14.
15.
ж3	2a2 ж2	a2
1
- Li2
2ж
2 arctg —
а
- Ы2(ж) +
+ - In2(l + ж2) - ln A - ж) ln A + ж2).
. 2 ln a	ж 1 , / 2 2\	^1TT /a + гж
- rfa» = 	arete:	1	ln 4(ж + a ) arete	Im L12
a	a 2a	a a	V 2a
(ж + a) In [(ж + aJ + b2
(ж + aJ + c2
2 Ll2 I (ж + aJ + c2 I " 4 ¦

198
Гл. 1. Неопределенные интегралы
[1.6.8
16.
>-y)lni-yT^F riyj1_y/1_
--С12(тг-20)
1 „,
bd
(a^cJ + 62 + d2J '
2d(a - с)
x + с
tgi] =
1 + e cos B(9 - 2<^) - л/1 - e2
1.6.8. Интегралы вида \x m In (ж + Vr±
1. J /(ж) In (ж + Va;2 + a? ) <fa = -2a In a J / (^j) (t2 _ A
2at
t2 -1'
a + Vx2 + a2
2.
-4a /
2/B/-2) Jy2(y-2J
; a >0 .
¦In z dz
tA + 1
5 a > 0|.
. \xpln(x + Vx2±a2)dx=	In (x + V^2 ± a2 )	—
J	l	;	p + 1 l	; p + 1 J
. In (ж + \/ж2 ± a2 ) dx = ж In (ж + V^^a2") — л/х2 ± a2 .
г	.		/ж2 a2\	.	 ж .
. ж In (ж + ^ж2 ± а2 ) dx = ( — ± — ] In (ж + ^ж2 ± а2 )	^ж2 ± а2 .
. ж2 In (ж + ^ж2 ± а2 ) dx = ^- In (ж
J	о
=Ь а2 ) -
. 2\3/2	2
j± ^
7. f ж3 In (ж + V^2 ±a2)dx= (—- —) In (ж + V^2 ± a2 ) -
J	\ 4 32 /	з
16
Ч
— а
32
8.
9.
п(ж
_
In (ж
=Ь а2
dx
(р - 1)хР-г	р - 1
In (ж + V^2 ± а2 ) ,	In (ж + V^2 ± a2 )	Vx2 ± а2
J
k Bn - 3)Bn - 5) . . . Bn - 2fe - 1) /a\2w
(=Fl)n
In
а + v xz + a
+
2T72
Ж
p2 _ n2
arctg -

1.6.10]
1.6. Логарифмическая функция
199
' In (ж + л/х2 ±а2) 1	г^——т;
10. I —	г——	 dx =	— In (ж + уж2 ± а2
л/х2 ± а2
Bп - 1Jп
Bn - 3)Bn - 5) . . . Bn - 2A; -
11.
12.
In (ж
,ll2
dx = In a • In ж ± - In
2
[±x/a > 1].
Bк)ПBк ^ IK \а
,' In (ж + л/х2 — а2 ) . . . .	1,2
13. | —1		^ dx = In |а| • In \x\ + - In
ж	z!
14.
п(ж
—^
dx =
In (ж + л/х2 ± a2 ) 1
In
In (ж + Vx2 ± a2 ) _ In (ж + ^ж2 ± а2
arctg ¦
± a2
ж
а
[\x\>
1.6.9. И нтегралы вида	- In (ж + ух2 ± 1) dx, 1пр(ж + ух2 ± 1'
J ух2 ±1	J
dx.
1.
2.
3.
4
2
In (ж + л/х2 ± 1) с!ж =
In (ж + 1/ж2±1) -
р^	р
2Х In (ж + ^ж2 ± 1) с!ж = i 1п2(ж
¦ In (ж + л/х2 ± 1) с!ж = ^ж2±1 In (ж + л/х2 ± 1) - ж.
. f 1пр(ж + ^ж2 ±1) dx = ж 1пр(ж + ^ж2 ± 1) -
- рл/х2 ± 1 \пр~г(х + ^ж
±1
г	1 [-/2]
. 1пп(ж + Vx2±l)dx =	 ^ (п + 1)п . . . (п - 2А;
J	п + 1
с2=Ы)^
[п/2]
6. 1п2(ж + ^ж2 ± 1) dx = ж 1п2(ж + ^ж2 ± 1) — 2л/х2 ± 1 In (ж + ^ж2 ± 1) + 2х.
1.6.10. Интегралы вида /(ж, In ж, еаш, sin ж, cos ж, . . .) dx.
1.	ха~ е~ах In ж с!ж = a~(Xry(a1 ax) In ж — а~~ ха 2^2@., а; а + 1, а + 1; —ах)
X
2.	е In ж с?ж = — [EI (—ах) — е In ж — In а — С].
J	a
[a, Re а > 0].

200
Гл. 1. Неопределенные интегралы
[1.6.10
. [ е^ах In х dx = - [е^ах In x - El (-ax)]
J	а
[Re а > 0].
4. | - e^ax In x dx = - [(C + In ажJ + (B) - 2 In ж El (-аж)] + V f
XL,	к
\fc+l
ж
5. [ e~ax In (ж + 6) dx = - [In 6 - e~ax In (ж + b) - eab Ei (-аб) + eab El (-аж - ab)].
j	а
о
J	tt
О
ж
7.	f In (&2 - ж2)е~аж dx = - {2 In b - e~ax In (b2 - x2) -
j	а
°	- е^а6[Е1 (аЬ) - EI (аб - аж)] - еаЬ[Е1 (-аЬ) - EI (-аб - аж)]}.
ж
Г. Г sin аж 1 . . 1 Г Г ci (аж) 1 . г cos аж]1 lflna + Cl
8.	1пж<	>dx = ±—\< ; :>—1пж<	>\	<	>.
J [соваж]	а I (si (аж) J	ismaxJJ a [ тг/2 J
I	1 1 /i \ (cos ах 1 . 1 г • / i	\
аж = =р— In (о — х)<	> ± — lei (ab — ах) —
a	I sin аж J a
, . Ч1 Г cos аб 1 1 г_. , .	ч _ , . Ч1 Г sin аб 1 1 Г In 6 1
-ci(ab)H . . Г + ^ Si a6^ ^Ь SI (ab)}\	.} + -{ n b
[smabj a	[cosabj a( 0 J
10. f - In A + ажп) ^ж = -i Ы2(^ажте).
J ж	n
о
/
^( - -ж
2 у 2
12. |1
J
14. In (cos ж) а*ж = — Ы2(^е2гж) — ж In 2	ж2.
15.	= 2J(-1) ——
16.	\llnSinX\dx = -Xln2T1-l Ch^ \.
J [In cos ж]	2 [ С12(тг — 2ж) j
о
a
17.	In (cos a — cos ж) dx = СЬBа) — СЬ(ж + a) — СЬ(ж — a) — (ж — a) In 2.
ж
ж
I i / •	i • \ i	•?•/ —i(x-\-a)\ • т • / —i(x — о.-4-7г)\
. In (sin a + sin ж) аж = —г Li2(e l ;) -«Li2(e l	) +
<тг].
< тг/2].
18. In (sin а
ia) + i U2(ei{a-ir)) - ж In 2 + - ж(ж - тг).

1.6.11]
1.6. Логарифмическая функция
201
X
19.	In (cos a + cos ж) dx = СЬ (тг + а — ж) + СЬ (тг — а — ж) — ж In 2.
о
ж
Г	111
20.	ln(tga; + tga) ^ж = -ж In cos а	С12Bж + 2а) + - С12Bа)	С12(тг - 2ж).
J	л	л	л
21
22
ж
. Г 1о A + 81пасо8ж)а*ж = ж In sin2 - - 77 In tg2 - - С12Bж) + С12Bж - 2rj) + Cl2Bf|)
о
[tgrj = sin «/(tg (a/2) + cosaj)].
-С12Bж) -C12Bcj) - 2ш In а
[tgu; = asinaj/(l — а cos a;)].
- - [U2{^e2i{^x)) - Li2(-e2i<p) - x(x - 2<p)]
Ь/а; M ^ тг/2; |y> - x\ ^ тг/2].
о
23. fin (acosx + bsinx) dx = ж In
ж
24. fl
25.
= (тг - 2<9) In [(I + л/l - а2 )/а] + 2ж In (а/2) -
- Ь(в - ж) + L(tt/2- 2ж)
тг/2;
= х In а — Ь[тг/2 + ж — arcsln A/а)] + Ь[тг/2 — х — arcsln A/а)]
[|ж| < тг/2; а| sin ж| < 1; а > 0].
26. I	^- dx =
1 — a2 sin 2ж
	^^^^ — In 2 + L@ — arccos а) — L@ + arccos а) — L(w/2 — 2 arccos а)
4аVI — «2 L^	J
- а2 ; 0 < ж < тг/2; |а| < ll.
28.
29.
sin In ж 1 . х , .
> аж = — iri
cos In ж J	2
n —1
27. I <J ""ж *" *" 1> с!ж = — (sin In ж =F cos In ж)
dx
(In x + a)
Z_S	1
~~Г~ = ^ПХ У^ —7	г	7	—
\Jj I	I & I # &	1 I , , , I 16	A/
¦Н(жеа).
In ж + а
fe=i
= е^аИ(жеа).
1.6.11. Интегралы вида
ln (aX
dx.
1.
2.
¦dx = \nx In2(l - ж) + 2 ln A - ж) LI 2A - ж) - 2 LI 3A - ж) + 2 LI 3A).
1 + Ж) dx = In ж 1п2A + ж) - - 1п3A + ж) -
Ж	о
1 + ж
1 + ж
' In Ж In A - ж)	т • / ч , т • / \
3. I	 dx = Ь1з(ж) — In ж Ь12(ж).

202
Гл. 1. Неопределенные интегралы
[1.7.1
4.
5.
6.
In2 Ж In A- ж)
LI
2 LI
- 2 LI
1 - ж
= -6Li4fo)
(^) ^3 In2 ж LI 2(ж) - In3 ж In A - ж).
+ 2 In A - ж) Li 3(ж) - In ж Li 3A - ж) + LI 3A) In :—
L	V1
—
+ 2 In ж In A - ж) Li 2A - ж) + — 1п2A - ж)[6 In2 ж + 4 In x In A - ж) - 1п2A - ж) - 2тг2].
8.
In A — ж) In A — ах)
- Li3(l -
1 —аж\ т . / 1 — аж
-Li
Li3(l/a) + Li3(l) + In A - ax)[U2(l/a) - LI2(ж)] +
+ In A - x)[U2(l - ax) - Li2(l/a) + тг2/6] + i Inaln2(l - ж).
Г In (ax + 6) In (еж + d) . .	f
9. —^	 / /#	; с!ж = In ^
J	+ /f
x + g/f
df-cg
+ In
bf-ag
In
In		In у + fin A - y) In A - %)^
df - eg bf - ag	J	у
[h = (c/a)(bf - ag)/(df - eg); у = a(fx + g)/(ag - bf); ag - bf ф 0; eg - df ф 0].
10.
11.
12.
= In
LI 2 (y) + In
In
In
- - bf) bf - ag
iln	^vrln2i/+ fln2/ln(l-2/)^
2 ag- - 6/	J	I/
In 2/ -
- df ф 0].
= In C/ LI2(z) + In a/ In
(df)	(df)
a(cg-df)
Inz - I In
2
In	Inz I In
a(cg^df) df - eg	2 df ^ eg
In2 z
- df ф о].
J
= - In - In2 v + - In3 v
z а	о
cg-df
[v = a(fx + g)/g; ag - bf = 0; eg - df = 0].
1.7. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
1.7.1. Введение.
Интегралы от обратных тригонометрических функций сводятся к интегралам от триго-
тригонометрических функций при помощи следующих формул:
Г ? ( \ arcsin х 1 \ j	, Г х (\ sin t 1 Л ( cos 11 »,	Г Г sin t 11
1. f ж, <	>]dx = ±\f[<	?, t]<	> dt	\x = <	> •
J \ [агесозж//	J VlcostJ /\slntj	L Icost/J
Ictgi/J
in х 1 \ j	, Г х (\ sin t 1 Л ( cos 11 »,
>]dx = ±\f[<	?, t]<	> dt
озж//	J VlcostJ /\slntj
Г / jarctg^n	fjftgtl	p
У \ ' \a,rcctgx f)	Г Vlctg*/'
/ arctg(a;/a)
iаrcctg(ж/a)
coet
sini
3

1.7.3]
1.7. Обратные тригонометрические функции
203
( f (ж), 1
J	J
.Z'f slot 1 /costl \/cost \ ,.
<	>,<	?, t I <	> dt
V\cost/' \slnt J ' /\sint/
ч Г arcsin ж 1
Н	г1
[ arccos ж J
fsint
,/ v f arcsin ж 1 . _.
f(x)\	\dx = F(x
[ arccos ж J
arcsin (ж/а) I _	I arcsin (ж/а)
> fi T — T <
[cost
F(a0 = J/0r)da:
arccos (ж/а)
{/ / \
arcsin (ж/а)
Я arcsin (x/a) 1 r
arccos (x/a) j
arcsin (x/a) \n~
(x/a)
arcsin
arccos (x/a)
arcsin (ж/
arccos (ж/
arcsin (ж/aj [
arccos (x/a) j
a) I2
a)/
±
arcsin
arccos (ж/
arcsin (x/a)
arccos (x/a)
arcsin (x/a)
arccos (x/a)
arcsin (x/a)
arccos (x/a)
ln J arcsin (x/a)
[ arccos (x/a)
arcsin (x/a) 1	жте+1 / arcsin (x/a)
dx = ж
±
arcsin (x/a)
arccos (x/a)
arcsin !ж//а!
arccos (ж/а)
Г
1.7.8. Интегралы вида ж
J
аж =
аж.
arccos (x/a)
arcsin (x/a)
arccos (x/a)
xn+1 /
ra + l\
те+1
а*ж
с!ж =
arccos (x/a)
2n+1 ( arcsin (ж/а)
Bn + lJ
2n+ij arcsin (ж/а)
' + 1 \ arccos (x/a)
2n \~^	2k+1n(n — l)...(n — k)
arccos (ж/а)
2п+2
_
аж —
- 1)Bп - 3) . . . Bга - 2k -
arcsin (ж/а)
±
rt2n+l
2n + 2 [ arccos (ж/а)
J^ Bra + l)Bra - 1) . . . Bra - 2k -
Bra + l)!!
Bга + 2Jn+!(fi + 1)!
arcsin (ж/а)
arccos (ж/а)

204
Гл. 1. Неопределенные интегралы
[1.7.4
4.
5.
6.
arcsln (x/a) 1 /ж2	a2 \ J arcsln (x/a) 1 ж
arccos (ж/a) J \ 2	4 / [ arccos (ж/a) J 4
arcsln (x/a) \	. x
arccos (x/a) J	3
3j arcsln (ж/а) 1 /ж4	За4\ J arcsln (ж/а)
arccos (ж/а)/ \4	32 J \ arccos (x/a)
arcsln (x/a)
xn \ arccos (x/a)
arcsln (x/a)
dx =
arcsln (ж/а)
а1ж
J_ f
ж2п \
ж2п \ arccos (x/a)
(n — 1)жтет1 [ arccos (x/a) J n-1 I <г>п-1л
arcsln (x/a)
Bn - 1)ж2те™1 \ arccos (ж/а) '
Bn-l)Bn-2) [«
Bn-:
l	l
arccos (ж/а)
Bn - 3)Bn - 5) . . . Bn - 2k - 1)
2k(n - 2)(n - 3) . . . (n - к - 1)
x I -
k ж
Bn-3)!!
9.
1 f arcsln (ж/а) 1 .	1
^ dx = —
ж2п+1 ^ arccos (ж/а)
/ 9	9~ Г	-1
уа2 — ж2 | 1
2пж2п [ arccos
a	{n i).
In (x/a) 1
os (ж/а) j
In
2nBn-l) [а2ж2п
10.
11.
ix2n{
arcsln (x/a)
2n+1 Ife^i ^2n ~ ^2n - 5) . . . Bn - 2A; - 1)
2пж2п \ arccos (x/a) J 2na2n ^ 2n — 2k —
n-1
A;
—fc —1/2
1 f arcsln (ж/
ж \ arccos (ж/
a)/
с!ж =
J arcsln (x/a) 1
[ arccos (x/a) /
, arcsln (x/a) \ . . a"
= 1пж<	: ;, : > ±ln-
=F 2Im LI 2 [ г
12.
13.
14.
15.
BA; - 1)!!
2fc + l
2ж
7Г f 0
' 11 In ж
¦ arctg ¦
±2Im Li-
ж
ж + га + iy a2
1.
arcsln ж . 1 _.. ,	ч	.
	аж = - Cl 2 B arcsin ж) + arcsin ж In 2ж.
Ж	zl
1 J arcsln (x/a) 1	if arcsln (x/a) 1 1
ж2 \ arccos (ж/а) J	ж \ arccos (ж/а) J а
1 J arcsln (ж/а) 1	1 J arcsln (ж/а) 1
ж3 \ arccos (x/a) J	2ж2 \ arccos (x/a) J 2а2ж
pt >i тл-	f/i i \±n+i/2 f arcsln ж 1
.7.4. Интегралы вида A ± ж) ; <	> б!ж.
J	[ arccos ж J
inx\dx = -J— A + ж)"+з/2 f arcsin x | ±
os ж J	2n + 3	[ arccos ж J
9n+^, /1 	 o> ? -
(-1)
+1/2 агсипх ж =
arccos ж I	2n + 3

1.7.5]
1.7. Обратные тригонометрические функции
205
2. [A - ж
J
п+1/2
	2_ _ +8/а Г arcsin*
2п + 3	[ arccos ж
±
3.
resin ж 1
A + ж)те+1/2 X arccos ж j
2
n + 1\
j
Bп-
Г
х \2п^
J arcsin x 1	^/1 — ж
+ ж)"-1/2 \ arccos ж J T Bn - l)Bn - 2J™
V Bп - 3)Bп - 5) . ¦ ¦ Bп - 2fc - 1) n-2-fcn ^ . ,
^ Bп - 4)Bгс - 6) . . . Bгг - 2k - 2)	l	j '
Bfi-3)!!	1
±
4.
1
{arcsin ж 1
arccos ж J
Bn-2)!!
°'
/TTx
A — ж)п+1/2 \ arccos ж
2	I arcsin ж
Bп^
arccos ж j ^ Bn - l)Bn - 2J^
y.2 Bn - 3)Bn - 5) . . . Bn - 2k - 1) n^2^fcf
^ Bn-4)Bn-6)...Bn-2ife-2)	l
Bn-2)!!
°
n_2
^2 -
5.
6.
7.
8.
бJ
2	/F-а)A-ж)
¦ arctg л i	}-
°
ж arcsin ж
Ь) ал/а2 - Ь2
arcsin ж	1
- ж)
с+ 1ж
[с > -1].
[с < -1].
А<
1.7.5. Интегралы вида жрA — х2)ч+1^2\
J	[ arccos ж ^
Интегралы этого пункта выражаются через элементарные функции в следующих слу-
случаях:
1)	р, г = 0, 1, 2, . ..; q = -1, 0, 1, 2, . ..;
2)	г = 1; р = 0, 1, 2, . . . ; д = -1, -2, . . . ;
3)	р= -2, -4, ...;
4)р = 0, 9 = -1-
2.
_ж2 +1/2f arcsin я:" м^
X arccos x
[ arccos ж
2ra + 3 \ arccos ж/ 2n + 3
' \ к
к ) 2к + I'

206
Гл. 1. Неопределенные интегралы
[1.7.5
3.
4.
5.
6.
7.
{arcsln ж 1 .
> dx
arccos ж J
arccos ж
2n - m + 4 Г A - ж2)п+1/2 Г arcsln ж
J
dx.
га- 1 \га/2- 1
к ] 2k — m + 2
то
In |ж
dx.
Если к = га/2 — 1, то соответствующий член в сумме следует заменить на
1 / п + 1
8.
иг — 1
2)n x/2 J arcsln ж 1
%~2 X arccos ж /
Если к = т/2 — 1, то соответствующий член в сумме следует заменить на
(-1)
9.
10.
11.
12.
13.
14.
т/2-1
га- 1 \т/2- 1
In |ж
Ж	[
dx =
2n
fc=0
п + 1 1
arcsin ж
arccos х
+
=р
)те 1^2 J arcsln ж 1
\ arccos ж J
A — ж2K/2 [arccosж
arcsln ж
A — ж2)п+1/2 [arccosж
¦1
} dx =
; j
arcsin ж
arccos ж
-ij (i-ж2

1.7.6]	1.7. Обратные тригонометрические функции	207
arccos ж J
J A — ж2)п+1/2 X arccos ж J	Bга — m)(l — ж2)"™1/2 \ arccos ж
1 f xm^1 dx m —1 f жт"~ I arcsin ж
2тг — m J A — ж2)п 2n — m j A — ж2)п+1/2 \ arccos ж
. «, , arcsin ж 1 ж J arcsin ж 1
1"- I (i _ ж2\п+1/2 i 	i dx = 7777 777^ _9\n-i /9 l 	r ^
1 Г жт 1 а*ж m-1 f xm 2 ( arcsin ж 1
T 2ra - 1 J A - x2)n ~~ 2n - 1 J A - ж2)«/2 \ arccos ж J Ж"
I	JL	I 1ЛХ \^LJJ.JLA *AJ I	.	-1-	1 Sl^UJL V/Slll Ж I	,
J- • • I 	/_	n \ — i i in i	f t*X	7	~^ ^ T~7~Z	n \ „ i /o i	f ^J^
COS Ж I
arcsin i I	1	I arcsin ж
^mfi _ ^2\n+l/2 } ягггпч - I	~~ (m _
If	о*ж	2п + тп^2Г	1	f arcsin ж
m - 1 J ж"^! - ж2)те	m-1 J жт™2A - ж2)п+1/2 [arccosж
f 1 f arcsin ж 1 _ 1	f arcsin ж 1
18. 	j- <	> аж = 	7- <	> =p
а*ж.
а*ж f 1	f arcsin ж , .
+ ^^	ox^ i/n	} dx.
2ra - 1 A - x2)n \ x(l- ж2)«/2 arccos ж
arcsin ж 1 . I arcsin ж 1 .
> с!ж = ж^ \ ±
arccos ж J [ arccos ж J
arccos ж
arcsin ж Г'	, i \ f / arcsm ж
i	c*°	• 2fc
i аж	, ,	ч v-^ / x h arcsin ж
20. 	:	 = In (arcsin ж)+> (-1)
^
arccos ж
fc=0
-i ^ * тж	f pf arcsec (ж/а) 1
1.7.6. Интегралы вида ж <	> аж.
J [ arccosec (ж/а) J
1. \ x arcsec ™аж= 	arcsec — =p	 ,	=¦	< > <
J	«	p + 1	a ^ p + 1 j V^2 - a2	LU/2J
x Гтг/2
arcsec — «^ J
2. | ж arccosec — аж = 	arccosec — ±
a	P+1	а р+
0 ,
J> < arccosec —
-я"/2.
/a)J
2ra + 1 \ arccosec (ж/с
2fc + 2-i
2п-Уж2-а2 Г уГ Bга - 1)Bга - 3) . . . Bга - 2А; - 1) /а\2fc+2l
2nBn + l) [ + ^ Bга - 2)Bга - 4) ... Bга - 2А; - 2) \ж J JT
arcsec (ж/а) 1^1
\ arccosec (ж/a) J 2j
„2n+i J arcsec (ж/а)
arccosec (ж/а)
2raBra - 2) . . . Bга - 2A;)	^а
ж
^ Bга - 1)Bга - 3) . . . Bга - 2А; -

208
5.
6.
7.
Гл. 1. Неопределенные интегралы
[1.7.6
arcsec (ж/
2п + 2 \ arccosec (ж
X2n{
, arcsec (x/a)
o< { у/ i <
arccosec (ж/a) J 2_
arcsec (ж/а)
arccosec (ж/а)
dx = —
arcsec (x/a)
Bn — 1)х2п~г [ arccosec (x/a)
^2 \fc
± ¦
IZllI/	JL J I*	<yL "
1 f arcsec (x/a)
arccosec (x/a)
2k + l\ к
ж2 - а2 Г y^ Bn - l)Bn - 3) . . . Bn - 2fe - 1) /ж\
пJаж2те [ + ^ Bn - 2)Bn - 4) . . . Bn - 2A; - 2) \а/
arcsec (x/a)
arccosec (x/a)
1 J arcsec (x/a) 1
2пж2п \ arccosec (ж/а) J
arcsec (x/a)
arccosec (ж/a) J 2J
Bn — 1)!! f arcsec (x/a
Bn)U2n 1 arccosec (x/a
ж	ж
arccosec — dx = ж arccosec — ± а In
а	а
О^	""Г9	'Т*	|
ж arcsec — dx = — arcsec — q= -уж2 — а2
а	2	а 2
2
Jb j	el/	db , iJb / ^
ж arccosec ~аж= — arccosec -±-уж -
а	2	а 2
< arccosec — <
x I тг/2
< arcsec — <
—-тг/2 I	a i тг
2	ж , ж	ж аж / п 7z , а 1 ,	/ ^
ж arccosec — аж = — arccosec — ± —ух1 — а1 ± — In ж + ух1 — а
3	6	б1
ж j тг/2
< arccosec —	< <
-тг/2 I а I 0
2fc + l
Bife-l)!! /а\
1 ж , тг , . а
— arcsec — dx = — In x\-\	\-
ж	а	2 ' ж
[0 < arcsec (ж/а) < тг/2].
[—тг/2 < arccosec (ж/а) < тг/2].
. . < arcsec — <
/2J	а I тг
1	ж _	1	ж
—г- arccosec — аж =	arccosec —
а	ж	а
ж I тг/2
< arccosec — <
-tt/2 J	а I 0
—тг arcsec — аж =	 arcsec — ±
	rp	I	у	^
arccosec — dx =	 arccosec — "f
а	2ж2	а	4аж2
ж Гтг/2
< arccosec — <
а 1 0
19

1.7.8]
1.7. Обратные тригонометрические функции
209
1.7.7. Интегралы вида [(ж =Ы)±п+1/2{ агс8есж X dx.
I arccosec ж J
f arcsec ж 1 ж
Условие: 0 < \	\ < —.
I arccosec ж J 2
arccosec ж
2n + 3
arccosec ж
2.
агс8есж
arccosec ж
2n + 3
arccosec ж
1	J arcsec ж 1
x + l)n+1/2 larccosecx J
2	j arcsec ж 1
arccosecx J X^ Bn - 1) (ж + 1)те™1/2 \ arccosec ж J
j arcsec ж 1
)те™1/2 \ arccosec ж J
4.
J arcsec ж
J
(ж — l)n+1/2 I arccosec ж
Bn — 1)(ж —
2n-l?jJ (|/2 + 2)^
г arcsec ж 1
"jn-i/2 \ arccosec ж /
fe=0
arccosec ж
\ dXm
J
1.7.8. Интегралы вида [ жт(ж2 - 1)±п+1/2|
.,	г arcsec ж 1 ж
Условие: 0 < <	> < —.
I arccosec ж J 2
тж	f m/ 2 .ЧП+1/2Г arcsec ж I1
Интегралы |ж (ж — 1)	^ _	 > ах при целых т, п, I с помощью подста-
j J sin 2/ 1 2n+2 J cos у 1 ^Bn+m+3^
arccosec ж
ау.
г arcsec ж 1	i
новок |/ = <	> сводятся к интегралам вида \ у <	} <	>
I arccosec ж J	J Icos I/ J	I sm У J
Результат выражается в виде комбинации элементарных функций в следующих случаях [18]:
1) I > 1, п^-1, т^-2п-3;
2I = 1, п < -1, m^-2n™3;
3)	I = 1, m — нечетное, m ^ ^2n — 3;
4)	m = — 1, п = — 1.
ff arcsec» I ,2 1)П
Jl arccosec ж/
+1/2 ^ ^ (ж2 - 1)"+1/2
2(n + 1)
)"+1/2ж f arcsec ж i
+ 1) 1 arccosec ж/
1 j
arccosec ж
агсзесж
агссо8есж
1 2 _ vn-1/2
/1Ж j
,
2.
Ж )dx =
arccosec ж J
агс8есж
arccosec ж
m + 2n + 2
fc=O
тп-2/ 2
A; / m^2Jb^l
n+i/2( arcsec ж
2_ +1/2r
I
arccosec ж
> с!ж.
14 А. П. Прудников и др., т. 1

210
Гл. 1. Неопределенные интегралы
[1.7.8
3.
arccosee ж
2п + 3 I arccosee ж
n+1
(ж2-1)п+1/2 г arcsecж 1 _ (ж2 - l)n+3/2 r агезесж l
/	(га — 1)жт^1 I arccosee ж 1
Г (ж2-1)п+1/2 г
J	жт	1
arccosee ж
га —1
2к — га + 1	га —
+ 4 Г (ж2 — i)n+1/2 r arcsec ж ] .
¦z		Чу	{	\dx.
1 J xm~A I arccosec ж J
(га -
+1/2( агенесж 1 (^l)n
т^1 I arccosee ж/ га-1
2п
7.
8.
(ж2 - 1)те
ra — 1
(ж2-1)п+1/2 г arcsec ж
к/ 2k - m +
(ж2 - l)n™1/2 r arcsec ж
arccosec ж -
r arcsec ж 1
<	> ax.
I arccosec ж J
j агезееж 1 _ (ж2 - 1)те+1/2 f агезесж 1
1 arccosee ж /	2п + 1 1 arccosee ж /
— 1 f arcsec ж ] .	If arcsec ж ] 2 r^	 r arcsec ж 1
J	2 1 arccosee ж J	I arccosee ж J
ж I arccosee ж
( arcsec ж 1 . 1 rn_1 , o r arcsec ж 1
^< > с!ж = —ж vж2 — 1 < >
i L arccosee ж J ra	I arccosee ж J
g f x f агезесж 1
J (ж2 - 1)^+1/2 1 arccosec ж J
arccosec ж J Bn - 1)(ж2 -
m(m — 1)	ra
— 1	J arcsec ж 1
n — 1)(ж2 — l)n^1/2 X arccosec ж 1 '
2 r arcsec ж 1
1 ^ arccosee ж J
±
. arccosec ж
2n-l
In-
C2^l
10.
11.
12.
13.
14.
15.
1	r arcsec ж l ,
x2 — i)n+i/2 [ arccosec ж J
жт(ж2 - 1)
(m -
I
m - 1 J xm(x2 -l)n	m-1 J жте^2(ж2 - 1)
arcsec ж 1 , \/ж2 — 1 r arcsec ж
r arcsec ж l
I arccosec ж J T
1	j arcsec ж 1
™ 1)те+1/2\ arccoSec ж J
1 j arcsec ж 1
a^2 _ i \ arccosec ж /
[m —
1
arccosec ж
m-2
}
J
a;Vr —
1 f arcsec ж l .
^^^ i > dx =
C2 _ ]_ I arccosec ж J
(ra — 1Jжт^1 га —
ж2 — 1 ( arcsec ж
arccosec ж
2 I	* 	J агс8есж i ^
1 J xm~2-^x2 — 1 I arccosec ж 1
ж r arcsec ж l
/ж2 — 1 I arccosec ж i
= yx2 —
¦{,
- r arcsec ж 1
. ^	^=р1пж.
I arccosec ж J
(ж2 - 1)
- IK/2 I
1	j arcsec ж 1
— i)n+i/2 \ arccosec ж J
}
— l)^1/2 1 arccosec ж i
±
2ra - 1 J (ж2 -
(ж2 — IK/2 I arccosec ж -
Brc - 1)(ж2 - l)n^V2 I arccosec ж.
с!ж	2n — 2 Г	1	j arcsec ж 1
2n — 1 J (ж2 — lO1^1/2 1 arccosec ж J
ж r arcsec ж 1 . 1 . x — 1
{	\ ± — In	.
Ж2 _ -^ [ arccosec ж J 2 ж + 1

1.7.9]	1.7. Обратные тригонометрические функции	211
Г хт с arcsec ж 1	хт~г ( arcsec ж 1
J (ж2 — l)n+!/2 \ arccosec ж / Bга — гаг)(ж2 — lO1^1/2 X arccosec ж X
1 Г xm~2dx m-
(ж2 - 1)те 2п - m J (ж2 - 1)
1 Г хт 2 г arcsec ж 1
rra J (ж2 — \)п+1/2 \ arccosec ж /
arcsec ж 1	1
_	х	г arcsec ж 1
~ ^B1)B l)^1/2 I	/
г arcsec ж 1
^-1/2 I arccosec ж/
т~2
arccosec ж X 2п — 1 J (ж2 — 1)п
гаг — 1 Г хт^2 ( arcsec ж 1
+ 2га- 1 J (ж2 - 1)«/2 1 arccosec x)
, - Г arcsec ж 1 _	1 г arcsec ж 1 .
18. I —^-^	-ч.. , , /о ^	Г«ж = ^7^	7Т7"^	1Хэт 1/91	f±
' I arccosec ж J	Bга — 1)(ж2 — I)™-1/2 I arccosec ж J
ж(ж2 — 1)п+1/2 \ arccosec ж J	Bга — 1)(ж2 — 1)п~
1 Г dx
fir arcsec ж l .
2n — 1 J ж(ж2 — 1)те J ж(ж2 — 1)тет1/2 1 arccosec ж X
^ л f 1	f arcsec ж l . .If arcsec ж l 2
19. —	<	> dx = ±-<	> .
J жуж2 -- 1 I arccosec ж J	2 I arccosec ж J
1.7.9. Интегралы вида \ xpI	\ , \ \ dx.
J { arcctg (ж/а) J
f „Г arctg (ж/а) 1 . жр+1 f arctg (ж/а) 1 a f жр+1 dx
1. жр<	\ . ч > с/ж = 	<	\ . ч > =F	 —^	T-
J [ arcctg (ж/а) J	p + 1 [ arcctg (ж/а) J p + lj x2 + a2
2n Г arctg (ж/а) 1	ж2п+1 Г arctj
\ arcctg (ж/а) J	2ra + 1 \ arcctg (ж/
la))
arctg (ж/а) 1	ж2те+2 J arctg (ж/а) 1
arcctg (ж/а)/	2n + 2 \ arcctg (ж/а) J
2fe-l
4. f f arCtg (;/a\ } dx = x\ &rCtg (;/a\ U - In (x2 + a2)
J \ t (/)/	\ t (/) J ^ 2 v	;
arcctg (ж/а)/	\ arcctg (ж/а) J ^ 2
[J arctg (ж/а) 1	ж2 + a2 f arctg (ж/
J [ t (/) j
1
arcctg (ж/а) j 2 [ arcctg (ж/
6. [2
а) "I 1
i \ ? -\- — ax.
а) j 2
3 [ arcctg (ж/а) J 6 6
[ arcctg (ж/а) J	4V	; \ arcctg (ж/а) J 12	4
1 J arctg (ж/а) 1	—if arctg (ж/а) 1	a f	б?ж
8 \—{ ar€tg ^^a^ 1 dx =	-1 { aFCtg ^X^a^ 1 ± а
J xn X arcctg (ж/а) J	(ra — 1)жп^1 \ arcctg (ж/а) j ra —1
9 \ —I arctg ^Ж//а^ 1 йж =	!	f arctS (ж/а) i
1 ж2п \ arcctg (ж/а) j	Bra - 1)ж2п^х \ arcctg (ж/а) /
2 i 2 "
г_1. ж +а
Lln-
10# | 1 f arctg (ж/а) I ^ =	1 f arctg (ж/а) ^±
c2n+1 \ arcctg (ж/а) J	2nx2n \ arcctg (ж/а)
,/-,4nf arctg (ж/а) 11
l } \ arcctg (ж/а) J J'
\ arcctg (ж/
14*

212
Гл. 1. Неопределенные интегралы
[1.7.10
2к+1
13. j-
16- I - 1	W / N
ж [ arcctg (ж/а)
17.
is.
2 ( In
ж2 [ arcctg (ж/а)
ж3 [ arcctg (ж/а)
arcctg (ж/а)/ 2а ж2 + а2 *
2 \ж2 а2 у \ arcctg (ж/а) J 2аж *
J (ж + бJ \ arcctg (ж/а)
|
Г
а — 6ж
а(ж + 6)
./°
cx + d
lcl	1	_
2	2
[tg 99 = ad —¦ be; tgO = ax -\- b].
dx.
1.7.10. Интегралы вида [жр(ж2 + a2)q I	^\
J	[ arcctg (ж/а)
Интегралы этого пункта выражаются через элементарные функции в следующих слу
чаях [18]:
1)р, г = 1, 2, 3, ...и(/< -р/2-1;
2)	г = 1, р — четное;
3)	г = 1, 2, р — нечетное, </ = —1, 0, 1, 2, ...;
4)	р = 0, д = -1.
f
{
2.
arcctg (ж/а)
g (ж/а) 1 ^
1 arccte (ж/а) Г ^ V А;
X arcctg (ж/а)
к=0
Жв
arctg (s/а
2m + 1/\ arcctg (ж/а)
2 2fc
A;
3.
arcctg (ж/а)
2т+4
a2m+4
arctg (ж/а)
2[ т + 1 ' т + 2 ' (m + l)(m + 2) J \ arcctg (ж/а)
J \

1.7.10]	1.7. Обратные тригонометрические функции	213
2т + 3	3	т	2fe 2m,^2fc + l
аж	_	а	х~^/ -\fctt ж
+ 2)Bт + 3) ^ 2(га
¦ а2)те Г arctg (ж/а)
, а*ж =
arcctg (ж/а)
Oil С^ US-L I tX/ / (Jj I	I	Ж	Л f # €/ | \AJ	tAy	Ж	Л	<UL>	i i V \ 1 €ЛУ	у
/п\ Г
l' ^ J
arcctg (ж/а)
Если fc = (га — l)/2, ^ = 0, 1, ..., гг, то соответствующие слагаемые в суммах заменя-
заменяются на а п^гг'
k) a X arcctg (ж/а)
5# , -	/arctg (ж/а) \^_	ж—1	/
(ж2 + а2)те [ arcctg (ж/а) /	2(п - 1)(ж2 + а2O1™1 [ arcctg (ж/а)
а Г хт^г dx	га —1 Г жто^2 / arctg (ж/а)
2(n-l) J (ж2 + а2)п + 2(n-l) J (ж2 + а2)" \ arcctg (ж/а)
6. I _ 1 ., Iarctg(ж/а) 1 dx = _. ^ * ., , Iarctg{х':\ \ ±
х/а) 1
(ж/а)/
(ж2 + а2)те [ arcctg (ж/а) J	2(n - 1)а2(ж2 + а2)"^1 [ arcctg (a
1	2n-3 f	1	/ arctg (ж/а) 1
2 -1- а2)"™1 \ arcctg (ж/а) /
4(п- 1Jа(ж2 + а2)те™1 + Bп - 2)а2 J (ж
-dx =
x2 + ал)п	а
"^ Bfi-2Jb-2)!!Bn^3)!!	ж	1 Bn - 3)!!
а [^ Bп - 2)!!Bп - 2к - 1)!! а2Л;(ж2 + а2)^ + 2а2^^! Bп - 2)!!
а ^4 B?г - 3)!!B?г - 2fe - 2)!!
2 ^ Bn^2)!!Bn-2ife
8.
(ж2 + а2)п X arcctg^/a)
1 [ arctg (ж/а) U B^3)f?	, ±
±
2(n-l) \ arcctg (ж/а) j [Bn - 2)!!а2"-2 (ж2 + 02)^
Bn-3)Bra-5)...Bn-2fc-l)
. жп / arctg (ж/а)
ж2 + а2 X arcctg (ж/а)
^ Bn - 4)Bn - 6) . . . Bn - 2k - 2) \ а
_ | n^2J arctg (ж/а) 1	2 f xn 2 / arctg (ж/а) .
[ arcctg (ж/а) J	J xA + a2 [arcctg (ж/а)
10 | ^ f arctg (ж/а) 1 ,a. = ±(-l)wa2w-1f arctg (ж/а)
ж2 + а2 [ arcctg (ж/а) j	2	[arcctg (ж/а)
1 arcctg (ж/а) J ^l j	2^ — 1 +^	2fe - 1	J ж2 + а2
^	6 \ / ; j k=1	k=1	j
^2w+1 ( arctg (ж/а) Ьж= If arctg (ж/а) ]^(_ir*fl^V
ж2 + a2 [arcctg (ж/а) J Ж 2 \ arcctg (ж/а) J ^l }	к
f 1
12.
j 2^ж	, ж f arctgCx/a) 1
2 ^	Jfe	J ж2 + a2 ^ l j	J ж2 + a2 \ arcctg^/a) J
1 / arctg (ж/а) lda. = ±J/ arctg (ж/
ж2 + а2 \ arcctg (ж/а) /	2а \ arcctg (ж/
/а) I2
/а) J

214
Гл. 1. Неопределенные интегралы
[1.7.10
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
ж J arctg (х/а) 1	1 \/ж2 + a2 J arctg (х/а) 1
ж2 + а2 \ arcctg (ж/а) j	2	2а \ arcctg (х/а) /
а + ix\ _ . fa — i
—^	 -Li2 —^
+ а2 [ arcctg (ж/а)
^ arcctg (ж/а)
ж = xl
2а J	V 2а
а Г In (ж2 + а2) ,
1	¦ dx.
О
8 \1п(ж2 + а2) /'
[ arcctg (
/a) 1 т«
ж/а) J 2
J arctg (ж/
а 1
/ ^ж =
/а)]
ж2 + а2 ( arcctg (ж/
= ^аж 1 2 2xf arctg (х/а)
~~ 2 2^Х п }\ arcctg (ж/а
1	/ arctg (ж/а) 1 da.=
(ж2 + а2J \ arcctg (х/а) )
х	( arctg (ж/а)
2 [ arcctg (ж/а)
J arctg (х/а)
- а2 X arcctg (ж/а)
х/а) 1 2
(ж/а)/
2а2(ж2 + а2) \ arcctg (х/а)
±
1 J arctg (х/а) 1
4а3 \ arcctg (х/а) /
± ¦
arctg (х/а)
arcctg (
arctg^/а)
arcctg (х/а)
1 J arctg (х/а)
х/а) 1
х/а) /
t2 + а2	х тт. /а + ^
	arctg	а Im Li 2
2а	а	\ 2а
4-1
жа I	О
2 . 2\
In (ж + а ) J
1 Г arctg (ж/а) 1 г
ж2 + а2 [ arcctg (ж/а) J	(г + 1)а \ arcctg (х/а)
1 J arctg (х/а) 1	1 J arctg (ж/а)
ж2 + а2 \ arcctg (ж/а) /	а \
ж Г arctg (х/а)
?jf ?р == —J- 	 ]
dx =
arcctg (ж/а) J
/а2 - ж2 1 arcctg (ж/а)
¦/ arctg (х/а)
[ arcctg (х/а)
х arctg ж
: а arcsln	h ¦
а
/- f arctg [\/2ж(а2 - ж2)
) ' ]
arcctg
/2ж(а2 -
arctg ж
¦ а*ж =
[а > Ц.
[6 > а].
1.8. ОБРАТНЫЕ ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
Неопределенные интегралы от обратных гиперболических функций вычисляются по
формулам раздела 1.6 после следующих замен:
Arsh ж = In (ж + v ж2 + 1),
Arch ж = ± In (ж + \/ж2 — 1 ^
Arth ж = - In
2 1-ж
1	ж + 1
Arcth ж = — In
2	ж — 1
Arsech ж = ±1п(- + 4/47^1
1
Arcosech ж = In (
ь ж
[ж > 1],
[\*\ < У,
[0 < ж ^ 1],
[ж > 0].

Глава 2. ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
2.1. ВВЕДЕНИЕ
2.1.1. Предварительные сведения.
В этой главе содержатся определенные интегралы от элементарных функций. Интегра-
Интегралы, у которых один или оба предела интегрирования являются переменными, в случаях,
когда подынтегральная функция от них не зависит (в частности, интегралы от иррацио-
иррациональных функций, сводящиеся к эллиптическим интегралам), помещены в главе 1.
Указанные в формулах условия сходимости интегралов обеспечивают их существование
либо в обычном смысле, либо как несобственных интегралов, либо в смысле главного
значения [20].
В начале соответствующих разделов помещены интегралы общего вида, зависящие от не-
нескольких параметров и позволяющие получать более общие результаты, чем содержащиеся
в последующих пунктах. Эти интегралы выражаются через функции Vj , Vj, приведенные
в приложении III; параметры, входящие в них, указаны в каждой формуле в фигурных
скобках.
В качестве примера вычислим интеграл
L dx
¦ x2 (bx + c)
= /
[а, Ь, О 0].
В силу формулы 2.2.2.5,
vr,
с	1	а"
где у = —, г = 2, р = -, р = 0. Пусть, например, \у\ ^ 1 (с ^ аЬ)\ тогда / = —^- Vt .
Подставляя значения г, /3 и р в параметры Е^, и, аз, 6з, сз, z функции V{~ и учитывая,
что р = 2, q = 1, получаем
'{a + ft)/2>
,A + « + Л)
1, ДB, 1 + h), ДA, (а + А)/2); (-j
ft!2
4
ДB, 1 + ft),
а/2
; +2;v
Таким образом,
a
xa dx
	= ^/згГ «/2 1 рЛ a. g + i. a2b2
^F^^(bx + c) 2c V L(l + «)/2j 4 2' 2 ' C2
а/2
г
[Кеа>0,а>0,
<7T .

216
Гл. 2. Определенные интегралы
[2.1.2
Функции Ух+ + У2+ и V\ B формуле 2.2.2.5 аналитически продолжают друг друга, поэтому
полученная формула справедлива не только при
ab
1, но и при
arg
ab
< тг. Подставив, в частности, в эту формулу а = 1 и используя соотношения ГA/2) =
(a, fe; fe; 2) = A -
получим
dx
/a2 - x2 (bx + c) 2c
2.1.2. Общие формулы.
Некоторые свойства определенного интеграла:
Ь	a	b
1. /(ж) с/ж = — f(x) dx. 2. /(ж) dx = /(ж) da? + /(ж) dsc.
Формула Ньютона-Лейбница:
3.
4.
Интегрирование подстановкой:
Ь	C
]f(g(t))g'(t)dt
[a = g(a), b = g(f3), g(t), gf(t) непрерывны, g1 (t) ф 0 и a < x = g(t) < b при а < t < /3].
Интегрирование по частям:
b	b
. f(x)g'(x) dx = f{x)g(x)\ha - g(x)f(x) dx.
Теоремы о среднем:
ь	ъ
6.
b	?
7. f(x)g(x) dx = f(a) g(x) dx
ь
=f(b)jg(x)dx
8.
ь	i
9. \f{x)g{x)dx = f{a)
[f непрерывна на [a, b], g(x) > 0, о ^ ? ^ 6].
[/ ^ 0, монотонна и не возрастает; а ^ ? ^ 6].
[/ ^ 0, монотонна и не убывает; а ^ ? ^ 6].
+ /(&) U(x)dx
[/ монотонна; а ^ ? ^ 6].
10.	= Л ^(ж) dx + в\ g(x) dx
[Л ^ /(а + 0), J5 ^С /F — 0), если / монотонно убывает;
А ^ /(а + 0), I? ^ /F — 0), если / монотонно возрастает; о ^ ? ^ 6].

2.1.2]
2.1. Введение
217
Дифференцирование интеграла по параметру:
ъ	ь
11. i
12.
13. —\f(x)dx = -Ha).
Некоторые формулы замены переменной:
14.
15.
ad — bc-\-(b — а)х
16.
dx.
dx
17. I /(ж) dx = [/(ж) + f{-x)] dx = O
о
18.
A + жJ"
= 2\f(x)dx
о
a	a	a
Г	f	If
19.	/(ж) daj = f(a - x) dx = - [/(ж) + /(a - ж)] dx.
oo	о
2a	a
20.	/(ж) с!ж = [/(ж) + /Ba - ж)] dx = О
о	о
a
21.	=2 [/(ж) da
о
Лт21 г/т*	Г / 1 — ii^
х ) их	 _ \ f I L У
[/Bо-з) = -/(*)].
[fBa-x) = f(x)\.
dy
О
23. J/(x,
— а , V о — ж ,
1
о
7Г/2
4(Ь^а)
(i + 2/2:
2/2K
¦ dy.
24.
25.
26.
F — a) /[a+ F™ a) sin y?5 V6 — a sin y?, V& — a cos y?] sin 2ip dip.
о
оо
= F - а) J /
О
а + by I (b — а)у jb — a
1 + 2/

218
Гл. 2. Определенные интегралы
[2.1.2
27. /(ж, -^ж2 - с2
28.
ydy
О < с ^ а < 6, а =
-,Р =
\COS (f	J COSZ (f
/3
а + с '	6 + с
[О < с ^С а < 6, cost* = с/а, cost? = с/6].
29. [/(ж,
30.
31.
) ^ж = 2с f/(-
2су
dy
[-с ^ а < b ^ с, а = а^г{с- \/с2 -а2), /3 = Ь^- \/^2 - с2 I.
V
/(с sin (ji9, с cos (f) cos у cf^?	[—с ^ сь < 6 ^ c, sin it = а/с, sin г? = 6/c].
[/(ж, r) = Re F(z), z = r(cos x + г sin ж), ^(г) аналитична при |z| ^ r].
32.
33.
Xg(x, Г)	7Г
dx=- [F(re-a) - F@)]
x(x2 + a2
(ж, г) = ImFf»; см. 2.1.2.31].
[см. 2.1.2.31].
[см. 2.1.2.31].
+ \/х2 + у
т/2
36. /(ж)	с!ж =
J	х
о
о
){ г \dx
{ cos ж J
8Г. [ЛМ_лм,ж = [/@)_/(+оо)]1п1
о
38.
[р, g > 0; /(ж) непрерывна на [0, оо), /(+оо) = lim /(ж) — конечная величина].
оо
Г	Г	1
Р? Я > 0; /(ж) непрерывна на [0, сю), и существует ж"~1/(ж) о*ж, Д > 0 .
L	J	J
т/2
39. [/(x)-/Bx)]ctga;da; = /@)ln2
40. f(x)e {ax
о
[a > 0].

2.1.2]
2.1. Введение
219
ж±1/2/
41.
«¦
43.
44.
45. - f - + -
46.
47.
48.
ac)/a f f
J
^e^2 dy
[a = 1 или г; a > 0].
[A; = 0 или 1; a, b > 0].
^) dx =
[a, b > 0].
ab)sf{y
a} b> 0; 6 =
ж V а ж
— f ( ж Н	I arete x dx
х \ xj
1 , /ж а
ж V а ж
О,
а > 0].
оо
4 J ж
f [ х -\— I dx.
1	гр I
р
/
х \а
1 Jхр а\л ,	па Г 1
- / — + — In х dx = 	 - /
х \а хр J	p j х
па Г 1 Jхр а
/	+
/
p j х \ а
о
dx
[а, р > 0].
In ж
с!ж = 0.
а, 6 > 0; аж	= =ру Г1РИ[
50.
51.
52.
53.
54.
оо
a J
[а, Ь > 0].
~^\ )dx =
abffiy^dy
a, 6 > 0; 8 =
2 , ,
У + ab
[a, b > 0].
T
; = |— f(x)dx	[ab > 0].
-оо	— оо
со	оо
/(ashж + бсЬж) sh ж dx = 2а /#(sgn6Vfe2 — a2 ch ж) sh2 ж dx.

220
Гл. 2. Определенные интегралы
[2.1.2
56
57.
58.
59
60.
61
Ь+Bп + 1)тг
а + Bп
Ь+(п+1/2)тг
а + (п + 1/2)тг
г х
- /(аж + бл/l + ж2 ) с/ж.
J л/1 + ж2
-оо
6 + 27ГП
. /(sin ж, cos ж) dx =	/(sin ж, cos ж) с/ж.
а+2тгп
I	+ / 	 Q1 И ОГ>		 fbf\Q SY* 1 /I ОТ*
I	I 1	Olll el/ •	L-Uu tJL/ J fJ>«J^ »
+ 1/2)*
/((^l)n+1 совж, (^1)та sin ж) ^ж
+ 1/2)тг
/(sin ж, cos ж) dx = /(sin ж, — cos ж) с/ж.
-1/2)тг	О
-3/2)тг	7г/2
/(sin ж, cos ж) с/ж = /(— sin ж, — cos ж) с/ж.
+ 1)тг	О
+ 2)тг	тг/2
/(sin ж, cos ж) dx = /(— sin ж, cos ж) dx.
Bп + 3/2)тг	О
птг	тг/2
62. a;/(sin ж) <ix = ттп f(sinx)dx
Bп+1)тт
2п + 1/2)тг
2п + 3/2)тг
Bп+1)тг
Bп+2)тг
о
тг/2
63.
тг/2
7г/2
64. /(sin ж, cos ж) с/ж = /(cos ж, sin ж) с/ж.
65.
= /(ж,
dx
66.
67.	/(вт2ж) cos ж dx = /(cos2 ж) cos ж с/ж.
о	о
7г/2	7Г
Г	1 Г
68.	/(sin2 ж, cos2 x) dx = — /(sin2 ж, cos2 ж) dx.
тг/2
70.	f(sin2x.cos2x)cosa~2xcosaxdx=- f\
J	2 J J Vl
[п = 0, ±1, ±2, ... ].
(-*) = /(*)].
с/ж

2.1.2]	2.1. Введение	221
тг/2	ж
71. f [f(eix cos ж) + f(e^ix cos ж)] dx = - l[f(eix cos x) + /(е^*ж cos ж)] dx =
О	7Г	0
= - /(егж cos ж) dx = тг/ I — I	/ (	) аналитична при |z| ^ 1 .
72.
т/2	.	.	тг	.
(е*ж cos ж) + f(e^tx cos ж)
a2 cos2 ж + б2 sin2 ж	2 J a2 cos2 ж + б2 sin2 ж
о	о
2 J а2 cos2 ж + б2 sin2 ж ab
аналИТИЧНа ПРИ Z ^ 1 •
7Г
- J/(a t- 2U{x+v~tx) (i -bcos ж) dx=ж[Па+ь)+/(a)]
о
[ |6| < 1; f(z) аналитична в \z — a\ ^ 1].
[ |6| < 1; /B) аналитична в |z — a\ ^ 1].
tt/2
76. /(sin ж, cos ж) <^ж = [/(sin ж, cos ж) + /(sin ж, — cos ж)] dx.
о	о
Г	Г •
J	J
о	о
тг	тг
78. f /(п)(со8ж)8т2пж^ж = Bга- 1)!! [ /(cosж) cosnx dx.
о	о
тг	тг
Г	• 2
J
.	/(sin ж, cos ж) dx = [/(sin ж, cos ж) + /(— sin ж, cos ж)] dx.
-ж/2	0
ж/2	тг/2
.	/(созж)с1ж = 2 f(cosx)
-тг/2	0
2тг	тг
82.	/(sin ж, cos ж) с/ж = [/(sin ж, cos ж) + /(— sin ж, cos ж)] dx.
о	о
тг/2
83.	= [/(sinж, со8ж) + /(з1пж, — созж) + /(™ sin ж,
О
тг/2
л / •	\.*ф/*	\.jfs/»	Ч . л /	•
, — cos ж)
о

222	Гл.2. Определенные интегралы	[2.2.1
2тг	2тт
84. /(a sin ж + 6 cos ж) dx = f(Va2 + б2 sin ж) dx.
85.
86.
87.
*
QQ
О «7*
*
91.
•tfZi.
93.
94.
95.
96.
0
= 2
оо
/(sin ж)
J x
0
7/(sin ж)
2
0
оо
J x
0
CO
f /(sin ж)
T
J л
0
CO
Г /(sin ж)
J Ж2 _|_ Z2
0
CO
/(cos ж)
2 _i_ 2
0
7Г
0
dx =
с!ж =
COS Ж
ж
da -
oo
Г xf(sinx) cos
ж24
0
6
г
-z2
]/(Ж)[?(Ж)]А1п
a
f
/(ж) ln i
J
a
6
|/(жIпп;
a
1
J /(ж) In (s
0
*(x)c
Ых--
1П7ГЖ
/^ +
тт/2
Г i
j
0
T"
0
sh2z
2z
sh z
z
X dr
	a x
ng(x
= f j
) dx =
62
(sir
sin
(sir
sin
7Г/2
J
0
т/2
r
J J
0
0
cos ж) с?ж.
ix)
ax
X
/(Sin Ж) 2
sin ж
' Г
J
0
oo
f ^
J
0
i dx
\
n
\)
/(sin ж) л
ch2 z — cos2 ж
(cos ж) cos ж с?ж
ch z — cos ж
тт/2
f 1 1 Г /(sin ж) sin ж cos25 ж
if 2 2
0
ь
/ л \n f
a
-y[/(x)[gr(x)]Adx
A=0*
a
ь
\xxf(x)dx\x=0.
a
1/2
+ a) /(ж) In (sinTra;) dx
0
A
(—x) = -fix); 5 =
[f(l — x) = af(x)].
2.2. СТЕПЕННАЯ И АЛГЕБРАИЧЕСКАЯ ФУНКЦИИ
2.2.1.	Введение.
Интегралы от степенной и алгебраических функций представляют собой широкий класс
интегралов, к которым с помощью замен переменных сводятся многие интегралы, содержа-
содержащие различные элементарные и специальные функции.
2.2.2.	Интегралы общего вида.
В этом пункте помещены формулы, которые позволяют находить интегралы содержа-
содержащие степенную и алгебраические функции. Некоторые частные случаи этих интегралов,

2.2.2]	2.2. Степенная и алгебраическая функции	223
соответствующие конкретным значениям входящих в них параметров, приведены в после-
последующих пунктах. Интегралы общего вида представляются с помощью функций Vj , Vj, j =
= 1, 2, 3, . . ., помещенных в приложении III. Конкретные значения параметров, входящих
в эти функции, приводятся в фигурных скобках после каждого интеграла. Значения инте-
интегралов этого пункта при \у\ = 1 получаются предельным переходом при \у\ —^ 1. Кроме
того, г = р/g, где р и q — взаимно простые натуральные числа, если не указаны другие
условия.
min(l,y)
s = rj + Q; + 7 — l, it = 7 -— /i — 1, ai =rj + o:, 6i = l-—/3 + j,
ci = 7 + rj + a, «3 = 1 — 7 + /i, 63 = (a + h)/r, c3 = /3 + (a + /i)/r, z = yp l
[Re a > 0 и Re 7 > 0 (при 0 < у < 1), или Re /3 > 0 (при у > 1), или Re (/3 + 7) > 1 (ПРИ У = 1)] •
2.
max A, у)
г	-—1/	\1г
Г2 =гГ[ ц-г-^ц-Л-а-^^-Л ' Й2 =Г[ /3-j,i-a + r(l-p + j) J'
t = h, v = j-\-a — 1 — r(l — /3 + j), 02 = 1^7 + ^, 62 = 1^/3 + г^хA — 7 — a + /1),
C2 = 1 + r^x(l — 7 — а + /1), «4 = 1 — 7 — 0 + r(l — /3 + j), 64 = 1 — /3 + j,
C4 = 1 — а + r(l — /3 + j), z = yp
[Re (a + 7 + r/3) < 1 + г и Re /3 > 0 (при 0 < у < 1), или
R > 0 (при у > 1), или Re (C + 7) > 1 (при у = 1)].
3. I жа 1A — жг) 1(ж — |/O 1 с!ж = V^ + F2"
У f	Г/3,7,1-7-а-^1 i^+.irf /3, 7, ^"'(T + a-l-
L	J ^	Г[
s = rj + а + 7 - 1, t = h, a\ = а + rj, 61 = 1 - /3 + j, ci = 7 + a + rj,
a2 = 1-7 + h, b2 = 1-/3 + rml(l - 7 - a + /1), c2 = 1 + г~гA - j - a + /i), z = |/p
у	[0 < 1/ < 1; Re^, Re 7 > 0].
4.
1
Er = -r'^>7j ^
и = j — h — 1, v = 7 +a — r(l-/3 + j) — 1, a3 = 1 —7 + /1, 63 = (a + h)/r, c3 = /3 + (a + /i)/r,
«4 = 1 — 0 — 7 + r(l — /3 + j), 64 = 1 — /3 + j, C4 = 1 — a + r(l — /3 + j), z = 2
1	f	[y > 1; Re^, Re7 > 0].
5. I жа"!A - xr)l3^1(y + x)p^1dx = < x	2	Ll2/| ^ J'
[|2/l > 1]
a, l — p — a — rjl 1 1/3, r (a + p — /i — 1), 1 — p + /1

224
Гл. 2. Определенные интегралы
[2.2.2
1Г/3 (а
г
fti = 1 -
О» I fly	11 ~т~ <Ь
J
0
|5 s = rj-\-a-\-p— \^ t = h, и = p — h — 1, a\ = rj -\- a,
ol + rj + p, a2 = 1 — p + h, &2 = 1 — P + rml(l — p — a + /iM
[|argy| < тг; Re a, Re/3 > 0].
-l ,	Vi + VV"	[It/I ^ 11,
dx = i _ _	u ' J'
i/i + V2	[|i/| > l]
=Г
i-.,_i-p
1 - G, 1 - p
- o- - (a + /1)
1 — cr + j, a — r(l ^ cr + j), 1 ^ p ^ a + r(l — cr + j)
о 	 ftp» л 	i	 /""V 	j	 /~% 	 I	g 	 # f% § 	 /°% 	 I 	 jhs f§ 1 	 /~% 	[	 /""V 	 I 	 T9 I 1 	 /"V 	I	 >Q 1 /^s -& 	 ffp* si 	[	 /~\i
^ — I j —|— ?j/ —|— jy	± 5 L — /1 j Li — jj	±	§ & j и — jj ^r t-л	J-	# I ±	О П^ «/ / 5 ^*1 — ' J >^ ^* 5
61 = 1 — cr + j, ci = p + a + rj, a2 = 1 — p + /1, 62 = 1 — cr + r^ A + h — a — p),
C2 = l + r A + Л- — a — p), аз = 1 — p + /1, 63 = (a + h)/r, сз = о* + (a + h)/r,
[ I argy| < тг; Re а > 0; Re (a + ar + p) < 1 + r].
r3+ + V4+	[0<y^l],
7. ж"^-/)^1
2/ -
8.
P — J J	Г\	Г	J	Г \	Г
= rj + a-l, t = h, u = -h-l, ai = l-P + j,a,2 = l-P + (l + h- a)/r,
62 = 1 + A + Л - a)/r, a3 = (a + /i)/r, 63 = P + (a + /i)/r, z = yp 1
[Re a > 0 и Re^ > 0 (при у ф 1), или Re^ > 1 (при у = 1)].
_ГЧР-1 ^ _fv3+ + V4+	[о < у ^ 1],
^
l + h - a
г \ г	г J	[ I — р J
s = ск + rj — 1, t = hj и = —/i — 1, ^ = 0 — 1 — гA — р),
ai = 1 - р + j, a2 = 1 - р + A - а + h)/r, 62 = 1 + A - а + /i)/r,
9. ж°
о
а3 = (а + /i)/r, 63 = р + (а + ^)/г? а4 = 1 - р + j, z = (-1)д|/р
[2/ > 0; Re a > 0; Re (a + гр) < 1 + г].
da;
[0 < у < i],

2.2.2]
2.2. Степенная и алгебраическая функции
225
i=o
[y > 1], [0 < Rea < 1 + r].
10.
dx
, J> + a, l-<r-2a-2jr
<T + 2a-2ft\ [ft-g/2, 1/2-ft
V
2r
l-a/2-h
(l-g)/2 + /t, -1/2 -ft
Ь5 =	А
, s = a/2 +a
г	V ' г у [l + /i- o-J
и = «т/2 — /i, ai = jr + a, &i = a + j> + a, c\ = 1 — /3 + j, rfi = 1 + a/2 + j> + a,
;i = A + a)/2 + jr + a, a2 = /i - cj/2, 62 = <r/2 + /i, c2 = 1 - ^ + B/i - 2a - a)/Br),
d2 = 1/2 + /i, e2 = 1 + B/i - 2a - <r)/Br), a3 = A - <r)/2 + h, b3 = A + a)/2 + /i,
c3 = 1 - /3 + B/i - 2a - a + l)/Br), d3 = 3/2 + h, e3 = 1 + Bh - 2a - a + l)/Br),
«4 = /i — cr/2, 64 = A — <j)/2 + /1, C4 = (a + h)/r, d4 = 1 — cr + /1,
e4 =
< тг; Rea, ReC > 0].
11. ^(l-/)^^
0
I _,_
IT7 1	r
- J ^5
v;+ + Ve
, 2a + 2jr, ^a/2 - a - jr
1 — cr + h
1/2-h, h^a/2
-1/2-h, A-a)
Л
s = a/2 + a + jr, t = h, u = a/2 - h, ui = (a - l)/2 - h, сц = jr + a, 61 = 1/2 + jr + a,
ci = 1-^+j, rfi = Ц-сг/2 + jr + a, ei = l-cr/2 + jr + a, a2 = h-a/2, b2 = (l-cr)/2 + /i,
c2 = 1 - /3 + BЛ - 2a - a)/Br), d2 = 1 - a + /1, e2 = 1 + B/i - 2a - a)/Br), a4 = h - a/2,
64 = <t/2 + h, c4 = (a + h)/r, d4 = 1/2 + h, e4 = /3 + (a + h)/r, a5 = A + <j)/2 + h,
65 = A - <r)/2 + /1, c5 = Ba + 2/i + l)/Br), rf5 = 3/2 + /1,
e5 = /3 + Ba + 2/i + l)/Br), z = (^
argt/| < тг; Rea, Re/3 > 0].
12.
l-
j,jr-\-a, -2jr-2a-a
В
2r
<r-l + 2a-2h
-(т/2, 1/2-h
15 А. П. Прудников и др., т. 1

226
Гл. 2. Определенные интегралы
[2.2.2
,1 — /9 —
л Г
г	г ) |_1-<t +
1- p + j, a + r(p-j- 1), 2r(l-p +j) -2а-<т
s = cr/2 + a + jr, t = /i, ti = 1/2 + h, u = a/2 - h, v = a/2 + а - r(l - p + j),
ai = а + jr, bi = a + a + jr, ci = 1 — p + j, rfi = 1 + cr/2 + а + jr,
i = A + <t)/2 + a + jr,a,2 = h- <т/2, b2 = a/2 + h, c2 = 1 - p + B/i - <j - 2a)/Br),
rf2 = 1/2 + Л, e2 = 1 + BЛ - o- - 2a)/Br), a3 = A - <т)/2 + Л, 53 = A + <r)/2 + h,
сз = 1 - p + B/i - a - 2a + l)/Br), rf3 = 3/2 + Л, e3 = 1 + B/i - <r - 2a + l)/Br),
a,4 = h- cr/2, 1L = A - <t)/2 + /i, c4 = (a + /i)/r, d4 = 1 - <r + /i,
e4 = p + (a + /i)/r, a6 = r(l - p + j) - a - a/2, 66 = r(l - p + j) - a + A - a)/2,
= l-p +j, rf6 = l^a + r(l^p + j), e6 = l^cj^a + r(l^p + i), z = (^l)9+p|
13. ха^г
о
¦ dx =
->v*+
Vf + Vf
= (-I)'
| argy| < n; Rea > 0; Re (a + pr + cr/2) < r].
v7+	ro < « < n,
a + Jr? ^°" ~~ 2o — 2jr
1 — cr — а — jr
2r
-ctg
2r
2r
2r
l-a/2-h
~a)/A--f-tij —1/-^ — "-
-ст - 2a + 2r(l + j), а -
s = <j/2 + a + jr, t = h,ti = 1/2 + /i, и = <j/2 - h, v = a/2 + a - r(l + j), ai = a + jr,
6i = cr + a + jr, a = 1 + j, rfi = 1 + cr/2 + a + jr, et = A + cr)/2 + a + jr, a2 = h - a/2,
fe2 = o-/2 + /i, C2 = 1 + B/i - 2a - o-)/Br), d2 = 1/2 + /i, e2 = c2, a3 = A - <r)/2 + h,
bs = A + <t)/2 + /i, c3 = 1 + B/i - 2a - G + l)/Br), d3 = 3/2 + h, e3 = c3,
a4 = h — a/2, 64 = A — сг)/2 + Л,, С4 = (a + h)/r, d^ = 1 — a + /1, 64 = C4,
«6 = r(l + j) - a - <r/2, 66 = r(l + j) - a + A - a)/2, c6 = 1 + j, d6 = 1 - a + r(l + j),
), m = 2p или 2p+ 1, z = (^
[|/, Re a > 0; Re (a + tr/2) < r].
14. I x~
о
V8~ + Vf + Vtо
1 - a - a J
E+= v
.
2a
7-aJ
I I + 7 -a -cr/2 J
+ 7 - cr - 2a 1
J
7
а-7/2,7-^-
a- G-
si = a + <j/2, s2 = 0, s3 = 1/2, s5 = a + (a - j)/2, s6 = a + (a - 7 - l)/2,
S7 = cr/2, ai = a, &i = cr + a, ci = 7/2, rfi = A + 7)/2, ei = 1 + cr/2 + a,
/1 = A + a)/2 + a, g-i = 1 + 7, a2 = -<r/2, 62 = cj/25 c2 = G - <r)/2 - a,

2.2.2]
2.2. Степенная и алгебраическая функции
227
rf2 = A + 7 - о-)/2 - а, е2 = 1/2, /2 = 1 + 7_а- с/2, ^2 = 1 - а - с/2, а3 = A - <т)/2,
Ьз = A + <т)/2, сз = A + 7 - <г)/2 - а, d3 = 1 + G - ^)/2 - а, е3 = 3/2,
/з = C - с)/2 - а + 7, gs = C - с)/2 - а, а5 = G - ^)/2 - а, Ь5 = A + 7 - ^)/2 - ">
с5 = т/2, db = -т/2, е5 = 1 - а + 7/2, /5 = 1-<т-а + 7/2, ^5 = 1/2,
а6 = A + 7 - <^)/2 - а, Ьб = 1 - а + G - ^) А с6 = A + 7) A d6 = A - 7) А
е6 = C + 7)/2 - а, /б = C + 7)/2 - ст - а, ^Гв = 3/2, а7 = -а/2, Ь7 = A - с)/2,
15. х
о
с7 = a, d7 = а - 7, е7 = 1 - а, /7 = 1 + а - 7/2, g = A - 7)/2 + а, * = 2/
[|argy| < тг; Re а > 0; Re Bа + а - 7) < 0].
+ у/1-\-Х)^
~^(т - 2а - 1, а+ 1/2
1/2-а-с
т, G-ст)/2^а
2а + <т - 1, G - с + 1)/2 - а
^"--2	-' 1^^а + 7/2 ]'
		I	iс\			\ ( I 1 \ /О		 О		 1 /О		 /	1 \ /О I		 /О
ai = a, 6i = а + a, ci = —7/2, ^i — 7 A ei = 1 + сг/2 + а, Д = A + с)/2 + а,
gl = 1/2, а2 = а + 1/2, 62 = с + а + 1/2, с2 = A - 7) A <fe = A + 7)/2,
е2 = C + с)/2 + а, /2 = 1 + с/2 + a, g2 = 3/2, а3 = -с/2, 63 = с/2, с3 = G - <т)/2 - а,
d3 = -G + <т)/2 - а, е3 = 1/2, /3 = 1 - а - c/2, g-3 = A - с)/2 - а, а4 = A - с)/2,
Ь4 = A + с)/2, с4 = A + 7 - с)/2 - a, d4 = A - 7 - ^)/2 - », е4 = 3/2,
J4 = C — с)/2 — a, g = 1 — с/2 — а, ав = G ~~ °")/2 — ск, &5 = A + 7 ~~ °*)/2 ~~ tt5
с5 = 7/2, d5 = A + 7) А е5 = 1 + 7/2 - а, /5 = 1 - а - а + 7 A ^5 = 1 + 7,
а6 = -с/2, 66 = A - с)/2, с6 = a, d6 = а + 1/2, е6 = 1 - с, /6 = 1 + а - 7 А
[|argy| < тг; Re а > 0; Re Bа + а - у) > 0].
/2/ + ж
?, а + jr, 1 — а — 2а — 2jr
Р - j, I - с - а - jr
EJ =
2<х^2
V
с + 2а - 2fe -
/
а + 2а - 2h -
2г
l-c + 2/i
1 - с)/2 + h, 1/2 - h
A-<т)/2-Л
- с/2 + fc, -1/2 - /1
a3 = 1
e3 = 1
-с/2-
r	v • г ...... ,,в = (с-1)/2 + а+^г,* = Л,
= /i + 1/2, и = (с — 1)/2 — Л,, ai = а + jr, 61 = а + а + jr, ci = 1 — /3 + j,
A + с)/2 + а + jr, ei = c/2 + а + jr, а2 = A - ff)/2 + /1, Ь2 = A + c)/2 + Л,
1-^ + A-с-2а + 2h)/Br), d2 = 1/2 + /г, e2 = 1 + A - a - 2a + 2h)/Br),
- a/2 + /i, fe3 = 1 + c/2 + /l, c3 = 1 - /3 + B - с - 2a + 2/i)/Br), d3 = 3/2 + h,
+ B - a - 2a + 2Л)/Bг), a4 = A - c)/2 + /1, 64 = 1 - c/2 + h, c4 = (a + h)/r,
i4 = 1 - cr + /1, e4 = /3 + (a + h)/r, z = {-yf
argy| < тг; Re a, Re/3 > 0].
15*

228
Гл. 2. Определенные интегралы
[2.2.2
dx =
{е}-2*
fV + x	{ Vf + V6
"/3, 2a + 2jr, A - с
Ы > 1]
-a- jr
В
2r	y* |_1-* + й Г
1/2-h, (l-cr)/2 +
A - cr)/2 - h
2/i + l\^[^l/2-/i, l-cr/2 + Л
-O-/2-/1
27
s = (cr - l)/2 + a + jr, t = /i, w = (a - l)/2 - h, m = a/2 - 1 - /i, ai = a + jr,
6i = 1/2 + a + jr, ci = 1 - /3 + j, di = A - <r)/2 + a + jr, ei = A + a)/2 + a + jr,
a2 = A - <j)/2 + Л, 62 = 1 - cj/2 + Л, С2 = 1 - )9 + A - o- - 2a + 2/i)/Br), d2 = 1 - a + Л,
e2 = 1 + A - a ^ 2a + 2li)/Br), a4 = A - <r)/2 + h, b4 = A + a)/2 + /i,c4 = (a + /i)/r,
, e4 = /3 + (a + /i)/r, a5 = 1-<t/2 + /i, 65 = 1 + <t/2 + /i, c5 = B
18.
= 3/2 +Л, e5 =/3 + Ba + 2/i + l)/Br), z = (-|/)p >	[|arg3/| < тг; Rea, Re/5 > 0].
02/1 > 1]
•V7~
^+ = 2<T+2a+2irrri - P + j, 1 - <t - 2a - 2jr, a +jrj
L	1 - p, 1 - a - a - jr	J'
cr + 2a - 2Л - 1>\г,[A - a)/2 + /i, 1/2
(l-a)/2-h
2r
-,1-p-
2a-2Л-
-a/2-h
1-СГ + 2Л] _ /a + /i
p + j, a — r(l — p + j), 1 — .
j) -2a
8 = (a - l)/2 + a + jr, t = /1, ti = 1/2 + h, и = (a - l)/2 - /i,
v = (cr — l)/2 + a — r(l — p + j), ai = a + jr, 61 = cr + a + jr, ci = 1 — p + j,
di = A + <t)/2 + a + jr, ei = a/2 + a + jr, a2 = A - <r)/2 + /i, 62 = A + <r)/2 + h,
C2 = l^p+(l^{j^2a + 2/i)/Br), d2 = 1/2 + /i, e2 = 1 + A - о- - 2a + 2/i)/Br),
a3 = 1 - <т/2 + Л, 63 = 1 + <т/2 + Л, c3 = 1 - p + B - o- - 2a + 2h)/Br), d3 = 3/2 + /1,
e3 = 1 + B - cj - 2a + 2/i)/Br), a4 = A - c)/2 + /1, 64 = 1 - a/2 + /1, c4 = (a + Л)/г,
d,4 = 1 — cr + h, e4 = p + (a + /i)/r, ae = A — cr)/2 — a + r(l — p + j),
b6 = 1- a/2 - a + r(l - p + j), c6 = 1 - p + j, d6 = 1 - a + r(l - p + j),
e6 = 1 - cr - a + r(l - p + j), z = (~l)q+p
[ I arg t/1 < тг; Re а > 0; Re Ba + 2rp + a - 1) < r].
19.
A -
v8- + vf
irj^ [l — cr — 2a — 2rj, a + rj
1 — a — a — r j
1-<т-2а


2.2.2]
2.2. Степенная и алгебраическая функции
229
¦ = ^Vctg
2 - cr - 2a-
2r
7Г I I
-a/2 + h, -1/2™ h
^a/2^h
I- a + 2h
j), a-
s = (<т - l)/2 + a + j>, t = /i, ti = /i + 1/2, u={a - l)/2 - /i,
v = (cr - l)/2 + a - r(l + j), ai = a + jr, &i = cr + a + jr, ci = 1 + j,
di = A + (t)/2 + a + rj, ei = <j/2 + a + rj, a2 = A - <т)/2 + Л,
b2 = (a + l)/2 + Л, c2 = e2 = 1 + A - <r - 2a + 2/i)/Br), rf2 = 1/2 + h,
a3 = 1 - <r/2 + /i, 63 = 1 + a/2 + h, c3 = e3 = 1 + B - <r - 2a + 2h)/Br),
ds = 3/2 + /i, a4 = A - a)/2 + /1, 64 = 1 - cj/2 + /1, c4 = e4 = (a + /i)/r,
d4 = 1 - a + fc, a6 = A - <r)/2 - a + r(l + j), 66 = 1 - <^/2 - a + r(l + j),
c6 = 1 + j, rf6 = l-a + r(l +j), e6 = l-<r-a + r(l +j), z = (-y)p\
[\argy\ < тг; 0<Rea<r + (l- Re<r)/2].
20. ж
(л/У
A +
Ы > 1]
|i^8+=2CT+2"^B(a, l-<r-2a),
[a + (a - l)/2, 7 - 2a - cr + 1
^i+o = 2
v
2-G-2a
7 - a
- G + l)/2, 2-2a-
8i = (a- l)/2 + a, s2 = 0, s3 = 1/2, s5 = (cr - l)/2, s6 = (<r - 7 - l)/2 + a,
s7 = (a - 7)/2 + a - 1, ai = a, 61 = cr + a, ci = 7/2, di = A + 7J/2,
ei = A + cr)/2 + a, /1 = cj/2 + a, gl = 1 + 7, a2 = A - cr)/2,
&2 = A + cr)/2, c2 = A - a + 7)/2 - a, d2 = 1 + G - cr)/2 - a, e2 = 1/2,
/2 = C - cr)/2 - a + 7, gr2 = C - cr)/2 - a, a3 = 1 - cr/2, 63 = 1 + cr/2,
сз = 1 + G - cr)/2 - a, d3 = C + 7 - cr)/2 - a, e3 = 3/2, /3 = 2 + 7^a^ a/2,
g-3 = 2 - a - cr/2, a5 = A - cr)/2, 65 = 1 - cr/2, c5 = a, d5 = a - 7, e5 = 1 - a,
/5 = 1 + a - 7/2, 5Гб = A — 7)/2 + a, a6 = A - a + 7)/2 - a, 66 = 1 + G - cr)/2 - a,
c6 = 7/2, d6 = -7/2, e6 = 1 + 7/2 - a, /6 = 1 - a - a + 7/2, #6 = 1/2,
a7 = 1 + G - (t)/2 - a, b7 = C + 7 - <r)/2 - a, c7 = A + 7)/2, d7 = A - 7)/2,
21. Z
0
- a - a, /7 = C + 7)/2 -<*,g7 = 3/2, z =
[ I argyl < тг; Re а > 0; Re Ba + a ~~ 7 - 1) < 0].
- da? =
V+ + V
= -2<7+2a+17 В (а + |, -<т - 2a Y
о-- 1,A + 7 -<т)/2- a

230
Гл. 2. Определенные интегралы
[2.2.2
2а, 7/2 - а
22.
Е9 =2a+a 7B(a - 7/2, 1 - a - 2a+ 7),
Sl = (o- _ i)/2 + a, s2 = <t/2 + a, s3 = 0, s4 = 1/2, s5 = (a - l)/2,
= (cr - 1 - 7)/2 + a, ai = a, 61 = <j + a, ci = 7/2, di = -7/2, ei = A + a)/2 + a,
Д = a/2 + a, g! = 1/2, a2 = a + 1/2, b2 = a + a + 1/2, c2 = A - 7)/2,
d2 = G + l)/2, e2 = 1 + cj/2 + a, /2 = (<r + l)/2 + a, g2 = 3/2, a3 = A - (r)/2,
Ьз = A + a)/2, c3 = A - a + 7)/2 - a, d3 = A - <r - 7)/2 - a, e3 = 1/2,
/з = C - <r)/2 - a, #3 = 1 - a/2 - a, a4 = 1 - <r/2, 64 = 1 + a/2,
c4 = 1 + G - <j)/2 - a, d4 = 1 - G + a)/2 - a, e4 = 3/2, /4 = 2 - a/2 - a,
#4 = C - a)/2 - a, a5 = A - <r)/2, 65 = 1 - <r/2, e5 = a, d5 = « + 1/2,
e5 = 1 + 7/2 + a, /5 = 1 - 7/2 + a, #5 = 1 - a, a6 = A - a + 7)/2 - a,
be = 1 - {a - 7)/2 - a, c6 = 7/2, d6 = G + l)/2, e6 = 1 + 7, /6 = 1 + 7/2 - a,
g6 = 1 - (j - a + 7/2, z = y>	[|arg2/| < тг; Rea > 0; ReBa + cr -7 - 1) < 0].
F+ + V9+ + F+
s" + VJ- + Vio	[|y| > 1]
^+ = 2a+2a^7 В (a, 1 - a - 2a), E$ = 22"+<т^7^1 В (a + (a - l)/2, 2 + 7 - 2a - a),
iq = 2	а В (a + cr/2 — 1, 3 + 7 — 2a — <r), Eg =2	В (a, 1 + 7 — 2a),
Eg = 2a+2a-'r-1 В (a - G + l)/2, 2 - cr - 2a + 7),
^ = ^2a+2a^7^27 В (a - 7/2 - 1, 3 + 7 - <t - 2a),
81 = (a- l)/2 + a, s2 = 0, s3 = 1/2, s5 = (a - l)/2, s6 = a + (o- - 7)/2 - 1,
s7 = a + {a - 7 - 3)/2, ai = a, 61 = a + a, ci = A + 7)/2, di = 1 + 7/2,
ei = A + (t)/2 + a, /1 = <j/2 + a, #i = 1 + 7, a2 = A - <r)/2, b2 = A + <r)/2,
c2 = 1 + G - a)/2 - a, d2 = C + 7 - <r)/2 - a, e2 = 1/2, /2 = C - <r)/2 - a,
?2 = C _ a)/2 + 7 - a, a3 = 1 - cr/2, 63 = 1 + cj/2, c3 = C + 7 - <r)/2 - a,
* = 2 + G ~~ a)/2 - a, e3 = 3/2, /3 = 2 - a/2 ~~ a, ^3 = 2 + 7 - a/2 - a,
a5 = A - cr)/2, 65 = 1 ~~ a/2, c5 = a, d5 = a - 7? e5 = 1 - a, /5 = A - 7)/2 + a,
gb = a- 7/2, a6 = 1 + G - <r)/2 - a, b6 = C + 7 - <r)/2 - a, c6 = A + 7)/2,
de = A - 7)/2, e6 = C + 7)/2 - a - G, /6 = 1/2, ge = C + 7)/2 - a,
«7 = C - <j + 7)/2 - a, 67 = 2 + G - a)/2 - a, c7 = 1 + 7/2, d7 = 1 - 7/2,
e7 = 2^cr^a + 7/2, Д = 3/2, g-7 = 2 + 7/2 - a, z = 1/}
[ I arg?/| < тг; Re a > 0; Re Ba + <r — 7) < 1].
23. x
(у/У
/y + x,
В
= 2Л
-x)(y + x)
- a - 2a), E$ = ™2сг+2а+17В(а + 1/2, -a - 2a),
"ffQ В (o- + 2a - 1, 1 - a + G - a)/2),
2, C + 7 - a)/2 - a), Eg" = 2^2а+1 В Bа, A + 7)/2 - a),
E1™ = 22a+CT~2l~1 В (a - G + l)/2, 2 + 7 - a - 2a),
Sl = (a - l)/2 + a, s2 = <j/2 + a, s3 = 0, s4 = 1/2, s5 = (a - l)/2,
s6 = a + (о- - 7)/2 - 1, ai = a, bi = a + G, ci = A + 7)/2, di = A - 7)/2,
ei = A + G)/2 + a, /1 = a/2 + a, gi = 1/2, a2 = a + 1/2, b2 = a + a + 1/2,
c2 = 1 + 7/2, d2 = 1 - 7/2, e2 = 1 + a/2 + a, /2 = (a + l)/2 + a, g-2 = 3/2,
аз = A - <7)/2, 63 = A + a)/2, c3 = 1 + G - <т)/2 - a, d3 = 1 - G + cj)/2 - a,
ез = 1/2, /3 = C ~~ a)/2 -a,g3 = l-a/2-a,a4 = l- a/2, b4 = 1 + a/2,
c4 = C + 7 - a)/2 - a, d4 = C - 7 - cj)/2 - a, e4 = 3/2, f4 = 2-a/2- a,
#4 = C - <7)/2 - a, a5 = A - o-)/2, 65 = 1 - a/2, c5 = a, d5 = a + 1/2,
e5 = 1 - <7, /б = A - 7)/2 + а, йГб = A + 7)/2 + a, a6 = 1 + G - a)/2 - a,

2.2.2]	2.2. Степенная и алгебраическая функции	231
66 = C + 7 - <т)/2 - а, се = A + 7)/2, * = 1 + т/2, е6 = C + 7)/2 ~~ а,
/6 = C + 7)/2- а - ex, ?6 = 1 + 7, z = у}	[|argy| < тг; ReBa + <т - 7) < 1; Re« > 0].
*1
у2 + 2ху cos 7 + х2	{V12	Ы > 1]
¦ dx ^^
[|argj/| < тг; Re а, Re/9 > 0; | —у| < тг; г > 0 произвольное].
_ \ V+ + у+	[\у\^1],
у2 + 2xycosj + x2	[ V12 + V13	[Ы > 1]
sin 7
г sin 7 |_	^ ~~ Р
[ | arg|/| < тг; Re а > 0; Re (а + гр) < г + 2; \j\ < тг; г > 0 произвольное].
J 1 — хг у2 + 2ж|/ cos 7 + ;
о
sin [(a + lr)n] y	r
[0 < j/ ^ 1],
в_Р_|г_я МУ /« + / \ g.n
r	\ r J
[У > 1],
[0 < Re а < r + 2; | —у| < тг; г > 0 произвольное].
I/+
л— | .. а — ± v -*- ! V -•- i "^ У	j __	I П4 Г у 1 f
[|з/1 > Ч
\-Cii4 -- —2	тг(—сгJij -^15 ^2	<tf Г|—сг Н™ 2т (/ -|- 1 — ^)j5
[ | argt/| < тг; Re a > 0; Re Bа + <хг) < 2; | —у| < тг; г > 0 произвольное].
28. |Ж^^	^d!B = J Vii + Vxt
{B+ = -2ст+2(а-2)/гтгA - аJ;, ??+ = _2"+2(а-2)/'>-1Г[1 - ff + 2r-x(/ + 1 - a)],
E{4 = _2ст+2(а-2)/г-17г, Ей = 2'+4a-V'rr-1, z = 2-2/ry, h = -a}
[ I arg|/| < тг; Re a > 0; Re Bа + егт) < 2 + r/2; | —у| < тг; г > 0 произвольное].
29
| argy| < тг; 0 < Re а < 2r + 2; | —у|, |A| < тг; г > 0 произвольное].

232	Гл.2. Определенные интегралы	[2.2.2
30. 1 ^о^1	У^ ш I	 Агг, — ) ?Г2 " 3 I *18 i 9	1\У\ ^ 1]?
Еп = 	^Г	, w \у ,Еп =	1
12 2rsin37 [P + (a + l)/r\y ' 18	2г
[|argy| < тт; Re a, Re/3 > 0; | —у| < тг; г > 0 произвольное].
A + хг)р~г	, IUU Vi"? + VA + '
dj; =
—о	 \ -L — №114 1 JL:i1 Ч —	о	А I	V 1
2sin37	2rsin37 '	n "	'
1 п[1-р-(а-/-1)/г
У"
I-/»	J ' 13 2 sin2 7'
"ie	2r'L	I-P
[ | arg|/| < тг; Re a > 0; Re (a + pr) < r + 4; | —у| < тг; г > 0 произвольное].
oo
32. —	 —	—	— = - (ysinj)~2U + 17*	[cm. 2.2.2.26],
0
(a + Ir — 1) cos [7@ + /r — 2)] a+|r^4
2 sin2 7^1	sin [(a +/г)тг]
I cos G - I7) ctg f °^	тг ) i/1^3 1	[0 < 3/ ^ 1],
V r	/I
i=o
A - a + r + rl) cos [7@ - r - rl - 2)] a^r^rl^4
2 sin2 7 ^-^1	sin \(a — r — rl)w]
(/ + l)cosG/ + 27)ctg (^±1 Лу-'-4\	[у > 1],
[0 < Re о; < г + 4; | —у| < тг; г > 0 произвольное].
33 Г д;"-! (l + vTT^r dx = f V + V + V + V
J	\
9o-+2(a-2)/r-l	9a+2(a-2)/r-l
9o-+2(a-2)/r-l	9a+2(a-2)/r-l
	—2	 (-*hiy-\ E+ =	 . 2 aT\-<r + 2r~\l + 1 - a)],
^ 7	ry2 sin7
2(hy\	2
sin^ 7	ry2 sin7
= 2a+2(a-4)/r-\(-aJi, E+ = -2ст+2^-4)/'-1GГ-1Г[-<7 + 2^A + 1 - a)],
E = ™_r+2{a-2)/r-2 2 ? =	ff 2,+2(a-2)/r-l -2
sin 7	rsin 7
?2-0 = -2"+2(a-4)/p-27ra, ??2"i = 2"+2^-4^r-1ar-\ z = 2~2'ry, h = -A
[ | arg^/l < тг; Re a > 0; Re Ba + от) < 4; | —у| < тт; г > 0 произвольное].

2.2.2]
2.2. Степенная и алгебраическая функции
233
34. х°
о
¦ 2xycosj + ж2J
^14 = —г^—*
sin 7
+ УГ6 + V2o + V2
г sin 7
Е7Л = —
J14 —	Г^~~
sin 7
^15 —	Г^ '
г sin 7
- a)],
, h = 1 - o-
35.
[ | arg 2/| < тг; Re a > 0; Re Ba + err) < r + 8; | —у| < тг; г > 0 произвольное].
2a;rcosA + x2r)(y2
I arg 2/| < тг; 0 < Re a < 2r + 4; [-y|, |A| < тг; г > 0 произвольное].
36.
xa~1dx
2rJ(l/2 + 2iC|/cos7 + ж2)
(—1L/ + 1) cos (AI + 2A)
— =BsIn2A) 1U1 + Ul	[см. 2.2.2.35],
4 sin2 A sin2 7 \~J	sin [(а + 1г)ж]
x [8in[7^r)] - (a + Ir - 1) cos [7(« + /r - 2)]] »«-•
^ rsin[(a-/-lOr/r]
^ (^l)lIcos(AI^ A)
со	si
Si
4sin2 Asm2 7 \_ sin [(a — Ir — г)тт
l)cos[7(<
°° (-l)'[(a + l)/r - 1] cos [Ar-X(a + I - 2r)]
1/	ч	г /	\i Sin Г7(а — /Г — Г — 1I1 a-r-lr-4
x I (a - Zr - r - 1) cos [7@; - /r - r - 2)]	^-^	:	^ U/	+
sin 7	J
E-
1=0
r sin [(a + 1)тг/г]
sin 7
I arg2/| < тг; 0 < Re a < 4(r + 1); | —у I, |A| < тг; г > 0 произвольное].
min A, y)
37.
a-l/! _r4/3^llV^ + Л/У^Х)
/У~х
¦ dx =
[0 < |s/| s= 1],
[\у\ > 1]
{Е+ = (-iy2->+2a+2jr(l - /З),- В (a + jr, 7 + a + jr),
Eg" = 27-2/lr-1G - 2Л)Ь В (/3, г'1 (а + ft)),

234
Гл. 2. Определенные интегралы
[2.2.2
Её = 2-2Лг-1(-7 - Щн В (/3, г^(а + 7 + Л)),
s = а + j> + G - 1)/2, гг = G - 1)/2 - h, гц = -A + 7)/2 - /i, ai = а + jr,
6i = а + 7 + J^, ci = 1 — /3 + j5 di = a + 7/2 + jr, ei = a + G + l)/2 + jr,
a4 = 1 - 7/2 + Л, 64 = A - 7)/2 + /i, c4 = (a + /i)/r, d4 = 1 - 7 + h,
e4 = ^ + (a + /i)/r, a5 = 1 + 7/2 + Л, 65 = A + 7)/2 + /1, c5 = (a + 7 + h)/r,
d5 = 1 + 7 + Л, e5 = /3 + (a + 7 + /i)/r, z = 2/p}
[|/, Re a, Re (a + 7) > 0 и Re^ > 1/2 (при t/ = 1), или Re/3 > 0 (при у > 1)].
38.
- (у/у - л/У - х ]
/У
Vf
^G - Щи В (/3, 1 - /3 - г~х(а + Л)),
(^7 - 2Л)Л В (/3, 1 - /3 - г^(а + 7 + Л)),
- /3), В (а - гA - /3 + j), 7 + а - гA - /3 + j)),
гг = G - 1)/2 -h,m = -A + 7)/2 - Л, v = а + G - 1)/2 - гA - ^ + j),
а4 = 1 - 7/2 + /i, &4 = A - 7)/2 + /i5 с4 = (а + /i)/r, rf4 = 1 - 7 + h,
е4 = Д + (а + /i)/r5 «5 = 1 + 7/2 + ^, Ьб = A + 7)/2 + Л, с5 = (а + 7 + Л)/г,
rf5 = l + 7 + ^, е5=/3 + (о; + 7 + Л)/г, а6 = 1 - т/2 - а + гA - ^ + j),
66 = A - 7)/2 - а + гA - ^ + j), с6 = 1 - /3 + j, d6 = 1 - а + гA - /3 + j),
е6 = 1 — Т ™" « + ^A "" /^ + j), ^ = 2/Р}	[У>
0].
V*
v7-
. в
E5 =
(
(-7 -
- p
, p
A - p)j В (a - r(l - p + j), 7 + « - r(l - p + j)),
s = G - l)/2 + a + jr, м = G - l)/2 - /1, ui = -A + 7)/2 - h,
v = a + G - l)/2 - r(l - p + i), ai = a + jr, bi = 7 + a + jr, a = l- p + j,
di = 7/2 + a + jr, ei = G + l)/2 + a + jr, a4 = 1 - 7/2 + h, b4 = A - 7)/2 + h,
C4 = {a + /i)/r, d4 = 1 — 7 + /1, e4 = p + (a + /i)/r, as = 1 + 7/2 + h,
65 = A + 7)/2 + h, c5 = (a + 7 + /i)/r5 rf5 = l + 7 + ^, e5 = p+(a + 7 + ^)M
ae = 1 - 7/2 - a + r(l - p + j), 66 = A - 7)/2 - a + r(l - p + j), c6 = 1 - p + j,
(l-
, e6 = l-7-
[Re a, Re (а+ 7) > 0].
40.
л/У ~ х
¦Vr
[о< \y\^i],
Ы > 1]
= " ctg
r
>7Л/
= ^2"
4-7-2ft)hCtgfa + 7 + fe7r
B (Q _ r(i + 1}> 7 + a _ r(i + 1)})
s = a + G - l)/2 + jr, и = G - l)/2 - h, щ = -A + 7)/2 - /i,

2.2.2]
2.2. Степенная и алгебраическая функции
235
v = ('у - 1)/2 + а - r(j + 1), сы = а + jr, 6i = 7 + « + J>, ci = 1 + j,
= 7/2 + a + jr, ei = G + l)/2 + a + jr, a4 = 1 - 7/2 + Л, 64 = A - 7)/2 + Л,
c4 = e4 = 1/2, d4 = 1 - 7 + /i, a5 = 1 + 7/2 + h, b5 = A + 7)/2 + /1,
c5 = e5 = 1/2, d5 = 1 + 7 + h, a6 = 1 - 7/2 - a + r(l + j),
be = (l-7)/2-a + r(l +j), се = 1 + j, d6 = l-a + r(l+j),
e6
= 1 - 7 - a + r(l +j), z = |/p I
[Re a, Re (a + 7) > 0].
41.
(i
ly-v	I ^8 + V9 + V10 + Vtl
" В (a, 7 + a), E% = 27+<T+2a В (a + a/2, a + 7 + a/:
У+^+га-!^ B (a + C. _ iy2l 7 + a + (a ¦
9a + 2a+7 г
+ 7, -a - 2a - 271
— a — a J	[ 1 ~ G ~ a ~ 7 J
si = a + G - l)/2, s5 = a + G + a - l)/2, s6 = a + G + a)/2 - 1,
s7 = G - l)/2, s8 = -A + 7)/2, ai = a, 61 = 7 + a, ci = -a/2,
di = A - a)/2, ei = 7/2 + a, /1 = G + l)/2 + a, g"i = 1 - a,
«5 = 1 — о — G + a)/2, 65 = A — 7 — a)/2 — a, C5 = a/2, ds = —a/2,
e5 = 1 - a - a/2, /5 = l^7^a- a/2, #5 = 1/2, a6 = C - a - 7)/2 - a,
b6 = 1 - G + a)/2 - a, се = A - a)/2, d6 = A + a)/2, e6 = C - a)/2 - a,
/6 = C - a)/2 - 7 - a, ?6 = 3/2, a7 = 1 - 7/2, 67 = A - 7)A c7 = a + a, d7 = a,
e7 = 1 + a/2 + a, /7 = A + a)/2 + a, #7 = 1 - 7, a8 = 1 + 7/2,
&8 = A + 7)/2, eg = a + a + 7, dg = a + 7, eg = 1 + a/2 + a + 7,
г/
42. (V
о
/8 = A + a)/2 + a + 7, g-8 = 1 + 7, z = -1
+ д/l/ - X O + (^/y - y/y - Ж O
[Re a, Re (a+ 7) > 0].
(л/ж
= 27+2a
В (a, 7 + a), E? = 27+2a+V В (a + 1/2, 7 + a + 1/2),
В (a + ct/2, 7 + a + a/2), tf9" = -fa,r
[2a + 27, ^a - 7 - a/2
8l = a + G - l)/2, s2 = a + 7/2, s5 = a + (<r + 7 - l)/2, s6 = G - l)/2,
s7 = -A + 7)/2, ai = a, 61 = a + 7, ci = -cr/2, di = a/2,
ei = 7/2 + a, /1 = G + l)/2 + a, gl = 1/2, a2 = a + 1/2,
62 = a + 7 + 1/2, C2 = A - <r)/2, d2 = (a + l)/2, e2 = a + G + l)/2,
/2 = a + 1 + 7/2, g-2 = 3/2, a5 = 1 - G + a)/2 - a, ft5 = A - 7 - cj)/2 - a,
e5 = -a/2, d5 = A - a)/2, e5 = 1 - a - a/2, /6 = i-7-a- a/2,
#5 = 1 - a, a6 = 1 - 7/2, Ь6 = A- 7)/2, c6 = a, d6 = a + 1/2,
e6 = 1 - 7, /e = 1 + a/2 + a, g-6 = 1 - a/2 + a, a7 = 1 + 7/2, 67 = A + 7)A
c7 = a + 7, ^7 = a + 7 + 1/2, e7 = 1 + a/2 + a + 7, /7 = 1 - a/2 + a + 7,
7» * = -2/
43.
[Rea, Re (a+ 7) > 0].
¦Vi"

236
Гл. 2. Определенные интегралы
[2.2.2
44
-Cig — Zi	О 1 (i j J ^T *-*¦)•) ¦*-J$ — ^	*-*
Eg = 21+2а+а~2а В (a + (j/2 - 1, 7 + a + a/2 - 1),
tj1Q = z	d (a, 1 — d — Za), Ь1г = I	В (a + 7, 1 — a — lot — ^7),
si = a + G - l)/2, s5 = a + G + <j)/2 - 1, s6 = a + G + o" - 3)/2,
«7 = G ~~ l)/2, s8 = -A + 7)/2, ai = a, 61 = a + 7, ci = 1 - c/2, di = A - a)/2,
ei = 7/2 + a, /1 = G + l)/2 + a, 54 = 1 - <r, a5 = C - 7 - <j)/2 - a,
65 = 1 - G + <t)/2 - a, c5 = A + <r)/2, d5 = A - <r)/2, e5 = C - a)/2 - a,
/5 = C - o-)/2 - 7 - a, g-5 = 1/2, a6 = 2 - G + a)/2 - a, b6 = C - 7 - <r)/2 - a,
c6 = 1 + a/2, d6 = 1 - o-/2, e6 = 2 - cj/2 - a, /6 = 2 - d/2 - a - 7, #6 = 3/2,
a7 = 1 - 7/2, 67 = A ~~ 7)/2, c7 = a + a, d7 = a, e7 = A + <r)/2 + a,
/7 = a/2 + a, g-7 = 1 - 7, «8 = 1 + 7/2, b8 = A + 7)/2, c8 = <r + a + 7,
dg = ol + 7, e8 = 1 + 7, /8 = A + a)/2 + a + 7, gg = cr/2 + a + 7, z = —2/}
[Re a, Re (a+ 7) > 0].
(a, 7 +a),
= 27+2a+
V В (а + 1/2, 7 +a+ 1/2),
Ег = 27+2CT+2tt^1 В (а + (.г - l)/2, a + 7 + (o-
" = 27a+1 В Ba, A - a)/2 - a), Em = 21~2a~^ В Ba + 27, A - a)/2 ~а~7),
si = a + G - l)/2, s2 = a + 7/2, s5 = a + G + <r)/2 - 1, s6 = G - !)/25
S7 = -A + 7)/2, ai = a, 61 = a + 7, ci = A - cr)/2, di = A + a)/2,
ei = a + 7/2, /1 = G + l)/2 + a, gl = 1/2, a2 = a + 1/2, fe2 = 7 + a + 1/2,
C2 = 1 - a/2, d2 = 1 + (т/2, e2 = a + G + l)/2, /2 = a + 1 + 7/2,
g2 = 3/2, a5 = C - 7 - (j)/2 - a, 65 = 1 - G + ^)/2 - a, c5 = A - o-)/2,
= 1 - <t/2, e5 = C - a)/2 - a, /5 = C - a)/2 - a - 7, g5 = 1 - a, a6 = 1 - 7/2,
fee = A - 7)/2, c6 = a, d6 = a + 1/2, e6 = 1 - 7, /6 = A + <r)/2 + a,
^6 = A - <j)/2 + a, a7 = 1 + 7/2, b7 = A + 7)/2, c7 = a + 7, d7 = a + 7 + !/2,
e7 = 1 + 7, /7 = A + (t)/2 + a + 7, g-7 = A - <r)/2 + a + 7, z = -y}
[Re a, Re (a+ 7) > 0].
у
45. [ж1
о
«-1 (л/17 +
•(л/У ~ Vl/^
A + 2ж cos 7 + ж2
- dx = U2 =
г
-A-2/J'
46.
A + 2ж cos 7 + %2J\/у — х
A + 2(a-Z-
-2(a + 0/1
[Re a, Re (a + Л) > 0; | —y| < тг; г > 0 произвольное].
	dx = 2~1(i/sra7)™2fy2 -
0<l/^; см. 2.2.2.45
\-2*-i^r| A-I
Л — Zt
' 18
A + 2(a-/-'
-rl
[Re a, Re (а + Л) > 0; | —у| < тг; г > 0 произвольное].

2.2.4]
2.2. Степенная и алгебраическая функции
237
2.2.3. Интегралы от (жм ^ ам)р и (ам ^ ;
а
Г	/	1
1 \( V _ M\/3-l j _ -1 /*(/3 —1) + 1 р л _?_
J	V м
о
о Г/ 2	2^-1/2,	2„Г°" 1N"
2. (а — ж ) 7 ах = тга
2Bга)!!
о	/2	2\те i	2п+1
3. (а — ж ) ах = а у;
о
Bп + 1)!!
4. I (ж^ - а^1 dx = д-1^^-1^1 В A - /3 -
5.
6.
,М _|_ ^М^ Р ^х = ^ z №Р g A/|Х, р —
бЬ _ тг !^2таBп - 3I?
x2 + z2)« ~ 2 Z Bn-2)!!
о
2.2.4. Интегралы от ха(а(л zb x^)p.
х + а
с/ж
J Уж (ж + а)
о
4.
5.
e-
7.
= /п
/о =ln(l + >/2), h = а{л/2 -1), /2 = у
[а, /1, Re/З > 0].
[а > 0].
[а > 0].
[а, /х > 0; 0 < Re^ < 1 - 1/fj].
, > 0; fi\argz\ < тг; ft Rep > 1].
[Rez > 0; n = 1, 2, 3, ... ].
[a, Re a > 0].
[a > 0].
[a > 0].
[a, Re a > 0].
[a > 0; n = 1, 2, 3, . . . ].
[a, Re a > 0].
[a > 0],

238
Гл.2. Определенные интегралы
[2.2.4
1-т
2(n
8.
арГ1 В ( ^,
Q f 2m, 2 2^-1/2. 7ra2w+2wBm - 1)!!Bn - 1)!!
9. ж (а — ж ) 7 аж = 	]_ ... ,— 4t	—
[а, /х, Rea, Re/3 > 0].
[а > 0 .
L J
о
а
10. L2m+1(a2-x2)n-
о
11.
12.
тг/2
a dx =
13.
(a5 a)
' J (x+"l|
= В (Q + 1, /3
15.
x + 1
а > 0; S =
[а > 0; 0 < Re a < 1].
[а, Re а > 0].
[Re а, Re/З > -1].
[0 < Re а < 1].
16.	—dx =
J	+1
x +1
:
a sinaTr
17.
18.
19.
(жп + 1)г
(p/n-l)\(m-l-p/n)\
	;	—
(m — l)ln
m-1 / n sin (pn/n)
[m, n, p = 1, 2, 3, . . . ; mn > p; p/n нецелое],
ra, n, p = 1, 2, 3, . . . ; тете > p; p/n целое I.
, sin [(a - ^)тг/2] „ .
dx = 	p7	^; ;. В (a
sin [(a +/3)тг/2] l
20.
21.
1 -
dx = фШ + 1) - ^(a + 1)
dx = irctgair
0; Re a, Re^ > -1].
[Rea, Re^ > -1].
[0<Rea<l].

2.2.5]
2.2. Степенная и алгебраическая функции
239
22.
23.
24.
25.
1 — х
//-I/
dx = za рВ(а, р - а)
dx =
dx
x + z	sin атг
Г жа dx	_i
26. 	 = ^7гаа ctg атг
J ж а
27.
28.
29.
30.
1r
\x - а\р
dx =
(a- р/2)ж
cos(p7r/2)
В(а, р- а)
| argz| < тг; О < Re a < Rep].
[largzl < тг; О < Rea < 1].
[а > 0; 0 < Re а < 1].
[а > 0; 0 < Re а < Rep < 1].
т^с!ж = / ,, ,П
(ж - а)п	(п - I)!sina7r 11
k=1
-а
~ }	П (а - А;)	[а > 0; 0 < Rea < n; n = 1, 3, 5, . . . ].
11
|ж
x — а {sgn ж
[0 < UrgzI < тг; 0 < Re а < Rep].
а Ч 5 ^	1та = 0; 0<Rea< 1.
I 1 J
2.2.5. Интегралы от (ам±/)р(Г т/
Условия: а, 6, с, d — действительные числа.
ь
1. [(ж - а)а^(Ь - xf-1 dx = (b^ а)а+^г В (а,
[Re a, Re/3 > 0].
*
3.
Ж^
(fe- a)"
7
а{ас + d){hc + d)a
0; Re a > 0].
0; Rea>0].
J
(еж
n\ B(fc + 1,
к)
> 0; Re/3 > 0].
ь
- J
f>(bc +d)(ac

240
Гл. 2. Определенные интегралы
[2.2.5
в.
7.
8.
9.
а + х
(а2 - ж2)т _	m\2m+1
¦ dx =
Bт + 1)!!
— л/d — асJ
[0 < Re/3 < 2, p ф 1].
[d > |ac| > 0].
(d + icx)r
dx = n(d2 + а2
10. |	dx = ±ж sgn |/(|/2 — а2
ж - I/
11.
12.
13.
14.
-{*„"}
dx
= ln-
/a - x (x + y) Va + 2/
2 ln^±^±i
2	/ a
arctg ,
/a — x (x — y)	y/y ~~ а	у У ~ а
[m = 0, ±1, ±2, ... ].
[—oo < |/ < —а или а < у < oo].
[-a < у < a].
[0 < a < 1/].
[a > 0; | argy| < тг].
[у > а > 0].
15. 1	dж = ± sgn у (у2 — a2) 1^2 arccos I	) —
16.
a + у а2 — y2
/
0 J
[-—00 < у < -—а или а < у < оо].
[-а < t/ < а].
20.
21.
[cd > 0; ad
1
/ж + z (ж + a) ^z — а
dx
¦In
/z + V^ -
/z — \/ z — a
[0 ^ к < 1].
с; Re^ > 1].
[a, z > 0].
Bп-3)!!2/тг
(ж2
2(п - I)z2n(z2 + у2) (п - I)!2«z2«(z2 + у2)

2.2.6]
2.2. Степенная и алгебраическая функции
241
22.
23.
24.
25.
26.
27.
28.
29.
оо
(^l)^1 дп
dx
[у, Rez > 0; п = 2, 3, 4, ... ].
(
(ж2 + z2)(x + |/)те (п - 1)! о^1 [z2 + у2 V 2z
dx
¦In-
-У)
[Rez > 0; |argt/| < тг, n = 1, 2, 3, . . . ].
[Rez > 0; | arg3/1 < тг].
dx
-y2
¦ arctg •
= У
VVV
¦2 _
¦ In
I/
[Rez, Ret/ > 0; | arg (z2 - t/2)| < тг; z ф у].
[z = у; Ret/ > 0].
[Rez, Ret/ > 0; | arg (y2 - z2)\ < тг; z ф у].
(a2x2 + 62)(е2ж4 + d2) " 2(«4d2 + 64c2) [б I"" d ] \/ 2J	[a> 6' c' d > °]'
(ж
, r2 >0; 0< |0i| < тг, 0< \02\ < тг;
0;
= e exp [eiwp - i(p - /3)@i + 03)]
э,-/3)
П, ^2 > 0; p > C] гз = yr2 + r\ + 2riF2 cos @i — 6>2), гз sin 0з = r2 sin @2 — 0i),
-1, если 0 < 0i < тг, 0 < 6>2 < тг
r3 cos 0з = ri+r2 cos @2™0i); |03| < тг; e =
30.
31.
32.
1, если — тг < 0i < 0, -—тг < 02 <
[a, 6 > 0; Re (/i + i/) > 1].
= 0
(a + *
= 0
[об < 0; Re(/i + v) > 1].
[Re a, Re 6 > 0; Re (/i + i/) > 1].
2.2.6. Интегралы от j l(ak^x)Pk.
k=i
Условия: a, 6, c, d — действительные числа.
ь
f
г, /	n c(a-b)
x 2Fi a, ^7; a + /3; -^——~^
\	ac + о
16 А. П. Прудников и др., т. 1
^^~г(ае 4- г/17 R Гг> Я) X
[Re a, Re^ > 0; | arg (d + cb)/(d + ca)\ < тг].

242
Гл. 2. Определенные интегралы
[2.2.6
2.
3.
4.
5.
6.
7.
8.
9.
10.
у-а\Р\у-Ь\а
[Re a, Re /3 > 0; у < a < 6 или a < b < у].
Ь-у
х 2Fi( 1, 2-а-/3; 2-/3;
В (а, /3JFi 1, /3; а +/3;
\	Ь-у /
[Re a, Re C > 0; у < а < b или о < 6 < у].
4(а, р -1) х
[Rea, Re/3 > 0; /3 ф 1; a < у < b].
6-а
\ а —1 |
— а\ «ж
6 — ж / ж — у sin атг
Ь- 2/
тг I	/ у — а \а
I cos аж ( f	 ) + 1
Ь-у
— 1 ) [0<Rea<2;t/<a<6 или а < b < у].
[0 < Re a < 2; a < 2/ < b].
х - у
¦ dx =
sin атт(Ь — у)
a-y
b- у
(еж
(be
(сж + d)n
[0 < Re a < 1; у < a < b или о < 6 < у].
[0 < Rea < 1; a < у < b].
(b - a)"**3 ^ /n\ В (a + Jfe, P + n - A;)
^\k) (bc + d)k(ac + rf)n^fe
: + d) > 0; Rea, Re/3 > 0].
[c ^ 0; ac + d, be + d > 0],
/1 = —о Vflc + d — V6c + d) , /2 = —т
2c2 l	; '	2c2
2c2
2c2
/3 =
тг(б^аJ
y^ (n-
fc=O
12.
1)!1 (,2+V1	'
13.
[m, n, p = 0, 1, 2, . . . ].
га — A;
[m = 0, 1, 2, . . . ; n = -1, 0, 1, 2, . . . ].

2.2.6]
2.2. Степенная и алгебраическая функции
243
14.
15.
16.
17.
18.
(ex
,
(g + A;, m-fc
d) > 0; Re a > 0].
CLX — Q>	Z D [Oi..
_ Г(а-1)ГC/2-а)
2^?
i, p; a + /3; --
|argz| < тг; a, Re a, Re/3 > 0].
dx
= ±-
/ж(а — ж) (ж ± с)	у/с(с =Ь а)
ж"™1 dx
/а — ж ж + а
[y > a; 0 < Re a < 3/2].
a, c > 0
. с > a > 0
[a, Rea> 0],
, /3/4 = а/4тг/2, /б/4 = ^а/4[тг/2 -
20. ||4^)±1/2^L = TZL±
«2 + Ж/	Ж — у	2
У + а
±1/2
I/
/ а \
arccos I	1 [—оо < у < —а или а < у < ею].
21.
22.
23.
24.
25.
26.
i ±1/2
a + 1/a2 - y2
[-а < у < а].
(еж
6с + d)(ac
> 0, Re/3 > 0].
argz|, |argy| < ж; Re а > 3].
+ zYx dx = z~xya~p В (a, p + Л - a) 2Fi (а, Л; р + Л; 1 - ^
В (a, a)
|argz|, |argt/| < тг; 0 < Re a < Re(p + A)].
[Re a > 0; |argy| < тг].
= ttz Х(-у)а г В (а, 1 - a + A) 2Fi (a, A; 1 + A; 1 + -
[|arg(-3/)| < тг; 0 < Re a < 1 + Re A].
16*

244
Гл. 2. Определенные интегралы
[2.2.7
27.
28.
= ™тг ctg (a — Х)жуа (z + у)	¦— В (а, А — а) х
z
1, 1 - А; 1 + а - Л;
2/
[2/ > 0; 0 < Rea < 1 + ReA].
xa~1dx
[(х + г)(я
— Г	I [|argz|, |argy| < тг; Rea > 1].
la — i/zJ
1.
2.2.7. Интегралы от II (a^fe =t жм^j fe.
k=i
Условия: a, 6, c, <i — действительные числа.
п.
Ira
- dx = 0т(Ь7 а)
/1 - ж2
0o(bj a) = F((fij b)^ 0iF, а) = F{ip, b) -— E(ip, b) -\- a
Bm + lHm+iF, a) - 2mF2 + 1I
1-a2
, a) — Bm — lN2<9m^iF, a) =
0_iF, a) =
Bm + lN26
ч
, b)] + &a
6, a) - 2mF2 + lH_m(ft, a) + Bm - lHi_mF, a) =
2' 2
3.
A
*
5.
7.
8.
9.
a + x\ dx
-a2 2acos(/37r/2)
с!ж =
Bm
[0< a < fe < 1; m = 0, ±1, ±2, . . . ],
л/Ь2 — a2 1
= arcsm , /-,	2 »
6v 1 — a
j
[m = 1, 2, 3, ... ]
[m = 1, 2, 3, ... ].
[a, Rea, Re/3 > 0].
[|Re/3| < 1; a > 0].
[d > \ac\ > 0].
an — xn dx
-,-n-l n ф
те+1 ~~ а ^ к
[г, Rea > 0; |zar| < 1; n = 1, 2, 3, . . . ].
[n = 1, 2, 3, ... ].
6/x sin
xa~1dx
Зтг	2/'
,а-5/3
(ж + |/)(ж2/3 + |/2/3)	8 A — 4cos2 an) sin атг
3jLi	6
[0 < Rea < 5/i].
[|argt/| < тг; О < Rea < 5/3].
1 - ж2

2.2.8]
2.2. Степенная и алгебраическая функции
245
10.
xmdx
{x2 + z2){x±y)n ~^fc
г^к (Т1)Г
(п-к-1)\ дуп~к~г [z^+ у
Re z > 0;
argj/l < 7Г, n = 0, 1, 2, . . .
t/ > 0, те = 1, 3, 5, ...
п.
12.
13.
14.
ж — у
sm атг sm (а +/х)тг
[t/ > 0; 0 < Rea < 1; 0 < Re (a + /i) < 1].
- 1
dx =
dx =
7Г Sin (/!7г/А)
xx ~ x^x J	A[cos (jwtt/A) + cos (атг/А)]
ХЛ — X л / X
= 1п
,-A<Rea</i + Rea<A].
[0 < ^ < A],
117Г
15.
(ж - I)
(ж — 1) с!ж = тгГА ctg Атг + /i ctg /Х7Г — (/x + A) ctg (/i + А)тг] — 1
16.	= 2GT/XCtg^7T - 1)
n
2.2.8. Интегралы от f\ (аГ ± жМ|е)Р|г, п > 4.
Условия: а, 6, с, rf — действительные числа.
Re(/x + A)|, |ReA|, |Re/x| < 1].
[A = -/x; |Re/i| < 1].
Fc + d)a(ac +
d)n-kto
0; m ^C те; Rea, ReC > 0].
2.
(x-y)\x-<
i2)	(cirf2 — e2cfi) slnaTT [ Fci + di)a	Fc2 + с12)а J
[dd2 Ф c2di; (acj + dj)(bcj + dj) > 0, j = 1, 2; 0 < Re a < 1].
1	тг sgn B/ — c) ctg атг
\y - c\2a~r[(y - a)(b - у)]г~а
[r = 0 или 1; а<у<6; а < с < b; 0<2Rea<l + r].
(ж - у)\х - с
||/-с|2а r[(|/ - a)F - 1/)]1 a
[r = 0 или 1; a<i/<6; a < с < b; 0<Rea<(l + r)/2].

246
Гл. 2. Определенные интегралы
[2.2.8
5. ха (а — х) A — их) рA — vx) dx = аа+ В (а1 /3)Fi(a7 р, А, а + /3; иа, va)
о
[ | arg и| < тг или а|it| < 1; | arg v| < тг или a\v\ < 1; а, Re a, Re /3 > 0].
6.
dx =
= A 1[а1ф(а1/Х) + . . . + апф(ап/Х) - аоф(ао/Х)}
[a0 = a\ + a2 + • . - + an; A, Re oli > 0; г = 0, 1, 2, . . . , n].
7.
8.
9.
10.
11.
/-(n)/2 + . . . + xa~1/n - n/"
1 - x
dx =
:tg;
dx = nlnn	[Re a > 0; n = 1, 2, 3, . . . ].
7Г
1 + x + ж2 + . . . + x2m+2	2m + 3 & 2Bw + 3)"
x2m+2
¦ ^Ж = ^т	~^т Ctg —
2)
2) '
хп~гAх
1)Bж + 1) . . . (пх
к dx = а°
-a-/3, р, А,
[п = 1, 2, 3, ... ].
-а; гг/а, v/a)
[а > 0; | argit| < тг или |и| < а; | argv| < тг или \v\ < а; 0 < Re Д < Re (А + р -— а) + 1].
12.
(Ах + В)
ci — Лс/i
Л
In
qr
In
C3CI2
[p =
i, q =
i, r = C2CI3 —
> €2/^2 >
- 2/"(j/v - l)ctgi/7r -
[y > 0;
Re/x|,
О].
7Г J
¦")l<i]-
14.
x — у x —
1-2/ L тг
In 2/ - 2B/M -^ 1) ctg /Х7Г
[y >0; y
(сх + rf)n4
dn \n
dx =
ж ^ BА;-1)!!Bп-2А;-1)!!
п-1
- V,
>• 71к
[cd > 0].
[Rez >0].

2.2.9]
2.2. Степенная и алгебраическая функции
247
Вг){А2х2 + В2) . . . (Л>-1Ж2 + Bn_i)
- B1c1)(A2d1 - В2сг) . . .
7г f
2 1
- B2c2) • • ¦
. . . (cndi — dnci)
+ . . .
. . . (cnd2 — dnc2)
2dn^B2cn)...(.
in — d2cn) . . . (cn-idn — dn-\cn
> 0; Cidj Ф Cjdi; г, j = 1, 2, 3, . . . , n; n = 2, 3, 4, . .
18.
¦ dx = In
[Pn(x) =
In=
Мп
' п =
. . . + An-!, Qn(x) = Boxn + Bis"-1 + . . . + Bn;
все корни С^п(ж) лежат в верхней полуплоскости],
z
0
0
B2
0
B4 ..
B3 ..
0 ..
0
0
. вп
, А« =
Bi B3 B5 ... 0
Bo B2 B4 . . . 0
0 Bi B3 . . . 0
0 0 0
Мг = До, Ai = Bi; М2 = ^Ло + АгВоВ^1, А2 = Bi;
М3 = -Л0В2 + ЛхВо - BoBi^2B3m1, А3 = В0В3 ~~ ВгВ2;
М4 = A0(^BiB4 + В2В3) - B0B3Ai + B0BiA2 + BoB^M3(BoB3 - BiB2),
А4 = BqB3 + B1B4 — ВхВ2Вз.
19.
cfж =
etc
1)т

etc
1.
2.2.9. Интегралы от ха(ах2 + bx + c)pA(x).
Условия: a, b1 с — действительные числа.
Z	^л, . fe sin 7A: ctg7 + C0S7A!
ж2 + 2x cos 7 + :
a + k
[n>m + l].
[Re a > 0; Ы < тг].
2.
¦ dx =
[6 + с + (a - 2 + e)y/cy/a + 2& + c]22^°^e^Fr(a - 3 + e) J (a + 2b + c)
(о + с + усул + ^^ + с] ^I^Q; — o/il + ej
с, a + 26 + с > 0; а < (у/с + %/а + 26 + с
2; Rea>3-?, e =

248
Гл. 2. Определенные интегралы
[2.2.9
(ах2 + 2Ьх
¦ dx =
• + с +
а-°Г(а + 1/2 ^ d) | (а + 2& + с) 1/2
О
с, а + 26 + с > 0; а < (д/с + л/а + 26 + с J; Re а > ст; /3 = \ "
L	1а-
4.
4х =
-а/2
sin [7 — ct arctg [sin 7A/ + cos 7)
sh [7 — a Arth	]
х A + х COS7J dx ^—v/ чд
6.
7.
dx =
fc=O
Trsln @:7)
sin 7 sin (an)
+ bx + c)p
Г |argy| < тг; 0 < Rea < 1; |-у| < тг
1	|argy| < тг; 0 < Re а < 1
[ |-yI < тг; Rea > 0].
[0 < |7| < тг; | Rea| < 1].
a	a	1	b2\
2	2	2	ac/
[a > 0; 62 < ac; 0 < Re a < 2 Re p].
X<*-1
8. I -—:—^	— dx = B (a, 2p - a)(a2 - b2
9.
¦аJ -Ь2]р
x 2F1
ж"dx
[6 < a; 0 < Re a < 2 Rep].
(ax2 + bx +
= In
/0 =
, h =
[а, с > 0; Re a > 2n - 1; 6 > -y/ac],
a-1
=
a-3
a-3/2j'
10.
11.
12.
ж
m+2fe + l/2
) 7
[а, с > 0; 0
-l; n = 1, 2, 3, ... при б2 < ас и n = 1, 3, 5, . . . при 62 > ac].
(-1)'
- b2
arcctg ¦
/ос^б2
[62 <ac].
1	6 + V&2 - ac \
¦In-		1	[ac< 6^1.

2.2.9]
2.2. Степенная и алгебраическая функции
249
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
Bга-1)!
[ас = б2], [а, 6, с > 0; 0 ^ т + к ^ п - 1; п = 1, 2, 3, . . . ].
х dx
(-1)
п —1 ап-2
2(га - 1)! дсп^2 \(ас - б2K/2
( 1 \Ti —I on —2
Ъ	b
arcctg
In-
ас — б2 л/ас — Ъ2
'ас	1
2(п-1)! Яс» V(б2 - асK/2 А11 6 + л/Ь2 - ас л/ас - Ь2
[ас>Ь2]„
Гас<621.
" 2(п-
da;
[ас = б2], [а, 6, с > 0; п = 2, 3, 4, . . . ].
- 26ж + с)п (га —1)! ^сп"
1
1	.	Ъ
¦ arcctg ¦
(п - 1)! дсп~г
п — 1
а
Bга- l)^2"
In-
-ас ш b
[ас>621.
[ас<621.
[ас = б2], [а, 6, с > 0; п = 1, 2, 3, . . . ].
Ь)
т+г
_ (-2)
п—1 on—1
Bп - 1)!! ^а^
dx
+ Ь)
[m + 2ife = 2п - 1], [а, 6, с > 0; п = 1, 2, 3, . . . ].
1
2П - 1)! дсп
(ж2 + 2 ж 1/ cos 7 + 1/2)р
— (а — 1)| cos7| -
¦ь)
[а, 6, с > 0; п = 1, 2, 3, . . . ].
а	а\ „ [а	а 1 2
2
-1 3
2
; 2' COS 7
)}
24.
25.
26.
	 с!ж :=::::
ж2 + 2 а; 2/ cos 7 + У2
Trsln [(I — 0O]
(ж2 + 2ху cos 7 + У2J
dx =
2 J2 Ч2~' Р	2~; 2'
|arg2/| < тг; 0 < |-у) < тг; 0 < Re а < 2 Rep].
[| arg 2/| < тг; 0 < |7| < тг; 0 < Rea < 2; а^ 1].
[0 < |7| < тг].
7r{sin [A — аO] — A — a) sin 7 cos [B — аO]}
2у4^а sin3 7 sin атг
[| arg 2/| < тг; 0 < |7| < тг; 0 < Re а < 4; а ф 1, 2, 3].

250	Гл.2. Определенные интегралы	[2.2.9
со
27.	Г	^-
J (ж2 + 2ж|/соз
о
со
28.	'	XdX
о
О
(ж2 + 2хуcos7 + 2/2K
_ 27^
%3
sin 7
ч
- sin 27
sin3 7
' — 7 cos 7
I2 sin3 7
- sin 27
4ysln3 7
dx =
Г	х2 dx	27 sin 27
J (ж2 + 2Жусо87 + г/2J = 4j/Sin37	[° <
_ 7r{3sln[(l - 0O] -3A - a) sin 7 cos [B- 0O] - A - а)B - a) sin2 7 sin [C - 0O]}
I arg I/1 < тг; 0 < |7| < тг; 0 < Re a < 6; а ф 1, 2, 3, 4, 5].
127 — 8 sin 27 + sin 47	9 sin 7 + sin З7 — 127 cos 7
°^	32|/5 sin5 7	' 1^	32i/4 sin5 7	'
27B + cos 27) — 3 sin 27	9 sin 7 + sin З7 — 127 cos 7
2^	16t/3 sin5 7	' 3^	32|/2 sin5 7	'
I27 — 8 sin 27 + sin 47
4 ~~	32|/sln57	'
157 — sin7cos7A5 + 10sin 7 + 8sm 7)
^0 = 	z	7	¦
48y" sin 7
15 sin 7 — I57 cos 7^5 sin3 7^2 sin5 7
48|/6 sin7 7
' = 2p - 2a + 1 =p 1; Re a > A ± l)/2; Re (p - a) > (=pl - l)/2; у > 0; 6 > -у].
= 7.(±3-3)/2
У
о /	1±3	1±3
х В р-а+ —г—, а-
2 '	2
[/3 = 2р^2а + 1±3; Re a > (l±3)/2; Re (р - а) > (=рЗ - 1)/2; 3/, 6 + у > 0].
35.
аж2 + 2bx + с	а(^ — 2/) sinaTr	a"/2 sin атг sh у?
о
|"о < Rea < 1; 0 < ас < b2; ab > 0; ay = b - \/b2 - ас , az = 6 + \Л2 - «с, ^ = Arch (|6|/

2.2.10]
2.2. Степенная и алгебраическая функции
251
36.
37.
38.
г	2	^п
[0 < Rea < 1; ас > b2; ф = arccos (b/y/ac) 1.
L	J
a(t/ + z) sin атг
0 < Re a < 1; ac < 0; az = 6 + yb2 — ac , ay = —b + yb2 — ac .
7rsh[(l-a^c"/2-1
ctg атг =
ctg атг =	г
a(z — I/)	a"/2 sh 99
[0 < Re a < 1; b2 > ac > 0; ab < 0; ay = -b — \/b2 - ac , az = -b
39.
40.
41.
	dx	 _ 1. g(r%/c + gc- hb)
(gx + h)\Jax2 + 26ж + с r h(rx/a + gb - ha)
-, /1, a > 0; с ^ 0; 6 > -yfac\ r = ^ah2 - 2bgh + e^r2 > oj.
42.	= — arccos 1			-
r	I gh(y/ac + 6)
43.
44.
hyfa
, h, a > 0; с > 0; 6 > V«c; r = \/-ah2 + 2feg-/i - eg2 > oj.
[a/12 - 26g-/i + eg-2 =0; o, g-, /1 > 0; с > 0; g-6 - /ia ^ 0].
(аж2
(^l)m7ran-m-V
- l)\\Bn -2k- 3)!!(ас -
[а > 0; ас > б2; m = 0, 1, 2, . . . , 2п - 2; п = 1, 2, 3, . . . ].
45.
с)п Bп - 2)!!(ас - б2)^
а > 0; ас > Ь2; п = 1, 2, 3, ....
2.2.10. Интегралы от жа(аж4 + 2&ж2 + с)рА(х).
Условия: а, 6, с — действительные числа.
1
1.
3.
4.
ж4±ж2 + 1	2-У2
(аж4 + 26ж2 + с)^ 2
о	о
оо
ж с!ж
—• 2- f
2±1	J
1
ОО
1[, яо/а'
2 I (аж2 + 2&ж
ж4±ж2
¦ б?ж =
аж4 + 26ж2 + с
[см. 2.2.9.7].
[а, с > 0; Ь2 > ас],

252
Гл. 2. Определенные интегралы
[2.2.11
2у/2с(Ъ + у/ас)
/о =
1 . b + y/b2 - ас
h = ^ /wn	In	—	, h =
2y/b2 - ac
[c > 0; b > -y/ac],
5. хл
о
2y/2a{b + ^ac)
p-1/21
1.
2.
3.
2.2.11. Интегралы, содержащие А{\/ах2 + Ъх + с).
оо
ж""^	_ 2Ск^х/^1^^а^х/гГ a/2, i/ - a
ж dx
[c> 0; Rep > 1/2].
[Rez > 0; 0 < Re a < Rei/].
n(n — m — 2)!
xa dx
+ z2
(m + l)(m + 3) . . . Bn - m - 1)
[Rez > 0; m = 0, 1, 2, . . . , n - 2; n = 2, 3, 4, . . . ].
[Rez > 0; 0 < Re a < ±Rei/].
4.
5.
6.
7.
8.
+ x)n (n — m — l)(w — m + 1) . . . (n + m + 1)
[Rez > 0; m = 0, 1, 2, . . . , n - 2; n = 2, 3, 4, . . . ].
ГBа)ГA/ - а)Г^1A + a + i/)
)T^1(l + 2i/ - a)
xm dx
[ | arg z | < тг; 0 < Re a < Re v\.
nzm"n+12"mBm + l)!(n - m - 2)![(m + n + I)!]™1
2nBz)m"n+1m!Bn -2m- 3)![Bn -m- I)!]
[|argz| < тг; m = 0, 1, 2, . . . , n- 2; n = 2, 3, 4, . . . ].
dx
/x2 - b2 (x + V^2 - 62 )" i/
; |argz| < тг; 0 < Re а < Re i/1
[|6| ^ a; Re i/ > 0].

2.2.11]
2.2. Степенная и алгебраическая функции
253
9.
xa~1dx
2 i 2 I \ v
2 2. 2
X у + Z
а и — a\ „ (\ {v —
/1/- ОП I/ + 1	, 1
[Re у, Rez > 0; 0 < Re а < Rei/].
10.
/ж2 + z2 A/ж2 + z2 + г/)"
[Rez > 0; \arg(y/z + l)\ < тг; 0<Rea<Rei/
11.
12.
13.
/ж2 + z2 {л/х2 + z2 + zI
xmdx
[Re z > 0; 0 < Re a < Re v + 1].
n(n-m -1)!
¦ ~~ m — l)Bn — m + 1) . . . (rn + 1)
[Rez > 0; m = 0, 1, 2, . . . , n - 1; n = 1, 2, 3, . . . ].
14.
15.
16.
17.
18.
ж2 + z2
та^г(\/т2
= 2-aza-v-1B[a,
4-
+ z2
= /"Vb U
i/, a;
[Rez > 0; | arg (y + 1)| < тг; 0 < Re a < Re i/ + 1].
1 — a ± 1/л
[Re z > 0; 0<Rea<l±Rei/].
dx =
(n — m)(n — m + 2) . . . (n + m)
[Rez > 0; m = 0, 1, 2, . . . , n - 1; n = 1, 2, 3, . . . ].
xa dx
/2x + z (x
7za^I/^1/2B(a, 2i/-2a + l)
[|argz| < тг; 0 < Re a < Re v + 1/2].
xm dx
л/z2
,-m-l)!
|argz| < тг; m = 0, 1, 2, . . . , n - 1; n = 1, 2, 3, . . . ].
[ж + z + 1/ + 2y/y(x + z) ] " da; =
x + I, а.)ъЬ\ I i/ + 1 - a, i/ + -; 2i/ + 1 - a; 1 - -
V	^	z^
|argz|, | arg 2/|, |arg(t//z)| < тг; 0 < Re a < Rei/ + 1/2]

254
Гл. 2. Определенные интегралы
[2.2.11
19.
20.
21.
xa dx
¦ + 2z (x + z + л/х2
_	I
[|argz| < тг; 0 < Re а < Re ?/+ 1/2].
хт dx
2z (ж
^)те Bn - 2m - l)Bra - 2m + 1) . . . Bra + 2m + 1)
[|argz| < тт; m = 0, 1, 2, . . . , n- 1; n = 1, 2, 3, . . . ].
/x +
ж2/ + 2 + 2y/xy(x + z) ] v dx =
' В ( 2а, - + и - а\ 2Fi I а + -, v + -; а + i/ + -; 1 -
[|argz|, | argj/l < тг; 0 < Re a < Re v + 1/2].
22.
= 2 z
2 ' ' 2 ' f ' z
[ |t/| < |z|; | argz| < тг; 0 < Re a < Re v + 1].
23.
= 2~
ln/
В (a, ^-a
1 + i/;
24.
¦ [(z + Vtt — x Y + (z — V« — ж I/]
«	a-l/2 v ;
1^1/
2 '
< 1; | argz| < тг; 0 < Re a < Re i/ + 1].
[a, Re a > 0; z2 ? [q, a]].
a
25. f tX<*	[(a + Va2 - ж2 )" + (a - Va2 -ж2)"] dx = Ba)a+l/^1 В (-, i/ + -^
J Va2 - ж2 U	;i	JJ	li	V2	2/
[a, Re a, Re (a + 2v) > 0].
26.
¦ dx =
, Ret/ > 0; 0 < Re a < Re v + 2].
27.
+ z2)(^2|/2 + z2) (Vx2 + z2
[Re |/, Rez > 0; 0 < Re a < Re v + 2].

2.2.12]
2.2. Степенная и алгебраическая функции
255
28.
\и = v - \/v2 - 1 , 2vyz = с2 + t/2 + z2; с, Rez, Key > oj.
2.2.12. Интегралы, содержащие разности алгебраических функ-
функций.
1.
2.
3.
4.
1-х 1 — хЛ
dx = С + 1пЛ
ф\ — )
V А/
^ \ dx = тг ctg атг
= ^(<т) - ф(а)
| arg Л| < тг; Rea, Re (a - А) > 0].
[|argz| < тг; Rea, Re a > 0].
[|argz| < тг; 0 < Rea < 1].
[|argz| < тг; Rea, Re a > 0].
5. ж [(ж + z)F — хи \dx = z н В (a, 1 — a — p)
6.
(ж + z)px
-dx =
Ka-l \ aA-1'
Ж ЛЖ	i
	г Ыж = In A
1 — ж 1 — жл
о
8.
J
dx =
[|argz| < тг; Rea > 0; 1 < Re (a + p) < 2].
— ф(р — <т)]	[| argz| < тг; Rep > 0; Rep > Rea].
[|argA| < тг; Rea, Re (Aa - A) > 0].
у > 0 или | arg 2/| < тг "
1 dz xy у dz ж /	sin ai (^ cos сктг
0 < Rea < 1,
У > 0
a
\\(T _i_ riNl7™1f/i _ tI^™1 4- Гт 4- rtl/3™1fn — tI^1] fir — Bа)^+1~г R Г/9 ^
да I I I «X/ I U/ I	I IL*/	%Aj J	I I eJL/ j CX1 J	I IL*/	еАУ I	CJy «X/ 	 1 X^ СД/ I	I J I LJ) _ /I
0
1
J
10
11.
12.
[a, Re^, Re 7 > 0].
 В (a, /3)
[a, 6, Rea, Re/3 > 0].
/1 - x2^
(a
- (a + еж)
a(x + ay^x"-1 + &(^
= 2
= a'ln-
В (a, p)
[a, 6, с > 0; Rep < 0].
[a, b, Rea, Rep > 0].

256	Гл.2. Определенные интегралы	[2.3.1
14.
рх)	\ qxj
о
оо
15. I	zr 1	 =0	Га, в произвольные].
О
оо
16. Г|[1 + — 1 -и + — 1 I —=
У V	/ J	а	/3	\а 0J	а	р
[а, /3, Re у, Re z > 0; Re/x, Re i/ < 0].
2.3. ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ
2.3.1. Введение.
В этом разделе содержатся интегралы, в подынтегральные выражения которых входит
показательная функция. Одним из способов вычисления таких интегралов является сведе-
сведение их с помощью замены переменной к интегралам, содержащим степенную и алгебраи-
алгебраические функции. Кроме того, некоторые интегралы, содержащие показательную функцию,
могут быть получены из других интегралов с помощью предельного перехода по параметру;
например, если
= /(а,
о
то при соответствующих условиях
\
(р(х)е~рх dx = lim I ( 1 + — ) ф(х) dx = lim [aap/(а, —ар)].
0	0
2.3.2. Интегралы общего вида.
В этом пункте помещены формулы, которые позволяют находить интегралы, содержа-
содержащие степенную, алгебраические и показательную функции. Некоторые частные случаи этих
интегралов, соответствующие конкретным значениям входящих в них параметров, приведе-
приведены в последующих пунктах. Интегралы общего вида представляются с помощью функций
Vj, j = 1, 2, 3, . . . , помещенных в приложении III. Конкретные значения параметров,
входящих в эти функции, приводятся в фигурных скобках после каждого интеграла. Кроме
того, г = p/q, где р и q — взаимно простые натуральные числа, если не указаны другие
условия.
°	{#26 = г^1 В (/3, (а + h)/r), и = а + r(f3 ~~ 1) + h,
а = (а + h)/r, b = /3 + (а + h)/r, z = {-sy/p)p}	[y, Rea, ReC > 0].
оо
2.
У {^26 = г В A3, 1 - /3 - (а + /i)/r), ?J27 = (-1)J'A - /3),Т[а - r(l - /3 + j)],
и = a + r(f3 — 1) + h7 ui = rj, t>i = r(l — /3 + j) — a, a = (a + h)/r,
b = p + (a + /i)/r, ai = 1 - /3 + j, fti = 1 - a + r(l - /3 + j), 2 = (-st//p)p}
[y, Re/3 > 0; Re s > 0 (или Res = 0, Re (a + r/3) < r + 1)].
CO
Г a-1 r	r -1
3. xa (yr + жг)р e sa; с!ж = Vbe + V27
J
0
tt 	 "*" О
Г

2.8.2]
2.3. Показательная функция
257
и = а + г(р — 1) + /г, tii = rj, vi = r(l — p + j) — а, а = (a + h)/r,
b = p+(a + h)/r, at = l-p + j, ft! = l^a + r(l~p + j), z = (~l)p+
[Re a > 0; r|argt/| < ?r; Re s > 0 (или Res = 0, Re (a + rp) < r + 1)].
4.
V2
7Г j ,
Vl = r(l + j) - a, a = b = (a + h)/r, аг = 1 + j, fti = 1 - a + r(l + j), z = (-sy/p)p >
[y, Re a > 0; Re 5 > 0 (или Re s = 0, Re a < r + 1)].
5.
о- [i-a/2, 1/2- j,a-r(j- a/2)
а + h	\	r	r
и\ = jr7 U2 = (j + l/2)r, и = а + rcr/2 + /&, vi = (j — a /2)r — a, V2 = [j + A — cr)/2]r — a,
ai=j- a /2, fti = j + o-/2, ci = 1 - a + (j - <r/2)r, di = j + 1/2, a2 = A - <r)/2 + j,
b2 = A + cr)/2 + j, c2 = 1 - a + [j + A - cr)/2]r, d2 = 3/2 + j, a3 = (a + /i)/r,
[Re a > 0; r|argy| < тт; Re s > 0 (или Res = 0, Re (a + err/2) < 1)].
6.
E30 =	?_2-'(«+'0/-i в f 1 + 2 (a + h), -a- - ^±±) ,
Ul = rj, u = a + ra/2 + h, vt = r(j - (j/2) - a, ai = j - cr/2, ftx = A - cr)/2 +:
ci = 1 - a + r(j - cr/2M di = 1 - o- + j, a3 = (a + /i)/r, &з = (a + /i)/r + 1/2,
c3 = 1 + a/2 + (a + /i)/r, d3 = 1 - <т/2 + (a + /i)/r, z = (^l)p
[Re a > 0; r|argy| < тг; Re s > 0 (или Res = 0, Re (a + err/2) < 1)].
7.
j, 1/2-j, a-r(j
?-30 —
r	\ r	r
= rj, ui = r(j + 1/2), u = r(a- l)/2 + a + Л, «i = [A - (r)/2 + j> - a,
17 А. П. Прудников и др., т. 1

258
Гл. 2. Определенные интегралы
[2.3.2
ci = 1
c2 = 1
2 = A - (т/2 + j)r ~~ а, «1 = A - <т)/2 + j, 6i = A + а)/2 + j,
а + г[A-<т)/2 +j], di = 1/2 +j, a2 = l-c/2 +j, 62 = 1 + a/2 + j,
a + r(l - <j/2 + j), d2 = 3/2 + j, a3 = (a + /i)/r, &з = cr + (a + /i)/r,
<t)/2 + (a + Л)/г, rf3 = aj2 + (a + /i)/r, z = (^l)p
[Re a > 0; r|argi/| < тг; Re s > 0 (или Res = 0, Re(a + <rr/2) < r/2 + 1)].
2
В ^- (а
^ ( Л), —
= rj, и = г(<т-1)/2 + а + Л, vi = r[(l-<r)/2 + j]-a, ai = (l-o-)/2+j, 6i = l-a/2 + j,
ci = 1 - a + r[(l - <r)/2 + j], di = 1 - o- + j, a3 = (a + /i)/r, 63 = 1/2 + (a + /i)/r,
+ (a + Л)/г, d3 = A - <t)/2 + (a + /i)/r, z = {^l)p+q{sy/p)
[Re a > 0; r|argy| < тг; Re s > 0 (или Res = 0, Re(a + <jr/2) < r/2 + 1)].
9.
и = --
r sin 7
— dx = U,
/2r
{-II sin[7((g + Q/r- 1)]
I!	sm[(a + IOr/r]
sin 7
[Re a > 0; I7I, 2r\argy\ < тг; Re s > 0 (или Re s = 0, Re a < 2r + 1)].
10.
(x2r + 2(xy)r cos 7 + y2
U
sin [(a + 1)ж/г]
^ „ f4/cosG/-7) -
2 sin2 7 2r2 sin2 7^ I!
[Re a > 0; | -y |, 2r|argt/| < тг и Re s > 0 (или Res = 0, Re а < 4r + 1); U см. 2.3.2.9].
11.
r/2_
+ Vf-^f + (l/r/ - л/г/г-^Г]е"вя da = Узе
-В
7
r	\ г	г
и = г(а - 1)/2 + а + Л,, а3 = (а + /i)/r, b3 = a + (а + Л)/г,
i = ст/2 + (а + /i)/r, d3 = (о- + 1)/2 + (а + /i)/r, z = (-si//p)p I
[у, Re a, Re (¦
0].

2.8.3]
2.3. Показательная функция
259
12.
¦ (xr/2 -
sx dx = V2*
V*t
[a - r{\ - a
jC/30 —
2l-2(a+h)/r
= (a
13.
г	\ 2	г ' 2	г
i = rj, г*2 = r(a + j), ад = r(d — l)/2 + a + /i, vi = r[(l — cr)/2 + j] — a,
v2 = r[(l + a)/2 + j] - a, ai = A - <r)/2 + j, fti = 1 - ^j/2 + j,
-a + r[(l-(r)/2 +j], di = l^cj + i, a2 = A + cj)/2 + j, 62 = 1 + a/2 + j,
c2 = 1 - a + r[(l + a)/2 + j], rf2 = 1 + a + j, a3 = 1/2 + (a + /i)/r5
a)/2 + (a + /i)/r, d3 = A - <r)/2 + (a +
[y > 0, Re s > 0 (или Re s = 0, Re (a ± <rr/2) < 1 + r/2)].
- ) ; Rea, Rea, Res > 0|,
-(а + Л)/г Л
14. жа~
о
9-1
i=o
'Л
A(p, 1 + /i)
1; z
A(p, l-a + rj), A(g, 1 + j)
1*
[0 < r < 1],
[r > 1].
2.3.8. Интегралы от хае
00
1.	\xa
0
00
2.	f xne
0
dx = nlp^1
^px dx =
3.
A(g, 1 + (a + /i)/r), A(p, 1 + h)
a
I I
V
[Rea, Rep > 0] или [0 < Rea < 1, Rep = 0].
[Rep > 0].
[Rep>0].
0
7+гоо
7
. [
x —1 —-pz
dz =
Р>0
p<o
; Rea < 1; 7 > 0
17*

260	Гл.2. Определенные интегралы	[2.3.4
2.3.4. Интегралы от (ж±а)ре"рж.
со
г
1. (ж - af~xe~vx dx = р~0е~раГ@) [а > 0; НеД, Rep > 0 или @ < ЕеД < 1, Rep = 0)].
G P
2.	[ G P dx = pp 1epzr(l-p,pz)	[Rep>0; |argz| < тг].
J [X ~Т Z)p
о
со
3.	[ ^——dx = -epzW{-pz)	[Rep>0].
J x -\- z
о
со
4.	dx = ^+pepzEI(^pz)	[Rep^O; |arg^| < тг].
о
--co
гсхэ
2.3.5. Интегралы от (хп ± an)pe^px.
Условие: а > 0.
Г е~рж	/тГ
5.	dx = J— epz ericiJpz)	[|argz| < тг; Rep > 0].
J Уж + ^	у P
о
CO
6.	I ^ /2 dx = -^=r -2^pepzerfc(Vp^)	[|argz| < тг; Rep ^ 0].
J (Ж + Z) I	y Z
0
со
7.	f ^^dx = -e^pl/ El (py)	[y, Rep>0].
J ж - у
о
[Rep > 0; t/ ^ 0, Imy = 0].
1. |(а2-ж2)'3-1е-ра:с/Ж = 2'3-1/2^:Г(/3)(р/аI/2-/3//3_1/2(ар)	[Re/3 > 0]
2. [(а-ж)/3е"ржс1ж = (-р)"/3е"ар7(Д, -ар)	[Re/3 > 0].
о
3	1 / ^	2\р~ 1дШ j	/ т~1 //Э\/(Г1 / \ \ О — ± / А т	/ \\	Гт-& /is. /^1
I [а -— х ) е ах = у'71"-'- \Р)\^а/^)	Jp—i/2(Q"*)	[Rep > OJ.
— а
4. (ж — а ) е рх dx = —=-Г(/3) ( — 1	Kp-i/2(ap)	[Re/3, Rep > 0].
J	V71"	V V )
1/2-/3
[e = ±1; Re^ > 0, ± Re (iA) < 0 (или 0 < Re^ < 1, Re (iA) = 0)]

2.3.6]
2.3. Показательная функция
261
6.
7.
о
8.
9.
- dx =
dx = — e
1/2-p
-р)(^)	[Н1/2_р(р^)-У1/2_р(рг)]
[Re г, Rep > 0].
[Л, Rez > 0; 0 < Rep < 1].
[Rez > 0; ImA = 0].
[Re z2 > 0; Im Л = 0].
[Re z3 > 0; Im Л = Ol.
V2 4
2.3.6. Интегралы от ха(х±а)ре рх.
Условие: а > 0.
1.	lxa^1(a-xf^1e^pxdx = B(aJ/3)aa+f3^11F1(a; a + /3; -ap)	[Rea, Re/3 > 0].
0
a
2.	IV-^a - жH8"^185 dx = y^F(a)(a/p)a^1/2e^ap/2Ia^1/2(ap/2)	[Rea > 0].
3.
4.
dx=
'ж (ж + a)	2i/a
5.
6. I жа-х(ж - af^e-** dx = Г(/3)аа+/3^1е^арФ(/5, a + /3; ap)	[Re/3, Rep > 0].
[^-)	[Rea,ReP>0].
7.
/ж — a x
9.
+
px dx =
erfc (д/ор)	[R-eP > 0].
a, a + 1 — p; pz)	[Re a, Rep > 0; | argz| < тг].
10. I x"-1 (x + z)"-^-"" dx = -j=rr(a)(p/zI/2-aepz/2Ka^1/2(pz/2)
0
[Re a, Rep > 0; | argz| < тг].
11.
[Rep > 0; | arg z\ < «].

262
Гл. 2. Определенные интегралы
[2.3.7
-1/2
in, I a — I/ , \±l/2-a -рж j	n,a J V P/	l г/ \ рг/2
12. ж (ж + z) 7 e F йж = 2 < _xj2 \Y(a)ep 7
„«. I BP)
Z~
Re a, Rep > 0;
< тг; <5 =
13.
14.
15.
ж + z
ж +
е~рж da: = F(a)za~lepzV{l - a, pz)
[\argz\ < тг; Re a, Rep > 0 (или Rep = 0, 0 < Re a < 2)].
n
' dx = (-l)n+1znepz El (-pz) + У^(к - l)\(-z)n^kp^k	[Rep > 0].
[Rep > 0; |arg^| < тг].
16.
17.
18.
x - у
l; a; ~
ctga?re py
[y, Re a, Rep >0;a^ 1].
=F
)(РУ\
-V2 V 2 )
[y, Re a, Rep > 0].
eAziF!(cj; p + (j; -A(z~2/))^
ffA>°l;
L\ A < 0 j '
19.
2тгЛ2
B/
Re |/, Rez > 0, Re (p + tr) > 1 .
- J, 2 - p - a; \X\(y + z))
[Re y, Rez > 0; Re(p + <r) > 1; <5 = cr, 0 = у при Л<0, 5 = p, в = у при Л > 0].
2.3.7. Интегралы от ха(х2 ± а2)ре^рх и ха(а2 - х2)е^рх.
Условие: a > 0.
о
-
2
?
2' 2' 2 ' P' 4
i 1 ^2_2^
; ^
[Re a, Re/3 > 0].
3.

2.8.7]
2.3. Показательная функция
263
~'в /з,
2 ' 2' 2 ^р' 4
(a + 2/3-2)iF2(l-/3; 2-/3-?, ^ °
4.
5.
6.
7.
8.
n + 1/ 2	2\/3 —1 — рж i	/ i\n
+ (x -a f e dx = (-1)
2' 2	к' 4
1/2-0 IX
[Re/3, Rep > 0].
, Rep > 0].
X
n-3/2
\п—1 on—1
[Rep >0; n = 1, 2, 3, ... ].
[Rep > 0; n = 2, 3, 4, ... ].
a I — a
2' 2
¦p;
р
p 1+a_2p
[Re z. Re a > 0, Rep ^ 0; если Rep = 0, то добавляется условие Re (a — 2p) < 1].
9.
X
J-U.
х {za^2[eipz+7rai/2rB - a, ipz) + е-*р*-™/2ГB _ ^
[Re a, Rep, Re z > 0; n = 1, 2, 3, . . . ].
n-l
X
то --рж	/ i \m+n —I9I —n
11. ^^^™—^r™ dx =	-,	-r-t
— sin (pz)(l/2 — C(pz))]}
[Rep, Rez > 0; к = 0, 1, 2, . . . ; n = 1, 2, 3, . . . ].
n —1
X
12.
13.
¦1)! dpm\zdz/
X {z^1[sln (pz) cl (pz) — cos (pz) si (pz)]}	[Rep, Rez > 0; n = 1, 2, 3, . . . ].
dx =
[/	\	/
sin I pz	— I cl (pz) — cos I pz ¦
—J
si (pz)
[m/2]
[Rep, Rez > 0].
[Rep, Rez > 0].

264	Гл.2. Определенные интегралы	[2.3.8
15.
2sIna7T
m -px	q,™^1
Ж (еру+ cosaire~py)	[у, Rea, Rep > 0].
xz — yz	I
0	K = 1
[y, Rep>0].
о
+ 2 cl (py) sin ( py	— ) - 2 si (py) cos ( py -
fe=i
[y, Rep>0].
°°F7 xa~1eiXx
17.	—	— dx = 7riza^2e	г/2	[j, Rez > 0; A < 0; 0 < Rea < 2].
J x + z
— oo — i-y
2.3.8. Интегралы от xa I |(ajUfe dz x^k)Pke~~~px.
к
1. жат1(а - xf^ix + ^)"ре^рж dx = В (a, f3)z^paa+C^41(a, p, a + /3; -а/г, ар)
о
[a, Rea, Re^ > 0; |arg(l + a/z)| < тг].
OG
2. f Z4^ + ZyaBx + z)^1/2e"pa; da; = z~1/2epz/2r(a)[D^a(^)]2
о
[a, Rea, Rep > 0; | argz| < тг].
7
3. I „3 , 2xi X2 + жз dx = 2 jci(pM) sin \P2/	2~ ) +€OS (P2/	^
+ sgnysi(p|y|) sin Uj/- ^J ^cos f pj/- ^J - (~l)mepy Ei(-py)i
[Rep > 0; Imy = 0].
f A > 0
Re 1/, Re z > 0; Re <r > -1; I
I A < 0, у ф z
[{х<:ь«—¦'¦•¦¦¦¦]¦
oo —«7
f
7
6. f ^^
| GZ > 1; A, 7, Rezfe > 0; A; = 1, 2, . . . , n; Rea > -1; Re ( a + V afc ) < 1 .
[ I Re z < 0 J	V ^ / J

2.8.10]
2.3. Показательная функция
265
Т.
П
ixTke~tXX dx =
X, j, Rez, Rezk > 0; к = 1, 2, . . . , n; Re ( a + ^ ak j < 2; Re a > -11.
fe=i
2.3.9. Интегралы от xa(\/x ± z + ажм
/xTz±y/x)U ^px
dx = 22r
2. Z-
0
2' 2 ' ' ^ ' '	^ 2' J
[r = 0 или 1/2; Rea, Rep > 0; | argz| < тг
v-1
a + —— I x
l-i/ 3
2 ' 2 ' 2
x 2F2( 2r + ^, 2r -
a, 2
^; ^ + 2r, 1 + 2r - ^ - a;
1 + J/
/ж + z
4.
ж(ж + z)
[r = 0 или 1/2; Rep, Re Ba + i/ =p i/) > 0; | argz| < тг],
[Rea, Rep > 0; |argz| < тг].
da; = v 2 z epz i^i/4 ( -т- )	[Rep > 0; | argz| < тг],
2.3.10. Интегралы от
z2 + ax +
-2г a + ^^2r r [ «, Г - (tt ± I/) /2
Z	1
(a ± i/ - 2r) x
a±i/l=Fi/ — a	p2/
"i/? +Г	2~'	2 +r; ^^
[r = 0 или 1/2; Rea, Rep, Re z > 0].

266
Гл. 2. Определенные интегралы
[2.3.11
2.
3.
[J-v{pz)-3-v{pz]\
[Rep, Rez > 0].
i
/7ГЧЗ/2
dx=\2) *
pz
У_
^YJ'-iwKt)
, Re z > 0].
4. x"'1-
0
± *)" ^
^dx = (^I-2r2a^-1za^-2rr\.a
a 1
1 + a + i/zbi/ 3 ^
1
_ 2r. _
»2z2
2r
2r - i/ - a -
p1"a^I/(±2:i/Irr(i/ + a - 1) X
3	i/ + a
5 - - 2r, 1 - —,
+ a - Ar) x
5.
1. xa
о
C2 + Z2
2.3.11. Интегралы от ж°
zl	zl	zl	4
[r = 0 или 1/2; Rep, Re2, Re (a + v =p i/) > 0].
^ и _J_ v ьл Т^
— Ж
+
ж^ +
(а - х)г
eTvx dx =
а, i/ + а
X 2^2 1 «,
a
2. L"-
o
	ha, — + a + l — 2r; —ap )	[r = 0 или 1/2; a, Re a, Re (a + v) > 0].
Zi	Zi
a "" х Y — (^
х — \/а — ж
(a ж jr
Г. ! Л/Л2 _ T2 W2 _ /_ 1
px dx =
(а2 -
[г = 0 или 1/2; см. 2.3.11.3].
3. Ж
о
а-i (а
(a2 - ж2)^
- 2г

2.8.11]
2.3. Показательная функция
267
+ а
,—
а2р2
•; —
„+ce !_2r 1+а+„_2г Г(а
	 ZJ	lilt'	Я	I
L
2 - 2r
a + 3
-2r;
4. xa
2 ' 2 r ^' 2' 2	2	-
[r = 0 или 1/2; a, Re a, Re (a + i/) > 0].
2, Г - a -
1 — 2cii
x 2F2 ( a, - + a; 1 + a-r--, l + a+--r; -ap
/2~ar( a -r-^-\ x
A
• - - a; -ap ) +
I/ 1 + I/
+ -, ^^ +r;l + i/, l +
+ (-1I-2га"|/2|'рг//2"вгГа + | - A x
X 2^2 ( r - -, —	hr; I-!/, l + r---a; -ap )	[r = 0 или 1/2; a, Rep > 0].
5. ж
na^l (Vх + «
— a У - (^1
a - Vх - a Y -p
>2 - a2)r
' — VХл — <
(ж2 -a2
dx
[r = 0 или 1/2; см. 2.3.11.7].
6.
a - y/x^a)u]e~px dx = l-J Bay/2Kl//2(ap)
[a, Rep > 0].
(fY* j л / /уъ jL _____ j^s ~~\ 1	_„_ I ___ I 1	I /v^ ___ л / /уъ j?t _____ /*w —^ 1
'. ix- 	^^	rr™	e F dx =
(x2-a2)r
= 22>-aa°
2r-a-2 l-2rna
¦ - a)/2, r- (i/ + a)/2
1-a
i/ + a	a2p2
Г' + ~~2	Г' 4
a 3
3 + a
'
" V Vr+I/~ar(a ^ i/ ^ 2r) x
(-lI^2r2I/a^2l/p2r"I/"ar(a + !/ - 2r) x

268
Гл. 2. Определенные интегралы
[2.3.11
х 2F3( г- -,
и 1 — и
v + а 1 — i/ — а	а2р2
2 '	2 ^ ' 4
[г = 0 или 1/2; a, Rep > 0].
8.
9.
(ж + \/х2 — а2 У + (ж — у/х2 — а2 )и
с их —
/ / 9	9
ж уж — а
(ж +
/2ра,|
/ж2-а2I/ + (ж-^ж2-^)" _?
— )
[а, Rep > 0].
2 y""/*-v*v 2 /
= 2а1/А:1/(ар)	[а, Rep > 0].
. [[(ж + ^ж2 -а2 У - {х-л/х2 -а2У]е^рх dx = 2p~1vau Ки(ар)
10. [[(ж
[а, Rep > 0].
11. ж~
о
= ег \ х
(х - a)r	la=z
[г = 0 или 1/2; Rep > 0; |argz| < тг; см. 2.3.11.4].
12.
13. ж"
о
[Rep > 0; |argz| < тг].
и/2
^ ij ух ух а
14. ж
о
^г (ж + z + л/а^
(д>1 	 <22)г	\a=z
[г = 0 или 1/2; Rep > 0; |argz| < тг; см. 2.3.12.7].
—т	е рж ^ж =
сю
1 — у хл — ал
15.
16.
(ж2-а2)^	la=z
[г = 0 или 1/2; Rep > 0; | argz| < тг; см. 2.3.12.7].
[Rep, Re^ > 0].
Р
dx = 2z
о
[Rep, Re^ > 0].
17. жс
о
(х + 2z)\/x2 + 2гж + с2
-л/z2 -с2))

2.8.12]
2.3. Показательная функция
269
[Re a, Reр > 0; | arg z\ < тг].
1.
2.3.12. Интегралы от xa(eqx-\-z) e
оо
.	Г (а) ^ (k + l)n-i(-
[Reg, Re(p + gn) > 0; |z| ^ 1; z ф -1, Re a > 0, или z = -1, Re а > n; n = 1, 2, 3, . . . ].
, хе рх , In 2
2. т	—т^ dx = —
3.
4.
5.
. rfx = f_i)n-1p-2n-1B2n - 1)тг2п]
7.
2 \g
2n+l
[Re a, Reg, Re (p + g) > 0].
[Re a > 0; цф О].
[Reg, Re(p + g) > 0].
[9 7*0].
9.
10.
eqx
^?g
7*0].
¦ с?ж = (~l)n—— [z p p В (—p, p + p)l =
С/рте
= (—l)n —	 {z p p В (—p, p + p)[ln z + ф{—р) — Ф(р + p)]}
[|argz| < тг; -Rep < Rep < 0; n = 1, 2, 3, . . . ].
11.
12.
13.
(ex + z)m	(m — l)\ dpn
[ | argz| < тг; -m < Rep < 0; m = 1, 2, 3, . . . ].
m —1 ^	n —то —1
arg z\ <тг; m = 1, 2, . . . , n — 1; n = 2, 3, 4, ...].
= 2mz
m тте—n—1

270
Гл. 2. Определенные интегралы
[2.3.12
fe=l	fe=l
	2 ^	h 2 In 2 )	[|argz| < тг; ra = 1, 2, . . . , n; n = 1, 2, 3, . . . ].
^ (n — m — 1)! x
то	1	n--'m--l
Z + 2V— - V i-
/ .v <1 L 	 1	/ v L
14.
argz| < тг; m = 0, 1, 2, . . . , n- 1; n = 1, 2, 3, . . . ].
15.
— / ^m^m-n-e/3	(m~l)!
у 1 _
3
2
argz| < тг; m = 1, 2, . . . , n; n = 1, 2, 3, . . . ; e =
16.
= z (n — m — 1)
17.
n —то —1
1	% -v 1	о	7Г
< тг; m = 0, 1, 2, . . . , n - 1; n = 1, 2, 3, . . . ; e =
3'
:з1х
x
7*-7#*-Г±-
k=l	fe=l
z|<tt; ra = 0, 1, 2, . . . , n + 1 - e; n = e-l, 1, 2, ...; e =
-3
1
2
18.
(ex + z)n
(n-1)!
то — 1	n — m + 1 \ 2 то — 1	n — ?7i-1
argz| < tt; m = 1, 2, 3, . . . , n- 1; n = 2, 3, 4, . . . ].
19.
dx = 2mzm n
20.
(ex
[ | argz| < тг; га = 1, 2, . . . , n; n = 1, 2, 3, . . . ].
.- l)!!(n-m- 1)!

2.8.18]
2.3. Показательная функция
271
2	m	n-m-1	-I
V"^	-L	\~~"^ 1	^2
|argz| < тг; m = 0, 1, 2, . . . , n- 1; n = 1, 2, 3, . . . ].
21.
(е^ + г)"
- In г
(n-1)!
m —1 „	n — m — l „ \ / 2 m —1
то. —1 1	n —то —1 -, \ 3
V "Л 1	V ~Л	1
•m —1 _,	n — m — l
/ ^ JL2	/ -^ L2
fe=l	k=l
argz| < тг; m = 1, 2, . . . , n - 1; n = 2, 3, 4, . . . ].
_
ото m_n-i/2Bn-2m-l)!!(m-l)!
' = 2 Z	;	;	^rv:	— X
m — 1 .,	n — m
k=l	k=l
2 2
3" "
m—1 ^	n—m
-1
)
< тг; m = 1, 2, . . . , n; n = 1, 2, 3, . . . ].
23.
+ <*±ш^
fe=l l	;	fe=l
n-m-1
fe=l 4~'" ~'	k=l	fe=l
|argz| < тг; m = 0, 1, 2, . . . , n - 1; n = 1, 2, 3, . . . ].
2.3.18. Интегралы от х°
In 2
1.
(e* -
¦ с?ж =
[Rep<2,
2.
- еа)к[фA
[0 < a < In2].
A;!
-p +A;) + ln(ea - 1)] +^;(l + p)	[a > In2].

272	Гл.2. Определенные интегралы	[2.3.13
5.
О
хех
ln(V2 - 1)] = g - Ьп2(^ - 1), /(b^1) = ? - ^ln2(V5 -2).
e-
[Re(p + p) > 0; Rep < n + 1; n = 0, 1, 2, . . . ].
7. I -—^^tt^— d# = 	-,	Bn - l)!!Bm - 2n - 1)!! x
I (ex _ iy/2-n	2т^гт\
же"тж
Bm^ l)!!2n^m^1
о
/	m	_, m — n — 1 1 \
x(ln2^Vxv	7 + ^ У^ t)	[n = 0, 1,2, ...,m-l; m = l,2,3, ...].
fc=l	k=l
oo
жеж
0
= 0или1].
11.
(еж - 1)D+е)/з-п	2(m!)
0
12. 7 rZm d* = -3-r\n ^ ?'f 1 (m - n)! x
J (еж - 1)D+е)/з-п	2 [гтг + 2/3 - e/3jl	;
0
= 0,1,2,...,™, e = o™i].
[n = 0, 1, 2, . . . , m + e; e = 0 или 1].

2.3.13]	2.3. Показательная функция	273
со
х2е^тх	_ жBп - 1)!!Bга - 2п - 1)!!
(е. _ i)i/2-n	^Г^!	х
О
><V + >J^-4>: лПгЧч7+ 2>J^^r->:f-21n2	[п = 0, 1, 2, . . . , m].
(ех - l)V2-n
о
[п = 0, 1, 2, . . . , т - 1; т = 1, 2, 3,
+n_12+m Bn-2m-3)!l
2 ffm
n —m —1 1
2 ~ е ,
, — m	х
J-O»
(ex - l)V2-n
0
[п = 0, 1, 2, . . . , то].
19.
0
Bп-1)!!(т-п-1)!Г f.(l)
- 1)!!	j
m —n —1
fc=i	fc	i
n—n—1	то
k=l	k=l
i	m — n — 1 1
fe l
(
о
18 А. П. Прудников и др., т. 1

274
Гл.2. Определенные интегралы
[2.3.14
21.
dx =
n
z, a, " + 1
q
[m = 0, 1, 2, n - 1; n = 1, 2, 3].
[Re(p/g) > -1; |arg(l-s)| < тг, Re a > 0] или [|z| ^ 1, г ^ 1, Rea >0] или [z = 1, Re a > 1].
22.
[Rea>l;
л-п-1ли(п)(Р
-lin = 1,2,3,...
25.
27.
28-
_
6	Z)
= Г(а)[Ф(г, о - 1, p + 2) - (p + 1)Ф(г, о, р + 2)]
[Rea> 0; Rep > -2; |arg(l - z)| < тг].
р + 2)]	[Rea > 2; Rep > -2].
29.
^_
dx = 22n-\2n\B2n\
( i
n+m-l
(ri-l)!
[n = 1,2,3,...].
[a > 0; -1 < Rep < 0; m = 1, 3, 5, . . . , n = 0, 1, 2, . . . , а ф 1
(или Tn = 1, 3, 5, . . . , га < n + 1, n = 1, 2, 3, . . . , о = 1)].
2.3.14. Интегралы от (ae^qx + beqx + с)^1 f(z)
Условие: j — действительное число.
Т
8
[Rea>0].
3.

2.3.14]
2.3. Показательная функция
275
5.
6.
^
Г(а)
Г A + ix)n - A - ix)n ,	г
8. ^^	'-	^	J—dx =
J	+1
е7ГЖ +1
2n+1i
п + 1 п + 1
В
п+1
[n = 1, 2, 3, ... ].
г	,
[Rea > 1; |arg(l-z)| < тг].
[Rea>l].
[n = 1,2,3,...].
п = 1, 2, 3, ... .
L	J
9.
Ю
}
су
2ж^ V2tt/J	gz^^1 J
[Reg, Rez >0; n = 1, 2, 3, ... ].
[Reg, Rez>0].
12.
13.
[-каем<о].
14. ж
J
ех + 1
= — ж .
3
4г
б 1
dx
x
п = 1, 2, 3, ...; Rep > — 1 — Re (i/^ + ^i2 + • • • + ^ifc)? символ J]* означает, что k-R член
/ti\	...
содерж;ит { слагаемых, которые отличаются наборами индексов г\, %2, • • ., г д., взятых из
Vie/
множ:ества г^1, 2, ...,?г.
17.
dx
еж — 1
= - In (sin /1тг)
[0 < Re /i < 1].
18*

276	Гл.2. Определенные интегралы	[2.3.15
со
— таз 1	т	1
•п в	— 1	,	, ^г^ 1
18.
ех _
О
Г е	е	Ж
19. ж	с!ж = 	т,		[0 < Reju < 1].
J	ех 1	sin /1тг
о
ех — 1	sin /1тг
20- J х2П (в«-1)а da; = ^ " 1)Bя")а"|^2„|	[п = 1, 2, 3, ... ].
О
со
2еш -е~ж +2 _ 2тг2
о
со
хех	dx	2тг J arctg F/а) 1
J огеж — (а2 ± о1) л/ех — 1 ао [ in A + о/а) J
о
ln(c/
a)ll
}
О
[а, 6, с, d > 0; max (a, 6) < max (с, rf)].
со	со
24. 	^^	 = 1,1719536194... 25. —^	=—=0,3118211319...
о	о
[0 < ReW9) < 1; 0
2n + I)!sin7
28. I 	^^	 = >^2^^	1Ь\<тг}.
29
— oo
со
Г	dx	'"у
-5	о	 = 	^		[ 1т1 < тг; а> 0].
J а2еж + е^ж + 2а cos 7 а sin 7
—00
Г ж da? 7lna	г. 1
30.	-j——	——	 =	—.		7<тг;а>0.
J а2ех + е™ж + 2а cos 7	asm 7
—00
2.3.15. Интегралы от А(х)е	.
[Re/3, Rep > 0] или [Re^, Reg > 0, Rep = 0] или [Rep = Reg = 0, Imp ф 0, 0 < ReC < 2].
00
P
2.
0
3
. J ж«-1е-^2-^ dcK = Г(а)Bр)-а/2 ехр [g2
0
[	] [
[Re a, Rep > 0] или [Re a, Reg > 0, Rep = 0] или [0 < Rea < 2, Rep = Reg = 0, Imp ф 0].

2.3.16]
2.3. Показательная функция
277
4.
5.
dx = -J — ехр
2Vp
erfc
= -Jl exp (|-
2У P	8P
[Rep > 0] или [Rep = 0, Imp^O, Reg > 0].
М [Rep > 0] или [Rep = 0, Imp^O, Req^O].
8P
7. j x e p « dx
0
oo
8n — px -—qx j
же	dx =
— oo
[Rep > 0] или [Rep = 0, Imp ф 0, Reg > 0].
т?^1ехР( 7Z )erfc
p dqn
[Rep > 0] или [Rep = 0, Reg > 0].
I Я \
exp — =
1 /1 /v% I
11. f e
J
12.
13.
~px2~qxdx =
V
4p
[Rep>0].
- 4pqb + a(g2 + 2p)] exp I f
f
4p
[Rep > 0].
2.3.16. Интегралы от А(х)е рх q/x.
1.
2.
3.
4.
5.
P
pz+q/z
\x-q/xr dx = ^
[Rep, Reg > 0].
[Rep, Reg > 0].
[Rep, Reg > 0].
[Rep, Re g ^ 0; | argz| < тг].
[i/, g, Rep > 0].

278
Гл. 2. Определенные интегралы
[2.3.17
6. е
о
7.
i(\x-ii/x) «•? _ ,
X
о
7+ioo
f
J
8. | ж" Lepx q/x dx = 2wi (-) 3aB^fpq)
7 —too
2.3.17. Интегралы от A(x)e~b^x a ™f
00
1
[Ax, A > 0].
[A > 0; ц ^ 0].
[p, g, 7 > 0; Rea < 1].
1.
/x — a
- exp
— a2 — рж) <ix =
2a Г 1
2
1
— exp (-аур2 - 62 ) erfc (z-)	exp (a
s± = у a(p i л/р2 ~~ ^2) 5 R-e ^5
erfc(z+)
+ 6) > 0 .
2.
3.
4.
JL	/I/O	9	\I	^ J^	i ^-f-
4// 9 9Xo exP l^PVa; —a — рж] аж — i / Л1/4 o .—x/^. o
ij/(ж2 - a2K	V 7Г	\ A J	\ A
. = a(p± yV - b2 ); Re 6, Re (p + 6) > o].
V^ — ft (ж + a)
(ж + ftJ^
(ж2 - a:
exp
—^^—	/2
— a2 — px) dx = 2\ — epa erfc (z~) erfc (z+)
f a
4 = a(p± л/р2 - b2 ); Re 6, Re (p + 6) > o].
exp {—bVx1 — aA — px) ax =
[4 = a(p±^p2 ™fe2); Re6, Re (p + 6) > 0; Re/3 < 1/4].
¦ [(ж + i/ж2 — ft2 Y exp F1/ж2 — ft2 ) + (ж — у/ж2 — a2 )v exp (^&V^2 — a2 )]
5. 	,		 x
'2 2
6.
7.
[Re (p ± 6) > 0].
. = aF± л/62 -p2); Rea, Re b, Re (p + b) > 0 .
- exp (^&^ж2 + ft2 — рж) dx =
<
— exp (—
— p2
p2 ) erfc (^_)	exp {a\fb2 — p2 ) erfc
z+
= aF± \Jb2 -p2); Rea, Re 6, Re (p + 6) > 0 .

2.8.19]
2.3. Показательная функция
279
8.
9.
ехр (-Ьл/х2 + а2 - рх)	/2 аЪ е , , с , х
ч	— dx = 2\ — е erfc (z+) erfc (z-)
z\ = a(b± \fb2 -p2); Re a, Re b, Re (p + b) > oj.
(а-
)
ехр
z\ = а(Ь± л/Ь2 -р2); Rea, Re6, Re (p + b) > 0; Re/3 < 1/4].
10. l(\/x2 + а2 + xfehx + (л/ж2 + а2 - xf e^bx]e^c^
= 2a"(c + bf/2{c - Ь)~и/2К„(ау/с2 - b2 )	[Rea, Re (с ± 6) > 0].
2.3.18. Интегралы от eg{x)f(x).
kk
2.
0
00
3. \ e^peX dx = -Ei(-p)
0
4.
5. Г xe
00
»• J
dx =
= -C.
(A2 + lJ
- I - In p
i, Rea, Rep > 0].
[Rep>0].
[A > 0].
[/i, Rep>0].
1.
2.3.19. Интегралы, содержащие разности алгебраической и пока-
показательной функций.
fre1~x~r хр \dx #/ ч ,	г
г, Rep > 0].
1 — жг 1 — ж 7 ж
— In г
2. (е1
1-1/*
жA — ж)
3.
— = — In г
[Rep > 0].
[г > 0].
4.
dx = C.

280
Гл. 2. Определенные интегралы
[2.3.19
5.
Ы
dx = Г(а)р
оо
э. [ х^[е^х - (ж + 1УР] dx = ф(р)
	 I — = ln	'
1 + qx J x	p
8-
1 +
х	р
[Rep ^0; -n < Rea < 1 - п].
[Rep > 0].
[Rep > 0; | argg| < тг].
[Rep > 0; |argz| < тг].
[/i, Rep > 0; fi\argq\ < тг].
10.
11.
13.
рх	A
i, Re o", Rep > 0; fi\argq\ < тг].
^х - 1
12.
di 1 , тг
— = — In —.
ж 2 4
x 2
17.
18.
19.
[Rep>0].
[Rep > 0].
[Rep > 0].
[Rep, Reg > 0].
[Rep>0].
dx
^r«j_ _ ^r _ g^p\np^ (p_ r^g \n q^ ^ ^p)r \nr
x
[Rep, Reg, Rer > 0].
20. (p-9)e-~ + — (e
-ropa! - e~mqx
) I — =plnp-9ln9-(p-9)fl + ln —
I ж	\	m
[m, Rep, Reg, Rer > 0].

2.4.1]	2.4¦ Гиперболические функции	281
со
Я в qX в ГХ \ —пх
—	1	е р dx = ip(q + р) — In (r + р)	[Re (q + p), Re (г + р) > 0].
е ж - 1 ж /
о
22.
о
23.	1^еж^^	 м^ж	Ч— = 1пВ(р, g)	[Rep,
о
со
24.	[ (се Д+ Ь+Те-^ " сеР'У ^Te-"') Ч = с + ++ h '" ?	[Rep, Re, > 0].
о
со
е рпж _ е gnx	е ртж _ g gmx \ ^	ч , Ш
	^г = (д — р) In—	то, n, Rep, Reg > 0 .
га	гаг	/ ж2	п
о
26.
о
х ^ (—l)fc+m(p + Vix + Ui2 + . . . + i/^O1™1 In (p + ui± + i/j2 + . . . + uik)
О ^. т ^. щ Rep > 0; Rep > — Re (yix + ^«2 + . . . + Щк)', символ Yl* означает, что к-й член
суммы содержит ( слагаемых, которые отличаются наборами индексов *i, *2, •••,*&, взятых из
\к'
множ:ества г = 1, 2, . . . , п .
27. е
,^РЖЧ
(жг + |/г)ст] ж \r g/	q	r
о
[г, </, Rep, Re<j > 0; г| argу| < тг].
со
28. (е^рхЯ - е^кхГ)— — _2	5^		[r? gRe/i, Rep > 0].
29 7	^
lnG//3)
Xnia/pp)	ini^P/a)	1/я 1
7 ; A = у ; J ;	a, 6, p>0; 0 < C < a1^ <7 .
1п(т//5)	J
2.4. ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
2.4.1. Введение.
Этот раздел содержит интегралы, в подынтегральные выражения которых входят ги-
гиперболические функции. Для их вычисления можно использовать следующие свойства. Ин-
Интегралы, содержащие гиперболические функции, могут быть преобразованы к интегралам
от показательной или тригонометрических функций, если воспользоваться соответствую-
соответствующими формулами, приведенными в приложении I. Интегралы, содержащие функции shn bx
и chn bx, сводятся к интегралам от функций shbkx и chbkx, если использовать формулы
для степеней гиперболических функций (см. приложение I). В ряде случаев интегралы
от гиперболических функций с помощью замены переменной сводятся к интегралам от
алгебраических и других функций. Например,

282
Гл.2. Определенные интегралы
[2.4.2
а	а
1 Г	If	1 Г
(f(x) ch2 bx dx = — ip(x) dx -\— (p(x)e2bx dx -\— (p{x)e^2bx dx =
а
Г
J
0
ж) cos
0
ibx dx =
2
а
Г
J
0
0
- сЬ26ж) dx =
0
ch ab
И
" J
1
В разделе «Гиперболические функции» а, 6, с — комплексные числа.
2.4.2. Интегралы общего вида.
В этом пункте помещены формулы, которые позволяют находить интегралы, содер-
содержащие гиперболические, а также степенную, алгебраические и показательную функции.
Некоторые частные случаи этих интегралов, соответствующие конкретным значениям вхо-
входящих в них параметров, приведены в последующих пунктах. Интегралы общего вида
представляются с помощью функций Vj , Vj, j = 1, 2, 3, . . . , помещенных в приложе-
приложении III. Конкретные значения параметров, входящих в эти функции, приводятся в фигурных
скобках после каждого интеграла.
В п. 2.4.2 приняты следующие обозначения: г = p/q, где р и q — взаимно простые
натуральные числа, если не указаны другие условия:
1, если взят sh6x, _ I (^l)Ln/2J+ ^
с. _
О, если взят chbx;
если взят	,
если взят chbx;
1/2, если взят shn 6ж, га = 1, 3, 5, ...,
1={ 0, если взят shnbx, п = 2, 4, 6, ..., С =
О, если взят chn bx, n = l, 2, 3, ...;
^ + 7 + h
= у (п ~~ 2к).
w = a + 2r(/3 - 1), ai = ?,
- x2r
/2 2
2n rr(l/2 + 27 + /i)'
= /3 + С ci = 1/2 + 27 + /i, z = F/pJp|
[y, Re^ > 0; Re a > -<5n; |arg6| < тг]
/^i2r __ Ж2г \" f sh &Ж 1 П
f \
X ch bx j
J
dx —
a/Br), i/ + a/Br)"
= (i/ + l)/2 + С ei = 1/2 + 27 + /i, z =
[t/ > 0; Re a > -n?, Re a > -n5 - 2r Re v\ \ arg 6| < тг]
/22-n-l -а/Bг)
r[(n/2)!]2 \2r
2r/

2.4.3]
2.4- Гиперболические функции
283
[г = 1/2]
,u = -a/Br), Vl = 2(Л
2(п -
[Re s > 0; Re a > —-Sri; arg 6 произволен при г > 1/2 (n| Re 6| < Re s при г = 1/2)].
. , o „	,, ч f shte 1 CT
2.4.8. Интегралы от Л(ж)< % , > .
[ ch 6ж J
Обозначение: <5 =
1.
shea?
dx = /а
^ = |^1Г(«)С(«) = 2с-*Г(а) f; --1-
fe=0
2
7Г
/4 =
2.
ch еж
dx = Ja
[Re с > 0; Re а > 1],
[см. 5.1.4].
[Re а, Re с > 0],
a, i) - С (a, |
7ГЛЗ
J
[cm. 5.1.4].
[Re с > 0; Re a > 28],
I^<5Г(а)С(а - 1),
j	2n —2n —l/i ol —2n\l-
i2n+l = 7Г С	A ^ 2	J
dx
4.
5.
6.
7. (a2-*2)**
о
[n = l,2, ...]
[Re с > 0].
Br- l)!!s-
Br)!!2c
2a
[r = [n/2], 5 = n- 2r; Re с > 0; n = 2, 3, 4, . . . ].
; /3 + 1; ab) =F iFi(l; /3 + 1; -ab)]
[a, Re/3 > 0; |arg6| < тг].
[a, Re/3 > 0; |arg6| < тг].

284
Гл. 2. Определенные интегралы
[2.4.4
8.
x=^aa+^-1B(a, /3)[1F1(a; a + /3; об) Т
=F iFi(a; a + /3; -aft)]	[а, ЕеД > 0; Rea > -5; | arg6| < тг].
Г а-i/	.«-i
. ж (а-ж)
J
(chbx)
^/a\
Vft/
sh(aft)/2\	/aft
ch (aft/2) J	7 \2
—;
—; —
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
1	(shbx\	7Г /7 2 f ab
— < , , > rfa; = —Vb /+i/4
ж	dx
7T /ftz
= !-•
(ж2 + z2) ch
X
[a, Re a > 0; |arg6| < тг].
2.4.4. Интегралы от О
к
Обозначение: S = < >.
= 2i^2i(^l)n/2~
sh bkX 1
J *
1.
shbx
7Г	ЬТГ
[a, Re/3 > 0; Re a > -S; |arg6| < тг].
О
[а, Re/3 > 0; |arg6| < тг].
[а > 0; |arg6| < тг].
[Rez >0].
[bz = тг; Rez > 0].
[26z = тг; Rez > 0].
[46z = тг; Rez > 0].
[Rez > 0].
[bz = тг; Rez > 0].
[2bz = w; Rez > 0].
[4bz = тг; Rez > 0].
<7Г].
[Re с > |Re6|].

2.4.4]
2.4- Гиперболические функции
285
2.
sh2 bx . с — тгЬсЬк (Ьтг/с)
sh еж
2с2
Rec>
[Rec>|Re6|].
4.
chbx
—;
ch еж
2c
2c
chncx
,
37г ь1
)!
coSec[67r/Bc)]
Re(i/c > Re6 .
nRec> |Re6|; A=
6.
^1 bx ch^1 bx dx = ^- В (%, 1-
zo	2
[b>0; 0 < Re^ < 2 - Rei/].
L/sin[b7r/Ba)]
i-i/ ь Wi-" ь
2	2а/ V 2	2а
[a>0; -*
8. sh17"
о
>
/	^	f[/(
<	> dx = ±	^< : ')
\chbxj	4а2Л/ж \sin[67r/Ba
za
la
[а > 0; -б < Re {иа) < -| Re Ь\/а].
f sh ax ( sh 6ж 1 . тг / атг	бтг \ Г sin Fт
9. —	^	U^= — cos— +cos— { l
J Ь [ ch ож J	2с \ с
{ .	/
с / [sin(a7r/c)
со
Г (shaxshbx^ dx	тг f sin [атг/BсI sin [6тг/BсI 1 г , , ч /f . Ч1
10. N }		=-{ '.; : Lr 7Д (^ > cos(a7r/c)+ cosFtt/c)
J [сЬажсЬбж/сЬсж	с \ cos [атг/Bс)] cos [6тг/Bс)] J L l ; ; V / л
. shaxchbx .	1
11. |	dx = —
ch еж	4е
4с /\ 4с
2Trsin (атг/с)
4c / cos (атг/с) + cos Fтг/с)
12.
вЬаж shcx
	-^
сЬ2сж
2c2 cos [атг/Bе)]
[Re О |Rea| + |Re6|].
Зс-а-Ьл
4с
[Rec > |Rea| + |Re6|].
[Re с > |Rea|].

286	Гл.2. Определенные интегралы	[2.4.5
2.4.5. Интегралы от А(х) ГТ <	>
Обозначение: S = < >.
оо
, Г (а)
f х2п+а (shbx} , тг <92п+?Т бтг
2. —	i lt }dx = — _уо , tg—
о
oo
Г sh2 bx .	1 .	Ьж
3. —	dx =	In cos —
J ж sh еж	2	с
о
I -'aml J sh 6ж ,
ch еж I ch bx
Rea >
lite с
1 -
>l
S; Re с >
[Re с > 2
Re6|]
Re6|]
[Re а > -5; Re с > |Re6|].
5. f ^?L dx = In tg (Ь+Л Л	[Rec>|Re6|].
J xchcx	\ Ac J
о
7	2п+5
Л 7ж2п+5(8Ь6Ж1	тг д2п+5 Ьж	Г	fl
6.	—¦	< , , > dx = — 0f0 , , sec—	Rec >	Re 6 ; <5 = ^
J chcx [chbx j	2c db2n+s 2c	L	\o
о
7.	Z^ dx = Г(а) 5](^l)fc{[cBfe + 1) - &Па + [cBJb + 1) + 6]^"}
[Re а > 0; Re с > |Re6|].
oo
{ shbx ,	тг ^2 Ьж (	Ьж	Ъж\
8.	ж—ц	dx = —-sin —I 2csin	6ttcos—	2Rec> Re6.
J ch^ ex	4c3	2c \	2c	2c/
о
СХЭ
9.	\ ^—dx = 2^аBа - l)a~aF(a)((a)	[Rea > -1; Rea > 0].
J so ax
о
oo
10.	IV-1 J^^=^f //4 i	[Rec> 0; Rea >1; см. 5.1.4].
J	сЬ2сж	ca f-; BA; + I)"	L	J
о	k=0
11.	hcch/iaa;shaa;da; = -^^-Г, ^\ ,	[о > 0; Re/x < 0].
о
oo
f a_x сЬсж , 2Г(а) ^	1
12.	жа г^	dx= 	^^> —,	г	T	Rea>2; см. 5.1.4 .
J	зп2сж	с" ^{2к + 1)а^г	L	J
0	fe"™°
oo
( shaxshbx f lt cos \(a — 6)тг/BсI	.
13.	dx=^ln	^	 ( ')	Rec> Rea
J жвЬсж	2 cos [(a + 6)тг/Bс)]
о

2.4.6]
2.4- Гиперболические функции
287
Г sh2 ах ch Ьх . 1,
14.	dx = -\n
J	h	4
1 + cos (Ьж/с)
xshcx
4 cos Bатг/с) + cos (отг/с)
(shaxchbx . 1. cos \Ьж/Bс)} + sin law/Bc)}
15.	dx=-\n')	\
J	h	2
xchcx
2 cos[fe7r/Bc)] — sin[a7r/Bc)]
16.
17.
shk
Rec> Rea
Rec> Rea +
[Rez >0; Re с > Re 6 .
= (-1) —cos	h(-l) 	sin	In I 2 cos—	>	V sin
2n	с	пж	с \	с J пж ^ п — к	с
[cz = жп; Rec > |Reb|; Re z > 0; n = 1, 2, 3, . . . ].
Ъж
b Ъж с Ъж . (
18.	=	cos	1	sin — In I 2 cos
2	с ж с \	2c
19.	=csln—	-cos — In ctg (	7Г
2c ж 2c	\ Ac
20.
21.
22.
J	о • bz , ^ • к	Uk 1 ^ bz +
^;r^ ax = — 2 sin —- + — sin bz — ch oz in tg
x2 + z2 ch (тгжIz)	2 2	4
ж chk
2 ^
+ z1 shcx
1c
—
2cz
ll
(^l)fc cos (Ькж
^	^	-^
cz + кж
= w:Rec> Re 6.
= w;Rec> Re fell.
[z > 0; z\Reb\ < тг].
>0; Re с > Re fe .
23.	= — cos — - 1 + sin — In tg (	ж
2 2c	2c	\ 4c
[2cz = тг; Re с > I Re 61].
24"
chbx
ж2 + z2 ch ex
-ехр — п + - тг -гб + - In A + etb7r/c
1 L c V 2 / J L	7r
[i&7r/Bc)]	,
2c бтг с бтг 2с . Ьж . (b + c
25.	= — cos	cos	1	sin — In tg 	тг
тг 2c 2	с тг	с	\ 4c
2c бтг , / k\ , бтг
26.	= —cos — In 2 cos — + 6 sin —
ж 2c V	2c /	2c
2.4.6. Интегралы от (а + bchn bx + cshn bx)p\
a
ch bx dx
[cz = тг(?г + 1/2); Re с > |Reb|].
\cz = ж: Re с > Re 6 1.
[2cz = тг; Rec > I Re 61].
1
J *
[а > 0; Re, < 1; |arg6| < .].
2.
bdix
2	V^z ™ «z
¦^^^=- arctg	—
- a2	a + b

288
Гл. 2. Определенные интегралы
[2А6
3.
4.
5.
6.
7.
8.
9.
10.
11.
= а
dx
а + b sh ж
— i
•In
а + Ъ
+
¦In
а + Ъ
а + Ь - л/а2 + Ь2
7Г	&7Г	/6
;аж = —.	cosec — sh - Arch а
а + спсж	су«2 - 1	с Vе
тг	Ъж fb	\
—^=^=- cosec — sin - arccos а
сл/l-a2	с \c	J
dx =
жЬ
1 + ch ex	с2 sin (бтг/с)
ch bx
[0 < |6| ¦
[b = a].
[аб^О].
[a > 1; Rec > |Re6|].
[-1 < a < 1; Rec > |Reb|].
[Rec > |Re6|].
(a + chcsc)*
ch 6ж
у a
с у 2
^7^ sec —
cy2	c
¦b/c, «/-,
I/
ch 6ж а*ж	тг[6 sin ? cos (bt/c) — с cos t sin (fet/c)]
c2 sin3 t sin (Ъж/с)
"-1 ф^1)с2 + Ь2 п{ . Ь	b
(cost + спежJ
[a ? [-1, 1]; Re(i/±6/c) > 0].
[-1 < a < 1; Rec > 2|Reb|].
[2 Re с > |Re6|; \t\ < тг].
[Re i/ > 0; Re(i/c) > Re с + |Reb|].
13.
14.
. тг sin Г6(тг — t)/cl ж — t
dx =	^—-—Ц-^-	cos r
с sin t sin (Ъж/с) csint
[Rec > |Re6|; 0 < т < тг; 0 < t < тг].
shax shbx
dx
15.
тг / 26тг	2атг\
iif		 cos	cos		x
ch аж ch bx J cos t + ch еж с sin t \ с	с J
sin [а(ж — t)/c] sin [Ь(ж + t)/c] — sin [а(ж + t)/c] sin [6(тг — t)/c] ]
cos [а(тг — t)/c] cos [6(тг + t)/c] — cos [а(тг + t)/c] cos [6(тг — t)/c] J
[0 < |t| < tt; Rec > |Rea| + |Reb|; тг Re с > |Re(ct)|].
2тг
shax shbx 1
= ±
ch ax ch 6ж j 1 + ch ex	c2 [cos B6тг/с) — cos Bатг/с)]
x 6
16.
sin (атг/с) cos
cos (атг/с) sin
sh (ex/2) sh 6:
cost + спеж	2c cos Fтг/с) sin (t/2)
os (Ъж/с) 1 J cos (атг/с) sin (Ъж/с) 11
In (Ьж/с) J \ sin (атг/с) cos (бтг/c) J J
тг sin (bt/c)
[Rec > | Rea| + |Im6|].
[Rec> 2|Re6|; 0 < \t\ < тг].

2.4.6]
2.4- Гиперболические функции
289
, sh(cx/2)shbx .	жЬ
17. —±—Ц^	dx =
1 + ch ex
18.
19.
20.
21.
22.
23.
24.
25.
dx =
с2 cos (Ьж/с)
бтг sin (bt/c)
(cosi + ch-сжJ	с2 sin t sin (Ьж/с)
6 ch ж + с sh ex Jb2 - c2	6 + с
2	л/b2 - с2
arctg -
/с2 - б2
¦In
» + с + Vc2 - б2
6 + с - Vc2 - б2
ж ( b
shax shbx 1	dx
ch ax ch bx j ch 2ax + ch 2bx 4(a2 — Ь2) ( а
[Rec> 2|Re6|].
[Re с > | Re6|; |t| < тг].
[\Ь\>\с\].
[0 < |6| < с].
[Ь = с].
[Re a, Re 6 > 0].
dx
/a2 - 62 + c2
In
a + 6 ¦
a + b + с — у а2 — b2 + c2
2(a - 6)
c(a — 6 — c)
2
62 = a2 + c2; c(a-fe-c) <0].
л/b2 -a2 - c2
=¦ arctg	—r-	h етг
a + 6 + c
[62 > a2 + c2, s = 0 при F - a)(a + 6 + c)>0; e = 1 при (b - a)(o + 6 + c) < 0, a < 6 + c;
e = -1 при (b - a)(a + b + c) < 0, a > b + c].
[Rec> |Refe|].
¦ сЬсЖсЬбж ,	Ж	&7Г . I iy . ,
26. 	о	^ж = 	— sec — ch - In A ¦
1 + ch2 ex	2слД 2c I - l
27.
28.
тг /	. 6тг\ 1 6t
—	ах = — I sh 2^ sin — sh —
sh2 t + ch2 ex	с V	2c /	с
тг бтг
= _Sec—
+ ch2 ex
2cy/2
30.
31.
dx
6 ch2 x + с sh2 ж
¦In
с — \/—bc
[2Rec> |Re6|].
[Rec> |Re6|].
[2Rec> |Re6|].
[6c > 0].
[fee < 0].
19 А. П. Прудников и др., т. 1

290	Гл.2. Определенные интегралы	[2.4.7
2.4.7. Интегралы от А(х)(а + bchn Ъх + cshn bx)p П { ^°кХ V
^ [сЬс^ж J
а
Г	ж с!ж	тгу 2	. а	.
1. 			 = —;—г^ arcsin th —	\а > 0 .
J sh(a;/2)>/cha-cha; sh (а/2)	2	L J
о
со
2.	' /' = Ja	[Rea>0; |t|< тг],
J cos ? + ch ж
о
'2 ' 2тгУ] " slnt ^l ;	к-
tin2 - 2l(I)}, J3 = ^-Ц (^ - t2), J5 = -^ (тг2 - t2)G7r2 - 3t2).
\2/	3sint	15 sin t
sin t ^
CO	_-
Г xa~ fsh (ж/2) 1	«22а^з f sin (?/2) cos (атг/2) 1
J cost + chx\ch(^/2)j	\ cos (t/2) sin (атг/2) J
x
[Re а > 0; \t\ < тг].
CO
Г ж sh &ж тг . ^2 бтг / . Ъж	&тг\
4. 	аж = — sin — с sin	отг cos —	Re с > Re 6 1.
J 1 + ch ex	с3	с \	с	с J
о
5- 1Г1 + СЬсЖТ^Ж = ^2Й^6^Г1г/+?^^	[Re(,c)>|Re6|].
0
со
Г жсЬ(ж/2)с!ж _ 4 Гтг	/w + t\ /тг - ¦
J cos t + ch ж ~ cos (t/2) [	\ 4 j ~ \ 4
о
[t 7^ 7rBife + 1); fc = 0, ±1, ±2, ... ].
[Reс > 0; \t\ < тг],
_ 2Bn + l)! ^ (^l)^^1 sinkt	t	^ff^2^f2\
In — т.—To—:—г 7 	tt>—П	? ^o — ~~t:—:—r5 ii —
jr»^Ti~t~Zi O"ST| J" fa	m/	iU Z Ti ~f~ Jl	-^-^ *--*-* -*¦
ii	—ihv
СП ОЖ	7Г6
8. I ^^^-—ГТ7	——;	г dx =
. 7	-
J (cost
о
(ж2 + z2)(cos t + ch еж)	2z(cos cz + cos t)
стг ^ Г ехр [^1Ьтг[Bк + 1)тг - *]/(тгс)] ехр [^{Ьтт[Bк + 1)тг + *]/(тгс)] 1
^hi^\ c2z2- [7rBife + 1) - t]2	c2z2 - [7rBJfe + 1) + t]2 J
[Re с ^ |Refe|; |t| < тг; Re z > 0].
[2 Re c> |Re6|].
Х П+ fCX hb d ^^ ^J^ fsec — (
10. Г Х fCX Shbx dx = ^^ ^J^ fsec — ch (- In A + ^2 ))}	[Rec>\ Reb|].

2.4.9]
2.4- Гиперболические функции
291
11.
12.
ах =
Г(а)
2(а2 - б2)"/2 |_\а - 6
/2
7
— а/2п сю
7 ' —
у (-1)»
Ъ ch ж + с sh ж ~ 2те(
' П ' 2
[Re а, Refe > 0, Re а > -2; см. 5.1.4].
Ь, с > О].
2.4.8. Интегралы от Л(ж
Условие: а > 0.
sh л/а2 — x2
ch л/а2 — x2
ch (cv а2 — ж2
2(Ь2
а	/¦	,
Г chfeo; I sh (сл/а2 - ж	_
" J (а2 - ж2K/4 \ ch (cVa2 - х2 ) J
= (f
a
3. \fa2 — x2 ch (cVa2 — x2 ) ch bx dx =
- b)]/
/±1/4
. . ch (c\/a2 ~~ x2 )
4. —,	—- ch 6ж с!ж =
K/r(n2 — t2)
- с)] /_1/4 [| (V^T^ + с)] .
2.4.9. Интегралы, содержащие thax,cthax и разности гиперболиче-
гиперболических и алгебраических функций.
[Re а > 0; -1 < Re a < 0].
2.
3.
4.
= 21-аа-аB1-а-1)Г(а)С(а
^1 1	I
I cthax — 1 J
Ьж =
а > 0; Re a >
ж ch ex
о
f ch k - 1 .	.	Ьтг
5.	ах = — In cos —
J жяпеж	2с
о
6-
[Rep > 1].
[с > 0].
[Re с > |Re6|].
[Re a, Re 6 > 0].
19*

292
Гл.2. Определенные интегралы
[2.4.10
7.
.4.10. Интегралы от х е <
{
cm. —t>x I " OJL
е <
ch bx
vx (sh bx 1
о
7
2. e
J
о
3.
{chbx J
1 ( b)
p2 - b2 { p j
—
p(p
1	f 262 1
	j— { 2	Л
— 4b2) {p - 26 j
[n/2]
[Rep>|Re6|].
Rep>2Re6|.
[2a = 1 - (^1)те; Rep > n|Re6|].
Г	/	1
4. e"psBshI/~16a;daj = г^^б^1 В [ i/, -^- H	^
J	\ 2b 2
о
5 7,
5. j e
0
Г е
6. -—	dx = In
J ch еж
[Rei/, Re6 > 0; Rep > Re(i/6-6)].
2
[Rep > n| Re6|; n = 1, 2, 3, . . . ].
[Rep > -n|Rec|],
2тс
8.
1
fea? dx = - In
2
In
2 p-b
[Rep>|Reb|]
г —рх	-|	А А2
9.	sh2tec^ = --lnWl	-
J ж	2 У р2
о	f
ch bx
11.
px shn bx dx = 2^nml V f
^ V к J (p -
[Rep > 2|Re6|].
[Rep > n| Re6|]
L	IJ

2.4.11]
2.4- Гиперболические функции
293
12.
¦ shn bx dx = II
[Rep > n| Re b\] m ^ щ m, n = 1, 2, 3, . . . ],
In [P2 - 4(n -
Inp,
,2n+l
h
i
Bn - 2fc
p-b{2n-2k
2 p^2b 4'
13.
14.
15. x
Г(а)С[а,
2c
rift-
in+2
p + 36 4 p + 6 8 p2 - 362 '
[Re a > 1; Rep > -|Rec|].
[Rec > 0].
shea:
dx = -[ — )	7
[Rec > 0; n = 1, 2, 3, . . . ].
16. x
chcx
= 21-2"с-"Г(а)[с(а, 7 + ^ V С
4 4c
3 , P
17. ж0
18.
19.
chcx
chcx
¦ dx =
2n+2
ch еж	ссЬ[атг/Bс)
[Re а > 0; Rep > -|Rec|].
[Re a, Rec > 0; a/ 1].
[Rec > 0].
[a, Rec > 0].
2.4.11. Интегралы от e рх и гиперболических функций.
со
6	ртг
Ж = —Z	777 Ctff —
2.
3.
4.
[Rep > |Re6|].
[Rep > |Re6|].
[Rep > Rei/|Re6|].
[c, Rep > 0].
о
Г
5. e
J
о
rf» = 2^k(c

294
Гл.2. Определенные интегралы
[2.4.12
_r~.sh6a;
1 ж Ьж
t
, ^nX shpx . 1 — In2
7. I e —о	dx =
ch рж	р
[2Rec>|Re6|].
[Rep>0].
2.4.12. Интегралы от Л(х), е~рх и гиперболических функций.
"№ b.X}dx = ^- [Ik(ap + ab) T h(ap - об)]
I СII OX J	А
[к = О или 1; a, Rep > 0; | arg b\ < тг].
1.
2.
3.
4.
5.
6. \ xe~px cthpxdx = -r-[	1
J	P V 4
о
СХЭ
7. - e~px shaxshbxdx = - In ^r	7^	^
J ж	4 p2 — (a + bJ
0
[Rep > |Re6|; |argz| < тг].
, ^
4c
4c
4с
4с
4с
¦•?
[Rep > 0; Re a > -1].
[c, Rep>0].
[c, Rep > 0; Re a > 1].
[Rep > 0].
[Rep > | Rea| + |Re6|].
8.
^р
0 a,
4
shax shbx dx =
4
4
Re p > Re a + ^ 6 •
4 (p — bJ -a2 4 (p — aJ — b2 4 p2 — (a — bJ
[Rep > I Real + I Re 61; p2 + a2 ^ b2}.
L	J
00
9. I -e~pxshaxchbxdx = - In )P + a(o ~ f o
J x	4 (p — aJ — b2
0
2 psin@7r/
12. \-
J
лth
ж сЬрж 2
2л/2
[Rep>|Re6|].
[ReP>0].
[Rep>0].

2.4.13]
2.4- Гиперболические функции
295
2.4.18. Интегралы от ха(ех + а)ре~рх{ ^Ы \.
{ ch bx J
2.
Г
еах - 1 \ ch bx J
26 2asm(bw/a)\cos(bw/a)
Г ж ch bx .
4. 	dx =
J аж 1
2a2sln2(&7r/a) 2b2
6.
7.
8.
10.
^1 sh2 6

eax + 1
1 . / а бтг
-ln(—tg—
4 \Ьтг & a
	dx = --In ( -;—sin
еаш - 1	4 \2Ьж	a J
t
2а2 sin (Ьтг/а)
=
2n sh bx
' 2a
Re a > |°|; Re a > |Re6|
[Rea>|Re6|]
L	IJ
Rea> Re 6
L	IJ
[Reo > 2|Re6|].
L	in
Rea>2Re6|.
l	i и
[Rea>|Re6|].
[max(Rea, Rec) > |Re6|].
26 \ 1 J
^ c2Bk-2\J^
[Re {mc - 6) > 0; Re [(m - 2)c - 6] > 0; { ^O^^t ¦
tf =
±
si
+ Ь)Г(Р - о - 6) т Г(а - Ь)Г(р - a + b)],
ж	J cos атг sin бтг 1
sin (a — 6)тг sin (a + Ь)ж \ sin an cos бтг J'

296	Гл.2. Определенные интегралы	[2.4.14
±	ж	Г.	. J cos аж sin Ьж 1	J sin аж cos Ъж 11
sin (а — 6)?rsln (а + 6)тг |_	\ sin атг cos бтг J	\ cosaTrsIn Ьж J J'
/п = ^у [(п - 1 - а)/±_! - 6/^]	[п = 2, 3, 4, . . . ].
о ^ 1 а тж	« -рж f b + shaa? I a
2.4.14. Интегралы от х е <	} .
[ 6 + eh аж J
г
Г	/9
-I	—раз/ 1	1 \i/ —1 I	• /	1/тггт-1/ \ I г/ —1/2 /~\i/ — l/2/ I \
1.	е (сп ж — сп а) ах =—ъ\ — е Т(у)ш ' aQ _1y2(cha)
а
то	[a, Rei/ > 0; Rep > | Re i/ - 1|].
Г е™рж	1 Г1	^ f-l)fee^afe1
2.	—	—— dx = ——\- + 2p\ 2 J2	[a > 0; Rep > -1; см. 5.2.5].
J сЬж + cha	sha[p	Р — к2 J
о
dx =	\ + 2p\ 2 J2
сЬж + cha	sha[p	_ Р — к2
fe1
7 е^рж	2 ^ sinafe
3.	dx =	>		[Rep > -1; а ф ±2жп; см. 5.4.3].
спж- cos a	sin а ^-^ р + ак
ч_1 i / 2а + аж
4. 	аж = — (sin а sin атг) cos 	 х
J ch рж + cos а	\Р/	L V 2 /
о
X СA-а, ^Г-^) -cos( ^Ц-— )C(l-a, ^r^)	[Re«, Rep > 0; \а\ < тг].
V	27Г/	\2/\	27r/J
ею
Г ж"™1е™рж .	2Г(а) v^ sin afe
5.	rfa; = 	^^ > т,	r-	Rea, Rep > 0; a 7^ ±2тгп; см. 5.4.3 .
J сЬрж^сова	раша^ (Н1)а
а	к—0
6. \x2n+1-,	C-^dx = In	[Rep>0],
J	ch рж — cos a
о
* - ^ - ^) , /„ = 2Bn + l)!p-2"+2 ? g^	[см. 5.4.2].
7.	—	¦	—dx=-[-	 + —		Rep>0; a < тг .
J (спрж + cosaJ	p\sma 1 + cosa/
о
oo
Г	/	\
8.	e~px(chcx-l)" dx = 2"I/c В f --i/, 2i/ + l j [Rec > 0; 2 Ret/ > -1; Rep > Re(ci/)].
9. I u в	rfg = - u^6u (ch Ьж - e^2iab)	[a,
1 sh ж + sh a	sh 07Г ch a
2.4.15. Интегралы от хае^ах^сх{ ^\Х 1.
1 ch 6ж J
T "-i -a^/sh6a:\ . BaT^F/	/52\[n / 6 \	/ b \]
. ж e <	>dx = -—'-	Г(а)ехр ( — )\D-a [-—= =F D^a[ ^^
J	[chfexj	2	\8a/ [ V y/2a J	\\/2a J J
Re a > 0; Rea>~<|
2- J6 ich6xlfe = T2\/aeXPUH	^^"^	[К"а>0].
0

2.4.15]
2.4- Гиперболические функции
297
3. Г x
J
2n+se-a*2 [ Sh ЬХ ) dx = (-l)n+sis^2-2n-1-sa—1/2-s/2
[chbx)
4.
[R.e>0].
5. I -e~ax2 shbxdx = — erf
J x	2i
[Rea>0].
L	J
{	\dx=-[ — )
6. I x1/2e^ax Г*ГГ Ux=^l — \
3/2
b2\\T fb2\ т (Ъ2
— /Tl/4 — +/±3/4 —
Reo>0.
1/2 aX
1/2*aX
=Fexp
[Rea>0].
9.
d
\сЬ6ж/	2Bа)а/2
10. \ xe	<
J
1 [^ (
=	л / — s (с — 6) exp
4a
erfc
4 [ z
- eibz erf z A +
± e~lhz erf
ъеа, Re z > 0; 6 =
12. (Tax
i г/л
ch[Bn
^[1 ,
a [2
f ~ax2~c
13.	e
J
2 + c2\ f sh[bc/Ba)]
4a / [ ch [bc/Ba)\
[Re a > 0].
Rea>0.

298
Гл. 2. Определенные интегралы
[2А16
2.4.16. Интегралы от А(х) ехр (-руж2 + z2 )<	>.
[ ch аж J
2.
ехр
pvn (
) ch
= Ja
/р2 - b2 )	[Rep > |Refe|; Re z > 0].
[Re a > -1; Re z > 0; Rep > |Reb|],
J4 =
3. x
(p2 -
а-l exP (^
/ж2 + z2
= Ia
(p2 - 62K/2
[Re a, Rez > 0; Rep > |Re6|],
), h =
»2X3/2 L
¦ z2 ) f sh &ж 1
x2 +
\chbxf
= bs f?
Rez > 0; Rep > |Reb|; S =
2.4.17. Интегралы от ж"е <
rfx = u[e"t/2So,i/s
-ax3 j йЬбж) ^ _ Z Глтгг/2о	/„лЗтгг/2
\chbx j
)TS0,i/s(z)]
a~1/2; Re a > oj.
=F
fc 3)/4
exp(^2v/g(p
p + b)]	[Rep > |Re6|; Re q > 0].
})/4exp(^2%/g(p^6))T
[Aj = 1 или 3; Rep > |Re6|; Re q > 0].
,	x. (shbx] ,	,_.. .v.fsint
ехр(аж™е )<	> аж = =р Г(а — о) <
Fl	;\сЬ6ж/	^' l ;i\cost
-/ ч Г sh 6ж 1
2.4.18. Интегралы от /(ж)ехр<	>.
[ ch ож J
1. е
Обозначение: S =
со
-ash, (
I}-
1 ch 6ж
о
dx = ±|
[Jb(a) ^ Jb(a)] ^ - [Еь(о) + Уь(о)] = 65Я^,, ь(а)
[Re a > 0; b нецелое].

2.4.19]
2.4- Гиперболические функции
299
1 ch bx
3.
| ch
- —
a
J ж d x =
oo
I. fe^achiE
ch 6ж с/ж = /Сь
5. e^achxshbxshxdx= -Кь(а)
J	a
о
~асьж chbx
Га	/а\
у 2тг	V 2 /
/ch ж
о I ^асьж chbxshx
8. I е	у —	ах = Кь(а)
/ch ж у ch ж — 1
9.
о
sinpTr
10. e^asha;"
о
dx
I тта
2 V ~2~
- J
11. е
о
-осЬж-рж i
1	г / \
аж — ж1„(а)
CO
12. J e—-
13.
14.	^ гас x px ^^ _____ ^^g Ржг/ JLjr^/ T / |^
2.4.19. Интегралы от А(х)е
Обозначение: <5 =
:}¦
6ж
sh Va
. /—	;
ch Vax2 + bx
1.
¦ ch (ел/а2 - ж2
[Re a > 0].
[Re a > 0].
[Re a > 0].
[Re a > 0].
[a, b > 0].
[Re a > 0].
[Re a > 0].
[Re a > 0].
[Re a > 0].
[Re a > 0].
[Re a > 0].
|Rep| < 1; а > 0].
[±Re(ia) < 0].
2z± = ^/c2 + p2 ±c; а, с > oj.

300
Гл. 2. Определенные интегралы
[2А1Э
2.
- ch (с\/ах — ж2 ) dx = же ар'2 /о I — \/р2 + с2 1
V2	/
[а, с > 0].
7^\ Иг —
-a ) dx ~
п1+?гп?
^ 1
4.
5.
6.
e^px J sh(cVx2 -a2
ж + а | ch (су ж2 — а2 )
ж с
2
[е = 0 или 1; а > 0; Rep > |Rec|].
exp (^
[а > 0; Rep > |Ree|].
1
сп
I	/
аж = \ —
pyn I 	fi \ / Tl 	 f
2 V p2-c2	Pl VP
[а > 0; Rep > |Rec|].
dx =
/ж — а (ж + a)
ch (су ж2 — a2 ) I	fl\/c \ 2 ,
-a, ±1/4B-)	[z± = a(p± y7^^2); a > 0; Rep > |Rec|].
erfc B-)
z± = a(p± \/p2 - c2 ); a > 0; Rep > | Rec|j.
9.
10.
I— /9
уж уж2 — а
|;z± = a(p± \/p2 - c2 ); a > 0; Rep > |Ree|].
¦ ch (с\/ж2 - a2)dx = ^_ K1/4(z+)K1/4(z-)
2z± = a(p± \Jp2 - c2 ); a > 0; Rep > |Rec|].
¦ ch (суж2 - a2 ) dx =
a?p?
(p2 -
. (ж Н~ уж a j =p (ж уж а ) —pxj -— \- » - - / 1 1 __
1	' 9 9	e 1 1 / /9 9 - ' ax —
/хл - az
[e = 0 или 1; a > 0; Rep > | Rec|].
oil I ty л	CX I
= a"|l^=^l T!^1^)	\Kv{a^p2~c2)	[a > 0; Rep > | Rec|].
12
p -— с
sh(b\
ch(
p -— с
dx _
13. I e "~si:
0
Jl/4B-
с!ж =
p2 - b2
Zyi ±ib). Rez > o; Rep > |Reb|l.
J
[Rep > | Reb|; | argz| < тг].

2.4.20]
2.4- Гиперболические функции
301
14
рх ch (h\/r2
\ Г ~*~ V 	—- ехп \-(п- \/п2 - h2 )
[Rep > |Re6|; |argz| < тг].
15.
<	.
+ я I ch Fv ж2 + xz )
dx =
exp - (p -
[Rep > |Re6|; |argz| < тг].
16.
ch (б^ж2 + xz ]
); 2 Re a > -Я; Rep > |Re6|; \a,rgz\ < тг].
17.
ж + z) \ ch (б^ж2 + xz )
тг pz
dx = —^ ep erfc(z
Jerfc(z_
(z_)|
z| = z(p± л/р2 -b2); Rep > |Re6|; |argz| < тг].
18.
fx + z
o( ^VP2~b2 ) [Rep>|Re6|; |args|<7r].
19.
4^3/4^^^
ch (bVx2 + xz)
= z(p± \fp2 - b2); Rep > |Re6|; |argz| < тг!.
20.
— + ж + Уж2 + xz I q= I — + ж — Va;2
e F" x
_ ,z
\2
-b	\P-b
, ч ff-r» i -л [сж/(а2 — ж2I
2.4.20. Интегралы от А(х)еп } {	') 2 2^
1 ch [сх/(а — х )]
Обозначение: <5 =
[Rep > I Re6|; | argz| < тг].
1.
sh 1
[сЖ/(а2 -
Ml/4-
l/4-a/2, ±1/4
а2Ь2 - с2 - 2ab
[Re а > -5; 2ab > с > 0; а > 0].

302
Гл. 2. Определенные интегралы
[2.4.21
2.
- ехр -
b \ J sh[cx/(x2 -a2)]
a
x2 -a2J \ch[cx/(x2 -а2)]
a-l
exp
dx =
- а2с2 + 6]1/4 х
4-а/2, ±1/4
[Re а < 1 + 5; 6 > ас > 0; а > 0].
3.
- ехр
Ж2 + а2\ j sh[cx/(x2^a2)]
dx =
4.
- ехр -
b \ i sh[cx/(x2 + z2)]
/2аЬ- ^4а262 -с2
, ±1/4 (
ch[cx/(x2
ЖС
X
2а
[Re a < 1 + <5; 2а6 > с > 0; а > 0].
exp
Q/2-l/4,±l/4
[-5 < Re a < 1 + 5; 6, c, Rez > 0].
5.
о
x Г
Mi/4-
+c2
l/4-a/2, ±1/4
^а/2-1/4, ±l/4
[-5 < Re a < 1 + 5; 6, c, Re z > 0].
2.4.21. Интегралы, содержащие A(x)J e^x\ shg(x), chg(x).
oo
Ь){/-1	[Rep>|Rea|].
л [ ^px ( sha[x] 1
1. I e p	V с«ж =
[ ch a[x\ J
ep - ch a
p(e2P - 2beP ch a + 62) [ ep - 6 ch
{bsh a 1
ep — 6 ch a j
[Rep > In 6+ | Rea|; b > 1].
3. le—2{t^
I ch ex
dx =
1 / тГ
62
f she A
[chCf
4(c2^a2)'
}i/2 1 a + с	1
, 2C = - In	Дс; Re a > | Re c| .
2 a^c	J

2.4.22]
2.4- Гиперболические функции
303
4.
\ ch (bx +
c/x)
exD
(P-b)(q-c)
J{p-b)(q-c) \ f sh d \
s = tfq2 - c2 5 Rep > | Re 6|; Reg > |Ree| .
f sh bx 1
2.4.22. Интегралы, содержащие разности А(х), е рж, <	>.
[ ch bx J
[Rep > |Rea|].
1. e p 	dx = - In 1	-
о
СХЭ
0
3.
= -p In ¦
— a a p + a
	in
2 p- a
[Rep > | Rea|].
[Rep> 1],
2 "A p - 1'
_ 1
~ ^2
= « In ( 1	2 + ^ln
2 \ р2 J 2 р —
-?
¦р-1
-р
5. е
в.
7.
ж shx
V 2
о
8. ж"
о
(л	^XS2	о	r(n-l)/2
ch ж + cos (тж/п)	sin (тж/п) ^
Ьшг
П
[Rep>0].
[Rep > 0].
[Rep>0].
[Re a > 1; Rep > -2].
; + 2)/(rn), A;/(rn) 1
9. | xn
sh ж
= Jn,
т
Jl =
2 m —1	,
тж x-^ m — к
m -— k
•	= 2, m + n = 1, 3, 5, . . .
•	= 1, m + n = 2, 4, 6, . . .
If» '"¦ — x
4 3 v^4 ^^ "~
= 	 Т717Г	> 	---
60	2 ^ J h4
k=l

304	Гл.2. Определенные интегралы	[2.4.22
СО	_-.
10. х	—~	dx = ттг тг + > (—1) —г-^—•
СП X
о
со
и. ,.„1 + (-1Г«-ага*
ch2 ж
о
т — к	7тж 3 \-^ / х^т^«
— 1	,	и-,	4	« т — 1
fc=i
Г е echbx , 1, с5
13. 	dx=-\n	—	Rea > 0; Rec > Reb .
J	x	2	a1
о
7 e~ax - e~cx	1 c2 - b2
14. 	chbxdx = -ln^:	—	[Rea, Rec > |Reb|].
J	ж	2 a2 — b1
о
CO
г e^ax — e^cx	b c2 — b2 с c + 6 a a + 6
15.	shbxdx= -In—	-^ + -In	г-77 In	г	[Reo, Rec> | Re6|].
J	x2	2a2-b22c-b2a-b
о
f (i_ e~ax)(l — р^(а+1)ж)
17. Ui	^V^	}-dx = 2aln2	[Rea > -1].
J	x sh x
18.
oo
f 1/ ^6ж ^cxshax\ a c2 - а2 с
. - ae — e 	 аж = — In	1— In
) \	J	2	b2	2
ae	e	аж = In1Ina
x \	x J	2	b2	2c — a
[Reb > 0; Re с > |Rea|].
CO
1 2csin[a7r/Bc)l 1 v^, Л а2
[а < 2(п + 1)с; а < 2пс].
со
20.
ch ж — cos (тж/п) х
о
г(п —1)/2
-1) sin	In
sln(m7r/n) ^ l }
[_ _ ,	. fr = 2, m + n = 1, 3, 5, ..
Rea, Re 6 > -1; <
L	[r = 1, m + n = 2, 4, 6, . .
^ж ттг е аш sin (тж/п)
-eJL.	6 t?T
2n сЬж + cos (тж/п) J ж
= tg — ln(rn) + 2 g (-1) sm — *1пГ[	(a + Jfc)/(pn)
= 1, m + n = 2, 4, 6, ...

2.5.1]	2.5. Тригонометрические функции	305
22. [ е^рхСЪаХСЪЬХ dx = In	[Rep > | Rea|, |Reb|],
J	xn
1 . p2 — b2 _ p . p2 — a2 b . » — 6 a1w + a
23. e p	dx = Jn	[Rep>l],
J	xn
0
j	li P+l	P	ж	-,	Pi P+l	j
J=ln	J = 1ln	J =
24.	e 	^	shxcte = - In	—	Rep > 2 .
J	x2	4 p2
о
CO
0
,	«,*. z shcx — ce^hx shax . ас % h2 — a2 ch . h + a ab . 6
26.	cfe = — In —	 + — In	—In
x2	2 b2 - c2 ' 2 h-a 2Ь-с
[Re6> | Rec|; Re Л > |Rea|].
no
I 1 ch ax — ch 6ж	1 [J In cos [6тг/Bс)] — In cos [an/Bc)]
0
x emcx _ e(m^2)cx	2 [\ In sin [6тг/Bс)] - In sin [пЖ/Bc)]
c2Bk-2Xf -b2 f 0 11
П c2Bife~2AJ~a2 + \ In (a/6) J J
ч , ,	ч (A = 1/2, m = 1, 3, 5, ...
a < (m- 2)c; 6 < (m - 2)c; <	7
1	; '	l	; ' 1 A = 0, m = 2, 4, 6, ...
CO
Г -ax	~bx	1	1	1 Г / 6 \	/ a \1
28. (e — e ) cth ex dx =	1— \ф\ — — ф[ —	[Re a, Re b > 0].
J	b а с I \2cJ	\2c/J
о
2.5. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
2.5.1. Введение.
В этом разделе содержатся интегралы, в подынтегральные выражения которых входят
тригонометрические функции. Для их вычисления можно использовать следующие свойст-
свойства.
Интегралы, содержащие тригонометрические функции, могут быть преобразованы к ин-
интегралам от показательной или гиперболических функций, если воспользоваться соответ-
соответствующими формулами, приведенными в приложении I. Интегралы, содержащие функции
sinn bx и cos" bx, сводятся к интегралам от функций sin kbx и coskbx, если использовать
формулы для степеней тригонометрических функций (см. приложение I). В ряде случаев
интегралы от тригонометрических функций с помощью замены переменной сводятся к ин-
интегралам от алгебраических и других функций. Например,
а	а	а	а
(р(х) sin2 bx dx = - I ip(x) dx--{ (p(x)e2ibx dx - - I (f(x)e^2ibx dx =
0	0	0	0
a	a	sin ab
f M ,2 ., , 1 f / w-, o, u If 2 /атозтяЛ dx
= — (p(x)sh tbx dx = — \ <p(x)(l — co^2bx) dx = —	x ш\		г
J	2j^v	b J "V b J л/1-х2
0	0	0
[ab ^ tt/2].
20 А. П. Прудников и др., т. 1

306	Гл.2. Определенные интегралы	[2.5.2
2.5.2. Интегралы общего вида.
В этом пункте помещены формулы, которые позволяют находить интегралы, содержа-
содержащие тригонометрические, а также степенную, алгебраические, показательную и гиперболи-
гиперболические функции. Некоторые частные случаи этих интегралов, соответствующие конкретным
значениям входящих в них параметров, приведены в последующих пунктах. Интегра-
Интегралы общего вида представляются с помощью функций Vj, j = 1, 2, 3, . . . , помещенных
в приложении III. Конкретные значения параметров, входящих в эти функции, приводятся
в фигурных скобках после каждого интеграла.
В п. 2.5.2 приняты следующие обозначения: г = p/q, где р и q — взаимно простые
натуральные числа, если не указаны другие условия;
~ _ I 1, если взят sinox, _ I ( —1)	, если взят smox,
[0, если взят cosbx;	[ 1,	если взят cosbx;
1/2, если взят slnn bx, в = 1, 3, 5, ...,
7 = { 0, если взят slnn bx, n = 2, 4, 6, . . . ,
0, если взят cosn &ж, n = 1, 2, 3, ...;
С = г'1 (а/2 + 7 + h), b = by(n - 2к)/2.
у
Л I а-1/ 2г	2гч/3^1 Г Sin6iC 1
1. ж (у - ж f <	} dx =
о
аг = С, bi = /3 + С, ci = 1/2 + 27 + /i, z = (-Ь2/р2
[у, Re^ > 0; Re a > -8щ | arg 6| < тг]
I cos ож ^
У
^n B(/3, 1-^-0 о	^о-п^Г/3, 1-Ь2"
V2 = 2r(l — j3 + j) — a, di = (,, bi = p + ?, ci = 1/2 + 27 + Л,, «2 = 1 — /
= 1^7^ a/2 + r(l - P + j), c2 = A - a)/2 + 7 + r(l - /3 + j), z = (-1
[y, 6, Re/3 > 0; Re (a + 2r/3) < A - (^l)n)/2 + 2r
a-l/ 2r , 2rxp^l f Sir
3.
0
V2 = 2r(l — p + j) — a, ai = ^, 61 = p + ?, ci = 1/2 + 27 + h, 0,2 = 1 — p + j,
62 = 1^7^«/2 + r(l^p + j), c2 = (l^a)/2 + 7 + r(l^p + i), z = (^l)p+<?62pp":
[6 > 0; 2r| arg 2/| < тг; Re a > -<5n; Re (a + 2rp) < A - (™l)n)/2 + 2

2.5.2]
2.5. Тригонометрические функции
307
4-
1 + (-!)%.„.! «-2
rA/2
F [l-a2
Г[ 62
и = а - 2r, v2 = 2r(l + j) - a, ai = 1/2 + 27 + /1, «2 = 1 - 7 + К1 + J) - «/2?
Ь2 = A - «)/2 + 7 + r(l + j), z = {Л2/р2)А
[у, Ъ > 0; Rea > -?n; Rea < A - (-1)п)/2 + 2г].
5.
r[(n/2)\}2 sinGro-/2)
)fflв(|, 1 - g -
in[(q + rg)/Br)] /a _ _ j«
sinGro-/2)	V2^'	2^
и = a + 2r(cr — 1), V2 = 2r(l — <j + j) — a, ai = ^, 61 = cr + ?,
= 1/2 + 27 + /1, a2 = 1 - (T + j, b2 = 1 - 7 - a/2 + r(l - a + j),
c2 = A - a)/2 + 7 + A -
[1/, 6, Re<j > 0; Re a > -5щ Re (a + 2ra) < A - (™l)n)/2 + 2r].
0
= V35 +
V3
а/Bг), 2p-j/-a/r]
J
-I/)/2, -1/2 -J, 1-
n = a + r(i/ — 2p), г;2 = ^Bp — i/ + 2j) - a, v3 = rBp + 1 — 1/ + 2j) — a, ai = 1/ + ^,
= ?, ci = 1 - p + i//2 + C, dt = A + i/)/2 - p + ?, ei = 1/2 + 27 + Л, a2 = p - i//2 + j,
b2 = ^/2 + p + j, c2 = 1/2 + j, d2 = 1 - 7 + r(p - *V2 + i) ^ a/2,
e2 = A - a)/2 + 7 + r(p - и/2 + j), a3 = p + A - i/)/2 + j, 63 = A + i/)/2 + p + j,
сз = 3/2 + j, d3 = d2 + r/2, e3 = e2 + r/2, z = (-I)p+gF/pJp
[6 > 0; 2r|argy| < тт; -<Уп < Rea < 2rp - r Re и + A - (-l)n)/2].
7. х
о
л = v35 +
smbx}n
\cosbxj
2p^n^l^a/rf \l
r
p = 0,1/2,
LF ' 7 J'
~ ^/2 - a/Br), tt/r
-p-i//2 + a/Br)
20*

308	Гл.2. Определенные интегралы	[2.5.2
35 = ( } ~2
1 — ^ Ч- J, e2
и = а + г(и - 2р), v2 = гBр - и + 2j) - a, ai = С, &i = С + V2,
= 1 - р - I//2 + ^, di = 1 - р + I//2 - ^, ei = 1/2 + 27 + Л, а2 = р - i//2 +
b2 = Р + A - */)/2 + j, е2 = 1 - i/ + j, d2 = 1 - 7 + r(p - и/2 + j) - a/2,
e2 = A - a)/2 + 7 + Kp - i//2 + j), z = (~l)p+q(b/pfp
[6 > 0; 2r|argj/| < тг; -Sn < Rea < 2rp - r Re и + A - (-l)n)/2].
I sin bx\n
\ COS ЬХ j
22
fei = i/ + ?, ci = v/2 + ?, di = (y + l)/2 + ?, ei = 1/2 + 2j + h, z = (-1
[y > 0; Re a > —n<5»; Re a > — n5 — 2r Re v\ | arg 6| < тг].
oo	_	,		_	,	 _
9.
У
, A + i/)/2 - a/Br), A - i/)/2 - a/Br)
}
Г
r[{n/2)\]2 [	1-a/r
2_n_2t+1
l,e2 J	[ v ~ Ah ез
6i = ? + 1/2, ci = A - i/)/2 + C, di = A + i/)/2 + C, ei = 1/2 + 27 + Л,,
a2 = A + i^)/2 + j, 62 = 1 + v/2 + j, c2 = 1 + у + j,
аз = A - *0/2 + j, 63 = 1 - ^/2 + j, e3 = 1 - v + j,
is = 1^7 + ^[(l^^)/2 + j]^a/2, e3 = A - a)/2 + 7 + r[(l - i/)/2 + j],
[t/, fe > 0; Rea < r(l - |Rei/|) + A - (-1)те)/2].
7	x^	(sinbxy
J x2r + 2(xy)r cos /3 + y2r \ cos bx J Ж ~
°	= Vsb + V^39 - г + (^1Г o-n-ie-2r+a ^^? sin [0(a - r)/r]
2	r[(n/2)!]2 sln/3slnGra/r)
1	7T3/2	;r, ^39 = -2"n^™-, и = a - 2r, V! = 27 + 21, v2 = r(l + I) - a,
r	sinp	sinp
1 = /3B7 + 21 + a - г)г~г, bi = B7 + 21 + а)тг/г5 ct = 1/2 + 27 + I,
4 = 1 + 1- a/r, fi = 7 + a/2 - r(l + I)/2, gi = A - a)/2 + 7 + r(l + .
[y, b > 0; |Д| < тг; -те<5 < Rea < 2r + A - (-l)n)/2; r > 0 произвольное].

2.5.2]
2.5. Тригонометрические функции
309
со
Г
01-1 е-зх2г { Smbx Y
e \cos6x/
o-n-i -а/Bг)
n\	/ а
27
[r = 1/2]
27
•¦ - -
—2p
[Res > 0; Re a > —<$n; arg 6 произволен (при г > 1/2); 6 > 0 (при г < 1/2);
n| Im6| < Res (при г = 1/2)].
+ (-1)П п_1 а/Bг)
2	[
V4
2г
и = а/Bг), vi = 2(Л + 7), «2 = 2rj - а, tp = 26(n - 2fc)s1/Br),
1/2 + 27 + h, 6i = 1 + ?, а2 = 1 - 7 + rj - а/2, Ь2 = A - а)/2 + 7
\ *\	[6, Re,>0; Rea
13.
1
cos ox — с
[(m-l)/2]
x V
i //о \
l/2-a/Br)
a/2
2 "	[(m/2)!]2 ^ ~\kJ\n-2kJ
[г ф \(г = 1 см. 2.5.13.20-21); с = 1 при п = 2, 4, 6, . . . ; с = 0 при п = 1, 3, 5, . . . ],
п- 2А;
i=o

310	Гл.2. Определенные интегралы	[2.5.2
A(q,
J ai = 7 + a/2 + r(j + p), bi = A + a)/2 - 7 + r(j + p),
a(m - 21) f 2 V	iip+»
[a, b > 0; — Sn — arm — 2с < Re a < 0 (при га + п = 2, 4, 6, . . .), или
— ёп — arm — 2с < Re а < max A, г) (при га + п = 1, 3, 5, ...)].
S1nn X I da: = 7@, 0, 1)	[см. 2.5.2.13].
cos bx — с J
sin ах л п
cos bx — с
fe=0	" "" 1=0
,ff,r) = 21—* V ef?) V r(.||——-I x
—-се
1; z
Ь ci), A(g,
-^ r/i! r [1/2+ p + ^, 1/2 + 27 + Л,
XiF2p+2g( Л^ i „ , ^ л/^ 1/2 + р + ^5 д(р; 1 + /l)j Д(р? i/2 + 27 + /i)
{!}J^^ 5 T^^
= 1/2 + 2p + j, bi = 1 - 7 - a/2 + r(p + j), ci = A - a)/2 + 7 + r(p + j),
— 21 f 71 — 2к\Г	( 1чр+д ,2g ^2p ^
6—-— ,z = (^l)p^9^9p pq
\	A J
a, 6 > 0; ^2c - <5n - arm < Re a < f 	^	'— +
+	r
с = 1 при n = 2, 4, 6, . . . ; с = 0 при тг = 1, 3, 5, ...
Т,	i da = J@, 0, 1)	[cm. 2.5.2.15].
cos 6ж — с j

2.5.2]
2.5. Тригонометрические функции
311
17.
sinbx 1
}
cosbx
1	( . |
} ax = 1 icr
[r > 0],
и =
/ ОТ	w |
¦ cos I	h I arctg — ] x
\ 2	s A
.-2k
(
x Г
z= Ib
= 2
x Г
a) arctg ^1 x
(,2 + a2
7 + {ol-
при z < 1,
при |z| > 1
[a, Re s > 0; Re a > —or — <5n; 6 — произвольное (при г > 1), | Im b\n < Re s (при г = 1)
и 6 > 0 (при г < 1)] или [Re s = 0; a, 6 > 0; -от — c5n < Re a < max (r, 1) (при г ф 1)
или — err — Sn < Re a < 0 (при г = 1)].
¦	rv —1 — ЧТГ	T'	Sill
18. ж е cosa/1
19.
a —1 —-sx
X cos Ьж j
[I(o-) см. 2.5.2.17].
= J(^)|CT=1,
(a-/r)/2
x fe
n - 2k
х/ж v^ /^
^т Е ?(
хГ
2	2«[(n/2)!]2
[a, 6 > 0; Rea<r<T + (l- (-l)n)/2 и Re s > 0 (или Re 5 = 0 и Re a > -r - nS)].

312
Гл.2. Определенные интегралы
[2.5.3
20. ж е
J
21.
___ Г Sill ЬХ 1 П ,	w ч1
cosax <	> dx = J(a)\
\cosbxj	v Jl<J=0
dx = K(a)\ Л
\chbx
см. 2.5.2.19 .
L	J
[г > 0],
L J
E
/г=0
n-2/fc
а
- х
/ч
r4
llmncTT
7r /cjtt f ^ a\
- cos — + larctg - x
\ 2	j
> 1
[c — произвольное нецелое; a, Re s > 0; Re a > ^crr — en;
b — произвольное (при г > 1) или п + | Re 6| < Re s (при г = 1)].
22. f /-^"^ cos ажг| ^ ^ Г dx = К((т)\а=0
[см. 2.5.2.21].
2.5.8. Интегралы от ж <	> .
{ cos ox J
Обозначение: S = < >.
(a + l)/2l
тт/2
1.
2.
тг/2
О.	X
J
О
Г .
2 L «/2 + 1 J
Rea>-1.
[Л = 1 при 71 = 1, 3, 5, . . . ; Л = тг/2 при тг = 2, 4, 6, . . . ].
7^
(m-2ife -

2.5.3]
2.5. Тригонометрические функции
313
Г sin ж	1 ,
4- J —dX=2l
О
7Г
Г m Г sinna? 1
5. \x <	} dx
J { cos пж J
-1)!
т- S + 1
— m +
6. I аГ ~sin"
о
7. ж cos x dx =
ЖЧ1Т1	'Г8 И' Т*
OIII	tAy L4/еду
[Rea > 2-n; n = 2, 3, 4, . . . ].
2Bn)!! *
О
тгк
8.	ж sin" х dx =
о
I	"ТО	\ "^
9.	ж созпжаж = — у.
J	U	Г»
= 0, 2, 4, . . . ,
COS^-TT
10.
11
12.
а^1Гз1п&ж1	Г(а) Г sin (а7г/2)
\ cos Ъх )	ba \cos(a7r/2)
Sin Ьх .	7Г
ж
[n, / = 1, 2, 3, . . . ].
[6 > 0; ^5 < Rea < 1].
[b > 0].
[Im6 = 0].
ею
13. ж" sinn bx dx = /а; n
[Imb = 0; -n < Rea < 2Л; n = 1, 2, 3, . . . ; Л = A - (-l)n)/4],
при a / -2(X + k), k = 0, 1,2,.. .,
I-2\-2k,n = lim /a,n при a —>> ^2A — 2k,
^
h/2-m,2l = ( —1)
[(m
,-21 \Ь\
m-l/2
Bm-l)H^
[0 ^ m ^ 2/- 1],
[m = l, 2, ...,2Z],
Sgn 6, /-3/2, 2 = о
/-1/2, 3 =

314
Гл.2. Определенные интегралы
[2.5.4
/о, Bm+i)/Bn+i) = 2Bm-4"-1)/Bn+1)B(Bm + l)/Dn + 2), Bm + l)/Dn + 2))	[6 > 0],
2-"Ьготг [("^/21f_n[(«-i)/2]+i »!(» - 2jT
m'n т!Т(ттг/2) ^ l ;	j\(n - j)!
[ft > 0, T(x) = cos ж при п = 11 - 1; Т(ж) = sin ж при n = 2/, / = 1, 2, 3, . . . ],
ttI&j B/ - 3)!!	_ я-blbl	^B^-5)!!
/а>2 = -2"ar(a)|b|"acos(a7r/2)	[-2 < Rea < 0],
/a,3 = 2~2|6|~QC - 3"a)sin(a7r/2)r(a)sgn6	[-3 < Rea < 1],
/o,3 = "Г Sgnfe, /-1,3 = T ЫпЗ, /_2,3 = - 7Г6|6|.
14. | /-1 cos2n+1 bx dx =
[6 > 0; 0 < Rea < 1].
2.5.4. Интегралы от ж
тт/4
1.
/7г\^Г	4m	4mA
[т = 2, 3, 4, ... ].
ж/4
J f sin ж 1
о <	}
{ COS Ж J
тг/4
3.
4.
5.
в.
к-г /2_к
2
B[n/2]-l)H
B[п/2])Н
[п = 1, 2, 3, ... ].
тт/2
0
тг/2
1 I
fe = l
т/2
0
7Г/2

2.5.6]	2.5. Тригонометрические функции	315
8. —?— dx = ^4
J COS X
о
2.5.5. Интегралы от (х + z)^ I
\ cos bx
Обозначение: S = ,
;}¦
[a, Re/3 > 0; |arg6| < тг].
CO
2. ж-af	, Мж = ^/1 / , о /о f	[a, 6>0; 0< Re/3 < 1].
J	[cosfexj	&^ [cos(a6 + /37r/2) J
3-р
sin (ртг/2 +
CO
Г 1 (sinbx\	ПГ Г	.	, х Г sinoz 1	. . Г cos bz 11
4.	-< f > с!ж = 4/—г cos6z =р smbz ± 2C(bz)< , > — 2S(bz)< f >
J уж + z { cos ож J	у 26 |_	I cos "z J	I sm ®z J J
о
[6 > 0; |arg^| < тг].
CO
f 1 f sin bx 1 . , /, x f sin 6z 1	/f 4fcos6zl
5. 	^ , >^ = ±ciFz)^ f ^si(fez)^ . , }	6>0; arg^<7r.
J ж + z I cos bx J	[ cos 02: J	[ sin oz J
CO
f 1 f sin 6ж 1 . . f cos by 1 r ,. ч , f sin 6t/1
j ж-у( cos bx J	[ sin 6|/ J	[ cos 6|/ J
0
2.5.6. Интегралы от (я:2 ± а2)"/""^ Г, (а2 - x2)"(
[ COS ОЖ J	[
a-a!Y-1(8in^}da! = ^f^V/V(/3)(H^1/2,(ab,)
' {cosbxj	2 \bj	У '{Jf3-i/2(ab)
COS ОЖ
[a, Re/3 > 0; |arg6| < тг].
2. L2 - «у-1! si
J
{cosbxj	2 \bj	{Y1/2
.l3(ab) J
[a, 6 > 0; 0 < Re/3 < 1].
CO
- J
[6, Rep, Rez > 0].
[6, Rep,

316	Гл.2. Определенные интегралы	[2.5.7
5. [ 82Ш ЬХ2 dx = ^- [e^bz Ei (fez) - ebz Ei (-bz)]	[6, Re* >0].
J x + z	2z
о
cosbx ,	7re~bz ABmfc)!B6z)
+ ^)m+idg=BgJm+im!E kl{m-k)l	[6,Re*>0].
fe°
7. —	 dx = — [cos by Si (fey) — sin by ci (by)]	[b, у > 0].
0
Г cos bx	ж
8- J ^—2dx = -^smby	lb,v>o].
[6, У > 0].
[6, Rez > 0].
0
0
T l2n + 1 &	(l)"^1 I Bn+l)bz
-\- Z	A	I
fc"~u
B+1)Ь ^*1 (^t Л^^ Ei
13.
15.
со
0
со
Г 2 J
0
со
л 2п-
ж2 И
0
&ж
z2 4.
fe=i
7Г /
4
г
7Г
22n+lz
Обозначение:
1. f х-^а - xf-1! Sinf I da, = (-i)^-^-^-1 В (а, /3) x
J	|[ cos bx J
11. [jE^da-A_e-^)	[6,Re,>0].
J X Z	4Z
6,
L
о к .г о	«/ , xiifsintel a	XMfsin6x1
2.5.7. Интегралы от ж (ж±а)^<	>, х (а — ху {	>.
[cos 6ж J	[ cos 6ж j
е: 5 = < >.
О
X [iFi(a; а + /3; iab) =F iFi(a; а + /3; -tab)]	[a, Re/3 > 0; Rea > -6; |arg6| < тг].
~2~
f а-1/	ча™1[81п6ж1	^- / tt Л "^l/2 f sin (ttfe/2) 1
2. ж (а — ж) <	> с!ж = V71" ( т )	1 / i / \ г
J	[созбж]	\Ь/	[cos(a6/2)J
о
[a > 0; Re a > -5; | arg 6| < тг].

2.5.7]
2.5. Тригонометрические функции
317
1	J sin bx 1
/x(a- x) I cos bx J '
4.
3-i (sir
1 cos bx I
- а -/3 -
25 а + /3 + 1 а + р + 25 1
5
a2b2
/3 3-/3 3
;
'2-at-p
3-a-p a2b
x
2l2-
5. ж (ж - a)
dx = ±-— -
2 \bJ
a6\ f cos (аб/2) 1
2 /I sin(ab/2) /
6.
dx = E(a + S, p — a — S)b z
a + 1 „ 1
^! + 2'
b2z2
i . ? 3 3 + p
'' 2' 2' 2
'
7.
x + z
\cosbx J
dx =
2 ' 4
[b > 0; Re a > -5; Re (a - p) < 1; | argz| < тг].
ГA — a, —ibz) + e ГA — a, *oz)J
[6 > 0; |argz| < тг; -5 < Re a < 2].
[Ь>0;
9.
V 2
(si
[о- = 0 или 1; Ь > 0; | argz| < тг]

318	Гл.2. Определенные интегралы	[2.5.8
со
Г ж" f sin bx I ,	a_i	(sin by] ,2_а „,	ч Г sin (атг/2) 1
10. 	<	^da; =-тгг/ ctgaTr^	> - 6 %Г(а - 2I ) ' { } х
J ж — у { cos ож J	[ cos by J	( cos (атг/2) J
fcos(air/2)l J,.3-« , а. Ь
0
2y2
a
'	2'
2' 2'	)Tb ^"VUnianWt^X' 2' 1 2'
, 2/ > 0; -5 < Re а < 2].
11. J x2"[(/3 + ix)"" т (/3 - «)"i
0
[b, Re/3 > 0; 0 sC 2n < Ret/].
12. I x2n+1[{p + ix)~u ±(p- ixy{ ШП^Ж 1
J
^ 1 dx =
[COS 0Ж J
о
)\ 1522ЪCl2	[b, ReC > 0; ^2 - S < 2n < Re v - 1].
2.5.8. Интегралы от Ж-(Ж2 - a2f f Skl h* V xa(a2 - х'Г ( ^ f V
[ cos bx J	[ cos bx J
Обозначение: <5 =
>.
a-i, 2 2^_1/
(созбЛ	2
0
x iF2(^—; 2 +<5; ^ + ^^; ^^^) 'a> Re^ >0; Rea > ~S; 'arg6' < ^^
о f /2 2^1/sinb]	^	^+1/2()
J	[cGskcJ	2 \bj	{Щ+1/2(аЬ) J	2/3
[а, Re/3 > 0; |arg6| < тг].
a2b2
3. fa:(a!aY{
J	[ cos bx
, и ' 2 '" ' 2" 4
[a, 6, Re^ > 0; Re (a + 2Д) < 3].
4. l2 yil™b* )^ (^Y"/\lY
j-/3-i/2(ab)
[a, 6 > 0; 0 < Re^ < 1/2].
6.
7r^^OJi/2-/3
z sin ртг [	z
[a, b > 0; 0 < Re^ < 3/2].

2.5.9]	2.5. Тригонометрические функции	319
со
7 Г ^^ f slnbx X dx _ ±?L a-2 f tg (атг/2) sin 6f/ 1 _
J ж2 — у2 \ cos &ж /	2	\ ctg (атг/2) cos by J
CO
Г ж J sin bx 1	J	(tt/2)cos&|/	1
J ж2 — y2 X cos 6ж J	\ sin by Si (by) — cos by ci (by) f
о
о
ха Г sin bx I n
2.5.9. Интегралы от
Обозначение: S =
1.
ха
(ж2 +
2'
-1
' Z2)P
( sin bx 1
1 cos bx j
i jJ^P — °t F1 / 1 \ J L\
~T~ t? I I ?X — А О) \
iF(a+i f+
г
Rez
2
>
0;
^5<
^ h2z2
a
' 2 +
Re a < ]
\ ,
) l
L + 2 Re p]
¦ жа 1 J sin bx 1	wza 2 ( cos (an/2) 1
¦2 + z2 \ cos 6ж J X^ 2 \sin(a7r/2)J \ ch 6z ^
CO
0	[6, Rez > 0; Re p > n].
4 7 Ж2П+' (Sin^|ix^f	ir+g0F BzI/2-' д2П+1 \b'-1/2K
J (ж2 + ^)Н6 ]dx~{	^ V(){lZ)	db*»+i[b	KP-
(	)	]	V(p)
0	Г	(l
6, Re z > 0; Re p > те + 5/2; 5 = ^
, 7 ж hinbx\J _ (-i)\_TO / a \ 2n_1+, ^Ьг.
J (ж2 + ^2)-\со8бж/С|Ж^ (m1)!	""U^/	6
0
[6, Rez > 0; 7i = 0, 1, 2, ..., m- 1; m = 1, 2, 3, ... ].
Г ж2+5 f sin foci _ l + e-bz ^bz	Г	_Г1
J (ж + z j ^ cos bx J	4z	L	10
0
7.
о
1	«Л^ uiii f еду	,,
8. , o , „ч„ с?ж =
0	[6, Rez > 0; m = 2, 3, 4, ... ].

320	Гл.2. Определенные интегралы	[2.5.10
со
х sin bx . тг ^.hz
—	-dx = —e	[b,Rez>0].
о
со
f sin bx . тг Г e~bz , , Л	.
10. —г-г	r-77 da = —т 1	B + bz)	\b. Rez > 0].
I rnlrnA _|_ y?\A	Q <y4	*/
0
о
12. | ж cos 6^ж = _1 [e^b^ EI (fez) + ehz Ei (-62?)]	[6, Rez>0].
x -\- z	A
0
4
>-i/2,3/2-p(*&2)]	[6, Rez > 0; Re p > 1/2].
14. I 	>2 2—^ж = 22та+1 2^(-l) I , |e
0
"	2
о
Г" ^^л dx = A {2IC + ln (ЬгI - te""Z Ei (bz) + e"Z Ei (~6г)]>	[Ь, Re*>0].
2bz -
bfc6ZEi[Bfc2n-lN,]	[b,ReZ>0].
жт	(s'mbxI
2.5.10. Интегралы от	<	> .
anxn + an^1xn^1 + . . . + a0 [ cos bx J
CO
х2к~1+8 fsmbx] ^	Г	1-5 ,	тг	fi
x2n + z2n\cosbx )	[ '	2 ' ' B ' 2n'	10
о
со
2. —	^<	> rfa; = =p—z + те \^ exp [ —bz sin :	—
J x2n + z2n \cosbx}	2n	_	V	2n
0	|m0
1 MCOS^1
тг <	>
/\sint/
21 + X Bfc + 1 - S)w + fez cos 2l + X тг; 6 > 0; 0 ^ Jfe < те + -; |argz| < —; <5 = ' X
2n v	7	2n '	' "	2' ' ° ' 2ri	Ю
f a;fe sin bx	1	, » 1
3. —	-dx = Ik	\b > 0; arg^ < - ,
J ж4 + z4	I » s 1 , h
0

2.5.10]
2.5. Тригонометрические функции
321
4.
5.
6.
х cos bx
т	тг^2	( bz\( bz . bz
Ji±i = . о_г1 ехр	— cos —= =p sin —=
x sin 6ж
—	—
x -У
аж =	V	У ехр — ovsin — sm
?11	\	П /
dx = h
+ by cos —
П
[6, у > 0; 0 ^ k < n].
Ь, у > 0; k = -1, 0, 1, 2, 3],
I_1 = -^(e-»»+ cos б?/ -2),
/i±i = ^T P cos fe2/ Si Fy) - 2sin by ci Fy) T eb!/ Ei (-by) ± e'"* Ei (by)],
7.
dx = Jfc
[6, з/>0; ife = 0, 1, 2, 3],
x^r
I2 cos 6|/ ci ^ +2 sin 6|/ Si
Ei ^ ± eby Ei (^
8.
(x - z)
dx = - (e±lz - 1)
z
9.	= — (cos у — 1)
I/
10. f^l^rf^f e-*+*(±z^ sin A-b+{°\y cos A-b
[±1тг>0].
[z = у] Imy = 0].
, Key
x \±zlTl(A+sin A^b^- A^ cos A^b) + < >|/(Л+cos Л^б - A^ sin A^6)
| = л/z4 + 2/2 ±z2; 6, Rez, Rej/ > o].
Г сх + d Г sin bx 1	, /	 x Г f cos bq 1 cq - d f sin 6g 11
12.	—	<	> rfa; = тгехр (—b\/p — q2) c<	> + / 	<	>
J x2 + 2дж + p [ cos ож J	LI sin bq J д/ p — q2 [ cos og J J
— oo
/,«,« = 1,2,3,...].
14 7
" J
[/, m, n = 1, 2, 3, ... ].
21 А. П. Прудников и др., т. 1

322
Гл. 2. Определенные интегралы
[2.5.10
"•
хт sin bx dx
db с2ж + ex1 ±
:=:: "
[6, с > 0],
h = (^"^^(e0 - cos 6c) ± [e^bc El Fc) - ebc El (-fee) - 2 sin 6c ci Fc) + 2 cos 6c SI Fc)]},
/2 = 2^2 [e6c El (-6c) - e^bc El Fc) + 2 ci Fc) sin 6c - 2 SI Fc) cos 6c] ± тг(е^5с + cos 6c).
ifi I	XmSmbx
16.	, . n n n .—г «ж =
[a, 6, с > 0],
cos I 6
- sin I 6
7Г
2Ve4 - a4
h = t л	exp -b\l	 I sin I b\
COS [ 6
¦ sin ( 6
J
[a, 6, с > 0],
1	/ //.2
- cos
1	. I lc*-a*
¦ Sin 04
1	( \c*-a*
X	— COS 0 4
1	. I, lc*-a*
¦ Sin 04
18.
1	1	1 f sin 6ж 1 . 7Г ^hz f sin flH ,	,
7	\F^—^^7	i—^—гП , Ыж = -е l	и)[Ъ> 0; Rez > Imo .
(ж — aJ + zJ (ж + а)^ + ^2] [ cos bx J	z	[cosaoj
19.
(ж — aJ
_b,fsina6|	Re2>|Ima|].
I cosa6 J
20.
sin 6ж с!ж
Bn)! 22^
21.
cos 6ж dx
(ж2 + 12)(ж2 + З2) . . . [ж2 + Bп + IJ
Bn + l)! 22те^
[ь > о].

2.5.11]
2.5. Тригонометрические функции
323
2.5.11. Интегралы от ха(л/х2 ± z2 + ах + bz)v А(х)
Обозначение
: 5 = < >.
;}¦
1 I xa {	} I	> dx -
JL. I «?.	/ о	ON	1	if U"*/
(ж2 + z2jr [ cosbx J
\1 — 2r i 1 — а — v-гл/ i
) b	Г(а+ i/-
cos [(a + i/)tt/2]
sin [(a + ^)тг/2]
a + i/ 3 — a — i/ 62z2
sin[(a + i/)/2 - 2r]
cos [(a + u)/2 - 2r]
к/
, 2r - V - a -
V - a - 6]
E)/2 J
^'	2'1 +22Г;
[r = 0 или 1/2; b, Rez > 0; -Я < Re a < - Re v + 2r + 1].
2. ж
о
3.
a_i ^v ^'" + z2 + z)ly/2 a J sin bx
X cos 6ж
r.2 j_ y2
/ж' + z-
1 /2л/а + ^
4- z2 4-
+ z1
1 cos 6ж J	V 26
6? Re2: >0; Rea > ™5]"
b, Rez > 0; 5 =
. . a_i A/ж2 + z2 + ж) ( sm к )
4. ж -—г—г	гт—^< , > dx =
B + 2)г [б/
2 \ 2
5.
a + 1
2 '
г+<5гГа + J, r - (a + г/-
a -\- S — is	. , a +
i/ 1 — I/	^	I^f^q;
-,
+ z2 + ж)" Г sin bx
л
b2z
v -\- ol b2 z2
+ z2
[r = 0 или 1/2; 6, Rez > 0; -5 < Re a < - Re v + 2r + 1].
coste
k±l/4+i//2 |
[6, Rez > 0; Re i/ < 3/2].
Sin (IS7T/
COS (lSTT/
[6, Rez > 0; |Rei/| < 1].
21*

324
Гл. 2. Определенные интегралы
[2.5.12
Г (ж + z + \/х2 + 2xz У + (x + z- \/х2 + 2xz )и Г sin ЬхЛ _
\/х2 + 2xz	I cos 6ж /
v Г J COS (bz — 7Г1//2)
~~ ^Z sm{bz - жи/2) j'Jl/K ' [cos(
[b > 0; |Rei/| < 1; \argz\ < тг].
8.
(ж +
— ж2
ж2 Y + (ж —
9.
(ж +
Y ( sin bx \
{ cos bx j
{cosec (г/тг/2)
sec(i/7r/2)
— a2 )l/ + (ж — ^ж2 — a2 У f sin 6ж ,
	<	>йж =
I cos bx
. Г J cos (i/tt/2) \ т / i \ / sin C1771"/^)
[\sin(W2)J "ia)T\cc
[a > 0; |argfe|<7r].
cos (i/tt/2 J
f (ж + \/x2 — a2Y + (ж — ^ж2 — a2 I17 f sin 6ж 1 ,	ж
10. ^	/ x =	^< , } dx = - —
^B 2)	I cos bx J	2
/ж(ж2 — a2)
X |j4
^
±l/4-i//2
о к 10 тж	П f sintt^ I
2.5.12. Интегралы от <	>
11 [cosaj^J
тг/4
1.
2ж
1 ^
> ,
а, 6>0; Rei/
^±1/44-^/2 ^T
V z
[a, 6 > 0; |Rei/| < 3/2].
[-1/2 < Re/i < 0].
2-
3.
4.
о
7Г
s2n+l
J
dx =
о
tt/4
2Bп)!!
8 2Ж ,	1„/771 + 1
	г—;—n^— dx = - В ( 	,
соз2г/+"г+2ж	2 \ 2 '
[Re/i > -1].
[Rei/ > -1].
0
tt/4
Г slnm x cos^1/2 2ж _ (m - l)!!Bn - 1)!! / тг/2, m = 0, 2, 4, . . . ,
t) # I 	 (%X — 	\
г»п«2п4-т4-1 «,	(«v, _i_ On ill	I 1	m — 1 4 е!
J	LUO	л	{III ~f~ /jlbjl.	I 1,	##?/ — JL 5 О j «J j . . •
0
tt/2
[п = 1, 2, 3, ... ].
. Г sin»
J
0
7Г/2
n!! \тг/2, п = 0, 2, 4, ...
7.
[п = 2, 4, ...].

2.5.12]	2.5. Тригонометрические функции	325
8.	= тг/2	[п = 1, 3, 5, ... ].
9.
cos ж	v ; ^ 2к - 1
о	к^г
тг/2
11	I • Д-1 I Sin Ь- l j	о-
11. sin^ ж< , > ах = 2
Г sin (бтг/2) 1 6 Г	/х	1 Гсо8Fтг/2I
\cosFtt/2) j + 2 [l + (/x + 6)/2, l + (/x-b)/2_|\sinF7r/2) J
X
тг/2
12.
о
тт/2
13. sin ч
cos (/jtt/2) J
2n + 5\( к
к л	Г
I I	L
-т)UJ	L	Ю
о
14.	=0	[ш > те; 8 = | Х
15
\	/	Bп - 2т- 1)!!Bт + 2п + 1)!! \ 2т
о
1)?2-1 f
2п + 1)!! \
[т ^ те; S =
(п - 1)!2теBт - 2п -
- 1)!!Bп - 1)!! f	2п	1
)!!	[2m + 2n + lJ
¦1):
771 > Щ S =
тг/2
17. cos17™ ж sin 6ж с!ж = 7г&2~
X sF2^, ^, i; 1 + ^,1 + ^; lj	[Rei,>0; |arg6| < тг].
Т	_, .	1
I Г*ОЧ	Т* Ч1П I 17 —I— 1 1 Ф Н Т* ~~ —
J	V
тг/2
18.
о
тг/2	д..!
19. cosn ж sin mx dx = ^J —^г	^-ту	гут^ + i
0	i=0 {п-]).{т п)..
- n - 2j)\\
[A; = min (ra, n), в = 2 при т-те = 41 + 2>0; 9 = 1 при т-те = 21 + 1>0;
^ = 0 при 771 — п = 41 ^ 0 или т — те < 0].
тт/2
Г	1
20. cosn ж sin nx dx =
J
о
2n+1 ^^ 7
i=1

326
Гл.2. Определенные интегралы
[2.5.12
тг/2
21.
22.
23.
24.
25.
26.
Г cosu~1xsin
тг/2
/
cos17 a;cos(i/ + l)xdx = 0
/
Г	п!	Г 1
cosn х cos тж с/ж = -.	г-тт	г-т { /
J	(п-т)!!(п + т)!!\тг/2,
.>0; |аг8&|<тг].
[Rei/>0].
о
тт/2
п — гаг = 1, 3, 5, . . . ,
га- m = 0, 2, 4, ...
= В
га!
(т — га) (гаг — га + 2) . . . (?га + га)
те < га; В = 0, если га — п четно; В = ±1, если га — п = 4/ ± 1, 1 = 0, 1, 2, ...].
тт/2
[ sin/i~1a;cosI/a;da; = - В (-, -)
J	A \ A A /
о
тг/2
тга sina7r
[RejLi, Re i/ > 0].
[a > 0].
т/2
28.
29. sin"
cos (/i + 1/)ж J	2 [ cosec (дтг/2)
dx=
B(Ai,
Re i/ > 0; Re/z > -
Re i/ > 0; Re/x > -
30.
31.
32.
33.
35.
36.
sin пж cos шж
ax = 0
= 7Г
[ slnm жсо8п x dx =
J
[?г ^ f?i или те > тег; га + n = 2k\.
[n > га; га + 7i = 2A; - 1, fc = 1, 2, 3, . . . ].
[m + n = 0,2,4, ...].
dx=
34.
sin2rax
cosi
2k -
=
a_i J sin bx 1
\ cos bx J
, {ц-Ь
fsinF7r/2) 1
\cosFtt/2) J
[Re/j, > 0; | arg6| < тг].

2.5.13]	2.5. Тригонометрические функции	327
/
п f sin Bга + 1)ж 1 . _ Г . п Г sin Bгм +
na^ l	; }dx = 2 sinn a^ l
/
»_ Г • п f sin Bга + 1)ж 1 . _	Г	. п Г sin Bгм + 1)ж 1 .
37.	sinna^ l ; }dx = 2	sinn a^ l	; ^rfx [см. 2.5.12.13-16].
J [ cos2ina? J	J	I coszfTiic J
о	о
38.	sln2n ж cos 2mx dx = -—^	(	J	\n>m].
о
39.	=0	[n < то].
7T/2
Г n fslnma?! . r / xm+ni	Г n fsinmjcl .
40.	cos ж	}dx= 1=f(™1)	cos ж	> dx	см. 2.5.12.19-25 .
J	[ cos mx J	J	[ cos mx J
о	о
At 1 n	» ,	(-1)П81П67Г	/	6 + П	6 + П
41.	j cos ^eoskccte = 2n(n + M 2F1I -n,	—; 1	—; -1
(	; 1;
0	[6^0, ±1, ±2, ...].
7T
cosn x cos mx dx = 0	[ra + n = 1, 3, 5, . . . или то > n, m + n = 2, 4, 6, . . . ].
42
0
43.
(m + n)(Z — 1)!
лл Г • m	n , [l + (^l)m][l + (^l)n] D/m|l
44.	sin ж cos ж dx =	—^^BI
J	2
a
2.5.13. Интегралы от xa s!nM ax cos17 bx.
ж/4
sin'* ж .	7г 1 .//x + l\
ж	т:^с1ж =	/3 ——	Re/x>-l.
cos^1»	4/i 2/iM\ 2 /
0
тг/4
Г slnn x
2. жЖ
J
cosn+2 ж
4+
2 4
тг/4	тг/4
Г о sin ж In 2 тг тг	Г	о sin ж , 1 ,	,. , ,. „ _ .
3.	ж 	— dx =	1	.	4. ж 	— Жс = - 1	п2	1	h G .
J cos3 ж 2 4 16	J	cos4 ж	3 V 4 216
о	о
тг/4
,	ж dx
5.
о
тг/2
6.
tt/2
[^!	тг fl
О
тт/2
Г . 2п	,	1 Г	2Bп)!!
8. ж sin ~ — ~ л~ —	| —
В. ж sir
о

328	Гл.2. Определенные интегралы	[2.5.13
о
тг/2	тг/2
Г	2 COS Ж 7Г2 Г з COS Ж ЗТГ 7Г3
10. ж —ц—dx = 4G	. 11. ж —s—с!ж = —In 2	.
J	sin ж 4 J sin*5 ж 2 16
о	о
12. ж cosn ж sin ж с!ж =	г—;	г \
J	(га + 1)!!(га + 1)\тг/2, га = 1, 3, 5, . . .
7г/2
о
тг/2
~м~
Г г cos ж ] м-1 Г sin ж 1 м тг
13. ж .	^	i	с1ж = ±^	—	0<±Re/x<l.
J	I Sin Ж J	[COS Ж]	2/iCOS (/А7Г/2)
тг/2	/
1/(	Г	. n	2m-l ,	B(n/2, Ш + 1/2)	П-1	Г	,n^2	2m^l ,
14. ж sin ж cos	x dx = —\1	Lv^ H	ж sin ж cos	ж dx
J	2Bm + n-l) 2m + n-l J
о	о
[m, n = 1, 2, 3, ... ].
15.
r(y) ^	f/
2-+1 l ; Г I/ + 6 + 1 )/2 Г((iz-fe + l /2
0
[Re i/ > 0; -1 - Re i/ < Re 6 < 1 + Rei/].
16. Ж81пм	^Г(	)/1
J
о
/x L M/2 + 1 J
xn l^(^l)n B[(n
2	B[(п-
U
7Г
Г ein т>
18.
cos ж
о
2n + m- 1) \ 2 '
1Q Г • 2n-l	rn j
J
о
7Г
I	"^	I	• 2п —1	тге —2 i	г	-1 л о
Н	ж sin ж cos ж аж	?n, n = 1, 2, 3, ...
2п + m — 1 J
о
оо
ж" slnn аж slnm 6ж с!ж = /^'т,
20
о
fe=o
E
Ь 7 + а/2, Л - 7 + A + а)/2; 2Л + 1/2; t) + 2Л - 1} +
^^^	лГА + 7 + а/2 1
¦B7- Ш1Г1а^а{п-2кТаТ\	г/ 7Ч/ при 0 < t < 1,

2.5.18]
2.5. Тригонометрические функции
329
AM(t) = •
(l + a)/2; 27 + l/2; Г1)
xb^a(m~2iyar\ * +
при t > 1,
+
A - 7 + A - a)/2, 7 - A + A - a)/2, A + 7 - a/2
A+ 7 +a/2
Л =
-> 7 =
-; a, 6 > 0; —m —¦ n < Re a < 0 (—«г-—те < Re a < 1,
4 ' '	4
если одно из чисел m, n нечетно или если m, ?г нечетны и a ^ 6); тп, п = 1, 2, 3, . . . ;
.Li i,_ a + b
11 тг . . .
1_\ = -тт(а, 6);
z
/2, 1 		Г1	е-ъ ]	г2, 1 	 /л	fi ч п 1,
О		 		I ""^ ^"J 5	0			L "^	J5
[Ь Ф 2«],
1 a . 2a + 6 6 . |4a2 - б2
'i = "Г in —	77 + "Г in 	—
I^i = a In 2 [6 = 2a];
1-2,1	7Г
1^2 = ~ fl2 [6 ^ 2a]; J^2 = — mln (a, 6);
a. — 6 аб , о, + 6
	In
2 |a-6| L ^
/!'22 = a2 In 2 [b = a]; /!'32 = - ?ra2C6 - a) [a ^ 6],
а]; /03' Х = i In
а, 6^ За];
;a], J!.5!1 = - Ca - b) [a ^6^ 3a], 7^=0 [6 ^ 3a];
, 1
kfri
/ i\
/__^ = — а [6 = am, m ^ n, m = 1, 2, 3, ...
оо
21. f Z slnn ax cosm 6ж da; = J«'m,
= V 7Г 2
x[n/2] + k_
ife!(n-A;)!
x — m — n —a
[(m/2)!]
{l-a)/2\'	(m-202fe2'

330
Гл. 2. Определенные интегралы
[2.5.13
Bkl{t) = a~a(n - 2к)~аГ
х {2Fi(A + а/2, Л + A + а)/2; 2Л + 1/2; *) - 1 + 2Л} при 0 < t < 1,
Л+A-а)/2
+ BA-l)Dt)A[&(m~2l)]~aF
«/2, A + а)/2 - Л; 1/2; Г1) +
при t > 1,
^
Л =
; а, 6 > 0; —n < Re а < 0 (—n < Re а < 1, если m шли п нечетно);
т, и = 1, 2, 3, . . . ;
2а],
J^1 = О [6>2а]; Jq'2 = ^ [а < 26], Jq>2 = -k [a = 26],
4	8
Tl,2 Ж г	о,п	j2,2	2а — 6	2,2	^Л г /,
Jo :=: — [а > 2oj; J_]_ = 	ж [а ^ о], J—1 = 	 [а ^ I
Jo 
73,1
16
тЗ, 1	/l	г
.], 4Л = ~Т^ [6 = За], 4Д=0 [6>3а];
9а2 -
--In
(а + &K(За-&)
а, 6^ За],
/i'j1 = ^^ а [6 = а], Ji'i1 = - (In 3 - 2 In 2)а [6 = За];
3, 1	^ /o 2 i 2ч
= ^ (За - Ь )
3,1
=
' 2 = -
Jl'2 =0 [6 ^ За]; J*>z = - [26 < о],
/03'2 = 4тг [26 = о], J03'2 = ^- [а<26<3а],
4' =^^ [26 = За], Jo' =^ [26>3а];
32	8
31n3
16
9a2 -
a2 - 462
a, 26 ф За],
J\2= 31n3 + 21n2Q [26 = а]> J!'12 = 5(ln3^1n2)a [26 = За];
^'22 = ^ (За2 - 262) [26 ^ a], j!'22 = ?- [6а2 + (За - 26J] [а ^С 26 <С За],

2.5.14]	2.5. Тригонометрические функции	331
о
J^2 = — тга2 [26 ^ За],
0
72i,i Bj - 3)!! тга
[(ап-Ь)/Bа)]
-^a^ [b = a- k = 1,2,3].
22.
V 2 ',
о
[д > 1, i/ > 0; д = 2fc/BZ + 1), i/ = 2m/Bn + 1)].
23. ха 1 cosn ax cosm bx dx = л/ж
о
X
k=O
k\(n-k)\ 2^ l\(m-l)\Ckl{t)
4
(п -
t =
(m -
f' ^2~; 2' *"/ ПРИ t > lj
[a, b > О; О < Re а < 1; га, тг = 1, 2, 3, . . . , кроме случая, когда тип четны одновременно].
ж"
2.5.14. Интегралы от 2 —- s!nM аж cos1' 6ж.
со
Г жа^
1. —	 slnn аж sin bx dx = la ь	\a = 1, 2; a, 6, Re z > 01,
J ж2 + z2
о
/_ -^\Aj —1
C1^6	)	6	[fc = l, 2, ...],
S!l	aZ€	Щ — li Zi • • -\i

332	Гл.2. Определенные интегралы	[2.5.14
Г2к	( —1) 7Г azu	~2az\2k Л	~2azi	Т2к	(~1) Я" ,.	~2az\2k -.i
*2,Bfc-i)a = 22fc+1 e 1A-e ) -1-е J, h,2ka = 22fc+1 [A-е ) - 1J,
-4feaz ,2fc
б	Sh CLZ.
f ж
2. —	 slnn ax cos Ьж dx = J™ ь	[a = 1, 2; a, 6, Re z > 0].
J ж^ + z2
r2fc-l	_ (-1) 7Г r/-,	^2ezx2fc^l -.i	r, _	1
J2,Bfc^l)a^	^fe	 LI1 - 6	i	- Х]	[Л - 1, J, ...j,
о
) Ж \p2az(
(-1) 7Г	-2агч2Л-1 -2аг	г, _ - „	i
	уп	 V1 ~ e	J	6	L« - ¦•¦> ^> •••]»
[« — 1, J, . . .J,
j2fc _
-2az	j2k _ (^^^ -4feaz ,2fc
3. —г	 cosn ax sin 6ж dx = Ia ь	[a, 6, Re г > 0],
} хл + zl
0
^ Ё (") ['аг Ei ^2laz^ - e"laz Ei i-
i2,(n+2)a
/^	-oz/-| | —2az\n	r	^ r/i , ~2az\n -• i
M«+4« = ^Ie	(! + e	) ' 72,"" = ^fiKHe	) -1],
/2, (n-i)« = ^ ch аг[A + e-2az)n-1 - 1], /2,3no = I eaz chn аг [n = 1, 2, 3, ... ].
Г i
4. —	 cosn ax cos bx dx = h	[a, 6, Re 2; > 01,
J Ж2 + Z2
0
/^	—-2azf-\ , -2az\n	j-	^	—az/-i , —2az\n
(^+i)« = ^TT^e A + e )' I(n+i)a = ^TT^e (l + e ),
— 2az\n , -2az -,i
) +e 1]
[n = 1, 2, 3, ... ].
oo
[x cosn ax ( sin anx 1 . тг , ,*! п Г cos any 1 n-n-i с
5.	—	— ^	&=--!/ cos ay< . ^}-2 ёж
J x1 — у2 [созатгж]	2	[ sin any J
о
те = 1, 2, 3, . . .; a > 0; 8 = j
f 1 sin bx .	7Г sh 6z
6.	-^-j	 ^^	dx = — —		0 < b < a; Rez> 0 .
J x2 + z2 8ш1аж	2z sh az
о
7 ±1 ¦ и	ик
_	Ж	Sin 0Ж _	7Г „U-iSnOZ
7.	^	о 	dx = ^^ z	—		0 < 6 < a; Re z > 0 .
J ж2 + z2 cosax	2	ch az
о

2.5.15]	2.5. Тригонометрические функции	333
х cos bx . ж ch bz
	dx =
ж2 + z2 sin аж	2 shaz
8. —		dx = - —		0 < b < a; Re z > 0 .
0
1 cos bx	ж
ж2 + z2 соваж	2z ch az
9. | —		 dx =		[0 < b < a; Re z > 0].
о
f 1 sin 6ж .	7Г sin2Ft//2)
10.	—	dx =	.l У1 J	0<6<a;y>0.
J x1 — у1 зшаж	у sin ay
0
00 -1
Г x	sin 6ж .	.
11.	—	 	dx = 0	0<6<a;y>0.
J xA ~ yA есшаж
о
2.5.15. Интегралы от xa ||sinM а^ж cos17 bkX.
k
Обозначение: 8 = < >.
A^п)/2 f] sin ЬЛж daj = 0	6fc > 0; 60
7
7	7г	г	i
2. ж^п^1[]81п&й;жс1ж = ^f]6fc	6fe >0; b0 > ^] 6 J .
0
k=Q	fc=0
3. xa sin ax sin bx sin ex dx = Ia
[—3 < Re a < 1; a ^ 6 ^ с ^ О, исключая a = 6 ^ с = 0],
sin (^) [-(a + 6 + c)"a + (a - b + c)"a + (a + b - Cya - e\a - b - с\~а]
[а ф 0, —1, —2; e = sgn (a — b — c), e = 0 при о = 6 + с],
a + 6-c,	. a - 6 - с
	in (a + о — c) H	in a — о — с
f {a + b cf {a b + cf + e(a b cJ
/_2 = — [(a + 6 + cf - (a + 6 - cf - (a - b + cf + e(a - 6 - cJ].
oo
a —1 FT	f-f	I Sin cX
4. ж II sin a7-ж I I со8 0^ж< . > dx =
cos 4 ж
[A ^ - a - m)/2
1 3	3 1.	I ^i	^m^i
' *¦"' 2' 2' ""¦' 2' C2' '"' C2 ' C2' *"'
2 ' 2 ' 2' *¦"' 2' 2' ""¦' 2' C2
TO	fl
[ai, . . . , am, 6i, . . . , 6n, С > 0; С > ai + • • • + am + 6i + . . . + bn] —m — <S < Rea < 1].

334
Гл. 2. Определенные интегралы
[2.5.16
5. ж'
о
— т+21
sin а,-ж I I cosbkXi	> dx
11	1 cos ?х I
= 0
i, . . . , am, 6i, . . . , 6n, С > 0; С > «l + • • • + «то + Ь\ + . . . + bn;
oo
6. ж^^1 О sin ajX О cos bkX sin ^x dx = — жаг . . . пщ^1
7
7 1 П
. — FT
7. I —т I I cosPfe пкХ sin bx sin ж dx = —
„ ж2 А А	2
о
oi, . . . , am, 6i, . . . , bni С > 0; С
7Г
k=l
b > ^ ^ а^р^; а^, pfc > 0 .
k=i	J
2.5.16. Интегралы, содержащие (а
Обозначение: S = < >.
a
1. (cos ж — cos aI7™1 cos bx dx = у7г/2 sln17™1^2 ar(i/)P6_1T2l/(cosa)
2.
3.
4.
5.
1/2)ж ,	ж
dx =
^^ dx = —^ Pn
у cos ж — cos a	у 2
[b, Rei/ > 0; 0 < а < тг].
[a > 0].
т/2
dx
1	b
arccos —
а2 — b2
-In
b + x/b2 - a2
= I/a
[6 = а].
1 + sin x J 1 + cos x 2
о	о
тг/2
1 — a cos 2пж	m	.	тт
—- cos x cos тж ож =
тг/2	тг/2
sin ж е!ж Г cos x dx тг
7.
тт/2
Г	cosn ж sin nx sin 2ж , тг
8.	 dx = — , .
J	1^2acos2x + a2	4a I \ 2
о
2т+2
- 2
( , J а
\кп/
+ 2^т^ т
< 1; п = 1, 2, 3, . . . ].
tt/2
9.
1 — 2асоз2ж + а2
жсоз/Зж _ (^1)теттA^аJта^1 f 1
; /3 < l-2n .

2.5.16]
2.5. Тригонометрические функции
335
тг/2
dx
1
(а+ 6cos жJ а2 — Ъ2 \\/а2 — b2	a a
1
Ь2~а2\а Jb2 - a2
т/2
10.
11.
12.
ж/2
Г sln2m x cosM x cos/Зж .
13.	т-	—^-dx =
b Ь
- arccos
\а>
In-
[b > a > 0].
2п-1
|а| < 1; /3 < 2п
(-1)татгA - а)
2т\ Bп - k^ I - 2
= 2п - 2т - /z - 2; \а\ < 1; /i > -1].
"
14.
15.
16.
17.
19.
21.
J
0
тг/2
J
0
тт/2
1
Ж
1
-COSS
— sin ж
— cos ж
тг
2
Ж COS Ж «*Ж	71
1 + 2а sin ж + а2 2i
т/2
0
тт/2
о
тг/2
ж б!ж
1 + sin ж
ж cos ж с!ж
1 + sin ж
1 — cos ж
т/2
= 1п2. 18.
х dx	ж
=	In 2.
1 + cos ж 2
тг/2
20.
1
I ± cos ж
[(!::>:}]¦
, cos nx .	тг
22.	dx =
а + b cos ж
/a2 - б2
— б2 —
[a > 6 > 0].
23.
cos a — cos ж
аж =
[а/0],
24.
= —7ГП
sinn ж
: COS Ж
[п = 2, 3, 4, ... ].

336
Гл. 2. Определенные интегралы
[2.5.16
25.
а + Ъ cos х
Ъ2^{ 4Ъ2	I 2
n + 1-21
б2
Л = тгЬ^2(а - V'а2 - Ь2 ) при п = 2k + 2, Л = -In	 при п = 2k + 1, 0 < |6| ^ а .
Ъ а — Ъ
26.
sin nx sin ж dx тг ±n_i
2
1 — 2а cos х + а2 2
27.
28.
cos nx cos ж
(a +
Ж ±п —1 ^ +1
Ж ~ 2~а	|а2 -1|
_ тг(а2^62)^/2	/	а
" (l-M)n	Ч^^
a>
29.
Я Ж :=:::
fe=O
772 + fl — 1
30.
31.
32.
33.
34.
A - 2acosx + a2)n+1
dx =
2п\ атетг
71 / 1 - аг
7Г
A — 2a cos ж + a )n cos тпж dx = 0
п\ ( п — к
к ) V 772 + к
cos nx dx	жа
1 — 2a cos ж + a2 11 — a2
sin nx — a sin (n + 1)ж
1 — 2a cos ж + a2
dx = 0
> 1
: = 2n + m - 2, |o| < 1
1 + а2
[Т1 < 77lJ.
[п ^ 77l].
[{!::::}]¦
35.
dx
(a + 6 cos жJ (a2^62K/2
36.
37.
+ а2)п II — а2 2те^1 I 1 1^1 А;
38.
(a
71 = 771 — 1
71 = 771

2.5.16]
2.5. Тригонометрические функции
337
2п+1—6
Г	cos ж	J sm2nx 1
J 1 + (a + 6 sin жJ \ cos Bn + 1)ж J
о
г /	( e\ \ \	I—i г /1	/	"
= T^sln I 2n+ ^ > J arctg J- tg I - arccos W —
L = a2 _ fe2 _ i + y/(«2 ^52^ XJ +4a2. о > 0; n = 1, 2, 3, . . . 1.
7T
81пжз1пржс1ж	тгар"" c""p
40.
41.
42.
(a2 -
[0 < a ^ c; a2 < 6c; p = 1, 2, . . . ].
(a
M x^2 vVtt2 — ft2
[a > |6|; Re и > 0].
(a
Bn - 2A; - l)!!Bife - 1)!! /a
43.
. sin(n + 1/2)ж	тг , ,
44. I ,	' ; dx = -^ Pn(cosa)
a — b
1 + M 2
; a
2 ' 2 '
45.
46.
47.
48.
49.
50.
51.
i/cos a — cos ж
dx	2
:K
=Ь b cos ж
^ж^= 1 р2/Гь
/3 — cos ж 4vtt \ 4 y
[a > |6| > 0].
[|a| < 1; Re// > 0].
[a > 0].
[a > 6 > 0].
dx
V 1 dz 2a cos ж + а
sin ж с?ж
y/l dz 2a cos ж + a2
= 2K(a)
2
[{!:!;:}]¦
— 2a cos ж •
= = - [K(a) - E(a)]
- a2 a
+ 1
(a - y/a2 - b2 )
aibcosa; 2%/а2 - Ь2
[a > b > 0].
22 А. П. Прудников и др., т. 1

338
Гл. 2. Определенные интегралы
[2.5.16
52.
53.
55.
56.
57.
ж sin ж dx тг а + \/а2 — Ъ2
= — in -
а + бсоэж b	2(a — b)
ж — sin ж .	ж cos ж
	^ж = 2. 54.
1 — cos ж	I I + sin ж
Ж Sin Ж б?Ж	7Г
1 — 2а cos ж + а2 а
± )
(а + 6 cos ж)
тг / 1
¦ аж = —
6 \а - 6 Ja2 - Ъ2
ж е/ж
1 — cos ж
= 4тг1п2.
58. ж
о
2тг
(а + b cos ж)'
, 2тг	2(а - Ь)
¦ dx = —- In ¦ v 7
а + л/а2 - Ъ2
59.
о
2тг
61.
dx
2тг
60
fe)!
J
о
2тг
(к\J(п - к)\
A -
2na
63.
1 — 2а cos ж + а2
ж =
[|а
о
2тг
64.
о
2тг
= 0
65.
о
2тг
cos Bn + 1)ж J a + b sin ж
sin Bn + 1)ж 1 dx	(-1)п+52тг(а - л/а2 - b2 Jn+s
66.
о
2тг
cos 2пж I a + 6 sin ж
sin (пж/2) sin (ж/2) 1
/а2 - b2
dx
cos (пж/2) cos (ж/2) j 1 — 2a cos ж + a^
= 0
67.
Ьо.
sin(n-l/2)a;sin(aj/2) . тгат
dx =
[а > \Ь\ > 0].
[{!::::}]¦
[0 < |Ь| < о].
[0 < |6| < о].
«| > 1.
. = 0, ±1, ±2, ... ].
1 — 2a cos ж + a2
1 + a
[m = n — 1 при |a| < 1; m = — n при |a| > 1; n = 1, 2, 3, . . . ].
cos (га — 1/2)ж cos (ж/2)	тга"
аж :=:::
1 — 2a cos ж + a2
1 - a|
= n ¦— 1 при |a| < 1; 77i = — n при |a| > 1; n = 1, 2, 3, . . . ].

2.5.16]
2.5. Тригонометрические функции
339
69.
с + cos ж	4 ,
- dx =	,	К
(а — Ь cos жK/2
b\/a + Ъ
26
а + 6с
а + 6 I a — b
Е
26
а + 6
, ж sin ж . . 2тг . а + л/а2 — Ь2
70. 	dx = ±—In ¦
а ±6 cos ж	6	2(а ± 6)
[а > b > 0].
[а > |6| > 0].
о
2тг
71. | ——¦	dx =
а± о cos ж
2тг
/а2 - б2
п[(а + ^а2 - б2 )п - (а - Va2 - б2 )n] In
^л i х cos пж .	2тг
72. ——	dx =
о
2тг
а ± 6 cos ж	^а2 _ 52
а - л/а2 - б2
/а + 6 + v а - 6
[а > |6| > 0].
[а > |6| > 0].
73.
ж sin ж da?	2тг
1 — 2а cos ж + а2 а
о
2тг
74.
1 — 2а cos ж + а2 1 — а2
ы	±1
п —1 _^fc	д.
±1\ . V^ а — а
п — к
_„ I _i	81ПЖ	7Г
75. ж —г^	-— dx =
2л/а2 - б2
76.
со
77.	Jx-S
о
схэ
78.	[ж
79.
= 0
. тг 1 — а п
тг 1 + о-2о[ч+1
— 2а cos ж + а2	2 A — а2)A — а)
- 2 _
[Ь]
2 A^
80.
81.
sin (mx/2) dx
= 0.
! 81П2Ж 1
[|а|<|6|].
[0 < а < 1; 6/0, 1, 2, .. . ].
[а > 1; 6/0, 1, 2, ... ].
L-,^ Г 8111(^/2I
4а \ cos (/хтг/2) /
82.
х И +sgn(a2 -1)
	f tga 1
- а2)те+1 [sin ж/
1 + a
dx =
211-a2
1
22*

340
Гл. 2. Определенные интегралы
[2.5.17
83. | ж
84.
tga;
a + bcoskx	2\fa2 — b2
= 0
[к = 2, 4; \a\ >
[к = 2, 4; \a\ <
85.	¦—- dж =
1 — 2a cos ж + a2
1 - а
2m-l 2m , ,k
86.
A - 2a cos ж + а2)"
1 + а
da; =
-E
(-1)* ГГ m + 1/2 1 4kak
A;! [1/2 + m, ^ jfej A + а
тгп!
87.
88.
89.
90.
2«+1Bm + n-
x Bm + 2k - 1)!! 2Fi ( m + n ~~ к + 3/2, i/;
7Г	1 + aeTcz
.-k)\
4a
1 — 2a cos еж + a2 ж2
- a2) 1 -
—
dx
Trasin cy
1 — 2a cos ex + а2 ж2 — |/2	|/|1 — a21A — 2a cos cy + a2)
[c, 2/ > 0; H ^ 1].
cos bx
dx
- 2a cos еж + а2 ж2 + z
- a2) 1 -
6, c, ReO 0;
cos 6ж
dж
1 — 2a cos ex + а2 ж2 — |/
- a21 sin % + 2a±F+c)/c sin cy
1 — 2a cos cy + a2
91.
92.
e h'c
ж sin 6ж	dx	ж е z
.-2acoEcx + a2 x2 + z2 ~ 2 A - ae^cz)(l - aecz)
b, с, у > 0;
c, 6, Rez > 0;
ж sin 6ж	dж
7Г	a±6//c — cos by
1 — 2асозсж + а2 ж2 — у2	2|1 — a2| 1 — 2a cos cy + a2 \a
, 1 — cos аж . sin ay
93.	—;	-dx = 7T
1.
x(x-y)	у
— oo
2.5.17. Интегралы, содержащие (a cos ж + 6sln ж + c)p.
In
cos ж + tg a sin ж cos ж	tg a
b,c,y>O;t a,
[a > 0; Imy = 0].
[a > 0].

2.5.17]
2.5. Тригонометрические функции
341
тг/2
2.
cos ж + tg a sin ж sin ж
dx /тг . .
= т + fl In
т/4
Г Л cos ж + В sin ж	Л6 — Ва (а + 6) Ла + ВЪ ж
' J acosx + bsmx Ж = 2(а2 + б2) ° 2а2 + а2 + Ъ2 ~4
о
тт/4
cos х — sin х	тг	G
ж	;	аж = -7 2
J cos ж + sin ж	4
о
тг/4
[а > 0].
[Ъф-а].
4.
2
т/4
5.
6.
8.
0
тг/2
9. f ж
cos ж + sin ж I cos ж
8
(тг/4 — ж) da?
cos ж — sin ж cos ж
тг/4
ж tg ж	dsc тг тг
=
тг тг .
=	In 2
4 8
In 2
cos x + sin ж cos ж 4 8
о
тг/4
ж dx
1	а-
In —
а2 + б2
4 (а2 + 62)(а-
тг/2
[а, 6 > 0].
cos ж =р sin ж

cos ж ± sin ж
1 о
10.
(cos ж ± sin ж) sin ж 4
т/2
11.
х dx
(a cos ж + Ъ sin ж) vsln2ic
/ I——
arctg I J -у
- arctg I \/ — - 1 I - arctg -
[a, b > 0].
7Г/2
12.
13.
x dx
о
tt/2
о
тг/2
(sin ж + cos ж) vsin 2ж
x dx	1/6 тга
(a cos x + 6 sin жJ а2 + б2 \ а 26
14.
0
2tt
(a cos ж + bsl
- dx =
[а, 6 > 0].
[а, 6, Re/x, Re i/ > 0].
15. (a cos ж + 6 sin x)n dx =
0
2тг
16.
dx
2	(n)!!
2тг sgn a
52
17.
18. I x
о
= 0.
-n-l/2 • n
sinn ж(соз ax + sin аж) dx =
тгл/2 iA
Bn-l)H^;
-l)*B)(n-2fc + a)
n-1/2
[a > n].

342
Гл. 2. Определенные интегралы
[2.5.18
2.5.18. Интегралы, содержащие (acos2 ж + 6sln2 ж + с) п.
тт/4
1.
2.
ж sin ж dx
(a2 cos2 ж + Ъ2 sin2 ж)\/cos 2ж
ТГ .	/ ТГ arCCOS 6 \	ТГ .	/ ТГ
= — In cos	1	In sin I —
2 J
¦ In sin I	h
тт/2
dx
(a2 cos2 ж + b2 sin2 ж)п
= /n
ж ( 5	3	3	5
т/2
3.
4.
6.
7.
8.
9.
10.
11.
12.
о
7Г/2
(а2 cos2 ж + b2 sin2 ж)те+! V п У Ba6Jn+1
- с!ж =	B(/i, v)
(a2 cos2 ж + b2 sin2
т/2
cosp+2n ж cos рж dx
(a2 cos2 ж + b2 sin2 ж)те+1
2n~ k\ fp + k - 1
тг/2
с!ж
тг . а + b
In ¦
a2 cos2 ж + Ь2 sin2 ж а2 — б2 26
т/2
COS /1Ж COSF Ж
о— dx =
о
тг/2
a2 cos2 ж + b2 sin2 ж	2а(а + 6)**
sin их cosM ж sin ж
a2 cos2 ж + &2 sin2 ж	2Ь(а +
т/2
in •
bk
тг/2
ж sin ж с!ж
а2 cos2 ж — b2 sin2 ж	Ьх/а2
г/2
о
тг/2
1 - b2 sin2 ж	2л/Г
A cos2 х + В sin2 ж
(а2 cos2 ж + &2 sin2 жJ
4ab\ a2 + Ъ2)
arccos bЛ
2 J
a2 + 62 = 1].
[a, b > 0],
[а, Ъ > 0].
[а, 6, RejLi, Ret/ > 0].
[а, Ь > 0; р > -2п- 1].
[а, 6 > 0].
[а, b > 0; /i > -1].
[а, 6, /i > 0].
[а, 6 > 0; А; = 1 или 2].
[а, 6 > 0].
[а, Ь > 0].

2.5.18]
2.5. Тригонометрические функции
343
тг/2
13. I Ж
ТГ
¦ ах = —-
-1
О
тг/2
A + 6 sin2 жJ	26 1 + 6
14.
15.
dx =
о
тг/2
О
тт/2
(a2 cos2 ж + б2 sin2 жJ
ж cos3 ж dx
sin ж(а2 cos2 ж + б2 sin2 жJ
2а62(а
4а3(а
,	2 cos ж A — а2 + sin2 х) ,	ж2 4 ^л sin [BА; + 1) arcsin а]
1Ь.	ж - - - — ах =	- — + у -г— ¦ ттт
J	(а2 — cos2 жJ	4а2 а ^^ Bk + IJ
о	fc=0
7Г
, ж sin ж dx	ж	b
17. I ——	— = -р=- arctg у -
а + 6 cos2 ж ^*	у -
18.
19.
20.
ж dx
a2 cos2 ж + б2 sin2 ж 2а6
ж з!п2ж dx
2тг . а + Ь
In ¦
а2 cos2 ж + б2 sin2 ж а2 — Ь2 2а
[6 > -1].
[а, Ь > 0].
[а, Ь > 0].
[а, Ь > 0].
> -Ь> 0].
[а, Ь > 0].
[а, Ь > 0].
21.
ж с!ж
а2 - cos2 ж
- 1
о
22.	=0
ж cos ж dx
23.
24.
25.
26.
. sin [BА; + 1) arccos а]
а1 - cos^ ж
/TZr^fo
¦dx = тг1п[4A-а2)]
= 2тг In [2A - а2 + ал/а2 - 1)]
! -1 ^а
ж2з1п2ж .	2
¦ аж = тг
(а2 — cos2 жJ
а(а2 -
о- I 2 1 — а2 + Bа2 — 1) sin2 ж
27. | ж^	г^	^^	dx =
28.
29. ж
о
(а2 — cos2 жJ
= 2тг1п[2A-а2 + \а
2 cos ж (а2 — 1 — sin2 ж)
(а2 — cos2 жJ
тг . 1 — а
тг .
^^ 	 1П
1П
а 1 + а
И > Il-
Ilia > 1].

344
Гл. 2. Определенные интегралы
[2.5.19
, 1 sin ж cos 2mx cosn х . ж Ъ2
30.	_ , о dx =
ж a2 cos2 х + б2 sin2 х	2а (а + ЪJ
[а, 6 > 0; тг = 2га или 2т — 1].
31.
с/ж
a2 cos2 ж + b2 sin2 ж cos 2ж
[а, 6 > 0],
/i'° =
32.
2аЪ Ь2 + а2 '
dx
rl, 1 _ rl,2 _
2а а2 + б2 '
26 а2 + б2 "
b a
2 \
ж2 + z2 а2 cos2 ж + б2 sin2 ж 4z(l?2 sh2 2 — а2 ch2 z) \a b $h2z )
[a, b,Rez > 0; thz ^ a/6].
33.
34.
(ж2 + z2)(a2 cos2 ж + b2 sin2 ж) ~ 2F2 sh2 z - a2 ch2 z) \b + a
(a2 cos2 ж + b2 sin2 ж)т ж
= /,
к, I
[а, b, Rez > 0].
[а, Ъ > 0],
ri,o _ ,1,-1
Ji — Ji
r3,-l _
1-2, 0 ______ 1-3, 0
26(а + 6)'
1, 2
2а(а-
rl,0 _ rl,-l _ ^ Q + &	тЗ,0 _ 1-3,-1 _
4ab3'
i2 — J2 —
16
r3,o ______ ,3,-i ______ n_ 3a + b	i5i _ i. 2 ______ jtt_
3 " 3 " 16 a365 ' 3 " 3 ~ 16
a +36
16
16 a5
i,o _ ?_
4' ^32
5,o _ ,5,-1 _____ тг
4 ~ 4 ~ 32
5a2
3;0 _ ,3,-1 _
' 4' ~ 4> ^
1,1 _ i,2 _ ^ a^
' 4 ~ 4 ^32
i>3 _- ri>4 _
14 — Ч
гЗ
а765
тг а2 + 562 г3,1 _ з, 2 _ тг а2 + 62
32
= IT = —
4 32 аЧ5
1 A — cos ж) cos ж а*ж
ж (а2 cos2 ж + б2 sin2 x)m sin ж
г° - JL г2 _ JL 1
1	О L '	1	О	I L '
о тг a2 + 62
2a a+ 6'
i-U "
io — —
г2 ______ ТГ	ж0 ______ ТГ
2 ~ 4а36' 3 ~ 16
2 _ тг
4 ~ 32
тг а2 + 362
16
32
4 _ тг а2 + 562
"' /4^32
[a, b > 0],
2.5.19. Интегралы, содержащие (acos ж + bsin ж + с) / .
1.
ЬШ X \ f ^ Cf ?H fbf^G.*" /V3	riim,^ ,
a cos2 ж — sin2 ж
2tga
In
тг - 2a
\а > 0].

2.5.19]
2.5. Тригонометрические функции
345
2.
3.
4.
ж sin ж dx
cos2 х у tg2 а cos2 x — sin2 x 4 cos а
A - cos а)
х sin ж d ж
= =
cos2 жг/sin2 а — sin2 ж ^ cos а
тг	о а
sin -
[а > 0].
[0 < а < тг/2].
ж sin ж с!ж
A — sin2 b sin2 ж) у sin2 а — sin2 ж
/о	L Г-t	• 2l • 2 \-1 1
= B cos 6 v 1 — sin 6 sin а) тг In
-1 1 COS 6+ лЛ - Sin 6 Sin a
тг In
2 cos a cos2 F/2)
тт/2
ж cos ж с!ж	тг
/
у si
sin ж — sin а
тг/4
о.
7.
8.
тг/2
Г 2 X
cos х у cos2 ж + k2 sin2 j
+ sin2 x
= 2V1 - к2 - 2E(ife) + K(ife)
— Дг2 sin2 x
¦к/2
10.
тг/2
12.
=г с!ж =
V1 — fe2 sin2 ж	k
Г/2
dx =
л/1 - ^2 cos2 ж	к
dx = i [7Г _ 2E(ife)]
к2 L	l л
[а > 0 .
< тг/2].
[0 < к < 1].
[0 < к < 1].
0 < к < 1; Л' = VI-
[0 ^C	к	< 1].
[0 <	к	< 1].
[o <	fc	< i].
L	J

346	Гл.2. Определенные интегралы	[2.5.19
. / sin ж 1 2 /	2 f sin ж 1 2 \	dx
lo. <	> 1 — а
о
= 2(kry2S(sin 2/3^1 - A;'2 sin2 /3 )~1/2 [| - Ж(к)ЕЦЗ, k')-E(k)F(P, kf) + K(fc)F(/3, A;')]
а2 = 1 - kf2 sin2 $ }	, у	 г Г 1
^ 0 < А; < 1; к' = VI - ife2 ; 5 = ^
20
21
22.
23.
24.
25.
26.
f
J
n
Г
J
0
CO
P
I
0
CO
f
I
0
oo
0
CO
л
I
ft
OO
I
0
5
с с?ж
A:2 sin2
x sin ж
sin ж
x у
1
"Eg Ж /
x у
sin ж I
ж I
/
1
ж
ж у
ж 1
к2 sin2
/
1 L
1+{й
1 с
ж
ж
f ein т 1
\ COS Ж J
Г sinrsc "
1
[ cos rx j
•
X cos x J
2\
4
^ cos rx j
2K(k)
(-l)nnn 1
Ik lnl
2
[2
I
2X-V2
1 A "K
/
-1/2
1
V2
\
-A;
+ k
0
sin ж cos" ж
7Г
16.	sin пх{\/1 - к2 cos2 х )±г dx = 0	[0 < к <С 1; п = 2, 4, 6, . . . ].
о
17.	=| bF2(tI, \, 1; i + |, i-|; fc2)	[o<*^i; n = i,3, 5, ...].
18.
о
7r(n-3)!!fc" f -
=	\
. cosn«(Vl - ife2cos2 ж)±Х с!ж = 0	[0 < к < 1; п = 1, 3, 5, . . . ].
[0 < к < 1; n = 2, 4, 6, . . . ].
[0 < к < 1].
[0 < к < 1].
1; r = l, 2].
28.	7	^^ Л^= fn	0 < ife < 1; kf = Vl~k2 ,
J ж^1-^281п2ж	L	J
/i = /2 = fc[E(fe)^fc/2K(^)],
/3 = /4 = 3^^[B - 3^2)ife/2K(ife) - 2(ife/2 - k2)E(k)].

2.5.19]	2.5. Тригонометрические функции	347
со
Г sin ж cosn ж
29. —	= dx = Jn	[О < k < 1],
J жу 1 — k2 cos2 ж
о
Ji = J2 = AT2 [K(ife) - E(fc)],
^4	2	- 2A + к2)Щк)].
30. - sir
о
, 2\ -V2
31. -si:
J ж	\l cos x
0
\r = 1, 2; 0 < к < 1; &' = лЛ - ^2 ] •
CO
Г	Gin ПГ* f*r\G 1»	1
32.
зз. / -—- = da; = _i
J жу 1 — к2 cos2 2ж	4«
о
CO	/	,
Q, [1.3	L , f sin2a;\'
34. — sin ж cos ж 1 + <	>
J ж	II cos 2ж J
о	v
35. Г fnxtsx=dx = -^ [K(fc) - E(fc)]
J ж\/1 — fe2 sin2 x	*
0
36 i sIn2жtgж
Г J \
жу 1 — fe2 cos2 ж
1	Л
J ж	в у \cos2^J J	k2{ Е(к)-Щк) J
[0 < к < 1].
38.
о
if sin a;tgs [/ 2[со8Ж12\ /
<
о
Jy' I ~ < Л _ x^ /^ /ox H -1 - Л 1 „:_ ™, j I
< 4 , ,v 1M .
ж I cos ж tg (ж/2) J \	I sin x
- 2(k'2 - k2)E(k)]	\0<k<l; kf =
[0< к < 1].
41-	/i » t9 ^=^[B-^)E(fe)-2d-
J жу1-к sin 2ж	о/с

348	Гл.2. Определенные интегралы	[2.5.20
4- + *Лп(-, _4-, к)^к2ж(к)]
h2 z	J V2 sh2 z' /	l ;J
[Re^ > 0; 0 < к < 1].
= -cth^nf -, —«—, A; )	[0 < A; < 1; Re z > 0].
z	2 sh'z /
43
44
f
J
0
CO
f
J
0
oo
f
-
X'
+
k2
1 +
X
sin2
z2
da
)Vi
sin i
X
-k2
с dx
1
1z
sin2^
2.5.20. Интегралы от
sin аж I I cos (ox + с) I
cos аж j \ sin (bx + c) j
, N f sin ax 1 ^ f sin (bx + c) 1 ^
\ cos аж J \ cos (bx + c) j '
dx = c{slnt[#i(t - ас) -
[х -j- z)
о
фх(^) = t" cost + si (t), Ф2(?) = t^sint - cl(t)
[t = c(z + а); а, с > 0; | arg z| < тг].
Г	x dx	о» л	г	/ -i
2. 	7	- =	In cos а	[0 < а < тг/2].
J cos x cos (а — ж)	sin а
о
, f . n_x r , ., , Trcos[rn(a -
4. sin ж cos [ra(a — ж)] ax = 	^	—
2n-inB
тг cos [ra(a — тг/2)]
n — m -
2 '	2
[n ^ ra; ra, n = 1, 2, 3, . . . ].
2тг
•3m
Г г , ., (	41I/fsinraa,l ,	2?ri3m 2 ,2ч1//2 Г sin cm I m
5. а + «6cos (а — ж) 1 <	> dx = 7	ч—(а + 6 ) 7 <	>Р^, (с)
J	[cosma^J	(l + i/)m ч	7 [coscm j v ;
coscm
[c = а/\/а2
2tt
Г
6. [а+ 6 cos (с- ж)]1/(
о
0
7# | Xa^l/Sln(te + C)
8.
I ^ =	Г sin (c + W2) 1	[6 > 0; 0 < Rea < 1].
|	l ;\cos(c + a7r/2) J	L	J
a 1 sin (жа/2 — bx)
ж |/
0
/	[у, 6>0; 0<а<2].
/

2.5.22]	2.5. Тригонометрические функции	349
0	г о-! тж	f sin (ажр + 6жд + с) 1
2.5.21. Интегралы от < . _	„ ; >.
F	\ cos (ажр + Ъхч + е) J
1.	ха sin (аж2 - 2аж) dx =	{SI (а) - тг[G2(а) + S2(a)]}	[а = 0 или 1; а > 0].
J	A
а
оо
2.	- sin (аж2 - 2аж) а*ж = - si (а) + — [1 - G(а) - 5(а)]	[а > 0].
J ж	2	2
1
. sin (аж2 + 26ж) |	1 ГтГ ( Ь2	62\
3.	<	о	>аж = -W — cos — q= sin —	fo > 01.
1	1 ___/_..2 , oL..4 r	2 V 2a I a ^ a /	L J
4. - sin (аж2 =F 2аж) dx = -\-- Сл(а) - S\a) =F С (а) Т 5(а)	[а > 0].
J ж	2 [2	J
о
5. Los (ж3 Т ах) dx = ^f { -J-1/8iC! + ^ }	[« > 0; с = 2(а
о
оо
f Г sin (аЖр + Ьа,') 1	1 ^ (-Ь)^ -(*,+!)/„Г( kq±±\ f sin с
J isCa^ + bx")/	p^ *!	V P \
2P
1
тг; а, 6, p, g > 0 .
J
2	1
Г sin (ax + 26ж + c) f	/Trfsindl	Г тг ас - б2	1
7.	<	9	} dx = а — <	}	\d=-^	;	а >0 .
J I cos (аж + 2&ж + с) I	V а Icos rf J	[4	a	J
— oo
oo
8.	smaV\x\ s^nx dx = ж(стауЩ +е <»л/1ЙТ 1	[a > 0; Imt/ = 0].
J	x — у	V	/
— oo
a ( sin ажр sin bx 1 a f з!пажр cos &ж 1
2.5.22. Интегралы от х {	v , >, ж <	„ , >.
[ cos аж cos bx J	[ cos аж sin bx J
Обозначение: S = < >.
	 Г f	_ о . .	. _ Л	~	У	_ о .	. _ 4	f t'l
Ь
X- J 1coSax2fSm6:Brfa;-V2a И sin [Ь2/DаI Г \4a ) ± \ coslb2/Ua)} Г\4а
0
[a, b > 0].
2.
[ cos аж
0
b _(e+1)/2 /a-hl\fcos[(l-aOr/4]l F/«±3 a±± 13 5	fe4 \
2	V 2 ylsin[(l-aOr/4]J V 4 ' 4 ' 2' 4' 4' 64a2 J
j
a + з\ ( cos [A + а)тг/4] j /5 + a 3 + a 3 5 7	6^\
2 J\I[(l + )/4] J2 3V 4 ' 4 ; 2' 4' 45 642 J
^12	V 2 Д sin [A + а)тг/4] J " a \ 4 ' 4 '2' 4' 4' 64a2/
[a, b > 0; -1 -25 < Re a < 2].
f ^1/2[81паж21 ...	тг /6 / . b2	b2 \	(b2 \
3. ж ; <	2 sm^da; = T-i - sin-±cos- Jim -	a, 6 > 0 .
J	[ cos аж J	4 V a \ 8a	8a J i \ 8a J
о

350
Гл. 2. Определенные интегралы
[2.5.22
И sin аж2 1 , , 1 /7/ б2	б2
2 > cos bx dx = — а — cos — =р sin —
cos ax J	2 у 2а \ 4a	4a
о
[a, b > 0].
е Г а_х Г Бтаж2 1
5. ж <	2 cosoa? ax
J	[ cos ax J
~J^_ /a\fsin(a7r/4)l Ff2 + a a. 1 1 3
2 V 2 / \ cos (атг/4) J 2
64 Л
4 ' 4' 2' 4? 4' 64а2/
Ь2 а/2_! /а ч/со8(атг/4I /а 2 + а#3 3 5_ б
[а, 6 > 0; -25 < Re a < 2].
6. ж ' <	2 r cosfea? а*ж = =F^
J	[ cos аж J	2 Па 1 cos с
о
7.
8a
8V2 \a
cos[F2 -тга)/(8а)]
2
[c = (б2 ^
тга)/(8а)]
0]
sin [(б2 + тга)/(8а)]
8. —г- sin аж2 cos bx dx = — \S\ — ] — С ( — 1 + \/тга sin
J ж2	2 |_ \4a/	\4a/	4a J
о
oo	.
ИЗ 3 • I Л I l Г А7
sin а ж sin ox \ ж о \ /ч /ч у 6	( ч
зз	> йж = —\\— Л/з с + «>-1/з(с) Т	^i/з(с)
cosa ж cos6jcJ	6а V За [	тг ;
о
со
Г	Г * I» 1	/	 Г ( rf
10. ж^1у^2 sin Bа^ж ) sin cxl , >а1ж = 4/^	~- к
J	[costej	у 2(с ~ ^) Llcos^
а); а, 6 > 0].
[а, 6 > 0].
[a, b > 0].
>аK/2; а, 6 > о].
J
[smrf
11.
c>6>0; a>0; d = ——, /i =
6
[с = b > 0; a > 0].
f si
— 1/2	/	/—\	I B111 v<b i
12. ж ; smBa\fx) coscxi	} dx =
cos 6ж J
e>6>G; a>0; d = ——, h =
6
13.
1 /F|lcos[a7Bc)
[с = 6 > 0; а > 0].

2.5.28]
2.5. Тригонометрические функции
351
14. I ж^1/2соз
/о /~\- (smbx\	I / ж , , i . ,ч
2ауж smcs<	>аж=-4/^	г-(cos а dz sin а)
V	;	I f ne IW I	9 A/ 9(r* h\ X	'
(cos /i db sin h)
15.
16. I ж
о
17.
/ /	,
= =р — 4 / — cos — ± sin —
4? I 2	2
с > 6 > 0; а > 0; d= ——, /г = ——
Ъ	+
• = с > 0; а > 0].
-1/2	/о ^\	f S1Tlbx\ j
1 со8Bауж)созсж^	^ с!ж = -., _, , ,,
[соэбж J	2 Y 2(c + 6)
1
cos rf)
(cos /i =F sin h) +
0; а > 0; d=
1 /тГ/ а2 .а2
= 7 А/ ~ cos T^ T sm 77"
4 V с V 2с	2с
[6 = с > 0; а > 0].
., . f sin (аж + b/x)
2.5.28. Интегралы от A(x){ x	' '
[ cc
Обозначение: S =
1.
2.
t{
аж + а/ж)
ж2 + 1 1 cos (аж + а/ж)
к cos (ax + Ь/х)
[4/х = -1 - 2а - 28, 4i/ = 3 + 2а - 2<f; а > 0; -l<Rea< 2].
sin (аж — а/ж) .	, ,. „,
/1^ж2 \соз(аж-а/ж) [ Х^ТУ^'
3.
sin (аж + а/ж) sin (аж — а/ж) 1 а*ж	тг Г sin (—2а)
cos (аж + а/ж) cos (аж — а/ж) j 1 ^ ж2 4 \ ехр (—2а)
[Re а > -1; а > 0].
[а > 0].
сх-)	/о
\Х \сов(аж + 6/ж) J Х^^\а) \
sec (атг/2)
cosec (атг/2)
- Г	1/2{8т(аж + 1
о. ж < .
J	[ cos (аж +
о
.	/тг" Г sine 1
dx = * — <	>
у а [ cos с J
6. ж
о
7.
-3/2/ sin (аж + Ь/х)
cos (аж + 6/ж)
тГ Г sine 1
— <	}
о { cos с J
О
— Ь/х)
а/2
зт(атг/2) 1 .
3os(a7r/2) j J
Г _i/2f вт(аж-Ь/ж)
о.	Ж	<	,	i / \
J	[ cos (аж — Ь/х)
о
9. ж"
о
sin (аж - Ь/х)
±JaBVab)}
[а, 6 > 0; |Rea| < 1].
[с = 2л/аЬ + тг/4; о, 6 > о].
[с = 2л/а6 + тг/4; а, 6 > ol.
[a, b > 0; I Rea| < 1].
[a, 6 > 0].
[a, b > 0].

352
Гл. 2. Определенные интегралы
[2.5.24
10. ж
sin (ах — Ь/хJ
cos (ax — Ь/хJ
dx = —а —
26 V 2
[a, b > 0].
11.
sin (ах ~~ Ь/х)
х2 + z2 { cos (аж - b/x)
ж х-1
2
а, 6, Re^ > 0; ? =
tt, sin (а/ж) sin bx 1 а f sin (а/ж) cos 6ж 1
2.5.24. Интегралы от ж< , , (	>, х < , ' \	>.
\ cos (а/ж) cos bx J	[ cos (а/ж) sin ож J
с»
f а-i f sin (а/ж) sin 6ж 1
L. ж <	>
J	[ cos (а/ж) созож J
sin (с
¦2тг~
ab > 0; | Re a <
CO
Г 1 f sin (а/ж) sin 6ж 1 . . f
J ж [ cos (а/ж) cos 6ж j	2
о
oo	^___
3. ж 7 < ; :	^ж = ±-4/— sinBVab)-cosBVab)±e
J	[ cos (а/ж) соэбж J	2 у 26
0
4. ж"
о
Sin (а/ж) Sin &Ж 1
cos (а/ж) соэбж J
1	Гп~ r .
-4/—
2	у 2а
sin Bva6) — cos Bva6) ± e
S =
[a, 6 > 0].
[a, b > 0].
[a, 6 > 0].
со
Г a_i Г cos (a/x) sin 6ж 1
J	[ sin (a/x) cos ож J
= -(-)
4 16/
а)а/2
cos (an/2)
± 2ж^г sma7rKaB\/ab)]
[a, 6 > 0; I Rea| < 1].
a f -1/2 f cos (а/ж) sin 6ж 1	1 Гп" . , ^-гч	, ГТ\^ -2V^6i
6.	ж ; < , , ч , ? dx = -\ — [sin Bva6)+cos Bva6)±e
J	[ sin (а/ж) соз&ж J	2 у 26
о
со
7.	I ж^:
о
sin (a/x) cos 6ж J	2 у 2а
sin (сл/а2 ± ж2 ) sin 6ж 1
[a, 6 > 0].
[a, b > 0].
2.5.25. Интегралы от Л(ж)
sin (сл/а2 ± ж2 ) cos 6ж ]
cos (cva ± ж2 ) sin 6ж j
i (сл/а2 ± ж2 ) cos 6ж j '
1. sin (cs/a2 — x2 ) cos bx dx =	^^=^^ J\ (a\/b2 + c2 )
J	2 у62 + c2
2.
(a2 - ж2K/4
- cos bxdx = -A — J1/4 - (V c2
6)]
- 6)] J1/4 [|
1/4
[a > 0].
¦«]
[a > 0].

2.5.25]
2.5. Тригонометрические функции
353
о ,' cos (с\/а2 - ж2 )	ж ( rryr-—г-.
3. I 	,—- cos bx dx = — Jo(a\/b2 + с2 )
cos (с\/а2 — х2
5. Va2 — х2 cos (cV«2 — ж2 ) cos bx dx =
6.
7.
8.
9.
10.
2 b2 + с2
cos bx dx =
\/b J_i/4
¦ sin ex dx = — sin cy
- c)] J1/4 [|
2 + у2
7ГС _Ь
= — e
2
2 + |/2

sin (су ж2 + у2
cos bx dx = — JQ(yVc2 — b2
2
3/2 /- г 2/ ^^-^^ ] rw
V6 J-i/4 - (C - VC2 - 62 ) J1/4 - I
sin (с^ж2 + у2 ) cos 6ж	тг е аЬ sin {c^Jy2 — a2 ]
JLJL.	¦	¦ t	uX — —
[а > 0].
)]	[a > 0].
[с, У > 0].
[6 > у > 0].
с > b > 0
6 > с > 0
; 2/>о .
/|/2 - а2
12.
[с > b > 0; у > 0].
[6 > с > 0; а, |/ > 0; а ^ 2/]-
[6 > с > 0; а = у > 0].
13. |ж
5 cos
у2 ) Г sin 6ж 1	тг ^аЬ	^
^<	}dx =	е cos (cV2/
-1/2
ж2 + a2 lcostej
I/2 ) / Sin 6Ж
6 > с > 0; a, |/ > 0; ё =
15.
+ у2
- cos bx dx = Ko(yyb2 — c2
[с > 6 > 0; у > 0].
[6 > с > 0; у > 0],
[с > 6 > 0; у > 0].
23 А. П. Прудников и др., т. 1

354	Гл.2. Определенные интегралы	[2.5.26
I tff лх I
2.5.26. Интегралы, содержащие <	>.
[ ctgax J
е: S = < >.
Обозначение:
2 1 t mxdx= x ^	[ Ж ) V	(^1)"	Г Г0, 2, 4,
' J g	4	lln4/^m-2A;-l	L 11, 3, 5,
о	fc=o	l i , , ,
tt/4
3.
0
7Г	1 7Г ,	G
5. жtgm xdx = /m,
1 T/kxix-V
4. j ж tgxdx- 2^
о	fc=1
f n	, 1/тгч" 2 ^ (Bk)
x ctff ж яж =: 	I 	 I 	 	 у 	 		\n = 12 3 1
о
•T
T	7Г	G
6. x ctgx da? =	— In 2 H	.
J	8	2
о
tt/2
9. ж tga; с!ж = — In 2. 10. ж tga; с!ж = ^тг In 2.
11.
ж
о
12- jtg
о
сов2ж	2 8
о
тг/2	_г
Г и Г gin 2ж1 . . тгя f sin (шг/2) 1
J	[2]	2 [ cos (/17г/2) j
[n = 1,2,3, ...].
0
7Г/2

2.5.26]	2.5. Тригонометрические функции	355
15. [ gTJ
J	[	J	I sin с
0
tg"(»/2) _ 1 U[(M + 2)/3] -
2±i	"з
0
Т
[2c = (/1 + 1/)тг; Re/i < 1; Re (/л
- ^[(/, +
2)/3]
1 + cos (/тг/п) sin ж
О	!
1	— fc-1 fc/
— 1) sin — тг r0
;;г / ( 1) sin 7Г h/> I	I w
2nsin(/7r/n) ^l ;	n l\ 2n J *\ In
[l + n = 1, 3, 5, . . . ].
to	!	n^^^ / i\fe-i • kl \ .(n + m-k
18.	= —^-r-—-^ > (-1) sin — 7т\ф\
tt/2
19.
0
n sin (/тг/п) ^ l ;	n L V n /	V n
[/ + n = 0, 2, 4, ...; m = 1, 2, 3, ... ].
i/2 f sin i/ж I , f cos (дтг/2) 1 .	x
^cos17^^	\dx = \ . / 7/o( ^B(/x + i/-l, l-/x)
[cosi/a^J	[ sin (/iTr/2) J
[Reju < l + <5; Re(/i + i/) > 1].
/
. ctga^cos^™ ж sin их dx = тг/2	[Rei/>0].
20
о
21. '
22.
cos 2x	4
о
tt/2	_^
2 dx=^j
sm^	2/icos(/i7r/2)
о
тт/2
23.
о
xdx	321/Зтг2
25. [ y
J у tg2 a — tg2 ж (tg2 b ~~ tg2 ж) cos2 ж
6 - tg2 a
COS 6	7Г i	.
a + arctg	- -	[0 < a < b < тг/2].
у sin (о — a) sin (b + a) ^
Г tsr^ о.ж 7Г
26-	2 , 2dx= ^	7	7^thflaz	[a, Rez >0; |Re/i| < 1].
J ж2 + z2	2zcos(fi7T/2)
0
27. ,
Ж2
о
23*
x ( tgax 1
+ z2 \ ctg аж J
2 [cthazj

Bга)!
> = 1, 2, 3, ...].
356	Гл.2. Определенные интегралы	[2.5.27
со	о
Г -2n 2n-l	n-l2 — 1 2п-1
28. ж sin ж cos Bn — 1)х tga; ^ж = ( —1) —;—гт™2 тг| .Вгп
J	Bn)l
со
ж^п sin2m ж cos 2тж tg ж dx = 0	[п = 1, 2, 3, . . . , 2т + 1].
о
со
ж~те sin2™1 ж cos 2тж tg ж dx = 0	[п = 1, 2, 3, .. . , 2т].
29
о
30
о
2.5.27. Интегралы, содержащие тригонометрические функции
от тригонометрических функций.
Обозначение: S =
тг/2
sin (a sin ж) sin Bп + 1)ж 1 . тг _ . ч	Г|
/ v	? dx = - J2n+5(a)	arga<?r.
cos (asm ж) cos 2nx J	2
о
r/2
If ab yfcosF7r/2)
6 \1 - ^2/ \sinFTr/2)
о
'<5 +1	6 + <5	<f - fe a2\ , ,4i^Afcos(
2 '	2 '	2
2. f {81п[аШ8ЖЦШ86жс1ж=1(т^) {
J [ cos (a cos ж) J	b \1 — b2 J {
x
Г	f sin (a cos ж) 1	. тг Г Г sin (птг/2) 1 _ / ч Г cos (птг/2) 1 _ / ,
3.	< ,	, >cosnxdx=—\< , ' \ >Jn(a) =F \ / / ч ?Ете(а
J	\ cos (a cos ж)/	2 [\ cos (гатг/2) j 1 ; ^ \ sin (гатг/2) j l '
о
тг/2
Г	f sin (птг sin ж) cos ж 1 , . 1 _ , ч (=pl)n+1
4.	ж< ;	;	> dx = ±—Jn(n7r) + ^»L^		п = 1, 2, 3, ... .
J	[ sin [пж cos ж) sin ж J 2n 2n
о
тг/2
5.	sin (ztga; — их) sin17™ ж dx = 0	[Rei/> 0; | argz| < тг].
6.
[Rei/ > -1
тт/2
0	[Re^ > -1; |argz| < тг; 7 + ?/ ф -2, -4, -6, ... ].
7. cos (z tg ж + их) cos17 ж с!ж = 2^1/^1же^г	[Ret/> —1; | argz| < тг].
о
ж/2
8.	cos (z tg ж — i/ж) cos17 ж с!ж = —-;—г с zz17	[Re v > 1; | arg г| < тг].
о
тг/2
I	Г*ОЧ	НГ	IT
9.	siп(?гtgж + их)	:	dx = —	[Rei/> 0; п = 1, 2, 3, . . . ].
J	sin ж	2
о
тг/2
10.	cos(z tga; — 2х) dx = Trze z	[| argz| < тг].
J
0

2.5.28]	2.5. Тригонометрические функции	357
тг
Г ,	ч Г sin Ъх 1 .	бтг Г sin Fтг/2) 1 , ч
11.	sin (a sin ж) < , >te = 2cos—^ ; ' s0)i, а	6>0.
J	[созбж]	2 [cosFtt/2) j v 7
о
тг
Г ,	ч Г sin bx I .	. Ьж Г sin Fтг/2) 1	. ч
12.	cos (а sin ж)^ . Ыж = -2б8ш—< l/f 7. ; }s^! b(a)	[b > 0.
J	[сов&ж]	2 [cosF7r/2)j
о
тг
sin (а sin ж) sin пж\ , _ м ^. ^^тг 7 , ,
13. N .	dx=iTi
J [ cos (asmж) cosns J	2
о
14. ,,
^cos(
о
7Г
. к Г f sin (a cos ж) 1	fsin(n7r/2) 1 7 . ,
J [ cos (a cos ж) J	[ cos (тгтг/2) J
о
(г/ж —a sin ж) I .	fEI/(a)l	^^ Г /	ч ,	т / ч
16.	7	; > аж = тг< , ч г-	17. cos (пж — asm ж) аж = 7rJn(a).
(их — asinx))	[J^ajj	J
о "	о
тг
Г Г sin (a cos ж) 1
18.	< ;	; > вттгжа'ж = 0.
J [ cos (a cos ж) J
— 7Г
ТГ
Г f sin (a cos ж) 1
19.	^ )	М
J [cos (a cos ж)]
sin (птг/
cos (птт /
2.5.28. Интегралы, содержащие жа и тригонометрические
функции от тригонометрических функций.
тг/2
х{ sin(atSx) Ъж = ±^е"а[С + 1пBа)те2аЕ1(^2а)]	[а > 0].
|чсо8(о^ж^ж J	4
о
тг/2
2. ж cos (a tg ж) . Х = -^- Ei(-a)	[a > 0].
J	8ш2ж	4
о
тг/2
3. ж sin (а^^ж)^^— = 	тг	[а > 0].
о
тг
4.	ж cos (пж cos ж) sin х dx = So, птг-
о
тг
Г	In
5.	ж sin (пп cos ж) sin ж dx = — [(^l)n — Jo{nn)\	[n = 1, 2, 3, . . . ].
J	ТЬ
о
оо
6.	\ -sm(atgx)\ г \dx = - A - е^а)	[а > 0].
J ж {cos ж J 2
о
со
7. [±si
J ж
о

358	Гл.2. Определенные интегралы	[2.5.29
8. [^(atg^tg^^
О
0
T 1 f sin3 ж 1 тг	f 41
10.	— cos(atga;)< 2 > dx =—(l-a)e	a< > [a > 0].
J ж [sin жtgжJ 16	[1J
о
oo
11.	жз1п(о^2ж)^	 = ~~ [exP i^a thz) — e^a]	[a, Rez>0].
J	x -\- z A
о
CO
12. I cos (a tg2 ж) cos ж —	- = —[chzexp (—ath z) — e ashz]	[a, Rez>0].
о
f cosfater2 ж) с?ж	тг	/14
13. ж	V^f	" 2 , 2 = о uo exp(-ath^)	[a, Rez>0].
J	8ш2ж ж2 + z2 2sh2z
о
CO
14. ж cos (atg2 ж) tgж^	2™ = —-—[e^a chz — exp (—ath z) shz]	[a, Rez>0].
J	Ж "г" Z	А СП Z
0
со
Г	/	2 ч , 2fc	^Ж _ 7Г j.	fe	,	. _ _a^
J	Ж2 + Z2 2
0
[Jfe = 1 или 2; a, Re z > 0].
2.5.29. Интегралы, содержащие разности тригонометрических
и алгебраических функций.
a
1. 	dx = С + In (afe) - cl (a6)	[a, b > 0].
о
а
Я1 \
	ctg х ) dx = In		[а > 0].
ж J sin a
о
Г 1 — cosn ж . жт Bт\	Г Г^ +
3.	аж = 		ш, =
J	ж2	4- V rn J	L L 2
о
п-1
1	^ 		I	п/ I У,	I
4.
[ !a)
0	fc"™°
[6 > 0;	-2 < Re a < 0; n = 1, 2, 3, . . . ].
5. l—(^^\	^^\	a/4
о
[6 > 0; 0 < Rea < 1; п = 1, 2, 3, . . . ].
жп — slnn ж
6. 	^т^	dx = Jn	[n = l, 2, 3, ...],
J ^
2. ("I) (J("fc) , Л = Т, ./2=3,
3, ^3 ^, ^4

2.5.29]	2.5. Тригонометрические функции	359
со	со
Г /cos ж — 1	1 \ dx С 3	Г /sin ж	1 \ dx
* J V ^ + 2A +ж)у "ж" = ? ~ 4* * J \^ TT^JV= ~ •
о	о
со
9.	[(ш8Ж	^—]— = -С	[k = l, 2].
J V	1 + ж*у ж	L ' J
о
со
10.		с1гж— = —.
о
1
Ка\ dx	тг Гехр(—аI
созаж±со8- ——5- = -i	f	[a > 0].
ж/1±ж2 2[ sma j
о
12.	rfln2+
J соз2ж	8	2
о
тг/2	тг/2
.„ f	l-sdga; тг	Г	4ж2 cos ж + (тг - х)х 2l o
13.		9 с?ж = —.	14.	— dx = тг In 2.
J sin ж 4	J sin ж
о	о
а	со
Г 1 — cos Ъх . Г cos bx t _, . , . ч
15. 	с!ж - 	dx = С + In (ab)	[а, 6 > 0 .
J ж	J ж
о	а
со
Г cos ах — cos bx . ,6
16. 	dx = In -	a, b > 0 .
J	ж	а
о
_ Гсозажсоэбж	тт., ч	.
17.	dx = -(b-a)	[о, 6>0].
J	ж	2
о
со
,о Г cosn ах - cosn 6ж . Г 1 + (-1)п (п - 1)!!] . Ъ
18. 	dx= 1	-±	'— ~	тг^ In -	а, 6 > 0; п = 1, 2, 3, . . . .
J	ж	I	2	nil \ а
о
чЛ 7 sln2n аж - sin2n 6ж ,	Bп-1)!!. Ъ
19. 	с/ж = -±-,	—^- In -	а, 6 > 0; п = 1, 2, 3, . . . .
J	ж	Bn)!! a	L	J
о
со
Г a sin 6ж — 6 sin аж ,	, , а
20.	dx = ab In -	а, 6 > 0 .
J	ж2	&
о
со
Г cos ах — cos bx . 1 Г . , ч	. , ч .	. ,. ч
21. 	т	г	аж = — ci (az) cos az + si (az) sin az — ci (oz) cos bz —
J ж(ж + ^)	z[ l ;	l ;	l ;
0
— si (bz) sin 6z + In —	[a, b > 0; | arg z| < тг].
23.
о
0
cos аж ± sin аж

360	Гл.2. Определенные интегралы	[2.5.29
24.
о
1 _ У ^Ж	2 _ К
1	з 5	з 23 27	8 47
Л	J	13 ^
ln310' Л1927Г' J8 280 11201п3' ^
ок f34sina^ . 2 , In2
25. 	sin ax ax = 		[а ^ 0].
J	ж	2
о
со
Г /	I ax dx	fexp(—a)l
26.	(cosaa;±cos-)—¦—- = ж< Fl J}	[a > 0.
J V	ж/ 1 ± ж2	[ sin а J
о
тг/4
^_ Г	sin ж —ж cos ж 1 Г л/2 — 1 /- . /-Ч1
27.	.	с1ж = ——2	7г-л/2 1пA + л/2) .
J	(ш2жK/2 2%/2 L 2 J
о
тг/4
Jo> I I — — Ж I tiff Ж — ctff Ж 	 :=::	in А.
I L V 2 /	J cos 2ж	4
о
°р 1 п	п	Г	п	1
29. — Л аь cos bhX dx = -> ftfclnfet.	\bk > 0, )> at = 0 .
J ж ^	^	I	k^i	\
CO
Г cosn аж cos (anx) — cosn Ьж cos (bnx)	, о-там ^
«¦JO. 	c/x* :=:: A — L J In —
J	ж	а
0	[a, 6 > 0; n = 1, 2, 3, ... ].
CO
31 f (sinx-
], /з=| [b = l]\
= f B ~ Ь2) [6<2], /з2 = -^ [6 = 2],
24	|4^&2| 6 |6-2| 6
/5 = — b(b3 - 12b + 16) [b ^
/ = ^ A926 - 8063 + 3064 - 6е)

2.5.30]
2.5. Тригонометрические функции
361
32.
(sin ж — ж cosa?)n
= Jl
> 0],
], 4=0
4=0
2.5.30. Интегралы от е
-рж f sinbx 1 n
[ cos ox J
[n/2]
Bk
[n/2]
fe=i
J42=0
Л = 1/2, n = 1, 3, 5, . . .
A = 0, n = 2, 4, 6, ...
)l 1
J J
5 |argp| < 7г .
2.
i. je sin .
3. I e px sln^ x dx =
о
4.	Те— E1ППЖЬЖ =
J	[ cos nx J
о
тгт
5.	e^px mnn x dx = nip
о
[p2 + Bife
(p2 + 4A2)(p2 + 4(A + IJ) . . . (p2 + 4(A + k - I
A = 1/2, n = 1, 3, 5, ...
A = 0, n = 2, 4, 6, ... /'
' 2
argp| < 7Г .
[Re и > -1].
[n/2]
fe=o
7r(m+l/2)
6.
A = 1/2, n = 1, 3, 5, ...
A = 0, 7i = 2, 4, 6, ...
[n/2]
argp| < 7Г
tt/2
3=0
A = 1/2, 7i = 1, 3, 5, ...
A = 0, 7i = 2, 4, 6, ...
; |argp| < 7Г

362
Гл.2. Определенные интегралы
[2.5.31
7.
[п/2]
dx = Ап\е-р*/2 Ц [р2 + Bk + 2АJ]-1
x il + 6
D + 2A)!
+ 4А2][р2 + BА + 2J]„..[р2 + (^:
= р, А = 0, п = 2, 4, 6, ...	|	\0
8.
^юж Г sin bx
. f e^px sin2 bxdx = 2Ь2р~г(р2 + 462)^X
[ReP>|Im6|].
[Rep > 2|Im6|].
[n/2]
10. I e~px slnn bx dx = bnp1~2Xnl fl [p2 + Ь2Bк + 2AJ]
fe=0
. = 1/2, n = 1, 3, 5,
11.
[Rep > n|Im6|; n = 1, 2, 3, . . . ].
1 sir
2.5.31. Интегралы от хае~рх< *"*" к
[cos bx J
Обозначение: S =
>.
1 + p2
Г n
J
о
da? = ( —1
n rf / х_д 1 + ep
1) -— p 	т
; dpn V	1 + P2
3.
/2
Г(а)
5. ke
J
0
; Re a > -8; Rep
2k+5

2.5.32]
2.5. Тригонометрические функции
363
со
6. f xne^px sinbxdx = In
Т	. Ь r	b
/_i=arctg-, /о = т^—о
p	ft2 + p2
246p(p2 - fe2)
[Rep > |Im6|; п = -1, 0, 1, 2, 3, 4],
2pb	2feCp2 - ft2)
(p2 + 62J	F2+p2K
00
7. жпе
cosbx dx = Jn
P_ , = P2-b2	f = 2p(p2 - 3fe2)
+ fe2' J F2+p2J' 2 F2+p2K '
J4 = ^
- 10P262
[Rep>|Imb|],
8. I x~3/2e~px sin bx dx = \[Ък {
о
оо
п-1/2 ^pX/sIn6
I cos bx
9.
b2 + p2
1 2
Rep> Im6.
L	IJ
10.
cos Ьж
dx =
11.
l + ( 1) 2-np-ap(a)
slnn bxdx = I%i
: = a arctg [6(n — 2A;)/p]; Re a > —5; Rep > n| Im 6|].
[Rep > n| Im&|; ттг^тг; m, ?г = 1, 2, 3, •••],
2.5.82. Интегралы от А(х)
Обозначение: S =
е"рш< sin ж 1
[ cos &ж J
{/0[a(p - i6)] T /o[a(p + i
[a, Rep > 0; | arg6| < тг]
2.
^ \dx=l_ a3ih[a(p - ib)} T h[a(p + гб)]}
cos bx J	2
[a, Rep > 0; |arg6| < тг]

364
Гл. 2. Определенные интегралы
[2.5.33
^е s
, 4^ni -п-1
= (-1) op
° 1 r-n-2fe-l
2py
- cos рж dx = —г- е
—	j cos рж dx = — —г е sin pi/
[Rep > |Im6|; \argz\ < тг].
[p > 0; | argz\ < tt/4].
fo, P > 0].
О
тт/2
егрж s!nM ж cos17 ж о*ж = 2 M v 1x
0
P^ M^ ^. 1+ P^ ,
-;-i)
2.5.33. Интегралы от /ер
тг/2
sin аж 1 M f sin bx 1 ^
><	>
cos ax J \ cos 6ж J '
[Re/x, Re 1/ > -1].
s!nM аж cos17 6ж.
f ei(M+l/)a; sln^^1
, i/) =
s!nM х ж cos17 1 ж dx =
отгг(р-1/)/2
^p fl — IS +
+ 1; 1 +
рж sin^™1 ж cos x dx =
(/i2+p2)B
/i + ip /i —
" \ cos bx
¦ exp
2 ' 2
' b + ip +
[Re/л, Re i/ > 0].
, Rei/ > 0].
[Re/x > 0].
5. e
,	1 \.
dx = — \ф
sin еж	2сг \
[п/2]
ip
2c
2a
n + 1
c — b — ip
	-
2c
> — ip + па %
2a
a, 6, Rep > 0; <5 =
[6, Rep > 0; с ф 0].
[Rep>0].

2.5.34]
2.5. Тригонометрические функции
365
0].
8.	— е~рх sin аж sin Ъх dx = - In ^	;	~т^	[Rep>|Ima| + Im6|l.
J ж	4 р2 + (а — бJ
о
со
Г 1 ^юж	, , a	2pb	b	2pa
9.	-е ^ sin аж sin ож йж = -arctg —	— + - arctg —
J ж2	2	р2 + а2 — Ь2 2	р2
о2 + б2 - а2
оо
10. J I в""" sin ax cos te dx = \ arctg
2°Р
р2 +_ fl2
2.5.34. Интегралы от xaR(eax)\ , L
[ cos bx J
Обозначение: S = < >.
2.
3.
4.
5.
sin bx
26 2ash(b7r/a)
"™1 fstntel
1
1 t
eax _ I \cosbx J
sin bx
x cos bx
ж . бтг 1
= —cth
2a a 26
7.
2a2sh2F7r/a)
o 1 /f^
2a2shF?r/2)
[Re a > -5; Re a > |Imb|].
Rea> Imfel.
L	IJ
[Rea>l-E; Re a > |Imb|].
[Rea>|Im6|].
L	IJ
[Reo>|Im6|].
L	IJ
[Rea>2|lm6|].
[Reo>|Im6|].
L	IJ
[Rea > 0; Rep > |Im6|; Re^ > -S]

366
Гл.2. Определенные интегралы
[2.5.35
Г sin bx .	1
9. 	dx =
J ax cx
а — ib
dx =	rW	)ф(
ax - ecx	2г(а-с)\_ \а-с J \a- с
-ф
max (Re a, Re с > |Im6 .
х2пв\пЬх
7r/Bc)]
_ j_/o\_
= 0, 1; 6, c> 0;
' ' '	'
b2 + c2Bk-2XJ
A = 1/2, m = 1, 3, 5, . . .
Л = 0, m = 2, 4, 6, . . .
Г cos атт sh бтг 1
sin2 атт ch2 бтг + cos2 аж sh2 бтг \ sin атт ch бтг /'
.	.Г cosaTrsh^TT I J sin атг ch Ъж 11
\ sin (^атг) ch бтг J \ cos атт sh бтг J J '
sin2 аж ch2 Ьж + cos2 аж sh2 бтг
In=^[(n-l-a)lti
2.5.85. Интегралы от /(ж, еах, sin Ьж, cos Ьж).
со
1. е™ж sgn (sin ж) dx = — th —.
[n = 2, 3, 4, ...
2.
cth
cth
p ~\~ О	Ли
[Rep
со
. J
[2 Rep > Rei/|Imb|].
"
ж ( b
a2 cos2 ж + b2 sin2 ж
о
7Г/2
r
[a,6>0].
7. I eipx cos^1 x{a2ei
dx =
p
+ /*-i/ + l)/2, (^ + /хТР + 1)/2)
с = max (a, 6); Re ц > 0;

2.5.36]	2.5. Тригонометрические функции	367
8. [ (а + cos xfeinx dx = , 2ж ч (а2 - l)^2/^ f 7 Q ^	[а > 1].
J	(i/ + l)n	\v«2 — 1 /
л „ лл „	^аж2_сж Г sin 6ж 1
2.5.36. Интегралы, содержащие е	<	>.
I cos ож J
Обозначение: S =
1. \е^ах {	}dx = J— e^° '^a)i	L /v v /J	[Reo>0].
J	[совбж J	|; A"	'	л	'
0
о
Jbf.	Ц «Ay	1U	-\	,	/-U/Oy 	 „I*	I |	„	11*11	„	' V ' Г) '
[Rea > 0; Re a > -S].
„ f _• i Л	_ / l	/ i 2 \	/ i 2 \
-1/2 —ate
3.	ж ' e <	> dx = —W— exp	M+i/4 —	Rea > 0 .
J	Icosfexj	2 V 2a F\ 8a / ± 7 \ 8a J	L	J
о
oo
4.	[x1/2e-a°2
0
[Rea > 0].
J	[cos bx
0
Rea > 0; S = .
oo	L	I o
Г 1 -аЖ2	7Г	/ 6 \
6. — e	sin bx dx = — erf ( ^_ J	[Re a > 0].
J ж	2
о
7. |же-2со8б^х=А + ^^ехр(-?)егг(^)	[Rea > 0].
0
8. L	il\
J	[cos bxJ
о
= 7J- < exp ^—	^ erfc ^^ T exp ^—	^ erfc —^ )\	Rea > 0 .
a-i ^ax2^cxf sin 6ж
Л T a-i ^ax2^cxf sin 6ж 1 ,	гГ(а)
9. же	^ f > б?ж = ——^7 exp
J	\со8&ж/	2Bа)а/2 F
J	\/	()	\ 8a
о
ibc\ ^ (
V
X exp — U>-a ^ Texp -—- D^a ^	Rea > 0; Rea > -Я .
10. же	cx < , > с/ж =	4 / — < (с + ib) exp	— erfc ( 	—
J	[costej	8а\/«1	L 4a J	V 2i/a
о

368
Гл.2. Определенные интегралы
[2.5.37
11. ж
J
о
12.
2
^аж fsinbx
<
f
	 <	> ах
z2\cosbx)	4
± ebz erf
ах = — z e ^e erf zJ a
4	L
±
cosBn + l)xseca;
2л/а
2
ch bz
00
. f
J
13. f xe~ax2 tgcxdx = -\ — y^(
J	а у a ^^
о	fe=1
1-2ссо8Ж
2.5.37. Интегралы от х°е-г>«-ч/«[АпЬ*\.
(cos bx J
Обозначение: <5 =
;}¦
I COS ОЖ
/п Г
Ot I A
exp
exp
2.
3
о.
4.
\-«/2i
>
cos ож J
[Re a > 0].
[Re(c2/«)>0].
Rea>0;
H > 1
[Ь, Reg > 0; Rea < 1].
[Rep> \lmb\; Req > 0].
; Re g
}]
= л/р2 + 62 ±p; Rep > |Im6|; Re g > o].
-а/ж2 а^/ш f Sin &Ж 1
2.5.88. Интегралы, содержащие е ' , e v , <	>.
[cos bx J
Обозначение
: <5 = < >.
F(a)fsin(aff/2I „Л_« l^a. a^
6« lcos(a7r/2)/°^4 2' 2 ' 4
I't)	[6,Rea>0;Rea<l].

2.5.38]	2.5. Тригонометрические функции	369
3.
4.
со
Г —2
0
со
J
0
со
|Vpv
0
cos bx dx —
x i > dx = <
CO
.=0
7Г
2
*!B*4
fe=0
J f
Гр + 1)/2]
/|6-3/2{|sin,l
r> —1 / /jL _i_ I \
1 L J
T
Re а > 0].
Rea> 0].
о-т*/4
6. ж e	<	/ dx = ^ — 4 / — U/i/4 I — I i • f i У1/4 I — I \	f
J	I cos bx J	2 у 6 I \86/ I sin с J	\8o/ I coscJJ
0
тг/8; 6, Rep > 0].
-pVZ	[i	I2 fi
7. 	smbxdx = тг - - C(^) + тг - - 5(z)	[z = p2/D^); ^5 Rep>0]
j ж	L2 J L2 J
о
0
f cos bx .
9. 	t=	dx =
8. |^_^ = /F)-1 + /(^)^	[с. 2.6.38.9].
j егтг^^!	8тг2	J e27Tv^ _ l	64 \2 тг тг2/
о
со
Г ж2сов2тгж .	1/^55
12. 	—	dx = 	 1
j е2п^ _ 1	256 V	7Г 7Г2
о
со
Г ж^шфгж/2) _ Г7 _ 87 35 105
J е27г^^1	16 ~	+
О
со
. ж3со8(тгж/2) ,	8 7 35 873
14.	п I l} dx = ^— + — + +
Зтг ' тг2 ' 2тт3 ' 16тт4°
о
15. Г с"" 3(Sinf )^ = ^И450 1/3(ге8"'/4)Те-"Ч 1/3(ze-3^4)}
J	[ cosoa? J	2o L	'	J
0	Г.. *,, ,очЗ/2..-1/2. Rea>0]
24 А. П. Прудников и др., т. 1

370
Гл. 2. Определенные интегралы
[2.5.39
Т1	А(х)	Г s"m ^х i
2.5.89. Интегралы, содержащие е 1 ; и <	>.
I cos ох I
Обозначение:
-й-
1.
¦ехр 1 b
Z1 + X1 I I COS СЖ
Ма/2_1/4,
X Ma/2-i/4,±i/4(b — vb2 - c2z2 )	[6, с, Rez > 0; -S < Rea < 1 + S].
2.
z2)cosbxdx =
pz
3. xa~
о
4. жа"
о
5. jx
О
6.
+ z2
p2 + <
Sin Ьж с!ж = Ja
- b2 )	[6, Rep, Rez > 0].
[6, Rep, Rez > 0; Rea > -1],
+
[6, Rea, Rep, Rez> 0],
exp (— b\/x2 + z2 ) <
, f sin Ьж 1
	=	L{ , > dx ¦¦
p2 _U r2	^ cos 5Ж j
/ж2 + z2
+
2.5.40. Интегралы, содержащие показательную функцию от
„ Г sin bx I
показательной и тригонометрических функции и <	>.
I cos bx J
1. ехр (ах — е
Г Sin 6ж 1 ,	._.	,, ч . f Sin 09 1
I	\dx = \Г(а + гЬ)\\ Т }
{ cos bx J	[ cos (p J
T(z)	1
= argT(a + гб), argT(z) = -г In —^^; Rea > | Im6|
lr(z)l	J
7Г/2
2.	xez sln x собх dx =—[ch z - h(z)
ж
[|argz| < тг]
[|argz| < тг]

2.5.41]	2.5. Тригонометрические функции	371
тг
4. же2СО8Ж sin ж dx = — [h{z) — e^z]	[| argz| < тг].
о
. [ eizcosx cos nxdx = inirJn(z)	[|arg*| < тг].
5
о
6. ег* cos ж sin" ж dx = утг ( — j	Г( — ) JA/_i)/2(^)	[Rei/ > 0; | argz| < тг].
о
7.
о
7Г
8. {e	— e	zsmш } dx = 2tt[Ji/(z) + iEI/(z)]	[| argz| < тг].
о
14. е
tg2 д.
9.	z	;—;	r = 2тг 7 e aJo{kyb2 + c2 )	[a, 6, с > 0].
J 1 — exp (—a — го cos ж — icsmx)	~
10.	ei{nx~zsinx) ^x _ 2qiJn{z)	[ | argz| < тг; n = 0, ±1, ±2, . . . ].
a
oo	oo	/ L \
11.	e-{px-zsmx) dx _ _ +2^ —	— Jkl — 1	[Rep > 0; |argz| < тг].
о	fe=i
7Г/2
0
[Re 7, Re/j, > 0].
13.	2те+2	fc?rct 	 = ^	'-	I ^2	\	\k=) f5 ^ = 1, 2, 3, ... .
о
oo
ж cos2 ж 2
о
[ sin (аж2 + 6ж + с)
2.5.41. Интегралы, содержащие Л{х), е ^х , <	2	+i
I cos {ax + bx + с)
Г 1 1
Обозначение: S =
.	__ . _ чЬж + с) 1 ,	1 / Г sine I r cosci\
ож + с) J	р2 + о2 \ [ cos с J I sin с J J
о
' sinalx
cos Fa
1 f	ep - 1	f sin a 1
? б?ж = —г-г	r<^ „	>	[a, Rep>0].
j	p(e2p — 2ep cos a + 1) ^ e — cos a J
2.
о
oo
r
cos a[x] j	p{e2p — 2bep cos a + &2) \ ep — b cos a J
о
[a > 0; 6^1; Rep > In 6].
24*

372
Гл. 2. Определенные интегралы
[2.5.41
l-XJ	су
4. \e-p*fsinbx
J \cos6x2
о
5.
ж
26 1 cos z
[z = p2/Db); b, Rep > 0].
\/2b	J)
f!2
I COS OX
[6, Rep > 0; Re a > -25].
sin с
cose t
¦тг/8; 6, Rep > Ol.
26
8.
9.
Г
10. \ xe
J
0
; 6, Rep > 0].
; 6, Rep > Ol.
sin Fж2
<
I
smbx2smpx\	p П
( p
> о?ж = 4 / exp —iL-
f	4V263 F V 26
[b > 0; Re a > — S; |argp| < тг/4].
[6 > 0; |argp| < тг/4].
11. [ x2e^px[sln (bx2 ± px) ± cos Fж2 ± px)] dx =
F - p2) exp (-^r
[b > 0; |argp| < тг/4].
Г ^a
12. e a
J
Л =
1	/ 7Г	_ад [n f sin сЛ 1	_ f COS cA 1 1
2	V « + c2	[I cos Cy^ J	I sm c^ J J
л/ж	^ал( Sin D 1
T^^W e 1 cos D J
V2
±аI/2, 2D = arctg (с/а) - Лс; 6 > 0; Rea > | Imc| .
J
B f з!пFж + с/ж) 1 ^
\ cos (bx + с/ж) J
e^2rs cos
Г 8Ш d 1
\cosd/
2rs8in(A + B), r = t/p2 + b2 , e = v7^2 + с2 , 2Л = arctg (b/p),
2B = arctg (c/q); Rep > | Im6|; Reg > | Imc|l.
14# Г x-s/2e
J
-s/2e-px-q/x f sin Fж + с/ж)
f sin Fж + с/ж) 1
\ cos (bx + с/ж) J
sin /
cos /
[/ = В + 2r5sln(/l + Б), r, s, Л, Я см. 2.5.41.13; Rep > |Im6|; Req > |1тс|].

2.5.42]
2.5. Тригонометрические функции
373
sm (qx
cos (qx
(п-2к)Ш ^
+ г)\, ( 1\"/?
> ах =	а / — ехр
+ r) J	\ 2а/ V «
n^2^\ 2fc^ -Jsln/il
4а
16. е^{ах +ЬаН
sin (px2 + gx + r
cos (рж + дж + г
dx =
a(b2 - Aac) - (aq2 - 2bpq + 4cp2)
4(a2+p2)
sin |~1	p p(q2 — Apr) — (b2p — 2abq + 4a2r)
cos 2	a	4(a2 + p2)
[Re a > 0].
17.
sin ex
cos ex3
2.5.42. Интегралы от А(х)е
Обозначение:
='-{!}•
cos Vаж2 + 6ж + с j
1.
/ж у а1 — x2
2.	— cos (cv аж — ж2 ) ax = тге ; Jo ( — <
J \/a.T — ж2	^2
3.
4.
dx =
hz± = c± \fc2 - p2 ; а, с > о].
j	[а, с > 0].
[A; = 0 или 1; а > 0; Rep > | Imc|].
5.
6.
sin (сл/х2 — a2) dx =
7Г	С
2 л/^Т^2
- cos (cv ж2 — a2 ) с/ж = * / —
/ж - a l	;	V 2 V p^ + с
рУ1/2 exp (-aVp2 + c2 )	[a > 0; Rep > |Imc|].
2^2 exP(^aVp2 + c2)
[a > 0; Rep > |Imc|].
cos (cv ж2 — a2 )
2±V2
s
+ 77
\z± = a(\/p2 + c2 dip); a > 0; Rep > |Imc|l.

374
Гл. 2. Определенные интегралы
[2.5.42
7.
8.
9.
10.
ж - a (ж + a) | cos (с ^ж2 — a2 ) J	\/2a
dx = /_ е Perfc(z+K v ;>
sin (с^ж2 — a2
cos (с^ж2 — a2 ^
= a(x/p2 + c2 dip); a > 0; Rep > |Imc|].
с2 dip); a > 0; Rep > | Ime|j.
уж уж2 — а2
z± = - (^/j^Tc2" ± c); a > 0; Rep > | Imc|l.
¦e px cos (с^ж2 — a2 ) dx =
[m = 0 или 1; a > 0; Rep > | Im c|].
sin (с^ж2 — a2 '
cos (с^ж2 — a2
/<	iiiT^faVp2 + c2 )	[d = i/arctg (c/p); a > 0; Rep > | Imc|].
[ cos a J
12.
sin (б^ж2 + z2
x2 + z2 1 cos (б^ж2 + z2
dx =
4 ^ [1 J1/4(,+ ) |Jl/4^-) T { Y1/4(Z+)
kz± = г{л/Ь2 +р2 ±6); Rez > 0; Rep > |Im6|l.
13. e^pxsmFVx2 + :
о
14.
[Rep > |Im6|; |arg^| < тг].
exp |-- (%/p2 + b2 -p)J
[Rep > |Im6|; |argz| < тг].
1 --^ (^P2 + ft2 ~ P)	[Rep > |Im6|; |argz| < тг].
J.O.	Л	A '
cos [by хл + xi
Z±=2l
±р); 2Rea > -<5; Rep > jlmfcj; |argz| < тг].
-1

2.5.48]
2.5. Тригонометрические функции
375
17.
г<	,	 > dx = —= ер erfc (z+){
ж + *) 1 cos (б^ж2 + ж*) I	>/i	l 4	1
4 = ^i
). Rep>
z| < тг L
CO
18. \ ^ ** cos (Ъл/х2 + xz)dx = epz/2K0 (-x/p2 + 62 )
J Vxvx +z	v2	;
[Rep > |Im6|; |argz| < тг].
1O f/ 2 . х
19. \{x +xz)
J
r^
cos (byx1 + xz )
); Rep>
г\<*].
СО
20.	- (—Ь ж + ^ж2 + xz ) =р (—h ж — \/х2 + xz)
J уж2 + xz LV2	/ \2	/ J
x e
[d = is arctg (b/p); Rep > | Im 6|; | argz| < тг].
2.5.43. Интегралы от A(x)e
™
Обозначение: <5 =
;}¦
cos [cx/(x ±a )]
1.
sin [сж/(а2 — ж2)]
а2 — ж2 J 1 cos [сж/(а2 — ж2)]
с2 I 2
2.
- exp -
262 + c2 +2a&
b \ J з1п[сж/(ж2 - а2)]
q/2-1/4, ±1/4
[а, 6, с > 0; Re а > -5].
x2 — a2 J | cos [сж/(ж2 — a2)]
dx =
4-а/2, ±1/4
[а, 6, с > 0; Re а < 1 + 5].
3.
- exp
da; =
+2abf/A x

376	Гл.2. Определенные интегралы	[2.5.44
xz + zz	V ж^г/ I cos еж/ ж + z
0
/4a262 + c2 + 2a6 1	/ V4a262 + c2 - 2a6'
	 I Ml/4-a/2,±l/4l
[a, b, с > 0; Re a < 1 + 5;
sin [сж/(ж2 + z2)]
2
5.	7	exp ^
J V2 + 2	V
X Mi/4_Q/2)±i/4 	r~?	 pi/4-a/2,±l/4 	^
\	AZ	J	\	AZ
[6, c, Rez > 0; -5 < Re a <
2
X Mi/4_a/2)±i/4	 )Mi/4-
2
'2z6-
2z	j-4*-<*/*,=4*y	2z
[b, c, Rez > 0; -S < Re a < 1 + 5].
2.5.44. Интегралы, содержащие показательную и тригонометриче-
тригонометрические функции от тригонометрических функций.
Обозначение: 8 =
>.
cos (z sin ж)]	[ — si(—r
0
tt/2
2	1 z cos ж I "*" V'-' "iAi •"/ I j	J *-"***¦ \^/ i	r	-	i
.	e	< / . ч Г dx = 1	f	argz < тг .
zcosa, f sin (z sin ж) 1	f2shl(z)
\ cos (zsin ж) J
sin (zsin ж) sin nx
COS (zsin ж) J	\	7Г
о
Г zcosa; f sin (z sin x) SIH ПХ 1 .	7TZ
3.	\ezcosx\	.	M^ = VT	argz| <тг; n = 1, 2, 3, ... .
J [ cos (zsm ж) cos nx J 2n!
о
4.	ez cos ж cos (z sin ж + bx) dx = z^b sin {Ъж)^{Ъ1 z)	[ \ arg z, | arg 6| < тг].
о
7Г
5. Ге2со8шсо8(^81пж + ж/2)с1ж = J- erf (v^)	[|argz| < тг].
0
os bx+cos ex) Г Sin (Z Sin 6ж) Sm (z Sm Cx) 1 ^ = ТГ ул	^(&+C)fc	Г 0 1
\cos(zsin&x)cos(zsincx) J Ж ~~ 2 ^ ГA + 6А;)ГA + ck) \ тг J
7.
о

2.5.44]
2.5. Тригонометрические функции
377
О	2СО8Ж	/	•	^SlnZfгЖ	V^
8. е	cos B sin ж)	dx = ж > -
J	v	; sins	^ Bife-
0	fc™°
9.
0
7T
10. \ez
0
11.
Sin Ж)
COS Ж + С
^| < тг].
[|argz| < тг].
|argz| < тг; \c\ > 1].
sin bx
12.
о
13. I e
1 — 2a cos bx + a2
1 — a cos 6ж
2a
1)
. тг
(IT = —
2
a z
(IT =	>
- 2a cos 6ж + a2	2 ^ T(kb + 1)
fe=i v	'
[ | arg2:| < тг;
argz| < tt;
1].
1].
pacoSx + bsinx(sl
\ c
cos (p cos ж + q sin ж + nx)
= (^iM7r[(p - bf
Г асо8Ж + Ь51пЖ
в
J
^n/2[(A + iB)n/2In(VC - iD ) Т (Л - iB)n/2/n(VC + Ш )]
[(p - 6J + (g + aJ > 0; Л = a2 - b2 + p2 - g2, В = 2(a6 + pg),
cos (o cos ж — asm ж + nx)
—
i
n\
cxj	1
Г 1	Г !^—i k n
15.	— ea cos x sin (a sin ж) cos nx dx = — ea — \^
J ж	2 [ ^ k\ 2n\
T	г»-1 к
16.	— ea cos x cos (a sin ж) sin nx dx = — ^J — H
J Ж	L	аП.
0	fc=0
17. -,
J x
0
sin (asm ж + пж) аж = — e
2
1
\ COS (fi J
[y? = narctg (b/a)\.
[a > 0].
[a > 0; n = 1, 2, 3, . . . ].
[a > 0].
18.
19.
20.
sin (a sin еж)
— у2 \ cos (a sin еж)
> аж — ± у е
_г a cos ac
е
cos (a sin ас) \ же
sin (a sin ac) J 2
же	f sin (a sin еж + bx) \	ж S-i
———^< v	/\dx = T-z
ж2 + z2 { cos asinca; + bx)
а, с, у > 0; 5 =
a, 6, c, Rez > 0; <5 =
sin (a sin сж +еж) I ,	ж
(ж2 + z2) sin еж [ cos (a sin еж + еж)
dx = w^rzz le<1 - exP (ae " -
a, c, Re г > 0; 5 =

378	Гл.2. Определенные интегралы	[2.5.45
ГХГ)
a cos еж sin(as'mcx) ТГ	г а	/ -сгм
	1	L А г» — 	 \Ра _____ PYn (пр cz\\	\п r Dp у \ о
о
оо
а cos еж
О
sin (a sin еж) ,	тг
^о 	^	" dx = о	~
х1 — у1 sin еж	2у sin су
«л	е	sin ^usinca;; ,	vi	г а	а cos су	/ .	м	г	л1
22- I „3.,а	L- da;= о..„:-„. [~е +е "cos (а sin су)]	[о, с, »>0].
i ж 1 — eacosciE Cos (a sin еж) .	тг г а	, CZ41
23-	2^ 2 	:	 dx = —— [еа - exp ae^cz	[а, с, Rez>0].
1 х2 + z2	sin еж	2shcz
о
ею
о>| Г ж 1 - еасозсжсо8(а81псж)	тг acoscy . . . ,	.	.
24. —	 dx = 	е ff sin (a sin су)	а, с, у > 0 .
J ж^ у2	sin еж	2 sin су
I/2	sin еж	2 sin су
о
со
р а cos еж
25. —	 sin (а sin еж) tg 1 еж dx = ±—th 1 cz[exp (ae™cz) — еа]	[а, с, Rez>0].
о
26.
2
о
[i/ = 1/2 - /i или I/ = 1 - 2/Lt; p, Re д > 0].
тг/2
27. е	cos х cos [2ptgж — (i/ + 1)ж] с!ж =	Г(	р 7 е sin —
J	2 \ 2/	2
0	[Rei/ < 0; р > 0].
2.5.45. Интегралы, содержащие разности функций А(ж), е рх,
J sin 6ж 1
\ cos 6ж J
со
Г 1 — е^ах
1.	sin bx dx = In	[Re a, 6 > 0],
°	r	a	b bf a2
h = arctg -, h = a arctg - + - In 1 + —¦
о	a 2 \ b1
о
Г 1 е	1 / a\
2. 	совбж^ж = -In I 1 + —I	[Reo, 6>0].
} x	2 \ b J
3. I I —	-) cosbxdx = lnb^ -ЩгЬ)^-ф(-гЬ)\	[b > 0].
J \еж - 1 ж/	2
о
со
4. e F 	аж = - In Ц		Rep > Imo .
J	ж	2 V P
о
0
p 2 V P:
a2
5. e p	dx = a arctg	 In 1 + —	Rep > Imo .
6. e px	dx = In	[Rep > 0],
J	&
о
/i = p™1 — arcctgp, /2 = 2™1 In A + p™2) + parcctgp — 1,
/3 = 2™ [—p In A + p~ ) + A — p ) arcctg p — p].

2.5.45]
2.5. Тригонометрические функции
379
1 — cos ах
а 1 . 1 — е
[а > 0].
8.
9.
10.
11.
- I rJ.T, =
ех - 1 х )
cos аж-е
az \ . / az \
~7f;smv71"y
dx = — In ¦
¦ cos bx dx = ~~ In —	-
2 b2 + a2
[а > 0; | argz| < тг/4].
[Re а > 0; Re с > |Imb|].
[Re а, Re с > |1тЬ|].
12. I	sin bx dx = — In
"±1O —^ + earctg	a arctg —	[Rea, Rec > I Imbl].
2 o2 + a2	c	a
1O f 1/ -ьж ^сжз1па
13. — I ae — e
} x \	x
а
а. а2 + с2	а
da? = — In	\- с arctg	а
2	b2	с
14.
1 — cos ax
x[e2ncx _ е2(п^1
• dx = — ]
2Csh[fl7r/Bc)
[Re b > 0; Re с > |Ima|].
2
. ^nX cos аж — cos bx .
15. e 	аж = /«
[о, с > 0; n = 1, 2, 3, . . . ].
[Rep > | Ima|,
2 + 62
1 ,
h = - In
2
p , p2 + a2	6	a
In г, I2 = - in	+ 6 arctg	a arctg -.
2 p2 + a2	2 p2 + 62	p	p
p2 + 6
i -юж sm ж - ж cos ж .
16. | e p 	dx = Jn
[Rep>0],
Ji = arcetgp	^у, J2 = l-parcctgp, J3 = - [(p2 + 1) arcctgp - p].
17.
18.
sin аж . ас . а2 + /i2 .	/i .	6
аж= — In ^r	-17 + ch arcctg	ab arcctg -
2 c2 + b2	а	с
[Re b > |Imc|; Re/i > |Imo|].
1
- йж = —
1	Г f In ch [Ьтг/Bс)] - In ch [атг/Bс)] '
2	[I In sh [6тг/Bс)] - In sh [а7г/Bс)] _
- E m-
a = 1/2, m = i, 3,5,...
10 1 ^рж 2ж cos ж - sin ж .	р / 4
19. I e F	sm x dx = ^ In I 1 -\—-
[Rep>0].

380	Гл.2. Определенные интегралы	[2.5.46
со
Г _~.ъ 2ж cos ж — sin ж	, л/тг , -1Ч
20. е		j	sin a? da; = ^— A-е ).
J	ж	2
о
п _ . .	т,	тт Г sha^ 1 Mfe Г sin 6*. ж 1 "fc "гт- Г яЬа^ж 1 Mt f cos6fc
2.5.4b.	Интегралы от ¦ ¦ <	><	г > I I i	fi-
i	fife v	«-/v	^ ^	fe
Г 1 1
Обозначение: S =
^р}11 П \<? + B^ + 2AJ62]
sh[a7r/B6)]j 1=1
Л = 1/2, n = 1, 3, 5, . . .
are 61, arera < тг: ,
1	! A = 0, n = 2, 4, 6, ...
2e f^da.= ^Lth^L	[Rec>|Im6|].
J shcx	2c 2c	L	IJ
о
7r6cthF7r/c) — с	г	I-.
	V—f-t	 [Rec>|Im6|].
Г sin bx , i Г . /с — ib\ ./с + г6\1 ж . Ьж
4. 	 da; = — Ш 	 I - ф[ ——	th—	Rec> Im6 .
J сЬсж	2cl\ 4c J ^\ 4c )\ 2c 2c	L	IJ
о
CO
Г cos bx _ ж , бтг
5. 	ax = — sech—	Ree> Imfel.
J сЬсж	2c	2c
о
(n — 1)!	[ cosech [Ъж/{2с;1 J _
sech[67r/Bc)]
J ) k=i
X = 1/2, n = 1, 3, 5, . . .
те Rec > Im 61: ,
171 Л = 0, n = 2, 4, 6, . . .
CO
f sh ax ( sin 6ж 1	ж г , , ,	, . 41_i Г sh Fтг/с) 1
8. —	<	> da; = — ch (Ьтг/с) + cos (атг/с) < . l V, +
J зЬсж [совбж]	2c	(sin (атг/с) J
о
CO
_ Г ch ax . . . тг	sh(&7r/e)
9. —	81п6жAж = —	\ ; ;	rT	Rec> Reo+ Im6 .
J shcx	2c ch (Ьж/с) + cos (атг/с)
о
k -l
Г J sh ax sin bx 1 da; ж ( sin [атг/Bс)] sh [6тг/Bс)] 1 / Ьж	аж\
J [спажсозож] chcx с [ cos [атг/Bс)] ch [ott/Bc)J J \ с	с J
о
[Rec > | Rea| ¦
со
Г J sh аж cos bx 1 dx	1 J 1
J \ chax sin bx J спеж	\
о

2.5.47]	2.5. Тригонометрические функции	381
1 о
13.
14.
., LCc-e-
+
СО
Г J sin аж sin bx
J \ cos ax cos 6ж
0
oo
J shcx ы"'
0
CO
f shcx sin 6ж .
I п т
ib\
1 in
) *
27Г[СО8(С
| dx
| спеж
2c[ch
2c2 ch
V 4c J M
^/c)+ch(Wc)]-
7Г Jsh[a7r/Bc)]sh
c\ch[a7r/Bc)]ch
7Г sh (a7r/c)
(air/с) + ch (Ьтг/с)
[6тг/BсI
^Зс-а +
, 4c
[Ьтг/Bс)]
[Ьтг/Bс)]
1
ib\ /Зс + а
) ^ V V 4c
¦/с)} [ReC>
1 / . атг . бтг
J V c c
[Re с >
[Re с >
|Rea| +
v1
J
|Ima| +
|Ima| +
[Re с >
Im6|].
Imb|].
Ini6|].
Im6|].
-ik f i f-i ( s'mbx 1
15. sh аж<	>dx =
J	[ cos ож J
0
fsh[ft7r/Ba)]l Г (y + 6)/2 1/1 — ^ ib\ (l-v ib
7Г \сЬ[6тг/Bа)]/ [(l + S ^u)/2j \ 2	2aJ \ 2	2a
[Re и > -6; Re [О - l)a] < -|Imb|].
16. sh ажспаж< f > dx =
J	[ cos ож J
о
_ b ГсЬ[6тг/Bа)]1 Г (и + ё)/2 Л f ib - ua\ f ib + va\
~ 4a2^tt \ sh [б7г/Bа)] J [(l + J-i/)/2j \ 2a J \ 2a J
[Re i/ > -5; Re(i/a) < -|Imb|].
-г- 1 Г, fthaall . . . 1 7Г fcosech[67r/Ba)]l
17.	1 - «{ , \\smbxdx = T	1 , г, // м Г	6, Rea>0.
J [ [ cth аж J J	b 2a i cth[o7r/ Ba)J J
o r .- тж	«TT f shafc^ 1 Mfe f 81п6^ьж 1 ^
2.5.47. Интегралы от ж I I <	> <	> ,
^¦¦¦[сЬа^ж] [cosOfca?J
I
Обозначение: <5 = <J >.
1 / ib\~\ A 1 / гб
a, — I 1 H	I TCa? ^1
[Re a > 1 - 8] Re с > |Imfe|].
oo
ГЖ2П+	fslntel ,	, xn 7Г ^2n + 1™<5	кж	Г	П
2. 	i	> dx = (-1) — o o , , . th—	Rec > Im6 ; <5 = «I
J зЬсж [ cos ож J	2c cFfc»^n+1^d 2c	L	10
о
3. ]^L^dx = lXnchbJL	[Rec>2|Im6|].
I xshcx	2	с
о

382
Гл. 2. Определенные интегралы
[2.5.48
. ха г Г sin Ъх 1 .
4. I —	<	\dx =
СП СХ { COS OX J
isr(a)
Dc)"
5.
СП СЖ I COS OX I
4с
sech —
2c
±С а
-С «,
4с
[Re а > -8; Re с > |1тЬ|].
1'
Re с > |Im6|; S =
о
Г sin Ъх ,	Г /6тг\1 тг
6. 	ах = 2 arete exp —
о
со
7.	ж —ц	dx = —г- cosech — [ бтг ch	2с sh —
J ch еж	4е3	2е \	2с	2с
о
8.
cos Ъх
ж
shaxsin&x
Ьж
—
4а
О
аж . бтг
7Г I — In ch
2c
f sin аж sin b .	if. ,
10. 	с?ж	= - In ch I
J жэпеж	2[ V 2c
0
со
Г ch bx sin2 ax	1 ch Bатг/с) + cos (Ъж/с)
JL JL # I (JL Ju	— ™~°" 111 , / \
J ж sh еж	4 l + cos(o7r/c)
о
shaxcosbx	1 ch [6тг/Bс)] + sin [атг/Bс)]
12. I 	;	ax = — In ¦
[Re с > |Im6|].
[2 Re с > |Im6|].
[6, Re а > 0].
[Re с > | Rea| + |Imb|].
[Rec > |Ima|
ж ch еж
13.
2 ch \Ъж/{2с)] - sin [аж/{2c)]
sh[67r/Bc)]
dx = arctg f77(t
жтеж	ch[a7r/Bc)j
[Re с > |Re6| + |Ima|]
[Rec > | Rea|
[Rec > |Ima|
1.
2.
3.
4.
5.
2.5.48. Интегралы, содержащие А(х)(а + &ch x)
a
СОвбж	/тГ ГA - I/) „„-1/2,1 ч
:	г— аХ = а		P., 1 /o(ch tt)
.	7Г	, бтг (Ь , . \
аж = —^^^^ cosech — sin — Arch а
сЬсж	c\/a? - 1	с \c	/
. 6ТГ . \Ъ д . ,
cth — sin - Arch ( — a
с [с	К
sin еж
СО8СЖ
ж	„Ьж (Ь	\
—.	cosech — sh - arccos a
c\/l - а2	с \с	J
cosbx
dx =
тгб
1 + ch еж	с2 sh (Ъж/с)
[а > 0; Rei/ < 1].
[а > 1; Rec > |Imb|].
[а < -1; Rec > |Im6|].
< а < 1; Rec > |Im6|].
[Rec > |Imfe|].

2.5.48]	2.5. Тригонометрические функции	383
со
cos bx	еж1с 2	и/2 \u-ib/c\ Ы/с( a "\
dx = 	(a — 1	i	\(J,, i I —,
[6, Re(ci/) > 0; a ? [-1, 1]].
b. ;:
J {a + chcx
0
f	COS Ьх	Ж	, 67Г „	, ч
7.	— dx = —— sech — Pib/0-1/2@)	-1 < о < 1; Rec > 2|Imb .
J у a + ch еж	су 2	с
о
CO
——	гг ch еж dx = 	В \v -\	, 1/	„чо n . ,o
[Rei/ > 0; Re Ос) > Re с + |Im6|].
со
Г xs'mbx ж 2 Ьп ( Ьж	Ьтт\
9.	dx = — cosech — отг ch	csh —	[Rec > | Imb ].
J 1 + СПСЖ	С6	С \	С	С J
0
X
2те+5 fslntel ,	(-l)^" д2п+5 Г , . ^^, гб
Re(i/c) ;
Hsh aa; sin 6x 1 с!ж тг / . 26тг 2атг\^
>	 = 	 ch	cos	 x
ch ax cos bx J cos t + ch еж с sin t\ с с J
0
sin [а(тг — t)/с] sh [6(тг + t)/c] — sin [а(тг + t)/c] sh [6(тг — t)/c] 1
cos [а(тт — t)/с] ch [6(тг + t)/c] — cos [а(ж + t)/c] ch [6(тг — t)/c] J
[0 < |t| < тг; Rec > |Rea| + |Imb|; тг Re с > |Re(ct)|].
sh ax sin bx 1 б?ж	2тг
12.	—
k ch ax cosbx J 1 + сЬсж e2[ch B6тг/с) — cos Bатг/с)]
f sin (атг/с) ch (Ьтт/с) 1	f cos (атг/с) sh (biz/c) 11	.
) /(uk /(Kal '/ /^^ /W	Rec> Rea
[ cos (атг/с) sh (oTT/c) J	[ sin (атг/с) ch (отг/с) J J
о
X
со
f sh еж sin 6ж . тт . bt	. Ьж	.	. .
13.	^ж = — ch — cosech —	6, с > 0, 0 < \t\ < тг .
J cos t + ch еж	с с	с
о
со
Г ch еж cos bx .	ж . bt	. Ьж	.	,
14.	dx =	sh — ctgt cosech—	[6, с > 0; 0 < ? < тг .
J cos t + ch еж	с с	с
о
со
Г ch еж cos bx .	жЪ	. бтг	.
15. 	dx =	— cosech —	6, с > 01.
J 1 + ch еж	e2	с
о
со
Г sh (cx/2) sin bx .	тг sh (М/с)
Ш	/¦ Ч	rfg= о WJ» / /• ^/оч	Rec>2 Im6; 0< t < тг .
J cost + сЬсж	2ech (бтг/с) sin (t/2)
о
со
f sh (еж/2) sin 6ж ,	тгб
17. 	V^	rfg =	[Rec>2|Im6|].
J 1 + сЬсж	с2 ch (бтг/с)
о
Г 8Ьсжз1п6ж .	b7rsh(&t/e)	.	,
18. \-	^^^	чо ^ = о ¦ ^ и // / ч	Rec> Im6; t <тг.
J (cost + chc«J	с2 smtsh (Ъж/с)
о

384	Гл.2. Определенные интегралы	[2.5.49
cosbx	.	же
d
.	же
dx =	h
2(	+ t)
dx =
(ж2 + z2)(cos t + ch еж)	2z(cos cz + cos t)
о
en ^ ( exp [^6тг[B^ + 1)тг - *]/(тгс)] ехр [-Ьтт[Bк + 1)тг
+ shJ^f e2z2- [тгBА; + 1) - t]2	c2z2-[TrBife + l
[Re с ^ |Im6|; |t| < тг; Re z > 0].
2.5.49. Интегралы, содержащие Л(ж)(а + 6ch2 xY I
{COS СЖ
Г cos 6ж .	тг	. бтг . 61n(l + v2)
1. 	s	ax = 	=¦ cosech — sin		2 Re с > Im6].
J 1 + сЬ2сж	2с^2	2с	с	L	и
0
о f chcx	l j	ж	,к 61n(l + v^)	ro	T Lll
2. 	^	 cos к аж = 	— seen — cos		Rec> Imbl.
J 1 + сЬ2сж	2c^2	2c	с	L	IJ
о
cosbx . тг { . . b7r\~ . bt
d	h2th
f cosbx . тг { . . b7r\	. bt
3.	—t>	о	dx = —\sh2tsh—	sin—	2Rec> Imb.
J sh21 + ch2 еж	с V	2c у	с	L	IJ
о
oo
f	cos bx	. тг . Ьтт _	/ i Л \
4.	z^^fe = — sech — Pib/Bc)-i/2(ch2t)	[Rec>|Im6|].
J Vsh2t + ch2cx	2c	2c
1/2	ДГ^	1/2 kn
5-
0
6. 	^	smbxdx = ( — l) 	-= „, o ,., sech — cos
[2 Re с > |Imb|].
^smbxdx = ( l)	= „, o ,., sech cos
1 + ch2 еж	l ; 2c^2 ^&2n+1 L 2c	2c
0
[Rec > |Im6|].
2.5.50. Интегралы, содержащие Л(ж)(сЬаж ± cos 6ж)^ <	>.
[ cos еж J
oo
Hshaxsmbx^	dx	тг J 61
ch ax cos 6ж J ch 2аж + cos 2bx 4(a2 + 62)\aJ
о
2. -r^:	:	7Z7^ dx =
сЬ2аж + соз2ож	(а2 + о2)а/2 V	a
о
[6, Re a > 0; Re a > -2].
Г	sin nx	, тг
3.	^^	^dx=—	n = l, 2, 3, ... .
J ж(сЬж + cos х)	4
о
Г ж	sin 6ж	. 6 Ь2 + 2с2	6
4.	—	 —	— dx = —	- arctg -	6у = 2тг; 6, Rec > 0 .
J хЛ — у1 ch еж — cos bx	2с о^ + с1	с
о
Г ж sin 6ж	.	6 Г ^6е^ 1
5. ^г		-— dx = ± arctg- + < 2 ,2ч-1 г	PI/ = Щ t/, Rec > 0 .
J ж2 у2 ch еж =р cos bx	с у Ъс(с + Ъ ) J
о
sin 6ж	.	6
^г	-— dx = ± arctg- + < 2 ,2ч
ж2 — у2 ch еж =р cos bx	с у Ъс(с + Ъ )

2.5.51]	2.5. Тригонометрические функции	385
со
f ж ch ax sin bx .	b
6. \ —z	j -—	^-—<ix = -	у6 = тг; 6, Reo >0.
J x2 — у2 d\2ax — cos2hx	2a(a2 + о2)
о
2.5.51. Интегралы, содержащие (ж2 + z2)^1^	> <	>,
[ ch ax ) { cos bx J
/2	2\—1 I D11 "Л I	f COS &Ж 1
(Ж +Z ) <	f	1 • L Г'
[ ch аж J	[ sin ож J
, 1 sin bx j	тг	же
~bz
о
[Re с > | Im 6|; Re z > 0; cz ф тгп].
1 ;	2
^^ n - к
fe=i
ln
[
3.	= --ch — + ^sh — In ( 2ch— )	[cz = тг; Rec > |Im6|].
2 с тг с \ 2c J
[cz = тгп; Rec > |Im6|; Re z > 0; n = 1, 2, 3, .
ch + sh In ( 2ch )
2 с тг с \ 2c J
,Ьж 2с ,Ьж	( Ьж\
4.	= с sh	ch — arete; sh — =
2c тг 2c B\ 2cJ
= ^[eb^2c)arctge"^/Bc) -e"^/Bc)arctgeb-/Bc)]	[2c^ тг; Rec>
5.	= ^ ce-*«™ + ^^ sh ^ In chN/DC)] + l
тг	4c ch[67r/Dc)]-l
, бтг	1
cch — arete: —^		\4cz = тг; Ree> Imfel.
4c S y^ Sh [6ir/Dc)]
J 2 + г2 chcx
о
sinbx	2f fc (fe + 1/2Jе-"г - (fc
^( '	7T2(/fc
[Rec > |Im6|; Rez > 0; cz ф тт(тг + 1/2)].
7.	= —2 sh	1	sh	2 ch — arctg th —	\cz = тт; Re с > Im 611.
2c 2 с	с	4c
~ ^2 6	v^	ПсЬ[1?7г/Dс)] -1/л/2
— ^2 ch — arctg —r=		[4cz = тг; Re с > | Im 6|].
ж cosbx	тге z	2 \~^ (— 1) ke ж'с
x2 + z2 shcx	2slncz	^ 7T2k2 — c2z2
о	fc=1
[Re с > | Im 6|; Re z > 0; cz ф irn].
~ ^2 12c€	€Vn^ 6	' ~
~ ^^c S V ~ 2 2 € V
11.	= 2 sh — arctg (е^б7Г/Bсм _|	e^b7T/Bc) — 1 = — ch	1 + sh — arctg sh —
2c	2	2 2c	2c	2c
[2cz = тг; Rec > |Im6|].
25 А. П. Прудников и др., т. 1

386	Гл.2. Определенные интегралы	[2.5.51
т
12' Т2
J «^
0
13.
14.
15.
1 coste,
+ z2 ch еж
(-1)п
се~Ьж/Bс) *
тгBгг + 1) jj
2с бтг
= — ch
тг 2с
-^(п + 1/2)тг1
С J
~г ( л\к
\^ ^ ' ~Ъкж/с
-ок-п
еЪж'с arctg (e^b7T/
2с . Ьж . ,
— ch — In A +
+ 1/2ft
ттЦк
\b+-\n
L тг
' i
1 тгBтг
/Bс)) - е
е-2б7г/сч
+ 1/2J-с^2
[Rec > |Im6|; Rez >
A + е-6^)] +
Ff« I 1
[cz = ж(п +
-"/с arctg (еь-/Bс))
[cz
[2cz
0; сг
1; п-
1/2);
= тг;
= тг;
ф тг(п 4
f 2; -е
Rec >
Rec >
Re c>
-1/2)].
_bw/c
Im6|].
Im6|].
Im6|].
тг	4c
бтг сЬ[6тг/Dс)] + 1/^2
ch — In	——	——	[4cz = w;Rec> Imfe.
тг	4с сЬ[6тг/Dс)]-1/л/2
oo
Г th ax sin bx , . . Ьтг 2a , к , / , k\
17.	— dx = b ch	sh — In 2 sh —	\2az = тг; 6, Re z > 0 .
J ж2 + z2	2a тг 2a \ 2a J
о
18.	= -— ebz + ^^ In cth—+ ^ch 6z arctg ehz	[4az = тг; 6, Rez > 0].
2z	z	2 z
Г icthaa?cos&ic .	. ^bz . . . . ^26z\
19.	dx = ^bze ^ch6zln(l^e )	[2az = ж; b, Rez > 0].
J	Ж "Г Z
0
20.	= ^e6z +ch6zln cth — + 2 sh bz arctg ebz	[Aaz = тг; b, Re z = 0].
oo
f cth аж sin 6ж . 2а , к, . бтг
21.	— dx = — sh — In cth —	\2az = тг; 6, Re ^ > 0 .
J x2 + z2	тг 2а	4а
о
Г жсШажеоз&ж .	тг ^bz . . . . bz	. .	^fez
22.	dx = ^2+-e + ch 6z In cth	h2sh6zarctge
J ж + z	2	2
о
[Aaz = тг; 6, Rez > 0].
oo
Г 1 J sh аж cos bx 1 rfaj	тг e~ J sin az 1
J 2 + 2 X h i b j h	2z sin cz \ cos az j
о
J
ж2 + z2 X ch аж sin bx j shcx
1^exp(-fe67r/c)/sin(afe7r/c
1 j
/sin(afe7r/c)\ , f 0 1
\CoS(akw/c)j + {7rBcz2y1)
[Rec > | Rea| + |Im6|; Re ^ > 0; c^ тгп].
1	/ 6тг\ Г . . f sin (аж/с) 1	f cos (атг/с) 11
2	V C/L [cos (атг/с)]	[ sin (атг/с) J J
с f ch (Ьтг/с) sin (атг/с) 1 , Г	/ &тг\ атг	/ 26тг\1
+ — { ,;. 7, ( ) 7/Нп 1 + 2ехр	cos—+ехр
2тг [ sh (Ьж/с) cos (атг/с) J |_	\ cj	с	\C/J
с Г sh (Ьж/с) cos (атг/с) 1	sin (атг/с)
Т-{ А, / ч • / / М arctgl 7 j
тг [ ch (отг/с) sin (аж/с) J
exp (отг/с) + cos (атг/с)
= 7г; Rec> Rea

2.5.52]	2.5. Тригонометрические функции	387
/ Ьп\ ( sin[a7r/Bc)]
25.	= ±сехр	)i г V/ ч
с (ch [Ьтг/Bс)] cos [атг/Bс)] 1 ch [Ьтг/Bс)] + sin [an/Bc)]
Tn\sh[b7T/Bc)]sin[a7T/Bc)] J П
n\sh[b7T/Bc)]sin[a7T/Bc)] J П ch [Ьтг/Bс)] - sin [атг/Bс)] +
2с f sh [Ьтг/Bс)] sin [an/Bс)] 1	cos [атт/BсI	г	,
—\ U\h По \\	По М Г arCtg u га / Д М	2cz = *¦; Re с > Re а + Iin 6 .
тг [ ch [67r/Bc)j cos [an/Bc)] J	sh[&?r/Bc)j
1 J sh ax sin bx 1
\
x2 + z2 \ ch аж cos 5ж J ch ex
sin [air/Bc)] \ J cos [air/Bc)]
+ \sin[a7r/BC)]
с f sh Ьтг/Bс) sin атг/Bс)П i Г	( Ьп\ атг	/ 2Ьж\
T—S	// м г V/	п 1 + 2ехр	cos	Ьехр
эт\сЬ Ьтг/Bс) cos атг/Bс) J [	Vе/	с	V с У
с Г ch [6тг/BсI cos [атг/BсI 1	Г	sin (атг/с)
тг X 2 sh [6тг/Bс)] sin [аж/Bc)] J	[ 1 + ехр (^бтг/е) cos (атг/с) \ ехр (^6тг/с)
[2cz = тг; Re с > |Rea| + |Im6|].
f	1	11
\ ехр (^6тг/с) J J
Г ж J sh аж sin bx 1 с!ж
J ж2 + z1 \ ch аж cos bx J sh еж
о
J sin az 1 2 ^>/ 1\fe ^ exP (^кЬтт/с) ( sin (актт/с) 1
\cosaz/	^^	n2k2 — c2z2 \ cos (актт/с) j
[Re с > | Rea| + |Imb|; Rez > 0; c^ тгп].
J
2slncz\cosaz/	^
2c	V C/L lcos(a7r/c)J	[ sin (атг/с) J 2[1J
1	f sh (Ьтг/с) sin (атг/с) 1 . Г о / Ьж\ аж ( 2Ьж\Л
=Fxi ,;, '[ ) '\\\n\l + 2exv[	cos—+ ехр
2	[ ch (Ьтг/с) cos (атг/с) j [	Vе/	c	\C/J
ch (Ьтг/с) cos (атг/с) 1	sin (атг/с)	.	.
,), ' [ . ; ;(> arctg	 / ч ,	/	ГТ	cz = tt; Re О Rea + Im6 .
sh (Ьтг/с) sin (атг/с) j	ехр (Ьтг/с) + cos (атг/с)
0
1 fee
" 2 \si
cos [an/Bc)] sh [6тг/Bс)] 1 ch [Ьтг/Bс)] + sin [an/Bc)]
sin [атг/Bс)] ch [Ьтг/Bс)] J ch [Ьтг/Bс)] - sin [атг/Bс)]
." sin [an/Bc)] ch [6тг/Bс)] ]	cos [an/Bc)]
T {	/L , , L ч Г arctg L /Л /;	2Cz = тг; Re с > Re a + | Im 6 .
1 cos атг/Bс) sh 6тг/Bс) j	sh 6тг/Bс)
30.	Ж	[(rh
Vch2 ж — 1	ch бтг + cos vn
[b, Re i/ > 0].
2.5.52. Интегралы, содержащие ^(ж), эЬбж, епбж, этаж2,	2
жп J sin тгж"
1.	—	<	2 МЖ = /n ,
J зптгж [ совтгж J
0
/+ = — /+ = — /- = - г = ^^г
1 4тт' 3 16тг' Х 8' 3 1
25*

388
Гл. 2. Определенные интегралы
[2.5.53
2.
ж Г sin тгж
1
1	2
ch тгж [ cos тгж
1 Г 1
{
{ >=.
8 [ 2тг J 8y2
Г sin bx Г sin ax 1 . . тг	_ бтг I sin [6 тг
3. —¦	<	2 } dx = ± — cosech — < ., 2
J впсж {cosax J	2c	2c cos [6 тг
о	L1
/Dc2)]
/Dc2)] J \ch(bVBc))
[атг = с2; а, 6, Rec > 0].
fcosfexfsinax 1 ^
4. —	<	2 \ dx =
J h [	J	c
0
—	<	2
chcx [cosax
ехр
А 6тг1 Г sin dk I
2/ с J \ cos rffc J "
атг2
——
с
тг 6 c2/ 1\
= -r--r + —[k + -] ; a, 6, Re c> 0 |.
4 4a a	J
9
Г cos bx ( sin аж 1 , тг . бтг Г Г cos <i 1	1
5. —	< 2 \dx = — sech ¦— N .	Т~7
J ch еж [ cos ax j 2c 2c |Д sin a J	y2
Г з!п&ж Г sin тгж2 1 	1 bj sin [тг/4 + 62/Dтг)]
2 2
oo
_ Г sh 6ж Г зштгж 1 . . 1
7. —	<	2 ? <ia? = zb-
J shTTX i costtx J	2
¦ ch 6ж f sin тгж
8. I —	\	2
b
cosec -
sIn[62/DTr)]
2 I cos F/2)-cos [67 Dтг)]
ch тгж I cos тгж
cos[62/Dtt)]
sin[62/DTr)]
[d = 62тг/Dс2), атг = с2; а, Ь > 0].
[6 > 0].
[|Re6| < тг].
ЦЯеЬКтг].
- 1
9.
1 + 2 ch Bхж/лД) I cos тгж
= ± I 4 ch ^^ — 2
J cos d 1
\ sincf j
^^3
1
;
12 4тг
1
4
[a > 0].
J sh (Va2 — x2 ) sin bx 1
2.5.53. Интегралы от Л(х)<	,		>,
I ch (va — ж2 ) cos bx I
A(x)
ch (Vft2 — x2 ) sin 6ж j
1. sh (cva2 — x2 ) cos bx dx =
о
2	= тга2с
4
тгас
3.	= —	. Jii
[0 < 6 < c; a > 0].
[6 = с > 0; a > 0].
[0 < с < 6; a > 0].

2.5.54]
2.5. Тригонометрические функции
389
. ' sh (c\/a2 - x2)	ж /тгс	га ( ,	N, , «,
4. ! -т^;	^o/, ; COS^flb = -i/^r- Jl/4 - F- V62 - C2) Ji/4 - I
L z!
(;2 _ ж2K/4
5.
6.
7.
8.
ch (c\Ja? — x2
- cos bx dx = — /o(aVc2 — fe2
7Г
2°
[a > 0].
[0 < 6 < с; а > 0].
[6 = с > 0; a > 0].
[0 < с < 6; a > 0].
ch
(а2 - ж2K/4
\3/2
a
9. Va2 — ж2 ch (cVa2 — ж2 ) cos bx dx =
10.
11.
2(c2 -
2
жа
Io(aVc2 -b2) -
MaVb2 -
ac2\/c2 — b2
h(aVc2 -i
[a < 6 < с; а > 0].
[c = 6 > 0; a > 0].
[0 < с < 6; a > 0].
,' ch (c-\/a2 — x2 )
3/2
2.5.54. Интегралы, содержащие тригонометрические функции
от гиперболических функций.
со
1. cos (ach ж) с!ж =	Уо(а)
2.
3.
[Ima = 0].
[Ima = 0; \Re(i\ < 1].
cos bx fslnfacha?)] .	тг3//2 /^a
eh ж [соз(асЬж) J
4 V 2
f sin 6ж f sin (ash ж)
4.	< ) л \
J УзЬж [cos (ashж)
о
dx =
г /тга r
= ^2 ? ~2~ [
^J ±1/4+i5/2\^/ ~
[a, 6 > 0].
[a, 6 > 0J.

390	Гл.2. Определенные интегралы	[2.5.55
со
Г совбж f sin (ashж) 1 .
5.		< ;	\ > dx =
J yshx [cos (ashж) J
о
1 1жа г	/' a \	/ a \	/' a \	/ a M
['±1/4-г6/2 ^ J ^±l/4+i6/2 ^ J + J±l/4+i6/2 ^ 2"J ^±1/4^*6/2 (^J j	К & > °1 •
2.5.55. Интегралы, содержащие гиперболические функции
от тригонометрических функций.
тг/2
cos ж I /	2
о
тг/2
О
тг/2
sin Bп + 1)ж 1	( i\n7r
cos Bn + 1)ж J	2
J	2 \aj V 2 / М/2
о
тг/2
Г ГзЬ(асо8жI созбж	/тг\3/2 >—	/а\г	/а\
1 ch (a cos ж) I /	~ = V 2/	i±i/4+b/2 ^J i±i/4-6/2 ^J	[a, 6 > 0].
о
тг/2
5.	ch (a cos ж) cos (c sin x) dx = — Jo (Vc2 — a2 )	[а, с > 0].
о
6.	ch (a sin ж) cosnx dx = {—l)n'	— тг/та(а).
о
7.	ch (a cos ж) sinM ж dx = v^" I — j ГI 	 1 /M/2(a)	[Re a > 0; Re/i > —1].
8.	ж ch (a cos ж) sin ж dx = — sha	[а Ф 0].
J	a
о
CO
Г sh (a sin ж) .	i\n-i ^ra2"™1 L ,	a2 1
9.	—	 sin ж 8т2тгж cos (a cos ж) dx = (—1) —7	гт 1 H	7	r
J	ж	8Bn — 1)! |_ 2nBn + 1)J
[a > 0].
CO
Г V, ( " \	1п — 1 Г	2	1
10.	—	 sin ж cos Bn — l)x cos (a cos ж) dx = (^1)те™1 —-;	— 1	-
о
[а > 0].
-- I sh (a sin ж)	/	х
11. | —	 cos ж соз2ггж cos (a cos ж) dx =
о
BAj Ч-1)! + 8Bп-1)! [ 2п(п
i-^?^t [»>o].
f ch (a sin bx) f sin (a cos bx) 1 .	тг f cos (a cos by) 1 . . . . ч
12. 	h-	^{ )	J\dx = T7r\ • /	/ sh asmfet/	a, 6, y>0.
J ж2 — |/2 [ cos (a cos ож) J	22/ [ sin (a cos by) J
0

2.5.56]	2.5. Тригонометрические функции	391
оо
ж sh (a sin bx) ( sin (а cos bx) ] ,
( si
X co
cos (а cos bx) j
и
тг Г Г cos (a cos by) 1 ,.,,ч Г 1 11
= =F77 И • /	L \ Г ch (а sin б?/) - <	>	а, 6, у > 0 .
2 [ [ sm (а cos оу) J	[а cos 6y J J
схэ	f	2 x
Г ch (а sin 2a;) J sin Bа cos ж) I	тг J sin а11
J б2 cos2 ж + с2 sin2 ж ) cos Bа cos2 ж) [	26с \ cos d)
о	к	}
[d = 2аф + с); а, Ь, с > 0].
оо
Г sin (а sh ж) / 1 \ , тг
15.	 sm (ach ж) аж = — sm а	Га > 01.
J shx	2
о
2.5.56. Интегралы, содержащие е™рж, shax, сках, slnbx, cosbx.
^.n-r f sh еж sin еж 1 ,	ю f 2c 1
e p <	da;=-p—^< 2 >	[Rep > | Rec| + | Imc|].
о
oo
f ^vx ( shcx cos ex 1 , c(p2 q= 2c2)
2. e p ^ 1	.	1с1ж = XF. ^A . ;	Rep> Rec|+ Imc| .
f sin 6ж 1
z<	} dx =
{COS ОЖ J
-fic-ib)/Bc) 1 Г (р-Мс + г6)/Bс)
J+ [
Rep > \Re(fic)\ + |Im6|; Re/x > -1 - ?, <5 = | X
о
oo
Г _rTsink , тг , бтг 1
5.	e 	da; = —cth		6, Re с > 0 .
J	shcx	2c 2c b
о
oo
, shaa;sin6a; .	b	ж	shB67r/c)
6. 	—dx = ^—	 '	\ I )
2c ch B6тг/с) — cos Bатг/с)
[b > 0; Re с > |Rea|].
тг	sin(a<77r/c)	f ch (b
ecx ± 1	^ 2(a2 + b2) ac ch B6тг/с) - cos Bатг/с)
о
a = \ j>; 6 > 0; Re с > |Rea||.
ch аж sin Ьж	&	тг	sh (&сгтг/с)	Jcos(a?r/c)
ecx ± 1	2(a2 + b2) ^ ac ch B6тг/с) - cos Bатг/с
о
{cos (aTi
1
<т = <{ }¦; 6 > 0; Rec > |Rea||.

392	Гл.2. Определенные интегралы	[2.5.57
2.5.57. Интегралы, содержащие е ' , shax, спаж, sinbx, cosbx.
со
Г ^РХ2 ( shcxslnbx} , 1 /тГ / с2 -Ъ2\ ( sin[bc/Bp)l I
1.	\е рх i	\dx = -J- exp	 {	'.)/; i	Rep > 0 .
J	[спсжсозож]	2 у p	\ Ap J [ cos [oc/Bp)J J
о
CO
Г 2 -ю2 f sh сж sin сж) . 1 / 7г	Г Г sin d 1 . c2 ( cos d 11 r 9 ,, v	i
2.	ж2е рж {	иж= / J	Л±^ . И [d = c2 Bр ; Rep>0 .
J	[ ch сж cos сж J	4 у F	L L cos " J P I sm « J J
о
. -1/2 vjshcssincxb	^ /^ t /c2\ Jcos[c2/Dp) + 7r/4]
3.	I ж ' e p { ,	> йж = 77774/- i-1/41 t" H . г 2 //. ч /л
sin [с /Dр) + 7T/4J
[Rep>0].
4.		пт" I ^J-1 i-'b^ 0111 i/bt/ I	л/ /1	I ^ — ijc 1 I 1 Sin u	I COS CL I
J	[зпсжсоэож]	Ар6/1 \ Ар J [ [cosdj [ sm a J
0
[d = 6c/Bp); Rep > 0].
CO	^__
Г ^„Ж2 f сЬеж sin сж 1 .	с /тГ / с2 . . с2\
5. же <	> аж = —4/ — I cos — ± sm —	[Rep > 0].
J	[япсжсовсж]	4р у р \ 2р	2р/
о
со	Г	2
Г -1/2 -и2 Г ch сж sin сж 1 . . тг Гс т (с2 \ I cos [с /Dр) — тг/4]
о. ж е <	> аж = ± к/л\ ~~ с/1/41 — Is	2
0	' [Rep>0].
7. ж™2е™рж shpic2 соэбж dx = W— exp I	I	erfc I 	 J	[6, Rep > 0].
-рЖ2 1 Г sin 6ж 1 ,	фг	Г рс2 Ifsindl
0
6c2
9. \ x ' e px (shcx ±81псж)с1ж = —a — /1/4 — <	2	>	[Rep > 0].
J	4y2p \8pJ I sh[c /(8p)]
10.
0
00
11.	е™асЬш sh (ж/2) sin 6ж с!ж = Im К'х^+гьС0')	[a, 6 > 0].
0
CO
12.	f е^асЬжсЬ(ж/2)соз6жAж = Re K1/2+ib{a)	[a, b > 0].
13. е^рж sh —	 )dx = 7rec p\0d 2cp, ^ + 03( 2cp, ^
J	\СПС~СО8Ж/	[ \	27Г/	V	*7
0
[Rec, Rep > 0],

2.6.2]
2.6. Логарифмическая функция
393
2.6. ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ
2.6.1. Введение.
В этом разделе содержатся интегралы, в подынтегральные выражения которых входит
логарифмическая функция. С помощью замены переменной они могут быть преобразованы
к интегралам от показательной и степенной функций. Некоторые интегралы от логарифмов
молено получить путем дифференцирования по параметру. Например,
CXJ	CXJ
f Z lnn(l + х) dx = f хпех(ех - l)^1 dx =
y dx
р=0
[-п < Rea < 0].
р=0
2.6.2. Интегралы общего вида.
В этом пункте помещены формулы, которые позволяют находить интегралы, содер-
содержащие логарифмическую, а также степенную, алгебраические, показательную и триго-
тригонометрические функции. Некоторые частные случаи этих интегралов, соответствующие
конкретным значениям входящих в них параметров, приведены в последующих пунктах.
Значения параметров, входящих в интегралы общего вида, приводятся в фигурных скобках
после каждого интеграла; г = p/q, где р и q — взаимно простые натуральные числа, если
не указаны другие условия.
у
In (еж + d)
1.
In \cx — d\
dx =
p-i
,.а + гв — г
2.
dya^r-r-
OL-h-1 A	d\H
	, /3 =F— X2
r	J\ cyj
- I 7Г
с ,
> I — Хз +
кСУ/
[\cy\>\d\].
l Если r > 0 — произвольное, то р = q = оо и Xj — 1? j — 1? 2, 3; если r > 0 — рациональное
(	/)
(r = p/q), то
q+2 q
(h
X2 —
h-P),(a-
Rea, Re/5 > 0;
arg (еж + d)\ < тг при 0 < ж < у
с, d > О
}]¦
3.
In |сж — d\
dx =

394
Гл. 2. Определенные интегралы
[2.6.2
\n{dx
4.
In \cx — d\
p-i
0 < Re^ < 1-Rea/r;
> dx =
-,i-p-
| arg (еж + d)\ < тг при ж > у
с, cf > О
cy\h
-— 1 i
\d)	Ж
(—l)h(l —
cosec [(r — rp — а + гЛ,)тг] 1 /cy\rh
ctg [(r - rp - a + г/1)тг] JvT/
-,1-р-- lnd	[|cy|<|d|].
5.
= ?|r(p-i)
A-PM-I)h f cosec [(a + гЛ)тг] 1 /d
1
cr ^-^ h + 1 \ r
< Если r > 0 — произвольное, то р = q = oo и %j = 1, j = 1, 2, 3, 4; если r > 0 —
рациональное (r = p/q), то
1, (Л + 1)/р, А(д, (а-
X2 —
l, Д(д, 1-/9 + Л), (l-/» + /i)9-1-ap-1;
. _1	_i
A(q, h + 1), 1 + A - p + h)q - ap
l,
1, A(q, 1 - p + A + h - a)r^1), (h + l)/p; z^1
cyy
Re a > 0, Re (a + rp) < r; r| arg y\ < тг;
f | arg (еж + d)\ < тг при 0 < ж < со
I
с, d > 0
6.
In (еж + d)
dx = —
rrf ^^ h +
h=0
cy\h	2 ( c
/i=0
1	/ cosec [(r + гЛ, — а)ж] 1 /cy\r
\ [(	)] ~j)
ctg[(r + rh - а)ж] j\ d
ж а^г аж
	у cte	In d
r	r
X2 ¦

2.6.2]	2.6. Логарифмическая функция	395
cosec [(a + гк)тт] 1 / d V
ctg [(a + гк)ж] j \cy J
h^a \f d\h
	тг if —
Ctg 	 7Г T— X4 -
— ттг^2уа^г ctg	 r In (cy) — 2тг cosec — тг	[ Icyl > d].
r [	r J
{Если r > 0 — произвольное, то р = q = 00 и %j = 1, j = 1, 2, 3, 4; если r > 0 —
рациональное (г = p/q), то
Xi = 2*i(l, (ft + l)p-1; 1 + (ft + l)p"x; г),
X2 = 2-Fi(l, (r + r/i — a)p-1; 1 + (r + rft — a)^; z),
Xi = 2^1A, (a + rh)p^; 1 + (a + rft)?; г),
X4 = 2FXA, (ft + I)?; 1 + (ft + l)p-x; г), г = (тсу/d)"}
' \	e, d > 0
[p = 0, 1/2],
8. J,-
0
/
Up 2 I
i (гЛ/2 + V*r + У)" P»» («я-«0
(ЖГ + Г)" \bcx-d\
-\-rv/2-pr+l Р^З 91' + 2('г + а + 1)/г /
dr ^ ft + 1 U,
i 1 — 2p / i т/2 — то ^"
~г ^ 7Г1 — J V /
J cosec [r(l — i/)/!
X\ ctg[r(l-i/)/2
2r -a-ri//2 <)~1
J cosec [Bp — i//2
X 1 ctg[Bp-i//2-
,ч a q-1 , -|\h//-i \
/ d Yh d a+riy/2^Pr^i
X \cy) X4+ сУ
у к У п 1
V r
-\- v v 2 I —
/ dX — LJ p
^Л!C/2-
\ 1 — 2p
1 \/
2p)h{r{l-v)/2
2 + hr — а]ж 1 / су \rh
+ hr-a\<ir j\~d) X2 +
("l)hBp
+ /i)r — a]?
f /i)r — а]тг
'2U2P-U,
h(a + rh)
1-1 r+2(a-
- r J
i/r Vp
r + a J
-v/2)h{2p + v
Л(слх\3 +
j\d J X
ВI —, 2p — и
/2)h / cosec (a -
1 t ( 4-
1 Ur + Л-
V С2/У
В ( —, 2p- i/ -
I r
_v)/2)h
+ hr-a]
/2)h
) 1 /Ч
2a\
rj
- rhOГ 1
\l-2p
2a\
— x
r /

396
Гл. 2. Определенные интегралы
[2.6.2
2p~?/~ — ) + ф(-
г J \г
- и - -
г
1Ы > \d\].
2aN
r J \ r ,
l Если r > 0 — произвольное, то p = q = oo и Xj — 1> i — 1? 2, 3, 4, 5; если r > 0 —
рациональное (г = p/q), то
Х2 —
Х4 —
Х5 =
;
, | - 2р + A A(g5 Л + 1), 1 + (J(l - i/)
+ Лг - а) ^
P
—; z
, 1
A(g, 1 - г/ + /i), A(g, 1 + /г), 1 + (а + rh)-
Rea > 0;
d J
f I are (еж -f d)| < тт при ж > О
i/r) < 2rp; r argy < 7г; ^ '
[	с, d > 0
}]¦
oo
-rpff pr-r«/2-a-ll
1JK
¦ In (же? + с) i
2рг — 2а
10.
p = 0 или 1/2; Re a > 0; Re Ba + vr) < 2rp; r\ arg y\ < тг;
i (ex + d)
In \cx — d\
dx =
h=0
2r(l - 2p)
rv + 2pr — 2a
arg (еж + d)\ < тг при ж > 0
с, d > 0

2.6.3]	2.6. Логарифмическая функция	397
Г cosec (a + hr)w I f dr s\	^2 _а/Гтп/а\ Г i	i , //аМ
х<	Л , / И 	 X2 + r s ' Г — fine - Ins + ё — .
[ ctg (а + пг)ж ) \ cr J	Vr/L	Vr/J
< Если г > 0 — произвольное, то р = д = оо и %i =%2 = 1; если г > 0 — рациональное
(г = p/q), то
^ 1 + (h + 1)р-\ А(д5 1 + A + Л - а)^1) J '
Ы
Re а, Res > 0;
с,
\
/
| arg (еж + d)\ < тг при ж > 0 11
О	JJ*
11. I жа 1з1п6жг<| |	, [> б?ж = (/(<5)
о
р-1
s (d\a+rS Г.1(^l)hf cosec (a + 2/ir + Sг)
7Г V	^
¦OГ}( —
су ^-^ /i!(<5 + 1/2)h(а + 2Лх + <5г) [ ctg (а + 2/ir + ёг)ж j \2ег
^ — ос/г / (х\	j*$ — (х Г	/О\	/
Н	г- Г ( — cos	тг 2r In с - 2 In 6 + i/> [ — 1 + (tg
2r2 \r/	2r I	\r / \ 2r .
i Если r > 0 — произвольное, тор = д = оои%1 =Х2 = 15 если r > 0 — рациональное
(r = p/Bq)), то
. A / 1 1 ., , ч\д/ -, /i + l-a
X2 =
p
1 + (a + h + гс5)р^\ A(g, /i + 1), A(g, /i + 6 + 1/2) I'
•=<-<№)'}
cj \2g
[_ ^	,	f | ащ(сж + d)\ < 7Г при ж > 0 11
— r<5 < Re a < r; b > 0; <	>
' I	c, d > 0	J J
12. Тж-1сО8^A1п;сж+^Ьж=^)
J	[ ln|c»-d| J
о
2.6.3. Интегралы от ха 1пст ж.
[U(S) см. в 2.6.2.11].
5=1
ж ln°" — с!ж = a a a Г(сг + 1)	[a, Re a > 0;
о
l
2.
о
l
. [жа^11ппжс1ж = (-lO1^^71^1^!	[Rea>0].

398
Гл. 2. Определенные интегралы
[2.6.4
, a In A + bx) — 6 In A + ах)	а
3.	ах = аи in -—
xz
[a, b > 0].
о
2.6.4. Интегралы от
a-l
1.
ж"
ж
о
??0 к\(а
Е
2
1 г" In т
3. I 	dx = /м
-L ~т~ Ж^
[a, /i, Re а > 0; Re a > -1].
[/1, Rep > 0; /i| argz| < тг].
[/i, Re а > 0],
4.
/i2 cos2(?r//i) *
[/i, Rea > 0; n = 1, 2, 3, . . . ],
Ja,n =
*, 21
х,2/-1
=
J^/2'2I=(^) i
r3M/4,2 _
252/x6
61/ttV
2
127 /тг
401 д
5-
та"! lnn т
*, Rea > 0; n = 1, 2, 3, . . . ],
»1--^	гЗ/х/2,1 _ 7Г
/i2
i-n/x, l y—-1-;
12	^-^ A^2
fe=i
2 ( "
2^ '
1
7тг4
120
7тг4
ЗО/i5

2.6.5]
2.6. Логарифмическая функция
399
a-1in	i / а \п
6. I *	HL^ da = - '	^
['"-'<¦ >-t)\
> 0; /Lfc| argz| < тг; 0 < Re a < ц Re p].
7.
1 In ж
dx =
1 In
9.
In ж
В ( —, p	/i In z + ^ ^ - ^ I P
[/i > 0; fj,\ argz| < тг; 0 < Re a < fi Re p].
m-l
/X In Z — ^J ———	7Г Ctg ::i:i
tb fli	ft	fJj
> 0; ц\ argz| < тг; 0 < Re a < jura; m = 1, 2, 3, . . . ].
771 — 1
(m - l)!/i2
2«l/2 —m
2m - 1
|argz| < тг; m = 1, 2, 3, . . . ].
10. | f 11П'Ж с!ж =
(ж^ + z^)^
11.
12.
13.
14.
ire
15.
16.
¦dx = 2 ^ /x
. > 0; fi\ argz\ < тг; 0 < Re a < fi Re p].
l,.x^,li	[|i, Rep>0].
¦da? = 0
dx = —
+ z^	/i c?ftn sin (an/fi)
[fJL > 0].
[/* > o].
> 0; /i|arg2;| < тг; 0 < Re a < fj].
+ z^
sin (an/
2 2	«ТГ
In z — 2тг/1 In z ctg	1——
2 а7Г
1 + cos
¦ In — dx = 0
sin2 (аж
> 0; /i|arg;z| < тг; О < Re а < /i].
[z > 0; а - д < 2].
1.
2.6.5. Интегралы от 7
жа^11ппж , а^^г) дп
dx =
/i dan
fa
a BIB,—
[a, /i, Re a, Re^ > 0 (Re^ > -тг при a = 1)].

400	Гл.2. Определенные интегралы	[2.6.5
а
Р	пг	( 1 \ к
2 1 а — 1/и,	и\т 1 п «^ I	/ -i\n I a + tiTO \ "^ / "^ \	\ -*-J	г	л1
. \х (ег^ — ar ) In — dx = ( —1) га! а р > I O—-—;ч .1	а, ц > 0 .
J	v	;	а	1 ;	^ V к ) (а + /ifc)n+1	L	J
771 ( 1 \k (
о
[a, /i, Re a > 0; Re <r > — то — 1].
4. —:	——dx=	В [p, - /ilna + ^ - )^ф [P+-
[a, д, Re а, Re^ > 0 (Re/З > -1 при а = 1)].
Г таЧ In2 т
«L	III X
5. 7	——- ax =
[a, /i, Re a, Re^ > 0 (Re/3 > ^2 при a = 1)].
1
6. —	In" ^dx= l t, j У f—г	[к| >1; /x>0;
о	к=1
Г ж" - 1	.^.i /	а .
7. 	In — da? = Г(сг + l)/i	{I <т + 1, — J	[Re а, Re<j > О].
J 1 — x^ x	\	/iy
о
1
8. f Ж	1пст i с!ж = Г(G + l)^"^"^^ + 1)	[/x, Rea > 0].
H, П tCX, П	—П —1
1 = M
9. 	Inn xdx = /"'n, /"'n = -Д n iA(n) I — I	[u, Rea > 0; n = 1, 2, 3, ... I,
0
"«^-irri-^i	[» = i,2,3,...:
4 fe=i
i, 1 , Tk-m, 1 _
2M2'
i Г n^1
r(n+l)/z,3 _ J- L\^__J___ Я" I	r(n+l/2)/z,3 _ J- o^ ^^	x	4 I
63

2.6.5]
2.6. Логарифмическая функция
401
10.
11.
1-х*
\n2n~1xdx =
12.
1 -
1п2
)!/i^2n^1B2n+1 - 1)СBп
13.
> 0; п = 1, 2, 3, . . . ].
> 0; 7i = 1, 2, 3, . . . ].
[/х > 0; n = 1, 2, 3, ... ].
[pt, Rea > 0; 7i = 1, 2, 3, . . . ],
' п — к — 1 тг2
jfe2"	б"
/M/2,1_ ж(п
"'2 -
"
'2 -
2 J'
гг — к
Bnf
2/л-
2m+l
/I 4
15/i5
, 2m
/ о \2
_ / ^ \
— 1	I
-Мпп;
/1 У /1
ctg —
[О < Rea < /ига; тг ^ га; то, тг = 1, 2, 3, . . . ].
15.
16.
- 1
27Г) ' П4
[/х > 0].
dx =
, ж08 In ж , тгг/а"м
17. 	дж =	—
/ ctg
тг . атг
- /х In j/ ctg
sin (атг//х)
i, у > 0; 0 < Rea
j,, у > 0; 0 < Rea < /i].
is.
О7Г \	2 2
1 fl J
i, t/ > 0; 0 < Rea < /i].
26 А. П. Прудников и др., т. 1

402	Гл.2. Определенные интегралы	[2.6.6
ха 1па ж
2.6.6. Интегралы от
ах1 + ох + с
(а + бJ
Г In ж , тг , G	г
2. —г——- dx = — In a		о > 0 .
J ж2 + а2	4а	а
о
1
3. I —,	г 1па -dx= у ' > f ,
х1 — lux cos 7 + a	x	sm7 ^ [a + Aj — 1)
о
[a > 1; 0 < 7 < 2тг; Re a > 0; Re <j > -1].
l
4. —	 dx =
19	Oi^
ж2 — 2аж cos 7 + a2	oan {	sin атг
о
[a > 0; 0 < 7 < 2тг; Rea > 0].
l
In2 ж	, 7G - 2тг)G^ тг)
x2 — 2жсо87 + 1	6sin7
о
4	^
Г	In ж	, 7G 2тг)G тг)
5. —	TTdx=	a - 	"	[0<7<2тг].
J x2 — 2жсо87 + 1	6sin7
6-
2
ж2 —
о
Ж 1П Ж	_ fe, n
J ж2±ж1
о
/+'1 = -0, 7813024129 . . . , /°'1 = -1,17195361935 . . . ,
/+'1 = -0,15766014915 . . . , /i'г = -0, 3118211319 . . . ,
9.
10.
11.
12.
f ^ ~
} x ¦— 2i
о
i
Г (ж + ,
J ж 2,
0
l
J-~'i
0
0
1
ж""
J 1
0
ж"аIп
x cos 7 -
x ) In
71
ж1пж^
1 1» i
1 + (a
-j
-
j0,2 8тг
. ж л тг sin [G — тг)а] f
Ь 1 sin 7 sin атг
2
sln7sina7r l ; ^ }"
пж | с!ж i'( \ 1
- ж У 1 — ж ^r v^;
dx тг2
1 - ж 6
— 1) In x ж In ж
I i J
f0,2 Ю7Г
+ 27rctga7r 7
/ // \ -1
[аG^тг)]}
[0 < 7 < 2тг; | Rea| < 1].
[0 < 7 < 2тг; | Rea| < 1].
[Rea>0].

2.6.6]
2.6. Логарифмическая функция
403
13.
14.
ire
15.
16.
ж(ж — z)
In
dx =
(z)
|arg(l - z)\ < тг, Re о- > -1] или [z = 1, Re «т > 0].
^	1 ГТГ2	/l\	1 2
;г da = - — - Li2 I - I - - In у
x(x-y)	у [ 3	\2/y 2
dx = - Li3 I - - - In j/ + — In 2/
2/ [ V2// 6	3
1пте x dx
= /„
[У
[Imo = lmb = 0],
/o =
а — 6 '
¦In
/i =
2(a-6)
(In2 \a\ — In2 |6| + A sgn а)	[Л = 0 при ab > 0; Л = тг2 при аб < 0],
/2 =
3(а - 6)
Aп3
[В = In |а/6| при а, 6 > 0; Б = In (ab2) при а > 0, b < 0;
Б = - In (а26) при а < 0, 6 > 0; В = 2 In |Ь/а| при а, 6 < 0].
17.
18.
х2 — 2ах cos 7 + «2	sin 7 ^«n
[а > 0; 0 < 7 < 2тг, 0 < Rea < 2].
dU 111 «I/ , П Uj
	 ?|^p ==
ж2 — 2аж cos 7 + a2	sln7sln2a7r
19.
20.
21.
x {In a sin an sin [(a — 1)G — тг)] + 7 sin атг cos [(a — 1)G — тг)] + тг sin [7@ — 1)]}
[a > 0; 0 < 7 < 2тг; 0 < Re a < 2, a ф 1].
In ж	(тг — 7) In a
ж2 — 2аж cos 7 + «2
a sin 7
ж2 — 2ж cos 7 + 1
х1 — 2ж cos 7
dx =
2тг sin Г
L
sin 7 sin атг
22.
23.
In2 ж
ж2 — 2аж cos 7 + о2	a sin 7
= О
c2 + 6ж + 1
[a > 0; 0 < 7 < 2тг].
¦ {тг ctg атг - G - тг) ctg [0G - тг)]}
[0 < 7 < 2тг; |Rea| < 1].
[аG — 7г)] — •
[0 < 7 < 2тг; |Rea| < 1].
[a > 0; 0 < 7 < 2тг].
|6| < 2; ?г = 1, 2, 3, . . . ].
26*

404
Гл. 2. Определенные интегралы
[2.6.7
2.6.7. Интегралы от ха(а — х ) 1пта ж.
1	1/п —1/ 2	2\—1/n i
I. ж	(a — ж j In
о
2 ^-i/n^^ 21na^7rctg[7r/Bn)]p^ 1 1
8a1/^cos[7r/Bn)] \ 2n ' 2n
[a >0; n = 2, 3, 4, ... ].
[n/2]
3. | flnx dx = Аа
/2 2
a > 0; jB = тг/2, r = 0 при n = 1, 3, 5, . . . ; В = 1, r = 1 при n = 2, 4, 6, . . . ].
-1) In 2 + In a+ (^1)
Jfe
[a > 0; Л = тг/2 при m = 0, 2, 4, . . . ; A = 1 при m = 1, 3, 5, . . . ].
а
1. Ж У W
2 — ж2 In ж с!ж =
= Аа
m+i(m-l)!!
(m + 2)!!
[a > 0; Л = тг/2 при m = 0, 2, 4, . . . ; A = 1 при m = 1, 3, 5, . . . ].
[a > 0; jB = тг/2, r = 0 при n = 1, 3, 5, . . . ; В = 1, r = 1 при n = 2, 4, 6, . . . ].
тт In2 т	fw — 1 VI
, «?, III X	m yill LJ..
6. , ^	dx = Aa ±	tt^
[a > 0; Л = тг/2 при m = 0, 2, 4, . . . ; A = l при m = 1, 3, 5, . . . ].
7.
1.
In Ж
dx =	In 2	.
8	2
2.6.8. Интегралы от Л(ж) lnn ж.
6
1пжс1ж	1 т^ / \/Ь2 — а2
26
1п(а6)
[0 < а < 6].
2.
In ж dx
1	I / a
/а2 + .
Г	In ж с!ж	1 [„/йЛ, / , v тгт;г.
3.	/	= — К ( - J In (ab)	К
J ^f(a2 -х2)(Ь2	-х2) 2&L \Ы	2
. f 1 + ж , ,	1 тг2	Г 1±а? , ,	3±1 2
4. 	In ж ах = 1	. *>а 	д In ж dx =	— тг .
J 1 — ж	о	J 1ТЖ	^ •
о	о
[a, Rez > 0].
[0 < а < 6].

2.6.8]
2.6. Логарифмическая функция
405
6.
In х
(ж2 +
- dx =
¦In-
2zVz2 + 1 я + л/z2 + 1
[Rez >0].
7.
2 In ж dx
A-ж2)A + ж4)	16B +л/2)'
[О < Rep < 1].
9. х1"
i
¦ In ж dx = ±-
10.
In ж dx
15.
\n(zy)
K
[±Rei/ < 0; /x > 0].
[* > 2/ > 0].
\1 —2r	an
/x
a//x, 2r- i/ - 2a//x"
[r = 0 или 1/2; /i > 0; ft Re (±i/ - t/)/2 < Re a < fir - fi Re i//2].
¦Inx dx =
\ol/fi + (i/ =F l/)/2, 2r — i/ — 2a/fi]
[r = 0 или 1/2; /i > 0; /i Re (±i/ - v)/2 < Re a < fir - fi Re i//2].
n / _2в/мг Г2а//х,
[r = 0 или 1/2; /z > 0; 0 < Re a < =F/i Re i//2 + fir].
[r = 0 или 1/2; /i > 0; 0 < Re a < fir =p /1 Re i//2].
[r = 0 или 1/2; /i, Re a, Re (a + fiv) > 0].

406
Гл. 2. Определенные интегралы
[2.6.9
16.
/X,
1 — 2r I >	[г = 0 или 1/2; /i, Re a, Re (a + jxi/) > 0].
it.
[r = 0 или 1/2; jla, Re a, Re (a + /л/) > О].
is.
f
21n2
[r = 0 или 1/2; /i, Re a, Re (a + [lv) > 0].
2.6.9. Интегралы от ж" 1пп(аж + 6).
а
¦*	ос — 1 1 / 1^ \ j 	 о; — iri / с\ \ о ( |_ 1 \\
J
а п г n/i\fc i/i\п 1
5. хп~г In (а + ж) dx = — (^lO1™1 \j -——*¦	h In а -\	— In 4
Jo	n L k=1 k	2 J
[a > 0; Re a > 0 (Re a > -n при о = 1)].
[a > 0; Re a > 0 (Re a > -1 при a = 1)].
In 41	[a>0].
4. жга
о
. lxa^1lnn(a^x)dx = aaj—[a^B(aJ /3 + 1)] ^=0
[a > 0].
[a. Re a > 0 (Re a > —n при a = 1)].
6. ^lnn(l^
J ж
о
a
7. ж"^1 In (a - x)dx = a~1aa[lna - С - ф(а + 1)]	[a, Rea > 0 (Rea > -1 при a = 1)].
8.
¦In 2.

2.6.9]
2.6. Логарифмическая функция
407
9.
11.
In (I ± ж)
1/2
тг2
_
1пA-ж) J In2 2 тг2
In 2.
12. [ж"1п2(а + ж)dx = ааа^1BAпа - С)[1п2 - /3(а + 1)] + In2 а + 2а V
J	I	^
^ *(<* + *) J
[а > 0; Re а > 0 (Re а > -2 при а = 1)].
а
13. f ж"1п2(а - ж) с!ж = ааа{[1п а - С - -0A + а)]2 + тг2/6 - ^'A + а)}
[а > 0; Re а > 0 (Re а > -2 при а = 1)].
15.
16.
о
п+1
+
17. I" In [ж] da; = ln(n!).
i
J	l	;
18
19.
= аа V
i ______
ln
20. x~n~1\n{x + a)dx =
а
со
J
lna+
In4
21
{
asm an { cos аж
22.
[а > 0; Re а < 0].
[а > 0; Re а < 0].
[а > 0].
[-1 < Re а < 0].
[а > 0].
23. f Z1п2(ж + a) dx = а~гаа ll (С + - - In a) [In 2
J	1 V ft /
00	f
24. f ж"1п2(ж -a)dx = ^а^аа\ [С + ф(-а) - In a]
2
-а) - In a]2 + —
[а > 0; Re a < 0].
[а > 0; Re a < 0].

408
Гл.2. Определенные интегралы
[2.6.10
2.6.10. Интегралы от ха(ах + ЬI3 1пп(сж + d).
[а > 0; Re а > 0 (Re а > —п при о = 1)].
2-
1п"(а+x)dx=(-1)n
[Re/3 > 0 для 1ппA -ж)].
Ф(Р)} - аа
5-
Г In (а + ж) In 2	2ч
6. —	 dx = 	In Bа )
Q, "т" Ж	Z
7.
[а > 0; Re а > 0 (Re а > -1 при а = 1)].
[а>0; рф\\.
[а > 0].
[a > 0].
8-
In2 2
9-
72
11.
9 24
k)(ln a
[а > 0; Re а > 0 (Re а > -2 при а = 1)].
1П2A +
2) "

2.6.10]
2.6. Логарифмическая функция
409
15.
.-х)
16.
A-я)
0-1
¦ In A + ж) dx = - 3F2A, 1, 1; 2, /3 + 1; -1)
[Re/3 >0].
17.
х)р
2)"
2) + 2C)"
18.
¦ dx = a 1 p x
¦fc) + (C + ^B + fc))'
20.
- '¦" '•
[Re/3 >0].
22. ж
/ж 1 + ж	4
-;—	T—t- dx = d
a^B{a, f3 + lJFi (p, a; a + /3 + 1; -^
[a, Re a > 0, | arg (еж + d)\ < тг при
24.
a
25. [^(a'
26.
(I _
[a, Re a > 0, | arg (ex + d)| < тг при 0 ^ ж ^ a, |ae| < \d\].
-1 lnn(a -x)dx = a" ^ [a^B(a, /3)]
[a, Re/3 > 0; Rea>0(Rea>-n при a = 1)].
 In (a — ж) dx = aa B(a, /3)[ln a + i^(/3) — ^(a + /3)]
[a, Re/3 > 0; Re a > 0 (Re a > -1 при a = 1)].

410
Гл. 2. Определенные интегралы
[2.6.10
28.
29.
а
.Г -1(a-*)/3-1ln"(
= а	В(/3, а){[ф(/3) — Ф{Р + о) + In a] + ф'(/3) — ф'(/3 + о)}
[а, Re/З > 0; Re а > 0 (Re а > -2 при а = 1)].
— р, а; а + /3; —-
^I
а / Jp=o
[а, Re а, Re^ > 0; | arg (еж + rf)| < тг при 0 ^ ж ^ а].
а	а
["(а - ж)^ In (еж + d) dx = f ж^ In (ас + d - ex) dx.
30. [in
31.
1 + ж dx In2 2 тг2
2 1-я	2	12
[ ха-г(а - xf'1 In (еж + d) dж = аа+/3^1В(а, /3) 1
+ cd аа В(а + 1, /3) з-^Ъ(ск + 1, 1, 1; 2, O + /3 + 1; —ac/d)
[a, Re a, Re/З > 0; | arg (еж + d)\ < тг при 0^ ж ^ а].
In d
32.
33.
34.
35.
36.
37.
38.
39.
)х /а + о ах	а	2/г
7=^	 =	т=г arccos V о
/ж	а — ж	л/а
In (а -ex)	1 + л/1 - с
^J y = с!ж = 2тг In	h тг In а
dx = тга In
- л/d + ас
/ж л/1 —
[о > 0; 0 < 6 ^ 1].
[0 < с ^ 1].
[а, 6, с > 0].
[0 < с < 1].
ж л/1 — ж
^(р^а
Р - а	V	ас
[Re (а ¦— р) < 0; | arg (еж + d)| < тг при а ^ ж < ею].
d
ас
(Р)*
^(p-a + k)k!\ ас/ [' ^	р
[Re (а — р) < 0; | arg (еж + d)| < тг при а ^ ж < ос, |d| < |ас

2.6.10]
2.6. Логарифмическая функция
411
40.
41.
(еж + d)p
д/Зп
d
ас
/3=0
42.
{ex +
p — a
[Re (a — p) < 0; a > 0, | arg (еж + d)\ < тг при a ^ ж < oo].
(In a - CJFi ( p, p - a; 1 + p - a; -— ) -
(p-a
ф(р-а
[Re {a -— p) < 0; a > 0, | arg {ex -}- d)\ < ж при а ^ ж < oo, |d| < |ac|].
oo
43.	ха~г{х — а) 1пп(ж — a) dx = a"'1— [a B(/3, 1 — ex. — /3)]
[a, Re/3 > 0; Re (a + /3) < 1].
oo
p
44.	ж (ж — a) In (ж — а) с!ж = a	B(/3, 1 — о — /5) [In a, ¦
45. жа 1
a_i 1п2(ж — a)
dx =
= aa+^1B(l^a^/35
[a, Re/3 > 0; Re(a + /3) < 1].
- a - /3) + In a]2 + ф'(/3) + ^A - « - /3)}
[a, Re/3 > 0; Re(a + /3) < 1].
46.
x [(acf B(/3, 1 - a - /3 - pJF1{~p1 1 - a - p - p; l^a-p; -d/(ac))]p=0
[a, Re/3 > 0; Re (a + /3) < 1; | arg (еж + d)| < тг при а ^ ж < oo].
oo
47. f /^(ж - af^1 In (еж + d) dx =
= aa+/3mlB(/3, 1 - a - p)[\n {ас) + ф{1 - a) - фA - a - /3)] +
+ dcaa+/3B(^, 2 - a - /3KF2B - a - ^, 1, 1; 2, 2 - a; -d/(ac))
[a, Re/3 < 0; Re (a + /3) < 1; | arg (еж + d)\ < ж при а ^ ж < oo].
48.
49.
d) d!B = (-1)" (I
(cx
(a, P - a)}
[Re a, Re {p ¦— a) > 0; | arg (еж + d)\ < тг при 0 ^ ж < oo].
- а)]
[Re a, Re {p ¦— a) > 0; | arg (еж + d)| < тг при 0 ^ ж < oo].

412
Гл. 2. Определенные интегралы
[2.6.10
СХ —L	JCX — L
50. | 	In (ex + d)dx = 	[In d - С - фA - a)}
51.
52.
53.
сх + d
CL)"
54e j У+ЖУ^ = -^(Р)
о
55.
[0 < Rea < 1; |arg(caj + d)| < тг при 0 < ж < оо].
[0 < Re a < 1; | arg (еж + d)\ < тт при 0 ^ ж < оо].
[Rep > 0].
'B(q!, p — Qj){['0(p) — Ф(р — Си) + In tt] — ф (р) -\- ф (р — С*0}
[ | arg а\ < тг; Re (а - р) < 0; Re а > 0 (Re а > -2 при а = 1)].
[Rep > 0].
) + р^/#(р+1)	[Rep > 0].
56. /4 Ш 1Ж +4Dj с!Ж = аа~рВ(а, р - а) х
Р
57.
58.
[Re (а — р) < 0; | arg а|, | arg 6| < тг; Re а > 0 (Re а > —1 при 6 = 1)].
,1,1; 2,р+1; 1-а)]
[Re р > 0; | arg а\ < тг].
(ах + i
¦1пп(сж + d)dx =
59
t j:— [a ki{ct, p + а ¦— ct) 2-i4i{o щ ® + р; I — аа/(ocj)Jp=o
[Re (а — а) < 0, Re а > 0; | arg (еж + d) \, | arg (аж + 6) | < тг при 0 ^ ж < оо].
жа^1(ж — а) In (х + а) dx =
= аа+^т1{В(/3, 1 — а — /3)[1п а + ^A — а) — -0A — а — /3)] +
В(/3, 2^a^^KF2B^a^^, 1, 1; 2 - а, 2; -1)}	[а, Re/5 > 0; Re(a + /5) < 1].
О О # I /	v 111 | С^ JL/ ""у" О/ | Сл«Х/ —— I ™"™" J U	JL/1 Lx « С/ ~~""~ Lx | \ III Сл "~~" 11/ I С/ "~~" LX | "~Г"
+ -г-
[Re (a - <j) < 0, Rea > 0; |1 - od/Fc)| < 1; | arg (еж + d)\, \ arg (ax + 6)| < тг при 0 ^ ж < оо].

2.6.111
2.6. Логарифмическая функция
413
, In (еж + d) .	2тг . ^ad +
61. I —p^7	~~ dx = 	 In
/ (	b)
ax + b)
v a
62. x
[ I arg (еж + d)|, | arg (ax + b)\ < ж при 0 ^ ж < oo].
Ы(СХ+^ dx = na-^%-1^2 ( In	^— т
(аж + bJ
¦ In la — ж| ,	тг , , , ч
63. | —^-r.	l- dx = —= In (a + b)
| arg (еж + d) |, | arg (аж + b) | < тг при 0 ^ ж < ос].
[а, b > 0].
2.6.11. Интегралы от ха(ах2 + 6)^ In (еж + d).
а
Г In (с2 + аж)	1	а Г	1 2 2
1. —™г	т-^- аж = - arctg — In с + - In (а + с )
J с2 + х2	с	с I	2
1пA ± ж)	тг
[а, с > 0].
Г In (еж + d) , тг . d + Vd2 — а2 с2 Г ж dж	.	. .
4. I —^z^^^^ аж = — in	h —		[а > 0; 6 = arcsin (ac/d); d > а
A	A	J Sin Ж
5.
Г In (a dz ж) . тг . а . _
6. /	; dж = - In - ± 2G
J а2 - ж2	2 2
_ . In (еж + 1)	тг2 1	2/ ч
7. I —, , _- аж =	^— arccos (ас)
жл/а2 - ж2	8а 2а
а, d > 0; ас^ б!; йг = Arch — .
d -J
[а > 0].
[а > 0; |ас| ^ 1].
8. | х—,	dx = — [Tr(d — Vd2 — а2с2 ) + 2Vd2 — а2е2 arcsin (ас/d) + 2аеAп d — 1)]
р2	Ус
9.	= — Tr + 2Va2c2 - d2 In ¦
2с
2ac(ln d — 1)
[d > o|c|; a > 0].
[0 < d ^ a|c|; a > 0].
Gl	_ f 1п(ж-1) _ тг1пЗ
11.
In (еж + d)
(ах + Ъ)л	hc~ad\a a b
1 / с 6с d
\	b
ln rf
dx =
[be ф ad; | arg (еж + d)\ < тг при 0 ^ ж < ею].

414
Гл. 2. Определенные интегралы
[2.6.12
13.
14.
15.
a2d
1п|1±ж
(lnd+1)
= -\n2±G.
4
[6с = ad] | arg (еж + d)\ < тг при 0 ^ ж < ею].
1п(аж
¦ J a
2 , 2 'dX = T
2 + с2	о
113 3 aV
11. Ь Ь + ас тг / а2с2
+ — I In — In	 In ( 1	—
2c ас 6 — ас 2
' 2' 2' 2' 2'
+ тг In b I	[Re с > 0; I arg (аж + 6) I < тг при ж > 0].
16. ж
о
In
F +жJ
zo
, ж In сх + rfl .
17. ^^	-ттг1 dx =
1п(а + 6)±
In
а + b
nd d2
2cz c2z2
m d
[a, 6 > 0].
[d, Rez > 0; Imc = 0].
2.6.12. Интегралы от ха(агх + 6i)/3(a2aJ + 62O 1пте(сж + d).
Ь|Я-у|
J I A	U I	\U	XI
b-y
L, а; 1 + а; -г
[a < у < 6; 0 < Rea < 1].
о i i' x - a \ i	i л	/l ЛпF-а) + ^(а + 1) + С-:
2. I [ 	 \n x — y\dx = 7та(Ь — a)—	^^
. о — ж /	sin атг
^тг^	Ьтг Q, . fa- a) F-J/) 2F1 1, a; 2 + a; --
sin атт	a + 1
In |ж — 2/|	,	. 6 - a
1 cf ж = тг In
v
[Re a = 0, а ф 0; a < у < b].
[a < у < b].
о
l
f
5.	ln(H
J
о
a
6.	ж"™1(
0
a
f -
7- J (
0
= 2 in 2
[a. Re a, Re/3 > 0; | arg (еж + d)\ < тг при 0 ^ x ^ a].

2.6.12]
2.6. Логарифмическая функция
415
, a; a + /3; -^) [In а
[а, Re а. Re /3 > 0; |ос| < d; | arg (еж + rf)| < тг при 0 ^ ж ^ а].
f р, а; а + /3; — ~г )	[а, Re а, Re^ > 0; | arg (еж + d)| < тг при 0 ^ ж ^ а]
о та~г(а — т)
О».	J/	l (Л	J/ J
(еж
10. i51-g.^.A+gAdx =
11.
ж2IпA
(а2 + ж2)(а2ж2
¦ da? =
[a, Re a, Re/3 > 0; |ac| < |d|; | arg (еж + d)\ < ж при 0 ^ ж ^ а].
1 f 1 \a + b. / L4 In 6 lnal 41n2
¦ln(a + feb^^^J+^^2.
[a, 6 > 0; а ф b].
[a > 0].
ln aj
, 1 + р - а - /3) 2Fi f p, 1 + р - а - /3; 1 + р - а;
[Re (р - а - )9) > -1; Re/З > 0; | arg (еж + d)\ < ж при а ^ ж < оо]
, I + р - а -
a-/9)|2Fi(p,
1 + p- a - /3; 1 + p - a;	x
ac /
14.
^0 (l + p^ajfc^!
[Re (a + )9 - p) < 1; a, Re^ > 0; \ac\ > \d\; | arg (еж + d)\ < ж при а ^ ж < оо]
ч/з-i 1пп(еж + A)
(еж +
¦ d ж =
, 1 + р - a - /3) 2Fi p, 1 + р - a - /3; 1 + р - a; —
[Re (а + /3 — р) < 1; Re/З > 0; | arg (еж + d)\ < ж при а ^ ж < оо].
dx = a
,l + p^a^^)x

416
Гл. 2. Определенные интегралы
[2.6.13
х J 2Fi(p, 1 + р-а-0\ 1 + р-а;	] [In (ас) + ф{р)] -
_q-/3+	_а+
k=0
¦p-a)kKl \ ас
[Re (а + /3 - p) < 1; a, Re^ > 0; \d\ < \ac\; | arg (еж + d)\ < ж при а ^ ж < оо].
16.
[Ееа > 0; Re (а - а - р) < 0; | arg(aa: + 6)|,
а; ст + р; 1 - -
)| < тг при 0 ^ ж < оо].
17.
, а; сг + р; 1	X
Re (a - а - р) < 0; Re а > 0;
1
ad
be
I
< 1; I arg (еж + d) I, I arg (аж + 6) I < тг при 0 ^ ж < оо .
J
18.
In (ж + 2а) dx = ак+а^р2а^р(а + р - l)fc x
х Г ["'
[In Bа)
- а - *) - Л(а + Р - I)
[к = 0 или 1; Re а > 0, Re (а - р) < -fe; jargaj < тг].
19.
h)
2тг
In 1
b \ У da
Vd(bg-ah) IV h
20. I ^'"^ + d) dX = 2^
(ax + b)(gx + h) """ 6g" — а/i I V «rf I V ad
тг In d
bh (yah + yfbg)
[bg ф ah; a, 6, e, d, g, h > 0].
Ttlnd
1-х2 1пA
1
(ax + bJ {bx + aJ	ab(a2 - b2) °a
In 1 +
: a/i; a, 6, c, d, g, h > 0].
[o^ 6; a, 6 > 0].
2.6.13. Интегралы от ха ln?
. I Ж + 6с1ж 1,26
1. I In	= — In —
ж + a x 2 a
ь ах + b
ex + d'
2. In
с + ж
dx
тг / .6a
= — F arcsin -, —
6 V	со
[0 < a < b].
[\b\ < \c\, a < b].

2.6.18]
2.6. Логарифмическая функция
417
3. In"	dx = aBni)nBn j -
4. xn
a — ж	n ¦
5. In
a + ж dx тг2
a — x x 4
[а > О].
[а > О].
[а^О].
5#	ln F^ ж = ~ ~ 2
1-4- т Hi* тт	1
П 1 - ж V ~ 12" ~ 6
(>/Б-1)/2
J	1 — ж ж
тг2 3
о . -1/2,
9. ж ; ш
а — &ж л/а — ж
= 2тг In ctg
тг — arcsin 6
Г. b + ж	da;	тг .а
10. In	/	= — arcsin ^
J b	/2 2	Ь
- x хл/а2 - ж2
11.
12.
dx = 2аГ((т
(-1)*
[-1 ^ b ^ 1; а > 0].
[О < а ^ Ь].
[Re а > 0].
/2
а - х (а2 - ж2
а-х Jo? - ж2
14. xa 1 In	dx =	и/? I
1	ж-a	a Г1 2
+C + ln4
15. In
I
16. ж
17.
ж + a ^ж тг
ж — a ж 4
¦ dx =
A;!
[Re<j > -1; Rep < 1; a > 0].
[Rea <1, афО] а> 0].
[a > 0].
ж — a	n — .
dx = 2аГ(о-
^
[о > 0; п = 2, 3, 4, ... ].
[Re а > 1; а > 0].
18. In
о- ж + а da;
[a > 0; Rep < 1; Re (cr + 2p) > 1].
27 А. П. Прудников и др., т. 1

418
Гл. 2. Определенные интегралы
[2.6.14
19. In
20.
21. I ж08 In
22.
ж + п dx	ж
- а х/х2 - а2 ~ 2
ex + о	a sin an
ex + d , n(da — ba cos an)
ex — b
x + a
dx =
acQ sin сгж
x — a
7П2	О7Г
	tg —
23. In
x + a
ж — a
7Г2
~2
24. f In
x + a dx n
x x + a 6
25. f In
26.
27. I In
x — b
x - у
dx
= 0
x(x2 + z2)
2.6.14. Интегралы от A(x)ln(ax
Обозначение: к' = л/l — к2 , 0 < А; < 1.
' In (а + 6ж2)	In а
2. I ——;—, ч» dx =
[a > 0].
[6, c, d > 0; 0 < Re a < 1].
[6, c, rf > 0; 0 < Re a < 1].
[a > 0; | Rea| < 1, a ^ 0].
[a > 0].
[a > 0].
[3/ < a < Ь или у > 6 > a].
[a < у < 6].
[a, Re^ > 0].
3.
c{c + d)
b	Га	[b be — ad . a + 6 с . c + cl
,2 , , о 24/т arctgW- + . . ., In	2-In
ad2 + be2 \ \ b	У a b(c + d) a	d с
a + л/a2 - b2
(а + Ьх)у/1 — x2
¦ dx =
¦In-
/a2 - 62 a
[a, b, c, d> 0].
[a, 6 > 0; a 7^ 6].
4.
5.
In A - JfeV) da = B - к2)Щк) - B - In Jfe')E(A:).
In A - ^2ж2) dx = k~2(l + ife/2 - к'2 In ^)K(fe) _ B - In ^)E(ife).
6.
)dx = = ь ^к _ 7ГK ,
-А;2ж2)	k K ' 2 l ;

2.6.14]
2.6. Логарифмическая функция
419
7.
Ml*
= !ln^K<*>-iK<*'>-
8.
9.	._ ., x_
0	1
= —- {(^2 + lljfc2 - 6k4 + 3Jfc/2 ln k')K(k) + [2 - lOJfe2 - 3A - 2k2) ln ife']E(A;)}.
l
10.	[ ,.lnA~.fc2a;2)^^ = ^ [(k2 - 2)K(Jfe) + B + ln fc')E(fc)].
11.
0
1
12. [ж
0
2
- k2x2)dx
к2
13.
14.
15.
In (a +
In 6
c +
= —— [B + ln A;')E(ife) - A + k'2 + k'2 In k')K(k)}.
- 2 + ln ^)К(^) + B - In к')Щк)].
[a, 6, c, rf > 0].
[a, 6, c, d > 0].
/a с с ad . a
b d d be b
ln
^1 In (ж2 + z2) dx = ^^ [ln Bz2) - A - a) sin ^ /3
- B - a)cos —
A
16.
[0 < Re a < 1 при z ф 1] -2 < Re a < 1 при з = 1; Re z > 0].
JL i •
/X \/t — X
dx ж2 arccos2 b
x=~6	2
— dx = 2тг In
IJ + a
18. Тж-11пA + 26ж + ж2)с1ж=27ГШ8(ааГСШ8б)
19. I ln (a2 -
ж2)
= - In (z2
— oo
1/2
20.
27*
dx
[0 < 26 < a ^ 1; c = 1 + 26-a].
[-1 < 6 ^ 1; -l<Rea< 0].
[a, Rez > 0; -1 < 6 ^ 1].
[n = 1,2,3, ...],

420
Гл. 2. Определенные интегралы
[2.6.15
2.6.15. Интегралы от А(х) In ¦
1
п -\-
2.
3. ж
_i / атг
) аж = тга etc;
[Re а > -1, а ^ 0].
[-1 < Re а < 0].
. Г In (Ж ± Ж)	7Г	Г Ж In (Ж ± Ж)	7Г	G
4. —	—- dx = — C ± 1) In 2. 5.	 dx = —In 2 ±—.
J 1 + 2	8 l ;	J 1 + 4	16	4
6.
1 + ж2
In (ж ± ж 1)
1 + ж4
7.
1 + ж4
16
16
(а + жJ
= 1п2а
A - аж)A + ах2) dx	1
—	- arctg л/а In (I + а)
10.
11.
12.
13.
J1"
о
со
Г
J
J
0
со
I
0
со
Г
I
In
In
ха
A
л т
2 i
ж2-
ж2-
=
— ал
2
-а2
0
(х-
,2J
1ж =
с!ж
ж —
faJ
f бJ
(о
У
+
1
С2
С2
	г- — 	7=г си ь
+ аж2 2^/а
0J7T
±7Г
7
asIn(aTr)
[Re а > -1; а > 0],
[а = 0; а > 0].
[а > 0].
[а, 6^0].
[0 < а < ±у < Ь].
[±у ? [а, 6]; 0 < а < Ь].
ь
(а2 + c2)a/2cos fa arctg-]	[0 < Rea < 1; а, 6, с > 0].
i a-i i a + 2а6ж + ж . 2тга [cos (a arccos 6) — 1
14. | ж In	—	dx =	^
(a + xJ	ct sin an
1K i ! A + x)(x + a ) dx 2
15. | In ^	 /v 	'- — = In a
(ж + aJ x
| Rea| < 1; -1 < b <C 1; a > 0].
[a > 0].
2.6.16. Интегралы от А(х) \па(у/ах^ + bz^ + ex17).
1.
In (V^2 ^ С2 + Ж) dx
—	^—
(	7ГЛ	1
I arccos c + ip	I In с H— L (arccos a-\- (p) ¦
V	2 /	2
= I arccos с
1
2
cos y? =

2.6.16]
2.6. Логарифмическая функция
421
2.	= (arccosc — тг/2) In с
a
3.	xa In (v a2 — ж2 + a) с!ж =
о
п.
v.Ot-1
ex (	/— Г	/о 1 i 1
a X	2 L(a + 1)/2J ttJ
[a = c< 1].
[a, Re a > 0].
4.
ж"
0
. 2M)r
dx =
i/=0
5.
/х» +
¦ln(
[r = 0 или 1/2; a, /i, Re a > 0; /л\ arg z| < тг].
a^\k
— 1 x
a
3. (V^
а
7. [in (Уж2 + а2 +ж)с!ж = а[1 - лД +1пA + л/2) + In а]
о
2	-к)к
— In a 1 — '
[a, /i, Re a > 0; fi\a,rgz\ < тг].
In BzM/2) - /i^^ (a In a - 1)
2	J
[a, /I, Re a > 0; jLt|argz| < тг].
[a > 0].
8.
9.
10.
In [\Jx2 + a2 + ж)
V^2 + a2
x = i In A + л/2 )[ln A + \/2 ) + 2 In а]
- 1) In п + л/9 In
[а > 0].
[а > 0].
f In (ах + л/1 — 62ж2 ) с!ж тг . _ rtr/arcsina\ _ _ /тг — arcslna\
0
ln
2L(arcsIn b) =р [2ЬG) — L(arcsln 6 + 7) + b(arcsln b
1
ln b — 7)] >
л/l + c2 - a2

422
Гл. 2. Определенные интегралы
[2.6.16
13.
1пA±
In A;
~2~
+*|-И
-А:2ж2
4 w 8 l ^ ; l ;
\о < к < 1; к' = у/l-к2].
< к <1; kf = y/l-к2].
15.
. 1 + ay/1 — x2 dx
In			 = тг arcsin a
16. In
1 + ал/1 — ж2 а* ж
- ал/1 - ж2" ж2 + ^2
а + z\/T^
- а^ - л/1 -
17. ж In
: + л/1 - Ж2
• - х/1 - х2
dx	тг
18.
19. In
1-х2 4
da;
' a-byf(l-x2)(a2 -x2) л/1-х2
— тг In
20.
VaF^Wx2 - xy/l^b2 dx 1	2,
In	= - arcsin b
а — x	x 2
1/2
|а| < 1; Rez > О].
\а\ < 1; О < & < 1].
[а > 0; |6| ^ 1].
21.
22.
23.
п In (ж + v ж2 — а2 ) dx = 	I In a +
(n-2)!!
[а > 0; Re а
а > 0; В = ж/2 при п = 1, 3, 5, . . . ; В = 1 при п = 2, 4, 6, . . . ].
[а > 0].
1п(а + \/ж2 + а2)—¦ = -[2-л/2 + In A + V2 ) + In а]
ж2 а
24.
25.
[Re/3 < 1/2; Re (a + /3) > 0].
-1)
ж2 - 1 4
26-
[a > 0].

2.6.16]
2.6. Логарифмическая функция
423
27
сю
. f xk(x2 - а2)а^(х ± л/х2 -a2I7 In (ж ± л/х2 ~a2)dx =
2k]
—j
[А; = 0 или 1; а, Re а > 0; Re Bа ± i/) < 1 - А;].
28.
Llnz + 2/ЗМ -2- J - (l=FlOrctg (— J	[/x >O, 0 < Rea < /i/2, /i|argz| < тг].
29. | жа —^—,	^ж =	2 а/мВ( —,	/ilnz±7rtg
30.
[fi > 0, /i|argz| < тг; 0 < Re а < /х/2, z 7^ 1 (|2 Re а| < д при z = 1)].
In (л/х^ + 1 ± жм/2) с/ж _ , тг2
31. [ Z In
32.
9 ,
х2 +
±
-dx =
тг	2G
2z nZ+ T"
> 0; -/i<2Rea< 0].
[Rez > 0].
\п{л
0
34. ж"-
о
[Re а < 1; Re (a + 2a) > 0].
35.
36.
^2^2р^2р^4
- In УЖ_ + ^_ ±^ ^ = ?	1-	В(р-1, p-1)	[Rez>0; Rep>l].
p-1
	^^ In -
В
2 '
rtW Г . V^ + z2 + a	dx	.a
37. In .	=	.	= тг arcsin —
J V2 + z2 - a2 Vx2 + z2	^
[Rez > 0; Rep > 1].
[0 < a < |z|; Rez > 0].
38.
а^{1п {a2 + b2 + ж2 + ^/[ж2 + (a + 6J][ж2 + (a - 6J] } - In Bab)}
dx =
ab	[a/2, C-a)/2, C - a)/2
r[	l-a/2
fe2 + a2
[0<Rea<l].

424
Гл. 2. Определенные интегралы
[2.6.17
39.
• + z*y
х =
j-	/ „^
zfl) - 2ф(и - 2-
1^ - 2гI
J
[г = 0 или 1/2; /1 > 0; 2 Re а > /х Re (±i/ - i/); Re (//t/ + 2а) < 2jur; /i| argz| < тг].
40.
In
/i
( j
± x) dx =
x Ulnz
2 /x
^, г т у -
ii	2 fi
2 + м"Г
-1(l-2r)l
• = 0 или 1/2; jtt > 0; Re Ba ± fiu) < 2r/j; /x| arg z| < тг;	Re a > 0 B Re a > -ц при 2 = 1)].
41. | / nX оч. [(^ж2 + z2 + ж)" In (^ж2 + z2 + ж) +
Ж I If! Iv 7*2 __L- y5"^		 'T* ll Hi*
I 111 I у tJL/	jP /6	eiL/ I CI/eiL'
p-1
в
X
2 ¦ r; rv 2
[fc = 0 или 1; Rez > 0; 2 Re p > к + 1 + |Rei/|].
42.
^	[(^ж2 + 2z2 + ж)" In (^ж2 + 2z2 + ж) +
+ (-l)k(Vx2 + 2z2 - xf In (^ж2 + 2z2 - x)] dx =
u-2k + 2p 2p-u-2k
Р-1
4 ) T \ 4
[k = 0 или 1; Rez > 0; 2 Re p > 2A; + | Reu\].
2.6.17. Интегралы, содержащие А(х) и —-—.
In ж
1. (жр - ж7
J1
с!ж /3
	= In
Мпж	7
, Re7 > -1].
[nRea > -1; n = 1, 2, 3, . . . ].
3- l^f r^ = bj.
ж2 + 1 In ж	4

2.6.17]
2.6. Логарифмическая функция
425
4.
dx
ж2 — 1 In ж
	 = — In (cos ртг)
|Re/3| < 1/2].
5.
ТР _ Т7 JT	/9 + 1 ж^
«?/	«?/	\JbJu	- L/ jp JL Ж"^
A - сж)п In ж ~~ 7 + 1 _
¦ А; — 1 \ k ¦,
с In-
7 +
*
da;
Ins
c| < 1; Re^, Re7 > -1].
/i > 0; Re^, Re7 > -1].
7.
"™1 -ж da; , / атт\
	—^	 = In tg	 1
+ 1 In ж
1 с/ж . 7Г
= In —
1 In ж	2
> 0; 0 < Re a < 1].
> 0].
10.
11.
12.
3=0
X In [a + 7(wi — j) + Р{п — A;)]	[Rea > max @, — riRe/3, -mRe7, — те Re /3 — mRe7J].
^(n-A;) + aN
7
[Rea > max@,
- nRe/3)].
da;
in ж
[Rea > max@, -Re/3, -Re7, -Re/3 - Re7)].
x — 1	dx
о
i
14. Гж°
о
15.
_ In 2
(ж2 + 1Iпж ~ ~2~'
y*P	1 ||ж7	11 dx
x^ — 1	In ж
(ж — 1)	di
13. ж
ж + 1 (ж2 + 1Iпж
> 0; Rea > max@, -Re/3, -Re7, -Re/3-Re7)].
1 + 2ж cos (тж/п) + ж2 In ж sin (тж/п) ^
x In Г
2n	'
Jfe + 1
p	 rp
' 2n '
2n
^к + 2 rkl
2n ' 2i
rp
p
2n ' 2n
[m < те; r = 1 при m + n = 2Z-l, r = 2 при m + n = 2/, / = 1, 2, 3, . . . ].
16.
i
— 1
= 1пГ
тж	[7
[Re/3, Re7 > -1].

17.
18.
Ji-
Jiff*'
{ х
0
1
-1 -
м _
(ж
1
1
*-1){х
ж — 1
т/3 1 >
Ж — 1 у
'-1I
J
I dx
' ж In ж
dx
ж In ж
426	Гл.2. Определенные интегралы	[2.6.17
= 1пВ(/3, 7)	[Re/3, Re7 > 0].
i/З	[д, Re/3 > 0].
Я1 жд \
:	 +	 dx = -<ф(Я)	[Reg > 0].
In ж 1 — ж у
о
20. Т [(м-1)^-1) _ I + J_l _^_ = ,„гЫ	[м > о].
J [	ж2	ж ж^_|(ж-1Iпж
1
оо
О1 Г^-ж7 с!ж	/ /3 + 1 \	/ /3 + 1 \
21.	= ± In sin	тг —In cos	тг q=
J ж"±1 In ж	V 2ц J	V 2^ J
о
=pln (sln^^TT ) +ln (cos^^tt ]	[/x > 0; Re^, Key > -1].
\ 111 J	\ 2/i /
CO
22.	^
24.	In A + ex) dx = > -— In —	 + In —¦	Re a, Re C > 0; с < 1 .
1	In ж	v	;	f^k в + к	в	l.m.i	j
/id. I Ж	—Ту	 aX — I— II	7 I — -L j I , J X
In ж
0
fc=O
x ^(-1)^ Ш ) [a + (n - Л)/3 + (m - jO] In (a + (n - k)fi + (m - j)
[Re a > max @, —n Re b, —m Re7, —n Re/3 — m Re 7)].
26.
In ж
0
= a In a - (a + /3) In (a + /3) - (a + 7) In (a + 7) + (a + /3 + 7) In (a + /3 + 7)
[Re a, Re(a + /3), Re (a+ 7), Re (a + /3 + 7) > 0].
27. [ (Ж ^2 Ж7) с!ж = B7 + 1) In B7 + 1) - 2G + /3 + 1) In G + /3 + 1) + B0 + 1) In B/3 + 1)
j ю ж
0	[Re7, Re/3 > -1/2].
28.
[In2 ж A-ж)
о

2.6.17]	2.6. Логарифмическая функция	427
1
30. Jlz"^ - г) + *«"> - р) + хр-х(Р - д)]^ =
о
= p(q — г) Inp + q(r — p) In q + r(p — q) In r	[p, q, r > 0].
i
f Г	TP	T9-l	„.^-l
32# 	~	I	~	I	±	|_
" J UP - Я)(Р - r)(P - s) (q~ p)(q - r)(q - s) (r- p)(r - q)(r - s)
о
ж3™1	1 dx 1 Г	p2 Inp
(s — p)(s — q)(s — r)\ In2 ж 2 [(p — q)(p — r)(p — s)
q2lnq	r2lnr	s2 In s	1
+ 1	77^	77	7 + 7	77^	77	7 + 7	Г?	77^	7	[Pj q, r, s > 0 .
(q - Р){Я - Г)КЧ - 8) {г - p)(r - q)(r -8) (8- p)(s - q)(s - r)\
32.
о
l
33.
о
l
34. [жа[г^+ ; ' " |-^ = -1пГ(а)+ (а-- ) Ina ^ а+ 1пл/2ж	[Rea>0].
о
0
36e i |"j_+sC-a01 dx _ 1пBтг)
In ж 2A™ ж)] ж In ж	2
о
37. f( 1 +l±?!)^ = ln2-1.
j упж 1 —- хг J In x
о
1 1 \ p_i] dx A \,	1пBтг
Г, , ,ж1пж + 1-ж . . 4
39.	In A + x)	ц	dx = In —.
J	Ж In2 Ж	7Г
0
схэ
40.	J x- In A + ,-) [(p + a)." - (, + a),' + *^f] ?. = _Q ln (tg g ctg g)
0
[p + a, 9+ a < 0; p, 9 > 0].
42.
l
i
J1
0
l
p i
II
0
f Л 1
L \ у
я
xlnx
\ о 1
1 'г* 4- f
/ + 21
1

428
Гл.2. Определенные интегралы
[2.6.18
xq -I	q
dx q3
[<? > 0].
11
45.
] —
Ju 111 «X/
2.6.18. Интегралы от
г/т
In x + a
In ж + a
2-
K"e"a Ei
a, Re a>0, n = l, 3, 5, ...
a, Rea > 0, n = 1, 2, 3, . . .
4.
In ж + а2
а оап
5.
[sin aa ci (aa) — cos aa si (aa)l
+ cos aa ci (aa)
[a, Re а > 0].
[а, Re а > 0].
7.
8.
9.
10.
11.
=iLD-7r)
О7Г
/xln2
[a/x = тг].
[тг + 2 In {y/2 ^ 1)]
с!ж	тг т-л, .
V(l)
^	 =_
n^ ж + а2 1 ^ ж2 a
г
а + Дгтг
а>0; Rea<l.
In ж	dx	I
In2 ж + а2 1 — ж2 4
12.	=1B-тг)
13.
-тг + 21п(л/2 -1)]
[2о = тг].
[4а = тг].

2.6.19]
2.6. Логарифмическая функция
429
15.
In x	dx
0 2	| O\O 1
n x + aA)A 1 — a
Г In A - жм) da;	тг . _
16. —^-s	 = - - In Г
J жAп2ж + а2)	а
	 Ы	In (afi) - " ( In	hi
[Re а > 0].
[Re а > 0].
[а, ц > 0].
2.6.19. Интегралы от произведений логарифмов.
1. I In ж In A ± ж) dx = 2	±— тг - A ± 1) In 2.
2. f жп1пж1пA±ж)с1ж =
¦ + т -
ife/ 24
¦In 2.
3.
= /
n = 1, 2, 3, . . . ],
Im,n =
4.
2
1
5.
6.
ч dx
- In A - &жм)—
X	X
1	/¦
(сг +1) .
v	; L
^„2*Md*
a + 2 (Ь)
> 0; Reo- > -1; \b\ < 1].
7. In" - In A - 2bx^ cos7 + Ь2ж^)— = ^2Т{а + :
0
8. I ж" In ж In-
b cos
9. | In ж In -
а (ж — 1)(ж — a) (a — 1) sin2 aw
dx	In a
а (ж — 1)(ж — а) 6(а — 1)
2 , 1 2 ч
¦a 1J2
k = l
[fj, > 0; Rea > -1; |6| < 1].
 + 1) In a — 2ж(аа~1 — 1) ctg an]
[a > 0; a ^ 1; 0 < Rea < 2; a ф 1].
[a>0,a^ 1].
10.
1п|1±ж
(ж + аJ
1	/, 2
In a -
0
[a > 0].

430
Гл. 2. Определенные интегралы
[2.6.20
In х dx 2 2
7r
f In ж . ,	2ч,	^ / \па\
12. —г- In A + аж ) da; = тг^а 1
J ж2	V 2 У
, , , х + а ,	Д	Л а
13. In ж In —	 аж = тг о ^ а + In —r
х2 + б2	V	&
[Re а > 0].
[а, Ь > 0].
, . . а + 2Ьх + х dx	. b
14. I In ж In —	 — = 2тг In a arcsin —
a1 — 2bx + xl x	a
15.
dx 2тг
ж2 b
[а, 6, с > 0].
16.
17.
^ = — [ас(а +с) + а3 In а + с3 In с-(а3 + с3) In (а + с)
Ж4	О
[а, с > 0].
ас) In F + ас) -6 In Ъ- ас]
2.6.20. Интегралы, содержащие In In ж.
[а, Ь, с > 0].
[1тЛ = 0].
о	K=1
i
2. Г In In — _^_ = ^Cln2-
J	ж 1 + ж
о
г In к
~к~'
3. In In - ¦
J x
о
dx
4. In In - ¦
dx
ж 1 + 2ж cos 7
5. In In
J	ж 1 + ж2 + ж4
о
2 + ж4
2n
7Г7Г27Г
аж = 	tg	In —
x2n	2n + 2 &2n + 2 r
n/r
6.	ж In In — In -аж = а
J	ж ж
о
i
7.	In In - -
[r = 2 при n = 2/, r = 1 при n = 2/ - 1, / = 1, 2, 3, . . . ].
(G + 1)[^(G + 1) ^ In a]	[Re a > 0; Re a > -1].
\fe+i
2)г/1пA/ж)
_L_
lnBfc + l) + 21n2

2.6.22]	2.6. Логарифмическая функция	431
2.6.21. Интегралы от хае^рх1Л 1пп х.
^))	[/х, Rea, Rep>0].
о
fi\da
2.	I /^e"^' Inxdx = /i^2p^a/Mr(a//i)[^(a//i) -lnp]	[/x, Rea, Rep > 0].
о
CO
3.	xne~pxlnxdx = ^гг(У"^ -С-lnp]	[Rep > 0].
Г _	1
4. e р{В1пжЖс = -- (C + lnp)	[Rep>0].
J	P
о
0
5. lxn-^e->-lnxdx=v^- Г 2> -— -C-lnDp)	[Rep > 0]
fe=l
6. J ^=rlnxdx = ~J::lG + lnDp)]	[Rep>0].
о
[/x, Rea, Rep > 0].
°°	/
I	-I	JU.Q	A	/	/ Ql \	/ ft \
ft I Ж G	lo X dx ^^ U T)	Г 1 	 1 \ ib I 	 I 	 In T) ~\~
+ ЦФ\ — I - lnpU> I — I +Ф' i — H	[/x, Rea, Rep > 0].
2.6.22. Интегралы от xaeax + ж lnn x.
о
[Rea, Rep > 0] или [Rea > 0, Rep = 0, Reg > 0] или [0 < Rea < 2, Rep = Reg = 0, Imp ф 0].
2.
fe
. I xa-1e-px2-2qx\nxdx = -2"ар"а/2Г(аIпрФ(а/2, 1/2;
_9 -(a+i)/a /a + 1\ ^ ((a + 1)/2)„ф((а + l)/2 + fc)
2P	I 2 jjj	C/2)fcfc!
[Rea, Rep > 0] или [Rea > 0, Rep = 0, Reg > 0] или [0 < Rea < 2, Rep = Reg = 0, Imp ф 0].
oo
Г / 2	-.4 ™рЖ2+2дЖ1	,	1 , g /7Г	, 2/ чм , r/ / ^м
4. ж(рж — дж — L)e	In ж ax =	1	л — exp (q /pj[l + erf (q/\/p )\
J	4p 4p у р
[Rep > 0].

432
Гл. 2. Определенные интегралы
[2.6.23
со
п	/ (Л \ П
О.-—1 —рх-—а/х % п j	oil
. ж е	' In х dx = 21 ——
\да
о
со
5. [ xa~1e~px~q/xlnxdx = ^
о
7Г
а/2
[Rep, Req > 0].
sin атт \_\р
со
а/2
6. xne
n —px — q/x
g
In х dx =
fe=O
[Rep, Reg > 0; a^O, ±1, ±2, ... ].
2 й*!<*-
x [In2 g - In2 p - 2 In цф(к + n + 2) + ф2(к + n + 2) - ф2(к + 1) +
1) - ^(A; + n + 2)] + p^
k=0
7.
с!ж	q
x	p
" (n - ЩФ(п - A; + 1) - lnp]
[Rep, Reg > 0; n = -1, 0, 1, 2, ... ].
[Rep, Reg > 0].
. 7
j
9.
[Rep, Reg > 0].
[Rep, Reg > 0].
2.6.28. Интегралы от xae^px ln B + bx).
l
1.	жеж ln A — ж) с?ж = 1 — e.
о
CO
p -рж	-i
2. 	ln Fж - аб) dx = - Е12(^ар) - ln (аб) El (^
j x	2
[a, b, Rep > 0].
¦\nn(a-
. [ xa^e^px In (a+ bx)
J
, 1-p + a; -y
[Re p > 0; | arg (a + баз) | < тг при ж ^ 0; Re a > 0 (Re a > — n при a = 1)].
7Г
dx= (y
b
b/ asman
u; a + 1;
о /
[Rep > 0; | arg (a + bx)\ < ж при x ^ 0; Re a > 0 (Re a > -1 при a = 1)].

2.6.24]
2.6. Логарифмическая функция
433
5.
})dx=
а — Ьх\)	p
Rep > О;
|arg(a/ft)| < тг
a, b > О
6. f — In A + Ьх) dx = \ fin2 f + 2С In f + С2 +
7. е~рж In (ж + а + 6) [ 	+	 ) dx = A + In а In b) In (а + b) +
x + а ж + 6
+ e~(a+6)p{Et (-ар) El (-Ьр) + [1 - In (aft)] El (-ap - bp)}	[a, 6, Rep > 0].
8.
f -v
J
0
x In
X
X
+ a
— a
dx = — [shl (ap) ch (ap) — chi (ap) sh (ap)]
2.6.24. Интегралы от A(x)e px In (ax2 + bx + c).
[a, Rep > 0].
1.
2.
i г /	mj	-ар/2 [тг Л. (ъар\ ( а	\ (ар
In [ж(а - ж)] da = тге р/ - Yo —- + In — - С /0 ( —
¦ In (ж2 — a2) dx = — ( С + In ¦
[a, Rep > 0].
[a, Rep > 0].
a + b
3. I —— In [(ж - a)(x - b)] dx = EI (-ap) EI (-ftp) - In (aft) EI (-ap - bp)
[a, 6, Rep > 0].
= ep(a+b){EI (-ap) EI (-ftp) - In (aft) EI (-ap - bp)}
[Re p > 0; | arg (a + b) | < тг].
[Re a, Rep > 0].
4.
1 x + a + b
5. e px In (ж + a ) dx = — [In a — cl (ap) cos ap — si (ap) sin ap]
J	P
о
6. e
In
In (ж2 -а2
dx = -[2\na- eap EI (^ap) - e^ap EI (ap)}
7.
\|Imo| > OJJ
[Re a, Rep > 0].
CO
8. 	In ll — а2ж2| dж = EI ( — ) EI (
J ж	Va/ V a
о
[a, Rep > 0].
28 А. П. Прудников и др., т. 1

434
Гл. 2. Определенные интегралы
[2.6.25
2.6.25. Интегралы от е рх\пА(х).
2.
3.
4.
= - [К0(ар) + In ае~ар]
e~px In (^T^ + л/x^i) dx = — [Ко(ар) + In Bа)е~ар]
+ ^)dx=±[ePz^Koipz/2).
+ Vx-ib)dx = — [Н0Fр) - Y0(bp) + In V26]
[a, Rep > 0].
[а, Rep > 0].
[Rep > 0; \argz\ < тг].
[6, Rep > 0].
5. e~px In (Vx2 + z2 + ж) dx = — [Ho(pz) - У0
lnz
6. | xne~px In (V^2 + z2 +
7.
+ - In 2
ТГ J
[Rep, Rez> 0].
8.
9.
2 +2zx
In (V^2
= - [epz K0(pz) + In z]
= ? In
[Rep, Rez > 0].
[Rep > 0; |arg^| < тг].
1.
2.
3.
2.6.26. Интегралы от R(ex)lnx.
In ж	_i
	dx = a
Г(а)
ex In ж
cos 7 + 1	2 sin 7
[Rep, Rez > 0].
l-Ka^l].
(a) - ln(ife + n)]
[Rea > 0; n = 1, 2, 3, ... ].
	G1пBтг) - тг1птг + тт1п cos- + 2тг In г( П + 7) \
ш 7 I	2	V 2 / J
[0 < 7 < тг].
n- 1)!
J
ex In ж	С 1, тг

2.6.29]
2.6. Логарифмическая функция
435
2.6.27. Интегралы, содержащие жа, е
1
1.
2.
3.
4.
6.
о—рх л»
In ж
пп(ж + а)
[Re а, Re/9 > 0; | argp| < тг].
k=Q
V*TTZ = Z [ЧР, « - 1) - А(р, /3 - 1)]
11 о?ж
ж) J ж
In2 Ж + 7Г2
2.6.28. Интегралы от ж" In (a + be px).
о
со
2.	жп1пA - ,
J
о
со
3.	fln(l±e~Q
о
B.
n+2
(п + 2)(п-
С(п + 2)
= -1пГ — + ^
2тг	4
Г .
4. In
J
о
—
4z
б?ж	а . p
= In	 In —
+ b
а + b q
2.6.29. Интегралы от xaR(shx, ch ж) In ж.
[Re a, Re^, Rep > 0].
[Reg > 0].
[Reg >0].
[Rep > 0].
[a > 0; n = 0, 2, 4, ... ].
[a > 0; n = 1, 3, 5, ... ].
ln
2тг
[a, Rez > 0].
[o + 6, pg > 0].
1.
тг тж . 2тг тг
In ж da; = —tg	In	h -
2n & 2n г п
/ \k-i •
(-1) sin
ктж . _ Г(п — (^l)r,fc)r
	In Г l v ,/ Л
n	L	kr/Bn)
[r = 1 при m + n = 2/-l, r = 2 при те + п = 21; I = 1, 2, 3, . . . ].
, сЬпгж . .	тг . /2тг\ ттгтг
2. I —	In x ax = — In — sec	h
chnx	2n \ r I 2n
[r = 1 при m + n = 2/ - 1, r = 2 при m + n = 21, i = 1, 2, 3, . . . ].
28*

436
Гл. 2. Определенные интегралы
[2.6.30
3.
dx =
dx
ch ax	2а
[Re а > 0].
4.	— da; =
J уж ch x
о
5. —5— аж = in	С.
J eh2 ж	4
о
/	1 \^
\ }
/2Дг
[In Bk + 1) + In4 + С].
, In ж
6.	^ж
7.
ch x + с
In ж
2 ch2 ж -
(Z?	7Г	f f Ж -\- W \	(Ж — ^ \ 1
= ,	In тг Н	,	In 	 I — In 		\(p = arccos c].
xfl^	x/T^ L V 2тг )	V 2тг Л	W	J
жк
2V 3
Vk
. a^-iOichx - x^hx	f x
8. I ж 	2	1пжа^ж = 2Г(а)
ch x
, 2n B?г + 1) ch ж — ж яЬж . .	. ..
10. | ж	—о	In ж б?ж = — I тг
ch ж
о
со
11.	ж
о
сх
12.	f ж
о
2n-i
— аж
sh2 ax
2п—1 2пе""аш sh аж — аж
sh2 аж
In ж а*ж =	( —
. оn 2аж ch аж — Bп + 1) sh аж . , А , ,.
13. ж 	^	In ж da; = — —
sh3 аж
а\а 7
о
со
14. | ж
о
2п 2аж sh аж — Bп + 1) ch аж
ch3 аж
i n^i аж ch аж ^ nsh аж , .
15. х 	о	1пжс?ж =
sh аж
-) \Вп
а/
16.
2.6.30. Интегралы от A(x)R(shx, спж) In A(x).
1.
2.
(а + 6ж2)	2тг
^	 dx = —In Г
ch еж	с
с +
[Re а > 0].
[а > 0; п = 1, 2, 3, . . . ].
[а > 0; п = 1, 2, 3, ... ].
[а > 0; п = 1, 2, 3, ... ].
[а > 0; п = 1, 2, 3, . . . ].
[а > 0; п = 2, 4, 6, . . . ].
[а > 0; п = 1, 3, 5, . . . ].
ж	с
	In
sh еж
с	, / с _\
^Ф
жл/Ь J
[а, 6, с > 0].
[Ь, с > 0].

2.6.31]
2.6. Логарифмическая функция
437
3.
chcx
—о
sh еж
. /1 , 4с2 2\ .
In Ц	т х ) dx =
V	2 )
л 1 сЬсж 1
4. —ц	In
sh еж \	тг
= ^ [kV2 - 4 + 2^2 In A + л/2 )]
5.
sh (тгж\/б)
\п(а + Ьх )dx = \ - In Г
ГеЬеж + сжзпсж /4с 2\ , 4с
6.	—5	In Ц	— х I dx = —In 2
J ж2 ch еж	\ жг J	тг
о
7.
ch ex +
ж2 ch2 еж
In
2 \
[с > 0].
[с > 0].
This
о
[а, 6 > 0].
[с > 0].
[с > 0].
Р"РЖ у	 т _|_ л/т2 — о2	1
— sh (ov ж2 — а1 ) In	аж = — In
In ^
2 р — о
[а > 0; Rep > |Reb|].
9.
л/х2 + 2^
sh (буж2 + 2^ж ) In
zp р + 6	^^	—
dx = е р In	 K0(z\fp2 - b2
p-b
[Rep > |Re6|; |arg^| < тг].
2.6.31. Интегралы, содержащие логарифмическую функцию
от гиперболических функций.
1. е^рж1п(8паж)с!ж = ^^
о
2.
+^(^) -c
р \2aJ
— [ln2+ — + ф(п) + С
Ina	2п
о
3. е^рж
о
\n(chax)dx = -\р( — ) - -
р[ \2а/ р
dx
4. | ж In ch ж с!ж = 0. 5. In ch ж	 = 0.
J	IX
о
оо
6. I Inch ж—— =	—In 2. 7. In thxdx = -ж2/S.
1	сЬ2ж 2 8
[а, Rep > 0].
[а > 0; n = 1, 2, 3, ... ].
[а, Rep > 0].
8. I xa 1\nthxdx =
a sin (атг/2)
[Re а > 0].
9. In
=	In 2.
2
^=
спж	2

438	Гл.2. Определенные интегралы	[2.6.32
со
1П Г a_i. cha^ + shft	/2\a тга+1
Ю. ж In-	—dx = -[-) ——	тгт- х
" ch ax — sh b	\a J asIn(a7r/2)
С(-"» ^^ ) -С(-а, —ПГ™ I +С(-а, ,„ ) -С(-а,
[Re а > 0; 26 > тг].
2.6.32. Интегралы от А(х){8тЬ,Х\\ппх.
{ cos bx J
# fЬГ(а) (	\
dan [ l ; \ cos (атг/2)
Г > 0; jH < Re а < lj.
пте Ж dx =
Г a_1(smbx^\. . Г(а) Г sin (атг/2) 1 г ., ч _ , тг Ti атг]
2. ж Ч , >1пжс1ж=^^^ ) 7. ; >U(a) - lnbzb - tgT
J \со8&ж/	ba \cos(a7r/2) J L^1 ;	2 & 2 J
о
¦*{-.'}
b > 0; { ^ J> < Re а < 11.
3.
ж
0
4.
0
i a-i f sin ^ж 1 i 2 , Г(а) f sin (атг/2) 1 f г . / ч _ _ . тг Ti атг]5
5- ' X < • >Ы ХаХ-~Ь^\со8(атг/2)]\[Ф{а)~1пЬ±21ё ~Y\
тг2 fsm(an/., K K	,,. n. , -, .Rea
r v y 4 \cos(a7r/2)
CO
6.
Г-11
0; \ }
I 0 j
Ж
0
7. 	^1пжс1ж =	[C + lnB6)-l]	[6>0].
J ж	z
о
со
8.	\^^t~—Un(ax)
J Ж2 + Z1 { COS 6Ж J	z,
0
[6, Rez > 0; | arga| < тг].
CO
Г 1 f x sin k] . , ч .
9.	—	-<	}ln(ax)dx =
J x2 — у2 у cos bx J
0
тг (±i-i)/2 \.( cos by
2	[I sm by
CO
fcos ax —cos ^ж i i i a Г^ 11 / i \ i
10. 	In ж rf» = In т С + - In (ab)	[a, b > 0].
J	ж	6 [_ 2	'
о

2.6.38]
2.6. Логарифмическая функция
439
Г cos ах — cos 6ж , , ж г, , ч, ^ ч ,	, , ,,
11.	In х dx = - [(а - 6)(С - 1) + a In а - 6 In 6]
j	x	2
о
[a, b > 0].
2.6.88. Интегралы от А(х){	>\пА(х).
I cos bx J
1.	sin bx In (a — x) dx = — {In a — sin a6 SI (aft) — cos aft[ci (aft) — С — In 6]}
о
oo
2.	f ^^^ In A + аж) da? = i [si2 f-^ + ci2 f-
J x	2 [ \aj	\a
о
r
3.	sin 6ж In
о
oo
f
4.	cos bx In
0
, cos bx .
5. 	In
X
X
X
X
+ а
— a
+ а
— с
dx = —- sin aft
ft
1 Г7Г
[a, b > 0].
[a, b > 0].
[а, 6 > 0].
ж + a
dx = ^ I — (cos ftc — cos aft) + cos 6c SI Fc) + cos ab SI (aft) —
— sin 6c ci Fc) — sin ab ci (aft)
ж — a
а|ж = — ж si (aft)
6. I cos bx In (a2 - x2) dx =
ci Baft) — С — In —	— Si Baft)
aj 6
7.
¦ In (a2 - x2) dx = — Yo(ab)	Jo(ab) ( С + In —
Г sinfta ,	2ч j	п. f ft
8. 	In A + ax ) dx = ^тг Ei	—
J ж	V /о
9.
10.
COSftiE
In A + ax ) dx = 7Г 6 Ei	— + v6
L V «
exp
0
11. cos 6ж In ( 1
J	V
о
12.
13.
j da; = ^ A -
J	b
x2
2 , _2
^2™
da; = — [1 — cos (by)]
¦ dx = — (
ft
14. ж sin 6ж In ¦
[a, b, с > 0].
[a > 0, 6 > 0].
[a, b > 0].
[a, 6 > 0].
[a, b > 0].
[a > 0, b ^ 0].
[6, Rez > 0].
[6, Re^ > 0].
[6, 2/ > 0].
[6, Re a, Re с > 0].
[6, Re a, Re с > 0].

440
Гл. 2. Определенные интегралы
[2.6.34
. sinbx . a2 + x2g2	\ ( ab\ _ ('ab
15. 	ln-r	Sizdx = ж Ei ^— - Ei
x	a1 +
о
16. sin bx In •
о
17.
сJ
2тг ^
, 2тг ^a6 .
с!ж = —e sin Fc
6
18.
г*оч Лт*
19.
_ 1 y> 2ф{к) + %к^ -2 In F/2)
~ 4^	fe(Jfe!J
2.6.34. Интегралы, содержащие In < , >.
I cos bx J
[6, g, h,Rea> 0].
[6, Re a > 0; |Imc| ^ Re a].
Lo(bz)]}	[b, Rez > 0].
[6, Rez > 0].
[6 > 0].
V
CBfc)
7Г/4
о
7Г/4
3.
о
tt/4
sin ж
cos ж
128
7Г
'
ТГ	7Г
8" ^32
G
—•
2
/
Г sinn ж . f sin ж 1 .
4.		т^ In <	> da;
J	cosn+2 ж [ cos ж J
|
4 Iln4/
|
7Г/4
5. cos17 2ж sin 2ж In sin ж
1) + In 2]
о
7Г/4
Г 1
6. cos17™1 2ж tg2ж In cos ж dx = —7	^ j3(y)
0
7.
о
тг/2
7г/2
8. InJ 8ШЖ I da; = --1п2. 9. ж In
J I cos ж]	2	J
о	о
\ COS Ж J	16
Re а >
[Re i/ > 0].
[Re и > 0].
[Re a > 0].

2.6.34]
2.6. Логарифмическая функция
441
тг/2
ю.
11.
о
тг/2
±7-1
м	Г sin ж 1
In <	У dx
[ cos ж J
и/2
1)/2
/3(и)
[Re/x > 0].
12.
(
cos ж] [cos ж
[A = 1, если n = 1, 3, 5, . . .; A = тг/2, если n = 0, 2, 4, . . . ].
{sin ж 1 . f sir
In
cos ж J [со:
, , sin ж . sin ж , .
13. \ i	In	Idx = \n2-1.
, cos ж I I cos ж
о
0
тг/2
0
cos ж J I sin ж
[Re/x > -2].
. = -2, -1, 0, 1, 2, ... ],
8 v '	n	2 nil
[А = ж/2, r = 0, В = 2 In 2, если n = 2, 4, 6, . . . ; A = 1, r = 1/2, В = 0, если n = 1, 3, 5, . . . ].
тг/2
Г „_i	,,_! , fsina;! , \ (и v
16. sin^ ж cos ж1п<	>аж=-В™,™
[ cos x J	4 12 2
о
tt/2
(и/2) j
17.
18.
т/2
о
7Г/2
Г	Г sin ж . .
19.	xl In
J	I cos ж J l sin x
о
7Г/2
.	.	1 ., / v \
In cos x dx = -- ф [ — ]
4 \2/
{Sin Ж 1 .	7Г f 1 1
}dx = - — < f л,п \
cos ж J	4n [ (—1) J
Г Re/j, > 0, Re i/ > -2 '
I Re i/ > 0, Re/x > —2 /J *
[Rei/>0].
[n = 1, 2, 3, ... ].
20. cos17 1 ж sin г/ж sin ж In cos ж dx = 2 v 2?r[C + t^(^) — \/v — In 4]
[i/> 0].
о
7Г/2
- 7—:	ГТ	^ln^	\dx=
J (asm ж + осозжJ [cosxj	a2 + о2
о
sin ж I .	1
йж =
In
[a > 0; 6^0, Im6 = 0].

442
Гл.2. Определенные интегралы
[2.6.34
тг/2
22.
23.
1
sin ж 1 .	тг
dx =
1 Г&
т/2
о
тт/2
a2 slnz ж + b2 cos2 ж [ cos ж J	2ab \ a + b \ a
з!п2ж
(asm2 ж + 6cos2 жJ [cosж J	2F — a) \ a"
2 • 2	i 2	2
a sin ж — о cos j
а, Ь>0.
а, 6>0.
0
тг/2
25.
26.
27.
28.
30.
32.
\/l -
cos ж]	2
smM 1 ж In sin x dx = —V^1 Г
о
ж sln^™1 ж In sin x dx =	В ( —, —
J	2 V2' 2
) + i A =f 1) In A -
/3(/х)
[0 < к < 1].
[Re/i >0].
[Re// > 0].
о
7ГП
( 8ШЖ \dx = -— In 2. 29. [ж2 In sin ж Лж = -— In 2 - - (C).
I COS Ж J	A	J	о	2i
о
2 2	^
ж In | sin x\ dx =	In 2. 31. з!п
о
}
sin \Bn + 1)ж] In sin x dx
2 /	n1 1
(In 2 - 2 V
ТГ
33. f cos [Bn + 1)ж] In sin ж dx = 0.
J
34. cos 2пж In sin ж с!ж =
J
2n
7Г
35. sinM ж cos /if	ж J In sin ж б?ж = — 2™мтг In 2
[n = 1, 2, 3, . . . ].
[/i > —1].
36.
37.
38.
fsin2n
2ж cos 2ж In sin ж с!ж = ~~ -
тг Bn-l)!!
тг . л/а2 — б2
In
7	In
«2 - b2 a + V«2 -
1
}
а > 0, а > b].
In
совож]
dx =
In
[n = l, 2; y? = sgn(l-|a|), |a| ф 1]

2.6.34]
2.6. Логарифмическая функция
443
39.
cos ж In sin x dx тг
1 — 2a cos x + a2 2a
I-
|a| ф\; ip = sgn(l -
40.
COS Ж	f Sin (ж/2) 1	7Г	r/	241 /-,	фч о 1 + ф i rtl
In < ; ' ; } dx = —:	— A + a ) In A qp « ) - 2a In 2
\ (/2)/	2|l2|Ll	/ v ^ ;	j
о
2тг
; ; } dx = :
cos (ж/2)/	2a|l~a2
L. I "	"		,	2 1П 1	А МЖ = 0
J 1^2асозж + а2 1со8ож1
о
2тг
42.
cos2(a?/2) In sin (ж/2)	тг
1 — 2a cos ж + a2	2a
a - 1
¦In 2
43.
45.
V 1 + sin2
-
44
Г	Sin3 ;
3 - , . , In 2 - 1
In sin x dx = 	.
sin ж
In
о
46. In
о
sin аж
cosax
	.
л
dx	ж ,
= — In ¦
47. In
о
OG
cosbx
sin аж
cosax
ж2 + z2 2z "* 2
а*ж	A dz 1)тг2 тга
=
48.
In | cos аж аж = — (о In 2 — a)
[a, Rez > 0].
[а, у > 0].
[a, b > 0].
о
49. CO°S Жо In I cos ax\ dx = — [ch 6z In A + e 2az) - e 6zln2]	[0 < 6 < 2a; Rez > 0].
J ж2 + z2	2z
0
50.
cosbx
xn{x2 + z2)
In
dx = /«
[a, b, Rez > 0],
/2 = -
2 "
ТГ __я
In 2 - az - ch bz In A + e~2a*)].
51.
52. I —In
1
sin bx In cos аж dx = тг In A + e az)z sh &z — z +ttz e z In 2
[0 ^ b < 2a; Re z > 0].
-
2
53.
1 f ж sin bx 1
	~{	\
+ z2 [ cos &ж J
sh 6z
z^ ch bz
In 1
[Rez > 0; 0 < b < 1].

444	Гл.2. Определенные интегралы	[2.6.35
со
Г 1 Г ж sin bx I _ ,	ч .	Г sh bz I . , ^Z4
54. —	-<	MnB - 2совж)йж = =Ftt4 _i , , > In A - e )
J ж2 + z1 { cos bx j	[ 2: ch bz J
0
[Re^ > 0; 0 < 6 < 1].
I о 1 y\ h Hf9 I
2.6.35. Интегралы, содержащие lnn <	>.
[ cos ож J
1.	tg x ln2n cos 2ж dx = 2n+1 Byi)!(Bn +1)	[n = 1, 2, 3, . . . ].
0
2.	f tg ж ln2n+1 cos 2ж dx = \72Л, тг2п+21B2
0
7Г/4
f	1
52n + 2 •
0
т/4
3
4(n + l)
1
2
0
тг/4	/
Г . u-i	/7T \ n.	f (-I)n2^1n!((n + 15 r.7 t
r±»	I sill	Zi«i/ Lg I	ZE. Л I 111 sill ZiX ИЛ — \		-, (n\	(	[rlc /Л ^> UJ.
J	v 4 /	\	A p \Av
0	v
17тг4
5. 1п2Bзтж)с1ж= 	. 6. ж In2B sin ж) с!ж =
25 920'
7* ' "x >О8Ж [ "" 2 V" ~ ' 12
0
tt/2
8.
0
tt/2
9.
0
7r/2
10. I ж In B sin x) dx = ж Li4 I - I + ^r
. Г ж
2/ 24	 8	"v 7 2880
0
7Г/2	7T
7тг'
ix = —
/
Г	1	Г
11. In2 B sin ж) In B cos ж) с!ж = - тгС(З). 12. ж2 In2Bsin ж) dx ^гт^.
J	8	J	z40
о	о
2.6.36. Интегралы от Л(х, sin ж, cos ж) In (a cos ж + &sln ж + с).
ж/2	тг/2
1. f ln(l±sina;)da; = --ln2ib2G. 2. f In A ± cos ж) dx = -- In 2 ± 2G.
о
тг/2	_i
Г i Л Г sina; 1 \ Г sina; 1	. тг2 1	2	Г1	П
3. In 1 + а	> <	>	dx =	arccos а	а < 1 .
J \	i cos x j J { cos ж j	8 2
0
Г sina; 1 \ Г sina; 1
> <	>
i cos x j J { cos ж j

2.6.36]
2.6. Логарифмическая функция
445
тг/2
Г cos ж In (I ± a cos x) .
4. I	\	L dx =
1 — or cos^ ж
1 I _ / тг	\ arccos a .
L ( тг — arccos a 1 —
l=Fl
а + л/а2 ~~ Ь2
ал/1 - a2 L V2
5.	In (а ± 6 cos x) dx = ж In
о
Г	с/ж
6.	In A + Ъ cos х)	 = тг arcsln b
J	cos ж
О
со
7. [ Ж Sm bX2 In A ± cos x) dx = ~ж sh bz In A ± e^z) - - eThz In 2
J ж + z	2
о
8.
ln(l±cosx)dx = -
2
±
- e~bz In 2
тг
9. In (a — 2a& cos x + b ) dx = 2тг In
[a, 6 > 0].
[6, Re г > 0].
[6, Rez > 0].
sin (ж/2) I	. , 2ч i i жа
) ' { }	\n(l - 2acosx + a ) dx = ± —
cos (ж/2)/	1 ; 2
о
11.	= 7rln|a| ±тг/Bа)
Л"
1 In A — 2a cos x + a2) dx	2тг
12.
l-26cosx
| X —
¦\n(l-ab±l)
\b\<l
4
13.
±г
7ГП
14. Г In (a
In а -Ь
2 — 2a6 cos x + b2) dx = 2жп In
0
7ТП
15. cosmx In A — 2a cos ж + a2) dx =	a
J	m
о
[{
Г f sin ж sin шж 1 , ,	2x , 7ГП / , bm+1 b771^1
16. i	> ln(l - 2a cos ж + a ) dx = 	 ±
J [ cos ж cos mx J	2 \ m + 1 m-1
о
17,
". [ cos{(m- 1/2)ж]1пA
— 2a cos ж + а ) с!ж = 0
о
2тт
18. I { "'" ^'"( ""ж '^ Нп A - 2а cos ж + а") йж = 0
J { cos (ж/2) cosf-гж J
о
> 1

446
Гл.2. Определенные интегралы
[2.6.37
19.
sin(a/a)sin[(n-l/2)a;] 1 . (л o	, 2ч ,	Г,ЬП
, . ' г/	. ; ; > In A — 2а cos х + а Ыж = тг±
cos (ж/2) cos [(п^ 1/2)ж] J v	;	[ п
6=
< 1
а|
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
In A - 2а cos ж + а2) 2 Ж 2 = - In A - ае z)
= — In (\a\ - sgnae^z)
|а| ^ 1; Re z > 0].
\a\ ^ 1; Re^ > 0].
= ^ 1п(|а| - 8gnae~z) -
sgn F ^
|о| ^ 1; Re^	> 0].
\а\ > 1; Re z	> 0].
[6 > 0; |a|	< 1].
[b > °;
CO°S Жо ln A - 2a cos ж + a2) dx = — < ch bz ln A - ae z)
x2 + z2	z [
— sh [zF -
к
< 1; b, Rez > 0].
7г Г
z I
a
^^ sh [zF — k)] — sh 6z ln \a
> 1; 6, Rez > 0].
tt/4
ln (cos ж ± sin ж) с!ж =	In2±—G.
8	2
о
2тг
f 1п(а
о
2.6.37. Интегралы, содержащие In
= 2тг1п[(а + л/а2 - Ъ2 - с2 )/2]
ai cos ж + &i sin ж + <
0,2 COS Ж + &2 Sin Ж + С2
тг/2
Г
1. ш
J
1пж с!ж	. Ь
	= тг arcsin —
а — о sin ж sin ж	а
г/2
2.
3.
. а + b cos x dx	b
ln	=тг arcsin-
а — о cos x cos ж	а
[|6h
[jfeK|a|].
о
тг/2
cos ж ,1 + 6 cos x .	тг	, 1|а&+ л/A — а2)A — б2)
In	dx = 	,	ln ¦
™ а2 cos2 ж l-focosx	2ал/1 - а2 1 - ab + д/A - а2)A - б2)
[0 < 6 < а < 1].

2.6.38]
2.6. Логарифмическая функция
447
, . 1 + sin x dx	2
4. I In	= arccos a
1 + a sin ж sin ж
5.	sin Bга -
о
2тг
Г
6.	СО8?71ж1п
1 — 2a cos x + a
dx = (-1)
n 2тга±Bп+1)
2тг
	 dx = — (na
a2	m
2тг ±ш/п
о
2тг
7. ctg-ln
ж 1 + 2a cos ж + а
2 1 + 2а cos nx + а2
= 0
[{!:!;:
[Ima = 0].
8. In
1 + sin ж dx 7Г2
1 — sin ж x 2
9. In
cos ж + sin x
cos ж — sin ж
dx 7Г2
10. In
1 — 2а cos bx + a dx
1 — 2а cos еж + а2 ж
ff '^a<1
LI \a\ > 1 или a = -1
2.6.38. Интегралы, содержащие In (acos2 ж + 6sin2 ж + с).
Обозначение: k! = \/l — к2 , 0 < к < 1.
тг/2
. f In A + bsln2 ж) dx = (~г' п\ A - 2~n~2) ((n + 2)
2. <	> In A + b sin ж) ^ж = — In	q= -
J \со8ж/ l	;	2 V	2^2
т/2
In A — а2 cos2 ж)	-
о
тг/2
4. I In (а2 cos2 ж + Ъ2 sin2 ж) б?ж = ж In
In
/
-62 + л/1-а2
r	n •	L , 2 J Sin Ж
5. ж sin ж cos ж II —« i
Л, = _L [37r| fc'3A " j5111 fe') | ± B2fe'2 + Qk4 - 3fe'2 In k')K(k) T
=F B-
- D - In A')E(fc)] + 7rfc-

448
Гл. 2. Определенные интегралы
[2.6.39
тг/2
Г 1 /l + sin G9COS2 ж\ .	. 1 + sin (ф/2)
6.	In	Г-?1	^МЖ = 7Г1П-
1 — sin (p cos2 ж
cos ((p/2)
[\<p\ <тг/2].
7.
-1/2
dx =
8.
sinn ж cos1 х i _ l2
J sins) \
<	>	In
[ cos x ) I
- к
/1'Г1 = /If = B^ k2)K(k) - B ^ In к')Щк), J*'0 = /11' =lnA;'K(A;),
к
/i' ml = /i'° =
1'0 = /31' -1 = kf~2[(k2
[2 -
- B -1пА;')
fe2 - 2 + ( \ \ In Jb;)Щк) + B - In кг)Щк)],
з1'0 = /31' -1 = kf~2[(k2 - 2)K(fc) + B + In кг)Щк)},
'2 ±^{
/33'0 = /33' ^ =
^ B + In ^)
k2 + I ^ I In Jfe'Wfc) - B + In ife#)E(ife)l.
9. I In (a2 cos2 ex + b2 sin2 сж)^	 = — [In (a ch cz + b sh zc) — zc]	[a, 6, c, Rez > 0].
x -\- z z
tg (ж/2) In (sin2 ж + F cos2 ж)	1 2(kfK/2
10.
— ^2 cos2 ж
оо
Г 1	f to-r 1 1
-1-1	J О ^ I J
J ж	[ sin ж J
(sin2 ж + к' cos2 ж) л^ _ 1 }n 2(VkI K
Vl — к2 cos2 ж
2 1
t/2
, In (sin ж + \/sin2 ж — sin2 ^>)
12.	dx =
1 — a2 cos2 ж
1
arctS
/l_a2 ylnsinV + -ln-
1 + Vl - a2
a2 + 1/I - a2 cos2 y? j
[|a| < 1; 0 < y> < тг/2].
2.6.89. Интегралы, содержащие lnA(tgx).
тг/4	тг/4
1. lntgicrfa; = —G. 2. в!п2ж In tgx с!ж = —— In 2.
o.
0
тг/4
Intgx
cos2a?
7Г2
8 '

2.6.39]
2.6. Логарифмическая функция
449
тг/4
4.
cos 2ж
4а
(тг =F arcsin a)
о
ж/4
, cos 2ж In tg ж .	ж
5. 	^— dx = —
1 ± asm2 2ж
тг/4
6. ln(l±tg<E)da; = -1
о
ж/4
sin \/Щ
tt/4
7. In tg т±ж)^— = ± —. 8. In
4 /si
с!ж	i71"
Ьк2ж ~ 16'
о
tt/4
9.
Г	|
(n + l)Bn
7Г/4
[
10. lntg(^±^)(lntg^Jn
J	V 4	/	SI
= ±-
¦Bn)!CBn-
0
тг/4
11.
,1-2"
0
7Г/4
, sin 2slntga; .	1
12.	n . o „ rfg = 	=
о
7Г/4
13.
1 — a2 sin2 2ж
sin 4ж In tg ж dx
[L(arcsln a) — arcsln a In 2]
(sin2 (p + tg2 v sin2 2ж)%/з1п2 2ж — sin2 <
2
ж cos2 f sin г; + у 1 — cos2 у? cos2 v
2 sin^slnv
7Г/2
14. f In tgжdж = 0.
о
¦In
+ sin v)
[0 < 9? < тг/2; 0 < v < тг/2].
15.	cosa 1 ж cos (a + 1)ж In tga; с!ж = —
J	Zifl
0
тг/2
16.	cos*^1 ж ctg ж sin (a + l)x In tg ж с!ж = — [С + ф(а + 1)]
о
тг/2
17.	Г tg»ln tg(aj/2)(ln со8ж)пс1ж = (-1)п^12^п^2п!((гг + 2, 1/2).
[а > 0].
[а > -1].
о
тг/2
18.
In tg ж
y/l - k2 sin2 ж
[0 < fc < 1].
29 А. П. Прудников и др., т. 1

450
Гл.2. Определенные интегралы
[2.6.40
19.
21.
j
In tgX
о
22. In
о
23.
1 -
ж = ^1п2 + С 20. I ж In |
о
ax ж
~x ~ T
| dx = 0.
[Re*>0].
cth az
K6,Re.>0].
2.6.40. Интегралы, содержащие показательную, логарифмическую,
гиперболические и тригонометрические функции.
vx[smbx\, ,	1
i
n
[Rep > |Im6|].
2.
2
p
с = a arctg —; Re p > I Im 61; Re a > <
P	I 0
3.
4.
^ \nxdx = - arctg - [c + - In (p2 + 62
ж	p [ 2
[Rep > | Im 6|].
7Г
1
[Ь, Reg > 0].
OO
5. sin bx In A ¦
со
3. [ sir
26
7.
8.
9.
262 26sh(fe7r/a) [ch(fe7r/a)
[6,	Re a > 0].
[6,	Re a > 0].
[6,	Rea> 0].
[6,	Re a > 0].

2.7.2]
2.7. Обратные тригонометрические функции
451
10.
11.
12.
ch x
ch x + sin a

спж — sin a
^—~	—""
спж + cosc
(ch — -chafe)
b sh бтг \ 2	у
dx =
ж shab
6сЬFтг/2)
dx = f ,^, 4(chcfe^ chafe)
feh(fe)
о
13. I e
о
14.
Чп^
тг
15. feacosa;[ln
[b > 0; | Rea| < тг].
[b > 0; 2|Rea| < тг].
[b > 0; | Rea|, |Rec| < тг].
[Rep>0].
[Rep > 0].
[a > 0].
16.
17.
-l)dx = zrctg[-)Kob
2ax
sin (буж2 + 2аж ) In
а + x +
dx =
[Rep > |Imfe|].
[Rep>|Im6|].
oo
18. [а,-1е-{8!п(/Ь1па!)Л
J	[ cos (oln ж) J
sin F In ж) 1 . ,_..	,v, f sin are; Г(а + ife)
) ; }dx = \r(a + ib)\<	)	{
cos (Ып ж)/	' l	;i\cos
Re а > | Im 6|; arg Г(ж) = -i In
^
|г(ж)
2.7. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
2.7.1.	Введение.
В этом разделе содержатся интегралы, в подынтегральные выражения которых входят
обратные тригонометрические функции. Они могут быть преобразованы к интегралам от
логарифмической функции и от степенных функций, если воспользоваться соответствую-
соответствующими формулами, приведенными в приложении I. В ряде случаев интегралы от обратных
тригонометрических функций с помощью замены переменной сводятся к интегралам от
тригонометрических функций. Например,
1	1	тг/2
arcsin ж dx = —г In (ix + л/t — х2 ) dx = ж cos ж dx.
oo	о
2.7.2.	Интегралы общего вида.
В этом пункте помещены формулы, которые позволяют находить интегралы, содержа-
содержащие обратные тригонометрические, а также степенную, алгебраические и тригонометриче-
тригонометрические функции. Некоторые частные случаи этих интегралов, соответствующие конкретным
значениям входящих в них параметров, приведены в последующих пунктах. Интегралы
общего вида представляются с помощью функций Vj, j = 1, 2, 3, . . ., помещенных в при-
приложении III. Конкретные значения параметров, входящих в эти функции, приводятся
29*

452
Гл.2. Определенные интегралы
[2.7.2
в фигурных скобках после каждого интеграла. В п. 2.7.2 приняты следующие обозначения:
г = p/q, где р и q — взаимно простые натуральные числа, если не указаны другие условия;
с. I 1, если взят sin6x,
О, если взят соз&ж;
7 =
I (—l
n/2] + fc
1,
1/2, если взят slnn bx, n = l,3, 5, ...,
О, если взят slnn bx, n = 2, 4, 6, . . . ,
0, если взят cosn bx, n = l, 2, 3, ...;
если взят	,
если взят соэбж;
Л f a^ifsin6a^l	. /ж\_ r/
1. ж <	> arcsin ( — 1 ах = На
ry
o , a_i f slnbx 1 n	/ж .
2. | ж <	> arccos I — I аж =
[ COS ОЖ J	\ I/
1, t/q, A(^5
1/2 + а/Bг)
1/2 + h)
ft)
[3/, b > 0; Re а > -rcr -
[cm. 2.7.2.1].
3. x
a_i f sinb 1 n
Г 81П&Ж 1	• fVY j	r/ \
{	> arcsin I — с!ж = J(cr)
[ cos 6ж J	V ж /
^ r

2.7.2]	2.7. Обратные тригонометрические функции	453
ГA/2
/2 + 27 + /i), A(p5 l +
[C = 1 - 7 + jr + (г - а)/2; у, 6 > 0; Re a < О].
со
4. ж0^1! Sm ,Ж > arccos (-Y dx = J(a)L=o	[см. 2.7.2.3].
J	[ cos bx)	\x/
У
У
f • l Л п	Г	/\Г1
a_i I sin ож	I	/ ж \ . ,w м
<	> sm i/arccos I — 1 аж = /v(<j)L=i,
j	[	\yj J
5. ж
J
[а/Bг) + (i/ + 1 + а)/2, а/Bг) + A + а - и)/2\'
35 \2
у2г\
2) 2«"!г	[e + (l + a + t/)/2, C + (l + o--t/)/2, 27
« = а + г((Т - 1), ai = С, 61 = С + 1/2, ci = ?, + A + <т + i/)/2,
di = | + A + о- - г/)/2, ei = 27 + 1/2 + h, z = (-Ь2/р2)р\
[у, Ь > 0; Re а > —6п].
у
6. [ж^1^2" - ж2Т1/2( 8ШбЖ Fcos Larccos f^Yl с!ж = K(a)|CT=0	[см. 2.7.2.5].
J	[costej	[	\У 1
_ Г а^1(81п&ж1п . г	fy\rl j r/ \i
7. \ x <	> sin i/ arccos I — J \ dx = L(cr)L=i,
J [ cos 6ж J L	V x J J
1-T -а/Г	1
n-"/2-e/Br),l-i//2-a/Br)J'
1/2 + h\'
6 = 7T U I	I	,
(l/2)j L1 - «2, 1 - 62, e2j
__ 3/2 (T^l^n-cr (^1)J
a + r(cr — 1), г;2 = ^A — cr + 2j) — a, V3 = rB — cr + 2j) — a, ai = ? — i^/2,
^/2, ci = A + <t)/2 + ?, di = ^j/2 + C, ei = 27 + l/2 + /i, a2 = A - и - a)/2 + j,
62 = (l + i/-o-)/2 + j, c2 = l/2 + i, rf2 = i-7-a/2 + r[(l-<7)/2 + j],
e2 = 7 + A - a)/2 + r[(l ^ a)/2 + j], a3 = 1 - (<т + i/)/2 + j,

454
Гл.2. Определенные интегралы
[2.7.2
ез = 7 + A - а)/2 + гA - <т/2 + j), * = ("*
[2/, 6 > 0; Re а < гA - <т)].
8.
- 2/2r)-1/2{ Sin^ Г
[ cos ox J
cos [^arccos (^Yl с/ж = L(<r
L	V x / J
[см. 2.7.2.7].
a-1/ 2r 2r\i//2 I sm "ж I	• I x
9. ж (ж +2/ ) i Г	sin i/arctg [ -
J [cos6a?J	[_ V 2/
о
(T)/2_QBr)
j-i 2 v "тг
= rBj — 1/) — a, V3 = rBj + 1 — 1/) — a, ai = cr/2 + ^5 6i = A — сг)/2 + ^,
//2 + C, di = (l + i/)/2 + ?, ei = 27 + 1/2 +/1, а2 = (с - i/)/2 + j,
i-7-a/2+r(j-i//2), c2 = (l-
2 + j, c3=3/2 + j, d3 = l-7-a/2
- a)/2 + 7 + r[j + A
^, У > 0; -n? -
1 _ (^i
pp^2p J
1
r Re v .
10.
+
^/2 Г 8
[совбж
i/arctg ( — | \ dx = Mia) L=o	[см. 2.7.2.9].
\y) J
Г	_2€
)
, 27
i
v2 = rBj + <r - i/) - a,
a2 =
1/2 + ?
- u)/2
= A + a + i/)/2 +
62 = A + a ~~ u)/2
c2 = 1/2
[6, |/ > 0; -n<f < Re a < A - (~l)n)/2 + ra - r Re i/].

2.7.4]	2.7. Обратные тригонометрические функции	455
12. \ха^{х2г+ у2гу/2{Ш1"^ \ cosli/arctgf^) \ dx = N (а) \а=0	[см. 2.7.2.11].
J	Icos ^x J	L	V ж / J
о
_	f arcsln bx
2.7.8. Интегралы, содержащие <	,.
[ arccos bx J
l
1. arcsln (el(px) dx = sgn (cos cp) arcsln (y^l — sin (p ) — cos <p + ^/2 sin tp cos [B(p + тг)/4] +
о
+ г{Aп y/l + sin (p + -\/sm (p ) + sin y? — \J2 sin cp sin [Btp + тг)/4]}	[0 ^ (p ^ тг].
l
1
2.	жа"Ч	^da = —N ^Т^Г Г ' 7	Rea>-1
J	\агссо8ж/	2aLlOJ V^ L1 + «/2JJ	L	U
о
Г	ж	f arcsln йж 1 .	тг I In л/t — k2 I
3.	^<	f }dx = T^\ , / ,ч >	0 < fe < 1 .
J ^(i _ я.2)(! _ рж2) \ arcCoS А^ж J ^2^1 In A + A;) j L	J
0	^	^
l
4.	е^рж arcsln x dx = — [Io(p) — ^o(p) — e™P]	[ I argp| < к]-
о
l
5.	же~рж arcsln x dx = —- f/o(p) — Ьо(р) + pLi(p) — pli(p) — A + p)e~p] -\—
J	2p2	p
о
[|argp| < тг].
l
f . / \ f arcsln ж 1 .	1 г/ чп т / m
6.	sin (пх7т)<	} dx = =F— (=Fl) - Joinn)]	n = 1, 2, 3, . . . .
J	[arccosж J	2n
о
l
Г f arcsin т 1	f тг/21
7.	1пж<	Ыж = ±B-In 2) - { ' У
J [ arccos ж J	[ 0 J
о
Г arccos ж _ ^ Bife — 1)!! In BJb + 2)
1	k=o	'	+
l
Г ax ( arcsin ж], ,7гГГсЬа1г/ч]
9.	e <	> dx = dz— < ^a } — Io(a)	[а Ф 0 .
J	[ arccos ж J	aLleJ	J
l
10.	ch ax arccos ж с?ж = — sh а	[а ф 0].
J а
-i
i
ii. < . ч > arccosжаж — — <	>	[п — i, -4, о, ... j.
-1
д / ч Г агс1жж 1 г
2.7.4. Интегралы от Л(ж), <	?
[ arcctg ж J
1. 1^аГС*8(е1Ж)Ьх=^-С°^
^ arcctg (ег1рх) |	4	2
dz — — In	;	h sin y? In B cos (p) — (p cos y? |	[ 1^1 < 7r/2]-
Л \Jt JL Sin <^i?

456
Гл. 2. Определенные интегралы
[2.7.4
2. | arctg2 ж dx = — + - In 2 - G.
3. Ua-ifarctg^/
[ arcctg (ж/
a) 1 , aa Г
, \ > dx = — тг
/a)i	4a L
a > 0; Rea> -
4. I — arctg (ж/а) dx = G.
пП( arctg (ж/а)
\ arcctg (ж/а)
5. ! x
?Hi*<-»'
со
6. arcctgn x dx = In
[(n l)/2] (_i)fc
[n = 2, 3, 4, ... ],
-1Г 1
(-l)kir2kB
7.
8.
arctg bx
71 i
= — In
2a
2a cos (атг/2)
'l + a2b2'
a
Г ж Г arctg bx 1
J Va2 - ж2 I arcctg 6ж j
йж = — I
46
2)
[0 < ipRea < 1].
[a, Re 6 > 0].
[a, Re 6 > 0].
10.
ж arctg 6ж .	тг	I	_	/ 1 + a262
- dx = 	,	arcctg by — arctg ^
/a2 - ж2 (ж2 - у2)	2^/у2 - a2
ii i ж arctg ж	,
11. I , . .^—	г™ аж = 7(а, с,
/с2 — ж2 (ж2 — у2)
[0 < а < t/; Re 6 > 0].
[0 < а ^ с < у],
= ^^5 7A, л/27 л/3) = -^.
. arctgn 6ж
12. —r-s—— dx = In
[6, Rez > 0],

2.7.5]
2.7. Обратные тригонометрические функции
457
13.
g Ж
^	. da = =
уж (x + ^)	v ^
Az L 6
[arctg
f arctg ax — arctg bx , тг . a
15.	dx = - In T
J	ж	2 6
7	тг
16. arcctg ax arcctg bx dx = — In
J	2
о
CO
1(, Г arctg аж - arctg bx	I 21 «
17.		2	2	arcctg ex dx = - ж In—
J	ж	2 b
- arctg (v 2bz — 1) — arctg bz]
[b > 0; \argz\ < тг].
[6, Rez > 0].
[a, b > 0].
[a, b > 0].
[a, 6, с > 0].
18.
arcsln ax arctg 6ж . Ьж . а + i/а.2 +
	— dx = — In
2	2
In1	1	In
2	aVa2 + b2	2
6 + V^2 + б2
arete —
2	&а
20.
arctg аж arctg 6ж	тг (а + 6)а+
	-2	dx = -ln aabb
( 1	arctg х) dx = —.
ж2 \ ж	)	4
а
[a, b > 0].
[о,6>0].
2.7.5. Интегралы от А(ж), е^рж, / arctSЬж
l ;	\ arcctg bx
1.
2.
arctff6ж
7
7rf0l.lr
arcctg bx j	2p
7
arcctg bx
6, Rep>0.
а(а + l)sin(a7r/2) X
жЪ~~~а	fa 1
2acos(Q:7r/2) X 2\2"' 2'
2'
^5 ^tW
2 4&2
b, Rep>0; Rea > -1 .
4 \ re
о. же
J
arcctg bx
-	x
—	— х
2

458	Гл.2. Определенные интегралы	[2.7.6
СО	/„
4. j х е
. j х
2acos(a7r/2) 12'	2 ' b2
1 „ 3 3 — a K !	r_
0; Rea > -1].
2b	{ 2 Г ЛГ " 2' 2 '
1
о
{x*
, aretgte . тт^^/счс —тгб.с с 1 i /л \ i
6. 	™	daj = - 1пГ(	 I	—In	 H	1пBтг)	6, Re c> 0 .
1 icx-l	c\ \2ттЬ/ 2тгЬ 2ттЬ 2ттЬ 2 l n	L'	J
_	= I
8
oo
9.
g
J \тг	ж
о
oo
oo
10. —-^		dx = - 1пГ(—— ) - 1пГ(	- -In		6, Re с > 0 .
J shc«	с [ \2тгЬ/	\ 2тгЬ / 2 с J
о
о
а/ \ f sin аж 1 I arctg&a:
2.7.6. Интегралы от А(х), {	> я
Обозначение: S =
Г a^tf smbx\
. \ x <	> arctg аж аж =
J	[cos bx J
_ irbsa-a-s ( sin (атг/2) 1
~ 2(a + <5) \cos(a7r/2)J
1
о
-1 (a + 8	а + ё	1 ^\
2 '	2	2' 4a2/
+ Ь—^- Г(а)\ Sm а7Г/;	M < Rea < 1; a, b > 0].
2	[cos (атг/2) J
CO
2.	Ж arctg аж а'ж = - — Ei (	J	[a, 6 > 0].
J ж	2 V a/
о
CO
3.	sin bx arcctg аж dx = — A — e ' )	[a, b > 0].
J	2o
о
oo
Г	1 Г ^b/a fb\	b/a ( bX\
4.	cos bx arcctg ax dx = —\e ' Ei I — ) — e ' Ei		[a, 6 > 0].
26	V a /	V a /
e I a-i Г sin&x 1	a
5. ж <	> arctg — a% =
1	cos bx J	ж

2.7.8]
2.7. Обратные тригонометрические функции
459
b5aa+87T ( sin(a7r/2) 1 ~г (а + 6
C0S(Q7r/2)
6. cos bx arete; -- аж = - i
7.
8.
sin еж	a _ 7Г . d + 1 + V^2 — 1
	arctg — ax = — In	^^^
coscic + rf	ж	с e"ac + d + v^2 -
. 2 ^ 2g
sin ж + с2 cos2 ж	ж
со
К 2 1	\ dx
— arctg	cos bx) — = С + In b
Ж X	J X
Ж	X
Х 3 1 а 3~а a2l}
[-(J < Re a < 2; a, b > 0].
[a, 6 > 0].
[a, с > 0; d > 1].
[a, b, с > 0].
[6 > 0].
2.7.7. Интегралы, содержащие arctgaa? и логарифмическую
функцию.
[\	,	In 2 7Г2	7Г
1. In ж arctg ж аж = ——\- — — —.
J	Z 4o 4
о
°°	2fe
х	х
3.	f In71 жAп х + п) arctg ж da = (^2)"nw!B"n - l)((n + 1).
о
со
4.	— In A + а2ж2) arctg bx dx = — [a6+ (а2 - б2) In (а+ 6) + 62 In &^ а2 In а]	[а, 6 > 0].
-"•3/4)" «-"¦
arcctg/(ж)
1. | sin ож arctg —	 dx = — e v
oo
2. f Z arctg (ae^x)dx = 2^а^1аГ(а)Ф(-а2, a + 1, 1/2)
3.
-r-—- arctg —¦	dx = - In A + ae cz)
x2 + z2	Х + асовеж	2
[a, 6, c> 0].
[a, Re a > 0].
[a > -ecz].

460	Гл.2. Определенные интегралы	[2.7.9
Г/ 1х \
4- Г^2	2	arctS (*
J \№ — X J
F(X, *){ J}	[0 < fc < 1].
Г СО8П Ж	a Sin Ж	.	7Г . г/	ч/	x2n^li
6. 	arete	с/ж =	In (I - а)A + а)	п = 0, 1; а > 0 .
sin ж	1-асозж	2
о
тг/2
! J arctg(a^l - Р81п2ж) |	dx	ж (	F(arctga,
\ arcctg (a \/l - k2 sin2 ж ) J yj\ - k2 sin2 ж 2 I F(arcctg (ал/l - k2 , A;)).
[О < к < 1].
2.7.9. Интегралы, содержащие /(<	>).
V 1 arcctg x)J
no
sin (i/ arcctg ж + с)
cos (i/ arcctg ж + с)
Г f sin (p/2 + c) 1	/p\ f cos (p/2 + c) 1	/p\l
[\ cos (p/2 + c) J y+1/2\2J \sin(p/2 + c)J "+1/2 V2/J
[Rep > 0; Re i/ > -1].
sin (f arctg ж)	1	C(^)
,	1	Ct1')
^ + WЛ 1)^=2(^1)- У	[Rei/>1]-
0
sin (i/arete аж)	. Civ, a)	1	1
^Р^1)& = ^ЧМ	[Rea>0;Re,>l].
0
(х _|_ iW2
4.	p™	e рж созбж cos (j/arctg
J уж
0
[6, Rep>0].
5 [(ж2 _i_ 2)^^/2(ж2 + Z2)^I//2/ sinbarctg(^/l/)]sin[l/arctg(^/^)] I
J	\ cos [//arctg (ж/2/)] cos [i/arctg (ж/z)] J
о
sin Bp arctg [a sin А/(ж + a cos A)]) 1
ж2 + 2аж cos A + a2)p \ cos Bp arctg [a sin А/(ж + a cos A)]) J
о
*' 2p - a)<! cosF- Л\\ >	[0 < Rea < 2Rep; a > 0; 0 ^ Л < .].

2.7.9]	2.7. Обратные тригонометрические функции	461
2.8. ОБРАТНЫЕ ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
Интегралы, содержащие обратные гиперболические функции, сводятся к интегралам,
содержащим гиперболические функции, с помощью подстановок вида у = Arsh ж, у =
= Arch ж, у = Arth ж, у = Arcth ж.
Кроме того, они могут быть сведены к интегралам от логарифмической, степенной и дру-
других функций, если воспользоваться формулами, приведенными в приложении I. Полученные
таким образом интегралы отнесены в соответствующие разделы.
Например, с помощью формулы
ch {у Arsh х) = - 1(\/х2 + 1 + xf + (л/х2 + 1 + х)~и]
получаем
жс^1е^ржсп(|/Аг8пж;Мж =
[Rea, Rep > 0].

Глава 3. КРАТНЫЕ ИНТЕГРАЛЫ
3.1. ДВОЙНЫЕ ИНТЕГРАЛЫ
3.1.1. Введение.
В этом разделе помещены двойные интегралы и указаны некоторые способы их приве-
приведения к одномерным интегралам. Кроме того, указаны различные системы координат на
плоскости, которые могут быть использованы при вычислении двойных интегралов.
Отметим, что основным способом вычисления двойных интегралов является сведение
Г Г
их к повторным [20]. Например, для вычисления двойного интеграла /(ж, у) dx dy его
G
можно свести к одному или нескольким повторным
Ь Х2(у)	b х2(у)	Ъ Х2(у)
f{x,y)dxdy=\l /(ж, y)dx\ dy = I dy f(x,y)dx,
a xi(y)	a xi(y)	a x\(y)
ИЛИ
/9У2(ж)	/3 y2(x)	/3	y2(x)
f(x,y)dydx=\l f(x,y)dy)dx=\dx f(x,y)dy;
aVl(x)	ol j/i(aj)	ol	2/i (ж)
при этом сначала вычисляются внутренние интегралы.
В частности, если G — треугольник, ограничнный прямыми ц = 0,|/ = жиж = а(а > 0),
то
ах	а а
Г /(	\	Г /(	\
/(ж, y)dxdy = ( /(ж, у) dx I dx = ( /(ж, у) dx I dy.
g	оо	о у
Кроме того, часто используется метод замены переменых интегрирования [20].
Пусть задано взаимно однозначное отображение ж = х(и, v), у = у(и7 v), области Г
плоскости переменных и, v на область 6г плоскости переменных ж, у, причем
а)	ж, у как функции и, v непрерывны в Г вместе с первыми частными производными;
б)	якобиан
дх/ди dx/dv
ду/ди dy/dv
Тогда справедлива следующая формула:
ИГ Г
/(ж, у) dx dy = f[x(u, v), у (и, v)]\A\dudv.
G	Г
Приведем некоторые системы координат на плоскости (dl — элемент длины, dS —
элемент площади) [16].
1)	Полярные координаты:
х = и cos v, у = и sin v,
0:$Jii<oo, 0^v< 2тг (обычно используются обозначения и = р, v = у?),
dl2 = dii2 + и2 dv2, dS = ududv.
2)	Обобщенные полярные координаты:
х = аи cos v, у = bu sin г;,
а, 6 > 0, 0 ^ и < оо, 0 ^ г; < 2тт,
А =
/0 в Г.

3.1.2]	3.1. Двойные интегралы	463
&%?ус\?ус\сус%?у	су	*гу	&у	с%	су	try
dl = (a cos v + b sin v) du +F — a )ixsin 2v du dv + (a + sin v + b cos v)u dv ,
dS = abu du dv.
3) Эллиптические координаты (х, у > 0):
а? - b2 \ ' У [ Ь2-а2
0^6 < а , --6 < и < оо, —а < v < -—6 ,
2	1	^ — ^	2	^ — ^	2
dl = —	diz — 	dt> ,
dS = —		du dv.
4:y/—(u + a2)(u + 62)(v + а2) (г; + b2)
4)	Вырожденные эллиптические координаты:
x = ch ix cos v, |/ = sh гх sin t;,
0 ^ и < oo, 0 ^ v < 2?r,
dl2 = (ch2 гх — cos2 v)(du2 + dv2), dS = (ch2 гх — cos2 v) du dv.
5)	Параболические координаты:
x = и -— v , |/ = 2гхг;,
—	oo < гх < oo, 0 ^ v < oo,
dl2 = 4(ti2 + v2)(du2 + dv2), dS = 4(tx2 + v2) dudv.
6)	Биполярные координаты:
sh и	sin f
ch гх + cos v '	ch гх + cos t;'
—	oo < и < oo, 0 ^ г; < 2тт,
> dS =
(chw + cos г?)^	(спи +
3.1.2. Общие формулы; интегралы от алгебраических функций.
В этом пункте предполагается, что все рассматриваемые интегралы существуют; a, b > 0.
JJ ¦-v-/[(=r+(fл<¦*
0
(f )"+(бГ^1	[a, p,p,q> 0].
1
2. \l f(ax + /3|/ + 7) dx dy = 2 f л/l - t2 f(t^/a2 + p2 + 7) dt
[a +/3 t^ 0; a, /3,7 — действительные числа].
3.	И f(x + y)dxdy= I /(*) dt.
11	1
4.	f f /(sy)(l - x)a^ya(l - yf-1 dx dy = B(a, /9) f f(t)(l -
11
/(sy)(l - x)a^ya(l - yf-1 dx dy = B(a, /9) f f(t)(l - t)^^1 dt
00	0	[Re a, Re/3 > 0].
1	1
5. J J^-y-^l - ^-^(l - yy-*-\l - xyzy dxdy =
7, 7
[Re7 > Rea > 0; Re7 > Re^ > 0; |arg(l - z)\ < тг].

464
Гл. 3. Кратные интегралы
[3.1.3
в.
7.
8.
9.
A -
10.
= гГ'^'
Fi(a, /3, /3#5 75 w,
= гГ'м'
: dx dy =
[Re/9, Re/3', Re G-/3-/3') > О]
vy)^a dx dy =
;, ReG-/3 -ДО > О]
dx dy =
7, 7
[Rep, Re/3', Reft - p), ReG'-/3') > 0].
*1'-?-1 dx dy
— UX — V|/)«+^™7-7/ + l
У» 7	J
[Re a, Re^, Re G - a), Re(jf - C) > O].
[p, g, Re a, Re/3 > 0].
11.
xy	ab
¦dxdy= ——r
/ж2 + I/2
12.
da? dy
1 - a L
7Г In A ¦
fa = 11.
3.1.3. Интегралы, содержащие показательную функцию.
Условие: a, 6, р, g > 0.
сю оо
1. f I f(ax + by)e~px~qy dxdy ¦¦
о о
оо оо
pq(bp - aq)
[о©	00
aq J f{x)e-px/adx-bp^ f(y)e-qv/b dy I.
2-
0 0
00 сю
+
3. | | f(xy)e
4.
dt.
0 0
00 00
xy
1 dx dy =

8.1.3]
3.1. Двойные интегралы
465
5.
)*e-r*-*vdxdy =
у + Л + 2)
Fi[ -Л, /x + 1;
I/ + 2; ^—
P
[Re/i, Re i/, Re (д + i/+ Л + 2) > 0].
[Re/i, Re 2/ > 0].
[Re i/ > 0].
16.
17.
18.
19.
30 А. П. Прудников и др., т. 1

466
Гл. 3. Кратные интегралы
[3.1.3
20.
I/4
1/	/g\ 2^2 ГE/4)р^/4 /1 /	/?
21.
2/(ж + уI
1/4
1 dx dy =
4>/2 Н
/1/ _ /?
[V2	V
22.
(ж
^ е
1 dx dy =
23.
ХУ
0 О
со со
(X
24.
о о
со сю
1 dx dy =
25.
о о
со со
26.
о о
со со
Аху
27.
'dxdy=
1 dx dy =
- Y0(y/pq)].
¦In
р + q
+
о о
со со
g _
28.
О О
со со
29.
О О
со со
30.
31.
32.
J J
0 0
со со
Г Г (V
J J
0 0
со со
+
т
У2
е рх чу dx dy =
-px-qy ^^ ^ _
-px-qy ^^ ^ _
P+
2аж|/ + у2
1 dx dy =
n3/2
[O-l].

8.1.3]
3.1. Двойные интегралы
467
33.
о о
со оо
34.
-px-qy-x
О О
оо оо
35.
у dxdy = ~e
xv j i	t-i/ \ -v/2 и/2 — 1 pq/21Xr
y dxdy = Y(v)p ' q ' eP4/ W-u/2,(i-u
о о
OO CO
36.
37.
y,e-px-qy-x2y dxdy= ^	2-u-S/2pBu-
o-px-qy-x
[-1/2 < i/ < 0].
о о
oo oo
38.	ye
39.
-px-qy-x у
dxdy = -
о о
со oo
} dx dy = — (cot. —
¦ ajjlac — b ) '
[a > 0; ac > b2].
40.
41.
xnyne~(X2^axy+y-)/l2(l-a2)] ^ dy = ^^ _ ^(n+D/2^
о о
oo oo
42.
о о
oo oo
— e
I/
-px-qy-(x/y)
43.
о о
oo oo
/x у
pq
44.
о о
CO CO
л/У
. rf =
[|arga| < тг/4].
4,
0 О
CO CO
.
46.
о о
oo oo
47.
dx dy =
о о
7 7
— q
sh I u Arch ¦
48.
aj d = /Z ln
|arga| ^тг/4; а ф 0].
Л	[|Rei/|<l].
9 >«]•
30*

468
Гл. 3. Кратные интегралы
[3.1.4
49
-px-qy-xy/(x+y)
dxdv-
О О
со со
50.
о о
со со
х + у
2pq(p + q
+ IK/2 '
51
0 0
со со
{ХУ){2
dx dy =
53.
о о
со со
54.
о о
со со
55.
p<7 - а2
l/ ±
2 V
±
2 V л/vq
56.
О О
со со
57.
_
[Rej/>-l/2J.
[р, > а2].
3.1.4. Интегралы, содержащие гиперболические функции.
Условие: а, 6, с, р, g > 0.
со со
1.	/;(asha? + 6ch x shy + cch ж chy) ch ж dx dy
—-co —-oo
c2 - a2 - b2
lim
2.
„
chxchy dxdy
ln(l + \/2)
A — fe2 shx shy)у sh x shy A — sh ж)A — shj/)
ch ж ch i/ rfx d|/
~ sh2 У)
2
. [7 yd2
J J у ch
v
у ch x —
v
=E(k)-(l-k2)K(k).

8.1.5]
3.1. Двойные интегралы
469
к оо
5.
о о
оо оо
ch жусп ж-f
- 2A -
6.
P + q
о о
оо оо
7.
о о
оо оо
8.	ch
e~v*-4v
dx dy =
4pg —
о о
оо сю
9. f [ — (ch ЛШ - 1)е~рх~чу dx dy = -2 arcsln2
J J xy
oo
4Dpg - 1)^3/2 arcsln
10.
О О
оо оо
sh y/xy e px qy dx dy =
4	1
arcsin
11.
[pq > 1/4].
2y/pq
9 Г
= - |1 - Dpq - 1I/2 arcsln
И > 1/4].
12.
о о
oo oo
13.
ch(ay/x2
/ж2 + |/2
• е рх qy dx dy =
¦ e^px^qy dx dy =
•In
pg — a\fp2 + q2 — a2
pq + aJp2 + q2 -a2
¦In
p2 + pg + q2 + (p + g)
q2 — a2 — a2
3.1.5. Интегралы, содержащие тригонометрические функции.
Условия: а, 6, с, р, q > 0; к2 < 1.
тг 2тг	1
Ир
/(а sin ж sin у + bcosx sin у + с cos у) sin у dx dy = 2тг f{t\/a2 + b2 + с2) dt
0 0	_i
функция /(t) непрерывна при |t| < \/а2 + б2 + с2 .
7Г 7Г
о Г Г j.// ,	6COS|/-C\ rfxrfy	2?TSgnC	^^	r	Г9\
2. /I actgж	 —ту	— =			/(sgncvc2 — a2 — b2 )
J J у	sin ж sin у / sin ж sin у	ус2 — a2 — б2
с2 > a2 + 62; lim f(t) = 0 .
L	t^ + oo	J
OO 7Г
3.	/;(acos ж shy + 6chy) shy dx dy =		¦ /(sgn Ьл/b2 — a2 )
b2 > a2; lim f(t) = 0 .
t> + oo
OO 27Г
4.	/'[(a sin ж + 6 cos ж) shy + cchy] shy dx dy =		/(sgn г-\Л?2 — a2 —
J J	v c2 — a2 — 62
л/с2 - a2 -
c2 > a2 + 62; lim f(t) = 01.

470
Гл. 3. Кратные интегралы
[3.1.5
Ир
/(a cos ж sh t/ + bchy) sin ж sh у dx dy = 2 /(sgn feVb2 — a2 ch y) sh у dy
0 0	Or	-|
62 > a2; lim /(*) = 0 .
тг/2 тг/2
Г Г	7Г2
6.	cos Ba sin ж sin у) dx dy = —Jq(®)-
о о
7Г 7Г
7.
4 — a2(l — cosa;)(l — cosy) 2a \a
7Г/2
[a > 1].
f f 2 /
В.	cos ж у
1 — sin2 ж sin2 у dx dy = —К j 	 I.
о о
ж/2 тт/2
9. f f cos2 ж cos2 yy/l - sin2 ж sin2 у dxdy= — 20K2( —J - 9тг2К~2 f — J .
о о
ж/2 тг/2
10.
11.
12.
о о
тг/2 тг/2
in у у 1 — й;2 sin2 ж si
ж sin у
О О
ж/2 7г/2
cosy
о о
тг/2 7г/2
13.
1 - к2 sin2 у
у 1 — fe2 sin2 ж sin2 |/
dx dy
sin2 у
dx dy = K(Jc).
"
о о
тг/2 у
¦и-
\/l — sin2 ж cos2 у
ctgydxdy	ж
о о
тг/2 тг/2
15.
16.
sin у dx dy
О О
ж/2 тг/2
sin2 a sin2 ж sin2 у
с!ж dy
- kf sin2 x — k\ sin2 у 1 + \/l —
гК
__ L2 _ /i __ L2 __ L2
fcl	V -1 ^1 ^2
хК'
- fcf + ^1 - k\ - k\
*!<!].
тг/2 тг/2
17.
18.
cos2 ж а*ж <
о о
тг/2 7г/2
у 1 — sin2 ж sin2 |/
cos2 х cos2 у dx dy I LT^2
sin2 ж cos2|/
2

3.1.5]	3.1. Двойные интегралы	471
7Г/2У
Г Г	sin 2y dxdy
A — к2 sin2 y)yl — к2 sin2 х	4А;
rfsc rf2/	_ ^2(<Р, А;)
20.
— к2 sin2 ж)A — к2 sin
21.
тт/2 2/
dx dy
In2 ж)A — к2 sin2 i/)	2
[fe2 cos2 ж + A — к2) cos2 i/] с!ж (% ж
~ k2 sin2 x)[l ~ A ~ k2) sin2 у] ~~2'
0 0
7Г/2 7Г/2
p p [>2 __2 _ i /-j |Л2\ лл„2
22.
'¦Шт
— fe2 sin2 |/
о о *
ir/2y
о о
тг/2
fi/1 _ f2Sj
24. J fi/1 f2Sj^ sin2y dxdy = ^{B - fc2)K(fc) - [2 + ^ In A -
, , /1 — к2 sin2 ж
25
о о
Г f /1-A;2 sin2 ж	f ,	7Г
4 /	о— sin г/ аж dy = —.
J J V 1 - к2 sin2 у У У 2л/Т^
f
26.
/2тг/2
sin x) A + sin I/)	da? c%
sin ж sin у	1 — 1г2 sin ж sin у
о о
27.	f f г/д/l - |/2 sin2 x dx dy = i [A + ^2)E(^) - A - A;2)K(A;)].
0	о
1	тг/2	1 тг/2
Г Г /		1	f f I		тг2
28.	yl — |/2 sin2 x dx dy = G + —. 29.	у cos2 x + i/2 sin2 x dx dy = —
JJV	2JJV	8
о о
к ч>
Я i
j/v/l - у2 sin2 x dxdy =
= | [A + A2)B(v>, fc) - A - A;2)F(^, A) - A -
31.
33
35
j
J
0
k
r
J
0
f
J
0
к
p
J
n
J
0
тг/2
Г
J
0
I
0
7Г/2
0
7l
1
ycos
У
Vi-
y2 sin2 x dx
- y2 sin2 x
~y2 dm
dxdy
2 x + y2 sin2
аж а г/
¦ |/2 sin2 x
• 2
sin (f
ay
j, jqi b\C(l
7Г2
ж 4
:E(A;) A-
> - cos <p + 1
34 f f -
J J \
0 0^
i 2\|Z-/jL\
dxdy
/I — y2 sin
1 ?>
P Г
36 f-
J J •
0 0
2 ж
У*
- 2G
зж ay 1 — cos (/?
у2 sin2 ж sm У

472
Гл. 3. Кратные интегралы
[3.1.5
37.
- 1) ctg
о о
к у
38.
i ydxdy = E(^, k)-(l- k2)F{ip, k) + (Jl-k*sin*<p - 1)
Vl-^sin^a;
у dx dy
A — a2 sin2 ж) у 1 — у2 sin2 ж
к*/2
39.
= (к2 -а2)П(^, а2, k) + E((p, к) - F(tp, к) + (yjl - к2 sin2 <р - l)ctg<p.
I/ с!ж с/у
0	о
1	у
40.
41.
A — а2 sin2 ж) у 1 — г/
I/ ^ж
y	= (к2 - аГ)П(тг/2, а2, к) - Ж(к) + E(fc).
1 — I/2 sin2 ж
A — a2 sin2 ж) у 1 — у2 sin2 ж
= A — а )П(у?, а , 1) — а П(у?, a , 0) + A — cos у?)/ sin у? — In (tg <p + sec у?).
/2
J J	2
О О
оо оо
42.
- |/2sln2 ж
cos ax cos fey dx dy = —
о о
OO OQ
43.	e рж ^ sin (ж + у) dx dy =
о о
оо оо
44.	e px qy cos (ж + у) dx dy =
рд -1
о о
оо оо
45. | | e px qy cos (жу) dx dy = sin (pg) cl (pq) — cos (pq) si (pq).
1
о о
оо оо
46.
о о
оо оо
47.
о о
оо оо
/х + у
1
/ж + у
рж^д;у .	Ху	in
F чу sin	dx dy = a —
e^p^9l/cos^^
48.
о о
оо оо
sin {x^fy ) dx dy = . /— — тгрер д erfc (p-\/q ).
49.	e-p*-™ cos (Жл/у) с!ж dy = ^pep q El (^p2g).
о о
оо оо
50.
*-'» sin (yv^)dx dy =
О О
оо оо
э jl. Ill/ e	h111 iyV ^J' j «л at/ — А/ о P

8.1.5]
3.1. Двойные интегралы
473
52.
53.
54.
55.
56.
dxdy = пу1Л {pq + a) 3/2.
0 0
oo oo
yne~px~qy sin y/^y dxdy =
о о
со со
о о
CO OO
dy = — ep g erfc (p-^/q ).
о о
oo oo
_ e px qy sin Bxfaxy) dx dy = ^ a
у	v	p V РЧ -
— e-px-qy sin {xy/jj)dxdy = -ep2qEi(-p2q).
57-
58.
59.
60.
61.
62.
63.
о о
со со
	e	sm {2xfaxy ) аж at/ =
/27	vv^/	^рд +
0 0
oo oo
0 0
oo oo
1	2
	e~px~qy cos (x-^/y) dx dy = жep q
v2/
cos л/ху dx dy =
2тгBn)lqn
0 0
CO CO
„n-l/2
	o px qy cog ^2^/axy ) dx dy = —==
о о
CO CO
cos2y2a|/ с!ж dy = тг(
0 0
oo oo
2Е
/pg + a2
x-l/2e-ap/(pqr+l)
-K
/pg + a2
64.
o2)/4K
lib
65.
—
xy
/ sin Jx^ dx dy = 2tt In
l + — +
4

474
Гл. 3. Кратные интегралы
[3.1.6
66. I I e
О ~
— y(a-\-ib cos ж + icsin ж)
dx dy =
2тг
«2 + б2 + с2
67.	—(cos
J J xy
о о
со со
Г f
68.	cos
о о
px qy dx dy = ^2 Arsh2
dx dy =
4pg + 1
69.
1
4	1
Arsh
Dpq + 1)
70.
Arsh
3.1.6. Интегралы, содержащие логарифмическую функцию.
Условие: а, р, g > 0.
о о
со со
2.
о о
CO CO
3.
1
РЧ
q Inp — ping
pg(p - q)
4.
2p(Inp — ln g) ¦
5.
yx-ya
ln у
11	1
' dxdy = X(qep, a). 6. f f exyln{xy) dx dy = f xx dx.
3.1.7. Интегралы, содержащие обратные тригонометрические
и обратные гиперболические функции.
Условие: р, q > 0.
со со
„-px-qy,,_ 2дAпд^1пр) + тгр
' dx dy =
о о
CO CO
2. Jjarctgyfe—
0 0
3. I I Arsh - e~px~qy
dx dy =
¦ln
P + g + у p2
P\fp2 + ^2 P + 9 ~~ vV+?

3.2.1]	3.2. Тройные интегралы	475
3.2. ТРОЙНЫЕ ИНТЕГРАЛЫ
3.2.1. Введение.
В этом разделе помещены тройные интегралы и указаны некоторые способы их при-
приведения к одномерным интегралам. Кроме того, указаны различные системы координат
в пространстве, которые могут быть использованы при вычислении тройных интегралов.
Отметим, что основным способом вычисления тройных интегралов является сведение
их к повторным [20], которые находят путем последовательного интегрирования по каждой
из переменных в отдельности.
Кроме того, часто используется метод замены переменных интегрирования. Пусть за-
задано взаимно однозначное отображение ж = х(и, v, го), у = у(и, г?, го), z = z(u, v, w)
области О пространства переменных и, г?, го на область V пространства переменных ж, г/,
z, причем
а)	ж, у, z как функции и, v, го непрерывны в О вместе со всеми первыми частными
производными;
б)	якобиан
дх/ди дх/dv	dx/dw
ду/ди ду/dv	dy/dw
dz/ди dz/dv	dz/dw
Тогда справедлива следующая формула:
Г Г Г
/(ж, у, z) dx dy dz =	f[x(u, v, го), у (и, v, го), z(u, v1 го)]|А| du dv dw.
v	n
3. Некоторые системы координат в пространстве (dl — элемент длины, dS — элемент
площади, dV — элемент объема) [16].
1)	Цилиндрические координаты:
х = ucosv, у = гл sin г;, z = го,
0 ^ и < оо, 0 ^ v < 2тт, ^оо < го < оо,
,,2	j 2 , 2 i 2 . i 2
dl = du + и dv + dw ,
dS2 = (и du dvJ + (du dwJ + (u dv dwJ,
dV = ududv dw
(обычно используются обозначения и = р, v = <p,w = z).
2)	Сферические координаты:
x = и cos v sin го, у = и sin v sin го, z = и cos го,
0 ^ и < оо, 0 $^ v <С 2тт, 0 ^ го ^ тт,
dl = du + и sin го dv + и dw ,
dS = (и sin wdudv) -^(ududw) + (и sin wdvdw) ,
dl/ = и sin го rfix dv dw
(обычно используются обозначения и = р, г» = <?>, го = t/>).
3)	Обобщенные сферические координаты:
ж = агх cos г? sin го, у = bu sin v sin го, z = си cos го,
0 ^ и < оо, 0 ^ v < 2тт, 0 ^ го ^J тт,
til/ = abcu2 sin го с1г^ dv dw.
3')
х = аи cosTO v slnn го, у = bu sinm г? sinn го, z = си cosn го,
dV = abcmnu cosm™ vsinTO~ г? cosn™ го sin n~ wdudvdw.

476	Гл. 3. Кратные интегралы	[3.2.1
4) Эллипсоидальные координаты:
2= (и + a2)(v + a2)(w + а2)	2= (и + b2)(v + 62)(w + Ь2)
Х ~~ (Ъ2 - а2)(е2 - а2) ' ^ ~ (а2 - 62)(с2 - Ь2)
2 _ (ti + c2)(v + c2)(w + c2)
Z
О ^ с2 < б2 < а2, ^а2 < го < -b2 < v < -с2 < и < оо,
l2
dl2 = - [/х(гх)(гл — v)(u — го) du2 — fi(v)(u — v)(v — w) dv2 + fi(w)(u — w)(v — w) dw2],
2
dS2 = — [—/jl(u)ijl(v)(u — vJ(u — w)(v — w)(dudvJ +
16
+ fi(u)(i(w)(u — v)(u — w) (v — w)(du dw) —
— fi(v)fj,(w)(u — v)(u ~~ w)(v — wJ(dv dwJ],
dV = — у —-fi(u)fi(v)fi(w) (u — v)(u — w)(v — го) du dv dw,
8
5)	Вырожденные эллипсоидальные «вытянутые» координаты:
х = sh и cos v sin w, у = sh и sin г» sin го, z = ch u cos го,
dl = (sh и + sin w)(du + dw ) + sh ixsin го dv ,
dS2 = (sh2 и + sin2 w) sh2 и, sin2 w(du2 + dw2) dv2 + (sh2 и + sin2 wJ (du dwJ,
dy = (sh ii + sin w) sh г* sin w dti dv dw.
6)	Вырожденные эллипсоидальные «сплюснутые» координаты:
ж = ch гх cos v sin w, у = chu sin v sin w, z = shu cos w,
0 ^ w < oo, 0 ^ v < 2?r, 0 ^ w ^ 7Г,
dl2 = (sh2 n + cos2 w) (dii,2 + dw2) + sh2 и sin2 w dv2,
dS2 = (sh2 и + cos2 w) ch2 wsln2 w(du2 + dw2) dv2 + (sh2 и + cos2 w)(du dwJ,
dV = (sh2 г^ + cos2 w) ch и sin w c/гх dv dw.
7)	Сферо-конические координаты:
2 _ u(v + a2)(w + a2)	2 _ u(v + 62)(w + 62)	2 _
Ж —	- - —гт - , у —	т—т	, Z -
(ft — О )CL	(О — ft H
dl = —	X(v)u(v — w) dv + X(w)u(v — w) dw ,
4 I u	J
52 = — [-X(v)(v - w)(dudvJ + A(w)(v - w)(dudwf - X(v)X(w)u2(v - wJ(dvdwJ],
1
dV = — \J—uX(v)X(w) (v — w) du dv dw,
о
X(t) = [i(t + a2)(t + 62)n\
Парабоидальные координаты:
x = 2uw cos г?, у = 2г1,го sin г?, z = и -— го ,
0^г*<оо, 0^г?< 2тт, 0 ^ го < оо,
dl = 4[(и + го )(сш + aw ) + u w dv j,
d52 = 16[(гг2 + w2)u2w2(du2 + dw2) dv2 + (u2 + w2J du2 dw2],
dV = S(u + го )uw dudv dw.

3.2.2]	3.2. Тройные интегралы	477
9) Тороидальные координаты:
sh и cos v	shu sin v	sin го
-, У =
ch и — cos w '	ch и — cos го '	ch и — cos w '
0 $J и < oo, 0 ^ v < 2тт, ^тг ^ го ^ тг,
dl2	(dti2 + sh2 и dv2 + dw2),
(спи — coswI
dS2 = —	-r [sh2 u(du2 + dw2) dv2 + du2 dw2},
(chu — coswL
sh n.
rfV = -г-.	r^ rfix dv dw.
(chu — coswL
10) Биполярные координаты:
sin и cos v	sin гл sin v	sh го
, У =
, У =	, а, 		,
ch w — cos г*	ch го — cos и ch w — cos г*
O^ii,<7r5	0^f< 2тт, ™oo < го < oo,
df =	2 22 2
(dti + sl
(спгу — cos иI
dS2 = —	r^r [sin2 u(du2 + dw2) dv2 + dii2 dv2],
(ch го — cos uL
dV = 7—¦	r^ du dv dw.
(chw — cosu)d
3.2.2. Общие формулы; интегралы от алгебраических функций.
Условие: а, 6, с, р, д, г, а, /3, 7 > 0.
1.
о
[при условии, что интеграл справа сходится абсолютно].
¦P/q
а а —аз a — x — y
000	0
4.
[при условии, что интеграл справа сходится абсолютно].
xyz dx dy dz
—9" ~T~ ITT "T —9"
az bz cz	2 1 2 2	Г
«ОС	,2 2, С 2 2, fl , 2,2, H
oc in-r + c a In —V a b In — .
5.	dx dy dz =
8(a2 - 62)F2 - c2)(c2 - a2) [	6
а3Г4A/4)
48^-^

478	Гл. 3. Кратные интегралы	[3.2.3
л	Г Г Г	dxdydz	4 з/ 2 . ,2 , 2x^1/2
6.	—f = - тгг (а + о + с ) ;
JJJ	^(	J + ( ЬJ + ( J 3
_	Г Г Г	dxdydz	2жаЪс _/ . V«2 — с2 Iа2 — Ъ2
7.	=	F —	;
л/х2 + y2 + z2 Va2 - с2 \	a 'Vo^-i
[a > b > c].
i i i	xvz	. . . 1 2,2 2 db + be + ca
8.	У 	dcr.dydr. = —n2h2r2
^x2 + 2/2 + z2	"	15
3.2.8. Интегралы, содержащие показательную, гиперболические
и тригонометрические функции.
Условие: а, 6, с, р, д, г > 0.
y2^(z^aJ dxdydz =
3/2 Г	/	\
(V/2 ILL L f !^) erf
oooooo
2.
0 0 0
[Re и > -2].
/3/3/3
о ГГГ	ch ж ch у ch z da; c% dz		„2/M
JJJ A ~~ sh x sh i/ sh z) ^A - sh2 ж) A - sh2 y){\ - sh2 z)
[a = In (>/2 - 1), C = In (л/2 + 1)].
OG 2ТГ 7Г
4.	/{[(a cos |/ + b sin i/) sin x + с ch ж] sh z + rf ch z} sh2 z sin ж dx dy dz =
0 0 0
oo
= 4тг f /(sgn dVd2 -a2 - b2 - c2 ch t) sh2 t dt	[d2 > a2 + 62 + c2; lim /(*) = ol.
J	L	t^ + oo	j
7Г 7Г 7Г
5. f f f	<fa<fy<**	= 4?rA8 + 12^2 - 10V3 - 7^6 )K2[B - V3 )(y/s - л/2 )].
J J J 3 — cos ж cos |/ — cos z
0 0 0
6.
7T 7Г 7Г
7Г
3 — cos ж cos у — cos ж cos z — cos i/ cos z	V 12
0 0 0
7Г 7Г 7Г
7.
47гК(
1 — cos ж cos у cos z	\ 2
0 0 0

3.3.2]
3.3. Многомерные интегралы
479
3.3. МНОГОМЕРНЫЕ ИНТЕГРАЛЫ
3.3.1. Введение.
Обозначения: х = (х±, ж2, • • • , хп), а = (ai, . . . , an), x2 = ж? + х\ + . .
+ 122Ж2 + . . . + а„жп, cfx =
= л/х\ + ж2.
п , ах =
ж2 ,
. . dxn.
Замена переменных (сферические координаты):
xi = pcos (р,
Х2 = р sin (fi cos у>2,
ж3 = р sin (/?i sin *^2 cos срз,
Хп-1 =
xn = p sin <pi sin v?2 • • . sin <^n^2 sin y?n^i,
0 ^ p < 00, 0 ^ <^fc ^ 7Г, A; = 1, 2, . . . , n - 2, 0 ^ y?n_i < 2тг,
rfV = p71^1 sinn^2 <pi sinn^3 (f2
n^3 sin 99^-2 rfp d(pi dcf2 . • . dipn~\ — элемент объема.
При х ^ 1 можно использовать формулу
/(x)dx =
7Г	7Г
= (^1)п • • • /(cos 0i, sin 0i cos 02, sin 0i sin 02 cos 0з, ...
о о
. . . , sin 0i sin 02 ... sin 6n-i cos 0n) sinn 0\ sin^1 02 ... sin2 0n-i sin 0n <
dx2 . . .
Г	Г
1.	vixi) dx\
J	J
a	a	a
X	XI	Xn-l	Xn	X
2.	f dxi f с!ж2 . . . [ dxn f /(*) dt = — f
жп)с1жп I f(t)dt= ^
3.
О	ж2
-2n)!
¦1)!
3.3.2. Интегралы по области x\ + x\ + . . . + ж2 ^ r2.
2. J ... j /(ax) dx = ,п + 1ч J (^ " *2)(n)/2/(|a|t) Л
Г	)
м-
2тг(п~1)/2 Г	7
/(x2, ax)dx= —^	^ It^dt /(t2,
4. I... I /(ax +
rfx =
[Imafe = 0; к = 1, 2, . . . , n].
¦ b)(r2 — j.2\Brn + n-l)/2 ^^

480
Гл. 3. Кратные интегралы
[3.3.2
5. ••• /(х , ах, bx)dx =
x2<r2
dt
f du f vn~3f(t
2 . 2 . 2
|a|?,
6.
U
1
C = rab, 7 =
 dy J g(\*\t){t - t2)^
8.
9. • • • dx =
(n-i)/2
00	r2/. , • л	n OO
j- —7—	П e^(t+iu)a;feFfc(a^)da^
fe=i ^__
[t > 0 — произвольный параметр].
l
p
t^1 dt ei|a|tti(l - ii2)(n^3)/2dti.
10. ... | (ax;
X2<1
Г(п/2) + Г
2m . _ Bm - 1)!!	тг"/2
11. Г.. f(axJm+1 rfx = 0.
12. f...
2 '-... + anx2)m(bxJ1dx =
ft
ftc
У = 0
14. •••
(axJ
21
2m + 1
n/2)'
[m + 1, n/2 + m
«•I-
(axJ
/, n/2 + m — i/ + 1,
r"
2 \ m
[m > 1; 0<i/<m + n/2; 6fc > 0, к = 1, 2, . . . , n].
16. ••• eaxdx=B7r)n/"|a
n/2 ~n/2

3.3.3]	3.3. Многомерные интегралы	481
17. [ • • • fA - х2)реах dx = Bп)п/22рГ(р + 1)|аГр-"/2/р+п/2(|а|).
18. |...
19. f... (Va/A^x2) dx = J(a, n)
X2<1
rBm+l)/2	/m+±\ J^/m^(m--\	_k
J(a, 2m+ 1)= *,; ' e- m + 2	? (?)
jrn-k
X 	г
 h(i) - MI)]}=<-')"^ty-•"'— (I)
2
^aEt(^a)]},
J(a, 2) = тге^а[1 + ae^a EI (-a)],
¦/(«, 3) = Пр e^a/2 [Ba + 1) ATx (|) - Ba + 3)^0 (f )].
I I '¦ ir	it	I - О	О >. / я!--» 1 \ / О * I n I i
?k\J % 1***1 11 i^vJo Ujhdjh tlJL 		f	ч	I I #	I/ J	С	t*?/
^ ^	[Imafe = 0, к = 1, 2, . . . , n].
3.3.3. Интегралы по области —	1	—Ь • • • H	'^— ^ 1.
d\	0,2	0>n
Условие: r, a*., 6^, ад., /3fe, г/д. > 0, A; = 1, 2, . . . , n.
°°	"	-1/2	1	/	n	,2 чп/2-p-l
X
У0	*0	'"""
г n 52
to = /_] 	~; 1/0 = 0, если 6i, 62, • • • , &n принадлежат области интегрирования; в противном
б2	б2	Ь2	1
случае у о — положительный корень уравнения 	г- -\	г- + . . . -\	— = 1 .
2/0 + а{ уо + а|	2/0 + «n J
Г Г		_	Г и*
2.
31 А. П. Прудников и др., т. 1

482
Гл. 3. Кратные интегралы
[3.3.3
3.
¦...+
П1/ь —1
afefc
4.
= Г
[t\ = 1, t2 = +СЮ, —СЮ ¦
= 0, t2 = 1, uk > О при О:
dx
5.
ртг
п/2
Г(р
00 при О: (/)	(/)	(/)
+ (x2/a2f2 + . . . + (хп/апHп ^ 1; А; = 1, 2, . . . , п].
п/2-Р п
п
[О < р < те/2; 2/о см. в 3.3.3.1].
V	1	2	•	n / ^_-j_
6.
= r
dx
_
7.
, ^/«2, • • • , ^n/oin
+ U2/OL2 + . . . + J/n/ttn J M —
П^1
[e = 1, —00 < 1/1, . . . , i/n < 00, fj, > l/i/ai + u2jot2 + . . . + un/an
при О: ж + ж + . . . + х%п ^ 1] или
. . . + i/n/'an и i/i, . . . , un > 0 при О: ж + ж^2 + . . . + ж"та ^ 1].
хх \ ^1
1 _|_ Tai 4- та2 -4- 4- татг
, V2/0L2, • • • , ^п/«п,
/3, (/3 + 2)/2
[/3 =
ilai, • • ¦ , vn/an, /3/2l _
/3, (/3 + l)/2	J
^/«2 + • • • + Vn/oLn]-
8.

3.3.4]
3.3. Многомерные интегралы
483
3.3.4. Интегралы по области sci j? О, Ж2 ^ О, . . . , жп ^ О,
. • - + хп ^ а.
j_ c e«(*+n/) dy ^
2тг
2.
n
fe=i i
[а > 0; t> 0 — произвольный параметр].
(ах
k=i
du
[a > 0; t > 0 — произвольный параметр].
4.
fe ^ 0, A; = 1, 2, . . . , n; 6 > 0].
5.
Щ <fe~1
sci^O, ж2^0, ..., жта^0
6.
i^n, к = 1, 2, . . . , ii — 1; sn = /in].
X2 + • • • + XnJ \X2 + Жз + • • • + Xn
X4 + • • • + Xn\	(	X
... Fn_i
П Г
f] t;fc-x(i - tk^-^Fk-^tk)dtk
[при условии, что интеграл в правой части равенства сходится;
• • • + "п, Imi/fe = 0, А; = 1, 2, . . . , n].
0-1 О-2 • • • ®>п
[а* >0, г = 1, 2, ..., п].
+ ...+
«2	«тг
(ж) = (ж - а\){х - п2) • • • (ж - on)J.
31*

484
Гл. 3. Кратные интегралы
[3.3.4
9.
10.
11.
12.
13.
14.
к	к
5^ Am + ^ ат + А;,
п = 1	т=1
к	fe + 1
m=l	m=l
к
xk =
= 1, 2, ..., 71 .
= г
1/1, i/2, ...
n	n
wife + ^ I/fc + 1
Lfe=i
• - • u
П=У2 = --- = У1=0
а2}2
. . . + «f }2/ь г = 1, 2, . . . , t; i/, > 0, j = 1, 2, . . . , n]
= Г
l , l/2 , • • • ,
У\ + ^2 + • • • + Уп - М+ 1,
(ЬхГ
(c0
CO
2 + ... + i/n + m+l
1/1, 1/2 , ...
- 1/2 + • • • + b
[ад., I/fe» M» ^1 +
n
О Х1к^ die =
1 > 0].
dx
• • • xn(l — ах)
(n+l)/2
7Г	|-r 1/2
> 0, к = 1, 2, . . . , n].
= Г
(ах + b)»
+ . . . + I^n - ,
[afe, 6, i/o, i/,
nvh — l
> 0; i/0 + i/i + . . . + i/n > M; A; = 1, 2, . . . , n].
= Г
Щ +
[ад., 6, i/Q, ffe
> 0; i/Q + i^i
^n = fJ>", к = 1, 2, . . . , n].

3.3.5]	3.3. Многомерные интегралы	485
15.	=(-l)mrf	4>."i. •••."»	|х
L^o + v\ + • • • + Уп — /i + га, /xj
{	1 + (fl* + Ь)*Г"*} dt
[ад., 6, i/q, i^fe, /i > 0; i/o + "l + • • • + ^n < /л; A; = 1, 2, . . . , n].
16.
17.	f • • • f	eax dx = V	^ (eafe - 1)
[у?(ж) = (ж - oi)(a; - аг) . . . (ж - ап)].
ь ь
3.3.5. Интегралы вида . . . /(х) rfx.
оо
. J . . .
а	а
оо	оо
. . . хп)х\/пх
\/пх\/п
п)х\х\
) "
CO	CO
4-Ж2 + --. + ж«) 1/n 2/n	(n — l)/n
f	Г
. . . .
оо	оо
3.
— со	—оо
Г( —-— j Vaift2 . . . ата о
[ofe > 0, A; = 1, 2, . . . , n; r = 6?/ai + ^/«2 + • . • + Ъ2п/ап].
CO	CO
I	I	J-	h ?~Т	—-I
4. ... т	г~ е^ Х I I Х1к^ ^х =
I (ао + ax)^	11 й
0	0	fc™1	оо	п
kj Ьд., i/, ft > 0 и либо ао > 0, либо ао = 0 и i/i + 1/2 + • • • + vn > /j].

486
Гл. 3. Кратные интегралы
[3.3.5
оо оо
5.
Vn, Ц,
fe=l
по
оо со
6.
_
- 4
1//XI,
[ад., /х, г/д. > О, А; = 1, 2, . . . , те].
те
к=1
11 Mfe afe
> 0, A; = 1, 2, . . . , n].
CO	CO
7.
—/2
, Rei/>0].
CO	CO
8.
o2 + (x - aJ]("+1)/2[<?2 + (x - bJ]("-1)/2
— оо --оо
9.
-co	-co
/ nx 1/2
положительно определенная квадратичная форма, aij =
A = det Q = det (ai;7-), В = det
оо	со
10.
1 1
11. Г.. [/(Ж1Ж2...ЖП)A-
О	О
= -rL= Bff)n/2e-(n+1)/e	[a > 0].
Vn + 1
1 dx =
= Г
[при условии, что интеграл в правой части сходится абсолютно].

8.8.5]
3.3. Многомерные интегралы
487
12.
13.
14.
[Re a, Re/3 > 0; Re z > max(-l/n, -Rea/(n- 1),
2	nCfl + 1)
-Xn) ^Х^	—	.
- 1))].
15.
3/OS	* # • X fi — ]_
x\xl...x
/1	«X/ *~)
E
2 2	2
ж...хк
(n + 1H + 2) ^ (n - ? + i)(ra - A; + 2)
0; |arg(l - z)\ < тг].
¦ 1)тг(п'
3/2)'

Глава 4. КОНЕЧНЫЕ СУММЫ
4.1. ВВЕДЕНИЕ
В этой главе помещены некоторые конечные суммы, содержащие различные элемен-
элементарные функции. Отметим, что для вычисления конечной суммы ^ пк можно ввести
вспомогательную сумму ^а/гЖ (или привести данную сумму к такой форме), записав
ее в виде обобщенного гипергеометрического ряда и получить ответ в виде обобщенной
гипергеометрической функции. Иногда может оказаться полезной следующая формула
замены индекса суммирования:
J2 ак= Y1 а*-*>
k = Tl\	к = П —712
в частности,
k=Q	k=0
Всюду в этой главе I, га, п = 0, 1, 2, 3, ..., если не указаны другие условия; кроме того,
по определению
= 0 при П2 < п\.
4.1.1. Суммы вида
3.
4.
5.
6.
7.
8.
[Bm+i(n + 1) - Bm+1]
9.
здесь
[m = 1, 2, 3, . . .
[m = l, 2,3, ...
-целая часть (n + l)/2]
fc=l
10.
11.

4.1.1]	4-1- Введение	489
k=l
14. J^k5 = ^n2{n + lf{2n2 + 2n- 1).
fei	12
15.
-!)*-^6 = i [1 + (-l)nEn2 - Бп4 - 2n5 - 1)].
k=l
1
16. 5](A; + a)m = ——- [Bm+1(n + 1 + a) - ?m+i(a)].
fc=o	m + I
fc=o
17. f](^l)fc(fe + a)m = i [(-l)nEm(a + n
fcO
18. f]B^ + l) = (n + lJ. 19. f](
fc=O	fc=O
20.
21. ]T(^l)fcBJfe + IJ = (^l)n2(n + IJ -
k=0
22.
23. ^
' ~ (^k (b - ayk[Bk+m+1(n + b + 1) - Bk+m+1(b)].
n	-.
24.	J2(k + a)(^ + b) = ~ n(n + Ш2п + 1 + 3(a + b)] ¦
A	1
25.	Y, k(k + X) • • • (k + w) = 	n(n + 1) . . . (n + m + 1).
A	l	A	l
26.	V A;(A; + 1) = - n(n + l)(n + 2). 27. V A;(/c + 1)(Aj + 2) = - n(n + l)(n + 2)(n
^^	3	Jr^'	4
28.	^ A;(A; + 3)(A; + 6) = i n(n + l)(n + 6)(n + 7).
29.	V A;(A; + 4)(A; + 8) = \ n(n + l)(n + 8)(n + 9).
30.
k=o	8 8
14 1
7) +
31.	^C^ + l)Cfc + 4)Cife + 7)	+
k=o	3 12
n	n
32.	Yjkkl = (n + l)!-l. 33.	^2k\(n-k)\ = Sn, Si = 2, 5n =
fc=l	fc=O

490	Гл. 4• Конечные суммы	[4.1.2
\к
/1-1 \к
4.1.2. Суммы вида у j -	—.
2- Е ^ = ^Т)? W^^U) - ^т-1}(п + 1)]	[т = 1, 2, 3, .. . ].
п
3. ?)
3 11	25	137 147
Si-1, St--,	Ss-y,	S4--, 5s-—, Л-—,
1089 2283	7129	7381
6	*	5 A
4- Е
5- Е^ =
49 205 5269
fe = l
7- E ^ = (^i)! (-ir^-^a) - (-i)-^^-4^+1)].
k=l
n
8. V-
319 rr 533 JT 1879 rr 1627
^	У	U
420' ^8840' Ув2520' Ul° 2520
31	115	3019
= ^6' V4=144' Ve
2n
10. V
V(i)	V^
ti k hk
4.1.8. Суммы вида
/ 1 -t\k
(k + a)s°
n
2. ^
з. У

4.1.5]	4-1- Введение	491
^ (к + a
\ /З'(п + « +
//Л
/II \fe
4.1.4. Суммы вида У^ ——¦—ту™™™
у^ (±l)fc = 1 Г/ С 1 Г^(а + 1I _
* 2^k(k + a) a[\-ln2J ^\^(а + 1)/ l j
(га + а + 1) - 0(п
1 2m
2 V	-	 ^^
fu^l	лЗ^^Х	fe^^l	fb^l
El П \—~\ 1
	=	 у
1 Л/ ~j~~ I I V j \ fb J~ {) I	III/	I/	111/ """I™" t f i ЛЬ ~g l> ~J #1/1
5 T	X	= X	г
^ (ка + b)(ka + a + b) ab a(na + a + b)'
m-j-n
ш	->»	I	I	# ж	-%	I
6.
^ (ka + b)(ka + ma + b)	ma U-' ka + b ^ ка + Ъ )'
k=0 x	/ x	/	\k=0	k = m	I
J^	1	1
k=0
1	1
a2 = ^ [^(^ - а + 1) - ^(га + а + 1) + ^(а) - ^(-а)
•
12.
-21) 2(m-Z) Jjrj	\ife + 2I ife + 21-
4.1.5. Суммы вида Л
1>(Ь)
1/3F)
' /	1\/	L\ К	/	1 /Э/	I к I 1 \ I	I Q(U\ I	'
}]+c)
n + c)/ \/3(c)JJ-
^	1	гг [1 Л 1	1 ^ 1
" ^ к{к + )(к + 1	^	^
m-l [l ^ к(к + п)

492	Гл. 4• Конечные суммы	[4.1.6
з У	1	l	l
k=l
n
4. V-
g \
^-^ (mk + l)(mk + ?n + l)(mk -
1 Г 1	1
2т [1(т + I) (тп + т + 1)(тп + 2т + I)
1	1
2а(а + 1) 2(п + а + 1)(п + а + 2)"
1
12
9 V	X	- П
4.1.6. Суммы	вида /^пПл и ДРУгие-
J^ ^	1 mn+1
^ {к + т)\	(га — 1)! (га + п)\
1	1 Г 1
2 V
4^ А;(А; + 1) . . . (А; + га) га [га! (п + 1)(п + 2) . . . (п + га)
п
^—>
(А; + а) (А; + а + 1) . . . (А; + а + га)
1 Г	1
4
k=0
/ J
fc=l
n
fe = l ^
v^1
Г
(fe-
tlI
кк
2
-*)
fc+i
-1)!
¦ к
m [a(a + l)(a + 2) . . . (a + m - 1) (n + a + l)(n + a + 2) . . . (n + a + m)
(п + а + 1)	Г(а)
Г(а + 1)Т e. V,,,,1 ,=i *
V 1
^ т
т=1
fc 1	n! n_i
2 B + l)! '
2 Bn + l)! '	^l j (n-k)UklJ ^ m n2'

4.1.7]
4.1. Введение
493
--
"
АЛЛ. Суммы вида
1.
3.
1~а;П
2. J2 kxk = A - x)~2[x + (nx - n - l)
x) - xn+1[(n + IJ - Bn2 + 2n -
n+1]
4. > к х = хA — х)~ х
х [ж2 + 4ж + 1 - (п + 1Kжп + (Зтг3 + 6п2 ~~ 4)жп+1
п
6.
7.
^
-Zn2-3n + l)xn+2 + n3xn+%
п + 2)хп+2-п{п + 1)хп+3].
о /*i I 	 f^y*	CD I ^Т* © *Л 	1	Л 	1	 § 1
1
8. ^ " ^ = - 1п A - х) -
A - х) - хп+1 Г(
J
- х + жГГ^1 dt.
(-1)" ("
- Уп+1/2Bх)].
[п/2]
Bfc - 1)!!
=2™
[n/2]

494
Гл. 4• Конечные суммы
[4.1.8
21
2n+l
Bп)!Г( i - n
)\ 2h_2x» (
п п\2х
r2k+s
Tin 1 1
)!(n - k)\
[6 = 0 или 1].
= 0 или 1].
(s-4)"
2n
26.
k=O
1	/ X]
r» + l 4 2/'
* ^оBк + 1)\(п^к)Г
4.1.8. Суммы вида ^(±1L-.
Всюду в этом пункте [а] означает целую часть а.
[п/2]
fe=l
,[п/2]
,
[n/2]
E [f
Г/
2(-Dl

4.2.1]	J^.2. Биномиальные коэффициенты	495
п — 1 г-	. -т.
7. Л^ X Н	= [пж] -\	(га — 1)(п — 1)	[то, п — взаимно простые числа].
fc=o L -^
4.2. БИНОМИАЛЬНЫЕ КОЭФФИЦИЕНТЫ
Обозначения: a, b — любые комплексные числа, при которых биномиальные коэффи-
коэффициенты существуют (относительно определения и свойств биномиальных коэффициентов
см. приложение I); /, m, n = О, 1, 2 . . .
4.2.1. Суммы вида У^(±1)*(?
и-.
k=Q	fc=O	fe = l
n	n	/	-1
3 \^(-l)k(U") — S	4 \^(-l)k(m\ — (~l)n( m ~
k=0	fc=O	^
6. >
^ \tiJ	4	\n/'
п
1(п-1)/2]
cos
4
/
12. > ^ f^l)R( '" ) =2n/zsln —
П7Т)	ire	V
fc=O —"•	^	fc=O
[n/3]
n/4]	[n/m]
f n ) = ?- V cos" ^
fe l
)	\2 + 2сав]. 18.	V f )	V cos	cos
\4ife/	4L	4 J	^ Ufe/ m ^^	w	m
k=0	fc=0	fe = l
E/	n \ 1 v^ те кж (n —
(	j=g2COS	COS
20. yVl)*f	mi) = (m1). 21.
\'^i»^/	^ - «	-^- j.	^	\'^	*^

496
Гл. 4- Конечные суммы
[4.2.2
[п/2]
22.
23.
24.
25.
=22п-2
Y> / n - к\ _ A + yS) - A - у5)
^	)
n+1
к —
а — п\
Ъ + 1 )'
а + п + 1
771 + 1
т
4.2.2. Суммы вида V^ ад.
[m < n].
4.
5.
1)!.
9.
10.
11.
15.
=0

4.2.2]
4-2. Биномиальные коэффициенты
497
k=0
17.
18.
=0
[m = l, 2, ...,
19. ?(-l)*(m + k)n+1 Q = (-1)" (m + \)(n + 1)!.
20.
[3n2 + A2m
•12m2l.
22.
k=0
f
Г1/2Г (n + X-
oo
x Г {cos [(n + 2a)t] - sin [(n + 2a)t]}t~n
~n~1/2 slnn
23.
=0
24.
k=Q
кфп/2
2k)n±2m+1(n) = 0
[a < -n < 0].
[m = 0, 1, 2, . . . ].
[m = 1, 2, 3, . . . ].
25.
26.
27.
28
29.
) -
к / tt
Or f t—1 si
J
sin" tdt
[n = 1, 2, 3, . . .; -1 < s < n].
[n/2]
2)!.
2 '
30.
fc=0
9
31. ^ (-l)k(n ~~ 2k)m f^|=0
/
32.
32 А. П. Прудников и др., т. 1
[m + n нечетное число, m = 0, ±1, ±2, ... ].
[0 < s < 2n].

498	Гл. 4• Конечные суммы	[4.2.2
пл	/2п\ 1
33. УД-1) (п-к) [ )=-Bп)!	[п^1].
34. ^(-1)*(п - JbJm {^f\ =0	[m = 1, 2, . . . , п - 1].
ЧК \ k\hn~K \ \ — <п	Чп \ l
НО» / К, I foil 1»! — »*•	ODi > I
k=l
37. 5D(zbl)feifer1r*-1-|B (^) = ±(n±l)n-1	[n^l].
= 2n	[n > 2].
38. ^A;"-*-1
40.	^Г(п-кУ
41.	V(^l)fc(o
у^ 1 /n\ _ f	Jw!(-l)m 2n
- k)\(n + k)\\ '
ж^ ( —1) fn\ 1 /^тг + пл^1 ж^ (—1) fn\	n\
44- 7	4" , = ^	•	45. > ^	— , = —.	-г	7	г
/-^ m + k \k/ m V m J /-^ «fe + avfe/	a(a -\-1) . . . (a -\- n)
fc=0 fc=0	v / v	/
46.
тк\к)	\m)\ k
fe=0	V fe l
49
50	=
/fc + l U/ n + l' '	f^Q2k + l\kJ Bn + l)!!'
П + 1 ^	n к ^ ^
1	! 1
у (-1) + f"
k=l l	7
53 V *+1Г^
53-
54. > ^	-
a ~~ к
j 1, ^ - 2^ + B„-1)!Г
1)^	[n = 3m],
55. 2^
fc=0
a-n\n)'	' ^a + ifc\ к ) al\ n ) J'

4.2.3]
4-2. Биномиальные коэффициенты
499
57.
[афО, -1, -2... ].
+ lJ\k) n + l^k'
4.2.3. Суммы вида \^ аи \ \хк.
^ \Ск/
2.
[п/2]
fe=O
5»
[п = Зга],
[п^Зт].
[п = Зга],
1, 6га+ 2],
[п = 6т + 4, 6га + 5].
[n/2]
>• E
fc=O
[n/2]
7.
4ж )
[n/2]
fc=O
2n + l
Bж + 1 ± -
10
2k
А 1
' 22к
2k
15. У^(—1) I	)ж2 = sec (arcsin — J cos Bn + 1) arcsin — .
k=0	X	7
16.
17.
n
18. g
32*

500
Гл. 4- Конечные суммы
[4.2.4
19
к=о
п	п(Зп +
' * = 3 S°' Л = 	15
20.
к + а \к
О
k=Q
[п/2]
23.
24.
25-
26.
2Г-
2fe
Ж =
\n + l
.-к V A;
¦ [A
2ж
)n + A - л/1-4ж2)п]
[«/2] gfc
30.
.*!/а\_ (
fe=O
1Vlfc + 2fc + ... + nfc)=(n
4.2.4. Суммы вида >^ ад.
ж	1	n + l/2 ж/2 |^	/ж\
6Л
-l
¦ E
к I	a - 1
-l
a l/a
а + к
771
Ш, / a — 1
771 — 1 V 771 — 1
тг + а
771 — 1
-1, ..., -п].

4.2.5]	J^.2. Биномиальные коэффициенты	501
5. V(-l)*~
2 \п
2n-l	/л X -1
И
n + 1
2n-l
10
1
2n+l	7	ч_i fe	2n+2
11. У(-1)*^2п + 1^	l2n±2
*
k-1 k
13. T^ ^
fc/ ak \ I ck
bkj\dk
n+1 n Л	k /-t ,
к=г k V*
4.2.5. Суммы вида V(±l)* f
b uj -2U
2 V ^ У	4	W2
7
^	2n \2l/4n
2k + l) i\2n)	4
- — a\ /'b + n — A;
7i
fc=O
13. V(")f 6,) = fe + fe
^4 \k)\n-k \ n

502	Гл. 4• Конечные суммы	[4.2.5
14
\(	\	(	\ (
V к у \т + кJ а — т\ п J \т + п
-ёо(„-л)=-ё о („-л)-
k=O	V	7	к=т+1	V	7
18 y
^&\А	( 1)	m ) \п - т - )
[п ^ 2; 1 ^ га ^ п- 1].
23. >ч-ir(:и- : i = ^^—[o+l >J( a/o 11 Д I
2	\n/2)\a )\a )
25. \
a \( a i 1 I 2a
)	)
*
fe=0
„. ^r kBn\Bn + 2a\
2m-n+l
34. 53 (-i)"C;][ _ ." ,)=o.
fc=O

4.2.5]	J^.2. Биномиальные коэффициенты	503
35.	V(-l)fcf2nV 2m )=( 1)" Bта)!Bп)!
36.	f(« + ^p + n-t\ = /« + H« + l
,. , , „ , k\ (Ь -
<О»Т.
38. Y(-i)k(a + k)(a + n *
^ V a J \ a J \ n/2
n — m / | \ /	|
on v^ / k\ ( n - k
m
n — m
40. V(
4\.4tIf*/lIsls/|Sj<l	f f ^ 1 I 	I	 & 1 '^ »'i'
I
4л. /.I	I (	,
43*^-' A; Jl, n - А; У ^V^1^^
44 V(a + ^/m-a-^ |6m+!(°^lj	[0^m^n-l],
A; /I n —
45. 2^(~^
47. V(^l)fcf?)fa + M) =(~l)nbn§n,m	[O^m^n].
fc=O	\	/	\	/	fc=m	x 7
п\(к/2\ - n on-2m{n-m-l
J^ J^2 ^ m_i
:!;')-(-!)•(„:,
2ra -"-

504	Гл. 4• Конечные суммы	[4.2.5
55. i2(i)k(r!)(a + k) (i)n( a
^ (Ап\ Bп - к\ 22n+1 /Зп
?U)( « ) =(„
k=Q
60. ^P(
k=0
Ik — l\ /m\
1	J = \n)'
68. > (-Г
', + n-2
74. ТDк)DП^4к) =22n
\ n
n-1
fc=0
[n/2]
76 V^ / a л / а
2kJ\n-2kJ 2\n J	4	V^/2
lMo ,=2m(. 64. v(-iri:ir: "]=2r
«/ \ 2n — m
65 y^1/ ^^kfn\f2n-2k + a\ _ fn-a-2
k=0
[n/2]
лл v^/ ^k(m\(m + n-2k-
bb.
^^ v ' \fc/\	m -
fc=0

4.2.5]	J^.2. Биномиальные коэффициенты	505
.y(a
?f\2k
rry(a)( a
2n-2kJ 2\2nJ	2 \n
n \ (rn + k\ /2m+ 1
" V n - 1
к=О
[п/2]
Г9. Vfn
2k
п - 2т
n-m-1
a АЛ =_a_22n/a + ny
4a — n/ a -\- n \ 2n J
81. y-pa + lWa-fe\= 2n/a + n^
82.
84.
2n
la,/a
l V 2
( 2a
,n-2m-l/w - m - 1
m
^\2k + lJ\) 2 + l V 2n
^/ n W n-l \ l/2n-l\
^ V2fe + 1 \22k) 2\2 + l)
^ V	/ \) 2\2m + l)	2
93 KnV/27 a V 2n"a
94. 5^	Л
fc=O

506	Гл. 4• Конечные суммы	[4.2.6
4.2.6. Суммы вида \^
ск/\ек
k=0
n/2n\	2/2n-2
^ = П I
2 \ п J	\ п — 1 J	2 \ га — 1
5.
h=1 ч m A m J	2 [\m + lj\m + lj \ m + 1 J\m + 1
^	\k/\m — kj	'\n-\-lJ\m — n
8. V^fm-*V")=0	[2n<m]
9- b(
k=O
и
^ n + k\kJ\ n ^ m n2
k=0	x	f m=l
1
rra
(-1)"
ra
ra
12 y^ 1 /2k\f2n-2k\ _ 2П Ba + l)Ba + 3) . . . Ba + 2w - 1)
^ a + k\ k J\ n-k )~	a(a +1) . . . (a + ra)
=
2k J	a
n-m + 1 Bm\Bn-2m
ra — 1
ra — к J 2(ra + 1) \ттг7\тг^ш' + 1
2ra + lN
n — k
1 \ n

4.2.7]
J^.2. Биномиальные коэффициенты
507
'
19
*
2k\ /2n-2A;\ _ Bn
2k\ Bn^2k
2АЛ/2п
А; Д n~
1Г22п/1
—^	,24n^
nBn + 1)	\ n
П — 1
6 —
p + qk	p{a + b ~ nc) + naq f a + b
n
fka\fna — ka\
J	)
^ k(n — k)\ k J \ n — k
2a\fna\
n )\ n )
na — n + k'
9	f
^^ (rnk + l)(rrm — fills +1) \ k
Y^ 2k + l (a- k-l\(a + kX _ /a\2
^ n + A; + 1 \a — n — 1/ \a — n/ \n/
^
[2n/3]	[fe/2]
4.2.7. Суммы вида
ад. I If \x
k=O
fe=O
n	„	n
- sr^ fn\2 k ST fi
o (":*
fe=0
(-')
-*
1 + Ж
1-Х
8.
to (i)-1=(:)¦-<¦

508 Гл. 4• Конечные суммы	[4.2.7
13- 2^-25-(л]и + «;= 	&	V(n-m)/2j	[гг - m четное число].
k=0
15. 5\
¦ (^l)n] (n + m\ /n + 2ra\ fn + m
n/2 J \ m J \ n
"•jb^'UA m J*
l +l j
^(l)^/2nW2n + 2fe\ 1 /2n
[Bm-n)/2]	7
20. V ^fm)f Ш^^ ]=2n"
fc=0	V
f« _ m\ /o
fc=m	••- \- ••-/	-	xl71 mi/z
24. y(-2)*fn)f2n-2M = fn). 25. У(-1)*2П(
^^v ; \к)\2т-к \m)	^K ' \k)\ n-k
k=0	ч	'	k=0	ч
In
29. ^
fc=0
n
30. ^j (": ")i"' т 11r-^ i = , 2"-,-- ^
fc=0

4.2.8]
4-2. Биномиальные коэффициенты
509
{-l)kfn-k\fk
32.
33.
34.
35.
к J\mJ	2n \2m-
k\(n+l
mil 2k J x ~' \ 2m J^ 2m + 1"
m \ 2m
2m
22n
[n/2]
1 (In
39.
a \ ( a — 2k
2n ^
2n-k\kJ\ n
40.
/ „/
2nfn-l-a/2
n
r»2fe + l
2A;4-1/V гг — /с
2a+ 2
42
44.
2k
^ (n - k
k = m x
nx (n + к
k)\ n
n	\2ra
[n/2]
n Y
m/
4.2.8. Суммы вида /J flfe
\^ /CL\ (b\^	6 + 1
45.
ek
b — a + 1 I \m/ \ m
fc=0
-l
n — к
к
4-
4
k fn\ ('к + т
I /n + m
n + I V m —
fe=i
1/ U + l
A; + a — 1
-1	n-l
к + a*
2(n

510	Гл. 4• Конечные суммы	[4.2.8
к=0	\—-/ ••-	-V- -v	fc=0 ¦— х ^ + а /	2а+ 1 \а
п + 2а\	2а + п + 1/2а
fe=O
11. ^(_1)k(^Bn + 2ay1 = (a + n^Bay1Ba+^-1
/а + п\ Г2а\~г (
\ п )\а) \
к ) -Ьт,
а
2п- 1)'
k=l
п
17. V(
18" ' ¦" \kJKk
k=Q
п
21. V-
— 1
ifc	"Ч 4JU	|	ft/	j	JL.	?шй 8 4J ? "LJU \ 8 \JU	j	S C/	#1/1
a + n + l™,fc\^y
fc=O
24.
l-2n
¦l^-1

4.2.9]	J^.2. Биномиальные коэффициенты	511
_i m i п^г -i
fc=O
29. Y
к/ \ к
4.2.9. Суммы вида
' J "\ckj \ek/ \gk
2	U/2A п
n\2 (а +k\ _ /а\2	ч?~. /п\2 (а + 2п -
) { 2п ) - {) ¦ 3- ]L{) {
4. 2^
k=0
n + k\2 (In
*¦ §(-')*(Т)B::Г)"
2n —m\ Bn — mx
k=0	x - / x ¦- - /	V m / V ^
n v^/ ^k/n\/a\( a
k=o	... .... xn^fc/	2
a
m — I I \m/
f{ } \k){ m + k )\l-m-k) { } \l-mj\l
)\
kj\n + kj \l + k J	llmlnl
2m \( 21
v ; l\m\n\{l + m)\{l + n)\{m + n)V
m + n + k^
k=0
m\ (a + m + n + k\ /a + m + n\ /a + m + n
w + n / V n / V m
n\ /m\ /ш, + n + I — k\ (m-\-1\ (n-\-1
m J \ n

512	Гл. 4• Конечные суммы	[4.2.9
а + п\ (b + n
п
к=0
+ п — т
п — т
к=0
19. У(П)( й )(т-к
^—' \к/ \т — к / \ п ) \т
к=0	х
»*,.-». т \ (а + п — к\ (а\(а
к=0
min (m, п)
к=0
т
22. "~
а \ / а\
-п)\п)'
/а\/а\
\т)\п)'
а\ ( b \(а^Ь^п^к\ ( а + пг\ /'Ъ + п
п ) I m
__	^п — к ) \т —
п
гт — а + Ъ\ (п + а — ЪХ ( а + к
II	1[
к )\ п-к )\т + п)~	?^о(т + ку.(п-к)\-
а + га — 2\ /а — к — 1
24.
Ка — п —
с)( )(*¦-*
Ы	/2/ •
28 Х^ (^1
29" S V fc A m A m - 1 / V п
п
30.	^(-1)
fc=0
п {
31.	^^
- (-1)*
т)\ т
2п-1\ (п
^ к + а \ к
U
/2n\ /2n-fe\2 _ 1- /2п\ /2п + а\ /а + пу1
\ к ) \ п ) а\п )\ п )\ п )
32.
¦ЯН» в %J	В 9J	j	_Л-	^в»/у^	# ?/	^	^nJ В ij
к=0
{^ 1 / п\ Bк\ ( к\ 1 (п \ Bп ~~ 2тЛ
^ (^l)fe /п\ (п + к\ ( 2к \_ (^l)n + (^l)m / п + т \( п^т
" ^ 22* иД А Дл + у	22"+x	V(n + m)/2 Д (n -

4.2.10]	J^.2. Биномиальные коэффициенты	513
-1
-—-	/ r>i \ / n j \ / Ti ^
4.2.10. Суммы вида
' " " \CkJ \ekj \gk/
у aJb^ f dk\ f fk
i
Y =
k '	(mn-n)\(mn + n)\'
—(J (*
^п(а-1\(Ъ-1\и + Ъ-1\ г
n 1 I n J V n
[m < n\.
a J\ b
7 X
m —1 ^	n ^
33 А. П. Прудников и др., т. 1

514	Гл. 4• Конечные суммы	[4.3.1
1
--.„. ,..,-.„.	Х2ж
'2тл
22 ^
оч V" (-l)fco2^n4/g + fc\/^fcA'1 22" /п-о-1/2
/ 		III	II	I	— 	 I
a + A; U/\ fe )\k )	a \2nJ\n
fe=l fe=l
4.3. ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
4.3.1. Суммы вида > afc< ;	: >.
^^ [ ch (А;ж + a) J
^(sh(te + a)l	. ж . n + 1 f sh[(nx/2) + a]
1- / i , /,	ч ? = cosech — shж< :; ;
^{h(k + ) J	2
sh
^o{( + ) J	2	2
sech
2
Q/2) Г Г sh [a - (ж/2)] 1	Г sh [Bпж + х + 2a)/2] 11
2 [\ch[a-(x/2)]J ^ ^ \ch[Bnx + x + 2a)/2]jj
. 2 ж Г/ ^ч f sh (пж + a) 1	f sh (пж + ж + a) 1 f shall
= —cosech — (n + 1)< , ,	i г — n\ * )	i t — \ * f\-
2 [v	/[ch(nx + a)j \сЬ(пж + ж + а)| [chajj
. v^, iXfe» f 8ЬAгж + a) 1	,2 ж Г п
4. > (-1) A;< . ;.	; > = sech — (-1) in +
^v ; \ch(te + a)J	2 [v ; v
+ (- г\пп(Б11(пх + х + а)\ _ f shall
\сЬ(пж + ж + a) J \chajj

4.4.1]	4--4- Тригонометрические функции	515
— 2n chn —
2
sh[(rc_c/2) + a]
..„. ._...„_ . -, ,	-	» ch Г(пж/2) + а]
^2 sh —
2
^^sm2n^ + 22r^1sh2n^.
¦ 4t	_<
8 Vf-l)fc I ^ I sh Г2г? - 2A- 4- 1W - 22n sh2n+1 т
fc=O	V
^(±l)kf2n\ w I4	an-i Г ГсЬ(ж/2I2п , (±l)n/2n\
tf» / ———————— §	Ml M — ft/ I Ju — ?a	I л	/ § \ ? iJbJu — ———————— 1	I ti/.
^n-feV^/	J\sh(x/2)J	2 \n
»—о	n
11. ]P	/ 2^ + ! \ 8ьBт1^2^ + 1)ж = 22п [сЬ2п+1жс1ж.
k=0
n-l
n/2
13# \ '„fef зЬ^ж] _	1
fc=O
[ ch kx J 1 — 2r ch ж + r2
[n_i_i f sh (n — t)x 1 теГ8Ь?гж1 . fshajl f 0 11
r < ^	\ г ~ ^* i	> ±r<	> -f- < >.
4.3.2. Суммы, содержащие зесЬж и thж.
1.	Yj 2^ sedl2 2fc^ = cosech2 x ~ 22n cosech2 2теж.
fe=O
2.	>^ ^r^ sech2 — = ^r™ cosech2 — — cosech2 ж.
/ ,./ fYlk	'Jk	2	2n
та	n-l
ftj # J^ ——— |j J_ j_	_____ ^^ и JL JL €ау ™~~~ _-_-_-_-_. |^^ |j J. 1. ¦—--—— ^	™_^ ^ * ^j Li JL Ji ^i e?y
/ j 2^ 2	2n 2n	v
fc=l	fc=O
r V X th2 Ж -rth2T 2fi	X "\	X rth2 Ж
fc=l	v	7
4.4. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
cos («ж + a) J
rf2m ^ J sin (kx + a)
fc=o v ™v"^ ' ^7 ^	Ш fc=o
33*
™	с!ж2т ^ \ cos (А;ж + a)

516
Гл. 4• Конечные суммы
[4.4.1
^ 2
i2m+1 y, fcos(kx + a)'
Гуъ 2аТП~Т~ 1 Zhi	м/ 1 О11П I I4 ""У* 	1	 /-$ \
[e = ±1, если т нечетное; е = =pl, если га четное].
sin (&ж + a)
i/sIn(fca; + a)
\ cos (te + a)
5. V(Slr
^ [cos
1 ^-^	\ sin (kx + a)
: = il, если т нечетное; е = ^1, если га четное].
x ^ . sin (kx + a) 1	ж . (n + 1)ж f sin Г(пж/2) + a]
5. > { ,	; > = cosec - sin	^< Lr, ' ; i ,.
Kcos(kx + a) j	2	2 \cos[(n»/2) + a] j
ir^. .fej sin (kx + a) 1	ж . (n + 1)(ж + тг) J sin [n(x + тг)/2 + a]
o. "/ ( Ij \ /	ч / = sec — sm
^^	cos (kx + a
7.
^ { cos («ж + a)
2
= - cosec —
[, .J sm (ггж + a) 1	f sm (пж + ж + a) 1 f sin all
(n +1)< ,	- n ,	; > — <	> .
[ cos (ггж + a) J	{ cos (ггж + x + a) J [cosaJJ
18ес2^Г (_1)П(П
4	2 [v ; l	;
9 X^ (n) f sin (kx + a) X = 2n cosn
4 ^ \(fe + ) J ~~ C°S
|8т(пж + ж + а) If small
l ; \со8(пж + ж + а) J [cosajj
[«/2]
. V (
^ \2fe
1
2 \cos[(nx/2) + a] J
}
соэ^ж J
. E
= 2'
cosBife
гг \ f sin А;ж 1
: + 1/ \ cos А; ж /
_i[ n x ( sm[(n^ 2)x/4]
n x J sin [Bп7г + пж - 2ж)/4]

4.4.2]	4--4- Тригонометрические функции	517
V
Лк
п \(smkx\_ 9n-i[/ Пп . те тг + ж f cos [(Зптг + пх - 2ж)/4]
J2 [A] 8Ш	{
п 7Г + X ( COS [(П7Г + ПХ — 2ж)/4] 11
=F cos — | ^ ^^ + пх ^ 2ж)/4] J J"
^	sinBn-2k
,n 2n Г cos ж i2^
{ } Xsinxi
^
^	/ о \	j2m —1
19. > ( —1)	)/г	sm2o= -1 2	—	-sin x	\m > 1].
^ ' \n-kj	da;2971
о
20. УA)*(
n-k)	v '	dxi™
П	/О 4- 1 \	j2m-l
21.	5^(^l)fc(	|B^ + 1Jт^1со8B^ + 1)ж = (^l)m+122n—2^TTsin'
re = O	^	^
22.	^(^l)fc f2W + X) Bk + lJm sin Bfe + l)x = (^l)m22n^^ sln2n+1 ж.
X	n
23.	> ^	^( , )sin(n-A:)a; = (±l)n22n N . ) '[) dx-
2n+1
0
) !} dx
sinOc/2j	2
{sin Bn -
к )\
2k + l)x \	n_x 2n f rcosx-,2^+1
2k + l)xj^( '	Jlsin»/
25.
k=0
^ кКп - кУ-
27. ^^
^—' [ cos (А;ж + а)
2 Г sin a 1 f sin (ж + a) 1 n+2 f sin (пж + a) 1 n+i f sin [(n + 1)ж + a] 11
\cosa/ \ cos (ж + a) J	\ cos (nx + a) J	\ cos [(n + l)x + a] /J"
f sin А;ж 1 T
x \-r
4.4.2. Суммы вида ) а^< , > .
v^ 1 sinb I	1 x-^/ xfc/ 2m \ cos (n + 1Iгж smnkx . n /2m
m — к
sin
cos [{2k + l)(n + 1)ж/2] J sin[BA;

518
Гл. 4• Конечные суммы
[4.4.3
з.
k=l
j "
_ г VV 1.fc / 2w \ coste + (~l)n~1cosBn + l)kx l-(-l)n/2m\
2m /_^	\m — к I	cos kx	2Im+l \ m /
4
\coskxf
m — к
sin[B*!
cos[Bk
n^1/sln[Bn + l)Bife-
5.	> (±l)kakp< , i =[a-— ) > (±l)ka
??[	X coskx)	\ da) ^ ;
v-^ f sin кхЛ n 1 .
6.	> <	> = — q= - 81
^ \ cos ifex J 2^2
f • i \ t
¦ *• sin ra
ka{	}
пж cos (n +
f si
3	. пж
=-sin— cosec-
4	2	2
x { sin [(n + 1)ж/2] 1
2 \cos[(n + 1)ж/2] j
T
П ( ' h 1 4 1
8. У^	? = — [3n
^ { cos kx J 8
(n
9.
S V = 2
1 . $пх	Зж Г sln[3(n +1)ж/2]
- sln2na? cos2(n + l)x cosec2a;].
[m = 0, 1, 2, . . . , n- 1].
fc=0
[n/2]
11. \^ cos2
2m
m
^4 I sin Bтг^2/п) I дЛг / птг . птгч
14. > <	J } = -— 1 + cos	=F sin	1.
^[cosB7rife2/^) J 2 V ^ 2 ^ 2)
{ sin bkX 1 m
>k\	} •
I COS 6fca? J
4.4.8. Суммы вида
1. \^ 22fe sin4 —г- = 22те sin2	sin2 ж.
k = l
2.
3*
=3r Ц)^ 3
n+iJ
J
m < 2n .
L	J
[m, I = 1, 2, 3, . . . ; ml < n].

4.4.4]
-4- Тригонометрические функции
519
з-Е-
- cos 2 x =
k=l
. . . _	v^ (smkx\ ( smky\
4.4.4. Суммы вида > afe<	><	> .
jL^t { cos л;ж J [ cos ky J
^^ . 1кж . ткж
1. > sin	sin	 = 0
2.
3.
2"
n

Ытг
4. 7 sin	cos	 = 0
jL^1	n	n
fc=O
5.
6.
7.
8.
fc=O
n-l
E
fe=O
cos
COS
ткж
n
21кж
n
n
= ~2
= n
cos
COS
kin _
— и
n
2ткж
— 0
n
л \™^ • ^wtt . к1ж 10, m Ф I,
9. > sin	sin ¦ — '
n	n
либо числа I — га, 1 + тне делятся на 2те, либо оба делятся на 2те].
[I — т делится, I + га не делится 2п].
[I — т не делится, I + тег делится 2п].
[тег ±1 — целые и не делятся на те].
[га, I — целые; га + I, тег — I не делятся на те; т ф I].
[ Z — га, i + тег не делятся на те ].
[ лишь одно из чисел I — тег, I + ттг делится на те].
[ I ¦— га, I + тег делятся на те].
[тег, I < те].
n, m = I / 0
v-^ ктж Ыж
10. > sin	cos	 = 0
Ч(к	Л	f f 1/1 I/ II	§\f V /I
11. > cos	cos	 = 0
n	n
12.
13.
14.
k=0
[п/2]
= 2n
n кж n ( n >
(-1)" cos	cos — = —
v ;	n	n 2n\mJ
[тег, I < те].
[га, I < n; m ф 1].
[m = l не делится на те].
[ т = I делится на те].
[1 ^ га ^ те — 1].
[/]
15. V (^l)fc ( П ) sm
х = cosnx.
' х = smnx.
17.
18.
= 2п sin	sin 2ж.
2п 4
4 = -
2 8

520	Гл. 4• Конечные суммы	[4.4.5
4.4.5. Разные суммы, содержащие sin ж, cos ж.
^	(-1)*	. 2m+1 2fc + l	. 2m
1.	^/^	 ' , —sin		тг = п sec пж sin ж	[т < п].
к=0 COS Ж — COS 	ТГ
2п
о у^	(~1)*	. 2fc + l	m 2fe + l	m
2.	Л_^	~7уГ	1—sm	тг cos 	тг = п sec nx cos ж	[га < п].
fe=0 COS Ж — COS 	ТГ
2п
о V^	(^!)fe	2т ^	1	Ж/	Ж	2т-1 Ж\
3. >	;— cos — = — cosec — cosec	2п cosec nx cos	—
^	for	2rc 4	2 V	2	2/
fe = l COS Ж COS
n
fe = l COS Ж — COS
n
[1 ^ m ^ n].
fe = l COS Ж — COS
1	ЖГЖ	Ж о Ж1
= - cosec — cosec	Bn + 1) cosec Bn + 1) — cos m —	[ra < n].
p* \ ^	v /	"^	• 2m "^	/m i -i \	(^72 "г 1)Ж , 2m —1 *^
5. >	——.	cos	sm 	 =	Bn + 1) cosec	—sm	—
^	2ктг	2n + 1	2n + 1	4	2	2
A; = l COS Ж — COS
[ra < 2n + 2].
n~1	(—l)k	2k + 1	«д."-1
6- У^	 oi , i	sin ^^ тг =	—.
^^ - o	2A; +1	9	2n	1 + x2n
fe=o 1 — 2ж cos	тг + xl
2n
7. \^	-p-j	z— cos	ттг sin	тг = n cos mx sec nx	[ra < n].
^^	Ik +1	2n	2n
k=0 COS Ж — COS 	Ж
2n
о	V^	!	П	x ПЖ	! Гi / i\ni 2 Ж
8. > 	г^™	—г^ = — cosec ж tg	1 — ( —1) sec — .
^ cos ж ^cos[BJfe + 1)тг/га] 2	B 2 8L l ; J	2
E2fc	к	2п	п	sin ж
' 2cosB^)^l Sm ( X) = 2-со8B-ж) + 1 8Ш ( Ж) "
fe=O
n fe-1
10. V П sin^ = 3-^±|.
k = 2 m = l
n k — 1
2-^ 11 cos h ~ к . 9
n
n 2k
15. 7 I—I)	II COS 	 = 	 — —.
Z—Jy '	II	9JU_L,1	Q . An	*3
fc=l	m=0

4.4.6]	4-4- Тригонометрические функции	521
п k-l	, .,
k = l m=0
Е/ t\k-i FT • Am-\-I A ( —lj
(—1)	II Sin 	 7Г =	h -	—
JL A	2k	3 3 • 271
jfe = l	m=0
n A; —1	_	^	^
E П
on V^n
20- Ell
n 2fc 1
- e д -'
^^71 + 1	, 4/	2	— ( — 1)
д ^^ 2[2 ;1)]
4.4.6. Суммы, содержащие sec ж, cosecic.
1. > sec— = 0. 2. > sec
ra	^^ 2n +1
fc=O	fc=O
v-^	2 I кж	\	2	2 fn7T	\
3. > sec — + x = n cosec 	 + nx .
^ \ n	/	V 2	/
4.
n —1	.	2	Lvr
\^ 2 «7Г ra — 1	^c™^ 2 ^^	J- / 2 n \
5. > cosec —	= 	.	6. >	cosec —	= — (n — 1)
z—^ ra 3	z—^ ra	6
fe=i	fc=i
7. V cosec2 2k + 1 ж = !L + I Г(^1)п _ Ц. 8. V cosec2 ¦
E. J sec [ж + (&тг/га)] 1	2/cosec [пBж + тг)/2] 1
\ cosec [ж + (кж/п)] J	\	cosec ггж	j
	 "I	О	«л
Г	Г _i_ toi* I W ~\	i	Г	Г /о _i_ \ /ol 1
^^ \ cosec [ж + B/гтг/га)] / 2	\	cosec пж	j
sec [(I
cosec (nx
2 Г cosec [Bгаж + тг)/4] 1 2
1	x/2) J
k=i
n — l	r	/	Ъ 1 \ ~\	/	L I \
12. \^ cos Bm + 1) I x -\	I cosec ( ж -\	J = ra ctg nx
fc=o L	^	n )\	V	n /
[m = 0, 1, . . . , 7i — 1; Inn — взаимно простые числа].

522	Гл. 4• Конечные суммы	[4.4.7
1О V^	( . klT\	з / , ^"ТГ Л	з	3
13. Л cos х -\	cosec ж -\	= п cos тгж cosec nx.
^ V	п J	V	п J
14 V J sec (А;ж + a) sec [(к + 1)ж + а]
J~f [ cosec (kx + а) cosec [(A; + 1)х + а]
\^/ i\fc I sec (kx + a)	sec [(к + 2)ж + a]
^ [ cosec (kx + a)	cosec [(& + 2)x + a]
1	j sec (x + a)	sec a I , Л xn j sec (nx + a) sec \(n + 1)ж + а]
= — sec ж К	/ — (~1) S
2	|
sec ж К	/ A) S
2 |Д cosec (ж + a) cosec a j [ cosec (nx + a) cosec [(n + l)x + a]
n
Ж ^—v 1 2 Ж	2 1 2 Ж
ctff ——— сЫх. 17. > -тгг sec —г- = cosec ж	— cosec —
2n+1 ^-^ 22fe 2fe	22n 2n
fel
Y^ 1 . 2 ж x 1	1
Z Sm
2к 2
. >^ —гт- sin — sec3 — = —т— cos — cosec3 — ^8 cos 2ж cosec3 2x.
4.4.7. Суммы, содержащие tga^, ctga^.
-1" ' (WI1=TI1
[m, n — взаимно простые числа].
^r tgN + (Wn)] I2 2	2Гс1ё[Bпж +
^0\ctg[x + (k7T/n)]j	\ CtgH
[(n-l)/2]
5.	^ tg2^ = i(nn
n-l ,	[(nl)/2]
6.	E ctg2 — = | (" " 1)(^ " 2)-	7. E с^ —
fe=i n s	k=i n
8. 2^i
k=l
Ects4 ^гтт = ?Bn)D + 1On"
k=l
11. V i-tg4 = — ctg— -2ctg2a;.
/ ^ 2fc 2fc 2n 2n
E ± tg2 ^ = ^3T B2"+2 - 1) + 4ctg2 2X - 2-a» ctg2
k=0
у
ctg (nx + a)

4.4.8]	4-4- Тригонометрические функции	523
п—1	п—1
14. ^tg-^т sec^- = tg,x - ter —. 15. Y^ 2k sin -^- tg2 —^— = to ж - 2n tg —.
[(n —1)/2]
г. Е (-i
г = tg ж tg. 15. > 2 sinг tg ггт = tg ж 2 tg
2k	2n	J	2k 2fc+1	2n
fc=O	fcO
[n/2]
fc=O
n 2fe
18. V П
fc = l m = l
n n
X—^ 1—Г	/	\	• Thn
и л	л	2
k = l m = l
тфк
x ¦¦>	1 I	,	v	. (П "г" JLJ7Г	, ^\n+l I I
?ta.» / ^^& "-'к I I ^^& {•Jbk "->tn) — oiii	\^ I J-J	I I
2
fe = l	m = l	k = l
тфк
4.4.8. Суммы, содержащие логарифмы.
nt	1
2.	V(a +fe)ln(o +Л) = 1пГ(а + t) dt + (n + I)a + - (n + l)(n - 1п2тг)	[а ^ О].
*=o	Jo	2
3.	^(-l)*B)ln(fta + 6)= [(l-i"I1^-1^	[o, 6>0].
a-l)n^"nai^	[a>0;b>nx].
\m —lo2n —2m —1 Bwi)! Г .—2m —1 • 2n
) 2	wj* s.n
?1(п-к)\(п + к + 1)\ l	J \ J	Bn + l)! J
re — и	q
[m, n = 1, 2, 3. . . ].
7. f>mln(fc!) = ^[	^l
n	n + 1
8.	X) In (A;!) = (n + 1) In (n + 1)!- ^ A; In A;.
fc=2	fc=2
9.	^ fc In (fc!) = W^ + X^ In (n!) - - ^ fc(fc - 1) In fc.
k=2	fc=2
n	n	1 n
10.	53 fc2 In (A:!) = - (n + l)Bn + 1) In (n!) - - J3 ^(^ ~ х)B^ ~ x)ln fc-
fc=2	fc=2
... ^i t,/, i4 ТГЛ , n-l \ _t	n	l^e^nat	(i-b)t]dt
11.	5:ьГ(* + 6)	(bl +	j «	+	^ «*
e	^ +	^
12. f](^l)^1lnr(fea + 6)= [(l-t)^0^ d/	[a<0; 6 > -na].

524	Гл. 4• Конечные суммы	[4.4.9
1/2
sin2nxt cteтг? dt.
J	5
14.	> cos kx In sin — = —
In	2x
0
v^	2ткж . . кж 1г.	. f m\ _1 тг тж
15.	>	cos	In sin — = — In2n + t/ч — + С H	ctg
^	n	n 2 L	\n J J 4	n
fe=i
[m = 1, 2, ..., n- 1; n = 2, 3, 4, ... ].
[(n^/2] mBife + l) , . 2A; + 1	1 л/т\ тг	ттг
16.	> cos —	 тг In sin	тг =	p — H	cosec
^^	n	2n	2 \ n J 4	тг
k=0
[m = 1, 2, ..., n- 1; n = 2, 3, 4, ... ].
4.4.9. Суммы, содержащие арктангенсы.
A	2 тг
1. У, arctg tj =	arcctgn — arcctg (n + 1).
- E arctS i + fc(jfea+l)a2
П-1
arctg i + a(fca + to + (ы + ы = arctg (na + b) ~ arctg 6-
. ^	2fc
4. > arctg	—	— = arctg
^ &2 + ^2 + fe4	ь
n + n2
2n	/	„,
5. V^ arctg | ж sec	 1 = arctg {sh Bn Arsh x) sech [Bn + 1) Arsh ж]}.
^	4n + l/
+
nml	ж — cos	тг
6.	X)(-l)* arctg —^
fe=O	Sin 	7Г
2n
. 2fc + l
n^!	Ж Sin 	7Г
7.	^(-1)* arctg	||T_= arctg ж«.
fc=O	1 — Ж COS 	7Г
2

Глава 5. РЯДЫ
5.1. ЧИСЛОВЫЕ РЯДЫ
5.1.1. Введение.
В этом разделе приведены суммы рядов вида ^ttfc, где аи — комплексные числа или
к
функции некоторых параметров, причем зависимость от параметров такова, что они не
записываются в виде степенных рядов (см 5.2) или тригонометрических рядов (см. 5.4).
В некоторых случаях для вычисления суммы ряда \^ а к можно ввести вспомогательную
к
сумму ^ пкХ , а затем воспользоваться формулами из E.2) и теоремой Абеля.
к
сю	оо
Пусть ряд ^2 ak%k сходится при \х\ < 1. Если сходится также ряд ^ ад.иО<ж<1,
к=0	к=0
к=0
При суммировании рядов могут оказаться полезными следующие формулы, в которых
функции /(ж), F(x), 6г(ж), М(х) и <р{х) связаны соотношениями
оо	оо	оо
F(x)= le~xtf(t)dt, M(s)= lts^G(t)dt, F(s)r(-s)= \ e~8tip[t)dt.
где
h(x, y)e~px dx = e~
J
оо	оо
2. ]Р F(k) = f {^ dx. 3. J2(-l)kF(k) = - f 4^"
1
4. ?G(fe + a) = —
6. fp,^/., • J
с — гоо
k = l
OO	1
2^F
о о
E F(lnfe) = J
fc^1	o
oo
c+too
fc=O

526	Гл.5, Ряды	[5.1.2
	 со
v-^ .-I/I \ к /2 f , , > 1 — ж cos at
8. VF(fca)a =4/- /c(t)	ч dt.
f-" l ;	V 7Г I JW1-2ж cos at+ ж2
0
n™^ r-i/i ч л /2 f - / ч 1 — x sin at
^^	y - '	Л — 2ж cos at + ж2
2 T./x	, Л2
/ 2 Г	/ 2 Г
где F(s) = J- fc(t) cos xt dt = \ — f8(t) sin xtdt.
V 7Г J	V 7Г J
0	0
(±1)*
5.1.2. Ряды вида \^
OO	°°
^ 1 ,,	1
[« = 2,3,4,...],
n2n-l 2n
jB2n|	[n = 1,2,3,...],
_2	_4
7Г	7Г
52 = — = 1, 64493407, 53 = 1, 20205690,	S4 = — = 1, 08232323,
6	90
6
55 = 1, 03692776, S6 = — = 1, 01734306, 5T = 1, 008349277,
8	к 98 10
= 	 = 1, 00407736, Sg = 1, 00200839,	S10 = —	 = 1, 00099458.
OO
3- E V- = Bl"s)c(s) = -щ J ^ndt = Ts	[Res> 0]'
k — l	q
T2n = B^jlA" з2")^"!^»!	[" = i, 2,3,...],
2
Ti = -In2 = -0, 69314718, T2 =	= -0,82246703, T3 = -0,90154268,
T4 = - ^r = -0, 94703283, T5 = -0, 97211977, T6 = - ^^ = -0, 98555109,
-| eyrj 8
T7 = -0, 99259382, T8 =	= -0, 99623300,
128^50
7^
T9 = -0,99809430, T10 =	= -0,99903951.
5 • 33 • 81 • 512
4. Vizl)^ = ^_Iln2. 5.
^ к	42
=	ln2. 5. f;	= +
к	42	^^fc + 1	4 2
fc=0
(_l)[/]
6. V^	'-	 = -0,5154.
k=i к
6.1.3. Ряды

5.1.4]	5.1. Числовые ряды	527
00	j.a-1
3. Г-	пг = -	\ntdt.
f (* + ) J Х *
о
[п = 2, 3, 4, ... ].
[Re s > 0].
		g Mw 	t	 # I i *-"	I	\	Ж I	\	J"	Si	Ш t <L2 I	l	Ш 	I	 ?-J	*s
k=O
. у. 7Т	 Vm = (	\\ P W	[m = 1, 2, 3, ... ].
7. Y^ jj	-— = ——	—-—^y cosec аж	[n = 1, 2, 3, . . . ].
1
(^l)fc _ f Г^1
8. у ¦}1\, =-	Intdt.
5.1.4. Ряды вида E
E
2»
2	4
Л2 = —- = 1, 23370055, Аз = 1, 05179974, Л4 = — = 1, 01467803,
о	Уо
6
А5 = 1? 00452376, А6 = 	= 1, 00144708, А7 = 1, 00047155,
960
1 7тг^	4,1 тт"'"®
As = 256 630 = 1, 00015518, Л9 = 1, 00005135, А10 = ^ gl 1Q24 = 1, 00001704.
fc=0
/7Г\2те
-	1	/7Г\"
Л2п+1 = —;	г- —
+ 2Bn)! V2/
M = j = 0, 78539816, A2 = G = 0, 91596559, Л3 = — = 0, 96894615,
к 5
A4 = 0, 98894455, A5 =	 = 0, 99615783, A6 = 0, 99868522,
64 • 4!
A7 = 6l7F , = 0, 99955451, A8 = 0, 99984999,
256 • 6!
A = 1385?Г f = 0, 99994968, A10 = 0, 99998316.
= Cs [Re 8 > 0],
г	ЫГ*2п+1 Го
„ _ nV2	ЗтгУ2	19тг^2	_
Cl - ~4~' Сз - 27 ' 6 ~ ~~2i»—'	5 • 218 '

528	Гл.5, Ряды	[5.1.5
• Ь
)j 2 ^6~' 4
~ _ 361тгУ2 - _
15 21Б '
15 • 21Б '	9 • 35 • 220
5. ±tlfH=*JL.
?	j су JL i_ -I	-| cy
/	-J \k
5.1.5. Ряды вида ^^
kn + ra
2.
In	n n ?-?	Ll	; n J
[n = 2, 3, 4, ...; ra = 1, 2, ..., n — 1; см. приложение 1.11].
(-1)*
^-^ кп + ra- ^^ fcn + ra
fc=O	fc=O
k=0	fe = l	fe=O
5.1.6. Ряды вида
oo	X	1
о о
^ (±i)	i jv>(fo)V(«)\	r . .141
2. у —	г—	— = ±-	<	>	[a = 6см. в 5.1.3].
^(fe + a)(fe + 6)	6-a\/3F)-/3(a)J
"¦

5.1.7]
5.1. Числовые ряды
529
6
т.
8
9-
у	= у
^ (кп + т){кп + га/ + га) га/ ^^ А;га + гга
^^ (А; га + т)(кп + гаг + и)
= If2f Jzl?__ll
га ^^ кп + гаг гаг
L fc=o	J
k + Г
10
^Щ + а) а\ р(а + 1) - In 2
со
. > 771	7 = —ИМ —+
?	g/ к* ( §ст$ -4- тп I	тп	\ т)
А/ I ГЬ § & | § § & I	##|>L	\ § (/
^	1	п
^-^ А;(А;га + га/ + га) га/ + г
(±1)" ^ 1	7Г fcosTra-i
(fe + a) a2 asinTral 1 J
1
w ^^ ^(fen + гаг)J
»•?¦
(±1)к
5.1.7. Ряды вида
n2\p'(m/n)j'
fe(fen + гга)
oo
El
fc=i
7
= 5 4
4' *
=й- «¦
1	ОС	°°
(-l)fe	5 2
= Л _ _1п2.
18 3
48'
3 7Г
2) " 4
34 А. П. Прудников и др., т. 1

530	Гл.5, Ряды	[5.1.8
0
щгпг!
4
25 ' 10 v^ '^~ 51
49 14
5.1.8. Ряды вида V]	\
^^ (A; + Z)(A;n + m)
oo	1 ra —1 1	oo
1. V^	 = 	 ^ -	2. V^	 = 2 In 2
^ (A; + l)(k + m) w - 1 ^ A;'	^ (к + 1)BA; + 1)
—r =	In 2.
2	'	* ?j(fc + l)Cfc + l) 4
5. > ——. ^ w^ ,—-77 = 	^--	6. > t;—. „4 /^,—~^ry = — In3 —
/ i \ к
9- E
»¦ E
oo

5.1.9]	5.1. Числовые ряды	531
9.
13.
34*
оо
со
k2°{2k +
оо
/ j f2A* -4-
fc=O ^
оо
к=0 ^
rBfe+
*ЦB* +
оо
^ "\
/ J (Г) h.
rBfe
/?	,/ / О L,
^	^ /о г,
fc=O
оо
ЧЦГ ^\
^_	^ (Oh
ОО
fc=O ^
оо
^ BА;-
1
¦1К2* +
¦1)C* +
1
¦1)C* +
1
¦ 1)DА; +
1
1)Dк +
1
+ 1)D*-
1
Ч- 1)DА; -
+ 1)(8А;-
1
-f l)(Sk-
+ l)(Sk-
1
+ 3)Dfc-
+ 3)D*-
1 A**
3)
2)
2)
X)
3)
1-3)
h5)
1-5)
Ь7)
h 1)
h3)
h5)
h 7)
h 1)
h 1)
1
2
2y^
2V3
7Г
7Г
4
i
4
2
3
3
2
15
12
1
5
5
'2k + I)
2. ]
9 In
3 2
V3
1
2
21П-
Kl V z
7Г
12
¦ + Ж (
+ 20
'л/2 "
'л/2 '
КУ Л
1 20 '
. 20
(kn + m)
^ f l)fc
1
^ V2
In °
iolni-
' 3 6
V2
3 6
10 n2°
+ 5v^ln'
7Г
4
1
2

532	Гл.5. Ряды	[5.1.10
20#	3) = 3 ~ 12 + 61П2"
B.
5.1.10. Ряды вида V
... , |W/ ,	г.
(ЗА; + /)(А;гс + га)
2 V	С)	= 1п2
* ^C^ + 1)C^ + 2) 3 '
^	1	_ 1	^	(^l)fc	1 2^3 7г 2
* ^ (ЗД + l)Cfe + 4) ~ 3'	" ^	+	+
^	4) ~ 3'	" ^ Cife + l)Cife + 4) ~ 3+ 27
5 V	г	=г i ж б V ()fc
f^Ck + l)Ck + b) 8 l2>/3'	^C^
^	1	7Г	2
^Cfe + l)Ffe + l) ^V +3 ° •
to ^
2 / ж
11. \ 	=	.
12. V,, (-V. .t=-^-l. is. V
?^ Cfc + 2)Cfe + 4) 3-^3 2'	* ^ CJfe + 2)CJfc + 5) 6'
2 / 7Г
2тг 2
5.1.11. Ряды вида Vy— (±1)
Y-	i	_ i y; i
* 4 DA + )Dfc + 41 + ) ~~ 41 ^ 4fe + '	'
. ^.„ , ..„..^.„ г 4/+ га) 4,1 ^ 4к + т'	^ Dк + 1)DА; + 3)
4^ Dfe + l)Dfe + 5) 4'

5.1.13]
5.1. Числовые ряды
533
в.
10.
13
„	ОО
= ^ + ^ т. у
18 24'	f^{4k
1 ж
2^8"
14
40
fc = 0
_	i_r_ _\fc
5.1.12. Ряды вида
со	1 * """ 1
4^ EА; + т)E& + 51 + т) ~~ 51 ^ Ък + т'
2
*
6
18'
=15- 5-
10"
-1 * /1
 10V ' У5 ¦
7
20'
5.1.13. Ряды вида
1
=
5) 24 '

534	Гл.5. Ряды	[5.1.14
°°	к	1	°°
= 4^f 1П B + )s 4" 2Ffe
[§к + 5)
(^l)fc	1	7Г |	1
~ ^6 + 18 ^
k=Q x
оо
II V"	±	 — _ _ " v "	7
^ (	)(	) 2 12	# ^ F^ + 5)F^ + 7) 6 2"
8 f-0	*	_ г
' ^ FА + 5)FА + 11) 30'
1 1
/1-1 \fc
5.1.14. Ряды вида \^	) /
1)(кп + т)
1-1
m)
k=0 x~'" ' -/V-" ¦' 5)	32	16
оо
)(8fe + 5) = 16 ^ ~ ^' 5* ^ (8Jb + l)(8Jb + 7) = 48 ^
7- i:,o, ,.wo, ,7) = ^-YlnA+V2
9) = 2 ~ ^
fc=O ч
оо
9. ^
fc=O
(±l)fc
1.15. Ряды вида V] —	 l
^^ (/га + 6)(/га
5.1.15.
(/га + b)(ka + с)(/га + d) *
i г/ i
= dw dz 	In2 ж da;.
1^1	1 -i- ™П.
2- ^т^т^
)	)
0 0 0
3_ y.	(±1)*	_ ±1
F - a)(c -a)\ /3(a) J + (a - b)(c - b)\ /3F) J + (a - c)F - c)\ /3(c)
F - aJ \ /3F) - /3(a) J Т 6-a{/3'F) J "

5.1.16]
5.1. Числовые ряды
535
4.
^ (к + a)(jfe + a + l)(fe + a + 2) 2a(a + 1)
(—l)fe
6
{k + a)(fc + a + i)(fe + a + 2)
1
Та + 2a(a
1
[a^O, -1, -2, ...].
[«#0,-1,-2,...].
+ m)(kn + ra + n)(kn + m + 2n) 2mn(m + n) *
m)(kn + m + n)(kn + m + 2n)
|
|
2mn2 2(m
'
^^	1	2 тг /	тга \
10. > yy^—¦—чо = -«	г ctgTrai—	).
^1 feffe + аJ а3 а2 V	sin тга/
И
7Г / 1 | ТГ ^ ^ \
a2 a	/
feffe + aJ a3 sin тга la2 a
5.1.16. Ряды вида
/ 1 ixfe
l J
r.
ГП2)
(-1)"
7
^fe(fe + l)(fe + 3) 36
со	_
^ fe(fe + 2)(fe + 3) ~ 36
7	8 V
36'	' ^
13 2ln2
36 3
^fe(fe + l)(fe + 3) 36 3'
^ fe(fe + 2)(fe + 3) ~ ^36
[cm. 5.1.5.2].
4	7
3ln2~ 9"
(-l)fc
17 тг 4
= ?^з^з1п2-

536	Гл.5. Ряды	[5.1.17
5 УЗ 9
+ ^ 1п2
оо
оо
k=l ^
оо
оо
сю
оо
оо
оо
to"
оо
k=l v
сю
оо
оо
1
fe + l)Cfe 4
fe + l)[bk-\
к + l)(Ak -\
к + l)Dfc H
1
к + 1)DA; H
fe + t)Dk -\
1
(—l)fc
lk + 1)CA;
1
2"+ ^
1
2* + l)D*
2" + ^
2Jfe + 1)DАг
1
4A? + l)Dfc
Ь2)
h 1)
h 1)
1-3)
ьз)
+ 3)
+1)
+1)
+ 2)
+ 2)
+ 1)
+ 1)
+ 3)
+ 3)
+ 3)
5,г
3	3
+ f4
9 3 3	3
5 2, n _ ^	f-l)fc	11 7Г
9 3 1П2' М" ^ ifeBife + l)Bfe + 3) ? ? 3
7Г
=6+ 2
31 V
' ^feBfc + l)Dfe + 3) 9 3
• Z JbDfe + l)D^ + 3) 9 3
5.1.17. Ряды вида V
(/г + 1)(кп\

5.1.17]	5.1. Числовые ряды,	537
о V	5dУ	= 1-1п2
• ^(fc l)Bfc l)Bfc 3)
5- g (fc + l)Bfc + l)Cfc + 2)
6- Е
7 V	1	= И
?^ (к+- Л\О.к -I- Л\(Ак + 1) 3 '
Y-	1	 = ^тг 8	8
* ^ {к + 1){2к + 1){Ак + Ъ) 3 3° 3"
»•
13 V	1	^	, 8
' t^Q (k + l)Bk + !)Dfe + 7) 5	15 45'
15 + 5ln2^ 5'
> - - --. . .w.. . 3, 3Ш^ 3 3.
v^	1	= !L^__3
2(fc + 1)Cfc + l)Cfc + 2)	4 4П
!L

538	Гл.5. Ряды	[5.1.18
g {к + i)Cfc + 2)Cfc + 4) = 2 °П 3 1}-
22 V"	v 1>>	 = --21п2	24
' ^(fe + l)CJb + 2)CJb + 4) 2	'	'
5)
12
31п2^ 27"
81-
5. V	^ J	= 3- In 2 - Уз lnB-
^ (A; + 1)FA; + 5)FA; + 7^
5.1.18. Ряды вида Л
BА; + т)(кп1 + mi)(kn2 + гаг) *
1	°°
= — 2 V
12'	^
2 V=
12'	^ Bfc + l)Bfe + 3)Bfe + 5) 8 3'
180'	^ Bife + l)Bife + 8)Bife + T) 24 45
^	1	^^ 1 ^?
* f^Q{2k + l)Bk + 3)DA; + 1) ~ 10 + 5 П 10'
6 g	?	+
CO	-I	-I
7- V^	7Г	1 .	1
* ^QBk + l)Bk + 3)DA; + 3)"б~3П ~ 6"
3) =\

5.1.18]	5.1. Числовые ряды	539
^1=5_^_1, ,
5) 6 6 3'
7	1
30 ~ 10 + 5
iq
^	1	^^ 1	1
^Bfe + l)Dfe + l)Dfe + 5) ~ 12 + 6	6*
1-1
^v	1	7Г	1 .	1
* f{2k + 1){Ак + 1)DА + 7) ~ 30 + 10 ° ^45'
12
5)
11
20 ~ 10 1п2^ 30'
* ^ BJfe + l)DJfc + 5)DJfc + 7) ~ 15 15 30 П '
15 30 1п2 15'
" ^Bfc + 3)Dfc + l)DA + 5) ~ 10 20 10 " '
j	-1
^	1	4	1	7Г
* f^Bk + 3)DJfe + 1)DА + 7) = 45 + 10 П ~ 30'
(-1)*	я- /3^2 \ 3 3^2
20 \	3 / 45 10
2 тг 1, n

540	Гл.5. Ряды	[5.1.19
5) 12V^V^ ^ 3' 6
i
6 ~ 12
= 4 + ^ ^ + f'"*1
- g B* + 3)(ife + 3)Dfc + 7) = 4 + ^ ^ + if
5.1.19. Ряды вида
77777r.
(ЗА; + га) (ЗА; + mi)(ЗА; + ra2)
1тгУз 1
1. >
^ {Ък + 1)(ЗА; + 2) (ЗА; + 4) 18 6"
оо	(_-\\к	1	о
тг	1
24"
7 - '"' ' -w"' ' ЛЧ/"' ' ™ч 4 36л/3 36
5 y^	1	= ^ 1
^ Cfe + l)Cfe + 2)Cfe + 7) ^ 60'
6 \^	l1)	= ^1^2^^
* f^ Cfe + l)Cfe + 2)Cife + 7) 15	40'
т V	\	= 1.
^ (ЗА; + 1)(ЗА? + 4) (ЗА; + 7) 24'
Е(— 1)	^тг	А	11
Лч^ -+. iV.4fc + 4V.4fc -+- 7) ~~ 27-^3 + 27 П ^72"
9 V	г	1
10 у	til!	= ^z^Aln2^2i
^Cfe + 2)Cfe + 5)Cfe + 8)	^ 27	180"
5.1.20. Ряды вида У
DA; + m)DA; + mi)DA; + m2)
16 8 s
f^l)fc	1	7Г	1
2- E Dfc + 1)Dfc + 3)DA + 5) = 8 " Wf + Wf 1П C
00
о v	-	= ^^L
' ^ Dk + l)Dk + 3)Dk + 7) 48 72"
1	7Г
7)

5.1.21]	5.1. Числовые ряды	541
5. V	I	= X_JL.
^ Dfc + l)Dfc + 5)DJfe + 7) 72 48
к—О
i(l +л/2).
6' ^ DЛ + 1)DЛ + 5)D* + 7) = 48^2 72
^ Dfc
24 16"
тг	5
5.1.21. Ряды вида
5)DА + 7) = I^/f 24
I- Е-
Z_-/ (h 4- п\(к 4- л 4- 1 \(к -4- л 4- 9Vfc 4-ni^	Ч/if/i 4- 1 Un 4- 9^
[а/0, -1, -2, ...].
00	( л\к	л °° ( i\k	t-7	о
2. / 	 = — Л* 	— — +	—	.
< J {к + оЛ\к + а + 1)(/Ь + ft + 2)(л + <2 + 3) 3 *^ к + о» бо. 3(о. + 1) 6(о. + 2)
*
(а)-/3F)/ F-а)Н/?'(а) + /3'(
1 2 v2
/ -/ JU2/JU _i „\2	^ЭТ2	„2 / -/ L2	„3 / j L. '
? ^L"+^=Ь[i - (-i)n] in 2 -12^[i+(-i)n]+
k2 '
.v^.^-ii. 9><-.'
12 16'	* ^гк2{к + 2J 16 24°
8 4
2)(к + 3) = 18" 11# ^ fe(fe + l)(Jb + 2)(fe + 3) = 9
17 8
3) = ? ~ 3ln2'
13 V	(^	=5 " ¦ 2lo2
" ^ ife(A + l)BA + l)BA + 3) 9 3 3
•	>	. ,.	.x^.	.x^.	_2x	4	2 7Г.
T
2
6 "

542	Гл.5. Ряды	[5.1.21
17 у	(-1)"	о , т ^
' ^(fc + lJBfc + l)Bfc + 3)	"*"	12"
1Я у	1	= ?_^з _^
(fc + lJCA + 2)CA + 4) 2 2	6'
' hd (* + 1J(ЗА + 2)(ЗА + 4) ~ 2+	12"
8	5
3) = 31П2^ 3*
21 V	^)	=5 ^ 2
' ^(J l)(Jb 2)BJb l)B^ 3) 3 3 3
оо
22 V	-	 = -
' ^(к + 1)(к + 2)Bк + 1)Bк + 5) 9"
5) 9 3
Y^	I	_ 1 2тг 2
* f{k + l)Bfc + 1)BА + 3)DА; + 1) ~5+15~5П "
5V 3 V ' 15
' ^ (fe + l)Bfc + l)Bfc + 3)Djfc + 3) ~ T ~ У " +3'
28 у-	1	=2тг 10	13
*	^^ (^ + 1)BA; 4- 1)BA; + 3)DA; + 5) 3 3	3"
Y>	1	_ 7Г 10	4
*	(^Q{k + l)Bk + l)Dfc + 3)DA; + 5) "I"!"	+ 3*
3°* ^ (A; + 1)BA; + l)Dfc + 1)DA; + 3)
1	2 2
(A; + l)Bife + l)Dfc + l)Dife + 5) =	3 ^ 3 ln2"
1=	^ ____ 14	2
3)	5 15	15°
Y^	1	 _ 4тг 6	8
* ^ (A; + l)Bife + 3)DJfe + 1)DA; + 5) ~ 15 + 5 ° ~ 5"
V	г	- Ж 10 2 10
" ^ (A; + 1)BA; + 3)DA; + 3)DA; + 5) ~ ? + У ° ~ Т*

5.1.22]	5.1. Числовые ряды	543
36' ^ (к + l)Cfc + l)Cfc + 2)C* + 4) = 2
37 vtil!
12 ^1п2+ 2*
39. >	 = — --. 40.
^ Bfe + lJBJfe + 3J 16 2
fc=0
41 V	-	 = ?--*	42
^ Bfc + 1JBA + 5J 64 9'
43. V	^	= !L_!L
^B^ + lJDfc + l)Dfe + 3) 2 8
1
~ 2 ~
4°
7Г
8""
11
~ 144
45. V	 = -L + ^-ln2- —
^ Bfe + l)Bib + 3)Dib + l)Dib + 3) 30 15	30
V2
1	/2
*	^ BA; + l)Bife + 3)DA; + l)Dife + 5)	~ 15 + 15 ° 30"
00
ir^	1	7Г	1
*	-^ BA; + l)Bk + 3)DA; + 3)DA: + 5)	= ? ~ 2'
ул 	1	 ^^G^TT 7Г^ 1
" ^ BA; + 1)DA; + l)DJfe + 3J ~ 2 8 + 16 + 2 ° '
5°* ^	5)	= 6ln2^ 24 + 12'
' Bfe + 3)DA: + l)DA: + 3)DA: + 5) 120 30	60'
k=O
)(	)( 7) 96
54
4 V4 V
53' 1,D^ + 1JD^ + 3J 32	• 54' JL
^ 1 5	G ^
* ^ Dfe + 3JDife + 7J	~ 288	16 + 128"
5.1.22. Ряды вида V
• • • {КП5
1	5тг2
7

544	Гл.5. Ряды	[5.1.22
°°	1	3
2' ^	!JB^ + 3J = 2
>•?¦
*
^	1	_ 22	4тг 1
* ^ (А; + 1)BА; + l)Bfc + 3)DJfe + 1)DAj + 3) ~ 15 ° ~ Тб ~ 15"
* ^ (Jfe + l)BJfe + 1)BД + 3)DJfe + 1)DД + 5) ~ 15 15 15° '
	 = —-	In 2
(A; + 1)BA; + l)Bk + 3)Dk + l)Dk+ 7) 135 15
^ 0 + 1)BA; + l)Bfe + 3)Dfe + 3)Dfe + 5) 3 3
7.	V^		= —	In 2
^—' (jfe + l)BJfe + l)Bjfe + 3)DJfe + 3)Djfe + 7) 15 15	45'
fc=O
^	1	4тг 22 ,	83
8.	> 		=	1	In 2
^ (fe +1)BA; +1)B^ + 3)D^ + 5)D^ + 7) 15 15	45'
*	1	_ 4	7Г	1
• о) о	о о
(A; + 1)BA; + 1)DA; + 1)DA; + 3)DA; + 5)
f.	1	 = _8_ 2_JL_J_
* ^ (ife + l)BJfe + l)DJfe + l)Dife + 3)Dife + 7) 15 П 10 135"
12 v	^	= i^^±in2^^L
^ (^ l)Bfe l)Dfe l)Dfc 5)Dfc 7) 135 15	30"
13 v	^	= ^L^lEin2 + ^
* ^ (jfc + l)BJfe + l)Dfe + 3)DJfe + 5)DJfe + 7) 30 15	45'
14.	> 	 = — -	-In 2.
^ (к + l)B^ + 3)DJb + l)Djfe + 3)Djfe + 5) 15 30 15
°°	1	4	14
15.	\^	 = —¦	1п2Н	—.
^ (к + l)B^ + 3)DJb + l)Djfe + 3)Djfc + 7) 30 15	135
^л	1	_ ж 8	91
17 V	X	- ^ 41 2 13
" ^ (A; + 1)BA; + 3)Djfe + 3)DA; + 5)DA; + 7) ~ ? + 3 ° ~ У'
54
1
15
' 3
In 2.
7Г
20 H
2
1 15

5.1.23]	5.1. Числовые ряды	545
22
24
5.
6.
7.
я
9.
10
12
13
16
35
oo
oo
^_	j /Q JL
OO
oo
oo
5.1.23.
fc = l
oo
oo
oo
oo
r(fc+
oo
' f^Q(k~
oo
Z.	¦¦¦/ f I?
oo
oo
X v /OL
oo
+ 1)B*
+ 1)B*
+ 1)B*
+ 1)D*
+ 3)Dife
Ряды
1
1
+ 1JBJ
1
+ 1JB!
1)B* +
1)B* +
М)B*-
f 1)BДг -
1
+ lKBi
+ lJBi
1
+ 3)Dife + 1)DАг Ч- 3)DЛ
1
+ 3)Dfc + 3)Dfc + 5)DA
1
+ 3)Dife + l)Dife + 5)DA
+ 1)DAj + 3)DJfe + 5)DA
+ l)D^ + 3)D^ + 5)DA
вида > , ч/
^^ («ni + mi)(
7Г2 39
+ 2J 4 16"
7-2 O4
l)Bfc + 3)Dfc + l)Dfc +
1
l)B* + 3)D* + l)D* +
M)B/c + 3)D/c + 3)D/c
1
1 Зтг2
fe + 3K 2 ' 64 '
1 _ Зтг2
fe + 3JBfe + 5J 256
1
?-jj Bk + 1)BA; + 3)DA; + 1)DA; + 3)DA
А. П. Прудников и др., т. 1
: + 7)
; + 7)
; + 7)
; + 7)
^ + 7)
(±1)'
1
45 '
7Г
20 '
60 '
180
60 '
kn2 + тп-г) • •
«о.
¦3)DA; +
¦ 3)D/г +
¦5)Dife +
+ 5)Dife-
+ 5)D*-
OO
14. ?
1
9'
: + 5)Dfe
5)
7)
7)
f7)
f 7)
f 7)
Bk -
+ 7)
1
15
15
15
I In
1 30ln
In r-
30 '"*
. (krii -\
1 9 In
5
67
135
47
45
5
52
135
MKBi
1
18
i ж
J 60
1
J 5"
i
45
2-6"
!
15
15
7Г
15
15
J 30
7Г
30
fe + 3)^
7Г
60
i-6, 7, 8, 9.
7Г 7
24 16
3
5'
135"
6 In 2.
5
135"
-Hta2.
1 ЗТГ 7Г3
5 2 ' 32 ' 128"

546	Гл.5. Ряды	[5.1.24
17 ул _	1	Зтг Зтг , тг
^J Dfc + lKDJfe + 3K 64 128 256"
00	1	ко	о	о 2
-jo V^	i	 = bS i Д С	Л7Г
* ^ Dfe + 3KDJfe + 7K 13824 256	2048"
оо
19. ?
^ (А; + 1)BА; + 1)BА; + 3)DА; + 1)DА; + 3)DА; + 5)DА; + 7) 5	135'
20. ± 1	=^ + Ни!_з5. 21. V	I	= ^_Ш_
^к4(к + 1L 45 3	^ [Щ + 1)Aг + 2)О + 3I2 54 216
оо	2	-,
22 V^ 	^	 _ ж /2 , оп\ ?
fc=0
oo
23. x:-
Bfc + lLBfe + 3L 768
(-1)*	 = _«;	7_
[B/fc + l)B/fc + 3)Bfe + 5)Bfe + 7)]2 1728 4050
24- Ё (iFTTRifeTsF = isk7гGг3п2+30n ~60)-
^	1	35тг2 6217
25. /
5.1.24.
648 11664
(±l)fc
1.24. Ряды вида V у—	—4	™	7Г-1	г
^ (к + ai)(A; + a2) . . . (A; + an)
oo	n n
l. у	1	= (-1)» у n
"i-—' (A; + ai)(A; + 02) • • • (A; + an)	^—^ A A аь — o>\
k=Q x	' v	7	v	7	k = l 1 = 1
[a» 7^ U, —1, —2, . . . ; o,i ^ щ при г т^ /j.
1
_х_^	1 Г tb"(l — t)"
2* ^ (A;a + 6)(A;a + b + 1) . . . (ка + 6 + n) ~ n\ J l^t0 *	[a, 6 > 0].
fe—0	Q
1	г
4.	V—	-.	— = \ta~1e1~tdt	[Reo>0].
^a(o + l)...(o + fc) J
00	JU	f fa/2-1
5.	V —;	г—'—,	-r = 	dt	[Re a > 0].
^a(a + 2)(a + 2fe) J 1 + t	L	J
=- g ^d+-) - e [^A+a) - ь<*'A+аи -
- j^ [с1гфA + 7<) " с2гф'A + 70 + ^ ^"A + 7<)],
где
gi(^) = (A; + ai)(k + a2) . . . (A; + am),
= (A; + /3iJ(^ + /32J . . . (A; + /9rJ5
= (к + 7iK(^ + 72K - . . (к + 7sK,
p(k) — многочлен степени не выше т + 2г + 3s — 2, все постоянные а$, /Зг, 7« различны и

5.1.24]
5.1. Числовые ряды
547
р(к)
= V ai +ST
qi{k)q2{k)qa{k) j^ к + оц fr{[k + Pi (к +/3
b2i
C3i
ъ (к + ъJ (к + ъ)'Л У
f>
г=1	i=l	i=l
'•Е
^ [к(к
— *bm, n-)
8.
Bn - 1)!!2" Гтт2
6
-A;-l
к
n- 1
10.
(~1)к
^ (п-2А;)!BА;)!
m + к - 1
к
2k { }
n-1
k=0
n-1
=2(-1)п e
n-1
2 In 2.
2т + п
лк(п + к- 1
к
m + kk~l)i2-^l)Cin^k)-
A; -
i\2»4
13
"•Е-
Е
fe=O
Bn^2ife^l)!B7rJfeB2fc^
(n-2A;)!BA;)!
^ + A;-l\fcr/
л	1-2 К(п-Л, 4
fe=O
~"
2m ??Л к
2 +
"' 4
г + гг - 2
гтг — 1
35*

548
Гл.5. Ряды
[5.1.25
9	9,	9ч.
5.1.25. Ряды вида
(fc2 ±
Щ {
[Res > 1/2; |o| < 1].
- 2,
7гГ/
сЬ2тг6\
(sh2nb\
i
*
1	1 7Г JcthTml
7Г J cosech жа
\
к2 dt а2	2а2 2а 1 cosec жа J
k=l
кфп
jfe2 - 4n2 16n2 '
oo
• E ferr = -°
= -°'26961L
E Р
= -0,516128.
14-
a2) 2a2 \ /3A + m) + ^A - m) - 2/3A) J '
oo C_i\fe
г = 0,671866. 15. V , До ; ч = ^0,423567.
l) '	?^k(k2 + l)
oo	oo
- E Щ^^ = О, 993317. 17. g
= 1,2,3,...].
[n = 1, 2, 3, ... ].
g
19.
= "О. 708078.
= -1,227411.

5.1.25]	5.1. Числовые ряды	549
= —AпЗ —1). 21. > . ,. »
= J_ . J^_	W cth тта 1
а2) 2а4 6а2 2a3\ctgTraj*
*
2а4 + 12а2 2а3\81птта
r1
^л	1	1	тг J cth тта 1 тг2 J cosech тта 1
^-^ Aг2 ± а2J 2а4 4а3 1 ctg тта Г 4а2 1 cosec тга Г
fc=O
\-^	1	тг	1 / Г cthTr&l f cth тга! \
Z_^ /i 2 -L	2WL2 .L L2\ = 9™T ~~2	K2" I a I	f ~~ I	f )
^л f^l)fc	1	tt fcosechTral /	fcthTral\
27- / no , 9X9 = 7Г-Т + T^i	>1 + тга^	И.
^^ (fc2 ± a2J 2a4 4a3 I cosec тта J V	I ctg тта J /
fc=O ч	;	v	^x	\ о	j /
= °>397117- 30- Е (Ftw = 0> 825042-
g (srpijj °>397117- 30- Е
^л	1	тг2 1 Зтг JcthTral тг2 JcosechTral
* ^ к2(к2±2J = б^4 ^Т	T
^^ «^(«^±a^J^ 6a4 ab 4a5 [ctg тта J 4a4 [ cosec тга J
00
1 тг2	тг JcosechTral /	JcthTral\
-^ Jfe2(ife2±a2J = об ~ 12a4 T 4a5 f cosec тта J \ + ?Га| ctg тта jj "
x , .«/	tt / . f cth тга 1	f cosech тта 1
^^ (Is2 ± a2J	4a I	\ ctg тга J \ cosec тга J
я^> (^l)kk2	тг /	J cth тга 1\ J cosech тга
^^ (к2 ± a2J	4a \	\ ctg тга J/\ cosec тга
\^ 1	1	, Зтг2 JcosechTral
^ (к2 zb a2K	2a6	16a4 \ cosec тта J
Зтг J cth тга 1 тг3 J cosech тга 1 J cth тга
16a5 \ ctg тта J 8a3 \ cosec тга J \ ctg тга
^л к2	тг JcthTral тг2 JcosechTral /	JcthTral\
^^ (fc2 zb a2K 16a3 \ ctg тга J 16a2 \ cosec тга J \	\ ctg тта J/
тг fcosechTral /22	2 2 fcosechTral	f cth тга! i
= ^TT1	U T7TV ~ 2тт2а^	} +1 + жа\	И.
16ал [ cosec тга J I	[ cosec тга J	[ctg тта] I

550	Гл.5. Ряды	[5.1.26
¦¦«
у,	1	тг /thGra/2)
' ^B^ + lJ±a2 ~ 4a\tgGra/2)J-
3 у (-1)" = 1 [ ^	ofl/a
" ^ Bfc + IJ - a2 4oLcosGro/2) P
BTWTI	? B*+^+1/4
- ?
*
Y" (^l)fcBfc + l) _ jr_ Г sech (тга/2)
^ BA; + IJ ± a2 ~ 4a \ sec (тга/2)
•
тг Г J sech(?ra/2) 1
о2] = 4а? [ ~ \ Бес(жа/2) J
B.
14 V	tl)	 = 21n2 15
" ^B^ + l)[B^ + lJl/4]	"	•
^ BA; + lJ[BJfe + IJ ± a2]	8a2 + 4a3 \ tg (тга/2) J '
17 V
' ^B^ + l
4a3 L V 2 / V 2 )\ 4a2
^0(	)[(	)/]	^(	)[(	1J-1] 4 4"
ie V1^ JL/th(W2)l

5.1.26]	5.1. Числовые ряды	551
^	1	тг fth (тга/2)} *г2 fsechGra/2)- "
' ^ [Bк + IJ ± а2]2	8а3 \ tg (тга/2) J 16a2 \ sec (тга/2)
± а2]2
^ (^l)fcBfc + l) _ jr^ Г sech (тга/2) th (тга/2)
" ^ [BJfe + lJ±a2]2 ~ 16a \ secGra/2)tgGra/2) /'
_ 7г2 Зтг fthGra/2)l тг2 f sech (тга/2) 1 2
~ 8a1 ~ 8a^ {tg (тга/2) J + 16a4 \ sec (тга/2) J *
= тг (thGra/2)| тг2 [ sech (тга/2)
*
* ^ [BА; + IJ ± а2]2 ~ 8а \ tg (тга/2) / 16 \ sec (тга/2)
_ тг Г 1 — sechGra/2)l тг2
~ 4a1 \ 1 - sec (тга/2) J T 16c
2 Г sechGra/2)thGra/2)
. - sec (тга/2) j 16a3 \ sec (па/2) tg (тга/2)
ЧЬ(тга/2)
1J±а2]2 " 16 1 secCW2) JV т ltg(W2)
тг / fthGra/2)l	Г sech (тга/2) 1 \
/2^ ' '-^-{secwVlj-
¦1J +а2]2
тг , тга 1 nfl + ia\ 1 Г_,/1-га\ , п, f 1-\-га
Ыа	2 4ia ^ V 2 / 16
1
37 V	X	= ^^ x
01 • Z-/ [Bife + lJ±a2]3 64a5
fsechGra/2I2 f th (тта/2) 1 2 2 f sech (тга/2) 1 2 f th (тго/2) 1
^1 secGra/2) J + \ tg (тга/2) j + ^ a \ sec (тга/2) j \ tg (тга/2) J
_ тг fthGra/2)l тг2 Г	fthGra/2)ll f sech (тга/2) 1
32^\^(>а/2) J 64^2 [ T7ra\tgGra/2) Jjt secGra/2) J

552	Гл.5. Ряды	[5.1.27
5.1.27. Ряды вида yj	4w •
ir~^ 1	1	тг sh л/2 тга + sin л/2 тга
к^ок4 + а4 2аА ^а^у/2 сЪлДжа-соБхДжа
^\ (~l)fc	1	тг sh л/2 тга + sin л/2 тга	тг sh (тга/л/2) + sin Gга/л/2)
^а3 ch л/2 тга — cos л/2 тга 2л/2 а3 ch (жа/л/2 ) — cos (жа/у/2 )
~ 1	7 тг
4- Е
fc=2
(-1)* -1 тг ,	, ч
=	(cosecTra + совесптга).
k=0
^у	1	1	Зтг sh ^2 тга + sin ^2 тга тг2 sh ^2 тга sin ^2 тга
'•Е-
а' ch V^ тга — cos л/2 тга 4а6 (ch л/2 тга — cos л/2 тгаJ
1	Зтг sh л/2 тга + sin л/2 тга тг2 sh л/2 тга sin л/2 тга
J 2а8	8^2 а7 ch лД тга - cos ^2 тга 4а6 (ch \Д тга - cos ^2 тгаJ
Зтг	sh(Tra/V2)+s!n(Tra/V2) тг2 sh (тга/л/2) sin (тга/л/2)
8^2 a7	ch (тга/1/2 ) - cos (тга/^2 ) 8а6 [ch (тга/^2 ) - cos (тга/л/2 )]2 '
— а4J 2а8
-l)fc	1	Зтг
2
H	 (cosecтгаctgтга + cosechтгаcthтга).
^	2fc + 2a + l		1
* h ffe2 + ^2 + !)^ + 2 ++&2]2 +fe2 ~ 2 +
• Bа + l)jfe + а2 + а + б2]2 + б2 а2 •
(^1)к[к2 + Bа + l)jfe + а2 + а + б2]
'
^ [к2 + Bа + 1)А; + а2 + а - Ъ2]2 + Bк + 2а + 1)Ъ2 2(а2 + о2)"
\~^ (^l)fc[fe2 + Bа + l)k + а2 + а + Ь2]Bк + 2а + 1)	а
14 V
k=i
5.1.28. Ряды вида
^^	1	тг sh л/2 тга + sin л/2 тга	тг sh (тга/^2 ) + sin (тга/^2 )
* ^ B^
а4 ~ 2л/2 а3 ch л/2 тта - cos л/2 тга Ал/2 а3 ch (тта/^2 ) ~~ cos (тга/^2 )'
2	2	к^о Bife + 1L + 1
4. V . f (~7	^ = 0,930130. 5. V . f ^~7	^ = 1,055602.
4^ BА; + IL + 1/4 '	^ Bife + IL - 1/4

5.1.30]
5.1. Числовые ряды
553
OO
в. У	-	=
Зтт sh \/2 жа + sin \/2 жа
Зтг sh
+ sm(Tra/\/2)
a7 ch \/2 жа — cos \/2 жа 16^2 a7 ch (тга/ л/2 ) — cos (жа/у/2)
ж2 sh \/2 жа sin л/2 жа	ж2 sh (тга/ \/2) sin (тга/ л/2)
7- Е
4а6 (ch>/2 тга-cos
—Зтг / тга
16а6 [ch (т
Е [Bfc
тга	тга\ тг2 / 2 тга
-у - th -) + -^ (sec -
, 2 тга
-sech -
1п .
5.1.29. Ряды вида У
Обозначение: д = ехр [—т
у (zlTn^ = _l I	2
2тг
oo	n
- E I^V = 2^
l
5-
n=l
°°
E
9-
7- E A _ g2nJ = 24
( g)	24 +
00 /I2n+1	1
E (i + g2n+x)a	= ^
00 /,2n+1	1
k=i
--1	9
"T4
\
\e1(x,q)j
,
dx\e1(x,q)j\ctgx
12.
1.
5.1.30. Ряды вида
OO
V—= 1,291285997.
ki к
J —.
OO / -|\fc
2. V l J = -0,78343051.
k=i к

554
Гл.5. Ряды
[5.1.31
3. ^— = 1,87985386. 4. ]P(
к=1	k=l
5.1.31. Ряды вида /^ ^т-
^ к\
См. также ряды вида
= ~G, 65583160.
— х (в п. 5.2) при х = ±1.
2
к=0
So = Si = 1, S2 = 2, S3 = 5, 54 = 15, Я5 = 52, Яе = 203,
S7 = 877, S8 = 4140, 5n+i =
kn 1
k=0
i = -1,
5.1.32. Ряды вида V^ a,k
N(k)
3.
7Г
360°
4.
5.2. СТЕПЕННЫЕ РЯДЫ
5.2.1. Введение.
В этом разделе приведены суммы рядов вида \^akX . Ряды, в которых пк содержит
тригонометрические функции, логарифмы и т.д., помещены в соответствующих разделах
этой главы.
Многие ряды могут быть записаны в виде обобщенных гипергеометрических рядов
Е°°
A;!
г, Ь2, . . . , 6д; ж)
и суммируются тем самым к соответствующей обобщенной гипергеометрический функции.
Отметим, что в теории степенных рядов естественно возникает понятие гамма-функции,
частным случаем которой является факториальная функция (Г(к-\-1) = к\)] в связи с этим
было сочтено целесообразным поместить в этой главе некоторые степенные ряды, коэффи-
коэффициенты которых содержат гамма-функцию. При этом могут быть полезными следующие
формулы (см. также приложение 1.6):
1 (L — а — к)

5.2.3]	5.2. Степенные ряды	555
)! = (l)*Q) 22fc, Bfc + l)! = (!)*(§) 22\
к + а = Г(^ДХ) (a,+,1)fc, (а + 1)(а + 2) . . . (а + к) = (а + l)fc.
Если известна сумма ряда
к=0
то с помощью почленного интегрирования и дифференцирования (в области сходимости)
можно найти также следующие суммы:
оо	х
ir-л Qfc	пк + т _
оо
]Г (nA; + m)afcxnfc+m = x^~ [xm+1S(xn)
k=0
и
оо	f й
Eim	к ___ I Q
Другие способы суммирования степенных рядов изложены в [20, 23, 42].
5.2.2. Ряды вида
Условие: х < 1.
ОО	-1
1. Y хк = ——. 2.
to
a \^ lз fe _ жA + 4ж + ж)	4 fc _
О. У К X — 	у-	г~.	.	Т. / гС Ж —
к = 1
10.
к=о
5.2.3. Ряды вида ?
ОО
~ Ж^	If te~1e~at
1. > т	г" — —г^ 	7 dt = Ф(ж, 8, а)
f^(k + a)s V{s) J l^xe-t	K ' ' )
V{s)
q
[Re a > 0; -1 ^ ж < 1; Re s > 0; если ж = 1, то Re 5 > 1].

556	Гл.5. Ряды	[5.2.4
ОО	?
3- Е Jr = Ы-(Ж)	^ ? 2, |*| ^ 1; п = 1, -1 < а < 1; ].
00 Tfc + «	f та-1
4.	У f	 =	dx	[Re а > 0; -1 <: х < 1].
fc^o	0
оо
5.	\^ 	e*fe7rb = тг cosecaTrexp [iBm ^ 6 + 1)атг]
/г = —оо
[га — целое число, для которого 2т < а < 2т + 1].
6. ^_^ —	ег ^ = тг cosec атт ехр [гBт — 6)атг]
[га — целое число, для которого 2т — 1 < а < 2га].
-^—-— ж .
пк + in
1/*, . 2к7Т
1. > ~~;	х =—х ' 2 > sm	тг arctg	—
^—' nfe + т	п	?—"'	п	ч1/
fc=0	L	fe = l	1 — Ж1/пСО8
/	oi	\
[ 2/n о l/n	^«^ , 1 \ i /-,	1/пч ,
cos	In ж 7 — 2ж 7 cos	h 1 I — In A — x ' ) +
n V	n /
m+1 X + ^г^ In A + x1/n)]	[\x\ < 1; ш^тг; w, n = 1, 2, 3, . . .].
2.
+ m	жта/п ^	т — кп
[(n-2)/2]
2 \™^ . 2 A; +1
> sin
. 2 A; +1	n
> sin	W7T arctg	', , Л
n ^^	n	°	-, /эт 2^ + 1
fe=0	1 — Ж1/n COS 	7Г
n
— > cos
n t^o	n
^tl Ш7Г in ( ж2/« _ 2ж1/п cos 2k + 1 тг + 1 ) +
V	п	J
In A + х1/п)	[га, n = 1, 2, 3, . . . ; -1 < ж ^ 1].
oo
3. V
4- Еьття!*+1 = Е
fc=0	fc=l
f	2n
тп — 1
/	ч	1Г~^ J- к
\л(\	х) 	 / 	ж	[—1 <Сж<1" m - 1 2 3 1
E( — 1) ol i m ж—л , ч и 1 ж ттг 1 ттг , ,	о,
_v	^ ж2/г+т = у^ (^lr^1	h sin	 arctg ж	cos	In A-я)
fc=l
e. f -B^ ж— = х;(-1)-?T!i + ? sin - arctg
fc0	fel
	cos f^~ In (ж2 - x + 1) +	In A + ж)	[-1 < ж ^ 1].
о	«5	«5

5.2.5]
5.2. Степенные ряды
557
к=0
Е
fc-i xm 4k 1 . ттг
х	1 . Зттг	х
—=	V - sin —-— arctg —=
л/l ^x 2	4	6^2+ж
In (ж2 - xV2 + 1) + i cos ^ In (ж2 + xV2 + 1)
8.
- COS 	 1П IX~ — ХУ'А + I) +
4	4	4
-11п[A + ж)/A-ж)]
arctg ж
\x\
ж + 2
10.
= б1пA^жЗЬ21пA^ж)^7Г arctg^
12.
¦ ж4/с+1 = - In —— + - arctg ж
4 1 — ж 2
arete
ж < 1].
ж < 1].
[\x\ < 1].
In-
4^2 1 -
\—л	1	4fc4-3	1	1 + Ж	1
13. > 	ж = - In	arctg ж
^4^ + 3	4 1 - ж 2 Б
ггл/2
arctg
< i].
ln"
15.
.21 / i^^6fc+i
-l)kx6k+1 1
=
5.2.5. Ряды вида
Условие: |ж| ^ 1.
^	1
1-ж2
12
1	ж	1 .
6 ar€tg Г^^ + тт^ 1п :
1	Ж1/З
— arctg	-
1 — x1
[-K ж ^ 1].
< 1].
	^	r-.
{nk + m){lk + j)
•^fc =
n-l
x J/ > exp
f4
in 1 ~~ x ' exp —— -
/ V	l
5 m/n ^ exp i	j In I 1 - ж 7 exp	 1 + I
fc=o V n / V	n / ;
2.
з.
[га ^ те; nj — Im ф 0; s — целое число, для которого si < j ^ (s + 1I].
nidi,	g/ ?-t I ?^ 	I	 fy% 1	/у*	/v^ jj,	m/ 1^9
fl/ I It/ ™j § i/ I	8 If	I $J	fb
^7^ (^ + m)(A; + n)
00 k
n	m fc
In A - x) - xn^m In A - ж) + Y^ - xfc - xn^m У2 ~~
fe=l	fe=l

558	Гл.5, Ряды	[5.2.5
00 1
7- Е fc(fc
(±l)fc	f Athaj
кBк-\-1)	\arctga?J
2fe+3	2 2
l(^T^)" =-3- + -r-Tln(l-x)-
3fe+3	v3 2	, ЖуЗ	1 , 2 . оч 1 /-,	3\ 3 2
=Ж arCtg+(a; +2)ln(lx)r
2)ln(l-x)-r In(l-x).
у,	(±1)"	fc+2 _ 1 Г	3/2 Г Arth ^
? (d^ ж"+1 = 1J iln H ^ 4 ^ ^ - u> (->]•
16. 2^ -
k=0
17 V	-	rsh+4
¦ ^Ck + 2)Ck + 4)
• E Dfe
f + ^ A - *2)[31n A-х)- In A - Xs)] - ^=- A + Ж2) arctg
- Е Dfe
4 16
ж	1 , л.(л ж~ + жу^+1	ж л/2
-I	(Л 4- ср \ I In	к 9. я.гс±(г —
4
1	ль-\-ъ х 1 , 2 ч , 1 + ж 1
5) Ж = 2 + 8 (Ж - Х) 1П Г^ - I

5.2.6]	5.2. Степенные ряды	559
ZjDfc + 3)D* + .
1 / 2 -.x , ж л/2	1 , 2 iX1 1-
¦(x -1) arctg-	г^^-^-(ж +l)ln-
2 4^2 l	; &1^ж2 8^2 l	' 1-;
= 12 + 16 ^ ~
25. V_^
k=0 v
ae. vT^^a;« = i-a.|!ilL!lL*dt.
tt	;	uy l / ,	Ti	;	r, J > 2.
(кпг + ?m)(A;n2 + ^112) • • • {krij + mj)
Условие: |ж| ^ 1.
00
E	ж"+1 = (x - !)ln A " *) + *[Li2 (^) " 1].
-	E fc2(fe + 1) ж
OO
-	E fc(fc + iJ ж"+1 = 2x + (l-x) In A - ж) - Li2
1-ж
4. V yy-	^—	 a:2fc+]L = Зж - f ж + -} ln A - ж2) + 2 ln
^ Аг(/е + 1)BАг +1)	\ ж/
4l(A + l)Bfc + l)Bfc + 3)	V h ;h I	;\ arctg ж
¦Ж4*+5
6. V-
2™1/2 ln [(ж2 + ж>/2 + 1)/(ж2 - ж^2 + 1I
(±1)"	w_l[( Y[Arthx|
X	[3A T Ж ]	)
2 1/z arctg
[( Y[|
+ 3)B* + 5) X -24 [3A T Ж ] 1 arctg x)
• ¦^Dfc + l)Dfc + 3)DA; + 5)
= ^ [a -
= ^ [^2 (ж4 + 2ж2 - 1) In ^±^±1 + 2^2 (ж4 - 2ж2 - 1) arctg
" ХIп С1 " ж) " Зж + (ж + Х) Li2

560	Гл.5, Ряды	[5.2.7
11- Е ЛТ = 7 (^ + 1) Li2 (х) + \ (Ж2 - 1) In A - х) - *- - gg.
Z-^t k2(k + 2J 4
oo
^ k{k + l)(k + 2)(k +
g k(k + l)(k + 2)(k + 3)	36
fc+2	f	24
EF(H 1)a(fe + 2J = 4 [A + 4Ж + 4ж) Lb (Ж) 4X T
5.2.7. Ряды вида ^^ Е ^
1	fc	1
k— один из корней степени те из 1 : 0д. = Л^Т = cos	\- i sin	 = е2гк7Т/п
те	те
00 к	°° 1 к
к=0	к=0
Aj_
1 к
тк -пх
cos (x/\2
ртТ!)	зe зe cos (V
•
Dfc)!
1
U * co * +ch *
14 л - у—/ 4fc+2 _ J 2 (сЬж-совж)
/ //II	\Т
14. > . /Л, , „ч, ж = ^^ sin —^ ch —=¦ - cos —^ sh —=¦ .
к=0 х	f
00 ^,4fc+3
?3*T7i)x =зе е ; «""(V-W-)	[? = 1или:
(±1)' 4*

5.2.8]	5.2. Степенные ряды	561
erfc(-x)
у, (±1)	h
18 V ^^ ^+i_c^(erf(x)]
^Г(^ + 3/2)Ж -е \fi(x)J-
erfi(
k=Q '
\к
1	x2
2	Le
20.
5.2.8. Ряды вида V] 7—--	г^-——- хк.
ГIl	1
2. ^) l ^ Ж" = ^(^ж)п[^(п + 1)^1пЖ]^ЖпГ(^п, х)	[|arga|<7r].
кфп
3. V ^^- xk = -C - In ж + El (±ж) = [ i (e^ - 1) dt.
k=i к'к	I t
fc=0
к=0 v " 7	fc=O
00	,	n —I д.
т V^	^	fc + n /	\ ж , /	\ V"^ ж ,
Y	>		 «Т	— I Т* 	 11 ) Р -4- I TJ — Т 1 > 	 -\-
/ ^/	/fill	^	'	^	"^ / ^/ f I
^ (±l)	2fc+1= ^?Гегй(ЖI
• 2k\Bk + l)	2 \erf(x)J-
erfi (x)
10. У	??= = -?=\ехр(хе-*2 -t2)dt.
?^к\^/кТТ у/к )
"• E D+B)ж" = 2x"a [rBa) cos M -1t2a"cos
00	r4fc+l
E
12.
k=0
36 А. П. Прудников и др., т. 1

562
Гл.5. Ряды
[5.2.9
14. V
°'
х2к = 2х~2а -Г Bа - 1) cos тга - [ t2a sin tdt\.
L	J	J
Si
16.
4fe+2
3/2) = f
ж/2
23.
24.
(I2 -
Bk + 2)!
2k+2	¦ ч !
x = ch (arcsinxlsecfarcsina;) — 1.
. . . [Bk - If - v2] 2k 1 .
x
BA; + 1)!
5.2.9. Ряды вида \
Обозначение: х = ae~a.
00 /» 1 i\n	jn
> ^^ж =
(A; + m)!
п
kl
dtn
exp Ft + же
2k 1 . .	. . Л
x = —sinfi/arcsinjc) — 1.
их 1	;
2. > --ж = ж^ е = Sn.
?^1 kl	\ йж/
= x(x + l)ex, S3 = x(x2 + Зж + l)ex.
аBа
5.
6.
1.
o(l-o)
- 2a + 4aea - e2a
4a2
0< a < 1 .
L	J
2aea - e2a
2a2

5.2.10]
5.2. Степенные ряды
563
5.2.10. Ряды вида ^J
3
•
'
"
(n - к)/2]
1 Г
Ж =2[ 2ЬегBж)
F(ka + b)F(kc + d)
>
r f2rl I *
^2(п + 1)/2е^Ж2/8^^
()(
2\ 2beiBx)
4fc+3 = 1
2
J'0Bx)
2Ьег'Bж)
'
^Г(^ + 3/2)Г(^ + 1/ + 3/2)
^ Г(А;/2 + n/2 + 1)Г(А;/2 - n/2 + 1)
oo	k
Н,Bж)
*=о
(-l)kx2
3A:
M= ГЬе1„Bх)
\bB)
- n)
- in ,] -
17
36*
[ t^Jv{t) dt	[Re/i < 1/2, /i + i/ = -2n - 1].
2ж
Ж J *	H
[Re i/ > 0].

564
Гл.5. Ряды
[5.2.11
18
кфп-1
х |1пж- - ф[ п+ - 1 - -ф[ п-
[Re/л < 1/2, ц +и = -2п].
5.2.11. Ряды вида
V{kc
¦х\
2.
гп Л х
A -
j.
L^i
-1
гп + к — 1 i
х
^ (m + fc)! fc _ m!
о» / 	г";;	 Ж —
A-^
4
_i/m-l\ 1
+ -
^i к — In + 1 n ^^	n
1 = 1	1 = 1
21
sin — (А; + 1)тг arctg -
,11
— Ж1/" COS —7
1 [(n)/2]	9/
+ - V
п ^	п
9/	/	9/	\
cos — (к + 1)тг In ж2/п - 2ж1/п cos — тг + 1 ) +
+ - In A - х) + (-l)*+ll + ( 1)П1п A + ж)] .
5
k=0
1 ;
[\х\ ^ 1; /х, 1/ > 0].
+
k=l
- t)]dt

5.2.18]
5.2. Степенные ряды
565
12.
13.
14. V
А;!
= exp (
о
[O^<1].
D; 0 < Re i/ < 1].
fc!
15.
(*) J 6
(A; + i/
[Rei/, Ree>0].
x\^l] хф1 при i/ > 0].
1; ж ^ 1 при i/ > -1/2].
5.2.12. Ряды вида \^ —	г—;	г—:	 xk.
^ r(ka^b)F(kc^d)F(ke +f)
er2 Bx) + bel2 Bж)
- Е
2
¦ i/+ 1)ГBА: ¦
ж4Л;
1r\O1lP' I 9ф I Г\С11 f 9ф I 	 ГЛОТ* f 9-1P I r\?3i1 I
I Lit; 1 |/ IZjXJ lJt;l|ylZjXf UtJl ^IZsel/j Ut3i|/ I
T* I ^) ЛР ! ГЪОТ* I *) ^T3 I 	I	 Г\С11	I ^У fYb \ r\|Zll	I О /тэ 1
¦i//2 + l)r(ife/2-
5.2.13. Ряды вида
V{kc + d)V{ke + f)
Bk-
fc_
" A 4Ж)
[-1/4 ^C Ж < 1/4].
[-1/4 ^ ж < 1/4].
3.
g (±Я!)* =
1/2
¦ X = — J
^ [2 In 2 - In
± Ах]
T 4ж2 )] In (I
- л/1 Т 4ж2
2Ы
»• E
BЛ)!
[-1/4 ^ж< 1/4].
[-1/4 $C x < 1/4].

566
Гл. 5. Ряды
[5.2.13
7.
BA;)!	2fe+i _ 1 \ f arcsin (t) 1 dt
[k\J{2k + lJ X ~ 2 J \ Arsh(t) J T
^	Bfe)!	г*-! 1	2 1/2
8- ^(fc^afc-l)^ =-(l-4x)/ +2arcsm(.
BЛ)!
\[
= ; l-a--
arcsin Bж)
2 \ Arsh Bж)
14.
15.
ч5/2
ж -24|t>JT l
A ~~
B/с
_8г
" 3Г
. Е
19- Е^Л
1/2v
(	j J
BА)!
¦ ж21г+3 = - |4ж - 2жA ~~ 4жУ7" - arcsin Ba?;
2*+з _
I/a f arcsin Ba;;
• Е
ч-3/2
2I " ~ 2х2 ' 2ж2
22
23-
Bfc
к+4
25.
1 < 1/4].
[NKV4].
[-1/4 ^ ж < 1/4].
[|Ж|<1/4].
[-1/4 ^ ж < 1/4].
[-1/4^ ж < 1/4].
[-1/4^ х < 1/4].
[|жК1/4].
у); \х\ <2/33/2].

,<,=0 l^«;j
5.2.15]	5.2. Степенные ряды	567
2в- ? 1ШШГ *" = МA - 4х)-3/2 + A + 4Ж)-3/2]	[-1/4 < х < 1/4].
i/ + 1/2) fe
+ 2«/ + 1)а!
fe
00	life	^
- g r(fc-, + 3/2)r(fc + , + 3/2) - 2 ^/2 J ^
g
t^
31
2Lj Г(А; +/x - i/+ 1/2)Г(А; +/x + i/+ 1/2)
5.2.14. Ряды вида
TVfr 4- f)
Arsh (x/2)
*(*!L,»+! _ ±4f4 2)i/2 Г arcsin (ж/2) 1	f arcsin (ж/2)
Ж	±4D T X j	/ + 2X\
±4f4 )
+ 3)! Ж - ±4D T X j \ Arsh (x/2) / + 2X\ Arsh (x/2)
1)! 2k+S _ ±2 2(i 2,i/2 f arcsin (ж/2)
3)!	±2жТ2DТж) |
k=Q	v	' 7
5.2.15. Ряды вида
T(ke + f)r(kg + h)
ж/2
к=0

568	Гл.5. Ряды	[5.2.16
' -	x/2
5.2.16. Ряды вида E
^ KF(kd1 + e1)...F(kdj + ej)
2k _ T2,r
E
/x -
5.2.17. Ряды вида VafcfV (±1) )xk.
t—1 V nl + mj
¦x)	[\x\<l].
2. у If у ±)хк = -\п2{1-х)	[-1^ж<1].
00	/ 2fe —1
5.	> ^	'-	 > 	 )x = <	}	[lacl < 1].
_x к VTfr/02m + 1/	[arctg ж]
6.	^ j^~\ Ё ^)x2k+1 = ln(l + ж2)arctgж - ж arctg2 ж + f arctg2 tdt	[\x\ < 1].
x\ < 1].

5.2.18]	5.2. Степенные ряды	569
k=Q	x m=0
, к
ЕтГХ
Jfe = l ^
11. > 	 >	— = —e erf (ж).
то=О
к
12- Ef?"
k=l
13* ' ^^М^""* ^^^"^ 1\ЛBх)-(тг/2I-оBЖ)/^
\" (-1) Г \" — "\ ^4fc = W (9,-гЛ -^ fr,^l\nx) ber Bж) - - bei Bж).
1
m	C+-lnx
m=l /	^
^ (klJ /Л П 2fc + 2	2	4 Ж
> ,	4, I > —=¦ laT + = -arcsin -.
^^ B^ + 2)! V ^^ m2 J	3	2
fc+1
5.2.18. Разные ряды вида
3J -
3) ¦
2
3 Л ov т —		-	p™lln a^/^4^ dt	Г ж! < 1- 0 < а < 11
fc=l	Q
оо	1
4. V^ —- хк = ж I t™33* dt.
fe = l	о
s- E[E?^f,^)l^+1 = (i + -2)p-ctgx.
с1I3 In A + ж).
m=O
[fc/2]

570	Гл.5, Ряды	[5.3.1
к=п
к Г п	/ с\	-I
Е (n+
/ t \ к Г
Е 7^I Е м
1{
' ~1; а;
ч л «,	If sin (t In b) ~~ x sin (t In ab)	. .	1	.
16. Л --г	г = T	—r^	^	T1 cosech 7rt dt + ^7		a, b > 0 .
J/ I I bl/	All/I J-	tl/ J
5.3. РЯДЫ С ПОКАЗАТЕЛЬНОЙ И ГМПЕРБОЛМЧЕСКМММ
ФУНКЦИЯМИ
5.3.1. Ряды вида J2
enk,
• Е е.» _ (_!)* = ^ B'n " 1)В
00 I 4n+l
2 4n + 2
1 1
24 ~ Stt'
*
96 + 6^ (-1)те -chwTr + 32
/•_ \4ri4-3 2fi-f-2
00
8-E
1L +
_ 7Г	(-1)П-СЬП7Г
^ BA; + IJ -

5.8.3]
5.3. Ряды с показательной и гиперболическими функциями
571
5.3.2. Ряды вида
Условие: \q\ < 1.
o7r2/Ing4i -1/2 _
4.
5.
6.
г{а, q)
[0 < q < 1].
7. f (_i
[0 ^ q < 1].
8.
exp
-1-) cosec2Vi dt.
Яо = 0, 38631860, S2 = 0, 37247207, S4 = 0, 36902569.
То = 0, 34968710, Т2 = 0, 36331424, Т4 = 0, 36673624.
= 0, 36800285, Ui = 0, 36792058, C/2 = 0, 36789315, U4 = 0, 36788096.
12. 5J(-
fc=O
oo
14.	]Ге
oo
15.	?
fc = ^o<
=0,36775603. 13.
211/4^.3/4 \ 4
± ) =0,04321392.
16. 53 (±l)';a2'Jg'j
';a2'Jg'j(*;+1) -
1 f (92(-ilna,
a \ i6i(—i lna5
9)
Я) У
5.3.3. Ряды, содержащие
El к (sh kx 1 . . / г sha?
TfN , , > =Arth#
fe=lk ^chk
1 — r ch x /10
	In A — 2r ch ж + r2
a|elRea;l < 1
sh(rsha) 1

572
Гл.5, Ряды
[5.3.4
k=0
chnx
dnu —
2(a
. = ch-
Im Arch a\ < Re x
cos at — r cos (a — b)t
sh (t arccos 6) cosecnTrt at
5.3.4. Ряды вида У^ an cosech &пж.
2
, А; < 1.
Обозначение: ж =
(-l)"^1 cosech In- -Jx = -Щк). 2. ^ ncosechnaj = —K(A;)[K(A;) - E(A;)].
(-1)n~ln cosech пж =
1	1
	 cosech Bn^ l)x = --ln(l - к2).
cosech2
-1 o/o 	 r,2
°°	/ 1 \	2
^cosech2 f n- - ]ж = — Щк)[Щк) -
n=l	^	^
^ (^1)W+1 /	,	, ПЖ\	1 /7Г	\
> 	 cosech no — cosech	 = —I	a)
^ n \	a J 2\a J
n=l
5.3.5. Ряды вида У^ аи cosech кж.
oo
^ Jfe cosech ктт =
[a > 0 ].
k=i
^
(~l)fcfc4n+1 cosech ifeTT = 0
[n = 1, 2, 3, . . . ].
)
Г
cosech кж = тг4^3 -
[
Dn + 4)!
г i о о
[„ = 1, 2, 3, ...
1)	, .	7Г
	 cosech кж =
ife3	360
cosech fc7r =
6.
к7
cosech кж =
453 600
cosech кж =	cosecTracosechTra.

5.3.7]
5.3. Ряды с показательной и гиперболическими функциями
573
9. У cosech2 Ьг = --
^	6
. 10. У cosech2 ?^±
6 2тг	^	2
+
2тг 16тг3
11.
1	1	/	2 2 ТГ \
-™	— cosech кж cosech (к + 1)тг = — cosech тг I 2 + 2тг cth тг — тг th — J.
12.
-,	оо	1 1 1	1	¦ /1 \
cosech JfeTr cth кж = — . 13. V cosech4 J^tt =	+ — +	« Г8 ( - ).
5.3.6. Ряды вида ^ an sech 6пж.
Обозначение: x =
, « < 1.
2.
Ж(к)
_ 2
х
= -K(ife). 3.
K'(fc)
11тBа/ж)|
_ jt,2\ 1/2
K(A;).
4.
1 \	91*
- -|ж= — K(ife). 5.
4
= — K(A;)E(A;).
6. У sech2
n=l
7. V 2±2n sech2 2±пж = ± cosech2 ж + -L / ° 1
n=o	ж I!i
5.3.7. Ряды вида ^ ajt sech б^тг.
=0
[n = l, 2, 3,
2fe
2fc
+ 1)9
(-1)"
8.
sech
23тг9
1 720 320'
—. 9.
24
" cos
[га = 1, 2, 3, ... ].
sech^l7r^ = _JL_.

574	Гл.5, Ряды	[5.3.8
\-^ (—1) Bк + 1) , 2к + 1	тг тга	тга
10.	> —	—	— sech	тг = — sec — sech —.
?j BA; +1L - а4	2	8	2	2
^—v	(~1)	1,^^ + 1	тг / тга i жа Л
11.	> ^^	чг/ т —^	^т sech	тг = —т sec — sech	11.
^Q{2k + l)[{2k + lL-a4]	2	8а4 V 2	2 )
JL jy да / ,	ч г /	ч .	.- оСъИ	#1	j 1
^ (	)[(	)	]	L	(/^ ) + ch
+ ^Г(). 14. Esech	. = .
V 7	fc0
+ +^
16. > sech 	тг =	 Г - I.
^	2	Зтг 384тг6 \4J
5.3.8. Ряды вида У^ afc th бд,.
^	1	, 2fc+l
l- E BA8 + lLn+.th^-' =
Пп+3
тг4
2 *fo
тг =
^Bk + lf	2	32"
о^ 2Jb + l	,2Jb + l	тг тга , тга	Л ^ 1 . х	.	1
5. ^2fc(l-th2fca!) = cthx-l	[ж > 0].
fc=0
Т^ 1 , 2 Ж	,2	1	2
5.3.9. Ряды вида У^ Qfc cth ктг.
к = 1	, . .	от»	i
lZ7ri	I D	i 04n+2 4n+3 \^ 	I — -1;	 о	о
°° 1	7	°° 1	19
^-^ Jb3	180	^ к7	56 700
fci	fei
v~^ /г	, ,	тг ch (тта^2) + cos
f^k4 + 4 С Ж ~
^^4^a4 ^"№" ^4тта4 4а2
2 ch (^^/2 ) _ cos (жал/2 ) 4тга4 '
	о ctg тга cth тга.
4а2 &

5.4.2]
5.4- Тригонометрические ряды
575
5.4. ТРИГОНОМЕТРИЧЕСКИЕ РЯДЫ
5.4.1. Введение.
В этом разделе помещены ряды, содержащие различные тригонометрические функции,
с том числе ряды Фурье. Отметим, что в некоторых случаях тригонометрические ряды
сводятся к рядам другого вида, например, к степенным рядам E.2), к рядам, содержащим
показательную и гиперболические функции E.3).
При суммировании тригонометрических рядов могут оказаться полезными следующие
формулы:
оо	^
^2 F(k) s'm kx = - sin x
k=i
1
chi-cosx
2тг],
^„/П ,	1 f cosa:-
У j F\k) cos kx = -
2 J ch t — cos x
0
f{t) dt
где
oo
F(x) = f f(t)e~xt dt.
Ряды, содержащие логарифмы, приведены в 5.5.1.
Г А «Ъ ГЪ	V^ i^1^ ( Sil1 кХ 1
5.4.2. Ряды вида > -^——^
El j smb 11
oofs
_х/ Л sinxl f О
2?r)s f cosecGrs/2)
i{ sec(W2)
4Г(в)
- r(e)
cosecGrS/2)
secGrS/2)
27Г
dt
[0
Res > 0 или |ж| > 0, Re s > 1].
[Re* > 1; 0 < x ^ 2тг].
[Re*>Oj.
2тг
[Res > 1; —л- < ж < тг].
[0 ^ ж ^ 2тг при п = 1, 2, 3, . . . ; 0 < ж < 2тг при п = 0].
Ё fck cosfca; = BBn)! B7ГJПВ2"(
[-тг < х ^ тг; п = 0, 1, 2,
[0<x^2W; « = 1,2,3,

576
Гл.5, Ряды
[5.4.3
9.
10.
11.
12.
ж — х ( cos а 1 .
	1	^-ln
2 I sin а/
ж \ I sin а
2/ [cos а
El j sin (kx + a
к X cos (kx + a
E°° (^l)^^1 f sin (kx + a) 1 , ж f cos a ] . /	ж
	\ , [ > = ± — < > + In B cos —
к [cos(te + a)J 2 I sin a J V	2
(±l)k . ,	Г /2sin(*/2)\
- sin А; ж = - In I	/ ; > d*
[ 2 cos (*/2) j
sin а
cos а
0 < ж < 2тг .
L	J
[-тг < x < тг .
L	J
k2
(±l)k
^
.	1 f
cos fca? = —<
12\
- бтгж + 2тг2
2 2
ЗЖ -7Г
^ ^ (±l)k . ,	ж
13. >	' Sinb=--
^ fc3	12
5.4.3. Ряды вида
(si
ж f x2 ^Зтгж + 2тг21
--	2 2	f
(k + a)s \ cos (kx + 6) J
k—0
(=
a)s\coskx ) F(
i r	V11
(s) J	1 - 2e^*
[Re a > 0; Re s > 0 при ж ф 0, Re s > 1 при ж = 0].
2
3.
4.
7.
1 f sin /гж 1
7Г
ч f sin (тг — x)a 1 Iff sin Г^жа + (a — 1/2)*1 1	* ,
d) j	/\-_l	 \ j i	v	/ cosec	dt
; \ cos (тг - x)a J 2 J \ cos [-xa + (a - 1/2)*] J	2
fSina,j±l ffooej-xa + jal/^n t
l ;[со8аж] 2 J \ sin [-жа + (a - 1/2)* J 2
Q
>
1 { ш\кх\
<	>
= тг cosec тга
f sin fBn + 1)тг — ж]а 1
\cos[Bn + 1)тг - x]a j
[2жп < x < 2ж(п +1) .
E°° (^l)fc f sin Д;ж 1	f sin Bптг — ж)а ]
)—^{ . ^ =тг cosec тга^ l	' ^	Bn - 1)тг < ж < Bn + 1)тг .
fe + a [соэ^ж]	[ cos Bпж - x)a j
1 J sin (kx + a)
+ a \ cos (kx + a) J ж sin
тг	J sin [Bn + 1)тга/ж] 1
in (тга/ж) \ cos [Bn + 1)тга/ж] j
Bn + 2)тг].
v^ 1 Г sin (А;ж + a) 1 =Fl v^ г/ ,	ч
> 	< ,	; > = ^-^г > \Bk — т)ж
^^ km + n [ cos (kx + a) j 2m2 ^^
cos fa ^ (ж + 2^
г )
sin a - ж +
sin [a — (ж + 2кж)п/т]
m ^ X cos Га — (ж + 2кж)п/т]
fe=O V	L	V	III
El J sin (a — kx) X
km — n X cos (a — kx) J
OO	_,	f • ( 1	X \	t ТП — 1
\~^ 1 I 8ш(А;ж + а) I =Fl v^
\ 	1 )	\ \ = —— >
^ km -n [ cos (А;ж + a) J 2m2 ^^
In 2
m > 0; 0 < ж < 2тг;
+ S(n — m) x
1, n > fn
0, ri ^ m
m ~ \ cos [a + (ж + 2^тг)гг/г7г]
ln [2
х + 2кж
2т
cos a + (ж + 2кж)п m]
sin [a + (ж + 2кж)п/т]
1
— п X cos
[т > 0; 0 < ж < 2тг; те/m ^ 0, 1, 2, . . . ].

5.4.4]
5.4- Тригонометрические ряды
577
9
^—' km + п 1 cos (А;ж + а
fe=O
m-l
=Fl v^r/o,	, -.x , i Г cos [а - (ж + 2кж + тг)п/ш] 1
= ^^7 / fBA; — га + 1)тг + ж к ; ;	f	ч , w
2m2 Z^ lv	/	J\sina- ж + 2А;тг + ж)п m] J
sin [a — (x + 2А;тг + тг)п/га]
-^ 1 cos fa — (ж + 2fe?r + 7г)п/гм
=O v	L	\	/ /
)
In 2 sin
— (ж + 2А;тг + 7г)п/га]
- BJfe + 1)тг
2m
кт-
k=0
f
km — n I cos
{sin (а — kx) 1
cos (а — А;ж) /
sin (kx + а) I
cos (kx + а) /
m > 0; -7Г < x < тг; 5(n - m) =
+ §(n — m) x
1, n >
0, n
— m + 1)тг
fc=O
¦ 2А;тг + 7г)п/га]
1 цг-^ j sin [а + (ж +
га ^-^ \ cos [а + (ж + 2Аж + тт)п/т
iy-л (^l)fc J sin (kx + а
In 2 sin
cos [а + (ж •
sin [а + (ж ¦
¦1)тг
- 7г)п/га]
^-^ fern — n I cos (А;ж + а)
fc=O	v	v	7
El I sin kx \ \ ,	ч r cos пж l ^r^ 1
1	л » r = ^Gr^^)i	r "" / тS1
_ A; + n [ cos А; ж J 2	ismii^J ^^ «
In
2sin—
V 2 /
1 i
-coskx\
A;	J [ cos пж
7i > 0; ^тг < ж < тг; те/m ^ 0, 1, 2,
}
n = 1, 2, 3, . . .; 0 < ж < 2тг .
,nL ( x\
(-l)n lnBcos-)
x\
-) +
2)
тг Г cos
{
l)	,
/ cos fca;
к	J [ cos nx
14
n = l, 2, 3, ...; -тг < ж
P < * <
5.4.4. Ряды вида
V^ 1 ГзтА;ж1
ED
п(ж/2) \	2 ж
M(Ж/2)/1пС^ 4
2/^ + ^^ тг Г sin (ж/2) 1
4 [sin (ж/2)] n€tg \^) Т1\со8(ж/2)|
(±1)к
[—7Г < Ж < ТГ]
+
( sin А;ж
I 1 COS ^Ж J
2.
2 \ sin (ж/2)
2 \ cos (ж/2)
[-тг ^C ж ^ тг].
37 А. П. Прудников и др., т. 1

578	Гл.5, Ряды	[5.4.5
о V^	1	fslntel	1 г	.	. . ,(81пж1
3. >	<	> = ±- 1 + (Ж - тфтжК	?-
^ А; (А; + 2) [ сов^ж J	2	[cos ж]
1 /о • ж\ Г sina
- sin ж In I 2 sin — 1 <	. , .
V 2 / [ cos ж j 4 11
\^ 1 /вт(А; + 1)ж1	. ж/cos (ж/2) 1 / . ж
^ А; (А; + 1) 1 cos (А; + 1)ж /	2 [sin (ж/2)/ V 2,
[cos ж/	2 [cos (ж/2)
Е°° (™l)fc (sin(A; + l^l	ж Г cos (ж/2) 1 Г sin ж 1
А; (А; + 1) [ cos (А; + 1)ж /	2 \ sin (ж/2) / [cos ж/
ж Г sin (ж/2) 1
2 [cos (ж/2)/
6.
v^ (™l)fc Гвш^ж] 1 1 й	. ч(81пж1 . . / жлгсозж] 1 Г 01
^ к (к + 2) [cos ^ж J	2V	;[со8ж]	V	2/18тж] 4[lj
1	Г sin А;ж 1 1 . ж . 2 х (cos ж ', .
- ™-lnctg -{ ^^}±
' ^oBk + l)Bk + 3)\coskxj 4 2
. тг . ж Г sin ж 1 if sin ж
Tsm^	fToi	Г	0<ж<2тг.
4 2 I cos ж I 2 1 cos ж '
1^л	(™l)fc	J Sin ^Ж 1	1	Ж	2
?j Bifc + 1)BA + 3) \ cos kx J = I C°S 2 tg
{sin ж 1,1/ sin ж 1
cos ж / 2 [ cos ж /
КАК ТЗ	^	(f /\
5.4.5. Ряды вида > у—™—г-™г<	>.
^^ (fc2 ± a2)m [ cos кх J
. V 2
^^ (fc2 ± a2)m [ cos кх
ж 1 ch [(тг — x)a] cosechTra
^a I cos [(тг — ж)а]
2.
тг / ch ax cosech тт 1 1
1	\
к ± a	2a [ cosas cosecira J
cosnx (тг--ж) sin пж
кфп
[ —7Г ^ Ж ^ 7Г].
(-l)fe , 1 1	ж sin ж
^2 _ ! cos kx = 2 ~ 4 СШ Ж	2—	[-тг ^ ж ^ тг].
E°° Is	.	тг f sh (тг — x)a cosech?ra 1
7rr-7smb = - • / \	Г	0<ж<2тг.
«2 ± a2	2 [ sm (тг — x)a cosecTra J
°° Jb	1	1
6» /* v^	о sin kx = - (ж — x) cos пж	sin nx	[0 < ж < 2тг; п = 1, 2, 3, ... 1.
^^ k2 — n2	2	4n
fci
_ ^ ^	i	1 COS Ж
к=2
i	1 COS Ж	/ . Ж\
COS =	COS Ж V sm ~~ j	[0 < ж < 2тг].

5.4.6]	5.4- Тригонометрические ряды	579
о V"V i\k+i к • ,	тг f sh аж cosech тт 1
8.	> (-1)	81пА;ж = -^ .	>	-тг < ж < тг .
^^	fe2 ± а2	2 [ sin аж cosec тга J
СО / -, \ k 1
v—v ( —1) As	Sin Ж Ж COS Ж
9.	> . -гц	 sin кх = —	1		-тг < ж < тг .
A;	.	1 1 ж . ж
7^	7 cos «ж = — - — - cos —¦ In tg —	0 < ж < 2тг .
4k2 — 1	4 4 2	4
1	тг J cosechTra 1 Г J ch (тг — х)а
Z^ (U2 + О2\2 —'"" — ТГ~1 + 77,31 спчрс тга I I гоч Гтг - тЬ
fc=O X	J	K	J LK	\	/
i 2
тг f cosech тга 1 f ch аж
1 coseC7ra J
{sh (тг — ж)а 11 тт2
sin (тг — х)а J J 4a2
1	тг Г cosech тга 1 Г Г ch аж 1	Г sh аж 11
ч v,^ ,.^ — ——г + -—г-<	> <	>^а(ж + тг)< .	>
а2J	2а4 Аа6 [ cosec тга J [ [ cos аж J	[ sin аж J J
12. 2^
k=0
тг2 J cosechTra 1
4a2 X cosec тга J
^2
тг2 J sh аж If cosech тга 1 тгж J ch (тг — x)a cosech тга 1
^ (к2 ± a2J ° """ 4a \ sin ax J \ cosec тга J 4a \ cos (тг — x)a cosec тга J
[О ^ ж ^С 2тг].
(~l)hk . _	тг2 Г sh (ж + тг)а 1 f cosech тга 1
smkx = Ti
тг2 Г s
4a [ si
^^ (Is2 dz a2J	4a [ sin (x + тг)а J { cosec тга J
тг .	x { ch аж cosech тга 1
— ж + тгН	>.
4a	[ cos аж cosec тга J
kn
5.4.6. Ряды вида Л ak
^ 1 fsinBfc + l)<El _ 1 fsinxl Г ^^(lzbe)
^ (fe + )s \ BA + l) J r() \	J J 1 2f 2 + 2t
a)s \ cos BA; + l)x J r(s) \ cos ж
Q
[Re a, Res > 0].
1 f sin Bfc + l)a; ^ _ 1 ? \G \cos3x j [c
ks \ cosBk + l)x) Г(в) J
1	r%
k=L	-	•	' "	• • q
OO
3. Г--	r—— slnB^ + l)x =
[-тг/2 ^ x ^ тг/2; n = 1, 2, 3, . . . ].
37*

580
Гл.5, Ряды
[5.4.6
lfO
[-тг/2 < ж < тг/2; п = О, 1, 2, . . . ].
f	[0 < ж < тг].
+
t
« In tg -
Z J	Z
тг(тг - ж)/4
1 Г	t
J lt
к=0
'•Е-
15.
16.
17.
Ч
Е ,/,
sin BА; + 1)х = sin ж — 2 sin ж In B sin ж)
sin BA; + 1)ж = sin ж - 2ж cos ж
k=i (
- cos Bк + 1)ж = cos х — ж sin ж + 2х sin ж
cos B^ + 1)ж = cos ж - 2 cos ж In B cos ж)
- Е
22.
= \ cos 2ж
23- E
- l)Bfc + 3)
Ь-/2 ^ Ж ^ тг/2],
[тг/2 ^ х ^ Зтг/2].
[-7Г/2 ^ « ^ тг/2].
[—тг/2 ^ ж ^С ^/2]»
[О < ж < тг].
[-тг/2 < ж < тг/2].
[О < ж < тг].
[-тг/2 < ж < тг/2].

5.4.7]
5.4- Тригонометрические ряды
581
24. V(-1 )k
g
si
BАг + IJ ± a2
1	/«I
l)»±a» C°S B*
g
g Bfe + 1)» ± ^
i\	тг fshaa? sech(a7r/2)l
+ l)s= — < .	; ; / >
4a { sin аж sec (атг/2) J
^ fshGr/2~x)a sech(a7r/2)
= Та { sin У/2 - *)« sec («./2)
тг ГсЬ(тг/2-ж)о sech(a7r/2)
\ cos (./2 - x)a sec (aJ/2)
-*У2 < ж < тг/2 .
BA;
^ (Jba + b)(ka + 6 + 1) . . . (ifea + 6 + n) \ cos [Bife + 1)ж
4 [ cosax sec (air/2)
J
1 fsin»! }tb
nl\cosxj J 1
о
1(l-t)n(l±ta) ,
L^^ dt	[a, b > 0; 0 < x < ж]
t2a	L	J
t2a
sin [Bж + тг)/4] 1 fsln^l
cos [Bx + тг)/4] J \ cos x J
sin (
cos
[0 < X < 7Г].
[-тг/2 < ж < тг/2].
5.4.7. Ряды вида
1 Г sin Дгж 1
-	>.
A;! [coslcx J
El
1 Г sin kx 1
— <	>
! I cos kx I
cos xf sin (sin ж)
^ cos (sin ж) J
(^l)fc Г sin kx
k\ \coskx
=
sin (sin ж)
cos (sin x) j
1 J sin 1гж 1 J sin [sin (ж/2)] sh [cos (ж/2)] 1
J2k)i\coskx j ~ [ cos [sin (ж/2)] ch [cos (ж/2)] J
(^X)fc Г Sin А;ж 1 _ f sin [cos (ж/2)] sh [sin (ж/2)] 1
BA;)! [coste J ~ T\ cos [cos (ж/2)] ch [sin (ж/2)] J'
f sin kx
ж J sin [sin (ж/2)] ch [cos (ж/2)] 1
~ €OS ~ \ [ (/)] h [ (/)] j
2 \ cos [sin (ж/2)] sh [cos (ж/2)] J
f sin kx
ж J cos [sin (ж/2)] sh [cos (ж/2)] 1
~2 { sin [sin (ж/2)] ch [cos (ж/2)] J '
_ ж f cos [cos (ж/2)] sh [sin (ж/2)] 1 . ж Г sin [cos (ж/2)] ch [sin (ж/2)] 1
	/	>ir: cjn 	I
2 \ sin [cos (ж/2)] ch [sin (ж/2)] j	2 \ cos [cos (ж/2)] sh [sin (ж/2)] /

582	Гл.5, Ряды	[5.4.8
г а о т^	^ 1 Г sin (kx + a) 1
5.4.8. Ряды вида } -< ,,	; >.
^-^ к\ ( cos (kx + a) J
V™^	1	fsintel 1.	ЧГ f sinail . /o	ч
1. > vr^	гут	r<	, > = - A ~~ COS Ж) =F<	> In B - 2 COS Ж) =p
, ч f cos ж]1 3 f 0 1 . if sin ж 1
T(k-x)\ .	+711^^1	Г	0<ж<2тг.
I sin ж J J 4 ^ 1 J 2[ cos x j
J sin (А;ж + а) 1
n) \ cos (&ж + a) J
^ (kr + b)(kr + b + 1) . . . (kr + 6 + :
t	[r, 6 > 0].
n!j 1- 2?rcosa; + t2r
о
+ b)(kr + 6 + 1) . . . (kr + b +
cos (А;ж + а) /
sin a 1 J sin (ж —
\ cos (ж -
а) 11
a) J J
v^ Bk — 1)!!	/ жч™1/2 ж — x
k=i ^ '"
<sr-y	Bjfe +1)!!	/ xx^1/2 x
6. ^C^1) Bfc4||J°°coskx= Bcos^j cos^^l	[-тг<я;<7г].
- [Bfc)?]2 f sin Bк + 1/2)ж 1 1 f К [sin (ж/2)] ]
*	^ (^!L24fe 1 cos BA; + 1/2)ж J ж \ К [cos (ж/2)] j	L X Щ
у Bfc)!Bfc + l)! (sinBfc + 3/2)^] = 4 f E [sin (ж/2)] 1 2_ f К [sin (ж/2)]
*	k^o (к1K(к + 1)!24fc I cos Bk + 3/2)ж )	Ж\Ж lcos (x/2)} 1 T ^ 1 E tcos (x/2)]
[0 < x < ж].
Q y^ (/x)fc(/A + ^- l)fc /sin (/i + i/ + 2^ - 1)ж 1
Г(^тг±1/2	1/2Л РГзУ^^ж) 1
0 < x < ж .
2m)l(k + m + n)!(fc + n + 1)?
(sin ж) Qn (cos ж)	[0 < ж < тг; m, n = 0, 1, 2, . . . ]
Esin kx	тг Г ch ax cos а (тг — ж) + cosaa; ch а(тг — жI
^4 + 4a2 ~ 16a4 I	chTra + cosTra	I	^ ^ ж ^ 4

5.4.9]	5.4- Тригонометрические ряды	583
12.
^ Г(|/ + 1 + А;)ГA/ + 1 - A;)	rBi/ + 1) \ sin (ж/2) J	2Т2{и + 1)
[не„>-±; |
у.	<±1^	fsinBfc + l)s] = 22-1 [sins]
• iL r(i/ + k + 3/2)ГA/ - A; + 1/2) [ cos BA; + l)x J ГB*/ + 1) \ cos ж J
1 j — 7Г < Ж < 7Г
2' 1 0 < ж < 2тг
2i/ —1 Г • 1 2i/
If 0 < ж < ?r
Re i/ > --; <
2 [ -тг/2 < ж < тг/2
„	^-^ rk f sin А; ж 1
5.4.9. Ряды вида У у———<	>.
^^ (к + a)s [cos kx J
Условие: г I < 1.
1	I г I r
2	\ 1J L
СО	h	f • i	\
x—v г [ smh ]
кеч- aiu i rns #с*.т* i	/, i i i
fc=O
[ж ф 0, Res > 0] или [|ж| > 0, Re 5 > 1].
k(8inkx\ ,л
1 Г , Г sin ж 1 fOll
1\±r{	\ + \A\°
f sl
<
2x2 . 2 2 i-
) 4r cos ж
A v^ 2fc+i f slnBfe + 1)ж 1 , 2U/1 , 2x2 . 2
4. 7 r < ,	; > = r(l dz r ) A + r ) — 4r cos
^	\cosBife + l)xj l	;Ll	;
i
ж
J
i[sinaj|
\cos ж/
5. У(^1)^2^(81п^ + 1)Ж1=гAТг2)[A + г2J^4г%1п2ж]^(81пЖ1^
I LU5 I aa fb \~ JL I ??/ J	I LUS JU J
E, t. sm кж г	/9ч sm ж	,	. U
kr { , ^ = t	*vT О--*1 Л	? - 2r(l - r cos ж К И.
[cos «ж] A — 2r cos ж + г2J [	[cos ж]	[1JJ
CO	U	f • i	\
7. > 	<	i- =
^-^ km + n [ cos А;ж j
_	1 T^1 Гсоз[?г(ж + 2А;7г)/т]1	r1/m sin [(ж + 2ктг)/т]
~ mrn/m Z^ I gin [п(д. + 2^7r)/w] J аГС g 1 - rl/m cos [(ж + 2^7г)/ш]
sin Гп(ж + 2^7r)/?nl 1 . /	i/m х + 2кж 2/m
HZ 	1	 / \	у ,	14/11 I —	COo 	 "T" Ct	J —(—
кг™^	1	J sin А;ж 1
^-^ rk(km — n) X cos А;ж j
[<5(n — m) = 1 при n > ra, <5(n — m) = 0 при n ^ ?ri; m > 0; 0 < ж < 2тг].
CO	l,	Г • i	Л
v^ т* i sm А;ж I
^ km — n \ cos А;ж j
г1/т81п[(ж + 2^7г)/т]
m ^ \ sin [п(ж + 2Аж)/т] j	1 - r1/^ cos [(ж + 2кж)/т]
Г sin [„(« + 2*w)/m] | /	1/
\[( + 2^)/] j \
r_ >;<{ -.,.,_ . -¦--г/-, frin[l-2rA'T"cos- ¦ -" +r^ +

584
Гл.5. Ряды
[5.4.10
[п/т]
1 Sm X L
У -г—	1	L
^^ few — n [ cos kx J
[п/т ф 0, 1, 2, . . . ; т > 0; 0 < ж < 2тг].
(^l)ferfc Г sinte 1
1	Г
1	~г	1 i Г = 7 1	1	1 , /	[
km ± п { cos «ж J ^—' яга ± n [ cos fe (ж + тг)
[т >0; -тг < а: < тг].
10.
к + n
k=l
n — к
sm kx + cos пх arete
11.
к + n
±1 n г n ±1 n-fe-l
n-fe-ln-fe-1
+ sin пж arctg
12. > -— sm А;ж = arctg
^ A;	\ 1 — r cos ж
1	1
± - sm nx In A q= 2r cos ж + r ) .
2	J
1	. ,	2\1
=F — cos nx In A =F 2r cos ж + r ) .
2	J
^-^ r	.	1, /	2ч
13. > -— cos «ж =	In A — 2r cos ж + r ).
^ к	2
14
f sin fcx 1 = 1 ? Г arctg Г_2г_ Г sin (x/2)
\	2 2|Arth [l Tr2 [cos (x/2)
1 . x fArth Г 2r (cos (ж/2)
TSlnU
•
(_l)V
Vfc+i
2r f sin (ж/2)
1 . ж j arctg
T2Sm2|Arth
2r Г co
l?^* I si
cos (ж/2)
sin (я/2)
r2fc+1
"
__1
~ 2 Г
к л in о	v^ rfc f sin Aгж + а) 1
5.4.10. Ряды вида > ут< ). , \>.
^-^ к\ [ cos («ж + a) J
г cos ж / sin (r sin ж + а)
cos (r sin ж + а) J '
^ k\ \ cos (kx + a)
fc=0
^> r2fc J sin 1гж 1 J sh [r cos (ж/2)] sin [r sin (ж/2)] 1
^ BA;)! 1 cos ^ж j \ ch [r cos (ж/2)] cos [r sin (ж/2)] /'
E°° (—1)кг2к ( slnkx 1	J sh [rsln (ж/2)] sin [rcos (ж/2)] 1
Bjfe) I [eGstej	\ ch [r sin (ж/2)] cos [rcos (ж/2)] J*
~ r2fe+i J sin ^ж 1 ^ Jch [rcos (ж/2)] sin [rsln (ж/2)] 1 ж
^ Bfe + 1)! \ cos Лж J ~ \ sh [r cos (ж/2)] cos [r sin (ж/2)] J C°S ~2
sh \r cos (ж/2)] cos Гг sin (ж/2)] 1 . ж
L	v / /j	l	\ / /j i gin
ch [r cos (ж/2)] sin [r sin (ж/2)] j 2 '

5.4.12]	5-4- Тригонометрические ряды	585
^1^y	Г gin kx |	f gh [r gin ^y2jj cog [r сш ^y2jj 1	^
* ^ Bfe + 1)! 1 cos kx J [ ch [r sin (ж/2)] sin [r cos (ж/2)] J C°S 2 T
{ch [r sin (ж/2)] sin \r cos (ж/2)] 1 . ж
1	V / /J	L	\ / /J I
sh [r sin (ж/2)] cos [r cos (ж/2)] j 2 '
v^ r2k+1 ( sin BA; + 1)ж 1 J sin (r sin ж) ch (r cos ж)
^ Bk + 1)! \ cos Bk + 1)ж J \ cos (r sin ж) sh (r cos ж) J'
sin B/г + 1)ж 1 _ f cos (r cos ж) sh (r sin ж
\
sin 1 r1'n sin ¦
X	Я	k_* -K. J. Л. I	S	KJ JL JL JS.
1/n 2ктт - x \ J \	n
=F exp r ; cos	 H /	oi
cos r	; sin
5.4.11. Ряды вида > ttfeg l ; <	>.
^^	( cos kx J
Условие: |g| < 1.
) f sinBfc + l)
5.4.12. Ряды вида > ake kai , >.
^^	[ cos kx J
^/ , -4fc ™fca . ,	1	Sin Ж
. > (±1) e 81пА;ж =	.
^	2 cos ж =F ch a
2.	?(±i)ecosfca: =
3.	V (±l)*e-Bfc+1)e sin Bk + 1)ж = 	^	( А а V
^ }	l	; сЬ2а=рсоз2ж \ sh a j
4. У:(±1)^со8B^ + 1)ж=	(l
^l ;	l	;	Ь22 \chaj

586	Гл.5. Ряды	[5.4.13
5.	V^ -——*— е~ а sin As ж = — arctg	.
^ к	cos х =р еа
°° (±l)fe ^ka	a 1
6.	\^ -——!— е а cos кх =	In [2(ch а =р cos ж)]-
V

k=l
y, _(±l? Bt+1)a f Sin Bfc + 1)* 1	1	Г J_ f Si
Z^2fc + 1	\cosBfc + l)x/ 2 8Lsha lc
Sin X
smr
cos ж I У 4 i ~ ~ 1 cos,
5.4.13. Ряды вида > a^r <	>
^^	[ cos А; ж J
1. > ~г{ , ? = ^^ > ( —1)	, I In A — 2rcosfea? + r ) —
fe=i	ч
"in B*4-1),
^ A;	2 ^	\/	т(	)
[-Ц г ^ 1].
3- g^^^Efr^l
[-Ц r ^ 1].
(-l)*^ (slnkx\2m 1
/1,	j	JL	I r>^o L* *у* f	^2^ /1	j ^	^ I /rri 	 JU
k=i	l	-1	fe=i
• f sin (/гж + а)
[f 1	/ 1 Ч\Г
a sin [(m — 2А;)ж] + (га — 2k)a -~-<
1 1
> .
5.4.14. Ряды вида > —¦
Обозначения: q = е-к'(*)/к(*)^ ^ = Ш!; Qq = ГТ A _ q2n^
Условия: \q\ < 1, |A;| < 1.
(±t)nqn . _	.ifctgxl 1т,/,чГ enгАdnиns^
LLsm2ra = ±^	> =F—K(ife)< ,	2x
x J 2tt l ;\ A - A; ) snnnc wndii
p|,m*|<Re(-ln,)].
3.

5.4.15]
5-4- Тригонометрические ряды
587
7.
8.
9.
Ifctgxj J_
4\tgzJT27r v ;\ Vl- k2 sew
[2Цт„|
[Цтх|
1{вг(Х,
1 д
lfctgx]
cos2na; =
sin 2ns =
K(ife)E(A;)
^ [A;K(A;)
[2|1тж| < Re (-
[2|1тж| < Re (-
Ing)].
[2\lmx\<Ke(-\nq)].
^	2n
n=1
J
11.
12.
iA (±l)ngn
= - In f -
[2|1тя:| < Re(
[2|1тж| < Re (
cos 2nx =
1	fsnui 1 f slna? 1 1. /o i/4,
- In <	}	In < 4/	—	>	In Bflf 7 A;
2	I en n X 2 \ л/1 - ife2 cos x j 2 l?
Ing)].
i/24
; )
[2|1тж| < Re (- Ing)].
n=l
ею
14. V
. - q2n)
1	fin sinx-ln0i(a:/7r) ]
2	[In cos* — 1пУ2(ж/7г) J
E
= ±j cosec x ^ K(fe){
= ±- sec ж
4
[2|1тж| < Re (- Ing)].
5.4.15. Ряды вида \, afe I I sin ^xj I I cos kyi.
1.
sin Ы sin % = i In
4
y)/2]sec[(x-y)/2]
±2/^0, 2тг, 4тг, ...
iy^TT, Зтг, 5тг, ...

588	Гл.5. Ряды	[5.4.15
^ (±1)к	1	2i	Г Г ж ±t/^0, 2тг, 4тг, ...
2. >^ -——^— cos «ж cos «у = — — In [4(со8ж =р cost/) J	<
	 к	4	|_ ^ ж zt j/ у2- тг, «Зтг, 5тг5 . . .
ею	х/ z?	U <k Л <k у,
3# Е J,s'mkxcoskV = \ (тг - 2у)/4, ж = 2/,	[0 < I/ < тг].
Цтг — ж)/2, 2/ < ж < тг
о©	f
— sin «ж sin «2/= <	[0 < |/ < тг].
5. ^J	-~™	 81П^Ж81п^|/= 		[ \х ± у\ ^ ТГ].
fc=l
fe=i ^2	12 [3f/2 +3(ж - тгJ -тг2, у ^ ж ^ тг
сю / -I \fe	if<5/'24-2^	2	f	) < <
i • J/	r™^ COS /С Ж COS /С 2/ ""^	\
[0 < |/ < тг].
8. \J -—г^	sin ^ж cos ку = — (тг2 — ж2 — 3|/2)	[ |ж ± у\ ^ тг].
1 , 0г[(х + y)/2, g] 1 , f sin [(ж + у)/2] cosec [(ж - у)/2] 1
, g] 4 1 со8[(Ж + у)/2]8ес[(Ж-2/)/2] J
1
2
г = <| l; |1тж| + |Imy| < -- Re \nq\.
12. > --smbsm A;2/ = \
k=i	[0,
тг/4, 0 < х < 2у,
'	*"	[0 < ж; у < тг].
2у < х < ж
г
2(тг - 2/)ж,
4
5. ^ tj sin А; ж sin ку cos А; 2 = - i (ж + ^ _ zOr _ 2ж|/, г/-^<ж<|/ + г5
\2(тг — жJ/,	|/ + z < х < тг
[0 < z <y < тг/2].
14. \j -—~™	sin Д:ж sin ky sin fez = 	.
к	Л
k = l
[Точка (ж, t/, z) лежит внутри многогранника |ж| + ||/| + \z\ < тт.]
оо
15. \j — sin2 Д:ж sin2 ку = 		[0 ^ ж ^ t/ ^ тг/2].
л	4

5.4.16]
5-4- Тригонометрические ряды
589
16. ^ — sin4 te sin2 % = —
k=lk	8
оо	3
17. У2 Тлs™4 ^x s'in-2 ^у= —
л	О
fcl
оо	п [(п-1)/2]
18. Е^" = -^Г Е (-1)*
fc=O
~~ i (-l)n/2[l + (-l)n] [(I)»] тгп
19.
[О ^С у±2х ^ тг].
(I)]	[0 < x < 2тг при n = 1; 0 ^ x ^ 2ж/п при п > 1].
n+2m Jbx = — ёт, о	[ M < 7r/Bm + n); n = 1, 2, 3, . . . ].
20.
n+2m
П
sin
i=o
n+2m
^ j | < тг при m = 0; \™^ |
3=1	3=1
тг при т > 0 .
\
n+2m
П
n+2m	p
3=1	1=1	I
1.
5.4.16. Разные ряды, содержащие тригонометрические функции.
Уз*8т34 = -(ж-8шЖ). 2. V 22к sin4 4
I1
k = l
oo / 2fc
2. ^22*sin4 ^ = Ж2-3т2Ж.
fe = l
k = l
4.
3fe
5.
22fe
oo	,	i,	2	2-i
V^ COS ^Ж SeC Ж7ГЖ112/лч
6- E	Щ-2	 =u~Y~2ln Bcosx)
7.
cos kx
= (x - —)
1 1
cos4 2fex = 1- - i cos2 2x.
20 4
г,
[-7Г/3 < x < 7Г/3].
[тг/3 < ж < 2тг/3].
= l Vm=l
°° 1	X	1
10- E ой sec2 о* = cosec2 x - -Zi ¦
oo
11. V
,
— Щк)\ SUU
ж	l г сп
г спи
[ж = -i7rK'(ife)/K(fc), it = tK'(Jfe) -
тг; | Im (it/K(ife))| < Re (~Kf (к)/Ж{к))].

590	Гл.5. Ряды	[5.5.1
12. У —^— msec (кжл/2 ) =	l j
I	1 о о	1
[n = l, 2, 3, ...].
-1	-i о
-г cosec K?rv2 =
14. > — tg —r- =	ctgsc.
Й2 2
	-=. 14. > — tg —r-
360^2	1Й2 2
2
= cosec ж "
2fe
18.	Y^ (-1I ctg (/ж + a) = —K(fc) dn и	[ см. условие к 5.4.16.11].
l = —oo
oo	/ -i i /r" \	3	oo2fe
19.	> — ctg 	kw =	—. 20. > I I ctg —	 =	1.
t^k3 V 2	/	45V5	f^H S2^ + l 4
21. f]1kt кЖ	^ j1/Bn + 1)»	X
+ l), ж некратно2тг/Bп + 1)
[m— целая часть Bn + 1)ж/Bтг); n ^ 1; 0 < ж < 2тг].
5.5. РЯДЫ С ЛОГАРИФМИЧЕСКОЙ И ОБРАТНЫМИ
ТРИГОНОМЕТРИЧЕСКИМИ ФУНКЦИЯМИ
5.5.1. Ряды вида \^а
3. V^	^lnife = Cln2	. 4. V^	'— In A; = 0,096615.
oo
5- ? ro^ ,iJ" Bfc + !) = -2'SC(^) In 2 - A - 2-3)C'(.).
00 / 1\k
6. V ^	'— In BAj + l)a = - In a	f In t sech t dt.
^ 2k + 1 v	; 4	4 4 J
fco
fc=o
oo
у (^l)fc ln [Bife + 1J 2 + 1] = Ц\\ sech *!L
^2ife + l Ll	;	J 2 J t	2a
8.
fc— 1
Q
\ dt

5.5.1] 5.5. Ряды с логарифмической и обратными тригонометрическими функциями 591
10. ^(-l)k(Jj^xk\nj±^ = ^ln™ + (t0-1-*6)^-
0
fc=l
11.
.
k + a
tint"
k=i
k\
In
= Г(а)
13.
Int
arccos t
Int
dt.
15.
1С
16.
Av	At.
= In (тга cosec air).
17. X) (-l)
18.
19.
тга 2
A; + a
= С + In (a ¦
21.
ж
1°
22. ^ [2 - BJb + 2a + 1)] In k + a + 1 = In 2тг + Ba - 1) In a - 2 In Г(а) - 2a.
п
23.
= i 0" -
¦ In BA; + a + 1)тг =
T
v^ 1 • i i i 1 / \ (*-* i a \ ж i
24. > — sin ra In ka = — (ж — тг) ( С — In — H	In
r -^ #?»	9	\	Х-7Г /	У.
k = l
00 ( I\fe
1
—
ж
sin
X
—
2
тг1пГ( —) [0 < ж < 2тг].
\2тг/
2,
[0 < Ж < 7Г].

592	Гл.5. Ряды	[5.5.2
оо	I
27. ^ sin Bк + !)ж ln I	 = - cos ж + [^ (-) + С + In 2тг1 sin ж	[0 < ж < тг].
§ъ ~™г™ JL	^	L \ 7T /	J
fc=O
5.5.2. Ряды вида У^ Qfc arctg Ьи-
оо
^ (^l)fe	,	а тг Г	1	, *тг ,
1. 2, 		arctg /га =	1		- cosech — at.
	 nj	Л A j	ь	а
fei
3.	Y, rrCtg{~kTb) ^ITbl =a^(b)^ar^r(b + ia)	[6 + ia^O, -1, -2, ...].
. ^ ...чЛ , / а \ а] ( arctg (th атт ctg бтт) 1	a
4.	> (±1) arctg	 — — = <	,\	, y. >- arctg —.
д,^^	[	V^ + 6/ ^J 1 arctg (sha7rcosec&7r)J	Bb
2а6	а f arctg (th атг ctg бтг)
= arctg ^	sv	/
v^z . xfc 2а6	а f arctg (th атг ctg бтг) 1
5. V (ibl fc arctg		— = arctg ^ ^ ^	sv	/Л'
^	Is2 + a2 — b2	b у arctg (sh an cosec бтг) j
CO /r» I i -1 \	°°
v^/ \fc B/г + 1)а	\-^/ \fc+i 4fea
7. ^(-1)" arctg Л ¦ _ 2 = arctg о-тг.	8. ^J(-l)fc+1 arctg = arctg а.
k=l	k=l
v^, xfe BJfe + 26 + l)a	а
9. g(-D* -ctg k2 + {^b + l)k + b>+b_a2	= -ctg -.
11.
13. Л, arctg -—	г^	— = arctg (th атг tg отг).
fc=O	l	;
. атг V3 атг
sh —r- sec
4	4
15. >( —1) Bk + 1) arctg -r—	Г7Г = 4п(^1)Пм1 arctg (e^n7T).
^	Bk + IJ
16 Vf^-nnarctffon+1/2 - - arcsini^	flul < 1- о - exn / 7rK'(fc)
1IJ- /^i x/ агстё9	— , arcsintf	мд| < i, g - exp< -
n=0
5.6. КРАТНЫЕ РЯДЫ
со со .,	со со

5.5.2] 5.5. Ряды с логарифмической и обратными тригонометрическими функциями 593
k=l1=1
oo oo
oo oo oo
8.VVV (*1т+Г°! ж/С+'+ГО = т\~	[-1 < - < 1/3].
k=0 1=0 m=0
oo oo
g W	Х	= Ж V3	10
' А^А^ ^2(^2 Л/ Ч /2)	30 "	*
0	W
^(^ Л;/ Ч /)	30 "	*	А^А^ k6(k2 + P) 113400"
|g — X I — X	Is — X I — X
оо оо	4
»• ЕЕ
^0 ^ B* + IJ [Bfc + IJ + B1 + IJ] 128 •
8
+ lJ + B^ + lJ] 92160'
рк =ж	" - B/-lJ-Bfc-lJ	.г
B/- IJ - BfcJ	I
BQ2-Bfe-lJ 1
k=01=0
сю оо
18 v^ (<*)k+i{P)k(P )i k i _ , 0 Ql	,	,
xV = fi(«, a', /3, /3', T, x, V)	[H.
k=01=0
OO OO / v	/ /э\
fc=0 1=0
Другие ряды вида A7)-B0) см. в [1, т. 1].
22-ЕЕ
0
23-
Е
к\\кч\. . . ^те!Г(^1 + ^2 + • • • + кп + v + 1) 1
«ее еХ/ ф-j
38 1/2 А. П. Прудников и др., т. 1

Глава 6. ПРОИЗВЕДЕНИЯ
6.1. КОНЕЧНЫЕ ПРОИЗВЕДЕНИЯ
6.1.1. Степенная и алгебраические функции.
п	п
к=1	k=l
п /	2 \	1
П/	CL \	I	ч
к = 1 ^	'	^П'^
3\ Г2/3 + а\ /З^а
2
fc = 2 x	7 fc = l k = l y '
9ТТ /-||_ 2fe\ 	 -i Ж	|—Г ,	2тг kifn\ 	 n -.
JLJL i^ot»	JL JL
fc=O X ^	fc = l
6.1.2. Тригонометрические функции.
i. тт / «n [« + (W«)n	=2i-»( «nnx \ 2_ nrfsinbL = 2i-nn.
I I I гпя Гт -I- fJ^Tr /n^l I	I ein Гп^9'г -I- >n-W9l I II n
n
k=l
[(n-l)/2] , .	.	f	1/2
fsin(fc7r/")l_2(I-n)/2j	«
/2 |i±^iL
о J sin [x + 2тг^/п] 1 ( . !_n J cos [nBx — tt)/2] — cos (п7г/2) 1
Ajl \cos[x + 2тг^/п] j ^	[	-cos(fi7r/2)+cosx	j*
k=0
2n-l
_ 2(t-n)/J
6. f] cos—=21-2n[(-l)"-l].
*=1
7.	]~T L2^2a6cosf^ + —) +621 =a2n^2an6ncosnx + 62n.
fc=о L	V	n /	J
n —1
8.	П
A / 2	2жк	\ a2n+1 - 1
9. И!»- 2a cos	hi I = 	.
к-г V	2n + 1 /	a - 1

6.2.1]	6.2. Бесконечные произведения	595
6.2. БЕСКОНЕЧНЫЕ ПРОИЗВЕДЕНИЯ
6.2.1. Степенная и алгебраические функции.
6 + 1
2)/2, (Ь-а
k=l
(а + 1)тг
¦ sin -
5 ftfl
-r
k=l
1	1	7Г
 1 [
BJc + lJJ \cosGra/2)J	" А_Д [ Bife + lJJ 4
12. П ( 1 + j^— ) ( 1 - y^ ) = ir^ sin F - а)тг cosec бтг.
14.
OO
ft
• П
c/\	k + b
a \ ft	a \ __asin7ra
/	4 \	1 J ch \/2 тта — cos V2 тта
" 1Д V Fj =
Д V	j 2тг2а2 | 2sln7rash7ra
18 П f	a"
21 2cosGm/2)chGm/2)
20. FT ( 1 - — ) = --L
/"; n = 2, 3, 4, . . . 1.
21 П 1	^	 =	( - У	Е2 i
* III	Г9^-ИМ2п+1)| 9Г9пЛ1\9/	2n|'
38 i/2*

596
Гл. 6. Произведения
[6.2.2
22. П fi + ("-^—У! f
AJL [ \k-\-bJ \[
k-b
[п/2]
п)
х ]Q[1- 2ак cos (b + 0к) + al]1/2[l
fe=i
[0 < b < 1; afc = exp(-27rasin[Bfc - 1)тг/п]),
cos F - /Зк) + a?]1/
2?racos [BA; - 1)тг/п]]
6.2.2. Произведения, содержащие A ± хп)т.
Обозначение: х = ехр [—тгЛ.9 (к) /К.(к)], 0 < к2 < 1.
oo	r	-| 1/12
1. ЦA-х2п)= \-тт-6к2A-к2)Кв(к)\ .
П = 1	1»Ж	J
оо
n=l
oo
3.	П A - xnf = 4ж-3х~1/4к1/2A - k2)K3(k).
n=l
oo	1	,	oo
л FT /i	2n\3	-L -1/4 « л /	\	ш, П
4.	Y\{l-x ) =-x ' Та6Ла,х) ¦ 5. П
n=l	«=0	n=l
oo
6.	Yl A - Ж2п)в = 2тг-3Ж-1/2/кA - ib2I/2K3(fe).
n=l
oo
7.	П A + x2n+1N = 2x1/4k~1/2(l - к2)-1'2.
n=0
8.	П A - Ж2"+1)в = 2Ж1/4А:~1/2A - fe2I/2.
П = 1
9.	f] A + ax2n + ж4п) = i ж-1/6B^I/3A - к2I/6 х
- arccos	Kffcj^i™ arccos	1, ж -
L2	V 2/J	L2	V 2; Jb
2n\6
x ) =
^^1/2ife(l^ife2I/4.
x cosec -
\1
6, ж)
ь=о.
, ж).
10. Y\(l + ax
2n+1 + x4n+2
x4n+2) =
= 21/3х1/12к~1/вA - fe2
, x).
11.
12.
2\l/2
, x). 13.
= 1Фо(а,

6.2.4]	6.2. Бесконечные произведения	597
00 -1 _ П	°°	-| _ П
14. Ц —^ = 04(О, ж). 15. [] 1_а;П_1/2 =[Bтг)Ж
п=1
17. fj
n=l
n=l V	7
00 /	2n
-1/2 >о й f^S)(i *a)i/a
_ /i _ i.
n=l \~ ' ~	/	n=0
6.2.8. Показательная функция.
oo
11	1-х
k=Q
2. Л A + ae~2 ) = - A + cth a)	[a > 0].
fc=i
4. ПA - е^27гЛ;/^) = з1/4е^%/з/18_ 5^ ГГ[1
OO
7. П ( 1 ¦
8.	П 1+ -y^— ) e~a/k = ^^ sin Ma + ft)] cosec тгб.
Ж1\ k + b J	a + b
k= — oo x	7
oo
9.	П (l±-)e^a/k = —smna. 10.
11 V k/	na
fe=--OO
6.2.4. Тригонометрические функции.
со	со
1. П sec T = 8,70003663. 2. П — Bfc + l)sin y ^ =0,18055054.
3- П |1- -^т) sec- = 0,86885742.
4. 11 cos — =
k=i
4

Приложение I. НЕКОТОРЫЕ ЭЛЕМЕНТАРНЫЕ
ФУНКЦИИ И ИХ СВОЙСТВА
1.1. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
1. Некоторые соотношения.
= — sin (—ж) = ±\/l — cos2 ж = ±у — A — cos 2х) =
= 2 cos'
2 (? _ 1
V 2 4
l + tg2^/2)	2г
1 = cos ( — ж) = =Ьу 1 — sin2 ж = ±4 / — A + cos 2ж) =
Т»	I	Т СТ IT» /Л
= 2coS2^l=^tS2 Ж/
2	l + tg2(ж/2)
sln2x
tg ж = — tg (—ж) = 	 = ±v sec2 ж — 1 = —
cos ж	1 + cos 2ж
'	_ 2tg(x/2) _ .eix-,
1 + cos 2ж
sin ж ^v ~ ~	з1п2ж
ctg ж = — ctg (—ж) = —	 = ±v cosec2 ж — 1 =
2tg(x/2)
огж 	 р-гж
sec ж = sec (—ж) = 	 = ±у 1 + tg2 ж =
cosec ж = — cosec
СО8Ж --v- . -S - - 1_tf?(x/2y
( x !	/i,^2	! + tg2(^/2)
(—ж) = 	 = =bvl + ctg2 ж = 	 , \ ' ,
1 ; sins	v	Б	2tg(x/2)
sin ж + cos ж = 1,	sec ж — tg ж = 1,	cosec ж — ctg ж = 1.
2. Формулы дифференцирования.
d sin ж	d ter ж	о
= cos ж, —	 = sec ж,
ах
cos ж,	sec ж,
ах	ах	ах
d cos ж	d ctg ж	2	^ c
= Sin Ж	COSeC
g	2
= —Sin Ж, 	;	 = — COSeC Ж,
ах
Sin Ж,	;COSeC Ж,	;ту.
ах	ах	ах	sin x
3.	Формулы Эйлера и Муавра.
ez+tx = ez (cos ж + г sin ж),
(cos ж + -г81пж)те = совпж + i sin пж	[п = 0, ±1, ±2,
4.	Связь с гиперболическими функциями.
sin (гж) = г sh ж, сов(гж) = сЬж, tg(ia?) = ithx,
ctg (гж) = —г ^Ьж, sec (гж) = sech ж, cosec (гж) = ^г

1.1.8]	1.1. Тригонометрические функции	599
5. Формулы сложения.
sin (ж ± у) = sin х cos у zb sin |/ cos ж, cos (ж ± г/) = cos ж cos у =р sin ж sin y,
sin (ж db iy) = sin ж ch у zb г sh |/ cos ж, cos (ж zb %) = cos ж ch 2/ qp i sin ж sh y,
tg(x±y) = "S"—s» , ctg(x±y)= 7T; ,
1 =F tg ж tg 2/	tg ж zb tg у
, . . v tgжzbith|/ 8т2ж±*8п2м
tg(x±22/)=	* -
ctg (ж zb %) =
1 =F г tg ж th 2/
1 zb i ctg ж cth |/ sin 2x =p * sh 2у
— ctg ж zb г cth |/ ch 2|/ zb cos 2ж
6. Формулы приведения.
sin (ж zb пж) = (^l)n sin ж, cos (ж zb пж) = (^l)n cos ж,
tg (ж zb пж) = tg ж, ctg (ж zb пж) = ctg ж,
• ( _L 2П+1 ^ _L/ 1^ / _L 2П + 1 ^	/ ^n •
Sin ( X ± 	 7Г I = ±( —1) COS Ж, COS I X ± 	 7Г I = =p( —1) Sin Ж,
ж=Ь —-—7Г 1 = -ctgж, ctg f x± —-—7Г I = -tga;,
sin ( ж zb — J = —- (sin ж zb cos ж), cos ( ж zb — 1 = —- (cos ж q= sin ж),
/ . тг \ sin ж zb cos ж tg ж zb 1
tg(*±I)-
ctg (x ± J
cos ж =p sin ж 1 =p tg ж '
cos ж =p i
sin ж zb cos ж 1 zb ctg ж *
7. Суммы и разности тригонометрических функций.
X zb 1/	Ж -F- 1/
sin ж zb sin у = 2 sin	cos	,
cos ж zb cos y = ±2 \C°S !!Ж
sin (ж zb i/)	sin (ж zb y)
tg ж ± tg у = 	, ctg ж ± ctg у =	;	;	,
cos ж cos у	sin ж sin i/
cos (ж + i/)
tg X - Ctg I/ =	;	,
cos ж sin i/
a cos ж + 6 sin ж = г sin (ж + у) = r cos (ж — ф),
где
г = \/а2 + б2 , sin (f = a/r, cos^9 = 6/r, sintp = b/r, cos 1/? = a/r,
sin ж — sin у = cos i/ — cos ж = sin (ж + у) sin (ж — у),
sin ж — cos j/=—cos (ж + 2/) cos (ж — у), sec ж + cosec ж = sec ж cosec ж.
8. Произведения тригонометрических функций.
sin ж sin у = — [cos (ж — у) — cos (ж + |/)],
А
cos ж cos у = — [cos (ж — 2/) + cos (ж + у)],
sin ж cos у = — [sin (ж — 2/) + sin (ж + |/)].

600	Прил. I. Некоторые элементарные функции и их свойства	[1.1.9
9. Степени тригонометрических функций.
sinx]2n	I ^, ^„._fc/2n\ л/ ,х . 1 (In
cos ж
sin ж
cos ж ^
sin ж I	1	1
1
cos ж/ ^2	2'
sin ж 1	if sin Зж 1 3 f sin ж
cos ж J	4 \ cos Зж / 4 \ cos ж
113
. = — cos 4ж q= — cos 2ж Н—,
cos ж I 8	2	8
sin ж I	1 Гз1п5ж1 5 Гз1пЗж1 5 J si
{sin x 1
cos x ) '
_ 1	3	15	5
^T32COS х+щст xT^2COS Ж+1б'
10. Тригонометрические функции кратных аргументов.
		\ к,
k=0	Ч
Ж,
fe=0
fc=0
г п^х
sin 2пж = 2n cos ж sin ж + V^ (^1)Л
L	fe=i
= 1 + ^(-1) —	; L
fe=i	^ '*
sin Bn ¦
х Ism ж + у д
, 2^ + 1^, 1 ,fc Bn - fe)Bn - fc - 1) . . . Bn - 2k + 2) o2n^2fc+1 . 2
H	-	^V-1;	JLJ	^	81П

1.1.11]	I.I. Тригонометрические функции	601
cos Bn + 1)ж = сояжх
x
t:	<2*>'
. Bw - fe)Bw - A; - 1) . . . Bn - 2k + 1) O2n~2fc . 2n~2k t
	~	?	sin	',
sin 2x = 2 sin ж cos ж, cos 2ж = 2 cos2 x — 1,
cos Зж J	~ I cos ж J [ cos ж
sin 4ж = cos ж D sin ж — 8 sin3 ж),
cos 4ж = 8 cos4 ж — 8 cos2 ж + 1,
fsin5a;l _ J sin ж 1 ^/sin^l i(iis'mxX
J	[ COS Ж J	[ COS Ж J	[ COS X J
f
cos 5ж
sin 6ж = cos x F sin x — 32 sin3 ж + 32 sin5 ж),
ж ~ 48 cos ж+ 18 cos ж — 1,
11. Тригонометрические функции некоторых углов.
f sin (тиг/2) ]	,n/21lT(-l)" П7Г l-(-l)"
¦ \cos(n7r/2)J l ;	2 ' 8 2 l + (_l)n
\cos
3.
четное 11 >
нечетное J J
f/n четное li
LI71 нечетное J J '
+ П7Г / i\[O+2)/3] ^3 Г , 1ч[(п + 1)/3]1	г i
tg — = (^l)Ll ;/ J — [1 - (^l)Ll ;/	Jj [n четное],
= (^l)^/3] ^ [l + (_l)[(»+D/3]]	[n нечетное].
4. sm^ = (-l)^^^1)[n/21	[n четное],
/ i\[(n-l)/4] 1	г i
= (--ljLV " J —=¦	[n нечетное],
mr	[n/41i + (-i)l"/»l
cos	 = ( —1)		[n четное],
нечетное]
/ i \[Bп + 1)/41	г	!
= ( —1)	[n нечетное].
39 А. П. Прудников и др., т. 1

602
Прил. I. Некоторые элементарные функции и их свойства
[1.1.11
= 0
sin = (.
6
N + ^-
= (-1)
[n/3]
УЗ[1 + (>1)[(«+1)/з]]
7. sin
пж
*т=(-1
= 0
ctg ^ = ^5 + 2 V5 , ctg ^ = ^
sinGr/12)l_ 1 /^ /^ (sinE7r/12)]_V3zfcl
tg(*7
ctg (ж/
sinG7r/12) 1
cosGtt/12) J
(
sin (Птг/12) 1 _ J
cos (Птг/12) /
[те ф 0, 5, 10,	... ],
[n = 0, 5, 10,	... ],
[п ф 0, 5, 10,	... ].
[п = 0, 5, 10,	... ],
[те четное],
[те нечетное],
[те четное],
[те нечетное],
[те четное],
[те нечетное].
[те четное],
[те нечетное],
[те четное],
[те нечетное],
[п = 0, 8, 16, ... ],
[те нечетное].
(

1.1.11]
I.I. Тригонометрические функции
603
10. sin ^- = I [-л/3 (л/5 - 1) + у10 + 2л/5 1
15 8 [_	J
tg ^ = -. C -
15 4
7Г	1 ,
Ctg15 = 4AH
cos -^ = - I ^5 + 1 + V3
tg — = - C + л/5 ) f -2л/3
ctgf = i(^5-l)BV3
п.
12.
14. sin^ = i [-(л/5 + 1) + лД\Jm - 2л/5 ),
COS 5 = I
-2>/3J,
sin ^ = | [-
cos ^ = I
2 +1),
39*

604	Прил. I. Некоторые элементарные функции и их свойства	[1.2.1
ctg ill"= iC
1.2. ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
1. Некоторые соотношения.
sh х = - sh (-ж) = ±\/сп2ж - 1 = ±4 /- (ch 2ж - 1) =
V 2
ch ж = ch (-ж) = \/sh2 ж + 1 = Ji (ch 2ж + 1) = 2 ch2 ^ - 1 = ^-±J
\ A	A	A
th ж = — th (—ж) = u _ =
cth ж = — cth (—ж) =
¦L/J.A tX/ \^I1 ^™j ejfy j JL о A A ^j еду	С* j (з,.
сЬж _ вЬ2ж _сп2ж + 1 _ ех + е^ж
n h /-уз /"»Г! *) О^ 	 1 Г^г! ^) О^	iO 3? 	 л "~~ Ж
oil ely V/II Zd JL/ JL \_/il j^j Ju	С С
sech ж = —— , cosech ж = —— ,
ch ж	sh ж
ch ж — sh ж = 1, th ж + sech ж = 1, cth ж — cosech ж = 1,
сЬж)п = shnx + сЬггж	[п = 0, ±1, ±2,
2. Формулы дифференцирования.
d sh ж . rf cosech ж ch ж rf ch ж .
~^	 =сЬж,	 =-—^—, —	 =зЬж,
«ж	аж	sh ж	«ж
d th ж	. о	rf sech ж	sh ж	d cth ж	. 2
= sech ж 5	 =	— , 	:	 = — cosech ж.
h
dx	'	с/ж	ch2 ж '	с!ж
3.	Связь с тригонометрическими функциями.
sh (гж) = isina?, сп(гж) = со8ж, th(ix) = itgx, cth (гж) = —г ctga!.
4.	Формулы сложения.
sh (ж ± у) = зпж chy dz shych ж, ch (ж ± у) = ch ж ch у dz sh ж shy,
sh (ж zb гу) = sh x cos у ± г sin у ch ж, ch (ж zb гу) = ch ж cos у zb г sh ж sin у,
„у.	ч	LO Ж 	1	 "СП i/	SO JLQu 	1	 SO ?&%!
th (ж ± y) = 1±thxth2/ = сЬ2ж + сЬ2|/ '
th (ж zb гу) =
1 dz г ^ж tgy
=F isin2y
— cos 2y
cth (ж ± iy) = ^^

1.2.8] 1.2. Гиперболические функции	605
5. Суммы и разности гиперболических функций,
sh ж ± sh у = 2 sh	 ch	,
uu\ Cthx±cthy = ±uu\
ch ж ch у	sh ж sh у
sh2 ж — sh2 у = ch2 ж — ch2 у = sh (ж + у) sh (ж — у),
sh ж + ch |/ = ch (ж + |/) ch (ж — у).
6.	Произведения гиперболических функций.
sh ж sh у = - [ch (ж + г/) — ch (ж — у)],
ch ж ch у = - [ch (ж + у) + ch (ж - у)],
sh ж ch у = - [sh (ж + |/) + sh (ж — |/)].
7.	Степени гиперболических функций.
{chx\
fshxl2n+1_ 1 ^
tchas/ =2(ch2a:=Fl)' \chx/ = 4
fshccl4 1,., , .„ o4 fshsl5 1 f sh5a;-5sh3a:
\ch4 =8(сЬ4ЖТ4сЬ2х + 3), |c^| = ^ (сЬ5ж + 5сЬЗж + 1ОсЬж
f sh т 1	1
^	\ = —
[ ch ж j 32
8. Гиперболические функции кратных аргументов.
ж,
& — l\ un-2fe-l
1 СП	Ж,
"о	\ * /
[п/2]
in-2*-2a!,
сп2ж = 2сп ж —
\ ch Зж J \ ch ж J	\ ch х ) '
8sh ж), сп4ж = 8сп ж^8сЬ ж

606
Прил. I. Некоторые элементарные функции и их свойства
[1.3.1
ch 6ж = 32 ch6 x - 48 ch4 ж + 18 ch2 x - 1.
1.3. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
1.	Некоторые соотношения.
Главные значения обратных тригонометрических функций определяются неравенст-
неравенствами
^тг/2 ^ arcsln ж ^ тт/2; 0 ^ arccos х ^ тг	[—1 ^ ж ^ 1],
^тг/2 < arctg ж < тг/2; 0 < arcctg ж < тг	[^оо < ж < оо].
arcsln (—ж) = — arcsln ж, arccos ( — ж) = тг — arccos ж,
arctg (—ж) = — arctg ж, arcctg (—ж) = тг — arcctg ж,
sin (arcsln ж) = ж, cos (arccos ж) = ж, tg (arctg ж) = ж, ctg (arcctg ж) = ж.
arcsln (sin ж) = ж — 2птг	[2тетг — тг/2 ^ ж ^ 2тетг + тг/2],
= ^ж + Bп + 1)тг	[Bп + 1)тг - тг/2 ^ х ^ 2(п + 1)тг + тг/2].
arccos (cos ж) = ж — 2птг	[2птг ^ ж ^ B?г + 1)тт],
= -х + 2(га + 1)тг	[Bп + 1)тг ^ ж ^ 2(п + 1)тг].
arctg (tg ж) = ж — птт	[птг — тг/2 < ж < птг + тг/2].
arcctg (ctg ж) = ж — птг	[птт < х < (п + 1)тг].
lim arctg ж = ±тг/2, lim arcctg ж = тг/2 =р тг/2.
х—>±оо	аз—->zbcxD
2.	Связь с логарифмической и обратными гиперболическими
функция ми.
arcsln z = —г In f iz
= —i Arsh (iz
arccos z = —г In f z + Vz2 — 1 1 = —г Arch z.
i
arctg z =	In
JL — % Z
= ^% Arth (s
/i	4 T 	 \
arcctg z =	In	 = г Arcth (iz).
? JL Z "T" JL
3. Формулы дифференцирования.
d	Id
— arcsin ж = ,	,
dx	i/l - ж2
d	1
— arctg ж = ———- ,
< arcsec ж <
/2
[{ о }<~-<
тг/2
/211
тг J J
° !1
г/2}|-
4. Связь между обратными тригонометрическими функциями.
тг
arcsin ж =	arccos x
2
= arccos Vl — ж2
= — arccos y/l — х2
= arctg ^J==
[0 ^ ж ^ 1],
[—1 ^ ж ^ 0],

1.3.4]
1.3. Обратные тригонометрические функции
607
= arcctg
=	arcsln ( 2хл/Т
=	arcsln 12x\/l — •
A A	V
7Г
arccos ж =	arcsin ж,
= 7Г + arctg
= arcctg
= - arccos Bж2 — 1)
A
= ж	arccos Bж2 — 1)
arctg ж =	arcctg ж,
= arcsln ¦
4
1
I
1
2
!
~ 2
7Г
3
I77
Ж
,tg
,tg
,tg
1
2 2
arcsln
1
— — я
ъ&1 +
arctg
2ж
2ж
arcsli
2ж
1 + ж
rfsin -
¦ ж
1-
1 +
(Г
А
2
2ж
ж
ж
7Г
7Г
2
>ж
Ьж2
[0 < ж ^ 1],
-1 ^ ж < 0],
< ж ^ 1],
[0 ^ x ^ 1],
[-1 ^ x ^ 0],
[0 < x ^ 1],
[-1 ^ x < 0],
[-1 ^ ж ^ 1],
[0 ^ x ^ 1],
[-1 ^ x < 0].
[ж ^ 0],
[ж ^С 0],
[x > 0],
[ж < О],
[ж > 0],
[ж < 0],
[^ > -1],
[х < -1],
N < 1],
[^ > 1],
[^ < -1],
[ж ^ -1],
1 ^ ж <: 1],
[ж > 1],

608
Прил. I. Некоторые элементарные функции и их свойства
[1.3.5
1	1-х2
= - arccos	-
2	1 + ж2
1	1-ж2
arcctg ж =	arctg ж,
1
= arcsin ,
= тг — arcsin ¦
[x
[x
[x
[x
>
<
0],
0].
0],
0],
P2 '
= arctg —
ж
1
[ж > О],
[ж < 0].
5. Суммы и разности обратных тригонометрических функций.
[жу ^ 0 или х2 + у2 < 1],
= тг + arctg —
ж
arcsin ж + arcsin у = arcsin ( x\/l — у2 + |/Vl — ж2 1
= ±7г — arcsin (азу 1 — t/2 + у у 1 — ж2
ж,
= ± arccos у A — ж2)A — у2) — ху
— у2 + ул/1 — х2
ж, у
ж, у
;:}]¦
= arctg
у/A-Х2)A-у2)ху
[жу ^ 0 или ж2 + у2 < 1],
жл/l — у2 + уу/\ — ж2
= arctg ,,		± тг
у/{1-Х2)A-у2) -
arccos ж + arccos у = 2тг< > ± arccos азу — уA — ж2)A — у2)
arccos ж — arccos у = =f arccos ж у + \/A — ж2)A —
У >
У <
у<0)У
arctg ж + arctg у = arctg
ж + у
1 - жу
= ±7г + arctg
х + у
1 - ж у
arctg ж — arctg 2/ = arctg
ж — у
1 + жу
[жу > -1],
= ±7г + arctg
х - у
1 + жу
[{:::}¦
1.4. ОБРАТНЫЕ ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
Arsh z = In (z +
1.	Связь с логарифмической и обратными тригонометрическими функ-
функциями.
= —ъ arcsin (iz), Arch z = In f z + \/г2 — 1 ) = i arccos^,
Arth z = — In	 = —i arete (iz), Arcth z = — In	 = —i arccte (—iz).
2 1-z	Sl ;	2 z- 1	6l ;
2.	Функции отрицательного аргумента.
Arsh ( — z) = — Arsh z, Arch ( — z) = Arch 2:, Arth (—z) = — Arth z, Arcth ( — z) = — Arcth z.
3.	Формулы дифференцирования.

1.4.5]
Ц. Обратные гиперболические функции
609
dx
d
dx
d
dx
d
dx
Arch
Arth
Arcti
a
ж
a
X
a
X
a
yx
yx
a2-
a2
2 + a2
±1
2 ^a2
a
^ж2
a
~ж2
[Arch (ж/a) ^ 0, x/a > 1],
[ж2 < а2],
4. Связь между обратными гиперболическими функциями.
Arsh x = Arch yx2 + 1 , Arch ж = Arsh у ж2 — 1 ,
= Arth ¦
/ж2 + 1
Arth ж = Arsh -
= Arth ¦
= Arch -
2 '
x ± t/
vy ± 1
У ± x
у ± x
/1-х
= Arcth —.
x
5. Суммы и разности обратных гиперболических функций.
Arsh х ± Arsh у = Arsh ( ж у 1 + |/2 ± у\/1 + ж2 ),
Arch ж ± Arch у = Arch |
Arth ж ± Arth 2/ = Arth
Arsh ж db Arch у = Arsh
= Arch
Arth ж ± Arcth 1/ = Arth
= Arcth
- 1],
xy ± 1
1.5. БИНОМИАЛЬНЫЕ КОЭФФИЦИЕНТЫ
-a)k a(a — 1) . . . (a — A; + 1)
_ /_ 1
= 1,
ife!
-ife
ife!
= 0
те!
.-k
[k = 1, 2, 3, ... ].
[ife = 1, 2, 3, ...; a^ -1, -2, -3, ... ],
[ife = 1, 2, ... те],
[A; = -1, -2, -3, ... или к > те],
[n^ k^ 0],
Г(а
a-b
a \	a /a — 1
+ lJ ~ 6 + 1
+ а\Г b
n J \n + a
a — b /a
" 6 + 1 \&/J V
b\/b-n\ _ /6\ /6-a
n)\ a J \a)\n
[Ъф—k, k + a, где ife = -1, -2, -3, . . . ],
/a +

610	Прил. I. Некоторые элементарные функции и их свойства	[1.4.5
-1/2\ = (-Г?Bп\ =	Bп-1)М
)	U	Bп)!! '
1/2 \ = (-1)п~1Bп-2\ =	! Bп-3)Н
/n + l/2\ ,
i 1 — ( —
\2n + l) ^{
/ n \ 22п+г
\1/2J
1.6. СИМВОЛ
1)та2"п" II
\ n / '
Bn\-1 ( n \
\n) > \n/2)
ПОХГАММЕРА
/2n4
V i
22n
7Г
(«)fc
-l/2\
f f
l(n-
~ \ 2n
1 Y1
l)/27 '
Г(а)	У r(l-a-fe)
(aH = 1, (a)-fe = ^, ,— = 7-	7-	[a^l, 2, ..., Л; Л = 1, 2, 3, ...],
Г(о)	(l-o)fc
(n + fe-1)!
Wife = —;	tti^5 (l)fc = «!,
(n-1)!
o-2*B* + l)!
{a)n+k = (a)n(a + n)fe, (a)n_fe =
A - a - njfe '
(a)nk = (-)
k
(a + mk)nk = ; ^—, (a + fc)fc = Y^, (a + m)fc =	v 	'—,
Wrnk	\a)k	{a)m
(a - mk)nk = (^l)mk(a)nk^mk(l - a)mk	[n ^ m],
= (-1)"* A"°)m*	[n<m],
(I a)
(a + k)n^k =
(a)fe	(a)mfc
i=o
,	,4	(-l)(a)n(l-a)mfe r
(a - mfc)n^|fc = —	, (a -
(I a n)
, (a k)n^k =
(I - a - n)ik+mk	(I - a - nJk

Приложение И. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ
ФУНКЦИИ И ИХ СВОЙСТВА
II.1. ГАММА-ФУНКЦИЯ T(z)
О п ре д е л ение:
: V{z) = Г taf-1e~t
[Rez > 0].
При Re z $C 0 функция T(z) определяется как аналитическое продолжение интеграла.
F(z) — аналитическая функция во всей 2-плоскости, за исключением точек z = 0, —1, —2, . . . ,
в которых она имеет простые полюсы.
T(z + 1) = zF{z), Г(п + 1) = п!, ГA) = ГB) = 1.
Bn-l)!!' V 2
1
/ 2\
Г(п+ - I =
\	4
2-5-8...Cn-1) /2
/2
), Г( -
4/	\4
= 1,354118.
Г(г)Г(-г) =	^
Z Sin
2 J \2
V{z
Г(го + l)F(z -w-
V{nz) = Bтг)A"п'
TBz) = ^^r(;
w)	Y{z)
n-l
x sh тгж '
|2
оЗг-1/2
ch тгж'
4	J сЬтгж + г
II.2. ФУНКЦИЯ
О п ределение:
i/?(z) — аналитическая функция во всей z-плоскости, за исключением точек
в которых она имеет простые полюсы.
= 0, —1, —2, . . . ,

612	Прил. II. Некоторые специальные функции и их свойства
1
фA + Z) — ф{\ — Z) =	TTCtgTTZ,
z
1 n^1 ( k\	11.
ф(пг) = —у \l)[z-\	1+ Inn, фBг) = - ^(z) + - ф ( z + - j + In 2.
n т~^ \ n J	2	2 \ 2 /
Кеф({х) = КефA — ix), 1тф{гх) =	1	€Й.птгж.
1тфA + гж) =	1	cth тгж, 1тф I —h ix) = — thirx.
2ж 2	\2	У 2
n x
i/?(n + 1) = -C + 5Z —? ^A) = ™c-
n-1
- -In3,
2л/3 2
2
р\	, ч тг ртг [(д^/2] 2рктт	ктг
?1 = _С - In Bq)	ctg — + 2 > cos —	In sin
qJ	2	q	^	q	q
[p = 1, 2, . .., 9-l; 9 = 2, 3, 4... ].
oo	^
= -C + („ - 1) g (fc + 1)(fc + ,}	[см- 5.1.7, 5.1.8].
(")A) = (-l)n+1n!C(n + 1)	[n = 1, 2, 3, ...
()
_,
2 n —1 _,	то —1
то —1	^
^i)nn! ? (fc+,)
fe=l	fe=O v	;
\) = (~l)n+1n!Bn+1 - l)C(n + 1)	[n = 1, 2, 3, . . . ;
2	^ Bk - IJ
II.3. ФУНКЦИЯ /3(z)
Определение:
2[ V 2 У rV2/J'
l
> = f ——dt	[Re^ > 0],
0

11.6. Числа Бернулли Вп	613
P(z) = V 		[см. 5.1.9].
р17, — 1 / . ч L	i	-1
A - 2) = ^—-/8(г), /3(* + п) = (-1)" ^ (~ ' + C(z)\,
п = 2,4,6,. 11
n = l,3,5,. /J'
C(n + 1) = (-1)" in2 + (-1)" ? tl)!Lt CA) = ln2.
o^P\	7Г	Qt	Bfc + l)P7Ti /
/3 I — I =	у cos	In I 2 — 2 cos
\/ 2i(/) ^	\
q
[p = 1, 2, 3, ..., g- 1; g = 2, 3, 4, ... ].
II.4. ДЗЕТА-ФУНКЦИЯ РИМАНА ?(z)
Определение:
oo .,
fc=l k*
При Re z ^ 1, z t^ 1, CC2-) определяется как аналитическое продолжение этого ряда.
22п-1_2п
СBп) =	|Д2п|	[п = 1, 2, 3, . . . ],
СA - 2п) = ^^^	[п = 1, 2, 3, . . . ],
С(-2п) = 0	[п = 1, 2, 3, ... ],
((п) = ^2 —	[п = 2, 3, 4, . . . ; см. 5.1.2].
к=1 кП
П.5. МНОГОЧЛЕНЫ БЕРНУЛЛИ Вп(х)
О п ределение:
fpxt	°°	fk
^ТТ = Е^(*)^	[|*|<2т
^)ля:п-*	[см.П.
к=о
1	Я2(ж) = ж^Ж+^
2	о
3
В3(ж) = х3 - ^ ж2 + I ж, Б4(ж) = ж4 - 2х + ж - ^,
В5(ж) = Ж5 - ^ ж4 + 5 Ж3 _ I	Б (ж) = Х6 _ Зж5 + 5 4 _ I 2 + ^
1 ;	2	3	6	l ;	2	2	42
Вп@) = Bnj ВпA) = (~1)пВп, вп(^) =-A~21~п)Вп.
II.6. ЧИСЛА БЕРНУЛЛИ Вп
Определение:
1 = V нк^.
к к!

614	Прил. II. Некоторые специальные функции и их свойства
2П^ fi2n+l=0	[n = l, 2, 3,
2^
„	1 я	б	691
jog :—•	1 -010 :::::::: 	1 -012 :™::	•
30'	66'	2730
II.7. МНОГОЧЛЕНЫ ЭЙЛЕРА Еп(х)
Определение:
Eq(x) = 1, E\(x) = ж — —, E%{x) = x — ж,
О	1
#з(ж) = ж3	ж2 + -, ^4(ж) = ж4 - 2ж3 + ж,
#5(ж) = ж5	х4 + - ж2	, ,Бб(ж) = ж6 - Зж5 + 5ж3 ~~ Зж.
II.8. ЧИСЛА ЭЙЛЕРА Еп
О п ределение:
to
?J0 = l, ?J2 = -l, E4 = 5, ?J6 = -61,
Е8 = 1385, ^ю = -50 521, Е12 = 2 702 765.

Приложение III. ТАБЛИЦА ФУНКЦИЙ V{ И V^
Обозначение: г = p/q; р и q — взаимно простые числа; т = 2р -\- q -\- 1; п = р -\- q -\- 1.
(_l)	/!,
2 "^o"^	V Д(р,
1	"fct-o~^"	' " Ч А(Р, 1 + Л), Д(9)С8)
2	? ~	2 " " У
(^	/1,
V3, — z_^ '
p-i
/i=0
Q —1
V+=vt
w+ _ у С'1)'' p+ t F _ f1' Л(Р' а2), Д(р,
в	Л, л,	вУт г 1^ д(р] 1 + л)) д(р
_ ^ (-i)fe	ti	/1, А(р, аз), А(р, 68), Д(</, сз); z
7 ^0 М 7У т т Ч Д(р, 1 + Л), Д(р, d8), Д(9, е8)
. А(р, о4), Д(р, Ь4), Д(9, С4); г
h\ Е*У ™F™-\ Д(р, 1 + Л), Д(р, rf4), Д(,, е4)
l, Д(р, ав), А(р, 6s), Д(в, св); г
в2/ т "*"
А! в2/ т "*"Ч Д(Р, 1 + Л), Д(Р, rfe), Д(9, е8)
tDL p- v р Л- А(Р. «в), А(р, Ьв), Д(«, св); г"
), Л(р, с6),
[fc = 1, 2, 3, 4],
[Л = 5, 6, 7, 8],
efc ? Jfe 5 8 к	/

616	Прил. III. Таблица функций Vi и Уг
= Е Ч
г=о
?	^РЖ1)' Bin[7(al + r(pfl))] +г(р_(_1Ь2
sin7|^	l\	1Л sin[(a + r(p-Z-1))тг]
_ \p C^1I E+	sin[(lr + a - 1O]	^r+a_2
~ ^ I! 14A - (t)i sin [(/г + а)тг] sin 7
sin 7
(-1I _ sin [(a - lr/2 - hr/2 - \
16 " tS j
Г (a + Q/2, fe - 2(a
sin 7 1
r ^J	sin A sin [(a — I — 1)тг/г] sin 7
~jj	sin A sin 7 sin [(a — r — 1г)тг]
OO	/ 1 \ . r » —1/ I\
r ~j	sin A sin 7 sin [(a + 1)тг/г]
18
« + ^ - 1) cos [7(g + Ir - 2)]
sin27sm[(a + lrOr]
^ ~ f ~ X VcosG* ~ 7) 1-3
r J sin2 7
sin2 7
1=0	oo	X ' 7
-	7Г	^^ (— II A — p)l[0L — r(l — p + /) — 1] COS [7(« — r(l — p + I) — 2)]
19 ~ о„;«2 л, Z_^	l!sin[(a - r(l - p +1))тг]1/гA+|™^)™а+4	'
/ =XSZ±LE
20 ^ I! 20 si
21 sin27
F^ (a - r(h + l)/2 - 1) cos [7(a - r(h + Q/2 - 2)]
20 sin27sin
= 7г v^r у
22 2f^ j
smAsm27sin[(a + lrOr]	У
7)sin[Ar(a - f - 1 - r)] |m3
sin A sin2 7 sin [(a -/- 1)тг/г] У '
(a - r - rl - 1) sin (XI) cos [7(a - r - rl - 2)] a_r_r/_4
l (^ + !) CQS G^ + 27) sin [Ar-^r - a - /)] _,_4
)	a + 07r/H

Прил. III. Таблица функций Vi и V{	617
« ^ 1)] а+|г+Лг_2
У
<* ~ ^ COS
sin[(lr
i=0 ,.	чА(р, 61), A(g,
. ax);
'1,
^А(р, cfc),
gr, аз), A(g, 6з);
/i=0
1,
^^^^^	«+iF'+24a(9, bi), Д(р, ex), д(р,
1, Д(9, a2);
fc=o ¦"" i=o -	^-v» a2)' Л^'
), A(p,
, A(g, ai), A(g,
л 2g+li12qr+2p I ,
fc=O	K j=0 3'
¦=K"e/al«(?
X
L, A(<|, «2M A(g, 62);	2:
X ljo+i -*' ~Aa-\-'Z'D 1 . ,	\л/	\л/	1\л/	\J'
A(^, l + jM A(</, C2J5 A(p, «2), A(p, 62)/
j=0 3-	/ 1, A(g, a3), A(9, 63);
x 2F22^
^ = »« E
Vi0= ?
^ /пч^AУ	/1, Д(р, а2), Д(р, 62);
[()/] /n
= ? ?(,
40 А. П. Прудников и др., т. 1

СПИСОК ЛИТЕРАТУРЫ
1.	Бейтмен Г., Эрдейи А. Высшие трансцендентные функции. — М.: Наука, 1965, Т. 1; 1966,
Т. 2; 1967, Т. 3.
2.	Бейтмен Г., Эрдейи А. Таблицы интегральных преобразований. — М.: Наука, 1969, Т. 1;
1970, Т. 2.
3.	Брычков Ю. А., Прудников А. П. Интегральные преобразования обобщенных функций. —
М.: Наука, 1977.
4.	Ватсон Г. Н. Теория бесселевых функций. Ч. I. — М.: ИЛ, 1949.
5.	Градштейн И. С, Рыжик И. М. Таблицы интегралов, сумм, рядов и произведений. —
Изд. 5-е. — М.: Наука, 1971.
6.	Двайт Г. Б. Таблицы интегралов и другие математические формулы. — Изд. 4-е. — М.:
Наука, 1973.
7.	Диткин В. А., Прудников А, П. Справочник по операционному исчислению. — М.: Выс-
Высшая школа, 1965.
8.	Диткин В. А,, Прудников А. П. Интегральные преобразования и операционное исчисле-
исчисление. — Изд. 2-е. — М.: Наука, 1974.
9.	Егорычев Г. П. Интегральное представление и вычисление комбинаторных сумм. — Но-
Новосибирск: Наука, 1977.
10.	Зинин Н. Н. Различные приемы приведения кратных интегралов и главнейшие приме-
применения этих приемов. — Варшава, 1892.
11.	Лебедев Н. Н. Специальные функции и их приложения. — Изд. 2-е. — М.—Л.: Физматгиз,
1963.
12.	Маричев О. И. Метод вычисления интегралов от специальных функций (теория и таб-
таблицы формул). — Минск: Наука и техника, 1978.
13.	Математические таблицы / Под ред. В. В. Карпенко, Е. Т. Колесова, Ю. С. Яковлева. —
Изд. 3-е. — Л., 1978.
14.	Смолянский М. Л. Таблицы неопределенных интегралов. — М.: Наука, 1967.
15.	Сонин Н. Я. Об одной формуле приведения кратных интегралов // Варш. у нив. изве-
известия. — Варшава, 1889.
16.	Справочная математическая библиотека / Под общ. ред. Л. А. Люстерника, А. Р. Ян-
польского. Математический анализ (дифференцирование и интегрирование). — М.: Физ-
Физматгиз, 1961.
17.	Справочник по специальным функциям с формулами, графиками и математическими
таблицами / Под ред. М. Абрамовица, И. Стиган. — М.: Наука, 1979.
18.	Тимофеев А. Ф. Интегрирование функций. — М.-Л.: ГТТИ, 1948.
19.	Уиттекер Э. Т., Ватсон Д. Н. Курс современного анализа. — Изд. 2-е. — М.: Физматгиз,
1962. Т. 1; 1963, Т. 2.
20.	Фихтенголъц Г. М. Курс дифференциального и интегрального исчисления, Т. 1—3. — М.:
Наука, 1966.
21.	Хаджи П. И. Функции вероятности. — Кишинев: Ин-т прикладной физики АН Молд.
ССР, 1971.
22.	Янке Е., Эмде Ф., Леш Ф. Специальные функции. Формулы, графики, таблицы. — Изд.
3-е. — М.: Наука, 1977.
23.	Bromwich Т. J. An introduction to the theory of infinite series. — London: Macmlllan ann
Co. Ltd, 1949.
24.	Byrd P. F., Friedman M. D. Handbook of elliptic Integrals for engineers and physicists. —
Berlin: Springer-Verlag, 1954.
25.	Davies H. T. Summation of Series. — San Antonio: Texas, 1962.
26.	Gould H. W. Combinatorial identities, a standardized set of tables listing 500 binomial
coefficient summations. — Morgantown: West. Wirg. Univ., 1972.
27.	Grobner W., Hofreiter N. Integraltafel. Teil I. Unbestimmte Integrate. — Wien und New
York: Springer-Verlag, 1975.
28.	Grobner W., Hofreiter N. Integraltafel. Teil II. Bestimmte Integrate. — Wien und Innsbruck:
Springer-Verlag, 1958.

Список литературы	619
29.	Hansen Eldon R. A table of series and products. — Englewood Cliffs.— London: Printice-Hall,
1975.
30.	Jolley L. B. W. Summation of series. — N.Y.: Dover Publication Inc., 1961.
31.	Lewin L. Dilogarithms and associated functions. — London: MacDonald and Co., 1958.
32.	Luke Y. L. Integrals of Bessel Functions. — N.Y.: McGrawHIll Book Company, 1962.
33.	Magnus W., Oberhettinger F., Soni R. P. Formulas and Theorems for the Special Functions
of Mathematical Physics. — 3 ed. — N.Y., Berlin: Springer-Verlag, 1966.
34.	Mangulis V. Handbook of Series for Scientists and Engineers. — N.Y.: Academic Press Inc.,
1965.
35.	Mathai A. M., Saxena R. K, Generalized Hypergeometric Functions with Applications In
Statistics and Physical Sciences // Lect. Notes Math. — 1973. — V. 348.
36.	Oberhettinger F. Tabellen zur Fourier Transformation. — Berlin: Springer-Verlag, 1957.
37.	Oberhettinger F., Badii L. Tables of Laplace Transforms. — Berlin, Heidelberg, New York:
Springer-Verlag, 1974.
38.	Oberhettinger F. Fourier expansions. A collection of formulas. — N.Y.: Academic Press, 1973.
39.	Oberhettinger F. Tables of Mellin Transforms. — N.Y., Heidelberg, Berlin: Springer-Verlag,
1974.
40.	Ramanujan A. S. Collected Papers. — N.Y.: Chealsea Publishing Co., 1962.
41.	Riordan J. Combinatorial Identities. — N.Y.: John Wiley and Sons Inc., 1968.
42.	Schwait I. J. An Introduction to the Operations with Series. — N.Y.: Chealsea Publishing
Co., 1924.
43.	Slater L. J. Generalized Hypergeometric Functions. — London, N.Y.: Cambridge Univ. Press,
1966.
44.	Wheelon A, D. Tables of Summable Series and Integrals Involving Bessel Functions. — San
Francisco: Holden — Day Inc., 1968.
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
1.	Гобсон Е, В, Теория сферических и эллипсоидальных функций. — М.: ИЛ, 1952.
2.	Грей Э., Мэтъюз Г. Функции Бесселя и их приложения к физике и механике. — М.: ИЛ,
1953.
3.	Демидович Б. П. Сборник задач и упражнений по математическому анализу. — М.:
Наука, 1977.
4.	Дёч Г, Руководство к практическому применению преобразования Лапласа и z-преобра-
зования. — М.: Наука, 1971.
5.	Диткин В. А,, Прудников А. П. Операционное исчисление по двум переменным и его
приложения. — М.: Физматгиз, 1958.
6.	Журавский А. М. Справочник по эллиптическим функциям. — М.-Л.: Изд-во АН СССР,
1941.
7.	Кампе де Ферье Ж., Кемпбелл Р., Петьо Г., Фогель Т. Функции математической физи-
физики. — М.: Физматгиз, 1963.
8.	Коренев Б. Г. Введение в теорию бесселевых функций. — М.: Наука, 1971.
9.	Корн Г., Корн Т. Справочник по математике. — М.: Наука, 1977.
10.	Кратцер Л., Франц В. Трансцендентные функции. — М.: ИЛ, 1963.
11.	Кузнецов Д. С. Специальные функции. — М.: Высшая школа, 1965.
12.	Кузьмин Р. О. Бесселевы функции. — М.-Л.: ГТТИ, 1933.
13.	Люк Ю. Специальные математические функции и их аппроксимации. — М.: Мир, 1980.
14.	Морс Ф. М., Фешбах Г. Методы теоретической физики. — М.: ИЛ, 1958, Т. 1; 1960, Т. 2.
15.	Оберхеттингер Ф. Преобразования Фурье распределений и их обращения. — М.: Наука,
1979.
16.	Сегё Г. Ортогональные многочлены. — М.: Физматгиз, 1962.
17.	Сикорский Ю. С. Элементы теории эллиптических функций с приложениями к механи-
механике. — М.-Л.: ОНТИ, 1936.
18.	Снеддон И. Преобразования Фурье. — М.: ИЛ, 1955.
19.	Слейтер Л. Дот. Вырожденные гипергеометрические функции. — М.: ВЦ АН СССР,
1966.
20.	Сонин Н. Я. Исследования о цилиндрических функциях и специальных полиномах. —
М.: Гостехиздат, 1954.
21.	Титчмарт Е. Дзета-функция Римана. — М.: ИЛ, 1947.
22.	Титчмарш Е. Введение в теорию интегралов Фурье. — М.: Гостехиздат, 1948.
40*

620	Список литературы
23.	Трантер К. Дэю. Интегральные преобразования в математической физике. — М.: Госте-
хиздат, 1956.
24.	Эфрос А. М., Данилевский А. М. Операционое исчисление и контурные интегралы. —
Харьков: ГНТИУ, 1937.
25.	Янушаускас А. И. Двойные ряды. — Новосибирск: Наука, 1980.
26.	Appell P. Sur les fonctlons hypergeometrlques de plusleures variables. — P.: Gauthler-VIIlars,
1925.
27.	Appell P., Kampe de Fernet J. Fonctlons hypergeometrlques et hyperspheriques. — P.:
Gauthler-Vlllars, 1926.
28.	Artin E. Elnfiihrang In die Theorie der Gamma-Funktlon. — Leipzig, 1931.
29.	Bailey W. W. Generalized hypergeometrlc series. — Cambridge, 1935.
30.	Bierens de Haan D. Nouvelles tables d'integrales definies. — N.Y.: Hafner Inc., 1957.
31.	Buchholz H. Die konfluente hypergeometrische Function. — Berlin: Springer-Verlag, 1953.
32.	Campbell G., Foster R. Fourier Integrals for practical applications. — N.Y.: Van Nostrand,
1948.
33.	Carlitz L. Generating functions. — Duke University, 1969.
34.	Colombo S. Les transformations de Mellin et de Hankel, applications a la physique
mathematlque. — P.: CNRS, 1959.
35.	Colombo 5., Lavoine J. Transformation de Laplace et de Mellin. Formulalres. Mode
d'utilisation. — P.: Mem. Scl. Meth., 1972.
36.	Doetsch G. Handbuch der Laplace-Transformation. — Basel, BIrkhauser Verlag, 1950-1956.
Bd. I-IV.
37.	Doetsch G., Kniess H., Voelker D. Tabellen zur Laplace-Transformation. — Berlin; Gottingen,
Springer-Verlag, 1947.
38.	Erdelyi A. Operational calculus and generalized functions. — N.Y.: Holt, Rlnehart and
Winston, 1962.
39.	Exton H. Multiple hypergeometrlc functions and applications. — Chlchester (Sussex): Hor-
wood, 1976.
40.	Exton H. Handbook of hypergeometrlc integrals: theory, application, tables, computer pro-
programs. — Chlchester (Sussex): Horwood, 1978.
41.	Kampe de Fernet J. La fonctlon hypergeometrlque. — P.: Gauthier-VIllar, 1937.
42.	Knopp K. Theory and applications of infinite series. — L.: Blackle and Son, 1951.
43.	Knopp K. Infinite sequences and series. — N.Y.: Dover Publ. Inc., 1956.
44.	Lindman С F. Examen des nouvelles tables d'integrales definies de M. Bierens de Haan. —
N.Y.: Hafner Publ. Co., 1944.
45.	McBride E. B. Obtaining generating functions. — В.: Springer-Verlag, 1971.
46.	McLachlan N. W. Bessel functions for engineers. — Oxford: Clarendon Press, 1955.
47.	McLachlan N. Wn Humbert P. Formulaire pour le calcul slmbolique. — P.: Gauthier-VIllar,
1950.
48.	McLachlan N. W., Humbert P., Poli L. Supplement an formulaire pour le calcul symbolique. —
P.: Mem. Sci. Math., 1950.
49.	Meyer zur Capellen. Integraltafeln. Sammlung unbestlmmter Integrate elementarer Funktlo-
nen. — Berlin, Gottingen, Heidelberg, 1950.
50.	Neville E. H. Jacoblan elliptic functions. — L.: Oxford Univ. Press, 1957.
51.	Nielsen N. Handbuch der Theorie der Gammafunction. — Leipzig: Teubner, 1906.
52.	Nielsen N. Theorie des Integrallogarithmus and verwandter Transzendenten. — Leipzig:
Teubner, 1906.
53.	Norlung N. E. Sur les fonction hypergeometrlques d'ordre superior. — Kobenhavn, 1956.
54.	Oberhettinger F., Magnus W. Anwendung der elliptiscen Functlonen In Physik und Tech-
nlk. — В.: Springer-Verlag, 1949.
55.	Pierce B. O., Foster R. M. A short table of integrals. — 4-th ed. — Ginn, 1956.
56.	Petiau G. La theorie des fonctlons de Bessel. — P.: CNRS, 1955.
57.	Rainville E. D. Special functions. — N.Y.: Macmlllan Co., 1960.
58.	Roberts G. E., Kaufman H. Table of Laplace transforms. — Toronto: McAinsh and Co.;
Philadelphia; London: W. B. Saunders Co., 1966.
59.	Sneddon J. The use of Integral transforms. — N.Y.: McGraw-Hill, 1972.
60.	Tricomi F. Elliptische Funktionen. — Leipzig: Academlsche Verlagsgesellschaft, 1948.
61.	Tricomi F. G. FunzionI Ipergeometriche confluenti. — R.: Edizonl Cremonese, 1954.
62.	Voelker D., Doetsch G. Die Zweldimensionale Laplace Transformation. — Basel: BIrkhauser,
1950.

УКАЗАТЕЛЬ ОБОЗНАЧЕНИЙ ФУНКЦИЙ И ПОСТОЯННЫХ
А(х) — алгебраическая функция или степенная функция с произвольным показателем
am и
am 11 = am (it, к) — эллиптическая функция Якоби, и =	—~^^^^^^^^=-
J yl - к2 sin2 cp
arccosz, arccosecz, arcsecz, arcsinz, arcctgz, arctg z — обратные тригонометрические функции
Archz, Arcosechz, Arcsechz, Arshz, Arcthz, Arth z— обратные гиперболические функции
argz — аргумент комплексного числа z (z = \z\etargz)
Bn — числа Бернулли
Bn{z) — многочлены Бернулли
beiu(z), Ьег„(г), bei(z) = bei0 (z), her (z) = ber0 (z) (Ьег„ (z) + i bei», (z) = Jv(e3iri/4z)) -
функции Кельвина
Г 1	l
С = 0, 5772156649 . . . — постоянная Эйлера С = lim V	In n
X
6 (ж) = 	 —j=- at — косинус-интеграл Френеля
у2тт J yi
0
oo
C(xj a) = ya~'1 cos tdt [Re a < 1] — обобщенный косинус-интеграл Френеля
X
Cn(z) = 	— 2-^1 I ^^j fb + 2Л; AH—; 	 J — многочлены Гегенбауэра
cd и = 	, en и = cos (am it) — эллиптические функции Якоби
dntt
ch z =	гиперболическая функция
chi(ж) =
= С + In ж -f 	 dt — интегральный гиперболический косинус
о
оо
Г cost
ci (ж) = — 	dt — интегральный косинус
X
Z
Ob (z) = — In f 2 sin — J dx — интеграл Клаузена
J ^	2 /
о
e%z + e~~%z 1 cos z
cos z = 	, cosec z = 	, ctg z = 	 — тригонометрические функциии
2	sin z	sin z
1	chz
cosech z = 	, cth z =	гиперболические функции
sh z	sh z
тг/2
T)(k) = —,	= D\ —. к) — полный эллиптический интеграл
1 ^ J л/1 - к2 sin2 if	V2' J
0 v	-r
sin (f dip
	 — эллиптический интеграл
- л/l — к2 sin2 <,p
Djj{z) = 2v'2e~~z /4Ф(	, —; — I — функция параболического цилиндра
л	dnn	Г	. 2	"	dnw
dc it = 	, dn it = \/1 — re sin (am it) , ds it = 	 — эллиптические функции лкоои
en it	v	sn«

622	Указатель обозначений функций и постоянных
тг/2
E(fc) = yl — k2 sin2 (f dip — полный эллиптический интеграл 2-го рода
о
j k) = у 1 — к2 sin2 (p d(f — эллиптический интеграл 2-го рода
о
Еп — числа Эйлера
En(z) — многочлены Эйлера
"Eju(z) = — sin (vip — z sin (p) dip — функция Вебера
7Г J
О
°°	zk
Ep(z; /i) = \™^ 	 [p > 0] — функция Миттаг-Леффлера
^ iX/i + fcp-1)
X
Г et
Ei (ж) = — dt — интегральная показательная функция
— оо
е = 2,718281828459 . . .
ez = exp z — показательная функция
интеграл вероятности
2 Г 2
erf (ж) = —= e~~l dt —
о
oo
2 Г 2
erfc (ж) = 1 — erf ж = —= e~~t dt —
V?r J
дополнительный интеграл вероятности
2 Г 2
rfi (z) = —=¦ e* eft — интеграл вероятности мнимого аргумента
О
dip
- V 1 — к2 sin2 (
0 v
— эллиптический интеграл 1-го рода
F(a, 6; с; z) = 2Гг(а, b; с; z) = ^ ^ff^ ^	[kl < 1],
l
г	ir
= Г С	*/3~1A — *)с-ь~1A — t«)~a dt	[I Re c> Re 6 > 0; |arg(l-^)| < тг]
[b, с - 6J J
о
— гипергеометрическая функция Гаусса
щенная гипергеометрическая функция
СО / ч	Д,
а; 6; z) = /	вырож:денная гипергеометрическая функция
Fc (a, b; ci, . . . , cn; zi, . . . , zn) — обобщенная гипергеометрическая функция
Fj(. . . ; ^, () [j = 1, 2, 3, 4] — функции Аппеля
Fl{a, Ь, Ь>; с; ,, С) = f ^g^^'
6, b ; с; z, С) = 2^
+ vicf < 1]

Указатель обозначений функций и постоянных	623
G = У^	 = 0, 9159655942 ... — постоянная Каталана
^0 Bк + IJ
Н„(г) = -^(^V+1	\	1F2(l; 3/2, iz + 3/2; -z2/4) - функция Струве
//^ ^(z) = Ju(z)-\-iYl/(z), Ну (z) = Ju(z) — iYl/(z) — функции Бесселя 3-го рода (функции Ганкеля
1-го и 2™го рода)
2 (?П __ 2
Hn(z) = (-—l)nez 	е z — многочлены Эрмита
dzn
i
hniU(z) = -	—	 2^2A, /i + 3/2; /x-i/ + 2, /z + i/ + 2; 2z)
hei^ (z), her,, (z), hel (z) = hel0 (z), her (z) = her0 (z) (her,, (z) + i hei^ (z) = Hi1}(e37ri/4z)) —
функции Кельвина
Iu{z) = —	 f — J o^l (^ + 1; — ) = e"i/?rJ'2Jl,Be"'2) — модифицированная функция
Бесселя 1-го рода (функция Бесселя мнимого аргумента)
Im z — мнимая часть комплексного числа z = х + Щ (Im z = у)
(Z\v	I	/	Z2\
Ju{z) = ( — 1 	 o^i k + l;	— функция Бесселя 1-го рода
V2/ Г(|/ + 1)	V	4 /
Jl/(z) = — cos (i/y? — z sin (p)d(f — функция Ангера
7T J
о
тг/2
Г	^^	/ тг \
К(/е) = —,	= jP ( —, /е I — полный эллиптический интеграл 1-го рода
/1 19 • 2	\ О /
J yl —«^sin ^	v^ 7
/С„(г) = 'KV-vW ~ Ivtz)\ г ^ ni /Сп(^) = lim /^„(г) [п = 0, ±1, ±2, . .. ] — функция
2slnuw	v-^n
Макдональда (модифиированная функция Бесселя 3™го рода)
к, к' [0 ^ к ^ 1; к' = у 1 — fc2 ] — модуль и дополнительный модуль в эллиптических интегралах
ky{z) = —j-p	г- Wv/2 i/2Bz) — функция Бейтмена
г( + 1)
kei^ (z), ker^ (z), kei (z) = keio (z), ker (z) = kero (z)
(kerv (z) likely (z) = e^l/7ri/2i^l/(e7ri/4z)) — функции Кельвина
X
L(x) = — In cost dt — функция Лобачевского
о
L|/(z) = е~"^+1^7Г*' 2Hl/(e7Tt/z) — модифицированная функция Струве
Ln(z) = b^(z) — многочлены Лагерра
z~v' ez dn
ULiz) =	(zn+I/e""z) — обобщенные многочлены Лагерра
n\ dzn
	 [Re s > 0; | arg A — z)| < тг] — полилогарифм порядка s
J e z
A E
0
li (z) =
ж
= Ei(lnz), li (ж) = 	 — интегральный логарифм In z = lnlzl + iargz — натуральный
J lnt
0
логарифм [z = \г\е{^2+2жк\ k = 0, ±1, ±2, . . . ]
^W>f, ju(z) = z^ I e^z' 1 i^iA/2 — >c-\-/z; 2/z + l; z) — вырожденная гипергеометрическая функция
"Уиттекера
nc ti, nd ti, ns и, nc = 	, nd и = 	, ns и = 	 — эллиптические функции Якоби
спи	dnti	sn it

624	Указатель обозначений функций и постоянных
On(z) = — / 	( — 1	— многочлены Неймана
4 ~	k\	V2/
2~™n dn
Pn(z) =	(z — 1)те — многочлены Лежандра
п\ dzn
Pv{z) = P®{z) = 2Fi l -и, 1 + v\ 1; —-— J [| arg A + z)\ < тг] — функция Лежандра 1-го рода
ч/х/2
-щ 1-М; ^—^) [|arg(z±l)| <тг]
ГA-^) \z^
/1 j_ ^.\м/2
2-Fi[ —1/, 1 + i/; 1 — /i; 	 I [—1 < ж < 1] — присоединенная
()
функция Леж:андра 1-го рода
A ^ ^)"аA + z)^— [(I - z)a+n(l + zf+n] - многочлены Якоби
dzn
р \z)	A ^)A + z)
2п?г!	dzn
Qjj{z) = Q^(z) — функция Лежандра 2-го рода
' + 3/2
(/i + i/)/2 + l; i/+ 3/2; z^2) [|arg(z±l)|, |argz|<7r],
-i0) + ei^7T/2Q^(x-i0)] =
[x) COS/iTT — Г
2 sin fiw
— присоединенная функция Лежандра 2-го рода
R(x) — рациональная функция
Re z — действительная часть комплексного числа z = х + гу (Re z = ж)
X
S(x) = 	 —-=- dt — синус-интеграл Френеля
у2тг J v t
о
со
S(x, a) = t"^1 sin t dt [Re a < 1] —обобщенный синус-интеграл Френеля
с („\ _ о /г\ _|_ 9J"^1
— функция Ломмеля
	 1^2A; (д —1/ + 3)/2, (д + 1/ + 3)/2; —z2/4) —функция Ломмеля
ж
Si (ж) = 	dt — интегральный синус
О
si (ж)
о- / \ Ж	Г S'mt .,
= bi (ж)	= — 	at — интегральный синус
2i	J t
sec z = 	 — тригонометрическая функция
cos z
sech z = 	 — гиперболическая функция
ch z
{1, ж > 0,
0, x = 0,
- 1, ж < 0
ez - e^z
sh z =	гиперболическая функция
ж
shi z = 	 dt = —i Si (газ) — интегральный гиперболический синус

Указатель обозначений функций и постоянных	625
eiz _ e-iz
sin z = 	;	тригонометрическая функция
sn и = sin (am и) — эллиптическая функция Якоби
Tn(z) = cos (narccosz) = — [(z + у z2 — 1 )n + (z — у z2 — 1 )n] — многочлены Чебышева 1-го рода
slnz
tg z =	тригонометрическая функция
cos z
sh z
th z = 	 — гиперболическая функция
ch z
sin [(те + l)arccosz]
Un{z) =	многочлены Чебышева 2-го рода
oo	, \v + 2k
Ui/(z, () = J_^( —1) I — I	Jv+2k(C) — функция Ломмеля двух переменных
j ij,(z) = -г^+1/2е~;/2ФA/2 — ж-\- /i, 2/i + 1; z) — вырожденная гипергеометрическая функция
Уиттекера
Mz)^JAz) {y ф n]j Yn{z) = lim nw [n = 0? ±lj ±2> e>> j _ функция
u()	{ ф ]j n{)
Sin 1/7Г	v—»-
Неймана (функция Бесселя 2-го рода)
yn(z) = 2^?o("^'"'? «• + 1; —z/2) — многочлены Бесселя
В(а, /3) = ———у — бета-функция
= f taf~1e~t rft [Rez > 0] —
гамма-функция
о
oo
Г(а, ж) = ta^1e"~t dt — дополнительная неполная гамма-функция
ж
X
j(a, х) = Г(а) — Г(а, ж) = ta"e'™t dt — неполная гамма-функция
1=1
аа+1	a+k-1
АB, а) = -,	——
v ; 2	2
- /О,	тфп,
dTOj n = 4	— символ Кронекера
11,	т = п
оо .,
C,{s) = 2_^ —	[Re z > 1] — дзета-функция Римана
k=l kS
OO	-
^(s, v) = 2_] 7	Г™ [Re 5 > 1; v 7^ О? ~1> ~~2, . . . ] — обобщенная дзета-функция Римана
00
fe=O

626	Указатель обозначений функций и постоянных
6»3(ж, q) = 1 + 2 ^ Я
k=i
04(ж, g) = 9q(x, q) — эллиптические тэта-функции
Л(ж, а)
= f ж-*
о
со
/ ч	Г	Ж
|/(ж) = 	at
о
,",*)= [
J A-1/ Si
. (l-i/sin2y?)v/l- fc2sin2
— эллиптический интеграл 3-го рода
K i; v ^ o, -l, -2, ...
it	i	\	x " \-~j-/q, k\~"*/q к • " • \^r)q к fc r
i, a2, • • • , ar; oi, 02, ... , os; z) = >^	—-—™™-!J	—™--!J— 2: — базисный гипер™
геометрический ряд
Ф(а, с; z) = Г	iFi(a; с; z) + Г	z1" iFi(l + a — с; 2-е; z) — вырожденная
Ц + а - с\	L « J
гипергеометрическая функция
Y'(z)
ip(z) = [lnr(z)]; = —г	пси-функция

УКАЗАТЕЛЬ ОБОЗНАЧЕНИЙ СИМВОЛОВ
(а)к = о(о + 1) • • • (а + к — 1) [к = 1, 2, 3, . . . ], (а)о = 1 — символ Похгаммера
тг! = 1 • 2 • 3 . . . (тг - 1)тг, 0! = 1! = 1
Bтг)!! = 2-4-6...Bп) = 2пп\
Bп + 1)!! = 1 • 3 • 5 . . . Bп + 1) = ^^ Г (п + -) = (-\ 2п
л/тг V 2 / V 2 / „
Bк)\\,
n^ _ n(n-l)...(n-A; + l)
тг>
О!! = (-1)!! = 1
к\
Ы(п^к)!	к\
¦ — биномиальные коэффициенты
= 1
Re a, Re b > с Re a > с и Re b > с
[ж] = п [п ^ ж < п + 1, п = 0, ±1, ±2, . . . ] — целая часть числа х
-z = х - iy [z = x + iy]
\x\ =
ж, ж ^ О,
-ж, ж < О
«fc = «m«m+i •••««, [тг ^ ттг]
= 1	[тг < ттг]
оо
п
k=l	k=l
п
/ j ®k = ат + CLm+1 + • • • + ап [п ^ т]
к = т
= 0
тг < т\

УКАЗАТЕЛЬ РАЗЛОЖЕНИЯ НЕКОТОРЫХ ФУНКЦИЙ
В РМДЫ
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
A + x)v 4.2.3.1, 5.1.29.12-13, 5.2.2.1-10, 5.2.10.8,
5.2.11.17
A-ж)~п 5.2.11.3
A - х)±п/2 5.2.13.1-2, 5.2.13.6
A + ж + ... + жт)р 5.2.18.12
ех 5.2.7.2
ах 5.2.7.3
бЬж 5.2.7.6, 5.4.5.8, 5.4.6.24-25
sh2n+1 х 4.3.1.8
бп2пж 4.3.1.10
сЬж 5.2.7.5, 5.4.5.1-2, 5.4.6.26-27
сЬ2пж 4.3.1.12
созеспж 4.3.2, 5.1.25, 5.1.27.5, 5.3.5.8, 5.3.6.7,
5.4.5.5, 5.4.5.8
cosech2 х 5.3.6.7
эеспж 4.3.2, 5.1.26
th ж 4.3.2, 5.1.26, 5.1.28.1
ctha;4.3.2, 5.1.25, 5.1.26.16,5.1.27.3-4,5.3.8.4-6
erchxsh(rshx) 5.3.3.2
erchxch(rshx) 5.3.3.2
sh ax sechy 5.4.6.24
chasechy 5.4.6.27
sech x sec ж 5.3.7.10-11
(l/ж2) thxtga^ 5.3.8.3
A/ж2) cthjcctgcc 5.3.9.5
sin ж 5.2.7.6, 5.4.3.4-6, 5.4.5.8, 5.4.6.19-20,
5.4.6.24-25
sin2n x 4.4.1.16, 5.2.18.8
sin2n+1a; 4.4.1.17, 5.2.18.10
cos ж 5.2.7.5, 5.4.3.4-5, 5.4.5.1-2, 5.4.6.21-22,
5.4.16.4, 5.4.6.26-27
cos2 ж 5.4.6.25, 5.4.16.5
cosn x 4.4.1.16-18, 5.2.18.9
ежз1пж 5.2.7.4
е^созж 5.2.7.4
shicsina: 5.2.7.13
сЬжэтж 5.2.7.7
эпжсовж 5.2.7.7
сЬжсозж 5.2.7.10
sh ж — sin ж 5.2.7.15
shx + sin ж 5.2.7.11
сЬж + СО8Ж 5.2.7.10
ch ж — cos ж 5.2.7.13
5.4.12.1
cos ж ± ch a
e cos x sin (s
sin ax sect/ ?
cos ж sect/ 5.'
(cos^)/2s
5.4.
.12.2
\ e±COS?C
i.4.6.24
4.6.27
• 5.4.6.30
cos (sin ж) 5.4.7.1-2
(со8ж)^1/2со8- 5.4.6.30, 5.4.8.6
соэесж 5.1.25, 5.1.27, 5.2.3.5-6, 5.3.5.8, 5.4.5.5,
5.4.5.8, 5.4.16.10, 5.4.16.16
sec ж 5.1.26.3, 5.1.26
tga; 5.1.26
^ж 4.4.7.1, 4.4.7.4, 5.1.6.4, 5.1.25.4, 5.1.25.22,
5.4.16.14
cosnx 4.4.7.16
4.4.7.17
cosn ж
1пA±ж) 5.2.4.3-4, 5.3.4.4
A- жпIпA-ж) 5.2.5.2-7
A- ж)^11пA-ж) 5.2.17.1
1пA - ж + ж2) 5.2.18.7
lni±5 5.2.4.8, 5.2.4.13
1-х
In (I - 2r cos ж + г2) 5.4.9.13
A + ж|)р1пA + ж) 5.2.18.6
In2 (I - ж) 5.2.17.2
1пA + жIпA - ж) 5.2.17.4
in sin ж 5.4.2.9
In cos ж 5.4.2.10
In ctga: 5.4.6.7-8
sin ж In sin ж 5.4.6.15
cos ж In cos ж 5.4.6.18
cos ж In sin (ж/2) 5.4.5.7
cos ж In tg(x/2) 5.4.5.10
sin ж In ctg^ 5.4.3.13-14
cos x In ctg2 ж 5.4.3.13-14, 5.4.5.10
In2 cos x 5.4.16.6
агсвтж 5.2.13.10
A ± ж2I/2 arcsin ж 5.2.14.2, 5.2.14.5
arcsin2 ж 5.2.14.3
arcsin4 ж 5.2.17.16
4.4.9.6-7
arctg2ж 5.2.17.5

Указатель разложения некоторых функций в ряды
629
5.2.18.5
5.2.17.7
In
arctg
агс^ж 5.2.17.8
п т.
5.4.9.12
1 — r cos ж
Arsh x 5.2.13.10, 5.2.13.19, 5.2.14.1-5, 5.2.16.3
A ± ж2I/2 Arsh x 5.2.14.2, 5.2.14.5
Arsh2 ж 5.2.14.3
Arth x 5.2.5.8-15, 5.2.6.7
Arth2 x 5.2.17.5
СПЕЦИАЛЬНЫЕ ФУНКЦИИ
ати 5.4.14.10
Вп 5.1.2.2, 5.1.2.4, 5.1.4.1
Вп(х) 5.4.2.5-8
bei (ж) 5.2.10.5, 5.2.17.14-15
Ье1;(ж) 5.2.10.4
ж~"Ьеи,(ж) 5.2.10.15
ber (ж) 5.2.10.3, 5.2.17.14-15
Ьег'(ж) 5.2.10.6
х~иЪети (ж) 5.2.10.15
ж~2г/[ЬеГ2 (ж) + bei2 (ж)] 5.2.12.1
ж~~21/~~1[Ьег1/ (ж) ber 'и(х) — bei 'u(x) bel^, (ж)]
5.2.12.2
ж1"^,, (ж) Ьег',, (ж) + bei,, (ж) bei ^(ж)]
5.2.12.3
С{х) 5.2.8.17
С^(созж) 4.4.1.26
жпС^A/ж) 4.1.7.20
С2пП(х)> С2п+^1(Х) 4-1.7.24, 4.2.10.17
Сп 1/^1/2A - 2ж) 4.2.10.15
xnC^t/^n(l/x) 4.2.10.19
хпСп~П+1/2A - 2/ж) 4.2.10.13
Н1/(ж) 5.2.10.22-23
Но(ж) 5.2.15.3, 5.2.15.6-8
жН0(ж) 5.2.15.1
Hi (ж) 5.2.15.2, 5.2.15.5
ж^^Н^ж) 5.2.10.10
жп[Еп+1A/ж) + Нте+1A/ж)] 4.1.7.17
жп[Е^п^1(ж) + H_n_i(x)] 4.1.7.18, 4.2.3.33
Нп(х) 4.1.7.13
жпЯпA/жL.1.7.12, 4.2.7.45
exh^^{x) 5.2.18.2
/п(ж) 5.1.25.1, 5.2.10.1
J'2{x) 5.2.10.13
x~uJu{x) 5.2.10.7
/|(ж) 5.2.16.2
Jv(x)J-u(x) 5.2.16.4
ж1^^/м^1/(ж)^^1(ж) 5.2.16.5
In(x) 5.2.10.1
ж^1//?/(ж) 5.2.10.7
е±а%(ж) 5.2.14.27, 5.2.16.1
/о(ж)±/о(ж) 5.2.10.3, 5.2.10.5
Ji(x) + h(x) 5.2.10.4
JoW + ^oW 5.2.10.6
/,MJ_^) 5.2.12.4
x^2iJJ1J{x)IjJ{x) 5.2.12.1
^2n+1[/!n-i/2W " /S+i/2(*)] 4-1.7.21
K(ife)E(ife) 5.3.6.5
K(fe) 5.1.9.2, 5.1.9.4, 5.2.16.6, 5.3.6.2, 5.4.8.8,
5.4.14
кЩк) 5.3.4.1, 5.3.6.4
A 5.3.3.4
Kn+1/2{x) 4.1.7.19
кег(ж) 5.2.17.14-15
L0(aj) 5.2.15.5
ж-^Ь^ж) 5.2.10.9
^П+1/2[/-п-1/2(ж) - Ln+1/2(a)] 4.1.7.14
Ь^(ж) 4.1.7.11
Lin (ж) 5.2.3.3, 5.2.5.4, 5.2.5.13, 5.2.6, 5.2.17.3,
5.2.17.9
жп+1Оп(ж) 4.1.7.15
Pn(x) 4.1.7.23, 4.2.10.18, 4.4.1.25
РпA + 2ж) 4.2.7.12
жпРпA/ж) 4.2.7.11, 4.2.10.20
хпРпA-2/х) 4.2.10.10
хпРп
4.2.7.38, 4.2.10.16
4.2.7.30
1те(гж) + гЕп(гж) 5.2.10.10
Jl/(x)cos7ii/ + EI/(jc)sin7ri/ 5.2.10.12
x^n[Jn(ix) - гНп(гж)] 5.2.10.11
5.4.8.9-10
5(ж) 5.2.8.19
«^«/(ж) 5.2.18.1
Shi (ж) 5.2.8.15
Si (ж) 5.2.8.15

630
Указатель разложения некоторых функций в ряды
ТпA-ж/2) 4.1.7.26
Т„A/ж) 5.2.3.25
ТпA^ж2/2) 4.2.10.12
хпТпA/х) 4.1.7.22, 4.2.3.28
Un(l-x) 4.1.7.27
xnUn(l/x) 4.2.3.7, 4.2.10.21
Uu(x, 0) 5.2.7.21, 5.2.11.8-9
C(х) 5.1.3.6, 5.1.5.1, 5.1.6.5, 5.1.6.10, 5.1.15.5,
см. также 4.1.2.7-9, 4.1.3.2-5, 4.1.4.1, 4.1.4.8,
4.1.4.11, 4.1.5.1, 4.4.8.16, 5.1.3.6, 5.1.6,
5.1.15, 5.1.21.3, 5.1.25.10, 5.1.25.13, 5.1.25.24,
5.1.26.3, 5.1.26.17, 5.1.26.33
^пЦх) 5.1.3.6
f3(b) - P(a) 5.1.6.2
ж~а7(а, ж) 5.1.31.1, 5.2.8.1
хпГ(п, ж) 5.2.8.2
ехГ(п, ж) 4.1.7.10
С(ж) 5.1.2.1
B^ж -х)С{х) 5.1.2.3
A^2ж)С(ж) 5.1.4.1
С(ж, v) 5.2.3.1, см. также 4.1.2.6, 4.1.3.1,
5.4.2.1-2
01(ж, q) 5.1.29.10, 5.3.2.5, 5.3.2.16, 5.4.11.1
<92(ж, q) 5.1.29.10, 5.3.2.3, 5.3.2.6, 5.3.2.16, 5.4.11.1
03(ж, q) 5.1.29.11, 5.3.2.1-2, 5.3.2.15, 5.3.3.3,
5.4.11.2
<94(ж, q) 5.1.29.11, 5.3.2.2, 5.3.2.15, 5.4.11.2
Ф(ж, в, v) 5.2.3.1-2
ф(х) 5.1.6.10, см. также 4.1.2.2-5, 4.13.2-6,
4.1.4.1, 4.1.4.7, 4.1.4.9, 4.1.5.1, 4.2.10.28, 4.4.8.15,
5.1.3.2, 5.1.6.2, 5.1.6.12, 5.1.6.16, 5.1.15.2-3,
5.1.15.9, 5.1.21.3, 5.1.24.1, 5.1.25.2, 5.1.25.13,
5.1.25.28, 5.1.26.12, 5.1.26.23, 5.5.1.19, 5.5.2.3
ф{п\х) 5.1.3.2
ф(Ь) -ф(а) 5.1.6.2
зтх1ф(х/тг) 5.5.1.27

УКАЗАТЕЛЬ ИНТЕГРАЛЬНЫХ ПРЕДСТАВЛЕНИЙ
НЕКОТОРЫХ СПЕЦИАЛЬНЫХ ФУНКЦИЙ
ЧЕРЕЗ ЭЛЕМЕНТАРНЫЕ
С{х) 1.5.53.3
С(х, а) 1.5.41.21
С12 (ж) 1.6.4.6-7, 1.6.10.16, 1.7.4.13
сЫ(ж) 1.4.21.8
о(ж) 1.3.3.34, 1.5.41.13, 1.6.10.8, 2.5.29.1
Du(x) 2.3.6.12
Щк) 2.2.5.18, 2.5.19.13, 2.5.19.23-24
Е„(ж) 2.5.27.3, 2.5.27.14
Е1(ж) 1.3.2.14, 1.3.2.22, 1.3.2.33, 1.3.3.13, 1.5.1.15,
1.6.10.3, 2.3.4.3, 2.3.4.7, 2.3.18.3, 2.3.19.8,
2.5.28.2, 2.6.33.8, 2.7.6.2
Ei (ж) Ei (—ж) 2.6.24.8
erf (ж) 1.3.2.16, 1.3.3.1, 2.4.15.2, 2.5.44.5
erf2 (ж) 2.3.6.4
erfc(a;) 1.3.2.19, 1.3.3.3, 2.3.4.5
erfc2 (ж) 2.3.6.8
егй(ж) 1.3.2.15, 1.3.3.2
iFi(a; 6; ж) 2.3.6.1, 2.3.6.18
Н„(А?) 2.5.6.1, 2.5.8.2
Я^1}(ж), н12)(х) 2.3.5.5, 2.3.6.17, 2.4.18.14
Нп(х) 2.3.15.10
1и(х) 2.3.5.1, 2.3.6.2, 2.4.3.9, 2.4.3.11
/2/4(ж) 2.4.3.12
Jv(x) 2.3.5.3, 2.3.16.8, 2.5.6.1-2, 2.5.8.2, 2.5.27,
2.5.55.1-7
J*/4(x) 2.5.7.3
Зи(х) 2.5.27.16
Зи\х) - Ju{x) 2.3.11.2, 2.4.18.9, 2.5.12.8
Щк) 2.2.5.18, 2.5.16.47, 2.5.19.20-26, 2.6.8.1,
2.6.8.10, 2.6.14.8, 2.6.38.10-11, 2.6.39.18
Ки(х) 2.3.5.4, 2.3.5.7, 2.3.6.7, 2.3.10.5, 2.3.11.8-
12, 2.3.16.1, 2.5.6.4, 2.5.9.11, 2.5.11.6, 2.5.23.7,
2.6.22.9
К^1/4(х)К^1/4(х) 2.3.11.8, 2.4.18.7
К*/4(х) 2.3.7.8
^) 2-3.7.7
К1/4(хI1/4(х) 2.5.9.7
Ъу{х) 2.4.3.11
Ь^^ж) - Iv{x) 2.5.6.3, 2.5.9.3, 2.7.3.4
L%(x) 2.5.7.11-12
Lls (ж) 1.6.5.9, 1.6.6.8, 2.3.14.5
Н(ж) 1.6.2.3
Рп{х) 2.5.16.2, 2.5.16.44
Pv{x) 2.4.6.10, 2.4.6.28, 2.5.48.7, 2.5.49.4
РЩх) 2.4.6.1
QJJ(as) 2.4.14.1, 2.5.48.6
S(x) 1.5.53.3
S(x, a) 1.5.41.21
бЫ(ж) 1.4.21.8-9, 2.5.44.2
Si (ж), si (ж) 1.3.2.34, 1.5.41.12, 1.6.10.8, 2.6.33.5
si2 (ж) + ci2 (ж) 2.6.24.7, 2.6.33.2
Yv(x) 2.5.6.2, 2.5.8.4, 2.5.54.2, 2.5.54.7
У12/4(ж) + ^2/4(ж) 2.3.7.12
Yt/4^)Jt/4^) 2.5.8.5
Y0(x) -Но(ж) 2.6.25.5
/3(х) 2.2.4.1, 2.3.12.6, 2.4.10.6, 2.5.12.27, 2.6.31.3,
2.7.4.3
Г(а, ж) 1.3.2.4, 1.5.40.20, 2.3.4.2
7(а, ж) 1.3.2.3, 1.5.40.19, 2.5.44.4
С(ж) 2.3.14.2, 2.3.14.6, 2.4.10.17, 2.6.5.8, 2.6.19.4,
5.6.31.8, 2.7.9.2
С(ж, v) 2.3.13.22, 2.4.10.13, 2.4.12.5, 2.4.22.7,
2.6.5.7, 2.6.9.6, 2.7.9.3
Ф(ж, s, v) 1.2.4.2, 2.3.13.21
ф(х) 2.2.4.20, 2.2.5.17, 2.2.12.2, 2.2.12.4, 2.3.19.1-
2, 2.3.19.6, 2.4.22.5-6, 2.6.13.15, 2.6.17.19,
2.6.17.45, 2.6.18.14, 2.6.31.1, 2.6.34.5,
2.6.34.14, 2.6.34.17, 2.6.34.20, 2.6.39.16
Ф(а, 6, ж) 2.3.6.6, 2.3.6.9

Научное издание
ПРУДНИКОВ Анатолий Платонович
БРЫЧКОВ Юрий Александрович
МАРИЧЕВ Олег Игоревич
ИНТЕГРАЛЫ И РЯДЫ
Том 1
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
Редактор Е.Ю. Ходан
Корректор Л. Т. Варъяш
Оригинал-макет: В. В. Худяков
ЛР №071930 от 06.07.99. Подписано в печать 17.10.02.
Формат 70x100/16. Бумага офсетная. Печать офсетная.
Усл. печ. л. 51,2. Уч.-изд. л. 77,16. Тираж 3000 экз. Заказ №
Издательская фирма «Физико-математическая литература»
МАИК «Наука/Интерпериодика»
117997 Москва, Профсоюзная, 90
E-mail: fizmat@maik.ru
Отпечатано с готовых диапозитивов в ПФ «Полиграфист»
160001, г. Вологда, ул. Челюскинцев, 3.
Тел.: (8172) 72-55-31, 72-61-75, факс (8172) 72-60-72.
E-mail: pfpv@vologda.ru http://www.vologda/~pfpv
EBN 5-9221-0323-7
9 785922 10323