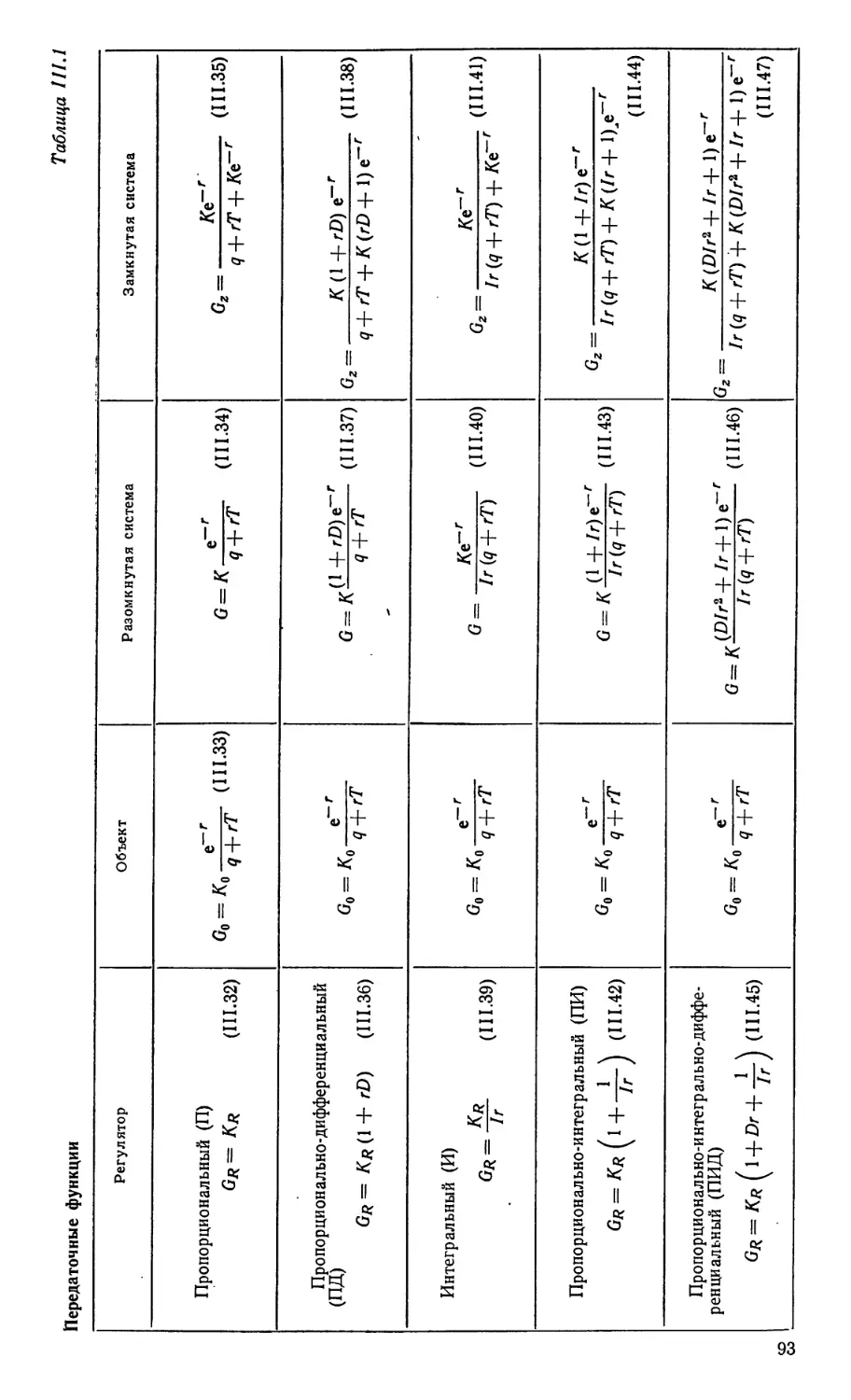
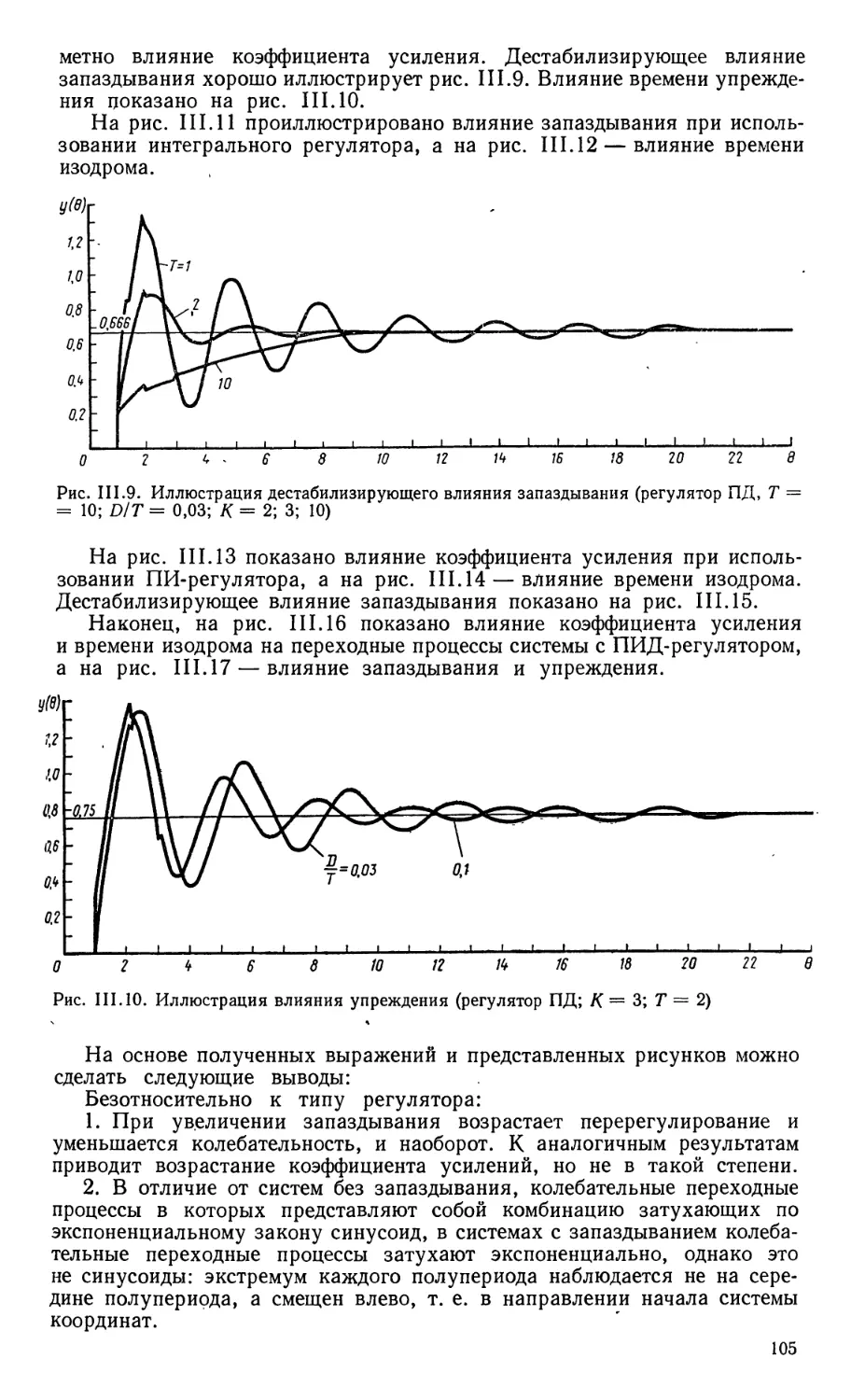
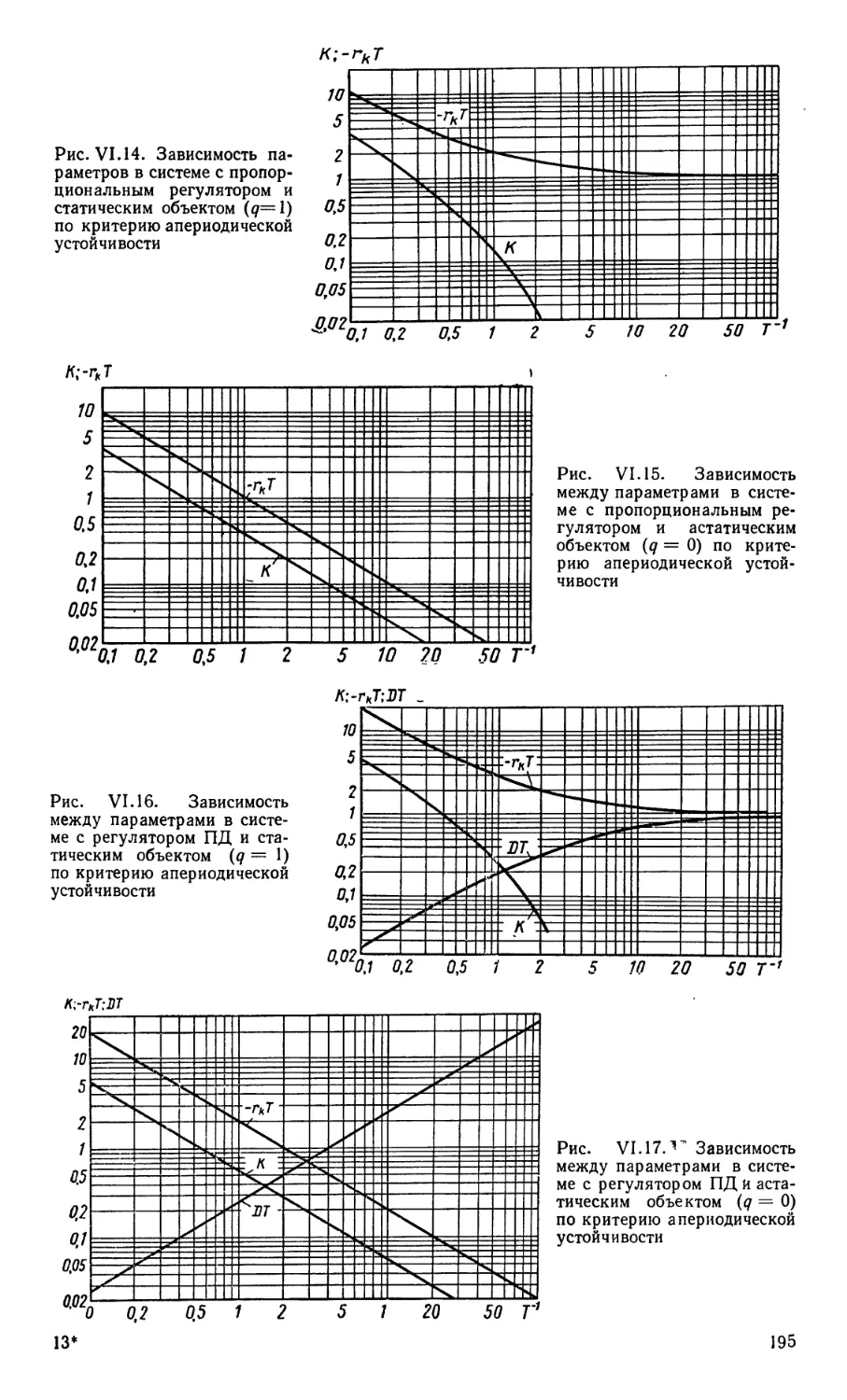
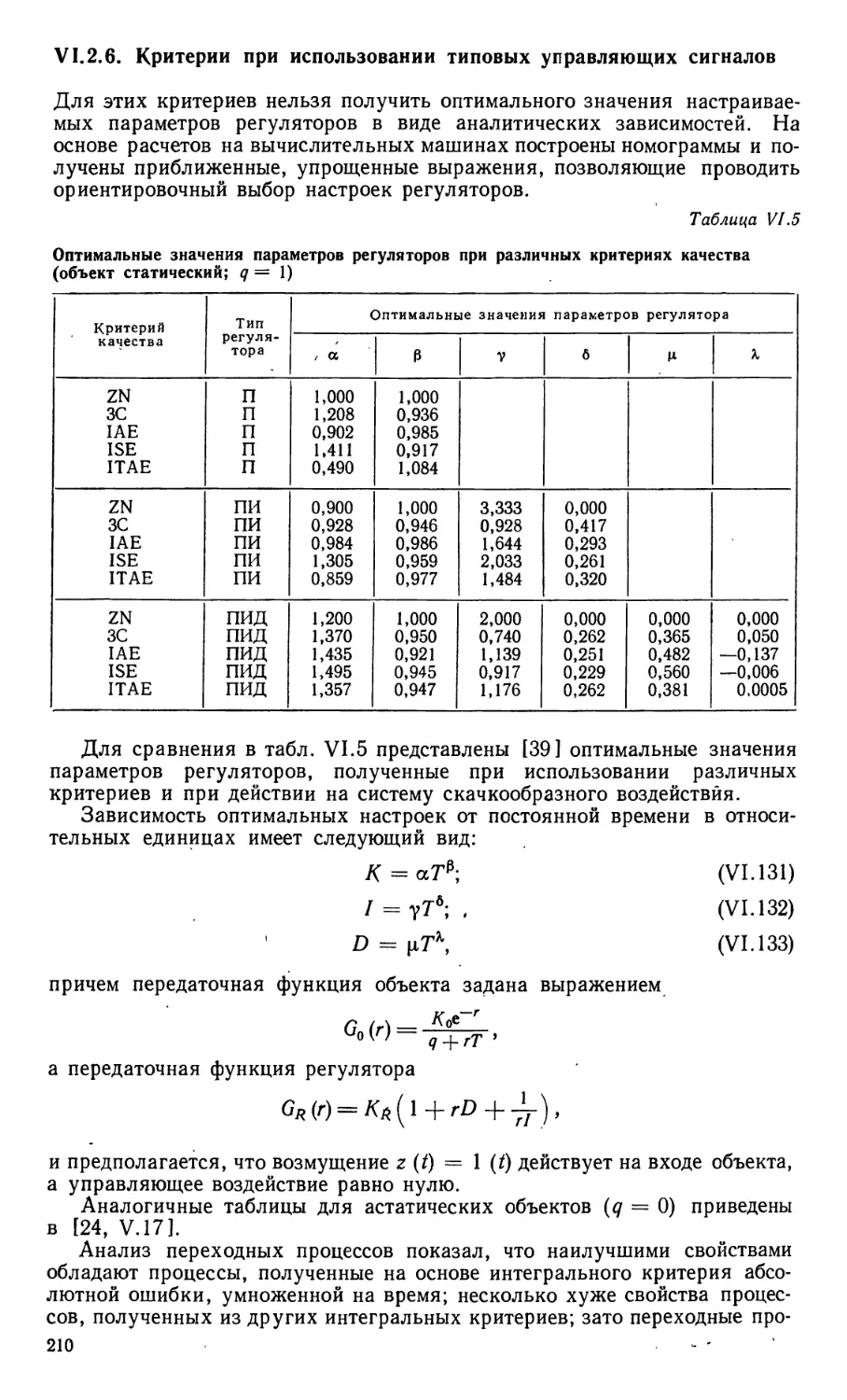
Текст
X. Гурецкий
Анализ и синтез систем
управления с запаздыванием
HENRYK GORECKI
Analiza i synteza ukladow
regulacji z opoznieniem
WYDAWNICTWA NAUKOWO-TECHNICZNE • WARSZAWA
X. Гурецкий
Анализ и синтез систем
управления с запаздыванием
Перевод с польского
канд. техн. наук доц. А Я. Дмитриева
Москва • « Машиностроение » 1974
Г 95
УДК 62—501.224
Турецкий X. Анализ и синтез систем
управления с запаздыванием. Пер. с польского. М.,
«Машиностроение», 1974, 328 с.
Книга посвящена изложению методов анализа
линейных, нелинейных и импульсных систем
автоматического регулирования с запаздыванием и
методов выбора параметров типовых регуляторов.
Большое внимание уделено математическому
описанию и идентификации объектов регулирования
с запаздыванием. Изложение сопровождается
многочисленными номограммами, таблицами и
графиками, которые могут оказать большую помощь
инженерам и научным работникам, занимающимся
разработкой и исследованием систем
регулирования с запаздыванием. Этому же способствует
обширная библиография.
Табл. 25. Ил. 238. Список лит. 438 назв.
© Издательство «Машиностроение», 1974 г.
Предисловие
В последнее время наблюдается повышенный
интерес к системам управления с запаздыванием. Это
объясняется тем, что в большинстве
производственных процессов имеются запаздывания, которыми
нельзя пренебречь, ибо их влияние на динамику
процесса весьма велико. Однако до сих пор
отсутствовали работы, целиком посвященные этой
проблеме, что объясняется достаточно большими
трудностями теоретического характера,
встречающимися при исследовании этого типа систем. В
данной книге сделана попытка охватить все задачи,
относящиеся к классическому регулированию. Но
в ней не рассматриваются ни вопросы теории
оптимального управления объектами с запаздыванием,
ни построение систем управления с запаздыванием
с изменяемой структурой. Эти. вопросы в
настоящее время весьма мало разработаны, а
проблематика так обширна и трудна, что потребовала бы
для своего решения отдельного объемистого тома.
Для тех, кто интересуется этими вопросами, в конце
книги представлен обширный список литературы.
Автор принял следующий порядок
представления материала: вначале приводится теория
линейных систем, потом — теория нелинейных систем,
причем сначала рассматриваются вопросы,
относящиеся к системам непрерывного регулирования,
затем — к системам импульсного регулирования.
Системы с чистым запаздыванием требуют для своего
описания математической модели в виде
дифференциально-разностных уравнений, а системы с
распределенным запаздыванием — в виде
дифференциальных уравнений в частных производных. Эти
модели имеют достаточно общий характер и
содержат в себе в качестве частных случаев как диффе-
5
ренциальные, так и разностные уравнения. Принята
следующая последовательность изложения: вопросы
выбора математической модели, примеры моделей
с запаздыванием, методы идентификации,
определение переходных процессов, вопросы устойчивости,
критерии качества регулирования и коррекции
регуляторов.
Все утверждения и формулы или доказываются,
или указывается литература, из которой они
заимствованы и в которой имеются доказательства
цитированных утверждений. Выводы, как правило,
иллюстрированы соответствующими графиками и
номограммами, помогающими разработчику быстро
выбрать оптимальные параметры регулятора и оценить
их влияние на динамику рассматриваемых систем.
Приношу сердечную благодарность доценту
доктору инженеру Анджею Вербицкому за
многочисленные замечания, благодаря которым удалось
избежать многих ошибок в моей книге.
АВТОР
Краков, сентябрь 1970 г.
Введение
Математические модели
управляемых процессов
Зход
и
Состояни
Дина
Связи.
не зависящие
от памяти
ex i
1
i
Память
мический npi
?цесс
Выход
У
Рис. В.1. Понятия входа, выхода и состояния
динамического процесса
§ В.1. Основные понятия
Первым понятием, необходимым для анализа воздействия обобщенных
сил на объект, являющийся предметом воздействия, есть понятие
математической модели.
Под моделью понимается математическая абстракция,
характеризующая физический, биологический, экономический процесс или процесс
другой природы. Модель представляет процесс через математические
связи между тремя совокупностями переменных: переменными входа,
переменными выхода и
переменными состояния.
Переменные входа или
выхода называются также
входными или выходными
сигналами. Часто для
краткости говорят о входе или
выходе и о состоянии.
Вход представляет в виде
явных функций времени
обобщенные внешние силы,
действующие на процесс,
динамику которого,т.е. поведение
во времени, надлежит исследовать. Аналогично выход представляет
непосредственно наблюдаемый ход процесса во времени. Вход и выход
имеют причинно-следственную связь, однако в зависимости от природы
процесса эта связь может быть сильной или слабой.
Характерной чертой каждого динамического процесса является то,
что его. поведение во времени определяется не только силами,
действующими в данный момент, но зависит также от воздействий, которые
существовали в прошлом. Можно сказать, что динамический процесс имеет
память (рис. В.1), в которой накапливаются последствия прошлых
воздействий. Для характеристики этой памяти вводится понятие состояния
процесса, т. е. совокупности числовых величин, полностью
характеризующих последствия прошлых воздействий на процесс. В зависимости
от природы процесса эта совокупность может иметь конечное число
элементов (тогда и говорят о текущем состоянии или просто о состоянии
процесса) или бесконечное число элементов, состоящих, например, из
функций, определенных на некотором интервале времени [t0 — т, t0]
(тогда говорят об обобщенном состоянии). Знания состояния процесса
(текущего или обобщенного) в момент времени t0, а также знания
внешних воздействий, т. е. входа на интервале [t0, ^], достаточно для
определения выхода и состояния процесса на полуоткрытом интервале [t0,
7
/J. В текущем состоянии содержится дополнительное требование, чтобы
модель процесса была без предсказания (или иначе — физически
реализуемой), т. е., чтобы ее состояние и выход в момент времени t < t-i не
зависели от состояний и входов в последующие моменты времени t > tx.
Иначе говоря, процесс без предсказания не реагирует на изменение своих
входных сигналов до их возникновения г.
Среди входных переменных различают обычно две разновидности:
переменные, представляющие собой целенаправленные воздействия,
именуемые управлениями (обозначаются через #), а также переменные,
представляющие собой беспорядочные воздействия, именуемые помехами
(обозначаются через г). Входные переменные процесса и особенно помехи
могут иметь случайный характер. Модель процесса называется
детерминированной, если в описывающих ее математических выражениях
отсутствуют случайные величины или случайные функции. Если такие
величины или функции присутствуют в модели или, что равнозначно, если
принимается во внимание случайный характер входных переменных,
то модель называется недетерминированной или стохастической.
Следующими важными понятиями являются пространства входных
и выходных величин и пространство состояния. Пространство входа U
представляет собой совокупность всех возможных значений входа и
данного процесса. Аналогично пространство состояния X представляет
собой совокупность всех возможных состояний процесса х, а пространство
выхода Y — совокупность всех возможных значений выхода К.
Совокупность значений времени, для которых и, х и у определены, есть
пространство времени 8. Пространства U, X и Y являются действительными
конечно- или бесконечно-мерными множествами либо подмножествами таких
пространств. Пространство Э является множеством или подмножеством
действительных чисел.
Если пространство времени непрерывно, то процесс или его модель
называются непрерывными во времени. Но если векторы входа и
состояния определены только для дискретных моментов времени tk9 причем k
принимает целочисленные значения, то пространство времени
дискретное, и модель называется дискретной или импульсной.
Очень важно различать функции, аргумент которых дискретен, т. е.
функции дискретной переменной от тех функций, которые принимают
значения из дискретного множества (изменяются на дискретном
множестве). Последние называются квантованными по уровню.
Следовательно, в непрерывных моделях вход, состояние и выход могут
быть определены для любого множества времени t £ 0, так как
пространство времени Э непрерывно, и могут принимать любые значения и £ £/, х Ё X,
так как пространства U и X также непрерывны (рис. В.2, а).
В моделях, дискретных во времени, пространство времени дискретно,
в связи с чем как вход, так и состояние не могут быть определены для
произвольных моментов времени, а Только в определенные, дискретные
моменты времени, однако они могут принимать любые значения и £ £/, хс- X
(рис. В.2, б).
В моделях с квантованием по уровню пространство времени
непрерывно, поэтому вход и состояние системы х могут быть определены для
прЪизвольного момента времени t, но только из строго определенного
множества дискретных значений по уровню (рис. В.2, в).
В системах с квантованием по времени и по уровню (именуемых далее
цифровыми) как пространство времени, так и пространство входов и
состояний дискретны. В связи с этим вход и и состояние х могут быть
1 В действительности существуют особые процессы и технические устройства, которые
осуществляют прогнозирование переменных входа, выхода или переменных состояния,
однако, строго говоря, и эти процессы не обладают свойствами предсказания, так как
прогноз будущих значений опирается на прошлые знания, а также на модель процесса и
может не соответствовать действительным будущим значениям переменных (Прим. авт.).
8
определены только для определенных дискретных моментов времени
и могут принимать только определенные значения из дискретного
множества (рис. В.2, г).
На рис. В.2, г обозначены множества возможных значений функции и
или х и показаны виды одной и той же функции, определенной в этих
\u(t);x(t)
ku(t);x(t)
u(t);x(t)
шит
в)
>—<
.
Г
?
б)
г)
Рис. В.2. Непрерывная функция времени (д); дискретная функция, квантованная по
времени (б); функция, квантованная по уровню (в); функция, квантованная по времени
и уровню (г)
множествах. На рис. В.2, а множеством возможных значений является
вся плоскость; на рис. В.2, б множеством возможных значений являются
равноотстоящие вертикальные линии; на рис. В.2, в множество
возможных значений — равноотстоящие горизонтальные линии, а на рис. В.2, г
множество возможных значений представлено совокупностью точек,
являющихся узлами решетки.
§ В.2. Математические модели процессов
Управляемые процессы — это процессы, подвергающиеся
целенаправленным воздействиям, а системы управления — это совокупность процессов
и устройств для реализации целенаправленных воздействий на эти
процессы.
Для анализа и синтеза систем управления необходимо знать их
математические модели.
Как строить математические модели? Выбор математической модели
зависит от целого ряда причин, важнейшими из которых являются:
1. Цель, которой она должна служить.
2. Потребная точность описания моделью реального процесса.
3. Ограничения, которые имеют процессы в действительности.
4. Наличие математических методов, а также вычислительных
возможностей, позволяющих проводить анализ модели за допустимое время,
т. е. возможность получения решения исследуемой задачи.
9
5. Степень изученности физических явлений в исследуемом процессе.
6. Возможности проведения измерений процесса.
7. Принятый показатель точности аппроксимации процесса с помощью
модели.
Процесс нахождения математических связей между данными,
получаемыми на основе измерений, можно осуществить двумя различными
способами:
а. Для первого из них отправной точкой служат данные измерений,
скрытые связи между которыми отыскиваются формальными способами
«чистой математики». К сожалению, чаще всего бывает так, что одна и
та же совокупность полученных данных математически может быть
интерпретирована достаточно большим числом способов. Здесь необходимо
обратить внимание на то, что для инженера проблема прежде всего
состоит в составлении уравнения, описывающего процесс, и лишь потом —
в нахождении его решения, в то время как для математика первой
проблемы вообще не существует, а важно исследование свойств каким-либо
способом полученного готового уравнения.
б. Для второго способа отправной точкой служит наличие изящных
понятий и связей в духе «чистой математики», среди которых
отыскиваются математические формулы, наиболее полно отражающие
действительность. Так, например, в настоящее время можно заметить
многочисленные попытки интерпретации понятиями функционального анализа
физических понятий таких, как расстояние, сигнал, амплитуда сигнала,
мощность, энергия и т. д. Способ этот обладает тем достоинством, что
одно абстрактное понятие может представлять несколько аналогичных
понятий, проявляющихся в различных областях техники.
В.2.1. Детерминированные модели процессов
Рассмотрим детерминированную систему, находящуюся в покое до
момента времени t0.
Выход системы определяется векторной функцией
~У1 (О"
у(0 =
U„(0J
а вход системы — векторной функцией
"«1 (О
(В.1)
(В.2)
Lu,{f)J
Статические модели. Если значения выхода системы у (t) для каждого
момента времени t£ 0 являются только функциональными значениями
входа и (f), т. е. если для всех u£U и ££0 существует зависимость
Ф МО, У (01 = О, (В.З)
причем
-фг
ф=
|-ф„
(В.4)
то говорят, что поведение системы полностью определено.
Система, описываемая уравнением (В.З), называется статической или
безынерционной. Если связь Ф между и (t) и у (f) линейна с точки зре-
10
ния обеих переменных, то и система называется линейной, и соответственно,
если Ф нелинейна, то система называется нелинейной.
Во многих случаях нелинейную систему (В.З) можно с достаточной
для практики степенью приближения рассматривать как линейную.
Для этого система (В.З) линеаризуется * относительно истинного
положения равновесия (и0, у0):
дФх дФг
дуг ' ду2 '
дФ2
dyi
дФ2
ду2
дФг
дуп
дФ2
дуп
дФп
дФп
дФп
dyi ' ду2
' дФг дФг
дих ' ди2
дФ2 дФ2
дУп А и = и{
дФ±
диг
дФ,
"Aft"
Ау2
у = у° L АУп А
дих ' ди2
диг
дФп дФп
дФп
диг
у = у° L-A^r-
и = и°
Aul
Аи2
(В.5)
L диг * ди2 у '
или в компактной форме
АуЛу = Аи° = Аи. (В.6)
Если существует обратная матрица Л^1, то можно определить
однозначно Ау в зависимости от Аи. ,
Динамические модели. Обыкновенные дифференциальные уравнения.
Для того чтобы определить развитие процесса во времени, в простейшем
случае принимается гипотеза о том, что будущее состояние процесса
(т. е. при t > t0) зависит только от состояния в момент t0 и от
уравнения и [t0> t], а мерой изменения процесса во времени служит
производная вектора состояния по времени
irx(t)=f1(x(ty9u(t)).
(В.7)
Это уравнение является уравнением состояния системы, связывающим
состояние системы с входом, причем для его решения должно быть
известно начальное состояние
х (t0) - с (В.8)
и управление
я (ад, е,= и0, п.
Обычно состояние не представляет сразу выход системы, поэтому
для полного описания системы необходимо еще уравнение выхода
У(*) = /2 [х (01- (В.9)
В большинстве случаев нелинейную модель процесса, описываемую
формулами (В.7) и (В.9), можно линеаризовать так же, как в случае
статической модели. Поступать таким образом следует особенно в тех
1 При этом должны существовать производные
d<bi I дФс
ду\ [и°. у
duk
где у, i = 1, 2 п; k = 1, . . ., г {Прим, авт.).
11
случаях, когда входы ограничены до малых вариации относительно их
средних значений.
Уравнения состояния для линейной системы имеют вид
±x(f) = A(f)x(1) + B(f)u(1);
*('о) = с; у (0 = C(t)x(t), (В. 11)
причем матрица А размерности пХп представляет собой векторную
производную векторной функции /х относительно вектора х при х = х°у
и = и0; аналогично матрица В размерности пХг — векторная
производная векторной функции/х по и при х =х°> и = и0, а матрица С
размерности р X п — векторная производная функции /2 по х при х = х°, и = и0.
Размерность п вектора состояния х называется порядком системы,
а произведение размерности г вектора входа и и р вектора у —
размерностью системы.
В частном случае одномерного процесса, т. е. с одним входом и одним
выходом, уравнение процесса может иметь вид
^л-1
dt
л-1 I
+ а1^Г + аоУ =
— h *"и _L h dm~lu
df71-
+
+ 61"5Г + 6°И»
(B.12)
с известным начальным условием у1 (/0); i = О, 1, . . ., п — 1.
Коэффициенты ai9 bt — постоянные величины.
Дальнейшие рассуждения будем проводить в предположении, что
т = п, ибо при т < л достаточно принять, что соответствующие
коэффициенты Ъь равны нулю.
Если управление и (t) есть функция порядка Ст~1 (это значит, что
она непрерывна до (т — 1)-й производной включительно), то за
координаты пространства состояния можно принять функцию и производные
выходные сигналы у (f). Однако часто функция управления и (t) не
непрерывна: например, скачкообразный входной сигнал имеет разрыв
непрерывности в точке /0- Тогда за координаты состояния нельзя принять
просто функции у (t) и ее производные, так как координаты пространства
состояния имели бы неограниченные по амплитуде скачки и нельзя было
бы вычислить каждое последующее состояние на основе предыдущего.
В таком случае координаты состояния можно определить, например,
следующим образом:
У = *i + с0и\ *
Xi — X<l -\- C±U\
Х2 == Х% -(- C2U\
Xп-1 — *п ~Г сп-1и'>
хп-= — ах
п-1лп'
Хп-л
+п-2лП-1
а±х2 — а0хг + спи
(В.13)
или в матричной форме
О, 1, 0, '.
О, 0, 1, .
.. О
.. О
1_— а0у —аъ —а2у
II Х1
*2
•
)хп_
+
Сх
с*
•
(В. 14)
*n-l A L_An _L _ _L
12
с начальными условиями
*i (*о) = У (to) —Co и (/0);
*2 (t0) = У (t0) — с0и (t0) — сги (t0);
х (to) = Уп^1 (to) — c0un-1 (to) — . • . — сп_2и (t0) — сп_г и (t0).
Дифференцируя п раз уравнение
у = хг + с0и
и используя выражение (В. 13), получим
• • • • • • •
У = *2 + coU + CXU\ У = Х3 + C0U + C±U + C2U\
уп-1 = хп + с0ип~1 + с±ип-2 Н \- сп.ги\
п
yW = —ап_ххп — ап_«хп_х агх2 — а0хг + S ^^n-i).
Подставляя результат в уравнение (В. 12) и приравнивая коэффициенты
при функции и и ее производных, получим уравнения, позволяющие
вычислить искомые коэффициенты ct: f
Со = Ьп\
С1 = fr/t-l an-lCo\
Сп ^0 ап-1Сп-1 ап-2Сп-2 ' * ' ^0^0
или коротко
с0 = *л>
1-1
ct — 6n-i— S <VWnk, ' = 1, 2,.. ./i.
*=o
Этот подход можно распространить на нестационарные системы, когда
коэффициенты at\ Ъ} в уравнении (В. 12) не постоянны, а являются я-кратно
дифференцируемыми функциями времени
at (t) и bj (t) (i = 0, . . ., n — 1; / = 0, . . ., n).
Тогда выражения, аналогичные выражению (В. 15), принимают
следующий вид:
со (t) = Ьп (0;
c'i(О = bn^t)- J S {?\tn-\)\ a«-i+k+s{t)°k(S)(°- (B-I6)
k=0 s=0
Разностные уравнения. Математические модели этого типа описывают
процессы управления, дискретные во времени, и, следовательно, процессы
импульсного управления. При постоянном шаге А дискретизации во
времени уравнения состояния системы аналогичны уравнениям для
непрерывных систем:
x[k+ll=f1(x[k]tttlk]9k),k = 0flf2,...;
дг[0] = с
y[b]=Mx[k])f (В. 18)
причем
x[k] = x(t0 + kA), у(Щ = у{и + Щ и т. д.
13
(В. 15)
(В. 17)
В частном случае линейных систем уравнения (В. 17) и (В. 18) имеют
вид
х [k + 1 ] = A [k] х [k] + В [k] и [k]\ (В. 19)
х[0] = с;
y[k] = c[k]x[k]. (В.20}
Уравнения (В. 17)—(В.20) можно также принять за первое
приближение уравнений (В.7)—(В. 11), позволяющих простым способом
находить приближенное решение этих уравнений. Полагая k = 1, 2, . . .
в уравнениях (В. 17)—(В.20), можно при известных л:(0) и и [k]
определить последовательность х [1 ], х [2], а также у [11, у [2], ... и т. д.
Вектор состояния, определенный уравнениями (В.7) или (В. 10),
а также (В. 17) или (В. 19), полностью характеризует процесс, ибо он
обладает тем свойством, что если для произвольного tx (t0 < tx <: f)
известны x(t^)9 #(9), a 9( [tl9 t]> то можно определить состояние для
всех t > t±. Знание x(tx) позволяет получить полную информацию
о состояниях и управлениях на отрезке t £ [t0, ^J, когда состояние при
£> tx зависит только от x{t^) и и (0), 0 = [tl9 t].
Резюмируя, скажем, что вектор состояния в момент tx содержит
полную информацию о предыстории процесса, т. е. для t < t±. Это основное
свойство систем без последствия и без предсказания позволяет относить
их к процессам марковского типа.
Дифференциально-разностные уравнения. В моделях большинства
промышленных процессов, таких как транспортные, тепловые и др., следует
учитывать запаздывание воздействия управления на состояние и выход.
Уравнения таких процессов могут, следовательно, иметь вид
^*(') = Л (■*«,*('), u(t-tJ9...\tt(t-%A9t)9 . (B.21)
где Tk > . . . > тх > 0 — времена запаздывания.
Для решения уравнения (В.21) на отрезке [t0, t±]9 очевидно,
недостаточно знать x(t0) и #(0), 0 = [t09 *il"» eu*e необходимо знать #(|);
£ = [t0 — Tk9 t0]. Поэтому за обобщенное состояние процесса,
характеризуемого уравнением (В.21), надлежит принять состояние x(t) и
векторные функции »(£/), I/ = U — тЛ; /]. Кроме того, пока управление
есть известная функция времени, до тех пор наличие запаздываний в
уравнении (В.21) ничем не усложняет его решения — это обыкновенное
дифференциальное уравнение.
Если, однако, процесс в уравнении (В.21) будет охвачен обратной
связью, делающей зависимым управление u(t) от состояния x(t)9 то
в окончательном уравнении системы управления появятся запаздывания
состояния. Уравнения системы могут быть представлены в виде
4г*® = Л(*i(')• *('-ТЛ>■ ■•.*('-**)*W..-.,"(<-ч),0;' (B.22)
j>(0 =/•(*(<))■ (B.23)
Уравнения этого вида» называются дифференциально-разностными.
Будем предполагать в дальнейшем, что %k > . . . > тх > 0, т. е.
уравнение (В.21) описывает процесс без предсказания с запаздыванием. Если
бы тЛ <. . . < тх < 0, то мы имели бы дело с процессом «с
упреждением», «с предвидением», который может быть положен в основу
формальной модели системы прогнозирования. В более общих моделях можно
также исследовать зависимость времени запаздывания т1э . . ., %k от
времени t и даже от состояния х. Процессы с запаздыванием (а также
с «опережением») не являются процессами марковского типа; для
определения их в будущем при t > t0 недостаточно знания состояния x(t0)
и управления и (0), 0 = [t0t t]. Здесь еще необходимо знать векторные
14
функции лг(Е), л 6» 6 = t*o — ть hh которые вместе с вектором х (t0)
определяют обобщенное состояние процесса.
Совокупность данных X
X = [х (*0); х (t) при / 6 6; и (t) при te I = Но - та, 'о1Ь (В.24)
определяющая начальные условия для уравнения (В.22), имеет
бесконечное число элементов, когда на полуоси можно выделить бесконечное
множество значений /.
В случае линейной системы уравнения (В.22), (В.23) принимают вид
± X (t) = | А. (t) X{t- xt) + Bt (t) tt(t- Tt); t0 = 0; (B.25)
y(t)=c(t)x(t). (B.26)
Дифференциально-разностные уравнения в частных случаях
вырождаются либо в разностные, либо в дифференциальные уравнения, являясь
тем самым общим видом вышеназванных математических моделей.
Интегро-дифференциальные уравнения. При описании процессов, для
которых вся «предыстория» играет существенную роль при определении
будущих состояний, необходимо использовать математические модели
в виде интегро-дифференциальных уравнений.
Уравнения состояния имеют вид
t t
х (t) и (0, J К (х (s), и (s), tts)ds,...9 jkp[x (s), и (s) /, s],
dx(t) = f1
dt
L ~CQ
y®=f*(x®). (B.28)
В частном случае в левой части уравнения (В.27) вместо производной
вектора состояния может присутствовать сам вектор состояния. Тогда
получаем не интегро-дифференциальное, а интегральное уравнение,
которое является его частным случаем.
Дифференциальные уравнения в частных производных. В случае систем
с распределенными в пространстве параметрами, таких как длинные
линии, трансокеанские кабели, теплообменники и т. п., для надлежащего
их описания следует применять математические модели, значительно более
сложные, чем представленные ранее. Уравнения состояния для примера
могут иметь следующий вид:
у (0 = /• (х (0),- (в-30>
где / — координата расстояния.
Эти модели характеризуют процессы с распределенным
запаздыванием. В частном случае линейные модели процессов могут описываться
так называемыми параболическими, гиперболическими и эллиптическими
уравнениями.
В последующей главе этот тип математических моделей будет
проиллюстрирован на конкретных примерах.
В общем случае уравнения (В.29), (В.30) могут содержать не
скалярные, а векторные функции с большим числом переменных, но анализ
этого типа очень труден.
В.2.2. Стохастические, игровые и адаптивные модели
Стохастические модели. Детерминированные модели, описываемые
уравнениями (В.7)—(В.30), рассматривались выше в предположении, что
на процесс не влияют никакие случайные воздействия. Однако такая
15-
идеализация действительности в весьма большом числе случаев
недопустима, и возникает необходимость учета влияния случайных факторов.
Пусть z (I) представляет собой вектор случайных воздействий с
известным законом распределения (чаще всего это нормальный закон
распределения с известной дисперсией). Подставляя z (t) в функции fl9 стоящие
в правой части уравнений (В.7)—(В.29), получим статистические модели,
описывающие соответствующие стохастические процессы. При
подстановке в них случайной переменной эти зависимости перестают быть
функциональными зависимостями и становятся статистическими. Для того
чтобы их можно было в дальнейшем применять, часто приходится
отказываться от использования наивыгоднейших законов распределения,
так как зависимости усредняются и последующие вычисления проводятся
так же, как и в детерминированных моделях. Однако при этом следует
помнить, что используются не величины строго детерминированные,
а лишь их средние значения.
Игровые модели. Эти модели находят применение, когда ничего не
известно о законе распределения вектора случайных воздействий z (t).
В этом случае делается грубое предположение, что вектор z (t)
изменяется наихудшим образом с точки зрения достижения цели управления.
Затем полагают, что вектор z (t) является как бы управлением
противника с противоположной целью управления. Таким образом, задача
управления сводится к проблеме теории игр. Используя основные
положения теории игр о наличии седловой точки, можно в ряде случаев
определить вектор оптимального управления и (t). Оптимальный процесс
управления, реализованный на этой основе, в наихудшем случае будет
лучше любого иного. Предположение о полной неизвестности закона
распределения вектора воздействий z (t) приводит, однако, к
дорогостоящим системам, которые к тому же могут работать в среднем хуже, чем
обычные системы управления^ Кроме вышесказанного возникает задача
получения информации о воздействиях z (f) в процессе управления.
Адаптивные модели. В этих моделях предполагается, что вид функции
распределения вектора z (t) известен и лишь не известны точно величины
ее параметров, таких как, например, среднее значение или дисперсия.
Для более точного определения величин, характеризующих систему,
вначале принимаются априорные вероятные значения и затем на основе
формулы Байеса после выполнения необходимого числа измерений
уточняются величины параметров. Повторяя этот процесс многократно,
получаем значения параметров, которые полно характеризуют данную систему.
Из этого обзора видно, что всегда стремятся свести стохастические,
игровые и адаптивные модели к детерминированным моделям. Выбрав
модель, необходимо проверить с помощью вычислений соответствие
модели реальному процессу.
§ В.З. Вычислительные аспекты
Процесс получения численного решения в настоящее время является
в сильной степени интуитивным, и в век математических машин его не
следует отождествлять с получением аналитического решения.
В процессе решения задач (на рис. В.З представлен этот процесс)
могут возникать три вида трудностей: аналитические, вычислительные
и принципиальные.
Аналитические трудности. На начальной стадии процесса
предполагается, что задача уже сведена к задаче решения системы уравнений.
Однако во многих случаях результаты решения не могут быть
представлены в виде элементарных функций или хотя бы в виде табличных. Тогда
с целью получения численных результатов следует применить различные
приближенные методы вычислений, такие как методы Пикарда, Ритца,
16
Монте-Карло и др. При этом непрерывные операции должны быть
заменены операциями в конечных разностях. В некоторых случаях такие
операции могут не приводить к получению решения. За этим исключением,
однако, аналитические трудности относятся к простейшим.
Вычислительные трудности. О них уже частично говорилось, но
с точки зрения применения вычислительных машин осветим их более
подробно.
Одним из парадоксов техники вычислений с помощью вычислительных
машин является тот факт, что может не быть никакой пользы от
получений решения в явном виде. Хорошей иллюстрацией этого факта является
решение системы линейных уравнений по правилу Крамера в виде
частного от деления двух определителей. При больших значениях этих
определителей в результате вычитания одного из другого могут возникать
весьма большие ошибки, особенно, если значение главного определителя
1 Задача
I ?
*
Конец
Существует
необходимость
упрощения
нет
До
— '' »1
Нет
Нет
Да
Проверка
результата
в исходной
задаче
Да
т.
1
Задача
упрощена
Процесс
решения
Проверка
б упрощенной
задаче
Да
Результат1
решения
ш 1
Проводилосьли
упрощение
задачи
i
Нет
Рис. В.З. Структура процесса решения задачи
близко к нулю. Аналогичные трудности имеются при вычислении сумм
слабо сходящихся бесконечных рядов.
В этих случаях применение итерационных методов и повышение
скорости сходимости является делом первостепенной важности.
Большие быстродействующие машины позволяют использовать
алгоритмы, которые нельзя реализовать на малых машинах, а также
позволяют решить практические задачи, характеризующиеся весьма большим
числом переменных. Здесь существует опасность использования машин
этого типа для выполнения простых задач, решение которых можно легко
получить с помощью карандаша и бумаги. Роль вычислительных машин
как инструмента не должна низводиться до положения панацеи от всех
вычислительных бед.
Принципиальные трудности. Основные трудности без учета
технических, экономических и иных аспектов заключаются всегда в четкой
математической формулировке задачи. Эти трудности лежат на более высоком
уровне, чем вышеназванные, которые всегда можно преодолеть с помощью
метода аппроксимации.*
Это пока скорее искусство, чем наука: как пройти «узкой тропинкой,
ведущей между трясиной сложности и пропастями упрощений»?
1 Кроме того, следует помнить, что нередко за сложность модели
платить приходится упрощениями в методах вычисления, и неизвестно,
какая из ошибок больше — ошибки метода вычислений или ошибки от
несовершенства модели.
Список литературы
1. Беллман Р. Процессы регулирования с адаптацией. М., «Наука», .1964.
2. Freeman H. Dicsrete—Time Systems. New York, J. Wiley, 1965.
3. Turowicz A., Gdrecki H. Sterowanie optymalne. WiadomoSci Matematyczne, Seria II,
XII, 1969, str. 115-149.
2 X. Турецкий
Глава I
Примеры объектов
с запаздыванием
Стремительный рост требований к темпам производства и качеству
продукции способствовал бурному развитию автоматизации
производственных процессов. Повышение темпов привело к тому, что управляемые
величины стали изменяться во времени, причем с большими скоростями.
В этих условиях стало играть важную роль время, которое проходит
от момента измерения значения регулируемой величины до момента
принятия решения и выдачи сигнала управления. Эффект запаздывания при
наличии обратной связи особенно ярко проявляется при автоматическом
управлении высокоскоростными самолетами, ракетами и большими
системами при наличии больших расстояний. Запаздывание реакции
управляющей системы на возникшее нарушение процесса приводит, как
правило, к возникновению автоколебаний в замкнутой системе, а нередко —
и к потере устойчивости системы. При необходимости учитывать время
запаздывания в математической модели следует использовать уравнения
в форме, более общей, чем дифференциальная, а именно —
дифференциально-разностные уравнения, представляющие собой более общий
класс функциональных уравнений.
Дифференциально-разностные уравнения впервые появились в XVIII в.
в работах Лапласа и Эйлера, однако проявление интереса к ним и
развитие их теории в связи с потребностями практики относятся ко времени
второй мировой войны. Основополагающей работой по теории
устойчивости систем, описываемых уравнениями этого типа, является работа
Л. С. Понтрягина [70]. К наиболее известным публикациям относятся
работы Р. Беллмана и К. Кука [III. 1] *, А. Д. Мышкиса [56], Э. Пинни
[68], А. Халанаи [32], Л. Э. Эльсгольца [22]. В теории оптимальных
систем управления с запаздыванием к важнейшим принадлежат работы
Н. Н. Красовского [51*]**, Л. С. Понтрягина и Болтянского [69]„
М. Н. Огюсторелли [IV.30J, М. Е. Салуквадзе [791 , Ф. М. Кирилловой
[40, 44 *], Г. Л. Харатишвили [34], Д. Чанга и Е. Ли [21 *].
Математическая модель в виде дифференциально-разностных
уравнений охватывает в частных случаях процессы, описываемые
дифференциальными уравнениями (т. е. непрерывные системы регулирования), и
процессы, описываемые разностными уравнениями (т. е. импульсные
процессы регулирования). Кроме чистого запаздывания, рассмотрение
которого приводит к дифференциально-разностным уравнениям, в систе-
* При ссылке к спискам литературы других глав к номеру библиографического
источника прибавляется римская цифра, обозначающая номер главы.
** Ссылка на источник, помещенный в конце книги в дополнительном списке
литературы, сопровождается звездочкой.
18
мах управления встречаются так называемые распределенные
запаздывания. Это запаздывание наблюдается в системах с распределенными
параметрами, описываемыми дифференциальными уравнениями в частных
производных [121. В теории регулирования встречается также понятие
эквивалентного запаздывания, которое используется при замене
дифференциальных уравнений высокого порядка дифференциально-разностными
уравнениями низкого порядка или нелинейных дифференциальных
уравнений линейными дифференциально-разностными уравнениями [86].
В данной книге речь будет идти о системах, которые можно описать
при помощи дифференциально-разностных уравнений; затем о таких,
в которых наблюдается чистое запаздывание, и о таких, в которых
присутствует распределенное либо эквивалентное запаздывание, но которое
достаточно точно можно описать дифференциально-разностными
уравнениями.
Возникает вопрос, какие явления с точки зрения пригодности теории
и методов исследования требуют применения математической модели
в виде дифференциально-разностных уравнений или же введения времени
запаздывания, определяющего неоднозначность между управляющим
сигналом и выходной реакцией.
Оказывается, что явления этого типа наблюдаются не только в
технике, но также в биологии, экономике и других областях.
Типичными здесь являются процессы: транспортные, перемешивания,
горения, эволюции, экономические, организационные.
Распределенное запаздывание, как правило, наблюдается в длинных
линиях, таких, например, как электрические, тепловые, гидравлические,
пневматические.
Однако вообще модели длинных линий достаточно точно можно
аппроксимировать при помощи дифференциально-разностных уравнений.
§ 1.1. Объекты с чистым запаздыванием
1.1.1. Транспортные процессы. Регулирование количества угля
на ленточных транспортерах
Система регулирования (рис. 1.1) должна обеспечить постоянство
поступления угля в мельницу. Уголь подается из бункера А с помощью
ленточного транспортера В на весы С, откуда он ссыпается в мельницу D. Тре-
Рис. 1.1. Регулирование
количества угля на
ленточном транспортере
77V7 V УТУРТУТСуХ
W С ' ■** '
I 1 1 *■ R
f I I
t'^t Ju
буемый вес угля w может быть задан массой груза, помещенного на
левом плече^весов. Разница между заданной величиной w и
действительной массой угля у подается в виде сигнала ошибки 8 на регулятор /?,
2* * 19
который формирует управляющий сигнал и на мотор М, перемещающий
заслонку Y.
Изменение -количества угля, поступающего из бункера А на
транспортер В в момент времени /, измеряется не сразу, а спустя некоторое
время т, в течение которого этот уголь будет перемещен на весы С. Этот
интервал времени зависит от скорости транспортировки угля v и
расстояния I точки измерения от точки управления. При постоянной
скорости v интервал времени т можно определить из выражения
V
(1.1)
Управляющий сигнал и проходит без искажений, а лишь с
запаздыванием т. При скачкообразном
изменении сигнала и реакция
процесса показана на рис. 1.2.
llmG
*l
<7
п
0
\
53
\
\
J
г
i
,
1
to
г
~о
1
=»
^
Ч
t
1
t
\ит=я
ит=г^
0
c)T=j л
ьк
or=f
&
:/ит=
1 ReQ
Тит*0
1 т-!
>ит=0.55
1
Рис. 1.2. Реакция объекта на единичное
{воздействие
Рис. 1.3. Амплитудно-фазовая
частотная характеристика объекта с
запаздыванием
Связь между приращениями Ау и Аи относительно положения
равновесия, заданного требуемой величиной w9 имеет вид
Ay (t) = КАи (t — т),
.а передаточная функция объекта регулирования
AY(s)
AU(s)
:G(s) = /Ce-^.
(1.2)
(1.3)
Полагая s = /со, получим соответственно частотную характеристику
G (/со) = /Се-/Т = К (cos сот — /sin сот), (1.4)
вид которой показан на рис. 1.3.
Из выражения (1.4) следует, что действительная и мнимая
частотные характеристики есть соответственно косинусоида и синусоида.
Так как ординаты характеристик не стремятся к нулю с ростом частоты со,
то в этом случае нельзя говорить об ограниченной полосе пропускания.
Неограниченность полосы пропускания гармонических составляющих
следует, очевидно, из факта, что запаздывание только смещает входной
сигнал во времени и не искажает его.
20
1.1.2. Система стабилизации толщины листа при холодной прокатке
Рассмотрим систему стабилизации, представленную на рис. 1.4. Так как
датчик толщины листа по конструктивным соображениям не может
находиться под валками, а только на - некотором от них удалении /, то тол-
щиномер измеряет толщину листа с некоторым запаздыванием т = —,
где v — скорость прокатки листа. Из-за этого выходное напряжение дат-
А
Рис. 1.4. Система стабилизации толщины холоднокатаной ленты
чика ир, пропорциональное разнице между заданной б2 и измеренной
толщиной б, запаздывает относительно действительного значения
толщины. Это напряжение усиливается усилителем /С, выход которого
подключен к обмотке возбуждения электромашинного усилителя.
Электромашинный усилитель управляет работой двигателя постоянного тока
с независимым возбуждением, который изменяет положения валков
прокатного стана.
Аналогичное временное запаздывание в передаче информации
наблюдается в магнитофоне в зависимости от расстояния между головками
записи и воспроизведения.
1.1.3. Двигатель постоянного тока с независимым возбуждением
Рассмотрим двигатель постоянного тока с независимым возбуждением
(рис. 1.5). Предполагается, что в обмотке возбуждения течет.постоянный
ток определенной величины, а напряжение и, подводимое к клеммам ротора,
является управляющим сигналом.
Двигатель нагружен моментом г. Управляемыми
величинами являются угловая скорость
двигателя со и электрический момент т.
С целью упрощения рассуждений
положим, что такие нелинейные эффекты
как насыщение, гистерезис, трение можно
не учитывать. Полагаем, однако, что
ротор двигателя не может вращаться
под действием внешнего момента г,
например из-за наличия стопора. Наличие
этого ограничителя вносит некоторый
нелинейный эффект. Будет показано, что
этот эффект может быть заменен
эквивалентным запаздыванием.
Анализ работы двигателя будет проведен в два этапа. На первом этапе,
когда на клеммах двигателя уже появилось напряжение сигнала и, течет
ток i и нарастает электрический момент /п, ротор не вращается, т. е.
21
Рис. 1.5. Схема двигателя
постоянного тока с независимым
возбуждением
о) = 0, так как момент нагрузки z еще превышает электрический момент /п.
На втором этапе начинается вращение с угловой скоростью ш.
Уравнения движения двигателя имеют следующий вид:
Этап I, 0 < t < т.
Уравнение напряжений
u(t) = i(t)R + L^P~. (1.5)
Уравнения моментов
т (t) = kmi (t); (1.6)
г (t) = г„ (1.7)
где R и L — соответственно сопротивление и индуктивность обмотки
ротора двигателя; km — коэффициент пропорциональности между
моментом и током.
Преобразуя уравнения (1.5) и (1.6), найдем передаточную функцию
п (s) - M(s) - ^ = — (I 8)
где Тх = L/7? — постоянная времени обмотки ротора. Полагая, что
управляющее напряжение постоянно при t > 0:
и (t) = U0 = const, (1.9
находим на основе уравнения (1.8) при нулевых начальных условиях
. = тД1-е г')
т(0 = тД1-е Г'Г (1.10)
где tnz = -g-km — пусковой момент двигателя.
Для определения времени, по истечении которого двигатель
начинает движение, приравниваем электрический момент и момент нагрузки:
m(T) = m2[l-e~Tl) = Zs- (Ml)
Из уравнения (1.11) видно, что время запаздывания т зависит от
величин mz и ms и, следовательно, является эквивалентным
запаздыванием для некоторого нелинейного эффекта:
Тх = 7Уп Ц-. (1.12)
пг2
Из уравнения (1.12) следует, что для того, чтобы двигатель как можно
лучше отрабатывал управляющий сигнал, т. е. чтобы время т было как
можно меньше, величина пускового момента должна быть значительно
больше величины момента нагрузки.
Так как двигатель начинает движение в момент равенства
электрического и нагрузочного моментов, т. е. через время т, то нарастание угловой
скорости (о происходит с запаздыванием на т относительно управляющего
сигнала.
Этап II, /:Ь>т.
Принимая упрощающее предположение, что изменение скорости
вызывается изменением напряжений и токов в течение времени,
предшествующего т, находим уравнение напряжений
u(t-<T) = i(t-<v)R + Ldiit-T)+e(t), (I.13)
где электродвижущая сила имеет вид
e(t) = ke<o(t), (I.14)
a ke — коэффициент пропорциональности.
22
Уравнение моментов
m(t — T) = kmi (t — x);
Z(t-T) = Z9(t-T) + J
dcojt)
dt
(1.15)
(1.16)
в которых J — момент инерции, приведенный к валу двигателя.
Уравнения (1.13)—(1.16), преобразованные по Лапласу, имеют вид
U (s) е-« = / (s) Re~ST + Lsl (s) e~sT — Li (т) е~" + E (s); (1.17)
E(s) = keQ(s); (1.18)
M (s) e-* = kmI (s) e-ST; (1.19)
Z (s) e-s* = Zs (s) e-« + JsQ (s), (1.20)
где i (т) — величина тока в момент равенства моментов.
Приравнивая между собой уравнения (1.19) и (1."20), определим
величину тока в момент времени, когда моменты двигателя и нагрузки равны:
/(s)er-«=AW.e-"+^sQ(s).
(1-21)
Подставляя формулы (1.21) и (1.18) в выражение (1.17) и учитывая, что
после преобразования получим
(U (s) - Щ^) е-« - *, (7\7^2 + T2s + 1) Q (s),
где Т2 = JRIkekm — электромеханическая постоянная времени;
-г^- = со0 — скорость холостого хода;
(1.23)
ke
Асо — уменьшение угловой скорости, вызванное
статической нагрузкой;
<йп — <*>о — Асо — номинальная скорость.
Тогда уравнение (1.23) с учетом формулы (1.9) можно записать в виде
^^^(W+ks + ir (L24)
По конструктивным соображениям у большинства двигателей
Т2 > 47\. (1.25)
С помощью обратного преобразования уравнения (1.24), учитывая
неравенство (1.25), получим
( 0 при /^т;
ш(*) =
t-T
<*п 1
Ti-T,
+
?2
(1.26)
при /:
где
Т[ 1Тг V \ 27\)
J
Г2
ГЛ
7У2 •
(1.27)
23
Выражение для момента на основе формул (1.10), (1.15), (1.16) и (1.26)
можно записать в виде
m(t)-
т2\\
— е Т%) при 0^/^т;
t-x t-x\ ПрИ T^t.
2S+
Jton
п
?2
(1.28)
Г1-Г2
Момент достигает максимального значения, когда dm (t)/dt = 0, т. е.
te=%+ TlT2 , lrw, / (1.29)
и его величина равна
т2
(1.30)
Величина момента при / = тив установившемся состоянии при t = 00
равна zs.
На рис. 1.6 представлены переходные процессы по угловой скорости
со (t)An моменту m (t).
Заканчивая рассмотрение двигателя, следует подчеркнуть, что там,
где речь идет о разгоне при полной нагрузке, всегда будет наблюдаться
запаздывание. В случае
управления мощными установками,,
например в прокатном
производстве, запаздывания могут
оказывать значительное
влияние на качество процесса.
1.1.4. Другие процессы
Запаздывание, которым нельзя
пренебречь, наблюдается во*
многих процессах. Например,
в работе [15] рассматривается
процесс горения в жидкостном
реактивном двигателе.
Временем запаздывания здесь
является время, которое
необходимо для впрыскивания
топлива в камеру сгорания и
достижения требуемого
давления. Запаздывание этого типа
очень часто служит причиной
больших трудностей при
управлении производственными
процессами, в которых
присутствует горение.
Значительные запаздывания наблюдаются в процессах сушки. При
сушке известняка во вращающихся печах [58] запаздывание от
изменения влажности до изменения температуры достигает нескольких
десятков минут. На рис. 1.7 представлены экспериментально снятый
переходный процесс при скачкообразном воздействии и частотная характеристика
вращающейся печи как объекта управления. Автор представляет
передаточную функцию такого процесса в виде
G (S) = /Се—«V(l + sT)\
Рис. 1.6. Изменение угловой скорости
двигателя (а); изменение момента двигателя (б)
24
где входом является изменение влажности, а выходом — температура
в печи. Постоянная времени равна приблизительно 2 мин, а время
запаздывания — 30 мин.
Другой очень интересный пример управления процессами с
запаздыванием описан в работе [83]. 3hro процесс производства бумаги. На
многих этапах этого производства присутствуют запаздывания, по величине
значительно превышающие постоянные времени, что создает большие
трудности при управлении процессом. Упомянутая работа содержит
блок-схемы^ передаточные функции и экспериментальные данные,
полученные при управлении с помощью вычислительных машин.
Применение вычислительных машин позволило уменьшить разброс в составе
бумажной массы, повысить выход продукции и другие экономические
показатели.
Is
eg
to
0,86%
40 60 мин
т i 1 1 1
Рис. 1.7. Характеристики процесса сушки кирпича:
а — реакции на скачок; б — частотная характеристика
Еще одним важным технологическим процессом, имеющим большое
время запаздывания, является производство стекла. Опыт управления
этим процессом при помощи вычислительных машин описан в
интересной работе [8]. Авторы приводят приближенную модель процесса в виде
передаточной матрицы и результаты исследований, полученные при
экспериментальном управлении с помощью управляющих машин, и
сравнение с ручным управлением.
Запаздывание часто встречается при управлении в химической
промышленности. Классическим примером нелинейного процесса,
содержащего чистое запаздывание, является регулирование показателя рН
какой-нибудь жидкости. Анализ системы этого типа дан в работе [82].
Система регулирования показателя рН представлена на рис. 1.8.
Статическая зависимость между значениями рН раствора и количеством
реагента существенно нелинейна (рис. 1.9). Но систему можно приближенно
представить с помощью линейной модели, полагая малыми отклонения
от заданного значения рН. Управление обычно осуществляется с помощью
пропорционально-интегрального регулятора, а процесс приближенно
может быть представлен передаточной функцией
G (s) = Ke-*V(l + sT).
Величины постоянных времени и запаздывания имеют примерно один
и тот же порядок.
Другим примером процесса, содержащего запаздывание, может
служить производство серной кислоты. Запаздывание в подобных
химических процессах возникает в связи с тем, что химические реакции требуют
25.
прежде всего перемешивания реагентов, а перемешивание растворов
обычно происходит достаточно медленно. Резюмируя,- можно сказать,
что все процессы, связанные с перемешиванием, содержат запаздывание.
В системах управления, где одним из элементов является человек,
Бее чаще возникает проблема скорости реакции человека на внешние воз-
Жидкость
Реагент Электроды
Рис. 1.8. Схема системы регулирования рН
действия. Это имеет особое значение при больших скоростях протекания
процессов, например при управлении современными самолетами или
ракетами. В связи с этим проведено большое число исследований с целью
приближенного определения математической модели реакции человека.
Вообще говоря, эта модель весьма сложна, однако для проведения
приближенного анализа часто достаточно воспользоваться линейной моделью
с запаздыванием (см. например, работы
Макруэра [49], Макдоннела [361 и
работы [7, 36, 45, 53, 57]). Большинство
авторов предполагает, что если входной
сигнал наблюдается пилотом визуально и
имеет случайный характер в достаточно
широкой полосе частот, а выходным
сигналом служит мышечная реакция пилота,
то поведение пилота может быть
приближенно представлено с помощью
передаточной функции
рН
10
\м
о
10 мп
GP(s)-
/Се~
l+sTt
1+sTi l+sTs
(1.31)
Рис. 1.9. Статистическая
характеристика изменения рН 2%-ного
содового раствора в 100 мл 0,2%-
ного раствора фосфата
где запаздывание т характеризует время,
необходимое для того, чтобы визуально
полученный сигнал достиг центральной
нервной системы, а оттуда на
конечности пилота поступил сигнал управления. Оно обычно равно 0,15—
0,25 с и достаточно постоянно для каждого человека.
Постоянная времени Тг характеризует ограниченность скорости реакции
мускулов и равна приблизительно 0,1 с. Постоянные- же времени Т2
и Т3 в большей мере зависят от вида входного сигнала. Наибольшие
значения постоянной времени достигают 2—3 с. Коэффициент усиления
также может изменяться, однако для конкретного человека — в не очень
26
широких пределах. Постоянные времени Г2, Т3 и коэффициент усиления К
характеризуют адаптивные возможности пилота к действующему
входному сигналу.
На рис. 1.10 показана блок-схема системы управления, включающая
пилота [451. На рис. 1.11 представлен для примера вид частотных харак-
Внешняа обстановка
Надигация
Органы управления
Программа полета
hr©H
Приборы
ффф
Динамика самолета'
(-)
Регулятор
а)
i(t)
~Ф
<->
eft)
Человек как элемент
системы управления
Шумовой
сигнал
Cp(ju) =
(ke-J"Tn(UjuTL)
(i+jtjTN)(i+ju)Tj)
*е
pit)
Линейный оператор
Технические
устройства
Gs(jcj)
■Ф
z(t)
6)
Случайные внешние
воздействия
Рис. 1.10. Функциональная схема системы управления пилотируемым самолетом (а);
блок-схем а системы (б)
теристик различных пилотов при одном и том же входном сигнале, а на
рис. 1.12 — частотные характеристики одного пилота при различных
входных сигналах. Из рисунков видно, что получение хорошей модели
в сильной степени зависит как от вида сигнала, так и от индивидуальных
особенностей различных пилотов. Работы в этой области в настоящее
время проводятся достаточно интенсивно в связи с тем, что даже при
полной автоматизации процессов человек играет решающую роль в
ответственных ситуациях. Очевидно, эти исследования важны не только
в авиации, но также и при автоматизации производственных процессов.
27
Время запаздывания присутствует также при построении
математических'моделей некоторых биологических процессов, таких как рост
популяции и др. [171. Колебания роста популяции относительно некоторого*
заданного значения требуют введения для их описания дифференциально-
разностных уравнений.
1т0
1
-2 -У
xj^3*4/
-/
\
-2'
-3
v;.
-6
-7
-в
-9
-to
^^zIL
-12
_ 0,3
1
'
-ftf
-
_
-
-
-
-
-
*=3S.0b ^\0,6
i\V i i л, i
2 A3 *45 6\7
°'5l o.s\ 0.7X
1
Ret
Рис. 1.11. Частотные характеристики
различных пилотов при одинаковых входных
сигналах
Рис. 1.12. Частотные характеристики
пилота при различных входных сигналах
Стоит, наконец, заметить, что многие экономические задачи,
являющиеся в настоящее время предметом исследования, также требуют для
двоей правильной постановки применения математических моделей в виде
сифференциально-разностных уравнений (см., например, в книге Минор-
ского [54], экономические модели Колецкого и организационные задачи^
Ракарда). Задачи эти в настоящее время играют большую^ роль при
получении алгоритмов оптимального управления экономикой страны.
§ 1.2. Объекты с распределенным запаздыванием
Рассмотренные выше процессы содержали чистое запаздывание, и их
можно было описать дифференциально-разностными уравнениями.
Однако в большинстве тепловых процессов, а также процессов, в которых
происходит передача сигналов на расстояние при помощи длинных
электрических, гидравлических и других линий, наблюдается запаздывание,
распределенное по всей длине линии. Это запаздывание, в отличие от
чистого4 запаздывания, приводит к искажению передаваемых сигналов.
Процессы этого типа требуют для своего описания дифференциальных
уравнений в частных производных.
- Прохождение сигналов через объекты с распределенными параметрами
при помощи некоторых упрощающих предложений можно свести к
задаче прохождения сигнала относительно только одной координаты —
расстояния. Так бывает, как правило, в случае электрических и
гидравлических длинных линий и иногда в теплопередачах. В этих случаях
рассматриваемые объекты можно описать при помощи линейных
уравнений в частных производных первого или второго порядка.
28
Дифференциальные уравнения второго порядка вида
+ Ьх (0 -^ + К (/) -g- + с (/) * = ц (/, о (1.32)
подразделяются на три типа:
1. Гиперболическое уравнение, для которого
ад»-(х)2<0' (1-33)
^представляет собой волновое уравнение. В простейшем случае оно имеет
вид
2. Параболическое уравнение, для которого
«ia3-(^-)2 = 0, (I.35)
представляет собой уравнение теплопроводности или уравнение
диффузии. В простейшем случае оно имеет вид
Wr-W = °- (L36>
:3. Эллиптическое уравнение, для которого
^з-(-|-)2>0, (1.37)
представляет собой уравнение потенциалов. В простейшем случае оно
имеет вид
Ж + |г-0. (1.38)
1.2.1. Длинная электрическая линия
Длинная линия является примером объекта с распределенными
параметрами, в которых проявляется распределенное запаздывание. Объекты
этого типа вызывают как запаздывание сигналов, так и их искажение.
Дальнейшее рассмотрение будет проведено на основе работ [94, 97].
Пусть будет задана однородная длинная электрическая линия, т. е.
такая, у которой на единице длины сопротивление/?;-, индуктивность Ly,
утечки Gj и емкость С/ постоянны независимо от координаты /.
На рис. 1.13 изображен начальный отрезок длинной линии.
Уравнение напряжений можно записать в следующем виде: .
u(t, /)- [u(t, /)+*ИШ<и] =R{dU(t,r) + Ltdl££±. (I.39)
Аналогичный вид имеет уравнение токов
i (t, l) - [i (t, l) + 2Ш dl] = G, dlu (t, I) + C, dl Щ^-. (1.40)
29
После преобразования получаем два основных уравнения длинной
электрической линии:
Qj— — Hi* (h 4 + Li —Qf- >
«tti-cw.o+c,*^
dt
(1.41)
(1.42)
Дифференцируя уравнение (1.41) по переменной / или /, а уравнение
(1.42) — по переменной / или t и складывая при этом левые и правые
Рис. 1.13. Эквивалентная схема участка длинной линии
части, после преобразований получим дифференциальные уравнения вто*
рого порядка относительно только одной переменной:
дЧ LiCi 4£ - (R/Cj + G,Lt) %■ - GjR,u = О
либо
дЧ
dl*
•*П dt2
Lfii -gr - (Rfi, + GjLj) *■ - Gfri = 0.
(I.43>
(I.44>
Это уравнения гиперболического типа и, следовательно, это волновые
уравнения напряжений и токов.
Систему дифференциальных уравнений в частных производных (1.41)
и (1.42) преобразуем дважды по Лапласу. Преобразуя относительно
переменной /, получим
- -^Jr*1 =7 (*. 01*/ + *Ч\ ~ LM0,0; (i.45>
~ ^dT- = U <S' l) [Gi + sC/] _ CiU (°> l)- <L46>
Используя далее преобразование по переменной /, получим
qU (s, q) + [Rj + $L,] I (s, q) = U (s, 0) + L,I (0, q); (1.47).
[G, + sC;] U (s, q) + ql (s, q) = C,U (0, q) + / (s, 0). (1.48)
Искомые преобразования U (s, q) и / (s, q) найдем, решая систему из.
двух линейных уравнений:
///- п\ — Я\Ц (* О + Ljl (0. q)] - (Rj + sL,) [CjU (0. q) +1 (a. 0)1 . ,, 4qY
tin „\—4 ICfU (0. Я) + / («. Ql ~ (G/ + «Су) [t/ («. 0) + Lfl (0, g)) ,, ^
Характеристическое уравнение имеет вид
<72 - (G, + sCf) (Rj + sL,) = 0.
(I.51>
30
Обозначим два его корня через
Яг. 2 = ±V> (1.52>
где
у (s) = YiGj + sC^Rj + sLj) (I.53)
называется волновой постоянной.
Для упрощения исследований предположим, что в момент / = О
не было запасенной энергии в линии на протяжении всей ее длины за
исключением только начальной точки / = 0.
При этом предположении
U (0, q) = I (0, q) = 0, (1.54)
а уравнения (1.49) и (1.50) с учетом выражения (1.53) упрощаются:
U («, Я) = ^^ U (s, 0) - «±±^-1 (s, 0); (1.55)
1 & Я) = -^ ' (*, 0) - "|r=f- U (s, 0). (1.56)
Делая обратное преобразование по переменной q, получим
U(s, /) = eV'+e~V< U(s, 0)-еУ'-2е~У1 ZI(s, 0); (I.57>
I (s, /) = ^ I(s, 0) ^ y^, (1.58)
где
г^=уЩЩ <LS9>
— волновое сопротивление линии.
Уравнения (1.57) и (1.58) можно представить в другой форме записи:
U (s, I) = U(s, 0) cosh?/ — / (s, 0) Z sinhy/; (1.60)
/(s, /) = /(s, OJVoshvZ —-^|^-sinhv/. (1.61)
Полагая в уравнениях (1.57) и (1.58) I = lki можно определить
передаточную матрицу ненагруженной длинной линии, у которой в точке lk
ток имеет величину / (s, /Л), а напряжение U (s, lk). Так как
coshy/*, — Zsinhv/Д ,ц(8 о)
ч-
то, вводя обозначения
/1/(8. W \ _ / COsh^« ~ZslnhV/A m(s, о) \
U(s, /*) / "\-4-sinhv/, cosh?/* l\/(s, 0) j < ' '
можно записать, что
где
'ЧТО-
G (s) К = X, (1.65)
fcoshylk, —Zslnhylk \
G(s) = \ l , . , . , (1-66)
w у ^-slnhv/ft, coshv4 у
«есть передаточная матрица. Таким образом, линии этого типа являются
элементом с двумя входами и двумя выходами. Ее блок-схема
представлена на рис. 1.14.
Если вместо условий в начале линии О (s, 0), / (s, 0) известны условия
в конце линии U (s, 4)> I (s, 4), то уравнения (1.60) и (1.61) преобразуются
так, что / заменяется на 4 — /ив связи с изменением положительного
направления оси / изменяются знаки токов / (s, /) и / (s, lk — I):
U (s, I) = U (s, lk) cosh y(lk — l)+I (s, lk) Z sinh у (lk — /); (1.67)
7(s, l) = T(s, /Jcosh7(4-/) + i%^sinhy(4-/).. (1.68)
Теперь рассмотрим случай, чаще всего встречающийся на практике,
когда на обоих концах линии находятся элементы с сосредоточенными
u(st0)
COShylK
Ф
*-*4-fsmhylh
1(5.0)
Г+Л-ZsinhylK
иШк)
coshylK k»<±>
/Js.U)
Рис. 1.15. Длинная линия с
сосредоточенными элементами на входе и
выходе
JU(s,OJ ) —*^--*J*- /U(S.IK)\_
Рис. 1.14. Блок-схема длинной линии
параметрами (рис. 1.15). Система описывается следующими уравнениями
в операторной форме:
Е (s) — I (s, 0) Zx = U (s, 0) — в начале линии; (1.69)
'U (s> lk) = J (s> 4) Z2 — b конце линии. (1.70)
Исключая в уравнении (1.67) ток / (s, 4), при помощи выражения
(1.70). получаем
U(s,l) = U(s, /ft) [coshтЛ - 0+-£-slnhT(/*-/)]• (1.71)
Полагая в выражениях (1.67) и (1.68) / = 0 и используя формулу
(1.69 , найдем
E(s)-I (s, 0)Z1 = U (s, lk) [cosh 74 + 4; Sinh yl*] (1 '72)
' (s, 0) = t/ (s, 4) [^ cosh 74 + -j slnh ?'*]
(1.73)
Из уравнений (1.72) и (1.73) исключаем ток / (s, 0), получаем
выражение для U (s, 4) и подставляем его в уравнение (1.71). Тогда окончательно
получаем
t/(s,/) = -f
Z2 cosh у (k — /) + Z sinh у (lk — I)
(1+A)C0ShY<ft+(-| +4)sinhV/ft'
(1-74)
32
Аналогично можно получить
Е cosh у (Ik — О + -f sin h у (lk — /)
/(s'/)=x'(1+t)cosh^+(i+^)slnh^' (I'75)
Если сопротивление нагрузки Zz равно волновому сопротивлению
линии или если линия бесконечно длинная (lk = оо), то выражения (1.74)
и (1.75) значительно упрощаются:
* u(s'Q=YTzTEe~yll Г(176)
/^/) = TTzT£e"v/» <L77>
так как не наблюдается явление отражения волны в конце линии.
Дальнейшие упрощения выражений (1.76) и (1.77) можно
осуществить, полагая, что сопротивление источника напряжения равно нулю
(Z1 = 0), т. е.
U (s, 0 = £e-v<; (I.78)
/(s, /) = -§-e-Y/. (I.79)
На основе выражений (1.78) и (1.79) рассмотрим подробно
разновидности длинных линий.
Длинная линия без потерь на сопротивление и утечки. Rf = Gy я« 0.
Волновая постоянная определяется из выражения (1.53):
у = 8У"ЦСг (!-80)
Учитывая, что скорость распространения волны
получим
Y = -f. (I.82)
Волновое сопротивление на основе выражения (1.59)
г=У^. (1.83)
Передаточные функции линии определяются соответственно
выражениями
<*<«. 0 = -?$--•"•': С-84)
о-ЛО-ад-^.-'"! (1-85)
отсюда видно, что такая линия в точке, лежащей на расстоянии 1г = хпг
от начала, представляет собой элемент с сосредоточенным запаздыванием
Ti = IJV> T- е- не Дает искажений сигнала.
На основе выражений (1.84) и (1.85) находим
U(s, l) = E{s)e *s; (1.86)
I(s, 1) = У^Е{з)<Г^* . (1.87)
о X. Турецкий 33
ШЩ
f
г -к
1
\
,
f
f
/
«->'"!
r.ywj
*;
Рис. 1.16. Реакция длинной линии на скачок
(/?;. = Qj ?& 0) (а); сечение волны напряжения
на некотором расстоянии 1г (б); сечение
волны напряжения для определенного момента
времени тх (в)\ частотная характеристика линии на определенном расстоянии /х (г);
частотная характеристика для определенного момента времени тх (д); блок-схема линии с точки
зрения изменения длины / (ё)
Полагая, что входное напряжение единичное, и используя теорему
смещения в области действительной переменной, на основе выражений
(1.86) и (1.87) можно определить реакции на выходе линии:
u(t, l) = E\(t-{)
i(U)=YfEl(t-±)
при t:
u(tf l) = i(t,l) = 0
при t< — ,
(1.88)
(1.89)
Реакции на скачок, определяемые соотношениями (1.88) и (1.89),
представлены на рис. 1.16, а. Форма входного напряжения Е не
изменяется ни при изменении времени, ни при изменении длины /. На
рис. 1.16, а сделаем сечение в момент времени г1 и получим вид волны
34
в зависимости от длины линии / при неизменном времени хг. С точки
зрения переменной длины эта линия представляет собой два усилительных
звена с одинаковыми коэффициентами усиления и обратными знаками,
соединенных параллельно и смещенных на величину / = тг. На
рис. 1.16, бив показаны сечения соответственно при постоянной длине
и при постоянном времени тх.
Теперь рассмотрим частотные характеристики. При подстановке в
выражение (1.84) s = /со можно найти частотные характеристики, которые
определяют поведение линии во времени на данной постоянной длине 1г
(рис. 1.16, г). Это характеристика звена с постоянным сосредоточенным
запаздыванием, равным Ti = IJv. Для получения выражения.,
определяющего характеристику с учетом изменения, длины / в данный момент
времени Tj, необходимо преобразовать по Лапласу соотношение (1.88):
ч
00
U(t, ?)=j£l(/—i)e-«'tf =
О
l=(v
= J E\(t— ±)е-*'Л=-|-(1 —е-*'"). (1.90)
Соответствующая передаточная функция имеет вид
G" ('• Ч) = -Щ0- = > (1.91)
где Е (q) играет роль функции Дирака в.поле Е. Полагая в выражении
(1.91) q = /со, можно найти характеристику, определяющую поведение
линии вдоль длин / в данный момент времени r1 = IJv (рис. 1.16, д).
Соответственно амплитудная и фазовая характеристики равны:
V2
\G0(t% аО| = -^1/1-008 0^; (1.91а)
W
ф('ь ^) = -arctgl_cos^ii;. (I.916)
Блок-схема линии показана на рис. 1.16, е.
Длинная линия без искажений. Если предположить в выражении (1.59),
что
то волновое сопротивление длинной линии имеет постоянную величину*
-не зависящую от s, и определяется выражением (1.83) так же, как в
случае линии без потерь. Волновая постоянная на основе выражений (1.53),
(1.92) и (1.81) запишется так:
y = VTjCi{s + a)=±±?-. (I.93)
Теперь из выражений (1.78) и (1.79) получим
U(s, l) = E(s)e "ae - s; (I.94>
/(s, l)=y jlE(s)e »ae "\ , (1.95)
Уравнения (1.94) и (1.95) отличаются от уравнений (1.86) и (1.87)
_i_
только множителем е v , который не зависит от оператора s. Поступая
3* 35.
аналогично предыдущему, найдем открытый Хевисайдом сдвиг во
времени без искажений:
* ' - V
I
при. *5* ~' (I-96)
«(/, Q = £l(f—i)e
u(t, l) = i{t, /) = 0 при f<lf (1.97)
но волна затухает вдоль линии экспоненциально с возрастанием длины /,
причем постоянная затухания
Т, = ±. (1.98)
Из выражений (1.94) и (1.95) прямо следует, что передаточные функции
линии имеют вид
GHS,/) = ^=]/fe-^V^s. (1.100)
На основе выражения (1.96) на рис. 1.17, а изображена реакция линии
на скачкообразное воздействие. Соответствующие сечения представлены
на рис. 1.17, б и е.. Следует заметить, что такая линия при изменении t
ведет себя как элемент с постоянным сосредоточенным запаздыванием,
равным тх = IJv при заданной длине lv Однако усиление в этом случае
не равно единице, как было ранее, а зависит от длины и равно е v .
Для определения поведения линии при изменении длины в данный момент
времени t найдем передаточную функцию на основе соотношения (1.96):
так как
со l=tu
U(t, q)= fE\ (t — 4)«Г^'' е-»'dl= \ El (t l~) e~ % ' е-"1 dl =
о о
= Е-^Г , (Ы01)
Т + *
то передаточная функция определяется выражением
Gu (t, q) = —^, = -£ • -^ [ 1 - е-«'е-</<° . (1.102)
Из соотношения (1.102) видно, что поведение линии в функции длины
в данный момент времени t± можно представить в виде блок-схемы,
показанной на рис. 1.17, г,—соединения инерционного звена с постоянной
Tt = via и звена запаздывания по длине 1г = t±v с коэффициентом
усиления е-**. На основе выражений (1.99) и (1.102), полагая соответственно
s = /со и q = /со, находим частотные характеристики, представленные
на рис. 1.17, дне.
36
т
Ujl
ff
\u(t.l)
и
ЙГ:
1—
(t,0)
t
t
j У 1
a ^/, + f
\
1
в-«ье-мА
iltju)
ImG
0.1 0.2 0.3 OA 0,5 0.6 0.7 Ofi ReG
\ uft.lt)
]
\J'-v _
t
6)
h(tui)
ReGfjcS)
Рис. 1.17. Реакции длинной линии без искажений RjlLj = G//C/ на скачок (а); сечение волны
напряжения на некотором расстоянии 1г (б); сечение волны напряжения для определенного
момента времени тг (в); блок-схема линии с точки зрения изменения длины 1г (г); частотная
характеристика линии для определенного момента времени тг (д); частотная характеристика
линии на определенной длине 1г (е)
Из формулы (1.99) следует, что амплитудная характеристика
определяется выражением
|G(/lf со)Г=е >,
а фазовая характеристика
Ф&, ©) = — ю-^-.
Аналогично на основе выражения (1.102) получим
(-«) +i
(1.99а)
(1.996)
(1.102а)
„-«<,
sin ш^и
Ф ft, «,) = -( arctg - w + arctg } _ e_0, ^ ^
(1.1026)
37
Кабель без индуктивности и без утечек. Томпсон (лорд Кельвин)
в 1855 г. впервые определил, каким образом изменяется ток вдоль
длинных морских кабелей, применяемых в телеграфии. В таком кабеле (за
исключением участка вблизи начала) ток изменяется относительно
медленно, что объясняется отсутствием эффектов, вызываемых наличием
индуктивности L. Потери на утечки в таком кабеле с учетом малых частот
также невелики.
Если принять в выражениях (1.43) и (1.44) Lj = G; = 0, то получим
уравнения
*•—*£,*. = <); (I.103)
-S—*£,-£ = 0. (1Л04)
Это уже не гиперболические волновые уравнения, а уравнения
параболического типа, аналогичные теплопроводности и диффузии. Волновая
постоянная на основании соотношения (1.53) определяется выражением
y(s) = VRfifi. (I.105)
Волновое сопротивление найдем из уравнения (1.59):
На основании соотношений (1.78) и (1.79) получим
U(s, I) = Е (s) e"1^ C/S; (I.107)
Г&О-ЩШе-'У^?. (1.108)
Передаточные функции линии при изменении времени равны
соответственно:
Ои(*,1) = Щ± = е~1^; (1.109)
C/(-./)-^-^e-^W. (1.П0)
При подаче на вход постоянного напряжения е (f) = Е = const из
выражений (1.107) и (1.108) получим
U{syi) = E±—s ; ' (i.iii)
!^-ЕУ%^-7Т— (1Л12)
Используя табл. 1.1, находим
W(U) = £erfc(-^Mj, (I.113)
где
38
erfc ir*fii_x_0liVRfii\ (1Л14)
называется дополнением функции распределения вероятности Гаусса,
причем
— функция распределения вероятности Гаусса.
Аналогично для тока получим выражение
'<'•«=* Vlhrs?'"^- (1Л16)
Подставляя в уравнение (1.116) / = 0, получим величину тока в начале
линии
'«•0)=ЕУМ'т*- (1Л17)
Вводя безразмерный параметр
ч=-щсг- а-п8)
выражения (1.113) и (1.116) можно представить в виде обобщенных
кривых, вид которых не зависит от параметров линии Rj и С;:
^^ = Ы(Л)=1-Ф(^); (1.119)
ч'-^жт*1^ (1Л20)
i(T,) = -J=,e~i. (I.121)
На рис. 1.18 и 1.19 изображены реакции на скачкообразное воздействие.
Изменение тока во времени в начале линии, определяемое соотношением
(1.117), показано на рис. 1.20.
Полагая в соотношении (1.109) s = /со, можно найти частотную
характеристику, которая изображена на рис. 1.21.
Для определения передаточной функции линии с учетом изменения
длины преобразуем обе части уравнения (1.107) и, подавая на вход
постоянное напряжение £, получим
U(s9 q) = —, Er v ■ (Ы22)
V,V/ s{q + VRjC}s) V
Из таблицы находим, что обратное преобразование по s равно
U(t tq)=E. \e-4t ±=^&l. (1.123)
Из выражения (1.123) находим передаточную функцию и частотную
характеристику:
^••>-ткК*гй%* (U24)
О
00
G„((,W = ,_%|e-*,-T^=r. (...25)
о
39
Преобразования Лапласа
Таблица 1.1
по
пор.
F(s) = fj e-s'/«)<*/
fit)
s
JI+1
(+-■)
n V's
S(8-l)
1
sVs
Vs
s(s — a)
1
sVs(s — a)
s\Ts
(л>0)
1
{Vs + a)s
s
Vs {Vs + a)
VI
(V~s + Va)(s-b)
{Vs + aYs
Vs
sVs + a)
1
(Vs + V'a)2
1
Ks+a
1
_____ / a — s \n
Vs + a \a + s )
(a + s)"^1 Vs + a
Vs + a+b
(s + a — b)Vs + a — b
Vnt
2ntn
Vrt ' 1-3.5... (2л-1)
V
e' erf /7
—J=- ea< erf (Ka<)
a-^ea'erf(^)-^l
.2
2nnle2D2rt4.1(Vr2^)
.(2л+1)! jAf
(l—ferlcaVt)
1
_J_ ata4 eri ca V't
Vnt
a — b
ea< erfc {Vat)
ГЛ _.____.«
a—fc
erfc(K^)-
|+(и4и"«*(./Э) + |^
ea'' erfc (a V't)
1 -2 l/-^- + (1 — 2a<)ea'[erf (Vat) — l]
«-<»<
Vnt
Dsn(2Vat)
.-at
2nr(n + ±-}V~t
2nn\Dy,+l{2V'a~t)
Vna(2n+\)\
{[(l + 2bt)l0(bt)+2btl1(bt)])
Продолжение табл. 1.Г
по
пор.
F(s)= f e-s* f(t)dt
О
fit)
19
20
21
22
23
24
25
26
27
28
29
30
31
1
Vs + a — Vs — a
1
Vs2 + OS + b
1
s Vs2 + a2
1
1
2n+l
(S2 + A») 2
1
1
K'S2— a»
1
1
(s + a) Vs2 + as
1
l^(s + a)(s + 6)
1
(s + 6) V{s + a){s + b)
Jo (at)
I .(at)
at
2
1
sin (a/)
a/ Vr2nt
2
2
С (at)
S(at)
1.3-5
^г(т)"'-м
n Jn (at)
an' t
Io(at)
at
2
(1)
a+b A
.-^'•{,.(-t,)+fl(-t,)}
Линия без утечек. Случай этот важен, ибо на практике часто можно
пренебречь утечками; при этом результаты теоретических исследований
не отличаются от данных эксперимента. Подставляя Gf = 0 в выражение
(1.53), получаем волновую постоянную
7 = V(Rj + sLj) sCj (1.126)
и волновое сопротивление на основе выражения (1.59)
Z=YRi + sLi. (I.127)
На основе выражений (1.78) и (1.79) получаем
y(Rj + sLj)sCj
(1.128)
(1.129)
41
Учитывая, что здесь /?/£/ = ах/2 [см. выражение (1.92)] и v =
■= 1/VLjCi, получаем
U(s,l) = E(s)e ° l 2j l^' (I-130)
/(s, l) = E(s)l/%- str . (1.131)
Вначале определим ток i (t, /), так как потом легче будет найти напря-
Рис. 1.18. Реакция на скачкообразное
воздействие и в кабеле Томпсона
* i(U)
Рис. 1.19. Реакция на
скачкообразное воздействие i в кабеле Томпсона
ilmu(jcj)
ReG(ju)
Рис. 1.20. Изменение тока во
времени в начале кабеля Томпсона
Рис. 1.21. Частотная характеристика кабеля
Томпсона
жение и (t, I). Полагая входное напряжение постоянным Е = const,
получим
/<!,/).
УЩ^^1
(ч-*)Т(' + *)"-(*)'
На основе теоремы смещений в комплексной области
где функция К (t, I) — обратное преобразование Лапласа:
K(t,l) = 2?-1\
'-&*-(*)*
V--W
(1.132)
(1.133)
(1.134)
42
Так как
-У'-ffl .4*ZVffi«
(1.135)
то на основании табл. 1.1 и теоремы, об изменении масштаба получим
''•['* У^Щ\ ■п»'»Т'
О
при t <
(1.136)
где /0 — функция Бесселя первого рода нулевого порядка от мнимого
аргумента.
Окончательно ток определяется выражением
На рис. 1.22 представлена временная характеристика изменения
тока i (/, /), определяемая выражением (1.137).
. Для нахождения напряжения и (t, l) на основе выражений (1.130) и
(1.131) можно записать
1 dl (s, /)
U(s, /) = ■
Cjs
dl
(1.138)
и потом окончательно
t
u(t,l) = -Ev$e a2^I0[j±yi«-(-Lf]l(t-±)dt (1.139)
Учитывая, что
dI0(tJ)
dl
= M'. 0.
(1.140)
где /i — функция Бесселя первого рода, первого порядка, можно
выражение для и (t, l) преобразовать далее. Из уравнения (1.137) в момент
времени t = IIv величина тока
■•(-И=£П<"Т'
а1 1_
v
(1.141)
так как /0 (0) = 1.
Подставляя выражения (1.140) и (1.141) в формулу (1.139), получим
.*.! Г /^-4
е 2 »—
u(t,l) = E
w&**Vr-w
при *> —,
dl
(1.142)
так как можно доказать, что изменение производной в момент
времени t = l[v не изменяет величины интеграла в выражении (1.142).
43
Полагая
-f£ = 0, f%-t = T и^-± = в,
2 v
получим окончательно
и (Г, 6) = £ e-e-jy^gr/V^K^-e») Ши
ри Т^Э;
а (Г, в) = 0 при Т < 9. (1.143)
Из соотношения (1.130) следует, что передаточные функции по перемен-
ной / равны соответственно
(1.144)
ьь ^(^Г-W
/(■+*)'-(*•)'
(1.145)
Подставляя s = /со в выражения (1.144) и (1.145), получим
соотношения, на основе которых можно определить частотные характеристики.
ilmG
и>=-2
Рис. 1.22. Изменение тока во времени Рис. 1.23. Частотная характеристика линии
в линии без утечек С/ «* 0
Например, имеем
без утечек С/ *=^ 0
-<4^Н
Ос/(/©,*) = «
тогда амплитудная характеристика
2 /fa, и
е » ,
.^yV1
Ы
а фазовая характеристика
Ф((0)
I
-а!©.
(1.146)
(1.147)
(1.148)
Вид характеристики (1.146) показан на рис. 1.23. Как и ранее, можно
получить передаточные функции по переменной /, которые, однако, имеют
достаточно сложный вид.
44
Общий случай. Рассмотрим сейчас случай, когда /?.- Ф 0; L. ф 0;
Gl Ф 0 и Сj Ф 0. Обозначим
a-L(*L4-^\
а~ 2 U/ + C/J'
где а — коэффициент затухания, и
Р 2 V L/ С/ У *
(1.149)
(1,150)
где Р — коэффициент искажений.
Тогда волновую постоянную на основании выражения (1.53) можно
записать в виде
_1_
v
Y = ^K(s+a)*-p*, (I.151)
а волновое сопротивление линии на основании выражения (1.59) — в виде
(1.152)
v(sC, + Gj)
В связи с этим из соотношений (1.78) и (1.79) следует, что
/ (s, /) = Е (s) v (sC. + G.) * =-.
v * ' w v ' ^ " J^(s + а)2 - р2
(1.153)
(1.154)
Поступая так же, как в предыдущем случае, предполагая, что Е ~
= const и учитывая выражение (1.134), получим
5r>[e-«</C (/,/)] =
-f K(s+a)*4*2)
Следовательно,
#(/, 0=-
/о(/Р^г-(4)2) при/^1;
при /<7
(1.155)
(1.156)
и из уравнения (1.154) получим
i(l, t) = E УЦ1е-«<фУ?-(±)2) +
t
Ijv
При определении и (/, /) следует иметь в виду, что
или
(1.157)
(1.158)
(1.159)
45
Окончательно после преобразований приходим к выражению
м (/, 0 = 0
при/>1; I <1Л60>
при / < 4 .
Из выражений (1.157) и (1.160) можно определить временные
характеристики.
Из соотношений (1.153) и (1.154) можно получить передаточные
функции
Gu{s,D=^VT^^; (I.161)
G7(s, 0 = o(sCy + G.) % —, (1.162}
на основе которых, полагая s = /со, находим частотные характеристики.
Характеристика Gy (/со, I) подобна характеристике, представленной на
рис. 1.23 для предыдущего случая, когда G, = 0.
Если в уравнениях (1.41) и (1.42) вместо тока i (/, 0 принять расход
жидкости q (t, I) в трубопроводе, а вместо напряжения и (t, I) — напор
h (t, О» Т0» полагая Rj = G, = 0, получим уравнения, аналогичные
уравнениям, описывающим гидравлическую линию. Очевидно, вместо емкости
Cj и индуктивности Lj следует поставить их гидравлические аналоги.
Для того чтобы не учитывать отраженных волн, следует предположить, что
в конце трубопровода имеется резервуар с соответствующим клапаном.
Трение в трубопроводе учитывается подстановкой в уравнение,
аналогичное уравнению (1.41), коэффициента, соответствующего сопротивлению R}.
С учетом того, что уравнения расхода жидкости нелинейны, линейную
модель можно принять только при условии малых изменений давления
относительно заданной рабочей точки. Результаты экспериментальных
исследований подтверждают хорошее совпадение с результатами, полученными
на основе данных уравнений.
При исследованиях теплопередачи в химических реакторах после
проведения линеаризации используются уравнения, аналогичные уравнениям,
описывающим движение тока в кабеле Томпсона [30]. Полную аналогию
с предыдущим можно заметить также при анализе паропроводов [96].
Так как одним из наиболее часто встречающихся объектов с
распределенными параметрами являются теплообменники, далее на основе работ [60]
и [18] будут достаточно подробно рассмотрены объекты этого типа.
1.2.2. Теплообменники
В работах [60, 18] показано, что неустановившийся процесс
теплообмена в теплообменниках типа «труба в трубе» можно с достаточной
степенью приближения описать следующей системой уравнений:
-§- + xi^L = ^i(9s-61); (I.163)
^ + X2^=xs2(9s-e2); (I.164)
dt ' 2 dl
ае5
dt
= ^(0i-9s) + ^s(92-es), a-165)
46
где 9Х — температура первой среды; 82 — температура второй среды;
0S — температура стенки, разделяющей среды; х — коэффициенты
теплопередачи между средами и стенкой; X — коэффициенты, характеризующие
соответственно случаи работы теплообменников в режимах тока и
противотока.
Для режима тока
*i = уь ^2 = v2; (1.166)
для режима противотока:
*i = vl9 Я2 = — v29 (I.167).
где v — скорости сред.
Уравнения (1.163), (1.164) и (1.165) после преобразований принимают
вид
(s + xsl) 9Х (/, s) + кг ^± _ Х§А (/, s) =
= 4 [(es С о)-0i 0. о))-^-^г1]; а-168)
(s + xs2) 9, (/, s) + Я2 Щ^ - xs29s (/, s) =
= т [ftft 0)-е2(/, о))-х,*1Ш]; (1.169)
(s + x2s + xu) es (/, s) - xls ex (/, s) - x2se2 (/, s) = | [xls (ex (/, o) - es (/, o» +
+ x2s(e2(/,o)-es(/, o))]. (1.170)
Полагая, что граничные условия 0j (/, 0,) 02 (/, 0) и 0S (/, 0)
выполняются, уравнения процесса стационарного теплообмена получим из
уравнений (1.163), (1.164) и (1.165) после приравнивания в них всех
производных по времени к нулю.
Тогда можно записать уравнения для OT^OHeHnfls температур от
стандартного состояния в следующем виде:
(s + xsl) Л6, (/, s) + X1d АУs) - xsl A6S (/, s) = 0; (1.171)
(s + xs2) A92 (/, s) + К d A6^(/'s) - xs2 A9S (/, s) = 0; (1.172)
(s + xls +*2s) Д65 (/, s)-xls A9X (/, s) -x2$ A92 (/, s) = 0, (1.173)
где
A01(Zf8) = e1(/.s)-^M; (1.174)
A92(/,s) = 92 (/,*) —^&°>; (1.175)
A9^/,s) = 9s(/,s)-^^-- (L176>
Решая систему уравнений (1.171), (1.172) и (1.173) относительно
интересующих нас отклонений температур А9Х и А92, получим
A0i (4, s) = Glx (s) А92 (0, s) +G21 (s) A92 (0, s); (I.177)
А92 (/„ s) = G12 (s) Д0! (0, s) + G22 (s) A92 (0, ,s), (1.178)
где lk — полная длина теплообменника.
47
Таким образом, структурная схема теплообменника (рис. 1.24)
полностью соответствует схеме, полученной при исследовании электрической
линии (рис. 1.14). В отдельных случаях, однако, передаточные функции
имеют достаточно сложную структуру.
При работе в режиме тока справедливы формулы
Gu (s) = eAM cosh В (s) — J^- sinh В (s);
£>i(s) Ms) sinh в ($)
G,i(s):
1+s —
X2S
а для случая работы в противотоке
B(s)
G21(s) =
Gn(s) =
eA(s)
1+S
1
K2s
cosh В (s) -
sinh В (s)
В (s)
C(s)
B(s)
sinh В (s)
1
cosh В (s)
C(s)
где
A(s) =
5(s) = i/ C2(s)
B(/)
sinh В (s)
Di(s)D2(s)
\ *2S ) \ «IS /
£ /<Л = Sfri — ^2)+^l(g)— A» 00
^iW = Tr
«2S«1S
1+S
Al X1S + X2S
Z>2(S) = -L. '*1*«
2W X2 Xis + X2s
K2s
i+»
l
1+s
X1S + X2S
1
X1S
1+S
1
X1S + X2s
ABtlQ)
m
Ш0)
•m
Gf/
&12
621
бгг
Л!
vJ
i
m У
ч 4*/ftJ
J ■
t
f , .
k 4*Лг)
Lr
Tt =
T,=
1.179)
1.180)
1.181)
1.182)
1.183)
1.184)
1.185)
1.186)
1.187)
1.188) ,
1.189)
Передаточные функции G22 (s)
и G12 (s) образуются заменой
индексов 1 и 2 в полученных ранее
выражениях. Это следует из сим-,
метрии уравнений (1.171), (1.172)
и (1.173). Если в найденных урав-
АВг(1к) нениях xls и x2s стремятся к
бесконечности, что означает
отсутствие влияния стенки, разделяющей
Рис. 1.24. Блок-схема теплообменника среды (тонкостенный
теплообменник), то это приводит к
значительным упрощениям. Уравнения для такого упрощенного случая приведены
в работе [601. В этой работе с помощью вычислительной машины для каждого
•случая получены логарифмические амплитудные и фазовые частотные
характеристики (рис. 1.25 и 1.26). Они показывают, что для теплообменников
48
характерна колебательность. При аппроксимации математической модели
теплообменников при помощи передаточной функции в виде рациональной
функции оператора s и элемента с сосредоточенным запаздыванием
можно получить значительные ошибки, возникающие из-за
пренебрежения постоянной времени перегородки между средами. Учет постоянной
времени разделяющей перегородки весьма существен в случае
теплообменников, работающих в режиме тока.
Теперь рассмотрим способ [18] аппроксимации математической модели
теплообменников при помощи рациональных функций оператора и
элемента с сосредоточенным запаздыванием.
Для получения приближенной передаточной функции теплообменников,
работающих в режиме противотока, преобразуем формулу (1.181):
Gn(s) =
1
coshS+^sinh* "Hi+i)^+!(!--!>■
1 1
С \ -В-А
к1+4к-л
Выражение
1 +
в
•JL е-2Б '
(1.190)
1 4- В~~ С е-2в
В + С
стремится к единице, когда s —» оо,
следовательно, для больших частот справедливо следующее соотношение:
Gn(s) = -
1 +
1
/;
4£>iP2
(1.191)
(1 + Si)(1+S^)4C2
причем в выражениях (1.183), (1.184) и (1.185) следует заменить т2 на
(—т2) и D2 (s) на —D2 (s). Кроме того,
Л В= s(x1 + t2) + D1(s) + D2(s) 1 х
*Y-
4С* (s) +
WJ)2
= _st1-D1(s)-C(s) l-i/ 1 +
Oi (s) D2 (s)
1
(1.192)
Разлагая в ряд найденную рациональную функцию при | s\ —> оо,
получим, что
Gn(s) = e-STi-D^ra)
1+^iM
"is
S + *is + "2s
+
+ ^Г
1 D\ (00) x\s
+
2 (s + "is + x2s)2
-st,—a, (00)
Pi (00) "is
+
+ •
• *i (s) + Щ (s) +
)]■
(1.193)
Так как область высоких частот характеризует ход процесса в
начальные моменты времени, то из формулы (1.193) следует, что реакция
4 X. Турецкий 49
-2-10 1 J/s
Рис. 1.25. Вид амплитудной характеристики теплообменника
I/S О
Рис. 1.26. Вид фазовой характеристики
теплообменника
50
теплообменника на скачок hlx (f) может быть охарактеризована
запаздыванием Тх, скачком в начальный момент времени h1± (хг + 0) = е-^*00)
и двумя производными
Ли (ti + 0) = e-^i ^Юхоони\ (1.194)
hii(T1 + 0) = e-*(<°>xl9Pl[oo) [Dl(~)Xls-Xi,-x2s]- (1.195)
Вторая производная может быть как положительной, так и
отрицательной* причем, если К[\ (хг + 0) > 0, то ею можно пренебречь.
Для малых значений s можно представить бц (s) в следующем виде:
G"(s)=nSe-st' (1Л96)
где
T = —!—^lnGu(s)\s=0. ч (1.197)
Таким образом, для аппроксимации динамики теплообменника во всем
диапазоне частот можно использовать следующее соотношение:
Ou(«)-Cu(0)((l+g^;^ern,, . (I.198)
причем Т{ при / = 1, 2, 3, 4 определяется на основе двух первых членов
разложения G1X (s) в области низких частот и трех первых членов
разложения в области высоких частот.
В частном случае теплообменника, работающего в режиме
противотока, в области низких частот имеем
Cu(s) = Оц (0) (1 - 8Т1г)*-ъ9 (1.199)
откуда после приравнивания выражений (1.198) и (1.199) получим
Т1г = ТВ+Т,- (7\ + Г2), (1.200)
а для высоких частот, раскладывая G1X (s) и беря три члена
разложения, получим три уравнения для определения постоянных времени Т.
Поступая подобным образом, можно получить остальные
передаточные функции G12; G21 и G22.
При определении приближенных передаточных функций
теплообменников, работающих в режиме тока, рассуждают аналогично случаю
противотока, однако здесь необходимо учитывать возможные особенности
реального вида реакции теплообменника на скачок. На рис. 1.27 и 1.28
изображены реакции на скачок для этого случая в зависимости от
величин хг и т2.
Когда хг > т2, передаточная функция приближенно определяется
выражением
Оц (s) = К 72S2 + 2\Ts + 1 e~STl + k<l T2s2 + 2%Ts + 1 ' (1.201)
а когда тх < т2 — выражением
Gn(s)=[a0 + klT2s^+T]+l] ег«.+А,яг^Т7. (1-202)
Шесть параметров а0, kly k2t ТгТ, £, которые необходимо найти,
определяются с использованием реакций на скачок (рис. 1.27 и 1.28), при
этом учитывается следующее:
а) величина скачка а0 в момент времени t = тг\
б) значение первой производной в момент времени t = хг + 0;
в) значение второй производной в момент ^ = тх + 0;
г) величина реакции на скачок в установившемся состоянии;
д) величина реакции на скачок в момент t = т2.
4* 51
Аппроксимация передаточных функций системы с распределенными
параметрами при помощи передаточных функций систем с
сосредоточенными параметрами необходимо и при анализе сложных технологических
процессов. Хотя процессами этого типа в настоящее время управляют при
помощи цифровых машин, однако без предварительного упрощения
математической модели реализация управления этого типа была бы невозможна.
Рис. 1.27. Реакция теплообменника на скачкообразное воздействие
Интересный пример анализа динамики блока котел—турбина описан
в работе [781. В ней приведены передаточные функции для отдельных
составляющих процесса, таких как экономайзеры, пароподогреватели, котел,
турбина и т. п.; блок-схема объекта вместе с системой управления и
результаты, полученные при управлении тепловой электростанцией.
т,<т2
А
т,>т
/
/
/
у
г
^^'^0'
Рис. 1.28. Реакции теплообменника на скачкообразное воздействие и
вспомогательные кривые
Объекты с запаздыванием встречаются также в металлургии [11]
в электрических приводах, управляемых с помощью выпрямителей [85,
1021, и прежде всего в химических процессах. Типичными примерами
здесь являются дисцилляционные колонны [9, 33, 74, 75]. В работе [78]
приведены величины времени чистого запаздывания и постоянных
времени для приближенных передаточных функций. Интересный подход
к описанию динамики колонны ректификации приведен в работе [101].
В работе [55] даны сравнительные таблицы приближенных параметров
математических моделей больших дистилляционных колонн.
Список литературы
1. Амелин А. Г. и др. Автоматизация в химической промышленности. М., изд. АН СССР,
1955.
2. Baeck H. S. Hydraulic on—off servo: simple, rugged positioner. Control Engineering,
December 1967, pp. 79—82.
3. Баклушин П. А., Киселев И. К.» Кубасова Л. И. Автоматизация теплоэнергетических
установок. М., Госэнергоиздат, 1960, с. 191.
52
4. Ball В. J., Rekoff M. G. An analysis of the distributed lag. ISA Transactions, April
1966, Vol. 5, No 2, pp. 146—155.
5. Bauer H. Berechnung von Regelkreisen mit nichtrationaler LJbertragungsfunction.
X Internationales Wissenschaftliches Kolloquium. Regelungstechnik, Heft 5, 1965, S.
217—223. Technische Hochschule Ilmenau, VEB Verlag Technik.
6. Беллман Р., Гликсберг И., Гросс О. А. Некоторые вопросы математической теории
процессов управления. М., Машгиз, 1962, с. 23—25.
7. Bekey G. E. Discrete models of the human operator in a control system. Proc. Il-nd
IFAC Congress, Basel 1963, London 1963, Butterworth.
8. Bublitz А. Т., Monly R. I., Thomas R. L. Computer control of a discrete glass
manufacturing process. Session 22, Proc. Ш-rd IFAC Congress, London, 1966.
9. Buckley P. S. Reflux cycle in destination columns. Session 32, Proc Ш-rd IFAC
Congress, London, 1966.
10. Buckley P. S. Techniques of process control, Chapter 12, New York. 1964, J. Wiley.
11. Burovoy I. A. Automatic control of processes in a fluidized bed in the non—ferrous
metallurgical industry. Automatic and Remote Control, Vol. IV. London, 1961, Butter-
worth, pp. 446—474.
12. Бутковский А. Г. Теория оптимального управления системами с распределенными
параметрами. М., Физматгиз, 1965.
13. Chaussard R., Grauvogel J., Davoust G. Rational adjustment of controls of a thermal
power station. Session 21, Ш-rd Congress IFAC, London, 1966.
14. Churchil R. V. Operational Mathematics. New York, 1958, McGraw-Hill.
15. Цянь-Сюэ-Сень. Техническая. кибернетика. М., Изд-во иностр. лит., 1956.
16. Crochettiere W., Vodobnik L., Reswick J. В. The design of control systems for
electronic activation of human limb movements, J. А. С. С, 1967, pp. 51—57.
17. Cunningham W. J. Analiza ukladow nieliniowych. Rozdz. 8. Warszawa. 1962, WNT.
str. 200—221.
18. Девятое Б. Н. К вопросу о приближенных представлениях передаточных функций
теплообменников. В кн.: «Автоматическое управление непрерывными процессами».
Новосибирск, Изд-во Сибирского отделения АН СССР, с. 29—41.
19. Девятое Б. Н. Переходные режимы работы непрерывнодействующих теплообменников
с толстыми стенками. Докл. АН СССР, 1960, т. 130, № 1.
20. Dudnikow E. G. Determination of the optimal setting—up of industrial automatic
control system from experimental data. Automatic and Remote Control, Vol. IV. London,
1961, Butterworth, pp. 360—364.
21. Elkind J. L., Miller D. C. On the process of adaption by the human controller. Session 30,
Proc. Ш-rd IFAC Congress, London, 1966.
22. Эльсгольц Л. Э. Введение в теорию дифференциальных уравнений с отклоняющимся
аргументом. М. «Наука», 1964.
23. Engel W., Jaschek H. Obungsaufgaben zum Grundkurs der Regelungsthechnik. Munchen,
1964, R. Oldenburg.
24. Euler K. Regelsysteme mit Lauftzeit. Regelungstechnik, 1959, Heft 3, S. 89—92.
25. Filipovic V. D. An approximate method of analising systems with distributed parameters.
Session 6, III—rd IFAC Congress, London, 1966.
26. Frey A. L., Deem W. В., Altpeter R. J. Stability and optimal gain in
extremum—seeking adaptive control of a gas furnace. Session 48. Proc. Ш-rd IFAC Congress, London,
1966.
27. Fujii S., Kanda N. An optimalizing control of boiler efficiency. Proc. H-nd IFAC
Congress, London, 1963, Butterworths.
28. Gascoigne D. Control matching of engines and intakes on supersonic aircraft. Session 44,
Proc. Ш.-rd IFAC Congress, London, 1966.
29. Герасимов С. Г. Теоретические основы автоматического регулирования тепловых
процессов. М., Госэнергоиздат, 1959, с. 210—278.
30. Gilles E. D. Dynamic und Regelung chemischer Rohrreaktoren. Messen Steuern, Regeln,
1966, Heft 5, S. 158—166.
31. Грицков В. И. Исследование сырьевой мельницы как объекта регулирования. В кн.:
«Автоматизация производственных процессов», М., Изд. АН СССР, 1958, с. 133—138.
32. Halanay A. Differential Equations A. P. New York, 1966.
33. Hale J. C, Updike О. L. Dynamics of pulsed—column extractors. Session 32, Proc. Ill-rd
IFAC Congress, London, 1966.
34. Харатишвили Г. Л. Принцип максимума в теории оптимальных процессов с
запаздыванием. М., ДАН, 1961, Т. 136, № 1
35. Heller G. Analogiegerat fur Totzeiten Regelungstechnik, Heft 8, 1959, S. 266—269.
36. Jex H. R.f McDonnell I. D., Pharak A. V. A critical tracking task for manual control
research. IEEE Trans. Human Factors in Electronic, 1966, No 4, pp. 138—145.
37. Кац А. М. Автоматическое регулирование скорости двигателей внутреннего сгорания.
М., Машгиз, 1956, с. 7 и 26.
38. Kessler С. Ein Beitrag zur Theorie mehrschleifiger Regelungen. Regelungstechnik, Heft 8,
1960, S. 261—266.
39. Kindler H„ Pohl G. Kleines regelunstechnisches Praktikum. Berlin 1967, VEB Verlag—
Technik.
53
40. Кириллова Ф. М., Чуракова С. В. К проблеме управляемости линейных систем с после-'
действием. — «Дифференциальные уравнения», 1967, Т. III, № 3.
41. Кисля ков В. С. Некоторые вопросы теории систем автоматического регулирования с
запаздыванием, отображаемых линейными дифференциальными уравнениями с
запаздывающим аргументом. «Автоматическое управление». Изд. АН СССР, 1960.
42. Коган Б. Я. Электронные моделирующие устройства и их применение для исследования
систем автоматического регулирования. М., Физматгиз, 1963.
43. Копелович А. П. Автоматическое регулирование в черной металлургии. Краткий
справочник. М., Машгиз, 1963.
44. Kopielowicz A. P. Dobor regulatorow automatycznych. Metody obliczeri. Warszawa,
1964, WNT.
45. Kreil W., Schweizer G. Der Mensch als Regler. Regelungstechnik. Heft 2, 1968, S/49—56.
46. Кремлевский П. П. Теплоэнергетические и химико-технологические приборы и
регуляторы. М., Машгиз, 1961. •
47. Kylstra F. J. Contrallability and allowable compresor capacity of a Flare gas recovery
system. Proc. H-nd IFAC Congress, London, 1963, Butterworth.
48. Masakaru Mats u bar a. On the equivalent dead time. IEEE Transactions on Automatic
Control, October 1965, Vol. AC—10, No 4, pp. 464—466.
49. McRuer Duane T. Graham Dunstan, Krendel Ezra S. Manual control of single—loop
systems. Part I. J. Franclin Inst. 1967, No I, p. 1—29.
50. Мееров М. В. Синтез структур систем автоматического регулирования высокой точности.
М., Физматгиз, 1958, с. 107—122.
51. Метод Гольдфарба в теории регулирования. Сб. статей, М., «Госэнергоиздат», 1962,
с. 96—99; 198—202:
52. Merz L. Die Begriffe Schwierigkeit, Leistungsfahigkeit und Durchfuhrbarkeit in der
Regelungstechnik, Teil I. Regelungstechnik, 1954, Heft, 2 S. 31—37.
53. Mesch F., Schweizer G. Practical application of statistical methods or reducing flight
test data. Session 44, Proc. IH-rd IFAC Congress, London, 1966.
54. Minorsky N. Drgania nielinieowe. Rozdz. 21, Warszawa, 1967, PWN.
55. Moczek J. S., Otto R. E., Williams T. J. Approximation models for the dynamic response
of large distillation columns. Proc. Il-nd IFAC Congress, London, 1963, Butterworth.
56. Мышкис А. Д. Линейные дифференциальные уравнения с запаздывающим аргументом.
М.—Л., Гостехиздат, 1951.
57. Naslin P., Raoult J. С. Modeles continus et echantillonnes des Toperateur humain place
dans une boucle de commande. Proc. Il-nd Congress IFAC 1963, London, 1963,
Butterworth.
58. Naumann K. Temperaturregelung einer Trockentrommel fur Kalksteinsplitt.
Regelungstechnik, Mai 1965, Heft 5, S. 240—247.
59. Nicholson H. Dynamic optimisation of a boiler-turboalternator model. Proc. Instr. Electr.
Engrs., 1966. No. 2, pp. 385—399.
60. Noldus E. Analytische Untersuchung der LJbertragungsververhaltens von Gleich und
Gegenstromwarmeaustauschern. Regelungstechnik, Marz 1967, Heft 3, S. 112—117.
61. Oetker R. On the control of sectors with dead time. Automatic and Remote Contol, 1961,
Vol. I, Butterworth, pp. 22—25.
62. Okori T. Inzynierskie metody doboru i strojenia regulatorow konwencjonalnych dla obi-
ektow z monotoniczna charakterystyka skokowa. Praca dyplomowa w Katedrze Auto-
matyki i Elektroniki Przemyslowej AGH, Krakow 1962.
63. Oldenburg R, Goodson R. E. Hydraulic line dynamics. Proc. Il-nd IFAC Congress,
London, 1963, Butterworth.
64. Ольденбург Р., Сарториус Г. Динамика автоматического регулирования. М.,
Госэнергоиздат, 1949.
65. Orcutt J. С, Lamb D. E. Stability of a fixed deb catalytic reactor system with feed-
effluent heat exchange. Automatic and Remote Control, Vol. IV, London, 1961,
Butterworth, pp. 274—281.
66. Основы автоматического регулирования. Под ред. Солодовникова В. В., М., Машгиз,
Т. I, Теория. 1954, гл. XIII, XXI.
67. Perret R., Rouxel R. Principle and application of a extremal computer. Prof. Il-nd
IFAC Congress, London, 1963, Butterworth.
68. Пинни Э. Обыкновенные дифференциально-разностные уравнения. М., Изд-во иностр.
лит., 1961.
69. Понтрягин Л. С. и др. Математическая теория оптимальных процессов. М., Физматгиз,
1961.
70. Понтрягин Л. С. О нулях некоторых простых трансцендентных функций. Изв. АН
СССР, 1942, 6, 115.
71. Profos P. Dynamisches Verhalten von KHmakanalen. Messen Steuern Regeln, April
1967, Heft 4, S. 117—123.
72. Prochnicki W. Dobor regulatorow i korzystnej struktury regulacimocy i cisriienia bloku
kociol-turbina. Prace IV Krajowey Konferencji Automatyki, z. 7, Krakow 1967»
str. 159—160.
73. Pulaczewski J. Dobor nastaw regulatorow przemyslowych. Warszawa, 1966. WNT.
74. Rees N. W. Dynamic indentification and optimum control studies on a pilot distillation
column. Session 32, Proc. Ш-rd IFAC Congress, London, 1966.
54
75. Rijnsdorp J. E., Van Kampen J. A., Bollen H. Automatic feedback controlof two product
qualities of distillation column. Session, 32, Proc. IH-rd IFAC Congress, London, 1966.
76. Ротач В. Я. Расчет настройки промышленных систем регулирования. М., Госэнерго-
издат, 1960. Приложения, с. 318—336.
77. Ruer D. Т. Мс et al.: System performance and operator stationarity in manual control
systems. Session 30, Proc. IH-rd IFAC Congress London, 1966.
78. Ruschinski V. M. D.ynamics of the automatic control of a boilerturbine unit. Automatic
and Remote Control, Vol. IV, London, 1961, Butterworth, pp. 365—372.
79. Салуквадзе М. Е. К задаче синтеза оптимального регулятора в линейных системах
с запаздыванием.— «Автоматика и Телемеханика», 1962, № 12.
50. Schone A. A special class of transfer functions for the description of the dynamic
behaviour of heat exchangers. Session 10, Proc. IH-rd IFAC Congress, London, 1966.
51. Shearez J. L., Scher R. S., Reid K. N. Standards for linear control systems. Control,
1961, 4, No. 39, pp. 115—116.
82. Silva L. M., Noebels H. J., Kehoe T. J. Analytische Bechandlung der pH-Regelung.
Regelungstechnik, Heft 4, S. 118—123.
83. Smethurst J. A. Direct computer control of production changes on a simulated quality
paper machine. Session 22, Proc. IH-rd IFAC Congress, London, 1966.
84. Смит О. И. М. Автоматическое регулирование. М., Физматгиз, 1962, с. 393—464.
85. Stahl К. Limiting control of electrical driver. Automatic and remote Control, Vol. IV,
London, 1961, Butterworths, pp. 180—186.
86. Strejc B. Naherungsverfahren fur aperiodische Obergangscharakteristiken.
Regelungstechnik, 1969, Heft 4, S. 124—128.
ST. «Техническая кибернетика». «Теория автоматического регулирования», Книга 1, под
ч ред. Солодовникова В. В., М., «Машиностроение», 1967, с. 199—210.
88. «Техническая кибернетика», «Теория автоматического регулирования», Книга 2, под
ред. Солодовникова В. В., М., «Машиностроение», 1967, с. 431—458, 517—576.
89. Tustin A. Feedback. Scientific American, September 1952, No. 9.
90. Ursoki M., Vamos T. Some questions reading control of power systems. Automatic and
Remote Control, Vol. IV, London, 1961, Butterworth pp. 93—98.
91. Voelker D., Doetsch G. Die zweidimensionale Laplace-Transformation. Basel 1950,
Verlag Birkhauser.
92. Воронов А. А. Элементы теории автоматического регулирования. М., Оборонгиз,
1954, с. 326—331.
93. Воронов А. А. Основы теории управления. Часть II. Специальные линейные и
нелинейные системы автоматического регулирования одной величины. М., «Энергия»,
1966, с. 7—48.
"94. Wagner К. W. Rachunek operatorowy i przekstalcenie Laplace'a. Warszawa, 1960,
PWN.
95. Weiss L. On the controllability of delay—differential systems. SIAM Journal on Control.
November 1967, Vol. 5, No 4, pp. 575—587.
96. Weller W. Methoden der mathematischregelungstechnischen Beschreibung von Stro-
mungsleitungen. Messen, Steuern, Regeln, 1967, Heft 6, S. 228—232; 1967, Heft 7,
S. 257—263; 1967, Heft 10, S, 327—377.
97. Wegrzyn S. Przebiegi nieustalone w elektrycznych liniach i ukladach lancuchowych.
Warszawa, 1958, PWN.
98. Wilczyriski Z. Zastosomanie maszyn analogowych w zakresie urzadzen cieplnych. Mas-
zyny Analogowe w Energetyce. Gliwice 1965, Energopomiar, str. 5—34.
99. Wunsch G. Die Entwicklung und die wichtigsten Verfahren der industriellen Regelung.
Regelungstechnik, 1953, Heft 3, S. 52—56.
100. Wunsch G. Podstawy automatyki. Warszama, 1961, PWT.
101. Zavorka J. The dynamic properties of rectification stations with plate columns. Proc.
Il-nd IFAC Congress, London, 1963, Butterworth.
102. Zygmunt H. Niektore zagadnienia optymalizacji przekstaltnikowych napedow pradu
stalego. Prace IV Krajowej Konferencji Automatyki z. 7, Krakow 1967.
Глава II
Идентификация объектов
с запаздыванием
Нахождение связи между входом и выходом на основе экспериментальных
данных носит в автоматическом управлении название «идентификация» и
служит для определения математической модели объекта.
В отличие от специалиста-физика, для которого основной целью
является нахождение структурной модели (что представляет собой, вероятно,
«оптимистический самообман»), для инженера-управленца очень часта
достаточно нахождения функциональной модели.
Под структурной моделью понимается такая математическая модель,
в которой структура уравнений отражает физическую структуру объекта.
Под функциональной моделью понимается
такая модель М (рис. II. 1), которая для
определенного класса входных сигналов (общих для
объекта и модели) дает на выходе
приблизительно такой же сигнал, что и объект О. При
этом не требуется знать физической структуры
объекта, который в этой ситуации часто назы-
y(t)*y(t)
uei/
м
Рис. II.1. Модель функци- вается «черным ящиком». Тем не менее под этим
онирования объекта подразумевается нечто вполне конкретное —
математическая структура модели объекта.
Последние исследования Калмана [16, 17] в этой области приблизили
конец эпохи «черного ящика». Насколько нахождение структурной
модели позволяет лучше понять различные стороны физических
явлений, происходящих в объекте, и более детальную идентификацию
объекта, настолько нахождение функциональной модели обычно позволяет
проводить лишь коррекцию регулятора.
Чтобы автоматизировать технологические процессы, необходимо прежде
всего их познать. Весткотт [57] образно сказал, что для того, чтобы съесть
вкусный черепаховый суп, необходимо прежде всего поймать черепаху.
Проведение процесса идентификации требует решения двух проблем:
технических измерений и аппроксимации.
Здесь речь будет идти исключительно о задачах аппроксимации.
Принципиально можно выделить четыре метода определения математической
модели объекта:
а) на основе реакции объекта на детерминированный входной сигнал
(чаще всего на единичный скачок);
б) на основе частотных характеристик, полученных в установившемся
состоянии при синусоидальном входном сигнале;
в) на основе моделирования реального объекта на математических
машинах при дальнейшем уточнении параметров модели заданной
структуры;
56
г) на основе корреляционного анализа входа и выхода.
Методы а) и б) можно считать классическими. Так как метод б) обычно
очень трудоемок, то будем вести речь только о методе а). Метод в) в
настоящее время наиболее перспективен и является предметом интенсивных
исследований как для детерминированных, так и стохастических входных
сигналов.
Для объектов большой размерности существуют методы аппроксимации
их при помощи моделей, содержащих запаздывание, о чем речь будет идти
в конце этой главы.
§ ИЛ. Определение математической модели
по временным реакциям
Разработанные в настоящее время методы позволяют, вообще говоря,
определить только постоянные коэффициенты линейного
дифференциального уравнения. Выявление же полной структуры и порядка уравнения
вообще невозможно 1. Здесь будут рассмотрены несколько методов
определения коэффициентов уравнения, когда известна выходная реакция
объекта; чаще всего это реакция на единичное скачкообразное воздействие.
В случае возникновения трудностей при использовании скачкообразного
воздействия можно применить сигналы другого вида, а затем при
вычислении характеристик пересчитать [50] их так, чтобы получить реакцию на
скачок.
II. 1.1. Определение параметров объекта первого порядка с запаздыванием
Пусть требуется определить параметры т, /С0, Т объекта, описываемого
уравнением
Ty(t) +y(t) = K0u(t-T)t r/ (0) = 0,
причем вынуждающая сила имеет вид
И^О;
0* <0.
Реакция объекта на это воздействие показана на рис. II.2.
"(0 = 1 (0 =
(ИЛ)
(II.2)
1
1
J
\
0
iy=h(t)
т Т
« ** ,Г
^—■ "
«о
1
t
Рис. II.2. Реакция объекта
первого порядка с
запаздыванием на скачкообразное
воздействие
И
Решение уравнения (IIЛ) имеет вид
(II.3)
1 В настоящее время разработаны методы идентификации нестационарных объектов и
методы определения порядка дифференциального уравнения квазистационарных объектов.
(Прим. перев.).
57
На рис. П.2 можно непосредственно определить величины
интересующих нас параметров.
Время запаздывания т — это интервал времени от момента подачи
воздействия до момента, когда начинает нарастать сигнал у (t). Следовательно,
в течение этого интервала времени и (t) Ф О, а у (t) = 0 *.
Постоянная времени Т — это время tk — т, в течение которого у (t)
достигает величины (1 — е"1) у (оо), что приблизительно равно 63,2%
от установившегося значения у (оо).
Коэффициент усиления /Со определяется отношением
А°~~ и(оо)
(ПА)
и, следовательно, отношением выхода ко входу в установившемся
состоянии.
II. 1.2. Определение параметров объекта второго порядка
с запаздыванием
Вначале рассмотрим объект с апериодической реакцией.
Уравнение, описывающее объект, имеет вид
ТгТ2 у (t) + (Tt + Т2) у (t) +y(t) =
= KQu(t-4), Тъ Г2>0. (US)
Полагая, что у (0) = у (0) = 0, а входное воздействие описывается
уравнением (П.2), получим решение
y(t) = h(t) = K0 И
Ti—To
t-x
т1-т2
t-x
)■
t
:T.
(II.6)
Реакция объекта на скачок h (t) представлена на рис. II.3. Время
запаздывания т и коэффициент усиления определяются, как и в случае
iy=h(t)
h(oo)
в Рис. П.З. Реакции
• объекта второго
порядка с
запаздыванием на
скачкообразное воздействие
объекта первого порядка. Для нахождения постоянных времени 7\ и Т2
введем новую переменную 9 = / — т. Тогда из формулы (II.6) получим
в m в
ме>~*.(1-^е ^+фгг* т')> е^°-
01.7)
* При условии, что объект до момента действия управляющего сигнала находился
в состоянии равновесия и в нем отсутствовала запасная энергия (Прим. перев.).
58
Дифференцируя уравнение (П.7) дважды, найдем
6(в)=тАГ(е~ТГ-е~¥Г), Э^О; (II.8)
1 1 л 2
Приравнивая вторую производную к нулю, получим абсциссу точки
перегиба
ep=r^rVlnlL (П1°)
' * 2 * 1 * 1
и, используя формулы (П.8) и (НЛО), найдем
Ч%)=^{^) Га_г'; (П.И)
/ т _h T _ М
i 2 * 1 ' 2
Из рисунка видно, что
Т *м>
Л(вр)
(11.13)
Ts=/Coj=LMe£)# (II 14)
h (Эр)
Подставляя в формулы (11.13) и (11.14) соотношения (11.11) и (11.12),
получим
Та^Т^У'-7* (11.15)
и
TS = T1+T2 (II.16)
или в относительных единицах
\ т т
(11.17)
(11.18)
На основе соотношений (11.17) и (11.18) получены номограммы,
представленные на рис. II.4. Порядок определения постоянных времени Тг и
Т2 следующий:
1) проводим касательную в точке перегиба экспериментально снятой
[реакции объекта на скачок (рис. II.3);
2) определяем величины Та и Ts и находим отношение TJTa\
3) для найденного TJTa отыскиваем на номограмме (рис. II.4)
соответствующую прямую;
4) координаты точек пересечения этой прямой с кривой определяют
искомые величины TJTa и Т21Та. Зная Та из пункта 2), легко находим
Тг и 7Y
Из рисунка видно, что для Ts = Та = 2/е = 0,73 прямая является
касательной к кривой, откуда следует, что критическое демпфирование
наблюдается при Тг = Т2.
59
Рассмотрим объект с колебательной реакцией *. Уравнение объекта
имеет следующий вид:
T*'y(t) +2\Ty{t) +y(t) = KoU(t-x). (11.19)
Пусть коэффициент демпфирования имеет величину 0< £ < 1/1^2,
Т > 0, у (0) = у (0) = 0 и входное воздействие описывается уравнением
(II.2). Решение уравнения (11.19) имеет вид
y(t) = h(t) = K0[l
Р-б <*-т)
СОп
ол
0,2
[<х>п COS (О (t — т) + .
+ б sin <о„ (^ — т)] J, t^> т,
(11.20)
где
VI — &2
(11.21)
— собственная частота
затухающих колебаний, а
73
VS
в =
I
vV
(11.22)
Шч
^
hi"
&ч
— относительная постоянная
демпфирования.
На рис. II.5 дан пример
О*—" 0 2 ' оь ' fl'g flfl"'^ /т вРемен1*°й характеристики.
; а Время запаздывания т и коэф-
~ тт , „ фициент усиления можно опре-
Рис. II.4. Номограмма для постоянных времени ^ ' „ „ Л vrn „
объекта второго порядка делить непосредственно из
рисунка. Для нахождения частоты
колебаний о и постоянной демпфирования б введем новую переменную
9 = t — т, тогда из выражения (11.20) получим
h (0) = /Со | 1 — — [со„ cos (D„e + б sin co„9]l ,9^0. (II .23)
Дифференцируя выражение (11.23) по 9, получим
уф) = К0*— (62 + (o^)sin>9, 9^0.
(11.24)
Приравнивая у (0) к нулю, найдем^абсциссы локальных экстремумов:
Qek = k^-, *=о, 1,2,.
(11.25)
С учетом точности выражений найдем экстремумы только при k = 1,2:
А1=уфе1)-\=К0<Г^П\ (H.26)
б
Л2 = 1—у(в,я) = /Сое" ^Я
(11.27)
1 Для колебательного звена, не имеющего перерегулирования в реакции на скачок,
когда коэффициент демпфирования лежит в границах 1/"^2 < £ < 1, необходимо применить
другие методы идентификации (Прим. ред. оригинала).
60
Беря отношение
и учитывая, что
А*
«>п
—
ефп
2я
где Т0 — период собственных колебаний, находим
4-бТ0=1пА. (П.ЗО) 1у-НЮ
Рис. II.5. Реакция
колебательного объекта второго
лорядка с запаздыванием
ч
(11.28)
(11.29)
f.
Теперь можно определить коэффициент демпфирования
1 =
-т6т°
In
At
V<+# ]/*
2 , 1 0^2
V"!+'-2t
(11.31)
На основе соотношения (11.31) получен график, представленный на
рис. II.6. Норядок определения частоты колебаний ып и относительного
демпфирования б по
экспериментально снятой характеристике
следующий:
1) по характеристике определяем
период колебаний Т0 и находим (йп
по формуле (11.29);
2) вычисляем Аг и Л2> находим
отношение A J A 2 и с помощью
графика определяем величину \.
Величину постоянной
демпфирования находим на основании
выражения (11.31) из соотношения
Рис. II.6. График для определения
коэффициента демпфирования
6 =
Так как
б
vwwn
то из формулы (11.22) можно определить
1
Т = -
V~$T<
(11.32)
(11.33)
(11.34)
61
Таким образом, найдены значения параметров объекта.
Далее будут рассмотрены общие методы, при помощи которых можно*
определить коэффициенты уравнений производного порядка.
II. 1.3. Метод площадей
Пусть имеется устойчивая линейная система, реакцию на скачок которой'
обозначим через у (t) = h(t).
Из графика реакции на скачок определим величину запаздывания т;.
остается найти параметры а1у . . ., ап и Ь0, . . ., Ьт дифференциального
уравнения, описывающего систему:
dny(t)
dtn
+
+ а* dt
У =
и dmu(t~%) , . , du(t~ т) , и ,, v
т d^~i+'"+fti dt ' + М(*-*)«
(II.35>
Теперь можно исследовать систему без запаздывания т, памятуя о
необходимости смещения шкалы времени вправо на величину т.
Тогда передаточную функцию системы можно представить в виде
0(5) = ^ + ^^ + ''-+^ + ^, п>т. (Ц.36>
ansn + an^sn ^ h axs + 1
Используя известную теорему операционного исчисления о предельном?
переходе [41, 42, 501, получим
Ко = Пт G (s) = b0;
s->0
Кг = lim Gx (s) = 1 im -^ [^0 - G (s)] = - bx + K0ai;
s+Q
s->0
/C2 = lim G2 (s) = lim 4- [/Ci — Gx (s)] = fc2 + /Ca — A>2;
(II.37>
Kr=limGr(s)=\im^-[Kr.1-Gr_1(s)} =
= (- 1)' br + Kr^fh - *r-A + •••+(- l)'-1 K0an
где br = 0 при r > m и аг = fcr = О при г > гг.
Таким образом, при порядке системы г = m + л получим (т + я + Д)'
уравнений для определения (гг + m + 1) искомых коэффициентов аь . | ..
. . ., ап и й0, . . ., Ьт.
Например, при п = 3 и m = 2 получим следующую систему уравнений:
в матричной форме:
*о
0 0 0
(11.38)*
/Сх —/Со 0 0
/С2 —Кг К0 0
_ Къ —Кь К3 —К2 _
В частном случае системы, когда Ьг = Ь2 = • • • =Ьт = 0, искомые-
значения (п + 1) параметров b0i au . . ., ап можно определить из первых.
(п + 1) уравнений системы (11.37).
62
-1 -
ах
а2
_аз_
" ь0~
-6i
0
0
0 _
Неизвестные еще значения коэффициентов /С0, . . • , Кг найдем
последовательным интегрированием реакции h (t) (рис. II.7), так как
существуют зависимости
4 К0 = Hm G (s) = Hm h (/);
s+0
*->><X>
/d = Hm Gx (s) = Hm -L[K0 — G (s)] = Hm hx {t) = Hm J [K0 - h {%)] dx;
t
K2=limG2(s)=\imh2(t) = \im\[K1 — h1(T)]dT,
t
Kr = 1 im Gr (s) = Hm J [*,_! - К_г (т)] Л.
s->0
^<»o
(II.39>
Из рис. 11.7 видно, что коэффициенты Кп определяемые формулой:
(11.39), есть площади, заключенные между кривыми /Cr_i — К-\ С) и-
осью времени. Благодаря
этому путем
последовательного интегрирования
(например, графического)
можно легко их вычислить
по экспериментальным
данным.
Вышеприведенная
процедура на основе принципа
суперпозиции может быть
использована для
многомерных систем и в случае,
когда входной сигнал и (t)
и выходной сигнал^ у (t)
имеют произвольный вид
[41, 50]. Таким образом,
этот метод обладает
достаточной универсальностью
и мало подвержен
действию помех, так как в
процессе интегрирования
происходит усреднение
результатов и сглаживание
кривых.
II. 1.4. Метод моментов
"I
0
Рис. II.7. Результаты интегрирования реакции нз>.
Пусть Задана передаточ- скачкообразное воздействие
ная функция объекта
G (s) = J g (t) e-*< dt.
(11.40)
Моментом i-го порядка импульсной переходной функции называется
выражение
т, =
= |^(0
dt.
(11.41)
63.
Разлагая в выражении (11.40) e~s' в ряд Тейлора, получим
00
G(s) = l[l-st + s^-s^+..-]g(t)dt.
(11.42)
Таким образом, используя формулу (11.41), можно выражение (11.42)
записать в виде
G(s) = m0 — sm1-\--^m2
3!
Щ +
(11.43)
Предположим, что время запаздывания т предварительно определено
из импульсной реакции и что импульсная переходная функция g (t) уже
соответственно смещена и отвечает системе без запаздывания. Тогда
передаточная функция есть рациональная функция (11.36) оператора s.
Подставляя выражение (11.36) в формулу (11.43), получим
(m0 — sm1 + 4rm2 —-Ц- т3-\ )(1 +
+ alS + a2s2+ ••• +ansn) = b0 + b1s + b2s*+ ... + bms>".
(11.44)
Приравнивая коэффициенты в обеих частях уравнения (11.44), можно
определить искомые значения коэффициентов аъ . . ., ani b0i . . ., bm
на основе известных значений моментов функции g(t). Например, при
п = 3 и т = 2 получим для коэффициентов следующее матричное
уравнение:
т0
пг1
1
"зГтз —
-4Гт*~
0 0
— т0 0
— Ш1 — Ш0
1
-2f т2 Щ
1 1
-ЗГтз-2\"12
0
0
0
— т0
— /пх
5!
/П5-
4!
7-/П4-огт3—<>rmi
' 1 "
Ь2
О
О
О
(11.45)
II. 1.5. Определение импульсных переходных функций
объектов управления с помощью метода моментов
Постановка задачи следующая [45]: требуется найти импульсную
переходную функцию g(t) объекта управления на основе известных временных
реализаций сигналов входа и (t) и выхода у (t) *.
Предположим, что сигналы и (t) и у (t) определены на интервале [О, Т].
С практической точки зрения за пределами этого интервала переходный
процесс должен закончиться. Это значит, что импульсная реакция у (t)
не должна превышать (2—5)% от максимального значения. Для того чтобы
теоретически упростить исследования, будем полагать, что Т =оо .
Для получения максимально возможной точности при аппроксимации
импульсной переходной функции g (t) применяется некоторая функция
веса w (f).
1 См. статью В. В. Солодовникова, А. Н. Дмитриева, Н. Д. Егупова, Е. С. Лобусова
«Идентификация линейных систем автоматического управления с распределенными
параметрами и запаздыванием». В кн.: Автоматическое управление и вычислительная техника,
№ 10 М., «Машиностроение», 1972, стр. 41—58, которая является дальнейшим развитием
работы [45] применительно к системам с запаздыванием (Прим. перев.).
64
Преобразование входного сигнала с весом w (t) имеет вид
00
Uw (s) = J w,(t) u (t) e-s< dt. (11.46)
о
Аналогично для выходного сигнала с весом w (t) можно записать
00
Yw (s) = J w (t) у (t) е-** dt (11.47)
и преобразование импульсной переходной функции с весом w (t)
00
Gw (s)= $ w (t) g (t) e-s< dt. ' (П.48)
о
Полагая начальные условия нулевыми в момент времени (0 ), можно
записать, что
Yw (s) = Gw (s) Uw (s). (11.49)
Подставляя формулы (11.46), (11.47) и (11.48) в выражение (11.49),
получим
00 00 00
j w(t)у (t) e~s< dt= \w(t)g(t) e-s*dt \w{t)u(t) t~st dt. (11.50)
Разлагая в ряд функцию е-55' под знаком интеграла в выражении
(11.50), получим
00 Г 00
J 2<-'>"з?-
О Ln=0
w(t)y(t)dt =
оо Г °э
= i 2<-i)v4isv и')*(')я| 2(-i)m^s"
О Lv=0
О Lm=0
w(t)u(t)dt. (11.51)
Полагая, что функции w (f), g (t), у (f) и и (t) интегрируемы в
пространстве L2 (0, оо), можно утверждать, что ряды в выражении (II.51)
абсолютно сходятся, и в связи с этим можно менять местами операции
суммирования и интегрирования.
Назовем
00
jxv = \ Р w (t) g (t) dt, v = 0, 1, . . ., (11.52)
моментом функции q (t) с весом w (f)\ аналогично для функций у (t) и и (t)
' оо
а»= { tn w(t) у (i) dt, n = 0, 1, . . .;
оо
Ьт = J V* w (t) и (0 dt% m == О, 1,
(11.53)
(11.54)
Моменты, определяемые формулами (11.53) и (11.54), можно вычислить,
так как сигналы у (t) и a (t) могут быть измерены, а функция веса w (t)
выбирается заранее, о чем речь будет идти ниже.
Подставляя выражения (11.52), (11.53) и (11.54) в соотношение (11.51),
получим
ОО 00 00
2(-i)^s«=2(-I)v^rsVS(-1)m^sm- ~(IL55)
П=0
5 X. Турецкий
v=0
m=0
65
Следовательно,
ОО 00
£(_l)n.jLs«= J] (-ir+m^S^. (11.56)
n=Q v, m=0
Беря v + т = п и приравнивая коэффициенты при одинаковых
степенях s, получаем
ОО 00 00
n=0 n=0 v=0
(-^f-S^1)" v!(»-"v)) <II58>
v=0
и окончательно имеем
a
JL (n\ v=0, 1, ...;
Из системы уравнений (11.55) на основе определенных ранее моментов
входа и выхода находим моменты импульсной переходной функции
°п ~~ D ( Мя-v
^-^ , п = 0, 1,... (11.60)
Теперь рассмотрим вопрос о том, как по известным моментам \in можно
приближенно определить импульсную переходную функцию g (t) данного
объекта и его передаточную функцию G (s).
С этой целью рассмотрим вопросы наилучшей аппроксимации
функции g (t) в пространстве L2 [0, оо ] с весом w (t) при помощи функции g(t).
Искомая функция g (t) должна обладать следующими свойствами:
1. Аппроксимирующая функция g (t) и импульсная переходная
функция g (t) при функции веса w (t) должны иметь одинаковые моменты до
/г-го включительно:
ОО
J Pg{t)w{t)dt=\i^ 0<v</z (11.61)
о
[сравните с выражением (11.52)].
2. Функции ф; (0, являющиеся базисом для функции
ё(0=£с,<мо, (H.62)
следует выбрать так, чтобы они представляли собой последовательность
ортонормированных функций, т. е. чтобы
? (0 при i=t=i\
J 4>i(t)<Pj(t)w(t)dt = t[l п^ . = h (11.63)
3. При этом коэффициенты С,- доставляют минимум функционалу
00
/ = J w(i) [g(t)-g(t)]2dt. (11.64)
66
Подставляя в выражение (11.64) g (f) из формулы (11.62) и
приравнивая далее производные dIldCt к нулю, с учетом выражения (11.63)
получим соотношение, определяющее коэффициенты Фурье:
С,= J w(t)g\t)q>i(t)dtt i = 0, 1,
., /г.
(11.65)
Теперь необходимо определить связь между коэффициентами Ci и
моментами \ii при заданном базисе <р( (t) и функции веса w (t).
Вначале рассмотрим случай, когда функции ср, (t) являются
полиномами Лягерра.
Аппроксимация многочленами Лягерра. Из определения многочленов
Лягерра
Ф,(0 = М0 = -^е
и
at.
d (at)
7[(otf)'e
—аП
(11.66)
После дифференцирования на основании формулы Лейбница для /-й
производной произведения двух функций [39] соотношение (11.66) можно
записать в виде
%W-t,M-V5g(J)^f. <И.«1
Чтобы выполнить соотношение (11.63), необходимо принять функцию
веса в виде
ш(0 = е-а'. (11.68)
Используя выражение (11.67) в соотношениях (11.65)., получим
Ci-V^J^-^^{l\\ S{t)w{t)t^JdU i = 0, 1, ...,/г. (11.69)
Подставляя в формулу (11.69) соотношение (11.52), получим связь
между коэффициентами Ct и моментами fjtf.:
/= О N ' I
= 0, 1,2,
(11.70)
Коэффициенты С,-, определенные на основе соотношения (11.70), имеют
следующий вид:
Ci = Va [\i0 — afxj;
(11.71)
. Следовательно, окончательно получим
(11.72)
67
или с учетом соотношений (11.62) и (1Г.67)
г(о~2^£(.;)Ш±> ("-7з>
причем Ct определяется из соотношения (11.70).
Передаточная функция объекта, следовательно, приближенно равна
0,s)»2cv«i:(;)j5^- ("•«>
Аппроксимация функциями Лягерра. Из определений функции Лягерра
dl
(at)
,,(« = KSe-^2(;)±=^. (I..76)
Коэффициенты Ct определяются на основе соотношений (11.63) и (11.76):
I . 00 Qfl
% (0 = -пг е * -^-. [(а*') е-«], (11.75)
т. е
at
i
/=0
Для того чтобы интегралы в формуле (11.77) привести к виду
моментов \it_j в соответствии с соотношением (11.61), необходимо принять
w (t) = ea'/2, тогда
ci=fV^2(!)-77=flf'i<-/'i=l'2, •■•*"• (IL78)
/=0 \ * г
Легко видеть, что соотношение (11.63) выполняется.
Импульсная переходная функция имеет вид
п at * / •
t=0 /=0 \ I I
Приближенная передаточная функция является рациональной
функцией оператора s:
0(8)~Уъ С, V~a ,YS~Jji+l • - (Н.80)
1 У+l
I I—s+-
i=0
(-i-b-J-)'
Коэффициент а определяется на основе оценки величин модулей
наименьшего и наибольшего полюсов передаточной функции G (s).
Способ определения иллюстрирует рис. 11.8. Следует нарисовать
окружность, которая должна охватывать все полюсы передаточной функ-
68
ции G (s) и располагаться в левой полуокружности. Из начала координат
проводится касательная к окружности. Длина этой касательной равна ос/2.
Аппроксимация показательными функциями. Рассмотрим зависимость
между передаточной функцией и импульсной переходной функцией g (t)
с весом w (t) (II.48):
Gw(s)=\ w{t)g(t)e-stdt.
Ядро преобразования Лапласа представляет собой полную систему
функций е~г', г = 0, 1, 2, ... в пространстве L2 [0, оо] с весом w (t).
Полагая в выражении (11.48) s = О, 1, 2, . . ., получим моменты \ir
функции g (t) с весом w (t) относительно системы функций e~rt:
,ir=J w(i)g(f)t-'*dt, r = 0, 1,2,
(11.81)
вид
где
В соответствии с формулой (11.62) аппроксимирующая функция имеет
*(') = 2с|Ф,-(0,
/=о
Szft+JD
^ = 2j7'e *-0, 1,2, ...,„,
/=o
а функция веса
w (t) = e-'.
(11.82)
Рис. 11.8. Определение масштабного
коэффициента по расположению корней
(11.83) передаточной функции
Коэффициенты у) получим ортогонализацией системы (11.82) методом
Шмидта, используя уравнения (11.63) и (11.83).
Система (11.82) в развернутом виде запишется так:
фо = то;
= yS + vie"';
ф2
Ф1 =
= Yo + Y?e^ + vle~2/;
Используя метод Шмидта, получим
vo = ± Кз;
На основе соотношений (11.65), (11.82) и (11.83) запишем выражение
для коэффициентов С£:
00 СО
c' = je W е~'ф« (0 d' = J ё (О Ы + vie""' + vk-2' +
00 00
+ • • • + v'e-") d (e"<) = уЦ g(t)d (е-') + Vf J g (0 e~' rf (e~<) +
б о
oo oo
+ Y21 g (0 в"2' d (e"') + • • • + yl f g (/) e~" d (e"<).
(11.84)
69
Учитывая соотношения (11.82), (11.81) и (11.84), получим
Ci = ylQ\io + y[\ii + yl2\i2-\ bvta. i =0,1,2, ...,л. (11.85)
Таким образом, на основании известных моментов \х{ можно
определить из системы (11.85) искомые коэффициенты Сг
Запишем систему (11.85) в развернутом виде:
п 0 .
Со = VoM'O»
Ci = yl\i0~\-y\\iu
С2 = yl\iQ + YiM-i + 72^21
(11.86)
Сп = Уо 1Ю + YiV i + 72 ^2 + h УпЦп-
Зная коэффициенты Ct и функции cpt. (/), можно найти
аппроксимирующую функцию
g(t)~~g(t)=tCityj*4t- (П.87)
t=o /=о
Передаточная функция имеет вид
ад«2с*Ет'тп- {IL88)
t=0 /=0
Схема идентификации объекта методом моментов, таким образом,
состоит в следующем:
1) определяется время запаздывания т;
2) выписываются моменты сигналов у (t) и и (t)\
3) определяются моменты импульсной переходной функции на
основании выражения (11.60);
4) вычисляются коэффициенты Фурье Ci системы ортогональных
функций у. (t) из выражения (11.65);
5) находится аппроксимирующая функция g (t) как линейная
комбинация функций ф£ (t)\
6) определяется (если в этом есть необходимость) передаточная
функция
G(S)~G(s) = L{£(0).
В заключение следует заметить, что метод моментов можно также
использовать для идентификации объектов с распределенными
параметрами. Последовательность операций и основные зависимости, а именно:
(11.52), (11.53), (11.54), а также (11.60), (11.70) и (11.71) те же, только
коэффициенты С, и моменты \i{ — не постоянные функции времени,
а являются функциями длины I. Вследствие этого функция g (t),
аппроксимирующая импульсную переходную функцию системы, также является
функцией длины /, т. е. имеет место следующая зависимость:
gn(tJ)=tci(t)%(t). (H.89)
t=0
§ II.2. Идентификация объектов с помощью модели
с настраиваемыми параметрами
В последние годы уделяется много внимания методам определения
особенностей динамики физических систем с использованием моделей с
настраиваемыми параметрами. Много исследований посвящено разработке
способов автоматической настройки параметров для того, чтобы иденти-
70
zlt)
utt)
Cue те па
git)
Модель
9(t)
»
, 1
уШ\ли
*\V
m(t)
r- 1
1 n-„. 1
d
Критерий
ошибки
устройство
Рис. 11.9. Метод модели с настраиваемыми
параметрами
фикатор можно было включать в самонастраивающуюся систему
управления. В большинстве работ представлены аппаратурная реализация моделей
' и способы настройки их параметров. Во многих случаях такая
аппаратура для настройки параметров необходима, а в случае модели, которая
настраивается на оптимум аппроксимации вручную, можно использовать
достаточно простое оборудование [4].
Способ использования модели с настраиваемыми параметрами показан
на рис. II.9. Требуется оценить динамику некоторой настраиваемой
физической модели, например импульсную переходную функцию g (/),
при использовании пробного сигнала и (f) в течение конечного интервала
времени 7\ Выходной сигнал системы может содержать помеху z (/),
так что измеряемый
сигнал п (t) = у (0 + г (*).
Модель системы
сконструирована так, что
входной сигнал может быть
одновременно подан на
вход как системы, так и
модели. Обычно модель
имеет постоянную
структуру с несколькими
настраиваемыми
параметрами. Выходной сигнал
модели т (t) сравнивается с
выходным сигналом п (t)
системы в соответствии
с некоторым критерием
ошибки, и параметры
модели подстраиваются до
тех пор, пока ошибка не достигнет минимума при использовании
соответствующей стратегии настройки. О найденной таким образом модели
говорят, что она оптимальным образом аппроксимирует систему.
Настройка параметров должна основываться на измерении ошибки. При
автоматической настройке модели аппаратура настройки включается
в цепь обратной связи (рис. И.9). В простейших случаях эту аппаратуру
может заменить человек.
Практическое использование моделей с настраиваемыми параметрами
требует исследования большого числа конкретных вопросов, о некоторых
из которых речь буде^ идти ниже.
Важнейшим вопросом, который возникает при использовании
настраиваемой модели, является следующий: какова должна быть структура
модели?
Решение задачи идентификации может иметь различные подходы:
1) Задан физический объект, структура которого известна, но не
известны параметры. Для определения значений этих параметров
структура модели должна быть выбрана так, чтобы она в точности
соответствовала структуре объекта. Если даже необходимо некоторое упрощение
модели, то обычно известно, какую аппроксимацию структуры следует
использовать.
2) В другом случае объект может быть «черным ящиком», структура
которого до некоторой степени известна, но может быть и совсем не
известна. В этом случае динамический объект аппроксимируется некоторой
математической моделью с определенной структурой. Передаточная
функция модели может содержать, например, два полюса, один нуль и время
запаздывания. Модель, отвечающая таким требованиям, может быть
построена различными способами и совершенно отличаться от структуры
реального объекта, даже если порядок числителя и знаменателя
передаточной функции объекта был выбран правильно. С другой стороны,
71
хорошо известно, что структура модели в значительной степени влияет
на точность и скорость сходимости процесса. Выбор структуры модели,
следовательно, должен производиться с учетом сказанного. Модель
также должна быть выбрана в зависимости от характера требуемой
информации. Если, например, требуется определить импульсную переходную ,
функцию объекта, то следует использовать модель, обеспечивающую
аналогичную временную характеристику. В результате можно получить
хорошую аппроксимацию импульсной переходной функции g (/)>
несмотря на то, что передаточная функция модели будет совершенно отлична
от передаточной функции объекта.
П.2Л. Модель в виде дифференциально-разностнога уравнения
Пусть р = dldt обозначает оператор Хевисайда, а е~Рх — оператор
сдвига на величину т. Тогда линейный объект с запаздыванием можно
описать уравнением
{а„рп + ап_грп'х -\ Ь (hP + *о) У (0 +
+ ФтРт + Ьт^р^ + .. • + Ьф + Ь0) е-Р*и (0 = 0. (II.90)
где п ^ т.
Параметры а0, . . ., ап, &0, . . ., Ьт и время запаздывания т не
известны, но предполагается, что известен порядок пит.
Требуется построить модель с настраиваемыми параметрами а,; Ру;
а; i = 0, 1, . . ., п\ j = 0, m, уравнение которой в случае идеальной
настройки'параметров совпадало бы с уравнением (11.90). Если в
уравнение модели, аналогичное уравнению (11.90), но с коэффициентами ai9
Ру, а, подставить те же функции у (t) и и (/), то правая часть этого
уравнения не будет равна нулю, а будет определять ошибку аппроксимации
объекта моделью:
КРЛ + <*,z-iPrt"x H baiP + ao)#(0 +
+ ФтРт + (W1-1 + • • • + PiP + Ро) er»u (t) = 8 (/). (П.91>
Уравнения (11.90) и (11.91) нормализуются так, чтобы их коэффициенты
не превышали единицы. Чаще всего нормализация проводится
относительно а0 и а0.
Предположим, что уравнения (11.90) и (11.91) уже нормализованы
и а0 == а0 = 1.
Из уравнения (11.90) получим
У (0 = ФтРт + ^m-iP™-1 + • • • + Ьур + Ь0) е~Р*и (0 +
+ (апр» + ап_гр^ + ... + ajp) у (0- (Н.92>
Аналогично из уравнения (11.91) получим
- в (/) + У (0 = ФтРт + Pm-lP^1 + ' • • + PiP +
+ р0) е-р*и (t) + (ajP + an_lPn-x + ... + аф) у (t). (II.93)
Вычитая соотношение (11.93) из выражения (11.92) и деля на рпу
окончательно получим
-^- = - ФтРт-П + fW"-»-1 + • • • + PlP-/Z+1 +
+ Pop-") е-^м (/) + {Ьтр™-п + bm.lP^n-i +
+ • • ■ + ^iP-"-*-1 + ^оР-") e"^it (0 + К«я - «J +
+ (ct^ - д^) p-i + ... + (a, - aj p-^1] у (t). (П.94)
Уравнение (11.94) моделируется на аналоговой машине, а сигнал
г1 (t) = г (t)lpn подается на квадратор и далее интегрируется в пределах
от 0 до 7\ На выходе, как показано на рис. 11.10, получаем некоторый
показатель ошибки /.
72
Проиллюстрируем это на примере системы второго порядка. Пусть
п = 2, т = 1 и а0
ап = 1.
Из уравнения (11.94) имеем
8(0 _
^- е~р°и (t) Ц- е~р°и (t) + -^- егР^и (/) +
+ "Э" е-^а (0 + а2у (0 - а2у (t)
а из уравнения объекта (11.90) при п
получим
2 и m = 1 после деления на р2
■i^- = 4-е-рт"(0 + -She-^W
Подставляя уравнение (11.96) в соотношение (11.95), получим
уравнение, пригодное для моделирования на аналоговой машине:
8(0
^+ -^0(0 +«*(/)•
-§-е-Ги(0-
-Ь-е-^а(/). (11.97)
На рис. 11.11 показана схема моделирования уравнения (11.97).
Благодаря такому виду уравнения изучаемый объект моделируется полностью^
без применения нежелательных дифференцирующих звеньев.
\z(t)
u(t)
Объект \
9(t)
Модель
git)
y(t) Xn(t}
1
J
m(t)
W" ,
\1
[/,
e?W
0 \
Рис. 11.10. Настройка модели на основе критерия минимума среднего квадрата ошибки
Из уравнения (11.95) видно, что когда все параметры модели
достигают своих оптимальных значений (а( = ait (3,- = bj, а = т), то е (/)
равно нулю либо равно величине возмущения z (t). Следовательно, при
оптимальной настройке параметров модели величина е (/) не зависит ни
от вида входного сигнала и (t), ни от функции п (t). Однако практически
никогда мы не достигаем оптимума, и тогда сходимость метода зависит
как от и (/), так и от п (t). Когда, например, возмущение приложено
к выходу у (t), то для данного вида модели получаем приближения
параметров в смысле минимума интеграла от квадрата ошибки. Для
устойчивых объектов все коэффициенты аь должны иметь одинаковые знаки
и отличаться от нуля. В случае минимальнофазового объекта
коэффициенты bi также должны иметь одинаковые знаки, .а при неминимально-
фазовом объекте они могут иметь разные знаки.
11.2.2. Модель в виде комбинации ортогональных функций
Модель объекта можно также построить в виде ортогональных
функций (см. метод моментов). Импульсную переходную функцию модели
можно тогда описать уравнением
g(t)
(11.98)
Блок-схема системы моделирования представлена на рис. 11.12. При
произвольном входном сигнале и (t) выходы отдельных элементов, реали-
7а
u(t)
Г"
Объект
г
|»й
1 1
.до
m
D^T
p ,
f I
\ аг\ \ С
T '
**J/M
1
00
/
Ъ4 i
^
4
г
a2y(t)
[ j
«ty(t)
p
yd)
P2
■m
Гг4-
1——
г^-
-hume-'*
ГЫ
V-
й й !
j
U(t) |
тщ "Г"
£>
I
.»Ше-1>ег " \j/ Sn® -ре
Модель,
Рис. 11.11. Блок-схема аналогового вычислителя для решения уравнения (11.97)
uit)
Объект
9(t)
x(t) ~ e(t)
КЭ *
Т(->
ф
rn.it)
-J
цЮ
m2(t)
\Еи
е*М
feW
ftffl
m„(t).
-/
I I
I I
I I
mil)
EF-U
Рис. 11.12. Аппроксимация импульсной переходной функции объекта
с помощью модели, основанной на разложении в ряд по ортогональным
функциям ф/ (t)
зующих ф,. (/), обозначены через mt (t). Можно доказать [25], что
линейная независимость ф,- (f) обеспечивает линейную независимость mi (t).
Ошибки в этом случае определяются зависимостью
в (0 = У (0 - т (t) = х (t) - t См (О, (И.99)
а критерий ошибки
Т 7* Г п
I = } е2 (/) dt = И */(/) - 2 С,т, (О
2
Л. (11.100)
Процедура настройки Ct. в данном случае сильно упрощается, так как
функции ф£ (f) взаимно ортогональны.
Однако выбор структуры модели не исчерпывает всех задач, связанных
с практическим использованием данного метода. Важнейшими из этих
задач являются следующие.
Изменение масштаба. Многие промышленные объекты имеют
настолько большие постоянные времени, что очень трудно моделировать
их с помощью аналоговых машин. В этом случае необходимо проводить
моделирование в ускоренном масштабе времени. Это требует регистрации
входных и выходных сигналов объекта и последующего их ускоренного
воспроизведения.
Критерий ошибки. Для оценки точности аппроксимации объекта
с помощью модели предложено большое число различных критериев.
Обычно они являются функционалами ошибки
8(/) = n(t) — m(t). (II.101)
Наиболее часто встречающимся критерием является интеграл от
квадрата ошибки
т
/^ \s2(t)dtj (II.102)
о
который приводит к выбору параметров на основе минимума выражения
(11.102). Следовательно, если входной сигнал модели m (t) есть линейная
функция параметров модели, то мы получим параболический минимум
выражения (11.102), что имеет большое практическое значение. Однако
в системах, содержащих запаздывание т, минимум в зависимости от
величины т имеет специфическую чашеобразную форму.
Начальные условия. Когда настройка модели производится по
реализациям сигналов, зарегистрированных на конечных интервалах времени
и затем циклично повторяемых, что обычно имеет место, возникает
проблема, как учесть в каждом отдельном случае начальные условия. Если
это возможно, то измерения должны проводиться при нулевых начальных
условиях в объекте. Иногда, однако, например при измерениях в объекте
во время его нормальной эксплуатации, это оказывается невозможным.
Когда начальными условиями нельзя, пренебречь или их нельзя учесть
отдельно, следует включить эти начальные условия в модель как
дополнительно настраиваемые параметры. Другая возможность заключается
в проведении измерений в течение достаточно длительного времени (если
такая возможность представляется с точки зрения сохранения
стационарности объекта) по сравнению со временем протекания переходных
процессов, вызываемых ненулевыми начальными условиями, с тем, чтобы
этими процессами можно было пренебречь. Еще одна возможность
заключается в подаче на систему (если это допустимо с точки зрения линейности)
входных сигналов и (t) с такой большой амплитудой, чтобы эффектом,
названным ненулевыми начальными условиями, можно было пренебречь.
75
Стратегия настройки. Способ отыскания оптимальных значений
параметров модели имеет большое значение и будет рассмотрен более
обстоятельно. При п настраиваемых параметрах критерий ошибки /
представляет собой поверхность в /2-мерном пространстве, имеющую
абсолютный минимум на множестве значений настраиваемых параметров.
Стратегия настройки должна однозначно приводить к достижению этого
минимума при старте из произвольной начальной точки. Возможные
источники трудностей здесь заключаются в следующем:
в наличии локальных минимумов;
в малой чувствительности критерия к изменению некоторых
параметров;
в слабой сходимости алгоритма отыскания минимума для некоторых
структур модели или для некоторых стратегий;
в отсутствии ортогональности модели, объясняющемся существованием
зависимости между оптимальным значением одного из параметров с
другими параметрами.
Если величины настраиваемых параметров существенно отличаются
от их оптимальных значений, то критерий аппроксимации / в некоторых
пределах может почти совсем не зависеть от изменения величин этих
параметров, так что нельзя заметить практически никаких изменений
в величине /, когда значения параметров лежат в области, отстоящей
отточки оптимальности. Эффект этот наиболее отчетливо и ярко выражен
в случае, когда идентифицируемый объект содержит запаздывание. Если
настраиваемая величина времени запаздывание в модели далека от
величины, существующей в объекте, то сигналы т (t) и п (t) не коррели-
рованы между собой независимо от того, какие значения принимаюг
остальные настраиваемые параметры.
Интеграл /, вообще говоря, является функционалом входа и (t)r
импульсной переходной функции g (/), возмущения z (t), времени
наблюдения Г, а также функций настраиваемых параметров а19 а2, . . ., ал.
Следовательно, можно написать
I = I (g, и, z, 7, а19 а2, . . ., ап). (П.103>
Для определенных значений g, и, z, T этот интеграл представляет
собой гиперповерхность в я-мерном пространстве параметров а. и
достигает минимума в той точке, где все параметры а. имеют оптимальные
значения.
Для того чтобы проиллюстрировать это графически, рассмотрим
двумерный случай. На плоскости параметров аъ а2 можно изобразить
кривые равных значений /, аналогичных линиям равных высот на
географической карте. Чаще всего эти линии бывают замкнутыми (рис. 11.13).
Задача заключается в отыскании стратегии, которая позволяет,
двигаясь из произвольной точки Р0, достичь точки М, где интеграл имеет
минимальное значение. Целесообразно выбрать такую стратегию, которая
не только позволяет из точки Р0 достичь точки М, но и обеспечивает
наименьшее время движения. Следовательно, необходимо двигаться из
точки Р0 в точку М вдоль линии наискорейшего спуска. Если движение
должно происходить во времени непрерывно, то траекторию можно
описать следующей системой уравнений:
1ЕГ = -*-ёг» '=1.2, ...,п, (И.104).
где dajdt — составляющие вектора, характеризующие непрерывное
изменение настраиваемых параметров во времени; д11да( — составляющие
вектора градиента /. Уравнение (11.104) выводится из условия, чтобы
увеличение интеграла / во времени было минимальным, т. е. чтобы ска-
76
= min.
(11.105)
лярное произведение вектора градиента / и вектора скорости daldt было
.минимальным:
dI — ( dI da \ — V д! d0Li
dt "" \ да ' dt ) ~~ Zj dat " d/
1=1
Скалярное произведение (11.105) достигает минимума, когда вектор
daldt пропорционален со знаком «минус» вектору градиента /, т. е. когда
-%- = — £grad/. (II.106)
На рис. 11.14 графически изображена стратегия движения вдоль
линии наискорейшего спуска, т. е. линии, касательной в каждой своей
-точке к вектору градиента с измененным знаком.
а,
1=const
gradl
I^const
da/dt
«1
Рис. 11.13. Типичные кривые
равных значений показателя настройки.
/ на плоскости настраиваемых
параметров а1 и а2
Рис. 11.14. Метод наискорейшего
спуска
Легко видеть на основании выражения (11.104), что если / —
квадратичная форма относительно а£., то at (t) непрерывно убывает во
времени.
Стратегия наискорейшего спуска выглядит приблизительно
следующим образом. Начинаем из исходной совокупности значений
параметров а10, а20, . . ., ап0. Далее каждый из параметров изменяется от
значения а10 на величину Да, и одновременно определяется изменение /
*(в двумерном случае это делается графически). Частные производные
можно аппроксимировать через
&-&• (iuo7)
и все значения параметров далее определяются в соответствии с
соотношением
A U Ы
(11.108)
Можно заметить, что.метод имеет два недостатка:
1) неизвестно, как выбирать. коэффициент пропорциональности k\
2) определение всех производных А//Да, трудоемко.
Для частичного устранения недостатка, отмеченного в пункте 2),
часто пользуются модифицированной стратегией наискорейшего спуска.
При этом не будем определять непрерывно значения градиента / или Да£
.и двигаться вдоль линии наискорейшего спуска, а будем двигаться вдоль
77
линии, просто определяемой по величине градиента в начальной точке
до тех пор, пока / не достигнет локального минимума. Проверить,
достигнут ли локальный минимум, можно некоторым числом шагов Да.. Когда /
достигнет своего локального минимума, в этой точке определим новое
значение градиента / и будем продолжать двигаться до тех пор, пока /
не достигнет нового локального минимума. Модифицированная стратегия
наискорейшего спуска изображена
на рис. 11.15. При движении с
постоянным градиентом интеграл /
достигает локального минимума
в точке, где вектор da/dt =
= — grad / становится
касательным к одному из контуров равных
значений /.
Однако, когда настройка
параметров осуществляется
вручную, даже этот метод становится
трудоемким.
Для определения параметров-
можно использовать
безградиентную стратегию, например
стратегию Гауса—Зейделя. Из точки Р0,
определяемой начальными
значениями параметров а.0, изменяется только один параметр, например
alf до тех пор, пока / не достигнет своего локального минимума.
Сохраняя теперь величину параметра аг постоянной, равной найденному
оптимальному значению aia, изменяем далее последовательно величину
параметра а2 до тех пор, пока / не достигнет локального минимума
относительно а2, и т. д. до параметра ап.
Рис. 11.15. Модифицированный метод
наискорейшего спуска (пунктирная кривая—/;
штриховая кривая — /х)
Рис. 11.16. Метод Гаусса—Зейделя
Затем возвращаемся к параметру аи потом а2 и т. д., пока не придем
к абсолютному минимуму. Вышеприведенная стратегия для двумерного
случая иллюстрируется рис. 11.16.
Эта стратегия аналитически может быть интерпретирована при помощи
системы уравнений
^7=0, /=1,2, ..., п. ' (11.109)
Уравнения (11.109) линейны только тогда, когда / есть квадратичная
форма at., а итерационный процесс приводит к абсолютному минимуму,
когда квадратичная форма / положительно определена. Если / не является
квадратичной формой, а имеет более сложный вид, то уравнения (11.109)
78
линеаризуются в некоторой окрестности абсолютного минимума.
Определение локального минимума относительно одного из параметров <xt
соответствует решению одного из уравнений системы (11.109).
Весьма существенна последовательность настройки параметров.
Запишем уравнения (11.109) в развернутом виде:
Pll<*l +Pl2<*2 +
р21<*1 + р22&2 +
+ Plnan = Сг\
+ Р2пап = <Y,
Pnlal + Рп2<*2 + ' • • + Pmfln = Сп.
(11.110)
Система (11.110) решается легче, когда коэффициенты рн при
элементах а/£> стоящих на диагоналях, значительно больше
коэффициентов ри или рп, i ф j. Опытным путем на каждом этапе можно определить
S.6
I
0,005
0,00k
0.003
0.002
0.001
О
II
\
\)\ Л
мк
1Г Т1
0,90 0,2k 0,9в 102 кв
Рис. 11.17. Зависимость интеграла / от
запаздывания а (числовой пример)
Рис. 11.18. Зависимость
интеграла / от настраиваемого
параметра а0 (числовой пример)
те параметры, которые в наибольшей степени изменяют величину 7V
Однако лучше всего на каждом цикле вычислений отбрасывать те
параметры, которые в предыдущем цикле оказали наименьшее влияние на
величину /.
Очень важно, чтобы вся исходная информация использовалась для
определений начальных значений параметров а,. Так как / может иметь
плоский экстремум, то при значительном удалении от оптимальных
значений параметров часто требуется вначале осуществить «случайный
поиск» для локализации кратеров в гиперповерхности / (аь . . , ап)
и только потом использовать описанную выше стратегию.
Например, в случае линейных объектов с запаздыванием зависимость
интеграла / от времени запаздывания о имеет чашеобразную форму
(рис. 11.17), тогда как от остальных параметров (например, от
настраиваемого параметра а0) эта зависимость параболическая (рис. 11.18).
Порядок экспериментального определения параметров линейных
объектов этого типа следующий:
1. Находится оптимальное значение параметра, характеризующего
время запаздывания в модели, т. е. отыскивается локальный минимум /
с точки зрения заложенного в модель запаздывания а.
2. Находится оптимальное значение параметра а0, представляющего
собой коэффициент в уравнении объекта, обратно пропорциональный
коэффициенту усиления.
3. Далее последовательно отыскиваются значения параметров,
представляющих собой коэффициенты, стоящие при возрастающих
производных в уравнении состояния объекта.
Зависимость интеграла / от параметров <xiy представляющих собой
коэффициенты, определенные в пунктах 2) и 3), — квадратическая, т. е.
79
в пространстве параметров кривые равных значений / являются
эллипсами. Скорость сходимости описанной процедуры Гаусса—Зейделя за-,
.висит, следовательно, от угла ф между осями эллипса, что хорошо
иллюстрируется рис. 11.16.
Влияние возмущений. На практике
выходной сигнал объекта всегда в
большей или меньшей степени «размыт»
помехами. Вследствие этого необходимо
отыскивать такие оценки параметров,
модели, которые будут оптимальными
при наличии помех.
При непрерывной оптимизации
модели экспериментально подтверждается,
что интеграл / содержит случайные
флюктуации, вызываемые
возмущениями (рис. 11.19). Это приводит к
некоторой неопределенности в определении
действительного минимума интеграла /.
Дисперсия о"! может быть определена
известными способами, а, как показывает рис. 11.19, при
графическом способе усреднения даже при относительно небольшом числе
измерений эту- неопределенность можно значительно уменьшить.
1/
/ ^
i
f
—^
(*i)opt *
,Рис. 11.19. Случайный разброс,
вызываемый возмущениями
§ II.3. Идентификация линейных объектов
на основе корреляционного анализа случайных сигналов
u(t)\
I
git)
x(t)
S(t-r)
Объект
\x(t-
z(t)
y(t)
Если требуется осуществить идентификацию объекта в процессе его
нормальной эксплуатации, т. е. в присутствии помех, на основе знания
только случайных реализаций сигналов входа и выхода, то в общем
случае необходимо использовать^ статистические методы. Основой этих
методов ядляется корреляционный анализ
сигналов. Эти методы требуют
проведения большой вычислительной работы и
характеризуются значительно меньшей
точностью, чем описанные выше.
Рассмотрим линейный объект (рис.
11.20), причем предположим, что объект
асимптотически устойчив, а помеха z (t)
не коррелирована с входным
сигналом и (t).
Тогда выходной сигнал у (t) определится уравнением
Рис. 11.20. Блок-схема
паздыванием
объекта с за-
у (t) = z (t) + J g (X - т) и (t - X) dK
(11.111)
где импульсная переходная функция удовлетворяет условиям
\k(t — т) при t^>x
g(t) =
0
при /<т.
(11.112)
Теперь определим среднее во времени значение произведения у (t— ft) X
X и (f). Величина эта будет функцией только временного сдвига сигнала у
.so
относительно и. Эта функция называется взаимокорреляционной
функцией г Ryu (ft) сигналов у (t) и и (f):
т
/?iW(*) = lim-^r- J y(t + Q)u(t)dt =
00 00
= \ \ g{b — T)u(t + u — X)u(t)dkdt. (II.113)
00 —00
Среднее значение произведения г(/+д) и (t) равно при этом нулю,
так как предполагается, что сигналы не коррелированы с помехой.
Поступая аналогично, можно определить автокорреляционную
функцию сигнала и (/):
т
Ruu($) = Hm 4r J"(' + *)"(') dt. (Ц.114)
Используя выражения (11.113) и (11.114), уравнение (11.111)
можно записать в следующем виде:
оо
*»«(*)= jg(X-T)RU®-4d%. (п.115)
оо
Это уравнение аналогично уравнению (11.111), только вместо
выходного и входного сигналов выступают соответственно взаимо- и
автокорреляционные функции.
Обозначая
X — т = ц, (11.116)
'на основании выражения (11.115) найдем зависимость
оо
Ryu (*) = | g (V) R«uW - х) - ц] rf|i. (11.117)
—00
Решая уравнение (11.117) известными методами [46, 55], получим
импульсную переходную функцию объекта R (t)y а временной сдвиг
между взаимо- и автокорреляционными функциями, как это видно из
уравнения (11.117) при графическом изображении этих функций,
представляет собой время чистого запаздывания т. Точность при этом будет
тем большей, чем сильнее Ruu (f) по форме приближается к функции
Дирака, а следовательно, чем ближе входной сигнал по своим свойствам
приближается к белому шуму. Имея импульсную переходную функцию,
легко найти передаточную функцию [46, 551.
§ II. 4. Аппроксимация объекта высокого порядка
с использованием модели, содержащей запаздывание
11.4.1. Аппроксимация при помощи модели первого порядка
с запаздыванием
Простейшая модель, которая пригодна только для анализа устойчивости
простых систем управления, может быть представлена уравнением (II.3).
Передаточная функция этой модели имеет следующий вид:
G(s) = 4fir- (И-118)
1 Точнее говоря, функция корреляции есть среднее значение произведения двух
сигналов не по времени, а по совокупности реализаций этих сигналов; она равна среднему
значению по времени при условии их эргодичности с точки зрения моментов второго порядка
этих сигналов (Прим. ред. оригинала).
6 х. Турецкий &1
Аппроксимация реакции объекта на скачок при помощи этой модели
была предложена в 1924 г. Купфмюллером [24]. Через точку перегиба
реакции проводится касательная, которая отсекает на оси времени t
величину, эквивалентную времени запаздывания т2, а на прямой у (t) =
= h (со) — величину постоянной времени (рис. 11.21). Хотя обе реакции
могут сильно отличаться одна от другой, но на устойчивость системы
(см. гл. IV) это мало влияет.
Н.4.2. Аппроксимация при помощи модели я-го порядка
при одинаковых постоянных времени с запаздыванием
Отправной точкой предположенного в работе [511 метода является
экспериментально снятая реакция объекта на единичный скачок (рис. 11.22).
На этой реакции отыскивается точка перегиба, определяются ее координаты
и параметры /*., ti9 Тю Тт с помощью касательной к кривой в точке
i
С
ky(t) = h(i)
1 Т -■
'bs:
1
t
и к
,
?
-*=
'
1
f?
1
1
i
-С|
Т
,
1
/
1УЙН
Ml)
1
V=o/
г*—**
-«—
^
V
* *
'Q
То
^
t
ui
1=0
Рис. 11.21. Метод аппроксимации Купфмюл» Рис. 11.22. Метод аппроксимации
лера
Стрейка
перегиба (рис. 11.22). На основе полученных величин определяется
эквивалентная модель с одинаковыми постоянными времени.
Реакция на скачок модели с п одинаковыми постоянными времени
и с коэффициентом усиления, равным единице, определяется выражением
t п-\
v=0
Дифференцируя выражение (11.119), получим
h(t) = e T
п-1
л-1
1 у /v у Л-1
т Zj vir Zj (v-i)i:
v=0 v=l
= e т
Г/i-l n—2
VI f VI Л
Zj virv+* Zj v\tv+x
Lv=0 v=0
t^O
или
82
— in-i
(n-l)lT» *
t^O.
(11.120)
Аналогично при п = 2 вторая производная реакции имеет вид
ч
или
/г (0 = е т
{П-2
/Я"1 1
(л — l)!^1]'
^0
(л~1)!Г« (л
A(0 = e-^1Jj^^[l-TjZ^T], /^0. (11.121)
В точке перегиба Q имеем
h(tt) = 0. (11.122)
Таким образом, приравнивая правую часть выражения (11.121) к нулю,
А = /г—1. (11.123)
получим
Подставляя выражение (11.123) в формулу (11.119), получим координату
точки перегиба
*&) = /», = 1 -e-(»-D ^ -^Г1- (ПЛ24)
v=0
Из рисунка видно, что
Т h(tt) (n—1)«-A
или
Тд __ (п- 2) 1 е^-1
Г (Л 1)/2"2
(11.125)
Из рисунка также видно, что
или
т.-*>-Ъ-*-ЧГ-т-Ь=$г[^ -|0^
Г ' ' /_ пя-2
(п-1)Л
п-1
«я—1
S(n-l)v
v!
v=0
В результате имеем
Тщ _ Тд . 7*ц ^
/Т1 /TI 1 <Т» <Т»
(11.126)
(11.127)
Подставляя выражения (11.123), (11.125) и (11.126) в формулу (11.127),
получим
Тт _ (/1-2)! \У (n-l)v
_ (/г — 2) 1 VI
(п_1)л-2 ^
v!
(11.128)
v=0
Разделив выражение (11.126) на (11.125), получим
л-1
(п—\)п-1-(п — 2)\
L v=o J_
Та (л_2)!ел-1
Аналогично при делении выражения (11.127) на (11.125), имеем
(11.129)
л-1
^ ~"е 1л vl
v=0
6*
(11.130)
83
На основе формул (11.123), (11.130) получена таблица для п = 1,
2, . . ., 10 (см. табл. II.1).
Последовательность нахождения модели по имеющейся
экспериментальной характеристике следующая:
1. На графике реакции объекта на скачок определяются величины
t[> hit Тш Тау Тту причем реакция должна быть нарисована в таком
масштабе, чтобы h (оо) = 1. Для этого прежде всего определяются:
точка перегиба;
отрезок %и = Ти/Та.
Таблица 11.1
Значения TJT, TJT, Tu/T, t£/T, q>/, TJT, TmITa
п
1
2
3
4
5
6
7
8
9
10
TJT
1
2,718
3,695
4,463
5,119
5,699
6,226
6,711
7,164
7,590
i TJT
0
0,282
0,805
1,425
2,100
2,811
3,549
4,307
5,081
5,869
Tu/Ta
0
0,104
0,218
0,319
0,410
0,493
0,570
0,642
0,709
0,773
и
0
1
2
3
4
5
6
7
8
9
Ф/
0
0,264
0,323
0,353
0,371
0,384
0,394
0,401
0,407
0,413
TmlT
1
2,000
2,500
2,888
3,219
3,510
3,775
4,018
4,245
4,458
TmlTa
1
0,736
0,677
0,647
0,629
0,616
0,606
0,599
0,593
0,587
2. По табл. 11.1 на основании найденного отношения Ти1Та
определяется порядок модели /г, причем, если найденная из рисунка величина
Ти1Та лежит между двумя соседними строками, то необходимо
уменьшить Ти за счет введения эквивалентного времени запаздывания тг.
Tt=0.87
TU=2J0
Рис. 11.23. Реакция объекта третьего порядка (7\ = 1; Т2 = 5; Т3 = 10) на
скачкообразное воздействие, аппроксимированная реакция модели второго
порядка с постоянными времени Т = 7,35 и запаздыванием т2 = 0,87
3. Постоянная времени Т находится на соответствующей строке
столбца ttIT\ столбцы TJT и TJT служат для контроля.
Для иллюстрации рассмотрим пример аппроксимации объекта третьего
порядка (рис. 11.23) с постоянным времени 1; 5 и 10. Из рисунка находим,
что Та = 20,00 и Ти = 2,10, а отрезок Ти = Ти1Та = 0,148. В табл. 11.1
число 0,148 лежит между числами, соответствующими объектам второго
и третьего порядка. Полагая, что объект второго порядка, из таблицы
находим Ти1Та = 0,104, что при Та = 20,00 дает Ти = 0,28, следова-
34
тельно, вводится запаздывание х2 = 2,95 — 2,08 = 0,87. Из рисунка
находим, что координата точки перегиба для объекта второго порядка без
запаздывания равна tt = 7,35, а так как из таблицы следует, что tJT = 1,
то постоянная времени объекта Т = 7,35. Таким образом, передаточная
функция модели
e-0,87s
G № = (7,35s+ 1)2 '
Из предыдущего рассмотрения следует, что, вообще говоря, объект
/г-го порядка с монотонным переходным процессом без перерегулирования
заменяется моделью, реакция которой на скачок равна
t—х2 п—1
Л(*)==1_е- —£!l=Jgi, t^r2, (И.131)
V=0
а передаточная функция имеет вид
G (s) = e~ST* п , (11.132)
v' (l + sT)n x
Если объект обладает чистым запаздыванием т, то модель будет иметь
суммарное запаздывание т2 + т.
Список литературы
1. Ball В. J., Rekoff M. G. An analysis of the distributed lag ISA Transactins, April 1966,
Vol. 5, No. 2, pp. 146—155.
2. Беллман Р., Гликсберг И., Гросс О. А. Некоторые вопросы математической теории
процессов управления. М., Изд-во иностр. лит., 1962, с. 23—35.
3. Blandhol E., Balchen J. G. Determination of system dynamics by use of adjustable
models. Proc. 11-nd IFAC Congress, London 1963, Butterworth.
4. Blandhol E. On the use of adjustable models for determination of system dynamics.
Trondheim 1962. Inst, for Reguleringsteknikk Norges Tekniske Hogskole, Tech. Rept.
62—5—D.
5. Бодров В. И., Чертков Н. К. Определение дифференциального уравнения объекта по
его временной характеристике. В кн.: «Анализ и синтез систем автоматического
управления», М., «Наука», 1968, с. 384—391.
6. Девятое Б. Н. К вопросу о приближенных представлениях передаточных функций
теплообменников. В кн.: «Автоматическое управление непрерывными процессами».
Новосибирск. Изд. Сибирского отделения АН СССР.
7. Dmowski R. Badanie ukladow regulacji zl ozonej z regulatora rzeczywistego i modelu
obiektu. Konferencja Techniki Analogowej 1966, str. 1—8.
8. Edelmann H. Ein Kriterium fur die aperiodische bzw. rein oszillatorische Stabilitat und
der Zusammenhang mit Reaktanztheorem. Regelungstechnik 1954, Heft 11, S. 264—267.
9. Fieger K., Middel J. Vereinfachte Behandlung linear Abtastregelkreise.
Regelungstechnik, 1967, Heft 10. S. 445—450.
10. Findeisen W. Technika regulacji automatycznej. Rozdz. 3 i 9. Warszawa, 1965, PWN.
11. Герасимов С. Г. Теоретические основы автоматического регулирования тепловых
процессов. М., Госэнергоиздат, 1949, с. 210—278.
12. Gorecki H. Teoria liniowych ukladow automatycznej regulacji. Archiwum Automatiki
i Telemechaniki. 1961, torn VI, z. 2—3, str. 153—184.
13. Gorecki H., Turowicz A. Extremalne przebiegi przejSciowe w liniowych ukladach
automatycznej regulacji. Zeszyty Naukowe AGN, Automatyka, 1966, z. 1, nr 112.
14. Gorecki H., Turowicz A. Optimum transient problem in linear automatic control system.
Automatic and Remote Control. Proc. I—st IFAC Congress. Moscow, 1960, pp. 59—61.
15. Grunwald E. Entwurf von Reglern und Ruckfuhrungen. Regelungstechnik, 1955, Teil I,
Heft 6, S. 147—152; Teil 11, Heft 7, S. 172—180.
16. Kalman R. E. On canonical realizations. Archiwum Automatyki i Telemechaniki, 1963,
torn X, z. 1.
17. Kalman R. E. On structural properties of linear, constant, multivariable systems. Ill-rd
IFAC Congress, London, 1966.
18. Kessler C. Ein Beitrag zur Theorie mehrscheifiger Regelungen. Regelungstechnik, 1960,
Heft 8, S. 261—266. <
19. Kindler H., Buchta H., Wilfert H. H. Zadania z techniki regulacji automatycznej.
Warszawa, 1968, WNT, str. 122—131.
20. Копелович А. П. Автоматическое регулирование в черной металлургии. Краткий
справочник. М., Машгиз, 1963.
85
21. Kopielowicz A. P. Dobor regulatorow automatycznych. Metody obliczeri. Warszawa,
1964, WNT.
22. Krzyianowski R. Metody wyznaczania charakterystyk amplitodowo—fazowych pew-
nego typu obiektow о parametrach rozloionych. Prace IV Krajowej Konferencji Auto-
matyki, Krakow, 1967, Z. 1, str. 215—232.
23. Kuhne Ch. Uber den Zusammenhang der Zeitkonstanten einer Regelstrecke 2. Ordnung
mit hierzu korrespondierten Totund Anlaufzeiten. Regelungstechnik, 1967, Heft 6, S. 206—
207.
,24. Kupfmuller K. Uder die Dinamik der selbsttatigen Verstarkungsregler, ENT S, 1928,
S. 456—467. Zeitschrift fur Techn. Physik. 1928, 9, S. 469—472.
25. Levin M. I. Estimation of the characteristics of linear system in the presence of noise.
Dr. Sc. Engn. diss. Dept El. Engn. Columbia Univ., New York, Juli 1959, pp. 113—114.
26. Loeb J. Les erreurs systematique et aleatoires dans la determination experimentale les'
functions de transfert Proc. 11—nd IFAC Congress. London, 1963, Butterworth.
27. Masacaru Matsubara. On the equivalent dead time. IEEE Trans, on Automatic Control,
October 1965, Vol. AC—10, No. 4, pp. 464—466.
28. Moczek J. S., Otto R. E., Williams T. J. Approximation model for the dinamic response
of large destination columns. Proc. 11—nd IFAC Congress, London, 1963, Butterworth.
29. Мотулевич Д. Ю., Тагаевская А. А. Виды возмущающих воздействий при
экспериментальном исследовании объектов регулирования. В кн.: «Автоматизация
производственных процессов». М., Изд. АН СССР, 1958.
30. Mtiller J. A. Regelstreckeanalyse mittels adaptiver Modelle. Messen, Steuern, Regeln,
1968. Heft 2, S. 78—80, Heft 4, S. 146—152.
31. Ольденбург Р., Сарториус Г. Динамика автоматического регулирования. М., Госэнерго-
издат, 1949.
32. Печерина И. Н. Расчет систем автоматического управления. М., Машгиз, 1962.
33. Popek L. Badanie przebiegow przejSciowych w liniowych u. a. r. metoda obnizenia rz§du
rownania rozniczkowego. Praca dyplomowa magisterska, Katedra Automatyki i Elek-
troniki Przemyslowej AGN, Krakow, 1960.
34. Pulaczewski J. Dobor nastaw regulatorow przemyslowych. Warszawa, 1966, WNT.
35. Qvamstrom B. An uncertaintly relation for linear mathematical models. Proc. Il-nd IFAC
Congress, London, 1963, Butterworth.
36. Radtke M. Zur Approximation linearer aperiodischer Obergangsfunctionen. Messen,
Steuern; Regeln, 1966, Heft 6, S. 192—196.
37. Рущинский В. М. Экспериментальное определение амплитудно-фазовых характеристик
регулируемых объектов по переходному процессу при возмущениях в виде
прямоугольного волнового импульса. В кн.: Автоматизация производственных процессов»,
Изд. АН СССР, 1958, с. 65—73.
38. Рущинский В. М. Определение приближенного выражения передаточных функций
регулируемого объекта по его экспериментальным частотным характеристикам. В кн.:
«Автоматизация производственных процессов». М., Изд. АН СССР, 1958, с. 74—82.
39. Ryzyk I. M., Graastejn I. S. Tablice calek, sum, szeregow i iloczynow. Warszawa, 1964,
PWN, str. 28.
40. Сагайдак Н. А. Определение постоянных времени звена второго порядка с
запаздыванием. В кн.: «Автоматизация производственных процессов». Вып. III. M., Изд.
АН СССР, 1960, с. 87—89.
41. Salamon M. Berechnung der Konstanten von Ersatzregelstrecken aus Betriebsmessungen.
Zeitschrift fur Messen, Steuern, Regeln, 1960, Heft 5, S. 200—205.
42. Schmidt H. Cfber die immittelbare Bestimmung von Polen und Nullstellern aus der
Obergangsfunktion. Messen, Steuern, Regeln, 1967, Heft 6, S. 201—207.
43. Shearer I. L., Sher R. S., Reid К. К. Standards for linear control systems. Control, 1961,
No. 39, pp. 115—116.
44. Смит О. И. М. Автоматическое регулирование. М., Физматгиз, 1962, с. 393—464.
45. Солодовников В. В., Дмитриев А. Н., Егупов Н. Д. Ортогональный метод анализа и
синтеза линейных систем автоматического управления на основе понятия моментов.
В кн.: «Автоматическое управление и вычислительная техника». Вып. 8, М.,
«Машиностроение», 1968, с. 30—36.
46. Солодовников В. В., Усков А. С. Статистический анализ объектов регулирования,
М., Машгиз, 1960.
47. Шигин Е. К. Классификация динамических моделей объектов регулирования химико-
технологических процессов. — «Автоматика и Телемеханика», 1968, № 6, с. 145—162.
48. Southwell R. V. Relaxation methods in engineering science. London, 1940; rowniez* w:
Nowoczensna mafematyka dla inzynierow, red. E. F. Beckenbacha, T. I. Rozdz. 17.
Warszawa, 1962, PWN.
49. Strejc V. О moznostech vyssiho vyuziti theorie regulace v praxi. Praha, 1958, Publikace
С Vedecke Technicke Spolecnosti pro Elektrotechniku.
50. Strejc V. Auswertung der Dynamischen Eigenschaften von Regelstrecken bei gemessenen
Einund Ausgangssignalen allgemeiner Art. Zeitschrift fur Messen, Steuern, Regeln, 1960,
Heft 1, S. 7-11.
51. Strejc V. Naherungsverfahren fur aperiodische Obergangscharakteristiken.
Regelungstechnik, 1959, Heft 4, S. 124—128.
86
52. Strejc V. Neue Methods der Naherung der Differentialgleichungen von Regelstrecken bei
Algemeihem Eingangssignal. Acta Technika, 1958, Nr 4.
53. Strobel H. Das Aproximazionsproblem der experimentallen Systemanalyse. Messen,
Steuern, Regeln, 1967, Heft 12, S. 460—464; Heft 1, S. 29—34; 1968, Heft 2, S. 73—77.
54. Strobel H. Cber die durch stochastische storsignale und Messfehler bedingten Grenzen
der Kehnwertmittelung im Zeitbereich, Messen, Steuern, Regeln 1968, Heft 2, S. 54—56,
55. «Техническая кибернетика». Кн. I «Теория автоматического регулирования», под ред.
Солодовникова В. В. М., «Машиностроение», 1967, с. 199—210.
56. Turowicz A., Gorecki H. On the experimal transient processes in linear systems. Bulletin
del/ Academie Polonaise des Sciences, Ser. des. sci. math., astr. et phys., 1966, Vol. XIV,
No. 11.
57. Westcott J. H. The Second International Congress of IFAC, Control, October 1963,
pp. 187—188.
58. Wolny J. Analyza i synteza ukladow automatycznej regulacjiz regulatorami konwencjo-
nalnymi i obiektami I rze du z czasem martwym. Praca doktorska, Katedra Automaty-
ki i Elektroniki Przemyslowei AGN, Krakow 1962.
59. Wozniacki W. О pewnej metodzie znajdowania parametrow krzywej aproksymujacej
okreslonego typu. Pomiary, Autumatyka, Kontrola, 1968, Nr. 8, S. 357—359.
Глава HI
Непрерывное автоматическое регулирование
линейных объектов с запаздыванием
§ III. 1. Введение
Общий вид дифференциально-разностного уравнения n-го
дифференциального и £-го разностного порядка с управлением и следующий:
/ [ty х (0, * (t — т), . . ., x(t — тк), х (/), х (t — Тх), , . .,
. . ., xW (0, *<"> (t - тх), . . ., *<»> (t - тк), и (О,
U (t — Tj), . . ., U (t — XK)t U (t — Тх), . . ., U (t — 1К)У . . .,
. . ., иС»>(* —тх), . . ., uW(t — TK)] = 0. (III.1)
Эта функция зависит от 1 + (£ + 1) Ця + 1) + (т + 1)1
переменных. Дифференциальный порядок п обычно определяется наивысшей
производной, присутствующей в уравнении, а разностный порядок k
равен числу различных аргументов переменной х.
Величины смещения аргумента ть . . ., хк могут быть постоянными,
а в более сложных случаях — функциями времени t или переменной
х (t). Смещение аргумента может наблюдаться либо только в переменных
состояния ху либо только в переменных управления и, либо в обеих
переменных. В зависимости от того, как смещен какой-либо из аргументов
переменных ху . . ., лг<л> в уравнении (III.1) относительно аргумента
наивысшей производной, в работе [161 рассматриваются следующие три
случая:
1) если в наивысшей производной xW присутствуют различные
аргументы, то уравнение (III. 1) называется нейтральным;
2) если в наивысшей производной х^ присутствует только один
аргумент, а аргументы в остальных слагаемых переменной состояния х меньше
этого аргумента, то уравнение (III. 1) называется уравнением с
запаздывающим аргументом;
3) если в наивысшей производной #<") присутствует только один
аргумент, а аргументы в остальных слагаемых переменной состояния
больше этого аргумента, то уравнение (III. 1) называется уравнением
с упреждающим аргументом.
Например, уравнение
ею* (0 + 0ii* (' — Т) + 0оо* (0 + «01* (t — т) = и (0 (Ш.2)
является дифференциальным и разностным уравнением первого порядка.
Оно нейтральное, если а10 Ф 0 и аг1 ф 0. Оно будет с запаздыванием,
если а10 Ф 0, а а1г = 0, и оно будет с упреждением, если а10 = 0,
а аг1 ф 0.
88
При исследовании систем управления уравнения вида (III. 1) обычно
можно свести к системе уравнений первого порядка в векторной форме
х (t) =f [t, х (0, х (t — т), x(t — т), и (t) ] (Ш.З)
— это нейтральное уравнение; или
x{t) =f[tfx(t)yx(t — x)9u(t)]y т>0 (III.4)
— это уравнение с запаздыванием; или
x(t) = f [t,x (0, x(t+%bu(f)h т>0 (III.5)
— это уравнение с упреждением.
В системах уравнений чаще всего наблюдаются уравнения с
запаздыванием, причем вид их обычно проще уравнения (III.4), т. е. имеет
линейную форму
x(t) = А0х (t) JrA1x{t — x) +B0u(t) + Вги (t — т),
(III.6)
где запаздывание управления (Вг Ф 0) присутствует обычно в уравнениях
объекта и уравнениях разомкнутой системы управления, а запаздывание
состояния (Аг = 0)— в уравнениях замкнутой системы управления.
Это уравнение может быть нелинейным с одной нелинейностью
x{t) = А0х(t) + Аг х (t — т) + df (cTx (t — т))ч +
+ B0u(t) +Вги{1-т)у (III.7)
где стх — скалярное произведение постоянного вектора с и вектора х\
Л0, Аъ В — постоянные матрицы; d— постоянный вектор. О функции
обычно предполагается, что она удовлетворяет некоторым дополнительным
требованиям, которые будут описаны позже.
§ Ш.2. Вычисление переходных функций
Задача Коши для уравнений с запаздывающим аргументом отличается
от аналогичной задачи для дифференциальных уравнений тем, что в ней
необходимо определить начальные функции, а не начальные условия.
Для иллюстрации рассмотрим
простое скалярное уравнение со
смещенным аргументом
*(t) = f U, x{t)y x(t — T)]. (III.8)
Задача Коши для уравнения (II 1.8)
состоит в определении непрерывного
изменения х (t) при / > t0 в
предположении, что х (t) = ф0 (t) при
t0 — х ^ t < t0 (рис. III. 1), причем
Ф (0 известная априори непрерывная
функция, известная начальная
функция. Отрезок tQ — т < t < t0y на
котором функция ф (/) определена, называется начальным множеством
Eto. Обычно предполагается, что ф (*0) = x (t+0). Если уравнение (III.8)
является векторным с векторными функциями х (t)> / и ф (t), то это
соответствует решению задачи Коши для системы уравнений. Как будет
показано ниже, используя методику последовательного интегрирования на
интервалах [/0 + "\ t0 + (i + 1) т], i = 0, 1,. . ., можно свести проблему
решения уравнения (II 1.8) к проблеме последовательного решения
дифференциальных уравнений, а следовательно, уравнений без смещения
аргумента. С этой точки зрения, за исключением особых случаев, теорему суще-
Рис. III. 1. Решение методом
последовательного интегрирования
89
ствования и единственности решения для уравнений с запаздывающим
аргументом можно свести к аналогичной теореме для дифференциальных
уравнений.
В случае изменяющегося во времени запаздывания т (t) необходимо
найти решение уравнения
x(t) =/ [*, x{t)y X(t — x)(t)] (III.9)
при />/0в предположении, что х (t) равно заданной начальной
функции фо (t)y определенной на начальном множестве Et , состоящем из
точки t0 и тех величин t — х (t)y которые
меньше t0 при t ^ 0 (рис. III.2).
II 1.2.1. Метод последовательного
интегрирования на интервалах
(метод шагов)
При интегрировании уравнения (II 1.8), когда
время изменяется в пределах
*о< t^ t0 +т, (ШЛО)
аргумент 6 = t — т изменяется в пределах
t0 — r^Q^t0. (III. 11)
На интервале (III.11) справедливо,
однако, соотношение
*(6) = Фо(е), (IIL12)
в котором ф0—известная, априори заданная, начальная функция.
Таким образом, на интервале изменения /, определяемой формулой
(ШЛО), т. е. для Еи можно вместо уравнения с запаздыванием (Ш.9)
решать равнозначное ему дифференциальное уравнение
(ЩЛЗ)
Рис. II 1.2. Определение
начального значения при решении
уравнения t — т (/) = О
x'(t) =/ It, x(t), <p0(*-T)J
При t0^ts^t0-\-TUX (t0) =. фо (*о).
После решения этого уравнения получаем х (t), которая на следующем
интервале Ett при t0 -+- т =s£ t «g: t0 + 2т
будет играть роль начальной функции,
т. е.
'o<0i«*o+t; (П1.14)
х (вх) = ф1 (в,). (III. 15)
Рис. III.3. Блок-схема
регулирования
системы
Следовательно, можно вместо уравнения (IIIЛ3) решать теперь
уравнение
'x(t) =/ [t, x(t), <px(t — x)] (111.16)
при t0 +x <!* «< U + 2т и х (t0 + пх) = фл (t0 + пх).
Поступая таким образом, можно получить, что на интервале Etfi
*{t)=f [t, x(t), <pn(t — x)] (111.17)
при t0 -{- пх ^ t ^ t0 + (п + 1) х и х (t0 + пх) = фл (t0 + пх).
Пример. Используем метод шагов для определения выходной реакции
системы автоматического регулирования, блок-схема которой изображена
на рис. III.3.
Уравнение регулятора:
и (t) = KRe(t). (III.I8)
90
Следовательно, имеется идеальный пропорциональный регулятор.
Уравнение состояния и выхода объекта (л: = у) запишем так:
T0y(t) +y(t) = K0u(t-r). (111.19)
Следовательно, объект является объектом первого порядка с
запаздыванием.
Обозначая через К = Kr К0 коэффициент усиления разомкнутого
контура системы автоматического регулирования, после подстановки
соотношений (III. 18) и (III. 19) в уравнение элемента сравнения с
s(t) = w(t)—y(t) (III.20)
получим следующее уравнение всей системы автоматического
регулирования:
Т0У (t) +y(t) + Ку (t - т) = Kw (t - т). (111.21)
Предполагается, что на начальном множестве Eto начальная функция
равна
У (t) = Ф° W = °; ) (III 22)
У (0) = Фо (0) = 0,| . <Ш"">
а воздействие w (t) — единичная функция, т. е.
1, *>0;
( 1, *>0;
Подставляя выражение (III.22) в формулу (111.21) при 0 <: * <т,
получим уравнение
T0y(t) +y(t)±=0, (111.23)
решение которого
у (0 = 0. (111.24)
В пределах т < t <з 2т на основании формул (II 1.21) и (III.24) получим
T0y(t) +y(t) = K, */(т) = 0, (111.25)
а его решение после интегрирования в пределах от т до t имеет вид
y;(0=-tf(l-e-~*L). (III.26)
Далее в пределах 2т </ <3т на основании (III.21) и (III.26) можем
записать
Т0У (t) + у (t) + К2 (1 - е~ -*Г) = К\ (111.27)
у (2т) = #(г-е~~£г). (Ш.27)
Решение этого уравнения интегрированием в границах от 2т до t имеет
вид
у$ = /с(1-е~^)Л/<ф_е~^(1^ (Ш.28)
Поступая аналогично, получим в пределах Зт < t < 4т
y(/) = ic(l-e"^)-/Ca[l-e"^(l+-^^)] +
+ ^{1_е-^[1+1^+^(-^)2]} (Ш.29)
и т. д.
91
111.2.2. Метод разложения передаточной функции
замкнутой системы в ряд
Теперь рассмотрим общую методику решения
дифференциально-разностных уравнений, описывающих линейные непрерывные системы
автоматического регулирования. Метод основан на использовании
передаточной функции разомкнутой системы. С помощью этого метода получим
общие формулы, определяющие выходные реакции в системах с типовыми
регуляторами и инерционным объектом первого порядка с запаздыванием.
Для систем автоматического регулирования, блок-схема которых,
представлена на рис. II 1.3, можно составить таблицу передаточных функций.
Для общности рассмотрения введем относительные единицы, отнеся
все величины ко времени запаздывания. Пусть:
6 = tlx — относительное время;
г = sx — оператор Лапласа;
Т = Т0/х — относительная постоянная времени;
D = Tdlx — относительное время упреждения регулятора;
/ = TJx — относительное время изодрома;
К = Kr Ко — коэффициент усиления разомкнутой системы;
= 11 для статического объекта;
^ ~~ \0 для астатического объекта.
Передаточная функция
пропорционально-интегрально-дифференциального регулятора (ПИД-регулятора)
Gfi(s) = KR(l+sTd + -Jr-), (III.30)
а передаточная функция объекта
°°® = т£Йг- <ш-31>
Тогда можно составить таблицу передаточных функций системы
с объектом вида (III.31) и типовыми регуляторами:
пропорциональным (П), пропорционально-дифференциальным (ПД), интегральным (И),
пропорционально-интегральным (ПИ),
пропорционально-интегрально-дифференциальным (ПИД).
Теперь получим формулы, позволяющие проводить вычисление
выходных реакций для систем, передаточные функции которых представлены
в табл. III.1.
Операторное выражение для выходных реакций системы
автоматического регулирования при единичном воздействии w (t) = 1 (/) имеет вид
Y(s) = ^-G2(s) (HUB)
S
или в относительных величинах
XJfL = ±-Gz{r), (HI.49)
где Gz (r) — передаточная функция замкнутой системы.
Учитывая, что
g'W~,tt8W' (IIL50)
где G (г) — передаточная функция разомкнутой системы, и
раскладывая G2 в ряд, получим
Gz(r)= 2 (—l)n[G(r)]n+1. (IH.51)
л=0
92
Передаточные функции
Таблица III Л
Регулятор
Объект
Разомкнутая система
Замкнутая система
Пропорциональный (П)
(111.32)
G0 = /Со
д + гт
(II 1.33)
G = K
q + rT
(111.34)
Gz=: **— (111.35)
q + rT + Kt-r
Пропорционально-дифференциальный
(ПД)
GR= Kr(1+ rD) (111.36)
G0= K0-
q + rT
G^K(l+rf^ ' (111.37)
q + rT
K{\+rD)t-
q + rT + K(rD+l)t
— (111.38)
Интегральный (И)
«.-£
(111.39)
G0= Ко-
q + rT
G =
Kt~
Ir(q + rT)
(111.40)
Kt~
Ir(q + rT) + Kt
— (111.41)
Пропорционально-интегральный (ПИ)
G«=K*(l+-i-) (111.42)
G0= Ко
q + rT
a-Ki)rV+% (I"-43)
G2 =
K(l+Ir)tr
Ir(q + rT) + K(Ir+\)jTr
(111.44)
Пропорционально-интегрально-дифференциальный (ПИД)
0Л=Кц{\ + Ог+-У) (III
45)
G0= Ко
q + rT
°-«{°'"^'++гтГ <'"*>
K(Dlr* + lr+\)t~
/r fa + /T) + К (Z)/r2 + Ir + 1) e~r
(111.47)
Следовательно,
Ш- = V (_ \)п -J- [G (r)]»+l. (IH.52)
Делая обратное преобразование, получим
У(в)
{00 \ 00
2 •(- 1)п-г [G (г)]^1 = 2 <- о" ^_l [4- [G<r)n+1] •
п=0 J /i=0
(111.53)
Справедливость вышеприведенных рассуждений доказывается
следующим образом.
Найдя величину разности
л=0
N N
О (г)- £ (-l)nGn+1(r)- ^ (-l)"^2^)
л=0 л=0
l + (G(r)
_ ^ (_i)«+itf»+2(r)_ ^ (_i)«Grt+2(r)
n=0 л=0
1+G(r)
^ (-l)»Gn+2(r)- 2 (-l)nG"+2(r)-Hl)^^2(r)
n=0 n=Q
l+G(r)
__ (l)N+lGN+2(r)
l+G(r)
можно показать [5, стр. 71], что если
G(r)= L(r) e-'
то
с+усо
С—/ 00
Следовательно, возможность вычисления неустановившихся
переходных процессов при помощи рассмотренного метода доказана.
Необходимым условием применимости метода является наличие
запаздывания.
Введем обозначение
уп (г)=4-[G wn+l=-г[Gb {r)]n+l e~r (n+1)=F*(r) e"r (n+1)'(IIL54)
где
/7n(/-)=4-fG^r)]"+1' (IIL55)
причем Gb (r) — передаточная функция разомкнутой системы без
запаздывания.
Соответственно обратные преобразования имеют вид
Л. (в) = а*-1 [/=; (г)] (Ш.66)
94
Уп (в) = 2-1 \Yn {r)]=g-i [Fn (r) e-Mn+D] =
=/я Ю-(л + 1)1, в^п+1, (111.57)
откуда следует, что
Подставляя выражения (III.54) и (II 1.58) в формулу (III.53), получим
окончательно
-^-= £(-!)" Уп (в). (Ш.59)
Из выражения (III.58) следует, что в формуле (II 1.59) суммирование
для конкретного 0*, N* <- 0* <: N* + 1 осуществляется не от 0 до сю,
а лишь от 0 до Л^* — 1, так как при 0* <*N* + 1 все выражения для
у (0*) при n^zN* [см. формулу (111.58)1 равны нулю. Следовательно,
из-за наличия запаздывания у (0) вместо бесконечного ряда представляется
усеченным рядом. Благодаря этому рассматриваемый метод точен и не
требует предположения, что | G (/ю) | <31.
Система с пропорциональным регулятором. Передаточная функция
разомкнутой системы [табл. III.1, формула (III.34)] имеет ряд
(111.60)
(111.61)
Для отыскания обратного преобразования воспользуемся методом
вычетов
в
связи
На
[ с чем
основании
F. (г) =
(111.55)
±(^Л
Gb =
имеем
\ л+1 _
1 1+гТ '
К
1 + гТ '
:(Ку+
L (9) = SB'1 [Fa (г)] = Res Fn (г) е* + Res Fn (г) е* 6^0. (II 1.62)
г=0 1
Из выражения (III.61) следует, что
RJ.1-.W- - (£ f ("Д [(f + |°r+.]) = ^' <ШЮ>
т
/
. Используя формулу Лейбница для /г-й производной произведения двух
функций, получим
•£[>']= 2.(0 (t/"~'V>«\ (Ш.65,
95
но (п — 0-я производная функция \1г определяется выражением
(±)(я-° =(_!,-< _£^_, (Ш.бб)
а i-я производная функции еге — выражением
(е*)(0 = е'е*. (111.67)
Используя соотношения (III.66) и (III.67) в формуле (III.65), получим
п
= (-1)" -р^г ег6 2 ( 1) (-1)' in - 0! (гв)'. (111.68)
1=0
Подставляя выражение (III.68) в формулу (III.64), получим
Res Fn(r)erQ =
i
е п
i=0
= (т)Л+17ГГ(-1)2"+17",+1е"* S (|)(-1)Ч«-0!(-|-У(-1У =
i=0
0 л
= _^+i_L ""г V л1(п —pi / е у
Л /г! е Zj Л (л —01 W / *
t=0
Окончательно можем записать
Res Fn{r)z* =^Kn+lt T 2ti (т)'" (IIL69)
Подставляя выражения (III.63) и (III.69) в формулу (III.62), получим
/»W-^ч"1 [»-*"* 2 тггСт)1]' е^°- {IIL70)
На основании соотношений (III.58) и (IIJ.70) имеем
8—(га+1) _п
1-е
Уя(в) = /Г
= А"'+1
2_L(ird£±i)yl, e^n + i. (Ш.71)
t=0 J
Подставляя соотношения (III.71) в формулу (III.59), получим
выражение, определяющее выходные реакции:
п=0 I f=0 J
(111.72)
Расписав выражение (III.72) для п = 0, 1, 2, . . ., легко убедиться,
что оно совпадает с соотношением, полученным ранее методом шагов.
96
Выражение (III.72) в размерных единицах, т. е. с учетом того, что
6 = //т, а Т = Т0/т, имеет вид
»(0-^н^ 11 -г*^^ Р-13-^1'
■2^r['-=w
, (111.73)
/^=(rt-f- 1)т.
При вычислении величины у (t*) для данного момента времени t*
обозначим целочисленные значения t*h через [/*/т] = N* и получим
формулу
ЛР—1 /• , п
X?ft — (n+l)x-\t 1
У
1\~—1 I
ю=2(—1)Я/ся+1
я=0
/-(я^рт
1-е *"•
t=0
"J п
, (Ш.73а)
*S*(/i+1)t,
где все слагаемые у [t* — (п + 1) т] на основании выражения (II 1.58)
при п ^ N* равны нулю.
Система с пропорционально-дифференциальным регулятором. Из табл.
III.1 [формула (III.41)] берем выражение для передаточной функции
разом кнутой системы
в связи с чем
<Ь(г) = *-г±7Г
(111.74)
Подставляя выражение (III.74) в формулу (III.55), находим
изображение функции
Г j-_LT+1
Fn(r) = T[K1fjr\ ={^г) 7hr ' (IIL
оригинал которой имеет вид
fn (в) = Res Fn (г) е* + Res F„e"f 0 ^ 0.
r=0
75)
(111.76)
Поступая аналогично предыдущему, найдем
1 \п+1
ResFn(r)^=(^)n+1\im
г +
D
г +
1
*гв
\=Kn+l (Ш.77)
Используя формулу Лейбница
£[('+^Г>]-2(;)[('+-ггГГ'(М" («..тч
1=0
и учитывая, что
■yl^] =7WTe'eS(p)(-1)'"',(''-'')l('*)' (Ш'81)
р=0
7 X. Турецкий 97
получим
=S(")^f('+T)'+,'-s(;)<-"'-'<i-rt|(^<iii-82>
t=0 p=0
Подставим выражение (III.82) в формулу (III.78):
Res Fn(r)erQ =
l
e
1=0 p=U
X(^P)!(4-)P(-1)^ =
/Д-Р \/»+i 1 "F ^! (/г + 1)1 /Л_ 1 Y+1V t!(t-p)! /_6\P
V T ) n!e *!(n-i)l (i + l)!\D 4 JLp\(i-p)\\T)
p=0
и получим окончательно
^w—Wr'-ttWHi-triMlY-
r=—— i=0 p=0
r (111.83)
Подставляя выражения (III.77)'и (III.83) в формулу (III.76), получим
I 1=0
=<(-S--I)'+,S^r(T)i.^0. ,....84)
p=0 )
бразом,
fc(8»-^|i-(^r.-t^2;(::.,)x
l i=o
(r_l).+.^(^±i,)»U> e&„ + 1 (Ш86)
D=0 i
X
Используя формулу (III.59), получим окончательно
/z=0 1
xSC+DCt-O^SttC-511^)'}-•»"+'• (I,i:86)
i=0 p=0
или в размерных величинах
t-(n+l)x
X
л ' 1 \ if./
л=0
У (0 = 2 (-W-И 1 - (^)n+1 e Я"
n=0 I
t=0 o=0 /
X
7=0 ■ - - - —0
98
Система с интегральным регулятором. Передаточная функция
разомкнутой системы на основании табл. III. 1 [формула (111.40)1 записывается так:^
G(r) = . К'"
П(1+гТ)-
Следовательно,
G»C-) = 77(tW <IIL88>
Поступая аналогично предыдущему, получим изображение функции
'.«-?• [4-ToWr- lwr^{r^r опт
и ее оригинал
fn (9) = Res Fn (г) е* + Res F„ (г) е*. 0 ^ 0. (111.90)
г=0 1
После преобразований получим
*. ,.„,. - - но» (^Г2 (2;+,'г/) £ (4)' <-»-' тип
1=0
И
_К_ез^„(г)е^(-1)»(^)"+'е-тУ(^-')^(^)'. (Ш.92)
г т
Таким образом,
'я+1
Ме)-(-.)"(^Г2<-')'-(^,'-;)1т(т)' +
I t=0
+«~f2(*.++r'U(-J-)'}.'»° <ш.И)
t=0
2n + l — i\ 1 / 6 у
7=о
и
I t=0
+ е_.-±п|, „ ^ ^^^^ 1 &n + L (ш94)
t=0 )
t=0
Окончательно запишем
ГЛ+1
«=о w=o
+ е-^Г^ 2 (2\++Г1) ^Г [^=^^-]£}нв-(п+ 1)] (111.95)
t=0 ' i
i=0
или в размерных единицах
(п+1
л=0 I i=0
+ е ^^2(2ft^\~H[^^]T[/-(n+1)Tl- (IIL96)
£=0 ° )
99
Система с пропорционально-интегральным регулятором. Передаточная
функция разомкнутой системы на основании табл. III. 1 [формула (II 1.43) I
имеет вид
К
(1-/г)е-г
/г(1+гГ) '
откуда
Gb = K-
\ — Тг
(111.97)
Jb — ^ Ir(l + rT)
Поступая аналогично предыдущим случаям, определим преобразование
1 \п+1
(111.98)
F,M = (^)"+' ('+^
гП+2
('++)
1 \л+1
и оригинал
с т\ (К \n+1 J I- d"+1
(я+1)1 ;io ^"+1
tz
,гв
+
, 1 ,. d"
/г I J
drn
ЫЕ-
г/г+2
, е^о.
(Ш.99)
После довольно сложных преобразований получим окончательно
fc=0
i=o
^«^^'(Г)'].^» ("MOO,
fc=0 J
100
л=0 V t==o
X
S'-d'
k (n + i-k)\ Г 6 —(/г+ 1) 1fe |
&о
+ е 7 ij (я_0!(/ + 1)1 \ / 1)
i+i
X
t=0
fc=0 J
или в размерных единицах
yW- f; (-d-^js (-D- .-.(Д4-,1-,). (-%-)' &-■>• х
/г=0 li=0 £=0
Х k\(i-k)\ L Т0 J ^е ij(n-0!(* + l)l
i=o
i
/ Т0 Л1+1П fn -U 1 4- / — АЛ! Г/ — f« Л_ П r1 fc
XV77~V __
fe=0
Система с пропорционально-интегрально-дифференциальным
регулятором. Передаточная функция разомкнутой системы на основании
табл. III. 1 [формула (111.46)1 запишется так:
Q==zK (Dir* + lr + \)e-r
(тЬ'ГЕ (№li(/tV' [^^-T ue-(n + i)b (Ш.102)
/г(1— гГ)
откуда
G> = * !+гГ - (HI-ЮЗ)
Найдем преобразование
Оригинал определяется' из приведенного выражения, но его трудно
использовать практически:
ш=(4^HI;Vo< (-1') (4 Г~'*
I t=0
k
k=0 /=0
X (л + 1_/)|(2/_Л)| {~d) +e r2j(— ^"X
х(ПШ-'2(-^(П"+,'Д',^"х
ft=0
х V /_n/ (_LV V f—1Г ( * ^ (я + О/1 х
?=0
(тП1-f)'^}. e>°- (Ш.Ю5)
Для выходных реакций получим следующее выражение:
, (6)=г 2 (-1)" (^-)n+1 s м)' (я+!) (^±^)п+1-1' х
71=0 1=0
Х S(_1)40 ^Г^' (т-)* 2 (*) (п+1-/)!(2/-А)! Ш'Х
£=0 /=0
101
e-(n+i)
■ xs<-D'(i) ,"+j:;lTt" Ъ->Нт)'Ь-»та)х
k=0 j =0 m=0
xl„+l_i„i;+^)„;_„)l(4r('-4-)'-mne-(.+1)l
(III. 106)
и в размерных единицах
-*<о=2<-1>"(^Г2<->>'(Т)><
71=0 i=0
ft=0
X\^7J 2l \ i ) (n+ 1 -/)! (2/-*)! (tJ~) X '
/=0
XI /_(я+1)т] + 2е г. (^)+Х
71=0
x2(;)F=^r2<-44i)*
t=0 . /e=0
(III.107)
Полученные выражения не являются приближенными, а позволяют
точно определить переходные процессы в любой произвольный момент
времени t. Так как в хорошо спроектированных устойчивых системах
переходные процессы заканчиваются достаточно быстро, то уже при
сравнительно небольшом числе шагов п величина у (t) постоянна.
' На основании выражений (111.72), (111.86), (111.95), (III.101) и (III.106)
в качестве примеров вычислены выходные реакции для нескольких типов
регуляторов при различных значениях настраиваемых параметров. Для
того чтобы можно было сравнить переходные процессы различных
регуляторов при относительной постоянной времени Т, на рис. III.4 изображены
выходные реакции' при следующих параметрах: К = 2; DIT = 0,1;
I/T =1; Т = 1; на рис. III.5 — при значениях параметров К = 2;
DIT = 0,1; IIT = 1; Т = 2 и на рис. III.6 — при К = 2; DIT = 0,lj
I/T =1; Т = 10. На рисунках можно проследить влияние постоянной
времени Т.
Кроме того, на рис. II 1.7 представлены выходные реакции
пропорционального регулятора при Т = 10 и К = 2, 3, 10. По рисунку можно
оценить влияние коэффициента усиления.
На рис. III.8 изображены переходные процессы системы с ПД-регуля-
тором при значениях Т = 10, DIT = 0,03 и К = 2, 3, 10. Хорошо за-
102
О 2
Рис. II 1.4.
У(В)\
1Л
k 6 8 10 12 1k 16 18 20 22 2k 26 28 30 32 3k
Переходные процессы при использовании различных регуляторов при К = 2; DIT = 0,1; I/T = 1; Т= 1
И.
36
о
00
0 2
Рис. III.5.
U 6 8 10 12 1k 16 18 20 22 2k 26 28 30 32 3 k
Переходные процессы при использовании различных регуляторов при К = 2; D/T =0,1; II'Т =1; Т = 2
36 в
Рис. 111.6. Переходные процессы при использовании различных регуляторов при
К = 2; D/T = 0,1; I/T = 1; Т = 10
U
10
0.8
0.6
ОМ
0.2
Г /
Г 0.909 I
Г °>75 /
Vл
=ю
V о.ббб 1 ъ~*
\ \
_J 1 J
1 F_—i '
-J 1
4J ^000000- "*
4z
-J 1 1 l_
1 1 1 1 1 1 1 1
10
1U
Рис. 111.7. Влияние усиления на характер переходных процессов в системе
с пропорциональным регулятором (Т =10; К = 2; 3; 10)
Рис. II 1.8. Влияние усиления на характер переходных процессов
системы с регулятором типа ПД (Т = 10; D/T = 0,03; К = 2; 3; 10)
104
метно влияние коэффициента усиления. Дестабилизирующее влияние
запаздывания хорошо иллюстрирует рис. II 1.9. Влияние времени
упреждения показано на рис. ШЛО.
На рис. III. 11 проиллюстрировано влияние запаздывания при
использовании интегрального регулятора, а на рис. III.12 — влияние времени
изодрома.
Рис. II 1.9. Иллюстрация дестабилизирующего влияния запаздывания (регулятор ПД, Т =
= 10; D/T = 0,03; К = 2; 3; 10)
На рис. III. 13 показано влияние коэффициента усиления при
использовании ПИ-регулятора, а на рис. III.14 — влияние времени изодрома.
Дестабилизирующее влияние запаздывания показано на рис. III. 15.
Наконец, на рис. III. 16 показано влияние коэффициента усиления
и времени изодрома на переходные процессы системы с ПИД-регулятором,
а на рис. III.17 — влияние запаздывания и упреждения.
0 2 4 6 8 10 12 /4 16 18 20
Рис. ШЛО. Иллюстрация влияния упреждения (регулятор ПД; К — 3; Т = 2)
22
На основе полученных выражений и представленных рисунков можно
сделать следующие выводы:
Безотносительно к типу регулятора:
1. При увеличении запаздывания возрастает перерегулирование и
уменьшается колебательность, и наоборот. К аналогичным результатам
приводит возрастание коэффициента усилений, но не в такой степени.
2. В отличие от систем без запаздывания, колебательные переходные
процессы в которых представляют собой комбинацию затухающих по
экспоненциальному закону синусоид, в системах с запаздыванием
колебательные переходные процессы затухают экспоненциально, однако это
не синусоиды: экстремум каждого полупериода наблюдается не на
середине полуперирда, а смещен влево, т. е. в направлении начала системы
координат.
105
III.11. Влияние запаздывания в системе с регулятором И (IIT — 4/8)
1Л
1А
0,3
0,6
ол
о
Рис.
Г /^ ^\
Г / f ^^^v^
Г 1/ /^^^
I \^&>^7 ! JL_.ri I I L L_l 1 1 L_
—I J—
-J L.
J.
t t \ t i т _
■ ' ■ ' ■ ' ■ ■ ■ ' ' ■ '
III. 12. Влияние времени изодермы на характер переходных процессов (регулятор Я, Т = 2)
Рис. III. 13. Переходные процессы в системе с регулятором ПИ при различных значениях
коэффициента усиления (Т = 2; IIТ = 1)
Рис. III. 14. Переходные процессы в системе с регулятором ПИ при различных значениях
//Г(/С= 1,2; Г= 2) n
О 2 ** 6 в Ю 12 74 16 1в 20 22 в
Рис. III.15. Влияние запаздывания на систему с регулятором ПИ (К— 1,2; I/T = 1)
107
3. Логарифмический декремент затухания
D = 1п\ Аг/А2\,
где А! и А 2 — амплитуды соседних колебаний относительно
установившегося значения, есть величина постоянная, как и в колебательных
системах без запаздывания.
В зависимости от типа регулятора:
4. Пропорциональные регуляторы могут работать совместно только
с объектами с большой относительной постоянной времени (малым
запаздыванием), так как, с одной стороны (с точки зрения устойчивости),
коэффициент усиления ограничен, а с другой стороны, слишком малень-
1М
1,2
1,0
0,6
ОМ
0,2
г J
у f
[ I I
Г ///
I i
Гу\^/<=0,5; у =0,5
/ l \
^K=0,S; у = 1 к=1,2; у=1
I . I I ,.!,_. I I I 1 ..!___!,.,._] 1.
1 1 - 1 1 __1 1 1 1 ! 1
10 г 12
14
16
18
20
22
Рис. III. 16. Влияние усиления на переходные процессы в системах с регуляторами ПИД
(Т= 1; DlT= 0,1)
кий коэффициент усиления приводит к большим ошибкам в
установившемся состоянии. Как это будет показано ниже, предельная величина
коэффициента усиления определяется соотношением
-f ~/, (Ш.108)
а установившаяся ошибка, как известно, обратно пропорциональна
величине (К + 1). Из выражения (III.72) легко заметить, что первый,
наибольший экстремум находится в пределах отрезка Е [2, 3 J при 0^,
удовлетворяющем соотношению
egl-2
(flCeO .'
(III.109)
Время появления первого экстремума сдвигается к началу отрезка Е
[2, 3], т. е. к величине 0 = 2, весьма быстро, пропорционально значению
т
когда уменьшается относительная постоянная времени, т. е. когда
возрастает запаздывание или уменьшается постоянная времени Т0 (рис.
III. 18). Это время уменьшается по гиперболическому закону при
возрастании коэффициента /С. Колебания отличаются от синусоидальных, они
близки к релаксационным. Из выражения (II 1.72) на основании
выражения (III. 109) можно также определить величину первого экстремума,
а следовательно, величину перерегулирования. Она равна
Уфе1) = Къ
1
е re Kj—K
108
v(*l
О 2 4 6 8 W 12 1k 16 18 20 22 в
Рис. III. 17. Влияние запаздывания и упреждения на переходные процессы в системах с регуляторами ПИД (К = 0,5; I/T = 0,5)
о
со
На рис. III. 19 изображена зависимость у (8^)»как функция
относительной постоянной времени при различных значениях К.
5. При работе с объектами, имеющими запаздывание, обнаруживаются
интересные особенности ПД-регуляторов. Влияние времени упреждения
на характер переходного процесса не одинаково на различных этапах
хода процесса. В начальной фазе, т. е. при малых значениях времени 0,
с ростом упреждения ,D наблюдаются малое демпфирование и склонность
к колебательности, однако в более поздней фазе протекания переходных
процессов наблюдается обратная тенденция, т. е. с ростом относительного
упреждения процессы быстро затухают. В связи с этим по сравнению
с системами, работающими с пропорциональными регуляторами, приоб-
2 3 <* S 6T
у{ве,)
К=1,2
2.0
US
0.5
О
Sv^
'-10
^чКс2
^у/
yfot)
К=10
10
5,0
IS
6Т
Рис. III.18. Зависимость времени
появления первого экстремума Qe от постоянной
времени Т (пропорциональный регулятор)
Рис. II 1.19. Зависимость экстремального
значения у (Qe ) от постоянной времени Т
(пропорциональный регулятор)
ретается весьма важное свойство, так как уменьшается
перерегулирование с одновременным сокращением области колебательности.
Момент появления первого, максимального перерегулирования легко
получить из выражения (II 1.86), приравнивая производную у (0) к нулю,
т. е. используя соотношение
6.-2
= (/СеО
— 2
ТФ D.
(ШЛИ)
На рис. II 1.20 изображена зависимость 0^ от DIT при различных
значениях 7\ а на рис. II 1.21 — зависимость экстремума от DIT.
Если же
то
Т = D,
е„ = 0;
у (в,,) = к.
(III.112)
(III.113)
Однако при выполнении зависимости (III. 112) система находится уже
за границами области устойчивости. Это объясняется следующим.
Дифференциально-разностное уравнение, описывающее работу
рассматриваемой системы с ПД-регулятором, не является уравнением с запаздывающим
аргументом, а является нейтральным уравнением
K{w(Q—l)-y(B—iy +
) +У(в-1)]}. (ШЛИ)
по
Ту (0) + у (6)
+ D [w(Q
Вследствие этого, как легко заметить на рис. III.8—ШЛО,
переходные процессы не гладкие, а содержат скачки. Полагая в выражении
(II 1.86) Э = 1, 2, 3, . . ., можно найти величины скачков как разность
значений справа и слева:
8п=(-1)п(ЩП+\п = 0, 1,2,3,...,
где s0 — величина скачка при 0=1.
(III.115)
Рис. II 1.20. Зависимость времени Q6i от
отношения D/T в системе с регулятором
типа ПД (К = 1)
1.0 13/Т
Рис. II 1.21. Зависимость экстремума
у (6е ) от отношения D/T (регулятор ПД)
Необходимым условием устойчивости системы, как это будет показано
ниже, является выполнение неравенства
4£<ь
(ш.пб)
Кроме того, величина скачка s0 при Э = 1 наибольшая, а потом она
.убывает с ростом (п + 1). Как следует из соотношения (III. 115), скачки
эти могут быть и положительными, и отрицательными. Соотношение
(III. 116) можно рассматривать с другой точки зрения. Если потребовать,
чтобы с течением времени скачки переходного процесса уменьшались,
то необходимым условием будет KD/T < 1. Условие уменьшения скачков
является, очевидно, необходимым условием асимптотической
устойчивости: если бы объект описывался дифференциальным уравнением
выше первого порядка, то в переходном процессе у (t) отсутствовали бы
скачки, но тем не менее условие (III. 116) осталось бы в силе применительно
к скачкам производной у (/).
Условие (III. 112) совместно с (III. 116) приводит к требованию, чтобы
К <1. (III.117)
Однако тогда установившаяся ошибка превысит 50% от
установившегося значения. С этой точки зрения условие (III. 112) практически
не реально. Малые отклонения от соотношения (III. 112) при большом
значении К привели бы к неустойчивости, исключительно к
колебательному режиму работы.
6. Регуляторы И и ПИ могут достаточно хорошо работать с объектами
с запаздыванием. Как известно, установившаяся ошибка в системах
с регуляторами этого типа теоретически равна нулю. Время изодрома
111 _
регулятора, с одной стороны, не может быть слишком маленьким, так как
величина экстремума сильно возрастает при уменьшении IIT (рис. III.22);
одновременно чрезвычайно сильно уменьшается время появления первого
экстремума (рис. II 1.23). С другой стороны, слишком большое время
изодрома приводит к затягиванию переходного процесса.
/ 1
^Т=2
1-
/
I/T
Рис. II 1.22. Зависимость экстремума
у (Qe ) от отношения IIТ в регуляторе
типа И
Рис. III.23. Зависимость времени
0е от отношения IIТ в регуляторе
типа И
С этих позиций наилучшими свойствами для работы с объектами t
запаздыванием обладают регуляторы ПИ. Пропорциональная составляющая
значительно ускоряет ход процесса в начальной фазе его протекания,
однако интегральная составляющая ликвидирует установившуюся ошибку
и ускоряет ход процесса в заключительной фазе.
!/(0е,)/К
Рис. II 1.24. Зависимость нормированного экстремума у (6eJ и времени 6ej от
отношения IIТ в ПИД-регуляторе (D/T — параметр; Т = const)
7. Регуляторы ПИД наиболее универсальны, обеспечивают
исключительно сильное сокращение времени протекания переходных процессов
по сравнению с ПИ-регуляторами. Соответственно и настройка их для
объектов с запаздыванием достаточно трудна. Как и з случае с
регуляторами ПД, в переходных процессах наблюдаются скачки, качественно и
количественно аналогичные.
112
На рис. II 1.24, а и б приведены зависимости первого экстремума
у (вв1) и времени его появления вв1 от IIT при различных D/T, а на рис.
'. 11.25 — от DIT при различных ЦТ для ПИД-регуляторов.
y(fef)/K
х1/Г=!/2
Рис. II 1.25. Зависимость нормированного экстремума у (&е ) (а) и времени Qe (б)
от отношения I/T в регуляторе ПИД (Т = const)
II 1.2.3. Метод, основанный на знании полюсов
передаточной функции замкнутой системы
Переходные процессы в системах с запаздыванием можно определить
с помощью уравнений, аналогичных уравнениям Хевисайда для систем
без запаздывания. Для этого необходимо найти корни характеристического
уравнения. Как известно, характеристическое уравнение системы с
запаздыванием является трансцендентным и имеет бесконечное множество
корней. Корни, расположенные вблизи мнимой оси и слева от нее,
характеризуют степень устойчивости и поведение системы вблизи установившегося
состояния, а корни, значительно удаленные от мнимой оси, влияют на
поведение в начальной фазе переходных процессов. Во многих задачах
автоматического регулирования установившееся состояние вообще не
рассматривают, а вопросы поведения системы на начальной
стадий-переходных процессов приобретают первостепенное значение. С другой
стороны, во многих задачах первой пары комплексно-сопряженных корней,
ближайших к мнимой оси, часто является достаточным для приближенного
определения поведения1 системы.
Характеристическое уравнение замкнутой системы. На "основании
табл. III. 1 можно составить табл. II 1.2 характеристических уравнений
для систем, блок-схема которых представлена на рис. III.3.
Теперь рассмотрим приближенный метод отыскания корней
трансцендентных уравнений. Это рассмотрение сопроводим подробным анализом
характеристических уравнений, представленных в табл. II 1.2.
Трансцендентные характеристические уравнения систем управления
можно записать в следующей общей форме:
SaA"^ = 0.
(III. 123)
Метод нахождения асимптотических корней. Как уже упоминалось,
корни, отстоящие далеко от начала координат, будем называть
асимптотическими корнями. При определении асимптотических корней уравнения
(III. 123) следует вспомнить, что каждая его составляющая имеет вид
/*e~* = e<i*ln'-*r\ ' (III. 124)
а ее модель
j г^е-^ | = е<^ 1п 1л I - 6 Re (г»# (III.125)
8 X. Турецкий 113
Характеристические уравнения
Таблица II 1.2
Тип
регулятора
П
пд
И
пи
пид
Характеристическое уравнение замкнутой системы
• q + rT+ КеГг= 0 (III. 118)
q + rT+ K(rD+ 1)е~г= 0 (III.119)
r(q + rT)+-j-*-r = 0 (III.120)
r(q + rT) + K(^r+-~^e-r = 0 (III.121)
r(q + rT) + k [r2Dv+r + -±-\ e-r = 0 (III.122)
Примечания
Для статического
объекта q = 1,
для астатического
У 1
Следовательно, это монотонно возрастающая функция переменной
(И In | г | — 6 Re (г)).
Соотношение (III. 125) можно записать еще в одном виде, а именно:
(u-tRe(r) )
j^e^|;=kl ln|r| . (III.126)
На плоскости ((г, £) (рис. III.26) заданы две точки: Р = (£, \х) и Q =
= (—Re (г), 1п|г|). Легко заметить, что показатель степени модуля г в
выражении (III. 126) равен отрезку OR. Следовательно,
OR = p _i-^L = f (g, £ ф), (Ш.127)
где
^<Р = SiW' 0<Ф<.я. , (Ш.128)
В зависимости-от угла ф доминирующей в уравнении (III. 123) является
то одна, то другая составляющая. Преобладающим, очевидно, будет тот
член, для которого величина OR наибольшая. Следовательно, в качестве
слагаемых (III. 125) суммы (III. 123) следует брать на плоскости ([х, I)
только те точки, которые лежат на концах выпуклой ломаной (рис. III.27).
Из уравнений (III. 127) и (III. 128) и рис. III. 127 следует, что всего точек,
лежащих на отрезке Ls при <р Ф я/2, существует
B* = -!*.*tgq>. +/.tgq>„ (Ш.129)
а уравнение (III. 123) после исключения \sk принимает вид
e-/s *ф/ ^kask(rerieq>sYsk [1 +0(8,)] = 0, (III.130)
где О (es) — символ Ландау, и соответствует тем точкам, которые лежат
внутри области, ограниченной выпуклой ломаной кривой. Члены, для
которых | г | —> оо, отбрасываются.
114
Теперь через р обозначим какой-нибудь корень алгебраическопГурав-
нения
£*ад^* = 0. . (III.131)
Сравнивая уравнения (III. 130) и (III. 131), видим, что асимптотические
корни должны удовлетворять уравнению
rertg<ps = р [1 + 0(es)]. - (III.132)
Для решения уравнений (III. 132) рассмотрим три случая:
Q=[-Re(r)% 1пИ]
Рис. II 1.26. Геометрическая интерпретация Рис. II 1.27. Выпуклая ломаная на пло-
модуля функции /*V~rfc на плоскости |£, \i скости ц, |.
1. Если <ps = 0, то уравнение (III. 132) дает непосредственно
r = p. ' (III.133)
2. Если <ps = rt/2, то tg <ps = оо и из соотношения (III. 129) видно, что
Ц,* = /,. . * ("1134)
На рис. III. 126 в этом случае будет присутствовать горизонтальная
линия, соответствующая уравнению \isk = const.
Кроме того, из уравнения (III. 127) следует, что все \xsk равны. Тогда
в уравнении (III.123) можно вынести за знак-суммы r**k и получить
следующее:
Теперь, полагая
е-' = р [1 + О (es)],
получим уравнение, аналогичное уравнению (III. 131):
£* askpl*k = 0.
(111.135)
(111.136)
(111.137)
Логарифмируя уравнение (III. 136), найдем "
—г = ln|p| + jargp ± 2mnj +0 (es), m = 1, 2, . . . (III.138)
и окончательно
г = —ln|p| + /(±2/ия — argp) + О (es), m = 1, 2, . . . (III.139)
3. Если cps ф я/2, то, логарифмируя уравнение (III.132), получим
, In r + r tg <ps = lnp ± /.2тя + О (es), m = 1, 2, . . . (III.140)
8* 115
Следовательно, приближенно имеем
rtgVl=±/-2jim + (« + /»)tgVf + 0(eJ + o(4^), m= 1, 2, ....
(Ш.141)
где дополнительный множитель (и + /о) играет роль поправки.
Подставляя уравнение (III.141) в выражение (III.140), получим
In (±/ctg<ps-2/nn-f и + А>) + (и + Д>) tg<ps± /-2/пл =
= \пр± /.2/тш + О (es) + О (-^)
или
In
[(±/-2mnctg9s)(l + ±/,L+ftg(ps)] +
+ (M + /I>)tg9s=lnp + 0(es) + 0(-^-);
ln(2^|ctgVs|)+ln(±/1^r)+ln(l±_|+>
2тя ctg
фг) +
+ (« + /t;)tg9s=lnp + 0(es) + 0(i^-)
Разложим In
(' +
u + jv
;—J в ряд1 относительно 1 и сохраним
:/.2mrtctg<
только первый член разложения, так как величина 2тп достаточно велика.
Тогда окончательно получим
In (2/тш | ctg <ps |) ± / \ sign ctg<ps ± ±/JS + ggq)< +*
' +(u + jv)tg4>s=lnp + 0(es) + 0(^): (III.142)
Приравнивая действительные и мнимые части, получим систему
уравнений относительно Неизвестных и и v:
^(f>sU + ^rv=ln\p\ + ln-2mn\ctg4>s\ + (Es) + Q(^); (III.143)
-tg
±2тл
%-u + tg<psv = argp+ ^-signctg9s + 0(es) + 0(-^r-). (III.144)
Главный определитель этой системы уравнений
tg<P
tg <Ps
±2тя
а определители
4т2я2 + 1
l ъ (л , 1 \ 4~2 4т2я-5 +
Ai =
In
|р|
tg<Ps
argp
2тя | ctg ф5
_ я
±2тя
sign ctg <ps tg <ps
tg
<Ps [In
2тя | ctg <ps|
arg p =й ~y sign ctg <ps
2тя
i ln(l +x) =
1!
2!
■ +
116
tg<Ps
—tgq>s
±2тя
In
2тя | ctg (ps |
я_
T
In :
argp -ь -£-sign ctg <ps
— я . "" 2тя I ctg (Ps I
argp + -2" sign ctg <ps ± ulm/ Ts
= tgq>,
Следовательно, искомые неизвестные определяются выражениями
А, -х__ 4mW |,_ |р| _ (argp + ^-sign ctg ф5)
tt =
Ctg <ps
4т2я2 +
г
In
Л, , 4т2я2 1п
J—"" rl±-
X" — Ctg ф* 4т2я2 +
Ы
2тя | ctg ф51
\Р\ ■
2тя | ctg <ps1
2тя
2тя
(III.145)
+(
argp + -J- sign ctg q>s)J
(III.146)
Подставляя выражения (III. 145) и (III. 146) в формулу (III. 141), после
упрощений, основанных на том факте, что т велико, получим искомое
выражение для определения асимптотического корня:
ip- +/[± (2m— -Lsign ctg <ps) я + argp]} +
■=ctg«pe{:
In
2mn | ctg q>s I
- +0(es) + 0(i^i), m = 'l, 2,
(III.147)
С помощью полученных выражений теперь можно найти корни
уравнений (III.118)—(III.122) из табл. III.2. Для этого необходимо, во-первых,
привести их к виду выражения (III. 123), затем определить коэффициенты
°:sk> M'sft» £sfc и начертить на плоскости [i, % ломаную выпуклую линию,
которая характеризует доминирующие слагаемые в выражении (III. 123).
В табл. III.3 приведены величины коэффициентов askJ \isky %sk.
Случай пропорционального регулятора. Учитываются только те
слагаемые уравнения (III. 118), которые лежат на прямой Ls, а уравнение (III. 131)
приобретает вид
Тр +К = О, (III.148)
откуда
p = --f. (HI.149)
Подставляя выражение (III. 149) в уравнение (III. 147), а также
учитывая соотношение tg <р2 = 1 из табл. III.3, получим окончательно
Т
/W = —ш
2/Ш1
/(2m ~)л, m=l, 2, ... (III.150)
Случай регулятора ПД. Из эскизов в табл. III.3 видно, что следует
учитывать слагаемые, лежащие на прямой Ls, и слагаемые, характеризуемые
прямой Ls2.
Для прямой Lsl, для которой ф2 = 0, из уравнения (III. 133) имеем
г = ру - (III.151)
а уравнение (III. 131) примет вид
К +KD'Pl = 0 (III.152)
или
1
ri = Pi = —
D
(III.153)
117
Значения коэффициентов
Таблица II 1.3
Тип
регулятора
Значения коэффициентов
Вид ломаной
Примечания
П
<*1 = q> Vi - О, lt = О
«2= 7\ |Ц= 1, Ев = О
а3 = К, [i3 — О, £3 = О
£ = 1, 2, 3;
tgq>i= 1;
я , я
пд
<*!= <mmi= о, Si == о
«2= Т, li2= 1, 62= О
«з = К, ц3 = 0, ls = 1
а4= tfD,fi4= l.E4= 1
1 ^<+г
\ I
Ь i ^
Л= 1,2,3, 4;
Ф1= О;
я
Ф1 = -7Г
И
<*i= <7, M^i = 1» Si = О
я2 = 7\ Ц2 = 2, £2 = О
«3= —» ^=0, £3 = 1
£= 1, 2,3;
Ф1 + -2"
ПИ
«i= <7, Цх= 1, £х= О
а2 = ТУ [i2 = 2, £2 = О
аз = —. Из = 0, g3 =т 1
а4 = ^»Ц4= 1» ^4= 1
k = 1,2, 3, 4;
Ф1= 0;
я , я
ф2 = Т^Т"
fli= <7> 14= 1» Ei= о,
«2 = 7\ № = 2, £2 = О,
ПИД | а3 = —, fx3 = 0, £3 = 1
а4 = #> М<4= 1, ^4= 1
а5= /ф,ц5=2, E5= 1
2-
•k
'«>*?
-С&1
.____.ф
к
.*
k= l, 2, 3, 4, 5;
Ф1=0;
я
Ф2 = ^-
118
Для прямой Ls2, <p2 = я/2 уравнение (III. 137) имеет следующий вид:
T-+KDp% = 0, (III. 154)
откуда
p*=~td- (»L155)
Подставляя выражение (III. 155) в соотношение (III. 139), получим
формулу для определения асимптотических корней:
r2m = —\n^-±j(2m—l)n. (III.156)
Интегральный регулятор. В этом случае tg <px = V2 и уравнение
(III. 131) имеет вид
7>2+-£- = о, (III.157)
откуда
!Л,2=±/)/-£-. (Ш.158)
Подставляя выражение (Ш.158) в формулу (II 1.147), получим
'imV= —2 In *?— ± i-4rrm, (III.159)
V-w x
/•2m = — 2In 4^!_ ±/-2(2m— 1)я, m=l, 2,... (III.160)
Регулятор ПИ. Этому случаю соответствуют две прямые: Lsl, у которой
<рх = 0, и Ls2, у которой tg <p2 = 1.
При ф! = 0 на основании выражения (III. 133) имеем
г = р. (III.161)
Корень определяется из уравнения (III. 131):
~Т + Крк=0, (111.162)
т. е
" — " — —,
ri=Pi—4-» (ШЛ63)
а при tg <p2 = 1 уравнение (III. 131) принимает вид
Кр+Тр2 = 0у (III. 164)
откуда
р2 = 0. (III.165)
Из формулы (III. 132) следует, что
г2 = 0 (III.166)
и
/>з = —Г' ,(111.167)
Подставляя выражение (III. 167) в формулу (III. 147), получим
гш = — Ui-Jr 2mn±i(2m |-) я, т=1, 2, ... (III.168)
119
Регулятор ПИД. Из табл. II 1.3 видно, что имеем две прямые: Lsl, у
которой cpi = 0, и Ls2, у которой ф2 = я/2.
При фх = 0 из уравнения (III. 133) получим
г = р, (III.169)
а корень определяется из уравнения (III. 131):
\ + Kp + KDp* = Oy (III.170)
т. е.
/•i,2 = P,,2= -25 —■ (Ш171)
При ф2 = я/2 уравнение (III. 137) принимает вид
T+KDp = 0, (III. 172)
откуда
Pz = -TD- '(HI.173)
Подставляя выражение (III. 173) в формулу (III. 139); получим
окончательно
r3m = — 1п-^±/(2/п-1)л, m=l, 2, ... (III.174)
Выводы и вопросы повышения точности. Полученные выражения
определяют значения корней тем точнее, чем больше их модули. С этой точки
зрения указанные выражения целесообразно применять тогда, когда речь
идет об определении поведения системы в начальной фазе переходного
процесса, т. е. при малых значениях t.
Формулы, приведенные в табл. II 1.4, позволяют сделать интересные
выводы:
1. Мнимые части корней при возрастании номера корня т растут
быстрее, чем соответствующие действительные части. Следовательно, по мере
возрастания т колебательность системы увеличивается, что хорошо видно
на рис. III.28 и 111.29.
2. Демпфирование, которое характеризуется действительными частями
корней, возрастает с ростом относительной постоянной времени и
уменьшается с ростом коэффициента усиления.
3. Самовыравнивание q не влияет на поведение системы в начальной
фазе переходного процесса.
4. Интегральная составляющая в регуляторах ПИ и ПИД не влияет на
ход процесса в начальной его фазе.
5. Поведение систем в зависимости от типа регулятора можно
подразделить на две группы:
А) демпфирование в системе с регуляторами типов П, И и ПИ (см.
рис. III.28) возрастает с ростом т\
Б) демпфирование в системе с регуляторами типов ПД и ПИД
постоянно независимо от величины т\ все корни имеют одинаковую
действительную часть (рис. II 1.29).
Таким образом, выявляется сильное влияние демпфирующей
составляющей на поведение системы в начальной фазе переходных процессов.
Системы, как это следует из рис. II 1.29, проявляют большую склонность
к колебательности.
6. С возрастанием дифференцирующей составляющей D уменьшается
демпфирование системы.
7. С возрастанием интегральной составляющей I'1 демпфирование
системы уменьшается.
120
8. Как известно, линейная система с постоянными параметрами
асимптотически устойчива, если действительные части всех корней ее
характеристического уравнения отрицательны. Из соотношений, представленных
в табл. III.4, для случая регуляторов типов ПД и ПИД получим
неравенство, удовлетворяющее вышеприведенному условию. С этой целью примем
во внимание пару корней, ближе всего расположенных к мнимой оси, т. е.
при т = I In T/KD <0 или K'D/T < I. Это известное уже неравенство
(III.116), гарантирующее уменьшение скачков в переходных процессах
систем с регуляторами типов ПД и ПИД.
1 hrr?=S
\*
\3
\л
>ч^/
Многократный X
корень Ч \
N
4 -J -2 ~1\
/*
и
А
1з
У*?77=-/
1
л/
10
\т = 7
г
о
-2
-4
-6
-8
-10
-1Z
Рис. II 1.28. Расположение корней
характеристического уравнения систем с
регуляторами типов П, И, ПИ (/С = 1;
/= 1)
XI
-1,о
**•
^
*j
I
*-/
I
1-2
-o.s
I
I
■f
jy
JO
20
10
40
-20
-30
-40
Рис. 111.29. Расположение
корней характеристического
уравнения систем с регуляторами
типов ПД и ПИД (Г = 1; К= U
D = 0,5)
Соотношения (III. 132), (III. 139) и (III. 147) показывают, что можно
повысить точность формулы, увеличивая значения корней на некоторую
постоянную величину. Эту величину можно определить, если имеется
какая-то дополнительная информация о системе, или же на нее
накладываются некоторые условия. В частности, можно увеличить точность
формул в табл. II 1.4, если известны точно значения хотя бы одной пары
комплексно сопряженных корней.
В качестве иллюстрации вышесказанного будет рассмотрена система,
состоящая из пропорционального регулятора и астатического объекта
(S = 0), находящегося на границе устойчивости.
Точный метод определения корней характеристического уравнения.
Пусть известно характеристическое уравнение [табл. III.2, формула
(111.118)1
q + rT + Ktrr = 0.
Полагая
r = x+jyf (III.175)
121
Формулы для определения асимптотических корней
Таблица 111 Л
Тип
регулятора
п .
пд
и
1
пи
пид
Выражения для корней
Т / 3 \
г2Ш = — In -jT- 2тя ± / ( 2т ^-) я, т = 1, 2,...
1
Г1~~"~б"' 1
Т
r<m = — In~Fn" ±'/(2m~" 0 я. т=1, 2,...
П1 4тя , .'
Г1т — ■ ■ Z III _ _L / ' '1/7Н1, |
г — о In .. 1. 1.9 (9m -. П Л ги— 19
" f^" ""
1
г2 = 0;
гзт as= — In -jT- 2тя ± / f 2/n д- J я,- /n = 1, 2,...
T
r3tn = — In -щ + / (2m — 1) я, m = 1, 2, .. .
лолучим
— (? + хГ) == Kt-X cosy;
yT == Kerx sin у.
Из системы уравнений (III. 176) имеем
x = — -y- — yrtgy;
sin у
& ctg у
-(*
я \-1
а после логарифмирования полудим
f'(y) = у ctg-y +In
sin у
In * л~
(Ш.176)
(III.177)
(III. 178)
(III.179)
q
К ~Г
Когда ~y~ е. > 0, то решение у лежит в пределах (2/с -г- 2/с + 1) я,
/с = 0, 1, 2, ... На рис. III.30 представлен вид функции / (#).
122
к
т
Зная величину -~- е из рисунка, можно найтй^в соответствии с
соотношением (III. 179) величину мнимой части у, а затем из формулы
(III. 177) — величины действительных частей х комплексных корней
уравнения (III. 118).
В соответствии с предположением, что q = 0 и х■ = 0, для первой пары
корней и первого соотношения системы (III. 176) получим
Уг,2=±^> (Ш.180)
а из другого соотношения
Т
я
(III.181)
Для значения KIT = -~- из рис.
II 1.30 найдем величины остальных
корней. Они сведены в табл. III.5.
Модифицированный метод
приближенного определения корней
характеристического уравнения.
Используя условие, что на границе
устойчивости (т. е. при х = 0) у == я/2
и KIT = я/2, увеличим точность
приближенного выражения. (III. 150).
На границе устойчивости первая
пара корней при пг= 1 должна иметь действительные части, равные нулю.
Следовательно,
— 1п[-^-2я — А] =0, » (III.182)
где А — постоянная х величина, которую необходимо определить.
Таблица II 1.5
Значения корней из формулы (III. 185)
Рис. 111.30. График
= '*/ctg*/+ In| sinr/11/
кривой / (у) ■■
Метод
Точный
Приближенный
m=l
.±l-f
.±l-f
m==2
— 1,5446 ±
± /• 2,4374я
—1,5978 ±
± /-2,5я
m = 3
—2,19678 ±
± /-JL, 4503л
—2,19466 ±
± /-4,5я
m = 4
—2,56213 ± ,
± /-6,46я
—2,56197 ±
± /-6,5я
Одновременно должны быть равны мнимые части, полученные точным
и приближенным методами:
(2—f )* + Я=-|-. (Ш.183)
Из соотношения (III. 182) получим
А = 2п-±г — 1,
(III.184)
123
а с учетом соотношения (III. 181)
А = 3
и из соотношения (III. 183)
В = 0.
Кроме того, теперь можно переписать выражение (III. 150) в более
точном виде:
гт2 = —\п (4т-3) ± j (4т-3) ~у т=1, 2, ... (III.185)
Следует заметить, что мнимые части корней в приближенном
выражении образуют арифметическую прогрессию с шагом d = 4я/2, а
действительные части являются логарифмами последовательных значений этой
прогрессии. Максимальная ошибка в процентах от точного значения
наблюдается при т = 2 и равна для действительной части 3,45%, а для мнимой
части — 2,58%.
Для сравнения рассмотрим устойчивую систему для случая, когда
ближе всего к мнимой/оси расположен двойной действительный корень,
а) Точный метод. Полагая, что q = 0 в уравнении (III. 118), и
дифференцируя это уравнение относительно переменной г, находим систему
уравнений
гТ + К?гг = 0;
Г-*г- = 0. I (ШЛ86)
Решая эту систему, получим
rkr = -U (Ш.187)
-^ = е. (III.188)
Остальные комплексные корни находятся из рис. III.30 при Т/К = е.
б) Модифицированный приближенный метод.
Используя соотношения (III. 187) и (III. 188), можно записать
—In [2яе — А]= — 1, (III. 189)
а также
(2 |-)я+Я = 0. - (III.190)
Из этих соотношений получим
А = 2яе — е;
R— Л
и выражение (III. 150) в модифицированном виде
/*2т = — 1п[2яе(т — 1) + е] ± / (4(/п— 1)-у), т= 1, 2, ...
(III.191)
В табл. III.6 даны точные и приближенные значения корней.
Из приведенных примеров следует, что использование приближенных
выражений, представленных в табл. III.4 для определения переходных
процессов, допустимо, если используются точные значения пары корней,
ближе всех расположенных к мнимой оси, а затем определяются величины
остальных асимптотических корней сдвигом на постоянную величину.
124
Значения корней
Таблица II 1.6
Метод
Точный
Приближенный
т=1
—1 ± /0
—1 ± /0
т = 2
—3,087383 ±
± /-2,3751л
—2,97683 ±
± /-2,5л
т = 3 '
—3,7189 ±
± /-4,4179л
—3,60406 ±
±/-4,5я
т = 4
—3,99063 ±
± /-6,4374л
—3,98448 ±
±/•6 5л
Обозначая через гт корни, найденны,е с учетом сдвига, можно
определить переходные процессы в системах управления с запаздыванием из
формулы, аналогичной формуле Хевисайда:
*®=Щ+ЪШ5'"^ <Ш192>
m=l
где L (rm) и М (гт) — значения соответственно числителя и знаменателя
преобразований, представленных в табл. III. 1 при г = гт.
Суммирование обычно ограничивается парой первых членов, так как
коэффициенты степенного ряда быстро уменьшаются, а показатели
степени быстро возрастают по модулю, сохраняя знак «минус».
Вопросы определения точных значений корней трансцендентных
уравнений будут еще рассматриваться в одной из последующих глав.
Список литературы
1. Bellman R., Cooke Kenneth L. Differential—Difference Equations. New York, 1963,
Academic Press.
2. Bellman R.,Kalaba R. Quasilinearisation and Nonlinear Boundary — Valus Problems.
New York, 1965, American Elsevier Publishing Company Inc.
3. Блох Е. Ш. Переходные процессы в линейных системах автоматического
регулирования. М. Физматгиз, 1961, с. 107—125.
4. Corduneanu С. Theoremes d'existence globale pour les systemes differentiates a argument
retarde. Качественные методы теории нелинейных колебаний, т. II, с. 195—201.
5. Курант Р., Гильберт Д. Методы математической физики. Т. I. М.—Л., Гостехиздат,
1951.
6. Cunningham W. J. Analiza ucladow nieliniowych. Rozdz. 8. Warszawa, 1962, WNT.
7. Cerny J. Poznamka k diferencialnym systemom s oneskorenym argumentom, pricom one-
skorenie zawisi od riesenia systemu. Souhrn Praci о Automatisati С. А. V. Praha 1961,
s. 255—265.
8. Эльсгольц Л. Э. Введение в теорию дифференциальных уравнений с отклоняющимся
аргументом. М., «Наука», 1964.
9. Gorecki H., Turowicz A. Metoda miejsc geometrycznych pierwiaskow rownari charakte-
rystycznych. Archiwum Automatyki i Telemechanyki, 1965, torn X, z. I, str. 11—27.
10. G5recki H. Pewne zagadnienie dynamiki ukldow redulacji zawierajacych czas martwy.
Archiwum Automatyki i Telemechaniki, 1965, torn X, z. 3, str. 303—318.
11. Jorgens E. Miejsca geometryczne biegunow transmitancji ukladow redulacji
automatycznej z czasem opoznienia przy kryterium optymalnego modulu. Praca dyplomowa
inzynierska, Katedra Automatyki i Elektroniki Przemyslowej AGH. Krakow, 1966.
12. Коган Б. Я. Электронные моделирующие устройства и их применение для
исследования систем автоматического регулирования. М., Физматгиз, 1963.
13. Kossowski M. Okreslenie przebiegow przejsiowych w ukladach automatycznej regulacji
obiektow inercyjnych 1 rze.du z rzeczuwistym opoznieniem przy zastosowaniu regulatora
P, PI, I. Praca dyplomowa magisterska, Katedra Automatyki i Elektroniki Przemyslowej,
AGN. Krakow, 1967.
14. Kowalski T. Okreslenie przebiegow przejsciowych w ukladach automatycznej regulacji
obiektow inercyjnych 1 rzfdu z rzeczywistym opoznieniem przy zastosowaniu regulatorow
PD oraz PID. Praca diplomowa magisterska, Katedra Automatyki i Elektroniki
Przemyslowej, AGN, Krakow, 1967.
125
15. Minorsky N. Drgania nieliniowe. Rozdz. 21: Drgania wywolane dzialanami opoznymi.
Warszawa, 1967, PWN.
16. Мышки с А. Д. Линейные дифференциальные уравнения с запаздывающим аргументам.
М.—Л.,1 Гостехиздат, л 1951.
17. Норкин С. Б. Дифференциальные уравнения второго порядка с запаздывающим
аргументом. М. Физматгиз, 1965.
18. Nowacki P., Szklarski L., Gorecki H. Podstawy teorii ukladow regulacji automatycznej.
T. I. Warszawa, 1958, T. II, 1962, PWN.
19. Ольденбург Р., Сарториус Г. Динамика автоматического регулирования. М.,( Госэнер-
гоиздат, 1949.
20. «Основы автоматического регулирования», Т. I, Теория, под ред. Солодовникова В. В.„
М., Машгиз, 1954. ч
21. Pai M. A.. The operational solution of difference—differential equatins using the modified
«z» trarisformi IRE Trans, on AutoMatic Control, October 1962, No. 5,. p. p. 124—125.
22. Peterka V. Eine einfache numerische Methode zur Berechnung der Obergangprozesse-
in linearen Regelkreisen.
23. Пинни Э. Обыкновенные дифференциально-разностные уравнения. М., Изд-во иностр.
лит., 1961.
24. Попов Е. П. Динамика систем автоматического регулирования. М., Гостехиздат, 1954,.
Гл. XI.
Глава IV
Анализ устойчивости линейных непрерывных
систем автоматического регулирования
с запаздыванием
§ IV. 1. Определение устойчивости в малом
Система, описываемая векторным уравнением вида
x{t)=f\t, x(t), л: (/-МО), ..., *(*-тА(0)Ь (IV. 1)
после отыскания решения лгф (f), соответствующего начальной функции
х (t) = у (t), на начальном множестве t £ g называется устойчивой в
малом, если для каждого е > 0
существует такое б (е) > 0, что из
неравенства
|ф(0-Ч>(0|<8(в),
t£l = [t0— тахт,,
t0] i = 1, . . ., k (IV.2)
следует неравенство
||*ф(0-*Г(0И<е, t^t0 (IV.3)
для последующих моментов времени
t> причем ty(t) — произвольная,
непрерывная начальная векторная
функция. Знак ||-|| обозначает норму
соответствующего вектора.
Таким образом, говоря о системе,
что она устойчива в малом,
утверждается только наличие точки, лежащей в окрестности е, и не
определяются границы этой окрестности. На рис. IV. 1 дана геометрическая
интерпретация определения устойчивости на фазовой плоскости для системы
второго порядка.
Рис. IV. 1. Геометрическая
интерпретация определения устойчивости
§ IV, 2. Определение асимптотической устойчивости
Система, соответствующая решению д:ф (/), называется асимптотически
устойчивой, если
Нт|хф (0-*♦(*) 1 = 0 (IV.4)
t-+co
при произвольной непрерывной начальной функции я|э (t)y
удовлетворяющей при достаточно малом бх >> 0 условию
|q>(0-*(OI<ei.
127
Таким образом, в случае устойчивости в малом от системы не требуется
достижения положения равновесия, а только не очень сильного
отклонения от положения равновесия; зато в случае асимптотической устойчивости
положение равновесия должно быть достигнуто.В случае линейных систем
с постоянным запаздыванием и постоянными остальными параметрами
каждая устойчивая система либо устойчива асимптотически, либо ее
параметры бесконечно мало отличаются от параметров асимптотически
устойчивой системы. '
Необходимым и достаточным условием асимптотической устойчивости
линейных систем с постоянным запаздыванием является расположение
всех корней характеристического уравнения в левой полуплоскости
комплексного переменного, т. е. чтобы существовало неравенство
Re [st.] <е при i = 1, 2, . . ., (IV.5)
где е > 0 — произвольная положительная малая величина, но не равная
нулю; s. — корни характеристического уравнения вида
F (s; e~s) = 0. (IV.6)
Так как уравнение (IV.6) является трансцендентным, то число корней
будет бесконечно большим, что коренным образом отличает системы с
запаздыванием от систем без запаздывания. Нахождение корней уравнения
(IV.6) затруднительно, поэтому рассмотрим критерии устойчивости, не
требующие знания величин корней, но гарантирующие, однако, их
расположение в левой полуплоскости комплексной переменной.
§ IV. 3. Аналитические критерии
Критерии устойчивости для систем с запаздыванием, аналогичные
критериям Гурвица и Раусса, основаны на результатах работ Л. С. Понтрягина
[1.70], а также Н. Г. Чеботарева и Н. Н. Неймана [51 и В. Н. Капы-
рина [21 ].
IV.3.1. Критерий Понтрягина
Критерий Понтрягина применим к характеристическим уравнениям в виде
квазиполинома
F (s, es) = S al/e-V = 0
4 (IV.7)
(t = 0, 1, 2, . . ., n; j= 1, 2, 3, . . ., k),
где au j — величины действительные или комплексные; т;- —
рациональные положительные числа.
С учетом невысокой точности измерений и технической реализации
при вычислениях можно ограничиться рациональными величинами т;-
типа
т/ = P/flV-
Чтобы привести уравнение (IV.7) к виду, удобному для дальнейших
исследований, умножим ,его на eT/nS, где
тш = max Ту. (IV.8)
Тогда получим эквивалентное уравнение в виде
F (s, es) = E az/s'eV = 0
'. / (IV.9)
(i = 0, 1, 2, . . ., п\ /= 1, 2, . . ., k).
128
Определение. Старшим членом квазиполинома (IV.9) называется
выражение a/;s'e /s, в котором показатели степени i и Я;- имеют наибольшие
возможные значения из совокупностей
(i = О, 1, . . ., п и i = 1, 2, . . ., k).
Пример.
F (s, es) = 3s2e43 + 2ses + 1
имеет старший член 3s2e4s.
Однако не каждый квазиполином имеет старший член, например,
F (s, es) = s?e3s + ^е2*5 -f 1 не имеет старшего члена.
Теорема 1 (Понтрягина). Квазиполином F (s, es) без старшего члена
имеет бесконечное множество корней с произвольно большой
положительной действительной, частью.
Из этой теоремы следует вывод, что необходимым условием
устойчивости системы, характеристическое уравнение которой имеет вид
квазиполинома (IV.9), является наличие в этом уравнении старшего члена. *•
Теперь исследуем квазиполином F (s, es), полагая s = /со. Как из-.
вестно [III. 18], радиусы-векторы, выходящие из мест расположения нулей
и концами скользящие по мнимой оси, в случае нулей, расположенных
слева от мнимой оси, при изменении со от —оо до +°° очерчивают
положительные углы, т. е. в направлении, обратном движению часовой стрелки.
Следовательно,
F (/со, е/«) = Р (со) + /Q (со) (IV. 10)
и
Ф = arg F (/со, е/«) = arctg -£gL. f (IV. 11)
Таким образом, если все нули квазиполинома лежат слева от мнимой
оси, то угол, очерченный вектором F (/со, е''0), будет положительным, и
должно выполняться неравенство
Ж>° flV.12)
/
ИЛИ
» '<»>^--^«<»>
>0, (IV. 13)
da — р2 (со) + Q2 (со)
ИЛИ
Р (со) Q' (со) — Р' (со) Q (со) >~0 (IV. 14)
при всех действительных значениях со.
На основе вышеприведенных рассуждений можно доказать следующую
теорему.
Теорема 2 (Понтрягина). Необходимым и достаточным условием
асимптотической устойчивости систем, характеристическое уравнение которых
имеет вид квазиполинома (IV.7), или необходимым и достаточным условием
того, чтобы все нули этого квазиполинома лежали слева от мнимой оси,
является выполнение одного из трех следующих условий:
1) неравенство (IV. 14) должно выполняться по крайней мере для
одного значения со, а нули Р (со) и Q (со) должны быть действительными и
кратными;
2) все нули Р (со) должны быть'действительными, и для каждого из них
должно выполняться неравенство (IV. 14);
3) все нули Q (со) должны быть действительными, и для каждого из них
должно выполняться неравенство (IV. 14).
Обычно третье условие наиболее употребительно.
9 X. Турецкий / 129
Пусть задана система, состоящая из идеального пропорционального
регулятора с коэффициентом усиления Kr и объекта с передаточной
функцией
G0 (s) = /C0e-ST/s70.
Характеристическое уравнение замкнутой системы имеет вид
F (s, es) = sT0 + Ke~sx = О,
где К = KRK0.
Умножив это уравнение на eST, получим
T0st" +K = 0. (IV. 15)
Уравнение (IV. 15) имеет старший член, следовательно, необходимое
условие устойчивости выполняется.
Полагая теперь в уравнении (IV. 15) s = /со, получим
Р (со) + /Q (со) = /С — Т0со sin сот + JT0^ cos сот = 0 (IV. 16)
и, следовательно,
р (со) = — 7> sin сот + К\ (IV. 17)
Q(co) = 70cocoscoT. (IV. 18)
Дифференцируя уравнения (IV. 17) и (IV. 18), получим
р1 (со) = —Г0 [sin сот + ™ cos сот J; (IV. 19)
Q' (со) = Г0 (cos сот — сот sin сот). (IV.20)
Исследуем знак неравенства (IV. 14) при со = 0:
Р (0) Q* (0) - Р' (0) Q (0) = КТ0 > 0. (IV.21)
Таким образом, неравенство выполняется, так как и коэффициент
усиления, и постоянная времени объекта Т0 всегда положительны.
' Теперь определим нули функции Q (со):
70со* cos со*т = 0, (IV.22)
т. е.
со0 = 0;
™*+1 =-J-+ fcrt, 4 = 0, 1, 2, ...
Уравнение Q (со) = 0 имеет только действительные корни; в
соответствии с третьим условием рассмотрим неравенство
ЛК+i) Q' (*>**) - Р' К+1) Q К+1) =
= [^—r-(-f+**)] (-1) (тг +kn) > °- (IV-23)
Допустимая величина коэффициента усиления будет наименьшей,
когда k = 0. Следовательно, можно получить условие устойчивости в виде
К<1Г-1Г- ' <IV-24>
Из рассмотренного примера видно/*что использование второй теоремы
.Понтрягина на практике затруднительно, поэтому в дальнейшем анализе
прибегнем к другой теореме.
Теорема 3 (Понтрягина). Число корней действительного
квазиполинома г F (/со, e'#0)), имеющего старший член апт (/со)" е/°)Ш и целочислен-
1 Квазиполином с действительными коэффициентами {Прим. ред. оригинала).
130
ные показатели степени Xf внутри прямоугольника А с длиной
горизонтальной стороны 4я&, равно
4mk + п. , (IV.25)
Вывод. Для того чтобы корни действительного квазиполинома со
старшим членом апт (/со)" е^т и целочисленными показателями степени Лу
были действительными, необходимо и достаточно, чтобы их число в
пределах (—2nk + e, 2nk + е), где k — произвольное большое целое число,
было точно равно 4mk + п.
Третья теорема позволяет использовать теорему 2. Следует только
обратить внимание на то, что условием кратности корней сор функции Р (со)
и корней со,, функции Q (со) является постоянство знака выражения
Q(M п =
Р' <©р)
или выражения
Р{*я)
, р=1, 2, 3, ... (IV.26)
Щ-> 9=1.2,3,... (IV.27)
Теорема 4. Если все корни квазиполинома
F(s)=fi (avs2v + bvs2*+l) (IV.28)
v=0
с действительными коэффициентами av, bv имеют отрицательные
действительные части, то все коэффициенты av, bv имеют одинаковый знак.
Нормируя знак при F (s) так, чтобы а0 > 0, получим ' *
*v>°' v = 0, 1,2, ... ) (IV.29)
bv > О,
В частности, для квазиполинома .
F (s) = (а0 + axs -\ |- ansn) cosh s +
+ (bo + bxs H h bnsn) sinh s (IV.30)
после разложения в ряд cosh s и sinh s получим
artS>0, 6rt>0;
a0 > 0;
«i + b0 > 0;
(IV.31)
)
Для отыскания неравенств, аналогичных определителям Гурвица для
систем с запаздыванием, можно поступить следующим образом: 1)
проверить наличие старшего члена в квазиполиноме F (s, es); 2) полагая в
квазиполиноме F (s, es) s = /со, исследуем, имеют ли квазиполиномы Р (со) и
Q (со) только действительные кратные корни. Для этой цели используются
теоремы 3 и 4 и образуется последовательность Штурма для
квазиполиномов Р (со) и Q (со).
Система с регуляторами типов П и ПД. Характеристический
квазиполином в относительных величинах имеет вид (табл. II 1.2)
F (г, е-') = (Tr+q)+K (Dr + 1) е-' = 0, (IV.32)
причем
0
1.
9* 131
(IV.33)
Умножая выражение (IV.32) на ег/2 и полагая г = 2г, получим
F (г, е2) = (2Tz + q) & + (2KDz + К) е~* = 0. (IV.32а)
Учитывая, что
е2 = cosh г + sinh z;
е-2 = cosh z — sinhz,
после преобразований выражения (IV.32a) получим
F(z, e*)=[2T(l' + ^)z + (K + q)]coshz +
+ [2Т(1 *j*-}z + (q-K)] sinhz. (IV.34)
Таким образом, как при D Ф 0, так и при D = 0 имеем случай
квазиполинома п = m = 1, который можно записать в следующем виде:
F (г, е2) = [агг +а0] cosh г + [pxz + p0J sinh z. (IV.35)
В рассматриваемом случае коэффициенты alf a0, plf ро являются
действительными-членами, однако для многомерных систем [341 могут
быть также числами комплексными. Поэтому ниже будет рассматриваться
общий случай, когда .
ос0 = ао + ja'o, ах = ах + ja\\ l
р0 = bo +/66, Pi = 6i + /«. J (IV'36)
Для определения устойчивости положим в уравнении (IV.35) z = /со и
получим два уравнения, которые должны иметь только действительные
кратные корни:
Р (со) = (—а[ cos со — b\ sin со) со — 65 sin со + ао cos со; (IV.37)
Q (<*>) = (tfi cos со — Ь{ sin со) со + 6о sin со + a'o cos со. (IV.38)
Составляя для уравнений (IV.37) и (IV.38) последовательность Штурма
~и вводя обозначения
А = aoai — аоа{\ |
В = Ъ'оа\ + aob\ — b0a{ — aob'u | (IV. 39)
С = 6o6i + 666i, J
получим следующее необходимое и достаточное условие устойчивости:
если
В2 — 4ЛС <0, - (IV.40)
то
но
то
и
или
если
также
aibi+aib[ > 0; ]
ami + аф.1 > 0, J
Яа — ААС > 0, (IV.42)
афх +а{Ь{>0;
, • '^n i (IV-43>
сш\ + аФг > 0 J
k2 = ks (IV.44)
aibi + aibi > 0; (IV.45)
a-octi + ahai < 0;
—*.+*, = —!; (IV.46)
J32
причем
ki = E \^-±.Щ^-) + 1, t- = 2, 3, . (IV.47)
где Е (x) обозначает целую часть числа х;
1^= arctg
Ьл
%г = arctg
т3 = arctg
—b + Vb2 — 4АС-
2С '
—в — VW-
•4АС
2С
(IV.48)
(IV.49)
(IV.50)
Частные случаи:
I. до = clq = 0 — квазиполином имеет нулевой корень и система
находится на границе устойчивости;
II. а\ = а{ = 0 — система неустойчивости;
III. Ь\ = Ы = 0 — система неустойчива;
IV. bo = bo = 0 — система может быть устойчива; необходимые и
достаточные условия устойчивости имеют вид
aibi +a[b[ >0; )
a0ai+a'oai>0; (IV.51)
k3 = 0 J
или
aibi+a{bi>0\ \
aoai+'afai <0; (IV.52)
&з = sign (aobi — aobi). J
V. do = a{ = bo = 6i = 0 (случай действительных коэффициентов) —
система может быть устойчива, а следовательно,
(IV.53)
(IV.54)
Необходимые
при
должно быть
а при
должно быть
Т2,3 —
± arctg |/-
«;
gpfli
Ml
и достаточные условия приобретают вид
а0Ь0> 0
агЬг > 0;
а0Ь0 <0
«l^i >0;
а0аг > 0;
^2 == ^3> .
,
причем
*1 = £[-J-(arc,gj/-^+il/-^)] +
(IV.55)
(IV.56)
(IV.57)
(IV.58)
1; (IV.59)
(IV.60)
133
или
k2 = О, (IV.61)
или также
а1Ь1>0; )
/п (IV-62)
aodi <0; J
—k2 +k3 = —l, (IV.63)
но этот случай не стоит принимать во внимание, так как k2 = —k3 и
является целым числом, а следовательно, уравнение не может быть
выполнено.
Таким образом, полагая, например, что
с0 > О, (IV.64)
(IV.65)
(IV.66)
i (IV.67)
а1>0;
получим, что
должно быть
а при
должно быть
при
ь0>о
fli>0;
&i>0,
k2 = 0. (IV.69)
В случае систем с регуляторами типов П и ПД, определяя на основе
выражения (IV.34)
а0 = К + q\
b0 = q — К;
(IV.70)
получим следующие условия устойчивости.
Регулятор Я. При D = 0 и q = 1, когда
/С<1, (IV.71)
система всегда устойчива, так как Т > 0.
Зато, когда
К> 1, (IV.72)
из выражений (IV.69) и (IV.59) следует
Для q = 0 уже получено соотношение 0 < К < Т -^- [см. формулу
(IV.24)].
Регулятор ПД. При q = 1, когда
&о>0,
имеем
/С<1. ' (IV.74)
134
Из выражений (IV.18) и (IV.70) получаем
KD
при
имеем
<1;
ьо<0
К>1;
(IV.75)
(IV.76)
KD \
IT
1 Г -1/(*+1)(1 +
1. arctgl/ )
('-#)
<1.
(IV.77)
При q = О случай &0 > 0 невозможен, так как К > 0. Рассматривается
только случай 60 <0, для которого
К>0;
/CD
<Л;
0<^г
Я"
2Т( 1
^ arctgj/ —
/CD
/CD
ЯГ»
('-¥)
/CD
Г J
1<1.
(IV.78)
Системы с регуляторами типов И, ПИ, ПИД. Характеристический
квазиполином в относительных единицах при использовании ПИД-регу-
лятора имеет вид (табл. II 1.2)
F (г, е-') = Ir{q + гТ) + К (DIr2 + plr + 1) е"' = О, (IV.79)
причем
__ | 0 для объекта без самовыравнивания;
^— \ 1 для объекта с самовыравниванием;
_ } 0, если нет пропорциональной составляющей;
-{?:
если есть пропорциональная составляющая.
Умножая выражение (IV.79) на ег/2 и полагая г = 2г, получим
F (z, ег) = [4/Гг2 + 2Iqz*\ ег + [4/CD/z2 + 2KIpz + К] егг = 0. (IV.80)
Используя выражение (IV.33), после преобразований получим
F (z, ег) = [4/Г (,1 + ^-) z2 + 21 (q + рК) г + /с] coshz +
+ [4/T(l --^-)z2 + 2/(<7-p/C)z-/t]sinhz = 0.
(IV.81)
135
Таким образом, это случай квазиполинома п = 2, т = 1 вида
F (z, ег) = (a2z2 + я г* + я<>) cosh z +
+ (М2 + 6iz + 60) sjnh ^ = О, (IV.82)
где а2, аъ а0> b2, bl9 b0 — действительные числа.
Необходимые условия следуют из неравенства (IV.31) в таком виде:
я0>0;
а2 > 0;
62>0;
аг + Ь0> 0;
«2 + 4- + fti>°-
(IV.83)
Эти условия будут использованы позже для определения устойчивости
систем регулирования.
Для анализа устойчивости положим в выражении (IV.82) г = /со и
получим два уравнения, которые в соответствии с теоремами Понтрягина
должны иметь только кратные действительные корни:
Р (со) = —а2со2 cos со — 6хсо sin со + я о cos со; (IV.84)
Q (со) = —Ь2со2 sin со -f- fli® cos со -J- b0 sin со.
(IV.85)
Из уравнений (IV.84) и (IV.85) по методике Чеботарева можно
получить искомые условия устойчивости.
Из неравенств (IV.83) видно, ^то существует только шесть комбинаций
знаков коэффициентов а2> . . ., Ь0 *. В системах, описываемых
уравнением (IV.81), знак изменяется только при коэффициенте и в этом типе
систем возможны две комбинации.
Теперь рассмотрим частные случаи. Пусть
а0 > 0, а2 > 0, &о > 0, Ь2 > 0,
тогда в зависимости от комбинации знаков коэффициентов можно выделить
четыре подварианта:
fli > 0, Ьг> 0;
01 <0, Ьг <0
01 > 0, Ьг <0
«1 <0, &i>0.
а1Ь1 > 0 (IV.86)
Если]
I Va0b2 — У a2b01 < У a±bv
(IV.87)
то необходимые и достаточные условия устойчивости можно выразить
неравенством (IV.83) и требованием, что,бы
fli>0.
(IV.88)
Резюмируя, необходимые и достаточные условия устойчивости можно
представить в виде следующих неравенств:
* В работе [5] ошибочно исключены два случая из-за неправильного вывода, что из
b2i> 0 следует Ь0$> 0. С практической точки зрения наиболее интересны случаи ai£> 0,
b0<$0, &i£>0 и ах5>0, 60<0, &i < 0- (Прим. автора).
136
или
Случай I.
а0 > 0;
fli > 0;
а2 > 0;
&о>0;
Ьг > 0;
&2>0;
I"У аЛ — У <*A I < У «Л
а0 > 0;
ai > 0;
я2 > 0;
Ьо > 0;
&i>0;
&2>0;
\Va0b2 — Vd2b0\^Va^bv j
Тогда дополнительно должно выполняться условие
L я ' я адг + V>2 tg2 *i J
— El T2 ] 1 . (в<Л — ДЬЛ) tg T2 I _0
L я "Г я ад* + М>2 tg2 т2 J
С л у ч а й II.
'
\
а0 > 0;
fli <0;
а,2 > 0;
&о>0;
Ь1<0;
&2>0;
а2 + -^ + &1>0;
С]
1 УоЛ-
*[-*+■
£[-тг +
. + Ьо > 0;
- У^А 1 s^-У^Л .
1 (а062 — а2Ь0) tg тх I __
я • аха2 + ЬХЬ2 tg2 тх J
1 . К&2- ^0)tgl
я ajOa + ЬХЬ2 tg2 т2
4-1 = 1.
J
Случай III.
а0> 0;
ai>0;
а2 > 0;
Ьо>0;
&i<0;
62>0;
(IV.
(IV.90)
(IV.91)
(IV.92)
(IV.93)
(IV.94)
137
*[■
я "• я * фг + ^ tg2 TX J "r
_j_ £ Г __ i _l J_ (<hbt — g2^o)tgT2 ] 2
"^ L Я "Г я ■ аха2 + Ms tg2 т2 J
Случай IV.
(IV.95)
а0>0;
fli <0;
a2 > 0;
6o > 0;
&i>0;
b2 > 0;
0i +*>o>0
(IV.96)
£ Г Tx . 1 _ fa6« — fl26Q)tgT1 I
L я "Г" я яхя2 + M2 tg2 *i J "1"
_L£ Г та . 1 ■ (Q062 — a260)tgT2 1 __|
причем
tgTs
— в — Кв2 — 4лс
2C
-B+KB2 — 4ЛС
2C '
(IV.97)
(IV.98)
(IV.99)
а коэффициенты Л, 5, С связаны с коэффициентами af., 6^ соотношениями
А\=аоа\а2\ (IV. 100)
В = «i&i (a0b2 + aa60) —<(aob2 — а2&0)2; (IV. 101)
С = &0&1&2»
(IV. 102)
Следует заметить, что при выполнении вышеприведенных неравенств
выражения под знаком радикала всегда положительны.
Из уравнения (IV.81) следует, что из рассмотрения выпали наиболее
интересные случаи, когда Ь0 = —К <0. Как упоминалось, они из-за
допущенной ошибки не рассматривались в работе [21] (см. [5] стр. 276,
277).
Необходимые и достаточные условия устойчивости для этих случаев
получены автором. Для них существует следующее соотношение
коэффициентов, получаемое приравниванием выражений (IV.81) и (IV.82):
KD
а2 = ш(1+Щ;)
аг = 2I(q + pK);
а0 = К;
Ь2=4Щ(1-^-);
bt = 21 (q- рК);
ь0 = -к.
(IV. 103)
138
С учетом того, что параметры и регулятора, и объекта неотрицательны,
можно сразу записать неравенства, которые всегда выполняются для
рассматриваемых систем:
а2 > 0;
ai >0*;
а0 > 0;
&о<0.
(IV. 104)
Кроме того, из необходимых условий (IV.83) следует, что должно
выполняться условие
62>0 (IV. 105)
или
откуда следует, что
4IT
(1-^)>0,
^-<1.
(IV. 106)
Это уже известное условие наличия скачков в переходном процессе,
вызываемое эффектом дифференцирования.
На основе уравнения (IV.83) можно записать
01 +Ь0>0
или
и окончательно
2/ (q + рК) - К> 0
(IV. 107)
(IV. 108)
XIV. 109)
или
4/r(l +
KD\ . К
Т ) "*" 2
+ 2/(«7-ptf)>0.
(IV. ПО)
Принимая во внимание неравенства (IV. 104) и (IV. 105), можно
заметить, что в этих случаях либо Ьг > 0, либо Ьх < 0. Тогда условия
устойчивости получают следующий вид:
Случай V.
а0 > 0;
fli>0;
а2>0;
«1 + Ь0 > 0; i
62>0;
Ъх > 0;
60<0
v Г Tt . 1 (a„fe2 — а2&0) tg тх I _
L Я ^ Я а^ + Ma tga тх J
ага2 + ЬХЬ2 tg2 т2 J '
(IV. Ill)
(IV. И 2)
* Случай, когда q = 0 и р = 0, приводит, как это будет показано позже, к структурной
неустойчивости и поэтому здесь не рассматривается (Прим. автора).
139
где
tgr
tgxt =
— В — VB2 — 4ЛС,
2C
— В — УВ2 — 4ЛС
2C '
(IV. 113)
(IV. 114)
а постоянные Л, Ву С определяются из зависимостей (IV. 100)—(IV. 102).
Случай VI.
а0 > 0; )
ах > 0;
а2> 0;
01 + &о > 0;
я2 + ^ + &1>0;
4 &2 > 0;
&i<0;
60<0
(IV. 115)
£ Г Т1 1 (flpft, — fl,60) tg Тх 1 ,
L я ~ я аха2 + Мг tg2 тх J "r
4-£ r_J^J-_L .(flo^i —^o)tgT8 1 о
(IV. И 6)
а тх и т2 определяются из соотношений (IV. ИЗ) и (IV. 114).
Следует обратить внимание на то, что в выражениях, стоящих под
знаком Еу предполагается, что они не целочисленные. Случаи, когда эти
предположения не выполняются, могут быть рассмотрены особо, однако
они не имеют практического значения, так как величины параметров
системы известны всегда приближенно и в определенных пределах
изменяются.
На основе полученных неравенств теперь можно найти области
устойчивости в пространстве параметров для различных типов регуляторов
и объектов.
Из уравнений (IV. 100)—(IV. 103) определим вспомогательные величины
В=КТ[2-£(д-р1Р)-1];
C = -I(q-PKf(l-A^);
tgTltl =
(IV. 117)
(IV. 118)
(IV. И 9)
21(д-рК)2(1-Щ '
(IV. 120)
140
Система с регулятором типа И (р = О, D = О, q = 1),
Из уравнений (IV. 103) получим необходимые и достаточные условия
устойчивости в виде
а2-4/Г; )
ах = 2/;
а0 = /С;
&2 = 4/Г; I (IV.121)
*i = 2/;
*о = -/С.
Из соотношения (IV. 108) следует, что
— >1
(IV. 122)
из соотношения (IV. 112)
Е Г Ti I. ' . ^ . tg^i 1 _
L я ~ я / 1 + tg2 тх J
= £ Г Ti I 1 - А" - tgt, 1
L я ^ я / 1 + tg2 т, J '
а из формул (IV. 113) и (IV. 114)
•"■-^i/W^B?-1)'
То — JT — Ti •
Соотношение (IV. 123) с учетом зависимости (IV. 124) можно
в виде двойного неравенства
^ я я / 1 + tg2 хг
tg*l
<1
(IV. 123)
(IV. 124)
записать
(IV.125)
или
•x-^j/^dA+(£)■-!)+
(IV. 126)
Система с регулятором типа ПИ.
а) р = 1, D = 0, q = 1.
На основании уравнения (IV. 103) необходимые и достаточные условия
устойчивости имеют вид
с2 = 4/Г;
а, = 2/ (Я + 1);
а<> = К;
&2 = 4/Г;
6Х = 2/ (1 - К);
Ь0'=-К.
Если
/С < 1 (IV. 128)
141
I
(IV. 127)
то должно выполняться неравенство
2/
7Г (*+!)> 1
0<Jl_±4
tg*l
(/C+l) + (l—^tg2^
<1,
где
l^=/WMf ■ + F^2-]* - ■)•
Если же
К>\,
то, используя соотношения (IV. 129) и (IV.83), получим
\К , 2Г
4/ </С— 1) ^ X —1
>1,
(IV. 129)
(IV.130)
(IV.131)
(IV. 132)
(IV. 133)
так как соотношение (IV. 116) выполняется всегда,
б) р = 1, D = 0, q = 0.
Из соотношений (IV. 103) получим
а2 = 4IT;
аг = 2IK;
а0 = К;
Ь2 = 4/Г;
&! = —2/tf;
6о = -К.
(IV. 134)
Тогда из соотношения (IV.83) найдем условия устойчивости в виде
/>4-
2
2Г
4/
+ -тг>1.
(IV. 135)
(IV. 136)
а соотношение (IV. 116) выполняется всегда. Кроме того, из соотношений
(IV. 135) и (IV. 136) следует, что отношение Т/К не может стать меньше
граничной величины
К > 4 '
Система с регулятором типа ПИЛ.
а) р = 1, q = 1.
На основе соотношения (IV. 103) имеем
а2 = 4/г(1+ «£-); ]
а1 = 2/(1 +Я);
а„ = Я".
ь0 =—К;
(IV. 137)
(IV. 138)
142
из соотношения (IV.83) получим условия
(IV. 139)
2/
-£-(1+К)>1.
(IV. 140)
Но условия зависят от знака коэффициента bv Если Ьг > 0, т. е.
К<\, (IV.141)
то должно выполняться неравенство
О ^JEl __!_._* tg^i
л л 41
<1, (IV. 142)
где
(l+A)(l + ^)+(l-tf)(l-^)tg*
tgrx =
/Сг[2^-(1—/С2) — l] +
+ |//(2T2[2-^-(l-^)-l]2 + 4/41-/C2)2[l-(^-)3]
2/
<i-*>-(i-4£)
Если же 6Х <0, т. е.
/С>1,
то условия устойчивости получим из соотношения (IV. 115):
ТГ(1+Я)>1
4/ (/С — 1) ^ /С—1 V ^ Т )-> 1ш
(IV. 143)
(IV. 144)
(IV. 145)
(IV. 146)
б) р = 1, <7 = 0.
Из соотношения (IV. 103) получим
e, = 4/7*(l+-^-);
«1 = 2//С;
а0 = К;
Ь1=—21К;
Ь0 = —К.
На основании соотношения (IV.83) условия устойчивости имеют сле-
(IV. 147)
дующий вид:
KD
<1;
i+i(>+f)»-l
(IV.148)
143
Таблица IV.
Области устойчивости в пространстве параметров
Тип%-
регуля-
тора
Области устойчивости Объект
П
* <1
или
К> 1
и
1" . i/rK+1 1 K—l-i/~K+l^,
0<-arctg J/Tii__.-Sf-yiriT<l
т
<1
или
K>1;
°<i|arctg]/
*■(■-?) r cic-i)(i-^)J<
<K-l)(l-^)
№-<i; о<^х
T ^ ' ^ я
[•V^f-^/
<7 = 1
Г ^ 2 ' v
K< 1
<7= 1
1+JW.l I ?=0
?= 1
Неустойчива ' I <7 = 0
Продолжение табл. IV. 1
Тип
регулятора
Области устойчивости
2/
К
К<\;
(К+1)>1;
0< JL_-iL.A.
tg^l
<i;
л Г КГ 1-лГ. . Г27(1-Л:2)12 \
или
пи
/С> 1;
2/ ^
к
27
4/ (/С—1) ^ /С —1
>1
/>
1 47+ 3
2 47+ 4
К < 47 + 3
4/ ^ К >
К<4Т
пид
к< i;
KD
<i;
-^-(Т + 1)>1
о<
1 /С
X
я я 4/
<1 + *>(1+?)+<1-*)(1-?)^
<i;
tgxx
дгг [2^[-(i-/:«)-i] +
/~ лрг» [2^(i-^)-i]2 +
]/ +4/2(i-W[i-(f)2]
2/
-|-(*+1)>1
(l_/0»(l—^-)
D<
* 2Г (,,KD\\
8Г-Ь3
а: < 8г + з
18Г + 3
28Г+4
/CD
<1
7>-Г
4/
'+Т(
tfD
>1
D<
1
/>
/С<87
1
10 X. Турецкий
145
Основные зависимости сведены в табл. IV. 1. Они позволяют
ориентировочно оценить расширение областей устойчивости из-за наличия
дифференцирующей составляющей. Сравнивая регуляторы ПИ и ПИД,
видим, что введение этой составляющей почти в 2 раза расширяет область
устойчивости.
На основе полученных зависимостей построены номограммы на
рис. V.l—V.25, которые дают возможность очень быстро
проанализировать устойчивость и произвести подбор параметров и типа регулятора
для данного объекта с точки зрения обеспечения устойчивости системы.
Список литературы
1. Бессекерский В. А. и др. Сборник задач по теории автоматического регулирования. М.,.
Физматгиз, 1963, Гл. 8, с. 215—221.
2. Брин И. А. Об устойчивости некоторых систем с распределенными и сосредоточенными
параметрами. —«Автоматика и телемеханика», 1952, Т. XXIII, № 7, с. 863—871.
3. Цыпкин Я. 3. Устойчивость систем с запаздывающей обратной связью. —«Автоматика
и Телемеханика», 1946, Т. 7, № 2—3, с. 107—128.
4. Cypkin Ja. E. LJber die obere Grenze des Stabilitatsgrades von I, PI, PID Reglern Rege-
lungstechnik. 1957. Heft 2, S. 49—50.
5. Чеботарев Н. Г., Нейман Н. Н. Проблема для полиномов и целых функций, Труды
Матем. ин-та им. В. А. Стеклова, Т. XXVI. Изд. АН СССР, М., 1949.
6. Edelman H. Ein Kriterium fur die aperiodische' bzw. rein szillatorische SJabilitat und
der Zusammenhang mit Reaktanztheorem. Regelungstechnik, 1954, Helf 11, S. 264—267.
7. Effertz F. H„ Ко 1 berg F. Einfuhrung in die Dynamik Selbsttatiger Regelungssysteme.
Dusseldorf 1963, VDI—Verlag.
8. Eisenberg L. Stability of linear system with transport lag. IEEE Trans, on Automatic
Control, April 1966, vol. AG11 No. 2, pp. 247—254.
9. Ellingsen H. V. Die Behendlung von Totzeiten bei rtumerischen Stabilitatsuntersuchungen
von Regelkreisen. Regelungstechnik, Dezember 1964, Helf 12, S. 535—541.
10. Engel W.t Jaschek H. LJbungssufgaben zum Grundkurs der Regelungstechnik, Munchen
1964, R. Oldenbourg.
11. Euler K. Regelsysteme mit Laufzeit. Regelungstechnik, 1959, Heft 3, S. 89—92.
12. Findeisen W. Technika regulacji automatycznej. Warszawa, 1965, PWN, str. 93—99,.
329—356.
ГЗ. Финкельштейн С. М. Об устойчивости систем автоматического регулирования с
длинным импульсным трубопроводом. В кн.: «Автоматизация производственных процессов».
Вып. Ill, M., Изд. АН СССР, 1960.
14. Follinger О. Zur Stabilitat von Totzeitsystemen. Regelungstechnik, April, 1967,.
Heft 4, S. 145—149. •
15. Герасимов С. Г. Теоретические основы автоматического регулирования тепловых
процессов. М., Госэнергоиздат, 1949 с. 210—278.
16. Gdrecki H. Zagadnienie stabilnej wspolpracy regulatorow PID z obiektem inercyjnym
n—tego rze,du. Zeszyty Naukowe AGN, Automatyka (w druku).
17. HalanayA. Some problems in the qualitative theory of the systems with time lag.
Качественные методы. Т. II, Киев, изд. АН УССР, 1963, с. 394—408.
18. Hale I. К. Asymptotic behaviour of the solutions of differential—difference equations.
Качественные методы. Т. II, Киев, изд. АН УССР, 1963, с. 409—426.
19. Jastrzejbska M. Problemy stabilnoSci i dopasowania ukladow automatyki zawierajacych
elementy о stalych rozloionych. Prace IV Krajowej Konferencji Automatyki, Krakow,
1967, AGN, z. I.
20. Jeffrey A. The stability of interacting control systems Automatic and Remote Contro.„
Vol. I, London, 1961, Butterworth, pp. 126—131. ^
21. Капырин В. Н. К проблеме Турвица для трансцендентных функций. Диссертация,.
Казань, 1944.
22. Kindler H., Buchta H.> Wilfert H. H. Zadania z techniki regulacji automatycznej.
Warszawa, 1968, WNT, str. 122—131.
23. Krall A. M. Stability criteria for feedback systems with a time lag. J. Soc. Industr. and
Appl. Math. 1964, Vol. A2, No, 2, pp. 160—170.
24. Краснов M. JL. Макаренко Г. И. Операционное исчисление. Устойчивость движения.
М., «Наука», 1964, с. 36—43.
25. Мансуров К. И. Об устойчивости линейных систем с запаздыванием. В кн.:
«Исследования по дифференциальным уравнениям и их применению», Алма-Ата, Изд. АН
СССР, 1965, с. 190—199:
26. Mufti I. H. A note on the stability of an equation third order with time lag. IEEE Trans.
. Automat. Control, 1964, Vol» 9, pp 190—191.
27. Мышкис А. Д., Шиманов С. Н., Эльсгольц Л. Э. Устойчивость и колебания систем
с запаздыванием. Качественные методы Т. II, Киев, Изд. АН УССР, 1963.
28. Неймарк Ю. И. Структура D-разбиения пространства квазиполиномов и диаграммы
Вышнеградского и Найквиста. М., ДАН 60, 1948< с. 1553—1560.
29. Nowacki P., Szklarski L., Gorecki H. Podstawy teorii ukladow regullacji automatycznej.
T. I., II, Warszawa, 1962, PWN.
30. Oguztoreli M. N. Time—lag. Control Systems. New York, 1966, Academic Press.
31. Ольденбург Р., Сарториус Г. Динамика автоматического регулирования. М.э Госэнерго-
издат, 1949.
32. Oppelt W. Poradnik techniki regulacji. Warszawa, 1958, PWT, str. 291.
33. «Основы автоматического регулирования», под ред. Солодовникова В. В., М., Машгиз,
Т. I, 1954, с. 673—683.
34. Paszkowski S. Stabilnosc wielowymiarowych ukladow ze sprz§zeniami zwrotnymi
miedzykanalami. Archiwum Automatyki i Telemechaniki, 1959, torn IV, z. 3—4.
35. Пятницкий Е. С. О структурной устойчивости одноконтурных систем регулирования
при наличии запаздывания. — «Автоматика и Телемеханика». 1962, Т. XXVIII, № 7,
с. 852—862.
36. Porter В. Stabylity Criteria for Linear Dynamical Systems. London, 1967, Oliver and
- Boyd, Edinbourg, pp. 139—166.
37. Satche M. Discussion of a previous paper. J. Appl. Mech. ASME, 1949, No. 16, pp. 419—
420.
38. Смит О: И. М. Автоматическое регулирование М., Физматгиз, 1962, с. 393—464.
39. Smith О. I. M. Feedback Control Systems. New York, 1958, McGraw-Hill.
40. Шиманов С. Н. Устойчивость систем с запаздыванием. Труды II Всесоюзного съезда
по теоретической и прикладной механике. М., «Наука», 1965, с. 170—180.
41. «Техническая кибернетика». Кн. 2: «Теория автоматического регулирования», под
ред. Солодовникова В. В., М., «Машиностроение», 1967, с. 431—458, 517—576.
42. Воронов А. А. Основы теории управления. Ч. II. Специальные линейные и нелинейные
системы автоматического регулирования одной величины. М., «Энергия», 1966, с.
7—48.
43. Walker I. A. Stability of feedback systems involving time—delays and timevarying
non-linearity. Int. J. of Control, 1967, No. 4, pp. 365—372.
44. Wang P. K. C., Bandy M. L. Stability of distributed—parameter processes with time—
delays. J. Electron, and Control, 1963, No. 4, pp. 343—362.
45. Wang P K. C. On the almost sure stability of linear timelag systems with stochastic
parameters. Int. J. of Control, 1967, Vol, II. No 5, pp. 433—440.
46. Yuan— Xun Qin, long—Qing Lian, Lian Kang. Effect of timelags on stability of dynamical
systems. Automatic and Remote Control, Vol. I, pp. 26—32. London 1961, Butterworth.
Глава V
Номограммы для определения областей
устойчивости на плоскости параметров
объекта и регуляторов.
Графические методы анализа устойчивости
Разработанные номограммы позволяют определить значения параметров
регуляторов типов П, И, ПИ, ПИД для объектов первого порядка с
запаздыванием. С учетом того, что в типичных промышленных объектах
величина запаздывания чаще всего меньше величины постоянной времени,
номограммы построены в относительных единицах с отнесением всех
параметров не ко времени запаздывания, а к постоянной времени. Это
значительно уменьшает ошибки вычислений. Связь между безразмерными
параметрами на графиках и безразмерными параметрами в предыдущих
исследованиях имеет следующий вид:
К = К&К0\
(V.1)
1 0
Г)' Td _ Td m х _
Т0 т Т0
г г Ti Tt т
То т То
D
Т
I
Т
Процедура использования номограмм такова:
1. Из графика реакции объекта на скачок или на основе других
данных находится величина отношения 7" = 1/Т и коэффициента объекта К0-
2. На основании найденной величины 7" и требований к величине
статической ошибки выбирается тип регулятора, и для данного типа
регулятора на соответствующей номограмме определяются области допустимых
значений параметров регулятора, таких как: время изодрома /', время
упреждения D и коэффициент разомкнутого контура К = К$К0-
Определив величины Г, D', К и зная величины 7",/С0, на основании
соотношений, представленных в табл. IV. 1, определяем значения Т.,
Td и KR.
Так как применимость номограмм, представленных на рис. V.l—V.25,
ограничена системами управления с объектами первого порядка, дальше
будут рассмотрены другие методы анализа устойчивости с запаздыванием.
§ V.l. Графические критерии устойчивости
Среди графических методов можно выделить два основных:
1. Метод амплитудно-фазовых характеристик. Этот метод является
аналогом критериев Михайлова и Найквиста для систем без запаздывания.
Наибольшее развитие метод получил в работах Цыпкина [81 и Сетча .[40].
2. Метод D-разбиения. Этот метод разработан Неймарком [32] и
Пинни [1.68].
148
wo
50
20
10
lljN^
ииптпема
устпойчи
вп
Система
регулирования
неустойт'Яп
ы
*-—оо при К
I I LU
_Ш
;
0,01 ОМ
0,5 0J 0,2
0.5
Г
Рис. V.I. Граница устойчиюсти в системе с регулятором типа П
и инерционным объектом с запаздыванием (q = 1)
К
100
50
20
10
5
1
1 х^ —
У
г*
сто
^Г
/ ч
VbTT
йч
ива
Не
>ус
тойч
ива
-
001 ОМ 0,05 0,1 ОЛ
0,5
Т1
Рис. V.2. Граница устойчивости в системе с регулятором типа П
и астатическим объектом с запаздыванием (q = 0)
К Т'=0 при К=10
/I 1 1 1 1 1 1 I II 1 1 1 1
0.1 0,2 0.5 1 2 >Т'
Рис. V.3. Граница устойчивости в системе с регулятором типа ПД и инерционным
объектом с запаздыванием (q = 1)
Т'=0
при K-W
Рис. V.4. Граница устойчивости в системе с регулятором типа ПД и астатическим объектом
с запаздыванием (q = 0)
150
к/i1
0.5
OX
0,1
0,05
OflZ
0.01.
г -"*
п
L
J ## -
\Усгниичива
Неустойчива
10
20
50
100
Рис. V.5. Граница устойчивости в системе с регулятором типа И
и объектом с запаздыванием (q = I)
Рис. V.6. Граница устойчивости в системе с регулятором типа ПИ и объектом с
запаздыванием (д = 1) при различных значениях /'
151
///'
50
20
10
5
2
1
0,5
0.2
0,1
Уст
ойчи
т
=т
да
1 к=г
[ гиххЧ/Ч-Г\_
Ж^Щ
N \\ч\> I4
\ \\\ VN
N \ \Nj\S
и
\ \
о\\\\15 \Ю \7 \5
|sj Неустоичида III
\[HJJ\
Ш^
\\ \\\
\\\\\
Г V
If 1
- 1 1 1 1 Ijl
Гч; III
ш
' 0.01 0,02
0,5 0.1
0.2
0,5
Т'
Рис. V.7. Граница устойчивости в системе с регулятором типа ПИ и объектом
с запаздыванием (q = 1) при различных значениях К
Рис. V.8. Граница устойчивости в системе с регулятором типа ПИ и
астатическим объектом с запаздыванием (q = 0) при различных значениях /'
152
20
10
5
2
f
0,5
0,2
0.1
гз
^
^сгпойчи
да \
|
K=2o\
%
П
\ \
\ )
1 '
J
]_
\15
— \ f
a
^r
\ \
\ \
\ w
Ш
ill
IN Неустойчива
чТГ\
ш \
14l\
N \
\ \ >
\\\ \
\\\ \
\\\ \
7\ W5 \J \2 I
ll I;
уф
зр
\
л
К
'\
J
0.02
0,05
0,1
02
0.5
2
V
Рис. V.9. Граница устойчивости в системе с регулятором типа ПД
и астатическим объектом с запаздыванием (q = 0) при различных
значениях К
Т'=0 при к*/00
Рис. V.10. Граница устойчивости в системе с регулятором типа ПИД и
объектом с запаздыванием (q= 1) при различных значениях /'; D' = 0,01
153
л
/О
to
5
2\
и
Т'=0 при
К=50
Чг
тойч
ива
к
II
[[
¥•
Ml \ \ \N
\ \ \\
и\ \ \
\ \ \
\ \ \
\ \
\ \
i'soj\o.t\ ол
\\
\
ч
Неустойчива
IX
sll \ 1
0,01
0,02
0.05
0,1
0,2
0,5
2 . Т'
Рис. V.11. Граница устойчивости в системе с регулятором типа ПИД и объектом с
запаздыванием (q = 1) при различных значениях /'; D' = 0,02
20
10
1 т1 п
1 / -4/
при К=33
Ус
\зз
moU4ut
la
1
г' m\ \ \
1 1 \ \
—1—1 1" Гд
1 1 1 \
II \ \
\ол-\—\
1 \
1 1 V—-~
о,зз-^\
ь
L—
Неу
-0,5
о\^
стойче
i6a
0,01
0,02 '
0,05
0,1
0,2
0.5
Г
Рис. V.I2. Граница устойчивости в системе с регулятором типа ПИД и объектом с
запаздыванием (q = 1) при различных значениях /'; D' = 0,03
154
к
w
5
2
X
Г=0 при K=20
\ |
Устойчива \
\ 1
\1
\0.2
[
\0.33
\о.
5
-[
Неустойчива
n/ ^ЧЧ?
^^ 1
0.1
0,2.
0,5
Г
Рис. V.13. Граница устойчивости в системе с регулятором типа ПИД и объектом с
запаздыванием (q = 1) при различных значениях /'; D' = 0,05
При Т'=0 К=10
1 V
' \
г—————-
\м
Устойчива \
/ \о,Н \
'0,2
' \
\азз
\ *
0,5
1\
^2
у.
'
Неустом
шва
г
0,1
0,2
0Л
Г
Рис. V.14. Граница устойчивости в системе с регулятором типа ПИД и объектом с
запаздыванием (q = 1) при различных значениях /'; D = 0,1
155
J'
0,5
0.2
-
Устойчива
"0,1
0,0
5
4r
/07В=ОО]
V 0,0?
"0,03
/\
Неустойчива
0,1
02
0,6
V
Рис. V.15. Граница устойчивости в системе с регулятором типа ПИД и объектом с
запаздыванием (<7 = 1) при различных значениях D; К = 1
/
1
0,5
0,2
Устойчива
/"
- 7?'-
~ И -(
1.01<
0,0?^
0,03^
0.05^
0,1 >6
W
уууу
у/
h
/
/А
Ш
ш
У
leyci
i
У//
и
у
пой
чиб
Г]
а
0,1
ол
0.5
Рис. V.16. Граница устойчивости в системе с регулятором типа ПИД и объектом с
запаздыванием (<7 = 1) при различных значениях D'\ К = 2
156
Рис. V.17. Граница устойчивости в системе с регулятором типа ПИД и объектом
с запаздыванием (q = 1) при различных значениях D'\ /С = 3
47 0.2 Т
Рис. V.18. Граница устойчивости в системе с регулятором типа ПИД и объектом
с запаздыванием (q = 1) при различных значениях D'\ К = 5
157
К для V=0; K=WO
Рис. V.19. Граница устойчивости в системе с регулятором типа ПИД и астатическим
объектом с запаздыванием (q = 0) при различных значениях /'; D' = 0,01
При Т'=0; К=50
0,0J 0,05 0,1 0%2 0,5 IT'
Рис. V.20. Граница устойчивости в системе с регулятором типа ПИД и астатическим объектом
с запаздыванием (q = 0) при различных значениях /'; D' = 0,02
/
158
При Т'=& K=33J3
Рис. V.21. Граница устойчивости в системе с регулятором типа ПИД и астатическим
объектом с запаздыванием (q = 0) при различных значениях /'; D' = 0,03
*V
/
0,5
0Л
°'1W 0.1 0.2 0,5 Г
Рис. V.22. Граница устойчивости в системе с регулятором ПИД и астатическим объектом
с запаздыванием (q = 0) при различных значениях D'; К = 2
159
0.5
ОЛ
0.1
Устойчива
1
1*=0,01^
| к
п п? /i
U,u£ ^/ ж
о.оз V//
0^0.05
*0.1
У
Неустойчива
' 0,05
0,1
ОЛ
0,5
7"
Рис. V.23. Граница устойчивости в системе с регулятором ПИД и
астатическим объектом с запаздыванием (q = 0) при различных значениях D'\ К = 3
0,5
ОЛ
0,1
Устойчива /
Л'-0,07 у i
п п? / /
' *Jf /
/7/77 /ft
» >7 / /
^ А
777/
^fo,05
^0,1
1еустойчиЬ
'а \
0,05
0,1
ОЛ
Г'
Рис. V.24. Граница устойчивости в системе с регулятором ПИД и астатическим
объектом с запаздыванием (q = 0) при различных значениях £>'; К = 5
160
Рис. V.25. Граница
устойчивости в системе с
регулятором ПИД и
астатическим объектом с
запаздыванием (q = 0) при
различных значениях D'\
/С = 10
V. 1.1. Критерии Сетча и Цыпкина
как аналоги критериев Михайлова и Найквиста
Идея этих методов основана на так называемом принципе аргумента.
Принцип аргумента гласит, что если функция F (s, es) аналитическая
и отлична от нуля в точках, лежащих в некотором замкнутом контуре С,
а вне этого контура имеет конечное число особых точек, являющихся
полюсами Р, и конечное число особых точек, являющихся нулями Z этой
функции, то имеет место зависимость
1
2я
;/ J F (s,
es)
ds^Z — P,
(V.2)
причем как полюса, так и нули следует подсчитывать с учетом их кратности.
Геометрический смысл этого утверждения состоит в следующем:
приращение аргумента функции F (s, es) при однократном обходе контура С
в положительном направлении (против хода часовой стрелки) равно
A arg F (s, е8) = 2n(Z — Р). (V.3)
Это означает, что число полных проходов угла 2я вектором F (s, es)
вокруг начала координат, когда s один раз обойдет контур С, равно
N = Z — P, (V.4)
т. е. равно разности числа нулей и полюсов функции F (s, ,es), охваченных
контуром С.
Критерий Сетча как аналог критерия Михайлова. С целью получения
условия, гарантирующего отсутствие в характеристическом
квазиполиноме F (s, es) корней с положительной действительной частью, применим
принцип аргумента к контуру CR, состоящему из отрезка мнимой оси
(—/Я; JR) и полуокружности радиуса R с центром в начале координат и
лежащему в полуокружности Re [si > 0 (рис. V.26). До этого необходимо
убедиться, что квазиполином не имеет корней на мнимой оси.
Из выражения (V.4) на основе принципа аргумента найдем Nc
и если
lim NCr = 0,
(V.5)
то это означает, что все корни квазиполинома удовлетворяют условию
Re [si <0, если только число полюсов функции F (s, es) внутри
контура Соо равно нулю (Р = 0).
11 X. Турецкий 161
В качестве примера рассмотрим характеристический квазиполином
системы управления с пропорциональным регулятором и астатическим
объектом с запаздыванием (табл. III.2):
F (г, е-') = г + /Се"' = О, (V.6)
где
Г = ST.
Пусть теперь аргумент, т. е. переменная г один раз обойдет
полуокружность CR\ для этого необходимо, чтобы при R —> оо
г = Яе/*, _-*-<Ф<-£.. V.7)
Тогда из выражения (V.6) Z7 (г, е"г) [также [очертит на плоскости
(Im F, Re F) полуокружность с бесконечно большим радиусом, а мнимая
1
6J = +oo
!
0
cj=-oo
^с
' v
^
0
\
- ] _
/ •
у
/с„
Рис. V.26. Иллюстрация
принципа аргумента
Рис. V.27. Вид контура С/?
на плоскости F (s, es) при
различных значениях
коэффициента усиления К
ось характеризуется соотношением
F (/со, е'®) = /со + /Се-/®, ' — оо < со < оо. (V.8)
С учетом того, что функция eri® является периодической функцией
переменной со с переходом 2я, получим кривую, повторяющуюся
бесконечное число раз вдоль мнимой оси. На рис. V.27 приведены три кривые
для различных значений коэффициента /С.
Легко заметить, что кривая при К = 1 не охватывает начала
координат, следовательно, система устойчива; кривая К = я/2 проходит через
начало координат, следовательно, представляет собой систему,
находящуюся на границе устойчивости, имеющую чисто мнимые корни; а кривая
при К = 2 дважды охватывает начало координат в направлении,
противоположном движению часовой стрелки, следовательно, характеризует
систему, которая в правой полуплоскости имеет два корня. Резюмируя,
можно сказать, что система будет устойчива, и то асимптотически, если
162
Вид таких кривых достаточно сложен, однако, как показал
Я. 3. Цыпкин, а позже Сетч, можно их упростить, если разделить
квазиполином таким образом, чтобы одна' его часть была рациональной
функцией оператора s, а другая часть — показательной функцией e~s
оператора s. В обычно встречающихся системах автоматического регулирования
это можно сделать. Оказывается, вместо изображения всей кривой
(рис. V.27) можно, что значительно проще, нарисовать отдельно
характеристический полином разомкнутой системы без запаздывания и
исследовать его положение относительно кривой e-~',fi>, представляющей на
плоскости окружность единичного радиуса. Тогда выражение (V.8) запишется
в виде разности двух векторов, зависящих от со:
F (/со, е/®) = G (/со) — Н (/со), (V.9)
где
G(/co) = /co; (V.10)
Я(/со) = —/Се-/®. (V. 11)
Теперь окончательно, используя принцип аргумента, можно
сформулировать следующую теорему:
необходимым и достаточным условием асимптотической устойчивости
системы с характеристическим уравнением вида (V.6) является равенство
нулю приращения аргумента вектора, объединяющего кривые G (/со) и
Н (/со), при изменении со от —сю до сю.
Зависимость (V.10) в общем случае является полиномом п-п степени
относительно /со, а зависимость (V. 11) представляет собой окружность
с центром в начале координат и с радиусом /С. Следовательно, кривая
G (/со) не должна пересекать кривую Н (/со).
Критерий Цыпкина как аналог критерия Найквиста. Здесь, как и в
классическом критерии Найквиста, анализируется знаменатель передаточной
функции замкнутой системы в виде
М2 = 1 +G(s) = О, (V.12)
а заключение об устойчивости замкнутой системы делается на основании
исследования поведения амплитудно-фазовой характеристики G (/со)
разомкнутой системы относительно точки (—1, /0).
Под амплитудно-фазовой характеристикой разомкнутой системы
понимается граничное положение при /?—> сю контура CR (рис. V.26), который
находится из передаточной функции разомкнутой системы
G(s>=we"ts- (V-13)
Приравнивая соотношения (V.12) и (V.13), видим, что нулю функции
Mz (s) соответствуют точки, в которых G (s) = —1. Применяя, таким
образом, принцип аргумента к функции G (s), необходимо определить число
обходов амплитудно-фазовой характеристики вокруг точки (—1, /0),
а не вокруг начала координат. Так как функция G (s) может иметь полюсы
в правой половине плоскости комплексного переменного, число обходов
амплитудно-фазовой характеристикой точки (—1, /0) или N = Z — Р
должно быть равно —Р, чтобы Z было равно нулю. Полуокружность,
являющаяся частью контура CR, вырождается в точку, ибо для
физически реализуемых систем порядок L (s) не выше порядка М (s). Кроме
того, отображение мнимой оси следует находить при изменении s = /со
не от —сю до сю, а от О до сю. Нахождение отображения мнимой оси
осуществляется в два приема:
находится амплитудно-фазовая характеристика, соответствующая
up М (/со) ' к ^'
11*
163
т. е. для системы без запаздывания (рис. V.28), а далее для отыскания
характеристики системы с запаздыванием, соответствующей
G (/<°) = -шй-еЧт=gp (M e-/<4t-
М (/ю)
(V.15)
достаточно учесть влияние множителя e^/0)t, приводящего к повороту на
угол —cojt без изменения модуля вектора Gp (/со). Следует обратить
внимание на то, что с помощью точек пересечения / и /' характеристик
Gp (/со) и G (/со) с единичной окружностью е-'шт (штриховая линия) можно
,
^'"""
у
/
/ _.-
/ ^^-*"^
I / f
if 1 s*
I / of.
1 / I 17
* 1 >/V
\ / ГЧ
\l >^ V
«/СГ N. w/t
' V \1!\
\\ ^*-^
\v
x>^
\lmCp
\^
\
\
)ШШЩ^ \
^4V \
Л I *
\ 1 1 1
\ 7 / 1
tm\S '
ш~^\ 1
\ ' s
ч. \ /xGpO'J ^/У*
^S<r \ /У \ ^''s
— Л l ^^
^ tJ; ^>T
""" _^^%<W
u=0
BeGp
Рис. V.28. Построение амплитудно-фазовой характеристики
системы с запаздыванием
найти граничные условия устойчивости, из которых определяется
критическая величина времени запаздывания тЛ, когда
' | G (/со) | = 1; (V.16)
arg [G (/со) I = arg [Gp (/со) I — (сот ± 2пК)
= _Я) k = 0, 1, 2, . . .
(V.17)
Подставляя соотношение (V.14) в формулу (V.17), видим, что
критическая величина времени запаздывания, т. е. наименьшая величина т,
удовлетворяющая соотношению (V.17), равна
Я — Фал + &т ■+■ 2#Я
** = ^Г^= > *=0,1,..., (V.18)
где
^L arClg Re[L(/co)] '
(V.19)
(V.20)
На основе этих условий можно исследовать устойчивость системы двумя
способами: либо, принимая граничные условия по модулю, анализировать
фазу, либо, принимая граничные условия по фазе, исследовать модуль.
Обычно принимается способ, основанный на задании граничных
условий по модулю, т. е. исследуются фазовые сдвиги системы в точках
пересечения характеристики Gp (/со) с единичной окружностью. Тогда
1М/Ч)| = 1, (V.21)
164
и если
Ф Ы = arg [G Цщ)] > — я,
то система устойчива; если
Ф (со*) = arg [G (/©л)] = — я,
то система находится на границе устойчивости, а если
Ф (со*) = arg [G (/соЛ) J <—я,
(V.22)
(V.23)
(V.24)
то система неустойчива.
Вышеприведенные рассуждения хорошо, иллюстрируются рис. V.29.
Обычно поступают следующим образом: из условия (V.21) находят
критическую частоту соЛ, которую далее подставляют в условие (V.22),
Рис. V.29. Анализ устойчивости с определением критической величины времени
запаздывания
и определяют, будет ли время запаздывания, полученное из этого условия,
меньше, чем реальное время запаздывания в объекте.
В качестве примера рассмотрим систему, состоящую из идеального
пропорционального регулятора и инерционного объекта первого порядка
с запаздыванием.
Передаточная функция разомкнутой системы ,
Следовательно, условие (V.21) имеет -вид
Из соотношения (V.26) определяем критическую частоту:
'о
Из выражения (V.25) следует, что
Ф (<ok) = —arctg a)kT0 — соЛт ± 2kn.
(V.25)
(V.26)
(V.27)
(V.28)
Подставляя теперь выражения (V.28) и (V.27) в условие (V.22),
гарантирующее устойчивость, получим при k = О, что
arctg VW=\ +f^-l<n.
(V.29)
165
Из соотношения (V.29) окончательно получим
т ^ я-arctg VK2-l У '
Легко заметить, что выражение (V.30) представляет собой иную форму
записи условия (IV.74), полученного ранее другим методом.
V.I.2. Метод D-разбиения
Как и в случае системы без запаздывания, нули характеристического
квазиполинома являются непрерывными функциями его коэффициентов.
Предполагается при этом, что коэффициент при старшем члене всегда
отличен от нуля. В пространстве коэффициентов всегда будут
существовать такие области, в которых находится постоянное число корней. В
каждой такой области число корней будет различно. Естественно,
предполагается, что области, содержащие одинаковое число корней, соединяются
между собой. Нас интересует только одна область — область
устойчивости, которая содержит все корни квазиполинома, и эти корни имеют
отрицательные действительные части. Кроме того, необходимо, чтобы при
изменении коэффициентов квазиполинома при переходе полинома через
мнимую ось корни меняли знак действительной части с минуса на полюс.
Следовательно, граница между областью устойчивости и другими
областями представляет собой гиперповерхность, а в двумерном случае —
кривую, на которой лежат только чисто мнимые корни квазиполинома.
Не всегда при непрерывном изменении имеющихся в распоряжении
параметров (или при непрерывном изменении выбранных коэффициентов
квазиполинома) в области этих параметров будет существовать область
устойчивости. Для выяснения того, является ли найденная область
областью устойчивости, достаточно проверить для любой точки, имеют ли
корни характеристического квазиполинома отрицательные
действительные части.
Штриховка областей и нахождение особых прямых (или плоскостей)
осуществляется так же, как и для систем без запаздывания, с той лишь
разницей, что роль главного определителя выполняет якобиан вида
дР дР
Jo =
dQ dQ
ф ' dv
(V.31)
где |if v — переменные параметры; Р (со, pi, v) — действительная часть
характеристического квазиполинома F (/со, еусо) замкнутой системы;
Q (со, [г, v) — мнимая часть этого полинома.
Например, для анализа устойчивости системы автоматического
регулирования в квазиполином, который имеет вид выражения (V.6),
подставим г = /со и будем считать коэффициент усиления К переменным
параметром. И пока будем полагать, что К может принимать как
действительные, так и комплексные значения. Тогда из соотношения (V.6)
получим
К (со) = —/сое'40 = со sin со — /со cos со, (V.32)
где со изменяется от —оо до -f- сю, или
Re [/С (со) J = со sin со; (V.33)
Im IK (со)] = —со cos со. (V.34)
На рис. V.30 изображены области постоянных чисел корней,
определяемых уравнениями (V.33) и (V.34) на плоскости одного комплексного
параметра. Очевидно, что представляет интерес только область устойчи-
166
вости D (0) и прежде всего заключенные в ней пределы изменения
действительных значений К- Допустимая, с точки зрения устойчивости,
величина коэффициента усиления, получаемая из рисунка, находится в
следующих пределах:
0<K<^, (V.35)
что согласуется с результатами, полученными другими методами.
JLlmK
и=2п
Рис. V.30. D-разбиение на плоскости комплексного параметра
В качестве другого примера рассмотрим характеристический
квазиполином, встречающийся при анализе вибраций
металлообрабатывающих станков и вертикальных мельниц:
F (s, es) = Is2 + r\s + 1 + а (1 — e~s) = 0. (V.36)
DO)
91
n
.91
n
[ M»
г >0<х, ЛГ
1 DM
1(2)
' 1
n*
D(0)
r$
яг
$^£
^
w=o
Рис. V.31. D-разбиение на плоскости двух действительных
параметров
Полагая в выражении (V.36) s = /со, получим систему уравнений
_со2£ + 1 + а (1 — cos со) = 0;
сот] -f а sin со = 0.
(V.37)
Якобиан У0 (со) = —со3, если | и ц считать изменяемыми параметрами.
167
Если J о (а) ф О, то
1 + а (1 — cos со)
—а sin со
Эти уравнения определяют области постоянных чисел корней на
плоскости двух действительных параметров, которые представлены на
рис. V.31. Из рисунка видно, что если параметр £ > (1 + 2а/я2, а т) > О,
то система асимптотически устойчива.
Аналогично система будет асимптотически устойчива, если £ > О,
ат)> —a cos 9, где 9 — корень уравнения tg со = со, лежащий между|гс
и 2тс. На основании этих граничных значений можно сделать интересные
выводы о конструктивных параметрах рассматриваемых устройств.
§ V.2. Структурная устойчивость
одноконтурных систем регулирования с запаздыванием
Методы структурной устойчивости дают такие условия, при которых
можно обеспечить устойчивость системы соответствующей коррекцией
величин параметров без нарушения структуры системы.
Итак, структурно устойчивой системой является такая система, для
которой существует область устойчивости в пространстве параметров
Неймарка.
Условия структурной устойчивости характеризуются простотой, а их
неудовлетворение означает, что необходимо изменить структуру системы..
Если условия структурной устойчивости выполняются, то в целом это
не означает, что анализируемая система при данных значениях
параметров устойчива, а означает только, что имеет смысл проведение
детального анализа с целью определения области устойчивости в пространстве
параметров и последующий выбор из этой области соответствующих
значений параметров системы.
Доказательства высказанных здесь утверждений можно найти в
работе [381.
Рассмотрение ограничим системами, характеристическое уравнение
которых имеет вид
е™М (s) + L(s) = О,
где
m
M(s)= П Afv(s);
V=l
m
L(s)=ULv(s), (V.41)
V = l
Предполагается, что Mv (s) и Lv (s) — полиномы не выше второго
порядка, т. е. типа cfis2 + b0s + cv\ причем в каждом из них, по
крайней мере, один из коэффициентов а, Ьу с отличен от нуля и, кроме того,
коэффициенты av, cv в полиномах Mv (s), Lv (s) положительны.
V.2.1. Основные теоремы
Примем следующие обозначения для полинома М (s): пг — порядок
полинома, а — кратность нулевого корня, Хг — число корней с
отрицательной действительной частью, 8± — минимально возможное число положи-
168
(V.38)
(V.39)
(V.40)
тельных действительных корнейг. Аналогичные обозначения вводим
для полинома L (s): n2, ^2, б2. Кроме предположения о неравенстве нулю
коэффициентов cv в полиномах Lv (s) полином L (s) не должен иметь
корней, равных нулю.
Теперь обозначим
п = пг + п2 (V.42)
и определим числа \i± и \i2 следующей зависимостью:
Хг + ^ = Х2 + \i2 = пг. (V.43)
Пусть рх обозначает целую часть дроби щ/2, т. е.
Pi = E[&-]. . (V.44-)
Системы, которые не содержат Mv (s) и Lv (s) с 6^0, а < 0, с ^ 0,
называются системами нормального типа (V.39);
В соответствии с теоремами Понтрягина в квазиполиноме (V.39)
должен существовать старший член, и, кроме того, можно получить
необходимое условие в виде
пх ^2: /i2. (V.45)
В дальнейшем изложении будем предполагать, что это условие всегда
выполняется.
Сейчас рассмотрим основную лемму, необходимую для последующих
исследований.
Лемма, Если в уравнении (V.39) все корни расположены в левой,
полуокружности, то существует целое число т0 ^ 0 такое, что для всех т >
> т0 полином
Fa(s)=(l +■%■)" M(s) + L(s) = 0 (V.46)
является полиномом Гурвица, т. е. имеет корни с отрицательными
действительными частями.
Вышеприведенная лемма позволяет утверждать, что из структурной
устойчивости систем с запаздыванием следует структурная устойчивость
одноконтурных систем автоматического регулирования, имеющих
характеристическое уравнение вида (V.46), если только т > т0. И наоборот,
если записать условия структурной устойчивости одноконтурных
систем, имеющих характерстическое уравнение в виде (V.46) при
достаточно большом /я, то получим необходимое условие структурной
устойчивости системы с запаздыванием.
Сначала рассмотрим системы без введения производных в закон
управления, т. е. L (s) = const. В этом случае имеет место следующая
теорема.
Теорема 1. Для структурной устойчивости одноконтурной системы
автоматического регулирования с запаздыванием, но без введения
производных в закон управления, необходимо и достаточно, чтобы эта
система была нормального типа и выполнялось неравенство
а+б1<2. (V.47)
Для аналогичных систем, но без запаздывания, кроме приведенных
условий теоремы 1 должно выполняться неравенство
п > 4Pl, (V.48)
1 Каждый полином Afv (s) вида bs — с или as2 + bs — с увеличивает 6Х на единицу.
При определении 6Х не учитываются множители as2 — bs+ с. Предполагается, что а, Ь, с
больше нуля (Прим. автора).
169*
Следовательно, введение запаздывания может обеспечить
структурную устойчивость системы без запаздывания, для которой не выполняется
только неравенство (V.48). Это означает, что введение запаздывания в
системы регулирования без запаздывания не приводит в полиноме М (s)
к увеличению числа нулевых корней и корней с положительными
действительными частями. Но отпадает условие, связанное с числом чисто
мнимых корней или комплексных корней с положительной
действительной частью полинома М (s).
Таким образом, если рассматривать системы, состоящие из
астатических, неустойчивых и колебательных инерционных звеньев, то из
теоремы 1 следует, что в одноконтурной системе без введения производных
как при наличии запаздывания, так и при его отсутствии не может быть
более одного астатического или неустойчивого инерционного звена.
Зато число консервативных звеньев гг в системе, с запаздыванием
может быть произвольным, в то время как в системе без запаздывания оно
ограничено неравенством (V.48).
Теперь рассмотрим более общий случай одноконтурной системы
управления, имеющей производные в законе управления, т. е. системы,
характеристическое уравнение которых имеет вид (V.39), но ограничимся
рассмотрением систем только нормального типа. Для систем более
общего вида можно получить только необходимые, но недостаточные
условия.
Для нормальных систем можно сформулировать следующие
необходимые и достаточные условия структурной устойчивости.
Теорема 2. Необходимым и достаточным условием структурной
устойчивости одноконтурных систем нормального типа, имеющих
характеристическое уравнение (V.39), является одновременное выполнение двух
неравенств:
п2^о +Ьг—\У (V.49)
где знак равенства допустим только при четных б2;
п2>о +б2— 1, (V.50)
где знак равенства допустим только при четных 8±.
Кроме того, должно быть выполнено одно из трех следующих условий:
К>-т; (V.51)
К>^-\ (V.51a)
Х2>^--\. (V.516)
Неравенство (V.51) должно выполняться, если Хг + \х2 четно и о =
= 4 k при четном Ьг или а = 4 k -f- 2 при нечетном 8г.
Неравенство (V.51a) должно выполняться при четном кх + Щ в
оставшихся случаях.
Наконец, неравенство (V.516) должно выполняться при нечетном
Хг + ц,2.
Полученные условия являются необходимыми и достаточными, тогда
как аналогичные условия для систем без запаздывания [3] (теорема 7) —
только необходимые. Сопоставляя, однако, теорему 2 и теорему 7 [3],
видим, что можно найти такие случаи, когда введение запаздывания
позволяет добиться устойчивости системы, которая без запаздывания
является структурно неустойчивой. Так, например, будет в случае,
когда для системы без запаздывания выполняются условия теоремы 2,
но не выполняется условие
">4Pl +цу (V.52)
170
где г] = 0, ± 1, ±2 входит как необходимое условие в теорему 7 работы [31.
Система без запаздывания в этом случае структурно неустойчива, а
система с запаздыванием структурно устойчива.
Справедливость всех вышеприведенных утверждений станет
очевидной, если уравнение (V.39) представить в относительных единицах,
полагая sx = г. Тогда
т т
е'П (^r* + -^r + clv) + Y\ (^/-2 + -^r + c2v) = 0.
v=l v=l
(V.53)
Теперь рассмотрим следующие примеры:
1. Существует ли возможность совместной работы регуляторов типа П
и типа ПИ с инерционными объектами т-го порядка с запаздыванием?
В этом случае характеристическое уравнение замкнутой системы
имеет вид
т
Т^ П (1 + sTf) + К = 0. (V.54)
/=i
Следовательно, в соответствии с принятыми обозначениями: пх =
= m + 1 или, когда используется только регулятор П, пх = т\ сг = 1
или, когда используется только регулятор П, а = 0; Ях = /п, когда
постоянные времени положительны;
6i = 0;
п2 = 0;
К = о
62 = 0.
Уравнение (V.52) имеет старший член, система является системой
нормального типа, следовательно, из теоремы 1 должно быть
а = бх <2
или
1 +0 <2,
или с пропорциональным регулятором
0 +0 <2.
Таким образом, системы этого типа структурно устойчивы, и с этой
точки зрения существует возможность совместной работы регуляторов
типов П и ПИ с инерционными объектами /п-го порядка с запаздыванием.
2. Существует ли возможность совместной работы регулятора ПИД
с вышеназванными объектами?
Характеристическое уравнение системы имеет вид
т
T{se" П (1 + sTj) + К (TtTds2 + 7\s + 1) = 0, (V.55)
и, следовательно,
п± = т + 1;
* = 1;
Хх = т, так как Tf > 0, / = 1, . . ., m;
бх = 0;
п2 = 2;
к2 = 2, так как Г., Td > 0;
б2 = 0.
171
Используя теорему 2, получим
1) п2 ^ о + S2 — 1,
т. е.
2^1 +0.— 1;
2) Л2 ^ <Т + 6а — 1,
т. е.
2^ 1 +0— 1,
3) К > ^y~ , Hi = пг — kL = m + 1 — 1 = т\
|ы2 = п2 — Я2 = 2 — 2 = О,
о-. 1 — 1
т. е. 2 > —о—» когда т четно,
или Я2> ~2 1, когда /п- нечетно,
т.е. 2>-±--1.
Таким образом, все условия выполняются, и система структурно
устойчива.
Регуляторы типов ПИ и ПИД также могут работать совместно с
консервативными или астатическим объектами. Это хорошо иллюстрируют
следующие рассуждения.
Пусть характеристические уравнения систем имеют вид
т
s7\eST П (ТУ + 1) + К = 0; (V.56)
пг
s37teST П (T)s2 + 1) -f К (TiTds2 + r,s + 1) = 0. (V.57)
/=i
Так как параметры /С, 7,, 7^ положительны, то легко убедиться,
используя теоремы 1 и 2, что системы структурно устойчивы.
§ V.3. Анализ устойчивости систем регулирования
с распределенным запаздыванием
V.3.I. Аналог критерия Найквиста
Так же, как и в случае с чистым запаздыванием, и здесь для анализа
устойчивости применим прежде всего критерий Найквиста.
В практических исследованиях, если передаточная функция
разомкнутой системы с чистым запаздыванием представляет собой
трансцендентную функцию, следует определить величину критической частоты из
условия устойчивости по мбдулю | G (/со) |, а затем найденная величина
частоты подставляется в условие по фазе ф (coj << —я. гарантирующее
устойчивость замкнутой системы. Если же передаточная функция
разомкнутой системы с распределенным запаздыванием представляет собой
иррациональную или трансцендентную функцию, поступают наоборот:
критическая частота сол определяется из граничного ус/ювия по фазе
Ф (<*>к) = —п и затем подставляется в условие по модулю | G (/со) | < 1>
обеспечивающее устойчивость замкнутой системы.
172
Пример 1. Задана замкнутая система автоматического регулирования
из идеального пропорционального регулятора с коэффициентом
усиления Кк и объекта с передаточной функцией
Со(5) = ЛГ0е->^. <V-58)
Такую передаточную функцию могут иметь некоторые тепловые объекты
или 7?С-цепи.
Передаточная функция разомкнутой системы имеет вид
G(s) = tfe-^, (V.59)
где
К = ^С^о-
Используя граничное условие устойчивости по фазе, получим
arg[G (/со)] = arg [/Се"Vi**T\ + 2кл = -я, k = 0, 1, 2, ... (V.60)
Полагая
]/"/0)Г= б +/Р (V.61)
и возводя выражение (V.61) в квадрат, получим
/соГ = б2 — р2 + /2бр (V.62)
или
б==р (V.63)
б=]/^. (V.64)
Подставляя соотношения (V.63) и (V.64) в формулы (V.61) и (V.60),
можно написать
argL#e r . ' ' " J=— У -^ + 2Ь = -я.
(V.65)
Считая k — 0, из условия (V.65) получим
]/^=я. (V.66)
Условие устойчивости по модулю в этом случае имеет вид
(V.67)
1 <?(/»)! =
или
/Се К 2
-//-¥
/С<е
= ЛГе К 2 <1
2
(V.68)
Подставляя соотношение (V.66) в выражение (V.68), получим
окончательно
К <ея. (V.69)
Следовательно, коэффициент усиления разомкнутой системы должен
быть меньше, чем 23, 14, независимо от постоянной величины 7\ а ошибка
в установившемся состоянии в процентах равна
е°° = -j^rr 100<4,2 о/0. (V.70)
173
Видим, что объекты этого типа с точки зрения ошибки в установившемся
состоянии могут работать совместно с пропорциональными регуляторами
только тогда, когда допустима величина ошибки порядка 5%.
Пример 2. Задана система автоматического регулирования, состоящая
из пропорционального регулятора с передаточной функцией
^ = тт^ (V'71)
и объекта с передаточной функцией
G0 = —-*° . (V.72)
Передаточная функция разомкнутой системы имеет вид
G (s) = -= ^ . (V.73>
Ks(l + sTR)(\+sT0) y
Полагая в выражении (V.73) s = /<о и учитывая, что
У^=Уй±±±, (V.74).
получим следующее выражение для частотной характеристики:
К V2 11 - со (т0 + tr) - <o*TRT0] - j [ 1 + со (Г0 + tr) - cd2t>t0]
G (/<»):
УЪ 2 [(1 - G)*7>T0)2 + a>2 {Tr + ro)2]
Из граничного условия устойчивости по фазе имеем
(V.75>
ИЛИ
argC</ffl) = -arc,gi±^±^££' = * (V.76>
<*lTkTo - со, (T0+ TR) - 1 = 0, (V.77>
откуда граничная частота
_ T0 + TR + VTl + 6T0TR + TR (V 78)
Щ 27^ •
Теперь, используя выражение (V.77) и условие устойчивости по
модулю для замкнутой системы, получим следующее неравенство,
определяющее коэффициент усиления разомкнутой системы:
|G0»)I = T7=^-77<1. (V-79>
Окончательно, с использованием соотношения (V.78), получим
K<V~2(TR + T0)
]"\
2
° ' (V.80)
2TrT0
V.3.2. Аналог критерия Михайлова
В работах [5, 7] с использованием подстановки s = w2, где w = /со,,
получен критерий устойчивости, аналогичный критерию Михайлова для
систем без запаздывания.
Теорема 1. Если знаменатель передаточной функции замкнутой
системы имеет вид
1+°и=Ш)' (VW>
174
где L (w) и M (w) — полиномы относительно переменной w = Vs* то
для устойчивости системы этого типа необходимо и достаточно, чтобы
все корни wlt w2, • . ., wn полинома М (w) удовлетворяли условию
(рис. V.32)
largofc!>-}-, *=1, 2, .,
(V.82)
Теорема 2. Для того чтобы замкнутая система, характеристическое
уравнение которой имеет вид *
М (w) = О, (V.83)
■U*)
была устойчива, необходимо и достаточно, чтобы вектор М\
при непрерывном изменении действительного параметра р от нуля до бео
i //77 IV
Рис. V.32. Иллюстрация
теоремы об устойчивости
систем, имеющих
передаточную функцию в виде
иррациональной функции
оператора s
конечности сделал точно я/8 оборотов вокруг начала координат на
плоскости комплексной переменной [Re [All, / Im [АЛ] в направлении,
противоположном движению часовой стрелки.
Доказательства этих теорем можно найти в работе [7].
Список литературы
1. Ahrendt W. К., Taplin I. F. Automatic Feedback Control. New York, 1961, McGraw—
* Hill, p. 91.
2. Айзерман М. А. Теория автоматического регулирования. М., «Наука», 1966, с. 178—
184.
3. Айзерман М. А. Теория автоматического регулирования двигателей. М., Гостехиздат,
1952, с. 413—418.
4. Althein H. J. Optimale Regelung einer Regelstrecke mit Ausgleichsgrad, Anlaufzeit
und Totzeit. Regelungstechnic, 1963, Heft 10, S. 232—235.
5. Ball B. J., Rekoff M. G. An analysis of the distributed lag. ISA Transaction, April
1966, Vol. 5, pp. 146—155. No 2.
6. Бессекерский В. А. и др. Сборник задач по теории автоматического регулирования.
М., «Физматгиз», 1963, гл. 8.
7. Брин И. А. Об устойчивости некоторых систем с распределенными и сосредоточенными
параметрами. — «Автоматика и телемеханика», 1952, Т. XXIII, №7, с. 863—971.
8. Цыпкин Я. 3. Устойчивость систем с запаздывающей обратной
связью.—«Автоматика и телемеханика», 1946, т. 7, № 2—3, с. 107—128.
9. Cypkin Ja. E. Ober die obere Grenze des Stabilitatsgrades von I, P, P—I, P—D, P—I—D
Reglern. Regelungstechnik, 1957, Heft 2, S. 49—50.
10. Чеборатев Н. Г., Нейман Н. Н. Проблема Рауса—Гурвица для полиномов и целых
функций. Труды Мат. Инст. им. В. А. Стеклова. Т. XXVI. АН СССР, 1949.
11. Edelmann H. Ein Kriterium fur die aperiocisdhe bzw. rein oszillatorische Stabilitat und
der Zusammenhang mit Reaktanztheorem. Regelungstechnik, 1954, Heft 11, S. 264—267.
12. Effertz F. H., Kolberg F. Einfuhrung in die Dymamic Selbsttatiger Regelungssysteme.
Dusseldorf, 1963. VDI—Verlag.
13. Eisenberg L. Stability of linear systems with transport lag. IEEE Trans, on Automata
Control, April 1966. Vol. AG 11, No 2, pp. 247—254.
175
14. Ellingsen H. V. Die Behandlung von Totzeiten bei numerischen Stabilitatsuntersuchungen
von Regelkreisen. Regelungstechik. Dezember 1964, Heft 12, S. 535—541.
15. Engel W.t Jaschek H. Obungsaufgaben zum Grundskurs der Regelungstechnik. Munchen,
1964, R. Oldenburg.
16. Euler K. Regelsysteme mit Laufzeit. Regelungstechnik, 1959, Heft 3, S. 89—92.
17. Findeisen W. Technika regulacji automatycznej. Warszawa, 1965, PWN., s. 93—99,
329—356.
18. Финкельштейн С. М. Об устойчивости системы автоматического регулирования с
длинным импульсным трубопроводом. В кн.: «Автоматизация производственных
процессов», вып. III. АН СССР, 1960.
19. Folinger О. Zur Stabilitat von Totzeitsystemen. Regelungstechnik. April 1967, Heft 4.
S. 145—149.
20. Герасимов С. Г. Теоретические основы автоматического регулирования тепловых
процессов., М., Госэнергоиздат., 1949, с. 210—278.
21. Gorecki H. Zagadnienie stabilnej wspolpracy regulatorow PID z obiektem inercyjnym
n—tero rzedu. Zeszyty Naukowe AGH, Automatyka (w druku).
22. Halanay A. Some problems in the qualitative theory of the'systems with time lag.
Качественные методы. Т. II, Киев, изд. АН УССР, с. 394—408.
23. Hale I. К. Asymptotic behaviour of the solutions of differential—difference equations.
Качественные методы. Т. II, Киев, Изд. АН УССР, 1963, с. 409—426.
24. Jastrzebska M. Problemy stabilnosci ukladow о stalych rozloionych. Prace IV Krajowej
Konferencji Automatyki, z. 1, s. 175—185. Krakow, 1967 AGH.
25. Jeffrey A. The stability of interacting control systems. Automatic and Remote Control,
Val. 1, pp. 126—131. London, 1961, Butterworthis.
26. Kindler H., Buchta H., Wilfert H. H. Zadania z techniki regulacji automatycznej.
Warszawa, 1968, WNT, s. 122—131.
27. Krall A. M. Stability criteria for feedback systems with a time lag. J. Sos. Inbustr. and
Appl. Math., 1964. Val. A2, No 2, pp. 160—170.
28. Краснов М. Л., Макаренко Г. И. Операционное исчисление устойчивости движения.,
М., «Наука», 1964, с. 36—43.
29. Мансуров К. И. Об устойчивости линейных систем с запаздыванием. В кн.:
«Исследования по дифференциальным уравнениям и их применению», Алма-Ата, Изд. АН СССР,
1965, с. 190—199.
30. Mufti I. H. A note on the stability of an equation of third order with time lag. IEEE.
Trans. Automat. Control. 1964, Vol. 9, No 2, pp. 190—191.
31. Мышкис А. Д. Шиманов С. Н., Эльсгольц Л. Э. Устойчивость и колебания систем с
запаздыванием. Качественные методы, ч. II, Киев, Изд. АН СССР, 1963, с. 241—269.
32. Неймарк Ю. И. Структура D-разбиения пространства квазиполиномов и диаграммы
Вышнеградского и Найквиста. М., ДАН 60, 1948, с. 1553—1560.
33. No was k i P., Szklarski L„ G6reski H. Podstawy torii ukladow regulacji automatycznej
T. I, II. Warszawa, 1962, PWN.
34. Ольденбург Р., Сарториус Г. Динамика автоматического регулирования. М.,
Госэнергоиздат, 1949.
35. Oppelt W. Poradnik techniki regulacji. Warszawa, 1958. PWT (отс. 291).
36. Основы автоматического регулирования. Под ред. Солодовникова В. В. М., «Машгиз»,
Т. I., Теория, 1954, с. 673—683.
37. Paszkowski S. Stabilnoic wielowymiarowych ukladow ze sprzezeniami zwrotnymi skros-
nymi miedzy kanaiami. Archiwum Automatiki i Telemechaniki, 1959, torn IV. z. 3—4.
38. Пятницкий Е. С. О структурной устойчивости одноконтурных систем регулирования
при наличии запаздывания.—«Автоматика и Телемеханика», 1962, Т. XXIII, № 7,
с. 852—862.
39. Porter В. Stability Criteria for Linear Dinamical Systems. London, 1967, Oliver and
Boyd, Edinburgh, pp. 139—166.
40. Satche M. Discussion of a previous paper. Journ. Appl. Mech. (ASME), 1949, 16,
pp. 419—420.
41. Смит О. И. М. Автоматическое регулирование. М., «Физматгиз», 1962, с. 393—464.
42. Smiht О. I. M. Feedback Control Systems. New York, 1958. McGram—Hill.
43. Шиманов С. Н. Устойчивость систем с запаздыванием. Труды II Всесоюзного съезда
, по теоретической и прикладной механике. М., «Наука», 1965, с. 170—180.
44. «Техническая» кибернетика», «Теория автоматического регулирования», Кн.2, под ред.
Солодовникова В. В., М., «Машиностроение», 1967, с. 431—458, 517—576.
45. Воронов А. А. Основы теории управления. Ч. II: Специальные линейные и нелинейные
системы автоматического регулирования одной величины. М., «Энергия», 1966, с. 7—48.
46. Walker I. A. Stability of feedback systems involving timedelays and timevarying non-
linearity: Int. J. of Control, 1967, No 4, pp. 365—372.
47. Wang P. K. C, Bandy M. L. Stability of distributed—parameter processes with time-
delays. J. Electron, and Control, 1963, No 4, pp. 343—362.
48. Wang P. К. С. On the almost sure stability of linear time—lag systems with stochastic
parameters. Int. J. of Control, 1967, Vol. 11, No 5, pp. 433—440.
49. Yuan—Xun Qin, long—Qing Lian, Lian Kang. Effect of time—langs on stability of
dynamical systems. Automatic and Remote Control, Vol. I, pp. 26—32. London 1961, But-
terworths.
176
Глава VI
Параметрический синтез
типовых регуляторов
В этой главе ограничимся исследованиями, связанными с нахождением
типового регулятора и определением оптимальных, в смысле выбранного
критерия качества, настроек его параметров. Речь идет о
параметрическом синтезе, так как здесь не определяется оптимальная структура
регулятора, а выбирается лишь один из пяти типов регуляторов с
заданной структурой, и только в рамках выбранного регулятора определяются
оптимальные значения его параметров. Задача определения
оптимальной структуры регулятора для данного объекта и принятого критерия
оптимальности может быть решена в* рамках структурного синтеза.
Пусть задана блок-схема системы автоматического регулирования,
представленная на рис. VI.1.
Вообще говоря, можно сказать, что
кЫ
w x-x^ I A I у У
i_zzl±T
на систему воздействуют два типа
внешних сигналов:
1) управляющие сигналы и или до;
2) возмущающее воздействие г.
Система регулирования , должна Рис. VI.l. Блок-схема одноконтурной
удовлетворять ДВуМ ОСНОВНЫМ требо- системы регулирования
ваниям:
а) с максимально возможной точностью отрабатывать управляющий
сигнал, т. е. должна существовать зависимость у (t) ^ до (t), и при этом
необходимо, чтобы система была легко управляемой, т. е. производная
dyldw должна быть достаточно большой во всем диапазоне изменений до;
б) по возможности не реагировать на возмущения z (t), т. е.
ошибка е (t), возникающая под действием возмущения, должна быть
наименьшей, а уж если она возникает, то ее необходимо максимально
быстро ликвидировать. Система должна слабо реагировать на
возмущения, т. е. производная dyldz должна быть по возможности малой.
Из сформулированных требований следует, что ^основными
показателями для оценки переходных процессов в системах автоматического
регулирования могут быть следующие:
— максимальное отклонение ех или ух\
— время регулирования tn называемое иногда временем протекания
переходных процессов.
Ниже эти показатели будут рассмотрены более подробно.
В зависимости от назначения системы на первый план выступает либо
требование, сформулированное в пункте а), либо в пункте б), либо оба
эти требования играют одинаковую роль.
В системах стабилизации сигнал до (t) = const, и для этого типа систем
важно требование, сформулированное в' пункте б).
12 х. Турецкий 177
В системах программного управления на первый план выступает
требование пункта а), так как система должна возможно точно отработать
сигнал программы w (t).
В следящих же системах обычно оба требования имеют одинаковое
значение.
На основе главных требований, стоящих перед системами
автоматического регулирования, формируется показатель качества либо в виде
явной функции, либо в виде функционала. Далее следует выбирать
параметры регулятора так, чтобы функция или функционал, при помощи
которых оценивается работа системы, достигали своего экстремального
значения. Однако часто мы ограничиваемся выбором параметров,
определяемых некоторым эквивалентным критерием; при таком выборе не
достигается экстремальное значение данного показателя качества, но
гарантируется достаточно хорошая работа системы в различных условиях
при различных возмущениях z и управляющих сигналах w.
§ VI. 1. Критерии качества систем автоматического регулирования
Различают два основных класса критериев в зависимости от того,
хороши ли они при определенном виде действующих сигналов или они
универсальны, т. е. применимы при любых сигналах, действующих на
систему.
а. Универсальные критерии. К ним относятся:
критерий устойчивости (S)*;
критерий апериодической устойчивости (SA);
критерий, именуемый показателем управляемости (WR);
критерий оптимального модуля (ОМ).
б. Критерии при действии типовых внешних воздействий (чаще всего
это скачкообразные воздействия). Среди них можно выделить:
параметры реакции системы на скачок, и кроме того, критерии, а
точнее интегральные показатели:
интеграл ошибки (IE);'
интеграл от квадрата ошибки (ISE);
интеграл от суммы квадратов ошибки и ее производных (ISEG);
интеграл от модуля ошибки (IAE);
интеграл от модуля ошибки, умноженный на время, (ITAE) и
другие критерии:
критерий Зиглера и Никольса (ZN);
критерий требуемого демпфирования (ЗС) и много других, которые,
вообще говоря, равноценны вышеприведенным.
Первой проблемой, с которой сталкиваются при выборе регулятора
и значений его параметров, является выбор критерия или показателя
качества.
Следует отдавать себе отчет в том, что все критерии качества в
определенной степени произвольны. Наличие в реальных системах
автоматического регулирования различного рода нелииейностей,
нестационарности, возмущений, приложенных в различных точках системы,
приводит к тому, что более или менее точно определенные «оптимальные»
параметры регулятора всегда отличаются от значений, которые были бы
наилучшими для данной реальной системы. Поэтому полученные значения
настроек регулятора, что очень важно, имеют только ориентировочный
характер и должны корректироваться в процессе эксплуатации системы.
При выборе критерия качества следует иметь в виду два основных
аспекта: с одной стороны, необходимо учесть спектр входного сигнала,
* Буквенные названия критериев образованы из первых букв английских
наименований. В отечественной литературе эти обозначения практически не используются (Прим.
перев.).
178
а с другой стороны, согласовать с ним передаточные особенности, т. е.
амплитудно-частотную характеристику данной системы регулирования
с точки зрения оптимального выполнения задачи, возложенной на
систему.
В наиболее распространенных системах автоматического
регулирования максимум амплитудной характеристики, т. е. максимум модуля
передаточной функции, лежит в области
низких частот, поэтому эти системы можно
считать фильтрами низких частот.
На рис. VI.2 изображена типичная
амплитудная характеристика системы и
обозначена резонансная частота со0,
соответствующая максимуму модуля, и граничная
частота со/, определяющая полосу
пропускания системы.
Помехи и возмущающие воздействия
имеют максимум спектра обычно в достаточно
высокочастотной области, лежащей на
границе полосы пропускания системы.
С точки зрения возможно точной
отработки управляемых сигналов система
должна иметь широкую полосу пропускания, но
с точки зрения парирования возмущений
полоса пропускания должна быть узкой, согласованной со спектром
возмущений так, чтобы максимум этого спектра лежал вне полосы
пропускания системы.
Рис. VI.2. Типичная
амплитудная характеристика системы
регулирования
VI. 1.1. Критерий устойчивости
Этот наиболее простой критерий определяет в общем условия
работоспособности системы. Основывается он только на использовании
знаменателя передаточной функции замкнутой системы, и в нем не
используется числитель передаточной функции, т. е. не вся имеющаяся
информация о системе. Критерий этот одинаково применим как к системам типа
а), так и к системам типа б). Экстремализация этого критерия
основывается на таком выборе параметров, чтобы корни знаменателя
передаточной функции (т. е. характеристического уравнения), приравненного
к нулю, возможно дальше отстояли от мнимой оси. Это приводит к
быстрому затуханию переходных процессов, т. е. к достаточно хорошей
отработке управляющих сигналов и быстрой ликвидации отклонений,
вызванных возмущениями.
Для замкнутой системы, представленной на рис. VI.1,
характеристическое уравнение имеет вид
1 +GR(s, A,)G0(s) = Of (VI. 1)
где kt — параметры настройки регулятора.
Через sf. (k() обозначены корни уравнения (VI. 1), лежащие вблизи
от мнимой оси слева от нее. Надо так выбрать параметры регулятора kn
чтобы действительная часть была максимальна:
max|ReSl|, (VI.2)
причем одновременно должно удовлетворяться неравенство
О > Re Si ^ Re s2 ^ • - • ^ Re sn, n = 1, 2, .... (VI.3)
Можно показать [V.29], что экстремализация этого типа приводит
к появлению в характеристическом уравнении корней большой крат-
12* 179
ности. В случае трансцендентных характеристических уравнений,
имеющих бесконечно большое число корней, это приводит к другому критерию
качества, именуемому критерием апериодической устойчивости. [671.
VI. 1.2. Критерий апериодической устойчивости
Этот критерий требует, чтобы ближайший слева к мнимой оси корень
был действительным и имел максимальную кратность. Он обеспечивает
апериодические переходные процессы без перерегулирования с
минимальной длительностью tr среди аналогичных переходных процессов.
Переходные процессы этого типа требуют реализации слабого управляющего
воздействия со стороны регулятора [24]; это означает, что величины
коэффициента усиления Kr и времени упреждения Td должны быть
малыми, а время изодрома Ti — большим. Слабое управляющее
воздействие желательно тогда, когда оно непредсказуемым образом влияет на
другие регулируемые величины в многомерных системах за счет
перекрестных связей.
Этот критерий может применяться ко всем системам автоматического
регулирования, т. е. и к таким, основная задача которых заключается
в парировании внешних возмущений, и к таким, основная задача которых
состоит в возможно более точном воспроизведении управляющих
сигналов, и, наконец, к таким, которые в равной степени решают обе задачи.
Критериями, которые используют информацию, содержащуюся и в
знаменателе, и в числителе передаточной функции системы, являются
показатель управляемости и критерий оптимального модуля.
VI. 1.3. Показатель управляемости
По аналогии со статической ошибкой, которая равна
вводится относительное динамическое отклонение, именуемое
показателем управляемости [V.l, V.17, 151:
| п (:(1л | = | в (/о) | (с регулятором) = 1 Vy -*
1 ч KJ > I | е' (/со) | (без регулятора) | 1 +GR (/со) G0 (/со) | ' * 1'°>
Легко видеть, что в установившемся состоянии при со —> 0
выражение (VI.5) преобразуется в выражение (VI.4).
Следовательно, формулы (VI.4) и (VI.5) показывают, во сколько раз
уменьшается спектр ошибки при наличии регулятора по сравнению со
спектром ошибки без регулятора при том же входном сигнале. В работе
[661 показано, * что для линейных систем справедлива зависимость
ы
1
1+<?*(/©) Со (/©)
Жо = 0. (VI.6)
1 Кратко доказательство зависимости (VI.6) состоит в следующем.
Применим теорему Коши к функции In q (s).
Областью интегрирования будем считать область, охваченную замкнутым контуром
справа от мнимой оси. Предполагаем, что рассматриваемая система устойчива и,
следовательно, не имеет корней в правой полуплоскости комплексного переменного. Кроме того,
известно, что для физически реализуемых систем интеграл вдоль полуокружности равен
нулю. Из этого следует, что интеграл по всему замкнутому контуру в соответствии с задачей
Коши равен нулю и при определении этого интеграла достаточно интегрировать вдоль
мнимой оси, хак как интеграл по всему замкнутому контуру можно разбить на интеграл вдоль
мнимой оси и интеграл вдоль линии, охватывающей правую полуплоскость комплексной
переменной. Далее можно положить, что s = /со. Учитывая, что ln| q (/со) | —функция чет-
оо . оо
ная, I In | q (/со) | da> = 2 In | q (со) | dco, а фаза ф (со) — функция нечетная и, кроме того,
180
Рис. VI.3. Вид показателя
мости
управляв-
то целесообразно увеличивать
резонансную частоту, так как при этом
возрастает полоса пропускания
системы и, как следствие, уменьшается
длительность переходных процессов.
Системы автоматического
регулирования технологических процессов,
как правило, характеризуются
относительно малыми граничными
частотами, поэтому вышеприведенной
рекомендацией мржно пользоваться.
Рассматриваемый критерий
применим как в системах программного
для которых следует найтиРихэкстоему1ГнЯп НекотоРые показатели,
вать, чтобы граничная частотя *S? У НапРимеР- можн° потребо-
величин паоаметппв * ™ Ла максимально возможной с учетом
вос?иГИЧЬ МаКСИШЛЬН0Й величины «о при выполнении условий устойчи-
достичь min | q (0) I и а' (0) == а" (0) - .. - n „ *
число производных #'9(со)/^4 = о До1н"о быть"равно нуГГоГчно6
VI. 1.4. Критерий оптимального модуля [35]
XZ^^eSaSВабТ Шб0Р ПараМ6Тр0В ^ЛЯТ0Ра »» основании
возм1жГширПоРк°оТКаНИЯ СИСТШЫ ДЛЯ П°ЛеЗНОГО СИГНала должна бы-
а бытГпТЛ13* хаРактеРис™ка не должна иметь резонансного пика
3 бЫТЬ П° возм°жности монотонной, убывающей. Следовательно вид
CD
£ Ф (о) dco = 0, окончательно получим формулу (VI.6). Наличие запаздывания учить,-
вается в функции о (s) наличием составлятпшу *—sx ,жлтт„
вательно, выражение (VI.6) охваГГГ^мь, с з^^зГе^ЖГ ГГр^).'^
181
амплитудно-частотной характеристики должен быть таким, как показано
на рис. VI.4. Условия, обеспечивающие такой вид характеристики,
получены в работах [60, V.33]. Здесь мы дадим их в следующем виде:
dec*
От
G(/«>)
+ G (/©) ! J и=о
где
0. Л=1. 2.
(VI.7)
Рис. VI.4. Желаемый вид амплитудной
частотной характеристики замкнутой
системы
я(М\
G (/со) - GR (/со) G0 (/со), k = 2/;
/ — число настраиваемых параметров
регулятора.
Этот критерий предназначается для
систем, которые должны возможно
точнее воспроизводить полезный сигнал.
Однако его можно модернизировать
для систем, основной задачей которых
является быстрая ликвидация
отклонений под действием возмущений. Между
показателем управляемости и модулем
передаточной функции замкнутой
системы существует следующая связь:
1 —
1 + G (/со)
(VI.8)
Переходные процессы систем автоматического регулирования,
спроектированных с использованием критерия оптимального модуля,
отличаются малым временем протекания и малым перерегулированием. Эти
достоинства критерия позволяют рекомендовать его для широкого
применения.
VI. 1.5. Параметры выходной реакции системы
на скачкообразное входное воздействие
Для того чтобы можно было сравнивать между собой различные системы,
принято рассматривать выходные реакции, вызываемые скачкообразным
изменением величины внешнего управляющего сигнала или возмущения.
Вообще можно считать, что этот вид сигнала для системы является
наиболее трудным, за исключением сигналов, вызывающих в системе
резонансные явления [У,44].
Ниже будут рассмотрены основные показатели качества переходных
процессов, вызываемых скачкообразным изменением входного сигнала
или возмущения.
Максимальное динамическое отклонение уг = —ех. Этот показатель
является одним из важнейших при оценке качества переходных
процессов. На рис. VI.5 и VI.6 изображены переходные процессы регулируемой
величины у при скачкообразном изменении входа w. В частности, на
рис. VI.5 изображены переходные процессы при управлении со
статической ошибкой ги 4= 0, а на рис. VI.6 — переходные процессы при
астатическом управлении, т. е. при еи = 0. На рис. VI.7 и VI.8 изображены
переходные процессы при скачкообразном изменении возмущения г.
Во многих технологических процессах недопустимы даже
кратковременные большие отклонения, и с этой точки зрения очень важна
максимальная величина отклонения. На основе максимального отклонения
определяется перерегулирование в процентах:
yx—w
100.
(VI.9)
182
Динамический коэффициент управления Rd. Этот коэффициент
характеризует управляющие способности регулятора, работающего совместно
с данным объектом при скачкообразном возмущении системы. Он
определяется как отношение максимального отклонения уъ вызванного возму-
Рис. VI.5. Переходные процессы в системе
автоматического регулирования при
скачкообразном изменении входной величины:
/ — реакция объекта; 2 — реакция замкнутом
системы; 3 — изменение входной величины
Рис. VI.6. Переходные процессы в
астатической системе автоматического
регулирования при скачкообразном изменении
входной величины (обозначения те же,
что и на рис. VI.5)
щающим воздействием z, к максимальному отклонению у0 от требуемого
значения wt вызванного тем же возмущением, действующим на объект
в разомкнутой системе без регулятора (рис. VI.8):
г, _ Уг (VI.10)
Rd~-y7-
п
и
\Ут-
-е
1/ ^
f
т
ь*—
2\
\ / ^^- ^Уч
^-^ <з\*
А-
±L
Рис. VI.7. Переходные процессы в
статической системе автоматического регулирования
при скачкообразном изменении
возмущающего воздействия:
/ — реакция объекта регулирования; 2 — реакция
замкнутой системы регулирования; 3 — изменение
возмущения
IV"
г*Х
■С
и ^
у
Л^Г
г^
2\
' X
"^1
5?
* tr У-
—^ ?
3»J
т
к
Рис. VI.8. Переходные процессы в
астатической системе автоматического
регулирования при скачкообразном изменении
возмущения (обозначения те же, что и
на рис. VI.7)
Зависимости Rd от Т = Т0/т при различных критериях качества для
одноконтурных систем управления приведены в работе [24].
Колебательность d. Она характеризует склонность системы к
колебаниям и определяется как модуль отношения амплитуды второго
колебания к амплитуде первого колебания (рис. VI.9):
d% = 1^-1 100. (VI. 11)
Ух
Время регулирования tr. Это время, за которое регулируемая
величина у (t) в переходном процессе начинает отличаться от установивше-
183
гося значения w менее, чем на заранее заданную величину А. Обычно
принимается, что А = 3%-т-5% w. В непрерывных системах с типовыми
регуляторами это время бывает минимальным при так называемых
критических апериодических переходных процессах. Дальнейшего
уменьшения времени регулирования до абсолютного минимума можно достичь
при- использовании специальных оптимальных, в отношении времени
переходного процесса, нелинейных систем управления.
Ошибка в устандвившемся состоянии, или статистическая ошибка ги
(рис. VI.5 и VI.7). В некоторых системах автоматического регулирования
наблюдается ошибка, которая не исчезает даже по истечении длитель-
ky-e
*г»
г х
I ^
^
\ \
tr
^1
/*
\У
а
1
t
I r
Рис. VI.9. К понятию колебательности
ного интервала времени. Эта ошибка не должна превышать некоторой
наперед заданной величины. Для регуляторов без интегральной
составляющей это определяется как
1 (IV. 12)
е„ =
1+***о
■w.
У регуляторов с интегральной составляющей ошибки в
установившемся состоянии теоретически равны нулю, но практически
незначительные ошибки могут существовать из-за неидеальности интегрирования в
регуляторе, дрейфа нуля, наличия зоны нечувствительности и т. д.
VI. 1.6. Интеграл от ошибки
Этот показатель можно представить в виде
Л = К(*)Л =
= lim[e0(/)
e~stdt
!imep(s)
s->0
= lim Г-
s->o L
-G2(0)
Gz(s)] =
_ dG2(s)
ds
ls=o
= _£(0). (VI. 13)
Таким образом,.этот критерий требует минимализации величины
первой производной функции Gz (s) при s = О в зависимости от параметров
регулятора. Он очень удобен с вычислительной'точки зрения, однако его
можно использовать только в тех случаях, когда имеем дело с
переходными процессами без перерегулирования.
VI. 1.7. Интеграл от квадрата ошибки
00 00 ,00
G2(0)-G2 ()'<*)
/CD
dco. (VI. 14)
Этот критерий используется чаще всего, ибо приводит к системам,
малоподверженным влиянию случайных возмущений. Однако для системы с
запаздыванием его не удается выразить в аналитической форме. Он дает
сильно колебательные- переходные процессы и требует значительного
184
управляющего воздействия, т. е. оптимальные значения усиления и
времени упреждения должны быть' большими, а время изодрома — малым.
Величина перерегулирования может достигать 45%.
VI. 1.8. Обобщенный интеграл от суммы квадратов ошибки
и ее производных
Для уменьшения колебательности переходных процессов применяется
критерий, позволяющий минимизировать интеграл от суммы квадрата
ошибки и квадратов производных с соответствующим весом:
00
/2И = J (4 (t) + M '4 V) + • • • + K*pk) 2 (0 dt. (VI.15)
о
В результате получаем более монотонные переходные процессы. Однако
определение оптимальных значений параметров результатов на^основе
этого критерия связано с большими трудностями.
VI. 1.9. Интеграл от модуля ошибки
со
'ui = J|e„(OI#. (VI.16)
О
Этот критерий обеспечивает переходные процессы с хорошими
свойствами, особенно в части малых амплитуд отклонений. Он более
чувствителен при малых отклонениях, чем квадратичный критерий, зато он менее
чувствителен при больших отклонениях.
VI. 1.10. Интеграл от модуля ошибки,)
умноженной на время
Для улучшения свойств предыдущего критерия, особенно для больших
интервалов времени, применяется критерий
00
'ni/ = J'IM*)|#. (VL17)
Очевидно, что все интегральные критерии применимы ко всем трем
. типам систем: стабилизации, программного управления и следящих
систем.
VI. 1.11. Критерий Зиглера—Никольса
Этот критерий требует, чтобы отношение двух последовательных
экстремумов переходного процесса yjyi было равно V4. Он не позволяет
одновременно определить все три параметра регуляторов ПИД.
На аналогичном требовании основан критерий Кахена—Куна. Для
ликвидации неоднозначности в определении параметров применяется так
называемый критерий трех ограничений.
Все эти критерии не опираются на предпосылки оптимизации в смысле
«сближения» реального переходного процесса к желаемому за счет
минимизации какой-либо функции ошибки гр (/), и поэтому они применяются
все реже.
Приведенная выше 'краткая характеристика критериев качества имеет
целью сориентировать читателя в проблеме выбора одного из них. Однако
выбор регулятора еще зависит от большого числа других факторов,
которые коротко будут охарактеризованы при рассмотрении общей методики
выбора регулятора.
185
§ VI.2. Общая методика выбора регуляторов
с заданной структурой
и сравнение их параметров
Выбор типа регулятора и определение его настроек зависит от следующих
факторов:
A. Типа объекта, т. е. его статических и динамических характеристик.
Здесь особенно существенны:
а) время запаздывания т;
б) постоянная (либо постоянные) времени Т0 в зависимости от того,
имеются одна или две доминирующие постоянные времени;
в) наличие самовыравнивания q = 1 (объект статический) или его
отсутствие q = 0 (объект астатический)у
г) порядок объекта или его приближенной модели;
д) линейность или нелинейность объекта.
Б. Места приложения возмущающего воздействия z, его вид и
продолжительность.
Чаще всего принимается, что возмущение представляет собой
скачкообразную функцию с известной амплитудой и приложено ко входу объекта
либо ко входу регулятора. Реже принимается, что возмущение
является стахастическим с известными статическими характеристиками
или является так называемым наиболее неблагоприятным сигналом
с ограниченной амплитудой, но вызывающим в системе резонансные
явления.
B. Принятого критерия качества.
Выбор критерия качества зависит от требований к характеру
переходного процесса со стороны технологии процесса. Решающими
показателями здесь являются:
а) допустимая ошибка в установившемся состоянии ги или статическая
ошибка; обычно требуется, чтобы она была в пределах 0—5% амплитуды
управляющего сигнала w или возмущения z;
б) допустимое время регулирования tn т. е. время, за которое
отклонение не уменьшится до 3—5% от требуемого значения;
в) допустимое динамическое отклонение; здесь обычно подразделяются
три вида процессов:
процессы, которые не допускают перерегулирования и должны быть
апериодическими;
процессы, которые допускают одно перерегулирование с амплитудой
рорядка 0—10% от величины управляющего сигнала. Такие процессы
встречаются чаще всего;
процессы, которые допускают большие перерегулирования с
амплитудой до 40% от заданного значения;
г) чувствительность переходного процесса к возмущениям (как
внутренним, так и внешним), к изменениям параметров;
д) чувствительность показателя качества к величине ошибки гр (она
должна быть высокой) и к флюктуации параметров системы (она должна
быть малой, чтобы работа в области оптимума была устойчивой).
ч
VI.2.1. Выбор типа регулятора в случае объекта с одной
доминирующей постоянной времени Т0
и временем запаздывания т
1. Аппроксимируя реакцию реального объекта на скачок, определим его
эквивалентную передаточную функцию
186
Постоянные К0, тиГ0 определяются по реакции на Скачок способом,
описанным в гл. II. Для улучшения аппроксимации постоянную времени
можно определить из соотношения
Т0 = to — т. (VI. 18)
Величины t0 и т определяются графическим методом, который
проиллюстрирован на рис. VI. 10. На рис. VI. 11 для примера изображена
реакция /, полученная методом аппроксимации Купфмюллера [30], и реакция 2,
полученная за счет уменьшения постоянной времени в соответствии с
соотношением (VI. 18).
(/)
0
\
\0,632Ко
' jrm
^.
«тL
То
* г'
« °
Точ*
?регс
и
а £
i6a
_-.L
\
<
t
yi
ю
0,8
0,6
ол
0,2
0
i
-
т
f
i i i i
2 V 6 в
-^1
Рис. VI. 10. Определение
эквивалентной постоянной времени Т и
времени запаздывания т по реакции
на скачкообразное воздействие
Рис. VI.11. Аппроксимация по
методу Купфмюллера и на основе
. формулы (VI. 18)
2. Оценим влияние возмущения на объект, которое характеризуется
отношением установившегося значения отклонения, вызванного
максимальны^ возмущением zm, действующим на объект без регулятора, к
установившемуся значению отклонения, вызванного управляющим
воздействием wy приложенным к объекту без регулятора:
m=J/£^
Уют
(VI. 19)
В случае объекта без самовыравнивания это влияние будет оцениваться
отношением производных основных величин в установившемся состоянии:
m
Угш
Угапг
(VI.20)
Свойства объекта характеризуются относительной постоянной времени
qr ^о
1 ~ т >
а переходный процесс характеризует относительное время регулирования
"Г- (VI.21)
Тг =
Требование, предъявляемое к системам автоматического
регулирования в установившемся состоянии, представляет собой отношение еи%/пг,
причем в системах с регуляторами П и ПД ги% является статической
ошибкой, возникающей из-за наличия зоны нечувствительности.
3. Выбор типа регулятора производится с помощью номограммы из
работы [33] (рис. VI.12). Области применимости каждого типа регулятора
заштрихованы. Из рисунка видно, что область применения регулятора
187
типа И ограничивается объектами, допускающими большое время
регулирования Т и большие установившиеся ошибки из-за наличия зоны
нечувствительности.
Пропорциональные регуляторы П могут использоваться в случаях,
когда допустимы либо большое время регулирования, либо большая
величина ги%/т. Малое время регулирования Тг порядка 5т при ejm
меньше 10% может быть получено только в случае объекта с малым
временем запаздывания т <20 Т0.
Регуляторы типа ПИ практически могут
использоваться при достаточно
произвольных требованиях к установившемуся
состоянию и произвольных возмущениях, если не
требуется, чтобы время регулирования было
меньше, чем 6т.
Время регулирования порядка (4—6) т
можно получить при использовании
регуляторов ПИД.
Дальнейшее уменьшение времени
регулирования до теоретически возможной
границы G, равной 2т, возможно только при
использовании специальных регуляторов
Смита или Ресвика, о чем речь будет идти
ниже.
При выборе регулятра к объекту с одной
постоянной времени наиболее существенную
роль играет пропорциональная
составляющая, меньшую —дифференцирующая
составляющая, зато при наличии
пропорциональной составляющей желательно введение
интегральной составляющей, так как при
этом не требуются большие величины коэффициента усиления. И
совершенно не рекомендуются интегральные регуляторы в связи с тем, что
переходные процессы при этом протекают очень медленно. Таким
образом, наиболее желателен регулятор типа ПИ.
VI.2.2. Выбор типа регулятора в случае объекта с двумя доминирующими
постоянными времени T0i и Т02 и времени запаздывания т,
а также без доминирующей постоянной времени
Аппроксимируя реакцию объекта по методике Ольденбурга и Сарториуса
[11.31], получим эквивалентную передаточную функцию
16 20
Рис. VI. 12. Номограммы для
выбора типа регулятора
Go(s)~ (l+sr01°)(l.+ sr02)
(VI.22)
Выбрать регулятор в этом случае поможет график из работы [12],
который получен на основе исследований систем этого типа на аналоговых
вычислительных машинах. График построен в координатах Т2 = Т02/х
и тг = Т01/х (рис. VI. 13).
Граница между областью применения регуляторов И и областью
применения регуляторов ПИ является геометрическим местом точек, в
которых коэффициент при интегральной составляющей К/1 в 2 раза больше,
чем для интегрального регулятора, что и обусловливает применение
регулятора ПИ. Аналогично граница между областями применения
регуляторов ПД и ПИД соответствует точкам, в которых коэффициент усиления
регулятора ПД в 2 раза больше, чем коэффициент пропорционального
регулятора П. Интегральная составляющая опущена, так как влияние ее
в регуляторах этого типа мало в сравнении с влиянием пропорциональной
и дифференцирующей составляющих. Штриховыми линиями обозначены
188
геометрические места точек, в которых коэффициент усиления
разомкнутой системы с регуляторами П и ПД равен 30, что соответствует
статической ошибке порядка 3%. Для объектов этого типа желательно наличие
дифференцирующей составляющей, ибо она сдвигает резонансный пик
в область высоких частот, благодаря чему обеспечивается хорошее
управление в области низких частот. Таким образом, здесь наиболее
употребительны регуляторы типа ПД или ПИД, так как можно избежать больших
усилений.
В случае, когда объект имеет передаточную функцию вида
G0(s)= K°e S . я>2,
ow (l+sT0)n' ^
т. е. не имеет доминирующей постоянной времени, использование
пропорционального регулятора невозможно; не помогает и введение
дифференцирующей составляющей, зато весьма
желательно наличие в этом случае
интегральной составляющей. Следовательно,
здесь наиболее употребимы регуляторы
типа И и ПИ.
После вводных замечаний по выбору
регулятора интегрального типа
приступим к определению оптимальных
значений его параметров. Для одного и того
же объекта они зависят от принятого
критерия качества. Общие соображения
по выбору критерия качества были
высказаны ранее.
Вообще все критерии, кроме критериев
оптимального модуля, показателя
управляемости и апериодической устойчивости,
в случае систем с запаздыванием не
приводят к аналитическим зависимостям
между параметрами регулятора и
параметрами объекта. Этот их недостаток не позволяет проводить точный
анализ систем автоматического регулирования данного типа. Кроме
того, критерии оптимального модуля и апериодической устойчивости
обеспечивают переходные процессы с ценными, с практической точки
зрения, свойствами: с малыми перерегулированиями и с малым временем
регулирования.
Оптимальные значения настраиваемых параметров при
неаналитических критериях найдены путем моделирования систем на аналоговых
машинах и путем кропотливых вычислений на цифровых машинах.
Сейчас рассмотрим подробно выбор оптимальных значений
настраиваемых параметров типовых регуляторов на основе критериев качества.
Области значений настраиваемых параметров, обеспечивающих
устойчивость систем, были рассмотрены ранее.
Рис. VI. 13. Выбор типового
регулятора
VI.2.3. Выбор величин настраиваемых параметров
на основе критерия апериодической устойчивости
Для определения границы апериодической устойчивости необходимо'
найти условия, при которых характеристическое уравнение (III. 122)
(см. табл. III.2) имело действительные кратные корни. Можно легко
показать, что найденные при этих условиях действительные корни
расположены в левой полуплоскости комплексного переменного вблизи от
мнимой оси.
189
Итак, рассмотрим знаменатель передаточной функции замкнутой
системы
М (г) = (Т + KDz-r)r* + (q + Ke-r) r+2<_e-rt (IV.23)
Если функция (VI.23) имеет нуль кратности га в точке г = rki то и ее
производные до (п — 1)-й включительно будут иметь тот же нуль. С
учетом того, что в случае регулятора ПИД имеются четыре параметра: /С, Ь, /
и 7\ сделаем предположение, что функция (VI.23) может иметь не более
одного четырехкратного нуля. Для определения кратности нуля найдем
производные функции (VI.23):
М (г) = 2г (Т + KDe-r) — KDr4~r + (q + Ke~r) — Kre^-fj-e~r. (VI.24)
Для упрощения дальнейших вычислений сложим левые и правые части
выражений (VI.23) и (VI.24):
М (г) + М (г) = Tr2 + qr +
+ 2 (Т + KDe-0 r +(q + /Се-')- (VI.25)
Дифференцируя функцию (VI.25), получим
. м (г) + М (г) = 2 (Т — KDe-r) r +
+ 2 (Т + KDt~') + (q - /Се-'). (VI.26)'
Продифференцируем выражение (VI.26):
М (г) + М (г) = 2KDre~r f 2 (Т — 2KDe~r) + Ke~r (I V.27)
и далее продифференцируем функцию (VI.27):
М (г) + М (г) = — 2KDre~r + 6KDe~r — К*-r. (IV.28)
Сложим левые и правые части выражений (VI.27) и (VI.28) и получим
окончательно
М (г) + 2М (г) + M(r) = 2 (KDe-r + T). (VI.29)
В случае существования пятикратного нуля функции (VI.23) должно
быть одновременно
М (rk) = 0; )
М (rk) = 0;
М (rk) = 0;
М (rk) = 0;
М (rk) = 0.
Таким образом, приравнивания к нулю правую часть выражения
(VI.29), получим
KDe-r + 7 = 0. (VI.31)
Так как параметры /С, D и Т всегда положительны, то
уравнение (VI.31) не может быть выполнено. Отсюда можем сделать вывод, что
в случае регулятора ПИД функция (VI.23) может иметь нуль кратности
не более 4. Поступая подобным образом в случае регулятора ПИ, т. е.
полагая D = 0, получаем, что не только выражение (VI.29), но и (VI.27)
никогда не может быть равно нулю, или в этом случае функция (VI.23)
должна иметь нуль с кратностью не выше трех. Аналогичный результат
получаем и при использовании регулятора ПД. Для регуляторов П и И
нуль имеет кратность два.
190
(IV.30)
Таким образом, в случае регулятора ПИД кратные нули функции
(VI.23) можно найти, приравнивая к нулю М (гк), М (г/,), М (rk) и М (rk),
т. е. из следующей системы уравнений:
М (г) = (7V2 + qr) + ( KDr2 + Kr + -у-) е~' = 0; (IV.32)
Ml (r) = (27V + q) + [—KDr2 + (2D — 1) Кг + К (1 }-)] e~' = 0;
(VI.33)
Mn(r) = 2T+ [KDr2 — (4D— \)Kr + 2(D— \)К + ^-} e-' = 0; (VI.34)
Mm(r)= \—KDr2 + (6D—l)Kr — 3(2D—l)K — -j-]e-r = 0. (IV.35)
Решая систему уравнений (VI.32)—(VI.35), получим следующие
зависимости между параметрами и искомым корнем:
/ =
^-УЗ+Щ,-(8+^), (VI.36)
(«'+■») Vf'+(^)'-[' + ^-+W]
[»+«#+(+ЛУг'+(-*-)'-[»+»++Ч+),+(+Л'
(VI.37).
D = — / y2JJ- ; (VI .38)
•{(«++)/•+(+)'-[•+++(*)']}
/
_ [.9 + -А. + ( JL.)2]} е [ VW" (3+ ^)]. (vi.39)
Для объекта без самовыравнивания (q = 0) зависимости (IV.36)—
(VI.39) сильно упрощаются:
/•* = /3-3; (VI.40)
/ = 2 + У~3; (VI.41)
Z> = 3+8КЗ ; (VI.42)
К = 6Г (2 /3 — 3) е^3-3. (VI.43)
Поступая таким образом, можно найти зависимости между параметрами
для остальных типов регуляторов.
Для регулятора ПИ, полагая в выражениях (VI.32)—(VI.34) D = 0
и решая эту систему из трех уравнений, получим
/ =
rk = ]/2 + (4-)2 - (2 + -£-); (VL44)
[»+*)+Ч*)'+(+Л - [»+W] /2+ Шг'
(VI.45)
191
К=2т[у2 + (-<т)2- l]eK2+(^)8-(2+^), (VI.46)
а для объекта без самовыравнивания (q — 0)
гА*=/2 —2; (VI.47)
/ = 3+21/2; (VI.48)
К=2Т(У~2— l)eVY~2- (VI.49)
Аналогично получим для регулятора И:
^ = 2г[)ЛТЩ-1]. (VI.51)
Устойчивая работа регулятора И с объектом без самовыравнивания
невозможна, в чем можно убедиться после подстановки в выражения (VI.50)
и (VI.51) q = 0:
rk = 0; ) '
Для регулятора ПД, приняв в уравнениях (VI.32)—(VI.34) / = оо,
после решения системы уравнений получим
= _2(l+^r); (VI.53)
/С = 2г(2+^)е~2(1+^г). (VI.55)
D = —.—! г; (VI.54)
С объектом без самовыравнивания
г* = -2; (VI.56)
(IV.57)
К = 47е-2. (VI.58)
В простейшем случае пропорционального регулятора имеем
r4 = -(l+2-i-); (VI.59)
УС^Ге""^2^)- (VI.60)
Выражения (VI.59) и (VI.60) при ц = 0 имеют следующий вид:
r* = -l; (VI.61)
K = Tt-K (VI.62)
Полученные результаты сведеы в табл. VI.I.
192
Области апериодической устойчивости в пространстве параметров
Таблица VIA
Тип
регулятора
'
п
пд
и
пи
Область апериодической устойчивости
'. — ;■++);
• ,-*-('-+)
rk = — 1;
К =Ге-1
. * — (»++):
4 + 1г
К = (1 + 47) е ^ г /
г* = — 2;
D = -b
У( = 47е"2
г,= |/1+[^;2-(1 + -^-';
f—(К' + ЬЬЧ
Система структурно неустойчива:
'* = 0; |
•1 / / i '2 f 1 '
i + '-L-2
Г 1 1 2 / ' 31 '
[3+"2Т"+4^"27"У +'"27~jJ_
-[2+(-^//2+(^)2
, Г./77ПТ f-j.
*-«■[!/.+(^r/-.J.lv '+ы l'+
(VI.63)
(VI.64)
(VI.61)
(VI.62)
(VI.65)
(VI.66)
(VI.67)
(VI.56)
(VI.57)
(VI.58)
(VI.68)
(VI.69)
(VI.52)
(VI.70)
(VI.71)
""2Г )\
(vi.72);
Объект
q= 1
' 9=0
q= 1
9=0
<?= 1
?=0
9= 1
13 X. Турецкий
193
Продолжение табл. VI. 1
Тип
регулятора
Область апериодической устойчивости
ПИ
rk = V2-2;
/ = 3 + 2 V~2\
(VI.47)
(VI.48)
(VI.49)
ПИД
*= Кз+Ыг/-(з+
1 \ .
2Т )9
(VI. 73)
/ =
1 2
2Г i
[зб + 9^ + б(^-)2+(4,)3]
(VI.74)
D:
V«+W-'
(VI. 75)
'-"■{(•+т)Уг'+(т)"
[9+_^+(4,)']).l^S+<^)'-(*+^)] ,V,.76,
D
^=1^3-3;
/ = 2 + /3;
з + Кз .
18
/С = 6Г (2 КЗ — 3)e(^3-3)
(VI.40)
(VI.41)
(VI.42)
(VI.43)
VI.2.4. Номограммы для определения областей устойчивости
на плоскости параметров объекта и регулятора
Введем безразмерные параметры, определяемые выражением (VI. 1), и на
основании соотношений (VI.61)—(VI.76) построим номограммы,
изображенные на рис. VI. 14—VI.22.
Критерий устойчивости и критерий апериодической устойчивости
основаны на соответствующем выборе знаменателя передаточной функции
замкнутой системы. Вследствие этого критерии не зависят от места
приложения возмущающего воздействия, следовательно, оптимальные
значения параметров, определенных на основе этих критериев, не зависят
ни от вида, ни от места приложения воздействия, а только от структуры
данной линейной системы.
Однако на качество переходных процессов место приложения
возмущений оказывает сильное влияние, и то, что этот фактор не учитывается
194
Рис. VI.14. Зависимость
параметров в системе с
пропорциональным регулятором и
статическим объектом (q=l)
по критерию апериодической
устойчивости
10 \
5
2\
7
0,5
ОЛ
0,1
0,05
&20.1 ОЛ
к-
ж
->кт\
НК
0,5 1
10 20 50 7"
Я,-г»Т
10
5
2
/
0.5
0,2
0.1
0,05
0,02^
щ
5п
\\\\к'
щ
Ш
4111 'X
11
91
Рис. VI. 15. Зависимость
между параметрами в
системе с пропорциональным
регулятором и астатическим
объектом (q = 0) по
критерию апериодической
устойчивости
■0.7 0,2 0,5 1 2 5 10 20
К;-гкТ;1)Т _
10
5
2
1
0,5
ол
OJ
0,05
50 Г
Рис. VI. 16. Зависимость
между параметрами в
системе с регулятором ПД и
статическим объектом (q = 1)
по критерию апериодической
устойчивости
K\-rHT;m
20\
10
5
2
1
0.5
ОЛ
0.1\
0,05
ОМ
^—?
и
fH-kr.T"
тЧГГ Л.
WIT TYT '
ГК ^ ч
птг к
"\—Н
—I—J-LLU
—I—11 iii
0%1 ОЛ 0,5 1
10 20 50 Т'1
0,02,
к;—
X.
^
^J.| 1
II |
I ij i
Н11~г*г'
jfp
тП "
^[Т
ITT
"sJ
|ч[
1 Т^ч] 1 1 1
1 1 rbsJ
о
ОЛ 05 1
20
50 Г1
13*
Рис. VI.17.4"" Зависимость
между параметрами в
системе с регулятором ПД и
астатическим объектом (q = 0)
по критерию апериодической
устойчивости
195
-rHT;KT/I
0,5
0.2
0.1
0.05l
0.02,
С
ft/ 0.2 0,5 12 5 10 20 50 TV
Рис. VI. 18. Зависимость
между параметрами в
системе с регулятором типа
И и статическим объектом
(q = 1) по критерию
апериодической устойчивости
Рис. VI. 19. Зависимость между
параметрами в системе с регулятором
ПИ и статическим объектом (<7 = 1)
по критерию апериодической
устойчивости
~rJ:K;I/T
10
5
2
1
0,5
0,2
0.1
0,05
0,Q2i
I I 11
k^J
Г*ТШ
/pSLL
F— Ti
— I/i 4-1-4-
гтТт
M| 11 L
ж—I
JffK'
1 "Ч-
Jill
I i 1 Iit
[mil
0,1 0,2 0,5 1 Z 5 10 20 50 Г'
-rhT;K;I/T
20
10
5
г
1
0,5
0,2
0,1
0,05
0,02
rvN
—
^
ч
гут?
Lr
,И\
~-j~t"JI
HtPn
П PvN
^
К
1рт
ли
4v
zzx~",pfc
FJte^
[ffip 1
Щ-Г*т
■=+dp$fc
Рис. VI.20. Зависимость
между параметрами в
системе с регулятором ПИ и
астатическим объектом (q = 0)
по критерию апериодической
устойчивости
0,1 0,2 0,5 1
10 10 50 Т
-;
-ГИТ;К;1/Т;1)Т
Рис. VI.21. Зависимость
между параметрами в
системе с регулятором ПИД и
статическим объектом (q = 1)
по критерию
апериодической устойчивости
ОМ
196
в критериях устойчивости, является их существенным недостатком.
Поэтому теперь рассмотрим критерии качества, которые учитывают место
приложения возмущения в системе. Оптимальные значения параметров
в них определяются с учетом не только знаменателя, но и числителя
передаточной функции замкнутой системы.
-гмТ;К;1/Т;ДГ
Рис. VI.22. Зависимость между
параметрами в системе с
регулятором ПИД и астатическим
объектом (q = 0) по критерию
апериодической устойчивости
20 \
ю\
г\
о,г\
оЛ
ош
ОМ
щ£
р5^
-N
7
7
р___
\s
7Г;
s
Ры III
I I
11^—
LHiii
I jf111
4V
NL^
lit
Tj| ^
^
4^
*
4
^
Ц-ff-l-fj
hjhii
OJ 0,2 0,5 1 2 5 10 20 50 T'1
VI. 2.5. Выбор регулятора и его параметров
на основе критерия оптимального модуля
В работе [34] приведены условия, обеспечивающие выбор параметров
регуляторов, работающих совместно с линейным объектом без
запаздывания, на основе критерия оптимального модуля. Этот критерий очень
удобен с практической точки зрения и приводит к получению переходных
процессов с малым перерегулированием. В работе [35] он обобщен на
случай линейных систем с запаздыванием. Исходя из условий (VI.7)
можно просто получить аналогичные условия для систем с запаздыванием.
Пусть
°.0-«)-Т$Ь ,(VL77)
где L (/со) и М (/со), вообще говоря, могут быть трансцендентными
функциями переменной со.
Дифференцируя зависимость
|L(/cd)|2 = L(/cd)L(-/cd)
(VI.78)
и используя формулу Лейбница, получим
dm
da>m
[ \L (/о) |2] = £ (1) Lim-k) Mw (-/«)• (VI-79)
*=0
Аналогично поступаем для | М (/со) |2.
Легко убедиться разлагая L (/со) и L (—/со) в степенной ряд, что
J— [L (/со)] = (—l)m Jt— [L (—/©)]•
d(dm dcom
Из соотношений (VI.79) и (VI.80) получим
m
dm [ I L (/со) |2] = ^ (-1)" (1) Lim~k) 0"ш)Lik) №•
da"
k=o
Аналогично можно записать для М (/со).
(VI.80)
(VI.81)
197
Условия (VI.7) в силу выражения (VI.81) принимают следующий зид:
т
2(_1)* (*) jL(m"*> (/<в) L(*} °"в)
k=0
£(-!)*( 7 )M(m~Л)(Усо)^)(/со)
k=0
= [Щ?Ь -«■ (V,-82)
о)=0
где т = 2, 4, . . ., 2/, причем / — число определяемых параметров
регулятора.
Теперь на основании соотношения (VI.82) найдем оптимальные
настройки регулятора ПИД. Согласно соотношениям (III.45) и (III.33)
(см. табл. III. 1) существует следующая зависимость, определяющая
передаточную функцию замкнутой системы:
G =
/с(яг* + г+4-)
^е-
/c(Dr* + r + -j-)
(гТ + q) + К (Dr* + г +-1) е-' г (rT + q)tr + К (л* + г + -j-J
(111.47)
Числитель передаточной функции
L(r) = K(Dr2 + r+-]-), (VI.83)
а знаменатель
Л1 (г) = г (rT + q)<tr + K (О/-2 + г + -J-) ■ (VL84)
При использовании регулятора ПИД определяются три параметра
регулятора. Поэтому в уравнении (VI.82) следует принять, что m = 6, и
дифференцировать функции (VI.83) и (VI.84) по г 6 раз, а затем в полученных
производных положить г = 0. Таким образом,
Iх (0) = К;
Ln (0) = 2KD;
Lul (0) = LIV (0) = Lv (0) = LVI (0) = 0
(VI.85)
Af(0) = -f;
M' (0) = AT + flr;
Af"(0) = 2/Ф + 2 (7* + ?);
^
•in
Min (0) = 3 (27 + (7);
riv
M1V (0) = 4 (37- + </);
Mv (0) = 5 (47 + q)\
MV1 (0) = 6 (57* + <7).
(VI.86)
Подставляя зависимости (VI.85) и (VI.86) в соотношение (VI.82),
получим:
при m = 2
К =
T{T + q)-2q
(VI.87)
198
при т = 4
*=-i—-„ т^- т ; (v*-88)
при т = б
-l(f + 5)+20D(-fr+3) = 5(4-+4). (VI.89)
Из этих соотношений после преобразований получим:
J_ _ 15<7(2Г+1)(6Г2 + ЗГ+ !)
/ "~ 180Г4 + 2ЩТ* + 135^Г2 + 42дТ + 7?'
(VI.90)
60Г' + 60?Гз + 27(?Г2 + 1дТ + д „1 ОП
180Г4 + 240^Гз + 135^Г2 + 42?Г + 7? * l '
Аналогично можно получить для регулятора ПД при m = 2
-[■±(д + К)]2=к[±(д + К)(±+2)-(Лг+Ц+«£-)]2, (VI.92)
а при m = 4
-5-+ 4
D = —l. (VI.93)
Из соотношений (VI.92) и (VI.93) окончательно определим
к_ (6Т + д)(\2Т*-д) (Щ g„
А~~ 2 (48Г2 + 30?Г + 5?) ^ L^
ИЛИ
D = ^WTW' <VL95>
На основе соотношений (VI.87), (VI.90), (VI.91), (VI.94) и (VI.95)
составлена таблица оптимальных настроек регуляторов, а на рис. VI.23—
VI.31 изображены номограммы.
Использование критерия оптимального модуля для инерционных
объектов n-го порядка с одной постоянной времени и запаздыванием приводит
к получению аналитических выражений для определения оптимальных
параметров регуляторов [60]. Его также можно использовать для
инерционных объектов второго порядка с разными постоянными времени и
запаздыванием. Однако для объектов с запаздыванием порядка выше
первого регулятор ПД не может быть использован, так как из условий
устойчивости нельзя применить большего усиления.
Поступая аналогично для объекта с передаточной функцией
Go{r) = J^-, (VI.I12)
0W (l + rT)n'
получим соотношения, представленные в табл. VI.3.
На основе выражений из табл. VI.3 построены номограммы,
изображенные на рис. VI.32—VI.37. Они позволяют быстро выбирать
оптимальные настройки различных регуляторов.
Эти номограммы основаны на аппроксимации объекта при помощи
одинаковых постоянных времени. Модели этого типа находят применение
для объектов, чаще всего встречающихся в химических и тепловых
процессах, как объекты с распределенными параметрами. Зато в
автоматическом приводе часто приходится иметь дело с двумя доминирующими,
отличными друг от друга, постоянными времени. И в этом случае можно
для объекта второго порядка с запаздыванием и различными
постоянными времени найти соотношения для оптимальных настроек регуляторов.
199
Таблица V/.2
Оптимальные, в смысле критерия модуля передаточной функции,
значения параметров регуляторов для объекта G0 (r)
Я + Тг
Тип
регулятора
Оптимальные значения параметров
Объект
п
к =
f2
2Т+ 1
к = -
(VI. 96)
q= 1
(VI.97)
<7=0
ПД
К =
(67+1) (12Г2— I).
2(48Г2 + 30Г + 5) '
4Г+1
D =
4(ЗГ+ 1)
(VI.98)
(VI.99)
(VI. 100)
(VI.101)
д= 1
q=0
И
/
1
2(Г+1)
Система неустойчива
/С = 0
(VI. 102)
(VI. 103)
q= 1
q=0
ПИ
К
6ГЗ + 6Г2 + ЗГ+1.
: 4(ЗГ2 + ЗГ+1) '
1 = 6Г2 + 6Г + 3
/ ~6Г2 + 6Г2 + ЗГ+1
(VI. 104)
(VI. 105)
Я = 1
ПИД
*(--)-)■
к =
1
(Г+1)-2
1 _
D =
(IV. 106)
15(2Г+1) (6Г2 + ЗГ+1)
180Г4 + 240Г3 + 135Г2 + 42Г + 7
60Г4 + 60Г3 + 27Г2 -\-7T-\-l
180Г4 + 240Г3 + 135Г2 + 42Г + 7
(VI. 107)
(VI. 108)
(VI. 109)
д=0
Я = 1
К = -
- + 2(D-1)
+ 12Z) = 4
(VI. ПО)
(VI.111)
<7=0
200
/
0,5
0,2
V
0,05
€02
fc=T=E
[Е5г~Ег
h-^--
p
- " L h
~-rJ \ p
■ i "pf=
№=s
fjf^
1—j—1=
~ 1 |:
' 1
ihm
итт
а/ ол o,s 1
5 10 20
К
5
2
7
0,5
0,2
0,1
0,05
SO TJ «",
Рис. VI.23. Зависимость между параметрами в
системе с регулятором П и статическим объектом
(q = I) по критерию оптимального модуля
F=
V 02
J_\
Я
w\
■rtii
I 1 H
05
t
1 2
f
| } ;
5
SB
ьн-j
i!!
Щ
r1
Рис. VI.24. Зависимость между
параметрами в системе с
регулятором П и астатическим объектом
(q = 0) по критерию оптимального
модуля
К;ЛТ
20
10
5
2
1
Ot5
0,2
0,1
OflS
ОЖ
\г~~
г^
I ^
г
—77"
/С
ЮТ
\у
Ww^
гп\
fe
^
\
\
У
L_
^
-^
I U+T
4м
я./ яг
«5
/0 2(7
50 Г"
Рис. VI.25. Зависимость между параметрами в системе с регулятором
ПД и статическим объектом (q = 1) по критерию оптимального
модуля
K;DT ^
~OJ 0,2 0,5
Рис. VI.26. Зависимость между параметрами в системе с
регулятором ПД и астатическим объектом (q = 0) по критерию
оптимального модуля
201
KI/T
0.5
0,2
0,1
0,05
0,02
HJJ п
^ш
0,1 0,2 0,5 1
10 20 - Т
-;
Рис. VI.27. Зависимость, между параметрами в системе
с регулятором И и статическим объектом (q = 1) по
критерию оптимального модуля
К;1/т
1
20\
1СЦ
5
2
1
1
0,5
ол
0,1
и, и о
п по
Ч^
I/T
H-U—
I 111
Jill '
I I J-+T11
4fi[t|i
{ i i 111
| | [\Щ
"0.1 0.2
0.5 1
10 20
50 T"1
Рис. VI.28. Зависимость между параметрами в системе с
регулятором ПИ и статическим объектом (q = 1) по критерию
оптимального модуля
I/T
20
10
0,5
0,2
0,1
005
ОМ
I .« I I I I
1
\ц\
^ш
\k=w \—рр
Цлг=; =
jjffr
шш
щ
1 LKIIIH
ицр
0,1 0,2
0,5
10
20
50
Рис. VI.29. Зависимость между параметрами в системе с регулятором ПИ
и астатическим объектом ((7=0) по критерию оптимального модуля
202
K;T/I;BT
0,1 0,2 0,5 1 2 5 10 20 50 T'1
Рис. VI.30. Зависимость между параметрами в системе с
регулятором ПИД и статическим объектом (q = l) по критерию
оптимального модуля
I/TlDT
'0,1 0,2 0,5 1 2 5 10 20 Т
Рис. VI.31. Зависимость между параметрами в системе с регулятором ПИД
и астатическим объектом (q = 0) по критерию оптимального модуля (сплошная
линия для //Г, штриховые — для DT)
203
Таблица VI.3
Оптимальные, в смысле критерия модуля передаточной функции,
значения параметров регуляторов для объекта GQ (г) — °
Тип
регулятора
П
И
пи
пид
Оптимальные значения параметров
пТ2
А п(п— 1)Г2 + 2лГ+1
К 1
/ 2(пТ+\)
(VI. ИЗ)
(VI. 114)
Г3(л3 + Зл2 + 2л)+ЗГ2(л2 + л) + ЗГл+1 .
А 4[(л3-л)Г3 + ЗГ2л2 + 37л+1] '■ <V1110'
1 3[Г3(л3 + л2) + ЗГ2(л2 + л) + ЗГл+П
/ (пТ + 1) [Т3 (/г3 + Зл2 + 2л) + ЗГ2 (л2 + п) + ЪТп + 1]
-2KU+D (VM16)
„ Р.Г» + Рб^5 + Р^4 + Р.** + Р.7* + PiT + Ро / V, , I 7 J
А_ аеГб + а^+а^ + сСз^ + а^+^Г + ао ' 1г1Л1'>
где
Р6 = 7п6 + 30л5 + 25л4 — 30л3 — 32л2;
р5 = 42л5 + 120л4 + 30л3 — 120л2 — 72л;
р4 = Ю5л4 + 180л3 — 15л2 — 90л;
Рз= 140л3 + 120л2 — 20л;
р2 = Ю5л2 + 30л;
Pi = 42л;
Ро = 7;
а6= 16лв — 80л4 + 64л2;
а5 = 96 л5 —240л3+ 144 л;
а4 = 240л4 — 240л2;
а3 = 320л3 — 80л;
а2 = 240л2;
ах = 96л;
а0=16;
1 2К+1 .
I 2K(nT+\) '
(VI.118)
(VI. 119)
4/( [(пТ + I)3 - лГ3] - ЦпТ + I)3 + Зл (лГ3 + Т2) + 2лТ3] /л/т 10лч |
L 12/((лГ + 1)3 (VI. 1.0)
>
204
ось
20]
10]
ОЛ ОМ Ofi Ofi 1,0 1ЛТ'1
Рис. VI.32. Зависимость между
параметрами регулятора П для
статического объекта n-го порядка
Рис. VI.33. Зависимость \между
параметрами регулятора П для
астатического объекта n-го порядка
ОЛ ОМ 0,6 0,8 1,0 1Л 1М 7~
im к
12
10
8
в
4
2\
20
'0
5
- 4
3
" 2
^ /
ав\
0,6 \
0,5 \
ом\
с
аз\
125 {
1 пЛ1°— — ~~
1 . ——— """ £ ———
L-—■""■""-~"~_£ ■—-
сР:Н":Ь::
T-~^^~~~J~~~~~
^--~"~~ \j?*/
^\£ ^Ч.
^--*/N*^
!5-^1^^Л^^*^^^чч^
ii5Si£ii=^£ill
'•56789 ri=10
Рис. VI.34. Зависимость между
параметрами регулятора И для
статического объекта n-го порядка
Рис. VI.35. Зависимость между
параметрами регулятора ПИ для
статического объекта n-го порядка
205
K;KT/I
0.2 0,Ь 0,6 0.8 1.0 1,2 1%UT-i
Рис. VI."36. Зависимость между
параметрами регулятора ПИД для
статического объекта /i-го порядка
пп/т
©о
5
k
3
1
0.9
0,в\
0.7
0,6
рч
к
F
у
N. \
, X \ :
. 1 L 1 L
п=10
———- </
Q
" 7
■—, S
\ J
1 1 1___ 1
О 0,2 ОЛ 0.6 0.8 1.0 U2 1J*T'1
Рис. VI.37. Зависимость между
параметрами регулятора ПИД для
статического объекта п-го порядка
0.2 О.Ь 0,6 0,8 1,0 12 Т~
Рис. VI.38. Зависимость между
параметрами регулятора П для статического
объекта с двумя различными
постоянными времени
Пусть передаточная функция объекта
K(s)- ^
(\+sT01)(\+sT02)
или в относительных единицах
где
а (г) = ^°е
1 1—n"T"»
т2 =
1 02
Т
(VI.121)
(VI. 122)
(VI. 123)
Соотношения, определяющие оптимальные значения параметров
регуляторов, сведены в табл. VI.4. По формулам, представленным в этой
таблице, с помощью цифровых машин [60] построены номограммы
(рис. VI.38—VI.44).
Таблица VIА
Оптимальные, в смысле критерия модуля передаточной функции,
значения параметров регуляторов для объекта
Тип
регулятора
Оптимальные значения параметров
П
К =
п+п
2T1T2 + 2(Tl + T2)+i
(VI. 124)
И
К
1
2(7\ + Г2 + 1)
(VI. 125)
ПИ
К-
г[2(т1 + т1тг + т*) + 2(т1 + т2т1 + т21) + (т2 + т1)] + \ ш
12 (7\ + Т2) (ТХТ2 + 7\ + Т2 + 1) + 4
(VI. 126)
JL = 2K+l (VI 127)
/ 2К[Т1 + Т2+\] ivi.iz/.
ПИД
ЗбОГ^ (Т% + ЗТХТ22 + ЗТ2Т2Х + T\) +
+ ЗбОГ^з (Т\ + ЪТ{1% + &Т2ХТ22 + ЪТ\Т2 + т\) +
+ 180 (7^ + 1ТХТ\ + 167^ + Ш\Т\ +
+ 7Т\Т2 + Т\) + 60 (7Т\ + 2ЪТХТ\ + Ш2ХТ22 +
+ 2ЪТ\Т2 + 7Т\) + 5 (757^ + \11Т{Г\ +
+ \11Т\Т2 + 1ЬТ\) + 3 (Б9Т1 + 987\Г2 + 597^) +
к== +49(7\ + Г2) + 7 .
720 (Тх + Г2)2 Т\Т\ + 720 (Тх + Т2) ТХТ2 (Т22 + '
+ ЗГ^з + Т\) + 240 (Тх + Т2)2 (Т2 + 6ТХТ2 +
+ Т\) + 240 (Тх + Т2) (2Т\ + ЪТХТ2 + 2Т2Х) +
+ 336 (7\ + Г2)2 + 112 (7\ + Т2) + 16
1 1+2К
I 2К(Т1 + Т2 + \) '
4К [3 (7\ + Т2) {2Т2 + 7\ + 1) + 1] -
-3(Тх + Т2)[2(Т2 + Т2) + 3]-б(Т2+Т2Тх + Т2)-\
\2К[{Т1 + Т2)(Т1 + Т2 + 2)+\]
(VI.128)
(VI. 129)
(VI. 130)
207
о
с»
Рис. VI.39. Зависимость между пара- Рис. VI.40. Зависимость между пара- Рис. VI.41. Зависимость между
метрами регулятора И для статиче- метрами регулятора ПИ для статиче- параметрами регулятора ПИ для
ского объекта с двумя различными ского объекта с двумя различными статического объекта с двумя раз-
постоянными времени постоянными времени личными постоянными времени
oo
20
10
S
k
3
15
2
18
?A
12
1
0,9
0,8
0f7S
I
\
_l I I I I I I
f Ъ/Т,'
I 1 ._.! 1 J
16
.o.s
-j i i
0 0,2 OM 0,6 0,8 1t0 1,2 1M T'1
Рис. VI.42. Зависимость между
параметрами регулятора ПИД для
статического объекта с двумя различными
постоянными времени (коэффициент
усиления)
to
о
со
Рис. VI.43. Зависимость между пара- Рис. VI.44. Зависимость между
параметрами регулятора ПИД для стати- метрами регулятора ПИД для
статического объекта с двумя различными ческого объекта с двумя различными
постоянными времени (время изодрома) постоянными времени (времени
упреждения)
VI.2.6. Критерии при использовании типовых управляющих сигналов
Для этих критериев нельзя получить оптимального значения
настраиваемых параметров регуляторов в виде аналитических зависимостей. На
основе расчетов на вычислительных машинах построены номограммы и
получены приближенные, упрощенные выражения, позволяющие проводить
ориентировочный выбор настроек регуляторов.
Таблица VI.5
Оптимальные значения параметров регуляторов при различных критериях качества
(объект статический; q = 1)
Критерий
качества
1 ZN
ЗС
IAE
ISE
ITAE
1 ZN
ЗС
IAE
ISE
ITAE
ZN
ЗС
IAE j
ISE
ITAE
Тип
регулятора
п
п
п
п
п
пи
пи
пи
пи
пи
пид
пид
пид
пид
пид
Оптимальные значения параметров регулятора
/ а
1,000
1,208
0,902
1,411
0,490
0,900
0,928
0,984
1,305
0,859
1,200
1,370 |
1,435
1,495
1,357
Р
1,000
0,936
0,985
0,917
1,084
1,000
0,946
0,986
0,959
0,977
1,000
0,950
0,921
0,945 |
0,947
V
3,333
0,928
1,644
2,033
1,484
2,000
0,740
1,139
0,917
1,176
б
0,000
0,417
0,293
0,261
0,320
0,000
0,262
0,251
0,229
0,262
и
0,000
0,365
0,482
0,560
0,381
А,
0,000 1
0,050
—0,137
—0,006
0,0005
Для сравнения в табл. VI.5 представлены [39] оптимальные значения
параметров регуляторов, полученные при использовании различных
критериев и при действии на систему скачкообразного воздействия.
Зависимость оптимальных настроек от постоянной времени в
относительных единицах имеет следующий вид:
К = аТр; (VI. 131)
/ = уТ6; , (VI. 132)
D = [лГ\ (VI. 133)
причем передаточная функция объекта задана выражением
а передаточная функция регулятора
GH(r) = K*(l+rD+±-),
и предполагается, что возмущение z (t) = 1 (/) действует на входе объекта,
а управляющее воздействие равно нулю.
Аналогичные таблицы для астатических объектов (q = 0) приведены
в [24, V.17].
Анализ переходных процессов показал, что наилучшими свойствами
обладают процессы, полученные на основе интегрального критерия
абсолютной ошибки, умноженной на время; несколько хуже свойства
процессов, полученных из других интегральных критериев; зато переходные про-
210 . - - '
цессы при настройках регуляторов по критериям Зинглера—Никольса
и трех ограничений имеют значительно лучшие показатели качества [39].
Анализ запасов по фазе и амплитуде систем с параметрами, выбранными
на основе этих критериев при скачкообразном воздействии, показал, что
запас по фазе колеблется в достаточно широких пределах (16—80°), зато
запас по модулю находится в очень узких границах (3—9 дБ) [14].
Аналогичный анализ для систем, находящихся под воздействием
скачкообразного управляющего сигнала, выявил колебания запаса по фазе
в пределах 40—65°, а запаса по модулю — в пределах 12—20 дБ [14].
* Следовательно, системы автоматического регулирования,
спроектированные для возможно более точного воспроизведения управляющего сигнала,
более устойчивы, чем системы, основной задачей которых является
парирование внешних возмущений.
Рис. VI. 45. Блок-схема системы с обратной связью по ур
Одним из наиболее полных исследований по выбору оптимальных
настроек регуляторов является исследование, проведенное под
руководством Я. 3. Цыпкина и наиболее полно представленное в работах [V.17, 24]
, В них содержатся номограммы для определения оптимальных настроек
регуляторов и графики показателей качества, таких как динамический
коэффициент усиления Rd и время регулирования tr Исследования
выполнены для трех критериев качества, а именно: критерия апериодических
переходных процессов, для которых время регулирования tr минимально,
критерия 20%-й колебательности и критерия минимума интеграла от
квадрата ошибки. Но графиками можно пользоваться только при
справедливости предпосылок выбранного критерия качества, вида и места
приложения внешнего сигнала и типа объекта.
Если объект можно представить в виде двух частей, из которых одна
является инерционным объектом без запаздывания с передаточной
функцией G0 (/со), & другая содержит запаздывание т, то, измеряя сигнал ур
на входе звена запаздывания, можно значительно улучшить работу
системы автоматического регулирования. Тогда система замыкается с
помощью обратной связи по ур (рис. VI.45). Благодаря тому, что регулятор
получает информацию без запаздывания, можно значительно лучше и
быстрее ликвидировать отклонения, вызываемые действием
возмущений z. Построение таких систем возможно, если возмущения z не действуют
непосредственно на часть объекта, содержащую запаздывание. Если же
возмущение действует на вход элемента с запаздыванием, то и в этом
случае можно улучшить процесс управления, но необходимо использовать
двухконтурные системы управления.
§ VI. 3. Двухконтурные системы автоматического
регулирования
Чаще всего используются так называемые каскадные системы
автоматического регулирования (рис. VI.46). Название объясняется тем, что имеется
регулятор GRl первичный, который соединен последовательно с
регулятором GR2 вторичным. Обычно вторичный регулятор является
пропорциональным. Он улучшает характеристики части объекта Gb, не содержащей
14* 211
запаздывания. Благодаря тому, что информация о действии
возмущений гх приходит в регулятор GR2 без запаздывания, происходит
значительное улучшение процесса управления. Возмущение г2 достигает
регуляторов GR1 и GR2 с запаздыванием т, поэтому реакция на это возмущение
^не столь сильна. Звено HR необходимо для коррекции характеристик
'звена Gb.
Это можно легко проиллюстрировать исследованием системы с
разомкнутой обратной связью первого регулятора. Операторное уравнение,
(-)
г>£
\
вщ
^{TsSLj
1
J-
GR2
"*
г
Объект
Gb
Ур Ур^
1
г 2
f
\у~
ГР
G0e-sr
1
i
\У У
1*'
1 '
J
'у
Рис. VI.46. Блок-схема каскадной системы автоматического регулирования
связывающее выходную величину Y (s) с входной 8 (s) и возмущениями
Zx{s) и Z2 (s), имеет следующий вид:
У(^= °Г^£Г*(«) + Л%1оь ZAs) + G0e-«Z2(s). (VI.134)
Для упрощения исследований примем передаточные функции в виде,
часто встречающемся на практике:
HR = 1; •>
G(a. = ^иъ
Gb
G0 =
/Со
1
(VI. 135)
Подставляя выражение (VI. 135) в формулу (VI. 134), получим
Y(s)
KR2Kq
i+«g^s>
■E(s) +
1 + Kr3K<,
{l+sT+^iro)il+sT-)
(1 + st+w;)(1+sT<*)
z^+jt^ZAs)- (VL136)
Аналогичное уравнение для одноконтурной системы без регулятора G#3
и без обратной связи HR имеет вид
Y (s) = GRlGbG0e-"E (s) + GbG0t^Zl (s) + G0e~"Z2 (s), (VI.137)
а с учетом выражения (VI. 135) получим
Y(s) = K0GRl(s) (1+sToei)(1+sro8) £(«) +
e— st e-sx
(VI. 138)
Сравнивая соотношения (VI. 136) и (VI. 138), видим, что возросла
скорость протекания переходных процессов, вызываемых изменением управ-
212
ляющего сигнала w или величины возмущения гь так как уменьшилась
в (1 + Kr2K0) раз постоянная времени Т01. Во столько же раз
уменьшилась амплитуда'возмущающего воздействия гг. Но введение каскадного
регулирования не влияет на возмущающее воздействие z2, приложенное
вне внутреннего контура системы. Действие этого возмущения
компенсируется цепью обратной связи основного контура.
Если возмущающие воздействия можно измерить, то эффект,
вызываемый как воздействием zl9 так и z2, может быть скомпенсирован при
использовании так называемых комбинированных систем, т. е. разомкнуто-
замкнутых систем. В них реализуются два принципа: принцип обратной
связи для ликвидации последствий действия всех видов возмущений как
измеряемых, так и неизмеряемых, и принцип компенсации измеряемых
возмущений. На рис. VI.47 представлена система этого типа. Учитывая
(
1
нк
Gr
1
1
1
Объект '
Сь
Z
If
c0e-sr
■tf ——_———_
| У ^ У
_J I
'</
Рис. VI.47. Блок-схема разомкнуто-замкнутой системы
трудности борьбы с возмущениями z при помощи цепи обратной связи
(так как возмущения действуют на часть объекта G0e_ST, содержащую
запаздывание), вводим цепь компенсации и определяем условия выбора
передаточной функции Hk этой цепи.
В операторной форме связь между Y (s), W (s) и возмущением Z (s)
имеет следующий вид:
Y(s)= Wo*"" W{s)+ (HGRGb+l)G0*-« z
Видно, что возмущение будет скомпенсировано при условии
1
H(s) =
Gr (s) Gb (s)
(VI. 139)
(VI. 140)
Это условие выполнить трудно, в чем можно убедиться, если
рассмотреть соотношение (VI. 135) и взять, например, простейший идеальный
пропорциональный регулятор с передаточной функцией Gr (s) = Kr.
Тогда
H(s) =
\+sT0
KrK0
(VI.141)
Следовательно, необходимо реализовать идеальный
дифференцирующий элемент.
Кроме дополнительных трудностей, связанных с измерением
возмущений, и того факта, что дифференцирующие элементы порождают в
системе сигналы с большими амплитудами, которые при наличии на входе
регулятора зоны насыщения срезаются, видно, что полная компенсация
возмущений невозможна. Действие некомпенсированных возмущений
уменьшается в процессе управления за счет наличия обратной связи.
213
Если объект регулирования с запаздыванием таков, что невозможно
измерить никакой величины, не содержащей запаздывания, то
используются специальные регуляторы Смита [1] или Ресвика [471. Идея этих
регуляторов основана на следующем. Если ни одна вспомогательная
величина, не содержащая запаздывания, недоступна для измерений, то ее
-Ф&&Ц
Рис. VI.48. Блок-схема системы с регулятором Смита
следует создать искусственно. С этой целью необходимо достаточно точно
знать математическую модель объекта и той ее части, которая не содержит
запаздывания, а также необходимо знать точно величину запаздывания.
Знание реакции системы без запаздывания позволяет регулятору
«предвидеть» будущее поведение системы.
1 Регулятор Ресвика II.
!?(Т>-
м
1
1
1
i
У
Та
Хс
S
1
IX -" -' ' - *^~
\
Jie'rs
^
\
»IL_
1
1
J
Объект
6„e-rs
1
У \ У
1
J
У
Рис. VI.49. Блок-схема системы с регулятором Ресвика
С целью упрощения анализа системы с регуляторами Смита и Ресвика
представим их блок-схемы (рис. VI.48 и VI.49).
Вначале проанализируем работу регулятора Смита. На основе блок-
схемы можно записать систему уравнений выхода
W — Y = Е;
Ег = Е-Ур(1- е-");
U = G&i,
(t/+Z)G„e-» = y;
UG0 = Yp.
(VI.142)
214
Исключая промежуточные переменные, получим зависимость между Y,
W и Z:
у /,д _ GR (s) G0 (s) e"sT w ,, G0e~ST(l + GR (s) G0 (s) - Gg (s) G0 (s) e~ST ,
Г W - 1 + GR (s) G0 (s) ^ W "Г 1 + GR (s) G0 (s) Z Is'■
(VI. 143)
В полосе частот, где | GR (/со) G0 (/со) | > 1, на основании
соотношения (VI. 143) можно приближенно записать
Y (s) « e-s*r (s) + G0 (s) (e~ST — e-2s*) Z (s). (VI. 144)
Таким образом, переходные процессы, вызванные скачкообразным
изменением управляющего сигнала, заканчиваются за время, равное
времени запаздывания т, а переходные процессы, вызванные скачкообразным
изменением возмущения, если объект содержит только запаздывание
G0 (s) = /С0, заканчиваются в течение 2т. Следовательно, регулятор
оптимален в смысле минимума времени регулирования, так как дальнейшее
уменьшение времени невозможно. Убедиться в этом можно с помощью
следующего рассуждения: на прохождение через объект с одним
запаздыванием т возмущающее воздействие затратит время т. Таким образом, только
через время т регулятор «узнает» о действии возмущения. Если регулятор
вырабатывает оптимальный управляющий сигнал, то этот сигнал после
прохождения через объект, т. е. опять через время т, ликвидирует
появившуюся ошибку управления, вызванную возмущением; следовательно,
в сумме окончание переходного процесса может наступить через
минимальное время, равное 2т.
На аналогичном принципе строится регулятор, предложенный Ресви-
ком (рис. VI.49). Этот регулятор труден в реализации, так как в нем
применяется оператор I/G0, обратный оператору, представляющему часть
объекта, не содержащую запаздывания. Элемент «предвидения»
регулятора Ресвика основан на системе с вспомогательной обратной связью,
причем в цепи обратной связи находится элемент с запаздыванием.
Уравнения выхода на основе блок-схемы имеют следующий вид:
Е = W — Y;
Up G0'
U = f/p+Pe-Ч/, р <1;
(U + Z) G0e-« = Г,
[ . (VI. 145)
где р < 1, так как при больших значениях р система была бы неустойчива.
Из соотношений (VI. 145) получим
Y(s) = !р — W(s) + G°(s) e~~STT(l ~ Pe~ST) Z (s)- (VI. 146)
w l+e-sT-pe-ST w^ l+e-sT-pe-sT w v ;
В случае, когда P = 1 и система находится на границе устойчивости,
получим
Y (s) = t~"W{s) + G0 (s) (e~s* — e-2sT) Z (s). (IV. 147)
Следовательно, соотношение совпадает с выражением (VI. 144) для
регулятора Смита, поэтому выводы полностью совпадают с предыдущими.
Оба регулятора имеют существенный недостаток с точки зрения
практической реализации элемента запаздывания. Если иметь в виду, что
запаздывание реальных объектов может быть от нескольких секунд до
нескольких часов, то видно, что практическая реализация элемента
запаздывания, у которого время запаздывания могло бы изменяться в таких
широких пределах, весьма затруднительна.
215
Теперь рассмотрим временное характеристики идеальных регуляторов
Смита и Ресвика. Полагая, что G0 = /C0 и GR = Kr, получим для обоих
регуляторов на основе соотношений (VI. 142) и (VI. 145) идентичную
зависимость
U(s) =
1
=«-*(*>•
Ко 1
При Е (s) = 1/s, разлагая 1/(1 — e~TS) в ряд, получим
U(S): ™ -
(VI. 148)
(VI. 149)
^0s п=0
или переходный процесс в области времени (рис. VI.50) записывается
в виде
«(/) = -!- £ 1(* —лт).
^0 п=0
(VI. 150)
Кои
*Ь
2\-
0 1г 2Г 3r 4r t
Рис. VI.50. Переходные процессы в
идеальных регуляторах Смита и
Ресвика
Таким образом, переходный процесс подобен тому, который
получили бы в импульсном регуляторе с экстраполятором нулевого порядка.
Положительные результаты применения
регулятора этого типа для управления
реальными процессами приведены в
работах [34, 411. Анализ качества системы
с регуляторами Смита дан в работах
[V. 17, 41, 681. Полученные результаты
говорят о том, что в некоторых случаях,
особенно когда речь идет об уменьшении
действия возмущений, с регулятором
Смита может конкурировать типовой
регулятор ПИД. Это в наибольшей степени
относится к тем объектам, у которых
относительная постоянная времени Т = 70/т
больше единицы [411.
В заключение этой главы приведем
общие соотношения для применения
конкретного типа регулятора в зависимости
от величины относительной постоянной
времени Т = Т0/х:
когда 5 < 7, достаточно релейного регулятора;
когда 1/5 < 7 <5, достаточно импульсного регулятора;
когда 1 < Г, достаточно типового регулятора непрерывного действия;
когда 0<7<1, необходимы специальный регулятор (например,
Смита) или другие методы компенсации запаздывания.
Список литературы
1. Baeck H. S. Hydraulic on—off servo: simple, rugged positioner. Control Engineering,
December 1967, pp. 79—82.
2. Баранчук Е. И. Проектирование и настройка электронных регуляторов. М., «Машгиз»,
1963, с. 268—290.
3. Bauer H. Berechnung von Regelkreisen mit nichtrationaler iibertragungsfunction. Rege-
lungstechnik, 1965, Heft 5, S. 217—223, Technische Hochschule Ilmenau, VEB Verlag
с Technik.
4. Bauer H. Ein Naherungsverfahren zur Reglereinstellung an Regelstrecken mit
nichtrationaler Obertragungsfunktion. Messen, Steuern. Regeln, 1967, Heft 8, Heft 11, S. 405—409.
5. Buckley P. S. Automatic control of processes with dead time. Automatic and Remote
Control, Vol. 1. pp. 33—40. London, 1961, Butterworths.
6. Бакклей П. С. Автоматическое регулирование процессов с чистым запаздыванием.
Труды I Конгресса ИФАК. Теория непрерывных систем. М., Изд. АН СССР, 1961,
с. 95—111.
7. Buckley P. S. Techniques of Process Control, Chapter 12. New York 1964, j. Wiley.
216
8. Eisenberg L. A controller design method for linear feedback control systems with
transport lag by parameter plane and dominant root methods. ISA Trans., 1967, No 3,
pp. 225—233.
9. Forys J. Dobor Qptymalnych nastaw regulatora P—I—D wspolpracujacego z obiektem
z czasem martwym. Praca diplomowa madisterska, Katedra Automatyki i Elektroniki
Przemyslowej AGH, Krakow, 1968.
10. Giloi W. Die Regelung von Totzeitstrecken nach dem Prinzip der Erganzenden Ruck-
fuhrung.
11. Gorecki H., Popek L. Analiza ukladow regulacji z opoznieniem (praca nieopublikowana)
Krakow, 1960.
12. Grabbe E. M.t Ra S., Wooldrige D. E. Handbook of Automation Computation and Control.
Vol. 3, New York. 1961, J. Wiley.
13. Hanny J. Bedingungen der practischen Optimums fur eine Regelstrecke zweiter Ordnung
mit Totzeit. Regelungs—technik, 1954, Heft 8, S. 191—197.
14. Isawa K., Hayashibe S. Optimum adjustment of control system. Regelungstechnik.
Moderne Theorie und ihre Verwendbarkeit. Munchen, 1957, E. Oldenbourg. S. 294—300.
15. Jansenn I. M. L. Control system behaviour expressed as a deviation ratio. Trans. Am. Soc.
Mech. Engrs., 1954, 76.
16. Емельянов А. И., Емельянов В. А., Калинина С. А. Практические расчеты в автоматике.
М., «Машиностроение», 1967.
17. Jex H. R., McDonnell I. D., Phatak A. V. A critical tracking task for manual control
research. I. E. E. E. Trans. Human Factors Electron, 1966, Vol. 7, No 4, pp. 138—145.
18. Junkier B. Das Verhalten idealisierter stetiger Regler und Regelstrecken mit ausgleich.
Regelungstechnik. 1955, Teil I, Heft 3, S. 54—58; Teil II, Heft 4, S. 80—84.
19. Кац А. М., Гоня к Н. Ф. Оптимальная настройка процесса изодромного регулирования
при различных видах запаздывания. В кн.: «Теплоэнергетические приборы и
регуляторы». Под ред. Кремлевского П. П. М., «Машгиз», 1960.
20. Kessler С. Ein Beitrag zur Theorie mehrschleifuger Regelungstechnik, 1960, Heft 8,
S. 261—266.
21. Kjndler H., Pohl G. Kleines regelungstechnisches Practikum. Berlin 1967, VEB—Verlag
Technik.
22. Кисляков В. С. Некоторые вопросы теории систем автоматического регулирования
с запаздыванием отображаемых линейными дифференциальными уравнениями с
запаздывающим аргументом. В кн.: «Автоматическое управние». Изд. АН СССР, 1960.
23. Копелович А. П. Автоматическое регулирование в черной металлургии. Краткий
справочник. М., «Машгиз», 1963.
24. Kopielowicz A. P. Dobor regulatorow automatycznych. Warszawa, 1964, WNT.
25. Корневский Д. Г., Колонец В. Г. Некоторые вопросы теории нелинейных колебаний
квазилинейных систем со случайным запаздыванием. — «Математическая физика»,
Киев, Изд. АН СССР, 1967, с. 91—113.
26. Кремлевский П. П. Теплоэнергетические и химико-технологические приборы и
регуляторы. М., «Машгиз», 1961.
27. Круг Е. К., Минина О. М. Электрические регуляторы промышленной автоматики.
Гл. V. М., Госэнергоиздат, 1962.
28. Кринецкий И. И. Основы автоматического регулирования химических процессов.
Киев, Гостехиздат, 1958.
29. Kuhne Ch. Ober den Zusammenhang der Zeitkonstanten einer Regelstrecke 2. Ordnung
mit den heirzu koresposdierten Tot und Anlaufzeiten. Regelungstechnik, 1967,
Heft 6, S. 206—207.
30. Ktipfmuller K. Accuracy limits of feedback control systems. Proc. I—st IFAC Congress,
Automatic and Remote Control, Vol. I, pp. 1—7. Lonbon 1961, Butterworths.
31. Kwakernaak H. Die optimale Regelung von einfachen chemischen Prozessen.
Regelungstechnik, 1968, H. 2, S. 57—62.
32. Kwakernaak H. Optimal filtering in linerar systems with time delays. IEEE Trans.
Autom. Control. 1967. No 2, pp. 169—173.
33. Лернер А. Я. Введение в теорию автоматического регулирования. М., «Машгиз»,
1958, с. 249.
34. Lubfer D. E„ Oglesby M. W. Applyng dead—time compensation for linear predictor
process control. ISA Journal, 1961, Vol. 8, No 11, pp. 53—57.
35. Marsik J. Eine schnelle Berechnung des Regelungsoptimums nach Oldenbourg und Sar-
torius, auch fiir Regelkreise mit transzendenten Frequenzgang. Regelungstechnik, 1958,
Heft 6, S. 217-219.
36. Мееров М. В. Синтез структур систем автоматического регулирования высокой точности.
М., Физматгиз, 1959.
37. Merz L. Die Begriffe Schwierigkeit, Leistungsfahigkeit und Durchftihrbarkeit in der
Regelungstechnik. Regelungs—technik, 1954, Teil I, Heft 2, S. 31—37.
38. «Метод Гольдфарба в теории регулирования», М., Госэнергоиздат, 1962, с. 96—99,
198—202.
39. Miller I. A. et al. A comparison of controller tuning techniques. Control Engineering,
Desember 1967, pp. 72—75.
40. Nicholson H. Control of sequential subsystem processes interconnected with transport
delays. Proc. Instr. Electr. Engrs. 1967, No 10. pp. 1562—1568.
217
41. Nielsen G. Control of system with time—delay. Materialy IV Kongresu IFAC, Warszawa,
1969.
42. Okori T. Inzynierskie metody doboru i strojenie regulatorow konwencjonalnych dla
obiektow z monotoniczna charakterystyka skokowa.Praca diplomowa. Katedra Automatyki
i Elektroniki Przemyslov ej AGH, 1962.
43. Przeworka—Rolewicz D., Rolewicz S. On control of linear periodic time lag systems.
44. Пухов Г. Е., Жук К. Д. Синтез многосвязных систем управления по методу обратных
операторов. Гл. VII. Киев, Изд. АН СССР, 1966.
45. Ragg В. С. Necessary conditions for the optimal control of a systems with
time—varying transport lags. IEEE Trans. Automat. Control, 1966, Vol. 11, No 4, pp. 738—740.
46. Reinisch K. Formel zur Bemessung von Regelkreisen einschlisslich Totzeit unter Einwir-
kung determinierter aperiodischer Storungen. Messen, Steuern, Regeln, 1964, Vol. 7,
No 3, pp. 94—101.
47. Reswick J. B. A delay—line controller. Materialy I Kongresu IFAC, Moskwa 1961.
48. Roberts A. P. Lagging filtering and progressive interpolation. Int. J. Control — 1967,
No 5, pp. 461—479.
49. Ротач. В. Я. Расчет настройки промышленных систем регулирования. М., Госэнерго-
издат, 1960, Гл. V.
50. Schliessmann H. Die Einstellung der Regel para meter fur Regelstrecken mit uberwiegen-
der Totzeit. Regelungstechnik, Marz 1962, Heft 3, S. 97—102.
51. Schliessmann H. Ober die optimale Bemessung von Regelsystem mit Laufzeit.
Regelungstechnik, 1959, Heft 8, S. 272—280.
52. Schliessmann H. Uber ein Verfahren zur optimalen Regelung von Systemem mit Totzeit.
Regelungstechnik, 1959, Heft 12, S. 418—421.
53. Schmidt C. Vergleich verschiendener Totzeitregelsysteme. Messen, Steuern, Regeln,
1967, Heft 2, S. 71—75.
54. Schmidt J. Dobor optymalnych parametrow nastawczych regulatorow P, I, P—D w
ukladach automatycznej regulacji obiektow inercyjnych pierwszego rzedu z rzeczywistym
czasem opoznienia. Praca dyplomowa magisterska. Katedra Automatyki i Elektroniki
Przemyslowej AGH, Krakow 1968.
55. Shearer I. L., Scher R. S., Reid K. N. Standards for linear control systems. Control,
1961, Vol. 4, No 39, pp. 115—116.
56. Simpson R. S., Monts R. С A difinition of average time delay for a linear system. Proc.
IEEE, 1967, No 10, pp. 1773—1734.
57. Soliman J. I., Al—Shaikh A. A state—space approach to the stability of continuous
system with finite delay. Control, Part I, 1965, No 88t pp. 554—556; Part II, 1965, No 89,
pp. 626—628.
58. Strejc V. Adjustability of derivative and intergal time constants in P—I—D controllers
with interaction. Acta Technica, 1960, No 5.
59. Strejc V. MoZnosti a dosavadni vysledku tabelovani optimalnych regulacnich pochodku.
Praha, 1962, Ustav teorie informace a avtomatizace CSAV.
60. Strejc V. О mozonostech vyssiho vyuZiti Theorieregulace v praxi. Praha, 1958, С S. T.S.E.
61. Strejc V. Possibilities and present achievements of tabulating optimal control processes.
Automatic and Remote Control, Vol. I, pp. 46—54. London, 1964, Butterworth.
62. Strejc V. ijnni: Teoria regulacji automatycznej. Warszawa, 1962, WNT.
63. Syrbe M. Ober die optimale Einstellung von Reglern auf Grund geometrischer Daten
der Regelstrecken — Frequenzgange. Regelungstechnik, 1963, Heft 7, S. 160—166.
64. Stiepan J. Podminky autonomnosti a invariantnosti kotelni regulace. Souhrn Praci о
Automatisace. Praha, 1961, 6. A. V. s. 303—316.
65. Weinmann A. Die bestimmte und verallgemeinerte Vorhersage von Signalen in linearen
Regelungssystemen. Elin—Z., 1965, Nr 1—2, S. 18—55, 11—111.
66. Westcott I. H. The development of relationships concerning the frequency bandwidth
and the mean square error of servo systems from properties of gain—frequency
characteristics. Automatic and Manual Control. New York, 1952, A. Tustin Editor Academia
Press, pp. 45—64.
67. Wolny J. Analiza i synteza ukladow automatycznej regulacji z regulatorami konwencjo-
nalnymi i obiektami I—go rzedu z czasem martwym. Praca doktorska, Katedra
Automatyki i Elektroniki Przemyslowej AGH, Krakow, 1962.
68. Wrobel Cz. Regulacja obiektow z czystym opoznieniem przy zastosowaniu regulatorow
P—I—D i specjalnych. Praca diplomowa. Katedra Automatyki i Elektroniki
Przemyslowej Krakow, 1964, AGH.
69. Wunsch G. Podstawy automatyki. Warszawa, 1961, PWT.
Глава VII
Импульсное управление объектами
с запаздыванием
§ VII.1. Определение переходных процессов
и анализ устойчивости
Математическое описание импульсных систем управления сводится к
разностным уравнениям, и когда они линейны, их решение можно найти,
используя различные методы: дискретное преобразование Лапласа [3],
[61, операторы Брауна [4], [47], z-преобразование [181 или
модифицированное z-преобразование [34], [431, [45], осуществленное Баркером [21,
[17], [23]. Для анализа импульсных систем с запаздыванием наиболее
подходящим является метод модифицированного z-преобразования.
Поэтому в этой глав,е будет использован именно этот метод. Следует
упомянуть, что для анализа переходных процессов в нелинейных импульсных
• Импульсный регулятор
Рис. VI 1.1. Блок-схема импуль- i *> (Т) £ 1 о^о | »
сного регулятора (—ЛТ^ \ h ! "
Р
£
>
*С
И
и
-J
системах наиболее приемлемым методом является использование
цифровых машин, что объясняется наличием рекурентных соотношений при
описании динамики систем данного типа.
Ограничимся рассмотрением систем с экстраполяторами нулевого
порядка, так как именно этот тип системы чаще всего встречается на
практике.
Рассматриваемый импульсный элемент состоит из двух частей
(рис. VII.1):
а) импульсного модулятора /р, который через определенные интервалы
времени Тр, называемые периодом повторения, выдает на выходе
импульсные сигналы с теоретически бесконечно малой длительностью и с
амплитудой et., равной величине непрерывного сигнала s(t), поступающего на
вход импульсного элемента в данный момент времени. Таким образом,
+ С-
8. (nTp)= J 8 (0 б (t - пТр) dt, (VII.1)
— со
где б (t — Тр) — импульс Дирака;
б) удерживающего элемента Р, который до момента появления
следующего импульса запоминает и выдает на выходе постоянный сигнал е
с амплитудой гг Этот сигнал далее поступает на непрерывную Rc или
дискретную часть Rd регулятора, где окончательно формируется
управляющий сигнал и.
219
Процесс образования сигнала е из 8 (/) с помощью сигнала е.
изображен на рис. VII.2.
Связь между отдельными сигналами выражается следующей
зависимостью:
со оо
£(s) = Ji(Oe-«'<tt=S J ё(/)е-'Л=2 J е(кТр)*-*< dt =
О k=Q kTp k=0 kTp
со оо
2 eW(-{)[rf+"^j;eft)e-*a(l-e-4 (VII.2)
k=Q
k=0
где предполагается (рис. VII.2),* что на каждом отрезке [kTp + (& +
+1) 7^1 функция 8 (&ТР) постоянна.
Так как на основе выражения
(VII.1)
Ei(s)=f>e(kTp)e-sTPk, (VI 1.3)
k=0
*/,
0
i
/
/
У
/
г
£
-«—
N
|Ч7—-<1
\
Г
г —
t
то окончательно
E(s) = ±(l-e-sTp)El(s). (VII.4)
С учетом формул (VI 1.2) и (VI 1.4)
передаточную функцию
удерживающего элемента можно представить
следующим образом:
GJs)-
Et(s) s yl
sT,
)■
(VII.5)
Теперь введем обозначение
Рис. VII.2. Преобразование непрерывного
сигнала в ступенчатый
г = esV
Тогда уравнение (VI 1.3) можно записать в следующем виде:
Е,(г)= £ e(kTp)z-k.
*k=0
(VII.6)
(VII.7)
Зависимость представляет собой операцию» известную как z-преобра-
зование, которое получило широкое распространение. Однако обычное
z-преобразование, определяемое зависимостью (VII.7), имеет
существенный недостаток. Если осуществить обратное преобразование для
отыскания 8 (/) из Е. (z), то обнаружим, что точные значения г (t) получаются
только при / = kTp, а промежуточные значения функции е (/), т. е. между
моментами времени t = кТри t = (k + 1) Тр, могут быть получены только
интерполированием. Этот недостаток ликвидируется так называемым
модифицированным z-преобразованием, с помощью которого можно получить
значения функции г (t) для произвольного момента времени.
Для иллюстрации модифицированного z-преобразования рассмотрим
систему, изображенную на рис. VI 1.3.
На этом рисунке представлено звено запаздывания, а штриховой
линией — фиктивный импульсный элемент на выходе, работающий
синхронно с прерывателем на входе. Фиктивный прерыватель необходим
220
для однозначного определения передаточной функции импульсной
системы. Передаточная функция, как обычно, представляет собой отношение
преобразования выходного импульсного сигнала yxi (t) к преобразованию
входного сигнала ei (t). Пусть Gb (s) обозначает передаточную функцию
непрерывной части системы, не содержащей запаздывания, a e_TS —
передаточную функцию звена запаздывания. Тогда
Ух О =y(t-i) = y(t- Wp); (VII.8)
% = ■
(VII.9)
УпУ)
£oy(kTp-XTp)8(t-kTp).
(VII.10)
Вообще говоря, в зависимости от
величины запаздывания могут существовать три ^«|
случая.
Gb(s)
y(t)
-TS
ffjt)
Ут№
Рис. VII.3. Иллюстрация модифицированного преобразования
Случай первый: К — целое число.
Обозначая через Е (z) и Y (z) преобразования сигналов г (t) и у (t)
и учитывая формулу (VII.6), получим, что
У, (г) = Z \y (t - %Тр)\ = S х (kTp - 1Тр) г-»=
/2=0
= S У (kTp - ХТр) г- (*»Л) 2-я = 2-%у (г),
k=0
(VII.11)
где z обозначает z-преобразование.
Таким образом, импульсная передаточная функция системы равна
Ох(г)
-= Ух (г) х Y(z)
E(z) E(z)
= Z"4?(z),
и окончательно
Gx(z) = z~b S g(kTp)z~k,
k=0
(VII.12)
(VII.13)
где g (kTp) — дискретные значения реакции импульсной системы без
запаздывания.
Из соотношения (VII. 12) следует, что для учета запаздывания
величиной т = КТр необходимо передаточную функцию G (z) умножить на z-%.
Случай второй: К — правильная дробь.
Пусть
шТр + КТр = Тр или К = 1
где пг заключено между 0 и 1.
Тогда уравнение (VII. 10) принимает вид
/72,
(VII.14)
Ух, (0=S? WP + («- 1) Тр] б(/- kTp).
k=0
(VII.15)
221
Применяя к уравнению (VII. 15) z-преобразование, получим
Ух (*) = z-1 S У ikTp + mTp) z-K ■ (VII. 16)
Аг=0
Значения запаздывающего сигнала ух (t) в дискретные моменты
времени равны соответствующим значениям выходного сигнала у (t) в
моменты тТр, тТр + Тр, . . . Эти значения обозначим через yL (t, m).
Символически можно написать
yr(kTp)=y(kTpt m); (VII. 17)
Vxi (0 = Vi (<■ ")• (VII.18)
Следовательно, величина # (&Гр + пгТр) соответствует величине у (t)
в момент времени t = kp + >яГр, лежащий между &7^ и (& + 1) Тр.
(кЩ t
Рис. VI 1.4. Импульсный сигнал и запаздывающий импульсный
сигнал
Вышеприведенные рассуждения хорошо иллюстрирует рис. VI 1.4.
Таким образом, уравнение (VII. 15) можно переписать в следующем виде:
00
yt(t,m)= E y[(k + m)Tp-Tp\b(t-kTp). (VIJ.19)
Когда m изменяется от 0 до 1, то уравнение (VII. 19) дает все значения
на этом отрезке. Применим к уравнению (VII. 19) z-преобразование.
Получим
Y (z, т) = z-1 £ У {kTp + тТр) г-*;
k=0
(VII.20)
р i "«" р/
это и есть модифицированное преобразование, которое обозначается Zm:
Zm [у (t)] = Y (z, m). (VII.21)
Легко заметить, что при пг = О
Vi (t, 0) = S У (kTp-Тр) б(/-kTp)
k=0
ИЛИ
У (г, 0) = г -1 S У №) г* = г-1 Г (г).
k=0
(VI 1.22)
(VII.23)
Это означает, что при пг = О сигнал */ (*) запаздывает на период
повторения Тр.
При пг = \
У, (', 1) = Е У («Те) б (t - kTp) = yt (t)
k=0
Y(z, l) = z^ S y(kTp + Tp)z-* = Y(z).
k=0
(VII.24)
(VII.25)
222
Следовательно, при т = 1 имеет место обычное z-преобразование.
Вышеприведенные рассуждения справедливы при условии, что у (t) в
промежутках между моментами замыкания прерывателя представляет собой
непрерывную функцию.
По аналогии с формулой (VII. 12) можно ввести понятие
модифицированной передаточной функции
со
G (г, т) = ^pJ«L = z-i 2 * (kTp + тТр) *-*. (VII.26)
E(z)
/г=0
Случай третий: К — непрерывная дробь.
Предположим, что
(л—1)<Ь<я, X = n — m, (VII.27)
где п — целое число; т — правильная дробь.
Запаздывающий сигнал
Ух (0 = У Ш + тТр) - пТр]. (VII.28)
В связи с этим • 4
Ус (/, гп) = S У К* + т) Гр - пГр] б (t - кТр). (VII.29)
fe =0
После применения модифицированного z-преобразования к
выражению (VI 1.29) получим
00
Y (z, m) = Z-" 2 у (£ГР + тГ„) z~*. (VI1.30)
/г =0
При т = 1 уравнение (VII.30) переходит в уравнение (VII.20).
Помещенная в конце главы табл. VII.И содержит оригиналы и
соответствующие z-преобразования. С помощью этой таблицы можно быстро
по оригиналам определить их z-преобразования и наоборот.
В общем случае применимость формулы (VI 1.30) зависит от возможности
быстро находить сумму бесконечного ряда. Когда при использовании
формулы (VI 1.30) и в последующем отыскании с помощью таблицы
оригиналов, соответствующих данным преобразования, встречаются
значительные трудности, можно использовать иное определение
модифицированного z-преобразования.
Пусть G (s) обозначает непрерывную передаточную функцию с п
некратными корнями si в левой полуплоскости комплексной переменной.
Тогда соответствующая ей модифицированная импульсная передаточная
функция определяется соотношением
G (*, т) = г"1 V %g_I Res G (s) |s=v (VII.31)
Выражение (VII.31) является аналогией известных формул Хевисайда
для непрерывных систем.
Оригинал для G (z, m) находится из соотношения
g (kTp, m) = -^ <J> G (z, m) z*-1 dz, (VI1.32)
г
причем контур Г должен охватывать все особые точки функции
G(z, m) z*-1.
Другим, часто используемым на практике методом определения
переходных процессов является разложение в степенной ряд относительно z"1
и последующее отыскание оригиналов для отдельных членов разложения.
Метод этот приближенный, однако легко реализуется на цифровых
машинах и позволяет легко учесть ошибки аппроксимации. Принимая т за
постоянный параметр, делим числитель передаточной функции G (z, га)
223
на ее знаменатель. Полученные таким образом коэффициенты при zrk
являются функциями т и определяют функцию g (kfpy m) в k-u периоде
при изменении т от 0 до 1. В работе [211 можно найти описание
программы на языке Fortran-II вместе с примерами.
Для иллюстрации методов, применяемых для анализа и синтеза
импульсных систем, рассмотрим типовую импульсную систему
регулирования. Система, блок-схема которой представлена на рис. VI 1.5, состоит
из прерывателя и экстраполятора нулевого порядка, непрерывной части
(чаще всего типа ПИД) и инерционного объекта первого порядка с
запаздыванием.
Полученные выше соотношения относятся к двум основным задачам:
а) воспроизведение управляющего сигнала, который может
представлять собой, например, скачкообразное изменение величины w\
б) ликвидация отклонений, возникающих из-за действия возмущений,
например скачкообразного изменения z.
VI 1.1.1. Анализ систем по управлению
Пусть передаточная функция непрерывной части регулятора системы,
показанной на рис. VI 1.5, имеет вид
где
Р =
О,
1.
GR(s)=KR(p + c-±r + rTds),
когда пропорциональная составляющая отсутствует;
(VI 1.33)
с =
когда пропорциональная составляющая присутствует;
О, когда интегральная составляющая отсутствует;
. (VII.34)
(VII. 35)
={■:
1, когда интегральная составляющая присутствует;
О, когда дифференцирующая составляющая отсутствует;
когда дифференцирующая составляющая присутствует.
(VI 1.36)
-»<^о » GR *А G0 —»♦ »
1 1 I 1 L
Рис. VI 1.5. Блок-схема одноконтурной импульсной системы
Пусть передаточная функция объекта
G0(s)
q+sT0
где
(VII.37)
(VII. 38)
0 для астатических объектов;
1 для статических объектов,
а передаточная функция экстраполятора нулевого порядка определяется
соотношением (VII.5).
Следовательно, на основе выражений (VII.5), (VII.33), (VII.37) можно
написать соотношение для передаточной функции разомкнутой
непрерывной системы
и (S) ~ Ei (s) ~" ~тГ
***о (\ _ e~sTp)\ rTd 4-
+
1
+л. .(.+^) ,(s+t)
il
(VII.39)
224
Из блок-схемы, представленной на рис. VII.5, следует такая система
уравнений:
Y(s) = G(s)E. (s); (VII.40)
Е (s) = W (s) — Y (s). ' (VII.41)
Исключая Y (s) из этих уравнений, получим
Е (s) = W (s) — G (s) E. (s). (VII.42)
Зависимость между преобразованиями импульсных сигналов Wt (s)
и Et (s) на основе соотношения (VI 1.42) имеет вид
Et (s) = Wt (s) - G, (s) Et (s) (VII.43)
или
' - •• Wt(s)
£,(«)'
(VII.44)
v M _ Gt (s) Wt (s)
riW- l+Q,{8)
l+G,-(s) *
Таким образом, окончательно из формул (VII.44) и (VII.40) получим
Y®=°i+Zl}$- (VIL45)
Преобразование последовательности импульсов выходного сигнала на
основе соотношения (VI 1.45) будет иметь вид
(VII.46)
z-преобразование выражения (VII.46) определяется соотношением
Модифицированное же преобразование Y (z, m), которое необходимо
из-за наличия содержащегося в Gi (s) запаздывания, определяется на
основе формулы (VII.46):
это преобразование совпадает с обыкновенным z-преобразованием для
систем без запаздывания. Оно не может служить для нахождения
произвольных значений Y (z, m) между моментами замыкания прерывателя.
Найдем передаточную функцию G (z, m) (например, из табл. VII. 11),
соответствующую преобразованию G (s) (VI 1.39):
(?(«,«)- . ^.Jff-'-^'fr-
(*-.
D+
сТп
1
+ f [(г - e-'Vr«) + e4«V. (* - 1)] + -^
(г — 1) (z — e-"Vro) -J-
Теперь введем относительные величины:
Г[^.(г-е-^^.) +
(z— 1)2 . (VII.49)
Y =
D =
1 =
К =
' X '
' X '
. Td .
Tt .
т '
KrK0
15 X. Турецкий
(VII.50)
(VII.51)
(VII.52)
(VII.53)
(VII.54)
225
Очевидно, что К является статическим коэффициентом усиления
разомкнутой системы. Предполагается, что относительный период
повторения у ^ 1- Это означает, что период повторения не меньше времени
запаздывания. Рассмотрение случая у <1, т. е. когда период повторения
меньше времени запаздывания, малоинтересно, так как во все моменты
времени, меньшие времени запаздывания, не может быть передана
никакая информация с объекта на регулятор, и, следовательно, регулятор не
может «знать», в каком направлении управлять системой г.
С точки зрения наилучшего использования информации за оптимум
следует принять у = 1, т. е. равенство периода повторения и времени
запаздывания. Независимо от этих принципиальных соображений
теоретическое исследование случая у < 1 весьма сложно.
Подставляя обозначения (VII.50)—(VII.54) в соотношение (VII.49),
получим модифицированную передаточную функцию разомкнутой
системы в следующем виде:
G <*• т) = 2 (,-%/*) {г"т е~*("~1)/r{z~l) + fl(z~*~qylT)~'
_ е_„ (Y_1)/r {z_l)]+c^_r _L_ J" JL {z _ e-,Y/r} +
(VII.55)
Для упрощения записей введем следующие обозначения:
ф1= i-(l — e-*<v-i)/r); (VII.56)
Фо = — (е-* <тМ>/7 — e-*v/*); (VII.57)
ч
^2=jr(e-giy-l),T+q(y^l)- l); (VII.58)
Ъ = Т {у- ~ (1 + *-"'$ [^Y^1 ~1]- 2е~й (V_1 )/Г}; (VIL59)
ф0 = ±- [е-я(v-D/r + (^zzii_ i) eL^v/r _^L e-„,r] .
(VI 1.60)
Обозначая в выражениях (VII.56)—(VII.60)
i__
£ = e" T , (VII.61)
сведем их в таблицу (см. табл. VII. 1) при q = 1 и q = 0.
Подставляя формулы (VI 1.56)—(VI 1.61) в соотношение (VI 1.55),
получим окончательно выражение для передаточной функции разомкнутой
системы:
G(z,m) = г(г*Еяу} ['•-^-£^-1>(г-1) + р(ф1г + Ф.) +
+ С~ПГ'Т=Т ^ + ^z + *o)] • (VII.72)
1 Если импульсный характер системы следует из того, что используются прямое
цифровое управление и аналого-цифровые преобразователи, преобразующие непрерывный
сигнал в цифровой код с периодом повторения Тр, то с учетом многоканальности
преобразователя и его технической реализации часто случается, что Тр <^ т и у <g 1 и,
следовательно, период повторения Тр значительно меньше времени запаздывания. Однако в этих
случаях динамика импульсной системы чрезвычайно близка к динамике непрерывной
системы, и поэтому анализ системы управления можно вести с помощью понятий и методов,
используемых в непрерывных системах с запаздыванием (Прим. ред. оригинала).
226
Таблица VILI
9i
9o
^2
*i
^0
q=l
1_£Y-1
£•7-1 _ £V
£v-i_1+Vjzl
1 + ^ + £V_XzlL£y_
£Y-1_£V_._|!_
(VII.62)
(VI 1.63)
(VI 1.64)
-2£v-! -
(VI 1.65)
(Vll.66)
q=0
1
2
1
2
v-i
Г
1
T
\ T )
V2 + 2v — 2
T2
1
2Г2
(VII.67)
(VI 1.68)
(VI 1.69)
(VI 1.70)
(VII.71)
Кроме соотношения (VI1.48) передаточная функция замкнутой системы
будет иметь вид
Gw(z) =
К [г ^г Е« <V-D (z- 1) + р (ф12+ Фо) + с -L.. _L- (г|>2г2+ ф12 +я|)0)]'
Г
1 1
z (г-Е**) + К [r-^Eq (1M) (г- 1) + р(сР1г+ Фо) +
+ ^77r#T=rr(^22 + ^2 + «] (VII.73)
VII. 1.2. Анализ системы по возмущению
Теперь определим передаточную функцию системы при скачкообразном
изменении возмущающего воздействия. Блок-схема системы изображена
Рис. VI 1.6. Блок-схема
системы с возмущением,
приложенным ко входу
объекта
ЧУ
на рис. VI 1.6. Поступая аналогично предыдущему случаю, получим
следующее выражение передаточной функции замкнутой системы по
возмущению:
tfo(<PiZ + 9o)
G2(z)
l 1
г (г - I™) + К [г Цг Е-" <v-D (z-\) + p (9lz + Фо) + с J/T z _ {
(VII.74)
Группируя слагаемые числителей и знаменателей в выражениях (VI 1.73)
и (VII.74) по степеням z, можно показать следующее:
15* 227
1. Числитель передаточной функции замкнутой системы по
управляющему воздействию w имеет вид
Ьг = В2г2 + Вгг + В0. (VI 1.75)
2. Числитель передаточной функции замкнутой системы по
возмущающему воздействию имеет вид
L2 = C2z2 + C±z + С0. (VII.76)
3. Знаменатель передаточной функции замкнутой системы независимо
от места приложения возмущающего воздействия имеет вид
М = Л3г3 + А2г2 + Ахг + А0. (VI 1.77)
Для единообразного представления систем как с непрерывной частью
типа ПИД, так и ПД в выражениях (VII.73) и (VII.74) числители и
знаменатели умножим на C(z — 1) и получим однотипные выражения для
коэффициентов Aki Bk и Ck.
Теперь с помощью выражения (VI 1.32) можно найти переходные
процессы рассматриваемых систем.
Преобразование реакции системы на скачкообразное изменение
управляющего сигнала определяется из формулы (VII.73) и табл. VII.2:
Y. (*.")= АЛ7ЛХг°+Ай -Т=Т- №88)
Таблица VI 1.2
Коэффициенты Л&, £& и Ck
Az = c (VI 1.78)
А^с^^ + с^Къ + г-^&^-ЕЧУ]-! (VII.79)
Л1 = с^г|>1 + с[р/СФо-г^£^^^
(VI 1.80)
A0 = c-^r%- [pK^-r-f-E*^]
Вг-с-^Ъ + с [pKih + r-tg-eHW]
(VII.81)
(VI 1.82)
B^c-^^ + c [рКщ-rJ^- Е«^] - [рКъ + г-!£-1*™]
(VI 1.83)
В. = с-^-♦.-[рКфв-г^-£»«*-»] - (VII.84)
C2 = cK0<Pi (VI 1.85)
Ci^cK&o-KoVi (VI 1.86)
C0 = -Ko<Po (VI 1.87)
228
Аналогично определяется реакция системы на скачок возмущения:
Y> <*. «> = АЛглЛХ%А0 • 1=т ■ <vii-89>
Как и в случае непрерывных систем, эти преобразования представляют
собой некоторые рациональные функции переменной z.
Если преобразование реакции записать в общем виде
y^^=Wt't^t^ ' <VII-9°)
то, зная корни уравнения
М (г) = О, (VII.91)
выражение (VII.32) можно свести к виду, эквивалентному формуле Хе-
висайда для непрерывных систем:
k
Y(NT )= L(1) -*- V ^ zN 4-
r=\
n—k
+ S 2 I (*-$(««) 11г<1"cos ("e< + *«)• <VIL92)
где zr — действительные корни; zi — комплексные корни
уравнения (VII.91), а их сумма, очевидно, равна степени полинома М {г).
Пусть
z, =а, +/р,. (VII.93)
Тогда, очевидно,
e. = arctg|^ (VII.94)
и
Ф, = arg L (zt) - arg (z. - 1) - arg M (г.), (VII.95)
Формула (VI 1.92) справедлива, когда М (z) имеет только некратные
корни. В случае кратных корней из выражения (VII.92) за счет
предельного перехода zr —> zr+1 можно получить соотношение, справедливое
для этого случая.
Первое слагаемое в правой части выражения (VI 1.92) характеризует
установившееся состояние; второе слагаемое — апериодическую
составляющую переходного процесса и третье — колебательную составляющую.
Так как zr и z. с ростом времени дают выражения (| zr S)N (| zt \)N , то для
того, чтобы переходные составляющие затухали, все корни должны лежать
внутри круга единичного радиуса, а для устойчивости линейной системы
необходимо, чтобы внутри круга единичного радиуса на плоскости z
лежали все корни уравнения (VII.91).
Методы вычисления переходных процессов в импульсных системах
подробно описаны в работе [28].
На рис. VI 1.7 изображен вид переходных процессов в зависимости от
расположения корней.
Для определения максимальной динамической ошибки приравниваем
к нулю первую разность у (NTp) (рис. VI 1.8):
Ar/ (NmTp)~= у [(N + 1) Тр] - у (NTp) = О, (VII.96)
предполагая, что вторая разность для данного N отрицательна, т. е.
^У(МтТр) <0. (VII.97)
229
Однако может случиться, что одна и та же максимальная величина
наблюдается в двух следующих друг за другом моментах времени
(см. рис. VII.9), тогда величина Nm9 полученная из уравнения (VII.96),
У\
"W-v.
Л
/
птЦ
■щртг /
Rez
Рис. VI 1.7. Виды переходных процессов в зависимости от расположения корней
характеристического уравнения
не будет целым числом и, следовательно, за момент появления максимума
следует взять число
N = Е [Nm+Ut (VII.98)
где Е [Nm + 11 означает, что надо взять целую часть числа Nm + I.
У1
h Щ
NTn
Тр 27р NTp(N+1)Tp t
Рис. VI 1.9. Максимальное динамическое
отклонение в моменты / = NTP и t = (N + 1) Тр
Рис. VI 1.8. Максимальное
динамическое отклонение в момент
времени t = NTP
§ VII.2. Вопросы устойчивости
Для анализа устойчивости импульсных систем можно использовать как
критерий Найквиста, так и аналитические критерии, например, критерий
Шура—Кона, являющийся аналогом критерия Гурвица.
VI 1.2.1. Критерий устойчивости Найквиста
Так как передаточная функция разомкнутой импульсной системы в общем
случае представляет собой рациональную функцию оператора г, то,
используя известный принцип аргумента, можно сформулировать критерий
Найквиста по аналогии с непрерывными системами.
230
Пусть знаменатель передаточной функции замкнутой системы имеет вид
= cnzn + cn_1zn-l+-..+c1z + c0 m (VII.99)
и пусть N — число нулей, а Р — число полюсов функции М (z). Анализ
выражения (VII.92) показывает, что необходимым и достаточным условием
устойчивости замкнутой импульсной системы является расположение
всех нулей полинома М (z) внутри круга единичного радиуса.
Из принципа аргумента следует, что если z один раз очертит на z-пло-
скости окружность единичного радиуса с центром в начале координат
против хода часовой стрелки, то конец вектора М (z) на плоскости
Im [M (z)], Re [M (z)] охватывает начало координат
Q = Z1 — P1 (Vir.100)
раз, где Z1 и Рг — соответственно нули и полюсы функции М (z),
находящиеся внутри круга единичного радиуса. Но полюсы функции М (z)
одновременно являются полюсами функции G (z). Уравнение,
преобразующее z-плоскость в М (z), имеет вид
М (z) =0, (VII.101)
а уравнение, преобразующее z-плоскость в плоскость G (z),
G(z) = —1. (VII.102)
Если замкнутая система устойчива, то все нули функции М (z) лежат
внутри окружности единичного радиуса, а число их, следовательно, равно
порядку числителя функции М (z), т. е.
Nx = п. (VII. 103)
Так как охват начала координат концом этого вектора можно заменить
охватом концом вектора G (z) точки (—1, /0), то можно сформулировать
следующий критерий устойчивости.
Замкнутая импульсная линейная система будет устойчива, если число
обходов точки (—1, /0) концом вектора G (z) равно
Q = n — Plt (VII.104)
когда z обойдет 1 раз начало координат по кругу единичного радиуса
в направлении, противоположном ходу часовой стрелки.
Если все полюсы разомкнутой системы также находятся внутри
единичного круга, т. е. если
Рг = п, (VII.105)
и, следовательно, если разомкнутая система устойчива, то число обходов
точки (1, /0) концом вектора G (z), чтобы замкнутая система была
устойчива, должно быть равно %нулю:
Q = n — n = 0. (VII. 106)
VI 1.2.2. Критерий Шура—Кона и Гурвица
V
Задано характеристическое уравнение замкнутой линейной импульсной
системы
М (г) = anzn + ап_^п-1 + : - - + агг + а0 = 0. (VII. 107)
Для исследования устойчивости системы, представленной
уравнением (VII. 107), записывается определитель 2&-го порядка, где к = 1,
231
2, . . ., n, a n — порядок уравнения (VII. 107):
Д* =
о
0
0
. . 0
. . 0
<*п
0
«п-1 •
ап .
• ■ ая-А+1
• • an-k+2
<tk-l
ап
an-i
a>k-2
0
^
Я/е-З
.
0
• • а0
. . 0
. . 0
0
а0
0
0
~ах
Rl
О
ап-к+1 an-k+2 an-k+3
о о
&h-
• ak_2
(VII. 108)
Здесь ап — коэффициенты сопряжения с ап.
Определить А^ имеет 2k строк и 2k столбцов.
Теорема/Все корни уравнения (VII. 107) находятся внутри единичного
круга, если определители (VII. 108) из коэффициентов уравнения (VII. 107)
удовлетворяют следующему неравенству:
Ak <0 при k нечетных
Ak > 0 при k четных
лх |
(VII. 109)
причем при k = 1 ак_г = а0 и an_k+1 = ап.
Например, при п = 1
М (г) = агг + а0;
при /г = 2
Д,=
Ai =
ап ал
= а«ап
(hfh < 0;
а0
«2
а0
ах
а*
\
а2
а0
С
а
С
а
= ^о^о — <
> , Я 2 <*1
о 0 а%
~а0 "flj
2 0 «0
>о
и т. д.
Использование этого критерия требует вычисления определителей очень
высокого порядка, поэтому часто используется преобразование
единичного круга в левую полуплоскость комплексного переменного, благодаря
чему далее можно пользоваться либо критерием Рауса, либо критерием
Гурвица.
Последовательность преобразований показана на,рис. VII. 10.
Полагая
2 =
1 +W
(VII.110)
232
перейдем от единичной окружности на плоскости z к левой
полуплоскости w. Служащая грайицей на плоскости s мнимая ось в плоскости z
преобразуется в окружность с единичным радиусом, а в плоскости w гра-
/ А > S S S
/Дополни- /Л
у тельная ^/А
', плоскость /X
v
» Ч X N \\N
Осно6*ная\^\
плоскость
Я
/Дополни- /А
у тельная '/Л
.плоскости /У
у тельная '/Л/ >с
' плоскость/X//
Т,
ImS
2
ScSs
VA'
3us
2
Рис. VII. 10. Последовательность преобразований области устойчивости
ницей снова служит мнимая ось. Более подробно этот критерий рассмотрен
в работе [281 (стр. 181).
Далее определим границы областей устойчивости систем, описываемых
соотношениями (VI 1.88) и (VI 1.89).
§ VII.3. Области устойчивости
на плоскостях настраиваемых параметров
С учетом соотношения (VII.77) положим в уравнении (VII.91)
z = a +/р (VII.Ill)
и получим
Л3а3 +Л2а2 +Аха + А0 — ЗЛ3сф2 — Л2Р2 = 0; (VII. 112)
/Р (ЗЛ3а2 + 2Л2а — Аг — Лзр2) = 0. (VIIЛ13)
На основе уравнений (VII. 112) и (VII. 113) можно рассмотреть
следующие два основных случая.
VI 1.3.1. Определение границы апериодической устойчивости
На границе устойчивости должно выполняться соотношение
\г\ =а2 + р2 = 1 (VII.114)
и, кроме того, для апериодической устойчивости должно быть
. Р =0. (VIIЛ15)
Тогда из формул (VII.114) и (VII.115) следует, что
а = +1; (VII.116
а = —1. (VII.117)
Подставляя (VII. 115) и (VII. 116) в выражение (VIIЛ12), получим
А3 +А2.+ Аг +Л0 = 0, (VII. 118)
а на основе табл. VII.2 уравнение (VII. 118) можно записать в виде
(с-1)[1-^ + р/С(Ф1 + Ф0)]+^№о + ^1 + %)==0. (VII.119)
Соотношение (VII. 119) как для статических (q = 1), так и для
астатических объектов (q = 0) может быть выполнено только при К = 0,
следовательно, этот случай не представляет интереса.
233
Но, подставляя выражения (VII. 117) и (VII. 115) в соотношение (VII. 112)
и также пользуясь табл. VI 1.2, получим, что
(c + l)(l+£«v)
/С =
(с + 1) [р (ф! - Фо) + 2г^- Е" <v-D] + с jL- (t|)a - Ъ + t|>0)
(VII. 120)
Из табл. VII.1, полагая в (VII.120) q = 1, получим формулу для
статических объектов
К =
1
('-т^)+**-
Еу
—1
(VII. 121)
х
г *м
\+Е? С+1 //Г
<('++)]
X
и аналогично для q = 0
1
7 — 2 . D
Р ХГ + 'Т
g(Y-l)"
(VII. 122)
(с+1)/Г
На основе соотношений (VII. 121) и (VII. 122) в табл. VII.3 и VII.4
представлены формулы для всех типовых регуляторов.
VI 1.3.2. Определение границы колебательной устойчивости
Используя в уравнениях (VII. 112) и (VII. 113) соотношение (VII. 114),
после некоторых преобразований получим, что на границе колебательной
устойчивости, т. е. при ($ ф 0, выполняется следующая зависимость
лг2^2 + /с[?1(1+с^)+5з]-^(1-^)=о, (Vii.i33)
где
t3=c-jjryl)1 + c(g0 — giyi J (VII.134)
£о = РФо — г-£-£(у-1м;
Вид формулы (VII. 133) при ^ = 1 и q = 0 для различных типов
регуляторов представлен в табл. VII.5 и VII.6.
На основе табл. VII.3—VII.6 составлены номограммы, представленные
на рис. VII. 11—VII. 18, которые позволяют выбирать параметр
регуляторов с точки зрения устойчивости.
С помощью представленных номограмм можно сделать много
интересных выводов.
Кривые границ устойчивости вблизи граничной кривой, обозначенной
штриховой линией, очень резко падают с обеих сторон от точек,
соответствующих максимально допустимому усилению. Из этого следует вывод,
что работа вблизи от указанных точек небезопасна, так как при изменении
относительного запаздывания Т~г во времени система очень легко может
потерять устойчивость и могут появиться опасные для системы колебания
с большой амплитудой. Работа с максимальным усилением была бы
возможна только в случае применения автоматической подстройки величины
234
Таблица VII.3
Граница апериодической устойчивости (q = 1)
пид
я-1 = 1
2tl'T D 2tl<T
1
ev/r+i ^ T ev/r+I '/Г
X
ev/r+i 27"
(VI 1.123)
ПИ
ге1'7" , 1 / 2^т
/f-i = 1 " 1
ev/r +1 W/Г \ ev/r + 1
/ 2е'/г y-2 \ <уилщ
U^ + i + 2Г 1)
И
л //г \
2е1/г , у — 2
^г + 1
2Г
(VII.125)
ПД
К'1 = 1 -
2ех/г , D ге1'2"
8V/r + 1 ^ T <У/т + 1
(VII. 126)
П
К"1=1
ге1^
г"т + 1
(VI 1.127)
Таблица VIIА
Граница апериодической устойчивости (q = 0)
пид
■пи
и
ПД
п
Я-^^ + ^-^Д (VII.128)
К"1=^=Д-^=Д- (VII.129)
J('i = — -^^- (неустойчив) " (VII. 130)
*~1=Х2Т^+Т" (VII.131)
К-*=1=Л (VII.132)
упреждения D при изменении относительного запаздывания Т"1. Из
рисунков также видно, что с точки зрения статической ошибки
совместная работа регуляторов типа П и ПД допустима только с объектами,
относительное запаздывание которых не превышает 0,6. Рисунки хорошо
иллюстрируют положительное влияние упреждающей составляющей Z),
так как допустимое усиление при использовании регулятора ПД в 4 раза
больше, чем допустимое усиление с регулятором П.
235
Таблица VI1.5
Граница колебательной устойчивости (q — 1)
пид ,
пи
и
ПД
п
t
/(2^2+^Ui(l+£v) + y-[l-^v] = 0 (VII.135)
£2 = т/г"(г|?0" *я)""(Фо + 9l);
(VI 1.136)
^Eifii + ^feO + ^ + bl-n-^l^o (Vii.137)
%2 = jjf №o - *8) - (Фо - Фх);
6з=7/7Г'*1 + (ч>0~ф1)
(VI 1.138)
K^xla + X & (1 + £v) + Ы - [1 - £*] = 0
1
Бг =777г№о~г1?2);
5з = 7/f *i
/с —
e1/7,(i_ D/71) — 1
_ ev/^
*~ е^_1
(VII.139)
(VII.140)
/\/тт ып 1
Из рисунков видно также, что если Тр = 2т, т. е. у = 2, то граница
устойчивости опускается, и область устойчивости уменьшается в 2 раза.
Из этого следует, что наилучшие условия создаются, когда период
повторения Тр точно равен величине запаздывания т, т. е. т = 1-
Для объектов, у которых относительное запаздывание Г"1 превышает
0,6, регуляторы типа ПД вообще неприменимы, так как максимально
допустимое здесь усиление для них К = 7, а это приводит к статической
ошибке 12,5% от установившегося значения. Для объектов с
относительным запаздыванием Т"1 > 0,6 следует рекомендовать регуляторы И и ПИ,
но особенно типа ПИД.
В случае использования регуляторов ПИД видно, что область
настраиваемых параметров регулятора можно разделить на три части в
зависимости от относительного запаздывания Г"1:
236
Таблица VII.6
Граница колебательности устойчивости (д = 0)
пид
к =
Т + 2
2/
№-')(*
2/Г ' Т
-+)
(VI 1.142)
ПИ
Y + 2
2/
/ Y
2/ + 1 ) \ 2/Г Г )
(VI 1.143)
И
2(у + 2)Т*
//Г
-Y-2
(VII.144)
ПД
/С:
1— D
(VI 1.145)
П
К = Т
(VI 1.146)
первая часть при Г"1 < 2, в которой составляющая 1// возрастает,
улучшая динамику системы по сравнению с регуляторами ПД;
вторая часть при 2 < 71-1 < 10, в которой составляющая 1/1
практически постоянна;
20
W
7
г
1
ол
I I
lr V
[о *
У
\
ол
ум I
\ |>|
fill
Мгг
^
/I I I I I I I
J J II 11
3?57
o,i ол
0,4 ОЛ 1
a)
7 Г
20
70
7
г
1
ол
k
\
[#/N
Щ1
\0%5
1
S-
§
SN.
sjgM
NT
ТТт
Ш
IF
Ж
tf^
W—i
Hfb-
I.LLJ
^
'г I
0,1
ОЛ Or1* ОЛ i
/С)
7Г
Рис. VII.И. Граница устойчивости системы с объектом с
самовыравниванием (q = 1) и регулятором ПД:
а — у = 1; D/T — var; б) V = 2; D/Г = var
третья часть при Т'1 > 10, в которой составляющая III уменьшается,
отчего динамика системы ухудшается, и регуляторы этого типа в этом
случае неприменимы.
Особенно сильно это проявляется в случае объектов без
самовыравнивания q = 0. Как и в непрерывных системах, объекты с запаздыванием
Г"1 > 0 требуют применения специальных регуляторов.
Сравнение максимально допустимых значений усиления в системах
с непрерывными регуляторами И идентичных систем с импульсными
регуляторами дает кажущееся преимущество применения к объектам
237
TK/I
7
/
0,7
ОМ
ОЛ
^fl^/f/zw/rRfflf
0,1 ол ол о,7 1 г (* 7 г
10
7
2
1
0,7
ОЛ
0,2
|L
.J \о
^Ef£
м SL
х Ph
_tk
Зт
1Й
/*п
is\\
0,1 0,2 ОЛ 0,7 1 I k 7V
6)
Рис. VII. 12. Граница устойчивости системы с объектом с
самовыравниванием (q = 1):
а — с регулятором И (v = 1); б — с регулятором ПИ (v = 1); Т/1 = var
И
20
10
7
h
г
1
ол
F I
/v
0
j
ч
\ р
ни п.
\\LO,5
11L^V>«.
"■"*'
^
=5*
-Ш
-TTJ /С
?0
Я ^
4Н 7
тп ^
"Гп
III ^
]п 7
1 ОЛ
\0,1
/v
0 *
i—
Ч
ч I I I
ол\
yd
\ р
Wt^5"
ITr"
III
0,1 ол ол ол 1 г
а)
4 7 Г1
0,1 ОЛ ОЛ ОЛ 1 2 Ч IV
6)
Рис. VII. 13. Граница устойчивости ^системы с объектом с
самовыравниванием (q = 1) и регулятором ПИД:
а — у = 1; Т/1 = 1; D/T = var; 6 — 7=1; Т/1 = 0,2; D/T = var
К
20
10
7
Ч
2
1
ол
I
V'
/\i
0
\
Л2\
Шл?5
»I i 111 i
Д/Ш1
'IINIII
§гШ
NJ^! \l Ift
Я
2tf
/0
7
Ь
7
/
///
\^7
/V
.0 —
i—
»
^v
Д2\
_\_|4_
m>^ /7
j\y
*» nrti
N 1 1 1 1 III
\b
l ill If
[Ш\\\
\ \ м F
\ \ \\
\\ V \
ьЛ1Л. aLLLL
0,1 ОЛ 0Л 0,7 1 2 k 7T'1 0,1 ОЛ 0Л 0,71 2 4 7Vr
a) ' 6)
Рис. VII. 14. Граница устойчивости системы с объектом с
самовыравниванием (q = 1) и регулятором ПИД:
a —v=l; D/T = var; 6—7=1; Т/1 = 1; D/T = var
238
20
10
7
1
0,7\
_... „
У Vs
Г 1
1
V
Щ
ffl
1 и
Л
405
к;
\Л\
N
\[| ЦП
N
.1±Ш1
К
on
10
7
л
1
1
0,7
к
щ
ц
Чу! 11
ж^
Ч\гс?'
vvfc
ш
'I III
Шм
-
; 1
К Н4+
111
0,1 0,2 Ofi 0,71 2 k 7T~
а)
0,1 0,2 ОЛ 0,71 Z * 7Г
6)
Рис. VII. 15. Граница устойчивости системы с объектом без
самовыравнивания (<7 = 0) и регулятором ПД:
а — у = 1; D/T = var; 6 — 7 = 2; D/T — var
К
7
Ч
2
1
0,7
#Л
0,2
I '
/1
W \v
М\ V
\\\ \
\
\оЛ о,
А
i 1
i 111 i 1 Пу
К
7
г
1
0,7
ОМ
0.2
I ;||
I ill
||v \
oj\\ оЛ
III
\пч?,
> IVi Лк
0,7 0,2 ДО 0.7 7 2 V 7Г' ^,/ 0,2 ОЛ 0.7 1 2 U 7Г
а)
б)
Рис. VII. 16. Граница устойчивости системы с объектом без
самовыравнивания (<7 = 0) и регулятором ПИ:
а — у = 1; Т/1 — var; 6 — 7 = 2; Т/1 = var
«0
к«;
[я \
4v
ч
\
St
А
^1 /7
Г^»
J \
ч[
I Г \;
4L/\X\
mvsSl\
Гх\\
^v
III N^
V- г
ж
\
\
Ч,\
v
\
\
\
_}
к
_
Ш
ьо
20
10
7
\\o.t.
ЧЛ
%2
\
^
v
4/7
5
>J
ГК 4
%v /
IlxSl
х
t
\
JlJ
1 ~ j 1 1
0,1 0,2 ОЛ S0J 1
а)
1
0,7
2 k 7 Г1 0.1 0,2 ОЛ 0,7 1
6)
7 Г'
Рис. VII. 17. Граница устойчивости системы с объектом без самовыравнивания (q = 0)
и регулятором ПИД:
а — у = 1; Т/1 = 0,1; D/T = var; б — у = I; T/I = 0,2; D/T = var
239
запаздыванием импульсных регуляторов, так как получаем большее
допустимое усиление при том же запаздывании. В действительности
оказывается, что если учесть ограничение на динамические ошибки в
переходном процессе, то, вообще говоря, импульсные регуляторы хуже
аналогичных регуляторов непрерывного действия.
• Теперь определим оптимальные значения настраиваемых параметров
непрерывной части импульсных регуляторов на основе критерия крити-
к
ьо
20
10
7
/
0,1
iy
V \N
г
ч<
п
14
N
"Ч| 1
N
]v
vJ|
'
J.J
ч 1
,Г Н.
IX
ш
ИЛ 1
yWi
МЛ1
ГуМ
1Ж
/
к
20
т
7
J
0,7
\\o.i
V \N
[ 2 У
гХ
L_a^__
^Ал 1 1 1 1
/Lull
-
4s I
'0,J\1\
\A\
Г I
0,1
ол
ОЛ 0,7 1
а)
7 Г
0.1 0,2
ОМ 0,7 1
6)
7 Г
Рис. VII. 18. Граница устойчивости системы с объектом без самовыравнивания (q = 0)
и регулятором ПИД:
а — V = 0; Т/1 = 0,5; D/T = var; б — у = 1; 77/ = 1; £>/Г = var
ческой апериодической устойчивости. Здесь можно обеспечить окончание
переходных процессов в определенное время, чего нельзя достигнуть в
непрерывных системах управления с типовыми регуляторами.
§ VII.4. Параметрический синтез импульсных регуляторов
Параметрический синтез, как и в регуляторах непрерывного действия,
основан на оптимальном выборе параметров.
Прежде всего рассмотрим выбор параметров непрерывной части типа
ПИД в импульсных регуляторах на основе критерия минимального
времени окончания переходных процессов и на основе критерия
оптимального модуля.
VI 1.4.1. Критерий критической апериодической устойчивости
Как и в случае непрерывных систем, потребуем, чтобы знаменатель
передаточной функции имел один сомножитель (z — zk) болыйой кратности.
В этом очень важном случае можно выбрать параметры непрерывной
части регулятора так, что»
zk = 0, (VII.147)
и тогда переходные процессы будут затухать в заданное время.
Для примера рассмотрим знаменатель передаточной функции,
определяемый соотношением (VI 1.77):
М (z) = Л323 + A2z2 + Axz + A{
240
Требуется, чтобы этот полином имел один трехкратный сомножитель.
Тогда первая и вторая производные должны содержать тот же
сомножитель. В .связи с этим можно написать следующую систему трех уравнений:
A3z* + A2z2 +Агг +А0 = 0; (VII. 148)
3A3z2 + 2A2z + Ах = 0; (VII. 149)
3A3z +Л2 = 0.' (VII. 150)
Так как необходимо определить четыре неизвестных /С, D, / и zkt
а в распоряжении имеются только три уравнения, то принимается, что
zk = 0, ибо это оптимальная величина, обеспечивающая протекание
переходных процессов в установленное время.
Используя соотношение для Ak из табл. VII.2 и уравнение (VII. 147),
можно из системы уравнений (VII. 148)—(VII. 150) получить соотношения,
определяющие оптимальные значения параметров регулятора ПИД:
,г_ (1 + £*<*) (Ь + Ъ+*о) - (ЧУ-^о). д/тт icn
/ ^ (l+^)(ft + ft + *«)9«-0h-4>o)
Т Ф1 + Фо
(VII.152)
Л = (1 + EW) (фа + fr + ф0) ф0 — (4>2ф0 + ^оф1) vn - - .
*" Ki + fi^W. + ti + tJ-^-Wl^^^ ' lv"-1M'
Для двух типов объектов q = 1 и q = 0 в табл. VII.7 и VII.8
представлены формулы для определения настроек типовых регуляторов.
В случае регулятора ПИ необходимо определить только три
неизвестных, так как D = 0. Из формул (VII. 148), (VII. 149) и (VII. 150) получим
4 = -Зг, = 7|гг|)2 + /Сф|-(1-^); (VII.154)
Аг = 3zl = JL Ь + К (Фо - фО + Еуд; (VII. 155)
i40 = —4 = -^г*о-Кфо. (VII.156)
Поступая аналогично в случае регулятора типа И, легко убедиться,
что могут существовать только один кратный корень и один некратный,
и, выбирая значения параметров /Си/, нельзя найти корень кратности 3.
Для регуляторов с непрерывной частью типа ПД знаменатель
передаточной функции упрощается к виду
М ($ = A2z2 + Агг + Л о, (VII.157)
так как коэффициент А3 = с = 0.
Для этого случая необходимо определить три неизвестные величины:
/С, D и zk. Требуя существования кратного корня zki необходимо решить
систему двух уравнений
A2z2 + А гг + А0 = 0; (VII. 158)
2A2z +A1 = Q« (VII 159)
Полагая гк = 0, полупим следующие соотношения, определяющие
параметры К и D:
—Аг = /Сф! + кЦг E(v~l) я — Еуя = 0; (VII.160)
— A0 = Ky0-^EW = 0. (VII.161)
16 X. Турецкий 241
Для регуляторов с непрерывной частью типа П необходимо определить
только два неизвестных: К и zk, которые непосредственно находятся из
уравнений (VII. 158) и (VII. 159):
к= ,._ ,?w _.ча; (vii. 162)
гк =
(Уъ + Уъ + ъ*4)
^Фо+Кфо + Ф!^
(VII. 163)
По формулам, помещенным в табл. VII.7, построены номограммы,
показанные на рис. VII. 19—VII.22 для различных значений параметров.
Эти номограммы позволяют находить значения настраиваемых параметров
к; D/T
4
2
0,7
ол
0,2
0J
0,07
1
i
I
1
i
5
NJ _^*
\\\^у^
^
7Г
п/тЩ
K;Zk
If.
2
1
0,7
ол
0,2
0,1
ол
К
Шн
0.1
0,2 ОЛ 0,71
а)
k 7 Г
0.1
цг w ол
6)
4 7Г1
Рис. VII. 19. Оптимальные значения параметров по критерию
апериодической устойчивости системы с объектом с самовыравниванием (q = 1) :
а — с регулятором ПД (V = 1); б — с регулятором И (V = 1)
К, D и /, обеспечивающих критическую апериодическую устойчивость
или бесконечно большую степень устойчивости для регуляторов ПИД и ПД.
Из вышеприведенного рассмотрения следует вывод, что для
реализации бесконечно большой степени устойчивости необходимо наличие
дифференциальной составляющей. Получение переходных процессов с
заданным временем протекания возможно только в случае регуляторов типа
ПИД и ПД. Тогда выражения для передаточных функций упрощаются:
для регулятора ПИД
В2 _-; , Вг
Л3
Gw(z) = -
г- + ^-г-
G.WHE-**.
-^-z"2-
-^-z"3;
для регулятора ПД
Mz)=4-z_1
В„
Ci ,-1
°Лг)=^-^+^г-
(VII. 184)
(VII. 185)
(VII. 186)
(VII. 187)
Из приведенных рисунков следует, что при принятом критерии можно
выделить две области работы регулятора ПИД:
первая область при Т'1 < 4, в которой усиление К и составляющая
1/1 сильно уменьшаются, а составляющая D сильно возрастает;
вторая область при Т'1 > 4, в которой К и D почти постоянны, а VI
сильно уменьшается. Эта область характеризует слабое влияние пропор-
242
k;t/i;zh
Ы ол ол opt
о)
4 7Г
*
2
0,7
0.1
ОЛ
0,1
0.07
V
^
^
■■j 1
1
Ц// 1 11 llll
fe^
[HL^
111 и in
|рЦ] F
| | \\Щ
OJ 0Л 0Л 0,7 1
6}
k 7Г
Рис. VI 1.20. Оптимальные значения параметров по критерию
апериодической устойчивости системы с объектом с самовыравниванием
(q = 1) и а — регулятором ПИД (у = 1); Zkr = 0;
б—регулятором ПИ (y= 1)
К; S/T
*;**.
ч-
2
1
ол
и,ч
UJ
0J
0,07
SF^
^
ЛГГ
Я/ту\ | |
Щ
k
1
ОЛ
ол
ОЛ
01
0,07
\
\
к
_5
чгН4
Л.
XI
7l
*
0J ОЛ ОА ОЛ 1
о)
7Г
0J ОЛ ОЛ 0,7 1
6)
7Г
Рис. VII.21. Оптимальные значения параметров по критерию
апериодической устойчивости системы с объектом без самовыравнивания (q=0)
и а — регулятором ПД (у = 1); Zkr = 0; б — регулятором П (q = 1)
А; Л/Т; Т/1
*:zk;r/i
4
7
С
1
РЛ
пи
Ч¥
/7?
OJ
0,07
ч?';
Ч
<Z7/T
у | |
H1L/
Т/1'
\
PNJIII
mJ
МП
ш
ШШ
и
2
1
1
ол
ОЛ
ОЛ
OJ
0,07
\\\ Ll
■llLiLjL.
plL/f -
yj^r/i
OJ 0,2 ОЛ OJ 1
о)
7 Г
OJ ОЛ ОЛ ОЛ 1
6)
7 Г
Рис. VI 1.22. Оптимальные значения параметров по критерию апериодической устойчивости
системы с объектом без самовыравнивания (? = 0) и а — регулятором ПИД (у = 1); Zkr = 0;
б — регулятором ПИ' (у = 1)
16*
243
Оптимальные значения параметров, определенные на основе
критерия критической апериодической устойчивости (q = 1)
Таблица VII.
ПИД
К =
(1+Г)еУ/гИг-1)-у
/ =
Y(eV/r_l)2
(1+Г)е^г(е^г-1)-у
ev/r(ev/r_l)
р ет/Г(еу/г_1) + т(е-1/г_1)
Т (1+Г)ет/Г(е7/Г-1)у
(VII.164)
(VI 1.165)
(VII.166)
ПИ
К = -^[Т^Т-~1) O-^' + ^j1 (VIU67)
/ = 77^ГГ[т(е^-0(Т^)3+(7'е1/7--Г-1)]; (VII.168)
I еТ/г ' е'/г \п -г I eT/r-el/r *1
+ 3zft =
e^r+l
„у/т
(VII.169)
ПД
1
е"Г-Г
J/t
(VII.170)
(VII.171)
-I. = (V(JIT - 1) e^ + W/r - 1) e'/r)2;
П
2k
= ev/r +
/;
v+l ev/r—1
т
e^-l
(VI 1.172)
(VII.173)
Оптимальные значения параметров, определенные на основе
критерия критической апериодической устойчивости (д = 0)
Таблица VIL8
ПИД
Зу + 2
*- 2Y2 Г'
D =
2
Зу + 1
Зу + 2
(VII.174)
(VII.175)
(VII. 176)
ПИ
К = Т Г
<'-**>' +z»
2v2
]=
(VII.177)
(VII.178)
(VII.179)
244
Продолжение табл. VI 1.8
ПД
Т
D= 1
(VI 1.180)
(VII.181)
П
К =
Zk
(i+Ky)2/
1
(VII.182)
(VI 1.183)
циональнои и интегральной составляющих и очень сильное влияние
дифференциальной составляющей регулятора. Анализируя переходные
процессы, легко убедиться, что критерий бесконечно большой степени
устойчивости может приводить к большим перерегулированиям порядка 100%.
Переходные процессы с малыми перерегулированиями можно получить,
если выбирать величины настраиваемых параметров регуляторов на основе
критерия оптимального модуля [39, 36].
VI 1.4.2. Критерий оптимального модуля
Этот критерий рекомендуется применять, когда требуется, чтобы система
возможно точнее воспроизводила управляющий сигнал.
Пусть задана импульсная система управления, описываемая
передаточной функцией
°и=Ш
Полагая в этой формуле
= J<*Ti>
e'w,
получим частотную характеристику в виде
G(itA—L{lu)
и('и>— M(ju)>
а квадрат модуля частотной характеристики в виде
]G(ju)\* = G(ju)G(-ju) = fflli1-™ =^-
или в зависимости от z
1 u " Af (z) Л1 (—z) U=/«
(VII.188)
(Vll.189)
(VII.190)
(VII.191)
(VII. 192)
Аналогично случаю непрерывных систем оптимальные значения
параметров определяются из условий
d2k Ti ч
d2k
du*k
M(u)
и = о
£(Q)
М(0)
(VII. 193)
где k = 1, 2, ... выбирается в зависимости от числа подлежащих
определению параметров.
Из соотношения (VII. 189) следует, что когда
и = о, то z= 1. (VII.194)
245
Таким образом, можно написать
1(0) _ L(u)
М (0) М (и)
а = 0
L(z)L(i-i)
М (гУМ (z-i)
г [ад- <VIU95)
Так как функции L (г) и Л4 (г) являются полиномами переменной г, то
можно записать
f(2)= S /«*". (VII.I96)
т=0
Сопряженная с ней функция
* F{*~1) = S /т2"т. (VII. 197)
т=0
i
Умножая функции одну на другую, после преобразований получим
F (z) F (z-ij = Ф0+ S Фт(гт + г—), (VII. 198)
где
я—т
Фт= L Шт- (VII.199)
/
В связи с этим интересующее нас выражение
определится следующим образом:
пусть
Wm (z) = z<* + згт, (VII.201)
тогда производная Wm (z) равна
^^_=^(£)_.^_=т(2т_1_г_т_1)(.2)=/тГ(я(г) (VII202)
и
d2k Wm(z) = {jmf"Wm(z). (VII.203)
du*k
Подставляя выражение (VII.203) в формулу (VII.200), получим
НргЙ">= S (/т)2*ФтГт(2). (VII.204)
Ul* m=l
В частности, при и = 0, т. е. z = 1, имеем
d2* ^
^ (а) |и=о = 2 (/)2* S ^2"Фт. (VII.205)
**** т=1
На основе соотношения (VII.205) условие (VII. 195) можно записать
в виде
т
= [^iy] ' k=\,2,S, ... (VII.206)
i=l
1=1
Рассмотрим систему, для которой L (г) и М (г) определяются
соотношениями (VII.75) и (VII.77).
246
Условия (VI1.206) примут в этом случае вид
К + 4*А,2
Hi + 4*^2 + 9*fi3
=(а0вЛ+Х+а3У> k=i>2>*> (™-207>
где
Хг = В0Вг + ВхВ2»
[хх = Л0Л! + ЛИ2 + Л2Л3;
[х2 — А0А2 -j- ЛхЛз^
[Хз — AqA^»
(VII.208)
(VII.209)
(VIT.210)
(VII.211)
(VII.212)
Используя зависимости для Bt и А, из табл. VII.2, можно правую часть
соотношения (VII.207) записать в виде
2 \ 2
/%Bi
i=0
3
c-^ry + (c-\)pk
——
(VII.213)
\-=o
Учитывая, что с может быть равно только нулю или единице, получим,
в частности, что
2>
1
при с = 1;
(VII.2I4)
Подставляя соотношение (VII.214) в выражение (VII.207) при с = I,
получим при k = 1, 2, 3 систему из трех уравнений:
14 + 4*14 + 9*1*, -1' *—*.
ваявшая эту систему уравнений, получим
щ = а2; |
[х3 = 0.
(VIL215)
(VII.216)
Подставляя в формулу (VII.212) соотношение (VII.208) и соотношение
для коэффициентов В. и At из табл. VII.2, получим
К
ЦТ
% — Кф0
KD
£(v-i)^==0;
^Ъ + *(ф0-Ф|)-2^£<^>*=-
-^-^ + Кф1 + -^-£^1)<7=1.
■£W;
(VII.217)
Решение этой системы уравнений дает оптимальные значения
настраиваемых параметров:
при q = 1
/ ~~
D =
1 +Т
1
г
1 + Г'
(VII.218)
(VII.219)
(VII.220)
247
при q = О
f-Oi
D = 1.
(VII.221)
(VII.222)
(VI 1.223)
Для регулятора ПИ из соотношения (VII.215) при k = 1,2 получим
только два уравнения, из которых следует:
при q = 1
(Г + 1) (е^г - I)2 + Ttl'T (Зе™" - 1)
К
у (еТ/Г _ !)2 + (? + 2) е1/Г (3eV/r _ ,)
(eV/r_,)2
Г=1 +
при q = О
(еТ/Г_1)2 + е1/Г(3еУ/Г_
А Y + 2'
*-••
О
(VII.224)
(VII.225)
(VI 1.226)
Для регулятора И при & = 1 из формулы (VI 1.215) получим:
при q = 1
-f=if+W; (VIL227)
при q = О система структурно неустойчива.
Подставляя в соотношение (VII.207) выражение (VIL214) при с = 0,
получим случай регулятора ПД и следующую систему двух уравнений:
К + &К _( К \2 ,__ < 9
1*1+ 4*||,+ 9*11, -V^ + КУ' Л-1,^.
(VII.228)
Аналогично предыдущему из,-системы уравнений (VII.228) получим
формулы для определения оптимальных значений параметров:
при q = 1
Т
,у/т_1 '
е"г-1 .
при <7 = 0
0 = 1.
(VII.229)
(VII.230)
(VII.231)
(VII.232)
Для регулятора П из системы уравнений (VI 1.228) при k = 1 имеем
только одно уравнение
^i=(^)Vi + 4(rpr)V2,
из которого окончательно получим:
при q = 1
при q = 0
248
t2y/T + e(v+D/r _ 2ev/r + j + 2е2/т- - зе1'7-
/с=
Т + 2
(VII.233)
(VII.234)
(VI 1.235)
Оптимальные значения параметров по критерию
оптимального модуля (д = 1)
Таблица VI 1.9
ПИД
К =
1 + Т,
1 + Т '
D^
\ + Т
К:
ПИ
(Т+\)(еУ/т-\)2 + Т*1'т№'т-\) ,
Y (ev/r _ 1)2 + (Y + 2) е1/7 (Зе*'г - l) '
ev/7-_2)2
/=1
(eY/^1)2 + ei/r(3ev/r_l)
И
д-
1
2Г + у + 2
ПД
К-
1
D
B1^-!
e^-l '
J/7-
П
/c =
eV^eV^^e^+O
e2Y/r + e(Y+l)/r _ 2eY/r + j + 2е2/Г _ Зе1/Г
Таблица VI1.10
Оптимальные значения параметров по критерию оптимального модуля (q = 0)
ПИД
пи
i И
! ПД
п
Остальные параметры, как в регуляторе типа ПД
К = —; D=l
Y '
Т
Полученные зависимости сведены в табл. VII.9 и VII. 10, и построены
номограммы, представленные на рис. VII.23—VII.25.
Из рисунков видно, что в зависимости от запаздывания Г"1 можно
выделить три области.
Область /:
Г"1 < 0,3 с регулятором типа ПИД;
Г"1 <: 1 с регулятором типа ПИ.
В этой области пропорциональная составляющая уменьшается,
дифференциальная возрастает, а интегральная почти неизменна. Эта область
наиболее предпочтительна.
Область //:
0,3 < Г"1 < 5 с регулятором типа ПИД;
Г"1 > 1 с регулятором типа ПИ;
Г"1 < 2 с регулятором типа ПД.
В этой области пропорциональная и интегральная составляющие
уменьшаются, а дифференциальная возрастает. Эту область использовать
можно.
249
к:№
/,
7
С
1
0,7
о Л
0,1
0,0)
1
1
1
1
1
ш
ш=
\
\
я>
11111
ш
ж
еёи
4
2
0,7
ол
0,2
0,1
0,07
\
\
=z
^
14 ] III]
0.1 0,2 ОЛ 0,7 1
а)
7 Г
0,1 0,1 ОЛ 0,7 1
б)
7Г'
Рис. VI 1.23. Оптимальные значения параметров по критерию оптимального
модуля системы с объектом с самовыравниванием (q = 1) и а — регулятором
ПИ (у = 1); б — регулятором П (у = 1)
fi;B/T; T/I
к; т/1
4
2
1
0,7
ОЛ
0.2
0,1
0.07
±=
5^
т
1
1
i
-L
V I 1 1
>и
Пг
п!к1
IP
TriLr^
Iffl^u
Т ^
т/i-
:22
ч.
N
^Htth
1 1 1 111
ч
И
с; яг
4* 57 /
а)
7Г>
4
0,7
ОЛ
0,2
0,1
OJ37
МП г//
к
I III*
0,1
0,2 ОЛ 0,7 1
б)
7Г
Рис. VII.24. Оптимальные значения параметров по критерию оптимального модуля системы
с объектом с самовыравниванием (q = 1) и а — регулятором ПИД (у =\);б — регулятором
ПИ (7=1)
кщ/т
01
7
4
г
1
0,7
.
ол
ОЛ
кп
I I 11 ч
-ni
ч
\
А
N_
ш\\
ш
0,2 ОЛ 0,7 1
а)
7 Г'
7
4
2
1
0,7
ол
ОЛ
0,1 ОЛ ОЛ 0.7 1
4 7 Г'
Рис. VII.25. Оптимальные значения параметров по критерию оптимального
модуля системы с объектом без самовыравнивания (q = 0) и а —
регулятором ПД (у = 1); б — регулятором П (у = 1)
250
Область ///:
е Т"1 > 5 с регулятором ПИД;
Т"1 > 2 с регулятором ПД.
В этой области пропорциональная и дифференциальные составляющие
постоянны, а интегральная уменьшается. Таким образом, работа здесь
вообще невозможна.
Значения параметров регулятора при критерии оптимального модуля
меньше, чем при критерии конечной длительности переходного процесса,
что понятно, так как последний требует очень энергичного воздействия
регулятора.
VI 1.4.3. Критерий при использовании типового управляющего сигнала
Так же, как и в случае систем автоматического регулирования
непрерывного действия, для определения оптимальных значений настраиваемых
параметров в импульсных системах могут применяться либо
интегральные критерии, либо критерий 20%-ной колебательности. При этом
предполагается, что возмущение имеет вид единичной функции. Но, вообще
говоря, получаемые результаты несколько хуже, чем в случае
непрерывных систем.
Зависимость двух основных показателей качества переходных
процессов — колебательности и времени регулирования — от критерия качества
можно охарактеризовать следующим образом.
При использовании интеграла от квадрата ошибки переходные
процессы имеют большую колебательность и большое время регулирования.
При использовании интеграла от модуля ошибки, умноженного на время,
переходные процессы сильно демпфированы и время регулирования мало.
Использование же в качестве критерия интеграла от модуля ошибки дает
переходные процессы с промежуточными свойствами. Запас устойчивости
системы при квадратичном критерии меньше, чем при критериях с
интегралом от модуля ошибки. '
Соответствующие зависимости оптимальных значений параметров от
величины запаздывания, периода повторения и вида критерия качества
можно найти в работах [24], [25].
§ VII.5. Параметрический синтез импульсного регулятора
общего вида
Рассмотрим систему управления, структурная схема которой представлена
на рис. VII.26.
Передаточную функцию объекта вместе с экстраполятором обозначим
через G0l (z), а передаточную функцию регулятора — через GRi (z).
Тогда передаточная функция замкнутой системы
°^=тШШг- <VI,-236>
Если передаточная функция замкнутой системы, т. е. определена
с использованием показателей качества переходных процессов на основе
наших исследований, то из формулы (VI 1.236) можно найти
передаточную функцию регулятора
°^—ЩШ^оШ' (VII237)
Зависимость (VI 1.237) является основной при синтезе, но только нужно
обратить внимание на следующие два обстоятельства:
1. Передаточная функция Gt (z) должна быть определена так, чтобы
регулятор был физически реализуем. Например, если принять, что G, (z) =
= 1, то, как легко видеть, для реальных G0l (z) регулятор реализовать
251
нельзя. Это означает, что алгоритм регулятора не может содержать
элементов таких, как положительные степени z и выражения вида esa при
а> 0.
2. Если передаточная функция объекта G0 (0) содержит нули в правой
полуплоскости комплексного переменного, т. е. G0/ (z) содержит нули вне
единичной окружности, то передаточная функция регулятора GRi (z)
не может иметь полюсов, компенсирующих эти нули, так как это приводит
к неустойчивости замкнутой системы,
Импульсный
регулятор
Запоминающий
элемент
Объект
Рис. VI 1.26. Схема импульсной системы регулирования
Поэтому пусть передаточная функция объекта
п /у\ — Lo (*) (z — zk)
где \zk\ > 1, а передаточная функция регулятора
*Rl
(Z):
MR(z)(z — zk) '
Тогда характеристическое уравнение замкнутой системы
(г - zk) Ш0 (z) MR (z) + L0 (z) LR (г)] = 0,
(VII.238)
(VII.239)
(VII.240)
т. е. это уравнение имеет корень zky лежащий вне окружности единичного
радиуса.
VI 1.5.1. Компенсация запаздывания
Из соотношения (VI 1.236) следует, что если передаточная функция объекта
содержит запаздывание, то оно будет присутствовать как в числителе, так
и в знаменателе передаточной функции замкнутой системы.
Сначала рассмотрим случай [5], когда относительное запаздывание Я,
определяемое соотношением (VI 1.9), является целым числом. В частном
случае оно может быть равно единице. Это означает, что период повторения
равен времени запаздывания.
Таким образом, пусть передаточная функция объекта будет
G0 (z) 2f* = G0 (z) г~\
GK{z)
(VII.241)
т. е. время запаздывания т в п раз больше периода повторения.
Подставляя выражение (VII.241) в соотношение (VII.236), получим
передаточную функцию замкнутой системы
GR G0 (z)z~n
G(z) = .
(VII.242)
l + GR{z)G0(z)z-n *
Знаменатель передаточной функции показывает, что запаздывание
повышает порядок характеристического уравнения. Под компенсацией
запаздывания понимается синтез такой структуры регулятора GR (z),
чтобы запаздывание не приводило к увеличению порядка
характеристического уравнения. Это означает, что при синтезе такого регулятора
знаменатель передаточной функции замкнутой системы не содержал
запаздывания. Запаздывание будет присутствовать только в числителе
передаточной функции. Такой синтез смягчает ограничения, которые существуют
из-за наличия запаздывания, например, с точки зрения условий устойчи-
252
вости. Но из-за наличия звена запаздывания в числителе передаточной
функции замкнутой системы в целом реакция системы будет сдвинута на
время запаздывания относительно момента приложения внешнего
воздействия. В такой скомпенсированной системе уже можно использовать
критерии качества для определения настроек корректирующих звеньев
таким же образом, как и в системах без запаздывания. На этом основано
применение регуляторов Смита и Ресвика для компенсации воздействия
запаздывания на системы непрерывного действия. Компенсация
достигается за счет введения моделей объекта с запаздыванием и без
запаздывания.
Из вышесказанного следует, что передаточная функция замкнутой
системы G/? (z) после компенсации должна иметь вид, аналогичный
формуле (VI 1.242), но должно отсутствовать звено запаздывания в
знаменателе передаточной функции:
«м-тШйта-- <VI1-243»
На рис. VI 1.27 изображена блок-схема нескомпенсированной системы,
а на рис. VI 1.28 — структура скомпенсированной системы.
Какой должна быть цепь, компенсирующая запаздывание, показано
на рис. VII.29. На схеме изображен компенсирующий элемент Gk(z),
подключенный параллельно объекту G0 (z) z~n. Для того чтобы получить
блок-схему, представленную на рис. VII.28 при исходной структуре
рис. VII.27, необходимо, чтобы передаточная функция компенсирующего
элемента удовлетворяла следующей зависимости:
G0 (z) z-" + GK (z) = G0 (z) (VII.244)
или
GK(z) = G0 (z) (1 - г-»). (VII.245)
Зависимость (VII.245) можно реализовать структурно регулятором
Смита. Тогда получим блок-схему, представленную на рис. VI 1.30,
впервые предложенную Я. 3. Цыпкиным. Управляющая часть системы
выделена штриховой линией. Теперь, используя критерий качества, можно
определить параметры регулятора G# (z).
Для завершения синтеза дискретного корректирующего устройства
с передаточной функцией G# (z) предположим, что на выходе объекта
сигнал тоже дискретный. На самом деле этот сигнал непрерывный, так как
объект составляет непрерывную часть всей системы; однако при синтезе
дискретного компенсатора можно сравнивать и компенсировать только
дискретные значения регулируемой величины у (t). Из-за наличия
запаздывания в объекте регулируемая величина и импульсная переходная
функция gon объекта сдвинуты на величину запаздывания п (рис. VII.31).
Из соотношения (VI 1.244) следует, что для получения импульсной
переходной функции до скомпенсированного объекта необходимо
определить импульсную переходную функцию с запаздыванием gon и
импульсную переходную функцию gk. Заметим, что
00 00
Gon (z) = 2 g0 (A) z~kz~n = £ go (*) г~* (VII.246)
fc=0 k=n
и
GK(z) = "ig0(k)z-k. (VII.247)
Если импульсную переходную функцию можно, как обычно,
представить в виде
*о(*)= Я***, (VII.248)
v=l
253
Z^-L~>e^
(->!
• Ъ
ff»«
7>
G0(z)
»
Г"
У ,
1
p—v v— —
f
Рис. VII.27. Блок-схема нескомпенсированной системы импульсного регулирования
Рис. VI 1.28. Структура импульсной системы со скомпенсированным временем запаздывания
0Я М
Wr\
ТР
GQ (г)
ОnU)
г-с^о—
г I * t *
■Ф
Рис. VI 1.29. Блок-схема системы с компенсирующим звеном
I 1
тр (-VA
Gr(i) b*~°^
God)
Go(z)
I f
I
Регулятор Цыпкина
I
Рис. VI 1.30. Система с регулятором Цыпкина
К,
х^
>?"
-9-"?-
/7
>
V^
V
Чк
Рис. VII.31. Импульсная переходная функция с
запаздыванием п
254
то, учитывая, что z = е р [см. формулу (VII.6), получим
Go„(z)= S £<*&"* = £ cv £ e(sv-s)V =
k—n v=l v=l /г=л
/ /
°2-ic'T3?^>-2jc' ,",-,v, ; <VIL249>
v=l
v=l
аналогично
Gk (г) = "S S CvafcT* = S Cv S* e(sv"s> V = '
fc=0 v=l V=l £=0
! _е(^^5)ГР(,г~^ e<V-s)7P
s7V> «vV* -S(n-l) ^n
V=l
■s)т-р <n-i) e< Vs) tp ^-\ esTp _ esvve"s (
v=l
(VII.250)
Сумма выражений (VII.249) и (VII.250) равна
G0(2) = G0n + GK=2jC- sf-vfrEi**!^' <VIL251)
V=l V=l
т. е. в соответствии с формулой (VII.248) g0 (k) = 2 cv г*-
v=l
Функцию бЛ%(г) в соответствии с соотношением (VII.247) можно
смоделировать на цифровой машине как дискретный фильтр. Блок-схема
такого фильтра изображена на рис. VI 1.32. Коэффициенты g0 (0), g0(l)t. . .
Рис. VI 1.32. Блок-схема дискретного фильтра
• • •> go {п — 1) представляют собой дискретные значения импульсной
переходной функции непрерывной части системы в моменты времени
k = 0, 1, . . ., (п — 1). Далее можно потребовать, чтобы функция Gon (z)
удовлетворяла условию
Gon (z) = G0(z)z-"Gp(z)y
где Gp (z) — передаточная функция экстраполятора.
(VI 1.252)
255
Теперь, подставляя соотношения (VII.251) и (VII.249) в выражение
(VII.252), получим выражение для передаточной функции экстраполятора
/
уПу— (П—1)
2 — Zv
GP(z)
V=l
(VII.253)
v=l
Передаточную функцию Gon (z) можно также представить как
линейную комбинацию функции G^iz) и ее производных порядка от 0 до / —1:
/-1
Gon(sTp) = e~SJPnG0(sTp)
t=0
(sTPY =
i-\
2^2]а<№>'^Ре
sTn-nsTn
e p _ esvTp
v=l i=0
Приравнивая соотношения (VII.249) и (VII.254), получим
esvV =
/-1
1^.(^)^=1, 2,
• J.
(VII.254)
(VII.255)
Из полученной системы / уравнений можно определить I неизвестных
коэффициентов аг
Главный определитель этой системы является определителем Вандер-
монда:
D =
1 SlTp, s\rp,
1 s2Tp, slTl,
1 stTp sjTl,
(S2TP)'-1
(siTP}
/-1
/-1 /
= П П (qt.
Qkl qt = siTP
(VII.256)
После вычисления коэффициентов a.y i = 0, 1, . . ., /— 1, функция
Gon (sTp) полностью определена. Кроме известной функции G0 (sTp)
определена также передаточная функция Gp (sTp).
Дискретный экстраполятор можно реализовать либо как дискретный
фильтр, либо в виде модели с передаточной функцией (VI 1.253).
Различные варианты экстраполяторов можно найти в работе [51.
Для иллюстрации рассмотрим вопросы компенсации запаздывания
в простейшем сулучае, когда необходимо управлять инерционным
объектом первого порядка с запаздыванием, а время запаздывания кратно
периоду повторения. Передаточная функция объекта с экстраполятором
равна
Go(*) = -rfe
l-e-sr"
а г — передаточная функция (табл. VII. 11)
_ 1-<Гтр1то
^о (2) — До _т it **
2-е Pf °
(VII. 257)
(VII.258)
256
^ Преобразования Лапласа и г-преобразования
Таблица VI 1.11
G(s)
t-kTs
1
1
s
1
s2
1
s3
1
s4
1
s*+!
1
s — (1/Г)1па
*tt)
b(t — kT)
6(0 |
"(0
*
2!
3!
— **
a4r
С (г)
г-*
1 ИЛИ Z~°
z
z — 1
Tz
(z-1)2
T2z(z+1)
2(z—l)3
r3(z2 + 4z+ 1)
6(z-l)4
lim (~!)" - d* / Z \
аХЬ Ь\ dak \z — fTaT}
1 z
z — a
G (г, m)
zm-l-k
0
1
z—1
mr 1 r
z—1 ' (z—1)2
T2 Г m2 2m + 1 2 1
2 L г—l ' (z — l)2 ' (z— l)3 J
Г3 Г m3 3m2 + 3m + l
6 L 2Г— 1 ' (z—1)2 '
6m+ 6 б"]
1 (z—1)3 l (z—1)4 J
lim (-D*. a* / e-^ \
a->o *! «fo* \z — eTaT)
am
z—a
00
Продолжение табл. VI 1.11
| G(s)
1
s + a
1
(S + Of
1
(s + a)*
1
1 (s + a)^1
1 а
5 (s + а)
1 а
s2 (s + а)
1 а
5*(* + «)
g(t)
t-at
fc-at
*2 е-а/
2
1-е-"
a
2! V
2 , , 2 2 _
a a2 a2
-о
GU)
г
г-е-аГ
Гге-аГ
(г-е*7)2
T\~aTz , Г2е-2аГг
2(г_е-07)2 ' (г-е-аГ)3
(- \)kdk / z \
k\dak \ z-t~aT )
(|-е~аГ)г
(г-1)(г-е-°0
Гг (1 — е-аГ) г
(г-1)2 а(2-1)(2-е-аГ)
Г2г (аГ —2)Гг
(г—I)3 + 2а (г— I)2 +
1 2 2
' «2(г-1) а2(2-е-аГ)
G (г. т)
е-атТ |
г-е-аГ
7,е_атГ[е-аг + т(2_е-аГ)]
(2_е-аГ)2
2
(2/п+1)е-а
+ (z-fTaTf
(- i)fcafe
Ша/г
Г т2 1
z-t~aT '
г 2е-2аГ 1
1 (г_е-аГ)3]
/ e-am:r \
[,-.-г) |
1 t~amT
г-1 г-е-аГ
Г пгТ-
(г—I)2 + г-
1
(2-1)» 1
Г2/л2/2 — Тпг/а -
+ г—1
-1/а , е-ап,г
-1 ' а(2-е-"г)
(т+ 1/2) —Г/а ,
(г-1)2 '
f 1/а2 е-""'7"
a2(2-e-"r)
1=2
vo
I
a.
a
X
+
+
+
X
CO
В t
+
+
X
M
о
3
6
1
с
ел
+
*■*
з
Б
с
ел
-^
+
F-.
о
3
ел
о
(N
1
1
м
м 1
^
1 з
1 £
ел
М
+
о
SCO
о
м
1
! 1
1 **
з
+
I
о.
3
Н
о!
з|
?
I
+
, о
3
■с
°
з
J2
+
о
3
1-е
со
О
+
з
°
з
+
°
з
+
I
+
о
3
ел
О
+
■*!« ^
+ -
+
| 7
п
+
(МО
з
1 +
CNO
3
+
|СМО
з
(МО
3
(NO
3
CNO
3
17*
259
О
Продолжение табл. VI1.11
G(s)
S(s2+G>g)
git)
а — a sec 0 cos (со0* + 0),
где e=tg"*-^-
G{2)
az az2 — az sec 0 cos (w0T + 0)
2—1
22 —22COSC00T+ 1
G (2, m)
a sec 0 {2 cos (тщТ + 0) -—
or — cos[(l—m)(oor + 0]}
2—1 22 — 22 COS ЩТ + 1
6 —a
(s + a)(S+6)
t-at_t-bt
2-е
-ar
2-е
-&г
t—amT e—btnT
2-е
-ar
2 — e
-ьт
(b-a)(s + c)
(s + a)(s+b)
(c — a) e"ar + (b — c) e
-to
(c — a)z (b — c)z
(c_a)e-q^ , (6 —c)e-
■bmr
2-е
-ar
A-fr7
a&
s(s + a)(s + 6)
62
1+ * e"«
a + b
a — b
^__е-ы
2-1 (a-b){z-t-aT)
az
(a — b) (z — e-*7")
6e-amr
2+1 (a_6)(z —e-er)
p—bmT
(a-b)(z-e~bT)
ab (s + c)
s(s + a) (s+b)
b(c-a) -a,
1 a — 6
a (6 — с) w
C2
■ +
b(c — a)z
2-1 (a-6) (2 — e-ar)
+
+
a (6 — c) 2
(a-6) (z —e-*r)
2—1
+
6 (с — а) е
—atnT
+
(*-*)(z-e-^)
a (b — c) e"
(в_6)(г_е-»0
+
-btnT
a%2
s*(s+a)(s+b)
abt — (a + b) b^—r t~at +
a — b
abTz (a>+b)z
(Z— 1)2 Z— 1
bh
(a - 6) (2 - e-^) ^ (a - 6) (2 - <TbT)
abT , д&тГ — (a + 6)
(z-1)2 n
fa-amT
2—1
+ ■
a\-bmT
(a-b)(z-t~aT) ' (a-6)(2-e-6r)
Продолжение табл. VI1.11
G(s)
a2b2 (s + с)
s*(s + a)(s + b)
g(t)
abet + [ab — с (a + b)] —
b*(c -a) at
a-b e "~
G (z)
a*(b-c) uT
a — b
abcTz
(z-1)2
(a
, ab —
1
b2(c-
-b){z-
a2(b
-c(a + b)z
z—\
a)z
-e-aT)
-c)z
(a-b)(z-t-bT)
abcT
G (z, m)
ab(\ -\-cmT)—c(a + b)
(z-1)2 ^ z—1
Ь2(с — а)*ГатТ
(a-b)(z-e~aT)
a\b-c)e-bmT
(a-b)(z-e-bT)
1
(s+a)(s + b)(s + c)
»-at
+
(b — a) (c — a)
1" (a-b)(c-b)
(a — c) (b — c)
+
{b-a){c-a){z-<raT)
Z
+
+
(a — b)(c — b)(z — e_&r)
z
(a-c)(b-c){z-<rcT)
-—amT
(b — a)(c—^(г — e-"7)
+
(a — &)(c — &)(z — e-6r)
1
(a-c){b — c)(z-e-cT)
s+d
(s+a)(s + b)(s + c)
d — a
(b — a) (c— a)
d — b
(a — b) (c — b)
d — с
*" (а —с) (b — c)
e~at +
,-Ы +
a~cT
(d — a)z
aT\ ~Г
+
(b — a)(c — a){z — t-aT)
(d — b)z
+
(a — b)(c-b)(z — e-bT)
(d—c)z
+
(a-c)(&-c)(z-e-cr)
(d_a)e-ewr
+
<6-a)(c-a)(z--e-er)
(d — b)e~bmT
+
+
(a — b)(c—b)(z — e-bT)
(d — c)e-cmT
+
(a — c)(6 —c)(z — e~cT)
to
о
to
Продолжение табл. VI1.11
о is)
git)
G{z)
G (z, m)
be
(b — a) (c—a)
<Tat-
abc
s(s + a)(s+b)(s + c)
(c-b)(a-b)
ab
(a — c)(b — c)
<Tbt-
*r-ct
z
z
1
(c
bcz
(b — a)(c— a)(z-
caz
— b)(a — b)(z — e-
abz
-e~aT)
~bT\
1
bee
—aniT
(a — c)(b — c){z — t-cT)
2—1 (b — c)(c — a){z — e-fl7)
ca<TbmT
(c — b)(a — b){t — <TbT)
аЬе~стТ
(a — c)(b — c) (z — <TcT)
abc (s + d)
s(s + a)(s + b)(s + c)
d _ (bc)(d — a) ^at _
(b — a) (c — a)
__ ca(d-b) bt _
(c-by(a-b)
ab (d •— c) _^ci
- {a-c)(b-c) e
dz
be (d — a)z
z—\ (b — a)(c — a)(z — eTaT)
ca (d — b)z
~~ (c — b) (a — b) (z — <TbT) ~~
ab (d — c)z
~ (a — c)(b — c){z — <TcT)
be (d — a) e"
-amT
2 — 1 (b — a) (c — a) (z — e~aT)
ca (d — b) e
—bmT
(c — b)(a — b)(z — e-bT)
ab (d — c) e-cmT
(a — c)(b — c)(z — e-cT)
(abc)2
s*(s + a)(s+b)(s + c)
abet — (be + ca + ab) +
+
bW
(b — a) (c — a)
--at
+
+
c*a*
(c — b)(a — b)
a4*
(а —с) (b — с)
e-« +
а.—**
abcTz (be + ca + ab) z
(z— l)2 ~~ z— 1
Wz
(b — a)(c — a)(z — e~a7)
c2a2z
+
+
(c — b)(a — b)(z — *TbT)
а*Ь*г
(a — c)(b — c)(z — ercT)
jibcT abcmT — (be + ca + ab)
— П*
(2-1)
2—1
ьчч-атпТ
(Ь — а) (с— a){z — <raT)
c*a4-bmT
\c_-b)(a — b){z — <rbT)
a44-cmT
+
+
+
(а —с) (b — c)(z — e-cT)
Продолжение табл. Vll.il
G±(s)
gU)
G(z)
G (z, m)
(abc)2 (s + d)
s2(s + a)(s+b)(s + c)
abcdt + [abc — (be -\- ca + ab) d] +
b2e2(d-a) at
~*~ (b-a)(c-a) "r
cW(d-b) ы ,
I" (c-b)(a-b) ^
■ a2fr2(d-c) c-c/
^ (a— c)(6 — c)
abc dTz [abc — (be + ca + a&) d/z]
i 1 i 1-
(z—l)2 [ z—1
b2c2(d — a)z
+
+
(b — a)(c— a)(z — e~a7)
c2a2(d — b)z
(c—b)(a — b)(z—e-bT)
a2b2(d — c)z
+
+
{a-c)(b-c)(z~e-cT)
abcdT
+
+
(z-l)2
abc (dmT + 1) — (be + ca + ab) d
+
(b
+
z—1
b2c2(d— a)e-amT
— a)(c — a) (z -
c2a2 (
a)(c — a){z — *TaT)
•a2(d — b)eTbmT
b)(a —6) (z-e"67)
Л2А2 /w __ „\ Л-ст7
(c — b)(a — b) (z
a2ft2 (d — с) е
(a-c)(6~c)(z —e-cr)
s (s + a)2
1-(1 +fl/)e
r-at
z-l 2-e-fl:r
a7e-a7z
+
1
aTe
1 + amT
z — e
-aT
(z-*-aT?
-amT
a2 (s + b)
s (s + a)2
bz
bz
b — be~at + a(a — b) te
-at
z-l z-e~ar '
a (a — b)Te~aTz
+ ■
(z-e"^)
-0П2
+
Z— 1
aT(a— b) e
шгсГ (л —ft)--fr
z —e
аГ
(*-
-oA2
a—amT
a*
s2 (s + a)2
(ar + 2)z —2z2
at —2 +(at + 2) e
-a*
(z-l)2
+ -
+ ■
2z
z —e
-fl7
aT<raTz
(Z-e~aT)2
aT
(z-l)2
amT —2
z —e
,-er
amT —2
z-l
АГе-°г
(z-e-07)2
-amT
+
О)
ч
I
о.
^
£
I
«I
>*—'I
м
И3
к
I
+
S
£1
I
« I
^
s
+
I
+
I
+
+
+
W ^ч
1—
«3
1
1
0)
ь.
а
1-1 1
м
к
сз
+
I
к I
I '
I
I ?
ъ —
& I
+ X
+
1+
+
b
•о
1
С*4
•О
1
1
N
S4
1
Q
|
1
N
+
^
SJ
N
1 •'—^
1
1
**
1 ^"^
г*
1
1 Q
г*
1
1 N
+
-о
+
5
«
+
£Г
м
3
«о,
1
а>
1
|
1
1 •
+
N
-о
1
1
2,
-о
+
1
а>
1
1
-О
1
сз
К
5
|
о
» 1
IN
1
Й
£"^
«
i
N
1 1
О
**
а
|
4>
•О
©*
1
й)
1
1
N
^
1
а
+
+
-I- S
I S
+
+
|+
+
264
\о
со
н
О)
Я
X
П
I
о,
а
+
' С?
^ + ^
'=• +
■ I
I X
N
6
^ L
+
4-
.о
г*
1
In
еч
1
1 Q
—
1
1
S4
1
2,
*с>
+
а
1
<о
«3
1
0)
1
1
N
С*
•ft
|
1
С1
•——*
ч
+
6
о
3
+
о
с
+
о
3
ел
О
и
I
+
+
•О N
i СЧ
I
й
+
о
3
+
I +
+
•О I
I ^
+
+
ел
+
+
+ 3
2,
+ „
•ft «
л +
I «
е»
•о
о
**~>
«3
+
ел
-О
+
о»©
3
1 +
5
+
I
265
to
О)
О)
Продолжение табл. VI 1.11
G(s)
g(t)
t~ot — e~at sec 0 (w0* - 0),
где
8 = tg"i
b — a
G (2)
2 —ze
2-е
г-ЬТ
sec 6 cos ((о0Г — 0)
z2-2z<TaTcos(oQT + er2aT
G (z, m)
-bmT
z-t-bT
sec 0 {2 cos (тщТ + 0) —
<ГаТ cos [(1 — m) (о0Г — 6]) <TamT
z2-2zt-aTcos(oQT + e-2ar
[(a-b)2 + (Q20}(s + a)
(s+b)[(s + a)2 + (u20]
(a-
-6)e-w —(a —ft)e~fl/
X sec 0 cos (co0/ + 6),
X
(a—b)z
(a—6) с
-бтГ
где
2-е
-^
^ (a — a) (6 — a) + cog
g (a-6)(o0
(a — b) [z2 — z€~aT sec 9 cos (щТ + 6)]
z2-2zt-aTcos<*QT + e-2aT
z^<rbT
(pc — 6) sec 0 {z cos (m(u0T + 8) —
«-ar
cos[(l—т)(о0Г + 6]} е
—amT
z2-2z<raTcosxDQT+e-2aT
[(a~b)2 + (4]x
X(s2 + as+P)
(s + 6) X
X [(s + af + u2}
где
+ £2e~a' sec 6 cos (w0* + 0),
(b2 — fra+P)*
k2 = a2 + (4 — 2ab + ba-
л-ьт
6=tr1
•P;
afc2 - (a2 + со2) x
X (a —6) + P (2a-6)
(D0£2
+
fe2 [г2 — 2е~аГ sec 6 cos (щТ + 6)]
22_-22е-а7,со8(о0Г + е-2а7,
(ft2 — fra + P) 2
fc2 sec 6 {2 cos (тсооГ + 0) —
-gr cos 8 [(1 — m) со0Г + 8]} е"0™7,
22-22e-^cosco0r-be-2fl7,
s
w
<3
N
<3
~
ЪО
"с/Г
о
*""
£
о
'•
^ ф4
•ч
з 3
1 £ 1
1 О '
Ф О
о <->
J
1
CN
+
С
3
СЛ
О
о
^
|
ы
см
1
см
ф4
+
к
о
3
СЛ
N
i О
1 °
1 ш
—*» О
1 CD
CO
LL ь*
И* а
1
1
CN
1
ъ
4-
Е^
3*
ел
О
^
о
1
см
1
ям
1
1
ф4
+
° 1
*-' Q 3
СЛ 1
о ^
Ф Ъ£
о ■*-•
8 II
"а Ф
|
1
»—•
£
и
CNO
3
CNO
3
+
CN
'S4
со
со
b.
Б
а
| "а.
ш4^
<ЗХ
+
в
1
1
ь + +
'« S 1
1 its
n ш '—
СЛ
о о
CD и
w к,
1
1
_ 1
1
Т
М
N
<ЗХ
+
в
•О
I
1
в*
, 3,\
СЛ
°
1 8
1 а
1 I
N 0)
1
— |
М
*** 1
CN
1
cy
+
3
СЛ
*""
<3
1
CN
1
CM
-4
а
га
1
'си
+
^
3*
СЛ
о
-N
а
1
ы
см
1
«Vi
+
^
^ 1 «
1 i i "•"ч ^
+ + 8 *§» SS
»о о | со.
1 S + + 4-
*> ' CN П^
__ СЛ ^ «
«■8 £ V*
-РФ 1 1 1
о «и cno **£ о
J ? + х
о
3
* II Sf
"Г 1е II
CD *TN
и
X ^
, ,«32.
"3° +
+ 8
Ъ +
1 •£■
в X
3
X +
/—4 °*
+ +
>_• CO
1—,
X
^
5
а
1~
ф4 S4
^ц
-^ сл ^
О I
1 s I
1 N ~<
о о
1 1
V
1
<3
\\
\ +
г*
3
1 сл
°
^
"3
1
см
1
+р 1
^
<=>
сл 1
N
°
О
ф
1 ^
к t-
^ а
1
1
N 1
0)
+
о
3
СЛ
о
"*•
сз
1
N
СМ
|
ч*
1 1
1
Ф4
+
J Нз
СЛ iH
О '
о 130
Ф о
а> ев
й* У
1
|
^_и
м
CNO
3
+
CN
<N О
3
+
см
+
со
*—*
со
267
_
_i
1—1
>
t?
ие таб<
жен
1
о
О,
с
?
N
-
^n7
о
ъо
"** 1
•о
*■•
5
1
ф 5
_+4
•8
^ и 7
1 S 1
о о
О) О
I
к-
°
V
■ +
3
18
О
' 1
СМ
1
1
Г4
1
8
р 1
N
•С>
1
1 Ф
1— W
CU
'«1
1
*\» к
n
»с> 1
"ч
3
1
+
О
3
со
О
и
3
1
1
1
N»
1
1
ф »о
Q (МО
3 з
1/1 7
о _|-
>—'' <м
Ф СЗ
О
3
со ед
? 1
1 со
* II
1 ®
О)
*=*
* U
^
+
со
^_,
(NO
3
+
СМ
CNO 1
3
+
CN
'с?
+
со
со
*""
5
1 '
3
+«
М 1
1 1
/*"*s '
СМО »-*
3 w
+ 4f
' ' -L
-f- 1 «W
1 Ф4 ^
п
~ ^ 1Г
^ ° .
И 1J.
*W ф !___
О СО
со £3
1
0>
1 1
к-
°
см
J
0)
+
°
3
со
О
Гч*
СМ
1
I
(М
+
Ф
см |
СМ
1
N
см
+
смо
3
+
ем 1
Q
- +
о
со
О
о
Ч>.
N О
—« со
1 &
N I
~ 8
1
ем
N
СМ
см
1
+
о
3
(О
О
U
СЗ
1
ей
1
Nv
tM
+
/»-«ч
ф
1 1 см
"Г ^ «
а £ i
1 s ^ Г
ж* О 1
/^^ч Ф ,Н
о
3
м
°з° S «•
СО о
1 СЗ СО
^ 1
+
3i
**
с_
ем
(МО
3
+
смо1
3
+
ем
"3
+
со
<м
со
К
s
1 а
, i I
•ft» ^
смо ,
3 С
~Г CNO
" +
1 1 a)
1 ф4 ^ц
1 3 °
1 3
1 Й 1
w ф ii
о со
си О
Й у
04 к.
•fti о
1
0)
1 1
Ф
i 1 +
% 1
+
tv»
CM |
•ft»
1
1
смо
3
+
см 1
^4
о
3,
со
о
о
Ф
- 3
1 *-
" 1
1
N
•ft*
(^
СЗ
см
+
о
3
со
О
и
сз
см
'1
1
СМ
Гч»
см
1
+
°
3
со
о
и
сз 1
I
ей
1
см
Гч>
^_« CNO
Ф4 3
1 + i«+
+ r i i
-^ о см о 4-
^-^ u 3
3 0 "Га
4- Si см
^ ? II
С4
•fti
3
1
н 1
eu см ьл 1
•fti а
1 •*
II
Si ф
e=C
u 1
+
CO
CM
(NO
3
+
^2^
"3° '
+
CM
СЗ 1
+
со
rsj
со
268
Для того чтобы регулятор был физически реализуем, необходимо, чтобы
числитель передаточной функции скомпенсированной системы имел
порядок не выше, чем знаменатель этой передаточной функции. В
рассматриваемом случае это будет выполнено, если потребовать, чтобы знаменатель
передаточной функции скомпенсированной системы был на два порядка
выше, чем числитель. Следовательно,
G, (г) = К0 U / zpjf- z~\ Tp < Г0. (VII.259)
(2— l)(z — e P' °
Подставляя формулы (VII.258) и (VII.259) в выражение (VII.237),
получим соотношение, определяющее передаточную функцию регулятора:
(l_e-^V)(2_e~VV)z
GR (z) = 7 т lт^, т ,т^ T1 Пм ЛГхл • (VII.260)
(l-e^/ro)(z_e-V^o)(2_1)_/Co(1_e-V7'o)2-^-1) V
В работе [8] даны реализация импульсных систем автоматического
регулирования, показатели качества и временные характеристики систем
со скомпенсированным запаздыванием.
К системам с амплитудной импульсной модуляцией в соответствии
с работой [121 можно свести системы с широтно-импульсной модуляцией
за счет применения разностных уравнений, а вообще говоря, и
нелинейные импульсные системы [301. В фундаментальной работе [30] приведены
оптимальные значения настраиваемых параметров импульсных
регуляторов на основе квадратично-интегрального критерия.
Список литературы
1. Analiza i synteza ukladow regulacji impulsowej i cyfrowej. Warszawa, 1962. Biuro
Ksztalcenia i Doskonalenia Kadr Naukowych PAN.
2. Barker R. H. The pulse transfer function and its application to sampling servo-system.
Proc. IEE, Desember 1952, Vol. 99, Pt. IV, pp. 302—317.
3. Gischpoff H., Thomas I. Ein Approximationsverfahren fur zeitoptimale Regler in li-
nearen Abtastregelkreisen mit Totzeit. Messen, Steuern, Regeln, 1967, Heft 8, S. 287—
291.
4. Brown В. М. Application of operational methods to sampling and interpolating systems.
Proc. I IFAC Congress, Automatic and Remote Control, Vol. I, pp. 270—276, London
196Г, Butterworths.
5. Цыпкин Я. З. Компенсация влияния запаздывания в импульсных автоматических
системах. В кн. «Теория и изменение дискретных автоматических систем». М., Изд.
АН СССР, 1960, с. 156—171.
6. Цыпкин Я. 3. .Теория линейных импульсных систем. М., Физматгиз, 1963.
7. Cypkin Ja. Z. Ober die Beseitigung des Einflusses von Totzeit auf die dynamischen
Eigenschaften von nichtlinearen Impulsregelsystemen. Regelungstechnik, Juni, Heft 6,
S. 196—198.
8. Dalhin E. B. Designing and tuning digital controllers. Instruments and Control Systems,
June 1968, pp. 77—83.
9. Fol linger O. Synthese von Abtastsysytemen in Zeitbereich. Regelungstechnik, Juni 1965,
Heft 6, S. 269—275.
10. Gessing R. Rownania roznicowe neiliniowych ukladow impulsowych z rzeczywistym cza-
sem opoznienia. Prace IV Krajowej Konferencji Automatyki, z. 1, Krakow 1967, AGH,
s. 115—133.
11. Grabbe E. M. at al. Handbook of Automation, Computation and Control. Vol. 3. Los
Anglelos, California 1961, J. Wiley, pp. 1201—1209.
12. Гришук В. П., Дамоиленко Ю. И. Приближенная методика выбора оптимальных
настроек систем прерывистого регулирования. — «Автоматизация и Приборостроение».
Киев, 1959, с. 80—87.
13. Haberstock F. Adaptive sampled data system for achieving minimum settling time in
systems with time varying parameters. Proc. Ш-rd IFAC Congress, London, 1963,
Session 45. #> 4
14. Haberstock F. Ober die Synthese von Abtastreglern fur Regelkreise beliebiger Ordnung.
Regelungstechnik, Teil I, Mai 1965, Heft 5, S. 235—239; Teil II, Juni 1965, Heft 6,
S. 281—286.
15. Izawa K. Discontinuous feedback control systems with sampling action. Automatic and
Remote Control, Vol. I., pp. 321—327, London, 1961, Butterworths.
269
16. Емельянов А. И., Емельянов В. А., Калинина С. А. Практические расчеты в
автоматике. М., «Машиностроение», 1967.
17. Jury E. I. Synthesis and critical study of sampled—data systems. Trans. AIEE. July
1956, Vol. 75, Pt. II, pp. 141—151.
18v Jury E. I. Przeksztalcenie Z i jego zastosowania. Warszawa, 1970, WNT.
19.' Kondo В., Iwai S., Saga M. Finite settling—time response in sampled—data control
systems with saturation. Automatic and Remote Control, Vol. I, pp. 305—310, London,.
1961, Butterworths.
20. Kopielowicz A. P. Dobor regulatorow automatycznych. Metody obliczen. Warszawa,
1964, WNT.
21. Kosorok I. R. Program for obtaining inverse Z-transforms Instruments and Control
Systems. June 1968, pp. 70—71.
22. Kuo В. С Analysis and synthesis of sampled—data control systems. New York, 1963,.
Prentice—Hall E. E. Series Englewood Cliffs.
23. Lago G. V. Additions to Z-transformation theory for sampled—data systems. Trans.
AIEE, January 1955, Vol. 74, Pt II, pp. 403—407.
24. Lopez A. M., Murrill P. W., Smith C. L. Optimal tuning of proportional digital
controllers. Instruments and Control Systems, Oktober 1968, pp. 96—102.
25. Lopez A. M. Ph. D. Dissertation. Lousiana State University 1968.
26. Моругин Л. А. Импульсные устройства с запаздыванием обратной связи. М.,
«Советское Радио», 1961.
27. Neumann В. Ein Beitrag zur Pulsregelung. Regelungstechnik, Oktober 1960, Heft 10,
S. 348—352.
28. Nowacki P., Szklarski L., Gorecki H. Podstawy teorii ukladow regul'acji automatycznej.
Warszawa 1962, PWN.
29. Ольденбург Р., Сарториус Г. Динамика автоматического регулирования. М., Гос-
энергоиздат, 1949.
30. Основы автоматического регулирования. Под ред. Солодовникова В. В. М., Машгиз,
Т. I., Теория. 1954, гл. XXI.
31. Pai M. A. The operational solution of difference—differential equations using the
modified «z» transform. I. R. E. Trans, on Automatic Control, October 1962, No 5, pp. 124—125.
32. Peinke W. Regelkreise mit periodisch anfallenden Istwert. Regelungstechnik, Mai 1961,.
Heft 5, S. 188—194.
33. Popek L. Dobor optymalnych parametrow regulatorow w ukladach impulsowych. Praca
doktorska, Katedra Automatyki i Elektroniki Przemyslowej, AGH, Krakow, 1963.
34. Ragazzini J. R., Franklin G. F. Sampled—Data Control Systems. New York, 1958,
McGraw-Hill.
35. Ротач В. Я. Импульсные системы автоматического регулирования. М.—Л., «Энергия»,
1964..
36. Strejc V. i inni. Teoria regulacji automatycznej. Warszawa, 1962, WNT.
37. Strejc V. Synthese von Regelkreisen mit Prozessrechnern. Messen, Steuern, Regeln, 1967,
Heft 6, S. 201-207.
38. Strejc V. Synthese von Regulungssystemen mi tProzessrechnern. Praga 1967, Academie
Verlag, S. 271—282.
39. Strejc V., Salmon M., Koteek Z„ Balda M. Zaklady teorie samocinne regulace. Rraha,
1958, SNTL.
40. Ширанков Г. Д. О новом принципе регулирования быстродействующим нелинейным
регулятором производственных процессов с большим запаздыванием. —
«Автоматизация и Приборостроение», Киев, 1959, с. 75—80.
41. Tait К. Е., Stanton R. В. The inter—relation on sampling aud transport lag in
determining control system stability. Internat. J. Control. 1967, No 2, pp. 97—122.
42. «Техническая кибернетика», Кн. 2 «Теория автоматического регулирования», под
ред. Солодовникова В. В., М., «Машиностроение», 1967, с. 431—458, 517—576.
43. Той J. Т. Digital and sampled—data control systems. New York, 1959, McGraw—Hill.
44. Труды международной конференции 'по многомерным и дискретным системам
автоматического управления. Прага 9—12 июня 1965.
45. Траксел Дж. Синтез систем автоматического регулирования. М., Машгиз, 1959.
46. Tschauner J. Einfunring in die Theorie der Abtastsysteme. Munchen, 1960, R. Olden-
bourg, S. 138.
47. Волгин Л. Н. Элементы теории управляющих машин. М., «Советское радио», 1962.
48. Weinmann A. Die bestimmte und verallgemeinerte Vorhersage von Signalen in linearen
Regelungssystemen. Elin—Z., 1965, Nr 1—2, S. 18—55, 11—111.
Глава VIII
Устойчивость и автоколебания в нелинейных
системах автоматического регулирования
с запаздыванием
Г) еп
г
А
Регулятор
Объект •
У У
'
\я
В предыдущих главах рассматривались линейные системы,
представляющие собой некоторую идеализацию реальных систем, ибо в
действительности каждая система является нелинейной.
Нелинейности, встречающиеся в системах, можно подразделить [11],
например, наследующие:
а) нежелательные нелинейности, которые, однако, нельзя по тем или
иным причинам ликвидировать; к ним относятся трения, люфт, насыщение
и гистерезис;
б) нелинейности, специально вводимые в систему и прежде всего в ее
управляющую часть.» Эти нелинейности вводятся для улучшения качества
Рис. VIII.1. Блок-
схема системы ре*
гулирования
работы системы, например, в оптимальных или экстремальных системах
или для упрощения технической реализации системы. Примером могут
служить релейные системы.
В этой главе будут рассмотрены две задачи:
1) определение условий устойчивости нелинейных систем;
2) определение амплитуды и частоты автоколебаний.
Рассмотрение ограничим случаем, когда на систему действует
постоянный по величине входной сигнал, представляющий, например, заданную
величину в системах стабилизации (рис. VIII. 1). Исследуя ошибку
е = w — y (VIII. 1}
и принимая такие координаты состояния х системы, чтобы в положении
равновесия, например при 8 = 0, обязательно было х = 0, изучим
поведение системы вблизи начала координат, т. е. изучим так называемое
тривиальное решение х (t) = 0. Но здесь не будем рассматривать подробно
очень важный в других отношениях вопрос устойчивости системы при
постоянно действующих возмущениях с ограниченной амплитудой.
Эта задача будет решаться тремя методами:
1) методом Ляпунова, развитым Н. Н. Красовским [9];
2) методом В. М. Попова [81, [13];
3) методом описывающей функции [10].
Метод фазовой плоскости, применимый для анализа систем второго
порядка, рассматривается в главе, посвященной релейным системам.
271
§ VIIIЛ. Второй метод Ляпунова
Как и в случае систем без запаздывания, основной идеей метода является
отыскание функции V [х (t)> t], играющей роль обобщенного расстояния
от начала системы координат, такой, чтобы ее производная dvldt вдоль
траектории уравнения, описывающего движение системы, была
положительна: dvldt 5> 0.
Формулировки теоремы Ляпунова об устойчивости и об
асимптотической устойчивости аналогичны теоремам для систем без запаздывания,
однако с их помощью мало что можно сделать. Но здесь существенный
вклад внес Н. Н. Красовский [9], который предложил вместо функции
Ляпунова рассматривать функционалы, обладающие лучшими свойствами.
Определение!.
Функционал
V [хг (s), х2 (s), . . ., хп (s), /] = V lx (s), /I, — т ^ s < 0,
t^t0 (VIII.2)
называется положительно определенным, если существует такая функция
<р (г) > 0 при г Ф 0, что
V[x(s), /]^ф[||д:(5)||т]. (VIII.3)
Норма [| х (s) || векторной функции х (s) может быть определена в
различных пространствах. Чаще всего норма берется в пространствах L2
или С0. А в случае нейтрального уравнения надо брать норму в
пространстве С\. Норма | х (s) ||т в пространстве Со и норма || х (s) ||T2
в пространстве L2 имеет вид
ll-*(s)!r= sup K(s)l;
—T<s<0
!•*№ =
} J A (r) ds
-TI=1
1/2
(VI11.4a)
а соответствующие им нормы вектора х выражаются формулами
11*1= sup |*.|; )
1<£</г
11*Ь = ]/|^-
(VIII.46)
Определение II.
Функционал V [х (s), t] имеет мажоранту, стремящуюся к нулю, если
существует непрерывная функция срг (г) ^ 0, срг (0) = 0, такая, что
V [х (s), t] < ф1 [|| х (s) у (VIII.5)
Опираясь на вышеприведенные определения, можно сформулировать
следующую теорему.
Теорема об устойчивости (обобщение второго метода Ляпунова).
Тривиальное решение системы
dxt (t)
dt
■ = fi(t, МО,.-., МО, М'-М*)],..., *nlt-
"МО!
ГС, (VIII.6)
*n['-*i(0L-.., xn[t — Tn(t)]), i=l, 2, .-.., л,
где т ^ T; (t) ^ 0, устойчиво, если существует непрерывный,
положительно' определенный функционал
V [х (s), t]y — т ^ s < 0, t^ t0;
||jt||(s)|[T<tf, Я>0, V\0, 0 = 0,
272
имеющий мажоранту, стремящуюся к нулю, такой, что его производная
неположительна:
dVlXn (t + s), t]
1 *dt <°» (VIIL?)
где x (t -f s) — решение уравнения (VIII.6), определяемое начальной
векторной функцией Ф (/), t0 — т ^ t ^ t0. Доказательство теоремы
можно найти в работе [9].
Первая теорема Н. Н. Краеовского об асимптотической устойчивости.
Тривиальное решение уравнения (VII 1.6) асимптотически устойчиво, если
существует непрерывный положительно определенный функционал
V [х (s), t] при t ^ t0 и ||* (s)t|| < Я, Н > 0, имеющий мажоранту,
стремящуюся к нулю, такой, что производная dV [xo(t -f s), t]/dt
отрицательно определена. Функция Хф (t + s) является решением уравнения
(VII 1.6), определяемым начальной векторной функцией Ф (/), где | Ф (/0 +
+ s)x || < б, а б > 0 достаточно мала.
Л\ожно доказать обратную теорему.
Вторая теорема Н. Н. Краеовского об асимптотической устойчивости.
Решение уравнения (VII 1.6) асимптотически устойчиво, если существует
функционал V lx (s), t], удовлетворяющий условиям
V [х (s), t] < Wx Qx (0) ||) + W2 Qx (s)||x2); (VIII.8)
Vlx(s),t]^Wqx(0)\\); (VIII.9)
lim sup4r<-cpfl*(<>)D. (VIII.10)
где W± (г) и W2 (г) при r ^ 0 монотонно возрастает, причем Wx (0) =
= Wo (0) = 0, а функции W (г) и ср (г)-непрерывны и положительны при
r> 6.
Доказательства этих теорем можно также найти в работе [91.
Теперь рассмотрим примеры, иллюстрирующие возможности
применения этих теорем для анализа устойчивости нелинейных систем
уравнений.
Пример 1. Заданная система уравнений описывается системой
нелинейных дифференциальных уравнений
-^L=aax1 (/)+•••+ ainXn (0 + ft (*i С), •••,*» (0;
Xi(t-ha),...,xn(t-hin)t), ;=l,...,n, (VIII. 11)
где а/у = const, htl = const, а функция f. удовлетворяет условию
| /, (xlt . . ., xn; ylt . . ., yn, t) | < p (|| x || + | у I). (VIII.12)
Предположим, что все корни X характеристического уравнения
a2i, . . ., й2п
artl, . . ., ап
= 0 (VIII.13)
имеют отрицательные действительные части.
Тогда в качестве функционала V можно взять квадратичную форму
V(xu ...,*„)= t btixtxh (VIII.14)
удовлетворяющую условию
£=У.£г(У«л1—У*?- (VIH.15)
273
Производная dvldt вдоль траектории системы уравнения (VI 1.11
имеет вид
dv VI dv I \S \ .
/=i \ /=i
n
+ S|-M'i ^«; *i(t-hu),...9xn(t-hu),t). (Vin.16)
/=i
Для того чтобы были выполнены условия второй теоремы, достаточно,
чтобы производная dvldt была функцией, отрицательно определенной на
кривых х{ (£), (I > 0), удовлетворяющих условию
V (хг (0), . . ., хп (0)) > qV (хг (g), . . ., хп ф (VIII.17)
при
£ < 0, 0< ? < 1, ? = const.
Кривые xi (£), удовлетворяющие условию (VIII. 17), в каждом случае
будут содержаться в семействе кривых, удовлетворяющих неравенству
п п
2*?(6)>*"£гЕ*?(6)' (VIIU8)
i=i max i=i
гДе Pmm и Ртах — наименьший и наибольший по модулю корни уравнения
bll — р, . . ., ь1п
62iv • . ., b2n l (VIII.19)
ЬП1> ч. •, Й/г
Следовательно, достаточное условие асимптотической устойчивости
решения х = 0 уравнения (VIII.11) сводится к тому, чтобы правая часть
уравнения (VII. 16) была функцией, отрицательно определенной на
кривых xt (£), удовлетворяющих неравенству (VIII. 18).
Пример 2. Задано уравнение второго порядка
5-+,(Р(-5Г'0+/[х(/~/1Й)1 = О' (VHI.20)
где / (х) — функция, относящаяся к пространству Сг и удовлетворяющая
условиям
-^ > а >0, | Г (x)\<L при ^0, (VIII.21)
а ф (у, 0» h (t) — непрерывные периодические функции времени,
удовлетворяющие неравенствам
-5^9- > Ь > 0 при уФ 0; (VIII.22)
г/
Л(0^0, Л (*)<*. h = const, (VIII.23)
Полагая, что движение системы началось при / <: 0, можно при / > О
записать уравнение (VI 11.20) в таком виде:
dx
274
„ - <f(D(l).t)-f(x,l)+ J f <*<( + »)) !/(< + »><»• (VIII.24)
A—„„ ,
-MM
Функционал берем в виде
V((x(0)f x(*)) = 2jf(E)dg + ^ + (-f)2 J (j2!^*^.
о x ' -h \о, /
(VIII.25) '
Находя производную lim Av/At вдоль траектории (VIII.20), можно
доказать, что условием ее отрицательности, а это и есть достаточное
условие устойчивости решения х = 0, у = 0 уравнения (VI 11.20), является
наличие неравенства
а
Л<-£-. (VIII.26)
Пример 3. Задано уравнение первого порядка
dx
dt
• = f[*(t — h(t))%t\% 0<Л(/)<Л, (VIII.27)
причем предполагается, что / (х, t) — непрерывная функция двух
аргументов относительно переменной х — принадлежит пространству Сг и что
a/|<L, I = const. (VIII.28)
дх
Если взять в качестве функции Ляпунова V = я2, то можно доказать,
что достаточными условиями асимптотической устойчивости решений х = 0
уравнения (VIII.27) являются
/ (*, /)/* + ^2Л (0 < -Y, 7 > 0, х Ф 0, (VIII.29)
где у — достаточно малое положительное число.
Пример 4. Задано нелинейное уравнение второго порядка
у = *L9 h>0 = const, (VIII.30)
где функции / и ф удовлетворяют условиям
/ (*> У) — f С*» 0) ^ f(x, 0) ^ , , п # л
7 1 у; ' 1 ; < —а, ' ^ ; < —Ь при х Ф 0, у Ф 0,
(VIII.31)
причем а и b — положительные постоянные и
|Ф(*Л t)\^L\y\. (VIII.32)
Выберем функционал V в виде
х 0
У (*(*). y(*)) = _J/(Ef o)dE + ^- + ^- J jf ©«. (VHI.33)
0 ; -Л
Достаточные условия устойчивости решения х = 0, г/ = 0
уравнения (VIII.30) принимают вид
а>1. (VIII.34)
С помощью теоремы второго метода Ляпунова можно доказать теоремы
об устойчивости в малом аналогично теоремам первого метода Ляпунова
дли нелинейных систем без запаздывания.
18* ' 275'
§ VIII.2. Первый метод Ляпунова
Анализ устойчивости в малом нелинейных систем с запаздыванием для
широкого класса систем можно свести к анализу устойчивости в малом
линейных систем с запаздыванием, т. е. к анализу устойчивости в первом
приближении.
Пусть система описывается системой нелинейных дифференциальных
уравнений
-^W~ = fi [*i (0, . •.. хя (0, * (/-т,), ..., ХпУ-тД, ...
.... *i(*-Ta), -..,**('-**)], '=1, 2,..., л, (VIII.35)
где ть . . .,' xk — положительные постоянные.
Полагая, что функции ft вблизи исследуемого положения равновесия
имеют первые, производные относительно всех аргументов xi9 уравнение
(VIII.35) можно представить в виде
^- = tx S0 ЪМ (f - т,) + /?, [хг (0, ...,хп (О,
*1 (t — Тг), . . ., Хп (t — Ti), . . ., Хг (t — Тл), ...
• - •> xn(t — Tk)l i = 1, 2 л; т0 = 0, т,^0, (VI 11.36)
где функция Rt зависит от производных выше первой функции /- по всем
xit а коэффициенты aui представляют собой величины первых
производных функции fL по хг в положении равновесия.
Тогда анализ устойчивости в малом нулевого решения системы
уравнений (VIII.25) аналогичен анализу устойчивости в малом нулевого решения
линейной системы, называемой системой первого приближения для
системы (VIII.35):
4P~ = t E *,/!*/('-*/). i=l> 2 *■ (VIII.37)
Теперь можно сформулировать следующие теоремы.
Теорема 1. Нулевые решения системы уравнений (VIII.35)
асимптотически устойчивы, если:
а) все корни X характеристического уравнения системы первого
приближения (VI 11.36)
2 Ар-™ - U
1=0
= 0 (VIII.38)
имеют отрицательные действительные части, где матрица At = {at-//},
/ — единичная матрица того же размера; I — определенная постоянная;
б) остаток Rt в уравнении (VI 11.36) можно определить из выражения
n(k+l)
|Я,("ь "t. .... М*+1))|<» Е Kl> (VIII.39)
где а — достаточно малая постоянная, все | Uj| достаточно малы: \uj\ < Н
и t ^ t0.
Теорема 2. Если хотя бы один корень характеристического
уравнения (VI 11.38) имеет положительную действительную часть и не
выполняется условие а) теоремы 1, то тривиальное решение уравнения (VIII.35)
неустойчиво. В случае, когда характеристическое уравнение имеет корни
с нулевыми действительными частями, об устойчивости судят по
нелинейному остатку Rr
276
§ VIII.3. Устойчивость при постоянно
действующих возмущениях
Пусть на систему автоматического регулирования действуют постоянные
возмущения в виде некоторых функций времени / и координат хг С учетом
этого перенесем в правую часть системы уравнений (VI 11.35) явные
функции времени / и дополнительные звенья.
Задана система уравнений
d-^==fc[t,xj(l-Tl(t))], i= 1, 2, . .„ л. (VIII.40)
Решение хь = 0 (i = 1, 2, . . ., п) системы уравнений (VI 11.40)
называется устойчивым при постоянно действующих возмущениях, если для
каждого е > 0 существуют такие бх (е) > 0 и б2 (е) > 0, что решение
системы
^^ = U V, X, (t - Т, (t))] + R, [t9 X; (t - T, (t))l
i, j = 1, 2, . . ., n; / = 1, 2, . . ., k (VIII.41)
удовлетворяет неравенству \xt (t) | < e, / = 1, . . ., n\ t ^> t0
при
I Ri: I < Sx (e), \xt (s) | < 62 (e), — т < s < 0,
t = 1, 2, . . ., n,
причем в функции Ri аргументы \xf (t — xz (f)) \ < Я, Я > 0.
Теорема. Если решение xt. = 0 (t = 1, 2, . . ., /г) системы (VIII.40)
единственное, асимптотическое, устойчивое, и функции ft удовлетворяют
условиям Липшица г относительно всех аргументов, начиная со второго,
то решение устойчиво при постоянно действующих возмущениях.
§ VIII.4. Метод Попова
Этот метод считается наиболее эффективным среди точных методов анализа
нелинейных систем управления [1], [2].
Если говорят, что нелинейная система устойчива в малом, то этим
констатируется только факт существования некоторой «области притяжения» G
(рис. VII 1.2) вокруг данной особой точки О, являющейся положением
равновесия системы. Однако ничего не говорится о границах «области
притяжения», которая, вообще говоря, может быть достаточно малой.
Через L обозначим область возможных начальных отклонений от особой
точки, которые накладывают технические условия эксплуатации системы.
Если область L полностью лежит в области притяжения, то говорят, что
система устойчива в большом. На рис. VII 1.3, а представлен фазовый
-портрет системы устойчивой в малом, но неустойчивой в большом, а
на рис. VIII.3, б — фазовый портрет системы, устойчивой в большом.
Если область притяжения G особой точки или область устойчивости не
ограничена и охватывает все фазовое пространство, т. е. если система
устойчива при любых начальных отклонениях от положения равновесия,
то о такой системе говорят, что она устойчива во всей области.
Нелинейные системы, имеющие одно положение равновесия,
устойчивые во всей области, составляют класс нелинейных систем, равноценных
с точки зрения топологической структуры линейным системем.
1 Функция / (х) удовлетворяет условиям Липшица, если существует такая постоянная
К £ (0, сю), что при всех х1у х2в рассматриваемой области изменения аргумента х
выполняется неравенство
I / fai) — / ta) I < К (*i — х2). (Прим. ред. оригинала).
277
Пусть задана нелинейная система, описываемая при помощи/системы
уравнений
£ [a^/(0 + *^/C —T)]+V[a(/—т)], f=lf 2, .. ., я, (VIII.42)
° = 2 ад*.
л=1
(VIII.43)
Все aih bih hL и ck постоянны; некоторые из них могут быть равны
нулю. В частности, если все постоянные ck равны нулю, за исключением
Рис. VIII.2. Фазовые траектории
системы, устойчивой в малом
Рис. VIII.3. Фазовые траектории системы,
устойчивой в большом (а); фазовые
траектории системы, устойчивой в малом, но
неустойчивой в большом (б)
*г
Г \\\\V>
sxXj»
1
ш$>
УЩ
x\^v
*1
ф
одной, например съ то нелинейная функция зависит только от одной
координаты, например / (хг). Теперь предположим, что при некоторых
значениях коэффициентов aih bljy ft. и ck и при некоторой определенной
функции / (а) система устойчива во всей области. Кроме непрерывной
зависимости решения от коэффициентов и от функции / устойчивость во всей
области сЬхранится и при других функциях / (а), мало отличающихся от
первоначально заданной, когда величины коэффициентов аи-, btj, ht и ck
остаются теми же.
Рассмотрим кривую и = f (a), обозначенную на рис. VI 11.4 сплошной
линией. Соответствующая ей система устойчива во всей области. Другая
кривая, показанная штриховой линией, «возмущена». Очевидно, каждой
кривой / соответствует другая система вида (VI 11.42). Возникает задача,
важная как для теории, так и для практики: в каких пределах и как сильно
можно «возмущать» кривую / (а), не нарушая при этом устойчивости во
всей области системы?
278
Система (VIII.42) абсолютно устойчива, если остается устойчивой во
всей области при произвольной характеристике у = / (а),
удовлетворяющей неравенству
f(o)
К><
< #2,
(VI11.44)
где Ki и /С2 — постоянные заданные величины (Кг < /С2).
Следовательно, кривая / (а) должна целиком находиться ' внутри
заштрихованного угла, ограниченного прямыми у = К\в и у = /С2а
(рис. VIII.5). В этом случае считается, что система абсолютно устойчива
в угле (КгК2)- Простая
замена переменных
= / (а) - КгС
= х (VI 11.45)
Рис. VIII.4. Иллюстрация возмущений нелинейной
статической характеристики
Рис. VII 1.5. Иллюстрация понятия
абсолютной устойчивости. Область
допустимых деформаций
нелинейной статической характеристики
преобразует систему (VI 11.42) в систему того же типа, но с
характеристикой, удовлетворяющей неравенству
f(o)
0<
;*.
(VIII.46)
где К = К2 — Кг.
Систему (VI 11.42) можно записать в матричной форме
clx(t)
dt
= Ах (t) + Вх (t — т) + hf [a(t — т)] о = стх, (VIII.47)
постоянные векторы; стх —
где А и В — постоянные матрицы; hue
скалярное произведение.
'Предположим, что система (VI 11.47) удовлетворяет условиям
устойчивости в первых линейных приближениях, т. е. все корни ее
характеристического уравнения
det (А + е-^Я — XI) = О (VIII.48)
расположены в левой половине плоскости комплексного переменного.
Тогда существует обратная матрица (А + еиВ — XI)-1.
Теперь можно сформулировать теорему, являющуюся обобщением
теоремы В. М. Попова на нелинейные системы с запаздыванием.
Первая теорема об абсолютной устойчивости. Если все корни
характеристического уравнения
det(4 + e-4B —Л,/) = 0
расположены в полуплоскости Re X ^ —а < 0 и если в этой
полуплоскости существует такое конечное число q > 0, что
-^- + Re (1 -f- j(oq) e-i^c* (A + e-i<**B — /со/)-1 h:
:0,
(VIII.49)
279
то для каждой функции /, характеризующейся тем свойством, что
существуют такие /Ci < /С2 < К, что
К\о2 < of (a) ^ К2о\
(VI 11.50)
тривиальное решение системы (VI 11.47) абсолютно устойчиво.
Вторая теорема об абсолютной устойчивости. Рассмотрим систему
без запаздывания в переменной а, т. е. такую, которую можно описать
уравнением
*^ = Ax(t) + Bx(t-i) + hf[o(t)]; (VIII.51)
(J=CTX,
где А и В — постоянные матрицы; h и с — постоянные векторы.
I ^
_^г
Тл
(-))
-U |
Ч-Jr
г lS
it/
L.
i—На}^
^ » 1 h I *
i ■■■ ^ ^7 " *■
•
•
—*4 лл }-*■
L
*' Г7~~1
1ПП *Г
^ 1 ^^^ V
: : j
• •
■i|ir|—'
1
6"
1 |
У ,
г
1
1 1
G'
Рис. VIII.6. Блок-схема системы с передаточной функцией,
определяемой уравнением (VIII.57)
Теперь можно сформулировать следующую теорему: если все корни
характеристического уравнения
det (4 + е-**Я — XI) = 0
лежат в полуплоскости Re А, <: — а<0 и если в этой полуплоскости
существует такое конечное число q > 0, что
-j^ + Re (1 + j(oq) cT (A + t-i^B — /со/)-1 h ^ 0, (VIII.52)
то для каждой функции, для которой существуют такие Кг < К2 < К, ЧТО
/гго2 ^ of (a) ^ &2а2,
тривиальное решение системы абсолютно устойчиво.
После такой обобщенной формулировки теоремы Попова остается
открытым вопрос о возможном выборе числа q так, чтобы выполнялось
неравенство (VIII.48) или (VIII.50). Но мы используем здесь простую
геометрическую интерпретацию теоремы, предложенную Поповым.
Для этого рассмотрим блок-схему, изображенную на рис. VII 1.6.
Линейная часть L системы, имеющая передаточную функцию G,
определена из уравнений (VI 11.47) и (VI 11.48) следующим образом.
Через р = dldt обозначим оператор Хевисайда, который здесь удобно
использовать, а благодаря тому, что начальная функция предполагается
равной нулю, удается избежать ошибок.
Тогда систему уравнений (VI 11.47) можно записать в следующем виде:
(А + е~^В — pi) х + hue-P* = 0; 1
где
u=f(o). (VIII.54)
280
Умножим первое равенство системы (VIII.53) на (А+е~рхВ — р1)~г
и получим
х = — (А + е-р*В — pi)-1 he-p^u. (VIII.55)
Умножим выражение (VI 11.55) на ст> используем вторую зависимость
из системы (VIII.53) и получим
а = ст (А + ef>xB — р1)~1 Ае-'* (—и). (VIII.56)
Передаточную функцию линейной части системы запишем в виде
J G (р) = -^ = С (А + t-P^B—pI)-1 ht~p\ ' (VI11.57)
Полагая р = /со, найдем частотную характеристику
G (/со) = e-/'wcT (Л + е-'<от# _ /со/)—1 Л. (VI11.58)
Соответственно для системы уравнений (VI 11.51)
G (уя|>) = ст (А + е-/<^# + /со/)-1 А. (VI11.59)
Следовательно, условия (VI 11.49) и (VI 11.52) обеих теорем примут
следующий вид:
Re (1 + jcoq) G (/со) ф ±- ^ 0. (VI 11.60)
Теперь найдем видоизмененную частотную характеристику
G* (/со) = Re GO"©) +/<o ImG (/со), (VIII.61)
которая получается из характеристики G (/со) умножением ординат на со,
оставляя абсциссы без изменения.
Обозначим
P = ReG(/co);
Q = со ImG (/со); } (VIII.62)
G* (/со) = Р + jQ.
Следовательно, на основе соотношений (VI 11.62) и (VI 11.60)
Re (1 + jqco) G (yco) -j- -i- = Re G (/со) — po Im G (/со) + -L,
т. е. условие Попова можно записать следующим образом:
P-qQ+^>0. (VIII.63)
Уравнение
P — ^Q-L-l-^0- (VIII.64)
на плоскости Р и Q определяет прямую, проходящую через точки Р =
= —Ilk и Q = 0 с наклоном tga = l/q.
. Благодаря вышеприведенной геометрической интерпретации получили
простой критерий абсолютной устойчивости: для того, чтобы система,
описываемая уравнением (VIII.47) или (VIII.52), была абсолютно
устойчива, достаточно, чтобы на плоскости Р, Q через точку —l/k, лежащую
на действительной оси, можно было провести прямую (не горизонтальную)
так, чтобы видоизмененная частотная характеристика G* (/со) не
пересекала эту прямую. На рис. VII 1.7 для примера показаны взаимные
положения прямых и характеристик G* (/со) абсолютно устойчивых систем,
а на рис. VIII.8 — примеры, когда критерий Попова не выполняется,
т. е. когда система не может быть устойчива в большом.
281
к
Г
\ ^
\ (с
) ч
1
Л
))}
V
s p
Рис. VIII.7.. Геометрическая интерпретация теоремы Попова об
абсолютно устойчивых системах
1 \
У*.
i
д) I
J "р
Рис. VII 1.8. Примеры амплитудно-фазовых характеристик
разомкнутых систем, неустойчивых в большом
282
Критерий Попова дает только достаточные условия, однако о его
достоинствах говорит тот факт, что все известные в настоящее время
критерии абсолютной устойчивости удовлетворяются, если удовлетворен
критерий Попова.
§ VIII.5. Метод описывающей функции
Этот приближенный метод, который основан на видоизмененном Е. П.
Поповым [121 критерии Найквиста, позволяет выяснить возможность
возникновения автоколебаний и определить их амплитуду и частоту. Конечно,
результаты, полученные с помощью этого метода, являются приближен-
i
<С1
'
^У
0
а
JW
а
Г"
\
i
б
г
-ь
/WJ
— -«--
0
-а
i
Г
I
1
1
а
i
b
I
1 <Ч
Рис. VII 1.9. Однозначная нелинейная
характеристика с насыщением и зоной
нечувствительности
Рис. VIII. 10. Неоднозначная нелинейная
характеристика с петлей гистерезиса и
зоной нечувствительности
ными и в некоторых случаях могут быть даже неверными. Однако для
большинства систем автоматического регулирования он дает правильные
результаты. Сущность метода заключается в замене автоколебаний
эквивалентной гармонической составляющей. Из этого следует, что ошибка
в определении амплитуды и частоты тем выше, чем сильнее форма
автоколебаний отличается от
гармонической.
Из-за существенных нелинейно-
стей, встречающихся в системах
регулирования (чаще всего
нелинейности имеют релейный характер с
зоной насыщения и зоной
нечувствительности или зоной неоднозначности
из-за наличия гистерезиса или люфта)
(рис. VIII.9 и VIII. 10), нелинейная
часть системы генерирует высокие
гармоники со значительными
амплитудами. Доказательство
применимости метода описывающей функции,
учитывающего только первую
гармонику, основывается на
фильтрующих свойствах линейной части системы автоматического регулирования.
Если линейная часть системы удовлетворяет гипотезе фильтра, т. е.
ее амплитудная частотная характеристика имеет такой вид (рис. VIII. 11),
что частота основной гермоники со0 меньше, чем граничная частота со/, а
все гармоники имеют частоты выше, чем cof, то высшие гармоники
подавлены, и в системе установятся автоколебания, близкие по форме к
гармоническим. Это и обеспечивает применимость метода описывающей функции.
Следовательно, требования к частоте автоколебаний имеют вид
Рис. VII 1.11. Условия применимости
метода описывающей функции
-5-< ©о < <of, k = 2, 3,
(VIII.65)
283
и представляются одновременно двумя неравенствами
С00 < (Of,
U ^ U О Q I (VIII.66)
k(o0 > ©у, k = 2, 3, » х
Для более детального рассмотрения метода исследуем систему
регулирования, описываемую системой нелинейных
дифференциально-разностных уравнений вида
dxi (/)
к /=1
= S а'Л' W + *//*/ С ~" т/) + М */ С — т/)1« * = 1> 2' * ' ' Л»
(VIII. 67)
где aih bu- — постоянные коэффициенты.
В соответствии с основным положением метода предполагается, что
Xj (t — т7) = Aj sin (o(t — т;). (VIII.68)
Периодична не только функция х} (t — т;), но и функция fif [xj (t — тД],
следовательно, ее можно разложить в ряд Фурье
п
f [A sin со0 (t — т)] = с0 + Е с* sin [&©0 (t — т) + <рЛ]
(VI 11.69)
и учитывать только основную гармонику.
Тогда вместо системы нелинейных уравнений получим систему
линеаризованных уравнений
(VIII.70)
где коэффициенты си- и dil представляют собой коэффициенты
разложения Фурье:
2я
си = -^т J ///И/sin со (/ - тД sin co/d (©01; (VIII.71)
о
2я-
d/y = ^- J ДуЛу sin© (/ —т,)cos©W (©/)]. (VIII.72)
о
Описывающая функция, таким образом, представляет собой отношение
символической амплитуды первой гармоники выходного сигнала к
символической амлитуде выходного сигнала:
J = с + /d.
Подставляя в соотношение (VIII.71) выражение
sin (ot =-- sin [© (t — Ту) + ©т7-] = sin © (/ — тД cos ©Ту +
+ cos (о (t — т;) sin ©Ту,
получим
2л
са = ~Ш7 I fu [Aisin ® $ ~ Т/М sin ® ^ — т/^ cos ^ ^ +
1 _
/
о
2я
+ -^ J fa lAJsin ® ^ — T/)lcos ® С — T/)sin ^ ^
о
284
или
си = cos сотуб, \fu\ + со sin (otjkc [fij]. (VII 1.73)
Аналогично, подставляя в соотношение (VI 11.72) выражение
cos со/ = cos со (t — Tj) cos coxy — sin со (/ — Ту) sin coxy,
получим
7 О
2я
+ ^5" J ^[ AiSin ® (/ — Т')] Sin ®(/ ~~ т/> Sin ®т^((0/)
или
sin cot/
^у = С08СОТу^П/,/1-^^^{/,/1,
(VIII.74)
где коэффициенты kc и &s определяются из известных соотношений для
нелинейных систем без запаздывания:
2я
k* <М = 1^7 1 ^/ (Л/sinЧ»)sin*^ (VIII.75)
о
2я
ММ = 1ЙГ 1 ^ (Л/81Пф)С08фЛр. (VIII.76)
7 о
Коэффициенты ct/- и d.y линеаризованной системы (VI 11.70) в системах
с запаздыванием зависят от частоты со, что не наблюдается в нелинейных
системах без запаздывания за исключением случая нелинейных систем
с гистерезисом.
После определения коэффициентов сп- и di}- можно приступить к
исследованию системы уравнений (VIII.70).
Характеристическое уравнение системы (VIII.70) имеет вид
det (A + C + Be-* + ХО — Щ = 0, (VI 11.77)
где е—и представляет собой матрицу вида
(VIII.78)
Матрицы А и В — постоянные, а матрицы С и D зависят от частоты со
и времени запаздывания т7-; матрица / — единичная.
Дальнейшее упрощение анализа системы (VI 11.67) можно получить,
если учесть возможность замены линейных звеньев с запаздыванием типа
bijXj (t — ту)
линейными звеньями без запаздывания путем гармонической
линеаризации, как и для линейных звеньев.
Таким образом, будем иметь
е-А,т =
£ hlx £ ^1
£—А,тв £—Ад2 .
:
e~un e-Kxn ■
• • е~^т>
. . А—^г
• • е~Кхп
dt
(VIII.79)
285
Коэффициенты c]j и dly, определяемые на основе выражекий (VI 11.73)
и (VIИ.74), имеют вид
с*ц = Ьцcos (оту; (VIII.80)
4 = _hL^lL. (VIH.81)
Следовательно, системы уравнений (VI 11.67) окончательно примут вид
^=^(«1/+*;^^ *=i. 2,..., п.
(VIII.82)
Характеристическое уравнение системы (VIII.82)
det (А + С* + С + kD* + Я/> — к/) = 0, (VIII.83)
где матрица Л постоянна, а матрицы С*, С, /)*, Z) зависят от
параметров О) И Ту.
Определение частоты автоколебаний и их устойчивости.
Периодические колебания в линеаризованной системе (VIII.82) возникают в том
случае, когда параметры системы выбраны так, что она находится на границе
устойчивости. При этом определители Гурвица для уравнения (VIII.83)
должны удовлетворять следующим неравенствам:
#У>0, /= 1, 2, . . .; /г-2; (VIII.84)
ЯЯв1 = 0. (VIII.85)
Частота автоколебаний cos на границе устойчивости легко определяется
из зависимости
0)5=^0^2^-, #о=1; л^З. (VIII.86)
ПП-2
Коэффициент а0 — свободный член характеристического уравнения
(VII 1.83), которое можно записать в виде
£ at7J = 0. (VIII.87)
Зависимости (VIII.85) и (VIII.86) содержат (п + 1) неизвестных Ajy
j = 1, . . ., п и (ds. Чтобы их определить, необходимы еще (п — 1)
уравнений. Эти уравнения легко определяются из линеаризованной системы
(VIII.82). Неизвестные (п — 1) амплитуды Л7 можно найти следующим
образом. Полагая в уравнении (VI 11.82)
получим
Atk = £ (аи + с) + сц) Aj + ((fa + dti) А {к. (VIII.88)
Отнесем все амплитуды к А
п*
*i=-%r> *»=!- (VIII.89)
Тогда после подстановки выражения (VI 11.88) в формулу (VI 11.87)
получим систему из (п — 1) линейных уравнений относительно
неизвестных к.:
/i-i
S и/ (я*7 + сц + cij + d]{k + dijl — 8И1) =
/=i
— —Щп — Cin — Cin — dink — dinky i = 1, 2, . ..., n — 1,
(VI11.90)
286
где
f 1 при i = /
i! \ 0 при i Ф j
— символ Кронекера.
Полагая
* = /Ч; / = V—l*
из уравнений (VIII.86) и (VIII.90) можно определить п неизвестных
величин ху- и (os.
Решение системы уравнений (VII 1.90) можно найти, используя,
например, правило Крамера
х/ = 7^' /==1' 2' ••" n~l> (VIII.91).
где главный определитель системы (VI 11.89)
DN = det (A + С* + С + /cosD* + /cosD — /©/)„_',. (VIII.92)
Матрица определителя имеет размерность определителя (VIII.83).
Определитель DN получается из определителя (VI 11.83) при вычеркивании
в нем последней строки и последнего столбца. Определитель Dj
получается из определителя DN заменой в нем /-го столбца столбцом (—а:п —
— cin — cin — d*inX — dinh), i — 1, 2, . . ., n — 1.
Величины xf комплексные. Это означает, что между максимальными
значениями (амплитудами) отдельных координат х}- имеются фазовые
сдвиги, которые легко определить, беря отношение мнимой части х;- к "ее
действительной части. Однако эти фазовые сдвиги не имеют существенного
значения, так как приводят только к изменению пределов интегрирования
в выражениях (VIII.71) и (VIII.72). В дальнейшем нас будут интересовать
только отношения амплитуд. Очевидно, что в качестве амплитуды Ап
можно взять действительную величину
|Л,| = 1x,1л, /= 1, 2, . .., /г-1. (VIII.93)
Уравнения (VIII.85) и (VIII.86) и система (VI 11.93) образуют (п + 1)
уравнения, необходимые для определения (п + I) неизвестных, т. е^
(os и Aj (/ = 1, 2, . . , /г).
Для того, чтобы определить, являются ли найденные автоколебания
(если таковые существуют, т. е. если (o2s — величина положительная)
устойчивыми, необходимо исследовать близость границы устойчивости.
Баутин Н. Н. ввел понятия опасной и безопасной границ устойчивости.
Находится ли система в области устойчивости, определяется путем малых
изменений значимой амплитуды Aj. Уравнения (VIII.93) можно записать
в общем виде:
Ai = 8i (An), j = 1, 2, . . ., n - 1, (VIII.94)
тогда каждому значению амплитуды Ап в пространстве параметров Л7
соответствует некоторая точка, которая при изменении амплитуды Ап
смещается вдоль кривой, являющейся графиком описывающей функции J
в зависимости от Л. По взаимному расположению кривой J и границы
устойчивости [11 ] можно судить об интересующих нас свойствах системы.
Чтобы в системе могли возникнуть автоколебания, кривая, заданная
уравнением Нп_г = 0, и кривая /должны пересекаться. Кривая Нп_г = 0'
проградуирована значениями параметра со, а кривая J — значениями
параметра А. Следовательно, их точка пересечения определяет частоту и
амплитуду автоколебаний при условии, что колебания удовлетворяют
неравенству (VIII.65), которое необходимо проверить, изобразив харак-
28?
теристику | G (/со) j. Если кривые не пересекаются, то автоколебания либо
вообще не возникают, либо колебания не являются гармоническими.
Аналитические результаты можно получить, исследуя определитель Гур-
вица в зависимости от амплитуды Ап = А.
Анализируя знак производной
(VIII.95)
можно установить важнейшие свойства системы:
1. Определяемые уравнениями (VIII.85), (VIII. 86) и (VIII.93)
колебания устойчивы, если
[^к.ш>0' (уш-9б>
где Aw — амплитуда автоколебаний, определяемая из уравнения Нп_1 =
= 0. Если знак неравенства обратный, то колебания неустойчивы.
2. Граница устойчивости будет безопасной в малой области, когда
вблизи границы устойчивости имеет место неравенство
№■]*-» >°- <VIII-97>
Неравенство (VI 11.97) означает, что точка А = 0 находится вблизи
границы устойчивости и что определитель имеет тенденцию к возрастанию,
следовательно, колебания в системе стабилизируются по мере возрастания
амплитуды. Обратный знак неравенства свидетельствует о том, что
граница устойчивости опасна.
3. Граница устойчивости безопасна в большой области, если
[t-L.>°- <VIIL98>
4. Говорят, что система легко возбуждаема, если
#„_!(())< 0 (VIII.99)
и если в интервале амплитуд А — 0, А = Aw нет других периодических
решений. Из этого также следует, что система, имеющая только один
устойчивый предельный цикл, должна быть легко возбуждаемой.
5. Система относится к трудно возбуждаемым, если кроме найденной
амплитуды Aw автоколебаний существует еще одно значение амплитуды
Ат < AWf которой соответствует неустойчивый предельный цикл.
Геометрическую интерпретацию вышеприведенных утверждений можно
найти в работе [111.
В заключение рассмотрения этого метода необходимо обратить
внимание на следующие его характерные особенности:
1. Метод не приводит к желаемым результатам, если не выполняется
неравенство (VIII.64). Это означает, что в системе могут присутствовать
колебания, вызванные высшими гармониками.
. 2. Если статистическая характеристика нелинейного элемента не
является симметричной нечетной функцией, либо замкнутая система есть
система статического регулирования, то в выходном сигнале системы кроме
периодической составляющей появится постоянная составляющая. В этом
случае отыскание предельного цикла в виде формулы (VI 11.68) приводит
к значительным ошибкам. Тогда следует искать решение в установившемся
состоянии в виде
Xf (0 = Aj sin cot + А0. (VIII.100)
288
В этом случае коэффициент разложения в ряд Фурье с0 необходимо
определить из формулы
2л
сю —
= ^ f fa Ио + At sin со (/ - т,)] d (со/) = ci0 (Л0, Af).
(VIII.101)
Величина дополнительного неизвестного А0 определяется так, как
показано в [И] для системы без запаздывания.
После линеаризации системы, очевидно, кроме критерия Гурвица
можно применить другие критерии устойчивости, используемые при
анализе линейных систем. Наиболее удобен с точки зрения
вычислительных процедур обобщенный критерий Найквиста.
Пример 1. Исследуем возможность возникновения автоколебаний
в системе автоматического регулирования, состоящей из идеального
пропорционального регулятора с передаточной функцией
GR = KR (VIII. 102)
и объекта с передаточной функцией
G0=/Co4^- (VIII.103)
Передаточная функция замкнутой системы имеет вид
Г = GRGo = KRK0e"sx К e~ST _ Y (s)
Uz 1 + GRG0 sTo + /C*/C0e-ST T0 $ + jK_e_ST W (s) •
To
(VIII.104)
Дифференциальное уравнение, описывающее систему на основе
формулы (VIII. 104), имеет вид
Ш. + ^- y(t—t) = ^7w(t-t), K = KRK0. (VIII.105)
Вводя в уравнение (VIII. 105) новую переменную
е(*_т).= w(t — x) —y(t — т) (VIII. 106)
и полагая, что w (t — т) = const, получим
-^- + -£-е(/-т) = 0. (VIII. 107)
0
Периодическое решение получим, если
е (t) = a cos at + b sin со* (VIII.108)
удовлетворяет уравнению (VIII. 107).
Подставляя выражение (VIII. 108) в формулу (VIII. 107), получим
к к
—асе sin со/ + b® cos со/ + -=r- a cos to (t — т) + -~— b sin со (/ — т) = 0
* 0 * 0
(VIII.109)
или
к к
—асо sin tot -f few cos tot + -£- a cos со/ cos сот + -=r- a sin со/сот +
* о ' о
+ -£-6 sin со/ cos сот — -^-6 cos со/ sin cor = 0, (VIIIЛ10)
'о 'о
19 x. Турецкий 289
После приравнивания коэффициентов
к к
-у-a sin сот+ —6 cos ют — а© = 0; (VIII.111)
-f-acoscoT — -J-& sin сот + &<» = О (VIII.U2)
* О 'О
из уравнений (VIII. 111) и (VIII. 112) получим
cos сот = О (VIII.113)
или
<» = -%Г±^Т-> я=0' !• 2-- (VIII.114)
Подставляя выражение (VIII. 114) в формулу (VIII. 111), получим
© = -£-, (VIII.115)
* О
а амплитуда остается неопределенной, так как система линейная.
Применяем метод описывающей функции л
^e(*~T) = cI*(/) + d*-^, (VIII.116)
коэффициенты ci и di определяются из уравнений (VIII.80) и (VIII.81):
(VIII. 117)
К
С\ = -~— cos сот;
'о
d=-
о
К sin сот
Т0 ' со
Таким образом, получаем обычное дифференциальное уравнение,
соответствующее дифференциально-разностному уравнению (VIII. 107):
dz(t) К sin сот de(t) . К Л Л ,,ч Л /лгттт 11 о\
- * -+ -~—cos соте (/) = 0. (VIII.118)
dt 7*0 со dt
Для того чтобы уравнение (VIII. 118) имело периодическое решение,
должно одновременно выполняться
л К sin сот Л
-~— cos сот = 0.
'о
(VIII.119)
После решения системы уравнений (VIII. 119) найдем частоту
автоколебаний, которая равна частоте, полученной точным методом [формула
(VIII. 115) .
Пример 2. Исследуем рассмотренную в первом примере систему
регулирования, только вместо пропорционального регулятора применим двух-
позиционный релейный регулятор, характеристика которого показана
на рис. VIII. 12.
Теперь дифференциальное уравнение, аналогичное уравнению
(VIII. 107), будет иметь вид
-^- + A-signe(/-T)==0. (VIII.120)
Решение уравнения (VIII. 120) легко получить, если учесть, что
te(0 _T *
dt "*" Г0
^iSL=n: JL (VIII.121)
290
или что
1 О
(VIII.122)
Положим е0 = 0 тогда решение имеет пилообразный вид (рис. VIII. 13).
Амплитуда этих колебаний
Л = -£-т, (VIII.123)
а их частота °
*> = -£-• (VIII.124)
Приближенное решение методом описывающей функции требует
определения коэффициентов Фурье функции -~- sign г (t — т).
1
*с
1
'
>т
i
*С
1
е
А
~7
\
0 г ZxS^
1
Зт
у/ЬТ
t
Рис. VIII. 12. Релейная характе- Рис. VIII. 13. Вид решения уравнения
ристика (VIII.122) при е0 = О
Для функции -7f- sign e (/) имеем
■'о
/С
К \f\ = о.
(VIII.125)
Тогда для функции -^- sign e (t — т) из соотношений (VIII.73) и
* о
(VIII.74) получим
^=^C0S(DT'
пА(оТ0
Sin ют.
(VIII.126)
Следовательно, линеаризованное уравнение, соответствующее
уравнению (VII 1.120), имеет вид
dt
1
4/С
sin <
(DT) + 8(/)^~cosa)T = 0. (VIII.127)
ЯА(ОТ0
Приближенное решение этого уравнения возможно лишь тогда, когда
одновременно выполняются условия
4/С
1
яА<йТ0
4/С
пАТ0
Sin сот = 0;
cos шт = 0.
(VIII.128)
Так как амплитуда — величина положительная, то из соотношения
(VIII. 128) получим
> = 4(-f ±2wl)' "=1'2' ■■•: (VIII.129)
4/С 4/Ст
(0:
Л==
П(оТа
я(|±2Ля)г0
19*
(VIII.130)
291
При п = О частота, определяемая выражением (VIII. 129), точно равна
частоте точного решения (VIII. 124), но при амплитуде А вместо
коэффициента 1 имеет место коэффициент 8/я2, т. е. на 18,9% меньше.
Пример 3. Рассмотрим систему автоматического регулирования,
состоящую из объекта первого порядка с запаздыванием
Go(s) = 7tSv (VIII.131)
исполнительного двигателя с передаточной функцией Gs = l/s и двух-
позиционного регулятора с коэффициентом усиления /О
Дифференциальное уравнение замкнутой системы имеет вид
To^L + J^L + Ksigne(t-'z) = 0. (VIII.132)
Вначале найдем точное решение уравнения (VIII. 132).
При г (t — т) > 0 имеем
-g. =Вхе-*/т> —К\ (VIII.133)
8 (t) = _ ВгТ0е-«т* — Kt + 52, (VIH.134)
где Bl9 В2 — постоянные интегрирования. При е (t—т) <0 получим
аналогичные выражения, необходимо только вместо К подставить (—К).
Так как решения являются периодическими, то следовательно, должно
быть
е(/х) = —8(0); (VIII. 135)
dt \tt ~ ~dt
s(t1 — t)=0. (VIII. 137)
(VIII.136)
Условия (VIII. 135) и (VIII.136) отражают наличие симметрии решения,
а условие (VIII. 137) определяет время tu по истечении которого решение,
определяемое формулами (VIII.133) и (VIII.134), утрачивает силу. При
этом время tx равно половине периода колебаний.
Из соотношений (VIII. 133)—(VIII. 137) определяем постоянные
интегрирования Вг и В2:
2К
1 + е-
Дх- . ■ Д/г,; (V"1-138)
B2 = KT0 + -%rt1 (VIII.139)
и получаем уравнение для определения неизвестного времени
переключения t±:
t, - 2 (т + Т0) tt + ^ff/г. = 0. (VIII.140)
После вычисления времени tx по формуле Лагранжа [7] или
итерационным методом находим частоту колебаний:
я
«> = --. (VIII.141)
de_
dt
Амплигуда полученного решения определяется из уравнений -тг
= 0, е (t0) = А. Из соотношения (VIII. 133) находим
292
^0 = _Гв1п^-, (VIII.142)
а из соотношений (VIII.134) и (VIII.142)
A=tBt-KT9(l-\n-g-) ' (VIII.143)
и с учетом соотношений (VIII.128) и (VIII.139) получим окончательно
Л = /({А + г01п[^(1+е-<./г.)]}. (VIIL144)
Частота со не зависит от усиления /С, а амплитуда А зависит от него
прямо пропорционально.
Проводя анализ приближенным методом описывающей функции [10],
можно заметить, что выражения для коэффициентов сх и dx идентичны
выражениям предыдущего примера. Следовательно, эквивалентное
уравнение имеет вид
^^^-(J-W8111^)^!^-008^)8^0- (VHU45)
Определитель Гурвица равен коэффициенту при е
^=1-W8inWT = 0' (VIII.146)
а квадрат частоты со равен отношению коэффициента при г (t) к
коэффициенту при е (t):
со2 = -^-. cos сот. ' (VIII.147)
Исключая из соотношений (VIII. 146) и (VIII. 147) амплитуду, можно
записать уравнение для частоты со
tgcoT=-^r-. (VIII.148)
Так как амплитуда А может иметь только положительные значения,
то физический смысл имеют только те решения, в которых cos сот > 0
и sin сот > 0.
После определения со из уравнения (VIII. 148) из выражения (VIII. 146)
получаем амплитуду '
Л= 4*^ют . (VIII.149)
Как и при точном решении, амплитуда А пропорциональна условию,
а частота от него не зависит.
Для определенных значений К и Т0 можно найти ошибку по частоте Асо
и амплитуде АЛ приближенного решения в процентах как функцию
времени запаздывания т (рис. VIII. 14).
Для исследования устойчивости и выяснения, является ли граница
устойчивости безопасной, берем производные
dHx дНг . дНг dm_
dA ~ ЗА * дм " dA '
На основе соотношения (VIII. 146) получим
dH1 4K . coTWsin сот — тcos сот) /лтт ici\
—ГТ- = 75—Sin СОТ т-^г : : f . (VIII.151)
dA яЛ2со А (2 cos сот + т sin сот) v
Знак этого выражения при Ях = 0 легко установить, используя
соотношения (VIII.148) и (VIII.149):
(VIII.150)
dH,
dA
Т0 + 1 + ™%
2^2
0
Я,=0 Л(2Г0+т)
>0. (VIII.152)
948 293
Следовательно, автоколебания устойчивы.
Далее, исследуя выражение
&нл
dA
А=0
= + ©о,
(VIII. 153)
легко установить, что граница устойчивости безопасна в малой области.
Исследование
dHx
dA |л=оо
= 0.
(VIII. 154)
приводит к выводу, что граница устойчивости опасна в большой области.
Однако при достаточно большой, но конечной величине А выполняется,
неравенство (VIII. 152), и поэтому автоколебания всегда устойчивы.
ЛА.Аш, °/о
0
/С
\
_ АЛ
^v^/)6J
0,5
si
Рис. VIII. 14. Характер ошибок в
определении амплитуды и частоты
автоколебаний методом
описывающей функции (к примеру 3)
Рис. VIII. 15. Анализ системы по взаимному
расположению границы устойчивости Нг = О
и графика описывающей функции
Уравнение (VIII. 145) можно переписать в виде
ё + Ье + Ь*г = 0.
(VIII.155)
Коэффициенты by b* находятся из уравнения (VIII. 145)^делением era
на Т0. На рис. VIII. 15 представлено взаимное расположение границы
устойчивости (VIII. 146) и кривой J в координатах Ь и &*. На кривую J
нанесена шкала параметра Л, а на границу устойчивости Ь* = 0 — шкала
частот со. Кривые пересекаются в точке, где амплитуда автоколебаний
равна А = 1,12, а частота со2 = 0,740. Так как существует только одна
точка пересечения кривых, то системы относятся к легко возбуждаемым..
Список литературы
1. Айзерман М. А., Гантмахер Ф. Р. Абсолютная устойчивость систем регулирования
М., Изд. АН СССР, 1963.
2. Айзерман М. А. Теория автоматического регулирования. Гл. V. М., «Наука», 1966-
3. Баутин Н. Н. Поведение динамических систем вблизи границ области устойчивости.
М.—Л., Гостехиздат, 1949.
4. Cremer L. Zeitschrift fur angewandte Mathematik und Mechanik, 1947, Nr 25/27, S. 16K
5. Эльсгольц Л. Э. Введение в теорию дифференциальных уравнений с отклоняющимся^
аргументом. М., «Наука», 1964.
6. Гольдфарб Л. С. К вопросу о теории вибрационных регуляторов. В кн.: «Метод Гольд-
фарба в теории регулирования», М., Госэнергоиздат, 1962.
294
7. Goursat E. Kurs analizy matewatycznej, T. I. Warszawa, 1914, Wyd. Kasy Pomocy
dla Osob Pracujacych na Polu Naukowen Imienia Dra I. Mianowskiego.
8. Halanay A. Differential equations, stability, oscillation, time lags. Chap. 4, Academie
Press, New York, 1966.
9. Красовский Н. Н. Некоторые задачи теории устойчивости движения. Гл. VI и VII.
М., 1959.
10. Magnus К. Stationare Schwingungen in nichtlinearen dynamischen Systemen mit Tot-
zeiten. Ingeneur—Archiv, Band XXIV, 1956, p£. 341—350.
11. Nowacki P., Szklarski L., Gorecki H. Podstawy teorii ukladow regulacji automatycznej.
T. 11, Warszawa, 1962, RWN.
12. Попов Е. П., Пальтов И. П. Приближенные методы исследования нелинейных
автоматических систем. М., Физматгиз, 1960.
13. Попов В., Галанау А. Об устойчивости нелинейных систем автоматического
регулирования с запаздывающим аргументом. — «Автоматика и Телемеханика», Т. XXIII,
1962, с. 849—851.
Глава IX
Релейное регулирование объектов
с запаздыванием
Это наиболее простой способ регулирования. В качестве регулятора
используется реле, причем в основном применяются двухпозиционные
и трехпозиционные реле.
При использовании двухпозиционного реле его выходной сигнал
может принимать только два значения, а выходной сигнал трехпозицион-
ного реле может принимать три значения. Оба типа реле могут
воздействовать на объект непосредственно или с помощью сервомотора, который
является интегрирующим звеном.
Для улучшения регулирующих свойств иногда используют релейно-
импульсные регуляторы. Релейные системы управления охотно и широко
применяют благодаря простой конструкции даже с объектами, имеющими
большие постоянные времени, и, следовательно, чаще всего при
управлении тепловыми процессами.
§ IX. 1. Двухпозиционные системы регулирования
В двухпозиционных системах автоматического регулирования
управляющий сигнал на объект принимает одно из двух крайних значений.
Характерной особенностью двухпозиционного регулятора является то, что
регулируемая величина у периодически изменяется в некоторых пределах.
I ■ 1 Т° 1«
дет
0\ 1 *—»
t-«—^ ^ з»
Рис. IX. 1. Блок-схема системы
регулирования температуры
Рис. IX.2. Упрощенные переходные процессы
при нагревании и охлаждении:
/ — процесс при включении нагревателя; 2 — процесс
при выключении нагревателя
Заданным значением в двухпозиционном регуляторе является та величина
регулируемого параметра у, при которой происходит изменение значения
управляющего сигнала. Если существуют два таких значения
регулируемой величины у для двух направлений движения, то заданным значением
является среднее арифметическое от этих двух величин.
296
Примером может служить система регулирования температуры,
показанная на рис. IX. 1. Если температура регулируется с помощью
контактного термометра, то при достижении заданной температуры контактный
термометр включает обмотку контактора, что приводит к выключению
нагревателя.
^На рис. IX.2 приведены переходные процессы регулируемого
параметра (температуры) при включении и выключении нагревателя. Кривые
переходных процессов хорошо аппроксимируются экспонентами и чистым
запаздыванием.
IX. 1.1. Определение переходных процессов в системе,
состоящей из двухпозиционного регулятора с зоной
неоднозначности и астатического объекта с запаздыванием
Рассмотрим переходные процессы в системе регулирования, блок-схема
которой изображена на рис. IX.3..
Передаточная функция объекта имеет вид
G0(s) = Ko
(IX.1)
Статическая характеристика регулятора представлена на рис. IX.4.
Видно, что она имеет зону необходимости (гистерезис). Ее можно описать
следующими зависимостями:
11 = 1$! при | или
{ —&<е<&, если ранее было и = Вх\
е<; — Ъ
■ — В2 при | или
— 6<e<6, если ранее было и = В2.
(IX.2)
В частном случае, когда Вг= В2 = В, характеристика симметрична.
"»г
V»
1
г
_ц
1
\J
и
i Ш
е'5Х
**—
(
1
1
[
Рис. IX.3. Блок-схема
двухпозиционной системы
регулирования
Так как регулятор реагирует на изменение выходной величины объекта,
то наличие запаздывания в объекте приводит к тому, что амплитуда
колебаний в установившемся состоянии будет больше, чем это было
необходимо при наличии только зоны неоднозначности регулятора. При
симметричной характеристике регулятора время нарастания tx
определяется из уравнения (IX. 1) и блок-схемы, представленной на рис. IX.3.
Имеем
у(*)-к e~ST
Дифференциальное уравнение имеет вид
т).
!=*.«</■
(IX.3)
в.
Если на входе объекта появится постоянный сигнал величиной и
то из соотношения (IX.3) следует, что на его выходе будем иметь
y(t) = KoB(t-r) +C. (IX.4)
297
Для определения времени tx достаточно иметь уравнение без
запаздывания (штриховая линия на рис. IX.5)
.yi(t) = K0Bt +C. (IX.5)
В момент времени t = %
ух (т) = КоВх +С = -Ь
или
С = — Ь + К0Вт.
Окончательно уравнение (IX.5) можно представить в виде
ух (t) = K0Bt -^Ь- К0Вт. (IX.6)
\
1
- «О
1
,
"J
!
ь !
1
^
i
i
b '
Ди '
1
1
\ '
1
С
Рис. IX.4. Статическая характеристика
двухпозиционного регулятора с петлей
гистерезиса
Рис. IX.5. Установившиеся колебания в
двухпозиционной системе регулирования
с симметричной статической
характеристикой с гистерезисом (объект без
самовыравнивания)
Следовательно, в момент времени tx на основе уравнения (IX.6) можно
записать
Ух d) = K<>bti — Ь — К0Вт = b + К0Вт
или
b
'1=2(1
к0в
)•
Период автоколебаний
6 = 4
Нт£г)
(IX.7)
(IX.8)
Размах автоколебаний
Ау = 2 (b + К0Вт). (IX.9)
В частном случае двухпозиционного регулятора без гистерезиса
b = 0, и период автоколебаний
0 = 4т, (IX.10)
а их размах
Ау = 2К0Вт. у (IX.11
Если регулятор имеет несимметричную статическую характеристику
с зоной неоднозначности, то, поступая аналогично, можно определить
длительность tx импульса положительной полярности -на выходе реле:
''~т0+£) + т§Г- (1ХЛ2)
298
Соответственно длительность отрицательного импульса
*>=<1+%)+-&• (1ХЛЗ)
я период и размах автоколебаний определяются выражениями
Ау = 2Ь +К0т(В1 +В2) (IX. 15)
Положительная амплитуда автоколебаний
АУ1 = Ь +К0Вхт, (IX. 16)
.и отрицательная амплитуда автоколебаний
. Ау2 = Ь +К0В2т. (IX. 17)
С учетом того, что амплитуды не равны, среднее значение
регулируемой величины не равно нулю и определяется выражением
Ays = К,т (В, - Я2). (IX.18)
Из формулы (IX. 18) следует, что при наличии в системе запаздывания
и несимметричной статической характеристики регулятора необходимо
настраивать регулятор не на заданное значение, а на значение
w + Ays.
Наконец, следует заметить, что из формулы (IX.И) можно определить
ошибку от действия на систему постоянного возмущения:
е2 = К0чг- (IX.19)
Чем больше запаздывание в системе, тем больше ошибка, возникающая
от действия возмущений.
IX. 1.2. Определение реакций в системе,
состоящей из двухпозиционного регулятора с зоной
неоднозначности и статического объекта с запаздыванием
В этом случае передаточная функция объекта имеет вид
Go(s) = /C0 ^о . IX.20)
При симметричной статической характеристике регулятора, поступая
.аналогично предыдущему, можно с помощью рис. IX.6 определить все
интересующие нас параметры переходных процессов.
Дифференциальное уравнение в этом случае имеет вид
То% + У = КбиУ-т). * (IX.21)
Если входная величина равна нулю, то реакция системы симметрична
я время нарастания t± равно времени спада t2:
tl = t2 = r + T0 In. 2K°B ~ (ff Z? е~Т/Г° • (IX-22)
Период и размах автоколебаний определяются выражениями
е = 2 [т + т0 ш 2К°В ~ jffij/> е~*/г' ]; (ix.23)
Ау = 21К„В (1 — е-*/*) + be.-*'?.]. (IX.24)
299
В этом случае автоколебания симметричны относительно заданного
значения. Если же характеристика регулятора не симметрична
относительно оси е, то выходная реакция имеет вид, представленный на рис. IX.7.
Соответственно время нарастания равно длительности положительного
импульса
IS /Г» | Г» Ч /IS О U\ ~ — Т/ТЛ
(IX.25)
4 _т I Г In *° (В* + йг) ~ (*°В2 ~ Ь) е~Т/Г'
*1 — Т + Г0 Ш А-.Д.-6
а время спада равно длительности отрицательного импульса
*, = т + 7\,1п
*б (Д1 + в2) - (/(«Bt - Ь) е-т/г°
K0s2 — ft
(IX.26)
1
1
/
1 /
ч\
'0
1 s'
/1
t /у
/ /
1 \>
1 \v
\\y\y
^ \
\ \
\
\
A/
/ /\\
/ / 1 \
//1
f\
r
L-Z^j
/ i
. ** ,
e
i
\
'
'
i
ч
? \j
. *.
b
0
-b
Рис. IX.6. Установившиеся колебания в
двухпозиционной системе регулирования с
симметричной статическбй характеристикой
с гистерезисом (объект с
самовыравниванием)
Рис. IX.7. Установившиеся колебания
в двухпозиционной системе
регулирования с несимметричной статической
характеристикой с гистерезисом (объект с
самовыравниванием)
Период автоколебаний определяется соотношением
"~ZT ' У°1П <Ko*i-*)(KiA-*)
-т/Г§
(IX.27)
(IX.28)
(IX.29)
(IX.30)
а размах автоколебаний — соотношением
АУ = К0 (В, + Я2) (1 — е-*/7"-) + 2Ь*-*т..
Положительная амплитуда регулируемой величины
ЬУх = К0Вг (1 — е-*/^) + fce-^o,
а отрицательная амплитуда
Д^2 = /С0В, (1 — е-^о) + 6е-*/г..
Среднее значение регулируемой величины определяется формулой
А^ = /С0(В1-В2)(1-е-^о), (IX.31)
а ошибка, вызываемая действием на систему возмущения z, — формулой
Аг/2 = /С0г(1-е-^о). (IX.32)
Если статическая характеристика регулятора не содержит зоны
неоднозначности, то в выражениях (IX.22)—(IX.30) следует положить
Ь = 0.
300
Уравнения (IX.28)—(IX.30) можно записать в более компактной
форме [21 ]
Л=1—(1—5)е-^о,
(IX.33)
где
либо
или
Аналогично
ч
либо
или
~*0
А-
А —
" *о
S-
С-
АУ
(В± + В2) >
A^i
*o*i
&у2
КоВ2
2Ь
(Вг + В2) '
b
~ *<А
b
0.1
в зависимости от того, какое из выражений (IX.28)—(IX.30) исследуется.
Зависимости (IX.33) можно изобразить графически при различных
значениях т/Г0 (рис. IX.8). Следует заметить, что размах отклонений
регулируемой величины должен быть
больше отрицательного значения
зоны неоднозначности1:
Ау^ — b. (IX.34)
Это ограничение обозначено на
рисунке штриховой линией. Кривые
позволяют быстро находить размах
и амплитуды отклонений
регулируемой величины. Из рисунка видно,
что размах и амплитуды
положительных и отрицательных
отклонений увеличиваются с ростом
запаздывания и зоны неоднозначности
двухпозиционного регулятора.
Минимальные отклонения
регулируемой величины можно было бы
получить, если бы удалось
реализовать двухпозиционныи регулятор
с отрицательной зоной
неоднозначности. Это возможно при использовании
в регуляторе соответствующей положительной обратной связи. Из
формулы (IX.32) следует, что в системе с двухпозиционным регулятором
наблюдаются статические ошибки так же, как и при непрерывном
регулировании с помощью регуляторов типа ПД. Уменьшение отклонений
регулируемой величины Y за счет уменьшения зоны неоднозначности
0.01
1*с—
N.
Г'
>-f
Г
Тп
=11
пг
\?
\ J
\/
~xj
,
11
)
I
1
1
_|
Г0,0
ол
го J
0,00
и/ ~
г
т
^
'
-08
-ОЛ
ол
0.8 S
Рис. IX.8. Зависимость размаха
отклонений регулируемой величины и
положительной и отрицательной амплитуд от
зоны неоднозначности
1 Это относится к случаям, когда специальной конструкцией двухпозиционного реле
достигается отрицательная величина петли гистерезиса для уменьшения размаха
отклонений. (Прим. ред. оригинала).
301
[см. формулу (IX.9)] одновременно приводят к уменьшению периода
колебаний [см. формулу (IX.8)] или к увеличению числа срабатываний
реле в единицу времени., Это общая черта всех релейных систем.
IX. 1.3. Определение выходных реакций в системе,
состоящей из двухпозиционного регулятора с зоной неоднозначности
и объекта с распределенным запаздыванием
Пусть частотная характеристика объекта имеет вид [21]
Go(/0) = /toe-^'w°. - * (IX.35)
Сигнал и, подаваемый с реле ria объект, имеет вид прямоугольной
волны (рис. IX.5). Этот сигнал можно разложить в ряд Фурье в виде
u(<) = -g-f] ^^п+1)Ш) (1Х36)
/1=0
Выходной сигнал у можно найти из соотношений (IX.35) и (IX.36).
Так как модуль частотной характеристики <
|G0(/co)[ = /C0e v 2 > (IX.37)
а фаза
Фо И = arg [Ge (/со)] = - ]/" *pL, (IX.38)
то выходной сигнал получим, умножая амплитуду каждой гармоники
входного сигнала на К0е~ К®г0/2 и сдвигая фазу каждой гармоники на
угол — |/соГ0/2:
_^_ -j/^-(2,1+1) со
У(0=^\^» 2^+Т sin [(2л+1)ш/+]/-^ (2л+1)/о
/г=0
(IX.39)
Из выражения (IX.36) и рис. IX.5 видно, что срабатывания реле
происходят в момент времени, когда
<otp = kn, k = 1, 2, . . . ' (IX.40)
В момент срабатывания реле отклонение регулируемой величины равно
(—\)k+lb. Подставляя эти значения и формулу (IX.40) в выражение
(IX.39) и учитывая, что со = 2я/0, получим
л=0
Формула (IX.41) позволяет определить зону неоднозначности в
зависимости от заданного относительного периода переключений Э/70 и
амплитуду первой гармоники А, отнесенной к Ко&- Вычисления по
формуле (IX.41) не представляют трудности, так как ряд быстро сходится.
На рис. IX.9 представлены результаты вычислений. Как и ранее, период
колебаний возрастает с ростом зоны неоднозначности и так же
увеличивается амплитуда их первой гармоники AIKqB. В этом случае также можно
302
использовать отрицательную зону неоднозначности для уменьшения
периода колебаний при одновременном уменьшении отклонений
регулируемой величины.
а/к0в (в/То)'1
Рис. IX.9. Зависимость
амплитуды и периода
автоколебаний от зоны
неоднозначности при двух-
позиционном
регулировании объекта с
распределенным запаздыванием
ОЛ
0,1
0,05
0,ОЬ
0,03
0,02 h 2
0,0!
0,005 L 0,5
20
h 10
5
3
Г /
4
—7"
/
V
\г
\
1
FV
\
—^
у
/
v^
1L
S
А/К0д
mj0/
ом о
0,0k
0,08 0,11 b/К0 В
В случае объектов более высокого порядка при наличии
запаздывания для определения амплитуды и периода автоколебаний используется
метод описывающей функции, рассмотренный в предыдущей главе.
§ IX.2. Анализ релейных систем на фазовой плоскости
Рассмотрим систему регулирования с трехпозиционным реле с
гистерезисом, которое вырабатывает управляющий сигнал на сервомотор,
являющийся интегрирующим звеном. Сервомотор управляет инерционным
7N е.
1
л
—»"
\ Г
_а_
—i
1
,
и
1
ш.
^
e-ST
К° 1+sTQ
У У
1
]У
(-)
Рис. IX. 10. Блок-схема системы регулирования с трехпозиционным
реле
объектом первого порядка с запаздыванием. Блок-схема системы
изображена на рис. IX. 10. Статическая характеристика трехпозиционного реле
изображена на рис. IX.И. Описывающие ее уравнения имеют следующий
вид:
и = В sign Ф, (IX.42)
где
Ф = sign [2 (е — а) + а (1 — г\) (1 — sign e) ] +
+ sign [2 (е + а) — а (1 — г)) (1 + sign e) ],
(IX.43)
1 Описание трехпозиционного реле в зависимости от производных его выходного
сигнала е справедливо только в предположении, что при v\a<^e,<^a или—а^:е<—г\а
выполняется условие ^ <0, если | и\ = В, и условие ^ ^0, если и=0. Предпо-
dt
tit
303
а через sign x обозначена функция
II при х > 0;
0 при х = 0; (IX.44)
— 1 при х <0.
Так же, как и ранее, здесь через В обозначена амплитуда выходного
сигнала реле. Зона нечувствительности обозначена через а, а зона
неоднозначности — с помощью коэффициента т), удовлетворяющего неравенству
|т) | <; 1. При т) = -fl имеет место трехпозиционное реле без гистерезиса,
но с зоной нечувствительности. При rj = —1 имеем двухпозиционное
реле с гистерезисом. Полагая а —* 0, получим в пределе двухпозиционное
реле без гистерезиса, если г) =
"I
-7*
Па
= —1, и идеальное
трехпозиционное реле без зоны
нечувствительности, если г) > —1.
Объект регулирования вместе
с сервомотором описывается
следующей передаточной функцией:
G(s) = K0sTi{f"sTo), (IX.45)
постоянная интегриро-
Рис. IX. 11. Статическая характеристика
трехпозиционного реле с гистерезисом
где Т.
вания.
Так как в линейной части
системы можно переставлять звено
запаздывания с другими звеньями, то будем рассматривать систему,
блок-схема которой представлена на рис. IX. 12.
Уравнение, описывающее линейную часть системы без запаздывания,
имеет вид
КоЩ. ■ (IX.46)
'о'; dt2 "Г * i dt
где
в
о
—В
и начальные условия у (+0) = у0, у (+0) = у0.
(IX.47)
ложение это выполняется для рассматриваемых далее систем регулирования. Однако
характеристику, показанную на рис. IX.11, необходимо представлять следующим
соотношением:
+£, если а < г
или если v\a << е ^ а, но ранее было и = +В\
0, если | е | ^ | т|а |
или если | е | ^ а, но ранее было и = 0;
—В, если е < —а
или если —а ^ е << —т), но ранее было и = —В.
Это соотношение можно записать иначе, подчеркивая роль положительной обратной
связи в формировании статической характеристики реле:
и = В sign 6; £ = и ■
В
п\
-{
е — a sign e, | е| > а;
0 I е I sc а-.
Переменная v здесь соответствует е после прохождения через систему с зоной
нечувствительности. Зависимость £ от выходной переменной реле и соответствует положительной
обратной связи, необходимой для формирования характеристики с зоной неоднозначности
(Прим. ред. оригинала).
304
Для упрощения дальнейших рассуждений введем новые переменные
'о
х = Тру;
%о = Т0у0;
х = К0-тг-их.
Тогда уравнение (IX.46) примет вид
Лс(О)
Л>
+ *(Ф) = х,
(IX.48)
(IX.49)
(IX.50)
(IX.51)
(IX.52)
-1д
■ц
<-»,
■ч'.
'у
1
JT|
Ln~.
а
. е""
*
^
*<7
STi(1+sT0)
У
1
У
f£/
У
Рис. IX. 12. Блок-схема системы со звеном запаздывания
решение которого дает
*(д) = х(1— е-*)+.лг0е"*; (IX.53)
у(*) = х[*-(1-е-*)] + у„ + дг,(1-е-*). (XI.54)
Для анализа системы на фазовой плоскости запишем уравнения
dym
dfl
dx(&)
dft
'*(*);
■х(Ф) + х.
Из уравнений (IX.55) и (IX.56) получим
dx _ х ,
~dy~~~x~~~ iy
(IX.55)
(IX.56)
(IX.57)
(IX.58)
решение которого имеет вид
у = С — л; — и In | л; — х |,
где постоянная С определяется из начальных условий.
Для нахождения амплитуды и периода автоколебаний можно
положить w = 0, и тогда
8 = — у. (IX.59)
Линии переключения, на которых выходной сигнал реле изменяется
скачком, получим из условия
sign ф = 0.
Тогда уравнения линий переключения запишем в виде
У = —Щ
у = а
У = W
у = —а
20 X. Турецкий
при *>0,
при х <0
(IX.60)
(IX.61)
(IX.62)
(IX.63)
(IX.64)
305
Из-за наличия в системе запаздывания т' = т/Г0 переключения в
системе не наступает при достижении фазовыми траекториями линий
переключения, определяемых уравнениями (IX.61)—(IX.64).
Рис. IX. 13. Фазовые траектории для трех значений х
Для определения линий переключения с учетом запаздывания тг
уравнения (IX.61)—(IX.64) преобразуются к виду
у(Ъ-г') = -г\а\ ^л (IX.65)
у{Ъ-т>)=а )ПРИ*>°; (IX.66)
у(ф —т') = щ ) (IX.67)
у(д_т') = _а)при*<0. (1Хв68)
(У9РХ81)
Рис. IX. 14. Сравнение
фазовых портретов
системы с запаздыванием и той
же системы без
запаздывания: сплошная линия—
траектория системы без
запаздывания;
пунктирная — траектория
системы с запаздыванием
Учитывая, например, что в уравнении (IX.65) у (ft— т') изменяется
в соответствии с уравнением (IX.54), если в нем вместо ft подставить
ft — т', получим
x[d_T'_(l_e^-^))] + r/o + Jc0(l-e-(^T')) = -ria. (IX.69)
Уравнение линий переключения должно выполняться для всех ft и,
в частности, для ft = 0. Это уравнение должно быть справедливо для
произвольных х0 и у0, следовательно, вместо них можно просто писать хиу.
306
Принимая во внимание эти замечания, получим окончательно
уравнения линий переключения с учетом запаздывания в следующем виде:
а при х = О
у = (ет — 1) (х — и) + хт' — ца, * > О,
у = а + х(е1' — 1), х>0
у = (ех — 1) (х + х) — хт + Щ
У-
— a + x(ev— l), x = 0
*<0.
(IX.70)
(IX.71)
(IX.72)
(IX.73)
Линии переключения делят фазовую плоскость на три области, в
которых в зависимости от х имеют место разные фазовые траектории
(рис. IX. 13). На рис. IX. 14 для сравнения изображены фазовые портреты
устойчивой системы без запаздывания и той же системы, но с
запаздыванием. Хорошо видно дестабилизирующее действие запаздывания.
IX.2.1. Условия существования предельного цикла
Как известно, для того чтобы в системе существовали устойчивые
периодические движения, необходимо, чтобы на фазовой плоскости
присутствовали соответствующие им фазовые траектории в виде замкнутых кривых.
С учетом симметрии принятой
статической характеристики трех-
позиционного регулятора
предельный цикл должен представлять
собой симметричную замкнутую
кривую относительно начала
координат.
Для предельного цикла всегда
должно выполняться условие
*|<|х|. (IX.74'
Рассмотрим предельный цикл,
изображенный на рис. IX. 15. Из
уравнения (IX.58) траектория,
проходящая через точку (yfl, ха),
лежащую в области, где х < 0,
соответствует уравнению
«><) к
/
/
/
/
/
/
/
/
I «I
1
1
1 г
Jr *
/i /
/ '
/ /
U-
-Па 0
Ч^'Лг)
/
/
/ '
,/
по
/
/
/
/
/у
/
/
/
/
/
/
/
. /
7 *рГп 7
^V"*^)
(У'па'-х'па) '
У = У а + Ха — X + X 1П
Рис. IX. 15. Предельный цикл
Х + X
*+ха
(IX.75)
Это должно также выполняться для точки с координатами {уцл\ —хц^у
лежащей на этой же траектории:
Уг\а = Уа + Ха + ХПа + К Ь ■
(IX.76)
к + ха
Но из уравнений (IX.53) и (IX.54) также следует, что
^а = _х[т'-(1-е""х')]+^а-^а(1-е-х'); (1X77)
— х'ъа = — х(1 — е~т) — Хпа£~х у (IX.78)
где точка с координатами (уца\ —Хщ) принята в качестве начальной, из
которой фазовая траектория через время запаздывания т' при х <0
достигает точки {у^ —х'т).
20* 207
Складывая уравнения (IX.77) и (IX.78), получим
Уч\а — Хца = — Ю + Уча — Х^а- (IX.79)
При х = 0 фазовая траектория представляет собой прямую линию,
проходящую через три вышеназванные точки: (уца; —хпа), (—у.л* —ха),
(—у'а, —Ха) (см. рис. IX.15). Следовательно, можно записать такие
уравнения
Уа + Х'а = Уа+Ха\ " (IX.80)
—Уг\а + ХЦа = Уа+ Ха- (IX.8 1)
Из уравнений (IX.53) при х = 0 и х0 = —ха получим
—ха = —ха*Г'1'. (IX.82)
Подставляя соотношения (IX.80) и (IX.82) в 'уравнение (IX.76),
получим
УПа = Уа + *а +"*ца + * Ь -^ ^г . (IX.83)
X ~г X(fi
Объединяя выражения (IX.81) и (IX.79), получим
хщ = ха +уа + Уф — хт'. (IX.84)
Подставляя соотношения (IX.84) в формулу (IX.83) и учитывая, что
У а = я; Уца = Л» получим окончательно
2 (а + *в) = хт' + х In „ , *+*?Г! , . (IX.85)
4 ' а/ ' х(1 +т ) —а(1 + т)) —*а v '
После введения относительных величин
v=^-\ (IX.86)
Ха
а
~*а
w = — (IX.87)
получим
2 (I+w)=,[-'+in p(l+t,;+;7+4)-i] • <IX-88)
Теперь введем эквивалентный коэффициент усиления разомкнутой
системы:
т0 в _ х
/С=/Со^-4- = 4-- (IX.89)
Таким образом, если точка с координатами (v[9 w() лежит на кривой
предельного цикла, то эквивалентный коэффициент усиления разомкнутой
системы можно найти из соотношений (IX.86), (IX.87) и (IX.89):
К=%-. (XI.90)
Отсюда как амплитуду, так и период автоколебаний в системе можно
представить в виде функции коэффициента усиления /С.
IX.2.2. Определение амплитуды колебаний
Наибольшая амплитуда у = ут имеет место при х = 0 (см. рис. IX. 15).
В связи с этим из уравнения (IX.75) при у = ут получим
ут = уал-ха + х1п—*-1г. (IX.91)
308
С учетом уравнений (IX.80), (IX.82), (IX.86) и (IX.87) получим для
относительной амплитуды следующую зависимость:
у Ут .
1 т п у
F/n=l+_L + JLin_i^
т l w ' w и + е~"х
(IX.92)
(IX.93)
Уравнения (IX.88), (IX.90) (IX.93) определяют зависимость от
коэффициента усиления /С.
IX.2.3. Определение периода автоколебаний
Период автоколебаний 0' — это время обхода изображающей точки
кривой предельного цикла.
Время, необходимое для перехода изображающей точки из точки (Уа\
ха) в точку (у^а\ —*ла), обозначим через дх, а время, необходимое для
Рис. IX. 16. Зависимость периода 9' и амплитуды Ут колебаний от коэффициента
усиления К при т' = 0
перехода изображающей точки из точки (—уа\—ха) в точку (у'па; —х'ца)> —
через Ф2; тогда время для обхода изображающей точкой всего
предельного цикла
&' =-г~\
(IX.94)
0' = 2дх + 2*2 + 4т'. (IX.95)
Время $г можно определить из уравнений.(IX.53) с учетом
соотношений (IX.82), (IX.84), (IX.86) и (IX.87):
#х=1п-
fl + e'
-т'
(IX.96)
1и(1+т') —ш(1+11) —1*
Время ft2 получим из уравнений (IX.53), (IX.86) и (IX.87):
А2=1й{у — е-х'[у(1+т') -я/(1+г))— 1]}. (IX.97)
Следовательно, безразмерный период автоколебаний 0' можно
определить через переменные v и w как функцию коэффициента усиления /С.
Эта зависимость достаточно сложна. Графически она представлена на
рис. IX. 16—IX.20. На рис. IX. 16—IX. 19 изображены зависимости
309
Ym-B1
Рис. IX. 17. Зависимость периода 9' и амплитуды Ym колебаний от коэффициента
усиления К жри т' = 0,26
Рис. IX. 18. Зависимость периода 6' и амплитуды Ym колебаний от
коэффициента усиления К при т' = 0,6
310
амплитуды и периода автоколебаний от коэффициента усиления К при
определенных значениях параметра rj и постоянных значениях
запаздывания т.
Из рисунков видно, что при большом усилении все кривые стремятся
к граничной кривой при tj = —1, т. е. при больших коэффициентах
30
10
L-/
*П'-0.6
brS---
-0
вЧ(к)\
0,8
0,в/ V
I
I
I
I
/
fyy/
Ут=т
'.
W
/
10
30
Рис. IX. 19. Зависимость периода 0' и амплитуды Ym колебаний от коэффициента
усиления К при т' = 1,0
усиления система работает так, как она работала бы с двухпозиционным
реле с гистерезисом. При значениях rj > 0,8, обеспечивающих наличие
петли гистерезиса, штриховые кривые становятся многозначными. Однако
экспериментальные исследования не
выявили существования автоколебаний /и-
в этой области.
границы
IX.2.4. Определение
устойчивости
На рис. IX.16—IX.19 можно найти
критические значения усиления /С,
т. е. те наименьшие значения
коэффициента усиления, при которых могут
возникать устойчивые автоколебания.
Пока кривые остаются однозначными,
эти значения совпадают с
обозначенными на рисунках асимптотами. Эти
значения с учетом зависимости (IX.80)
можно определить аналитически,
переходя в соотношении (IX.88) к
пределам
(IX.98)
—1<т)<0,8.
ат'-2/К.
').
""1—V—1
1^1
И щ
/
ш
1 /
w\
щ\
-as
-0.2 0 0,2
0.6
Рис. IX.20. Зависимость критического
коэффициента усиления К от
коэффициента петли гистерезиса т)
311
На рис. IX.20 изображена зависимость критического значения
коэффициента усиления /С0 от параметра г\ и времени запаздывания. В области
—1 <3rj <0,8 усиление К0 определяется соотношением (IX.98)
(сплошные линии), а в области 0,8 <tj < 1 эти значения определены из
рис. IX.16—IX.19 (штриховые линии).
Для практического использования при определении критического
значения коэффициента усиления можно воспользоваться формулой
Ко = -^$-> -Кл<1, (К.99)
которая получена из выражений (IX.98) и (IX.20).
§ IX.3. Релейно-импульсное регулирование объектов
с запаздыванием
Из вышеприведенного анализа следует, что если запаздывание имеет
большую величину, то использование релейных регуляторов даже
теоретически без гистерезиса может приводить к недопустимо большим, с точки
зрения требований технологии, отклонениям регулируемой величины.
Рис. IX.21. Процесс нарастания регули- Рис. IX.22. Процесс спада регулируемой
руемой величины у при релейно-импульс- величины у при релейно-импульсном регу-
ном регулировании инерционного объекта лировании инерционного объекта с запа-
с запаздыванием здыванием
Поэтому для улучшения качества работы систем этого типа
применяется релейно-импульсное регулирование.
Двухпозиционное релейно-импульсное регулирование осуществляется
с помощью регуляторов, состоящих из:
релейной части со статической характеристикой без зоны
нечувствительности и без гистерезиса;
312
импульсной части, формирующей на выходе регулятора
последовательность импульсов с постоянной амплитудой, знак и длительность
которых определяются знаком и величиной сигнала на входе регулятора.
i Знак выходного сигнала с релейной части регулятора противоположен
знаку входного сигнала, т. е. +В при е < 0 и —В при е > 0. Знак
выходного сигнала с импульсной части регулятора совпадает со знаком
входного.сигнала на регулятор; сигнал постоянен по величине и равен
+ (Вг + В2) при е > 0 и — (Вг + В2) при е <0. В результате выходной
сигнал регулятора представляет собой сумму выходных величин с обеих
частей регулятора и имеет характер импульсов с длительностью /2, а пауза
между ними равна t±. Переходные процессы в регуляторах этого типа
изображены на рис. IX.21 и IX.22.
Резюмируя, можно сказать, что переходный процесс в релейно-импульс-
ной системе можно определить, зная реакцию системы на прямоугольный
импульс с известными амплитудой и длительностью и осуществляя
суммирование составляющих переходных процессов этого вида,
происходящих от каждого импульса с известной длительностью и знаком и
постоянной амплитудой. Следовательно, специфика релейно-импульсного
регулирования заключается в том, что на объект регулирования воздействует
последовательность импульсов, знак и длительность которых зависят от
направления^ и величины отклонения регулируемой величины у от
заданного значения. Благодаря тому, что с импульсной части регулятора
на объект поступают сигналы противоположного знака нежели с релейной
части, регулирующие переходные процессы в системе более плавные,
а отклонения регулируемой величины от заданного значения меньше.
На основе исследований, проведенных в предыдущем параграфе
относительно двухзначного регулирования, можно написать, что регулируемая
величина изменяется в соответствии со следующими соотношениями:
Д&= tfoto + B^U ~еГо 1- ад\1 ~е7'° j= /С0ВД1 -ги ) ; (IX. 100)
-АГоМ1-е-Т7).; (IX. 101)
Ьу, = КоВ1{1-*~^)\1+е~^)-КоВ1[1-<Г17)<Г'*: ; (IX. 102)
A</4=A"<AU-e т')(е г<,+'е т> )- К0В2(\ - t и) х
x(l+e fr_); (IX. 103)
—КоВ,\1-ъ г,Д1+е T° Je T\ (IX.104)
Методом индукции можно доказать, что положительная амплитуда
Аг/гл+i. т- е. после прохождения (2л + 1) импульсов, равна
^еди^-е /o)(i+j^
(n-k+l) (tt+t2)
То
(n-k) (tt+tt)
e To (IX.105)
-K0B2[l-e T°)e T°Y
948 313
или
1-е
(IX. 106)
Аналогично отрицательная амплитуда At/2m+i после прохождения
(2т + 1) импульсов равна
/ • _ _U_\ _ J± m _ (m-k) U3+tt)
AW = /C,AU-e r'je T' Ve r» -
/ -АД Г т (m-fe+1) (fr-MJ "]
■_едД1-е r#/h+2e
или
'°2e Гв -^oB2ll-e 4
(IX.107)
(IX. 108}
X e r° V e
где /3 — длительность отрицательного управляющего импульса на объект
при положительном сигнале на входе регулятора; tA — соответственно
длительность положительного импульса.
Рис. IX.23. Сравнение установившихся процессов при обычном
двухпозиционном регулировании и при релейно-импульсном
регулировании инерционного объекта с запаздыванием
На рис. IX.23 для сравнения изображеньк установившиеся процессы
при двухпозиционном регулировании и при релейно-импульсном
регулировании.
При двухпозиционном регулировании положительная амплитуда
Ay1 = K0B1{l-i"f7)'y (IX.109)
это следует из формулы (IX.29) при 6 = 0.
314
Аналогично отрицательная амплитуда
Ау2 = К0В2\1 - e-T7j . (IX.НО)
Из рис. IX.21 и IX.23 видно, что наибольшая положительная
амплитуда при релейно-импульсном управлении будет
ЬУи = *У*»ь (IX.111)
где п — число целых периодов длительностью (tx -f t2), уменьшающихся
во времени запаздывания объекта т.
Учитывая это, можно записать
и обозначая
получим
т = (tx + t2)n-t2y (IX.112)
-£- = «. (IX.113)
tl = 1T—{ ; (IX. 114)
1 (l+a)n — a' v '
t2 = "т . (IX. 115)
1 (1 + а) п— а v '
Подставляя зависимости (IX. 114) и (IX. 115) в соотношения (IX. 106)
и (IX. 108), получим окончательно
[/ т_ 1 \ т_ а
вД 1 _ е Го ' "+«"-«j е г« ' "+ап-а +
+ В2[ 1 - е~ Гв 'л+ал~аjjе" Го "п+ад~а Ye" г°
2_. (1+аЬ(я-Л)
п-\-ап—а
(IX. 116)
Поступая аналогично, найдем величину отрицательной амплитуды.
Л#!
.„ = 7(0вД 1 — е т° ' m+pm-p ) — /СоUi( 1 - е т' ffl+pm-p) —
где
'« =
1 I m
i
(l+P)m-p '
рт
/i i a\ ~, a •
(1+3) (m-
m-f-flm-
-k)
>
(IX. 117)
(IX. 118)
(IX. 119)
(IX. 120)
Период колебаний
Ау( = Ауи + Ау2г (IX. 121)
На основе соотношений (IX.116)—(IX.121) можно утверждать, что
при двухпозиционном релейно-импульсном регулировании без
гистерезиса статического объекта с запаздыванием область колебаний
регулируемой величины относительно заданного значения при надлежащем выборе
315
коэффициентов аир может быть существенно уменьшена (теоретически
до нуля), и это возможно даже при достаточно большом запаздывании
в объекте.
Наконец, на рис. IX.24 изображен установившийся процесс в двух-
позиционной релейно-импульсной системе регулирования астатического
объекта с запаздыванием. Статическая характеристика двухпозиционного
реле несимметрична, однако гистерезис отсутствует.
Рис. IX.24. Сравнение установившихся процессов при двухпозиционном
регулировании и при релейно-импульсном регулировании астатического объекта с
запаздыванием
Соответствующая положительная амплитуда в этом случае
Ьуи =
_ К^[(В1 — аВ2)п + В1]
(IX. 122)
(1 + а) л — а ' ]
?огда как при обычном двухпозиционном регулировании [из
формулы (IX. 16) при 6 = 01 лэна равна
АУ1 = К0Вхх (IX. 123)
Следовательно, в случае использования релейно-импульсного
регулирования амплитуда уменьшается в
раз.
(IX. 124)
Аналогично отрицательная амплитуда при релейно-импульсном
регулировании
ЬУч (1+P)m-P ' (IX. 125)
а отрицательная амплитуда при обычном двухпозиционном
регулировании, как это следует из формулы (IX. 17),
Ьу2 = К0В2г. (IX. 126)
Отсюда уменьшение отрицательной амплитуды колебаний
М,
(1 + P)m-P .
(l-PB^m+r,
(IX. 127)
316
Из соотношений (IX. 124) и (IX. 126) видно, что наибольшее
уменьшение размаха колебаний регулируемой величины происходит тогда, когда
значения параметров а и |3 близки к максимальным
«m--fj-; (ix.128)
Р« = т£- (1ХЛ29)
В этом случае амплитуды уменьшаются в
М1т = (1 +am)/z-am, (IX.130)
М2т = (\ +К)п-К (IX. 131)
раз.
В случае симметричной статической характеристики реле
*т = К- 1, (IX.132)
тогда, например, при п = 10 из соотношений (IX. 120) и (IX. 131) получим
Мхт = М2т = 19. Таким образом, имеем 19-кратное уменьшение
амплитуды колебаний.
Если на систему регулирования действуют возмущения, то нельзя
выбирать а и р из соотношений (IX. 128) и (IX. 129), так как регулятор
не будет компенсировать отклонений, возникающих от действия
возмущений. В этом случае оптимальные значения коэффициентов а и Р
определяются выражениями:
ао=|^; (1ХЛЗЗ)
Во
max
$о = 1г^, (IX-134)
#1 max
где Вх min и В2 mm — минимальные значения сигнала с регулятора на
объект соответственно при включении и выключении регулятора при
максимальной величине возмущений; 5Jmax и В2тах — максимальные
значения сигнала с регулятора.
Список литературы
1. Алексеев А. С. Двухпозиционный регулятор температуры с зоной опережения.
Памяти А. А. Андронова. Изд. АН СССР, М., 1955, с. 45—76.
2. Bottcher W. Optimales Verhalten von Zweipunktreglern mit Ruckfuhrung. Regelung-
stechnik. October, 1964, Heft 10, S. 340—344.
3. Bottcher W. Vergleich vol. Dreipunktreglern mit linearer und nichtlinearer
Ruckfuhrung. Regelungstechnik, July 1964, Heft 7, S. 297—305. '
4. Flugge— Lotz I. Discontinuous Automatic Control. Princeton 1953, Princeton
University Press.
5. Gagelmann H. Zur Untersuchung kontinulerlicher und diskontinuierlicher Relaissysteme
mit Totzeit in der Phasenebene. Messen, Steuern, Regeln, 1967, Teil I, II, Heft 7, S. 246—
250, 369—372.
6. Gessing R. Rownania roznicowe nieliniowych ukladow impulsowych z rzeczywistym czasem
opoznienia Prace IV Krajowej Konferencji Automatyki, z. 1, AGH, Krakow, s. 115—133.
7. Hegstenberg I., Sturm В., Winkler O. Messen und Regeln in der Chemischen Technik.
Berlin—Gottingen—Heidelberg 1957, Springer—Verlag.
8. Irawa K., Weaver L. E. Relay—type feedback control system with dead time and
sampling. AIEE Applications and Industry, May 1959, No*42, pp. 49—54.
9. Емельянов А. И.,, Емельянов В. А., Калинина С. А. Практические расчеты в
автоматике. М., «Машиностроение», 1967..
10. Кампе-Немм А. А. Автоматическое дв\'хпозиционное регулирование. М., «Наука»,
1967.
11. Кампе-Немм А. А. Динамика двухпозиционпого ре^лироваиия. М., Госэнерго-
издат, 1966.
317
12. Кампе-Немм А. А., Трусов А. Н. Простой метод увеличения точности двухпози-
ционного регулирования температуры. В кн.: «Теплоэнергетические приборы и
регуляторы». Под ред. Кремлевского П. П. М., Машгиз, 1960, с. 76—93.
13. Kashiwagi Y., Fliigge—Lotz I. Periodic solutions of differential equation with relay
control. Internat. J. Control, 1967, Vol. 6, No 1, pp. 1—25.
14. Kindler H., Rohl G. KHenes regelungtechnisches Praktikum. Berlin, 1967, VEB Verlag
Technik.
15. Клюев А. С. Двухпозиционные автоматические регуляторы и их настройка.
Библиотека по автоматике. М., «Энергия», 1967.
16. Копелович А. П. Автоматическое регулирование в черной металлургии. Краткий
справочник. М., Машгиз, 1963.
17. Kopielowicz A. P. Dobor regulatorow automatycznych. Metody obliczen. Warszawa,
1964, WNT.
18. Кремлевский П. П. Теплоэнергетические и химикотехнологические приборы и
регуляторы. М., Машгиз, 1961.
19. Круг Е. К.. Минина О. М. Электрические регуляторы промышленной автоматики.
Гл. V. М., Госэнергоиздат, 1962.
20. Oguztoreli M. N: Relay type control systems with retardation and switching delay.
J. Soc. Industr. and Appl. Math. Control, 1963, No 3, pp. 275—289.
21. Ольденбург Р., Сарториус Г. Динамика автоматического регулирования. М.,
Госэнергоиздат, 1949. '
22. Попов Е. П., Пальтов И. П. Приближенные методы исследования нелинейных
автоматических систем. М., Физматгиз, 1960.
23. Schumann F. Konstruktionsverfahren fur die Regelgrosse bei Relaistystemen mit linear-
asymptotischen Strecken. Messen, Steuern, Regeln, 1967, Heft 9, S. 317—322.
24. Skrzywan A. Regulacja dwupolozeniowa. Podstawy Automatyki. Pod red. S. W§gr-
zyna, skrypt, Warszawa, 1960, PWN, s. 253—279.
25. Strejc V. i inni. Teoria regulacji automatycznej. Warszawa, 1962, WNT.
Список дополнительной литературы
1. Бакакин А. В., Уткин В. И. Системы с переменной структурой с запаздыванием в
переключающих устройствах. В кн.: «Системы с переменной структурой и их применение
в задачах автоматизации полета, под ред. Б. Н. Петрова и С. В. Емельянова. М.,
«Наука», 1968.
2. Banas J. F., Vacrou A. G. On linear systems with a time-varying delay and isoperimetric
constraints. IEEE Trans, on Automatic Control, August 1968.
3. Banks H. T. A maximum principle for optimal control problems with functional
differential systems. Bull. Amer. Maht. Sci., 1969, 75, pp. 158—161.
4. Banks H. Т., Jacobs M. Q. The optimization of trajektories of linear functional
differential equations, SI AM J. Control, 1970.
45. Banks H. T. Necessary condition for control problems with variable lags. SI AM J. Control,
1968, Vol. 6, No 1.
6. Banks H. T. Variational problems involving functional differential equations. SIAM
J. Control, Februar 1969, Vol. 7, No. 1
7. Beck M. S., Gough N. E. A model reference adaptive control system using a cost
function criterion for driers and other dead time processes. Internat. I. Control, 1967, No 1,
pp. 55—76.
3. Berndt A. Zastosowanie metody plaszczyzny fazowej do analizy cyfrowych ukladow regu-
lacji bez taktu zewne,trznego. Prace Instytutu Automatyk PAN, z. 32, Warszawa, 1966.
9. Бей ко М. Ф., Бейко И. В. Численный метод построения оптимального управления для
одной системы с распределенными параметрами, «Вычислительная и прикладная
математика», Вып. 5. Изд. ЮГУ, 1968.
10. Bischoff H., Thomas J. Ein Approximationsverfahren fur zeitoptimale Regler in linearen
Abtastregelkreisen mit Totzeit. Messen, Steuren, Regeln, 1967, Heft 8, S. 287—291.
11. Buckalo A. F. Explicit conditions for controllability of linear systems with time lag.
IEEE Trans, on Autom. Control, April 1968, Vol. 13, No 2, pp. 193—195.
12. Буякас Б,- И., Пионтковский А. А. К аналитическому конструированию регуляторов
для систем с запаздыванием в исполнительном механизме. — «Автоматика и
Телемеханик а», 1969, № 2.
.13. Бутковский А. Г., Доманицкий-С. М. О синтезе управляющей части оптимальных систем
для некоторых объектов с запаздыванием. «Теория и применение дискретных
автоматических систем», М., Изд. АН СССР, 1960, с. 27—35.
14. Бутковский А. Г., Лернер А. Я. Об оптимальном управлении системами с
распределенными параметрами. — «Автоматика и Телемеханика». 1960, Т. XXI, № 6, с. 682—691.
15. Бутковский А. Г. Оптимальные процессы в системах с распределенными параметрами. —
«Автоматика и Телемеханика», 1961, Т. XII, № 1, с, 17—26.
16. Бутковский А. Г., Полтавский Л. Н. финитное управление системами с
распределенными параметрами. — «Автоматика и Телемеханика», 1969, № 4, 23—33. •
319
17. Бутковский А. Г. Теория оптимального управления системами с распределенными пара-
метрами. М., «Наука», 1965, с. 474.
18. Хараташвили Г. Л. Оптимальные процессы с запаздыванием. Тбилиси, Изд. Месне-
рева, 1966. ,
19. Хараташвили Г. Л. Принцип максимума в теории оптимальных процессов с
запаздыванием. Доклады АН СССР, 1961, Т. 136, № 1.
20. Chyung D. H.$ Lee Е. В. Delayed action control problems. Preprints of IV IFAC Congress,
Session 13, Warszawa, 1969.
21. Chyung D. H., Lee E. B. Optimal systems with time delays. Proc. Ill IFAC Congress,
London, 1966. Session 7.
22. Chyung D. H. Linear time—lag systems with side constraints. Preprints of JACC 1967, •
pp. 470—473; IEEE Trans, on Automatic Control. August 1967, V. Ac-12, No 4,
pp. 434—435; «Системы Автоматического Управления», 1968, № 4, стр. 49—57.
23. Cynningham W. J. Analiza ukladow nieliniowych. Rozdzial 8, Warszawa, 1962,
WNT.
24. Cypkip Ja. Z. Elements of theory of numerical automatic system. Automatic and Remote
Control, Vol. I, pp. 286—294. London, Butterworths.
25. Чинаев П. И. Анализ и синтез самонастраивающихся систем. Киев, 1960, с. 183—186.
26. Dancewicz J. Dynamika procesu zeliwiakowego. Pomiary, Automatika, Kontrola 1969, ni I
s. 30—34.
27. Дралук Б. Н., Хинайс'кий Г. В. Системы автоматического регулирования объектов,
с транспортным запаздыванием. М., «Энергия», 1969, с. 70»
28. F511inger О. Synthese von Abtastsystemen in Zeitbereich. Regelungstechnic, june, 1965,.
Heft 6, S. 269—275; «Системы Автоматического Управления», М., 1965, № 37,
v с. 1 — 17.
29. Frank P. M. Vollstandige Vorhersage im stetigen Regelkreis mit Totzeit. Regelungstechnik,.
Marz 1968, Heft 3, Teil I, S. 111 — 116.
30. Габасов Р., Чуракова С. В. Достаточные условия оптимальности в?системах с
запаздыванием.— «Автоматика и Телемеханика», 1967, № 1, 1968, №2.
31. Габасов Р., Чуракова С. В. К теории управляемости линейных систем с
запаздыванием. — «Техническая Кибернетика», 1969, № 4.
32. Габасов Р., Чуракова С. В. Необходимые условия оптимальности в системах с
запаздыванием.— «Автоматика и Телемеханика», 1969, № 1, с. 45—64.
33. Габ.асов Р. Об одной задаче теории оптимальных процессов. — «Автоматика и
Телемеханика», 1967, № 8.
34. Gessing R. Rownania roznicowe nieliniowych ukladow impulsowych z rzeczywistym-
czasem opoznienia. Prace IV Krajowej Konfereffcji Automatyki, z. 1, AGH Krakow,
1967, s. 115—133.
35. Gorecki H., Turowicz A. On switching instans in minirnumtime control .problem. Bull-
Pol, des Sciences, ser. de Sc. Techn., 1968, Vol. XVI, No 2.
36. Gorecki H., Turowicz A. N0 pewnym ukladzie adaptacyjn,ym sterowanym optymalnie,
Prace IV Krajowej Konferencji Automatyki. z. 1, AGH Krakow, 1967, s. 147—163.
37. Isobe Т., Totani T. Analysis and design of a parameter-perturbation adaptive system
for application to process control. Proc. Il-nd Congress IFAC, London, 1953 r
Butterwoth.
38. Емельянов G. В. Системы автоматического управления с переменной структурой. М.,
«Наука», 1967, с. 86—93.
39. Kalman R. E. Contribution to the theory of optimal control. Boletin de la Sociedad
Matematica Mexicana/ 1960, Vol. 5, pp. 102—119.
40. Каменский Г. А., Хвилов Э. А. Необходимое условие оптимального управления для
'систем с отклоняющимся аргументом нейтрального типа. — «Автоматика и
Телемеханика», <N9 3, 1969. ^
41. Келенджеридзе Д. Л.-Об одной задаче оптимального преследования.—«Автоматика»
и Телемеханика», 1962, Т. XXIII, № 8, с. 1008—1013.
320
"42. Kinnon D. Mac. Optimal control of systems with pure time delays using a variational
programming approach. IEEE Trans, on Automat. Control. June 1967, Vol. AC-12, No 3,
pp. 255—262.
43. Kjpiniak W. Dynamic optimization and control a variational, approach. New York, 1961,
MIT Press and J. Wiley, pp. 51—63.
44. Kirillowa F. M. Applications of functional analysis to the theory of optimal process.
SiAM J. Control, 1967, Vol. 5, No 1.
45. Кириллова Ф. М., Чуракова С. В. К проблеме управляемости линейных систем с
последействием. «Дифференциальные уравнения», 1967, Т. III, № 3.
46. Kirillowa F. М., Czurakowa S. W. Relative controllability in systems with time—lag.
Dokl. АН СССР.
47. Кириллова Ф. M. О направлении в теории оптимальных процессов. — «Автоматика
и Телемеханика», 1967, №Л1.
48.- Кириллова Ф. М., Полетаева И. А., Чуракова С. В., Габасов Р. Управляемость и
синтез - оптимальных динамических систем. Preprints of IV IFAC Congress, Session 7,
Warszawa, 1969.
49. Коган В. Я., Петренко Ю. И., Чернышев М. К. О моделировании иррациональных,
передаточных функций.—«Автоматика и Телемеханика», 1968, № 7, стр. 118—132.
50. Красовский Н. Н. Об аналитическом конструировании оптимального регулятора
в системе с запаздыванием времени. —.«Прикладная математика и механика», -1962,
№ 1, с. 39—50.
51. Krassowskij N. N. Optimal processes in systems with time lag. Proc. Ш-rd IFAC Congress,
London, 1963, Butterworth.
52. Красовкий Н. Н. Теория управления движением. М., «Наука», 1968, с. 349—374.
53. Крин едкий И. И. Основы автоматического регулирования химических процессов.
Киев, 1958, Гос. Изд. Техн. Лит. с. 205—209.
54. Кринецкий И. И. Расчет нелинейных автоматических систем. Киев, 1962, Гос. Изд.
Техн. Лит. с. 187—203.
55. Круг Е. К., Минина О. М. Об оптимальных переходных процессах в системе
автоматического регулирования с ограничением положения регулирующего органа. —
«Автоматика и Телемеханика», 1958, Т. XIX, № 1, с. 10—25.
ч
56. Kwakernaak К. Optimal filtering in linear systems with tyme delays. IEEE Trans, on
Automatic'Control, April 1967, Vol. AC-12, No 2, pp. 169—173.
57. Lee E. В., Markus L, Foundations of Optimal Control Theory. Appendix В., pp. 521—529/
New York, 1967. J. Wiley.
58. Lee E. B. Variational problems for systems having delay in the control action. IEEE
Trans, on Autom. Control, Desember 1968.
59. Manitius A. Optimum control of linear time lag systems. Preprints of IV IFAC Congress,
Session 13, Warszawa, 1969.
60. Manitius A. Optymalne sterowanie procesami z opoznieniem zmiennych stanu. Praca
Doktorska, Kaiedra Automatyki i Telemechaniki Politechniki Warszawskiej,
Warszawa, 1968.
61. Маркушин Э. М., Шиманов С. Н. Приближенное решение задачи аналитического
конструирования регулятора для систем с запаздыванием. — «Автоматика и
Телемеханика», 1968, ЛЬ 3, с. 13—20.
62. McCausIand I. Time—optimal control of a linear diffusion processes. Proc. Inst. Electr.
Engrs., 1965, No 3, pp. 543—548; «Системы автоматического управления», 1965, № 27,
с. 16—30.
63. Милуткин В. П. Принцип миксимума для задач с запаздыванием и фиксированным
временем и свободным правым концом траектории. — «Автоматика и Телемеханика».
1968, ЛЬ 6, с. 37—45.
21 X. Турецкий 321
64. Mishkin E., Braun L. Adaptive Control Systems. New York, 1961, McGraw Hill.
65. Mitsumaki T. Modified optimum non-linear control. Automatic and Remote Control.
Vol. I, pp. 520—528; Proc. I-st Congress IFAC, Moscow 1960, London 1961, Butterworths.
66. Oguztoreli N. N. Optimal pursuit strategy processes with retarded control systems. J.
Soc. Industr. and Appl. Math. 1964, No 1, pp. 89—105; «Системы автоматического
управления», 1965, № 6, с. 1—11.
67. Oguztoreli M. N. Time—Lag Control Systems. London, 1966, Acad Press, s
68. Осовский Л. М. Идентификация по ФЧГ и АЧГ одномерных нелинейных объектов
управления, имеющих эффект чистого запаздывания. —«Автоматика и Телемеханика»,-
1968, № 8, с. 159—168.
69. Павлов А. А. Динамика быстродействующих релейных сервомеханизмов с
запаздыванием.— «Техническая Кибернетика», 1963, № 1, с. 172—180.
70. Павлов А. А. Синтез релейных систем, оптимальных по быстродействию. Метод
фазового пространства. М., «Наука», 1966.
71. Perret R., Rouxel R. Principle and application of extremal computer. Proc. H-nd IFAC
Congress, London, 1963, Butterworth.
72. Przeworska— Rolewicz D., Rolewicz S. On periodic solution of non-linear differential-
difference equations.
73. Ragg В. С Necessary conditions for the optimal control of a system with time—varying
transport lads. IEEE Trans. Autom. Control, 1966, No 4, pp. 738—740; «Системы
автоматического управления», 1967, № 19, с. 1—7.
74. Ragg В. С, Stepleton С. A. Time optimal control of second—order systems with
transport lag. Internat. J. Control, 1969, No 3, pp. 243—257; «Системы автоматического
управления», 1969, № 16, с. 8—26.
75. Roberts A. P. Lagging filtering and progresive interpolation. Internat. J. Control, 1967,
No 5, pp. 461—479.
76. Roberts J. D. Extremum of hill-climbing regulation a statistical theory involving lags,
disturbances and noise. Proc. Inst. Electr. Engrs., 1965, No 1, pp. 137—150.
77. Sakawa Y. Solution of an optimal control problem in a distributed—parameter system.
IEEE Trans. Automat. Control, 1964, No 4, pp. 420—426; «Системы автоматического
регулирования», 1965, № 20, с. 1—16.
78. Sebesta H. R., Clark L. G. On the optimal control problem for dynamical process with
variable delays. Preprints of JACC, 1967, pp. 326—334.
79. Strejc V. Synthese von Regelkreisen mit Prozessrechnern. Messen, Steuren, Regeln Juni
1967, Nr 6, S. 201—207.
80. Шигин Е. К. Автоматическое регулирование объекта с чистым запаздыванием
регулятором с переключаемыми параметрами. Гл. I — «Автоматика и Телемеханика»,
1965, № 10, с. 1644—1671; гл. II — «Автоматика и Телемеханика», 1966, № 6,
с. 72—81.
81. Шигин К. К. Классификация динамических моделей объектов регулирования химико-
технологических процессов.—«Автоматика и Телемеханика», Л968, № 7,
с. 160—174.
82. Валеев К. Г. Линейные дифференциальные уравнения с синусоидальными
коэффициентами и стационарными запаздываниями аргумента. Качественные методы теории
нелинейных колебаний. Киев, 1963, Изд. АН СССР, Т. II, с. 100—119.
83. Вежбицки А. Принцип максимума для процессов с нетривиальными запаздываниями
управления. — «Автоматика и Телемеханика». 1970.
84. Walker I. A. Stability of feedback systems involving timedelays and timevarying
non-linearity. Internat. J. Control, 196?, No 4, pp. 365—372.
322
S5. Wang P. K. C„ Bandy M. L. Stability of distributed — parameter processes with time
delays. J. Electron, and Control, 1963, No 4, pp. 343—362.
86. Wang P. К. С. Optimum control of distributed parameter systems with time delays. IEEE
Trans. Automat. Control, 1964, No 1, pp. 13—22; «Системы Автоматического
Управления», 1964, № 27, с. 1—18.
87. Weiss L. On the controllability of differential systems. Si AM J. Control, Novembre
1967, Vol. 5, No 4, pp. 575—587.
88. Wierzbicki A. Zasada maksimum a synteza regulatorow optymalnych, cz. I. Archiwum
Automatyki i Telemechaniki, 1968.
89. Wierzbicki A. Zasada maksimum a synteza optimalnych urzadzeri sterujacych. Rozprawa
habilitacyjna. Katedra Automatyki i Telemechaniki Warszawskiej, Warszawa, 1967.
90. Wrobel Cz. Regulacja obiektow z czyctym opoznieniem przy zastosowaniu regulatorow
PID i ukladow specjalnych. Praca dyplomowa magisterska. Katedra Automatyki i Elek-
troniki Przemyslowej, AGH Krakow, 1964.
Оглавление
Предисловие автора о
Введение. Математические модели управляемых процессов 7
§ В.1. Основные понятия 7
§ В.2. Математические модели процессов 9
8.2.1. Детерминированные модели процессов . . . . 10
8.2.2. Стохастические, игровые и адаптивные модели 15
§ В.З. Вычислительные аспекты 16
Список литературы 17
Глава I. Примеры объектов с запаздыванием 18
§ 1.1. Объекты с чистым запаздыванием 19
1.1.1. Транспортные процессы. Регулирование количества угля на
ленточных транспортерах 19
1.1.2. Система стабилизации толщины листа при холодной прокатке ... 21
1.1.3. Двигатель постоянного тока с независимым возбуждением .... 21
1.1.4. Другие процессы . . 24
§ 1.2. Объекты с распределенным запаздыванием 28
1.2.1. Длинная электрическая линия 29
1.2.2. Теплообменники 46
Список литературы 52
Глава II. Идентификация объектов с запаздыванием 56
§ II.1. Определение математической модели по временным реакциям 57
11.4.1. Определение параметров объекта первого порядка с
запаздыванием : 57
II. 1.2. Определение параметров объекта второго порядка с
запаздыванием 58
II. 1.3. Метод площадей 62
II. 1.4. Метод моментов 63
II. 1.5. Определение импульсных переходных функций объектов
управления с помощью метода моментов 64
§ II.2. Идентификация объектов с помощью модели с настраиваемыми
параметрами 70
11.2.1. Модель в виде дифференциально-разностного уравнения 72
П.2.2. Модель в виде комбинации ортогональных функций 73
§ П.З. Идентификация линейных объектов на основе корреляционного анализа
случайных сигналов 80
324
§ 11.4. Аппроксимация объекта высокого порядка с использованием модели,
содержащей запаздывание . . . . 81
11.4.1. Аппроксимация при помощи модели первого порядка с
запаздыванием 81
11.4.2. Аппроксимация при помощи модели п-го порядка при одинаковых
постоянных времени с запаздыванием 82
Список литературы 85
Глава III. Непрерывное автоматическое регулирование линейных объектов с
запаздыванием 88
§ III. 1. Введение . . . . 88
§ II 1.2. Вычисление переходных функций 89
111.2.1. Метод последовательного интегрирования на интервалах (метод
шагов) 90
111.2.2. Метод разложения передаточной функции замкнутой системы
в ряд 92
111.2.3. Метод, основанный на знании полюсов передаточной функции
замкнутой системы . ИЗ
Список литературы . 125
Глава IV. Анализ устойчивости линейных непрерывных систем автоматического
регулирования с запаздыванием 127
§ IV. 1. Определение устойчивости в малом 127
§ IV.2. Определение асимптотической устойчивости 127
§ IV.3. Аналитические критерии 128
IV.3.1. Критерий Понтрягина 128
Список литературы 146
Глава V. Номограммы для определения областей устойчивости на плоскости
параметров объекта и регуляторов. Графические методы анализа
устойчивости 148
§ V.I. Графические критерии устойчивости . 148
V.l.l. Критерии Сетча и Цыпкина как аналоги критериев Михайлова и
Найквиста 161
V.I.2. Метод D-разбиения 166
§ V.2. Структурная устойчивость одноконтурных систем регулирования с
запаздыванием 168
V.2.I. Основные теоремы 168
§ V.3. Анализ устойчивости систем регулирования с распределенным
запаздыванием 172
V.3.I. Аналог критерия Найквиста 172
V.3.2. Аналог критерия Михайлова 174
Список литературы 175
Глава VI. Параметрический синтез типовых регуляторов 177
§ VI. 1. Критерии качества систем автоматического регулирования 178
VI. 1.1. Критерий устойчивости 179
VI. 1.2. Критерий апериодической устойчивости 180
VI. 1.3. Показатель управляемости 180
VI.1.4. Критерий оптимального модуля . . . 181
VI. 1.5. Параметры выходной реакции системы на скачкообразное входное
воздействие 182
VI. 1.6. Интеграл от ошибки 184
VI. 1.7. Интеграл от квадрата ошибки 184
VI. 1.8. Обобщенный интеграл от суммы квадратов ошибки и ее
производных 185
325
VI. 1.9. Интеграл от абсолютной ошибки 185
VI. 1.10. Интеграл от абсолютной ошибки, умноженной на время 185
VI. 1.11. Критерий Зиглера—Никольса 185
§ VI.2. Общая методика выбора регуляторов с заданной структурой и
сравнение их параметров 186
VI.2.1. Выбор типа регулятора в случае объекта с одной доминирующей
постоянной времени TQ и временем запаздывания т 186
VI.2.2. Выбор типа регулятора в случае объекта с двумя
доминирующими постоянными времени Т01 и Т02 и времени запаздывания т,
а также без доминирующей постоянной времени 188
VI.2.3. Выбор величин настраиваемых параметров на основе критерия
апериодической устойчивости 18$
VI.2.4. Номограммы для определения областей устойчивости на плоскости
параметров объекта и регулятора 194
VI.2.5. Выбор регулятора и его параметров на основе критерия
оптимального модуля 197
VI.2.6. Критерии при использовании типовых управляющих
сигналов • 21G
§ VI.3. Двухконтурные системы автоматического регулирования 211
Список литературы 216
Глава VII. Импульсное управление объектами с запаздыванием 219
§ VII. 1. Определение переходных процессов и анализ устойчивости 219
VII. 1.1. Анализ системы по управлению 224
VII. 1.2. Анализ системы по возмущению 227
§ VII.2. Вопросы устойчивости 230
VI 1.2.1. Критерий устойчивости Найквиста . 230
VI 1.2.2. Критерий Шура—Кона и Гурвица 231
§ VI 1.3. Области устойчивости на плоскости настраиваемых параметров . . . . 235
VII.3.1. Определение границы апериодической устойчивости 233
VI 1.3.2. Определение границы колебательной устойчивости 234
§ VI 1.4. Параметрический синтез импульсных регуляторов 240
VII.4.1. Критерий критической апериодической устойчивости 240
VI 1.4.2. Критерий оптимального модуля 245
VI 1.4.3. Критерий при использовании типового управляющего сигнала . . 251
§ VI 1.5. Параметрический синтез импульсного регулятора общего вида .... 251
VI 1.5.1. Компенсация запаздывания 252
Список литературы 269
Глава VIII. Устойчивость и автоколебания в нелинейных системах автоматического
регулирования с запаздыванием 271
§ VIII. 1. Второй метод Ляпунова 272
§ VIII.2. Первый метод Ляпунова 276
§ VII 1.3. Устойчивость при постоянно действующих возмущениях 277
§ VIII.4. Метод Попова 277
§ VII 1.5. Метод описывающей функции 283
Список литературы 294
Глава IX. Релейное регулирование объектов с запаздыванием 296
§ IX. 1. Двухпозиционные системы регулирования 296
IX. 1.1. Определение переходных процессов в системе, состоящей из
двухпозиционного регулятора с зоной неоднозначности и астатического
объекта с запаздыванием 297
IX. 1.2. Определение реакций в системе, состоящей из двухпозиционного
регулятора с зоной неоднозначности и статического объекта с
запаздыванием 299
326
IX. 1.3. Определение выходных реакций в системе, состоящей из двухпози-
ционного регулятора с зоной неоднозначности и объекта с
распределенным запаздыванием 302
§ IX.2. Анализ релейных систем на фазовой плоскости 303
IX.2.1. Условия существования предельного цикла 307
IX.2.2. Определение амплитуды колебаний 308
IX.2.3. Определение периода автоколебаний 309
IX.2.4. Определение границы устойчивости 311
§ IX.3. Релейно-импульсное регулирование объектов с запаздыванием .... 312
Список литературы 317
Список дополнительной литературы 319
X, Турецкий
Анализ и синтез
систем управления
с запаздыванием
Редактор издательства Е. В. Григорин-Рябова
Технические редакторы: Е. П. Смирнова, Н. В. Тимофеенко
Корректор Ж. Л. Суходолов а
Переплет художника А. Я. Михайлова
Сдано в набор 29/1II 1974 г.
Подписано к печати 8/VII 1974 г.
Формат 70Xl08Vie Бумага типографская № 2
Усл. печ. л. 28,7
Уч.-изд. л. 25,9
Тираж 6000 экз. Заказ 948. Цена 2 р. 68 к.
Издательство «Машиностроение»
107885, Москва, Б-78, 1-й Басманный пер., 3
Ленинградская типография № 6 Союзполиграфпрома
при Государственном комитете Совета Министров СССР
по делам издательств, полиграфии и книжной торговли
193144, Ленинград, С-144, ул. Моисеенко, 10
X. Гурецкий
£j? r
>*-
-л-'ЧЙЬ. _fw
' 11^
S„4
..*