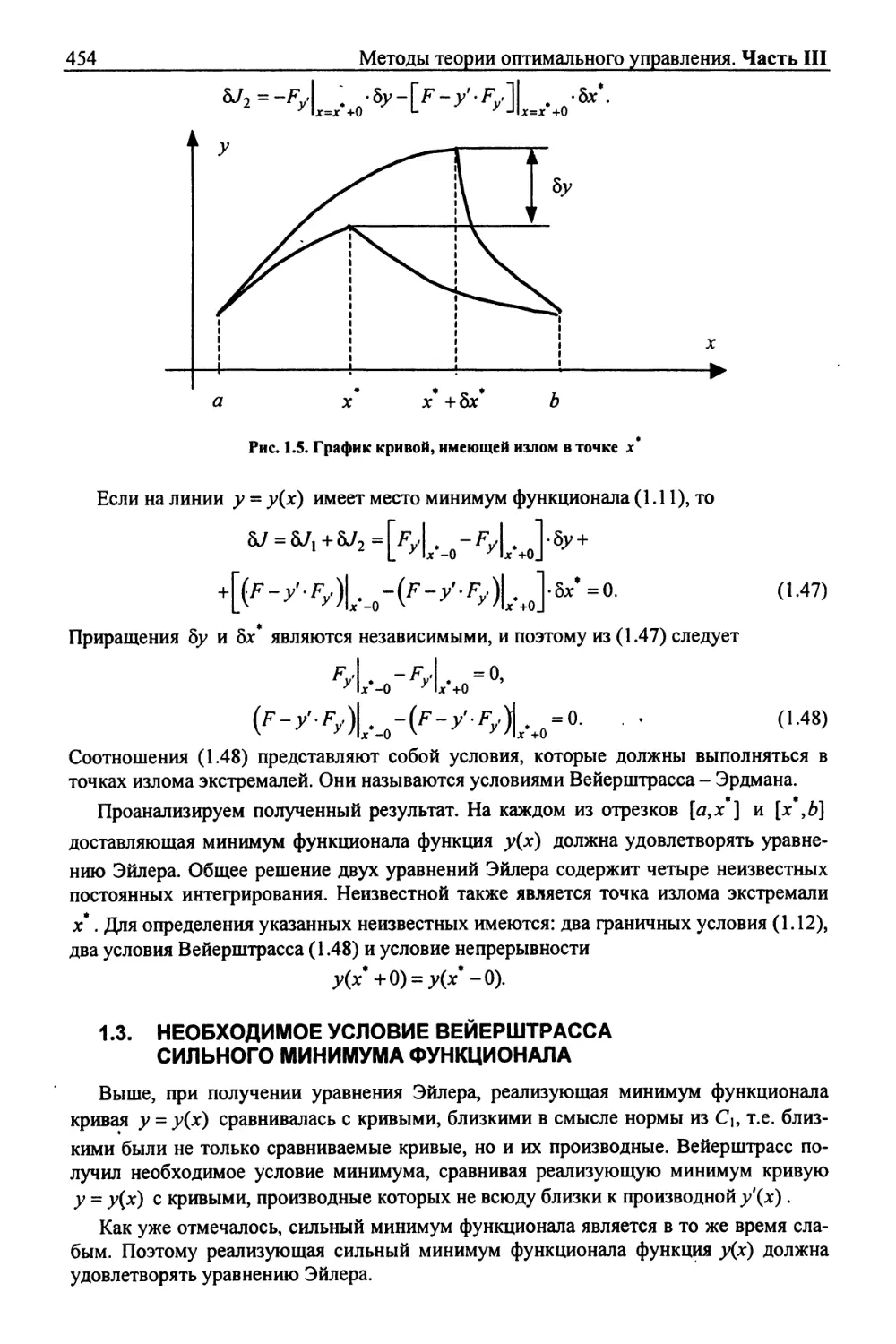
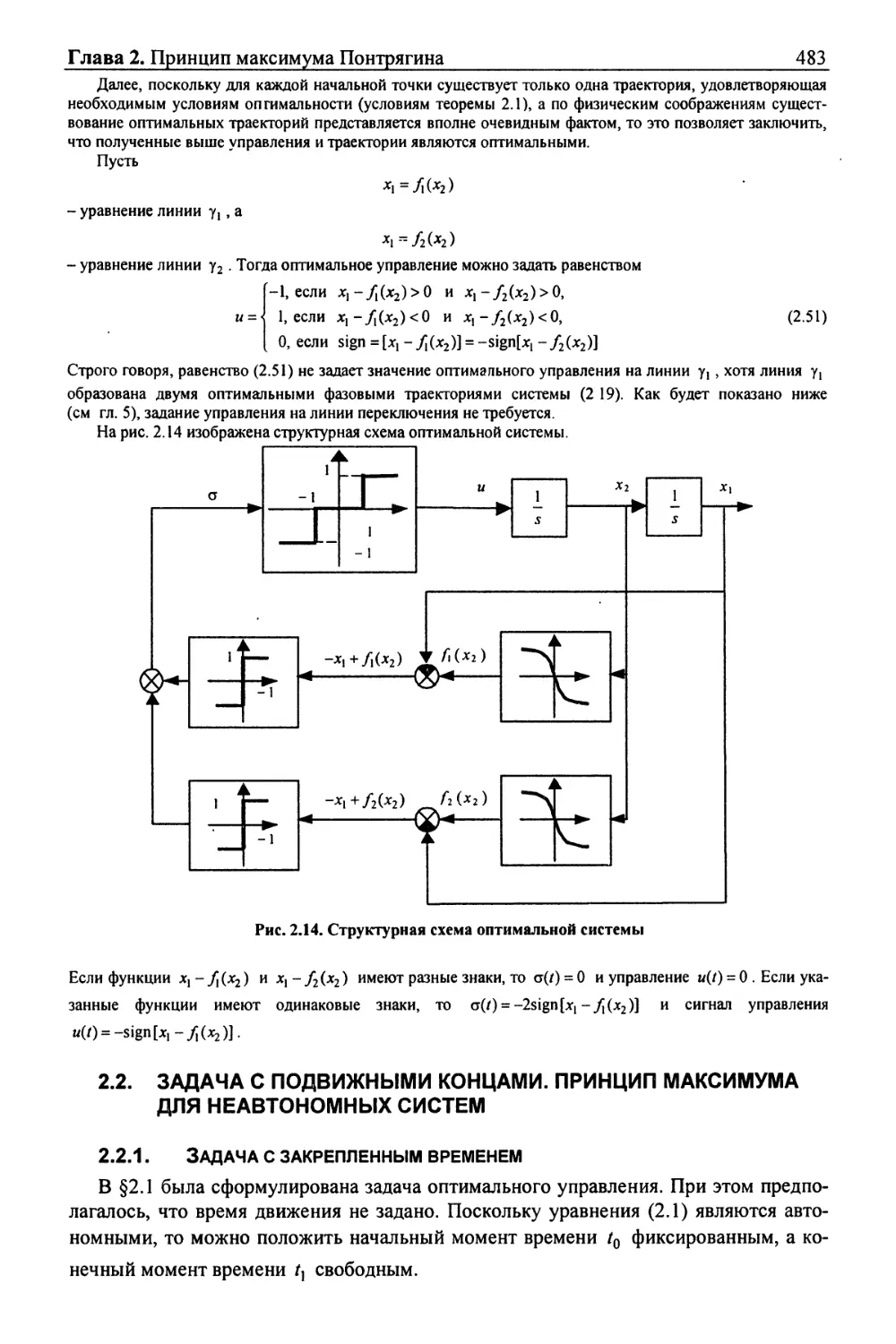
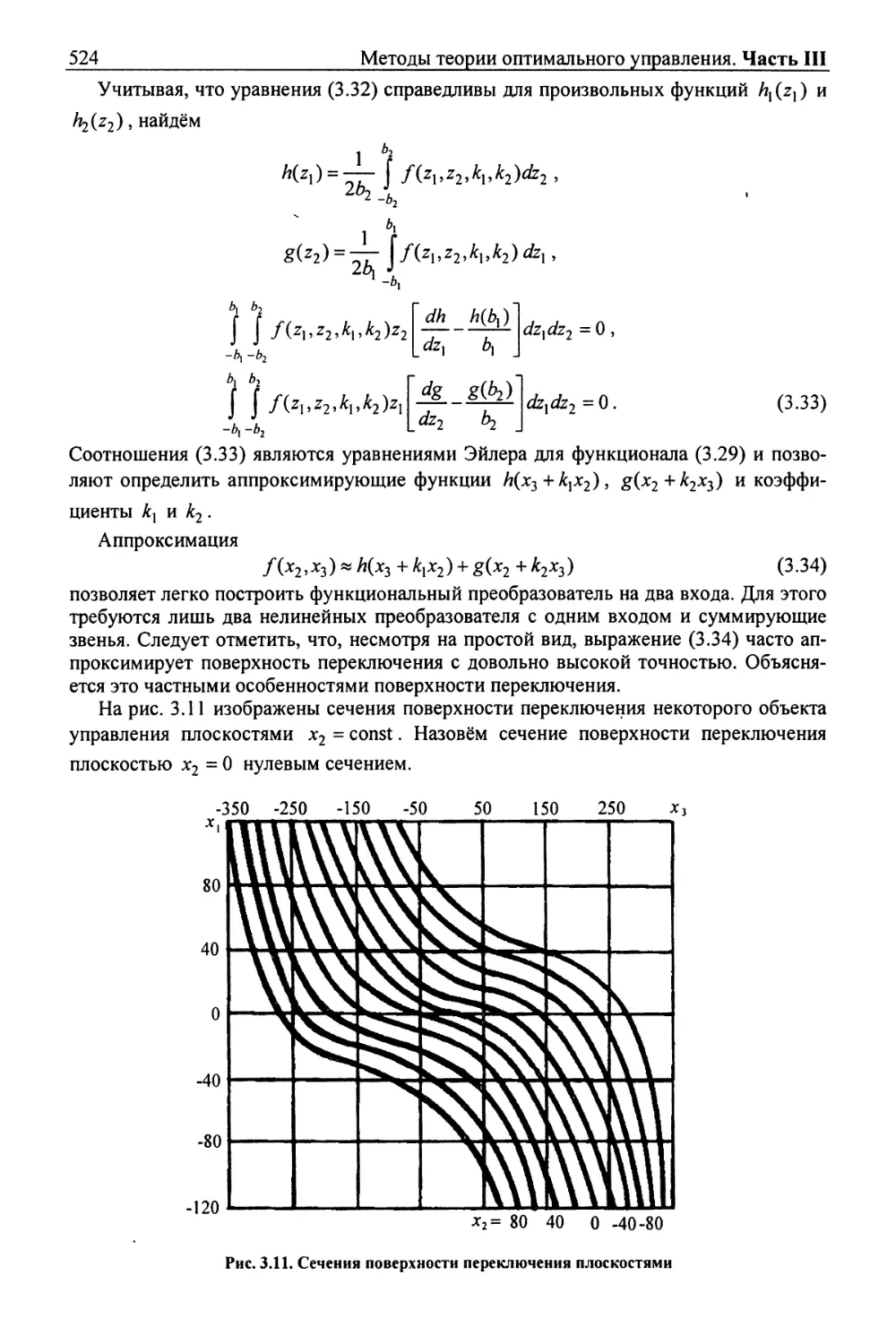
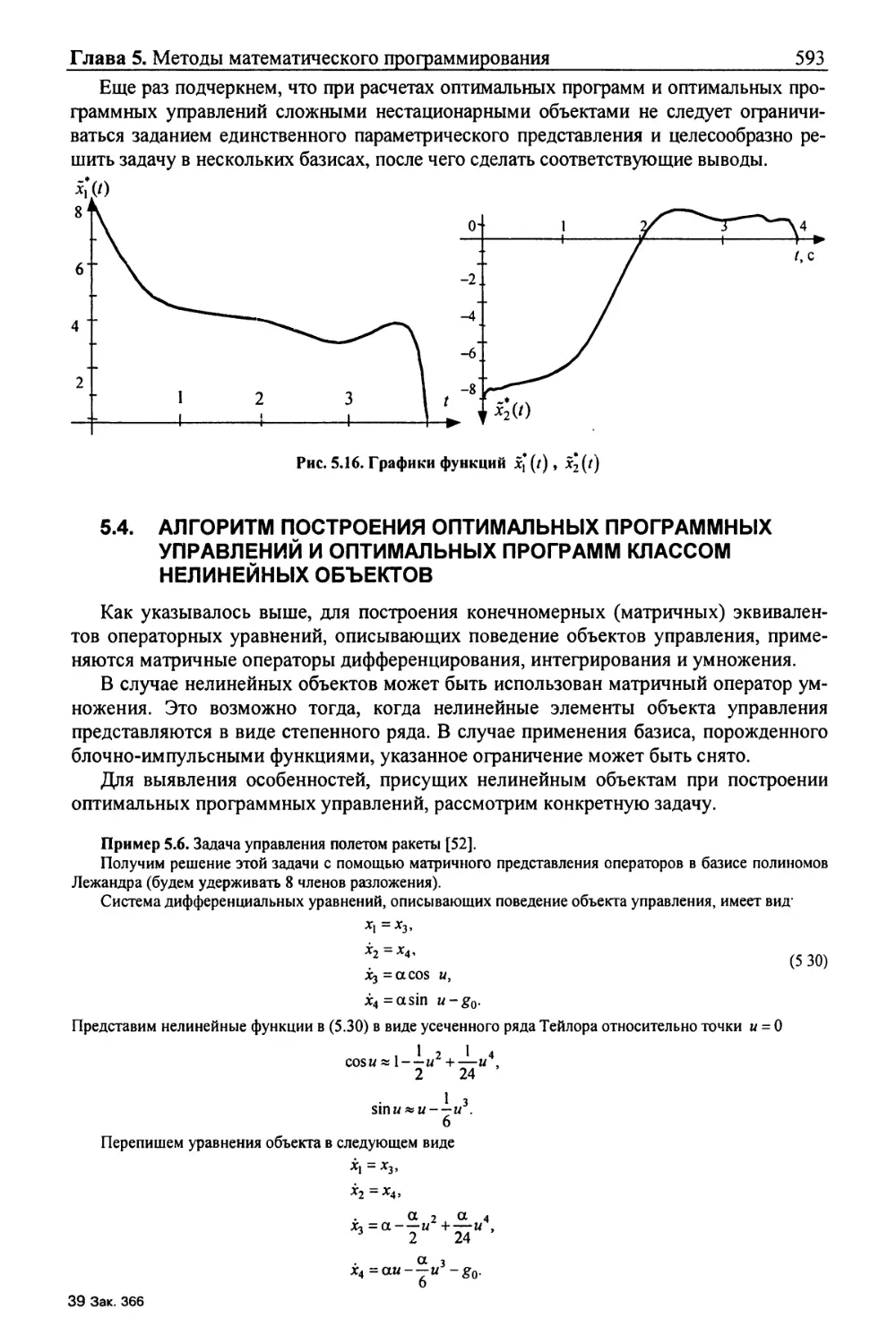
Текст
МЕТОДЫ ТЕОРИИ
АВТОМАТИЧЕСКОГО
УПРАВЛЕНИЯ
Цикл учебников и учебных пособий
основан в 1997 г.
Под общей редакцией заслуженного деятеля науки РФ,
доктора технических наук, профессора
К.А. Пупкова
МЕТОДЫ КЛАССИЧЕСКОЙ
И СОВРЕМЕННОЙ ТЕОРИИ
АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Учебник в трех томах
ТОМ 2
СИНТЕЗ РЕГУЛЯТОРОВ
И ТЕОРИЯ ОПТИМИЗАЦИИ
СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Под редакцией заслуженного деятеля науки РФ,
доктора технических наук,
профессора Н.Д. Егупова
Рекомендовано Министерством образования Российской Федерации
в качестве учебника для студентов высших учебных заведений,
обучающихся по машиностроительным
и приборостроительным специальностям
Москва
Издательство МГТУ им. Н.Э. Баумана
2000
УДК 681.5:681.3(075.8)
ББК 14.2.6
М54
Рецензенты:
1. Академик РАН ЕЛ. Попов;
2. Кафедра автоматических систем Московского института радиотехники,
электроники и автоматики (заведующий кафедрой, член-корреспондент
РАН Е.Д. Теряев).
Авторы:
Д-р техн. наук, проф. К.А. Пупков, д-р техн. наук, проф. Н.Д. Егупов,
д-р техн. наук, проф. A.M. Баркин, д-р техн. наук ЕМ. Воронов, инженер
Э.П. Козубов, канд. техн. наук, доц. ВТ. Коньков, канд. техн. наук, доц.
В.И Краснощеченко, канд. техн. наук, доц. А.П. Курдюков, канд. техн.
наук, доц. В.И. Пилишкин, д-р техн. наук, проф. В.М. Рыбин, канд. техн.
наук, доц. В.И. Сивцов, канд. техн. наук, доц. Я.В. Слекеничс, д-р техн.
наук, проф. А.И. Трофимов, д-р техн. наук, проф. Н.В. Фалдин
М54 Методы классической и современной теории автоматического управления:
Учебник в 3-х т. Т.2: Синтез регуляторов и теория оптимизации систем
автоматического управления / Под ред. Н.Д. Егупова. - М.: Изд-во МГТУ им.
Н.Э. Баумана, 2000. - 736 с; ил.
ISBN 5-7038-1627-0 (Т.2)
ISBN 5-7038-1579-7
Центральной проблемой расчета и проектирования систем автоматического управления
является проблема обеспечения высокого качества ее функционирования, включая оптимизацию по
тем или другим критериям; это - проблема синтеза САУ.
Второй том учебника посвящен изложению методов синтеза регуляторов, обеспечивающих
заданное качество процессов управления и позволяющих определить состав, структуру САУ и
параметры всех ее устройств из условия удовлетворения заданному комплексу технических
требований в классе линейных (стационарных и нестационарных), нелинейных, дискретных и
многомерных систем Отражены основные положения модального управления.
Изложены основы теории оптимальных систем классическое вариационное исчисление,
принцип максимума Л.С Понтрягина, динамическое программирование Р Беллмана,
аналитическое конструирование регуляторов (АКОР)
Рассмотрены проблема моментов, предложенная и обоснованная Н.Н Красовским, и
нашедший широкое применение метод математического программирования
Отражены подходы, позволяющие синтезировать оптимальные системы с ограничением на
фазовые переменные Материал является частью общего курса теории автоматического
управления, читаемого студентам МГТУ им. Н.Э. Баумана, ТулГУ, ОИАТЭ и других вузов
Учебник предназначен для студентов вузов; он может быть также использован аспирантами и
инженерами, а некоторые положения - научными работниками, занимающимися автоматическими
системами.
УДК 681.5:681.3 (075.8)
ББК 14.2.6
ISBN 5-7038-1627-0 (Т.2) © Пупков К.А., Егупов Н.Д., Баркин АИ и др , 2000
ISRN 5 7(ПЯ 1S70 7 ® МГТУ им. Н.Э. Баумана, 2000
loom э-/ш>о-1э/?-/ 0 ИзДательство МГТУ им. Н.Э. Баумана, 2000
Нашим учителям
посвящается.
ОБЩЕЕ ПРЕДИСЛОВИЕ К УЧЕБНИКУ
I. Особенности учебника.
Учебник издается в трех томах, состоящих из четырех частей и заданий для
самостоятельной работы. Для него характерно следующее:
1. Учебник охватывает основные положения, составляющие содержание
теории автоматического управления. Изложение материала начинается с
основных понятий и определений (сущность проблемы автоматического управления,
определение системы управления, фундаментальные принципы управления, основные
виды и законы автоматического управления и др.) и заканчивается детальным
рассмотрением содержания некоторых современных направлений теории
автоматического управления.
Поскольку курс теории автоматического управления включен в учебные планы
различных инженерных специальностей и является одним из важнейших элементов
общетехнического образования, учебник может быть рекомендован студентам,
заново приобретающим знания в области теории автоматического управления, и
специалистам, которым приходится эти знания восстанавливать. Учебником могут
пользоваться также студенты тех специальностей, для которых курс является
профилирующим, определяющим квалификацию инженера.
При изучении курса студент или специалист должен сделать выборку материала,
определяемого конкретной задачей и возможностями общего плана обучения.
2. Содержание учебника имеет инженерную направленность, поэтому
изложение ведется с инженерной точки зрения: подчеркиваются главные идеи, лежащие в
основе методов, но не всегда приводятся строгие математические доказательства.
Учитывая, -но без освоения технического аспекта изучение методов теории автоматического
управления не приводит к нужному результату (часто имеют место трудности в
постановке и решении инженерных задач даже при хороших знаниях теоретических
положений), физическая и содержательная сторона дела подчеркивается в течение
всего курса. Более того, значительное внимание уделено рассмотрению конкретных
промышленных систем управления. Например, в главе 7 тома 2 рассмотрены
системы управления теплоэнергетическими параметрами атомных электростанций; в
заданиях для самостоятельной работы описаны системы управления, применяемые в
атомной промышленности. Примеры, иллюстрирующие теоретические положения и
методы расчета, тесно связаны с решением конкретных инженерных задач в таких
отраслях, как атомная энергетика, производство летательных аппаратов и др.
3. Методы теории автоматического управления, рассмотренные в учебнике, в
большинстве своем ориентированы на применение ЭВМ.
Интенсивное развитие процессов автоматизации проектирования систем
автоматического управления, обусловленное развертыванием высокопроизводительных
вычислительных комплексов в проектно-конструкторских организациях,
перемещение центра тяжести процесса проектирования от аппаратного обеспечения к
алгоритмическому и программному обеспечению приводят к необходимости разработки
нового методологического обеспечения, включая соответствующие вычислительные
технологии [136].
Для содержания книги характерна, в известной мере, «вычислительная окраска»,
поскольку возможности современных ЭВМ позволяют значительно ускорить сроки
проектирования САУ и, таким образом, налагают свой отпечаток на вычислительную
часть ТАУ. Успех в решении поставленных задач расчета и проектирования с
использованием ЭВМ зависит от многих факторов, основными из которых являются: степень
адекватности математической модели системы; степень эффективности численных
методов ТАУ, используемых в алгоритмическом обеспечении; наличие
высококачественного программного обеспечения; от того, насколько успешно используется
творческий потенциал исследователя-проектировщика. При этом решающий фактор остается
за человеком, который может решать многие неформализованные задачи.
Поскольку системы автоматизированного проектирования (САПР) являются в
настоящее время одним из наиболее эффективных средств повышения
производительности инженерного труда и научной деятельности, сокращения сроков и улучшения
качества разработок, то в главе 8 (том 1) кратко отражены соответствующие положения, в
том числе изложены численные методы (аппарат матричных операторов).
Рассмотренное в трехтомнике методологическое обеспечение, ориентированное
на применение ЭВМ, может служить базой для решения весьма сложных задач
инженерного проектирования САУ.
4. В учебнике с единых позиций изложены как основные методы классической
ТАУ, так и положения, определяющие содержание некоторых современных
направлений теории управления.
При рассмотрении материала учитывался тот факт, что периодизация развития
ТАУ не является установившейся и общепринятой [136].
К классическим можно отнести положения, базирующиеся на рассмотрении
линейных и нелинейных дифференциальных и разностных уравнений с постоянными и
переменными коэффициентами применительно к описанию систем, исследованию их
устойчивости и качества процессов.
К классическим положениям также можно отнести и описание процессов в
пространствах состояний, поскольку в классической теории широко применялось
описание движения в фазовом пространстве.
В конце пятидесятых - начале шестидесятых годов появились известные работы
Л.С. Понтрягина, Р. Белмана, Р. Калмана, в которых заложены основы теории
оптимального управления: принцип максимума, динамическое программирование,
функционально-аналитические методы и др. Хорошо известно, что многие идеи теории
оптимального управления сформировались на инженерном уровне в классический
период ТАУ.
Важнейшие результаты теории оптимального управления можно отнести к
классическим положениям ТАУ.
Все указанные положения с необходимой глубиной и полнотой изложены в
первых двух томах учебника.
Методы современной ТАУ, интенсивно разрабатываемые в настоящее время и
включающие аппарат синтеза грубых систем автоматического управления в
пространстве состояний, #°° -теория оптимального управления, задачи оптимизации
многообъектных многокритериальных систем с использованием стабильно-
эффективных компромиссов, синтез систем автоматического управления
методами дифференциальной геометрии (геометрический подход), использование нейро-
компьютерных управляющих вычислительных систем, основные положения теории
катастроф, фракталов, хаоса, а также задачи исследования и проектирования
адаптивных и интеллектуальных систем отражены во 2-м и в 3-м томах учебника.
Таким образом, учебник охватывает наиболее важные разделы теории
автоматического управления; вместе с тем он не претендует на всесторонний охват
проблематики теории автоматического управления. Не затронуты такие важные направления,
1редисловие
;ак инвариантность, теория чувствительности, методы и алгоритмы оценивания ди-
юмических процессов, идентифицируемость и методы и алгоритмы идентификации
отражены лишь содержание проблемы и подходы к ее решению), системы со слу-
[айной структурой, стохастические системы, теория нелинейной фильтрации и др.
5. Основное содержание и структуру учебника определил коллектив авторов,
включающий представителей разных российский школ науки об управлении:
(.А. Пупков (МГТУ им. Н.Э. Баумана), А.И. Баркин (Институт системного анализа
>АН), Е.М. Воронов (МГТУ им. Н.Э. Баумана), Н.Д. Егупов (МГТУ им. Н.Э. Баумана),
З.Г. Коньков (МГТУ им. Н.Э. Баумана), А.П. Курдюков (Институт проблем управле-
1ия РАН), Л.Т. Милов (Московский государственный автомобильно-дорожный инсти-
уг (МАДИ)), В.Н. Пилишкин (МГТУ им. Н.Э. Баумана), В.И. Рыбин (Московский
государственный инженерно-физический институт (МИФИ)), В.И. Сивцов (МГТУ им.
1Э. Баумана), Я.В. Слекеничс (Обнинский институт атомной энергетики (ОИАТЭ)),
^.И. Трофимов (Обнинский институт атомной энергетики (ОИАТЭ)), Н.В. Фалдин
Тульский государственный университет); этими авторами написана большая часть
рехтомника.
II. Методические вопросы. Необходимо указать, что никакой учебник не может
щть окончательных рецептов для решения широчайшего спектра задач, порожден-
шх практикой проектирования сложных систем автоматического управления.
Изложенный в книгах материал призван служить базой, фундаментом, позво-
тющим с большей скоростью и эффективностью находить пути для решения задач
грактики.
Вместе с тем материал излагается таким образом, чтобы читателю были видны
тути практического применения рассматриваемых методов. В большинстве своем
методы доведены до расчетных алгоритмов, приводятся таблицы и другой
вспомогательный материал, облегчающий их применение. Положения, изложенные во всех
разделах, иллюстрируются подробно рассмотренными примерами, связанными с зада-
iomu расчета и проектирования конкретных систем.
Весьма важным является вопрос методики изучения курса «Теории автоматического
травления» с целью стать специалистом в этой области, пользуясь циклом учебных
тособий и учебников, издаваемых указанным выше коллективом авторов.
Весь цикл учебников и учебных пособий можно условно разбить на три серии:
1-я серия - базовая; эта серия включает три тома настоящего учебника.
2-я серия - базовая повышенного уровня, в которой основное внимание уделено глу-
5окому и достаточно полному изложению методов, определяющих содержание
современных направлений теории автоматического управления.
3-я серия - серия учебных пособий, посвященная полному и глубокому изложению
теоретических положений конкретных направлений ТАУ, например, статистической
динамике нелинейных САУ и др.
Сказанное выше иллюстрируется рис. В.1.
Базовый уровень приобретается изучением предлагаемого учебника, в котором
систематически изложены методы классической и современной теории управления и дано
достаточно полное представление о проблематике и путях развития науки об управле-
-ши техническими объектами.
Содержание каждого из томов учебника серии базового уровня иллюстрируется
эис. В.2.
После освоения базового уровня можно приступить к специализации в той или
другой области теории автоматического управления, изучая соответствующие тома 2-й се-
эии, а также статьи и монографии по специальным проблемам теории управления.
Цикл: Методы теории
автоматического управления
1-я серия учебников "Методы
классической и современной теории
автоматического управления" - серия
базового уровня
Том 1 Анализ и статистическая
динамика
систем автоматического управления.
М.: Изд-во МГТУ, 2000. - 748 с.
♦
Том 2: Синтез регуляторов
и теория оптимизации систем
автоматического управления
М. Изд-во МГТУ, 2000. - 736 с.
♦
Том 3 Методы современной теории
автоматического управления.
М . Изд-во МГТУ, 2000
♦
2-я серия учебников - серия
повышенного базового уровня
Том 1* Методы синтеза
оптимальных систем автоматического
управления. М.: Изд-во МГТУ, 2000. - 512 с.
♦
Том 2* Оптимизация многообъектных
многокритериальных систем.
М.. Изд-во МГТУ, 2001.
♦
Том 3: Адаптивные, робастные
и интеллектуальные системы
автоматического управления.
М.: Изд-во МГТУ, 2001.
3-я серия - серия учебных пособий,
в которых отражены конкретные
направления ТАУ (специализация)
К.А. Пупков, Н.Д. Егупов,
А.И. Трофимов. Статистические
методы анализа, синтеза и
идентификации нелинейных систем
автоматического управления
М: Изд-во МГТУ, 1998 - 562 с
*
К.А. Пупков, Н.Д. Егупов,
В Г. Коньков. Методы анализа, синтеза
и оптимизации нестационарных
систем автоматического управления
М: Изд-во МГТУ, 1999 - 684 с.
Рис. В.1. Структура цикла учебников и учебных пособий «Методы теории автоматического управления»
Тредисловие
1 том: Анализ и статистическая динамика систем автоматического управления
В этом томе изучаются
Математическое описание классов систем, отраженных
на приводимой ниже структурной схеме
1 САУ, 2 Линейные САУ, 3 Нелинейные САУ, 4 Непрерывные САУ,
5 Дискретные САУ, 6 Непрерывно-дискретные САУ, 7 Стационарные САУ,
8 Нестационарные САУ, 9 САУ с сосредоточенными параметрами,
10 САУ с распределенными параметрами
Анализ и статистическая динамика САУ:
Детерминированный
анализ систем
1 Устойчивость,
2 Качество
в переходном
режиме,
3 Качество
в установившемся
режиме и др
Статистический
анализ линейных
и нелинейных
систем
Линейная фильтрация
(фильтры Винера -
Колмогорова,
фильтры Калмана -
Бьюси), нелинейная
фильтрация
Идентификация
объектов
управления
линейных
и нелинейных
систем
t
2 том: Синтез регуляторов и теория оптимизации
систем автоматического управления
^ _-— Методы и задачи* —-^.^^^^
Синтез систем по заданным показателям
качества
Методы синтеза регуляторов
1 Группа методов, основанная
на принципе динамической
компенсации,
2 Группа методов, использующая
аппарат математического
программирования,
3 Частотный метод,
4 Модальное управление,
5 Методы синтеза грубых систем
управления
6 Метод моментов и др
Синтез оптимальных систем
Методы оптимизации
1 Вариационное исчисление,
2 Принцип максимума, включая
управление при ограничениях на фазовые
координаты,
3 Динамическое программирование,
4 Аналитическое конструирование
регуляторов,
5 Нелинейное программирование,
6 Метод моментов,
7 Синтез оптимальных обратных связей и др
3 том: Методы современной теории автоматического управления:
1 Оптимизация многообъектных многокритериальных систем,
2 Нп- теория оптимального управления,
3 Адаптивные системы,
4 Синтез систем методами дифференциальной геометрии,
5 Основные положения теории катастроф, фракталов и теории хаоса,
6 Нейросетевые методы для решения задач проектирования вычислительных систем,
7 Интеллектуальные системы и др
Рис. В.2. Структурная схема, иллюстрирующая содержание трехтомника
«Методы классической и современной теории автоматического управления» (базовый уровень)
\0
Если специализация предусматривает расширенное изучение статистической
динамики нелинейных систем автоматического управления, то можно воспользоваться
учебным пособием К.А. Пупкова, Н.Д. Егупова, А.И. Трофимова «Статистические методы
анализа, синтеза и идентификации нелинейных систем автоматического управления». -
М.: Издательство МГТУ им. Н.Э. Баумана, 1998. - 562 с. (под редакцией д-ра техн. наук,
проф. Н.Д. Егупова), в котором систематически изложено содержание основных
положений статистической теории нелинейных систем, методов их анализа, синтеза,
оптимизации и идентификации.
При специализации в области систем автоматического управления с переменными
параметрами полезным может оказаться учебное пособие К.А. Пупкова, Н.Д. Егупова,
В.Г. Конькова, Л.Т. Милова, А.И. Трофимова «Методы анализа, синтеза и оптимизации
нестационарных систем автоматического управления». - М.: Издательство МГТУ
им. Н.Э. Баумана, 1999. - 684 с. (под редакцией д-ра техн. наук, проф. Н.Д. Егупова).
Этот труд представляет собой первое учебное пособие в отечественной литературе,
специально посвященное рассмотрению методов математического описания,
детерминированного и статистического исследования, синтеза и оптимизации
нестационарных систем. Работа включает две части: в первой части изложена теория линейных
систем с переменными параметрами; вторая часть посвящена разработке алгоритмов
исследования, синтеза и оптимизации сложных нестационарных систем, поведение
которых описывается скалярными и векторно-матричными дифференциальными
уравнениями высокого порядка. Алгоритмы предназначены для решения задач, имеющих
место в повседневной инженерной практике при расчете и проектировании систем
управления одноконтурными и многоконтурными сложными объектами с переменными
параметрами.
Авторы выражают глубокую благодарность рецензентам - академику РАН
Е.П. Попову и коллективу кафедры «Автоматические системы» Московского
государственного института радиотехники, электроники и автоматики (МИРЭА), руководимой
членом-корреспондентом РАН Е.Д. Теряевым, за ценные замечания, способствовавшие
улучшению содержания книги. Авторы благодарят заслуженного деятеля науки и
техники РФ, д-ра техн. наук, проф. А.С. Шаталова, заслуженного деятеля науки и техники
РФ, д-ра техн. наук, проф. Б.И. Шахтарина (МГТУ им. Н.Э. Баумана), которые своими
советами позволили значительно улучшить структуру учебника, углубить изложение
отдельных теоретических положений, улучшить окончательный вариант рукописи.
Авторы благодарят концерн «Росэнергоатом», научно-исследовательский центр
космической системотехники, департамент образования и науки Правительства
Калужской области, а также Издательский Дом «Манускрипт» за помощь в издании учебника.
Большой объем книги и широта охваченного материала вызвали большие трудности
при ее написании. Конечно, эти трудности не всегда удавалось преодолеть наилучшим
образом. Читатели, вероятно, смогут высказать много замечаний и дать свои
предложения по улучшению книги.
Авторы заранее признательны всем читателям, которые не сочтут за труд указать
на замеченные неточности, ошибки, на пути совершенствования структуры учебника
и его содержания.
К.А. Пупков
Н.Д. Егупов
Предисловие П
ПРЕДИСЛОВИЕ К 2-МУ ТОМУ
Настоящая книга представляет собой 2-й том учебника «Методы классической и
современной теории автоматического управления», посвященный изложению
содержания и методов решения двух центральных проблем теории автоматического
управления:
1) проблемы синтеза систем автоматического управления по заданным
показателям качества:
• обеспечение устойчивости (стабилизация);
• повышение запаса устойчивости (демпфирование);
• повышение точности управления в установившихся режимах;
• улучшение переходных процессов (уменьшение перерегулирования и числа
колебаний, увеличение быстродействия и др.) [92, 139 - 141];
2) проблемы оптимизации управления, состоящей в выборе такого закона
управления, который, удовлетворяя четко заданной системе ограничений,
обеспечивает при своей реализации оптимальное значение того или иного показателя
качества работы системы.
Этот том содержит положения как классической, так и современной теории
автоматического управления.
Решение первой проблемы достигается синтезом регуляторов, включающим
рассмотрение вопросов определения его структуры и параметров, места включения,
исходя из обеспечения требований к качеству процессов управления. Предметом
изучения рассматриваемой проблемы является направление, формулируемое как методы
научного проектирования систем с заданными показателями качества.
Вторая же проблема - проблема оптимизации - по существу является
вариационной задачей, когда требуется получить экстремум функционала, который избран в
качестве критерия оптимальности системы.
Что касается первой проблемы, то во втором томе учебника детально рассмотрены:
• краткое введение, отражающие основные результаты решения проблемы;
• базовые принципы синтеза регуляторов (глава 1);
• методы синтеза регуляторов, применяемые при решении широкого спектра
инженерных задач (глава 2);
• технические аспекты проблемы синтеза регуляторов, позволяющие с нужной
эффективностью ставить и решать конкретные, порожденные практикой
задачи (с этой целью во втором томе помещена глава 7, в которой описаны
принципиальные, функциональные и структурные схемы систем управления
теплоэнергетическими параметрами атомных электростанций; в примерах,
иллюстрирующих применение методов, рассмотрены задачи синтеза регуляторов,
применяемых в летательных аппаратах и др.);
• особенности решения задач синтеза регуляторов в классе нестационарных,
нелинейных и многомерных систем (главы 2 и 4);
• частотный метод В.В. Солодовникова, который основывается на соответствии
между логарифмическими частотными характеристиками разомкнутой
системы и ее статическими и динамическими свойствами в замкнутом состоянии
(глава 3);
• широкие возможности аппарата нелинейного программирования,
позволяющие произвести синтез регуляторов, обеспечивающих диктуемые
содержанием задачи ограничения (глава 2);
п
• основы теории модального управления;
• \ метод синтеза грубых систем автоматического управления.
Вторая часть тома посвящена изложению теории оптимизации систем
автоматического управления. Основное внимание уделено принципу максимума Л.С. Понтря-
гина, который применим к задачам с уравнениями общего вида, и динамическому
программированию Р. Беллмана. Достаточно подробно рассмотрены методы
редукции задач оптимального управления к задачам конечномерной оптимизации. Переход
к конечномерному описанию непрерывных задач открывает перспективу для
использования аппарата нелинейного программирования.
Если на некоторые из координат фазового вектора накладываются ограничения,
то принцип максимума в том виде, как он сформулирован в главе 2 части III,
несправедлив. Формулировка принципа максимума при наличии ограничений на фазовые
координаты намного сложнее; она вынесена в приложение 1.
Кроме того, в приложения вынесены основные положения нелинейного
программирования и алгоритмы построения оптимальных программных управлений и
оптимальных программ с ограничениями на фазовые переменные методом
математического программирования.
Для лучшего уяснения излагаемого материала приведены примеры синтеза
оптимальных систем, работающих по принципу обратной связи с использованием
принципа максимума и динамического программирования; рассмотрено значительное
число задач по построению оптимальных программных управлений и оптимальных
программ методом математического программирования с использованием описания
систем автоматического управления матричными операторами в ортонормированных
базисах (глава 5 части III).
В случае линейных объектов общая теория задач оптимального управления,
основанная на использовании результатов решения проблемы моментов, предложена и
обоснована Н.Н. Красовским (§5.5 части III).
Характерным для задач оптимального управления является то, что точные
аналитические решения удается получить лишь в редких случаях. Сложность или
невозможность получения аналитических результатов для задач в достаточно общей
постановке привели к развитию вычислительных и приближенных методов построения
оптимального управления (они отражены в главе 5, а также в приложениях 2, 3,4).
Соавторами отдельных разделов 2 тома являются д-р техн. наук, проф. А.А. Гре-
шилов (прил. 2), канд. техн. наук, доц. М.Ю. Адкин (§2.3 части II), канд. техн. наук,
доц. В.И. Краснощеченко (глава 3 части II), канд. техн. наук, доц. А.К. Карышев (§2.7
и 4.4 части II), инженер Д.В. Мельников (§2.7 и 4.4, примеры в главе 2 части II), д-р
техн. наук, проф. Л.Т. Милое (§5.6, 5.7 части III). Примеры синтеза оптимальных
программ методами нелинейного программирования части III рассчитаны инженером
А.Н. Бурлакиным.
Авторы выражают признательность инженерам К.И. Желнову, К.Ю. Савинченко и
МЛ. Трубачеву за помощь при подготовке рукописи к изданию и создание оригинал-
макета учебника.
Список используемых аббревиатур и обозначения
13
СПИСОК ИСПОЛЬЗУЕМЫХ АББРЕВИАТУР
АСУ
АФЧХ
АЧХ
ГОС
ду
ИПФ
ИУ
ИУр
КУ
КФ
ЛАЧХ
лп
ЛФЧХ
мм
мнк
МП
МПФ
нч
ок
ОНБ
онс
ОС
ОУ
п
пд
пи
пид
ПС
ПФ
пх
р
САУ
СП
СПл
СПФ
СУ
СФ
сх
ТАУ
тп
ФС
фф
ФЧХ
- автоматизированная система управления
- амплитудно-фазовая частотная характеристика
- амплитудно-частотная характеристика
- гибкая обратная связь
- дифференциальное уравнение
- импульсная переходная функция
- исполнительное устройство
- интегральное уравнение
- корректирующее устройство (регулятор)
- корреляционная функция
- логарифмическая АЧХ
- линейное программирование
- логарифмическая ФЧХ
- математическая модель
- метод наименьших квадратов
- математическое программирование
- матричная передаточная функция
- неизменяемая часть
- основной канал в многомерных системах
- ортонормированный базис
- ортонормированная система
- обратная связь
- объект управления
- пропорциональный регулятор
- пропорционально-дифференциальный регулятор
- пропорционально-интегральный регулятор
-пропорционально-интегрально-дифференциальный
регулятор
- перекрестная связь в многомерных объектах
- передаточная функция
- переходная характеристика
- регулятор (корректирующее устройство)
- система автоматического управления
- случайный процесс
- спектральная плотность
- стандартная (эталонная) передаточная функция
- система управления
- случайная функция
- спектральная характеристика относительно ОНБ
- теория автоматического управления
- технологический процесс
- фундаментальная система
- формирующий фильтр
- фазочастотная характеристика
14
ОБОЗНАЧЕНИЯ
А - оператор системы
А((о) - амплитудная частотная характеристика
Л(усо) - амплитудно-фазовая характеристика
А(/), В(/) - матрицы коэффициентов векторно-матричного
дифференциального уравнения
5(/) - дельта-функция
y(t) - входной скалярный сигнал
Y(/) - входной векторный сигнал
*(/) - выходной скалярный сигнал
Х(0 - выходной векторный сигнал
W(s) - передаточная функция скалярной системы
W(s, t) - параметрическая передаточная функция
W(s) - передаточная функция системы в пространстве
состояний
F(s) - преобразование Лапласа функции fit)
£(т) - импульсная переходная функция скалярной
стационарной системы
k(t,i) - импульсная переходная функция скалярной
нестационарной системы
К - коэффициент усиления системы или элемента
К(т) - матричная импульсная переходная функция
К(/,т) - матрица ИПФ нестационарной системы в пространстве
состояний
К(/) - матрица коэффициентов обратной связи
Р(со) - действительная частотная характеристика
Q((o) - мнимая частотная характеристика
ф(со) - фазовая частотная характеристика
Цш) - логарифмическая амплитудная частотная характеристика
е(/) - сигнал ошибки системы
jcc(O - свободная составляющая выходного сигнала (свободные
колебания)
хв(/) - вынужденная составляющая выходного сигнала
(вынужденные колебания)
h(t) - переходная характеристика
n(t) - помеха
m(t) - полезный входной сигнал (управляющее случайное
воздействие)
Список используемых аббревиатур и обозначения rj_
I - единичная матрица
j = V-1 - мнимая единица
т - порядок числителя передаточной функции
п - порядок знаменателя передаточной функции
Ту - время переходного процесса
Т - постоянная времени
E(s) - преобразование Лапласа для сигнала ошибки
£ - коэффициент демпфирования
А., - корни характеристического уравнения
соср - частота среза
р(х,у) -метрика
I? (Q), С[0, Т] - функциональные пространства
||х| - норма элемента х
F = {fk(t): к = 1,2,...} -линейно независимая система
ф = {(рД/): к = 1,2,...} - ортонормированный базис или ортонормированная
система
ск - коэффициенты Фурье
С(/) - матрица уравнения наблюдения
Ск - коэффициенты ошибок
С^ - одностолбцовая матрица коэффициентов Фурье функции
/(О
Wal(/:,/) - к-я функция Уолша
/*э(0 - эталонная переходная характеристика
Я(\|/, X, Y) - функция Гамильтона
/(/?) - функционал качества
W3 (s) - эталонная ПФ замкнутой системы
W^(s) = W*{s) - стандартная (эталонная) передаточная функция
разомкнутой системы
W0(s), Wm(s) - передаточная функция объекта или неизменяемой части
системы
Wp(s) - передаточная функция разомкнутой системы
WKy(s) - передаточная функция корректирующего устройства
(регулятора)
М - оператор математического ожидания
Rxx (/j, t2) - корреляционная функция случайного процесса ДО
&xyih>h) ~ взаимная корреляционная функция случайных процессов
ДО и Г(0
$хх С00) ~" спектральная плотность случайного сигнала ДО
gx (t) - среднеквадратическое отклонение случайного сигнала
ДО
Дсо - эффективная полоса пропускания системы
\6
o(t) - случайный сигнал ошибки системы
Х(0) = Х° - начальное состояние системы
Х(Т) = ХТ - конечное состояние системы
Х(/) - вектор-функция состояния
Хв(г) - вектор-функция выхода
Хф (/) - фундаментальная матрица
Sc - матрица управляемости по состоянию
SB - матрица управляемости по выходу
Lo - матрица наблюдаемости
1х - линейный функционал
Х; - моменты функции относительно системы функций
и* (t) - оптимальное программное скалярное управление
и* (/, Х(0) - оптимальное скалярное управление, реализующее
принцип обратной связи
U* (г) - оптимальное векторное программное управление
U* (Г, Х(0) - оптимальное векторное управление по принципу
обратной связи
ЧАСТЬ II
МЕТОДЫ СИНТЕЗА СИСТЕМ
АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
ПО ЗАДАННЫМ ПОКАЗАТЕЛЯМ КАЧЕСТВА
Зак. 366
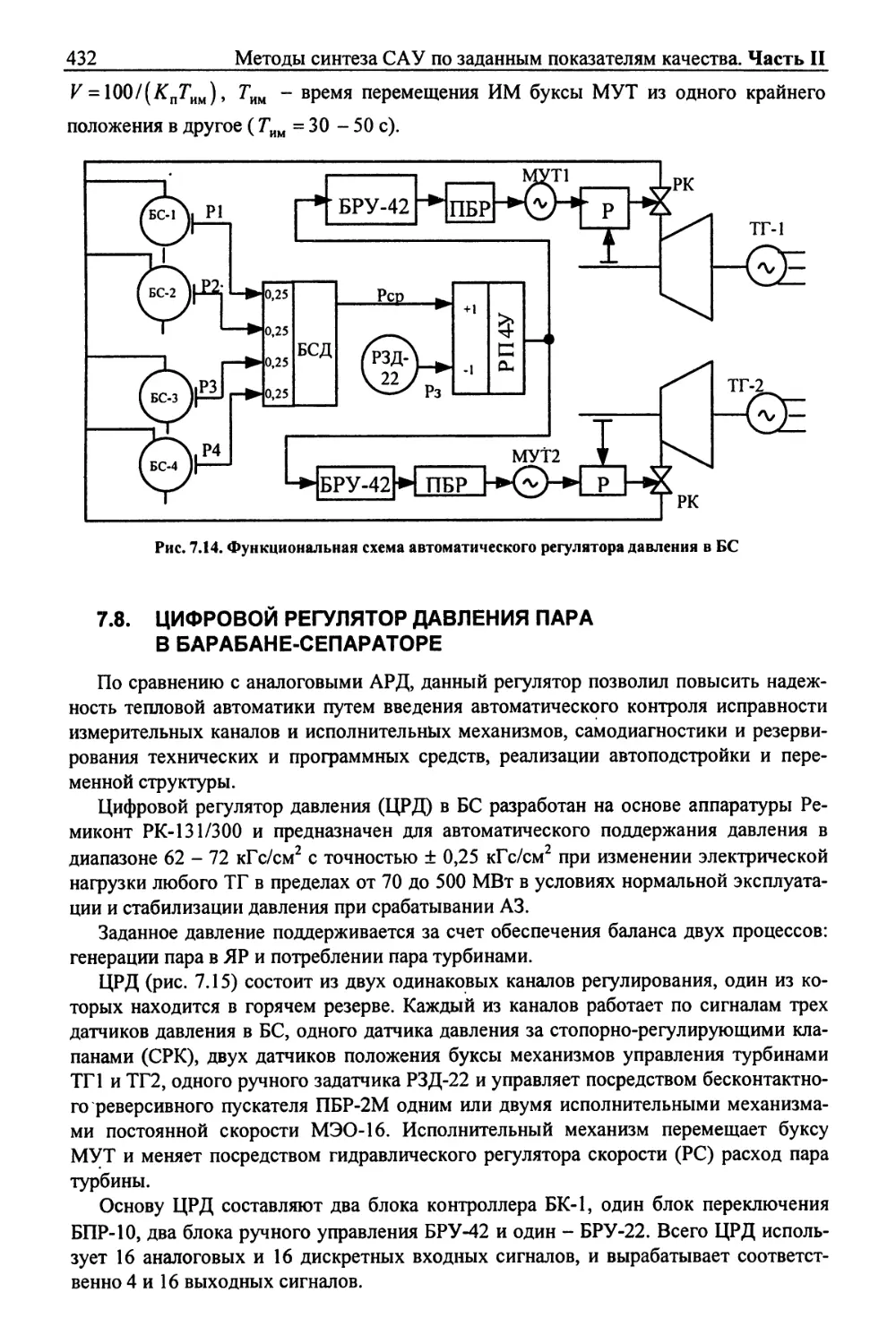
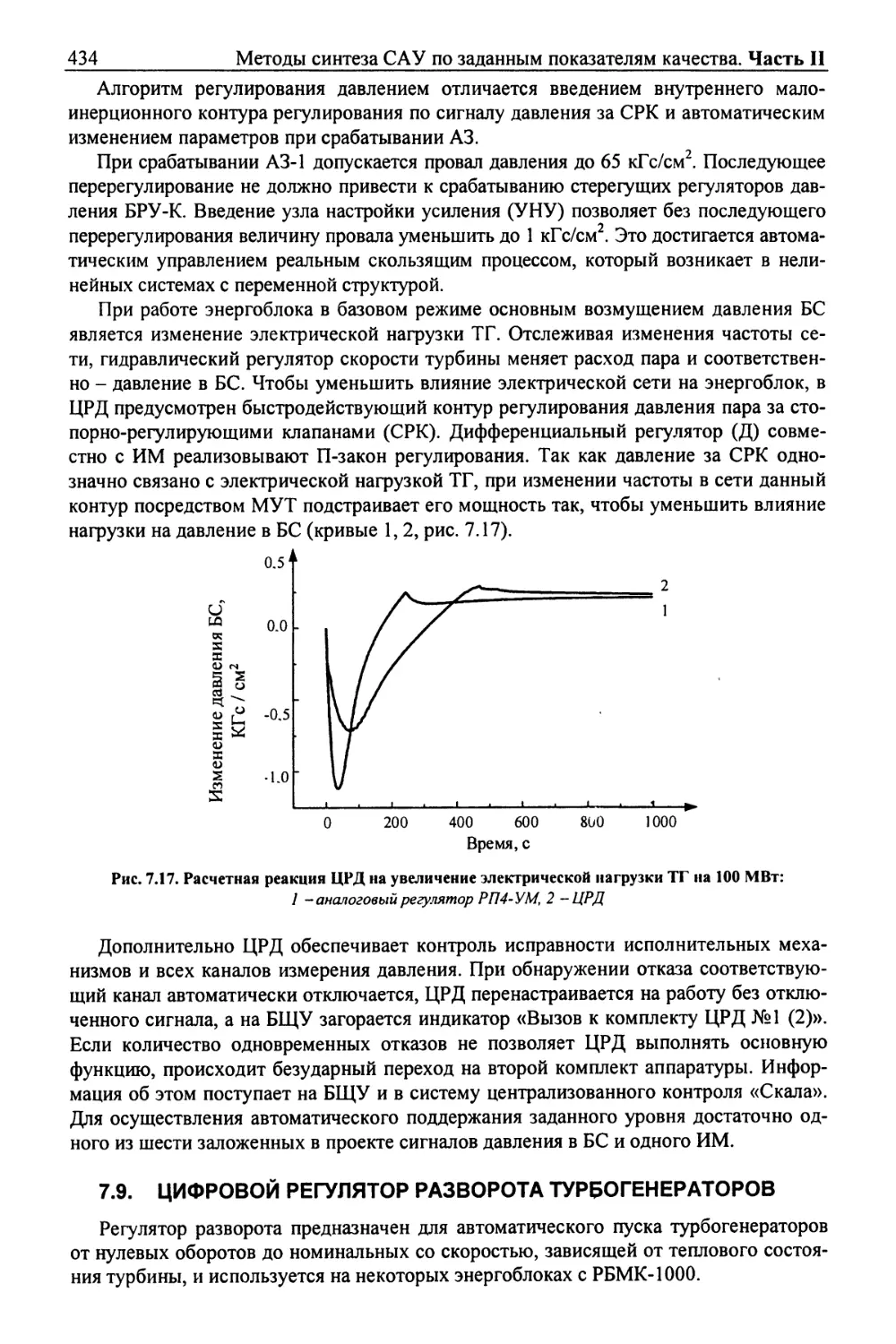
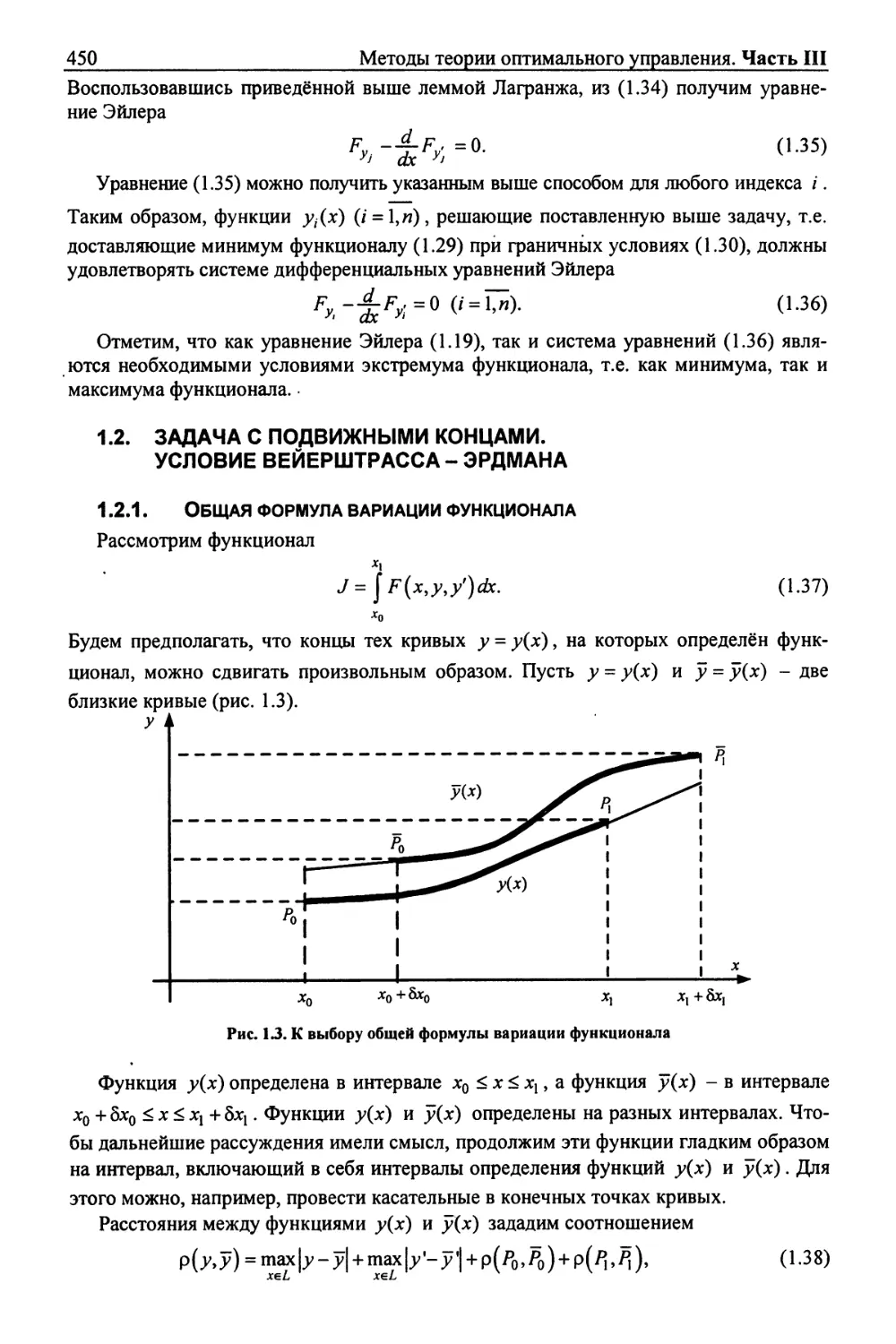
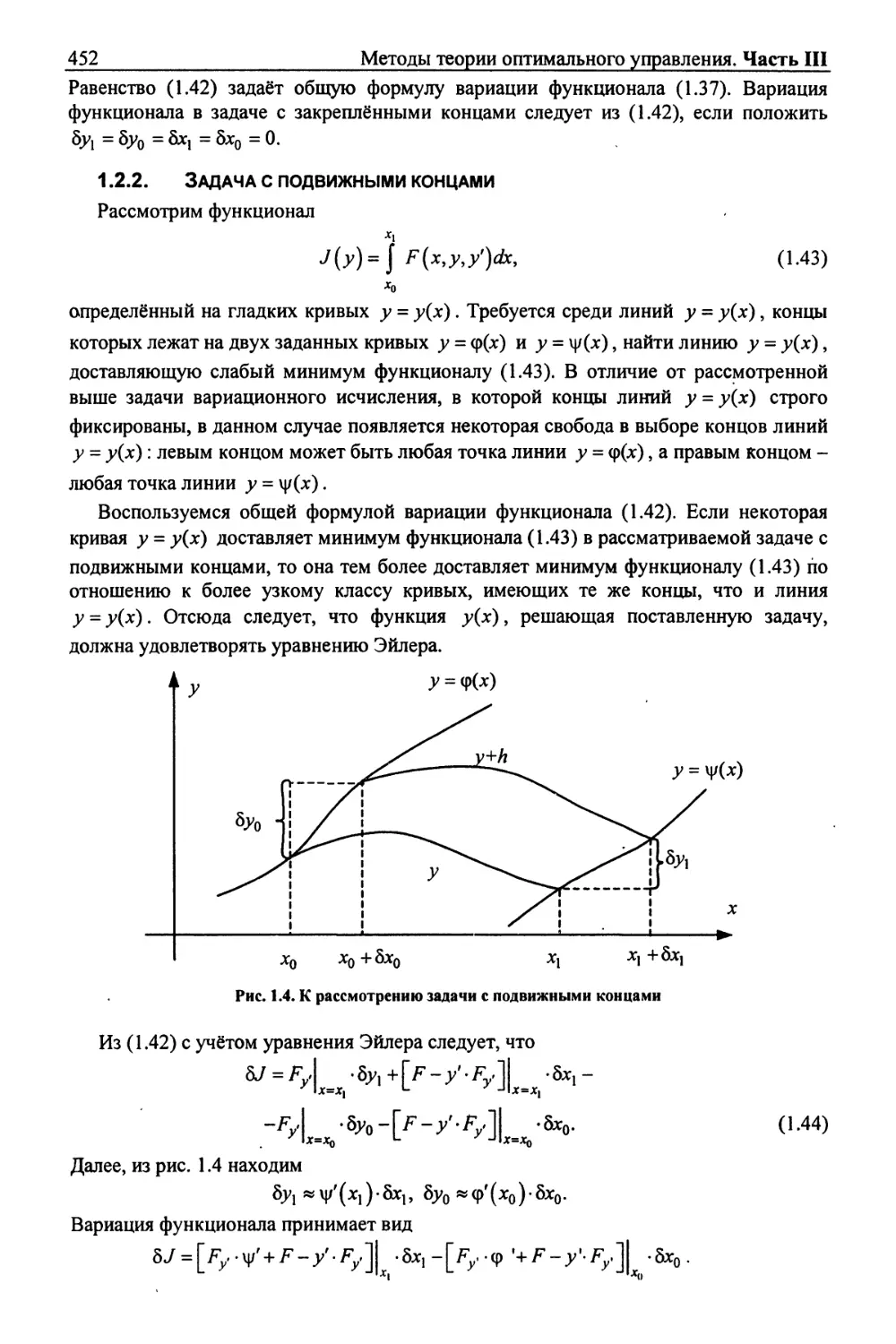
18 Методы синтеза САУ по заданным показателям качества. Часть II
ВВЕДЕНИЕ
Одной из центральных задач теории автоматического управления является задача
синтеза систем, в результате решения которой определяется состав, структура
САУ и параметры всех ее устройств из условия удовлетворения заданному комплексу
технических требований: обеспечение устойчивости {стабилизация) и качества
переходных процессов (увеличение быстродействия, недопустимость больших
перерегулирований и др.)\ повышение точности управления в установившихся режимах и др.
Далее под методами синтеза СЛ У по заданным показателям качества
понимаются методы решения задачи синтеза регуляторов {корректирующих устройств),
позволяющие определить место его включения, структуру и параметры, исходя из
требований к качеству процессов управления.
На основе располагаемой априорной информации об объекте управления и
номенклатуре измерительных преобразователей рассматриваемые далее методы
позволяют решить задачу синтеза системы, алгоритмы работы которой далее подвергаются
моделированию; завершающей же стадией синтеза является отладка при натурных
испытаниях.
Разработкой методов синтеза регуляторов занимались ученые России и
зарубежных стран.
Г. В. Щипановым сформулирована задача синтеза систем, позволяющих
компенсировать действие возмущений; B.C. Кулебакиным и Б.Н. Петровым указаны пути
практической реализации принципа компенсации.
А.А. Красовским, Ф.А. Михайловым, А.А. Фельдбаумом разработаны методы
выбора параметров СА У, имеющих заданную структуру и основанных на
использовании интегральных оценок; получены результаты и по другим аспектам решения
указанной задачи.
Ценные результаты, связанные с проблемой выбора эталонных передаточных
функций, получены в работах В.А. Боднера, Б.Н. Петрова, В.В. Солодовникова,
А.А. Красовского, Г.С. Поспелова, Т.Н. Соколова, СП. Стрелкова, А.А. Фельдбаума.
При решении задач синтеза САУ, подверженных воздействию случайных
процессов, важную роль играет нахождение динамических характеристик оптимальной
(эталонной) системы. Большое значение в решении этой проблемы имеют работы
Н. Винера, Л. Заде и Дж. Рагаццини, В.В. Солодовникова, B.C. Пугачева, П.С.
Матвеева, К.А. Пупкова, В.И. Кухтенко, B.C. Медведева, Ю.М. Астапова и др.
В частотном методе, разработанном В.В. Солодовниковым и получившем широкое
распространение в инженерной практике, расчет производится с использованием
типовых логарифмических амплитудных частотных характеристик, для которых построены
подробные номограммы показателей качества процессов управления [141]. С помощью
этих номограмм можно построить эталонную амплитудную частотную характеристику
синтезируемой системы, определить ее передаточную функцию, найти частотные
характеристики и передаточную функцию корректирующего устройства.
В.И. Сивцовым и Н.А. Чулиным получены результаты, позволяющие решать
задачи автоматизированного синтеза систем управления на основе частотного метода
[118]; В.А. Карагановым, Ю.И. Бородиным и А.Б. Ионнисианом рассмотрены
некоторые задачи обобщения частотного метода на класс нестационарных систем. В
русле этого направления лежат работы В.Г. Конькова и Л.Т. Милова. Частотный метод и
его место в теории автоматического управления отражены в [141], а также в книге
В.В. Солодовникова, В.Н. Плотникова и А.А. Яковлева [130].
Введение 1_9^
Метод, разработанный Н.Т. Кузовковым, позволяет использовать связь основных
показателей качества процесса управления с величинами доминирующих полюсов и
нулей синтезируемой системы, а также установить связь этих полюсов и нулей с
варьируемым параметром.
В.В. Солодовниковым, В.В. Семеновым и А.Н. Дмитриевым разработаны
спектральные методы расчета и проектирования САУ, позволяющие построить
конструктивные алгоритмы синтеза регуляторов [127, 131].
Решение задачи компенсации в виде функциональных степенных рядов расмотре-
но Г. Ван-Трисом в [25]. Там же построены алгоритмы определения
компенсирующих ядер в прямой цепи и цепи обратной связи.
В [109] К.А. Пупковым, А.С. Ющенко и В.И. Капалиным систематически и с
единых методологических позиций изложена теория нелинейных систем; разработаны
методы синтеза регуляторов в классе нелинейных систем, поведение которых
описывается функциональными рядами Вольтерра. Класс систем со случайными
параметрами исследован в работах Е.А. Федосова и Г.Г. Себрякова, а применение теории
чувствительности - в работах P.M. Юсупова.
Аппарат многомерных ИПФ, ПФ, частотных характеристик, а также
многомерных интегральных преобразований Лапласа и Фурье позволил О.Н. Киселеву,
Б.Л. Шмульяну, Ю.С. Попкову и Н.П. Петрову разработать конструктивные
алгоритмы идентификации и оптимизации нелинейных стохастических систем, включая
синтез регуляторов [51]. Я.З. Цыпкиным и Ю.С. Попковым рассмотрены методы синтеза
регуляторов в классе дискретных систем [157].
А.С. Шаталовым, В.В. Барковским, В.Н. Захаровым рассмотрен широкий спектр
вопросов по проблеме синтеза систем автоматического управления; результаты
отражены в [13]. Аппарат обратных задач динамики управляемых систем использован
П.Д. Крутько для синтеза оператора обратной связи, а также для решения ряда
других задач [64].
Аналитический метод синтеза САУ объектами с нестабильными параметрами
разработан Н.И. Соколовым и его коллегами. Он дает обоснованные рекомендации
по формированию эталонной математической модели синтезируемой системы с
учетом условий ее физической реализуемости [92].
Теоретические положения, являющиеся основой решения задачи синтеза
регуляторов, нашли отражение в работах Е.П. Попова и В.А. Бесекерского.
Широкий спектр подходов к решению рассматриваемой задачи рассмотрен
А.А. Первозванским [93]. Конструктивные алгоритмы синтеза регуляторов для
широкого класса систем с использованием аппарата математического
программирования предложены И.А. Дидуком, А.С. Орурком, А.С. Коноваловым, Л.А. Осиповым и
отражены в [7, 91]. К.Ф. Теодорчик, Г.А. Бендриков, СП. Стрелков, Г.В. Римский
рассмотрели методы корневых подграфов [139].
Чрезвычайно трудной является проблема синтеза регуляторов в многомерных
системах. В работах, рассматривающих вопрос о разрешимости задачи синтеза
регуляторов при выполнении известных требований, получены соответствующие условия
резрешимости (Р. Брокетт, М. Месарович). В.В. Солодовниковым, В.Ф. Бирюковым,
Н.Б. Филимоновым получены результаты, направленные на решение задач синтеза
регуляторов в классе многомерных систем; ими предложен критерий качества,
который адекватно отражает динамическое поведение многомерных систем;
сформулированы условия, при которых задача синтеза разрешима. Ценные результаты
получены А.Г. Александровым и отражены в [3]. Многими авторами (Б. Андерсон, Р. Скотт
и др.) рассмотрен подход, в основу которого положено «модельное соответствие»
синтезируемой системы и желаемой модели. В этом же русле с использованием
метода пространства состояний находятся работы Б. Мура, Л. Силвермана, В. Уонема,
з
20 Методы синтеза САУ по заданным показателям качества. Часть II
А. Морзе и др. Используется «геометрический подход», рассмотренный В, Уонемом
и Д. Персоном.
Одной из проблем, связанной с синтезом регуляторов в классе многомерных
систем, является проблема «развязки» каналов. В русле решения этой проблемы
находятся работы Е. Джильберта, С. Уанга, Е. Дэвисона, В. Воловича, Г. Бенгстонз и др.
Вопросы синтеза регуляторов в многомерных системах с использованием разных
подходов изложены в работах Е.М. Смагина, X. Розенброка, М, Явдана, А.Г.
Александрова, Р.И. Ивановского, А.Г. Таранова.
С. Канг и Т. Калат изучили «проблему минимального проектирования». Вопросы,
связанные с диагональной доминантностью, изучались О.С. Соболевым, X. Розен-
броком, Д. Хаукинсом.
Отдельным вопросам проблемы синтеза многомерных систем посвящены работы
М.В. Меерова, Б.Г. Ильясова.
Часть II содержит 7 глав, в которых отражены основные подходы к решению
проблемы синтеза регуляторов.
В первой главе изложены принципиальные положения, являющиеся фундаментом
нашедших применение в инженерной практике методов синтеза регуляторов.
Вторая глава целиком посвящена рассмотрению основных методов синтеза регу*
ляторов в классе одномерных систем, включая стационарные, нестационарные и
нелинейные.
В третьей главе детально изложен частотный метод, а в четвертой - основные
подходы к решению задачи синтеза регуляторов в классе многомерных систем,
В пятой главе отражены основы теории модального управления.
Шестая глава посвящена изложению основных положений одного из
современных направлений теории автоматического управления - методу синтеза грубых сие*
тем управления.
Если в предыдущих главах в основном изложены теоретические положения,
связанные с проблемой синтеза регляторов, то целью последней, седьмой, главы
является обширная иллюстрация практического использования ранее изложенного
материала. В частности, приведены конкретные приложения, связанные с синтезом
регуляторов в системах управления теплоэнергетическими параметрами атомных
электростанций, а в [148] описаны технические средства аналоговых и цифровых
регуляторов. Особое внимание уделено вопросам синтеза и настройки аналоговых и
цифровых регуляторов, которые внедрены на атомных электростанциях [148],
При таком методическом изложении материала вдумчивый читатель имеет
возможность изучить не только теоретические положения, составляющие содержание
широкого спектра методов, но и познакомиться с конкретными техническими
реализациями, аппаратной частью, конструкцией всей системы автоматического
управления. Это будет способствовать более глубокому освоению методов синтеза
регуляторов и их практическому применению.
Глава 1. Общие принципы 2л_
ГЛАВА 1. ОБЩИЕ ПРИНЦИПЫ,
НА КОТОРЫХ БАЗИРУЕТСЯ РЕШЕНИЕ
ЗАДАЧИ СИНТЕЗА РЕГУЛЯТОРОВ
Синтез регуляторов (корректирующих устройств) САУ - одна из важнейших
задач, изучаемых теорией автоматического управления. Эта задача является весьма
сложной, неоднозначной, требующей творческого подхода при ее решении. Если
многие важные задачи теории управления изучаются и другими науками, то задача
синтеза - это задача, собственно, теории управления. Указанная задача должна
учитывать особенности работы конкретных систем управления, их конструкции,
технические характеристики и т.п.
Рассматриваемую задачу решает, как правило, большой коллектив разработчиков:
специалисты по отдельным элементам систем; специалисты, изучающие объект
управления и строящие его математическую модель; математики (специалисты по
численным методам) и др.
Проблема синтеза КУ в большинстве случаев точно не решается. Даже если
можно построить алгоритм нахождения точного решения, то такой алгоритм интересен
лишь с точки зрения выявления тех трудностей, которые необходимо преодолеть
при решении задачи.
При решении сложных инженерных задач общую задачу синтеза регуляторов
часто рассматривают как совокупность частных задач, которые вытекают из
проектируемой системы и степени сложности задачи синтеза регулятора. К частным можно
отнести следующие задачи:
• стабилизация объекта управления и повышение запаса устойчивости;
• обеспечение необходимой точности воспроизведения воздействий в
установившемся режиме;
• обеспечение заданного качества в переходном режиме.
Решение указанных задач базируется на некоторых общих принципах, которые
кратко изложены в настоящей главе.
Общие принципы указывают пути достижения высокого качества работы САУ
как в переходном, так и в установившемся режимах.
1.1. ОСНОВНЫЕ ЭТАПЫ РЕШЕНИЯ ЗАДАЧИ СИНТЕЗА
РЕГУЛЯТОРОВ В КЛАССЕ ЛИНЕЙНЫХ
СТАЦИОНАРНЫХ СИСТЕМ
Изложим основные этапы решения задачи синтеза регуляторов, определяющие
содержание этой сложной проблемы.
1-й этап. Постановка технической задачи. На этом этапе постановка задачи
делается в содержательных терминах. Ведется обсуждение с использованием таких
понятий, как возможные режимы работы системы (установившийся или
переходный), необходимая точность, ограничения, ориентировочное время работы системы и
др. Формируется функциональная схема системы, рассматриваются энергетические
вопросы, обсуждаются вопросы выбора типа исполнительных элементов и
усилительных устройств и т.д.
2-й этап. Математическое описание технической задачи и ее постановка. На
этом этапе строятся математические модели всех элементов, входящих в систему.
22
Методы синтеза САУ по заданным показателям качества. Часть II
выбирается структура регулятора и место его включения. Задается эталонная система
или эталонный выходной сигнал. Выбирается критерий приближения к эталону.
Для систем, работающих в переходном режиме^ эталонный выходной сигнал
может быть задан в виде переходной характеристики, определяемой параметрами:
время регулирования Гр, перерегулирование а %, частота колебаний со = 2п IT, п -
число колебаний и др. (рис. 1.1). Часто Лэ(/) - эталонная переходная характеристика
задается в виде апериодического переходного процесса (рис. 1.2)
/1,(0 = £(1-*"«>') = *э('). (Ы)
*(')t
maxl
1
п ' S
о
7
1
7_
0
2Д
К
Л(оо)
Рис. 1.1. Переходная характеристика
к
0,95Л:
и т t
р
Рис. 1.2. Эталонный переходный процесс
Параметр аэ определяется заданным временем Т?. Поскольку Гр представляет
собой момент входа переходного процесса в 5%-ую трубку относительно установив-
шегося значения, то очевидно, что
Лэ(Гр) = 0,95/: = /:(1-^7р); (1.2)
откуда имеем
in0,05 3
а„=~
Т Т
(1.3)
Эталонную переходную характеристику колебательного типа можно задать в форме
Глава 1. Общие принципы
23
Аэ(/) = [я0 + (Я1-Я0)е-^со8рэ/]1(0, (1-4)
где Нх - амплитуда желаемого процесса при / = +0, Но - значение /гэ(/) при / = оо
(астатизм системы).
Если Нх=0,Н0=\ (астатизм первого порядка), то
А,(0 = [1-е-^со8Рэ/]1(/). (1.5)
Задаваясь параметрами аэи (Зэ, можно строить процессы разной длительности,
колебательности, перерегулирования.
Кроме этого, могут задаваться ограничения на скорость и ускорение процессов на
выходе, а также на управление u(t). В самом деле, например, требования в
отношении быстродействия должны учитывать мощность исполнительного элемента.
Поэтому в общем виде, если объект задан описанием в пространстве,состояний
Х = АОХ + Вои, (1.6)
то X(t) € Хп, где Хп - разрешенная область возможных значений вектор-функции
X{t) V/ е [0,Г], a u(t) e U], где Vх - разрешенная область значений управления u(t)
V/e[0,r].
Рис. 1.3. К постановке задачи синтеза КУ:
I - изменяемая часть системы, включающая последовательное (/) и параллельное (4)
корректирующие устройства (может быть или (/), или (4), или и то и другое),
II - неизменяемая часть системы, состоящая из усилителя 2, исполнительного элемента 3.
объекта управления 5 и измерительного элемента б (неизменяемую часть называют объектом)
Требования к системе могут быть определены заданием эталонного оператора
системы (эталонной системы). Эталонный оператор системы определяет
качество системы как в переходном, так и в установившемся режимах.
Для систем, работающих в установившемся режиме, информация о точности
задается с помощью допустимых значений коэффициентов ошибок
с с с
^0доп'^1 доп»^"2доп># • • •
Типовая постановка задачи может быть сформулирована так: произвести синтез
регулятора, который обеспечил бы следующее [140]:
1) нулевую установившуюся ошибку при подаче на вход сигнала вида y(t) = \(t);
2) перерегулирование сттах% в системе не должно превышать сгдоп%;
3) время переходного процесса Гр не должно превышать Гр доп';
4) максимальное ускорение выходной переменной при заданных условиях не
должно превышать допустимого значения.
24
Методы синтеза САУ по заданным показателям качества. Часть II
Часто задаются добротность по скорости и по ускорению (например, САУ должна
иметь добротность по скорости Дс и по ускорению Ду). Часто говорят, что
переходная характеристика должна находиться в «коробочке» В.В. Солодовникова (рис. 1.4).
Й(М
'уст
^\\\\\XVsNXSN
Рис. 1.4. Область допустимых значений переходной функции («коробочка» В.В. Солодовникова)
На этом этапе выбираются (если они известны) или строятся (если они
неизвестны) математические модели всех элементов, входящих в систему. Выбирается
структура и место включения регулятора. Этот этап является наиболее сложным в том
смысле, что менее всего поддается формализации. Здесь нельзя предложить каких-
либо однозначных рекомендаций. Если неудачно выбрана структура КУ, то никаким
подбором параметров не удастся получить реакцию скорректированной системы,
близкую к желаемой. Корректирующие устройства могут быть последовательными,
параллельными (дополнительные местные обратные связи, рис. 1.3) и представлять
собой неединичную главную обратную связь (ГОС).
Достоинством последовательных КУ является простота их реализации (RC-цепи и др.).
Недостатки [130]:
• при применении последовательных КУ недопустим значительный «уход»
параметров неизменяемой части (НЧ) и КУ от эталонных;
• применение дифференцирующих RC-цепей для уменьшения колебательности
приводит к «подчеркиванию» (усилению) помех в системе.
Параллельные КУ характеризуются следующими достоинствами:
• степень «грубости» системы больше, чем для последовательных КУ;
• нет технических проблем с питанием параллельных КУ;
• как правило, параллельные КУ включены после низкочастотных элементов
(например, после исполнительного устройства), на выход которых помехи,
имеющие достаточно высокочастотный спектр, практически «не проходят» и,
таким образом, не поступают на вход КУ.
Недостатки: параллельные КУ - это чаще всего отдельные технические
устройства (однако не исключаются и RC-цепи) и, следовательно, это дорогостоящие и
громоздкие элементы (тахогенераторы, дифференцирующие трансформаторы и т.д.).
Часто последовательное корректирующее устройство заменяется на два:
последовательное и параллельное [139]. Рассмотрим САУ с последовательным КУ (рис. 1.5)
и эквивалентную систему с последовательным и параллельным включением КУ
(рис. 1.6).
Глава 1. Общие принципы
25
yit)
Г *
[
"(О
x{t)
Рис. 1.5. САУ с последовательным включением КУ
y^l+^l
Щ*)
W^x{s)
_i
У
i
«2(0
—►
W2(s)
/2\s) щ
Рис. 1.6. САУ с последовательным и параллельным включением КУ
Положим, что рассчитано последовательное КУ с передаточной функцией
WKy](s) . Поскольку WKy](s) реализуется с использованием сложных схем, заменим
его на два более простых элемента с ПФ w'KyX(s) и w'Ky2(s) [139]. Имеем
WWKyl =
wwt
ку1
i+иуг^
w = w}w2w3.
Отсюда находим
w> WKy,{s)-WKyX{s)
^ку2^^ ~
(1.7)
(1-8)
W2(sWKy](s)
Если выбрана w'^^s), то с помощью (1.7) можно рассчитать передаточную
функцию последовательного корректирующего устройства WKy](s). С помощью
равенства (1.8) легко найти WKy2(s), если выбрана WKyl(s).
3-й этап. Синтез регулятора. На 2-ом этапе была выбрана возможная структура
регулятора. На 3-ем этапе решается задача синтеза регулятора, состоящая в расчете
его параметров.
Методы синтеза можно условно разбить на две группы. Первая группа включает
методы, в которых эталоном является выходной сигнал. При использовании этого
подхода в качестве эталона чаще всего задается желаемая переходная характеристика
/?э(0, а параметры регулятора выбираются из следующего условия: реальная
переходная характеристика системы должна возможно меньше, в известном смысле,
отличаться от эталонной h^it). Вторая группа методов использует понятие
эталонного оператора. При этом подходе задача ставится так: надо подобрать параметры
регулятора таким образом, чтобы оператор системы возможно меньше, в
известном смысле, отличался от эталонного оператора.
4-й этап. Анализ полученного решения. Полученные на предыдущем этапе
значения параметров регулятора подставляются в уравнения системы, и проводится ее
анализ на предмет устойчивости. Если система устойчива, то строится ее переходная
2 Зак. 366
26
Методы синтеза САУ по заданным показателям качества. Часть II
функция и другие характеристики, по которым проверяется соответствие
скорректированной системы требованиям, сформулированным в техническом задании. Если
система не удовлетворяет предъявленным требованиям, то необходимо вернуться ко
второму и третьему этапам.
5-й этап. Аппаратная реализация регулятора. Результатом реализации этого
этапа является принципиальная схема регулятора, построенная в соответствии с
выбранной структурой и рассчитанными параметрами. Если предполагается реализация
регулятора на базе специализированной ЭВМ, то формируются требования к ЭВМ,
работающей в контуре САУ в реальном масштабе времени; строится
алгоритмическое и программное обеспечение ЭВМ.
6-й этап. Испытания системы.
1.2. ОБЩИЕ ПОЛОЖЕНИЯ, ОПРЕДЕЛЯЮЩИЕ
ПУТИ ОБЕСПЕЧЕНИЯ ЗАДАННОГО КАЧЕСТВА
И СТРУКТУРУ РЕГУЛЯТОРА
В КЛАССЕ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ СИСТЕМ
При проектировании регуляторов необходимо иметь в виду некоторые общие
положения, которые могут облегчить решение конкретных задач. Можно указать
следующие пути обеспечения заданного качества работы САУ в переходном и
установившемся режимах:
• введение в прямую и обратную цепи системы дифференцирующих звеньев для
обеспечения заданного качества работы в переходном режиме;
• введение в прямую цепь интеграторов для обеспечения заданной точности
работы САУ в установившемся режиме;
• введение в прямую цепь усилителя с таким коэффициентом усиления, который
рационально влиял бы на качество как в переходном, так и в установившемся
режимах.
Имеют место и другие положения принципиального характера.
Изложим содержание сформулированных общих принципов обеспечения
высокого качества работы САУ.
1.2.1. Стабилизация и обеспечение заданного качества работы
СИСТЕМ В ПЕРЕХОДНОМ РЕЖИМЕ ВВЕДЕНИЕМ ОБРАТНОЙ СВЯЗИ
ПО ПРОИЗВОДНЫМ
Положим, что известно некоторое эталонное расположение полюсов замкнутой
системы, обеспечивающее необходимое качество управления (рис. 1.7). Например, по
расположению полюсов на комплексной плоскости можно судить о качестве работы
САУ в переходном режиме.
Мнимая i
ось
s5*
*-» л*
S :с
О
Действительная
ось
Рис. 1.7. Комплексная плоскость
Глава 1. Общие принципы 27^
Иногда полагают, что наилучшие, в известном смысле, динамические свойства
система имеет, когда ближайшей к мнимой оси будет пара комплексно сопряженных
полюсов. Если система второго порядка имеет комплексно сопряженные полюса
sl2 = -So ±j$0, то время переходного процесса Гр и перерегулирование а связаны
следующими формулами с а0 и Ро :
ао «i-; с = *-"*•'*■.
'р
Ясно, что на основании заданных показателей качества Грио можно рассчитать
положение определяющей пары полюсов САУ на комплексной плоскости.
Добавление третьего ближайшего к мнимой оси вещественного полюса обычно улучшает
качество переходного процесса [139].
Изложим метод реализации заданного расположения полюсов САУ на
комплексной плоскости.
Положим, что -su-s2,..'9~sn -заданные полюса. Тогда эталонное
характеристическое уравнение замкнутой системы имеет вид
D9{s) = (s+s0{s+s2)..4s + sH) = s" +aH_xsn-^... + als + a0. (1.9)
Пусть неизменяемая часть системы (объект) представлена на рис. 1.8 и имеет ПФ
Уо(д)- . . *, -• 0.10)
s"
+ <*-!
К
+ ...
+ d0
x(t)
Рис. l.S. Структурная схема неизменяемой части системы
Охватим объект обратной связью с передаточной функцией вида
Тогда структурная схема принимает вид, изображенный на рис. 1.9. Найдем ПФ
системы
К
к(ко + k]S+k2s2 +...+Kn_]Sn~])
s"+dn_]s"-]+... + di
„_!•> -t-...-r«0
К
s" +(dn_l+KKn_l)s"-] +... + {dx+KK])s + (d0 + KK0)'
Запишем характеристическое уравнение скорректированной системы
D(s) = sn +(dn_l+KKn_])sn-]+... + {dl+KKl)s + {d0 + KK0). (1.12)
Сравнивая (1.9) и (1.12), получим условия равенства (1.12) эталонному
характеристическому уравнению (1.9) [93]:
di+KKi^a,; AX, =a,-</,, / = 0,л-1.
Тогда
*;=^^-,/ = 0,л-1. (1.13)
К
28
Методы синтеза САУ по заданным показателям качества- Чисть II
i
9 •
\
+4,
Рис. 1.9. Структурная схема скорректированной системы
Изложенное выше позволяет заключить [93]: введение обратной связи по выходу
и его производным позволяет вместо характеристического уравнения вида
D0(s) = sn +dn.is"-1 +dn_2s"-2 +... + </,*+4, (Ы4)
получить характеристическое уравнение
где путем изменения коэффициентов К09К}9...,Кп^ можно добиться равенства
(1.12) эталонному характеристическому многочлену (1.9).
Таким образом, введением ОС по выходу и его производным до (п-\) порядка
можно обеспечить заданное расположение полюсов на комплексной плоскости [93].
Из (1,12) ясно, что для стабилизации объекта можно использовать ОС лишь по
нескольким производным, но необязательно до (л-1) порядка включительно [93].
Важно лишь, чтобы многочлен (р < п -1)
имел нули в левой полуплоскости.
Мнимая t >
ось
*=~г
Комплексная
плоскость
0 Действительная ось
^=52=0
Рис. 1.10. Полюса системы на комплексной плоскости
W-a
Пример 1.1 [93]. Имеем разомкнутую неустойчивую систему с ПФ вида
J
s\Ts + \)'
Полюса системы имеют следующие значения:
5, =о, s2 =0, 53 =-1/7\
Замкнем систему ОС (рис 111)
WOC = K0 + Kls + K2s2.
Тогда ПФ замкнутой системы имеет вид
Глава 1, Общие принципы
29
W{s)--
№ + *) 1
, | KQ + KiS±K2s2 Ts3 + (\ + K2)s2 + Kls + K{)
Ts* + *2
*v
1
l
s2(Ts + \)
x(t)
Рис. 1.11. Структурная схема системы
Запишем характеристическое уравнение замкнутой системы
Выберем эталонный многочлен (рис. 1.12) вида
D3(s) * (& + af = 0 ; $j ~ -a ; 52 = -а ; s3 = -а .
Тогда
(j + a)3 * 53 + 352a + Зш2 +a3 = 0 .
(1.16)
(1 17)
Приравнивая коэффициенты в (1.16) и (1.17) при одинаковых степенях 5, получаем формулы,
определяющие К{),КЬК2:
~± = Ъа\ 1 + А:2=37а; *2=37Ъ-1,
£- = з<х2; A:1=3ra2;~f = a3, /Г()=а3Г
Мнимая
ось
a
О
Комплексная
плоскость
Действительная
ось
Рис. 1.12. К решению задачи (пример 1.1)
Обеспечим устойчивость системы введением более простой "ОС (рис. 1.13) Запишем формулу,
определяющую ПФ замкнутой САУ:
W(s) =
V(Ts> + s2)_
Ts3 + s2
y(f) +
1
s2(Ts + \)
KQ+K]S
x(t)
Рис. 1.13. К примеру 1.1
30
Методы синтеза САУ по заданным показателям качества. Часть II
Используя критерий Льенара - Шипара, получим необходимые и достаточные условия устойчивости
системы, имеющей характеристическое уравнение
aos3 + а,52 + a2s+а3 = 0 ,
(здесь а0 = Т , а, = 1 ; <х2 = К,, а3 = Ко ).
Необходимые и достаточные условия устойчивости имеют вид
а0 > 0 ; otj > 0 ; а2 > 0 ; а3 > 0 ; Д2 > 0 .
Здесь
- главный определитель Гурвица; из него найдем Д2:
А =
0
«3
<*2
0
0
«3
1 к
<*2
= а,а2 - а()а3 = Щ - ТК{) > 0; К, > ТК{).
Теперь легко записать соответствующие неравенства
Т > 0; К, > 0; Ко > 0; Кх > KJ .
Таким образом, для обеспечения устойчивости нет необходимости вводить вторую производную по
выходу.
Большой класс объектов описывается уравнениями второго порядка. Поэтому
продолжим рассмотрение вопроса применительно к колебательному звену.
Рассмотрим системы, структурные схемы которых представлены на рис. 1.14.
Л
К
Т2
> <').
s2+2T& + \
x(t)
а
К
T2s2+2T$s + \
Рис. 1.14. Структурные схемы систем
Положим, что колебательное звено (рис. 1.14, а) имеет небольшое значение £ и,
таким образом, является сильноколебательным. Охватим это звено ОС с ПФ
Woc = Kos. Найдем такое значение Ко, которое обеспечило бы заданное значение £э
(например, 4э=0Л):
l +
KKos
'т2„2
2 „2
T2s2+2T^s + \
Tlsl +(2T£> + KK0)s + \ Tlsl +27V + 1
Найдем ^э:
2Г^ + ЛА:0=2Г^э; 4э= — ^ ~2Т~-
Глава 1. Общие принципы
31
Таким образом, охват колебательного звена ОС с ПФ Woc = Kos дает
возможность увеличивать коэффициент демпфирования до нужного значения, не изменяя
структуры объекта [100].
Этот результат чрезвычайно важен, поскольку, не изменяя конструкции элемента,
введением гибкой обратной связи можно добиться уменьшения его
колебательности [100].
Пример 1.2. Рассмотрим структурную схему канала управления креном ракеты (рис 1 15) [77]
Передаточная функция канала управления креном определяется формулой
W(s) —VA—
(1 18)
Процесс установления крена ракеты с использованием системы управления, структурная схема
которой представлена на рис. 1.15, носит колебательно-затухающий характер, причем процесс является
медленно затухающим
Я') = Ук
Kh
~ S(/)
Г
5,=и(0
Ку
s(Tys + \)
Ik
= *(')
Рис. 1.15. Структурная схема системы
Приведем (1 18) к виду
045) =
s2+2^(uOKs + a2OK
19)
где соок =
- собственная частота колебаний ракеты по крену,
4 = :
- коэффициент демпфирования
Параметром, с помощью которого можно изменять качество управления, является коэффициент передачи
К1у чувствительного элемента. Очевидно, для увеличения £ (увеличения затухания) коэффициент Kiy надо
уменьшать. Однако можно показать, что с уменьшением К1у увеличивается установившаяся ошибка [77]
Поэтому такой путь получения желаемых характеристик контура управления креном оказывается
нецелесообразным [77].
На практике используется введение обратной связи по скорости, причем сигнал x(t) = yK(t)
формируется с помощью скоростного гироскопа.
Структурная схема канала управления креном с введением сигнала крена и его производной
представлена на рис 1.16.
Я0 = Уо(0|
УкзиО +
5,(0=1/(0
Kv
s(Tys+\)
*(O = Y*(g
Рис. 1.16. Структурная схема системы
32
Методы синтеза САУ по заданным показателям качества. Часть II
Для структурной схемы, представленной на рис 1 16, передаточная функция имеет вид (1 19), однако
коэффициент демпфирования изменяется, он определяется формулой
1 + лппл\,л^ ^ КпрКуКу
<U=:
vnpiVYiVY _
= ^+:
- = *> + **,
(120)
Как следует из последней формулы, изменяя Ку, можно в достаточно широких пределах менять
характер установления угла крена
Из изложенного можно сделать вывод, с помощью дополнительного сигнала, сформированного в
автопилоте, можно изменять динамические характеристики системы «ракета-автопилот», не меняя
аэродинамической формы ракеты.
Далее рассмотрим структурную схему канала управления продольным движением ракеты (рис 1 17)
Здесь, помимо сигнала обратной связи по углу тангажа, сформированного позиционным гироскопом,
введены два дополнительных сигнала [77].
Один из них, измеряемый скоростным гироскопом, пропорционален угловой скорости вращения
продольной оси ракеты & , а второй - датчиком линейных ускорений, пропорционален углу атаки а
»»(').
Ъ As
э
9 *
i
п
к
V
«в
\
s2 +2^соо5 + о)о
а
1
+
i
Рис. 1.17. Структурная схема системы
Из структурной схемы (рис 1 17) следует дифференциальное уравнение вида [77]
о(0 + (2^соо + а6КпрКв№) + (e)J + аьКпрКа + ±.asKttpKJa(t) =
= а5/:прл:э(83-э)
Из рассмотрения последнего уравнения следует сигнал скоростного гироскопа искусственно изменяет
коэффициент демпфирования ракеты и собственную частоту ее колебаний [77].
1.2.2. Целенаправленное изменение динамических свойств систем
путем введения дифференцирующих звеньев в прямую цепь
Рассмотрим систему, структурная схема которой представлена на рис. 1.18.
Регулятор
К
Ъ
^)
Неизменяемая
часть
«(О
иэ
о
Щ*)
x(t)
Рис. 1.18. Структурная схема системы
"лава 1. Общие принципы
33
Из-за наличия дифференцирующего звена регулятор формирует сигнал
управления u{t) с прогнозом: если амплитуда e(f) увеличивается, производная е(/)
положительна и сигнал u{t) усиливается. С момента уменьшения сигнала е(/) сигнал
i(t) < О и сигнал u(t) интенсивно ослабляется (рис. 1.19).
Рассмотрим пример и изложим математическую сторону вопроса. Положим, что
неизменяемая часть системы является колебательным звеном с малым значением % ,
г.е. неизменяемая часть - сильноколебательный элемент.
8(0-
8(/)
управляющий
сигнал м(/)
усиливается _
^управляющий
сигнал м(0
ослабляется
Рис. 1.19. Сигнал ошибки е(/)
Ш*0Ш
р
Рис. 1.20. Структурная схема системы
Передаточная функция системы имеет вид
Wis)= ТЧ+К2Т^ + Х ~
T2s2+2TZ,s + \
K3+K'3s
Kc+Kus
T2s2+(2T^ + Ka)s + Kc+\
(1.22)
р2„2
?;V+2r,^+r
где
;^ =
к„
Il + Ke 2Tjl + Kc
Выбором коэффициентов Ка и Кс можно целенаправленно изменять
динамические свойства замкнутой системы, в том числе увеличить \ до нужного значения.
34
Методы синтеза САУ по заданным показателям качества. Часть II
1.2.3. Влияние коэффициентов усиления разомкнутой системы
и интеграторов в прямой цепи на качество работы сау
в установившемся режиме
Известно, что установившаяся ошибка работы САУ определяется выражением
б(0 = с0Я0+с,Я0+^с2Я0+...+—стУ(т) (0, (1.23)
2! т\
где Со, Сх, С2 ... - коэффициенты ошибок.
Если W(s) - ПФ замкнутой САУ, то справедлива формула
Сп=^т[1-№Щ , к =0,1,2,.... (1.24)
Обычно называют: Со - коэффициент статической ошибки; С] - коэффициент
скоростной ошибки; С2 — коэффициент ошибки по ускорению и т.д.
Из формулы (1.14) находим
C°=7TF' (L25)
1 + А
где К - коэффициент усиления разомкнутой системы (рис. 1.21).
Из (1.25) следует, что уменьшение установившейся ошибки достигается
увеличением коэффициента усиления К. Вместе с тем с увеличением точности в
установившемся режиме уменьшаются запасы устойчивости и при некотором К > К^
система становится неустойчивой.
Рассмотрим систему (рис. 1.21). Имеем
К
W(s)= ао*3+(У2+а2* + 1 *
1 + -
К
aQs3 +aj52 +a2s + l
а0^3 + а^2 + a2s +1 + К
К
ао534-а152+а25> + 1
*(£
Рис. 1.21. Структурная схема системы
Воспользуемся критерием Льенара - Шипара; пусть
а! а3 0
А =
а0 а2 0
- главный определитель Гурвица.
0 ах а3
Необходимые и достаточные условия устойчивости можно записать так: сс0 > 0;
ctj > 0, а2 > 0, а3 = 1 + К ;
А2 =
a, oti
а0 а2
щ i + a:
а0 <х2
= а!а2 -ао(1 + /С) = а1а2 —cxq -OqK >0 .
Отсюда получаем
аха2-а0 >а0К ;
далее запишем выражение, определяющее критический коэффициент усиления К^:
Глава 1. Общие принципы 35_
а1а2~а0 _jt
При К > Кф - система неустойчива.
Из изложенного легко заключить: при увеличении точности работы САУ в
установившемся режиме путем увеличения К необходимо помнить: запас устойчивости
системы уменьшается и существует К = К^, при котором система становится
неустойчивой. Однако существуют такие структуры систем, которые допускают
неограниченное увеличение К [156].
Для достижения нужного запаса устойчивости используют введение в прямую
цепь дополнительных звеньев, например, апериодического звена, постоянная времени
которого значительно больше постоянных времени имеющихся апериодических
звеньев.
Пользуясь (1.24), легко показать, что если в прямой цепи имеется один
интегратор, то Со = 0.
В самом деле, если в прямой цепи имеется один интегратор, то ПФ разомкнутой
системы имеет вид
F s
Найдем ПФ замкнутой системы
»о(*)/
Запишем зависимость для коэффициента Со
C0=(\-W(s))\ =1-М>)=1-1 = 0.
Аналогичным образом легко показать, что если в прямую цеп$ включены два
интегратора, то Со = 0, Q = 0; для трех интеграторов имеем Со = 0, С, = 0, С2 = 0 .
Как и в предыдущем случае, когда увеличение коэффициента усиления в прямой
цепи разомкнутой системы понижало запас устойчивости, так и введение
интеграторов приводит к аналогичному результату.
Повышение статической точности путем введения интегрирующих звеньев
требует проведения мероприятий по сохранению запасов устойчивости САУ.
Из изложенного выше можно заключить, что введением в прямую цепь
интеграторов, включением в прямую цепь и цепь обратной связи дифференцирующих
звеньев, а также изменением коэффициента усиления разомкнутой системы можно
добиться высокого качества работы САУ в переходном и установившемся режимах.
1.2.4. Влияние местных ОС
Основные виды ОС определяются ПФ (рис. 1.22):
• жесткая обратная связь (действует на систему как в переходном, так и
установившемся режимах)
0^(5) = /^; (1.26)
• инерционная жесткая ОС
Kc(s)=-^-; (1.27)
• гибкая обратная связь (действует лишь в переходных режимах)
36
Методы синтеза САУ по заданным показателям качества. Часть II
инерционная гибкая ОС
0^(5) «Кос*;
K^s
CL
(1.28)
(1.29)
Рис. 1.22. Структурная схема системы с обратной связью W0Q(s)
Проиллюстрируем основные свойства ОС при охвате ими различных типов
звеньев [100].
Пусть IVO (*) =
К
Ts + \
T3s + l
где
Кэ=-
К
-. гэ=-
(\ + КК0С) ' (\ + КК0С)
Вывод: жесткая отрицательная ОС не изменяет структуру апериодического
звена, но уменьшает его инерционность (уменьшает постоянную времени).
Тем самым она улучшает качество переходного процесса в САУ и оказывает
стабилизирующее действие, т.е. превращает неустойчивую замкнутую систему в
устойчивую.
is
Если же W0(s) = -—-, a fl^Cs) = K0Gs , то
7i + l
W(s) =
К
ГЭ5 + Г
где
T3=T + KK0G.
Таким образом, гибкая отрицательная ОС не изменяет структуру и не влияет на
передаточный коэффициент апериодического звена. Она лишь увеличивает его
инерционность (увеличивает его постоянную времени).
Положим теперь, что
ад = -,а^0С(*) = К0С.
В этом случае получаем
T3s + \
где
Кэ= —, 7\ =
Э IS *
ккп
Глава Ь Общие принципы j/_
Итак, под действием жесткой ОС теряется интегрирующее свойство звена и
оно превращается в апериодическое с коэффициентом усиления, который
определяется Кос. Постоянная времени Тэ будет мала при большом К .
Рассмотрим случай, когда
ВД = ->^ос(*) = ^7-
s Tocs + \
Имеем
где
W{s)'~Ty+T2^i'
Следовательно, интегрирующее звено превращается в звено второго порядка;
при большом К охват интегрирующего звена инерционной жесткой обратной
связью эквивалентен усилительному звену с введением производной.
Если же W0(s) = -, а Жос(.у) = £ocs , то
s
S
где
К
(1 + КК0С)
Таким образом, гибкая обратная связь не изменяет структуру интегрирующего
звену, но уменьшает его передаточный коэффициент (увеличивает постоянную
времени Тэ = — ).
Рассмотрим практически важный случай, когда
Передаточная функция замкнутой системы имеет вид
где
W(s) = —ri-
T3V+2Гэ£э.я-1
к К т - Т т. - -§
1 + ^ос ф^ККо, J^KKZ
Вывод: жесткая отрицательная ОС не изменяет структуру колебательного
звена, но уменьшает постоянную времени и коэффициент демпфирования, при этом
уменьшается коэффициент передачу.
Если же колебательное зэено охватывается отрицательной ОС С ПФ
W0C(s) = K0Cs,
2Т{\-%)
то при л:ос <
W№—*
rV+2r^5 + l
3& Методы синтеза САУ по заданным показателям качества. Часть II
где
КК
£э = £ + ~ (этот случай рассматривался выше).
2Г(1-£)
Если же K0Q > —-—~, то
К
{T]S + \)(T2s + \y
где
7, =0,5fr + Vr2-4r2>j; Г2 =0,/г-Vr2 -4Г21; r^l^T + KK^.
Следовательно, сильная отрицательная ОС превращает колебательное звено в
последовательное соединение двух апериодических звеньев.
IS
Легко показать, что если W0(s) = К ; Woc(.s) = —а£—, то
W{s) = K9(T,s + l),
где
к К Т Тос
т.е. инерционная отрицательная ОС превращает идеальное усилительное звено в
реальное дифференцирующее звено, с помощью которого можно получить
производные входного сигнала.
Последовательный регулятор, имеющий ПФ
и объединяющий в себе введение интеграла и производной, называется изодромным.
Использование изодромного регулятора позволяет получить необходимый порядок
астатизма, сохраняя устойчивость и качество системы в переходном режиме.
А теперь рассмотрим случай, когда объект с ПФ
»;(*)=■ к
охватывается ОС с ПФ
rMmw
Пользуясь структурными преобразованиями, получим ПФ замкнутой системы [100]
у(д)в *i(p + l) ш
s(Tis2+Txs + \)
где
к __ % Т2 _ TT0Q т _ Т + Тос
1 1 + ККое' 2 \ + КК0С' 1 \ + КК0С'
Вывод: при сохранении интегрирующего свойства звена получается эффект
введения производной, т.е. интегрирующее звено становится изодромным {постоянные
времени 7J и Т2 могут быть уменьшены за счет увеличения К ). Инерционное
запаздывание в ОС может быть использовано для улучшения^ качества переходных
процессов (получается эффект, аналогичный введению производной в прямой цепи).
В заключение рассмотрим условие сохранения порядка астатизма охватываемого
звена.
лава 1. Общие принципы
Если Wo(s) = -^-W'(s) и 1Уос(5) = Кос5^с(5),то
S
w(s) =. *оВД
Отсюда следует, что для сохранения v-го порядка астатизма необходимо выпол-
1ение условия ц > v .
Общий вывод: применение далее простейших отрицательных обратных связей
позволяет существенно изменять свойства типовых звеньев. Если же элементы
регулятора могут быть охвачены ОС, то динамические свойства этих элементов
могут быть изменены в направлении обеспечения заданного качества работы
замкнутой САУ[100].
Изложенные здесь положения лежат в основе подходов к выбору рациональной
структуры регулятора для каждого конкретного случая. При проведении инженерных
расчетов целесообразно принимать во внимание следующее. Уменьшение
установившейся ошибки достигается увеличением добротности системы (передаточного
коэффициента разомкнутой системы). Вместе с тем при увеличении коэффициента
усиления в большинстве случаев уменьшаются запасы устойчивости и при К > Ккр
система становится неустойчивой. Поэтому при повышении точности работы САУ в
установившемся режиме путем увеличения К необходимо предусмотреть
мероприятия для обеспечения достаточного запаса устойчивости. Увеличение точности
путем обеспечения астатизма (включение интеграторов в прямую цепь) также
требует реализации мероприятий по сохранению запасов устойчивости САУ.
Для получения астатизма целесообразно использовать изодромные звенья с ПФ
wKy(s) = K»(T"s+lKi+bL>
У . S S
где
ТИ = постоянная времени изодрома.
Если ТИ - достаточна велика, то запас устойчивости может быть сохранен
неизменным [130].
Неединичная обратная связь — один из путей реализации астатической системы.
Демпфирование с подавлением высоких частот - еще один путь обеспечения
устойчивости или повышения запаса устойчивости. Этот путь реализуется введением
апериодического звена, постоянная времени которого значительно больше
постоянных времени имеющихся апериодических звеньев разомкнутой системы
is
Жр(5) = (715 + 1)(Г2, + 1)(Г3, + 1)-
Устойчивость и необходимый запас устойчивости могут быть обеспечены
введением форсирующего звена при любой ПФ исходной системы. При этом
увеличивается быстродействие системы, вместе с тем увеличивается и влияние помех.
1.3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ И СТРУКТУРНЫЕ СХЕМЫ
РЕГУЛЯТОРОВ
1.3.1. Математические модели
В предыдущем параграфе была показана роль операций усиления,
интегрирования и дифференцирования: с помощью изменения величины коэффициента усиления
j40 Методы синтеза САУ по заданным показателям качества. Часть II
в прямой цепи, введения местных обратных связей, включения интегрирующих и
дифференцирующих звеньев можно добиться заданного качества работы САУ (в
пределах возможностей, которые определены структурой используемого регулятора).
В соответствии с этим положением строятся математические модели регуляторов,
цель которых - формирование управляющего воздействия (команды управления) на
объект (рис. 1.3).
Здесь пока ограничимся рассмотрением наиболее распространенных
математических моделей линейных регуляторов по отклонению непрерывного действия. В этих
простейших законах управляющее воздействие u(t) линейно зависит от сигнала
ошибки е(/) (включение в прямую цепь усилителя), его интеграла (включение
интегрирующих звеньев) и первой производной (включение дифференцирующих звеньев).
Сказанное выше позволяет ввести в рассмотрение следующие виды управляющих
устройств (регуляторов):
1) пропорциональное управляющее устройство (П-у правление)
КуЮ = К; (1.30)
2) интегральное управляющее устройство (И-управление)
0;y(j)=^eJ-,KH=:-L; (1.31)
3) пропорционально-интегральное управляющее устройство (ПИ-управление)
WKy(s) = K + ^- = K + -^-; (1.32)
s TKs
4) пропорционально-дифференциальное управляющее устройство (ПД-управ-
ление)
^Ky(5) = K+V = *+^; О-33)
5) пропорционально-интегрально-дифференциальное управляющее устройство
(ПИД-управление)
WKy(s) = K + ^- + KRs. (1.34)
s
Вводя кратное интегрирование и дифференцирование, можно получить более
сложные законы управления.
1.3.2. Анализ динамических характеристик регуляторов
Кратко рассмотрим основные характеристики приведенных выше регуляторов, следуя [88].
С использованием П-регулятора комплексная частотная характеристика (КЧХ) разомкнутой системы
имеет вид
Wp{j<u) = KW0U<i>). (135)
При подключении к объекту П-регулятора КЧХ объекта увеличиваются на каждой частоте
пропорционально в К раз
На рис. 1 23 приведены КЧХ разомкнутых систем с П-регулятором При К = 1 КЧХ разомкнутой
системы совпадает с КЧХ объекта регулирования. При К > 1 КЧХ разомкнутой устойчивой системы
приближается к точке В (- 1 ,у0); при К < 1 КЧХ отходит от этой точки.
На рис. 1.23 в качестве примера изображены две КЧХ разомкнутой системы, при К - К{ -1,5 и при
а: = а:2 = о,5.
Выходной процесс в П-регуляторе описывается выражением
м(0 = *£(/), (1.36)
где е(/) - входное воздействие регулятора, u(t) - управляющий сигнал, поступающий на объект
управления. Как выше отмечалось, чрезмерное увеличение запаса устойчивости С ухудшает качество регули-
рованияу т.к. при этом затягивается переходный процесс в системе (увеличивается время переходного
процесса (см. §1.2)), увеличивается установившаяся ошибка.
Глава 1. Общие принципы
41
С.
Р(ю)
Рис. 1.23. Характер изменения КЧХ разомкнутой системы при изменении ее коэффициента
С учетом сказанного для системы с П-регулятором существует некоторое оптимальное значение
коэффициента его передачи К*., которое и следует выбирать при настройке системы [88]
При использовании И-регулятора выходная величина u(t) - команда управления, пропорциональна
интегралу от входной величины е(/)
и(/) = Кн}е(т)</т
(1.37)
Коэффициент передачи Ки является параметром настройки И-регулятора, определяется формулой
(138)
со
Комплексная частотная характеристика разомкнутой системы с И-регулятором имеет вид
(139)
Из (1.39) следует, что в системе с И-регулятором вектор КЧХ объекта на данной частоте
увеличивается в Ки/& раз и поворачивается по часовой стрелке на 90°.
В качестве примера на рис. 1.24 построена КЧХ разомкнутой системы с И-регулятором по КЧХ
объекта управления
На рис. 1.24 каждый вектор разомкнутой системы связан с КЧХ выражением (1.39), например
OE]=£*-e-JiU2OAl
со,
(140)
Так как при со -> 0 отношение К„ /со -> оо , то КЧХ разомкнутой системы с И-регулятором при со —> 0
уходит в бесконечность, асимптотически приближаясь в третьем квадранте к отрицательному
направлению мнимой полуоси [88]
Основное назначение закона И-регулирования - ликвидация установившейся ошибки управления
В качестве самостоятельных И-регуляторы применяются достаточно редко из-за медленного
нарастания управляющего сигнала U(t) при отклонении регулируемой переменной (при увеличении ошибки е(/))
Очень часто закон управления используется блоком или устройством, конструктивно являющимся
составной частью регулятора, реализующего более сложный, например, пропорционально-интегральный
закон управления.
Выше отмечалось о реализации законов управления, учитывающих производную от сигнала z(t)
Если П- и И-регуляторы не могут упреждать (прогнозировать) ожидаемые отклонения регулируемой
величины, реагируя только на уже имеющиеся в данный момент нарушения технологического процесса, то
с помощью введения производной возможен процесс прогнозирования, при формировании управляющего
сигнала, поступающего на объект управления
Регулятор, использующий ё(/) (Д-регулятор) при большой скорости отклонения регулируемой
величины (когда в начальный момент П-регулятор оказывает слабое управляющее воздействие на объект, а И-
регулятор только начинает наращивать управляющее воздействие) оказывает существенное управляющее
воздействие на объект, ликвидируя тем самым отклонение регулируемой величины (уменьшая ошибку
е(/)), причем чем больше возмущающее воздействие на объект (чем больше ошибка е(/) ), тем быстрее
42
Методы синтеза САУ по заданным показателям качества. Часть II
будет отклоняться управляемая величина от заданного значения и тем значительнее будет управляющее
воздействие регулятора на объект, направленное на нейтрализацию возмущающего воздействия [88].
Реализация Д-регулятора в чистом виде практически неосуществима. В связи с этим в качестве
Д-управляющих устройств используются дифференциаторы с передаточной функцией [88]
(V+D
(1.41)
JQW
WJja)
Рис. 1.24. Комплексные частотные характеристики объекта Жо(усо)
и разомкнутой САУ W?(j<a) с И-регулятором
Для комплексного использования преимуществ законов П- и И-регулирования в автоматических
системах широко применяются регуляторы, формирующие законы как П-, так и И-регулирования
одновременно. Такие регуляторы называются, как было сказано выше, пропорционально-интегральными, или
сокращенно - ПИ-регуляторами
На практике используются ПИ-регуляторы, имеющие ПФ вида
Ки
■w-*+£"*+-f
(142)
- параллельное соединение П-регулятора и И-регулятора (£„=—-; Тн называют постоянной времени
'и
интегрирования).
Если при настройке ПИ-регулятора установить очень большое значение постоянной времени Т„ , то он
превратится в П-регулятор.
Если при настройке регулятора установить очень малые значения к, то получим И-регулятор с
коэффициентом передачи по скорости \/Ти = К„ .
Часто используются ПИ регуляторы с ПФ [88]
'из5
(143)
где Тю - постоянная времени изодрома.
Переходная характеристика ПИ-регулятора с передаточной функцией (1.42) представлена на рис. 1.25
(прямая 1) [88].
В (1.42) К и» Ти - параметры настройки; в (1.42) имеют место взаимосвязанные параметры настройки
статической и астатической частей по коэффициенту усиления К. Так, при настройке коэффициента
усиления К будет изменяться и постоянная времени интегрирования:
T=TUJK. (1.44)
лава 1. Общие принципы
2Кг0
Кг0
0
1
N
/
У
2
J
t
т т
Рис. 1.25. Закон ПИ-управления регуляторов с передаточной функцией (1.42) (прямая 1)
и с передаточной функцией (1.43) (прямая 2) при поступлении на вход постоянного сигнала е0
и при одинаковом значении коэффициента передачи К регуляторов
Постоянной времени изодрома регулятора с ПИ-законом регулирования называется время, в течение
-оторого от действия интегральной (астатической) части регулятора удваивается пропорциональная
статическая) составляющая закона управления.
На рис. 1.26 приведены переходные характеристики в ПИ-регуляторах, выходной сигнал которых оп-
)еделяется зависимостями [88]
u(t) = Kz(t) + ±-jz(T)dT
• и /ч
(1.45)
"(О
К = К3г(
К — л2в0
о
( 1 ' 1
u(t) = KU(/) + — Je(x)^T .
K = 2K2eq
K=2Kxz,
K = K2s0
t
(146)
a U б
Рис. 1.26. Характер изменения законов ПИ-управления
при различных постоянных значениях коэффициента усиления К регуляторов:
а - для регуляторов с ЛФ WKy (s) = К+— ; б - для регуляторов с ПФ WKy (s) = —^-^ -
Из рис. 1.26, а видно, что при законе ПИ-регулирования скорость нарастания интегральной
составляющей на выходе регулятора при изменении К не изменяется При законе ПИ-регулирования в случае
изменения К пропорционально изменяется и скорость нарастания интегральной составляющей на выходе
регулятора
На практике нашли применение ПД-регуляторы с ПФ
1¥ку(*) = К + Клз, (147)
а также с ПФ
WKy(s) = K{\ + Tnms)9 (1.48)
где ТП9 - постоянная времени предварения.
44
Методы синтеза САУ по заданным показателям качества. Часть II
И, наконец, запишем ПФ ПИД-регуляторов [88]
WKy(s) = K + — + Клз = К + ^ + Кдз
THs s
(1.49)
»;yW = i«:h+^+rnijj=^i+b.+rn.jj d 50)
- ПИД-регулятор с общим коэффициентом усиления для различных составляющих закона управления
При скачкообразном изменении регулируемой величины идеальный ПИД-регулятор в начальный
момент времени оказывает мгновенное бесконечно большое воздействие на объект регулирования,
затем величина воздействия мгновенно падает до значения, определяемого пропорциональной частью
регулятора, после чего, как и в ПИ-регуляторе, постепенно начинает оказывать свое влияния
астатическая часть регулятора.
К, Ти и Кд - параметры настройки ПИД-регулятора.
ПИД-регулятор по своим возможностям является более универсальным по сравнению с другими
регуляторами. С его помощью можно осуществлять различные законы управления.
Характеристики типовых ПИ-, ПИД-регуляторов и дифференциаторов приведены в табл. 1.1.
Таблица 1.1
Вид
характеристики
Характеристика регулятора типа
ПИ
ПИД
Дифференциатора
Уравнение
Hx+riz"
'«,' at
У T«i
'■!"■«;
Передаточная
функция
«1 + :
Tu,s
*11 + 7?+Г-
МО
Переходная
характеристика
h{t)
№)
Щ)
КЧХ
Уб(со)
со = 0 ^(g)
ijQW
Jc
(О
k ш
JW
У^л7
0) = 0
*.
10)
J
= 00
/»(tt)
i ,Л(©)
АЧХ
nA(a)
■J-
LA(a)
И«> (0 = ±
ФЧХ
ф(<0)
1,Ф)
^♦ф(©)
лава 1, Общие принципы
1.4. ОБЩИЕ ПРИНЦИПЫ, НА КОТОРЫХ БАЗИРУЮТСЯ
ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ МЕТОДОВ
И АЛГОРИТМЫ РАСЧЕТА ПАРАМЕТРОВ
В ЗАДАЧАХ СИНТЕЗА РЕГУЛЯТОРОВ
Положения, изложенные в предыдущем параграфе, позволяют определить пути
беспечения заданного качества работы синтезируемой системы автоматического
правления и на этой основе найти математическую модель и структурную схему
>егулятора, место его включения, а также варьируемые параметры.
Однако на этом этапе не рассматривается вопрос расчета численных значений па-
>аметров регулятора рх, р2,..., рг.
Цель настоящего параграфа - изложение общих принципов, позволяющих
построить методы и алгоритмы расчета параметров Р\^Рг^^рг регулятора
WKy{s,pup2,...,pr).
1.4.1. Принцип динамической компенсации
В соответствии с этим принципом в результате решения задачи синтеза
регулятора определяются как его структура, так и параметры /?i,/?2»•••>/?/•• Поэтому в
рассматриваемом случае структура и параметры регулятора не задаются, а определяется
лишь место его включения,
Изложим основные положения принципа динамической компенсации.
Разделение задачи синтеза регуляторов на два этапа:
• нахождение эталонной динамической характеристики Аъ {например,
передаточной функции);
• синтез регулятора, обеспечивающего равенство эталонной и реальной
динамических характеристик (т.е. нахождение оператора и параметров
регулятора 4у).
Рассмотрим систему (рис. 1.27),
т
«(0
Рис. 1.27. Структурная схема системы
На структурной схеме использованы обозначения; Ао - оператор неизменяемой
части системы (объекта управления), Л^ - оператор регулятора, Аэ - эталонный
оператор замкнутой системы.
Далее будут использованы положения операторной алгебры, в соответствии с
которой имеют место следующие действия:
1) сложение операторов А + В = С \
2) умножение операторов АВ = С\
3) умножение оператора на скаляр Ак = В или кА = В .
Кроме этого, справедливы правила:
1) операция сложения коммутативна
А+В=В+А\
2) операция сложения и умножения ассоциативны
46 Методы синтеза САУ по заданным показателям качества. Часть II
А + (В + С) = {А + В)+С и а{ВС)=(АВ)С;
3) операция умножения не коммутативна
АВ * ВА .
Для системы (рис. 1.27) справедливы зависимости
6(0 = yif) - *(0, *(0 = Aou(t), и(0 = 4* е(0.
Из этих формул имеем
*(0 = 4АуБ(0,
или
где Лр = /^о^ку "~ оператор разомкнутой системы.
Имеет место соотношение s(0 = y(t)~- A0A^z(t) и, следовательно,
6(0 + 4,4*6(0 = (/ + 4>4у )е(0 = ЯО •
Отсюда находим
е(0 = (/ + 4Ау)Л(0.
Поскольку
д:(/) = 4,4*6(0 = Л^ку (/ + 4^ку)"! ЯО,
то оператор замкнутой системы определяется формулой
А = А0Аку(1 + А0Аку) .
Теперь легко найти выражение, определяющее оператор регулятора через
операторы А и 4) • Имеем
Л (/ + 4)4<у ) = ^ + АА0Аку = 4Ику •
Из последней зависимости следует
/4 = 4)4<у ~АА0Аку =(Л~^Л)4у =(^""^)Л^ку •
Отсюда находим
аку=[{1-а)а0]-1а = а;]{1-аУ1а.
Поскольку оператор замкнутой системы должен равняться эталонному оператору,
т.е. А = АЭ, то окончательная формула, определяющая оператор регулятора,
запишется так
4<у=Ло1('-ЛэУ"1Л\ (1.51)
В последней формуле Аэ и AQ известны, поэтому принципиально возможен
расчет оператора А^ , при этом определяются структура регулятора и численные
значения его параметров рх, р2,..., рг.
Проверим анализ основной формулы. Из нее следует, что синтез регулятора в
соответствии с рассматриваемым принципом предполагает компенсацию динамики
объекта; процесс компенсации иллюстрируется рис. 1.28.
Из рассмотрения схемы (рис. 1.28) можно записать
1/(0 = ^о1(/-^э)"^э]б(0
Глава 1. Общие принципы
47
it) = Aou(t) = ^AoAo](l-A3YA^z(t) = (l-A')~lA\
X0+/Ov£(0
^=^(1-^ А*
x(t)
Рис. 1.28. Структурная схема скорректированной системы
Из последней формулы следует, что основным содержанием принципа
динамической компенсации является возможность не учитывать динамику объекта при
синтезе регулятора, что обеспечивается наличием в операторе регулятора
сомножителя Aq1 .
Формально зависимость, определяющая А^ , дает точное решение задачи синтеза
регулятора. В большинстве же случаев физически элемент с оператором А^
реализовать не удается.
Важным является следующее положение: содержание большого числа
инженерных методов синтеза регуляторов сводится к топ или другой форме аппроксимации
соотношения
AKy=Aol(l-A3)']A\
Такая аппроксимация направлена на:
1) упрощение структуры регулятора;
2) возможность получения физически реализуемых элементов;
3) обеспечение устойчивости замкнутой системы;
4) повышение свойства грубости и др.
(см. параграф 2.2, в котором изложен принцип динамической компенсации
применительно к классу стационарных линейных объектов).
В связи с этим при решении практических задач центральными следует считать
две формулы:
А\ = Л^ку И Аэ = А0Аку i1 + А0Аку ) >
где А* - эталонный оператор разомкнутой системы; Аэ - эталонный оператор
замкнутой системы.
Задача синтеза формулируется как задача расчета оператора регулятора А^
из условия приближенного выполнения {не обязательно за счет наличия звена с
оператором Aq ) одного из двух равенств:
А* « Ар или Аэ « А,
где Ар и А - реальные операторы соответственно разомкнутой и замкнутой систем.
При использовании принципа динамической компенсации достигается точное
равенство реальных операторов эталонным операторам за счет сомножителя Aq1 .
В инженерных расчетах указанное равенство не достигается, поэтому целесообразно
найти соответствующую оценку погрешности, определяющую ухудшение качества
процессов управления.
Вместе с тем при проведении расчетов необходимо помнить, что многие методы
в неявной форме реализуют принцип динамической компенсации.
^8 Методы синтеза САУ по заданным показателям качества. Часть II
1.4.2. Оптимизационный принцип синтеза регуляторов,
предполагающий достижение приближенного,
в известном смысле, равенства реального выходного
СИГНАЛА хр(t,Р\,р2,'~,Рг)ЭТАЛОННОМУ ПРОЦЕССУ *э(/)
В основе реализации этого принципа лежит аппарат нелинейного программирования.
Основное содержание этого принципа состоит в следующем: задается оператор
регулятора, зависящий от параметров р],р2,...,рг, т.е. Аку(рир2,...,рг);
задаются эталонное воздействие y3(t) и эталонная реакция на это воздействие x3(t).
Проблема синтеза состоит в подборе таких значений параметров рх 9р2,...,рг,
которые обеспечили бы близость, в известном смысле, реального выходного сигнала
хр{*>Р\>Р2>->Рг) и эталона x3(t).
Обсудим этот подход; положим, что мерой близости выбрана метрика
пространства с[о,г], т.е. задача формулируется так:
1\{*>Р\>Р2*--->Рг) = *№\хр{*>Р\>Р2>-»>Рг)-Хэ{*)\-> miQ--
OutuT ■ pt,i=],r
Если же воспользоваться метрикой пространства L2 [о, Т], то
1г(*>РьР2—Рг) = ][хр{1,Р\,Р2>»'>Рг)-х9к)] А-> mia_.
В функционалы 1Х и /2 входит функция xp(t,pup2,...,/?r). Она определяется
зависимостью
A(P\>P2>->Pr)Xp(t,P\,P2>->Pr) =
= [ЛАсу(А>/>2>"->/0(/ + ^о4у(/^^
где А(рх,р2,...9Рг) - оператор замкнутой системы, зависящий от параметров
РиР2>->Рг регулятора.
Из последней формулы находим
Хр{^Р\,Р2,^Рг) = ^оАку{РиР2^^Рг)^ + АОАку{РьР2^^Рг)) | Уэ(0 = ,} $2)
= А-1(р{,р2,...,рг)уэ(0.
Полученная зависимость позволяет сделать следующий вывод: для реализации
рассматриваемого принципа необходимо знать обратный оператор замкнутой
системы, явно зависящий от параметров регулятора. Это - чрезвычайно сложная
задача, решение которой возможно лишь в исключительно простых случаях (см. §2.6).
1.4.3. Оптимизационный принцип синтеза регуляторов,
предполагающий достижение приближенного, в известном
смысле, равенства правой и левой частей операторного
уравнения, описывающего динамику замкнутой
скорректированной системы
Содержание этого принципа состоит в следующем. Пусть y3(t) - заданное
(эталонное) воздействие, x3(t) - желаемая реакция; тогда имеет место зависимость
\АпАжу(Р1>Р2'->Рг)(1 + 4>Ач{Р\>Р2>->Рг)) 1 '*э(')« У,(0. С1-53)
F\(t,P\,P2>->Pr)
Рг(*,Р\,Р2">Рг)
Глава 1. Общие принципы 49^
В последней формуле стоит знак приближенного равенства. В идеальном случае,
правильно подобрав структуру и значения параметров регулятора рх, р2,..., рг, мы при
подстановке в операторное уравнение скорректированной системы эталонного,
воздействия y3(t) и желаемой реакции x3(t) получили бы тождество, т.е. д:э(0 была бы
решением операторного уравнения системы при правой части y3(t). Идеальный же
подбор регулятора, в общем случае, невозможен, поэтому имеет место невязка
E(t,pl,p2,...,pr) = Fl(t,p],p2,...,pr)-F2(t,p],p2,...,pr). (1.54)
На основе невязки можно построить соответствующие функционалы и
сформулировать задачу синтеза регулятора так:
'з(р\>Pi>->Pr)= max|£(/,P\,p2,.~,pr]-> miu- ;
т
U {р\ э Pi >•••> Рг) = J Е2 ('> Р\,Рг^рМ-+ min_
- при соответствующих ограничениях, связанных с устойчивостью и качеством
работы системы.
Достоинство последнего подхода состоит в том, что он не требует нахождения
обратного оператора А~] (р}, р2,..., рг). Это - принципиальное упрощение задачи.
Этот подход можно применить к широкому классу систем, включая линейные
нестационарные и нелинейные системы, системы с опаздыванием и т.д. Как и в
предыдущем случае, аппарат нелинейного программирования является основным
инструментом реализации этого принципа.
1.4.4. Принцип, лежащий в основе группы методов,
использующих понятие моментов
Для иллюстрации рассмотрим основную идею одного из методов.
Если выбрана так называемая моментная система f\(t),f2{t)^.,,ff(j), то на основе
(1.53) можно записать систему равенств
}[><О^(Я1»Р2э»-.Рг)(^ + ^^(Р1эР2э».эРг))"11*э(ОЛ(ОЛ =
0L J
т
=фэ(0Л(0* к = Ц; 1>г.
о
Решая систему (1.55), можно определить значения параметров р*\,р2,.~,р*г.
Метод применим к широкому классу систем, включая и нелинейные
автоматические системы [7]. Реализация этого принципа также базируется на аппарате
нелинейного программирования.
В [7] приведено решение задачи синтеза нелинейных систем с использованием
рассматриваемого принципа по заданным показателям качества (быстродействие,
перерегулирование, степень колебательности). При этом безусловно обеспечивается
абсолютная устойчивость и грубость системы по варьируемым параметрам. Введены
условия, обеспечивающие абсолютную устойчивость синтезируемой системы.
Весьма удобным для этой цели является критерий абсолютной устойчивости В.М. Попова
в его алгебраической форме. Исследованы ограничения, накладываемые на
синтезируемые параметры системы; подробно рассмотрен алгоритм синтеза с применением
нелинейного программирования.
Рассмотренные далее методы в той или другой мере базируются на теоретических
положениях, определяющих содержание изложенных четырех принципов.
5 Зак. 366
_50 Методы синтеза САУ по заданным показателям качества. Часть II
В заключение отметим, что в большинстве своем методы синтеза регуляторов
не имеют строгого математического обоснования. Построение вычислительной
системы (алгоритма), предназначенной для решения задачи синтеза регуляторов,
есть лишь первый шаг в создании теории метода. За ним должно следовать
выяснение условий сходимости алгоритма, определение скорости сходимости, нахождение
оценки погрешности априорной и апостериорной, выработка способов улучшения
сходимости, если последняя окажется недостаточно быстрой.
С указанной точки зрения, применяемые в инженерной практике методы в
большинстве своем принадлежат к классу эвристических. В такой ситуации приходится
прибегать к любому из методов, который выглядит полезным. Мы неизбежно
обращаемся к проверкам всяких догадок, удачных идей или любых разумных способов
решения рассматриваемой задачи.
Другими словами, процесс синтеза регуляторов является творческим, поскольку в
приведенных ниже методах описаны лишь вычислительные схемы; остальные же
этапы обоснования можно рассмотреть лишь при решении конкретных задач синтеза
регуляторов.
Глава 2. Методы синтеза регуляторов в классе одномерных систем 5J_
ГЛАВА 2. МЕТОДЫ СИНТЕЗА РЕГУЛЯТОРОВ
В КЛАССЕ ОДНОМЕРНЫХ СИСТЕМ
Для случая, когда объект линеен и стационарен, а система - скалярна,
разработано большое число методов синтеза регуляторов. Каждый из этих методов имеет свои
достоинства и недостатки.
Содержание этой главы имеет ярко выраженную инженерную направленность,
поскольку при решении конкретных задач проектирования регуляторов можно
воспользоваться одним из изложенных здесь методов; при рассмотрении основных
положений уделено внимание физической стороне вопроса; поскольку методы
ориентированы на применение ЭВМ, подробно излагается вычислительная технология.
Практически каждый из методов иллюстрируется примерами, взятыми из
инженерной практики.
Для того чтобы изложение не воспринималось в отрыве от запросов практики, в
главе помещен материал, отражающий применение регуляторов в системах,
предназначенных для управления конкретными процессами.
Большинство из изложенных здесь методов в той или иной мере используют
аппарат математического программирования как наиболее конструктивный путь
решения задач расчета параметров регуляторов с большим числом ограничений,
связанных не только с задачей синтеза по заданным показателям качества, но и с
необходимостью обеспечения большого числа ограничений.
Более того, постановка задачи синтеза регуляторов является естественной при
использовании терминов математического программирования, при этом не
исключается и случай, когда невозможно получить целевую функцию и ограничения в виде
явных выражений от варьируемых параметров регулятора рь р2,..., рг.
Вместе с тем изложение часто носит эвристический характер, оно не всегда имеет
достаточно полное теоретическое обоснование, но, тем не менее, метод позволяет
пр;: вдумчивом подходе получить конструктивные результаты при решении
инженерных задач.
2.1. МЕТОДЫ ПОСТРОЕНИЯ ЭТАЛОННЫХ ПЕРЕДАТОЧНЫХ
ФУНКЦИЙ ЗАМКНУТЫХ СИСТЕМ
Как было показано выше, задача синтеза регулятора может быть поставлена
следующим образом.
Задана система автоматического управления (рис. 2.1).
Заданы передаточные функции эталонной системы W3(s) и объекта управления
5*
Рис. 2.1. К постановке задачи синтеза регулятора
52
Методы синтеза САУ по заданным показателям качества. Часть II
Задача заключается в нахождении ПФ регулятора WKy(s).
Но прежде чем переходить к нахождению WKy (s), необходимо определить W3(s)
- передаточную функцию эталонной системы исходя из требований технического
задания.
Изложим некоторые подходы, связанные с определением W3(s).
2.1.1. Построение передаточной функции эталонной системы
в классе оптимизационных задач
Рассмотрим структурную схему замкнутой системы (рис. 2.1).
Сформулируем задачу нахождения эталонной ПФ замкнутой системы следующим
образом [156]: определить ПФ W3(s) замкнутой системы таким образом, чтобы
показатель оптимальности вида
00
/ = J[e2(0 + A.V(0]* (2Л)
о
достигал экстремума.
На первом этапе построим решение задачи без выполнения условия физической
осуществимости.
Имеем
+00
1=i I {1£С/(й)12+х* \uv°f}dOi- (2-2)
Поскольку
s(t) = y(t)-x(t),
Е(уа>) = УС/а») - W(j<a)Y(ju) = 0 - 0Чусо))Г(/о),
*С/а>) = »;Оа>)С/(У<«>),
^оО©) КО®)
то функционал (2.2) принимает вид
_1_
2п
I = j- J |1 - WQof |Г(уш)|2 + X2 |^(уш)|2
УОш)
ВДю)
</со.
(2.3)
Введем следующие обозначения для известных функций переменной <о:
5/©) = |УО(о)|2;
2
5Л«) =
У(у(0)
rr0Un)
(2.4)
Тогда соотношение, определяющее функционал, запишется так:
(2.5)
Далее воспользуемся следующими зависимостями:
|1 - W{j(»tf = (1 - WUa>)){\ ~ П-М) = [1 - »"(-» - »W + Ж(»^(-уо))] =
= 1 - (^(-» + W(J<b)) + ^(уа^С-ую)
Глава 2. Методы синтеза регуляторов в классе одномерных систем 53_
и
5э((о) = 5/со)+5„(со). (2.6)
С учетом (2.6) выражение под интегралом (2.5) можно записать так:
[s/co) + WU&W (~>>)]S,(co) - (W(yco) + W(-yco))S,(a)) +
.^-^ = ко-со)5э(со)-^(со)12-1-+^(^(ЮП (27)
Преобразования, которые были приведены выше, позволили получить
зависимость, в которой искомая частотная характеристика W(j&) входит только в одно
слагаемое.
Теперь функционал, экстремум которого требуется найти, принимает вид
+00 |
+ -
2л
-со
Tfi |2 I Sv(co)SM(co)l
jjwiMSM-sM —+-L_Ji_j<ftD. (2.8)
Поскольку слагаемые в подынтегральном выражении неотрицательны, то
минимизация / сводится к минимизации слагаемого [156]
Или, что то же самое,
Л(ю) = ^Ою)5э(й))-5^ш)|2. (2.10)
Очевидно, / достигает минимума, если
Щусо)5э((о)-^((о) = 0.
Отсюда находим
^(» = -
S,(P)
5/со) + 5а(ш)
но
W0(Jvi)
тогда
,|2
--, КУ°*
^3(7со)= ■ Г " ., , (2.11)
1+КоО«)|
2nl\KU«>)\ 2+Х2
Таким образом [156], оптимальная, в указанном смысле, частотная
характеристика замкнутой системы определяется частотной характеристикой объекта
управления и весовым множителем X2.
При нахождении k(t) = L~l yV3(s)\9 где W3(s) определяется (2.11), не
выполняется условие физической реализуемости k(i) = 0 при / < 0.
Например, если [156]
1 + усо7]
54
Методы синтеза САУ по заданным показателям качества. Часть II
то
W\ja>) =
__к23 _ к3
*э
l + X2|l + 7y<of 1 + 7>2 l + TJm l-TJco
Кэ=-
1 + /L2
- Т — •
Или, что то же самое,
W3(s) =
-*L
1
/1 + Х2
т
2 I гэ^+1 1-т;5
Тогда
*(') =
^"^^о,
(2.13)
^^
е'\ t<0.
Из последнего равенства следует, что ИПФ не удовлетворяет условию
физической реализуемости k(t) = 0 при t < 0.
Поэтому важной является задала определения таких W3(yo>) и WJ(s), которые
удовлетворяли бы условию физической реализуемости.
Проведем соответствующие рассуждения, следуя [156].
Воспользуемся операцией факторизации
S» = |T(»|2 = ^Осо)^(-У(о),
где Ч^усо) имеет верхние нули и полюсы, а Ч'С-у'ш) - нижние нули и полюсы.
Тогда
2
Л(ш) =
ИЧусоЩУш)-
Sy(u)
Т(-уш)
5э(со).
(2.14)
Представим второе слагаемое в последней зависимости в виде (воспользуемся
операцией расщепления)
S»
Т(-усо) ЧЧ-ую)
5у(ш)
«Р(-ую)
(2.15)
причем первое слагаемое имеет верхние полюса, второе - нижние
После проведенных преобразований следует зависимость
S» у \ 5/(0)
Л(ш) =
Отсюда имеем
Ж(усо)Т(усс.)-
^э(уш) =
^(-yo))J [^(-yco)
1 f 5/ш) 1 +
5э(ш).
¥(у(0) Т(-у(о)
(2.16)
(2.17)
- оптимальная устойчивая частотная характеристика.
Так как
кш
(|fro(y(o)|2+X2),
Глава 2. Методы синтеза регуляторов в классе одномерных систем 55_
то для устойчивого, минимально-фазового объекта и типового задающего
воздействия можно записать соотношение
^-Ш*****!-
Зависимость, определяющая оптимальную реализуемую частотную
характеристику, запишется так:
^э(усо) =
W0<Ja)
YU<u)[K(j(of+X2]^
YUvWoH*)
tyoU'nf+Ь2]_
(2.18)
В [156] приведен пример и задачи, иллюстрирующие применение рассмотренного
подхода.
2.1.2. Построение передаточной функции эталонной системы
В КЛАССЕ НИЗКОЧАСТОТНЫХ ФИЛЬТРОВ БАТТЕРВОРСА
Предписанные или желаемые динамические свойства замкнутых систем задаются
соответствующим положением нулей и полюсов ПФ замкнутой системы. Рассмотрим
постановку задачи и методику выбора желаемой ПФ, основанную на использовании
теории низкочастотных фильтров Баттерворса (Баттерворта). Проведем
предварительные рассуждения с учетом принципа фильтрации [93].
Положим, что входной сигнал содержит гармонические составляющие в полосе
О < со < соо.
Условия отработки воздействия без ошибки можно записать в форме
HrWM.)-!!4"0"1-- (219)
1 [0 при со >соо.
Если факт, отраженный зависимостью (2.19), выразить терминами
гармонического анализа, то система с ПФ (2.19) идеально пропускает гармоники с частотами, не
превышающими соо> и идеально подавляет гармоники с частотами со > соо .
Известно, что система с АЧХ вида (2.19) физически не реализуема в классе
систем, имеющих дробно-рациональные ПФ. Однако приближенно такую систему
реализовать можно. Важно помнить о том, что «хорошая» замкнутая система, имеющая
необходимую точность в установившемся режиме и заданные параметры
переходного процесса, должна быть, как правило, близка по своим свойствам к идеальному
низкочастотному фильтру с АЧХ вида (2.19) [93].
Выполним в (2.19) нормирование по частоте и положим сон =со/соо; тогда АЧХ
идеального низкочастотного фильтра будет иметь вид (рис. 2.2). Поскольку, как уже
говорилось, фильтр с АЧХ вида
(1 при 0 < со < 1,
А(а> н) = \ F H (2.20)
v н [0 присон>1
физически не реализуем, то его можно построить, если задать приближение Л2(сон)
в виде (здесь и далее индекс «н» в сон будем опускать) [93]
К(Усо)12=Л2(со)= . 2 . '4 ГЗГ = -Г7Т7- <2'21)
l + ^or+^co 4+...+6„йГп Я„(<о )
56
Методы синтеза САУ по заданным показателям качества. Часть II
Л(*>„) '
1
1
Рис. ?.2. АЧХ идеального фильтра
В последней зависимости требуется найти численные значения Ь^^,...,6Л и п\
Ьо -1, поскольку при этом условии
Запишем формулу для ошибки в полосе частот [0,1]
£>„(©) = !-
1 W)-l
Ви(со2) Вп(о>г)
Или, что то же самое,
D ■ Уо2+^а)4+...+6,,со2" _ у + 6^2+...+У
1 + Ai©2 +U2CO4 + ... + bn®2n l + ^z + ^z2 + ... +V"
(2.22)
(2.23)
где z = со .
Теперь задача стоит в том, чтобы из условия обеспечения, в известном смысле,
минимума Д,(со) подобрать коэффициенты 6^ 62> -А- Например, таким условием
может служить хорошее приближение ЛЧХ идеального фильтра функцией Лдсо) в
области со = 0 и менее точное воспроизведение спада частотной характеристики в
области со = 1. Может быть поставлена задача найти такую аппроксимирующую
функцию Д,(со), которая носила бы колебательный характер с равными амплитудами
колебаний около АЧХ идеального фильтра.
Для того чтобы обеспечить аппроксимацию АЧХ эталонного фильтра функцией
Лл(со) в области со = О, необходимо воспользоваться разложением зависимости,
определяющей ошибку D(z), в ряд Тейлора при z = 0 и коэффициенты разложения
приравнять нулю.
Запишем ряд Тейлора для функции D(z):
D^z) = D^0) + D;(0)^ + d;(0)^ + ... + D^40)^£^ + .... (2.24)
Ряд (2.24) определяет ошибку приближения АЧХ идеального фильтра функцией
(2.23); потребуем, чтобы ряд (2.24) при удержании «и» членов разложения был бы
равен нулю, что равносильно
Dn(0) = /Ш = D;(0) =... = Ztf-^O) = О. (2.25)
Вычисляя производные от функции (2.23) при z = 0, можно показать, что при
аппроксимации Dn(z) рядом Тейлора (л-1)-го порядка все первые коэффициенты
6,, Ь2,..., Ьп_х с учетом (2.25) обращаются в нуль, т.е. ^ = ^ =... = Ьп_х = 0 .
Глава 2. Методы синтеза регуляторов в классе одномерных систем
57
Тогда
At — =
1 + М^
In #
(2.26)
Обычно полагают Ъп -1, поскольку в этом случае граница полосы пропускания
фильтра соответствует значению 0,707. В этом случае аппроксимирующее
выражение принимает вид
1 |тт, / . \\2
a2 -2L
г^=ЫН-
(2.27)
Фильтр, у которого квадрат АЧХопределяется последней формулой, называется
фильтром Баттерворса. Комплексный коэффициент передачи фильтра Баттерворса
будем обозначать через IVE (yco).
На рис. 2.3 и 2.4 приведены АЧХ фильтров, передаточные функции которых
определяются зависимостью (2.27) при различных значениях п.
0,4
0,2
0 0,5 1 1,5 2 2,5 3
Рис. 23. Амплитудно-частотная характеристика фильтров Баттерворса
Для нахождения ПФ фильтра воспользуемся леммой о факторизации [93]
|^Б(у©)|2 = WE(j<oWE(-j<i>) = ^б(*)0б(-4«,» •
Поскольку
1
111 J* 1
Uo>oJ
1
l+(-l)np2n
1+
s
р=—
©о
1
U)
>
I
In
О)2"
l
t \2n
— 1
JTeyCD
(2.28)
4 Зак. 366
58
Методы синтеза САУ по заданным показателям качества. Часть II
то полюсы последней зависимости определяются из уравнения
р2п = ±1, (2.29)
причем (+) соответствует нечетным значениям п, а (-) - четным.
0
1 П
30
40
■20LgA.-.
ДБ
-::
1
|\ ^
IV
\2
\
V 3
\
Д
7Я\\\\ \4
8^\\\\\ \
9^\\\\|\ 5\
\\\\\
к
\
\
\
V
\
со
соо
0,2
0,5
4 5
Рис. 2.4. Логарифмическая амплитудно-частотная характеристика
фильтров Баттерворса
Представляя единицу в комплексной форме, получим
рк =±coscpA iysincp*,
где
при четном п ц)к=(-\)к\ я; к = 0,1,2,..., (л-1);
\ 2п )
при нечетном п ср^ =(-1)Ч — я; к = 0,1,2,..., (л -1).
(2.30)
(2.31)
Таким образом, полюсы лежат на окружности единичного радиуса с центром в
начале координат.
Фильтр Баттерворса, из известных соображений, должен иметь полюсы в левой
полуплоскости, поэтому полюсы такого фильтра определяются зависимостью
рк =-cos(j>£ ±ysinq>£. (2.32)
Численные значения полюсов представлены в табл. 2.1.
Таблица 2.1
1
2
1
2
3
Действительная часть полюса
Мнимая часть полюса
л = 2
-0,7071067812
-0,7071067812
-0,7071067812/
-0,7071067812/
А7 = 3
-1,0000000000
- 0,5000000000
-0,5
0,0000000000/
0,8660254038/
- 0,8660254038/
Глава 2. Методы синтеза регуляторов в классе одномерных систем
59
Окончание табл. 2.1
1
2
3
4
1
2
3
4
5
1
2
3
4
5
6
1
2
3
4
5
6
7
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
10
-0,9238795325
-0,3826834324
-0,3826834324
-0,9238795325
- 1,0000000000
-0,8090169944
-0,3090169944
-0,3090169944
-0,8090169944
-0,9659258263
-0,7071067812
-0,2588190451
-0,2588190451
-0,7071067812
-0,9659258263
- 1,0000000000
- 0,9009688679
-0,6234898019
- 0,2225209340
- 0,2225209340
. -0,6234898019
-0,9009688679
- 0,9807852804
-0,8314696123
-0,5555702330
-0,1950903220
-0,1950903220
-0,5555702330
-0,8314696123
- 0,9807852804
-1,0000000000
-0,9396926208
-0,7660444431
- 0,5000000000
-0,1736481777
-0,1736481777
-0,5000000000
-0,7660444431
-0,9396926208
- 0,9876883406
-0,8910065242
-0,7071067812
-0,4539904997
-0,1564344650
-0,1564344650
-0,4539904997
-0,7071067812
-0,8910065242
-0,9876883406
/7 = 4
л = 5
п = в
п = 1
/? = 8
/2 = 9
л = 10
-0,3826834324/
0,9238795325у
-0,9238795325/
0,3826834324/
0,0000000000/
0,5877852523/
-0,9510565163;
0,9510565163/
-0,5877852523/
-0,2588190451;
0,70710678127
-0,9659258263/
0,9659258263/
-0,7071067812/
0,2588190451/
0,0000000000/
0,4338837391/
-0,78183148257
0,9749279122/
-0,9749279122/
0,7818314825/
-0,43388373917
-0,1950903220/
0,5555702330/
-0,83146961237
0,9807852804/
- 0,9807852804/ .
0,8314696123/
-0,5555702330/
0,19509032207
0,0000000000/
0,34202014337
-0,6427876097/
0,8660254038/
-0,98480775307
0,9848077530/
-0,86602540387
0,6427876097/
-0,34202014337
-0,15643446507
0,4539904997у
-0,7071067812/
0,8910065242/
- 0,9876883406/
0,9876883406/
-0,8910065242/'
0,7071067812/
-0,4539904997/
0,1564344650/
j60 Методы синтеза САУ по заданным показателям качества. Часть II
Если Ьп Ф1, то р2п = ±— и
рк = р(-cosф* ± jsinфк\ (2.33)
где р = 2п\— .
\О„
Величина неравномерности частотной характеристики учитывается множителем р .
Если известны полюса Р\, р2, •••, Рп »то ПФ может быть представлена в виде
W^p) = т V( Ц—; г. (2.34)
КР-Р\){р-Рг)-\Р-Рп)
При п четном последняя зависимость принимает вид
1
ОЛР)
Wb(p) = -2 = ^7Т7' (2-35)
п
а если п - нечетное, то
ШР) = д = -7Г77Т> (236)
1 =
Dn(p)
(p+<Ji)f[(p2+quP+<ioi)
где
D](p) = p + \;
D2(p) = p2 +1,4142/7 + 1;
D3(p)^(p + \)(p2+p + \);
D4(p) = (p2 +0,7654/7 + l)(p + 1,8478/7 + 1);
D5(/7) = (/? + l)(/72+0,6180/? + l)(/?2 +1,6180/7 + 1);
^6(P) = (p2+0^176/7 + l)(/72+l,4142p + l)(/72 +1,9319/7 + 1); (2-37)
D7(/?) = (/7 + l)(/72+0,4450/7 + l)(/72.+ l,2470/7 + l)(/72+1,8019/7 + 1);
D8(/7) = (/72+0,3902/7 + l)(/72+l,llll/? + l)(p2+l,1663p + l)(/72 +1,9616/7 + 1);
^9(P) = (p + 0(/?2+0>3473/? + 1)(/72+^ + 1)(/?2+1'5321p + l)(/72+l,8794p + l);
Ao(/?) = (p2+o>3129p + 1)(p2+O'9O8°/? + 1)(^2+1'4142^ + 1)x
x(p2 +1,7820/?+ l)(p2 +1,9754/7 + 1).
Зависимости, определяющие D|(p), D2(p\..., D10(/7)?можно переписать в виде
Dn(p) = \ + d]P + d2p2 +d3p3 +... + рп, (2.38)
причем do=dn =1.
Полином Dn(p) называется полиномом Баттерворса
Коэффициенты полиномов Баттерворса d]y d2, ..., dnm.x вычислены; их значения
до п = 10 приведены в табл. 2.2.
Глава 2. Методы синтеза регуляторов в классе одномерных систем
61
Таблица 2.2
4
dx
4
4
4
4
4
4
4
4
4o
л = 2
1
1,41421
1
w = 3
1
2
2
1
л = 4
1
2,61313
3,41421
2,61313
1
л = 5
1
3,23607
5,23607
5,23607
3,23607
1
/i = 6
1
3,8637
7,4641
9,14162
7,4641
3,8637
1
л = 7
1
4,49396
10,0978
14,5918
14,5918
10,0978
4,49396
1
л = 8
1
5,12583
13,1371
21,8462
25,6884
21,8462
13,1371
5,12583
1
я = 9
1
5,75877
16,5817
31,1634
41,9864
41,9864
31,1634
16,5817
5.75877
1
/2 = 10
1
6,39245
20,4317
42,8021
64,8824
74,2334
64,8824
42,8021
20,4317
6,39245
1
Из приведенных выше формул следует, что фильтр Баттерворса - каскадное
соединение звеньев с ПФ вида [75]
^Б,(Р) =
/>2+2$,соо//? + с4
(2.39)
где о)О/ - собственная частота звена, £ - коэффициент демпфирования, причем
соО/=7^"Д/=гТ=- (240)
2V<3ro/
Для звена первого порядка можно записать
^б/О>) = -^Ч 0)0,= ?,, (2.41)
/? + ю0,
Поскольку полюса ПФ известны, то можно рассчитать и нормированные
переходные процессы. Переходные функции фильтров Баттерворса показаны на рис. 2.5.
ь Л„(со0г)
1,2
0,8
0,6
0,4
0,2
-0,2
0 2 4 6 8 10 12 14 16 18 20
Рис. 2.5. Графики нормированных переходных характеристик фнлмроь < л.г^ъмуъл
62
Методы синтеза САУ по заданным показателям качества. Часть II
Ненормированное время определяется выражением / = т/со0 и, следовательно,
Тр(п) = т0(и)/со0 - время переходного процесса п -го фильтра Баттерворса.
Фильтры Баттерворса имеют АЧХ, близкую к идеальной низкочастотной (и
быстро стремящуюся к ней при л-»оо), причем граница, вплоть до которой АЧХ близка к
единице, почти совпадает с частотой соо (или равна единице, если частота
нормированная). Однако с ростом п растут фазовые искажения.
Рассмотрим фазочастотные характеристики фильтров Баттерворса. Фазовые
сдвиги, вносимые звеньями первого и второго порядка и определяющими фильтр
Баттерворса как их каскадное соединение, могут быть представлены соотношениями
со
со/
Ф/ — = ~arctg
юо [ ш i
Фу — ="arctg
1 соо
2^,сОоЛ
со0
©О/"
(2.42)
тогда, например, фазочастотная характеристика фильтра Баттерворса для четного п
определяется зависимостью [75]
со | ^ со0
— =-£arctg—
Ф
СОл
/=1
«о/-
2'
(2.43)
Характеристикой фильтров Баттерворса является и время групповой задержки t3,
определяемой формулой [75]
'э =
, СО
^Ф
(2.44)
Соответствующие фафики приведены на рис. 2.6 и 2.7.
1
и
400
600
со
Ч
ш
щ
\
Si
S
ч
ч
N
Ч
ч
ч
ч
ч
к.
\
'^
ч
Ч
ч
Ч
ч
п
ч
ч
S
= 2
хм*
4
5
7
8
ч
К»
■^*
*ч»
«^*
mm
*^
■*■
BS=
**.
=5
**•
•ма
«мм
1^
•««
ч«
■NM.
СО
со0
0,5
1,0
1,5
2,0
Рис. 2.6. ФЧХ фильтров Баттерворса
Глава 2. Методы синтеза регуляторов в классе одномерных систем
63
Из рисунка, на котором представлены фазочастотные характеристики, следует, что
с ростом п растут фазовые искажения и на частоте соо ф — может существенно
• , V^o/
отличаться от нуля, что является отрицательным свойством фильтров Баттерворса.
В заключение отметим, что для аппроксимации АЧХ идеального фильтра могут
быть использованы полиномы Чебышева (равноволновая аппроксимация) и
полиномы Лежандра (фильтры класса L). О их возможностях можно судить по рис. 2.8 -
2.11, на которых представлены АЧХ и ФЧХ указанных фильтров [75].
О
0,1 0,2 0,5 1 2 3 4
Рис. 2.7. Характеристики времени групповой задержки фильтров Баттерворса
i
0
5
10
15
20
п = 2
/
5
/
4
q
1
1\
-
1 \
1 \
\
11 \
\
\
0,7647
со
со0
1 ■►
0,1 0,2 0,5 1 2
Рис. 2.8. АЧХ чебышевских фильтров
3 4 5
64
Методы синтеза САУ по заданным показателям качества. Часть II
400
600
0,1 0,2
2 3 4
Рис. 2.9. ФЧХ чсбышсвских фильтров
1
Л
10
20
30
40
■1
■
ш
ш
i
\V\
\\\ X
\\\
\\\
\\\
\\>
\\
\ \
\
\ > \
\ \ \
\ Pv
\ \
\ 1 ^
ч
ч
\
0)
(O0
0,1 0,2 0,5 1 2 3 4
Рис. 2.10. АЧХ фильтров класса L
Основы подхода к выбору и и соо изложим, следуя [93].
Положим, что требования, связанные с качеством работы системы в
установившемся режиме, т.е. с точностью отработки воздействия, сформулированы так:
1. Замкнутая система должна быть устойчивой.
2. Замкнутая система должна иметь заданную точность в установившемся
режиме при обработке линейного сигнала: если у(О = уо+у^ и l^j^yf -
предельная скорость изменения сигнала y(t), то установившаяся ошибка не
должна превышать некоторого наперед заданного значения 8], т.е. |е(г)| < г*
при / £ Гр, где е£ - предельная допустимая ошибка обработки y(t).
Аналогичные условия можно сформулировать для гармонического
полезного сигнала и помехи, частоты которых заданы на промежутках Qm и Qn .
Глава 2. Методы синтеза регуляторов в классе одномерных систем
65
3. Пусть обрабатываемое воздействие определяется формулой
/w(/) = /wcosco/ и т<тд
для любых со е Qm ; тогда
\г(0\<глт при/>Гр,
где тл - заданная предельная амплитуда сигнала m(t), a е* - заданная
предельная допустимая ошибка.
4. Помеха определяется зависимостью
где «л < л£ - предельная амплитуда помехи, а на вызванную наличием n{t)
ошибку накладывается требование
|е(/)|<е* при t>Tp,
причем ел - заданная величина.
i
0
200
400
600
4-)
т
i
S
V
N
S
S
s
^^ л = 2
-■■ ■
СО
0,1 0,2 0,5 1 2 3
Рис. 2.11. ФЧХ фильтров класса L
Условия 1 - 4 можно рассматривать как требования к качеству системы.
Выполнение указанных требований связано с рядом неравенств, вывод которых
приводится в [93]:
\2
1
1 —
1 + 1^-
С0л
1
2л
**•""■•
Dn\^
i<(«-)"l
©<©„,.
(2.45)
(2.46)
С учетом сказанного выше алгоритм выбора соо и п в фильтрах Баттерворса
заключается в том, чтобы выполнялись условия [93]
66 Методы синтеза САУ по заданным показателям качества. Часть II
sin^coo >maxfe^|, с0 <ш„| ^ | , (2.47)
причем величины у*, ют, тА, cow, п* - характеризуют допустимые по
техническим условиям воздействия, а параметры е* и е* определяют требуемую точность.
Что касается требований к качеству работы системы в переходном режиме, то для
фильтров Баттерворса значение для величины перерегулирования от(п) = max/*„(/)-1
и времени переходного процесса тр(л) = (о0Гр(л) можно определить по графикам,
представленным на рис. 2.5.
При проведении расчетов необходимо помнить, что с увеличением п
перерегулирование растет (см. рис. 2.5), но является практически удовлетворительным до
п - 5 ; наименьшее время переходного процесса имеет место при « = 2и
г,*.)-*».
Дополнительное ограничение на выбор параметров вида
ТрОО
СОп >
тр
соответствует предельно допустимому времени переходного процесса.
2.1.3. Метод стандартных коэффициентов построения
эталонной передаточной функции
Между характером переходной и передаточной функций системы существует
сложная, но тем не менее вполне определенная связь. Вид переходной функции
определяется значением нулей (корней числителя) и полюсов (корней знаменателя)
передаточной функции. Для любой конкретной формы передаточной функции может
быть найдено некоторое «оптимальное» распределение нулей и полюсов, при
котором переходная функция будет наиболее благоприятной с точки зрения динамики
рассматриваемой системы. Каждому такому оптимальному распределению нулей и
полюсов соответствует вполне определенное значение коэффициентов полиномов
числителя и знаменателя передаточной функции, которое назовем стандартным.
Далее построим изложение, следуя [47, 62, 102].
Любой характеристический полином замкнутой САУ:
D(s) = ansn +an_xsn~x +an_2sn-2 +... + <v + a0 (2.48)
можно записать в виде
D(s) = sn -f^L-co^-1 +^-L.co^2 +... + _Lco^ + co2, (2.49)
апщ апщ а„©о~
где ш0 = п\
Или, что то же самое,
где
(2.50)
Глава 2. Методы синтеза регуляторов в классе одномерных систем
67
В качестве первой типовой функции можно взять передаточную функцию вида
cog
ЖЭ(5) = -
(2.51)
s" +/*1Gv"~1 +A2(o20s"-2 +...+ An_]Q)n0-]s + (on0 '
Для системы с ПФ (2.51) можно получить переходный процесс без
перерегулирования, когда корни знаменателя все вещественны. При всех вещественных корнях и
при 0)0 = const наименьшее время регулирования будет, если все корни будут
кратными. В этом случае коэффициенты Л15 Л2,..., АпА окажутся коэффициентами
бинома Ньютона (s + 1)". В табл. 2.3 приведено значение этих коэффициентов для л,
равного 1,2, 3, 4, 5,6.
Таблица 2.3
п
1
2
3
4
5
6
Коэффициенты знаменателя
1 1
1 Л г*2 1
1 Л,=ЗЛ2=3 1
Ы,=4Л2=6Лз=4 1
Ыг=5Л2=10Лз=10Л4=5 1
1 ^,=6^2=15^1=20^4=15^5=6 1
То
3
4,8
6
7,9
9
10,6
Введем в рассмотрение безразмерное время переходного процесса т0 = со0Гр.
Действительное время переходного процесса определяется зависимостью
Гр = т0 /со0 . В табл. 2.3 приведено время переходного процесса т0 для систем
различного порядка.
На рис. 2.12 представлены графики переходных функций, ПФ которых
определены стандартными коэффициентами, приведенными в табл. 2.3.
Если в переходной функции допустимо некоторое перерегулирование, то корни
можно взять комплексными, благодаря чему сокращается также время управления.
Полином знаменателя передаточной функции W{s) замкнутой системы
представляется в форме произведения nil одинаковых квадратных трехчленов
Д5) = (5Ч2^ю05 + сй^)"/2=5/7+^о)05л"1+... + 4_1(о^15+(о2. (2.52)
10
Рис. 2.12. Графики переходных функций для систем с передаточной функцией
типа (2.51) и коэффициентами, определяемыми по табл. 2.3
68
Методы синтеза САУ по заданным показателям качества. Часть II
Значение £ = 0,75. При п нечетном знаменатель передаточной функции W(s)
состоит из (л-1)/2 квадратных трехчленов и одного двучлена первой степени. Св'о$од<-
ный член этого двучлена принимается равным единице. Значения коэффициентов
Ах,А2,...,АпА приведены в табл. 2.4.
Таблица 2.4
п
2
3
4
5
6
Коэффициенты знаменателя
1 1,5 1
1 2,5 2,5 1
, 1 3 4,25 3 1
1 4 7,25 7,25 4 1
1 4,5 9,75 12,375 9,75 4,5 1
то
2,9
4,4
5,15
6,20
6,7 '.
В табл. 2.4 приведено безразмерное время регулирования т0 для систем
различного порядка. Сравнивая это время с его значением для систем, имеющих
коэффициенты, определяемые табл. 2.3, видим, что при одинаковых значениях п время
регулирования в последнем случае существенно меньше.
На рис. 2.13 представлены графики переходных функций для систем, определе*
ных стандартными коэффициентами, приведенными в табл. 2.4.
*(тУ
1,0
0,8
0,6
0,4
0,2
у
J
Д = 0,05
д'
/
у
/
п
4
/
/
т~
/
/
/
/
/
И
1
г
1
1
1 1
1 1
о
1
8
4.
Рис. 2.13. Графики переходных функций для систем с передаточной функцией
типа (2.51) и коэффициентами, определяемыми по табл. 2.4
Рассмотрим передаточную функцию, имеющую один нуль:
хя-1
W3(s) = .
А-1в>0 ■у + с°0
sn + Axa>osn-l+... + An_yo Л + coS
(2.53)
Чтобы уменьшить выброс, вызванный влиянием нуля, надо замедлять скорость
нарастания переходной функции. Это можно сделать «разведением» корней
полинома знаменателя по действительной оси.
При передаточной функции с одним нулем корни рекомендуется располагать на
отрицательной вещественной полуоси по арифметической прогрессии./Значения
коэффициентов полинома знаменателя в формуле (2.53) для такого распределения ко^ .
ней приведены в табл. 2.5.
Глава 2. Методы синтеза регуляторов в классе одномерных систем
69
Таблица 2.5
п
1
2
3
4
5
6
1 -й член прогрессии
0,5
0,183
0,098
0,063
0,039
0,039
Разность
прогрессии
-
1,5
1,517
1,138
0,86685
0,717
Коэффициенты знаменателя
1 1
12,5 1
1 5,1 6,35 1
17,22 16,3 11,83 1
192938 18 1
1 11 45,8 92,3 82,3 27,7 1
На рис. 2.14 представлены графики переходных функций для систем,
определяемых стандартными коэффициентами табл. 2.5.
0,2
8
Рис. 2.14. Графики переходных функций для систем с передаточной функцией
типа (2.5Э) и коэффициентами, определяемыми по табл. 2.5
Рассмотрим передаточную функцию с двумя нулями:
*Г(5):
.хЛ-2„2
.л-1.
4.-2PQ S +4,-1в>0 * + Щ
(2.54)
Чтобы уменьшить влияние нулей, рекомендуется располагать корни полинома
знаменателя на отрицательной вещественной полуоси по геометрической прогрессии.
В табл. 2.6 приведены значения коэффициентов полинома знаменателя А^, А2,
..., 4м для такого распределения корней.
Таблица 2.6
п
3
4
5
6
1-й член
прогрессии
0,182
0,185
0,075
0,038
Знаменатель
прогресси
5,5
3,08
3,63
3,7
Коэффициенты знаменателя
1 6,7 6,7 1
17,9 15 7,9 1
1 18 69 69 18 1
136 251485 25136 1
Т()
1,5
3,3
9,2
-
70
Методы синтеза САУ по заданным показателям качества. Часть II
-f
3 / 4 / 51
!
//
У/
/
(-
/
/
п = 6
/
/
/
/
f
А
► s
штяшаш—л
"-■ ■—
кД = 0,05
—t-
"■ —.
"*- *•
1——.
"I1 —
1,2
1,0
0,8
0,6
0,4
0,2
Рис. 2.15. Графики переходных функций для систем с передаточными функциями
типа (2.54) и коэффициентами, определяемыми по табл. 2.6
Метод стандартных коэффициентов нашел широкое применение при решении
задач проектирования систем управления летательными аппаратами [22, 47]; подробно
с основными положениями метода можно познакомиться в [47, 62,102] и др.
В настоящем параграфе изложены лишь некоторые подходы к определению
эталонных ПФ замкнутых систем. Следующей важной задачей является построение
таких регуляторов с ПФ W^is), которые обеспечили бы приближенное в общем
случае равенство реальной ПФ замкнутой системы W(s) и заранее выбранной
эталонной ПФ W3(s). Этот вопрос подробно рассмотрен ниже.
2.2. ПРИНЦИП ДИНАМИЧЕСКОЙ КОМПЕНСАЦИИ И АНАЛИЗ ЕГО
ЭФФЕКТИВНОСТИ ДЛЯ КЛАССА СТАЦИОНАРНЫХ СИСТЕМ
В параграфе 1.4 было введено понятие принципа динамической компенсации.
Основная формула, определяющая оператор регулятора, имеет вид (формула (1.51))
Ац = А;х(1-А9уХА\ (2.55)
В настоящем параграфе подробно обсудим вопрос применения принципа
динамической компенсации к классу стационарных линейных скалярных систем.
Пусть W*(s) - эталонная передаточная функция замкнутой системы; она выбрана
из условия обеспечения необходимого качества работы САУ в переходном и
установившемся режимах (параграф 2.1).
Найдем передаточную функцию эталонной разомкнутой системы (рис. 2.16).
Имеем
W[5) uw;{,y
Глава 2. Методы синтеза регуляторов в классе одномерных систем
71
тогда
w>(,)(i+w;{s))=w;(s).
Отсюда находим
w(s)+w(s)w;(,)=w;{s),
или, что то же самое,
w>(,)-rr;{,)-w>{s)tr;{')-w;{s)(i-w{,)).
Легко записать выражение для эталонной ПФ разомкнутой системы
Рис. 2.16. Структурная схема эталонной системы
►us/ w
W3(s)
W3(s)
1
x(t)
Рис. 2.17. Структурная схема эталонной системы
Задача синтеза регулятора иллюстрируется рис. 2.18.
yd)
Г
(s)
W
*
)
(')
x(t)
Рис. 2.18. К постановке задачи коррекции
Из анализа структурных схем 2.16 и 2.18 сразу же следует, что задача коррекции
получает решение при выполнении следующего условия
W>(s) = lVKy(s)W0(s). (2.57)
Поставим следующий вопрос: при каких условиях имеет место равенство
передаточных функций W*(s) и ^(s)? Очевидно, такое равенство справедливо, если ПФ
объекта управления WQ(s) = 1, т.е. объект безынерционный. Равенство WQ(s) -1
может быть достигнуто, если скомпенсировать динамику объекта, вводя в прямую цепь
дополнительное звено, имеющее ПФ, обратную ПФ объекта управления (это звено
называют компенсатором); тогда имеет место равенство
W0{s)W-\s) = \
и структурная схема скорректированной системы принимает вид (рис. 2.19).
72
Методы синтеза САУ по заданным показателям качества. Часть II
y(t)
*(')
Рис. 2.19. Структурная схема скорректированной системы
Или, что то же самое (рис. 2.20).
аЕ(0*
г
г
\
\-W\s)
1
I
Рис. 2.20. Структурная схема скорректированной системы
(динамика объекта скомпенсирована)
Таким образом, исходя из физических соображений, получено формальное
решение задачи синтеза регулятора с эталонной передаточной функцией замкнутой
системы W3(s) (ПФ компенсатора можно рассматривать как часть ПФ регулятора, тогда
WKy(s) = W3(s)W^l(s) (рис. 2.19)). Формальные рассуждения приводят к тому же
результату.
Поставим задачу так: полагая известными ПФ неизменяемой части WQ(s) (как
уже принято, WQ(s) называют ПФ объекта; сюда же входят ПФ исполнительного
элемента, усилительных устройств, измерительных систем и т.д.) и W3(s), найдем
ПФ W^(s) корректирующего устройства (регулятора) (рис. 2.18). Справедлива
зависимость для fV3(s)
V ' \ + Wv{s)W0(s)'
(2.58)
Тогда
*Г(,)(1 + ^(,)*0(*)) = ^у(*)»'в(*).
Отсюда получаем соотношение
-WKy(s)Wo(s)W^s) + WKy(s)Wo(s) = W3(s).
Или, что то же самое:
^(s)[W0(s) - W0(s)W >(s)] = W \s).
Из последней формулы следует
*Г3(*) _,„-!,
*М*) = "
rw-l(s)w;{s).
(2.59)
W0(s)(\-W>(s))
Из формулы (2.59) легко заключить, что ПФ корректирующего устройства (КУ)
состоит из двух частей: первая часть включает W3(s) и определяется
зависимостью (2.56); вторая же часть имеет ПФ9 обратную передаточной функции
объекта. Структурная схема системы с КУ, определяемым формулой (2.59), представлена
на рис. 2.19.
"лава 2. Методы синтеза регуляторов в классе одномерных систем
73
Поскольку W*(s) определяется выражением (2.56), то окончательно структурная
схема скорректированной системы имеет вид, представленный на рис. 2.21.
Поскольку W~l(s)W0(s) = 1, то имеет место структурная схема (рис. 2.20),
которая совпадает со схемой, представленной на рис. 2.19.
ЧЛ/ 1-й"
(£L
w*№
w;\s)
W0(s)
W(s) = l
Рис. 2.21. Структура регулятора, имеющего ПФ WK (s)
Изложенный способ синтеза называют методом Динамической компенсации [64, 93].
Такое название обусловлено тем фактом, что ПФ корректирующего устройства
содержит сомножитель W~l (s), обратный передаточной функции неизменяемой части.
7~\i
За счет введения сомножителя Wo (s) компенсируются динамические свойства
неизменяемой части (рис. 2.21).
Пример 2.1.
Рассмотрим задачу синтеза регулятора на примере канала крена, полагая:
а) К1у=1; КпрКу =62; Гу=0,3 с; Гр=2,4 с, W0(s) = -
*пр*Т
s(Tys + Kly)
б) Эталонную ПФ замкнутой системы найдем, воспользовавшись методом стандартных
коэффициентов; она имеет вид (см. табл. 2.3):
»"(*)=
S2 + AxGiQS + Gil
Поскольку coo=-SL = -i- = 2 ,то
Тр 2,4
v ' 52+4j + 4
Учитывая, что
- ПФ замкнутой системы.
-.■«■^••'••1М-*Г1-
можно определить ПФ регулятора:
Пример 2.2 [93].
Положим, что
К(*) =
Ts + \
, К>0, Г>0,
а эталонная ПФ определяется зависимостью
s + K
т, К >0.
Тогда ПФ регулятора может быть записана в форме (2.59). Поскольку
к'
у.М- »"(*)
(2.60)
(2.61)
(2 62)
(2.63)
(2.64)
74
Методы синтеза САУ по заданным показателям качества. Часть II
то
^•>=¥44'К}
Последняя ПФ определяет ПИ-управление
u(t)^T е(*) + 1|в(т)Л .
(2.65)
(2 66)
Обсудим полученный результат с точки зрения эффективности применения
принципа динамической компенсации для синтеза корректирующих устройств.
1. КУ является весьма сложным, поскольку должно включать две части:
компенсирующую (обратная передаточная функция объекта) и эталонную (ПФ разомкнутой
эталонной системы).
2. Регулятор в общем случае содержит дифференцирующие звенья, входящие в
составляющую W~x(s). Эти звенья физически трудно реализуемы. Приведем один из
вариантов реализации [93]. Найдем ПФ замкнутой системы, представленной на
рис. 2.22.
ЛЬ
^Ц8Н
к
кп
Г05 + 1
Рис. 2.22. К вопросу реализации форсирующего звена
W{s) =
К
_ K(Tos + \)
\ + KKo/(Tos + \) Tos + \ + KKo
K(Tos + \)/(l + KKo)K3(Tos + \)K
Tos/(\ + KKo) + l T3s + l Л ° h
(2.67)
поскольку Тэ -> 0 при К -> <х>. Отсюда легко сделать вывод: охват усилительного
звена с большим коэффициентом усиления инерционной отрицательной обратной
связью с ПФ W^s) = Ко /(TQs +1) позволяет получить реальное форсирующее звено,
выходом которого является производная от входного сигнала. Кроме того, отметим
известный факт: дифференцирующие звенья усиливают влияние помех на качество
работы системы.
Однако при некоторых условиях регулятор оказывается физически реализуемым,
т.е. он не содержит дифференцирующих звеньев.
В самом деле, пусть
Пусть т - степень полинома числителя передаточной функции WQ{s);
п - степень полинома знаменателя передаточной функции W0(s);
р - степень полинома числителя передаточной функции W^{s);
q - степень полинома знаменателя передаточной функции ^ку(^).
Передаточная функция замкнутой эталонной системы
(2.68)
(2.69)
Глава 2. Методы синтеза регуляторов в классе одномерных систем 75_
Пусть а - степень полинома числителя передаточной функции W3(s)\ р -
степень полинома знаменателя передаточной функции W3(s).
Для реализуемой W3(s) должно быть р>сх.
Передаточная функция регулятора будет реализуема, если q> p . Пусть тип
фиксированы. Определим, какие условия надо наложить на а, Р, чтобы q> p . Так как
,,(,,. '•W-14, (2.70)
то
W {Л W'(s) P{')A(s) _R(s)
W"{']* W0{s)[l-W>{s)] B(s)[D(s)-P(s)] C(s)- (2-?1)
Откуда
p = a + n\ ^ = /w + p; p^q, если a + n < m + P,
или P~a>n-m.
При таких условиях передаточная функция последовательного корректирующего
устройства при заданной неизменяемой части системы будет реализуема [123].
3. Из-за неточного знания W0(s), а также вследствие влияния нелинейностей
системы полная компенсация никогда не достигается, и это порождает новые колебания
в системе.
4. При сокращении нулей и полюсов система не обладает свойством грубости
(при малых отклонениях параметров системы отклонения величин, характеризующих
состояние системы, могут быть достаточно большими [64]).
5. Система в некоторых случаях может оказаться неустойчивой [64, 93].
Рассмотрим этот вопрос более подробно.
Найдем характеристическое уравнение замкнутой системы.
Поскольку
"W C(s)'
а
o{)~A(s)'
то
R(s) B(s)
Щ"Щ R(s)B(s)
[)~l + M.M C(s)A{s) + R(s)B(,y Ц12)
C(s) A(s)
Характеристическое уравнение имеет вид
N(s) = C(s)A(s) + R(s)B(s). (2.73)
Так как
т
1 D(s)
16 Методы синтеза САУ по заданным показателям качества. Часть II
то ПФ регулятора определяется зависимостью
W> B(s) (D(s)-P(s)) C(s)'
и, следовательно,
R(s) = A(s)P(s), (2.74)
C(s) = B(s)(D(s) -P(s)). (2.75)
Последние соотношения позволили выразить передаточную функцию регулятора
через A(s) - знаменатель ПФ объекта и B(s) - числитель ПФ объекта. Здесь
необходимо обратить внимание на тот факт, что ПФ регулятора определяется через ПФ
объекта управления, т.е. через полиномы A(s) и B(s) (это следует из формулы (2.75)).
Подставив (2.74) и (2.75) в зависимость, определяющую характеристическое
управление замкнутой системы, найдем
N(s) = A(s)B(s)(D(s)- P(s)) + B(s)A(s)P(s) = A(s)B(s)D(s). (2.76)
Отсюда следует: поскольку характеристическое уравнение скорректированной
системы содержит A(s) и B(s), определяющие ПФ объекта в соответствии с формулой
(2.68), то наличие правых нулей и (или) полюсов объекта приводит к тому, что
характеристическое уравнение скорректированной системы будет иметь правые полюса, и,
таким образом, эта система при указанных условиях становится неустойчивой.
Другими словами, метод динамической компенсации применим лишь в том
случае, если объект не содержит правых нулей и (или) полюсов.
Область применимости метода, использующего принцип компенсации, можно
расширить, если с помощью внутренней обратной связи провести стабилизацию
объекта управления [93].
Имеют место и другие «подводные камни», анализ которых проводится в [93];
там же рассмотрены специальные процедуры стабилизации и приведен общий
алгоритм синтеза закона управления произвольными объектами, включая неминимально-
фазовые.
Из сказанного выше следует, что применение принципа динамической
компенсации требует большой осторожности. При расчете конкретных систем необходимо
провести анализ влияния указанных выше факторов на качество работы, системы.
Метод интересен с той точки зрения, что приводит формально к точному решению
поставленной задачи. Из изложенного можно сделать вывод, что метод решения
задачи синтеза регуляторов следует искать в классе приближенных (аппроксимацион-
ных) методов, использующих аппроксимацию основной зависимости во временной
или частотной областях. Такой подход позволит получить методы, дающие хотя и
приближенное, но физически реализуемое решение, обеспечивающее качество
работы САУ, близкое к заданному.
2.3. РАСЧЕТ РЕГУЛЯТОРОВ С ПОМОЩЬЮ УРАВНЕНИЙ СИНТЕЗА
В ряде работ предложен подход, позволяющий решить задачу синтеза
регуляторов с устранением некоторых недостатков, присущих принципу динамической,
компенсации [64].
Идея подхода состоит в том, что передаточная функция замкнутой эталонной
системы при предположении, что
^о(*) = ^> (277)
A(s)
"лава 2. Методы синтеза регуляторов в классе одномерных систем п_
юлжна удовлетворять следующим условиям:
W 3(s) = ^ = —— - ПФ замкнутой эталонной системы; (2.78)
D(s) D(s) У
C(s)A(s)
1 - W э(.у) = - ПФ ошибки замкнутой эталонной системы, (2.79)
где
D(s) = do + d]s + d2s2 + ...+d2n_ls2n-l+s2n
- эталонный характеристический полином;
В ($) = Ьо + bxs + b2s2 + ... + bn_x sn'x;
A (s) = a0 + axs + a2^ 2 + ... + sn.
Полиномы Л(^) и A(s) - известны, они определяют динамические свойства
неизменяемой части; эталонный полином D(s) выбирается специальным образом,
например, методом стандартных коэффициентов, но так, чтобы были реализованы
предписанные динамические свойства замкнутой системы. Это достигается тем, что
D(s) является характеристическим уравнением замкнутой системы, а расположение
корней характеристического уравнения Si,s29---9s2n в левой полуплоскости
комплексной области определяет параметры переходного процесса:
• быстродействие (время переходного процесса);
• колебательность (число колебаний и их частоту);
• перерегулирование а% и др.
Таким образом, в качестве эталона задается только полином D(s), на числитель же
соответствующие требования не накладываются. Вместе с тем изображение
переходного процесса выражается зависимостью
H{s)J_RW')mlUL. (2.80)
V ; s D(s) sD(s) K '
Если корни характеристического уравнения простые, то зависимость для />(/) -
переходного процесса имеет вид
где sk - корни уравнения D(s) = 0.
Как видно из (2.81), элементарные колебания hk(t) = eSk' определяются корнями
sl9s2,...,s2n и полностью характеризуют структуру сигнала h(t). Однако
амплитуда элементарных колебаний определяется как полиномом D(s), так и числителем
P(s); в связи с этим необходимо анализировать динамические свойства замкнутой
системы после ее синтеза. Например, если решается задача коррекции в классе
систем не содержащих интегратор в прямой цепи, то найденный регулятор может
.обеспечить заданные быстродействие, степень колебательности и перерегулирование, при
наличии недопустимо большой установившейся ошибки.
ПФ корректирующего устройства определяется зависимостью
где
IS Методы синтеза САУ по заданным показателям качества. Часть II
R(s) = ro + rxs + r2s2 + ...+rn_xsn~];
C(s) = co + c]s + c2s2 + ...+cn_ls"-l+s";
коэффициенты полиномов R(s) и C(s) подлежат определению.
Для ПФ замкнутой системы справедливо соотношение
ММ
,rf;) *(*W. C(s)A(s) R(s)B(s)
^W l + MM C(s)A(s) + R(s)B(s)-
C(s) A(s)
Из зависимости (2.82) находим
D(s) = A(s)C(s) + B(s)R(s). (2.83)
Последнее уравнение называется уравнением синтеза, поскольку оно позволяет
найти неизвестные го,гх,...,гп_х,со,сх,...,сп_х [64].
Уравнение синтеза при строгом рассмотрении вопроса находится из соотношений
(2.78) и (2.79), поскольку
R(s)B(s) C(s)A(s)
D(s) - D(s) ' ,
Отсюда сразу же следует (2.83). Синтезированная описанным методом система
устраняет некоторые недостатки, присущие принципу динамической компенсации и
обладает свойством грубости [64].
Определим систему алгебраических уравнений для нахождения неизвестных
коэффициентов г0, гх,..., гп_х, с0, с,,..., с„_,. Из (2.83) имеем
(а0 + axs + a2s2 +... + an_\Sn~] + sn j(c0 + c^s + c2s2 +... + cn_}s"~] + s" j+
+(6o+z?15+v2+---+Vi's'l"1)(ro+v+v2+---+v^AJ"1)=:
= do+d}s + d2s2 +rf3^3 +dAsA +... + dln_xs2n-x +s2n ;
отсюда получаем систему алгебраических уравнений
Яосо + ^ого = ^о >
«oc1+fl1co+Vi+Vo = rfi5
аос2 + ахсх + а2с0 + V2 + *1П + Й2^о = d2 \
аос3 + ахс2 + а2с, + а3с0 + bor3 + 6,r2 + fe2r, + 63^о = ^з • (2-85)
В линейной системе алгебраических уравнений 2я неизвестных; число
уравнений также равно 2п.
Решение системы (2.85) приводит к нахождению численных значений
неизвестных коэффициентов ПФ регулятора. Назначая соответствующим образом корни
характеристического уравнения D(s) = 0, можно добиться хорошего качества работы
системы в переходном режиме. Для этой цели можно использовать метод
стандартных коэффициентов или фильтры Баттерворса. Качество работы в установившемся
режиме определяется наличием интеграторов в прямой цепи. В связи с этим введение
интеграторов в прямую цепь изменяет структуру корректирующего устройства, и его
передаточная функция будет выражаться зависимостью
'•>м-£$гу (286)
Глава 2. Методы синтеза регуляторов в классе одномерных систем
79
Для удобства проведения расчетов поступают так: интегратор (или интеграторы, в
зависимости от порядка астатизма) вносят в структуру объекта (неизменяемой
части), и тогда эквивалентная схема принимает вид (рис. 2.23).
Я')
1
C,(s)
sA(s) = Ax(s)
I
Рис. 2.23. Структурная схема эквивалентной системы
Обозначим
sA(s) = Ах (s) = s (а0 + axs + a2s2 +... + an_xsn~] + s n J =
= aos + axs2 + a2s3 +... + я,,.^" + sn+\
Степень Ax(s) равна л + 1. Запишем уравнение синтеза
/i1(5)C(^) + ^(5)/?(^) = D(5). (2.87)
Для определения неизвестных коэффициентов с, и гу получим систему уравнений,
аналогичную (2.85); для этой цели введем обозначения:
R(s) = rQ + ^s + fys2+... + rnsn;
C(s) = c0 + cxs + c2s2 +... + cnsn +... + sn+l;
D(^) = t/0 + c/15 + ^2+... + rf2/J52w+... + ^2{w+1); (2.88)
^i(s) = aos + a^2 + a253 +... + я„.,.у" + 5Л+1;
Л(^) = fe0 + bxs + V2 + • • • + bnAs"-1.
С учетом (2.88) уравнение синтеза принимает вид
(aos + axs2 +a2s3 +... + an_xsn +sn+x Vc0 +cxs + c2s2 +... + cnsn +^n+1)+
+ (b0 +bxs + b2s2 +... + 6и5И)(^о +rxs + r2s2 +... + rnsn>)= (2.89)
= do+dxs + d2s2 +... + d2ns2n +s2{n+]).
Можно видеть, что задача, когда в прямой цепи имеет место один интегратор, в
точности совпадает с предыдущей, с тем лишь различием, что вместо степени п в
уравнении синтеза берется степень п +1. Аналогично изложенному следует поступать и в
тех случаях, когда требуется синтезировать систему, обладающую астатизмом более
высокого порядка.
Пример 2.3 [82]. В системе, структурная схема которой представлена на рис. 2.24, обозначим
x(t)
№ +
Wm{s)
WM)
Wm{s)
пу
KM
где
Рис. 2.24. Структурная схема системы автоматического управления
Wy(s) = K2 - ПФ усилителя;
J50 Методы синтеза САУ по заданным показателям качества. Часть II
fVny(s) - —- - ПФ исполнительного механизма;
IS
Wl(s) - —r-т ПФ объекта управления.
T2s2+2T£4s + \
Заданы параметры системы [82]
К2 = 2; К3 = 50, КА = 10; Г42 = 0,64; 2ГД 4 = 0,8.
Рассмотрим систему, в структурную схему которой не включено корректирующее устройство.
Передаточная функция замкнутой системы имеет вид
W(s) = ——7 Ы£л
(T2s2+2T£4s + \)s + K2K3K4
Исследуем устойчивость не скорректированной системы с помощью второй формулировки критерия
Михайлова [82]. Имеем
c(<i>) + jd(G>)
где
с(ю) = -27-444с>2+£2/:зА:4>
^(ю) = со(-Г42©2 + 1).
При ф>) = 0 со2=^^^ = 2-252; следовательно, юи = ±25^2 и ю,=25>/2.
2Г4^4
Если же d(a>) = 0,то ©2=0 и со3 = 1,25 .
В соответствии с критерием Михайлова система устойчива, если с(0)>0 и <аГ(0)>0 И уравнения
с(ю) = 0 и d((u) = 0 имеют все действительные и перемежающиеся корни, т.е. если между каждыми двумя
соседними корнями б^(со) = 0 лежит корень уравнения с(ю) = 0 или между двумя соседними корнями
с(со) = 0 лежит корень уравнения d(<o) = 0 .
Критерий перемежаемости корней формулируется так* для устойчивости системы корни должны
перемежаться и быть вещественными, а сумма корней должна быть равна порядку уравнения п.
В рассматриваемой системе условие чередования корней уравнений с(со) = 0 и d(<a) - 0 отсутствует,
следовательно, система неустойчива.
Поскольку
W (j)= К*К*К* - 100° -B(S) •
s(TA2s2 + 2ГД45 + 1) s(0t64s2 + 0,85 + 1) A(s)*
B(s) = b0 = 1000;
A(s) = s(aQ + axs + j2),
то
D(s) = do+dls+d2s2+dys3+d4s4+dsS5 + s6;
W^> r° + ^rf з ■
* co + cls + c2s2+s3
Воспользовавшись методом стандартных коэффициентов, в качестве эталонной ПФ выберем ПФ вида
,х6
W\s) =
56 + 6co055 + 15o^4 + 20(oJs3 + 15a)^2 + 6a)Js + cuJ
6 •
Положим, что Гр = 10,6, тогда ю0 = — = 1 и
W\s)-.
= P(s)
' s6+6ss + \5s4 + 20s* + \5s2 + 6s + \ D(s)'
Уравнение синтеза в развернутой форме имеет вид:
{aos + a]s2 + s*)(cQ + cls + c2s2 + s3) = bQ(ro+ri! + r2s2) =
= dQ+dxs + d2s2 +d3s3+d4s4+d?5 + s6.
Отсюда получим систему линейных алгебраических уравнений для расчета неизвестных коэффициентов:
Глава 2. Методы синтеза регуляторов в классе одномерных систем
81
(2 90)
Vo = <*о>
fl0C1+fl,C0 + V2 = ^2'»
aoc2+alC]+co = d3;
ao+alc2 + cl=d4;
a]+c2=d5.
Если ввести в рассмотрение одностолбцовую матрицу
Ч = (со,с„с2,го,г„г2),
го систему (2.90) для определения неизвестных коэффициентов можно переписать так.
(а0 0 0 0 Ьо
а, а0 0 0 0
1 ах а0 0 О
1
или, что то же самое,
3125
2
3125
0 Ьп 0
3125
0^
Ьо
0
0
0
0,
С|
<?2
''о
Г\
J2j
dx I
^2
d4-a0
db-ax
I ^o J
'О = 1;ТЬ+ 2
г, =6.
25
5 25 ,. 5
2 '■2^c0+-.c, = 15;c0+-.c1+-.c2 = 20;
5 25 ,. 5 ,
С'+Гг-1Г15;С2+Г6
Найдем решение последней системы и построим h{i) и Л(со).
Формула, определяющая ПФ регулятора, имеет вид
W^s)= r° + V + V
-де
co + cxs + c2s*+sJ
ro=6,41O^, c0 = 3,2031,
г, =6,36 10"4 , С! = 7,5,
г2«0, с2=4,75.
На рис. 2 25 приведены графики h(t) и Лэ(г).
1,4
1,2
0,8
0,6
0,4
0,2
МО
/
Лр(О
>
/
'/■
и
10
12
14
16
Зак. 36IS
Рис. 2.25. Графики эталонной и реальной переходных функций
скорректированной системы
82
Методы синтеза САУ по заданным показателям качества. Часть II
0,5
Л(и)
ЛМ
4 (со)
0 0,5 1 1,5 , 2 2,5
Рис. 2.26. Графики эталонной и реальной АЧХ скорректированной системы
Формулы для определения hp{t) и Лэ(/) имеют вид:
/?p(0 = l + 5,9810-3/5e-'-7 10-2/4ew-0,166/3e-/-0)5r2e-/-/ew-e-/;
Лэ(/) = 1-8,Зе-3/5е-/-4,16е2/4е-/-0,166/3е-/-0,5/2е"/-/е-/-е"'.
Структурная схема системы с найденным регулятором имеет вид (рис. 2.27).
-2£U®--*
Регулятор
6,36 10~4j + 6,4 10~4
.$3+4,75s2+7,5*+ 3,2031
Неизменяемая часть
100
s
10
0,64s2 +0,85 + 1
—►
Рис. 2.27. Структурная схема скорректированной системы
Пример 2.4.
Рассмотрим систему, задача синтеза регулятора которой по корневым годографам рассмотрена в [139].
Напомним, что траектории, описываемые на комплексной плоскости корнями характеристического
уравнения замкнутой системы при изменении одного из параметров от 0 до оо, называют корневыми
годографами [139]. При построении теории корневых годографов основополагающие результаты получены
К.Ф. Теодорчиком и развиты Г.А. Бендриковым и СП. Стрелковым (1948 - 1949 гг.), Г.В. Римским.
Если известен корневой годограф, то очевиден подход к решению задачи синтеза регулятора:
выбирается такое значение варьируемого параметра, которое обеспечивает выполнение требований к качеству
синтезируемой системы.
ПФ объекта управления имеет вид
^о(5) = 5(0,Ь + 1)(0,055 + 1) '
Регулятор, включенный последовательно, должен обеспечить выполнение следующих условий: Тр <0,7,
20%<а<30%.
Выбор параметров и синтеза корректирующих устройств по корневым годографам включает
следующие этапы
1 Поскольку основополагающее положение метода состоит в том, что динамика замкнутой системы
определяется парой комплексно-сопряженных полюсов
5,э2 = -ао±уо)о,
то отсюда следует вывод, эталонной ПФ замкнутой системы является колебательное звено с ПФ вида.
_*0
W,(s) = -
Г0У + 2Г0^ + 1
Глава 2. Методы синтеза регуляторов в классе одномерных систем
83
Б рассматриваемом случае установлены зависимости, связывающие а0 и соо с Гр и а , они
записываются так:
Поскольку в соответствии с постановкой задачи Гриа известны, то по приведенным формулам
легко рассчитать полюса s*2 , они равны [139]
5,3i2=-6±yil,2
2 На комплексную плоскость наносятся полюса 5,э2 и полюса неизменяемой части системы
5, =0; s2 =-10; s3 =-20.
3 Для выбора значения передаточного коэффициента К разомкнутой системы сроится корневой
годограф при изменении К (способ построения корневого годографа разработан очень детально, см [139]).
Чтобы траектория корней скорректированной системы при изменении К проходила вблизи полюса 5,э,
используется динамическая компенсация ближайших к мнимой оси полюсов ПФ объекта управления. В
этом случае обеспечивается определяющее влияние полюсов 5,э2 на динамику замкнутой системы. Из
сказанного легко заключить, что метод принципиально предполагает использование положений принципа
динамической компенсации, что порождает известные трудности. В рассматриваемой задаче можно
скомпенсировать ближайший к мнимой оси полюс s2 неизменяемой части, ПФ компенсатора имеет вид
0^(5) = (0,1*+ 1).
Вводится дополнительный полюс s4, так, чтобы полюс sj* находился на траектории корней
скорректированной системы [139]. В рассматриваемом случае, звено регулятора ПФ которого имеет полюс s4,
запишется так:
WK2(s) = -
0,0425 + 1
4. Вычисляется значение К.
В рассматриваемом случае К = 12 .
5. Составляется ПФ последовательно включенного регулятора; она имеет вид-
"* 0,042^ + 1 к к
Структурная схема системы представлена на рис. 2.28.
—*vv *
- т
12
O,br + 1
0,042-s+l
)
1
j(0,1j + 1X0,05.y + 1)
x(t)
Рис. 2.28. Структурная схема САУ
Поскольку ПФ замкнутой САУ определяется зависимостью
го- п 565°
"5(0,05j + 1)(0,0425 + 1) + 12 (s + 34,5)(.у2 +9^ + 164)'
то /ip(/) = l-0,157e"34'5/ + l,14^-4'5/sin(12/-2,31) .
График Лр(0 представлен на рис. 2.29.
Из рис 2 29 следует, что Гр = 0,635 , а а = 27% .
Построим решение рассматриваемой задачи с помощью уравнений синтеза
Имеем:
W0(s) =
12
A(s) s(0,\s + l)(0,055 + l)
- передаточная функция объекта управления;
^KyW = 77T = -T-i—Г1 ' ПФ регулятора
7 C(S) 5J+C2.r+C,5 + C0
84
Методы синтеза САУ по заданным показателям качества. Часть II
Эталонный характеристический многочлен получим, воспользовавшись аппаратом стандартных
коэффициентов
Ш)
/,4f
0,25 0,5 0,75 t,C
Рис. 2.29. График переходного процесса
Поскольку 7*р = 0,7, то соо = —^— = 15,14 и характеристический многочлен замкнутой системы при-
нимаетвид(см §2 1)
D(s) = s6 + d5s5 + d4s4 +d3s3 +d2s2 + dxs + d0 ,
где
d5 =90,857, dA =3439,59; d3 = 69446,997;
d2 = 788719,446; dx =4777386,485; d0 = 12057213,51.
Теперь легко записать уравнение синтеза
K(r2s2 + rls + r0) + s(T]s + \)(T2s + \)(s3 + c2s2 +clS + c0)=>
= se+d5s5 +d4s4 +d3s3+d2s2 +dxs+dQ.
Система алгебраических уравнений для расчета неизвестных коэффициентов ПФ регулятора
запишется так:
r°K-d-
ТХТ2 If
г2К + с0Т2+сх+с0Тх .
= «i,
Чг
cJiT2+clTi+c{T2 + c2_
Чг
с1Чг + с2Т1+с2Т2 + 1_.
Чг
с2Г,Г2 + Г|+7-2_
Чг
Отсюда находим
го = 5023,8385; с0 = 14859,24;
г, =752,3075; с, = 1413,877;
г2= 25,0690; с2 =60,8571.
Структурная схема системы управления представлена на рис. 2.30.
На рис. 2.31 приведены графики эталонного переходного процесса и реального переходного процесса
на выходе системы с регулятором, рассчитанным по методу уравнений синтеза.
Глава 2. Методы синтеза регуляторов в классе одномерных систем
85
^*<8к
25,069 2 752,3075 5023,8389
14859,24Л 14859,24' 14859,24
1 з, 60,8571 2 1413,877
14859,24 14859,24 14859,24
—►
12
s(0,\s + 1)(0,05.у + 1)
*(')
Рис. 2.30. Структурная схема САУ
1
0,9
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0
'МО
/
/
/
МО /
У
/
/ /
/ /
/
/
/
/
/
/
"^мо
^—■
~- —
/, с
о
0,2
0,4
0,6
0,8
1,2
Рис. 2.31. Графики эталонного /гэ(/) и реального hp(t) переходных процессов
На рис 2.32 представлены графики АЧХ эталонной системы и системы, регулятор которой рассчитан
методом уравнений синтеза.
1
0,9
0 8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
•А(а)
V
\
\
Л
\\
/\
N
^ \
\
\
\
_
СО
0 5 10 15 20 25 30 '
Рис. 2.32. Графики эталонной и реальной АЧХ скорректированной системы
86
Методы синтеза САУ по заданным показателям качества. Часть II
2.4. МЕТОД ЭТАЛОННЫХ ПЕРЕДАТОЧНЫХ ФУНКЦИИ
ЗАМКНУТЫХ СИСТЕМ УПРАВЛЕНИЯ
Содержание этого метода заключается в следующем. Положим, что синтезируется
последовательно включенный регулятор. ПФ объекта управления известна и равна
вд=
B(s)
^(s) =
R(s)
- передаточная функция регулятора, коэффициенты
A(s)' ■"" C(s)
которой подлежат определению (на степени полиномов R(s) и C(s) никаких
ограничений не накладывается).
Если структура регулятора выбрана таким образом, что ПФ замкнутой системы
имеет вид
Щ{р)
W(s) = -
(2.91)
sn +alx(p)sn-] +al2(p)s"-2 + ... + aop(/>)'
где p = (pvp2,-~,Pr) ~ неизвестные параметры регулятора, то выбирая эталонную
ПФ вида
W>(s) =
сог
sn+A]<»osn-]+A2(ulsn-2 + ...+ А„_1®п(1
(2.92)
irt_iwo S + (UQ
легко получить систему алгебраических уравнений для расчета неизвестных
параметров риръ ...,/?г:
a^ip) = Ахщ,а12(р) = А2а>1..., аЦр) = cog. (2.93)
Если решается задача выбора п параметров, т.е. г = п, то она сводится к решению
системы уравнений (2.93). Как указано в [62], часто имеют место трудности,
поскольку получающаяся система уравнений оказывается несовместной или ее корни
оказываются комплексными. Рассматриваемый метод пригоден обычно в тех
случаях, когда достаточно велико число варьируемых параметров и когда каждый
коэффициент ПФ зависит от малого числа параметров [62].
Проиллюстрируем основные положения метода на примерах.
Пример 2.5 [62]. Рассмотрим систему стабилизации скорости вращения двигателя, структурная схема
которой представлена на рис. 2.33.
1 +-<-* I К* I I к. I У(0
К,
иггы
Ts
75 + 1
Рис. 233. Структурная схема системы стабилизации скорости вращения двигателя
Пусть К2 = 15 с"1, А:, =0,2 с"1; задача состоит в нахождении Кг,г и Г
ПФ разомкнутой и замкнутой системы соответственно имеют вид:
КхКгКг(Т* + \) ,
^}~Ts3H\ + rK2T)s2>
J\. i А. л/С •»
W(s) = .
KxK2Kys + -
3+(- + rK2]s2 + K}K 2K3s +
Выберем эталонную ПФ вида:
И"(»)
а>о
А. |Л. лЛ -1
©J
s3 +у4,соо52 +A2(ols + (dl 53 + 5,lo)(>y2 + 6,35coJs + cOo
Глава 2. Методы синтеза регуляторов в классе одномерных систем
87
Если Гр = 2,5, to =5, то
>=4
Для вычисления Кз,Тиг имеет место система алгебраических уравнений
А1ы0 = — + гК2, или 5,1-2 = —+ г-15;
А2<д20 = К]К2К3, или 6,36-4 = 0,215Л:з;
з КЖ2К3
или 8 = —2 —.
Отсюда находим:
£з«8,5;7«3,18с;г«0,66.
Пример 2.6 [47]. Рассмотрим задачу управления центром тяжести крестокрылого снаряда в боковом
движении.
В качестве примера выбора параметров автопилота для управления движением центра тяжести
рассмотрим крестокрылый снаряд, стабилизированный по углу крена. Эта задача поясняется рис. 2.34
V Заданная
траектория
N
8V
Рис. 2.34. Схема угловых и линейных координат, характеризующих положение
снаряда относительно прямолинейной траектории в боковом движении
Пусть MN - заданная прямолинейная траектория, по которой должен двигаться снаряд. В этом случае
заданное значение координаты центра тяжести снаряда по оси oz% есть z-^-zq.
Рассмотрим систему управления боковым отклонением центра тяжести крестокрылого снаряда,
учитывая переходные процессы в угловом движении снаряда. Система уравнений имеет вид [47]
d\ ф/ <ф „ s ДА/,
dt
■ = И.(Ч»-Ю;
К=ч[^-^\ + Фг-г*) + *г\{Ч-гг)*-
(2.94)
Исключая из уравнений (2.94) все переменные, кроме zg, найдем следующее общее уравнение системы
управления боковым отклонением центра тяжести снаряда:
dbze , ,dAzR d3ze
d2z.
<k.
+M2 + i№.)^£ + i2b2Ve -L + q2b2Vezg =
dz
'- + q2D2Yez3—r-
У
(2 95)
d\ .
dt
Структурная схема представлена на рис. 2.35.
= izb2Ve^ + izb2Ve^ + q2b2Vez3- j л
k$Ve dAMb
Методы синтеза САУ по заданным показателям качества. Часть II
-аа®*
izs +izs + qg
AFm
1
Jy\
AM.
►&h^S^
1,
I'v
l\s + b2
)
Рис. 2.35. Структурная схема, соответствующая системе уравнений (2.94)
Рассмотрим задачу выбора параметров системы управления центом тяжести методом стандартных
коэффициентов
В качестве объекта управления возьмем снаряд, параметры которого приведены в табл. 2 7.
Таблица 2. 7
ч
1
с
0,34
"Р
1
с2
13,5
ЛР
1
с
0,1
1
с
0,205
1
с2
5,6
<*\
1
с
0,645
а2
1
с2
13,6
ь\
1
с2
5,6
Ьг
1
с2
1,9
i¥
с
0,865
Ту
с
2,95
1
с
0,124
т„
с
0,256
0,707*
Пусть скорость снаряда Ve = 300 м/с .
Необходимо выбрать параметры системы управления так, чтобы Тр = 15 с .
Передаточная функция для системы управления центром тяжести на основании уравнения запишется
Wi
<./■>«=:
iMS+Wt+чМ.
(2.96)
s5+(a] +1^)5* +(а2+1уЬ2+1уЬх)з* + (iyb2+izb2Ve)s2 +izb2Ves + qzb2Ve
Коэффициенты числителя и знаменателя перед s2 отличаются друг от друга на небольшую величину
iyb2 <к izb2Ve. Характеристическое уравнение эталонной ПФ имеет вид:
s5 +18соо54 +69ш?53 +69<*ls2 +18©Jj + ®J =0 . (2.97)
Приравнивая соответствующие коэффициенты знаменателя передаточной функции (2.96)
коэффициентам характеристического уравнения (2.97), получим систему алгебраических уравнений [47]
в,+/„,&, =18ш0;
а2+ iyb2 + iybx = 69(0 J,
/V|//>2+U>2Ke=69coJ; \ (2 98)
izb2Ve=\Su>l
gzb2Ve=(ol
Значение «собственной частоты» системы соо определяем на основании соотношения
со =1о=М = 0613с-19
7р 15
где т0 = 9,2 взято по кривой стандартного переходного процесса для системы пятого порядка
Подставляя полученное значение соо в уравнения (2.98) и решая их поочередно, начиная с первого,
получим следующие значения передаточных чисел автопилота-/у = 1,86 с; /у = 1,58; iz =0,023 рад-с/м =
= 1,33 градс/м; i2 =4,53- 10"3рад/м = 0,26 град/м; ^г = 1,54.10~4рад/мс = 8,8310"3град/мс .
В качестве эталонной ПФ не обязательно выбирать ПФ со стандартными
коэффициентами. При проектировании конкретных систем управления эталонной ПФ может
Глава 2. Методы синтеза регуляторов в классе одномерных систем 89^
служить любая ПФ, обеспечивающая заданное качество управления в переходном и
установившемся режимах.
В [91] рассмотрен метод расчета параметров регулятора, обеспечивающий
приближение ПФ замкнутой системы, содержащей q неизвестных, к эталонной ПФ
W3(s)9 с введением области заданного расположения полюсов изображения W{s)
синтезируемой системы.
Пусть W3(s) = — эталонная передаточная функция; W(s) = — - пе-
редаточная функция замкнутой системы управления, содержащая q искомых параметров.
Положим, что ПФ эталонной системы сконструирована таким образом, что
выполнено равенство тх+п2=т2+щ.
Тогда из равенства
*=0 *=0
ЫО Аг=О
из которого следует соотношение
U-o ) U-o ) U=o ; U-o )
сразу же можно записать следующую систему алгебраических уравнений
bla2 + b?a} + b\a0 -аъ0Ь2 - a\bx -a\b0 = 0;
Ъ1хая%-а1гЪтг=0.
Поскольку эталонную ПФ можно построить таким образом, чтобы были
выполнены неравенства
^r-2</w2+«i,
то подход может оказаться полезным для решения конкретных задач. Однако
необходимо помнить, что в общем случае искомые параметры нелинейно входят в
соотношения, определяющие коэффициенты bk(pl9p2,..,pr), п = 0,т2 и ак(рьр2,..,рг),
п = 0, п2, что усложняет алгоритм поиска параметров.
В [91] изложен метод приближения W(s) к W3(s) с одновременным введением
полюсов изображения синтезируемой системы W(s) внутрь заданной области, чем
обеспечиваются необходимые степень и запас устойчивости и колебательность системы.
6 Зак. 366
jH) Методы синтеза САУ по заданным показателям качества. Часть II
Пример 2.7 [91].
Изучим режим малых колебаний при регулировании возбуждения синхронного генератора. Генератор
работает через дальнюю передачу на систему U = const. Используются уравнения генератора в
упрощенной форме Лебедева - Жданова, учитывается постоянная времени цепи возбуждения. Постоянными
времени возбудителя и дифференцирующих звеньев пренебрегаем.
Пусть 0(/) - угол между вектором ЭДС и вектором напряжения U\ изображение приращения 0(/) при
внезапном малом изменении нагрузки записывается так [91]:
щз) = У+у+й. .
aAs +a$s +a2s +als + a0
где b2 = 0,287 -O,38902-0,632y2 ;
6, =4,86-0,3890,-0,632y, ,
/>о = Ю,2;
a4 =(1,21-1,6302 -2,65y2)10~2 ;
я3 = (20,5-1,630,-0,124p2+ 2,65у1+0,201у2)-Ю~2,
a2 =(56,8-0,1240,+29,3P2-0,201y,-39,9y2)10-2,
a] =2,13 + 0,2930, -0,399y, ,
a{ =6,57.
Приведенные зависимости соответствуют номинальному режиму 0 = 67°. Величины 0О и у0,
являющиеся коэффициентами усиления при регулировании по отклонениям тока и напряжения от их
номинальных значений, приняты равными 0о = 1,О;уо=-15,О
Задача ставится следующим образом
1) Д0($) должно быть близким к эталонному изображению
чем обеспечивается апериодичность переходного процесса с Гр =2,5 с при максимальной скорости
протекания процесса, не превышающей 2,5 рад/с .
2) система должна быть слабоколебательной (при колебательности tg vj/, где vj/<70°).
Из соотношения
(b2s2 + bls + b0)(s2 +22.S + 40) = 62(a4sA + a2s3 +a2s2 +a{s + a0)
получаем систему алгебраических уравнений
62а, =22*0+406,;
62a2=b0+22bl+40b2;
62аг = Ьх+22Ь2\
62а4 -Ь2.
Из последней системы находим систему так называемых условных уравнений
0,6у, =287-33,650,;
13,78у, +0,5у2 = 82,0-8,450, -33,702;
2,28у, +14,02у2 =-1,54 + 0,6210, -8,6302,
-1,003у2 =-О,463 + О,63102.
Воспользовавшись методом наименьших квадратов, получим решение системы (2 99) относительно
У\ и Y2-
у, =6,85-0,7250,-2,4402;
у2 =-1,25 + 0,1670, -О,22102
Теперь характеристическое уравнение системы может быть записано в виде
D(5) = 6,57 + (-O,61 + O,5920,+O,97502)5 + (l,O52-0,06670, +О,38602)*2 +
+(0,381-0,03520,-0,066702>3+ (4,53-0,4420,-1.О4502)1О-254.
Исходя из обеспечения заданного запаса устойчивости в [91] найдены численные значения параметров
0, и 02 , они равны 0, = 5,3; 02 = 1,9 .
Отсюда получаем у, = -1,63; у2 = -0,78.
Глава 2. Методы синтеза регуляторов в классе одномерных систем 91_
Можно показать, что допустима вариация параметров в пределах (20 - 25)%, при которой полюса
остаются внутри заданной области плоскости S.
Проверка приводит к следующему результату:
поскольку
ju=-l,66±yl,57,
53>4=-15,15±yi9,53,
то (второй составляющей пренебрегаем):
Д9(/) * 1,56 - 2,27е"|>66' sin(l,57/ + 43°30')
Вывод* рассчитанные параметры обеспечивают заданное качество управления.
2.5. МЕТОД ЭТАЛОННЫХ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
РАЗОМКНУТЫХ СИСТЕМ
При рассмотрении принципа динамической компенсации были использованы
взаимосвязанные соотношения
И
В эти зависимости входит эталонная передаточная функция разомкнутой системы
W*(s). Выше (см. пункт 2.1.3 в §2.1) был рассмотрен метод стандартных
коэффициентов построения эталонной передаточной функции W3 (s) замкнутой системы.
Алгоритм синтеза регулятора упрощается, если пользоваться эталонной (стандартной)
передаточной функцией разомкнутой системы W* (s), которую легко найти, зная W3 (s).
Если
п
W>(s) —
sn + Ax®osn-1 + А2ф +... + Л-1°>о" s + К
то
ум, у'(') , <
pW l-W(s) s(s"-l+Al<»oSn-2+... + An_yo-1)'
Последняя ПФ имеет один нулевой полюс и, следовательно, реализуется система
с астатизмом первого порядка.
Если же в качестве эталонной ПФ замкнутой системы имеет место ПФ вида
W3 / ч = ЛчСОрЛ + сор
Jlt+i4,(D05'l"1+...+ /(r|_1©3"lJ + G)S '
то эталонная ПФ разомкнутой системы запишется так
цгэ /s\ = ^(Рр'^ + Юр
PV 52(^2+40)0^-3+... + Л-2<"2)
и, таким образом, система имеет астатизм второго порядка.
Аналогично, если
w* is\ = Л-2<Оо"2^+Лч<"^-ю>о
то
И'э (о) = Ап-2(*"° * Лп~х^ * ^
6*
92
Методы синтеза САУ по заданным показателям качества. Часть II
Пример 2.8. Найдем эталонную передаточную функцию разомкнутой системы при следующих
условиях, первый член прогрессии равен 0,063 ; разность прогрессии 0,867 и т0 = 13 ; система должна иметь
астатизм второго порядка
Изтабл 2.5 имеем:
И"М = -
18©fc + ©%
.s5+9©o.s4+29©?.s3+38©o52 + 18©4)5 + ©o
Тогда формула, определяющая W* (s), имеет вид:
^э / ч = 18cog^-Kog
р l ' *5+9©(/ + 29©?.у3 + 38©3352 '
Аналогичным образом можно рассчитать и построить таблицы, ориентированные
на решение класса задач синтеза регуляторов. Приведем одну из таких таблиц (см.
табл. 2.8, она составлена на основе данных, приведенных в табл. 2.5).
Таблиг
№
п/п
1
2
3
4
5
6
7
8
9
10
11
12
m
1
1
1
2
2
2
2
2
2
2
2
2
п
2
3
4
2
3
4
5
6
7
8
9
10
а, %
5
8
10
10
10
10
10
10
10
10
10
10
К
©0
1,4
©0
2
©о
2,6
со?
Од
5,1
со?
16
со?
38
со?
73
coi
163
313
со?
587
со?
988
со?
52 + 1,4cooj
53 + 2соо52 + 2со?5
coS
54 + 2,6юо53+3,4аф2 + 2,6со?5
2,5соо5 + ю?
S
6,3co?5 + cdJ
J3+5,lC0052'
ll,8©j5 + (Oo
54 + 7,22©053+16,3©?52
18©о^ + соо
*5 + 9(й054 + 29со ?*3 + 38со fc 2
25(^5+©!;
/ + 11ю055+43ю?54 + 83©3>у3 + 73©4д2
44c4y + coj;
л7 + 13ю0*6 + 66ю?*5 + 173ю3/ + 238ю^3 + 163©^2
68©?5 +
58 + 15©о^7+92©?56 + 299со3>у5 +
+©s
+554©^4+579©^у3+313©^2
1О6©5$ +
s9 +17©058 +121©?57 +476ю?56 +
+©о
+1114©^5+1581©^4 + 1320©^3 + 587©^2
151©?5 +
510 + 19ю059 + 152©?58 + 691©^7 + 1941©^6+
+со'°
+3464©^5+3908©^4 + 2666©^3 + 988©^2
fa 2.8
5
7
9
7
9
11
13
15
17
19
21
23
Глава 2. Методы синтеза регуляторов в классе одномерных систем 93_
Перейдем к изложению содержания метода. Исходные данные:
• структурная схема системы (WQ (s) - ПФ всех функционально необходимых
элементов);
• порядок астатизма;
• величина перерегулирования а% ;
• время переходного процесса Гр.
Основной идеей метода является приближение с помощью подбора структуры и
параметров КУ реальной ПФ к некоторой эталонной, причем последняя обладает
необходимым порядком астатизма (что обеспечивает заданную точность в
установившемся режиме работы) и включает параметр ©0, который обеспечивает
необходимое быстродействие через нормированное время переходного процесса.
Величина перерегулирования а%, не превышающая известной величины, заданной в
процентах, обеспечена подбором коэффициентов эталонной ПФ.
Эталонная ПФ некоторых разомкнутых систем приведены в табл. 2.8. Если
заданы: время переходного процесса Тр; перерегулирование а%; порядок ПФ
(согласуется с порядком ПФ неизменяемой части), то по таблице можно найти нужную
эталонную ПФ разомкнутой системы, причем относительное время переходного
процесса т0 = со0Гр.
Поскольку со0 =то/Гр, т0 находится из таблицы, а Гр - задано, то можно
рассчитать значение параметра соо и, следовательно, ПФ разомкнутой системы. Таким
образом, эталонная ПФ разомкнутой системы, обеспечивающая заданные параметры
переходного процесса и значение динамической ошибки замкнутой системы,
известна. Обозначим ее
K4s)=bmS +tm-lS , +- + Ь°. (2.100)
В (2.100) все численные значения коэффициентов числителя Ш, bf,..., b?n\ и
знаменателя (а^, af,..., аъп\ известны.
Далее подбирается структура наиболее простого КУ таким образом, чтобы имело
место равенство
Пусть
^(^•^(^,)=6'-(A)5m+ViUK;'+-+6o(A), (2..01)
О\/ КУ \ »rl } / \ П /\ /7-1 / \ ч
где Pi - параметры КУ, подлежащие определению. Для расчета /?, можно
воспользоваться следующими соображениями.
Одно из них состоит в следующем. Поскольку в идеальном случае справедливо
равенство
blsm +bl_xsm-x +...+bl _ bm(Pi)sm +bm.l(Pl)sm-i +... + *ь(л)
anV+anV"''+- + *o ая(р1у+а,,_х(р1у-1+... + а0(р1) '
то отсюда легко записать:
j)4 Методы синтеза САУ по заданным показателям качества. Часть II
<*>(а) = «о. а\(Р*) = а\> ■••> an{Pi) = °l,
А)(р,) = ^, b{Pl) = b?, ..., bm{Pi) = bl.
В последней системе имеют место следующие факторы: система относительно
Р\> Рг* •••» Рк> как правило, нелинейна; число уравнений не всегда совпадает с
числом неизвестных, что вызывает известные трудности [17].
Пример 2.9. Рассмотрим простейший пример, иллюстрирующий алгоритм расчета параметров
регулятора методом эталонной ПФ разомкнутой системы
Пусть ПФ разомкнутой системы имеет вид:
Задача заключается в нахождении таких параметров Ке> Г,, 7"2, которые обеспечили бы время
переходного процесса Гр < 1,5 с , а величину перерегулирования а < 10%
В качестве эталонной ПФ разомкнутой системы выберем ПФ вида:
I 5,1соо
Из сравнения Wp (s) и Wp (s) легко получить следующие равенства:
*e=ft; ri=^; Гг=5>;-
Поскольку юо= —= — = 6с"1,то Ке = 7,05с-2, ^ =1,05с, Г2=0,032с.
Пример 2.10. Рассмотрим канал управления креном ракеты (рис. 1.15). ПФ замкнутой системы без
регулятора определяется зависимостью
W(s)= /""^ .
TS+s + K^K,
IS
Пусть WKy(s) = K+—- - последовательный пропорционально-интегральный регулятор (положим,
что К1у = 1). Тогда передаточная функция разомкнутой системы с регулятором определяется формулой
Кп?КуК^ КпрКуКн
( ч_(^ + ^и)^пР^у _КПрКуК5 + КпрКуК„ _ Ту Ту
^
Т1
Положим, что порядок астатизма равен 2, а < 10%, а время переходного процесса Гр - задано.
Как и в предыдущем примере, эталонная ПФ имеет вид
Г1/э/.\_6,3(0()5 + (0%
Л JV+5,lov2'
Из равенства Wp (s) = W* (s) следует система уравнений:
1 КпрКуК
/у /у
В рассматриваемом подходе величина со0 зависит от известной постоянной времени ракеты по каналу
крена Ту, из этого следует.
С другой стороны, через величину <оо определяется время переходного процесса Т?; оно равно
Глава 2. Методы синтеза регуляторов в классе одномерных систем
95
Гр=-^- = 45,9Гу.
Последней формулой при принятой структуре регулятора определяется время переходного процесса
канала управления креном 9
Из соотношений, приведенных выше, сразу же находим численные значения параметров регулятора
К и Ки ; они равны
к 6,3ofrr к _ e)fc
Если Ту = 0,03 с ; Кп?Ку = 300, то
соо=--!—= 6,5359; АГ = 0,0269; /:и=0,0279; Гр = 45,9 0,03 = 1,377с
5,1Гу
На рис. 2 36 - 2.39 приведены1 переходные характеристики и амплитудно-частотные характеристики
системы управления каналом крена ракеты
■*(0
О 0,2 0,4 0,6
Рис. 2.36. График переходной характеристики нескорректированной системы
J
3,5
? S
1 5
1
0,5
0
1
/
\
\
\
\
-
со
100 200 300
Рис. 2.37. АЧХ нескорректированной системы
400
Известно, что наиболее конструктивный путь решения задач синтеза регуляторов
это использование методов нелинейного программирования. При этом показатели
96
Методы синтеза САУ по заданным показателям качества. Часть II
качества стационарного и переходного режимов обеспечиваются приближенно при
безусловном обеспечении устойчивости и грубости (по варьируемым параметрам)
системы с синтезированными параметрами. Кроме этого, могут быть наложены
ограничения на параметры, колебательность и др.
4*ю
0,5
1
1
■ .
-
•
-2*.
0 0,5 1 1,5 2
Рис. 2.38. График переходной характеристики системы с регулятором
0,5
1 И(ю)
\
—■
со
0 20 40 60
Рис. 239. АЧХ системы с регулятором
Во многих достаточно сложных случаях применение метода эталонных ПФ
позволяет использовать аппарат нелинейного программирования (см. Приложение 2).
Пример 2.11. На рис. 2.40 приведена структурная схема системы автоматического управления.
Г к"у | Г
у«) лочвю!
ОУ
вд
W0
W2(s)
W3(s)
Wa(s)
1Д
i : i
Рис. 2.40. Структурная схема системы автоматического управления
Глава 2. Методы синтеза регуляторов в классе одномерных систем
97
На рисунке передаточные функции имеют следующий вид: Wx (s) - передаточная функция синтези-
К К
руемого регулятора (корректирующего устройства); W2 (s) = К2; W3 (s) = —- ; WA (s) = —у-^
s 7^5 + 2c^ 4T4S +1
Пусть передаточная функция регулятора имеет следующий вид:
'•<•>■«■•;#•
где Кь т,, Г, - неизвестные параметры регулятора, подлежащие определению.
В этом случае передаточная функция разомкнутой системы автоматического управления, после
соответствующих преобразований, будет следующей:
ад-
К1К2К3КАх1 К1К2КгК4
Щь Ш±
г,г42 г,г42 г,г42
В качестве стандартной передаточной функции выберем ПФ вида
(2.102)
(2.103)
"55+9cuo/ + 29(o^3 + 38(u^2 '
где юо = хо/Гр.
Приравняв соответствующие коэффициенты выражений (2.102) и (2.103), получим систему уравнений.
^^ = 9соо;
/,/4
/,/4
У,/4
Для решения системы уравнений воспользуемся оптимизационными методами. Для этого введем в
рассмотрение следующие функции, зависящие от искомых параметров регулятора.
8ilAi,T|,iiJ —3 18Юо>
/1/4
с (К т Т\- ^4 +^4^4^1 лт .
бз^Л,,!,,/,) —j VCOO,
/,/4
ММ
e,(A:I.t,.r1)--lT-3toi
ММ
Функционал определяется зависимостью
/(*i.t,.r,)-te?(A:I,x1.r,)
/=1
Таким образом, поставленную задачу синтеза регулятора можно сформулировать в терминах
нелинейного программирования:
при соответствующих ограничениях.
_98 Методы синтеза САУ по заданным показателям качества. Часть II
2.6. ОПТИМИЗАЦИОННЫЙ МЕТОД СИНТЕЗА РЕГУЛЯТОРОВ
В ЧАСТОТНОЙ ОБЛАСТИ
Рассматриваемый ниже метод основан на использовании второго принципа,
изложенного в §1.4. Этот принцип предполагает, что параметры регулятора
рассчитываются из условия приближения выходного сигнала x(t) на заданное воздействие
у3 (/) к некоторому эталону хэ (г). Критерием близости может быть выбрана
метрика пространства L2[0,oo).
Основная формула имеет вид (см. §1.4)
/(/>„ /?2,...,/?г) =
= 1\ХЛ')-\АоАку(Р\>Р2-»'А-)(/ + ААу(/>1>Р2—>Pr)) 11 УъЩ<Ь-> min •
о I L J J Pit ыГг
В последней зависимости:
Ао - оператор объекта;
Аку(р],р2,:.,рг) - оператор регулятора, зависящий от изменяемых параметров
Р\>Р2>—>Рг'у
уэ (/) - эталонный входной сигнал;
хэ (/) - эталонный выходной процесс.
Принципиальная трудность применения рассматриваемого подхода заключается
в том, что записанный выше функционал, подлежащий минимизации по параметрам
регулятора P\->Pi,..~>pr> требует знания обратного оператора замкнутой системы
[АоАку(Р\>Р2>->Рг)(* + АоАку{Р\>Р2>->Рг)) J >
явно зависящего от параметров регулятора ри р2,-.., рг -
Как уже указывалось, реализация этого подхода возможна лишь в простейших
случаях.
К таким случаям относится класс линейных стационарных систем, когда
критерием, определяющим степень близости реального выходного сигнала
х?{РъР2>-~>Рг) к эталонному процессу x3(t), служит функционал
°° 2
/(Pi,P2>".,/V> = f [x3(t)-x?(t,pup2,...,pr)] A. (2.104)
о
Рассмотрим задачу синтеза регуляторов в общей постановке: заданы входной
сигнал y3(i) и эталонная реакция на это воздействие x3(t); необходимо построить
алгоритм расчета параметров регулятора (при известной структуре) исходя из
следующих условий
• 1(Р\,Рг>->Рг)-> mil^_;
PiMs
• X(t)e Xn Vfe[0,r], где X(f) - вектор-функция состояния системы; Хп -
заданная область;
Частным случаем X(t)eX" V/e[0,T] является принадлежность
переходной характеристики h(t) «коробочке» В.В. Солодовникова.
Глава 2. Методы синтеза регуляторов в классе одномерных систем
99
• u(t)eU], u(t) - скалярное управление, поступающее на объект; U] -
заданная область;
• р?<Рх <ру9...,р?<рг<ру.
• C0<C0jxon, Cj <С1доп,...,
где Со, Си... - коэффициенты ошибок.
Конкретная постановка задачи может быть сформулирована так: при заданной
структуре регулятора (предполагается, что регулятор с заданной структурой обладает
соответствующими возможностями) найти параметры р = (р\,Р2>-,Рг) из условия
наилучшего приближения реального выходного сигнала xp(t,pup2,...9pr),
являющегося реакцией на д>э(О = КО> к эталонной переходной характеристике с заданными
показателями качества: быстродействием, колебательностью, максимальным
отклонением в переходном режиме при обеспечении устойчивости системы и
приближенном обеспечении заданной точности в установившемся режиме.
В качестве эталонной переходной характеристики можно задавать процесс,
изображение которого определяется зависимостью [91]:
яэ(*) = с,
^-5 + 1
2
°а252+а,5 + 1
НА, (О,
где GQ определяет статизм системы, а, и а2 - параметры, связанные с временем
переходного процесса Гр и максимальным отклонением в переходном режиме Лртах1
формулой
<*2
ч
^pmaxl
1 Со
^)maxl
Со
-1
2
2
бои
(Xi = -.
Сказанное выше можно записать в следующей форме: найти параметры
Р\у Рг> •••» Рг > обеспечивающие выполнение условий:
1) функционал (2.104) принимает минимальное значение;
2) обеспечивается устойчивость системы (в вычислительном отношении для
проверки устойчивости системы наиболее удобен критерий Раусса);
3) если >>э(/) = 1(/), то Аэ(0 ~ эталонная переходная характеристика; функция
. Ар (/,/?) должна находиться в «коробочке» Солодовникова, т.е.
а)|Ар(/,/?)-Ауст|<Д,
где А - постоянная величина, значение которой в техническом задании
задается в процентах от установившегося значения выходного процесса
Vr = M'>/>)Uoo;
б) аО/оgW'M-Vr100%<а0/0доп9
Ауст
т.е. перерегулирование не должно превышать допустимого значения (обычно
^%доп =00-30)%);
100 Методы синтеза САУ по заданным показателям качества. Часть II
в) Гр < Трлоп, т.е. время переходного процесса не должно превышать
допустимого значения Трдоп.
Кроме этого, могут быть заданы ограничения на производные выходного
процесса, на число колебаний Ар (t,p) (при проектировании систем допускают
число колебаний равным (1-2), реже (3 - 4); иногда колебания недопустимы) и др.
4) выполнены ограничения, обусловленные требованиями к точности системы в
установившемся режиме. Требования к точности должны быть предъявлены в
виде ограничений на коэффициенты ошибок:
С С
Тогда, записав передаточную функцию по ошибке через передаточную
функцию замкнутой системы и выполнив деление полинома числителя на полином
знаменателя, поучим следующие ограничения:
—(яо-60)<с0доп;
—(а1-*1)-^-(а0-гЪ)<С1доп;
ао а0
—{а2-Ь1)^{ах-Ь{)^{а^Ь,)^{а^Ь,У<С2АОП,
ао а0 а0 а0
которые ввиду зависимости коэффициентов ai9 / = 1,и и bj9 у = l,w от
искомых параметров Р\,Р2>—>РГ также являются ограничениями на параметры.
Область допустимых значений варьируемых параметров обычно ограничена
условием их технической реализации
Pim^Pi^PiM* / = 17.
Использование приведенных соотношений позволяет задачу определения
варьируемых параметров ph / = 1, г, обеспечивающих наилучшее приближение к
эталонной переходной характеристике, сформулировать следующим образом: требуется
минимизировать функционал (2.104) при ограничениях 1), 2), 3), 4).
Рассмотрим решение поставленной задачи для частного случая, когда
y3(t) = l(t),x3(t) = Ky(\-e-a>'). (2.105)
Запишем формулу, определяющую переходный процесс через неизвестные
параметры корректирующего устройства:
Лр^р)^!-1!^,/?)-!, (2.106)
где
Wo (s) - ПФ объекта; W^ (s,p) - ПФ регулятора. В формуле (2.107) /?,, /?2,..., рг -
параметры корректирующего устройства; подбором этих параметров достигается
заданное качество переходного процесса. Таким образом, реальный переходный про-
Глава 2. Методы синтеза регуляторов в классе одномерных систем Ш1_
цесс определяется зависимостью (2.106), в которую входят неизвестные параметры
Запишем формулу для невязки
Тогда функционал качества имеет вид
l{Pi.P2,~,Pr) = ][**{.t)-bp(t,PJf<* ■ (2Ю8)
о
Преобразуем подынтегральное выражение в (2.108) по Фурье
Ky(l-e-4)-hp(t,pl,p2,...pr)r*
.*„ Ку Wv{ja>,p)W0{j*) 1 (2-Ю9)
• усо ую + о, 1 + ^(М/»)»;(уа))^) U '^'
Воспользовавшись равенством Парсеваля, зависимость (2.109) перепишем в виде
00 2
l(Pl,p2,...,pr) = l[x3(t)-hf>(t,p)]dt:
0 (2.110)
00
Je2(/,p) = — J E(ja>,p)E(-j<o,p)de>.
о 2lt-«>
Преобразуем(2.109) следующим образом:
£(y(0 p)^^ ** Ьт(рХМт+... + №) 1 __
уй> ую + о, an(pXj®)m+... + ao(p)j<>>
ck (pXJtif + сы jpXjuf'1 +■■■ + со(р) _ CQ(0,p)
dk ipXJaf + <*k-i (PXM*-X +... + do(p) MJ*> P)'
где
4 (P) = <t,+i (p) = (an (p)Ky +an (p%..., co(p) = Kya3ao (p)+bo (p)a3,
dk(P) = dn+2(P)= в„0»).-» </,(р) = ао(Р)«э. do(p) = O.
Перепишем (2.110) в виде
/(А,/>2,-,/У) = -1 СУ*>Р™-*л-Р>*тш] gki~Mp) do, (2.112)
где
/4(д/>)=Ль(р)(»* +а1о>)Осо)*-1 +...+л,(р) ;
&С/^р)=л(рХ»2*'2+л(рХ;в))2*"4+...+&-|(/»).
Как уже указывалось ранее, чрезвычайно важным является тот факт, что для
значения интеграла (2.112) можно записать точную формулу. Таким образом,
функционал (2.1 \0) удается представить в виде функции, явно зависящей от переменных
К(Р\ *Н(Р)>•••»К(Р\ 8о(Р)> 8\(Р)>•••» 8к(р) и> следовательно, явно зависящей от
параметров /?,, ръ ..., рг, т.е. I(p) = I(P\,p2>...,Pr) •
Эта формула имеет вид (см. приложение в первом томе)
(-0**4
ш^ЩрЖк-
где
102 Методы синтеза САУ по заданным показателям качества. Часть II
Мк = " " " , mkr = h,k_r{p)\ К{р) = 0 (v < 0,v > к),
тк\ тк2 - ткк
Nk - определитель, полученный из Мк заменой элементов первого столбца
величинами go(p% g\(p), ..> gk-\(p) •
Таким образом, здесь центральную роль играет равенство Парсеваля,
позволяющее полунить следующее основное соотношение
1 7 gkU*.Pi,P2,...,Pr) Jm. (2Л13)
2я4АА(Ую,/?1,р2»»->Л)А*(-МЛэЛэ-..»л)
H)*+4(fl.ft,---,Pr) min
2K(P\>P7>->Pr)Mk(PbP2>~'>Pr) (Pi>Pi> -Л)
при указанных выше ограничениях.
Если же эталонная переходная характеристика задана Яэ ($), то
ЕШ в p)-G fU<°) + l Ьт(рХЛ»Г+... + Ьт(р) 1 _
" ' °а2С/о))2+о,0-ю) + 1 а„(рХМ)т+... + а„(р)М
% (pXj®)kl +...+со(р) cc/<D,j>)
и функционал, подлежащий минимизации, имеет вид
а;„ „ и\ ' f C(MP)C(-Mp) .
1{Р^-Р^Тп1о^рш-М^-
Так как параметры р],р2,...,рг входят в коэффициенты изображения,
определяющего невязку, нелинейным образом, то сформулированная задача расчета
pi9 i = l,r, является задачей нелинейного программирования и может быть решена с
использованием известных методов (см. Приложение 2, а также [37]).
Ввиду сложности приведенных выше ограничений для решения задачи
нелинейного программирования можно использовать процедуру численного направленного
поиска; в частности, может быть использована процедура случайного поиска [7].
Дополнительно может накладываться ограничение на колебательность системы. В
[7] приведены зависимости, определяющие ограничения, накладываемые на
коэффициенты характеристического уравнения.
В каждом конкретном случае проектирования регуляторов можно для некоторых
ограничений записать явные соотношения, зависящие от параметров, для других же
реализуется поиск параметров, удовлетворяющих нужным ограничениям, при этом
показатели качества на каждом шаге направленного поиска могут определяться по
результатам интегрирования дифференциальных уравнений, описывающих динамику
системы.
Глава 2. Методы синтеза регуляторов в классе одномерных систем
103
Пример 2.12 [144]
Рассмотрим систему автоматического управления перегрузки летательного аппарата с перестройкой
параметров регулятора в зависимости от высоты и скорости полета (рис 2 41)
V
н
t
nw
*®4
*t(y+ixy+o
*(У + 1)
*V*)
■&а>
*6№*+1)
♦-►
1
Kl Гс5 + 1
Летателы ый аппарат
КМ
Рис. 2.41. Структурная схема системы автоматического управления
Значения параметров объекта в зависимости от скорости и высоты полета приведены в табл. 2 9.
Таблица 2.9
Режимы
полета
1
2
3
4
Я, км
0
6
10,5
13,5
М
0,2
0,6
1,2
1,8
к*
0,067
0,298
0,274
0,229
кь
0,555
0,882
0,432
0,242
Т, с
0,741
0,378
0,182
0,178
0,388
0,301
0,160
, 0,094
Гс.с
2,76
1,89
1,8
2,59
Постановка задачи: рассчитать параметры последовательно включенного регулятора системы
управления перегрузкой летательного аппарата в зависимости от высоты и скорости полета, обеспечивающие
устойчивость и заданные показатели качества в различных режимах полета (см. табл. 2.9)
Найдем ПФ объекта управления [144]:
KZ(Tcs + \)
= ГУ + 27^ + 1 Кп К.
1 +
кЛгк%(тс5+\) KZ(Tcs+\) Л2+(2Д + /:дг^гс)5+(1 + /:дг^)
T2s2 + 2T$s + l
К»
АО
' O\s +\)(T2s +1) ejj2 +а,°5 + а00'
где К,
) \
т^+ы&у
д , КЛУК1ТС | _jl.
)
к,кр.) ,
Положим, что Кдг = 0,8 - глубина обратной связи по угловой скорости тангажа, теперь можно
рассчитать численные значения параметров Г, ,Г2,Кн для всех режимов полета (см. табл. 2 10).
Таблица 2.10
Режимы полета
1
2
3
4
0,0463
0,175
0,204
0,191
2,02
' 1,78
0,63
0,96
0,068
0,081
0,050
0,068
104
Методы синтеза САУ по заданным показателям качества. Часть II
ПФ регулятора, включенного последовательно, будем находить в виде
*t(V+ixy+i)_ ф*+ф,+ф
"У4 ' ./т .j.n /»«Уг24.с
(2.114)
где А? = KkTkTki;U? = *(7^ + W" = **;«? = П,-
С учетом изложенного выше структурная схема системы управления может быть представлена так
(рис. 2.42).
?
*t(V+iXV+1>
5(П,* + 1)
(r,j+ixr2j+i)
«(0
Рис. 2.42. Структурная схема системы управления перегрузкой ЛА
Поставим задачу синтеза регулятора, который обеспечит следующие параметры переходной
характеристики
Гр<5с; а%<20%
во всех режимах полета.
В качестве эталонной переходной характеристики выберем процессы, определяемые формулами:
/t,(0 = l-cos(p3*Ta'');
я>(,)Л—£±аь
где аэ = 1,1;Рэ = 1>2-
Поскольку
Щ*) = -
s (j + a,)2+^!
by$s2 + b?s + bF$
то преобразование Фурье невязки примет вид
1>,(/>)0«>)'
E{j<u) = H\s)-W(sY- = if .
где
с3(/>) = Й^в? - *gb? + cfoV + а,а№ + a,a»;
c4(p)=a3a2°af;
</,(р) = (аэ2 +рэ2)(во0+60°^)+2аА\к)';
^(р)-(^+ЙХ«^+*?г+аГг)+2«ц(Ц|+«|5^)+«8»Гг;
4(р)=(<ч2+Р'Х^+4)+2аэ(А4'+*№ + -?)+°о°+W;
rf4(p) = (a,2 +P2)a2°a?' +2а,(щ°а? +<£)+<&? +Ь°0Ь? +в?;
rf5(p) = 2a3a2°af+ai44'+''2;
Отсюда следует (см. формулу (2. Ill))
1 7 gt0o,P)
7<"'ft P') = 1Z\
2* *hkUw,p)hk{-jw,p)
dm,
Глава 2. Методы синтеза регуляторов в классе одномерных систем
105
где
go=O; Si=c42; g2=2c2c4-c32,
g3 = 2coc4-2c]c3 + c22; g4 = 2c(f2-c2], gs=c2&
Ao=flf6; hx-db\ h2=d4; h± = d3; h4=d2\ /%=</,; h6=d0 .
Функционал, подлежащий минимизации, может быть записан так:
где
М(р) =
ho(p)
0
0
0
0
go(p)
bo(P)
0
0
0
0
f(n\ -
I\P) ~
h2(P)
ho(p)
0
0
g,(p)
fh(p)
h,(p)
Up)
0
0
Nk(p)
2Иъ(.р)Мк(р) '
Чр)
A4(P)
Ыр)
Щр)
hx(p)
Up)
gi(p)
Up)
h,(p)
Up)
hip)
Up)
0
Up)
hs(p)
Up)
Up)
Up)
ёг(р)
Up)
Up)
Up)
Up)
Up)
0
0
0
Up)
Up)
Up)
g*(p)
0
0
Up)
Up)
Up)
0
0
0
0
0
Up).
SbiP)
0
0
0
0
Up)
N(/>) =
Минимальное значение функционала с соответствующими ограничениями находилось с
использованием пакета Matlab (при проведении конкретных расчетов необходимо учитывать факт многоэкстремаль-
НОСТИ фуНКЦИИ 1{р ,/?2, . ,рг))
На рисунках, которые приведены ниже, представлены графики переходных характеристик системы без
регулятора, эталонной системы и системы с синтезированным регулятором.
Для 1-го режима получены следующие численные значения коэффициентов ПФ регулятора и
параметров Кк, Ткх, 7^ и7^ :
6^=218,1548; 6^=323; 6^ =107,99; ^=1,88;
Кк = 107,99; Ткх = 1,021; 7^ = 1,98; Г*. = 1,88.
Л(/)и
12 3 4 5 6 7
Рис. 2.4Э. Графики переходных процессов (режим 1)
Для 2-го режима имеем*
V? = 31,2; Ь? = 59,8, Ь$ = 26; а1? = 3,4;
К* =26; 7^=1,5; 7^ =0,8; 7^ =3,4;
106
Методы синтеза САУ по заданным показателям качества. Часть II
соответствующие графики приведены на рис. 2.44.
1,4
j2| I I ■*£—'
1 2 3 4 5 6 7 8
Рис. 2.44. Графики переходных процессов (режим 2)
3 режим: коэффициенты и параметры имеют следующие значения:
У? = 12,8; if = 34,5; Iff = 23; а? = 2;
Кк = 23; Ткх = 0,8; 7^ = 0,7; 7^ = 2,
а графики имеют вид (рис. 2.45).
1,4
1,2
0,8
0,6
0,4
0,2
Т У~\ Т
I I
I I ...
\ И{() - реальный переходцрй процесс
I y/l
—-!-V4
L 1
—f—
:xq
4.-
4 1
Ш/) - ndpexoAHujft npousci без регулятора
4 1
^,c
Рис. 2.45. Графики переходных процессов (режим 3)
4 режим: коэффициенты и параметры имеют следующие значения:
Глава 2. Методы синтеза регуляторов в классе одномерных систем
107
6^=22,68; ^=46,8; 4^=24; я£у=2,01;
^ =24; 7* =1,05; 7^=0,9; 7^ =2,01,
а графики переходных процессов имеют вид (рис. 2.46)
Л(/)п
т-
12 3 4 5 6 7
Рис. 2.46. Графики переходных процессов (режим 4)
2.7. ОПТИМИЗАЦИОННЫЙ МЕТОД СИНТЕЗА РЕГУЛЯТОРОВ
ВО ВРЕМЕННОЙ ОБЛАСТИ
Сделаем предварительные замечания. В §1.4 рассматривался подход к решению
проблемы синтеза регулятора, не требующий знания обратного оператора замкнутой
системы. Общая формула, определяющая решение задачи, имеет вид (см. вывод
формулы (1.54)):
т 2
Л[4оЛу(ЛэЛ...,л)(/ + 4>Лу(ЛэА-»Рг))"1 |*э(0-л(0) <*-> тщ_,
л \L J ) Pi >' — !»''
где Ао - оператор объекта управления,
Аку (Р\ у Р\•••» Рг) - оператор регулятора,
уъ(г) - заданный вход, хэ(0 - эталонный (желаемый) выход.
В настоящем параграфе изложим этот подход применительно к решению задачи
синтеза регуляторов в классе линейных одномерных стационарных систем.
Рассмотрим систему (рис. 2.47).
Пусть заданы: WQ(s) - передаточная функция неизменяемой части САУ; место
включения и тип корректирующего устройства; W^{s,p) - передаточная функция
корректирующего устройства; Р\,Р\,—9рг - параметры КУ, подлежащие
определению в результате решения задачи синтеза.
108
Методы синтеза САУ по заданным показателям качества. Часть II
y{t) +,-. е(/)
Стационарный
линейный регулятор
* с регулируемыми
параметрами Р\,Ръ *Рг
Изменяема часть (стационарная)
u(t)
Стационарный
линейный объект
управления
Неизменяемая часть
*(/)
Рис. 2.47. Структурная схема линейной стационарной системы
Тогда Wp(s,p)-WKy(s,p)lV0(s) - передаточная функция разомкнутой системы.
Отсюда находим ПФ замкнутой САУ:
W(s р)- Wp(s>p) ^bm(p)sm+... + b0(p)
К'Р \ + Wp(s,p) an(p)sn+... + a0(p)
(2.115)
р = {/?!,...,pr} - множество неизвестных параметров КУ.
Перейдем от передаточной функции к дифференциальному уравнению системы
2>v(/>)*(v) =f>4(/0/4) • (2.П6)
v=0 к=0
Коэффициенты уравнения зависят только от р( - параметров корректирующего
устройства. Далее положим ап(р) = 1.
Рассматриваемый метод принадлежит к классу методов, использующих
приближение к эталонному выходному сигналу хэ (t), являющемуся реакцией на заданное
воздействие y3(t).
Для класса стационарных систем уэ(() может быть единичной ступенькой, т.е.
y3(t) = \(t), а хэ(/) = Лэ(0 - эталонная переходная характеристика.
При идеальном выборе структуры и параметров регулятора должна иметь место
зависимость
£аЛр)х?\{)=£ьк{р)у[к\0. . (2.117)
v=0 k=0
Другими словами, при подстановке в ДУ скорректированной системы y{t) = y3(t)
ее частным решением при Х° =(;с(0),У(0),...,д:(л"1)(0)) должна быть функция
jc(r) = jc3(/) и, таким образом, должно быть выполнено тождество (2.117). Однако
идеальный выбор КУ практически невозможен. Поэтому задача синтеза КУ состоит в
том, чтобы подобрать параметры КУ, обеспечивающие минимальное значение невязки
между правой и левой частями ДУ (2.116) при подстановке в него желаемых
воздействия и реакции [7].
Пусть y3(t) - заданное воздействие, хэ(/) - желаемая реакция; тогда уравнению
(2.116) эквивалентно интегральное уравнение вида [147]
хэ (/) +1 kx (t, т, р)х3 (т) dx =[ к у (t, т, р)у э (т)</т,
(2.118)
где
Глава 2. Методы синтеза регуляторов в классе одномерных систем 109^
Перепишем (2.118) в виде
*>(')+1оЛ")!^;^[('-1)""']'-МЛ-
'■(-D* *' (2'20)
-£М')!?^^[<'-1)""Ь(1)Л=£"''>)-
ше обозначение:
J(«-l)!c/xvL j3
0
Введем следующие обозначение:
0 ' ' (2.121)
f(-D* d"
С учетом введенных обозначений (2.120) принимает вид
.*э(') + Zflv(p)^(0-£6*(p)^(0 = E(t,p); (2.122)
v=0 Jfc=0
в последней зависимости функции D*(t), v = 0,«-l и D%(t), k = 0,m известны.
Пусть
п-\
F,(/,p) = x,(0+Sev(p)^(0;
v=0 (2.123)
Тогда невязка E(t, p) определяется соотношением
E(t,p) = Fl(t,p)-F2(t,p). (2.124)
Последняя формула имеет вид функции, явно зависящей от параметров
рир2, -,рг регулятора.
Рассмотрим конкретный случай, когда y^(t) = l(t), а х^(1) = Ку(\-е~а>') -
эталонный переходный процесс.
Тогда зависимости, определяющие Fx(t,p) и F2(t,p) принимают вид
izi"zk-] (-i)>
^«>Р) = Ку(\-е-а*') + Ку% 2 et(/»)-
*-о у-о w у (2 125)
х/"->-*-:
^■r^VHW"- (2Л26)
Формула, определяющая невязку E(t,p), явно зависящую от параметров
регулятора /?!, р2, ..., рг, может быть записана так:
110 Методы синтеза САУ по заданным показателям качества. Часть II
E{t,px,p2,...,Pr) = KJ\-e-^) +
(£»£■■ (_iy
+*,Z I 77
"к {РъРъ-<Рг)—7гЪК (риР2,-,Рг)
ку
,„-*_
»Лп-^ {-\у , . .. . .... (2.127)
ыо н> 0>1)!(л-у-*-1)!
Л—1 /7—Л—1 f—iW
-^vX Y Г~^ <*k{PuPi>~*Pr)*n~J~M +
jt=O 7=0 \аэ )]An-J-K-i)\
n-\n-k-\ j (-.\\J
+^Z Z Z ,-,„., "). k ak{Px,Pl,...,Pry-^e-^.
кшо j=o /=оаэ v\n-j-k-\)\
Для расчета параметров регулятора можно использовать функционалы вида
Л(/?1)Р2-..рг)=тах|£(/,/71,/?2,...,/7г)|. (2.128)
Последняя зависимость трудно реализуема и на практике применяется весьма
редко. Более простой как с аналитической, так и с вычислительной точек зрения
является квадратичный функционал
т
I2(pl,p2,:,Pr) = lE\t,pbp2i...,pr)dt. (2.129)
о
В некоторых случаях целесообразно использовать функционал вида
со
1ъ{РмРъ^Рг) = \Е2^РиРъ->РЖ*)<Ь> (2-130)
о
где р(0 - весовая функция; примером весовой функции является экспонента, т.е.
р(О = е-с'.
Значение Т выбирается из условия Т = (5 - 8)Гр.
Задачу синтеза регулятора можно сформулировать так: найти минимум
квадратичного функционала
00
I(p) = I2(Pi,P2>'~>Pr)=\E2(t>P\>P2>-,Pr)e~ctd-+ mio_ (2.131)
при следующих ограничениях:
1) синтезируемая система должна быть устойчивой;
2) hp(t,pbp2,...,pr) - реальная переходная характеристика должна находиться в
«коробочке» В.В. Солодовникова;
3) Со ^С0доп, Сх ^С1доп, ..., т.е. коэффициенты ошибок не должны превышать
некоторых допустимых значений.
Сформулированная задача относится к классу задач нелинейного
программирования [37]. Зависимость, определяющая 12(Р\,р2,...,рг), является
многоэкстремальной, поэтому расчет глобального экстремума встречает значительные трудности.
Минимизация 1{р) может быть выполнена с помощью программ минимизации
функций, которые присутствуют в научно ориентированных пакетах прикладных
программ. Предпочтительнее выбирать программы, специально предназначенные для
минимизации квадратичных функций. На параметры, по которым ведется
минимизация, должны быть наложены ограничения, вытекающие из какого-либо критерия
устойчивости.
Например, можно воспользоваться критерием устойчивости Льенара - Шипара,
который сводится к ограничениям типа неравенств.
Глава 2. Методы синтеза регуляторов в классе одномерных систем Ш_
К ограничениям, обусловленным требованиями устойчивости системы,
добавляются ограничения, обусловленные требованиями точности работы системы в
установившемся режиме.
Минимизация функционала 1(р) не гарантирует принадлежности реального
переходного процесса «коробочке» В.В. Солодовникова, поэтому дополнительно
добавляются соответствующие ограничения.
Минимизация функции многих переменных при указанных выше ограничениях -
достаточно сложная и трудоемкая задача.
Ввиду того что рассмотренный метод не требует знания обратного оператора,
а невязка E(t,pbp2,..>,pr) порождается разностью между левой и правой частями
дифференциального уравнения системы, он обобщается на нестационарные,
нелинейные и многомерные системы, системы с запаздыванием; дает возможность
учитывать ограничения как на параметры системы, так и на характеристики
процессов на выходе; при попадании в область неустойчивости процесс расчета
продолжается. Метод позволяет учитывать требования, связанные с устойчивостью
и точностью работы в установившемся режиме и использовать разные критерии
качества, в том числе и логические. В заключение отметим, что при расчетах можно
использовать стандартное программное обеспечение, реализующее аппарат
математического программирования, причем степень сложности расчетов слабо зависит от
степени сложности синтезируемой системы.
Пример 2.13.
Для системы управления технологическим процессом передаточная функция определяется
зависимостью [91]
Щж) —у+у+ь+\ 9
a6s +a5s +a4s +a^s +a2s + a,.s + a0
где
bQ = l,22p4; bx = l,22/>3; b2 = l,22/?2; b3 = l,22p,;
до = 1,22р4; 5j =l,22/?3; a2 = l + l,22/?2;<53 = 5 + 1,22/?,; 54=9; <55=7,4; <56=2,25.
Пользуясь рассмотренным выше методом, требуется рассчитать параметры Р\,Р2,Рз,Р4 >
обеспечивающие приближенное выполнение условий с% й 30%, Гр «(20 - 30) с [91 ].
Найдем ДУ, определяющее переходную характеристику
• *<64o+i*v(/>)*(v)=i>(/>b'<*)>
v=0 *=0
где
, ч 122 , ч 122 , ч 4 122
а° Р 225Р4' в1(р) = 225л; *2 9 + 225Р2;
, ч 122 20 . ч . , ч 148
225Pl+~9~; fl4^= ; а5^=И5' °в
, ( ч 122 , , ч 122 . . ч 122 ... 122
°^=225P4i ^P) = 225Pii 2(/?)=225/?2> з(/?)= 225Pl'
При произвольных значениях параметров регулятора /?,, р2» Рз> Р* имеет место зависимость,
определяющая невязку £(/,/?):
£(/,/?) = хэ(/) + 2av(p)Dxv(t)-Xbk(p)Dyk(t),
v=0 ^=0
где
0№)-i^|r[('-')!]lW".
причем дсэ(/) = 1-е"а>/.
112
Методы синтеза САУ по заданным показателям качества. Часть II
После элементарных преобразований легко получить соотношение для невязки
E(t,Pup2,p3,p4) = \-e-a^-— /4+ — /3-2/2+ — /-
122
1
1 /2
_ 1 £_ _ _
~225Р4[п0 '^7~24 *^ + 6 al~2 '^V~'~
122 Г_1_ _И___[ j^_ _[ il_ JL jl
225Рз[24'аэ 6а2+2'^ а<+а5э]
122
1 t3 1 /2
"1~+2^/?2Лб"а~~2'^+^"^
а'
(20 122 "jfl /2 / / 1 . Г / 1 ] 148 1
4 122 20 122
_122 р4 122 Рз 9 + 2Г5Ра , J+225Pl
225 с^ 225 а^ а4 а^
4 148
45 аэ
Поскольку Гр = 20 с, то аэ « — = —; функционал определим зависимостью
Гр 20
1(Р\>Рг>Рз>Р4) = \Е2(*>Р\>Р2>Рз>Р4)е *dt.
Соотношение, определяющее функционал, можно переписать так:
I(pl,p2yp3,p4) = 0t023Z75p3 + 010lp4+0,\p]+0t000&79pl +
+0,00227-р]-2-р}р2 + 0,05-р2+0,00035 р2 + 0,00043 рър4 +
+0,00014 • pi + 0,0007 • р4 • р, + 0,00058 • р4 • р2 + 0,001 •p3/?2+0>0013fVPi +12744.
При принятых условиях процесс оптимизации при ограничениях на коэффициенты
характеристического уравнения, реализующих критерий устойчивости Льенара - Шипара, позволил получить следующие
значения параметров регулятора:
р\ = 1,2; р\ = 0,81; р\ = 0,12; р\ = 0,001.
Графики эталонного и реального переходных характеристик представлены на рис. 2.48.
0 10 20 30 40 50
Рис. 2.48. Графики переходных процессов
Был проведен также расчет параметров регулятора для следующих условий:
Гр = 10 с, а%£30%.
Поскольку в этом случае аэ = — = — , то функционал принимает вид:
Глава 2. Методы синтеза регуляторов в классе одномерных систем
ИЗ
ЦРиРг'РэуРл) = °>°087 Ра +0,00012- р\ -0,02-р3 + 0,00036 р4-/?3 +
+0,08 • /?, + 0,04 • р2 + 0,00058 • р4 • /?, +0,001 \рърх +0,0019 /?,2 +
+0,000298• р\ - 0,0005 -р4'Р2+ 0,00075• р\ + 0,0023 • рх • р2 +
+0,0009 -рур2 + 0,9724.
Функция веса определяется формулой
В результате оптимизации получены следующие значения параметров регулятора*
р* = 2,1; /?2 = i>6; Рз=о>6'> />J = o,O2i.
Соответствующие графики, определяющие /?р(0 и Лэ(0, приведены на рис. 2.49.
Л(0"
0,2-
5 10 15 20 25
Рис. 2.49. Графики переходных процессов
Пример 2.14.
Рассмотрим задачу синтеза регулятора в системе автоматического управления газоперекачивающих
агрегатов [56].
Большинство крупных газовых месторождений отстоят от промышленных и коммунальных
потребителей на несколько тысяч километров и несмотря на то, что природный газ на выходе из скважин имеет
давление более 10,0 МПа, транспортирование его за счет естественного давления возможно только на
коротких участках газопровода
Увеличение пропускной способности газопроводов достигается путем установки на расстояниях
100 - 150 км друг от друга промежуточных компрессорных станций (КС). КС восстанавливают давление
газа на участке газопровода до расчетного значения. Компрессорные станции оборудуются комплексом
технических средств, обеспечивающих надежную работу газоперекачивающих агрегатов (ГПА), обычно
включенных в последовательные и параллельные группы.
ГПА состоит из нагнетателя и привода, в качестве которого преимущественно используются
газотурбинные установки (ГТУ). В нагнетателе, который представляет собой лопаточную машину сжатия,
энергия внешнего источника сообщается газу, за счет чего и повышается его давление. Задачей системы
регулирования является поддержание одного или нескольких параметров на требуемом уровне В ГПА
регулируемыми параметрами являются либо частота вращения нагнетателя лйбр давление газа на выходе из КС.
Газотурбинная установка с нагнетателем и газопровод представляют собой динамическую систему
(объект регулирования), которую можно представить в виде отдельных элементов или звеньев.
Уравнения движения элементов ГПА составляют, исходя из условий баланса мощностей (моментов) и
законов сохранения массы, энергии или других свойств. Основными характеристиками любого звена
являются динамические константы, определяемые расчетным или экспериментальным способом.
Применительно к решению задач устойчивости и определения качества переходного процесса будем
рассматривать только малые колебания динамической системы около равновесного положения. Это
означает, что математическая модель включает только линейные дифференциальные уравнения с постоянными
коэффициентами, или, что то же самое, из-за малости отклонений параметров от состояния равновесия,
нелинейную зависимость при разложении в ряд Тейлора представляют только первыми членами
разложения (учитываются только линейные члены). Изменение искомых величин и независимых параметров
удобно представить в безразмерном виде в относительных координатах:
9 Зак. 366
114
Методы синтеза САУ по заданным показателям качества. Часть II
5j =_!Q—£_1552 =ii2o—£l;5ir=ilQ>—£lL;52r =i-2ni—E2L _ относительные изменения давления
P\o P20 Piro Ргт
на входе и выходе из компрессора (или нагнетателя). Индекс «О» обозначает,значение параметра в
установившемся режиме;
54 =ii4o_£_±j g5 -Еш—El. _ относительные изменения давления на входе и выходе турбины
НИЗКОГО
го давления (ТНД),
Р50
7Vn-7;
^40 "" Та . _ Г<п - Тк
З.т =iiO
У30 - '40 У50
сокого давления (ТВД) и входе и выходе ТНД.
В качестве масштабов приведения величин к безразмерному виду целесообразно принимать их
значения в равновесном состоянии.
Заданный режим работы объекта нарушается вследствие возмущающих воздействий Для ГПА это, в
основном, изменение потребления газа, приводящее к изменениям крутящего момента нагнетателя и
связанной с ним турбины. К возмущающим воздействиям для ГПА следует отнести и изменения температуры
и давления окружающей среды. На рис. 2.50 представлена функциональная схема САУ. Возмущением
системы является относительное изменение потребления газа X в выходном участке газопровода.
Регулируемой величиной является относительное изменение давления газа на выходе нагнетателя 82Г , а
регулирующим воздействием является относительное открытие топливного клапана ц
Я
Jib
УЛ.
Рис. 2.50. Функциональная схема автоматического управления ГПА:
/ - чувствительный элемент; 2 -усилитель; 3 - главный сервомотор; 4 - ГПА
Структурная схема САУ имеет вид (рис. 2.51).
Тах s+au
<J>l(*)
М*)
X(s)\ Вход Выход
ф-В-Ф^
»4<*)
Рис. 2.51. Структурная схема ГПА с двухвальной ГТУ
Приведем численные значения параметров [56]:
Глава 2. Методы синтеза регуляторов в классе одномерных систем 115
ап =2,1, я,2 =1,12, а13 = 0,7,я,4 =0,5;
«21 =15,3, а22 = 2, а23 = -19, а24 = -19, а^ = 0,5;
я3, = 0,5 с, я32 = 1, аъъ = -1,1, я34 = 0,5, а35 = 0,35, а36 = 0,07;
Гт = 0,03 с, я4, = 1,16, а42 = 2,1, д43 = 0,5, а^ - 0,07, а45 = 0,02, а^ = 0,04;
Тп = 0,02 с, я5, = 1,01, а52 = 1,08, а53 = 0,5, Л54 = °>й
^3 = 14 с, аех = 21,7, а62 = -20,5, я63 = 15,1;
^4 = 9,54 с, а1Х = 24,8, а12 = -20,5, л73 = 15,1;
6,, = 0,314,621 =0,201.
ПФ корректирующего устройства имеет вид
жи(,)=-*2>-- ±
^ S2r(j) Г^Г^Лзбр*3 + (7>3Л, + Ts2Ts3 + 752Г5, )8р^2 + (7j, + 7>2 + 753)8р5 + 6р '
где Tslt Ts2, Ts3> Ьр - параметры регулятора.
Пользуясь известными методами, можно получить следующее дифференциальное уравнение,
описывающее поведение САУ:
Хау(,)*<*>=£м/>>*<*\
v=0 *=0
где
x(t) - выходной сигнал (62Г(/)); y(t) - входной сигнал (Я.(0);
а0 = 6155,2961808р +493,8437521;
5, =(79535,363154-6155,2961807>3+6155,29618075, +
+6155,296180752)6р + 6834,487720;
а2 =(79535,363157>3+312706,1214 + 79535,36315Г52 + 79535,36315Г5, +
+6155,296180Г51Г52 + 6155,296180751753 + 6155,2961807^2Г53)5р+ 12562,75068;
а3 = (79535,36315^,^2+6155,2961807^,^2753 + 312706,1214753 +395952,3304 +
+79535,363157527i3+312706,121475,+79535,36315Г5,Г53 + 312706,1214752)8р +
+521,3389;
54=(312706,1214Г5,Г53 + 79535,361575,Г52753+312706,1214Г5,Г52+ 57417,2539 +
+312706,1214752753 + 395952,330475, + 395952,3304752 +395952,3304753)8р +
+0,4546266779;
а5 = (395952,330475,753 + 395952,3304752Г53 + 312706,1214Г5,752Г53 +1859,0647 +
+395952,330475,Г52 + 57417,25395752+57417,25395Г5, + 57417,2539395Г53)8р,
а6 =(57417,25395Г5,753 +57417,25395752753 +4,82864623 + 57417,25395Г5,Г52 +
+1859,064703Г52 +395952,330475,Г52Г53 + 1859,06470375, + 1859,0647037j3)Sp;
ап = (57417,2539575,Г52753 + 1859,064703Г5,Г53 + 4,82 8646229 75 3 +
+1859,064703Г5,752+ 1859,064703Г52Г53+ 4,82864622975,+4,828646229752)8р;
58 = (4,828646229Г5,752 +4,828646229Г5,Г53 + 1859,064703Г5,752Г53 +
+4,828646229752753)8р;
а9 =4,82864622975,Г527538р;
Ьо = -1228,2112888р; '
й,= (-1228,21128875,-12176,49993-1228,211288753-1228,211288752)8р;
й2 =(-29655,43270-12176,49993Г53-12176,4999375,+1228,211288Г5,753-
+1228,211288 75,752 -1228,211288 Ts2Ts3 -12176,49993752)8р;
Ьъ = (-12176,49993Ts{Ts2 -12176,4999375,753-29655,43270Г5, -5522,08536-
-1228,21128875,752753 - 2965 5,43270 75 2 - 29655,43270753 -12176,499 75 2Г53)8р,
Ь4 = (-29655,4327075,Г52 -193,5547424 - 5522,085360753 - 29655,4327Ts2Ts3 -
-5522,085360Г5,-12176,49993Г5,752753-29655,43270Г5,Г5з-5522,0853752)8р,
116 Методы синтеза САУ по заданным показателям качества. Часть II
Ь5 = (-29655,432707j,7j27j3 - I93,55474247j3 - 193,55474247j2 -05061474040-
-5522,085360752Г53-5522,0853675,^2-193,5547424Г51-5522,085375|Г5з)6р;
Ьв = (-5522,0853607^,^2^3 - 0,5061474040752 - 193,554742475,7$3 - 0506147404075, -
-193,554742475,7*2-0,50614740407*3 - 193,55474247527i3)5p;
Ь7 = (-193,554742475,752753 - 0,50614740407i2753 - 050614740407i,753 -
-0,506147404075,752)6р;
Ьъ =-0,506147404075,Г52Г538р;
р -параметры регулятора (75,,752,753,6р).
Эталонный переходный процесс определим выражением лсэ(/) = Ку(\ -е~а^').
Имеем
E(t) = Fl(t,p)-F2(t,p) = Ky(\-e-a>l) + Kyj^g}ak(p)-±-bk(p) L8"* -
Аг=О L КУ J
-Ку^ак{р)^щ^-к-^Ку^2как(р)е-^\
*=0 7=0 *=0
где
1 1 1 1 1 =J_. =1[. =J_.
go " 3628800'g| " 40320'8l " 5040'*3~ 720'g4~l20'8s 24><&6 " 6'g? " 2>gs ~ '
1 1 _ 1 1 1 1 1 1 _ 1
a^ a? a37 aj aj aj aj aj аэ
1 11 11111
1 11111
co3O = ; co3, = -; o32 = —=-, co33 = j; cd34 = —r; co35 = —jr;
30 120аэ 3I 24al 32 6a3 33 2a43 а5э а^
1 1111
26аэ 6аэ2 2а^ аэ4 а^
1 111
6аэ 2аэ2 а3 аэ4
J_ l l
2a.
«60 =T~;o)6i =—2->о)б2 =т;
1 1
o70=—;co7, =—2*;
аэ аэ2
1
®8o= — •
аэ
Тогда
F,(^)-^p)=M.-e-)+^[^«-t)+s(ai-t
5040[ 2 ^J 720[ 3 ^J 120[ 4 A:J 24[ 5 Ky
t4 t5 t6 t1 t% \ ( \ t t1
24a^ 120a4 720a^ 5040a2 40320a3J [ a] a] 2a^
Глава 2. Методы синтеза регуляторов в классе одномерных систем 1_Г7^
+_^___^_+_^ t6 | /7 ] Jj !_+jL+jL+
+ 6al 24a< + 120aJ 720a? +5040a, /' +[c^ aj + 2a^+6a< +
I* r5 /6 1 f 1 / t2 l3
+ r-r 7 + - <Z2 + Г + —Г 7 +
24a J 120af. 720a2 J ^ a* a* 2a* 6af, 24a* 120a*
f 1 / t2 /3 /4 1 f 1 / /2 /3 "I
[a\ at 2*1 6al 24a\) { a', a> 2a? 6aJ
|,а3э a2 2aJ ^ a2 a3j аэ J '[аэ' а8э a^ aj c^ а4э
а3 аэ2 aj
где
av(P>oy(p)/an(p), v = 0,l,..8;
bk(p)^bv{p)yjan(p)1 v = 0,l,...8.
Анализируя ДУ, описывающее поведение САУ, можно определить установившееся значение
выходного сигнала хуст при заданном входном воздействии ул •
= ^ 1228,2112886 р
^3
а0^3 6155,295186 р+ 493,8437521
Но а0 и Ьо зависят только от одного параметра КУ, а именно от степени неравномерности регулятора
Ьр . Обычно принимают 6р = 0,05, поэтому хуст =-0,07660916735^. При ^=0,1 желаемую реакцию
зададим в виде*
хэ(/) = -0,00766091673(1 -e^3t), т.е. ^ = -0,00766091673; аэ=0.3
Функционал, подлежащий минимизации, запишем в виде
200
/(Гд„Г52,7>3)= j E2(t,Tsl9Ts2Js3)dt .
о
Или, что то же самое,
I(TsuTs2Js3) = 2531,00537Й7^| + 5223,412078Г5,7д3 + 5223,4220787527*3 +
+206,2287806752Г^з +206,2287806^^ + 206,22878067j,7>32 +
+206,2287806752Г532 + 206,228780675,27i2 +2531,0053787i22 +
+2531,0053787*? + 206,2287806^, Г^22 + 15,80914574752Г52Г52 +
+0,32975575127532752 + 15,8091457475|Г53Г51 +0,30297552Г5|Г^Гд, +
+15,809145747*, Ts]Ts2 +4,217651863752Г532 +4,217651863Г52Г532 +
+0,30297557527*27s3 +0,0054693627j12r^7532 + 4,217651 MTsfTsj +
+3946,9114667*, +3946,911466^, +3946,911466^ +
+624,4817541^,7*2^3+5223,41207875,752-1544,167750.
Так как при синтезированных параметрах система может оказаться неустойчивой, были введены
ограничения на устойчивость системы.
Решение задачи было получено с использованием метода нелинейного программирования, причем
исходными данными для решения задачи на ЭВМ были: параметры эталонного процесса; функция,
определяющая невязку и зависящая от параметров регулятора; ограничения на искомые параметры Г5,,752,75з,
заданная колебательность системы.
В результате минимизации были получены следующие значения параметров регулятора
Г.У, = 0,028748 «0,03; Ts2 =0,072578 «0,07; Ts3 =0,153567«0,15 .
Проведем, анализ скорректированной системы Передаточную функцию системы с найденными
параметрами регулятора можно записать в виде
или, что то же самое,
118
Методы синтеза САУ по заданным показателям качества. Часть II
^(5) = (-0,797182161610-5j8-0,0034812422457-0,2587889956-7,633197755-
-104,2509790/ -657,2274284/-1636,02800s2 -624,1776385-61,4105644)/
(0,0000760511781 b9 + 0,3340876159/ +2,5 54180149/ + 78,807744243/ +
+1154,133273/ + 8089,33787b4 +24295,88162/ +29197,51156/ +
+10888,197085 + 801,6085611).
Найдем реакцию системы 62Г(0 на заданное входное воздействие X = 0,1.
Известными методами получим выражение, определяющее выходной сигнал:
82Г(/) = -0,007660916734 - 0,0012&Г351'8750908' + 0,48096е-33'38008687' +
+0,33888 • i(rV23'62691103' + 0,0002815496096е-12'60350525/ cos(2,l 67470826/) +
+0,0002682842784е-12'6О350525/ sin(2,167470826/) - 0,005362514165<Г2'87840526/ +
ч^01401796355е-1753Ш916'-0,00403779^^
На рис. 2 52 пунктирной линией показан эталонный выходной сигнал, а сплошной линией показан
реальный выходной сигнал.
0(111111111
1 I I I I I I
10 20- 30 40 50 60 70 80 90 100
-0,001
U с
Рис. 2.52. Эталонный и реальный выходные сигналы скорректированной системы
2.8. ПРОЕКЦИОННЫЙ МЕТОД СИНТЕЗА РЕГУЛЯТОРОВ
Этот метод по существу является одной из форм реализации метода,
рассмотренного в предыдущем параграфе, т.е. метод относится к классу оптимизационных во
временной области.
Положим, что в зависимости (2.122) коэффициенты av(p\ у = 0,я-1 и
Ьк{р), к = 0,т зависят от параметров регулятора. Воспользуемся обозначением
-av(p) = Cv(p\ у = 0,и-1; bk(p) = Cg(p), g=;fl,w + m + l;
-£>*(/) = Z)v(/)> v = 0,h-1; D£(t) = Dg(t), g = w,/7 + w + l.
Тогда соотношение (2.124) можно записать так
£(^) = *3(/)-£cv(/>)Z),(p).
(2.132)
v=0
Задача заключается в нахождении таких коэффициентов Cv(p), у = 0,л+/и,
которые обеспечивают минимум функционала
Глава 2. Методы синтеза регуляторов в классе одномерных систем 119
J *,(O-£cv(p)Dv(p) Л. (2.133)
0L v=0 J
Сформулированную задачу можно трактовать как задачу приближения функции
x3{t) линейной комбинацией элементов D0(t), D}(t), ..., Dn+m(t), причем должна
быть обеспечена сходимость в среднеквадратичном. Другими словами,
коэффициенты Со(/?), С}(р), ..., Сп+т(р) подбираются из условия минимума
среднеквадратичной ошибки.
Если же рассчитаны Cv(p), v = 0,л+ m, то далее решается задача нахождения
параметров регулятора ри р2, —,рг- Задача имеет наиболее простое решение, если
параметры р{9 р2, ..., рг входят линейно в коэффициенты С0(р)9С1(р)9...9Сп+т(р).
Тогда путем группировки в (2.132) членов относительно неизвестных параметров
Р]> Рг> •••> Рг указанное соотношение (2.132) можно записать в виде
E(t,pl,p2,...,pr) = f0(t)-plflit)-p2f2(t)-...-prfr(t). (2.134)
Функционал (2.129) принимает вид
т
/(p) = f[/o(0-Pi/i(0«P2/2(0-.-.-Pr/r(0]2*. (2.135)
о
Из последней зависимости следует, что задача безусловной минимизации (2.135)
свелась к задаче приближения известной функции /0(Г) комбинацией известных
функций /,(0,/2(0,...,/г(0.
Если через Lr < /i(0>/2(0>—>/r(0 > обозначим линейную оболочку
(подпространство в I? [О, Т]), то сформулированная задача по существу будет задачей проектирования
/0(0 на линейную оболочку Lr < f\(t)9f2(t)9...9fr(t) > . Другими словами, это -задача
квадратичного приближения функции /0(/) функциями f\(t\f2(t\...,fr(t)\ В связи с
этим по своему содержанию метод является проекционным.
Минимум квадратичного функционала можно найти, если вычислить его частные
производные по параметрам р],р2,...,рг и получить систему уравнений, приравняв
их к нулю:
■^■=2}|Е/,(0л1/1(г)Лв0:
Ф1 bUo /
др2
oV/=o J
дРг {VU j
Данная система уравнений относительно неизвестных параметров КУ является
линейной системой алгебраических уравнений, которую можно переписать в виде
а\ \Р\ + a12/>2 + - + a\rPr = b\ у
<*ъ\Р\+аг2Рг+- + а2гРг = Ъ2\ (2.136)
<*r\P\+<*r2P2+- + arrPr=br-
120
Методы синтеза САУ по заданным показателям качества. Часть II
Решая последнюю систему, получим численные значения оптимальных
параметров Р\9 р1> —, Р*г- Если число параметров рх, р2, ..., рг невелико, то система
(2.136) будет хорошо обусловленной и трудности при ее решении не возникают.
Структурная схема алгоритма синтеза приведена на рис. 2.53.
Выбор структуры и параметров регулятора, выбор
места включения регулятора
Нахождение дифференциального и эквивалентного
интегрального уравнений замкнутой системы
X
Построение функций F\(p) и F2(p)
_L
Построение невязки £(/,/?)
X
Построение функционала 1{р)
X
Построение и решение системы алгебраических
уравнений
L
+. Р =\РиРг>->Рг)
Рис. 2.53. Структурная схема алгоритма синтеза регуляторов
Рассмотрим еще один подход. Положим, что система стационарна и ее ДУ имеет
вид
п-\
*(n)(0+2>v(/>)*(v) = I>v(/0/v); (2.137)
v=0 v=0
кроме того заданны у3 (/), х3 (t).
В общем случае у3 (/) - некоторый сигнал, подлежащий отработке, а хэ (/) -
желаемая реакция на у3 (/).
Перейдем от дифференциального уравнения (2.137) к эквивалентному уравнению
вида
гэ(0 + J*(/, т, p)z3(т)Л * § bv (p)y(3v) (0 - х<я-!> (6)an_{ (p) - (х["-]) (0)/ +
v=0
+x^2)(0))an_2(/?))-...-L"-\0)^£^ + xr2(0)^[+x,(0)jad(^ (2.138)
где
А^т,р) = Х*у(/»)(/ Т)>> 1м' гэ(0 = хэй(0,
to (я-v-l)!
(2.139)
причем хэ(0), х'э(0),..., х^п {)(0) - ненулевые начальные условия эталонного
выходного сигнала. Обозначим
r\n-2(t) = xi"-2)(0)t+xln-2\0), (2.140)
,п-\
tn-2
г1о(0 = 4"'1)(0)7Ц- + 4я"2)(0)-Ц- + ... + ^э(0).
(«-1)! (я-2)!
Глава 2. Методы синтеза регуляторов в классе одномерных систем \2\_
С учетом введенных обозначений (2.138) принимает вид
п-\
*э(о+2Хоо
v=0
Г Т)" ' г,(т)</т + лУ(0
(и-v-I)!
«ЕМ/О^Ю- (2.141)
v=0
Обозначая
U0 = K' Т)" ' Mt)dx + r\v(t), v = 0,/i-l
0(n-v-l)!
- известные функции, из (2.141) следует
п-\ т
r,(0+ Sflv(^v(O - £6,(P)^V)(O. (2-142)
v=0 v=0
В идеальном случае при соответствующем выборе параметров рх, р2, ...,рг
уравнение (2.142) превращается в тождество.
Поскольку такая ситуация в общем случае недостижима, то, обозначая
п-\
F,(/,/7) = 2э(/)+2>V(P)W) ,
v=0
F2(t,p) = f,bv(p)yiv\t), (2.143)
v=0
получим незязку
E(t,p) = F](t,p)-F2(t9p). (2.144)
Далее, как и в предыдущем случае, задача формулируется так
г
I(p)=\E2(t,p)dt-^mm. (2.145)
Jo '
Последняя задача может быть сведена к задаче аппроксимации в пространстве
L2[0J].
Если уравнение имеет вид
Х*уЫ*(и)(0 = ;К0.а >>,(/) = 1(0, x3(t) = h3(t) = ky(\-e-a>'),
v=0
то
Fx(t,p) = (-1)" ссГ1*-*''* Е^(Р)}(-1Г МГ1 ^Г^в"аЭ^Т;
^2^^) = К0,
и задача становится чрезвычайно простой и ее решение сводится к задаче
аппроксимации в L2[0,T].
Пример 2.15.
Рассмотрим канал управления креном ракеты (рис. 1.15), полагая:
К]у = \; КщКу=62;Ту=0,3 с; у, = \(,);
*э(/) = 1 - е~2'496' - желаемый (эталонный) выходной сигнал;
is
Wку = К + KAs + —и- - последовательно включенный ПИД-регулятор.
Задача состоит в расчете численных значений коэффициентов К,Кди Кн - ПИД-регулятора
методом аппроксимации в пространстве L2[0,T].
На рис. 2.54,2.55 и 2.56 показаны соответственно импульсная переходная функция, переходная
характеристика и амплитудно-частотная характеристика системы без регулятора (нескорректированной
системы). Причины наличия сильноколебательных процессов подробно рассмотрены в [17].
8 Зак. 366
122
Методы синтеза САУ по заданным показателям качества. Часть II
В соответствии с описанными выше теоретическими положениями найдем ПФ замкнутой системы с
последовательно включенным ПИД-регулятором:
W(s) =
KAKnpKys2 + KKnpKys + КнКпрКу
Tys3 + (1 + КЛКП9КУ + KKnpKys + КиКпрКу '
О 0,5 1 1,5 2 2,5 3 3,5 4
Рис. 2.54. Импульсная переходная функция нескорректированной системы
0 0,5 1 1,5 2 2,5 3 3,5 4
Рис. 2.55. Переходная характеристика нескорректированной системы
А А(а)
Рис. 2.56. АЧХ нескорректированной системы
Или, что то же самое,
Глава 2. Методы синтеза регуляторов в классе одномерных систем
123
ЛппЛ. * .„ КппКу .„ КппК
vnpyvy Л
W(s)--
з (\ + КлКпрКу) 2 KKnpKy K»KnpKy'
Дифференциальное уравнение имеет вид
х(з)(/)+(1 + ^^р^)Л/)+:^1у(0+М!1Л
х(/)=
кппкУ
к*пк.
кппк,
ч ч ч
^ ^ % hi,
Последнему уравнению эквивалентно интегральное уравнение Вольтерра 2-го рода
'-А(-0* dk
*з(0+11^^Ь(<-т)2]0-'-2486')^
' 2 /|ч* WA
Запишем формулу, определяющую невязку:
'у 'у
Ч 'у 'у
'у 'у \ 'у
/у /у
/о(О
/i(0
-К±КпрКу (D[(t) - D,r(/)) - K±KnpKy (DUO - DUO),
'У У
/0(0 = 1-е-1''+ 1,667
/,(/) = 3,333-^^ >-
(2а,,еа'' + 2)е-^ 3;333
а, а,
ЛС)
МО'ХЗЗЗК^
(,(1^4-
а 2
1-2аэ/ + аэ2/2-н2| If3
2 а^ 6
Система алгебраических уравнений, определяющая неизвестные коэффициенты К, Кли К„, имеет вид
124
Методы синтеза САУ по заданным показателям качества. Часть II
где
а2\Ка + аг1К + а23Кп = Ьъ
а3]Кл+а32^ + а33Кн=Ьг,
о
т
о
Поскольку матрица системы - матрица Грама линейно независимых элементов, определитель которой
отличен от нуля, решение существует и оно единственно.
Расчет приводит к следующему операторному уравнению с матричным оператором.
'28777,879 66322,474 99312,298
66322,474 194887,513 326260,178
99312,298 326260,178 580468,349
Отсюда находим, искомую одностолбцовую матрицу
3018,113
8648,335
14336,586
к'
<
=
0,212
0,403
0,102 10"8
ИПФ, ПХ и АЧХ скорректированной системы представлены на рис. 2.57, 2.58 и 2.59.
25-.
Л С
0.1 0 2 0 3 0 4
Рис. 2.57. ИПФ скорректированной системы
А МО
',с
Рис. 2.58. Переходная характеристика скорректированной системы
Глава 2. Методы синтеза регуляторов в классе одномерных систем
125
i. A(a)
20 40 00 80 100
Рис. 2.59. АЧХ скорректированной системы
2.9. СПЕКТРАЛЬНЫЙ МЕТОД СИНТЕЗА РЕГУЛЯТОРОВ
С ИСПОЛЬЗОВАНИЕМ ФУНКЦИЙ ЛЯГЕРРА
2.9.1. Постановка задачи*
Пусть Ф(/) = (ф! (г),ф2 (г),...,ф/(/),...) - ортонормированный базис. Полагаем,
что задана эталонная ПФ замкнутой системы W*(s) и ПФ объекта W0(s), причем
L-{{W3d(s)} = k3(i)eL2[0,oo) и L'] {WO(s)} = ко(т)е1? б[0,оо). Представим *э(т) и
к0 (т) в виде разложения по ОНБ:
*,(*) = IcfrPvM и *oW = Z^v(t). (2-146)
V=l V=l
Матрицы С*э = (с^, с*э,...,с)э,.. \ и С*° = (cf°, с*°,..., cf°,...) называются
спектральными характеристиками соответственно эталонной системы и объекта
управления в выбранном базисе Ф(/).
Положим, что построены алгоритмы, позволяющие рассчитать спектральную
характеристику Ск*>' skrf"1,^,...,^,...) регулятора, если известны С*эи С*° при
условии, что кц (т) € L [0,оо), а все элементы ф; (t), / = 1,2... преобразуемы по
Лапласу и возможна физическая реализация в аналоговой или цифровой форме
элементов, имеющих ИПФ Ф, (т), / = 1,2...,/,.... Если построена ИПФ регулятора в виде
*KyM=i>v%vM>
v=l
то ПФ регулятора может быть представлена так:
v=l
(2.147)
* Перед рассмотрением настоящего параграфа необходимо изучить соответствующие положения
первого тома учебника
126
Методы синтеза САУ по заданным показателям качества. Часть II
Поскольку известна структура регулятора в форме (2.147), то структурную схему
регулятора можно изобразить в следующем виде (рис. 2.60).
—►
ф,(,)
Регулятор
К(*)
Рис. 2.60. Структурная схема системы
Далее рассмотрим алгоритм синтеза системы, структурная схема которой
представлена на рис. 2.60, используя в качестве базиса функции Лягерра.
2.9.2. Функции Лягерра
Ортонормированные на полуоси [0,оо) функции Лягерра определяются формулой
1 ' S(«-v)! (v!)2
(2.148)
к - масштабный множитель, который выбирается таким образом, чтобы ускорить
сходимость ряда; т = 0, 1, 2,—
Переписав (2.148) в виде
Л
U') = I<W'Ve2. (2149)
v=0
где ст
= Jk-
"Ч-*У
(w-v)!(v!)2
Лягерра:
_kj_
L0(t) = Jk-e~2;
, получим зависимости, определяющие первые 10 функций
*<
Ц(() = ^к-е~2 (\-kt);
Ь{1) = у[к-е~ -(l-l-k-t + ^-tA;
Li^^Jk-i^ (\-3-k-t+-k2 -t2 --к* -А;
L4(t) = yfk-e~ (\-4-k.t + 3-k2 -t2 --к* ■? +~k4-t*\
М0 = ^.Л.(1-5.Ь(+5.*Ч2-^./3Д^^-^./5);
Глава 2. Методы синтеза регуляторов в классе одномерных систем
127
L6(t) = V* -e~2' .fl-6.*./ + -.*2 ./2 --к3 ./3 + -*4 -/4 -
\ 2 3 8
20 720
L7{t) = Jk.e~ki.(l-7.k.t + ^.k2.t2-^k3.t3A4.t4-
^W V 2*6 24
__1*5.,5+^6.,6_ * /Л Л
40
720
5040
-к1 -V
Ut) = y[k.e~* -{х-Ъ.к.г + ХА.к2-?-— *3./3+ — *4-/4-
^W I 3 12
Z_£5 ^5 + _jL#6 .f6 - * '-7 -7 - Х '-8 '8
15
180
—к1 -tU—— *»./»•
630 40320
L9(t) = yfk-e 2 • l-9^-/ + 18-it2-/2-14^3./3+— Л4-/4-
-21Jk3e/3+^il6./6_JLt7./7+. 1 ,8 .,в
20 60 140 4480
Перепишем (2.150) в матричной форме:
O = U F,
-*8./5--
1 -*9-/9
362880
где
ф=(1о(0.М0.М<).-)т.
I _*1 -tL -LL
U =
10 0 0 0
1-10 О О
1 -2 - О О
1 -з 2 -I о
2
1 -4 3
1 _5 5 -- — —^~
6
2 J_
3 24
5 J_
3 24
/о(0
О
О
о
о
о
120
о
о
о
о
о
о
1
j _6 15 _]0 5 _^J_
2 3 8 20 720
1 -7 — -— — -— —
2 6 24 40 720
/i(0
О
О
О
О
О
О
О
1
Л(0
1 -8 14 -
28 35
3 12
15 180
О
О
О
О
О
О
О
О
1
5040
J_
"бЗО 40320
1 1
, -9 18 -14 21 .21 X .
4 20 60 140 4480
О
О
О
О
О
О
О
О
О
1
362880J
(2.150)
(2.151)
(2.152)
(2.153)
128
Методы синтеза САУ по заданным показателям качества. Часть II
Графики А)(0' А (0» •••» ^9 (О "Р11 ^ = * и ^ = Ю "представлены на рис. 2.61 и2.62.
1 23456789 10
Рис. 2.61. Графики первых 10-и функций Лягерра при к = 1
М)
О 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
Рис. 2.62. Графики первых 10-и функций Лягерра при к = 10
2.9.3. Построение спектральной характеристики объекта управления
1. Рассмотрим случай, когда объект задан его передаточной функцией.
Глава 2. Методы синтеза регуляторов в классе одномерных систем
129
В [126, 127] рассмотрены задачи численного обращения одномерного и
многомерного преобразования Лапласа.
Положим, что [127]
^о (s) - —7\ ~ ^^ объекта управления. (2.154)
N\s)
Представим
г>0(,)}=*0(')=2>Н(<)>
t
/=0
где
причем
О v=0 о
v=0
^ = ]tvK{t)e~>dt
(2.155)
(2.156)
(2.157)
- моменты ИПФ объекта управления.
Из формулы (2.156) следует, что для расчета элементов спектральной
характеристики объекта управления в базисе функций Лягерра необходимо построить
алгоритм расчета моментов ц0, щ, ц2» •••> Ц/> ••• •
Изображение Wo (s) является регулярной функцией комплексного аргумента s в
полуплоскости Re5>0, в которой дифференцирование W0(s) можно выполнять
под знаком интеграла Лапласа. Поэтому из формулы, определяющей интеграл
Лапласа, имеем
о
Сравнивая (2.157) и (2.158), находим
Hv=H)X(v)
к
Дифференцируя (2.154) по s, получим зависимости
(2.158)
(2.159)
(2.160)
Все равенства этой системы справедливы при Re s > 0. Отсюда можно записать
новую систему, полагая
s = k/2 (k>0,keRl);
" Г А£(£)'
Если W0(s) имеет вид формулы (2.154), то моменты ц; можно найти следующим
образом. К выражению M(s) = W0(s)-N(s) применим формулу Ньютона -
Лейбница для п -ой производной от произведения двух функций:
J^(/)e"^-Hy^|
4=ц„ (/ = 0,1,2,...).
130
Методы синтеза САУ по заданным показателям качества. Часть II
M(i)(s) = W0(s)N{i)(s) + iW;(s)N{i-}) (*) + ...+
(2.161)
где
с =-
(i-m)\m\
Из последней формулы можно получить зависимость, позволяющую вычислить
моменты сколь угодно высокого порядка:
Л)~ N{s)
(2.162)
Отсюда следует
(-\j»i=(-lj]t%(t)e~idt =
d*
Ъ*Л')
ds
к ~
*=2
= Yi_JioPL_l|-^pM+ ... + c>mp/m+ ... + /ц._,р|])
(2.163)
где
.t^m^W
*; P,=^(0W
s'i
k, (/ = 0,1,2,...).
s-
(2.164)
Полагая, что матрица моментов
М = (цо,ц,,ц2,..., ц,,...)Т
вычислена, а матрица ортогонализации U, соответствующая функциям Лягерра,
известна, получим матрично-операторное соотношение для расчета матрицы-столбца
это соотношение имеет вид
C*°=U-M. (2.165)
Или в развернутом виде
VT-
1
1
1
1
1
1
-к
-2к
-Ък
-4*
-5к
—к1
2!
2!
2!
2!
3!
3!
3!
-it*
4!
4!
5!
Но
Из
"coV
(2.166)
Существенное влияние на сходимость ряда (2.155) оказывает масштабный
множитель к, методика выбора которого изложена в работах [18, 127].
Глава 2. Методы синтеза регуляторов в классе одномерных систем 131
Пример 2.16. Положим, что изображение Wo (s) имеет вид [127]
w /у 0,441Q-V+0,841710-V + 0,12434j3 +
°^~0,1910"6/ + 0,51310-457 + 0,676610"256 + ""*
_^ +8,05385 s2 +3,631 5 + 2
0,502 s5 +16,45111 s4 +11,312 s2 + 3,631 s +1
Построим оригинал ko(t) в виде проекции на линейную оболочку Ц (Аь---, £7), где к = 1 Для
этого воспользуемся алгоритмом, описанным выше.
Сначала необходимо рассчитать матрицу моментов М, для чего следует найти численные значения
моментов {pv: v = 0,1,...,7} и {yv : v = 0,l,...,7}. Соответствующие формулы имеют вид [ 127]'
$Q=[a%s* +a1s1 +aes6+asp5 + a^4 +aj53 + a:s2 + a^ + a^j/s = к/1,
Pi =(8a857+7a7j6 + 6flf655 + 5a^4+4a^3 + 3flrjS2 + 2flf ^s + a^/s = k/2;
p2=(56a856 + 42a755+30a654 + 20a^3 + 12fl452 + 6a^ + 2a2)/5 = it/2;
Рз = (з36а855 + 210а754 + 120а&у3 + 60а^2 + 24а^ + 6а3)/л = Л/2;
p4=(l680agj4+840e7J3 + 360a652 + 120asS + 24a4)/5 = it/2,
p5 = (б720д853 + 2520a7j2 + 720flr65 + 120a5)/j = kl2\
P6 = (20 160<v2 + 5040а75 + 720a6)/5 = к /2;
P7 = (40 320<v + 5040a7)/j = it/2;
моменты {у v} (где v = 0, l,.,.,7) рассчитывают по формулам
y,=(5^4+4V3 + 3^2 + 2^25 + />1)/5 = it/2;
у 2 = (20^3 +12&4*2 + 6635 + 2b2)/s = к /2;
Уз = (б0&5.*2 + 24*45 + &>з)/5 = т,
y4 = (120V + 2464)/5 = kl2\
Y5 = 12065;
Y6 = 0,
Yt=O.
Формулы, определяющие элементы одностолбцовой матрицы М, можно записать так:
Ро Ро
Ро Ро
Ро Ро
Ро Ро
Матрица-столбец моментов имеет вид
132
Методы синтеза САУ по заданным показателям качества. Часть II
м =
0,685088
1,3808949
3,6295890
10,322243
22,393210
-60,779604
-1648,02198
-19422,6728
Воспользовавшись матрично-операторным соотношением
"1
1 -1
-2 1/2!
-3 3/2! -1/3'
-4 6/2! -4/3! 1/4!
-5 10/2! -10/3! 5/4! -1/5'
-6 15/2! -20/31 15/4» -6/5! 1/6!
-7 21/2! -35/3» 35/4! -21/5! 7/6! -1/7!_
рассчитаем матрицу-столбец коэффициентов Фурье
Ст =[0,6850883 -0,6958065 -0,2619067 0,266514 0,101832->
->-0,103429 -0,040019 0,0408939] .
7
Отсюда следует к0 (/) = ?х^ц А) x{t) = £ckv°Lv (/)
щ
Из
Из
С2
В табл. 2.11 приведены дискретные значения функции ko(i) и £0(/).
2. Рассматриваемый случай предполагает, что передаточная функция объекта
неизвестна, однако известно следующее:
• объект линеен и стационарен;
• *о(т)е£2[0,«>).
В этом случае необходимо провести детерминированную или статистическую
идентификацию объекта.
Положим, что для определения спектральной характеристики объема Ск° имеется
возможность подать на вход объекта пробный сигнал у (/) и зафиксировать
соответствующую реакцию x(t). Тогда для расчета С*0 можно воспользоваться равенством ,
x(') = lbo(t)y('-*)d*> (2Л67)
о
при этом предполагается:
y(t)eL2[0,oo); *(/)e Z,2[0,oo); ko(t)eI?[0,<*>); Х° =(х(0),х'(0),...,х^)=0 ,
т.е. объект до подачи на вход сигнала у (/) находился в состоянии покоя.
Поскольку рассматриваемые далее положения будут применяться при решении
задач статистической идентификации и коррекции, воспользуемся обобщенным
соотношением вида
/(0«}/iW/i('-t)A.
(2.168)
Представим f(t), f](t) и f2(t) так:
Глава 2. Методы синтеза регуляторов в классе одномерных систем
133
/('ЫХМО; /i(')= Z<'M'); Л(')= Z<2M0- (2-169>
Таблица 2.11
v=0
v,=0
v,=0
Обозначение
v=0
Численные значения функций £0(/) и ko(t)
(дискретность Д / = 1 с)
0,000000
0,130787
-0,060724
0,020157
0,000000
0,131697
-0,059810
0,021734
0,386412
0,003161
-0,026882
0,012673
0,383134
0,001984
-0,028992
0,017221
0,556206
-0,079365
0,000347
0,005253
0,553371
-0,079934
-0,004223
0,011695
0,557003
-0,116593
0,011786
—
0,557572
-0,114955
0,012447
—
0,447747
-0,117306
0,025603
—
0,452205
-0,113379
0,025262
—
0,289434
-0,094361
0,025422
—
0,293490
-0,091273
0,023720
—
Подставив (2.169) в (2.168), запишем
(2.170)
v=l oU«l ) U=1 )
Или, что то же самое,
v=0 у,=0у2=0 о
Умножая последовательно последнее равенство на Lo(t)9 А(0' *-Л(0' ••• и
интегрируя на промежутке [0, с»), получим
ср = Ё Ё<чМК(тК('-^тМ')<*> р=о, 1,2,....
Vj=0v2=0 0 0
Имеем
cf=Y У cfxcflcp 0 = 0 1 2
(2.171)
v,=0v,=0
134
Методы синтеза САУ по заданным показателям качества. Часть II
Можно показать, что
\\LV{(x)LVi(t-x)dxLp{t)dt =
00
1
Тк
, если Vj + v2 =/? + ! и Vj ^p,v2 ^/?;
—7=-, если Vj+v2 = p и Vj <p,v2 </?; (2.172)
у/к
0, во всех остальных случаях.
Таким образом, система (2.171) является треугольной.
Поскольку в практических расчетах используется конечное число членов
разложения, то система (2.171), эквивалентная интегральному соотношению (2.16*8),
принимает вид
v,=0v2=0
Так как задача решения уравнения (2.168) поставлена некорректно, то, очевидно,
система (2.173) плохо обусловлена, т.е. при её решении имеет место вычислительная
неустойчивость.
Зависимость (2.173) решает задачу идентификации в виде (2.155), а (2.173), как
указывалось выше, представляет собой треугольную систему алгебраических
уравнений (c^v =0 для всех v, и (или) v2 >p) относительно элементов спектральной
характеристики объекта ск° в базисе функций Лягерра.
Рассмотрим метод статистической идентификации, предполагающий разложение
корреляционных функций Rxy{t) и fyr(T) в ряды по функциям Лягерра [18, 147].
В этом случае предполагается следующее:
• процессы Y(t) и X(t) являются стационарными, обладающими свойством
эргодичности ;
• RYY (т) £ L2 (-оо, +оо) ; Rxy (т) е L2 (-со, -ко) ; *0 (т) 6 L2 [0,оо).
Если известны функции Ryy (т) и RYY (т), то ИПФ может быть определена путем
решения уравнения Винера - Хопфа [122]
Ллт(т) = |%(т->.) ko(\)dX, -оо<т<оо.
(2.174)
Последнее уравнение может быть решено с использованием разложений
корреляционных функций Rxy (т) и RYr (т) в ряды по функциям Лягерра:
RYy(x) =
*ir(T) = 2XnM*), 0<x<co;
v=l
Rh (x) = I>v"Lv (т), -оо < т < 0;
v=l
^(т) =
(2.175)
*М*) = 1^МТ)> 0<т<со;
V=l
^W = £c^Iv(t), -oo<t<0.
v=l
%(T) = j[jm-Jr(/)r(/-T)*f (2.177)
Глава 2. Методы синтеза регуляторов в классе одномерных систем В5_
Разработаны специализированные вычислительные устройства для нахождения
cR)y v = 07* cR™ v = 07* cR~X7 v = 0~/
С теоретическими положениями, а также с аппаратной реализацией можно
познакомиться в [69, 147]. Здесь изложены лишь принципы построения соответствующих
вычислительных устройств.
Поскольку
00
cRn =cRn = J/?;v(T)Lv(T)</T, v = 0, 1,..., /, (2.176)
о
а
= lim
Г-юо
то отсюда следует зависимость
& =cv«" =3limijy(/)}y(/-T>Lv(T) Лй =
~*°° О О
1^°
= lim -\Y(t)Jv(t)dt, v = 0, 1,..., /, (2.178)
где
Jv(/) = Jf(;-i)Lv(T)</T (2.179)
о
- установившейся выходной процесс фильтра, имеющего ИПФ Z,v (т).
Таким образом, общая формула для расчета коэффициентов разложения RYY (т)
как при т > 0, так и при т < 0 имеет вид
1 т °
№ =*? =-Jr(/>/v(O*- (2Л8°)
о /
Коэффициенты с"п представляют собой оценки коэффициентов Фурье разложения
RYY (т) по функциям Лягерра.
Показано, что математическое ожидание оценки
Л/[с^] = J%(t)4,(t)</t, v = 0,1,2,...J
о
совпадает с истинным значением, т.е. оценка является несмещенной.
. Дисперсия оценки коэффициентов с/г определяется зависимостью [69]
При практических расчетах необходимо помнить, что с увеличением числа членов
разложения / дисперсия оценки корреляционной функции увеличивается [69].
Структурная схема вычислительного устройства для расчета v -го коэффициента
Су™, v = O,l, ..., / представлена на рис. 2.63, а соответствующее вычислительное
устройство для нахождения eft™, с***,..., of™ - на рис. 2.64.
136
Методы синтеза САУ по заданным показателям качества. Часть II
iw
Фильтр Лягерра
сИПФ1Дг)
■МО
Множительное
звено
Интегратор
Жуу
Рис. 2.63. Структурная схема вычислительного устройства для нахождения с\
Рхх
Н')
Блок фильтров Лягерра,
имеющих ИПФ
£0(r),L, (r ),..., L,(r)
МО
X
МО I
X
•МО
X
Блок умножителей
1 п
й«*
±}м*
Блок интеграторов
М
г*Ь
Рис. 2.64. Структурная схема вычислительного устройства
для расчета коэффициентов Фурье автокорреляционной функции Rn (т)
Вопросы аппаратной реализации вычислительного устройства отражены в [18, 69].
Здесь отметим лишь следующее. Поскольку ПФ функций Лягерра имеют вид
М*)-
к
S + 2
( кХ
S~2
к
, v = 0, 1, ...,/,
(2.181)
то, очевидно, каждый следующий фильтр Лягерра может быть получен из предыду-
щего последующим подключением к нему звена с ПФ V (s) =
s —
к
S + 2J
; нулевой же
фильтр - апериодическое звено. Звено с ПФ Z? (s) - фазовращатель, поскольку [18]
(2.182)
к
1Э (уо)) = ~ = cos9 + ysin9 = e7(p.
7CD+2
Отсюда следует, что при прохождении сигнала через звено Z? (s) амплитуда его
не меняется, но происходит задержка по фазе, зависящая от частоты.
Глава 2. Методы синтеза регуляторов в классе одномерных систем
137
С учетом сказанного структурная схема (рис. 2.63) принимает вид
Ш
JL
к
V + l
X
_*
*л
X
*
к
Л + 2
X
X
Ш*
ij<*.
£}м*
у п
с«"
,Я/г
cf»
,Л)+)
Рис. 2.65. Структурная схема вычислительного устройства
Схемы, связанные с аппаратной реализацией функций Лягерра, представлены на
рис. 2.66.
а
Рис. 2.66. Структура ортогональных фильтров Лягерра (а) и звенья, ее образующие:
инвертирующее апериодическое (б), фазовращающее (в)
В [69] принципиальная схема представлена в виде (рис. 2.67) (здесь к =
2
фильтр с точностью до постоянного множителя -j= имеет ПФ вида
4к
RC
138
Методы синтеза САУ по заданным показателям качества. Часть II
к_
2
к'
Jk
Вход
ф
а
3
о
и
н
в
е
?
о
Р
С =
С =
р
^ г^
■I) Н)\
Ш
У
с
и
л
и
т
е
л
ь
|Г
XV /
\\ /
//R \
II
У
с
и
л
и
т
е
л
ь
Рис. 2.67. Принципиальная схема функций Лягерра
D +
Аналогичным образом строятся вычислительные устройства для расчета cvAT и
rRXY
(2.183)
При этом необходимо учесть следующее. Поскольку левая ветвь R^ (т)
взаимной корреляционной функции определяется формулой
т
то для коэффициентов Фурье <$** имеет место зависимость
& = 'imiF {t)\L^)h^)d^t = \\m^\°X(t)jvY{t)dt.
о о
Запишем рабочую формулу
I о
& =±\x{*VA*)*>
(2.184)
где JvY (t) = \Lv(i)Y(t-%)d'z - выходной сигнал v-го фильтра Лягерра в устано-
о
вившемся режиме. Структурная схема v -го канала соответствующего
вычислительного устройства имеет вид (рис. 2.68).
Xif)
Фильтр Лягерра
сИПФ4(т)
Лг(0
Множительное
звено
Интегратор
r^YY
Рис. 2.68. Структурная схема вычислительного устройства
На основе приведенной на рис. 2.68 структурной схемы легко построить
вычислительное устройство для вычисления коэффициентов с^п, v = 0,1, 2, ...,/.
Глава 2. Методы синтеза регуляторов в классе одномерных систем
иу
Правая ветвь Л£у (т) может быть представлена так:
(2.185)
v=l
где
<#< = limify(/)jLv(T)i(/-T) rfx* = ify(/>/vjr(/)A, (2.186)
причем JvX (f) = \Lv{x)X{t-x)di - установившейся выходной сигнал v-гофильт-
0
о
ра Лягерра при воздействии на вход сигнала X(t). Соответствующая структурная
схема представлена на рис. 2.69.
X(t)
Y(t)
Фильтр Лягерра
сИПФХДг)
•МО
Множительное
звено
t
Интегратор
rKYY
Рис. 2.69. Структурная схема вычислительного устройства
Далее будем полагать, что с помощью вычислительных устройств найдены
корреляционные функции RYy (т) и Rxy (т) в виде разложения по функциям Лягерра.
Вернемся к уравнению Винера - Хопфа. Во многих работах процедура
идентификации сводится к решению аппроксимирующей это уравнение системы линейных
алгебраических уравйений вида
^(/A) = AX*0(yA)%[A(^y)]5 ' = 0, l,...,tf-l, (2.187)
7=0
где Af - порядок системы алгебраических уравнений, равный числу
восстанавливаемых точек ИПФ; i,j - целые числа, определяющие номера отсчетов
корреляционных функций и ИПФ, отстающих друг от друга на интервал дискретизации А.
В матричной форме (2.187) имеет вид
AK0=Q,
где
' RYY(0) RyY(A) ... Ryy((N-l)A])
д= Ryy(A) RYY(0) ../ RYY((N-2)A) ^ ^igg)
RYY((N-\)A) ... %(0)
Ko=(*(0), *(А),...Д((^-1)А))Т; (2Л89)
Q^(RXY(0)yRXy{A)iRXy{2A)^.9RXy((N-\)A))\ (2.190)
При построении ко(т) по результатам решения системы (2.187) имеет место
сильный разброс значений &(/Д), / = 0, 1,...,Л^-1, обусловленный низкой точно-
140
Методы синтеза CAY по заданным показателям качества. Часть II
стью определения RYY (т) и R^ (t) по данным нормальной эксплуатации
вследствие малой длительности и нестационарности реализаций случайных процессов X(t)
и Y(t), низкой точности измерений и др.
В связи с этим уравнение Винера - Хопфа целесообразно решать, используя
разложение RYY (т) и Кху (т) по функциям Лягерра.
Поскольку уравнение Винера - Хопфа имеет вид интегрального уравнения
(2.168), то система алгебраических уравнений, связывающая коэффициенты Фурье
разложения функций RYY (т) и R^ (т) по функциям Лягерра с элементами с*0
спектральной характеристики объекта С*0 =(co°>cf°>c20> ••• >cf°) будет иметь вид,
аналогичный системе (2.173). Основы такого подхода отражены в [147]. Число членов
разложения / имеет смысл, обратный параметру регуляризации [18]. Очевидно, при
/ —> оо аппроксимация
(2.191)
v=0
становится сколь угодно точной и факт, характеризующий разброс (2.191) йерегуля-
ризованного, решения, сохраняется. При / -» 0 имеет место сглаживание, но
аппроксимация (2.191) может быть совершенно неудовлетворительной из-за большой
погрешности. Поэтому выбор /, играющий роль параметра регуляризации,
осуществляется из компромиссных соображений [18, 147].
Эффект сглаживания с помощью функций Лягерра иллюстрируется рис. 2.70 [18],
а роль сглаживания в задаче идентификации показана на рис. 2.71 [59].
1,0
график сглаженной корреляционной
функции
график корреляционной функции
' процесса /Ьт(т), найденный путем
решения уравнения (2.187)
Рис. 2.70. К иллюстрации процесса сглаживания с помощью функций Лягерра
'лава 2. Методы синтеза регуляторов в классе одномерных систем 1/и_
В качестве начального значения множителя к при аппроксимации временных ха-
к
>актеристик можно выбрать — = (2-10)Г3, где Г3 - время затухания аппроксими-
зуемой функции.
Задача идентификации значительно упрощается, если Y(t) - белый шум. В этом
:лучае, поскольку RYY (т) = 2тыо8(т),
4(т) = 2Ч(^0(^)8(т^)Л = 2я5Л(т).
(2.192)
График ko(t\ полученный в результате
решения задачи идентификации
40 60 100
80'
0,6
0,4
0,2
ko(t) - график сглаженной ИПФ 0
co(t) -0,2
-0,4
-0,6
-0,8
-1,0
Рис. 2.71. К иллюстрации процесса сглаживания при решении задачи идентификации
с помощью уравнения Винера - Хопфа (в качестве аппроксимирующих полиномов Чебышева,
ортонормальные на системе п+\ равноотстоящих точек и определяемые выражением
>Л(т)
г-1,0
4-0,8
\
J
20
\
/
40
J
Ryy(t)
/ cj
60 80 100
RxyW
CXGY
/u')~V(«+*+ir>£( ) UJIt-J^t
Структурная схема системы идентификации для построения 2nsоко (т) в форме
2^0A0W = Z4<>iv(T)
/
v=0
представлена на рис. 2.72.
ПО
RYY(x) =
-2nso8(x)
Объект
управления
Блок фильтров Лягерра, имеющих
ИПФ^СтХ^т),...,^)
Ы01
—Нх|
АЛО
-Их
Ы0
-Нх
x(t)
й-)*
iJ(->*
4
*
Рис. 2.72. Структурная схема системы идентификации
(2.193)
142 Методы синтеза САУ по заданным показателям качества. Часть II
Известно, что ИПФ, определяемая из уравнения Винера - Хопфа, оптимальна по
критерию минимума среднеквадратической ошибки
M[(X(t)-XM(t)f] =min,
где Хм (0 - выходной сигнал системы с найденной ИПФ путем решения уравнения
Винера - Хопфа.
В связи с этим легко построить алгоритм расчета элементов спектральной
характеристики объекта из следующего условия
1{ФУМ *(/)-£^|Мт)К(/-т)лЦтт.
[_ v=0 - о J Су°
f)l(rk° rk° гк° гкЛ
Из условия — т = 0, / = 0,/ легко получить
дск>
)x{t))LVx (х)Г (/-т)ЛЛ = If N ^ (т)У (г-т)Л/^а (X)Y {t-\)dX \dt.
0 0 v=OoLo 0 J
Обозначая
Vv2 = J V (0V {t)dt, Rx,n =}^(0 JVlr {t)A , (2.194)
о о
легко найти следующую систему алгебраических уравнений
Кл7=КлС*°. (2.195)
Откуда следует
C^RJJR^. (2.196)
В зависимостях (2.194) Г- интервал осреднения, а бесконечный предел означает,
что фильтр работает в установившемся режиме.
Последняя система далее будет получена из других соображений.
Если построены RYY(^) и Rxy (t) в форме разложения по функциям Лягерра, то
можно построить ПФ объекта управления в виде [18]
Ъ,(*)-я-„(,)
оК> R^(s)-RyY(s)'
[Ryy (т),т<0; ПК' 1^(т),х<0,
a R^y (s), R'xy (s), RyY (s), Ryy (•*) - преобразования Лапласа (изображения) от
соответствующих функций.
Пример 2.17.
Положим, что с помощью вычислительных устройств, структурные схемы которых описаны выше,
получены следующие результаты (используется один канал и, следовательно, удерживается только
нулевой член разложения Lo(x)):
Глава 2. Методы синтеза регуляторов в классе одномерных систем
143
л*гМ =
*2l
Ы
кх, к2 - масштабные множители функций Лягерра. Преобразуем по Лапласу приведенные выше
зависимости; изображения имеют вид:
г*гг FT rfyr [Г
RYY (s) = ь > RYY \S) = 1—.
kx
^jrrW = к » rxy(s) = 1—
5-
Отсюда находим ПФ объекта управления
к2
2
»;(*)•
м-)-^"*^-*1
ИПФ имеет вид
Обратимся еще к одному подходу, результаты моделирования которого показали
работоспособность и Достаточно высокую точность при решении задачи статической
идентификации в условиях нормального функционирования объектов управления [18].
Имеем
X(t) = ]ko(*)Y(t-T)dx,
или, с учетом спектрального представления ИПФ,
*(/)-Zc*.jMT)r(f-T)rfT.
v=0 о
Поскольку ./v(f) = J Lv{x)Y{t-x)dx - установившийся выходной сигнал v-ro
фильтра Лягерра, то
*(0=1*лМ-
(2.197)
v=0
Умножив обе части последнего равенства на Jp(i) и вычислив математическое
ожидание полученного произведения, найдем
M[x{t)jp{t)\=±ckv*M[jv{t)jp{t)\.
v=0
Или, что то же самое,
v=0
На практике используется конечное число членов разложения; тогда
v=0
или в матричном форме
144
Методы синтеза САУ по заданным показателям качества. Часть И
Ryj=RnCk%
где
RA7 - (Ялу0,Ялу,, Д;^ , •••>^Л7/) I
v.p=()
(2.198)
(2.199)
Приближенная спектральная характеристика объекта управления определяется
формулой
C^RJJRk,, (2.200)
совпадающей с зависимостью (2.196).
Структурная схема системы идентификации представлена на рис. 2.73.
Y(t)
Рис. 2.73. Вычислительное устройство статической идентификации динамических
объектов в условиях нормального их функционирования
Она содержит блок фильтров Лягерра, а также /+1 умножителей и /+1
интеграторов. Детально с описанной системой идентификации можно познакомиться в [18].
При использовании любого метода идентификации необходимо помнить, что
решение задачи идентификации поставлено некорректно. Развиваются методы решения
некорректных задач, позволяющие алгоритмически осуществлять отбор возможных
решений по дополнительной информации о них [18]; среди этих методов наибольшей
Глава 2. Методы синтеза регуляторов в классе одномерных систем 14^
общностью и возможностями выделяется метод регуляризации А.Н. Тихонова,
использующий лищь качественную информацию о гладкости восстанавливаемой функции.
В спектральном методе, основанном на разложении ИПФ по ОНБ,
неустойчивость решения, свойственная задаче идентификации, проявляется в связи с выбором
числа членов разложения /. Для повышения точности восстановления ИПФ
необходимо увеличивать /, но при этом проявляются отмеченные особенности и ошибка
идентификации возрастает. С другой стороны, при малых / восстановленная ИПФ
будет слишком гладкой. Повышение точности и устойчивости результатов
идентификации достигают применением ОНБ в сочетании с тестовыми воздействиями и
сглаживанием информационных сигналов.
Пример 2.18.
В [18] исследованы вопросы точности идентификации с помощью подхода, предполагающего
нахождение спектральной характеристики объекта по формуле (2.200)
Объект идентификации имеет ПФ вида.
,Г(А- 4^ + 1)
oV ' 0,012^3+0,252 + 0,95 + l
Входной сигнал, поступающий на объект управления, формировался фильтром
где £ = 0,5, Т- , / - частота среза.
Принимались следующие значения / . 0,25Гц, 0,5Гц, 1Гц, 2Гц Из известных соображений следует,
что сигнал y(t), поступающий на вход объекта, отличен от белого шума Значения — принимались
равными 2 и 3.
В результате проведения эксперимента находились матрицы Rjj и Ryj, а по формуле (2 200)
рассчитывалась приближенная спектральная характеристика объекта:
С*-=(С*°,с^,Сз\с*°)Т.
Поскольку передаточная функция W0(s) известна, то по приведенным выше формулам можно
рассчитать точную спектральную характеристику объекта; обозначим ее так
c?.=(cfe.^.<4>4,c£)T.
Так как С*0 и С*° известны, то относительная погрешность коэффициентов разложения находилась
по формуле
А_А
Av = Cy ^.100%, v = 0,4;
CVT
а в качестве критерия точности идентификации был принят функционал
e=[i(*-cfc)2l:t4
l_v=0 J v=0
Результаты расчетов приведены в табл 2.12. Величина Q во всех вариантах идентификации не
превышала 0,005, поэтому можно сделать следующий вывод: изложенный подход является работоспособным и
позволяет получить достаточно высокую точность ИПФ объекта управления в условиях нормального его
функционирования При идентификации объектов управления с ПФ вида [18]
5(0,2, + 1)
01W " 0,04*40,5.+ 1
И
02^'" 0,01s3 +0,1655 + 0,75* +1
на выходы подавался псевдослучайный двоичный сигнал единичной интенсивности Шаг интегрирования
был выбран равным 0,01, а масштабный коэффициент функции Лягерра/: = 1
Результаты экспериментов приведены в табл 2.13
Описанные выше результаты экспериментальной проверки метода подробно изложены в [18]
11 Зак. 366
146
Методы синтеза САУ по заданным показателям качества. Часть II
Таблица 2.12
к/2, с[
Т,с
/Гц
4
<£
4-
с",-
д.
Д3
д..
д5
о
Т,с
/Гц
&
с40
А.
Д2
Аз
А4
А,
0
0,25
1,416
-0,7277
-0,2137
-0,0946
-0,0260
0,61
-3,П
-17,5
-39,7
-71,1
0,004015
1
1,420
-0,7184
-0,2646
-0,0954
-0,1121
0,9
-4,4
2,2
-39,2
24,9
0,00210
2
1,407
-0,7515
-0,2591
-0,1568
-0,0898
ЗС
0,5
1,423
-0,7246
-0,2185
-0,1056
-0,0398
1,12
-3,58
-15,6
-32,7
-55,6
0,002917
8
2
1,413
-0,7279
-0,2815
-0,0998
-0,1487
0,45
-3,1
8,7
-36,4
65,6
0,00295
0,25
1,219
-1,068
0,0487
-0,0963
0,0139
-0,1
-0,09
36,6
-23,5
-173,2
0,0008
1
1,228
-1,062
0,0456
-0,1057
-0,0156
0,69
-0,67
27,7
-16,0
-17,8
0,00024
3
1,220
-1,069
0,0357
-0,1259
-0,0198
0,5
1,225
-1,056
0,0568
-0,0969
0,0069
0,46
-1,27
63,7
-23,0
-136,4
0,000845
2
1,229
-1,069
0,0374
-0,1110
-0,0321
0,72
-0,06
4,6
-11,8
69,3
0,00018
Таблица 2.13
J
0
1
2
3
4
6,4815
2,2634
1,2703
0,8244
0,5493
с>
6,4817
2,2648
1,2788
0,8230
0,5480
А%
0,003
0,06
-0,12
-0,17
-0,24
3,0864
-2,7435
-0,9907
-0,1101
0,1402
3,0857
-2,7426
-0,9907
-0,1128
0,1417
Д%
-0,02
0,03
0,01
-2,45
1,07
В заключение изложим основные положения метода идентификации, в основе
которого лежит понятие модели объекта с настраиваемыми параметрами (рис. 2.74)
[135].
Глава 2. Методы синтеза регуляторов в классе одномерных систем
147
ИоМ
«(')
Рис. 2.74. Структурная схема системы идентификации с помощью модели
с настраиваемыми параметрами: ВКО - вычислитель критерия ошибки;
ВП - вычислитель параметров
Сущность метода состоит в том, что входное воздействие y(t) подается на
идентифицируемый объект и его модель (рис. 2.74). Структура модели объекта с
настраиваемыми параметрами с,м учитывает структуру реального объекта. Выходной сигнал
объекта х(/) сравнивается с сигналом выхода модели xM(t), и в соответствии с
выбранным критерием ошибки z(t) = x(t)-xM(t) осуществляется настройка
параметров модели с,м.
Структура выбранной модели объекта оказывает большое влияние на точность и
скорость настройки параметров, которая в значительной степени определяется
взаимосвязью, существующей между ними.
Как и в методах, описанных ранее, ИПФ модели объекта представляется в виде
Ut)=2>vmLv(t) = (cm)TL(t),
v=0
где См =(cq, с[\ ..., С/м) -настраиваемые параметры модели,
L(t) = (Lo(t),L, (t), ... ,£/(?)) - одностолбцовая матрица функций Лягерра.
Для расчета матрицы См можно воспользоваться методом вспомогательного
оператора. Если / = F(s) - критерий, характеризующий степень близости модели и
объекта, то имеет место соотношение [135]*
с™(п = Х = Х—— , /=0,/,
' U дс? dz dcf
где X - некоторый коэффициент.
Поскольку
E(s) = [wo(s)-Wm(C,s)]y(s),
где W0{s) - ПФ идентифицируемого объекта, WM(CM, s) - ПФ модели,
представляющей собой каскадное соединение элементов с ИПФ, являющимися функциями
Лягерра, то [135]
дг
дг
11*
* В [135] детально изложена теория систем с настраиваемыми моделями
148
Методы синтеза САУ по заданным показателям качества. Часть II
Структурная схема системы идентификации, основу которой составляет
последняя формула, имеет вид (рис. 2.75).
ВКО
Рнс. 2.75. Структурная схема системы идентификации
Система идентификации представляет собой вычислительное устройство,
осуществляющее следующие операции:
• преобразование входного сигнала y(t) звеньями, представляющими собой
фильтры Лягерра с ПФ L0(s), L^s), ..., L/0);
• дифференцирование сигнала, являющегося выходом элемента, формирующего
значение F(e(t))\
• умножение сигналов Z*(/) и Z^/);
• интегрирование с коэффициентом усиления X.
Из структурной схемы (рис. 2.75) следует, что настройка модели производится
независимо по параметрам с$ , cf, ..., с;м .
2.9.4. Алгоритм расчета регулятора
Положим, что задана эталонная ПФ замкнутой системы W3 (s); тогда
Wv(s)W0(s)
>K)-1 + Wv(s)iro{s)'
(2.201)
где W (s)- ПФ регулятора, W0(.s) - ПФ объекта управления. Поскольку
справедливы зависимости
W3(s) + W,(S)WKy(s)lV0(s) = lVKy(S)W0(s)
Глава 2. Методы синтеза регуляторов в классе одномерных систем 149^
то
WJ(s) = WKy(s)We{s), (2.202)
где Wc{s) = W0(s)-W0{s)W,{s).
Обозначая
k,(x) = L-x{W3{s%kc{*) = ^{W0{s)-W0(s)W,{s)},
можно записать интегральное уравнение, определяющее ИПФ регулятора:
Аэ(0 = }*с(/-т)*ку(т)</т. (2.203)
о
Предполагая, что
A,(0eL2[0,oo), *c(r)6L2[0,oo), к^(t)e £2[0,co),
и представляя их в виде
v=0 v=0
v=0
легко записать систему алгебраических уравнений для расчета неизвестного вектора
С** - (ск" Л Л Л У
Эта система имеет вид (см. вывод формулы (2.173)):
v,=0v2=0
Как уже говорилось выше, последняя система является треугольной; в этой
системе одностолбцовые матрицы
г^с _. (Л Л Л с^с f
известны.
Таким образом, формулой
v=0
определены структура и параметры регулятора.
Пример 2.19.
Пусть объект управления определяется ПФ
1,4
W0(s) = :
T^ + ^TZ + Tiy + iT^lT&s + X
Г, =0,4; Г2=0,3, £ = 0,4
Переходная характеристика
£)
нескорректированной системы представлены на рис. 2.76 и 2.77.
ь IVUriV 1 Г11Х4Л
150
Методы синтеза САУ по заданным показателям качества. Часть II
Ш
0 2 4 6 8 10
Рис. 2.76. График переходной характеристики нескорректированной системы
Л КО
0 2 4 6 8 10
Рис. 2.77. ИПФ нескорректированной системы
В качестве эталонной выберем передаточную функцию замкнутой системы вида
и^-г-гг2 •
s + l,4coo.s + coo
причем со() = — , если Гр = 5 , то соо = 1 и, следовательно
11среходная характеристика эталонной системы имеет вид (рис. 2.78).
40
1,5
0123456789 10
Рис. 2.78. Переходная характеристика эталонной системы
Глава 2. Методы синтеза регуляторов в классе одномерных систем
151
Спектральная характеристика ИПФ эталонной системы, найденная с помощью рассмотренного выше
алгоритма, может быть записана так (масштабный множитель функций Лягерра выбран равным 6, т е к - 6 )
0,1724992
-0,366864661
0,3429111181
-0,236532666
0,126453367
-0,045870733
0,000035366
0,018696084
-0,021080456
0,016116197
С*' =
Таблица 2.14
', с
0
1
2
3
4
5
6
7
8
9
10
0
0,455438924
0,341804301
0,144212313
0,0239421611
-0,017593526
-0,019108016
-0,010001946
-0,02794425
0,00036925
0,000966217
*э(')
0,015585998
0,454389076
0,342599771
0,146322122
0,022093306
-0,019525404
-0,013159707
-0,004309597
-0,000986046
-0,000178641
-0,0000274
ИПФ k3(t) эталонной системы и ее аппроксимация k3(t) с помощью функций Лягерра
(удерживалось 10 членов разложения) представлены на рис. 2 79, дискретные значения приведены в табл 2 14
КС)
0 2 4 6 8 10
Рис. 2.79. Графики ИПФ эталонной системы £э(/) и ее аппроксимация кэ(/)
Для реализации алгоритма необходимо знать ПФ Wc (/); она записывается в форме
Wc(s) =
3500s2+4900*
90s5 + 59 b4 + 234 b3 + 5205s2 + 5100s + 2500
152
Методы синтеза САУ по заданным показателям качества. Часть II
Запишем спектральную характеристику кс (/) = L~l [Wc (s)}; она имеет вид
' 0,572724874'
-0,975829066
-0,173914715
1,012815751
-0,39049937
-0,067170956
-0,070279766
0,100893516
0,045777287
1^-0,070683042,
Дискретные значения kt(i) и kc{t) приведены в табл. 2.15.
СК =
Графики kc(t) и kc(t) имеют вид (рис. 2.80).
Таблица 2.15
t, с
0
1
2
3
4
5
6
7
8
9
10
МО
0
0.958683938
-0 885688855
-0 290145299
-0.147690903
0.00117876
0,026767303.
0,022554218
0,009613417
0,001836034
-0,001039297
Ш
-0,039597192
0,966204896
-0,878854658
-0,294748187
-0,1488007781
0,003027259
0,027652086
0,012021285
0,003120536
0,000607778
0,0000975
0 2 4 6 8 10
Рис. 2.80. Графики функций kc(t) и kc(t)
Система алгебраических уравнений (2 204) для рассматриваемого примера запишется так
Глава 2. Методы синтеза регуляторов в классе одномерных систем
153
А,,
Аи
А22
Г Л 1
А"
*
\с"Л
где
А„ =
0,23381
-0,63219
0
0,23381
0
0
0,32738 -0,63219 0,23381
0,48448 0,32738 -0,63219
0,48448
1,-0,5729
А„ =
0,132 -0,5729
-0,0012692 0,132
0,069881 -0,0012692
-0,022501
(,-0,047545
0 О
О О
О О
0,23381 О
0,32738 -0,63219 0,2338lJ
ГО 0 0 0 0}
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
о о о о о,
0,48448 0,32738 -0,63219^
-0,5729 0,48448 0,32738
0,132 -0,5729 0,48448
-0,0012692 0,132 -0,5729
0,069881 -0,0012692 0,132
0,069881
-0,022501
0,23381 0 0 0 0
-0,63219 0,23381 0 0 0
0,32738 -0,63219 0,23381 О О
0,48448 0,32738 -0,63219 0,23381 О
1,-0,5729 0,48448 0,32738 -0,63219 0,2338lJ
Одностолбцовая матрица, определяющая спектральную характеристику регулятора, имеет вид
(0,737762982^
0,425744646
1,584745637
1,148445338
2,35263977
1,899905493
3,110075917
2,655168552
3,866129189
Д410934455,
Переходная характеристика и НПФ скорректированной системы практически совпадает с переходной
характеристикой и ИПФ эталонной системы (рис. 2.80).
Структурная схема скорректированной системы представлена на рис. 2.81.
ЮЗак.366
С*" =
154
Методы синтеза САУ по заданным показателям качества. Часть II
{ »
Л.
Регул
.
ятор
s-k
и.
ч
2J
г
,
J--
5 + —
1 !
ш
«(')
14
7/+(2Щ+?)|>+(ЗГ+2Й1+1
Объект управления
Рис. 2.81. Структурная схема САУ
*0
2.10. МЕТОД МОМЕНТОВ СИНТЕЗА РЕГУЛЯТОРОВ
Метод моментов нашел широкое применение в математике и приложениях, в том
числе в теории автоматического управления*. В [4, 5, 125, 126, 127] методом
моментов получили решение задачи численного обращения одномерного и многомерного
преобразования Лапласа, идентификации и синтеза самонастраивающихся систем.
Напомним, что /-м моментом функции x(t) относительно ht(t) системы Н
называется интеграл вида
ц,=|*(/)йД;)<*> / = 1,2,...,/, (2.205)
п
где #(/) = {й,(/), / = 1,2,...,/} - моментная система функций, Q - множество, на
котором определены функции А, (/) и x(t).
Множество М = {\ik : k = 1,/} называется множеством моментов.
В предыдущем параграфе подробно рассмотрены аспекты применения моментов
ц,- = 1,2,...,/, когда
_kt_
Л/(/) = ///2,аО = [0,о)).
Показано, что если известны моменты функции x{t) e Z? [0,оо), то эта функция с
любой степенью точности в метрике Z2[~0,oo) может быть представлена в виде
где
ct=Y.Ci]K{t)x{t)dt,
(2.206)
(2.207)
v=0 о
* Приложение метода моментов в теории оптимального управления отражено в третьей части учебника.
Глава 2. Методы синтеза регуляторов в классе одномерных систем
155
to
причем c/v-элементы матрицы ортогонализации, йД/) = /уе 2,v = 0,l,...,/
-функции моментной системы.
Таким образом, окончательная формула, определяющая функцию x(t) через ее
моменты, имеет вид [126]
/mO L V-0 J
Можно ввести в рассмотрение моменты вида [126]
00
ц,-|*(|)Г*Л,
(2.208)
(2.209)
где #(/) = {А, (/) * е~с//, / я 1,2,...,/} - экспоненциальная моментная система.
Если известны экспоненциальные моменты вида (2.209) функции x(t) е Z,2 [0,оо),
то x(t) может быть восстановлена с любой степенью точности в метрике I? [0,оо).
В самом деле, известна следующая теорема (теорема Саса): положим, что KC = qk -
комплексные показатели, обладающие свойством: Re% >— и среди них нет
равных. Тогда система F. - Ь?к: к = 1,2,...} полна в I2 [0,1] в том и только том случае,
если
£ReM)
*-1
1+
:ОО.
(2.210)
Если воспользоваться заменой % = е~', то из теорема Саса следует утверждение:
система Я|е"?*': к «1,2,...; Imqk > 0> полна в I2 [о,») в том случае, если
tfl+lftl2
Ортонормированную систему, порожденную системой экспоненциальных
функций, можно записать в виде
v щ{1) = с2Хе-«+с21е-2а\ (2.211)
Ф/ (0 = C/ie'C' + c/2«f2e' +...+с„е-'с'.
Или в матричной форме
Ф2(0
с21 с22
0^
e~2cl
е~1а
(2.212)
ю*
156 Методы синтеза САУ по заданным показателям качества. Чэсть II
В работах В.М. Амербаева [4, 5], а также в книге В.И. Крылова и Н.С. Скобля [65]
построен аппарат численного обращения преобразования Лапласа с использованием
понятия моментов.
В.М. Амербаевым задача обращения преобразования Лапласа сформулирована как
классическая проблема моментов Хаусдорфа: по заданным / моментам функции x(t)
00
^=Jx(/)«-wdff / = U, (2.213)
о
построить ее приближение *(/), такое, чтобы / первые моменты *(/) совпадали с
известными моментами ц/5 / = 1,/ функции *(').
Если известно изображение X(s) функции x(t), то очевидна справедливость
системы моментных равенств
, /-U. (2.214)
s=ic
ц,=|*(/)в-*Л
О
Полагая известным изображение X(s) функции #(*)е/,2[0,ао), легко найти мо*
менты вида:
? Л
И/ =Jrfe 2x(t)A9 / = 0,1,...,/,
о
00
li^je'ictx(t)dt9 / = 1,2,...,/
о
по следующим формулам
Ц, =(-1)'*<'>(*)[_4 ИЛИ Ц, -W(4**> ^-215>
а затем построить приближение x(t) в виде разложения по ортонормированному
базису [65,126]
/=0 Lv=0
- разложение по функциям Лягерра;
1=0 L v=o
- разложение по ортогональным экспоненциальным функциям,
Этот подход обобщается на многомерное преобразование Лапласа [125],
Последними двумя формулами определяется минимизирующий в I? [0,ео) элемент редшия
проблемы моментов. Другими словами, норма функций х(() в пространстве
I2 [0,оо) является минимальной, т.е. || х ||^2г0 лч= min.
Из сказанного выше можно сделать вывод: если известно необходимое число
моментов функции x(t) относительно моментной системы Я, то функцию x(t)
можно восстановить с любой степенью точности (например, в метрике Z,2 [0,оо)), т.е.
Lv(t) (2.216)
Ф;(0 (2.217)
Глава 2. Методы синтеза регуляторов в классе одномерных систем 157_
знание моментов функции x(t) дает возможность ее восстановления с
необходимой точностью.
В ряде работ рассмотрены вопросы определения моментов звеньев САУ, расчета
моментов по данным активного эксперимента и по данным нормальной
эксплуатации; сделаны обобщения на системы с распределенными параметрами.
В [7, 91] близкое по содержанию понятие получило другую трактовку.
Следуя [7, 91], приведем определение; характеристикой мнимых частот
процесса *(/)== X(s) называется функция, получаемая в результате придания аргументу
изображения X(s) йещественных значений s = st. Очевидно, значения
характеристики мнимых частей представляют собой моменты функции x(t) относительно
экспоненциальной моментноЙ системы. При практических расчетах удается получить
совпадение заданных и полученных характеристик X(s) не во всем бесконечном
множестве точек, а лишь в некоторых точках s = sf. Таким образом, при решении
конкретных задач используется конечное число моментов
Ц,=*(*)и,,/==1,2,..., /. (2.218)
В [7, 91] приведена формула, определяющая функцию x(t) по характеристике
мнимых частот.
А теперь обратимся к задаче синтеза регуляторов с учетом принципиально
важного фактора: знание необходимого числа моментов функции x(t) полностью
определяет ее во временной области.
Приведенное обстоятельство широко используется в тех случаях, когда переход
из пространства изображений в пространство оригиналов сопряжен с преодолением
серьезных затруднений. Один из примеров - случай, когда изображение не является
дробно-рациональной функцией и принадлежит, например, к классу
трансцендентных изображений, которым описываются процессы в системах с распределенными
параметрами.
Очень удобный операционный метод в применении к уравнениям в частных
производных приводит к необходимости решения обыкновенного дифференциального
уравнения относительно изображения. Отсюда изображение функции X(z,s) будет
уже не дробно-рациональным, а трансцендентным. Наличие трансцендентных
функций приводит к тому, что оригинал в этом случае находится в виде бесконечного
ряда, т.к. число корней характеристического уравнения является бесконечным.
Наличие трансцендентных функций в формуле, определяющей X(z9s), в задачах
анализа практически не приводит к каким-либо затруднениям при использовании
метода моментов.
Пример 2.20 [91].
Рассмотрим процессы, имеющие место в телеграфной линии, считая линию однородной, длины / с
распределенными постоянными, километрические значения которых: r,Lycyg .
Будем исследовать уравнение тока, описывающего переходный процесс в приемном реле,
определяемом параметрами г' и V в конце телеграфной линии, полагая, что при включении цепь находится под
действием постоянного напряжения Uo.
В [91] подробно рассмотрены процессы, имеющие место в исследуемой системе, и приведены
соответствующие математические модели. Изображение тока в конце линии при z-\ определяется формулой
/(5) = ^2 (2.219)
К) pshY/ + /?(5)chy/' *
где R(s) = r'+sL' - операторное сопротивление нагрузки, причем
158 Методы синтеза САУ по заданным показателям качества, Часть II
/(0) = /(оо) = 0; /(оо)*/(0).
Приведем численные значения параметров [91]:
- провод стальной, диаметром d = S мм,
- r = 7°^; g = lO-«—L_; £ = 910-^; c-9-l^i;
км Ом км км км
- длина линии / = 500 км; UQ = 1 В;
- приемное реле: г' = 300 Ом; V = 1 Гн.
Как указано в [91], попытка найти оригинал /(/) .== I(s) с помощью формулы разложения
наталкивается на весьма серьезные трудности.
Применение метода моментов значительно упрощает решение поставленной задачи, Можно
использовать два подхода.
Если ошибка е(/) = i(co) - /(/) е I? [0,оо), то соотношение, определяющее е(/), можно записать в виде
^)-JH^('lLc]h(t). (2.220)
«р
где ф, (/) - элементы ОНБ, E(s) ==' s(t), причем цу = £($)|^w в Гe(/)e~*Vf - моменты, легко рассчиты-
о
ваемые по изображению E(s).
В [91] рассматривается подход, состоящий в аппроксимации 1(з) дробно-рациональным
изображением вида
причем
Из условия равенства моментов можно записать зависимость
. A^L-n*,). *-*. i-ui3. (2.22I)
Для отыскания неизвестных коэффициентов имеют место уравнения
st{si+W) = F(st)(sf+2Posl+t20), i = \Xl. (2.211)
Приведем численные значения рассчитанных параметров [91]
6j=l,125102i; W = 281,7~; p0 -1,125 \02- .
ее с
Далее рассмотрим вопрос применения метода моментов для решения задачи
синтеза регуляторов.
Согласно постановке задачи известна эталонная динамическая характеристика:
или W3(s) - эталонная передаточная функция, или /*,(/) - эталонная переходная
характеристика. В первом приближении в качестве W3(s) или Ьъ(() можно принять
характеристики системы второго порядка, что равноценно аппроксимации сложного
процесса основной составляющей второго порядка.
В необходимых случаях в качестве эталонного может быть принят процесс более
сложного вида*
Поскольку задача синтеза при регулярных воздействиях заключается в выборе
структуры и параметров САУ, которые обеспечивают заданные показатели качества
и точности, то исходя из известных соображений определяются типы и варьируемые
параметры последовательных, параллельных или последовательно-параллельных
корректирующих устройств. Так как W0(s) и структура W^ (s,p) известны, то легко
найти ПФ замкнутой системы в виде
Глава 2. Методы синтеза регуляторов в классе одномерных систем
159
w(s в,Шг+Ьш-Мг-х+...+ь{р)
(2.223)
где р = (р\,Рг,->Рг) - варьируемые параметры регуляторов, относящиеся к одному
или нескольким звеньям и подлежащие определению.
Теперь постановка задачи синтеза регулятора методом моментов может быть
сформулирована так [7]:
Необходимо минимизировать целевую функцию
П2
>ы-*ж\'£:У,:£:-:УЫ*)
p(j,), (2.224)
где Sj = ic - показатели экспоненциальной системы
# = {*"*:/ = 1,2,...,/; о О},
/ - число моментов, р(^) - весовые множители, при следующих ограничениях:
1) pim<Pi<piM, / = 1,г - ограничения на значения варьируемых параметров
Pi, обусловленные условиями их физической реализуемости;
2) А, > 0, где А, - определители Гурвица (/ = 1, п -1) - ограничения на
устойчивость системы;
3) Со < С0дон; Сх < С1доп;... - ограничения на коэффициенты ошибок,
обеспечивающие требуемую точность системы в стационарных режимах при
произвольных медленно изменяющихся воздействиях;
4) а;>0, / = 0,л; y(/t,v|/) = —^—>у(л,ц/°), / = 1,л-1,где у(л,v|/) -параметр,
ai-\ai+\ v y
характеризующий колебательность (см. табл. 2.16).
Это ограничение обеспечивает колебательность tg\|/ не выше заданной tgvj/0 .
Таблица 2.16
п
2
3
4
£5
\|/,град
0
4
4
4
4
30
3
3
3
3
45
2
2,41
2,41
2,41 •
60
1
2
2
2
90
0
1
1,41
1,465
Легко заметить, что поскольку
„/. )_bm(p)s'»+bm_i(p)sr1+...+b0{p)^
К"Р)-аш(р)4+а_1(р)'4-*+...+а0(Р)-
оо оо
= \к(т,р)е-*х* = \к{х,Р)е-^х = и, (р),
О О
00
a W3(sj)= | K3(x)e~tcx = |Lt^, / = !,/; - моменты ИПФ замкнутой системы с
регулятором, a \i* - моменты ИПФ эталонной системы, зависимость (2.224) может быть
переписана в виде
160 Методы синтеза САУ по заданным показателям качества. Час
/ 2
/(p) = min]£[|i,(p)-(if] р(*,). (2.
А м
Итак, в сформулированной постановке задачи исходными данными для реш
задачи синтеза регулятора являются: параметры эталонного процесса (эталонная
W3(s)); ПФ замкнутой системы, включающая ПФ WQ(s) объекта управления и
^ку is) регулятора с варьируемыми параметрами /?,, / = 1,г ; ограничения на ус
чивость (реализуется критерий Раусса); ограничения на искомые параметры pi
данная колебательность и, наконец, заданные коэффициенты ошибок.
Если в качестве эталонной динамической характеристики задается Аэ (/), то i
вая функция принимает вид
или, что то же самое,
I{p) = min[ixf{p)-^]2p(si)> ■ (2.
Рк L J
где \xht (р) и ц^э - моменты переходных характеристик синтезируемой и этало!
систем.
В простейших случаях можно получить систему алгебраических уравнений ви
ЬЛрУ +bm_l(p)s'»-i+...+b0(p) -
an(p)s°+aMpV-l+- + "o(p) (Д (
причем />г, и решить последнюю методом наименьших квадратов othochtcj
неизвестных коэффициентов ПФ W[s).
Поскольку Sj = ic, то важным является вопрос выбора значения с (в общем
чае можно выбирать значения s]9 s2, s3,..., Sj, не подчиняя закону s, = ic).
В [7] рекомендуется следующий подход к выбору значений sl9s29s39...9si
предлагается располагать по закону геометрической прогрессии
*v=si?'v
со знаменателем профессии q = 2. При этом основная часть значений su s2, s$,.
должна входить в промежуток 0 < si■ < sx, где W3 fa) может быть выражена в д<
Жэ(^,)тах : ^э (^, ) = ^э(^)тах. Как правило, * = 0,2-0,3, если W3(st) - фуш
убывающая, и А = 0,7-0,8 - если возрастающая.
Рассмотренная задача синтеза регуляторов решается методом нелинейного i
граммирования (см. Приложение 2). Варьируемые параметры регулятора опред
ются решением задачи нелинейного программирования, заключающейся в мин»
зации функционала (2.224) (или функционала (2.226)) при ограничениях 1), 2), 3)
при выполнении критерия устойчивости Рауса, применяемого к характеристическ
уравнению замкнутой системы. Алгоритм имеет алгебраический характер и нет
обходимости интегрировать дифференциальные ураьпгния системы для каждого
четания варьируемых параметров или решать систему в конечно-разностной фор\
В [7] детально рассмотрены методы синтеза нелинейных систем, использую
Глава 2. Методы синтеза регуляторов в классе одномерных систем
161
идентификации класса линейных стационарных объектов. Этот метод целесообразно
применять и при решении задачи синтеза регуляторов, когда ПФ объекта неизвестна.
Если на вход объекта подать ступенчатое воздействие y(t) = \(t) и зафиксировать
в какой-либо форме реакцию h(t), а также положить, что ПФ объекта имеет вид
wo =
bZsm"
a°sn°+a° /"-Чао0
(2.229)
причем коэффициенты bf, i = 0,mo и o°, j = 0,no подлежат определению, то
указанные коэффициенты могут быть рассчитаны путем решения следующей системы
алгебраических уравнений
од
__о
\-e-s''dt
i = l,l.
(2.230)
Моменты
*?-/*(')
e~sUu / = !,/,
(2.231)
легко рассчитать, если с необходимой точностью зафиксирована переходная
характеристика h(t) (в общем случае вход y(t) может отличаться от ступеньки и выбран
в классе наиболее информативных процессов).
Поскольку / > п0 + т0 +1, то систему (2.230) с целью исключения влияния шумов
и других факторов целесообразно решать методом наименьших квадратов.
Пример 2.21.
Рассматриваемый ниже пример носит методический характер; его цель - показать основные этапы
синтеза регуляторов методом моментов. При полном использовании возможностей метода моментов
можно получить решение задачи синтеза сложных регуляторов для объектов высокого порядка, включая и
класс нелинейных систем [7] Рассматриваемый ниже пример, иллюстрирует также тот факт, что метод
моментов не накладывает ограничений на место включения регулятора.
Рассмотрим следующую систему летучих ножниц, описанную в [50, 141] Далее изложим этапы
расчета параметров регулятора.
1 -й этап: Построение структурной схемы системы, выбор места включения регулятора, определение
его структуры и варьируемых параметров.
Рассмотрим случай, когда динамика системы корректируется двумя корректирующими устройствами,
одно из которых имеет ПФ ^^(s) и находится в прямой цепи системы, второе с ПФ W^^s) - в цепи
местной обратной связи. Структурная схема системы представлена на рис. 2.82.
У^ ' ^ /С^ ^ ттг / \ ^ | и/ /_\ |"Т" jC^X I гжг / \ . иг ( _\ V /
^HgK wM
f»iW
i
2{')
Рис. 2.82. Структурная схема следящей системы летучих ножниц
162
Методы синтеза САУ по заданным показателям качества. Часть II
На структурной схеме Wx (s), W2 (s) и W3 (s) - ПФ элементов, входящих в неизменяемую часть
системы, ^1(5) и W^2[s) - передаточные функции корректирующих устройств.
Передаточные функции Wx(s), W2(s) и W^(s) определяются зависимостями [50]:
w,(*)-k, ;w,(*)=-
Л*
;»з(*) = -
к.
чь
(7> + 1)(Г,, + 1)(7)* + 1)(Гм* + 1)' 3W 5(V + 1)(V+1)'
Приведем численные значения параметров
£W=31,4H/A; А:9А=0,65 радДсВ); 7) =0,002 с; К,/:п=3,9; 7^ = 0,085 с; Гм=0,02с;
Кх = 0,0394; /:г = 2,8 В/А; Гг = 0,69 с; Tg = 0,0068 с; /^ = 1,8 Ом; 7^ = 0,0525 с.
Построим переходную характеристику объекта управления. Его ПФ имеет вид
Wx(s)W2(s)WAs) = Wo(s) =
73178014
0,01256/ +9,1б56 +1616,0755 + 91458,1б54 -
+1850386,553 + 1284450052+ 150000005 + 73178014'
Переходная характеристика определяется формулой
^(/) = 1-3,6.10-^в-5^+ЗЛ-10^.е-147|-9Д.10^.в^+0,26.в-|7'-0,358-в-К8'-
-0,9-е"0-1* •cos(2,49/)-0,434e"0'15' sin(2,49/);
график переходной характеристики представлен на рис. 2.83.
4 МО
М<)
2 4 6 8 10 12 14
Рис. 2.83. График переходной характеристики объекта управления
Для отражения методического содержания подхода, с целью упрощения дальнейших рассуждений и.
расчетов выберем простейшие передаточные функции W^s) и W^2(s) корректирующих устройств.
Положим, что
iytvl{s) = K+-JL - пропорционально-интегральный регулятор (ПИ-управление);
^куг(5) = —" инерционная жесткая обратная связь.
7^,5 + 1
При решении конкретных инженерных задач учитываются возможности регулятора с точки зрения
достижения заданного качества работы системы в переходном и установившихся режимах, "а также пути
его реализации.
2-й этап: Нахождение ПФ замкнутой системы с учетом ПФ И^!^) и W^2(s).
Если воспользоваться обозначениями: Кр = /?,, Тр = р2, \/Ки = р3» ^ = 1, то ПФ следящей
системы летучих ножниц принимает вид
b2s2 + bls + b0 .
W(s) =
a9s9 + а858 + a-fS1 + a6s6 + ass5 + a4s4 + a3s3 + a$s2 + axs + a0 *
где
Глава 2. Методы синтеза регуляторов в классе одномерных систем
163
60 = 73178014; 6, =73178014/>3 + 73178014/?2; ^ = 73178014,
а0 = 73178014; а, = 73178014-/?3 +73178014 р2;
а2 = 2857400000- ръ р} + 73178014р3 р2 4-15000000 р3;
а3 = 262309320 • р3 ■ рх +15000000 • рг • рг +12844500 • ръ\
а4 = 1651577,2р3р1 + 12844500р3/?2 + 1850386,5р3;
Л5 = 91458,165 р3 +1850386,5-рург\
а6 = 1616,074р3 + 91458,165/?3р2;
а7=9,1623р3 + 1616,07/>3р2;
а8 = 0,0125 рг + 9у\6ргр2\
а9 = 0,0125 /?3р2.
3-й этап: В соответствии с параметрами, характеризующими качество работы системы, выбирается
или эталонная ПФ W^(s), или эталонная переходная характеристика hy(t)
Положим, что Тр <, 7 с; а £ 20%.
Выберем в качестве эталонной ПХ, установившееся состояние которой имеет, место при Ту > (6- 7) с .
Для описания такого процесса можно воспользоваться зависимостью
/t,(/) = l-e-°'5'cos(0,9/).
Изображение этой функции имеет вид
ад-Ц (*+0>5)
s (5 + 0,5)2 + 0,8Г
4-й этап: Составляется система алгебраических уравнений вида
2>(*К
1 1
fo+0,5)
ЕМрК
st st (s/ + 0,5)2+0,81
(2.232)
Рассматриваемый этап требует творческого подхода, поскольку строгих рекомендаций к выбору
конкретных значений 4 = J|, s = s2>... нет. В общем случае необходимо выбрать sit / = 1,р по методике,
которая изложена выше, причем р > г , т.е. число уравнений вида (2232) больше числа неизвестных
параметров. Далее систему алгебраических уравнений можно решить известными методами, например,
методом наименьших квадратов. Решение системы (2.232) можно свести к задаче оптимизации известными
подходами.
В рассматриваемом достаточно простом случае положим *, = 0,4; s2 = 0,8; 53 = 1,2
5-й этап: Решение системы алгебраических уравнений (2232).
Приведем результаты решения:
р\ = 0,0165; р\ = 0,052; р\ = 8,06.
6-й этап. Анализ скорректированной системы.
График переходной характеристики представлен на рис. 2.84.
А МО
в 10 15
Рис. 2.84. Графики переходных процессов
164
Методы синтеза САУ по заданным показателям качества. Часть II
Если же уменьшить время переходного процесса до Гр «(4-5) с , то перерегулирование достигает
40% (рис 2.85) и в этом случае необходимо выбирать регулятор с другой структурой.
' kH{l) Лэ(0=1-е-'СО5(1-2/)
Л,
у-Л-/^
*Р(0
5 10 15
Рис. 2.85. Графики переходных процессов
(параметрырегулятора р, =0,0066; р\ =0,42; ръ =75,87 )
/> с
20
Пример 2.22. Рассмотрим пример синтеза регулятора системы управления, структурная система
которой представлена на рис. 2.86.
4%%|
K}+K2-s
Регулятор
I
I
I
Г
I
I
I
м
I
Неизменяемая часть |
^эму
7J-5+1
)
«2(0
KyS
-
^ред
1
1
J
1
1
*(0
Рис. 2.86. Структурная схема системы автоматического управления
Параметры системы имеют следующие значения [82]
Т№ = 0,5 с; Тх =0,165 с; Кэ = К^К„Кт = 240 .
Задача синтеза заключается в нахождении параметров Кь К2, К3, таких, которые обеспечили бы
Гр<0,8с, а%<10%.
Найдем параметры К]у К2, Къ из условия приближенного равенства ПФ замкнутой системы
W(5y-
K3K2s + K3K{
г,гда53+(г,+гдв)52+(i+лгэа:2+агэаг3)5+агэаг,
эталонной ПФ вида
где соо = — = 7,5 .
^W=-
coj
53+Зю0$2+3<Оо$ + Сй<)
Воспользовавшись методами моментов и полагая sx =0,3; s2 =0,6; 53 =0,9, получим систему
алгебраических уравнений вида
0,889 =
72*2 + 240*!
0,36208 + 72*2 + 72*з + 240*ч '
Глава 2» Методы синтеза регуляторов в классе одномерных систем
165
0,79383 =
144*,+240/:,
0,85722 + 144А-2 +144*3 + 240*, '
216*2 + 240*,
0,71178 = —
1,4988 + 216*2 + 216*з + 240*,
Решение последней системы приводит к следующему результату
*,* = 0,01075; *2 = 0,00552; К\ = 0,000138 .
Графики А,(/).—^(j) и Лр(/) скорректированной системы представлены на рис. 2.87.
4 МО
0.8
Об
0.4
0.2-
МО
МО
t, С
0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 ^
Рис. 2.87, Графики переходных процессов
При решении задачи расчета параметров регулятора в качестве эталона можно выбирать не эталонную
передаточную функцию (эталонный оператор), а эталонную переходную характеристику Лэ (/).
Пример 2.23.
Рассмотрим еще один подход к синтезу регуляторов методом моментов, предложенный в [91].
Положим, что заданно изображение вида
X(s) = = J4 > (2-233)
Qt4s +p2s +P\S + S
где pi и рг - варьируемые параметры. Эталонный процесс задается формулой
*.(')' , ,°'32, . (2-234)
a\s +a,5 + l
Полагая, что *(°°) = дгэ(оо), а в изображении, определяющем эталонный процесс, коэффициенты а\ и
д,э также могут меняться исходя из необходимости расположения полюсов изображения X(s) внутри
заданной области, чем обеспечивается необходимая степень и запас устойчивости, а также
колебательность системы.
Из (2.233) и (2.234) имеем
0,32(0,4j3 + p2s2 + p]S + 5) = 1,б(<ф3 + rfs +1) .
Отсюда получаем
0,4$3 + p2s2 + р\$ + 5 = 5a2V + 5а? s + 5,
или, что то же самое,
p2s + рх = 5a\s + 5а,э - 0,452.
В соответствии с методом моментов комплексному переменному 5 будем придавать действительные
значения
5, = 0, s2 = 0,1; 53 = 0,2; s4 = 0,3; ss = 0,4; $6 = 0,5; 57 = 0,7; л8 = 1,0; л9 = 1,5; $10 = 2,0;
su = 5,0; sl2 = 7,0; s,3 = 10,0.
Отсюда получаем системы уравнений (первые пять уравнений снабжены весовыми множителями,
равными соответственно 10,10,5,3,2):
166
Методы синтеза С АУ по заданным показателям качества. Часть II
(2.235)
Юр, = 5(ЦЭ;
Юр, + р2 = 5(ЦЭ + Sal ~ О»04»
5р, + р2 = 25д3 + 5д2 - 0,08;
Зр, + 0,9р2 = 15л,3 + 4,5^ -0,108;
2р, + 0,8р2 = Юа,3 + 4^ -0,128;
р,+0,5р2= 5^ + 2,5^-0,1;
р, + 0,7р2 = 5д,3 + 3,5^ - ОД96;
p,+p2 = 5a,3 + 5a3-0,4;
р1+1,5р2 = 5а1э+7,5а2э-0,9;
р, + 2р2 = 5д,э + Юя2 -1,6;
р, + 5р2 = 5я3 +25л3.-10,0;
Pi + 7p2 = 5a,3 + 35fl|-19,6;
p,+10p2 = 5fl,3 + 50a|-40,0.
Из последней системы можно получить следующие уравнения [91]
24,7р, + 5,0р2 = 123,5а,3 + 25,0а| - 7,778;
5,0р, + 19,44р2 = 25,0fl,3 +97,22^ - 60,33;
отсюда следует
р,=5л,э + 0,328;
p2 = 5fl23-3,18.
Теперь характеристический полином изображения, определяющего эталонный процесс, принимает вид
Л^(5) = 0,453 + (5^-3,18)52+(5д3 +0,328)5 + 5.
Таким образом, характеристический полином эталонного изображения зависит от двух
коэффициентов а,3 и а\, которые можно менять из условия обеспечения заданного качества управления.
Уравнения
э = 3,04 +15,9а,3 э = _0064 аз = 0636
2 25а,э + 1,64 ! 2
определяют соответственно границы области устойчивости и двух асимптот этой границы (рис. 2.88).
1.5
(2.236)
1.0
0.63<
0.5
Обла ль устойчш ости
/7Т
"г
0,064
Рис. 2.88. Плоскость в координатах аэ и я2, на которой показана
граница области устойчивости и область допустимых процессов
Глава 2. Методы синтеза регуляторов в классе одномерных систем
167
В соответствии с методикой, изложенной в [91], значения коэффициентов а,э = 1,8 и а\ = 0,8
обеспечивают монотонный процесс, при этом р\ = 9,33; р\ = 0,82 .
Переходные процессы приведены на рис. 2.89.
>
0.28
0.20
0.12
0.04
i *1
/>
10-
/
/
У
/
/
у
/
/
-у
к
л
>^:
^—
4(0
—-;
/, с
0.4 1.2 2.0 2.8 3.6 4.4
Рис. 2.89. Графики процессов дс,({) и x(l)
2.11. МЕТОД МАТРИЧНЫХ ОПЕРАТОРОВ
Основным положением метода является описание регулятора и объекта в
пространстве состояний системами ДУ и эквивалентными им матричными операторами.
Положим, что объект управления и регулятор имеют соответственно ПФ вида
(2.237)
.(2.238)
На основе ПФ (2.237) и (2.238) легко получить эквивалентные системы в
нормальной форме Коши.
Например, для (2.237) система имеет вид
^_ =
а
хм+к°и, / = 1,1%-1;
dx,
(2.239)
— = -,
dt
где
<-i4 -<-24-i —--- —0в-*| +*^и.
to to _о lo _о to.
К2 ~ °то-2 ~ ап0-1К\ " аПо-2К0 э
/-1
/и=0
168
Методы синтеза САУ по заданным показателям качества. Часть II
Аналогичную систему легко записать и для ПФ, определяющей регулятор.
Теперь можно записать векторно-матричные ДУ, описывающие поведение
объекта и регулятора
Х(/) = АОХ + Вои; х = С0Х; (2.240)
Хку(/) = Аку(р)Хку+Вку(р)б; w = CKyXKy. (2.241)
Во
Рис. 2.90. Структурная схема системы автоматического управления
Перейдем к рассмотрению спектральных характеристик временных сигналов и
динамических характеристик системы относительно выбранного ортонормированно-
го базиса Ф(г) = [q>j (/),ф2 (/)>.• -,Ф/ (0]? •
Рассмотрим векторно-матричное дифференциальное уравнение (2.240). Перейдем
от описания объекта и регулятора векторно-матричными дифференциальными
уравнениями к их описанию матричными операторами*.
Уравнение (2.239) эквивалентно уравнению с матричным оператором вида:
п0
С*' + ]Г А* -С*' = А? -С", / = 1,/7о, (2.242)
v=l
или
I + ^AJ 1с?=АГ-С-.
(2.243)
v=l
Из выражения (2.243) можно определить спектральную характеристику / -го
элемента вектора Х(/)
1-1
С*' =
"♦I
Afv -А"-С", / = 1,«о .
(2.244)
v=l
Следовательно, систему уравнений (2.239) можно записать в виде векторно-
матричного уравнения следующего вида:
С*2
Af,
^12
АХ аХ
21 А22
AWoi АЛо2
А^
1"о
х
2п0
*ПоПо
сх2
с^
А1
0
0
0 ...
Л и
А2 ...
0 ...
0
0
А^
С"
С"
' Теория матричных операторов изложена в главе 9 первого тома учебника.
Глава 2. Методы синтеза регуляторов в классе одномерных систем
169
или
где
Сх =
сх1
сх2
С4
Ах
Ах
С
=
Х=А"
A«»i
•с",
Ах22
А"02
••• АН
••• А2п{)
Ах
''' "о"<
А" =
А? О
О
О А^ ... О
О 0 ... А^
; с" =
с"
с"
г*.
Спектральная характеристика выходного сигнала определяется из соотношения
"о
или с учетом выражения (2.244)
"о
C-S4
/=1
1 +
1>;
-1
•A;tt.Cw;
тогда
где
7=1
СХ=А См,
-1
/=1 [ 7=1 .
Проводя аналогичные преобразования, получим уравнение, связывающее
спектральные характеристики сигнала управления м(/), формируемого регулятором, и
сигнала ошибки е_(/), причем спектральная характеристика сигнала u(t) будет
зависеть от искомых параметров р:
1-1
С»(р) = ^.1 + £А%(р)
v=l
м
•К(р)-с\
или
где
Си(р) = Ар(^)-СЕ,
Ар(р) = ^.1 + ^(р)
-1
•а;(р).
v=l |_ ц=1
Воспользовавшись структурными преобразованиями, можно найти выражение,
связывающее спектральные характеристики входного y(t) и выходного x(t) сигналов:
Cx(p) = A{l + A-Ap{p)Jl-A-Ap(PyCx.
170 Методы синтеза САУ по заданным показателям качества. Часть II
Численные значения параметров регулятора находятся из условия
г
1{p) = l[xp{',p)-x,{t)fdt^mm (2.245)
о
при следующих ограничениях:
• обеспечивается устойчивость системы;
• X(/) е ХП{) V/ е [0,Т], ХП() - заданная область;
• u{t) eU] V/ е [0, Г], Ux - заданная область;
• рГ<Р1<р^ / = п;
• С, < С, доп, где С, - коэффициенты ошибок.
Сформулированная задача решается методами нелинейного программирования,
причем функционал (2.245), учитывая спектральную форму описания процессов,
имеет вид
/(р) = }[с^(р)-^]Т.ф(т)-Фт(т).[с^(р)-С^Л.
0
Отсюда имеем
I(p) = [c*(p)-Ctj {С*(р)-С*3]. (2.246)
Таким образом, в результате перехода к рассмотрению спектральных
характеристик временных функций и динамических свойств системы автоматического
управления функционал (2.245) свелся к виду (2.246). Это значительно упрощает
вычисления, поскольку операции над матрицами и векторами значительно проще реализовать
на ЭВМ, чем операции над функциями.
Пример 2.24.
Рассмотрим канал крена (рис 1 15).
Пусть.
КЩК, =62, Г, =0,03 с; W^(s) = K + ^;
х,(1) = \-е"^; сц=3, Тр=\.
В качестве меры близости будем использовать функционал
1(К,К„) = 1[хр(1,КЛ„)-х,(1)~}2А,
О
где Т - интервал интегрирования Значение Т выбирается значительно превышающим время
переходного процесса
Пусть Г = 5Гр = 5
Рассмотрим объект управления; запишем его дифференциальное уравнение
Тух(1) + х(1) = К„!>К1 ■«(/), (2 247)
ИЛИ
x(t) + arx{t) = bQ-u(i),
где я, = — * 33,3, Ьо = -^-L « 2066,7
Ту Ту
Введя в рассмотрение обозначения x](t) = x(t), x2(t) = xl(t), уравнение (2 247) можно записать в
виде системы дифференциальных уравнений первого порядка
*.(') = *2(')>
x2{t) = b0-u(t)-arx2{t)*
Глава 2. Методы синтеза регуляторов в классе одномерных систем
171
Последнюю систему уравнений можно записать в виде векторно-матричного дифференциального
уравнения
Х(/) = А0-Х(/) + В0-и(/), х(/) = С0-Х(/), (2249)
где
Го
*<•>■::!: • ч: -1,j l.
-Ц
Во =
О
2066.
,} ЧЯ
В результате Сфуктурную схему системы автоматического управления можно представить в виде,
приведенном на рис 2 91
И') +/С>е(0
ууч^Ц
(2 250)
:''1_го о "I Гсж-1 Го о~| Гс"1
Рис. 2.91. Структурная схема системы автоматического управления
Если перейти к рассмотрению спектральных характеристик и воспользоваться аппаратом матричного
представления операторов в выбранном ортонормированном базисе, то систему дифференциальных
уравнений (2 248) можно записать в виде
СХ'=РСХ2, |
CX2=^0PCw-a1PCXj,J
где Сх' - спектральная характеристика *,(/), СХ2 - спектральная характеристика *2(/), С" -
спектральная характеристика u(t), Р - матрица оператора интегрирования.
Последнюю систему можно записать в следующем виде.
Гс-
[с-
или
ri -р I ГсХ|1_Г° о] |~с
Здесь I - единичная матрица Из последнего уравнения находим спектральные характеристики элементов
вектора Х(/)
|СХ'|_Г1 -Р
Спектральная характеристика выходного сигнала определяется следующим образом
Cx=dlCx*+d2Cx> .
В векторно-матричном уравнении (2 252) спектральная характеристика С" сигнала управления будет
зависеть от искомых параметров К и Кн :
Си(К,Кн) = [К.\ + Ки?]'Се.
Таким образом, спектральная характеристика выходного сигнала также будет зависеть от искомых
параметров К и К„ .
Тогда функционал (2.246) можно записать в следующем виде:
1(К,КЯ) = [СХ(К,КК)-СХ>]1[С'(К,КЯ)-С'] (2 253)
и поставленная задача принимает форму:
1-го о|Гс"
PJ [О Ь0Р}[с-
(2 251)
(2 252)
172
Методы синтеза САУ по заданным показателям качества. Часть II
1(К,К„)^> min (2 254)
В качестве ортонормированного базиса использовались функции Уолша и удерживалось 32 члена
разложения В базисе функций Уолша оператор интегрирования на интервале исследования [0,5] имеет
следующий вид (приведена клетка размерностью 8x8)
р
В качестве начальных значений искомых параметров регулятора были приняты К{> = \, КЦ = \ В
этом случае значение функционала (2 253) равно
7(ЛГ°,Л:") = 4,8854 1О"2 .
Минимизация функционала (2.253) осуществлялась с использованием алгоритма Нелдера - Мидда -
алгоритма безусловной минимизации функции многих переменных Точность расчета задавалась равной
0,01 % В результате решения задачи были найдены следующие значения параметров регулятора
АГ* =4,0195 10~2, АГ* =2,7243 10"* ,
а значение функционала равно
/(**,/^5,1736-КГ4 .
На рис 2 92 представлены графики эталонного и реального переходных процессов
♦ *э (')»**(')
1,2
2,5
-1,25
0
-0,625
0
0
0
-0,3125
1,25
0
-0,625
0
0
0
-0,3125
0
0
0,625
0
0
0
-0,3125
0
0
0,625
0
0
0
-0,3125
0
0
0
0
0
0
0,3125
0
0
0
0
0
0
0,3125
0
0
0
0
0
0
0,3125
0
0
0
0
0
0'
0,3125
0
0
0
0
0
0
0
1
0,8
0,6
0,4
1,2
График {кальной переходной •
характеристики !
График эталонной переходшй
1 j
{-
—►
0 12 3 4 5
Рис. 2.92. Графики эталонной и реальной переходных характеристик
Пример 2.25. Структурная схема системы представлена на рис 2.93
Г
Регулятор
к
S
i
У
Неизменяемая часть
Рис. 2.9Э. Структурная схема системы
Глава 2. Методы синтеза регуляторов в классе одномерных систем
173
Поведение САУ описывается следующей системой дифференциальных уравнений
аГи'(') + «(Х') = *2Куе-(') + *Г8'(/) + ^е(/),
где входной сигнал регулятора с(/) определяется зависимостью
г(1) = у(,)-х(!);
y(t) и x(t) - соответственно входной и выходной сигналы системы управления При этом выходной
сигнал определяется дифференциальным уравнением
fljv(/)+я 2v(f)+«?*'(')+*<>(')=WO+*о»(0
Коэффициенты дифференциального уравнения объекта имеют следующие значения
flJ = l, ej=3,l, я,0 = 2,9, а%=3, />,° = 2, />(?=3,
£1^=1; aJy=0.
Требуется определить оптимальные, в известном смысле, значения коэффициентов Ь™ , bf* , Ь™
дифференциального уравнения корректирующего устройства, которым соответствуют параметры Кл , К ,
A'j, ПИД-регулятора, исходя из условия обеспечения минимального отклонения выходного сигнала
системы дср(/,/?) от эталонного дгэ(/) Эталонный процесс хэ(/) = 1-е~3' задан как желаемая реакция на
ступенчатый входной сигнал .уэ(/) = 1(0 •
С помощью метода матричных операторов определены следующие оптимальные значения параметров
регулятора
К*И=(Ь?)* =2,4810,
К*=(Ь?)* = 1,4669,
К1 = [Ь?)* = 1,5697
В качестве стартовой точки поиска экстремума были взяты следующие значения параметров
Ки=0,1, К = \, Кл=0
На рис 2 94 представлены графики эталонного и реального переходных процессов до выполнения
оптимизации (стартовая точка) и график для найденных оптимальных значений параметров ПИД-регулятора
И')
1
0,9
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
Эталрнньф пер6ходн|ый гцЬоцесЬ x,(j)
0 0,5 1
4,5
Рис. 2.94. Эталонный и реальный выходные сигналы системы
до оптимизации параметров регулятора и после оптимизации
174
Методы синтеза САУ по заданным показателям качества. Часть II
2.12. МЕТОДЫ СИНТЕЗА РЕГУЛЯТОРОВ В КЛАССЕ
ОДНОМЕРНЫХ ЛИНЕЙНЫХ НЕСТАЦИОНАРНЫХ СИСТЕМ
В предыдущих параграфах были рассмотрены методы синтеза регуляторов в
классе стационарных систем. Задача принципиально усложняется, если объект и
регулятор имеют переменные параметры, т.е. находится решение задачи в классе
нестационарных систем. В настоящем параграфе делаются обобщения рассмотренных в
предыдущих параграфах методов, ориентированных на решение задач синтеза
регуляторов в классе стационарных систем, на нестационарные системы.
2.12.1. Основные положения принципа динамической компенсации
при описании системы и ее элементов импульсными
переходными функциями
Рассмотрим дифференциальное уравнение системы с переменными параметрами
v=0 v=0
Введем в рассмотрение линейные дифференциальные операторы
v=0
dt
(2.255)
Тогда уравнение (2.255) можно записать так
Lx(p9t)x{t) = Ly{p9t)y(t). (2.256)
Последнее уравнение в символической форме принимает вид [141]
x(t) = L? (p,t)Ly (p,t)y(t) = Ay{t). (2.257)
Из (2.257) следует, что выход системы x(t) является результатом воздействия
оператора А на вход y(t).
Оператор Е] = Lx (/?,/) =
1
обычно называют интегрирующим, а опера-
Lx(p,t)
тор Е2 = Ly(p,t) -дифференцирующим.
Можно ввести в рассмотрение обратные операторы. Если АВ = I, где I - единичный
оператор, то оператор В называют обратным по отношению к оператору А ; тогда
АА~]=1. (2.258)
В частности, обратными друг другу являются операторы интегрирования и
дифференцирования.
Lx(p,t)
Рис. 2.95. Последовательное соединение обратных друг другу операторов
Если два нестационарных элемента описываются уравнениями (рис. 2.95)
Lx(p,t)x](t) = Ly(p,t)y(t) и Ly(p9t)x(t) = Lx{p9t)xx(t),
Глава 2. Методы синтеза регуляторов в классе одномерных систем
175
„ ММ
то первому из них соответствует оператор А = ———-
Lx(p,tY
а второму - оператор
A~] = Lx)Pjt\ . Тогда xx(t) = Ay(t) и *(/) = Л"1х1(/) = у4"1^(/) = Iy(t); отсюда
ММ
*(/) = ,(')•
После введения понятия оператора системы с переменными параметрами легко
сделать постановку проблемы синтеза регулятора нестационарной системы,
рассматривая в качестве примера конкретную задачу.
На вход системы (рис. 2.96) поступает полезный нестационарный случайный
сигнал m(t) и нестационарная помеха n(t).
г
1
1
+ П
1
1
|
1
1
1
1 _
У
i,
Корректирующее
устройство
с оператором А^
«(0
А3
Нестационарный
объект -i
с оператором Ао
Рис. 2.96. Структурная схема системы
Статистические характеристики сигналов m(t) и n{t) известны: Rmm(t\,t2),
Rnn(t\,t2) ~~ корреляционные функции соответственно полезного сигнала aw(/) и
помехи /?(/) (положим, что m(t) и n(t) - не коррелированны).
В рассматриваемой задаче полагаем известными и уравнения, описывающие
динамику нестационарного объекта. Задача заключается в нахождении структуры и
параметров нестационарного корректирующего устройства, такого, которое
обеспечивало бы выполнение следующего условия
MUm(t)-X(t)f~\-> min.
Решая уравнение Винера- Хопфа, можно найти эталонный оператор А3
замкнутой нестационарной системы.
Таким образом, в рассматриваемой постановке задачи А3 и Ао - известны, а Аку
подлежит определению.
В §1.4 приведено решение поставленной задачи в терминах принципа
динамической компенсации; оно имеет вид
AKy=A-o](l-A3j]A3. . (2.259)
С использованием введенных выше дифференциальных операторов,
определяющих оператор А, задача синтеза сводится к нахождению Lu (p,t) и Lz (p,t),
определяющих дифференциальное уравнение
Lu(p,t)u(t)=Le(p,t)z(t). (2.260)
Тогда
и(г) = Ау£(') = С» (Л'К (А'МО • (2-261)
176
Методы синтеза САУ по заданным показателям качества. Часть II
Реализация рассмотренного подхода связана с преодолением значительных
трудностей; получение конструктивных результатов возможно лишь в простейших случаях.
Рассмотрим решение поставленной задачи с использованием аппарата
импульсных переходных функций.
ИПФ разомкнутой системы, включающей последовательное соединение
регулятора и объекта управления, определяется зависимостью [141]
т
где
£ку(/,т) - ИПФ регулятора;
к0 (/,т) - ИПФ объекта управления.
Предварительно отметим, что наряду с обратными операторами можно ввести в
рассмотрение и обратные ИПФ (рис. 2.97).
l*i (О
у(') = Ь(1-х)
*М
*"М
*(') = 6(/-т)
Рис. 2.97. К определению понятия обратной ИПФ
Имеем
х(/) = |л-(/,т)х1(т)Л = |/:-1(/,л)/:(л,т)^Л. (2.263)
О т
Поскольку элементы являются обратными, то
*(/) = |*-1(/,л)*(л,т)</п = 5(/-т),
следовательно
J*(/,T,)*-0b*)*l = 5(/-T).
т
Из (2.262),умножая обе части на к~ (/,т) и интегрируя, найдем
t i п
или
т
Соответствующая структурная схема имеет вид (рис. 2.98).
Рис. 2.98. К задаче нахождения ИПФ регулятора
(2.264)
Глава 2. Методы синтеза регуляторов в классе одномерных систем
177
В задаче синтеза в качестве эталонной задается ИПФ замкнутой системы k(t,i);
она связана с ИПФ кр (t,x) очевидной зависимостью
*(м) = Ар(/,т)-|Ар(М1)*(п,т)^П.
(2.265)
Последнее соотношение представляет собой интегральное уравнение,
позволяющее найти ИПФ k(t,x) замкнутой системы по ИПФ kp(t,x) разомкнутой системы
управления.
Алгоритм синтеза регулятора включает следующие этапы:
• задание из соображений обеспечения заданного качества работы системы
эталонной ИПФ k3(t,x) замкнутой САУ (например, она может быть найдена
путем решения уравнения Винера- Хопфа);
• нахождение эталонной ИПФ £р(/,т) разомкнутой системы путем решения
интегрального уравнения
t
k,(t,x) = k;(t,x)-jk;(t,r\)k,(r\,x)dr\; (2.266)
расчет ИПФ регулятора по формуле
Агку(/,т) = |Л:рэ(л,т)А0-1(/,п)^.
(2.267)
С учетом сказанного структурная схема системы с регулятором может быть
представлена так (рис. 2.99).
ИО+к*!6*'
<да.
*РЭМ
Регулятор
—Р
*о"М
I I Объект i
i ! , , i
I i
*оМ
I
I
I •
I -— ' , , j
М''т)
х{1)
Рис. 2.99. Структурная схема нестационарной системы с регулятором с ИПФ к^ (/,т)
Как и в предыдущих случаях, в которых рассматривались стационарные системы
(§2.2), при решении задачи синтеза регуляторов в классе нестационарных систем
имеет место принцип динамической компенсации.
Трудности реализации подхода, использующего аппарат ИПФ, состоят как в
необходимости решения достаточно сложных интегральных уравнений, так и в
отыскании и реализации обратных импульсных переходных функций.
2.12.2. Основные положения принципа динамической компенсации
при описании системы и ее элементов
матричными операторами
Достаточно конструктивное, с вычислительной точки зрения, решение задачи
синтеза регулятора с использованием принципа динамической компенсации
позволяет получить аппарат матричных операторов (см. главу 9, том 1).
В терминах метода матричных операторов задача синтеза может быть
сформулирована так: найти матричный оператор корректирующего устройства из условия
13 Зак 366
178
Методы синтеза САУ по заданным показателям качества. Часть II
равенства матричного оператора замкнутой системы эталонному матричному
оператору.
Приведем основные этапы синтеза системы методом матричных операторов:
• определение эталонного матричного оператора Аэ замкнутой системы,
• определение эталонного матричного оператора А3р разомкнутой системы и
матричного оператора корректирующего устройства;
• реализация схемы корректирующего устройства, имеющего требуемый
матричный оператор.
В общем же случае эталонный оператор замкнутой системы Аэ выбирается из
условия обеспечения необходимого качества работы САУ.
Найдем матричный оператор эталонной разомкнутой системы, полагая, что
известен матричный оператор эталонной замкнутой системы (рис. 2.100). Имеем
A3=a;(i + AJ)"\ (2.268)
су
1
1
! Ч
6(0
р'
К 1
1
| *(0
!QX
Рис. 2.100. Структурная схема эталонной нестационарной системы
Умножим левую и правую части последнего выражения справа на матрицу I + Ар
и, приняв, что (i + Ар ) (i + Ар ) = I (I - единичная матрица), получим
a'(i + a;)=a;.
Отсюда находим
АЭ , А Э а Э А Э
+ А Ар = Ар,
или, что то же самое,
A3=A>-A>A'=(I-A>)a>.
Теперь легко записать выражение для эталонного матричного оператора
разомкнутой системы
A^I-A^A3. (2.269)
Теперь структурная схема эталонной системы принимает вид, представленный на
рис. 2.101.
y(t)
с?
Г
Аэ
1
0
-А')"'А1 ■
! с
Рис. 2.101. Структурная схема эталонной системы
На рис. 2.102 представлена структурная схема нестационарной системы,
включающая объект и регулятор.
Глава 2. Методы синтеза регуляторов в классе одномерных систем
179
ЛО
С
е(0!
<8h^
п С£
Аэ
Аку
«(/)
Ао
(i-a')-'a' = a;
x(t)
—►
с1
Рис. 2.102. К постановке задачи коррекции
Пользуясь структурными преобразованиями, получим зависимость (рис. 2.102)
А0Аку=(1-Аэ)-1Аэ. (2.270)
Отсюда находим (см. формулу (2.259))
Аку=(А0)-1(1-Аэ)-1Аэ=(А0Г1А^. (2.271)
Из последней формулы легко заключить, что матричный оператор
корректирующего устройства состоит из двух частей: первая часть включает Ар и определяется
зависимостью (2.269); вторая же часть имеет оператор, обратный оператору
объекта. Поскольку для Ар справедлива формула (2.269), то структурная схема
скорректированной системы может быть представлена в виде, изображенном на рис. 2.103.
г—
i
i
i .
i
i
i
i
Регулятор
(■-*•)■
Аэ
-ку
(А0Г
А=1
Объект
i
i
i
x(t)
—►
Рис. 2.103. Структурная схема скорректированной системы
Изложенный метод синтеза регуляторов реализует принцип динамической
компенсации в спектральной области [83].
Следуя [84], сделаем некоторые пояснения. Реализация принципа динамической
компенсации с целью решения задачи синтеза корректирующего устройства для
сложных систем (см. пример в §2.7) может оказаться очень трудной; схему решения
задачи можно значительно упростить, если воспользоваться алгоритмом
декомпозиции [84]. Содержание алгоритма декомпозиции иллюстрируется примером,
представленным на рис. 2.104.
После определения алгоритма декомпозиции последовательно рассчитываются
операторы звеньев, получаемых в результате объединения звеньев с известными
операторами и содержащих корректирующее звено, в том числе (на заключительном
этапе) оператор этого звена. При этом необходимо решать все или некоторые из
следующих задач [84]:
• звенья 1 и 2 соединены параллельно; известны их операторы; требуется найти
оператор соединения в целом;
• звенья 1 и 2 соединены последовательно; известны их операторы; требуется
найти оператор соединения в целом;
• звено с известным оператором включено в циклическое соединение; требуется
найти оператор этого соединения;
з*
180
Методы синтеза САУ по заданным показателям качества. Часть II
звенья 1 и 2 соединены параллельно; известны операторы звена 1 и
соединения в целом; требуется найти оператор звена 2;
звенья 1 и 2 соединены последовательно: звено 1, за ним звено 2; известны
операторы звена 1 и соединения в целом; требуется найти оператор звена 2;
в той же схеме соединения известен оператор звена 2; требуется найти
оператор звена 1;
звено 1 охвачено положительной обратной связью; известен оператор этого
циклического соединения, требуется найти оператор звена.
Задача
ч
J
1
ч /
К
' \
2 ■
3 '
\7
V \
А Свертывание
1
—►
i
4
2
Б. Декомпозиция
4 -?► 3
К J
\ 7
ч /
т
6
Л
Л
4
I/ \
N 7
I/ M
-И»^
/ \
-и8^
\7
"Им
"-► 7
7
1Л
z7
Ч^ 7
5
Л
Рис. 2.104. К определению алгоритма декомпозиции:
| | - звенья с известньши матричными операторами; К - корректирующий фильтр,
I - звенья, содержащие корректирующий фильтр
Все эти случаи представлены на рис. 2.105, где диагональными чертами помечены
звенья, характеристики которых подлежат определению.
Глава 2. Методы синтеза регуляторов в классе одномерных систем
181
-й
ф^-нЕ>**
X
й
X
-с
-►
1
т
-►
ч /
-►
1
\ /
/ \
►
т
ч"
2
■►
1
Рис. 2.105. Элементарные задачи вычисления матричных операторов и вычислений:
| |- звенья с известными матричными операторами,
\^^\ - звенья, матричные операторы которых подлежат определению
-Hg>-
4 •
т
Л
т
/ \
*ч~~
/ \
\ /
/ \
Б Декомпозиция
\7
6
/ \
N 7
6
Х\
¥тСГ
■^►-^S)^
т
\ У
4
V \
\ 7
^7
■^ 1
Рис. 2.106. Сложный случай определения алгоритма декомпозиции:
П I - звенья с известными матричными операторами, \^^\ - звенья,
матричные операторы которых подлежат определению; К- корректирующий фильтр
182 Методы синтеза САУ по заданным показателям качества. Часть II
Решение перечисленных задач с использованием аппарата матричных операторов
затруднений не вызывает. Как указано в [84], в процессе последовательного
определения матричных операторов неизвестных звеньев могут возникнуть случаи, когда
корректирующий фильтр содержится одновременно в двух звеньях. В этих случаях
процедура расчета усложняется и приводит к необходимости решения
дополнительных задач. Это иллюстрируется примером, приведенным на рис. 2.106. На первом
этапе декомпозиции можно получить последовательное соединение с двумя
неизвестными звеньями. Используя преобразования 2-4, матричный оператор звена 6
можно выразить через оператор звена 3. Далее надо обратиться к задаче 1. Теперь
она уже может быть решена, т.к. остается одно неизвестное - матричный оператор
звена 3. Решив эту задачу, переходим к задаче 5, которая дает решение задачи в
целом - определяется матричный оператор регулятора.
О степени эффективности принципа динамической компенсации применительно к
классу нестационарных систем можно отметить следующее: КУ является всегда
сложным, поскольку должно включать две части: компенсирующую, описываемую
оператором, обратным оператору объекта, и эталонную (описывается оператором
разомкнутой эталонной системы).
Техническая реализация звена с оператором, обратным оператору объекта, очень
сложна. При его реализации необходимо учитывать не только формальное описание,
но и физику процессов, протекающих в объекте. Оператор (Aq)"1 в общем случае
включает в себя матричные операторы дифференцирующих звеньев и операторы
умножения.
2.12.3. Оптимизационный метод синтеза регуляторов
во временной области
Предварительно необходимо отметить, что применение оптимизационного
принципа синтеза регуляторов, предполагающего достижение приближенного равенства
(например, в L2 [0,Т]) реального выходного сигнала x?(t,pup2,...,pr) к
эталонному процессу с использованием формулы (1.52), трудно реализуемо, поскольку в
общем случае обратный оператор замкнутой системы неизвестен (см. §1.4).
Поэтому при решении задачи синтеза регуляторов в классе нестационарных систем
целесообразно пользоваться оптимизационным принципом, предполагающим
достижение приближенного равенства правых и левых частей операторного уравнения,
описывающего динамику скорректированной системы (см. формулу (1.53) в §1.4).
Если дифференциальное уравнение регулятора записать в виде
|>r(0«(v)=ZTOeW> (2-272)
v=0 v=0
где
^(o-i/^w. '=°'"';
v=l
то параметрами, подлежащими расчету, являются
(2.273)
с*1' i = 0, /7i; v = 1,/;
\ . _|_ 1_ (2.274)
с%', / = 0,m,; v = l,/.
Глава 2. Методы синтеза регуляторов в классе одномерных систем \83_
Таким образом, число неизвестных параметров определяется зависимостью
r = /x(/?j +l) + /x(/wj +1).
Неизвестные параметры будем обозначать через pi, / = \9г .
Если Ао - оператор объекта, Аку(р],р2,...,рг) - оператор последовательно
включенного регулятора, то выходной сигнал системы при подаче на вход у3 (/)
определяется зависимостью
хр(*>Р\>Рг> — >Рг) =
Г / \-П~] (2-275)
= [ЛЛу(а>л>--->а)(/ + 4Лу(а>А2>---'А-)) J ^э(0-
Тогда неизвестные параметры регулятора pl9 р2, ..., рг могут быть определены
путем минимизации квадратичного функционала, т.е.
т
•/(/?,, /?2>--->/v) = J{*p {*>Р\>Рг> ->Рг)-хЛ*)^л =
о
Т f
= lU3(t)-^A0AKy(pup2,...,pr)(l+A0AKy(pup2,...,pr))'i^ y3(t)
О ' v '
[ Xp(t,P\,P2*-,Pr)
—> min .
Последнюю зависимость можно рассматривать как общий подход к решению
поставленной задачи. Приведем конкретные соотношения.
Положим, что с помощью известных методов [84] получено уравнение замкнутой
системы с учетом уравнения регулятора в виде
/7-1
x(")(t,pl,...,pr) + y£dav(t,pl,...,pr)x(v)(t,pl9...,pr) =
v=1 (2.277)
= Zbk(t,P],...iPr)yM(t).
Этому уравнению эквивалентно интегральное уравнение
т
x(t9pl,...,pr) + lKx(t,T9pu...,pr)x(x,p],...9pr)dT =
т ° (2.278)
= j Ky(t9z9pl9...9pr)y(x)d^9
.2
dt-> (2.276)
где
Кх(^Рь...,Рг) = ^-±^^
Ky(t9T9Pl9...9pr) = Y,( ,ч, , k\bk(*>P\>->Pr)(t-t)n~l I
причем P\, p2, ...,pr - неизвестные параметры регулятора.
Поскольку эталонные входной сигнал y3(t) и выходной процесс x3(t) известны,
то можно записать соотношение, определяющее невязку:
184 Методы синтеза САУ по заданным показателям качества. Часть II
E(t,pb...,Pr) = x3(t) + JKx(t,T,p]9...,pr)x3(T)d'z-
0 (2.279)
-|^(М,Д,...,л)^э(т)Л.
о
Для нахождения неизвестных параметров ри ръ ..., рг можно воспользоваться
методами нелинейного программирования; алгоритм имеет вид:
т
/(/?,, p29...9pr)=\E2(t9pl9p29...;pr)dt = min (2.280)
о Л
при ограничениях, определяемых содержанием рассматриваемой задачи.
Многие положения, изложенные в §2.7, справедливы и для рассматриваемого
случая.
Для получения соотношения, определяющего невязку, может быть использована
зависимость вида
о v=o
-^av{t,p,...,Pr)xf){0)-f-.
v=0 *=v V /•
В последней формуле неизвестные коэффициенты pl9 р2, ..., рг не находятся
под знаком производной, что упрощает алгоритм расчета Вместе с тем требуется
знание п -ой производной от эталонного выходного сигнала z3 (t) = xy (t), причем
выходной процесс хэ (/) может быть отличен от переходной характеристики и
включать соответствующие производные при t = 0 .
2.12.4. Метод моментов
В соответствии с формулой (1.55) (см. §1.4) при наличии зависимости (2.279)
неизвестные параметры определяет следующая система алгебраических уравнений
т
JE(t9Pl9p29...9pr)fk(t)dt = 09 *=п; 1*г. (2.281)
о
Если / = г , то имеет место система алгебраических уравнений; если же / > г, она
может быть решена методом наименьших квадратов.
Задача может быть решена методами математического программирования;
алгоритм имеет вид
/ т'
/(/?,,р2,...,/?г) = У (
*=i о
хэ(*)+ |*,(/,т,Д,...,рг)дгэ(т)Л \fk{t)dt-
I
-JKy(t^P]i...,pr)y3(T)dTfk(t)dt
о
(2.282)
= Е[цИа>'">/>г)-^э(Р1>-">/0] =™п>
Глава 2. Методы синтеза регуляторов в классе одномерных систем
185
где
О
Т t
fk(t)dt, * = 1,/;
И*ЭЫ = ||^(^т,л,...,рг)уэ(т)Л.Л(/)Л, * = 1,/,
о о
при ограничениях, диктуемых содержанием конкретной задачи.
2.12.5. Метод матричных операторов
Все положения, изложенные в §2.11, справедливы и для рассматриваемого случая;
отличие заключается лишь в том, что в алгоритм дополнительно вводится матричный
оператор умножения (см. главу 9 в 1-ом томе учебника).
2.13. МЕТОДЫ СИНТЕЗА РЕГУЛЯТОРОВ
В КЛАССЕ ОДНОМЕРНЫХ НЕЛИНЕЙНЫХ СИСТЕМ
2.13.1. Принцип динамической компенсации
Здесь рассматривается класс систем, задачи синтеза которого излагаются на единой
методологической основе, какой является описание систем функциональными рядами
Вольтерра [25, 51, 109]. Теория, в основе которой лежат ряды Вольтерра, называемая
обычно аналитической теорией нелинейных систем, имеет целый ряд привлекательных
черт: она применима для решения широкого круга нелинейных задач и опирается на
строгий математический аппарат [25, 51, 109]. Понятия ИПФ и ПФ, которые являются
эффективным инструментом анализа и синтеза линейных систем, распространяются и на
нелинейные системы - тем самым вносится методологическое единообразие при
построении методов расчета и проектирования систем в рамках аналитической теории.
Рассмотрим основные положения задачи синтеза регуляторов, пользуясь
аналитической теорией нелинейных систем (детальное изложение этой теории можно найти в
[25, 51, 109]). Структурная схема нелинейной системы автоматического управления
представлена на рис. 2.107.
►
Нелинейный
регулятор
«(/>
Нелинейный объект
управления
*(<)
Рис. 2.107. Структурная схема САУ
Положим, что элементы САУ (рис. 2.107) описываются рядами Вольтерра:
оо t ' t
v=l 0 0
- ряд Вольтерра, описывающий поведение регулятора;
00 t t
^(^) = 2I J--J^o(Ti'T2--^)е(/~т1>(/-т2)...е(/-т/)^/т1с/т2 ...d/x,
'=1 0 0
- ряд Вольтерра, описывающий поведение объекта;
00 t t
Х^) = 2 J**'J^^Tl'T2---^)8(r~Tl>(/-T2)---e(/-^)^Tl^T2---^'
7=1 О О
12 Зак. 366
186
Методы синтеза САУ по заданным показателям качества Часть II
x{t)^\-\k"(xux2,...xp)y{t-xx)y{t-x2)...y{t-xp)dx,dx2...dxp
Л=1 О О
- соответственно ряды Вольтерра, описывающие поведение разомкнутой и
замкнутой системы.
Воспользовавшись понятием многомерной передаточной функции (1-й том
учебника), определяемой зависимостью
00 00
W{sus2,...,sn)=j-jk(xl,T2,...zny^e-s^...e-^dxldT2...d4,
О О
можно заключить, что в рассматриваемой задаче имеют место следующие
передаточные функции:
И^Ы> ^к2у(*М2)> W^y(s],s2,s3)y...,W1Zy(sx,s2,...,sv) - ПФ регулятора;
^o(5i)> wo{s\>s2)> ^o{s\^s2^s3)y^K{sbs2^"^si) - ПФ объекта управления;
fl'pfci), W^(s],s2)9 W*(s],s2,s3),..., Wj(s]9s2,...,Sj) -ПФ разомкнутой системы;
W{(s}), W2(sbs2), W3(sl,s2is3),..., Wp (sus2,...,sp} - ПФ замкнутой системы.
Задача синтеза регулятора заключается в нахождении его передаточных функций,
таких, чтобы замкнутая система обладала эталонными динамическими
характеристиками. Таким образом, постановка рассматриваемой задачи полностью совпадает с
задачей синтеза регуляторов в классе линейных систем. Предполагается, что
неизменяемые элементы системы (объект управления) представляют собой соединение
линейных инерционных и нелинейных безынерционных звеньев. При этом линейные
элементы предполагаются минимально-фазовыми, а нелинейные - аналитическими
функциями, имеющими обратные для всех возможных входных воздействий. Такое
предположение обусловлено положениями принципа динамической компенсации.
Поскольку предполагается, что заданы эталонная система, имеющая ПФ W\ (s^),
W*(sbs2), W*(s{,s2,s3),..., W*(s],s2,...,sk), и объект управления, описываемый
ПФ Wq (s] ), W2 (s] ,$2), •. •, то задача синтеза сводится к нахождению ПФ
регулятора W^y(s],s2,...,si), / = 1, 2,.... Сказанное иллюстрируется рис. 2.108.
+ ^
1
р-
+_
-3
• •;;;'№•"
W£(Sl,S2,...,SN)
г
Л
9
Ч
Регулятор
Объект
г
7\
4
Рис. 2.108. К постановке задачи синтеза регулятора ,,
Глава 2. Методы синтеза регуляторов в классе одномерных систем \87_
В [25, 51, 109] разработан аппарат структурных преобразований на основе
многомерных передаточных функций, аналогичный тому, который широко используется
для решения линейных задач.
Запишем формулы, связывающие ПФ замкнутой и разомкнутой систем [109]:
W2{suS2) = -
1 + ^.)'
Wp2(sus2)
[l + K(sl+s2)]Yl[l + W}(sr)]
1
Г=1
Учитывая, что в задаче синтеза регулятора для ПФ замкнутой системы должны
быть выполнены равенства
W\Sl) = W^(s,), W2(Sl,s2) = W2(Sl,s2),...y WN(sus2,...sN) = W,N(sus2,...,sN),
находим
i+Wp'fo)'
W2(s{,s2) = -
0УМ2)
[i+^,+*2)]n[i+<w]
1
Из последних соотношений легко получить формулы, определяющие ПФ
разомкнутой системы через ПФ замкнутой системы:
Wf{sbs2) =
W,2(sus2)
[l-W^+a2)]l[l[\-Wi(sr)]
r=\
Поскольку разомкнутая система представляет собой последовательное соединение
регулятора и объекта управления, то справедливы зависимости [109]:
^(S|.S2)<(Sl)<fe)+f.'(S|+«2)<(S|,S2) = MfL^ii ,
[i-^+^jnt1-^)]
Теперь легко найти соотношения, определяющие ПФ регулятора:
чы-Ш)®1^ •
12*
188
Методы синтеза САУ по заданным показателям качества. Часть II
ЪМ— ^Щ1 W(si+s2)jl-
[i-^+^rK1-^)]
\-i
ПММ
K(s^s2)Y\w:(sr)\ ,
r=\
Полученные формулы представляют собой решение поставленной задачи. По
поводу рассмотренного выше подхода необходимо сделать следующие замечания:
• как и в линейных стационарных и нестационарных задачах, в классе
аналитических нелинейных систем имеет место компенсация динамических
характеристик объекта за счет его обратных ПФ, т.е. принцип динамической
компенсации, справедлив и для рассматриваемого случая;
• реализованная по рассмотренной методике система не будет в точности
совпадать с эталонной ввиду того, что при определении ПФ регулятора дважды
производилось усечение ряда Вольтерра;
• совершенно аналогично решается задача синтеза регулятора и в случае, если
последний включен в цепь обратной связи.
Рассмотрим систему, структурная схема которой имеет вид (рис. 2.109).
—*&к->
Регулятор
«W
К(*)
п
f(z) = alz + a3z3
Объект
*(0
Рис. 2.109. Структурная схема САУ
Для последовательного соединения регулятора и линейного звена с ПФ Wo (s)
имеют место зависимости [109]
<ым*1)»<(*1.*2.*зК !>...•.
3
ПФ разомкнутой системы можно записать так:
г=1
Далее легко получить равенства
Г
ЪЧ*1'*г>*з)
i-d£*'
, r=l
г
г=1
№-*'(*,)]
Глава 2. Методы синтеза регуляторов в классе одномерных систем
189
Из последних соотношений получаем ПФ регулятора:
км=
^'Ы
W^(si,s2,s3) = -
<hKM[l-^(*x)]'
#ofcf
3^
I"*? I*,
, r=\
г
r=\
«№?('')
3 ^ 3
I
«УЕ'Ш-^м]
Если эталонная система линейна, то ПФ регулятора определяется так:
w.
«ы~\3щш°>)]~'■
i
\-l
Из последних зависимостей легко сделать вывод, что в соответствии с принципом
динамической компенсации регулятор можно рассматривать как последовательное
соединение безынерционной нелинейности f~x, обратной к /, и инерционных
линейных звеньев с ПФ
Ai
1 — W\ [S\ )
Соответствующая структурная схема представлена на рис. 2.110.
^ЭД
K(s)
1-ад
г1
W? (s)
Регулятор
*o(s)
f
Объект
^(0
Рис. 2.110. Структурная схема САУ с регулятором, реализующим
принцип динамической компенсации
В заключении рассмотрим систему, структурная схема которой имеет вид
(рис. 2.111).
190
ПА) >
Т
Методы синтеза (
Регулятор
«(0
ЗАУ по заданным показателям качества
z{t)
Объект
Часть II
Рис. 2.111. Структурная схема САУ
Пользуясь рассуждениями, которые были приведены выше, легко получить
зависимости, определяющие ПФ регулятора при условии, что эталонная система является
линейной:
Я,
\-1
*М^2>*з) =
г=\
ПМыГ '
atUW<> M
Структурная схема системы с регулятором, реализующим положения принципа
динамической компенсации, представлена на рис. 2.112.
i-^(5)
Г1
Регулятор
/
К(*)
Объект
КО
Рис. 2.112. Структурная схема скорректированной системы
Таким образом, если неизменяемая часть системы образована последовательным
соединением линейной инерционной и безынерционной нелинейности, а эталонная
система линейна, то регулятор реализуется последовательным соединением
инерционных и нелинейных безынерционных звеньев.
00
Если f(z) задана степенным рядом, т.е. /(z) = ^flf-z' , то коэффициенты ряда,
/=1
г-1
описывающего функцию / , определяются с помощью формул обращения
степенного ряда [109].
и 1 А. а2 h _ 2a2 ~а\аЪ
ах а{ а{
Достоинства и недостатки принципа динамической компенсации для линейного
случая обсуждались выше. Возможности принципа динамической компенсации для
систем, рассматриваемых аналитической теорией, учитывая известные факторы,
ограничены. Например, рассмотренный метод трудно реализовать для достаточно
сложных систем. Его можно применять для определения ядер невысокого порядка,
Глава 2. Методы синтеза регуляторов в классе одномерных систем \9\_
поскольку соответствующие уравнения получаются очень сложными.
Самостоятельной задачей является проблема аппаратной реализации регулятора.
2.13.2. Оптимизационный метод синтеза регуляторов
во временной области
Очевидно, методы синтеза регуляторов в классе нелинейных систем, требующие
знания обратного оператора замкнутой системы с целью нахождения зависимости,
определяющей выходной сигнал в функции параметров регулятора рх, р2, ... /?г,
практического интереса не представляют. При решении конкретных задач весьма конструктивные
алгоритмы можно разработать, пользуясь оптимизационным принципом синтеза
регуляторов, предполагающим достижение приближенного равенства правой и левой частей
операторного уравнения, описывающего поведение замкнутой скорректированной
системы с неизвестными параметрами регулятора [7]. Такое равенство достигается за счет
изменения параметров регулятора при подстановке в операторное уравнение эталонных
входного y3(t) и выходного x3(t) сигналов (см. §1.4, формула (1.53)).
Положим, что поведение замкнутой нелинейной системы с регулятором,
имеющим варьируемые параметры р{, р2, ...рг9 описывается уравнением
п-\ т
x^+jjav(pl,...pr)x^ + F(x) = ^tk(pl,...pr)P. (2.283)
v=0 k=0
Этому уравнению эквивалентно интегральное уравнение
+(^l('~Tr'F(*(T))rfT= (2-284)
t Г т / -\к £ 1
-j|g^&M«....*)<'-.r]*>]*.
Пусть уэ (/) - эталонный входной сигнал, а хэ (/) - эталонный выходной
процесс. Тогда, воспользовавшись обозначениями:
F^/,A,...pJ = X3(0/j(|i^^[^(A.---Pr)('-TrI]^(T)U +
О [к=0\ г )
+riu^t-^'lF^^dx' (2285)
^(',л.-л)-||£^^г[4(л,...л)(/-хГ1]лЦ.
можно записать соотношение для невязки
E(t9pl9...pr) = Fl(t9Pl9...pr)-F2(t9pl9...pr). (2.286)
Далее задача формулируется в терминах аппарата нелинейного программирования:
т
1(ри...рг)= [£2(/,д,.../7г)Л=тш (2.287)
J Pk
192
Методы синтеза САУ по заданным показателям качества. Часть II
при ограничениях, диктуемых содержанием задачи (например, безусловно должна
обеспечиваться абсолютная устойчивость и грубость системы по варьируемым
параметрам [7]).
Здесь были изложены положения, являющиеся обобщением выводов,
рассмотренных в §2.7 для класса стационарных систем. Если продолжить рассмотрение
применительно к классу нестационарных нелинейных систем, то обобщение легко получить,
пользуясь зависимостями, приведенными в §2.12. Очевидно, невязка для класса
нелинейных нестационарных систем может быть представлена так:
E(t,pi,...pr) = x,(t)+JKx(t,T,pi,...pr)x3(-[)fc +
о
+7^f(M"~^(*))*-fM^A.-"*)*(T)*-
(2.288)
о о
Одной из форм реализации рассмотренного выше подхода является
проекционный метод. В некоторых случаях он позволяет построить достаточно конструктивные
алгоритмы синтеза регуляторов.
2.13.3. Проекционный метод синтеза регуляторов
В §2.8 задача синтеза регуляторов сведена к задаче аппроксимации в
пространстве Z,2 [О, Г]. Подход, изложенный в §2.8, можно обобщить на нелинейные системы.
Задачу синтеза регулятора будем рассматривать для нелинейных следящих
систем, примеры структурных схем которых представлены на рис. 2.113 - 2.115.
Особенностью этих систем является наличие одного нелинейного элемента в прямой
цепи или цепи обратной связи.
*1&щ
(s)
и{1) -
+ ^
- i
—
►
')
п
*(<)
Рис. 2.113. Структурная схема системы с нелинейным элементом в цепи местной ОС
*W4
М»)
u(t)
K(s)
*(<)
irM
Рис. 2.114. Структурная схема системы с нелинейным элементом в цепи главной ОС
Полагая, что Wx = ,\, WQ= °;(, Woc = ос; ; - передаточные функции
Ау(*) Ms) W)
корректирующего устройства, объекта и обратной связи соответственно, по
структурным схемам легко записать дифференциальное уравнение системы: для систем,
структурные схемы которых представлены на рис. 2.113 и 2.114, - относительно вы-
Глава 2. Методы синтеза регуляторов в классе одномерных систем
193
ходной координаты *(/), а для системы (на рис. 2.115) - относительно сигнала
ошибки е(/):
(4АсЛу + ЯкуЗЛс )х + bob^f{x) = ЯкАЛс^ > (2.289)
ЛсЛуЛ^ + B0QB^B0F{X) = В^В^Г,
(A0AKy + B0BKy)E + B0AKyF(E) = A0AKyY.
(2.290)
(2.291)
^%н
8(0
F(8)
i
+ i
<8>—-
ед
44
Рис. 2.115. Структурная схема системы с нелинейным элементом в прямой цепи
Анализируя (2.289), (2.290) и (2.291), можно сделать вывод, что после
нормировки относительно коэффициента при старшей производной движение
рассматриваемых нелинейных систем описывается дифференциальными уравнениями вида
Jn)(tht,«,J4t)+tcJF*J4*)=tbJ'k)(t)> (2-292)
/=о у=о *=о
где и<п-\, т<п, y{t) - входное воздействие, x{t) - реакция системы, F(x) -
аналитическая нелинейная функция.
Задачу синтеза регулятора нелинейных систем будем решать в следующей
постановке. Движение нелинейной системы задается уравнением (2.292), причем
коэффициенты уравнения aj(P),Cj(P),bk(P) зависят от Р - параметров регулятора
системы. Далее факт зависимости коэффициентов уравнения системы от параметров
регулятора указывать не будем. Требуется определить параметры регулятора системы
исходя из условий приближенного обеспечения заданных показателей качества
работы системы.
На первом этапе, в соответствии с требуемыми показателями качества работы
системы, выбирается желаемый переходный процесс: Положим для определенности,
что это - переходная характеристика Лэ(/). Для большинства задач синтеза
регулятора в качестве эталонной можно выбрать зависимость вида:
/b(/) = ^(l-e"a^cosco/),
причем
где Тр - время переходного процесса.
Далее, применяя известный подход, осуществляем переход к интегральному
уравнению, эквивалентному исходному нелинейному дифференциальному уравнению системы:
t t t
x(t)+ JKx(t,x,P)x(x)dT+ JKf{t,x,P)F(x(x))dx= \Ky(t,x,P)y(x)dx, (2.293)
194 Методы синтеза САУ по заданным показателям качества. Часть II
где
Введем следующие обозначения:
FXi(t,P)=x3(t)+)Kx(t,T,P)x,(z)di,
о
■FXi (t,P) = JKf(t,x,P)F(x,(x))dT, (2.294)
О
Fx{t,P) = FxXt,p) + FX2{t,p)
И
F2(t,P)= \Ky{t9x9P)y9(x)dx. (2.295)
о
Тогда невязку можно записать в виде:
b(t,P) = Fx(uP)-F2{t9P). (2.296)
На основе формулы, определяющей невязку, можно построить функционал 1(Р),
в качестве которого удобно использовать метрику пространства L4[0,T]:
(т V/»
/(/>) = Р*[о.И|ЕМ'Л1 • <2-297)
Параметр Г в (2.297) выбирается исходя из длительности Гр; практика
показывает, что Г«(3-5)Гр.
Оценка вектора Р может быть произведена, как было показано выше, в
результате минимизации функционала:
/>*=min/(/>). (2.298)
Проблема нахождения Р* может быть сведена к задаче аппроксимации в
пространстве L2[09T].
Введем в рассмотрение вспомогательный вектор параметров Р :
P = {ai(P)J=0^\,cJ(P)J=^Mnk = 0~^.}, (2.299)
элементами которого являются коэффициенты уравнения (2.292). Ясно, что оценив
вспомогательный вектор Р, можно получить зависимости для расчета параметров
регулятора.
В рассматриваемой постановке задача синтеза эквивалентна задаче аппроксимации в
пространстве 12[0,Г]. Методы синтеза, основанные на минимизации функционалов
Глава 2. Методы синтеза регуляторов в классе одномерных систем 195
типа метрик функциональных пространств по параметрам вспомогательного вектора
Р , по своему содержанию являются аппроксимационными или проекционными.
Далее положим, что входной и выходной сигналы системы аппроксимируются
полиномами Лежандра или Чебышева, т.е.
Я/) = (С)ТФ(О; *(/) = (с*)ТФ(/), /€[0,Г], (2.300)
где Ф(/) = {ф0 (f),(Pi (*)»—>Фм (t)} - используемый ортонормированный базис.
После группировки членов относительно 1,/,/2,...,/м зависимость (2.300) можно
переписать в виде
y(') = Itf''=(c')Te(/); *(0=Z^=(c)Te(0, (2.30D
/=0 /=0
где
в(/)={»о(0.»1(0.-»м(0}т. (2-302)
причем 8,-(*) = /', / = 0,/-l. Данное предположение не ограничивает общности
рассуждений, поскольку существует матричный оператор, позволяющий переходить от
базиса Ф(/) к базису ©(/). Далее положим, что нелинейная функция имеет вид
^(*(')) = 1Л**(')- (2-303)
Найдем выражения для слагаемых, определяющих невязку (2.296). Имеем
^[('-^r^TVO^^^V-^-1^. (2.304)
Для FXi(t,P) можно записать
.'jg, А-У__£_
0v=0
или
/^(r,^)=*(O+Z^av(O. (2-305)
v=0
где
Аналогично для FX2(t,P) имеем
М'^)=2ЛРу('). (2-307)
v=0
где
Отметим, что если заданным сигналом .уэ(') является воздействие з;э(/) = 1(/),
формула для расчета функций Pv(f) принимает вид
^('^)"(')+||»,(^^[('-Г']«Н^
196 Методы синтеза САУ по заданным показателям качества. Часть II
a (t) = tn~v У *—}- = - (2 309)
Перейдем к нелинейным зависимостям. Для случая, когда F(jc(t)) - кусочно-
линейная функция, ее можно представить так:
F(x(t)) = F+0(t)1(t) + X[/:;;(t)-F.,(t)]i(t)) (2.310)
/=1
где т, - моменты переключения кусочно-линейной нелинейности; F+i (т), F_t (т) -
аналитические выражения нелинейной характеристики звена до и после момента
переключения нелинейности т,; s - число переключений, которое зависит от вида
характеристики F(x) и процесса на входе звена х(т).
Тогда
Очевидно, что реакция нелинейного элемента после / -го момента переключения
может быть записана в виде линейной комбинации
F+i(x) = */x(T) + rf|.=*/X^r+rf/. (2.312)
/•=0
Подставляя (2.312) в (2.311), получим окончательное выражение для Fx (/, Р):
M'.^Z^vtO. (2-313>
v=0
где
Yv()'S§y!(»-v-y-i)!fey+r+iL'« '' J+y+iL'« '' \\-
Учитывая, что ts+} -1, перепишем последнюю формулу в виде
tf(0 = <(')+Y£(')+<(')> (2-314)
где
М) ^s y!(W_v-y-i)!<[{^ls;(y+r+i)Lf*1 ' JJ
+77Т^-'' J|-2-(,+r+1)'. -« y+1
'w»w"^Sy«(»-v-y-i)!(y+'-+i)f
, (_1)V-4
Yv'U 74s.y!(«-v-y-l)!(y + l)"
Глава 2. Методы синтеза регуляторов в классе одномерных систем 192.
Рассмотрим вариант, когда /^(т)) - аналитическая и гтредставима рядом (2.303).
Запишем нелинейную функцию как функцию времени. Для этого воспользуемся
матрицей умножения для полиномиального базиса. Найдем эту матрицу.
Пусть z(f) = *(/)/(/) и x(t) = {cxje(t), /(/) = (СУ)Т0(/). Тогда для z(t)
справедливо
z{t) = (cx)Je{t)QT (t)cf =(cxjci(t)cf,
где
n(0-
©1,0 Wl,l
©0./-1
©I./-1
_coM>o ©/-u ... coMM_
причем
0)^=0)^=9^,=»^; /,y = 0,/-l. (2.315)
В (2.315) аргумент опущен для краткости. Учитывая (2.315) и отбрасывая
элементы матрицы £l(t) с индексами, большими чем /-1, имеем
a(t)cf=
&0 9j ... 9М
»! S2 ... 0
9М 0 ... 0
d
<£
■1.
Но аналогичный по структуре вектор 3(/) можно получить иначе
а(Ф
с0 с, ... см
0 с( ... с{_20
0 0 ... 4
д,
9/-.
= АУ(/)0(О>
следовательно, z(/) = (сг)Т в(/) = (с^)1 А^ (/)©(/) иСг = А^ (Z)C1.
А^, (/) определяет структуру искомой матрицы умножения для степенного базиса.
Теперь можно записать выражения для коэффициентов разложений старших
степеней функции x(t):
x'(t)=(c"JAy(x)Q(t) = (c^&(t),
х3 (t) = (С*2 )Т А, (,)в(0 = (С )Т А, (х)А, (х)е(/) =
= (С^)Т (Ay(x))20(t) = (&]0(t), (2.316)
**(t)-(e)T(A,(x)f-le{,)-(c*]e(t).
198 Методы синтеза САУ по заданным показателям качества. Часть Н
Полученные равенства (2.316) позволяют представить нелинейную функцию в виде
^(*W) = ZZ/*<^- (2-317)
Принимая во внимание (2.317) и (2.303), найдем требуемые выражения для Fx (/, Р):
'-» (-i)v dv
и п-\1-\ г ( i\v
=0j=0k=
и Л-1/-1 г /_i\v '
=Z-vZZZt^vc«-./^; r^\.Wd,= (2.318)
v=0 i=0j=0k=2\n Ч- О *
ИЛИ
v=0 /=0 7=0^=2^ V! V + J)
v=0
где
Таким образом, все аналитические выражения, определяющие невязку (2.296),
найдены.
Используя полученные выше зависимости для невязки, функционал (2.296)
можно записать в виде
/(p)=fU,(0+Z^Hav(0-ZA,HPv(0+Z^HY{(0 * (^=2)- (2-319)
0 \ v=0 v=0 ' v=0 J
Функционал (2,319) относительно вспомогательного вектора Р может быть
записан так:
Т ( п+т+и+\ • Л
l(P)=Ux3{t)- X ЛЛ(0 \dt, (2.320)
0 \ v=0 J
где pv - компоненты вспомогательного вектора; параметры pv и функции fv(t)
определяются следующим образом:
Pv =
-av, v = 0, л-1,
V = «,A7 + /W, (2.321)
-cv_w_m^!, v = w + w + l,w + w + i/ + l;
av(/), v = 0,/i-l,
/v(0 = -
Pv-ЛО» v = «,« + w, (2.322)
y^v_n_mJi (/), v = fi + nf + l,/i + m + i/ + l.
Анализируя выражение для функционала, записанного в форме (2.320), можно
сделать вывод, что рассматриваемая задача сведена к задаче аппроксимации функции
хэ(/) линейной комбинацией функций /o(0>/i(0>-**>A(0> k=m + m + u + \.
Глава 2. Методы синтеза регуляторов в классе одномерных систем 199^
Такой подход позволяет свести задачу определения неизвестных параметров
вспомогательного вектора к решению системы линейных алгебраических уравнений.
Действительно, учитывая, что
dl(P) Ч к
d~Pi
требуемую систему алгебраических уравнений запишем в виде
WP = R, ' (2.323)
где W = |wy, Uj = 09k\ - матрица, элементы которой определяются формулами
L-2j(x3(o-£a,/v(')Wm'> «=p.
<Л v=o 7
и R = (/•;, i = 0,k) - вектор-столбец правой части:
о
Решая систему (2.323), получим численные значения оптимальных параметров
~* «,* ~*
Пример 2.26.
Структурная схема статической нелинейной системы имеет вид, представленный на рис. 2.116.
Нелинейный элемент типа «насыщение» находится в цепи местной обратной связи:
0,5 при х>0Д
F(x)= х при |*|<0,5, (2 324)
-0,5 при х<0,5.
Известны параметры звеньев системы, относящихся к функционально-необходимым элементам
7] =0,15с, А, =10с"1. Требуется определить параметры регулятора: к2,к3,к4, которые обеспечивают в
системе апериодический переходный процесс - реакцию на 1(/) при нулевых начальных условиях, причем
время переходного процесса должно составлять Гр « 0,5с , при статической ошибке не превышающей 5%.
Прежде всего запишем дифференциальное уравнение, описывающее движения САУ. Это уравнение
имеет вид
7x(0+(i+*A)i(/)+M2*(0+*A^(*W)s!*i*2>'(0+*Ay(0.
или, с учетом известных параметров и нормировки,
x(t) + (6,66 + 66,66*з)*(/) + 66,66*2*(/) + 66,66*4F(*(/)) =
= 66,66*2j(/) + 66,66Jy>(/).
Выберем желаемый переходный процесс. По условию задачи он должен быть апериодическим,
амплитуда процесса при / -> оо равна единице Этим условиям удовлетворяет процесс вида
А,(/) = (1-в^).
Показатель экспоненты оц определим исходя из заданного времени переходного процесса и
статической ошибки
1-е-а>05>0,95;
откуда аэ > 6 . Выбираем аэ = 6.
В системе во время переходного процесса будет иметь место один момент переключения
нелинейности при hj (/) = 0,5 . Момент переключения найдем из уравнения
1-е"0'5 =0,5,
откуда /( =0,116с . Следовательно, нелинейная функция F(x(t)) для /^(/) согласно (2.310) представима
в виде
200
Методы синтеза САУ по заданным показателям качества. Часть II
F(/) = (l-e-*)l(/)-(l-e-«')l(/-rI) + 0,5[l(/-/1)]
Теперь запишем квадратичный функционал
<W 1 I \2
/(P)=Jk(T)+I^av(T)-Z^PvW + coy|f(x) Л,
(2 326)
где
ао(т) = 0,999923т3-1,498680т4 + 1,789349т5-1,750703т6 +
+ 1,399029т7 -0,878324т8 + 0,400624т9 -0,115882т10 + 0,015705т11,
а, (т) = 2,999769т2 - 5,994723т3 + 8,946747т4 - 10,504223т5 +
+9,793208т6 - 7,026594т7 +3,605518т8 - 1,158823т9 + 1,727650т10,
Р0(т) = 0,5т2; р,(т) = т;
у^ (т) = 9,253338• 10"4 - 2,557094• 10"2т + 0,250000т2
Представим /i>(/) в полиномиальной форме:
Л,(/) = 5,999539т- 17,984171т2 + 35,786988т3 -52,521115т4 +
+58,759253т5 -49,186158т6 + 28,844947т7 -10,429411т8 +
+1,727650т9.
Далее, решая задачу аппроксимации функции /ц(т) элементами ау(т), ру(т) и у{(х), получим
к*2 = р\ = 0,606847, к\ = я* = 0,907425, к\ = р\= 0,003054.
Анализ полученного решения показал, что в данном случае обеспечивается 10%-я грубость по
варьируемым параметрам.
На рис. 2.117 показаны эталонная переходная характеристика и переходная характеристика
скорректированной системы, а на рис 2 118 - абсолютная погрешность z(t) = ft> (t) -h^ (t) Легко заключить, что
погрешность не превышает 0,25%.
1 ' *(<)
к2 + k3s
—Ьф
4,tiS + i)
F(x)
Рис. 2.116. Структурная схема нелинейной системы
. М')Л(')
075
05
025
f
1
/
1
О 05 1 15 2
Рис. 2.117. Эталонная ПХ h^(t) и ПХ скорректированной САУ h^(t)
Глава 2. Методы синтеза регуляторов в классе одномерных систем
201
0.00249633
в(0 = А,(/)-Лр(/)
1 /
/
t,c
•000327477
0 05 1 15 2
Рис. 2.118. Ошибка приближения эталонного процесса
Пример 2.27. Структурная схема нелинейной САУ приведена на рис. 2 119 Заданы значения
параметров системы.
Тдв = 0,5 с, Г, = 0,165 с , к = £эму£Д|Лред = 240 Нелинейный элемент в системе реализует квадратичную
зависимость F(x) = x2(t)
Необходимо определить значения параметров нелинейной системы kh k2, к3 таким образом, чтобы
удовлетворялись следующие требования.
• при скачкообразном внешнем воздействии y(t) = l(/) время переходного процесса в системе
должно составлять Гр * 1 с , а перерегулирование а < 23%;
• обеспечивалась грубость системы по параметрам не менее десяти процентов
Структурная схема системы, представленная на рис 2 119, относится к схемам с нелинейным элементом
в цепи местной ОС Дифференциальное уравнение системы относительно выходной координаты запишется
гак
После нормировки уравнение принимает вид.
x(t) + ^06O6x(t) + k4(\ + kk2)x(t) + kk}k4x(t)
+kk3k4j;[F(x)] = kk]k4y(t) + kk2k4y(t), *4 = 12,1212
(2 327)
(2 328)
Выберем желаемый переходный процесс в виде /i, (/) = £>, (1-е a^coscon Параметры процесса найдем,
исходя из предъявленных требований к показателям его качества
Полагая, что Т = 2л/о) - период собственных колебаний процесса, можно записать выражение для
максимального отклонения переходной характеристики
/W^dl-e^U (l-/n"UJl-/M,
эткуда легко определяется колебательность процесса и его частота:
со тг 7саэ
ц = — = -. г, со = !——.,
аэ In A In A
где А =
L-l
Известно, что время переходного процесса Тр связано с коэффициентом затухания приближенным
равенством
202
Методы синтеза САУ по заданным показателям качества. Часть II
Из приведенных выше зависимостей следует
3 .
а,- « — « 3 ,
Т?
со «/^Ц* 6,093* 6.
|1пД|
Пользуясь описанным выше методом, определяем искомые параметры.
А:* =0,0417862, £2* = 0,0176393, *3* = 0,00095812
Эталонный переходный процесс и процесс в системе при найденных параметрах показаны на
рис 2 120 Анализ полученного решения подтвердил, что при этих параметрах заданная грубость обеспе-
ytt)j(2\4t)t
кл + kos
-Ф
к к к
эму дв^ред
5(Т„5 + Щ* + \)
k3s
Fix)
Рис. 2.119. Нелинейная следящая система
1.5
1.13
-Г
/
t S
tj
ti
if
t $
tj
pl'J
1—fe.
*(0.
0 0.5 1 1.5 2
Рис. 2.120. Эталонный h^(t) и реальный /?р(/) переходные процессы
0.198865
iM')-*p(<)
•0.01^799
Рис. 2.121. Ошибка приближения эталонного процесса h^{t)
Глава 2. Методы синтеза регуляторов в классе одномерных систем 203
2.13.4. Метод моментов
Положим, что известна зависимость, определяющая невязку (2.286), причем для
функций F\{t,P\,Pi--'Pr) и ^i{^P\^P2-"Pr) справедливы соотношения (2.285).
Пользуясь положениями, изложенными в §1.4 (см. пункт 1.44), запишем систему
равенств
г
\E(t,px,p2...pr)fk{t)dt = O,k=U. (2.329)
о
В §2.10 при рассмотрении класса линейных стационарных систем используется
экспоненциальная моментная система:
H = \ekct\ к = 1,2,...; се/?1}; (2.330)
в [7] также рекомендуется использовать систему (2.330), причем приведены
конструктивные-алгоритмы решения задач синтеза регуляторов для широкого класса
нелинейных систем. Там же построены алгоритмы, использующие понятие обобщено
линеаризованных систем. Из (2.329) легко получить систему алгебраических
уравнений для расчета неизвестных параметров регулятора.
Пример 2.28 [7]
Рассмотрим систему, структурная схема которой представлена на рис. 2 116, а ее поведение
описывается уравнением (2 325), где нелинейный элемент имеет вид (2 324). Постановка задачи совпадает с той,
которая приведена в примере 2.26. Положим, что эталонные входной и выходной процессы определяются
зависимостями
>,(/) = !(/), хэ(/) = А,(/) = 1-в-61. (2331)
а задача синтеза заключается в нахождении параметров *2, къ, к4
Перепишем (2 325) в виде
л(/) + а,(Аз)х(0 + ао(*2)^(') + ^(*4)/г(^(')) = 6,(*з)Я') + *о(*2Ь(') (2332)
Приведем зависимости, определяющие функции F](t,pl,p2. pr) и F2(t,p^p2 • Рг)> определяемые
(2 285)
о 1*=о
hj0-T)4*4)F[(i-*-f>')}/T,
+J
о
о U=o "т J
Отсюда следует соотношение для невязки
E(t>k2,k3yk4) = Fl(t,k2,k3,k4)-F2(l,k2,k3,k4). (2 333)
Элементы моментной системы определяются формулами [7]
/,(') = '"" ,Л(') = ^'2'- (2334)
т
Тогда JE(i,k2ik3,k4)ft(t)dt = 09 / = 1,2
о
После проведения соответствующих расчетов имеет место система алгебраических уравнений [7]
0,208*4 - 0,833*2 - 5*з + 0,95 = 0,
0,243*4 - 0,555*2 - 6,667*з + 0,933 = 0,
отсюда следует
*2 = 1,972*з+ 0,4223,
*4 =31,94*з-2,8762
Необходимо обратить внимание на следующее обстоятельство Поскольку неизвестных параметров
три, то, следуя изложенным выше положениям, необходимо выбрать три моментных функции
204 Методы синтеза САУ по заданным показателям качества. Часть II
/iM'/iM и/з(0 и> таким образом, получить три уравнения для расчета параметров регулятора
к2, к3, к4
В [7] рассмотрен подход, позволяющий получить два уравнения (2 336), при этом имеет место
возможность изменять параметр къ таким образом, чтобы были выполнены важные ограничения,
определяющие качество работы системы В [7] детально изложен вопрос выбора параметра къ из условия
получения абсолютной устойчивости системы, а также обеспечения статической ошибки, не превышающей
5%. Кроме того, значение параметра къ выбирается из условия получения положительности параметров
къ к3, к4 и максимальной грубости системы по этим параметрам С учетом выполнения указанных выше
условий к3 =0,091, рассчитанные по формулам (2 336) значения параметров к2 и кА равны к2 =0,6017,
Л4 =0,0303
При найденных значениях параметров регулятора в системе имеет место монотонный переходный
процесс, заканчивающийся практически к моменту времени Тр = 0,5 с , и статическая ошибка системы не
превышает 5%
Легко видеть, что если / > 3 , то, построив систему равенств
7
\Е(1,к2Лз^4)М1)Л = ^(кък3,к4)-\ху,(к29к^к4) = 09 v=l,2 />3,
о
Т 7
где ^(M3.*4) = jM'.*2,*з>*4)Л('К HJ(M>*4) = \Fi(*>k*kэ*4)/Д'У'>
о о
задачу расчета коэффициентов къ кг, к4 можно сформулировать в терминах нелинейного
программирования
-.2
1(к2Л,Л4) = £[»1(к2Л3,к4)-»!(к2,к,Л4)]2 = кпн^
при соответствующих ограничениях
Как уже указывалось, рассмотренные выше методы, использующие аппарат
нелинейного программирования, предполагают задание ограничений в виде явных
выражений от варьируемых параметров P\,Pi,.--,pr- Если такие зависимости не
получены, то на каждом шаге направленного поиска параметров рьр2,...,рг необходимо
интегрировать дифференциальные уравнение, описывающие динамику системы с
учетом уравнения регулятора.
Глава 3. Частотный метод синтеза корректирующих устройств 205
ГЛАВА 3. ЧАСТОТНЫЙ МЕТОД СИНТЕЗА
КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
Частотные методы синтеза корректирующих устройств относятся к числу
наиболее разработанных и широко применяемых на практике. Это объясняется, прежде
всего, их физической прозрачностью, гибкостью и инженерной направленностью.
Среди ряда частотных методов синтеза (см., например, [17, 141]) мы рассмотрим
частотный метод синтеза последовательных корректирующих устройств, базирующийся
на концепции желаемой логарифмической амплитудно-частотной характеристике,
предложенной В.В. Солодовниковым [141]. Данный метод широко используется для
синтеза следящих систем. Основная идея метода - это связать логарифмические
частотные характеристики разомкнутой системы, вещественную частотную
характеристику замкнутой и показатели качества переходного процесса (перерегулирование и
время переходного процесса), формирующие так называемую «коробочку Солодов-
никова». Наиболее просто эта связь находится для минимально-фазовых систем,
поэтому нами будут рассматриваться только такой класс систем. В первой части главы
будут получены соотношения, определяющие данную связь, далее рассмотрен
алгоритм синтеза желаемой логарифмической амплитудно-частотной характеристики и,
наконец, подробно разобран пример.
3.1. ОПРЕДЕЛЕНИЕ ИМПУЛЬСНОЙ ПЕРЕХОДНОЙ ФУНКЦИИ (ИПФ)
ПО ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ ЗАМКНУТОЙ СИСТЕМЫ
Пусть W(s) передаточная функция замкнутой устойчивой системы. По
определению ее ИПФ имеет вид
C+ja
1 ^
*(/) = f W(s)estds. (3.1)
2 л/ J.
J с- /оо
Так как по условию все полюсы левые, абсциссу сходимости с в интеграле (3.1)
можно принять равной нулю (с = 0), тогда
1
k(t) = — ( W(s)estds. (3.2)
Сделаем в (3.2) замену переменной s = yco . В этом случае интеграл (3.2) можно
представить в виде
1
k(t) = — f W(j®)eJ(utdo). (3.3)
271 J
-00
Выражение (3.3) представляет собой обратное преобразование Фурье. Оно опре-
00
деляет функцию k{t) на интервале 0 < / < оо , если интеграл J k(t)dt абсолютно схо-
-00
дится. Это условие для устойчивой системы выполняется.
Представим комплексную частотную характеристику Ж(усо) в виде:
ЖО(о) = Дсо) + уе(о)), (3.4)
где Р(ю), б(ш) -вещественная и мнимая частотные характеристики соответственно.
1
*(-т) = — f W(ja)e-jmda, 0 < т < оо . (3.7)
1
0 = — f (/5(co) + yg(co))(coscoT-j/sino)T)Jco .
206 Методы синтеза САУ по заданным показателям качества. Часть II
Подставляя (3.4) в (3.3) иучитывая, что em - cos со/ + j sin со/, получим
k(t) =— f (P(co)cosco/-g(o))sinco/)^/co + y— f (/>(w)sintt/ + 0(co)cosco/Wco. (3.5)
—CO —00
Функции P(co), cos со/ являются четными функциями от со, а (?(со), sin со/ -
нечетными функциями от со [115], поэтому подынтегральная функция во втором
интеграле (3.5) является нечетной функцией со и ее интеграл в симметричных пределах
равен нулю. В первом интеграле подынтегральная функция является четной
функцией, поэтому выражение (3.5) можно окончательно записать в виде
-СО - 00
k(t) = — f />(co) cos co/dco — f g(co) sin со/б/со . (3.6)
Необходимо отметить, что преобразование Фурье (3.6) определяет k(i) в пределах
-оо < / < оо , а по условию физической реализуемости k(t) = О при / < 0 . Учтем этот
факт следующим образом. Пусть / = -т . Выражение (3.3) в этом случае имеет вид:
1
2п
—со
Согласно сделанного замечания к(-т) = 0 , поэтому (3.7) можно представить в виде:
271
—со
Или, используя факт четности и нечетности соответствующих функций, получим
00 j ОО
— J P(co)coscotc/co = —Jg(co)sincoTc/co. (3.8)
С учетом (3.6) и (3.8) получим следующее окончательное выражение для ИПФ
устойчивых физически реализуемых систем:
j 00 ^ 00
k{t) = - [ />(со) cos co/<ico = — f 0(co) sin со/dco, / > 0 . (3.9)
ni ni
3.2. ОПРЕДЕЛЕНИЕ ПЕРЕХОДНОЙ ХАРАКТЕРИСТИКИ
ПО ЧАСТОТНОЙ ХАРАКТЕРИСТИКЕ ЗАМКНУТОЙ СИСТЕМЫ
После нахождения выражений, связывающих вещественную или мнимую
частотные характеристику с ИПФ, важно получить аналогичную связь и для переходной
характеристики, т.к. чаще всего при синтезе систем определяющим является вид
желаемой переходной характеристики.
Пусть, как и прежде, W(s) - передаточная функция устойчивой физически
реализуемой системы. По определению переходная характеристика данной системы может
быть найдена из выражения:
A(0 = JL J Ше-А. (3.10)
2я/ J s
С-усО
W(s)
Наличие одного нулевого корня в выражении —— не позволяет нам ввести абс-
s
циссу сходимости с = 0, поэтому сделаем следующие тождественные
преобразования формулы (3.10):
Глава 3. Частотный метод синтеза корректирующих устройств 20/
c+jco
h{t) = W{0) + ±- ^ЬМе«4 (3.11)
2тг/ J s
c-jao
где W(fi) - статический коэффициент передачи.
R W(s)~W(0)
Подынтегральное изображение имеет все полюсы в левой полуплос-
s
кости, что проверяется непосредственной подстановкой вместо W{s) дробно-
рационального выражения
т
W(s) = *f = Ш,Щ0) = Ь.. (3.12)
£a,s> °{S)
/=0
Представление (3.11) позволяет использовать абсциссу сходимости с = 0, сделать
замену переменных s = у со и с учетом (3.4) получить следующее выражение для h{t):
A(O^(0)+If!Wfl^es
2л _J yco
-00
=Р^+П{о^.со,ш+5^т%[пш]м+ (злз)
2ti_j у, со о) )
+J -^-L ^^-COS0)/+ Sill (0/ rf(O,
2ti j^v со со ^
где учтено, что W(0) = Р(0). Ранее было отмечено, что Р(со), cos со/ - четные
функции, g(co), sin со/ - нечетные функции частоты со, функция является нечетной
со
функцией со, поэтому первый интеграл в формуле (3.13) имеет четную
подынтегральную функцию, а второй - нечетную. Это позволяет представить (3.13) в виде:
/г(0 = Р(0)Д[^со5со/-ьР(СО)-/?(0)51по)/Усо. (3.14)
7TJ0V CO СО )
Условие физической причинности, определяющее, что h(t) = 0, / < 0 , по
аналогии с формулой (3.8) приводит нас к следующему соотношению:
^_т) = 0 = 1?дасовт-^ЬМ8Ь1ЮТЪа),о<т<со,
ft о V ® со
или
— ^ coscoTflfco = — —^^ ^-^sincoxJco . (3.15)
Подставляя (3.15) в (3.14), получим
2?/>((о)-Я(0)„;я
/7W = />(o)+£f£i^2z£Wsin(0^(0 =
■п- J f л
nJ со «J 0)
208 Методы синтеза САУ по заданным показателям качества. Часть II
где использована формула [40]
I со 2'
Выражение (3.16) определяет связь между частотными характеристиками
замкнутой системы и ее переходной характеристикой. Из этого следует, что для устойчивых
систем переходная характеристика определена либо вещественной Р(со), либо
мнимой g(co) частотными характеристиками системы, поэтому между этими
характеристиками, в свою очередь, также должна быть определенная зависимость и она
определяется преобразованиями Гильберта [115]:
Q(u)
п J и-
du,
1 •? p(u)
e((0)=ij£W^.
71 J W-CO
СО
(3.17)
Обозначая через Л(со) модуль функции W(jw), а через ф(со) ее аргумент, будем
иметь:
W(j(o) = А((о)еМ(й), (3.18)
откуда следует
In W(j®) = In A((o) + у'ф(со). (3.19)
Функции 1п/4(со) и ф(со)связаны с функцией \nW(j(u) таким же образом, как
связаны Р(ю) и (?(со) с функцией Ж(усо) (формула (3.4)). Поэтому аналогично
формуле (3.17) можно утверждать, что если все полюсы функции \r\JV(s) расположены в
левой полуплоскости комплексной переменной s, то функции \пА((й) и ф(со) также
связаны преобразованием Гильберта
1 г ф(и)
я J и-
-00
1 7 In Л(со)
Так как
. 1 г In Л((л,,
ф(0)) = ~ ^^-flfO).
71 J W-CO
СО
(3.20)
ln^Cs) = \n^- = \nB(s)-\r\D(s), (3.21)
D(s)
то к числу особых точек функции \nW(s) относятся не только нули функции D(s)
(полюсы передаточной функции W(s)), но и нули B(s) (т.е. нули W(s)).
Таким образом, формулы (3.20), позволяющие определить А(ю) через ф(со) и
наоборот, будут иметь место лишь в том случае, если все нули и полюсы W(s)
располагаются в левой полуплоскости, т.е. W{s) является передаточной функцией
минимально-фазовой системы (МФС). МФС отличаются тем, что из всех систем, имеющих
одну и ту же амплитудно-частотную характеристику, они дают наименьший сдвиг
фаз между входными и выходными сигналами, при этом существует взаимно
однозначное соответствие между амплитудно-частотной и фазочастотной
характеристиками, определяемое формулами (3.20). Далее мы будем рассматривать только
минимально фазовые системы.
Глава 3. Частотный метод синтеза корректирующих устройств 209
3.3. ОЦЕНКА КАЧЕСТВА ПЕРЕХОДНОЙ ХАРАКТЕРИСТИКИ
ПО ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ
При оценки качества переходного процесса в некоторой системе автоматического
регулирования воспользуемся полученной ранее интегральной зависимостью между
переходной характеристикой h(t) и вещественной частотной характеристикой Р(со)
A(O = -f^^sina)/rfo). (3.22)
71 £ СО
В работах В.В. Солодовникова (см., например, [130]) получены наиболее важные
оценки качества переходной характеристики h(t), связанные с формой вещественной
частотной характеристики Р((£>). Основными из них являются следующие.
1. Установившееся значение А^ переходной характеристики определяется
начальным значением вещественной частотной характеристики:
й(со) = Р(0). (3.23)
Это легко доказывается по теореме о предельном значении оригинала
Э)8
А(оо) = lim А(0 = Km sH(s) =lims\ —— \ = W(0) = Р(0).
/-»со v->0 .v->0 у S J
2. Начальное значение Ао = А(0) переходной характеристики определяется
конечным значением вещественной частотной характеристики:
А(0) = Р(оо). (3.24)
Доказывается аналогично на основании свойства о начальном значении оригинала.
3. Следующее соотношение базируется на теореме о масштабировании (теореме
подобия): двум вещественным частотным характеристикам, сходным по форме, но
отличающимся масштабом по оси абсцисс в Qo раз (Qo >0), соответствуют
переходные характеристики, также сходные по форме и отличающиеся масштабом по оси
абсцисс в — раз. Покажем это.
Qo
Пусть известна некоторая переходная характеристика А(т), связанная с
вещественной частотной характеристикой Р(со') зависимостью
2f/W) •
А(т) = - f-^isin((o'x)^co'.
7Г J fiV
Введем новую переменную со по формуле
co' = Q0co,
получим
А(Т) = ffi(Qo<n)sin((DQoT)Qo<ft> =
где введены новая переменная
и масштабированная вещественная частотная характеристика
P(co) = P(Q0(o).
5 Зак. 366
210
Методы синтеза САУ по заданным показателям качества. Часть II
Если Qo > 1, то P(co) определяется сжатием в Qo раз по оси абсцисс
вещественной частотной характеристики F(co) (для Q.o < 1 соответственно растяжение). При
этом масштаб по оси абсцисс для h{i) (переходная характеристика для Р((о))
увеличивается в Qo раз (см. рис. 3.1).
Р(со), Р(со)
МО, МО
КО
МО
^0
On
Рис. 3.1. Масштабированные вещественные частотные характеристики
и их переходные характеристики
4. Двум вещественным частотным характеристикам, сходным по форме, но
отличающимся масштабом по оси ординат в (3 раз, соответствуют переходные
характеристики, также сходные по форме и отличающиеся масштабом по оси ординат в Р раз.
Это очевидно и непосредственно определяется формулой (3.22).
5. Разрыв непрерывности вещественной частотной характеристики
свидетельствует о том, что система находится на границе устойчивости. Разрыву при со = 0
соответствует апериодическая граница устойчивости (наличие нулевого корня
характеристического уравнения, т.е. интегратора) и разрыву при со ф 0 - колебательная
граница устойчивости (наличие пары чисто мнимых корней характеристического
уравнения, т.е. консервативного звена).
Глава 3. Частотный метод синтеза корректирующих устройств
211
6. Острый пик вещественной частотной характеристики при угловой частоте
со0 (с"1) свидетельствует о медленно затухающих колебаниях переходной
характеристики с частотой, близкой к — (Гц) (наличие резонанса).
2ti
7. Если вещественная частотная характеристика является непрерывной
положительной функцией (/'(со)), ее производная - неположительной функцией — < 0 ,
то время переходного процесса определяется неравенством
— </пп< —, (3.25а)
а перерегулирование не превышает 18%,
а%<18%, (3.256)
где соп - интервал частот, в котором ?(со)>0 (интервал положительности
вещественной частотной характеристики) (рис. 3.2 б, в).
/>(0)
Рис. 3.2. Типичные вещественные частотные характеристики
На рис. 3.2 представлены типичные вещественные частотные характеристики.
Частота сос ограничивает так называемый интервал существенных частот. При со > сос
ординаты функции Р(со) пренебрежимо малы и при расчетах не учитываются.
Отбрасываемая часть вещественной частотной характеристики на рис. 3.2 показана
пунктиром. Для монотонных функций вида (рис. 3.2, в), где на интервале 0 < со < сос = соп,
dP
Р(со) > 0, — < 0, имеет место следующий результат: а% = 0% , т.е. переходная ха-
с/со
15*
212 Методы синтеза САУ по заданным показателям качества. Часть II
рактеристика монотонна. Для характеристики общего вида (рис. 3.2, а) оценка времени
переходного процесса может быть получена только снизу:
'пп> —, (3.26)
а перерегулирование может быть приближенно оценено по формуле [160]:
ao/o<U8Pmax+0?277Pmin^(0)1Q()O/
Р(Р)
причем для Pmin - 0, Ртах = Р(0) имеем оценку (3.256).
Чтобы пояснить свойство 7, рассмотрим следующую идеализированную
вещественную частотную характеристику:
|>0, О<со<шп,
[0, со> соп.
В этом случае переходная характеристика принимает вид:
., ч 2^(0)) . , 2 _ 7 sin со/ ,
п{ СО 71 i СО
Интеграл
(3.28)
я J со/
SKx)jE}Mdu (3.29)
о м
называется интегральным синусом, который имеет следующее свойство [40]:
si(00)=f£»^U=£. (з.зо)
J и 2
Из выражений (3.27), (3.29) видно, что
*(oo) = Si(oo) = />0,
что было получено ранее (см. свойство 1). С учетом обозначения (3.29) и
соотношения (3.30) формула (3.28) примет вид:
*(/) = -/>0Si(<Dn/).
71
Если обозначить соп/ = т и принять Ро = 1, соп = 1, то получим следующую
формулу:
Л|—] = A(T) = -Si(T), (3.31)
где назовем /г(т) нормированной переходной характеристикой или h-функцией, при
этом график Л(т) имеет следующий вид (см. рис. 3.3).
Для данной вещественной частотной характеристики (Ро - 1, соп = 1) /^-функция
имеет следующие показатели: а% < 18%, /пп < An (это будет показано ниже).
В.В. Солодовников [130] ввел более общий вид базовых вещественных частотных
характеристик - единичную трапецеидальную вещественную характеристику Р(со)
(рис. 3.4).
Глава 3. Частотный метод синтеза корректирующих устройств
213
12Г
1,05
1
0,95
08
06
04
02
0
Л(т)
А
/ \
"'"г N
/
/
I
V" -/—--
о
10 т„п«4д15 сопг = т 20
Рис. 3.3. График //-функции для Р{) = 1, />(со) =
Р(), 0<со< 1,
0, (о>1
/>(со)
со„
<?„=!
со, с '
—►
Рис. 3.4. Единичная трапецеидальная вещественная характеристика
Здесь параметр только один:
х = ^ f°<x<i
С0п U = C°a
называемый коэффициентом наклона (выше была рассмотрена единичная трапеция с
X = 1). Имеем:
1, 0 < со < соа = х,
Л(со) =
1-0)
, Х<ю^1>
1-Х
0, ш>1.
(3.32)
214
Методы синтеза САУ по заданным показателям качества. Часть II
Для единичной вещественной трапецеидальной частотной характеристики (далее
просто единичная трапеция) /г-функция принимает вид (см. формулу (3.28)):
*х(т) = -Г
2 г sin сот
d® +
2 г 1-со sin сот
' о
со
7lJ l-
d(o =
со
-flsKx.)- '
, |si(.)-si(i[.)+C0"-CM*TU
(3.33)
где индекс x для Ах(т), ^х(со) показывает зависимость/г-функции, Р(со) от одного
параметра х- hx -функция (3.33) затабулирована и имеется во многих работах (см.,
например, [116, 130]). Графики h% -функций при различных коэффициентах наклона
X приведены на рис. 3.5.
12
1.18
1.05
1
0.95
08
Об
04
02
W
I
./..■■у,
-с
УХ
«я
/
>
^^
у — 0
^
ттах «|
1пп ^
4я
°0 2 4 6 8 10 12 14 w
Рис. 3.5. Графики /^ -функция при различных коэффициентах наклона х
Из рис. 3.5 видно, что для типовой единичной трапеции при изменении 0 < х ^ 1,
нормированное время переходного процесса находится в пределах (% = 0,2)
7г < тпп <4я (х = 1), при этом 0 < а < 18% .
Если аппроксимировать заданную вещественную частотную характеристику
/Хсо) совокупностью трапецеидальных характеристик, т.е.
т т
Р(со)« Х^(«) = ЕроД,^)' (3-34)
/=1
/=1
.^а,
где X/ =—L5 i = U*n - коэффициент наклона /-й трапеции, w - число трапеций, POj
П/
- высота /-й трапеции, то на основании свойств 3 и 4 получим:
Глава 3. Частотный метод синтеза корректирующих устройств 215
где т. - нормированное время , т.е. время для соп = 1.
Как следует из формулы (3.27), величина перерегулирования тем больше, чем
больше максимальная ордината Ртах. В случае, когда система находится на
колебательной границе устойчивости, величина Ртах =оо и вещественная характеристика
при со = со0 (см. свойство 5) терпит разрыв.
Из соотношений (3.26), (3.27) следует, что при использовании для оценки
качества системы автоматического регулирования вещественной частотной
характеристикой /5(со) быстродействие системы характеризуется интервалом положительности
соп, а запас устойчивости - максимальной ординатой Ртах . Для увеличения
быстродействия следует увеличивать интервал положительности соп, а для увеличения
запаса устойчивости - уменьшать максимальную ординату Ртах.
Эти качественные выводы широко используются при синтезе корректирующих
устройств частотным методом, о котором речь пойдет ниже.
3.4. СВЯЗЬ ПОКАЗАТЕЛЕЙ КАЧЕСТВА ЗАМКНУТОЙ СИСТЕМЫ
С ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ РАЗОМКНУТОЙ
При синтезе корректирующих устройств частотным методом используются
логарифмические частотные характеристики разомкнутой системы, поэтому важно найти
соотношения, связывающие показатели качества (в частности, перерегулирование,
время переходного процесса) замкнутой системы с логарифмическими амплитудно-
частотными и фазочастотными характеристиками (ЛАЧХ, ЛФЧХ), частотой среза
разомкнутой системы.
Пусть W{s), 0{s) - передаточные функции соответственно разомкнутой и
замкнутой систем, причем
\ + W(s)
Пусть
W(ja) = <У(со) + уУ(со) = Z(coy0(to), (3.36)
Ф(усо) = />(ш) + У2(со) = А(фМ(а)= W(J^ (3.37)
Из (3.35)-(3.37) получим:
= Z(co)cos8(co) + 7Z(co)sine(co) = ^ + (3Jg)
1 + Z(co) cos 0(co) + y'Z(co) sin 0(co)
Из выражения (3.38) найдем:
а) вещественная частотная характеристика замкнутой системы:
Z^KZC^coseCc^
Z2((o) + 2Z((o)cos0(o)) + l
б) мнимая частотная характеристика замкнутой системы:
Z(co)sin0(co)
Z2(co) + 2Z(cu)cos0(g)) + 1
Геометрическое место точек Р(со) = const = Рс согласно (3.39) определяет уравнение
&*> „2, .TrrZ. . ■• (3.40)
Z2((o) + Z(co)cos0(co)
Z2(co) + 2Z(co)cos0(co) + l~ c'
216
Методы синтеза САУ по заданным показателям качества. Часть II
или
Z(co)cos0(co)(l-2/5c) = Z2((o)(Pc-l) + /)c.
Аналогично для мнимой части:
Z(co) sin 0(co) - 20cZ(co) cos 9(co) = Qc + QCZ2 (со).
(3.41)
(3.42)
В соответствии с выражениями (3.41), (3.42) можно построить номограммы: (3.41)
- для определения Р(со), (3.42) - для определения Q(v>) по амплитудно-частотной
Z(co) и фазочастотной Э(а)) характеристикам разомкнутой, причем по оси абсцисс -
фаза 6(со) в градусах, по оси ординат - амплитуда Z(co) в децибелах (номограмма
приведена во многих учебниках и справочниках, в частности, см. [116]).
На рис. 3.6 представлен фрагмент данной номограммы.
А,дБ
30
6 (град)
-350 -300 -250 -200 -150 -100
Рис. 3.6. Номограмма для определения Р(со) замкнутой системы по ЛАЧХ и ФЧХ
разомкнутой системы. Цифры при кривых определяют Рс
В формуле (3.41) Z(o)) = 10°'05L(co), L(o)) = 201gZ(co). Ось абсцисс данной
номограммы охватывает значения 0 от 0 до -360°, ось ординат охватывает значения от
- 28 дБ до +28 дБ. При L > 28 дБ Р « 1 и при L < -28 дБ Р « 0; при Рс = 0,5 имеем
L(co) = 0 для любых частот со и любого угла Э(ш).
Чтобы выяснить связь показателей качества замкнутой системы с частотными
характеристиками разомкнутой, рассмотрим вещественную частотную характеристику,
аппроксимируемую двумя трапециями. Для удобства представим ее в
масштабированном виде (рис. 3.7), где индекс 1 определяет первый вариант трапеции, ^(со) ха-
0).
рактеризуется тремя параметрами: основным коэффициентом наклона х= > коэф-
фициентом формы X = —- и дополнительным коэффициентом наклона ха = ~~^" • Из
соп
0)ь
характера данной трапеции видно, что система с такой вещественной
характеристикой имеет астатизм первого порядка Ро - 1, кроме того, мы далее предполагаем (как
было сказано выше), что она является еще минимально-фазовой.
Глава 3. Частотный метод синтеза корректирующих устройств
217
Рассмотрим второй вариант трапеции Р2((Ь), который отличается от РДсо) тем,
что интервал положительности Р(со) определяется частотой среза соср, причем, как
было показано выше, Р(соср) = —. Для масштабированной трапеции: Р2(&) введем
еще один параметр (относительную частоту среза) хс •
Хс =
0)п
где частота среза соср определяется следующим выражением:
©сР=Хс«>п. ^с) = --
■=^
Ра = \
.Р,(ю)
^а. ^ «J. 1 = ®п.
-^
(3.43)
Рис. 3.7. Вещественная (нормированная) частотная характеристика,
аппроксимируемая двумя трапециями
Масштабированная трапеция ^2(^) имеет следующий вид (рис. 3.8). Из
геометрических построений (рис. 3.8) получим:
(Ртах -0,5)(1 -х)
Хс = Х+-
max
А(&)
^а. ^b. ^d. ^ср
соп
0)п
соп
0)п
СО
Рис. 3.8. Вещественная (нормированная) аппроксимированная
частотная характеристика Р2((Ь)
(3.44)
14 Зак 366
218
Методы синтеза САУ по заданным показателям качества. Часть II
Данный вид трапеции позволяет определить погрешность, вносимую заменой
соп-»соср.
И, наконец, введем еще один вид трапеции Р3(&), который учитывает реальный
вид вещественных частотных характеристик. Для большого количества минимально-
фазовых объектов вещественная частотная характеристика имеет следующий вид
(рис. 3.9), где сос - полоса существенных частот.
kP(<D)
V
11 п
V
G)
Рис. 3.9. Типовая вещественная частотная характеристика
Из данного графика следует, что в реальных условиях необходимо учитывать и
отрицательную часть вещественной частотной характеристики. Мы рассмотрим
следующую трапецию Р3(с6) (рис. 3.10), где (3>1 - коэффициент, определяющий
интервал существенных частот сос, сос = (5(оср.
'max
Р = 1 - Р
1 min * * max
tf>2(©)
0)а
^=^
\1
соп
соп
Рис. 3.10. Аппроксимация типовой вещественной характеристики
Проведем сравнение переходных характеристик для 3-х масштабированных
вещественных аппроксимированных частотных характеристик: ^(ш),..., Р3(^) •
На рис. 3.11 представлены графики Л(т) для следующих параметров: X = % = 0,8 ,
Xa=l,Xc=0,9091,p = 2,/>max = l,l.
Глава 3. Частотный метод синтеза корректирующих устройств
219
12
1
08
06
04
02
0
Л(т)
-0 2
1
1
/ I
1 i
7
Tnn*
O%<
2,23ti
ИдлГ!:
/>(w)
,Р2(Й) —
Д(ш)
20%
т = соп/
0
10
12 .
Рис. 3.11. Переходные характеристики для 3-х видов вещественных
частотных характеристик
Расширим полосу существенных частот, сделав Р = 4 , при сохранении остальных
параметров неизменными. Получим следующие переходные процессы (рис. 3.12).
1 2 *(Т)
1
08
06
04
02
-0 2
//
1
\
{..
V
1 ^
— ~Р\
р
— h
(со)
(со)----
(©)
а% < 20%
«2,471
т = соп/
10
12
Рис. 3.12. Переходные характеристики с параметрами рис. 3.11,
но с расширением полосы существенных частот ((3 = 4)
Из сравнения этих графиков видно, что ошибка в переходных характеристиках,
вызванная аппроксимацией трапеций ^(со), Р3(со) трапецией Р2((Ь), как по
перерегулированию, так и по времени переходного процесса незначительна.
Оценим влияние других параметров. На рис. 3.13 представлены переходные
процессы для А. = 0,7, х = 0,7,ха=0,6, хс =0,8636, р = 2 , Ртах =1,1.
220
Методы синтеза САУ по заданным показателям качества. Часть II
1 2
1
08
06
04
02г
А(т)
-0 2
i
/
/
/
/
/
Tnn ~
I
г
Г
o% < 2
2,7ti
!(©)
'2(«) ---
)%
T = CO/
0
10
12
14
Рис. 3.13. Переходные характеристики вещественных частотных характеристик
/i(co),..., /\(d>) для А. = 0,7, х = 0,7, ха=0.6, хс = 0,8636, р = 2, ^=1,1
Из сравнения графиков (рис. 3.11 - рис. 3.13) видно, что при значительных
изменениях отдельных параметров перерегулирования а% остается практически
неизменным, лишь незначительно изменяется время переходного процесса тпп.
Оценим теперь влияние Ртях . Сохраним все параметры предыдущего примера
неизменными, но Ртак возьмем равным 1,2 (т.е. увеличим по сравнению с предыдущим
вариантом). Получим следующие переходные процессы (рис. 3.14).
1 2
1
08
06
04
02
0
-0 2
1
/
/
/
/
/
V
N
—
\j£r J
__-__-_J
— Pl(&)
■■■--p2 (©)"■-
P3(co)
G% < 26%
тпп«3,18тг
T = (D /
'0
10
12
14
Рис. 3.14. Переходные характеристики вещественных частотных характеристик
£,(ю) Р}{&) Для Х = 0,7, Х = 0,7, Ха=0'6' Хс=°^636, р = 2, ^=1,2
Глава 3. Частотный метод синтеза корректирующих устройств
221
Данные графики показывают, что изменение Ртлх существенно влияет как на
перерегулирование, так и на время переходного процесса: при увеличении Ртах растет
а% и тпп. На основании многочисленных исследований были получены
усредненные графики, характеризующие собой зависимость относительного времени
переходного процесса тпп и перерегулирования а% от максимального значения
вещественной частотной характеристики Ртак, причем, т.к. переходные процессы для Р}((Ь)
и Р2{&) отличаются незначительно, то принято шср =соп. Данные зависимости
приведены на рис. 3.15 [116, 130].
Из рассмотренных выше графиков можно сделать следующий вывод: если
реальная масштабированная вещественная частотная характеристика Р((Ь) не превышает
по абсолютной величине графика Р^(&), то переходной процесс реальной системы
будет удовлетворять следующим условиям
/пп</*п, о%<о*%,
где (•)* -значения аи tnn , полученные из графиков (рис. 3.15).
Это приводит нас к следующему заключению: если характеристика Ц0(со))
разомкнутой системы не заходит в прямоугольник, включающий линии уровня
Рс - Ртах и Рс = 1 - Ртах на номограмме для определения Р(ш) замкнутой системы
по ЛАЧХ и ФЧХ разомкнутой системы (рис. 3.6), то замкнутая система будет иметь
показатели качества не хуже f *п, а*%. На рис. 3.16 это показано для Ртах =1,2,
/>min=-0,2.
40
35
30
<*%. V»
о*
Кр'п
25
%
20
15
10
.Г
«С
—
__^^
^Г
I
р V<^--n
1 11 12 13 14
Рис. Э.15. Графики зависимости относительного времени переходного процесса
тпп = соср/пп и перерегулирования а% от максимального значения /^
вещественной частотной характеристики при % < 0,8, к > 0,5 , ха ^ 0,4
Обозначим одну сторону прямоугольника через 2у, а вторую - 2q и определим q
как запас устойчивости по амплитуде (в Дб), а у - запас устойчивости по фазе (в
град.).
222
Методы синтеза САУ по заданным показателям качества. Часть II
£,ДБ
9 (град)
-350 -300 -250 -200
Рис. 3.16. График Z,(9((o)) разомкнутой системы, у которой переходной процесс
удовлетворяет показателям качества (/пп < /*„, а% < а*% )
Из графика (рис. 3.16) видно, что прямоугольник огибает так называемая средне-
частотная, т.е. в окрестности частоты среза соср часть кривой Ц0(со)).
Построением прямоугольников, включающих в себя различные линии уровня
Рс = Ртач, РС2 = 1 - Ртах, были получены следующие графики для определения
необходимых запасов по амплитуде q (Дб) и фазе у (град.) (в зависимости от Ртях),
которые обеспечивают требуемые показатели качества (рис. 3.17) [116, 130].
<7, дБ у, град
60
50
40
30
20
10
'max
—-*ч;
^—- q
1 —-^_
11
1 2
1 3
14
Рис. 3.17. Графики определения минимальных запасов устойчивости
по амплитуде q (дБ) и фазе у (град.)
Глава 3. Частотный метод синтеза корректирующих устройств 223
Из графиков рис. 3.16 можно сделать следующий вывод: для того, чтобы кривая
Ц9(а>)) не заходила в прямоугольник со сторонами 2q и 2у, необходимо и
достаточно, чтобы избыток фазы
ju(co) = 18O -нв(со)
на интервале q > L(co) > -q изменения ЛАЧХ разомкнутой системы был не менее у, т.е.
ц(со) > у, Vco: q > L((o) > -q .
3.5. ОПРЕДЕЛЕНИЕ ЧАСТОТЫ СРЕЗА ЛАЧХ РАЗОМКНУТОЙ
СИСТЕМЫ ПРИ НАЛИЧИИ ОГРАНИЧЕНИЙ
НА МАКСИМАЛЬНОЕ УСКОРЕНИЕ В СИСТЕМЕ [133]
Во многих практических задачах объект управления является инерционным
механическим объектом и подчиняется второму закону Ньютона. Для такого класса
объектов можно решать задачу оптимального по быстродействию перевода системы из
одного состояния в другое при ограничении на максимальное ускорение (в терминах
теории оптимального управления - при ограничении на управление). Пусть объект
управления описывается системой второго порядка:
х = и, |w|<wmax, x(0) = i(0) = 0, *(*,) = *„ >0, *(*!) = <>. (3.45)
Необходимо определить структурную схему оптимальной по быстродействию
системы управления данным объектом.
Решим первую часть задачи с использованием принципа максимума Понтрягина [99].
Для этого представим уравнение (3.45) в форме Коши:
х _и. M*"U. (3-46)
*,((>) = *2(0) = 0, (3.47)
*i('i) = *im *2(О = 0- (3-48)
Требуется найти оптимальное ограниченное управление u°(t), переводящее
систему из состояния (3.47) в (3.48) и минимизирующее функционал
/ = min/,. (3.49)
I/
Данная задача имеет простое графическое решение и определяет следующее
оптимальное управление:
71
и°(0 =
0</<_m!IL
2
71
min
<t*Ttm, (3.50)
max > л
[0, t>Tmm,
где 7"mm = min /, - оптимальное по быстродействию время перехода. Переходной
процесс имеет следующий вид (рис. 3.18).
Данный переходной процесс аналитически можно представить следующим образом
+\^{t-Tmm)2\[t-Tmn], (3.51)
где 1 [/] - функция Хависайда.
224
Методы синтеза САУ по заданным показателям качества. Часть II
x(t)
*о(О
Разгон
"орможение
Рис. 3.18. Оптимальный по быстродействию переходной процесс при w = >vmax
Найдем преобразования Лапласа для (3.51). Имеем:
тт1П_
и>
2wn
V /»ч — max ^rrmaxfc
л о \s) ~ —з
- + W,
И>
s
max 3
(3.52)
-^f|l-2e" 2 +e-7'-"' .
По теории о предельном значении оригинала найдем хм :
хп = х0 (t) = lim sX0(s) = 1 im s Wmax7°"" = wmaxrmin
(3.53)
Последнее выражение получено разложением е 2 и е 1min's в ряд Тейлора до
второго порядка включительно в окрестности 5 = 0. Итак, для того чтобы система
обладала астатизмом первого порядка, при условии, что объект переводится из
состояния х(0) = 0 в состояние х(Тт{п) = хп за минимальное время, необходимо, что-
w T-
бы на ее вход подавалась ступенька с амплитудой тах т1П
4
По определению:
g{t)=^f^\[t)=gM-
X0(s) = 0o(s)G(s) = 0^)^_™l
(3.54)
(3.55)
Сравнивая (3.55) и (3.52), получим оптимальную передаточную функцию (она
является трансцендентной):
. , ч 4 1-2е 2 +e~7minS
(3.56)
причем выполнено условие астатизма
ПтФ
Найдем частотные характеристики для 0o(s) : <I>q(j(u) = Po(®) + jQo(®) • Имеем:
ПтФ0(5) = 1.
"лава 3. Частотный метод синтеза корректирующих устройств
225
ад=
т2
1 mm
Т ■
1 1П1
l-2cos М*-ю +cos(rmin(o)
-со
Go(*) = -
<2sin^o)j-sin(rminco)'
-О)
(3.57)
(3.58)
Если передаточная функция Фо(5) имеет единичную обратную отрицательную
связь, то оптимальная передаточная функция разомкнутой системы определится как
/ т \
4
Т2
1 min
1-2е 2 + <г'»»°(
0o(s) = Лшп
°" 1-ФоМ , 4 '
52-
г2
1 mm
1-2е 2 +в"
(3.59)
Выражение (3.59) позволяет построить ЛАЧХ и ЛФЧХ разомкнутой системы, но
нашей задачей будет найти частоту среза соср опт для данной ЛАЧХ. Легко находим,
что для системы с единичной отрицательной обратной связью справедливы
соотношения (об этом уже говорилось выше, см. §3.4):
' |Ц(;<»,т| = 1ДК„) = о, (3.60)
/i К «0 = 0,5. (3.61)
Подставив (3.61) в (3.57), получим следующее трансцендентное уравнение
-^min^cp опт +cos(^min«cp опт)-2™*
из которого находим
Т ■
ср опт
+ 1 = 0,
(3.62)
(О
ср опт
(3.63)
Используя выражения (3.54) и (3.63), получим окончательную формулу,
связывающую частоту среза соср опт, максимальное ускорение wmax и величину
отрабатываемой ступеньки g0, при которых переходной процесс имеет максимальное
быстродействие и астатизм 1-го порядка
со
ср опт
(3.64)
3.6. МЕТОД ЛОГАРИФМИЧЕСКИХ АМПЛИТУДНО-ЧАСТОТНЫХ
ХАРАКТЕРИСТИК (ЧАСТОТНЫЙ МЕТОД СИНТЕЗА
ПОСЛЕДОВАТЕЛЬНЫХ КОРРЕКТИРУЮЩИХ
УСТРОЙСТВ В.В. СОЛОДОВНИКОВА)
Как уже было показано выше, свойства систем автоматического регулирования
(САР) полностью определяются частотными характеристиками ее разомкнутой цепи.
Если все элементы системы минимально-фазовые, то достаточно рассмотреть только
амплитудно-частотную характеристику (АЧХ) (см. §3.2) или ЛАЧХ. Построить
226 Методы синтеза САУ по заданным показателям качества. Часть II
ЛАЧХ не сложно, поэтому метод синтеза САР, использующий ЛАЧХ, широко
применяется в инженерной практике.
Рассмотрим один из подходов синтеза последовательных корректирующих
устройств (ПКУ), использующий желаемые ЛАЧХ, разработанный В.В. Солодовнико-
вым для следящих систем с астатизмом 1-го порядка [17, 116, 130].
Сущность этого метода заключается в следующем. Сначала строят
асимптотическую ЛАЧХ £н(со) неизменяемой (основной) части системы. Затем составляют
желаемую ЛАЧХ Ьж((й) разомкнутой системы. Разность
ZJco)-LH(co) = LKy(co)
определяет ЛАЧХ последовательного корректирующего устройства (ПКУ).
Построение желаемой ЛАЧХ £ж(со) осуществляют, исходя из графиков и
соотношений, полученных нами ранее (см. §§3.2 - 3.5, и требований, предъявляемых к
синтезируемой системе.
Желаемую ЛАЧХ условно разделяют на три части: низкочастотную, среднечас-
тотную и высокочастотную. Низкочастотная часть определяет статическую точность
системы - точность в установившемся режиме. Среднечастотная часть является
наиболее важной, т.к. определяет устойчивость, запас устойчивости по фазе и амплитуде
и, следовательно, качество переходных процессов, о чем мы подробно говорили
выше. Основные параметры среднечастотной асимптоты - это ее наклон и частота среза
соср. Чем больше наклон среднечастотной асимптоты, тем труднее обеспечить
хорошие динамические свойства системы. Поэтому наиболее целесообразен наклон -
20дБ/дек.
Частота среза соср определяет быстродействие системы. Чем больше соср, тем
выше быстродействие, тем меньше время переходного процесса tm.
Высокочастотная часть желаемой ЛАЧХ незначительно влияет на динамические
свойства системы (см. §3.5, варьирование частоты шс =Рсоср). Вообще говоря,
лучше иметь возможно больший наклон ее асимптот, что уменьшает требуемую
мощность исполнительного органа и влияние высокочастотных помех. Иногда при
расчете высокочастотную ЛАЧХ не принимают во внимание (что будет использовано в
примере, см. ниже).
Построение желаемой асимптотической ЛАЧХ по В.В. Солодовникову [17,
130] (для следящих систем с астатизмом 1-го порядка).
Предположим, что низкочастотная асимптота желаемой ЛАЧХ ^ж(со) совпадает с
ЛАЧХ £н(со) и имеет наклон -20 дБ/дек (т.е. неизменяемая часть имеет астатизм 1-го
порядка) и необходимый статический коэффициент усиления К; в этом случае может
быть реализовано пассивное ПКУ с К^ < 1; в противном случае ПКУ должно
включать усилитель.
Исходными данными при синтезе ПКУ могут быть следующие требования. По
заданной передаточной функции WH(s) неизменяемой части разомкнутой системы
требуется выбрать ПКУ, обеспечивающее получение следующих характеристик
качества замкнутой системы в переходном и установившемся режимах:
1) система должна обладать астатизмом 1-го порядка;
2) коэффициенты ошибок по скорости Сх и ускорению С2 не должны
превышать С*, С*2 ;
3) длительность переходного процесса /пп не должна превышать заданного
значения /1;
Глава 3. Частотный метод синтеза корректирующих устройств
227
4) перерегулирование а% в системе также должно быть ограничено некоторой
величиной <j*%;
5) максимальное ускорение в системе (для инерционных механических объектов)
не должно превышать wmax при начальном рассогласовании g0.
Построение желаемой ЛАЧХ £ж(о), отвечающей 4-м из 5 вышеуказанных
требований по правилам связи между ЛЧХ разомкнутой системы, вещественной частотной
характеристикой замкнутой системы и показателями качеств замкнутой, мы уже
можем осуществить на основании проведенного выше анализа. Единственным не
охваченным пунктом остается пункт 2, т.е. обеспечение заданной точности в
установившемся режиме. Здесь необходимо найти частоту сопряжения со, низкочастотной
асимптоты. Рассмотрим один из вариантов решения этой задачи. Пусть для
определенности низкочастотная и среднечастотные части желаемой ЛАЧХ разомкнутой
астатической системы имеют вид (рис. 3.19).
Цсо), дБ
-20дБ/дек
Низкочастотная
асимптота
-40дБ/дек
Среднечастотная
-20дБ/дек асимптота
со tfg)
Рис. 3.19. ЛАЧХ разомкнутой системы
Если среднечастотная ЛАЧХ достаточно велика, тогда для низких частот можно
записать следующую передаточную функцию разомкнутой системы:
АГ(т$ + 1)
W(s)*
5(75 + 1)
(3.65)
причем Ш] = — , со2 = —. Коэффициенты ошибок для замкнутой системы имеют вид:
0 ' к к к2
1
(3.66)
Если К достаточно велико, то членом —г- можно пренебречь. Тогда из соотно-
К2
шения (3.66) получим:
k>-L,(c{<c;),
С2'<(Г-т)С,\(С2<С*),
(3.67)
или
£l<±
(3.68)
С, СО, С02
При со, <<со2 частоту со, можно найти по следующей приближенной формуле:
с'
(0,=
_"-i
С
(3.69)
228
Методы синтеза САУ по заданным показателям качества. Часть II
Теперь рассмотрим алгоритм построения желаемой ЛАЧХ £ж(со).
1. Выбирают частоту среза соср , обеспечивающую получение требуемых
динамических характеристик. Она должна удовлетворять неравенству
«>ср(>пп)^ср ^ср оптКлах) • (3-70)
Здесь соср(/*п) - значение частоты среза, при которой время переходного
процесса не превышает заданного значения /*п. Значение соср(/*п) определяют из графиков
рис. 3.15: по заданному значению о % определяют Ртах , а затем по Ртдх находят
(о)ср/пп)*, после чего определяют соср(/*п)
(°Упп)*
wCD('nn) = -
■Чрч'пп
(3.71)
где (соср/пп) - значение оср/пп , полученное для найденного Ртах .
Правая часть неравенства (3.70) - это максимально допустимое значение частоты
среза при заданных значениях максимального ускорения wmax регулируемой
координаты и начального рассогласования g0 (напомним, что рассматриваются следящие
системы). соср опт^тах) находится из формулы (3.64).
Если окажется, что
со
(Wmax)<(Ocp('nn)> T0 НуЖНО Выбирать
ср опт\ггтах>
соср < соср onT(wmax)» конечно, заданное время переходного процесса в этом случае не
будет получено, но максимальное ускорение w не превысит wmax .
Выбранное значение соср наносят на график (рис. 3.20).
2. Строят среднечастотную асимптоту. Ее проводят через точку соср с наклоном
-20дБ/дек. Меньший наклон трудно осуществить, а при большем наклоне трудно
обеспечить требуемый запас устойчивости (рис. 3.20).
/-(со), дБ -40дБ/дек
/(-60дБ/дек)
-бОдБ/дек
Рис. 3.20. Построение желаемой ЛАЧХ
3. Среднечастотную асимптоту сопрягают с низкочастотной. По графикам
(рис. 3.17), используя найденное'значение Ртах, определяют необходимые запасы
устойчивости по амплитуде q и фазе у, чтобы обеспечить требуемые динамические
характеристики. Определяют частоты со2: 1ж(со2) = q ; со3: £ж(о)3) = -<7. Через
точку (1ж(со9), со 2) проводят асимптоту с наклоном -40дБ/дек или -бОдБ/дек до Пересе-
Глава 3. Частотный метод синтеза корректирующих устройств 229
чения с низкочастотной асимптотой в точке (Аж((о,),со1). Если в точке (1ж((о,),со,)
с*
имеем —V<co,, то условия пункта 2 по точности в установившемся режиме будут
выполнены.
4. Среднечастотную асимптоту сопрягают с высокочастотной частью ЛАЧХ LH(co)
неизменяемой части системы. Сопряжение осуществляют через точку (£ж(со3) ,со3)
прямыми с наклонами -40дБ/дек, -бОдБ/дек, -80дБ/дек, так, чтобы высокочастотная
часть желаемой ЛАЧХ мало отличалась от высокочастотной асимптоты £„(оо).
5. Проводят проверку правильности выбора среднечастотной асимптоты, частот
сопряжения и асимптот сопряжения £ж(со), что должно обеспечить выполнение
требований по переходному процессу. Это условие определяется требованием, чтобы
кривая /,ж(0ж(со)) не заходила в прямоугольник со сторонами 2у и 2q (см. рис. 3.16),
что будет выполнено, если избыток фазы |и(со) будет больше у в диапазоне Vw:
M°>2) = Я ^ Мю) *-q= £ж(с°з). М(°>) > Y •
Если при выбранном сопряжении избыток фазы |д(со2)<у, ц(о3)<у , то
сопряженную частоту со2 смещают влево, со3 вправо или уменьшают наклоны асимптот
сопряжения. При больших запасах |и(со)изменения проводят в противоположном
направлении.
Замечание. При сопряжении следует стремиться к тому, чтобы £ж(со) возможно
меньше отличалась от 1н(со). Чем меньше различие между формой этих ЛАЧХ, тем
проще необходимое корректирующее устройство.
После построения £ж(со) находят ЛАЧХ последовательного корректирующего
устройства
^ку(со) = 1ж(со)-1н(ш).
Если ПКУ получилось пассивным, то для многих характеристик £ку(о)
существуют готовые схемы (R, С - четырехполюсники), которые можно использовать для
практических реализаций синтезируемого ПКУ (см. [116, 130]).
Рассмотрим пример.
Пример 3.1. Передаточная функция неизменяемой части позиционной системы автоматического
регулирования с механическим инерционным объектом имеет вид
*.(,)« ™
*(0,15 + 1)(0,0(Ш + 1)
Требуется выбрать ПКУ, обеспечивающее получение следующих показателей качества замкнутой
системы
1) система должна обладать астатизмом 1 -го порядка (Со = 0 ),
2) коэффициенты ошибок по скорости и ускорению не должны превышать С,* = 0,004 с, С*2 = 0,02 с2,
3) длительность переходного процесса /пп < /*п = 0,4 с,
4) перерегулирование а%<<т*% = 25%,
5) максимальное ускорение регулируемой величины должно составлять 250 рад/с2 при начальном
рассогласовании go = 0,15 рад
Решение
Рассмотрим исходную систему Передаточная функция замкнутой системы при отсутствии ПКУ
(IV^ (s) = 1) имеет вид
ом-т^т-
300
I + ^hOO 0,0003s 3+0,103s 2 + 5 + 300
230
Методы синтеза САУ по заданным показателям качества. Часть II
Полюса замкнутой системы s] = -342,13 ; s2 3 = -0,6 ±./54,06 Из чего можно заключить, что
исходная система имеет высокую колебательность. На рис 3 21 - 3 23 показаны ее временные и частотные
характеристики. Заметим, что вещественная частотная характеристика /'„(со) (рис 3 22) имеет скачок на
частоте со0= 54,06 с~1 Перерегулирование составляет а% = 95,2%, время переходного процесса
/пп = 4,89 с , что значительно превышает требуемые показатели Поэтому требуется синтезировать ПКУ
Строим асимптотическую ЛАЧХ неизменяемой части LH(co) (рис 3 24)
~0 1 2 3 4 5 6
Рис. 3.21. Переходной процесс для нескорректированной системы: /пп = 4,89 с, а% = 95,2%
20
15
10
5
0
-5
-10
-15
-20
-25
-an
' 0 20 40 60 80 100
Рис. 3.22. Вещественная частотная характеристика Рн(со) нескорректированной системы
Построим желаемую асимптотическую ЛАЧХ Прежде всего найдем частоту среза соср Из графиков
(рис. 3.15) имеем: для а*% = 25% получим Ртах =1,18, что соответственно дает (соср/пп)* =10. Откуда
для /*п = 0,4 с находим
К
1
/
/
- - - -
<°cp('nn) = -
-Я-£-25с-.
^пп 0,4
Глава 3. Частотный метод синтеза корректирующих устройств
231
Получена левая граница возможных значений соср Правая граница определяется из выражения (3 63)
cocpon>max) = J^ = J| = 40,82<r'
U (ДБ)
100
50 --■}-
-50
;;;;;;;
iSiki
!!I!
::::
!!
;
!!!!
„и
'■!!!!
:::::
Ч
::::::
ч
!!!!!
::::::
::::iNv
::::::
\
;;;;;;
s;::::
'(lg)
«(Ig)
10J
Рис. 3.23. а) ЛАЧХ нескорректированной системы; б) ЛФЧХ нескорректированной системы
J iL, дБ
А, (а)
» (lg)
80
Рис. 3.24. Определение ЛАЧХ последовательного корректирующего устройства
232
Методы синтеза САУ по заданным показателям качества. Часть II
Выбираем соср = 30 с ' и наносим на график (рис 3 24) среднемастотную асимптоту с наклоном
- 20 дБ/дек
По графику (рис 3.17) для Ртах = 1,18 получаем необходимые запасы устойчивости q = 17 дБ, у = 46
Определяем по q и -ц точки сопряжения о)2=5с"' и со3 = 200с"1 Асимптотой сопряжения с наклоном
- 40дБ/дек сопрягаем среднечастотную асимптоту с низкочастотной Получаем частоту сопряжения
со, = 0,625 % 0,63 с"1 Заметим, что данная частота позволяет удовлетворить требованиям по коэффициентам
ошибок С* и С2 , т к минимальная требуемая частота в этом случае равна
1 С2 0,02
а частота сопряжения со'2 = 1,8 с"1
Для того чтобы упростить ПКУ, выбираем правую границу среднечастотной асимптоты равной
со'з =80 с"1 (а не 200с"1), что, конечно, приводит к пересечению кривой £ж(Ож(со)) прямоугольника со
сторонами 2у и 2q, но в силу малости коэффициентов передачи системы для о> со'3 (-10 дБ и менее) это
не окажет заметного влияния на переходной процесс Итак, считаем, что £ж(со) = /.„(со) для
Разность
/,к>(со) = Аж(со)-£н(со)
дает следующую передаточную функцию ПКУ
W (;)- I5 АЮ
• ( 1 ,Yi 1
5 + 1 5+1
1,0,63 Д80
Передаточная функция разомкнутой системы с ПКУ имеет следующий вид
W«W = -
300|-5 + 1
^5
.(<UX* + I)(^ + l)(JL, + l
Соответственно замкнутой системы
605 + 300
0,000154+0,024б53 + 1,602852 + 615 + 300Л
полюса которой 5, =-173,22, 52=-5,7, 534 = -33,54 ±у43,75
Коэффициенты ошибок С, =0,0033 < С,* =0,004, С2 =0,0094 <С2 =0,02
Временные и частотные характеристики замкнутой системы с ПКУ приведены на рис 3 25 - 3 28
1 Ч
12
1
08
06
04
02
0
п о
• -/-
I
I
I
I
I
02
04
06
08
Рис. 3.25. Переходная характеристика скорректированной системы: /пп = 0,205 с, сг% = 20,5%
Глава 3. Частотный метод синтеза корректирующих устройств
233
12W
1
08
06
04
02
0
-0 2
-0 4
'0б0 20 40 60 80 100 120
Рис. 3.26. Вещественная частотная характеристика Яж(со) скорректированной системы
50-
\
\
\
\
\
\
\
----
_ _ ._
-50--Т-
-100
::TSL
7
!!m
1 ми
;;:;:
;:;;::
i i inn
4
s
1 III
....
to(lfi)
10"
101 10° 101
a
10z
10J
-50
-100
-150
-200
-250
6Ж (фад)
-300
iiiiii
. I! !<!
i ... .и
41!!!!!
* 111■■
<^
i mi
\,„
' Л!!
\
i.V
N
::::::
!!!!!!
•! МП
' I''!!
!! iH?
'(lg)
102 101 10° wM01 ^"'ю2
б
103
Рис. 3.27. а) ЛАЧХ скорректированной системы, б) ЛФЧХ скорректированной системы
Из рис 3 27, б имеем следующие избытки фаз' ц(со2) = 50°, ц(соср) = 50 , ц(оУ3) = 15 Недостаток
избытка фазы для (о = со'3 приводит к пересечению кривой Аж(Эж(со)) прямоугольника (см рис 3 28) Од-
234
Методы синтеза САУ по заданным показателям качества. Часть II
нако при этом /пп = 0,205 с < /пп = 0,4 с, <т% = 20,5% < а % = 25% , т е. все требования к системе
полностью выполнены
100^
80
60
40
20
-ц
-20
-40
-60
"?§00 -250 -200 -150 -100 -50
t
У
У
/
<
I ^^
г\~ "
!
г- 2у ,
—i
•
!
>
)
/ "
ивж(о))
0ж(оз), фад
Рис. 3.28. График зависимости 1ж(8ж(со)) для скорректированной системы. Прямоугольник
отображает область, куда не должен входить данный график при идеальной коррекции
Перейдем к практической реализации данного ПКУ Из [116] находим, что пассивное интегро-
дифференцирующее звено вида (рис 3.29) имеет следующую асимптотическую ЛАЧХ (рис 3 30), что
совпадает с видом L^ (со) и имеет передаточную функцию
(7ft + l)(7fr + l)
W^s) = -
т;т;*2+\тЛ\+^\+ц\з+\
где T!=R,Ct, Ц = ЯгС
Рис. 3.29. Электрическая схема ПКУ
Для выбора параметров ЯС-цепочки ПКУ необходимо использовать следующее равенство
(7ft + l)(7>+l)
7]T2V+ Г,'
i^h
=«'„(•)■
Отсюда получаем следующие уравнения*
Г=/?.С, =- сек, Г2' = /?2С2 = — с,
(3 72)
(3 73)
Глава 3 Частотный метод синтеза корректирующих устройств
235
10-
-10-
\ RJ 2 1 \ Rj 2 2 0,625 80
L, дБ
(3 74)
т;
т;
-20дБ/дек
20дБ/дек
Рис. З.Э0. Асимптотическая ЛАЧХ интегро-дифференцирующего звена
Уравнения (3 72) - (3 74) имеют 4 неизвестные, поэтому один параметр выбираем произвольно Пусть
емкость С, = 10 nF, тогда сопротивление Я, =(l/5)/(l0 10"6) = 20kQ
Из уравнений
2 2 10
я,
получаем /?2 = 131,25 kQ , С2 =0,7619 nF« 0,76 ^F
0,625 80
236 Методы синтеза САУ по заданным показателям качества. Часть И
ГЛАВА 4. МЕТОДЫ СИНТЕЗА РЕГУЛЯТОРОВ
В КЛАССЕ МНОГОМЕРНЫХ ЛИНЕЙНЫХ
СИСТЕМ (ОСНОВНЫЕ ПОНЯТИЯ)
В предыдущих главах было изложено содержание методов синтеза для случая,
когда объект имеет один вход и один выход (одномерные объекты).
В этом случае ставится задача синтеза регуляторов в классе одномерных систем.
Задача принципиально усложняется, если объект управления имеет т входов и т
выходов и, таким образом, имеет т каналов.
Например, в системе управления турбореактивным двигателем можно указать
следующие каналы [92]: управления скоростью вращения турбины; управления
количеством подаваемого топлива; управления температурой газов перед турбиной и
др. При применении методов синтеза регуляторов в классе одномерных систем
должно быть выполнено условие: каждый канал должен быть «развязан» от
остальных каналов, независим, автономен - и только в этом случае можно применить
описанные выше методы.
Но через объект - турбину - эти каналы влияют друг на друга. Такая
взаимозависимость, неавтономность каналов, порождают принципиальные трудности при
синтезе систем управления многомерными объектами.
Центральной проблемой при синтезе регуляторов в классе многомерных систем
является «развязка» каналов. Если эта проблема в каждом конкретном случае
получила решение, то на следующем этапе применяются методы синтеза регуляторов в
классе одномерных систем.
В этой главе кратко рассмотрим вопросы математического описания
многомерных объектов, постановку задачи синтеза регуляторов и подходы к ее решению.
4.1. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ МНОГОМЕРНЫХ СИСТЕМ
АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Многомерными называются системы, у которых вход и выход - вектор-функции.
В системе автоматического управления турбореактивным двигателем
управляемыми переменными являются: скорость вращения турбины, количество подаваемого
топлива, температура газов после турбины и др.
Для управления каждой из переменных конструируется свой канал. Эту систему
можно представить структурной схемой, показанной на рис. 4.1. На схеме Y(/) -
векторный входной сигнал. В данном случае
У(/) = (л(/),л(0,л(0,...),
где, например, у} (/) - заданное (нужное) значение скорости вращения турбины и т.п.;
XB(/) = (xjB(/), **2(0> *з(0> *4(0>—) - векторный выходной сигнал,
где **(/) - реальное значение скорости вращения турбины и т.д.
Для упрощения рассуждений рассмотрим всего два канала; тогда более
развернуто схему можно представить в виде, изображенном на рис. 4.2. Здесь y}(t) и y2(t) -
управляющие сигналы; x*(t) и *?(0 ~ реальные значения регулируемых величин. В
хорошо спроектированной системе каналы y\(t)->x*(t) и ^(О-^^гСО - независи-
Глава 4. Методы синтеза регуляторов в классе многомерных систем 2У7_
мы, т.е. выход *■(*) управляется только сигналом >;.(/) и х?(/)- сигналом y2(t)
(сигнал yx(t) не влияет на x\(t) и y2{t) не воздействует на x*(t)).
+~ ■Г~~Ь>[
Y(/
Регулятор
Объект
ш
Рис. 4.1. Структурная схема системы управления турбореактивным двигателем
ъ *
рж
КУ2
OKi
xfft)
Рис. 4.2. Структурная схема двумерной системы
В реальных же системах наряду с основными каналами ОК! и ОК2 часто имеют
место перекрестные связи nCj (сигнал yx(t) воздействует на выход x\(t)) и ПС2
(сигнал ^2 (0 воздействует на выход Jcf(O).
При исследовании подобного рода систем, а также при синтезе регуляторов
(корректирующих устройств KYj и КУ2) необходимо учитывать перекрестные связи ПС,
иПС2.
Объект называется автономным, если за счет налагаемых дополнительных
связей исключается взаимное влияние каналов (ПС] и ПС2 отсутствуют).
Рассмотрим методы математического описания многомерных систем с помощью
дифференциальных уравнений. Эти уравнения можно записать следующим образом:
L[\X*+... + L[pxBp=L[lyl+... + L[mym;
£21*,в+... + Ь2рхър=Ь21у1+... + 12тут;
(4.1)
Lp\x* +... + Lppxp = lpXyx +... + 1ртУт,
где LirLi} -линейные дифференциальные операторы:
in Лп~^
u,dr
jr-\
at at
Каждый оператор воздействует на функцию xk следующим образом:
LiJxl=al?-xl+alx^xl+... + alxl
at at
Положим, что коэффициенты линейных дифференциальных операторов не
зависят от времени, т.е. имеет место стационарная линейная многомерная система.
238
Методы синтеза САУ по заданным показателям качества. Часть II
Преобразуя по Лапласу обе части (4.1), находим
Lll(s)Xf(s) + ... + Llp{s)Xtp(s)=lll(s)Y,(s) + ... + llm(s)Yll,(sy,
L2X(s)Xf(s) + ... + L2p(s)XBp(s) = L2l(s)Yl(s) + ... + L2m(s)Ym(s);
Lpl (s)X? (5) +... + Lpp(s)X;(s) = lpX (s)Y, (5) +... + lpm (s)Ym (s).
Или, что то же самое,
Ink) hi(s)
[Lpl(s) Lp2(s)
1ррЩх'р(з)
X?(s)
Xfc)
L(s)
/Z11(5) Li2(s)
4,(5) ^(s)
X(A)
[Lpi(s) lpl{s) -. Lpm(s))
Y2(s)
Ws).
С учетом введенных обозначений (4.2) запишется в виде
L(s)X.(s) = L(s)Y(*).
Из (4.3) сразу же следует
X.{s) = u4s)L{s)Y(S),
где
L-'(,) =
Ч>)
(au(s) ... aip(s)^T
a2](s) ••• a2pis)
api(s) ••• apPis
pp\ ) J
(4.2)
(4.3)
atJ{s) - алгебраическое дополнение Ay (s) матрицы L(^); №(•?)
-присоединенная матрица.
Или, что то же самое,
/ ..о / Ч\
x!(s)
Wn(s) Wu(s) ... Wlm(Sy
W2X(s) W22{s) ... W2m(s)
KX'p(s)j WM Wpi(s) - Wpm{s)J
Y2(s)
x.(,) w(0 "~^Г
С учетом введенных обозначений (4.4) принимает вид
X.(S) = W(*)Y(5),
где W(i) -матричнаяПФ (передаточная матрица).
Переходя в (4.4) во временную область, получим
(4.4)
(4.5)
Глава 4. Методы синтеза регуляторов в классе многомерных систем
239
*5(0
-J
f*n(/-x) ... ^(/-т)^
ч*„(/-т) ... *„,,(/-т),
К(|-т)
Гл(т)"
Л ft)
v
Y(t)
dr.
(4.6)
Из последней формулы следует
Х.(г) = }к(/-т)¥(т)Л,
(4.7)
где К(т) - матричная ИПФ многомерной системы.
Так же, как и для одномерных систем, можно ввести понятие частотных
характеристик. /
Если САУ нестационарна, зависимость (4.6) принимает вид
*,в(0
x\(t)
K*№.
i
k2X{t,x) ... Л2и(/,т)
,*„(/,т) ... ^(/.т^
Л(т)
J* (т),
Л.
х.(')
Или, что то же самое,
К(г,т
Y(t)
Хв(/) = |к(г,т)¥(т)Л.
(4.8)
(4.9)
Пример 4.1. Рассмотрим систему, описываемую уравнениями вида
x?+xf+x*2=y2.
Перейдем к изображениям
{s2+s)x;(s) + Xi[s) = Yl{s).
{s + \)X?(s) + sX'2{s) = Y1(s)
Или в матричной форме
((s>+s) \)(х;(*)\ (\ оуу.ш
{(s + l) s)(xi(s)){0 Ч{Уг('))
Найдем L'1 (s); имеем4
|ь(5)| = (52+ф-(5 + 1) = 53+52-5-1 = (^ + 1)(52-1);
au(s) = s'y fl,2(j) = -(5 + l); fl2I(j) = -l; a22(5) = 52 + 5.
Отсюда находим
*н- ' ' ' -'
Выражение для изображения выхода принимает вид
' s 1
Л, [S
X'2(s)
(s + \)(s2-\) (i + l)(52-l)
s + l
{ (s + l)(s2-l) (s + l)U2-l))
УЛ>).
240
Методы синтеза САУ по заданным показателям качества. Часть II
Из последней формулы находим
u+i)(*2-i)
*;(*)=--гт»н,)-
*i(')-
1
^-i
(S + I)(i2-1)
*i(').
(4 10)
(^ + 1)(52-1)
(4 11)
X'2(s) = W,l(s)Yl(s) + W22(s)Y2(S)
Зависимости (4 10) и (4 11) учитывают не только прямые (основные) каналы, но и перекрестные связи
(рис 4 3)
Wn(s)
WM(5)
xffi)
Рис. 4.3. К описанию многомерных систем с помощью передаточных функций
4.2. ПОСТАНОВКА ЗАДАЧИ СИНТЕЗА РЕГУЛЯТОРОВ
В КЛАССЕ МНОГОМЕРНЫХ СТАЦИОНАРНЫХ СИСТЕМ
Многомерная система автоматического управления, реализующая принцип
обратной связи, показана на рис. 4.4. Здесь X е R" - состояние объекта; U(/) -
управляющий вход объекта; Y(t) - задание регулятору (уставка); e(/) = (s1(/),...,6ot(/)) -
рассогласование (ошибка управления), компоненты которого определяются
формулой е*(0 = л(0-*2(0, * = U™-
Объект управления объединяет всю неизменяемую часть системы:
исполнительный элемент, объект, измерительную систему и т.д.
Положим, что объект описывается уравнениями состояния
X(0 = AX(0 + BU(0, (4.12)
где А = const; В = const, и выхода
ХВ(/) = СХ(О. (4.13)
Пользуясь приведенными выше методами, связь между входом и выходом можно
представить в виде (в матричной форме)
XB(0 = W(s)Y(s),
или в развернутом виде
'X?{s)\ fWu(s) Wl2(s) ... WXm{s)
Xl(s) _ W2X{s) W22{s) ... W2m{s)
.M*) W»4(s) - K,n,{s),
(hi')'
Уг(')
U,(4
(4.14)
Проведем некоторые рассуждения, касающиеся качества управления в классе
стационарных систем.
В одномерных системах критерий качества характеризовался параметрами
переходного процесса, такими как время регулирования, перерегулирование, точность
работы системы в установившемся режиме и др. [130].
Глава 4. Методы синтеза регуляторов в классе многомерных систем
241
*/ft>
Рис. 4.4. Структурная схема многомерной системы
В многомерных объектах не удается найти единый критерий, который бы
наиболее полно и всесторонне характеризовал систему.
В одномерных системах для оценки качества работы СЛУ достаточно провести
один эксперимент.
В многомерных САУ, если представление о качестве будет строиться на
концепции проведения одного эксперимента (на все каналы одновременно подаются
ступенчатые воздействия и анализируются соответствующие реакции), то разработка
методов синтеза, использующая такую концепцию, к удовлетворительному
результату не приводит.
В большинстве своем многомерные системы имеют т выходов и т входов.
Каждая входная уставка (воздействие) предназначена для отработки «своим» каналом.
Что касается идеальной системы, в которой все каналы развязаны, в ней
осуществляется управление по каждому каналу автономно, т.е. каждому индивидуальному
скалярному выходу соответствует свой индивидуальный вход у, (t) (своя уставка).
Таким образом, размерность входа Y(/) всегда совпадает с размерностью
выходного процесса Хв (/).
Отсюда легко сделать вывод: любую замкнутую систему управления
многомерным объектом можно рассматривать как квадратную систему (рис. 4.5).
У г»)
Ут®
1
Z
/77
^ -О —Jr»e- mm ^Ч^
«/
2
/77
xfu)
xf(*J
xia)
Рис. 4.5. Квадратная система
В квадратной системе имеют место т2 одномерных каналов (с учетом
взаимозависимости каналов), соответствующих всевозможным парам (у,**), /,у = \,т .
Важным является следующее положение: т параллельно работающих каналов
.у,(О-»*Г(О> .У2(О->*2 (')>...> Л, (0->*,"('), т.е. «вход уДО -выход х,в(/)»
являются собственно каналами управления выходом, а остальные перекрестные каналы
>>,(/) -» xbj(t\ (/ ф j) следует рассматривать как возмущения.
При таком рассмотрении вопроса динамическая точностью качество многомерной
системы тем выше, чем точнее и качественнее в системе по каждой выходной
переменной xf(t\ i = \,m отрабатывается свой индивидуальный вход yt(t) и чем меньше
при этом на нее влияют другие входы (чем меньше влияют перекрестные связи).
Исходя из предыдущих рассуждений, качество управления может характеризовать
критерий, предложенный В.В. Солодовниковым и Н.Б. Филимоновым. Этот критерий
наиболее адекватно отражает динамическое поведение многомерных систем.
17 3ак 366
242
Методы синтеза САУ по заданным показателям качества. Часть II
Динамическое качество многомерной СЛ У тем выше, чем точнее она
отрабатывает входной сигнал у jit) для каждой выходной переменной x*(t), i = \,m и чем
меньше при этом влияние на другие выходные переменные xf(t), i ^ j объекта.
Качество управления определяется матрицей переходных характеристик Н = (hlJ(t))"1 ^
системы посредством задания областей допустимых значений выходных переменных.
Переходный процесс /?„(/), i-\,m по каждому каналу, являющийся реакцией на
1(0, ограничивается такой же областью, как это принято в теории одномерных
систем, причем параметры этих областей для каждого канала - свои (рис. 4.6).
Переходный процесс hl}(t) (влияние yf(t) на выход x*(t)) ограничивается
областью, симметричной относительно оси времени, причем высота ее определяется
допустимым взаимным влиянием каналов ст/7тах(/^у); ширина одна и та же для всех
выходов и определяется наиболее инерционным перекрестным каналом (рис. 4.6).
<5/ -
had)
1 ■
~бц/пах
///////////,
& 1/ "У
ЧШ1Ж1
шли
7///////Л
7-1
l.roax
W77W7/I
п
—»- О
-Gijitiax
//////////////
2й
//////А'///
///////////////
Рис. 4.6. К определению критерия качества многомерных систем
Сказанное выше математически можно выразить следующим образом [76]:
-а^тах </2,(О5П + ^тах, 0<t<Timax; (4.15)
|А,(0-1|<А,7>7;тах; (4.16)
/*,Д0|<а/7тах, i*j, 0<t<T; (4.17)
Ии(0\<А, i*j9 t>T\
fO, /Vy,
^H = 8|/ =
1, / = У,
(4.18)
(4.19)
где A - малая постоянная величина; T = max Т1тяк; ajmax ,a//max , 7;max, a//max (/ * j)
\<t<m
- заданные максимально допустимые значения прямых показателей качества
управления: максимально допустимое положительное перерегулирование, отрицательное
перерегулирование и время регулирования /-го выхода, максимально допустимая
величина влияния / -го входа на j -й выход системы (влияние перекрестных связей).
Н(0 - матричная переходная характеристика, представляющая собой квадратную
функциональную матрицу с элементами htj{t).
Такой подход к формированию критерия качества учитывает, с одной стороны,
качество отработки системой воздействия собственно по каждому каналу, с
другой стороны - допустимое взаимное влияние всех перекрестных связей.
Глава 4. Методы синтеза регуляторов в классе многомерных систем
243
Кроме ограничений на процессы hH(t) и htJ{t), часто необходимо накладывать
ограничения на их производные соответствующего порядка, например, типа
модульных ограничений:
tfto
Если объект описывается уравнением (4.12), то ограничения можно записать в
виде
Xs(t)eXm We [0,7],
\J(t)eUm V/e[0,r],
где Хт и Um - допустимые области.
Могут быть наложены ограничения и на вектор-функцию Х(7). В
установившемся режиме каждый канал должен обеспечивать заданную точность воспроизведения
входных сигналов, что достигается заданием допустимых значений коэффициентов
ошибок по каждому каналу.
Сделаем постановку задачи, пользуясь описанием объекта управления и
регулятора в пространстве состояний:
X(0 = AoX(0 + BoU(0, Хв(/) = СоХ(0 -уравнение объекта,
Хку (0 = А^Х^ (0 + В^еСО, U(/) = С^Х^ (0 - уравнения регулятора,
c(0 = Y(/)-XB(0.
Структурная схема многомерной системы автоматического управления
представлена на рис. 4.7.
Общая постановка задачи: необходимо найти матрицы А^, В^С^, такие,
которые обеспечили бы заданное в известном смысле качество управления (например, с
учетом ограничений на управление U(0 и переменные состояния).
х.(0
'х.(0
Регулятор
Объект управления J
Рис. 4.7. Структурная схема многомерной системы автоматического управления
Можно сформулировать конкретную постановку задачи синтеза системы
управления многомерным объектом: требуется синтезировать устойчивую систему,
удовлетворяющую требованиям (4.15) - (4.19) и требованиям точности в
установившемся режиме [76].
Наиболее простая структура реализуется безынерционными звеньями или
звеньями, описываемыми передаточными функциями, степень полинома числителя
которых меньше степени полинома знаменателя.
Задача синтеза в сформулированной постановке разрешима при условии
функциональной управляемости объекта по выходу, т.е. должны быть выполнены
требования:
1) размерность выхода объекта не должна превышать размерности его входа;
2) передаточная матрица объекта должна иметь полный ранг;
17*
244
Методы синтеза САУ по заданным показателям качества. Часть II
3) объект не должен иметь правых передаточных нулей.
Требования 1 и 2 тесно связаны с возможностью выполнения условий
автономности контуров объекта.
Регулятор
Ы*)
x(t)
Рис. 4.8. Структурная схема многомерной системы с регулятором,
ycipoiicTBOM развязки каналов и стабилизирующим устройством
В структурную схему многомерной системы (рис. 4.8) входят следующие
элементы: стабилизирующее устройство, необходимое для решения задачи стабилизации
исходного объекта управления, компенсатор, или устройство развязки каналов,
предназначенный для решения задачи динамической развязки контуров управления
каждой выходной переменной объекта, и, наконец, регулятор, цель которого -
решение задачи коррекции показателей динамического качества отдельных контуров
регулирования.
4.3. ДИНАМИЧЕСКАЯ И СТАТИЧЕСКАЯ РАЗВЯЗКА КАНАЛОВ
(ОБЩИЕ ПОЛОЖЕНИЯ)
Для асимптотической устойчивости линейной системы дифференциальных
уравнений с постоянными коэффициентами необходимо и достаточно, чтобы
вещественные части корней характеристического уравнения были отрицательны, или
собственные значения матрицы А должны располагаться в левой полуплоскости
комплексной плоскости.
Справедливость этого положения вытекает из равенства, определяющего свободные
колебания систем. Если же система неустойчива, то ее необходимо стабилизировать.
Пусть объект описывается уравнениями
X(/) = AX(/) + BU(/); (4.20)
ХВ(О=СХ(/). (4.21)
Воспользуемся стационарной обратной связью вида [93]
U(f) = -KX, (4.22)
где К - матрица размером тхп .
С учетом (4.22) уравнение объекта запишется так
Х(/) = АХ(/) - ВКХ(/) = [ А - ВК] Х(/). (4.23)
Одномерный стационарный объект можно застабилизироватъ с помощью
введения отрицательной обратной связи по производным до (п -1) порядка.
Аналогично, для многомерного стационарного объекта введение обратной связи
по состоянию и соответствующий выбор матрицы К может обеспечить любое
заранее заданное расположение собственных значений матрицы [А - ВК] на
комплексной плоскости.
Глава 4. Методы синтеза регуляторов в классе многомерных систем
245
Практический интерес представляют такие характеристические многочлены,
корни которых расположены слева от мнимой оси. В этом случае замкнутая система
является асимптотически устойчивой.
Таким образом, сказанное кратко формулируется так: если задан вещественный
характеристический многочлен
А(Х) = А./1+Ся.1Х/|-1+... + С0, (4.24)
то с помощью выбора линейной обратной связи и(/) = -КХ(/), где К -
действительная постоянная матрица размером тхп , можно обеспечить равенство
характеристического многочлена А - ВК с многочленом (4.24).
Необходимым и достаточным условием разрешимости проблемы размещения
собственных значений с помощью линейной обратной связи является выполнение условия
rankJB AB А2В...А/Мв} = л. (4.25)
Поскольку с помощью выбора матрицы К можно обеспечивать любое наперед
заданное размещение собственных значений, то отсюда легко сделать вывод:
указанной процедурой можно обеспечить не только устойчивость, но и качество свободных
колебаний системы.
Однако здесь необходимо учесть появление ряда нежелательных факторов, таких
как возможность появления большого уровня управляющих воздействий; могут
также иметь место большие «забросы» значений некоторых переменных при большом
смещении собственных значений в левую полуплоскость [9].
Уравнение стабилизированного объекта можно принять следующим
Х(/) = [А - ВК]Х(/) + U(/). (4.26)
Структурная схема объекта показана на рис. 4.9.
U(±) X
XtM
Рис. 4.9. Структурная схема стабилизированного объекта
Можно вводить и другие обратные связи. Однако во всех случаях необходимо
помнить о том, что для замыкания обратной связи необходимо знать вектор
состояния Х(/).
Последний же оценивается с помощью наблюдающих устройств. В связи с этим
реализация рассматриваемого принципа тесно связана с задачей получения
приемлемой оценки вектора состояния.
Существует направление в теории автоматического управления, изучающее
вопросы построения наблюдающих устройств. В этом направлении рассматриваются
критерии идентифицируемости, асимптотические наблюдающие устройства,
идентификаторы Люенбергера и др. Приведем лишь некоторые сведения об
асимптотических идентификаторах состояния.
Асимптотическое наблюдающее устройство определяется векторно-матричным
дифференциальным уравнением
X(/) = AX(/) + BU(0 + L(XB(/)-CXB(0), Хв(0) = Х^. (4.27)
Входными воздействиями здесь являются измеряемый выход ХВ(/)=СХ(/) и
вход и(/).
246
Методы синтеза САУ по заданным показателям качества. Часть II
Если матрицы Ат и Ст невырождены, то матрица L может быть выбрана так,
что будет выполняться условие
£(/)=|х(О-х(Оро
при любой ограниченной начальной ошибке.
В векторно-матричном уравнении (4.27) появление последнего слагаемого
L(XB(/) -СХв(ж связано с обеспечением работоспособности идентификатора при
неизвестном начальном состоянии Х° .
Идентификатор может быть реализуем на интеграторах и усилительных элементах.
Полезен и следующий факт [93]: если оценка вектора состояния Х(/) находится
как решение уравнения (4.27) и объект
X(/) = AX(/) + BU(/); Х(/) = СХ(/); Х(о) = Х°
замкнут обратной связью
U(/) = -KX(/),
то при выполнении условий
rankJB АВ...А"-1в} = л и rankjc1 ATCT ...(а7)""1 Ст|=л
возможен выбор матриц К и L таких, что замкнутая система будет устойчивой.
Структурная схема стабилизированного объекта имеет вид, представленный на
рис. 4.10.
</(/)
О
W(s)
А,В,С
xih>
Наблюдающее
устройство
Рис. 4.10. Структурная схема стабилизированного объекта
Пример 4.2. Стабилизация объекта управления [76] Пусть многомерный объект описывается
уравнением вида
X=AX+BU,
где
'-0,0297 0 1,0 0,0438 0 ^
-1,2155 -0,7923 0,1306 0 0
А= 0,4304 0,021 -0,0152 0 0 , В =
0 1,0 0 0 0
х 0 0 1,0 0 0,
Характеристическое уравнение матрицы А имеет вид
Л (X) = X5 + С4Х4 + С3Х3 +С2Х2 + СХХ + Со
Корни характеристического уравнения
А., =-0,95, Х2 =0,59, ^з ="0,45, Х4 =-0,06, Х5=0
Из анализа корней очевидно, что объект неустойчив и его необходимо стабилизировать
Построим линейную обратную связь по состоянию
и = -кх,
гакую, чтобы имел место следующий характеристический многочлен (некоторый гурвицев полином
стандартного вида)
0
-0,0402
0,3807
0
0
0
1,5671
-0,0671
0
0
Глава 4. Методы синтеза регуляторов в классе многомерных систем
247
Д(Я.) = X5 +2,8Х4+5,0^3 + 5,5Х2 +3,4^ + 1 (4 28)
Корни последнего полинома представляют желаемый спектр Л* замкнутой системы
А* ={-0,895, -0,376 ± j 1,292, -0,576±y0,534}
Матрица К выбирается из следующего условия* она должна иметь минимальную первую норму
||К|,= т,гф,,| (4 29)
Пользуясь алгоритмом, изложенным в [76], получим следующую матрицу
f5,864 -0,536 2,23 0,098 0,0 ^|
К~[б,817 0,806 2,79 1,019 -5,78J (4 }
С помощью введения обратной связи по состоянию корни характеристического уравнения
перемещаются следующим образом
X, = -0,95-► Х\ = -0,895, Х2 = 0,59-»Х\ = -0,376 + ./1,209,
Хъ = -0,45 -> Х\ = -0,376-;1,209, Х4 = -0,006 -> Я.4 = -0,576+ у0,534,
Х5 = 0,0 -> А.5 = -0.576 - J°>534
Матрица стабилизированной системы будет иметь вид
А = А-ВК (431)
Матрицы Л, В, К - известны В [76] показано, что матрица
(-48,35 7,089 4,1 4,67 54,294^
~[ 3,221 -0,828 -0,014 0,328 5,273 J
таюке решает задачу стабилизации, но последняя матрица имеет большее значение нормы (4 29), чем
матрица (4 30)
Далее положим, что объект управления является асимптотически устойчивым.
Изложим некоторые положения, касающиеся развязки каналов.
Связь между входом и выходом в объекте задана формулой
У" с
Wu{s) Wu{s)
W2i{s) W21{s)
к»
{>)
{'1
г1
щ
(s]
{'1
(4.32)
^nl(^) Wn2(s)
Рассмотрим 1-й выход объекта
X?{s)=Wu{s)Ul{S)+...Wln(s)Un(s). (4.33)
В многомерных объектах 1-й выход определяется 1-м входом (основным входом),
и, кроме этого, на 1-й выход оказывают возмущающее воздействие 2-й, ..., и,
наконец, /7-Й ВХОД.
Независимость выходных переменных от других входов, кроме соответствующих
входных воздействий, т.е. и, (/) -> xt (t), / = 1,и означает, что передаточные функции
перекрестных каналов должны обращаться в нуль.
Таким образом, необходимым и достаточным условием автономности
(независимости каналов) является диагоналъность передаточной матрицы объекта, т.е.
должна иметь место зависимость [113]
X\{s)
Ш')
о
*М
о
о
о
о
Wm{s)
U, Is)
(и Л*)
(4.34)
В реальных же системах перекрестные связи отличны от нуля и, следовательно,
качество работы каждого канала зависит как от свойств собственно канала, так и от
характера перекрестных связей.
248
Методы синтеза САУ по заданным показателям качества. Часть II
В связи с этим при постановке задачи синтеза регуляторов в многомерных
системах предъявляются требования не только к процессам в каждом основном канале, но
и требования, регламентирующие взаимные влияния каналов.
На практике применяются несколько путей «развязки» каналов.
Один из них - создание специальных устройств {компенсаторов), которые
включаются на входе многомерного объекта. Передаточные функции компенсаторов
(устройств динамической развязки каналов) выбираются таким образом, чтобы
получить или строго диагональные передаточные матрицы, или матрицы с
доминирующей в том или ином смысле диагональю. Матрица с доминирующей диагональю
позволяет ослабить взаимодействие между контурами регулирования. Условие
диагональной доминантности можно записать так [1, 76, 113]:
W,,
(ф I
/ = 1,7*'
^(4-)|;/ = 1,/я,
(4.35)
или
КИ> Ё K(4/=1'm (4-36)
7 = 1, /*'
для всех s e D .
Например, если / = 1, то условием диагональной доминантности является
неравенство
\щ. И > Ш4+К И+• -К И' <4-37)
или
\wu(s)\>\W2](s)\ + \W^(s)\ + ...\Wni(s)\. (4.38)
Матрицы, удовлетворяющие условиям (4.36) и (4.37), называются диагонапьно-
доминантными матрицами [1, 76].
Степень связности в многомерных объектах может быть охарактеризована и
другими способами. Одним из таких способов является использование матрицы
Бристоля [113]. Эта матрица определяет степень связности в статике и имеет вид
Л =
*!1
^21
Л12
х22
4/7
^2п
(4.39)
где
*//=■
(dxjdtij) все контуры разомкнуты
(dxjdut\ ьсе контуры замкнуты, кроме иу, /,у = \,п
Здесь Хч определяется как отношения производных: числитель - производная
установившегося значения выхода xt разомкнутой системы по управлению iij ;
знаменатель - производная установившегося значения выхода х, замкнутой системы по
тому же управлению иj.
Если взаимное влияние каналов отсутствует, то как матричная передаточная
функция разомкнутой системы, так и матричная передаточная функция замкнутой
системы, связывающей вход Y(/) и выход XB(f) системы, будут диагональными.
Этот факт чрезвычайно важен с той точки зрения, что каждый канал может
корректироваться независимо от других каналов и, таким образом, могут быть
использованы методы синтеза корректирующих устройств одномерных систем.
Глава 4. Методы синтеза регуляторов в классе многомерных систем
249
Рассмотрим систему, показанную на рис. 4.11. Для нее можно записать
следующие равенства [113]:
£(/) = Y(/)-XB(/);Z(s) = WKy(s)E(5);
V{s)=WK(s)Z{s);Xt(s) = V/o(s)V(s).
УМ £(t)
Регулятор
WK9(S)
lit)
Компенсатор
WK(s)
U(t)
F=3
Объект
Wc(S)
Xt(ti
t
(4.40)
(4.41)
Рис. 4.11. Структурная схема системы
Отсюда следует
XB(5) = W0(5)WK(^)WKy(5)E(,).
Тогда, подставляя E(s) = Y(s) -Хв (s) в последнюю зависимость, получим
■ XB(5) = W0(S)WK(5)WKy(5)[Y(5)-XB(5)] =
= W0(S)WK(s)V/Ky(s)Y(s)-W0{s)V/K(s)V/Ky{s)XB{s).
Из (4.41) следует
XB(s) + -W0(S)^K(s)WKy(s)XB(s) = W0(s)^K(s)WKy(s)\(s).
Или, что то же самое,
[l + W0(5)WK(^)WKy(.)]XD(S) = W0(5)WK(^)WKy(5)Y(5).
Из последней формулы находим основную зависимость
Хв (*) = [I + Wo (s) WK (s)^ (*)]"' Wo (s) WK (i)W4 {s)\ {s).
Условием воспроизведения сигнала Y(/) без ошибки (идеальная система),
очевидно, является
[l + W0(S)WK(5)WKy(5)]"1W0(5)WK(^)WKy(5) = I) (4.44)
где I - единичная матрица.
Это тот идеальный случай, к которому стремятся приблизиться конструкторы
систем управления.
Теперь, с учетом (4,44) и предыдущих рассуждений, рассмотрим выбор
передаточной функции компенсатора.
Пусть передаточная функция объекта управления имеет вид
'ВД »Й(,) ... ГГ£[з))
(4.42)
(4.43)
Wo(,) =
Передаточная функция регулятора является диагональной матрицей
V,7(*) о ... os
0 W%{s) ... 0
(4.45)
Wjs) =
0
0 ... W£{s))
(4.46)
16 3ак. 366
250
Методы синтеза САУ по заданным показателям качества. Часть II
Ясно, что если передаточная функция последовательного соединения
«компенсатор-объект» будет диагональной, то это будет означать, что каналы «развязаны»,
передаточные функции как разомкнутой, так и замкнутой систем будут иметь
диагональный вид.
Задача состоит в том, что надо подобрать передаточную функцию компенсатора
таким образом, чтобы было выполнено условие
W.
о
w°
/i2 \
ynn\
V*W wfM ... wt[s)~\
w}M ... w2kn(s)
W'(s)
Wn\(S) IVnk2(s) ... W^,[s).
0
KM
0
0
(4.47)
n 0 0 ... fVn°n(S)j
В последней формуле Wop(.s) - передаточная функция объекта с «развязанными»
каналами.
Перепишем (4.47) в виде
Wo (s) WK (s) = diag Wo (s) = Wop (s). (4.48)
Зависимость (4.48) сразу же позволяет найти передаточную функцию
компенсатора
WK(j)=W0-|(5)diagW0(5). (4.49)
Критический анализ изложенного подхода проведем на конкретном примере [113].
Пример 4.3. Пусть передаточная функция объекта имеет вид [113]
0,7
Wn(j) =
1+9*
2,0
1+85
2,0
0
0,4
1 + 65
2,3
0
0
2,1
(4 50)
U+ Ю5 1+85 1 + 75;
Динамический компенсатор будем сгроить таким образом, чтобы последовательное соединение
компенсатора и объекта имело диагональную матричную передаточную функцию
( 0Л
W0P(5) =
1 + 95
0
0
0,4
1 + 65
0
0
0
2,1
(4 51)
В соответствии с формулой (4 49) найдем обратную передаточную функцию объекта
w04W =
1,43(1+95)
-7,14(1 + 9д)(1 + 6д)
0
2,5(1 + 65)
7,82(1+95)(1+б5)(1 + 75) -1,5б(1 + 95)(1 + 75) -2,74(1+ 6j)(1+7j) Q4
(I+85)2 1 + ИЬ 1+8^ > \ )
Далее по формуле (4 49) находим передаточную функцию компенсатора
(4 52)
Глава 4. Методы синтеза регуляторов в классе многомерных систем
251
WK(*) =
1
-7,14(1 + 9л)(1 + 6д)
1 + 8.S
7,82(1 + 9s)(l + 6.s)(l + 75) -1,56(1+ 9s)(l +7s) -2,74(1+ 6j)(1 + 7j)
\ + \0s
(1 + fo)'
I+85
(4 53)
Структурная схема с динамическим компенсатором показана на рис 4 12
I уъ—^
Рсъулятор
Динамический
компенсатор
Рис. 4.12. Структурная схема системы с динамическим компенсатором
Передаточная функция замкнутой системы имеет вид
W(*)=[l + W0(*)W0-1(J)diagW0(J)WKy(J)]
xW0(,)W0-'(5)diagW0(.)WKy(5) =
г I
(4.54)
^I + diagW^W^JdiagW^W^*).
Из последнего выражения видно, что W"1 (.s)W0(s) = I и, таким образом, динамика
объекта компенсирована обратной передаточной функцией, передаточная матрица
прямой цепи является диагональной
Wp(5)=diagW0(5)WKy(^). (4.55)
Передаточная матрица замкнутой системы также будет диагональной и,
следовательно, синтез регуляторов молено проводить по каждому каналу самостоятельно,
пользуясь теорией одномерных систем.
Подобный случай нами уже был рассмотрен и посвящен синтезу регуляторов
одномерных систем (см. §2.2).
Все недостатки подхода, которые рассматривались в §2.2, имеют место и в
настоящем случае. Напомним их:
1. Подход требует точного знания передаточной матрицы объекта, что не всегда
возможно;
Если точная и приближенные модели объекта значительно отличаются друг от
друга, компенсации динамики объекта не произойдет (нули и полюса объекта не
будут компенсированы обратной передаточной функцией) и качество управления будет
плохим; замкнутая система может стать даже неустойчивой.
2. Для реализации передаточной функции компенсатора необходимо иметь
дифференцирующие звенья, которые точно физически не реализуются;
3. Если объект имеет звено запаздывания, то для реализации компенсатора
необходимо иметь звенья опережения, которые так же, как и дифференцирующие
звенья, точно не реализуются;
4. Если система работает в условиях помех, то дифференцирующие звенья будут
усиливать их влияние;
16*
252
Методы синтеза САУ по заданным показателям качества. Часть II
5. Если передаточная функция объекта управления содержит нули в правой
полуплоскости комплексной плоскости, то в компенсаторе эти нули оказываются
неустойчивыми полюсами и их неточная компенсация приводит к тому, что в
передаточной матрице замкнутой системы появляются неустойчивые полюса,
что приводит к неустойчивости системы. Часто для упрощения конструкции
компенсатора применяют компенсацию в статическом режиме.
В этом случае компенсатор будет включать лишь безынерционные элементы
(усилители). В самом деле, формула (4.49) будет иметь вид
WK(0)=Wo-l(0)diagWo(0). (4.56)
Пример 4.4 [76] Рассмотрим пример для статического режима работы системы Имеем
(0,1 О О Л, (0,7 0 0 Л,
Wo(0)= 2,0 0,4 0 , diagWo(0) = 0 0,4 0
[2,3 2,3 2,lJ [о 0 2,1
Тогда, рассчитав передаточную функцию YV"1 (0) , получим
( 1,43 0 0 1
W;1 (0) = 1-7,14 2,5 0
[ 6,26 -2,74 0,48j
Теперь легко найти передаточную матрицу компенсатора
( 1,43
WK(0)= -7,14
0
2,5
(0,7 0 0 ^ ( 1 0
0 0.4 0 И"7'14 1
6,26 -2,74 0,48 J
1^0 0 2,\) \ 6,26 -2,74 1 J
С помощью компенсатора WK(o) оказываются скомпенсированными все
перекрестные связи в статическом режиме. В переходном же режиме имеет место период
заметного влияния динамических связей.
Построим структурную схему с динамическим компенсатором [76].
С учетом того, что
\VK(*)WKy(s) =
=
w2\
[К
w\\
к
к
{') ȣ(*)
(s) w;2(s)
0
0
^(
'I
0
0
0
)wg(a)
0
W£{s)
0
0
0
0
0
>
а также принимая во внимание зависимость
т.е.
U2(s)
Щ{*и
W^s)W${s) 0
W2\[s)W*{s) W!2{s)W%(s)
О
о
е, [s
£■>
2W
/зВ,(^,7М W!2{s)W%[s) Wb[s)w3{s))
получаем
U,(S)=W^(s)Wir{s)B](s)+W^2(s)W^(s)s2(s)+W3Ki(s)W^(s)z3(s).
Глава 4. Методы синтеза регуляторов в классе многомерных систем
253
Теперь легко изобразить структурную схему (рис. 4.13).
дЙУ
Рис. 4.13. Структурная схема трехмерной системы с компенсатором
Структурная схема системы со статическим компенсатором следует из схемы
рис. 4.13 при s = 0.
В [76] предложен метод, позволяющий осуществить полную динамическую
развязку всех скалярных компонент вектора выхода, при этом не используется
компенсация передаточных полюсов и нулей объекта управления.
В соответствии с [76] к объекту со стороны его входа подключается специальное
звено, названное звеном динамической развязки (естественно, при / -» оо и s -> 0 это
звено может быть использовано и как развязка каналов в статическом режиме).
Указанное звено состоит из двух блоков: стабилизации и диагонализации передаточной
матрицы стабилизированного объекта, формирующего новые развязанные каналы
регулирования.
С алгоритмом диагонализации можно познакомиться в [76].
Пример 4.5 [76] Матричная передаточная функция объекта управления имеет вид
-L о -L'
5+1 5+1
1 5 + 2 1
W0(5) =
5 + 1 (5 + 1)(5 + 3) 5 + 3
Матричная передаточная функция диагонализатора запишется так
WK(5) =
-52-25-2
-1
252+85 + 8 -5-2
S2 -65-10 1
1
52+85 + 15
о
1
5 + 7 )
Передаточная функция последовательного соединения «диагонализатор-объект» имеет диагональную
передаточную функцию
-252-85-12
WK+0(*) =
(5 + 1)(52+85 + 15)
о
-5"-45-6
(5 + l)(5 + 3)(5 + 7)J
Пример 4.6 [76] Рассмотрим систему, описываемую уравнением вида
X = AX + BU, ХВ=СХ,
где
Х={хьхъхг,хл)\\) = {иьи2)\ Хв=(х1х»2)\
254
Методы синтеза САУ по заданным показателям качества. Часть II
А =
-0,16 0,177 -0,984 0,104^1
-18,191 -1,162
-0,158 -0,04
0 1,0
0 0,02 ^
-14,131 -0,554
-0,432 -0,966
0 О
Найдем многомерную передаточную матрицу объекта
0,82 0
-0,279 О
0,18 О
В =
с =
w0W =
-14,2b2 -6,565-6,4
0 0 0 1
10 0 0
0,38s2-l,15s-18,18
s4 + l,6s3+3,65s2+3,41s + 0,53 s4 + l,6s3+3,65s2+3,41s + 0,53
-2,08s2 -2,3s- 0,45
0,02s3 + 1,08s2 + 1,06s-0,09
U4 + l,6s3+3,65s2 + 3,41s + 0,53 s4 + 1,6s3 + 3,65s2 + 3,41s + 0,53,
Передаточная функция блока диагонализации, найденная по методу [76], имеет вид
'-0,03s3 -1,58s2 -1,56s + 0,13 0,23s2-0,69s-10,95^
WK(*) =
s3+3,41s2+0,91s
-3,05s2-3,38s-0,66
s3+3,41s2+0,91s
Введем обозначения.
s2+0,12s
8,56s2 + 3,95s+ 3,86
s2+0,12s
(s)__ K(s) Kb) w
w^W =
Тогда справедлива зависимость
или, в развернутом виде,
{ 0 Wg(s))
U(*) = W,(*)W1V(*)E(*).
KM K(s))(K(s) o )(zt(s
U2(s)) \WZ(S) И£(,)11 0
■)Ы°).
или, что то же самое,
{"г(*)J"[К {s)W (s) Wi,(s)W£ (s)j 1%(s))
Для каждой из компонент вектора управления можно записать
U2(s) = W2K,(s)WlY(s)sl(s) + lV^(S)W^(s)s2(sy
Последние две формулы определяют структуру системы от сигнала ошибки е(/) до сигнала
управления, поступающего на вход объекта Эта структура показана на рис 4 14 и 4 15.
(4 57)
8Р-
WJS)
1
Рис. 4.14. Структурная схема корректирующего устройства плюс диагонализатор
Глава 4. Методы синтеза регуляторов в классе многомерных систем
255
+ 4
Н
гула тс
Р
Диагонализатор
г—
^
L._*i
W",M
>
—ч
+1
utai
A,B,C
CmoSuAusupolauHtuii
о8%€кт
управления
xfc)
Рис. 4.15. Структурная схема двумерной системы управления
4.4. ОПТИМИЗАЦИОННЫЕ МЕТОДЫ СИНТЕЗА УСТРОЙСТВ
РАЗВЯЗКИ КАНАЛОВ И РЕГУЛЯТОРОВ
Рассмотрим пример [56]. Системы управления современных газотурбинных
двигателей (ГТД) имеют несколько регулируемых параметров и обычно столько же
регуляторов. Так, в авиационных однокаскадных турбореактивных двигателях (ТРД)
регулируемыми величинами являются частота вращения вала п и температура
газов перед турбиной Г, требуемые значения которых поддерживаются соответственно
изменением подачи топлива G и площади критического сечения реактивного сопла
F . При наличии форсажной камеры для сжигания топлива за турбиной число
контуров регулирования увеличивается до трех. Добавится еще один регулируемый
параметр - температура газов в форсажной камере и соответственно новое
управляющее воздействие - расход топлива для сжигания в форсажной камере.
Введение корректирующих устройств в контур систем автоматического
управления обеспечивает достижение заданных динамических свойств [56].
Приведем конкретные уравнения многомерного объекта. Так, ТРД без учета
инерционных свойств газовоздушного тракта описывается уравнениями:
т3 =aTG\x-aT^ + aTXT\T,
где
т3=АГз/Г3; Ф = До/со; /^ = AF^/F^ ; ^ = AG/G
- относительные изменения величин; Хп и Хт - внешние возмущения по частоте
вращения и температуре; апТ ...aTXi - коэффициенты усиления. Применив
преобразование Лапласа, получим
*э М = *гЛ {'№) - aT/lWw (зЩз) + атм WKC {s)XT {s)9
где »V(j) =1/(7^ + 1) ^kc(*)=1; М*)=^р(*)=^л(4 WT{s) - передаточная
функция ротора, WKC(s) - передаточная функция камеры сгорания.
Структурная схема объекта показана на рис. 4.16.
(4.58)
(4.59)
256
Методы синтеза САУ по заданным показателям качества. Часть II
an, r
От,*
-\ WXc(s)
ЛТИ)
Рис. 4.16. Структурная схема двумерного объекта управления (ТРД)
В качестве управляющего воздействия по частоте вращения можно использовать
интенсивность подачи топлива (AG ), а по температуре газов за камерой сгорания -
изменение площади критического сечения сопла (Д/7^). Тогда передаточные
функции регуляторов при наличии измерительного, усилительного и исполнительного
устройств (их передаточные функции равны единице) обозначим через fVpl (s) и
Структурная схема многомерной системы, включающей регуляторы и
неизменяемую часть (объект управления), показана на рис. 4.17.
Л* ft?
г*>
Рис. 4.17. Структурная схема системы управления турбореактивного двигателя
Задача синтеза регуляторов с передаточными функциями W^r(s) и W^n(s)
заключается в выборе таких параметров рх,р2,...,рг, которые обеспечили бы
независимость каналов управления (развязка каналов) и требуемое качество переходных
процессов по каждому каналу.
Глава 4. Методы синтеза регуляторов в классе многомерных систем 257
Рассмотрим решение задачи синтеза компенсаторов и корректирующих устройств
в общем виде.
Неизвестными являются параметры корректирующих устройств (или коэффициенты
дифференциальных уравнений, описывающих поведение корректирующих устройств).
Поскольку дифференциальные уравнения неизменяемой части и корректирующих
устройств известны, то можно записать систему дифференциальных уравнений,
связывающих векторный вход системы \(t) с ее векторным выходом Хв(/).
Естественно, эта система уравнений включает неизвестные коэффициенты, определяющие
поведение регуляторов. Их надо подобрать таким образом, чтобы обеспечить
заданное качество управления в многомерной системе.
Положим, что двумерная система описывается системой дифференциальных
уравнений вида
v=0 v=0 v=0 i>=0
v=0 v=0 v=0 v=0
В последней системе предполагается, что коэффициенты a]v](p), а\2{р), b"(p),
b]v2(p), а^(р), al2(p), Ь21(р), Ь22(р), т.е. они зависят от параметров компенсатора
и регулятора; п - максимальный порядок линейных дифференциальных операторов
L ij = 1,2; т - максимальный порядок линейных дифференциальных операторов
Наложим ограничения на переходные процессы /?„(/), / = 1,2 по всем каналам
системы (/?,,(/) ограничиваются такой же областью, как это принято в теории
скалярных систем; параметры областей - свои для каждого канала). Наложим также
ограничения на процессы й/Д/) (влияние входного сигнала >>,(/) на выход х^ (/)).
Качество многомерной системы тем выше, чем точнее по каждому выходу х,в, / = 1,2
отрабатывается свой индивидуальный вход у, (7) и чем меньше влияют на него
другие входы. Подадим на первый вход системы единичную ступенчатую функцию
у} (t) = \(t); при этом уг (t) = 0 . На выходе получим реакции Их, (/) и hn (t).
В эталонной системе должна иметь место следующая ситуация:
*,(')=*?.('). *2(')=*12(')-
Тогда система уравнений (4.60) приближенно принимает вид:
£al\p)h{ft,) + £a?(p)h№(t) = ±bl\p)lU(t),
v=0 v=0 ,=0 (46])
£aV(p)h№(t) + £a?(p)h${t) = £b?(p)\M(,).
v=0 v=0 v=0
Последняя система уравнений является приближенной в том смысле, что
hxj(t)Фh]x(t), a h]2(t)ФhX2{t), поскольку в общем случае невозможно подобрать
параметры р = {р],Р2>---->Рг) корректирующего фильтра, обеспечивающие равенство
*'(') = *п (').*! (О = *1Э2(')-
258 Методы синтеза САУ по заданным показателям качества. Часть II
Параметры корректирующего устройства необходимо подобрать таким образом,
чтобы при подаче на первый вход сигнала y\{t)= \{t) ее выходной сигнал д:,в (t)
возможно меньше отличался от И?) (/), а х2 (t) - от h\2 (/).
Повторим приведенные выше рассуждения применительно ко второму входу,
принимая yi{f)=\{t) (при этом ^,(/) = 0). На выходе получим реакции h2](t) и
h22(t). В эталонной системе при соответствующем подборе параметров Р\,р2,-..,рг
должны быть выполнены условия:
*.(')=M'Mli(')> x2(t)^h22(t)=hi2{t).
Можно записать следующие уравнения
tt\p)^{<)+±£{p)^{<)=b?{p){v\<\
v=0 v=0 v=0 (462)
^а1\р)^{1) + ^а?{р)${1)^Ь?{р)\(у){1).
v=0 v=0 v=0
От уравнений (4.61) и (4.62) перейдем к эквивалентным интегральным
уравнениям и заменим hy(t) на h?(t). В этом случае получим соотношения
т т т
z, (/, р) = \К хи (/, х, p)h^ (xVx + 1к *2 {l, т, p)h,э2 (t)A - IК уп {l, x, p)\(z)di,
0 0 0
T T T
z2{t9p) = \КХ2Х {t^Pyu (т)А+ \КХ22 {их,рУп (т)Л- \КУ2] (/,т,р)1(т>/т,
0 0 0
/ Т 7
s з (/, р) = \к;, (/, т, P)h], (т)л + Ja: *2 (/, т, Р)л2э2 (т)а - J* ^2 (/, т, p)i(t)a ,
0 0 0
г г г
е4 Ы = J/:^ (М,Р>2Э, (х)А+ \КХ22 {t^p)hl2 (т)А- J/:^ (/,х,Ж^.
0 0 0
Важным является тот факт, что компенсатор и регулятор должны иметь такую
структуру, подбор параметров которой Р\,Р2>--->Рг должен обеспечить малость в
известном смысле функций е, (/,/?), / = 1,4 .
Введем в рассмотрение функционал
/(/>)= \[z\{t,p)+zl{t,p)+zl{t,p)+z\{t,pidt. (4.63)
о
Будем выбирать вектор параметров р таким образом, чтобы обеспечить минимум
функционала (4.63), т.е.
/(/?)-» min
р
при соответствующих ограничениях.
Нахождение оптимальных значений параметров Р\,Рг,--- по указанному
алгоритму обеспечивает приближение переходных процессов hu(t) и h22(t) в двумерной
системе к эталонным, т.е.
МО**.'!'* h22{t)*hl2{t),
Глава 4. Методы синтеза регуляторов в классе многомерных систем 259
а также приближенную развязку каналов двумерной системы (при этом
предполагается, что корректирующее устройство обладает необходимыми возможностями).
Если анализ скорректированной системы покажет, что качество ее работы является
неудовлетворительным, в известном смысле, тогда необходимо использовать более
сложные компенсаторы и регуляторы, обладающие большими возможностями как в
плане реализации развязки каналов, так и в плане обеспечения качества переходных
процессов по ее каналам и качества работы в установившемся режиме.
Для решения рассматриваемой задачи высокую эффективность имеет метод
матричных операторов.
Дословно повторяя рассуждения, приведенные выше, можно рассмотреть
соотношения
^,(р)С*»+^2(р)С*«=^(р)СЛ,
Ab(py:h»+A;2(py:h»=Ab(p)c^,
Ab(p)Ch»+A{2(pY:h»=A{2(p^,
A^{p)Ch-+A^(p)Ch^Ay2(p)C^,
где Л (0 = 1(0 •
Далее, заменяя в последних соотношениях hu(t) = h^(t), hn(t) = h?2(t),
h2l (0 = A|, (0, h22 (t) = h\2 {t) и вводя в рассмотрение невязки
в1(/,/,)-(с"(/»))тф(О.в2('./')=(св*(р))тф(О.
вз (t.p) = (С" (р))Т Ф(/),в4 (t.p) = (С-(,))Т Ф(0>
легко получить функционал
4p) = tt[c!J(p)]2.
7=1/=1L
Задача математического программирования, приводящая к решению задачи
синтеза компенсатора и регулятора, формулируется так:
/(/?)-» min
р
при соответствующих ограничениях.
260 Методы синтеза САУ по заданным показателям качества. Часть II
ГЛАВА 5. МОДАЛЬНОЕ УПРАВЛЕНИЕ
В главе 5 изложены основные принципы модального управления.
5.1. ПОСТАНОВКА ЗАДАЧИ
Задача синтеза систем управления является одной из важнейших в теории
управления. Среди многочисленных подходов к решению поставленной проблемы
рассмотрим метод, использующий результаты линейной алгебры, а именно: синтез на
основе модального управления Модальное управление (синтез модальных
регуляторов) можно определить как задачу управления, в которой изменяются моды
(собственные числа матрицы объекта) с целью достижения желаемых целей управления [9].
При этом необходимо определить матрицу коэффициентов К динамической
обратной связи, обеспечивающей замкнутой системе требуемое расположение мод.
Часто управляемые объекты имеют лишь небольшое число собственных чисел,
которые с помощью обратной связи требуется сдвинуть в желаемые точки, оставляя
остальные собственные числа без изменения. В этом случае говорят об управлении
отдельными модами. Этот сдвиг подчас проще вычислить и обеспечить, чем
реализовать сдвиг всех характеристических чисел объекта. Такого рода задачи часто
возникают при управлении многомерными объектами.
При синтезе важную роль играет информация о векторе состояния объекта.
Вначале будут рассмотрены алгоритмы модального управления с полностью
измеряемым вектором состояния, а затем выявлены особенности, которые вносит
наблюдатель при неполных измерениях. Нельзя не отметить и различия в алгоритмах синтеза
скалярного и векторного управлений, о которых будет сказано ниже.
Рассмотрим формальную постановку задачи модального управления при
полностью измеряемом векторе состояния.
Пусть Gv ={X]9...,XS}, s<n - произвольный набор комплексных чисел, в
котором каждое комплексное число представлено вместе со своим сопряженным. Пусть
дА ={Х} ,...ДУДУ+1,...Д„} спектр матрицы А линейной системы управления.
Х(/) = АХ(/) + BY(0, X е R", Y е /Г . (5.1)
Пусть Л* ={GV,A.V+1,...,X;,} = {^,...а*ДУ+1,...Д„} - некоторый желаемый спектр,
сформированный из набора Gs и (n-s) корней матрицы А. Назовем систему (5.1)
модально управляемой по отношению к желаемому спектру А*, если существует
матрица коэффициентов обратной связи К
Y(0 = KX(/) (5.2)
размерности т х п, такая, что матрица (А + ВК) замкнутой системы
Х(/) = (А + ВК)Х(0 (5.3)
имеет спектр А*.
Очевидно, что если s < п , т.е. когда необходимо перевести только часть корней,
оставляя остальные на месте, не требуется, чтобы объект (5.1) обладал свойством
полной управляемости. Достаточно, чтобы он был модально управляем, т.е. допускал
бы закон управления Y(f) = КХ(/), изменяющий заданные моды объекта (5.1).
Если s = n и система (5.1) модально управляема по отношению к любому спектру
А , то она называется полностью модально управляемой
Глава 5. Модальное управление 26]_
Ясно, что полная модальная управляемость и управляемость системы (5.1) тесно
связаны друг с другом, о чем свидетельствуют алгоритмы, которые будут
рассмотрены ниже. И, более того, эти два понятия эквивалентны, о чем говорит следующая
георема [9].
Теорема 5.1. Пара матриц {А, В} управляема тогда и только тогда, когда она
полностью модально управляема.
Данная теорема говорит о том, что при полной управляемости можно получить
любой наперед заданный желаемый спектр замкнутой системы, и наоборот, если
можно выбором матрицы обратной связи К обеспечить любой желаемый спектр, то
система (5.1) полностью управляема.
Рассмотрим отдельные алгоритмы модального управления.
5.2. МОДАЛЬНОЕ УПРАВЛЕНИЕ ПРИ ПОЛНОСТЬЮ ИЗМЕРЯЕМОМ
ВЕКТОРЕ СОСТОЯНИЯ. УПРАВЛЕНИЕ ВСЕМИ МОДАМИ
5.2.1. Скалярное управление (т = 1)
Рассмотрим сначала случай скалярного управления, т.е. В = Ь, где b - «-мерный
вектор-столбец. Для решения поставленной задачи модального управления (всеми
модами) необходимо перейти от исходного описания объекта управления
Х(/) = АХ(0 + ЬЯ0 (5-4)
к преобразованной системе (новому базису)
£(0 = АХ(0 + 6у(0, (5-5)
причем матрица А является сопровождающей матрицей [9, 71]
характеристического полинома фА(А.) матрицы А, т.е. если
Фа(^) = Г + а„_1Г~1+... + а^ + я0, (5.6)
то
"О 1 0 ... О
0 0 1 ... 0
А =
0 0 0 ... 1
1~а0 -ах -а2 ... -ап_х
При этом Б = [0 0 ... 1]т . Представление исходной системы в виде (5.5)
называется каноническим представлением. Связь между описаниями (5.4) и (5.5) в случае
полной управляемости объекта (5.4) определяется матрицей перехода S
X = SX, (5.7)
где матрица S определяется из следующего соотношения [9, 73]
S = [6, АЬ,..., A"-lb][b, Ab,..., А^'ЬГ1 = %М;/ , (5.8)
где М^, М^ - соответственно матрицы управляемости в новом и старом базисах.
Напомним, что по условию полной управляемости detM^ Ф 0. Рассмотрим пример.
Пример 5.1. Пусть матрицы А и b объекта управления (5 4) имеют вид
Ранг матрицы управляемости
262
Методы синтеза САУ по заданным показателям качества. Часть II
м =
81
14J
равен 2, поэтому для А и b существует каноническое представление Найдем матрицу преобразования S
Характеристический полином для матрицы А
Тогда
ФА(А.) = Х-7А.-2 = 0
-в ;]• чз
s =
о i¥i
1 7 2 14
1
0
г
2
1
2 .
При этом непосредственной проверкой получаем
A = SAS"\ b = Sb
После предварительных обсуждений мы можем сформулировать алгоритм
модального управления.
Пусть линейная стационарная система (5.4) управляема и пусть
ц>\Х) = Хп+ап_1Хп~1+... + а]Х + а0 (5.9)
- произвольный нормированный полином с желаемым спектром А . Тогда
существует вектор обратной связи К = [К}... Кп]т, такой, что замкнутая система в
преобразованном виде
Х(О = [А + ЬКТ]Х(О (5.10)
имеет ф*(^) своим характеристическим полиномом. Покажем это. Пусть
ц>А(Х) = Х" +an_{kn~x +... + a{k + UQ - характеристический полином матрицы А.
Поскольку по условию пара {А, В} управляема, то, согласно рассмотренному выше
представлению, существует базис, в котором эта пара имеет канонический вид А, Б .
Выберем компоненты матрицы обратной связи по формуле
^/+1 =а/-а/-, / = 0,и-1. (5.11)
Подставляя выражение (5.11) в (5.10), получим
[А + ЬКТ] =
0
0
1
0
0
0
0
-а
0
0
0
-а,
1п-\
1
0
0
1
[ЛО -СХ0,ДГ, -СХ,,...,4ЯГЯ_, -0Ся_1] =
о
0
0 0
-а0 -а,
0
-а2
1
а это значит, что характеристический полином замкнутой системы
совпадает с полиномом ф (X).
(5.12)
(5.13)
Глава 5. Модальное управление 263
Теперь необходимо найти связь между коэффициентами регулятора К в
преобразованном базисе с коэффициентами К исходного. Используя соотношения (5.4),
(5.5), (5.7) и учитывая, что A = S~1AS, b = S~1b, получим
Х(0 = (А + bKTs)x(/) = (А + ЬКТ )Х(/), (5.14)
откуда
KT=KTS. (5.15)
Итак, процедура синтеза модального регулятора в случае полностью
управляемой системы со скалярным входом y(t) следующая:
1) вычисляем матрицу перехода S, связывающую исходную систему (5.4) с ее
каноническим представлением (5.5) (формула (5.8));
2) находим коэффициенты модального регулятора Кт в преобразованном базисе
(формула (5.11));
3) определяем коэффициенты обратной связи Кт для исходной системы
(формула (5.15)).
Пример 5.2. Пусть уравнение состояния объекта управления 2-го порядка со скалярным управлением
имеет вид
*(о=[б !]ад+[?Ь
Необходимо синтезировать для заданной системы модальный регулятор, который бы обеспечивал
замкнутой системе желаемый спектр Л* = {-3,-1}
Решение:
1 Проверяем управляемость системы
"1 31
А1б
31ь=Ркм,=Р 51,
Ч Ш U 20J'
rank My = 2 = п , следовательно исходная система полностью управляема и для нее можно синтезировать
требуемый регулятор
2 Характеристический полином матрицы А
ФА (X) = det (А - XI) = X2 - 9Х -10 = X2 + а{Х + а0 ,
Х]=\О,Х2 =-1
3 Сопровождающая матрица полинома фА (А.)
О 1 1 ГО Г
1-а0 -а,] [\0 9
при этом
Б
4 Находим матрицу преобразования S согласно формуле (5 8)
я S соглас!
■С Ж
1
35
11
35
2"
35
11
35
5 Определяем желаемый характеристический полином
у\Х) = {Х-Х\)(Х-Х2) = (Х + 3)(Х + \) = Х2+4Х + 3 = Х2+а1Х + а0
6 Вычисляем коэффициенты регулятора для преобразованной системы Кт =[К\ К2~\
К1=а1)-а0=-\0-3 = -\3,
^2=д,-а,=-9-4 = -13
7 Находим коэффициенты модального регулятора в исходном базисе
264 Методы синтеза САУ по заданным показателям качества. Часть II
39
1
35
11
. 35
2"
35
13
35.
KT = KTS = [-13 -13] ~35 35 X* -*
1 J 11 13 L 7 7
8. Проверяем, что замкнутая система имеет требуемый спектр. Имеем
Г 45 _57"
7 7
—Ч ИИ -?]■.« »
7 7
Убеждаемся, что фА+ькг (к) = \2 +4Х + 3 и АА+ькт = {-3,-1} = Л*, т.е. регулятор спроектирован верно
Замечание. Здесь и далее всюду под обозначением LT понимается
транспонированная матрица, если L - матрица, и вектор-строка - если L - вектор-столбец.
5.2.2. Векторное управление
В этом случае задача модального управления имеет, в общем, неединственное
решение и при этом могут быть предложены различные алгоритмы вычисления
матрицы К. Один из подходов [9, 73] предполагает приведение системы с многомерным
управлением к одномерному. Назовем этот подход алгоритмом 1. Он состоит из трех
частей.
Алгоритм 1
Находим матрицу обратной связи К у размерности тхп, такую, чтобы система
X(0 = (A+BKy)x(/) + b^y(0 (5.16)
(где bj - я-мерныйу-й столбец (j e [1.../и]) матрицы В, у/ -j-я компонента вектора
управления Y) была полностью управляема. Для этого необходимо и достаточно,
чтобы пара {а + ВК7;Ь7} была управляемой и любые две жордановы клетки
матрицы А имели различные собственные значения [73]. Далее предполагается, что это
условие выполнено, т.к. в противном случае скалярное управление недостаточно и
необходимо увеличивать размерность управления. Для существования такой
матрицы Ку необходимо и достаточно, чтобы пара {А,В} была полностью управляема и
Ь7*0 [9].
Без потери общности можно рассмотреть случай j = 1 (об особенностях
алгоритма для j * 1 будет сказано ниже).
Для нахождения матрицы К! сформируем матрицу управляемости
М>=[ь1,...>Ьда,АЬ1,...,АЬ|И,...,Ая-|Ь1,...,Ая-1Ьт]. (5-17)
Выберем из пхт столбцов этой матрицы п линейно независимых. Такие
независимые столбцы матрицы М^ существуют в силу полной управляемости объекта
(5.4). Имеется несколько способов такого выбора. Рассмотрим один из них [74].
Будем перебирать столбцы bl9 Ab]9..., AV] Ъ{ до тех пор, пока вектор AV|b, не будет
выражаться в виде линейной комбинации векторов Ъи Abi9..., A ] bj. Эта процедура
легко реализуется проверкой соотношений:
rank Bj =rank[b1,Ab1,...,AVl"1b1] = v1, (5.18)
rank[b1,Ab1,...,AV|b,] = v1. (5.19)
Глава 5. Модальное управление 265
Если v, =/?, то объект (5.4) полностью управляем с помощью управления^/), и
тогда переходят ко второй части алгоритма 1. Если Vj < п, то будем
последовательно присоединять к полученному набору (5.18) столбцы матрицы
В2 = b2,Ab2,...,AV2""1b2l до тех пор, пока вектор Av'2b2 не будет выражаться как
линейная комбинация векторов bj, Ab,,..., AVi~1bi,b2, Ab9,..., AV:~lb2, т.е.
rank[B,;B2] = v1+v2, (5.20)
rank[B,;B2;AV2b2] = v1+v2. (5.21)
Если v, + v2 <n, продолжается процедура присоединения к полученному набору
[Bj;B2] векторов b3, Ab3,..., AVi~!b3 и т.д.
Предположим, что для некоторого v3 имеем v, + v2 +v3 -n , т.е. получена
совокупность п линейно независимых векторов матрицы управляемости (5.17) и,
следовательно, матрица
Т^Ь^.^АЬ,,...^-1^^ (5.22)
невырождена, (det T * 0 , dim T = п х п).
Сформируем матрицу Р размерности тхп следующим образом
Р = [0,0,...,0,е2Д...,0,е3Д. .,0], (5.23)
где е2 -Vj -й столбец, е3 -(v, + v2) - столбец этой матрицы, общее число которых
равно Vj + v2 +v3 -n, а через е, (/=2,3) обозначен /-й столбец единичной матрицы
размерности тхт.
Теперь искомая матрица К\ может быть найдена из выражения
К^-РТ"1. (5.24)
Для того чтобы показать, что полученная матрица (5.24) определяет управляемую
пару {A+BKi; b}, перепишем матрицу Р = - К|Т в виде
P = -K1[b1,...,Ab1,...,AVl-1bI,b2,...,Ab2,...,AV2-1b2,b3,...,Ab3,...,AVi-!b3] =
= [0,0,...,0,е2,0,...,0,е3,0,...,0].
Это матричное равенство соответствует следующему набору векторных равенств:
К,Ь, = 0, К,АЬ, = 0, К!А2Ь, = 0,...,-К,AVl-1b, = e2,
К^ = 0, К,АЬ2 = 0, К,А2Ь2 = 0,...,-К,AV2"]b2 = е3,
К,Ь3 = 0,К,АЬ3 = 0, К! A2b3 = 0,...,-K, AvHb3 = 0.
(5.25)
Используя векторные равенства (5.25), легко показать, что пара {А+ВКь bj}
управляема, т.е. векторы bb [A+BKj]bi,..., [A+BK^'b] -линейно независимы.
Переходим ко второй части алгоритма 1.
2. Применяя к объекту управления
Х(0 = (А + ВК, )Х(/) + ЬхУ] (0 (5.26)
процедуру синтеза, рассмотренную ранее для скалярного управления, и вводя
обратную связь для (5.26) в виде
Ь,у,(О = BG(0X(/) = b,gf X(/), (5.27)
где матрица G имеет вид (dim G = т х п)
266
Методы синтеза САУ по заданным показателям качества. Часть II
G =
^ О 0 ... 0
И gj =[gU g\2-g\n]> ПОЛУЧИМ
X(0 = (A + BK,+BG)X(0.
Таким образом, полная матрица коэффициентов обратной связи К , т.е.
Y(0 = KX(/),
будет иметь вид:
K = K,+G.
Приведенный алгоритм 1 представляется наиболее простым как с точки зрения
компактности его изложения, так и с точки зрения удобства для практических
вычислений [9]. Однако при таком подходе исключается значительная часть
решений, которая может быть получена при проектировании систем управления. Ниже
будет рассмотрен алгоритм 2, который решает более общую задачу модального
управления. Но сначала рассмотрим пример.
Пример 5.3 (п = 3, т = 2)
Пусть матрицы А и В имеют следующий вид
А =
(5.28)
(5.29)
(5.30)
"1
0
1
0
1
0
г
0
1
, в =
"1
0
0
0"
1
0
Спектр матрицы А ЛА={0;1,2}. Необходимо, если это возможно, синтезировать модальный регулятор
так, чтобы спектр матрицы замкнутой системы А + ВК был равен Л*={-1, -2. -3}
Решение.
1 Проверяем управляемость системы
1 2 0 0 01
МЛ =[Ь1,АЬ|,А2Ь,,Ь2,АЬ2,А2Ь2] =
0 0 0 111
0 12 0 0 0
rank My - 3 , т е система полностью управляема и, значит, модально управляема
2 Считаем, что будем управлять с помощью первого столбца Ь| матрицы В, поэтому из матрицы
Mv выбираем 3 линейно независимых вектора, начиная с Ь| Отсюда получаем V| = 2, v2= 1 Формируем
матрицу Т
Т =
3. Формируем матрицу Р (размер 2x3).
Р =
"1
0
0
1
0
1
0"
1
0
"1
0
0
0
0
1
-1"
1
0
"о
0
0
0
1
0
о"
0
1
_Г0 0 0]
где пунктирная черта отсекает часть координат единичных векторов, длина которых превышает
размерность вектора управления (т = 2)
4 Определяем матрицу К {
К,=-РТ '=
0
0
0
-1
0]
J
1
о
о
0
0
1
-1
1
0_
0 0 0
0 0-1
5 Матрица объекта с частично замкнутой обратной связью
Глава 5. Модальное управление
267
А(1) = А + ВК,=
1
0
1
0
1
0
1
-1
1
кО>
Спектр матрицы А^' такой же, как у А , т.е
ЛАс„= {0,1,2}.
6 Приходим к объекту со скалярным управлением
X(/) = (A + BK1)X(0 + b1>;1(/) = A(I)X(/) + b^1(/)
7 Проверяем управляемость полученной системы
M<I> = (b1,A(')b,,(A<Vb,} =
"1
0
0
1
0
1
2"
-1
2_
0
0
0
1
0
-2
0
1
3
,ь =
0
0
1
rank M^ =3=> пара JA(1),b,J управляема
8 Синтезируем матрицу коэффициентов обратной связи G
а) Характеристический полином матрицы А^
фд(1)(А.) = X3 -ЗХ2 + 2Х = Х3 + а2Х2 + а{Х
б) Сопровождающая матрица полинома фА<п(Х)
А(1> =
в) Желаемый характеристический полином*
(р\Х) = (Х + \)(Х + 2)(Х + 3) = Х3 + 6Х2 + \\Х + 6
г) Матрица управляемости для пары jA(I),b}
М, = {Б,А(|)Ь,(А(|))2ь}-
д) Находим матрицу S
s = mv(m(vv =
е) Вычисляем коэффициенты регулятора g, для преобразованной системы.
gu =ао-ао = 0-6 = -в,
gl2=fl,-aI=2-ll = -9,
g,3=a2-a2=-3-6 = -9
ж) Матрица (строка) коэффициентов регулятора в исходном базисе
ГО 1 01
"О
0
1
0
1
3
1
3
7
"0
0
1
0
1
3
г
3
7
1
0
0
1
0
1
2"
-1
2
-1
=
"0
0
1
1
-1
-1
0"
1
2
gT=glS = [-6 -9 -9]
0 1 1
= [-9 24 -27]
1 1 2
9 Формируем матрицу коэффициентов обратной связи G
Г,П = Г-9 24 -27
L о J L ° ° °
10 Искомая матрица коэффициентов обратной связи.
11. Проверяем корни у матрицы замкнутой системы.
268
Методы синтеза САУ по заданным показателям качества. Часть II
А + ВК =
"1
0
1
0
1
0
г
0
1
+
"!
0
0
0"
1
0
-9 -24 -27
0 0 1
ЛА+вк ={-1.-2,-3},
Г-8 -24 -26]
0 1 1
^10 1
т е. модальный регулятор спроектирован верно.
Замечание 5.1. В случае выбора произвольного столбца матрицы В (Ьу) в
алгоритм 1 вносятся следующие изменения:
1) после проверки полной управляемости (rank М> =/7) формируют матрицу Т,
затем идет столбец кьдоА4'2"1!
начиная с
Ь, доАУ'"1Ь/
j] ди л ■ и, и т.д., пока
V| + v2 -Г... + v^ = n , где к <т ;
2) матрица Р выглядит следующим образом:
Р = [0,0,...,0,е1,0,...,0,е2,0,...,0,еу_1,0,...,0,е7+1,0,...,0,еь0,0],
где единичный вектор ej стоит на v} месте, е2 - (v,+v2) и т.д. Если
с = v, + v2 +v3 +... + v, > т , тогда все единичные орты, стоящие правее
столбца е, будут нулевыми, т.к. единицы в них появляются ниже т-й строки (см.
пример выше);
3) матрица G имеет вид
~ 0 0 ... 0
0 0 ... 0
G =
gj\ gj2
g
J>"
^0 0 ... 0
причем dim G = m x n .
Теперь рассмотрим другой подход модального управления для т > 1 [82, 113].
Алгоритм 2
В данном алгоритме модального управления, где исходная система (5.4) имеет
векторное управление (т>\) используется каноническое преобразование замкнутой
системы [82]. Предположим, что система (5.4) полностью управляема и в желаемом
спектре Л* выполняется условие Х*} ф\1 для/*у, i,j = 1,...,/?, т.е. жордановые клетки
матрицы замкнутой не имеют одинаковых собственных значений. Кроме того,
естественно потребовать, чтобы матрица В была матрицей полного ранга, т.е. rank В - т.
Напомним некоторые определения. Вектор R7 (соответственно L;) называется
правым {левым) собственным вектором матрицы А , если справедливы соотношения
AR,=XjRrj = ui, (5.31)
Ьт7А = ^Ьт7,у = ГЯ (5.32)
где Xj - собственное значение матрицы А. Сформируем 2 матрицы
R = [R,,R2,...,R/?]
и
Lj —
а-
Ll->
Глава 5. Модальное управление 269
которые соответственно состоят из правых и левых собственных векторов, причем
эти матрицы связаны условием
LR = RL = I, (5.33)
где I - единичная матрица размером п х п.
Стрелка -> подчеркивает, что левый собственный вектор L7 в матрицу L
входит вектор-строкой.
Пусть 9 = diag{X1 ... Хп) -диагональная матрица, состоящая из собственных
чисел матрицы А. Тогда выражения (5.31), (5.32) можно записать следующим
образом:
R8 = AR, (5.34)
0L = LA. (5.35)
Умножая (5.34) слева на L, а (5.35) на R с учетом (5.33), получим следующие
соотношения
9 = LAR, (5.36)
R8L = А. (5.37)
Из формул (5.34) - (5.37) получим для исходной системы (5.4) преобразованную.
Сделав замену переменных
X = RX, (5.38)
подставляя в (5.4) и учитывая из (5.33), что
L = R4, (5.39)
имеем
X(0 = eX(0 + LBY(/). (5.40)
Из условий управляемости следует, что в каждой строке матрицы LB существует
хотя бы один ненулевой элемент. Ненулевые элементы в строке LTyB информируют
нас о том, какими управлениями из У\,У29—>Ут-> образующими вектор Y, можно
изменять собственное значение А, матрицы А , соответствующее собственному векто-
ру Ц.
Пусть Х\, Х*2,...,Х*п - желаемые собственные значения замкнутой системы
Х(0 = (А + ВК)Х(/) (5.41)
и R*,R2,...,R* - соответствующие им правые собственные векторы. Тогда для
матрицы А + ВК замкнутой системы имеем
(A + BK)R* =A.*R*, (5.42)
или
(A-^I)R;=-BP7\ у=п, (5.43)
где
Р* = KR* j = ~n . (5.44)
- столбец размером т х 1.
Из уравнений (5.43), (5.44) определим неизвестные собственные векторы
R[,R2,...,R*, предварительно задавшись столбцами Pj*,P2,...,Py*. Нахождение
векторов R* и Р*, j = \,п зависит от того, является ли желаемое собственное значение
А,* собственным значением матрицы А или нет. Поэтому рассмотрим каждый
случай отдельно.
270 Методы синтеза САУ по заданным показателям качества. Часть II
1) Желаемое собственное значение X* не является собственным значением
матрицы А, т.е. det(A-A.*IW0. Тогда взяв любой ненулевой столбец Р* ^0,
но так, чтобы матрица Р была матрицей полного ранга (rank P = т) и
учитывая, что матрица В - матрица полного ранга (rank В = т), имеем
r* =-(a-x;.i)"1bp;, у=п,
р7 *о.
2) Х*; является собственным значением матрицы А , т.е. det(A-A,*Ij=O. Тогда
уравнение (5.43) будет иметь ненулевое решение относительно R*, если ранг
ее исходной системы будет равен рангу расширенной (теорема Кронекера -
Капелли), т.е.
rank(A-A.*l)=rank(A-X*I;-BPj). (5.46)
Если Lj - левый собственный вектор матрицы А , соответствующий
собственному значению X*, то, умножив слева (5.43) на L7,, получим:
Ъ](А-Х)1)К)=-Ъ]ВР]. (5.47)
Учитывая (5.32), имеем:
L](X]1)=X)L].
Тогда соотношение (5.47) примет вид:
L^BPj=0, (5.48)
или
QyPj=O, (5.49)
где обозначено Qy =L^B. Таким образом, все т -столбцы Р* должны для этого
случая удовлетворять соотношениям (5.49). В частности, здесь можно брать Р* =0.
Это означает, что при сохранении Xj в спектре замкнутой системы сохраняется и
соответствующий собственный вектор R*. Для систем со скалярным управлением
(w = 1) это имеет место всегда.
Получив весь набор собственных векторов R* (j = 1,л) и столбцов Ру (у = 1,л),
находим матрицу модального регулятора:
K = P*(RV, (5.50)
где р*=[р;,р2ф,...,?;].
Рассмотрим пример, который был решен ранее с использованием алгоритма 1.
Пример 5.4 (Алгоритм 2) (п = 3, /я = 2)
Итак, даны матрицы
Глава 5. Модальное управление
271
А =
"1
0
1
0
1
0
г
0
1
, в =
"1
0
0
0"
1
0
Спектр матрицы А ЛА = { 0 ; 1 , 2 }. Желаемый спектр Л* = {-1 , -2 , -3 }
Пара {А, В) управляема Это уже было показано Так как все собственные значения ЛА и Л*
различны, то для нахождения правых собственных векторов R* (у = 1, 2, 3) используем формулу (5 42)
Пусть Pj=[l 0] , у = 1,2 Тогда для Л.1* = — 1 имеем
r;=-(a-x;i)~'bp; =
Аналогично для А.2 = -2 получим
Т1
0
|_1
0
1
0
г
0
1
-
-1
0
0
0
-1
0
0"
0
-1
-1
1
0
1
0'
1
0
Til
-0,6667'
0
0,3333
-0,375"
0
0,125
Для Хз=-3 примем Р3* =[0 1] , чтобы матрица Р имела полный ранг 2 Тогда имеем
R-, =
0
-0,25
0
и R =
-0,6667
0
0,3333
-0,375
0
0,125
0
-0,25
0
Окончательно получим следующую матрицу коэффициентов-
"-0,6667 -0,375 0 "н
0 0 -0,25
0,3333 0,125 0
Проверим полученный результат Матрица системы с обратной связью
Г-4 0 -6
(А + ВК) =
• / .ч-1 П 1 01
-5 0 -7
0-4 0
0 -3
1 0
Спектр ЛА+ВК = {-1, - 2, - 3} = Л*, т е. модальный регулятор спроектирован верно
5.3. УПРАВЛЕНИЕ ОТДЕЛЬНЫМИ МОДАМИ
ПРИ ПОЛНЫХ ИЗМЕРЕНИЯХ
Рассмотрим задачу модального управления, в которой необходимо обеспечить
сдвиг собственного значения Хк матрицы А к Х*к , причем остальные собственные
значения остаются без изменения. Такая техника полезна при решении таких задач,
когда объект не является полностью управляемым, но он модально (по отношению к
Хк ) управляем и может быть стабилизирован с помощью модальной обратной связи.
Предположим, что все собственные значения матрицы А различны.
Алгоритм сдвига собственного значения Хк к желаемому Х*к основан на
следующей теореме.
Теорема 5.2. Для того чтобы в спектре матрицы А изменился корень Хк, а все
остальные собственные значения и правые собственные векторы, в том числе и Rk,
остались без изменения, необходимо и достаточно, чтобы строки матрицы
модального регулятора К были пропорциональны левому собственному вектору L^ матрицы
А , т.е.
272
Методы синтеза САУ по заданным показателям качества. Часть II
K = F,L', (5.51)
где F* - некоторый ненулевой столбец размерности тх\.
Доказательство. Нам необходимо показать, что существует непрерывный
путь, соединяющий матрицу А с А =А+ВК, если матрица К определяется
выражением (5.51), при этом Rj. = R^. Обозначим через RJ^ = R^ правый собственный вектор
собственных значений Хк матрицы A, a R^y) = R^ - соответственно матрицы А* для
По определению
(A + BK)Rj=X.X- (5-52)
Умножим слева левую и правую части (5.52) на левый собственный вектор \7к
матрицы А
L"J(A + BK)R;=^lJr;. (5.53)
Так как \7кА = Хк\7к , тогда имеем
(\;-^)lIr; = lt,bkr;. (5.54)
Если в выражение (5.54) подставить формулу (5.51), то получим
(\'к -Xk)\JkR'k = LjBFtLjR;. (5.55)
Когда Х*к = Хк , то R*k = R^ и \7кКк = 1. Но тогда в правой части (5.55) имеем
F*=0, что даст в соответствии с (5.51) К = 0.
При изменении Х*к (Х*к *Хк), произведение l[rJ^ =\(\<i<q) будет
постоянным согласно (5.33). Соотношение (5.55) будет выполнено, если можно подобрать
такой ненулевой столбец F^ , чтобы
X'k-Xk=LTkBFk. (5.56)
Это всегда можно сделать, если L^B * 0, что имеет место при модальной
управляемости по моде Хк . Таким образом, при выборе структуры регулятора вида (5.51) все
правые собственные вектора, включая R*, остаются неизменными, мода Хк сдвигается к
значению Х*к, если столбец F^ для (5.51) определяется из условия (5.56).
Пример 5.5. Рассмотрим пример, когда не имеет место полная управляемость, но существует
модальная управляемость. Итак, дано {п = 3, т = 2)
0,8571 8,8571 9,000'
-0,8571 -4,8571 -3,000
А =
1,000
в =
1
0,5714 2,5714
Спектр матрицы А ЛА = {0, -1, -2}
Необходимо сдвинуть корень Х\ = 0 к Х\ = -3
Составляем матрицу управляемости
Му =[b,,Ab,,A2b,,b2,Ab2,A2b2] =
-0,3 -0,2631
0,2 0,0526
0 0 0 1
0,0;0;-0,2631,-2
0 0 0 0,0526
1
-0,2631 1,4
O,O526J
-0,2631
0,0526
Ранг Mv = 1, т е система не является полностью управляемой
Находим правые собственные вектора матрицы А и составляем матрицу R
Глава 5. Модальное управление
273
R,
Ri
R =
. R2
l l l
-0,3 -0,2631 -1
0,2 0,0526 0,6667_
В соответствии с формулой (5 39) находим матрицу левых собственных векторов L
1,4287 7,1441 8,5727~|<-ЬТ
0 -5,4293 -8,1434
L = R1 =
-0,4286 -1,7148 -0,4243
Проверяем модальную управляемость
L[B = [1,4287 7,1441 8,5727]
1
1
-0,3 -0,2631
= [1 0],
0,2 0,0526
т е система модально управляема, т к LJB * 0 Подставим найденные матричные данные в формулу (5 56)
(-
(-3)-(0) = [l 0]F,=[l О][Д'] = /Г||-
Откуда Fu = -3, a Fu может быть любым, например F2i=0, тогда столбец Fi имеет вид
«■И
Полученный столбец F| позволяет найти матрицу модального регулятора
K = F,Lf= [1,4287 7,1441 8,5727] =
' Г-4,2861 -21,4323 -25,71811
~|_ о о о * }
что определяет матрицу замкнутой системы
"-3,4290 -12,5752 -16,7181
А =А+ВК=
0,4287 1,5725
-0,2850 -1,7150
4,7154
-4,1436
которая имеет следующий спектр Лд. ={-3,-1,-2} и Лд. совпадает с желаемым спектром Л*
Замечание 5.2. Если необходимо сдвинуть две и более моды, процедуру,
рассмотренную выше, необходимо проводить итеративно, сдвигая каждый раз по одной
моде, т.е.
А -> А* = А + ВК, -> А*2 = А* + ВК2 -> ... -> А*^ = А*р_} + ВК^ ,
и общая матрица модального регулятора К определяется выражением:
к = £к,,
(5.57)
/=1
где 1 <р<п-число сдвигаемых мод.
5.4. ОПТИМАЛЬНОЕ МОДАЛЬНОЕ УПРАВЛЕНИЕ
ОДНОЙ МОДОЙ ПРИ ПОЛНЫХ ИЗМЕРЕНИЯХ
Если в строке L[ В имеется более одного ненулевого элемента, при сдвиге моды
Хк = Х*к возникает неоднозначность в выборе столбца F^ . Эту неоднозначность
можно использовать для вывода оптимального модального управления с точки
зрения минимизации энергетических затрат по переводу моды Хк в Х*к . В качестве
целевой функции используем следующую квадратичную функцию
19 3ак 366
274 Методы синтеза САУ по заданным показателям качества. Часть II
т т
где ач > 0 - весовые коэффициенты матрицы усиления К модального регулятора.
Необходимо минимизировать функцию J по KtJ (/=1,..,/и,/=1,..,/и) при соблюдении
линейного ограничения:
-k\--kk=\}kWk. (5.59)
В выражении (5.58) число оптимизируемых параметров KtJ равно тхп . Но, с
другой стороны, матрица К определяется из соотношения (5.51):
K = F*LJ. (5.60)
Так как левый собственный вектор \7к матрицы А определяется самой матрицей,
тогда число оптимизируемых параметров в выражении (5.60) остается равным
dim F^ , т.е. т. В соответствии с этим, подставив формулу (5.60) в (5.58), получим
т п т п
/=1 7=1 1=1 7=1
Ограничение (5.59) представим в следующем развернутом виде:
/=i ч
где
Ql=LT,B. (5.63)
После этих преобразований задача оптимизации состоит в следующем.
Необходимо найти столбец (т + \) коэффициентов ¥ik (i = \,m), минимизирующий
функцию (5.61) при линейных ограничениях (5.62).
Эту задачу решим методом неопределённых множителей Лагранжа. Составим
функцию Лагранжа:
т п ( т \
£ = £Ea,4,FJ+J *;-А*-£йЛ , (5.64)
/=17=1 V /=1 )
где \\f -множитель Лагранжа для ограничения (5.62).
Условие минимума (5.61) при ограничении (5.62) - стационарность функции С
по оптимизируемым параметрам Fik , т.е.
дС =0,/ = ui. (5.65)
dFik
Формула (5.65) и ограничение (5.62) дают следующую систему (w + 1) линейных
уравнений относительно F*k (/ = 1,/и) и vj/:
£a942F*k - Wb = 0, ' = UJ, (5.66)
т
K~h=I,Qk,K- (5-67)
/=1
Учитывая простоту этих уравнений, их решение можно получить аналитически.
Пусть в т -й строке Qj для некоторого / = / (1 < / < т) элемент Qkl * 0. Выразим из
(5.66) для / = / множитель vj/:
Глава 5. Модальное управление 275
ЁчАК
v^=-ZzL- . (5.68)
Qki
Подставляя вместо vj/ правую часть (5.68) в уравнение (5.66), получим:
2£а<,4й п F*& =0' (569)
7=1 Ук1
где / = I, т и i' ФI.
Из (5.69) найдём оптимальные значения параметров в т -столбце Fk :
п
К = V Fl = Р,*^ , (5-70)
где i = \,m и / ^/, а
7=1
причём (3/А: = 1.
Из выражения (5.70) видим, что (w-1) коэффициент /<£ линейно зависит от
коэффициента F/^ , который мы определим из линейного ограничения (5.67).
Подставляя в уравнение (5.67) вместо F*k правую часть (5.70), получим:
т
^-Ь*=ЕШМй- (5-72)
/=1
Откуда:
F^=^^. (5.73)
"ЕйиРл
/=1
Таким образом, алгоритм нахождения оптимального столбца F^ и соответственно
оптимальной матрицы К* при переводе моды Хк матрицы А к моде Х*к следующий:
1 шаг. По заданным матрицам А и В определяем левый собственный вектор \Jk
матрицы А и условие модальной управляемости по моде Хк: L^B = Qj ф 0.
2 шаг. Выбираем произвольный ненулевой элемент строки Qkl ф 0. Заметим, что
если такой элемент единственный, то задача оптимизации отсутствует, т.к. F^
определяется однозначно.
3 шаг. Из соотношений (5.71) находятся элементы $ik , / = 1,т, / * I, Рд, = 1.
4 шаг. Из формулы (5.73) находим F*k .
19*
276
Методы синтеза САУ по заданным показателям качества. Часть II
5 шаг. Из выражения (5.70) находим Flk, / = 1,/и , / * /.
6 шаг. По формуле (5.60) определяем К*.
Пример 5.6. Пусть матрицы А и В объекта управления имеют вид
"1
0
1
0
1
0
г
0
1
, в =
"1
1
0
г
0
1
А =
Кроме того, заданы весовые коэффициенты матрицы К
п п Г1 2 °'31
1Ы = Ь 0,5 8J
Спектр матрицы А ЛА={0,1;2} Необходимо перевести корень Х3=2 в Х*3=-2 и при этом
минимизировать функцию (5 61)
Решение.
1 Находим матрицу левых собственных векторов*
l=lt;->
0,5 0 -0,5
0 1 0
0,5 0 0,5
и проверяем условие Х3 ~ модальной управляемости
l5b = qJ=[O,5 l]*0,
те объект модально управляем, причём оптимизация по примеру (5 61) возможна, тк строка Qj имеет
несколько (в данном случае 2) ненулевых элемента
2 Выбираем элемент (?31 = 0,5 , т е / = 1
3 Р,з=1,
з
^""^О (1 0,52 + 2 О2+0,3 0,52) ,
2>ЙЛ "(' °>52+0>5 °2+8 о-52)^1
4 Определяем fj3
Ъ=-,
^з-^з
-2-4
-=-5,0704
"■■4 «-KS:^ • »i-k;
Р.з2з1 + Р2зез2 1-0,5+ 0,28891
5 Находим оставшиеся элементы столбца F3
F2*3 = p23 F,*3 = 0,2889 (-5,0704) = -1,4648
6 Определяем матрицу оптимальных коэффициентов модального регулятора
f-2,5352 0 -2,5352^
',7324 0 -0,7324J
Проверим, что модальное управление проведено правильно Матрица
(-2,2676 0 -2,2676^
А* = А + ВК*= -2,5352 1 -2,5352
[ 0,2676 0 0,2676j
имеет спектр Лд. ={0,1,-2}, те матрица К* * найдена верно Определим значение функции J для
найденной матрицы К*
^=EZa'X=13'1831
Заметим, что если для выданных весовых коэффициентов ||а;у|| и матрицы Q3T выбрать другой
неоптимальный столбец F3, также переводящий d3 -> d\, то значение целевой функции J будет больше
Например, если
Г-41
F3=| |,то J = 14,2>/
Глава 5. Модальное управление 277
5.5. МОДАЛЬНОЕ УПРАВЛЕНИЕ ПРИ НЕПОЛНЫХ ИЗМЕРЕНИЯХ
Рассмотренные выше алгоритмы модального управления получены из условия,
что доступны для измерения все коэффициенты вектора состояния, что на практике
случается редко. Поэтому важно получить алгоритмы модального управления для
объектов, где не все компоненты вектора X доступны непосредственному
измерению. Ясно, что в этих случаях необходимо синтезировать устройство для получения
оценок X вектора состояния, т.е. построить наблюдатель.
Модальное управление с наблюдателем полного порядка. Рассматривается
задача модального управления для объекта управления с уравнением состояния
Х(/) = AX(O + BY(O,X е R\\e Rm (5.74)
и уравнением выхода
Хв(0 = СХ(/), Хв е RCJ < п , (5.75)
требуется построить модальный регулятор
Y(/) = KX(0, (5-76)
который обеспечит заданное расположение корней замкнутой системе (5.74), (5.75).
Оценку Х(/) вектора состояния получим на выходе наблюдателя полного порядка,
динамика которого описывается уравнением [57]
Х(/) = (А - КНС)Х(О + КНХВ(О + BY(0, (5.77)
где Кн - матрица (я х/) коэффициентов наблюдателя. Обозначим выбранный
характеристический полином наблюдателя полного порядка ф* (к):
9*(A,) = det(A-KHC-M). (5.78)
Так как вектор Х(/) недоступен для измерения, то попробуем заменить в цепи
обратной связи вектор X(t) на его оценку X(f). Многочлен ср* (к) можно выбрать по
своему усмотрению и тем самым получить произвольную динамику стремления
оценки X(f) к X(t) при / -» оо . При такой замене основной интерес представляют
два вопроса: 1). Матрица К выбрана в предположении, что известно состояние X(t),
а потом вектор состояния заменим его оценкой Х(/). Получится ли прежний
регулятор? Другими словами, будет ли система с обратной связью по-прежнему иметь
желаемый характеристический полином ф (к) ? 2). Какой эффект вносит в систему
наблюдатель? Оказывается, что выбранные характеристические числа системы с
обратной связью по состоянию и характеристические числа (собственные значения)
наблюдателя войдут в замкнутую систему без изменения. Справедлива следующая
теорема.
Теорема 5.3. Пусть дана полностью управляемая и наблюдаемая система (5.74),
(5.75). Пусть матрица К выбрана так, что спектр матрицы А+ВК совпадает с
желаемым Л , т.е. характеристический полином Фа+вк(^) = Ф (^)» и ПУСТЬ выбрана
матрица коэффициентов наблюдателя Кн, такая, что характеристический полином
матрицы А-КНС совпадает с желаемым полиномом ф* (к). Тогда характеристический
полином замкнутой системы (5.74), (5.77) (с учетом (5.75) и (5.76)) 2я-порядка
Х(/) = АХ(0 + ВКХ(0, (5.79)
Х(0 = (А - КНС)Х(О + ВКХ(0 + КНСХ(О, (5.80)
278 Методы синтеза САУ по заданным показателям качества. Часть II
который обозначим через щ(к), совпадает с произведением выбранных многочленов
Ф0(^) = Ф*(Х).ф*н(Х). (5.81)
Доказательство. Представим уравнения (5.79), (5.80) в виде системы 2л-порядка
Ж')) LK"C a-khc+bkJ[x(/)J 1x(/)J
= А° • k ; . (5.82)
Сделаем следующую невырожденную замену координат
LE(t)J 1x(oJ Li -УЖО.
(5.83)
где Е(/) = X(f) - X(t), I - единичная матрица размерности п х п. В новых
переменных:
Г*«1 РАор-|Гх(')1 рГ а вк 1,Гх«1_
[e(oJ LE«J LK«c a-khc+bkJ \m\
A + BK -ВК |Х(ОЪАооГХ(0|
Так как матрица преобразования Р невырожденная, то матрицы А00 и А0, свя-
• занные выражением
дОО = рдОр-1 ? (5 85)
подобны и, следовательно, имеют одинаковый характеристический полином, т. е.'
ФА- (М = Фа" (Х) = Фо (^) = Ф* (^)Фн (*) • (5-86)
Что и требовалось доказать.
Формула (5.86) имеет важное значение, т.к. позволяет задачу модального
управления с наблюдателем разделить на две независимые подзадачи:
1) построение модального регулятора;
2) построение наблюдателя полного порядка.
Решение 1-й подзадачи было рассмотрено выше, где можно использовать
алгоритмы 1 или 2 или провести оптимальный выбор коэффициентов К модального
регулятора. Что же касается 2-й подзадачи, то здесь для нахождения матрицы Кн
можно воспользоваться принципом дуальности для управляемости и наблюдаемости,
установленным Р. Калманом [31].
Пусть даны две системы, из которых одна описывается уравнениями
fX(0 = AX(/) + BY(0, (
_х.(О = сх(о,
а другая уравнениями
jz(o = ATz«+cTv(o, (588)
[g(/) = btz(0.
Такие системы называют двойственными, или сопряженными друг другу.
Очевидно, что условие
rank[B;AB;...;Aw-1B] = A7
является условием полной управляемости системы (5.87) и одновременно условием
полной наблюдаемости системы (5.88), а равенство
rank[cT;ATCT;...;(ATr'CT] = «
Глава 5. Модальное управление 279
- условием полной наблюдаемости системы (5.87) и одновременно условием полной
управляемости системы (5.88).
Воспользуемся этим принципом дуальности, чтобы задачу нахождения
коэффициентов Кн наблюдателя свести к задаче модального управления. Для этого во
вспомогательной задаче (5.88) необходимо найти такую матрицу коэффициентов
обратной связи Кн
V(0 = -KjZ(/), (5.89)
чтобы матрица (ат-СтК^| имела характеристический полином
ФАт_сткт (X) = ФА_К с(М » совпадающий с желаемым ф* [X). А это и есть задача
модального управления. И к ней можно применить все рассмотренные выше алгоритмы
синтеза.
Таким образом, задача синтеза алгоритмов модального управления с наблюдателем
полного порядка сведена к двум независимым подзадачам модального управления:
1) нахождение матрицы коэффициентов К управления с обратной связью
Y(/) = KX(0 системы (5.87), обеспечивающие желаемый полином замкнутой
системы ф* (X);
2) определение матрицы коэффициентов Кн управления с обратной связью
V(t) = -K^Z(/) системы (5.88), обеспечивающей желаемый полином
замкнутой системы ф* (X).
280 Методы синтеза САУ по заданным показателям качества. Часть II
ГЛАВА 6. СИНТЕЗ ГРУБЫХ СИСТЕМ
АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
В ПРОСТРАНСТВЕ СОСТОЯНИЙ
При управлении многомерными динамическими объектами часто встречаются
задачи, когда цель управления может быть сведена к некоторым ограничениям на
вектор состояния объекта. К таким задачам, в частности, могут быть отнесены:
• обеспечение программного режима движения объекта управления на этапе
проектирования системы автоматического управления объектом (задача про-
' граммного управления и стабилизации);
• перевод объекта из одного начального заданного множества в другое конечное
заданное множество (задача терминального управления);
• обеспечение допустимого (заданного) качества переходных процессов в
системе управления объектом;
• обеспечение принадлежности динамических характеристик системы
автоматического управления объектом заданному множеству в пространстве
состояний (задача управления фазовыми потоками (пучками траекторий),
определяемыми ограничениями в пространстве состояний).
Характерной особенностью подобных задач является то, что они формулируются
в терминах пространства состояний объекта. А это, в свою очередь, означает, что для
перечисляемых задач цель управления может быть сформулирована и представлена в
виде фазовых ограничений (т.е. в виде ограничений на координаты вектора
состояния). Предлагаемый метод фазовых ограничений позволяет для многомерных
динамических объектов синтезировать управление, обеспечивающее выполнение
заданной цели, которая может быть представлена в виде ограничений на вектор состояния
объекта.
6.1. КОНЦЕПЦИЯ ФУНКЦИОНАЛЬНО-МНОЖЕСТВЕННОЙ
ПРИНАДЛЕЖНОСТИ
В этой главе рассмотрены некоторые свойства и определения пространства
состояний. Вводится понятие меры близости и окрестности множества. Исследуются
способы задания окрестностей множества, а также их свойства в зависимости от
определения меры близости.
Приводятся модели систем управления и подходы к заданию возможных
неопределенностей. Показывается формирование общей цели управления для различных
задач синтеза и формулируется концепция ^функционально-множественной
принадлежности.
6.1.1. Понятие окрестности множества и функции или меры близости
Пусть рассматривается некоторое векторное нормированное метрическое
пространство Н с введенными на нем нормой Ц и метрикой ря (•), обладающими
всеми необходимыми свойствами [60, 145]. В этом пространстве Н предполагается
заданным некоторое замкнутое множество Q, т.е.
gctf.
Причем
Глава 6. Синтез грубых систем автоматического управления 281
FQ*0 и YQ<oQ. (6.1)
Введем понятие окрестности множества в пространстве Я. С этой целью введем в
рассмотрение некоторый функционал, называемый мерой близости или функцией
близости в Я.
Определение 6.1. Функционал y.H(h\h2), определенный для любых h\h2 еН
(D^ -HxH), будем называть мерой близости или функцией близости между
элементами A1, А2, если для него выполняются условия:
1. ц//(Л1,Л2)>0 Vh\h2eH при /г1*/*2; (6.2)
2. |дя(А\А2) = 0 при А!=А2. (6.3)
Нетрудно видеть, что мера близости ця() обладает более широкими свойствами,
чем метрика рИ (•), и поэтому ей соответствует более широкий класс функций,
удовлетворяющих свойствам (6.2), (6.3).
В частности, всегда в качестве \хн (•) можно выбрать функцию рн (•), т.е.
М-) = Ря(0. (6-4)
На основе ця(0 можно ввести s-окрестность произвольного элемента ИеН вида
О*(А) = {АеЯ: ММ)<е}, (6-5)
представляющую собой некоторое открытое множество в Я, все элементы которого
удалены от А в смысле меры близости \iH (•) не более чем на некоторую величину г .
Через O*(h) обозначим замкнутую 8-окрестность heH в смысле меры (iw(). Тогда
ГС£(А)сО*(/0,
где
ГО£(Л) = {ЛбЯ:ци(А,А) = б}. (6.6)
Используя введенную меру близости |ая()> можно задавать 8-окрестности
произвольных замкнутых множеств в пространстве Я. С этой целью вначале введем в
рассмотрение меру близости элемента h от замкнутого множества Q, которую
обозначим Ц//(А,0.
Определение 6.2. Функционал Д#(^>0» определенный для произвольного
замкнутого множества Q с Я и любого элемента А е Я , будем называть мерой близости
между элементом А и множеством £)> если для него выполняются условия:
1.Д//(Л,0>О VheH при Аг£; (6.7)
2.ЦЯ(Л,0 = О VheQ. (6.8)
Свойства (6.7), (6.8) позволяют задавать достаточно широкий класс функций,
используемых в качестве Ця (•). В частности, можно положить
ця(А,0 = т1п ця(А,А). (6-9)
heQ
Нетрудно видеть, что данная мера удовлетворяет услозиям (6.7), (6.8), которые
соответственно следует в силу соотношений (6.2), (6.3). Действительно, если hzQ,
то, согласно (6.2), \хн (А, А) > О У heQ, и потому
min а я (А, А) >0.
heQ
Если же A g Q, то в силу (6.3)
1Я 'З-а^ *5«ft
282
Методы синтеза САУ по заданным показателям качества. Часть II
min \iH(h,h) = \iH(h,h) = O.
he(J
В качестве \iH(-) в соотношении (6.9) согласно (6.4) можно выбрать, например,
одну из метрик. Вид функции £#(•) ,очевидно, при этом будет определяться не
только свойствами функции Ц//0) , но также и свойствами замкнутого множества Q.
Используя меру близости \xH(h,Q), введем понятие е-окрестности множества Q в
пространстве Н.
Определение 6.3. е-окрестностью множества Q в пространстве Н в соответствии с
мерой близости \хн{-) называется множество O^(Q) вида
(%{Q) = {heH: ]xH(h,Q)<s}. (6.10)
Очевидно, что Q с 0ц(0 и O^(Q) - открытое множество в Я. Тогда под
замкнутой с-окрестностью Q будем понимать множество
&=СШ) = {Л€Я:ц„(Л,0<е}
(6.11)
с граничными элементами h, образующими границу TQe. Для Qt справедливо
также следующее представление:
ее={Л = ^(Л,5): 5<s, heTQ]. (6.12)
Необходимо также отметить возможность использования в качестве меры \хн (•)
не функций, а некоторых функционалов.
На рис. 6.1 показано формирование е-окрестностей для пространства R2.
х2
ГЯ ^
8,<69
Рис. 6.1. 6 -окрестности множества Q
В дальнейшем для границы TQh будем использовать наименование е-окрестности
множества Qt .
6.1.2. Модели рассматриваемых объектов управления
в пространстве состояний
Будем считать, что объекты управления, рассматриваемые в арифметическом
пространстве R" , являются динамическими и в общем случае могут быть как
линейными, так и нелинейными, а также как стационарными, так и нестационарными.
В общем случае можно считать, что уравнения состояния объекта управления
представляют собой обыкновенные дифференциальные уравнения, которые
приводятся к нормальной форме или*к форме Коши [98, 128] и имеют вид
Глава 6. Синтез грубых систем автоматического управления 283
(6.13)
гуп+m + t +<:/ + !
V
_V
, и =
~щ '
, W =
, Р =
_Р</_
, а =
x = /a(x,u,w,p,/),j
х(/0) = х0,/>f0, ]
где х - /7x1 вектор состояния объекта; и - тх\ вектор управления; w - rxl вектор
возмущений; р - dx\ вектор параметров объекта; a - пх\ вектор индексов,
компоненты которого могут принимать произвольные вещественные значения из /?'; /"(•)
- некоторая пх\ вектор-функция, обеспечивающая существование и единственность
решения задачи Коши [98], с областью определения D,, с R"
Пусть
Тогда под /а(-) понимается следующее выражение
/aO = [yia'(x,u,w,p,0, ...,/wa-(x,u,w,p,/)]1 , (6.14)
где каждая компонента ai9ie\,n принимает значения из некоторого заданного
множества At a R], / е 1, п , т.е.
a, e A{, ie\,n. (6.15)
При этом
аеА. (6.16)
Предполагается, что в зависимости от значения а, компонента /а'(0 принимает
то или иное соответствующее выражение. Обозначим через Ft - множество
возможных выражений функции f^ (•) в зависимости от значения параметра а,, т.е.
Ff ={/«•(.): ахеА,}. (6.17)
В дальнейшем множество F, будем называть внешней шкалой структур для
функции у;а' (•).
Очевидно, для задания множества возможных структур функции /а() можно
воспользоваться метрикой или введенной выше' мерой близости в пространстве
функций.
Необходимо также отметить, что задание структур может осуществляться в
задачах формирования (проектирования) САУ (объектов управления), когда возможен
неоднозначный выбор структуры одного и того же объекта, и это необходимо учесть.
А задание структур целесообразно осуществлять в задачах управления при
неопределенности по структуре объекта.
6.1.3. Величины в уравнениях состояния объекта,
описание, допущения и ограничения
Рассмотрим те ограничения и предположения, которые используются о векторах
x,u,w,p в уравнении состояния объекта (6.13). Вектор состояния х должен
принимать ограниченные по норме значения в R" . Обычно предполагается, что для этого х
удовлетворяет следующим ограничениям. Пусть в Rn+] определены функции
ограничения v|/7(x,/), j e l,x, непрерывно-дифференцируемые по всем своим аргументам.
284 Методы синтеза САУ по заданным показателям качества. Часть II
Тогда формируется замкнутое множество Q(t) вида
Q(t) = {xeRn: i|/7(x,/)<0,y еп}, (6.18)
которое определено для каждого t>t0 на всем интервале функционирования объекта
(6.13). И также определены на этом интервале множества int Q(t\ TQ(t), TQ} (t), j e l,x .
В дальнейшем множества Q(t) обычно будем считать ограниченными.
Пусть в R" задана некоторая непрерывно-дифференцируемая пх\ вектор-
функция ф(х), т.е.
<р: R" -+R" и ф(х)=хеЛ". (6.19)
Тогда под ограничениями (или фазовыми ограничениями) на вектор состояния х
в пространстве R" будем понимать соотношение
ф(х)€б(О V/>/0. (6.20)
Заметим, что в качестве ф() могут использоваться не только вектор-функции, но
также и операторы определенного вида, являющиеся диффеоморфными
отображениями.
Рассмотрим характер ограничений, накладываемых на вектор управления. Пусть в
пространстве Rm задано некоторое замкнутое, в общем случае, неограниченное
множество U(t) допустимых значений вектора управления. Тогда ограничение на
значения вектора и имеет вид
ueU(t\t>t0. (6.21)
Часто требуется учитывать ограничения не только на значения, но и
непосредственно на вид (на структуру) формируемого алгоритма (закона) управления. С этой
целью можнб воспользоваться так называемыми шкалами сложности [14, 124, 134],
формируемыми по признакам сложности, характеризующими уровень сложности
структур синтезируемых законов управления.
Считаем, что в достаточно общем случае закон управления можно представить в
виде
u = uY(x,/), (6.22)
где uY(-) -некоторая тх\ вектор-функция заданного вектора, который
определяется выбором параметра у. О параметре у предполагается, что это некоторый g x 1
векторный параметр, значения которого характеризуют сложность структуры
соответствующего закона управления. При этом сложность можно понимать, как в смысле
сложности технической реализации согласно [14, 124, 134], так и в более широком
смысле - как некоторый признак или свойство, позволяющий упорядочить структуры
законов управления по тем или иным математическим характеристикам.
Пусть
G = {Gv}l,QRg (6-23)
- заданное множество значений параметра у, a Gv, v е 1, р - его подмножества. Тогда
шкала сложности по структуре управления имеет вид
P = {pvCi> (6.24)
где pv, v е 1, /7 - элементы шкалы сложности, представляющие подмножества вида
pv={uYQ: yeGy},vel^. (6.25)
лава 6. Синтез грубых систем автоматического управления 285
При этом р можно рассматривать, как внешнюю шкалу, a pv, ve\,p - как
нутренние, элементы которых допускают параметризацию. Возможно также, что р
- шкала сложности Iгорода [134], т.е. когда
рх ар2 с ... срг, (6.26)
\nw-2го рода, если
Pvil>v2=0 Vv,^v2Gi^. (6.27)
Тогда ограничения на структуру закона управления имеют вид
u = uY(-)Ep = jur(-): YgG}.
Рассмотрим ограничения на вектор возмущения w . В достаточно общем виде
:лучаи ограничения на вектор w можно представить, как ограничения на множество
допустимых значений w , т.е.
weW(t)aRr, t>tQ, (6.28)
где W[f) - заданное в Rr замкнутое ограниченное множество. Задать W(t) можно,
например, одним из следующих способов.
Пусть
некоторая заданная в Rr вектор-функция. Тогда:
1. ЩО = {w € Rr: |w, -w?\< %t (/), t > t0 J, (6.29)
где £,(/), /el,r - скалярные неотрицательные функции.
2.W(t) = \yv<=Rr: (w-w°(0,V(O-(w-w0(O))<i;(O, /S/o}, (6.30)
где \(t)>0 - rxr матрица; ^(/) -скалярная»неотрицательная функция;
3. W = {weH: ||vv-w°|| <^°1, (6.31)
где ^° > 0 - скалярная величина; | -||я - одна из возможных норм в векторном
нормированном пространстве Н.
Кроме указанных способов задания множества W(t) (6.29) - (6.31) может
использоваться также следующий подход. Предполагается, что возмущения, действующие на
объект управления, могут быть представлены в параметрической форме, т.е.
w = w(u,0, (6.32)
где w(),- некоторая гх\ вектор-функция заданного вида, являющаяся кусочно-
непрерывной и необходимое число раз дифференцируемой на интервале
функционирования объекта; и - / х 1 векторный параметр, значения которого могут изменяться
в пределах некоторого заданного R1 множества V, т.е.
иеК. (6.33)
Тогда для данного случая
W = lV(t) = {w = \v(uJ): ueV},t>t0. (6.34)
Рассмотрим ограничения на вектор параметров Р в уравнении состояния (6.13). В
достаточно общем случае можно считать, что допустимые значения dx\ параметра
р должны удовлетворять соотношению
286 Методы синтеза САУ по заданным показателям качества. Часть II
ре Я, (6.35)
где В - некоторое заданное в Rd множество.
При этом Р предполагается фиксированным на всем интервале функционирования
объекта, а соотношение (6.35) характеризует возможную параметрическую
неопределенность задания данного объекта.
6.1.4. Формирование цели управления
Для класса динамических объектов, описываемых уравнениями типа (6.13),
актуально решение следующих задач:
• перевод объекта из одного начального заданного множества So a R" в другое
конечное заданное множество Sk с R" . При этом допустимы ограничения на
время перевода. Это, так называемые, задачи терминального управления [34,
151];
• обеспечение программного режима движения объекта управления на этапе
проектирования системы автоматического управления (САУ) объектом. Это -
задачи программного управления и задачи стабилизации [122];
• обеспечение допустимого (заданного) качества переходных процессов в
системе управления объектом [89, 104];
• обеспечение принадлежности динамических характеристик САУ объектом
заданному множеству в пространстве состояний. Это, в основном, задачи
управления фазовыми потоками (пучками траекторий или потоками траекторий),
определяемыми фазовыми ограничениями в пространстве состояний [90, 123].
Характерной особенностью данных задач является то, что они формулируются в
терминах пространства состояний объекта или системы управления (СУ) и,
соответственно, требования к их выполнению (разрешимости) сводятся к тем или иным
эквивалентным требованиям, которым должен удовлетворять вектор состояний САУ. А
это, в свою очередь, означает, что для перечисленных классов задач цель управления
может быть формализована и представлена в виде тех или иных ограничений на
вектор состояния, т.е. в виде фазовых ограничений.
Действительно, пусть рассматривается задача 1, т.е. если при t = /0 х(/0) = х0 е So,
(причем х0 может быть произвольным элементом из So), то при / = tk (где tk -
необязательно задано) необходимо, чтобы \{tk)-\ eSk . Тогда заданное требование
можно представить в виде задачи по обеспечению фазовых ограничений следующим
образом.
Пусть Q* (/) с R" - такое множество, что для него выполняются условия:
1.5ос0Ч'о);
2. 3/ = Z1 > /0 такое, что
Q*(t)f)Sk*0 при fe[/V],
где /2<оо и tk e
,[^1
в частности, можно потребовать,
чтобы
Q\t)QS'k при*е|7,*2].
Тогда, вводя обозначение
(6.36)
Глава 6. Синтез грубых систем автоматического управления 287
6(0 =
Q\tlte[tQ,t1];
(6.37)
2*(0П^,/е[/\/2],
задачу 1 приведем к виду
x(t)eQ(t)9t>t0. (6.38)
Рассмотрим задачу 2. Пусть программный режим движения характеризуется
некоторой траекторией x*(t), которая с достаточной степенью точности должна быть
воспроизведена объектом (6.13). Пусть o(x*(t)) - некоторая замкнутая окрестность
траектории х*(/), определенная для всех / > /0 и содержащая все свои граничные
элементы. Окрестность Оух*(т = О*(t) задана в одной из рассмотренных выше метрик
пространства R" . Тогда, задавая приемлемые размеры данной окрестности, можно
считать, что траектория х*(/) воспроизводится с требуемой точностью, если объект (6.13)
в произвольной точке окрестности О* (О. Тогда задача 2 приводится к виду
x(t)eQ*(t),t>t0. (6.39)
При этом, когда задача 2 является задачей стабилизации, то программная
траектория х* (/) ее О е R" , а объект (6.13), как правило, - линеаризованный.
В задаче 3 качество переходных процессов определяется видом некоторой
области D(t), заданной в пространстве состояний R" на основе требуемых значений
показателей качества САУ. В этом случае задача 3 непосредственно сводится к
соотношению
x(/)eD(0, t>t0. (6.40)
Рассмотрим задачу 4. Пусть
X(t) = {x(t): x(to) = xoeXo}, (6.41)
где Хо - заданное замкнутое множество в R" , х(/) - множество значений пучка
траекторий, выходящих из множества Хо, в текущий момент времени /. Тогда задача
управления пучком траекторий состоит в обеспечении соотношения
X(t)eQ(t\ t>t0, (6.42)
где Q{t) - заданное замкнутое множество в R" , или, что то же самое,
x{t)eQ(t\ Vx(/o) = xoeXo, />/0. (6.43)
Вообще говоря, если динамические характеристики САУ могут быть
представлены через свойства траекторий х(/) объекта (6.13), то обеспечение ограничений на
данные характеристики также сводятся к некоторым фазовым ограничениям.
Таким образом, решение приведенных выше четырех задач сводится, собственно,
к обеспечению соотношений (6.38) - (6.40), (6.42), (6.43), которые представляют ни
что иное, как ограничение на переменные состояния объекта управления. Поэтому в
достаточно общем случае можно утверждать, что для широкого класса задач
управления, рассматриваемых в пространстве состояний, цель управления может быть
представлена в следующем виде
x(t)eQ(t), />/0, (6.44)
где Q(t) d Rn - заданное замкнутое множество.
288 Методы синтеза САУ по заданным показателям качества. Часть II
Соотношение (6.44) может быть обобщено и представлено следующим образом
Фо(х(0)е&(0, t*t09 (6.45)
где фо(-) -заданная пх\ вектор-функция, непрерывно-дифференцируемая в R" ;
Q0(t) с: R" - заданное замкнутое множество для всех t > /0.
6.1.5. Формирование концепции функционально-множественной
принадлежности (фмп) на элементах пространства состояний
В соответствии с изложенным в предыдущем параграфе, задача управления
объектом (6.13) состоит в обеспечении ограничений на вектор состояния, которые
сводятся к соотношению (6.44) или (6.45), характеризующему принадлежность в
пространстве Rn заданному множеству и называемому соотношением
принадлежности. При этом о самом объекте (6.13) предполагается, что при его задании возможна
параметрическая неопределенность вида (6.35), а также неопределенность при
описании структуры объекта либо в соответствии со шкалами структур (внешней и
внутренней), либо на основе множества структур, ограниченных по норме. Кроме того,
должны выполняться ограничения на вектор состояния (6.20) и вектор управления
(6.21), (6.27) при действии возмущений вида (6.28) - (6.34).
Поскольку цель управления (6.45) так же, как и ограничения на вектор состояния
(6.20), представляет собой ограничения на вектор х, то, считая данные ограничения
совместимыми, приведем их к единому виду
ф(х) = ф(х(0)еб(0, />'о> (6-46)
где пх\ непрерывно-дифференцируемая вектор-функция ф(-) и множество Q{t)aRn
выбраны так, чтобы из выполнения соотношения (6.46) следовала бы справедливость
соотношений (6.20) и (6.45).
Таким образом, для объекта управления (6.13) с возможными
неопределенностями по структуре, параметрам, возмущениям указанного вида решается задача
обеспечения соотношения принадлежности, приводимые к единому виду (6.46).
При реализации соотношения (6.46) необходимо учитывать следующие особенности:
• точное задание множества Q(t) и функции ф(х) во многих практически
важных случаях часто оказывается невозможным. Это обусловлено тем, что
обеспечение тех или иных ограничений обычно допускается с некоторой степенью
точности;
• при использовании математической модели объекта управления возможны
неопределенности по структуре и параметрам модели, а также по возмущениям
со стороны окружающей среды;
• существенные трудности, а иногда и невозможность обеспечения заранее
заданных ограничений. Это связано с тем, что задание тех или иных
ограничений, исходя из технических требований, накладываемых на задачу, обычно не
учитывает вид модели объекта управления (динамику объекта). Данное
обстоятельство и приводит к трудности обеспечения ограничений.
Таким образом, указанные особенности характеризуют трудности при реализации
соотношения принадлежности (6.46) для объекта (6.13). При этом невозможность
учета динамики объекта, а также неопределенность описания его модели приводит к
необходимости некоторого изменения ограничений для обеспечения их
разрешимости. Следовательно, для обеспечения цели управления, сводящейся к ограничениям
на вектор состояния, целесообразно соотношение (6.46) видоизменить так, чтобы
допускалась неоднозначность выбора данных ограничений непосредственно из зада-
Глава 6. Синтез грубых систем автоматического управления 289
ния цели управления (соотношения принадлежности). Для этого воспользуемся
введенным выше понятием е-окрестностей множеств в пространстве состояний.
Допустим, что при / = /0 вектор х(/0) = х0 удовлетворяет условию
ф(хо)е&о(/0), (6.47)
где £?Ео(Уо) ~ 8о -окрестность множества Q(t0), соответствующая некоторой
достаточно малой скалярной величине
80=е(х0)>0. (6.48)
Причем, согласно (6.48), для каждого х0 определена, вообще говоря, своя
величина е0, а значит, и своя 80-окрестность QZo(t0) (в частности, если е0 =0 для всех
возможных х0, то согласно (6.47) получим
Ф(ХО)€2(/О) (6-49)
при любом выборе х0 ).
Если, например, некоторая траектория х(/) удовлетворяет условию (6.49), то
обязательно существует такой отрезок времени 7Хх0), состоящий, по крайней мере, из
одной точки /0, что при /еГ(х0) справедливо соотношение (6.46). В случае, когда
Г(х0) не совпадает со всем интервалом функционирования САУ, то при teT(xQ)
условие (6.46) не выполняется, но вполне возможно, что
q>(x(0)e&(0,e>e0, (6.50)
т.е. х(Г) не выходит за пределы е-окрестности множества 0{t), где s - достаточно
малая величина. Следовательно, если соотношение принадлежности (6.46) для какой-
либо траектории х(/) объекта (6.13) не выполняется, то для данной \{t) вполне
возможно выполнение соотношения (6.50), в котором множество Qz{t), вообще говоря,
является достаточно малым расширением множества Q(t) за счет соответствующего
выбора величины е > 0. Но тогда, учитывая приведенные выше особенности при
реализации соотношения (6.46), можно считать, что выполнение соотношения (6.50)
при соответствующих значениях 8 на всем интервале функционирования САУ
равносильно выполнению цели, поставленной перед системой. При этом в качестве цели
вместо (6.46) принимается соотношение (6.50).
Множество допустимых значений величины е, для которых соотношение (6.50) с
достаточной степенью точности можно рассматривать в качестве цели управления,
обозначим через 8 . Очевидно, что
8 = [е",е+], (6.51)
где 8~ = 0, 8+ - некоторая заданная величина.
Используя введенное обозначение (6.51) и учитывая сказанное, можно расширить
понятие цели управления для объекта (6.13). Будем считать, что в достаточно общем
случае для объекта (6.13) цель управления обеспечивается тогда и только тогда (или
состоит в том), когда на его траекториях обеспечивается выполнение следующего
соотношения
<р(х(0)е&(0
при ее8, />/0,J
называемого аналогично (6.46) соотношением принадлежности. При этом можно
допустить, что величина 8 в (6.52) имеет не фиксированное значение из множества
290 Методы синтеза САУ по заданным показателям качества. Часть II
8, для всего интервала функционирования, а является, вообще говоря, некоторой
неотрицательной функцией следующего вида
б = б(х(/))=б(0, t>to, (6.53)
т.е. предполагается, что для каждого t > t0 текущему значению траектории х(/)
соответствует своя вполне определенная величина 8 = ё(/) е 8 .
Используя для 8-окрестностей определение согласно (6.11), выражение цели в
виде соотношения принадлежности (6.52) представим как следующее неравенство
цй,(ср(х(,)),£(О)<е1 (б54)
При 8 = 8(0^8, />/0J
где цлй - одна из возможных мер близости в пространстве R" , а б(/) определяется
согласно (6.53).
Таким образом, получим, что для динамического объекта, рассматриваемого в
пространстве состояний согласно уравнению (6.13), цель управления можно
представить в виде некоторого соотношения принадлежности, имеющего выражение (6.52)
или (6.54) и позволяющего учесть приведенные выше особенности при реализации
ограничений на х(/).
В соответствии с приведенными выше рассуждениями можно сформулировать так
называемую концепцию функционально-множественной принадлежности (ФМП).
Концепция ФМП: если произвольный динамический объект управления может
быть представлен посредством своей математической модели в пространстве
состояний, то стоящую перед ним цель управления всегда можно свести к тем или иным
ограничениям на вектор состояния объекта, определяющими характер
принадлежности вектора состояния некоторым множествам или их окрестностям в каждый
текущий момент времени.
Полученные выше соотношения (6.52), (6.53) являются одним из возможных
подходов реализации концепции ФМП для объекта управления вида (6.13). При этом вид
множеств их окрестностей определяется соответственно видом ,Q(t) и Qz(t), а
характер принадлежности им вектора х = х(/) - вектор-функцией ср(-).
В соответствии с концепцией ФМП цель управления формулируется следующим
образом: для любой траектории х(/) объекта (6.13), начинающейся в некоторой
80 -окрестности множества £?(/0), т.е. х(/0) = х0 е£?е(/), в каждый текущий момент
времени t > tQ функционирования объекта должна существовать такая s-окрестность
множества Q{t) при s e S, для которой x(t)eQz(t).
6.2. РЕАЛИЗАЦИЯ КОНЦЕПЦИИ
ФУНКЦИОНАЛЬНО-МНОЖЕСТВЕННОЙ ПРИНАДЛЕЖНОСТИ
В ПРОСТРАНСТВЕ СОСТОЯНИЙ НА ОСНОВЕ МЕТОДА
ОБОБЩЕННЫХ ФАЗОВЫХ ОГРАНИЧЕНИЙ
В данной главе дается общая постановка задачи синтеза с учетом введенного
определения окрестности множества и рассматривается подход к ее решению.
Приводится основная теорема метода фазовых ограничений, а также ее обобщенный
вариант для случая задания ограничений на функциональную зависимость от вектора
состояния. Даются варианты конструктивного использования основной теоремы, в том
числе с учетом ограничений на структуру законов управления. Исследуется случай,
когда ограничения задаются только на часть компонент вектора состояния.
Глава 6. Синтез грубых систем автоматического управления 291
6.2.1. Постановка задачи по формированию структуры системы
и алгоритмов управления на основе концепции
функционально-множественной принадлежности
В предыдущей главе был рассмотрен класс объектов управления, описываемых
уравнением состояния (6.13) и обладающих в соответствии с данным уравнением
следующими особенностями:
1) наличие неопределенности по структуре объекта, которую можно
охарактеризовать на основе использования шкалы структур F, а также множества
структур, ограниченных по норме;
2) наличие неопределенности по параметрам объекта;
3) отсутствие полной информации о возмущениях, действующих на объект
(неопределенность по возмущениям);
4) наличие ограничений на значения управления и его структуру в соответствии
со шкалой сложности р .
С учетом данных особенностей и цели управления дадим строгую постановку
задачи синтеза для рассматриваемого объекта.
Будем считать, что под неопределенностью по структуре, в соответствии со
шкалой F понимается возможность выбора требуемой (или наиболее предпочтительной)
структуры /а(-) объекта на некотором заданном множестве структур F, исходя из
тех или иных условий, определяемых поставленной целью. Т.е. в данном случае на
множестве F осуществляется выбор структуры /aQ, которая способствует
выполнению цели. В этом смысле выбор структуры может рассматриваться, как
управляющий фактор.
Если имеется неопределенность по множеству структур, ограниченных по норме
или по мере близости, то под этим будем понимать, что на всем указанном
множестве структур (т.е. для каждого элемента данного множества) должна выполняться
поставленная цель управления.
В общем случае возможно одновременное задание неопределенности в указанном
смысле. Рассмотрим, как в этом случае она может быть представлена.
Допустим, что по шкале структур F выбрана та или иная структура /а(-), т.е.
fa(-)e F. При этом относительно /а(-) предполагается, что ее задание
осуществляется с некоторой неопределенностью (погрешностью). Множество возможных
структур имеет вид
Ф 4/(')е*":М/аох/о)^а 1 (б55)
[Vx е 0о> Vu € U09 Vw е W09 Vp е B0,t > t0 J
где Uo, Wo, Bo - некоторые достаточно малые окрестности соответственно множеств
U(t), W(t\ B(t) V/ > t0; Qo - некоторая окрестность множества допустимых значений
вектора х , для которых справедливо соотношение принадлежности (6.52) или (6.54);
\iR>, (•) - некоторая мера близости в R" , в частности, совпадающая с одной из норм
пространства Rn ; 8a - заданная величина, принимающая достаточно малые
неотрицательные значения, которая определяет соответствующую величину погрешности
при задании той или иной структуры /"(•) е F .
Таким образом, каждой структуре fa(-)e F соответствует свое множество
возможных структур Фа, любой элемент которой может быть реализацией модели
объекта (6.13), если по шкале Fв качестве данной модели выбрана структура /а(). То-
292 Методы синтеза САУ по заданным показателям качества. Часть II
гда одновременное задание неопределенности можно представить следующим
образом. Предполагается, что в качестве структуры объекта (6.13) может использоваться
произвольный элемент
Л-)еФв, ]
где Фа имеет вид (2.1); \ (6.56)
/"OeF. J
Теперь с учетом имеющихся ограничений на структуру и параметры объекта
можно сформулировать общую постановку задачи синтеза: для класса объектов
управления, описываемых уравнением типа (6.13), требуется синтезировать такой
закон управления u = uY(x,/) и выбрать такую структуру /а() в соответствии со
шкалой структур F, чтобы при обеспечении ограничений на значения закона
управления и на сложность его технической реализации, задаваемой на основе шкалы
сложности р, для произвольного значения параметра (3 объекта, удовлетворяющего
ограничению (6.35), на всем множестве возмущений w(/), удовлетворяющих
соотношению (6.28) или (6.29), (6.43) при произвольной реализации /(•) структуры /а(-)
и множества Фа согласно (6.55), (6.56), обеспечивалась заданная цель управления,
сформированная на основе концепции ФМП в виде соотношения принадлежности
(6.52) или (6.54).
Таким образом, результатом решения поставленной задачи будет синтезированный
закон управления uy(x,f) ограниченной сложности и выбранная структура объекта
/а(), реализуемая с точностью до произвольного элемента /(•) множества Фа.
6.2.2. О МЕТОДЕ ФАЗОВЫХ ОГРАНИЧЕНИЙ И ЕГО ОБОБЩЕНИИ
Сформулированная в предыдущем параграфе задача требует привлечения такого
метода для её решения, который бы при учете всей совокупности ограничений и
указанных неопределенностей позволял получать соотношения, допускающие
неоднозначность выбора закона управления и его структуры, а также возможность
принадлежности вектора состояния объекта (6.13) различным окрестностям того или иного
множества. Как уже отмечалось, для решения поставленной задачи будем
использовать подход, развиваемый на базе метода фазовых ограничений [94, 95, 96] и
называемый в дальнейшем методом (£?,р) -разбиения пространства состояний [42].
Метод фазовых ограничений основывается на следующей теореме.
Теорема 6.1. Для объекта управления, описываемого уравнением
x = /(x,u,0, x(fo) = xo, />/0, ' (6.57)
где х, и - пх\, тх\ векторы состояния и управления, при наличии ограничений на
вектор управления вида
ue£/(x,f), (6.58)
где U(x,t) с Rm - некоторое заданное множество для каждого х и / > /0, для
выполнения следующего соотношения на вектор состояния
х = х(0еО(/),/>/05 (6.59)
Q(t) = {xeR": v|/(x,f)<o}, (6.60)
где i|/(x,0 - скалярная непрерывно-дифференцируемая по всем своим переменным
функция, достаточно, чтобы обеспечивалось неравенство
Глава 6. Синтез грубых систем автоматического управления 293
(VxMa/(x,u,/))<0
для каждого х е YQ(t) и хотя бы
\ (6.61)
одного соответствующего ему значения
u e U(x,t) при / > /0,
где TQ{t) = | х е R" : vj/(x,/) = 0> - фаница множества Q{f)\ Vxv|/ - градиент функции
v|/(x,/); (Vxv|/,/(-)) - скалярное произведение векторов Vxvj/,/(-) е /?" .
В [95] показана справедливость данной теоремы для достаточно широкого класса
многомерных объектов, в том числе нелинейных и нестационарных. При этом об
объекте предполагается лишь, что его можно представить в нормальной форме Коши.
Если цель управления объектом (6.57) приводится к более общему виду
у = Ф(х(0,0€ Q(t\t>t^ (6.62)
где ф(х,/) - некоторая заданная пх\ непрерывно-дифференцируемая вектор-
функция, а множество
е(0 = {уеЛя: М/(у,/)<0}, (6.63)
то метод фазовых ограничений может быть обобщен на основании следующей
теоремы.
Теорема 6.2. Для объекта управления (6.57) при наличии ограничений на вектор
и (6.58) для выполнения соотношения принадлежности (6.62) для вектора состояния
х достаточно, чтобы обеспечивалось следующее неравенство
~dt
VyV,Vx9-/(x,u,0 + ^|£0
для каждого у е TQ(t) и каждого х е М(у,t)
Г
(6.64)
и хотя бы для одного, соответствующего каждому х,
значения ueU(x,t), t>t0, J
где TQ(t) - фаница множества Q(t) Vyv|/ - фадиент функции vj/(y,/); Vxcp - яко-
. биан функции ф(х,0 , вычисляемый согласно (6.17); M(yj) - некоторое
многообразие, соответствующее у е TQ(t) и определяемое согласно зависимости
Л/(у,/) = jx6Rw: ф(х,/) = у}, (6.65)
при этом область значений £ф(0 функции ф(х,/) такова, что
0(/)сЯф(/) при t>tQ. (6.66)
Доказательство. Доказательство данной теоремы во многом аналогично тому,
как доказывается теорема 6.1. Действительно, пусть x(t) - некоторая траектория
объекта (6.57), такая, что
ф(х('о)>'о) = ф(хо>'о)ее('о)-
Допустим, что соотношение (6.64) выполняется, и при этом в силу (6.66),
обеспечивается условие
M(y,t)*0 Vyere(/), t>to.
Если Для выполнения соотношения (6.62) этого недостаточно, то это означает, что
для рассматриваемой х(/) в случае нарушения (6.62) должен существовать такой
момент времени
294 Методы синтеза САУ по заданным показателям качества. Часть И
/ = /*>/0,
для которого
Ф(х(/*), t*) = у (/*) = у * е TQ( t) , (6.67)
и для сколь угодно близких к /* значений / > t*
<p(x(t)j) = y(t)eQ(t). (6.68)
Согласно указанным свойствам M{y,t) условие (6.67) обязательно выполнится.
С учетом определения множества Q{t) (6.63) условия (6.67), (6.68) означают, что
v(y*/) = o и м/(у(0'/)>0 при />г*'
т.е. в момент / = / функция ср(у(/),/) является возрастающей на траектории х(/).
Поэтому
vjy(y*,/*)>0 (6.69)
нетрудно получить, что
V =fvy4/,V19-/(x,u,/) + ^j + ^. (6.70)
Но тогда в силу (6.69), (6.70)
VyV,VlV./(x.u,/) + |) + ^>o"
при t = t\ x(t* )e м(у*У),
что противоречит неравенству (6.64), которое должно выполняться Vxe Л/(у*,/*), а
значит и для х = х(/*). Отсюда следует, что сделанное выше предположение о
возможности нарушения соотношения (6.62) не справедливо. Тем самым теорема доказана.
6.2.3. Формирование эквивалентных соотношений
в виде максминных и минимаксных неравенств
Неравенство (6.64) можно представить в другом виде. Действительно, из
определения vj;(-), ф(-) следует, что Vyij/, Эф/9/, d\y/dt зависят непосредственно только от
у = ф(х,/) и от /. Поэтому выполнение неравенства (6.64) возможно тогда и только
тогда, когда за счет выбора управления и = и~(х,/)^^(х,0 обеспечивается
выполнение неравенства вида
для каждого yeTQ(t) и каждого хе M(y,t),t >f0,
где u~(x,/) определяется в результате решения задачи минимизации
min (V v|/,Vx9./(x,u,0) = (vy\|/,Vx9-/(x,u-(x,/),0). (6.72)
Очевидно, если (6.71) не выполняется, то тогда и при любом другом допустимом
u e U(\,t) неравенство (6.64) выполняться не будет.
Поскольку (6.71) справедливо для всех х е М(у,/), то оно будет выполняться
тогда и только тогда, когда выполняется соотношение
mm
ueU(\,t)x
(6.71)
Глава 6. Синтез грубых систем автоматического управления 295
max
хеМ(у
;oue^(v^'Vx9-/(x'M))+(v^'f)+f"0
(6.73)
для каждого yeTQ(t) и каждого хе А/(у,/),/ >/0.
Таким образом, получим, что неравенство (6.64) эквивалентно неравенству (6.73).
Это можно сформулировать как следствие к теореме 6.2.
Следствие 6.1. Для обеспечения соотношения (6.62) для объекта (6.57) при
ограниченных (6.58) достаточно, чтобы выполнялось неравенство (6.73), эквивалентное
неравенству (6.64).
Неравенство (6.73), не учитывает возможных ограничений на структуру закона
управления. Если необходимо это учесть, то соотношение (6.64) приводится к виду,
отличному от (6.73). Действительно, допустим, что желательно, чтобы
синтезируемый закон управления был реализован в виде (6.22), т.е.
u = uy(x,t)eU(x,t),
где параметр у е G и его значения определяют ту или иную структуру закона
управления.
Тогда, подставляя его в выражение (6.64), получим
v>lf,v>v./(«4,,,),o3>fSo (6?4)
для каждого у eTQ(t) и каждогох е Л/(у,/),/ >/0.
Очевидно, для выполнения (6.74) необходимо и достаточно, чтобы выполнялось
неравенство
™*:)(v,,y,v.n*,«>M.0){v,4,%y%s° (67;)
для каждого у е TQ[t)9t>t0.
Тем самым доказано следующее положение.
Следствие 6.2. Для обеспечения соотношения (6.62) для объекта (6.57) за счет
выбора допустимого закона управления согласно (6.58) желаемой (заданной)
структуры (6.22) достаточно, чтобы выполнялось неравенство (6.75), эквивалентное в этом
случае неравенству (6.64).
В важном частном случае, наиболее часто встречающемся на практике,
справедливо условие
, / (6.76)
VxeDv(t),t*t09\
где £>ф(0 - область определения функции ф(х,/), т.е. множество допустимых
значений управления U не зависит от текущего значения вектора состояния. Тогда без
учета ограничений на структуру закона управления можно показать справедливость
следующего утверждения.
Следствие 6.3. Чтобы для объекта (6.57) выполнялось соотношение (6.62) с
учетом ограничений (6.58), (6.76) достаточно выполнения неравенства
min max (Vvv|/,Vx©-/(x,u,0) + [ Vvvj/,—1 + —<0
для каждого у eTQ(t),t>t0, J
являющегося эквивалентным неравенству (6.64). При этом будет справедливо
следующее тождество
296 Методы синтеза САУ по заданным показателям качества. Часть II
min max (Vv\i/,VY(p- /Yx,u,/)) =
S TiPS min (V 1|/,Ухф./(х,и,0)
xeM(\,t) ueU(x,t)^ '
(6.78)
eM(),t) ueU(x,ty
VyeTQ{t),t>t0.
Доказательство. Покажем эквивалентность неравенств (6.64) и (6.77).
Действительно, пусть для некоторого и = и* е U(t)
Ч**ж,.л«м.о+£)+Ы (679)
Vyere(r) и VxeM(y,t),t>t0. J
Очевидно, данное неравенство выполняется тогда и только тогда, когда
max (vvM/,Vx9./(x,u*(x,0,O) + fvvM/,^V —^ol
хем(у,<)\ yV> x4WV' {ihJ) { yV'dt) dt (6.80)
Vyen2(/),/>/0. J
Если, например, (6.80) для некоторого и = u e U[t) не выполняется, то для й не
будет выполняться и (6.79). В свою очередь, для того чтобы существовало хотя бы
одно управление и*, удовлетворяющее (6.80), необходимо и достаточно, чтобы
min max (Vvij/,Vx(p-/(x,u,O) + | Vvvj/,-^ | + -^<0
Vyere(/), t>t09
т.е. должно выполняться неравенство (6.77).
Таким образом, показана эквивалентность неравенств (6.77) и (6.64) в том смысле,
что обеспечение неравенства (6.77) является необходимым и достаточным условием
разрешимости неравенства (6.64).
Покажем справедливость тождества (6.78). Прежде всего, заметим, что поскольку
неравенства (6.77) эквивалентны неравенствам (6.64), и неравенства (6.73) также
эквивалентны неравенствам (6.64), то отсюда следует, что (6.77) и (6.73) -
эквивалентны между собой, каждое из этих неравенств разрешимо тогда и только тогда, когда
разрешимо другое.
Для удобства дальнейших выкладок введем обозначение
a(y,x,u,0=(vyi|/,Vx9./(x,u,O) + ^Vy4/,^j + ^. (6.81)
Рассмотрим неравенство
a(y,x,u,/)<a0, (6.82)
где предполагается, что величина а0 может принимать произвольное вещественное
значение.
Очевидно, неравенство (6.82) имеет тот же смысл, что и неравенство (6.64).
Аналогично тому, как были получены неравенства (6.73) и (6.77), находим, что (6.82)
обеспечивается тогда и только тогда, когда разрешимо каждое из следующих
неравенств
max min a(y,x,u,/) <a01 (6.83)
xeM(yj)ueU(xj) W } 0|
VyerO{t),t>t0y
Глава 6. Синтез грубых систем автоматического управления 297
min max <j(y,x,u,/) <a0] -
ueU(xj)xeM(y,t) \ (6.84)
Vyere(/),/>/0. J
При этом, так же как (6.73) и (6.77), неравенства (6.83) и (6.84) будут
эквивалентны между собой при любом значении а0. Допустим, что в общем случае
max min a(y,x,u,/)* min max a(y,x,u,/). (6.85)
xeM(y,t)ueU(x,t) W } uel/(xj)xeM(y,t) l '
Пусть
max min a(y,x,u,?)=a;(y,/), (6.86)
xeM(y,t) ueU(x,t)
min max a(y,x,u,/) =a±(y,/). (6.87)
ueU(x,t) хеЛ/(у,/)
Тогда согласно (6.85)
Неравенства (6.83) и (6.84) примут вид
ат(у,0<<т0 Vyer6(0,/>/0 (^88)
и
а^у.О^ао Vyere(/), t>tQ. (6.89)
Предположим, для определенности, что
a:F(y,/)<a±(y,/).
Тогда всегда можно указать такое значение ао= ао\ что
ат(у,/)<а;<а±(у,/). (6.90)
Но (6.90) противоречит тому, что неравенства (6.83) и (6.84) или (6.88), (6.89)
эквивалентны между собой для любых значений a0 e R1, в том числе и для ао= а0*.
Поэтому и неравенство (6.90) невозможно, а значит, несправедливо
предположение (6.85). Отсюда следует, что обязательно должно выполняться равенство
a?(y,/)=a±(y,/)l
W } W }\ (6.91)
vy€re(/),/>/0,J
или, что то же самое,
Из (6.91), (6.92) получим справедливость соотношения (6.78). Что и требовалось
доказать.
6.2.4. Смешанные неравенства при структурных ограничениях
на управление
Выше было получено неравенство (6.75), учитывающее ограничение на структуру
алгоритма управления. Приведем его к более удобному виду.
Аналогично тому, как введена была функция a(y,x,u,/) , введем обозначение
a1'(y)x,O=(vy^Vx9./(x,u1'(x,/),/))+^VyV)^j^. (6.93)
Тогда справедливо следствие.
Следствие 6.4. Для выполнения неравенства (6.64) на классе законов управления
заданной, согласно (6.76), структуры необходимо и достаточно, чтобы выполнялось
неравенство
298 Методы синтеза САУ по заданным показателям качества. Часть II
min max max aY(y,x,/)<0|
yeG yeFQ(t) xeM{yj) I (6 9^
npwt>t0, J
и необходимо, чтобы
max min max aY(y,x,/)<0|
У€ф(0 yeG xeM(y,t) I (5 95)
при t>tQ. J
Доказательство. Действительно, согласно (6.75) получим
max oY(y,x,/)<0 1
хел/(у,г) I . (696)
\/yeTQ(t) при/>/0,)
где yeG. Очевидно, при фиксированном у е TQ{t), для существования на
множестве G требуемого у, для которого справедливо (6.96), необходимо и достаточно,
чтобы выполнялось неравенство
min max aY(y,x,/)<0,|
yzGxeM(y,t) I (697)
t>t0. J
При этом, поскольку, в зависимости от выбора yeG, функция uY() меняет свою
структуру, то в силу (6.93) aY(-) также будет менять структуру. Поэтому, вообще
говоря, различным у соответствуют различные функции aY (•). Обозначим
aY(y,/)= max aY(y,x,/). (6.98)
xeM(yyt)
Тогда неравенство (6.96) примет вид
+ VJ ; \ (6.99)
VyeTQ(t), t>t0 при yeG.J
Для фиксированного yeG (6.99) выполняется тогда и только тогда, когда
max aY(y,f)<0, t>to. (6.100)
уеГОД
Но отсюда следует, что для существования хотя бы одного значения yeG, для
которого справедливо (6.100), необходимо и достаточно, чтобы выполнялось неравенство
min max aY(y,/)<0,|
yeGyeTQ(t) [ (6.101)
что эквивалентно (6.94).
С учетом обозначения (6.98) неравенство (6.97) примет вид
mincY(y,/)<0, />/o1
у*° (6.102)
при уеГб(/). J
Пусть
minaY(y,/) = CTY;(y)(y,O, (6.103)
где у(у) eG и является решением задачи минимизации (6.102) при заданном
уеВД.
Глава 6. Синтез грубых систем автоматического управления 299
Тогда, если
alM-^M^'o} (6Ю4)
VyeT6(/), J
то это эквивалентно тому, что
max a*~(y)(y,/)<0, t>to, (6.105)
уеГ(?(/)
что эквивалентно неравенству (6.95).
Невыполнение (6.105) означает, что для некоторого у = у е TQ{t) не будет
выполняться неравенство (6.102), т.е.
mina* (у,Л >0
yeG
ИЛИ
a^(y,/)>0VyeG. (6.106)
Это, в свою очередь, означает невыполнение неравенства (6.75), эквивалентному
согласно следствию 6.2 неравенству (6.64). Отсюда следует необходимость (6.105)
или (6.95), что и требовалось доказать.
Заметим, что выполнение (6.105) означает, что для каждого у е TQ(t)
существует такой y~(y)eG, что закон управления uY ^у'(х,/) обеспечивает выполнения
неравенства (6.64) для данного у. При этом не следует, что uY ^(y,/) обеспечивает
(6.64) Vy eTQ(t). Поэтому (6.105) рассматривается в качестве необходимого
условия разрешимости.
Неравенство (6.94) может использоваться в качестве критерия разрешимости
задачи синтеза на множестве законов управления заданной (ограниченной) структуры.
При этом требуемый закон управления может быть непосредственно синтезирован в
результате решения неравенства (6.94).
6.2.5. О РАЗРЕШИМОСТИ ПРИ ОГРАНИЧЕНИЯХ НА ЧАСТЬ
КОМПОНЕНТ ВЕКТОРА СОСТОЯНИЯ
Полученные выше соотношения (результаты) основывались на том условии
(предположении), что функция a(y,x,u,/) при фиксированных у, u, t определена на
множестве M(y,t) и при этом для каждого хе M(y,t) принимает вполне
определенное значение. В более общем случае возможно, что при фиксированных у, и, /
функция a(y,x,u,f) не однозначна на множестве М(у,/). В частности, такая ситуация
возникает, когда функция a(y,x,u,/) зависит от таких компонент х,, /е 1,и,
вектора X, которые в явном виде не входят в задание множества M(yj) (например, а(-)
зависит от всех xl,x2,...,xn , а М(у,/) зависит только от х] их2, а оставшиеся
компоненты jc3 , л:4, , лгя в задании А/(у,/) не участвуют).
Рассмотрим именно этот случай. Введем для каждого у е П2(/) некоторое
множество Л/(у,/), представляющее собой совокупность только тех компонент вектора
X, которые не участвуют в задании множества M(y,t) (если, например, все
xh i el, n , участвуют в задании М(у,/),то А/(у,/) =0). Пусть
300 Методы синтеза САУ по заданным показателям качества. Часть II
\fyeTQ{t) M(y,t)*O,t>to. (6.107)
Выясним для данного случая условия разрешимости неравенства (6.64). При этом
заметим, что если хе А/(у,/), то полностью определены компоненты xt ,/j e /j, и не
определены (могут выбираться произвольными) компоненты х, ,/2 е /2, где /ь /2 -
некоторые множества индексов (/jfl/^O, /,U/2=l,rt). Если же хеА/(у,/), то
полностью определены х, ,/2 е /2, и не определены х, ,/j e /,. Поэтому для заданного
у е Fg(/) соответствующий ему вектор X является определенным, если указать
такое множество А/(у,/), что справедливо соотношение
xeM(y,t)nM(y,t),t>t0. (6.108)
Рассмотрим неравенство (6.64). С учетом обозначения (6.81) его можно привести
к следующему виду
a(y,x,u,/)<0
V уеГб(/), VxeM(y,t)
(6.109)
и хотя бы для одного u = u(x,t)eU(x,t),t>t0.
Поскольку выполняется условие (6.107), то на множестве M(y,t) функция ст(-)
является неоднозначной, разрешимость неравенства (6.109) теряет смысл из-за
неопределенности функции а(). ,
Неравенство (6.109) можно сделать однозначным (определенным), если х
рассматривать не как элемент множества M(y,t), а удовлетворяющим условию (6.108).
В этом случае при фиксированном векторе у е TQ{t) неравенство (6.109)
приводится к выражению
cr(y,x,u,/)<0
УхеЛ/(у,/)пЛ/*(у,/)
(6.110)
и хотя бы для одного u = u(x,/) eU(x,t)9 t>t0,
эквивалентному тому, что на указанном граничном элементе у е Г£?(')
обеспечивается выполнение соотношения (6.62) при t > t0. При этом предполагается, что для
данного уеГ<2(^) должно существовать хотя бы одно такое непустое множество
M*(y,t), что для всех элементов множества М(у,/) пЛ/*(у,/) обеспечивается
неравенство (6.100). Если такого М (y,f) не существует, то не разрешимо не только
неравенство (6.110) при заданном yeFg(/), но не обеспечивается разрешимость
поставленной задачи синтеза. Если же требуемое Л?* (у,/) существует, то тогда, как
правило, выбор его не однозначен, и для решения неравенства (6.110) можно выбрать
произвольное М (у,() из числа допустимых.
Таким образом, показана справедливость следующего утверждения.
Утверждение 6.1. Если для рассматриваемой системы (6.57) для некоторого
фиксированного yeTQ(t) М(у,()ф0 при />/о, то в точке yeFQ(t) ограничение
(6.62) не будет нарушено тогда, когда на всем классе множеств А/(у,/) найдется
хотя бы одно такое множество Л/* (у,/), что справедливо соотношение (6.110).
Глава 6. Синтез грубых систем автоматического управления 301
Приведенное утверждение дает достаточное условие того, что система (6.57) в
заданной граничной точке у е Г£)(/) не нарушает обобщенных фазовых ограничений (6.62).
6.2.6. УСЛОВИЯ РАЗРЕШИМОСТИ ПРИ НАЛИЧИИ ВОЗМУЩЕНИЙ
Полученные выше соотношения метода соответствуют уравнению объекта
управления вида (6.57) при отсутствии возмущений со стороны окружающей среды.
Рассмотрим как изменятся данные соотношения, когда данные возмещения должны
учитываться. Пусть уравнения объекта имеют вид
i = f(x9u&t)9x(t0) = x09t>t09 (6.111)
где % -г х 1 - вектор возмущений, о котором известно, что
$е£, (6.112)
Е - некоторое заданное множество в пространстве Rr. Считаем, что L задается на
основе детерминистской информации о возмущениях £. Тогда аналогично (6.81)
можно ввести следующую функцию
a(y,x,u^,/) = (Vyv|/,Vx9-/(x,u,5,/))+^Vyv|/,^j + ^, (6.113)
используя которую, так же как было получено выше неравенство (6.64), можно
показать справедливость следующего соотношения
a(y,x,u,5,/)<0
Vyerg(r) и VxeA/(y,f), 3ueU(x,t)
(6.114)
и V£gI, (>t0.
Если неравенство (6.65) выполняется, то этого достаточно, чтобы обеспечивалась
цель управления (6.62). Из (6.114) следует выполнение эквивалентного неравенства
вида
max min max a(y,x,u,q,/) <0l
xeM(yj)ueU(x,t) §eZ 'I (6.115)
Vyer<2(0, t>t0, j
или
max max min max a(y,x,u,£,/) < 0,1
y<=K2(t)xeM(y,t)ueU(x,l) Z,eZ I (6.116)
t>tQ. j
Для решения полученных соотношений могут использоваться различные
численные процедуры [30, 32, 39, 150], выбор которых существенно зависит от выбора
функции сг(-) и заданных ограничений. В дальнейшем для ряда важных случаев этот
вопрос будет рассмотрен подробнее.
Если вместо соотношения (6.62) рассматривать следующее
yeQe(t),t>t0, (6.117)
то аналогично (6.63) множество Qt (t) можно задать в виде
&(г) = {у6Л":ч/в(у,0£О}, (6.118)
где е предполагается заданной величиной, выбранной на некотором диапазоне
величин.
> Тогда, заменяя в полученных ранее соотношениях функцию vj/(-) на vj/£(),
получим требуемые неравенства на параметры системы.
302 Методы синтеза САУ по заданным показателям качества. Часть II
6.3. РАСШИРЕНИЕ МЕТОДА ФАЗОВЫХ ОГРАНИЧЕНИЙ
НА е-ОКРЕСТНОСТЯХ МНОЖЕСТВ
В ПРОСТРАНСТВЕ СОСТОЯНИЙ
В данной главе рассмотрены несколько подходов применения метода фазовых
ограничений в зависимости от характера задания е-окрестностей. При этом
s-окрестности предлагается задавать: как некоторые множества уровня функций
ограничения; с помощью некоторых отображений (стационарных и нестационарных)
границ заданных множеств; на основе проекционного подхода. Для каждого из
подходов получены конкретные соотношения для решения задач синтеза.
6.3.1. Постановка задачи и предположения метода
с учетом 6-окрестностей
Рассмотренный в предыдущей главе метод обобщенных фазовых ограничений,
основанный на введении s-окрестностей множеств в пространстве состояний, может
быть обобщен с позиции других подходов, используемых для систем, задаваемых в
пространстве состояний.
Считаем, что объект управления так же, как и в предыдущем случае, описывается
либо уравнением (6.57), либо (6.111). Вначале рассмотрим задание объекта
уравнениями (6.57), согласно которым
х = /(х,и,/),
х(/0) = х0, t>to.\
При этом уравнение и удовлетворяет ограничению (6.58), т.е.
u€t/(x,O, t*t0,
где, в частности, U(x,t) = U = const.
Вместо ограничения (6.59) на вектор состояния будем рассматривать ограничение
более общего вида (см. (6.52))
Ф(х) = ф(х(/))еее(0, '>'о>]
ееЕ,
где ф() - заданная пх\ функция, непрерывно-дифференцируемая в R" ; Е -
заданное в R] множество.
Требуется для объекта (6.57) синтезировать такой закон управления, который бы
удовлетворял ограничению (6.58) и при этом обеспечивал принадлежность вектора
состояния заданной с-окрестности в R" согласно условию (6.52).
Так же, как и в предыдущей главе, получим некоторые достаточные условия на
вектор управления, при выполнении которых обеспечивается (6.52).
Будем считать, что е принимает произвольное фиксированное значение на
множестве Е, т.е. соотношение (6.52) должно обеспечиваться в некоторой фиксированной
е-окрестности множества Q.
Кроме того, положим
Ф(х)гх. (6.119)
При этих допущениях будем синтезировать требуемый закон управления. Далее
для решения поставленной задачи рассмотрим два подхода, представляющие собой
обобщения метода фазовых ограничений: 1) метод обобщенных фазовых
ограничений; 2) метод (6»р) -разбиения пространства состояний, - и основанные на
использовании концепции ФМП.
Глава 6. Синтез грубых систем автоматического управления 303
Вначале рассмотрим первый подход - метод обобщенных фазовых ограничений.
С учетом (6.119) соотношение (6.52) принимает вид
х = х(/)еО.(0 ]
w *eW I (6.120)
при ее Е, / >/0.J
Сформулируем произвольную е-окрестность множества Q{t) вида (6.60), т.е.
когда Q(t) = lxeR": \\i(x,t)<o\. Для этого поступим следующим образом.
Произвольная е-окрестность множества Q(t) имеет вид
Qz(t) = [xeR": if/8(x,O<o}, (6.121)
где v|/E(x,/) - скалярная, предполагаемая непрерывно-дифференцируемой функция
ограничения, соответствующая данной е-окрестности.
Поскольку е может принимать произвольное значение на множестве Е = е~,е+ ,
то Qz - может быть произвольным множеством, удовлетворяющим соотношению
Qz-(t)eQG(OeQz.(t),t>to, (6.122)
где е~,е+ могут быть, в частности, определены аналогично (6.111).
На рис. 6.2 показано, каким образом можно выбрать допустимую е-окрестность Qz.
Возможные е-окрестности
множества Q
Q Ч-
Рис. 6.2. Выбор е-окрестности множества Q
Таким образом, задача синтеза требуемого закона управления может быть
сформулирована следующим образом: для объекта (6.57) построить такой закон
управления, удовлетворяющий ограничению (6.58), который бы обеспечивал выполнение
фазовых ограничений вида (6.120) хотя бы для одной е-окрестности Qz(t)
произвольного вида, сформулированной для множества Q(t) и удовлетворяющей условию
(6.122).
Заметим, что вид Qz(t) полностью определяется заданием той или иной функции
ограничения v|/e(x,/). Согласно (6.5) формирование е-окрестностей с теми или ины
ми свойствами для заданного множества Q определяется выбором некоторой мер
близости |ы(х,0, характеризующей близость или удаленность х от Q в том или ино^
смысле. В рассматриваемой постановке задачи синтеза вид и свойства ц(х,0
специально не оговариваются, и, в общем случае, для задания ц/е(х,/), обеспечивающих
(6.122), могут использоваться ц(х,0 с различными свойствами. Поскольку \уе(х,/)
304 Методы синтеза САУ по заданным показателям качества. Часть II
могут соответствовать различным |и(х,0, то в качестве Qz(t), ееЕ, допускается
использовать произвольное множество, удовлетворяющее (6.122).
6.3.2. Метод фазовых ограничений на б-окрестностях множества q
Рассмотрим решение задачи синтеза, сформулированной в предыдущем
параграфе. Очевидно, если для множества Q(t) определена некоторая мера близости
ц(х,0, то на ее основе для каждого е>0 всегда можно построить е-окрестность
Qz(t) с границей TQz(t) и соответствующую ей функцию ограничения vj/E(x,/).
Таким образом, в общем случае
\|/е(х,0 = С?(ц(х,е),е(0,е), (6.123)
где G(-) - некоторый оператор, определяющий однозначную зависимость от
заданных ц(х,0, Q{t) и s.
Если в общем случае зависимость (6.123) известна, то функция \|/е(х,/) является
заданной, и для решения поставленной задачи синтеза можно воспользоваться
сформулированной выше в предыдущей главе теоремой 6.1 с соответствующей заменой
е(/),ге(о,ч/(х,о на &(о,г&(о,ч/е(х,о.
Однако, если даже зависимость (6.123) не известна, то функцию i|/E(x,/) всегда
можно задать с учетом требуемых свойств (6.122). При этом меру близости ц(х,0
уточнять не обязательно.
Таким образом, будем считать, что для произвольной е-окрестности Qz(t),
удовлетворяющей (6.122), функция vj/e(x,/) может быть непосредственно задана и
предполагается известной. Тогда аналогично теореме 6.1 справедлива следующая теорема.
Теорема 6.3. Для объекта (6.57) при наличие ограничений на вектор управления
(6.58) соотношение (6.120) хотя бы для одной е-окрестности Qz(t),
удовлетворяющей (6.122), будет выполняться тогда, когда выполняется неравенство
(Vxi|/£,/(x,u,0) + ^<0 VxeraW,
хотя бы одного u = u() e U(x,t) и некоторой
(6.124)
v|/E(x,O, соответствующей Qz(t), t>t0.
Данная теорема представляет собой некоторое обобщение теоремы 6.1, однако
непосредственно пользоваться ею затруднительно, поскольку не определено, как
формировать допустимую функцию i|/e(x,f) и осуществлять набор х на границе
Г<28(0 произвольно выбираемой г-окрестности.
Рассмотрим, каким образом можно задавать функцию \|/Е(х,/), определяющую
произвольную допустимую е-окрестность множества Q. Для этого воспользуемся
свойствами поверхностей уровня функции i[/(x,f), c помощью которой задается
множество Q{t).
Известно, что поверхность уровня TQ{t) задается с помощью равенства
¥(х,0 = 0, />/0.
Пусть необходимо задать некоторую поверхность YQz(t). Считаем, что между
граничными элементами xeTQ(t) и xeFge(0 можно установить взаимно
однозначное и непрерывно-дифференцируемое соотношение вида
Глава 6. Синтез грубых систем автоматического управления
305
х = л(х,О, (6.125)
где г|()- пх\ вектор-функция с соответствующими свойствами. Тогда достаточно
произвольную поверхность TQz(t) можно представить в виде
Га(/) = {хеЛи:Т(л(х,/),/)=0}. (6.126)
Действительно, справедливость этого непосредственно следует из представления
Tg(r) и связи между FQ(t) и TQz(t).
Рассматривая на множестве TQz(t) теорему 6.3, получим, что для обеспечения
соотношения (6.120) на 8-окрестности^(0 достаточно, чтобы выполнялось
следующее неравенство, непосредственно получаемое из неравенства (6.124)
(V^.V^,/(x,u,0)-b(Vn^)T.|l + ^<0,
dt dt
\f\eTQz(t), хотя бы одного и = и(-) е£/(х,/),/ >/0J
где использовались соотношения
^е(х,/) = 4^(л(х,/),/),
(6.127)
dt "^ ' dt dt
(6.128)
Согласно определению функции л(0 поверхность rQz(t) можно представить в виде
щ(г)={х=л"1(^0>^еГе(0}> (6-129)
где ri"1 (•) существует в силу взаимной однозначности л() и в достаточно общем
случае предполагается известной.
Из (6.129) следует, что если х пробегает все множество YQZ (/), то вектор х
пробегает все множество TQ(t).
Поэтому, если в неравенстве (6.127) осуществить замену переменной х на
переменную х в соответствии с зависимостью х = г|~1(х,0> то получим соотношение,
эквивалентное (6.127), выполнения которого достаточно, чтобы обеспечить (6.120) на
некоторой TQz(t), и имеющее следующий вид
(V^-V^/Iiu,/)).^)7 -f + ^0
Vx € TQZ (/), хотя бы одного u = u(-) e O(i,t)yt > t0,
где использованы обозначения
У,л = Vxn(n-' (i,f).') ^„Ф = УпУ(л-' {x,t),t),
(6.130)
/(х,и,о=/(л (х'0'«.');^7=^ '
Таким образом, показана справедливость следующего результата.
(6.131)
21 Зак. 366
306 Методы синтеза САУ по заданным показателям качества. Часть II
Следствие 6.5. Для обеспечения соотношения (6.120) для объекта (6.57) при
ограничениях на управление (6.58) достаточно, чтобы существовала такая
взаимнооднозначная и непрерывно-дифференцируемая в Rn (или в Q + (/) V/ > /0) п х 1
вектор-функция г|(«) вида (6.125), для которой выполняется неравенство (6.130).
Заметим, что неравенство (6.130) является удобным для синтеза требуемого
закона управления, т.к. входящие в него величины полностью определены, а выбор
допустимой функции г|() не требует разрешения сложных ограничений.
6.3.3. Метод фазовых ограничений при отображении е -окрестностей
на заданное множество
Рассмотрим другой подход к заданию е -окрестностей, позволяющий получить
достаточно эффективные соотношения для синтеза управления. Произвольную
s-окрестность TQz(t) множества Q(t) будем задавать по аналогии с (6.125), но в
отличии от (6.125) считаем, что
хе=^М, (6.132)
где хЕ eYQz[t), %eYQ[t)\ £(•) - пх\ вектор-функция,
непрерывно-дифференцируемая и взаимно-однозначная между поверхностями TQ(t) и TQz(t).
Вначале рассмотрим случай, когда
TQ{t)=TQ^const, Г&(')=Г& -const, £(x,f)=S(x). (6.133)
Аналогично (6.129) можно записать
Г&={хЕ=^(х): xeTQ]. (6.134)
Изменяя вид функции £(х), для фиксированного множества Q можно получить
различные 8 -окрестности с границами TQZ. Для того, чтобы на Qz применять
теорему 6.3, получим выражение для Vy*Fe, зависящее непосредственно от Ух¥ с
учетом (6.132).
Из равенства
хЕ=^(х) (6.135)
получим следующее соотношение между дифференциалами хЕи dx
■c/xe=Vx£.rfx, (6.136)
где Vx£ - якобиан функции £(х).
Пусть Г = Г(х) - гиперплоскость в пространстве R" , касательная к поверхности
YQ в точке xeFQ. Аналогично определим гиперплоскость Ге =Ге(хЕ),
касательную к YQZ в точке хЕ е TQZ, которая выбирается согласно равенству (6.135). Если в
соотношении (6.136) вектор dx выбирать таким образом, чтобы
x + dxeTQ, где хеГ^, (6.137)
то в силу свойств функции £(х) получим, что
хЕ +</хе € га, где хЕ 6 га • (6.138)
В силу бесконечной малости векторов dx и dxB следует, что
x + dxeT{x)y хЕ+ЛЕеГЕ(хЕ), (6.139)
т.е. dx и dxz лежат соответственно в гиперплоскостях Г(х) и ГЕ(х). Известно, что
Глава 6. Синтез грубых систем автоматического управления ЗСГ7
У '}, V >\ (6.140)
VxeTQ J VxcereE. j
Поэтому для произвольных приращений А и dxe, удовлетворяющих (6.137),
(6.138), с учетом их ортогональности векторам V^T , Vx.vFE (6.140) получим
(Vx4',A)=0
(6.141)
Vc/x, что x + dxe TQ\)
\ x * I I (6.142)
Vc/xe, что xE+A£ergE.J
Равенство (6.142) с учетом (6.136) примет вид
(v^4',,a')-(v1,4',,v1§a)-((v^)tv],4',,a) = o| (6143)
Vrfx, что x + dxeTg. J
Сравнивая (6.141) и (6.143), в силу 4/е(х) произвольности вектора dx , получим
(V^)TVx^e=p(x)-Vx^, (6.144)
где р(х) - некоторая скалярная функция, определенная Vx e Fg (считая, что
функция также, как и ЧЧх) с возрастанием имеет расширяющиеся множества уровня, то
можно положить, что Р(х) > 0 Vx e TQ, т.к. вектор VxElFe будет ориентирован
относительно TQG).
Поскольку £(х), согласно определению, устанавливает взаимно-однозначное
соответствие между множествами TQ и TQZ, то такое же соответствие должно быть
между векторами (x + rfx) и (хБ Wxe), удовлетворяющими (6.137), (6.138).
Следовательно, взаимно-однозначное соответствие будет между рассматриваемыми
приращениями dx и dxz. А поскольку dx и dxz связаны соотношением (6.136), то
получим, что якобиан Vx£ VxeFQ представляет собой пхп невырожденную матрицу.
Отсюда находим, что и Vx^ также nxri невырожденная матрица. И потому из
(6.144) следует, что
V^^Pix^V^'-V/F. (6.145)
Введем обозначение
0(x)=l(Vx£) j -nxn матрица,
с учетом которого
УхСТе=р(х)-0(х)-Ух^. (6.146)
Кроме того, необходимо отметить, что согласно (6.134), если х пробегает все
множество Г<2 , то х8 пробегает все множество TQZ и наоборот. Тогда теорема 6.3
применительно к множеству Qz сводится к следующему результату.
Следствие 6.6. Для обеспечения соотношения (6.120) для объекта (6.57) при
ограничении (6.58) достаточно, чтобы существовала такая е -окрестность Qz,
связанная с заданным множеством Q посредством взаимнооднозначной и непрерывно-
21*
308 Методы синтеза САУ по заданным показателям качества. Часть II
дифференцируемой функции £(х) согласно (6.135), для которой выполняется
неравенство
P(x)(©(x)Vx4')/(^(x))u,/))<0 1
г (6.147)
VxeFg8(/) ихотябы одного и = и(-) е£/(£(х),/),/ >/0.1
Заметим, что поскольку скалярная функция Р(х) > 0 Vx е TQ, то неравенство
(6.147) можно рассматривать в виде
(0(x)Vx% /U(x),u,z))<0 | (6И8)
\/хеГ£)е(/) ихотябы одного u = u(*) €l/(§(x),/),f >/0.J
Полученные соотношения справедливы для стационарных фазовых ограничений
и функции §(•). Рассмотрим более общий случай, когда Q и £(•) являются
нестационарными.
6.3.4. Метод фазовых ограничений
при отображении на нестационарные 6-окрестности
При рассмотрении нестационарного случая можно непосредственно
пользоваться соотношениями, полученными в предыдущем параграфе. Пусть условие
(6.133) не выполняется, т.е.
Г0 = Г0(/), Щ=Щ(/),$(.) = $(х,/).
Поступим следующим образом. Сведем нестационарный случай к стационарному
путем введения новых переменных и расширения вектора состояния.
Обозначим
*„+,=> . (6.149)
Введем расширенный вектор состояния
х= - пх\ вектор (6.150)
L*/H-iJ
Тогда
Ч/(х,/)=Ф(х). (6.151)
Кроме того,
rg = {xe/?"+1: Ф(х)=0}. (6.152)
Вместо функции £(х), действующей в R", введем функцию £(х), действующую в
Rn+] следующим образом:
xE=S(x,/)l
ХП + \ * ХП+\
? = Ф), (6.153)
где £(х)-(и + 1)х1 вектор-функция, у которой
1U+I (*) = ^и+1 (xn+i) = хп+\ ■ (6-154)
Тогда, аналогично (6.134), можно записать
■щ={хЕ=!(х):х€Г£}. (6.155)
Таким образом, приходим к задаче, соответствующей стационарному случаю,
рассмотренному в предыдущем параграфе. Поэтому следствие 6.6, а значит и
неравенство (6.147) или (6.148), можно непосредственно применить к множеству YQZ.
Глава 6. Синтез грубых систем автоматического управления
309
(6.156)
Согласно (6.148) и введенных обозначений (6.150) - (6.154) получим, что в
рассматриваемом случае для обеспечения (6.120) должно выполняться соотношение
(e(x)VY4>,7(I(x),u))s0 |
\/хеГ£(/) и хотя бы одного и = и(-)е £/(•),f >/0,J
где 0(х)-(я + 1)х(яч-1) матрица, определяемая аналогично матрице Э(х); (л + 1)х1
вектор-функция /(•) с учетом дополнительного уравнения (6.149), приводимого к
виду хп+1 = 1, определяется согласно соотношению
'§(*),и,*я+1
1
/№)>") =
/
(6.157)
Приведем неравенство (6.156) к виду, непосредственно зависящему от исходного
вектора состояния х . Согласно определению
(6.158)
0(x) = ((v,f)TJ.
Якобиан VY£ имеет следующее выражение
VTs =
а*,
а?,
дх,
ах2
дх2
дх2
Ял
дхп
д\2
тп
din
ЗХп
94,
д\2
д\п
дхл
дх,
дхп дхп+
п+\
(6.159)
где с учетом определения ^п+\(\) (6.153) должны выполняться равенства.
^= =С±1=0;С±1_=1 (6160)
Очевидно, внутренняя, выделенная в (6.159), матрица представляет собой якобиан
Vx£. Тогда выражение (6.159) с учетом (6.160) можно привести к виду
тг\Т
(W =
.dt
(vx^)T
dt
... ^L
dt
0
0
0
i
1
.dt
в"1
dt
dt
0
0
0
1
= 0
_ j
(6.161)
Используя выражение (6.161), вычислим матрицу ((V^)T) !.
Воспользуемся известным обстоятельством, что если R - некоторая
невырожденная матрица, то обратная матрица R"1 имеет вид
310
Методы синтеза САУ по заданным показателям качества. Часть II
R-^-'1
detR
^11 R2\ ••* ^wi
Rn R22 "• Кг
(6.162)
где R; j - алгебраическое дополнение элемента rf} матрицы R .
i-l
Из структуры матрицы 0 следует, что
Кроме того
©,-] = 0,} при i,je\,n.
enl+l/ = 0 при je\9n
в-' =det0-1.
(6.163)
(6.164)
S-i
Определим выражения для алгебраических дополнений 0/w+J при ie\,n. Co-
-1
гласно (6.161) для произвольного 0; п+] справедливо выражение
er;+i =
ОГ1
?к Ё* ... ^к
dt dt dt
(-1)/+W+1,
(6.165)
где ©у1 - (я-1)хя матрица, полученная вычеркиванием /-й строки у матрицы 0 * .
Раскладывая детерминант (6.165) по последней строке, получим
v-l
0-',+1 =(-l)'+"+1 |(-,r'|L.det 0-> +(_ir^.det0-.
+ ...
\п+п д£,п
yj + v 3^v
... + (-1Г ^-det©"1 ^(-ly^Xl-ir^-det©-1 =
(6.166)
v=l
= Z(-l)'+V+l%-det0-',
V=l
dt
где G>il - (n-\)x(n-\) матрица, полученная вычеркиванием v-го столбца у
матрицы ©""'.
Соотношение (6.166) справедливо для всех алгебраических дополнений 0~),+,
при /е 1,я. С помощью полученных выражений (6.163), (6.164), (6.166) может быть
вычислено в соответствии с (6.162) матрица © вида (6.158).
Имеем
°=(И7'=
dete~'
©п1 ©г! - ®ы ®л"1и
©Г' ©^ - ©„1 ё-\12
®т! e;i
yln
2n
И"1
б"1
йг1 . йг1
0-1 /Л"1 (ы\~^ (2\~^
\,п+\ U2,w+1 *" ил,л+1 и/?+1,л+1
Глава 6. Синтез грубых систем автоматического управления
311
det0
-1
©г,1
©Г2'
©г»1
ей
- в;{
- e;i
- e-J,
- в;' ,
О
о
det©
-1
0
в, 02
в-
(6.167)
где
®.=£<-г'М,-п.
(6.168)
V-1
С учетом (6.149) - (6.151) определим выражение для вектора У^Ч* в неравенстве
(6.156). Имеем
У;Т =
Vx¥
La/ .
(6.169)
Согласно (6.156), используя (6.167)-(6.169), вычислим следующее выражение
01
0V;VP =
0
0, ©2
®„
VXT
dt
0VX^
У0Д+^
©v^
(0,VxT) + f
(6.170)
где
0 = [0, 02...0W]T.
Тогда неравенство (6.156) с учетом (6.157) принимает вид
(0(х)УхФ ,7($(х),и)) = (в{х)ЧхЧ ,/(4(x),u)) + (©,Vx4') + ^<0
(6.171)
(6.172)
Vx<=rQ(t) и хотя бы одного u =u(-) eU(£,(x),t),t>t0.
Неравенство (6.171) приводится к более компактной форме
(VxT,0T(x)./(^(x),u,/)+0) + ^<O
VxeTg(f) и хотя бы одного u =u(-) g(/(^(x),/),/>/0.J
Таким образом, показана справедливость следующего результата.
Следствие 6.7. Для обеспечения соотношения (6.120) для объекта (6.57) при
ограничении (6.58) достаточно, чтобы существовала такая нестационарная
6-окрестность Qz(t), связанная с заданным нестационарным множеством Q(t) с
помощью некоторой непрерывной дифференцируемой и взаимно-однозначной
функции £(х) согласно (6.132), для которой выполняется соотношение (6.172).
312
Методы синтеза САУ по заданным показателям качества. Часть II
В важном частном случае вектор-функцию £(х,/) можно выбирать стационарной,
т.е. £(•) = £(х). В этом случае неравенство (6.172) принимает более простой вид.
Действительно, т.к. согласно (6.168)
0,=О V/gU
поскольку
^- = 0 Vveu,
dt
то (6.172) приводит к выражению
(vx4>,0T(x)-/(^(x),u,O)^<O
dt \ (6.173)
Vxerg(f) и хотя бы одного и = и(-)е t/(^(x),/), />/0.J
В качестве функции £(•) может, в частности, использоваться функция
следующего вида*
5(x) = x + a(x)V/F, (6.174)
где х е TQ, а а(х) - скалярная непрерывно-дифференцируемая функция.
Тогда
" Vx£ = £ + a(x)V^ + Vx¥-(Vxa)T,
где
(6.175)
V^ =
а2т
Э2¥
д2Ч>
дх\дх„
д2У
dxl
- пхп симметричная матрица .
(6.176)
дхпдхх
Отсюда находим, что
0 = rE + a(x)V^ + Vxa-(Vx4/)Tl .
Выбирая достаточно произвольную функцию а(), можно задавать различные
допустимые £(•) вида (6.174).
В качестве ^() в ряде случаев целесообразно использовать следующее выражение
£(-) = Мх, (6.177)
где М-пхп невырожденная матрица (за счет этого обеспечивается
взаимно-однозначное соответствие между YQ и TQZ).
Тогда
VX£ = M, (6.178)
и
о = (мт)"'.
(6.179)
* Нетрудно убедиться, что данная функция удовлетворяет требованию, предъявляемому к ^(*) * т-е
обеспечивает взаимно-однозначное соответствие между YQ и YQZ
Глава 6. Синтез грубых систем автоматического управления 313
При этом условием для выбора той или иной матрицы М является обеспечение
неравенства
det М ф 0.
Полученные выше соотношения (6.171), (6.172) могут непосредственно
использоваться для синтеза требуемых алгоритмов управления. Возможные подходы на их
основе будут рассматриваться далее.
6.3.5. О ПРОЕКЦИОННОМ ПОДХОДЕ В ЗАДАЧЕ ОБЕСПЕЧЕНИЯ
ФАЗОВЫХ ОГРАНИЧЕНИЙ
Пусть так же, как и в предыдущих параграфах, рассматривается некоторое
замкнутое и ограниченное множество Q(t), определяемое
непрерывно-дифференцируемой функцией ограничения Ч^х,/). Обозначим через z(t) - действительную
траекторию объекта, описываемого уравнением (6.57). Через х(/) в данном случае
обозначим некоторую проекцию (отображение) траектории z(/) на границу TQ(t), т.е.
х(/)еГ0(*), '>'о. (6-180)
Отображение (проектирование) z(/) на TQ(t) осуществляется в соответствии со
следующей зависимостью:
z{t)=j)(x(t)j), <^'о> (6Л81)
согласно которой предполагается, что для каждого t > t0 фиксированному значению
z(/) на TQ(t) соответствует свое значение х(/) и наоборот. Кроме того, п х 1
вектор-функция г|() предполагается непрерывно-дифференцируемой.
Используя соотношение (6.136), определим уравнение для проекции х(/) е YQ(t).
Для этого продифференцируем по времени правую и левую части данного уравнения.
Имеем
z = VxTvx + fl, (6.182)
at
где Vxr| - якобиан функции г|().
Поскольку функция г|() предполагается взаимно-однозначной между
действительной траекторией z(/) и ее проекцией х(/) е TQ(t), то текущей скорости объекта
z должна однозначно соответствовать текущая скорость проекции х . А это
возможно только в том случае, когда Vxr| - невырожденная матрица.
Таким образом, поскольку матрица Vxr| - невырожденная, то из (6.182) получим
x = (V^)"'[z-f]. (6.183)
$ (6.183) следует, что
= (У1лГ1[/(ж,и,0-|-] = (УжлГ1[/(л(х,0,и,/)-|].
/e(x,u,0 = (V^)"l[/(n(x,0,u,/)-^j, (6.184)
Согласно уравнению (6.57) из (6.183) следует, что
Если обозначить
то последнее уравнение приводится к виду
x = /g(x,u,0,
(6.185)
х(/0) = х0, />/0,J
20 Зак 366
314 Методы синтеза САУ по заданным показателям качества. Часть II
где х0 определяется из условия
z('o) = n(x('o)>'o)- (6.186)
Однако из уравнения (6.185) не следует, что если х(/) - его решение, то в этом
случае обязательно х(/) е TQ(t), V/ > t0. Это связано с тем, что при формировании
уравнения (6.185) не учтены условия принадлежности х(0 к TQ(t).
Для того чтобы х(/) е Г<2(0, V/ > t0, очевидно, достаточно потребовать, чтобы
х('о)еГе(го)
, ч г (6.187)
И V(x(/),/)a0 V/>VJ
Указанное тождество будет выполняться тогда и только тогда, когда на проекциях
траекторий x(t) функция vj/() не изменяется во времени, т.е. должно выполняться
уравнение ~~^" .
vi/=(VxM/,x)+^ = 0, V/>/0. (6.188)
ot
Тогда (6.187) с учетом (6.188) примет вид
х('о)еГе(/о) 1 *
.(УЛЧ+Й-.о, ,„„.)- <6189)
Поскольку х удовлетворяет уравнению (6.185), то (6.189) приводится к виду
х(/о)еГ0(*о) 1
, \ 5ш [ (6.190)
и (Vx4/,/o(x,u,/)) + ^ = 0, />/0.J
Отсюда с учетом (6.184) получим
х('о)еГ2('о) ' 1
и [чМчЛх{л^л*А-Щ+^=о, v/^.| (6Л91)
Проанализируем выражение (б».Т91) относительно существования такой вектор-
функции т](х,<Х2^для^кс«<)рой траектория объекта, определяемая в соответствии с
(6;18l£ удовлетворяет тем или иным требуемым ограничениям.
Вообще говоря, соотношение (6.191) можно рассматривать в качестве некоторого
уравнения относительно функции ц(-).
Поскольку произвольную траекторию z(/) объекта (6.57) всегда тем или иным
образом можно отобразить на заданную поверхность YQ(t), то в общем случае
обязательно существует, по крайней мере, хотя бы одно взаимно-однозначное
соответствие определенным образом выбираемого вида, между траекториями z(0 и их
отображениями (проекциями) х(/) на данной поверхности TQ{t). Поэтому уравнение
(6.191) всегда должно иметь не менее одного решения г\(-). С другой стороны, если
уравнение (6.191) имеет хотя бы одно решение, то оно в силу соотношений (6.181),
(6.183) характеризует взаимно-однозначное соответствие между z(/) и х(/) е TQ(t).
Следовательно, если уравнение (6.191) рассматривать относительно г|(), то на всем
множестве решений обязательно найдется такое, которое согласно (6.181)
соответствует действительной траектории объекта (6.57).
Более того, можно утверждать, что если р - множество решений уравнения
(6.191), то произвольное решение rj(-) e p соответствует одной и той же траектории
Глава 6. Синтез грубых систем автоматического управления 315
z(/) объекта (6.57), определяемой согласно зависимости (6.181) и находящейся во
взаимно-однозначном соответствии с проекцией x(t)eTQ(t), своей для каждого
Действительно, справедливость данного утверждения следует из того, что
уравнение (6.191) получено в результате эквивалентных преобразований (6.188) - (6.190),
вытекающих из условия (6.187) и использования соотношений (6.182) - (6.185),
справедливых только при взаимно-однозначных функциях г|(х,/). Причем, поскольку для
объекта (6.57) начальное состояние z(/0) = z(/,z0), то ему соответствует своя траектория
z(t0) = z(/,z0). А согласно (6.186) вектору z0 соответствует вектор х0 е TQ(t0), свой
для каждой функции г|(-)ер. В силу (6.185) для каждых х0 и г\(-) определяется
своя траектория х0 е TQ(t0), V/ > /0. Следовательно, одной и той же траектории z(/)
взаимно-однозначно согласно (6.181) соответствуют проекции xoeTQ(to),
определенного для каждой г|(-) е р.
Рассмотрим, каким образом можно задавать функции г|(). Пусть г|() выбирается
в виде
Ti(x,0 = x + a(x,/)Vxi|/, хбГ6(0, (6Л92)
где а(-) - некоторая скалярная непрерывно-дифференцируемая функция, которая
заранее не определена и характеризует близость (расстояние) действительной
траектории z(t) от границы TQ(t) в каждый момент времени t > t0.
Очевидно, что в каждый фиксированный момент времени t>t0 произвольно
заданному вектору z = r|(x,/)e R" соответствует согласно зависимости (6.192) вполне
определенный вектор хеГ£)(/) и некоторое фиксированное число сс(-) (для
доказательства справедливости данного утверждения достаточно, чтобы множество Q(t)
было выпуклым). Следовательно, г|(х,0 вида (6.192) обеспечивает взаимно-
одьизначное соответствие между z(i) и х(г) и может использоваться в соотношении
(6.191). При этом
Ухл = ^ + а(х,/)У^ + УхМ;-(Уха)Т,
(6.193)
~ д д ч
(последнее соотношение справедливо в силу перестановочности операции — и —).
9/ ас,-
Подставляя (6.193) в (6.191), получим нелинейное дифференциальное уравнение в
частных производных относительно скалярной функции ос(-), которое в общем
случае может не иметь аналитического решения.
Для решения (6.191) относительно а(-) должны быть заданы начальные краевые
условия для ос(). Очевидно, они определяются из уравнения
xo+a(xo,/o).Vxv|/(xo,/o) = zo, (6.194)
20*
316 Методы синтеза САУ по заданным показателям качества. Часть II
где z0 = z(/0) - начальное состояние объекта (6.57). Причем, величина ct(xo,fo) = а0,
как отмечено выше, определяется однозначно. Таким образом, уравнение (6.191)
решается при наличии краевого условия
а(хо,/о) = ао, (6.195)
где а0 соответствует z0.
Справедлив следующий результат.
Утверждение 6.2. Уравнение (6.191) при заданном законе управления и = и() и
выбранной вектор-функции r\(\j) вида (6.192) имеет единственное решение сс(х,/),
удовлетворяющее краевому условию (6.195).
Доказательство. Действительно, в силу существования взаимно-однозначного
соответствия между траекторией объекта z(/) и ее проекцией xeTQ(t) уравнение
(6.191) должно иметь не менее одного решения ос(х,/)- Допустим, таких решений
несколько: ctv(x,/), v e N, где N - некоторое множество индексов, каждое из
которых такое, что
осу(х0,/0) = ос0 VveN.
Поскольку заданным а0 и х0 при г = /0 согласно (6.194) соответствует вектор
z0, то всем решениям av(x,/), veN соответствует одна и та же траектория z(t)
объекта (6.57).
Но выше было установлено, что при выборе r\(\J) вида (6.192) каждому вектору
z для фиксированного t > t0 соответствуют свои единственные значения а и х.
Поэтому для траектории z(t) в каждый момент / > t0 может соответствовать только
одно значение а(-) и одно значение x(t). Следовательно,
av(x,/) = a(x,/) VveN,
т.е. уравнение (6.191) при заданных краевых условиях и выбранном законе «(•)
может иметь только единственное решение ос(х,/). Что и требовалось доказать.
Рассмотрим требования, которым должна удовлетворять функция a(\J) (или в
общем случае г|(х,0), чтобы обеспечивалась цель (6.120). Согласно (6.120) должно
выполняться соотношение
ж(0еГ&(/) или \|/e(z(/),/)£0 V/>/0.
С учетом выражения (6.192) получим
x + a(x,0VxM/er&(0, x€rg(0l
или \|/E(x + a(x,OVx\|/,/)^0 Vr>/0. J
Условие (6.196) может быть проиллюстрировано на рис. 6.3.
Неравенство (6.196) можно привести к следующему виду
\|/8(х,<х(-),0*0
(6.197)
Vxere(0, t>to.\
Отсюда следует, что для обеспечения требуемых фазовых ограничений функция
a(x,0 должна удовлетворять следующему неравенству
a(x,0*ae(x,0 1
Vxere(0, t>to,\
Глава 6. Синтез грубых систем автоматического управления
317
где ос8(х,О - некоторая известная скалярная функция, определяемая из (6.196) или
(6.197) и принимающая, в общем случае, неотрицательные значения. Причем для
каждого допустимого ееЕ функция ссБ(х,/) может иметь свое выражение. Если из
(6.197) или (6.196) функцию ссе(х,0 с достаточной степенью точности определить
нельзя, то для оценки допустимости а(х,/) можно использовать неравенство (6.197).
Таким образом, показана справедливость следующего результата.
/да
fQ£(t)
Рис. 6.3
Утверждение 6.3. Для того чтобы для объекта (6.57) некоторый закон управления
и = и()€£/(•) обеспечивал заданные фазовые ограничения (6.120), достаточно,
чтобы функция а(х,0, являющаяся решением уравнения (6.191), удовлетворяла
соотношению (6.196) (или одному из эквивалентных соотношений (6.197), (6.198)) для
любого ао=а(хо,/о), определяемого согласно (6.194) при произвольном
*c€Ck(/o)/0(fo)-
Используя утверждение (6.121), можно решать не только задачу обеспечения
фазовых ограничений, но и, в частности, задачу обеспечения устойчивости объекта
(6.57) в R" . Для этого необходимо конкретизировать вид Q(t). Выделим два случая
задания Q{t):
l.OeeCO, '*'о; (6Л")
2.0*0(0, t>t^ (6.200)
где 0 е R" - нулевой элемент в пространстве R" .
Если, например, выполняется условие (6.200), то поскольку для устойчивости
объекта (6.57) в R" необходимо, чтобы
z(0 -> 0 при / -> оо j
для любого z0 = z(/0) e R",\
то, используя выражение (6.192), получим
x(0 + a(x(0,/)Vx\|/(x(0,0->°
при/-» оо для любого х0 =x(to)eTQ(to)
и любого ao=a(xo,/o), удовлетворяющего (3.96).
(6.201)
(6.202)
318
Методы синтеза CAY по заданным показателям качества. Часть II
(6.203)
Поскольку z0 может быть любым вектором, то в качестве а0 можно выбирать
произвольное неотрицательное число. Кроме того, если обозначить:
limx(0 = x°°,
/->00
limV1v(x(/),/) = VxV",[
то условие (6.202) приводится к виду
xoo+a-VJcv|/oo=0 ]
УхоеГ£(/о) и Vao>O.J
Векторы х00 и Vxv|/°° могут быть непосредственно определены. Действительно,
поскольку z(t) -» 0 при / -» оо, то z(oo) = 0 € R", и поэтому х00 может быть
определен, как расстояние от нулевого элемента 0 б R" до множества £?(<*>) (до границы
Г(?(°°)), которое предполагается выпуклым (см. рис. 6.4).
Отсюда следует, что соотношение (6.203) всегда разрешимо, т.к. векторы х00 и
Vxv|/°° коллинеарны, и поэтому из решения (6.203) всегда можно определить
значение а^ .
z(0
гее»)
a-Vx\|/(
Рис. 6.4
(6.204)
Тогда получим, что в случае (6.200) объект (6.57) является устойчивым в R" , если
a(x(/),/)->a00, x(0->x°° при /->оо|
Vxoere(/O) и Va0>0. ' J
Для проверки выполнения (6.204) можно воспользоваться уравнением (6.191) при
подстановке в него выражения (6.192) с учетом (6.193). Если условие (6.204)
выполняется для некоторого выбранного допустимого закона управления и = м(-), то это
означает, что для данного и() уравнение (6.191) должно выполняться при значениях
/ = оо, a(-) = ae, x = x°°. (6.205)
Кроме того, с учетом (6.193) должно выполняться условие
5а .
> 0 при / -> оо,
(6.206)
поскольку а^ - стационарная точка, к которой стремится функция сс(х,/).
Аналогично получим следующее соотношение
5a w. ;—
>0при /->оо \//е1,и
dxi
Глава 6. Синтез грубых систем автоматического управления 319
или
Vxcc -> 0 при t -» оо. (6.207)
Тогда, подставляя в (6.191) значения (6.205), а также в соответствии с (6.206) и
(6.207) значения
Ul I/=OO
получим алгебраическое уравнение, которое будет выполняться, если правильно
выбран закон управления м(-). Таким образом, решая уравнение (6.191) совместно с
использованием условий (6.204) можно формировать закон управления, обеспечивающий
устойчивость объекта (6.57). Притом необходимо отметить, что рассмотренный
подход, вообще говоря, может давать только необходимые условия устойчивости, для
получения достаточных условий требуется осуществить линеаризацию (6.191) в
окрестности х°° и аЛ и провести анализ поведения малых отклонений во времени.
Аналогично обеспечение устойчивости объекта (6.57) в R" можно рассматривать
для случая (6.200) на основе условий (6.201), (6.202). Однако при этом на а(х,0 в
отличие от (6.203) будут накладываться другие условия, выполнение которых также
исследуется с помощью уравнения (6.191).
Используемое в рассмотренном подходе отображение л(х>0 может иметь более
общий вид по сравнению с (6.192). Например, в качестве г|(х,/) можно использовать
вектор-функцию следующего вида
Л(х,/) = п(у(х,0,х,/), (6.208)
где fj() -некоторая пх\ вектор-функция заданного вида,
непрерывно-дифференцируемая по всем своим переменным; у(х,/) - скалярная
непрерывно-дифференцируемая функция, вид которой заранее не задан. При этом выбор той или иной функции
fj(-) вида (6.208) должен обеспечивать взаимно-однозначное соответствие между
z(t) e R" и ее проекцией \{t) e TQ{t). Нетрудно получить
Vxn=^(VxY)T+Vxfi(Y,x,O,
\ (6.209)
dfj^dfj ду | df\(y,\,t)
dt ду'dt dt '
где Vxfj(y,x,f), —Чу,х,/) - якобиан и частная производная по времени функции
dt
f\(y,x,t), когда скалярная функция у(х,0 рассматривается как некоторый
фиксированный параметр.
Подставляя (6.209) в (6.191), получим уравнение в частных производных
относительно функции у(х,0, которая имеет единственное решение для заданных краевых
условий у(хо,/о) = у0, определяемых из соотношения
*о=л(Уо>хо,'о)- (6-210)
Справедливость этого доказывается аналогично утверждению 6.2.
320 Методы синтеза САУ по заданным показателям качества. Часть II
6.4. ПОСТРОЕНИЕ ГРУБЫХ СИСТЕМ УПРАВЛЕНИЯ
ПРИ МОДУЛЬНЫХ ОГРАНИЧЕНИЯХ
В данной главе показано решение задачи синтеза при модульных ограничениях на
компоненты вектора состояния на примере линейных систем управления. Приведена
геометрическая интерпретация основной теоремы метода фазовых ограничений и
показано ее непосредственное использование. Рассмотрен синтез при ограничениях
на качество управления, приведены некоторые численные процедуры решения
задачи. Дан анализ разрешимости задачи синтеза с учетом преобразования поворота
фазовых ограничений. Показана связь кругов Гершгорина с разрешимостью задачи
синтеза и их использование для построения грубых систем управления. Введена оценка
степени грубости системы, с помощью которой предлагается синтезировать системы
заданной грубости. Показана связь полученных достаточных условий на параметры
регулятора со свойствами так называемых входных-выходных матриц. Рассмотрен
вопрос выбора допустимых фазовых ограничений на основе положительного
собственного вектора входной-выходной матрицы. Сформулирован критерий
разрешимости задачи синтеза. Приведена процедура синтеза системы управления на основе
управления максимальным собственным значением входной-выходной матрицы.
Предложен критерий управляемости данным собственным значением.
6.4.1. Постановка задачи синтеза линейной МСАУ
ПРИ МОДУЛЬНЫХ ФАЗОВЫХ ОГРАНИЧЕНИЯХ
В предыдущих главах были получены общие соотношения, позволяющие
формировать различные законы управления по заданным фазовым ограничениям для тех
или иных динамических систем. Рассмотрим решение задачи синтеза применительно
к линейным многомерным системам автоматического управления (МСАУ) при
фазовых ограничениях вполне определенного вида.
Пусть уравнение МСАУ имеет вид
*;ГВЙ> } (6.2,1)
x(/0) = x0,/>/0,J
где х, и - п х 1,т х 1 векторы состояния и управления.
А = А(0 = [а„Щи> В = В(/) = [Ьт(ОТ/;=].
Причем
u = u + y\ . (6.212)
где у1 =у!(0 - некоторое задающее управление (воздействие); и - управление,
формируемое по принципу обратной связи.
На рис. 6.5, 6.6 показаны возможные структуры, соответствующие МСАУ (6.211).
У
КУ
и
х = Ах + Вй
х
хп =Сх
-►
Рис. 6.5. МСАУ с КУ в прямой цепи
Здесь: КУ - корректирующее устройство, являющееся линейным безинерцион-
ным звеном; С - матрица измерителя размера Ып вида C = C(t) = [c^v(t)]l£
хв - / х 1 вектор выхода (измерения).
',v=l'
Глава 6, Синтез грубых систем автоматического управления
321
хв=Сх (6.213)
- уравнение измерителя; г = у-хв - /xl вектор невязки; y(/)-/xl вектор задающих
воздействий.
U
,1
х = Ах + Вй
К
Рис. 6.6. МСАУ с регулятором в цепи обратной связи
Здесь: К - /их/ матрица регулятора (обратной связи), которая в общем случае
может быть нестационарна, т.е.
K = K(/) = [^(0]"i=,;
и = Кх = КСх
(6.214)
- уравнение регулятора.
С учетом (6.212) - (6.214) уравнение (6.211) приводится к виду
х = Ах + Ву\ 1
x(/0) = x0,f>/0,J
где
(6.215)
(6.216)
А = А + ВКС
- матрица состояния замкнутой системы.
В общем случае ограничения на вектор состояния могут быть представлены
согласно рис. 6.7 (для случая п = 2).
х(/,4)
Q(<)
Рис. 6.7. Вид «фазовой трубки»
Здесь: QQ0\Q(tk),Q(t) - сечения «фазовой трубки» («пучка траекторий»)
ЭДУо>'*] в начальный /0, конечный tk и текущий / моменты времени; х]0 и *q, х\ и
х\ - начальные и конечные значения фазовых траекторий; Q[/o,^] - фазовая трубка,
представляющая собой совокупность множеств Q{t) допустимых значений вектора
состояния х и системы (6.215), определенных для каждого значения te[tQ,tk].
В достаточно общем случае множество Q(t) можно представить в виде
2(0 = fW), <6-217)
/=1
322 Методы синтеза САУ по заданным показателям качества. Часть II
где
0(/) = {хеЛя: 1|/,(х,0<0},/еп;
v|/,(x,0
- некоторые непрерывно-дифференцируемые в R" функции ограничения.
Г0(О = {хеЯл: м;/(х,/) = 0},/бп
- граница множества (?,(/). Считаем также, что TQ{t) - граница множества Q(t),
образованная участками границ TQt(t)9 /el,x, которые будем обозначать
ге(оПга>/бп.
Тогда для рассматриваемой МСАУ можно поставить следующие задачи:
1) требуется определить, существует ли для данного xoeQ(to) траектория
х(/,х0) системы (6.215) такая, что
х(/, х0) е 6(0 V t > /0 или V/ е Г, . (6.218)
и если существует, то какое допустимое управление u e Rm ей соответствует;
2) существует ли такое допустимое управление (допустимый закон управления)
u e Rm , которое обеспечивает выполнение условия
х(/,хо)е£(О Vx0e£(>0)]
и V/>/0 или V/еГ J'
где Т- некоторый заданный непрерывный отрезок времени.
В дальнейшем в качестве функций ограничения 1|/;(х), / = 1,Х рассматриваются
следующие функции
i|//+(x,0 = -<7/(0 + */,
vi/-(x,O = ^/(O-^, (6.220)
/е1,и,
соответствующие фазовым ограничениям вида
\x\<qi(t\ /еп, (6.221)
(7,(0 - непрерывно-дифференцируемые неотрицательные функции.
6.4.2. Геометрические условия обеспечения фазовых ограничений
Рассмотрим применение теоремы 6.1 для случая, когда фазовые ограничения
задаются в виде (6.217). Введем обозначения
L &i ^2 йг« J
/ = Ax + Bu1(0,
(^хМ;/'/) = Х"^'Л - скалярное произведение векторов Vx^ и/
7=1 ^
Тогда аналогично теореме 6.1 можно показать, что для обеспечения фазовых
ограничений (6.217) достаточно выполнения следующего условия.
Следствие 6.8. Для объекта управления, описываемого уравнением (6.57) (или, в
частном случае, (6.215)), для обеспечения ограничения
x(0efi(0 V>^0,
Глава 6. Синтез грубых систем автоматического управления
323
где Q(t) определяется согласно (6.217), достаточно выполнения неравенств
(Vxv|/,,/) + ^<0,
(6.222)
v*€ra(or|re('), /ei,x, t>t0.
Покажем, как в пространстве состояний R" может быть интерпретировано
данное неравенство. Допустим, что
v|/,(x,/)^v]/,(x), /еп, (6.223)
т.е. функции ограничения стационарны, отсутствует их явная зависимость от Л Тогда
неравенства (6.222) приводятся к виду
(VxM/,,/)<0 Vxerfip|r£, /ей, />/0. ' (6.224)
Согласно определению [45], градиентVxvj// представляет собой вектор,
ортогональный гиперплоскости, касательной поверхности уровня функции vj/,(x) в точке
касания.
Из определения YQt следует, что YQt является поверхностью уровня (нулевого
уровня) функции v|/,(x). Следовательно, в каждой точке \eYQt вектор vj/Дх) будет
ортогонален гиперплоскости, касательной к YQf в данной точке.
Здесь гиперплоскости, касательные к YQ{ в точках jc1, x2, являются прямыми. Но
тогда Vxv|// ортогонален к данной гиперплоскости и в каждой точке х е YQ^YQ.
Из (6.224) находим, что обеспечение фазовых ограничений (6.217) согласно
(6.224) эквивалентно тому, что в каждой граничной точке VxeFQp|rQ, /el,x,
вектор скорости х системы (6.57) или (6.215) должен быть направлен внутрь
соответствующего полупространства R" .
Но поскольку в каждой точке xeYQ^YQ гиперплоскость Г является
касательной к границе множества Q, а само множество Q с R" , то получим, что х найравлен
либо внутрь Q, либо по касательной к его границе. В этом и состоит геометрический
смысл условия (6.224), что отражено на рис. 6.8 для случая п = 2, х = 4.
Vxv|/3
щПге
Rz
VxM/2
щПге
Vxvj/4
щГ|ге
гаПге
I vxVi Q
Рис. 6.8. Геометрический смысл обеспечения фазовых ограничений
324 Методы синтеза САУ по заданным показателям качества. Часть II
6.4.3. Определение достаточных условий на параметры регулятора.
Частный случай экспоненциальных ограничений
Неравенство (6.222) не зависит от выбора конкретного значения х0 е Q(t0), т.е.
если (6.222) выполняется, то, каким бы ни было начальное условие х0 е Q(t0),
соответствующая ему траектория
х(/,хо)е2(/) V/>/0.
При этом в Rm можно выбрать закон управления, обеспечивающий это включение.
Если рассматривается сформулированная выше первая задача (6.218), то
воспользоваться соотношением (6.222) можно следующим образом. Построим относительно
заданного х0 некоторую достаточно малую окрестность 0(хо),т.е.
хо€0(хо)се(/о). (6.225)
Аналогично тому, как было построено множество Q(t), />/0, построим
множество б(/,х0), t>t0, такое, что
е(Г,Хо)сб(О, '>'о>1
е(/о,хо)=0(хо). ■ (6*226)
Тогда, применяя на множестве Q(t,x0) соотношение (6.222), можно решать
задачу (6.218).
Рассмотрим неравенство (6.222) применительно к линейной системе (6.215).
Подставим в (6.222) вместо/выражение из (6.215). Получим
(vxV|/,,Ax + Bu4o)+-^^0, />/0,|
УхеГеДОПШО, ielx.
Отсюда находим
vx€rfl.(onrew. /el>x, t>to\
Рассмотрим случай, когда
иЧО = О, (6.228)
а множество Q{t) формируется на основе ограничений (6.221). Тогда
(VxM;,Ax)<-^- ]
V ' dt I (6.229)
Vx e TQfr{ff\TQ(t\ i e п, t> /O.J
где A = [a/V^=1; x = n - для функций ограничения вида (6.220), (6.221); TQ?(i)y
г2Г(0 ~ границы множеств Qf {t\ QJ(t\ формируемых соответственно на основе
функций i|//"(x,0, М>/~0М) вида (6.220).
Множество Q(t) при t>t0 является гиперпараллелепипедом и может быть
представлено следующим образом (п = 2, рис. 6.9).
Преобразуем неравенство (6.229). С учетом (6.220) получим
'лава 6. Синтез грубых систем автоматического управления
325
vxv; =
0-010 ••• 0
Vxvj/,- =
0 ••• 0-10 ••• 0
, /el, л,
M^-,,(0, ,.п
га+пг0
0
92
"92
/
9i
га+Пге
х\
\
га+пге
Так как
Рис. 6.9. Вид модульных фазовых ограничений
|v=l v=l v=l
то с учетом выражений для Vxv|/^, Vxv|/^
(ViV*>Ax)=E2,v*v>
v=l
(vxv|/7,Ax) = -^5iVj:v, /е1,л.
v=l
(6.230)
(6.231)
Вектор x в неравенстве (6.222) рассматривается на участках границы
ге*(оПгео, /епт.е.
если хеГд;р|Щ то ^=9/(0, |^v|^9v(0, veu\/, 1
если xerg~p|rg, то x^-q^t), |xv|<qrv(O, ve1^\/.J
Подставляя (6.230) - (6.232) в (6.222), получим
(6.232)
п
^alvxv<qi(t)-aiiqi(t), t>t0, /el,/?, \xv\<qv(t);
v=l
n
-]Ta/v*v <q,iO-a^XO, t>t09 ie\,n, \xv\<qv(t).
v=l
(6.233)
326 Методы синтеза САУ по заданным показателям качества. Часть II
Очевидно, неравенства (6.233) преобразуются к виду
п
1Х5/у*у|^й(о-ад,-(о»
v=l
V*/
(6.234)
/е1,я, \xv\<qv(t) vel,w\/, t>t0.
Поскольку (6.234) должно выполняться для любых значений |xv|<^v(/),
v e 1,л\/, то оно должно выполняться и для такого х, которое доставляет максимум
левой части неравенства. Очевидно
п п п п
Z5'v*v ^ ZI5'v*v|=ZKI* W ^ ZI5*kv(o.
v=l
V*/
v=l
v=l
v=l
Кроме того, при xv = qv (Osign aJV, vel,w\ /,
iZ^v*j=ZI5/vMo.
v=l
v=l
tax ^ I Z5/v*v I = ZI5/vkv(0-
Следовательно,
max | >
|xv|<^vr/; v=
В результате (6.234) примет вид
п
2ffivkv(o^ft(o-fl,i*(o,
(6.235)
v=l
V9t/
v=l
(6.236)
Соотношения (6.236) в общем случае являются достаточными условиями для
выбора закона регулирования, обеспечивающего ограничения (6.221). Укажем частный
случай, когда (6.236) являются и необходимыми условиями.
Пусть qt{t) = d^, / € l,w, где dk > 0 - некоторые постоянные величины. Тогда
получим
Zkk^<^^-^^^,
/el, я, />/о,
v=l
ИЛИ
v=l
V9t/
(6.237)
/el,w, t>t0.
Если система (6.211) стационарна, то неравенства (6.237) также будут
стационарными. При этом согласно [95] их можно рассматривать как необходимые и
достаточные условия обеспечения экспоненциальных ограничений.
Глава 6. Синтез грубых систем автоматического управления
327
6.4.4. Анализ разрешимости достаточных условий обеспечения
фазовых ограничений
Согласно (6.216)
А = А + ВКС.
Выразим элементы aiv матрицы А через элементы a/v, 6/ц, к^, с^
соответственно матриц А, В, К, С. Нетрудно показать справедливость равенства
•/ т
_4-1 М
/el,и, vel,/7.
Подставив (6.238) в (6.236), получим следующую систему неравенств
относительно элементов синтезируемой матрицы К
(6.238)
v=l
V*/
/ т
"'v+ZZV^v
4=1 М
^v(/)<^(0- au +XZW^v \ЯМ
4-i n-i
(6.239)
/€1,л, />/0.
Проанализируем условия разрешимости данной системы неравенств. Из (6.236),
(6.239) видно, что левая часть каждого неравенства данной системы является
неотрицательной. Следовательно, для разрешимости необходимо, чтобы и правые части
неравенств также были неотрицательными. Кроме того-, для различных задач,
представляющих практический интерес, можно потребовать
й(/)<0, />/0, igU, (6.240)
т.е. чтобы q,{f) были монотонно невозрастающими функциями.
Таким образом, если выполняются неравенства (6.240), то из (6.236) следует
?,(')-я,,?, (0^0, /е!Я t>t0
или
5,<^<0, /GU, />/0.
9i(0
Отсюда
/ т
(6.241)
^+ZZVn4c4v^0'
НИ
i€l,/i, />/0.
Неравенства (6.241) представляют собой необходимое условие разрешимости
соотношений (6.239). Неравенства (6.239) проще обеспечивать, если матрица А имеет
главную диагональ с доминирующими отрицательными элементами au,i € \,п.
Рассмотрим геометрическое условие разрешимости неравенств (6.239), которое
для линейных систем может быть распространено на общий случай задания
произвольных линейных ограничений.
Действительно, пусть ограничения (6.217), задающие множество Q(t), являются
линейными, т.е. \|/Дх,0>*'€1,х - произвольные линейные функции. Тогда Q(t) -
некоторый многоугольник достаточно произвольного вида. Ограничения также
считаются технически реализуемыми, т.е. соответствующий им многоугольник Q(t)
328
Методы синтеза САУ по заданным показателям качества. Часть II
сжимается при t>t0. Используя геометрические свойства соотношений (6.222) и
известные результаты [29], согласно которым произвольная линейная форма
(^xV/'/)4"—L L / е 1,х» на линейных ограничениях (6.217) принимает экстремаль-
L & ]
ные значения в вершинах многоугольника Q(t), аналогично рассмотренному случаю
можно показать, что для разрешимости (6.222) требуется, чтобы в каждой вершине
М, многоугольника Q{t) вектор скорости х системы (6.215) был направлен внутрь
Q(t) (см. рис. 6.10).
М
М
мл
Рис. 6.10. Геометрическое условие разрешимости фазовых ограничений
Если, например, для некоторого заданного Q(t) геометрическое условие
разрешимости не выполняется в одной из вершин М (см. рис. 6.11), то обеспечить
разрешимость возможно путем деформации Q(t) за счет изменения вершины М.
*2 ▲
М
R1
Рис. 6.11. Деформация Q(t) за счет изменения вершин
6.4.5. Синтез МСАУ при ограничениях на качество регулирования
Рассмотрим применение условий (6.222) или (6.227) для решения задачи
построения МСАУ с заданными ограничениями на качество регулирования. Воспользуемся
определением качества регулирования согласно [104] и распространим его на случай
многомерной системы. Ограничения на качество регулирования примут вид
Глава 6. Синтез грубых систем автоматического управления
329
-Я,(/)£*, £j£(0, t>t09
/el, л,
В достаточно общем случае рассматривается МСАУ, показанная на рис. 6.12.
У +-
(6.242)
Объект управления
К
^-#*
Рис. 6.12. Схема синтезируемой САУ
Здесь: x = Ax + Bu; u = KxB; xB=Cx; е = у-и; й = £.
Отсюда получим уравнение МСАУ
х = Ах + В£ = Ах + В(у-и) = Ах + В(у-КСх)
или
(6.243)
х = Ах + Ву(О,х(/0) = х0,/>/0,|
А = А-ВКС.
Для рассматриваемого случая (6.243) соотношения (6.222) можно представить в
виде
(Vx^x)^-(VxV/,By(0)) (6244)
С учетом (6.242) функции ограничения определяются согласно зависимостям:
Vf (*,/) = *,-tf (0*0,'
Ч/-(х,О = -х(-?Г(Г)<0) (6.245)
/el, л.
Получим окончательный вид требуемых соотношений
п т
v=l ц=1
£ 5,vp;v s 9* (0 - Ы (о - £ VmO,
V=l ц=1
(6.246)
/el,я, />/0.
Соотношения (6.246) являются более общими по сравнению с (6.236) и могут быть
сведены к последним, если положить
<7Л') = 9ЛО Vveu; уц(/)«0, це!^, (6.247)
т.е. несимметричные фазовые ограничения заменяются симметричными, а задающее
воздействие обнуляется.
Допустим, что фазовые ограничения являются симметричными, т.е.
<7Л0 = ?у(0 = ?у(')>0, veu,
а
>>м(0*0 при |Д€1,/и.
330 Методы синтеза САУ по заданным показателям качества. Часть II
Тогда (6.246) принимает вид
2w)
Ц=1
п
^(')-a,,u(0-X|a,vk('),
v=l
(6.248)
V*/
/el, л, t>t0.
Нетрудно видеть, что неравенства (6.248) разрешимы тогда и только тогда, когда
разрешимы неравенства (6.236). А из (6.246) следует, что для разрешимости данных
неравенств необходимо выполнение соотношений
~ ч7 (О+чч!(0 * % (0 - *ия! (0,1 (6 249)
/еп, t>t0. J
В некоторых случаях неравенство (6.246) можно упростить. Допустим, что вы-
прлняется условие
Ву(0е1{А}, (6.250)
где l{a} - линейное подпространство в R" , натянутое на вектор-столбцы матрицы
А (или Z,{A}=ImA - область значений вектор-функции Ах при xeR" [145]). Тогда
существует такой вектор x*gRw, для которого
-Ах*=Вхв. (6.251)
В системе (6.243) вида
х = Ах + Вхв=(А-ВКС)х + Вхв
произведем замену переменной по формуле
х = х-х\ (6.252)
Имеем
х + х*=Ах + Ах*-ВКСх*+Вхв,
или, с учетом (6.251),
i = Ах - (х* + ВКСх* у (6.253)
Ограничения (6.242) примут вид
-q-(t)<Xi+x* <q+(t)9 ie\,n.
Отсюда
-д-(0-х*<Х;<д+(0-х1 /еп (6.254)
Считаем, что ограничения для xh /el,n, являются симметричными, т.е.
?;(0-х;=?Г(0 + ^=8/(0>0, /еп (6.255)
Тогда с учетом (6.254)
|^|<5Д/), /GU (6.256)
На рис. 6.13 ограничения (6.254) показаны для постоянного и переменного х .
Таким образом, приходим к задаче обеспечения симметричных фазовых
ограничений (6.256) для системы (6.253). Обозначим
х* +ВКСх* =z* =z*(K,0 - лх1 вектор. (6.257)
Тогда система (6.253) приводится к уравнению
£ = Ax-z\ x(/0) = x0, t>t0, (6.258)
лава 6. Синтез грубых систем автоматического управления
331
це вектор х должен удовлетворять симметричным ограничениям (6.256). Поскольку
истема (6.258) имеет такой же вид, что и (6.243), то для нее справедливы соотношения
max
п
1>
xv zi
v=l
^5/-я,А>
l€l,/l, t>t0.
(6.259)
*
0
5,
8,
5,
xi0
0
i
л
\
8,
s,
/
s
t
Рис. 6.13. Ограничения для постоянного (а) и переменного (б) вектора X
Из (6.259), с учетом того, что
max
tf/v*v-Z,
v=l
n
v=l
следует неравенство
\zi
n
v=l
(6.260)
/€l,/I, Г>Г0,
аналогичное (6.248) и удовлетворяющее тем же самым условиям разрешимости, что
и (6.248). При этом вектор ъ формируется согласно выражению (6.257).
6.4.6. О ДЕФОРМАЦИИ ФАЗОВЫХ ОГРАНИЧЕНИЙ
ДЛЯ ОБЕСПЕЧЕНИЯ РАЗРЕШИМОСТИ ДОСТАТОЧНЫХ УСЛОВИЙ
При решении неравенств (6.236) одним из приведенных в предыдущем параграфе
методов вероятен случай, когда выполнение соотношений (6.239) в классе линейных
законов управления (6.214) обеспечить невозможно. Но это не означает, что для
рассматриваемой системы (6.215) нельзя подобрать такие фазовые ограничения, при
которых соотношения (6.239) будут разрешимыми. Причем часто для разрешимости
требуется лишь незначительно сформировать (изменить) заданные ограничения. В
частности, так, как показано выше на рис. 6.11.
Допустим, что деформация Q(t) осуществляется за счет некоторого поворота
данного множества в пространстве R" без изменения геометрических соотношений
данного множества.
332
Методы синтеза САУ по заданным показателям качества. Часть II
Переход от множества Q(f) к множеству Q\t) за счет некоторого поворота Q(t)
на угол а называется преобразованием вращения [71] и характеризуется матрицей
вращения Ту, соответствующей повороту Q(t) в плоскости двух переменных jc, и jc7
При этом
"1 0 ••• 0 0 ••♦ 0 0 ••• О"
О 1 • • 0 0 ••• 0 0 ••• О
Т</ =
0
0
0
0
0 •
0 •
0 •
0 •
• COSCC
•• 0
• 0
•• since
0
1
0
0
... о
... о
... 1
... о
-sina ••
0
0
cosa ••
• 0
• 0
• 0
• 0
(6.261)
О 0-0 0 ••• 0 0 ••• 1
Матрица Т^ обладает свойствами ортогональной матрицы, согласно которым
TtfT.Tff=VTtfT-E,x.e.Tj=T;1.
Если в R" осуществляется несколько поворотов множества Q(t),
характеризуемых матрицами вращения %jl9%2j29---*%kJk9 т0 общий поворот 6(0 к Q'{t)
характеризуется матрицей вида
Тогда вектор х, полученный в результате поворота вектора х, равен
х' = Тх, (6.263)
а множество Q\t) определяется по формуле
Q' = т• Q = |х' е R" : х' = Тх, х е Q}. (6.264)
Фазовые ограничения для деформированного многоугольника будут следующими
х = х(/)€е'(/), />/0- (6.265)
Таким образом, вместо соотношения х(/) е Q(t), t>t0, где Q(t) задается
согласно (6.221), необходимо для системы (6.215) обеспечить деформированные
ограничения (6.265).
Данную задачу можно свести к рассмотренной путем соответствующей замены
переменных. Действительно, если исходный вектор х преобразовать к х' согласно
(6.263), то в новой системе координат деформированный многоугольник имеет вид
Q'(t) = jx' е R" : |х'| < qt (r), i е Щ, (6.266)
т.е. задается аналогично Q(t) в старой системе координат.
Кроме того, (6.215) примет вид
или
где
ТЧ^АТ"^'
х^ТАТ-^А'х',]
х'(/о) = хо, t>t0, \
(6.267)
Глава 6. Синтез грубых систем автоматического управления 333
А^ТАТ^ТАТ7 (6.268)
- согласно свойствам ортогональных матриц. В результате приходим к
эквивалентной задаче обеспечения фазовых ограничений (6.266) для системы (6.267), которые
будут выполняться тогда, если выполняется система неравенств
£fr|*v(f)s*(/)-ff;(to,(r)L
(6.269)
v=l
dt
(6.272)
ie\,n,t>t0,
где
аА,=а(;(К,а,,а2,...,аД /,veu, (6.270)
коэффициенты матрицы А', которые помимо матрицы регулятора К зависят от
углов поворота al,a2,...,o.k, определяемые матрицами вращения
TW.TW-T4A- <6'271)
При этом неравенства (6.269) разрешимы тогда и только тогда, когда для системы
(6.215) разрешимы соотношения (6.222) для деформированных фазовых ограничений
(6.265). Данное утверждение справедливо для произвольного невырожденного
линейного преобразования (т.е. не только для преобразования вращения).
Это непосредственно следует из сравнения неравенств
(V,¥,(v),t)+£^SO
(vxv,,(t-V4t^
/еп, t>tOi Vx = T-]x'erQ'{t)()rQ;{t).
Из (6.272) видна эквивалентность первого и второго неравенств, а значит,
утверждение верно.
Более того, можно показать, что если система (6.215) является полностью
управляемой, то за счет преобразования поворота (6.261) многоугольник Q{t) вида (6.221)
всегда можно деформировать таким образом, что соответствующие этому случаю
неравенства (6.269) будут разрешимы.
Для линейных систем вместо деформации всего многоугольника Q(t) можно
рассматривать деформацию (смещение) его отдельных вершин. При этом смещать
вершины необходимо таким образом, чтобы вектор скорости системы х в смещенных
координатах был направлен внутрь Q\t).
6.4.7. Использование кругов Гершгорина для анализа разрешимости
достаточных условий
Неравенства (6.236) можно рассматривать, как некоторое обобщение известных
результатов, полученных в теории матриц и используемых для локализации их
собственных значений.
Известным результатом, имеющим практическое значение, является теорема
Гершгорина [154] о локализации собственных значений произвольной матрицы А . В
соответствии с ней вводятся обозначения:
334
Методы синтеза САУ по заданным показателям качества. Часть II
п
Pi=Z|5/v|>/€l>'I>
v=l
G/(A) = {z6C:|z-fl//|<p/},
G(A) = UG,(A), '
(6.273)
где ру - радиус /-го круга Гершгорина G/(A) , заданного в комплексной плоскости С
(z - вектор на комплексной плоскости); G(A) - область Гершгорина.
Если Xj,ie\,n - собственные значения матрицы А , то согласно теореме
Гершгорина
^gG(A) V/eui. (6.274)
Известен более общий результат, связанный с использованием кругов
Гершгорина. Согласно [9] для произвольной матрицы А круги Гершгорина определяются
следующим образом
1 п
р/=—ZI5»vK
Pi v=l
G,(A) = {z€C:|z-a//|<p,},/el,w
(6.275)
С
Im z
\ pi
л
\
) °
пл. С
Rez
Gn(A) G2(A)
G,(A)
Рис. 6.14. Расположение кругов Гершгорина в левой полуплоскости
эквивалентно неравенствам (6.236)
При этом область G(A) имеет вид аналогичный (6.273) и обеспечивает условия
локализации собственных значений (6.274), а /?, >0, ie \,n - произвольные
неотрицательные числа. За счет соответствующего выбора /?, >0,/б1,л, можно добиться
хорошей локализации собственных значений матрицы А .
Допустим, что
^/(0 = А = const, /el,/i.
Тогда неравенства (6.106) приводятся к виду
1
(6.276)
(6.277)
Глава 6. Синтез грубых систем автоматического управления
335
или, с учетом (6.275),
р,<-5й, /е1,л, t>tQ,
т.е. к рассмотренным уже соотношениям.
Но при этом круги G,(A), / е 1, л формируются согласно (6.275)
Пусть круги Гершгорина имеют по-прежнему вид (6.275), но условия (6.276) не
выполняются. Тогда получим
, п •
9/ v=i Яг
или
р, <-а//+— ,/е1,л,/>/0.
(6.278)
В плоскости С введем новую переменную
£ = z-z,,/gU, (6.279)
соответствующую /-му кругу Гершгорина G,(A), где z, - некоторый заданный
вектор на плоскости С
z = z + zt
и круг G,(A) имеет вид
G/(A) = {f + z/GC:|z + z/-5//|<p/} =
= {zeC:|z-(a//-z/.)|<p/}, /сп.
Очевидно, что в новой системе координат у всех кругов СДА), / е \,п , центры
смещены на вектор (аи - z/) относительно нового начала отсчета (см. рис. 6.15).
л
аи - zi
/
k lmzJ
\
L Imz
пл.С Re z
0 Rez '
Рис. 6.15. Круги Гершгорина при смещении центра координат
Положим
В силу свойств qt{t)
Чг
1г eRl и z, <0 V/g1,a7.
(6.280)
(6.281)
Поэтому круги G;(A) в новой системе координат имеют вид согласно рис. 6.16.
336
Методы синтеза САУ по заданным показателям качества. Часть II
ОДА)
Рис. 6.16. Круги Гершгорина в новой системе координат
В то же время неравенства (6.278) можно представить в виде
р, < -(ап -z,), / е Ъп, t > t0. (6.282)
Следовательно, и в этом случае, так же как и в двух предыдущих, получим, что
неравенства (6.236) или (6.278) выполняются тогда и только тогда, когда для каждого
круга Гершгорина G/(A), / el,/i, представленного в новой системе координат (6.279),
каждый G,(A) расположен слева от прямой, параллельной мнимой оси и
проходящей через точку z, (см. рис. 6.16).
Таким образом, показана справедливость следующей теоремы, связывающей
разрешимость неравенств (6.236) с расположением на комплексной плоскости кругов
Гершгорина. ♦
Терема 6.6. Для разрешимости неравенств (6.236) необходимо и достаточно,
чтобы каждый круг Гершгорина G,(A) /е1,л, построенный для матрицы А системы
(6.215), располагался на комплексной плоскости С левее прямой, параллельной
мнимой оси и проходящей через точку z, = —,/ е \,п, лежащую на вещественной оси.
В соответствии с данной теоремой можно утверждать, что если для системы
(6.215) построены круги Гершгорина (6.275), каждый из которых на комплексной
плоскости расположен левее прямой, проходящей через точку z,= — е Rez и парал-
4i
лельной мнимой оси lm z, то будут выполняться ограничения
Рассмотрим частный случай экспоненциальных фазовых ограничений, т.е. когда
^(О^/А/еп.
Тогда радиус круга G,(A) равен
1 V"4~ I , X/ 1
(6.283)
v-l
V*/
vW
а величина z,- смещения мнимой оси
Глава 6. Синтез грубых систем автоматического управления
337
4i dtekt
*i
(6.284)
т.е. совпадает для всех кругов. При этом для обеспечения ограниченных значений
траектории х(/) величина X < О. Данному случаю соответствует рис. 6.17.
f Imz
Rez
GW(A) G2(A) G,(A)
Рис. 6.17. Требуемое расположениие кругов Гершгорина
при экспоненциальных ограничениях
Таким образом, для матрицы А можно обеспечить требуемое расположение
кругов Гершгорина в соответствии с теоремой 6.6, а тем самым будут обеспечены
заданные фазовые ограничения (6.221).
6.4.8. о связи управляемости системы с расположением кругов
Гершгорина. Оценка степени грубости (робастности) системы
Известно [15], что если система (6.211) является полностью управляемой, то
собственные значения матрицы А замкнутой системы (6.215) могут иметь
произвольное распределение (расположение) на комплексной плоскости С. Однако это
свойство управляемости систем еще не гарантирует, что круги Гершгорина G,(A), / = 1, л,
соответствующие матрице А , можно также расположить на комплексной плоскости
произвольным образом.
Для полностью управляемой системы можно найти такое невырожденное
преобразование системы координат (6.263), для которого в новой системе координат
неравенства (6.236) будут разрешимыми. При этом было показано, что в качестве такого
преобразования можно использовать преобразование вращения. В более общем
случае невырожденное преобразование должно быть таким, чтобы преобразованные
матрицы А и В обеспечивали возможность формирования матрицы А с
доминирующими диагональными элементами отрицательных знаков.
В частности, матрицу Т, соответствующую требуемому преобразованию, можно
выбирать следующим образом. Пусть
(6.285)
А' = ТАТ"!,В' = ТВ
- матрицы А и В в новой системе координат. Тогда необходимо, чтобы
диагональные элементы матрицы
А' = А' + В'КТ1 =Т(А + ВК)Т"1 =ТАТ1
могли принимать одновременно произвольные значения в R], а скорость их
изменения в зависимости от изменения К превосходила скорости изменения
недиагональных элементов. В дальнейшем будет рассмотрена одна из процедур выбора
требуемой матрицы К.
>3 Зак. 366
338
Методы синтеза САУ по заданным показателям качества. Часть II
Из анализа расположения кругов Гершгорина на комплексной плоскости следует
вывод не только о выполнении того или иного неравенства системы (6.236), но и о
степени грубости (робастности) системы управления при возможном разбросе
значений ее параметров. Пусть рассматривается /-е неравенство системы (6.278) т.е.
1 п
—УХ-|?у*-з«+—''-'°-
я, tr я,
Обозначим через К = К' - значение матрицы, для которого данное неравенство
обеспечивается. Считаем также, что некоторые параметры матриц А, В, С заданы не
точно (полная информация об их значениях отсутствует, а сами значения задаются с
некоторой, вполне определенной, погрешностью). Введем обозначения
6/ц = bt + AV
_ О Л
^v - c£v
(6.286)
где fl/vAn»^ и tf,°vA° ,c£v ~ действительные и номинальные значения элементов
матриц А, В, С; Ая/у,А6/ц,Дс£У - погрешности задания значений элементов, о
которых имеется информация вида
(6.287)
|Да,у| < ct/v,|A6/M| < Р/ц,|Ас^| < y4v #
где ос/у,Р;ц,у^у - некоторые заданные величины.
Тогда согласно (6.238)
/ т
(6.288)
Отсюда
/ /W
(6.289)
ИИ
/ m
Ай/У = AalV +ХЕ^Л V?v +*/цА^у + Д^цДс^)*^.
Соотношение (6.289) показывает, как неточность задания элементов матриц
А, В, С влияет на неточность задания элементов матрицы А при фиксированной
матрице К1. Из (6.289) нетрудно получить, что
K|<a/V) (6.290)
где, с учетом (6.287),
Используя представление аы в виде (6.288), получим следующее выражение для
/-го неравенства
1 V4~o . .- . . ~о ,~ ,1l, (6.292)
4i v=i
~0+д5,Ук^-5°-даг,,+-^,
Глава 6. Синтез грубых систем автоматического управления 339
где Aaty/iAau удовлетворяют (6.290), (6.291) и могут иметь в соответствии с этими
соотношениями произвольные допустимые значения.
Определение 6.4. Будем говорить , что система (6.215) является грубой (робаст-
ной) относительно фазовых ограничений для /-й координаты вектора состояния х
(для jcj), если существует такая матрица регулятора К = К0 , для которой
обеспечивается выполнение неравенства
|*,|<<7,(0, t*to>
при произвольных значениях элементов матриц А, В, С (6.286) с учетом возможного
диапазона их изменения (6.287).
Аналогично определим грубость системы для всего вектора состояния х .
Определение 6.5. Будем говорить, что система (6.215) является грубой (робаст-
ной) относительно фазовых ограничений для вектора состояния х , если существует
матрица К = К0, для которой на всем диапазоне изменений элементов матриц
А, В, С (6.286), (6.287) обеспечиваются неравенства (6.221).
Поскольку достаточным условием обеспечения ограничений (6.221) является
выполнение неравенств (6.236), то рассмотрим свойство грубости (робастности)
системы применительно к данным неравенствам. С учетом определений 6.2 система
(6.215) будет грубой относительно фазовых ограничений (6.221), если для каждого
/el,л выполняется неравенство (6.292) при разборе параметров системы согласно
(6.286), (6.287).
Неравенство (6.292) можно представить в виде
р?+дР,<-(г?,+Д2//)+^
я,
(6.293)
/el, л, t>tOi
где Ар, -погрешность в определении радиуса р, круга Гершгорина G,(A). Причем
|Ap,|<-!-^a/Wv /=ТЯ (6.294)
Я\ V=l
Тогда аналогично тому, как строились круги Гершгорина для неравенств (6.278),
можно построить круги G;(A° +AA), / = 1,я, для неравенств (6.293), как это
показано на рис. 6.18, где А0 - номинальное значение матрицы А , а ДА - допустимая
погрешность или возмущение матрицы А . Если неравенства (6.293) выполняются, то
возмущенные круги G,(A° + ДА), / = 1,л согласно теореме в.6 будут находиться
слева от прямых, проходящих соответственно через точки zf =—, i = \,n и лежащих на
вещественной оси qt плоскости С. При этом, чем больше величины
2,-=^-(52+Р?)> /е^> (6-295)
тем допускается большее параметрическое возмущение, при котором выполняются
неравенства (6.293) и, значит, обеспечиваются заданные фазовые ограничения (6.221).
Величину L, будем называть степенью грубости (робастности) системы (6.215)
по координате xh относительно фазовых ограничений (6.221).
23*
Методы синтеза САУ по заданным показателям качества. Часть II
G,(A°)
rio
аО
G,(AU+AAU)
Рис. 6.18. Допустимое расположение кругов Гершгорина при параметрических возмущениях
Величину
I =mjnl/
/el,л
(6.296)
будем называть степенью грубости (робастности) системы (6.215) относительно
фазовых ограничений (6.221).
Чем левее расположены на комплексной плоскости круги Гершгорина, тем
большие значения принимают величины £,,/ е 1,я и 2 , и следовательно, тем более
грубой является рассматриваемая система управления (6.215).
Для того чтобы обеспечить построение системы (6.215) с требуемой степенью
грубости Ео, необходимо обеспечить выполнение неравенства
Е>£0 . (6.297)
или, с учетом определений (6.295), (6.296),
Отсюда
Il-=^-(2ii+p/)^S0*Vi€l,/i.
4i
р, <-5;/+—-So>
(6.298)
ie\,n,t>t0.
Синтез матрицы К в соответствии с соотношениями (6.298) позволяет построить
систему управления с заданной степенью грубости по отношению к ограничениям
(6.221).
6.4.9. Входные-выходные матрицы и их связь с разрешимостью
достаточных условий
Для исследования свойств неравенств (6.236), анализа их разрешимости и
формирования процедуры решения могут эффективно использоваться так называемые
входные-выходные матрицы [138]. Согласно их определению, это такие матрицы
А* = [а*$*я\, элементы которых удовлетворяют условиям
atj >0 при /*У,
аи =
а;.-произвольная вещественная величина при i-j.
(6.299)
Рассмотрим неравенства (6.236). Очевидно, их можно представить в виде
Глава 6. Синтез грубых систем автоматического управления
341
\a2l\qi+a22q2+... + \a2n\qn<q2
M<7i + Mft + - + annqn < qn
который, в свою очередь, приводится к следующей векторной форме
где их л матрица А и их1 вектор q имеют выражения
Ы
а22
Ы
ы
, q = q(O =
<7i(')'
«72(0
(6.300)
(6.301)
(6.302)
при этом q = q(r) = \qx(0 <fi(t) ••• qn(/)]T . Нетрудно видеть, что элементы матри-
цы А удовлетворяют условиям (6.299). Следовательно, матрица А является
входной-выходной. Кроме того, вектор q(0 является положительным, т.к. V/el,/i
9i(0>0.
Известно [138] следующее свойство входных-выходных матриц: если А* - входная-
выходная матрица, то она имеет собственное значение Х+ с максимальной
вещественной частью (т.е. Re X+ =max ReXi9 где А,,, / е \,п - все собственные значения
матрицы А*), причем это собственное значение является вещественным (т.е.
Im А. = 0), а собственный вектор е+, соответствующий данному значению X*,
единственен и является положительным (т.е. ef > 0 V/ е 1, л, где е[, / е 1, п, - компоненты
Таким образом, для матрицы А справедливо
AV=AV
r=maxReA/, e+ =[<...<]т >0f*
/el,/?
(6.303)
Поскольку матрица А является входной-выходной, то для нее также должно
выполняться свойство (6.303). А с учетом зависимости aiv от матриц К и С, получим,
что А является входной-выходной для любых значений матрицы К. Поэтому для
матрицы А всегда можно указать такие
\+=X+(K)eRl
tf"iDq+=q+(K)>0,
что
Aq+=A+q+, (6.304)
где собственное значение X* имеет максимальную вещественную часть среди всех
собственных значений матрицы А, a q - соответствующий ему положительный
собственный вектор.
342 Методы синтеза САУ по заданным показателям качества. Часть II
Воспользуемся рассмотренным свойством матрицы А для анализа разрешимости
неравенств (6.236) или (6.301).
Справедливо следующее утверждение.
Утверждение 6.4. Для разрешимости неравенства (6.301) для практически
реализуемых функций ограничения, удовлетворяющих условиям (6.240), необходимо и
достаточно, чтобы собственное значение Х+ матрицы А удовлетворяло неравенству
Х+ < 0 . (6.305)
Действительно, справедливость этого утверждения непосредственно следует из
теоремы 6.6, согласно которой для практически реализуемых функций ограничения
все круги Гершгорина лежат в левой полуплоскости комплексной плоскости С, если
неравенства (6.301) разрешимы. Тогда все собственные значения Xnie 1,я, матрицы
А , также находятся в левой полуплоскости, т.е. Re Xt< 0 V/ е 1,п. И согласно
определению Х+ (6.303) получим, что Х+ < 0. В то же время, если выполняется
неравенство (6.305), то существуют такие практически реализуемые функции ограничения
q(/), для которых неравенство (6.301) выполняется. Тем самым показана
справедливость утверждения 6.4.
Таким образом, о разрешимости неравенства (6.301) для практически реализуемой
q(0 можно судить по знаку X* . Если выполняется (6.305), то при некоторой матрице
К обязательно найдется такая практически реализуемая q(t), для которой
обеспечивается (6.301), а значит и фазовые ограничения.
6.4.10. О ЗАДАНИИ РАЗРЕШИМЫХ ФАЗОВЫХ ОГРАНИЧЕНИЙ
В предыдущем параграфе было показано, что если для некоторой матрицы К
^.+ (К)<0, то найдется такая практически реализуемая q(/),. соответствующая
данной К, для которой справедливо неравенство (6.301). Рассмотрим, какого вида могут
быть указанные функции q(/) для рассматриваемой К, удовлетворяющие (6.301), и
каким именно образом их можно выбрать или построить.
Пусть q+(t) - нестационарная функция (это возможно при Х+ ф0). Согласно
утверждению 6.4 считаем, что А,+ < 0. Рассмотрим следующую задачу: для заданной
матрицы А , у которой Х+ < 0, требуется построить множество практически
приемлемых функций q(0, удовлетворяющих неравенству (6.301) (т.е. для которых
выполняются фазовые ограничения (6.221)).
Для решения данной задачи воспользуемся разложением произвольной функции
q(t) > 0 относительно функции q+(t). Поскольку в общем случае
9(0*P(0V(0, 9(t)>0,p(t)eR\
то q{t) можно представить в виде
q(t) = Pl(t).q+{t)-q\O, (6-306)
где величина множителя px(t) выбрана минимально возможной из условия, что
e(Ospi(o-6+(o, (6.307)
a q\t) - вектор невязки между векторами q(/) и Pi(0"4+(0-
На рис. 6.19 показано определение р^/) и ^(0-
Глава 6. Синтез грубых систем автоматического управления
343
PiQ+(O Q4<)
\ \
-х2
\
i
Q(t)
\
\
4*2
ч
\
0
<72=Р|<?2
/
/
I
г +
Я
Рис. 6.19. Разложение функции q{t)
Поскольку Q+(t),Q(t) - прямоугольные параллелепипеды в Rn, то pj(/) имеет
вид
Pl(0 = miQ{M).} = min{MI,...,M)l
Для определенности положим, что
*»-58
(6.308)
(6.309)
Тогда вектор невязки q] аналогично тому, как показано на рис. 6.19, в общем
случае можно представить следующим образом
?1(0 = Pi(0-?1+(0-?1(0, (6.310)
где пх\ векторы q*+(t),g\t) определяются согласно выражениям
<71+(0 =
о
, <?Чо=
*,-i(0
о
(6.311)
т.е. векторы qu(t\qx(f) являются ортогональными проекциями векторов q+(t\q(t)
на («-1)-мерное координатное подпространство/?^"1 ортогональное оси 0хп (или
вектору [0 0 ... 0 хп]т).
Таким образом,
ql\t)eR"n-\q\t)zK-x. (6.312)
С учетом (6.310) выражение (6.306) примет вид
(6.313)
(6.314)
<7(O = P,(O<7+(O-Pi(O<71+('W(O.
Вектор q\t) по аналогии с (6.306) можно представить в виде
q\t) = p2(tW+(t)-q2(t),
где множитель р2(/) выбирается минимально возможным из условия
344
Методы синтеза САУ по заданным показателям качества. Часть II
a(Osp2(o-a+(o, (6.315)
6i(0>6i+(0 ~ ортогональные проекции многоугольников Q(t),Q+(t) на
подпространство R"~].
Множитель р2(0 определяется с помощью соотношения
Для определенности можно считать, что
*в-М:
Тогда для <72 (0 по аналогии с (6.310) справедливо выражение
?2(0 = P2(0w2+(0-?2(0,
где
2+
<Г(0 =
<7.+(0
<7n+-2«
о
о
, <72(') =
9,(0
Чп-lit)
о
о
причем
?2+«еС- ?2(0б<;2-1.
(6.316)
(6.317)
(6.318)
(6.319)
(6.320)
где /??„_! - (и - 2)-мерное координатное подпространство, ортогональное осям 0х„ и
ох,
(6.321)
(6.322)
и-1 •
Подставляя (6.318) в (6.314), получим
Тогда выражение (6.313) примет вид
9(0 = Pi(0?+(0+(p2(0-Pi(0)9l+(0-P2(092+(0+92(0.
Продолжая и далее подобную процедуру разложения векторов, получим
«7й"2 (о=р„-. (0<7(л-2)+(о - р„_, a V"-1)+(о+9(""°(о. (6.323)
где
^-.)(0)<7(»-.)+(0еЛ.п1 з2|
^л, ,3 = ^з1*л,.,2 = ^2 ~ ДВУХ" и одномерное координатное подпространства,
построенные указанным выше образом;
(6.325)
(6.324)
Поскольку Л~ - одномерное подпространство, то в силу (6.324) получим
9""1(0 = Ри(0<7(""1)'(0, (6-326)
Глава 6. Синтез грубых систем автоматического управления 345
где
Р*(') = ^-. (6.327)
Согласно определению множителей pv(0, v е 1, л можно записать соотношение
Pl(/) < р2(0 <... < ря.,(0 < рМ (6.328)
рассматриваемое в текущий момент времени / > t0. Неравенства (6.328) будут
справедливы V7>f0, если считать, что геометрические соотношения между qt{t)Je\,n
также остаются неизменными V/ > t0 .
Аналогично можно получить выражение общего вида
к-\
I
v=l
Л. I
q (0 = Pi(0?+(0 + £ (Pv+i(0-Pv(0)9v+(0-P*(09*+(0 + 9*(0, (6-329)
где
як (0 = р*+, (0«?А+0) - р*+, (0«?(*+1)+ (0+ч(м) (0,1 (6.ззо)
1 < А<«-2. ]
Тогда для к = п-2 получим
?(О = р,(О?+(О+Х(р^(0-рЛ'))<Г(') -Рл-2О?<л-2)Х0 +
+p.-,(0V"2)+ -Р..,(0?("-'н(0+р.(0?(""|)+(0 = (6-331)
л-1
= P,(O^(O + Z(Pv+,(O-Pv(0)^v+(0.
Выражение (6.331) представляет собой разложение произвольной вектор-функции
<?(/)> 0 по элементам собственного вектора q*(t). Воспользуемся разложением
(6.331) для решения поставленной задачи по построению требуемых функций q(t). В
неравенство (6.301) вместо q{i) подставим выражение (6.331). Тогда получим
Aq<q или
pxkq+ +£0Vi -pv)A<f+ <pxq+ +p^+ +
v=l
+Z[(Pv+i -Pv)«7V+ +(Pv+i -Pv)«7V+]
V=l
Отсюда находим
Z(Pv+. -Pv)A<?v+ <p,9+ +2[(PV+. -Pv)?V+ +(Pv+i -Pv)<7V+} (6-332)
v=l v=l
Неравенство (6.332) можно непосредственно использовать для задания
требуемого класса функций q(t), соответствующих заданной матрице А . При этом решение
(6.332) осуществляется непосредственно относительно положительных функций
pv(/),vel,H, - удовлетворяющих условию (6.328), при фиксированных значениях
векторов
?v+(0, <Г (0, ?+(0, А<Г (0, vel^T) .
22 Зак. 366
346
Методы синтеза САУ по заданным показателям качества. Часть II
6.4.11. Построение допустимых фазовых ограничений
на основе разложения по элементам собственного вектора
Рассмотрим возможный подход к определению допустимых функций q(t),
удовлетворяющих (6.301), на основе неравенства (6.332). В общем случае можно записать
(6.333)
qv+=k+ ... qU о ... о] ,vei,(*-i).
Тогда, используя выражение (6.302), для А получим
Aqv+ =
аи - элементы матрицы А .
Обозначим
, vel,(rt-l),
Pv(0 = Pv+l(0-Pv(0, V€l,(/I-l).
В силу (6.328)
Pv(/)>0, Vvg1,(/I-1).
С учетом (6.334) рассмотрим левую часть неравенства (6.332).
Имеем
п-\ п-\
£PvAqv+ =XPv
v=l v=l
r i — v
i=i
n~ v
Z<W
/=1
n-\ n-v
Z Ем»?;
v=l /=1
n-\ n-v
I ZpA/<?,+
v=l /=1
В то же время правую часть неравенства (6.332) можно привести к виду
(W+Z(M.++iW)
v=l
Pl?2+Z(M2+M2)
v=l
n-\
m++Z(mv++mv+)=
v=!
Pl^+-l+(Pl^+-l+P.^-l)
Pl^+fZPvVr+flPvVr
Vv=l У Vv=l J
P.^++(ZPv]^+(ZPv]92+
Vv=l
Pi^-i+Pi?»-i+M»-i)
Pl^n
(6.334)
(6.335)
(6.336)
(6.337)
(6.338)
Глава 6. Синтез грубых систем автоматического управления
347
Подставляя (6.337), (6.338) в (6.332), получим следующую систему неравенств
относительно искомых множителей
п-\ (n-v \ (п-\ \ (п-\ \
XPV I<W Urn* + iPv к + ZPv k.
v=l
A7-1
/=1
w-v
LpJ L^tf NfW + ZPv № + iPv k-
v=l V/=l У Vv=l У Vv=1
v=l
/j-2
v=l
'w-2
л-1
v=l
n-\
n-v
ZPv Z^-i,/^ Npi9«+-i +Pi^-i +Р19„+-1)>
(6.339)
v=l V/=l У
Система неравенств (6.339) используется для непосредственного формирования
допустимых фазовых ограничений, соответствующих фиксированной матрице А .
Чтобы функция q(t) была монотонно невозрастающей с учетом разложения (6.331),
можно положить
0<^<-Г,Р/0>0. ]
Поскольку
то система (6.339) может быть преобразована следующим образом
п-\ (п-\ \ Г (n~i
(6.340)
ZPvO Е^О; U PlO^+ IPvO (^++^)
^0;» У'б1,Я.
(6.341)
v=l \i=\ J L Vv=l
На основе решения данной системы определяются требуемые множители.
Система является линейной относительно р10, Pv0, v e 1, (п -1), и ее можно решать многими
известными методами [70]. Более того, поскольку X < -Х+, то
х + х+ <о
и потому
max plo^-bX(Pvo)(^++^)
v=l
qtj =-Pio^+<7o7'
(6.342)
Поэтому, если для некоторого 0 < X < -Х+ величины р10 > 0, Pv0 > 0, v е \,(п -1)
являются решениями неравенств (6.191), то они также будут решениями следующей
системы
ZPvo|Z^oJ^-Pio^^oV
v=l V/=1 )
j G 1,12.
Отсюда следует, что можно решать более простую систему неравенств (6.343), а
полученные решения затем проверять на удовлетворение ими исходных неравенств.
При этом нетрудно видеть, что саму систему (6.343) достаточно просто решить. По-
12*
(6.343)
348 Методы синтеза САУ по заданным показателям качества. Часть II
скольку р10 > 0 и (Jv0 > 0,v e 1,(л-1) выбираются независимо друг от друга, то,
задавая р10 достаточно большим по величине, a Pv0 -достаточно малым, всегда
можно обеспечить разрешимость (6.343).
6.4.12. Критерий стабилизируемости системы управления
В соответствии с приведенным выше утверждением 6.4, для существования
практически приемлемых функций ограничения q(t), обеспечивающих заданные фазовые
ограничения вида (6.221), достаточно, чтобы существовала такая матрица К, которая
бы обеспечивала выполнение неравенства (6.305). Рассмотрим вопрос о выборе
матрицы К, для которой неравенство (6.305) разрешимо.
Введем следующее определение. Будем говорить, система (6.211) стабилизируема
относительно ограничений (6.221), если существует хотя бы одна такая матрица К,
для которой у матрицы А собственное значение Х+ = Х+ (К) удовлетворяет
неравенству (6.305), т.е.
Х+=Г(К)<0.
Тогда в качестве критерия стабилизируемости, с учетом введенного определения,
можно рассматривать уравнение
Х+ =Х+(К) = 0. (6.344)
Таким образом, если обеспечивается соотношение (6.344), то система (6.211) является
стабилизируемой и для нее всегда можно выбрать такую матрицу К, что Х+ (К) < 0 .
Пусть
а(Х) = det(XE - А) = а0 + ахХ +... + ап_{Хп'х + Хп = 0 . (6.345)
Поскольку Х+ является собственным значением матрицы А, то для проверки
стабилизируемости системы (6.211) молено воспользоваться соотношением (6.345)
при X* = 0
a(0) = det(-A) = 0. (6.346)
Однако непосредственное решение (6.346) относительно К в общем случае
связано с существенными трудностями. При этом заранее не известно, является ли
уравнение (6.346) разрешимым для рассматриваемой системы или нет.
Рассмотрим другой геометрический подход к проверке выполнения критерия
стабилизируемости, основанный на использовании кругов Гершгорина. Известно, что
если в ограничениях (6.221) функции qt{t\ie\,n, являются экспонентами с
показателем X, то достаточные условия, которым должна удовлетворять матрица К,
приводятся к соотношениям (6.237). Используя для этого случая обозначение
?(0 = ?о^>где?0=М d2 ... dn]T,
в соответствии с (6.301) неравенства (6.237) приведем к виду
AqQeXt<Xqoeh
или
Aqo<Xqo. (6.347)
Это означает, что все круги Гершгорина G;(A), /el,л, для рассматриваемой
системы расположены левее прямой, параллельной мнимой оси и проходящей через
точку (X,j-O) на комплексной плоскости. Если положить X = X+>q0 =<?o , то
неравенство (6.345) приводится к виду
Глава 6. Синтез грубых систем автоматического управления
349
что эквивалентно следующему расположению кругов Гершгорина на комплексной
плоскости, представленному на рис. 6.20.
Im z
пл. С
Rez
g;(a)
G2+(A) C,+ (A)
Рис. 6.20. Круги Гершгорина на компонентах положительного собственного вектора
-. п
Здесь: р* = —^|a,v|<7ov,/e 1,л (?ov>V€l>" ™ компоненты вектора qrj);
90i v=l
V9t/
G,+ (A), /el, я - круги Гершгорина, соответствующие величинам 1С w q$ .
Согласно рис. 6.20 все круги G*(A), /el, л, имеют общую точку касания
(А/,уО), лежащую на вещественной оси. При этом данная точка может находиться
как в левой, так и в правой полуплоскости комплексной плоскости. Отсюда нетрудно
получить геометрический эквивалент сформулированного выше критерия стабилизи-
руемости системы (6.211) относительно ограничений вида (6.221).
Действительно, система (6.211) является стабилизируемой, если каждый круг
Гершгорина G/"(A), /el,/!, построенный с помощью собственного вектора ^о » ка-
сается справа мнимой оси комплексной плоскости в начале координат (соответствует
Х+ =0).
Очевидно, для того, чтобы проверить, выполняется ли данный критерий стабили-
зируемости или нет, необходимо проверить разрешимость следующей системы
уравнений
ctii+Piг =0,/el, л,
или
1
Д,,+ — y|a,v|</v=0,/el,/!,
4£f
(6.348)
где предполагается, что X = Х+ = 0, а dv = q^v9 v е 1,п, р, = р,+, / е 1,л.
350
Методы синтеза САУ по заданным показателям качества. Часть II
Таким образом, геометрическое условие стабилизируемости эквивалентно
разрешимости системы алгебраических уравнений (6.348). При этом система (6.348)
решается одновременно относительно матрицы К, а также относительно собственного
вектора ql •
Заметим, что если для проверки стабилизируемости системы (6.211) использовать
уравнение (6.346), то помимо вырожденности матрицы А , обеспечивающей (6.346),
необходимо также потребовать, чтобы значение X = 0 имело максимально
возможную собственную часть среди всех корней характеристического уравнения (6.345),
кроме X = Х+ = 0.
6.4.13. Процедура синтеза системы управления '
на основе управления максимальным
собственным значением входной-выходной матрицы
Рассмотрим вопрос о том, каким образом может быть синтезирована матрица К,
обеспечивающая фазовые ограничения (6.221) с помощью введенного в предыдущем
параграфе критерия стабилизируемости и его геометрического и алгебраического
аналогов. Воспользуемся тем обстоятельством, что для любых значений т х п
матрицы К соответствующая ей входная-выходная матрица А обязательно имеет
вещественное собственное Х+ с максимальной вещественной частью. Притом, как было
показано в предыдущем параграфе, если q£ - соответствующий Х+ собственный
вектор (всегда положительный), to на комплексной плоскости С круги Гершгорина
GJ(А), / е 1,п , располагаются согласно рис. 6.21.
Выше отмечалось, что собственное значение Х+ =А,+ (К) непрерывно зависит от
матрицы К. Поэтому, непрерывно изменяя величину матрицы К, можно добиться
того, чтобы значение Х+ непрерывно изменялось (увеличивалось или уменьшалось).
Это соответствует тому, что на вещественной оси комплексной плоскости С точка
Х+ непрерывно перемещается вправо или влево (см. рис. 6.21).
Imz ^
пл. С
А.2=Ь+(К2) /Х\ = Х\К])
G+(A2)
G+(A,)
Rez
Х+0 = Х+(К0)
G\AQ)
Рис. 6.21. Управление собственным значением Х +
Здесь: Х\ < X] < Х+о - значения собственного числа Х+, соответствующие
матрицам K^K^Kq;?^1 ,X\\X+2 - скорости изменения величины Х+ в точках Х+0,Х\,Х+2 в
зависимости от матрицы К; G+(A0),G+(A1),G+(A2) - области Гершгорина при
K0,Kj,K2.
Глава 6, Синтез грубых систем автоматического управления 351
Следовательно, собственным значением Х+ можно управлять с помощью
матрицы К, непрерывно перемещая его вдоль вещественной оси комплексной плоскости
С. Тогда, если система (6.211) стабилизируема в смысле (6.344), то произвольную
начальную величину Х+о = Х+(К0) за счет непрерывного изменения матрицы К
всегда можно перевести в левую полуплоскость комплексной плоскости С по
непрерывной траектории вдоль вещественной оси. Обеспечив значение Х+ = Х+(К)<0,
далее можно продолжить поиск требуемой матрицы К, обеспечивающей
ограничения (6.221), либо, в случае неразрешимости последних для заданной q(t), попытаться
отыскать q(t), наиболее близкую в том или ином смысле к q(t), для которой (6.221)
выполняются.
Таким образом, для решения рассматриваемой задачи предлагается вначале
перевести собственное значение X* в левую полуплоскость комплексной плоскости С , а
затем скорректировать выбор матрицы К и, если необходимо, функции q(t).
Рассмотрим подход к решению задачи перевода Х+ в левую полуплоскость
плоскости С . Вначале необходимо найти начальное значение Х+о , из которого
осуществляется требуемый перевод. Выберем произвольную матрицу К = Ко и для нее
определим А0=А + ВК0С и Ао Тогда А,о=А.+ (Ко) - соответствующее собственное
значение матрицы Ао,
Значение Х+о можно найти из решения характеристического уравнения (6.345)
при А = Ао . Однако при этом не обязательно вычислять другие собственные
значения. Аналогично [61] можно утверждать, что если Х+о - вещественный корень
характеристического уравнения (6.345) с максимальной вещественной частью, то
справедливы соотношения
a{k\X+0)>0, *€0,(11-1), (6.349)
где ^(Х) - к-я производная многочлена а(Х).
Таким образом, величину Х*о можно определить как минимально возможное
вещественное значение, удовлетворяющее неравенствам (6.349). Величине ^о
соответствует свой собственный вектор #о = Яо (Ко) > который можно определить в
результате непосредственного решения следующего линейного алгебраического уравнения
Ао • <7о = ^о<7о или (^оЕ- Ао)(7о = 0 .
Определив указанным образом начальные значения X+0,qQ , можно решать
требуемую задачу управления собственным значением X* .
Для одновременного нахождения начальных значений ^о><7о > в отличие от
предыдущей процедуры, рассмотрим численный подход, обеспечивающий сходимость к
требуемым X*0,qQ . С этой целью воспользуемся неравенством (6.347)
А<7о ^ ^-<7о >
которое будет равенством только при X = Х+ ,q0 = q$ . Представим (6.347) в виде
352
Методы синтеза САУ по заданным показателям качества. Часть II
* и? * "3 - ип ^ л
«22 + «21 "Г + <*23 -1 +... + а2п -S- < X,
4
d2
Л dx Л d2 л dn_x
а„ а„ а„
(6.350)
Для определенности будем считать, что значения au,ie\9n можно упорядочить
следующим образом
К* ^ К-\*-\ ^ "• ^ а22 < аи . (6.351)
Введем обозначения
dn-\ _ dn-2 _ dx __
~1 - а1 »"3 - а2 »— >"Т" ~ aw-l'
*л-1
T.e.TiL- = aw_v,vGl,(«-l).
«V+1
(6.352)
С учетом (6.352) для величин dt I d} в неравенствах (6.350) можно получить
следующие выражения:
a*+i-aik+2--'av. ve(* + l),(/i-l);
1
71-*
-, veO,(*-l).
Отсюда нетрудно видеть, что
a/(a1,a2,...,aw_1) =
= «н +«/1 *a«-l •-•«/i-i+1 +5/2 *ал-2 •••••a«-/+l +- + Я/,/-1 -а«-М +
1
1 . 1
+ аи+] + аи+2
aw.; ая.гая.м
+ ... + **,-
-, 2<i<n.
(6.353)
(6.354)
Выражения (6.354) можно непосредственно использовать для построения
численной процедуры по одновременному нахождению начальных значений Х+ и q$ .
Выберем начальные значения положительных коэффициентов av,v€l,(fl-l)
достаточно малыми.
Начнем увеличивать коэффициент с^ от а{\ а другие коэффициенты оставим без
изменения.
При обеспечении равенства ап(•) = aw_|(•) значение aj фиксируется. Кроме того,
принимается, что
a^ =a1v,ve2,(>7-l).
Причем коэффициент а2 будем увеличивать, а остальные коэффициенты av
оставим без изменения. Тогда для некоторого значения a2 =cx2 >ot2 хотя бы одна из
возрастающих сумм сравняется по величине с одной из убывающих сумм. Допустим,
что совпадение по величине произошло с суммой <Зл_2(). В этом случае принимается
a|,=a;,vel,(/!-l)\2.
Глава 6. Синтез грубых систем автоматического управления 353
При этом коэффициент ос3 начнем увеличивать, а остальные оставим без изменения.
Далее повторяется процедура, описанная выше для коэффициентов а!,а2. Данная
процедура продолжается до тех пор, пока величина разности
*+/\ */\--/\ • */\ (6.355)
где а (•) = тахл/(0,а (•) = mma;(),
не начнет возрастать. Чтобы обеспечить убывание величины а0, выделяют такие
коэффициенты <xv,v e 1,(я-1), при изменении которых сумма а+ (•) уменьшается, а
(5"() - возрастает. Таким образом, повторяя процедуру требуемое число раз,
добиваемся того, что <5° (•)->(). Данная задача всегда разрешима и имеет единственное
решение при положительных коэффициентах av,vel,(«-l) в силу свойств
входных-выходных матриц.
Таким образом, в результате предложенного подхода можно одновременно найти
значения X+0,qQ , соответствующие матрице К = К0. Далее, необходимо
осуществлять управление собственным значением X*, перемещая его в левом направлении.
Укажем важное условие, которое можно эффективно использовать при управлении
значением Х+.
Утверждение 6.5. Для стабилизируемости системы (6.211) необходимо, чтобы
существовала такая матрица К, которая бы обеспечивала выполнение системы
неравенств
а„<0, /епк (6.356)
Таким образом, чтобы обеспечить разрешимость неравенств (6.347), необходимо
выполнение соотношений (6.356). Поэтому, прежде чем определять начальное
значение X* = Х+о , вначале необходимо выбрать такую матрицу К, которая бы
обеспечивала выполнение неравенств (6.356). Если такая матрица К = Ко найдена, то для нее
находят указанным образом значение Х+ = Х+о .
Управление перемещением Х+ в левом направлении предлагается осуществить
следующим образом. При фиксированной матрице К
£,-(•) = £/(<*), /€l,w,
где a = [aj a2 ... ослЧ]т - (п -1 )х 1 векторный параметр.
Обозначим через
a+=a+(K) (6.357)
значение параметра a, соответствующее собственному вектору q^ при
фиксированной К. Тогда
а;(а+) = Х+ V/eu. (6.358)
Поскольку коэффициенты a^J e\,n явно зависят от К, то можно записать
й/(0 = й/(а,К), /el,и
и
az(a+,K) = >.+(K), /<=п. (6.359)
354 Методы синтеза САУ по заданным показателям качества. Часть II
Рассмотрим вопрос, о том, как следует изменять матрицу К, чтобы обеспечить
равенства (6.359), а значение А.+ (К) при этом непрерывно перемещалось влево.
Обозначим через к векторный параметр размера (nl)x\, составленный из всех
коэффициентов матрицы К, например, следующим образом
* = [*!! - *1/ *21 - *2/ - *«1 - *»/Г. (6.360)
Тогда (6.359) примет вид
аДа+,*) = А.+ (*),1еп. (6.361)
Каждая из функций at(a,k)9iG\,n является непрерывно дифференцируемой по
всем компонентам параметра а и кусочно-непрерывной по параметру к. При этом
дифференцируемость яД) по компонентам параметра к нарушается на тех его
значениях, для которых хотя бы один из коэффициентов alJ9je\,n\i обращается в
ноль. Введем обозначения
X^eR-:*,(*)-0},1 ^
/ G 1,Л,У € 1,л\/. J
Очевидно, при к е Xy,j е 1,л\/, коэффициент а^(к) и функция а,(аД) не
дифференцируемы по Л. Допустим, что к0 £ Ху У/ е 1, л \ /,/ е 1, л . Для этого значения к0
определим выражение дифференциала функций аДссД0),/ е 1,л. Изменение к из
этого значения в произвольном направлении можно представить в следующем виде
к = к°+к* -у, (6.363)
где у - скалярный параметр, принимающий произвольное значение к , (тГ)х\ -
заданный вектор, определяющий направление изменения к (к* может выбираться
произвольным).
Тогда
^ = аЦаД°) = У-^-^- + У-^-^. (6.364)
Поскольку
dk^ _ ♦ Эа _ Г 9О|_ 5а2 9а/?,| ]
то
* ' [at, эа2 "" алт_/ j ' а' [ax, ^ '" за»-.
""' Эй, dav
y.
= (Vaa,,a;)
V:
и выражение (6.364) принимает вид
Глава 6. Синтез грубых систем автоматического управления 355
a'iy(a,k°) = (VkaiX) + (yaai,a'y)\
>• (o.JdjJ
/el, л. J
При изменении к согласно (6.363) (т.е. в направлении вектора к*) значение Х+(к)
изменяется со скоростью
т (6.366)
„ Л+ дХ+ дХ+ дХ+ I
где VkV =
_ЭЛ, дк2 дкт1\
Тогда для того, чтобы осуществлять непосредственное управление собственным
значением Х+ за счет соответствующего изменения параметра к, при котором Х+
непрерывно перемещается в левом направлении вдоль вещественной оси на
комплексной плоскости, необходимо таким образом изменять к, чтобы левая и правая
части уравнений (6.361) убывали с одинаковой скоростью (т.е. чтобы скорости
изменения (производные по направлению) этих частей были одинаковыми и имели при
этом отрицательный знак).
Таким образом, чтобы уравнения (6.361) обеспечивались, и при этом значение
Х+(к) непрерывно уменьшалось, должны выполняться следующие соотношения
' я'(a,Jfc°)= —<0 V/eu (6.367)
ду
или
(V4a,,*V(Vea,,a;) = (V4X+,**)<0J (6 36g)
V/епй, J
отсюда
(yaa,,a'y) = (VkX+,k')-(ykank')= .
= (V4r-VJkaj,*') = (vt(X+-e/),**), /еп,
т.е.
(Vea,,a;) = (Vt(a.+ -a,),**), /еп- (6.369)
Чтобы значение Х+(к) перемещалось влево по вещественной оси при к = к0,
необходимо и достаточно выполнение неравенства
rr'=(V^+,**)|^o<0, (6.370)
t
при этом само значение Х+у с учетом (6.370) можно выбирать произвольным.
Тогда в соответствии с (6.369) нетрудно видеть, что изменение параметра к в
направлении к* и заданного значения к0 обеспечивает непрерывное перемещение Х+
влево тогда и только тогда, когда существует такая отрицательная величина А,* , для
которой система линейных алгебраических уравнений (6.369) разрешима
относительно (и-1)х1 векторного параметра <х^, область допустимых значений которого не
ограничена (т.е. совпадает со всем пространством Rn~]).
356
Методы синтеза САУ по заданным показателям качества. Часть II
Действительно, если сформулированное условие справедливо, то это означает,
что при уменьшении собственного значения Х+ со скоростью \* параметр а
должен изменяться со скоростью а!^, а параметр к со скоростью у в направлении к*.
Поскольку вектор а может принимать только положительные значения, т.е. а > О
или, что то же самое, ctv > 0 Vv € 1,(/и-1), то при изменении к в направлении к*
необходимо, чтобы положительность а сохранялась. Для достаточно малых
изменений к (т.е. для достаточно малых значений у ) с требуемой степенью точности можно
записать
а = а +а
;•?>
(6.371)
где а = а° соответствует значению А:0. Тогда за счет малости у можно обеспечить
(6.232). Следовательно, сформулированное условие не противоречиво и его
выполнение обеспечивает равенство (6.222) при изменении к.
Уравнения (6.369) можно представить в виде
(Уаа„а'у) = Х* -(Ука„к*), i^h"-
Если воспользоваться обозначениями
(6.372)
Vaa =
УЛ.
-их(я-1) матрица; V^a =
V*<52
V*an
-nx(m-l) матрица;
, г / /-|T
Lt =|Av A; ••• Л; | -nxi вектор,
то система уравнений (6.372) приводится к виду
vaa.a;=L;'-v,a.*\ • (6.373)
(п уравнений относительно (п - 1) неизвестного, т.е. переопределенная система). Из
теории линейных алгебраических уравнений известно [52], что для разрешимости
переопределенной системы уравнений (число уравнений больше числа неизвестных)
необходимо и достаточно, чтобы избыточные (лишние) уравнения были линейно
зависимы от системы не избыточных уравнений (число которых равно числу
неизвестных). Нетрудно видеть, что система уравнений (6.372) или (6.373) переопределена,
если в качестве неизвестных аргументов использовать компоненты (л-1)х1 вектора
а' (матрицы Vaa,Vak известны, вектор к* задан, а вектор Ц можно задавать
произвольным с учетом неравенства (6.370)). Поскольку число неизвестных л, то для
разрешимости (6.372) или (6.373) необходимо и достаточно, чтобы одно
произвольное уравнение системы (6.372) было линейно зависимым от остальных (п- 1)
уравнений. В качестве такого уравнения можно, например, выбрать последнее.
Сформируем матрицу, составленную из всех коэффициентов уравнений (6.373) (т.е. из
коэффициентов левой и правой частей). Очевидно, данная матрица имеет вид
р = Гуаа (ц'-у,а-*')1 (6.374)
т.е. Р - п х п матрица, у которой хотя бы одна строка линейно зависима от других
строк.
Отсюда следует, что rank Р < п, и потому
Глава 6. Синтез грубых систем автоматического управления 357
detP = O. (6.375)
Равенство (6.375) можно рассматривать в качестве критерия управляемости
вещественного собственного значения Х+ в левом направлении относительно изменения
вектора к вдоль к*. Тогда, задав произвольное значение Ц , с учетом (6.370) и
рассматривая (6.375) как уравнение относительно к*, можно определить допустимость
того или иного направления к* при изменении вдоль него матрицы К. Затем,
согласно (6.373), определяется вектор а^, с учетом которого по формуле (6.371)
оценивается величина а, а также дальнейшая возможность использования направления
к" (т.к. необходимо, чтобы а > 0).
6.5. ПОСТРОЕНИЕ ГРУБЫХ СИСТЕМ УПРАВЛЕНИЯ
ПРИ КВАДРАТИЧНЫХ ОГРАНИЧЕНИЯХ
В данной главе осуществляется синтез грубых линейных систем при
квадратичных ограничениях с учетом и без ограничений на структуру закона управления. В
соответствии с основной теоремой метода фазовых ограничений для решения задачи
синтеза получены максимальное и минимальное неравенства, которые в дальнейшем
исследуются. Показано, что требуемый закон управления может быть найден в
аналитическом виде, но при этом должно выполняться некоторое условие на границе
допустимого множества, эквивалентное спектральным ограничениям для
соответствующей матрицы. Вводится оценка степени грубости системы управления, связанная
со спектром указанной матрицы. Получены соотношения для синтеза системы
заданной степени грубости. Показано, что разрешимость задачи синтеза эквивалентна
разрешимости некоторому матричному неравенству, обобщающему известное
неравенство A.M. Ляпунова. Рассматривается задача формирования двухуровневой системы
управления. Показано, как ее разрешимость связана с управляемостью некоторой
подсистемы исходной системы управления.
6.5.1. Постановка задачи синтеза при квадратичных ограничениях
Будем рассматривать систему управления того же вида (6.211), структурная схема
которой представлена согласно рис. 6.5 и 6.6. При этом считаем, что
y\t) = 0eRm.
Таким образом,
х = Ах + Bu,x(f0) = х0,/ > /0. (6.376)
При этом пхп и ихт матрицы А = А(/), В = В(/) в общем случае могут быть
нестационарными с непрерывно вещественными коэффициентами atJ{t), 6/v(/),
/€1,я,у el,H,vel,/w. Кроме того, предполагается, что ограничения на вектор
состояния
x(/,xo)6g(O V/>/0 (6.377)
и на вектор управления
ueU(x,t) W>/0 (6,378)
задаются с помощью некоторых квадратичных функций. Поэтому рассматриваемые
ограничения (6.377), (6.378) будем в дальнейшем называть квадратичными. Покажем,
каким образом могут быть заданы данные ограничения.
Без ограничения общности произвольную квадратичную функцию, стационарную
или нестационарную, можно представить в виде
358 Методы синтеза САУ по заданным показателям качества. Часть II
T(x,/) = (x,M(/)x)^(O = XZ/«,;(*i •*, -9(0, (6-379)
где М = М(0 - пхп вещественная симметричная матрица с элементами ти = /и/;-(/)>
/, У € 1, л (w;y =mjj), представляющими собой непрерывно-дифференцируемые
функции при / > /0; q(t) - некоторая непрерывно-дифференцируемая скалярная
функция. Воспользуемся квадратичными функциями вида (6.379) для задания
множества Q(t).
Пусть Q(t) имеет вид
Q(t) = {xeRn: *F(x,/) = (х, М(/)х) -q(t) < о}. (6.380)
Для того чтобы множество Q(t) было ограниченным, достаточно выполнения
следующих условий, которым должны удовлетворять М(/) и q(t)
М(/)>0 Vr>/0,
(6.381)
#>0V/>/0,1
т.е. функция q(t) должна быть положительной, а матрица M(f) - положительно
определенной [97] (матрица М является положительно определенной в R", если
V х е R" \ {0} выполняется неравенство (х, М х) > 0).
В общем случае будем считать, что пхп матрица М = М(/) при t>t0 является
невырожденной, т.е.
detM(/)*0 Vf>/0. (6.382)
Ограничения на управление представим в следующем виде
£/(х,0 = {neRm: 8(x,u,0 = (u,L(/)u)-p(x,t) < о}, (6.383)
где \j{t)-mxm вещественная симметричная матрица, о которой в общем случае
предполагается, что
detL(/)*O V/>/0, (6.384)
т.е. L(/) - невырожденная матрица V/ > t0.
Для того, чтобы U(\yt) было ограниченным множеством, необходимо
потребовать, чтобы L(/) и скалярная функция /?(х,/) удовлетворяли условию
l*»ft*W»0J 385)
V/>/0,Vxee(/).J
При формировании ограничений на управление
ueU0 (6.386)
обычно используют некоторое фиксированное множество Uo= const. Задание
£/(х,/) в виде (6.383) должно осуществляться из условия
C/(x,/)sI/o Vxe2(/),/>f0 (6.387)
и обеспечивать достаточно простой выбор допустимого закона управления того или
иного вида.
Кроме того, важным требованием, предъявляемым к синтезируемому закону
управления, является требование на вид (на сложность в смысле реализации) его
структуры. Пусть ^ - множество (шкала) возможных структур законов управления,
Глава 6. Синтез грубых систем автоматического управления 359
упорядоченных по тому или иному признаку. Например, по признаку сложности
реализации в соответствии с принципом сложности, приведенного в [134]. Т.е. можно
записать, что
s=(;«!£,. (6-388)
где ^ - £ -й элемент множества (шкалы) структур, представляющий собой некоторое
подмножество законов управления, соответствующих заданному уровню сложности
реализации (в общем случае - заданной характеристике признака, которая, в
частности, может означать: линейность или нелинейность; вид и свойства нелинейности;
статичность и инерционность; вид инерционности; стационарность или
нестационарность - и т.д.).
Тогда, если
ие£, (6.389)
то обязательно найдется такой элемент f^,£ e l,N, шкалы £, которому и будет
принадлежать управление и, т.е.
ue^eljf. (6.390)
При этом, согласно (6.390), управление и представляет собой некоторый закон
и*(х,0,т.е.
u = u*(x,/UeUV, (6.391)
со структурой, соответствующей заданному уровню сложности реализации (или
заданной характеристике некоторого признака, в частности, из числа перечисленных).
Под условием
uei/(x,0n? (6.392)
будем понимать выбор закона управления вида (6.391), принимающего допустимые
значения в смысле (6.378).
В результате, задачу синтеза управления можно сформулировать следующим
образом: требуется на множестве допустимых значений U(x,t) вида (6.383) и заданной
шкале структур р (6.388) синтезировать закон управления u = u(x,/),
удовлетворяющий условию (6.392) и обеспечивающий для системы (6.376) выполнение
фазовых ограничений (6.377) для множества Q(t) вида (6.380).
Для решения поставленной задачи, так же как и в предыдущей главе, можно
непосредственно использовать теорему 6.1.
6.5.2. Получение достаточных условий на управление
В соответствии с условиями теоремы 6.1 воспользуемся следующими
обозначениями
Ге(/) = {хбЛл:Ч'(х,О = (х,М(Ох)-9(О = 0};
Уж*Р=2М(/)-х;
5¥ ' ( (M(t) } dq(t) , . чч ./ч
сМ .
где под или М понимается
Л
производная матрицы М(г) по времени.
Кроме того, введем следующую скалярную функцию
(6.393)
360 Методы синтеза САУ по заданным показателям качества. Часть II
a(x,u,0 = (Vx%/(x,u,/)) + —, (6.394)
где /(x,u,/) = Ах+Ви, и в отличие от (2.27) рассматривается случай, когда
ф(х,г) = х.
Тогда в соответствии с теоремой (2.1) должно выполнятся следующее соотношение
V ' (6.395)
VxeTQ(t) и хотя бы одного и = й(х, t)eU(x, t), t>to,j
обеспечивающее фазовые ограничения (6.378) при допустимых значениях закона
управления.
Решение неравенства (6.395) можно осуществить на основе соотношений,
формируемых следующим образом.
Утверждение 6.6. Для разрешимости соотношения (6.395) необходимо и
достаточно, чтобы выполнялось неравенство
max min a(x,u,f)^0 V/>/0. (6.396)
Доказательство. Покажем справедливость данного утверждения. Для удобства
введем обозначение
c'(x,t) = min a(x,u,/). (6.397)
ueUyxj)
Тогда, если для некоторого t = t* >tQ (6.396) не выполняется, то найдется такой
вектор х = х* е TQ\t*J, для которого
a-(xV)>0.
Из определения (6.397) следует, что в этом случае
c(x*,u/)>cr(xV)= min a(x*,u/)>0 Vu€l/(xV)f
V / V ) U6f/(x-,/-) X ) V '
т.е. неравенство (6.395) не выполняется. Тем самым показана необходимость
соотношения (6.396).
Покажем достаточность условия (6.396). Действительно, пусть (6.396)
выполняется для всех t > t0. Тогда для произвольного момента времени t = i>t0 в сипу (6.396)
получим
max сГ(х,/)<0,/ >/о.
хеГ(#) V }
Поскольку для любого х g Г£)(?)
G~(xj)< max o~(xj),
V } xeTQ(t) V ;
то a"(x,f)<0 VxeTQ(t). Следовательно, для любого хеГ^(^) найдется такой
вектор u = u(x,f) € J7(x,f), для которого
min a(x,u,f) = a(x,u(x,f),f) = a"(x,f)<0.
Отсюда, с учетом произвольности i, следует достаточность условия (6.396). Тем
самым утверждение доказано.
Таким образом, неравенство (6.396) может рассматриваться, как критерий
разрешимости соотношения (6.395), и быть непосредственно использовано для синтеза
Глава 6. Синтез грубых систем автоматического управления 361
требуемого (допустимого) закона управления, которое определяется в результате
решения задачи минимизации
min а(х,и,/) = а(х,и~(х,/),Л]
»^М V (6.398)
xeVQ(t), t>tOi J
где u~(x,/) - решение задачи (6.398).
Особенностью использования максминного неравенства (6.396) для синтеза
управления является то, что формируемый при решении задачи (6.398) закон и" (х,/) будет
иметь структуру, полностью определяемую видом множеств U(x,t) и Q(t).
Для синтеза закона управления й(-) желаемой (заданной) структуры, вообще
говоря, отличающейся от структуры и"(-), целесообразно использовать непосредственно
соотношение (6.395). Получим соответствующие этому случаю условия на желаемый
закон управления. Пусть и = й(-) - некоторый закон из заданной шкалы структур р,
т.е. u()g p. Тогда, согласно (6.390), (6.391) й(-) можно представить в виде
Й(.) = и*(х,/),£бп7. (6.399)
Будем считать, что принадлежность й(-) тому или иному элементу р^^е \9N ,
шкалы структур р допускает параметрическое представление, т.е. произвольный
элемент
iH(x,/)ep^€EUV
имеет вид
u*(x,0 = u(x,yV),$eUV, (6.400)
где у^-Л^ xl векторный параметр, принимающий значения на некотором
множестве G^
Y*eG§, SgIJV. (6.401)
Таким образом, тот или иной желаемый закон управления будем искать в виде
й() = й(х,у*,О, 56UV. (6.402)
Для рассматриваемого закона управления соотношение (6.395) примет вид
а(х,и(х,у^О,0 = 5(*У.О*0
VxeT£(/) и хотя бы одного у*>еб^,> (6.403)
для которого u(x,yV)e(7(x,/), '^'o-
Введем множества
G^{y^eG^.u(x9y^t)eU(xj) Vxe0(/), ^>o}> (6-404)
полученные в результате пересчета исходных ограничений на управление (6.378)
непосредственно на ограничения для параметра у^, определяющего вид структуры
управления. Тогда вместо (6.403) получим следующие соотношения
а(х,у^,/)<0 1
с (6-405)
\/хеГ£(0 и хотя бы одного y^eG^, t>t$A
362 Методы синтеза САУ по заданным показателям качества. Часть II
обеспечивающего синтез требуемого управления.
Допустим, что для некоторого у^ = у^ е G^ выполняется неравенство
**-?№ 1 (6.406)
Vxere(/), t>to.\
Поскольку (6.406) справедливо для любого xeTQ(t), то (6.406) будет
выполняться и для того вектора х е TQ(t), на котором а(х,у V) принимает максимальное
значение на границе TQ(t), т.е.
max а(х, у *, /) = а+ (у* ,0^0, t>t0. (6.407)
xeVO(t)
Нетрудно видеть, что неравенства (6.406) и (6.407) эквивалентны друг другу, т.к.
из выполнения одного из них следует выполнение другого, и наоборот, если одно не
выполняется, то и другое также выполняться не будет.
Воспользуемся соотношением (6.407) для получения критерия разрешимости
(6.405). Согласно (6.407) параметр у^ = у^ определяет закон управления вида (6.402),
для которого обеспечивается соотношение (6.395). Пусть на множестве G^ выбран
произвольный параметр у^. Для него, аналогично (6.407), можно определить
функцию а+(у^,0, для которой проверяется выполнение неравенства
a+(y*,/)<0,f>/0. (6.408)
Данное соотношение можно непосредственно использовать, чтобы проверить,
обеспечивает ли управление (6.402) с данным у^ требуемые фазовые ограничения. С
учетом (6.408) условие (6.405) можно представить в виде
Зу^ eG*, для которого]
+ /Е \ (6409)
a+(yV)<0,>>/0. J
Тогда соотношение (6.409) целесообразно использовать в качестве критерия
выбора требуемых параметров у^ . При этом следует иметь в виду, что (6.409)
проверяется для каждого выбираемого тем или иным способом у^ . Если указать способ
перебора параметров у^ е G^ для проверки выполнения (6.409), то данное
соотношение рассматривается, как критерий разрешимости условия (6.395) относительно
желаемого закона управления на заданной шкале структур р.
В частности, в качестве возможного способа перебора у^ е G^ является перебор
у^ (формирование минимизирующей последовательности у^) в соответствии с
задачей минимизации
min а+(у^,/)/>/0. (6.410)
Тогда критерием разрешимости (6.395) относительно закона управления
желаемой структуры, с учетом (6.407), является следующее соотношение
min max a(x,yV)<0,/>*0, (6.411)
y*6G5 xeTO(t) V ' /
где индекс £el,jV может выбираться произвольным в зависимости от желаемой
структуры синтезируемого закона управления.
Глава 6. Синтез грубых систем автоматического управления 363
Действительно, пусть для некоторого £ е \9N на множестве G^ найдется такой
параметр у^ , для которого выполняется соотношение (6.411). Отсюда следует
справедливость (6.409), а значит, и (6.407). Значит, найдется такой закон управления
й(х,у^,п, для которого обеспечиваются неравенства (6.403) или (6.395). С другой
стороны, если на множестве G^ неравенство (6.411) не выполняется, то это означает,
что для любого у^ е G^
а+(у^,/)> min a+(y^,/)>0
для некоторых моментов времени t>t0.
Отсюда следует, что Vy^ e Gt max а(х,у^,/)>0 для некоторых / >/0, т.е. для
хеГО(0
каждого y^eG^ в данные моменты t>t0 обязательно найдутся такие векторы
х е YQ{t), для которых (6.403) не выполняется (а значит, и (6.395)). Поэтому синтез
желаемого закона управления й(х,у^,П на основе (6.395) или (6.403) осуществить
нельзя. Таким образом, показана справедливость следующего утверждения.
Утверждение 6.7. Для разрешимости соотношения (6.403) относительно закона
управления желаемой структуры й(х,у^,м на заданной шкале структур р
необходимо и достаточно, чтобы обеспечивалось минимаксное неравенство (6.411).
Для решения полученных неравенств: максминного (6.396), не учитывающего
ограничения на структуру управления, или минимаксного (6.411), обеспечивающую
желаемую структуру управления, можно, в частности, использовать известные
численные процедуры решения подобного класса задач, изложенные в [39, 150]. Однако
данные процедуры в общем случае могут быть достаточно громоздкими
(трудоемкими) для рассматриваемой системы, поскольку непосредственно не учитывают ее
свойств, позволяющих более эффективно решать поставленную задачу. Поэтому
далее предлагаются новые подходы к решению неравенств (6.396), (6.411) с учетом
свойств системы (6.376).
6.5.3. Построение закона управления на основе достаточных условий
Рассмотрим решение задачи синтеза законов управления, обеспечивающих
выполнение неравенств (6.396), (6.411). Для этого вначале требуется сформировать
функцию g(x,u,/) согласно соотношению (6.394). Подставив в (6.394) выражения
(6.393), получим
a(x,u,r) = (2M(/)x,Ax + Bu) + (x,M(r)x)-(7(0 =
= 2(M(/)x,Ax) + 2(M(/)x,Bu) + (x,M(/)x)-^) =
= 2(atM(/)x,x)+2(btM(/)x,u)+(m(/)x,x)~^(0 =
= ((m(/) + 2AtM(/))x,x)+2(btM(/)x,u)-^(/),
где использовалось равенство
(z,Ox) = (oTz,x),
хе R", ze R1, Ф-lxn матрица (/ - произвольное положительное целое число).
364 Методы синтеза САУ по заданным показателям качества. Часть II
Для упрощения дальнейших выкладок целесообразно ввести следующее
обозначение
v = v(x,f) = BTM(f)x, (6.413)
с учетом которого
a(x,u,/) = ((M(0 + 2ATM(r))x,x)+2(v,u)-(7(0- (6-414)
В том случае, когда управление синтезируется в виде (6.402), функция a(x,u,f)
принимает вид
д(х,у^/)=((м(/) + 2АтМ(/))х,х)+2(у,й(х,у^,/))-^(/). (6.415)
В важном частном случае
п(х,у<,/)=К4хх, (6.416)
где К^-тхп матрица обратной связи, которая, например, в зависимости от индекса
%, имеет вполне определенное число изменяемых коэффициентов.
После подстановки (6.416) в (6.415) или (6.412) получим
д(х)К4,/) = ((м(/)+2АтМ(/))х,х)+2(вт,М(г)х,К4х)-9(/) =
= ((м(/)+2АтМ(*))х,х)+2(к£втМ(/)х,х)-«?(/) = (6.417)
= ((м(г)+2(Ат + К^Вт)м(0)х,х)-9(г).
Воспользуемся выражениями a(x,u,/) и д(х,К^,/) для решения соответственно
неравенств (6.396), (6.411). Вначале рассмотрим решение задачи синтеза без учета
ограничений на структуру управления. Для этого докажем справедливость
следующего результата.
Лемма 6.1. Решением задачи минимизации (6.398) при используемых
предположениях о L(/)s p(\,t) является закон управления следующего вида
I
u = iT(M) = Р2^ , -L-'^v. (6.418)
Доказательство. Из выражения a(x,u,f) согласно (6.414) следует, что (6.398)
можно свести к следующей эквивалентной задаче
min a(x,u,f) = ((M + 2ATM)x,x)-<7 + 2 min (v,u),
. U€(/(x,/) V ' V^ / / ue(/(x,0 f
т.е. решается задача
min (v,u). (6.419)
Но поскольку (v,u) -линейная по переменному и функция, то свои экстремальные
значения она принимает, только на границе множества U(x,t) [29]. В результате
окончательно задача (6.419) приводится к виду
min(v,u) 1
\ (6.420)
при (u,Lu)-/? = 0 (L = L(/),p = p(/)).J
Глава 6. Синтез грубых систем автоматического управления 365
Для решения задачи (6.420) воспользуемся методом множителей Лагранжа [19].
Введем лагранжиан
L(u,p) = (S,u) + p[(u,Lu)-p],
где р - скалярный множитель Лагранжа.
Используя необходимое условие экстремума (VUL = 0), находим соотношение
VuL = v + 2pLu=0. (6.421)
Поскольку det L ф 0 , то из (6.421) следует
u = -—L~lv. (6.422)
2р
Подставляя данное выражение в (6.420), определим р
! (L-'v,v) I (L-'v,v)
р1=2-тг' р2="2"тг-
Заметим, что полученные величины определены Vvei?m. Действительно, т.к.
р > 0, то величина р2 определена. Кроме того, из L > 0 следует, что L"1
симметричная и положительно определенная MLT1 > 0 j матрица.
Поскольку L - невырожденная матрица, то \/xeRn вектор Lx пробегает все
пространство R", т.е. L~!>0. Тем самым показано, что выражения для
р,,р2 определены \/\eRm. Чтобы определить истинное значение множителя
Лагранжа, подставим pi,p2 в выражение (S,u) с учетом (6.422). В результате получим,
что минимальное значение (v,u) достигается при р = р], т.е.
где
„ЙavfB)-(v.--)--^(v,L"v)*,
1
u = u (х,/) = - -'L~l\ .
(L-'V,V)2
Что и требовалось доказать.
Полученное в результате решения задачи минимизации (6.398) управление
и" (х,г) вида (6.418) является требуемым синтезируемым законом управления,
удовлетворяющим максминному критерию (6.396). Однако, чтобы для данного закона
обеспечивались фазовые ограничения (6.377), его необходимо проверить на
выполнение неравенства (6.399).
Рассмотрим важный частный случай, когда управление u~ (x,f) вида (6.418)
имеет линейную структуру. Введем обозначение
o>(x,f) = ^ p. (6.423)
(L-v,vJ
|2
366 Методы синтеза САУ по заданным показателям качества. Часть II
Очевидно, со(х,/)- скалярная неотрицательная функция принимающая, в общем
случае, значения от 0 до +оо . Тогда согласно (6.418)
u~ (x,f) = -oo(x,f) L1 (/) v. (6.424)
Поскольку выражение (LT^vj линейно зависит от х, то для того, чтобы
и" (х,/) также линейно зависел от х , необходимо потребовать выполнения условия
со(х,/) s со0 = const > 0 . (6.425)
Тогда линейный закон управления, являющийся решением задачи минимизации
(6.398), имеет вид
и" (х,/) = -соо -L"(t)BT -М(/)х = К"(f)x, (6.426)
где
К" (/) = -соо -I/1 (/)BT -М(/). (6.427)
Причем К~(0-хе£/(х, /) \/xeQ(t), t>to.
Для того чтобы выполнялось условие (6.425), функция p(x,t) должна иметь вид
/?(x,0 = ^.(L-1(0v,vu). (6.428)
Аналогично тому, как было получено управление (6.424), для синтеза закона
управления й(х,у^,/) с желаемой структурой (6.416) будем решать неравенство
(6.411) с учетом найденной выше функции а(х,К^,/) вида (6.417). Для синтеза
управления необходимо решить задачу максимизации (6.407). Введем обозначение
S4(r) = М(/) + 2(Ат + К|[ВТ)М(/), (6.429)
с учетом которого функция а(х,К^,0 примет вид
а(х,К^,0 = (S4(/)x,x)-<7(0. (6.430)
Тогда в соответствии с (6.407) получим следующую задачу максимизации
max[(S§(Ox,x)-?(0]<0, t>t0, I
при (х,М(/)х)-<7(/) = 0 (т.е. xeTQit))]
Нетрудно видеть, что решение данной задачи полностью совпадает по форме с
решением задачи максимизации (6.399), обеспечивающей проверку выполнения
фазовых ограничений для синтезированного закона управления и~(х,/) вида (6.426). В
этом можно непосредственно убедиться, подставив (6.426) в выражение а(х,и,/)
(6.412). Поэтому решение указанных задач будет осуществлено одновременно и
приведено в следующем параграфе.
6.5.4. УСЛОВИЯ ВЫПОЛНЕНИЯ ФАЗОВЫХ ОГРАНИЧЕНИЙ
НА КЛАССАХ СИНТЕЗИРУЕМЫХ ЗАКОНОВ УПРАВЛЕНИЯ
Как отмечалось выше решение задач (6.431) и (6.399) аналогично друг другу,
поскольку максимизация осуществляется на одном и том же множестве TQ(t), а
выражения максимизируемых функций подобны друг другу, т.к. та и другая являются
квадратичными формами. Поэтому вначале рассмотрим решение задачи (6.399), а
затем полученный результат применим к задаче (6.431).
Определим выражение функции a~(x,f) для управления и"(х,/) с учетом (6.398),
(6.426). Имеем
Глава 6. Синтез грубых систем автоматического управления 367
a-(x,/) = ((M(0+2ATM(0)x,x)+2(BTM(Ox,K-x)-4(0 =
= ((м(0 + 2(ат + К-тВт)м(/))х,х)-^(0 = (6.432)
= (S(>)x,x)-<?(/),
где с учетом (6.427)
S(0 = M(0 + 2ATM(/)+K-TBTM(/) =
т , т (6.433)
= М(0 + 2АтМ(/)~2ш0М(ОВЬ"1(0-ВтМ(0.
В соответствии с (6.399) для обеспечения фазовых ограничений должно
выполнятся неравенство
max G~(x,t)<0 Vf>/0, (6.434)
хеГ£(/)
которое согласно (6.432), (6.433) приводится к виду
max[(S(/)x,x)-<7(0]^0 1
* J I (6.435)
при (х,М(/)х)-?(/) = 0, t>to.\
Сравнивая задачи максимизации .(6.435) и (6.431), нетрудно видеть, что они
подобны друг другу- Причем из (6.433) и (6.431) следует полная сходимость матриц
S(0 и S^(0, отличающихся лишь видом матриц К" и К^. Поэтому решение
данных задач основывается на одних и тех же положениях, тем более что та и другая
задачи определяют условия выполнения фазовых ограничений соответственно для
законов управления (6.426) и (6.416).
Для максимизации квадратичной формы (функции)*) на замкнутой поверхности,
также описываемой квадратичной функцией, можно воспользоваться методом
множителей Лагранжа. Решение данной задачи использует следующий результат [154].
Лемма 6.2. При каждом моменте времени t > t0 все собственные значения
матрицы M~](S+ST), где М = М(0, S = S(t) являются вещественными.
Используя лемму 6.2, получим, что собственные значения матрицы M~!(S^ +S^T)
также является вещественными (S^ формируется согласно (6.429)). С учетом
доказанной леммы, рассматривая решение задачи максимизации (6.435), данное решение
можно сформулировать в виде следующей теоремы [20].
Теорема 6.4. Для разрешимости задачи (6.435) необходимо и достаточно, чтобы для
каждого t>t0 собственные значения Xt;= Xt(0>/€ 1,и, матрицы M~l(/)(S(0 + ST(0)
удовлетворяли неравенству
X, (/) < X* = X* (/) = 2
<?(<)'
(6.436)
iel,n, t>t0.
Доказательство. В соответствии с методом множителей Лагранжа для задачи
(6.435) сформируем лагранжиан следующего вида, определенный для каждого t > tQ:
L(x,p) = (Sx,\) + p[(x,Mx)-q].
*) Произвольную квадратичную форму (x,Sx) = (STx,x) можно представить в виде
fs+sT ^ 1
(x,Sx) = х,х , где -(S + ST) - симметричная матрица.
368 Методы синтеза САУ по заданным показателям качества. Часть II
Тогда максимизация квадратичной формы (x,Sx) будет эквивалентна задаче
maxZ(x,p),
для решения которой воспользуемся необходимым условием экстремума VXZ = O.
Получим
VxZ = (s + ST)x + 2pMx = 0.
Отсюда следует, что максимизирующее значение х должно удовлетворять
уравнению
(s + ST+2pM)x = 0. (6.437)
А для определения значения множителя р необходимо воспользоваться условием
(х,Мх) = ?. (6.438)
Решением уравнения (6.437) является следующий вектор
M"l(S + ST)x = (-2p)x. (6.439)
Но соотношение (6.439) означает, что вектор х является собственным вектором
матрицы MT^S + S1), коэффициент к = -2р - соответствующим данному вектору
собственным значением матрицы M'^S+S7). Таким образом, максимум
квадратичной формы а~(х,/) на ограниченной квадратичной поверхности TQ(t) достигается
только на одном из собственных векторов матрицы M^S+S7). Пусть хс -
собственный вектор данной матрицы, является не тривиальным решением уравнения (6.439)
(после умножения такого решения на постоянное число вновь получим решение
уравнения (6.439)). Тогда, скалярно умножая на хс слева уравнение (6.437), получим
(xc,Sxc) + (xc,STxc)+2p(xc,Mxc) = 2(Sxc,xc) + 2p(xc,Mxc) = 0,
или
(Sxc,xc) = -p(xc,Mxc). (6.440)
Так как согласно (6.438) должно выполнятся условие
(хс,Мхс) = ?,
то (6.440) принимает вид
(Sxc,xc) = -p?, (6.441)
как отмечалось выше, значения коэффициента р связаны с собственными
значениями A,, ,/€l,w матрицы MT^S+S7) зависимостью
А.,=-2р, ,/еп. (6.442)
Тогда для собственных векторов х', / е 1, л , соответствующих Xh i e 1, л , с
учетом (6.441) получим
(Sx'y)^,?, /ей. (6.443)
Отсюда, очевидно, следует
max (Sx,x)= max fsx/,x/)=max -X^ \ =—q-max . (6.444)
ie\,n
Глава 6. Синтез грубых систем автоматического управления 369
Поскольку
m*x [(Sx>x)-<?(')]= m«(Sx>x)-^(/) = i9(0-mp^-9(0.
xeVQy)1- J х€Г(Д/) 2 ie\,n
то для выполнения (6.434) должно выполнятся неравенство
-tf(0nia_xА,,-<?(/)<(), '^'о>
2 /el,л
или
max^;<2^, t>t0.
ieln q[t)
Тогда окончательно получим, что для разрешимости задачи (6.434) необходимо и
достаточно, чтобы для каждого t>t0 собственные значения матрицы M'^S + S1)
удовлетворяли неравенству
Что и требовалось доказать.
В общем случае при М^О о разрешимости условия (6.434) также можно судить
по вещественным собственным значениям матрицы MT^S + S1). Однако при этом,
если для М } 0 теорема 6.4 даст необходимые и достаточные условие разрешимости
(6.434), то для М } 0 - только необходимые.
Заметим, что результаты теоремы 6.4 распространяются на случай, когда вместо
S используется матрица S^ вида (6.429), и при этом рассматривается разрешимость
задачи (6.431).
6.5.5. Анализ спектральных ограничений
по значениям характеристического многочлена
Полученные выше соотношения (6.436) можно непосредственно использовать при
синтезе требуемого закона регулирования. При этом, если матрица S формируется
согласно (6.433) с учетом выражения (6.427) для матрицы К = К~, выполнение или
невыполнение соотношений (6.436), эквивалентных выполнению или невыполнению
фазовых ограничений (6.377) для закона u~(x,f) вида (6.426), зависит только от
выбора допустимых матриц M,L и величины та0 >0.
Если же формируется матрица S^ вида (6.429), зависящая от К^ (заданной
структуры), то на выполнение соотношений (6.436) непосредственно оказывают
влияние матрицы К^ и М . Поэтому в первом случае обеспечение неравенств
(6.436), а следовательно, синтез системы управления, возможно осуществлять только
за счет выбора тех или иных допустимых матриц М и L величины ш0
(варьирование М , L , ш0). Во втором случае обеспечение (6.436) осуществляется либо за счет
варьирования коэффициентов матрицы К^ при заданной М , либо возможно
одновременное варьирование как коэффициентами К^, так и коэффициентами М .
Непосредственная проверка неравенств (6.436) при заданных М и L либо К^ и
М может оказаться достаточно сложной, т.к. требует вычисления всех
вещественных собственных значений матрицы М"1^ +S^).
9^ <*air 4ftfi
370 Методы синтеза САУ по заданным показателям качества. Часть II
Для упрощения процедуры проверки (6.436), а значит и процедуры синтеза,
необходимо включить сам процесс нахождения собственных значений. С этой целью
можно воспользоваться некоторыми известными свойствами характеристических
многочленов [61], позволяющими судить о распределении собственных значений
исследуемой матрицы по значениям, принимаемым соответствующим ей
характеристическим многочленам.
Рассмотрим процедуру проверки неравенств (6.436). Пусть при некотором t > /0
g(X) - характеристический многочлен матрицы M~](S^ +SJ[), т.е.
g(X) = detr^E-M-1(S + ST)] = detJM-irAM-(S + ST)l} =
. ./ j (6.445)
= detM"1-det[?iM-(S + ST)J = detM"1-g(A(),
где
g(X) = det[x,M-(S + ST)].
Так как detM l *0 (M ] - невырожденная матрица), то корни уравнений
g(X) = 0ng(X) = 0 (6.446)
совпадают, т.е. для проверки (6.436) вместо многочлена g(X) можно использовать
многочлен g(X). Чтобы установить, существует ли требуемое спектральное
распределение (6.436) для матрицы М"1^ +S^), воспользуемся известным результатом,
приведенным в [61] и который может быть сведен к следующей теореме [20].
Теорема 6.5. Если все корни Xi9iel9n, нормированного*) характеристического
уравнения
вещественные, то неравенства
gW^)>0,* = 0,U,/i-l, (6.447)
где g^k'(x) - к-я производная полинома g{x), X* - произвольное вещественное
число (А* € Rl J, выполняются тогда и только тогда, когда все Xt ,/е 1,л , расположены
слева от X*, т.е. когда
Xj <X* V/бпя. (6.448)
Доказательство данной теоремы, в частности, может быть осуществлено
аналогично тому, как в предыдущей главе проводилось доказательство неравенств (6.349).
Теоремой 5.2 можно непосредственно воспользоваться для проверки неравенств
(6.436). Действительно, пусть многочлен g(x) получен в результате нормирования
многочлена g(X). Тогда для произвольного t > t0 должны выполнятся неравенства
*w[*-<<»<u.5=i.l (6.449)
для всех t>t0. J
*) Многочлен gfa) считается нормированным, если коэффициент при старшей степени X равен
единице
Глава 6. Синтез грубых систем автоматического управления j/ i
Поскольку коэффициенты многочлена g(X) непосредственно зависят от матриц
М и L или М и К^, то неравенства (6.449) можно рассматривать относительно
параметров указанных матриц. Тогда, решая (6.449), относительно М и L или М и
К^, тем самым осуществляем синтез требуемой системы управления.
Если, например,
q{t) = const Vf>/0, (6.450)
то . Тогда А*(/) = 0, и (6.449) принимает вид
g<A>(0)>0, *eO,(/i-l)J (б451)
V/=>/0. J
Так как
g{X)=X" +g,.1^-1+... + g1?i + g0,
то нетрудно доказать, что
\п-к} (л-1-я/ . (6.452)
+ ^+1(* + 1)Х + ^*!,*€0,(/1-1).
Отсюда находим
g(k\o)=gk-k\,ke\J^. * (6.453)
Тогда, подставляя (6.453) в (6.451), получим
а*о, кеЦ^Т)) (6454)
т.е. все коэффициенты многочлена g(A,) должны быть неотрицательными. С учетом
определения g(A) и матрицы S (6.433) или S^ (6.429) следует, что
g*=^(M,L,co0)>0 или gk(M,K^ keO,(n-\),
где gk{) - некоторые известные функции, получаемые при вычислении полинома
В результате приходим к следующим соотношениям
gk=gk(M,L,<»0)>0 или gk(M,K^0, *е0,(л-1)| (g 455)
v/>;0, J
которые могут непосредственно использоваться для синтеза требуемого закона
управления.
Если матрицы А, В, М, L - стационарные, то система неравенств (6.455) от
времени не зависит. Эффективность (простота) решения неравенств (6.455) определяется
характером зависимости коэффициентов gk 9ke\,(n-\) от элементов матриц
М, L, К^. Чем проще зависимость, тем эффективнее решается система (6.455).
Упрощения зависимости можно добиться за счет выбора соответствующего базиса в
пространстве состояний R", в котором рассматривается система (6.376) и
ограничения (6.377), (6.378).
В общем случае при ^0 с учетом (6.452) неравенства (6.449) примут вид
25*
372 Методы синтеза САУ по заданным показателям качества. Часть II
/ . \п-к / л\. / . \n-\-k
(6.456)
При решении систем неравенств (6.455) или (6.456) относительно М, L, соо или
М, К^ важной является проблема существования решения (т.е. разрешимости
данных неравенств). Далее эта проблема будет рассмотрена.
6.5.6. Оценка грубости системы при квадратичных ограничениях
Полученные в предыдущем параграфе соотношения (6.455), (6.456) позволяют
синтезировать требуемый закон управления. Однако при этом важным является
вопрос, насколько синтезированный закон эффективен при тех или иных возмущениях
системы (6.376) - структурных, параметрических, внешних и т.д., то есть, будет ли
при наличии указанных возмущений обеспечено решение поставленной задачи
синтеза с учетом найденного закона управления. Для ответа на этот вопрос
целесообразно воспользоваться свойством грубости системы управления и оценить степень
грубости на основе предлагаемого подхода.
Как следует из теоремы 5.1, если синтезированный закон управления и~ (х,/)
вида (6.426) или й(х,у^,м вида (6.416) таков, что для него обеспечиваются неравенства
(6.436), то задача синтеза решена. Если же (6.436) не выполняется, то необходимо
выбрать другую матрицу К" вида (6.427) за счет изменения соо, М и L или
соответственно матрицу К^. Таким образом, от характера выполнения неравенств (6.436)
зависит, насколько эффективным является тот или иной синтезированный закон
управления. Причем, чем сильнее неравенства (6.436), тем, очевидно, эффективнее
будет закон управления. С учетом этого можно ввести в рассмотрение некоторую
меру, величина которой характеризует степень грубости синтезируемой системы
управления.
Обозначим через
Д = А(/) = А.*-шахХ|- = 2^{-тах\,
iei/i q\l) ie\,n
я(<)
(6.457)
t>t0,
степень грубости системы (6.376) относительно квадратичных фазовых ограничений
для закона (6.426) или (6.416).
Нетрудно видеть, что величина А характеризует грубость системы. Причем, чем
больше А, тем более грубой по отношению к различным возмущениям является система.
Таким образом, величину А можно использовать как некоторую меру,
характеризующую степень грубости системы управления. С помощью введенного определения
степени грубости можно обобщить поставленную задачу синтеза, если потребовать,
чтобы формируемый закон управления обеспечивал выполнение требуемых
ограничений (6.377), (6.378) с заданной степенью грубости Ао .
Под системой, обладающей заданной степенью грубости Ао по отношению к
квадратичным ограничениям, будем понимать систему (6.376), для которой
синтезированный закон управления обеспечивает выполнение неравенства
А = А(0>А0 V/>/0, (6.458)
Глава 6. Синтез грубых систем автоматического управления 373_
где Ао > 0 - некоторая заданная величина.
В результате получим, что при синтезе управления помимо ограничений (6.377),
(6.378) необходимо учитывать ограничение (6.458). Покажем, как достаточно просто
можно учитывать (6.458) на основе неравенств (6.449), (6.456). Согласно (6.457) находим
д = д(/) = д/-тах>1, >А0.
ie\/i
Отсюда
mbxMX--A0=2M-A0=d (6459)
Vt>t0. J
Для обеспечения данных неравенств можно воспользоваться теоремой 5.2. Тогда
аналогично (6.449) получим, что (6.459) выполняется тогда и только тогда, когда
выполняются неравенства вида
^[K-0(t))>0,ke0^-l) (6460)
для всех t>tQ9 J
где X*Q(t) = 2-^-^-Ао, а выражение для g^k\A) определяется согласно (6.452).
Подставляя выражение для Х*о (О В неравенства (6.460), по аналогии с (6.456)
получим следующую систему неравенств, которая используется для учета ограничений
на грубость системы управления
i { • \п~к / ,ч, / ■ \п-\-к
(п-кУ\ q ) {п-\-к)\\ q )
+&+iO(* + l)!|2^-A0 | + а(0*!^0
(6.461)
VAeO, (л-1), />V
Полученные соотношения (6.461) позволяют синтезировать закон управления
u~(x,f) или й(х, у^,0» не только из условия обеспечения ограничений (6.377),
(6.378) (в силу теоремы 5.1), но и из условия обеспечения этих ограничений с
некоторой степенью грубости.
Необходимо также отметить следующее свойство введенного определения
степени грубости (6.457): значение А не зависит от выбора базиса в неравенстве состояний
R", в котором рассматривается система (6.376). Действительно, это непосредственно
следует из того, что собственные значения произвольной квадратной матрицы
инвариантны к произвольному базису Rn, относительно которого может быть
представлена данная матрица [52]. Поэтому собственные значения А./5 ie\,n, а значит и
max Л; матрицы M~l(S + ST) остаются неизменными для произвольного базиса в
/el,и
Rn. А согласно (6.407) в этом случае остается неизменной и величина А.
6.5.7. Разрешимость задачи синтеза
в классе линейных законов управления
Выше (в 6.5.5) отмечалась важность проблемы разрешимости поставленной
задачи синтеза, т.е. прежде, чем непосредственно решать неравенства (6.455), (6.456) или
374 Методы синтеза САУ по заданным показателям качества. Часть II
(6.461), необходимо знать, а будут ли вообще данные неравенства разрешимы, и, что
необходимо сделать (как модифицировать ограничения) для обеспечения их
разрешимости. С этой целью рассмотрим вопрос об условиях разрешимости задачи
синтеза в зависимости от свойств матриц А, В, М, L . При этом считаем, что для
обеспечения разрешимости матрицами L и М можно варьировать. Будем рассматривать
случаи, когда должен осуществляться синтез закона и~(х,/) вида (6.426).
Как отмечалось выше (см. (6.434) или (6.431)), для того, чтобы синтезируемый
закон управления решал поставленную задачу, должно выполняться неравенство
max [(S(0,x)-<7(0]<0l max \(S,(t),x)-q(t)]<o]
xer<2(')L l или *ero(oL * J \ (6.462)
Vt>t0 J \/t>t0. J
Определим, при каких условиях выполняется первое неравенство (6.462). Для
этого можно воспользоваться следующей леммой [78].
Лемма 6.3. Для каждого t > t0 матрицу L > 0 всегда можно выбрать такой, что при
[КегВтм]пГ0*0,
для разрешимости неравенства (6.462) необходимо и достаточно, чтобы было разре:
шимо неравенство вида
max Г(8х,х)-<Л<0,/>/0, (6.463)
xe[KerBTMJnrOL J
где KerBTM -ядро матрицы ВТМ ; S = M + 2ATM .
В соответствии с доказанной леммой задача разрешимости первого неравенства
(6.462) сводится к задаче разрешимости более простого неравенства (6.463). Для
анализа разрешимости (6.463) целесообразно ввести следующие обозначения. •
Пусть
Я = КегВт czR" (6.464)
- некоторое подпространство в пространстве Rn. Считая, что размерность
подпространства Н равна г, т.е.
dim# = r (г>0 - целое число),
в Н зададим (выберем) произвольный базис из г векторов \pj Jr_ и образуем п х г
матрицу Р вида
Р = [А Pi "' Pr]> rankP=r.
То есть столбцы матрицы Р образованы из векторов выбранного базиса. Для
анализа разрешимости (6.463) потребуется использовать следующую лемму.
Лемма 6.4. Подпространство КегВтМ определяется равенством
КегВтМ = М"1-Я, (6.465)
где
Я = {х е R" : х = Pz, z e Rr) *). (6.466)
Покажем справедливость следующей леммы.
*) Справедливость представления И в виде (1.466) следует из того, что произвольный вектор хе Н
г
можно разложить по элементам базиса пространства Я, как x = £z;/?;5 ZjeR], или, что то же самое,
представить в виде x = Pz, z = [zj z2 ••• zr
Глава 6. Синтез грубых систем автоматического управления 375
Лемма 6.5. Матрица Р1!^"1? - симметричная и положительно определенная в
R" ,т.е. РтМ~1Р,если М>0.
Можно записать
(м^Ь, h)>0 VhG#\{0}. (6.467)
Поскольку Я - подпространство Rn, то последнее неравенство рассматривается
не на всем пространстве R", а только на некоторой его части (подпространстве Я).
Поэтому в общем случае возможно, что М"1 } О (т.е. М > 0), но при этом М имеет
также свойства, при которых (6.467) выполняется, а значит и в этом случае Р1!^'1?.
Выясним более общие условия, при которых выполняется неравенство (6.467), и
при этом, возможно, М >• 0.
Известно, что у произвольной симметричной матрицы МП1 >0 собственные
векторы т\т2,...,т" образуют базис уп'|/=1 в пространстве Rn [24]. Пусть \xniel9n
- собственные значения МГ1, соответствующие данным векторам (т.е.
Ы~хт1 =11,77*', где \ii ^0,\//е1,л в силу невырожденности М). Выделим
положительные ii*>Q,veN+, и отрицательные ц~ <0,s e TV", собственные значения
(здесь N+ и TV" - непересекающиеся подмножества индексов, причем
N+\JN~ = {l,2,...,w}), которым соответствуют собственные векторы ml,veN* и
mi,s e N~ . Согласно [97] каждое из множеств |m+ )ve^+ и yns_ )veAr представляет
собой совокупность линейно-независимых векторов, на основе которой может быть
образовано соответствующее подпространство в Rn H+ и Я", т.е.
Н+ +Н~ =R".
Тогда справедлива лемма.
Лемма 6.6. Для положительной определенности матрицы Р1^!"1? достаточно,
чтобы выполнялось условие
HqH+ . (6.468)
Данная лемма дает более общие условия положительной определенности
матрицы Р^^М"1?, которые, однако, являются только достаточными. Далее потребуется
также использовать следующий результат.
Лемма 6.7. Характеристическое уравнение
det(^iE-D-1F)=0, (6.469)
где D - симметричная вещественная матрица, D > 0, F = FT , имеет
неположительные корни тогда и только тогда, когда вещественная матрица F неположительно
определена, т.е. когда F < О.
Приведенные выше леммы позволяют сформулировать результат о разрешимости
неравенства (6.463). С этой целью проведем некоторые преобразования. Рассмотрим
неравенство (6.463). Для х е КегВтМ с учетом 6.4 получим
x = M"1Pz, zeRr.
Тогда
(Sx,x)= (SM"1Pz,M"1Pz)= ^MT^SM^P^zYl
, ч / ч Г (6'47°)
(x,Mx) = (M"lPz,M M~lPzJ={z9 P^^PzJ.
(6.471)
376 Методы синтеза САУ по заданным показателям качества. Часть II
С учетом (6.470) неравенство (6.463) примет вид
maxf^M^SM^Pz, z)-^l<0
при (z, PTM"1Pz)~(7 = 0, t>t0.
Анализ разрешимости задачи (6.471) основан на следующей теореме [78].
Теорема 6.6. Для разрешимости неравенства (6.471), эквивалентного
соотношению (6.463), необходимо и достаточно, чтобы выполнялось следующее матричное
неравенство
Pt[nAt+AN-(n + |/n)]p<0, (6.472)
где N = M"1 >0, ц*=^.
Я
При этом неравенство (6.472) является достаточным условием разрешимости
поставленной задачи синтеза для системы (6.376) при ограничениях (6.377), (6.378).
Доказательство. Рассматривается неравенство (6.471) аналогично неравенству
(6.434), разрешимость которого устанавливается на основе теоремы 6.1. Поэтому
результаты данной теоремы можно непосредственно применить к неравенству (6.471).
Тогда с учетом леммы 6.5 непосредственно получим, что для выполнения (6.471)
необходимо и достаточно, чтобы собственные значения ц7 ,j e \,г матрицы
(ptm"1pV1(ptm"1sm"1p+ptm"1stm~1p)=
\ (6.473)
= (ртм"]р) Vm-^s+s^m^p,
удовлетворяли неравенствам
jI7<2^,yGU. ' (6.474)
Ч
Обозначим ц = 2)1. Составим для матрицы (6.473) характеристический
многочлен. Имеем
detj ^E-(ptM"1p)"1PtM~1(s + St)m"1p| =
= 2det jlIE-(ptM"1p)"1PtM"1(m + AtM + Ma)m"1p|= (6.475)
= 2det
ДЕ-(РТМ"1Р)" РТМ-1(М-1ММ~14-М-1АТ+АМ-1)Р
Введем обозначение N = М х, с учетом которого получим
N = —M"1 =-М"1ММ"1
dt
(действительно, это следует, из тождества
0 = — Е = — (М-М'1)=М-
dt rf/V )
Используя новую переменную
0 = — Е = — (М-М"1)=М—М"'+(— m|M"'=MN+MM
dt dt^ ' dt {dt )
-1).
ц = ц-ц |Ц=-^ 1, (6.476)
выражение (6.475) приведем к виду
Глава 6. Синтез грубых систем автоматического управления 377
det||LiE + ^E-(prNP)"1pT(-N + NAT+AN)p| =
= detLE-(pTNP)"1rVPTNP + PT(-N + NAT+AN)pl|= (6.477)
= detLE-(pTNP)"1pT[NAT4-AN~(N + ^i*N)]p|.
Рассмотрим характеристическое уравнение
detliE-(pTNP)~1pTrNAT+AN-(N + ^N)lp|=O. (6.478)
С учетом (6.474), (6.476) получим, что корни уравнения (6.478) должны
удовлетворять неравенствам
^=A7-^=lfr7-W<0,yGU. (6.479)
Поскольку PTMP>0, a PT|~NAT + AN-(n + j/nYJp - симметричная, то
согласно (6.479) и лемме 5.7 следует, что матрица Рт NAT + AN-n4 + fi*Nj P -
неположительно определенная, т.е. справедливо неравенство (6.472). Тем самым
показана справедливость утверждения о необходимости (6.472) для разрешимости
(6.463). а поскольку выполнение (6.463) дает лишь достаточные условия для
разрешимости поставленной задачи синтеза для системы (6.376), то это означает, что и
(6.472) также дает только достаточные условия разрешимости. Тем самым теорема
доказана.
Теорема 6.6 рассмотрена для случая, когда М > 0 . Если же М > 0, то насколько
являются справедливыми результаты данной теоремы? Можно ли и в этом случае и
каким именно образом пользоваться матричным неравенством (6.472)? Поскольку
теорема 6.6 основывалась на использовании соотношения (6.463) леммы 5.3, то
нетрудно убедиться, что неравенство (6.463) будет выполнятся независимо от
положительной определенности М , т.е. она справедлива и при М } О .
Другим используемым при доказательстве результатом было условие РТМ~1Р > 0 ,
которое, согласно лемме 5.6, будет выполнятся и при М } О, если только
обеспечивается (6.468).
Кроме того, справедливость теоремы 5.3 основывалась на лемме 5.7. Из анализа
доказательства данной теоремы видно, что согласно лемме 5.7 следует неравенство
(6.472). При этом специально не требовалась положительная определенность М .
Поэтому неравенство (6.472) справедливо в общем случае, в том числе и тогда, когда
М > 0, т.е. неравенство (6.472) при обеспечении разрешимости задачи синтеза
должно выполняться для любых симметричных невырожденных матриц М . Но если
М > 0, то совместно с (6.472) должно рассматриваться условие (6.468),
определяющее выбор возможных матриц М .
Таким образом, неравенство (6.472) является критерием разрешимости задачи
синтеза без учета ограничений на структуру алгоритма управления. Рассмотрим, при
каких условиях разрешимо второе неравенство (6.462), учитывающее структурные
ограничения.
Воспользуемся выражением (6.429) для S^(/). Тогда
24 Зак. 366
378 Методы синтеза САУ по заданным показателям качества. Часть II
(s4x,x) = ([M + 2(AT + K£BT)M]x,x)=
= (Мх,х)+((Ат+К^Вт)Мх,х)+(М(А + ВК^)х,х)= (6.480)
= ((МА4 + А^М)х,х)+(Мх,х),
где А^ = А + ВК^ .
Согласно [27], если А^ - устойчивая матрица, то всегда можно выбрать такую
матрицу М^ > 0, что
R^=M4A^+A^M4<0.
Тогда, выбирая
м = рм4,
где (3 > 0, можно обеспечить неравенство
R = PR^ «0
за счет соответствующего значения р»0. Тем самым обеспечивается выполнение
второго неравенства (6.462).
Таким образом, одним из возможных условий разрешимости (6.462) является
стабилизируемостъ системы (6.376) (т.е. обеспечение устойчивости матрицы А^) на
множестве матриц обратной связи К^ заданной структуры.
Заметим, что анализ разрешимости (6.462) возможен и в более общем случае при
учете структурных ограничений.
Рассмотрим важный частный случай, когда М и q - соответственно не зависящие
от времени матрица и вектор.
Тогда
N = O, ц*=0,
где О - пхп нулевая матрица (случай стационарных фазовых ограничений).
В этом случая условие разрешимости (6.472) примет вид [34]
W = PTVP<0, 1
(6.481)
где V = NA' +AN.J
Образуем множество
G = {х е R" : (х, Vx) < о}. (6.482)
Справедлив следующий результат.
Лемма 6.8. Для выполнения неравенства (6.481) необходимо и достаточно, чтобы
выполнялось соотношение
KerBT = HqG. (6.483)
Очевидно, когда V < 0, то G- R", и (6.483) обеспечивается, поскольку
Н <z.Rn =G. Из теории устойчивости известен результат A.M. Ляпунова [15],
согласно которому
NAT+AN = V<0 и N>0,
то матрица А должна быть устойчивой. Однако в рассматриваемом случае
возможно, что G ф R", но (6.483) будет выполняться. При этом матрица А может быть и
неустойчивой. Следовательно, полученный результат (6.481), (6.483) можно
рассматривать, как определенное обобщение условиями устойчивости A.M. Ляпунова.
Глава 6. Синтез грубых систем автоматического управления 379
6.5.8. О ФОРМИРОВАНИИ ДВУХУРОВНЕВОЙ СИСТЕМЫ УПРАВЛЕНИЯ
ПРИ РЕШЕНИИ ОБОБЩЕННОГО МАТРИЧНОГО НЕРАВЕНСТВА
Полученное в предыдущем параграфе условие разрешимости задачи синтеза
сводится в общем случае к неравенству (6.472) или, в частном случае, при стационарных
фазовых ограничениях - к более простому неравенству (6.481). Неравенства (6.472),
(6.481) представляют собой некоторые обобщения известного матричного
неравенства A.M. Ляпунова [15], поэтому в дальнейшем их предлагается называть
обобщенными матричными неравенствами.
Поскольку неравенства (6.472), (6.481) представляют собой критерии
разрешимости задачи синтеза, то важным является вопрос о проверке выполнения данных
неравенств, и, если они не выполняются, - о возможности их обеспечения за счет
допустимой вариации фазовых ограничений (т.е. матрицы М и величины q).
Вообще говоря, как было показано выше, для проверки разрешимости задачи
синтеза и выбора допустимых ограничений на систему (6.376) можно непосредственно
использовать неравенства (6.456) и (6.461), учитывающие также и требуемую степень
робастности (грубости) синтезируемой системы. Однако соотношения (6.472) и (6.481)
являются более простыми и эффективными с (6.456) и (6.461), т.к. дают меньшее число
ограничений непосредственно на параметры рассматриваемой системы.
Рассмотрим возможные подходы к решению неравенств (6.472) и (6.481). Одним
из них является применение критерия Сильвестра [97] непосредственно к матрице
W, определяемой согласно (6.481) или в общем случае в виде
W = PTVP, 1
т /. * ч (6.484)
v = nat + an-(n+h nJj
(V принимает выражение (6.481) в стационарном случае).
Пусть
Тогда в соответствии с критерием Сильвестра [97] для обеспечения неравенства
W < О или W = -W > О
необходимо и достаточно, чтобы выполнялись следующие соотношения
detW,>0, detW2>0, ..., detWr>0, (6.485)
где
W,=-h,; W2=- " 12 ;
LW21 W2l]
w =-
wu wu ... wh
w21 >v22 ••• w2r
_wrX wr2 ••• wn
Решая неравенства (6.485) относительно параметров системы, можно определить
допустимые фазовые ограничения, которые будут обеспечиваться.
Другой подход к решению рассмотрим для случая стационарных фазовых
ограничений. Воспользуемся тем обстоятельством, что матрица Р формируется из векторов
произвольного базиса подпространства Я. Поэтому выберем такой базис в Я, для
которого неравенство (6.481) принимает, по возможности, наиболее простой вид. В
частности, в качестве такого базиса можно выбрать ортонормированный базис, для
которого матрица Р имеет вид
Р = [Е 1, (6.486)
?4*
380 Методы синтеза САУ по заданным показателям качества. Часть II
где Е - гхг единичная матрица, О„_г г - (п-rxr) нулевая матрица. А под матрицей Р
понимается матрица Р, полученная в результате некоторого невырожденного
преобразования Т при переходе в пространстве R" от исходного базиса к другому.
В исходном базисе согласно (6.376) система управления имеет вид
х = Ах + Ви.
Пусть в новом базисе вектор состояния xeRn связан с х зависимостью
х = Тх, detT*0.
Тогда
х=Ах+Ви,
где
А = ТАТ\ В = Т В.
Очевидно, что
Я = КегВт=Кег(ТВ)Т=Кег(втТт)=(тт)~1-Я (6.487)
(см. лемму 6.4). Матрицу преобразования Т необходимо выбрать такой, чтобы из
векторов базиса подпространства Н можно было сформировать матрицу Р вида
(6.486).
Р можно представить, как
Р = [Й р2 ••• рг]Т,
где /?,-, / е 1,г - векторы базиса подпространства И .
С учетом (6.487) получим
р = (тт)"]р
или
Й=(ТТ)'!-А, /el, r.
(6.488)
Поскольку Р должна иметь вид (6.486), то в соответствии с (6.488) решается
задача
/ тЧ-1 Г Е 1
(Тт) Р= , (6.489)
где под Р понимается матрица, составленная из векторов произвольного базиса
подпространства И.
На основе (6.489) определяется требуемая матрица преобразования Т, которая,
очевидно, может быть определена неоднозначно.
Фазовые ограничения в новом базисе примут вид
Ф(х, Г) = ^(Т"1х, О = (Т"1Х, МГ1х)-^ =
/ т ч (6.490)
= 1х, (Т"1) МТ-1х1-^г = (х,Мх)-(7,
где М = (Т~1)ТМТ~1.
Отсюда
N = M"! =TM"1TT (6.491)
(здесь использовалось то обстоятельство, что f T"! j = f TT j [97]).
Глава 6. Синтез грубых систем автоматического управления
381
Представим матрицы А и N в виде
А
ГА,, А121 R [Nil N121
[а21 A22J' LN2i N22J*
(6.492)
где N,, =N^1,
N22=N
22'
N12=Nlt.
Здесь: матрицы Аи, NH -rxr; A22, N22 -(л-г)х(и-г) ; A12, N12 -rx(w-r);
A21, N21 - (n-r)xr размеров соответственно. В результате для неравенства (6.481)
получим следующее выражение
PT(NAT+AN)p = fE ОГЯЛ-" -и •
V > L ^'JMn21 N22J
А[,
А?2
LA2I A22j
А,,
+1 -"
А2,
А, 2
А22
Nn N
N21 N
On-r,r
= [Е Or>n.f]x
(NnAf.+N^A^+AnNn+A.jNj,) (n, , Aj, +N12aI2 +A,,N12 + AI2N22)
(N^A^+NjaA^+A^Nn+AjiNi,) (Й21а5,+Я22а12 + А211Ч12+АиЙ22)_
Б
О„.
Г»Г-
= [(n11A?'1+N12A?"2+A1iNii+A12N21)x
(NnAl,+NuAl2+AuNI2 + A12N22)]x E =
= N1IA[I+AnNu+NI2A/'2+A12N21.
(6.493)
(6.494)
Тогда, используя (6.493), неравенство (6.481) представим в виде
NuA[, + AnNu <-(N12A72 + AI2N21).
Если, например, Nt2 = N2( = Ог и_г, то согласно (6.494)
UuAlx + AuUu<-(UnAj2+Al2Nn), (6.495)
т.е. получим матричное неравенство Ляпунова. Для описания уравнения (6.495)
относительно допустимой матрицы Nj j > 0 можно воспользоваться известными
методами [44], предполагая при этом, что Ап - фиксированная матрица. Согласно [15]
(6.495) разрешима тогда и только тогда, когда А,, - устойчивая матрица (т.е. все ее
собственные значения имеют отрицательные вещественные части). Поэтому для
анализа разрешимости неравенства (6.495) рассмотрим вопрос о том, при каких
условиях может быть обеспечена устойчивость матрицы Ах}, являющейся квадратным
блоком матрицы А.
Пусть управление и, синтезируемое для системы (6.376), в общем случае имеет
вид
u = iT(x,0 + u(x,0, (6.496)
где и~(х,/) определяется согласно (6.426), а
й(х,/) = К(Охв, хв=С(0х, (6.497)
хв -/xl вектор измерения; К(0,С(г) - их/, Ып матрицы.
382 Методы синтеза САУ по заданным показателям качества. Часть II
С учетом (6.496), (6.497) уравнение системы (6.376) преобразуется к виду
х = А(0х + B(f)iT(х,/), (6.498)
где А(0 = А(0 + В(0К(0С(/).
Тогда вместо А для системы (6.498), эквивалентной (6.376), в полученных выше
соотношениях (6.472), (6.481) можно использовать матрицу А , которой за счет
выбора матрицы К(/) (6.497) можно в зависимости от свойств управляемости и
наблюдаемости системы (6.376) придать те или иные свойства, требуемые для
разрешимости (6.472), (6.481).
Выбор управления в виде (6.496) в два этапа: вначале из условия обеспечения
требуемых свойств матрицы А (закон й(х,/)); а затем из условия обеспечения
разрешимости поставленной задачи (закон и~(х,/)), - представляет собой
формирование двухуровневой системы управления.
Покажем, как при формировании управления (6.496) можно обеспечить
разрешимость неравенства (6.495). С этой целью, как отмечено выше, необходимо обеспечить
устойчивость блока Aj, матрицы А . По аналогии с матрицей А через А будем
обозначать матрицу А , рассматриваемую в новом базисе пространства R" и
получаемую с помощью матрицы преобразования Т. При этом А так же, как и А ,
разобьем на четыре блока и выделим блок Aj, той же размерности, что и А,,.
Нетрудно показать, что
А = А + ВКС,где С = СТ"1. (6.499)
Если, например, С = Е (х = хв), то
Обозначим
А = А + ВК, К = КТ"1. (6.500)
D = BKC (или ВК). (6.501)
Очевидно, D - пхп матрица. Тогда, разбивая D на четыре блока тех же
размерностей, что и у матрицы А , получим
Ап = А,, + б,,. (6.502)
Покажем, как определяется матрица Dj,. Пусть
!.[?■], (6.503,
где В]9 В2 - соответственно гхт, (п-г)хт матрицы. С учетом определения В
следует, что
b4?']=tbJTiHTiB
М Lt2j да
т.е.
В, =Т,В, В, = Т,В, (6.504)
где Т,, Т2 -гхт, (п-r)хт матрицы.
Представим матрицу С в виде
С = [С, С2], (6.505)
Глава 6. Синтез грубых систем автоматического управления 383
где С], С2 - /хг, Ы(п-г) матрицы.
Тогда
с=[с, с2],
и с учетом (6.501), (6.503) получим
[b2Jl 2J LB2Kq в2кс2
где
Dn = В,КС1. (6.506)
Отсюда, в соответствии с (6.502), следует
А,, =А11+В1КС1. (6.507)
Согласно (6.495) рассматривается неравенство
ГЧцА?", + A, ,N, ,<;<), (6.508)
для разрешимости которого, как отмечалось выше, матрица Aj j должна быть
устойчивой. Поэтому анализ разрешимости неравенства (5.138) сводится к анализу
существования такой mxl матрицы К, которая обеспечивает устойчивость блока Aj l
вида (5.137). Для проверки устойчивости Al j можно использовать один из
алгебраических критериев устойчивости [149]. Например критерий Гурвица. И на основе
вытекающих из него соотношений подбирать требуемую матрицу К. Но прежде, чем
осуществлять подобный подбор К, необходимо знать, возможно ли вообще
обеспечить устойчивость Aj,. С этой целью целесообразно использовать следующий
подход.
С учетом (6.499), (6.505) получим
с»[с, с2]«ст-=о[(т^ (т-)2] = [с(т-), с(т-)2],
т.е.
С, =С-(Т"1) , С2 =С-(Т'1) , (6.509)
где (Т'1] , (Т"1] - соответственно пхг, пх(п-г) матрицы.
Кроме того, нетрудно видеть, что
■Tl1-A-[(T-V(r'),]-
i^TAT-'J '
;; ^(пуЫтЛ ^
TjAfr1} Т2А(т-')2
Отсюда следует, что
А.^Т.А^-1^.
В результате (5.137) приводится к следующему выражению
a^t.a^-'Wt.bkc^t-'U
^Т^А + ВКС)^"1) =Т,А(Т-')
384 Методы синтеза САУ по заданным показателям качества. Часть II
в соответствии с которым можно достаточно эффективно выделять исследуемый
блок матрицы А .
Используя матрицы А], и В,, можно установить возможность обеспечения
устойчивости Aj ]. Если, например, С = Е , то рассматриваемая задача сводится к
анализу управляемости пары матриц Aj, и 1^ .
Действительно, в этом случае Ап, В{, К^КГГ"1} -соответственно гхг,
rxm.mxz матрицы. Причем для любой допустимой матрицы Т можно придавать
произвольные заранее заданные значения матрице Kj, которым будут
соответствовать свои вполне определенные значения матрицы К (т.е. выбор допустимой Т не
влияет на область значений К]). Но тогда свойства матрицы
Ап = А11+В1К1
определяются парой матриц (An,Bj). Поэтому, если (ап,В]) -управляемая пара
[48] (т.е. для данных матриц выполняется критерий управляемости), то матрицу Ах 1
всегда можно сделать устойчивой за счет выбора соответствующей К] и тем самым
обеспечить разрешимость (5.138).
В более общем случае для обеспечения разрешимости (5.138) достаточно
потребовать, чтобы пара (An,Bi) была стабилизируемой [57] (т.е. неуправляемые
собственные значения матрицы Ап, должны находиться в левой полуплоскости
комплексной плоскости). Известно [71], как эти собственные значения выделяются.
Рассмотрим случай, когда С*Е. Тогда в выражении (5.137) Ап, Bj, К, С]
-rxr,rxm,mxl,lxr матрицы. Можно также потребовать, чтобы матрицы Ап, В1?
С! обеспечивали стабилизируемость Aj}. Однако, если
rank Cj =r,
то стабилизируемость Ап определяется только парой (An,Bj).
6.6. СИНТЕЗ РОБАСТНЫХ (л-РОБАСТНЫХ) СИСТЕМ УПРАВЛЕНИЯ
ПО НЕПОЛНОМУ ВЕКТОРУ СОСТОЯНИЯ
Покажем, как формируется закон управления, если система находится под
некоторыми внешними воздействиями. В этом случае уравнения состояния имеют вид
x = Ax + Bu + Dv, x(fo) = xo, />/0, (6.511)
где v-rxl вектор возмущения; D = D(t)-nxr матрица.
Кроме того, задано уравнение выхода (измерения) системы
хв=Сх, (6.512)
хв-/х1 вектор выхода (измерения); C = C(t)-Ixn матрица.
О возмущении v = \{t) предполагается, что это либо некоторая заданная
(известная) вектор-функция, либо вектор, являющийся элементом заданного множества
К = К(/)с/?/,т.е.
Глава 6. Синтез грубых систем автоматического управления 385
v(/)eF(/),/>/0. (6.513)
Считаем, что ограничения накладываются непосредственно на вектор выхода у, т.е.
xt = CxeQ(t) Vt>t0, (6.514)
где
е(/) = {хвеЛ/:ч;(Хв,/) = (хв-х°)м(хв-х°))-9(/)<0}.
Здесь 1x1 матрица М(/)>0 и скалярная функция q(t)>Q имеют тот же смысл,
что и в рассмотренном выше случае, а хв = хв(/) - некоторый /xl вектор, который
может быть задан в виде известной вектор-функции, либо выбирается произвольно
на некотором заданном множестве X® = X® (/) с R1, т.е.
xl(t)eX°(t) \ft>t0. (6.515)
Ограничения на управление имеют вид
u = u(-)e(/(x,/) VxB=Cxeg(/), />/0, (6.516)
где
(/(х,0 = {и€^:(и-и°,ь(и-и°))-р(х,0<о}.
Здесь и0 = и0 (/) - некоторый тх\ вектор, который либо является заданной
вектор-функцией, либо выбирается произвольно на некотором заданном множестве
U°=U°{t)czRm,TX.
u°(t)eU°(t) Vt>t0. (6.517)
Пусть х° =хо(/)-их1 вектор-функция, являющаяся решением уравнения
Сх = хв, (6.518)
которое предполагается разрешимым. В достаточно общем случае (6.518) разрешимо
не однозначно. Тогда в качестве х° (/) можно использовать произвольное решение
(6.518). Введем переменные
х = х-х°, u = u-u0, хв=хв-Хз. (6.519)
Тогда уравнения (6.511), (6.512) приводятся к виду
х = Ах + Вй + л, ]
\ (6.520)
хв=Сх, х(/0) = х0=х0-х (/0), t>tOi\
где
ц = п(/) = -х° (/) + Ах° (t) + Ви° (/) + Dv(/). (6.521)
Ограничения на векторы выхода и управления сводятся к следующим
x = x(/)6e(0 = {xe/?w:4/(x,r) = (x,Mx)-^(0<o}, />J
т / \ I (6.522)
М = С МС {в общем случае M>0J;
й = й(-)е^(х,/) = {йеЛш:(и,Ьй)-р<0} при xeQ(t),t>to
ч (6.523)
p = p{x,t) = p[x + x°(t),ty,
где
386 Методы синтеза САУ по заданным показателям качества. Часть II
и = и (•) = Кхв + Кх° - и0. (6.524)
Тогда, аналогично предыдущему, получим
о(х,и,/) = (У£ч/,Ах + Ви + ц) + ^ =
dt (6.525)
= (i(M + 2ATM)xV2(BTMx,u)+2(x,Mi])-^
И требуемый закон управления, определяемый в результате решения задачи
минимизации, рассмотренной выше, имеет следующий вид
u = й" (х,/) = £ —-L^Mx. (6.526)
(ь'^ш^мх)
Тогда для обеспечения линейности синтезированного закона (6.526) следует
положить
p(x,r) = (L"1BTMx,BTMx).
В результате чего получим
u"(x,/) = -L"1BTMx. (6.527)
Согласно (6.519)
u"-u°=-L"1BTMx.
Отсюда, с учетом выражений для х (6.519), М (6.522), находим, что
и" - и0 = -L"1BTCTMC(x - х°)= -L^BVMCx +
ч-Ц^С^МСх0 = -L~1BTCTMxB + L"1BTCTMx^.
Обозначим
Тогда
К" = -ir^C^M. . (6.528)
u--u°=KxB-K-x^. (6.529)
Если, например, положить
и°=К-х^, (6.530)
то требуемый закон управления, удовлетворяющий ограничениям (6.516) и
являющийся линейным, имеет вид
iT=K-xB. (6.531)
В общем случае, согласно (6.529),
и" = К" хв + и0 - К"х^, (6.532)
где ni°-K~xB) - некоторая известная тх\ вектор-функция, формируемая с учетом
ограничений (6.515), (6.517). При этом и°(), хв() можно выбирать в соответствии
с (6.515), (6.517) так, чтобы обеспечить заданные фазовые ограничения.
Рассмотрим случай, когда и" (•) имеет вид (6.531). Тогда, как показано выше, для
выполнения ограничений (6.514) должно рассматриваться следующее неравенство
sup а(х,й'(х,/),Л<0 V/>/0, (6.533)
где функция g(x,u~,/V получаемая путем подстановки закона (6.527) в выражение
(6.525), имеет вид
"лава 6. Синтез грубых систем автоматического управления
387
(6.535)
a(x,u-(i,/),/)=(x,Sx) + 2(x,Mii)-9. (6-534)
Здесь
S = М + 2 АТМ - 2MBL~1BTM.
Таким образом, задача (6.533) с учетом (6.534) принимает следующее выражение
sup[(x,Sx) + 2(x,Mi])-^]<0
при (х,Мх)-<7 = 0, t>t0,
отличающееся от соответствующей задачи максимизации для системы с
квадратичными ограничениями тем, что в выражении максимизируемой функции
a""(x,f) = a(x,u~(x,/),/)
имеется дополнительное слагаемое 2(х,Мтм.
Поскольку максимизация осуществляется на неограниченном множестве Г£)(/)
(в силу вырожденности матрицы М), то вначале необходимо определить условия,
при выполнении которых задача (6.525) имеет решение. Для определения условий
существования введем следующие обозначения:
Я = Кег М - ядро матрицы М ;
Я1 - подпространство в R" , являющееся ортогональным дополнением ядра Я ,
т.е. Я 0 Я1 = R" , Ф - знак прямой суммы подпространств.
В подпространстве Я сформируем произвольный базис {Д }f=1, из элементов
которого образуем пх% матрицу
P = [Aft...px].
Произвольный элемент хе R" можно однозначно представить в виде суммы
х = х]+х2, (6.536)
где х1 еН1, х2 е Я.
Преобразуем задачу (6.535) с учетом представления (6.536). С этой целью
подставим (6.536) в выражение (6.534). Нетрудно показать, что, с учетом определения х1,
х2, после подстановки и соответствующих преобразований получим соотношения:
(х,Мх) = (х',Мх1),
(iSx) = (iI,SxI) + (xlf(s + ST)x2) + I(x2,(s + ST)x2)i
здесь необходимо учитывать, что
I(i',(s+s*)i'Hi',si'),
(x,Mi|) = (il,M4).
Используя (6.537), приведем (6.534) к следующему выражению
(6.537)
388
Методы синтеза САУ по заданным показателям качества. Часть II
a(x)u-(x,/),<)=0-(x,/) = o-(x1+x2,/)=(x1)Sx1)+
2
+(i1,(s + ST)x2)fi(i2,(s + ST)i2)+2(i1,Mil)-9-
= a-(x1,/)+(x1,(s + ST)x2)+i(x2)(S + ST)x2)
(6.538)
Тогда задача максимизации (6.S3S) принимает вид
supra-(i1,r)+(xI,(s + ST)i2)+i(i2,(s + ST)x2)|sO
при (х',Мх')-9 = 0, tkt0.
Из (6.539) с учетом обозначения rQx(t) = k} е Я1 :(х',М(/)х1 )=?(*)} получим
(6.539)
эквивалентное выражение задачи максимизации
sup|a-(x^/)+(x^(s + Sт)x2)+I(x^(s + Sт)x2)j =
= sup Га-(ж1,/)+(ж1,(8 + 8т)ж2)+1(ж2,(8 + 8т)ж2)1^0.
(6.540)
6ro'(/)
i2eH
Нетрудно показать, что задача максимизации произвольной непрерывной
функции 0(x!,x2 J на некотором множестве 9*, которое можно представить в виде
где $1,9^2 -заданные множества, такие, что х1 е9^, х2 еЩ и ^i - ограниченное
множество, удовлетворяет условию
sup 0(x\x2) = max sup 0(x\x2).
х2е«2
i!6Wx2eK2
(6.541)
Действительно, для каждого фиксированного х1 е ^ можно определить
величину sup 0(x*,x2)>0(xl,x2) Vx2g^2.
х2еЩ
Тогда значение
max sup 0(xl, х2) > 0(xl, х2) Vx1 € ^,, Vx2 € Щ,
х'еЖ, х2б«2
т.е. соответствует абсолютному максимуму функции 0(х!,х2) на множестве SR и
потому является решением задачи максимизации.
С учетом (6.541) задачу (6.540) можно представить в виде
sup |"a-(x1,/) + (x1,(S + ST)x2) + ^(x2,(S + ST)x2)l =
х1 «=£'(<)
х2<=//
= max \ а (х1
,0+sup (х\
х2еЙ1
при(х1,Мх1)-<7(/) = 0,/>/0.
Согласно (6.542) вначале решается задача
(S + ST)x2) + ^(x2,(S + ST)x2)|y<0
(6.542)
Глава 6, Синтез грубых систем автоматического управления
389
sup[(x1,(S + ST)x2) + i(x2,(S + ST)x2)l,
(6.543)
а затем осуществляется минимизация по х1 е TQ] (/). Поскольку
S + ST = 2(M+ATM + MA-2MBL"1BTM),
то
(S + ST)x2 = 2(М+ МА)х2, (х2,(S + ST)x2) = 2(х2,Мх2),
и (6.543) приводится к виду
sup
x2etf
rzi
$2>
rz2
2(х\(М+МА)зГ) + (* >МэГ)
(6.544)
Очевидно, для того чтобы задача (6.542) была разрешимой, необходимо
потребовать, чтобы обеспечивалась разрешимость получения задачи (6.544). При этом под
разрешимостью задачи (6.544) понимается существование верхней грани на
подпространстве Н у функции
2(х1,(М+МА)х2) + (х2,Мх2) . Для анализа
существования верхней грани воспользуемся приводимыми далее результатами.
Лемма 6.9. Для разрешимости задачи (6.544) необходимо, чтобы
(х2,Мх2)<0 \/\2еН. (6.545)
Соотношение (6.545) можно представить в более удобном виде. Для этого
воспользуемся введенным выше базисом в пространстве Й и сформулированной из его
векторов матрицей Р размера пх% (х = и-rankC). Очевидно, что произвольный
вектор х е Н можно представить в виде
х2 =Рг,где zeRx. (6.546)
Тогда справедлива лемма.
Лемма 6.10. Неравенство (6.545) эквивалентно условию
РтМР<0.
Далее покажем справедливость следующей леммы.
Лемма 6.11. Решения уравнения
(z,PTMPz) = 0
образуют подпространство Кег Рт М Р.
(6.547)
(6.548)
Тл
« ПУТ
Доказательство. Известно, что симметричную матрицу Р МР можно
представить в виде Рт М Р = FTAF, где F~xxX невырожденная матрица, а А
-диагональная матрица
Пч о
х2
А =
0
390 Методы синтеза САУ по заданным показателям качества. Часть II
А.,-,/е 1,х - собственные значения матрицы РТМР, которые, как известно, являются
вещественными и неположительными (Х{ < 0).
Пусть
z = Fz=[f1,i2,...,zx] .
Тогда уравнение
(z, PTMPz) = (z, FT AFz) = (Fz, AFz) = (z, Az) = ]£ A.,i? = 0
имеет те же решения, что и уравнение
Az = 0.
Поскольку det F Ф 0, то последнее уравнение эквивалентно следующему
FTAz = FTAFz = 0 .
Но это в соответствии с определением ядра матрицы означает, что решения данного
уравнения образуют подпространство
KerFTAF=KerPTMP.
Что и требовалось доказать.
Далее сформируем подпространство
Z = P КегРтМР. (6.549)
С учетом (6.546) можно записать
Zc// = KerM. (6.550)
Тогда согласно лемме 3 для каждого элемента х2 е L будет выполняться
соотношение
(х2,Ш2 j = fpz,MPz) = (z,PTMPz) = 0 , • (6.551)
поскольку в этом случае в соответствии с (6.549)
х2 = Рг,где zeKerPTMP.
Лемма 6.12. Если выполняется условие (6.545) или (6.547), то для существования
верхней грани (6.544) (разрешимости задачи максимизации) необходимо, чтобы
обеспечивалось соотношение
(м + Ма)^сЯ. (6.552)
Покажем справедливость следующего результата.
Лемма 6.13. Если L-лхя симметричная матрица, то подпространство Я1,
являющееся ортогональным дополнением подпространства Н = Ker L в R" (т.е.
Rn = Я 0 Я1), будет инвариантным подпространством для £ , т.е. I • Я1 с Я1.
Из леммы 5 следует, что Я1 - инвариантное подпространство матрицы М .
Поэтому для произвольного вектора х = х1 + х2 получим
Мх = М (х1 + х2 )= Мх1 е Я1. (6.553)
Отсюда следует, что для любой матрицы А вектор
хА = Ах = Хд +£д , Хд е Ях,Хд еЯ1,
при каждом х g R" также будет удовлетворять аналогичному соотношению, т.е.
МАх = МхА = Мх^ е Я1, Vx б Я". (6.554)
Глава 6. Синтез грубых систем автоматического управления 391
Лемма 6.14. Условие (6.552) будет выполняться тогда и только тогда, когда
справедливо соотношение
ZcKer(M + MAJ. (6.555)
Доказательство. Прежде всего, отметим то обстоятельство, что
КегРт=Я1. (6.556)
Действительно, это непосредственно следует из того, что вектор-столбцы 1;,
/ g 1,х, матрицы Р согласно определению удовлетворяют условию I, е Я , V/ е 1,х ,
и потому I, 1Я1.
Тогда
Ртх = ... х = ... =0, УхеЯ1.
м
•х =
.М.
А это в свою очередь означает справедливость (6.556), поскольку других векторов
в R", удовлетворяющих данному равенству, не существует.
Пусть х2 е L . Тогда в соответствии с выражением (6.549) можно записать
х2=Рг,где zeKerPTMP.
Отсюда получим
PTMPz = PT(MPzj = 0,
т.е. MPz е Кег Рт . Или, с учетом (6.556),
МРг = Мх2бЯ1, Vx2eZ. (6.557)
Используя (6.554) и (6.557), находим, что
(м + МА)х2=Мх2 + МАх2еЯх, Vx2eZ, (6.558)
поскольку каждое из слагаемых принадлежит Я1.
Кроме того, согласно (6.552) можно записать
(м + MAJx2 е И , Vx2 е L . (6.559)
Так как подпространства Я1 и Я ортогональны друг другу, т.е. Я 1 Я1, то из
сравнения выражений (6.557), (6.558) следует, что один и тот же вектор (М + МА)х2
только тогда может одновременно принадлежать Я и Я1, когда он нулевой, т.е.
при выполнении условия
(m + Ma)x2=0, Vx2gZ. (6.560)
А это означает справедливость (6.555). Что и требовалось доказать.
Рассмотрим важный частный случай, когда матрица М является стационарной,
т.е. М = const. Тогда, используя лемму 6.4, можно показать справедливость
следующего результата.
Следствие 6.9. Если М - стационарная матрица, то для выполнения условия
(6.552) необходимо и достаточно, чтобы подпространство Я было инвариантно
относительно матрицы А. .
392 Методы синтеза САУ по заданным показателям качества. Часть II
Представим подпространство Н в виде
H = L®LL. (6.561)
С учетом (6.561) для произвольного вектора х2 е Н справедливо разложение
х2=х2Л+х2'2, (6.562)
где х2'1 е Z, х2'2 € Z1.
Подставим разложение (6.562) в выражение (6.544). В результате получим
2 [х1,1м + MA j х2 ) + (х2, Мх2 \ =
= 2(х\(м + Ма)х2И| + 2[х\(м (6.563)
+ (х2Л,1Йх2'2) + (х2^^
Согласно (6.551) имеем
(х2Л,Мх2Л) = 0.
Из (6.560) следует
(М + МА)х2л =0.
Кроме того, поскольку в соответствии с (6.557)
Мх2Ле#\
а в силу (6.561)
то х2'2 -L Мх2'1, и поэтому
(х2'2,Мх2Л) = (х2Л,Мх2'2) = 0.
В результате подстановки полученных соотношений в (6.563), задачу
максимизации (6.544) приведем к следующему эквивалентному виду
sup fox1, (M + МА)х2'2 ) + (х2'2, Мх2'2 )]. (6.564)
Поэтому вместо анализа разрешимости задачи (6.544) можно рассматривать
вопрос о разрешимости (6.564). Это устанавливается на основе доказанных выше лемм,
и результат формулируется в виде следующей теоремы.
Теорема 6.7. Для разрешимости задачи (6.564) (а значит и (6.544)) необходимо и
достаточно, а задачи (6.542) необходимо, чтобы выполнялись условия:
1.(x2'2,Mx2'2)<0Vx2'2gZx;1
> (6.565)
2.ZcKer(M + MA). J
Справедливость данной теоремы непосредственно вытекает из лемм 6.1 - 6.6.
Рассмотрим решение задачи максимизации (6.564) с учетом полученных
соотношений (6.565). С этой целью в подпространстве Z1 зададим произвольный базис
{р,}*=1, где % = d\mLL - размерность L1. Из векторов введенного базиса образуем
пхх матрицу
P = [>ift-/>x]'
с помощью которой произвольный вектор х • е L можно представить в виде
x2-2=Pz,ze/?*. (6.566)
Глава 6. Синтез грубых систем автоматического управления 393
Преобразуем выражение (6.564) с учетом зависимости (6.566). После
непосредственной подстановки (6.566) в (6.564) получим
supv(x^z)=supГ2(x^(lЛ + MA)Pz) + (z,PтlЙPz)l. (6.567)
Полученная задача представляет собой задачу безусловной максимизации,
решение которой должно удовлетворять следующему уравнению:
Vsv(x\z) = 0.
Отсюда находим
V£v = 2РТ (м + АТМ W +2PTMPz = 0. (6.568)
Так как согласно условию 1 теоремы 1
fx2'2,Mx2'2) = (z,PTMPzj<0 Vze/?*,
то матрица РТМР - отрицательно определенная, т.е. РтМР<0 , и, следовательно,
невырожденная. Поэтому решение уравнения (6.568) имеет вид
z = -(FMP)"1 F (М + А7»!)*1. (6.569)
Подставим (6.569) в (6.567). После соответствующих преобразований получим
следующее значение для верхней грани
supv(x1,z) = -(xl,Rx1), 1
2**x [ (6.570)
где R = (М + MA)P(FMP)"1 Рт (М + ATM)J
Поскольку матрица РТМР < 0, то отрицательно определенной будет и (J^MP)"1,
т.е.
(РтмРу1 <о.
Но тогда из выражения для R (6.570) следует, что для произвольного хе Rn
(x,Rx) = /Грт(М + ATM)xl(FMP)"1 |"F(M + АтМ)х1^< 0.
Следовательно,
R<0
или
(6.571)
-(^Rx1)^ Vx1 eH1.
Воспользуемся полученным результатом (6.571) для решения задачи (6.542).
Для этого в подпространстве Н размерности (п-%) (т.е. dim Я =п~х) зададим
произвольный базис {/?/}"_ +i • ^3 векторов данного базиса образуем пх(п-х)
матрицу
Тогда произвольный вектор х1 е Н1 может быть представлен в виде
х1 =Px,zeRn~x. (6.572)
С учетом (6.570), (6.572), а также выражения (6.534), задача (5.172) преобразуется
к следующему эквивалентному виду
394 Методы синтеза САУ по заданным показателям качества. Часть II
ццх [(z,PTSPz) + 2 (z,PT Мл) - q - (z,PTRPz)] =
= max[(z,PT(S-R)Pz) + 2(z,PTMn)-^]<0 (6.573)
при (z,PTMFz) = q, t<t0.
Для решения полученной задачи (6.573) воспользуемся следующим результатом,
устанавливающим свойства матрицы РТМР.
Лемма 6.15. Матрица РТМР является положительно определенной, т.е.
РтМР>0. (6.574)
Из леммы 6.15 следует, что задача максимизации (6.573) разрешима (существует
хотя бы одно решение), поскольку рассматривается максимизация непрерывной
квадратичной функции на замкнутом ограниченном множестве.
Решение задачи (6.573) можно осуществить, используя подход Лагранжа. Для
этого введем лагранжиан
a(z;p)=(z,PT(S-R)Pz)+2(z,PTMii)-^ + p[(z,PTMPz)-^. (6.575)
Тогда требуемое решение определяется из уравнения
VYa = 0, (6.576)
где
V-a = F (s + ST - 2R)Pz + 2РТ Мл + 2pPTMPz =]
\ (6.577)
= [PT(s + ST~2RjP + 2pPTMPjz + 2PTMn. I
Отсюда, если для множителя р справедливо неравенство
detO(p)*0, 1
где Ф(р)=Рт (S +ST -2R)P +2pPTMPj (6'578)
(т.е. матрица Ф(р) - невырожденная), находим вид решения
z = -2Ф"1 (р) РтМц. (6.579)
Значение множителя Лагранжа р определяется из условия
(z,PTMPz)= 4(фч (р)РтМл,РтМРф-1 (p)PTMii) =
. _ _ (6-58°)
= 4(т1,МРф-1(р)РтМРф-1(р)РтМ|]) = ^
Здесь использовалось то обстоятельство, что матрица Ф~Чр) так же» как и Ф(Р) >
является симметричной.
Преобразуем задачу (6.573) к более простому виду на основе соотношения
(6.577). Для этого умножим скалярно на вектор z правую и левую части уравнения
(6.577). В результате получим
(z,V7a)=(z,[pT(s + ST-2R)p+2pPTMP]z+2PTMn) = 0,
или
(zJPT(s + ST-2R)^) + 2p(z,PTMPz)+2(z,PTlVbi) =
= 2(z,PT(S-R)Pz) + 2p^+2(z,PTMn)=0.
(6.585)
Глава 6. Синтез грубых систем автоматического управления 395
Нетрудно видеть, что последнее уравнение получено с учетом того, что
(z,PTSPz) = (z,PTSTPz)
и
(z,PTMPz) = <7, (6.582)
тогда в соответствии с (6.581) находим
(z,PT(S-R)Pz)+2(z,PTMti)-g = -p(7 + (z,PTMTi)-(7- (6.583)
В результате задача максимизации (6.573) с учетом (6.579) приводится к
следующему виду
max -pq + (z,FTMr\\-q =
г / ч и (6.584)
= max т -рд-2(ф-{ (p)PTMii,PTMti)-<7 L
-2ф-'(р)РтМ||1- V ) J
Поскольку в последнем выражении варьируемыми параметрами могут быть
только скалярный множитель р и вектор т|, то в общем случае в соответствии с (6.573),
(6.584) получим
тахГ-р^-2(т1,МРФ"1(р)Ртп)-^1<0
при 4(т],МРФ'1 (р^МФ"1 (р)РтМт]) = q,t > t0.
Заметим, что условие (6.585) рассматривается в общем случае для каждого t>t0,
поскольку q = q(t) и ц = r\(t) - некоторая скалярная и векторная функции. Кроме
того, матрицы в данном выражении также могут зависеть от времени.
Таким образом, показана справедливость следующей теоремы.
Теорема 6.8. Для разрешимости задачи (6.542) необходимо и достаточно, чтобы
на всем интервале функционирования системы (6.511) была разрешима задача
(6.585).
Данная теорема дает ответ на поставленную в начале этого параграфа задачу: как
выбрать допустимый закон управления, который для системы (6.511), (6.512) при
наличии ограничений (6.513), (6.515) - (6.517) обеспечивает выполнение фазовых
ограничений (6.514). Действительно, если согласно теореме 2 задача (6.585)
разрешима, то это означает, что решением поставленной задачи синтеза является
линейный закон управления (6.531) с учетом предположений (6.518), (6.530).
В некоторых случаях использование условия (6.585) может быть существенно
упрощено. Действительно, если справедливо соотношение
PTMii = fi = const) (6.586)
то (6.585) преобразуем к выражению
тахГ-Р(7-2(т],ф-1(р)т1)-^]<0
р L _ _ (6'587)
при 4(л,Ф"1 (р)РтМРФ"1 (р)ч) = q,t > V
Нетрудно видеть, что в соответствии с (6.587) задача синтеза требуемого закона
управления сведена к максимизации скалярной функции на некотором множестве,
состоящем из конечного числа значений скалярной переменной р, которое
определяются в результате решения полиномиального уравнения в выражении
396 Методы синтеза САУ по заданным показателям качества. Часть II
(6.587). Решение данного уравнения основано на применении известных
(стандартных) вычислительных процедур и должно учитывать, что требуемое значение
переменной р является вещественным.
Соотношение (6.586) может быть, в частности, обеспечено, если
ц = r\(t) = % s const. (6.588)
Или, согласно (6.521), (6.530), (6.528), (6.518), должно выполняться следующее равенство
i,(r) = -xo(0 + Axo(0 + Bu°(0 + Dv(/) =
= -х0 (t) + Ах° (/) + ВК-1 xl (t) + Dv (/) = -х° (/) + Ах° (/) -
-BL"1BTCTMx° (t) + Dv (/) = -х° (/) + Ах° (/) - (6.589)
-BIT1 ВтСтМСх° (/) + Dv (/) = -х° (t) +
+ (А - BL-1Btm)x° (/) + Dv(f) = Ло ■ const.
Отсюда находим, что
х0 = (a-BITVmJx0 +Dv(/)-4o, (6.590)
где вектор х° согласно (6.518) удовлетворяет также уравнению
Сх°=х°в.
Из (6.590), (6.518) можно непосредственно получить условия, обеспечивающие
выполнение тождества (6.588). Действительно, если для некоторого вектора ц0
разрешима задача (6.585) при / > /0 , то синтезируемый закон управления имеет согласно
(6.531), (6.528) вид
и = и" (хв,/) = К"хв = -LTVc^Mx, =
= -L4BTCTMCx = -UlBTMx.
(6.591)
Подставим (6.591) в уравнение системы (6.511). Получим
х = (А - BL~1BTM)x + Dv. (6.592)
Тогда если для некоторого т\0 условие (6.587) выполняется, то на траекториях
уравнения (6.592) справедливо ограничение (6.516), т.е.
хв(/) = Сх(0еб(0, />/о>
а конкретный вид возмущений v = v(/) в этом случае не оказывает никакого влияния
на (6.516). Действительно, вычтем из (6.592) уравнение (6.590) и, с учетом (6.519),
получим
X = (А - ВЬ'^М)* + ц0. (6.593)
Поскольку (6.587) выполняется, то для x(t) справедливо (6.522), т.е. x(f) e Q{t)
при t>t0. А т.к. уравнение (6.593) не зависит от вида v(r), то в силу
эквивалентности (6.592) и (6.593) следует, что и (6.516) не зависит от v(f), а
определяется только значением вектора ц0. Однако при этом необходимо учитывать, что
решение уравнения (6.590) должно удовлетворять условию (6.518).
Выясним, для какого класса возмущений v(/) решение х° = х° (/) уравнения
(6.590) является также и решением равенства (6.518). Без ограничения общности
можно считать, что
rankC = /, t>t0. (6.594)
Глава 6. Синтез грубых систем автоматического управления
397
Представим С в виде
с=[с, с2],
где Cj,С2 - соответственно / х /, / х (л - /) матрицы. Причем
rankCj = /, t>t0.
Вектор х также представим в виде
х° =
„01
„02
(6.595)
(6.596)
где х°!, х02, / х 1, (и -1) х 1 векторы.
Тогда произвольное решение уравнения (6.518) определяется следующим образом
[с. с2]
„01
„02
^01
-Г vul 4-Г vuz - yu
-CjX +С2Х -Хв,
02 _ „0
ИЛИ
Г Y01 - Y0 Г Y02
Мх ~хв~^2х >
v01 г-\„0 ^-1^ 02 _ J, 0 , р v02
х =С, хв-С, С2х =F,xB + F2x ,
^02
где х может принимать произвольное значение из пространства R
,л-1
F, =Cj"l,F2 =-CJ"]C2 - /х/,/х(а?-/) матрицы.
Обозначим:
A = A-BL-1BTM=|.n А'2
А21 А
22
(6.597)
(6.598)
(6.599)
где А],,А|2,А21,А22 -соответственно 1x1, Ы[п-1), [n-l)xl, (n-l)x(n-l)
матрицы;
-И-
Ло
(6.600)
где D1?D2 - /ха% (n-l)xr матрицы; Цо,11о - /xl, (я-/)х1 векторы.
Очевидно
х01 =F1x2 + F1x2 + F2xO2+F2x02. (6.601)
С учетом (6.596), (6.597), (6.599) - (6.601) уравнение (6.590) можно представить в
виде
кО11 faiS + F^ + F^+V2'
^02 Г ^02
Л11 Л12
LA21 A22j
F^ + F.x
.02
^02
D,
<ni
X J |_ X
Отсюда находим
F,x£ +F,x° +F2x02 +F2x02 = А„Чх2 + A,,F2x02 + A12F2x02 + A12x02 +D,v-i,J,|
x02 = A21F,x° + A21F2x02 + A22x02 + D2v -itf. J
После соответствующих преобразований получим
D,v = (F2 -A,,F2 -AI2)x02 +F2xO2 +(F, -A11F1)xob + F1x2+i,')
D2v = -(A21F2 + A22)x02+x02-A21F,x»+i1?.
Запишем данную систему в виде
(6.602)
398
Методы синтеза САУ по заданным показателям качества. Часть II
rDi]v=rF2-AnF2-A12
[d2J [ -a2If2-a22
x02 +
О
-A2IF,
< +
О„_,
■и
П-I/l-l
*2+
хО2 +
где On_ln_hOn_tl -соответственно (n-l)x(n-l), (n-l)xl нулевые матрицы.
С учетом (6.600) и обозначений
" F,
R,=
F2-A,,F2-A12|)R2=| F2
.Ф.Л-*»*
-A21F, j
,Ф2 =
О
n-IJ
(6.603)
-A21F2-A22 J- ' L<W,_
последнее уравнение запишем следующим образом
Dv = RlX02 + R2x02 + Ф,х° + Ф2х° +т]0. (6.604)
Таким образом, класс требуемых возмущений F(/), обеспечивающих равенство
(6.518) для решений х°(/) уравнения (6.590), задается с помощью (6.604). Т.е., если
V(t) - произвольное решение (6.604), то для него обеспечивается (6.518) и (6.590).
Следует иметь ввиду, что х° =\°B(t), г|0 - заданные векторы, а х02 е Rn~] -
произвольный из рассматриваемого пространства, который, вообще говоря, может
выбираться в виде произвольной непрерывно-дифференцируемой по времени функции.
При этом, если Xg(/) - ограниченная функция (или вектор), то и хО2(/) целесобразно
выбирать также ограниченной. Тогда хО1(/) и х°(/) в силу (6.597), (6.596) также
будут ограниченными.
Получим условия, при выполнении которых уравнение (6.604) имеет непустое
множество решений относительно функций V(t). Пусть ot(D) - линейное
пространство, образованное вектор-столбцами матрицы
D = [^j d2 ... dr],dj,j el, r - nxl вектор-столбцы.
Очевидно,
dim ct(D) = rank D.
Тогда для разрешимости (6.604) необходимо и достаточно, чтобы
Обозначим
RlX°2 +R2x02 +Ф^ + Ф2х^ +T!0 € ct(D).
R = [R, R2 Ф1 Ф2* По] = [» R].
(6.605)
(О =
„02"
х02
1
О)
&Г
(6.606)
где R, R - матрицы, столбцы которых соответственно принадлежат и не
принадлежат подпространству ct(D); <о, ш - векторы, размерности которых согласованы с
матрицами R, R .
Глава 6. Синтез грубых систем автоматического управления
399
Тогда (6.605) принимает вид
Rco = Rw + R© e a(D). (6.607)
Поскольку
R©ea(D) V5,
то для обеспечения (6.607) необходимо выбрать такое значение вектора со , чтобы
R© е a(D). (6.608)
Найдем условия, при которых (6.608) будут выполняться. Для этого матрицу R
представим в виде
R = R"+R1, (6.609)
где R~ - матрица, образованная ортогональными проекциями столбцов матрицы R
на подпространство a(D); R1 - матрица, образованная столбцами, ортогональными
подпространству a(D).
Тогда согласно (6.608) получим
R© = R© + R1© e a(D), (6.610)
где R~©ea(D) V©, а R16±a(D) V© за исключением ©е KerRx(T.K. тогда
R1© = 0 € a(D)).
Отсюда следует, что (6.610) выполняется тогда и только тогда, когда
©eKerR1. (6.611)
Поэтому (6.611) является необходимым и достаточным условием разрешимости
(6.605) или же, что то же самое, (6.604). С учетом (6.611) уравнение (6.604)
приводится к виду
Dv = Ro5 + R~w,6 e KerR1. (6.612)
Если векторы ш,юе R1 содержат варьируемые координаты, то на основе (6.612)
задается множество возможных возмущений, соответствующих фиксированному
вектору t]0.
Если вектор % не является фиксированным (например, ц0 =щ(0 - некоторая
вектор-функция), то анализ разрешимости (6.605) можно осуществить следующим
образом. Пусть
R0=[R, R2 Ф, Ф2] = [Йо Ro],'
„02"
(О0 =
^02
А
ОХ)
©о
(6.613)
где матрицы Ro,Ro и векторы шо»^о обладают аналогичными свойствами, что и
матрицы R,R и векторы ©,©. Тогда (6.605) приводится к виду
Ro<*o +По = ^0^0 +^о^о +r\o e a(D)- (6.614)
Для матрицы Йо и вектора т]0 воспользуемся ортогональным разложением на
подпространство a(D) аналогично (6.609). Получим
400 Методы синтеза САУ по заданным показателям качества. Часть II
*°=^+*°'} (6.615)
где матрицы Rq,Ro строятся аналогично матрицам R",^1^ %,Ло -векторы, для
которых % е a(D),i|o I a(D).
С учетом (6.615) соотношение (6.614) приводится к виду
Ro«>o + По = ^ойо + Щ&о + ^о 6о + По + Ло =
(— _ ~_ -\ /• I I \ (6.616)
R0<o0 + R060 + ц0 J+ {Щ60 + Tio je a(D),
где RocSo +RqU0 +Цо e a(D) Vcio,V6o,Vno e a(D), a Rq60 +По -1-a(D)-
Отсюда следует, что (6.616) будет выполнятся тогда и только тогда, когда
Ro»o+tio=O. * (6.617)
Поскольку % не является фиксированным, то его всегда можно выбрать таким,
чтобы обеспечивалось равенство (6.617).
Уравнение (6.617) в общем случае является необходимым и достаточным
условием разрешимости (6.605) и (6.604). С учетом (6.617) получим следующее выражение
для (6.604)
Dv = R0c50 + RqU0 + no, (6.618)
где Цо е a(D),<o0 - произвольные векторы, ай0 - удовлетворяет (6.617). На основе
(6.618) задается множество возможных возмущений V(t), соответствующих
изменяемому вектору %(/).
Рассмотренный подход к формированию робастных систем управления позволяет
ввести понятия так называемых ц-робастных систем: система (6.511) имеет
г|-уровень робастности (внешний уровень) и сама является г|-робастной, если для
r\(t) = r\ s const V/>/0
обеспечивается соотношение (6.585).
При этом по заданному т| определяется вид множества возможных (допустимых)
возмущений, при которых обеспечивается выполнение требуемых ограничений.
6.7. ПОСТРОЕНИЕ НЕЛИНЕЙНЫХ РОБАСТНЫХ СИСТЕМ
ПРИ СТРУКТУРНО-ПАРАМЕТРИЧЕСКИХ НЕОПРЕДЕЛЕННОСТЯХ
Пусть уравнения движения некоторого объекта имеют вид
x = /a(x,u,w,0,
(6.619)
хв=Сх,
где x,u,w,xB - сответственно /?xl, /wxl, rxl, /xl векторы состояния, управления,
возмущения, выхода; /а(-) - их1 вектор-функция, определяющая единственность
решения задачи Коши, индекс (параметр) а характеризует степень точности задания
функции /а() по параметрам и структуре. Различным значениям а соответствуют
различные значения тех или иных параметров, входящих в состав /а0 . При этом
Глава 6. Синтез грубых систем автоматического управления 401
при изменении а в функции /а(-) могут происходить структурные изменения.
Характер структурных и параметрических изменений, как правило, является
неопределенным и зависит от окружающей среды. Поэтому точное значение параметра а в
общем случае указать нельзя, но можно считать, что
aeA(t\t>t0, (6.620)
где A(t) - некоторое допустимое множество значений а, определенное для каждого
t>t0.
О возмущении w известно, что оно является элементом некоторого заданного в
Rr множества W , т.е.
W=.y*(t)ew(t\ t>tQ, (6.621)
где предполагается, что w{t) определено в каждый момент времени / > /0. В
частности, под w(t) понимается множество возмущений вида
w(t) = {wе Rr: мГ(0м^<(0, Цеп}, (6.622)
где w~(/), w*(t), |i € l,r - некоторые заданные функции времени.
На вектор состояния системы наложено ограничение
x = x(t)eQ(t%
(6.623)
где Q(t) - заданное в R" замкнутое ограничение (для определенности, выпуклое)
множества.
Решаемая задача в общем случае формулируется в следующей постановке:
требуется определить такой закон управления u = u(xB,/), который бы обеспечивал
требуемые фазовые ограничения (6.623) для системы (6.619), подверженной действию
возмущений w(t) вида (6.621) (в частности (6.622)) и при структурно
параметрической неопределенности ее правой части вида (6.620).
Далее будем предполагать, что функция /а() известна с точностью,
определяемой соотношением (6.620), где A(t) - известное для каждого t>t0 множество.
В функции /aQ выделим линейные части по состоянию и управлению, т.е.
представим /а() в виде следующего разложения
/a(-) = Aax + Bau + Fa(x,u,w,0x, (6.624)
где Аа = Аа(/),Ва =Ва(/) -некоторые hxn.hxm матрицы; Fa(•) - hxn
матричная функция.
В общем случае представление /а (•) в виде (6.624) не единственно. В
рассмотрение принимаются только те разложения, для которых каждая компонента
матричной функции Fa (•) на границе FQ(t) множества Q[t) при всех t>t0 принимает
ограниченные по модулю экстремальные (минимальные и максимальные) значения
при допустимых значениях векторов u,w .
Допустимые значения w определяются согласно соотношениям (6.621), (6.622), а
под допустимыми значениями вектора управления и понимаются произвольные
ограниченные по величине значения u e Rm, если какие-либо другие ограничения на
вектор управления отсутствуют.
27 Зак. 366
402 Методы синтеза САУ по заданным показателям качества. Часть II
Практически достаточно произвольную функцию /а (•) можно с учетом
указанных требований представить в виде (6.624). Однако способы такого представления и
предпочтительность того или иного разложения не рассматривается.
Пусть управление и ищется в виде
u = kaOxB+kal(xB)xB, (6.625)
где ka0 =ka0(t)-mxl матрица, kal=kal(xB,/)-wx/ матрица, элементы которой
к*1 =к*1 (хв,г), т.е. являются некоторыми функциями вектора выхода, которые
могут быть как произвольными функциями (на вид матрицы-функции kaI (xB,/)
ограничения не накладываются), так и функциями вполне определенной структуры (на
вид kal наложены ограничения). Например полиномиальными, релейными и т.п.
функциями. В частности, можно считать kal (•) = Om/ -mxl нулевая матрица. Тогда
управление и согласно (6.625) ищется в классе линейных законов.
Воспользуемся соотношениями (6.624), (6.625), с учетом которых управление
(6.619) преобразуется к виду
x = Aax + Ba[ka°Cx + kal(Cx)Cx] +
+Fa (x,ka°Cx + kal (Cx)Cx,w,f)x =
= [(Aa +BakaOc)+Bakal(Cx)C+ (6.626)
+Fa(x,kaO,kal,w,/)]x =
= [Aa+Fa(x,ka0,kal,w,/)]x = Aax,
где
A =A +B\C' (6.627)
Fa=BakalC + Fa(-),j
а вид матриц Aa,Fa (•) следует непосредственно из (6.626), причем Аа (•) является
матрицей-функцией.
С учетом (6.625),(6.626) поставленную задачу можно сформулировать следующим
образом:
Требуется синтезировать такие матрицы ka0 = ka0 (/) kal = kal (xB,/), для
которых решения уравнения (6.626) удовлетворяло бы фазовым ограничениям (6.623) на
множестве возмущений (6.621) или (6.622) и структурно-параметрической
неопределенности матрицы Аа в силу (6.620).
Пусть множество Q(t), определяющее ограничения на вектор состояния х
системы (6.626), формируется аналогично тому, как это показано выше, т.е., если
i|/,(x,f), /el,и - непрерывно дифференцируемые,по всем своим переменным
скалярные функции ограничения, то
e(/) = {xe/?n:v|//(x,r)<0,/eu}. (6.628)
Введем ограничения вида
yi±(x;t) = ±xl-ql(t)<0,
Глава 6. Синтез грубых систем автоматического управления
403
соответствующие следующим фазовым ограничениям (6.623)
|х,|£ Я (/),! е!Я (6.629)
где qt [t)yi е \,п - непрерывно дифференцируемые для всех t положительные
скалярные функции.
Для того чтобы решение системы (6.626) удовлетворяло ограничениям (6.623)
вида (6.628), достаточно, чтобы для каждого t>t0 выполнялись неравенства
(vxy,,A«x)+^<0 1
^ хТ( > Ы \, (6.630)
xera(/)nre(/),i€Uj
где TQ(t) - граница множества Q{t), состоящая из участков
Г0 (t) = {х € R" : v, (х,/) = О},/еп. (6.631)
Неравенства (6.630) с учетом фазовых ограничений (6.629) аналогично (6.619)
приводятся к выражениям
п
v=l
Xj =qj,\xv\<qvyve\,n\j,t>t0
(6.632)
v=l
(6.633)
Xy = -?/>|*v| ~ ^v»V e hn\j,t>t0
где a"v = a"v (x,kflO,kal,w,/\;,v e l,w -элементы матрицы Aa (•). Причем
a?v =^v+//v(x,ka0,kal,w,/), (6.634)
где 5"v,//"(*) ~ элементы соответственно матриц Aa Гка0,t\ Fa (x, ka0, kal, w,tj.
Если, например, Fa (•) = Om , то Aa = АГка0,/j, и аналогично (6.619) можно
показать, что неравенства (6.632), (6.633) эквивалентны следующим неравенствам
п
Z|5yv|?v^9y-5^'' jel,n, t>t0, (6.635)
v=l
которые решаются непосредственно относительно матрицы ka0(f). Структурно-
параметрическая неопределенность для рассматриваемой линейной системы
соответствует отсутствию точной информации об элементах матриц Aa,Ba. Причем под
структурной неопределенностью линейной системы понимается возможность
изменения хотя бы одного из элементов я"у>^/ц матриц Aa-,Ba на интервале,
содержащем нулевое значение.
Пусть Fa (•) •£ От , тогда неравенства (6.632), (6.633) приводятся к виду
27*
404
Методы синтеза САУ по заданным показателям качества. Часть II
а;у = 5?у+7£(х,кв0,кв1,1м),
V=l
v*7
-Ё(^+/7ау)^^^-(^+Л>)^^7=-^,
v=l
v*7
у 6 l,/i|xv| <qv,ve\,n\j,t> t0.
Из (6.636) следует
(6.636)
где
v=l
v*7
"Ё(5> + /^)*v ^ <7/ " 25^/ +~1?>Х1= "Яг
v=l
v^7
^_ n
v=l
v^=7
(6.637)
(6.638)
(6.639)
т.е. /",// определены соответственно при ху = ^ и *7 = -^ . Из выражения (6.637)
непосредственно следуют необходимые условия их разрешимости, являющиеся
условиями существования закона управления (6.625), обеспечивающего решение
поставленной задачи. Эти условия можно получить путем сложения неравенств (6.637)
и приведения к виду
\xv\<qv,vel,n\j,t>t0.
Соотношения (6.639) могут быть использованы для первоначальной проверки
существования требуемого закона управления. Однако для синтеза управления (6.625)
предлагается использовать неравенства (6.637), представляющие собой достаточные
условия обеспечения фазовых ограничений (6.629).
С этой целью поступим следующим образом. Поскольку неравенства (6.637)
рассматриваются на всем множестве допустимых векторов X, то на их основе можно
получить более жесткие, но и более удобные для синтеза матриц ka0,kal неравенства.
Действительно, поскольку каждое из неравенств (6.637) справедливо в текущий
момент времени t > t0 соответственно для каждого
то (6.637) будут выполняться, если обеспечиваются соотношения
Глава 6. Синтез грубых систем автоматического управления 405
s^^er^г^^^4nn^^"й>'"/")-^"^'"г5'
v=l
v*7
xerQj(t)f]TQ(t),
~Y<a%xv- m?x
v=l
хеГО-ПГд
-!>>•
v=l
(6.640)
^Аъ-ъ*+я>ъ-***+~я>
хеГб;(/)Пге(^),у€1,л, />/„•
Неравенства (6.640) преобразуются к более простому виду. Действительно,
нетрудно показать, что
™^P>"-t№
x€RjJnr<?v=l
max
хеГО;ПГ(?
v=l
\
^v?
Z~a
aJvqv
v=l
v*7
(6.641)
v=l
v*y
А для правых частей (6.640), поскольку a^vJe\,n - только функции времени,
справедливо
min (q. - Щм. - ff ) = ^, - 5^ .■ + min Iff ) =
xerQjnVQ^ J M J J ' J JJ J xerO}nrQ\J >
С учетом (6.641),(6.642) соотношения (6.640) приводятся к виду
п __
(6.642)
v=l
v^7
Е|^^=^у-«>у+/Г'
v=l
v*7
(6.643)
у el,л, f>/0.
Поскольку неравенства (6.643) рассматриваются на всем множестве возмущений
(6.621), то, чтобы они были справедливы при любом возмущении w , достаточно
обеспечить следующие условия
v^7
-qj-fyj- max}/;+ шц-Ъд,-/**,
406
Методы синтеза САУ по заданным показателям качества. Часть II
i\a$>W*A(ij-afa+/г)=
v=l
(6.644)
= 9>-5S^+J™n)//-=^-5;9y+//-> jel,n, t>t0.
(6.645)
Неравенства (6.644) представляют собой достаточные условия обеспечения
фазовых ограничений (6.629) и могут быть непосредственно использованы для синтеза
матриц ka0,kal, поскольку в силу (6.642), (6.644)
/f+=max max ff (x,ka0,kal,w,/) =
=/;+(ka0,ka1,/),
/f"=min min /f (x,ka0,kal,w,>) =
= /;-(ka0,ka1,/),
и, кроме того, согласно (6.627) ajv = a*v (ka0, A jy v e l,/i', т.е. для каждого момента
времени t>tQ величины f*v+,f"v~, a*v9j,ve\9n зависят только от матриц ka0,kal.
При синтезе матриц ka0, kal неравенства (6.644) можно рассматривать при
произвольном значении a € A(t), t > t0, согласно (6.620), а затем, выбрав для этого a
матрицы ka0, kal использовать их с некоторой степенью точности на всем
множестве <A(t). Но можно непосредственно синтезировать ka0, kal, гарантирующие
ограничения (6.629) с учетом структурно-параметрической и внешней неопределенности,
на основе соотношений, эквивалентных (6.620), (6.644), вида
max
max
<xeA(t)
l|*?v|tfv+«X+#v+
v=l
*я„
X|5«v|«7v+aX-/,v
V=l
*4j>
(6.646)
jeln, t>tQ.
Необходимо отметить, что каждое из двух неравенств, соответствующих j'e \9n и
входящих в выражения (6.644) или (6.646), можно решать относительно ka0,kal
независимо от другого. Однако полученные в результате такого решения значения
матриц ka0, kal обязательно должны удовлетворять и другому неравенству.
Поскольку в выражениях (6.644), (6.646) от матрицы kal зависят только
величины //+,/ух",у б1,и, а затем выбирается kal из условия полного обеспечения
рассматриваемых неравенств.
В том случае, когда в разложении (6.624) Fa (•) = От , а управление и ищется в
виде (6.625), величины /уа+ * 0, /уа~ * 0, j е 1, л, т.е. также сохраняется пораздель-
Глава 6. Синтез грубых систем автоматического управления 407
ный синтез ка0, ка1. Однако, т.к. /7а+,/уа~,у е1,л, зависят от kal и не зависят от
ka0, синтез данных матриц может осуществляться не только независимо друг от
друга, но и одновременно.
В том случае, когда система (6.619) является линейной, структурно-
параметрическая неопределенность, как отмечалось выше, соответствует
неконтролируемым изменениям параметров системы на некоторых интервалах. Тогда
операция тах(«) согласно (6.646) соответствует непосредственно операции взятия
максимума от выражения (6.646) по неконтролируемо изменяемым параметрам.
Для нелинейных систем указанный случай структурно-параметрической
неопределенности также имеет место. Однако можно указать более общий случай
структурной неопределенности, не сводимой к тому или иному изменению параметров
системы. Пусть правая часть системы (6.619) имеет вид
/a(x,u,w,/) = /0p(x,u,w,r) + 9(x,0 (6.647)
или
/a(x,u,w,0 = /oP(x,u,w,/)(l + v(x,0), (6.648)
где /оР(#) - пх\ заданная вектор-функция с параметрической неопределенностью,
характеризуемой значениями параметра р на некотором допустимом множестве
Р(/);ф(/)-их1 неизвестная вектор-функция, соответствующая аддитивной
структурной неопределенности; v(x,/) - неизвестная скалярная функция,
соответствующая мультипликативной структурной неопределенности. Функции cp(x,/),v(x,/)
удовлетворяют тем или иным ограничениям, которые в достаточно общем случае
можно представить в виде
(p(x,f)eO,v(x,/)eF, (6.649)
где Ф, V - некоторые заданные множества. В частности, можно считать, что Ф или V
- это множество функций, ограниченных по величине. Например, Ф, V можно задать
аналогично тому, как задано множество W{t) (см. (6.622)). Тогда аддитивная ф(х,/)
и мультипликативная v(x,f) структурные неопределенности могут рассматриваться
по аналогии с возмущениями W{t), и операция максимизации на множествах Ф,К
аналогична максимизации на W[t) вида (6.622).
Возможны также и другие подходы к решению неравенств (6.646) с учетом того
или иного определения операции тах(») в зависимости от определения вида
множеств a e A[t), Ф,К . Но они в данной работе не рассматриваются.
6.7.1. Оценка робастности системы с помощью кругов Гершгорина
Для анализа разрешимости неравенств (6.646), а также для оценки робастности
системы (6.619) при синтезированном законе управления вида (6.625) можно
воспользоваться кругами Гершгорина [145].
Для пхп матрицы Аа, формируемой согласно (6.627), определены п кругов
Гершгорина Gj (Aa \ j е 1, и, объединение которых
g(a")=ug,(a°)
408
Методы синтеза САУ по заданным показателям качества. Часть II
содержит собственные значения матрицы Аа.
При этом
G,(A")=
1 ^
геС':|й5-*|£5,= — %\а%\р.
Pj v=l
(6.650)
где /?v, v e 1, /7 - произвольные положительные числа; SjJ e 1, л - радиус j -го
круга Gj уАа ]; С* - комплексная плоскость.
Сопоставим неравенства (6.644) с определением кругов Гершгорина (6.647). В
качестве положительных величин Pj примем функции ^(г),т.е. р} -q} (/), j е l,w.
Тогда для матрицы Аа круг G; (Аа j имеет радиус
S* = S
"У V / v=l
(6.651)
v*/
С учетом (6.651) неравенства (6.644)приводятся к виду
■а ,Ъ , 1 7а-
^s-,f;-,r.
(6.652)
je\,n,t>t0..
Поскольку z = ajj еС* является центрому - го круга Гершгорина, то левые части
неравенств (6.652) соответствуют крайней правой точке круга G} (Aa \ на комплексной
плоскости С*, являющейся точкой пересечения данного круга с действительной осью.
Тогда неравенства (6.652) означают, что они будут выполняться тогда и только
тогда, когда каждый круг Гершгорина G7 f Aa j, у el,« будет находиться слева от
прямых, параллельных мнимой оси на плоскости С* и проходящих соответственно
через точки z) =— —, z~ =— —,je\,n лежащие на действительной оси
4j qj 4j qj
(см. рис. 6.22).
Так как в общем случае zj,zj зависят от времени, то указанное требование должно
выполняться для всех t>t0. Положением кругов Gy (ka \ j е\,п на комплексной
плоскости С* можно управлять за счет выбора соответствующей матрицы ка0, так
как центр каждого круга, находящийся в точке а* , и радиус S* зависят только от
ка0. А положением прямых, параллельных мнимой оси, можно управлять как с
помощью ка0, так и с помощью kal, так как /7a+,/ya~,y € 1, л зависят от ka0 и kal.
Таким образом, перемещая с помощью выбора ka0 каждый круг Гершгорина
Gj (Aa ) влево и с помощью выбора kal соответствующие ему прямые, параллель-
Глава 6. Синтез грубых систем автоматического управления
409
ные мнимой оси, вправо, можно добиться требуемого расположения кругов Гершго-
рина на комплексной плоскости С* и тем самым обеспечения неравенств (6.644) или
(6.652).
ImS
пл.С*
zj Re S
Я, Я,
Я, Я!
Рис. 6.22. Геометрическая интерпретация обеспечения фазовых ограничений
Допустим, что для некоторых к?0, к?1 требуемое расположение кругов
Gj (Aa Y у е 1, л обеспечено. Тогда для синтезированного закона управления
iT = k?°xB + k?1(xB)xB можно говорить о степени робастности системы. Под этим
будет пониматься следующее. Под степенью робастности дляу-й компоненты
вектора состояния понимается расстояние от круга Gj (Аа ) (т.е. от точки z" = a* +S" ,
лежащей на действительной оси в С*) до ближайшей из двух соответствующих ему
прямых, параллельных мнимой оси (т.е. до точки zj или z~), которое обозначим
через а" и, согласно определению, равное
аа = min \z] - z*; z] - z? }, у е п. (6.653)
С учетом (6.653) под степенью робастности системы (6.619) при синтезированном
управлении и* будем понимать величину
аа=тша?. (6.654)
je\,n J
При обеспечении допустимого расположения кругов Гершгорина на комплексной
плоскости aa > 0. Причем, чем больше величина aa , тем более робастной является
система, т.е. фазовые ограничения (6.629) для синтезированного закона управления
будут обеспечиваться на более широких множествах структурно-параметрических и
внешних возмущений.
Заметим, что при синтезе требуемого закона управления вида (6.625) можно
дополнительно потребовать, чтобы обеспечивалась заданная степень робастности, т.е.
чтобы выполнялось неравенство
aa>cr ,
(6.655)
26 Зак. 366
410 Методы синтеза САУ по заданным показателям качества. Часть II
где а* > 0 - известная величина.
Эффективность решения задачи синтеза зависит от вида разложения (6.624)
функции /а (•), т.е. от свойств матриц Аа,Ва и функции Fa (•), тот или иной
выбор которых влияет на сложность: синтеза матриц ka0,kal обеспечения заданных
ограничений; требуемого размещения кругов Гершгорина на комплексной плоскости.
Пример 6.1.
Пусть уравнения движения некоторого объекта имеют вид
x = 3x + x2u + 2x2tt>tOt
где х, и - скалярные переменные.
Заданы фазовые ограничения |х| < е~',/ > /0
Необходимо синтезировать управление и - кох + кх (х) х .
Согласно (6 624) воспользуемся разложением
f(A = 3x + u + x2u-u + 2x3=3x + u+\ ux-- + 2x2\x .
W \ х )
Отсюда
F(.) = mx-- + 2x2, A = 3,B = \
Согласно (6 626),(6 627)
F(.) = BKl+F(.) = kl(x)^k0x + k](x)x)x-k°X + k^X + 2x2 =
= ko(x2-\) + kl(x)x2+2x2.
В соответствии с (6 638), (6 645)
max
г--1^Ше-2'-1)+к'(-е-Уь+2е'2'У}'
и-
те
Г =[кп(е-2' -1) + к,(е-)е-21 +2е-2']е-,
/-=-[*0(е-2'-1) + А,(-е-')г-2'+2е-2']е-'
Согласно (6 627)
А = А + ВК{)=3 + к0.
Тогда неравенства (6.644) примут вид
0<-^_(з + Л0)е-/-^0(е?-2/-1) + А1(г-/)^2Ч2е-2/]е-/,
0<-e"'-(3 + it0)^-[^)(^-l) + ^(-^)e-242^y/f
Отсюда после соответствующих преобразований следует
^(^)<-(^0+2)-4е2/,
^(-е-/)<-(^0+2)-4е2'^>/0
Пусть кх (х) ищется в виде
*1 (*) = *10+*11 —
Тогда неравенства приводятся к следующему
kl0+kulj<-(k0+2)-4e2tJ>t(),
для выполнения которого достаточно, чтобы
Глава 6. Синтез грубых систем автоматического управления 411
*1О<-(*о + 2),1
для любого к0.
Таким образом
*и*-4
и -кох + klox + kn- = (k0+ kl0)x + кп-у
где ко,к1О,ки удовлетворяют приведенным выше условиям.
Предложенный метод может быть использован для достаточно широкого класса
задач при построении управления различными объектами, о структуре и параметрах
объекта, возмущениях внешней среды. При этом цель управления может быть
сведена к достаточно общему виду фазовых ограничений. Данный класс задач особенно
характерен при разработки и формировании интеллектуальных систем управления
когда необходима быстрая обработка информации, выработка управления в реальном
режиме времени. При чем в этих задачах возможна неопределенность по цели.
Рассмотренный метод позволяет учитывать и ее. Необходимо также отметить, что
полученные соотношения метода (6.644), (6.652) могут быть эффективно реализованы на
основе известных численных процедур, в том числе и параллельных алгоритмов.
Возможен дальнейший анализ и обобщение неравенств (6.644), (6.652) с целью
упрощения и расширения их решения. Неравенства (6.644), (6.652) могут
использоваться при выработке алгоритмов управления. Поскольку полученные соотношения
допускают геометрическую интерпретацию с помощью кругов Гершгорина, то они
оказываются удобными в инженерных расчетах.
6.8. СИНТЕЗ СИСТЕМ НА ОСНОВЕ ГРАНИЧНЫХ ОТОБРАЖЕНИЙ
Рассмотрим одну из модификаций разработанного метода, основанную на
отображении реальной траектории на границу фазового множества и позволяющую
обеспечить необходимое функционирование системы с учетом различных
ограничений: на управление, вектор состояния, сложность технической реализации. При этом
множество допустимых управлений будет тем шире, чем менее жесткими являются
данные условия. Предлагаемый далее метод отображений позволяет получить
расширенные условия по сравнению с методом неравенств.
Пусть объект управления описывается управлением
Х = /(Х,и,0, ]
, , (6-656)
Х(/0) = Х0, f>/0,j
где X,u-wxl, тх\ векторы состояния и управления, /(-)-лх1 вектор-функция,
удовлетворяющая условию существования и единственности решения задачи Коши.
На состояние системы (6.656) наложено ограничение:
X(t)eQ(t) Vr>/0, (6.657)
где
е(/) = {Х€Я":м/(Х,/)<о}*0,
ij/(X,f) - непрерывно-дифференцируемая по X и Г функция. Ограничения на
управление имеют вид
ueU(X,t) VXeQ(t), t>t0, (6.658)
U(X,t)^0- замкнутое в Rm множество.
26*
412 Методы синтеза САУ по заданным показателям качества. Часть II
Учет ограничений на сложность технической реализации осуществляется с
помощью шкалы сложности £, формируемой на множестве технически реализуемых
управляющих устройств.
Требуется синтезировать допустимый закон управления заданной структуры из
£ , обеспечивающий условие: Х(/) е Q{t) \/t>t0, если только Хо е Q(t0).
Пусть Г<2(/)- граница Q(t), элементами которой являются векторы Z,T.e.
re(/) = {Ze/?":y(Z,0 = o}.
На пространстве Rn+1 определим непрерывно-дифференцируемую по всем
аргументам пх\ вектор-функцию g(Z,X,t), где Х- некоторая скалярная величина,
принимающая значения из замкнутого связного множества Л с R1. Считаем, что для
Q(t) можно выбрать такую g(Z,X,t), которая для любого t = t* >t0 определяет
взаимно-однозначное отображение
g(zXt*):rQ(t*)xA->R". (6.659)
При этом Л можно разбить на два таких непересекающихся подмножества А1 и
Л2, т.е. Л = Л] U Л2, что устанавливается взаимно-однозначное соответствие
g(z,X/):re(/*)xA,->e(/*). • (6.660)
Положим
X = g(Z,M). (6.661)
Тогда, если X е А}, то Хе Q(t), и если XеЛ2, то X £ Q(t). Допустим, что из
(6.661) в явном виде определяется зависимость
Z = G(X,M), (6.662)
G(-)- в силу свойств g(-) непрерывно-дифференцируема по X,X9t. Если Х(/)-
некоторая траектория системы (6.656), то согласно (6.659), (6.662) ей однозначно
соответствуют: непрерывно-дифференцируемая функция X = X(t) со значениями из
множества Л и траектория
Z(t) = G(X(t),\(t)9t)erQ(t) Vr>/0. (6.663)
Согласно определению
\|/(Z(f),/)sO W>/0.
Отсюда
d\\j
^=(vzi|/,z)+i|/;so, (6.664)
at v '
A</v
где (vzv|/,z) = ^~—-i^;- скалярное произведение векторов Z и
z L^arj""^] ' ¥r a/ '
С учетом (6.663)
Z = (VxGfX) + GiX + G;=(vxG(X(O,X(/),/ft ,,^ч
(o.ooj)
/(X(/),u(/),/) + Gi(X(/),A.(/),r)X + G;(X(/),X(/),/),
Глава 6. Синтез грубых систем автоматического управления 413
и(/)- управление, которому соответствует траектория Х(/). Используя (6.661),
(6.665) приводится к виду
z = Fx(z(t),u(t),x(t),t)+F2(z{t),\(t),t)i. (6.666)
После подстановки (6.666) в (6.664) получим
i у;(г(0,/)+(угМ>(г(04^(г(0»»(0»^(0>0)_
(vzy{z{t),t),F2 (Z(t),X(t),t)) (6.667)
=ф(г(/),и(ОД(О,О-
Предполагается, что (vzv)/(Z(/),/),F2(z(/),X(/),/))*0 Vf >/0. Из (6.660)
следует, что если X = X(t) е Л, Vf 2: /0 и удовлетворяет (6.667), то X(r) e Q{t) V/ > /0.
В соответствии с (6.667) рассмотрим дифференциальное уравнение
*■•(«<')...*.').} (6.668)
где Z(/) -произвольная траектория на TQ{t). Для получения достаточных условий
на управление воспользуемся теоремой.
Теорема 6.9. Если для некоторого допустимого управления и = й(-) е £, решение
уравнения (6.668) удовлетворяет условию:
X(t) € Л! для любой Z(t) e TQ(t) и для всех t>t0, (6.669)
то й(-) обеспечивает выполнение фазовых ограничений (6.657), если только
Хоеб(/О).
Доказательство. Пусть условия теоремы выполняются для некоторого
допустимого и = й(-) е £ , однако фазовые ограничения не обеспечиваются. Тогда
траектория Х(/), соответствующая данному управлению, в некоторый момент времени
t~t*>t0 выходит из QU j и, по крайней мере, на некотором интервале (t*,t* + т\
где Т > 0,
X{t)*Q{t).
Из условий (6.659), (6.660) взаимно-однозначного отображения g(-) следует, что в
этом случае
X(t)eA2 для всех te(t\t* + т).
А поскольку Л2 П Aj = 0, то приходим к противоречию с предположением о
выбранном законе управления й(). Следовательно, фазовые ограничения не
нарушаются. Что и требовалось доказать.
Рассмотрим применение для линейной системы, т.е. когда
/(X,u,/) = AX + Bu, A = A(/), В = В(г). (6.670)
Считаем, что для всех t^t0 Q(t)- выпуклое множество и нулевой элемент
О е Q(t). Тогда можно воспользоваться линейным отображением
X = g(ZA/) = )iZ, (6.671)
414
Методы синтеза САУ по заданным показателям качества. Часть II
где X е Л = [0,оо). При этом X е Q{t) только тогда, когда X е Л, = [0,1]. Нетрудно
проверить, что отображение (6.671) удовлетворяет условиям (6.659), (6.660).
С учетом (6.670), (6.671) уравнение (6.668) примет вид
Если и ищется в виде
и = п() = КСХ, К = К(Г), С = С(/),
то
(Vzh/.azJ+y;
х = х-
= Xq>(Z,K,r),
(6.673)
(VzV,Z)
X(to) = Xo, A = A + BKC.
Решением (6.673) является
Х.(/) = ехр]|ф(г(т),К(т),т)л1х0.
1
Пусть 0 < ^0 < 1. Согласно теореме: ехрНф(2(т),К(т),т)£/т|>А,0 е[0,1] для любой
I'» J
Z{t) e TQ[t) и для всех t>t0. Отсюда
ехр (ф(г(т),К(т),т)Л10<1 (т.к. >,0>0)
или
}ф(г(т),К(т),т)Л^-1пХ0.
(6.674)
Рассматриваемый подход может быть распространен на случай нескольких
фазовых ограничений. Пусть, например, ограничения имеют вид
ч,,(х,/)=|*,И(О*о.1
/ = 1Д...,л. J
Тогда при А.о = 1 на основе (6.674) для элементов матрицы А получим неравенства:
JW _ Л s o,
/ V=l
(6.675)
9yW
У = 1,2,...,я />/0,
являющиеся обобщением достаточных условий, полученных в [60]. Если (6.674) или
(6.675) выполняются при te[to,to +Г], то на этом отрезке обеспечиваются фазовые
ограничения.
Глава 7. Регуляторы основных теплоэнергетических параметров АЭС 415
ГЛАВА 7. РЕГУЛЯТОРЫ ОСНОВНЫХ
ТЕПЛОЭНЕРГЕТИЧЕСКИХ ПАРАМЕТРОВ
АТОМНЫХ ЭЛЕКТРОСТАНЦИЙ
В предыдущих главах в основном рассматривались теоретические положения,
составляющие содержание методов синтеза регуляторов. Цель настоящей главы -
знакомство читателя с так называемыми «живыми» регуляторами, т.е. регуляторами,
применяемыми в промышленности. Такой методический подход позволяет
«привязать» изложенные в главах 1 - 6 положения к решению конкретных задач. В главе
описаны особенности математических моделей регуляторов, их аппаратная
реализация, а также связь с физическими процессами, которые необходимо учитывать при
решении задачи. Детально излагаемые ниже положения рассмотрены в [148].
7.1. ОСНОВНЫЕ УПРАВЛЯЕМЫЕ ПАРАМЕТРЫ
ЭНЕРГОБЛОКОВ С РЕАКТОРАМИ ВВЭР И РБМК
Энергоблоки АЭС как объекты автоматизации имеют следующие особенности:
1) непрерывный характер основных технологических потоков (носителей
тепловой и электрической энергий) и дискретный характер вспомогательных
технологических потоков, обеспечивающих работу основных потоков;
2) значительные единичные мощности энергоблока, что приводит к
значительным потерям при профилактике, ремонте, авариях, а также усложнению
вспомогательного технологического оборудования;
3) сложность технологии, что требует большого количества измеряемых
параметров (около 30 тыс.), запорной и регулирующей арматуры (около 4,5 тыс.);
4) сложность технологического процесса и недостаточное его исследование не
позволяет ограничиться управлением по состоянию. Применяется комбинация:
управление по состоянию (логическое управление и регулирование) и
событийное управление в экстремальных ситуациях (блокировка, защита);
5) высокая экологическая опасность, необходимость обеспечения высокой
радиационной, ядерной, пожаро-, взрыво-, электробезопасности. Это требует
резервирования оборудования, применения вспомогательного оборудования.
Упрощенная однопетлевая технологическая схема энергоблока с реактором ВВЭР
приведена на рис. 7. Г. Через активную зону 1 реактора 3 прокачивается теплоноситель
первого контура с помощью главных циркуляционных насосов 2. Нагреваясь в
активной зоне реактора, теплоноситель поступает в парогенератор 4, где отдает тепловую
энергию теплоносителю второго контура. Полученный в парогенераторе пар во втором
контуре поступает в турбину 5, вращающую электрический генератор 6. Отработанный
в турбине пар конденсируется в конденсаторе 7: Конденсат с помощью конденсатных
насосов 8 подается через регенеративные подогреватели низкого давления 9 в
деаэратор 10. Очищенная от газов в деаэраторе питательная вода подается насосами 11 через
регенеративные подогреватели высокого давления 12 снова в парогенератор.
Для функционирования данного энергоблока все основные параметры отдельных
его агрегатов должны поддерживаться в заданных технологических пределах. В наи-
* С используемыми терминами, а также с техническими средствами аналоговых и цифровых
регуляторов, используемых в АЭС, можно познакомиться в [148].
416
Методы синтеза САУ по заданным показателям качества. Часть II
более часто применяемых режимах управления мощностью энергоблока в качестве
регулируемой величины выбирается давление пара перед турбиной. Поддержание
заданного давления пара осуществляется изменением электрической мощности
генераторов или тепловой мощности реактора с помощью перемещения управляющих
стержней исполнительным органом 13 системы управления реактора. При этом в
качестве управляющего воздействия используется также сигнал нейтронного потока
в реакторе. Частота сети поддерживается с помощью регулятора, воздействующего
на регулирующие клапаны 14 турбины.
Существует ряд параметров, которые не влияют непосредственно на выработку
электроэнергии, но влияют на режим работы блока. Одними из важных параметров
являются: уровень в парогенераторах, который регулируется изменением расхода
питательной воды с помощью регулирующего клапана 15; уровень конденсата в
регенеративных подогревателях, регулируемый с помощью клапанов 16; уровень в
конденсаторе турбины; уровень в деаэраторе, который регулируется подачей пара
через клапан 17.
Для поддержания давления и массы теплоносителя в первом контуре имеется
специальное устройство - компенсатор объема (давления) 18, в котором над уровнем
воды поддерживается паровая подушка с постоянным давлением.
бру
/
Рис. 7.1. Технологическая схема энергоблока с реактором ВВЭР
Давление в нем поддерживается изменением мощности нагревателя 19, а также
путем впрыска холодной воды клапаном 20 или сброса пара клапаном 21. При
снижении уровня воды в компенсаторе объема в первый контур подается
дополнительная вода с помощью подпиточного насоса 22. В аварийных ситуациях изменяется
давление пара перед турбиной путем сброса пара в конденсаторы через редукционно-
охладительные установки 23.
На рис. 7.2 показана технологическая схема энергоблока с реактором РБМК-1000.
В реакторе 1 расположены технологические каналы 2, через которые прокачивается
теплоноситель с помощью главных центробежных насосов 3. Пароводяная смесь из
технологических каналов поступает в барабан-сепараторы 4. В каждой паре барабан-
сепараторов они объединены по воде и пару. Расход воды через каналы регулируется
с помощью клапанов 6.
Пар из барабан-сепараторов по трубопроводам 7 поступает на турбину: цилиндр
высокого давления 8, сепаратор 9, цилиндры низкого давления 10. После турбины
Глава 7. Регуляторы основных теплоэнергетических параметров АЭС 417
пар попадает в конденсаторы 11. Вода из конденсаторов с помощью насосов 12 через
подогреватели низкого давления 13, деаэраторы 14, насосы 15 по трубопроводам 5
снова подается в барабан-сепараторы.
Уровень воды в барабан-сепараторах регулируется с помощью клапана 17. При
аварийном повышении давления пар сбрасывается в конденсаторы турбин через
быструю редукционную установку в конденсатор (БРУ-К) 18 или в барботер 19 через
(БРУ-Б) 20.
Реакторы типа РБМК обладают некоторыми особенностями: малое
саморегулирование, положительный паровой эффект реактивности. Эти эффекты выдвигают более
высокие требования к статической и динамической точности поддержания давления,
высокие требования к регулированию уровня в барабанах-сепараторах. В процессе
же работы имеют место колебания уровня. Необходимо также осуществлять
регулирование большинства тех же параметров, что и в энергоблоках с реакторами ВВЭР.
19
13
Рис. 7.2. Технологическая схема энергоблока с реактором РБМК
7.2. СТРУКТУРНЫЕ СХЕМЫ РЕГУЛЯТОРОВ АЭС
Несмотря на существенные различия энергоблоков с различными ЯР и
используемого в них энергетического оборудования, большинство регуляторов имеют
одинаковые структурные и функциональные схемы.
Среди регуляторов тепловой автоматики можно выделить две группы: регуляторы
уровня (АРУ) жидких сред и регуляторы давления (АРД) пара, которые существенно
влияют на режим работы ядерного энергетического блока.
Регуляторы уровня предназначены для поддержания заданного уровня
теплоносителя в компенсаторах давления (КД) и барабанах-сепараторах (БС), питательной
воды и конденсата пара в парогенераторах (ПГ) и регенеративных перегревателях.
Заданный уровень в АРУ поддерживается за счет обеспечения материального баланса
между притоком и оттоком вещества в регулируемом сосуде. Часто приток и отток
представляют разные фазы одного вещества. Например, приток - вода, отток - пар.
Для рассмотрения динамических свойств объектов регулирования (ОР) в АРУ,
используем уравнение материального баланса
^(РЛ+РЛ)=С„-С7П, (7.1)
где рв, VB - плотность и объем воды,
рп,Уп - плотность и объем пара,
418 Методы синтеза САУ по заданным показателям качества. Часть II
GBiGn - расходы воды и пара соответственно.
Так как для сосуда с постоянным поперечным сечением F и высотой Н объем
воды равен FB = hF , а пара - Vn = (Я -h)F , где h - уровень воды, то после
подстановки Vn и Vb в (7.1), получим зависимость уровня воды от расходов пара и воды
при постоянных их плотностей в виде:
^(PB-Pn)f = GB-Gn. (7.2)
Из (7.2) следует, что при сделанных допущениях уровень жидкости в ОР является
интегралом от материального баланса GB-Gn. При этом расход пара играет роль
возмущения, а расход воды является управляющим воздействием (рис. 7.3).
Рис. 7.3. Структурная схема объекта управления АРУ:
£ = 1/(рп-рв)//г — коэффициент передачи; s — переменная преобразования Лапласа
Для управления расходом воды применяют регулирующие клапаны (РК),
снабженные электрическим исполнительным механизмом (ИМ), который также
представляет интегрирующее звено с передаточной функцией
ад-fi^J-, (7.3)
где V(s) - изображение входного сигнала ИМ;
Гим - постоянная времени ИМ.
Легко показать, что охват двух интеграторов отрицательной обратной связью
(ООС) не обеспечивает устойчивость такой системы, поскольку характеристическое
уравнение THMs2 + k = О имеет чисто мнимые корни. Это вынуждает вместо И-закона
регулирования применять П-закон.
Простейшим способом обеспечения устойчивости АСР с астатизмом 2-го
порядка, является охват ИМ жесткой ООС по положению регулирующего клапана
(рис. 7.4).
Анализ приведенной одноимпульсной (импульс по уровню) структурной схемы
АРУ приводит к следующей зависимости уровня h от уставки А3 и возмущения Gn,
записанной в операторной форме:
TCMs2 +s + knk TCMs2+s + knk
Из последнего выражения следует, что одноимпульсный АРУ с местной обратной
связью по положению РК имеет статическую ошибку, вызванную возмущением. Так,
в установившемся ( s = 0) режиме h = А3 только при Gn - 0. Изменение расхода
пара, например на постоянную величину AGn, приводит к возникновению
установившегося отклонения уровня от заданного значения на величину ДА = AGn I kn, которое
называется неравномерностью регулирования. Неравномерность регулирования об-
'лава 7. Регуляторы основных теплоэнергетических параметров АЭС 419
>атно пропорциональна коэффициенту кп передачи П-регулятора. Одноимпульсный
\РУ с местной обратной связью по положению РК применяют для регулирования
объектов, не требующих высокой точности поддержания заданного уровня, например
>егенеративных подогревателей.
-4gb
■*&•
Щтци*)
ГгвЧ
Рис. 7.4. Одноимпульсный (двухимпульсный) АРУ с местной обратной связью
по положению регулирующего клапана (расходу питательной воды),
кп - коэффициент пропорциональности П-регулятора
Расход питательной воды GB зависит не только от положения регулирующего
слапана, но и от других факторов, например от напора питательного насоса. Поэтому
5олее совершенным является двухимпульсный АРУ, в котором местная ООС введена
ж по положению РК, но по расходу воды GB.- Заметим, что выражение (7.4), строго
говоря, соответствует именно двухимпульсному АРУ.
Для большинства регуляторов уровня выражение (7.2), описывающая ОР, имеет
Золее сложный вид, т.к. плотности воды и пара'зависят от температуры (в КД) и дав-
пения (в БС). Уровень питательной воды в ядерных паропроизводящих установках
^ЯППУ) зависит от подвода тепла. При увеличении мощности реактора возрастает
интенсивность парообразования, что снижает среднюю плотность воды и повышает
зе уровень даже при сохранении баланса между расходами пара и воды. К
аналогичному результату ведет резкое снижение давления пара в ЯППУ (эффект
«вспухания»). На практике имеет место известный парадокс, когда увеличение расхода не-
цогретой воды для питания ЯППУ, вместо увеличения уровня ведет к его
временному снижению из-за уменьшения интенсивности парообразования.
Ш
Рис. 7.5. Структурная схема трехимпульсного АРУ,
K^6(s) - передаточная функция регулирующего блока
В случае необходимости обеспечения высокой точности поддержания заданного
уровня (ПГ, БС, КД) применяют трехимпульсные АРУ. В таких регуляторах в
качестве местной ООС используется сигнал материального баланса e = Gu-Gn. В этом
случае реализовывается принцип комбинированного управления по отклонению и
возмущению.
Пусть ради простоты Kp6(s) = kn . Тогда для трехимпульсного АРУ справедливо
выражение
420 Методы синтеза САУ по заданным показателям качества. Часть II
V + Skn + knk ТШ52 + ^п + kuk
Из последнего выражения следует, что трехимпульсный АРУ не имеет статической
ошибки относительно установившихся возмущений расхода пара, т.е. h = h3 при
любой Gn = const. Заметим также, что данный вывод справедлив только в том случае,
если для формирования сигнала материального баланса измеряются все имеющие
место расходы воды и пара. В противном случае, неконтролируемые расходы, например
во время продувки парогенератора, вызовут отклонение уровня от заданного значения.
Для улучшения переходных процессов АРУ вместо П-закона в некоторых случаях,
например для регулирования уровня в БС, реализовывают ПИ-закон.
Автоматические регуляторы давления предназначены для поддержания заданного
давления пара в ЯППУ. При этом АРД должен обеспечить баланс между генерацией
пара и его расходом. Так как большинство энергоблоков работают в базовом режиме,
т.е. мощность блока задает ЯР независимо от нагрузки электрической сети, заданное
давление АРД поддерживают, подстраивая расход пара турбиной в соответствии с
его генерацией. Для этого в зависимости от сигнала рассогласования АРД
осуществляет воздействие на механизм управления турбиной (МУТ) и посредством
гидравлического регулятора скорости (PC) вращения турбины меняет расход пара.
Возмущением для АРД является изменение мощности ЯР и изменение расхода пара
вследствие реакции PC на изменение частоты в электрической сети.
АРД могут выполнять свои функции, если турбогенератор работает на
энергосистему в синхронном режиме. В противном случае, например во время пуска энергоблока
или в аварийных режимах, связанных с остановом ТГ, используются так называемые
стерегущие регуляторы - быстрые редукционные установки, сбрасывающие пар в
конденсатор (БРУ-К), деаэратор (БРУ-Д) или барботер (БРУ-Б). Функциональные схемы
этих регуляторов аналогичны АРД за исключением управляющих воздействий,
которые через исполнительные механизмы воздействуют на соответствующие клапаны.
Для стерегущих регуляторов устанавливаются более высокие (на 1 - 2 кГс/см2)
значения заданного давления.
Давление пара в ЯППУ зависит от мощности ЯР (подвода тепла), расходов
питательной воды и пара. При постоянной энтальпии питательной воды для небольших
приращений перечисленных технологических параметров справедливо уравнение
A^AP(t) = Ae + p,AGB -P2AGn, (7.6)
at
где АР - изменение давления; AQ, AGB, AGn - приращения подводимого тепла и
изменения расходов питательной воды и пара соответственно; Л, рь р2 -
коэффициенты пропорциональности.
В свою очередь, расход пара на турбину зависит как от его давления в ЯППУ, так
и от положения регулирующих клапанов. Данная зависимость в линеаризованном
виде может быть записана как
AGn=p3Ap + Az, (7.7)
где Az - изменения положения РК турбины,
Р3 - коэффициент пропорциональности.
Из последнего выражения приходим к уравнению инерционного звена 1-го порядка
T—AP(t) + AP(t) = klAQ + k2AGh-k3Az9 (7.8)
dt
где Т = А/($ф3), *,=1/(Р2Рз)> *2=Р./(Р2Рз), *з = 1/Рз-
Глава 7. Регуляторы основных теплоэнергетических параметров АЭС 421
Таким образом,, при регулировании давления ОР не обладает астатизмом, что
позволяет строить АРД по одноимпульсной схеме (рис. 7.6).
AG
г
[
1
THMs
Az*nn n^TVi it»
I_lJ ^cS'
i
7^ + 1
Рис. 7.6. Структурная схема одноимпульсного регулятора давления в ЯППУ
Регулирующее устройство с ПФ Kp6(s) совместно с исполнительным
механизмом \/(TnMs), как правило, реализовывают ПИ-закон регулирования.
Возмущениями для АРД являются тепловая мощность реактора и расход
питательной воды. Так как на расход пара АРД оказывает действие через гидравлический
регулятор турбины, электрическая сеть также оказывает влияние на давление пара.
Поэтому, строго говоря, расчет АРД должен проводиться с учетом динамики PC
турбины. Однако для уменьшения возмущения реактора со стороны электрической сети
через турбогенератор и АРД, его быстродействие ограничивают. Так как переходные
процессы PC длятся (1 - 2) с, в то время как переходные процессы АРД - (3 - 10) мин,
то это позволяет рассматривать оба регулятора раздельно.
На АРУ оказывает влияние АРД через изменение расхода пара. Поэтому сначала
настраивают АРД, а потом - регулятор уровня. В этом случае можно считать AGB = 0.
Практика эксплуатации АРД показала, что одноимпульсные регуляторы
удовлетворительно работают в условиях нормальной эксплуатации. Однако в нештатных
ситуациях имели место случаи, когда возникающие при этом перерегулирования
давления приводили к останову энергоблока. Поэтому в настоящее время
разрабатываются двухимпульсные АРД. Второй импульс в регуляторе вводится по давлению за
стопорно-регулирующими клапанами (СРК) турбины. Так как давление за СРК
отражает мощность ТГ, использование этого сигнала позволяет организовать внутренний
малоинерционный контур регулирования, позволяющий уменьшить влияние
электросети на энергоблок. Однако в двухимпульсных АРД проявляется неравномерность
регулирования давления при изменениях мощности ЯР, что устраняется посредством
ввода в регулятор сигнала по мощности реактора. Такой АРД по своей сути реализо-
вывает трехимпульсную схему регулирования.
7.3. РЕГУЛЯТОРЫ ПИТАНИЯ ПАРОГЕНЕРАТОРА
Автоматические регуляторы питания парогенератора (ПГ) предназначены для
поддержания материального баланса между расходом пара и подачей питательной
воды при заданном ее уровне. Поэтому наряду с термином регулятор питания часто
используется термин регулятор уровня ПГ.
Регулируемым параметром является уровень питательной воды в ПГ, управляющим
воздействием - ее расход, а возмущением - изменение расхода пара турбиной при из-
422
Методы синтеза САУ по заданным показателям качества. Часть II
менении ее мощности. На уровень воды в ПГ также оказывают влияние мощность
реактора, давление пара в ПГ, температура питательной воды и другие факторы.
В качестве примера рассмотрим автоматические регуляторы уровня
парогенераторов ПГВ-1000 энергоблоков с ВВЭР-1000. Каждый из четырех ПГ снабжается
двумя регуляторами уровня: основным РУПГ-1 (2,3,4) и пусковым РУПГ-1А (2А, ЗА,
4А). Оптимальный уровень воды в ПГВ-1000 h3 = 2050 мм в диапазоне мощности ЯР
0 - 30% поддерживается пусковым, а свыше 30% - основным регулятором уровня.
Наличие двух регуляторов обусловлено нулевым выходным сигналом блока
извлечения корня (БИК), работающего совместно с измерительным преобразователем
Сапфир-22ДД, при малых расходах (0 - 15% от номинального). Это приводит к
потере сигнала по материальному балансу и превращению регулятора в одноимпульсный.
Точность поддержания заданного уровня в стационарных режимах ±50 мм. При
повышении уровня на 300 мм свыше номинального РУПГ автоматически
переводится на дистанционный (ручной) режим управления регулирующим питательным
клапаном (РПК) и инициируется его закрытие. Если при этом рост уровня прекратился и
его превышение над заданным снизилось до 250 мм, снимается блокировка РУПГ,
который оператором может быть переведен в режим «Автомат». Повышение уровня
на 500 мм сверх заданного приводит к закрытию стопорных клапанов турбины, что
предотвращает заброс воды в турбину, и останову ЯР.
Снижение уровня питательной воды в ПГ на 150 мм от номинального уровня
вызывает включение аварийных питательных электронасосов и пусковых РУПГ-1 А
(2А, ЗА, 4А), на 500 мм - отключение ГЦН для предотвращения термических
напряжений трубчатки ПГ, на 650 мм - к останову энергоблока по сигналу АЗ-1.
Регуляторы уровня ПГ строятся по трехимпульсной схеме на основе КТС Каскад-2
(рис. 7.7).
ПГВ-1000
ПИТАТЕЛЬНАЯ
ВОДА
i
1111
=ssh
БСПТ
У 22
САПФИР
2000 1
t
БИК
Рис. 7.7. Упрощенная функциональная схема основного регулятора
уровня питательной воды ПГВ-1000
Глава 7. Регуляторы основных теплоэнергетических параметров АЭС 423
Входными сигналами РУПГ являются:
• уровень h питательной воды в ПГ (измеряется гидростатическим методом,
измерительный преобразователь Сапфир-22ДД, диапазон измерения 0 - 1000 мм);
• расход питательной воды (измерительный преобразователь Сапфир-22ДД,
максимальный расход 2000 м /час);
• расход пара на турбину (измерительный преобразователь Сапфир-22ДД,
максимальный расход 2000 м3/час).
Перечисленные выше входные сигналы суммируются блоком А05 с учетом их
знаков.
Уровень в ПГ задается посредством 13У11.
Сигнал с выхода импульсного регулирующего блока 2Р27 через блоки управления
(2БУ21) и включения регулятора (БВР) подаются на усилитель У22, управляющий
исполнительным механизмом регулирующего клапана.
Наряду с обратной связью по воде, в регулятор уровня введена жесткая обратная
связь (В 12) по положению регулирующего клапана и реализован дополнительный
контур коррекции статической погрешности, вызванной продувкой ПГ (23У11, 1Р27,
1БУ27,Д05).
В отличие от регулятора уровня компенсатора давления, в РУПГ не введены
сигналы расходов воды, используемой для продувки. Поэтому во время регулярно
проводимых продувок ПГ из-за нарушения материального баланса возникает
статическая погрешность поддержания уровня. Для ее устранения посредством 1БУ27
включают 1Р27, который добавляет к сигналу отклонения 2Р27 интеграл от небаланса
Н3-И.Во время продувки уровень ПГ корректируется задатчиком 23У11.
7.4. РЕГУЛЯТОРЫ УРОВНЯ КОМПЕНСАТОРА ОБЪЕМА
Рассматриваемые ниже автоматические регуляторы уровня (АРУ) компенсатора
давления (КД) применяется на энергоблоках с ВВЭР-1000 и предназначены для
поддержания необходимого уровня воды во всех режимах работы реактора. На блоке
устанавливаются два регулятора - штатный и пусковой.
На уровень воды в КД влияет термическое изменение объема теплоносителя в
первом контуре при изменении его температуры и нарушение материального баланса
между расходами теплоносителя на продувку и подпитку, подвода и слива уплотняющей
воды ГЦН. На уровень также оказывает влияние система поддержания давления в
первом контуре и работа второго контура. Минимальный допустимый уровень воды Ямин
равен 5470 мм. Понижение уровня воды ниже Ямин приводит к оголению и пережогу
трубчатых электронагревателей (ТЭН). Превышение максимального уровня #макс
(^макс = 8770 мм при 100 % мощности реактора) уменьшает объем паровой подушки
КД и нарушает работу системы поддержания давления первого контура.
Программа работы штатного АРУ рассчитывается, исходя из требования
сохранения постоянной массы теплоносителя в первом контуре. Так как уровень зависит от
температуры, для определения заданного уровня А3 воды в КД используется ее
средняя температура Гср в первом контуре. При изменении мощности реактора от 0 до
100% Тср меняется от 275 до 302°С, а номинальный уровень воды в КД от Ямин до
//макс. Следовательно, зависимость требуемого (заданного) уровня теплоносителя от
средней температуры может быть записана в виде /*3 (Гср ) = 5470+ F(rcp-275), где
F = (8770-5470)/(302-275) =122 мм/°С. На некоторых энергоблоках Ямин =6010 мм
при Гср = 280°С . В этом случае V = 138 мм/°С.
424
Методы синтеза САУ по заданным показателям качества. Часть II
В качестве Тср используется максимальная величина из средних температур
четырех петель (рис. 7.8, рис. 7.9).
Мтср)
Петля 1
Петля 2
Петля 3
Петля 4
Рис. 7.8. Схема формирования сигналов
максимальной средней температуры и заданного уровня
Для оценки Гср посредством термопар и нормирующих преобразователей Ш78
(пределы измерения 0-400°С) измеряется температура теплоносителя горячей и
холодной ниток каждой петли. Соответствующие сигналы усредняются сумматорами
А05, и из полученных сигналов блоками нелинейных преобразований Н05
выделяется максимальный - Ермаке- Блок ограничения и размножения сигналов А05
осуществляет формирование по Тсрмакс заданного уровня И3(ТСЛ.
В штатном регуляторе уровня посредством ручного задатчика ЗУ-11 предусмотрена
ручная корректировка заданного уровня теплоносителя в КД в пределах ±1000 мм.
Входными сигналами штатного регулятора уровня являются уровень в КД - h^,
заданный уровень - А3 (Тср) и сигнал материального баланса (местной обратной
связи) - е.
Уровень в КД измеряется гидростатическим образом измерительным
преобразователем «Сапфир-22 ДД» модели 2444 с максимальным избыточным давлением
400 кГс/см2.
Сигнал материального баланса формируется сумматором А05, который реализо-
вывает соотношение e = GTl+GBl-GT2-GB2. Соответствующие расходы G
измеряются:
• расход подпиточной воды, «Сапфир-22 ДД», пределы измерения 0-100 м3/ч;
• расход продувки, «Сапфир-22 ДД», пределы измерения 0-80 м3/ч;
• расход уплотняющей воды к ГЦН, «Сапфир-22 ДД», пределы измерения
0-16м3/ч;
• расход уплотняющей воды от ГЦН, «Сапфир-22 ДД», пределы измерения
0-12,5м3/ч.
"лава 7. Регуляторы основных теплоэнергетических параметров АЭС
—ч
кд
425
Аур
7кд
Сапфир
400
С
>
к пг
ЦТ<>)
СЗУ
ЯР
АО5
Ст2
БИК
Сапфир
80
Gb2
БИК
Сапфир
12,5
GtI
БИК
GbI
БИК
Сапфир
100
^_Сапфи|
16
ГЦН
^В систему
продувки-
подпитки
ГЦН1
УРС02
уплотнение
от ГЦН
На уплотнение к ГЦН
СКУ
Р27
УРСОЗ
УЛУ-Н
Из системы подпитки-
продувки
Рис. 7.9. Упрощенная функциональная схема регулирования уровня теплоносителя
в компенсаторе давления энергоблока с ВВЭР-1000
Выходной сигнал регулирующего блока Р27 через устройство логического
управления второго уровня (УЛУ-И) оказывает воздействие на регулирующие клапаны
TK32SO2 или TK32SO1, меняя расход подпиточной воды таким образом, чтобы
hyv = /г3(^Ср) • С помощью ключа, расположенного на БЩУ, один из клапанов
выбирается рабочим, другой - резервным. После полного открытия рабочего клапана
воздействие регулятора автоматически переключается на резервный. При этом закрытие
клапанов начинается с резервного клапана.
Программа работы пускового регулятора основана на поддержании заданного
объема теплоносителя в первом контуре во время разогрева и расхолаживания энер-
426
Методы синтеза САУ по заданным показателям качества. Часть II
гоблока. При этом критерием постоянства объема является неизменность уровня
воды в КД. Во время разогрева первого контура сильно (приблизительно на 300°С)
меняется его температура и, следовательно, давление. Вследствие этого для повышения
точности измерения уровня вводят коррекцию показаний уровнемера по температуре
воды в КД в виде Афа1СГ (Т^) = у2 (Гкд)+ ух (Tm)h^, где Афакт - фактический уровень
воды в КД при температуре 7^, °С, Аур - уровень по показанием уровнемера, ух (Т^)
и ^(^кд) ~ нелинейные функции температуры, зависящие от текущих значений
плотности воды и пара (рис. 7.10).
ifYl(T) 0iY2(T), мм
-100
-200
-300
-400
-500
-600
-700
-800
1,0
0,9
0,8
0,7
0,6
0,5
50 100 150 200 250 300 350
Температура воды в КД, град С
а
50 100 150 200 250 300 350
Температура вода в КД, град С
б
Рис. 7.10. Функции ^i(^) и /1факт (Г) для коррекции показаний уровнемера
с базой 6Э00 мм и учетом азотной подушки в интервале температуры 60 - 200°С
Для реализации требуемой зависимости Лфакт(Г) применяется схема коррекции
уровня (СКУ), которая работает по сигналам уровнемера Аур и температуры Тт воды
в КД (рис. 7.11). Нелинейные функции У\{Тп) и ^(^кд) реалиЗовываются блоками
нелинейных преобразователей Н05 способом кусочно-линейной аппроксимации.
В пусковом регуляторе предусмотрен ручной задатчик уровня (РЗУ). При
заполнении реакторной установки посредством РЗУ задается й3 = 11600 мм, во время
сброса азота - А3 = 1Ю00 мм> а затем - А3 =4570 мм. При расхолаживании первого
контура - А3 = 11000 мм.
САПФИР
400
hyp
Ш79
Н05
1Г
У1
А35
У1Аур
Н05
А06
Лфакт = ^2+>;1Лур
►
Рис. 7.11. Схема коррекции уровня
Аналогично штатному регулятору, сигнал от регулирующего блока Р27 через
УЛУ-И оказывает воздействие на пусковые регулирующие клапаны TK31SO2 или
TK31SO1.
Глава 7. Регуляторы основных теплоэнергетических параметров АЭС 427
7.5. РЕГУЛЯТОРЫ УРОВНЯ РЕГЕНЕРАТИВНЫХ
ПОДОГРЕВАТЕЛЕЙ
Система регенеративного подогрева питательной воды для ядерной паропроизво-
дящей установки (ЯППУ) состоит из ряда подогревателей, включенных
последовательно по воде. При этом подогреватели, включенные между деаэратором и
конденсатором, называются подогревателями низкого давления (ПНД), а между
деаэратором и ЯППУ - подогревателями высокого давления (ПВД). Для подогрева
питательной воды используется пар из отборов турбины (из выходных патрубков ее
цилиндров), который после отдачи теплоты основному конденсату в ПНД или питательной
воде в ПВД превращается в конденсат греющего пара. Уровень воды в ПНД и ПВД
не должен превысить допустимые пределы. Повышение уровня конденсата греющего
пара в подогревателях уменьшает поверхность теплообмена, что приводит к недогре-
ву питательной воды и снижению коэффициента полезного действия энергоблока.
Чрезмерно высокий уровень может привести к попаданию воды в систему отсоса
паровоздушной смеси или даже к ее вскипанию и забросу пароводяной смеси в
проточную часть турбины и, как следствие, вызвать аварию.
Для поддержания уровня конденсата греющего пара в заданных пределах
применяются автоматические регуляторы уровня ПНД и ПВД. В качестве примера
рассмотрим вариант схемы регулирования уровня группы ПВД типа ПВ2500-97-18А
(ПВ2500-97-28А), устанавливаемых на энергоблоках с ВВЭР-1000.
Объектами управления являются ПВД-6 и ПВД-7, включенные последовательно
по питающей воде и каскадно по конденсату греющего пара (рис. 7.12).
Уровни воды в ПВД зависят от материального баланса расхода пара на отборы с
турбины (расход на отборы зависит от общего расхода пара турбиной, т.е. от ее
мощности) и расхода конденсата греющего пара. При этом возмущением на уровень в
подогревателях является изменение расхода пара на отборы, а регулирующим
воздействием - изменение расхода конденсата греющего пара. Контроль уровня
конденсата начинается с отметки 4200 мм ПВД-6 и 3700 мм ПВД-7 от днища корпуса.
Номинальный уровень при 100% нагрузке энергоблока 4800 мм для ПВД-6 и 4000 мм
для ПВД-7. При повышении уровня до 5390 мм в ПВД-6 или до 4500 мм в ПВД-7
срабатывает защита на отключение данной группы подогревателей по пару.
Регенеративные подогреватели относятся к объектам, к которым не
предъявляются строгие требования по точности поддержания регулируемого параметра - уровня
воды. Так, например, уровень воды в ПВД-7 может колебаться в пределах от 3500 до
4500 мм. Это позволяет упростить регулятор уровня, реализовывая его по одноим-
пульсной схеме (сигнал по уровню) без ввода местной обратной связи по
материальному балансу (импульсы по расходам греющего пара и его конденсата). Однако для
обеспечения устойчивости такой системы приходится вводить жесткую обратную
связь по положению регулирующего клапана и осуществлять П-закон регулирования.
Такой регулятор имеет статическую погрешность по возмущению, но благодаря
интегрирующим свойствам объекта, сохраняет астатизм 1-го порядка, что исключает
установившуюся ошибку по задающему воздействию. Рассматриваемая схема
содержит один регулятор РУ-7 для ПВД-7 и два регулятора РУ6-К и РУ-6Д для
поддержания уровня в ПВД-6 (обозначения регуляторов условны). Аппаратура
автоматического регулирования построена на основе КТС Каскад-2 и УКТС. Все три
регулятора реализованы по схожим схемам. Основными входными сигналами являются
заданные Л3 и измеренные А уровни воды в ПВД. Выходной сигнал регулирующего
устройства через блок включения регулятора и тиристорный усилитель мощности
типа ПБР-ЗА подается на исполнительный механизм МЭО, управляющий
регулирующими клапанами типа Т-1496с или Т-1536с. Блоками БВР управляет оператор
посредством расположенных на БЩУ БРУ-32 (на схеме не показаны).
428
Методы синтеза САУ по заданным показателям качества. Часть II
от 1-го
отбора
от 2-го
отбора
ПВД-7
ПВД-6
кПГ
-с
сапфир
25
в конденсат* р
Ча
РК
РУ7
■fcrt-
РК
РУ6-К
БСГТГ
БРТ БВР
отТПН
>
сапфир
25
Т-1536С
ш—
РУ6-Д
БСПТ
А3=4000 ( зуи
в деаэратор
БВР
зу„)Л3=4800 (тЛ Л3 = 4770
Рис. 7.12. Вариант функциональной схемы автоматического регулирования уровня
в ПВД-6 н ПВД-7 энергоблока с ВВЭР-1000
Так как из-за каскадного включения ПВД по дренажу конденсата греющего пара
на уровень в ПВД-6 оказывает влияние регулятор уровня ПВД-7, для регулирования
уровня ПВД-6 используются два регулятора РУ6-Д (основной) и РУ6-К (стерегущий)
и вводится сигнал по положению регулирующего клапана ПВД-7. РУ6-К включается
в работу при превышении ошибки РУ6-Д заданного значения. Для этого у
стерегущего регулятора устанавливается более широкая зона нечувствительности и больший
заданный уровень Л3, что исключает явление «гонок» регуляторов.
7.6. РЕГУЛЯТОР ПИТАНИЯ БАРАБАНА-СЕПАРАТОРА
Данный регулятор предназначен для поддержания уровня воды в БС
энергоблоков с реакторами РБМК-1000 с точностью ±50 мм посредством изменения расхода
питательной воды регулирующими питательными клапанами (РПК). Регулятор
должен обеспечить материальный баланс между расходом пара на турбины и притоком
питательной воды от деаэраторов при заданном уровне воды в БС. При снижении
уровня на 200 мм и 1000 мм последовательно срабатывают аварийные защиты АЗ-1 и
Глава 7. Регуляторы основных теплоэнергетических параметров АЭС 429
АЗ-5 соответственно. АЗ-5 срабатывает также при повышении уровня на 150 мм.
Один регулятор обслуживает два БС одной половины энергоблока, связанных
водяной перемычкой. Всего на одном энергоблоке устанавливаются четыре регулятора
уровня в БС, два из которых являются пусковыми (включаются в работу только во
время пуска энергоблока). Каждый из регуляторов может воздействовать на один (в
режиме нормальной эксплуатации) или два (в аварийных режимах) РПК.
Рассмотрим функциональную схему автоматического регулятора уровня (рис. 7.13).
Регулятор выполнен по трехимпульсной схеме. Регулируемой величиной является
уровень питательной воды в БС. Так как оба БС соединены по воде, то, как правило,
ограничиваются измерением уровня в одном из них. Измерение производится
гидростатическим методом с применением двухкамерных уравнительных сосудов с базой 1600 мм
(+400, -1200). В качестве уровнемера используется дифференциальный манометр Сап-
фир-22ДД на номинальный перепад 1600 мм в. ст. При этом крутизна уровнемера равна
у у =0,00313 мА/мм Н2О или 0,05 мА/%. Сигнал измеренного уровня (оценки уровня)
h подается на регулирующее устройство РП4-УМ, где сравнивается с сигналом заданного
уровня й3 от ручного задатчика РЗД-22, расположенного на БЩУ. Кроме h и h3 для
формирования рассогласования е используется сигнал дополнительной обратной связи е,
вырабатываемый блоком суммирования и демпфирования E = h3-h + e.
САПФИР
16
г
РП4-У
БРУ-42
ФЦ0650
РПК
U
БРУ-42
ФЦ0650
ИМ
БСД
-0,5К
-0,5К
+0,5
+0,5
Св2
'п!
3-
БИК
БИК
БИК
БИК
САПФИР
100
САПФИР
100
САПФИР
160
САПФИР
160
"X РПК
t
ВОДА
Рис. 7.13. Упрощенная функциональная схема автоматического регулятора уровня
в БС одной половины энергоблока с РБМК-1000
Сигналы по расходу питательной воды GB поступают от блоков извлечения корня
(БИК) и двух измерительных преобразователей Сапфир-22ДД с диапазоном 0-100 кПа.
Дроссельные устройства по воде рассчитаны на перепад 1 кГс/см2 при объемном расходе
воды 1600 м3/ч. С учетом плотности воды 0,912 т/м3 при температуре 165°С крутизна
водомера равна ув=0,00336 мА/(т/ч) или 0,0538 мА/(% расхода воды).
430 Методы синтеза САУ по заданным показателям качества. Часть II
Сигналы по расходу пара Gn поступают от двух БИК и измерительных
преобразователей Сапфир-22ДД с диапазоном 0- 160 кПа, которые совместно с дроссельными
устройствами, рассчитанными на перепад давления 1,6 кГс/см2 при расходе 1600 т/ч,
обеспечивают крутизну паромера равной уп =0,0031 мА/(т/ч) или 0,049 мА/(%
расхода пара).
Так как сигналы по расходу питательной воды GB, отражающие действия РО, а
сигналы по расходу пара <7П, отражающие возмущение со стороны турбины на БС,
имеют отличные крутизны, при формировании сигнала е дополнительной обратной
связи необходимо учитывать их знаки и ввести масштабный коэффициент К, т.е.
e = 0,5Gnl +0,5Gn2 -0,5Af(GBl +Gb2) . Коэффициент К на соответствующих входах
БСД выбирается из условия АГ = (2уп -Yy#G)/2yB, где HG - неравномерность
показаний уровнемера HG = AA/AGb «-0,25 мм/%.
Выход РП4-УМ через блоки ручного управления БРУ-42 может быть подключен
к одному или двум исполнительными механизмами РПК. В режиме нормальной
работы блока один из ИМ получает сигнал от регулирующего устройства и
осуществляет автоматическое поддержание заданного уровня (его БРУ в положении «А»).
Другой ИМ находится в горячем резерве (его БРУ в положении «Р») и позволяет
осуществлять ручное дистанционное управление соответствующим РПК. В
аварийных режимах сигнал A3 инициирует переключение обоих БРУ в положение «А», что
обеспечивает двойную скорость изменения расхода питательной воды и позволяет
удержать уровень в допустимых пределах.
На динамику переходных процессов в БС влияет не только регулятор уровня, но и
регулятор давления. Однако влияние регулятора уровня на давление существенно
слабее влияния регулятора давления на уровень в БС. Поэтому вначале настраивают
АРД, что позволяет настраивать регулятор уровня, считая давление постоянным.
Приведем некоторые рекомендации по настройке регулятора уровня. Ширина
зоны нечувствительности А выбирается равной 10 мм, что обеспечивает такую же
статическую погрешность поддержанию уровня. С учетом крутизны уровнемера для
РП4-УМ Анч =0,63%. Постоянная времени демпфирования Т^ =0,5ГЛ/А, где Л -
амплитуда в мм, Т - период пульсаций уровня БС без автоматического регулятора в
с. Постоянная времени изодрома Гиз =(0,5ч-1)Гф. Коэффициент передачи
регулятора Кп = 100/(КГим), где Гим - время полного открытия РПК, а скорость связи
выбирают равной V = 400/Сув / (2 ч- 3) / Гим. Сигнал рассогласования в РП-4У формируется
в соответствии с выражением s = h2-h + Kee. В качестве оптимального Ке в [148]
рекомендовано значение Ке =уу/(09ЗуъК), где уу в мА/мм, а ув в мА/%.
Минимальная длительность выходных импульсов 0,3 - 0,7 с, что обеспечивает
оптимальное соотношение между точностью поддержания заданного уровня и частотой
срабатываний ИМ.
7.7. РЕГУЛЯТОР ДАВЛЕНИЯ ПАРА В БАРАБАНЕ-СЕПАРАТОРЕ
Автоматический регулятор давления (АРД) предназначен для поддержания
заданного давления пара в барабанах-сепараторах энергоблоков с РБМК-1000.
Давление в БС зависит от мощности реактора (генерация пара), мощности
турбогенераторов (потребление пара) и расхода питательной воды и регулируется путем приведе-
Глава 7. Регуляторы основных теплоэнергетических параметров АЭС 431
яия потребления пара в соответствии с его генерацией. АРД регулирует давление до
лчшорно-регулирующих клапанов (СРК) турбин и часто называется регулятором
давления «до себя» (РДС).
В условиях нормальной эксплуатации давление пара поддерживается равным
69 ±0,25 кГс/см2. Обычно на энергоблок устанавливается один или два АРД,
управляющие одним (в режиме нормальной эксплуатации) или обоим (в аварийных
режимах) механизмами управления турбиной (МУТ).
При АЗ-1 происходит управляемое снижение мощности реактора до 60%
номинальной, что вызывает провал давления. Допускается уменьшение давления до 65 кГс/см2.
Причиной срабатывания АЗ-2 является отключение одного из турбогенераторов.
Несмотря на то что при этом мощность реактора снижается до 50 - 55% нормальной
величины, тепловая инерция реактора приводит к росту давления в БС. При повышении
давления до 71,5кГс/см2 автоматически включаются «стерегущие» регуляторы давления,-
так называемые быстрые редукционные установки в конденсатор (БРУ-К),
сбрасывающие пар мимо турбин в конденсаторы. БРУ-К отличаются от АРД величиной заданного
давления и тем, что управляют не МУТ, а клапанами (четыре клапана на энергоблок)
сброса пара в конденсаторы. В случае дальнейшего роста давления в работу включаются
релейные регуляторы, которые открывают главные предохранительные клапаны,
сбрасывающие пар в барботер. Повышение давления до 73,5 кГс/см2 вызывает срабатывание
АЗ-5, приводящее к полному останову энергоблока.
АРД в стандартном исполнении строится по схеме одноимпульсного регулятора
(рис. 7.14).
Давление в БС контролируется с помощью двух - четырех манометров типа Сап-
фир-22Д с диапазоном 40 - 80 кГс/см2, сигналы которых подается на блок
суммирования и демпфирования. Выходной сигнал БСД Рср представляет среднее значение
давления в БС и подается на один из входов регулирующего устройства РП4-У. На
другой вход РП4-У поступает сигнал заданного давления Р3 от ручного задатчика
РЗД-22, расположенного на БЩУ.
Совместно с ИМ постоянной скорости МУТ, АРД реализовывает ПИ-закон
регулирования. Посредством БРУ-42 выходной сигнал регулирующего устройства может
быть направлен к ИМ МУТ одной или обеих турбин. В режиме нормальной
эксплуатации один из БРУ находится в положении «А», а другой - «Р». Пусть выход РП4-У
соединен с ИМ МУТ1. В этом случае ТГ-1 участвует в регулировании давления в БС.
Если, например, частота электросети уменьшится, то гидравлические регуляторы
скорости (PC) турбин приоткроют регулирующие клапаны и увеличат расход пара,
что вызовет уменьшение давления в БС. Однако возникший при этом сигнал
рассогласования Р3-Рср посредством РП4-У и ИМ переместит буксу МУТ1 в сторону
уменьшения мощности ТГ-1, что заставит его гидравлический регулятор скорости
закрывать регулирующие клапаны турбины до восстановления давления в БС. После
переходного процесса установится равновесное состояние при новой частоте в сети.
При этом мощность ТГ-2 возрастет, а мощность ТГ-1 уменьшится, а их сумма
останется без изменения. Таким образом, при помощи АРД электрическая мощность
энергоблока автоматически подстраивается под тепловую мощность реактора, т.е.
осуществляется базовый режим регулирования энергоблока.
Для настройки АРД в [148] рекомендовано ширину зоны нечувствительности
выбрать равной 0,3 кГс/см2, постоянную изодрома Гиз =20 с, коэффициент передачи
регулятора Кп =75/(иуд), где п - количество манометров в АРД, уд - крутизна
манометра, мА/% (для рассматриваемого АРД уд =0,063 мА/%), скорость связи
432
Методы синтеза САУ по заданным показателям качества. Часть II
V = 100/(КпТкм), Гим - время перемещения ИМ буксы МУТ из одного крайнего
положения в другое (Тим =30 - 50 с).
Рис. 7.14. Функциональная схема автоматического регулятора давления в БС
7.8. ЦИФРОВОЙ РЕГУЛЯТОР ДАВЛЕНИЯ ПАРА
В БАРАБАНЕ-СЕПАРАТОРЕ
По сравнению с аналоговыми АРД, данный регулятор позволил повысить
надежность тепловой автоматики путем введения автоматического контроля исправности
измерительных каналов и исполнительных механизмов, самодиагностики и
резервирования технических и программных средств, реализации автоподстройки и
переменной структуры.
Цифровой регулятор давления (ЦРД) в БС разработан на основе аппаратуры Ре-
миконт РК-131/300 и предназначен для автоматического поддержания давления в
диапазоне 62 - 72 кГс/см2 с точностью ± 0,25 кГс/см2 при изменении электрической
нагрузки любого ТГ в пределах от 70 до 500 МВт в условиях нормальной
эксплуатации и стабилизации давления при срабатывании A3.
Заданное давление поддерживается за счет обеспечения баланса двух процессов:
генерации пара в ЯР и потреблении пара турбинами.
ЦРД (рис. 7.15) состоит из двух одинаковых каналов регулирования, один из
которых находится в горячем резерве. Каждый из каналов работает по сигналам трех
датчиков давления в БС, одного датчика давления за стопорно-регулирующими
клапанами (СРК), двух датчиков положения буксы механизмов управления турбинами
ТП и ТГ2, одного ручного задатчика РЗД-22 и управляет посредством
бесконтактного реверсивного пускателя ПБР-2М одним или двумя исполнительными
механизмами постоянной скорости МЭО-16. Исполнительный механизм перемещает буксу
МУТ и меняет посредством гидравлического регулятора скорости (PC) расход пара
турбины.
Основу ЦРД составляют два блока контроллера БК-1, один блок переключения
БПР-10, два блока ручного управления БРУ-42 и один - БРУ-22. Всего ЦРД
использует 16 аналоговых и 16 дискретных входных сигналов, и вырабатывает
соответственно 4 и 16 выходных сигналов.
Глава 7. Регуляторы основных теплоэнергетических параметров АЭС
433
~рсЦ*Х
МУТ| ^г
РК-1
-1
1 - Ручной задатчик РЗД-22
2 - Блок питания БП-1А
3 - Блок переключения БПР-10А
4 - Блок ручного управления БРУ-22
5 - Указатель заданного давления
6 - Блок ручного управления БРУ-42
РК-2
Рис. 7.15. Функциональная схема цифрового регулятора давления в барабанах-сепараторах:
БС-1 - БС-4 -барабаны-сепараторы, ТГ~1, ТГ-2 -турбогенераторы
Заданное давление АР3 устанавливается оператором блока посредством РЗД-22.
Узел задания давления (УЗД) ограничивает скорость изменения уровня заданного
давления величиной 1 (кГс/см2)/мин и осуществляет непрерывный контроль
исправности РЗД. Далее АР3 сравнивается с измеренным давлением в БС АР6с и сигнал
рассогласования через ПД-регулятор, исполнительный механизм и МУТ управляет
расходом пара турбины.
U
W
<L>
CQ
<L>
0>
СО
К
о
1,0 J
0,0
-1,0
-2,0
-3,0
-4,0
-
-
л 1
V
1 , 1 . 1 1 1 . 1 1 1 ы.
200
400 600
Время, с
800
1000
Рис. 7.16. Ожидаемое отклонение давления при срабатывании АЗ-1:
У -аналоговыйрегулятор РП4-УМ, 2 -ЦРД
ПД-регулятор совместно с ИМ постоянной скорости реализовывают ПИ-закон
регулирования.
29 Зак. 366
434
Методы синтеза САУ по заданным показателям качества. Часть II
Алгоритм регулирования давлением отличается введением внутреннего
малоинерционного контура регулирования по сигналу давления за СРК и автоматическим
изменением параметров при срабатывании A3.
При срабатывании АЗ-1 допускается провал давления до 65 кГс/см2. Последующее
перерегулирование не должно привести к срабатыванию стерегущих регуляторов
давления БРУ-К. Введение узла настройки усиления (УНУ) позволяет без последующего
перерегулирования величину провала уменьшить до 1 кГс/см2. Это достигается
автоматическим управлением реальным скользящим процессом, который возникает в
нелинейных системах с переменной структурой.
При работе энергоблока в базовом режиме основным возмущением давления БС
является изменение электрической нагрузки ТГ. Отслеживая изменения частоты
сети, гидравлический регулятор скорости турбины меняет расход пара и
соответственно - давление в БС. Чтобы уменьшить влияние электрической сети на энергоблок, в
ЦРД предусмотрен быстродействующий контур регулирования давления пара за сто-
порно-регулирующими клапанами (СРК). Дифференциальный регулятор (Д)
совместно с ИМ реализовывают П-закон регулирования. Так как давление за СРК
однозначно связано с электрической нагрузкой ТГ, при изменении частоты в сети данный
контур посредством МУТ подстраивает его мощность так, чтобы уменьшить влияние
нагрузки на давление в БС (кривые 1,2, рис. 7.17).
0.5i
2
1
U
UQ
X
о
2
0.0
-0.5
-КО
200
400 600
Время, с
800
1000
Рис. 7.17. Расчетная реакция ЦРД на увеличение электрической нагрузки ТГ на 100 МВт:
У - аналоговый регулятор РП4-УМ, 2 -ЦРД
Дополнительно ЦРД обеспечивает контроль исправности исполнительных
механизмов и всех каналов измерения давления. При обнаружении отказа
соответствующий канал автоматически отключается, ЦРД перенастраивается на работу без
отключенного сигнала, а на БЩУ загорается индикатор «Вызов к комплекту ЦРД №1 (2)».
Если количество одновременных отказов не позволяет ЦРД выполнять основную
функцию, происходит безударный переход на второй комплект аппаратуры.
Информация об этом поступает на БЩУ и в систему централизованного контроля «Скала».
Для осуществления автоматического поддержания заданного уровня достаточно
одного из шести заложенных в проекте сигналов давления в БС и одного ИМ.
7.9. ЦИФРОВОЙ РЕГУЛЯТОР РАЗВОРОТА ТУРБОГЕНЕРАТОРОВ
Регулятор разворота предназначен для автоматического пуска турбогенераторов
от нулевых оборотов до номинальных со скоростью, зависящей от теплового
состояния турбины, и используется на некоторых энергоблоках с РБМК-1000.
Глава 7. Регуляторы основных теплоэнергетических параметров АЭС 435
Цифровой регулятор разворота (ЦРР) состоит из одного канала регулирования и
работает по непрерывным сигналам двух датчиков оборотов ТП и ТГ2, двух
датчиков температуры внутреннего корпуса цилиндра высокого давления ТП и ТГ2, а
также - по дискретным сигналам открытия стопорных заслонок и достижения
номинальных оборотов (рис. 7.18). Основу ЦРР составляет один БК-1А и четыре БРУ-42,
посредством которых осуществляется автоматизированный пуск ТГ.
Процесс разворота ТГ начинается после перевода соответствующего блока
ручного управления 8БУР в положение «А». Блок контроллера, воздействуя на
синхронизатор турбины, начинает поднимать давление масла в линии первого усиления, что
приводит к приоткрытию регулирующих клапанов и толчку турбины. Далее ЦРР
автоматически с ускорением 70 об/мин2 выводит обороты турбины на уровень 600 об/мин.
Дальнейший подъем оборотов происходит после перевода 9БУР в положение «А» с
ускорением 70 об/мин2, если температура внутреннего корпуса ЦВД не превосходит
100°С, и с ускорением 250 об/мин2 в противном случае. В любой момент процесс
разворота можно остановить переводом соответствующего БУР в положение «Р». В
этом случае ЦРД осуществляет стабилизацию достигнутых оборотов.
Рис. 7.18. Функциональная схема
цифрового регулятора разворота турбогенераторов:
/ - датчик оборотов ТГ; 2 -датчик давления масла в линии 1-го усиления;
3 - датчик температуры ЦВД; 4 - блок питания; 5 - индикатор оборотов ТГ
29*
ЧАСТЬ III
МЕТОДЫ
ТЕОРИИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
Введение 437
ВВЕДЕНИЕ
Проблема оптимизации является одной из важнейших проблем как науки, так и
повседневной человеческой деятельности, ибо человеку органически присуще
стремление к достижению наилучшего (оптимального) результата. С формально
математических позиций задачи оптимизации можно разбить на две группы: оптимизация
в конечномерном пространстве, или параметрическая оптимизация, и
бесконечномерная оптимизация. К последней группе относятся, прежде всего, вариационное
исчисление, принцип максимума, динамическое программирование и др. методы.
В задаче конечномерной оптимизации речь фактически идет об исследовании на
максимум и минимум функции многих переменных.
Показатель, по которому в задачах оптимизации оценивается качество
системы, называется критерием оптимальности. В задачах управления критерием
оптимальности, как правило, является функционал, т.к. конечный эффект определяется
всем процессом управления, т.е. зависит от управления как функции времени
Оптимальное управление может быть получено в двух видах в виде оптимсиь-
ноп программы и оптимальной стратегии. В первом случае управление является
функцией времени. Поскольку при программном управлении система оказывается
разомкнутой, то неточности в математической модели объекта управления,
неконтролируемые возмущения и т.п. приводят к тому, что реальная траектория движения
может отличаться от оптимальной*. Во втором варианте оптимальное управление
задается как функция фазовых координат и входного сигнала, и система управления
является замкнутой. Таким образом, сохраняются все достоинства системы,
построенной по принципу обратной связи.
Определение оптимальной программы является более простой задачей. В этом
направлении достигнут значительный прогресс [63]. Что же касается определения
оптимальной стратегии, то круг решенных задач здесь оказался существенно более
узким. Однако для специалистов в области автоматического управления основной
интерес представляет именно определение оптимального управления в виде функции
стратегии.
Если определена оптимальная стратегия, то можно говорить о полном решении
задачи оптимизации, поскольку в этом случае определяются не только параметры,
но и структура оптимальной системы.
Теория оптимального управления является сравнительно молодой научной
дисциплиной. Ее развитие началось с середины пятидесятых годов текущего столетия. У
ее истоков стоит известный российский ученый А.А. Фельдбаум [64], который
получил первые результаты по синтезу оптимальных по быстродействию систем.
Большой заслугой А.А. Фельдбаума является также то, что он одним из первых обратил
внимание на специфику задачи оптимального управления, на невозможность
решения этой задачи методами классического вариационного исчисления. Ему удалось
привлечь внимание к задаче оптимального управления крупнейших российских
математиков. Это привело к созданию в настоящее время весьма известного принципа
максимума Понтрягина [46].
Примерно в это же время американский математик Р. Беллман сформулировал
основные положения динамического программирования. Перед институтом, в
котором работал Р. Беллман, правительством США была поставлена задача рационально-
*Более подробно см. §5.8
438 Методы теории оптимального управления. Часть III
го размещения военных баз. Обдумывая эту задачу, Р. Беллман сформулировал
основные идеи динамического программирования.
В конце пятидесятых годов и в шестидесятые годы теория оптимального
управления развивалась очень бурно. В сферу ее интересов были вовлечены многие
математики мира. Это позволило в кратчайшие сроки обогатить теорию рядом методов.
Например, очень быстро удалось развить классическое вариационное исчисление и
сделать его пригодным для решения задач оптимального управления. И до настоящего
времени основными математическими методами теории оптимального управления
являются вариационное исчисление, принцип максимума Понтрягина, динамическое
программ ирование.
При синтезе оптимальной системы управления в основном решаются две задачи:
определение оптимального управления, которое, как правило, необходимо получить
в виде оптимальной стратегии, и реализация оптимального регулятора. Хотя
серьезные проблемы могут возникать и на этапе реализации оптимального регулятора,
наиболее сложной является первая задача. Поэтому в литературе, посвященной синтезу
оптимальных систем, основное внимание уделяется изложению математических
методов теории оптимального управления и их применению для определения
оптимального управления.
Построение точных решений в задачах оптимального управления возможно лишь
в немногих ситуациях. Основным же подходом к решению реальных задач является
приближенная численная оптимизация [4].
Проблеме, рассматривающей вычислительные методы синтеза систем
оптимального управления, посвящено огромное количество работ; здесь ограничимся лишь
общими понятиями и конкретными рекомендациями, лежащими в русле методов
математического программирования и параметризацией задач оптимизации с
применением проекционных методов.
Метод математического программирования (МП) решения задач оптимального
управления - это направление, в котором исходную бесконечномерную задачу
заменяют новой, параметризованной, относящейся к классу конечномерных задач
оптимизации. Далее переписывают все ограничения задачи в виде ограничений на
значения параметризованных функций; интегралы заменяют функцией, зависящей от
параметров вектора управления U(/) и фазового вектора Х(/). Таким образом, метод
МП включает редукцию вариационной задачи к конечномерной и ее решение
разработанными методами линейного или нелинейного программирования, т.е.
нахождение экстремума функции многих переменных при ограничениях типа равенств и
неравенств
Применение аппарата математического программирования и разработка
численных методов для решения конкретных задач оптимального управления относится к
60-м годам. Более того, к середине 60-х годов сложилось самостоятельное
направление - «Численные методы оптимизации», являющееся составной частью
вычислительной математики. В рамках указанного направления разработаны численные
методы для важных классов задач оптимизации, в том числе методы условной
минимизации в выпуклом или невыпуклом случаях. Установлена область применимости,
выяснена скорость сходимости. Американский ученый Л.А. Заде ввел
математическое понятие - нечеткое множество, обобщающее понятие обычного множества.
Теория нечетких множеств тесно связана с понятием системы с переменными
параметрами, поскольку нестационарную систему можно описать как стационарную,
если ввести в рассмотрение нечеткие параметры [67]. При таком подходе
классическое математическое программирование рассматривается, в значительной степени,
как нормативная методология эффективного выбора. Использование аппарата
нечетких множеств привело к разработке метода нечеткого программирования, которое
Введение 439
выделяет естественную множественность целей и значении, неточно определенных
подцелей и ограничений. Введено в рассмотрение робастное программирование. Оно
означает гибкость, устойчивость алгоритма по отношению к разбросу базовых
параметров. Робастная программа сравнительно малочувствительна к исходным
предпосылкам, но не столь эффективна, как «точная» программа, если эти предпосылки
выполняются. Трудности решения задач оптимального управления определяются рядом
факторов, главным из которых является размерность задачи, количество переменных
и количество ограничений [38].
Важным этапом является разработка конструкций вычислительных алгоритмов,
доведение расчетов до фактического решения задачи; рассмотрение совокупности
приемов, образующих вычислительную технологию. Как указано в [63], это очень
важная часть практической вычислительной работы, без грамотного оформления
которой никакую идею не удастся довести до успешного расчета. Задачу оптимизации
необходимо рассматривать не как проблему принципиальной возможности
приближенного решения, а как проблему фактической эффективности алгоритма. В [63]
рассмотрено много конкретных примеров, уделено внимание важности этапа
разработки вычислительной технологии; приведены примеры, когда решение задачи
сталкивается с серьезными трудностями, которые порождены именно вычислительной
стороной дела, указывается на необходимость уметь контролировать те результаты,
которые выдает та или иная программа, особенно претендующая на решение такой
задачи, как поиск минимума.
В настоящей главе приведены постановки конкретных задач оптимального
управления, алгоритмы их решения методами математического программирования и
примеры построения оптимальных программных управлений и оптимальных программ.
Как отметил ЯЗ. Цыпкин, «большую популярность завоевали принцип
максимума, метод динамического программирования, метод математического
программирования и ряд других методов, которые вошли в золотой фонд теории оптимального
управления» [52].
Основные положения методов, вошедших в золотой фонд, рассматриваются в
этой части учебника.
Вопросам оптимального управления посвящено большое число работ.
Библиография работ содержит свыше десяти тысяч наименований. Многие из указанных
работ ориентированы на математиков и они очень сложны для восприятия
специалистами, занимающимися разработкой систем автоматического управления, а
некоторые из них вообще не рассчитаны на практическое использование.
Работ, которые ориентированы на разработчиков систем управления и студентов,
обучающихся по соответствующим специальностям, сравнительно немного, и они не
охватывают всех разделов теории оптимального управления. Для этой категории
читателей можно порекомендовать работы [2, 4, 6, 7, 22, 32, 33, 46, 56, 69]. К этой
группе работ относится и настоящий учебник.
440 Методы теории оптимального управления. Часть III
ГЛАВА 1. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
Задача оптимального управления относится к задачам вариационного исчисления.
В начале пятидесятых годов, когда А.А. Фельдбаумом была сформулирована задача
оптимального управления, оказалось, что классическое вариационное исчисление, из-
за наличия в задаче оптимального управления ограничений в форме неравенств, не
позволяет определить оптимальное управление и оптимальную траекторию. Это
привело к появлению принципа максимума Понтрягина.
* После опубликования принципа максимума усилиями ученых разных стран удалось
быстро распространить вариационное исчисление на задачи оптимального управления.
Такое распространение выполнено в §1.5 настоящей главы. Однако получаемые таким
образом условия оптимальности оказываются аналогичными принципу максимума и
являются по сравнению с последним более слабыми. Именно, в вариационном
исчислении область допустимых значений вектора управления обязательно должна быть
областью в классическом смысле этого слова, т.е. должна удовлетворять свойству
связности. В принципе максимума данная область может быть любым множеством
векторного пространства, например, состоять из совокупности изолированных
точек. Это расширяет возможности принципа максимума. Можно, например, искать
оптимальное управление в классе релейных сигналов и т.п.
На практике при определении оптимального управления предпочтение, как
правило, отдается принципу максимума. Однако изучение вариационного исчисления
позволяет более глубоко понять содержание математических методов теории оптимального
управления и их возможности. На это в основном и нацелена настоящая глава работы.
Далее в работе принцип максимума выводится из вариационного исчисления.
1.1. НЕОБХОДИМОЕ УСЛОВИЕ ЭКСТРЕМУМА ФУНКЦИОНАЛА
Понятие .функционала является естественным развитием понятия функции.
Говорят, что в классе функций задан функционал, если указано правило, по которому
каждой функции из этого класса ставится в соответствие некоторое число*.
Например, интеграл
ь
J = lF(x,y(x))dx
а
каждой непрерывной функции у(х) ставит в соответствие число, т.е. является
функционалом.
Вариационным исчислением называется раздел математики, в котором
рассматриваются задачи определения максимума и минимума функционалов, а также
определения функций (кривых), на которых эти максимумы и минимумы
достигаются. Приведем простой пример вариационной задачи. На плоскости заданы две
точки с координатами (а, А) и (Ь, В). Требуется среди линий у = у(х) (а<х<Ь),
соединяющих эти точки, найти такую, которая имеет наименьшую длину, т.е. найти
функцию у(х), на которой функционал
ь .
y=JV1+(/)2^
а
достигав! минимума.
Глава 1. Вариационное исчисление 441
1.1.1. Функциональные пространства*
При изучении функционалов, как и при изучении функций, удобно использовать
геометрический язык. Каждую функцию у(х), принадлежащую определенному классу,
будем рассматривать как точку некоторого пространства. Пространство, элементами
которого являются функции, называется функциональным пространством.
Функциональное пространство R называется нормированным, если каждому
элементу у(х) е R ставится в соответствие некоторое неотрицательное число \у\ -
норма этого элемента. При этом должны выполняться следующие три аксиомы:
1) 1^11 = 0 только при условии, что у(х) = 0;
2) для любого числа X: \\Xy\\ = |А,|||>>||;
3) для любых ух е R и у2 е R: \\ух + у2\\ < \\ух \\+\\у21|.
Последнюю аксиому принято называть неравенством треугольника.
В вариационном исчислении используются три функциональных пространства.
Пространство С. Пространством С называют совокупность непрерывных
функций у(х), заданных на отрезке [а, Ь]. Норма в пространстве С задается равенством:
Ш=тах|у(*)|. 0.1)
Пространство Сх. Пространством Сх называют совокупность непрерывных
функций, заданных на отрезке [а, Ь] и имеющих на этом отрезке непрерывную
первую производную. Норма в пространстве Сх задается выражением:
. \у\ = max \у(х)\ + max \у'(х)\. (1.2)
Пространство Сп. Пространством Сп называют совокупность функций,
заданных на отрезке [а, Ь] и имеющих непрерывные производные до п-го порядка
включительно. Норма в пространстве Сп определяется равенством:
В нормированном функциональном пространстве R можно определять расстояние
между любыми функциями. Именно, расстояние р(у\,У2) между функциями у} и у2
задается равенством: p(>;i,>;2) = ||j;i "УгЬ Отметим, что в соответствии с
выписанными выше аксиомами нормы р(<у1, у2) = р(у2, у\), т.к. Ц^ - у21| = Ц^ - У\ \ •
Из соотношений (1.1) и (1.2) следует, что расстояние между функциями ух и у2
в пространствах С и Сх задается соответственно равенствами:
P(^i >Уг) = ll^i - Уг II = тах, \У\ (*) - У г М\»
а<х<,Ь
Р(У\ у Уi) = \У\ - Уг ||, = max | ух (х) -у2 (х)\ + max | у{(х) - у'2 (х)\.
Очевидно, что две функции близки в пространстве Сх, если близки как сами
функции, так и их производные.
1.1.2. Дифференциал функционала
Пусть R- некоторое функциональное пространство. Функционал J(y)
называется непрерывным в точке yoeR , если для любого г > 0 можно указать такое 5(е),
*См Приложение 2 в первом томе учебника.
28 Зак. 366
442 Методы теории оптимального управления. Часть III
что при любых у, удовлетворяющих условию \у~Уо\< 8, справедливо неравенство
\j(y)-J(yo)\<z. Функционал J(y) называется непрерывным в некоторой области
пространства R, если он непрерывен в каждой точке этой области.
Функционал J(y) называется линейным, если он удовлетворяет следующим
свойствам:
1) для любых ух и у2 J(y\+y2) = J{yx) + J(y2)\
2) для любого числа X J{Xy) - XJ(y).
Пример 1.1. Функционал
ь
J{y) = \r\(x)y(x)dx,
а
где г|(дс) - заданная непрерывная функция, является линейным Он непрерывен в пространстве С
По аналогии с дифференциалом функции можно ввести понятие дифференциала
функционала.
Пусть J(y) - некоторый функционал. Дадим функции уо(х) приращение h(x) и
запишем приращение функционала:
bAyo,h) = J(yo+h)-J(yo).
При фиксированном у0 AJ(yo,h) является функционалом относительно И.
Дифференциалом функционала J(y) в точке у0 называется главная линейная часть
приращения функционала &J(y0, И). Именно, если приращение A J(y0, И) можно
представить в виде
дал>*)=ф(*)+<*-1Н1>
где ф(А) - линейный функционал, а а -> 0 при |Л| -> 0, то ф(/*) называется
дифференциалом функционала J(y) в точке у0 .
Можно показать, что дифференциал функционала, если он существует,
определяется однозначным образом. Дифференциал функционала называют также вариацией
функционала и обозначают bJ(h).
Как и дифференциал функций, дифференциал функционала оказывается весьма
полезным при исследовании на максимум и минимум функционалов. В дальнейшем
в качестве основного варианта рассматривается минимизация функционалов. Вообще
необходимо иметь в виду, что между минимумом и максимумом функционала
существует простая связь:
max J(y)= - min( - J(y)).
Рассмотрим функционал J(y), определенный на элементах нормированного
функционального пространства R. Говорят, что функционал J(y) достигает в
точке у0 минимума, если найдется такое г > 0, что для всех у, принадлежащих
8 -окрестности точки у0 , т.е. удовлетворяющих неравенству
Ь-Уо1<*> (1-3)
справедливо соотношение
J(y)-J(y0)>0. (1.4)
Если в качестве функционального пространства R рассматривается
пространство С, то такой минимум называется сильным, а если в качестве R рассматривается
пространство Сх с соответствующей нормой, то минимум называется слабым.
Глава 1, Вариационное исчисление 443
В разграничении слабого и сильного минимумов функционала определяющая
роль отводится окрестности (1.3), которая однозначно зависит от нормы
соответствующего функционального пространства. В вариационном исчислении, например,
широко изучается функционал вида
ь
J = \F{x9y9y')dx9
а
который определен на дифференцируемых функциях у(х). Если имеет место сильный
минимум функционала, то условие (1.4) должно быть справедливо для
дифференцируемых функций >>(*), удовлетворяющих неравенству
max )>>(*)-.yo(*)|<e> (1-5)
a£x<b
а при слабом минимуме функционала - для функций у(х), удовлетворяющих
соотношению
тахь\у(х)-уо(х)\+таху(х)-у'о(х)\<е. (1.6)
Пространство С является существенно более богатым по числу входящих в него
функций у(х), нежели пространство Сх, т.к. любая функция у(х)еСх принадлежит
также пространству С, в то время как обратное утверждение неверно. Сильный
минимум функционала может достигаться на непрерывно дифференцируемой функции.
В этом случае, очевидно, всякий сильный минимум является в то же время слабым.
Действительно, из того факта, что имеет место неравенство (1.4) по отношению к
непрерывным функциям, удовлетворяющим условию (1.5), тем более следует, что
имеет место неравенство (1.4) по отношению к непрерывно дифференцируемым
функциям, удовлетворяющим соотношению (1.6).
Это обстоятельство имеет важное значение, т.к. позволяет заключить, что
необходимое условие слабого минимума функционала является в то же время необходимым
условием сильного минимума функционала. Слабый минимум функционала
определяется обычно значительно проще, т.к. в вариационном исчислении, как правило,
рассматриваются функционалы, которые являются непрерывными в пространстве Q
и не являются непрерывными в пространстве С. Создавая теорию слабого минимума,
можно пользоваться непрерывностью функционала.
Рассмотрим два примера.
Пример 1.2. Найти минимум функционала
J = ){y'fdx
о
при условии, что><0) = 0, у{\) = 1. Обозначим у'(х) = и(х). Тогда, очевидно, требуется найти минимум
функционала
1
\u\x)dx
о
при условии, что
1
ju(x)dx = y(\) = \ (1 7)
о
Покажем, что ио(х) = О есть минимум функционала. Проверим это Пусть и(х) = ио(х) + и(х) - 1 + v(x)
Тогда
1 1 til
J[ho(x) + и(х)]2 dfc = J[l + о (*)]2 ^ = 1 + ^ ^
О 0 0 0 0
18*
444
Методы теории оптимального управления. Часть III
т.к. в силу условия (1.7) Ju(jc)dbr = O. Таким образом, функция уо(х) = х реализует сильный минимум
о
исходного функционала, причем этот минимум является абсолютным, поскольку он имеет место по
отношению ко всем дифференцируемым функциям из С.
Пример 1.3. Найдем минимум функционала
J = \{y'fdx, у{0) = 09 Я0 = 1.
(18)
Обозначим, как и выше, у\х) = и(х) Исходная задача (1.8) эквивалентна задаче о минимуме
функционала
при условии, что
\u\x)dx
ju(x)dx = \ .
Покажем, что функция и(х) = 0 задает слабый минимум функционала. Рассмотрим
1 ill
J (l + о(*))3 ск = 1 + 3 J v(x)dx+3 J и2 (x)dx + J и3 (x)dx.
О 0 0 0
ь
Функция u(x) = uo(x) + v(x) = \ + v(x) должна удовлетворять граничному условию ^u(x)dx = \. Отсюда
а
следует, что
1
J\)(*)£k = O.
О
В результате получаем
1 1 1
j[\ + \>(x)fdx= l + 3JV(;c)dc+Jo3<fr.
О 0 0
Если |и| < б (е < 1), то о2 > |о3|, Зи2 > |и3| и, следовательно,
1
J(3u2-u3)c&>0.
о
Таким образом, доказано, что функция уо(х) & х (и(х) = 1) доставляет слабый минимум функционалу.
Посмотрим, является ли этот слабый минимум сильным? Будем выбирать и(х) в соответствии с
рис 1 1
Рис. 1.1. График функции и(х)
Как и выше, fu(x) = O. При л->оо, >\. Поэтому
Глава 1. Вариационное исчисление 445
При достаточно больших и (Зл - л2) < 0 и, следовательно,
1 1
3JV(;c)<ic+JiAk<0.
о о
Таким образом, если наложено ограничение на значение производной функции у(х\ то функция
Л 00 = х доставляет минимум функционалу (1.8). Если на значение производной у\х) не накладывать
ограничение, то на линии уо(х) = х минимум функционала не имеет место. Это позволяет заключить, что
функция уо(х) = х доставляет слабый минимум функционалу и не доставляет сильного минимума
Приведем необходимое условие экстремума функционала.
Теорема 1.1. Если функционал J(y) достигает в точке у0 минимума
(максимума), то дифференциал функционала, если он существует, в этой точке обращается
в нуль.
Доказательство. Пусть функционал J(y) достигает в точке у0 минимума. По
определению минимума
J(y0+h)-J(y0) = 5J(h) + a.\\h\\>0 (1.9)
для всех И, для которых норма h достаточно мала. Если дифференциал функционала
6 J(h) * 0, то при достаточно малых А знак суммы
8У(А) + а-|А|| (1.10)
будет полностью определяться знаком первого слагаемого. Но 5 J(h) - линейный
функционал, и потому 8J(-h) = -5У(А), т.е. знак суммы (1.10) может быть любым,
что противоречит условию (1.9). Поэтому 5У(А) = 0, и теорема доказана.
1.1.3. Простейшая задача вариационного исчисления
Рассмотрим простейшую задачу вариационного исчисления. Пусть задан
функционал
ь
J^F(x,y,y')dx. (l.ll)
а
Относительно функции F(x,y,y) будем предполагать, что она имеет непрерывные
частные производные по всем своим аргументам до второго порядка включительно.
Требуется среди гладких функций у{х), удовлетворяющих граничным условиям
у(а) = А9 у(Ь) = В, (1.12)
найти функцию, доставляющую слабый минимум функционалу (1.11).
Для решения поставленной задачи воспользуемся теоремой 1.1. Найдем
дифференциал функционала (1.11). Дадим функции >>(л:) приращение h(x) и найдем
приращение функционала
ь ь
AJ = lF{x,y + h,? + h')dx-lF(x,y9y')dx. (1.13)
а а
Так как функции >>(*) иу(х)+И(х) должны удовлетворять условиям (1.12), то
h(a) = h(b) = 0. (1.14)
446 Методы теории оптимального управления. Часть III
Принимая во внимание, что функция F(x,y,y') имеет непрерывные производные
по всем своим аргументам, приращение (1.13) можно записать в виде
ь
U = \\Fy{x,y,y')'h + Fy(x,y,y')'h'~\ax + ..., " (1.15)
а
здесь многоточием обозначены члены, имеющие порядок выше первого
относительно И и И. Интеграл, стоящий в правой части равенства (1.15), является линейным
функционалом относительно переменной h(x) и отличается от приращения Д J лишь
на слагаемое, имеющее порядок малости выше первого относительно Цй^ , т.е.
является дифференциалом функционала (1.11). Таким образом,
ь
bJ = \[Fy(x^y')-h + Fy,(x^ylyh']dx. (1.16)
Выполним интегрирование по частям:
)Frh'dx=Fy..h\-)h.j-Fy.dx.
dx
а а
Принимая во внимание граничные условия (1.14), дифференциал функционала (1.16)
перепишем в виде
SJ=]\Fy{x,y,y')~Fy(x,y9yf)lKx)dx. (1.17)
Если функция у(х) доставляет минимум функционалу (1.11), то в-соответствии с
теоремой 1.1 дифференциал функционала равен нулю. Таким образом, можно записать:
■h(x)dx = 0. ■ (1.18)
b-iF>]
а
Равенство (1.18) должно иметь место для произвольных функций й(х),
удовлетворяющих граничным условиям (1.14). Это возможно, если функция h{x) умножается
на нуль, т.е. если выполняется равенство
Fy(x,y,y')-4-Fy'(x,y,yt) = 0. (1.19)
ах
Математически строгий ответ на этот вопрос дает следующая лемма.
Лемма (лемма Лагранжа). Пусть г\ (х) - непрерывная функция. Если функционал
ь
Ли) = Jti (*)•*(*) Л == О
а
для любых функций h(x)eCx и удовлетворяющих граничным условиям (1.14), то
Доказательство. Пусть в некоторой точке xQ (a<xo<b) функция г|(;с)^О.
Положим для определенности, что Л (лг0) > 0 . Поскольку функция г\ (х) непрерывна,
то найдется интервал (£,, £ 2)с [а> b] и содержащий точку х0, в котором функция
ц (х) > 0 . В качестве h(x) выберем следующую функцию
Кх) = \^-Х)2-^-Х)2' ССЛИ *6Gl'$2).
[О, если *е(£,Д2)-
Глава 1. Вариационное исчисление 447
Легко видеть, что выбранная таким образом функция h(x) является непрерывно
дифференцируемой и удовлетворяет условиям (1.14). Однако на этой функции
Ь $2
\ф).И(х)ск=\у\ W.ft-x)2.(^x)2&>0,
Si
т.к. под знаком интеграла стоит положительная функция. Полученное противоречие
доказывает лемму.
Если теперь к равенству (1.18) применить доказанную выше лемму, то получим
уравнение (1.19). Уравнение (1.19) называется уравнением Эйлера.
Отметим, что приведенный выше вывод уравнения Эйлера справедлив, строго
говоря, если предположить наличие у функции у(х) второй производной. Однако, если
усложнить рассуждения, можно получить уравнение Эйлера, не делая
предположения о существовании второй производной функции >>(*)•
Таким образом, функция у(х), являющаяся решением поставленной выше
простейшей задачи вариационного исчисления, должна удовлетворять уравнению
Эйлера. Уравнение Эйлера является необходимым условием слабого минимума
функционала (1.11) при граничных условиях (1.12).
Выпишем уравнение Эйлера в развернутой форме:
Fy(xiy9y')-Fyx(x9y9y')-Fyy(x9yiyl)-y'-Fyy(xiyiyl)-y" = 0.
Уравнение Эйлера представляет собой дифференциальное уравнение второго
порядка относительно неизвестной функции у(х). Общее решение этого уравнения
содержит две произвольные постоянные, которые можно определить с помощью двух
краевых условий (1.12).
Функцию у(х), удовлетворяющую уравнению Эйлера, называют экстремалью.
Рассмотрим частный вид уравнения Эйлера, который соответствует случаю, когда
подынтегральная функция функционала не зависит явно от jc, т.е. когда функционал
имеет вид
ъ
J=lF(y,y')dx. (1.20)
а
Выпишем для функционала (1.20) уравнение Эйлера:
Fy(y,f) ~ Руу(У,У') ■ У ~ Руу{у,У) ■ у" = 0.
Умножим это уравнение на у :
y-/V-(yf-F/F-y.y-F/y=0. (1.21)
Непосредственной проверкой убеждаемся, что уравнение (1.21) эквивалентно
уравнению
^[F-/./y]=0. (1.22)
Из (1.22) следует
F-y'-Fy=c, (1.23)
здесь с - произвольная константа.
Пример 1.4. На плоскости заданы две точки с координатами (а, А) и (Ь, В) (рис 1 2).
Требуется среди гладких линий у = у(х), соединяющих концы этих точек, найти линию, которая при
вращении её вокруг оси х образует поверхность наименьшей площади.
При вращении элемента дуги dS (см. рис. 1.2) образуется поверхность, имеющая площадь
, . -^
dII = 2nydS = 2nyJ\+\
448
Методы теории оптимального управления. Часть III
а при вращении линии у=у(х) - поверхность, площадь которой
(1.24)
Таким образом, требуется найти минимум функционала (1 24) при выполнении граничных условий
у(а) = А, у(Ь) = В (125)
Так как подынтегральная функция функционала (1 24) не зависит отх, то можно записать первый
интеграл уравнения Эйлера в форме (1 23)
(£?
{dxl : = C. (.26)
в
А
^^
а
dS /
dx
b
Рис. 1.2. К решению задачи оптимизации
Из (1 26) следует
у2-С2
С2
Разделяя переменные и выполняя интегрирование, найдбм
Carcch^ = x + Cj,
здесь С, - произвольная константа. Окончательный результат имеет вид
y = Cch
x + Q
Произвольные постоянные С и С, определяются из условий (1.24), которые приводят к уравнениям
Л = С-сЬ£±Я, Я = Ссп^Я (1.27)
В зависимости от конкретных значений чисел а,А,Ь,В возможны следующие три случая.
1. Уравнения (1.27) имеют единственное решение, т е. существует единственная кривая вида
r = Cch^L, (1.28)
проходящая через заданные точки (а, А) и (Ь, В). Эта кривая и является решением задачи.
2 Уравнения (1 27) имеют два решения, т е существуют две кривые вида (1.28), проходящие через
заданные точки {а, А) и (Ь, В). В этом случае одна из этих кривых доставляет минимум функционала, а
другая нет Определить реализующую минимум функционала функцию у{х) можно путем непосредственного
вычисления интеграла (1 24) вдоль каждой из этих линий
Глава 1. Вариационное исчисление 449
3. Уравнения (1.27) не имеют решения. Это означает, что в классе гладких линий, проходящих через
заданные точки (а, А) и (Ь, В), нет линии, реализующей минимум функционала (1.24).
1.1 .4. Вариационная задача с п неизвестными функциями
Рассмотрим функционал
ъ
J = \F{x,yx,y2,...,yn,y[,yl2,...,yln)dx, (1.29)
а
зависящий от п неизвестных функций У\,у2,—>Уп • Пусть, далее, заданы граничные
условия
yi{a) = Aiiyi(b) = Bi9 / = п (1.30)
Найдём дифференциал функционала (1.29). Дадим функциям yfo) приращения
ht(x). В силу (1.30) приращения ht(x) должны удовлетворять условиям
/7,(а) = 0, / = п (1.31)
Приращение функционала _
ь
AJ = JF(x,y] +Ии...,уп+кп,у[+к{,...,у'п+1>1'п)сЬс-
-1р(х,У\,'~>Уп>У\>~'>Уп)<Ьс-
а
Выделим, как и выше, главную линейную часть приращения функционала:
Ь п
где многоточием обозначены члены, имеющие порядок малости выше первого
относительно ht и h\. Дифференциал функционала, таким образом, имеет вид
ai=\
Выполняя интегрирование по частям и учитывая соотношения (1.31), окончательно
получим
а '=1
Если функции yt(x) (i = \,n) доставляют слабый минимум функционалу (1.29), то
в соответствии с теоремой 1.1 дифференциал функционала равен нулю, т.е.
Jl(^-^)M*>*=°- (1-зз)
а /==1
Приращения ht(x) независимы между собой (они должны удовлетворять только
граничному условию (1.31)). Поэтому, зафиксировав индекс / (например / = у),
функцию hj(x) будем считать произвольной, а остальные h^x) (при /* j) положим
равными нулю. Тогда равенство (1.33) примет вид
Jfr-^bw*'0- (L34)
450
Методы теории оптимального управления. Часть III
Воспользовавшись приведённой выше леммой Лагранжа, из (1.34) получим
уравнение Эйлера
/г -4-/V =0.
(1.35)
у; dx у<
Уравнение (1.35) можно получить указанным выше способом для любого индекса /.
Таким образом, функции yt(x) (/ = 1,я), решающие поставленную выше задачу, т.е.
доставляющие минимум функционалу (1.29) при граничных условиях (1.30), должны
удовлетворять системе дифференциальных уравнений Эйлера
Fyi"dkF*=0 (/ = I^ (L36)
Отметим, что как уравнение Эйлера (1.19), так и система уравнений (1.36)
являются необходимыми условиями экстремума функционала, т.е. как минимума, так и
максимума функционала.
1.2. ЗАДАЧА С ПОДВИЖНЫМИ КОНЦАМИ.
УСЛОВИЕ ВЕЙЕРШТРАССА - ЭРДМАНА
1.2.1. Общая формула вариации функционала
Рассмотрим функционал
J=lF(x,y9y')dx. (1.37)
Будем предполагать, что концы тех кривых у = у(х), на которых определён
функционал, можно сдвигать произвольным образом. Пусть у = у{х) и у = у(х) - две
близкие кривые (рис. 1.3).
х0 хо+&хо Х} хх+5х}
Рис. 13. К выбору общей формулы вариации функционала
Функция у{х) определена в интервале х0 < х < хх, а функция у(х) - в интервале
х0 +5х0 <*<*, +5*!. Функции ><jc) и у(х) определены на разных интервалах.
Чтобы дальнейшие рассуждения имели смысл, продолжим эти функции гладким образом
на интервал, включающий в себя интервалы определения функций у(х) и у(х). Для
этого можно, например, провести касательные в конечных точках кривых.
Расстояния между функциями ^(jc) и у{х) зададим соотношением
p(^7) = max|y->?| + max|/-5?1 + p(Po^o) + p(i^). С1-38)
XE.L XE.L
Глава 1, Вариационное исчисление 45^
здесь р(/>0,/)0) и р(/>,,/>1) - расстояние соответственно между левыми и правыми
концами кривых у = у(х) и у = у(х), L - указанный выше интервал определения
функций у(х) и у(х). Обозначим координаты кривой у = у(х) соответственно
(хо>Уо) и (*1>Л)> a координаты концов проварьированной кривой у = у(х) -
(х0 +дх0, у0 +8у0) и (хх + 8*,, у, + 5^). Положим J(x) = y(x) + h(x). Функции ^(х)
и у{х) полагаются близкими в смысле расстояния (1.38).
Рассмотрим приращение функционала (1.37):
АУ= J F{x,y^Kyt^ht)dx-\F{x^yl)dx^
х,+&г,
= j[F(x,y + h,y> + h')-F(x,y,y')]dX+ J F(x,^ + Ay + A')*-
- \ F{x,y + h,y' + h')dx.
Воспользовавшись формулой Тейлора и применив теорему о среднем, получим
AJ = j [Fy (х,уУ) ■ h(x) + Fy (x,y,y') ■ h\x)]dx +
ь (1.39)
+F(x,y,y')\ ■&c]-F(x,y,y')\ -ахо+оОКу + А,;;)),
здесь
о(р(у + й,у))_Л
lim т ;—г— - v.
p->o р(^ + Л,^)
Выполним интегрирование по частям
\Fy.h'dx = Fy\x •h(x])-Fy.\x .h(xo)-lh~4-Fy,dx.
х\ xi
Тогда равенство (1.39) можно записать в виде
AJ = ][Fy(x,y,y')-jj-F/(x,y,y'j\Kx)dX +
+Fy
•А(л:1)-/у| +F -fixj-H •5x0 + o(p(y + A,^)).
(1.40)
Из рис. 1.3 видно, что
5^о «*(*о) + /(*о)Ч> йУ\ « A(*i) + /(*i)-&!• (1.41)
В равенстве (1.41) отброшены члены, имеющие порядок малости выше первого.
Из (1.40), отбрасывая слагаемые, имеющие порядок малости выше первого, и
принимая во внимание (1.41), окончательно получим
bJ = j[Fy(x,y,y>)-^Fy(x,y,y')^Kx)dK +
х» (1.42)
+Fy\ .8^+[f-/Fy]| .&,-Fy| •fyo-[^-^v]| S^o-
452
Методы теории оптимального управления. Часть III
Равенство (1.42) задаёт общую формулу вариации функционала (1.37). Вариация
функционала в задаче с закреплёнными концами следует из (1.42), если положить
6у, = 5у0 = дхх = 8*0 = 0.
1.2.2. Задача с подвижными концами
Рассмотрим функционал
J(y)=f F(x9y,y')dx,
(1.43)
•*о
определённый на гладких кривых у = у(х). Требуется среди линий у = у(х), концы
которых лежат на двух заданных кривых у = ср(х) и у = vj/(jc) , найти линию у = у(х),
доставляющую слабый минимум функционалу (1.43). В отличие от рассмотренной
выше задачи вариационного исчисления, в которой концы линий у = у(х) строго
фиксированы, в данном случае появляется некоторая свобода в выборе концов линий
у = у(х): левым концом может быть любая точка линии у = (р(х), а правым концом -
любая точка линии у = у(х).
Воспользуемся общей формулой вариации функционала (1.42). Если некоторая
кривая у = у(х) доставляет минимум функционала (1.43) в рассматриваемой задаче с
подвижными концами, то она тем более доставляет минимум функционалу (1.43) по
отношению к более узкому классу кривых, имеющих те же концы, что и линия
у-у{х). Отсюда следует, что функция у(х), решающая поставленную задачу,
должна удовлетворять уравнению Эйлера.
; У = Ф)
у = \|/(х)
х0 хо+дхо *i *i+S*,
Рис. 1.4. К рассмотрению задачи с подвижными концами
Из (1.42) с учётом уравнения Эйлера следует, что
Далее, из рис. 1.4 находим
Ьух *\ц'{хх\Ьхъ 5у0 «ф'(хо)-8го.
Вариация функционала принимает вид
5J = [Fy.M/4F--y.Fy]L.6x1~[Fy.9 4F~^'.F/][.5x0.
(1.44)
Глава 1. Вариационное исчисление 453
В соответствии с теоремой 1.1 запишем условие минимума функционала:
5J = [Fy4i' + F-y'-Fy.]\ .&,-
,*' (1.45)
-[F/-9' + F-y-Fy]|^-5x0=0.
Поскольку 5х0 и 6х, -независимые приращения, то из (1.45) находим
[Fy.tf + F-?.Fs]\^09
[Fy-9' + F-/.Fy]| =0. (1.46)
Равенства (1.46) носят названиче условий трансверсальности.
При решении вариационной задачи с подвижными концами необходимо сначала
решить уравнение Эйлера, общее решение которого будет содержать две
произвольные константы, а для определения указанных констант следует воспользоваться
условиями трансверсальности (1.46).
Иногда встречается смешанный случай, когда один конец кривой у = у(х)
закреплён, а второй - подвижен. В этом случае условие трансверсальности записывается
только для подвижного конца траектории.
1.2.3. Условия Вейерштрасса - Эрдмана
Выше, выполняя вывод уравнения Эйлера, мы предполагали, что реализующая
минимум функционала функция у(х) имеет непрерывную вторую производную.
Вообще, в вариационном исчислении доказывается, что экстремаль функционала
(1.11) является дважды непрерывно дифференцируемой функцией во всех точках
(х, у), в которых
Fyy(x9y9y')*0.
Однако встречаются вариационные задачи, в которых минимум функционала
достигается на кусочно-гладких линиях.
Рассмотрим простейшую задачу вариационного исчисления о минимуме
функционала (1.11) при граничных условиях (1.12), полагая, что допустимые кривые
у = у(х) могут иметь излом в некоторой точке х* (а < х* < Ь). На каждом из
интервалов (а,х*) и (x\b) функции у(х) являются гладкими и потому кривая,
доставляющая минимум функционалу (1.11), удовлетворяет уравнению Эйлера.
Представим функционал (1.11) в виде суммы двух функционалов
Ь х* Ь
J = \F(x^y')ax = Jx+J2 = \F(x,y,y')dx+\F{x,y,y')ax.
а ах*
Будем предполагать, что точка излома х* варьируется (см. рис. 1.5).
Вычислим вариацию отдельно для функционала У, и J2. Воспользуемся общей
формулой вариации функционала (1.42). Для функционала J} граничные условия
состоят в следующем: левый конец кривой закреплен, а правый свободен. Поэтому,
принимая во внимание уравнение Эйлера,
&/1=iy
с=/-0 L *J|jc=jc-0
Для функционала J2 закреплён правый конец кривой у = у(х), а левый свободен,
и, следовательно,
454
Методы теории оптимального управления. Часть III
&/2=-/у| ; .ey-fF-y-Fyll , .&с\
1 У\х*х+О L У-*\х=х+0
jc + &t
Рис. 1.5. График кривой, имеющей излом в точке х*
Если на линии >> = у(х) имеет место минимум функционала (1.11), то
+[^->''^)Lo-(^-/^y)Uo}^=o-
Приращения 5у и 8х* являются независимыми, и поэтому из (1.47) следует
(1.47)
Ч--о-Ччо = 0'
(F-y'Fs)\x._o-{F-y'Fy\.+o = O- • (1-48)
Соотношения (1.48) представляют собой условия, которые должны выполняться в
точках излома экстремалей. Они называются условиями Вейерштрасса - Эрдмана.
Проанализируем полученный результат. На каждом из отрезков [а,х*] и [х*,Ь]
доставляющая минимум функционала функция у(х) должна удовлетворять
уравнению Эйлера. Общее решение двух уравнений Эйлера содержит четыре неизвестных
постоянных интегрирования. Неизвестной также является точка излома экстремали
х*. Для определения указанных неизвестных имеются: два граничных условия (1.12),
два условия Вейерштрасса (1.48) и условие непрерывности
у(/+0) = у(х-0).
1.3. НЕОБХОДИМОЕ УСЛОВИЕ ВЕЙЕРШТРАССА
СИЛЬНОГО МИНИМУМА ФУНКЦИОНАЛА
Выше, при получении уравнения Эйлера, реализующая минимум функционала
кривая у = у(х) сравнивалась с кривыми, близкими в смысле нормы из Сь т.е.
близкими были не только сравниваемые кривые, но и их производные. Вейерштрасс
получил необходимое условие минимума, сравнивая реализующую минимум кривую
у = у(х) с кривыми, производные которых не всюду близки к производной у\х).
Как уже отмечалось, сильный минимум функционала является в то же время
слабым. Поэтому реализующая сильный минимум функционала функция у(х) должна
удовлетворять уравнению Эйлера.
Глава 1. Вариационное исчисление
455
Пусть на кривой у = у(х) реализуется сильный минимум функционала
ь
J = \F(x,yiy')dx. (1.49)
а
Выберем произвольно на кривой у = у{х) точку 1 и правее её точку 3 так, чтобы между
точками 1 и 3 кривая у - у(х) не имела угловых точек. Проведем через точку 1
произвольную гладкую линию у = Y (х) (см. рис. 1.6). Переменную точку 2 линии у = Y (х)
соединим с фиксированной точкой 3 линией Е23, определяемой уравнением у = у(х).
Линию Е23 будем выбирать близкой к линии у = у{х) в смысле нормы из Сх.
у = У(х)
В
«о
Рис. 1.6. К решению задачи нахождения необходимых условий
сильного минимума функционала
По условию кривая доставляет сильный минимум функционалу (1.49). Положим,
что точка 2 стремится к точке 1, пробегая значения линии y=Y(x). В соответствии с
определением сильного минимума значение функционала (1.49), вычисленного вдоль
линии А123В (рис. 1.6), должно быть больше (в крайнем случае равно) значения
функционала, вычисленного вдоль линии у=у(х\ т.е. должно иметь место условие
bJn = \F(xJJ')ck+\F(x,yJ)dx-\F(x^y')dx > 0. (1.50)
Найдем главную часть приращения ДУ13. Отметим, прежде всего, что
\F(xJX
)dx^F(xJJ')\bx^
где Sxj = х2 -хх. Далее, главную часть приращения
(1.51)
jF(x,p,f)A-jF(jc,y,/)tfe
Х2
можно найти по формуле вариации функционала в задаче с подвижным левым и
закрепленным правым концами. Так как функция у(х) удовлетворяет уравнению Эйлера, то
I F(x,y,y)dx- JF(x,y,y')dx*-[Fy.-Y'+F-y'-Fy.~]\x 5xv (1.52)
456 Методы теории оптимального управления. Часть III
В равенствах (1.51) и (1.52) опущены слагаемые, имеющие порядок малости выше
первого.
Введем обозначение
E(x,y,y\Y') = F(x,yJ')-F(<x,y,y')-(Y'-y').Fy,(xiyiyt).
Принимая во внимание (1.50) - (1.52), запишем
AJ13«£(x,*/,r)8xi*0.
Из данного неравенства вытекает, что
E(x^y\Y%>0. (1.53)
Так как точка 1 выбиралась произвольным образом, то условие (1.53) можно
переписать в виде
E(x,y,y'J')>0.
Таким образом, доказана следующая теорема.
Теорема 1.2 (необходимое условие Бейерштрасса сильного минимума
функционала). Говорят, что допустимая кривая у = у(х) удовлетворяет условию
Вейерштрасса, если в каждой точке х этой кривой выполняется неравенство
E(x,y,y'J')>0 (1.54)
для любого числа Y'. Если кривая у = у(х) доставляет сильный минимум
функционалу (1.49), то она удовлетворяет условию Вейерштрасса (1.54).
Как уже отмечалось, реализующая сильный минимум функционала кривая
у = у(х) удовлетворяет уравнению Эйлера. Поэтому сначала решается уравнение
Эйлера и находится экстремаль у = у(х). Затем на полученной экстремали у = у(х)
проверяется условие Вейерштрасса (1.54).
Пример 1.5. В п. 1.1. (пункт 3) были рассмотрены два примера и показано, что функция у'=х
доставляет сильный минимум функционалу
1
J = \{y')2dx
о
и только слабый минимум функционалу
о
Проверим для каждого из этих примеров выполнение условия Вейерштрасса сильного минимума
функционала.
Для первого примера
E(xyyyj') = (Y')2-l2-(Y'-\)2.
Функция Е представляет собой параболу. Исследовав эту функцию на максимум и минимум, легко
установить, что min Е - 0 и достигается в точке Y' -1. Таким образом, линия у = х удовлетворяет необходимому
условию Вейерштрасса сильного минимума функционала.
Для второго примера
Е(х9У9у\Г) = (Г)2-\г-(Г-\)'39
т.е. функция Е представляет собой кубическую параболу. Кубическая парабола может принимать
отрицательные значения, и, следовательно, линия у = х не удовлетворяет необходимому условию Вейерштрасса
сильного минимума функционала.
1.4. ЗАДАЧИ НА УСЛОВНЫЙ МИНИМУМ
В вариационном исчислении задачами на условный экстремум называют такие
задачи, в которых минимум функционала ищется не на произвольных функциях, а на
функциях, которые удовлетворяют некоторым дополнительным (кроме граничных)
условиям. Рассмотрим сначала наиболее простой вариант вариационной задачи на
условный минимум.
Глава 1. Вариационное исчисление
457
Задача Лагранжа. Пусть требуется найти минимум функционала
и
J = lF(x,yby2,...yn,y{9y'2,...,y'n)dx,
(1.55)
при условии, что допустимые функции у;(х) (/ = 1,л) удовлетворяют граничным
условиям
yi{a) = Ahyi{b) = Bi (/ = п) (1.56)
и к уравнениям связи
gl(x9yuy2^,yn) = 0 (/ = п), к<п. (1.57)
Предполагается, что граничные условия (1.56) не противоречат уравнениям (1.57), т.е.
g/(a,4,...,^) = 0,
g/(MP...A) = o, / = п
Пусть, далее, условия связи (1.57) являются независимыми, т.е. для всех значений
х>У\>Уг>—>Уп' удовлетворяющих условиям (1.57),
"dgi 3gj_ _ <&
дух ду2 дуп
rang
9gk dgk
ду{ ду2
дуп
= к.
В рассматриваемой задаче минимум функционала (1.55) ищется не на
произвольных функциях yt(x) (i = \,k), а только на тех из них, которые удовлетворяют к-
уравнениям связи (1.57). Сформулированная задача на условный экстремум
называется задачей Лагранжа с голономными связями.
Ниже для решения задач на условный экстремум используется некоторый
стандартный прием. Этот прием не будет строго обосновываться. Однако он является
очевидным на эвристическом уровне и позволяет очень просто получить
необходимые условия экстремума в форме уравнений Эйлера.
Рассмотрим вместо функционала (1.55) функционал
и
^(*> у У) + IX (*)#/*'у)
7=1
dx,
(1.58)
здесь Х,(х) - некоторые неизвестные функции (неопределенные множители
Лагранжа), у = (у\,...,уп) и у' = (У]9.--,у'п) - «-мерные векторы. Будем искать безусловный
минимум функционала (1.58), полагая, что он задан на функциях у^х) (/ = 1,я) и
Xj(x\j = \,n (на функции Xj(x) граничные условия не накладываются). Очевидно,
множество значений функционала (1.58) включает в себя множество значений
функционала (1.55) при ограничениях (1.57). Далее, если выполнены уравнения связи
(1.57), то функционал (1.58) совпадает с функционалом (1.55) при любых
множителях Лагранжа ^7(jc) (у = 1,А).
Функции yi(x) (/ = l,w) и А.у(х), j = 1,л, доставляющие безусловный минимум
функционалу (1.58), должны удовлетворять следующим уравнениям Эйлера:
458
Методы теории оптимального управления. Часть III
г.+£*■&-&*-<>- '->.».
У,
ду, dx y' ' ' ' (1.59)
gy(*,y) = o, у = п.
Из (1.59) следует, что безусловный минимум функционала (1.58) достигается на
функциях, которые удовлетворяют уравнениям связи (1.57), т.е. безусловный
минимум функционала (1.58) достигается в точке, в которой он совпадает с функционалом
(1.55). Поскольку при этом выполняются также уравнения связи (1.57), то, очевидно,
соотношения (1.59) следует рассматривать как необходимые условия экстремума
сформулированной выше вариационной задачи (1.55) - (1.57). Уравнения (1.59)
называются уравнениями Эйлера - Лагранжа.
Сформулируем окончательный результат. Итак, если функции у®(х) (/ = \,п)
доставляют экстремум функционалу (1.55) при граничных условиях (1.56) и ограничениях
(1.57), то найдутся такие множители Лагранжа \j(x) (у = 1Д), что функции
у®(х) (/ = 1,л) Д7(х) (у = 1Д) удовлетворяют уравнениям Эйлера-Лагранжа (1.59).
Соотношения (1.59) представляют собой систему из (п+к) уравнений
относительно (п+к) неизвестных функций yt(x) (/ = 1,л) и Х{(х) (j = 1,£). Далее, п из этих
уравнений являются дифференциальными уравнениями второго порядка. Поэтому
общее решение системы (1.59) будет содержать 2л произвольных констант, для
определения которых следует использовать 2п граничных условий (1.56).
Рассмотрим задачу на условный экстремум, когда уравнения связи содержат
производные.
Пусть требуется найти минимум функционала (1.55) при условии, что допустимые
функции yi (х) (/ = 1,я) удовлетворяют граничным условиям (1.56) и уравнениям связи
Ф/*,у,у') = 0 О = п), к<п. (1.60)
Как и выше, уравнения связи будем считать независимыми, т.е. будем полагать,
что следующая матрица
ЭФ,
ду\
дФк
ЭФ,
ду'г
дФк
5Ф,
ду'„
дФк
ду\ ду'2 ду'„
имеет ранг к вдоль кривой, доставляющей минимум, для всех х е [а,Ь].
Как и в предыдущем случае сформулированная задача на условный минимум
сводится с помощью неопределенных множителей Лагранжа к задаче на безусловный
минимум для функционала
Для функционала (1.61) уравнения Эйлера - Лагранжа имеют вид
дФ,
К i-l J A,, J*
<t>j(x.y) = 0,
dx
/V;+I>,
7=1
дФ,
= 0, / = 1,и,
(1.62)
Глава 1. Вариационное исчисление 459
Уравнения (1.62) являются необходимыми условиями экстремума функционала
(1.55) при наличии дифференциальных связей (1.60) и граничных условий (1.56).
Соотношения (1.62) представляют собой систему из (л+£) уравнений относительно
(л+к) неизвестных у, (х) (/ = 1, л), Xj(х) (j = 1, А).
Задача Больца. В классической постановке задача Больца формулируется
следующим образом: в классе функций
У;(х), / = 1,л, х} <х<х2,
удовлетворяющих дифференциальным уравнениям
Ф/*>У>У') = О, 7 = 1™, *<"
и условиям для концов
Ч>ц(^(*,)>*2>У(*2)) = 0> Ц = 1А /?<2л + 2,
найти функцию у(х), на которой функционал
J = g(*i> У(*1)>*2 > У(*2)) + J Л ^ У» У ')<&
достигает минимума. Здесь, как и выше, у и у' - векторы.
Задача Майера с подвижными концами является задачей Больца, в которой
функция/тождественно равна нулю, а задача Лагранжа - частный случай задачи Больца,
когда в выражение для функционала J не входит функция g.
С помощью простых преобразований легко убедиться, что задача Больца
приводится как к задаче Майера, так и к задаче Лагранжа. Действительно, задача Больца
эквивалентна задаче Майера относительно неизвестных функций
УМ> Уп+М, * = Ъ"> xl<x<x2,
удовлетворяющих (w+1) уравнениям связи
фу(*,у,у') = о, а=Г^),>>;+.-л*>у,у')=о,
(р+\) граничным условиям
Ч*ц (*i > У(*i X *2 > У(*2)) = 0, ц = 1, ру уп+1 (х,) = 0,
и функционал
J = g(x\>y(x\),x2,y(x2)) + yn+l(x}).
Далее, задача Больца эквивалентна задаче Лагранжа с неизвестными функциями
УМ,yn+l(x)9 / = 1,л, х, <х<л:2,
удовлетворяющими уравнениям связи и граничным условиям
Ф7(*>У>У') = 0» У'п+i = °> j = lm>
Уц(^1»У(^)^2>У(^2)) = °» Н- = 1>А Л-ы(^) ^—= 0,
х2-х,
и с функционалом вида
J=j[f(x.y,y') + yn+i]<b.
Из изложенного материала, таким образом, следует, что эти три задачи имеют
равную степень общности.
460 Методы теории оптимального управления. Часть III
1.5. РЕШЕНИЕ ЗАДАЧИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
МЕТОДОМ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
1.5.1. Формулировка задачи оптимального управления
Рассмотрим технический объект, движением которого можно управлять. Пусть
движение объекта задается системой дифференциальных уравнений в нормальной
форме Коши
—i- = fi(xb...,xn,ul,...,um), / = 1,я. (1.63)
at
Обозначим х = (xj,..., хп) - /7-мерный вектор состояния, и = (щ,..., ит) -
/w-мерный вектор управления. Относительно управления и будем предполагать, что
вектор и является кусочно-гладкой функцией, имеющей конечное число разрывов
первого рода. Управление и может принимать свои значения из некоторой
ограниченной области U. Область U можно задавать, например, неравенствами
A)<Uj<A2j, j = ljn. ' (1.64)
Векторное пространство с декартовыми координатами jcpjc2,...,*n обозначим X и
будем называть фазовым пространством системы (1.63). Каждому вектору х в
фазовом пространстве соответствует некоторая точка. Если задано управление
и(0 = (Hi(О,---.««(О), tQ<t<tx, и начальное условие х(/0) = х° = (х,°,...,х°), то
решение системы (1.63) будет определять движение объекта. В фазовом пространстве X
этому движению соответствует фазовая траектория \{t)-{xx(t),...,xn{t)). В этом
случае говорят, что управление и(/), /0 </</,, переводит фазовую точку из
начального положения х(/0) = х° в конечное положение х(^) = х1 (х1 = (х\,...,х\)).
Рассмотрим следующую задачу. Требуется среди управлений u(0 e V, t0 <t <tx
{моменты времени /0 и t{ нефиксированы), переводящих фазовую точку х из
заданного начального положения х° в заданное конечное положение х1, найти такое,
которое доставляет минимум функционалу
J = \Mxl9...,xn9ul9...9um)A. (1.65)
'о
Управление u(t), решающее поставленную задачу, называется оптимальным
управлением, а соответствующая ему фазовая траектория \(t) - оптимальной
фазовой траекторией.
Иногда вместо начальной и конечной точек фазового пространства задаются
начальные и конечные многообразия. Например, в фазовом пространстве X системы
(1.63) заданы многообразия s{) и s]9 определяемые системами уравнений
sQ: ф/(лг,,х2,...,д:;7) = 0, / = 1,/?, р<п,
5,: ру(х,,х2,...,л:„) = 0, v = l,*, k<n.
Требуется среди управлений u(t)eU, to<t<t{, переводящих фазовую точку с
многообразия s0 на многообразие s{, найти такое, которое доставляет минимум
функционалу (1.65). Такую задачу оптимального управления называют задачей с
подвижными концами.
Сформулированная задача оптимального управления является вариационной
задачей на условный минимум. По сравнению с классическим вариантом, данная зада-
Глава 1. Вариационное исчисление
461
ча усложнена наличием ограничений типа неравенств (см. (1.64)). Ограничения типа
неравенств практически всегда имеют место в задачах оптимального управления
техническими объектами. Однако путем несложной подстановки ограничения типа
неравенств могут быть легко сведены к ограничениям типа равенств, и тем самым
задача оптимального управления сводится к вариационной задаче на условный минимум.
Будем полагать, что функции
Дх,и) (/ = М), Ф/(х) (/ = VP), Pv(x) (v = U)
имеют непрерывные производные по всем своим аргументам. Пусть, далее область U
задается неравенствами (1.64).
Введем т дополнительных переменных v1,v2,...,vm и непрерывно
дифференцируемые функции
a/(urVj) = uJ-Xj(vj) = O, j = \,m.
Функции Xj(vj) должны удовлетворять следующим условиям:
max Xj(yf) = AJ;
min x,(vy) = 4.
На рис. 1.7 изображен график такой функции.
л)
г— 1
[
Рис. 1.7. График функции Xj(vj)
Рассмотрим следующую задачу Майера вариационного исчисления. Требуется
среди функций */(0,wy(/),v7(/),/ = 0,л, у = 1,л, to<t<t]9 удовлетворяющих
системе дифференциальных уравнений
gi(xi9x],...,xn9u],...,um) = xi-fi(xx,...,xn,u],...Jum) = O, / = 1,л, (1.66)
уравнениям в конечных соотношениях
oij(uJ,vJ) = uJ-x/(vJ) = 0, y = l,m, (1.67)
а также условиям на концах
fao(xoOo\xl(toX...,xn(to)) = x(to) = Q,
\<Pi(x\(t\)>—>xn(t})) = 09 l = lp, p<n\
Pv(*ift)^2ft)v,^(/i)) = 0, v = U, k<n, (1.69)
найти такие, которые доставляют минимум функционалу
J = xQ(tx). (1.70)
Сформулированная задача Майера эквивалентна поставленной выше задаче
оптимального управления с подвижными концами. Действительно, дифференциальные
уравнения в этих задачах совпадают. Условие (1.67) позволяет свести ограничения
(1.68)
462 Методы теории оптимального управления. Часть III
типа неравенств к ограничениям типа равенств. При этом дополнительные
переменные Vj(t) (у = 1,/и) не входят в управления (1.66). Из первого уравнения (1.66) и
первого условия (1.68) следует, что
'i
J = xo(tx) = j fo(xx,...,xn,u[,...9um)dt.
'о
В двухточечном случае, т.е. когда заданы начальные и конечные значения вектора
х, условия (1.68) и (1.69) принимают вид
U(/O)=o, ^(/o)-^°=o, (i7i)
\х,ах)-х]=о, ' = Пл.
Будем предполагать, что уравнения иу(/) и Vj(t) могут иметь разрывы первого рода.
1.5.2. Необходимое условие экстремума
Сформулированная задача Майера вариационного исчисления как аналог задачи
оптимального управления является задачей на условный минимум. Хотя условия,
наложенные на функции хДОэнДО^уДО» являются более сложными, чем это
рассматривалось в §1.4, общая идея решения задачи остается прежней: необходимо
воспользоваться неопределенными множителями Лагранжа. Обращение именно к задаче
Майера обусловлено желанием получить результаты, аналогичные принципу
максимума Понтрягина. Далее, в целях упрощения весьма громоздкого вывода
необходимых условий оптимальности, ниже мы будем использовать обоснование, которое по-
прежнему выполняется на эвристическом уровне, несколько отличающееся от
обоснования, изложенного в §1.4.
Рассмотрим функционал
т р
-^jiO-a^Uj^Vj^dt + ^pJ^ixoitol ... ,*„(>о))+ (1.72)
7=1 /=0
к
v=l
здесь Р/\РуД/(О> Цу(О - неопределенные множители Лагранжа. Если функции
xi(t)>uj(t)>vj(f) удовлетворяют уравнениям (1.66) - (1.69), то значение функционала
(1.72) совпадает со значением функционала (1.70) при любых р^, ру> ^/(0> Цу(О •
Найдем вариацию функционала (1.72). При определении указанной вариации
будем считать, что в интервале (/0>*i) имеется лишь одна точка разрыва управлений
w,(/), Vj(t). Наличие нескольких точек разрыва управлений приведет лишь к
громоздкости дальнейших выкладок, но не повлечет за собой изменения окончательного
результата.
Пусть t - точка разрыва управлений. Точка / разбивает интервал (/0>'i) на два
подынтервала U0J*f и (/*,tA, в каждом из которых управления uf(t)9vf-(t)
непрерывны. Обозначим x~(t\ u~(t), vj(/), ^,~(0> Иу(О соответствующие значения в
Глава 1. Вариационное исчисление
463
интервале (to,t*)9 а через */"(/), wj(/), v*(/), X*(t), \i*(t) -значение переменных в
интервале (t*, tx).
При получении вариации функционала сравниваются значения функционала на
функциях Xj(t)9Uj(t),Vj(t) со значениями функционала на близких функциях
Xj(t) + bxi(t\ Uj(t) + bUj(t), Vj(t) + 5vj(t). Будем также варьировать моменты времени
/ и /j. При этом необходимо различать «вариацию точки», например, А х* (t ) от
«вариации в точке» 8x,+ (f*):
Дх;(/*) = х;(/Ч8/*) + 8х;(/*+8/*)-х;(Г*)*8хГ(О + */+(О-8/ •
Вообще, имеют место следующие равенства:
dtL J
Выпишем разность
A J = *0+ (/, + 5/,) + &с0+ (/, + 5/,) - xl (/,) +
/=0
f *r ± rf&r
\t at at
-gl\-*--x •"
-ay(i/;,vj)]|df
'if*
У-1
/=o
i dx* d8x* . . + + .
/ +5/ I n
, dxt dbx: _ _ _ _ _ _
ш at
/=i j
/, ['=0
7=1 j
ft —^ + ——,x+ +5x+,w+ +5w+
/+5/'
- J iv
/=0
\ at at
464
Методы теории оптимального управления. Часть III
+2^РГ Ф/ (*о ('о ) + 8*о ('о X х~ Оо ) + 8*~ ('о ))н
/=0
+ZPv • Pv {x+ (/, + 5/,) + 5х+ (/, + 8/,))-
V=l
/=0 v=l
здесь X = (jcj, ...,*„) и 5Х = (5х!, ..., 8хп) - векторы. Выделим главную линейную
часть приращения функционала
AJ «5x+(h) + ~[xo (*,)]• Sr,+
/=0
Эх" л ^ах;
v=i 5м„
8«:
« (5a. 5a. ]
1=0 i=QUXi Uo) v=l /=1 VXi (t\)
v=l /=1 OXi V\)
(1.73)
Воспользуемся формулами
dbx'O)
,' ''(dXJ(t)
j x-(o-^^=x-(o-8x-(oi;o-j^-8x-Wc//=
'(dXJit)
= я.;(/*) • &c-(г*) - XJ(r0) • 8x"(/0) - J —iii• &Г(ОЛ.
J a/
, + ,.ч ^x,+ (O
rL Л1 + /
+ //ч 5:^//л ldK(O g,.+
/* /*
Из условия непрерывности функций *,(/) и х; (/) + 8х, (/) следует, что
Ах,+ (/*) = Ах," (/*) = Ах,-(/*). Далее, выразим в равенстве (1.73) Ьх~ (/*) и 8х,+ (t*) через
Ах,(/*). Тогда вариация функционала примет вид:
Глава 1. Вариационное исчисление
465
/7
aft
Л
-+Z*
а=0
Эх Г
•&г
5а,
^•Z^+^l+Z^-^-^K
7=1
-js
/* 1'=°
ди~
ди~
Н
Эу:
а=0
l/=0 "",
сюс ,
7=1
/7
•5vJ ^/ +
+Z(^r(^)-^;(^))-^/(^)+(i+^o(^))-64(/1)-
/=0
- Z^('*)/rc*)-Z^('*)-//+('*)|s'* +
L/=0 /=0
(1.74)
/=0
/=1
/=0 йяс,~('о)
Zp:-
зрч
v=l
dx!(t})
-К Со)
+ К(<\)
•Sx"(/0) +
•6^+(^,)+
*o('i) , ^
Л Л
+ i:-Zpv-Pv(^i)) -5/,.
v=l
При выводе вариации функционала (1.74) предполагалось, что время движения
{Q задано. Поскольку система является автономной, то движение системы не
зависит от того, в какой конкретный момент времени оно началось, а полностью опре-
1еляется временем движения. Поэтому при выводе вариации функционала (1.74)
гачальный момент времени /0 предполагался фиксированным, а варьировался
олько конечный момент времени ^ . Далее, если считать, что время движения за-
щно, т.е. фиксированы начальный и конечный момент времени, то соответствую-
цая формула вариации функционала по-прежнему задается равенством (1.74), в
ютором следует положить 5/, = 0.
Если функции хДг), Uj(t)9 vy(/) реализуют минимум функционала (1.72), то по
еореме 1.1 вариация такого функционала равна нулю, т.е. bJ = 0.
В силу уравнений связи (1.66), (1.67) и условий для концов (1.68) и (1.69) не все
[риведенные в равенстве (1.74) вариации переменных являются независимыми. Имен-
ю, зависимыми являются: 2(п +1) + 2т вариаций &с~, Ьх*, 6и~, 8wJ, 6v~, 5vJ, / = 0, п,
i = 1, т, из общего их числа 2(п +1) + Am ; (р +1) + к вариаций 6х, (/0), 5х, (t{), / = 0, п .
Выберем множители Лагранжа \J(t), V(0> Цу(О» V^(OJ = 0,n9j = \,m так, что-
ы в равенстве (1.74) коэффициенты при зависимых вариациях bx~(t), 5x,+ (/),5i/y(/),
>м|(0 обращались в нуль. Тогда
466 Методы теории оптимального управления. Часть HI
dX
а-° *'" (1.75)
+ Л fbf
- *' Ы' (1.76)
/=0 OUj dUj
Выберем множители Лагранжа р,~, р* при {р + \+к) зависимых вариациях
5х~(/0), 5л:/" (^), чтобы обратить в нуль коэффициенты при этих вариациях, и,
учитывая независимость (произвольность) остальных вариаций, найдем
ах,
. *, <L77)
условия Вейерштрасса - Эрдмана
\-(t*) = \;(t'), /=оЯ
(1.78)
г^у^-г^ч1--*
/=о ш /=о
и условия для концов
DVT?7--^('o) = O, i = 0,/i,
,=о ac-(ib) (179)
£р;-^-+^«.)=о,/=1Я
v=i Здг, (/,)
1 + Я.0(/,) = 0,
с// t// v=1
Преобразуем полученные соотношения в более удобную форму.
Введем функцию
п т
Я(Х, х, u, v, \i) = Hx(X, х, и) + Я^(ц,и,у) = ^^у;(х,и)+^ц7а/(и,у).
/=0 7=1
Здесь Х = (^0,...Д„), v = (v,,...,vOT), ц = (ц,,...,цш) - векторы. Тогда уравнения
(1.76) и (1.77) можно записать в виде
^1 = 0,^1 = 0,
ди, dv.
1 ] (1.81)
дН+ дН+ . —
— = 0,—= 0,у = 1,1и.
ди* dv*
То есть условия (1.76) и (1.77) совпадают с условиями экстремума функции Н.
Глава 1. Вариационное исчисление 467
Второе условие (1.78) выливается в условие непрерывности Нх и, следовательно,
функции Я (функция Яц в соответствии с уравнениями связи (1.67) равна нулю):
--('•ню
Уравнения (1.66) и (1.67) могут быть записаны в виде
£-*£./-<п (1.83)
dt dXt
^ = 0, j = l,m. (1.84)
Отметим далее, что вместо соотношений (1.75) можно записать уравнения
%■-%■ "^
Покажем, что на оптимальной траектории функция Я = const. Запишем производную
dt h^, dt &&, dt £du, dt %duJ dt %dvj dt'
Из (1.86), принимая во внимание (1.81), (1.83)-(1.85), найдем, что
dt
и, следовательно, функция Я, рассматриваемая как функция времени, постоянна.
Рассмотрим частный случай, когда левые и правые концы линий x,(t),i = \,n
закреплены. В этом случае условия для концов принимают вид (1.71), и из
соотношений (1.79), (1.80) следуют равенства:
РГ-А-7('о) = О> ' = 0Я
pt-Xt(/,) = O, / = ГЯ
1 + ^(0 = 0, О-87>
Из (1.87) находим, что
Ях(Г(/1),х+(/1),1/+(/1)) = 2;^1)-У-(х+(/1),и+Й)) = 0. (1.88)
Из (1.88), принимая во внимание, что Яц = 0, вытекает
Я(/)-0, /0^^^1- (1-89)
Если кривые ^-(r), w7(/), vy-(0 , i = Q,n ,j = \,m реализуют минимум функционала
по отношению ко всему классу допустимых линий, то они тем более реализуют
минимум функционала по отношению к линиям с закрепленными концами, т.е. по
отношению к более узкому классу линий. Отсюда следует, что условие (1.89)
справедливо и при граничных условиях (1.68), (1.69).
31*
468 Методы теории оптимального управления. Часть III
1,5.3. Необходимые условия Вейерштрасса
Для сформулированной в настоящем параграфе задачи Майера В.А. Троцким [57]
было получено необходимое условие Вейерштрасса сильного минимума, которое
заключается в следующем: если на функциях jcy(/), Uj(t\ v,(t), i = 0,n, j = \,m
реализуется сильный минимум функционала (1.70), то в каждой точке отрезка t0 < t < /,
должно выполняться неравенство
Я(х,и,УД,ц)<Я(х,и,уД,ц),
здесь векторы х, u, v соответствуют кривой, на которой реализуется минимум
функционала, a U и V - любые управления, удовлетворяющие условиям
a;(t/,-,K,) = 0, у=п.
Если вспомнить, что дополнительное управление v в функцию Нх не входит и
что #м = 0 , то условие Вейерштрасса сильного минимума можно записать в виде
Ях(х,иД)<Я^(х,иД). (1.90)
В неравенстве (1.90) и - оптимальное управление, a U - любое допустимое
управление, т.е. управление, удовлетворяющее условиям
A) <Uj <А], j=un.
Таким образом, на кривой, дающей сильный минимум функционалу (1.70),
функция Мх, рассматриваемая как функция вектора и, должна принимать максимально
допустимое значение.
Сформулированные в данном параграфе необходимые условия оптимальности,
как нетрудно видеть, практически полностью совпадают с принципом максимума
Понтрягина. Поэтому их можно успешно использовать для определения
оптимального управления и оптимальной траектории. Однако на практике целесообразно
пользоваться непосредственно принципом максимума, который обладает большей
общностью и который формулируется в удобной для практического использования
компактной форме.
Глава 2. Принцип максимума Понтрягина 469
ГЛАВА 2. ПРИНЦИП МАКСИМУМА ПОНТРЯГИНА
Принципом максимума называют математический метод, который был
разработан академиком Л. С. Понтрягиным и его учениками для решения задач
оптимального управления. Предложенная авторами метода математическая модель процесса и
чёткое компактное формулирование основного результата - сильных необходимых
условий оптимальности - оказались очень удачными. Метод пользуется большой
популярностью. Эгому в немалой степени способствовала изданная в 1961 г.
монография «Математическая теория оптимальных процессов», которая хорошо отвечала
духу того времени и была написана с большим педагогическим мастерством.
Несмотря на то, что первые публикации по принципу максимума появились уже более
сорока лет назад, принцип максимума и в настоящее время остаётся основным
инструментом для определения оптимального управления и оптимальных траекторий.
В данной главе рассматриваются задачи оптимального управления, когда заданы
ограничения только на вектор управления. Этому соответствует классический
вариант принципа максимума, который наиболее часто используется на практике. Наряду
с изложением условий оптимальности в форме принципа максимума, большое
внимание уделяется рассмотрению их применения для определения оптимального
управления и оптимальной траектории.
Строго говоря, принцип максимума ориентирован на определение программного
оптимального управления. Однако он часто позволяет легко выявить структуру
оптимального управления и вид оптимальных траекторий, что даёт возможность
выделить всю совокупность оптимальных траекторий. Таким образом, принцип
максимума молено успешно использовать для синтеза оптимального управления.
Большинство рассмотренных ниже примеров посвящены именно определению всей
совокупности оптимальных траекторий и, следовательно, синтезу оптимального управления.
Изложение материала начинается с формулировки задачи оптимального
управления, хотя она приводится и в первой главе работы. Однако такой способ изложения
позволяет читателю (особенно читателю, которого интересует прежде всего
прагматическая сторона - решение практических задач по определению оптимального
управления) изучить один из наиболее эффективных методов теории оптимального
управления, не изучая первой главы работы.
2.1. НЕОБХОДИМЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ В ФОРМЕ
ПРИНЦИПА МАКСИМУМА
В §1.5 были получены необходимые условия, которым должны удовлетворять
траектория и управление, реализующие сильный минимум функционала. В
настоящем параграфе они обобщаются и приводятся в компактной форме принципа
максимума.
2.1.1. Задача оптимального управления
Рассмотрим сначала конкретный пример. Пусть имеется двигатель постоянного
тока, который работает на механизм М Движением двигателя можно управлять,
изменяя напряжение ия, подводимое к цепи якоря (напряжение ив будем считать
постоянным). Из условия электрической прочности напряжение, подводимое к цепи
якоря, должно быть ограничено:
\иа\<А.
470 Методы теории оптимального управления. Часть III
Рис. 2.1. К постановке задачи оптимального управления
Пусть требуется осуществить поворот вала двигателя на некоторый заданный
угол. Интуитивно ясно, что существует бесконечное множество функций ия((),
которые решают поставленную задачу, т.е. обеспечивают поворот вала двигателя на
заданный угол. Но тогда естественно поставить ещё одну задачу: среди функций
мя(/)> решающих первую задачу, найти наилучшую в каком-либо смысле, например,
осуществляющую поворот на заданный угол за минимально возможное время или с
минимальной затратой энергии.
Сформулируем задачу оптимального управления.
Рассмотрим объект или процесс, который описывается системой
дифференциальных уравнений
at
или векторным уравнением
d\ ,
— = f(x,u),
dt
здесь х = (х,,х2,...,*„) и f = C/i,/2,...,/J - п-мерные векторы, u = (w,,w2,...,ww) -
т -мерный вектор управления. Вектор х называют фазовым вектором системы, или
вектором состояния.
Будем полагать, что вектор управления и может принимать свои значения из
некоторого множества U . В отличие от множества, рассмотренного в параграфе 1.5,
U может быть любым множеством т -мерного евклидова пространства, например,
оно может состоять из совокупности изолированных точек. На рис. 2.2 при т = 2
изображён пример множества U , состоящего из четырёх изолированных точек.
В этом, кстати, заключается существенное отличие принципа максимума от
вариационного исчисления (см. §1.5). Из-за принятого способа построения вариаций в
вариационном исчислении U может быть только областью в классическом смысле
этого слова, т.е. когда оно удовлетворяет свойству связности.
Будем предполагать, что в уравнениях (2.1) функции /• (/ = 1,л) непрерывны по
всем своим переменным и непрерывно дифференцируемы по переменным ху
(у = 1,л). В качестве допустимых управлений рассматриваются кусочно-
непрерывные функции uv(t) (v = 1,т), удовлетворяющие условию и (t)eU .
Глава 2. Принцип максимума Понтрягина
471
©-
©--
"1
Рис. 2.2. Пример множества 6/
Векторное пространство с декартовыми координатами xl,x2,...,xn будем
называть фазовым пространством системы (2.1) и обозначать X. Каждому вектору х в
фазовом пространстве соответствует некоторая точка (фазовая точка). Если задан
вектор и(/) и начальное условие х(/0) = х° =(x1°,jc2,...,x^), то систему уравнений
(2.1) можно решить. Разным вектор-функциям и(0 будут соответствовать различные
решения х(/) уравнений (2.1), т.е. выбором вектора и (О можно управлять
движением системы. Решению х(/), /0 -'-'i > в фазовом пространстве X соответствует
некоторая линия, которая называется фазовой траекторией системы.
Пусть в фазовом, пространстве X заданы две точки х° = (х,0,;^,...,;^) и
х1 = {x\,x\,...ix)l). Рассмотрим следующую задачу. Требуется среди допустимых
управлений и(/), (0<(<^,т.е. кусочно-непрерывных вектор-функций u(t)eU
(моменты /0 и tx не фиксированы), переводящих фазовую точку системы (2.1) из
заданного начального положения х° (х(Г0) = х°) в заданное конечное положение х1
(х( /j) = х1), найти управление и траекторию, доставляющие минимум функционалу
J = I fo(xbx2,...,xn,u],u2i...,um)dt. (2.2)
'о
Управление и(/) и траектория х(/), решающие поставленную задачу, называются
оптимальными.
Выбором функции /0(х,и) функционалу (2.2) можно придавать различный
физический смысл. Если, например, функция /0(х,и) задаёт секундный расход топлива,
то функционал (2.2) выражает общий расход топлива, затрачиваемый на движение от
точки х° до точки х1. Ниже особое внимание уделяется частному случаю, когда
/0 = 1. В этом случае функционал
J
= |Л = /,-|
(2.3)
задаёт время движения. Управление и траектория, минимизирующие функционал
(2.3), называются оптимальными по быстродействию.
Будем предполагать, что функции /0(х,и) и ——■— (/ = 1,я) являются непре-
дх,
рывными по всем своим переменным.
472
Методы теории оптимального управления. Часть III
2.1.2. Необходимое условие оптимальности
Введём (п + 1) -мерный вспомогательный вектор i|/ (0 = (Уо(0> У\(0>---> УДО)»
определяемый уравнениями:
• = о,
dt ^ "
*М, / = п
(2.4)
Если задано управление и(/), начальная точка и, в соответствии с уравнениями (2.1),
определена траектория х(/), то система уравнений (2.4) принимает вид
'd\\i0
dt
■ = 0,
<fy/(O_
= -5>,
^(x(/),u(Q) —
, / — 1, П,
(2.5)
dt % > дх,
т.е. является системой линейных однородных уравнений. Из теории
дифференциальных уравнений известно, что такая система при любых начальных условиях имеет
единственное решение, причем функция ц/(0, являющаяся решением уравнений
(2.5), непрерывна по t.
Введём функцию
Я(ч1,х,и) = Хч/,-У;(х,и). (2.6)
/=0
Функцию #(i|/,x,u) называют функцией Гамильтона. Непосредственной
проверкой убеждаемся, что уравнения (2.4) могут быть записаны в виде
rf$c)=Of
dt
dtf(i|/,x,u)
(2.7)
, / = 1,л.
dt дх,
Аналогичным образом можно показать, что уравнения (2.1) могут быть записаны
следующим образом:
dt
dtf(i|/,x,u) —
При фиксированных v|/ и х функция #(i|/,x,u) становится функцией вектора
управления и. Обозначим
M(vj/, x) = sup //(vj/, х, u).
U € (/
Если точная верхняя грань значений функции #(\j/,x,u) как функции вектора и
достигается в некоторой точке, принадлежащей множеству U , то
sup //(i|/,x,u) = max #(i|/,x,u).
uel/ uef/
Теорема 2.1 (принцип максимума Понтрягина). Пусть u(0, /0 -^-^i ~
допустимое управление, a \(t) - соответствующая ему траектория, переводящие
фазовую точку х системы (2.1) из заданного начального положения х в заданное
конечное положение х1, так что х(/0) = х° , х(^) = х1. Если u(t) и x(t) - оптимальное
Глава 2. Принцип максимума Понтрягина 473
управление и оптимальная траектория, то найдется непрерывная вектор-функция
\\i(t).удовлетворяющаяуравнениям (2.7), что:
1) в каждый момент времени /, /0 < t < Г,, функция H(\\f(t),\(t),u),
рассматриваемая как функция переменного и , достигает в точке и = и(/) максимума
Я(ч»(0, х(/), и(0) = А/(ч»(О, х(0); (2.8)
2) выполнено условие нетривиальности решения системы уравнений (2.7)
V(0*0; (2.9)
3) в конечный момент времени tx
Ч/0(О<0, Л/(М/(/1),х(Г1)) = О. (2.10)
Можно показать (см. параграф 1.5), что если выполняются соотношения (2.7) и
(2.8), то функции vj/0(/) и А/(\|/(/), х(/)), рассматриваемые как функции времени t,
постоянны. Поэтому соотношения (2.10) можно проверять не обязательно в
конечный момент времени /],ав любой момент времени / е [to,t\].
Отметим, что теорема 2.1 задаёт необходимые условия сильного минимума
функционала (2.2) в рассматриваемой задаче на условный минимум.
Доказательство принципа максимума в том общем виде, как он сформулирован
выше, в работе не приводится. Однако, если множество U задаётся неравенствами
|иу|<Л7., у=пь (2.11)
то практически все условия теоремы 2.1 следуют из рассмотренной в параграфе 1.5
задачи Майера вариационного исчисления. При этом вектору \[/ = (v|/0,vj;1,...,vj;w) в
задаче Майера соответствуют множители Лагранжа \0,\]9...,\п (уравнения (2.4)
совпадают с уравнениями (1.75)), функции #(ц/,х,и) - функция Нх(\0,Х]9...,\п,
щ,и2,...,ит). Некоторые дополнительные условия, которые имеются на первый
взгляд в задаче Майера, представляют собой подробно записанное (с применением
множителей Лагранжа) условие максимума функции Яя. Отметим далее: как
показывает анализ приведённого в параграфе 1.5 вывода необходимых условий минимума
функционала, его можно повторить практически при любом способе задания области
U . Необходимо только, чтобы U была областью в классическом смысле этого
слова, т.е. удовлетворяла свойству связности.
Единственное отличие теоремы 2.1 от условий оптимальности, приведённых в
параграфе 1.5, заключается в следующем: в соответствии с теоремой 2.1
уо(/) = const < 0 , а в задаче Майера X0(t) = -1. Однако это отличие не столь
существенно. Теоремой 2.1 вектор v|/(r) задаётся с точностью до произвольного
постоянного положительного множителя. Действительно, легко установить, что если
следующие функции \|/(0, х(0, и(0 удовлетворяют условиям теоремы 2.1, то и функции
ky(t), х(/), и(0, где k = const > 0, также удовлетворяют условиям теоремы 2.1.
Поэтому при \yo(t)*O всегда выбором k можно добиться выполнения соотношения
v|/0(/) = -l. Отметим, что ситуация, когда \|/0(г) = 0, встречается редко и связана с
понятием анормальности вариационной задачи [5].
Получим из теоремы 2.1 необходимые условия оптимальности в задаче на
быстродействие. Положим /о = 1. Тогда функция (2.6) принимает вид
Я(м/,х,и) = 1|;о+Х^(х'и)- (2Л2)
474 Методы теории оптимального управления. Часть III
Введём п -мерный вектор vj/ = (v|/1,vj/2,...,vj/w) и функцию
Я(у,х,и) = 5>,/(*,1|). (2.13)
В соответствии с уравнениями (2.7) вектор v|/ (О задаётся уравнениями
^ = _ая(у,х,«)л.=-
<# dxt
Обозначим
A/(\|/,x) = sup//(\j/,x,u).
U€t/
Из (2.12) и (2.13) следует, что если
A/(i|/,x) = #(i|/,x,u*),
то
М(\|/,х) = Я(\|/,х,и*).
Пусть и(/) и х(0 - оптимальные по быстродействию управление и траектория.
Как следует из (2.8), (2.10), (2.12) и (2.13), в этом случае
Я(у (0, х(0, и(0) = Щч (0, х(0) = А/(у (0, х(0)-v|/0 = -v|/0 > 0 .
Полученный результат сформулируем в виде ещё одной теоремы.
Теорема 2.2 {принцип максимума в задачах на быстродействие). Пусть n(t) и
х(0, t0 < t < /j, - допустимое управление и соответствующая ему траектория,
переводящие фазовую точку из заданного начального положения х в заданное
конечное положение х1. Если управление и(/) и траектория \(t) являются
оптимальными по быстродействию 1 то найдётся непрерывная вектор^функция
\|/ (0 = (vj/j (0, v|/2 (0> • • •»Wn (0) > удовлетворяющая уравнениям (2.14), ч/яо;
1) в каждый момент времени t, f0 < / < /j, функция Я(\|/ (/), х(/), и),
рассматриваемая как функция переменного и, достигает в точке и = и(0 максимума
Я(у(0,х(0,и(0) = M(i|/(0,x(0); (2.15)
2) выполнено условие нетривиальности решения системы уравнений (2.14)
4/(0*0;
3) в конечный момент времени tx
М{у{Щх(Н))>Ъ. (2.16)
Как и в случае теоремы 2.1, отметим, что если выполнены соотношения (2.14) и
(2.15), то функция М(\|/(0, х(0) постоянна. Поэтому соотношения (2.16) можно
проверять в любой момент времени / е [/0^il •
Проанализируем теорему 2.1. Покажем, что она содержит «полную систему
условий», т.е. число условий совпадает с общим числом неизвестных.
При решении задачи необходимо найти п функций хД0> (" + 1) функций ij/ДО и
т функций Uj(t), т.е. всего 2л + 1 + /и неизвестных функций. Для определения
указанных функций можно воспользоваться п, уравнениями движения (2.1), (я + 1)
уравнениями (2.7) и т условиями максимума (2.8). Условия максимума (2.8)
позволяют в каждый момент времени / определить управления Uj(t). Если, например,
Глава 2. Принцип максимума Понтрягина 475
максимум функции #(\|/(r),x(/),u(0) достигается во внутренней точке области U .
то должны выполняться соотношения
d#(i|/(0,x(0,u)
dUj
= 0, j = \,m.
Далее, In +1 из указанных уравнений являются дифференциальными. Общее
решение этих уравнений будет содержать 2л+ 1 произвольных констант. Неизвестно
также время движения /, -10, т.е. общее число неизвестных чисел равно 2п + 2 . Для
нахождения указанных чисел можно использовать 2/7 условий прохождения
оптимальной траектории через заданные точки /их1, условие
A/(Vft),x(/,)) = 0.
Выше уже отмечалось, что теоремой 2.1 вектор \|/(/) определяется с точностью до
постоянного положительного множителя. Поэтому всегда, например, можно положить
Таким образом, общее число условий совпадает с общим числом неизвестных.
Поэтому можно ожидать, что условия теоремы 2.1 позволят выделить одну или
несколько траекторий, проходящих через заданные точки х° и х1. Так как теорема 2.1
задаёт необходимые условия оптимальности, то оптимальная траектория будет
находиться среди выделенных траекторий.
К настоящему времени накоплен достаточно богатый опыт по применению
принципа максимума для определения оптимального управления и оптимальной
траектории. Этот опыт показывает, что задаваемые теоремой 2.1 (теорема 2.2 является
частным случаем теоремы 2.1) необходимые условия оптимальности являются сильными
в том смысле, что выделяемые ими управление и траектория, как правило, являются
оптимальными. Далее, известно, что принцип максимума, как необходимое условие
сильного минимума, не может быть усилен.
Рассмотрим несколько примеров.
Пример 2.1. Рассмотрим объект, движение которого задаётся уравнением
9-
здесь и - управляющий параметр, который должен удовлетворять условию
\и\<А, (2.18)
где А - заданное положительное число. В соответствии с формализмом принципа максимума представим
уравнение (2.17) в виде системы дифференциальных уравнений первого порядка
-ЗГ=х*'1Г=и- (2|9)
Будем решать задачу о наибыстрейшем переводе фазовой точки системы (2 19) из заданного
начального положения в начало координат (точку х1 = 0 ) В качестве начальной точки будем рассматривать любую
точку фазового пространства. Это позволит выделить всю совокупность оптимальных траекторий
Воспользуемся теоремой 2.2 Составим функцию Гамильтона
#(\|/,X,u) = y,*2+\J/2M.
Принимая во внимание неравенство (2.18), из условия максимума функции Гамильтона найдем
M = ^signv|/2(/). (2 20)
Вспомогательные переменные yx(t) и \|/2(0 находятся из системы уравнений
м=0>^=-„ (2.21)
Выпишем решение системы уравнений (2.21):
Vi(0 = Q, V2(O = -C,/ + C2,
где С, и С2 - произвольные константы Тогда условие (2.20) принимает вид
30*
476
Методы теории оптимального управления. Часть III
w = ^sign(-C,/ + C2) (2.22)
Графиком функции у2(0 является прямая линия, и поэтому функция vj/2(/) может изменять знак не
более одного раза Из (2 22), таким образом, следует, что оптимальное управление u(t) является кусочно-
постоянной функцией, принимающей значения А и -А и имеющей не более двух интервалов
постоянства управления Обратно, любая такая функция u(t) может быть получена из (2 22) при соответствующем
выборе постоянных С, и С2.
Найдем фазовую траекторию системы (2 19) при ы = А . Имеем*
x2 = At + sl9 *, =^Л/2+$,/ + .у2 (2 23)
Выразив из первого уравнения (2 23) время t и подставив его во второе уравнение, получим
_1_
' 2А
(2 24)
где s =57 sf - произвольная постоянная Аналогичным образом легко показать, что при и = -А
1А
фазовые траектории системы (2 19) являются параболами вида
xx=~x\ + s\ (2.25)
здесь s** - произвольная постоянная.
На рис. 2 3 и 2 4 представлены параболы семейств (2.24) и (2.25) соответственно.
*2
Рис. 2.3. Параболы семейства (2.24)
По параболам семейства (2 24) фазовая точка движется снизу вверх, а по параболам семейства (2 25) -
сверху вниз, тк в соответствии со вторым уравнением (2 19) при и- А координата х2 возрастает и при
и-~А убывает
х2
Рис. 2.4. Параболы семейства (2.25)
Глава 2. Принцип максимума Понтрягина
477
Рассмотрим фазовую траекторию, на начальном участке которой фазовая точка движется под
воздействием управления и = А по параболе семейства (2.24), а заканчивается движение под воздействием
управления и--А по параболе семейства (2.25). При этом заканчивается движение по той из парабол семейства
(2.25), которая проходит, через начало координат, т к конечной целью управления является перевод фазовой
точки в начало координат. Указанная траектория изображена на рисунке 2 5 (линия MRO ).
Если на начальном участке фазовая точка движется под воздействием управления и--А , а
заканчивается движение под воздействием управления и = Ау то движение происходит по траектории M'R'O,
которая симметрична относительно начала координат траектории MRO
*г
Рис. 2.5. График фазовой траектории
На рис 2 6 изображена совокупность всевозможных оптимальных траекторий Эти траектории
действительно являются оптимальными, т к. для каждой начальной точки х° существует единственная
траектория, удовлетворяющая необходимым условиям оптимальности (теореме 2 2), а по условию задачи ясно,
что оптимальное управление существует
*2
R'
Рис. 2.6. Графики оптимальных траекторий
Из рис 2 6 видно, что переключение управления происходит на линии ROR' Выше линии ROR'
оптимальное управление и = -А , а ниже линии ROR' оптимальное управление и - А . Линия RO является
частью параболы семейства (2 25) и задаётся уравнением
а линия R'O - частью параболы семейства (2 24) и задаётся уравнением
478 Методы теории оптимального управления. Часть III
Введем функцию
\-А выше линии ROR' и на линии RO,
[А ниже линии ROR' и на линии R'O.
Тогда в каждый момент времени / оптимальное управление
и = и(х(0).
Если в уравнениях (2 19) положить м = и(;с), то при каждом начальном условии решением системы
уравнений (2 19) будет идущая в начало координат оптимальная по быстродействию траектория
Пример 2.2. По-прежнему рассматривается объект, движение которого задаётся уравнениями (2.19)
Будем предполагать, что на управляющий параметр и наложено ограничение
\и\<\ (2.26)
В качестве критерия оптимизации рассмотрим функционал
7
J = \(k+\u\)dtt (2 27)
о
здесь к - некоторое положительное число
Функционал (2 27) является линейной комбинацией двух функционалов
т г
Jx=\dt и J2=j\u\dt,
о о
один из которых задает время движения, а второй - расходуемые на управление ресурсы Число к является
весовым коэффициентом, с помощью которого устанавливается компромисс между двумя этими критериями
Требуется найти управление и траекторию, переврдящие фазовую точку из заданного начального
состояния в начало координат и минимизирующие функционал (2.27). В качестве начальных предполагается
рассмотреть все точки фазовой плоскости
В соответствии с теоремой 2.1 функция Гамильтона
Н(\\1,х,и) = \\>0(к + \и\) + \у]х2+у2и . (2 28)
Вектор \|/(0 определяется уравнениями
^ = 0,^ = 0,^ = -*,. (229)
dt dt dt
Выше уже отмечалось, что теоремой 2.1 вектор \|/(/) определяется с точностью до постоянного
положительно! о множителя. Далее, поскольку \j/0(/) = const < 0 , положим vj/0(/) = -1. Тогда функция (2.28) примет вид
Н{уцух,и) = -к-\и\+\ц{х2 + v|/2w (2 30)
Для определения оптимального управления необходимо максимизировать функцию Гамильтона как
функцию управления, и, в соответствии с (2 30), максимизация функции Гамильтона выливается в
максимизацию функции
АН = -\и\ + \\>2и
Представим АН в виде
Г(м,2-.>,пРии>0( (2
1(4*2 +^U ПРИ U~®
Из условия максимума функции (2 31), принимая во внимание ограничение (2 26), найдем
1, если у2(/)>1,
-1, если у2(0<-1>
u\t) = • 0, если | v|/2(/) | < 1, (2 32)
€[0,1], если vj/2(/) = 1,
е [-1,0], если vy2(/) = -l,
здесь символом u(j) обозначено управление, максимизирующее функцию Гамильтона.
Введём в рассмотрение функцию «зоны нечувствительности» у = dez(jc), которая определяется
соотношениями
0, если |*| <1,
sign х, если |*| >1,
€[0,1], если jc = 1,
€[-1,0], если х = -\
У =
Глава 2. Принцип максимума Понтрягина
479
На рис 2 7 приведен график функции у = dez(x)
Равенство (2.32) можно записать в виде
*/(/) = dez(i}/2(/)) (2 33)
В конечный момент времени Т \{Т) = 0 , т к. конечной целью управления является перевод фазовой
точки в начало координат Покажем, что
|М/2(Г)|>1.
(2 34)
а У
-1
-1
Рис. 2.7. График функции dez(x)
Запишем равенство
Н(у(Т)ЖПи\Т)) = -к-\и\п\ + ЫТ)-х2(Т) + у2(Т) и\Т) (2 35)
Если |ц/2(Г)| < 1 , то в соответствии с (2.33) и(Т) = О и из (2 35) следует
Н(у(Пх(Пи(Т)) = -к*0 (2 36)
Соотношение (2.36) противоречит второму условию (2.10) При 1|/2(Г) = 1 и(Т) е [0,1], а при уг(Т) = -1
и(Т) е [-1,0]. Равенство (2.34) в этом случае также приводит к соотношению (2.36).
Из неравенства (2.34) следует, что в начало координат фазовая точка может попасть либо с
управлением u{t) = 1, либо с управлением u(t) = -1.
Проинтегрируем уравнения (2.29):
Vi(0 = Vi(0), v|/2(/) = -i|/,(O)/ + ij/2(O). (237)
Строго говоря, уравнения (2.29) допускают решение
Vi(0 = 0, \|/2(/) = ±l. (2.38)
В этом случае соотношение (2 33) не определяет управление u{t) однозначным образом. Однако решение
(2 36), как легко убедиться, противоречит условию
Л/(м/(О,х(/)) = 0
и поэтому его следует исключить из дальнейшего рассмотрения
В соответствии с (2.37) график функции \|/2(/) является прямой линией Вид этой прямой
определяется начальными условиями \j/j(O) и vj/2(O). Далее, если
\|/2(/) = vj/2(0),
то в соответствии с неравенствами (2 34) | у2(0) |> 1.
Рассмотрим оптимальное управление и оптимальную траекторию, соответствующие функции \|/2(/),
представленной на рис 2 8.
Управление u*(t) в этом случае имеет вид, изображенный на рис. 2.9.
Как следует из (2 24) и (2 25), при и = 1 фазовая точка движется по параболе семейства
(2 39)
*i = 2*2-
а при и = -1 - по параболе семейства
1 2 ♦•
Xl=--x2+s
здесь s* и 5** - произвольные константы. При u(t) e 0
(2 40)
480
Методы теории оптимального управления. Часть III
т е. при и s 0
*2(/) = *2(0),
xl(t) = x2(O)t + xl(Q),
точка движется по прямой линии
x2(t) = x2(O)
V2
-1
Рис. 2.8. График функции у2(/)
(2 41)
i
1
-1
i U
h
Т
1 /
1
Рис. 2.9. График оптимального управления
На рис 2 10 изображено семейство прямых (2 41)
Рис. 2.10. Графики прямых, определяемых уравнением (2.41)
Таким образом, траектория, соответствующая изображенному на рис 2 9 управлению и{1), состоит
из парабол соответственно семейств (2.39) и (2.40), соединенных между собой отрезком прямой (2 41)
(рис.2 11).
На заключительном участке фазовая точка движется по параболе семейства (2.40), причем по той из
парабол семейства (2 40), которая проходит через начало координат Эта парабола задается уравнением
I 2
а участок параболы, по которому фазовая точка переводится в начало координат, - уравнением
*i=--*2> *2^°
(2 42)
Глава 2. Принцип максимума Понтрягина
481
и = 0
и = \
к = 1
Рис. 2.11. График оптимальной траектории
Переключение управления с м*(/) = 0 на u*(t) = -\ происходит именно в точках участка параболы (2 42)
Таким образом, можно записать
Линию, которая задается уравнением (2 42), обозначим yj"
Найдем линию, в точках которой происходит переключение уравнения с u\t) - 1 на u(t) = О
Воспользуемся равенством M{y(t), x(/)) = 0 Для момента времени и имеем
-Л-|м(/2+О)| + м/,(/2)д:2(/2) + 1|/2(Гг)1/(/2+О) = О (2 43)
В соответствии с рис 2 8 и 2 9
i/(/2+0) = -l, vj/2(/2) = -l
Из (2.43) следует
к
\|/,(/2) = \|/,=-
*2«2)
(2 44)
Найдем время движения с управлением и (0 = 0 Так как \|/2(*,) = 1, vj/2(/2) = -1 , то из равенства
следует
2 ' V,
или, принимая во внимание (2 44),
/,-/, =-
2х2(/2)
(2 45)
В интервале t{ < t < t2 фазовая точка движется под воздействием управления u"(f) = 0 Поэтому
*i('2) = *2('l) Й-О + ^Й).
Поскольку дг2(О = *2 (h) >то можно записать
Точка v(/2) лежит на линии у|" и, следовательно,
Подставив (2 47) в (2 46), получим
*|('2) = -^*2('2)
*l('l) = -f^|]*2(y
(2 46)
(2 47)
Далее, учитывая, что jc2(/2) = x2(t\), можно записать
482
Методы теории оптимального управления. Часть III
*i«.) = -(j+f}*22('i)-
Итак, переключение управления с и*(0 = 1 на и'(1) = 0 происходит в точках кривой
(2 48)
Линию, задаваемую уравнением (2.48), обозначим у£
Рассмотрев управление u*(t), представленное на рис. 2.12, аналогичным образом можно показать, что
переключение управления с м*(/) = -1 на и*(/) = 0 происходит на линии
а переключение управления с и*(/) = 0 на м*(/) = 1 происходит на линии
(2 49)
(2.50)
Линии, задаваемые уравнениями (2.49) и (2.50), обозначим соответственно у2 и у2. Пусть, далее,
7i = УГ U уГ , а у2 = Уг U yj
L
1
-1
i U
h
' h
1
1
j ^
Т t
Рис. 2.12. График управления u(t)
Таким образом, на фазовой плоскости существуют две линии переключения у, и у2 (см. рис 2.13)
Выше линии у, и у2 управление м*(/) = -1, ниже линии у, и у2 управление м*(/) = +1 В промежутке
между линиями у, и у2 и*=0 На рис. 2.13 жирными линиями выделены две фазовые траектории,
которые удовлетворяют теореме 2.1. Только управления и траектории, задаваемые рис 2.13, могут быть
оптимальными.
и = -\
Рис. 2.13. Графики фазовых траекторий
Глава 2. Принцип максимума Понтрягина
483
Далее, поскольку для каждой начальной точки существует только одна траектория, удовлетворяющая
необходимым условиям оптимальности (условиям теоремы 2.1), а по физическим соображениям
существование оптимальных траекторий представляется вполне очевидным фактом, то это позволяет заключить,
что полученные выше управления и траектории являются оптимальными.
Пусть
*1=Ж*2)
- уравнение линии у,, а
X\^f2(x2)
- уравнение линии у2. Тогда оптимальное управление можно задать равенством
Г-1, если х]-/х(х2)>0 и х,-/2(х2)>0,
и = \ 1, если х1 -/,(х2)<0 и х,-/2Ос2)<0, (2.51)
[ 0, если sign = [х, - /,(*2)] = -sign[x, -/2(х2)]
Строго говоря, равенство (2.51) не задает значение оптимального управления на линии у,, хотя линия у,
образована двумя оптимальными фазовыми траекториями системы (2 19). Как будет показано ниже
(см гл. 5), задание управления на линии переключения не требуется.
На рис. 2.14 изображена структурная схема оптимальной системы.
а
li
А
1
-1
_L
-1
к
1
—
—
—►
-Л
-д
"Г.
1
-1
i+/i(*2>;
С
•l+/2(*2) d
\
и
' fi(x2)
5н—
i.
1
S
х
с
L
Щ
l
1
S
X
Рис. 2.14. Структурная схема оптимальной системы
Если функции х1 -/,(х2) илг/2(х2) имеют разные знаки, то <т(/) = 0 и управление u(t) = 0 . Если
указанные функции имеют одинаковые знаки, то a(/) = -2sign[x, -f\(x2)] и сигнал управления
i/(O = -sign[x,-y;(x2)].
2.2. ЗАДАЧА С ПОДВИЖНЫМИ КОНЦАМИ. ПРИНЦИП МАКСИМУМА
ДЛЯ НЕАВТОНОМНЫХ СИСТЕМ
2.2.1. Задача с закрепленным временем
В §2.1 была сформулирована задача оптимального управления. При этом
предполагалось, что время движения не задано. Поскольку уравнения (2.1) являются
автономными, то можно положить начальный момент времени t0 фиксированным, а
конечный момент времени t} свободным.
484
Методы теории оптимального управления. Часть III
Будем теперь считать, что моменты времени /0 и /j фиксированы. Обратимся к
рассмотренной в §1.5 задаче оптимального управления методом классического
вариационного исчисления. При фиксированных моментах времени /0 и ^ вариация
функционала будет по-прежнему задаваться равенством (1.74), в котором следует положить
5^ = 0 . Это, в свою очередь, приведёт к тому, что из необходимых условий минимума
выпадут условия (1.87) и, следовательно, равенство (1.88), доказательство которого
основывается на соотношениях (1.87). Если теперь совершить обратный переход от
приведенных в §1.5 необходимых условий оптимальности к принципу максимума
(теореме 2.1), то получим все условия теоремы 2.1, кроме соотношения
A/((/,),x(/,)) = 0. (2.52)
Таким образом, необходимые условия оптимальности для задачи с
фиксированным временем движения задаются теоремой 2.1, из формулировки которой следует
исключить условие (2.52). Отметим, что соотношение
Л/(у(0,х(0) = const
по-прежнему сохраняет свою силу. Однако функция M(\\t(t), x(t)) теперь не
обязательно должна равняться нулю.
2,2.2. Задача с подвижными концами
В §2.1 предполагалось, что начальное и конечное состояние системы строго
определены, т.е. в фазовом пространстве заданы начальная х° и конечная х1 точки,
которые следует соединить оптимальной траекторией. Рассмотрим более общий
случай. Предположим, что вместо начальной и конечной точек заданы начальное s0 и
конечное s} многообразия. Пусть многообразие sQ задаётся уравнениями
<(>/(*!, х2,...,*„) = О, / = 1,А р<п, (2.53)
а многообразие s, - уравнениями
pv(x1,x2,...,xJ = 0, v = U, k<n. (2.54)
Если л = 3, а /? = £ = 1, то многообразия sQ и sx представляют собой поверхности
в трехмерном фазовом пространстве. При п - 3, р = 2, к = 1 многообразие sQ задается
как множество, образованное пересечением двух поверхностей (рис. 2.15), т.е.
является линией в трехмерном фазовом пространстве, а многообразие s] по-прежнему
представляет собой поверхность.
Рис. 2.15. Начальное s0 и конечное S] многообразия
Глава 2. Принцип максимума Понтрягина
485
Функции ф/(х1,х2,...,хя) = 0 и Pv(x,,jc2,...,*„), l = \,p, v = l,k, будем полагать
непрерывно дифференцируемыми по всем своим аргументам. Введем вектор
м* Х1)-(<тш мл
^ ах, дх2 дхп )
называемый градиентом функции ф (х).
Многообразие sQ называется гладким, если в каждой точке xe.s0 следующие
векторы
УФ1(х),Уф2(х),...,УФя(х) (2.55)
линейно независимы. Условие линейной независимости векторов (2.55) эквивалентно
требованию, чтобы ранг матрицы
дц>} дщ Эф,
дхх
дф2
дхх
д<Рр
дх2
<3ф2
&г
дх„
5ф2
дх„
их, йх->
дх„
был равен р. Аналогичным образом определяется гладкость многообразия s{. В
дальнейшем многообразия s0 и sx полагаются гладкими.
Рассмотрим следующую задачу: требуется среди допустимых управлений и(/),
переводящих фазовую точку х с многообразия ^0 на многообразие 5,, найти такое,
которое доставляет минимум функционалу (2.2). Так как в поставленной задаче
концы траектории х(/) могут скользить по многообразиям s0 и s}, соответствующую
задачу оптимального управления будем называть задачей с подвижными концами.
Пусть и(0 и х(0> h -t -h ~ управление и траектория, решающие поставленную
выше задачу оптимального управления с подвижными концами. Но тогда найдутся
точки х° и х1, лежащие соответственно на многообразиях s0 и s} (рис. 2.15). Ясно,
что управление и(/) и траектория x(t) являются оптимальными и в смысле
рассмотренной в §2.1 двухточечной задачи оптимального управления, т.е. управление и(/) и
траектория х(г) должны удовлетворять принципу максимума (теореме 2.1).
Таким образом, принцип максимума (теоремы 2.1 и 2.2) остается в силе и для
задачи с подвижными концами. Однако в этом случае необходимо иметь некоторые
дополнительные условия, которые позволили бы определить положение точек х° и
х1 на многообразиях sQ и s}.
Для получения указанных дополнительных условий обратимся к параграфу 1.5, в
котором приводятся необходимые условия оптимальности, полученные методами
классического вариационного исчисления. Дополнительные условия задаются
соотношениями (1.79). Выпишем эти условия, используя обозначения, принятые в
принципе максимума:
, ч А - 5ср,(х)| . —
(2.56)
/=i
ix = x(/0)
486 Методы теории оптимального управления. Часть III
здесь р,~ и р/+, / = /,/?, v = l,£ - некоторые числа. Во избежание недоразумений
отметим, что имеющееся в (1.79) дополнительное условие вида
Vo('o) = Po (2.58)
в равенстве (2.56) опущено, т.к. Ро - произвольное число, и, следовательно,
соотношение (2.58) не несет какой-либо новой информации.
Будем говорить, что на левом конце траектории х(/) (в момент /0) выполнено
условие трансверсальности, если найдутся такие числа р,~ (/ = 1,р), что имеют место
соотношения (2.56). Аналогично, говорят, что на правом конце траектории х(/)
выполнены условия трансверсальности, если найдутся такие числа р* (у = 1,я), при
которых выполняются равенства (2.57). В смешанном случае, т.е. когда один конец
траектории закреплен, а второй подвижен, условия трансверсальности следует
относить к подвижному концу траектории.
Сформулируем окончательный результат. Необходимые условия оптимальности в
задаче с подвижными концами заключаются в следующем:
1) оптимальное управление u(t) и траектория x(t) должны удовлетворять
принципу максимума (теореме 2.1 или 2.2);
2) на подвижных концах траектории должны выполняться условия
трансверсальности.
Условия трансверсальности являются теми дополнительными условиями, которые
позволяют, в конечном счете, определить начальную и конечную точки, лежащие на
многообразиях s0 и sx. Действительно, координаты неизвестных точек х° и х1
вместе с р + k неопределенными множителями Лагранжа P/\Pv> / = 1,/?, v = l,я,
приводят к 2п + р + к неизвестным числам. Для определения указанных чисел необходимо
воспользоваться 2п условиями трансверсальности (2.56), (2.57) и р + к уравнениями
(2.53), (2.54), т.е. число неизвестных совпадает с числом уравнений.
Формально условиями трансверсальности можно пользоваться и в том случае,
когда в уравнениях (2.53) и (2.54) р = к = п. Уравнения (2.53) и (2.54) в этом случае
задают соответственно начальную х° и конечную х1 точки, т.е. имеет место
двухточечная задача оптимального управления. Использовать условия трансверсальности в
двухточечной задаче оптимального управления вряд ли целесообразно, т.к. это может
только усложнить решение задачи.
Выясним геометрический смысл соотношений (2.56) и (2.57). Для этого запишем
их в векторной форме:
vc('o) = tp/V9/(x)l=x(((|); (2.59)
v(<i)=£p;vPv(*)L((1)- <2-60)
v=l
Известно, что вектор
V«>'(X>IX = X(,O) (2-61)
Глава 2. Принцип максимума Понтрягина 487
ортогонален к поверхности*
Ф/(х)=0 (2.62)
в точке х = x(f0) . Многообразие s0 образовано пересечением р поверхностей (2.53).
Поэтому вектор (2.61), являясь ортогональным к поверхности (2.62), ортогонален и к
многообразию s0, которое принадлежит поверхности (2,62). Таким образом, правая
часть равенства (2.59) является линейной комбинацией векторов, каждый из которых
ортогонален многообразию s0. Поскольку векторы (2.55) линейно независимы, то
вектор (2.59) является ортогональным к многообразию s0 в точке х(/0) вектором
общего положения. Аналогичным образом можно показать, что вектор, стоящий в
правой части равенства (2.60), является ортогональным к многообразию s} в точке
х(/,) вектором общего положения.
Вектор Y называется ортогональным к многообразию s0 в точке х(/0), если он
ортогонален к плоскости, которая касается многообразия s0 в точке x(f0).
Касательная к многообразию s0 плоскость образуется пересечением р плоскостей, каждая из
которых касается в точке х(/0) одной из поверхностей
Ф/(х) = 0, 1 = 1р.
Обозначим Го плоскость, касательную к многообразию s0, а 7] - плоскость,
касательную к многообразию s{.
Условия трансверсальности можно сформулировать в следующем виде. Говорят,
что на правом конце траектории х(/) выполнено условие трансверсальности, если
вектор v|/(r,) = (\|/1(/,),v|/2(/,)>•••>У/ДО) ортогонален плоскости 7j. Аналогичным
образом формулируется условие трансверсальности и для левого конца траектории х(0-
Пример 2.3. Внесем некоторые изменения в пример 2.2 (§2.1). По-прежнему полагается, что движение
объекта управления задается уравнениями (2 19) при ограничении на параметр управления (2.26), и в
качестве критерия оптимизации рассматривается функционал (2.27) Однако вместо заданной конечной точки
(в примере 2 - это начало координат) будем рассматривать перевод фазовой точки на многообразие,
которое задается уравнением
дг,=О.
К условиям оптимальности, задаваемым теоремой 2.1, необходимо добавить условия трансверсальности на
правом конце траектории, которые имеют вид
Vi0O = P, Ч/2(7>0. (2.63)
Так как р является произвольным вещественным числом, то первое равенство (2 63) не накладывает
никаких условий на функцию \j/j(/) . Далее, в соответствии с (2 37) у2(0 - линейная функция, которая
может обращаться в нуль только один раз Поэтому в интервале 0</ < Т функция \j/2(0 не может
изменять свой знак
Как следует из (2.63) и (2 32), на заключительном участке фазовая точка движется под воздействием
управления м*(/) = 0 по траектории семейства (2 41). На начальном участке в зависимости от знака у2(0)
движение происходит либо под воздействием управления м* = 1, либо - м* = -1. Возможен также вариант
( ц;2(0) = 0 ), koi да на всей траектории движения u{t) = 0
На рис 2 16 изображены управление м*(/) и соответствующая ему траектория x(t) при vj/2(0)> 1
Найдем на фазовой плоскости совокупность точек, в которых происходит переключение управления с
«*(/) = 1 на м*(/) = 0
Запишем равенство
* Вектор (2 61) называется ортогональным к поверхности (2 62) в точке х = х(*0), если он ортогонален
плоскости, которая касается поверхности (2 62) в точке x(f0).
488
Методы теории оптимального управления. Часть III
Н(у(Т\ х(Т), и(Т)) = -к - \и\Т)\ + м/, (Т) • *2(Г) + м/2(Г) • iT(r) =
= -* + 1|/,(7Ул:2(7>0,
из которого следует, что
к
*,(/,) = V,(7>
х2{Т)
(2 64)
и
(
i
= 0
kJC2
а (
Рис. 2.16. Графики управления и фазовой траектории
В интервале /, < / < Т
V2(n = -Vi(/|)-(7'-/i) + M/2tt)
В соответствии с (2 32) м/2(/,) = 1 и, очевидно,
1
Г-Л=-
Так как уД) = у,(П , то из (2.64) следует
Т-и =
х2(Т)
(2 65)
В интервале tx<t<T u(t) = 0, и потому
х, (Г) «дггЙМГ-/, ) + *,(/!>.
Принимая во внимание (2 65) и равенство х\Т) = 0 , найдем
*,(/,) = ~-*2(/,)-дг2(71)
Но т.к х2(Т) - jc2(/j) , то окончательно получим
(2 66)
Равенство (2.66) задает на фазовой плоскости параболу. Однако, как следует из рис. 2.16,
переключение управления с и*(/) = 1 на м*(0 = 0 возможно только при *2(/,)>0 (в противном случае прямая хх =0
не может быть достигнута), т.е. уравнение (2.66) необходимо дополнить неравенством x2(t{)>0 .
Обозначим у* линию на фазовой плоскости, определяемую соотношениями
X,=---JC2.*2*0
Именно в точках линии у+ происходит переключение управления и (/) с+1 наО
Если рассмотреть управление u\t), вид которого представлен на рис. 2 17, и соответствующую ему
фазовую траекторию, то указанным выше способом легко установить, что переключение управления и (/)
с -1 на 0 происходит на линии у', которая задается соотношениями
*i=j-*22. ^2^0
Обозначим у объединение линий у* и у": у = у+ Uy' Для каждой фазовой траектории х(/)
переключение управления м*(/) происходит на линии у . На рис. 2 18 изображены линия «переключения» и вид
Глава 2. Принцип максимума Понтрягина
489
выделенных необходимыми условиями оптимальности фазовых траекторий. Только изображенные на
рис 2 18 траектории могут быть оптимальными траекториями
-1
Рис. 2.17. График управления u*(t)
Необходимые условия оптимальности непосредственно не могут гарантировать оптимальность
выделенных с их помощью управлений и траекторий. С другой стороны, оптимальная траектория и
оптимальное управление должны удовлетворять необходимым условиям Изображенные на рис 2 18 траектории,
несомненно, являются оптимальными, тк. каждой начальной точке соответствует единственная
траектория, а по условиям задачи существование оптимальных траекторий и управлений представляется вполне
очевидным
На рис 2 18 видно, что каждая оптимальная траектория целиком лежит либо в левой, либо в правой
полуплоскости
х(0)
Рис. 2.18. Графики оптимальных фазовых траекторий
Обозначим
*1=ф(*г)
уравнение линии у Оптимальное управление задается равенством
1, если jcj — ф(х2) < 0 и *1<0,
-1, если хх-<р(х2)<0 и хх >0,
О, если л:, - ф(дг2) > 0 и х, < О,
или xl-(p(x2)<0 ИХ|>О
2.2.3. Неавтономный случай
В отличие от §2.1 будем теперь считать, что движение объекта управления
описывается неавтономными уравнениями вида
— (2.67)
а вместо функционала (2.2) будем рассматривать функционал
—L = /•(*,,..., хю и,,..., ит, 0, / = Un,
at
J = J/o(*i> •••» х„, и,,..., ит, i)dt.
(2.68)
490 Методы теории оптимального управления. Часть III
Будем полагать, что момент времени /0 задан, а момент времени tx не задан и вместе с
управлением и(/) выбирается из условия минимизации функционала (2.68).
Ограничимся рассмотрением двухточечной задачи о переводе фазовой точки х = (х]9...,хп)
из заданного начального положения х° в заданное конечное положение х1 .
Введем еще одну переменную хп+]9 которая определяется уравнением
— = hXn+\{Jo) = to .
at
Очевидно, в этом случае хп+1 = /, и уравнения (2.67), функционал (2.68) можно
переписать в виде
-£ = fi(xi,...9xn,ul,...,um,xn+l),i = \,n,
ut (2.69)
dxn+l = ^
dt
J = \fo(xx,...,xn,ub...,um,xn+X)dt. (2.70)
'o
В результате получили автономную задачу оптимального управления.
Введем (я+1)-мерный вектор х = (*,,..., хЛ,х„+1) и (я-Н)-мерное фазовое
пространство X*. Автономный вариант исходной неавтономной задачи оптимального
управления выглядит следующим образом. В фазовом пространстве X* задана начальная
точка х° = (Xj°,..., x®,t0) и конечное многообразие 5,, задаваемое соотношениями
xv-xJ,=0,v=:u. (2.71)
Требуется среди допустимых управлений и(/), /0 </</,, переводящих фазовую точку
х системы (2.69) из заданного начального положения х° на многообразие (2.71),
найти такое, которое доставляет минимум функционалу (2.70).
Для сформулированной автономной задачи оптимального управления с
закрепленным левым и подвижным правым концами условия оптимальности задаются
теоремой 2.1 и условиями трансверсальности. Условия трансверсальности имеют вид
v|;/(/1) = p;(/=u),v|/,+1(/1) = O. (2.72)
Первые п соотношений (2.72) не накладывают никаких условий на
вспомогательные функции \\?j(t),i = 1,я, т.к. р;+, / = 1,и - любые вещественные числа.
Содержательным является последнее условие (2.72).
2.3. ОПТИМИЗАЦИЯ ПО БЫСТРОДЕЙСТВИЮ ЛИНЕЙНЫХ
ОБЪЕКТОВ УПРАВЛЕНИЯ
2.3.1. Максимизация функции Гамильтона
Рассмотрим оптимизацию по быстродействию линейного объекта управления,
движение которого задаётся системой уравнений с постоянными коэффициентами
dx п т
-jf = ZA*v+Z^M*'/ = 1'"- (2-73)
/=1 к-\
Запишем систему уравнений (2.73) в матричной форме
^ = Ах + Ви, (2.74)
at
Глава 2. Принцип максимума Понтрягина ' 491
где х = (х1,х2,...,л:Л) - «-мерный вектор состояния системы, u = (ul,u2,...,um) -
w-мерный вектор управления, А и В - матрицы, имеющие размерности
соответственно пхп и пхт . Векторы х и и являются векторами-столбцами.
Будем предполагать, что система уравнений (2.74) является нормальной, т.е.
следующие матрицы
Gy=[b7|Ab,|...|A"-'b7], j = \^i (2.75)
для всех у являются невырожденными, здесь by -у-й столбец матрицы В. Пусть,
далее, область управления U представляет собой w-мерный параллелепипед,
задаваемый неравенствами
A)<Uj <AJj = lm, (2.76)
где А) < О, А] > 0, j = пп.
В соответствии с теоремой 2.2 запишем функцию Гамильтона
п т п т
/=1 7=1 /=1 к=\
В матричной форме функция Гамильтона имеет вид
77(\|/, х, u) = v|/TАх + \|/тВи. (2.77)
Вспомогательный вектор v|/(/) определяется уравнениями
£ = -AV (2-78)
Оптимальное управление и(/) доставляет функции Гамильтона в каждый момент
времени t максимум. Так как первое слагаемое функции (2.77) не зависит от
управления, то максимизировать необходимо функцию \|/TB u , которую представим в виде
т Г п 1
VTB« = Z EV/^k- (2.79)
*=iL=i J
Так как компоненты вектора и в соответствии с (2.76) могут изменяться независимо
друг от друга, то из условия максимума функции (2.79) найдем
Uv =
п
А\, если XvA* >°>
п
А1к9 если ^]v|//^<0, k = \ym.
ых (2.80)
п
/=1
В соответствии с (2.80) оптимальные управления uk(t), к = \,т являются
кусочно-постоянными функциями, принимающими значения А\, А%. Покажем, что для
нормальной системы (2.74) соотношения (2.80) определяют оптимальное управление,
за исключением конечного числа точек, однозначным образом.
Как следует из (2.80), компонента ик вектора управления и определяется
неоднозначным образом, если
/=1
Вектор-функция v|/(/) - аналитическая функция, т.к. является решением системы
линейных однородных уравнений с постоянными коэффициентами. Но тогда анали-
492 Методы теории оптимального управления. Часть III
п п
тической является и функция У^ЧЛС)^ • Если функция ^^i(t)bik обращается в
*i=\ ,=1
нуль на бесконечном множестве точек t, то
1>,(')^=о.
/=1
Запишем это равенство в векторной форме
ЧЛ'Ж^О, (2.81)
где Ь* - к-\\ столбец матрицы В.
Продифференцируем тождество (2.81) (п-\) раз. Принимая во внимание
уравнение (2.78), получим систему уравнений
V(')b*sO,
VT(OAb,,0, (2>82)
Относительно вектора i|/(/) уравнения (2.82) являются системой линейных
однородных алгебраических уравнений. Определитель этой системы
det[Gj]*O,
т.к. по предположению система уравнений (2.74) является нормальной. Из (2.82)
следует тогда, что вектор
ч/(0 = о,
что противоречит пункту 2 теоремы 2.2.
Таким образом, из условия максимума функции (2.79) оптимальное управление
и(/) определяется однозначным образом (за исключением конечного числа точек).
2.3.2. Теорема о числе переключений
В соответствии с равенством (2.80) оптимальные по быстродействию управления
uk{t\ к = \,т, являются кусочно-постоянными функциями, принимающими значения
Ахк или Л% причем переключение управления щ(1) происходит в момент обращения в
п
нуль функции ^у t(t)bik . Выше было установлено, что указанная функция обраща-
ется в нуль конечное число раз, т.е. число таких переключений в интервале to<t<tx
конечно. Для определения оптимального управления очень важно заранее
располагать информацией о возможном числе таких переключений. Оказывается, что для
определённого класса линейных объектов управления удаётся получить такую
информацию.
Прежде чем формулировать основной результат в виде теоремы, сформулируем и
докажем следующую лемму [46].
Лемма. Пусть ХЬХ2,...,ХГ ~различные вещественные числа, a f\(t), f2 (t),...,/r (t)
-многочлены, имеющие степени соответственно кх, к2,..., кг. Тогда следующая
функция {квазимногочлен)
у;(/)ех''+/2(0^'+...+/г(/)еХ'-' (2.83)
может обращаться в нуль не более чем кх+к2+... + Аг + г -1 раз.
Глава 2. Принцип максимума Понтрягина 493
Доказательство. При г = \ лемма справедлива, т.к. функция /j(/)eX|'
обращается в нуль в точках, в которых обращается в нуль многочлен /, (/), и,
следовательно, имеет не более к\ нулей.
Предположим, что лемма справедлива, когда число слагаемых меньше г.
Покажем, что в этом случае она справедлива и при г слагаемых. Это утверждение докажем
методом от противного. Предположим, что при г слагаемых лемма неверна и
функция (2.83) имеет, по крайней мере, кх +к2+... + кг+г нулей. Умножим (2.83) на e~Xfi,
что не изменит её нулей. В результате получим функцию
A(t)e^-K>+f2(t)e(X>-KK... + fr_l(t)e{X'-<-X')'+fr(t). (2.84)
Продифференцировав функцию (2.84) г+1 раз, получим
gl(t)e(X'-X'Kg2(t)e^-X'K... + gr_l(t)e^-X'K (2.85)
здесь gv(t) - многочлены, имеющие ту же степень, что и многочлены fv{t).
Поскольку между двумя нулями функции лежит, по крайней мере, один нуль её
производной, то при каждом дифференцировании может «теряться» не более одного нуля,
т.е. функция (2.85) имеет не менее
кх +к2 +... + Лг + г-(£г+ 1) = А, + £2+... + &,._, +(г-1)
нулей. Но квазимногочлен (2.85) имеет г-\ слагаемых, числа {к^-\г) - различны.
По предположению для него справедлива лемма, и он может иметь не более чем
k\+k2+... + kr_l+(r-2) нулей. Получили противоречие, которое доказывает
утверждение о том, что если лемма справедлива для г -1 слагаемых, то она справедлива и
для г слагаемых.
Дальнейшее доказательство леммы следует из метода математической индукции.
Перейдём теперь к формулировке теоремы. Во избежание недоразумений
отметим, что рассматривается двухточечная задача оптимального управления, т.е. задача
о наибыстрейшем переводе фазовой точки системы (2.74) из заданного начального
положения х° в заданное конечное положение х1.
Теорема 2.3. Если входящее в уравнение (2.74) матрица А имеет только
вещественные собственные числа, а управления Uj(t), j = 1,/и удовлетворяют теореме 2.2,
то каждое из управлений Uj(t\ j = \,т является кусочно-постоянной функцией,
принимающей значения AJ9 А} , и имеет не более п-\ переключений, где п - порядок
системы (2.74).
Доказательство. Из равенства (2.80) следует, что управление Uj(t), j = \,m ,
является кусочно-постоянной функцией, принимающей значения A]j, AJ, а число
п
переключений управления совпадает с числом нулей функции ^М/Д/)^ . Таким об-
разом, для того чтобы определить максимально возможное число переключений
управления мД/), необходимо установить, сколько раз может обращаться в нуль
п
функция ^WjiWy .
Пусть р1,р2,..;Рп - различные собственные числа матрицы А. Тогда матрица
- Ат имеет собственные числа Х1,Х2,...,ХГ, где ^v = -pv (у = \,г). По условию тео-
494 Методы теории оптимального управления. Часть III
ремы матрица А имеет вещественные собственные числа. Но тогда и собственные
числа Xv матрицы -Ат также являются вещественными. Обозначим pv, v = l,r,
кратность собственного числа ^v . Очевидно, р, + р2 +... + рг = п.
Как известно из теории линейных дифференциальных уравнений с постоянными
коэффициентами, каждая функция ц/Д/),/ = 1,я, являющаяся решением уравнения
(2.78), имеет вид
V/(0 = /i(0eX|/ +/2(О^2' +... + /г(0еХ'', (2.86)
здесь /v(/), v = l,r - многочлены, причем степень многочлена /v(/) не превосходит
pv-l. Но тогда линейная комбинация ^T,\\ij(t)by будет иметь вид, аналогичный
(2.86). Запишем
Хч/ДО^ =а,(0^ +ст2(О^2/ +... + аг(/)^, (2.87)
/=1
здесь gv(/), v = l,r - многочлен, имеющий ту же степень, что и многочлен fv(t).
Применив к функции (2.87) доказанную выше лемму, найдём, что она может
обращаться в нуль не более чем
(р1-1)+(р1-1)+... + р_1+(г-1)=й-1
раз. Теорема доказана.
Данную теорему называют теоремой о числе переключений. Она находит
широкое применение при синтезе оптимального по быстродействию управления в задачах
с одним управляющим параметром. Далее, нетрудно убедиться, применив принцип
максимума для неавтономных систем, что теорема сохраняет свою силу, если вместо
уравнений (2.74) рассматривать уравнение
^ = Ах + Ви + у(/),
где у(/) - некоторая известная вектор-функция.
2.3.3. Достаточные условия оптимальности
Рассмотрим двухточечную задачу об оптимальности по быстродействию
управления объектом (2.74) при наличии ограничений (2.76). При этом предполагается, что
начальной точкой х° может быть любая точка фазового пространства, а конечная
точка х1 совпадает с началом координат, т.е. х1 = 0. Как и всюду в данном параграфе,
будем считать, что система уравнений (2.74) является нормальной.
Теорема 2.4. Пусть и (/) и \ (/), t0 < t < tt -управление и траектория,
переводящие фазовую точку х системы (2.74) из заданного начального положения х° в
начало координат. Если управление и*(/) и траектория х' (t) удовлетворяют
теореме 2.2, то они доставляют функционалу
J = jdt = tx-t0
'о
абсолютный минимум.
Доказательство. Запишем равенство
А ы] /=1 А А /=1 А
Глава 2. Принцип максимума Понтрягина 495
здесь х(/) - любая траектория системы (2.74), соответствующая допустимому
управлению и (г) и переводящая фазовую точку системы из заданного начального
положения х° в начало координат. Будем, далее, полагать, что траектории х(/) и х*(/)
исходят из начальной точки х° в один и тот же момент времени tQ .
Перепишем равенство (2.88) в векторной форме
ik^-)]=^-)^T|(x--x). (2.89)
Из (2.89), принимая во внимание (2.78) и (2.74), найдём
^[M/T(x^x)] = -H/TA(x^x) + M/T[A(x^x) + B(u*-u)]= (29o)
= утВ (и*-и).
Управление и*(/) и траектория х*(/) удовлетворяют теореме 2.2 и поэтому
управление u* (t) в каждый момент времени / максимизирует функцию v|/TB u , т.е. в
каждый момент времени / имеет место неравенство
v|/TB (iT(/)-u(/))>0.
Выше было показано, что для нормальной системы (2.74) управление и*(/) из
условия максимума функции \|/тВи определяется однозначным образом. Далее, если
х(/) *x*(f), то u(t)?u*(t), причём в каждой точке t (за исключением конечного
числа точек, а их можно не принимать во внимание), в которой u(/) * u (/)
v|/TB (u*(f)-u(f))>0. (2.91)
Обозначим т момент времени, в который приходит в начало координат
траектории х(/). Покажем, что
если х(/)^х*(/), здесь /, - момент прохождения траектории х*(/) через начало
координат. Предположим противное и положим и(/) = 0 при х </</,. Тогда
х(/) = О при х < t < /,. Проинтегрируем равенство (2.90):
ji[vT(x*-x)]* = JVTB(u*-u)rf/. (2.92)
'о 'о
Из (2.92), принимая во внимание неравенство (2.91) и соотношение x*(/j) = х(^) = 0 ,
найдём, что
0 = С, (2.93)
где С > 0. Полученное противоречие доказывает недопустимость предположения о
том, что х </,. Далее, поскольку на функцию х(/), которая сравнивается с функцией
х*(/), не накладывались никакие ограничения, то доказан абсолютный минимум
функционала J.
Теорема 2.5 (теорема единственности). Пусть х (/) и х (t) — две
оптимальные траектории, соединяющие начальную точку х° с конечной точкой х1 и
доставляющие абсолютный минимум функционалу
496 Методы теории оптимального управления. Часть III
'i
'о
Тогда x(t) = x~(t).
Доказательство. Будем предполагать, что в равенстве (2.90) вспомогательный
вектор \|/ = (vj/,(/),...,v|>w(/))t, существование которого гарантируется теоремой 2.2,
соответствует оптимальной траектории x\t). Если x**(/)*x*(f)> то имеет место неравенство
(2.91) и из (2.92) тогда следует противоречие (2.93), которое доказывает теорему.
В теореме 2.5, в отличие от теоремы 2.4, конечной точкой х1 может быть любая
точка фазового пространства.
Точку х1 будем называть точкой равновесия, если найдется вектор и0,
удовлетворяющий ограничениям (2.76), такой, что Ах1 + Ви° = 0.
При u(0=u° уравнение (2.74) имеет решение х(/) = х1. Анализ доказательства
теоремы 2.4 показывает, что она сохраняет свою силу, если конечной точкой х1
является точка равновесия (точка х1 = 0 является частным случаем точки равновесия).
При управлении техническими объектами, как правило, рассматривается перевод
фазовой точки системы в точку равновесия (обычно в начало координат). Именно
такая ситуация и рассмотрена в теореме 2.4. На самом деле теорема 2.4 сохраняет
свою силу и в том случае, когда х1 может быть произвольной точкой фазового
пространства. Однако в этом случае доказательство теоремы заметно усложняется.
Пример 2.4. Рассмотрим систему уравнений
*1=*2>
х2 =и-х1.
(2 94)
Будем решать задачу о наибыстрейшем переводе фазовой точки системы (2 94) из начальной точки
х° = (х1? ,х2) в начало координат за минимально возможное время, полагая, что на управляющий параметр
и наложено ограничение \и\ < 1 В процессе решения задачи в качестве начальной точки будет рассмотрена
любая точка фазового пространства
Легко видеть, что система уравнений (2.94) является нормальной Поэтому управление u(t) и
траектория х(/), удовлетворяющие теореме 2 2, в соответствии с теоремой 2 4, являются оптимальными
Запишем функцию Гамильтона
Я(ч/,х,м) = Ч/, x2+\\i2(u-xl)
Из условия максимума функции Гамильтона находим, что оптимальное управление
и(/) = sign \|/2(0 (2 95)
Вспомогательный вектор у2(0 определяется уравнениями
Из (2 96) следует уравнение
d\2
-^ + 4/2=0,
dt
решение которого имеет вид
¥2 (0 = с\cos/ + c2smt = R sin(/ - а),
здесь R(R> 0) и а - некоторые постоянные, причем 0 < а < 2л
В соответствии с (2 95)
w(/) = signsin(/-a).
Таким образом, оптимальное управление представляет собой кусочно-постоянную функцию,
принимающую значения +1 и -1 на интервалах времени длиною л Исключение составляют первый и последний
интервалы, длина которых зависит от а и /, (/0 полагается равным нулю) и может быть любой
величиной, не превышающей числа п
Глава 2. Принцип максимума Понтрягина
497
Найдем фазовые траектории системы (2 94) при и = 1 и и--\
При и = 0 из сравнения уравнений (2.94) и (2 96) следует, что
x2(t) = /?sin(/ + у), х,(0 = -Rcos(t + у)
Фазовые траектории представляют собой окружности вида
x2+xj = R2 (2 97)
Радиус R зависит от начальных условий и может быть любой величиной
При и = 1 уравнения (2 94) можно переписать в виде
d(x{-\)_ dx2_
В соответствии с (2 97) фазовые траектории системы (2 94) при и = 1 представляют собой окружности
(Xl-\)2+x22=R2 (2 98)
радиуса R с центром в точке О\ с координатами (1,0) Семейство окружностей (2 98) изображено на рис 2 19
Рис. 2.19. Графики окружностей, определяемых (2.98)
Аналогичным образом легко показать, что при и = 1 фазовые траектории являются окружностями вида
(x1 + l)2+jc22=/?2 ' (2 99)
с центром в точке О.и имеющей координаты (-1,0) Окружности семейства (2 99) представлены на рис 2 20
k Х2
Рис. 2.20. Графики окружностей, определяемых (2.99)
По окружностям семейств (2.98) и (2.99) фазовая точка движется по часовой стрелке с равномерной
скоростью, проходя за время п ровно половину окружности.
Рассмотрим оптимальную фазовую траекторию, которая соответствует управлению, представленному
на рис 2 21
На заключительном участке фазовая точка движется под воздействием управления и - 1 по дуге
окружности семейства (2.98), причем по той из окружностей семейства (2 98), которая проходит через начало
координат, т.к конечной целью управления является перевод фазовой точки в начало координат
Обозначим г| длину заключительного участка Очевидно r\ < n За время г| фазовая точка проходит дугу АО
окружности
33 Зак. 366
498
Методы теории оптимального управления. Часть III
(дс|-1)2 + дс2=1,
меньше половины окружности (рис 2 22)
1
1
-1
• и
а
я + а
2я+ а
1
1
/i
t
Рис. 2.21. Графики управления u(t)
В положение А фазовая точка попала, двигаясь в течение времени п под воздействием управления
и = -1 по дуге В А окружности семейства (2 99). За время п фазовая точка проходит ровно половину
окружности. Таким образом, точка В симметрична точки А относительно центра О.\.
Следующим участком оптимальной траектории (считая от конца) является полуокружность СВ с
центром ъ точке О), и, следовательно, точка С симметрична точке В относительно центра О\ и тд.
Изображенному на рис 2 21 оптимальному управлению соответствует оптимальная траектория DCBAO.
кх2
и = \\
Рис. 2.22. График оптимальной фазовой траектории
Если рассмотреть оптимальное управление (рис. 2 23), у которого на заключительном участке длиною
г| м(/)=-1, то получим оптимальную траекторию, симметричную траектории DCBAO относительно начала
координат (на рис 2.22 траектория D'C'BO)
Рассмотрим теперь, что представляет собой совокупность всех возможных оптимальных траекторий
Длительность заключительного участка г| может быть любым числом, лежащим в диапазоне 0 <г|<л
Поэтому точка А может быть любой точкой полуокружности ОМ\. Точка В симметрична точке А
относительно центра О_,, и поэтому она может быть любой точкой полуокружности NXN2 Аналогичным
образом можно показать, что точка С может быть любой точкой полуокружности М2М3 и т.д
Если рассмотреть оптимальную траекторию тапа D'C'B'A 'О, то указанным выше способом легко
установить, что возможные положения точки А' образуют полуокружность N\O, возможные положения точки
В' - полуокружность М\Мг, а возможные положения точки С - полуокружность N3N2 и т.д Но точки А,
В, С, А\ С' В 'являются точками фазового пространства, в которых происходит переключение
оптимального управления. Таким образом, переключения оптимального управления происходят' на линии
Л^зЛ^2iV|ОЛ/iЛ/2Л/3 ., составленной из полуокружностей единичного радиуса
Глава 2. Принцип максимума Понтрягина
i
> и
499
i ^
I
Рис. 2.23. Оптимальное управление
Введем функцию
v(*i,*2) =
(2 100)
1 выше линии...N3N2NlOM]M2My..u на линии Мр,
[-1 ниже линии...ЛуУ2#1<9Л/1Л/2Л/3---и на линии Np.
Из рис. 2 22 следует, что оптимальное управление u = v(xux2) Если в уравнениях (2 94) положить
и = v(xj,x2), то решениями системы (2 94) будут идущие в начало координат оптимальные по
быстродействию траектории
Пример 2.5. Рассмотрим систему уравнений
х2=и2,
полагая, что на управления щ и и2 наложены ограничения
| Wl|<l, К|<1
По-прежнему решается задача о наибыстрейшем переводе фазовой точки системы из заданного
начального положения в начало координат.
С помощью матриц (2.75) легко убедиться, что система уравнений (2.100) не является нормальной.
Это означает, что из условия максимума функции Гамильтона управление определяется неоднозначным
образом. Рассмотрим, как это сказывается на определении оптимального управления и оптимальных
траекторий.
Запишем функцию Гамильтона
tf(\|/,X,ll) = V|/j(M, +Х2) + Ц12и2.
Вспомогательные переменные \|/,(/) и ц/2(/) определяются уравнениями
Л dt У1
(2.101)
(2 102)
Из условия максимума функции Гамильтона находим, что оптимальное управление
M,(/) = signv|/,(/),
M2(/) = signvj/2(0,
здесь предполагается, что функция sign у не определена в точке у - 0.
Функция vj/2(/) не может тождественно равняться нулю, т.к. тогда, как следует из второго уравнения
(2 101), у,(/) = 0 , что противоречит пункту 2 теоремы 2.2. Однако уравнения (2 101) допускают
нетривиальное решение
М/,(/)^0, M/2(/) = vj/2(O),
которое приводит к тому, что управление м, не определяется однозначно из условия максимума функции
Гамильтона, т.е условию максимума удовлетворяет любое значение параметра их, лежащего в диапазоне
- 1 < Mj < 1
Уравнения (2.101) имеют решение
Vi(O = Vi(0),V2(O = -Vi(0)/ + V2(0)- (2 103)
Если начальное условие vj/j(O) * 0, то в соответствии с (2.101) управление щ на всем интервале движения
эстается неизменной величиной, равной 1 либо -1. Функция vj/2(/) может изменять свой знак только
эдин раз. Поэтому управление м2(0 является кусочно-постоянной функцией, принимающей значения +1
или -1, и допускается только одно изменение знака управления. Далее отметим, что если в оптимальном
!№ижении управление u2(t) изменяет свой знак, то, как следует из (2.103), на начальном участке движения
/правления u2(t) и ux(t) имеют одинаковые знаки.
500 Методы теории оптимального управления. Часть III
Необходимо рассмотреть два варианта у,(0 * 0, vj/,(/) = 0
Рассмотрим сначала первый вариант, когда vjy,(/) * 0 В этом случае справедлива теорема 2 4, и,
следовательно, управление и траектория, удовлетворяющие теореме 2 2, являются оптимальными, а
теорема 2 5 исключает возможность существования других оптимальных траекторий.
Найдем фазовые траектории системы (2 100), соответствующие различным сочетаниям управлений м,
и и2 Для этого решим уравнения (2 100), полагая щ и и2 постоянными величинами
Имеем
1 2
Х\ = ~и2* + и\* + С11 + С2>
здесь с, и с2 - произвольные числа Определим из первого уравнения время / и подставим его во второе
уравнение В результате получим равенство
x,=-^ + ^x2 + s, (2 104)
2w2 u2
2
где s = с—■ -с, - произвольная константа. Равенство (2.104) задает параболу, вершина которой
" 2и2 «2
лежит в точке с координатами s -, -м. Задаваясь различными значениями s, параболы (2 104)
I 2"2 J
можно произвольным образом сдвигать вдоль прямой
х2 = -щ
Рассмотрим оптимальные траектории, на которых управление u2(t) имеет переключение В этом
случае возможны следующие сочетания начальных условий для вспомогательного вектора ц/(/) vj/2(0)>0,
v|/,(0)>0,v|/2(0)<0,vj/,(0)<0
Для первого сочетания управление щ = 1, управление м2 на начальном участке равно 1, а на
заключительном участке равно -1 На начальном участке фазовая точка системы движется по параболе семейства
1 2
х\=~2 *2+*2+*>
вершина которой лежит на прямой
а заканчивается движение по параболе семейства
1 2
Xl=--'X2-x2 + s,
причем по той из парабол, которая проходит через начало координат
Для второго сочетания начальных условий управление щ =-1, управление м2 Д° переключения
равно -1, а после переключения равно 1 Оптимальная фазовая траектория состоит из примыкающих друг к
другу кусков парабол соответственно семейства
и семейства
1 2
1 2
*1 = 2 ^2-^2 + ^
Вершины этих парабол лежат на прямой х2 = 1
На рис 2 24 изображены две рассмотренные выше оптимальные траектории. Остальные оптимальные
траектории, соответствующие варианту \|/,(/) * 0 , аналогичны изображенным на рис 2.24.
Оказывается, что не все точки фазового пространства, рассматриваемые как начальные для
оптимальных траекторий, могут быть переведены в начало координат с помощью оптимальных траекторий,
соответствующих первому варианту (\|/,(/)*0) Предельной оптимальной траекторией типа А'В'О
(\|/2(0) < 0, i|/,(0) < 0 ) является траектория, у которой участок В'О равен нулю Очевидно, на этой
траектории управление u2(t) не имеет переключения (траектория LO на рис. 2.25) Предельной траекторией
типа АВО является траектория L'O, на которой м, = 1, и2 = 1 Фазовые точки, расположенные между
Глава 2. Принцип максимума Понтрягина
501
линиями МВОВ'М' и LOV, как следует из рис. 2 25, не могут быть переведены в начало координат с
помощью оптимальных фазовых траекторий, соответствующих первому варианту
/
1
о
[
1
-1 '
Рис. 2.24. Графики оптимальных траекторий
*7^ ' т Л ^7-v
Рис. 2.25. Графики оптимальных траекторий
Рассмотрим второй вариант, когда v|/t(/) = 0. В этом случае, как следует из (2 101) и (2 102),
управление u2(t) не имеет переключений Соответствующие оптимальные траектории лежат в области,
ограниченной линиями LOV и MOM'
Положим для определенности, что начальная точка х° лежит в области, ограниченной линиями LO и
МО . Как следует из уравнений (2 100) и рис. 2 25, фазовая переменная х2 может быть переведена в нуль
только с управлением u2(t) = -1, т е. необходимо выбрать vj/2(O) < 0 Переменная х2 обращается в нуль за
время
/, = jc2(O), (/0=0)
Анализ уравнений (2.100) показывает, что фазовая переменная х2 выбором управления м, (|м,|<1)
также может быть переведена в нуль за время /,, при этом управление м,(/) определяется неоднозначным
образом Очевидно, каждая из этих траекторий является оптимальной, т к. обращение в нуль фазовой
переменной х2 выполняется за минимально возможное время
Для того чтобы упростить окончательный результат, будем выбирать управление м,(0 постоянной
величиной, но так, чтобы фазовая переменная х, обращалась в нуль за время /, = х2(0) Тогда фазовые
траектории являются параболами вида
1 2 •
Xi=--x2-u]x2,
(2 105)
здесь символом щ обозначено соответствующее постоянное значение управления и, Разным точкам х
соответствуют различные значения управления Wj* . Так как фазовая точка движется по параболам (2 105),
то, очевидно, управление и\ можно задать равенством
502 Методы теории оптимального управления. Часть III
1 х,
Mi = Х->
' 2 2 х2
Это управление можно рассматривать как оптимальное
Таким образом, в области фазового пространства, ограниченной линиями LO и МО , оптимальное по
быстродействию управление задается равенствами
1 х,
I х2
И2=-1
Линии LO и МО представляют собой куски параболы (2 104) соответственно при щ =-1, и2 =-\ и
щ = 1, м2 = -1 и определяются уравнениями.
х]=---х1+х2,х2>0\
*,=-- х^-х2,х2>0.
Соответствующая оптимальная траектория на рис 2 25 изображена пунктиром
Аналогичным образом можно установить оптимальные траектории, лежащие в области, ограниченной
линиями НО и М'О Линия L'O определяется уравнением
а линия М'О -уравнением
х\ - ~Х2 +Х2 > Х2 - 0 '
*1=^*2-*2>*2*°-
Оптимальное управление в этой области задается равенствами*
1 jc,
I х2
и2 = \.
Пунктиром на рис 2.25 обозначена соответствующая оптимальная траектория.
Обозначим jc, =/|(*2) ~ уравнение линии LOV , а хх =/2(^) ~ уравнение линии MOM' Пусть,
далее, jc, =/3(jc2) - уравнение линии LOM\ xl =/4(*2) - уравнение линии МОП Из рис. 2 25 следует,
что оптимальное управление задается равенствами
-1, если хх - /3(х2) > 0,
1, если х, - /4(х2) < 0,
-—*2~—• еСЛИ *l-/l(*2)<0> *|-/2(*2)>°> *2>0'
2 х2
~тх2+—» если х,-/,(х2)>0, х,-/2(х2)<0, х2<0,
2 х2
{-1, если х,-/2(х2)>0,
[ 1, если х, -/2(х2)<0
2.4. СИНТЕЗ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
Принцип максимума ориентирован на определение оптимального управления в виде
функции времени, т.е. на определение управления в виде оптимальной программы. Если
управление ищется в виде оптимальной программы, то решение задачи с помощью
принципа максимума может быть сведено к определению начального значения для
вектора \|/. Начальный вектор \|/ должен быть выбран таким образом, чтобы
исходящая из начальной точки х° оптимальная фазовая траектория проходила через
заданную конечную точку х1. Так как часть условий задается в начальный момент времени
/0, а часть условий - в конечный момент tx, то получаем типичную двухточечную
краевую задачу для системы дифференциальных уравнений. Определение
оптимального управления в виде оптимальной программы рассматривается в [17].
Глава 2. Принцип максимума Понтрягина 503
Однако возможен другой способ задания оптимального управления. Во всех
рассмотренных выше примерах оптимальное управление задавалось в виде функции
вектора состояния. Такой способ задания оптимального управления не
ограничивается рассмотренными выше примерами, а справедлив для любого объекта управления,
движение которого задается уравнениями (2.1). Это и понятно, если в данный момент
времени / состояние системы характеризуется вектором х, то этот вектор
полностью определяет дальнейшее оптимальное управление, т.к. из оптимальности
траектории х(0 следует оптимальность и ее конечного участка. Для оптимизации
системы, начиная с состояния х, не важна предыстория, т.е. как система попала в
состояние х . Значение имеет лишь само состояние х .
Таким образом, оптимальное управление может быть задано в виде функции
u=v(x). (2.106)
Равенство (2.106) является векторным. В скалярной форме оно имеет вид:
mi=v1(jc,,x2,...,xw),
«2 — "2V Р 2»*"' /1/»
к„=уи(х1,х2,...,хя).
Функция v(x) задает оптимальное управление в виде функции вектора
состояния и называется синтезирующей функцией, или функцией стратегии, а задача
построения функции v(x) - синтезом оптимального управления.
Для специалистов по автоматическому управлению наибольший интерес
представляет определение оптимального управления в виде синтезирующей функции.
Синтезирующая функция v(x) полностью определяет оптимальную систему: она
показывает, какие следует взять обратные связи и как их следует преобразовать,
чтобы получить наилучшую (оптимальную) систему. Очень важно, что функция v(x)
позволяет построить управление системой по принципу обратной связи.
Строго говоря, принцип максимума, как уже отмечалось, ориентирован на
определение оптимального управления в виде оптимальной программы. Однако он
позволяет сравнительно просто выделить всю совокупность оптимальных траекторий, и
тем самым найти оптимальное управление в виде синтезирующей функции.
Пример 2.6. Рассмотрим в качестве примера управление параметрами газа в проточной полости.
Оптимальное управление будем искать в виде синтезирующей функции
На рис. 2 26 представлена принципиальная схема объекта регулирования Он состоит из ресивера 1,
проточной полости 3, впускного 2 и выпускного 4 регулируемых отверстий, нерегулируемого отверстия 5,
работающего на потребителя При построении математической модели, описывающей изменения
параметров газа в проточной полости, были приняты следующие допущения:
• термодинамическое тело - идеальный газ;
• теплообмен между газом и корпусом проточной полости отсутствует,
• регулирующие органы, осуществляющие изменение площадей впускного и выпускного отверстий,
являются безынерционными.
Изменение параметров газа в проточной полости задается следующей системой дифференциальных
уравнений:
f = f(7,G,-rC2-rC3),
dt W (2 107)
^ = ^[(кТр-ТЩ-(к-\)ТО2-(к-\)ТС,],
где Gh G2, G3 - массовые секундные расходы газа через отверстия, имеющие площади Sl9S2,S3
соответственно, R - газовая постоянная, W- объем проточной полости, к - показатель адиабаты; Рр,Тр - давле-
*Синтезу оптимального управления, или оператора оптимальной обратной связи, посвящен §3 1 2
504
Методы теории оптимального управления. Часть III
ние и температура газа в ресивере, Р, Т - давление и температура газа в проточной полости Секундный
расход газа через отверстия определяется соотношениями*
G\=Vis\ko-jjfirY(p.pp)> G2=»2S2kQ^Y(Pa,P),G2 = »2S2k0-1!LY(Pa,Pl
°7ятУ
°7W}
Y(Pi,P2) =
1 2к
к+\
1, если — <рь
Р' > * , если А>р„
здесь ц,,|д2,Цз - коэффициенты расхода газа через отверстия Sl,S2,S3 соответственно,
/^-атмосферное давление Коэффициент к0 вычисляется по формуле
2 W
PJ
Рис. 2.26. Принципиальная схема объекта управления
Таким образом, процессы, происходящие в полости, описываются системой нелинейных уравнений
(2 107)
Параметрами газа в проточной полости можно управлять, изменяя во времени площади S{ и S2
впускного и выпускного отверстий Площади Sl и S2 представим в виде
Sx =кхщ,кх =5,тах ,
S2 -к2иъ к2 =S2max,
полагая, что на управляющие параметры щ и и2 наложены ограничения
0 < м, < 1, 0 < и2 < 1
Рассмотрим оптимальный по расходу вывод параметров газа на заданный режим Для уменьшения объема
вычислений функцию Y(PltP2) аппроксимируем выражением
YM) = -
р
1, если — <рь
рг
1-
ы
I P
— если -^>рк.
Р2
0-Р*)
Конечное состояние газа (режим, на который необходимо вывести систему) определяется точкой
(Р°, Т°) Качество процесса управления будем оценивать функционалом
о V р
где /, - время управления Функционал (2 108) задает массовый расход газа из ресивера.
(2 108)
Глава 2. Принцип максимума Понтрягина
505
Оптимальное управление будем искать в форме оптимальной стратегии, т е требуется найти функции
v,(/\7"), v2(P,T), такие, что управления
— u^v^PJ), u2 = v2(P,T)
переводят фазовую точку (Р, Т) системы (2 107) из произвольного начального состояния в заданное
конечное состояние (Р°, Т°), и притом так, чтобы функционал (2 108) принимал свое наименьшее значение
Воспользуемся теоремой 2.1 Запишем функцию
H(v,PJ,ul,u2) = vvikluJc0-5=Y(P,Pp) +
>iRTp
kR P P
+V| — (7>М*о-г=ДЛ^)-Гц^^0-/==У(/>,,,/>)-ГОз)|+ (2 109)
—(T^^^-J-Y(P,P,,)-T^i,jtfr—Y(Pa,P)-TGiU-
W JRTn Vrt/ |
RT
+V2
Вспомогательный вектор vj/(/) = (vj/0(/), v|/j(/), vj/2(/)) задается системой дифференциальных уравнений
dt
d\\fi _
dt
d\\f2
~dT~~
Здесь
VeG,A/ + v,[^(GlW-G^-GJV)j + vl[-^(*7-|,-7-)G^ + (*-l)rc(G2 + G3)jJ, (2 110)
kR
RkTp-2RT\ 3y[RT
WP J 2 W
(k-\)(G2 + G3)
M = <
N = <
0
Y
1
P
p
при — <РЬ
2(Л^)(1-р,)2
при ^-<р„
0-Р.)2 г
PY2(Pa,P)
при —>Р^;
при-^>^;
L =
С =
1 при—-<рь
^hfc-W-fc*
/^Р' ,PJ
У^ЛЛ)
при—>рА,
0 при-^-<рь
Р2 Р Л -у
Ц—^ при^->р,
Y\Pa,P) P
Из условия максимума функции Гамильтона находим
kR
RT t
signr(p,p/J)^M,-7^^4^^^-7^^2—{ктр-туп,-1^\^
[kR P RT P \ 1
(2 111)
32 Зак. 366
506 Методы теории оптимального управления. Часть III
Поскольку оптимальные управления u{(t) и u2(t) являются кусочно-постоянными функциями,
принимающими значения 0 и 1, то синтез оптимального управления сводится к построению в фазовом
пространстве системы (2 107) геометрического места точек, в которых происходит переключение управления, тек
построению линий переключения.
Воспользуемся принципом попятного движения Фельдбаума Введем обратное время т = /,-/, где /,
- момент окончания процесса управления. Если (Р(/), Г(/)), 0 </</,, - некоторая траектория системы
(2 107), исходящая в момент /=0 из точки (Р*,Т*), проходит в момент tx через точку (Р°,Т°), то в
обратном времени т эта траектория проходит в обратном направлении, те Р(х = 0)=Р°, Г(т = 0) = Г°,
Р(х = /,) = Р\ Т(х = /,) = Т* Таким образом, в обратном времени т любая оптимальная траектория
должна исходить из точки (Р0, 7°)
Для решения уравнений (2 107) и (2 110) в обратном времени в них необходимо перейти к
производным по обратному времени т Между производными по прямому и обратному времени существует
простая связь
dy _ dy
~dt~~~dx
Обозначим \j/° = vj/(t = 0) вектор начальных значений Если вектор у0 удовлетворяет соотношению
tf(\|/o,^r°,w,(T = 0WT = 0)) = 0, (2.112)
то совместное решение системы уравнений (2 107), (2.110), (2.111) (для уравнения (2 107) начальное
значение определяется точкой (7*°, Г°)) задает некоторую оптимальную траекторию Полученная траектория
выделена с помощью необходимых условий оптимальности, которые, строго говоря, не гарачтируют ее
оптимальности Однако на практике такие траектории, как правило, являются оптимальными.
Определенные соображения на эту тему приводятся ниже Если перебрать все возможные значения век ;ора ц/°, то
получим совокупность оптимальных траекторий Очевидно, эта совокупность должна охватывать всю
фазовую плоскость системы (2.107) (или, по крайней мере, ее область управляемости) Таким образом,
построив оптимальные траектории, можно найти синтезирующую функцию v(P,T)
При реализации указанного способа целесообразно поступить следующим образом Так как согласно
принципу максимума (теоремы 2 1) вектор-функция \y(t) определяется с точностью до постоянного
положительного множителя, будем полагать, что начальные значения yjj и vj/J удовлетворяют соотношениям
!и>?)2='. (2Ш)
k so,
а величина у® определяется из уравнения (2 112) Задавая значения из диапазона -1 < vj/J < 1 и вычисляя
v|/[] и I}/" из соотношений (2 112), (2 113), строим однопараметрическое семейство оптимальных
траекторий Этим семейством исчерпываются все возможные оптимальные траектории системы (2 107) От одно-
параметрического семейства легко перейти к конечному множеству оптимальных траекторий, например,
равномерно распределив в интервале (-1,1) ряд значений величины ц/° Это множество позволяет по
точкам построить линии переключения
Поскольку в уравнение (2 112) входит управление, то соотношения (2.112) и (2 113) должны решаться
совместно с равенствами (2.111). Далее, т к. в соответствии с равенствами (2.111) возможны четыре
комбинации значений вектора и(т) = 0, то, задавшись одной из этих комбинаций и величиной vj/?, из
соотношений (2 113) и (2 112) находим Ч'о и Ч'г • Справедливость данной комбинации проверяется с помощью
равенств (2 111). Если равенства (2.111) не выполняются, то следует перейти ко второй комбинации и т д.
Одна из четырех комбинаций должна обязательно удовлетворять соотношениям (2.111)
По указанному выше алгоритму можно составить для ЭВМ программу синтеза оптимального
управления параметрами газа в проточной полости
Рассмотрим два варианта численного решения задачи:
• выход на установившийся режим Ро - 8 МПа, То = 300е К ;
• выход на неустановившийся режим Ро = 14 МПа, То = 320° К .
Исходные данные:
Рр=40МПа, Тр =300°К; Д = 287,1 ^r.K; Ц,=Ц2=Цз = 1>
А: = 1,4, Ж = 5010"4м3; S3 = 10-10"V, Кх =К2 = 1210"4м
Глава 2. Принцип максимума Понтрягина
507
Оптимальные траектории, полученные численно на ЦВМ, изображены на рис 2 27 и рис 2 28
Рис. 2.27. Графики оптимальных траекторий
.—
1
1
к
1
1
Г'
1
г
у
т к
A i
т
~
- —
— им.
—■ -*.
-*
30
РППй
Рис. 2.28. Графики оптимальных траекторий
Как следует из этих рисунков, фазовая плоскость системы (2.107) разбивается на три области, в
каждой из которых управления щ и и2 постоянны. Переход через линию ML сопровождается
переключением управления и,, а переход через линию MOL - переключением двух управлений м, и и2 Линии
переключения LO и N0 представляют собой оптимальные траектории системы, линия переключения LM -
траекторией системы не'является.
Изображенные на рис. 2.27 и на рис. 2.28 траектории получены с помощью необходимых условий
оптимальности, следовательно, только эти траектории могут быть оптимальными, если они вообще
существуют. Существование оптимальных траекторий представляется достаточно очевидным по физическим
соображениям.
32*
508
Методы теории оптимального управления. Часть III
ГЛАВА 3. ОПТИМАЛЬНЫЕ ПО БЫСТРОДЕЙСТВИЮ
СИСТЕМЫ АВТОМАТИЧЕСКОГО
УПРАВЛЕНИЯ
Одной из наиболее важных проблем теории оптимального управления является
проблема синтеза систем, оптимальных по быстродействию. Время регулирования
входит в число основных характеристик системы автоматического управления. Для
многих технических систем уменьшение времени регулирования, т.е. повышение
быстродействия системы, имеет большое практическое значение.
Синтезу оптимальных по быстродействию систем автоматического управления
посвящено большое число работ. Основоположником этого направления является
А.А. Фельдбаум [64]. Особенно много публикаций на эту тему выполнено в
шестидесятые годы.
В настоящей главе работы рассматриваются основные этапы синтеза оптимальной
по быстродействию системы: синтез оптимального управления, аппроксимация
поверхности переключения, учёт входных сигналов, исследование ошибок слежения,
приближённый метод синтеза систем высощго порядка.
3.1. СИНТЕЗ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
МЕТОДОМ ФАЗОВОГО ПРОСТРАНСТВА
3.1.1. Постановка задачи синтеза
Пусть задан некоторый объект регулирования, который будем называть также
неизменяемой частью системы (рис. 3.1).
Требуется выбрать структуру и параметры управляющей части, которые
обеспечивают в системе при любых входных воздействиях yo(t) и любых начальных
условиях оптимальные по быстродействию процессы.
Уо
W
УЧ
и
W
ОБЪЕКТ
У
Рис. Э.1. К постановке задачи синтеза
На практике задачу синтеза ставят обычно более узко. Рассматривают не
произвольные входные воздействия, а лишь некоторый подкласс, в который включают
наиболее существенные. Часто нет необходимости отождествлять множество начальных
условий со всем фазовым пространством, т.к. иногда заранее известна область
возможных начальных условий и эта область может быть весьма ограниченной.
Формулируя задачу синтеза, будем стремиться к некоторой идеальной системе.
Эта система не должна иметь ошибок при воспроизведении входных сигналов, т.е.
должна быть идеальной как следящая. Она также должна обеспечивать минимальную
Глава 3. Оптимальные по быстродействию САУ 509
длительность переходных процессов. Такую идеальную систему часто очень трудно
реализовать на практике. Однако весьма важно иметь представление о
принципиальной возможности построения такой системы.
Рассмотрим линейный объект управления, движение которого задаётся уравнением
у{п) +ап_}/"-]) +... + а]У' + аоу = ки , (3.1)
где а, и к (к > 0) - некоторые константы, у - регулируемая величина, и -
управление. На управление и наложено ограничение
\и\<А. (3.2)
В любой САР ошибка
где у0 - входное воздействие. Если имеет место идеальное слежение, то
№ = Уо«). (3.3)
Из (3.3) следует, что
/*>(*)* УР(О (3-4)
при любом /.
Если в начальный момент / = 0 не выполняется хотя бы одно из условий (3.4) при
1 < п, то соблюдение равенства (3.3) при / > 0 невозможно даже теоретически.
Действительно, скачкообразное изменение координаты y(t) или её производной dly\dtl
при / < п недопустимо, т.к. тогда старшая производная dnyldtn будет содержать
дельта-функцию, т.е. левая часть уравнения (3.1) окажется неограниченно большой, а
это невозможно, т.к. в силу (3.2) правая часть уравнения (3.1) ограничена. Поэтому в
данном случае в системе должен быть переходный процесс. Таким образом, для того
чтобы в системе, начиная с некоторого момента времени tx, имело место идеальное
слежение, необходимо выполнение соотношений
Я'О^ой). y{l\h) = y{o\h)> i=u^i.
Рассмотрим фазовое пространство с декартовыми координатами .у,У,...,.у('1~1).
Изобразим в этом пространстве траекторию уо(/) = (Уо(0,у'0(1),...,у^~1\()),
соответствующую входному сигналу yo(t). Пусть в начальный момент / = 0 фазовая точка
у(0) = (у(0)9уЩ9...9у{п~~Х)(0)) не совпадает с фазовой точкой уо(О) = О>0(0), у'0(0\...
Уоп~1\0))- Оптимальным называется такое движение (рис. 3.2), при котором фазовая
точка у совмещается с фазовой точкой у0 за минимально возможное время.
Вместо введённого пространства на практике целесообразно рассматривать
фазовое пространство ошибок с декартовыми координатами x = yQ-y, x' = y'0-yr, ...,
х(л-1) = y(n~V -y("-l\ в пространстве ошибок идеальному слежению соответствует
начало координат. Оптимальным является такое движение, при котором фазовая
точка x = (x,xf,...,x(w"1)) переводится из начального состояния в начало координат за
минимально возможное время (рис. 3.3).
В силу неравенства (3.2), идеальное слежение возможно лишь за такими
входными сигналами yo(t), которые удовлетворяют неравенству
и называются допустимыми.
510
Методы теории оптимального управления. Часть III
dy_
dt
dt2
Рис. 3.2. К определению оптимального движения
Из соотношения х = у0 -у выразим у и подставим в (3.1):
ИЛИ
где
х{п) + а„ V +... + ахх' + аох = -ки + ДО,
f(t) = у(оп) + а,.!^"0 + •.. + ^ + аоУо.
Если входное воздействие задано, то /(/) - известная функция времени.
х
х(0)
(3.6)
dx_
dt
Рис. 3.3. К определению оптимального движения
В соответствии со сказанным выше, для построения оптимальной системы
необходимо найти закон управления, который обеспечивает перевод фазовой точки
x = (jc,x',...,jc(w~1)) системы (3.6) из произвольного начального состояния в начало
координат за минимально возможное время. В решении указанной задачи большую
помощь может оказать теорема о числе переключений (см. 2.3).
3.1.2. Синтез оптимального управления
Будем сначала предполагать, что в качестве задающих воздействий выбирается
такой подкласс функций, для которого f(t) = 0. Для объекта
у' = ки
таким подклассом будут, например, функции
Глава 3. Оптимальные по быстродействию САУ
511
.vo(O = a' + &>>
где gx и g0 - произвольные числа. Вообще, если входной сигнал представляет собой
многочлен с произвольными коэффициентами, то он принадлежит к указанному
подклассу в том случае, когда степень многочлена меньше порядка астатизма объекта
управления. Для рассматриваемого подкласса входных воздействий уравнение (3.6)
имеет вид
х{п) + а„_}х{"-1) +... + ахх' + аох = -ки. (3.7)
Предположим, что уравнение (3.7) удовлетворяет теореме о числе переключений.
Тогда любую идущую в начале координат траекторию x(t) можно разбить на
участки, каждый из которых характеризуется управлением А либо -А. Совокупность
всевозможных идущих в начало координат оптимальных траекторий заполняет всё
фазовое пространство. Таким образом, каждой точке фазового пространства X
ставится в соответствие некоторый знак управления, а всё фазовое пространство
разбивается на две области, одна из которых характеризуется управлением и = А, а другая
- управлением и = -А . Границу, разделяющую эти области, обозначим S и будем
называть поверхностью переключения. Синтез оптимального управления сводится к
построению в фазовом пространстве поверхности переключения.
Будем сначала предполагать, что п = 3 . Выпишем уравнение
хт + а2хп + ахх + аох = -ки. (3.8)
В соответствии с теоремой о числе переключений оптимальная траектория x(t) в
этом случае разбивается на три участка, на которых знаки управления чередуются.
Так как управления принимают значения А , -А, то в начало координат фазовая
точка может попасть либо с управлением и = А, либо с управлением и = -А .
Предположим, что на заключительном участке и- А. Существует единственная
траектория, которая является решением уравнения (3.8) при и - А и проходит через начало
координат. Обозначим эту траекторию Ц (рис. 3.4).
ц
ц
Рис. 3.4. Графики фазовых траекторий
Если на заключительном участке и = -А, то соответствующую траекторию
обозначим Ц, Объединение линий Ц и Ц обозначим Ц :
ц=циц.
512 Методы теории оптимального управления. Часть III
Таким образом, заключительный участок любой оптимальной траектории
обязательно лежит на линии L,.
Если на заключительном участке и = А, то на участке, предшествующем
заключительному, и = -А . Конец предпоследнего участка оптимальной траектории в этом
случае лежит на линии Ц. Конечной точкой предпоследнего участка может быть
любая точка линии Ц. Совокупность траекторий, примыкающих с управлением
и = -А к линии Ц, обозначим L'{ (один штрих означает управление и = А, два
штриха - управление и = -А).
Если на заключительном участке оптимальной траектории и = -А, то
предпоследний участок характеризуется управлением и = А, причём конец предпоследнего
участка лежит на линии Ц. Совокупность траекторий, примыкающих с управлением
и = А к линии Ц, обозначим L2. Пусть 1^ = 1^ U L2.
Ясно, что совокупность L2 представляет собой поверхность в трёхмерном
фазовом пространстве.
Покажем, что L2 является поверхностью переключения, т.е. L2=S. Для этого
рассмотрим множество возможных первых участков оптимальной траектории.
Совокупность траекторий, примыкающих с управлением и = А к полуповерхности
(поверхность с краем) L2, обозначим Ц, совокупность траекторий, примыкающих с
управлением и = -А к полуповерхности L2, обозначим Ц. Отметим, что
L3 з L2 z> Ц . Очевидно, что совокупность L3 совпадает со всем фазовым
пространством системы.
Выше (см. 2.3) доказана теорема о том, что для линейного объекта оптимальная
по быстродействию траектория единственна. Это означает, что. оптимальные фазовые
траектории, имеющие одну и ту же конечную точку, не пересекаются. Но тогда
траектории, входящие в совокупность Ц, не могут пересекаться с траекториями,
входящими в совокупность Ц. Так как совокупность Ьъ = иг{}Ц совпадает со всем
фазовым пространством, то сказанное возможно лишь в том случае, если
совокупность L3 лежит по одну сторону от поверхности L2, а совокупность Ц - по другую
сторону от L2. Совокупность L\ характеризуется управлением и = А, а
совокупность Ц - управлением и = -А, т.е. по разные стороны от поверхности L2
оптимальное управление имеет разные знаки. Таким образом, для системы третьего
порядка L2=S.
На рис. 3.4 DBCO - пример оптимальной траектории. Рассмотрим теперь
исходное уравнение (3.7). Для данного объекта указанным выше способом строятся
совокупности Zq, L2, L3. Рассматривая четвёртый участок движения (считая от конца), в
полном соответствии с тем, как это делалось выше, строится совокупность 14 •
Продолжая этот процесс, путём последовательного перехода от рассматриваемого
участка к предыдущему получим совокупности L5, L6, ..., Ln_x. Совокупность Ln_x
представляет собой поверхность в п -мерном фазовом пространстве. Аналогичным
образом можно доказать, что Ln_x = S .
Отметим, что из приведённых выше рассмотрений следует, что поверхность
переключения состоит из «особых» точек фазового пространства, т.е. из таких точек,
которые переводятся в начало координат с числом переключений управления, меньшим
чем п -1.
Глава 3. Оптимальные по быстродействию САУ 513
На первый взгляд кажется, что для реализации оптимального регулятора
требуются не только основная перегородка - поверхность переключения, но и перегородки
внутри самой поверхности переключения, чтобы реализовать переключение
управления при переходе фазовой точки из многообразия Lp в многообразие £р_,. В
действительности, это не так. В реальной оптимальной системе фазовая точка движется
либо чуть выше, либо чуть ниже поверхности переключения, либо движение по
поверхности переключения осуществляется в скользящем режиме. Поэтому для
реализации оптимальной системы требуется «построить» только одну перегородку -
поверхность переключения.
Пример 3.1. Рассмотрим объект, имеющий передаточную функцию
W(s) =
(Ts + \)s
Такую передаточную функцию имеет, например, летательный аппарат по каналу крена на некоторых из
режимов полёта Движение объекта описывается уравнением
Т^^-ки (39)
dt dt
Будем предполагать, что на управляющий параметр и наложено ограничение
И £ А,
а задающее воздействие уо= g0, здесь g0 - произвольная константа
Ошибка
и уравнение (3 9) принимает вид
7-£f!* + *=-Jb, (3 10)
dt dt
Так как уравнение (3 9) имеет второй порядок, то S = L,, т е поверхность переключения имеет
размерность 1 и, следовательно, представляет собой линию на фазовой плоскости
Для определения линии переключения Ц воспользуемся принципом «попятного движения» Фельд-
баума. Введём обратное время т = /, -/, здесь /[ - конечное время, t - текущее время Если в прямом
времени траектория *(/) проходится от начала к концу, то в обратном времени т (0 < т < tx) - от конца к
началу Справедливы следующие соотношения
dx dx dx _dx dx _ dx
dt dt dx dx dt dx'
j2v A r^v"l А Г Л*Л А1*
£l-!L W-_A Г dxl_d2x
dt2 ~ dt\dt\~ dx\ dx\~ dx2 '
dnx ,ndnx
dxn dtn
Уравнение (3 10) можно записать в виде
Т^-^-Ы (3 11)
dx2 dx
Полагая и = const, найдём решение уравнения (3 11):
dx (3 12)
x = C]Te*iT+kux + C2
Перейдем в уравнениях (3.12) к производной по прямому времени
dx ' (3 13)
х = С1Тет/т+ких + С2
Так как в обратном времени траектории Ц и Ц исходят из начала координат, то постоянные
интегрирования С, и С2 найдём из условий.
514
Методы теории оптимального управления. Часть III
Окончательно получим
*■.-•• 3
^ = кие*т-ки,
dx
= 0
(3 14)
х = -Ткиех/т + ких + киТ
Уравнения (3.14) определяют (в функции параметра т) в фазовом пространстве с декартовыми
координатами — их при и- А линию Ц , а при и - -А линию Ц
dt
На рис 3 5 изображены линии Ц и Ц . Рассмотрев первые участки оптимальной траектории, легко
установить, что выше линии 1^ оптимальное управление и = А, а ниже линии L, оптимальное
управление и = -А .
ц
\
\
\
ч
и
ч
X
\
"\
= -А
<<
— —А
i
.
-—
■*--*^
-А
—
i л
и = А
■—-^^ ^» ^
"~~^^^\
--^"=^\^
\
\
ц
Рис. 3.5. Графики фазовых траекторий
Обозначим х = ср(х) - уравнение линии ^ . Тогда оптимальное управление будет задаваться
равенством w = ^4sign [лс — ф(дс')] ♦
На рис. 3.6 представлена структурная схема оптимальной системы
Рис. 3.6. Структурная схема оптимальной системы
Пример 3.2. Рассмотрим применение изложенной выше теории для синтеза оптимальной системы
третьего порядка
Пусть движение объекта задается уравнением
Л3"
(3 15)
Глава 3. Оптимальные по быстродействию САУ 515
На управляющий параметр и наложено ограничение
\и\<А.
Задающее воздействие имеет вид
7o = S2'2 + gi' + So>
гДе Si^SbSo - произвольные числа.
Введем ошибку
Из равенства (3.16) следует, что
x = yo-y = g2t2+git + go-y (3 16)
d3x = d3y
dt3 dt3
Тогда уравнение (3.15) можно записать в виде
$=-
В соответствии с теоремой о числе переключений, оптимальное по быстродействию управление ре-
пейно и в переходном процессе допускается не более двух переключений реле Так как уравнение (3 17)
имеет третий порядок, то в фазовом пространстве системы с декартовыми координатами х, dx/dt,
d2x/dt2 существует поверхность переключения S = 1^, по одну сторону от которой - оптимальное
управление и = А, а по другую - и = -А .
В обратном времени уравнение (3.17) принимает вид
£-«. (3 18)
ах
Найдем решение уравнения (3.18), предполагая, что и = const.
£х
dx2
ил _
fx=yC^>
х = и-7- + С,~ + С2т + С3, (3 19)
о 2
где Сх, С2 и С3 - константы интегрирования.
Перейдём в уравнениях (3.19) к производным по прямому времени
^Г-«+С„ f = -«y-Ci*-C2' * = <4+С,у+С2т+С3.
Константы С,, С2, С3 определяются из условий
d2x\ dx
dt2\ -*3o':d -*2о>*Ц-*ю-
у = мт + *3(
Окончательно получим
dt
dx x2
— -"Т-*зоТ + *2о,
т3 х2
* = My + X3oy-X2oT + X,<). (3'2°)
Уравнения (3.20) позволяют рассчитать любую траекторию, входящую в совокупность Z^ (см
рис. 3.4).
Назовем полутраекторией траекторию движения системы (3.17) (или (3 18)), соответствующую
постоянному знаку управления и . Будем предполагать, что обратное время х вводится отдельно для каждой
полутраектории. Структура оптимальной поверхности переключения представлена на рис 3.4
Положим, в уравнениях (3.20) дг,0 = х20 = %> = 0 Уравнения
(3 21)
d2x
dt2
= мх,
dx
dt
х2
= -и—,
2
X-
и
х}
—
6
516
Методы теории оптимального управления. Часть III
при и- А задают (в функции параметра т) линию Ц , а при и = -А - линию Ц Отметим, что параметр
т необходимо изменять от нуля в положительную сторону
В результате численных расчётов, выполненных с помощью уравнений (3 21), линия Lx = Ц[] Ц
задаётся совокупностью дискретных точек. На рис. 3.7 представлена проекция линии Lj на плоскость х = 0.
Если над каждой расчетной точкой записать соответствующее ей значение координаты х, то с помощью
рис 3.7 можно задать линию Ц .
Поверхность переключения образуют полутраектории, примыкающие к линии Ц Для определения,
например, полутраектории CD (рис 3 8), примыкающей с управлением м = -А к линии Ц , необходимо
в уравнениях (3 20) положить м = -Л,а в качестве начальных значений х]0 , х20 , х30 взять координаты
точки D . Параметр т при этом по-прежнему отсчитывается от нуля в положительную с |$рону.
Аналогичным образом строятся другие полутраектории, образующие совокупность L%
и = -А
и = А
Рис. 3.7. Результаты расчетов (задача 3.2)
Полутраектории, входящие в совокупность 1\, характеризуются управлением и- А и примыкают к
линии Ц Каждая из этих полутраекторий может быть рассчитана по уравнениям (3.20) Для этого в
уравнениях (3.20) следует положить и = А,а начальные значения должны совпадать с координатами
соответствующей точки линии Ц Легко видеть, что полутраектории, входящие в совокупность L^ ,
симметричны относительно начала координат полутраекториям, входящим в совокупность /^ .
На рис. 3 8 изображены проекции образующих поверхность переключения траекторий на плоскость
х = 0 . Рис 3 8 позволяет задать поверхность переключения. Для этого над каждой расчётной точкой
необходимо записать соответствующее ей значение координаты х. Отметим, что, с практической точки
зрения, результаты расчётов целесообразно оформлять в виде рис. 3 8
и = А
Ц
и = -А LI
Рис. 3.8. К построению поверхности переключения
Поверхность переключения часто задают в виде таблицы с двумя входами. Для получения такой
таблицы необходимо на рис. 3 8 наложить координатную сетку и с помощью интерполяции определить зна-
Глава 3. Оптимальные по быстродействию САУ
517
чения координаты х в узлах этой сетки. В верхней строке таблицы записываются значения координаты
d2x/dt2 , в левом столбце - значения координаты dx/dt, а на пересечении строки и столбца -
соответствующее им значение координаты х
Положим, что х = /(*', х") - уравнение поверхности переключения Нетрудно установить, что выше
поверхности переключения и = А, а ниже поверхности переключения и = -А Оптимальный закон
управления, таким образом, можно записать в виде
и = As\gn[x - f(x\x")\
На рис 3 9 представлена структурная схема оптимальной по быстродействию системы управления
Таблица 3.1
А
Х2
ХЪ
*;
х'т
*21
хл
*12
*22
*32
XJ1
*п,2
•^23
х33
XJ3
ХтЪ
X*
*1/
*21
X3i
ХЛ
xmi
х'
хи
*2s
*3s
ХР
Хш
l
А
-А
и
ОБЪЕКТ
Рис. 3.9. Структурная схема оптимальной по быстродействию системы управления
3.1.3. Обобщение задачи синтеза
Выше рассмотрен синтез оптимального управления и показано, что если /(/) = 0,
то в фазовом пространстве системы существует поверхность переключения S = Ln_x.
Если f(t) * 0, то поверхность переключения оказывается нестационарной. В этом
случае синтез оптимального управления целесообразно проводить в расширенном
пространстве, размерность которого зависит от заданного класса входных сигналов.
Именно в расширенном фазовом пространстве можно обеспечить стационарность
поверхности переключения.
Поясним это на конкретном примере. Рассмотрим объект, движение которого
задаётся уравнением (3.9). Пусть входной сигнал имеет вид
где gi и g0 - произвольные константы.
В соответствии с пунктом 3.1.2 перейдём в уравнении (3.9) к ошибке
518
Методы теории оптимального управления. Часть III
„ d2x dx .
T!F+lT-ku+b-
В это уравнение входит параметр gx, характеризующий входной сигнал. Поскольку
уравнение удовлетворяет теореме о числе переключений, то при любом
фиксированном gx в фазовом пространстве с декартовыми координатами jc, dx/dt можно
указанным в пункте 3.1.2 способом построить линию переключения. Разным значениям
параметра gx будут соответствовать различные линии переключения.
Увеличим на единицу размерность пространства: рассмотрим пространство с
декартовыми координатами х, dx/dt, dyo/dt. Каждому фиксированному dyo/dt в
этом пространстве соответствует линия переключения, а множество всевозможных
линий переключения образуют в расширенном фазовом пространстве поверхность
переключения (рис. ЗЛО). Эта поверхность задаёт оптимальное управление при
любом входном сигнале рассматриваемого класса.
/о
Уо = Ь
Рис. 3.10. К определению поверхности переключения
Таким образом, если /(/) ф 0, то синтез оптимального управления выполняется в
расширенном фазовом пространстве системы. В зависимости от заданного класса
входных сигналов в число дополнительных фазовых координат могут входить ряд
производных входного сигнала, а также время t. Для данного случая сохраняет свою
силу разработанная в пункте 3.1.2 процедура синтеза. Однако, поскольку
поверхность переключения в исходном фазовом пространстве является нестационарной,
необходимо многократное повторение указанной выше процедуры синтеза.
На практике входной сигнал обычно задают в виде многочлена. Будем считать,
что входной сигнал имеет вид
*>=£*/. <з-22>
/=о
где gt - произвольные константы.
Обозначим к порядок астатизма объекта управления (3.1). Нетрудно видеть, что
для объекта (3.1) при входном сигнале (3.22) синтез оптимального управления
должен осуществляться в расширенном фазовом пространстве порядка л + (г-£ + 1)х
х1(г-*) + 1(г-/;-1),где
Глава 3. Оптимальные по быстродействию САУ 519
[О при z<0,
\l при z>0.
Например, для объекта (3.9) при г = 2 синтез оптимального управления
осуществляется в пятимерном пространстве с декартовыми координатами х, dx/dt, dyo/dt,
d2yjdt\t.
Изложенный способ синтеза позволяет построить закон управления, который
гарантирует строго оптимальное управление при любом входном сигнале из заданного
класса. Однако он приводит к увеличению размерности пространства, в котором
осуществляется синтез. Так как с увеличением размерности пространства объём
необходимых вычислений нарастает лавинообразно, то в некоторых случаях это может
служить серьёзным препятствием для практического использования данного подхода.
Рассмотрим ещё один способ синтеза, который не требует увеличения
размерности пространства, и его можно применять при любых входных сигналах.
В следящей системе входной сигнал заранее неизвестен, но он должен быть
допустимым, т.е. должен удовлетворять неравенству (3.5). Неравенство (3.5)
гарантирует принципиальную воспроизводимость объектом (3.1) входного сигнала yo(t).
Однако реальная система должна не только обеспечить воспроизведение входного
сигнала, но и «догнать» его. Поэтому реальная техническая система проектируется
таким образом, чтобы её динамические возможности существенно превосходили те,
которые требуются для воспроизведения входных сигналов. Таким образом, для
любого технического объекта управления выполняется неравенство
УоИ) + ап-\Уо"~]) + • ■ • + <*\Уо + аоУо\ ^ *4 >
где Ах обычно существенно меньше А .
Задачу синтеза оптимального по быстродействию управления для уравнения (3.6)
будем рассматривать как дифференциальную игру, в которой один из игроков
распоряжается выбором управления и, а второй игрок - выбором управления 9 = /(/). На
управления и и Э наложены ограничения:
\и\<А,\Ь\<кАх.
Первый игрок выбором управления и стремится обеспечить наибыстрейший
перевод фазовой точки х = (х,*',...,х^"^) в начало координат, а второй игрок с помощью
управления в препятствует этому. Если второй игрок не в силах помешать переводу
фазовой точки х в начало координат, то он стремится увеличить время перевода.
Решение указанной дифференциальной игры задаётся с помощью поверхности
переключения, которая строится изложенным в пункте 3.1.2 способом. Однако в
данном случае при построении поверхности переключения ограничения (3.2) следует
заменить неравенством
\и\<А\
где А0 = А-Ах. Отметим, что поверхность переключения по-прежнему строится в
соответствии с уравнением (3.7).
Пусть х = ц>(х\х\...,х("~^) - уравнение поверхности переключения. Решение
(для первого игрока) дифференциальной игры задаётся равенством
и = A sign [х-ф',х\...,х{"-]))]. (3.23)
Закон управления (3.23) не является строго оптимальным, а построен по
принципу гарантированного результата: он обеспечивает минимальную длительность пере-
520 Методы теории оптимального управления. Часть III
ходного процесса при наихудшей функции /(0, т.е. при наихудшем (для данного
начального вектора х(0)) варианте входного сигнала yo(t). В остальных случаях
данный закон управления гарантирует длительность переходного процесса, которая
обязательно должна быть меньше, чем оптимальная при наихудшей функции /(/).
Практическое использование данного подхода показывает, что закон управления
(3.23) обладает высокой эффективностью. Так как фактически в данном случае имеет
место игра против природы, которая не отличается злонамеренностью, то реальный
результат оказывается существенно лучше гарантированного. С прикладной точки зрения
закон управления (3.23) часто вполне можно рекомендовать в качестве оптимального.
Разработанный в пункте 2 метод синтеза базируется на теореме о числе
переключений и, строго говоря, справедлив лишь в том случае, когда характеристический
многочлен
/?"+а„_1/?"-1+... + я1/? + а0, (3.24)
соответствующий уравнению (3.6), имеет только вещественные корни. На самом деле
данный подход можно использовать и при наличии комплексных корней. Однако,
если характеристический многочлен (3.24) имеет хотя бы одну пару комплексных
корней, то установленная в пункте 3.1.2 структура поверхности переключения (см.
рис. 3.8) справедлива не для всего фазового пространства, а лишь для некоторой,
включающей начало координат, области фазового пространства. На практике эта
область оказывается обычно достаточно большой и включает в себя начальные
условия, которые могут встретиться в реальной технической системе, т.е. при синтезе
оптимальной системы управления техническим объектом, как правило, можно
использовать метод синтеза, разработанный в пункте 3.1.2.
Точное выделение указанной выше области является весьма трудной задачей. В
качестве определённого ориентира в этом направлении можно привести следующий
результат.
Если характеристический многочлен (3.24) имеет комплексные корни, то
оптимальное управление также является релейным и задаётся с помощью поверхности
переключения, которую будем обозначать S . Если рассматривать поверхность S в
целом, то она отличается от поверхности S, структура которой изображена на
рис. 3.4. Однако в некоторой области, включающей начало координат, поверхность
S* имеет ту же структуру, что и поверхность S .
Обозначим /? = сс + /со комплексный корень характеристического многочлена
(3.24), имеющий максимальную по модулю мнимую часть. В соответствии с рис. 3.4,
поверхность переключения S состоит из траектории движения, по которым фазовая
точка системы переводится в начало координат. Любая точка поверхности S,
которая переводится в начало координат за время т, удовлетворяющая неравенству
т < я/|со|, принадлежит также поверхности S*. Отметим, что данный результат легко
следует из принципа максимума Понтрягина.
Иногда при синтезе оптимальной системы нельзя ограничиться отмеченной выше
частью поверхности S*. В этом случае синтез оптимального управления
осуществляется с помощью принципа максимума Понтрягина.
3.2. АППРОКСИМАЦИЯ ПОВЕРХНОСТИ ПЕРЕКЛЮЧЕНИЯ
На рис. 3.9 изображена структурная схема оптимальной по быстродействию
системы, из которой следует, что для реализации оптимального регулятора требуется
функциональный преобразователь на два входа. Число входов функционального пре-
Глава 3. Оптимальные по быстродействию САУ 521
образователя определяется размерностью пространства, в котором осуществляется
синтез оптимального управления. Например, если поверхность переключения
строилась в п -мерном фазовом пространстве, то для реализации оптимальной системы
необходим функциональный преобразователь на п -1 входов.
Поверхность переключения после соответствующих расчётов, как правило,
задаётся дискретно в виде некоторого массива чисел. Поэтому для реализации
оптимального регулятора необходимо выполнить аппроксимацию поверхности переключения,
т.е. получить для задания поверхности переключения аналитическую зависимость.
Вид аппроксимирующей функции существенно зависит от того, какие вычисли
тельные элементы будут использоваться при построении функционального пре
образователя.
Цифровые вычислители обладают большой универсальностью и в этом смысле не
накладывают практически никаких ограничений на формулу аппроксимирующего
выражения. Но в оптимальной системе вычислитель работает в реальном масштабе
времени, и поэтому при выборе аппроксимирующей функции следует стремиться к
тому, чтобы уменьшить объём вычислений, необходимый для формирования сигнала
управления. Аналоговый вычислитель мгновенно отрабатывает сигналы,
поступающие на его вход. Однако он накладывает весьма жёсткие ограничения на вид
аппроксимирующей функции.
Аппроксимация поверхности переключения для систем произвольного порядка
рассмотрена в [22]. Однако строгий синтез оптимальной системы для объектов
высокого порядка очень сложно осуществить на практике. Поэтому для систем высокого
порядка, как правило, используют приближённые методы синтеза, о которых речь
пойдёт ниже. На этом основании в данном параграфе мы остановимся на
аппроксимации поверхности переключения только для систем третьего порядка.
Для систем третьего порядка поверхность переключения задаётся равенством
*1=/(*2>*з)-
В процессе расчёта точек поверхности переключения легко построить сечения
поверхности переключения какими-либо плоскостями, например,
х2 = const.
На рис. 3.11 представлен вид таких сечений для одного конкретного объекта управления.
Каждое такое сечение можно аппроксимировать выражением вида
г
£а»з), (3.25)
у=о
здесь ф'Дхз) О' ~ номер сечения) - некоторые известные функции, а значения (п + \)
коэффициентов ос^, например, определяются по методу наименьших квадратов, т.е.
выбираются так, чтобы минимизировать среднюю квадратическую ошибку
т
Fl(a'0,alu...,a!a) = Yi
к=0
/(4,x3(*))-£a>^(x3(A))
7=0
(3.26)
В равенстве (3.26) х3(к) - расчётные точки. Коэффициенты ос^ определяются из
уравнений
|^- = 0 (у = М). (3.27)
Эос,-
Уравнение (3.27) приводит к системе линейных алгебраических уравнений (л + 1)
порядка.
522 Методы теории оптимального управления. Часть III
, На практике в качестве аппроксимирующего выражения (3.25) часто используется
многочлен, т.е.
п п
£а>^(хз) = £с#, (3.28)
7=0 у=0
здесь неизвестными являются (п +1) коэффициентов Clj. Коэффициенты С1}
многочлена (3.28) зависят от сечения, т.е. являются функциями х2. Рассчитав для каждого
сечения аппроксимацию (3.28), найдём, как зависят коэффициенты С^ от
переменной х2. Для коэффициентов С1}, в свою очередь, можно построить
аппроксимирующую зависимость, используя для этого, например, многочлены степени / с
неизвестными коэффициентами Ъ{. Коэффициенты b{, можно также определить по методу
наименьших квадратов. В результате получим аппроксимацию вида
/(vj)=tt^vi
7=0 v=0
Применение для аппроксимации сечений многочленов не всегда оправдано.
Вообще при выборе аппроксимирующих зависимостей необходимо учитывать частные
особенности сечений. В частности, весьма полезными могут оказаться
ортогональные разложения.
Остановимся подробно на ещё одном способе аппроксимации, который, на наш
взгляд, хорошо учитывает частные особенности поверхности переключения и
который позволяет получить достаточно точную и сравнительно простую
аппроксимирующую зависимость.
В дальнейшем будем считать, что f(x2,x3) - непрерывная функция, заданная в
некоторой области D . В силу симметрии поверхности переключения f(-x2;-x3) = -f(x2,x3).
Будем функцию f(x2,x3) аппроксимировать выражением
h(x3+kxx2) + g(x2+k2x3),
полагая, что h и g - непрерывные функции. Функции h и g и неизвестные числа
кх и к2 найдём из условия минимума функционала
J = Я [Я*2>*з)-Л(*з +*Л)-«(*2 +k2x3)]2dx2dxy (3.29)
Область D* (D* с D) представляет собой параллелограмм, ограниченный прямыми
x3=-klx2+bi,x3=-klx2 -й| ,
Х2 = —К2Х3 + с?2 , Х2 = —К2Х3 —1?2 ♦
Найдём минимум функционала (3.29). Выберем произвольные непрерывные
функции h(x3+kxx2) и g(x2+k2x3) и дадим h и g приращения zxh(x3+kxx2) и
z2g(x2 +k2x3), а коэффициентам кх и к2 - приращения е3 и е4. В результате
получим
y(s1,82,63,64) = JJ [/(*2>*з)-А(*3+*1*2+83*2)-
-гхЬ(х3 + кхх2 + г3х2) - g(x2 + к2х3 + г4х3) -
-s2g(x2 + к2х3 + s4x3)]2 dx2 dx3.
Глава 3. Оптимальные по быстродействию САУ
523
Отметим, что, хотя область D* определяется через неизвестные коэффициенты кх и
к2, она предполагается заданной. Поэтому коэффициенты кх и к2 в равенствах
(3.30) не варьируются. Задание области D* соотношениями (3.30) позволяет
существенно упростить окончательный результат.
Если функции И(х3+кхх2) и g(x2+k2x3) доставляют минимум функционалу
(3.29), то должны выполняться следующие условия:
а/
9si
= 2jJ [f(x2,x3)-h(x3+klx2)-g(x2+k2x3)]x
6,-4=0 D*
xhx(x3 + kxx2)dx2dx3 = 0;
— =2[f [f(x2,x3)-h(x3+kxx2)-g(x2+k2x3)]x
xh2{x2 + k2x3)dx2dx3 = 0;
л i = 2Я t^(*2.^з)-^(^з + *Л)~Я(^2 + кгхъ)]x
dJ\
b3le,.4-0 D*
[^з+^2) 2J 2 3
^П =>2Я [Л*2>*з)-М*зН*2)-£(*2+*2*з)]х
b4le,_4=0 D*
Lrf(x2+/:2JC3) 3J 2 3
(3.31)
Введём новые переменные:
zx=kxx2 +x3\ z2- k2x3 + x2.
Предположим, что ^^2 * 1 (в противном случае функции hug можно привести к
одному аргументу). Заменив в интегралах (3.31) переменные, получим
-ь
л
I (f(zuz29kuk2)-h(zx)'g(z2))ik2
~Ъг
\ (f(zltz2,kl9k2)-h(zx)-g(z2))dzx
-Ь
hx(zx)dzx=0,
h2(z2)dz2=0,
[f(zx,z2,kx,k2)-Kzx)-g(z2)] \~z2 \dzxdz2 +
dh
))
-bx -b2
bx b2
Щ f f [f(zbz29k]9k2)-h(zx)-g(z2)]—zxdzxdz2 =0,
J J dzx
(3.32)
-Ь-ь2
J l[f(zXiz2,kx,k2)-h(zx)-g(z2)] (-^Z]]dzxdz2
Л-1 V dz2 )
b\ b2
+kx J J [f(zbz29kX9k2)-Kzx)-g{z2)]^z2dzxdz2 =0.
J J az2
-Ь-ь2
524
Методы теории оптимального управления. Часть III
Учитывая, что уравнения (3.32) справедливы для произвольных функций h}(z}) и
/*2(z2), найдём
1
*(*i) = :
J f(zbz2,kl9
k2)dz2,
-ь2
2M
g(z2) = •£- jf(zbz2,kbk2) dzx,
J|/(rlfZ2^^)^[^-^]*.*2=O,
(3.33)
Соотношения (3.33) являются уравнениями Эйлера для функционала (3.29) и
позволяют определить аппроксимирующие функции h(x3+k]x2), g(x2+k2x3) и
коэффициенты кх и к2.
Аппроксимация
Дх2,*з) * А(*з + *№) + ^2 + ^2^з) (3-34)
позволяет легко построить функциональный преобразователь на два входа. Для этого
требуются лишь два нелинейных преобразователя с одним входом и суммирующие
звенья. Следует отметить, что, несмотря на простой вид, выражение (3.34) часто
аппроксимирует поверхность переключения с довольно высокой точностью.
Объясняется это частными особенностями поверхности переключения.
На рис. 3.11 изображены сечения поверхности переключения некоторого объекта
управления плоскостями х2 = const. Назовём сечение поверхности переключения
плоскостью х2 = 0 нулевым сечением.
-350 -250 -150 -50
50
150
250
*з
80
40
0
-40
-80
-120
\
1
х2= 80 40 0 -40-80
Рис. 3.11. Сечения поверхности переключения плоскостями
Глава 3. Оптимальные по быстродействию САУ 525
Из рис. 3.11 видно, что любое сечение может быть получено приближённо путём
сдвига (без вращения) нулевого сечения вдоль осей х3 и х}. Это даёт возможность
представить (приближённо) уравнение поверхности переключения в виде
*1=ф(*з+У(*2)) + Р(*2)- (3-35)
В равенстве (3.35) функция ф задаётся графиком нулевого сечения, функция у(х2)
учитывает смещение нулевого сечения вдоль оси лг3, а функция (3(jc2) - вдоль оси
jcj . Если считать функцию у(х2) линейной (а это обычно имеет место), то равенство
(3.35) является частным случаем аппроксимации (3.34). Этим и объясняется
достаточно высокая точность аппроксимации (3.34).
Для численного решения системы уравнений (3.33) можно рекомендовать метод
Ньютона, причём в качестве начальной точки поиска целесообразно использовать
соответствующие значения, полученные по «методу сечений». Хороший выбор
начальной точки обеспечивает быструю сходимость метода Ньютона.
3.3. ОШИБКИ СЛЕЖЕНИЯ В ОПТИМАЛЬНЫХ
ПО БЫСТРОДЕЙСТВИЮ САУ
Начиная с первых работ по оптимальному управлению [64, 65], в литературе
большое внимание уделялось синтезу оптимальных по быстродействию систем
автоматического управления. Однако, как следует из определения оптимального по
быстродействию управления, оно обеспечивает наибыстрейший перевод системы в
заданное состояние, т.е. оптимизирует в системе переходный процесс. При этом такая
важная характеристика, как точность регулирования (точность слежения), выпадает
из рассмотрения. Если при синтезе оптимального управления удаётся в полной мере
учесть возможные входные воздействия, то оптимальная система воспроизводит их
идеальным образом. Однако на практике такое встречается крайне редко.
Необходимо также иметь в виду, что в технических системах оптимальный закон управления
реализуется приближённо.
Рассмотрим объект, движение которого описывается уравнением
= ки + ЬтМ{т)+Ьт_]М{т-])+... + Ь{М' + Ь0М.
Здесь у - регулируемая величина; М - возмущающее воздействие; и - управление;
at, bj,, к (к > 0) - некоторые числа. Предполагается, что на управляющий параметр
и наложено ограничение
\и\<А. (3.37)
Введём ошибку х = уо-у, где yo(t) - входное воздействие. В случае идеального
слежения ошибка x(t) = 0 . Очевидно, идеальное слежение принципиально возможно
лишь за таким входным воздействием, которое удовлетворяет неравенству
уР + а»-!^"0 + • • • + <ЬУо ~ЬтМ(т) ~ ViM(m4) -...-Ьом\<кА.
Будем предполагать, что имеет место строгое неравенство
/оп) + <*я-1у1Г1) + •.• + Wo ~ЬтМ{т) ~Ьт-Мт~]) ~ • • •"Ь,М\ < кЛ . (3.38)
Подставим в уравнение (3.36) у = у0 -х
x(w)+a/1_1JC(w"1)+... + aox = -b + /(/), (3.39)
где
526 Методы теории оптимального управления. Часть III
/°(0 = J#° + а„.1^"-1) +... + а1У'о + аоУо,
f\t) = bmM(m) +bm_,M(m-X) +...+W+Ь0М.
Введём вектор х = (х,х',...9х^п"^). В векторном пространстве с декартовыми
координатами х, х , ..., х^"]) идеальному слежению соответствует начало
координат. Синтезом оптимального управления будем называть построение такой функции
Э(х,/), при которой управление и = 9(х,0 переводит фазовую точку системы (3.39)
из произвольного начального состояния в начало координат за минимально
возможное время.
В данном разделе всюду предполагается, что при синтезе оптимального
управления функция f{t) принимается равной нулю. Кроме того, в правильно
спроектированной системе в режиме слежения ограничители не достигаются, поэтому для
удобства будем считать, что они вообще отсутствуют.
Оптимальное по быстродействию управление задаётся равенством •
и = A sign (х-ф',х\...,х(п-1))). (3.40)
Здесь
х = ф\х",...,х("-])) (3.41)
- уравнение поверхности переключения. Если входное и возмущающее воздействия
таковы, что f(t) = 0, то система (3.36), (3.40) идеальным образом воспроизводит
входное воздействие, причём слежение за входным сигналом происходит в скользящем
режиме. Решение y(t) = yo(t) устойчиво в целом, или, по крайней мере, область
притяжения этого решения совпадает с областью управляемости системы (3.36), (3.40).
Если /(/)*0, но слежение за входным сигналом по-прежнему происходит в
скользящем режиме, то справедливо уравнение (3.41). Так как
Ф(0,0,...,0) = 0,
уравнение (3.41) допускает решение
х(0 = 0.
Таким образом, и в этом случае имеет место идеальное воспроизведение входного
сигнала. Следует иметь в виду, что в силу структуры поверхности (3.41) в
скользящем режиме движения траектории х(/) стягиваются к началу координат.
Остановимся на условиях существования скользящего режима. При получении
условий существования будем предполагать, что оптимальный закон управления
определяется равенством
и = A sign (х-ф',х',...,х^,-/м\-/к+2\...,-/-«)). (3.42)
Введённые здесь изменения по отношению к закону (3.40) объясняются тем, что при
синтезе оптимального управления входное воздействие обычно задаётся в форме
многочлена. Если указанный многочлен имеет степени к и к < п-\, то х^к+^ = -у^к+1\
х(*+2) __у*+2) ^ х(п-\) =.__д;("-1) Это даёт возможность представить оптимальный
закон в форме (3.42). В законе управления (3.40) используются производные входного
сигнала до (п -1) -го порядка включительно, получение которого удаётся далеко не
всегда. Поэтому оптимальный закон управления часто реализуют в форме (3.42).
В соответствии с работой [58] условия существования скользящего режима
задаётся неравенствами
Глава 3. Оптимальные по быстродействию САУ
527
— [x-(D(x' Х" Х{к) -V(*+1)>> -V(W-1}1 I -x'-OS-x'-ltLx--
\ X - ф^Х ,X ,.. •, X , у J,..., у - X X X
atL J \U=A ox ox
_ дф (Ar-i-l) 5ф
- dxWX Э(-/+1>)
5ф
/""'> +
+^^[b+/('bao3;"aiy"---"w(""1)1L-<()'
^^-Ф^л...,^,-^"),...,-/"-1)]! =*'-|v-|v-
"' 1и=-/1 "X СПС
__5ф_ (i+i) __5ф__ (*+2) 5ф
У"^
9ф
-[Аи + /(/)-аЬу-а|У-...-вя.,У"-1)]
М=-/1
Движение в скользящем режиме определяется уравнением
>0.
(3.43)
(3.44)
где х = уо-у.
Найдём из (3.44) х'(0 и подставим в (3.43). В результате получим неравенства
д<Р Г/, л . s*,^ ... ...« - «("-•)_ v(n)]<0
(3.45)
Оф
-^_^[_jM + /(0_ew>-eiy-...-flli.iy-i)_y-)]>0.
Условия (3.45), как легко видеть, эквивалентны следующим соотношениям:
У{п) +an_,/n-xU... + a<)y-f\t)\<kA,
9ф
д(-/"^)
<0.
(3.46)
х=х(/)
Здесь i(t) = (x(t),xXt),...,xik\t),-y{k+l\t),-y{W - n-мерная
вектор-функция, представляющая собой решение уравнения (3.44).
Отметим, что неравенства (3.46) проверяются на решениях вырожденного
уравнения. Первое из условий (3.46) представляет собой ограничение на выходной сигнал
y(t). Интересно отметить, что это ограничение совпадает с динамическими
возможностями объекта (3.36). Второе условие (3.46) задаёт ограничение на вид функции ф .
Если в равенстве (3.42) к = п-\, т.е. рассматривается закон управления в форме
(3.40), то второе неравенство (3.46) принимает вид
Как следует из структуры поверхности переключения, при любом порядке
системы (3.36)
дф
Э(-У-»)
= о.
(3.47)
х=0
528 Методы теории оптимального управления. Часть III
Так как условия (3.46) являются достаточными, то равенство (3.47) необязательно
приводит к срыву в точке х = О скользящего режима движения. Очевидно,
соотношения (3.47) не приводят к срыву скользящего режима движения, если управление
и- А переводит фазовую точку х из начала координат (точки х = 0) в область, где
х-ф(х) < 0 , а управление и - -А - в область, где лс-ф(х) > 0 . Данное условие
может быть проверено с помощью уравнений
/п)+ап_У"-]) + ... + а]у' + а0у = ки + /\О.
При реализации оптимального регулятора функция ф(х), как правило,
аппроксимируется некоторым выражением. Если используются аналоговые вычислительные
элементы, то полученные аппроксимирующие зависимости, в свою очередь,
аппроксимируются кусочно-линейными функциями. В конечном счёте получается
оптимальный (квазиоптимальный) регулятор, для которого условие (3.47) не имеет место.
Вместе с этим оказывается возможным, оценивая существование скользящего
режима, ограничиться проверкой неравенств (3.46).
Остановимся более подробно на законе управления в форме (3.40). В этом случае,
как уже отмечалось, скользящий режим обеспечивает идеальное воспроизведение
любого входного сигнала, удовлетворяющего неравенству (3.38). Так как в режиме
слежения х(/) = 0, то в каждый момент времени /
дф 1 =0
дх{п-%)-о
Из первого условия (3.46) вытекает, что
\f(t)\<kA, (3.48)
т.е. первое условие (3.46) совпадает с неравенством (3.38).
В окрестности точки х = 0 уравнение (3.39) можно приближённо представить в
виде
х(п) =-ки + /(0, (3.49)
т.е. можно считать, что в окрестности начала координат поверхность переключения
строилась в соответствии с уравнением
х{п)=-ки. (3.50)
Исходя из неравенства (3.48) и уравнения (3.50), нетрудно установить, что
управление и - А переводит фазовую точку х системы (3.49) из начала координат в область
х-ф<0, а управление и = -А - в область х-ф>0. Таким образом, для системы
(3.36), (3.40) при любом входном воздействии, удовлетворяющем неравенству (3.38),
в точке х = 0 всегда выполняются условия существования скользящего режима.
Как уже отмечалось, при реализации оптимальной системы вместо функции ф
используется аппроксимирующая функция ф . Аппроксимирующие функции могут быть
весьма разнообразными. Однако, если при реализации оптимальной системы
применяются аналоговые вычислительные элементы, то функция ф , как правило, является
кусочно-линейной, причём в окрестности точки х = 0 функция ф* линейна и
sN ■ *°- а51)
"* 1х=0
Пусть в окрестности точки х = 0 функция ф* задаётся уравнением
Глава 3. Оптимальные по быстродействию САУ 529
х = ^С,х«\ (3.52)
Непосредственно из соотношений (3.52) и (3.38) следует, что неравенство
рЬт . =с«-.<° <3-53>
Ш х=0
гарантирует существование скользящего режима в точках поверхности
переключения, принадлежащих некоторой окрестности начала координат. Поскольку при
любых малых отклонениях от начала координат гарантируются выход фазовой точки на
поверхность переключения и последующее движение (в скользящем режиме) по
указанной поверхности, то решение x(t) = 0 является устойчивым, если устойчиво
вырожденное уравнение (3.52).
Таким образом, если для объекта (3.36) оптимальный закон управления
реализуется в форме
и = A sign (х-у(х',х",...,х{"-1))), (3.54)
и ф* - кусочно-линейная функция, для которой справедливо неравенство (3.53), и,
кроме того, вырожденное уравнение (3.52) устойчиво, то в системе (3.36), (3.54)
любое допустимое входное воздействие воспроизводится идеальным образом. При этом
решение x(t) = y(t) устойчиво в малом.
Законы управления в форме (3.54) и (3.40) обеспечивают идеальное
воспроизведение входного сигнала, причём не требуется измерение возмущающего воздействия
M(t). Однако это возможно лишь при использовании чистых производных. Если
вместо производных выходной величины в законе управления применяются
«естественные» координаты объекта (ток, давление и т.п.), то возмущающее воздействие
через «естественные» координаты войдёт в вырожденное уравнение движения. В
этом случае идеальное слежение возможно только при измерении возмущающего
воздействия.
В отличие от соотношений (3.40) и (3.54), закон управления в форме (3.42) не
обеспечивает идеального слежения за произвольным допустимым входным
сигналом. Действительно, движение в скользящем режиме в этом случае описывается
уравнением
Уо-У = Фо-у',Уо-у",-Ак)-У(к\-/к+1\-У{к+2\^-У("-]))- (3-55)
Функция y(t) = yo(t) является решением уравнения (3.55) только при условии, что
Применение уравнений (3.55) для оценки точности режима слежения в общем
случае затруднительно. Однако, если в (3.42) к = 0, т.е. уравнение (3.55) имеет вид
>> + Ф(-/,-/,... г/И)) = ^о, (3.56)
то можно рекомендовать следующий подход. Вместо входного воздействия yo(t)
зададим выход системы y(t), который должен удовлетворять первому неравенству
(3.46). Используя уравнение (3.56), по заданному выходу легко найти
соответствующее ему входное воздействие yo(t) . Сравнивая y{t) и yo(t), можно сделать
заключение о точности слежения. Отметим, что указанный подход может быть
использован и в том случае, когда поверхность переключения задана численно в виде
таблицы, как это часто бывает после выполнения соответствующих расчётов по синтезу
оптимального управления.
35 Зак. 366
530 \ Методы теории оптимального управления. Часть III
Если в равенстве (3.55) ф - аппроксимирующая кусочно-линейная функция, то
анализ системы существенно упрощается, т.к. уравнение (3.55) может быть легко
проинтегрировано при произвольном входном воздействии. Однако и в этом случае
удобно задаваться не входом системы, а её выходом. Действительно, относительно функции
Уо(О уравнение (3.55) имеет более низкий к -й порядок. Функцию y(t) всегда можно
выбрать так, чтобы выполнялось первое условие (3.46). Так как второе условие в
оптимальных и квазиоптимальных системах, как правило, выполняется, то, следовательно,
удаётся исключить из рассмотрения участок выхода системы на скользящий режим
движения. Это, вообще говоря, сделать невозможно, если задавать входное воздействие
yo(t). Отметим, что, как следует из приведённых выше рассуждений, неравенства
(3.46) сохраняют свою силу и для кусочно-гладкой функции ф .
Если в оптимальном законе управления используются «естественные»
координаты объекта, то описанные выше приёмы оценки точности режима слежения можно
сохранить, воспользовавшись методом эквивалентного управления [58]. Очень часто
«естественные» координаты объекта можно легко выразить через выходную
координату и её производные. Это позволяет для оценки точности режима слежения
непосредственно использовать уравнение (3.44).
Сделаем одно уточняющее замечание. Следящую систему, которая без ошибки
воспроизводит любое допустимое входное воздействие, т.е. воздействие,
удовлетворяющее неравенству (3.38), назовём идеальной. Выше было установлено, что система
(3.36), (3.40) является идеальной следящей системой. При этом поверхность (3.41)
необязательно должна соответствовать оптимальному закону управления. Нетрудно
показать, что справедливо и обратное утверждение: если детерминированная
следящая система является идеальной, то её закон управления задаётся в форме (3.40).
Сформулируем последний результат более строго. Будем предполагать, что в
законе управления следящей системы может использоваться информация о входном и
выходном сигналах, а также об их производных и первообразных, т.е.
u = F(y,y',...,/i\y0,y'0,...,y^,/-]\/-2\...,/-k\yi-l\..y0-^). (3.57)
Соотношение (3.57) охватывает все возможные случаи применения линейных и
нелинейных корректирующих устройств. В равенстве (3.57) следует положить /<л,
т.к. в соответствии с (3.36) переменные y(t), /(/), • ., Ул)(0 однозначно задают
управление и . Справедливо следующее утверждение: если следящая система (3.36),
(3.57) является идеальной, то закон управления (3.57) имеет вид (3.40). Отсюда, в
частности, следует, что только релейный закон управления может обеспечить
идеальное воспроизведение любого допустимого входного воздействия.
3.4. ПРИБЛИЖЁННЫЙ СПОСОБ УЧЁТА МАЛЫХ ПОСТОЯННЫХ
ВРЕМЕНИ
Известно, что при синтезе оптимального по быстродействию управления объём
вычислений с увеличением порядка системы катастрофически возрастает. И дело
здесь, собственно, не столько в численном определении самой поверхности
переключения (хотя и это сопряжено с некоторыми трудностями), сколько в обработке
огромного массива чисел, дискретно задающих поверхность переключения, а также в
получении подходящей аппроксимации. Для систем низкого (второго и третьего)
порядков вычисление поверхности переключения и её аппроксимации обычно не
составляет большого труда. В соответствии со сказанным выше, для систем высокого
порядка большое значение приобретают приближённые способы, приёмы и методы
синтеза оптимального управления.
Глава 3. Оптимальные по быстродействию САУ
531
В настоящем разделе предлагается приближённый способ синтеза оптимального
по быстродействию управления. Этот способ позволяет при синтезе оптимального
управления приближённо учесть влияние малых постоянных времени. От других
известных в литературе методов данный выгодно отличается тем, что благодаря
аппроксимации системы высокого порядка системой низкого порядка с запаздыванием
он достаточно точно учитывает «вклад» малых постоянных времени в оптимальный
закон управления.
В передаточных функциях технических систем можно выделить большие и малые
постоянные времени. Звенья, содержащие большие постоянные времени, обычно
описывают силовую часть системы, а звенья, содержащие малые постоянные
времени, - управляющую часть. В дальнейшем будем исходить из следующего: малые
постоянные времени приводят к малым изменениям в поверхности переключения.
Передаточную функцию системы, полученную из исходной путём исключения
звеньев, содержащих малые постоянные времени, назовём базовой, а соответствующий
ей оптимальный по быстродействию закон управления - базовым законом.
Совокупность звеньев, не входящих в базовую передаточную функцию, образует систему,
которую будем называть дополнительной. Способы получения базового закона
управления рассмотрены выше. Остановимся на тех изменениях, которые следует внести в
базовый закон управления, чтобы учесть влияние малых постоянных времени.
Изложение указанного подхода целесообразно начать с рассмотрения
конкретного примера. При этом в целях упрощения будем предполагать, что ограничение
накладывается только на управление.
На рис. 3.12 изображена структурная схема объекта, причём пунктиром выделена
базовая передаточная функция. Пусть на управляющий параметр и наложено
ограничение
\и\<А.
Исключив звено с малой постоянной времени, легко определить оптимальный по
быстродействию закон управления. Он задаётся равенством
и = -As\gn(y3 -q>02)), (3.58)
где у3 - фО>2) - уравнение линии переключения.
1 Уъ
Рис. 3.12. Структурная схема объекта
Оптимальное по быстродействию управление релейное как в базовой, так и в
исходной системах. Однако в исходной системе на вход базовой передаточной функции
поступает координата yx(i), которая «сглаживает» релейный сигнал u{t) (рис. 3.13).
Так как Тх « Т2, то базовая система обладает существенно большей
«инерционностью», чем дополнительное звено, т.е. базовая система практически не реагирует
на форму быстрых изменений координаты yx(t), а «отслеживает» их среднее
значение. Это позволяет приближённо учесть влияние дополнительного звена, заменив его
звеном запаздывания. На рис. 3.12 пунктиром изображены запаздывающие моменты
переключения, компенсирующие влияние малой постоянной времени. Следует
отметить, что введение запаздывания является распространённым приёмом, который
используется при аппроксимации систем высокого порядка моделями низкого порядка.
35*
532
Методы теории оптимального управления. Часть III
и,ух
Л
с d I
Рис. 3.13. Графики оптимальных управлений
Воспользуемся известным способом синтеза систем с запаздыванием, который
заключается в том, что в законе управления (3.58) текущие координаты у3 и у2
заменяются упреждёнными на запаздывание т. Однако вместо традиционной для таких
задач схемы упреждения, основанной на использовании формулы Коши для решения
системы линейных дифференциальных уравнений, будем использовать ряд Тейлора
(траектория релейной системы не является аналитической функцией, и, строго
говоря, она не может быть представлена рядом Тейлора; однако ниже будут
использоваться только такие производные, которые для данной системы существуют и
непрерывны). Ограничиваясь первым членом ряда Тейлора, можно записать
at
at
Из передаточной функции системы следует, что
dy3 dy2 I , ч
Заменяя в законе (3.58) текущие координаты на упреждённые, получим
и = -A sign
Уз+У2*-Ч>\У2+—(У\-У2)*
(3.59)
Отметим, что в закон управления (3.59) входят все фазовые координаты объекта.
Из приведённых выше рассуждений следует, что при правильно подобранном
значении запаздывания х закон управления (3.59) достаточно точно учитывает влияние
малой постоянной времени 7j, т.е. его можно рассматривать в качестве
приближённого оптимального закона управления объектом, изображённом на рис. 3.13.
Остановимся на способе определения запаздывания х. Известно, что для
рассматриваемого объекта поверхность переключения представляет собой совокупность
идущих в начало координат оптимальных траекторий, на которых допускается одно
переключение управления. С другой стороны, в релейной системе (необязательно
оптимальной) движение по поверхности переключения возможно в скользящем
режиме. Так как оптимальная поверхность переключения состоит из траекторий
движения, то её можно рассматривать как предельную поверхность скольжения.
Значение запаздывания х будем выбирать так, чтобы поверхность переключения,
реализующая закон управления (3.59), также была предельной (в рамках заданной
структуры) поверхностью скольжения. Это является косвенным критерием близости по-
Глава 3. Оптимальные по быстродействию САУ 533
верхности переключения, входящей в закон (3.59), к строго оптимальной
поверхности. При таком выборе т траектории, порождаемые законом (3.59), имеют характер
строго оптимальных: фазовая точка объекта сначала выводится на поверхность
переключения, а затем по поверхности переключения переводится в начало координат.
В соответствии с работой [7] на поверхности переключения
Уъ + Уг*~ЩУг + — (У\ ~Л)т = ° > (3-60)
условия существования скользящего режима задаются неравенствами
Л
Уз+Уг*-Ч>\ Уг+—(Ух-УгК
Г2 'Аи-А
>0,
Уъ + ДЪ*-ф| Уг +—(Л -Уг)^ ] | ^ °-
уА\и=-А
Выполнив дифференцирование, получим соотношения
1— Ьъ+—>"i —- 1— —(^i ~yi)— —М-уО^о,
2J Г2 &^ Т2)Т2 dzT2Tx
*"f ]^ +f Л -f^fl-f If-Сл -Л) + |Е^^ + Л)^0, (3.61)
r2j r2 azl^ r2jr2 dzT2Tx
где
У2
Отметим, что неравенства (3.61) должны выполняться в каждой точке поверхности
(3.60).
Так как запаздывание т входит в условия существования скользящего режима
(3.61), то для определения предельной поверхности скольжения необходимо найти
такое запаздывание т°, любое малое изменение которого приводит к срыву
скользящего режима движения.
Обозначим левую часть соотношений (3.61) W(y]9y2,u,t) (для статического
объекта координата уъ также входит в условия существования скользящего режима; при
определении функции W(yx,y2,u,T) её необходимо выразить из уравнения (3.60)
через ух и у2). Из передаточной функции объекта следует, что фазовые переменные ух
и у2 изменяются в пределах
-Л < у} < А, -А < у2 < А . (3.63)
Область, выделяемую неравенствами (3.63), обозначим D . Пусть
R(x)= min W(yby2,T,A),
Я* 00= max W(yuy2,i,-A).
Нетрудно видеть, что
Д*(т) = -Л(т).
Величина запаздывания т°, при которой поверхность (3.60) является предельной
поверхностью скольжения, удовлетворяет уравнению
Л(т°) = 0.
534
Методы теории оптимального управления. Часть III
\
\
На рис. 3.14 изображён график функции Д(т) при 7J =0,02, Т2=\, А = \. Так
как dcp/dz = O в точке z = 0, то при z = 0 неравенства (3.61) не зависят от знака
управления. Для соответствующих у]9 у2, как непосредственно следует из (3.61) и
(3.62), левые части соотношений (3.61) при любом т равны нулю. Этим и
объясняется наличие на графике функции Л(т) участка, лежащего на оси т.
R
0,5
0 0,01 0,02 т, с
Рис. 3.14. График функции Д(т)
Другой способ определения запаздывания т основывается на приравнивании
площадей криволинейного треугольника acl и прямоугольника acdb (см. рис. 3.13).
Легко убедиться, что запаздывание т, если его определять указанным способом,
равно 7j. Более того, если дополнительная система состоит из к апериодических
звеньев, включённых последовательно и имеющих постоянные времени 7], Т2, ..., Тк , то
запаздывание т = 7] + Т2 +... + Тк . Отметим, что для рассматриваемого объекта оба
способа дают примерно одинаковый результат.
На рис. 3.15 изображена осциллограмма отработки системой (с законом
управления (3.59)) начального рассогласования по координате уъ. Из рисунка видно, что
координата yx(t) имеет два излома, что соответствует двум переключениям
управления. Длительность переходного процесса при этом практически не отличается от
строго оптимальной. Исследование на ЭЦВМ закона управления (3.59) при
различных значениях постоянных времени 7] и Т2 показывает, что указанный подход
можно успешно использовать при разносе постоянных времени в пять и более раз.
0,5
-0,5
ч
V
1
L
/
/
/
0,5 i,0 f,5
Рис. 3.15. Графики сигналов
t.c
Глава 3. Оптимальные по быстродействию САУ
535
Изложенный на конкретном примере способ учёта при синтезе оптимального
управления малых постоянных времени практически без изменений переносится на
случай любой базовой передаточной функции, а также на случай любого порядка
вспомогательной системы. При этом, упреждая координаты объекта, можно
использовать такое число членов ряда Тейлора, которое соответствует порядку
вспомогательной системы. Это позволяет включить в закон управления все фазовые
координаты объекта. Если при формировании упреждения используются к членов ряда
Тейлора, то такое упреждение будем называть упреждением к -го порядка.
На рис. 3.16 изображена структурная схема объекта, у которого базовая
передаточная функция остаётся прежней, т.е. 7J « Т2, То « Т2. Воспользовавшись для
упреждения координат двумя членами ряда Тейлора, по аналогии с действиями,
проведёнными выше, получим закон управления
и = -A sign | уъ + у2\ + -—(.у, - у2)^- - ф| у2 + —О, - у2)т +
if 1 1 (i
г\т<г2
Уо
Уг-
Щ
(3.64)
Запаздывание т определим рассмотренными выше способами. Необходимо только
иметь в виду, что не всегда выбором т можно обеспечить существование
скользящего режима на всей поверхности переключения. На практике существование
скользящего режима на всей поверхности переключения, вообще говоря, не требуется.
1
Tos + l
Уо
►
1
7^ + 1
У\
г—►
1
T2s + \
Уг
►
1
s
\ Уъ
-} ►
Рис. 3.16. Структурная схема объекта
Если дополнительная система состоит из апериодических звеньев, как на
рис. 3.16, то вместо упреждения £-го порядка можно использовать к упреждений
первого порядка. Сначала учитывается только одно апериодическое звено. С
помощью упреждения первого порядка для такой системы строится оптимальный закон
управления. Этот закон затем рассматривается как базовый для новой системы, в
которую включается другое апериодическое звено, и т.д.
На рис. 3.17 изображена осциллограмма отработки системой четвёртого порядка
(Го = 0,01, 7j = 0,02) начального рассогласования.
Оптимальный закон управления строился путём двукратного применения
упреждения первого порядка. Следует отметить, что получаемый таким образом закон
управления оказывается более близким к оптимальному, чем закон управления (3.64).
На рис. 3.18 изображена осциллограмма отработки начального рассогласования
оптимальной системой, базовая передаточная функция которой совпадает с
рассмотренной выше, а вспомогательная представляет собой колебательное звено с
параметрами Т = 0,02 (с), £ = 0,5 . При построении оптимального закона управления было
использовано упреждение второго порядка.
Если передаточная функция объекта содержит колебательное или консервативное
звено, то, как известно, оптимальные траектории образуют только часть поверхности
536
Методы теории оптимального управления. Часть III -
переключения. В этом случае при выборе времени запаздывания т по первому
способу необходимо ориентироваться именно на эту часть поверхности.
Ум.м
0.5
-0,5
-V)
^
1 \
i V
<
1 !
Л/"
л
Г
t
0 0.5 1,0 «,5
Рис. 3.17. Графики сигналов
у
•^1,2.3 I ~Т 1
0,8
0,4
0
-0,4
-0,8
-1,2
t-.e
~-—^.
|^:
v—
у» i
1
/
/
/ j
J
Уо
32
16
0
-16
-32
-48
0 0,5 1,0 1,5 ttc
Рис. 3.18. Графики сигналов
Описанный выше приём приближённого учёта малых постоянных времени может
эффективно использоваться и в более сложных задачах оптимального управления,
например, если требуется построить оптимальный закон управления при наличии
ограничений на фазовый вектор системы или при синтезе оптимального управления
для объекта с ограничителями и т.п. Необходимо, однако, иметь в виду, что в задачах
с ограничениями на фазовый вектор системы указанный приём приводит к
небольшому смещению граничного участка оптимальной траектории. Это может вызвать, в
конечном счете, нарушение (правда, незначительное) заданных ограничений. С
практической точки зрения такие нарушения вполне допустимы.
Глава 4. Динамическое программирование 537
ГЛАВА 4. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
И АНАЛИТИЧЕСКОЕ КОНСТРУИРОВАНИЕ
РЕГУЛЯТОРА
Динамическое программирование, наряду с принципом максимума, является
основным математическим методом, с помощью которого определяется оптимальное
управление. В отличие от принципа максимума, который формулируется таким
образом, что оказывается ориентированным, прежде всего, на определение оптимального
управления в виде оптимальной программы, динамическое программирование
позволяет определять оптимальное управление только в форме синтезирующей функции.
Динамическое программирование хорошо обосновано для дискретных процессов.
Обоснованное применение динамического программирования для непрерывных
процессов не всегда возможно. Это связано с тем, что при выводе функционального
уравнения Беллмана приходится делать предположение, непосредственная проверка
которого по уравнениям движения и функционалу невозможна. И только после
решения уравнения Беллмана можно проверить, выполняется ли сделанное
предположение или нет. Далее, функциональное уравнение Беллмана для непрерывных
процессов представляет собой дифференциальное уравнение в частных производных.
Это уравнение обычно имеет весьма сложный вид, и численное его решение часто
весьма затруднительно.
Если иметь в виду не только задачи оптимального управления, то необходимо
отметить, что динамическое программирование обладает большой универсальностью.
Его можно использовать для решения широкого класса задач оптимизации.
В настоящей главе излагается основное содержание динамического
программирования как метода оптимизации. Рассматриваются как дискретные многошаговые
процессы принятия решений, так и непрерывные процессы. Приводится ряд
примеров по решению задач оптимизации методом динамического программирования, в
том числе его применение к задаче об аналитическом конструировании регуляторов.
4.1. ДИСКРЕТНЫЙ МНОГОШАГОВЫЙ
ПРОЦЕСС ПРИНЯТИЯ РЕШЕНИЙ
Пусть состояние системы задается вектором р = (р\,Р2,—,Рп) - Обозначим
р° = (/?i°,/?2>--->Рп ) начальное состояние системы, р1 - состояние системы на
единицу времени позже и т.д. Последовательность ро,р\р2> -эР^ , где
р*+|=т(р'У), k=0,\,...,N (4.1)
задает изменение состояния системы в дискретные моменты времени.
В равенстве (4.1) Т = (7],Г2,...,Г„) - «-мерный вектор, u = (ul9u2,...,um) -
/w-мерный вектор. На изменения состояния системы можно влиять, выбирая на
каждом шаге вектор и из некоторого заданного множества U. Вектор и называется
вектором решения, вектором управления или просто решением. В силу особенностей
динамического программирования начальное состояние системы удобно обозначать
вектором р.
Последовательность
p,pV,...,p", uV,..,u\ (4.2)
34 Зак. 366
538 Методы теории оптимального управления. Часть III
где
p*+1=t(pV), * = o,u,#
называют многошаговым процессом принятия решений. Если N — конечное число, то
такой процесс называют конечношаговым, если число элементов в
последовательности (4.2) не ограничено, то - бесконечношаговым.
Будем качество многошагового процесса оценивать функцией
*(p,pV,...,p\uV,..,u"). (4.3)
Для дискретного многошагового процесса функция (4.3) является функционалом,
поэтому именно так она и называется в дальнейшем. За оптимальное будем
принимать максимальное значение функционала (4.3).
Равенство (4.1) представляет собой систему разностных уравнений. Строго
говоря, введенное здесь понятие многошагового процесса сводится именно к системе
разностных уравнений. Однако в динамическом программировании рассматриваются
многошаговые процессы, которые невозможно задавать системой разностных
уравнений. Пример такого многошагового процесса будет рассмотрен ниже.
Отметим одно свойство многошагового процесса, которое в дальнейшем играет
важную роль. Это свойство можно сформулировать так: для многошагового процесса
будущее в полной мере определяется настоящим. Если настоящее состояние системы
характеризуется вектором р*, то для будущего состояния pN неважно, каким
образом система попала в состояние р*. Оно полностью определяется многошаговым
процессом, который начинается из состояния р .
Введем важное понятие стратегии. Будем на каждом шаге вектор управления и*
задавать в виде функции вектора состояния р*:
u*=u*(pA). (4.4)
Функция (4.4) задает правило, по которому на каждом шаге выбирается вектор
решения и называется функцией стратегии, или просто стратегией. Стратегия,
которой максимизирует функционал (4.3), называется оптимальной. Возможность
задания оптимального управления в виде оптимальной стратегии непосредственно
следует из отмеченного выше свойства многошаговых процессов.
Сформулированный многошаговый процесс принятия решений не задает никаких
условий на конечное значение вектора состояния, т.е. речь идет о многошаговых
процессах со свободным правым концом. Именно такие процессы рассматриваются ниже.
Однако можно рассматривать многошаговые процессы, у которых конечное значение
вектора состояния фиксировано либо на его значение заданы какие-либо условия.
4.2. ПРИНЦИП ОПТИМАЛЬНОСТИ. ОСНОВНОЕ
ФУНКЦИОНАЛЬНОЕ УРАВНЕНИЕ БЕЛЛМАНА
В основу динамического программирования положен достаточно очевидный
принцип оптимальности Беллмана. Его можно сформулировать следующим образом.
Оптимальная стратегия обладает тем свойством, что независимо от того, каким
было первоначальное состояние и первоначальное решение, последующие решения
должны быть оптимальными относительно состояния, которое возникло после
принятия первого решения.
Поясним принцип оптимальности. Пусть и^и1,...,^ - оптимальная
последовательность решений для /V-шагового процесса, который начинается из состояния р.
Глава 4. Динамическое программирование 539
Тогда, очевидно, и1,и2,...,11^ является оптимальной последовательностью решений
для N-\ -шагового процесса, который начинается из состояния р1.
Рассмотрим многошаговый процесс принятия решений (4.2). Будем качество
этого процесса оценивать функционалом
y = f>(pV), (4.5)
к=0
здесь h - скалярная функция векторного аргумента. Функционал (4.5) для
дискретных многошаговых процессов играет ту же роль, что и функционал вида
т
J = jh(p,u)dt
о
для непрерывных процессов.
Максимальное значение функционала (4.5) однозначно определяется начальным
значением вектора состояния р и числом шагов N. Обозначим максимальное
значение функционала /#(р). Функцию fN(p) будем считать определенной для любого
значения вектора состояния р и любого числа шагов N.
Воспользуемся принципом оптимальности Беллмана. Пусть на первом шаге
выбрано некоторое решение и0, а в последующем в соответствии с принципом
оптимальности принимаются оптимальные решения. Тогда функционал
= л(р,и°)+Л,_1(р|)=А(р,и0)+/А,_|(т(р,и0)}
Для того чтобы оптимизировать //-шаговый процесс, необходимо, очевидно, вектор
и0 выбрать таким образом, чтобы он максимизировал правую часть равенства (4.6).
В результате получим соотношение
/w(p) = max[A(p)u°)+/w_1(T(p,u0))], N>1. (4.7)
К равенству (4.7) следует добавить уравнение
/о(р) = тахГл(р,и°)1. (4.8)
Функция /0 (р) задает максимальное значение функционала (4.5), когда он содержит
только одно слагаемое.
Равенство (4.7) связывает между собой максимальное значение функционала для
N-шагового процесса с максимальным значением функционала для (N-l)-utaaoeoeo
процесса и называется основным функциональным уравнением Беллмана.
Равенство (4.7) задает рекуррентное соотношение, которое решается
последовательно. Из уравнения (4.8) определяется функция /0(р) и подставляется в правую
часть равенства (4.7), положив N= \. Максимизировав правую часть равенства (4.7),
получим функцию /i(p). Затем по функции /i(p) определяется функция /2(р) и
т.д. При этом наряду с последовательностью функций /o(p),J/J(p)J/2(p))->
которые задают максимальное значение функционала, получим последовательность
функций uo(p),u1(p),u2(p), задающих оптимальную стратегию.
Последовательность u°(p),ul(p),... состоит из функций, которые максимизируют правую часть
уравнения (4.7) (при N = 0 - правую часть уравнения (4.8)).
34*
540 Методы теории оптимального управления. Часть III
Запишем уравнения (4.7) и (4.8), используя скалярные функции и скалярные
переменные:
+/м-\(Т\(Р\>'-->Рп>и\>-''Ут)^2(Р\>->Рп>и\>--'Ут)>''-
...,Гя(Л,...,/1||>1/10,...,^))], N>\;
fQ(p]9p29...,pN) = maxhfa,p2,...,pn9Ui9U2,...9u0m\
u eU v '
Отметим одну важную особенность метода динамического программирования.
Данным методом оптимальные решения определяются в виде функции стратегии.
Если использовать терминологию главы 2, то можно сказать, что метод позволяет
определять оптимальное управление только в виде синтезирующей функции.
Рассмотрим еще несколько функционалов.
Пусть качество многошагового процесса принятия решений (4.2) оценивается
функционалом
Принцип оптимальности Беллмана в этом случае приводит к функциональному
уравнению
/дг(р) = |тш/дг_,(т(р,и0)) N>\;
/о(р) = *(р).
Для вариационного исчисления весьма сложными являются функционалы вида
J= max g(pk,uk\ (4.9)
0<k<N ^ '
Обозначим /дг(р) максимальное значение функционала (4.9). Применяя принцип
оптимальности Беллмана, получим функциональное уравнение
/д,(р) = тах maxg(p,u°);max/^_1(T(p,u0)) .
|_u eU ч ' u eU ^ ч 7/J
Если рассматривается бесконечношаговый процесс, то функционал (4.5)
принимает вид
J = f>(pV). (4.10)
k=0
Будем предполагать, что ряд (4.10) сходится при любых значениях векторов uk eU .
Максимальное значение функционала (4.10) в этом случае однозначно определяется
начальным значением вектора р. Принцип оптимальности Беллмана приводит к
функциональному уравнению
/w(p) = max[/,(P)u0)+/(T(P)u°))].
Пример 4.1. Задача о замене оборудования. Пусть имеется некоторый комплект оборудования,
который характеризуется покупной ценой р и функцией ежегодного дохода n{t). Функция n(t) задает доход от
работы оборудования в течение одного года от момента / до момента t+\, здесь t - возраст оборудования в
годах / = 0, 1,2, Будем, далее, предполагать, что оборудование является специальным и не имеет
продажной цены. Требуется определить оптимальную политику замены оборудования, которая дает
максимальный доход для ^-летнего производственного процесса.
Обозначим /к (/) максимальный доход, который можно получить от /:-летнего производственного
процесса, если к началу этого процесса имеется оборудование, возраст которого / лет (t = 0, 1, 2, ). В на-
Глава 4. Динамическое программирование 541
чале каждого года можно принять одно из следующих двух решений: заменить оборудование или оставить
старое оборудование. Принцип оптимальности Беллмана приводит к функциональному уравнению
/t(/) = max[«(/) + /t.I(/ + l),-/> + «(0) + /t.1(l)], N>\ (4 11)
К равенству (4.11) следует присоединить уравнение для однолетнего производственного процесса
/,(/) = max [л (/);-р + л(0)] (4 12)
В равенстве (4 11) выражение, стоящее в квадратной скобке до точки с запятой, задает доход, который
можно получить от ^-летнего производственного процесса, если на первом году этого процесса принять
решение оставить старое оборудование при применении в дальнейшем оптимальной политики замены
оборудования. Выражение, стоящее после точки с запятой, задает доход от ^-летнего производственного
процесса, если на первом году принять решение заменить оборудование при применении в дальнейшем
оптимальной политики замены оборудования
Положим /?=4, n(t)=4-t Тогда уравнения (4 12) и (4.11) примут вид
|/(/) = шах[4-/,0],
1Л{») = тах[4-/ + Л.1(/ + 1).Л.1(1)]
Из первого уравнения (4 13) находим
, ч [4-/ при /<4, (С при /<4,
/l('H0 при ,>4; "'(') = 1Я при ,>4
Функция м, (/) задает оптимальное решение, здесь С - оставить старое оборудование, И - заменить
оборудование
Подставим функцию /, (/) во второе уравнение (4 13) Получим
[4-(/ + 1) при / + 1<4,
/2(/) = тах 4-/ + <
2W ' [0 при / + 1>4;
Перепишем это уравнение в виде
*М"| РТ £ э|
Из (4.14) находим, что
, ч Г7 - 2/ при / < 2, . ч [С при / < 2,
Л<Н при ,>2, "'«■{" при <>_2.
Продолжим этот процесс Запишем второе уравнение (4 13) для трехлетнего производственного
процесса
t\ Г (7"2(/ + 1) ПРИ ' + 1^2, 1
/3(/) = шах 4-/ + ^ v ; 5. (4 15)
3W L 1з при /+1>2' J
Из уравнения (4 15) следует, что
/9-3/ при /<1, \С при /<2,
/з(/) = |5 при />1. "Щи при t>_2
Для четырехлетнего производственного процесса второе уравнение (4 13) принимает вид
/4(/) = max 4-/ + < v ;
w [ [5 при / + 1>1,
или
/4(0 = т4{10-4/ ПРИ / = °' б1 (4 16)
■/4W L19~/ при r>0; J
Из (4 16) следует
10 при / = 0,
Л(0 =
. ч [С при /<3,
9-/ при /<3, иМ) = \
' \Н при />3
6 при />3; L
Этот процесс можно продолжать на пять лет и т.д. Ограничимся четырехлетним производственным
процессом. Получили последовательность функций /i(f)>/2(*)»/зМ»/4(0 » К0Т0Рые задают
максимальный доход в зависимости от длительности производственного процесса и возраста оборудования, которое
имеется на начало производственного процесса. Функции wl(/),w2(0>w3(/)'w4(0 задают оптимальную
стратегию, причем функция щ (t) задает оптимальное решение на первом году Ачпетнего
производственного процесса в зависимости от возраста оборудования
542
Методы теории оптимального управления. Часть III
Пусть, например, к началу четырехлетнего производственного процесса имеется оборудование,
возраст которого три года. Максимальный доход, который можно получить от производственного процесса,
равен 6 (/4 (3) = 6 ) Оптимальная стратегия, которая обеспечивает этот доход, не является однозначной, а
имеет следующие варианты '
а) первый вариант
Год от начала процесса
Оптимальное решение
Доход за год
1
С
1
2
Я
0
3
с
3
4
С
2
б) второй вариант
Год от начала процесса
Оптимальное решение
Доход за год
1
Я
0
2
С
3
3
с
2
4
С
1
в) третий вариант
Год от начала процесса
Оптимальное решение
Доход за год
1
я
0
2
С
3
3
Я
0
4
С
3
Все три варианта оптимальной стратегии эквивалентны между собой, если интересоваться только
четырехлетним производственным процессом, т к они обеспечивают один и тот же доход, равный 4 Однако
они не эквивалентны, если принимать во внимание состояние оборудования в конце производственного
процесса В первом варианте по окончанию производственного процесса оборудование имеет возраст 3
года, во втором - 4 года, в третьем - 2 года
Пример 4.2. Кратчайшие пути через сети [4] Рассмотрим сеть, состоящую из N узлов,
занумерованных 1,2, ,7V, и взаимосвязанных звеньев. Обозначим ttJ (ttJ >0) время прохождения звена (у) Будем
решать задачу о нахождении пути через сеть, который соединяет два заданных узла и время движения
вдоль которого минимально.
Данная задача имеет важное значение при выборе маршрутов движения автомобилей, самолетов по
транспортным сетям, передачи сообщений по сетям связи и т п Числа ti} могут необязательно означать
время прохождения звена (/, Д а, например, задавать расход топлива
Пусть конечным узлом, с которым следует соединить начальный узел, является узел N. В соответствии
с формализмом динамического программирования в качестве начальных узлов, необходимо рассматривать
все узлы сети
Обозначим щ время перевода системы из узла / в узел N по кратчайшему пути (/ = 1, 2, . , 7V-1).
Принцип оптимальности Беллмана приводит к функциональному уравнению
Uj =ттГ/,. +и.1, / = 1,2, ..,7V-1,
)Ф1 L J J J
(4 17)
Покажем, что уравнение (4 17) имеет единственное решение
Пусть щуи2, ,uN и UbU2y...,UN - два различных решения уравнения (4.17). Пусть, далее, т
является индексом, для которого разность Um - и„, достигает максимального значения. Покажем, что эта разность
равна нулю
В соответствии с (4.17) запишем
Очевидно,
tmr+Ur>tmn+Un.
Тогда из соотношений
Um<tmr+Uri
ит=*тг+иг
следует неравенство
Um-um<Ur-ur.
Поскольку для индекса т разность Um - um достигает максимального значения, поэтому
ит-ия =U,-ur,
причем г * т
Далее, рассмотрев разность Ur-ur, подобным образом найдем узел s (s * m,s * г), для которого
IJ -и =1Г -и =П -и
Глава 4. Динамическое программирование 543
Поскольку число узлов конечно, то, перебрав все узлы, окончательно получим
Um-um = UN-uN=0
Полученное равенство доказывает единственность решения уравнения (4 17).
Остановимся теперь на численном решении уравнения (4 17) Воспользуемся методом
последовательных приближений
В качестве начального приближения м,°, / = 1,#, положим
что соответствует времени прохождения звена (/,#), т е непосредственному переводу из узла / в узел N
(минуя другие узлы) Если звено (/, N) отсутствует или вообще отсутствует какое-либо звено (i,j), то
можно в качестве ^(/,у) взять подходящее большое число Таким образом удается очень просто решить
трудные вопросы связей между узлами.
Следующее приближение получим по формуле
и] = ттГ/„+м°1 i = \,N-l и^=0 (4 18)
Предусмотренную равенством (4 18) минимизацию следует выполнять путем непосредственного
сравнения встречающихся сумм, что быстро выполняется на ЭВМ Переход от к-го приближения к к+\
осуществляется с помощью соотношений
м*+1=тшГ/,, +ик.\ i = \,N-\, ukN+]=0
j*i IJ J J
Рассмотренный алгоритм имеет простую физическую интерпретацию. Величина и? соответствует
времени перехода непосредственно из узла / в узел N, минуя другие узлы Величина и] задает
минимальное время перехода из узла / в узел N при наличии не более одного промежуточного узла, величина и2 -
при наличии не более двух промежуточных узлов и т д Из этой интерпретации следует, что
последовательные приближения приводят к монотонному убыванию величины и' (/ = 1, N), т е
0<Wf+1<Wf,
что гарантирует сходимость последовательных приближений
4.3. МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
ДЛЯ НЕПРЕРЫВНЫХ СИСТЕМ
Рассмотрим применение динамического программирования для решения задачи
оптимального управления.
4.3.1. Автономная система
Пусть движение объекта задается системой уравнений
-j- = /1(х\,х2,.'.,хп,щ,и2,...,ит),1 = \,п,
at
или в векторной форме уравнением
^ = f(x,u), (4.19)
at
здесь х = (д:1,...,х„) - /i-мерный вектор состояния, и=(щ,...,ит) - w-мерный вектор
управления, f = (/},...,/„) - «-мерный вектор. Предполагается, что вектор и может
принимать свои значения из некоторого множества U, т.е. u(t) e U . В качестве
минимизируемого будем рассматривать функционал
т
J = JG(x,u)dt. (4.20)
о
В рассматриваемой задаче полагаем фиксированным начальное состояние,
которое будем обозначать через х и конечное состояние х*. Время перехода из начального
состояния в конечное не фиксируется. Так как целью оптимизации является получе-
544 Методы теории оптимального управления. Часть III
ние оптимальной синтезирующей функции (оптимальной стратегии), то начальной
точкой х может быть любая точка фазового пространства.
Минимальное значение функционала (4.20) однозначно определяется начальным
значением вектора х. Обозначим минимальное значение функционала
S(x) = S(xl9x2,...9xn).
Пусть х(/), 0<t<T - оптимальная траектория, переводящая фазовую точку из
начального положения х(0) = х в конечную точку х\ Тогда
S(*)=minb(x(0,u(/)H
1 ' о
Представим функционал в виде
jG(x(/),u(/))ift = jG(x(/),n(/))* + jG(i(/),u(O)A
о о д
Будем предполагать. Оптимальное управление и(/) кусочно-непрерывно. Условимся
за значения управления в точках разрыва принимать пределы справа.
Пусть в интервале (0,Д) выбрано некоторое управление и(/),ав дальнейшем в
соответствии с принципом оптимальности выбирается оптимальное управление.
Тогда
}g(x(0,u(,)H = s(x(a)).
А
В силу непрерывности траектории х(/)
х(Д) = х(0) + х(0)-Д + о(Д), •
где
Д->0 Д
Принимая во внимание уравнение (4.19), можно записать
x(A) = x + f(x,u)|r=0.A + O(A),
ИЛИ
x(A) = x + f(x,u)-A + o(A),
здесь и - значение управления в момент / = 0. Таким образом,
г
jG(x(/),u(/))A = S(x + f(x,u)-A + o(A)).
д
Далее,
д
jG(x(/),u(/))rf/ = G(x,u).A + o(A).
о
Если в начальный момент t - 0 выбрано управление u e U , а в дальнейшем в
соответствии с принципом оптимальности выбиралось оптимальное управление, то
функционал принимает значение
G(x,u)-A + o(A) + S(x + f(x,u)-A+'o(A)). (4.21)
Для оптимизации функционала надо минимизировать выражение (4.21). Таким образом,
5'(x) = min[G(x,u)^ + o(A) + 5r(x + f(x,u)-A + o(A))]. (4.22)
Глава 4. Динамическое программирование 545
Будем предполагать, что функция S(x) имеет непрерывные частные
производные по всем своим аргументам. Отметим, что справедливость всего последующего
вывода зависит от того, выполняется это предположение или нет. Заранее функция
£(х) неизвестна и проверить справедливость этого предположения по уравнениям
движения нельзя. Можно решить задачу и определить функцию S(x). Если она
окажется непрерывно дифференцируемой, то приводимые ниже результаты являются
справедливыми. Однако имеют место случаи, когда функция S(\) не является
непрерывно дифференцируемой.
Поскольку функция S(x) предполагается непрерывно дифференцируемой, то
S(x + f(x,u).A + o(A)) = 5(x) + —.f(x,u).A + —.о(А),
здесь в соответствии с правилами дифференцирования скалярной функции по
векторному аргументу
dS_(dS_dS_ j»'
dx \дхх дх2 дхп
- матрица-строка. Из (4.22) находим
[d*s 1
G(x,u)-A + S(x) + f(x,u)-A + o(A) ,
dx J
или
[d*s 1
G(x.,u) + — f(x,u) A + o(A). (4.23)
v ' ' dx v ;J v ;
Поделим неравенство (4.23) на А и перейдем к пределу при А -» оо. В результате
получим
Г dS 1
0 = min G(x,u) + f(x,u) . (4.24)
uet; [_ dx J
Равенство (4.24) является функциональным уравнением Беллмана. К уравнению
(4.24) необходимо присоединить граничное условие
$(х')=0. (4.25)
В частном случае, когда оптимизируется время движения, т.е.
т
о
уравнение Беллмана принимает вид
/УС
-l = min — -f(x,u), (4.26)
uetf dx V '
здесь функция S(x) задает минимально возможное время движения от точки х до
точки х*. Для уравнения в частных производных (4.26) граничное условие по-
прежнему задается равенством (4.25).
Решая уравнение в частных производных (4.24), наряду с функцией £(х),
задающей в зависимости от начальной точки х минимальное значение функционала,
определяется также функция и(х), которая задает оптимальную стратегию, или
оптимальную синтезирующую функцию.
546 Методы теории оптимального управления. Часть III
Уравнение Беллмана (4.24) задает необходимое условие минимума. Именно, если
функция S(x) является непрерывно дифференцируемой по всем своим переменным,
то она удовлетворяет уравнению Беллмана (4.24).
Пример 4.3. Рассмотрим объект, движение которого задается уравнениями
dx> dx-y
—Г = х2, ~г = и.
dt dt
В качестве конечной точки х* выберем начало координат, т.е. положим х*=0. Качество процесса
управления будем оценивать функционалом
т
J = l(xf+xl+u2)dt (4 27)
о
Таким образом, речь идет об определении оптимальной стратегии м = 9(*|,х2), которая обеспечивает
перевод фазовой точки из произвольного начального состояния в начало координат, и притом так, чтобы
на траекториях движения функционал (4 27) принимал наименьшее значение
Выпишем функциональное уравнение Беллмана
О = min xf+xl+u2 +—x2 +—u (4 28)
as ds 1
ax, дх2 J
Из (4 29) находим
и уравнение Беллмана принимает вид
2к +
и =
дх2
1 dS
2дх2'
ds lfasV л
Так как на управляющий параметр и не наложено никаких ограничений, то для определения минимума
необходимо продифференцировать правую часть уравнения (4 28) по w
(4 29)
(4 30)
(4 31)
Будем искать решение уравнения (4.31) в виде квадратичной формы
5(х) = С1дс12+С2^2+С3х22.
Тогда
|£ = 2СЛ+СЛ, ^- = С2х1+2С3х2
охх дх2
Уравнение (4 31) принимает вид
х\ + Х1 —(4Сз2*2 + ^С2Съх{х2 + С\х\ ) + 2С,х,л:2 + С2л:2 = 0
Коэффициенты Си Сг, Сз определяются из системы уравнений:
i-Ic|=o,
1-С32+С2 = 0, (4.32)
2С,-С2С, = 0
Система нелинейных алгебраических уравнений (4.28) имеет два вещественных решения
С2=2, С3 = >/3, С,=>/3,
с2=2, с3=-7з, с, = -7з
Эти решения в соответствии с (4 30) приводят к двум синтезирующим функциям
м = -дг1-л/3лс2, (4.33)
'!/ = -*,+>/Здг2 (4 34)
В результате получаем две линейные системы, причем линейная система, порождаемая функцией (4.34),
оказывается неустойчивой и, следовательно, не может обеспечить перевод фазовой точки в начало
координат.
Таким образом, оптимальная синтезирующая функция (оптимальная стратегия) задается равенством
(4 33). На рис. 4.1 изображена структурная схема оптимальной системы
Глава 4. Динамическое программирование
547
1
р
1
р
*\
Рис. 4.1. Структурная схема оптимальной системы
Пример 4.4. Рассмотрим простейшее уравнение
х = и-х,
полагая, что на управляющий параметр и наложено ограничение
М<1.
Будем решать задачу перевода переменной х из произвольного начального значения в нуль.
Как следует из (4.26), уравнение Веллмана имеет вид
• dS< \
-l = min—(и-х)
(4 35)
Оптимальное по быстродействию управление
. dS
и = -sign —
dx
Подставляя (4.37) в (4.36), получим уравнение
, dS dS . dS
-1 = -—х-— sign—
dx dx dx
Найдем решение уравнения (4 38), полагая — > 0 . Из соотношения
dx
(4 36)
(4 37)
(4 38)
£<->=-
следует, что
S(x) = \n(x + \) + C\
dS
S{x) =
(4 41)
(4 39)
здесь С* - произвольная константа При — < 0 аналогичным образом найдем
dx
S(x) = \r\(\-x) + C" (4 40)
Полагая, что равенства (4.38) и (4 40) справедливы при х=0, то в соответствии с граничным условием (4 25)
С'=С"=0
Функция S(x) задает минимальное время движения и может быть только положительной величиной
Из (4.39) и (4.40) следует тогда, что
{ln(jC-h 1) При Х>0,
1п(1-дг) при х<0
Оптимальное по быстродействию управление, таким образом, определяется равенством
[1 прих<0,
[-1 придс>0
Как следует из (4 41), производная —^—- имеет разрыв в точке х = 0. Это ставит под сомнение спра-
dx
ведливость функционального уравнения Беллмана (4.38). Однако, поскольку в оптимальном движении
переменная *(/) не изменяет знак, функцию S(x) можно отдельно рассматривать при х>0 и при *<0,
а в каждой из этих областей функция S(x) является непрерывно дифференцируемой Это позволяет
заключить о справедливости равенства (4.41).
Во избежание недоразумений отметим, что целью настоящего примера является не демонстрация того,
как с помощью динамического программирования можно осуществлять синтез оптимального по быстро-
548 Методы теории оптимального управления. Часть III
действию управления, а желание показать, что предположение о непрерывной дифференцируемости
функции S(x) является весьма существенным ограничением метода динамического программирования,
когда он применяется для непрерывных процессов. Этот пример также показывает, что для синтеза
оптимального по быстродействию управления целесообразно использовать принцип максимума Понтрягина
4.3.2. Неавтономная система
Рассмотрим неавтономную систему уравнений
-Г = fi(x\,X2,...,xn,ul9u2,...9um,t)9 / = 1,«. (4.42)
at
Будем, далее, предполагать, что подынтегральная функция функционала также
зависит от времени /, т.е.
г
J= J G(xl9x29...9xn9ul9u29...9um9t)dt. (4.43)
±о
По-прежнему рассматривается задача о нахождении управления, задаваемого в виде
оптимальной стратегии, которое осуществляет перевод фазовой точки
. х = (хх,х2,...9х„) системы (4.42) из заданного, но любого начального состояния, в
некоторую заданную точку х* =(дг1*,...,дс* j так, чтобы функционал (4.43) принимал
наименьшее значение. При этом начальный момент времени /0 предполагается
фиксированным. Однако, в соответствии с формализмом динамического
программирования, начальный момент времени /0 хотя и считается заданной, но может быть любой
величиной. Относительно конечного момента времени Т будем предполагать, что он
не задан, а определяется из условия прохождения траектории х(/),/0 <t<T, через
точку х*,т.е. х(Г) = х*.
Воспользуемся рассмотренным в параграфе 2.2 способом сведения неавтономной
задачи оптимального управления к автономной. Запишем уравнения (4.42) в
векторной форме
^ = f(x,u,/), (4.44)
здесь х = (х1,...,хЛ) и f = (/j,...,/„) - «-мерные векторы, и = (щ,...,ит) - w-мерный
вектор. Присоединим к уравнениям (4.43) уравнение
■ = и„+1 ('о ) = '<>• (4.45)
Ли+1
Л
Из (4.45) следует, что xn+l(t) = t.
Неавтономная задача оптимального управления (4.42), (4.43), таким образом,
сводится к автономной задаче для'системы дифференциальных уравнений
-£ = Г(х,и,*я+1),
dJ (4.46)
dxn+\ _ i
dt " '
и функционала вида
г
J = \G(x,u,xn+l)dt. (4.47)
'о
Так как конечный момент времени Т не фиксирован, то на конечное значение коор-
Глава 4. Динамическое программирование 549
Задача оптимального управления (4.46), (4.47) по терминологии главы 2 является
задачей с закрепленным левым и подвижным правым концами траектории. Это
обстоятельство, как легко видеть, не оказывает никакого влияния на вывод
функционального уравнения Беллмана, а находит свое отражение лишь в изменении
граничного условия. В соответствии с (4.24) для задачи (4.46), (4.47) функциональное
уравнение Беллмана имеет вид
O = min[G(x1u,Vl)+f-f(x,u!vI) + ^-.l|, (4.48)
ue(/ [ 0Х OXn+l J
здесь
3S_JdS_dS_ dS_
дх \_дх{ дх2 дхп
- матрица-строка. Поскольку хп+] = /, то уравнение (4.48) можно переписать в виде
К уравнению (4.49) следует добавить граничное условие
s(x*,r)=0. (4.50)
Так как хп+х(т)=Т может быть любой величиной, то условие (4.50) должно иметь
место для любого Т.
Последний результат нуждается в пояснении. Введем (л+1)-мерное фазовое
пространство X с декартовыми координатами xux29...,xn9t. Обозначим П прямую
линию, проходящую в пространстве X через точку (х*, 0) параллельно оси /. Граничное
условие (4.50) заключается в следующем: функция S(\,t) должна обращаться в нуль
в каждой точке прямой П. Это возможно, очевидно, только в том случае, когда
функция S(x,t) при х = х* не зависит от t.
Если конечный момент времени Т фиксирован, то граничное условие по-
прежнему задается равенством (4.50), в котором Г теперь - заданная величина.
4.4. . ЗАДАЧА ОБ АНАЛИТИЧЕСКОМ КОНСТРУИРОВАНИИ
РЕГУЛЯТОРА
Задача синтеза для линейных объектов управления, минимизирующего
квадратичный критерий, называется задачей об аналитическом конструировании
регуляторов. В этом случае оптимальный закон управления является линейным. Таким
образом, задачу об аналитическом конструировании регуляторов можно
рассматривать как метод синтеза линейных систем.
4.4.1. Автономный случай
Рассмотрим автономный линейный объект управления
— = Ах + Ви, (4.51)
dt
здесь А и В - постоянные матрицы, имеющие размерность соответственно
пхп, пхт, и=(щ,и2,...,ит) - m-мерный вектор управления, х = (х],х2,...,хп) -
«-мерный вектор состояния. Векторы и и х рассматриваются как векторы-столбцы.
Будем искать управление, минимизирующее функционал
J = -J(xTQx + uTRu)^, (4.52)
550 Методы теории оптимального управления. Часть III
где Q и R - постоянные матрицы, имеющие соответственно размерности пхп и
пхт. Матрица Q предполагается неотрицательно определенной, а матрица R -
положительно определенной. Пусть, далее, на вектор и не наложено ограничений, т.е.
он может быть любым.
Матрица Q называется неотрицательно определенной, если для любого вектора
х Ф 0 xTQx > 0 . Матрица R называется положительно определенной, если для
любого вектора и^О и Ru > 0. Матрица С называется симметрической, если
Ст = С . В соответствии с критерием Сильвестра [34], для того чтобы
симметрическая матрица R была положительно определенной, необходимо и достаточно,
чтобы все ее ведущие главные миноры были положительны. Ведущим главным
минором порядка k называют определитель, составленный из элементов матрицы R,
стоящих на пересечении первых к строк и первых к столбцов.
С помощью матриц Q и R в равенстве (4.52) заданы квадратичные формы xTQx и
uTRu . Поскольку любую квадратичную форму можно задать с помощью
симметрической матрицы, будем полагать, что матрицы Q и R симметрические.
В сформулированной задаче условия на правый конец траектории не налагаются.
Однако функционал (4.52) может быть конечным лишь в том случае, если х(/) —> 0
при /->оо.
Минимальное значение функционала (4.52) однозначно определяется начальным
значением вектора х . Обозначим минимальное значение функционала 5(х). Хотя в
рассматриваемой задаче оптимального управления правый конец траектории
свободен, приведенный в параграфе 4.3 вывод уравнения (4.24) сохраняет свою силу, т.е.
для рассматриваемой задачи функциональное уравнение Беллмана задается
равенством (4.24). Таким образом, уравнение Беллмана имеет вид
0 = min -xTQx + -uTRu+—(Ax + Bu) . (4.53)
Найдем уравнение, минимизирующее правую часть уравнения (4.53). Для этого
продифференцируем правую часть по и и приравняем полученную производную к
нулю. Справедливы следующие формальные правила дифференцирования по вектору и:
d_
du
4-ви1=^
du[dx
В результате получим уравнение
-^[uTRul = 2uTR,
dn L J
J dx
uTR + — B = 0. (4.54)
dx
Из уравнения (4.52) находим, что
' dx
ut=_^br-i
или
„ = -(fB.R-)T. ^ (4.55)
Используя известное матричное тождество (СМ) =МТ-СТ, равенство (4.55)
перепишем в виде
Глава 4. Динамическое программирование 551
■~("-)т-'(1Г-
Так как R - симметрическая матрица, то (r~1 j = R"1. Поэтому можно записать
u=-R-'BTWT. (4.56)
Kdx)
Управление (4.56) минимизирует правую часть уравнения (4.53). Действительно,
^rixTQx + IuTRu+^(Ax + Bu)l = AruTRl = R5
du2l2 2 dxK ;J A|L J
т.к. R - положительно определенная матрица. Таким образом, равенство (4.56) задает
оптимальное управление.
Подставим оптимальное управление в уравнение (4.53). Получим уравнение
IxTRx+I^BR-iRR-.BTWT+^fAx_BR-.BTWTl0
2 2 dx {dx dx\ {dx)
i^_1^br-.btWt+^Ax = 0.
ИЛИ
Vrx--—BR-'B1! — I + —Ax = 0. (4.57)
2 2dx {dx) dx У J
Уравнение (4.57) представляет собой уравнение в частных производных
относительно неизвестной функции S(x).
Решение уравнения (4.55) будем искать в виде положительно определенной
квадратичной формы, т.е. положим
S(x) = -xTKx,
v ; 2
где К - симметрическая матрица. По правилу дифференцирования квадратичной
формы
^ = хтК. (4.58)
dx
Подставим (4.58) в (4.57):
-xTQx --xTKBR"1BTKTx + xTKAx = 0. (4.59)
2 2
Равенство (4.59) можно переписать в виде
2
В левой части равенства (4.60) стоит квадратичная форма. Квадратичная форма
обычно задается с помощью симметрической матрицы.
Матрица Q является симметрической. Покажем, что матрица KBR~1BTKT также
является симметрической. Действительно, в соответствии с известным матричным
равенством (С • М) = Мт • Ст, можно записать
(kbr-^k7)т = (вткт)т (kbr1 )т = kb(r1 )t (кв)т = kbr-^k1.
Запишем в равенстве (4.60) квадратичную форму хтКАх с помощью
симметрической матрицы. Для этого представим указанную квадратичную форму в виде
~xt[q-KBR"1BtKt+2Ka]x = 0. (4.60)
552 Методы теории оптимального управления. Часть III
хтКАх = хт [-КА + -АТКТ |х,
где — КА + — АТК - симметрическая матрица. Тогда равенство (4.60) принимает
вид
-xT[Q-KBR"1BTKT+KA + ATKT] = 0. (4.61)
В левой части равенства (4.61) стоит квадратичная форма. Эта квадратичная
форма может равняться нулю только в том случае, если ее матрица равняется нулю.
Таким образом, получим равенство
Q - KBR^K1 + КА + АТКТ = 0. (4.62)
Уравнение (4.62) называется матричным уравнением Риккати. Матричное
уравнение (4.62) позволяет определить искомую матрицу К. Оно эквивалентно системе из
п2 уравнений.
Матричное уравнение (4.62) имеет не единственное решение. Из решений
уравнения (4.62) необходимо выбрать такое, которое задает определенно положительную
матрицу К. Такая матрица определяется однозначным образом.
Пусть К - положительно определенная матрица, являющаяся решением
уравнения (4.62). В соответствии с (4.56), оптимальное управление задается равенством
u = -R"1BTKTx. (4.63)
Равенство (4.63) задает линейный закон управления, и, следовательно, оптимальная
система (4.51), (4.63) является линейной.
Покажем, что для системы (4.51), (4.63) функция
S(x) = -xTKx
является функцией Ляпунова.
В самом деле, S(x) - положительно определенная функция. Ее полная
производная по времени, вычисленная в силу уравнений (4.51), имеет вид
i jo
—Six) = —[Ах + Bui = хтКАх - xTKBR"lBTKTx. (4.64)
dt dx
Из уравнения (4.60) следует, что
xtKAx=-xt[kBR~1BtKt-Q]x. (4.65)
Подставив (4.65) в (4.64), получим
—S(x) = —xTQx--xTKBR4BTKTx. (4.66)
dt 2 2
Принимая во внимание (4.63), равенство (4.66) можно переписать в виде
-^S(x) = -!xTQx-!uTRii.
dt V ; 2 2
Поскольку xTQx и uTRu являются положительно определенными квадратичными
формами, то, следовательно,
-5(х)<0
для всех х*0. В силу теоремы Ляпунова решение х(/) = 0 системы (4.51), (4.63)
является асимптотически устойчивым.
Глава 4. Динамическое программирование 553
Таким образом, синтез управления, минимизирующего функционал (4.52), приво-
цит к устойчивой линейной системе. Такую оптимизацию можно рассматривать как
эдин из методов синтеза линейных систем управления. Этот метод является
несомненно полезным для синтеза многомерных систем управления.
Основную сложность при применении данного метода составляет решение
матричного уравнения Риккати (4.62). В настоящее время разработаны стандартные
программы (см., например, математический пакет MatLab), которые позволяют легко численно
решить матричное уравнение Риккати, выделить положительно определенную матрицу
К и, таким образом, найти оптимальную синтезирующую функцию и(х).
Пример 4.5. Рассмотрим уравнение
^ = Ах + Ви,
dt
полагая, что матрицы А, В и вектор х имеют вид
ч: :]■ -й -и
и - скалярное управление Требуется найти управление, минимизирующее функционал
y = Ij(xTQx + ™2) dt,
2 о
где матрица
[О Яг J
г> Яь Яг ~ положительные числа
Матрицу К , с помощью которой задается функция S(x), представим в виде:
В соответствии с (4.62), запишем уравнение Риккати"
О Яг\ r[kn k22] [lj l ] [кп к22]
:,2 к22\ [О Oj Ll Oj [kt2 kn\
Из (4 67) следует система уравнений
*11-;*12*22=0- (4 68)
Яг-Х-кг22 +2*,2=0.
Система уравнений (4 68) имеет следующие решения:
1 V У (4 69)
kn=±yjqj^2±2y[^).
Выделим из (4 69) решение, соответствующее определенно положительной матрице К. Применяя
критерии Сильвестра, найдем, что таким решением являются
к22=^(я2 + 2фУ\)-
В соответствии с (4 63), оптимальное управление
и = —(*ц*1-*22*г)-
554 Методы теории оптимального управления. Часть III
4.4.2. Неавтономная система
Пусть движение системы описывается уравнением
^ = А(/)х + В(/)и, , (4.70)
at
здесь А(/) и В(г) - матрицы порядка пхп и п хт, х- «-мерный вектор состояния,
и - /w-мерный вектор управления. Как и выше, будем полагать, что на вектор и не
наложены никакие ограничения. Качество процесса управления будем оценивать
функционалом
1 Т
J=-j(xTQ(f)x + uTR(/)u)^, (4.71)
'о
где Q(t) - неотрицательно определенная матрица, a R(/) - положительно
определенная матрица. Требуется определить оптимальную стратегию и(х,/),
минимизирующую функционал (4.71).
При решении задачи оптимизации будем полагать, что конечный момент времени
Г фиксирован. Заданными считаются также начальное условие х(/0) и начальный
момент времени /0. Однако, в соответствии со спецификой динамического
программирования, начальные значения /0 и х(0) хотя и полагаются заданными, но могут
быть любыми (х(О)бХ, to>T). Будем, далее, полагать, что правый конец
оптимальной траектории свободен, т.е. на значение вектора х в момент времени Т не
накладываются никакие условия.
Для рассматриваемой задачи оптимального управления функциональное
уравнение Беллмана задается равенством (4.49), которое принимает вид
-| = min[lxTQ(0x+luTR(0u + £(A(0x + B(0u)]. (4.72)
Для определения минимума продифференцируем правую часть уравнения (4.72) по
вектору и. В результате получим уравнение
из которого следует
или
utr(,)+|Lb(,) = 0,
ОХ
от = -|в(0и-(').
u--(R-'(0)TBT(0(f)T. (4.73)
Как и выше, здесь матрицы Q(/) и R(/) полагаются симметрическими. Но тогда
R4(/) также является симметрической матрицей. Поэтому уравнение (4.73) можно
переписать в виде
u = -R-'(0BT(0[£]T. (4.74)
Так как вторая производная от правой части равенства (4.72) равна R(/), a R(/) -
положительно определенная матрица, то управление (4.74) доставляет минимум
правой части уравнения (4.72).
Глава 4. Динамическое программирование 555
Подставив управление (4.74) в уравнение Беллмана, получим
-|.I,TQ(/)l + I|B(,)R-'(/)R(')R-'(')BT(<)(f)T +
♦f(аС)»-«М«"М»тМ (If)
После преобразования подобных членов это уравнение принимает вид
-f4jlQ<')«-ifB<"R-1wBTw(f)T+fA<')1- («5>
Решение уравнения (4.75), очевидно, должно удовлетворять граничному условию
S(x(T)j) = 0. (4.76)
Решение уравнения (4.75) будем искать в виде положительно определенной
квадратичной формы
S(x,/) = ~xTK(/)xT, (4.77)
где К (г) - симметрическая матрица размерности пхп. Из (4.77) следует, что
3S I т dK т dS т„ / \
— = -х1 х1, — = х1К(л.
dt 2 dt dt w
Отметим, что матрица .— состоит из производных элементов матрицы К(/) и так-
dt
же является симметрической. Уравнение (4.75) тогда принимает вид
-ixT—x = ixTQ(Ox--xTK(OB(/)R"1(/)BT(r)KT(/)x + xTK(/)A(/)x. (4.78)
Перепишем уравнение (4.78) в виде
Квадратичная форма равняется нулю для любого вектора х лишь в том случае, если
равна нулю образующая ее матрица. Таким образом, получили матричное уравнение
^ = K(/)B(0R-1(/)BT(0KT(0-QW-K(0A(0-AT(0KT(/). (4.79)
В уравнении (4.79), как и выше, для получения решения в виде симметрической
матрицы К(/) выполнено преобразование
2К(/)А(0 = К(0А(0 + Ат(/)Кт(0.
Уравнение (4.79) представляет собой матричное уравнение типа Риккати. Его
необходимо дополнить граничным условием
К(7>0,
которое следует из условия (4.76). В соответствии с (4.74), оптимальное управление
„М-ц-'ЮвЧОВДх.
Оптимальное управление является линейной функцией х, т.е. оптимизация
управления линейным неавтономным объектом (4.70) по критерию (4.71) приводит к
неавтономной линейной системе уравнений
^ = [a(0-b(0r-'(0bt(0k(0]x.
556 Методы теории оптимального управления. Часть III
4.5. СВЯЗЬ МЕЖДУ ПРИНЦИПОМ МАКСИМУМА
И ДИНАМИЧЕСКИМ ПРОГРАММИРОВАНИЕМ
Установим связь между принципом максимума и динамическим
программированием.
Пусть движение объекта задается векторным уравнением
^ = f(x,u), (4.80)
at
здесь х и f - я-мерные векторы, и - /w-мерный вектор управления. Вектор и может
принимать свои значения из некоторого заданного множества U. Рассмотрим
двухточечную задачу оптимального управления. Будем полагать, что в фазовом
пространстве X системы заданы начальная х° и конечная х1 точки. Требуется среди
допустимых управлений u(t)eU (время движения не фиксировано), переводящих фазовую
точку х из заданного начального положения х° в заданное конечное положение х1,
найти такое, которое доставляет минимум функционалу
J = J/o(x,u)A (4.81)
'о
Соответствующая задача оптимального управления была рассмотрена в
параграфе 4.3. Основное функциональное уравнение Беллмана имеет вид
O = rain[/o(x,u)+^f(x,u)l. (4.82)
ueU L OX J
Будем предполагать, что функция 5(х) дважды непрерывно дифференцируема. Так
как минимум любой функции g(u) переходит в максимум функции -g(u), то
управление (4.82) можно записать в виде
о-ш[-/,и-|гм],
ИЛИ
0 = max
ueU
3S
-/o(x,u)-£—/y(x,u)
дх,
(4.83)
7=1 ил)
Пусть u(/) - оптимальное управление. Тогда из (4.83) следует уравнение
-/о(х>и)-1^/Лх>и) = 0- <4-84)
7=1 ^У
Продифференцируем уравнение (4.84) по хД/ = 1, л). Получим равенства
дХ, рдХ;дх/А > ^дХ; дХ, ■
В силу уравнения (4.80)
A d2S . , s d dS
/ /i(x.u) = >
я поэтому равенство (4.83) можно переписать в виде
_£dS_ _ a/0(x,u) _ ^dS_ dfj{x,u) ^
dt dxj dXj ~{dxj dXj
0, i = \,n. (4.86)
Глава 4. Динамическое программирование 557
Обозначим v|/, = и положим \|/0 = -1. Тогда из (4.86) следуют равенства
дх,
Л Ро J дх,
Именно такими уравнениями определяются вспомогательные переменные в
принципе максимума (см. уравнение (2.4)).
Далее, соотношение (4.83) можно переписать в виде
max#(ij/,x,u) = 0. (4.87)
ueif
Из равенства (4.87) следует, что оптимальное управление доставляет в каждый
момент времени / функции Гамильтона максимум и что-функция M(\j/(/),x(/)) = 0.
Таким образом, получены (с учетом сделанных выше предположений) все условия
теоремы 2.1.
558 Методы теории оптимального управления. Часть III
ГЛАВА 5. МЕТОДЫ МАТЕМАТИЧЕСКОГО
ПРОГРАММИРОВАНИЯ И МОМЕНТОВ
ПОСТРОЕНИЯ ОПТИМАЛЬНЫХ ПРОГРАММ
И ОПТИМАЛЬНЫХ ПРОГРАММНЫХ
УПРАВЛЕНИЙ. СИНТЕЗ ОПТИМАЛЬНЫХ
ОБРАТНЫХ СВЯЗЕЙ
Как указывалось во введении к части III, построение аналитических решений
разнообразных задач оптимального управления возможно лишь в крайне простых случаях.
Часто такие задачи могут быть сформулированы лишь благодаря далеко идущей
идеализации, когда фактически вместо поставленной задачи решается совсем иная.
Основным же подходом к решению реальных задач является приближенная
численная оптимизация, методы которой подробно рассмотрены в [44, 47].
Здесь мы ограничимся лишь методами нелинейного программирования для
случая, когда используется конечномерная проекционная аппроксимация объектов
управления [39].
5.1. АЛГОРИТМ ПОСТРОЕНИЯ ОПТИМАЛЬНЫХ ПРОГРАММНЫХ
УПРАВЛЕНИЙ И ОПТИМАЛЬНЫХ ПРОГРАММ МЕТОДАМИ
МАТЕМАТИЧЕСКОГО ПРОГРАММИРОВАНИЯ
С ИСПОЛЬЗОВАНИЕМ МАТРИЧНОГО ПРЕДСТАВЛЕНИЯ
ОПЕРАТОРОВ В ОРТОГОНАЛЬНЫХ БАЗИСАХ
Изложенные в восьмой главе первого тома учебника положения можно
рассматривать как подходы к решению задачи параметризации всех соотношений, которые
используются при построении оптимальных программных управлений и
оптимальных программ (редукция задачи оптимального управления к задаче математического
программирования). Основной является параметризация математической модели
объекта управления.
С математической точки зрения, параметризация математической модели объекта
означает разработку метода решения операторных уравнений объекта (в первую
очередь, дифференциальных и интегральных уравнений), позволяющего непосредственно
по операторным уравнениям объекта записать явное выражение их решения, пользуясь
символикой матриц, определяя все элементы в конечномерных пространствах.
Пользуясь понятиями блочно-импульсных функций и обобщенных блочно-
импульсных функций (ОБИФ), сеточные методы можно отнести при известных
условиях к классу проекционных, когда в качестве базисных функций (ф,(/)} берутся
функции с конечными носителями {финитные функции), т.е. такие функции,
которые отличны от нуля лишь на небольшой части той области, на которой
определено искомое решение задачи. Такой подход лежит в русле метода конечных
элементов [37, 39,47].
Таким образом, по идейному содержанию редукция задач оптимального
управления к задачам математического программирования может рассматриваться на
единой основе - проекционном подходе.
Глава 5. Методы математического программирования 559
Далее, рассмотрим общий подход к построению алгоритма расчета оптимальных
программных управлений и оптимальных программ на примере линейных
нестационарных объектов, поведение которых описывается векторно-матричным
дифференциальным уравнением вида
X = A(/)X + B(/)U, Х(0) = Х°. (5.1)
Воспользуемся следующими обозначениями:
/0 = 0; /, = Т; Х° = (х,(0),х2(0),...,хЛ(0))т
- начальное состояние объекта,
Хт =(х,(Пх2(Т),...,хп(Т))т
- конечное состояние объекта.
Предположим, что нестационарный объект (5.1) вполне управляем: для любых
Х° и Хг существует такая функция U(/,X°,X7), t e [0,Т], что решение X(f)
уравнения (5.1) при U(/) = U(/,X°,X7), удовлетворяющее начальному условию Х° при
t = 0 , пройдет через X7 при / = Т.
Этапы общего алгоритма [47, 48].
1-й этап: Техническая формулировка задачи. Техническую формулировку
задачи обычно делают в содержательных терминах, присущих рассматриваемой
инженерной задаче.
Например, при проектировании системы оптимального управления самолетом
вертикального взлета и посадки определяют физические переменные,
характеризующие состояние управляемого объекта, находят управляющие функции, также
представляющие собой физические параметры, изменяемые во времени (например, тяга
двигателя, угол атаки, угол крена и др.). На этом этапе важным является вопрос
выбора критерия оптимизации; последний целиком определяется содержанием
инженерной задачи. Например, достижение назначенной точки происходит с
минимальным расходом горючего или за минимальное время и т.д.
2-й этап: Постановка математической задачи оптимизации.
На этом этапе строится математическое описание физического объекта
(например, самолета) и процесса управления в рамках принятой степени полноты.
Техническая постановка задачи и ее математическая модель в процессе
исследования не остаются неизменными, а находятся во взаимодействии друг с другом.
Построение адекватной математической модели представляет собой итерационный
процесс, в ходе которого уточняются как постановка самой технической задачи, так и
формулировка математической модели [47,48].
Например, в задаче управления самолетом вертикального взлета и посадки
строится математическая модель в форме системы дифференциальных уравнений [48].
Переменные, входящие в эту систему уравнений (например, модуль воздушной
скорости, угол наклона траектории, угол поворота вектора скорости, координаты центра
масс в земной системе), могут служить фазовыми координатами, а тяга двигателя,
угол атаки, угол крена - управляющими функциями, которые подлежат определению
из условия достижения цели управления [47,48].
3-й этап: Выбор общего подхода к решению математической задачи оптимизации.
В нашем случае - это аппарат математического программирования.
Третий этап включает в себя следующие подэтапы [39]:
а) редукция математической модели объекта управления к конечномерному
эквиваленту. Параметризация вектор-функций Х(/) и U(/) осуществляется с помощью
спектрального представления компонент в ОНБ (удерживается конечное число
членов разложения) (см. главу 8 в первом томе учебника, а также [39, 47]):
560
Методы теории оптимального управления. Часть III
*,(<)=
0,(0=
M')=I«S4(0
v=0
5/./(0=Ес*"Фу(0
v=0
%(')=2>>v(')
v=0
M0=2X-<pv(')
v=0
(5.2)
(5.3)
где индекс /, как правило, будем опускать. Или, что то же самое,
*,(') =
ФТ(/)С
Фт(0с-
= ф(/)с*,п,(/) =
ФТ(/)С'
ФТ(/)С""
= Ф(/)С(/,
где
Ф(/)=
ф(0
ф(0
о
0
ф(0.
сх<
сх2
С"'
- клеточные матрицы.
Учитывая конечномерные представления вектор-функций X(f) и U(/), для
линейного нестационарного объекта (5.1) можно воспользоваться конечномерным
эквивалентом, представляющим собой уравнение с матричным оператором
С* = KXBUGU + А*Ф^ ; (5.4)
б) редукция функционала качества к конечномерному эквиваленту.
С учетом рассуждений, которые были приведены выше, функционал качества
можно переписать в виде
J = \f0(o{t)Cx,<t>{t)Cu9t)dt = j(c\Cu). (5.5)
о
Поскольку
X, (t) = <t>(t)C\Vl(t) = &(t)Cu,
а Сх = А* ЫиСи +Ф^г)= АА'ваС(; + А*Ф^ , то получим функционал, зависящий
только от спектральных характеристик компонент вектора управления
./(C) = J/0(o(0(a
*ВиС"+АдгФ°А,),Ф(0Си)Л;
в) редукция краевых условий к конечномерному эквиваленту.
При t = Т фазовая траектория X(t) должна «попадать» в область, близкую, в
известном смысле, к точке X , т.е.
р(х^ф(0[=гс*)<в.
(5.6)
Глава 5. Методы математического программирования 561
В идеальном случае имеет место ограничение типа равенства
Соотношение (5.6) определяет тот факт, что достаточно достичь желаемого
состояния Хт с некоторой точностью.
Начальные условия Х° автоматически выполняются, т.к. они учитываются
ограничением (5.4).
Ограничения, порожденные краевыми условиями, при использовании
рассматриваемого подхода приводят к необходимости исследования сходимости рядов
*|7(0«Фт(0с\ / = п (5.7)
на промежутке [0,7], включая точки /=0 и / = Т.
В связи с этим обстоятельством при реализации метода, использующего
спектральное представление компонент вектор-функции Х(/), необходимо обратить
внимание на рациональный выбор используемого ОНБ;
г) редукция ограничений типа неравенств к конечномерному эквиваленту.
Параметрическая форма этих ограничений имеет вид
O(t)Cx еХ" V/g[0,71,
- „ (5-8)
O(t)Cu eUm Vte[09T].
В частном случае ограничения, накладываемые на все или отдельные фазовые
координаты, могут иметь вид
|oT(f)C**|<Jcfn; /е[0,Г]Д=п, (5.9)
где х%оп - константы (модульные ограничения).
Совокупность ограничений вида (5.8) или (5.9) формирует в фазовом
пространстве область «разрешенных» значений фазового вектора.
В систему неравенств (5.8) и (5.9) входит непрерывное время /. Заменим эти
ограничения системой дискретных ограничений. Для этого на отрезке [0,7] введем
конечное множество Tg = itj :j = 1,2,..., g^ = 0,fg| = T9ti <ti+]\, которое назовем
сеткой ограничений. Точки tj будем называть узлами сетки Tg. Если расстояние
Atj =tj -tj_x между соседними узлами постоянно (не зависит от у), Д/у = At для
всех j = l,g\, то сетку Tg называют равномерной, в противном случае -
неравномерной. Вместо вектор-функции X(/) = (jcj (/),...,*„(/)) , определенной для всех
/е[0,Г], будем рассматривать сеточную функцию Х} =x(tA целочисленного
аргумента j = l,gi для узла tj сетки Tg .
В задачах оптимизации сетка Tg в общем случае является неравномерной, ее
можно выбирать экспериментально, причем реализуется следующая
последовательность [47]:
• на основе изучения динамических свойств объекта и опыта эксплуатации
систем, близких по свойствам к проектируемой, строят сетку ограничений;
• решают задачу оптимизации с построенной сеткой ограничений;
• строят оптимальную фазовую траекторию;
• проводят анализ полученных результатов; цель анализа заключается в том,
чтобы выяснить наличие таких моментов времени t е [0, Т], в которых траек-
37 Зак. 366
562
Методы теории оптимального управления. Часть III
тория системы находится в недопустимой области. Если это имеет место, то
строят новую сетку, причем в окрестности выхода траектории из допустимой
области интервал дискретизации уменьшается.
4-й этап. Выбор численного метода решения задачи математического
программирования.
Эти методы подробно описаны в [16, 17] (см. также приложение).
Если в результате решения задачи нелинейного программирования получены
одностолбцовые матрицы коэффициентов Фурье компонент вектора управления
С"1 ,CM2,...,C"W , то оптимальное программное управление определяют с помощью
зависимости щ (t) = Фт (t)CUk, к = \,т, а оптимальные фазовые траектории находят
по формулам х*к (t) = Фт (t)Cx'k, к = 1,л.
Далее будут приведены формулировки задач построения оптимальных
программных управлений и оптимальных программ с использованием описания объекта вектор-
но-матричным дифференциальным уравнением и его конечномерным эквивалентом.
ТаблицаЗ. 1
Бесконечномерная постановка задачи
т
y = J/0(X(/),U(/),/)<//->min,
0
a)U(f)€t/mV/e[0,r],{
6)X(t)eX"\/t€[0,T]\
- ограничения типа неравенств;
а) Х(0) = Х°,Х(Г) = Х7',1
б) X = A(/)X + B(/)U J
- ограничения типа равенств
Конечномерная постановка задачи,
ориентированная на применение математического
программирования
y(cu)->min,
а)Фт(</)(АхВиС1)+АхФ^)еЛГл,|
6)Фт(11)СЬ€и'" }
- ограничения типа неравенств;
а) ФТ(Г)СХ=ХТ, 1
б) АхСх = ВиСи+Ф°г]
- ограничения типа равенств
Проиллюстрируем применение изложенных выше положений для решения задачи
оптимизации, когда [39,47]
y = JuT(/)u(O^=||u||2,u(/)6C[o,r].
(5.10)
Управление U(/) должно обеспечить перевод объекта из начального состояния X
в конечное состояние Хг за промежуток [0,Г], причем критерий (5.10) должен
иметь минимальное значение. Потребуем, чтобы фазовые координаты хк (t)
находились в области допустимых значений, которая может быть задана соответствующими
неравенствами. Для примера потребуем, чтобы
W/max-|W/(/)|>0V/e[0,r],/ = i^; (5.11)
xJM'\xj(tp0>/te[09T]j^9 (5.12)
гДе w/max и xjmax ~~ заранее заданные скалярные величины.
Положим, что при заданных условиях существует единственная вектор-функция
U* (t). Для решения задачи выберем ОНБ, удовлетворяющий соответствующим
условиям, связанным со сходимостью приближенных решений к точным на [0, Г] и в
Глава 5. Методы математического программирования 563
точках / = 0 и t = Т. Обозначим Ф = (ф0 (f),9i (f),...,(p/ (*)) . Подставим компоненты
вектора управления в форме й^(г) = ^с"*фу(/) = Фт(^)С"* ; к = \,т\ компоненты
v=0
вектора состояния имеют вид хк (f) = Фт (/)С*А ; к - \,п.
Выразим критерий качества и ограничения через коэффициенты
ГЩ rU\ ГЩ ги1 rUn, *п
при этом
Т 7Т m "I m l 2
y-fuT(/)U(/)*-J S«5(r) U-ZZ(c?) =^(СУ). (5.13)
О oLv=l J v=lr=0
В рассматриваемой задаче имеют место ограничения типа равенств и неравенств.
Неравенства (5.11), в соответствии с постановкой задачи, должны быть выполнены
для всех f е[0,Г].
Построим сетку ограничений Tg = itj : j = 1,g). Тогда неравенства (5.11) и (5.12)
можно переписать в виде
w/max
xjmax
фт(^)с^|>оу^д=п,у=п.
Сформулированная задача построения оптимального программного управления и
оптимальной программы свелась к задаче квадратичного программирования
v=lr=<r ' С(/
при ограничениях вида:'
Оа)«/тах-Фт(г,)См' >0Д = п;/ = п?;
6)^max-kT(^)^
>Q,k = \,g'J = hn\
> - ограничения типа неравенств,
2)а)Фт(Г)С* «Хг, 1
> - ограничения типа равенств.
б)АхС^г=В(/Са+Ф^
Рассмотренный выще метод можно применять для класса нелинейных систем с
аналитическими нелинейностями. После разложения аналитических нелинейностей в
ряды будут иметь место операции умножения, которые имеют эквивалентное
спектральное представление, использующее матричный оператор умножения*. Кроме
того, он легко обобщается на случай, если объекты описываются
дифференциальными уравнениями с запаздыванием и в частных производных. Структурная схема
алгоритма представлена на рис. 5.1.
Преимущество введения параметрических представлений по сравнению с
другими приемами состоит в том, что отпадает необходимость решать уравнение для
сопряженных переменных, а для оптимизации могут использоваться стандартные
методы поиска в конечномерном пространстве. Кроме того, параметрические
представления можно использовать для оптимизации моделей сложных технологических
процессов по результатам экспериментов, планируемых и проводимых непосредственно
* См. главу 8 в первом томе учебника, а также [39,47].
37*
564
Методы теории оптимального управления. Часть III
самой системой управления. Это позволяет избежать усложнения используемых
моделей, что особенно существенно для практики [49]. Как указано в [49], анализ
конкретных задач оптимального управления показывает, что при решении практических
проблем не следует ограничиваться заданием единственного параметрического
представления.
с
Начало
D
Ввод исходных
данных
—*—
Расчет матричного
оператора системы
(расчет матриц
АХ,В1\Ф<>)
}
Нахождение
зависимости,
определяющей
критерий J(Cy)
у
Формирование
ограничений
типа равенств
Формирование
ограничений
типа неравенств
Решение задачи
нелинейного
программирования
Печать
результатов
расчета
и*(/)ихЧо
с
±
Конец
j
Рис. 5.1. Структурная схема алгоритма расчета
оптимальных программных управлений и оптимальных программ
Необходимо опробовать несколько моделей, чтобы убедиться в том, что
выбранная модель действительно является достаточно общей.
Глава 5. Методы математического программирования 565
Процедура параметризации управлений часто представляется достаточно
эффективной, поскольку она очень проста и позволяет применять стандартные приемы
поиска экстремума. Основной ее недостаток - трудности исследования вопросов
сходимости на промежутке [0, 7]. Небольшая скорость сходимости приводит к
отсутствию гарантии того, что параметризированное управление достаточно близко, в
известном смысле, к оптимальному, если, конечно, базис разложения не выбирается
каким-либо специальным образом.
Число членов разложения должно быть, с одной стороны, не слишком большим
(для того чтобы поиск был эффективным), а с другой - не слишком малым (для того
чтобы получить хорошее приближение к точному решению), и это противоречие
разрешается только практикой.
В следующих параграфах приводятся примеры решения конкретных задач.
5.2. АЛГОРИТМ ПОСТРОЕНИЯ ОПТИМАЛЬНЫХ ПРОГРАММНЫХ
УПРАВЛЕНИЙ СТАЦИОНАРНЫМИ ЛИНЕЙНЫМИ ОБЪЕКТАМИ
ПО КРИТЕРИЮ МИНИМАЛЬНОЙ ЭНЕРГИИ
В предыдущем параграфе был рассмотрен общий алгоритм построения
оптимальных программ и программных управлений. При решении конкретных задач могут
быть использованы различные критерии качества. Например, часто стоит задача
расчета управлений, имеющих минимальную энергию; в этом случае имеет место задача
оптимального перевода объекта из состояния Х° в состояние Хт таким образом,
чтобы функционал [39,47]
(т \К
J(U) = |JuT(0U(/)dr (5.14)
принимал минимальное значение. Постановка задачи: при заданных:
• уравнении объекта управления
X=AX+BU;
• ограничениях
Щтак-\щ^)\>ОЫе[О,Т]91 = Т^1,
xjmn-\xj(tp0Vte[09T]j = u;
• времени управления [0,Г];
• краевых условиях
Х°в(Ч(0)^(0),...Л(0))Т,
хг = (^ (г), jca (аг)э...эхя (зг))т,
требуется найти такие программное управление U* (/) и фазовую траекторию
(оптимальную программу) Х*(/), при которых критерий (5.14) принимает минимальное
значение.
Формальная постановка задачи:
т
y(U) = JuT(/)U(/)^-^min
о
при следующих ограничениях:
(5.15)
566
Методы теории оптимального управления. Часть III
- ограничения типа равенств,
(5.16)
l.a)X = AX + BU,
б)Х(0) = Х° =(Х1(0),х2(0),...,х„(0))Т,
в) Х(Г) = Хг = (хх {0),х2 (0),...,*и (0))Т
2.a)ulmK-\u,(tp0Vte[0,T], ' = п»»1 ■
. . } - ограничения типа неравенств.
б)*утах ~ЫфОУ;е[0,Г],./= 1,л J
Постановка задачи в терминах математического программирования при
использовании спектрального метода для параметризации соотношений, входящих в (5.16):
при следующих ограничениях
- ограничения типа равенств,
1. а)АхСх=ВиСи+Ф°м,}
б)Фт(Т)Сх =ХТ
2. а) итах-|фт(/,)С"'|>0 *=п, / = п?;1
\ - ограничения типа неравенств.
(5.17)
6)xjmax-\0T(tk)Cx
>0 k = l,g9j = l,n
Структурная схема алгоритма представлена на рис. 5.2.
Пример 5.1. Управление положением ротора двигателя постоянного тока [54].
Редукцию поставленной задачи к задаче математического программирования осуществим
спектральным методом, используя в качестве базиса функции Уолша.
В рассматриваемом случае известны функции, определяющие и* (/), х* (t) и х\ (/), они имеют вид [54]
м;(/) = -6 + 12/,
*;(/) = 1-3/2+2/3,
*;(*)=-6/+б/2.
Получим решение задачи методом математического программирования и сравним полученные
результаты с точными.
Для нахождения и (/), icj* (/), х*2 (t) перепишем уравнения объекта в виде
*2 (') = <ВД (/) + я22*2 (') + Ь21щ (/) + b22u2 (t);
после интегрирования имеем
t t i t
*l(0 = JflIIXl(T)rfx + Je12*2W^ + jAiltt1(x)flfT + J^2I«2(T)rfT + XI(0);
0 0 0 0
/ / / /
x2^) = ja2lxl(x)dx + la22x2(x)dx + jb2lul(T)dx + jb22u2(x)dT + x2(0).
0 0 0 0
Матрица интегрирования в базисе функций Уолша строится в соответствии с алгоритмом,
изложенным в главе 8 первого тома, и для Т= 1 с имеет вид (вырез матрицы размером 8x8):
0,5 0,25 0 0,125 0 0 0 0,0625"
-0,25 0 0,125 0 0 0 0,0625 0
0 -0,125 0 0 0 0,0625 0 0
-0,125 0 0 0' 0,0625 0 0 0
0 0 0 -0,0625 0 0 0 0
0 0 -0,0625 0 0 0 0 0
0 -0,0625 0 0 0 0 0 0
-0,0625 0 0 0 0 0 0 0
А =
Глава 5. Методы математического программирования
567
с
/
Начало
/Ввод исходных данных А, В,
Л , Л , М,тах, Л, тах
:>
—►
s
Выбор базиса и расчет матриц
Параметризация критерия качества
v=l /г=1
Формирование ограничений типа
равенств
а)А*С*-ВуСи+Ф°„
б) ФТ(Т)СХ =ХГ
t
Формирование оц
раве
",тах-|фТ(^)С"|
*Уи«-|фТ(^)С^
>аничений типа не-
нств
^0,^ = 1^;/ = !^
1 > ОД = 'ugj = М
♦
Решение задачи оптимизации с
использованием оптимизатора
Quattro Pro v.5.0
^
Печать результатов расчета
1Г(/)иХЧ0
с
Конец
о
Рис. 5.2. Структурная схема расчета оптимальных программных управлений U* (t)
и оптимальных программ X* (/) (критерий качества - энергия управления)
Уравнения объекта с использованием матричного оператора интегрирования можно записать так
С* =апАиС* +*12АИС* +6пАие" +*2АИС|* + Ф°„,
Сх> =а2,АиСХ| +а22АиСХ1 +Ь2]\НСЩ +622АИС"2 +Ф^.
Поскольку в уравнениях объекта
ГО <Г\
А =
0 1
•-С :)•
то матричный эквивалент можно переписать в виде
568 Методы теории оптимального управления. Часть III
:"J [с*) [с) U(°)<J
где А = " и - клеточная матрица размером (1п)х(1п).
\^0Аи OAHJ
Теперь постановка задачи в терминах математического программирования формулируется так
/
Ч2
V=l Cv
при следующих ограничениях
С" =Я[С | + В'
ГсМ+^,(о)-ф»1
[cj U(o)-</
х°=(фТ(')ис^1;фТ('1„СХ1я0)'
х^=(фт(4гс^о,фт(4гс^о)
- ограничения типа равенств.
Ограничения на управление и фазовые координаты не накладываются.
Для решения задачи воспользуемся оптимизатором, встроенным в табличный процессор Quattro
Pro v. 5.0 (в данном случае размерность базиса принималась равной 32).
Приведем результаты решения поставленной задачи: спектральные характеристики сигналов
С" ,СХ| ,С*2 определяются следующими одностолбцовыми матрицами:
С""' = [0,0488106; - 3,123064; - 0,102396, -1,510334; - 0,102396; 0,1023955; - 0,102396;
-0,703969, - 0,102396,0,1023955; - 0,102396,0,1023955; -0,102396; 0,1023955;
-0,102396,- 0,300787; - 0,102396; 0,1023955; - 0,102396, 0,1023955, - 0,102396;
0,1023955, - 0,102396; 0,1023955; - 0,102396; 0,1023955; - 0,102396; 0,1023955;
-0,102396; 0,1023955; -0,102396; -0,099195 ],
Сх' = [0,4881367; 0,3165846; 0,00470020,0,1331058; 0,0011563; - 0,025173; 0,0023376;
0,063415; 0,0002703; - 0,006274; - 0,0000249; - 0,003124; 0,0005656; - 0,012574;
0,0011563, 0,031326; 0,00004883; - 0,001549; - 0,0000249, - 0,0007624; - 0,0000249,
0,00002499, - 0,0000249; - 0,0003687; 0,0001226; - 0,003124; - 0,0000249,
-0,001549; 0,0002703; - 0,006274; 0,0005656; 0,015626],
Сх> =[-1,0001; -0,036201; 0,401582; - 0,017300,0,099195; 0,0015999; 0,199991;
-0,0078504; 0,0235989, 0,0015999; - 0,0015999,0,0015999; 0,0487978; 0,00159993,
0,0991956, - 0,0031252; 0,0046997; 0,001599; -0,001599; 0,001599; -0,001599,
0,001599, - 0,001599,0,001599; 0,010999,0,001599, - 0,001599; 0,0015999,0,023598;.
0,0015999; 0,0487978, - 0,00076266]
Выполняя над указанными массивами обратное преобразование Уолша, получим дискретные значения
управления м*(/) и оптимальной программы Х*(/) = (л£ (/),д£(/)1, которые приведены в табл 5.2.
На рис 5.3 представлены графики указанных функций и точного решения.
Пример 5.2 [25]. Оптимальное управление материальной точкой при заданных условиях.
Рассмотрим материальную точку массы т, движущуюся в вертикальной плоскости {£,л} в поле силы
тяжести Предположим, что в качестве управляющего воздействия к точке т приложена реактивная сила/
возникающая в результате отделения от нее частиц с элементарной массой \dmx\. Тогда масса точки является
величиной переменной m = m(t) и ее движение можно описать векторным уравнением Мещерского (рис. 5.4)
dv
Здесь т - да(/) = т0 + тх (t), где /720=cons/, да, (/) > 0 - реактивная масса точки; / = (s - v) dmx ldt\\ -
вектор абсолютной скорости точки т; s - вектор скорости частицы dm\ в момент t+dt после ее отделения,
так что a=(s - v) есть вектор относительной скорости отделяющейся частицы, р - вес.
Глава 5. Методы математического программирования
569
6
I I I I I I I I I I I I I К1* I I t I I I I I II I I I I Й
0,2
0,6
1 /, с
1 Л с
Рис. 5.3. Графики функций м*(/), и (/), ic,*(/), х\(/), Jcj (/), jcj (/)
36 Зак. 366
570
Методы теории оптимального управления. Часть III
Таблица 5.2
Дискретные значения u*(tk), u*(tk), x*x(tk), x\(tk), x\(tk), x\(tk)
h
0
0,03340
0,06681
0,1002
0,1336
0,1670
0,2004
0,2338
0,2672
0,3006
0,3340
0,3674
0,4008
0,434
0,467
0,501
0,534
0,567
0,6012
0,6346
0,6681
0,7015
0,7349
0,7683
0,8017
0,8351
0,8685
0,9019
0,93534
0,96874
1,00
-6,0981
-5,694
-5,291
-4,888
-4,485
^,082
-3,679
-3,275
-2,872
-2,469
-2,066
-1,663
-1,259
-0,856
-0,453
-0 05
0,352
0,755
1,159
1,562
1,965
2,368
2,771
3,175
3,578
3,981
4,384
4,787
5,190
5,594
5,997
-6,000
-5,599
-5,198
-4,797'
-4,396
-3,995
-3,594
-3,193
-2,793
-2,392
-1,991
-1,590
-1,189
-0,7887
-0,3879
0,0129
0,41375
0,81465
1,2155
1,6163
2,0172
2,4181
2,8189
3,2198
3,6206
4,0215
4,4224
4,8232
5,2241
5,6249
6,0
h
0
0,0156
0,0468
0,0781
0,1093
0,1406
0,1718
0,2031
0,2343
0,2656
0,2968
• 0,3281
0,3593
0,3906
0,4218
0,4531
0,4843
0,5156
0,5468
0,5781
0,6093
0,6406
0,6718
0,7031
0,7343
0,7656
0,7968
0,8281
0,8593
0,8906
0,9218
0,9531
0,9843
1,00
1,00
0,99851
0,99265
0,98123
0,96465
0,94329
0,91755
0,88782
0,85450
0,81798
0,77866
0,73692
0,69317
0,64779
0,60118
0,55314
0,50585
0,45791
0,41032
0,36347
0,31774
0,27355
0,23127
0,19131
0,15405
0,11990
0,08923
0,06246
0,03997
0,02215
0,00941
0,00212
-0,0001
0,00
1,00
0,99927
0,99361
0,98264
0,96672
0,94623
0,92153
0,89298
0,86095
0,82581
0,78792
0,74765
0,70537
0,66144
0,61623
0,57010
0,52342
0,47657
0,42989
0,38376
0,33855
0,29462
0,25234
0,21207
0,17418
0,13904
0,10701
0,078468
0,053764
0,033271
0,017356
0,006385
0.000724
0
0
-0,095283
-0,27954
-0,45121
-0,61028
-0,75675
-0,89062
-1,0118
-1,1205
-1,2166
-1,3001
-1,3709
-1,4292
_
,4749
,5079
,5284
,5363
,5316
,5142
,4843
,4418
,3867
,3189
,2386
,1457
,0402
-0,9221
-0,7913
-0,6480
-0,4921
-0,3236
-0,1425
0,14-Ю-6
0
b(<k)
0
-0,09228
-0,26806
-0,43213
-0,58447
-0,72509
-0,85400
-0,97119
-
-
-
-
-
-
-
-
-
-
,0766
,1704
,2524
,3227
,3813
,4248
,4633
,4868
,4985
,4985
-1,4868
-1,4633
-1,4282
-1,3813
-1,3227
-1,2524
-1,1704
-1,0766
-0,97119
-0,85400
-0,72509
-0,58447
-0,43112
-0,26806
-0,09228
0
Проектируя уравнение Мещерского на горизонтальную и вертикальную оси координат, получим
следующие уравнения движения [25]
jm(/)S = m^(').
}m(/)ij = wan(/)-/w(/)g,
где а^ и ац - проекция вектора а на оси £, и х\. Допуская, что абсолютная величина вектора а задана и
равна ст, запишем систему уравнений в нормальной форме.
х2=щ,
*4=М2-2>
• . т т
где *! =£,*2 =£,*з = л>*4 =11>wi =crcosar—,м2 =acosan— , cu,an - углы, составляемые вектором а с
щ т *
осями ^ и г|, причем
(• \2
т)
Будем считать реактивную силу управляющим воздействием
Для рассматриваемой системы сформулируем задачу оптимизации*
Глава 5. Методы математического программирования
571
J(U)= J[Ml2(x) + W22(x)}/x ->min
1/2
при следующих ограничениях:
*\(*) = хг{1)>
*2(') = wiW>
*з(/) = *4(<)>
x4(t) = u2(t),
Хт =(Xl(T),x2(T)MT)MT))
(будем полагать g = 0).
/
ограничения типа равенств;
^Л
/ *p=mg \^
I
fe°,n°)
kT^)
Рис. 5.4. Движение материальной точки массы m в вертикальной плоскости {^,г|}
в поле силы тяжести
Ограничения типа неравенств отсутствуют
Положим: Х° = (-1,0,0,0), Хг= (0,0,0,0), Г = 1с. Для нахождения u\(t),u\{t)X\(t)^\(t), 5j(/),jcj(/)
перепишем уравнения объекта в виде:
х2 = д2Л (/) + а22х2 (/) + а2зХз (/) + а24х4 (г) + Ь2]щ (/) + 622w2 (/),
^=аз^1(0 + Лз2^(0 + Лзз^з(0 + а34^(0 + М|(0 + М2(0»
ЛГ4 = а41^1 (0 + ^42^2 (0 + <*43*3 (0 + «44^4 (0 + Ml (0 + V<2 (0'
после интегрирования имеем*
/ / /
X\{t) = \auxx{x)dx + \anx2{z)dT + \anx^i)dx-^
0 0 0
/ / /
+jal4x4(x)dx + \bllui(x)dx + jbllu2(x)dx + xl(0),
0 0 0
t ( t
x2(t) = \a2lx](x)dx + \a22x2(x)dx + ja23x3(x)dx +
0 0 0
t I t
+ja24X4{*№ + jb2lUi(x)dx + \b22u2(x)dx + x2(0),
0 0 0
1 t I
X3(t) = ja3lxl(x)dx + janx2(x)dx + ja33x3(x)dx +
0 0 0
/ / t
+la34x4(x)dx + \b3]ul(x)dx + jb32u2(x)dx + x3(0),
0 0 0
1 t t
x4{t) = \a4Xxx{x)dx + \a42x2(x)dx + \a43xi(x)dx +
0 0 0
t I t
l+\a44x4(x)dx + jb4Xul(x)dx + jb42u2(x)dx + x4(O).
0 0 0
36*
572
Методы теории оптимального управления. Часть III
В качестве базиса будем использовать полиномы Лежандра. Матрица интегрирования в базисе
полиномов Лежандра на промежутке [0,7] запишется так [39,47]:
*-л>
-1/3 0
0 -1/5
1/3
о
о
1/5
о о
о о
о
1
2/W-3
О
1
2/и-З
1
2т -2
О
0,5
0,5
0
0
0
0
-0,1667
0
0,1667
0
0
0
0
-0,1
0
0,1
0
0
0
0
-0,0714
0
0,0714
0
0
0
0
-0,055
0
0,055
0
0
0
0
-0,045
0
Для Г= 1 с матрица интегрирования имеет вид (приведен вырез матрицы размером (6x6))
А =
Уравнения объекта с использованием матричного оператора интегрирования можно записать так.
С*1 = a,,AHCXl +а|2АиС* +я,3АиСХз + а14АиСХ4 +
^А^'+^А^+^ОК,
Сх' =д21АиСХ| +а22АиС*> +я23АиСХз + я24АиСх< +
+Ь2хАиС«+Ь22АнС'>+х2(0)Ф0„,
Сх" = я31АиСх' +а32АиСХ2 +я33АиСХз + я34АиСх« +
^Л.С'+^А^+^^Ф^
Сх< = а41АиСХ| +а42АнСх> +а43АиСХз +я44АиСХ4 +
+^41АиСы'+А42АиС^+х4(0)Ф^-
Поскольку в уравнениях объекта
А =
то матричный эквивалент можно переписать в виде:
0
0
0
0
1
0
0
0
0
0
0
0
0"
0
1
0
;В =
0
1
0
0
0"
0
0
1
с*
с*
сх>
= А
С1'
С*
С
с\
{с.
1
)
Xl(0)
«2(0)
^з(О)
U(o)
■ф%
■ф°„
■К)
где
А =
0А„
0Аи
0А„
0А„
в =
1А„
0Аи
0А„
0А„
ГО-А„
1АЯ
0А„
0А„
0-
0-
0-
0
0-
0-
0-
1
А„
А„
К
А„
А.]
А„
Аи
А..
0-
0-
1-
0-
_
А
А
А
А
- клеточная матрица размером (in) x (In),
- клеточная матрица размером (In) x (1т).
Глава 5. Методы математического программирования
573
Теперь постановка задачи в терминах математического программирования формулируется так*
\>/2
Vv=J v=l )
> mm
при следующих ограничениях:
С*'
с*
.сг
= А
С*'
сх>
с*
сх<
4е"1'
V.
1
)
ч(о)
Х2(0)
*,(0)
хЛО)
■К)
■К
С"' =
0,0123879"
-5,962708
0
0
0
0
0
0
0
0
г<г
0
0
0
0
0
0
0
0
0
; сх' =
С*2
'0,999978бГ
0,00619395
-0,9937846
0
0
0
0
' 0
0
0
; С* =
0
0
0
0
0
0
0
0
0
; сх: =
0
0
0
0
0
0
0
0
0
Хи=(фт(,)[=оС" -1; Фт(г)|1=оС *0; ФТ(/)|,=0С" *0;Фт(0|/=цС" -о),
х"^('tr^'и0; фТ(')|„гс12s0; фГ(')1тс*«o;i>T(OUc^o)
Для решения задачи математического программирования воспользуемся оптимизатором электронной
таблицы Quattro Pro v.5.0.
Приведем результаты решения задачи оптимального перевода объекта из состояния Х° в состояние
Хг без Офаничений на фазовые координаты. Одностолбцовые матрицы, представляющие собой
спектральные характеристики сигналов С1, С2, СХ|, С*2, С*3, С*4, имеют вид:
(-0,50104301^
0,59936777
0,001032325
-0,09937846
0
0
0
0
0
0
Следующие формулы определяют оптимальное программное управление и оптимальную программу,
полученные с помощью конечномерной оптимизации:
п\ (t) = 5,9750959-11,925416/;
й;(/) = 0;
х,* (/) = -0,999999-0,2397992 • КГ10 / + 2,98754/2 -1,9875/3;
jc^ (/) = 5,975/ - 5,962708/2,
*з(<)=°;
Метод множителей Лагранжа позволяет записать точные формулы, определяющие и* (/), и\ (/), х* (/),
Х2 W» *3 (О» Х4 (0 у 0НИ имеют ВИД:
«;(/) = 6-12/;
u2{t) = 0;
jc;(/) = -l + 3/2-2/3;
Зс;(/) = 6/-6/2;
x4(t) = 0.
В табл. 5.3 приведены дискретные значения компонент вектора управления и*(/), "2(0' "*(')> "г (О и
компонент вектор-функций X* (/) и X* (/). На рис. 5.5 и 5.6 представлены графики указанных выше функций
574
Методы теории оптимального управления. Часть III
Таблица 5.3
Дискретные значения u*{(tk), u\{tk), x\{tk), x*(tk), x2(tk)9 x2(tk)
h
0
0,053
0,105
0,158
0,211
0,263
0,316
0,368
0,421
0,473
0,526
0,579
0,631
0,683
0,736
0,789
0,842
0,894
0,947
1
Щ{*к)
5,9751
5,3475
4,7199
4,0921
3,4645
2,8369
2,2093
1,5817
0,9540
0,3263
-0,3013
-0,9289
-1,5565
-2,1842
-2,8118
-3,4394
-4,0669
-4,6949
-5,3229
-5,9499
6,0
5,3684
4,7369 '
4,1052
3,4736
2,8421
2,2105
1,5790
0,9473
0,3157
-0,3158
-0,9474
-1,5790
-2,2106
-2,8422
-3,4738
-4,105
-4,737
-5,369
-6,000
*Г('*)
-1,0000
-0,99201
-0,96922
-0,93334
-0,88614
-0,82933
-0,76467
-0,6939
-0,61872
-0,54092
-0,46222
-0,38429
-0,30904
-0,23807
-0,17308
-0,11604
-0,0684
-0,0320
-0,0087
-0,0001
-1,0
-0,99198
-0,96909
-0,93308
-0,88569
-0,82869
-0,76381
-0,69282
-0,61743
-0,53944
-0,46057
-0,38260
-0,30716
-0,23614
-0,17124
-0,11434
-0,0669
-0,0309
-0,008
0
0
0,29796
0,56287
0,79481
0,99362
1,1595
1,2923
1,3920
1,4588
1,4924
1,4931
1,4607
1,3953
1,2968
1,1654
1,0008
0,8033
0,5727
0,3090
0,0124
Ъ{'к)
0
0,29917
0,56508
0,79781
0,99726
,1635
,2964
1,3961
,4627
[,4958
,4958
1,4626
1,3962
,2963
,1634
0,9972
0,7978
0,5650
0,2991
0
0,01 ■•
-0,01"
-0,02
0,2 0,4 0,8
Рис.5.5. Графики функций u*(t),u\(t)
1 /,с
Глава 5. Методы математического программирования
575
-o,oi • •
-0,02^ f w
о|25 о',5 V.75- l'-c
Рис.5.6. Графики функций ъ{*)>*2(*)>ъ(*)>х1{*)
Построим решение той же задачи методом матричных операторов, но с ограничением на фазовые
координаты; положим
*2(/)<1,25,
Х° = (-1;0;0;0); Хт = (0,0;0;0); / = 10
- базис - полиномы Лежандра.
В результате реализации процедуры оптимизации получены следующие спектральные характеристики
оптимального программного управления и компонент оптимальной программы
х-(,)=(*;(,),*;(,),*-М>*;(<)).
576
Методы теории оптимального управления. Часть III
CXj =
1*
f 0,0243992'
-5,926432
0,0186509
-3,499914
0
1,3494825
0
1,2176168
-0,097307
^ 0,9268948,
0,99993 '
0,01033
-0,7377
0,001865
-0,31133
0
0,0207528
0,0028619
0,016195
-0,002861
. Си'г -
( 0 Л
0
0
0
0
0.
0
0
0
дыо-5,
, v^ —
0
0
0
0
0
0
0
0,773993810"9
0
-0,7739938 1С
;сх:
'-0,50175 '
0,57374
0,001588
-0,05647
0,000133
-0,01809
-0,000095
0,000321
0,00017
ч 0,000476,
*
0
0
0
0
0
0
0
0
-0,26315789
, о
Решение поставленной задачи имеет вид
и,* (/) = 390920,57964/7 -412493,086/6 + 261415,6494/5-101789,2880/4 +
+145,1339/-204047,65438/8 + 45065,6251/9 +5,878+ 23827,835/3 - 3056,65882/2;
й;(/) = -0,110-5+0,41184/7-0,42042/6+0,2522/5-0,09/4 +
+0,00009/- 0,21879/8 + 0,04862*9+ 0,01848/3 - 0,00198/2;
icj*(/) = 188,4884/7-189,8591/6 + 108,9/5-299,6/4-0,9999-
-0,03267/-102,019/8 +23,159/9 -2,5438/3 +4,5042/2;
х\ (/) = -2002,5835 /7 +2549,7894 /6 -1899,0891 /5 +829,523/4 +
48,5612/ + 834,6035/8-139,149/9-181,7539/3 + 0,12281/2- 0,2439;
х3*(/) = -0,00031/7+0,0003161/б-0,0001823/5 + 0,00006/4-0,26315 10-7/ +
+ 0,000169/8 - 0,0000376 /9 - 0,000011/3 + 0,947368 • 10"6 /2 - 0,29 • 10~21,
^(/) = 0,001354/7 -0,00221/6 + 0,00189/5 -0,00091/4 +
+0,18947 • 10"5/ - 0,000338/8 + 0,00024/3 - 0,000033/2 - 0,2631 • 10"7.
Графики функций щ (/), п\ (/), jc,* (/), х\ (/), хг (/), х\ (/) представлены на рис. 5.7. и 5.8.
".'(')81
б-
2-
О
-2-
-4'
«■но
0,02-
0,01- ■
Л С
0,4
-0,01' '
-0,02
/, с
0,25
0,5
0,75
Рис. 5.7. Графики функций £*(/), u*2(f)
Глава 5. Методы математического программирования
577
-0,2-
-0,4 •
-0,6-
-0,8'
-1
0.25 0,5 О275 1
^ \ с
у/ 0,9
/ 0,6
у/ 0,3'
_—-*^ 0
/ \
/ \
/ \
/ V'c
0,25 0,5 0,75 |
0,02*
0,01
-0,01 ''
-0,02
и 0,25 0,5 0,75 i'«c
Рис. 5.8. Графики функций ^(/),*2(0»*з(0»*4(0
Пример 5.3. Оптимальный заход на посадку транспортного самолета (рис. 5.9) [67].
Линеаризованное уравнение продольного движения самолета при заходе на посадку представляет
собой следующее дифференциальное уравнение [67]
в+2^ю0ё+К )2 е=кт0 (ш0 )2 л+к (соо )2 л,
где Э - угол тангажа, л - угол отклонения руля высоты, который осуществляет управление самолетом,
£ - коэффициент демпфирования угла тангажа, соо - собственная частота, То - постоянная времени, К -
коэффициент усиления системы «отклонение руля высоты - угол тангажа». При выводе уравнения
предполагалось, что путевая скорость v остается постоянной, а для путевого угла у выполняется условие
|у|«1. Если через h обозначить высоту полета, то зависимость между углом тангажа 9 и скоростью
снижению h самолета имеет вид
77* + /i = v6.
После некоторых преобразований получим
й 1 - 257>О Ail- 2£7qCD0 + (7qCoo )2 А 1-2^Госоо+ (7>О)2 ,• , ,2
(То)
(ТоУ
ГУ
Рис. 5.9. Условные обозначения при рассмотрении задачи захода самолета на посадку
578
Методы теории оптимального управления. Часть III
С введением переменных состояния xl=h,x2=h,x3 = Qyx4 = 9, переменной управления и = г| , а также
новых постоянных
__—^- +
V
а22 = - \/Т0; а23 = v/T0; а42 =
2§%+£«.
v(7i)2 vTi '
«43 = --^+^-Ы2;*44 =1 -2^0; *0 =*ГоК)2
полученное выше уравнение можно переписать в векторно-матричной форме
*2
*}
Граничные условия можно записать так:
*((О) = дг(О, Xi(T) = xiT=0, / = 1,2,3,4,
причем время Г является заданным. Заход на посадку транспортного самолета осуществляется в последней
фазе приземления до момента касания им посадочной полосы в общем случае по лучу; это означает, что
самолет должен выдерживать как можно более точно требуемую траекторию. Поэтому в критерий
оптимизации необходимо ввести отклонение действительной траектории от заданной. Кроме того, отклонение
руля должно находиться в заданных пределах, чтобы обеспечить комфортные условия для пассажиров.
Таким образом, имеем следующий функционал качества [67]
"0
0
0
0
1
«22
0
«42
0
«23
0
«43
0 '
0
1
«44
V
*2
*3
Х4
+ *о
"0"
0
0
1
Z/=l 0 L Ч J/ J
Коэффициенты р, (/ = 1,2,3,4), так же как аир, представляют собой весовые константы
Пользуясь ими, можно придать больший вес выполнению конечных условий, отклонению от заданной
траектории или отклонению руля.
Зададимся следующими исходными данными [67]:
х10 = 30,5 м; х20 = -6,1 м/с; х30 - -0,078 рад; х40 = 0 —;
с
а22 = 0,4 с; а2Ъ = 31,2 м/с2; а42 = 0,0097 —;
мс
a =-0,76-V; a44=-°>6 -S *о = -2,37 -Ь
с с с
Т = 20 с; а = р = 2; р/=1000 (/ = 1,2,3,4).
Решим задачу методом математического программирования с использованием положений теории
матричных операторов. Перепишем уравнения объекта в следующем виде
*,=х2(/),
*2 = «22*2 (') + «23*3 (').
*3=*4>
*4=«42МО + «43*ЗМ + «44*4(0 + *0"(')-
После интегрирования имеем
*,(/)=*, (0)+j*2 (*) ^
о
/ /
x2(t) = x2(0) + \a22x2(T)dx + \a23x3(x)dTy
о о
*(0 = *(0) + Ыт)Л.
X4(0 = *4(0) + J«42*2(T)«'X + J«43*3(T)«'X + }«44*4(T)«'T + }V(^«'^
0 0 0 0
В качестве базиса будем использовать функции Уолша.
Для Г= 20 матрица интегрирования имеет вид (приведен вырез матрицы размером 8x8)
Глава 5. Методы математического программирования
579
10
-5
0
2,5
0
0
0
-1,25
5
0
-2,5
0
0
0
-1,25
0
0
2,5
0
0
0
-1,25
0
0
2,5
0
0
0
-1,25
0
0
0
0
0
0
1,25
0
0
0
0
0
0
1,25
0
0
0
0
0
0
1,25
0
0
0
0
0
0
1,25
0
0
0
0
0
0
0
А =
Уравнения объекта с использованием матричного оператора интегрирования можно записать так
С"=АиС*+*1(0)-Ф°,>
С* =апАкС" +*ИАИС" + *2(0)Ф0„,
С>=АиС^+хэ(0)Ф^
Сх< =а42АнС +a4iAHC' + амАиС +*оАиС" +*4(0)Ф^.
Матричный эквивалент имеет вид
С*'
сх>
cxv
'0
0
0
о
0
*2зА„
0
а43Аи
0 ^
0
А„
44АИ>
<У
с*
с*
+
( о N
0
0
с +
*i(0)-<
Л2(0)Ф»
*,(О).Ф°
го /^с
1 - метод математического программирования
2 — сглаженная кривая
Рис. 5.10. Графики функций к*(/), *,*(/), x*(t)
580
Методы теории оптимального управления. Часть III
Теперь формулировка задачи в терминах математического программирования запишется так:
•/(c")4tp-Kc)Ucl'T-
Zv=l
при следующих ограничениях:
2ас?с,
~В)+
р(с:)2
-> mm
Сх'
Сх>
Сх'
сх<
ГО Аи
0 (322АИ
0 0
0 а42Аи
0
а23Аи
0
0
0
А„
а43Аи а4АК
С*
+
' 0 ^
0
0
ЛАи,
см +
*1(0)ф°„
*з(О)'ФЯ
/4(0) Ф^
Ф^О^С* «0; ФТ(')|,_гсХ4 *°-
Приведем результаты решения задачи оптимального перевода объекта из состояния Х° в состояние
Хт без ограничения на фазовые координаты. Одностолбцовые матрицы, представляющие собой
спектральные характеристики сигналов С"", СХ|, С*2, СХз, С*< , имеют вид:
С" =
'-0,016224'
-0,016167
-0,01487
-0,014922
-0,009856
-0,009821
-0,010679
-0,010716
-0,004042
-0,004028
-0,003705
-0,003718
-0,005629
-0,00561
-0,006099
-0,006119,
; Сх* =
f3,0683 '
3,0028
2,0295
2,7740
2,0556
2,6550
1,7944
2,3675
0,20915
0,37209
0,42233
0,67049
0,8905
1,2043
0,7443
1,0900 J
; cXj* =
^-1,7441 '
-1,1909
-1,9269
-1,4247
-1,0728
-0,6758
-0,5954
-0,3347
0,29992
0,48920
0,39435
0,43956
-0,39226
-0,16499
-0,24955
-0,09047,
; сХэ* =
0,027000 ^
0,028065
0,033165
0,038380
-0,0087879
-0,0115598
-0,0174542
-0,0110899
-0,0117272
-0,0112087
-0,0227866
-0,0204211
-0,0043889
-0,0050706
-0,0044227
-0,0017712
; Сх« =
0,0028341
0,0070762
0,0081128
0,0070220
0,0326736
0,0364587
0,0179340
0,0187635
-0,0120759
-0,0137741
-0,0022700
-0,0000164
0,0073976
0,0084526
-0,0007440
0,0004298
Выполнив над массивами С" и С*1 обратное преобразование Уолша, получим дискретные значения
функций управления и оптимальной посадочной траектории, которые приведены в табл. 5.4.
Графики функций u*(t),x*(t) и сглаживающей кривой £,*(/) представлены на рис. 5.10.
Пример 5.4. Стыковка космических объектов [3].
Вопросам стыковки посвящено большое количество работ; кроме того, успешное развитие
космической техники и реальные стыковки, неоднократно проведенные при полетах советских и американских
космонавтов, показывают, что проблема в общем решена [3].
Отличием космических объектов, движущихся по орбите, от приземных, движущихся в атмосфере или
гидросфере, является то, что они не взаимодействуют с внешней средой. Плотность внешней среды такова,
что ее влиянием на небольшом отрезке времени можно пренебречь и считать, что на объект действуют
лишь гравитационная сила и сила тяги реактивного двигателя, управляемого с помощью САУ. Кроме того,
можно приближенно считать, что тот небольшой участок круговой орбиты, который пролетают объекты за
время выполнения стыковки, прямолинеен. Действительно, его длина примерно равна 20Q - 400 км, что
составляет 0,5-1% от длины круговой орбиты, равной 41000 км.
Вектор силы тяжести при этом перпендикулярен траектории и не проектируется на ее направление.
Учитывая сказанное, запишем уравнения движения двух объектов вдоль оси L:
Глава 5. Методы математического программирования
581
*1=Я1>
4=V2>
где L\ и vi - координата и скорость перемещения цели (первого объекта) вдоль оси L\ L2 и v2 - координата
и скорость перемещения перехватчика (второго объекта) вдоль оси L\F- сила тяги двигателя
перехватчика; т = 2943 кг - масса перехватчика.
Дискретные значения функций и (/) и x\(t)
Таблица 5.4
/*,с
0
1,2500
2,5000
3,7500
5,0000
6,2500
7,5000
8,7500
10,000
11,250
12,500
13,750
15,000
16,250
17,500
18,750
20,00
м*(/*),рад
-0,14221
-0,064305
-0,029075
-0,013147
-0,005943
-0,002691
-0,001213
-0,000549
-0,000247
-0,000115
-0,000049
-0,000025
-0,9-10"5
-0,510"5
-0,310"3
-0,3 10~5
0
*1*('*)>м
25,350
14,144
4,2569
-0,25320
-0,053284
1,4908
2,0676
1,5653
0,90061
0,66649
0,78288
0,88972
0,74211
0,24501
-0,78119
-2,9228
0
Будем предполагать, что управляющая сила F перехватчика, создаваемая его реактивной двигательной
установкой, может менять направление и линейно зависит от перемещения управляющего органа
^=9810 6.
Возьмем астатический регулятор ускорения с законом управления
t = KF(u-v2),
где Kf=10,0 - передаточное число рулевого привода;
v2 - текущее ускорение перехватчика, измеренное вдоль оси L\
u = u(t) - текущее ускорение и, подлежащее определению.
Постановка задачи оптимального управления: определить закон управления ускорением u(t),
обеспечивающий плавную безударную стыковку двух космических объектов, при этом энергия управления
Т
где [0,7] - промежуток управления.
Сформулируем математическую постановку задачи.
Предварительно введем вектор состояния X = (jc,...j^)т , *, = Ц, х2 = v,, jc3 = Ц, jc4 = v^, д$ = 6 .
Задача заключается в переводе объекта, описываемого системой дифференциальных уравнений
*1=*2,
*3=*4,
. 9810
*4" 2943Х5'
• 1л( 9810 "I
582
Методы теории оптимального управления. Часть III
из начального состояния Х° =(xjo..j^o) в конечное состояние Хг за промежуток [0,71, ПРИ эт<>м
функционал качества
т
J = \u2(t)dt
о
должен принять минимальное значение.
Выберем величины констант [3]:
я, = 0 (цель движется без ускорения),
Т - 30 с (время процесса стыковки),
xl0 = Lj0 = 1200 м (начальная координата цели),
х20 = v,0 = 8000 м/с (начальная скорость цели),
Л'зо = £20 = Ю00 м (начальная координата перехватчика),
*4о = V2o = ^000 м/с (начальная скорость перехватчика),
х50 = б0 = 0 условных единиц.
Конечные условия:
ххг = х3г, или х[Т -х2Т =0 (координаты перехватчика и цели совпадают),
х2Т = х4Т, или х2Т - хАГ = 0 (скорости перехватчика и цели совпадают).
Ограничения типа неравенств отсутствуют. Перепишем уравнения объектов в виде
*1=*12*2(')>
*2=а„
х4 =045X5(0»
x5=aS5x5(t) + b5u(t).
После интефирования имеем
Х|(0 = Ь2Х2(т)о'1 + х|(0),
о
t
x2(t) = laldT + x2(0) = alt + x2(0),
о
Лз(0 = /а34Х4(0^Т + Лз(°)'
О
/
X4(0 = Jfl45XsWefT + ac4(0),
x5(t) = \aS5x5(x)dx + lbsu(x)dx + x5(0y
о о
В качестве базиса будем использовать полиномы Лежандра. Матрица интефирования в базисе
полиномов Лежандра на промежутке [0,7] запишется так [3]
Ам=~
1
1
0
0
0
0
0
-1/3
0
1/3
0
0
0
0
0 ...
-1/5 ...
0 ...
1/5 ...
0 ...
0 ...
0 ...
0
0
0
0
1
2т-3
0
1
0
0
0
0
0
1
2/и-З
0
2/и-З
Для .Г- 30 с матрица интефирования имеет вид (приведен вырез матрицы размером 8x8):
Глава 5. Методы математического программирования
583
А
Аи =
15
15
0
0
0
0
0
0
-5
0 -
5
0
0
0
0
0
0
-3
0 -2
3
0 2,
0
0
0
0
0
,142
0
142
0
0
0
0
0
0
-1,6666
0
1,6666
0
0
0
0
0
0
-1,363
0
1,363
0
0
0
0
0
0
-1,153
0
1,153
0"
0
0
0
0
0
-1
0
Уравнения объекта с использованием матричного оператора интегрирования можно записать в виде
CXj
сх>
сх<
Сх>
= *12А,
,сх>
+*(о)-фХ
= АиСа'+*2(0)Ф°г,
= а24А
= я45А
= а55А
Поскольку в уравнениях объекта
А =
0 1
0 0
0 0
0 0
0 0
«С*
«с*
0
0
0
0
0
+ х3(0).ф(
+ *4(0)Ф
h
)
V»
)
+ 65АиС + *5(0)
0 0
0 0
1 0
0 3,333
0 -33,33
, в =
•Ф°д
"0"
0
0
0
10
г-
то матричный эквивалент можно переписать в форме
сх«
с*
сх*
схг
= А
сх»
СХ2
СХз
сх<
СХ5
+
' 0 >
0
0
0
,ЮАИ>
С + А„Са' +
ч(о) •<
4.(0) •<
x3(O)0°N
*4(0)-<
(аиАн
где А =
а15Аи
a2sK
- клеточная матрица размером 5/х5/
^51 Аи . а55Аи)
Теперь можно поставить задачу в терминах математического программирования.
Ч2
■'И-ЕИ) ^™»
при следующих ограничениях:
Сх'
сх,
сх*
cxv
= А
CXl
сх>
СХз
сх<
cxv
+
' 0 Л
0
0
0
,ЮАИ>
4(0)-<1
4.(0)-<
С"+А.С^+ *,(<>)■<
" «4(0)-<
М°)ф0»)
Х° = (Фт(/)| Сх< * 1200; Фт(*)| С" «8000; Фт(/)| С * 1000;
ч '1г=О х 'll=0 v '1|=О
Фт(/)[ оСх< «8000;Фт(*)|( оС'! »0);
Хг=Фт(/)[ гСг'-Фт(/)[ гС^-0;
584
Методы теории оптимального управления. Часть III
Приведем результаты решения задачи оптимального перевода объекта из состояния Х° в состояние
Хт без ограничения на фазовые
С\ С\ С\ СХК С*\ Сх> имеют вид:
сХз* =
' 0,0034414'
-1,3230
0,0042198
0,0036758
0,0041684
0,0036008
-0,006116
, 0,13631 ,
' 121100,0 '
120120,0
0,38126
-19,874
-0,0069447
0,15616
0,030086
v -0,15126 ,
; С*
; Сх* =
координаты. Спектральные характеристики сигналов
'121200,0'
120000,0
0
0
0
0
0
, 0 ,
( 8006,7 '
0,078455
-6,6229
0,0051368
0,0029480
0,013164
-0,13109
-0,012135
; сх> =
'8000,0'
0
0
0
0
0
0
, 0 ,
' 0,0016924 '
-0,39492
0,00061667
0,0057549
0,00018549
0,0083949
-0,0031548
0,050773 J
Следующие формулы определяют оптимальное программное управление и оптимальную программу,
полученные с помощью конечномерной оптимизации:
м*(/) = 1,1849 + 0,2139110"7/7-0,2253810"5/6+0,000094034/4
+ 0,17631/-0,0019700/4 + 0,021641/3-0,11788/2;
1\ (0 = А (0 = 1200'° + 8000,0/;
v,(/) = X2 (/) = 7999,999;
4Sf) = ^з(0 = -0,23737 10-7/7+ 0,25305 10"5/6 +1000,3-
-0,00010534/5 + 7999,8/+ 0,0021518/4 -0,036848/3 +0,76897/2;
v2(0 = Х4(/) =-0,19044 10"8/7 +0,3379610'7/6+0,6785210-5/5 +1,5040/-
-0,00034676/4 +0,0065309/3 +7999,8-0,098087/2.
Практический интерес представляют выражения для разности координат и скоростей перехватчика и
цели:
^-^=^(/)-Лз70 = 199»7 + 0'2/ + 0»2373710"7/7-°>2530510--5^ +
+0,00010534/5-0,0021518/4 + 0,036848/3-0,76897/2;
v2 -v,= x'4(t)-xl(t) = -O,1904410-8+0,3379610~7 /6+0,67852 10'5/5 +
+1,5040/-0,00034676/4+0,0065309/3-0,2-0,098087/2.
В табл. 5.5 приведены дискретные значения функций Ц (/) -1^ (/) и v2 (/) - v, (/).
Можно сделать вывод, что разность координат и скоростей перехватчика и цели составляют малые
величины, т.е имела место плавная безударная стыковка. Графики функций и*(/), L\(t)-1^(()у
v2 (/) - v, (/) приведены на рис. 5.11. На рис. 5.11 также приведен график закона управления
„(,)=^i+to)
Г-/
используемый на практике. Недостатком этого закона является то, что он трудно реализуем при значениях
/, близких к Т. Поэтому, реализуя этот закон управления, необходимо прерывать автоматический режим
вблизи конечного момента времени и в дальнейшем стыковку осуществлять вручную. При использовании
найденного в этом примере закона u{t) эта проблема не возникает. Точность стыковки при найденном и =
- u(t) значительно выше, чем при используемом на практике.
Глава 5. Методы математического программирования
585
Таблица 5.5
Дискретные значения функций L\(t)-^(0 и v2(0"~vi(0
0
1,5789
3,1579
4,7368
6,3158
7,8947
9,4737
11,053
12,632
14,211
15,789
17,368
18,947
20,526
22,105
23,684
25,263
26,842
28,421
30,000
М'*)-М'*)>м
199,99
198,52
193,92
186,73
177,33
166,06
153,22
139,13
124,10
108,50
92,696
77,063
61,972
47,784
34,835
23,441
13,910
6,5607
1,7642
0,000013083
*2Ы-у,Ы,м/с
-0,16924
1,9844
3,7752
5,2898
6,5798
7,6696
8,5643
9,2566
9,7339
9,9834
9,9962
9,7699
9,3099
8,6279
7,7392
6,6563
5,3811
3,8935
2,1368
-0,31586-Ю*7
!/*(')> М/С
2 -
200-
160-
120-
80'
40-
N
7,5
\
15
\.
22,5
.. /, с
30
и'Ом/c2 i
«ft м/с2
1 •
Q.
-04"
-г
74
1 - используемый на практике
2 - найцентй методом
матеметичесюго
хрограммирования
1?Ч^ 224 30^
7,5 15 22,5 30 /,с
Рис. 5.11. Графики функций, характеризующие процесс оптимального управления
Приведем решение задачи при условии а\ =2м/с2, т.е. цель движется с ускорением. Все остальные
константы и алгоритм решения остается без изменения. Спектральные характеристики сигналов
С\ С\ С\ Сх\ С\ Сх; имеют вид:
586
Методы теории оптимального управления. Часть III
2,0033 "
-1,3356
0,0021329
0,0018579
0,0021069
0,00182
-0,008221
Д068896 J
; С*' =
121500"
120450
150,0
0
0
0
0
, 0 J
'8030,0'
30,0
0
0
0
0
0
, о ,
; С*3 =
г 121400 '
120570
150,41
-20,049
-0,011584
0,078801
0,029190
г0,076205,
сх« =
8036,7
30,083
-6,6819
0,0015510
0,0015598
0,010932
-0,066042
l,-0,014283j
;СХ' =
(0,060162
-0,39520
-0,00018009
0,013362
-0,00060334
0,020655
-0,0037137
0,047977
Lx-Lvu
22,5
Рис. 5.12. Графики функций и (/), L, (/) - L, (/), v2 (/) - v, (t)
Следующие формулы определяют оптимальное программное управление и оптимальную программу,
полученные с помощью конечномерной оптимизации:
м*(/) = 3,2624 + 0,011257/3-0,061969/2+0,000048113/5-
-0,0010156/4-0,11457 Ю-5/6+0,10812 Ю"7Р +0,051789/;
М/) = ^(/) = 1200,0 + 8000,0/ + /2;
v, (/) = Хг(/) = 8000,0+ 2,0/2;
l2(/) = xJ(/) = -0,026828/3+l,7291/2+ 1000,5-0,000054672/5 +
+0,0011379/4+0,1292710-5/6-0,1195910-7/7+7999,8/;
v2(/) = ^(0 = 0»002l074/3-0'065816/2-0»2128810"5/5"0'OM061538/4 +
+0,15164Ю6/6-0,2241410"8/7+7999,8+3,4182/.
Глава 5. Методы математического программирования
587
Запишем выражения для разности координат перехватчика и цели:
Z1(^)-L2(/) = ^(/)-^(/) = 199,5 + 0,2/-0,7291/2+0,026828/3+0,000054672/5-
-0,0011379/4-0,1292710-5/6+0,П95910"7/7;
v2(0-viM=*n0-*n0=0>0021074'3-^
+0,1516410-V-0,224141(rV -0,2 + 1,4182/.
В табл. 5.6 представлены дискретные значения функций Ц (/) -1^ (/), v2 (/) - v, (/).
Так как разность скоростей и координат перехватчика и цели при t=T достаточно мала, то можно
заключить, что произошла мягкая безударная стыковка космических объектов.
Закон управления, используемый на практике, в случае ах *0 обеспечивает v2(T)-vl(T) = 1,06 м/с,
т.е. требуется ручная стыковка на конечном этапе процесса [3].
Замечания:
• при я, * 0 точность управления несколько уменьшается;
• чтобы уменьшить потребное ускорение перехватчика, нужно увеличить заданное время стыковки;
• при ограничении на ускорение перехватчика при неизменяемом времени стыковки задача намного
усложняется.
На рис. 5.12 приведены графики функций «(/),£,(/)-1^ (/),v2 (/)- v^ (/).
Таблица 5.6
Дискретные значения функций L[(t)-L2(t) hv2(/)-V|(/)
0
1,5789
3,1579
4,7368
6,3158
7,8947
9,4737
11,053
12,632
14,211
15,789
17,368
18,947
20,526
22,105
23,684
25,263
26,842
28,421
30,000
М')-М<)>м
199,99
198,57
194,08
186,94
177,55
166,25
153,36
139,21
124,16
108,54
92,720
77,066
61,940
47,700
34,693
23,257
13,720
6,4188
1,7096
0,000077166
v2(')-vi(')>M/c
-0,15992
1,9230
3,7217
5,2702
6,5916
7,6987
8,5958
9,2811
9,7489
9,9924
10,006
9,7875
9,3383
8,6640
7,7732
6,6737
5,3683
3,8476
2,0800
-0,18386-Ю*5
5.3. АЛГОРИТМ ПОСТРОЕНИЯ ОПТИМАЛЬНЫХ ПРОГРАММНЫХ
УПРАВЛЕНИЙ НЕСТАЦИОНАРНЫМИ ЛИНЕЙНЫМИ
ОБЪЕКТАМИ ПО КРИТЕРИЮ МИНИМАЛЬНОЙ ЭНЕРГИИ
Постановка задачи совпадает с той, которая сделана для стационарных объектов
по критерию минимальной энергии управления. Отличие состоит лишь в том, что
объект описывается уравнением вида
X = A(/)X + B(0U. (5.18)
Формулировка задачи в терминах математического программирования и
структурная схема алгоритма ее решения подробно рассмотрены в §5.2.
Пример 5.5. Рассмотрим объект, описываемый уравнением
X = A(/)X + B(/)U, (5.I9)
588
Методы теории оптимального управления. Часть III
1,1 + / t-t1) \\ t
Задача формулируется так: перевести объект из состояния Х° = (9;-9)т в состояние Хг = О за
время Т = 4 с, при этом функционал качества
y(u)=)uT(/)u(/)d
it -> mm.
(5.20)
(5 21)
(5.22)
Для решения задачи параметризации воспользуемся матричными операторами умножения и
интегрирования (в качестве базиса используются полиномы Лежандра).
Перепишем уравнения объекта в виде
*i(0 = M0*i(0+M0*2(0 + M0^(0+M0w2(0>
*2О = *2l(0*l(0 + «22(0*2(0 + W0«|(0 + М0"2«,
* или в матричной форме
Сх- = АиАу(дп)Сх' + АиАу(а12)Сх' +АиАу(Ап)Си« + АиАу(а,2)Си' + Ф°,,
Сх> = АиАу(а21)Сх1 +АиАу(а22)СХ2 +АиАу(621)Си- +АиАу(622)Си^ +Ф°,
где Аи - матрица интегрирования,
Ау(я/У), Ay(bij)- матрицы умножения, порожденные коэффициентами Я/Д/), ^(0 •
Матрица умножения, порожденная функцией /(/), вычисляется по следующему алгоритму
1) вычисляется спектральная характеристика функции /(/) по базису Ф(/), т.е. одностолбцовая
матрица С7;
2) вычисляются вспомогательные коэффициенты а{ :
3) вычисляются вспомогательные коэффициенты и ljk
aflj-iQi-W 2ft + l
(5.23)
«ijk
2/ + 2/ + Г
k = i-j + 2l,l = 0...j9
i*j\
0,
k*i-j + 2l,l*0...j,
(5.24)
"y/*="/yb
4) вычисляется матрица умножения, порожденная функцией /(/):
Ау(/) =
т-\ . т-\ ,
I и cj j; M.10c/
/=0 /U0 /=0
m-\ , m-\ f
Vi=0 /=0
m-1 ,
m-1 ,
/=0
m-1 ,
I «/,/я-1,т-1С/
(5.25)
Тогда, если задана операция вида
*(0 = /««(0, (5.26)
то в спектральной области она может быть представлена так
Сх=Ау(/(/))С\ (5.27)
Сформулируем задачу: найти компоненты вектора
и*(о (йГ(о и й?«) .
переводящего объект из состояния Х°= (9, -9)т в состояние ХТ = (0,0)т за время [0; 4 с] при условии
т
y(U) = JuT(/)U(/)J/-»min.
о
Ограничения на компоненты *](/) и*2(/) не накладываются.
Далее приведем соответствующие матрицы:
Глава 5. Методы математического программирования
589
2,0 -0,6666 0
2,0 0 -0,4000
Ау(о„(0) =
0,6666
0
0
О
О
0,4000
О
О
О
О
-0,2857
О
0,2857
О
-0,22222
О -0,1818
0,22222 О
Ау(о,2(0) =
Ау(*21(0) =
Ау (aaW)-
Ау(*„(0) =
Ау(612(/)) =
Ау(М0) =
5,3333 2,6666 0,5333 0 0 0
8,0000 6,3999 3,2000 0,6857 О О
2,6666 5,3333 6,0952 3,4285 0,7619 О
О 1,6000 4,8000 6,0444 3,5555 0,8080
О 0 1,3714 4,5714 6,0259 3,6363
0 0 0 1,2698 4,4444 6,0170
О
О
-1,3333 -1,0000 -0,8571 О
О -1,2000 -1,0000 -0,8888
О
-1,1428 -0,9999 -0,9090
-1,1111
О
О
О
-1,0000
-1,0000 -0,6666 О
-2,0000 -0,9999 -0,8000
О
О
О О
О О О О
'3,0000 0,6666 0 0 0
2,0000 3,0000 0,8000 О О
О 1,3333 3,0000 0,8571 О
О 0 1,2000 3,0000 0,8888 О
0 0 0 1,1428 3,0000 0,9090
О О О О 1,1111 3,0000
-3,3333 -2,0000 -0,5333 О О О
-5,9999 -4,3999 -2,4000 -0,6857 О О
-2,6666 -4,0000 -4,0952 -2,5714 -0,7619 О
О -1,6000 -3,6000 -4,0444 -2,6666 -0,8080
О 0 -1,3714 -3,4285 -4,0259 -2,7272
О О О -1,2698 -3,3333 -4,0170
5,3333 2,6666 0,5333 0 0 0
8,0000 6,3999 3,2000 0,6857 О О
2,6666 5,3333 6,0952 3,4285 0,7619 О
О 1,6000 4,8000 6,0444 3,5555 0,8080
О 0 1,3714 4,5714 6,0259 3,6363
0 0 0 1,2698 4,4444 6,0170
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
1,0000 О О
0,9999 О
1,0000 О
1,0000 О
0,9999 О
О 1,0000
590
Методы теории оптимального управления. Часть III
Ау(*22(/)) =
'2,0000 0,6666 0 0 0 0
2,0000 2,0000 0,8000 0 0 0
0
0
0
0
1,3333 2,0000 0,8571 0 0-
0 1,2000 2,0000 0,8888 0
-
0 0 .1,1428 2,0000 0,9090
0 0 0 1,1111 2,0000
Ф^=[1 0 0 0 0 0 0 0 0 0]Т.
>
Далее с помощью указанного выше оптимизатора были найдены спектральные характеристики
сигналов щ(1),и2(0,х\(0 и x\(t)
матрицы:
С' =
'-3,706223 '
2,8535124
1,4486783
-0,619376
-0,227512
0,6288935
-0,100215
-0,150326
0,0666549
0,0367026
-0,025437
-0,007282
0,0074687
0,0009459
,-0,002503 ,
;
в базисе полиномов Лежандра. Приведем соответствующие одностолбцовые
' 0,2250842'
-0,202033
-0,201078
0,1634701
-0,027901
-0,079928
0,0536246
-0,003611
-0,011309
0,0029313
0,0021935
-0,0009
-0,000458
0,000264
ч 0,0001141,
; Сх'* =
' 3,903298'
-3,49393
-0,351640
-0,86703
0,96796
-0,320282
-0,15050
0,125750
0,087985
0,012963
0,01244
0,02343
0,017022
0,00993
^ 0,012857,
'-1,73489 '
5,87031
-4,156
-2,2038
2,26534
1,0611
-1,25004
-0,322895
0,481321
0,11444
-0,142268
-0,032763
0,04115
0,0133011
,-0,005193 ,
Теперь легко записать формулы, определяющие приближенные оптимальные компоненты ы*(/) и
u\(t) вектор-функции управления U (/) и функции x\(t) и x\{t) - компоненты оптимальной
программы X (/):
«,*(/) = 2,1659639 /-4,8081851 /2-0,000374 /14-52,861634 /6 +
+ 0,0106203 /13 -0,1337238 tn + 0,?820345 /n -4,6550049 /|0 +
+ 14,9017748/9 -32,837097 /8 +50,0920934 t1 +38,12492921 /5 -
-17,9818198 /4 +6,7198632 /3 -5,2821585;
u2(t) = -0,1791777 / + 0,160077 + 1,254432 /2 + 0,00001705 /м -
-0,0298878 /6-0,0004365 /13 +0,0048393 /12 -0,0302624 /" +
+ 0,1163214 /10 -0,27983728 /9 +0,40626469 /8 -0,3010298 /7 +
+ 0,34088079 /5 -0,16709678 /4 -0,837859 /3;
*,*(/) = -9,469607167 / + 12,68140888 /2 +0,00192148 /14 +296,20632226 /6 -
-0,0522618 /|3 + 0,63622909 /12 -4,57441658 /п + 21,580904 /10 -
-70,178476 /9 +160,7799626 /8 -260,655189159 /7 -230,43293737 /5 +
+117,56954321 /4 -38,1200928 /3 + 9,008594148;
x\(t) = 3,81124755 /-4,95461356 /2 -0,000776 /14 -140,2774129 /6 +
+0,0237918 /13 -0,31899588 /12 +2,46157017 /п -12,102045 /10 +
+39,67062479 /9 -88,4119356 /8 +134,7934138 /7 +97,593713 /5 -
-42,8138438/4 +13,36151169/3-9,001254.
Соответствующие графики приведены на рис. 5 13 и 5.14.
Глава 5. Методы математического программирования
591
о
1 ■ 2 ■3*4^ 7с
Рис. 5.13. Графики функций щ (/), &£ (')
Получим решение той же задачи, но с ограничением на фазовые координаты; в частности, положим,
что *2(f)<l.
▼ 3(0
Рис.5.14. Графики функций л'*(/), x2{t)
В результате решения задачи оптимизации получены следующие матрицы:
592
Методы теории оптимального управления. Часть III
'-4,151939'
2,3189397
-0,023501
-1,292123
-0,106938
0,7828009
-0,145021
-0,198926
0,0797213
0,0218755
-0,069851
-0,031321
0,0264711
0,0420974
0,0172125,
; с*;=
'-0,534755'
-0,157577
0,2768694
0,3199676
-0,158104
-0,890891
0,0829876
0,0151995
0,0083919
0,0503028
0,0358572
-0,026034
-0,049001
0,2436907
^1,709011 >
'3,9628
-2,43950
1,169724
-0,701665
0,3001
-0,765756
-0,436540
-0,183
-0,198965
-0,193170
-0,150147
-0,1511
-0,128953
-0,07515298
,-0,06509
'-2,716803
6,4073011
-2,115872
-2,3425
1,3707703
0,91124764
-1,1844
-0,3961362
0,3829967
0,05970736
-0,1736
-0,09498541
-0,1270025
-0,16575
0,1749695
(5.29)
Выражение для м,*(/), u\(t), **(/), x\(t) имеют вид:
Mi*(/) = -6,0500958-0,01230754r]O-12,2655068/2-28,7366069/6+48,753276616/5-
-49,029963/4 + 29,6963155/3 + 3,4399234/ + 10,20739/7 -2,1561345 /8 + 0,250208067 Л
Й2(/) = 0,0063179329/1О + 12,8596276/2 +0,3742452+9,7050199/6-14,89525237/5 +
+15,3616908/4-14,4454817/3-6,0892433/-3,86628688/7 +0,91108742/8 -0,1140289/9;
*,*(/) = -0,02645557/10 +8,93065678-8,93075649/2 -45,4630216/6 +75,393117/5 -
-77,368247/4+45,3055445/3-6,9444448/ + 17,11829538/7-3,905549665/8+0,4932839/9,
biO = -0,0305892308/'° -22,478360579/2 - 68,64929824/6 +113,040989/5 -110,2971457/4 +
+ 64,380356768/3 -9,076507814 +5,4445979/+ 24,943435/7 -5,340386975/8 +0,62285857/9.
Графики приведены на рис. 5.15 и 5.16.
о
Рис. 5.15. Графики функций и[ (/), п\ (/)
Глава 5. Методы математического программирования
593
Еще раз подчеркнем, что при расчетах оптимальных программ и оптимальных
программных управлений сложными нестационарными объектами не следует
ограничиваться заданием единственного параметрического представления и целесообразно
решить задачу в нескольких базисах, после чего сделать соответствующие выводы.
Рис. 5.16. Графики функций *,*(/), x\(t)
5.4. АЛГОРИТМ ПОСТРОЕНИЯ ОПТИМАЛЬНЫХ ПРОГРАММНЫХ
УПРАВЛЕНИЙ И ОПТИМАЛЬНЫХ ПРОГРАММ КЛАССОМ
НЕЛИНЕЙНЫХ ОБЪЕКТОВ
Как указывалось выше, для построения конечномерных (матричных)
эквивалентов операторных уравнений, описывающих поведение объектов управления,
применяются матричные операторы дифференцирования, интегрирования и умножения.
В случае нелинейных объектов может быть использован матричный оператор
умножения. Это возможно тогда, когда нелинейные элементы объекта управления
представляются в виде степенного ряда. В случае применения базиса, порожденного
блочно-импульсными функциями, указанное ограничение может быть снято.
Для выявления особенностей, присущих нелинейным объектам при построении
оптимальных программных управлений, рассмотрим конкретную задачу.
Пример 5.6. Задача управления полетом ракеты [52].
Получим решение этой задачи с помощью матричного представления операторов в базисе полиномов
Лежандра (будем удерживать 8 членов разложения).
Система дифференциальных уравнений, описывающих поведение объекта управления, имеет вид*
*1=*3>
х2=х4,
% = a cos и,
х4 =asin м-go-
Представим нелинейные функции в (5.30) в виде усеченного ряда Тейлора относительно точки и = 0
, 1 2 1 4
cost/ «1—и +—и ,
2 24
1 з
sinwww—и .
6
Перепишем уравнения объекта в следующем виде
*1=*3>
*2=*4>
a 2 a 4
Хл =a—и +—и ,
^ 2 24
(5 30)
а з
*4=aw--M -g0-
о
39 Зак. 366
594
Методы теории оптимального управления. Часть III
Запишем последнюю систему в матричной форме, применяя операторы интегрирования и умножения.
Имеем
Сх'=АиСХз+^(0)Ф^,
С^=АнС^+дс2(0)Ф^
С = АиСа -^АиАу(и)С" +|-Аи(Ау(и))3См +х3(0)Ф^
С*< = аАиС -^Аи(Ау(М))2С" - АИС*° + *4(0)Ф°„
(5.31)
50
50
0
0
0
0
0
0
-16,66
0
16,66
0
0
0
0
0
0
-10
0
10
0
0
0
0
0
0
-7,142
0
7,142
0
0
0
0
0
0
-5,555
0
5,555
0
0
0
0
0
0
-4,545
0
4,545
0
0
0
0
0
0
-3,846
0
3,846
0
0
0
0
0
0
-3
0
где Аи - матрица интегрирования в выбранном ОНБ. Матрица интегрирования в.базисе полиномов Ле-
жандра имеет вид
А =
В (5.31) Ау(м) - матрица умножения на функцию (в данном случае - на функцию м(/)). Матрица
умножения в базисе полиномов Лежандра имеет вид (поскольку коэффициенты с" неизвестны, матрица
Aj (м) является функцией переменных с" )
с," 0,333c£ 0,2cJ 0,\42с"4
0,999с£ 0,999с," + 0,4с; 0,4с^ + 0,25^ 0,25c$ + 0,19с?
с3" 0,66с£ + 0,428cJ| сЧ +О,28с5 + 0,285с? 0,428с$ +0,19си4 + 0,216си6
си4 0,6c?+0,44c5w 0,6^+0,26^+0,3^ с\ +0,26с> 0,18с5" + 0,23с?
(приведен вырез матрицы размером 4 х 4), Сх' ,Си,С",Cgo ~ спектральные характеристики
соответствующих функций и констант, Ф^ - вспомогательный вектор-столбец, необходимый для учета начальных
условий, размерностью / х 1
<=[1,0;...0]т.
Матричный эквивалент системы уравнений, описывающих поведение объекта (5.30), можно записать так.
Ау(и) =
С*'
С*
с*
сх<
о
о
о
'о о
о о,
о о
,о" о
(\ о
0 I
0 0 I
А„
0
С*'
С'
+
о
о
0 0 0
(о о
о о
о о
о о
о
о
Аи
0> -Ам
а
"б
О
О
Са
л о
О I
о о
,0 О
о о
о о
о о
о о
-!)
о
о
1а
О
О
А„
О
О
О
О
Ам
Го о
о о
о о
о о
о л
о
(АУ(И))3
О
о
Аи
О
O'i
О
о
Ам
А
0 ^
0
у(«)
с +
С" +
где I - единичная матрица размерностью 1x1
Глава 5. Методы математического программирования
и-
1 о;
•0.5-
Лс
595
Полученное векторно-матричное соотношение можно записать в общем виде Сх = F(C?J)
Рад 2i
*2,м
30000-
2ЛЗОО-
20000-
15000-
10000-
3000
б)
о
х4,м/с
600-
500-
400-
300-
200
100-
в)
JC, ,М
10000
20000
40000
дг3,м/с
200
800 1000
1200
Рис. 5.17. Графики функций, характеризующих процесс управления:
1 -решениеу полученное методом математического программирования,
2 -решение, полученное методом дискретизации Пирсона
Сформулируем задачу в терминах математического программирования:
У(Си) = тт[-|>?Ру(Г)
при следующих ограничениях:
1 Сх = F(C(/)
2.XT=<bJ(t)\(^Cx> «30000;Фт(0[_тСх< *0j
- ограничения типа равенств.
59*
596
Методы теории оптимального управления. Часть III
С" =
'0,7009748'
-1,199579
-0,748134
0,1096817
0,0295336
-0,024550
0,0364488
0,1318374,
ГХ|* -
"10542,64"
17103,96
8487,51
2453,11
182,098
-461,85
-92,333
, 40,3517,
• cxi -
'12444,91'
17307,83
3063,22
-2658,30
-1013,89
-121,548
39,0150
, 12,2698 .
'382,71 Г
515,576
203,161
14,7597
-75,8701
-16,8677
10,49144
^4,698661
. с*'л -
' 290,8048 '
125,7199
-276,7588
-135,5054
-19,670
10,120
3,1901
^ 2,0956 ,
Приведем результаты решения задачи оптимального перевода ракеты из состояния Х° в состояние X7
без ограничения на фазовые координаты. Одностолбцовые матрицы, представляющие собой спектральные
характеристики сигналов С" ,СХ| ,С*2 ,CXi ,CA, имеют вид*
'0,7009748^1 ^10542,64^ (12444,9 Г
-1,199579 17103,96 17307,83
-0,748134 8487,51 3063,22
„;_ 0,1096817 х;_ 2453,11 • -2658,30
0,0295336 ' ' " 182,098 ' * ~ -1013,89 '
-0,024550 -461,85 -121,548
0,0364488 -92,333 39,0150
0,1318374 J [ 40,3517; { 12,2698 ,
Приведенные ниже формулы определяют оптимальное программное управление и оптимальную
программу, полученные с помощью конечномерной оптимизации:
w*(O = 0,079r + l,00 + 0,45210"11/7-0,154l0"8/6 + 0,0004/3-0,0O00U4+0,2O8-10"6/5-0,008/2,
^(О = 14,319/-0,006 + 0,14510"8/7-0,610"6/6+0,094/3-0,004/4+0,000085/5 + 2,25/2,
^(/) = 0,173/-0,00086 + 0,44310Л7-0,117-10~6/6+0,007/3-0,00013/4 +0,687- 10~5/5+4,159/2,
Хз*(0 = 8,231/ + 0,007 + 0,16110"9/7-0,467-10"7/6 + 0,003/3-0,00015/4 + 0,44810"5/5-0,1655/2,
jc!(/) = 9,663/-0,004 + 0,719-10"10/7 -0,222-10"7/6+0,009/3-0,0002/4 +0,2856-10"5/5-0,1735/2
В [52] приведено приближенное решение задачи методом дискретизации Пирсона. На рис. 5.17
приведены графики оптимального управления u(t), х\ - /\(х\) и х*4 = f(x\), полученные двумя методами.
На рис. 5.18 приведены графики компонент вектор-функции Х*(/)} полученные методом
математического программирования с использованием матричного представления операторов в базисе полиномов
Лежандра
Построим решение той же задачи с использованием матричных операторов, но с ограничением на
фазовые координаты
*4(0<400q . (5 32)
(т е ограничим величину вертикальной составляющей скорости).
Заменим ограничения на всем промежутке [0,100с] дискретной сеткой; из рис. 5 18 можно заключить,
что целесообразно потребовать выполнения неравенства (5.32) в точках / =50,60, 70, 80 с.
Таким образом, к формулировке задачи в терминах математического программирования необходимо
добавить 4 ограничения типа неравенств
Фт(/)| Сх<<400,
1/=50
Фт(/)| С*4<400,
1/=60
Фт(/)| С*4<400,
1=70
фТ(/)[ =
СХ4<400.
В результате реализации процедуры оптимизации получены следующие спектральные характеристики.
С" =
Следующие формулы определяют оптимальное программное управление и оптимальную программу,
полученные с помощью конечномерной оптимизации:
u{t) = 0,0517/ + 1,29 + 0,493- 10"м/7 -0,1599-10~8/6+0,00041/3 -0,000012/4 +0,2015-10"6/5 -0,0071/2;
х,Ч/) = -3,260/ + 0,0007-0,60410~9/7+0,21210"6/6-0,084/3 + 0,0029/4-0,000033/5+3,0367/2;
'0,6585593'
-1,102337
-0,388532
-0,133186
-0,168734
0,0354228
0,139082
0,1438477,
> *-' —
'12118,89'
20991,85
10926,03
1953,77
-262,906
-150,934
0,383257
-15,6494>
• С*2 ~
> ^-* —
'11672,06^
15687,24
2228,90
-2253,75
-519,346
-113,737
-123,713
-24,6901
С* -
455,5808'
639,6091
178,7192
-37,2230
-29,9851
-0,65397
-4,06885
-1,00675,
• СХ4 ~
5 ^-* —
' 265,901Г
97,37931
-239,218
-84,8284
-24,9169
-19,0455
-6,41942
11,14279 .
Глава 5. Методы математического программирования
597
jc*(/) = 19,6381/-0,OO0O3-0,954110"9/7+O,20521O~6/6-h0,O766/3-0,00077/4 -0,00001/5 + 2,796/2,
Зсз(/) = 4,5482/-0,00028-0,345510-1О/7 + 0,83335-10-8/6 + 0,0056/3-0,000028/4-0,56310-6/5-0,132/2,
*4*(0 = 14,327 /-0,002 + 0,3824 -10"9/7 -0,139-10"6/6 + 0,048 /3 -0,0013 /4 +0,000019 /5 -0,825 /2
На рис 5.19 представдены графики оптимального управления u(t) (а), оптимальной траектории (б),
годографа оптимальной траектории (в), а на рис. 5 20 - графики компонент вектор-функции Х*(/)
**(/), м
•90000
x*2(t),M
30000
2XW
2000О
15ооа
10000-
5000
x](t),u/t
/,с
20 « 60 80 100
Рис. 5.18. Графики фазовых переменных
598
Методы теории оптимального управления. Часть III
Приведенный пример, заимствованный из [52], предназначен для иллюстрации
особенностей расчета оптимальных программных управлений и оптимальных программ.
Уравнения объекта отличаются относительной простотой, поэтому в качестве
базиса использованы полиномы Лежандра.
Рад
15-
0 5-
а) о"
-0*
-1
*2>м
30000
23000-
20000
15000
10000
3000
б)
х4 ,м/с
500-
400
300
200
100
/,с
20
40
60
JC| ,М
10000
20000
30000
40000
30000
60000
х3,м/с
200
400
600
800
1000
1200
Рис. 5.19. Графики функций, характеризующих оптимальный процесс управления
с ограничением на фазовые переменные
Глава 5. Методы математического программирования
599
*;(<)>ч
50000
30000
20000
x'2{t),u
зоооо-
2:5000
20СШ
13000
10000
5000
•*з>
м/с
1000
800
м/с
13сГ
/,с
0*" 20~ 4) бГ 8Ь 1<М
Рис. 5.20. Графики фазовых переменных
600 Методы теории оптимального управления. Часть III
Если же объект достаточно сложен, а оптимальное управление имеет разрывы
1-го рода, целесообразно использовать функции Уолша, блочно-импульсные
функции или обобщенные блочно-импульсные функции [39, 47].
Аналогичным образом решаются задачи построения оптимальных программ и
оптимальных программных управлений для других функционалов.
5.5. МЕТОД МОМЕНТОВ (ОСНОВНЫЕ ПОЛОЖЕНИЯ)
Проблема моментов, рассмотренная Крейном, получила название L -проблемы
моментов [26]. Результаты решения этой проблемы были использованы рядом
авторов для построения оптимальных программных управлений, а также для синтеза
систем, работающих по принципу обратной связи. Н.Н. Красовский использовал метод
L -проблемы моментов для решения задачи оптимального управления объектами с
сосредоточенными параметрами [25]. А.Г. Бутковский показал, что этот метод может
быть с успехом обобщен для решения более сложных задач, связанных с
бесконечномерной проблемой моментов и с задачами оптимального управления системами с
распределенными параметрами [9]. Метод оказался общим аппаратом решения
многих задач синтеза оптимальных управлений*. Он дает единый подход к рассмотрению
различных классов линейных управляемых систем, например, с сосредоточенными и
распределенными параметрами произвольного порядка. Куликовский получил
конструктивные результаты, связанные с решением задачи синтеза оптимальных
управлений, используя аппарат приближения в различных функциональных
пространствах. Особенно простые результаты получены при рассмотрении задачи в 12[0,Г]
[31]. Широкий спектр задач теории управления рассмотрен А.И. Морозом; он
получил решение с использованием L -проблемы моментов задач, связанных с
управляемостью и наблюдаемостью систем, с синтезом оптимальных управлений по ряду
конкретных критериев.
В [8] алгоритмы определения функций управления с минимальной нормой
сформулированы для линейных систем из более простых рассуждений, которые вытекают
из геометрической интерпретации в фазовом пространстве рассматриваемых задач
управления.
Метод L -проблемы моментов применим к классам систем:
1) непрерывных и дискретных4,
2) стационарных и нестационарных',
3) автономных и неавтономных',
4) с одним и несколькими управляющими воздействиями [9].
При этом допускается весьма разнообразные оптимизируемые функционалы и в
первую очередь функционалы типа норм в функциональных пространствах.
Как указано в [9], метод моментов часто позволяет найти вид управляющих
сигналов в замкнутой аналитической форме, а в тех случаях, когда это сделать невозможно,
дает единый алгоритм для построения точного или приближенного решения задач. При
этом сложность алгоритма мало зависит от числа управляющих воздействий, она зависит
лишь от порядка уравнения и характера собственно оптимальных задач [9].
5.5.1. Формулировка проблемы моментов и ее решение
Линейным функционалом в гильбертовом пространстве Н называется
отображение /, ставящее в соответствие любому х е Н число 1х, т.е. /: Н —> R , причем
отображение является:
Во второй главе второй части изложены положения метода моментов применительно к решению еще
одной важной задачи -- синтеза регуляторов
Глава 5. Методы математического программирования 601
1) аддитивным 1(х} +х2) = lxx +/jc2 ;
2) однородным l(cx) = clx, се R;
3) ограниченным \lx\ <с\\х\\н для всех хе Н .
Весьма важным для дальнейшего изложения является содержание следующего
факта [25]:
1) любому линейному функционалу в пространстве ^[0,7] (1<р<оо)
соответствует производящая функция и(т), которая определена почти всюду на [0,Г] и
u(x)eL"[0j], (l/p +1/4 = 1);
2) всякий линейный функционал 1х в пространстве i/j^T] может быть
представлен в виде
г
lx = (x,u) = \x(x) u(x)dx; х(т)е LP[OJ]9 и(т)е I?[0j], (5.33)
о
причем производящая функция м(т) однозначно определяется заданием
функционала /;
3) норма функционала равна норме производящей функции в пространстве
Z?[O,r]:
Кт)Ц.П=11/1 = <
llL'[0j]
J|«(x)|^rfT при/7>1, q<0;
(5.34)
vraio<t^r max|w(x)| при/? = 1, q = qo.
Множество линейных ограниченных функционалов, определенных на ^[О^],
называется сопряженным к ^[О,^] пространством и обозначается £я*[0,Г].
Из содержания приведенного выше факта следует два важных положения:
каждый функционал из 1я*[0,Г] представляется в виде операции интегрирования на
[0,Г] (формула (5.33)); норма функционала в L^* [0,7"] равна норме производящей
функции в Z?[0,r] (изометрический изоморфизм пространств Iя* и L4 (формула
(5.34)). Пусть
#(0 = {й*(0: * = 1Я WeIf[0,T] }
- некоторая система функций. /-м моментом функции w(t) относительно АД/)
системы #(/) называется интеграл вида
т
/А,=|М/)и(/)<//, / = 1,я. (5.35)
о
Система равенств (5.35) называется моментной системой (или системой мо-
ментных уравнений).
Система функций Н называется моментной системой функций.
Числа \iy / = 1,я называются моментами функции u(t) относительно
моментной системы Н.
Множество X = ixk: А = 1,л| называется множеством моментов.
38 Зак. 366
602 Методы теории оптимального управления. Часть III
Отметим, что равенства (5.35) - это функционалы, имеющие одну и ту же норму:
если hk{t)elf, /е[0,Г],то
Проблема моментов формулируется следующим образом [9, 25]. Заданы
моменты Хк функции u(t} относительно элементов моментной системы //(/). Число
заданных моментов может быть как конечным, так и бесконечным. Как показано в
[9], задание конечного числа моментов соответствует системе с
сосредоточенными параметрами. Для исследования управляемых систем с распределенными
параметрами необходимо рассматривать бесконечное {счетное) число моментов.
Требуется найти условия существования, единственности, а по возможности
вычислить или оценить производящую функцию u(t) {или, что то же самое,
необходимо найти функционал I e If* из набора моментных уравнений (5.35)). Так как
интеграл (5.35) можно рассматривать как линейный функционал, то последний
определяется порождающей функцией м(/), а функции hk{t) можно рассматривать как
элементы, на которых этот функционал определен, т.е. интеграл (5.35) записывается
в виде
lhk, Л = 1,2,3
Поскольку мы рассматриваем гильбертово пространство If [0,Г], как уже
указывалось выше, всякий линейный функционал записывается как скалярное произведение
lhi=(uyhi) = Xn i = ~n. (5.37)
Приведенные рассуждения можно обобщить на абстрактные линейные
нормированные пространства и рассмотреть проблему моментов в этих пространствах. Выше
было отмечено, что всякий линейный функционал можно рассматривать как элемент
сопряженного пространства. Для функциональных пространств функционал задается
производящей функцией u(t). Поэтому в наиболее общей форме проблема моментов
может быть сформулирована так: найти такой функционал I, который на заданной
системе элементов /^(Z),/^(/),...,/?„(/) принимал бы значения ^1Д2,.-.Д„, т.е.
/^=Х„/ = 1,2,3,...,и. (5.38)
Функционал, который удовлетворяет (5.38), называется разрешающим.
Известно [25], что сформулированная проблема моментов имеет не единственное
решение, т.е. существует много функционалов /, которые дают решение проблемы
моментов. Для получения единственности решения вводят дополнительные
ограничения. Например, можно поставить задачу об отыскании такого линейного
функционала /, который не только давал бы решение проблемы моментов (5.38), но и имел
бы минимальную норму (например, в пространстве Lp* [0,Г]).
Содержание L -проблемы моментов: ,L -проблема моментов формулируется
так: найти необходимые и достаточные условия для существования такого
функционала I, который дает решение сформулированной выше проблемы моментов и,
кроме того, удовлетворяется неравенство
(Т у/?
J|h(t)|*</t при/?>1, <7<°°;
№ =
<о
vraio<T£r max|w(t)| при/? = 1, q = оо.
<L. (5.39)
Глава 5. Методы математического программирования 603
Содержание оптимальной проблемы моментов: найти функционал leLp*[0,T]
(или, что то же самое, производящую функцию и{х)\ такой, который
удовлетворяет условиям (5.38) и имеет минимальную норму в If* [0,Г], т,е.
l/l^[o,r]:=lwlb[oj] = min- (54°)
Функционал I, удовлетворяющий условиям (5.38) и (5.40), называется
оптимальным разрешающим функционалом [25]. Такого рода задачи были рассмотрены Крей-
ном для конечномерной проблемы моментов. Далее будем рассматривать задачу в
Lp[0,T].
Можно показать справедливость следующей теоремы: проблема моментов
разрешима для любых Х,1Д2»—Д« тогда и только тогда, когда функции
h\ (0) ^2 (0> •••> К (0 линейно независимы.
Теорема, приводимая ниже, дает ответы на следующие вопросы [9, 25]:
1) существует и является ли единственным функционал / с минимальной нормой
11/11^[0,7']=^П?
2) как найти порождающую функцию u{t), дающую решение оптимальной
проблемы моментов?
3) как найти минимальную норму функционала / в LP* [0, Т] ?
Теорема [31]. Пусть
/*Д0е£р[0,Г];\,е/^/ = п;
u{t)eL*[0,T]; l/p + l/q = l
и задана система
т
jhk(t)u(t)dt = Xk, * = 1,л,
о
где hk (/) - линейно независимые элементы.
Тогда в пространстве ^[О,?1] существует единственный линейный функционал /,
такой, что выполнены условия
lhi=)hl(t)u{x)dx = Xh / = 1,л;
о
= ||и||,.гЛ,.1 =min.
nLO-[0j)-\n\L<i{0j]
Минимальная норма определяется равенством
l|/|L.m^i =maxT
v=l
1
,p,fnTl-maA]j и — |j r. -.
|2>А(0| min X^v^W / -
llv-i Il^[o7] v llv=i IIl"[oj]/ при %kvK~]
1 „ I,
lL9[0j]
|Z*>v(0| / .
lv-1 Щ0,Т]/ "РИ1ЛХ=1
»1
38*
604
Методы теории оптимального управления. Часть III
где
тш£*А(/)
К l|v=l Щ0,Т}/
f „ = mm
при XivXv=l *v
v=!
0 v=l
nV/>
dt
При X^v = l
(5.41)
Порождающая функция определяется выражением
1*Ж(о|
«м-
|Яэ(О|Г^[о,г]
l^wrsign^c/),
где
(5.42)
(5.43)
#э(0= Z*v4«.
v=l
Таким образом, в явном виде найдена зависимость для порождающей функции
функционала и, другими словами, найдено решение оптимальной проблемы
моментов. Кроме того, получена зависимость для расчета неизвестных коэффициентов
kx,...,k*. Заметим, что для нахождения указанных коэффициентов может быть
использован аппарат нелинейного программирования* Найдем
minJ = min fX*A(>) dt\ (5.44)
у(
(5.45)
(5.46)
при линейном ограничении
к{Кх +к2'к2 +-+кп\п =1.
Поскольку функционал J является нелинейным, то и задача поиска к{,...,к*
относится к классу задач нелинейного программирования.
Укажем еще один эффективный подход к решению оптимальной проблемы
моментов. Из соотношения
к{кх +к2Х2 +... + кпХп =1
находим
к{кх =1-^2^2 "~^з^з " — ~К^-п-
Отсюда
А1 Л1 К\ Л1
Перепишем зависимость
klh[(t) + k2h2(t) + ... + knhn(t),
учитывая выражение (5.46), в виде:
(5.47)
где
= т1Л1(О-А2|^(О-А2(о1-Аз[^(О-/ь(О|-...-
-к„\ ^(о-мо \ = Mt)-k2f2(t)-kiMt)-...-knfn(t),
* См Приложение 2.
Глава 5. Методы математического программирования 605
- известная функция;
Ж')-=т-*(0
л,
жо=^(о-л(ои=2,и
- известные функции.
Учитывая (5.47), интефал (5.44) принимает вид
J = \\Mt)-k1m-hMt)-...-kJn{t)\pdt. (5.48)
о
Из последней зависимости следует, что задача минимизации функционала J свелась
к задаче наилучшего приближения функции fx(t) линейной комбинацией функций
fi(0,/з (О>...»fn(О (в смысле метрики пространства I/ [0, Т]).
Метод решения оптимальной проблемы моментов, основанный на использовании
теоремы Крейна, обладает тем достоинством, что сводит проблему к задаче
аппроксимации, позволяя тем самым использовать ряд методов и готовых результатов,
известных в теории аппроксимации [31]. По условиям задачи система элементов в If [0,Г]
Aj(/),...,/^(0 обладает свойством линейной независимости. Отсюда вытекает линейная
независимость функций fx(t),f2(t),...,/„(t) . В пространстве Z,2[0,r] задача
нахождения ki,k29...,k* затруднений не вызывает и ее решение очевидно. В пространстве же
Z,1 [0, Т], когда функционал J, подлежащий минимизации, имеет вид
о
решение задачи неоднозначно.
Чтобы обеспечить однозначность аппроксимации в метрике пространства
Z?[0,r], необходимо наложить дополнительные ограничения на функции {^(t)) и
{/•(0} [31]. Положим, что система {/-(0} образует систему Чебышева, т.е. является
п
линейно независимой и количество нулей функции ]T£v/v(0 на промежутке [0,Г]
v=2
не превышает п. Тогда, используя известные из теории аппроксимации факты,
можно заключить, что решение задачи аппроксимации в £][0,Г] однозначно.
Достаточно полно изучен вопрос о том, какие системы функций образуют
систему Чебышева [26, 31].
5.5.2. Алгоритм синтеза оптимальных программных управлений
методом моментов для класса линейных одномерных объектов
Поставленная задача формулируется так: для линейного объекта, описываемого
дифференциальным уравнением вида
][>v(')*(v) =E*v(')«(v) . (5-49)
v=0 v=0
* Задачи оптимального управления объектами с распределенными параметрами подробно рассмотрены в [9]
606 Методы теории оптимального управления. Часть III
построить программное управление w*(/), переводящее объект из начального
состояния Х° = (х(О\хЩ9...,х(п~Х\о)\ в конечное ХТ = (х(Т\х'(Т)9...,х{п~1\т)\ за
промежуток [t0 =0,/j =7*], причем норма управления u(t) в пространстве 1^[0,Г]
должна иметь минимум, т.е.
(т ^
1иЬ[о.г]=ЦИОГ*1 -*min- . (5-5°)
Эта задача может быть решена с помощью метода моментов, основные положения
которого изложены в предыдущем параграфе.
Запишем векторно-матричный интеграл Коши для уравнения САУ (пока будем
полагать, что U(/) - вектор-функция):
Х = А(/)Х + В(0у. (5.51)
Он имеет вид
т
Х(0 - JХф(0Х2(x)B(x)U(x)«/x + ХФ(/)Х^(0)X° , (5.52)
о
где Х° - начальное состояние.
Обозначая
хф(0Х5!(т) = Ф(*,т),
перепишем (5.52)
Х(/) = J Ф(*, т)В(т)и(т)Л + Ф(/,0)Х°.
о
Поскольку
Xi1(T) = 1P(T), (5.53)
где Т(т) - фундаментальная система сопряженной системы, то (5.52) можно
переписать в виде
т
Х(/) = ХФ(/)Х° + |Хф(/тт)В(т)и(т)Л.
о
Умножая обе части последнего равенства на *F(/), получим
т
Т(0Х(0 = Т(/)Хф(/)Х° +Т(0Хф(0|*(х)В(х)и(х)Л . .
о
Учитывая (5.53), запишем
т
Т(/)Х(Г) = Х° + J *F(t)B(t)U(t)</t . (5.54)
о
Или, что то же самое,
J*F(t)B(t)U(t)c/t = Т(0Х(0-Х°.
о
Полагая верхний предел в (5.54) t = Т, находим
т
Jh(t)U(t)</t = A, (5.55)
о
Глава 5. Методы математического программирования 607
где
Н(т) = ¥(т)В(т); Л = ¥(Г)Х(Г) - Х°.
Равенство (5.55) выражает необходимые и достаточные условия, которым должна
удовлетворять функция U(t) , чтобы система (5.51) перешла из заданного начального
состояния Х° в заданное конечное состояние X7 .
Если же предыдущие рассуждения отнести к скалярному объекту (5.49), то
соотношение (5.55) в скалярной форме запишется так
т
J^(tMt)Jt = Xi;
jh2(x)u(i)dz = X2;
(5.56)
т
J/axMx)</T = V
о
Теперь, пользуясь вышеизложенными результатами, легко записать зависимость,
определяющую оптимальное управление:
п
и* (') = Т-^Тр 1Яэ(')Г' Sign Яэ(/), (5.57)
||Яэ(7)||Р1>[о,г]
где
#э(0 = !>Л(0. (5-58)
У=1
Управление (5.57) имеет минимальную норму в пространстве 13 [0,Т]:
(г \УЧ
IHL'[o,r]= IJMM ^min-
Важно обратить внимание на факт, который здесь используется: норма
функционала I в терминах теории управления является одновременно нормой входного
воздействия в пространстве Lq\0,T\, т.к. воздействие совпадает с производящей
функцией функционала. Норма функционала / в рассматриваемом подходе является
функционалом качества работы системы управления.
В формулу, определяющую оптимальное программное управление и* (t), входят
коэффициенты k*,k2,...,k*. Они находятся путем решения следующей задачи
нелинейного программирования:
min f Х*А(>)
*v I 0 v=l
dt
(5.59)
при ограничении
k{kx +^2 +... + kn\n=\. (5.60)
Эта задача может быть решена только на ЭВМ; результатом ее решения являются
числовые значения k^k^,...9k*.
608
Методы теории оптимального управления. Часть III
Следуя [9,25], можно указать последовательность решения задачи оптимизации:
1) описать объект линейным уравнением (5.49); задать все входящие в уравнение
параметры; перейти к нормальной форме Коши;
2) задать время процесса /0 = 0; tx = Т ;
3) задать начальное Х° и конечное Хг состояния;
4) задать минимизируемый функционал в виде нормы управления в пространстве
Lq[0j];
5) сформулировать задачу оптимального управления;
6) построить фундаментальную систему сопряженной системы и рассчитать
Я(т);
7) построить моментные функции hk(t) и рассчитать вектор моментов
Л = (л,1,а,29...,л,л) ;
8) записать задачу в виде эквивалентной проблемы моментов;
9) решить задачу нелинейного программирования (5.57) и, таким образом, найти
числа к{,к£9...9к*;
10) после расчета чисел к^к^^.^к*, полученных в результате решения задачи по
пункту 9, записать окончательный ответ в виде формулы для искомого
оптимального управления (см. формулу (5.57)) и его минимальной нормы
(т \Уя
т1п1ии[о,г]=1К«|=уК«г^^ .
Рассмотрим случай, когда p = q = 2. Функционал качества в рассматриваемом
случае имеет вид
(Т Л/2
J = \ju2W\ .
Реализуя последовательность решения задачи, получаем формулу для
оптимального программного управления в виде
"*(') = •
У=1
JLEOv(') л
0Vv=l
Ё*Я«
v=l
Signf I>v4(')j = (If)2 f I*v4(')j ,
т.к.
/ =
1
v=l Vv=l ) v=l
'«1 IL2[0,7']
Для нахождения оптимальных значений к^к^^.^кп необходимо решить задачу
т
minJ|*A(')|2<u
К о
при условии
£*Л,=1. (5-61>
v=1
Глава 5. Методы математического программирования
609
Последняя задача является классической задачей аппроксимации, а еще более
конкретно - задачей о наилучшем приближении в среднеквадратичном.
Учитывая рассуждения, приведенные выше, задачу (5.61) перепишем в виде (см.
формулу (5.48)):
miaJ = minj[fl(t)-k2f2(t)-...-kJn(t)]2 dt.
Оптимальные значения к^к^,...,к* находятся обычным путем: берутся от J
частные производные по кх,к2,...>кп и приравниваются нулю. Имеем
\^T = j[MO-k2Mt)-...-knfnU)]f2(Odt = 0;
Л. ОК-)
2 0
Т
1ТГ = 1Ш0-Ш<)---Ш<)]Л№ = 0;
юкг 0
(5.62)
1 а/
~ = l[A(t)-k2Mt)-...-knfn(t)]fn(t)dt = 0.
2dk,
п 0
£
I
т
«'(О
Рис. 5.21. Структурная схема алгоритма:
/ - входные данные; 2 - расчет моментов Xj Д 2»• • • Ля «' 3 ~ расчет моментных функций
Л1(/),Л2(/),...,/|„(/); 4 - расчет коэффициентов atJ и формирование системы алгебраических уравнении;
5 — решение системы алгебраических уравнений и нахождение к* ,к\,..., к*,
б - построение оптимального программного управления и (/)
Обозначая a{j - jfi(t)fj(t)dt, из (5.62) запишем
610 Методы теории оптимального управления. Часть III
а2гк2+а2Ъкъ+... + а2пкп =q2;
. , (5.63)
Поскольку f\(t)9f2(t),...9fn(t) линейно независимы, матрица системы (5.63) не
вырождена и, таким образом, система (5.63) имеет единственное решение. Структурная
схема алгоритма расчета u*(t) представлена на рис. 5.21.
Заметим, что если критерием качества является энергия управления, оптимальное
программное управление u*(t) е С[0,Г], т.е. является непрерывной функцией.
Пример 5.7 [9, 54]. Пусть объект описывается уравнениями
х,=*2;*2 = м,
где x](t),x2(t) - фазовые координаты объекта; u{t) - скалярное управление. Найдем управление u*(t),
имеющее минимальную норму в L2 [0, Г] (минимальную энергию) и осуществляющее перевод объекта из
нулевого начального состояния в конечное состояние с координатами Хт = (7\1).
Сведем задачу оптимизации к проблеме моментов. Имеем
i
x2(t) = ju(x)dx + x2(0\
о
/ /Гт- ]
xl(t) = \x2(T)dT + xl(0)=l\ Jntt)^ + *2ft) k* + *i(0) =
о о|_о J
/ I t
= j(t - x)u(x)dT + x2(0)t + х,(0) = -Jtm(t)^t + t\u(i)dx + jc2(0)/ + x,(0)
0 0 0
Отсюда находим
Ju(x)dx = x2{t)-*2(0); -\xu(x)dx = x,(/)-t\u{x)dx-x2(0)t + x\(0)
0 .0 0
При t = T получим
T T
jtu(t)dt = r, \u(t)dt = \.
о о
Последние два равенства представляют формулировку задачи оптимизации в терминах проблемы
моментов, причем }\(t) - /; /^(0 = 1; Xj = Г; Х2 = 1. Рассчитаем оптимальные значения коэффициентов к\,к2.
Имеем
Гт
min И(*,/ + *2)2Л
при условии кхТ + к2 = 1.
Пользуясь описанной выше методикой, получаем:
1 2Т' 2 2 .
Найдем норму функционала
и- '
Теперь можно записать формулу, определяющую оптимальное управление*
■•«"Кг-Э-КН-
В [9] для рассмотренного объекта поставлена и решена задача перевода объекта из нулевого
начального состояния в точку, которая в фазовом пространстве системы движется по закону
Глава 5. Методы математического программирования 611
за минимальное время при ограничении на значение энергии управления
(т \Уг
|Н| = \\u2{t)dt\ <L.
Ко )
Оптимальное управление по быстродействию имеет вид [9]
Следуя [25], сделаем одно существенное замечание. Метод моментов, помимо
решения задачи о нахождении программного оптимального управления, т.е.
управления и = u*(t) как функции от независимой переменной /, позволяет решить задачу
синтеза системы оптимального управления, работающей по принципу ОС, т.е. опрег
деление управления и* (xl(t\x2(t),...,xn(t)) как функции от фазовых координат.
При решении этой задачи используется принцип «размораживания» начальных
условий, т.е. каждый текущий момент времени / принимается за начальный и тем
самым, принимая x(t) за начальное состояние, соответствующее этому моменту
времени, можно получить значение м* искомого оптимального управления как
функцию координат xx(t),...,xn(t) управляемого объекта и* = м*(*,,х2,—>*„)•
Системы управления минимальной силой являются частным случаем оптималь-
1 1 ,
ных систем, рассмотренных выше, когда р = 1 и а = оо , поскольку — + — = 1.
Р Я
Величина
J = vraio<^r max |w(/)| (5.64)
называется силой управления скалярным объектом. Критерий (5.64) получается из
общей формулы
(Т \УЯ (Т \Усо
Выражение, определяющее оптимальное программное управление, в явном виде
следует из зависимости (5.57) при р = 1 и q = оо .
Имеем
я
и(0 = т
v=l
J EOvwU
О v=l |
1*Ж«
v=l
sign Х*Ж(0 = ||f sign 2>Ж(/) , (5.65)
v=l J \v=l
где оптимальные коэффициенты k\,k\,...Xn находятся из решения задачи
Т п I
ininj ZAA(0U
v 0 v=l I
при условии k{kx +k2X2 +... + AwXw =1. Эта задача может быть решена на ЭВМ как
задача математического программирования.
Рассмотренная задача расчета k\,k\^..,k*n может быть сведена к задаче
аппроксимации в Z,1 [О, Т].
612
Методы теории оптимального управления. Часть III
В самом деле, имеем:
•/=J[/l(O-*2/2(O-...-*ll/»(O]A
Необходимо найти такие значения коэффициентов kl9k2,...,*„, которые
доставляют minJ.
Это равносильно задаче аппроксимации функции fx(t) линейной комбинацией
функций М0,М0,...,/п(0 в Ll[Q,T].
п
Это классическая задача Чебышева о нахождении функции f\(t)-^kvfv(t),
v=2
наименее уклоняющейся от нуля.
5.5.3. Векторно-матричный вариант
Если объект управления является многомерным, а его динамика описывается
уравнением в пространстве состояний (5.51), то имеет место векторно-матричное
соотношение (5.55), или, что то же самое, .
i
/«2,(1) Аа(т) ... А,ш(т)
U.W М*) ... КпЮ)
=
Л,
(5.66)
Решение задачи имеет вид
U(0 = К |к*Н(/)|Р" Sign К*Н(/), 0 < t < Г, р > 1,
(5.67)
где вектор К* =Ш9к£,...9к*) и число Хп есть решение следующей задачи: найти
mm
к
ta[J|KH(o|p*
при условии ЛК = 1.
Норма оптимального управления определяется формулой [9]
М-с
Каждая из компонент вектора U* (т) может быть рассчитана по формуле (5.67). Или
Р~Х ( п \
sign £*;/»,*(') U=i>«,
л(0
-ЦИГ]Г|е^(/)
/=1
при этом оптимальные коэффициенты к*,/£,...,к* находятся как решение
следующей задачи: найти
mm
при условии
^j^j +^2*2 +.-. + ^Л*л =1 . •
Доказательства приведенного факта можно найти в [9]. Полученные результаты
могут быть использованы для построения оптимальных программных управлений и
оптимальных программ.
Глава 5. Методы математического программирования 613
5.6. УПРАВЛЯЕМОСТЬ ЛИНЕЙНЫХ СИСТЕМ
Выше были рассмотрены задачи оптимального управления: нахождение
оптимального управления U*(/), переводящего объект из начальной точки Х°в
конечную точку Хт, при этом критерий качества должен иметь минимум. Однако прежде
чем строить U*(0 необходимо убедиться, а имеет ли поставленная задача решение,
т.е. возможен ли в принципе перевод данного объекта, имеющего конкретную
математическую модель, из точки Х° в точку Хт. Другими словами, перед построением
оптимального управления U*(f) необходимо убедиться, обладает ли объект
свойством управляемости в указанном выше смысле.
То есть возможность приведения Л НС в любое требуемое состояние X(f) и к
любому требуемому значению выхода Хв (f) с помощью сигнала управления
отражается понятиями управляемости по состоянию и по выходу. В зависимости от
степени и характера этой возможности вводят в рассмотрение несколько
разновидностей понятия управляемости [39]. В теории стационарных систем наиболее широко
используется понятие полной управляемости, которое справедливо и для ЛНС.
Система называется полностью управляемой по состоянию (по выходу), если из
начального состояния Х(/о), соответствующего любому /0, она может быть
переведена в любое окончательное состояние X(tk) за конечное время tk -/0
ограниченным входным сигналом и(/)П|и(/)|| < ooj. Иначе говоря, существует такое
tk9 t0<tk<co,4TO X(tk) = Xk.
У нестационарных систем имеются такие свойства, которые заставляют чаще,
(чем в стационарном случае), использовать и другие, более тонкие понятия
управляемости, например понятия полной управляемости на интервале [to,tk];
абсолютной управляемости на интервале [to,tk] ,и т.п., предполагающие у системы наличие
свойств, указанных в определении соответственно на заранее заданном интервале
[to,tk] (в определении правый конец этого интервала заранее численно не задан); на
любом конечном подынтервале, принадлежащем заданному [/0Л] •
Критерии управляемости для ЛНС существенно отличаются от аналогичных
критериев систем стационарных. Рассмотрим методику их вывода на примере критерия
полной управляемости на интервале [to,tk] • Выводить этот критерий гораздо
удобнее для системы
Z(/) = D(/)U(r);l (5.68)
X.(/)-F(f)Z(/)J (5.69)
- многомерного интегратора, к которому исходная система приводится с помощью
линейного неособого преобразования, характеризуемого (пхп) матрицей Т(/):
Z(0 = T(/)X(/). (5.70)
Действительно, продифференцировав соотношение (5.70), имеем
z(/)=t(/)x(/)+t(0*(/),
614 Методы теории оптимального управления. Часть III
откуда
Подставим полученное выражение Х(г) в формулу объекта управления:
T-404(0-T~40*(0X(') = A(/)X(/) + B(/)U(/);
тогда, учитывая, что X(/) = T~1(/)Z(/) (см. формулу (5.70)), уравнения объекта
приведем к виду
z(t)»T(t)T-\t)nt)T-\t)z(i)+T(t)A(i)T-l(t)z(t)+T(t)B(t)m^
= [T(t)T-l(t) + T(t)A(t)T-\t)]z(t) + T(t)B(t)U(t);
(5.71)
XB(t) = C(t)T-](t)Z(t).
Если матрицу Т(/) выбрать так, чтобы выполнялось
f (t)T~x (t) + T(t) A(t)T~l (() = 0, (5.72)
то из формулы (5.71) получим (5.68), (5.69), где матрицы
d(/) = t(/)b(0; 1
\ (5.73)
Нетрудно убедиться, что матрица
Т(/) = Ф(/0,/), (5.74)
равная ПМ системы удовлетворяет условию (5.72); выполнив в левой части
уравнения (5.72) подстановку (5.74), получим
Ф(/0,/)Ф"1 (/0,/) + Ф(/0>/) А(/)ф-! (/0,/) =
= -Ф(/0,0 A(f )Ф"! (to,t) + <l>(tO9t) А(/)Ф"! (t09t) = 0,
т.е. уравнение (5.72) превратилось в тождество, и выражение (5.74) действительно
является решением уравнения (5.72) относительно Т(г). Поэтому согласно (5.73)
D(/) = O(/0,/)B(/); 1 (5.75)
F(r) = С(0Ф"' ('о,О = С(ОФ(г,/о)| (5-76>
Первая форма критерия управляемости ЛНС.
Критерий 5.1 управляемости по состоянию. Система (5.68), в которой D(/)e Z,2[/o,^], * полностью
управляема по состоянию на [/<>,/*] тогда и только тогда, когда (их л) матрица yXi('o>'*)~ неос°бая,
где
y*(W*) = jD(f)DT(/)A. (5 77)
'о
Достаточность этого критерия нетрудно доказать, если положить
. и(0 = Вт(/)8*, (5.78)
"Запись D(/)eZ?[/0,/A] означает, что каждый элемент матрицы D(/) принадлежит к классу функций,
интегрируемых с квадратом на [/ол] •
Глава 5. Методы математического программирования
615
где гх - неизвестный постоянный «-вектор. Тогда уравнение (5.68) примет вид
^ = D(,)DT (,)£,,
dZ(t) = D(t)DT(t)Zxdt;
интегрируя левую и правую части от /0 до tk, получим
Z(tk)-Z(t0) = yxl(t09tk)£x.
Это соотношение превратится в тождество (т.е. система переведется из состояния
Z(r0) в Z(tjc) за время tk-t0 управлением (5.78)), если вектор £х в управлении
(5.78) выбрать равным
£х=Ух1('о''*)№)-2('о)]- (5-79>
Но из (5.79) следует, что такой вектор, а следовательно, и такое управление типа
(5.78) существует лишь в том случае, если матрица УХ1 (to,tk) неособая, что и
требовалось доказать.
Несложно показать необходимость сформулированного критерия.
Следствие 1. Система (5.68) полностью управляема по состоянию на [/0Л] тогда и только тогда,
когда строки матрицы D(/) есть линейно независимые функции аргумента/.
Следствие доказывается на основе рассмотренного критерия методом от
противного.
Пусть матрица УХ1 (to,tk) особая, тогда существует такой постоянный ненулевой
л-вектор С = [сх,с2,...,сп]т , что
СтУХ1(/0Л) = (0 0...0) = (О^
(5.80)
где О - нулевая л-строка.
(1х„)
Действительно, в силу линейной зависимости строк УХ1 =[>;xi;l>;xi;2 -^xi,,,]
матрицы УХ1 (т.к. она особая), согласно определению линейной независимости
существует л таких чисел с,; / = 1, п, что
Z^-Д. (5.81)
Произведение в левой части формулы (5.80), представляющее собой л-строку
[п п п 1
Z с>Ух\п Z ЪУуап • • • Z ЧЛай .
/=1 ы\ /=1 ■ J
можно раскрыть в виде
'+с|Ла„ +ci>'xi12 ••• +с\У\\и
^TV _ +С2^Х1„ +С2Ухи, - +С2УХ1,
С УХ1 -
+с\Ух1,
+с2Ух12
+с„Ух1„
/=1
_+спУх\п1 +спУх\п1 ••• +спУх\т
откуда с учетом формулы (5.81) следует равенство (5.80).
Умножим слева и справа соответственно на Ст и С обе части выражения (5.77);
получим
616 Методы теории оптимального управления. Часть III
CTyXI(/0,/,)C = |cTD(/)DT (t)Cdt.
'о
Учитывая формулу (5.80), имеем
О = }хт(/)Х(/)Л = }[я.12(г) + ^(/) + ... + ^(/)]л^0, (5.82)
'о 'о
где Хт (/) = DT (/)C- и-вектор, но тогда равенство в выражении (5.82) может иметь
место только в том случае, если
XT(/) = CTD(/)= О . (5.83)
Отсюда следует, что строки матрицы D(/) линейно зависимы (см. формулу (5.80)).
Однако формула (5.83) получена из предположения о том, что матрица Ух\{(о>*к)
особая. Если же она неособая (т.е. если система (5.68), согласно рассмотренному
критерию, полностью управляема по состоянию на [to,tk ]), то такого вектора С, что
справедливо соотношение (5.80), а следовательно, и (5.83), не существует. Тогда по
определению линейной независимости строки матрицы D(/) линейно независимы,
что и требовалось доказать.
Критерий 5.2 управляемости по выходу. Система (5.68), (5.69), в которой F(tk)D(t)e Z^ffo,/*],
полностью управляема по выходу на ['о*'*] тогДа и только тогда, когда (г х г) матрица
Уп(1о,<к) = \Ц<к)Щ*>Т(<)*Т(<к)<1< (5.84)
неособая.
Достаточность доказывается аналогично тому, как это сделано при доказательстве
достаточности критерия 5.1, если положить
Y(t) = Dr(t)Fr(,k)£r,
где £у - постоянный г-вектор.
Поскольку состояния Х(/) и Z(/) (системы (5.68)) связаны неособым
преобразованием
z(0=o(w)x(0,
критерий 5.1 является необходимым и достаточным критерием полной
управляемости на интервале [to,tk] по состоянию и для исходной системы, а критерий 5.2 -
необходимым и достаточным критерием полной управляемости на интервале [to,tk] по
выходу и для исходной системы; нужно только матрицы управляемости УХ1 (to,tk) и
Уп(/0,^) выразить через параметры исходных уравнений. Сделать это нетрудно,
используя соотношения (5.75), (5.76).
Критерий 5.3. Система, в которой Ф(/0,^)В(г)е12[/0,//к], полностью управляема по состоянию на
[to,tk] тогда и только тогда, когда (г х г) матрица
Ух1(/о,^) = )ф(/о,0ВМвТ(0фТ(^о,0Л
'о
неособая.
Глава 5. Методы математического программирования 617
Критерий 5.4. Система, в которой К(/ь/) е /,2[/0,/*], полностью управляема по состоянию на [/ОЛ]
тогда и только тогда, когда (пхп) матрица
Ул(/0Л) = )к(/,,/)Кт(/*,/)Л (5.85)
'о
неособая.
Согласно соотношениям (5.75), (5.76) из формулы (5.84) получим
Уу1(/оЛ) = |с(/*)ф(^л)ф(%.0в(0вТ(0х
(5.86)
х[ф($к^)Ф(^)]т Ст (tk)dt.
Учитывая, что Ф(^,/0)Ф(г0,/) = Ф(^5*), вместо матрицы (5.86) получим матрицу
(5.85).
Вторая форма критерия управляемости ЛНС. В необходимых и достаточных
критериях полной управляемости ЛНС на интервале [to,tk] по состоянию и по
выходу (см. критерии 5.3, 5.4) используется матрица перехода системы, которая, как
правило, неизвестна. Для многих ЛНС на основе этих критериев могут быть
выведены алгебраические (использующие непосредственно матрицы уравнений состояния и
выхода системы) критерии управляемости [39]; правда, получаются они чаще уже в
виде лишь достаточных критериев.
Сформулируем в качестве примера достаточные алгебраические критерии полной
управляемости на ( доказательство см. в [39]).
Критерий 5.5. Пусть в системе А(/),В(/) - матрицы, дифференцируемые соответственно
(л-1), (п -2) раз почти везде на интервале [to,tk] • Для полной управляемости по состоянию на
интервале такой системы достаточно, чтобы (л х пт) блочная матрица управляемости
Ухн(0 = [в(/):а{В(/)}!...1А/1-1{В(/)}] (5.87)
имела ранги почти везде на некотором конечном подынтервале [*1,/2] интервала [/0,/*] Здесь А-
оператор
A = _A(,)+iL. (5.88)
at
Критерий 5.6. Пусть в системе А(/),В(/)- матрицы, дифференцируемые соответственно
(л-2), (п-\) раз почти везде на интервале [/0>'*] • Дл* полной управляемости по выходу на интервале
[/0,/*] такой системы достаточно, чтобы (гхпт) блочная матрица управляемости
Уун=с(^)[в(/):а{в(/)}:...;ал-1{в(о}]=с(/,)ухп(о,
d (5-89)
A = -A(/) + iL
dt
имела ранг г почти везде на некотором конечном подынтервале [fj,^] интервала [/0>'*]
Критерии 5.5, 5.6 становятся необходимыми и достаточными критериями
абсолютной управляемости соответственно по состоянию на [to,lk] системы, по выходу
на [to,tk] системы, если требования, предъявляемые этими критериями,
выполняются почти везде на интервале [/0»^] [39].
Пример 5.8. Пусть система имеет конкретный вид
618
Методы теории оптимального управления. Часть III
Поскольку скалярный вход воздействует на каждую координату вектора состояния независимо (так
как матрица системы А - диагональная), то интуитивно можно предположить абсолютную управляемость
системы по состоянию (этот факт и имеет место в случае стационарных систем с диагональной матрицей
А), однако в данном случае интуиция приводит к неверным результатам. Действительно, матрица
управляемости (см. формулу (5.87))
имеет ранг 1 * (л = 2), т.е. данная ЛЫС с диагональной матрицей не оказалась абсолютно управляемой.
Этот противоречащий интуиции результат можно разъяснить следующим образом. Уравнению (5.90)
соответствуют два апериодических звена с переменным коэффициентом передачи, работающие от общего
входа (рис.5.22). ИПФ апериодического стационарного звена
*(/,т) = е-°(/-т)1[/-т]
можно представить в виде
k(t,T) = e-at\[t-x]ea\
что соответствует структурной схеме рис. 5.23, в связи с чем исходная система эквивалентна системе
рис. 5.24.
«/©
*') 1
н
^-
е
«КО fc
"2(0
1
s+a
1
s+b
*/(0
Рис. 5.22. Структурная схема системы (5.90)
еа1
1
S
Рис. 5.2Э. Структурный элемент схемы
и С)
}
к»
1
1
S
Xlif)
X2(0
}
Рис. 5.24. Структурная схема системы
Отсюда явно следует, что л, (/) и х2 (/) при любом u(t) независимо изменяться не могут, т.к.
и, поскольку z{ (/) = z2 (/),
Л2(0=^(')«М)'-
Это соотношение на плоскости хх0х2 определяет линию, которую изображающая точка не может
покинуть при любом w(/), следовательно, система (5.90) не может быть переведена управляющим сигналом из
заданного состояния в любое требуемое, если оно не принадлежит указанной линии.
Для класса стационарных систем имеются более простые критерии,
использующие лишь исходную информацию о системе, даваемую матрицами А и В .
Критерий формулируется! так [39]: для управляемости стационарной системы п -го порядка
Глава 5. Методы математического программирования 619
X(/) = AX + BU (5.91)
необходимо и достаточно, чтобы ранг (пхпт) матрицы управляемости
Sc=(b|AB|...|Aw4b) (5.92)
был равен п, т.е. rankSc = п .
В самом деле, для стационарной системы справедлива формула
Х(/) = еА/ Х° + JeA('~T)BU(x)</T. (5.93)
о
Пользуясь теоремой Гамильтона - Кэли, е можно выразить в виде конечного
ряда
еА' = С01 + С1А/ + С2(А/)Ч... + С„_1(А/)"~1. (5.94)
Подставив (5.94) в (5.93), запишем
Х(/) = еА'Х° + [Гс0В + С1(/-т)АВ + С2(/-т)2А2В +
oL (5.95)
+...+С„.1(/-тГ1А"-|в]и(т)й?т.
Последнюю зависимость можно представить так:
C0U(i)
Х(/) = еА'Х<)+}[в|АВ|...|А''-1в]
C,(/-t)U(t)
dx.
Как выше уже указывалось, содержание понятия управляемости означает, что
вектор управления U(t) соответствующим образом воздействует на все компоненты
вектора состояния Х(0 . А это будет иметь место тогда и только тогда, когда
подынтегральное выражение в (5.95) обеспечивает такое влияние, т.е. когда ранг матрицы
Гв|АВ|...|А"~1В 1 равен п. Условие управляемости не по состоянию, а по выходу,
можно получить, если обе части уравнения (5.95) умножить на матрицу С :
Хв(О = СХ(/) = СеА/Х0 + [[С0СВн-С1(/-т)САВ + ...+
о (5.96)
+ С„.1(/-тГ1СА/1-1в]и(т)с/т.
С учетом таких же соображений, которые были приведены выше, можно показать
следующее: выход ХД/) будет полностью управляемым тогда и только тогда, когда
ранг матрицы управляемости по выходу
Sb =[CB|CAB|...|CAW"1B] равен р.
Пример 5.9. Имеем объект [39]
Тогда
620 Методы теории оптимального управления. Часть III
Найдем ранг матрицы
miab]-[; ;].
Отсюда делаем вывод: rankSc = 2 . Объект полностью управляем.
Пример 5.10.
Найдем произведение АВ:
ГО 1Y-1 1
АВ= 1 2JI 0 2
Тогда
т.е. rankSc = 2 . Объект полностью управляем.
Кратко остановимся на свойствах управляемости, стабилизируемости и нормали-
зуемости нелинейных объектов. Напомним, что свойство стабилизируемости
линейных объектов заключается в том, что с помощью регулятора в цепи обратной связи
все неустойчивые моды могут быть сделаны устойчивыми. Очевидно, устойчивый
объект стабилизируется тривиальным образом, а всякий управляемый объект стабиг
лизируем. Нормализуемость же представляет собой наиболее сильную форму
управляемости (каждая компонента вектор-функции U = (их (t),u2 (t),..,um (/)) в
отдельности обеспечивает управляемость объекта). Для линейных объектов получены
критерии управляемости, стабилизируемости и нормализуемости.
Строгие же условия управляемости, стабилизируемости и т.д. найдены лишь
для некоторых классов нелинейных объектов. Линеаризация нелинейных уравнений
объекта во многих случаях позволяет установить наличие или отсутствие указанных
выше свойств [49].
Пример 5.11(49).
Рассмотрим нелинейный объект, поведение которого описывается дифференциальными уравнениями
вида
dxx/dt = -*| - Daxx{2 + щ, (5.97)
dx2 Idt = Daxx} -x2-Dal(x1 )"2 + ^. (5 98)
Проведем линеаризацию этих уравнений в окрестности установившегося состояния jc,,,^2» >
задаваемого уравнениями u]s -\, u2s = 0 . Обозначим jc, = xt -xii3 щ = w, -uis (i - 1,2). Разложим уравнения (5 97),
(5.98) в ряд Тейлора, пренебрегая членами выше первого порядка. Результат с учетом введенных
обозначений запишется в форме:
dxxldt = -(\ + 2DaxxXs)xx +w,, (5.99)
cb^l dt = {2DaxxXs)xx-\\ + \l2{Da3l x2s)XI2^x1^u2, (5.100)
где xXsixls - решения уравнений, определяющих установившееся состояние
0 = -хи- Daxxh + 1,
' , х1/2 (5.101)
0=Оахх1-х25-Оа3(х25)1/\
Или в векторно-матричной форме X = АХ+ BU, где
~-(\ + 2DaxxXs) 0
А= ол ( 1 Da3 ) , (5.102)
2DaxxXs -|1+27~ фг
2(^2v)
Глава 5. Методы математического программирования
621
в
=[::]
(5 103)
Критерий управляемости состоит в том, что ранг матрицы управляемости должен быть равен 2. Имеем
0
1 0
0 1
-(1 + 2Яед,)
2Da{xXs
lc=[b;ab]=
2(X2s)
Очевидно, rank Lc = 2, из чего следует, что нелинейный объект будет управляемым в любом
установившемся состоянии.
Нелинейный же объект, описываемый системой дифференциальных уравнений
-± = -x{-Daxx\ + db
-± = Daxx\ -x2- Da3 (xj,)1'2 + и„
не является управляемым, поскольку ранг матрицы управляемости
0
LC=[B!AB]= °
■ , , 1 Ра
2(X2s)
равен единице.
5.7. НАБЛЮДАЕМОСТЬ ЛИНЕЙНЫХ СИСТЕМ
При синтезе систем, работающих по принципу обратной связи, в каждый момент
времени t необходимо знать вектор состояния Х(0 . Некоторые из компонент
вектора Х(/) могут быть получены с помощью различного рода датчиков,
измерительных устройств. В общем же случае можно наблюдать лишь вектор-функцию Хв(0 -
выход системы. Две вектор-функции Х(/) и Хв(/) связаны между собой с помощью
матрицы С:
ХВ(О = СХ(/). (5.104)
Размерность Х(0, как правило, выше размерности Хв(/).
В связи со сказанным выше в теории управления ставится задача: построить
алгоритм расчета вектора X(t), если на некотором промежутке известен вектор Хв(0 и
математическая модель системы.
Задача нахождения вектора X(t) состояния системы или отдельных компонент
указанного вектора по известным на некотором промежутке [/q>'i] вектор-
функциям Хв(/) и U(0* а также математической модели системы носит название
задачи наблюдаемости линейной системы.
Если задача наблюдаемости для линейной системы имеет решение, то система
называется полностью или частично наблюдаемой в зависимости от того, все или
часть компонент вектора X(t) удается определить.
Для линейной системы
Х(/) = А(/)Х(Г); (5.105)
Хв(/) = С(0Х(0
(5.106)
пара матриц A(t) и C(t) называется наблюдаемой, если можно решить задачу о
наблюдаемости для системы (5.105) по известному на некотором промежутке
вектору выхода Хв(0 (5.106).
622 Методы теории оптимального управления. Часть III
Для класса стационарных линейных систем построены конструктивные критерии,
позволяющие установить факт наблюдаемости системы. Если нет специальных
оговорок, то речь идет о так называемых свободных системах, т.е. о наблюдаемости
свободных колебаний, предполагая, что входное воздействие U(/) s 0 .
Справедлив следующий критерий: для линейных систем вида
Х(/) = АХ(0;
хв(0 = сх(/);
Х(0) = Х°
с постоянными матрицами А и С для полной наблюдаемости необходимо и
достаточно, чтобы ранг (пхпр) -матрицы наблюдаемости Lo был равен п :
Lo =
АТСТ
(at)2ct...|(at)"V
Покажем справедливость приведенного критерия [49]. Имеем для свободных
колебаний вектора состояния
Х(/) = еА/ Х° = (COI + Q/A +... + С,,./"1 А""1 )х° .
Выходной сигнал определяется формулой
Хв (0 = СХ(/) = (СОС + С,/СА +... + Сп.хГ1С А""1 )х°. (5.107)
Система наблюдаема, если все координаты вектора состояния в момент t = 0,
т.е. Х°, можно определить по информации о выходе Хв(/) на конечном интервале
времени. Если найден вектор Х°, то известна и вся исходящая из него траектория.
Другими словами, если получена зависимость, определяющая Х° (начальное
состояние), то по этой информации можно построить вектор состояния
Х(0 = еА'Х°.
Для решения задачи необходимо разрешить уравнение (5.107) относительно Х°
(эта процедура носит название псевдоинверсии).
Умножая обе части (5.107) на exp (A' j и интегрируя от 0 до Г, находим
"т т
|(с0С + С1/СА + ... + Сл_1/г;-1СА/7-1) х
Х° =
_о
х (СОС + QCA +... + С„_/'~1СА'1-1 )л] х
т т
xJ(c0C + C1rCA + ... + Cw.1rw4CAw-1) ХВ(ОА
о
Введем в рассмотрение матрицу М :
т
М
о
х (СОС + С,/СА +... + Cn.xtn~xCKn~x }dt.
Представим матрицу М в виде
= J(COCT +С^АТСТ +...+С„./-' (ATf' Ст]>
Глава 5. Методы математического программирования
623
M = J
АТСТ
-|КГст
QI
lV'i
[coifaa\.\c^t"-li\
с
СА
СА
п-1
(5.108)
ей.
В (5.108) 1-(рхр) - единичная матрица.
Перепишем (5.108) в форме
М= С
АТСТ
...|(ATf'cTljf*
С
СА
СА
п-1
Блочная матрица Т (прхпр) состоит из (рхр) диагональных блоков с
элементами (ckO,tktJ\ *,у = 0,1,2,...,л-1.
Потребуем, чтобы матрица М была невырожденной. Воспользовавшись
известными фактами из теории матриц, можно показать справедливость следующего
утверждения: для того, чтобы выполнялось равенство rank M = п, необходимо и
достаточно, чтобы rank Lo = n.
Рассмотрим следующую систему
(5.109)
(5.110)
f-*«
u(0 = c(/)Z(0;Z(0) = zu.
Можно показать [49], что для любой задачи управления можно построить такую
задачу наблюдения, что решение последней будет являться и решением задачи
управления и, наоборот, для любой задачи наблюдения можно построить
соответствующую задачу управления, причем решение последней будет решать первую
задачу.
Приведенное положение составляет содержание принципа двойственности. В
соответствии с принципом двойственности вопросы наблюдаемости для наблюдаемой
системы превращаются в вопросы управляемости для двойственной ей управляемой
системы. Приведем уравнение управляемой системы
X(0 = A(0X + B(/)U. (5.111)
Пусть
Щ0 = -А(/);С(0 = Вт(/). (5.112)
Системы (5.109), (5.110) и (5.111) называются сопряженными, если выполнены
условия (5.112).
Для разрешимости задачи наблюдения системы (5.109) необходимо и
достаточно, чтобы была разрешима двойственная ей задача управления, т.е. чтобы система
x(o = -dt(OX<o+ct(OU(O
(5.113)
была вполне управляемой. Воспользовавшись критерием (5.92), получим для случая
стационарной системы: система (5.109) и (5.110) является полностью наблюдаемой
в том и только том случае, если выполнено условие
624 Методы теории оптимального управления. Часть III
-И"'стЬ
rank CT DTCT
где п - порядок наблюдаемой системы.
Понятие наблюдаемости для нестационарных систем характеризует возможность
по выходу системы судить о ее состоянии. Как и в управляемости, существует
несколько разновидностей понятия наблюдаемости.
Система называется полностью наблюдаемой на интервале [/<>>**]» если ПРИ за~
данных /0 и tk начальное состояние Х(/о) свободной системы можно определить
по известному на [t^tk\ выходу Хв(/), когда наступит момент tk .
Критерий 5.7 - первая форма критерия наблюдаемости ЛИС. Система полностью наблюдаема на
интервале [/о,/*] тогда и только тогда, когда столбцы матрицы
Н(мо) = С(/)Ф(/,/о)
линейно независимы на интервале [tQ,tk].
Доказательство достаточности. Из уравнения выхода системы с учетом
приведенных выше формул при Хв(/) = О имеем
и(/) = С(/)Ф(Мо)Х(/о) = Н(/,/о)Х(/о) (5.114)
(rxl) (rx/j) (nxn) (nx\) (rxn) (их1)
(снизу в скобках указаны размерности соответствующих выражений), откуда вектор
Х(/о) определен быть не может в силу того, что выражение (5.114) представляет
собой систему из г уравнений с п неизвестными, где г < п .
Умножив левую и правую части (5.114) слева на
ФТ(Мо)Ст(/):
' Щ '
Фт(/,/о)Ст(0х(/) = Фт(/,/о)Ст(0Ст(0Фт(/,/о)Х(/о), (5.115)
1 (^7) '(гх1) ' (^) " (Ц ' (wxl)
получим систему из п уравнений, но вектор Х(/) из нее все-таки не может быть
найден, т.к. линейно независимых уравнений в ней лишь г (линейная безынерционная
операция, описываемая матрицей Фт(/,/0)Ст(/), может дать лишь линейную
комбинацию исходных соотношений).
Недостающая информация может быть найдена, если использовать значения
выхода, полученные и в другие моменты времени, например с помощью суммирования
членов типа (5.115) при различных tt, включающих значения выхода в эти моменты
времени:
ХВ(;,) = ХВ(/О+/Д/), / = 0,1,2,3,...,#-1;
NAt = tk-t0
(At- интервал, с которым производится наблюдение за выходом).
В случае непрерывного наблюдения сумма примет вид интегралов:
|фт(/,*ь)ст(Ох(О*-
|фт(/,<ь)ст(/)с(/)ф(/,<ьМ
.'о
Х(/о). (5.116)
Глава 5. Методы математического программирования 625
Свидетельством того, что в сформированном таким образом выражении
содержится достаточное для определения Х(/о) количество информации, явится тот факт,
что квадратная (пхп) матрица
AI(r0,/,) = JoT (мо)ст (t)c{t)o{t,tQ)a
'о
неособая, т.к. тогда из уравнения (5.116)
'о
Но если матрица A! (to,tk) неособая, то матрица имеет линейно независимые строки,
а матрица С(/)Ф(/,/0)- линейно независимые столбцы, что и требовалось доказать.
Доказательство необходимости критерия 5.7 приведены в [39].
Сравнивая содержание следствия и только что доказанного критерия, можно
заметить очень важное свойство ЛНС.
Свойство ЛНС. Система полиостью наблюдаема на [tQ,tk] тогда и только тогда, когда
сопряженная система полностью управляема по состоянию на [to,tk] .
Действительно, согласно следствию 1 и формуле (5.75) для полной управляемости
по состоянию сопряженной системы необходимо и достаточно линейной
независимости строк матрицы
Фс('с,л)вДО.
Но в соответствии с полученными выше результатами,
Вс (/с) = Ст (/с); Фс (/Со,/С) = Фт (tc,tCo),
поэтому линейная независимость строк матрицы
Фс('со^с)Ве(/с) = ФТ(/с>^)СТ(Гс)=[с(/с)ф(/с,/Со)]Т
означает линейную независимость столбцов матрицы С(/)Ф(/,/0), что совпадает с
требованиями критерия 5.7 полной наблюдаемости исходной системы на [to,tk ].
Это свойство ЛНС отражает, как и для стационарных систем, так называемую
дуальную связь (дуальность) между наблюдаемостью и управляемостью по
состоянию, согласно которой, используя известные уже алгебраические критерии
управляемости к сопряженной системе^ нетрудно получить вторую форму критерия
наблюдаемости.
Критерий 5.8. Система, где А(/),В(/)- матрицы, дифференцируемые соответственно (л-2),(л-1)
раз на интервале [to,tk] > абсолютно наблюдаема на интервале [/0,/*] тогда и только тогда, когда (пхпг)
составная матрица наблюдаемости
а11(/)=[ст(г);д{ст(<)}:...:д"-|{ст(/)}];
(где А = Ат (/) + — ) имеет ранг п почти везде на интервале [/0,/*] .
В определении 5.1 предполагается, что систему начинают исследовать в момент
£ = /0, т.е. понятие наблюдаемости связывается с возможностью определения со-
41 Зак. 366
626 Методы теории оптимального управления. Часть III
стояния по будущим значениям сигнала. Калман поставил задачу по-другому, более
естественно - определять состояние по прошлым значениям выхода, связав
возможность ее решения с понятием идентифицируемости, или восстанавливаемости.
Определение восстанавливаемости имеет вид определения полностью наблюдаемой
системы, в котором последняя фраза «....когда момент tk наступит» заменена на
фразу «если момент tk уже наступил» (т.е. исследование восстанавливаемости системы
начато при £ = tk ).
Пусть исследование системы начато при £ = t0, и оказалось, что она наблюдаема;
ясно, что отсюда не следует ее восстанавливаемость, т.к. для оценки
восстанавливаемости требуется располагать выходом системы при £,<t0, а факт наблюдаемости
информации о ее выходе для этих моментов не содержит. Так как матрицы
стационарной системы неизменны во времени, ее наблюдаемость означает и ее
восстанавливаемость и наоборот.
Развивая понятие инверсной системы
2^ = АМЪ('ы) + *ш(Ф(*и)>
Xu{tu) = Cu(tu)Xu(tu),
(5.117)
можно заметить, что инверсная система (5.117) в будущем (начиная с момента
tu = tuk = -tk) принимает значения, равные прошлым значениям исходной системы, а
в прошлом - будущие (рис. 5.25), поэтому: если исходная система полностью
наблюдаема на [/оЛ]> то инверсная система (5.117) полностью восстанавливаема на
[tQ,tk ]; верно и обратное утверждение.
0
t
V°
-о——
Q
tu tu—tU()—to tu—tUK—tk
Рис. 5.25. К пояснению работы инверсной системы
Экспериментальный способ анализа наблюдаемости ЛНС. Поскольку
исследование наблюдаемости по приведенным критериям связано с необходимостью
определять ранг матрицы наблюдаемости (а эта операция в реальных условиях
неконструктивна), в практических работах все чаще применяется довольно оригинальное
конструктивное решение этого вопроса. Правда, весьма громоздкое: необходимо
работать со сложной моделью, для реализации которой дополнительно требуется два
источника нормальных векторных гауссовых белых шумов q(/) и г(/)
размерностью соответственно (лх1) и (rxl) с нулевыми средними значениями и известными
матрицами их интенсивностей Q(/) и R(f).
(пу.п) (гхг)
Экспериментальный способ состоит в следующем. Поставим в соответствие
исходной системе новую стохастическую модель
Глава 5. Методы математического программирования
627
(5.118)
^l = A(/)X(/) + B(/)q(/),|
Z(/) = C(r)X(/) + r(f),
для которой рассчитаем сходящийся фильтр Калмана [39]:
^ = A(O*(O + K(O[Z(O-C(OX(O]; (5.119)
K(^)=p(r)c(0R"1(0; (5Л2°)
^ = A(/)P(/)+PWAT(/)-P(OC(/)R-1(/)CT(/)P(O+B(/)Q(/)BT(/); (5.121)
Р(0) = Р0, (5.122)
где Х(/)- оптимальная по Калману оценка вектора состояния системы (5.118);
К(/)- матрица коэффициентов оптимального фильтра Калмана, вычисляемая по
формулам (5.120), (5.121), (5.122); Ро ={P,jo)i,j' = \,n- заданное исходное значение
дисперсионной матрицы (матрицы ковариаций); P(f) - ошибки оценивания
Х(0 = Х(0-Х(/):
P(O = {^(O}/J.C;=^[X(OXT(O]; (5-123)
здесь М- символ операции математического ожидания.
Как видно из выражения (5.123), диагональные элементы матрицы P(f)
представляют собой дисперсии ошибок оценивания фильтром соответствующих
координат вектора состояния. Если в процессе работы фильтра окажется, что в
установившемся режиме /-й диагональный элемент Ри (оо) уменьшился в сравнении с его
исходным значением Ри (0) на 50% и более, то система (5.118) и исходная система
хорошо наблюдаема по /-й координате, т.к. из теории оптимальной фильтрации
известно, что фильтр Калмана работоспособен только при наличии свойства
наблюдаемости системы, для которой он строится. Обеспечить сходимость процедуры (5.119) -
(5.122) в данном случае достаточно просто ввиду того, что все ее параметры
известны точно.
Выше были введены понятия управляемости и наблюдаемости. В [22]
рассмотрены вопросы декомпозиции систем; показано, что многомерная система может быть
декомпозирована на четыре подсистемы: управляемую и ненаблюдаемую 5,,
управляемую и наблюдаемую S2, неуправляемую и ненаблюдаемую S3, неуправляемую и
наблюдаемую S4.
Управление системы можно записать следующим образом (рис. 5.26)
Аи
А22
А,з
А23
Азз
х*
хс
К;
хв=(о с2 о с4)(х0 х, хс х,).
A14N
А24
А34
А44>
хс
Ixj
А.
1
в2
0
,0,
и;
41*
628
Методы теории оптимального управления. Часть III
U
А24
Si
Л34
У13
Хв
Рис. 5.26. Структурная схема системы, декомпозированной на четыре подсистемы
5.8. НЕКОТОРЫЕ ПОДХОДЫ К СИНТЕЗУ ОПТИМАЛЬНЫХ
СИСТЕМ, РАБОТАЮЩИХ ПО ПРИНЦИПУ ОБРАТНОЙ СВЯЗИ
Напомним некоторые определения, связанные с проблемой синтеза систем с
оптимальными обратными связями.
Вектор-функцию U* (t), зависящую от t, называют оптимальным программным
(временным) управлением.
. Системы, в которых оптимальное управление U (/) является функцией времени,
называют системами программного управления, или незамкнутыми системами, или
системами без обратной связи.
Траектория X* (t), являющаяся решением уравнения объекта при U(/)= U* (/),
называется программной траекторией или оптимальной программой.
Ветор-функцию U (/,Х(?)), зависящую от вектора X(f), называют
координатным управлением, или законом управления.
Закон управления U*(r,X(/)) физически выражает известный принцип
обратной связи, согласно которому величина управляющего воздействия определяется на
основании измерения текущего состояния системы Х(/).
Сравним две линейные системы, представленные на рис. 5.27 и рис. 5.28. На
рис. 5.27 представлена разомкнутая система; такой класс систем может быть
реализован, если:
• известна с достаточной степенью точности математическая модель объекта
управления;
• объект не подвергается воздействию случайных возмущений;
о все каналы связи управляющей системы и объекта защищены от каких-либо
случайных влияний;
• известны и точно реализуются начальное Х° и конечное ХТ состояния;
• точно реализуется программное управление U* (t).
Глава 5. Методы математического программирования
629
Системы этого класса в большинстве случаев неработоспособны. В самом деле,
при создании систем приходится допускать некоторую погрешность, обусловленную,
например, ограниченной точностью изготовления их компонент. Динамические
характеристики могут меняться со временем из-за старения, изменения температурных
условий, атмосферных явлений и т.п. Это приводит к неточности задания
динамических характеристик, а последние определяют вектор-функцию U* (/).
Кроме того, имеют место внешние возмущения, которые часто не подлежат
контролю и не могут быть скомпенсированы.
Для некоторых систем, когда, например, неизвестно конечное состояние (задача о
перехвате цели), вообще невозможно построить системы программного управления.
Поэтому трудно представить процесс управления без обратной связи, который бы
имел сколько-нибудь существенное значение.
Входные
данные
Управляющее
устройство
Й.
в(0
X
i
ь
фх°
J
Qn(o
а(0
х(/)
С(0
Хв(0
Х0,Х7>[0,Г]идр.
Рис. 5.27. Структурная схема разомкнутой системы
Процесс управления с обратной связью (см. рис. 5.28) наблюдается везде: в
живых организмах, в социальных, экономических, хорошо работающих технических
системах. Однако синтез систем, работающих по принципу обратной связи,
представляет собой чрезвычайно сложную задачу.
Изложим некоторые подходы к ее решению, т.е. рассмотрим задачу синтеза
оптимальных обратных связей.
рх°
в(/)
u'(',xHWJ
\
J
А(/)
Управляющее
устройство
х(0
с«
хн(0
Наблюдающее
устройство
Рис. 5.28. Структурная схема оптимальной системы, работающей
по принципу обратной связи
Первый подход состоит в том, что для решения поставленной задачи
используются методы, позволяющие сразу же рассчитать координатное управление и, таким
образом, реализовать управление объектом по принципу обратной связи. К таким
методам можно отнести:
• метод динамического программирования;
• метод решения линейно-квадратичных задач;
• метод моментов.
Второй подход основан на использовании понятия двухэтапной оптимизации ГЗЯ1
630
Методы теории оптимального управления. Часть III
Выше были подробно рассмотрены методы расчета оптимальных программных
управлений U* (/) и оптимальных программ X* (/).
Расчет U* (t) и X* (t) представляет собой первый этап решения задачи синтеза
оптимальных систем.
Пусть X* (t) - оптимальная программа, U* (t) - оптимальное управление. Полагая,
что эквивалентные случайные возмущения малы, можно предполагать, что X (t)
получит некоторое приращение 5Х(/); тогда реальная фазовая траектория имеет вид
Х(/) = Х*(/) + 8Х(/). (5.124)
Для компенсации 5Х(/) реальная управляющая вектор-функция V(t) должна
иметь вид [38]
U(/) = U*(/) + 5U(/). (5.125)
Задача расчета 5U(f,X) носит название задачи проектирования оператора
обратной связи и составляет содержание второго этапа.
Таким образом, на втором этапе определяются параметры системы,
обеспечивающей максимально возможную точность достижения цели. Эта схема решения
проблемы управления носит название двухэтапной оптимизации.
Как указано в работе академика Н.Н. Моисеева [38], «схема двухэтапной
оптимизации, разделяющая процесс управления на два последовательных этапа - выбор
программы и построение механизма реализации этой программы, - является одним
из важных эвристических приемов современной теории управления. Он в равной
степени необходим и для управления техническими и технологическими, где он
возник, и для управления социальными и экономическими системами, где он сделался
основой программного метода управления». В [38] приведено обоснование
возможности использования идей двухэтапной оптимизации для решения конкретных задач.
Задатчик
программного
управления
Задатчик
программной
траектории X* (г)
мо=*;(')-*< (о
/ = 1,и
Рис. 5.29. Структурная схема оптимальной системы,
работающей по принципу обратной связи
Структурная схема системы, построенная с использованием двухэтапной
оптимизации, представлена на рис. 5.29.
В последующих параграфах основное внимание будет уделено методам
реализации схемы двухэтапной оптимизации.
Глава 5. Методы математического программирования 631
5.9. СИНТЕЗ ОПТИМАЛЬНЫХ ОБРАТНЫХ СВЯЗЕЙ
Выше был рассмотрен вопрос синтеза линейных систем по интегральному
квадратичному критерию. Принципиальным фактором при решении линейно-
квадратичных задач является возможность синтезировать системы, работающие по
принципу обратной связи. Эти результаты можно использовать для синтеза
оптимальных нелинейных систем, работающих по принципу обратной связи. Далее
изложим алгоритм решения этой задачи [44,49].
5.9.1. Расчет оптимальной программной траектории,
ИСХОДЯЩЕЙ ИЗ НАЧАЛЬНОГО СОСТОЯНИЯ Х(0) = Х°
Пусть нелинейный объект описывается векторно-матричным дифференциальным
уравнением
X = F(X(/),U(/)), X(0) = X° (5.126)
с критерием оптимальности
т
J = go(X(0) + J/o(X(0,U(/))A (5.127)
о
Для решения этой задачи можно применять методы математического
программирования, подробно рассмотренные выше и не использующие непосредственно
аналитический аппарат принципа максимума. Вместе с тем разработано большое число
алгоритмов, основу которых составляет совокупность необходимых условий
оптимальности.
Выбор того или другого алгоритма расчета оптимальной программы X* (/)
определяется конкретным содержанием задачи.
5.9.2. Линеаризация в окрестности оптимальной программы х*(/)
и программного управления u* (/)
Для вариации функционала путем разложения выражения (5.127) в ряд Тейлора в
окрестности X (/) и U (/) можно получить зависимость
&/ = (ago/axj5x(r) + l/25xT(r)(52go/ax2)|*5x(r)-
-Хт (Т)8х(Т) + \т (0)Ьх(0)+\\(дН /ди)\* &и +
oL (5.128)
+1/25ит(92Я/аи2)|*5и + (аЯ/ах)|*5х + 1/25хт(а2Я/5х2)|*8х +
+6хт (д2Н / dxduj 6u + (dkT I dt)bx\ dt,
где 5x = x-x*,5u = u-u*,H = f0 + \TF . Положим, что X*(f) и U*(/)
удовлетворяют необходимым условиям оптимальности первого порядка [49]
дН/ди = 0, dkT Idt = -(дН/дх)\*, Хт (Т) = (dg0 /дх(Т))\*, (5.129)
причем предполагается, что Х(0) = Х° задано (x(0) = X*(0) j, а Х(Г) свободно. В
этом случае X* (/) и U* (/) определяют оптимальную программу и оптимальную
траекторию. Тогда выражение (5.128) принимает вид
632 Методы теории оптимального управления. Часть III
&/ = ||1/28ит(а2Я/5и2Тби + 5хт(а2Я/5х5иТ8и +
о1- • (5.130)
+1/28хт(а2Я/ах2)|*8х]Л + 1/25хт(Г)(52а/5х2)|+8х(Г).
Учитывая свойство нелинейности объекта, оптимальная программа X* (/) и
оптимальное программное управление U* (/) рассчитываются для каждого начального
состояния Х(0) = Х°. Для решения этой задачи можно применить линеаризацию
уравнения (5.126) в окрестности X* (/) и U* (/) при Х(0) = Х°. В результате будет
иметь место уравнение в вариациях для возмущенного движения [1, 49].
Кратко опишем соответствующий алгоритм. Для компонент вектор-функций
X (/) и U* (/) справедливы соотношения
xi(t) = x*(t) + &ci(t)9 / = п nuk(t) = uk(t) + &uk(t)9 к = \,т.
Таким образом, U* (/) и X* (/) - оптимальное управление и оптимальная
программная траектория, X(f) = X*(/) + 8X(f),U(/) = U*(/) + 8U(f) - вектор-функции,
характеризующие реальное движение, определяемое уравнением. Положим, что
8х, (0) (i = \,n) - случайные погрешности при реализации заданных начальных
условий, для которых имеет место неравенство
£&c2(0)<s2, (5.131)
•/=1
где 8 - известное число.
При проведении всех последующих рассуждений полагается, что малость
начальных отклонений, определенных неравенством (5.131), гарантирует малость
отклонении X(t) от Х*(/) на интервале управления [0,Г], т.е. при всех Ге[0,Г].
Запишем уравнения, описывающие отклонения реального движения от
программного; имеем
*;(/)+&сД/)=/(дг;(о+&,(о,...,д:; (о+&и(о.
v (5.132)
ih(t) + bux(t),...,um(t) + bum{t),t),i = \,n.
Поскольку
*'(0 = //(*Ч').~.*»('). u\{t),...,um{t),t),i = u, (5.133)
то следующие уравнения определяют возмущенное движение
8*; (г) = 8/; (&, (г),...,б*„ (г), Ьщ (г),...,8ит (/), г), / = п, (5.134)
где
^(Sx^/) 5хя(/)95М1 (/)э-,би|И(/)э/) = у;(г;(/) + &1(/) х;(/) + &„,
w,*(r) + 8w1,...,w^(/) + 8wm,/)-/;(A:1\...,x*,w1*,...,w^,/).
Путем разложения функции bfM = \,n\ в ряд Тейлора в окрестности точки
х,*,...,х*,«*,...,м^ получим
Глава 5. Методы математического программирования
633
5Х(/) = ¥'х * ЪХ + % Г 5U+0{Ьх),
(5.135)
где
¥х\ =
¥х
дхх
ах,
dfx
дх2
дх2
dfx
■" дх„
а/2
а*
дх-у
щ =
аи,
аи,
ди2
Эхк
9/2
(5.136)
а^„
(5.137)
хдщ ди2\ дип
В приведенных выше формулах символ |* означает, что частные производные
находятся в точке
*,-=**,/ = 1,л, uk=uk9k = l9m; 0t(bxx ,...,5хя, 5^ ,...,8wm,/), / = 1,я
- зависимость, характеризующая члены второго порядка малости.
Уравнение (5.135) можно переписать так
4(5х(оь
л
Эх
д¥
5Х+— 5U,5X(0) = 5X°.
9u
(5.138)
Как уже отмечалось, это уравнение описывает движение объекта для начальных
условий, удовлетворяющих неравенству |5Х(0)| < е . Очевидно, качество управления
изменится; степень изменения, обусловленного возмущениями, можно рассчитать по
формуле (5.138).
Систему дифференциальных уравнений (5.135), описывающую отклонение
фактического движения объекта Х(/) от оптимальной программы X (/), можно
записать в виде
п т
7=1 *=1
5.9.3. Синтез оптимальной обратной связи
С помощью приведенных выше рассуждений исходная нелинейная задача (5.126)
и (5.127) свелась к линейной задаче (5.135) и (5.138). Положим, что функционал,
характеризующий степень близости траекторий Х(/) и X*(f) на промежутке [0,7],
является квадратичным
ЛГ\ о- , ОСС
634 Методы теории оптимального управления. Часть III
^=J[Z*&?(oV> (5Л39)
оЫ )
а на управление ограничения не налагаются.
Поскольку система (5.138) является линейной, а задача минимизации
функционала (5.139) является линейно-квадратичной задачей относительно неизвестных 8Х(/)
и 6U(/), то ее решение имеет вид
5U(/) = -K(/)5X(f) = -K(/,X°)5X(f). (5.140)
Последняя формула отражает факт управления по принципу обратной связи по
отклонениям от программы 8х, (/) = xt (t)-x* (/),/ = l,/i. Таким образом, по формуле
(5.140) можно рассчитать стабилизирующие управления 8u](t),8u2(t)9...,5um(t),
минимизирующие критерий (5.139) и уменьшающие «расстояние» в смысле критерия
(5.139) между Х*(/) и X(f).
Если найдены компоненты стабилизирующего управления 8wj(/),5w2(^),
...,5um(t),TO компоненты результирующей вектор-функции управления
определяются зависимостями ик (/) = ик (/) + 8иЛ (/), Л = 1,/и .
В практических задачах компоненты ик (/) обеспечивают основное движение
системы, а компоненты buk{t) «парируют» малые отклонения от программного
движения, обеспечивая если Т -> оо , устойчивость и требуемую точность реализации
программного движения. Поэтому обычно выполнено неравенство [1]
u'k{t)\>\buk{t%k = \^.
Если на стабилизирующее управление накладывается ограничение вида
г
J6u2k{t)dt<i;k,k = hm,
о
то критерием, определяющим качество стабилизации, может служить функционал [1]
oL=i *=i J
Поскольку введены критерии, характеризующие степень близости Х*(/) и Х(г),
то функции
Ъик (0 = гк \Ъхх (0,8x2 (/),...,8хя (t)],k = пг, (5.142)
при которых на движениях системы (5.138), возбужденных произвольными
начальными отклонениями из множества (5.131), показатель качества принимает
наименьшее значение, называются компонентами оптимального стабилизирующего
управления (при Г->оо оптимальное стабилизирующее управление при принятых
условиях обеспечивает асимптотическую устойчивость системы).
В результате проведенных рассуждений найдены компоненты (5.142) управления
с обратной связью, при котором при начальных условиях, удовлетворяющих
неравенству (5.131), квадратичный критерий качества (5.141) принимает минимальное
значение [1]. Важным является тот факт, что оптимальная программа X* (/) рассчиг
Глава 5. Методы математического программирования 635
тывается с учетом знания вектора Х° =(xj(O),^2(O),...,a:w(O)) и, таким образом,
матрица K(t) в формуле (5.140) также не зависит от Х° .
Расчет же стабилизирующего управления не требует измерения реальных
начальных условий, необходимо лишь выполнение условия (5.131) (малость начальных
отклонений). Приведем алгоритм реализации рассмотренного выше подхода [1]:
• вычисляется и запоминается набор оптимальных программ U*(/),X*(/) для
достаточно грубой сетки начальных условий Х° ;
• вычисляются и запоминаются матричные коэффициенты Ки,Х° j усиления
регуляторов, обеспечивающих оптимальную коррекцию для каждого
начального условия; ,
• определив наиболее близкое к фактическому начальное условие из числа
запомненных и используя соответствующую матрицу Ku,X°j, формируется
текущее управляющее воздействие.
Структурная схема оптимальной системы, работающей по принципу обратной
связи, представлена на рис. 5.29.
При наличии внешних возмущений N(/) = (/?,(/),...,ns (/)) уравнение (5.126)
имеет вид
X = F(X,U,N,f). (5.143)
Из последнего уравнения можно получить
&/ =Е<#)5*, +М(05м* +2>?v(0K, '=п с5-144)
j=\ k=\ v=l
i*
fir
где \|//v (t) = —4 , / = 1,л; v = 1,5.
onv\
Можно указать следующие случаи, определяемые объемом информации о 3nv :
• имеется полная информация о вектор-функции N(/), например, компоненты
пк (/) могут быть точно измерены в процессе движения объекта;
• известны статистические характеристики процессов 5лу (/), v = 1,5 ;
• известно, что |блу(/)| <5/7v, v = 1,5 , т.е. функции 5лу(г) ограничены
известными числами.
В зависимости от указанных трех факторов используется следующая
классификация оптимальных систем [1]:
• равномерно-оптимальные;
• статистически-оптимальные;
• минимаксно-оптимальные.
В первом случае мерой эффективности стабилизирующего упраэления
используется интеграл вида
oL/=i **i J
а во втором случае - интеграл
636 Методы теории оптимального управления. Часть III
J = M JlE^Sxf+XY^U ; (5.146)
toV/=i *=i ) J
стабилизирующие управления находятся из условия минимума функционалов (5.145)
и (5.146) на решениях системы (5.144).
В третьем случае, когда информация о N(/) отсутствует, находит применение иг-
ровой подход к определению оптимального управления, обеспечивающий наилучший
результат при наихудшем внешнем воздействии. Соответствующие системы
получили название минимаксно-оптимальных [1].
В заключение остановимся на некоторых обстоятельствах, которые необходимо
учитывать при решении задачи синтеза оптимальной нелинейной системы с
помощью рассмотренного здесь алгоритма, в основу которого положены следующие
ключевые моменты:
* известна оптимальная программа X* (t);
© задача сводится к синтезу оптимальной линейной системы по интегральному
квадратичному критерию с помощью линеаризации в окрестности
программной траектории X (/).
Одно из обстоятельств состоит в том, что алгоритм предполагает гладкость
характеристик нелинейных элементов. Другое обстоятельство - отсутствие
ограничений на U*(/,X(/)) и Х(/), т.е. на управление и фазовые переменные ограничения
не накладываются.
При теоретическом обосновании рассмотренного подхода для решения
конкретных задач важным является обоснование факта малости отклонения X(f) от
X (/) для всех ^е[0,Г], если имеет место малость начальных отклонений.
Рассмотренная схема имеет весьма широкое распространение; ее же теоретическое
обоснование требует проведения соответствующих исследований.
В заключение отметим, что для измерения переменных состояния необходимо
использовать наблюдающие устройства. В общем случае свойство наблюдаемости
нелинейных объектов установить весьма сложно. Поэтому на практике используют
линеаризованные уравнения: линеаризуют уравнения объекта в окрестности X* (/), а
затем уже применяют стандартные критерии наблюдаемости для линейных
нестационарных систем.
В заключение отметим, что в [44] рассмотрены задачи синтеза приближенно
оптимальных (субоптимальных) обратных связей при следующих гипотезах:
* гипотеза слабой управляемости объекта,
о гипотеза слабой нелинейности,
* гипотеза о разных скоростях изменения переменных состояния.
Пример 5.12 [49]
На практике часто встречается задача управления температурой в химическом реакторе с
непрерывным перемешиванием Управляющим воздействием является скорость подвода охлаждающей среды
Запишем дифференциальное уравнение объекта
pCpy(dT/d,-) = pCpF(Tf -Т)Ц-АН)П^-Е1ЯТ -Q,
Г(0) = Г,.
Если воспользоваться безразмерными переменными х = 777у, t-t'FIV, a = (-AH)k0V/pCpTfF ,
у = ЕI RTf , u = Q'/ pCpFTf , xo = To/Tf , xd=Td/Tf,TO исходное уравнение принимает вид
dx/dt = \-x + ae-y/x-u, x(0) = *b- (5.148)
Глава 5. Методы математического программирования
637
Минимизируемый критерий определяется формулой
J=\\[(x-xJ)2 + au2]dt
(5 149)
Предположим, что известны оптимальная программа Х*(/) и оптимальное программное управление
Линеаризованные динамика и критерий задаются матрицами
где
А = (д//дх)\= \-\Jay/x2)e-i/x' [в = (д//ди){ =-\,
О = (э2Я/ах2)[=1 + Шау^хм)-[2ау//31|^//,
R = (d2tf/dw2)f=a, N = 0,
И (X,IU,/) = -(XTQX + UTRU) + кт(АХ + BU)
- гамильтониан.
Уравнение Риккати для Р(/) имеет вид
р(т) = о,
или с учетом того, что X* = аи*,
\ + Х
ау2 2ау
(•Г И'
,-Г/х
dt
S-e-"' -I
•\2
И"
Р+^ 1-ссм
ay2 lay
W1 (^*)3,
*-Г/*
К(/) = -Р(/)/а.
Отсюда получается выражение для оптимального регулятора
,i(/)=«-(/)-k(/)[x(/)-x-(0]
(5 150)
(5 151)
(5 152)
638 Приложения
ПРИЛОЖЕНИЕ 1. ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ
ПРИ ОГРАНИЧЕНИЯХ
НА ФАЗОВЫЕ КООРДИНАТЫ
В данной главе работы по-прежнему рассматривается решение задачи
оптимального управления. Однако в отличие от главы 2 теперь предполагается, что
ограничения заданы как на вектор управления, так и на фазовые переменные системы.
Ограничения на фазовые координаты существенным образом усложняют определение
оптимального управления и оптимальной траектории.
Большое внимание уделяется изложению необходимых условий оптимальности.
Изложение начинается с рассмотрения условий оптимальности при ограничениях на
фазовые координаты произвольного порядка, а затем указываются те упрощения,
которые имеют место при ограничениях на фазовые координаты первого порядка.
Такой способ изложения позволяет избежать ненужной тавтологии, которая
обязательно имела бы место, если бы в начале рассматривались ограничения первого
порядка, а потом - любого порядка.
Как и в главе 2, большое место отводится оптимальному по быстродействию
управлению линейными объектами. Для таких задач формируются достаточные
условия оптимальности, рассматривается управление объектом с помощью
инерционного руля, приводятся примеры решения задачи синтеза оптимального по
быстродействию управления со специально подобранными модельными объектами.
П1.1. ПРИНЦИП МАКСИМУМА ПРИ ОГРАНИЧЕНИЯХ
НА ФАЗОВЫЕ КООРДИНАТЫ
При определении оптимального управления, наряду с ограничениями на
управление, часто необходимо учитывать также ограничения на фазовый вектор системы.
При управлении двигателем постоянного тока, например, ограничения могут быть
наложены: на величину управляющего напряжения, на величину тока якорной цепи,
на скорость вращения двигателя. Ограничения на фазовые координаты существенно
усложняют определение оптимального управления.
Необходимые условия оптимальности при ограничениях на фазовые координаты
в форме принципа максимума были получены Р.В. Гамкрелидзе [15] (см. также [3]).
По современной терминологии указанные условия относятся к случаю, когда
ограничения на фазовые координаты имеют первый порядок. Вообще следует отметить, что
установлению условий оптимальности при ограничениях на фазовые координаты
посвящено много работ [39], причем в подавляющем большинстве этих работ
рассматриваются ограничения первого порядка. При управлении техническими
объектами ограничения на фазовые координаты выше первого порядка встречаются весьма
часто.
В настоящем параграфе излагаются необходимые условия оптимальности при
ограничениях на фазовые координаты произвольного порядка. При этом мы не будем
останавливаться на доказательстве формулируемых теорем ввиду их громоздкости.
Рассмотрим объект, движение которого определяется уравнением
^ = f(x,u), (П1.1)
dt
здесь х = (хих2,...9х„), f = (/i,/2,...,/J - «-мерные векторы, и = (w1,w2,...,w,) -
/-мерный вектор управления. Вектор х будем называть в дальнейшем вектором со-
Приложение 1. Оптимальное управление при ограничениях на координаты 639
стояния или фазовым вектором системы (П1.1). Область U допустимых значений
управления зададим неравенствами
Лу(и)<0, у = п. (П1.2)
Предположим далее, что заданы ограничения на область значений фазового
вектора х. Именно, будем считать, что вектор х может принимать свои значения из
некоторой ограниченной области В , определяемой неравенствами
g,(x)<0, y=U. (П1.3)
Граница области В образована к поверхностями S}, заданными уравнениями
g,(x) = 0, j = \J.
Рассмотрим следующую задачу. Пусть в фазовом пространстве X системы (П1.1)
заданы две точки х° =(jc1°,X2,...,x^) и х1 =(х{,х\,...,х]п), каждая из которых
принадлежит области В . Требуется среди управлений u(/)еU, to<t<t{, переводящих
фазовую точку х системы (П1.1) из начального положения х(/0) = х° в конечное
положение x(/j) = х1 и притом так, что соответствующая траектория х(/) е В , найти
такое, которое доставляет минимум функционалу
J = J/o(x,u)A. (П1.4)
'о
Управление и траекторию, решающие поставленную задачу, будем называть
оптимальными.
Обозначим С точку выхода фазовой траектории х(/) на границу области В, а
через /** - точку схода траектории \{t) с границы области В в открытое ядро
области. Точку отражения, как и точку выхода, обозначим t*. Точки /* ,/** (точки
выхода, схода и отражения) называются также точками стыка траектории х(/). Ниже
рассматриваются только такие оптимальные траектории х(/), которые имеют
конечное число точек стыка. Далее, будем предполагать, что каждый граничный участок
оптимальной траектории x(t) не имеет точек, лежащих на пересечении двух и более
ограничивающих поверхностей.
А*
вычисленная в силу уравнений (П1.1), должна равняться нулю, т.е. имеет место
равенство
d dgix)
^(X)=^T/(X'U)=O-
Будем предполагать, что каждая из функций gy(x) дифференцируема по / - q}
раз, где qj - порядок производной, в которой впервые (в силу (П1.1)) появляется
явно управление и. При этих условиях ограничение
g/x)<0
назовем ограничением порядка q}. Обозначим
Если траектория х(/) лежит на границе Sj области В , то производная — gy(x),
■77s,oo=*;(x), v=uy-i,
at
640 Приложения
и будем предполагать, что для любого j q} <n, ибо в противном случае система
уравнений
gy(x) = 0,
(П1.5)
ф;(х)=о, v=Uj-\
может оказаться противоречивой.
Ниже широко используется понятие регулярной точки х . Это понятие относится
к переменной области управления и его удобно ввести для некоторой абстрактной
области, которая в работе конкретно нигде не используется. Рассмотрим такую
область. Обозначим ее через U(x) и зададим соотношениями
*,<*.")*<>, у-п (Ш6)
/>a(x,u) = 0, а = 1,к,
где функции Ry и Ра, у = 1,/, а = 1, к , непрерывно дифференцируемы по х и и.
Пусть (х,и) - произвольная пара, удовлетворяющая условиям (П1.6). Индекс
у, у = 1,/, назовем активным в точке (х,и), если
Лу(х,и) = 0.
Множество всех активных в точке (х,и) индексов у обозначим /(х,и). Точку
х* назовем регулярной, если для любого ueU(\) следующие векторы
graduPa(x\u), а = 1,к,
gradu/^(x*,u), y€/(x\u)
линейно независимы. Множество регулярных точек хеХ назовем областью
регулярности. Справедливо следующее утверждение.
Лемма. Если х° - некоторая регулярная точка и множество U(\°) ограничено,
то найдется такое г > 0, что окрестность х - х° < s принадлежит области
регулярности.
Доказательство леммы приводится в [16].
Предполагается, что функции /(x,u); /0(x,u);/?y(u), y = l,/, непрерывно
дифференцируемы по своим аргументам. В качестве допустимых управлений будем
рассматривать кусочно-непрерывные вектор-функции и(/), принимающие свои
значения из области U, определяемой неравенствами (П1.2). Пусть, далее, соотношения
(П1.2) удовлетворяют условию общности положения, т.е. для любого u eU
следующие векторы
grad/?y(u°), у б/(u°)
линейно независимы.
Введем функции
P/(X)u) = ^7g7(x) = [grad0j>-1(x)]T-/(x)u). (П1.7)
Обозначим ш* (х) переменную область управления, заданную неравенствами
Ду(и)<0, у = п
Л(х,и)<0.
Приложение 1, Оптимальное управление при ограничениях на координаты 641
Символом соу (х) будем обозначать область управления, определяемую
соотношениями
/?Y(u)<0, y = U
/>7(x,u)>0,
а через со7 (х) обозначим область управления, заданную условиями
/^(и)<0, у = п
/>,(x,u) = 0.
Так как соотношения (П1.2) удовлетворяют условию общности положения, то
отсюда следует: если х - некоторая точка, регулярная относительно области соу (х), то
она регулярна одновременно и относительно областей о>7(х) и со**(х). Это
позволяет единообразно ввести понятие регулярной траектории.
Если в некоторый момент t0 выполняются равенства g, (х(/0)) = 0 ,
ф;(х(/о))=о, v = w,-i,
а в интервале /0 < / < tx управление u(t) удовлетворяет неравенству
P,(x(0,u(0)<0, (П1.8)
то, как легко видеть,
g,(x(0)<0, to<t<tx.
Если неравенство (П1.8) заменить равенством
/>7(x(0,u(0) = 0,
то траектория х(/) целиком лежит на границе «S/.
Очевидно, в каждой точке t*a выхода на ограничение и в каждой точке ta схода с
ограничения должны выполняться соотношения (П1.5). Однако в точке отражения
траектории нет необходимости требовать выполнения всех равенств (П1.5). Точку t*a
назовем точкой отражения порядка qj (cjj < qj), если
<£j(x(>a)) = °> v = l,§y-l, q}<qP
или
Ф;(х(/а)) = 0, v = l,§7-l, 4j=qj-
Если qj < q}, то 'qj должно быть четно и, кроме того,
0j'(x(O)<<>- (ш-9)
Уравнения (П1.5) задают в фазовом пространстве X некоторое многообразие.
Будем считать, что для любого j указанное многообразие является гладким, т.е. в
каждой точке многообразия векторы
gradgy(x), grad0](x),...,grad0jy"1(x)
линейно независимы. Положим, далее, что функции Pj(x,u), определяемые
соотношением (П 1.7), имеют непрерывные производные по переменным х и и.
642 Приложения
Пусть х(/), /0 -'-'i - оптимальная траектория, соединяющая заданные точки х° и
х1 и принадлежащая допустимой области В . Точками стыков траектория х(/)
разбивается на ряд участков. Каждый из таких участков будем называть элементарным
процессом. Траекторию х(/) можно рассматривать, таким образом, как сложный процесс,
состоящий из нескольких последовательно протекающих элементарных процессов.
Рассмотрим следующую вспомогательную задачу. Пусть сложный процесс
х(7), to<t<tl9 точками /*,/**,...,/*,/** разбит на элементарные процессы. Каждый из
этих элементарных процессов описывается системой дифференциальных уравнений
(П1.1), причем на отрезках t*a<t<t", а = 1,5, управление и(/) может принимать
значения из области со* (х), а в остальных случаях - из области U. В точках t*a
переключения элементарных процессов должны выполняться соотношения (П1.5), если /*
-точка выхода на ограничения или точка отражения порядка q}, или соотношения
g,(*(0) = o,
если /* - точка отражения порядка cjj, q}<qr Относительно моментов /", а = 1,5
будем предполагать, что они могут выбираться свободно. Требуется так выбрать
управление u(r), to<t<t{, и моменты времени to,t],...,t*a,t",CL = Us, чтобы
соответствующая фазовая траектория х(/), соединяющая точки х° и х1, доставляла
минимум функционалу (П1.4).
При выводе необходимых условий оптимальности оптимальную траекторию
сравнивают с близкими (варьируемыми) траекториями. Обозначим t*a + 5/*^, /" +8/"
точки стыка варьируемой траектории. Если х(/)е£, то в соответствии с (П1.5) и
(П 1.8) близкие траектории х(/) + 8х(/) на отрезках t*a+8t*a<t<t*^-\-bt*^ также
принадлежат области В . И только в окрестностях точек стыка t*a, /" варьируемые
траектории вспомогательной задачи могут, вообще говоря, выходить за пределы области
В . Однако, как показано в [5] (см. §4.4), несмотря на отмеченное обстоятельство,
необходимые условия оптимальности вспомогательной задачи сохраняют свою силу
и для исходной задачи. Условия оптимальности для вспомогательной задачи можно
записать, воспользовавшись теоремой 4.4 [5].
Введем вспомогательный вектор Ч'(О = (м;о(О»Ч/1 (0>--->Ч*п(0) и скалярную
функцию
п
#(i|/,x,u) = £i|/,/(x,u) = [\|/] f(x,u),
/=0
где f(x,u) = (/0(x,u),...,/,7(x,u))-(« + l)-MepHbm вектор. Вспомогательную вектор-
функцию v|/(/), если она соответствует движению в открытом ядре области В ,
определим системой уравнений
rfVjL= ^ = _ЭЯ(у,»,ц) /е1Я
dt dt dXj
а при движении по границе области В - уравнениями
Приложение 1. Оптимальное управление при ограничениях на координаты 643
(П1.11)
d^ ^ = JH&,*9u) дР{ъ,и) -
dt dt dxt dXj
Траекторию t0 < t < /, будем называть регулярной, если регулярен каждый
граничный участок этой траектории, т.е. если регулярна относительно области шу(х)
каждая лежащая на границе области В точка x(t) данной траектории.
Будем говорить, что в точке t*a выхода на ограничение выполнено условие
скачка, если имеет место одно из выписанных ниже трех соотношений:
Vo('a+O) = 4>o('a-°)>
V/
дх,
v=l
Ч>о('а-О) = О,
,. m о dgj(x{fa)) ^ v дФ](х«*а)) . —
(П1.13)
v=0
Уо(^а+°):=О>(
a^7 v=, ел:,
(П1.14)
<//~1
ЕЮ2^о.
v=0
Аналогично, в точке отражения t*a выполнено условие скачка, если выполняется
одно из трех соотношений:
(П1.15)
^ +»). „й -„»„• 3effi£» /f <^*2p,, .^
5x
v=l
\|/0(/e-0) = 0,
,. m о dg7(x(Q) «H v 5Ф;(х(4)) . —
(П1.16)
ЕЮ2^0;
v=0
ч/о(/;+о)=о,
, 0ag;(x(O) ^' у<эф;(х(О) . —
МУД/а+О) = Ц°^ +^>a ^ , l = ln,
Oxi v=l ^
(П1.17)
ЕЮ2^;
lv=0
644 Приложения
здесь qj (cjj <qj) - порядок точки отражения.
Далее, будем считать, что в момент £ схода с ограничения выполнено условие
скачка, если
V(C+0) = i|>(C-0), (П1.18)
либо
М*о(С+О) = О.
дх,
9/"1
y(C-0)*kp»grad^(x(C))+tP«8rad<p;(«(C))j
Последнее соотношение (П1.19) должно иметь место для любых действительных
чисел Рд, v = 0,9,-1.
В равенствах (П1.12) - (П1.19) ju£, v = 1,<77 -1 - некоторые действительные чис-
. Для констант ii4ar , |l
следующие соотношения:
ла. Для констант ц^ , [i4aj , входящих в условия (П1.12), (П1.15), справедливы
Не' *0, (П1.20)
если t*a - точка выхода на ограничение;
ц^О, q}<qjy (П1.21)
если /* - точка отражения траектории;
цГ1=0, (П1.22)
если t*a - точка отражения траектории и выполняется хотя бы одно из двух
соотношений:
^(х(О,и(/;-0)) = 0,
ру(х(/;>,и(/;+о))=о.
Кроме того, в условии (П1.13), если оно применяется в паре с (П 1.18) (а это
возможно, когда qj > 1), а также в равенствах (П1.16) и (П1.17) при ^ = q}
справедливо соотношение (П1.22).
Далее отметим, что для одного и того же граничного интервала t*a < t < ta
условие скачка в форме (П1.14) может применяться только в сочетании с условием
(П1.18). Обратное утверждение неверно, т.е. условие скачка в форме (П1.18) может
применяться в паре с (П 1.12) либо (П1.13).
Интервал t*a<t< f ** назовем граничным интервалом первого рода, если в момент
t™ схода с ограничения выполняется соотношение (П1.18). Интервал t^ < t < t"
будем называть граничным интервалом второго рода, если в точке схода t"
выполняется соотношение (П 1.19). Интервалы ^*</</^*+1, а = 1,5-1, t0 </</,*, /**</</ls
соответствующие движению фазовой точки в открытом ядре области В, назовем
внутренними интервалами.
Приложение 1. Оптимальное управление при ограничениях на координаты 645
Теорема Ш.1. Пусть регулярная траектория х(/), t0 < t < tb принадлежит
области В и соединяет заданные точки х и х : Для оптимальности управления u(t)
и траектории х(/) необходимо существование непрерывной на отрезке 70 < t < t]
(за исключением, быть может, точек стыка) вектор-функции \|/(/), кусочно-
непрерывных функций X(t\ vy(/), у = 1,/, определенных в каждом из граничных
интервалов t*a<t<t", ос = 1,5, таких, что:
1) вектор-функция \|/(0 определяется на внутренних интервалах системой
уравнений (П1.10), на граничных интервалах - уравнениями (П1.11);
2) в каждом из интервалов движения функция
vj/0(/)<0;
3) на граничных интервалах выполняются соотношения
ая(м/(0,х(/),и(0) dPjWMO) X эят(и(/)) —
дщ дщ р} дщ
vr(/)/?y(u(0) = 0,vY(/)>0, y = U, г; </<С. (П1.23)
причем \(t) > 0, если ta < t <ta -граничный интервал первого рода',
4) в каждой точке стыка оптимальной траектории выполнено условие скачка;
5) выполняется условие максимума функции H(\\f(t), х(/), и(/)):
а) на внутренних интервалах
#(V(0,x(0,u(0) = max tf(y(0),x(0,u), (П1.24)
ueU
б) на граничных интервалах первого рода
Я(Ч»(/),х(0,1|(0)= шах Я(м»(/),х(0.«). (П1-25)
М€О)у(х)
в) на граничных интервалах второго рода
Я(«|»(0,х(0,и(0)= max Я(*|/(/),х(/),и); (П1.26)
U€COy(x)
6) в каждом из граничных интервалов выполнено условие нетривиальности
решения
V(O*(O,ji-grad0;'-1(x(O), (П1.27)
где \х - произвольное действительное число;
7) в каждый момент времени /, /0 < / < tx, вектор-функция \|/(/) ^ 0 (общее
условие нетривиальности решения);
8) функция
Я(ч1(/),х(0,и(0) = 0, tQ<t<tx.
Замечание 1. Условие скачка в форме (П1.12) можно отнести к точке схода /а ,
положив вектор-функцию \\f(t) непрерывной в точке t*a. Но тогда условие
максимума (П1.25) следует заменить соотношением
tf(M/(O,x(O,u(O)= max tf(i|/(/),x(/),u).
ueco, (x)
Теорема П1.1 задает необходимые условия оптимальности при ограничениях
произвольного порядка. Однако степень сложности условия скачка существенно
зависит от порядка ограничения. Для ограничений первого порядка условие скачка за-
646 Приложения
метно упрощается. Если ta - точка выхода на ограничение первого порядка (или
точка отражения), то, как следует из (П1.22), (П1.28), (П1.27), соотношения (П1.16),
(П1.17), (П1.14) оказываются принципиально невыполнимыми и их следует
исключить из условия скачка. Далее, в [3] доказывается, что в условии скачка,
соответствующем точке отражения, ^°а > 0. Из (П1.21) следует, что ^°а = 0, т.е. соотношение
(Ш. 15) принимает вид
4>('a+0) = i|/(/;-0). (П1.28)
Очевидно, условие скачка в форме (П1.28) можно отнести также и к теореме 24
[3]. Отметим, наконец, что условие скачка в форме (П1.13) может выполняться (для
одного и того же граничного участка) только в сочетании с условием скачка в форме
(П1.19).
Вместо регулярности траектории х(/) можно требовать ее слабую регулярность.
Пусть u(t), ta<t<ta , - некоторое управление, а х(/) - соответствующая ему
траектория системы (П1.1), целиком лежащая на границе 5; области В . Граничный
участок t*a < t < t** траектории х(/) называется слабо регулярным, если в каждый
момент времени /, t*a < t < t", следующие векторы
grad/?y(u(0), ye/(u(/)),
gradu/>,(x(0,u(0) (Ш'29)
линейно независимы. При этом в каждой точке t' разрыва управления u(t) (включая
и точки t*a,t") линейно независимыми должны быть как векторы (П1.29),
определяемые парой (х(/')> u(f'-O)), так и векторы, определяемые парой
(x(f' + 0),u(/' + 0)). Траектория х(/), to<t<t{, называется слабо регулярной, если
слабо регулярны все ее граничные участки.
Ниже, наряду с областью ш*(х), нам понадобится ее подмножество со* (х), такое,
что точка х регулярна относительно множества шу (х). Аналогичным образом
вводятся области со**(х) и 6>7(х)-
Теорема П1.2. Пусть u(/), t0 < t < tx, - оптимальное управление, а х(/) е В -
соответствующая ему траектория. Если траектория х(/) слабо регулярна, то
справедливы все условия теоремы П1.1, кроме соотношений (П1.25) и (П1.26), которые следует
заменить равенствами:
Я(ч1(/),х(/),и(/))= max tf(V(0,x(/),u), (П1.30)
ued)7(x)
/У0КО,х(О,и(О)= max tf(i|/(0,x(0,u). (П1.31)
иесоДх)
Для технических объектов области со* (х) и со7 (х) обычно совпадают с
замыканием множеств &*(х) и а>7(х). Но тогда условия максимума (П1.30) и (П 1.31)
можно заменить соотношениями (П1.25), (П1.26), т.е. в этом случае слабо регулярная
оптимальная траектория удовлетворяет всем условиям теоремы П1.1.
Теорему П1.1 можно усилить, если в качестве допустимых управлений
рассматривать кусочно-непрерывные, кусочно-гладкие вектор-функции и(/).
Приложение 1, Оптимальное управление при ограничениях на координаты 647
Теорема П1.3. Пусть допустимые управления и(/) представляют собой кусочно-
непрерывные, кусочно-гладкие вектор-функции u(/) e U . Если оптимальная
траектория x(r), t0 < t < tx, регулярна, то:
1) выполняются все условия теоремы П1.1;
2) на каждом граничном интервале в каждой точке дифференцируемости
функции X(t)
— <0. (П1.32)
dt
Замечание 2. В теореме П1.3 оптимальную траекторию х(/) можно считать слабо
регулярной. Это приводит к изменению пункта 1 теоремы. Именно, в пункте 1
ссылку на теорему П1.1 следует заменить ссылкой на теорему П1.2.
Сделаем замечание, общее для теорем П1.1 - П1.3.
Замечание 3. В теоремах П1.1 - П1.3 соотношения (П1.12), (П1.15), (П1.18)
являются главными в условиях скачка. Дело в том, что в нормальном случае vj/0(O *■ О,
и условия скачка в других формах оказываются невозможными.
Остановимся кратко на обсуждении полученных результатов.
В теореме П1.3 рассматривается более узкий класс допустимых управлений.
Однако это позволило получить дополнительное соотношение (П1.32). Опыт
применения условий оптимальности показывает, что неравенство (П1.32) имеет важное
значение. Можно привести достаточно простые примеры, в которых дополнительное
условие (П1.32) заметно облегчает синтез оптимального управления. Впервые
неравенство (П1.32) в числе необходимых условий оптимальности было получено в [3]
(см. теорему 2.5) для систем с фазовыми ограничениями первого порядка. Теорема
П1.3 устанавливает справедливость данного неравенства для фазовых ограничений
произвольного порядка.
Если теорему П1.3 записать применительно к ограничениям первого порядка и
сравнить с известной в теории оптимального управления теоремой 25 [3], то теорема
П1.3 отличается тем, что сочетает в себе сильное условие максимума (П1.25) с
неравенством (ГТ1.32). В теореме 25 приводится лишь слабое условие максимума (Ш .31).
Доказательство теоремы П1.1 приводится в [5], причем схема доказательства
данной теоремы заимствована из работы [17], в которой получены условия
оптимальности при ограничениях на фазовые координаты первого порядка. Возможность замены
условий типа «общности положения» более слабым требованием регулярности
оптимальной траектории непосредственно следует' из сформулированной выше леммы.
Далее, теорема П1.2 легко выводится из теоремы П1.1.
П1.2. ДОСТАТОЧНЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ
ПО БЫСТРОДЕЙСТВИЮ
В настоящем параграфе доказывается, что для линейного объекта полученные в
параграфе П1.1 необходимые условия оптимальности являются одновременно
достаточными или переводятся в разряд достаточных путем незначительного усиления их.
Будем предполагать, что движение объекта задается уравнением
— = Ax + Du, (П1.33)
dt
здесь А и D - постоянные матрицы, имеющие размерности соответственно п х п и
пхг,\ - «-мерный вектор, характеризующий состояние системы, и - г-мерный
вектор управления. Управление и может принимать свои значения из замкнутого
параллелепипеда U , определяемого неравенствами
648 Приложения
Axv<uv<Al, v = u, (П1.34)
где Alv < 0,aI > 0 . Пусть, далее, ограничение на фазовые координаты имеет вид
<М, (П1.35)
здесь к,,к2,...,кл и М - некоторые константы. Ниже предполагается, что
ограничение (П1.35) имеет порядок q. В силу линейности ограничения (П1.35) и
управления (П1.33) каждая из функций ф](х),Ф^(х),...,Ф^ч(х),. j = 1,2, также является
линейной. Положим
ф?-\х)=£С/х„ фг\*)=-2>л-
В тех случаях, когда речь идет о произвольной ограничивающей поверхности £у
будем использовать обозначение Фд~х(х).
Рассмотрим двухточечную задачу об оптимальном по быстродействию
управлении объектом (П1.33) при наличии ограничений (П1.34), (П1.35). При этом
предполагается, что начальная точка х° принадлежит открытому ядру области В , а конечная
точка х1 совпадает с началом координат. Отметим, что в данном случае функционал
(П1.4) имеет вид
J=\dt. (П1.36)
Ф.
<0
В настоящем параграфе в качестве допустимых управлений рассматриваются
кусочно-непрерывные, кусочно-гладкие вектор-функции и(/), удовлетворяющие
неравенствам (П1.34). Далее, оптимальная траектория предполагается слабо регулярной.
Такая траектория, очевидно, должна удовлетворять условиям теоремы П1.3 (см.
также замечание 2).
Выведем для сформулированной выше задачи из теоремы П1.3 ряд простых
результатов, которые будут использованы затем для доказательства достаточности
указанных условий.
Для объекта (П1.33)
#(i|/,x,u) = i|/0+\|/TAx + \|/TDu, (П1.37)
а функция
/>(х)= WAx+ WDu, (П1:38)
дх дх
здесь \|/ =(v|/1,v|/2,...,M/n) -«-мерный вектор. Из условия слабой регулярности
траектории х(/) следует, что при движении по границе области В управление и(/) не
может принимать вершинного значения параллелепипеда С/, а функции
не могут одновременно превращаться в нуль. Более того, в каждой точке /
граничного интервала t* <t< /** существует такое и = т , что
^^-Ч» * 0, А]т < Um < А2т . (Ш .39)
tr *,
Приложение 1. Оптимальное управление при ограничениях на координаты 649
В соответствии с (П1.38) уравнение
/>(x,u) = 0 (П1.40)
при фиксированном х определяет в пространстве Ег некоторую плоскость. Так
как вектор
grad/>(x,u)
не зависит от х и и, то область управления со*(х) является замыканием множества
со;(х). Аналогично область со^(х) представляет собой замыкание множества со7(х).
Отсюда, учитывая непрерывность по управлению функции (П1.37). находим, что на
слабо регулярной траектории x*(t) условия (П1.30), (П1.31) можно заменить
соответственно равенствами (П1.25), (П1.26).
Рассмотрим участок оптимальной траектории, принадлежащей границе области В.
Принимая во внимание (П1.39), разрешим уравнение (П1.40) относительно ит:
1 „^ УЛ/ д хх ^ ЧЛ/ , (П1.41)
ит =--
^dcp^ix)
V1
1а~
/=1
дх,
*im
дФч-\\) А ^&d0q-\x)J
ах
1=1 О=1
дх,
1
где символ 2^ означает суммирование по и от 1 до г, пропуская и = т . Под-
ставляя далее (П 1.41) в функцию
A#(i|/,u) = i|/TDu,
(П1.42)
найдем
п г(т)
ДЯ(ч/, u) = Atf<"4V,x,u) = ££4oW'.>- -
1
1=1 0=1
^ дх "■
;=1 ОХ1
дФ"-\х) -ZrxrVj дФ"-\х);
_p=l /=1 j=\ uxi p=\ /=1 v=l LXi
Здесь обозначение Я(т)(\|/,х,и) введено, чтобы подчеркнуть, что выражение (П1.43)
получается из (П1.42) при подстановке в последнее (П1.41).
Утверждение 1. Если max A#(i|/,u) достигается на управлении и , причем
U€CO*(x)
/=1 dxi
Am<Um<Am> V
dim^0, то управления w*, v = l,r, v^w, доставляют
/=1
max ДЯ(1|/,х,и). Здесь область U^ задается неравенствами (П1.34), из которых
ие(/
следует исключить индекс v = т .
Утверждение 1 непосредственно следует из равенства (П1.43).
На границе области В вспомогательный вектор \\r(t) находится из уравнений
d\\JQ
dt
= 0,
dy = 5Я(у|/,х,и) + дР(х,и)
dt дх дх
(П1.44)
650 Приложения
здесь скалярный множитель X(t), в свою очередь, определяется из уравнения
где Ra(u) = 0 -уравнение проходящей через точку u(/) грани параллелепипеда U
Учитывая (П1.39), из (П1.45) найдем
п
X(t) = l^—z . (П1.46)
Ar fa im
/=1 0Xi
Условимся считать, что в момент / определен скалярный множитель Xm(t), если
для данного / выполнено условие (П1.39) . Тогда скалярный множитель X(t)
определяется формулой (П1.46). Вообще говоря, в один и тот же момент времени t
может быть определено несколько множителей: lXm(t),XK(t\...,Xc(t), причем
Xm(t) = XK(t) = ... = Xc(t).
Пусть в момент /♦ непрерывности управления и(/) определен множитель ^с(/*).
Тогда в силу непрерывности и(/) и найдется такая окрестность точки
Эх,-
/*, что для L-z<t<L + z будет определен множитель Xc{t ). Пусть, далее, /* -
точка разрыва управления u(r) и пусть для и(/«,-0) определен множитель Хт(и),а
для и(и +0) - множитель А.к(/*). Тогда, очевидно, можно указать такие
полуинтервалы [г*,/*-6]),[/*,/*+s2), в каждой точке которых определены соответственно
^ш(/) и ^.к(/). Точку /' будем называть точкой переключения множителя X(t)
(множитель Xm(t) переключается на множитель XK(t)), если существуют два таких
интервала [t'j'-e^) и [/',/' + s2), что X(t) = Xm(t) при /е(/',/'-Б,) и X(t) = XK(t)
при te(/',/' + б2) и не существует такого интервала (/'-е,/' + е) и такого с, что
X(t) = Xc(t) при /е(/'-е,/' + е). Из заданного определения следует, что точка
непрерывности управления и(/) не может быть точкой переключения.
Утверждение 2. В каждой точке /' переключения множителя X(t) последний
остается непрерывным.
Из условия непрерывности функции #(\|/,х,и) следует, что управления и*(/'-0)
и и*(/' + 0) доставляют в момент t' максимум функции (П1.37). Соединим точки
u*(r'-0) и iT(/' + 0) в пространстве ЕГ отрезком П (П с co(x(f'))) • В силу
линейности относительно управления функция (П1.37) достигает максимума относительно
множества со*(х(/')) в каждой точке отрезка П. Учитывая утверждение 1, получаем,
что функции A#(m)(\|/,x,u) и Д#(к)(\|/,х,и) достигают на отрезке П максимума
относительно параллелепипеда U^ и £/(к) соответственно.
По определению точки /' имеем:
Al<um(t'-0)<A2m, um(t' + O)czAl\jA2m,
Al<u'K(t' + 0)<Al, u'K(t'-0)cAlK\jAl,
Приложение 1. Оптимальное управление при ограничениях на координаты
;=1 Oxi
651
^дФ<>-\х)
Z-
/=1
дх,
dlm*0.
Для любого управления и'еП (и'* и (/'-0), и'* и (/' + 0))
Al<u'm<A2m, A]K<u'K<A2K.
Из (П1.47), учитывая сказанное выше и (П1.43), получаем
П 1 Гл И Я^Л<И
У diK\Vi (О г
Г-
/=1
II^^™4«v« ...
дх,
Разделив (Ш .48) на
ld Lp-iw
L—^—d*
дХ;
(П1.47)
(П1.48)
/=i
дх,
и принимая во внимание (П1.46), найдем
МО-МО = о.
Таким образом, утверждение 2 доказано.
Сделаем некоторые преобразования. Подставив в уравнение (Ш.ЗЗ) um(t) из
(П1.41), получим
х = Атх + О/яй, (П1.49)
где
А =
da ~
din
^дФ"-\х)
U п
V
удФ"~\х) U дхр
PJ
i,j = \,n,
- матрица размерности ихи,
D =
</,„ —
Z
Л = 1
^аФ?-'(х)^
L ax, sm
pv
/•= l,w, v = l,r, vФт,
- матрица размерности «x(r-l), u - (г-1)-мерный вектор, получаемый из вектора
и путем исключения m-й компоненты. Подставим в функцию (П1.37) управление
um(t) из (П 1.41). Тогда
Я(1|/(0,х(/),и(0) = Vo +[^(0]Т Amx + [y(/)]T Dmu . (П1.50)
Раскрывая, наконец, множитель Xm(t) в уравнениях (П1.44), находим
dy
d\\f
s-- -Ji-^-
(П1.51)
Таким образом, из (П1.50), (П1.51) и утверждения 1 следует, что на каждом
интервале, на котором определен некоторый множитель Хт (/), относительно
уравнения (П1.49) должен выполняться принцип максимума в том виде, как он
формулируется для открытого ядра области В.
652 Приложения
Введем некоторое обобщенное условие общности положения (в смысле работы
[3]). Будем считать, что относительно уравнения (П1.33) и ограничений (П1.34) и
(П1.35) выполнено обобщенное условие общности положения, если:
1) для любого ребра к параллелепипеда U векторы
Dk, ADk,...,A""1Dk
линейно независимы в X ;
2) для любого /,/ = 1, г, и любого ребра к параллелепипеда 6/(/) векторы
линейно независимы.
Ниже мы будем предполагать, что соотношения (П1.33), (П1.34), (П1.35)
удовлетворяют обобщенному условию общности положения.
Пусть /,' и t'i+] - две соседние точки, в которых происходит переключение
множителя X(t). Из обобщенного условия общности положения вытекает, что в
интервале t] <t < t'i+l определен только один множитель Лагранжа, например Хт (t).
Разобьем точками переключения множителя X(t) отрезок [t*,t**] на сумму отрезков:
здесь N - конечное число, т.к. и(/) - кусочно-непрерывная, кусочно-гладкая вектор-
функция. Если множитель X соответствует отрезку As, то будем обозначать его X^s.
В силу непрерывности функции H(\\f(t),\(t),u(t))
H(y(t* -0),x(f*),u(r* -0)) = Я(1|/('* +0),x(f*),u(/' +0)). (П1.52)
Из (П1.52), условия скачка (П1.12), соотношений (П1.5) и равенства
/>(x(/*),u(f40)) = 0
найдем
j|>,w,V -о)(щ(Г -о)-«,(/' +о» + ...+
/=l (Ш.53)
п
+ £^rV/(/* -0)(«r(/* ~0)-иг(Г +0)) = 0.
/=1
В соответствии с условием максимума (П1.24) каждое из слагаемых (П1.53)
неотрицательно, т.е. равенство (П1.53) возможно, если каждое слагаемое равно нулю. '
Пусть в момент /* определен множитель Хт (t). Тогда
j^Vi('*-O) = O. (П1.54)
Если в момент t определен множитель XK(t ), то аналогичным образом можно
доказать, что
п
]Г<//ку,.(Г+0) = 0. (П1.55)
/=1
Пусть и*(/) и х*(Г), {q </ <fj, - соответственно управление и траектория,
удовлетворяющие условиям теоремы П1.3, причем предполагается, что
i|/0(0*(U0 </<;,. (П1.56)
Приложение 1. Оптимальное управление при ограничениях на координаты 653
В соответствии с замечанием 3 (§П1.1) в этом случае условия скачка допускаются
только в главной форме (Ш .12), (П1.15), (П1.18).
Будем говорить, что траектория х*(/) доставляет слабый относительный
минимум функционалу (П1.36), если
J(x\t))<JW)
для любых траекторий x(t), принадлежащих «классу» варьируемых траекторий
теоремы П1.3. Отличительными чертами этого «класса» траекторий являются:
1) траектория х(/) выходит на границу области В в близкие моменты t* +5/*,
причем выход на границу области В обязателен, если траектория х* (t) имеет
граничный участок;
2) в интервалах t* + 5f* </</**+ 5/** выполняется неравенство
Ф^ч(х(0)<0; (П1.57)
3) если /* - точка отражения порядка q (q < q), то траектория х(/)
удовлетворяет соотношениям
g(x(/4Sf*)) = 0,
ф'(х(/Ч5/*)) = о, у=п^Т.
Теорема П1.4. Пусть u*(f) и x*(t) - управление и траектория, переводящие
фазовую точку х системы (П1.33) из заданного начального положения х° в начало
координат. Если траектория х* (/) слабо регулярна и удовлетворяет условиям
теоремы П1.3 и равенству (П1.56), то на траектории х*(0- функционал (П1.36) достигает
слабого относительного минимума.
Доказательство теоремы. Условимся простоты ради считать, что траектория
х (/) имеет один участок, лежащий на границе области В . Положим для
определенности, что при t* <t < /** траектория х* (t) лелсит на границе
п
Введем обозначение
п
У = Хк'*' •
/=1
Для доказательства теоремы воспользуемся методом, изложенным в [16].
Запишем равенство*
j-^tx- -х^^ц,^; -х<) + ^(х; -х,)^, (П1.58)
/=о /=о /=о
где траектория x(t) близка к траектории х*(/) в указанном выше смысле. Равенство
(Ш .58) справедливо для любого /, t0 < t < tx, за исключением, быть может, точек стыка.
* Координата xQ(t) находится из уравнения
dx
dt =1,хо(/о) = О,
т.е. XqV^^J .
654
Приложения
Принимая во внимание условие скачка (П1.12), можно записать
/=1 /=1
°xi v=l VXi
Поскольку ограничение (П1.35) имеет порядок q, то
fd M^-Yd Ё*!«- -fd '
,=1 oxi ,=| oxi ,=1
Из (П1.59), (П1.54), (3 .46) находим, что
Далее, из (П1.55) следует равенство
дФч-2(х)
= 0.
(П1.60)
(П1.61)
Определим значение производной —— при t = t* через 8 -функцию. Именно, бу-
dt
дем считать, что вспомогательный вектор \|/(/) при движении в открытом ядре
области В определяется уравнениями
d\\J0 d\\r aT
dt dt V
^)) + §
M°Vg(x(^)) + X^vV0v(x(/*))
v=l
5(/-/*). (П1.62)
Подставляя в (П1.58) уравнения (Ш.ЗЗ), (П1.62), (П1.44), найдем
£!>,<*; -х,) = ач,тО(и' -n)^±^f^-X{t){xt -x,) +
dt]
+p\j/TD(u* -u) + l(t')[y'(-"-]) _y»-')]..5(/-/*) +
+ L0(/->') + ^vt'*v(O-^vw)
L v=i
8(/-/ ),
(П1.63)
где
а =
P =
{1 при to<t<t и /**</</b
0 при /* <t<t*\
[о при to<t<t* и /**</</,,
[1 при /* <t<t**.
Ha отрезке Ay
vTD(u-u)+jr\(tKx;-Xi)dP(*>ц )=11^\ч//(и:-«У)+
7 /=1 v=l
р=1
/=1 /=1
Прибавим к правой части соотношения (П1.64) выражение
dXj
(П1.64)
ч,£Тф'"(х'к-■
dlv(uv-uv)
/=1 v=l dxi
и вычтем его, чтобы не нарушить равенства. Тогда, принимая во внимание (П1.46),
(Ш.ЗЗ) и (П1.35), найдем
Приложение 1. Оптимальное управление при ограничениях на координаты 655
Тжч/ ♦ ч v^/ч/ • \дР(х,и)
\|/'D(u -u) + 2^UtXx,-xt)—\' ' =
ы\ dxi
п r(As)
d
= Z Z div4,i(uv-uv) + X(t)—[0"-\x'(O)-<l>4-]W)]- (П1.65)
/=1 v=l t*t
n r(As) ^sri\q-\/*\
ы\ ы\ dxi
[я (П1.65) в (П1.63) и учитывая (Ш/
/=1 /=i ^Л/
Подставляя (П1.65) в (П1.63) и учитывая (П1.46), получим
N п г(Дл)
x5(/-^) + p^l(A5)^^,vv//(«;-«v) +
Л = 1 /=1 V=l
+
р^(,х/(,-.) -у^^-р^-')-^-»]^-
« « ^) аф^1(ж«)
Л, ZZ Z ^ ^ 4v(«v -«v)Vp
Ь тг— а*&°
п ал«-1
дФч-\х')
+|и°(/(О-ЯО)+ХиУ(/(У)(О-УУ)«)
L v=i
Отметим, что в точке выхода t* справедливы равенства
y(t') = D,
м дх>
b(t-t'). (П1.66)
(П1.67)
/(v)('*) = 0, v = 1,9-1.
Представим траекторию х(/) в виде х(/) = х*(/)+8х(/). В соответствии с (П1.5)
y(t' +dt*) = y\t* +5t') + by(t' +8t') = D,
(П1.68)
y(vV +8/*) = /(v)(/* +5/*) + 8/v)(/* +8/*) = 0, v = l,<7-l.
Из (П1.68), принимая во внимание (П1.67), найдем
6'('*) + о(5'') = 0> (П1.»)
Sy(v\t*) + o(dt*) = 0, v = 1,(7-2,
P(x\t*)u\t* -0))6t* +by{g-]\t*) + o(bt*) = 0.
Здесь символом о(5/*) обозначена величина, имеющая порядок малости выше
первого относительно 5/*, т.е.
lim^ = 0.
Из условия слабой регулярности траектории х*(/) следует, что
Р(хУ),иУ-0))*0.
Из (П1.69) вытекает тогда
656
Приложения
5у(/') = о|бх(/*)|,
6yv)(/*) = o|8x(/*)|, v = u^2.
(П1.70)
Обозначим через т момент времени, в который траектория х(/) проходит через
начало координат. Покажем, что т > tx. Предположим противное и назначим u(f) = О
при т </</,. Тогда х(/) = х1, х </</,.
Проинтегрируем равенство (П1. 66):
«о <=° 'о <о .
'' /У Г чЛ '' N " Г(ДЛ>
х5(,-/>Ф^[цо(/(9Ч)^-'0]Мр11(А5)[£ S ^v/(«C-«v)-
2.2. 2. dPAs—г-—rf,v("v -*Оч>Р ,-+5,-
p=l<=1 v=l
dx,
АЭФ«ч(х)
2."
1=1
ax,.
d,
-]dt- J р[/(^)_^-п]^Л +
/Ajt
► J p[/('-1)-y('"1>]f-^)A + }L0O''(0-y(0)+SVvO'*(v)(/)-^v)(/))
/45/' \ dt ) ,o|_ v=l
xb(t-t*)dt. (П1.71)
Учитывая фильтрующие свойства 5 -функции и.(Ш.7О), можно записать
}L°(/(o-^(O)+Z^v(/(v)(o-yv)(/))
v=l
<7-2
S(/-/ )Л =
(П1.72)
= ^°6^)+ZhVv)(^) = o|8x4^)|.
v=l
Далее, если 5/* >0 , то в интервале t* <t<t* +8/* неравенство (П1.57) не
выполняется. Имеем
' 7 p(/(«-i _^-'))^:Л = 5>;(?-»(/')£(М^)5,- +0(6,-).
Из (П1.69) следует тогда, что
/*+5 /*
^/>.
J Р(/(^)-^))^А = о|вх(/Ф)|.
(П1.73)
В соответствии с условием максимума (П1.24) в каждой точке внутреннего интервала
\|/T(OD(u*(0-u(0)^0. (П1.74)
Далее, из утверждения 1 вытекает, что на граничном интервале
ZKA5)
5=1
п г(Да-)
ff^) 5Ф9Ч(х') , , . ,
Е Z ^vV/(«v-»v)-
р=1/=1 v=l
9*,
/=1 v=l
^дФ"-\х')
ых дх<
^■du»
>0. (П1.75)
Приложение 1. Оптимальное управление при ограничениях на координаты 657
Из (П1.71), принимая во внимание соотношения (П1.61), (П1.32), (П1.72) -
(П1.74), найдем, что
о = Ь9 (П1.76)
где 6>0. Противоречие (П1.76) доказывает недопустимость предположения о том,
что т < /,.
Если t* - точка отражения траектории х*(/) порядка q,q <q, то из уравнения
(П1.52), соотношений (П1.15), (П1.21), (П1.22) следует равенство
ц*"1 = 0.
Далее, при т < /, рассмотренным выше способом можно получить неравенство
(П1.76). Теорема П1.4, таким образом, доказана.
Если ограничение (П1.35) имеет первый порядок, то удается получить
существенно более сильный результат. При этом отпадает необходимость в дополнительном
условии (П1.56).
Теорема П1.5. Пусть \*(t) - слабо регулярная траектория, переводящая фазовую
точку х из заданного начального положения х в начало координат и
удовлетворяющая условиям теоремы П1.3; если ограничение (П1.35) имеет первый порядок, то
на траектории х (t) функционал (П1.36) достигает абсолютного минимума.
Теорема Ш.6 (теорема единственности). Пусть x*(t) - траектория,
удовлетворяющая условиям теоремы П1.5, а х (/) -любая другая оптимальная
траектория, соединяющая точку х° с началом координат. Тогда x**(f) = x*(O-
Доказательство теорем П1.5 и Ш.6 следует из равенства (П1.71). Так как теперь
у^~]\х) = у(х), то условие (П1.76) можно получить, не предполагая траектории x\t)
и х(0 близкими. Подробное доказательство теорем П1.5 и П1.6 приводится в [18].
Рассмотрим объект, движение которого задается уравнением
у^-ап_Уп-х)-...-аху'-аъу = ки, (П1.77)
здесь у - выходная координата, и - управляющий параметр, ait / = 0,л-1, к
-некоторые константы, причем к>0. Представим уравнение (П1.77) в виде системы
уравнений
*1=*2'*2=*3 *"-'=х"' (П1.78)
хп=ки- яох, -а}х2 -....- ап_ххп ,
где х, = у. Пусть на управляющий параметр и наложено ограничение |и| < А[.
Предположим, далее, что фазовые координаты системы (П1.78) должны
удовлетворять неравенству
| *л-1 - 4,-2*1,-2 " - " 4*1 \*М, (П1.79)
здесь di;, i = 1,п - 2, и М- некоторые числа.
Ограничение (П1.79) имеет второй порядок, причем граница допустимой области
В задается уравнением
«(х) = дгя.,+£/л.2д:л.2+... + 4*1-с = 0, (П1.80)
где с = ±М . Как следует из соотношений (П1.78), (П1.80), движение по границе
области В описывается уравнениями
*1 =*2'*2 =*3'"-'*л-3 ~хп-2' mi cn
, , , (111.61)
хп_2 =c-d]xx -d2x2-...-dn_2xn_2.
43 Зак. 366
658 Приложения
Траекторию движения х(/), /0 < / < tx, в задаче (П1.78), (Ш .80), (Ш .36) будем
интерпретировать как некоторый «эстафетный» процесс [5]. В этом «эстафетном»
процессе движение в открытом ядре области В задается уравнениями (П1.78), движение
по границе области В - уравнениями (П1.81). Переключение уравнений движения с
(П1.78) на (П1.81) происходит в момент /* выхода фазовой точки на (л-2)-мерную
гиперплоскость
g(x) = 0,
<P](x) = (xn+dn_2xn_l+... + dlx2) = 0.
Момент /** переключения уравнений движения с (П 1.81) на (П1.78) выбирается
свободно. В точках t и / фазовые координаты связаны соотношениями
х/(/*+0) = х|-(/*-0), / = 1,/!-2, (П1.82)
х,(Г+0) = ;с,(Г-0), / = 1,л-2,
Я(х(Г+0)) = 0, ' (П1.83)
Ф](х(Г+0)) = 0.
Последние два равенства (П1.83) определяют координаты хп_х (/** + 0), хп (t** + 0).
Для указанного «эстафетного» процесса необходимые условия оптимальности
задаются теоремой 4.4 [5].
Введем (я-2) -мерный вектор х = (дг1>х2,...,х/|_2) и (п-\) -мерный
вспомогательный вектор \j) = (v|/0, v|/j,..., v|/w_2), который определяется уравнениями
^ = 0, *2L = _WvAc)t /=1^Г2, (П1.84)
dt ■ dt dxi
здесь H(\\t,x,c) - функция Гамильтона, записанная относительно уравнений (П1.81)
и функционала (П1.36). Будем говорить, что траектория х(/) = (xx(t),x2(t),...,xn(t)),
t* </</**, целиком лежащая на границе области Д, удовлетворяет условию
оптимальности на границе, если найдется такая ненулевая непрерывная вектор-функция
ф(0, определяемая уравнениями (П1.84), что в каждый момент времени
t{t* </</**)
Я(м/(Г) ,х(/),с) = гпахЯ(ц/(0,х(0,^) = 0'
v|/0(/)<0.
Далее, участок траектории \{t), целиком лежащий в открытом ядре области В,
должен удовлетворять теореме 2.1 (принципу максимума Понтрягина).
Будем говорить, что в точке выхода t выполнено условие скачка, если
v|/o(/*-O) = v|/o(/*+O),
дх{ дх,
дхп_х Эх
/7-1
5хи a^w
Приложение 1. Оптимальное управление при ограничениях на координаты 659
Если t - точка отражения, то условие скачка будем задавать одним из соотношений:
yO'-O^vC'+O), (П1.87)
либо
i|/0(/*-0) = y0(/*+0),
^-0) = ^Ч0) + ц0^^ + И1^1^, / = п, (П1.88)
дх( • дх,
|u0signc<0, |i,signc>0.
Равенство (П1.87) относится к точке отражения первого порядка, равенство
(П1.88) - к точке отражения второго порядка. Причем в условии (П1.88) неравенство
ц j s ign с > О выливается в равенство
ц,=0, (П1.89)
если выполняется хотя бы одно из условий:
/>(x(f*),u(/'-0))=4 '
/>(x(f*),u(/*+0)) = 0.
Аналогично, в точке схода ?** выполняется условие скачка, если
Н/о(Г+О) = ч/о(/"-О),
^Г+о)^дГ-о)+ц2М^+Цз^!Ш)) /asI^2t
dxt • дх;
дх„_х Зх„_,
,„(,"+о).Й2«)+Ц]^С)1.
дх„ дхп
В равенствах (П1.86) - (П1.90) [io,[il^2^3 - произвольные действительные числа.
Выписанные выше условия, кроме неравенства jj.osignc7 < 0, вытекают из
теоремы 4.4 [5], записанной для сформулированного выше «эстафетного» процесса, а в
случае точки отражения - также из теоремы П1.1. Правда, условия скачка приводятся
здесь лишь в главной форме.
Будем предполагать, что в точке выхода /* и в точке схода /** выполняются
соотношения
*0, -^Yg(x(0) *0.
Эти соотношения, в известном смысле, эквивалентны требованию регулярности
или слабой регулярности граничного участка траектории x(t).
Теорема Ш.7. Пусть управление и(/) и траектория х(7), t0 <t<tx, переводят
фазовую точку х из заданного начального положения х° =(х,°,...,х^) в начало
координат. Если траектория х(0 удовлетворяет на внутренних интервалах движения
теореме 2.1, на граничных интервалах - условию оптимальности (П1.85), а в точках
стыка - условиям скачка (П1.86) - (П1.88), (П1.90), то на траектории х(/)
функционал (П1.36) достигает абсолютного минимума.
43*
660 Приложения
Теорема Ш.8. Пусть x*(t) = (x*](t),...,x*n(t)) - траектория, удовлетворяющая
условиям теоремы П1.7, а х (t) -любая другая оптимальная траектория. Тогда
x"(t) = x\t).
Теорема П1.7 задает достаточные условия оптимальности. В случае достаточных
условий обычно важно знать, не являются ли эти условия чрезмерно жесткими. Опыт
применения теоремы П1.7 показывает, что она с успехом может быть использована
для синтеза оптимального управления.
Доказательство теорем П 1.7 и П 1.8 аналогично доказательству теоремы П1.4. Оно
подробно приводится в [19]..
П1.3. ОПТИМАЛЬНОЕ ПО БЫСТРОДЕЙСТВИЮ УПРАВЛЕНИЕ
В СЛУЧАЕ ИНЕРЦИОННОГО РУЛЯ
В теории оптимального по быстродействию управления особое место занимает
теорема о числе переключений, полученная еще А.А. Фельдбаумом [20] и
обобщенная в известной монографии [3]. Именно на основании этой теоремы решено
большинство практических примеров по синтезу оптимального по быстродействию
управления. В данном параграфе (см. также [21]) теорема о числе переключений
распространяется на случай, когда управление объектом осуществляется с помощью
инерционного руля.
Итак, пусть движение объекта описывается уравнением
— = Ax + D6, . (П1.91)
dt
здесь 5 = (81,82,...,5r)-r -мерный вектор, каждая координата которого задает
перемещение соответствующего рулевого органа. На перемещение рулей наложены
ограничения
|57|<Я7, у=п. (П1.92)
Будем считать рули инерционными, полагая, что их движение описывается
уравнением
~ = ч, (П1.93)
dt
где и = (щ, и2,..., иг) - г -мерный вектор, задающий, безынерционное управление.
Пусть, далее, вектор и может принимать свои значения из-области U, которая
задается неравенствами
Uj\<AJf у=п (П1.94)
В неравенствах (П 1.92) и (П 1.94) Rj и А} - некоторые числа.
Ниже предполагается, что система уравнений (П1.91) является нормальной.
Именно, будем считать, что для любого j, j = \,r , следующие векторы:
- линейно независимы, здесь d7 - п -мерный вектор, представляющий собой j
столбец матрицы D. В этом случае, как показано в §2.3,'управление и(/) находится из
условия максимума функции Гамильтона (за исключением конечного числа точек)
однозначно.
В соответствии с уравнением (П1.93) каждый из рулей описывается
интегрирующим звеном, и, следовательно, о его инерционности можно говорить лишь условно.
Приложение 1. Оптимальное управление при ограничениях на координаты . 661
Однако во многих технических системах переходные процессы в приводе руля
оканчиваются весьма быстро (по сравнению с временем движения с постоянной
скоростью). В этом случае инерционный руль с достаточной для практики точностью
может быть описан соотношением (П1.93).
Рассмотрим задачу о наибыстрейшем переводе ф'азовой точки системы (П1.91),
(П1.93) из некоторого начального положения в начало координат. Будем
рассматривать эту задачу в двух вариантах. В первом варианте (назовем его вариантом Е)
конечное значение задается как для вектора х, так и для вектора б , т.е. х1 = 0, б1 = 0 .
Во втором варианте (вариант L) конечное значение задается только для вектора
х (х1 = 0). Что же касается начального состояния, то оно предполагается полностью
заданным, т.е. в начальный момент времени заданы векторы х и б .
Приняв переменные 8у, j = \,r за фазовые перем'енные, а вектор и -за
безынерционное управление, сформулированную выше задачу оптимального
«инерционного» управления сведем к задаче об оптимальном безынерционном управлении, но при
ограничениях на фазовые координаты системы.
Сформулируем сначала достаточные условия оптимальности.
Ограничения (П1.92) выделяют в фазовом пространстве X системы (П1.91),
(П1.93) допустимую область В, ограниченную поверхностями S] и S^(y = l,r),
причем поверхность S) задается уравнением
*)(в) = 57-Д,=0,
а поверхность S* -уравнением
g2j(6) = -8j-Rj = 0.
В дальнейшем наряду с обозначением S] и S* будет широко использоваться
обозначение Sj , где под поверхностью Sj понимается любая из поверхностей £j,
S2j. Уравнение поверхности Sj условимся записывать в виде
gy(«) = 0. , (П1.95)
В отличие от рассмотренного выше здесь допускается движение фазовой точки по
пересечению двух и более ограничивающих поверхностей Sj . Обозначим через р
множество индексов у , таких, что
= Rj,
если yep. При движении по границе области В
/>7(8(0,u(/)) = -^g/6(0) = ^(Osign57=0
для любого yep. Область управления, определяемую соотношениями
Uj \<АГ у = 1,г, РДб,и) = 0, уер,
обозначим сор. Будем считать, что при движении фазовой точки по границе области
В управление и принимает свои значения из области сор.
Обозначим tJ точку выхода на поверхность Sj, а через 7J - точку схода с
поверхности Sj . Точку отражения от поверхности, как и точку выхода, будем обозна-
662 Приложения
чать tJ. Так как возможен одновременный выход на две и более ограничивающие
поверхности, то допускаются соотношения
Аналогичные соображения справедливы и для точек схода и отражения. Более того,
одна и та же точка может совмещать в себе, например, выход на границы SJtSv и
сход с границ Sa и5р, т.е. возможны соотношения
tj =t* =7а=7К
Точки выхода, схода и отражения называют еще точками стыка траектории. Если
точка стыка представляет собой только точку выхода* или только точку схода, или
только точку отражения относительно некоторой ограничивающей поверхности Sj ,
то соответствующую точку стыка назовем простой. Каждую точку стыка, которая не
является простой, будем называть сложной. Будем, далее, предполагать, что сложная
точка стыка является точкой выхода на поверхности Sf для всех j e S, точкой схода
с поверхностей Sj для j е 0 и точкой отражения от поверхностей Sj для j е Г,
здесь S, 0 и Г - некоторые множества. Участок ij </<т2, на котором траектория
(х(/),5(/)) принадлежит границе области Б и не имеет других точек стыка, кроме
т, и т2, назовем простым граничным интервалом.
Введем векторы
V =(V|/],V|/2,...,V[/W), \|/2 =(V|/w+i,V|/w+2,...,V|/;]+r),
и составим функцию
Я(М/,х,6,и) = М/0+(1|/1)Т(Ах + В6) + (1|/2)Ти.
Вектор v|/(/) определим уравнениями
dt dt ' ■ (П1.96)
dy2
= -DTi|/'-
dt
При движении по границе области В нам понадобятся также вспомогательные
функции Xj (t), j ер , которые зададим уравнениями .
ая(ч,(,),х(,),8(о,и(о)= ару(»(/),ц(О)>
duj duj .
Пусть т, < / < т2 - простой граничный интервал. Будем говорить, что в
интервале Tj < / < т2 выполнено условие оптимальности на границе, если найдется такая
ненулевая непрерывная вектор-функция ц/(/) w такие вспомогательные функции
А., (0> У ер, что:
1) в каждый момент времени t, ix < t < т2, выполняется условие максимума
Я(м/(0,х(0,6(0,и(0) = тахЯ(1|/(0,х(0,5(0,и)^0;
иеюр
2) для любого ieo в каждой точке дифференцируемости
Приложение 1. Оптимальное управление при ограничениях на координаты 663
С/Х:
—^-<0; (П1.98)
dt
3) выполнено условие нетривиальности, т.е. решения системы (П1.96) вида
\|/0(0-0, уЧО-О,
i|/2(O = I>7grad gj№))>
jep
где [if - произвольные действительные числа, не допускаются.
Рассмотрим точку стыка т. Условие скачка в-этой точке зададим уравнениями*
Ч/о(т + О) = \|/о(т-О), v|/1(t + 6) = v|;1(t-O),
M/2(T + 0) = v2(^-0)+S^Srad^(5(T))' (П1"}
здесь \ij — произвольные действительные чисЛа.
Теорема П1.9. Пусть u(t),to<t<tx, - кусочно-непрерывное, кусочно-гладкое
управление, переводящее фазовую точку (х,5) системы (П1.91), (П1.93) из
заданного начального положения (х°,6 ) в начало координат, т.е. в точку х =0, 6 =0.
Если соответствующая управлению и (О траектория (х(/),б(/)) удовлетворяет на
внутренних интервалах движения принципу максимума Понтрягина (теорема 2Л),
на каждом простом граничном интервале - условию оптимальности на границе, а в
точках стыка - условиям скачка, то на траектории (х(7),§(0) функционал (П1.36)
достигает абсолютного минимума.
Теорема П1.9 задает достаточные условия. Однако эти условия являются, по-
видимому, также и необходимыми. Нетрудно видеть, что в случае скалярного 5
теорема П 1.9 совпадает с теоремой П1.3.
Теорема ШЛО. Если (х*(/),6*(/)) - траектория, удовлетворяющая условиям
теоремы П1.9, а (х (/),5 (/)) -любая другая оптимальная траектория, то
(х* (0,8* (0)=(х** (О,»" (0).
Для задания достаточных условий в случае варианта L необходимо к теореме
П1.9 присоединить условие трансверсальности
\|/и+у(/1) = 0>у=п. (П1.100)
При этом теоремы П 1.7 и П 1.8 сохраняют свою силу.
Доказательство теорем П1.9 и П1.10 аналогично доказательству теоремы П1.4,
причем в силу частных особенностей объекта (П1.91), (П1.93) оно сильно упрощается.
Легко видеть, что на каждом простом граничном интервале вектор v|/(/)
определяется условием оптимальности на границе с точностью до слагаемого
Vo(O = O, V(0 = 0,
M/2(0 = Z^gradg7(6(0).
yep
* Если X - простая точка стыка, то соотношения типа м/п+у(т - 0) = 0, м/п+7(т + 0) = 0 следуют из
непрерывности функции Я(\|/(/),х(/),б(0,и(0) в точке стыка, а условие непрерывности, в свою очередь,
вытекает из возможности варьирования момента Т. В силу особенностей системы (Ш 91), (П1 93) в
сложной точке стыка, например, при /* =/* =/" =/р*, моменты времени /*,/*,/",/р* варьируются
независимо друг от друга. Это позволяет записать последние два условия (П1 99)
664 Приложения
Это позволяет условие скачка в форме (П1.99) заменить условием скачка вида
у|/о(т-О) = м/о(т + О), v|/1(t-0) = ij/1(T + 0),
M/2(T + 0) = M/2(T-0)+X^grad^(5WX (П1.1О1)
Ч/„+/т + О) = О, ye0.
Условие скачка в форме (П 1.101) часто оказывается более удобным при
практическом применении, нежели условие (П1.99).
Будем предполагать, что матрица А имеет действительные собственные числа.
Тогда матрица Ат также имеет действительные собственные числа.
Теорема П1.11 (теорема о числе переключений). Если все собственные числа
матрицы А - действительны, а траектория (х(/),6(/)) удовлетворяет условиям
теоремы П1.7, то оптимальные по быстродействию управления Uj(t\ у = \,r,
представляют собой кусочно-постоянные функции, принимающие значения Aj, 0, - А}, и
каждое управление Uj (/) изменяет знак не более п раз, если рассматривается
вариант Е, и не более (п - /) раз, если рассматривается вариант L, здесь п -порядок
системы (Ш.91).
Доказательство теоремы П1.11. Из условия максимума функции
Я(\|/(/),х(/),6(/),и(0) находим, что при движении в открытом ядре области В
оптимальное управление
и)(0 = ^sign yn+j(/), у = п, (П1.102)
а при движении по границе области В
и, (0 = 0, yep,
w7(0 = ^sign 1|/и+у(0, yep-
Далее, в соответствии с (П1.97)
\/(0 = 4V/(0sign8,
и условие (П1.98) принимает вид
<Л|/Я+/
sign 6<0, yep. (П1.103)
dt
При доказательстве теоремы будем использовать условие скачка в форме
(П1.101). В соответствии с (П 1.101) и (П1.96) вектор \|/'(0 непрерывен и задается
вторым уравнением (П1.96). Далее, как следует из (П 1.101), (П1.95) и (П1.96), точка
стыка т вносит изменение лишь во вспомогательные функции \\tn+J(t) для всех
у g 0 и оставляет без изменения остальные компоненты вектора \y(t). Итак, если
рассматривать вспомогательную функцию \\in+J(t), то она определяется, кроме
уравнений (П1.92), только точками схода с границы Sj.
Пусть У\,У2>-->Ут ~ попарно различные собственные числа матрицы -Ат .
Предположим, далее, что собственное число уо имеет кратность £о, так что
kl+k2+... + km =п. Тогда на любом интервале, не содержащем точек стыка,
vw+y(0 = g/(0-^-4g^(0-^-4...+gi(0-eY-'4cy, у=п, (Ш.104)
1 при t>t<j,
Приложение 1. Оптимальное управление при ограничениях на координаты 665
здесь glit), и = 1,т, - многочлены, причем степень многочлена glv(t) (для любого
j) не превосходит kv -1, cj - некоторые константы. Равенство (П 1.104)
соответствует случаю, когда собственные значения матрицы А отличны от нуля. Если среди
собственных значений имеется число 0, то вид равенства (П 1.104) изменится, однако
полностью сохраняются все приводимые ниже рассуждения.
Так как для любого j вектор
v(/) = (vo(0, V(0, v2(0) = fo, о, ^ЪЬШШ),
V дЬ J
где Hj - произвольная константа, является тривиальным решением системы (П1.96),
то, как следует из (П 1.101) и (П1.104), в интервале t0 < t < 7J+y
Vn+j«) = S{ (t)ey>' + g{ (/)eTl'+... + gJm «У» '+col +
f > dgjW®)) ut rA (П1.105)
h J 56>
здесь
i(/-/7) =
c°j - некоторая константа.
Обозначим \|/jj+y(f) функцию vj//1+;(/), задаваемую равенством (П 1.104), если в
нем положить Cj = c°j . В соответствии с леммой §2.3 квазимногочлен \\i°n+J(t) имеет
не более, чем (к} -1) + (к2 -1) +... + (кт -\) + т = п корней, а квазимногочлен
— ^«+/(0 не более (я-1) корней. Таким образом, функция \\f°n+J(t) имеет не более
чем (л-1) точек экстремума и, следовательно, не более п участков монотонности.
График функции \y°n+J(t) при и = 4 изображен на рис. П 1.1.
График функции \\J°n+J(t) позволяет задать функцию yn+J(t). При этом, как
следует из (П 1.105) и последнего равенства (П 1.101), условие скачка в момент схода Ts'
может быть учтено параллельным переносом оси абсцисс так, чтобы она проходила
через точку vj/JJ+Дл/) . Этот перенос, очевидно, следует выполнять в каждой точке
схода с поверхности Sj.
В соответствии с (П 1.102) знак управления и} (/) совпадает со знаком функции
Wn+j (0 ' если ^j (t) I < Rj. Далее, т.к. wy (TSJ - 0) = -и} (7SJ + 0), то движение по
границе Si всегда приводит к смене знака управления. Если траектория движения
системы (П1.91), (П1.93) такова, что bj(t)\<Rj, to<t<t]9 то переключение
управления Uj{t) осуществляется в нулях функции v|;w+y(O = v|/^+7(/), и, следовательно,
управление и} (/) может изменять знак не более п раз.
Отметим, что функция y°n+J(t) имеет максимальное число нулей, равное п, если
каждый участок монотонности этой функции содержит один нуль, как это изображе-
42 Зак. 366
666
Приложения
но на рис. П1.1. Далее, в соответствии с (П1.103) в интервале // <t<7s' функция
vj/A?+y(/) и, следовательно, функция \\f°n+J(t) монотонна. Таким образом, число
граничных участков функции 5^(0 не может превышать число участков монотонности
функции \\fl+/(t). Если некоторый участок монотонности функции 1|/„+/(0 занят
нулем t*, таким, что bj(t*) </?,, то, как следует из предпоследнего равенства
(П1.101), он не может соответствовать граничному участку функции 5;(г).
i
/
/
/
Л
\ Г
\J
Рис. П1.1. График функции V|/rt+/-(0
Таким образом, число изменений знака управления Uj(t) не может превышать
числа участков монотонности функции \\f°n+J(t). Отсюда следует доказательство
теоремы для варианта Е. Попутно было доказано также, что функция 5у(7) не может
иметь более чем п граничных участков.
Для доказательства теоремы П1.11 в случае варианта L необходимо принять во
внимание условие трансверсальности (П 1.100). Это условие занимает нуль на
последнем участке монотонности функции 4fn+j(t), т.е. на последнем участке
монотонности функции \\jfl+J(t) теперь невозможно изменение знака управления. В этом
случае, как легко видеть, функция 57(7) может иметь не более (п-\) граничных
участков.
Замечание. Теорема П1.11, естественно, остается справедливой и в том случае,
когда конечная'точка х1 либо (х^б1) не совпадает с началом координат, но
принадлежит открытому ядру области В.
При г = 1, т.е. в случае одного управляющего воздействия, теорема П1.11
позволяет весьма просто осуществлять синтез оптимального управления. Именно,
сохраняет свою силу классический способ построения поверхности переключения,
предложенный в [20] для задач без ограничений на фазовый вектор.
(П1 106)
Пример П1.1. Рассмотрим систему
x + ^x + uqX^ k5,
5 = м
при ограничениях 5<R, и<А Будем решать задачу о наибыстрейшем переводе фазовой точки системы
(П 1.106) в начало координат (случай Е) Для данной системы поверхность переключения образуется
исходящими (в обратном времени х) из начала координат фазовыми траекториями, на которых координата
б(х) имеет вид ломаной линии ОМЫ либо 0MW (рис. П1.2) Возможные положения линий MN и M'N'
показаны пунктиром С помощью этой поверхности задается управление при движении фазовой точки в
открытом ядре области В
Приложение 1. Оптимальное управление при ограничениях на координаты
61
667
-R
\ \ \ J
-я
/ / лу / / / / /
/ / /*/ / / / / /
Рис. П1.2. К примеру I1I.1
П1.4. СИНТЕЗ ОПТИМАЛЬНОГО ПО БЫСТРОДЕЙСТВИЮ
УПРАВЛЕНИЯ ПРИ ОГРАНИЧЕНИЯХ НА СКОРОСТЬ
ДВИЖЕНИЯ И УСКОРЕНИЕ
1. Ограничение на ускорение. Рассмотрим объект третьего порядка
у + а{у + я? у + а$у = и. (П1.107)
Пусть заданы ограничения
\u\<A,\y\<D.
Будем, далее, предполагать, что характеристическое уравнение
л'3+а,52+а25 + а3 =0 (П1.108)
имеет только действительные корни.
Представим уравнение (П 1.107) в виде системы дифференциальных уравнений
*1 =;с2>:*:2 = Х3> *3 = и~а1х\ ~а2х2~а\хЗ- (П 1.1 09)
Область £ допустимых значений фазового вектора о задается неравенством
Сначала будут рассмотрены только регулярные оптимальные траектории. Поэтому
для синтеза оптимального по быстродействию управления воспользуемся теоремой II1.5.
Выпишем функции
Pj{xji) ~ (и-аъхх -а2х2 -a{x3)s\gnx3,
^(\|/,X,w) = Vj/0+Vji,.Y2 +1|/2*з +Уз.(*'-ЯзЛ'1 .-^2*2 -а\Х1У
Из условия максимума функции Я(\|/,х,г/) находим, что при движении в открытом
ядре области В
tt(O = ^signi|/3(O. (П 1.110)
При движении по границе области В
и - аъхх + а2х2 + яjX3 • (П1 111)
Движение на границе области В возможно лишь в полосе
| а3х} +а2х2 +a,x3 \s A . (П1.112)
В соответствии с условиями регулярности ограничимся рассмотрениями в
открытой полосе
| а3*1 +^2Х2 +#1*3 | < Л •
Вспомогательная вектор-функция \\f(t) определяется в открытом ядре области В
уравнениями
flfyo = 0 <hf\ =
dt
на границе области В - уравнениями
42*
d\\f2 aty3
: ^3^3'—Г" = "Vl + «2^3>—Г" = ~^2 + ^1^3'
(П1.113)
668
Приложения
^ = 0,^ = 0,^- = -^,^ = -^
dt dt dt ' dt
dX
Условие ^^ < 0 выливается в неравенство
dt
dt
signjt3 = -v|/2 signx3 <*0.
(П1.114)
(П1.115)
Далее, соотношения (П1.54) и (П1.55) принимают вид
у3(/;-0) = 0, ч/з(С) = О-" (П1.116)
Перейдем к обратному времени т. В соответствии с теоремой П1.5 в точках схода
т^* (каждой точке выхода t*a в обратном времени соответствует точка схода)
должны выполняться условия скачка
Далее, в точках выхода, очевидно,
V(x#a+0) = V(x;-0).
Соотношения (П 1.110), (П1.111), (П1.115)- (Ш. 118) и условие
Я(\|/(т = 0),х(т = 0),м(т = 0)) = 0
образуют полную систему необходимых и достаточных условий оптимальности,
которым должна удовлетворять регулярная оптимальная траектория.
Покажем, что исходящая в обратном времени из начала координат траектория
OMNQ (рис. Щ.З) оптимальна, а участки этой траектории ОМ и NQ, лежащие в
открытом ядре области Б, принадлежат поверхности переключения.
(П1.117)
(П1.118)
(П1.119)
Рис. П1.3. К задаче синтеза оптимального управления при ограничениях на ускорение
В соответствии с уравнениями (П 1.113) вспомогательные функции v|/3(t) и \j/,(t)
определяются в открытом ядре области В уравнениями
где
v|/3(t) = V|/?K(t) + v|/5k'(t) + 4/3K4t),
V, (т) = -\|/?К* (т) - а3ч/?К(т) - ДзЧ>?ЬС'(т),
4/?=i|/f.(T = 0),/ = 1,2,3,
(П 1.120)
K(t) = L
-1
53 + a,52 +a<>s + ai
Приложение 1. Оптимальное управление при ограничениях на координаты 669
К (x) = L
-i
-s -a]s-a2
2
s + ci\S + a2s + я3
атор обратного пре
(т[ <т<тГ)
L ] - оператор обратного преобразования Лапласа. На границе области В
4>о(т) = Yo(Ti )> v|/,(t) = v|/,(tI),
V|/2(T) = \|/i(T|)(T-Ti)4-V|/2(TJ>.
Далее, в интервале tJ"* < т < т2* (точка Мсоответствует т«*, точка N- т|*, точка £? - т2)
ч/3(х)=^(т;)л:(т-тГ)+[ч/,(х1)(т;*-т;)+у2(т;)]г(т-тГ)+ ^
+Ч/з(т;)*'(т-тГ),
или
^з(тО) = М/1оК(то) + ^2оК'(то) + м/зОКЧто) +
+[-Ч/1окф(т;)-£1зч/2ок(т;)-а3ч/з°к'(т;)](тГ-т;)к'(то-т|), (П1Л22)
здесь т° - время «свободного» движения, т.е. время, отсчитываемое только при
движении фазовой точки в открытом ядре области В.
Для любого т|* < т* < т2 (т* > т?* =tJ) можно так выбрать вектор начальных
значений i|/° = (v|/q , у®, v|/2, Уз)» что в интервале 0 < т < т* участок траектории
OMNQ удовлетворяет всем условиям оптимальности, а в самой точке т*
\|/3(тО = 0, .
т.е. соответствующая точка х(т«) принадлежит поверхности переключения.
Указанные числа \|/р v|/?f \|/з с точностью до постоянного множителя найдутся из системы
линейных однородных уравнений
^з(т;) = ч/,°К(т;) + ч;20К'(т;) + н/зОКЧт;) = 0,
vj/3(t,°) = v);1oK(t,o) + v);2()K'(t.o) + V3OK"(t,o) + [-x|;1oK*(t;)- (П1.123)
- а3V2°K(t; ) - а3v3°K'(x;)](хГ - < )К'(т.° - х!) = 0.
Покажем, что выбранный в соответствии с (П1.123) вектор \|/° ^(у?,^^ Уз) оп"
ределяет функцию у3(т), которая на отрезке 0 < т < т* не имеет других нулей, кроме
точек Tj,Tj ,т*.
При т|* < т <т* v|/3(t) не может обращаться в нуль, т.к. в соответствии с леммой
(см. §2.3) функция (П1.121) может иметь не более двух нулей. Предположим, что
vj/3Cx) имеет wy-Nb B интервале 0<т<т*. Тогда, как следует из указанной леммы,
функция
\|/з'(х) = ч/10К(т) + ч/20К'(т) + Ч/з°КЧт) (П1.124)
не может иметь нулей при т>т[. В равенстве (П 1.124) индекс «звездочка» введен,
чтобы подчеркнуть различие между ц/3(т) и функцией (П1.124). Это различие имеет
место при т > Т] . Если функции (П 1.124) соответствует управление м(т), 0 < т < Tj,
переводящее фазовую точку из начала координат на границу
670
Приложения
х3 = -D,
то
1|;3(т)<0 (П 1.125)
при т > т, .
Учитывая, что vj/^(T| ) = у-(т*) = 0, уравнение (П 1.124) можно переписать в виде
v|/,'(t) = v|/,(t;)K(t-t;) + v|;2(t;)K'(t-t;). (П1.126)
При т > 0 К(т) > 0, а для астатического объекта (о-, = 0) и К'(т) > 0. Для
астатического объекта функция К'(т) имеет вид, изображенный на рис. П1.4. Отметим, что
К(0) = К'(0) = 0,
К'(т) п (П 1.127)
Х^ооВД
= 0.
Из (П 1.127) вытекает, что при малых значениях разности т-ij знак функции
(П 1.127) определяется вторым слагаемым, а при больших - первым слагаемым.
Неравенство (П1.125) поэтому возможно только при
\|/,(т;)<0, ч/2(Т;)<0. (П1.128)
Для статического объекта будем дополнительно предполагать, что время движения
по траекториям NQ от одной ограничивающей плоскости до другой меньше т0, где
т0 - отличное от нуля решение уравнения
К'(т) = 0.
Из (П 1.128) и (П 1.121) находим, что функция (П 1.122) не может обращаться в нуль в
точке т*. Последнее противоречит уравнениям (П1.123). Таким образом, функция
1|/3(т) имеет нули только в точках т|",т**,т*.
Из совокупности решений (П 1.123) выберем решение, в котором \ц\ >0 .
Равенство (П1.119) удовлетворим соответствующим подбором числа \\Jq. Из (111.116) и
неравенства \|/? > 0 следует, что функция v|/3(t) убывает на отрезке 0<т<т1.
Поэтому
\|/2(т|)£0. (П1.129)
Далее, из соотношений
\|/3(тГ+О) = О, Ч/3(т.) = О •
вытекает, что
у,(тГ)>0, \|/2(тр)<0. (П1.13О)
К'
Рис. 111.4. График функции К'(т)
Приложение 1. Оптимальное управление при ограничениях на координаты 671
Из (П 1.129), принимая во внимание (П 1.130), (П 1.114), получим условие (П 1.115).
Таким образом, траектория NQ принадлежит поверхности переключения, причем
проводимые выше рассуждения распространяются на всю совокупность траекторий,
сходящих в обратном времени с линии MS. Далее, поверхности переключения
принадлежит также траектория ОМ и примыкающая к ОМ (с управлением и = -А)
совокупность траекторий (рис. П1.3).
На рис. П1.3 представлена лишь часть траекторий, образующих поверхность
переключения. Остальные траектории являются симметричными (относительно начала
координат) изображенным. FPNMO и LRQNMO - оптимальные траектории
соответственно с одним и двумя заходами на границу.
В заключение отметим, что выше был рассмотрен наиболее интересный для
приложений случай «жесткого» ограничения по ускорению, когда траектории,
образующие поверхность переключения, имеют участок (MS), лежащий на границе области В.
При менее «жестких» ограничениях, когда в силу (П1.112) в точке М невозможно
движение на границе области В, поверхностью переключения является изображенная
на рис. П1.3 совокупность траекторий, ограниченная линией ОМТ.
2. Ограничение на скорость движения. Рассмотрим теперь задачу синтеза
оптимального по быстродействию управления объектом (П 1.109), когда вместо
ограничения на ускорение задано ограничение на скорость движения, т.е. область
допустимых значений фазового вектора х задается неравенством:
|х2|<£>. ' (П1.131)
Неравенство (П 1.131) представляет собой ограничение второго порядка. Для
отыскания оптимальных траекторий и оптимального управления воспользуемся
достаточными условиями оптимальности, задаваемыми теоремой П1.7. Отметим, что в
соответствии с теоремой П1.7 движение по границе области В определяется
уравнением
я-,=С,
а функция
Ф(х) = х3.
Как следует из (П1.109), при движении по границе области В управление
и(0 = я3*1 +^2*2- (П 1.132)
В силу ограничения |н|<Л движение по границе области возможно только по
отрезкам прямых
х2=Д лг3=О, \a2D + djxx\<At (П1.133)
х2=-Д х3 =0, \агхх-а2й\<А. (П1.134)
Ниже в соответствии с условиями теоремы П1.7 вместо допустимых отрезков
рассмотрим интервалы, которые получаются из (П 1.133) и (П 1.135) при замене
нестрогих неравенств на строгие.
В соответствии с теоремой П1.7 определим функции Гамильтона при движении
по границе области В равенством
Я(м/,х,с) = н/0+М/1с, (П1.135)
где вспомогательный вектор ф = (Vo'Vi) определяется из уравнений
^ = 0,^- = 0. (П1.136)
а л
Из условия максимума функции (П1.135) находим
c-signvj/, >0. (П1.137)
672 Приложения
Как и выше, синтез оптимального управления будем проводить с использованием
обратного времени т . Выпишем условия скачка:
v|/o(t*+O) = v|/o(t*-O), vj/1(t40) = v|/,(t*-0),
♦ * (111. lie)
v|/2(T -0) = ц2, i|/3(t -0) = |i3;
v|/o(t**+O) = v|/o(tm-O), v|/,(t**+O) = \|/,(t**-O),
Ч/2(тМ+О) = цо, 1|/3(т**+0) = ц,; .
1|/0(т*+0) = \|/0(т'-0), V|/,(t*+O) = 4/1(t*-O),
v|/2(t40) = vj/2(t*-0) + |i0, v|/3(t*+O) = v|/3(t*-O) + m1; (П1.140)
|ii0signc<0, jLijSign с > 0.
Соотношения (П 1.138) соответствуют точке выхода на ограничение (в обратном времени
т), соотношения (П1Л 39) - точке схода, а соотношения (П1.140) - точке отражения.
Пусть т* - точка выхода на ограничение. Из уравнения
Я(Ч/(т* -0),x(t*),i/(t* -0)) = Я(чКт* +0),х(т'),с),
принимая во внимание (П1.138), найдем
\|/3(т'-0) = ц3=0. (П1.141)
Аналогичным образом можно показать, что в точке схода т*
\|/3(т**+0) = ц, =0. (П1.142)
Если т* - точка отражения второго порядка, то из уравнения
Н(у(т -0),х(т*),и(т* -0)) = Я(м/(т* +0),x(t*),w(t* +0))
и соотношения (П1.140) следует равенство
„ d2g(x(T))
+ Ч/3(т -0)(и(т +0)-и(т -0)) = 0. (П1.143)
т=т*+О
По определению точки отражения
dT2
signc<0.
т=т*+0
Из равенства (П1.140) находим тогда
</2g(x(x))
Иг
dx
2
<0.
т=т*+0
Далее, из условия максимума функции Н(\у,х,и) следует, чтр
\|/3(т* - 0)(i/(t* + 0) - w(t* -0)) < 0.
Таким образом, каждое слагаемое, стоящее в левой части равенства (П 1.143),
неположительно и, следовательно,
d2g(x(x))
Ц| * „•„
= 0, (П1.144)
vj;3(t -0)(w(x +0)-и(т -0)) = 0.
Из (П1.144) и (П1.89) вытекает, что
Соотношения (ШЛЮ), (П1.119), (П1.132), (П1.137) - (П1.142), (П1.145) образуют
полную систему достаточных условий оптимальности.
Приложение 1. Оптимальное управление при ограничениях на координаты
Отметим, что в соответствии с (П1.132) и условиями регулярности
673
Поскольку
signc
и(т +0)
|и(т"-0)
У2£(х(т))
а3хх(т*) + а2х2(х*)\< А ,
а3х}(т ) + а2х2(т )
<А.
dx1
<0, signc
d2g(x(T))
dil
<0,
(П 1.145)
т=т -0
(П1.146)
т=т +0
то из (П 1.110) и (П 1.109) получаем равенство
и(т* - 0) = и(т** + 0) = -Asign с .
Из (П1.146) следует, что при переходе фазовой точки с одной ограничивающей
плоскости на другую оптимальное управление и(т) должно иметь хотя бы одно
переключение. Из (П1.141) и (П1.142) вытекает тогда, что первая из функций (П1.120)
должна иметь не менее трех нулей. Последнее невозможно, т.к. в соответствии с
леммой (§2.3) указанная функция может иметь не более двух нулей. Таким образом,
оптимальная траектория х(т) может иметь только один участок, лежащий на границе
области В.
Покажем, что изображенная на рис. П1.5 траектория OMNPL принадлежит
поверхности переключения. Для этого достаточно показать, что для любого т*, Т| < т* < т7,
можно так выбрать вектор начальных значений v|/° = См^о^Ч^?»Ч^2>М7?) и число |л0,что
в интервале 0<т<т* выполняются условия оптимальности (П1.110), (П1.119),
(П1.137)-(П1.142), а в самой точке т*
1|/3(тО = 0. (П1.147)
Рис. П1.5. Графики траектории
Для статического объекта будем по-прежнему предполагать, что время движения
фазовой точки по траектории PL от одной ограничивающей плоскости до другой
меньше т0.
674 Приложения
Указанный выш
системы уравнений
Указанный выше вектор \|/° с точностью до постоянного множителя найдется из
v|/3 (T1) = v|/10K(T1) + i|;20K'(T1) + v|/30Kff(T1) = 0,
щ (t;)=M/1ok(t;)+vi/2ok'(t;)+m/3V(t;)=o,
Я(ч1(0),х(0),1/(0)) = 0, (П1.148)
где ij - момент первогр переключения (соответствует точке М). При т > тр
функция vj/3(t) определяется равенством
1|/3(т) = \|/1(т1)К(т-т1*) + ц0К'(т-тГ).
Число |i0 выберем таким образом, чтобы обесг!ечить выполнение уравнения
(П 1.147), т.е. положим
Ио=-У|(*;)*?'~Т1..)- (ПЫ49)
К (т* -Tj )
Из соотношений
Я(ч|(т|),х(т1),1/(т|)) = \|/о+ч/,(т|)х2(т|)=-О, уо'(т)<О
и уравнений (П 1.136) вытекает выполнение неравенства (П 1.137), выполнение
условий (П1.110), (П1.119), (П1.141), (П1.142) следует из уравнений (П1.148) и (П1.149).
Таким образом, доказано, что траектория PL (как и вообще любая из сходящих в
обратном времени с прямой NG траекторий) принадлежит поверхности
переключения. Далее, изображенная на рис. П 1.5 совокупность траекторий, примыкающих с
управлением и = А к линии OMF и не имеющих граничного участка, также
принадлежит поверхности переключения. Для завершения построения поверхности
переключения необходимо к траекториям, изображенным на рис. П1.5, присоединить
симметричные (относительно начала координат).
Изображенная на рис. Ш.5 поверхность переключения была построена, исходя из
достаточных условий оптимальности (теорема П1.7). Однако тот же самый результат
может быть получен, если воспользоваться необходимыми условиями
оптимальности, задаваемыми теоремой П1.7.
Далее, отметим, если ограничения на фазовый вектор имеют вид
ИЛИ
\x2+bxxx\<D,
то в первом случае поверхность переключения строится аналогично пункту 1, а во
втором - по аналогии с пунктом 2.
7. Обобщение задачи синтеза. В заключение остановимся кратко на случае,
когда одновременно заданы ограничения на скорость движения и ускорение, т.е.
область В задается неравенствами
| х3 | < D,, | х2 | < D2.
Для отыскания оптимального управления можно воспользоваться достаточными
условиями оптимальности (теорема П1.4) или необходимыми условиями
оптимальности, задаваемыми теоремой П1.7. На рис. П1.6 изображены траектории, задающие
поверхности переключения, причем рассмотрен наиболее интересный с
теоретической и практической точек зрения случай, когда траектория OMN нарушает
ограничение
|х3 |<D. (П1.150)
Приложение 1. Оптимальное управление при ограничениях на координаты 675
Если траектория OMN не нарушает ограничение (П 1.150), то поверхность
переключения образуется траекториями, изображенными на рис. П1.5 и продолжаемыми до
пересечения с границей области В. Правда, при этом линия MF может иметь
граничный участок, и тогда точка F лежит на пересечении плоскостей
х2 =-D2,x3 = D,.
Рис. П1.6. Графики траекторий
На рис. П 1.6 траектория OMNPQ касается ограничивающей плоскости х2 = D2 в
точке Р . Отрезок PG представляет собой траекторию движения системы (П 1.109)
по границе х-, = D2. Напомним, что движение по указанной границе возможно лишь
в пределах отрезка (П1.133).
Дополним исследование, проведенное выше, рассмотрением нерегулярных
траекторий. В целях упрощения будем предполагать, что в уравнениях (П 1.109) аъ =0,
т.е. рассматривается астатический объект.
Граница допустимой полосы (П 1.112) на плоскости х3 - -D задается прямыми
а2х2 -axD- А,
а2х2 -a]D = -A,
на одной из которых управление достигает значения А, а на другой -А
(см. рис. Ш .7). На плоскости хъ - D допустимая полоса ограничена прямыми
а2х2 + a\D = A,
а2х2 +a,D = -A.
Условие регулярности (слабой регулярности) траектории x(t) для
рассматриваемой задачи выливается в требование: на каждом граничном интервале управление
u(t) должно удовлетворять неравенству
\Ф)\<А>
т.е. траектория х(/) не должна содержать точек, принадлежащих границе полосы
(П1.112).
Так как движение системы (П 1.109) по границе полосы (П 1.112) невозможно, то
траектория \(t) может иметь лишь некоторое конечное число точек, в которых не
выполняются условия регулярности. Повторив рассуждения, приведенные в §1.2,
нетрудно показать, что для объекта (П 1.109) теорема П1.5 сохраняет свою силу и в
случае нерегулярных траекторий.
676
Приложения
На рис. П1.7 изображены траектории, задающие поверхность переключения,
построенную с учетом нерегулярных траекторий. Включение в рассмотрение
нерегулярных траекторий позволяет заметно расширить область оптимальной
управляемости системы. Именно, построенная в пункте * 1 поверхность переключения
(см. рис. Ш.З) дополняется совокупностью траекторий, примыкающих с
управлением и =-А к траектории ЕГ (рис. П1.7), где точка Е лежит на границе допустимой
полосы (П1.112) (x3=-D). Кроме того, поверхности переключения принадлежат
также траектории, примыкающие с управлением и = -А к отрезку JE' (точка Е'
симметрична относительно начала координат точке Е). Отметим, что отрезок JEr и
точка z лежат на границе допустимой полосы (П 1.112) (х3 = D).
Рис. П1.7. Графики траекторий
На рис. П1.7 представлена лишь часть траекторий, образующих поверхность
переключения. Остальные траектории являются симметричными (относительно начала
координат) изображенным.
Мы рассмотрели синтез оптимального управления в предположении о том, что
характеристическое уравнение (П 1.108) имеет только действительные корни. Нетрудно
видеть, что полученные результаты справедливы также и в случае комплексных корней
характеристического уравнения, если время движения по оптимальным траекториям от
одной ограничивающей плоскости до другой не превышает —Т , где Т- период
собственных колебаний системы (П 1.109). Пример синтеза оптимального по
быстродействию управления при ограничениях на фазовые координаты для системы, состоящей из
колебательного звена и интегратора, подробно рассмотрен в §4.3 [5].
В литературе [22], [23] выделен класс нелинейных объектов управления,
названных неосциллирующими, для которых выполняется теорема об (п-\) переключении
оптимального управления. Анализ задаваемых теоремой П1.3 необходимых условий
оптимальности показывает, что для неосциллирующих объектов третьего порядка
справедливы результаты, аналогичные изложенным в настоящем параграфе. Именно,
если ограничения на фазовые координаты имеют первый порядок, то структура
поверхности переключения, с помощью которой задается оптимальное управление при
движении базовой точки в открытом ядре области В, совпадает с изображенной на
Приложение 1. Оптимальное управление при ограничениях на координаты 677
рис. П1.7. В тех случаях, когда ограничения на фазовые координаты имеют второй
порядок, структура оптимальной поверхности переключения задается рис. П1.5.
Пусть, например, движение системы описывается уравнениями
*1 =/l(*l>*2)> *2 = /2(xl>*2>*3)>
*з =/з(*з>«) = *(*з)-« + *(*з)> (П1.151)
*(*з)>0>
и заданы ограничения
\и\<А, (П1.152)
|jc3|<D. (П1.153)
Будем предполагать, что функция /; u = l,3j непрерывно дифференцируема по
переменным x]tx2,x3. В соответствии с [22] система (П 1.151) является неосцилли-
рующей, если выполняются неравенства
MW>o,M>o.
дх3 дх}
Для объекта (П1.151) ограничение (П1.153) имеет первый порядок, и,
следовательно, в открытом ядре области В оптимальное управление задается с помощью
поверхности переключения, изображенной на рис. П1.7.
Заменим в соотношениях (П1.151) - (П1.153) неравенство (П1.153) ограничением
которое имеет второй порядок. Тогда структура оптимальной поверхности
переключения будет задаваться рис. П1.5. Здесь следует только иметь в виду, что линия
GPN , представляющая собой траекторию движения фазовой точки по границе
области В, в отличие от (П 1.134) определяется уравнениями
Х2 =-Д /2(*1,*2>*з) = 0-
Далее, движение по границе области В происходит под воздействием управления
n{t), которое вычисляется из условия
/>,(х(/),и(0) = 0.
Если система имеет второй порядок, то синтез оптимального управления (см. [5])
существенно упрощается.
678 Приложения
ПРИЛОЖЕНИЕ 2. МАТЕМАТИЧЕСКОЕ
ПРОГРАММИРОВАНИЕ
(ОСНОВНЫЕ ПОЛОЖЕНИЯ)
ФОРМУЛИРОВКА ЗАДАЧИ МАТЕМАТИЧЕСКОГО
ПРОГРАММИРОВАНИЯ
Задача математического программирования содержит некую целевую функцию,
оптимум которой следует определить, и систему равенств и неравенств,
описывающих условия-ограничения задачи. Общая задача математического программирования
состоит в определении вектора х* с координатами х[9х*2,...,х*п , который является
решением задачи:
оптимизировать
f{xuxl9...9xn) (П2.1)
при ограничениях
£,(*,,х2,...,х„)>0;
g2(x,,x2,...,jrw)£0;
(П2.2)
gm(xl9x2,...,xn)>09
/ц(х,,*2,...,хя) = 0;
h2(xl9x29...9xn) = 0;
(П2.3)
hp(xl9X29...9xn) = 0.
Используем понятие вектора как упорядоченной совокупности п действительных
чисел x = {xl,x2,...,xn}. Тогда выражение (П2.1) - (П2.3) можно записать в более
компактной форме:
оптимизировать /(х),
при ограничениях
g;(x)>0; / = l,/w;
й,(х) = 0; j = ~p.
Текущие индексы / и у пробегают все целочисленные значения от 1 соответственно
до т и р.
Координаты вектора х часто необходимо записывать не в виде строки, а в виде
столбца:
4N
(хих2,...,х„)Г =
Приложение 2. Математическое программирование (основные положения) 679
Общая задача математического программирования разбивается на задачи,
названия которых определяются видом функций, которые необходимо оптимизировать и
которые входят в условия-ограничения, типом переменных задач, алгоритмом
решения. Если функции /(х), g/(x), hj{\) в выражениях (П2.1) - (П2.3) линейны, то
полученную задачу называют задачей линейного программирования.
Если хотя бы одна из функций /(х), gt (x), hj (x) нелинейна, то (П2.1) - (П2.3)
называют задачей нелинейного программирования. Многие задачи, в свою очередь,
разбивают на подмножества. Так, если /(х) является квадратичной функцией, а
ограничения линейны, то получаем задачу квадратичного программирования (более
точно /(х) должна быть квазиопределенной квадратичной формой).
В сепарабельном программировании целевая функция /(х) представляет собой
сумму функций, различных для каждой переменной. Условия-ограничения здесь могут
быть как линейными, так и нелинейными, но все недиагональные элементы матрицы,
состоящей из вторых частных производных любой функции задачи, равны нулю.
Если координаты искомого вектора х являются только целыми числами, то
получаем задачу целочисленного программирования (линейного или нелинейного).
В задачах математического программирования требуется найти так называемый
условный экстремум (максимум или минимум) функции при наличии ограничений.
Рассмотрим задачу математического программирования, в которой есть только
ограничения в виде равенств. Пусть целевая функция задачи является функцией двух
переменных: z = /(х) = f(xx,x2). Ее аргументы связаны уравнением ф(х,,х2) = 0
(ограничения в виде неравенств отсутствуют). Если функции z-f[xx,x2) поставить в
соответствие некоторую поверхность, то в данной задаче необходимо найти
следующие точки:
а) принадлежащие линии пересечения поверхности z = /(x],x7) и цилиндра с
образующей, параллельной оси OZ, и с направляющей ф(х1?х2) = 0;
б) в которых функция z = f(xux2) принимает экстремальные значения
(рис. П2.1). Как видно из рис. П2.1, точки условного экстремума А и В не
совпадают с наибольшим или наименьшим значением функции z = /(х,,х2) - с
безусловным экстремумом функции f(xx,x2). Если из уравнения связи
ф(л-! ,лг2) = 0 можно выразить в явном виде одну переменную через другую,
например х2 = v|/(x,), то ^ = /(jc1,jc2) = /[x1,v|/(^1)] становится функцией
одной переменной хх и ее безусловный экстремум отыскивается
традиционными методами (приравниваем первую производную от /[*i,y(*i)] по хх
нулю). Безусловный экстремум функции /[*i,v|/(jci)] является условным
экстремумом для функции f(x]9x2) при ограничениях q>(xl,x2) = 0.
• Однако выразить в явном виде из условий-ограничений необходимую часть
переменных, как правило, не удаегся.
Лагранж предложил метод нахождения условного экстремума функции (метод
носит его имя). Пусть требуется решить следующую задачу: минимизировать
f(xx,x2,...,xn) при ограничениях h} (хх,х2,...,хп) = 0; j~\,p. По условию задачи
составляется функция Лагранжа
680
Приложения
F{xl,x2,...,xn) = f(xl,x2,...,xn) + YjXJhl(xbx2,...,xn).
7=1
Здесь Xj - неизвестные постоянные множители, подлежащие определению
(множители Лагранжа), т.е. требуется найти п неизвестных х]9х2,...,х„ и р множителей
Лагранжа Хх,Х2,...,Хр .
х
z =f(x]tx2)
(xvx2) = 0
Рис. П2.1. Геометрическая интерпретация метода Лагранжа
11 i
Л] т л2 1
-1
Рис. П2.2. Область допустимых значений л*, и х2
Для рассматриваемого примера
F{x\>x2) = f{xl9x2) + X<p(xux2).
Точки, в которых возможен экстремум, находятся как решение системы
алгебраических уравнений, полученной приравниванием нулю частных производных от
функции Лагранжа по искомым переменным (п уравнений) и включением в эту
систему р ограничений-равенств. Метод Лагранжа сводит задачу отыскания
условного экстремума функции /(х) к задаче отыскания безусловного экстремума
функции F[\,X).
Ограничения-неравенства еще более усложняют задачу. Дело в том, что
ограничения-неравенства задают область допустимых значений переменных. Например,
пусть требуется оптимизировать некоторую функцию /(х) при ограничениях
g1(x) = ^l-^>0,
Приложение 2. Математическое программирование (основные положения) 681
g2(x) = l-x2-x22>0.
Область допустимых значений переменных хх и х2 в этой задаче есть пересечение
области, лежащей «внутри» параболы хх = х\ с кругом единичного радиуса,
уравнение окружности которого имеет вид х\ +х\ -1 (рис. П2.2).
Пересечение цилиндра, направляющей которого является граница полученной
области D, с поверхностью z = /(x) может давать самые разнообразные варианты.
На рис. П2.3, а - в показаны поверхности, полученные в результате пересечения
цилиндра, направляющей которого служит граница области допустимых значений
переменных хх и х2, и поверхности, соответствующей целевой функции z = f(x],x2).
На рис. П2.3, а точка М безусловного экстремума функции z = f(x]9x2) является и
точкой условного экстремума задачи. На рис. П2.3, б точка М является уже
граничной и в ней целевая функция достигает своего наибольшего значения. На рис. П2.3, в
точка М не принадлежит области допустимых значений переменных, а целевая
функция имеет равные наибольшие значения по линиям ALB и АКБ (т.е. неясно, что же
брать за решение задачи). Эти неоднозначные результаты получены даже в случае,
когда поверхность целевой функции z = /(х) достаточно проста и обладает
единственным (глобальным) максимумом.
М.
z =Л*,,х2)
IV
м
?—-.
^*-—
\
Рис. П2.3. Точка экстремума М\
а-функции f(x\,x2) и задачи',
б - стала граничной,
в-не принадлежит области
допустимых значений х\ и х2
Наиболее полные результаты в задачах математического программирования
получены для выпуклых целевых функций, когда область допустимых значений является
выпуклым множеством. Множество точек D называют выпуклым, если для любых
точек Л/] и М2 , принадлежащих области D, отрезок МХМ2 принадлежит
множеству (области) D (рис. П2.4, а). Другими словами, любая точка ykMx +(l-^)M2]
682
Приложения
принадлежит области D для любого X, 0 < X < 1, и для любых точек Мх и М2,
принадлежащих области D. Причем пересечение конечного числа выпуклых множеств
выпукло.
На рис. П2.4, б показаны невыпуклые множества. Функцию f(M) называют
выпуклой на непустом выпуклом множестве Д если для любых двух точек Мх и А/9,
принадлежащих области Д и для любого числа X, О < X < 1, справедливо неравенство
f[XM,+{\-X)M2]<Xf{M,) + {\-X)f{M2).
а б
Рис. П2.4. Выпуклые (а) и невыпуклые (б) области (множества)
Функцию /(А/) называют строго выпуклой, если для О < X < 1 и МХФ М2
выполняется строгое неравенство
/[хм,+(\-к)м2]<х/{м,)+(\-х)/(м2). ■
Геометрически выпуклая функция лежит над своими касательными. Примером
выпуклой функции является парабола.
Сумма выпуклых на множестве D функций есть также выпуклая на D функция.
Функцию /(х) называют вогнутой на выпуклом множестве Д если функция
-/(х) выпукла на D.
Ограничения g/(x)>0; / = l,/w образует выпуклое множество D {выпуклую
область D), если все функции gt (x) вогнуты.
В математическом программировании выделяется важный класс задач - задачи
выпуклого программирования:
минимизировать /(х),
при ограничениях g, (х) > 0; / = 1,/и,
где /(х) - выпуклая функция, а все функции &(х) - вогнуты, т.е. рассматривают
выпуклые функции на выпуклых множествах.
Задачи выпуклого программирования обладают важным положительным
свойством: локальные минимумы целевых функций являются одновременно глобальными
{единственными).
Очевидно, что решить подобную задачу проще, чем в случае, когда целевая
функция /(х) и область D будут общего вида.
Приложение 2. Математическое программирование (основные положения) 683
НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ ОПТИМУМА
В ЗАДАЧАХ МАТЕМАТИЧЕСКОГО ПРОГРАММИРОВАНИЯ
В общем случае в задачах математического программирования ставится вопрос об
отыскании локального минимума (максимума) целевой функции, т.е. такого значения
х , что для значений х, принадлежащих некоторой окрестности этого значения х ,
выполняются неравенства f[x J>/(x) для строгого минимума (максимума) и
fix J~/(x) для нестрогого минимума (максимума). Как и для функций одной
переменной, в задачах математического программирования требуется сформулировать
необходимые и достаточные условия существования оптимума.
Рис. П2.5. Положение градиента V/(x) в точке решения х* и в точке х,
не являющейся решением задачи математического программирования
(знаками «+» и «-» указано направление возрастания значений линий уровня)
Если в задаче математического программирования множество D выпукло, а
функция /(х) дифференцируема в точке х* е D, то градиент V/Yx J, если он отличен от
нуля, составляет нетупой угол ф с вектором, направленным из х в любую точку
Xj е D. Другими словами, скалярное произведение (V/(x* Yxj -х *]>0 (рис. П2.5).
Для точки х, не являющейся решением задачи, всегда найдется такая точка х2, что
cpj будет больше я/2.
В тех случаях, когда решение х* принадлежит внутренней области Д градиент
V/(x*) = 0.
Сформулированное условие является необходимым условием локальной
оптимальности в задаче минимизации дифференцируемой функции на выпуклом
множестве (для выпуклой задачи оно является и достаточным условием глобальной
оптимальности).
Для области D в виде параллелепипеда, когда aj<Xj<bh
-оо < al < bt < +оо, / = 1,л данное (необходимое) условие следует понимать как
= 0, если а, <х* <bt\
> 0, если х* = at * -оо;
< 0, если х* = bj Ф +оо.
»('•)
дх,
684 Приложения
Здесь градиент «смотрит» внутрь области D.
Чтобы определить координаты возможной оптимальной точки, надо из
необходимых условий составить соответствующие системы уравнений и решить их.
В общем случае для задачи вида
/(x)->min; (П2.4)
g,(x)>0, / = UJ; (П2.5)
А7(х) = 0,у = 1^, (П2.6)
вводится функция Лагранжа
т р
где и, (i = 1,т\ Xj (j = 1,р) - множители Лагранжа, подлежащие определению
наряду с координатами вектора х. Множители Лагранжа А,7 для ограничений-равенств
могут иметь любой знак, множители Лагранжа ut для ограничений-неравенств -
неотрицательны. Если в задаче математического программирования (П2.4) - (П2.6)
множество Р9 xePaR", выпукло, функции /(х), g,(x), i = \,m выпуклы на Р и
дифференцируемы в точке х* е Д D = |х е Р\g, (х) > 0, / = 1,т, к} (х) = 0, j = 1,/?},
функции hj(x),j -\,p линейны и при некоторых u*,X*j выполняются условия
(VxZ,(x,u*,X.*\x-x* j>0 при всех хеР и M*g/fx*j=O, / = 1,то х* -(глобальное)
решение этой задачи.
Соотношения
(vxL(xV,X*),x-x*)>0 (П2.8)
при всех х е Р ,
«*ft(x*)=0, / = tw, (П2.9)
для задачи выпуклого программирования являются не только необходимыми, но и
достаточными условиями существования решения {условия Куна- Таккера):
а) если х является внутренней точкой области Р\ х е int P, то условие (П2.8)
эквивалентно VxZ,(x ,u Д )=0;
б) если область Р имеет вид параллелепипеда
P = lxeR" ak <xk <bki * = 1,л|,
где -оо < ak < bk < too, то соотношение (П2.8) эквивалентно следующему
условию: для любого к = \,т
= 0, если ак <хк <Ьк;
Ы
ir(x 'u •*•)
> 0, если хк = ак Ф -оо;
дхк
< 0, если xj^ = bk Ф +оо;
в) ecyjw P учитывает условие неотрицательности части (s) переменных и имеет вид
/> = {хеД"|;с* >0, к=Щ,
Приложение 2. Математическое программирование (основные положения) 685^
где 0<s<n, то условие (П2.8) эквивалентно совокупности условий:
—-(х ,и Д )>0,
хк^-(х\и, )/)=0, А=п (П2.10)
дхк v '
—-(х ,и ,Х )=0,А: = 5 + 1,«.
В отличие от методов отыскания оптимальных решений в задачах без
ограничений-неравенств здесь появляется дополнительное условие (П2.9), которое называют
условием дополняющей нежесткости'.
Это условие разделяет ограничения-неравенства на активные, которые в точке
оптимума обращаются в нуль (g,(x*) = 0, / = 1,/^ 1\ <т\ и пассивные \gt{\\^0,
/ = 1,^, l\ +l2 = wj. Для пассивных ограничений коэффициенты Лагранжа w*
должны быть равны нулю, при этом пассивные ограничения не оказывают своего влияния
на решение х*.
Рассмотрим случай, когда в функции Лагранжа присутствуют только
ограничения-неравенства: /(х) -> min, g, (x) < 0, / = 1,/и . Тогда в точке минимума
vx/(x>i>;vxg/(x*)=o,
ы
т.е. антиградиент целевой функции является неотрицательной линейной
комбинацией градиентов функций, образующих активные ограничения в точке х* (рис. П2.6).
№
Рис. П2.6. Связь направлений градиентов активных ограничений и антиградиента
*
целевой функции в точке решения X ив точке X, не являющейся точкой решения
На рис. П2.6 показано множество, образованное неравенствами gx (х) < 0,
g2(x)<0, g3(x)<0. Здесь же в точках х* и x указаны направления градиентов
активных ограничений и антиградиента целевой функции. Отсюда следует, что
точкой оптимума не может быть точка х, т.к. в ней не выполняется условие того, что
антиградиент /(х) есть положительная линейная комбинация градиентов активных
ограничений. Решением является точка х*, где данное условие выполняется.
686 Приложения
Мы рассмотрели некоторые условия существования решения, учтя производные
первого порядка. Как и для функции одной переменной, при анализе условий
оптимальности можно рассматривать производные высших порядков (в частности,
второго). В задачах математического программирования сформулированы и
доказаны условия оптимальности второго порядка, в которых оперируют вторыми
частными производными от функции Лагранжа.
В общем случае задачу математического программирования можно было бы
решать по следующей схеме:
1) записывание задачи в канонической форме вида (П2.4) - (П2.6) и составление
функции Лагранжа (П2.7);
2) составление системы условий, которые характеризуют решение (определяют
точки, где возможно существование оптимального решения - стационарные
точки): в развернутой форме записывают условия (П2.8), (П2.9), а также
условия, накладываемые задачей на допустимые значения х и на множители
Лагранжа. Например, для условия (П2.10) полная система для определения
стационарных точек имеет вид
л*>0; — (x,u,X)>0;**— (х,иД) = О, * =п;
8хк дхк
—-(х,и,Х) = 0Д=5 + 1,и;
ахк
z/, >0, g,(x)>0; w,g,(x) = O,/ = U;
&(x) = 0,i = / + l,/w;
3) решение полученной системы необходимых условий. Это удается сделать в
аналитическом виде лишь в редких случаях;
4) если удалось получить решение системы необходимых условий -
стационарные точки, надо провести исследование стационарных точек для отбора среди
них решений. Это сделать непросто. Иногда проще провести
непосредственное исследование поведения целевой функции в стационарной точке.
На последних двух этапах полезно привлечение физических и геометрических
соображений о возможном решении задачи математического программирования.
ТЕОРИЯ ДВОЙСТВЕННОСТИ И НЕДИФФЕРЕНЦИАЛЬНЫЕ
УСЛОВИЯ ОПТИМАЛЬНОСТИ В ЗАДАЧЕ ВЫПУКЛОГО
ПРОГРАММИРОВАНИЯ
В задачах математического программирования (П2.4) - (П2.6) молено указать
условия оптимальности, не прибегая к понятиям производных и градиентов, с
помощью так называемой теории двойственности. Особенно плодотворен этот подход в
задачах выпуклого программирования.
Будем рассматривать функцию Лагранжа (П2.7). Обозначим через / точную
нижнюю грань целевой функции задачи (П2.4) - (П2.6) на ее допустимом множестве
D: /* = inf/(х). Точка х* е D является решением задачи (П2.4) - (П2.6) в том и
только том случае, если /* = f(x \.
Введем вектор у с координатами ui\i-\,m\ и Xj (j -\,pj. Вектор у*
называется вектором Куна - Таккера задачи (П2.4) - (П2.6), если при всех хе D
Приложение 2. Математическое программирование (основные положения) 687
/s/(x)-Z«;&(x) + j>>,(x) = L(xy)
/=1 7=1
Любой задаче математического программирования можно поставить в
соответствие так называемую двойственную задачу оптимизации. Между прямой и
двойственной задачами имеются полезные связи.
Двойственной к задаче (П2.4) - (П2.6) называют задачу
ф(у)->тах; уеК,
где ф(у) = inf Z,(x,u,X) = inf
ш у
^={уее|ф(у)>-оо}.
Исходную задачу называют прямой. Если целевую функцию в двойственной задаче
ф(у) -> max заменить на -ф(у) -» min , то можно утверждать, что задача, двои-
ственная к произвольной задаче математического программирования, всегда выпукла.
Если в задаче математического программирования множество замкнуто и выпукло,
функции /(х), g,- (х), i = \,т непрерывны и выпуклы на D, функции hj(\), j -\,р ,
линейны или отсутствуют и решение прямой задачи конечно If > -оо \, в
частности, она имеет решение, то множество решений двойственной задачи непусто и
совпадает с множеством векторов Куна - Таккера прямой задачи. При этом справедливо
соотношение двойственности / = ф , т.е. минимум целевой функции прямой задачи
совпадает с максимумом целевой функции двойственной задачи. Учитывая, что число
переменных в двойственной задаче равно числу условий-ограничений в прямой задаче,
в ряде случаев двойственную задачу решить проще.
Получим необходимые и достаточные условия оптимальности в задаче выпуклого
программирования на основе теории двойственности. В этом случае изменится
только форма необходимых и достаточных условий (не будут участвовать производные),
но предпосылки в обоих случаях одинаковы.
Пара (х ,у JePxQ называется седловой точкой функции /,(х,у) на PxQ^eaiu
L[\ ,у* )=minZ,(x,y );
Z,(x\y*)=maxZ,(x\y),
т.е. L\\,y*\>L\x,y*\>L\x,y\ при всех хеР, yeQ.
Тогда точка х* е Р является решением прямой задачи в том и только том
случае, если существует вектор у &Q, такдй, что пара \х ,у 1 — седловая точка
функции Лагранжа L(\,y) на P*Q. Таким образом, если одновременно решать и
прямую и двойственную задачи, то к точке минимума (к решению) мы можем
приближаться с «двух» сторон.
Пример П2.1.
Рассмотрим пример.
минимизировать /(х) =| jc, - 21 +1 х2 - 21,
при ограничениях
£,(х) = х,-*22>0,
688
Приложения
А,(х) = *,2+;с22-1 = О
Прежде всего построим по условиям-ограничениям допустимую область D - множество точек
(х\,х2), удовлетворяющих ограничениям задачи. Ограничение gi(x) определяет область «внутри»
параболы jc, = х\ (рис. П2.7); ограничение Л[(х) - окружность единичного радиуса с центром в начале
координат (рис. П2.7). Допустимая область D этой задачи - дуга окружности ABC. Чтобы найти точку, в
которой функция /(х) принимает минимальное значение на допустимой области D, построим линии
уровня /(х) - штриховые линии. В точке (2,2) /(х) = 0; при /(х) = 1 и /(х) = 2 линии уровня образуют
квадраты. Градиент функции V/(x) направлен в сторону дуги ABC, и функция /(х) будет иметь
минимальное значение в точке касания линии уровня к дуге ABC. Так как линии уровня отсекают от осей х1 и
71 . . Я 1 ^
х2 равные отрезки, то координаты точки касания равны 1 cos— = I sin — = -т= . Решение задачи*
4- 4 V2
• _ 1 *_ 1 . , , ч_ ,
х\ -~75Г> хг~~гТ •> Jm\nW-J
■72'*2=7Г
1 1
= 2
ИЪГИ
-2
«2,6.
\
-1
Рис. П2.7. Графическое решение задачи математического программирования
Нетрудно видеть, что то же решение будет и в том случае, если вместо Л, (х) взять #2(х)= х\ + х\ ~ 1 - 0 •
Тогда допустимая область D будет заключена между дугами ABC и АОС (рис. П2.7). Но минимальное
значение функции /(х) в области D будет достигнуто в точках х\ =-?=* и х\ --т= .
МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ ЛИНЕЙНОГО
ПРОГРАММИРОВАНИЯ
При рассмотрении задач линейного программирования целесообразно их
подразделить на отдельные классы (виды) задач. Для каждого такого класса удаётся
сформулировать алгоритм решения, приемлемый только для данного класса задач.
Наиболее разработанными в математическом программировании являются задачи
линейного программирования.
В задачах линейного программирования целевая функция линейна, а условия-
ограничения содержат линейные равенства и линейные неравенства. Переменные
могут быть подчинены или не подчинены требованию неотрицательности. Одна и та
же задача линейного программирования может быть записана в различной форме.
Говорят, что задача линейного программирования записана в канонической форме,
если все её ограничения, кроме х} > 0 , j = 1, п, представляют собой равенства. Если
все ограничения имеют вид неравенств, то задача записана в стандартной форме.
Приложение 2. Математическое программирование (основные положения) 68У^
Для записи задачи линейного программирования в различной форме применяются
следующие приёмы:
1) точка минимума функции /(х) совпадает с точкой максимума функции
-/(х);
2) ограничения в виде неравенств
п
Y,auxJ>bi(i = \im)
7=1
можно представить в виде равенств, использовав новые переменные
Xj (/ = п +1, п + 2,..., т), xi > О, называемые слабыми:
п
YjaljXj-xi=bi.
7=1
Для неравенства 2^ ayxj - fy можно взять х, > О и получить равенство
7=1
п
3) ограничение в виде равенства ^OyXj =6,- можно заменить двумя неравенст-
7=1
п п
вами £а/Л^ >Ь,-, £eff*y ^Ь< •
7=1 7=1
Если имеется /w равенств ^Д//*у =6,- (/ = l,w), их можно заменить (w + 1)
7=1
неравенствами
п т п
Y,auxj *bt о=1>т)и ^lQlauxj "*/) ~°'
у=1 /=1 >=1
4) если на переменную Xj (у = 1,я) не наложено условие неотрицательности, её
можно заменить двумя неотрицательными переменными х* и jcJ , положив
*7 =JC) "^7'^7 -^'^7 ~^ *
Если имеется «таких переменных Xj (j = \,n), то их можно заменить
(л + 1) неотрицательными переменными *уИ д:0, положив х7- =jc] -х0 .
Система ограничений в виде равенств и неравенств образует выпуклое множество
- выпуклый многогранник. Это множество может быть ограниченным и
неограниченным. Целевая функция задачи линейного программирования - тоже выпуклая
функция. Таким образом, задача линейного программирования является частным
случаем задачи выпуклого программирования.
Рассмотрим систему ограничений задачи линейного программирования в виде
равенств
п
Yaaijxj =zbi(i = l9m)in>m . (П2.11)
7=1
45 Зак. 366
690 Приложения
Говорят, что система (П2.11) линейных уравнений совместна, если она имеет, по
крайней мере, одно решение. Система (П2.11) называется избыточной, если одно из
уравнений можно выразить в виде линейной комбинации остальных. Система
(П2.11) несовместна, если ранг матрицы latJ ; / = 1, j = \,п, равен г, ранг
расширенной матрицы этой системы (с присоединённым столбцом Ь{) больше г .
В системе (П2.11) число переменных (неизвестных х) п больше, чем число
уравнений т . Будем считать, что ранг этой системы равен т (система неизбыточна)
и что система (П2.11) совместна. Тогда т переменных из общего их числа п
образуют базисные переменные, а остальные (п-т) переменных называют свободными.
Система (П2.11) в этом случае будет иметь бесчисленное множество решений, т.к.
свободным переменным можно давать любые значения, для которых находят
значения базисных переменных. Решение системы (П2.11) называют базисным, если все
свободные переменные равны нулю. Если система уравнений имеет решение, то она
имеет и базисное решение. Решение системы уравнений (П2.11) называют
допустимым, если все его компоненты неотрицательны. Если система линейных уравнений
обладает допустимым решением, то она имеет и базисное допустимое решение.
Совокупность всех допустимых решений системы (П2.11) есть выпуклое множество,
или, другими словами, множество решений задачи линейного программирования
выпукло. Так как это множество образовано плоскостями (гиперплоскостями), то оно
имеет вид выпуклого многогранника. Базисное допустимое решение соответствует
крайней точке выпуклого многогранника (его грани или вершине).
Если существует оптимальное решение задачи линейного программирования, то
существует базисное оптимальное решение.
Целевая функция задачи линейного программирования есть уравнение плоскости
(или гиперплоскости для числа переменных больше трех). Пусть в вершинах
выпуклого многоугольника мы установили «столбы», высота которых определяет значения
целевой функции в данной вершине. На эти «столбы» наложим.плоскость (графическое
представление целевой функции). Очевидно, что максимальное и минимальное
значение целевая функция задачи линейного программирования достигает либо в вершине
выпуклого многогранника, либо на одной из его граней. Таким образом, решение
{решения) задачи линейного программирования лежит в вершинах выпуклого
многогранника и для его нахождения надо вычислить значение целевой функции в вершинах
выпуклого многогранника, определяемыми условиями-ограничениями задачи.
СИМПЛЕКС-МЕТОД - ОСНОВНОЙ МЕТОД РЕШЕНИЯ ЗАДАЧ
ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Рассмотрим задачу линейного программирования в канонической форме:
п
найти минимум функции /(х) = ^С/Л/
п
при условиях ^Г я^jcy = bt , i = l,m, m<n, Xj > 0, j = 1, л .
7=1
Предполагается, что решение этой задачи суд*ествует. Чтобы найти оптимальное
решение, надо найти допустимые базисные решения, а из них выбрать оптимальное
базисное решение. Для чего мы должны поочередно из столбцов матрицы
ILJ i = \,m, j-\,n выбирать т столбцов и решать систему из т уравнений с т
неизвестными. Такой метод требует решения С^=п]4 ,, _ ч^ уравнений, что
практически невозможно, даже для небольших значений т .
Приложение 2. Математическое программирование (основные положения) 69]
Для решения задач линейного программирования в 1949 г. американским
математиком Дж. Данцигом разработан симплекс-метод, ставший основным для решения
задач линейного программирования.
Разберем главные моменты симплекс-метода на небольшом числовом примере:
минимизировать /(х) = 3 - х4 + х5 при ограничениях
х2+2лг4+3х5-7 = 0,
хъ-х4 -Зх5 -2 = 0,
ЛГ| + х4 + х5 - 2 = 0,
х, > 0;х2 > 0;х3 £ 0;х4 > 0;х5 > 0.
Определитель, составленный из коэффициентов при неизвестных хьх2,хъ, имеет вид
0 1 0
0 0 1 и не равен нулю. Поэтому ранг матрицы ограничений равен 3, базисные
1 0 0
переменные - Х!,х2,х3, а свободные переменные - х4,х5. Выразим базисные
переменные через свободные:
Xj = 2 — Х4 ~ Х5 >
х2 = 7-2х4 -Зх5;
х3 = 2 + х4 + Зх5 •
Базисное решение (при нулевых значениях свободных переменных х4 и х5) в
данном случае х} = 2,х2 = 7,х3 =2 и является допустимым (значения xl5x2,x3
положительны). Значение целевой функции при таких значениях переменных /(х) = 3 . Но
оно может быть уменьшено, если увеличить значение переменной х4, входящей с
отрицательным коэффициентом. Очевидно, что увеличивать х4 можно до тех пор,
пока не будут нарушены условия-ограничения задачи, в частности, пока переменные
хх,х2 и хъ будут неотрицательны. Например, если х4=2,х5=0, то
Х] - 0, х2 = 3, х3 = 4 - новое допустимое решение. При ;с5 = 0 переменная Xj = 0,
если х4 =2/1=2; х2 = 0 , если х4 = 7/2 = 3,5; хъ - 0, если х4 = 2/(-1) = -2 . Чтобы ни
одна из переменных хих2 и хг не стала отрицательной, надо выбрать наименьшее
положительное отношение элементов столбца свободных членов к соответствующим
коэффициентам при х4 . Берем х4 - 2, хх становится равной нулю, т.е. х1 переводим
в свободные переменные, а х4 = 2 становится базисной переменной. Ограничения и
целевую функцию надо выразить теперь через хх и х5: из первого уравнения имеем
х4 =2-jcj -х5, из второго - х2 =3 + 2xj -x5; из третьего - х3 =4-х]+2х5 и
f(\) = 3-2 + xl +x5 +x5 =1 + jc! +2x5. В данном случае любое увеличение значении
свободных переменных хх и х5 ведет к увеличению (но не к уменьшению) значений
целевой функции, т.е. получили оптимальное решение:
Х] = 0, х5 = 0, х2 = 3, х3 = 4, х4 = 2,
Какие выводы можно сделать из этого примера? Во-первых, надо так разделить
базисные и свободные переменные, чтобы получить допустимое базисное решение, а
затем выразить базисные переменные и целевую функцию через свободные
переменные. Во вторых, по знаку коэффициентов при неизвестных в целевой функции следу-
45"
692
Приложения
em определить: а) не достигли ли мы уже оптимального решения (нет
отрицательных коэффициентов); б) значение какой переменной лучше увеличить, т.е. какую
переменную следует перевести в свободные. Другими словами, определяя
минимальное положительное отношение элементов столбца свободных членов к
коэффициентам при новой свободной переменной, находим переменную, которую необходимо
перевести из базисных в свободные. После чего выражаем условия-ограничения и
целевую функцию через новые свободные переменные.
Процесс повторяют до тех пор, пока не будет получено оптимальное решение.
Если среди коэффициентов при неизвестных в целевой функции есть
положительный, а все коэффициенты в условиях-ограничениях при нем неположительны, то
задача линейного программирования не имеет оптимального решения, минимальное
значение целевой функции равно - оо .
Рассмотрим геометрическую интерпретацию симплекс-метода.
В условиях одной из первых задач линейного программирования, для которых
Данциг разработал вычислительный метод, входили ограничения вида
п
Эти ограничения в «-мерном пространстве определяют симплекс. Симплекс
трехмерного пространства изображен на рис. П2.8. Рассмотрим неравенство хх+х2 <t\
при условиях X] > 0 , х2>0. Область решения этого неравенства показана на
рис. П2.9. Данное неравенство можно преобразовать в уравнение введением слабой
переменной х3. Тогда получим систему x]+x2+x3=bl, х, > 0, х2 > О, х3 > О .
Областью решений этой системы является треугольник А ЛВС, показанный на
рис. П2.8, если принять, что А-В = С-\\. Каждой точке треугольника области
рис. П2.8 соответствует точка области на рис. П2.9.
ху
Х2
Х\
Рис. П2.8. Симплекс трехмерного пространства
Соответствие можно устанавливать, проектируя эту треугольную область на
плоскость ххх2. Если придать слабой переменной хъ постоянное значение с, то х} и
х2 должны удовлетворять уравнению хх + х2 = 6, - с, которое является уравнением
прямой, параллельной x]+x2=bl. Если слабая переменная равна нулю, то
х\ + Х2 = Ь\ • Таким образом, значение слабой переменной может служить мерой
близости точки из треугольной области к границе x]+x2=bl полупространства,
определяемого исходным неравенством.
Приложение 2. Математическое программирование (основные положения) 693
Х2
О
В *i
Рис. П2.9. Область решения неравенства
В общем случае в симплекс-методе процедуру поиска начинают с допустимой
вершины, а затем переходят в соседнюю вершину так, чтобы значение целевой функции
«улучшилось». В пространстве векторов свободных переменных возрастание значения
одной из свободных переменных от нуля, при котором остальные свободные
переменные остаются равными нулю, соответствует движению из начала системы координат,
образованной свободными переменными, по одной из координатных осей. При этом,
поскольку (п-\) свободных переменных равны нулю, (л-1) ограничений задач
выполняются как равенства. Другими словами, все соседние с началом координат
вершины (которые соответствуют текущему решению) связаны с началом координат (п-\)
ребрами выпуклого многогранника. Возрастание от нуля значения некоторой
свободной переменной может привести к тому, что эта переменная станет базисной. Для того
чтобы получить в качестве решения вершину, необходимо заменить одну из базисных
переменных на свободную, т.е. произвести соответствующее перемещение вдоль одной
из координатных осей до тех пор, пока не будет достигнута другая вершина. Если
двигаться дальше, то будет нарушено условие неотрицательности переменных. Таким
образом, в симплекс-методе начинают с локальной координатной системы с началом
координат, соответствующим решению, и перемещаются вдоль ребра к соседней
вершине, в которой значение целевой функции «улучшается». После перехода в новую
вершину рассматривают новую систему координат с началом в этой вершине. Если
движение осуществляют согласно критерию (выбирают минимальный отрицательный
коэффициент при неизвестных в целевой функции), то это соответствует спуску по
самому крутому ребру из всех пересекающихся в начале координат. Величину изменения
целевой функции за одну итерацию определяют как углом наклона (крутизной) ребра,
так и длиной ребра. Более точно она равна минимальному значению по / величины
Icyfy/tfJ для данного у, где atj - соответствующий элемент вектора-столбца а} для
j -й свободной переменной.
Замечание. Итак, в симплекс-методе всегда считают, что в первую таблицу
внесено допустимое базисное решение. В задачах, описывающих реальные системы,
допустимое базисное решение подобрать трудно. Для этого решают
вспомогательную задачу линейного программирования, которая позволяет не только найти
допустимое базисное решение, но и установить, совместна ли система ограничений
исходной задачи.
Пусть система ограничений исходной задачи записана в следующем виде:
п
где bt > О, i = 1,/w. Этого нетрудно добиться, умножив при необходимости уравнения
на -1.
694 Приложения
Введем новые переменные
и рассмотрим целевую функцию
/(4) = X$/-»min. ' (П2ЛЗ)
/=1
Допустимое решение для задачи (П2.12), (П2.13) сразу задано. В процессе
решения задачи возможны следующие случаи:
1) min/(^) = 0, £,=0, i = \,m (все £,- стали свободными переменными) -
полученное решение Xj, j = 1,я , является допустимым решением исходной задачи
линейного программирования;
2) min /(^) > О - система ограничений исходной задачи несовместна.
В первом случае можно отметить две особенности:
1) целевая функция /(%) достигла своего минимума, равного нулю, а некоторые
из переменных £,- находятся среди базисных, хотя и равны нулю. При этом
нет необходимости обращать внимание на знаки в строке для целевой
функции (можно любую свободную переменную выводить в базисные), т.к.
значение целевой функции не изменится, но следует выполнять условия,
обеспечивающие допустимость нового базисного решения (рассмотреть минимальное
положительное отношение);
2) даже после выполнения предыдущего пункта в строке для базисной
переменной £,- нет положительных элементов (нельзя получить положительное
отношение). Это означает, что переменные, входящие в уравнение для £;- с
ненулевыми коэффициентами, должны быть равны нулю в данной задаче. В процессе
дальнейшего решения их надо исключать из рассмотрения.
Наряду с решением вспомогательной задачи линейного программирования
(П2.12), (П2.13) преобразуется и целевая функция исходной задачи, которая
приписывается в задаче (П2.12), (П2ЛЗ) в виде дополнительной строки.
МЕТОД ПОЛНОГО ИСКЛЮЧЕНИЯ ЖОРДАНА ДЛЯ РЕШЕНИЯ
СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
На каждом шаге симплекс-метода требуется определять новые «наборы» базис-
пых и свободных переменных, т.е. решать системы линейных алгебраических
уравнений. Задачи линейного программирования решают с помощью стандартных
симплекс-таблиц, формализующих алгоритм перевода базисных переменных в
свободные. Этот алгоритм и определяет конкретный вид симплекс-таблиц. Рассмотрим
симплекс-таблицы, преобразуемые с помощью метода полного исключения Жордана,
получившего наибольшее распространение в линейном программировании.
Рассмотри систему т линейных алгебраических уравнений с п неизвестными
а\\х\ +anx2+... + auxs+... + aXnxn =6,;
ai\x\ + ai2X2 + • • • + aisxs + • • • + атхп = Ь,;
ат\х\ + ат2х2 + • • • + amsxs + • • • + атЛ = К ■
Приложение 2. Математическое программирование (основные положения) 695
В методе полного исключения Жордана делают такие преобразования, в
результате которых в каждой строке и в каждом столбце матрицы системы линейных
алгебраических уравнений остаются по одному неизвестному с коэффициентами,
равными единице.
Например, мы хотим исключить переменную xs из всех строк за исключением /-и
строки. Элемент ajs - коэффициент, стоящий перед переменной xs, называют
генеральным элементом, i -я строка и s -й столбец - разрешающими. Прежде всего,
разрешающую строку делят на ais и она остается неизменной. Чтобы исключить xs
из первого уравнения, умножим разрешающую строку на {-ais) и сложим с первой
строкой. В результате получим первую строку с нулевым элементом на месте als.
Аналогично исключаем xs в остальных строках. Получим новую эквивалентную
запись системы алгебраических уравнений. В ней / -я строка имеет прежний вид, но
все коэффициенты у нее поделены на ais; s -й столбец состоит из нулевых элементов
(кроме единицы, стоящей в / -й строке). Остальные элементы матрицы системы и
столбец свободных переменных пересчитываются по правилу прямоугольника. На-
- Н aisal n ~ alsain
пример, новое значение элемента а1п будет равно aln=-
ais
аи- ~ ;*
УС
din
uis
I
\
\
.ЛЫ
din
а новое значение Ьт столбца свободных членов - b% = -Jh-JE 2LL-L
Г"
I
| * j. b,
ams bm
Из правил прямоугольника следует, что когда в разрешающей строке (столбце) есть
нулевые элементы, то элементы столбцов (строк), пересекающих эти нулевые
элементы, остаются без изменений.
В процессе решения задач линейного программирования симплекс- методом
возможно «зацикливание». Поясним его суть. Пусть в процессе решения задачи
линейного программирования на некотором шаге симплекс-метода наименьших положи-
696 Приложения
тельных отношений свободных членов к коэффициентам разрешающего столбца
оказалось больше одного, т.е. выбор разрешающего элемента неоднозначен. После этого
шага все упомянутые свободные члены, за исключением свободного члена
разрешающей строки, обратятся в нуль. Этот случай называют вырожденным: сливаются
две или большее число вершин выпуклого многогранника D, когда ребро (или
ребра), соединяющие эти вершины, стягиваются в точку.
В алгоритме симплекс-метода каждый шаг означает переход по ребру от данной
вершины многогранника D к соседней (расположенной на том же ребре), а при
вырождении - совпадении двух соседних вершин - алгоритм может потерять
монотонность, т.е. может случиться, что после указанного шага мы остались в той же
вершине, только выраженной с помощью другого набора из п уравнений, относящихся к
этой вершине. Если продолжать решение симплекс-методом, то не исключено, что
после некоторого числа шагов мы вернемся к уже взятой ранее вершине и процесс
начнет повторяться. Произойдет зацикливание. Если в процессе решения
проводилось запоминание уже испытанных ребер, то для прерывания зацикливания
достаточно сменить генеральный элемент.
Существуют алгоритмы, где автоматически предусмотрены меры против
зацикливания - «расклеивание» слипшихся вершин.
Приложение 3. Редукция задач оптимального управления нелинейными объектами 697
ПРИЛОЖЕНИЕ 3. РЕДУКЦИЯ ЗАДАЧ ОПТИМАЛЬНОГО
УПРАВЛЕНИЯ НЕЛИНЕЙНЫМИ
ОБЪЕКТАМИ К ЗАДАЧАМ
МАТЕМАТИЧЕСКОГО
ПРОГРАММИРОВАНИЯ
С ИСПОЛЬЗОВАНИЕМ МЕТОДА
СЕТОК И АЛГОРИТМЫ ИХ РЕШЕНИЯ
Приведенные в третьей части учебника зависимости определяют общую
постановку задачи оптимального управления, в которых имеют место ограничения типа
равенств и ограничения типа неравенств.
В сформулированной постановке задачи функции Х(/) и U(^) принадлежат
бесконечномерным пространствам.
Из формулировки задачи математического программирования следует, что
функции Х(/) и U(/) следует характеризовать конечным числом параметров. Только в
этом случае удается свести задачу оптимального управления к задаче
математического программирования.
Таким образом, первым этапом в задаче применения математического
программирования для нахождения оптимальных U*(/) и Х*(/) является этап редукции
задачи оптимального управления к задаче математического программирования*. Из
сказанного можно заключить, что структурная схема, характеризующая процесс
решения задачи построения U*(/) и Х*(/) (оптимальные вектор управления и
фазовый вектор), может быть представлена в виде, показанном на рис. П3.1.
Далее, рассмотрим методы параметризации функций, входящих в постановку
задачи оптимального управления. Обозначим параметризуемую функцию через /(/).
Проведем изложение применительно к решению классической задачи -
вариационной задачи с закрепленными граничными точками, которая тесно связана с задачей
оптимального управления.
Задача формулируется так:
m{inn/) = m(injF(/(O,/'(/),/)^ (П3.1)
при условиях /(0) = /°, f(T) = /7, Fu f — скалярные функции.
Сформулированная задача относится к классу краевых задач [3, 43].
Функция /*(*), доставляющая минимум функционалу (П3.1), определяется
известным уравнением Эйлера
F'f{f,f',t)-F;r{f,r,t)-Fjr(f,r,t)f-F;r(f,f\t)r=o. (пз.2)
* В главе 5 рассмотрены методы математического программирования, использующие проекционную
аппроксимацию уравнений и соотношений, определяющих постановку задачи оптимального управления
44 Зак. 366
698
Приложения
Здесь частные производные от F(f,f',t) берутся без учета зависимости / и
/'от t. Уравнение (П3.2) - уравнение второго порядка, и поэтому его общее
решение содержит две произвольные постоянные, которые определяются с помощью
краевых условий.
Входные данные
±
Формулировка задачи оптимального
управления в терминах бесконечномерных
пространств с использованием
аппарата дифференциальных уравнений
±
Редукция исходной задачи к задаче
математического программирования
(параметризация исходной задачи)
I
Решение задачи математического
программирования (расчет U*(/) и Х*(/))
и»,х*(0
Рис. П3.1. К постановке задачи оптимального управления
Дифференциальные уравнения вариационных задач интегрируются в конечном
виде лишь в исключительных случаях. В связи с этим широко используется редукция
бесконечномерной задачи к конечномерной задаче оптимизации.
Изложим содержание метода конечных разностей (или метода сеток).
Его популярность во многом объясняется относительной простотой перехода к
конечномерным задачам [43].
Идея метода сводится к следующему: область непрерывного изменения аргумента
заменяют конечным {дискретным) множеством точек {узлов), называемым сеткой.
Вместо функций непрерывного аргумента рассматривают функции, определенные
только в узлах сетки - сеточные функции (рис. П3.2).
При таком подходе функция f(t) характеризуется ее дискретными значениями -
параметрами /(/0), f{tx)9 ... , f{tN.x)9 f{tN).
Производные заменяют их разностными аналогами - линейными комбинациями
значений сеточных функций в узлах сетки. В результате, например, краевую задачу
(П3.1) заменяют дискретным эквивалентом — дискретной краевой задачей
(разностной схемой) [43].
Краевая задача (П3.1) заменяется дискретным эквивалентом вида
min/(/(0),/(/0,...,/(/H)'^*I^(/(O/(fM).r/(/|)
JVi) JVI) |=0 Ч "
при условиях /(0) = /°, f(tN) = fT.
->*i
(ПЗ.З)
Приложение 3. Редукция задач оптимального управления нелинейными объектами 699
/0=0/, /2 /;
N-\ \<V
Рис. П3.2. Сеточная функция f(tk ), к =0,N
Так как значения /(/0) и /('#) заданы, то задача сводится к отысканию
экстремума функции N-\ переменных f(t})9 f(h)> ••• > /(Ov-i)> стоящей в правой
части (ПЗ.З).
Таким образом, бесконечномерная задача сведена к конечномерной задаче
оптимизации. Несмотря на кажущуюся простоту метода, при его использовании
приходится решать ряд проблем. Например, следует иметь в виду, что для одной и той же
задачи можно построить большое число различных разностных схем, среди которых
далеко не все пригодны для использования на практике [65]. Самостоятельной
трудной задачей является выбор размерности задачи (выбор шага h) (размерность задачи
при практическом использовании этого подхода может оказаться очень высокой).
Перейдем к формулировке задачи оптимального управления в терминах аппарата
математического программирования.
Заменим область непрерывного изменения аргумента конечным (дискретным)
множеством точек (узлов).
Вместо функций непрерывного аргумента рассмотрим функции, определенные
только в узлах сетки, - сеточные функции.
Разделим промежуток [0,Г] на N равных подынтервалов [0,/,],[^,/2],...,[/yV_i,/A ]•
где*д,=7\ h = ti+l-tf.
К уравнению (ПЗ.З) с целью решения задачи параметризации можно применить
замену производной конечной разностью
d\ Х(/ы)-Х(/,)
dt ~ h
и, таким образом, сформулировать задачу в параметрической форме.
С учетом сказанного уравнение (ПЗ.З) заменяется простейшей разностной схемой
X(//+J) = X(//) + AF(X(//),U(/<),//);
для функционала (П3.6) можно записать зависимость
•/ = A]£/o(X(r,),U(0).
/=0
К уравнениям (П3.4) должно быть добавлено начальное условие
Х(0) = Х°
и условие на правом конце
Х(Г) = Х7' = Х(/„),
44*
(П3.4)
(П3.5)
(П3.6)
(П3.7)
700 Приложения
где X(/yV) - фиксированный вектор. Кроме того, на изменение управления U(/) и
фазового вектора наложены ограничения
U(tt)e\Jm V/ = (U7; X(/7)gXw V/ = l,yV-l. (П3.8)
Справедливы зависимости [72]:
X(,,) = X(/0) + AF(X(/0),U(,0)) = 0,(U(/0)),
Х(/2) = Ф1(и(го)) + Л^(Ф1(и(го))>и(/1)) = Ф2(и(/о).и('1)).
Х(/*) = Ф*-,(и(/0).и('1).-.и(/А_2)) +
+^(Фн(и((,),и((|),...,и(гм)),и(/н))=
= ф*(и(/0),и(/1),и(/2),...,и(/4_1)).
С учетом последних формул функционал (П3.5) можно записать в виде
y=X;j/(U(?0),U(O,.-,U(/,.))> (П3.9)
/=0
где
уДи(/0),и(^,..,и(О) = А^(фДи(/0),и(/1),...,и(/м),и(О)).
В последней зависимости функционал У, зависит только от первых (/ + 1)
неизвестных переменных.
Функции вида (П3.9) в [72] названы функциями с последовательным включением
неизвестных.
Редукцию задачи оптимального управления к конечномерной задаче оптимизации
можно реализовать с использованием так называемой элементарной операции [72].
Эта операция вводится следующим образом. Проведем в пространстве состояний
(X,t) плоскости t = tj=ih, которые обозначим через Е,. Точки Х(/,) являются
точками пересечения траектории системы у(/) с плоскостями Z;.
Пусть В(Х(^),Х(/;+1)) - оператор, который паре точек Х(/,-) и Х(//+,) ставит в
соответствие управление U(//), переводящее объект за время h из состояния Х(/,)
в состояние Х(^/+1); y(^,^+i) - участок траектории, который соединяет точки Х(//)
и Х(//Ч1). Отразим этот факт выражением
(y(/<,rw),U(//))=B(X(//),X(/w)). (ГОЛО)
Оператор В(х(/,),Х(*/+1)) называется элементарной операцией [72].
С учетом сказанного выше функционал (П3.9) можно представить так
j(x(0,u(/))=Xj/o(y('^,+1).u(0)^=ZR:(x(/,))x(//+1)).
/=0 / /=0
Если задан оператор B(x(r/),X(f/+1)), то траектория определяется конечным
числом точек Х(/;) - точек пересечения этой траектории с поверхностями 1;.
Проблема построения элементарной операции рассмотрена в [72].
Если от векторно-матричного уравнения (П3.4) перейти к эквивалентному
уравнению с интегральным оператором
Приложение 3. Редукция задач оптимального управления нелинейными объектами 701
X(/) = Jf(X(t),U(t),t)£/t+X°, (П3.11)
о
то конечной разностью (П3.4) можно не пользоваться, а применять эквивалентное
соотношение, например, вида
Х(/и) = АХ^(Х(х<),и(т/),т/)+Х°;
/=0
множитель h перед суммой выделен для того, чтобы коэффициенты At были
безразмерными величинами.
Формулировка задачи построения оптимального программного управления U* (/,)
и оптимальной программы X*(tt) с помощью аппарата математического
программирования имеет вид:
^ = S^(u(/0),u(/,),..,u(/,)) =
/=0
= ХА/г(ф.(и(/о).и('|).".,и(/(._,),и(/|)))->тт
/=0 VV'>
при следующих ограничениях:
а) Х(//+1)=Х(//)+Их(//)1и(/Д//); (П3.12)
б) U(/,)eUm;X(0eX";
в) Х° =X(o)eG°, XT =Gr eGr;
г) и(/,) принадлежит классу допустимых.
В обсуждаемом подходе задача построения оптимальных программных
управлений Uy) и оптимальных программ Х*(/) свелась к стандартной задаче нелинейного
программирования. Трудности решения этой задачи определяются многими
факторами, и главное - это ее размерность, количество переменных и количество
ограничений. Размерность возникающей задачи математического программирования
определяется в основном двумя обстоятельствами: размерностью вектора х(/) и
количеством интервалов N , т.е. произведением nxN .
Если N достаточно велико, то даже в тех случаях, когда размерность вектора
X(t) невелика, задача математического программирования оказывается чрезвычайно
трудоемкой. Число N определяется прежде всего требованиями точности [72].
Пример П3.1. Оптимальный вывод двухступенчатой ракеты на орбиту спутника
Рассмотрим задачу оптимального вывода многоступенчатой ракеты на орбиту спутника [118] Будем
исходить из предположения, что траектория полета первой ступени уже известна. Ограничимся рассмо!-
рением второй ступени Из условия равновесия сил и моментов (рис ПЗ 7) получим следующие уравнения
движения [118]
m'y = Ss\n(Q + c)-mg,
m'z = Scos(Q + c),
IQ = -Slsinc.
Аэродинамическими силами и кривизной поверхности Земли пренебрегаем Значения тяги S и
ускорения силы тяжести g принимаются постоянными. Выражая переменную во времени массу т и момент
инерции / в виде
Л! = /Я0-Ц0/, Ц0 = COnSt,
1 = mk0* k0 = const
702
Приложения
и при новых константах
а, = S/m0 , а2 = цо/то , аъ = Si/mQk0 ,
и новых переменных состояния х = [х{, ,д:6]т и управлении
хх=у, х2=у, x2=z. x4=z. x5=Q, х6=0,
w = a
указанная система принимает вид [118]
а\
\-a2t
х3=х4,
x2=—^-s\n(x5+n)-g.
x4=—±—cos(x5+ul
\-a2t
*5 = *6>
-sinw
" \-a2t-
с начальными условиями Х°, которые получаются из конечных условий первой ступени и задаются здесь
равными
хю =30-103м » х2о =1,48-103м/с; хзо=Ом,
.х40 = 260 м/с , х5о = 1,39 рад; д-60 = 0 рад/с
У
L Т
у'
/
/
/
' mg
Ч/и
/Is
С
траектория
полета
^-
Рис. ПЗ.З. К задаче вывода двухступенчатой ракеты на орбиту спутника
Задача оптимизации состоит в определении управления «(/) {угол управления двигателем) таким
образом, чтобы после окончания подъема ракеты параметры траектории у = х{ и z = x3 возможно
меньше отличались от заданных уТ - л*,7 и zT = хЪ1, m. e чтобы функционал
y = [.Y,(7-)-*17]2+[x3(7-)-*37.]2
принял минимальное значение.
Значения констант равны [118]
а1 = 13,33м/с, а2:=4,4410"31/с, дг3 =1,18 1<Г31/с,
дг,г=200103м; jc3r =500 Ю3м, Г = 100с
Рассмотрим решение поставленной задачи сеточным методом. Для этого перейдем к системе
уравнении с интегральными операторами
X, (/) = JjC2 (x)rfT + ДГ, (0),
о
x2(0 = }T^sin(x,(t) + ii(t))rft-e* + jC2(0).
x,(/) = j*4(t)rft + jr,(0),
Приложение 3. Редукция задач оптимального управления нелинейными объектами 703
*4(')=irbcos(*5(T)+''(T))rfT+*4(o)>
x,(0 = j**(t)rft + *,(O),
О
*f>(')=bi^sin("(T))rfT+*6(0)
Применим метод сеток: непрерывные функции м(/), *,(/) заменим их дискретными эквивалентами
u(tk), Xj(tk)- Используя простейшие квадратурные формулы, получим.
*i('*)=*5>i('.)+*i(o).
*j('*) = *tr£L-Sin(JC5('')+»(''))-«'*+*2(0)-
А-
*з('*)=Л2>4('Л+*з(о)>
*s('*)=*i>6(/,)+*3(o),
A:
**('*) = *Z-r£27*in(«('<))+**(0)
/=0 l ~ ^2'/
-1
-2
_3
-4 •
-5
u*(t), рад
20
40
60 80 100
1 -сеточный метод
2 - метод второй
вариации
/, с
-►
0 20000 40000 60000 80000 100000 120000
Рис. П3.4. Графики м*(/) и jcJx^J
Х3,М
704
Приложения
Теперь формулировка задачи оптимального управления в терминах математического
программирования имеет вид
-|2 г / ч -\2
J=J(u(h)) = [x\{tN)-xvi] +[*зЫ-*з/] ->min
при ограничениях типа равенств
• дискретный аналог интегральных уравнений, описывающих поведение системы,
• конечные условия
*i('*)=*ir»
*зМ=*зг-
Для решения задачи математического программирования воспользуемся оптимизатором, встроенным
в табличный процессор Quattro Pro v 5 0
Результатом решения задачи математического программирования является массив дискретных
значений u*(tk) и *,(/*), / = 1,2,3,4 Дискретные значения приведены в табл. ПЗ 1
Анализируя полученные результаты, можно заключить, что конечные условия не достигнуты Отсюда
следует, что с помощью второй ступени ракета не может достигнуть требуемых значений jc,7 и хзг Этого
можно добиться лишь с использованием третьей ступени
Задача также была решена методом второй вариации [118], были получены аналогичные результаты
Графики управления и* (t) и зависимости **7-(*зН приведены на рис ПЗ 4
Таблица П3.1
Дискретные значения и*(tk), x*(tk), x*2(tk), xl(tk)yx*4(tk)
tk, с
0,0
3,4483
6,8966
10,345
13,793
17,242
20,690
24,138
27,586
31,035
34,483
37,931
41,380
44,828
48,276
51,725
55,173
58,621
62,069
65,518
68,966
72,414
75,863
79,311
82,759
86,208
89,656
93,104
96,552
100,00
u*(tk), рад
-1,3240
-1,3656
-1,4179
-1,4826
-1,5616
-1,6492
-1,7723
-1,9103
-2,0711
-2,3714
-2,4456
-2,6445
-2,8387
-3,0253
-3,2064
-3,3914
-3,5937
-3,8302
-4,1190
-4,4336
-4,6382
-4,5497
-4,1053
-3,4421
-2,8440
-2,4854
-2,3664
-2,4215
-2,5684
-2,7161
*,*(/*), м
30025
40126
45028
49822
54506
59080
63539
67884
72102
76174
80103
83887
87523
91000
94319
97472
100440
103230
105780
108060
110040
111780
113350
114870
116560
118340
120290
122380
124630
127030
•/ \ м
с
1480,0
1453,0
1421,8
1390,3
1358,4
1326,5
1293,6
1259,7
1224,1
1180,1
1140,1
1097,9
1053,9
1008,7
962,47
914,45
863,49
806,65
740,05
662,02
577,64
499,48
450,45
449,73
481,72
522,38
563,70
606,40
651,74
699,66
*з('Д м
42,2
2269,7
3648,3
5192,6
6905,7
8790,3
10850
13086
15504
18102
20885
23858
27022
30376
33931
37686
41639
45795
50137
54642
59296
64124
69186
74465
79851
85240
90579
95867
101100
106290
264,15
352,40
399,75
447,88
496,81
546,55
597,16
648,64
700,99
753,32
807,24
861,87
917,26
973,51
1030,7
1088,7
1147,1
1204,8
1259,1
1306,5
1349,3
1400,5
1468,1
1530,9
1561,8
1563,1
1549.3
1532,1
1517,6
1505,0
Приложение 4. Редукция задач оптимального управления линейными объектами 705
ПРИЛОЖЕНИЕ 4. РЕДУКЦИЯ ЗАДАЧ
ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
ЛИНЕЙНЫМИ ОБЪЕКТАМИ
К ЗАДАЧАМ МАТЕМАТИЧЕСКОГО
ПРОГРАММИРОВАНИЯ
С ПОМОЩЬЮ МЕТОДА СЕТОК
И АЛГОРИТМЫ ИХ РЕШЕНИЯ
Пусть линейный объект описывается векторно-матричным уравнением вида:
X = A(f)X + B(/)U. (П4.1)
Рассмотрим простейший случай, когда А = const, В = const.
Изложим несколько подходов к решению задачи параметризации с
использованием метода сеток.
Первый подход связан с использованием конечной разности первого порядка; в
этом случае имеем конечномерный эквивалент уравнения (П4.1)
хГ(* + 1)А]-Х[*А]
—^ '-^ — = AX(kh) + BU(AA). (П4.2)
Для того чтобы замена операции дифференцирования взятием конечной разности
была правомерна, необходимо, чтобы А было мало по сравнению с наименьшей из
постоянных времени процесса.
Эта схема хорошо изучена и отражена, например, в [72, 104].
Для построения дискретного аналога используется формула вида [93, 104]
X(t) = eAtX°+\eA{t-x)BV{x)dx.
о
Определяя последовательно с помощью последнего соотношения Х(кИ) при
условии кусочно-постоянных управлений, будем иметь:
X{h) = eAhX° +}eA(/7-T)^BU(0),
о
Х(2А) = eAhX(h)+ JeA{2h~x)dT BU(A),
(Jfc+l) h
X[(* + l)A] = eA/?X(*A)+ J eA{(M)h'x)dxBV(kh).
к h
В общем виде дискретная модель может быть представлена так
Х[(* + 1)А] = Ф(*А)Х(*А) + ри(*А),
и
гдеФ = еА\р=фА(/7"т)</тВ.
о
706 Приложения
Отсюда находим формулу, удобную для практического использования:
А:-1
X(kh) = Ф*Х° +р]Гф*-1-/и(/7г). (П4.3)
/=0
В последних зависимостях выбор шага А не требует особого обоснования и,
вообще говоря, соотношения справедливБ1 при любых А.
И, наконец, редукция задачи оптимального управления к задаче математического
программирования может быть осуществлена с помощью формулы
X(/) = J(AX(t) + BU(t))</t + X° .
о
Задача построения оптимального программного управления в терминах
математического программирования может быть сформулирована так:
1(и(/Дх(,О) = А]Г/о(хЫ> "('*))-> min
при следующих ограничениях:
а) X{tk)eXn, k = 0jT~ly\
1) > - ограничения типа неравенств;
б) V(tk)eV", k = 0,N-l\
a) X((N) = X',
2)
б) X(tk+l)-e
Ah
4+1
X(tk)+le«"-x)dTBV(tk)
(П4.4)
- ограничения типа равенств.
Рассмотрим конкретный случай ограничений. Например, очень часто ограничены
абсолютные значения переменных состояния и управления, т.е. налажены
действующие в течении всего времени управления следующие условия в форме
неравенств [104]
ulM-\ui\>O,i = \^;i (п45)
xj М~
х,|>0, j = l,n,\
где w, м и Xj м - заданные скалярные величины. Неравенства (П4.5) представляют
собой одну из простейших форм ограничений, которые могут быть наложены на
переменные состояния и управления.
Задача построения оптимальных программных управлений в терминах
математического программирования формируется так же, как и в предыдущем случае, но
ограничения имеют вид (П4.4).
Если же объект имеет переменные параметры, то для параметризации можно
использовать конечные разности; тогда
X [(* +1) А] = Х(Щ + h [ А(*А)Х(*А) + B(*A)U(* А)].
Для решения рассматриваемой задачи может быть использовано интегральное
соотношение
Х(0 = Ф(/,/0)Х° + |Хф(ОХ^(х)В(т)и(т)Л , (П4.6)
о
где Ф(/,/о)= Хф(О'Хф1('о) - (п х п )-переходная матрица состояния, /0= 0,
Хф(/) - нормальная фундаментальная матрица,
Приложение 4. Редукция задач оптимального управления линейными объектами 707
(xu(t) *,2(/)...х|и(/)Л
ХФ« =
x2i(t) x22(t)...x2n(t)
(П4.7)
UrtW *«2 (0-•*„„(') J
причем X((7), Х2(/),...,Хи(0 ~ столбцы матрицы Хф(/) являются решениями уравнения
X = А(/)Х (П4.8)
при следующих начальных условиях
Х,(/) = (*,,(') *2,(/)...хя,(/))«(! 0 0...0),
(П4.9)
Хи(Г) = (х1я(0 х2и(/)...хпя(0)^(0 0 0...1).
Дискретный аналог (П4.6) имеет вид
Х(//) = Ф(/у,/у.1)Х(^1)+ J Ф(//_1,т)В(тУти(/7.1). (П4.10)
Ч-\
При решении задачи оптимального управления одну из точек Х° или X7 всегда
можно положить равной нулю.
В самом деле, выражение, определяющее выходной сигнал Х(/) при Х° ^0,
записывается в виде (П4.6).
Положим Х° = 0 ; тогда
Х(О = fxo(0Xi1(T)B(x)rfT = jK(M)U(x)rfx .
о о
Запишем формулу, определяющую X7 :
т
Хт = Ф(7\ 0)Х° + J Хф (Т)Х~Ф{ (т)В(т)и(т)Л. (П4.11)
о
Отсюда находим
7"
X7' = X7' -Ф(Г,0)Х° = |хф(Г)Х^(т)В(т)и(т)<Ут . (П4.12)
о
Поскольку, при Х° = 0 имеет место равенство
Х(/) = |хф(ОХф1(т)В(т)и(тУт,
о
и
г
Х(Т) = Jxo(DXi!(T)B(T)U(T)£/T , (П4.13)
о
то из (П4.11) и (П4.13) следует, что задача перевода объекта (П4.8) из произвольной
начальной точки Х(0) = Х° в точку Х(Т) = X7 равносильна задаче его перевода из
начальной точки Х(0) = Х° =0 в точку Х(Т) = Хт = Хт -Ф(Г,0)Х°.
Аналогично получаем
г
0 = Ф(7\ 0)Х° - X7' + J Хф (Т)Х~Ф1 (х)В(т)и(т)Л,
708 Приложения
из чего можно заключить, что задача перевода объекта (П4.8) из начальной точки Х°
в произвольное конечное состояние Хг равносильно задаче его перевода из
эквивалентной начальной точки Хз, определяемой соотношением
Хэ) = Х°-ф-1(Г,0)Хг = Х0-Х^1(Г)Х7' в точку Х7'=0.
Заметим, что для нахождения эквивалентных начального и конечного состояний
необходимо предварительно рассчитать фундаментальную матрицу, что для
нестационарных объектов представляет собой весьма сложную задачу. В связи с этим этот
подход используется лишь при решении простейших задач.
К более конструктивным результатам приводит применение дискретного аналога
формулы
Х(О = |[А(т)Х(т) + В(т)и(т)]Л + Х° , (П4.14)
о
требующей знания лишь матриц А(0 и В(/).
Задача построения оптимальной программы и оптимального программного
управления формируется так:
ЛМ }
*Х/о<х('*)>и('*)»-> min
Лг=О J X('*),U('*)
при ограничениях:
а) V(tk)eVm; к = 0^Г\\
1) > - ограничения типа неравенств;
б) X(/t)eX"; k = 0,N\ J
2) ограничения типа равенств:
а) Х(/„) = Х7',
б) дискретный эквивалент любой из формул, связывающий вектор-функции U(/)
и Х(0 (зависимости (П4.4), (П4.10)).
Пример П4.1. Управление положением ротора двигателя постоянного тока.
Система дифференциальных уравнений, описывающая поведение объекта, может быть представлена в
виде [107]
*(')8В*(0' (П4 15)
х2(/) = М0,
где к - коэффициент пропорциональности (в расчетах будем полагать, что к-Х).
Постановка задачи: при заданных'
• уравнении объекта
*1 = Х2 '■> *2 = и '
• отсутствии ограничений на управление \J(t) и фазовый вектор X(t);
• краевых условиях,
• Х°=(1;0), Х7'=(0;0);
• времени управления Т = 1 с требуется найти такое программное скалярное управление u{t) и
фазовую траекторию X* (/) = (х\ (/), х\ (0) , при которых критерий {энергия управления)
т
J(u) = Jw2(0^/-»min
и
Построим оптимальное программное управление и оптимальную программу с помощью одного из
алгоритмов оптимизации, применяя для редукции исходной задачи к задаче математического
программирования метод сеток
Переходим от рассмотрения непрерывных функций *,(/) к их дискретным представлениям x,(tk).
Тогда, используя известные квадратурные формулы, можно получить выражения для *,(/*), / = 1,л , к -1, Л'.
Приложение 4. Редукция задач оптимального управления линейными объектами
Имеем*
709
X1(/) = X1(0) + jx2(T>/T,
о
x2(t) = x2(0) + \u(r)dT
Полагая N-ЗО (количество точек дискретизации), вычислим шаг дискретизации h =
N-\
Используя квадратурные формулы для получения дискретного эквивалента интегральных уравнений,
найдем выражения для дискретных значений X\{tk) и x2(tk).
Задача оптимального управления в терминах метода сеточной редукции формулируется так. найти
оптимальный набор дискретных значений u*{tk), удовлетворяющий следующим ограничениям.
xl(T) = xl(0) + hYdx2(tk),
x2(T) = x2(0) + h^u(tk)
*=о
(при использовании более точных формул указанные выше зависимости принимают более сложный вид)
При этом функционал качества определяется соотношением.
N-\
J = J(u{tk)) = hYu2(tk) -» min .
hi u('*>
Дискретные значения и графики приближённого и точного решения задачи оптимального управления
приведены в табл П4.1 и на рис П4.1
Xftb J
Ufa
02 04 90
Рис. П4.1. Графики функций u{t)y w*(/), *>*(/),*,*(/), x*2(t),x*2(t)
710
Приложения
Таблица П4.1
Дискретные значения u(tk)9 п\(к), £,*(/*), x*x(tk)9 x*2(tk), x\(tk)
h
0
0,034483
0,068967
0,10345
-0,13794
0,17242
0,20690
0,24138
0,27587
0,31035
0,34483
0,37932
0,41380
0,44828
0,48277
0,51725
0,55173
0,58621
0,62070
0,65518
0,68966
0,72415
0,75863
0,79311
0,82760
0,86208
0,89656
0,93104
0,96552
1,0000
-5,983
-5,573
-5,160
-4,748
-4,335
-3,922
-3,509
-3,096
-2,683
-2,270
-1,858
-1,445
-1,032
-0,619
-0,206
0,2062
0,6191
1.0319
1,4448
1,8576
2,2705
2,6834
3,0963
3,5092
3,9221
4,3350
4,7478
5,1607
5,5736
5,9865
А* к)
-6,0000
-5,5862
-5,1724
-4,7586
-4,3448
-3,9310
-3,5172
-3,1034
-2,6896
-2,2758
-1,8620
-1,4482
-1,0344
-0,6206
-0,2068
0,2070
0,6208
1,0346
1,4484
1,8622
2,2760
2,6898
3,1036
3,5174
3,9312
4,3452
4,7592
5,1722
5,5862
6,0002
1
0,99644
0,98639
0,96994
0,94797
0,92084
0,88907
-0,85311
0,81347
0,77062
0,72510
0,67737
0,62789
0,57721
0,52580
0,47411
0,42269
0,37200
0,32255
0,27480
0,22926
0,18645
0,14677
0,11083
0,079030
0,051330
0,029830
0,013700
0,0036193
-0,000238
1
0,99651
0,98639
0,97010
0,94817
0,92106
0,88929
0,85334
0,81368
0,77083
0,72528
0,67752
0,62802
0,57729
0,52583
0,47413
0,42267
0,37200
0,32248
0,27468
0,22914
0,1828
0,14662
0,11066
0,0789
4,051 9
0,0298
0,0136
0,0035
0
*2('a)
0
-0,19926
-0,38434
-0,55519'
-0,71180
-0,85417
-0,98230
-1,0962
-1,1959
-1,2813
-1,3524
-1,4094
-1,4521
-1,4806
-1,4949
-1,4948
-1,4806
-1,4522
-1.4095
-1,3526
-1,2814
-U959
-1,0963
-0,98239
_ -0,85426
-0,71189
-0,55529
-0,38445
-0,19937
-0,00005
Aw
0
-0,19377
-0,38526
-0,55649
-0,71344
-0,85613
-0,98455
-2,0387
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-1
1,1986
1,2842
1,3555
1,4226
1,4554
1,4839
1,4982
1,4382
1,4839
1,4555
1,4126
1,3555
,2842
1,1986
,0987
-0,9846
-0,8561
-0,7134
-0,5565
-0,3853
-0,1998
-0,0001
Получили решение поставленной выше задачи с ограничениями на фазовые координаты. Потребуем,
чтобы
*2(/)>-1,43
Для этого к полученной ранее вычислительной схеме добавим ограничения для дискретных значений x2(tk)
л:2(/*)>-1,43, * = 0,jV-1
Результаты решения поставленной задачи приведены в табл П4 2 Графики функций оптимального
управления м*(/), а также компонент оптимальной программы £,*(/) и x*2(t) приведены на рис П4 2
Таблица П4.2
Дискретные значения u*(tk), xx{tk), x2{tk)
h
0
0,034483
0,068967
0,10345
0,13794
0,17242
0,20690
0,24138
0,27587
u\tk)
-1,4663
-5,6103
-5,194
-4,7792
-4,3636
-3,9480
-3,5325
-3,1169
-2,7013
*Г('*)
1
0,99913
0,99159
0,97786
0,95846
0,93387
0,90459
0,87110
0,83391
AW
0
-0,12202
-0,30831
-0,48027
-0,63791
-0,78121
-0,91019
-1,0248
-1,1252
Приложение 4. Редукция задач оптимального управления линейными объектами 711
Окончание табл. П4.2
0,31035
0,34483
0,37932
0,41380
0,44828
0,48277
0,51725
0,55173
0,58621
0,62070
0,65518
0,68966
0,72415
0,75863
0,79311
0,82760
0,86208
0,89656
0,93104
0,96552
1,0000
-2,2858
-1,8702
-1,4546
-1,0391
-0,6235
-0,2079
0,3897 Ю"14
-0,294 10"14
-0,0029
0,2618 10~14
1,7581
2,1736
2,5893
3,0049
3,4205
3,8361
4,2517
4,6673 ч
5,08296
5,49857
5,91418
0,79350
0,75039
0,70503
0,65796
0,60964
0,56060
0,51127
0,46198
0,41267
0,36340
0,31405
0,26687
0,22223
0,18066
0,14269
0,10880
0,079410
0,055130
0,036430
0,023739
0,017521
-1,2112
-1,2828
-
-
-
-
-
-
-
-
-
,3402
,3832
,4119
1,4262
1,4298
1,4298
,4299
1,4299
,3996
1,3318
,2497
,1532
,0424
-0,91729
-0,77784
-0,62407
-0,45595
-0,27350
-0,07673
8*ы
го
*1т
Рис. П4.2. Графики функций м*(/), x\(t), x\(t)
712
СПИСОК ЛИТЕРАТУРЫ КО 11-Й ЧАСТИ
1. Автоматизированное проектирование систем автоматического управления /
Под ред. В.В. Солодовникова. - М.: Машиностроение, 1989. - 546 с.
2. Автоматическое регулирование паровых турбин и газотурбинных установок /
Под ред. И.И. Кириллова. -Л.: Машиностроение, 1986. -446 с.
3. Александров А.Г. Синтез регуляторов многомерных систем. - М.:
Машиностроение, 1986.-384 с.
4. Амербаев В.М. Некоторые применения ортогональных многочленов к
численному обращению интеграла Лапласа // Труды 2-й Республиканской конф. по
математике и механике. 1959. - Алма-Ата: АН Каз.ССР. - С. 26 - 38.
5. Амербаев В.М. Операционное исчисление и обобщенные ряды Лягерра. -
Алма-Ата: Наука, 1974. - 500 с.
6. Амосов А.А., Дубинский Ю.А., Копченова А.Н. Вычислительные методы для
инженеров. - М.: Высшая школа, 1994. - 544 с.
7. Анализ и оптимальный синтез на ЭВМ систем управления / Под ред. А.А.
Воронова и И.А. Орурка. - М.: Наука, 1984. - 344с.
8. Аналитические самонастраивающиеся системы / Под ред. В.В. Солодовникова.
- М.: Машиностроение, 1965. - 500 с.
9. Андреев Ю.Н. Управление конечномерными линейными объектами. - М.:
Наука, 1976.-424 с.
10. Астапов Ю.М., Медведев B.C. Статистическая теория систем автоматического
регулирования и управления. - М: Наука, 1982. - 304 с.
11. Афанасьев В.К, Колмановский В.Б., Носов В.Р. Математическая теория
конструирования систем управления. - М.: Высшая школа, 1989. - 488 с.
12. Баранов В.Н., Захаров Ю.Е. Электрические и гидравлические вибрационные
механизмы. Теория, расчет и конструкции. 2-е изд., перераб. и доп. - М.:
Машиностроение, 1977. - 328 с.
13. Барковский В.В., Захаров В.Н., Шаталов А.С Методы синтеза систем
управления. - М.: Машиностроение, 1969. - 328 с.
14. Батенко А.П. Системы терминального управления. - М.: Радио и связь, 1984.
-160 с.
15. Беккенбах Э., Беллман Р. Неравенства. - М.: Мир, 1965. - 276 с.
16. Беклемишев Д.В. Дополнительные главы линейной алгебры. - М.: Наука, 1983.
-336 с.
17. Бесекерский А.В., Попов Е.П. Теория систем автоматического регулирования.
-М.: Наука, 1975.-768 с.
18. Бессонов А.А., Загашвили Ю.В., Маркелов А.С. Методы и средства
идентификации динамических объектов. - Л.: Энергоатомиздат, Ленинградское
отделение, 1989.-280 с.
19. Бирюков В.Ф., Пилишкин В.Н. Исследование разрешимости и решения задачи
синтеза управляющего устройства для линейного нестационарного объекта
при ограничениях вдоль траектории // Известия ВУЗов. Серия
приборостроение. 1992. №9.-С. 49-55.
20. Бирюков В.Ф., Пилишкин В.Н. Согласование ограничений вдоль траектории
при синтезе управляющего устройства для линейного нестационарного
объекта // Межвуз. сб. научных трудов: Обработка и преобразование информации в
задачах управления. - Рязань, 1984. - С. 103 - 107.
Список литературы ко Н-й части 713
21. Бщадзе А.В. Уравнения математической физики. - М.: Наука, 1976. - 296 с.
22. Боднер В.А. Системы управления ЛА. - М: Машиностроение, 1973. - 544 с.
23. Бутковский А.Г., Пустыльников Л.М. Теория подвижного управления
системами с распределенными параметрами. - М.: Наука, 1980. - 384 с.
24. Ванеев КГ., Финин Г.С. Построение функций Ляпунова. - Киев: Наукова
думка, 1981.-412 с.
25. Ван-Трис Г. Синтез оптимальных нелинейных систем управления. - М: Мир,
1964.-168 с.
26. Васильев Д.В., Чуич ВТ. Системы автоматического управления. - М.: Высшая
школа, 1967.-368 с.
27. Венгеров А.А., Щаренский В.А. Прикладные вопросы оптимальной линейной
фильтрации. - М.: Энергоатомиздат, 1982. - 192 с.
28. Воеводин В.В. Вычислительные основы линейной алгебры. - М.: Наука, 1977.
-304 с.
29. Воеводин В.В., Кузнецов Ю.Д Матрицы и вычисления. - М.: Наука, 1984. -
320 с.
30. Вопросы теории и элементы программного обеспечения минимаксных задач /
Под. ред. В.Ф. Демьянова, В.Н. Малоземова. - Л.: Изд-во ЛГУ, 1977. - 192 с.
31. Воронов А.А. Устойчивость, управляемость, наблюдаемость. - М.: Наука,
1979.-336 с.
32. Гавурин М.К, Малоземов В.Н. Экстремальные задачи с линейными
ограничениями. -Л.: Изд-во ЛГУ, 1984. - 176 с.
33. Гайскип В.А., Егупов Н.Д., Корнюшин Ю.П. Применение функций Уолша в
системах автоматизации научных исследований. - Киев: Наукова думка, 1993.
-212с.
34. Галиуллин А.С. и др. Построение систем программного движения. - М.: Наука,
1971.-352 с.
35. Гноенский Л.С., Каменский Г.А., Элъсголъц Л.Э. Математические основы
теории управляемых систем. - М.: Наука, 1969. - 512 с.
36. Горинштейн A.M. Численное решение задач радиотехники и техники связи на
ЭЦВМ. - М.: Связь, 1972. - 200 с.
37. Грешилов А.А. Прикладные задачи математического программирования. - М.:
Изд-во МГТУ им. Н.Э. Баумана, 1990.-280 с.
38. Д'Анжело. Линейные системы с переменными параметрами. Анализ и синтез.:
Пер. с англ. / Под ред. Н.Т. Кузовкова. - М.: Машиностроение, 1974. - 288 с.
39. ДанскинДж.М. Теория максимина. - М.: Сов. радио, 1970. - 200 с.
40. Двайт Г.Б. Таблицы интегралов и другие математические формулы. - М.:
Наука, 1978.-228 с.
41. Дейч A.M. Методы идентификации динамических объектов. - М.: Энергия,
1979.-240 с.
42. Демьянов В.Ф. Минимакс: дифференцируемость по направлениям. - Л.: Изд-
во ЛГУ, 1974.-112 с.
43. Деруссо /7., Рой Р., Клоуз Ч. Пространство состояний в теории управления. -
М.: Наука, 1970.-620 с.
44. Джури Э. Инноры и устойчивость динамических систем. - М.: Наука, 1979. -
300 с.
45. Динамика нестационарных линейных систем / Ф.А. Михайлов, Е.Д. Теряев,
В.П. Булеков и др. - М.: Наука, 1967. - 368 с.
46. Дмитриев А.К, Егупов Н.Д, Шестопалов A.M. Машинные методы расчета и
проектирования систем электросвязи и управления. - М.: Радио и связь, 1990.
-272 с.
714
47. Доброленский Ю.П., Иванова В.И, Поспелов Г.С Автоматика управляемых
снарядов. - М.: Оборониздат, 1963. - 386 с.
48. Евланов Л.Г. Самонастраивающиеся системы с поиском градиента методом
вспомогательного оператора // АН СССР. Техническая кибернетика. 1963. №1.
-С. 47-51.
49. Иванов В.А., Медведев B.C., Чемоданов Б. К. Математические основы теории
автоматического регулирования: В 2-х т. - М: Высшая школа, 1977. Т.1. -
518с.
50. Иващенко Н.Н. Автоматическое регулирование. Теория и элементы систем.
Изд. 4-е. - М.: Машиностроение, 1978. - 736 с.
51. Идентификация и оптимизация нелинейных стохастических систем / Ю.С.
Попков, О.Н. Киселев, Н.П. Петров, Б.Л. Шмульян. -М.: Энергия, 1976.-440 с.
52. Ильин В А., Позняк Э.Г. Линейная алгебра. - М.: Наука, 1974. - 296 с.
53. Казаков И.Е. Статистическая теория систем управления в пространстве
состояний. - М.: Наука, 1975.-432 с.
54. Казаков И.Е. Статистические методы проектирования систем управления. -
М.: Машиностроение, 1969.-262 с.
55. Калиткин Н.Н. Численные методы. - М.: Наука, 1978. - 512 с.
56. Карышев А.К. Динамика и управление газоперекачивающими агрегатами:
Учебное пособие. - М.: Изд-во МГТУ им. Н.Э. Баумана, 2000. - 160 с.
57. Квакернаак X., Сиван Р. Линейные оптимальные системы управления. - М.:
Мир, 1977.-652 с.
58. Киселев О.Н., Попков Ю.С. Некоторые вопросы синтеза одного класса
нелинейных фильтров // Автоматика и телемеханика. 1967. №11. - С. 29 - 38.
59. Кожинский О.С, Грабарь Л.П. Об одном методе идентификации линейных
объектов управления // Идентификация. Докл. II Всесоюзн. Совещ. по
статистическим проблемам теории управления. - М.: Наука, 1970. - С. 39 - 50.
60. Колмогоров А.Н., Фомин СВ. Элементы теории функций и функционального
анализа. - М.: Наука, 1976. - 544 с.
61. Кострикин А.И. Введение в алгебру. - М.: Наука, 1977. - 496 с.
62. Красовскип А.А., Поспелов Г.С. Основы автоматики и технической
кибернетики. - М.: Госэнергоиздат, 1962. - 724 с.
63. Красовский Н.Н Теория управления движением линейной системы. - М.:
Наука, 1968.-476 с.
64. Крутько П.Д. Обратные задачи динамики управляемых систем. Линейные
модели. - М.: Наука, 1987. - 304 с.
65. Крылов В.И., Скобля НС. Методы приближенного преобразования Фурье и
обращения преобразования Лапласа. - М.: Наука, 1974. - 224 с.
66. Кузовков Н.Т. Динамика систем автоматического управления. — М.:
Машиностроение, 1968.-386 с.
67. Кузовков Н.Т. Модальное управление и наблюдающие устройства. - М.:
Машиностроение, 1976. - 184 с.
68. Кузовков Н.Т. Теория автоматического регулирования, основанная на
частотных методах. - М.: Оборонгиз, 1960. - 448 с.
69. Куликов Е.И. Методы измерения случайных процессов. - М.: Радио и связь,
1986.-272 с.
70. Курош А.Г Курс высшей алгебры. - М.: Наука, 1965. - 412 с.
71. Ланкастер Л. Теория матриц: Пер. с англ. - М.: Наука, 1982. - 272 с.
72. Лапин СВ., Егупов Н.Д. Теория матричных операторов и ее приложение к
задачам автоматического управления. - М.: Изд-во МГТУ им. Н.Э. Баумана,
1996.-496 с.
Список литературы ко Н-й части 715
73. Ли Э.Б., Маркус Л. Основы теории оптимального управления: Пер с англ. -
М.: Наука, 1972.-576 с.
74. Литвинов А.П., Моршаков СП., Фабрикант Е.А. Основы автоматики / Под
ред. В.А. Бесекерского. - М: Машиностроение, 1967. - 272 с.
75. Маклюков М.И. Инженерный синтез активных RC-фильтров низких и инфра-
низких частот. - М.: Энергия, 1971. - 184 с.
76. Макашов B.C. Автоматизированный линейный синтез многосвязных систем
автоматического регулирования с заданным динамическим качеством: Дис.
кандидата технических наук. - М.: 1990.
77. Максимов М.В., Горгонов Г.И. Радиоуправление ракетами. - М.: Сов. радио,
1964.-386 с.
78. Малоземов В.Н. Линейная алгебра без определителей. Квадратичная функция.
- С.-Петербург, С.-ПГУ, 1997. - 78 с.
79. Матвеев П.С, Синщын А.Ф. Динамическая точность систем автоматического
управления со случайными параметрами // Автоматическое управление и
вычислительная техника. - М: Машиностроение, 1964. Вып.6. - С. 232 - 305.
80. Матвеев П.С., Синщын А.Ф., Глебачев ЮМ. и др. Оптимизация систем
автоматического управления с учетом нелинейностей, случайных параметров и
помех // Автоматическое управление и вычислительная техника. Частотные
методы. - М.: Машиностроение, 1968. Вып.8. - С. 239 - 282.
81. Машинные методы расчета и проектирования систем электросвязи и
управления / А.Н. Дмитриев, Н.Д. Егупов, A.M. Шестопалов и др. - М.: Радио и связь,
1990.-272 с. ,
82. Методические указания к курсовым работам по теории управления / Авт.-
сост.: Л.С. Диканова, О.М. Данченко, Л.Е. Зотов и др. / Под ред. В.В.
Семенова. - М.: Изд-во МАИ, 1992. - 60 с.
83. Методы анализа, синтеза и оптимизации нестационарных систем
автоматического управления / Пупков К.А., Егупов Н.Д., Коньков В.Г., Милов Л.Т. - М.:
Изд-во МГТУ им. Н.Э. Баумана, 1999. - 684 с.
84. Михаилов Ф.А., Терпев Е.Д., Булеков В.П. Динамика непрерывных линейных
систем с детерминированными и случайными параметрами. - М.: Наука, 1971.
-286 с.
85. Моисеев Н.Н. Математические задачи системного анализа. - М.: Наука, 1981.
-488 с.
86. Моисеев Н.Н., Иванилов Ю.И., Столяров Е.М. Методы оптимизации. - М.:
Наука, 1978.-420 с.
87. Мороз A.M. Курс теории систем. - М. Высшая школа, 1987. - 380 с.
88. Наладка средств автоматизации и автоматических систем регулирования:
Справочное пособие / Под ред. А.С. Клюева. - М.: Энергоатомиздат, 1989. - 368 с.
89. Овсянников Д.А. Математические методы управления пучками. - Л.: Изд-во
ЛГУ, 1986.-226 с.
90. Овсянников Л.В. Групповой анализ дифференциальных уравнений. - М.:
Наука, 1978.-400 с.
91. Орурк И.А. Новые методы синтеза линейных и некоторых нелинейных
динамических систем. - М.: Наука, 1965. - 208 с.
92. Основы теории автоматического управления / Под ред. Н.Б. Судзиловского. -
М.: Машиностроение, 1985.-452 с.
93. Первозванский А.А. Курс теории автоматического управления. - М.: Наука,
1986.-616 с.
94. Пилишкин В.Н. Алгоритмы робастного управления в интеллектуальных
системах // Вестник МГТУ. Серия приборостроение. 1998. № 1. - С. 23 - 34.
716
95. Пипишкин В.Н. Робастное управление в интеллектуальных системах на основе
формирования фазовых ограничений. - В кн.: Машиностроение,
приборостроение, энергетика. - М: Изд-во МГУ, 1996. - С. 239 - 248.
96. Пилишкин В.Н Управление в интеллектуальных системах на основе
концепции функционально-множественной принадлежности // Вопросы
радиоэлектроники. Серия АСУПР. 1995. № 3. - С. 23 - 28.
97. Поляк Б.Т. Введение в оптимизацию. - М.: Наука, 1983. - 384 с.
98. Понтрягин Л.С Обыкновенные дифференциальные уравнения. - М.: Наука,
1970.-332 с.
99. Понтрягин Л.С, Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф.
Математическая теория оптимальных процессов. - М.: Наука, 1969. - 384 с.
100. Попов Е.П. Теория линейных систем автоматического регулирования и
управления. - М.: Наука, 1978. - 720 с.
101. Попов Е.П. Теория нелинейных систем автоматического регулирования и
управления. - М.: Наука, 1988.-256 с.
102. Поспелов Г. С, Доброленский Ю.П. Метод стандартных коэффициентов для
выбора параметров линейных систем автоматического регулирования / Сб.
статей по автоматике и электротехнике. - Изд. АН СССР. 1956. - С. 53 - 61.
103. Пугачев B.C., Казаков И.Е., Евланов Л.Г. Основы статистической теории
автоматических систем. - М.: Машиностроение, 1974. - 512 с.
104. Пупков К А., Фалдин КВ., Егупов Н.Д. Методы синтеза оптимальных систем
автоматического управления. - М.: Изд-во МГТУ им. Н.Э. Баумана, 2000. - 512 с.
105. Пупков К.А. Основы кибернетики. Математические основы кибернетики. - М.:
Высшая школа, 1974.-416 с.
106. Пупков К.А. Основы кибернетики. Теория кибернетических систем. - М.:
Высшая школа, 1976.-416 с.
107. Пупков К.А. Статистический расчет нелинейных систем автоматического
управления. - М.: Машиностроение, 1965. - 404 с.
108. Пупков К.А., Егупов Н.Д, Трофимов А.И. Статистические методы анализа,
синтеза и идентификации нелинейных систем автоматического управления /
Под ред. Н.Д. Егупова. - М.: Изд-во МГТУ им. Н.Э. Баумана, 1998. - 562 с.
109. Пупков К.А., Капалин В.И., Ющенко А.С Функциональные ряды в теории
нелинейных систем. - М.: Наука, 1976. - 448 с.
ПО. Райниш К. Кибернетические основы и описание непрерывных систем: Пер. с
нем. - М.: Энергия, 1978. - 392 с.
111. Растригин. Л.А. Современные принципы управления сложными объектами. -
М.: Сов. радио, 1980. - 232 с.
112. Расчет и анализ движения летательных аппаратов: Инженерный справочник.
-М.: Машиностроение, 1971.
113. Рей У.Х. Методы управления технологическими процессами: Пер. с англ. - М.:
Мир, 1983.-368 с.
114. Римский Г.В. Основы общей теории корневых траекторий систем
автоматического управления. - Минск: Наука и техника, 1972. - 328 с.
115. РойтенбергЯ.Н. Автоматическое управление. - М.: Наука, 1978. - 552 с.
116. Сборник задач по ТАР и У / Под ред. В.А. Бесекерского. - М.: Наука, 1978. - 512 с.
117. Сейдж Э.П., Уайт Ч.С Оптимальное управление системами. - М.: Радио и
связь, 1982.-392 с.
118. Сивцов В.И., Чулин Н.А. Автоматизированный синтез систем регулирования на
основе частотного метода теории автоматического управления. - М.:
Машиностроение, 1982.-236 с.
119. Современные методы идентификации систем / Под ред. П. Эйхкоффа. - М.:
Мир, 1983.-440 с.
Список литературы ко П-й части 717
120. Соколов НИ. Аналитический метод синтеза линеаризованных систем
автоматического регулирования. - М.: Машиностроение, 1966. - 328 с.
121. Солодов А.В. Методы теории систем в задаче непрерывной линейной
фильтрации. - М.: Наука, 1976. - 264 с.
122. Солодовников В.В. Статистическая динамика линейных систем
автоматического управления. - М.: Физ.-Мат. Лит., 1960. - 656 с.
123. Солодовников В.В., Бирюков В.Ф., Пилишкин В.Н. Синтез регулятора для
многомерного объекта по ограничениям на вектор состояния // Труды МВТУ.
Системы автом. управ. 1979. № 314. Вып. 7. - С. 42 - 59.
124. Солодовников В.В., Бирюков В.Ф., Тумаркин В.И. Принцип сложности в теории
управления. - М.: Наука, 1977. - 342 с.
125. Солодовников В.В., Дмитриев А.Н., Егупов Н.Д Анализ и синтез нелинейных
систем автоматического регулирования при помощи рядов Вольтерра и
ортогональных спектров. - В кн.: Техническая кибернетика / Под ред. В.В. Соло-
довникова. Кн.З, ч.2. - М.: Машиностроение, 1969. - С. 223 - 254.
126. Солодовников В.В., Дмитриев А.Н., Егупов Н.Д Ортогональный метод анализа
и синтеза линейных систем автоматического управления на основе понятия
моментов. - В кн.: Автоматическое управление и вычислительная техника.
Вып. 8. Частотные методы. - М.: Машиностроение, 1968. - С. 30 - 86.
127. Солодовников В.В., Дмитриев А.Н., Егупов Н.Д Спектральные методы расчета
и проектирования систем управления. - М.: Машиностроение, 1986.-440 с.
128. Солодовников В.В., Матвеев П.С Расчет оптимальных САУ при наличии
помех. - М.: Машиностроение, 1973. - 240 с.
129. Солодовников В.В., Плотников В.Н, Яковлев А.В. Основы теории и элементы
систем автоматического регулирования. - М.: Машиностроение, 1985. - 608 с.
130. Солодовников В.В., Плотников В.Н, Яковлев А.В. Теория автоматического
управления техническими системами. - М.: Изд-во МГТУ им. Н.Э. Баумана,
1993.-492 с.
131. Солодовников В.В., Семенов В.В. Спектральная теория нестационарных систем
управления. - М.: Наука, 1974. - 336 с.
132. Солодовников В.В., Семенов В.В. Спектральный метод расчета
нестационарных систем управления летательными аппаратами. - М.: Машиностроение,*
1975.-272 с.
133. Солодовников В.В., Топчеев Ю.И., Крутикова Г.В. Частотный метод
построения переходных процессов: Справочное пособие. - М.: Гостехиздат, 1955. -
196 с.
134. Солодовников В.В., Тумаркин В.И. Теория сложности и проектирования систем
управления. - М.: Наука, 1990. - 166 с.
135. Солодовников В.В., Шрамко П.С Расчет и проектирование аналитических са-
. монастраивающихся систем с эталонными моделями. - М.: Машиностроение,
1972.-284 с.
136. Справочник по теории автоматического управления / Под ред. А.А. Красов-
ского. - М.: Наука, 1987. - 712 с.
137. Суетин П.К. Классические ортогональные многочлены. - М.: Наука, ГИФМЛ,
1976.-328 с.
138. Татевский В.М., Колтев Г.С. Элементарная теория линейных неравенств и их
приложения. - М.: Изд-во МГУ, 1973. - 160 с.
139. Теория автоматического управления / Под ред. А.А. Воронова. Ч. I, II. - М.:
Высшая школа, 1986. - 362, 382 с.
140. Теория автоматического управления. Изд. 2-е / Под ред. А.В. Нетушила. - М.:
Высшая школа, 1983.-432 с.
718
141. Техническая кибернетика. Теория автоматического регулирования / Под ред.
В.В. Солодовникова. - М: Машиностроение, 1967 - 1969. Кн.1 - 768 с. Кн.2 -
680 с. Кн.З, ч.1 - 608 с, ч.2 - 366 с.
142. Титчмарш Е. Введение в теорию интегралов Фурье. - М.: Гостехиздат, 1948. -
302 с.
143. Тихонов А.Н.,Арсенин В.Я. Методы решения некорректных задач. - М.: Наука,
1974. -420 с.
144. Топчеев Ю.И., Цыпляков А.П. Задачник по теории автоматического
регулирования. - М.: Машиностроение, 1977. - 592 с.
145. Трикоми Ф. Дифференциальные уравнения. - М.: Изд-во ИЛ, 1962. - 352 с.
146. Трофимов А.И. Автоматика, телемеханика и вычислительная техника в
химических производствах. - М.: Энергоатомиздат, 1985. - 512 с.
147. Трофимов А.И., Егупов Н.Д, Дмитриев А.Н. Методы теории автоматического
управления, ориентированные на применение ЭВМ. - М.: Энергоатомиздат,
1997.-654 с.
148. Трофимов A.M., Егупов Н.Д, Слекеничс Я.В. Принципы построения
автоматических регуляторов теплоэнергетических процессов АЭС. - М.:
Энергоатомиздат, 1999.-340 с.
149. Уонэм М. Линейные многомерные системы управления. - М.: Наука, 1980. -
376 с.
150. Федоров В.В. Численные методы максимина. - М.: Наука, 1979. - 280 с.
151. Федосов Е.А., Инсаров В.В., Селивохин О.С. Системы управления конечным
положением в условиях противодействия среды. - М.: Наука, 1989. - 270 с.
152. Федосов Е.А., Себряков Г.Г. Спектральный анализ систем управления со
случайно изменяющимися параметрами // Автоматическое управление и
вычислительная техника. Частотные методы. - М.: Машиностроение, 1968. Вып.8. -
С. 207-238.
153. Химмельблау Д. Прикладное нелинейное программирование: Пер. с нем. - М.:
Мир, 1975.-344 с.
154. Хорн Р.,Джонеон Ч. Матричный анализ. - М.: Мир, 1989. - 656 с.
155. Хофер Э., Лундерштедт Р. Численные методы оптимизации. - М.:
Машиностроение, 1981.-192 с.
156. Цыпкин ЯЗ. Основы теории автоматических систем. - М.: Наука, 1977. -
650 с.
157. Цыпкин ЯЗ., Попков Ю.С. Теория нелинейных импульсных систем. - М.:
Наука, 1973.-414 с.
158. Чаки Ф. Современная теория управления. Нелинейные оптимальные и
адаптивные системы. - М.: Мир, 1975. - 424 с.
159. Шаталов А.С. Отображение процессов управления в пространствах
состояний. - М.: Энергоатомиздат, 1986. - 256 с.
160. Шаталов А.С. Структурные методы в теории управления и
электроавтоматике. - М.: Госэнергоиздат, 1962. - 320 с.
161. Шахназаров Г.А. Программное обеспечение расчета систем автоматического
регулирования: Учебное пособие. - М.: Изд-во МВТУ им. Н.Э. Баумана, 1985.
-50 с.
162. Шахтарин Б.И., Шелухин О.И. Отработка негауссовских случайных
процессов с применением ПЭВМ. - М.: Изд-во МГТУ им. Н.Э. Баумана, 1992. -
178 с.
163. Эпкхофф П. Основы идентификации систем управления: Пер с англ. - М.:
Мир, 1979.-464 с.
Список литературы к Ш-й части 719
СПИСОК ЛИТЕРАТУРЫ К 111-Й ЧАСТИ
1. Александров AT. Оптимальные и адаптивные системы. - М: Высшая школа,
1989.-264 с.
2. Атинс М, Фалб П. Оптимальное управление. - М.: Машиностроение, 1968. -
764 с.
3. Батенко АЛ. Управление конечным состоянием движущихся объектов. - М.:
Советское радио, 1977. - 256 с.
4. Беллман Р., Калаба Р. Динамическое программирование и современная теория
управления. - М: Наука, 1969. - 118 с.
5. БлиссГ.А. Лекции по вариационному исчислению. - М.: Изд-во иностр. литер.,
1950.-348 с.
6. Болтянский ВТ. Математические методы оптимального управления. - М.:
Наука, 1969.-408 с.
7. Брайсон А., Хо-Ю-Ши. Прикладная теория оптимального управления. - М:
Мир, 1972.-544 с.
8. Бублик Б.Н., Кириченко Н.Ф. Основы теории управления. - Киев: Издательское
объединение «Вища школа», головное издательство, 1975. - 328 с.
9. Бутковский AT. Методы управления системами с распределенными
параметрами. - М.: Наука, 1975. - 568 с.
10. Бутковский AT Теория оптимального управления системами с
распределенными параметрами. - М.: Наука, 1965. - 456 с.
11. Васильев Ф.П. Численные методы решения экстремальных задач. - М.: Наука,
1988.-552 с.
12. Волин Ю.М., Островский Г.М. Принцип максимума для разрывных систем и
его применение к задачам с фазовыми ограничениями // Известия ВУЗов.
Серия радиофизика. 1969. № И. - С. 1609 - 1621.
13. Гамкрелидзе Р.В. Оптимальные процессы управления при ограниченных
фазовых координатах // Изв. АН СССР. Математика. 1960. № 3. - С. 315 - 356.
14. Гилл Ф., Миррей У., Райт М. Прикладная оптимизация: Пер. с англ. В.Ю.
Лебедева / Под ред. А.А. Петрова. - М.: Мир, 1985. - 340 с.
15. Гноенский Л.С, Каменский Г.А., Эльсгольц Л.Э. Математические основы
теории управляемых систем. - М.: Наука, 1969. - 512 с.
16. Грешилов А.А. Прикладные задачи математического программирования. - М.:
Изд-во МГТУ им. Н.Э. Баумана, 1990. - 280 с.
17. Дегтярев Ю.И. Методы оптимизации. - М.: Радио и связь, 1980. - 270 с.
18. Ермольев Ю.М., Гуленко В.П., Царенко Т.И. Конечно-разностный метод в
задачах оптимального управления. - Киев: Наукова думка, 1978. - 164 с.
19. Жевнин А.А., Крищенко А.П. Управляемость нелинейных систем и синтез
алгоритмов управления // ДАН СССР. 1981. Т.4. № 5. - С. 18 - 29.
20. Жевнин А.А., Толокнов В.И., Шевяков О.В. Программное управление посадкой
на Землю транспортных космических кораблей // Космические исследования.
1975. Т.13. Вып. 6. - С. 935 - 937.
21. Зельдович Я.Б., Мышкис А.Д. Элементы прикладной математики.- М.: Наука,
1967.-646 с.
22. Иванов В.А., Фалдин Н.В. Теория оптимальных систем автоматического
управления.-М.: Наука, 1981.-332 с.
720
23. Квакернаак X., Сиван Р. Линейные оптимальные системы управления. - М.:
Мир, 1977.-650 с.
24. Красин И.А., Котченко Ф.Ф. Неосциллирующие оптимальные системы
высокого порядка // Автоматика и телемеханика. 1968. № 6. - С. 148 - 151.
25. Красовский Н.Н. Теория управления движением линейной системы. - М:
Наука, 1968.-476 с.
26. Крепн М.Г., Нуделъман А. А. Проблема моментов Маркова и экстремальные
задачи. - М.: Наука, 1973. - 552 с.
27. Крищенко АЛ. Оптимальное управление нелинейными системами //
Автоматика и телемеханика. 1981. № 6. - С. 25 - 36.
28. Крищенко А.П. Стабилизация программных движений нелинейных систем //
Известия АН СССР. Техническая кибернетика. 1985. № 6. - С. 21 - 29.
29. Крутько П.Д. Обратные задачи динамики управляемых систем. Линейные
модели. - М.: Наука, 1987. - 304 с.
30. Крутько П.Д. Обратные задачи динамики управляемых систем. Нелинейные
модели. - М.: Наука, 1988. - 326 с.
31. Куликовский Р. Оптимальные и адаптивные процессы в системах
автоматического регулирования. - М.: Наука, 1967. - 380 с.
32. Куропаткин П.В. Оптимальные и адаптивные системы. - М.: Высшая школа,
1980.-288 с.
33. Клюев А.С., Колесников А.А. Оптимизация автоматических систем управления
по быстродействию. - М.: Энергоиздат, 1982. - 236 с.
34. Ланкастер П. Теория матриц. - М.: Наука, 1978. - 280 с.
35. Лесин В.В., Лисовец ЮЛ. Основы методов оптимизации. - М.: МАИ, 1995. -
340 с.
36. Ли Э.Б., Маркус Л. Основы теории оптимального управления: Пер. с англ. -
М.: Наука, 1972.-574 с.
37. Марчук Г.И., Агошков В.И. Введение в проекционно-сеточные методы. - М.:
Наука, 1981.-416 с.
38. Моисеев Н.Н. Математические задачи системного анализа. - М.: Наука, 1981. -
488 с.
39. Моисеев Н.Н. Численные методы в теории оптимальных систем. - М.: Наука,
1971.-424 с.
40. Моисеев Н.Н, Иванилов ЮЛ., Столярова Е.М. Методы оптимизации. - М.:
Наука, 1978.-420 с.
41. Мордухович Б.Ш. Методы аппроксимаций в задачах оптимизации и
управления. - М.: Наука, 1988. - 360 с.
42. Нелинейная оптимизация систем автоматического управления / Под общей
ред. Е.П. Попова. - М.: Машиностроение, 1970. - 308 с.
43. Олейников В.А., Смирнов Т.М. Оптимальное по быстродействию управление
нелинейными объектами // Автоматика и телемеханика. 1970, №12.-
С. 167-170.
44. Первозванский А.А. Курс теории автоматического управления. - М.: Наука,
1986.-614 с.
45. Поляк Б. Т. Введение в оптимизацию. - М.: Наука, 1983. - 384 с.
46. Понтрягин Л.С., Болтянский ВТ., Гамкрелидзе Р.В. и др. Математическая
теория оптимальных процессов. - М.: Наука, 1976. - 392 с.
47. Построение систем программного движения / Под ред. А.С. Галиуллина. - М.:
Наука, 1971.-180 с.
48. Расчет и анализ движения летательных аппаратов: Инженерный справочник.
- М.: Машиностроение, 1971. - 352 с.
Список литературы к Ш-й части 721
49. Рей У.Х. Методы управления технологическими процессами. - М.: Мир, 1983.
-368 с.
50. Справочник по теории автоматического управления / Под ред. А.А. Красовско-
го.-М.: Наука, 1987.-712 с.
51. Суетин П.К. Классические ортогональные многочлены. - М.: Наука, 1979. -
412 с.
52. Табак Д., Куо Б. Оптимальное управление и математическое
программирование. - М.: Наука, 1975. - 280 с.
53. Талдыкин А. Т. Векторные функции и уравнения. - Л.: Изд-во ЛГУ, 1977. - 344 с.
54. Теория автоматического управления / Под ред. А.А. Воронова.- 4.1, 2. - М.:
Высшая школа, 1986. - 362, 382 с.
55. Теория автоматического управления. Изд. 2. / Под ред. А.В. Нетушила. - М.:
Высшая школа, 1983.-432 с.
56. Троицкий В.А. Оптимальные процессы колебаний механических систем. - Л.:
Машиностроение, 1976.-248 с.
57. Троицкий В.А. Задача Майера-Больца вариационного исчисления и теория
оптимальных систем // ПММ. 1961. Вып. 4.
58. Уткин В.И. Скользящие режимы и их применение в системах с переменной
структурой. - М.: Наука, 1974. - 272 с.
59. Фалдин Н.В. Оптимальное по быстродействию управление линейным
объектом // Известия ВУЗов. Серия электромеханика. 1981. № 2. - С. 1351 - 1356.
60. Фалдин Н.В., Макаров Н.Н Условия общности положения в задачах
оптимального управления // Некоторые вопросы дифференциальных уравнений в
решении прикладных задач. - Тула.: ТулПИ, 1983. - С. 148 - 153.
61. Фалдин Н.В. Линейные быстродействия при ограниченных фазовых
координатах // Автоматика и телемеханика, 1967. № 1. - С. 23 - 33.
62. Фалдин Н.В. Достаточные условия оптимальности в одной задаче с
ограниченными фазовыми координатами // Известия ВУЗов. Серия радиофизика. 1969.
№7.-С. 1067-1075.
63. Федоренко Р.П. Приближенное решение задач оптимального управления. - М.:
Наука, 1978.-488 с.
64. Фелъдбаум А.А. Оптимальные процессы в системах автоматического
управления // Автоматика и телемеханика. 1953. № 6. - С. 712 - 728.
65. Фелъдбаум А.А. Вычислительные устройства в автоматических системах. -
М.: Физматгиз, 1959. - 800 с.
66. Флетчер К. Численные методы на основе метода Галеркина: Пер. с англ. - М.:
Мир, 1988.-352 с.
67. Хафер Э., Лундерштедт Р. Численные методы оптимизации. - М.:
Машиностроение, 1981.-192 с.
68. Шаталов А.С. Отображение процессов управления в пространствах
состояний. - М.: Энергоатомиздат, 1986. - 256 с.
69. Янг Л. Лекции по вариационному исчислению и теории оптимального
управления. - М.: Мир, 1974. - 488 с.
4fi Яяк. 366
722
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
1 А
Абсолютный минимум
Автоматический регулятор
Автопилот
Активный индекс
Алгоритмическое обеспечение
Амплитудно-частотная характеристика
Аппроксимация поверхности
переключения ...
1 Б
Базовая система
Баттерворса фильтр.
Беллмана принцип оптимальности
Бсллмана уравнение
— для непрерывных процессов
— для неавтономных систем . .
Больцазадача
Быстродействие . . . .
1 в
Вариационное исчисление
— простейшая задача .
Вариация функционала .
— общая формула.
Всйерштрасса - Эрдмана условия
Вейерштрасса условие сильного
минимума
Вектор ортогональный
Вектор состояния
Вещественная частотная
характеристика замкнутой системы.
Вспомогательная задача
1 г
Гамильтона функция . ...
Гладкое многообразие ..
Граница области ...
Гершгорина круги
1 Л
Динамическое программирование
Динамические характеристики
Дифференциальные уравнения. .
— объекта управления ....
Дифференциал функционала
Допустимое управление . . .
Достаточные условия оптимальности . ...
1 с
1 Е
Единственность теоремы
91
415
86
648
98
205
521
526
.55
539
540
544
550
460
469
1|
440
440
440
450
454
A s/l
490
469
205
648
ik
-А
469
648
648
тп
ik
538
48
21
21
440
469
490
i|
490
II ж
Желаемая ЛАЧХ
|| о
II з
Задача Больца
Задача вариационного исчисления
простейшая ...
— Лагранжа . ....
— тапера
— на условный экстремум
— с w-неизвестными функциями
— с подвижными концами
Задача вспомогательная
— об аналитическом конструировании
регуляторов
— о замене оборудования ..
— оптимального управления. .. .
— оптимального управления
с закрепленным временем.
— оптимального управления
с подвижными концами.
Задача синтеза
Задающее устройство
Запас устойчивости
— по модулю
— по фазе
Звено дифференцирующее
— интегрирующее . .
il 14
II и
Идеальная следящая система.
Инерционный руль.
Интервал граничный
— внутренний . ...
— второго рода
— первого рода
— простой ...
Исполнительное устройство .. . .
Исчисление вариационное
II к
Качество управления. .
— в переходном режиме
— в установившемся режиме .
Квадратичная форма. ..
Корректирующее устройство
— параллельное
—последовательное .
Коэффициент демпфирования
— ошибки
Критерий оптимальности
— квадратичный.
— Сильвестра
1
. 210
1
460
.. 440
... 456
456
..440
450
648
550
..539
. . 460
490
490
21
21
205
205
205
26
34
II
1
550
648
661
ас 1
661
661
661
668
.21
. . 440
\
..34
26,32
. 34
550
. , 21
. 21
21
. 26
26
544
544
550
Предметный указатель
■л »
Лагранжа задача.. 460
— лемма 440
— множители .... . . . 460
Лемма
— об области регулярности 648
— о числе корней квазимногочлена 502
Логарифмическая амплитудно-
частотная характеристика (ЛАЧХ) 210
— желаемая 210
— типовая 210
Логарифмические частотные
характеристики (ЛЧХ) .. 215
— анализ устойчивости 216
— метод построения 220
Лягерра функции . 126
723
— принцип динамической
компенсации во временной области 174
— принцип динамической компенсации
в спектральной области 177
Майера задача 460
Максимизация функции Гамильтона 483
Матричная передаточная функция 236
Метод
— динамического программирования 539
— матричных операторов 167
— моментов 154
— оптимизационный во временной
области 107
— оптимизационный в частотной
области 98
— построения эталонных ПФ . .. 51
— проекционный 118
— развязки каналов... . .... 244
— синтеза грубых систем 280
— спектральный 125
— уравнений синтеза 76
— частотный 205
— эталонных ПФ 86,91
Минимум абсолютный 483
— сильный 440
— слабый 440
Множители Лагранжа 460
Модульные ограничения. .... 320
| н ft
Наблюдаемость .. ... .. 622
Невязка 48
Нелинейная система
— метод моментов синтеза КУ 203
— постановка задачи синтеза
регуляторов 185
— принцип динамической
компенсации 185
— проекционный метод синтеза КУ 192
Непрерывный функционал 440
Нестационарная система
— метод матричных операторов 167
— метод моментов синтеза
регуляторов 184
— постановка задачи синтеза
регуляторов .... 174
46*
Область устойчивости
— построение 205
— САУ . 205
» Область управления .. 469
— на границе 648
— регулярности 648
Обратная связь . 21
Объект управления 21
Обобщенное условие .. 668
Оператор 45
Оптимальность по быстродействию 469
Оптимальная траектория 460
Оптимальное управление . . 460
Ортогональный вектор 483
Основное функциональное уравнение 538
Отклонение регулируемой величины 21
■ п
Параметры системы . 21
Пассивный корректирующий фильтр . 21
Передаточная функция
— определение 21
— ошибки 34
— САУ 21
Переменные состояния . 240
Перерегулирование ... 21
Переходная функция 48
Переходная характеристика
— реальная ... 48
— эталонная 48
Переходные процессы 48
Показатели качества управления . 98, 154
Поверхность переключения 521
Приведенное управление 509
Принцип
— динамической компенсации ... 45
— максимума Понтрягина . 469
— оптимизационный . 48
Простой граничный интервал 661
Пространство нормированное 440
— функциональное . ... 440
Процесс многошаговый 539
— элементарный . 648
Программирование математическое 679
Проектирование САУ... . 21
> -- '
Расчет САУ .... 21
Регулируемая величина 21
Регулятор
— давление пара в барабане-сепараторе 432
— математические модели 39
— ПИ,ПД,ПИД 39
— питания парогенератора 421
— питания барабана-сепаратора 4°Р
724
— пропорциональный (П) 39
— уровня компенсатора объема 423
— этапы проектирования 21
Регулярная
— область .. 639
— точка 639
— траектория .. . 648
Риккати матричное уравнение 550
Робастная система 384
Связь обратная 21
Сигнал
— входной 21
— выходной 21
— главной обратной связи 21
— ошибки 21
Сильвестра критерий 544
Сильный минимум функционала 440
Синтез оптимального управления 502
— по квадратичному критерию 544
Синтез корректирующего устройства 21
— параллельного 51
— последовательного 51
— постановка задачи 51
Система автоматического управления
(САУ) 21
— линейная стационарная 51, 70, 86,91
— линейная нестационарная 174
— нелинейная 185
Слабый минимум функционала . 440
Слабо регулярная траектория 648
Сравнивающее устройство ... .21
Стабилизация объекта 26
Структурная схема САУ 21
Теория автоматического управления 5
Теоремы единственности 490
— о достаточных условиях
оптимальности 502
— о необходимых условиях
оптимальности 469
— о числе переключений 502
Траектория оптимальная 460
— регулярная 648
— слабо регулярная 648
у
Управление допустимое 469
— оптимальное. 460
— оптимальное по быстродействию 469
Управление
— многомерными объектами 236
— модальное 260
Управляемость и наблюдаемость
— определение. 614, 622
— системы . 614,622
Управляющее воздействие . 21
Уравнение Беллмана 538
— для автономных процессов .. .. 544
— для неавтономных процессов .. 544
Уравнение матричное типа Риккати 550
— Эйлера 440
Уравнение
— динамики 21
— объекта управления 21
— ошибки .. 21
Условие
— Вейерштрасса сильного минимума 454
— скачка 639
Условия Вейерштрасса - Эрдмана 450
Условия оптимальности достаточные . .. 490
— необходимые . 469
Условия трансверсальности 483
в=ф Ik
.. 21
544
.440
.440
440
440
469
Функциональная схема САУ
Функционал
— квадратичный
— линейный
— непрерывный в области
— непрерывный в ючке
Функциональные пространства
Функция Гамильтона
Частота ....
— сопрягающая
— среза
Частотная характеристика
— амплитудная
— амплитудно-фазовая
— вещественная
— логарифмическая амплитудная.
— мнимая..
208
.209
215
.216
.217
218
.219
.220
Эйлера уравнение . .
Элементарный процесс.
Экстремаль
— первого типа
— второго типа
440
.648
.440
509
.509
Содержание • i_ib_
СОДЕРЖАНИЕ
ОБЩЕЕ ПРЕДИСЛОВИЕ К УЧЕБНИКУ 5
ПРЕДИСЛОВИЕ К ТОМУ 2 11
СПИСОК ИСПОЛЬЗУЕМЫХ АББРЕВИАТУР 13
ОБОЗНАЧЕНИЯ 14
ЧАСТЬ II. МЕТОДЫ СИНТЕЗА РЕГУЛЯТОРОВ 17
ВВЕДЕНИЕ 18
ГЛАВА 1. ОБЩИЕ ПРИНЦИПЫ, НА КОТОРЫХ БАЗИРУЕТСЯ
РЕШЕНИЕ ЗАДАЧИ СИНТЕЗА РЕГУЛЯТОРОВ 21
1.1. Основные этапы решения задачи синтеза регуляторов
в классе линейных стационарных систем 21
1.2. Общие положения, определяющие пути обеспечения
заданного качества и структуру регулятора в классе
линейных стационарных систем 26
1.2.1. Стабилизация и обеспечение заданного качества
работы систем в переходном режиме введением
обратной связи по производным 26
1.2.2. Целенаправленное изменение динамических свойств
систем путем введения дифференцирующих звеньев
в прямую цепь 32
1.2.3. Влияние коэффициентов усиления разомкнутой
системы и интеграторов в прямой цепи на качество
работы САУ в установившемся режиме 34
1.2.4. Влияние местных ОС 35
1.3. Математические модели и структурные схемы регуляторов 39
1.3.1. Математические модели 39
1.3.2. Анализ динамических характеристик регуляторов 40
1.4. Общие принципы, на которых базируются основные
теоретические положения методов и алгоритмы расчета
параметров в задачах синтеза регуляторов 45
1.4.1. Принцип динамической компенсации 45
1.4.2. Оптимизационный принцип синтеза регуляторов,
предполагающий достижение приближенного,
в известном смысле, равенства реального выходного
сигнала xp(t,pup2,...,pr)эталонному процессу x3(t) 48
1.4.3. Оптимизационный принцип синтеза регуляторов,
предполагающий достижение приближенного,
в известном смысле, равенства правой и левой
частей операторного уравнения, описывающего
динамику замкнутой скорректированной системы 48
1.4.4. Принцип, лежащий в основе группы методов,
использующих понятие моментов 49
726 Содержание
ГЛАВА 2. МЕТОДЫ СИНТЕЗА РЕГУЛЯТОРОВ
В КЛАССЕ ОДНОМЕРНЫХ СИСТЕМ 51
2.1. Методы построения эталонных передаточных функций
замкнутых систем 51
2.1.1. Построение передаточной функции эталонной
системы в классе оптимизационных задач 52
2.1.2. Построение передаточной функции эталонной
системы в классе низкочастотных фильтров
Баттерворса 55
2.1.3. Метод стандартных коэффициентов построения
эталонной передаточной функции 66
2.2. Принцип динамической компенсации и анализ
его эффективности для класса стационарных систем 70
2.3. Расчет регуляторов с помощью уравнений синтеза 76
2.4. Метод эталонных передаточных функций
замкнутых систем управления 86
2.5. Метод эталонных передаточных функций
разомкнутых систем 91
2.6. Оптимизационный метод синтеза регуляторов
в частотной области 98
2.7. Оптимизационный метод синтеза регуляторов
во временной области 107
2.8. Проекционный метод синтеза регуляторов 118
2.9. Спектральный метод синтеза регуляторов
с использованием функций лягерра 125
2.9.1. Постановка задачи 125
2.9.2. Функции Лягерра 126
2.9.3. Построение спектральной характеристики объекта
управления 128
2.9.4. Алгоритм расчета регулятора 148
2.10. Метод моментов синтеза регуляторов 154
2.11. Метод матричных операторов 167
2.12. Методы синтеза регуляторов в классе одномерных
линейных нестационарных систем 174
2 МЛ. Основные положения принципа динамической
компенсации при описании системы и ее элементов
импульсными переходными функциями 174
2.12.2. Основные положения принципа динамической
компенсации при описании системы и ее элементов
матричными операторами 177
2.12.3. Оптимизационный метод синтеза регуляторов
во временной области 182
2.12.4. Метод моментов 184
2.12.5.. Метод матричных операторов 185
2.13. Методы синтеза регуляторов
в классе одномерных нелинейных систем 185
2.13.1. Принцип динамической компенсации 185
2.13.2. Оптимизационный метод синтеза регуляторов
во временной области 191
2.13.3. Проекционный метод синтеза регуляторов 192
2.13.4. Метод моментов 203
Содержание 727
ГЛАВА 3. ЧАСТОТНЫЙ МЕТОД СИНТЕЗА КОРРЕКТИРУЮЩИХ
УСТРОЙСТВ 205
3.1. Определение импульсной переходной функции (ИПФ)
по частотным характеристикам замкнутой системы .205
3.2. Определение переходной характеристики по частотной
характеристике замкнутой системы 206
3.3. Оценка качества переходной характеристики
по частотным характеристикам 209
3.4. связь показателей качества замкнутой системы
с частотными характеристиками разомкнутой 215
3.5. Определение частоты среза ЛАЧХ разомкнутой системы
ПРИ НАЛИЧИИ ОГРАНИЧЕНИЙ НА МАКСИМАЛЬНОЕ УСКОРЕНИЕ
в системе [133] 223
3.6. Метод логарифмических амплитудно-частотных
характеристик (частотный метод синтеза
последовательных корректирующих устройств
в.в. солодовникова) 225
ГЛАВА 4. МЕТОДЫ СИНТЕЗА РЕГУЛЯТОРОВ
В КЛАССЕ МНОГОМЕРНЫХ ЛИНЕЙНЫХ СИСТЕМ
(ОСНОВНЫЕ ПОНЯТИЯ) 236
4.1. Математическое описание многомерных систем
автоматического управления 236
4.2. Постановка задачи синтеза регуляторов в классе
многомерных стационарных систем 240
4.3. Динамическая и статическая развязка каналов
(общие положения) 244
4.4. Оптимизационные методы синтеза устройств развязки
каналов и регуляторов 255
ГЛАВА 5. МОДАЛЬНОЕ УПРАВЛЕНИЕ 260
5.1. Постановка задачи 260
5.2. Модальное управление при полностью измеряемом
векторе состояния. управление всеми модами 261
5.2.1. Скалярное управление (т = \) 261
5.2.2. Векторное управление 264
5.3. Управление отдельными модами при полных измерениях 271
5.4. Оптимальное модальное управление одной модой
при полных измерениях 273
5.5. Модальное управление при неполных измерениях 277
ГЛАВА 6. СИНТЕЗ ГРУБЫХ СИСТЕМ АВТОМАТИЧЕСКОГО
УПРАВЛЕНИЯ В ПРОСТРАНСТВЕ СОСТОЯНИЙ 280
6.1. Концепция функционально-множественной
принадлежности 280
6 1.1. Понятие окрестности множества и функции
или меры близости 280
6.1.2. Модели рассматриваемых объектов управления
в пространстве состояний 282
6.1.3. Величины в уравнениях состояния объекта, описание,
допущения и ограничения -. 283
728 Содержание
6.1.4. Формирование цели управления 286
6.1.5. Формирование концепции функционально-
множественной принадлежности (ФМП)
на элементах пространства состояний 288
6.2. Реализация концепции функционально-множественной
принадлежности в пространстве состояний на основе
метода обобщенных фазовых ограничений 290
6.2.1 Постановка задачи по формированию структуры
системы и алгоритмов управления на основе
концепции функционально-множественной
принадлежности 291
6.2.2. О методе фазовых ограничений и его обобщении 292
6.2.3. Формирование эквивалентных соотношений
в виде максминных и минимаксных неравенств 294
6.2.4. Смешанные неравенства при структурных
ограничениях на управление 297
6.2.5. О разрешимости при ограничениях на часть
компонент вектора состояния 299
6.2.6. Условия разрешимости при наличии возмущений 301
6.3. Расширение метода фазовых ограничений
на 8-окрестностях множеств в пространстве состояний 302
6.3.1. Постановка задачи и предположения метода с учетом
s-окрестностей 302
6.3.2. Метод фазовых ограничений на s-окрестностях
множества Q 304
6.3.3. Метод фазовых ограничений при отображении
г-окрестностей на заданное множество 306
6.3.4. Метод фазовых ограничений при отображении
на нестационарные г-окрестности 308
6.3.5. О проекционном подходе в задаче обеспечения
фазовых ограничений 313
6.4. Построение грубых систем управления при модульных
ограничениях 320
6.4.1. Постановка задачи синтеза линейной МСАУ
при модульных фазовых ограничениях 320
6.4.2. Геометрические условия обеспечения фазовых
ограничений 322
6.4.3. Определение достаточных условий на параметры
регулятора. Частный случай экспоненциальных
ограничений : 324
6.4.4. Анализ разрешимости достаточных условий
обеспечения фазовых ограничений 327
6.4.5. Синтез МСАУ при ограничениях на качество
регулирования 328
6.4.6. О деформации фазовых ограничений для обеспечения
разрешимости достаточных условий 331
6.4.7. Использование кругов Гершгорина для анализа
разрешимости достаточных условий : 333
Содержание 729^
6.4.8. О связи управляемости системы с расположением
кругов Гершгорина. Оценка степени грубости
(робастности) системы 337
6.4.9. Входные-выходные матрицы и их связь
с разрешимостью достаточных условий 340
6.4.10. О задании разрешимых фазовых ограничений 342
6.4.11. Построение допустимых фазовых ограничений
на основе разложения по элементам собственного
вектора 346
6.4.12. Критерий стабилизируемости системы управления 348
6.4.13. Процедура синтеза системы управления на основе
управления максимальным собственным значением
входной-выходной матрицы 350
6.5. Построение грубых систем управления
при квадратичных ограничениях 357
6.5.1. Постановка задачи синтеза при квадратичных
ограничениях 357
6.5.2. Получение достаточных условий на управление 359
6.5.3. Построение закона управления на основе
достаточных условий 363
6.5.4. Условия выполнения фазовых ограничений
на классах синтезируемых законов управления 366
6.5.5. Анализ спектральных ограничений
по значениям характеристического многочлена 369
6.5.6. Оценка грубости системы
при квадратичных ограничениях 372
6.5.7. Разрешимость задачи синтеза
в классе линейных законов управления 373
6.5.8. О формировании двухуровневой системы управления
при решении обобщенного матричного неравенства 379
6.6. Синтез робастных (г|-робастных) систем управления
по неполному вектору состояния 384
6.7. Построение нелинейных робастных систем •
при структурно-параметрических неопределенностях 400
6.7.1. Оценка робастности системы
с помощью кругов Гершгорина 407
6.8. Синтез систем на основе граничных отображений 411
ГЛАВА 7. РЕГУЛЯТОРЫ ОСНОВНЫХ ТЕПЛОЭНЕРГЕТИЧЕСКИХ
ПАРАМЕТРОВ АТОМНЫХ ЭЛЕКТРОСТАНЦИЙ 415
7.1. Основные управляемые параметры энергоблоков
с реакторами ВВЭР и РБМК 415
7.2. Структурные схемы регуляторов АЭС 417
7.3. Регуляторы питания парогенератора 421
7.4. Регуляторы уровня компенсатора объема 423
7.5. Регуляторы уровня регенеративных подогревателей 427
7.6. Регулятор питания барабана-сепаратора 428
7.7. Регулятор давления пара в барабане-сепараторе 430
7.8. Цифровой регулятор давления пара в барабане-сепараторе 432
7.9. Цифровой регулятор разворота турбогенераторов 434
730 Содержание
ЧАСТЬ III. МЕТОДЫ ТЕОРИИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ 436
ВВЕДЕНИЕ 437
ГЛАВА 1. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ 440
1.1. Необходимое условие экстремума функционала 440
1.1.1. Функциональные пространства 441
1.1.2. Дифференциал функционала 441
1.1.3. Простейшая задача вариационного исчисления 445
1.1.4. Вариационная задача с п неизвестными функциями 449
1.2. Задача с подвижными концами.
Условие Вейерштрасса- Эрдмана 450
1.2.1. Общая формула вариации функционала 450
1.2.2. Задача с подвижными концами 452
1.2.3. Условия Вейерштрасса - Эрдмана 453
1.3. Необходимое условие Вейерштрасса
сильного минимума функционала 454
1.4. Задачи на условный минимум 456
1.5. Решение задачи оптимального управления
методом вариационного исчисления 460
1.5.1. Формулировка задачи оптимального управления 460
1.5.2. Необходимое условие экстремума 462
1.5.3. Необходимые условия Вейерштрасса 468
ГЛАВА 2. ПРИНЦИП МАКСИМУМА ПОНТРЯГИНА 469
2.1. Необходимые условия оптимальности
в форме принципа максимума 469
2.1.1. Задача оптимального управления 469
2.1.2. Необходимое условие оптимальности 472
2.2. Задача с подвижными концами.
Принцип максимума для неавтономных систем 483
2.2.1. Задача с закрепленным временем 483
2.2.2. Задача с подвижными концами 484
2.2.3. Неавтономный случай 489
2.3. Оптимизация по быстродействию
линейных объектов управления 490
2.3.1. Максимизация функции Гамильтона 490
2.3.2. Теорема о числе переключений 492
2.3.3. Достаточные условия оптимальности 494
2.4. Синтез оптимального управления 502
ГЛАВА 3. ОПТИМАЛЬНЫЕ ПО БЫСТРОДЕЙСТВИЮ
СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ 508
3.1. Синтез оптимального управления
методом фазового пространства 508
3.1.1. Постановка задачи синтеза 508
3.1.2. Синтез оптимального управления 510
3.1.3. Обобщение задачи синтеза 517
3.2. Аппроксимация поверхности переключения 520
3.3. Ошибки слежения в оптимальных по быстродействию сау 525
3.4. Приближённый способ учёта малых постоянных времени 530
Содержание 731
ГЛАВА 4. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
И АНАЛИТИЧЕСКОЕ КОНСТРУИРОВАНИЕ РЕГУЛЯТОРА 537
4.1. Дискретный многошаговый процесс; принятия решений 537
4.2. Принцип оптимальности. Основное функциональное
уравнение беллмана 538
4.3. Метод динамического программирования
для непрерывных систем 543
4.3.1. Автономная система 543
4.3.2. Неавтономная система 548
4.4. Задача об аналитическом конструировании регулятора 549
4.4.1. Автономный случай 549
4.4.2. Неавтономная система 554
4.5. СВЯЗЬ МЕЖДУ ПРИНЦИПОМ МАКСИМУМА
И ДИНАМИЧЕСКИМ ПРОГРАММИРОВАНИЕМ 556
ГЛАВА 5. МЕТОДЫ МАТЕМАТИЧЕСКОГО ПРОГРАММИРОВАНИЯ
И МОМЕНТОВ ПОСТРОЕНИЯ ОПТИМАЛЬНЫХ
ПРОГРАММ И ОПТИМАЛЬНЫХ ПРОГРАММНЫХ
УПРАВЛЕНИЙ. СИНТЕЗ ОПТИМАЛЬНЫХ ОБРАТНЫХ
СВЯЗЕЙ " 558
5.1. Алгоритм построения оптимальных программных
управлений и оптимальных программ методами
математического программирования с использованием
матричного представления операторов
в ортогональных базисах 558
5.2. Алгоритм построения оптимальных программных
управлений стационарными линейными объектами
по критерию минимальной энергии 565
5.3. Алгоритм построения оптимальных программных
управлений нестационарными линейными объектами
по критерию минимальной энергии 587
5.4. Алгоритм построения оптимальных
программных управлений и оптимальных программ
классом нелинейных объектов 593
5.5. Метод моментов (основные положения) 600
5.5.1. Формулировка проблемы моментов и ее решение 600
5.5.2. Алгоритм синтеза оптимальных программных
управлений методом моментов
для класса линейных одномерных объектов 605
5.5.3. Векторно-матричный вариант 612
5.6. Управляемость линейных систем 613
5.7. Наблюдаемость линейных систем 621
5.8. Некоторые подходы к синтезу оптимальных систем,
работающих по принципу обратной связи 628
5.9. Синтез оптимальных обратных связей 631
5.9.1. Расчет оптимальной программной траектории,
исходящей из начального состояния Х(0) = Х° 631
5.9.2. Линеаризация в окрестности оптимальной
программы X* (/) и программного управления U* (/) 631
5.9.3. Синтез оптимальной обратной связи 633
732 Содержание
ПРИЛОЖЕНИЕ 1. ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ
ПРИ ОГРАНИЧЕНИЯХ НА ФАЗОВЫЕ КООРДИНАТЫ 638
П1.1. Принцип максимума при ограничениях
НА ФАЗОВЫЕ КООРДИНАТЫ 638
П1.2. Достаточные условия оптимальности
ПО БЫСТРОДЕЙСТВИЮ 647
П1.3. Оптимальное по быстродействию управление
В СЛУЧАЕ ИНЕРЦИОННОГО РУЛЯ 660
П1.4. Синтез оптимального по быстродействию управления
ПРИ ОГРАНИЧЕНИЯХ НА СКОРОСТЬ ДВИЖЕНИЯ И УСКОРЕНИЕ 667
ПРИЛОЖЕНИЕ 2. МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
(ОСНОВНЫЕ ПОЛОЖЕНИЯ) 678
Формулировка задачи математического программирования .... 678
Необходимые и достаточные условия оптимума в задачах
математического программирования 683
теория двойственности и недифференциальные условия
оптимальности в задаче выпуклого программирования 686
Математическая постановка задачи линейного программирования ... 688
Симплекс-метод - основной метод решения задач линейного
программирования 690
Метод полного исключения жордана для решения систем
линейных алгебраических уравнений 694
ПРИЛОЖЕНИЕ 3. РЕДУКЦИЯ ЗАДАЧ ОПТИМАЛЬНОГО
УПРАВЛЕНИЯ НЕЛИНЕЙНЫМИ ОБЪЕКТАМИ
К ЗАДАЧАМ МАТЕМАТИЧЕСКОГО
ПРОГРАММИРОВАНИЯ С ИСПОЛЬЗОВАНИЕМ
МЕТОДА СЕТОК И АЛГОРИТМЫ ИХ РЕШЕНИЯ 697
ПРИЛОЖЕНИЕ 4. РЕДУКЦИЯ ЗАДАЧ ОПТИМАЛЬНОГО
УПРАВЛЕНИЯ ЛИНЕЙНЫМИ ОБЪЕКТАМИ К ЗАДАЧАМ
МАТЕМАТИЧЕСКОГО ПРОГРАММИРОВАНИЯ
С ПОМОЩЬЮ МЕТОДА СЕТОК И АЛГОРИТМЫ
ИХ РЕШЕНИЯ....' 705
СПИСОК ЛИТЕРАТУРЫ К 11-Й ЧАСТИ 712
СПИСОК ЛИТЕРАТУРЫ К Ш-Й ЧАСТИ 719
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ 722
733
ANNOTATION TO THE TEXTBOOK
"Classical and state-of-the-art control theory methods".
This textbook is published in three volumes.
I volume: "Analysis and automatic control systems statistic dynamics".
II volume: "Regulator synthesis and automatic control systems optimization theory".
III volume: "State-of-the-art control theory methods".
I. Characteristic properties of the textbook.
1. This textbook is addressed to the broad reading public.
a). Students who begin to obtain knowledge in the field of control theory. It should be
mentioned that this subject may be both an obligatory one evaluating the level of
engineer's proficiency and an optional one.
b). Students and specialists who have to resume studies in the field of control theory
because of expanding tasks of process automation for different purposes.
c). Students and specialists who want to refresh their knowledge studying the part of the
textbook, which has not been included into engineering specialities curricula.
The readers have to choose the material according to the particular tasks a), b), c) and to
general curriculum opportunities. Taking into consideration the purpose of this textbook it
should be noted that it presents sufficient material for the choice to be made.
2. Material introduction methods.
This textbook attempts to provide the readers with knowledge of control theory methods
from initial concepts of control theory (control aims and concepts, control systems analysis,
systems classification, analysis and synthesis of the main tasks and others) to its state-of-
the-art issues.
In other words, this textbook presents both fundamental concepts of classical control
theory and concepts determining the subject-matter of some state-of-the-art trends.
Thorough understanding of control theory is impossible within the limits of up-to-date
investigation programmes, that is why the subject-matter of some trends has not been included
into this textbook.
3. The level of readers mathematical background.
The authors of this textbook set out the material in easy and readily available way.
A scope of knowledge of higher mathematics required for the textbook contents
understanding is restricted to the programme for junior students at higher technical educational
institutions.
Concepts of functional analysis are implemented in this textbook. The necessary
information is given in a due corresponding section of the textbook. Owing to language
application and the results of functional analysis the subject-matter of each method is better
revealed, the opportunity of obtaining in - depth theoretical information is developed, the
connection between methods that seem to be different at first sight is clarified.
4. Technical character of the textbook.
The subject matter of the textbook is presented from the engineering point of view.
The author stresses the main ideas forming the bases of the methods but does not always
adduce strict methodological proofs. The subject-matter of the textbook is supposed to
form the base.
It is supposed that the material of the textbook will be the base for finding more easily
the ways of solving practical tasks. Besides, the material is presented in such a way that the
reader can imagine the ways of practical use of the methods under consideration.
734
In most cases the methods are reduced to the calculated algorithms, the tables and other
additional material, facilitating their application are given in the textbook.
The main merit of the textbook is the consideration of the particular control systems
being used in the atomic industry with the aim of regulating the thermotechnical processes:
• It presents principal, functional and structural circuits of the system.
• It illustrates the calculations using particular algorithms.
• It gives the analysis of the results, etc.
It is impossible to study control theory without mastering the engineering aspect. That is
why the engineering aspect of formulating and solving practical tasks is accentuated during
the whole course.
5. "Computing colouring" of the material.
The contents of the book is characterized by a certain "computing colouring" because
the present-day computers give the possibility of reducing the term of the automatic control
systems design and thus make an imprint on numerical methods of the automatic control
theory.
Successful solving of problems of computing and design with the use of computer
depends on many factors:
• The degree of the adequacy of the system mathematical model.
• The degree of the numerical methods efficiency being used in the algorithmic
provision.
• The presence of high-quality software.
• To what degree the creativeness of a researcher-designer is used.
The author of the textbook tried to take into consideration all these factors.
II. The contents.
1. Mathematical models of the automatic control systems.
The problems of the mathematical description of the singular and nonsingular linear and
non linear control systems, the systems with the distributed parameters, the continuous
discrete systems are considered in the textbook in detail. Considerable attention is paid to the
method of the state space in the linear system which gives basically new possibilities of the
system analysis and control laws synthesis. The description by the Volterra series is
considered in the non-linear system class.
2. Determinated analysis of the automatic control systems.
The system theory methods were studied for solving the following problems:
a). The investigation of the steady-state singular, non-stationary and non-linear systems:
- the criteria of stability are considered in detail;
- considerable attention is paid to non-linear system class;
(The original material concerning the problems of stability is given in a due chapter).
b). The study of the system performance in unstable mode and creation of output
processes.
. c). The investigation of performance accuracy in the stable mode.
3. Statistic analysis of the automatic control systems.
The technical methods of the broad class ACS statistic research, including non-linear
and stochastic system are considered in the textbook.
4. Filtration and control systems statistical synthesis.
This chapter includes the following methods:
a). Synthesis of optimal filters, using Kolmogorov - Wienner's theory as well as
R. Caiman and R. Busy,
b). Synthesis of optimal observers,
c). Synthesis of optimal analytical and non-linear filters, described by Volterra series
and so on.
735_
5. Numerical methods of complex control system analysis under determined and
random action.
Matrix operator method forms the bases of computerized control system investigation
useful for algorithmisation and programming.
6. Control objects identification.
Formulation of the problem of linear and non-linear objects class identification, main
problems, engineering approach to its solution are outlined in this textbook.
7. Control system synthesis based on quality (regulators synthesis).
Alongside with traditional methods of regulator synthesis (frequency, modal control,
dynamic compensation methods and other) great attention is devoted to mathematics
programming process application due to the fact, that the latter one determines general
approach to optimization problems solution and is computer oriented.
8. Synthesis of optimal automatic control systems.
The following problems were depicted:
a). Basis principles of calculus of variations;
b). Pontryagin's principle of the maximum including the problem of phase variables;
c). Dynamic programming;
d). Linear-quadratic problems;
e). Moments method;
0- Mathematic programming process as applied to optimal programmed controls
development.
9. Method of up-to-date CAD theory.
Method including the process of rough control systems synthesis, H - control theory
and robust methods as well as, the problems of multi-object and multi-criteria systems
optimization together with the application of effective compromises, calculation tasks and
design of adaptive and intellectual control systems, differential geometry methods
application in control theory and others.
Учебное издание
Константин Александрович Пупков
Николай Дмитриевич Егупов
Александр Иванович Баркин
Евгений Михайлович Воронов
Эдуард Петрович Козубов
Виктор Григорьевич Коньков
Владимир Иванович Краснощеченко
Александр Петрович Курдюков
Владимир Николаевич Пилишкин
Виктор Михаилович Рыбин
Владислав Иванович Сивцов
Янис Витальевич Слекеничс
Адольф Иванович Трофимов
Николай Васильевич Фалдин
МЕТОДЫ КЛАССИЧЕСКОЙ
И СОВРЕМЕННОЙ ТЕОРИИ
АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
В трех томах
Том 2
СИНТЕЗ РЕГУЛЯТОРОВ И ТЕОРИЯ ОПТИМИЗАЦИИ
СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Редактор С.Н. Капранов
Корректор КЮ. Савинченко
Компьютерная верстка КЮ. Савинченко, М.П. Трубачев
Изд. лиц. №020523 от 25.04.97. Подписано в печать 14.11.2000.
Формат 70 х 100 1/16. Печ. л. 46. Усл. печ. л. 59,8. Уч.-изд. л. 59,3.
Бумага офсетная. Печать офсетная. Тираж 2000 экз. Заказ № 366.
Издательство МГТУ им. Н.Э. Баумана
107005, Москва, 2-я Бауманская, 5
Оригинал-макет подготовлен редакционно-издательским отделом
филиала МГТУ им. Н.Э. Баумана в г. Калуге
Отпечатано с готового оригинал-макета в ГУП «Облиздат»
248640, г. Калуга, пл. Старый торг, 5
ISBN 5-7038-1 627-0
816.2































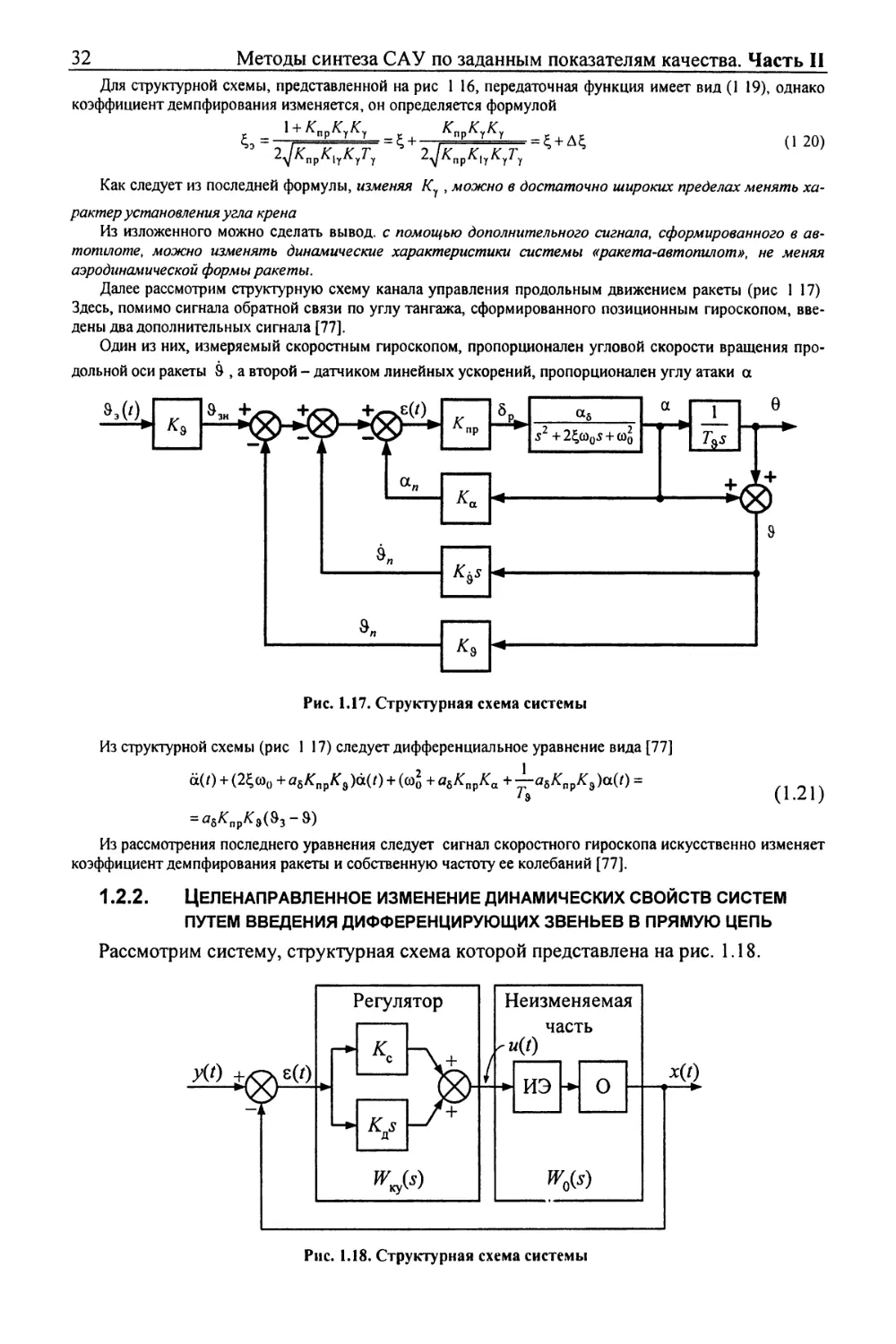

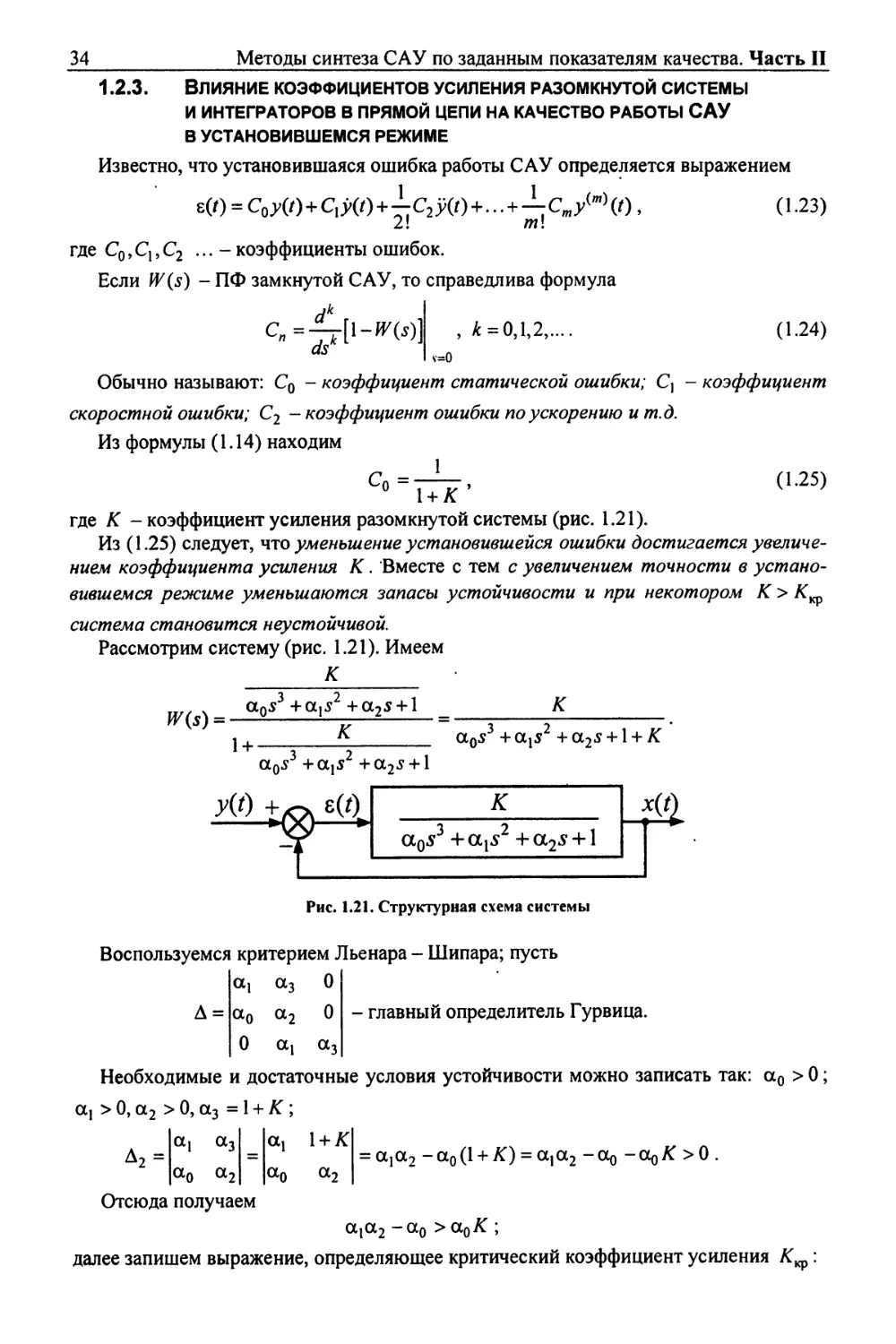



































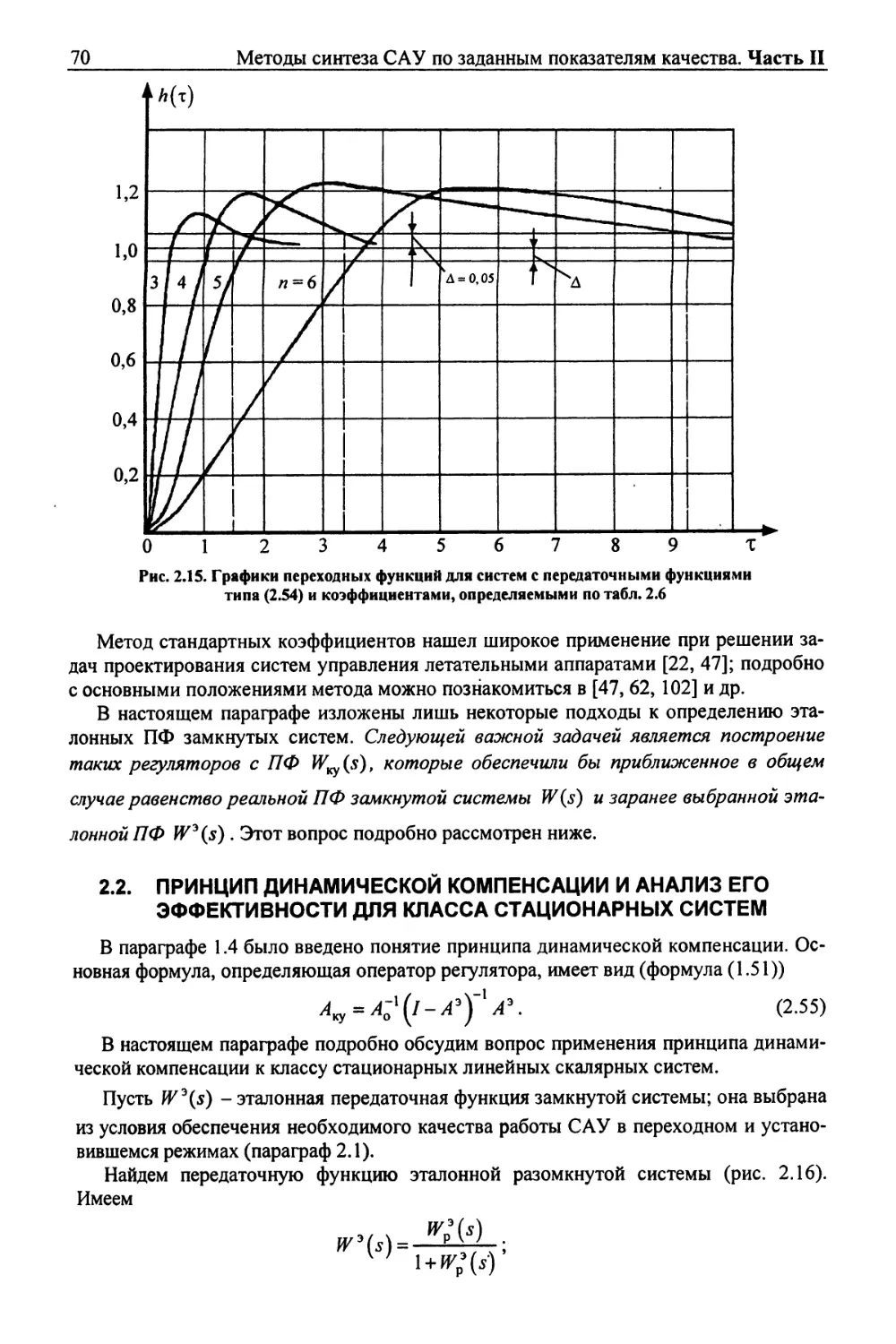




































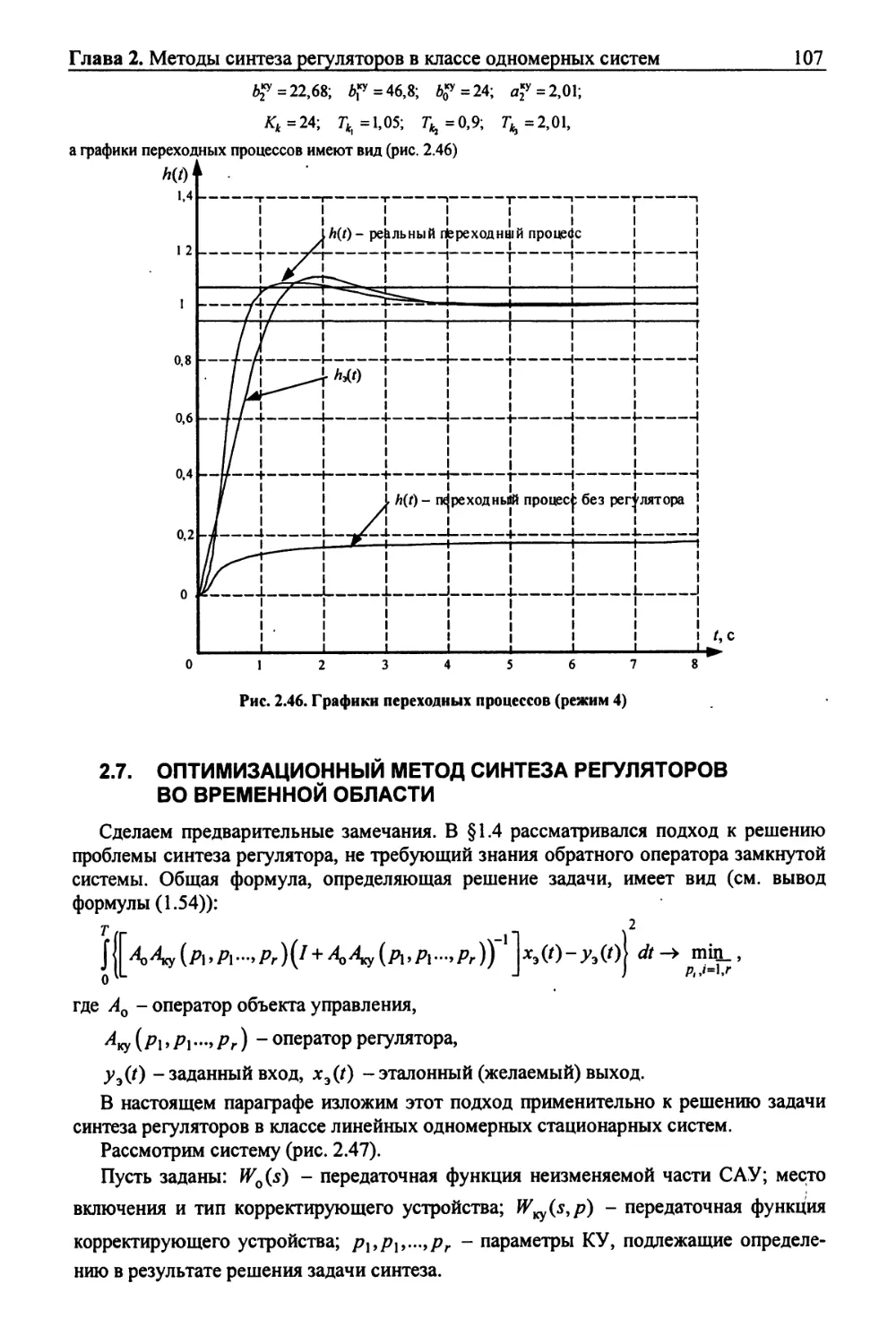










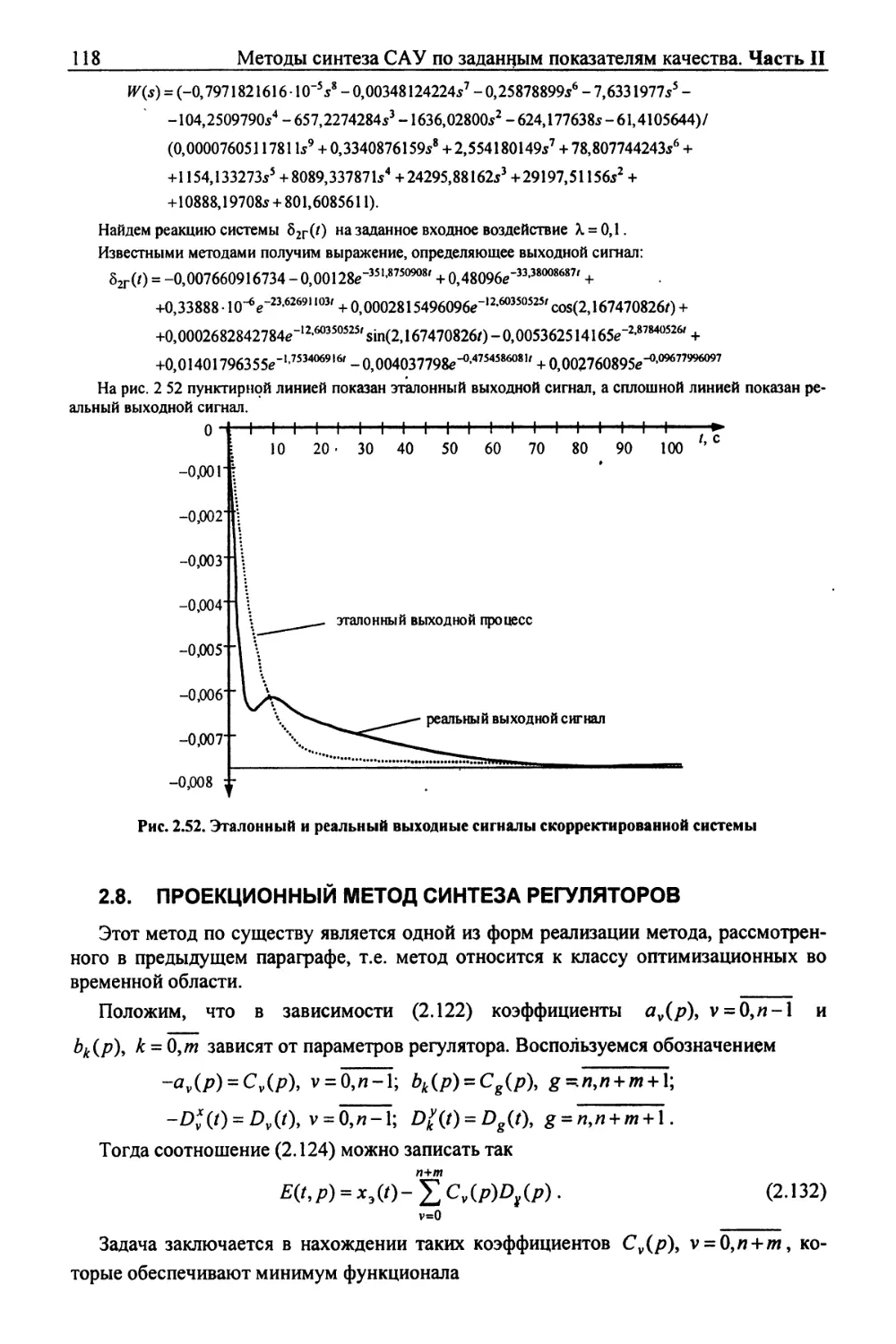







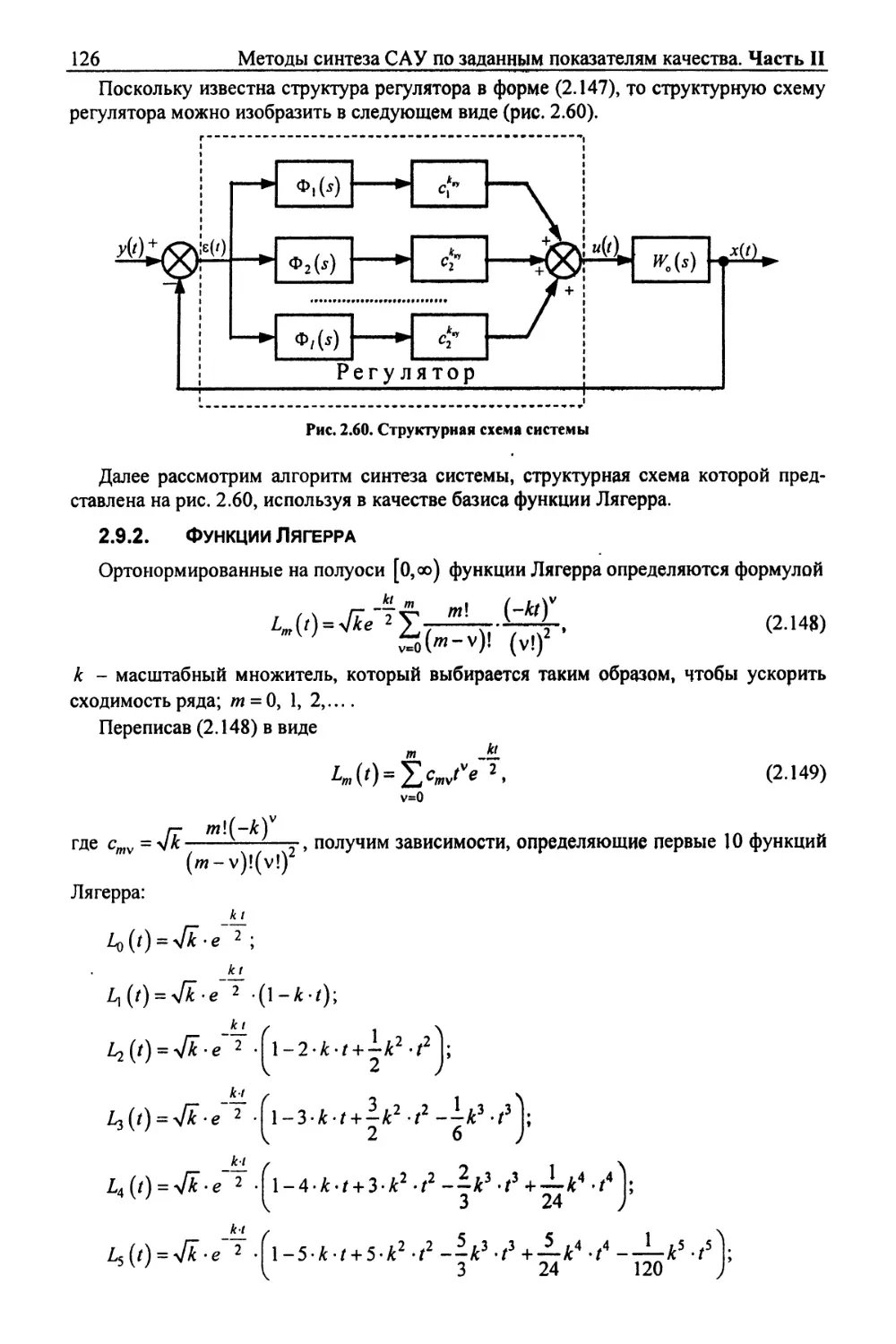

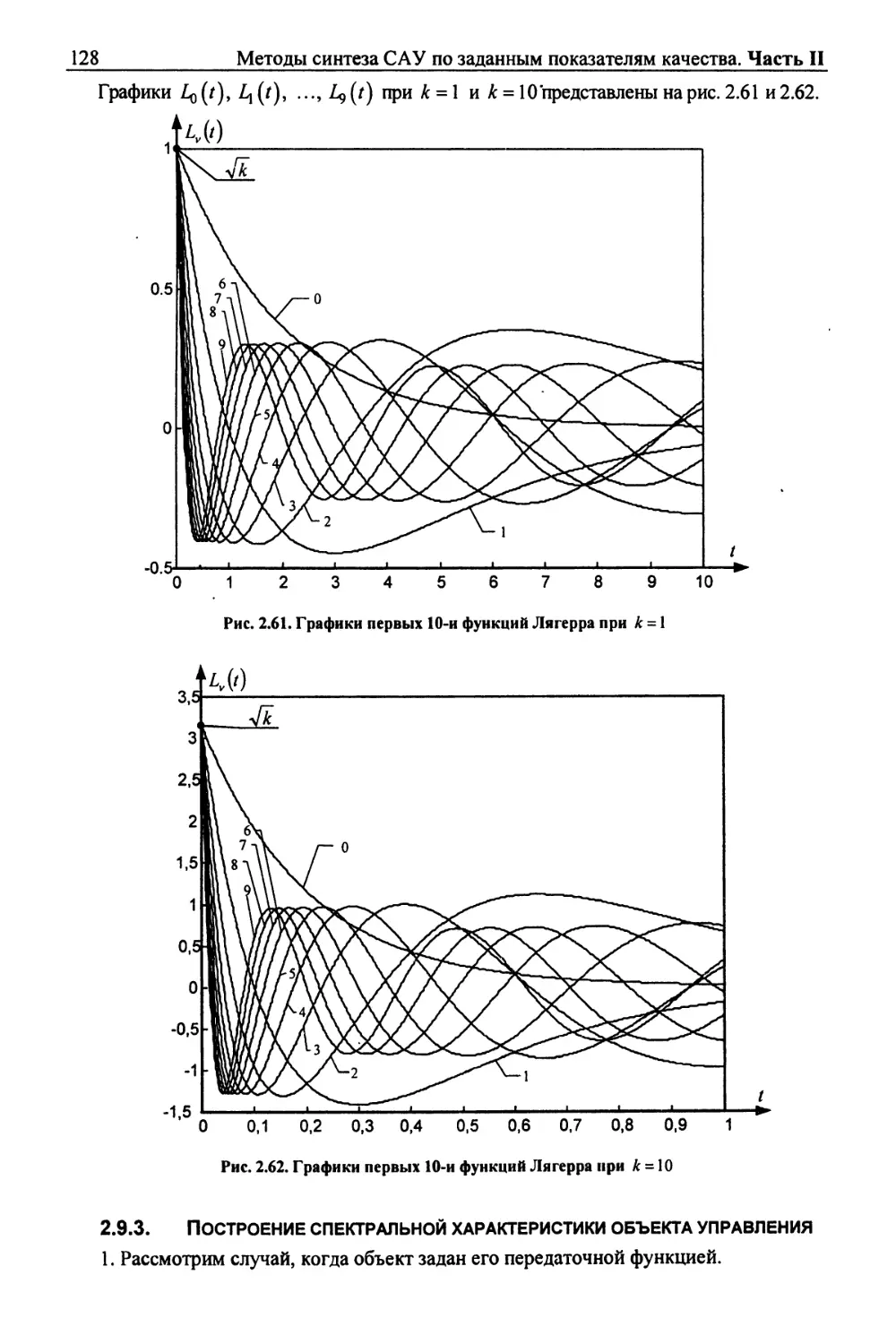

















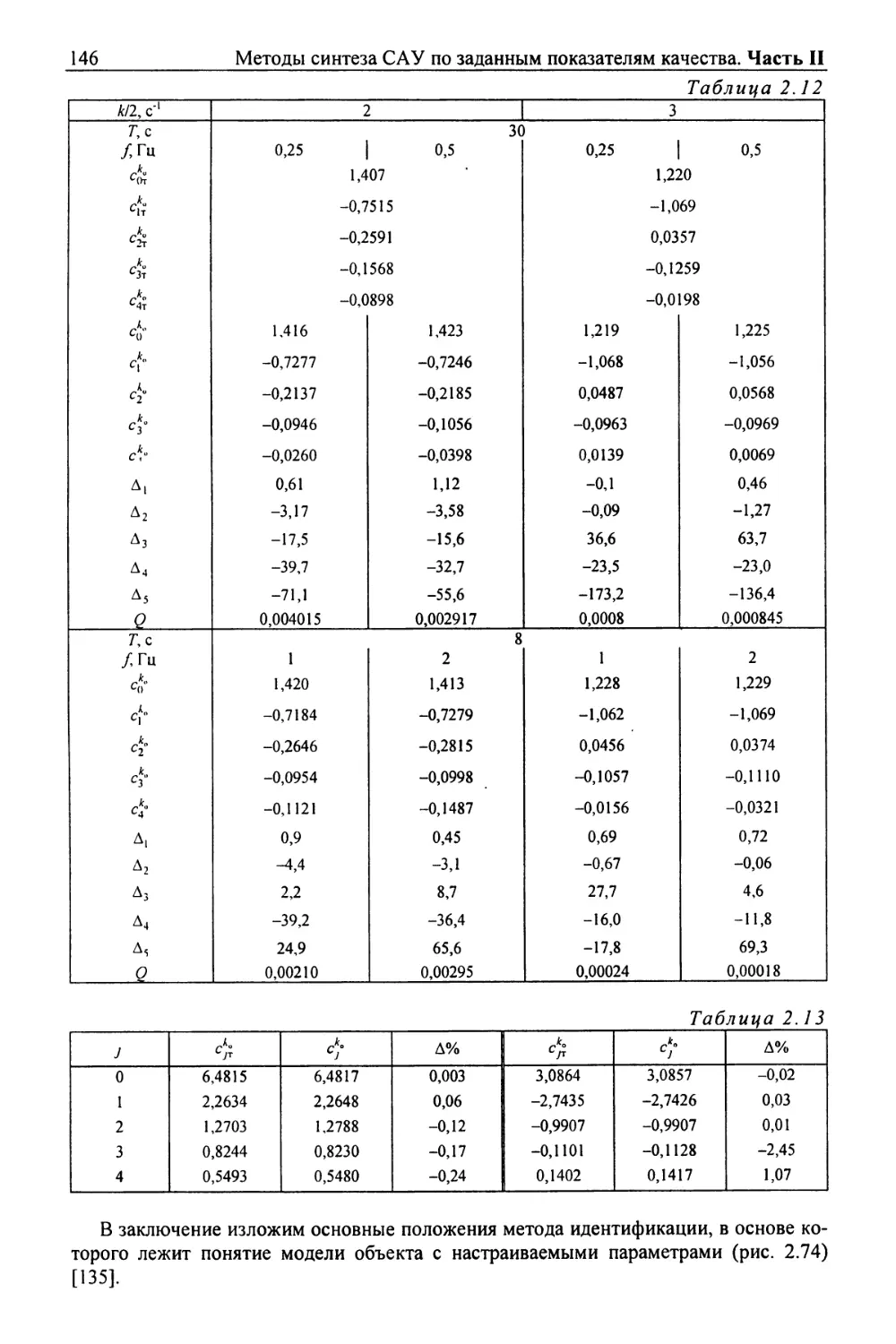

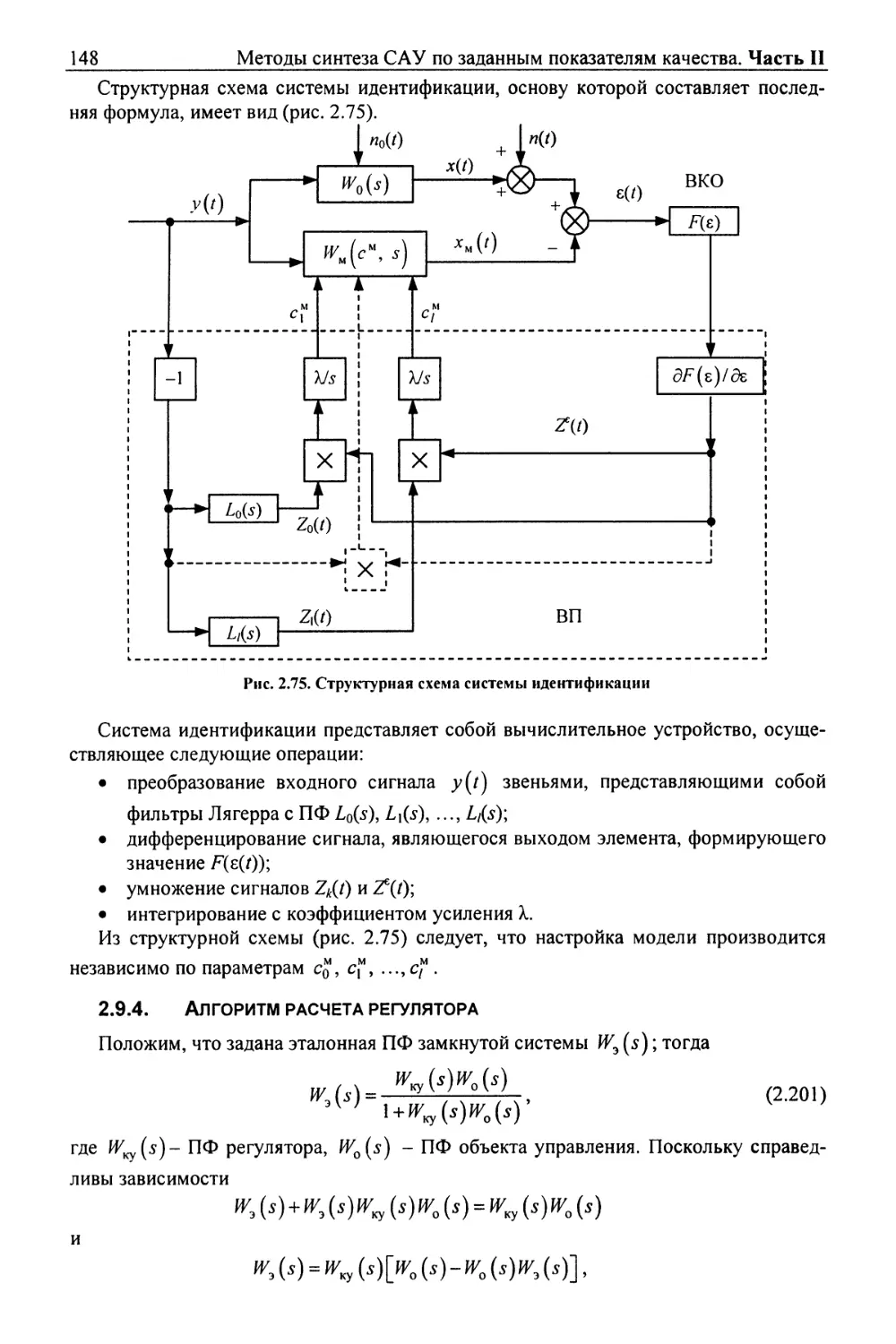


















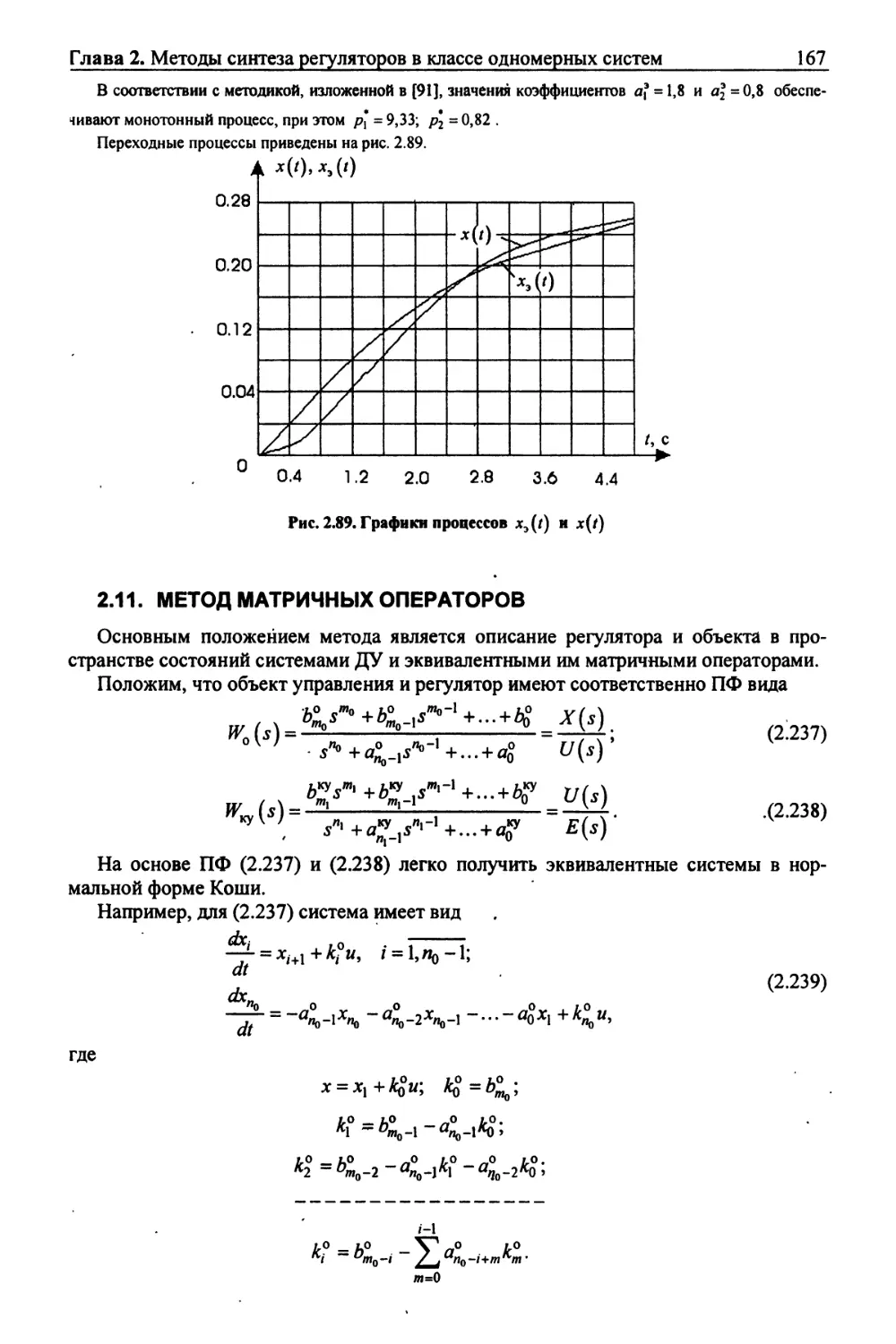



















































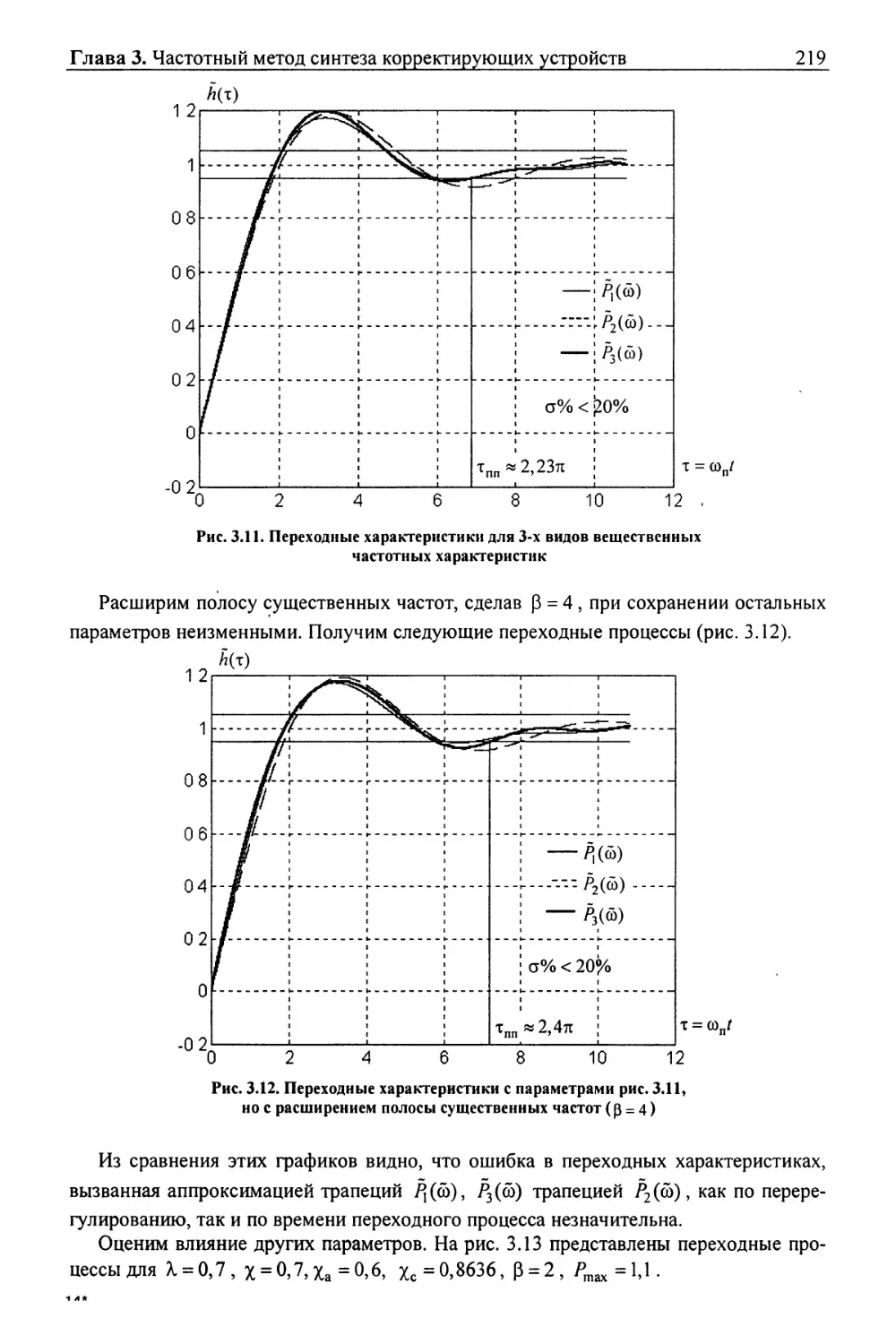



![3.5. Определение частоты среза ЛАЧХ разомкнутой системы при наличии ограничений на максимальное ускорение в системе [133]](https://djvu.online/jpg/S/G/v/SGvLnLaUmletH/223.webp)