РОССИЙСКАЯ АКАДЕМИЯ НАУК
СИБИРСКОЕ ОТДЕЛЕНИЕ
ИНСТИТУТ МАТЕМАТИКИ им. С. Л. СОБОЛЕВА
Современная математика — студентам и аспирантам
Новосибирск
Издательство Института математики
19 9 9
Ю. Г. РЕШЕТНЯК
КУРС
МАТЕМАТИЧЕСКОГО
АНАЛИЗА

УДК 517
ББК 22.16
Р47
Решетняк Ю. Г.
Курс математического анализа. Ч. I, кн. 1. — Новосибирск: Изд-во
Ин-та математики, 1999. — 454 с. — (Современная математика — студентам
и аспирантам).
ISBN 5-86134-066-8.
Учебник «Курс математического анализа» в двух частях написан на
основе лекционного курса, читавшегося автором в Новосибирском
государственном университете, и отражает опыт работы кафедры математического
анализа по совершенствованию преподавания этого предмета. Дается
оригинальное изложение ряда тем, составляющих традиционное содержание курса.
Читателю также представлены отдельные интересные вопросы,
примыкающие к основному материалу. Часть I, книга 1 учебника предназначена для
студентов первого курса математических факультетов университетов. Она
может быть полезна преподавателям математики в университетах и в других
высших учебных заведениях, где читается математический анализ.
Ответственные редакторы
ШВЕДОВ Игорь Александрович
ИОНИН Владимир Кузьмич
Издание осуществлено при финансовой поддержке
Российского фонда фундаментальных исследований
(код проекта 99-01-14013).
© Решетняк Ю. Г., 1999
© Институт математики
им. С. Л. Соболева СО РАН, 1999
'#
и
т-, 1602070000-06 rv__ -
Р Я82(03)-99 Бе3 объявл-
ISBN 5-86134-066-8

КУРС МАТЕМАТИЧЕСКОГО АНАЛИЗА
часть 1 * книга 1
Введение в математический анализ.
Дифференциальное исчисление функций
одной переменной
ОГЛАВЛЕНИЕ
От автора 7
Предисловие 9
Глава 1. Введение в математический анализ 11
§ 1. Понятие множества 12
1.1. Множество и его элементы 12
1.2. Логическая символика 14
1.3. Кванторы 16
1.4. Операции над множествами 16
1.5. Прямое произведение множеств 17
§ 2. Функции 19
2.1. Понятие функции или отображения 19
2.2. Образ и прообраз. Накрывающее и взаимно однозначное
отображения 20
2.3. Суперпозиция отображений 21
2.4. Обратное отображение 22
2.5. Сужение и продолжение функции 25
2.6. График функции 25
§ 3. Вещественные числа и числовые множества 26
3.1. Алгебраическая структура множества вещественных чисел 27
3.2. Порядковая структура множества 3R. 28
3.3. Расширенная числовая прямая. Промежутки (отрезки) 29
3.4. Абсолютная величина. Положительная и отрицательная части
числа 30
§ 4. Точные границы числового множества. Аксиома
непрерывности. Натуральные, целые и рациональные числа . 32
4.1. Понятия точной верхней и точной нижней границ
числового множества. Аксиома непрерывности 33
4.2. Признаки точной верхней и точной нижней границ
числового множества 35
4.3. Свойство монотонности относительно включения
точной верхней и точной нижней границ 37
4.4. Множества натуральных, целых и рациональных чисел 38
4.5. Существование квадратного корня 48
4.6. Сокращенные обозначения для суммы и произведения 50

4
Курс математического анализа, ч. 1, кн. 1
§ 5. Вещественные числовые функции 52
5.1. Алгебраические операции над вещественными функциями.
Монотонные функции 52
5.2. График вещественной числовой функции 53
5.3. Точные границы вещественной функции 55
§ 6. Комплексные числа 58
6.1. Понятие комплексного числа. Определение и основные свойства . 58
6.2. Вещественная и мнимая части комплексного числа. Модуль.
Сопряженное число 62
6.3. Геометрическое представление комплексных чисел 64
§ 7. Счетные множества 67
7.1. Определение счетного множества 67
7.2. Операции над счетными множествами 71
Задачи 75
Глава 2. Теория предела 81
§ 1. Определение и простейшие свойства предела 82
1.1. Понятие предельной точки числового множества 82
1.2. Определение предела функции на произвольном подмножестве R. 87
1.3. Понятие непрерывной функции 94
1.4. Теорема о предельном переходе в неравенстве. Единственность
предела 95
1.5. Существование предела и асимптотическая ограниченность 98
1.6. Теорема о зажатой переменной и ее следствия 100
1.7. Характеристика предельных точек числового множества 105
1.8. Понятия непрерывности и предела для комплексных функций .. 107
§ 2. Теоремы об операциях над пределами 109
2.1. Операции с бесконечно малыми 109
2.2. Теоремы об операциях с пределами. Случай конечных пределов. 112
2.3. Правила замены переменной под знаком предела 114
2.4. Теоремы о пределах суммы, произведения и частного. Случай
бесконечных пределов 119
§ 3. Признаки существования предела 125
3.1. Теорема о существовании предела монотонной функции 126
3.2. Критерий Коши — Больцано существования конечного предела 130
3.3. Критерий Гейне существования предела 135
3.4. Несчетность множества вещественных чисел R 137
3.5. Понятие одностороннего предела и классификация
точек разрыва функции на отрезке 138
§ 4. Теорема о разрешимости уравнения f(x)=h и ее
следствия 143
4.1. Теорема Коши о промежуточных значениях 144
4.2. Теорема о существовании непрерывной обратной функции 147
§ 5. Основные теоремы о непрерывных функциях 151
5.1. Теорема выбора Вейерштрасса 152
5.2. Теорема Вейерштрасса о наибольшем и наименьшем
значениях непрерывной функции 155
5.3. Понятие равномерно непрерывной функции 156
5.4. Топологические отображения отрезков в множество Ш 161

5
§ 6. Верхний и нижний пределы последовательности 163
6.1. Определение и простейшие свойства
верхнего и нижнего пределов 163
6.2. Критерий существования предела последовательности 167
6.3. Понятие частичного предела последовательности 170
6.4. Характеристика верхнего и нижнего пределов
последовательности 174
Задачи 176
Глава 3. Элементарные функции 187
§ 1. Показательная, логарифмическая и степенная функции.
Некоторые замечательные пределы 188
1.1. Существование и конечность предела lim (l+^)n 189
п—*оо
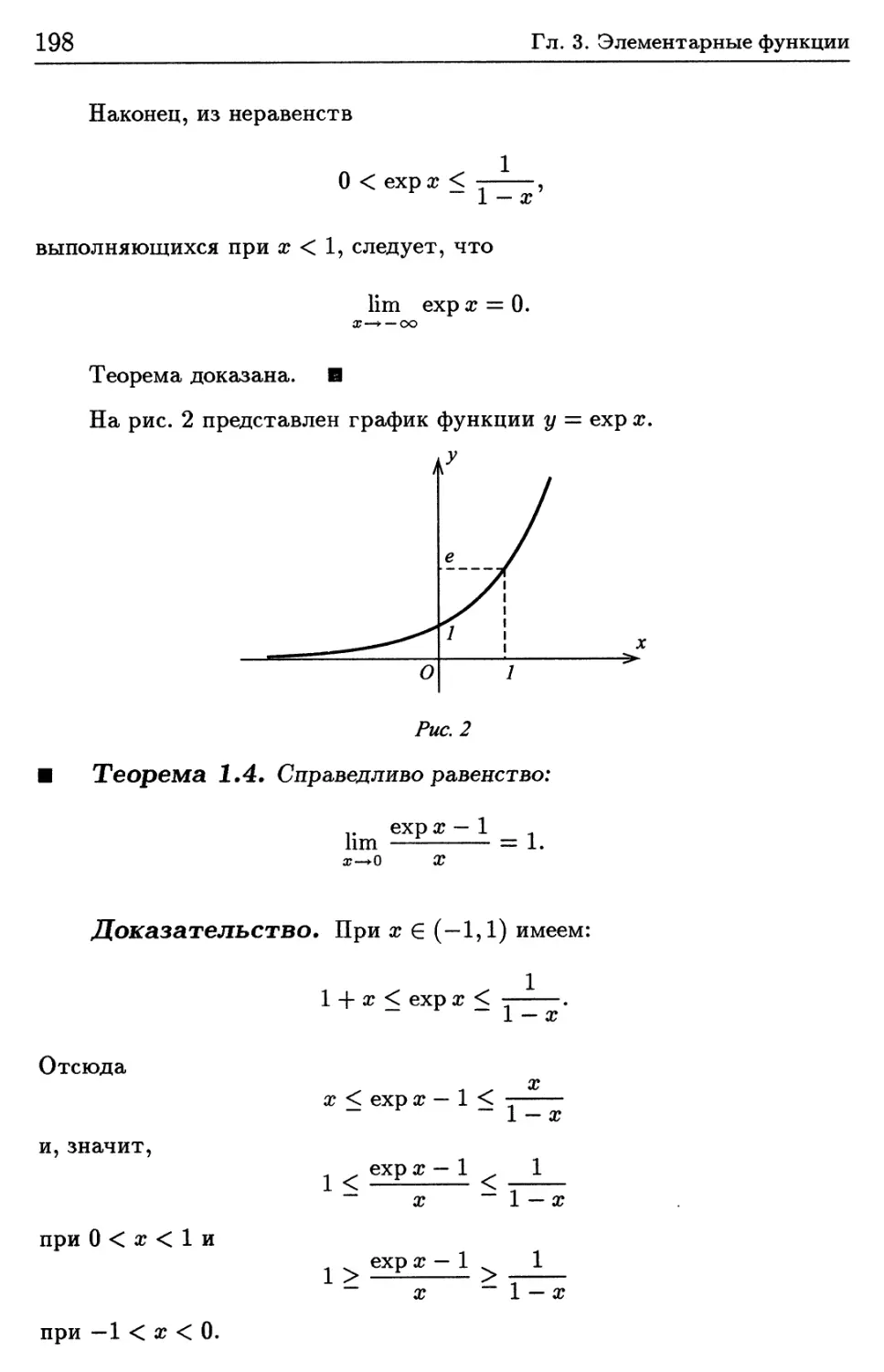
1.2. Свойства функции ехр 194
1.3. Функция — натуральный логарифм 199
1.4. Операция возведения в степень. Степенная функция.
Показательная функция 204
§ 2. Тригонометрические функции. Общее понятие
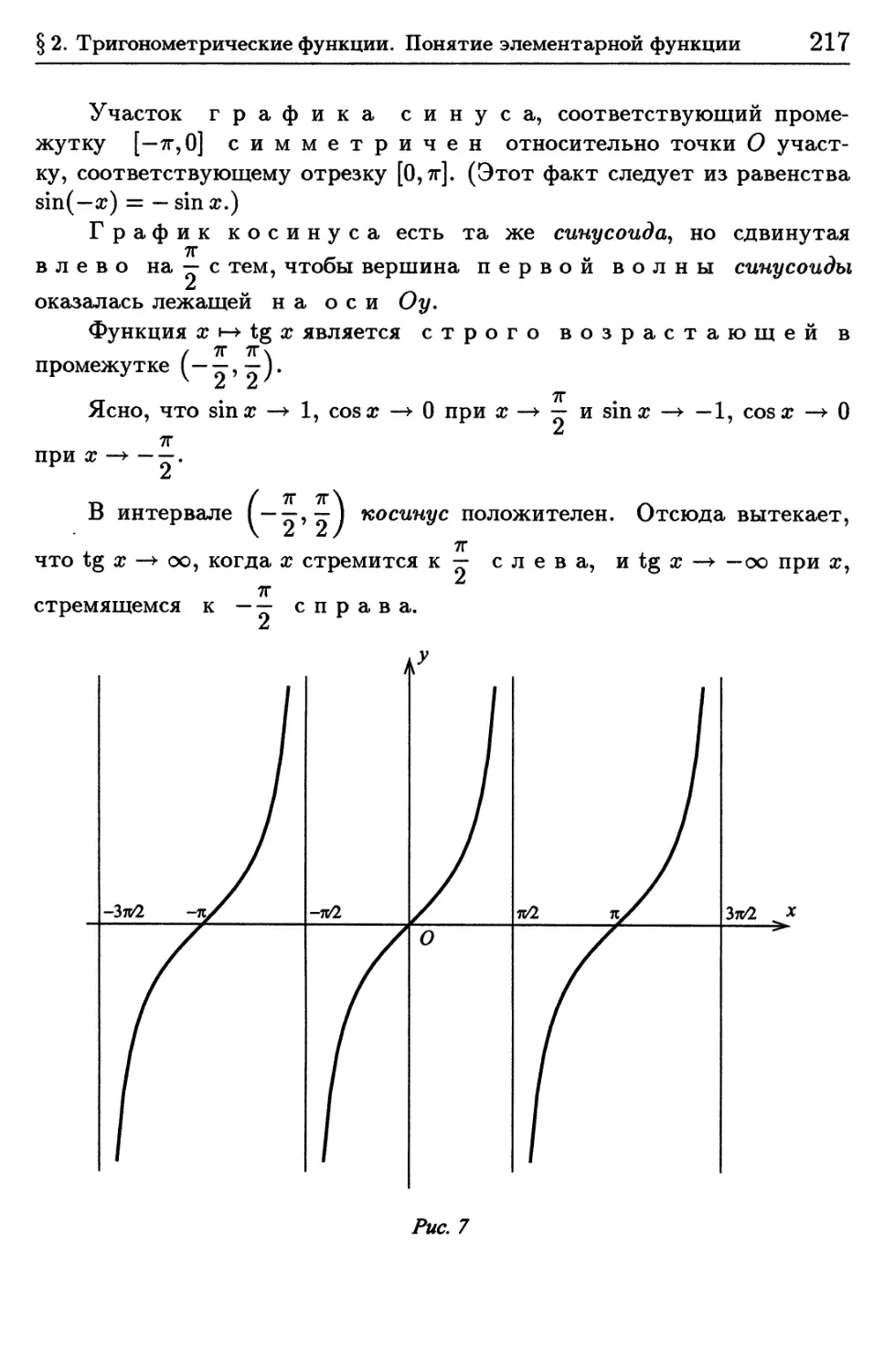
элементарной функции 211
2.1. Синус, косинус и тангенс 211
2.2. Предел lim ^ 219
х—► ()
2.3. Обратные тригонометрические функции 223
2.4. Показательная функция комплексного аргумента 226
2.5. Общее понятие элементарной функции 228
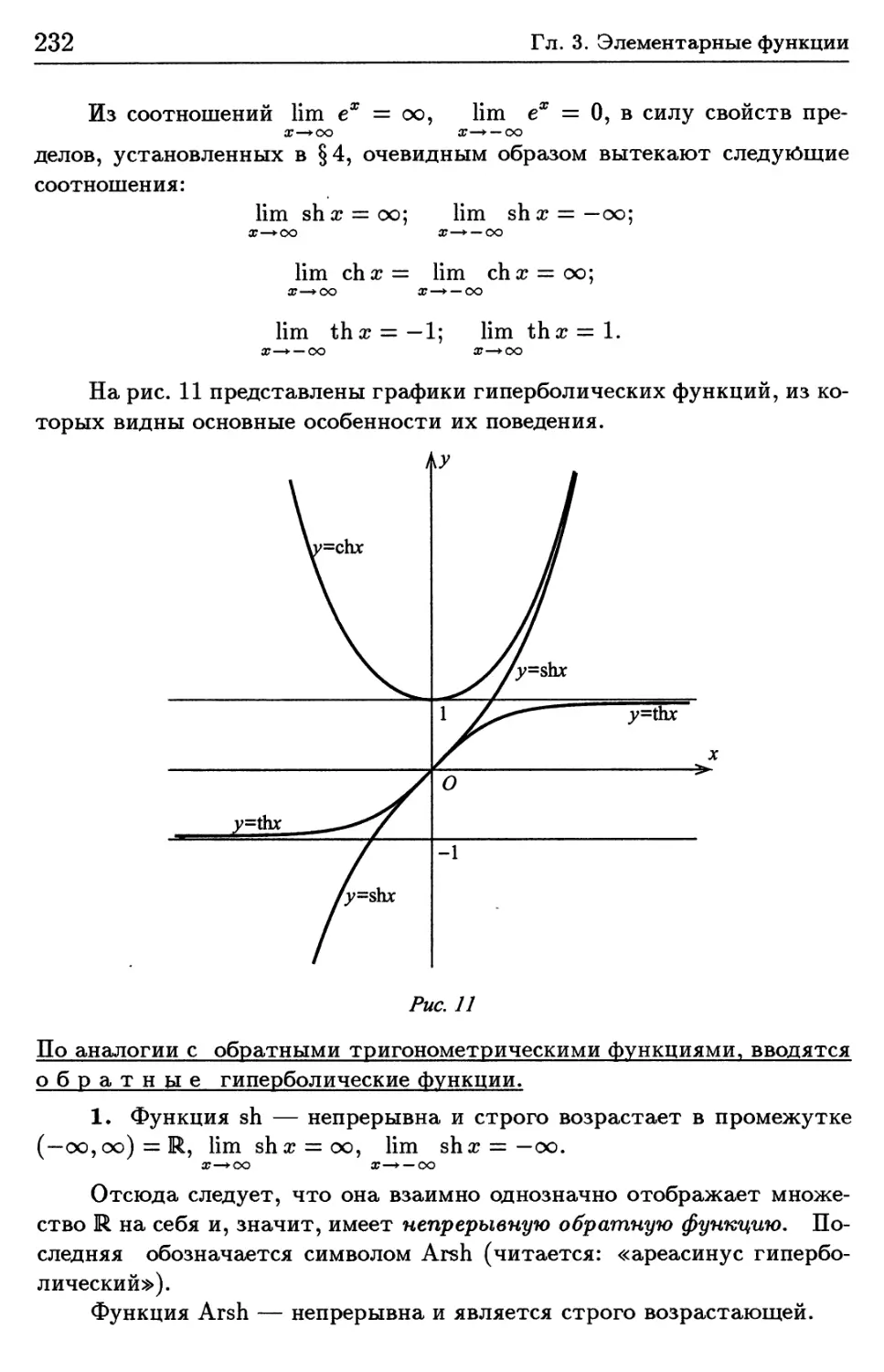
2.6. Гиперболические функции 229
§ 3. Сравнение поведения элементарных функций вблизи
концов области определения 234
3.1. Понятие об асимптотических соотношениях 235
3.2. Сравнение поведения основных элементарных функций
в концах области определения : 238
§ 4. Некоторые дополнительные сведения об элементарных
функциях 241
4.1. О функции ехр в комплексной плоскости 242
4.2. Функциональные уравнения элементарных функций 251
Задачи 261
Глава 4. Дифференциальное исчисление функций одной
переменной 263
§ 1. Определение и простейшие свойства производной 264
1.1. Понятие функции, дифференцируемой в точке. Определение
производной 264
1.2. Правила дифференцирования 267
1.3. Дифференцирование основных элементарных функций 271
§ 2. Некоторые приложения понятия производной 278
2.1. Касательная графика функции 278
2.2. Понятие параметризованной кривой. Касательная к
параметризованной кривой 279
2.3. Полярная система координат на плоскости. Графики функций
в полярной системе координат 297
2.4. Приложения понятия производной в физике и механике 301

6 Курс математического анализа, ч. 1, кн. 1
§ 3. Производные высших порядков 303
3.1. Определение производной высшего порядка 304
3.2. Производные высших порядков некоторых элементарных
функций 306
3.3. Теорема о произведении функций классов Dn и Сп. Формула
Лейбница 309
3.4. Теоремы об операциях над функциями классов Т)п и Сп 312
§ 4. Теоремы о среднем значении 315
4.1. Точки экстремума функции. Теорема Ферма 316
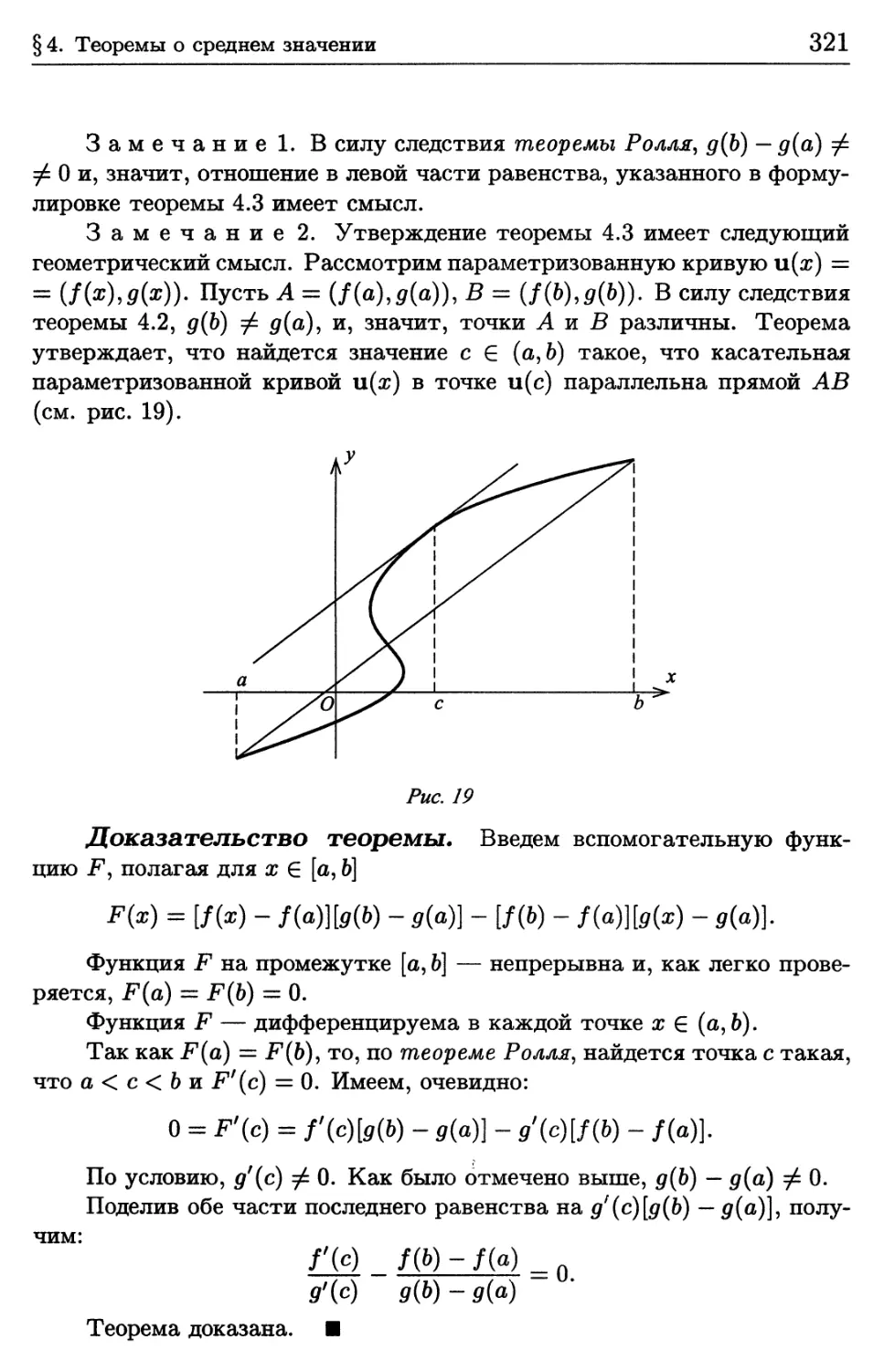
4.2. Теоремы Коши и Лагранжа о среднем значении 319
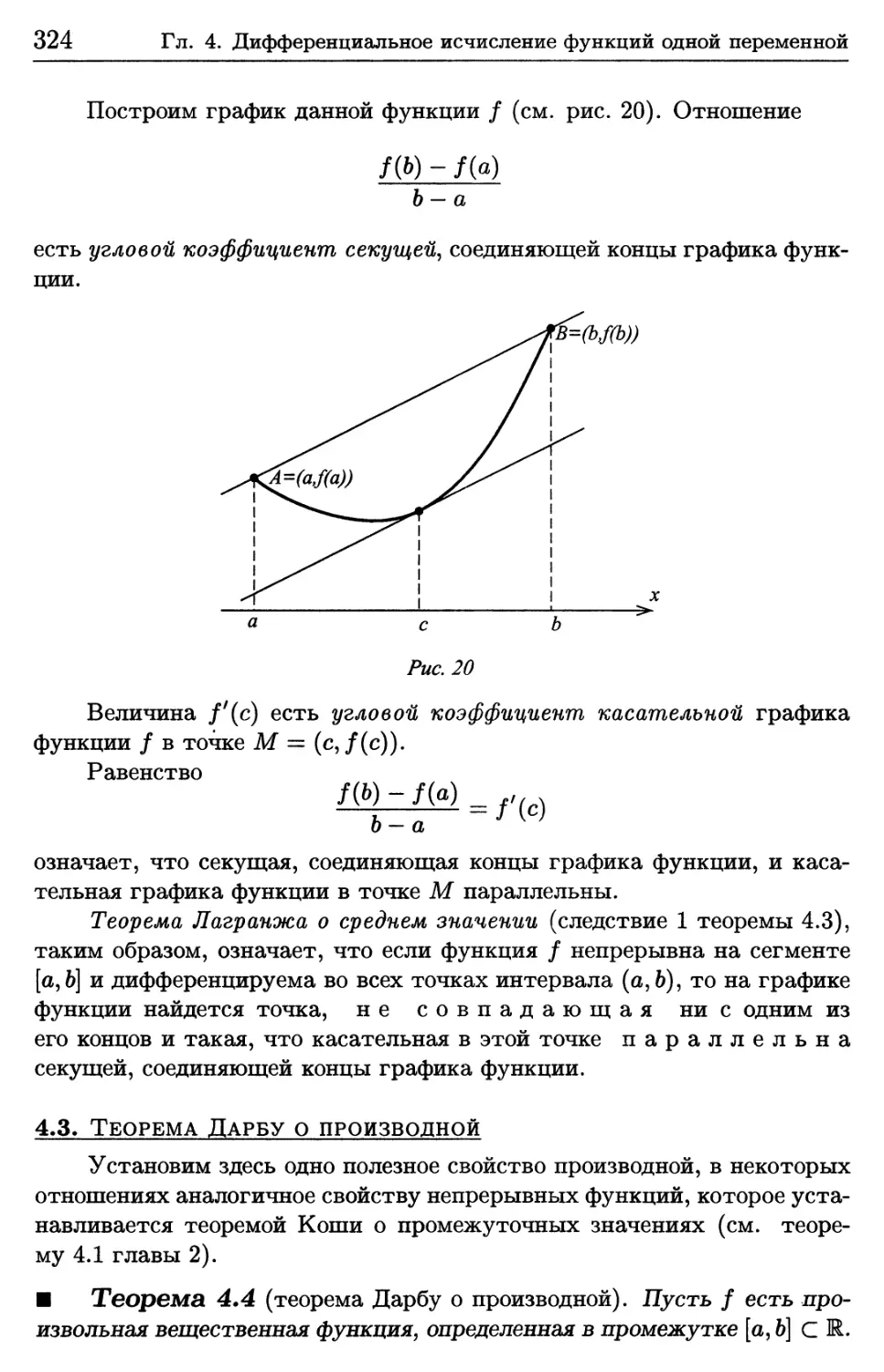
4.3. Теорема Дарбу о производной 324
4.4. Критерий монотонности функции 326
4.5. Ослабленный критерий монотонности функции 329
§ 5. Правила Лопиталя раскрытия неопределенностей 336
5.1. Неопределенность типа q 336
5.2. Неопределенность типа — 341
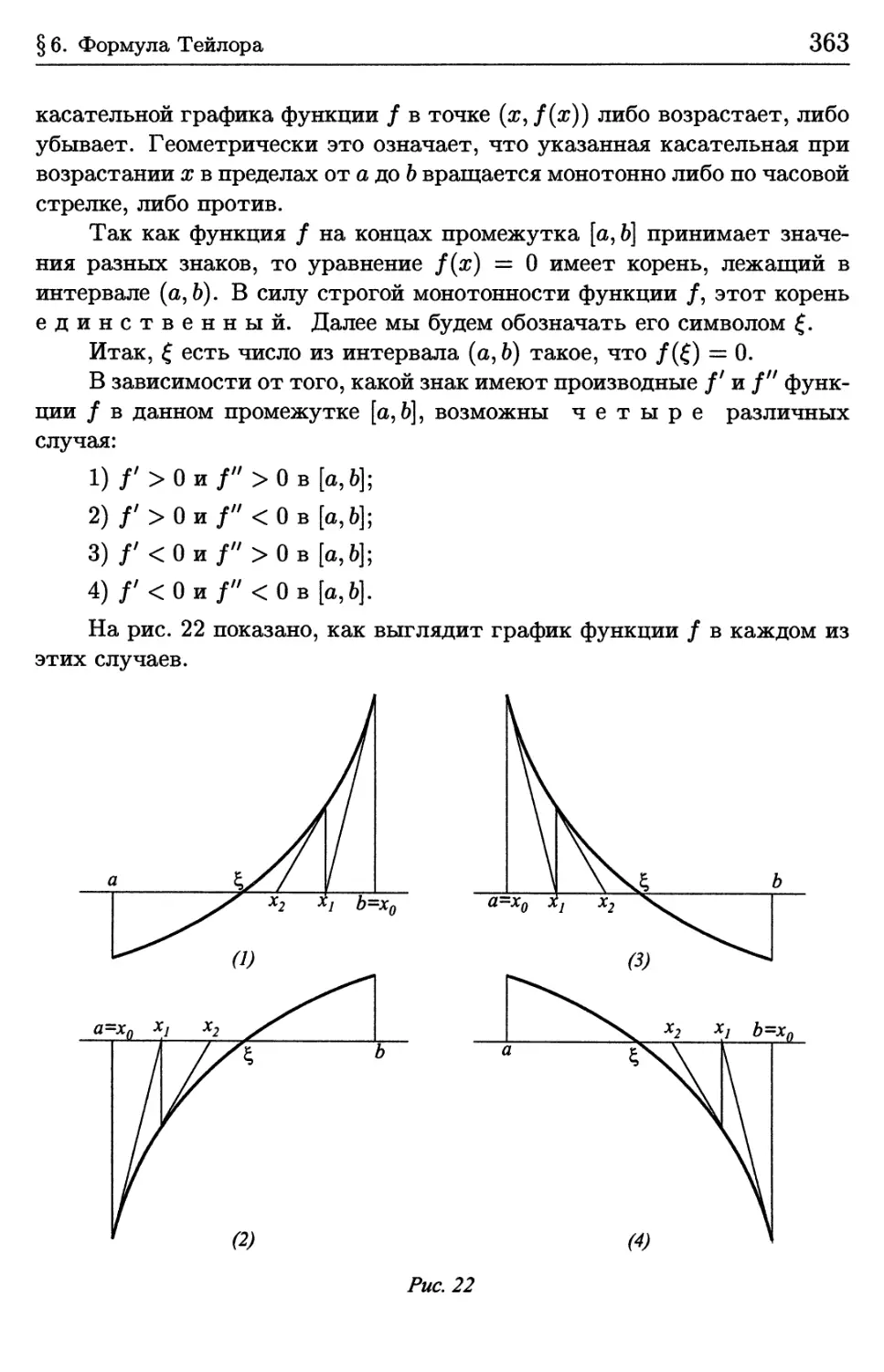
§ 6. Формула Тейлора 344
6.1. Некоторые сведения о полиномах одной переменной 345
6.2. Формула Тейлора с остаточным членом в форме Пеано 350
6.3. Оценки остаточного члена формулы Тейлора 354
6.4. Новое доказательство формулы Лейбница 358
6.5. Метод Ньютона (метод касательных) приближенного решения
уравнений 361
§ 7. Точки экстремума дифференцируемой функции 369
7.1. Необходимые условия экстремума 370
7.2. Достаточные условия экстремума 374
7.3. Достаточные условия экстремума для функции, П-кратно
дифференцируемой в точке 377
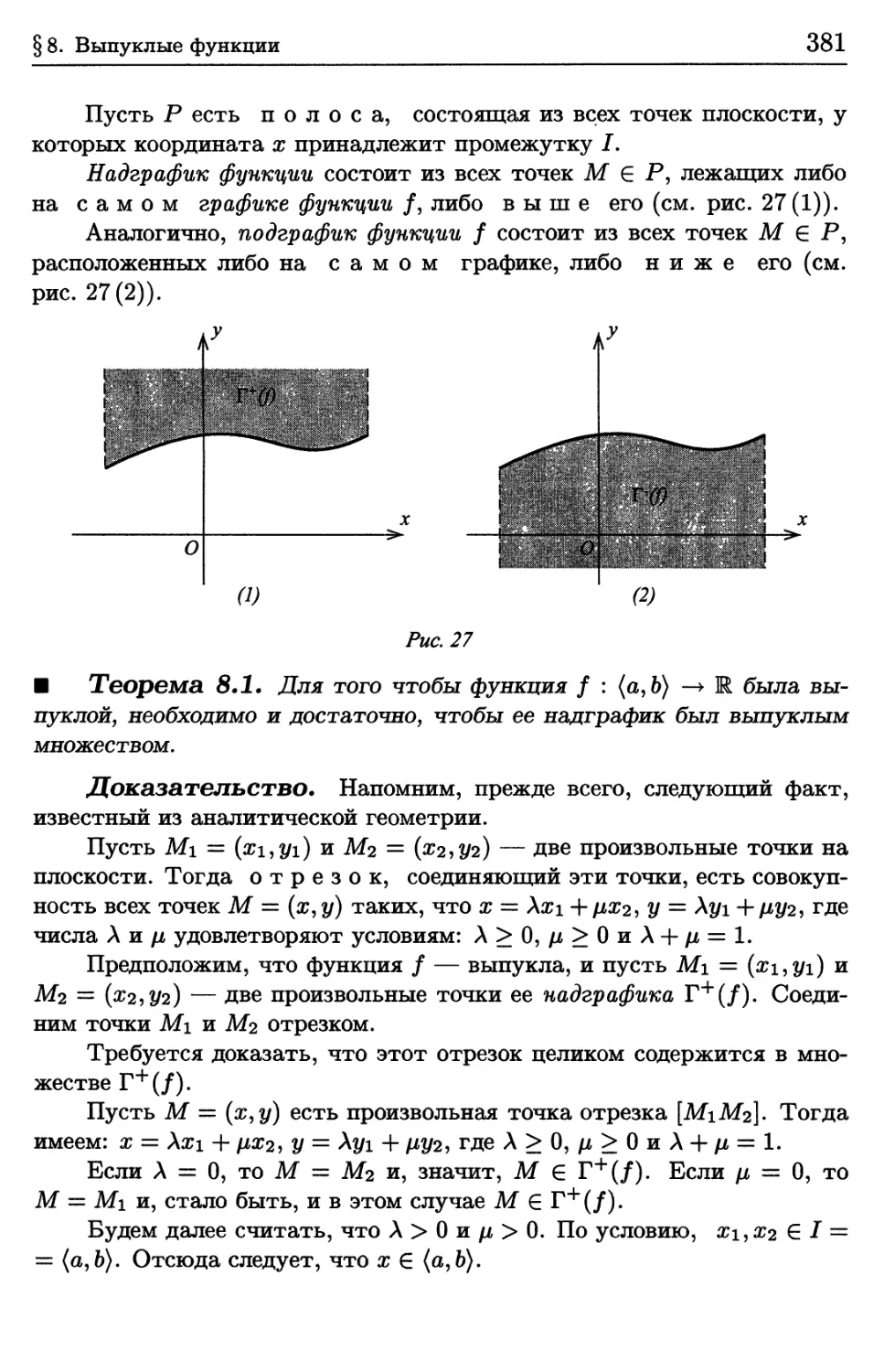
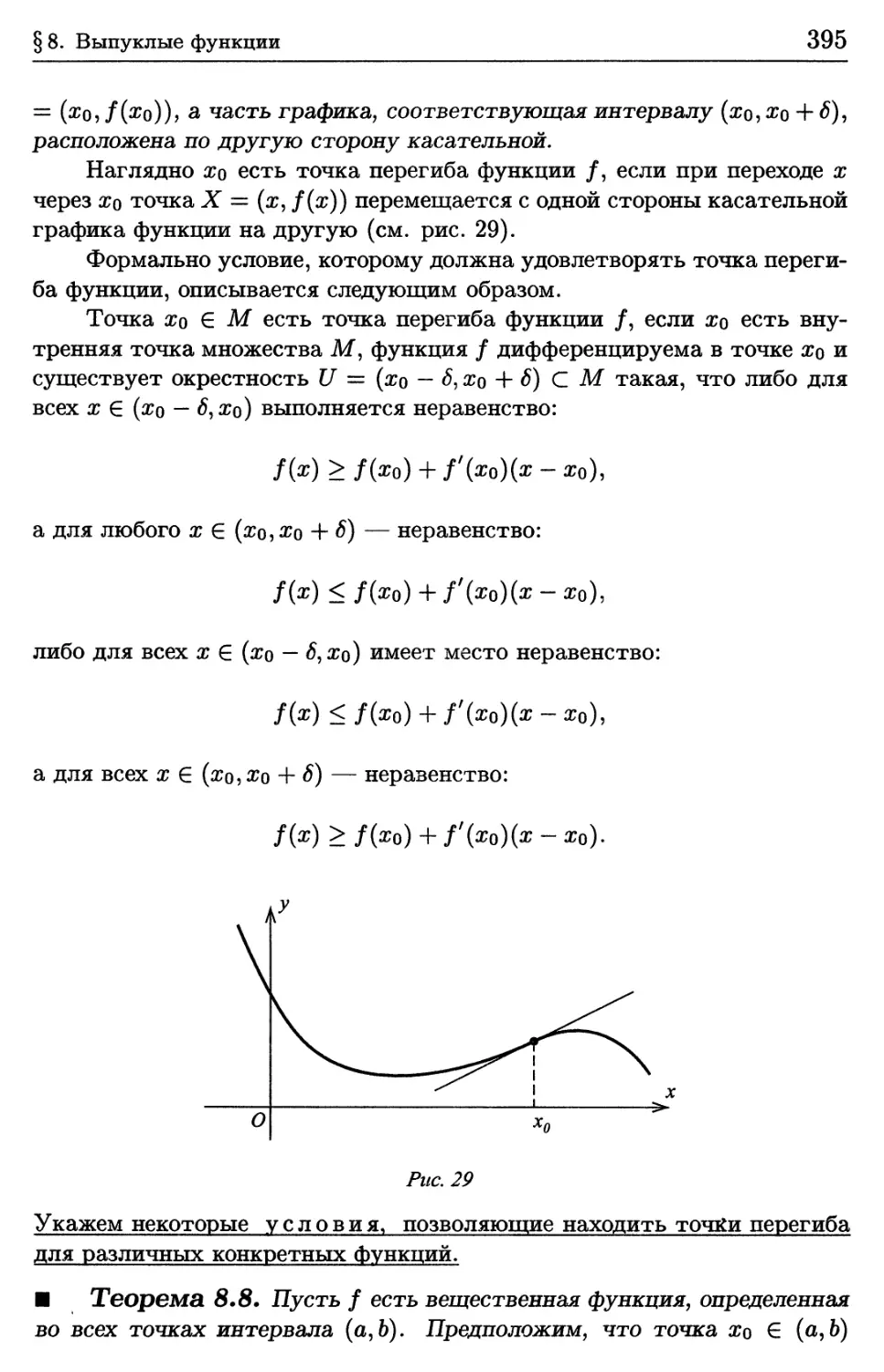
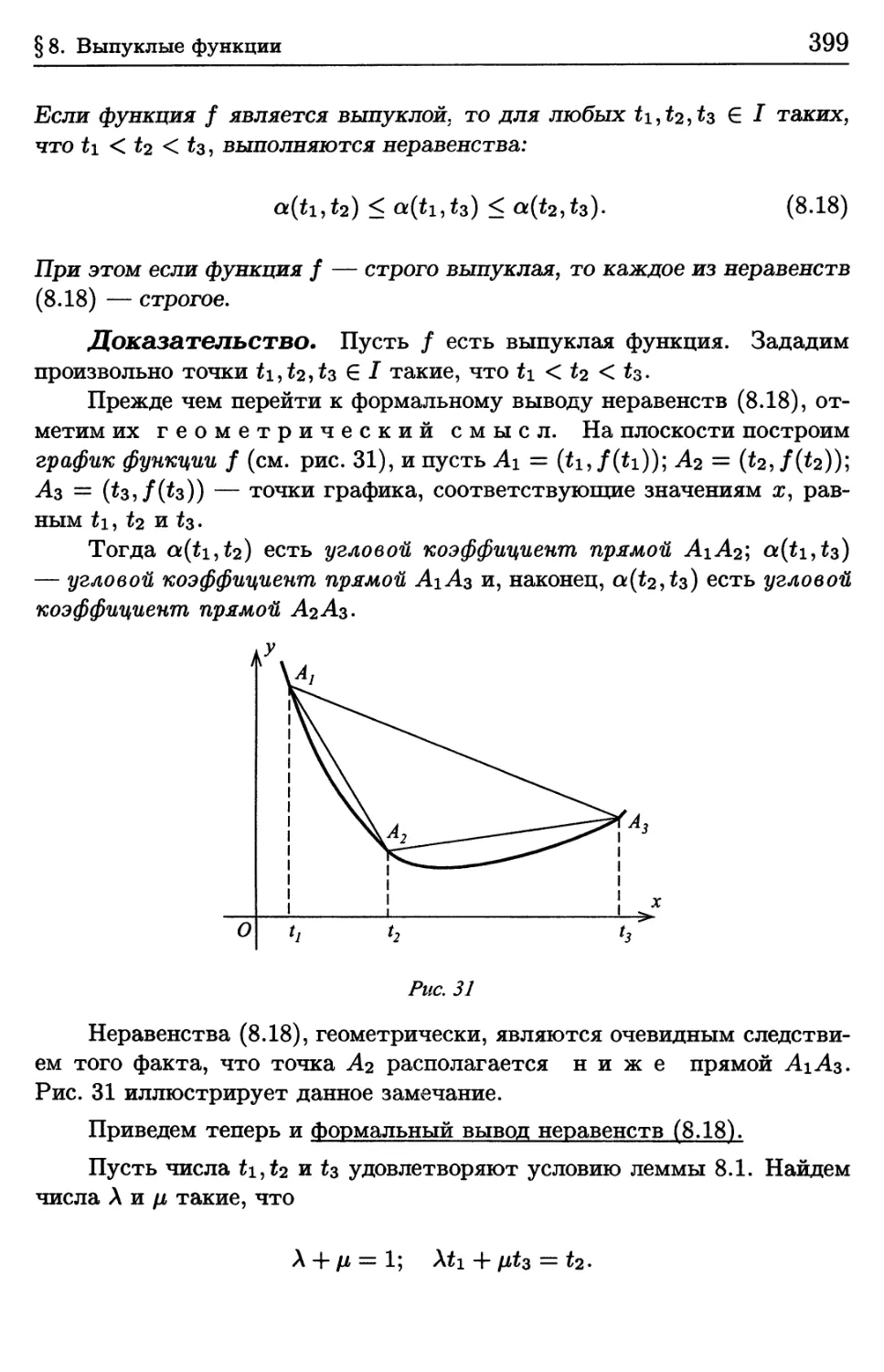
§ 8. Выпуклые функции 379
8.1. Определение выпуклой функции. Неравенство Йенсена * 379
8.2. Критерий выпуклости функции 384
8.3. Основные неравенства анализа 389
8.4. Точки перегиба функции 394
8.5. Критерий выпуклости функции в общем случае 398
§ 9. Исследование функции методами дифференциального
исчисления 406
9.1. Построение графика функции 407
9.2. Исследование алгебраических уравнений второй и третьей
степени 417
9.3. Исследование параметризованных кривых 423
Задачи 433
Указатель обозначений 443
Предметный указатель 445

Задача преподавания математического анализа есть одна
из труднейших задач науки и педагогики. Все
обстоятельства являются осложняющими эту задачу: и самый рост
науки с ее непрерывным обогащением новыми фактами, и
связанное с этим колеблющееся освещение, казалось бы,
прочно установленных начал, и, наконец, изменяющийся
уровень знаний и потребностей тех кругов, к которым
обращено слово педагога. *
Н. Н. ЛУЗИН
От автора
(к первой части книги)
Предлагаемый вниманию читателя учебник «Курс математического
анализа» (часть 1-я в двух книгах и часть 2-я) является итогом работы,
выполнявшейся мною на протяжении более тридцати лет на механико-математическом
факультете Новосибирского государственного университета (НГУ).
Содержание книги — основы дифференциального и интегрального исчислений в
вещественной области и смежные вопросы.
Дифференциальное и интегральное исчисления составляют основу
математического образования. В широком смысле «математический анализ»
означает часть современной математики, включающую в себя такие ее
разделы, как теория функций комплексной переменной, теория
дифференциальных уравнений, дифференциальная геометрия, теория функций вещественной
переменной, функциональный анализ, теория вероятностей и др. Эти
направления теоретической математики интенсивно развиваются в наши дни. Цель
книги — изложение тех начальных сведений из математического анализа,
которые необходимы для того, чтобы овладеть достижениями перечисленных
направлений математики и успешно работать в них.
Дифференциальное и интегральное исчисления имеют большое значение
также и с точки зрения приложений математики. Решение многих задач
естествознания, в частности, механики, физики, химии и других наук, основано на
методе математического моделирования различных явлений и процессов. При
этом применяются в основном математические модели, использующие понятия
дифференциального и интегрального исчислений. Эти дисциплины
представляют собой язык, на котором формулируется большинство законов физики и
механики. Не случайно один из основателей математического анализа Исаак
Ньютон является также основоположником современной физики.
В эпиграфе приводятся слова выдающегося российского математика,
академика Н. Н. Лузина. Когда в 1963 г. в Новосибирском университете мне было
предложено взяться за чтение лекций по математическому анализу, я в полной
мере ощутил те трудности, о которых говорил Н. Н. Лузин. К этому времени в
нашей стране уже было издано большое число прекрасных учебников по этому
предмету, и задача лектора, казалось бы, сводилась к простому озвучиванию
уже имеющихся руководств. Представлялось, что содержание курса
математического анализа однозначно определено тем положением, которое
дифференциальное и интегральное исчисления занимают в системе математического
образования. Исключить или, наоборот, включить что-либо в этот курс, было
непросто. Работая над курсом, я не имел каких-либо априорных установок
относительно того, каким должен быть курс математического анализа, кроме
одной: каждая отдельная тема должна наиболее адекватно отражать
«сегодняшнее состояние науки». За прошедшее время способ изложения отдельных
тем курса неоднократно пересматривался. Предлагаемая вниманию читателя
книга в двух частях есть результат этой работы.
«Успехи математических наук», 1989, т. 44, вып. 2(266), с. 3.

8
От автора
Усилия, затраченные мною на работу над курсом математического
анализа, в свое время были поддержаны моими старшими коллегами, из которых
я, в первую очередь, должен назвать тогдашнего заведующего кафедрой
математического анализа, члена-корреспондента АН СССР Алексея Андреевича
Ляпунова и первого ректора Новосибирского университета, академика Илью
Несторовича Веку а. Я вспоминаю о них с чувством глубокой благодарности.
Ранее учебные пособия по отдельным темам читаемого мною курса
математического анализа неоднократно издавались в Новосибирском
государственном университете. Выпуск книги, содержащей по возможности полное
изложение курса, планировался мною давно. Однако найти время для реализации
этой идеи мне удалось лишь сейчас. Автор ясно понимает, сколь
несовершенны результаты его труда, и критически настроенный читатель несомненно
сможет указать примеры, подтверждающие это. Тем не менее я надеюсь, что
книга станет полезным пособием для всех, кто собирается учиться сам или
намерен учить других математическому анализу.
Буду благодарен читателям за любые замечания и критику.
Различные аспекты курса математического анализа я неоднократно
обсуждал с коллегами по кафедре математического анализа. Обмен мнениями
имел для меня существенное значение. В связи с этим мне хотелось бы
поблагодарить сотрудников кафедры математического анализа Новосибирского
государственного университета, с которыми я работал многие годы, а также
коллектив преподавателей кафедры, ведущих практические занятия. Их
суждение всегда было для меня очень важным при выборе способа и порядка
изложения отдельных тем. Безусловно, я также благодарен бывшим студентам
— слушателям моего курса — за бесконечное терпение и благожелательное
отношение к моим усилиям. Я благодарю коллег — сотрудников Института
математики им. С. Л. Соболева СО РАН — за конструктивное обсуждение
проблем преподавания математического анализа. Я благодарю сотрудников
издательства Института математики СО РАН и, прежде всего, Кутатела-
дзе Семена Самсоновича, вложивших много редакторского труда в подготовку
учебника, Дятлова Владимира Николаевича, переработавшего первую главу
книги и сделавшего ряд полезных замечаний, а также благодарю других
сотрудников издательства, работавших над подготовкой книги к изданию.
Выражаю большую благодарность ответственным редакторам книги — Шведову
Игорю Александровичу, Ионину Владимиру Кузьмичу, прочитавшим первые
восемь глав книги и сделавшим много очень ценных замечаний, а также Во-
локитину Евгению Павловичу, выполнившему необходимые рисунки к книге
с помощью компьютерной программы. Профессору Игорю Александровичу
Шведову — моему коллеге по кафедре математического анализа НГУ и по
Институту математики СО РАН — я особенно признателен за обсуждение
взглядов на преподавание курса математического анализа, за обстоятельные
дискуссии на протяжении более двух десятков лет по различным вопросам
математического анализа как принципиального, так и технического
характера. Особо благодарю дирекцию Института математики им. С. Л. Соболева
СО РАН за практическую помощь в подготовке рукописи «Курса
математического анализа» и руководство Новосибирского государственного университета
и механико-математического факультета НГУ, где я работаю много лет. С
глубокой благодарностью, кроме упомянутых мною выше, я вспоминаю
академиков А. И. Мальцева, С. Л. Соболева и Л. В. Канторовича, которые, — в
те годы, когда я начал преподавать, — ознакомились и в целом одобрили мой
проект курса математического анализа на механико-математическом
факультете НГУ. Я благодарю Екатерину Григорьевну Решетняк за ее неоценимую
помощь при подготовке рукописи этой книги.
Издание книги финансировалось Российским фондом фундаментальных
исследований, грант № 99-01-14013.
Ю. Г. Решетняк

ПРЕДИСЛОВИЕ
Учебник — «Курс математического анализа» состоит из двух частей,
которые содержат 15 глав. Первая часть «Курса математического анализа»,
состоящая из двух книг, содержит материал, который обычно рассказывается
студентам-математикам на первом году обучения на
механико-математическом факультете Новосибирского государственного университета. В первых
главах автор стремился изложить материал в форме, по возможности,
доступной для начинающих, уделяя особое внимание мотивировке проводимых
рассуждений. Почему принято такое определение того или иного понятия, а
не другое, какие трудности возникают, если отойти от принятого автором
пути, а также какие трудности могут возникнуть, если пойти по этому
пути дальше? Какова роль тех или иных условий в формулировках основных
теорем? В какой мере здесь можно найти ответы на эти вопросы, — судить
читателю. В книгу включен также и разнообразный материал сверх того, что
должно рассматриваться как некоторый «обязательный минимум» для курса
математического анализа. По большей части, каждая отдельная тема из
этого дополнительного материала хотя бы один раз рассказывалась автором на
лекциях.
В книгу 1 части первой «Курса математического анализа» включены
первые четыре главы.
В главе 1 — «Введение в математический анализ» —
приводятся начальные сведения о теории множеств и о вещественных числах,
используемые при изучении свойств понятий предела и непрерывной функции. Начала
теории множеств, в том виде, как они изложены в книге, в настоящее время
называют «наивной теорией множеств». Знакомство с такой версией теории
множеств есть необходимый шаг при ознакомлении с ее более продвинутыми
вариантами (они в этой книге не используются). Теория вещественных
чисел излагается аксиоматически. Такой способ изложения в настоящее время
является, по-видимому, общепринятым. Основная задача, которая возникает
перед лектором на этом пути, — как сформулировать аксиомы,
характеризующие свойство непрерывности множества вещественных чисел. В настоящей
книге в качестве аксиомы непрерывности принято условие существования
точной верхней и точной нижней границ у всякого числового множества. В главе
1 определяется также понятие комплексного числа. Здесь излагаются
основные сведения о бесконечных счетных множествах (материал, относящийся к
этой теме, потребуется в главе 5, посвященной интегральному исчислению).
Глава 2 — «Теории предела». Понятие предела определяется
сначала для функции, областью определения которой является произвольное
подмножество множества всех вещественных чисел К. Понятие предела
последовательности появляется как частный случай, когда область определения
функции есть множество всех натуральных чисел. В этой же главе
определяется понятие непрерывной функции и устанавливаются основные теоремы
о непрерывных функциях вещественной переменной.

10
Курс математического анализа, ч. 1, кн. 1
Задача главы 3 — «Элементарные функции» — дать определение
основных элементарных функций — показательной, логарифмической и
степенной, основанное на строгой теории вещественных чисел. Сначала вводится
функция ехр ж, которая, как будет показано, есть показательная функция,
основанием которой служит число е = expl. Для произвольного х величина ехр ж
определяется как предел выражения (1 + ^)п при п, стремящемся к оо. С
помощью функции ехр последовательно определяются логарифмическая, степенная
и общая показательная функции. Автор не посчитал возможным включить в
курс «строгую» теорию тригонометрических функций в полном объеме, ввиду
ее громоздкости. За основные приняты те определения тригонометрических
функций, которые опираются на представления, относящиеся к элементарной
геометрии. В заключительной части главы 3 приводятся соображения
относительно определения тригонометрических функций, основанного на строгой
теории вещественных чисел. Предел, посредством которого была определена
величина ехр ж, существует также и в случае, когда х есть произвольное
комплексное число. Это дает возможность продолжить показательную функцию
ехр на множество всех комплексных чисел. Используя полученное
продолжение, можно определить синус и косинус вещественного аргумента, а через них
и остальные тригонометрические функции. В дополнение к основному
материалу, в главе 3 приводятся теоремы о характеристике основных элементарных
функций как решений некоторых функциональных уравнений.
Основы главы 4 — «Дифференциальное исчисление функций
одной переменной» — излагаются более или менее традиционным путем.
Приводится определение производной функции, описывается техника
вычисления производных, доказываются теоремы о среднем значении; даются
стандартные приложения теорем о среднем значении к выводу правил Лопиталя
и формулы Тейлора. Затем рассматриваются задачи об отыскании
экстремумов функции одной переменной. Описывается техника исследования функций
одной переменной методами дифференциального исчисления. Определяется
также понятие выпуклой функции и устанавливаются некоторые важные
неравенства. В той части главы 4, которая посвящена теории выпуклых функций,
вопрос о критерии выпуклости функции исследуется в общей форме.
О содержании следующих четырех глав части 1 — с 5-й по 8-ю — будет
рассказано в предисловии к книге 2 первой части «Курса математического
анализа».
В предисловии ко второй части учебника «Курс математического
анализа» будет описано содержание глав, входящих во 2 часть.
Каждая глава книги сопровождается задачами по теме этой главы.
Основную часть из них составляют те, которые включались в разное время в
экзаменационные билеты на механико-математическом факультете
Новосибирского государственного университета. При отборе задач автор старался
подбирать такие, решение которых способствовало бы лучшему пониманию
теоретических аспектов данного «Курса».
В книге принята следующая система нумерации. Главы делятся на
параграфы, имеющие порядковую нумерацию. В свою очередь, каждый параграф
разбивается на пункты (или разделы), которые имеют двойную нумерацию:
первая цифра — номер параграфа, вторая цифра — порядковая.
Формулируемые в книге утверждения (предложения, теоремы и леммы) и формулы имеют
— в пределах параграфа — аналогичную двойную нумерацию. Рисунки имеют
порядковую нумерацию в пределах главы. В конце книги приведены указатель
обозначений и предметный указатель.

Глава 1
ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Г
• Понятие множества, включение множеств, прямое
произведение • Общее понятие функции или
отображения • Взаимно однозначные (инъективные)
отображения и отображения «на» (сюръективные или надъ-
ективные), обратное отображение • Множество
вещественных чисел • Аксиомы действий над
вещественными функциями • Аксиомы порядка •
Точная верхняя и точная нижняя границы числового
множества • Аксиома непрерывности • Множества
натуральных, целых и рациональных чисел • Принцип
математической индукции • Принцип Архимеда •
Вещественные функции и алгебраические операции с
вещественными функциями • График функции •
Точная верхняя и точная нижняя границы вещественной
функции • Комплексные числа. Алгебраические операции
над комплексными числами • Модуль комплексного
числа, сопряженное число • Счетные множества,
свойства счетных множеств, теоремы об операциях со
счетными множествами •

12
Гл. 1. Введение в математический анализ
§1. Понятие множества
В этом параграфе излагаются некоторые элементарные сведения из
теории множеств и математической логики, которые будут
применяться в дальнейшем. Приводятся основные начальные сведения из теории
множеств. В частности, определяется понятие включения множеств,
описываются операции объединения, пересечения и прямого
произведения множеств. Операции эти обычно имеют простой наглядный смысл
и при доказательстве тех или иных их свойств следует каждый раз
попытаться сначала понять, что означает то или иное утверждение о
множествах наглядно.
Нужные сведения из математической логики не идут далее
описания логической символики, употребляемой в этой книге, как способ
сокращенного описания отдельных математических высказываний. В
современной математике понятие множества играет роль своего рода
строительного материала, из которого конструируются все основные
математические объекты.
1.1. Множество и его элементы
1.1.1. В курсе математического анализа обычно ограничиваются так
называемым «наивным» подходом к определению множества. Это
вызвано тем, что множество используется здесь как вспомогательный,
терминологический объект и не является предметом изучения. Мы также
не будем задаваться целью дать строгое аксиоматическое определение
множества, ограничившись разъяснением понятия множества и
описанием действий, в которых это понятие принимает активное участие.
Для нас множество будет одним из первичных математических
понятий, не выражаемым через другие математические понятия. Обычно,
говоря слово «множество», мы будем под этим понимать совокупность
объектов произвольного рода, рассматриваемую как единое целое.
Вместе с термином множество будут употребляться и его синонимы типа
набор, система, совокупность и т. п. Например, можно говорить о
множестве решений некоторого уравнения, о коллекции картин,
хранящихся в музее, совокупности точек круга и т. д.
Объекты, составляющие то или иное множество, называются его
элементами.
Множество считается заданным, если для любого объекта можно
установить, является он элементом данного множества или нет.

§ 1. Понятие множества
13
Множество иногда задается указанием всех его элементов. Если
таких элементов немного, то для их перечисления используют
обозначение: {#, у, 2,...} — это множество, элементами которого являются
объекты х, у, z и т. д. (их перечень должен быть достаточно ясен из
контекста). Кстати, порядок упоминания элементов при таком задании
множества несуществен (в отличие от упорядоченных наборов,
определяемых ниже). Более распространен способ задания множества путем
указания свойства, которому должны удовлетворять все его элементы:
запись
{о + а | х обладает свойством Р(х)}
выделяет те элементы множества X, которые удовлетворяют условию
Р(х).
Пусть А — произвольное множество, а х — какой-либо объект.
Если х есть элемент А, то говорят, что х принадлеоюит А и пишут х Е А
(читается: «х принадлежит А», «я — элемент А», «я из А»). Если же
х не является элементом множества А, то говорят, что х не
принадлежит А. В обозначениях последняя ситуация выражается следующим
образом: х £ А (читается: «# не принадлежит А» или «# не есть
элемент А»).
Удобно говорить о множестве, у которого нет элементов.
Множество, не имеющее ни одного элемента, называется пустым и
обозначается символом 0. Например, множество всех прямоугольных
равносторонних треугольников пусто, так как не существует ни одного такого
треугольника. Часто возникает такая ситуация, когда вводя
множество математических объектов, удовлетворяющих определенному
условию Р(х), мы заранее не можем сказать, существует ли хотя бы один
#, соответствующий этому условию Р{х). Существование или
несуществование таких х часто устанавливается лишь в конце исследования.
До этого приходится говорить о множестве {х | Р(х)}, не зная заранее,
будет это множество пустым или нет.
В теории множеств пустое множество играет роль, аналогичную
той, которая в арифметике принадлежит нулю.
1.1.2. Пусть А и В — произвольные множества.
Говорят, что А содержится в В или, иначе, А является
подмножеством или частью J3, если всякий элемент множества А является
элементом множества В. При этом используют либо запись А С J3,
либо запись В D А (первая читается «А содержится в В», вторая —
«J3 содержит А»). Тем самым для множеств определено отношение,
обозначаемое знаками С и Э и называемое включением.
Принято считать, что пустое множество содержится в любом
множестве, то есть 0 С А, каково бы ни было множество А.

14
Гл. 1. Введение в математический анализ
Говорят также, что элементы пустого множества удовлетворяют
любому наперед заданному условию, поскольку в пустом множестве нет
никаких элементов. (Как говорил один из профессоров, у которых автор
учился: «Все элементы пустого множества зеленые, так как у него нет
никаких элементов».)
Отметим очевидные свойства отношения включения.
(1) Для всякого множества А верно включение А С А.
(2) Если АсВиВсС,тоАсС.
Говорят, что множества А и В равны, и пишут А = J3, если всякий
элемент множества А принадлежит В и всякий элемент множества В
принадлежит А. Иначе говоря, А = В в том и только в том случае, если
А С В и В С А.
Отметим очевидные свойства равенства множеств.
(3) Для любого множества А имеет место равенство А = А.
(4) Если А = В, то В = А.
(5) Если А = В, В = С,тоА = С.
1.2. Логическая символика
Основное содержание математики обычно организуется в виде
отдельных утверждений, выражающих те или иные факты. Как и при
подходе к понятию множества, мы не будем задаваться целью дать
строгое определение тому, что следует относить к утверждениям, а опишем,
что под этим следует понимать.
1.2.1. Условимся называть высказыванием какое-либо
повествовательное предложение, в котором что-либо утверждается об упоминаемом в
нем объекте. О каждом высказывании мы должны знать, истинно оно
или ложно. Из высказываний по правилам логики образуются
составные высказывания или утверждения, истинность которых по
известным правилам определяется в зависимости от истинности
составляющих утверждение высказываний.
Пусть Р и Q — произвольные высказывания.
Конъюнкцией высказываний Р и Q называется высказывание «Р и
Q», которое истинно тогда и только тогда, когда истинны оба
высказывания Р и Q одновременно. Конъюнкция Р и Q обозначается символом
P&Q или Р Л Q.
Дизъюнкцией высказываний Р и Q называется высказывание «Р
или Q», истинное в том и только в том случае, когда истинно хотя бы
одно из высказываний Р или Q. Дизъюнкция Р, Q обозначается через
PVQ.

1. Понятие множества
15
Если Р — высказывание, то высказывание «не Р» (обозначается
-»Р) называется отрицанием Р. Отрицание Р истинно, если Р ложно,
и ложно, если Р истинно.
Хотя в дальнейшем мы обычно не употребляем термины
«дизъюнкция, конъюнкция», но достаточно часто используем зависимость
истинности составного высказывания от истинности его составляющих.
Утверждение «Р V Q» может оформляться также в виде: «либо Р,
либо Q».
1.2.2. Пусть Р и Q — высказывания. Под импликацией Р => Q
понимается утверждение «из Р следует Q», которое может также оформляться
одним из следующим равнозначных выражений:
• из Р вытекает Q;
• если выполнено Р, то выполнено Q;
• для выполнения Р необходимо выполнение Q;
• Р выполнено только в том случае, если выполнено Q;
• Р выполнено только тогда, когда выполнено Q;
или, если поменять порядок обращения к Р и Q, то одним из таких
равнозначных выражений:
• Q следует из Р;
• Q вытекает из Р;
• Q выполнено, если выполнено Р;
• для выполнения Q достаточно выполнения Р;
• Q выполнено в том случае, если выполнено Р;
• Q выполнено тогда, когда выполнено Р.
Импликация Р => Q ложна, если Р истинно, a Q ложно, и истинна
во всех остальных случаях.
Если из Р следует Q и одновременно из Q следует Р, то
символически этот факт записывают в виде Р <Ф=> Q и употребляют для его
словесного выражения одно из следующих равнозначных
словосочетаний:
• Р и Q равносильны;
• для того чтобы (было выполнено) Р, необходимо и достаточно,
чтобы (было выполнено) Q;
• Р выполнено тогда и только тогда, когда выполнено Q;
• Р выполнено в том и только в том случае, если выполнено Q.
Мы часто будем пользоваться тем фактом, что импликации «из Р
следует Q» и «из (не Q) следует (не Р)» равносильны. В этом легко
узнается хорошо знакомый прием доказательства, называемый
доказательством от противного.

16
Гл. 1. Введение в математический анализ
1.3. Кванторы
В математических утверждениях часто употребляются
словосочетания «для всякого», «для любого» и т. п., а также слова «существует»,
«найдется» и т. п. Иногда удобно вместо них использовать специальные
знаки, называемые кванторами. А именно, вместо словосочетаний «для
любого» и т. п. пишут знак V, а вместо слов «существует» и т. п. —
знак 3.
Мы будем применять эти символы, главным образом, при
следующих обстоятельствах.
Пусть дано множество X и мы составляем утверждение «для
любого элемента х из X выполнено условие Р». Тогда это утверждение
будем записывать в виде:
(Vx£X)P.
С другой стороны, утверждение «найдется элемент х множества X,
для которого выполнено условие Р» будет записываться так:
(Зхех)р.
Многочисленные примеры указанных употреблений кванторов
читатель найдет достаточно скоро.
1.4. Операции над множествами
Пусть А и В — некоторые множества.
А В
Рис. 1
Объединением множеств А, В называется совокупность всех
объектов х, каждый из которых является элементом, по крайней мере, одного

§ 1. Понятие множества
17
из множеств А и В. Объединение множеств А и В обозначается
символом: АиВ (см. рис. 1).
Пересечением множеств А и В называется совокупность всех
объектов #, каждый из которых принадлежит обоим множествам А ж В
одновременно. Пересечение множеств А, В обозначается символом А П-В.
Если у данных множеств А и В нет общих элементов, то их
пересечение АПВ представляет собой пустое множество: АПВ = 0. В этом
случае говорят, что множества А ж В не пересекаются или
дизъюнктны.
Разностью множества А и множества В будем называть
совокупность всех элементов А, не принадлежащих В. Разность множеств А,
В обозначается символом А\В (см. рис. 1). Из определения,
очевидно, следует, что для любых множеств А, В справедливы соотношения
А\ВСА,(А\В)ПВ = 0.
1.5. Прямое произведение множеств
1.5.1. Пусть даны два произвольных объекта х и у. Говорят, что они
образуют упорядоченную пару (ж,у), если объект х считается первым,
а у — вторым. Об упорядоченной паре нередко говорят просто как о
«паре», опуская прилагательное «упорядоченная». Первый элемент
пары называют иногда ее первой компонентой, а второй, соответственно,
— второй компонентой пары.
Отличительная особенность упорядоченной пары состоит в
следующем. Две пары (#i,yi), (#2,2/2) считаются совпадающими в том и
только в том случае, если х\ — Х2, yi = 2/2.
Мы подошли к понятию пары как к первичному понятию, хотя
нетрудно показать, что для любых #, у множество {х,{х,у}}
удовлетворяет указанному выше условию и тем самым упорядоченная пара может
быть определена как множество {ж, {х,у}}.
Пусть А, В — произвольные множества. Совокупность всех пар
(ж, у), где х £ А, у £ В, называется (прямым) произведением множеств
А и В и обозначается символом А х В (см. рис. 2).
Если множества Am В конечны, например,
А= {Ж1,Ж2,...,ЖП}, В = {yi,2/2,...,2/m},
то элементы прямого произведения могут быть выписаны в виде
таблицы:
(#l,yi) (Xi,y2) ... (Х1,ут)
(X2,yi) (#2,2/2) ... (Х2,Ут)
(Xn,yi) (#n,2/2) ... (#n,2/m).

18
Гл. 1. Введение в математический анализ
В том случае, когда одно из данных множеств А и В пусто,
произведение Ах В также пусто.
ill ii i
1 i—i i ' >-
I ч _^_ ^
А
Рис.2
1.5.2. Понятие упорядоченной пары распространяется на случай
любого конечного набора объектов. Это можно сделать, например,
следующим образом.
Пусть дано произвольное целое число п > 2. Предположим, что
каждому натуральному числу к такому, что 1 < к < п, сопоставлен
некоторый объект а^. В этом случае говорят, что задана упорядоченная
совокупность (ai,a2,... ,an) или, иначе, кортеж длины п или просто
упорядоченная n-ка объектов, состоящая из п компонент а&. При этом
afc называется fc-й компонентой системы (ai, аг,..., ап).
Пусть Ai, А2,..., Ап — произвольные множества.
Прямым или декартовым произведением множеств Ai, А2,.. •, Ап
будем называть множество
Ai х А2 х • • • х Ап =
= {(^1,Ж2,. ..,#п) | xi e Ai,X2 E Аг,.. чХп е Ап).
Прямое произведение множеств Ai, A2,..., Ап обозначается либо
символом
Аг х А2 х ••• х Ап,
либо посредством выражения:
п
A=XAi

§2. Функции
19
Данное определение не исключает случай, когда все множества Ак
совпадают.
Если А\ = A<i — • • • = Ап ~ А, то множество А\ х А2 х • • • х Ап
обозначается также символом Ап.
В соответствии с определением произведения множеств, Ап есть
совокупность всех упорядоченных наборов, у которых каждая компонента
является элементом множества А,
§2. Функции
Понятие отображения — одно из основных в современной
математике. С ним мы поступим так же, как с понятием множества, а именно,
воспримем его как первичное понятие математики, хотя нетрудно дать
определение функции (отображения), используя определения множества
и произведения множеств. Просто нам это в данном курсе не требуется.
2.1. Понятие функции или отображения
Пусть А и В — произвольные множества. Отображением f
множества А в множество В называется всякое правило или закон, согласно
которому каждому элементу х множества А соответствует один
определенный элемент у множества В. Этот элемент у обозначается символом
f(x) и называется значением отображения / на элементе х. Множество
А как совокупность тех объектов, на которые распространяется
действие правила /, называется областью определения отображения /, а
совокупность всех значений f(x) при х, пробегающем область
определения, — множеством значений отображения /.
Область определения отображения / нередко обозначается
символом D(f), а множество его значений — символом E(f).
В тех случаях, когда в качестве области определения и множества
значений отображения выступают множества определенной природы,
вместо термина «отображение» используют другие. Например, если
отображение определено на подмножестве числового множества и
действует в числовое множество, то вместо термина «отображение» обычно
используют термин «функция». В некоторых случаях вместо
отображения говорят об операторе, функционале и т. д.
Тот факт, что / есть отображение множества А в множество В,
символически записывается следующим образом: / : А —> В (читается:
«/ отображает А в В»). Для записи отображения / используют также
следующие обозначения: /(ж), у = f(x), f : х Е А i-> f(x) E В.
Ясно, что в обозначении отображения / типа у = f(x) или просто f{x)

20
Гл. 1. Введение в математический анализ
участвует не только правило /, то есть собственно отображение, но и
его значения на элементах х. Это обычно не вызывает недоразумений
и нередко достаточно удобно, поскольку здесь явно указывается символ
аргумента.
Отметим два частных случая общего понятия отображения.
Пусть дано множество А,
Отображение / : А —» А такое, что f(x) — х для любого х Е А,
называется тоэюдественным отображением множества А и обозначается
символом id^.
Отображение f : А—> В называется постоянным, если существует
Ь Е В такое, что f(x) = Ь, каково бы ни было х Е А.
2.2. Образ и прообраз. Накрывающее и взаимно однозначное
отображения
2.2.1. Пусть даны множества А и В и отображение / : А —* В.
Пусть Е — произвольное подмножество А. Совокупность всех
элементов у Е 23, каждый из которых является значением отображения / хотя
бы на одном элементе множества Е, называется образом множества Е
при отображении f и обозначается символом f[E]. Символически:
f{E] = {yeB\(3xeE)y = f(x)}.
Отображение / : А —► В называется отображением множества А^
на множество В, если f[A] = В (предлог «на», таким образом, несет
определенную терминологическую нагрузку). Иногда такое
отображение называют накрывающим.
Рассмотрим отображение / : А —> В и произвольное множество М.
Совокупность всех элементов х £ А, для которых значения f(x) при
отображении / принадлежат множеству М, называется прообразом М
при отображении /:4^Ви обозначается символом /_1[М]. В том
случае, когда множество М состоит из единственного элемента, то есть
М = {?/}, прообраз /~х [{у}] обозначается просто через /_1(у).
Заметим, что множество /_1[М] может быть пустым. Это,
очевидно, имеет место в том и только в том случае, когда
f[A] Г)М = 0.
В данном выше определении прообраза множества М при
отображении / : А —> В не требуется, чтобы М было подмножеством В.
Очевидно, что если В П М = 0, то /_1[М] — пустое множество и в общем
случае /_1[М] = /_1[М П В].

§2. Функции
21
Символически определения прообразов множества и элемента
выглядят так:
Г1[М) = {х е А | f(x) е м}; г1 (у) = {х е А \ f(x) = у}.
2.2.2. Отображение / : А —» В называется взаимно однозначным, если
для любых различных элементов Ж1,Ж2 Е А значения f(xi),f(x2)
различны. Иначе говоря, / : А —> J3 взаимно однозначно, если оно
удовлетворяет условию:
(Vsi Е А)(Уж2 Е A)(xi фх2^ f(xi) ф /Ы).
Ясно, что условие взаимной однозначности / можно
сформулировать так: отображение / : А —> В взаимно однозначно, если для любого
у £ В множество /_1(у) состоит не более чем из одного элемента.
Отметим следующую часто используемую терминологию.
Накрывающее отображение называют сюръективным, взаимно
однозначное — инъективным и, наконец, сюръективное и одновременно
инъективное отображение — биективным. ^
2.3. Суперпозиция отображений
2.3.1. Пусть даны отображения / : А± —> J3i, g : А2 —> В2.
Суперпозицией или композицией отображений /, g называют отображение
h : жи g{f(x)).
Суперпозиция отображений /, g обозначается символом g о f
(порядок, в котором записываются символы / и д, существен).
Область определения суперпозиции g о f является совокупностью
всех х Е -Ai, для которых f(x) E A2, то есть множество /_1[А2]
(возможно, пустое).
Отметим, что суперпозиция есть один из основных способов
построения новых функций из уже имеющихся.
2.3.2. Операция образования суперпозиции обладает одним важным
свойством, которое называется ассоциативностью.
Ш Теорема 2Л (об ассоциативности суперпозиции). Пусть даны
отображения / : А\ —> В±, g : А2 —> В2, h : A3 —> JB3. Тогда отображения
<р = h о (д о /), <ф = (h о д) о f совпадают, то есть имеют одну и ту же

22
Гл. 1. Введение в математический анализ
область определения и <р(х) = *ф(х) для всякого х из их общей области
определения.
Доказательство. Положим g о f = hi, h о g = fa. Требуется
доказать, что ho hi = fa о f.
Возьмем произвольно х Е Ai. Тогда hi(x) определено в том и
только в том случае, если у — f(x) Е Аг, и <р{х) будет определено для данного
ж, лишь если z — hi(x) = g(y) = g(f(x)) принадлежит Аз. При этом
ф) = h(z) = h(g(f(x))). (2.1)
Итак, область определения функции <р(х) есть совокупность всех
х Е А\ таких, что f(x) E А2, a g(f(x)) Е Аз, и для каждого такого х
значение <р(х) определяется формулой (2.1).
Область определения fa есть множество всех у Е Аг, для которых
д(у) Е Аз. Для х Е Ai значение ^(ж) определено, лишь если у = f(x)
принадлежит области определения Д, то есть если z — д(у) Е Аз. Таким
образом, область определения г/> есть совокупность всех х Е Ai таких,
что у = /(ж) Е А2, a z = д(у) = g(f(x)) Е А3.
Мы видим, что области определения функций <р и *ф совпадают.
При этом
tf(*) = Л №)) = %№))) (2-2)
на каждом ж, для которого ip(x) определено. Из равенств (2.1) и (2.2)
следует, что (р(х) = ^(ж) на каждом ж, для которого величины р(х) и
я/>(ж) определены.
Теорема доказана. ■
2.4. Обратное отображение
2.4.1. Пусть даны произвольные непустые множества А и J3 и
отображения f : А —> В, д : В -+ А. Отображение д называется левым
обратным к /, если для всякого х Е А выполняется равенство
g(f(x)) = ж,
и правым обратным к /, если для всех у € В
f(g(y)) = у-
Иначе говоря, отображение д является левым обратным к /, если
д о / = id а, и правым обратным к /, если / о д = ids, где id а и ids —
тождественные отображения множеств А и J3, соответственно.

§ 2. Функции
23
Ясно, что если д — правое обратное к /, то / является левым
обратным к д, а если д — левое обратное к /, то / является правым
обратным к д.
Отображение д : В —» А будем называть обратным к отображению
f : А —» Б, если # является одновременно левым и правым обратным
к /, то есть
#№)) = ж
для всякого х £ А и
f(g(y)) = у
для любого у Е В, или, что то же самое, если д о f — idA, f ° g = ids-
Отображение #, обратное к отображению /, обозначается Z""1.
2.4.2. Установим необходимое и достаточное условие существования
обратного отображения. Предварительно докажем следующее
утверждение.
■ Лемма 2.1. Пусть даны отображения (p:T-+Unil>:U—>T.
Еслифскр = idr, то ср взаимно однозначно, а ф есть отображение «на».
Доказательство. Возьмем ti,t2 Е Т, t\ ф t2. Пусть u\= <p(ti),
U2 = ^(^2). Тогда в силу условия леммы ф(и\) = t\, ф(и2) = fo. Отсюда
следует, что п\ ф U2b ибо в противном случае мы получили бы, что
h = £2, вопреки предположению. Итак, если ti ф ^2, то <p(ti) ф ^(fe),
то есть отображение <р взаимно однозначно.
Возьмем t £Т. Пусть u = <p(t). По условию ф(и) = ip(p(t)) = t.
Таким образом, для любого t Е Т существует и Е U такое, что
ф(и) — £, а именно и = (p(t) удовлетворяет указанному условию. Это
означает, что ф есть отображение U на Т.
Лемма доказана. ■
2.4.3. Докажем теорему об условии существования обратного
отображения.
■ Теорема 2.2. Пусть дано отображение f : А —> В. Для того
чтобы существовало отображение g : В —» А, обратное к f, необходимо
и достаточно, чтобы отображение f было биективным, то есть взаимно
однозначным отображением множества А на множество В. В случае,
если обратное отображение существует, оно единственно.
Доказательство. Необходимость. Предположим,
что отображение / имеет обратное отображение д. Тогда д о f = idA-
Отсюда, полагая в лемме 2.1 Т = J3, U = А, <р — /, ф — #, получим, что
/ взаимно однозначно. По условию имеем также / о д = ids- Полагая

24
Гл. 1. Введение в математический анализ
в лемме 2.1 Т = A, U = Б, ф = /, <р = 0, заключаем, что / есть
отображение «на».
Необходимость доказана.
Достаточность. Предположим, что / биективно. Возьмем
у £ В. Так как / — отображение А на Б, найдется х Е А такой, что
f(x) = у. Поскольку / взаимно однозначно, такой х — единственный.
Тем самым для всякого у € В существует и притом только один элемент
х множества А такой, что f(x) = у.
Пусть д — отображение множества А в Б, которое элементу у € В
сопоставляет х Е А такой, что f(x) = у. Докажем, что д есть
отображение, обратное к /.
Действительно, пусть у & В. Положим х = д{у). Тогда согласно
определению д имеем f(x) = у, то есть f(g(y)) = у для любого у Е Б.
Это означает, что д — правое обратное к /.
Далее, пусть х — произвольный элемент множества А. Положим
у = f(x). Отображение д по определению элементу у сопоставляет
элемент ж, то есть д(у) = х. Таким образом, g(f(x)) = х для всякого х Е А,
то есть д — левое обратное к /.
Итак, д является одновременно левым и правым обратным к / и,
следовательно, д есть обратное к /.
Достаточность установлена.
Докажем единственность обратного отображения.
Предположим, что отображение / удовлетворяет всем условиям
теоремы, и пусть д\ и #2 суть отображения, обратные к /. Возьмем у € В.
Пусть xi = 0i(у), х2 = 02(i/). Тогда /(ал) = у, /(ж2) = У-
Так как / взаимно однозначно, то х\ = #2. Значит, 0i(y) = 02 (у)
для любого у Е Б и, следовательно, отображения <д и 02 совпадают.
Теорема доказана. ■
Пусть д = Z""1. Согласно определению, это означает, что
отображение 0 является левым и одновременно правым обратным к /. Отсюда
следует, что / является одновременно правым обратным и левым
обратным к 0, то есть / — отображение, обратное к 0, / = д~г. Мы получаем,
таким образом, что / = (/""1)""1.
Поскольку, согласно теореме, необходимым и достаточным
условием существования обратного отображения является биективность
исходного, то тем самым обратное отображение, как и исходное, биективно.
Отметим, что мы используем один и то же символ как для
обозначения прообраза множества, так и для обозначения обратного
отображения. Ясно, что при рассмотрении прообраза, в отличие от обратного

2. Функции
25
отображения, не требуется взаимной однозначности данного
отображения. Как правило, использование символа /_1 в указанных ситуациях
не приводит к недоразумениям.
2.5. Сужение и продолжение функции
Понятие функции или отображения представляет собой
совокупность трех объектов: области определения, множества, в котором оно
принимает значения, и правила соответствия. Если хотя бы один из
указанных трех объектов меняется, то мы получаем другое
отображение. Это находит свое отражение, например, в том, что свойства
отображения быть взаимно однозначными или быть отображением «на»
при таких изменениях, вообще говоря, не сохраняются.
Полезно отразить в соответствующих определениях и обозначениях
некоторые ситуации, возникающие в тех случаях, когда меняются либо
область определения, либо множество, в котором принимаются значения
отображения. Здесь мы ограничимся только случаем, когда изменяется
область определения.
Пусть даны непустые множества А, М и В, причем М С А, и
отображения / : A—* J3, д : М —» В. Будем говорить, что д есть
ограничение или сужение отображения f на М, если f(x) = д(х) для каждого
х Е М. В этом случае будем также говорить, что / есть продолжение
g на А.
Сужение отображения / : А —» В на М будем обозначать g = /|м
или g = f\M. Пусть g = f\M- Тогда
g = foju,
где jm — вложение М в А, то есть отображение, определенное на
множестве М, действующее в А и сопоставляющее каждому
элементу х Е М этот же самый элемент (но рассматриваемый как элемент
множества А),
2.6. График функции
Пусть A is. В — произвольные множества. Рассмотрим их прямое
произведение Ах В. Предположим, что задано отображение f : А -> В.
Множество всех пар (ж, f{x)) Е А х Б, где х Е D(f), называется
графиком отображения f и обозначается символом Г(/).
Иначе говоря, график отображения / — это множество
упорядоченных пар (ж,у) Е А х В таких, что у = /(ж), х Е D(f) (см. рис. 3).

26
Гл. 1. Введение в математический анализ
ill ii i
1 1—I I 1 I >
Ч /
А
Рис.3
♦ Предложение 2.1. Множество Г С А х В является графиком
некоторого отображения f : А —► В в том и только в том случае, если
для любого х £ А существует у € В такой, что (ж, у) еГ ииз (х, у\) Е Г,
(#> 2/2) Е Г вытекает равенство у\ = У2-
Доказательство. Действительно, если множество Г — это
график некоторого отображения / : А —> J3, то оно, очевидно,
удовлетворяет данному условию.
Обратно, предположим, что для множества Г с А х В указанное
условие выполняется. Возьмем х Е А.
Согласно условию, найдется у Е J3, для которого (х,у) Е Г, причем
такое у единственно. Сопоставим каждому х Е А элемент у Е В такой,
что (х,у) Е Г. В результате получаем некоторое отображение
множества А в множество J3, графиком которого, очевидно, является данное
множество Г.
Предложение доказано, ф
§3. Вещественные числа и числовые множества
Числовые множества играют важнейшую роль в математике. Есть
несколько путей к определению таких множеств. В этом параграфе мы
остановимся на аксиоматическом подходе, при котором множество
вещественных чисел определяется как множество, на котором определены
алгебраические операции и отношение порядка, обладающие
свойствами, содержащимися в перечисляемых ниже аксиомах. Множество
вещественных чисел будем обозначать символом Ш.

§ 3. Вещественные числа и числовые множества
27
3.1. Алгебраическая структура множества вещественных
чисел
Будем считать, что на Ш определены операции сложения и
умножения. Это означает, что заданы некоторые отображения 5:lxR-^l
и р : Ш х R —» М, обладающие приводимыми ниже свойствами А.1—А.4,
М.1-М.4, AM. При этом для пары ж, у число s(x,y) обозначается
символом х + у и называется суммой чисел х и у, а р(#, у) — символом х • у
или просто ху и называется их произведением.
О свойствах операций s и р будем говорить как об аксиомах
алгебраической структуры множества Ж или аксиомах действий над
вещественными числами.
А.1 (ассоциативность сложения). Для любых ж,|/,2ЕК имеет
место равенство
(х + у) + z = х + (у + z).
А.2 (существование нуля). Существует число О Е М такое, что
для всякого х Е Ш
х + О = 0 + х = х.
А.З (существование противоположного числа). Для всякого
xGl существует число ~жЕ1 такое, что
х + (-х) = 0.
Число —х называется числом, противоположным х.
А.4 (коммутативность сложения). Для любых х,у еШ
х + у — у + х.
М.1 (ассоциативность умножения). Для любых х, у, z Е М
имеет место равенство
(х-у) • z = x-(y-z).
М.2 (существование единицы). Существует число 1 Е М такое,
что для всякого жЕ1
1. х = х • 1 = х.
М.З (существование обратного числа). Для любого х ф 0 из
R существует число — такое, что
х
1 1
X • — = - - X = 1.

28
Гл. 1. Введение в математический анализ
Число — называется числом, обратным к х.
х
М.4 (коммутативность умножения). Для любых х,у Е Ж
х-у = у-х.
AM (дистрибутивность). Для любых x,y,z Е Ж выполняется
равенство
х • (у + z) = х • г/ + ж • z.
Если a; G К, у Е К, то число ж + (—у) называется разностью чисел х
и у и обозначается символом ж—у. Если у ^ 0, то число ж— обозначается
ж
через — и называется частным х и у.
У
Перечисленные аксиомы достаточны для того, чтобы вывести
из них все известные тождества элементарной алгебры.
3.2. Порядковая структура множества Ж
3.2.1. На множестве Ж определено отношение, обозначаемое символом
< и называемое отношением порядка. Это означает, что для каждой
пары вещественных чисел ж, у указано, верно ли для нее высказывание
х < у или нет, и если оно верно, то будем говорить, что х не больше у,
или что х не превосходит у, или, наконец, что х предшествует у.
В случае, если х < у, будем также писать у > х и говорить, что
у не меньше х, или у больше или равно ж, или у следует за х. Таким
образом, высказывания х < у и у > х означают одно и то же условие.
Свойства отношения порядка в Ж описываются следующими
аксиомами порядка.
01. Для всякого жЕК справедливо отношение х < х.
02. Если ж, г/, z Е Ж таковы, что х < у и у < z, то х < z.
03. Если х < у и у < ж, то х = у.
04. Для любых ж, у G Ж всегда либо х < у, либо у < х.
ОА. Если х < у, то для любого г 6 R имеет место неравенство
х + z < у + z.
ОМ. Если х < у и 0 < z, то xz < yz.
Пусть х,у G Ж. Если х < у и х ф у, то будем писать х < у или
у > х и говорить, что х меньше у или что у больше х.

§ 3. Вещественные числа и числовые множества
29
Формулы, содержащие знаки <, >, < и >, называются
неравенствами. Неравенства, содержащие знаки < и >, называются строгими,
неравенства со знаками < и > — нестрогими.
3.2.2. Из аксиом порядка легко вывести простейшие свойства
отношения порядка, например, следующие.
(1) Для любых двух элементов х, у Е Ж выполняется одно и только
одно из следующих трех соотношений:
х < у; х = у; у < х.
(2) Пусть х, у, z Е Ж таковы, что либо х < у и у < z, либо х < у и
у < z. Тогда х < z. В частности, если х < у и у < z, то х < z.
(3) Если х < у, тох + zKy + z для всякого z E Ж.
(4) Если х < у, то xz < yz для всякого z такого, что О < z.
(5) Для любого х Е Ж имеет место неравенство х2 > 0.
3.3. Расширенная числовая прямая. Промежутки (отрезки)
3.3.1. В некоторых ситуациях, связанных с отношением порядка в Ж,
удобно использовать множество вещественных чисел, дополненное
двумя так называемыми бесконечными элементами. А именно, добавив к
множеству Ж два элемента — оо и +оо («минус бесконечность» и «плюс
бесконечность») такие, что — ос < х < ос для любого х Е Ж, мы
получаем расширенное множество вещественных чисел (или
расширенную числовую прямую), обозначаемое символом Ж. Считаем также, что
—ос < ос. Согласно определению, Ж = MU {—ос,+ос}. Вместо символа
+ос далее мы будем писать просто ос.
Элементы множества Ж также будем называть числами. При этом
число х Е Ж будем называть конечным, если х Е Ж.
Числа —оо и оо будем называть бесконечными элементами
множества Ж.
Определение бесконечных элементов по существу содержит
распространение отношения порядка в Ж на множество Ж.
Нетрудно проверить, что при этом выполняются утверждения
аксиом 01-04.
Соотношения х < у и х > у для элементов из Ж определяются так
же, как и для элементов из Ж.

30
Гл. 1. Введение в математический анализ
3.3.2. Пусть даны произвольные числа а Е Й и Ъ Е Ш такие, что а <Ъ.
Множество, обозначаемое символом (а, Ь) и совпадающее с одним из
множеств
(а,Ь) = {х Е Й | а < ж < Ь},
[а,Ь] = {ж Е К | а < ж < Ь},
[а, 6) = {ж Е К | а < ж < &},
(а, 6] = {ж Е R | а < х < Ь},
называется промежутком с концами а, Ь (расширенной) числовой
прямой.
При этом множество (а, Ь) называют открытым промежутком или
интервалом, а множество [а, Ь] — замкнутым промежутком или еег-
ментом с концами а, Ь. Промежутки [а,Ь) и (а,Ь] называют
полуоткрытыми.
Промежуток (а, Ь) будем называть ограниченным, если его концы
суть конечные числа, то есть —ос < а < Ъ < ос. Ясно, что [а,Ь] =
= (а, Ь) U {а} U {Ь}, [а, Ь) = (а, 6) U {а}, (а, Ь] = = (а, Ь) U {Ь}.
Отметим, что (—ос, а], где а < ос, есть множество всех чисел жЕК
таких, что х < а, а (—ос, а) есть множество всех ж Е М, для которых
х < а. Аналогично [а, ос) = {ж Е М | х > а}, (а, ос) = {х Е М | х > а},
где аЕК. Наконец, (—ос, ос) = М, [—ос, ос] = Й.
3.4. Абсолютная величина. Положительная и отрицательная
части числа
Абсолютной величиной или модулем числа х Е Й называется число
|#|, равное ж при ж > 0 и —ж при ж < 0.
3.4.1. Легко доказываются следующие свойства модуля.
1. Для любых х и у из Ш
|sy| = N-lvl-
В частности, для всякого х Е М
|-*| = |-1|Ф1=Ф1.
2. Яусть а Е К, a > 0. Тогда
а) неравенство \х\ < а равносильно системе неравенств
б) неравенство \х\ < а равносильно системе неравенств
—а < х < а;
—а < х < а.

§ 3. Вещественные числа и числовые множества
31
3. Для любых чисел ж,уЕК
\х + у\< \х\ + \у\.
Действительно,
-М <£< N; Чу1 <У < |у|-
Складывая эти неравенства почленно, получим
-(N + |y|)<a? + y<N + |y|,
откуда, в силу свойства 2, следует, что
|я + у| < \х\ + \у\-
4. Для любых ж, у Е К.
IW-|y||<k-y|.
Действительно, имеем ж = (ж — у) + у; у = (у — х) + ж. Отсюда, в
силу свойства 3,
\х\ < \х - у\ + |у|; |у| < |у - х\ + |ж|.
Из первого неравенства получаем
М-|у| < к-у|,
а из второго —
М- \у\ > —|ж —1/1-
Отсюда, в силу свойства 2, вытекает, что
N-|у|| < fc-y|.
3.4.2. Пусть жЕМ. Полооюительной частью числа х называется число
ж+, равное ж, если х > О, и 0, если ж < 0.
Отрицательной частью числа ж называется число ж", равное 0,
если ж > 0, и —ж, если ж < 0.

32
Гл. 1. Введение в математический анализ
4 Предложение 3.1. Для всякого х £ К справедливы равенства
х = х*—х~, \х\ = х* + х". (3.1)
Если х > О, то #+ = х, х" = 0, |#| = #, и оба равенства для такого
х верны. Пусть х < 0. Тогда #+ = 0, х" = —х, \х\ = —х, откуда ясно,
что и в этом случае равенства (3.1) верны.
Предложение доказано. 4
Из соотношений (3.1) для жЕМ вытекают следующие равенства:
+ Ы + # _ Ы—ж
2 ' 2
Для произвольного a;Gi полагаем
{1, если х > 0;
0, если ж = 0;
—1, если х < 0.
Величина sgn а; (читается «сигнум #», signum — знак (лат.))
называется знаком числа х.
Для всякого жЕМ, очевидно, имеем
\х\ = х sgn х, х = |#|sgna;.
§4. Точные границы числового множества.
Аксиома непрерывности. Натуральные,
целые и рациональные числа
Понятия точной верхней и точной нижней границ произвольного
множества вещественных чисел играют существенную роль в
математическом анализе. В этом параграфе приводятся определения этих
понятий и устанавливаются некоторые основные их свойства.
Число q называется верхней границей числового множества А, если
А расположено слева отр, то есть р > х, каково бы ни было х £ А.
Наименьшая из верхних границ есть точная верхняя граница множества А.
Аналогично определяется, что есть точная нижняя граница множества.
Утверждение, что среди верхних границ произвольного числового
множества есть наименьшая, однако, не вытекает из тех свойств
множества вещественных чисел, которые нам уже известны. Оно должно быть

§ 4. Точные границы числового множества
33
принято в качестве новой аксиомы множества К. Здесь приводится
точная формулировка этой аксиомы и тем самым завершается построение
аксиоматики множества М.
Свойство множества R, выражаемое приводимой ниже аксиомой,
наглядно представляет собой отсутствие «пробелов» в Ж. Можно
сказать, что совокупность всех вещественных чисел представляет собой
некоторую «непрерывную протяженность».
Кроме того, приводятся определения множества натуральных,
множества целых и множества рациональных чисел, опирающиеся на
аксиоматику множества вещественных чисел.
4.1. ПОНЯТИЯ ТОЧНОЙ ВЕРХНЕЙ И ТОЧНОЙ НИЖНЕЙ ГРАНИЦЫ
ЧИСЛОВОГО МНОЖЕСТВА. АКСИОМА НЕПРЕРЫВНОСТИ
4.1.1. Рассмотрим произвольное множество icK.
Число / Е Ё называется верхней (нижней) границей или
мажорантой (соответственно, минорантой) множества А, если для любого
х G А выполняется неравенство х < I (соответственно, х > /).
Всякое множество Act имеет хотя бы одну верхнюю (нижнюю)
границу, например, число оо (—оо) является верхней (нижней) границей
любого непустого множества А С Й.
Множество 4 СК называется ограниченным сверху (снизу), если
оно имеет хотя бы одну верхнюю границу, отличную от оо (—оо).
Множество ict называется ограниченным, если оно ограничено
сверху и снизу в множестве Е, то есть если существуют такие конечные
числа р и q, что для любого х Е А выполняются неравенства р < х < q.
Совокупность всех верхних (нижних) границ множества АсМ
будем обозначать символом Г+(А) (соответственно, Г~(А)). Множества
Г+(А) и Т~(А) непусты, так как -оо Е Г~(А), оо Е Г+(А).
Оказывается целесообразным считать, что всякое число рбК
является верхней и одновременно нижней границей пустого множества.
Пусть дано множество icl.
Число а называется наибольшим (наименьшим) элементом
множества А, если а принадлежит А, и является верхней границей множества
А, то есть если а Е А и для всех х Е А выполняется неравенство х < а
(соответственно, х > а).
Наибольший (наименьший) элемент множества А, если он
существует, обозначается символом max А (соответственно, minA) (max и
min от латинских слов maximum — «наибольший» и minimum —
«наименьший») .
Число — оо является наименьшим элементом, а число оо —
наибольшим элементом множества М.

34
Гл. 1. Введение в математический анализ
Для замкнутого промежутка [а, Ь] в Й левый конец а является его
наименьшим, а правый конец Ъ — наибольшим элементом.
Множество АсМ, вообще говоря, может и не иметь наименьшего
или наибольшего элемента. Например, интервал А = (0,1) не имеет ни
наибольшего, ни наименьшего элемента.
Действительно, возьмем произвольно точку а Е (0,1) и положим:
а а + 1
2' у 2
Очевидно, что 0<х<а<у<1. Тем самым а не может быть
ни наименьшим, ни наибольшим элементом промежутка (0,1), так что,
ввиду произвольности а Е (0,1), у множества А = (0,1) нет ни
наименьшего, ни наибольшего элемента.
Ясно, что множество Е не имеет ни наименьшего, ни наибольшего
элемента (имеется в виду в самом множестве Е).
4.1.2. Пусть дано непустое множество А С Й. Наименьшая из его
верхних границ называется точной верхней границей множества А
и обозначается символом sup A (sup — сокращение латинского слова
supremum, то есть — «наивысший»). Наибольшая из нижних границ
множества А называется точной нижней границей множества А и
обозначается символом inf A (inf — сокращение латинского слова infimum,
то есть «нижайший»).
Иначе говоря, q = sup А, если q есть наименьший элемент
множества Г+(А) верхних границ множества А, то есть если выполнены
следующие условия:
1) q > х для любого х Е А;
2) если q' есть верхняя граница А, то есть qf > x для любого
х Е А, то q < q'.
Аналогично р = inf А, если р есть наибольший элемент множества
Г~(А) нижних границ множества А, то есть если выполнены следующие
условия:
1) р < х для любого х Е А]
2) если р' есть нижняя граница А, то есть р' < х для любого
х Е А, то р > р'.
4 Предложение 4.1. Если множество А С М имеет наибольший
элемент, то этот элемент и является точной верхней границей
множества А. Если множество А имеет наименьший элемент, то он является
точной нижней границей множества А.

§ 4. Точные границы числового множества
35
Пусть а = max А. Тогда для любого х Е А выполняется
неравенство х < а. Это означает, что а есть верхняя граница множества А.
Пусть теперь q' — произвольная другая верхняя граница
множества А. Тогда для всех х Е А выполняется неравенство х < qf, в
частности, и а < q', так как а Е А. Таким образом, а — наименьший элемент
множества Г+(А), то есть а = sup A.
Часть утверждения, касающаяся точной нижней границы,
доказывается аналогично.
Предложение доказано. ♦
Если множество АсК пусто, то всякое число х Е Й является его
верхней и одновременно его нижней границей. Наименьший элемент
множества Е есть — оо, наибольший есть +оо.
Таким образом, в данном случае наибольшая из нижних границ
множества А равна +оо, а наименьшая из его верхних границ равна
—оо, то есть
inf 0 = +оо, sup 0 = —оо.
4.1.3. Завершим перечисление аксиом, характеризующих множество
вещественных чисел, а именно, сформулируем аксиому
непрерывности множества вещественных чисел.
Аксиома С. Всякое множество Ас! имеет точную
верхнюю и точную нижнюю границы.
Аксиома С утверждает, таким образом, что для всякого множества
АсЙ множество Г+(Л) его верхних границ имеет наименьший элемент,
а множество Т~(А) всех его нижних границ имеет наибольший элемент.
Аксиома С не может быть получена как следствие
сформулированных ранее свойств вещественных чисел.
4.2. Признаки точной верхней и точной нижней границ
ЧИСЛОВОГО МНОЖЕСТВА
4.2.1. Установим удобный в использовании критерий того, что данное
число является точной верхней (нижней) границей числового
множества.
■ Теорема 4.1. Пусть дано непустое множество АСЕ. Для того
чтобы q E M было точной верхней границей А, необходимо и достаточно,
чтобы выполнялись условия:
(a) q — верхняя граница множества А;
(b) для любого q' < q существует х Е А такой, что q' < х < q.
Для того чтобы р было точной нижней границей А, необходимо и
достаточно, чтобы выполнялись условия:

36
Гл. 1. Введение в математический анализ
(а') р — нижняя граница множества А;
(bf) для любого р' > р существует х Е А такой, что р' > х > р.
Доказательство. Мы ограничимся тем, что докажем
утверждение, касающееся точной верхней границы.
Необходимость. Пусть q = sup А. Тогда q есть верхняя
граница А, так что условие (а) соблюдено. Покажем, что q удовлетворяет
условию (ft).
Возьмем q' < q. Поскольку число q является наименьшей из
верхних границ множества А, то qr не является верхней границей А.
Следовательно, неравенство х < q' не может выполняться для всех х Е А, то
есть найдется х Е А, для которого это неравенство не выполняется и,
значит, для этого х будет q' < х.
Очевидно, х < q, поскольку q есть верхняя граница множества А,
и условие (ft) тем самым выполняется.
Необходимость доказана.
Достаточность. Пусть q удовлетворяет условиям (а), (ft).
Согласно условию (а), элемент q есть верхняя граница множества А.
Требуется доказать, что q — наименьшая из верхних границ.
Согласно условию (ft), любое число q' < q не является верхней
границей А. Поэтому если q' есть верхняя граница А, то q' > q, так что
q — наименьшая из верхних границ множества А.
Утверждение, касающееся точной нижней границы, доказывается
аналогично.
Теорема доказана. ■
А
(, ^
Я Я
Рис. 4
Наглядно смысл полученного результата таков: число q есть
точная верхняя граница множества А в том и только в том случае, если,
во-первых, q есть верхняя граница множества А и, во-вторых,
сместившись влево от точки #, мы обязательно перескочим через какую-то точку
множества А (см. рис. 4).
Аналогично, р есть точная нижняя граница А, если р есть нижняя
граница А и, сместившись вправо от р, мы обязательно увидим, что
слева оказалась какая-то точка множества А.
4.2.2. В качестве примера применения теоремы 4.1 докажем следующее
утверждение.

§ 4. Точные границы числового множества
37
■ Лемма 4.1. Пусть А = (а, &), а < Ъ, есть промежуток
расширенной числовой прямой. Тогда a = inf А, Ъ = sup A.
Доказательство. Очевидно, что х < Ъ для всякого х Е (а, 6),
так что Ь есть верхняя граница множества А.
Возьмем произвольно q' < Ъ и докажем, что найдется ж £ А такой,
что q' < х. Если q' < а, то в качестве требуемого х можно взять любой
элемент из А. Если же a < q', то А = (a, ft) содержит в себе интервал
(#', ft) и, значит, любая точка х £ ((/, ft) принадлежит А, при этом q' < х.
Тем самым Ъ удовлетворяет условию (ft) теоремы 4.1 и, следовательно,
Ь = sup(a,ft).
Аналогично устанавливается, что a = inf(a,b).
Лемма доказана. ■
▼ Следствие. Если числа a < b и с < d таковы, что имеет место
включение (a, ft) С [с, d], то с < а, Ъ < d.
Действительно, предположим, что а < ft и (a, ft) С [с, d]. Тогда
для всех х £ (a, ft) имеют место неравенства с < х < d и, значит, с
— нижняя, ad — верхняя границы интервала (a, ft). Следовательно,
с < inf (a, ft) = а, ft = sup(a, ft) < d, что и требовалось доказать. ▼
4.3. Свойство монотонности относительно включения точной
ВЕРХНЕЙ И ТОЧНОЙ НИЖНЕЙ ГРАНИЦ
■ Теорема 4.2. Пусть даны множества А С М и В С Й. Тогда в
случае А С J5 справедливы неравенства
inf A > inf Б, sup A < sup В.
Наглядно смысл теоремы таков: при увеличении множества его
точная верхняя граница не уменьшается, а точная нижняя не
увеличивается.
Доказательство теоремы. Если множество А пусто, то
неравенства выполняются очевидным образом.
Будем считать, что А — непусто. Тогда иВ/0.
Пусть р = inf JB, q = sup В. Тогда для всякого х Е В имеем:
р <х < q. (4.1)
Так как А С В, то любой элемент множества А является элементом
множества J5, и, значит, для всякого х Е А выполняются неравенства

38
Гл. 1. Введение в математический анализ
(4.1). Это означает, что р есть нижняя, a q — верхняя граница
множества А и, следовательно,
р < max Г~ (А) = inf A; q> min Г+ (А) = sup A.
Теорема доказана. D
4.4. Множества натуральных, целых и рациональных чисел
4.4.1. Выделим в R три подмножества, играющие определенную
самостоятельную роль.
Начнем с множества натуральных чисел.
Множество AcR назовем индуктивным, если 1 е А и для любого
х е А элемент х + 1 также принадлежит А.
Ясно, что множество R всех вещественных чисел индуктивно, так
что совокупность всех индуктивных множеств непуста.
Пересечение любой совокупности индуктивных множеств
является индуктивным множеством.
Действительно, единица входит в каждое из множеств такой
совокупности, и, значит, входит и в их пересечение.
Если же какое-то число х принадлежит пересечению, то оно
принадлежит и каждому из составляющих совокупность множеств, а
поскольку все они по предположению индуктивны, то и х +1
принадлежит каждому из этих множеств и, стало быть, их пересечению. Тем
самым пересечение любой совокупности индуктивных множеств есть
индуктивное множество.
Из доказанного, в частности, следует, что пересечение
совокупности всех индуктивных множеств есть индуктивное множество. Это
пересечение называется множеством натуральных чисел и
обозначается символом N {1,2,3,...}. Элементы множества N называются
натуральными числами.
Таким образом, можно сказать, что множество натуральных
чисел — это наименьшее из множеств А с R, содержащих единицу и
таких, что А + 1 с А, где А + 1 = {х+1\хе А},
В частности, если множество М с N индуктивно, то оно совпадает
с N, М = N.
Действительно, из определения N следует, что N с М. Из
соотношений М с N и N с М вытекает, что N = М.
4.4.2. Из данного выше определения вытекает следующее
предложение, называемое принципом математической индукции.
Ind. Пусть дано некоторое утверждение Р(п), истинность которого
зависит от натуральных чисел. Предположим, что

§ 4. Точные границы числового множества
39
1) Р(1) ИСТИННО]
2) из истинности высказывания Р(п) следует, что истинно также и
Р(п + 1). Тогда утверждение Р(п) верно для всех п е N.
4.4.3. Множество Z = N — N = {я - ?/ | х G N, ?/ G N} называется
множеством целых чисел.
Число х Е R называют рациональным, если существуют такие целые
числа р и <?, что q ф О и р — qx (то есть х есть частное p/q целых чисел р
и q). Поскольку при любом а ф О справедливо равенство
p/q = ap/aq,
можно считать, что q есть натуральное число.
Множество всех рациональных чисел обозначается символом Q.
Всякое число, не принадлежащее Q, называется иррациональным.
4.4.4. Установим несколько важных свойств множества N.
(1) Единица является наименьшим элементом множества N.
Действительно, промежуток [1,оо) является индуктивным
множеством и, значит,
Nc[l,oo).
Отсюда следует, что для всех п Е N выполняется неравенство п > 1 и,
стало быть, единица есть наименьший элемент множества N.
(2) Если п Е N и п > 1, то п - 1 G N.
Действительно, пусть М есть совокупность всех п £ N таких, что
либо п = 1, либо п — 1 € N. По условию, 1GM. Предположим, что п е М.
Тогда (п +1) -1 = п е N и, значит, п+1 е М. В силу принципа индукции,
получаем, что М совпадает с N.
Таким образом, всякое число n G N принадлежит М, то есть либо
п = 1, либо n-lEN, что и требовалось доказать.
(3) Если числа п е N и m Е N таковы, что п < ш, то разность гп — п
является натуральным числом.
Для п = 1 предложение верно в силу (2).
Предположим, что п € N таково, что для всякого натурального m> n
разность m-n принадлежит N. Пусть m>n + l, m€N. Тогда m > n и,
значит, m-n G N. В этом случае m-n > 1. В силу (2), отсюда вытекает,
что
m - (п + 1) = (т - п) - 1 G N.
Мы получаем, что если доказываемое утверждение верно для
некоторого п, то оно также остается верным, если заменить п на п+1. В силу
принципа индукции, предложение (3) доказано.

40
Гл. 1. Введение в математический анализ
(4) Пусть числа х € Z и у £ Z таковы, что х < у. Тогда разность
у — х есть натуральное число и справедливо неравенство: х < у — 1.
Замечание. Неравенство х < у — 1 равносильно неравенству
х + 1 <у. Предложение (4), таким образом, равносильно следующему.
Если числа ж, у £ Ъ таковы, что х <у, то у — х EN и х + 1 <у.
Действительно, пусть х и у суть целые числа, причем х < у.
Согласно определению, это означает, что х = р — q, г, у — г — s, где р, q, r, s
— натуральные числа. Имеем: р — q < г — s, откуда р + s < г + q.
Числа р + s и г + q — натуральные и, значит, согласно (3), разность
(р + s) — (г + q) есть натуральное число и потому (г + q) — (р + s) > 1.
Осталось заметить, что (г + q) — (р + s) = (г — s) — (р — q) = х — 2/, и
предложение 4 доказано.
Из предложения (3) следует, что если х есть целое число, то имеет
место одна и только одна из следующих трех возможностей:
а) х е N; Ь) х = 0; с) - ж е N.
Действительно, пусть xGZ, Тогда, по определению, х = m — п,
где m G N и n E N.
Если ж > 0, то m > n и потому согласно (3) х £ N, то есть имеет
место случай а). Если а; = 0, то мы имеем случай Ь).
Наконец, если х < 0, то m < п и —ж = п — m > 0. В силу
предложения (3), отсюда вытекает, что —х £ N, то есть для данного х выполнено
условие с).
Для произвольного множества А С К символом —А будем
обозначать множество всех х £ Е таких, что —х £ А. Формально:
-А = {я £ М | -ж £ А}.
Из доказанного нетрудно вывести, что выполняется равенство:
Z = NU{0}U(-N).
4.4.5. Следующее предложение, которое в соответствии с
существующей традицией мы будем называть принципом Архимеда,
характеризует расположение множества натуральных чисел среди вещественных.
■ Теорема. 4.3 (принцип Архимеда). Множество N не ограничено
сверху в Е.
Доказательство. Допустим, что N ограничено сверху в Е, и
пусть L = supN < оо. Для каждого п £ N имеем: п < L и, в частности,

§ 4. Точные границы числового множества
41
1 < L. Положим L/ = L — 1. Тогда L' < L и, значит, найдется n E N
такое, что L' = L — 1 < п. Отсюда L < п + 1.
Число п + 1 — это элемент N, и поскольку L = sup N, то п + 1 < L.
Итак, с одной стороны, L < п + 1, а с другой — п + 1 < L.
Полученное противоречие доказывает теорему. ■
▼ Следствие. Каковы бы ни были числа х > 0 и у > О, ж, j/Gl,
существует п £ N, для которого у <пх.
Доказательство. Множество N, согласно принципу Архимеда,
не ограничено сверху и, значит, число у/х не является его верхней
границей. Отсюда вытекает, что найдется п Е N такое, что у/х < п, то
есть у < пх, что и требовалось доказать. ▼
4.4.6. Определим общее понятие последовательности.
Предварительно опишем некоторый класс подмножеств множества
всех целых чисел Z.
Пусть к — произвольное целое число. Тогда символом Nk
будем обозначать множество всех целых чисел, удовлетворяющих условию
z > к. Формально данное определение можно записать так:
Nfc = {z e Z | z > к}.
Для всякого z G Nfc число z — к + 1 — целое положительное и,
следовательно, п = z — к + 1 есть натуральное число.
Обратно, если п е N, то г = п + £-1е N*.
Из определения следует, что & есть нижняя граница множества N&.
Его точная верхняя граница есть оо.
Действительно, возьмем произвольно число L < оо. В силу
принципа Архимеда, найдется п Е N такое, что L — к < п. Тогда L < п + к.
Число z — п + к — целое. При этом z > к и, значит, z E Nfc.
Мы видим, что здесь выполнены все условия критерия точной
верхней границы множества (см. §4) и, стало быть, оо = supNfc. Отметим,
что множество No, в частности, есть множество, получаемое из N
добавлением одного элемента — числа 0. Очевидно, что Ni = N.
Пусть М есть произвольное множество. Последовательностью
элементов множества М называется всякая функция ж, область
определения которой есть одно из множеств N*, а область
значений — множество М. Значение, принимаемое этой функцией
на элементе п Е N&, мы будем обозначать символом хп-
Часто говорят также, что хп есть n-й член последовательности и
число п называют номером этого члена.

42
Гл. 1. Введение в математический анализ
Для сокращенной записи последовательности
х:пе^ихпеМ
применяется одно из следующих выражений:
(хп е М)пещк; (хп)пещк; (xn)n=k,k+iy...
или, наконец, выражения:
(хп), п = fc, к + 1, fc + 2,...,
и
(xn), neNk.
Из принципа математической индукции вытекает следующий
принцип индукционного построения последовательностей.
Предположим, что для некоторого к е Z определен элемент хк
множества М и задано правило, которое позволяет указать хп+1 е М
в случае, если уже определено хп. Тогда последовательность хп
определена полностью.
Действительно, пусть М есть множество всех натуральных чисел п
таких, что £n+fc-i определено. Тогда, как нетрудно видеть, множество
М индуктивно и, значит, М совпадает с N.
Осталось заметить, что когда п пробегает множество N, то номер
n+fc-1 пробегает N&. Из доказанного поэтому следует, что хп определено
для всех п е Nfc.
4.4.7. Установим некоторые дальнейшие свойства подмножеств
множества всех натуральных чисел N.
■ Теорема 4.4. Всякое непустое подмножество множества N имеет
наименьший элемент.
Доказательство. Пусть Е с N, причем Е ф 0. Пусть fc = inf E.
Так как для любого п е N имеет место неравенство п > 1 (напомним,
что 1 есть наименьший элемент множества N), то fc > 1. В силу свойства
точной нижней границы (теорема 4.1, п. 4.2.1), найдется х е Е такое, что
к<х < fc + 1.
Пусть у — произвольный элемент множества Е. Докажем, что у > х.
Действительно, допустим, что у < х. Тогда, в силу (4), у < х — 1 < fc,
что противоречит тому, что к есть нижняя граница Е.
Итак, для всякого у е Е имеет место неравенство у > х. Это и
означает, что х есть наименьший элемент множества Е.
Теорема доказана. ■

§ 4. Точные границы числового множества
43
▼ Следствие 1. Для всякого числа х е R существует делое число р
такое, что р < х < р 4-1. Такое число р единственно.
Доказательство. В силу принципа Архимеда (теорема 4.3),
найдется m G N такое, что \х\ < т. Тогда —т < х < т и, значит,
О < х 4- т < 2т.
Обозначим через Е совокупность всех чисел п е N таких, что х+т < п.
Множество Е непусто, так как, например, 2га е Е.
Пусть и есть наименьший элемент множества Е. Тогда х+т < и.
Поскольку и есть наименьший элемент множества £?, то и — 1 ^ Е, и потому
условие, посредством которого определено £?, для и — 1 не выполняется,
то есть и - 1 < х 4- т. Число р = и-1-ти есть искомое.
Пусть р и q — целые числа такие, что p<x<p-\-lnq<x<q + l.
Тогда р < q 4-1 и, значит, в силу замечания к предложению (4) п. 4.4.4,
имеем р 4- 1 < q 4- 1, то есть р < q. Аналогично заключаем, что q < р,
откуда р = <?.
Следствие 1 доказано. Т
Замечание. Для произвольного х £ R число р еШ такое, что
р < х < р + 1, называется целой частью числа х. Обозначим его Е(х).
(В литературе целая часть числа часто обозначается символом [х].)
т Следствие 2. Каковы бы ни были числа а, Ь е R такие, что a < 6,
найдется рациональное число х, для которого а < х < 6.
Так как Ь - а > 0, то, в силу следствия теоремы 4.3, существует
значение n G N такое, что 1 < n(b — a).
Согласно следствию 1 (см. выше), найдется m e Z такое, что
m < an < m 4-1. Для этого m выполняются неравенства:
0<т4-1 — ап<1< п(Ь — а).
Отсюда
0<m + l- an < n(b — a).
Далее,
an < m 4-1 < bn.
Разделив обе части последнего неравенства на п, заключаем, что
Ш4-1 .
а < < Ь,
п
Ш4-1
так что число х = и есть искомое.
п
Следствие 2 доказано, т

44
Гл. 1. Введение в математический анализ
4.4.8. Покажем, как интуитивные представления о конечном
множестве и числе его элементов соотносятся с данным здесь определением
натурального числа.
Для произвольного п G N символом 1П далее обозначается
множество всех натуральных чисел га таких, что т < п, то есть
1П = {га G N | га < п}.
Множество 1п будем называть п-м отрезком множества всех
натуральных чисел N.
Если га < п, то тем более га < п + 1. Отсюда вытекает, что при
каждом п G N имеет место включение: 1П С In+i- Если га Е In+i и
га/п + 1, тога<п + 1и, значит, в силу предложения (4) п. 4.4.4,
га < п и, следовательно, га € In. Это позволяет заключить, что
In+l=InU{n + l}.
Непустое множество А называется конечным, если существует
число п G N такое, что А допускает взаимно однозначное отображение на
множество 1п. Это п называется числом элементов множества А.
Пустое множество также будем считать конечным множеством.
Число его элементов, естественно, считаем равным нулю.
Выясняя число объектов, образующих какую-либо совокупность
(например, число банкнот в пачке денег, число студентов,
присутствующих на занятиях, число автомобилей на стоянке и т. п.), мы по
очереди указываем на каждый из этих объектов, произнося при этом слова:
«один», «два», «три» и т. д. Когда будет указан последний из данных
объектов, слово «п», которое мы при этом произнесем, и будет
обозначать число объектов, входящих в данную совокупность.
Математически этот обычный процесс счета есть не что иное, как
построение взаимно однозначного отображения рассматриваемого
множества объектов на отрезок 1п множества N.
В связи с данным определением конечного множества возникают
некоторые вопросы, без ответа на которые это определение не может
считаться удовлетворительным. Главный из них таков:
не может ли оказаться, что для некоторого множества
существуют взаимно однозначные отображения на различные отрезки 1п и Im
множества натуральных чисел N?
Иначе говоря, не может ли получиться, что, подсчитывая число
элементов конечного множества в разном порядке, каждый раз мы будем
получать разные результаты?

§ 4. Точные границы числового множества
45
4.4.9. Покажем, что описанная неприятная ситуация не может иметь
места. Предварительно установим некоторые простые свойства
множеств Дп.
(К1) Всякое взаимно однозначное отображение множества 1п в себя
является отображением 1п на себя.
Действительно, в случае п = 1 множество 1п состоит из
единственного элемента — числа 1. Существует только одно отображение
множества Ii в себя — тождественное отображение Ii. Оно взаимно
однозначно и является отображением Ii на себя.
Предположим, что для некоторого п Е N справедливость
доказываемого утверждения установлена.
Пусть (3 : In+i —» In+i есть взаимно однозначное отображение In+i
в себя. Предположим, что /3(п + 1) = п + 1. Обозначим через а
ограничение Р на 1п.
Отображение a — взаимно однозначно. Если mGln, тош/п + 1
и, значит, a(m) = /3(га) ф /3(п + 1) = п + 1. Отсюда следует, что
а(га) < п, то есть а(га) Е In Для всякого га Е 1п и, следовательно, a
отображает 1п в себя. В силу индукционного предположения, а есть
отображение множества 1п на себя. Отсюда вытекает, что /3 есть
отображение множества In+i на себя.
Рассмотрим случай, когда (3(п + 1) ф п + 1.
Пусть /3(п + 1) = га. Зададим отображение т множества In+i на
себя, полагая т(га) = п + 1, т(п + 1) = га и т(к) = к в случае, если
к Е In+i отлично от га и п + 1.
Мы видим, что т есть взаимно однозначное отображение
множества 1п+1 на себя. Полагаем: j = т о (3. Очевидно, 7 есть взаимно
однозначное отображение In+i в себя. При этом 7(^ + 1) = т[/3(п + 1)] =
= г (га) = п + 1. По доказанному, отсюда вытекает, что 7 есть
отображение множества In+i на себя. Это позволяет заключить, что /3 также
является отображением множества In+i на себя.
В силу принципа индукции, предложение доказано.
(К2) Пусть даны числа п, га Е N. Если существует взаимно
однозначное отображение 1п в Im, то п < т.
Действительно, пусть a : In —» Im есть взаимно однозначное
отображение. Требуется доказать, что п < га.
В случае п = 1 это верно, поскольку 1 есть наименьшее
натуральное число.
Предположим, что для некоторого п данное утверждение доказано.
Пусть /3 : In+i —* Im есть взаимно однозначное отображение.

46
Гл. 1. Введение в математический анализ
Если Р(п + 1) = га, то ограничение /3 на 1П будет взаимно
однозначно отображать 1П в Im_i. В силу предположения индукции, отсюда
следует, что п < т — 1 и, стало быть, п + 1 < га.
Предположим, что к = /3(п + 1) ф га. Пусть г есть отображение
множества 1Ш на себя, определенное следующим образом: т(к) — тп,
т(гп) = к и т(г) = г в случае, если г Е Im отлично от & и га.
Очевидно, т есть взаимно однозначное отображение множества Im
на себя. Полагаем: j = г о /3. Отображение 7 множества In+i в Im
взаимно однозначно. При этом j(n + 1) = m. По доказанному, отсюда
следует, что п + 1 < т.
Оба требования принципа индукции здесь соблюдены и тем самым
предложение (К2) доказано.
Пусть А есть непустое конечное множество. Предположим, что
существуют биективные отображения а : А —»1пи/3:А—» Im. Тогда
/Зоа"1 есть взаимно однозначное отображение множества 1П в
множество Im. В силу (К2), это позволяет нам заключить, что п < т.
Аналогичным образом, ао/3"1 есть взаимно однозначное
отображение множества Im в 1П. В силу (К2), отсюда следует, что га < п и,
значит, га = п.
Таким образом, для всякого непустого конечного множества А
число п G N, такое что А допускает взаимно однозначное отображение на
множество 1П) единственно.
Предоставляем читателю доказать самостоятельно, что если
множества А и В суть произвольные непересекающиеся конечные
множества, п — число элементов множества А, га — число элементов
множества jB, то множество A U В имеет п + га элементов.
(КЗ) Всякое непустое подмножество множества 1П является
конечным множеством, то есть допускает биективное отображение на
множество Im для некоторого га Е N.
Доказательство будем вести с помощью принципа индукции.
Пусть п = 1. Имеем: Ii = {1} и всякое непустое подмножество Ii
совпадает с Ii, а потому конечно.
Предположим, что для некоторого п предложение доказано. Пусть
А есть непустое подмножество множества In+i.
Если п+1 не является элементом А, то для всякого k E А имеем к <
< п +1 и, значит, к < п. Отсюда вытекает, что А С 1П- Следовательно,
в силу предположения индукции, множество А конечно.
Предположим, что п + 1 е А. Пусть А' = А \ {п + 1}.

§ 4. Точные границы числового множества
47
Если А' пусто, то А состоит из единственного элемента — числа
п + 1. Полагая а(п + 1) = 1, мы, как очевидно, получим взаимно
однозначное отображение А на Ii, так что в этом случае множество А
конечно, в смысле данного здесь определения.
Если А' ф 0, то для всякого к Е А', очевидно, имеем: к < п + 1 и,
значит, к < п, то есть А! С 1п-
По предположению индукции, множество А! конечно.
Следовательно, существует биективное отображение а : А1 —» 1т. Продолжим а на
Л, полагая а(п + 1) = т + 1. В результате получим биективное
отображение А в Im+ъ
Тем самым конечность множества А доказана.
4.4.10. Установим некоторые свойства конечных подмножеств R.
■ Теорема 4.5. Всякое непустое конечное множество
вещественных чисел имеет наименьший и наибольший элементы.
Доказательство. Пусть АсК — конечное множество и п(А)
— число его элементов. Если п(А) = 1, то А состоит из
единственного элемента, который будет и наименьшим и наибольшим элементом
множества А.
Предположим, что утверждение теоремы верно, когда п(А) = п.
Пусть п(А) = п + 1. Возьмем произвольный элемент х £ А.
Множество А \ {х} состоит из п элементов и, по предположению, обладает
наименьшим и наибольшим элементами.
Пусть р — наименьший, q — наибольший элемент А \ {ж}. Тогда
меньшее из чисел х и р будет наименьшим элементом множества А.
Аналогично большее из чисел х и q является наибольшим
элементом множества А.
Теорема доказана. ■
4.4.11. Как приложение принципа математической индукции докажем
здесь одно неравенство, которое будет использовано в дальнейшем.
■ Теорема 4.6 (о неравенстве Бернулли). Пусть число х е R
таково, что 1 + х > 0. Тогда для любого натурального п справедливо
неравенство:
(1 + х)п > 1 + пх. (4.2)
Знак равенства при этом имеет место в том и только в том случае,
если: либо п = 1, а х > — 1 — произвольно, либо п > 1, х = 0.
Доказательство. Высказывание Р(п), истинность которого мы
должны доказывать для всякого n E N, состоит в следующем.
Если 1 + х > 0, то (1 + х)п > 1 + пх. При п = 1 имеем: (1 + х)п =

48
Гл. 1. Введение в математический анализ
= 1 + х >1 + х, так что высказывание Р(1) — истинно.
Пусть n G N таково, что высказывание Р(п) для данного п истинно,
то есть для всякого х G Ш такого, что 1 + х > О, выполняется неравенство:
(1 4- х)п > 1 4- их.
Число 1 + х — неотрицательно.
Умножая обе части последнего неравенства на 1 + х, получим:
(1 4- х)п+1 > (1 4- пх)(1 4- х) = 14- (п 4- 1)х 4- их2 > 14- (п 4- 1)х.
Это означает, что для данного п истинно также и высказывание
Р(п 4-1).
В силу принципа математической индукции, то есть — на
основании предложения Ind — из доказанного следует, что если 1 4- х > О, то
(1 4- х)п > 14- пх для любого п € N.
Для завершения доказательства надо рассмотреть еще, в каких
случаях в неравенстве (4.2) имеет место знак равенства?
Очевидно, что в случае п = 1 неравенство (4.2) превращается в
равенство.
Пусть п > 1. Тогда п — 1 е N и, следовательно,
(1 + х)п = (14- х)п_1(1 + х) > (1 + (п - 1)х)(1 4- я) = 1 4- пх + (п - 1)х2.
Отсюда видно, что если х ф 0, то
(1 4- х)п > 1 4- пх
(неравенство строгое!). Тот факт, что при х = 0 неравенство (4.2)
превращается в равенство, — очевиден.
Теорема доказана. О
4.5. Существование квадратного корня
Пусть дано число х > 0. Квадратным корнем из х называется
такое число у, что у2 = х, и арифметическим квадратным корнем из х
называется такое неотрицательное число у, что у2 = х.
Арифметический квадратный корень из х обозначается символом >/х, и если нет
поводов для недоразумений, то об арифметическом квадратном корне
говорят просто как о квадратном корне. То, что у, удовлетворяющее
данным условиям, существует, читатель воспримет как нечто само собой
разумеющееся. Этот факт, однако, нуждается в доказательстве, и
таковое не может быть дано без применения аксиомы непрерывности

§ 4. Точные границы числового множества
49
(см. п. 4.1.3). Позднее (см. гл. 2, §4) будет доказана общая теорема, из
которой, в частности, следует существование квадратного корня из
неотрицательного вещественного числа. Здесь мы дадим непосредственное
доказательство этого факта.
■ Теорема 4.7. Для всякого числа х>0 существует и притом только
одно у > О такое, что у2 = х.
Доказательство. Пусть дано х > 0. Если х = 0, то у = 0
удовлетворяет всем требуемым условиям. Если у\ и у2 таковы, что 0 < у\ < у2,
то у\ <у\. Отсюда следует, что может существовать самое большее одно
значение у > 0 такое, что у2 = х.
Пусть А — множество всех у € R таких, что у > 0 и у2 > х.
Покажем, что А непусто. Действительно, из верного для всякого
t > 0 равенства
5 К)
1
4
Г + 2ж +
£2
= х +
£(«-?)
следует, что
5 К)
>Ж
(4.3)
при всяком £ > 0, так что число у = - U+ -) для любого t > 0
принадлежит А и тем самым множество А непусто.
Положим у = inf А и докажем, что это у искомое.
X
Предположим, что у2 > х. Тогда у > —, откуда следует, что
1 / х
У>2{У+У
У1-
Полагая в неравенстве (4.3) t = у, получим, что у? > ж и, значит,
2/i е А. Это, однако, противоречит тому, что inf А = г/ > г/i. Тем самым
предположение о том, что у2 > х, ведет к противоречию и,
следовательно, у2 < х.
Допустим, что у2 < х. Положим y2 — y + h, где 0 < h < 1. Имеем
у2 = у2 + 2yh + h2 <y2 + 2yh 4- ft.

50
Гл. 1. Введение в математический анализ
X — V
Теперь выберем значение h такое, что h < и одновременно
^У + 1
0 < h< 1. Тогда
у\ < У2 + (2у + 1)Л < у2 + |^j?y(2y + 1) = х.
Так как у по условию есть точная нижняя граница множества А,
найдется у' Е А такое, что у < у' < У2- Поскольку у' Е А, имеем
(у')2>х.
С другой стороны, из неравенств 0 < у < у' < уг следует, что
(у)2 <у1<х.
Итак, допустив, что у2 < х, мы снова приходим к противоречию.
Значит, этот случай также не имеет места.
Остается единственная возможность: у2 = х.
Теорема доказана. ■
4.6. Сокращенные обозначения для суммы и произведения
4.6.1. Пусть даны произвольные целые числа га,п, причем т <п.
Предположим, что каждому целому числу к Е Z такому, что т <
< к < п, сопоставлено некоторое вещественное число х&. Сумма всех
чисел xm,Xm+i,..., хп обозначается символом
п
к=т
а их произведение — символом
п
П **• (4-5)
к=т
В случае п = т имеем единственное число #&, для которого Xk =
= хт = хп, и тогда будем считать, что каждое из выражений (4.4) и
(4.5) совпадает с этим числом Xk.
Из известных свойств операций сложения и умножения чисел
непосредственно вытекают следующие соотношения.
Пусть т,1,п — целые числа, причем т < I < п. Допустим, что
любому целому к такому, что т <к < п, сопоставлено некоторое число
%к-

§ 4. Точные границы числового множества
51
Тогда
i
п I п п / \ / п \
Х^Хк = 5ZХк + 11, Xkj ПХк = ( ПХк) ( П Хк)
fc=ra к=т fc=Z-f-l к=т ^ к—т ' ^ fc=Z+l '
4.6.2. Отметим еще одно свойство, которое называют правилом
замены индекса (суммирования).
Пусть га < п. Тогда
п п—г п+г
^2 Xk ~ ^2 Хк+Г = Х^ Хк-г, (4.6)
к=т к—т—т k=m+r
п п—г п+г
ПХк = П Xk+r = П rrfc"r' (4#7)
fc=m k=m—r k=m+r
Для доказательства достаточно заметить, что все три суммы в (4.6)
состоят из одних и тех же слагаемых и все три произведения в (4.7)
состоят из одних и тех же сомножителей.
Иногда удобно говорить о сумме и произведении пустого множества
чисел. А именно, сумму пустого множества слагаемых будем считать
равной нулю, а произведение пустого множества сомножителей —
единице.
4.6.3. Пусть п — натуральное число. Положим
п
п\ = Y[k = l 2 ... п.
к=1
Кроме того, условимся считать, что 0! = 1. Выражение п! читается
«п-факториал».
Введем еще одно обозначение.
Пусть п G N. Тогда символ п\\ (читается: «п дважды факториал»)
означает произведение всех не превосходящих п чисел одной четности с
числом п, то есть при п = 2га имеет место равенство п\\ = 2 • 4 •... • 2га,
а если п = 2га — 1, то п\\ = 1 • 3 •... • 2га — 1.
Как нетрудно видеть, при каждом га Е N имеют место равенства:
(2m)!! = (2m)m\, (2т - 1)!! = ^-l)\V

52
Гл. 1. Введение в математический анализ
§5. Вещественные числовые функции
В этом параграфе исследуется частный случай общего понятия
отображения, в котором областью значений является множество всех
вещественных чисел Е. Такие отображения называют вещественными
функциями или просто функциями. Для них можно определить
операции сложения, умножения и деления.
С помощью системы координат на плоскости график
вещественной функции, заданной на подмножестве Е, можно представить в виде
некоторого множества на плоскости.
Далее неоднократно будут использоваться понятия точной верхней
и точной нижней границ функции. Здесь приводятся определения этих
понятий и доказываются некоторые их основные свойства.
5.1. Алгебраические операции над вещественными
функциями. Монотонные функции
5.1.1. Пусть А — произвольное множество. Вещественной функцией
(или просто функцией) на множестве А называют всякое отображение
Функцию / : А —> Е будем называть конечной, если /(ж) G I для
всех х Е А.
В дальнейшем, если не оговорено особо, под вещественной
функцией всегда понимается конечная вещественная функция.
Пусть f:A-±Rn.g:A-±R — конечные вещественные функции,
определенные на множестве А.
Суммой и произведением функций / и g называют функции
s : А -> Е и р : А -> Е,
определенные следующим образом:
s(x) = f(x) + g(x), p(x) = f(x)g(x)
для всех х Е А. Функцию s обозначают символом / + #, а функцию р —
символом fg.
Для функций /', g определим их частное /г, принимая в качестве его
области определения множество всех х Е А, для которых д(х) ф О, и для
всякого такого х полагая

§ 5. Вещественные числовые функции
53
Пусть a G Е — произвольное число и / : А —> Е — числовая
функция, определенная на множестве А. Символами а/ и / + а будем
обозначать функции, определенные условиями
(af)(x) = a-f(x), (/ + о)(ж) =/(ж)+ о
для всякого х € А.
Если дана функция / : А -+ Ё, то символами |/|, /+ и /" будем
обозначать функции, определенные следующими соотношениями:
\f\:x»\f(x)\, f+:x»(f(x))+, f~ : х » (f(x))~.
Очевидно, что имеют место равенства:
f = f+-r, \f\ = f+ + r-
5.1.2. Пусть множество АсК непусто. Функция / : А -* Е называется
возрастающей или неубывающей, если для любых #i,#2 из А таких,
что xi < #2, выполняется неравенство /(ал) < /(#2)-
Функция / : А —» Е называется убывающей, если для любых #i,#2
из А таких, что х\ < Х2, имеет место неравенство f(xi) > /(#2)
Функция, удовлетворяющая этому условию, называется также невозраста-
ющей. Если для любых #i,£2 из А таких, что х\ < Х2, выполняется
неравенство f(xi) < /(#2) (неравенство f(xi) > /(#2)), то будем
говорить, что функция / строго возрастает (соответственно, строго
убывает).
Функция / : А —► Е называется монотонной, если она либо
возрастающая, либо убывающая. Если функция / : А —> Е строго
возрастающая или строго убывающая, то будем говорить, что / — строго
монотонная функция.
5.2. График вещественной числовой функции
5.2.1. При изучении вещественных функций, определенных на
подмножествах Е, полезны некоторые геометрические представления.
Осью на плоскости или осью в пространстве называется всякая
прямая, на которой указаны две различные точки, одной из которых
присвоено наименование нулевой, а другой — единичной.
Пусть I — произвольная ось, О — ее нулевая точка, Е — единичная
точка (см. рис. 5).
1 1 1 —I 1 1
ОМЕ МО Е
Рис.5

54
Гл. 1. Введение в математический анализ
Каждой точке М на оси / может быть сопоставлено некоторое
вещественное число ж(М), называемое координатой точки М на оси L
Число х(М) определяется следующим образом. Пусть £ > О —
отношение длин отрезков ОМ и ОЕ,
= |ОЛ^ >
* \ОЕ\ -
Тогда х(М) = £, если точки М и Е лежат по одну сторону от точки О, и
х(М) = — £, если М и Е лежат по разные стороны от точки О.
Справедливо следующее утверждение.
♦ Предложение 5.1 (первый основной постулат аналитической
геометрии). Отображение х : М е I ь-> х(М) взаимно однозначно отображает
прямую I на множество всех вещественных чисел R. ♦
P2(-L5,-l)
.Pi(3,2)
М(3.5,-.5)
Рис. 6
Аналитическая геометрия в своих построениях существенно
опирается на данное предложение. Обычно оно приводится без
доказательства, поскольку последнее возможно лишь на основе точного
аксиоматического изложения геометрии. В связи с этим мы и называем данное
предложение «постулатом».
5.2.2. Напомним понятие декартовой ортогональной системы координат
на плоскости, известное из школьного курса геометрии.
Зададим произвольный отрезок е. Проведем две взаимно
перпендикулярные прямые ОХ и OY, пересекающиеся в точке О (см. рис. 6).
На прямых ОХ и OY отложим отрезки ОЕх и ОЕУ1 равные отрезку
е, и будем считать точку О нулевой на каждой из прямых ОХ и ОУ, а
точки Ех и Еу — единичными.

§ 5. Вещественные числовые функции
55
Каждая из прямых ОХ и OY является осью и, следовательно,
определено понятие координаты для точек на этих осях.
Пусть М — произвольная точка на плоскости, М\ и Мъ — ее
ортогональные проекции на прямые ОХ и OY, соответственно. Пусть
х(М) — координата точки Mi на оси ОХ, у(М) — координата точки
М2 на оси OY. Точке М, таким образом, отвечает пара
вещественных чисел (х,у), где х = х(М), у = у(М), то есть некоторый элемент
множества I2 = 1 х Е.
Числа х и у называются координатами точки М. При этом число
х называют абсциссой, а число у — ординатой точки М.
Сформулируем теперь другой основной постулат аналитической
геометрии.
♦ Предложение 5.2 (второй основной постулат аналитической
геометрии). Отображение М «-» (х(М),у(М)) плоскости в прямое
произведение Е х R = R2 взаимно однозначно и является отображением
плоскости на множество Ш2. ф
Это предложение означает, что если точки Mi и Мъ различны,
то соответствующие им пары (xi,yi) и (#2,2/2) также различны, и для
любой пары чисел (х, у) существует точка М, абсцисса которой равна
х, а ордината равна у.
Отображение плоскости в множество пар вещественных чисел Ш2,
получаемое с помощью описанного здесь построения, называется
декартовой ортогональной системой координат на плоскости, а оси ОХ и
OY называются осями этой системы координат.
5.2.3. Пусть А С М, А ф 0. Пусть дана функция / : А —> Е. Зададим
на плоскости декартову ортогональную систему координат. Графиком
функции / в этой системе координат называется множество всех точек
М, у которых первая координата х(М) принадлежит А, а вторая
координата у(М) равна f(x(M)).
Использование графика функции часто позволяет представить те
или иные свойства вещественной функции в наглядной, обозримой
форме. График функции обычно изображается в виде некоторой линии на
плоскости. Следует сказать, что, вообще говоря, график вещественной
функции может оказаться множеством, мало поддающимся наглядному
восприятию. Впрочем, такого рода «плохие» функции, если и будут
представлены в дальнейшем, то лишь в качестве примеров,
иллюстрирующих те или иные ситуации общего характера.
5.3. Точные границы вещественной функции
5.3.1. Пусть дана функция / : М —> R, где М — произвольное
множество. Предположим, что А — непустое подмножество М.

56
Гл. 1. Введение в математический анализ
Число LER называется верхней границей функции / на множестве
А, если для всех х € А выполняется неравенство f(x) < L.
Аналогично К ЕЙ называется нижней границей функции f на
множестве А, если для всех х Е А имеем f(x)>K.
Ясно, что верхняя (нижняя) граница функции — это верхняя
(нижняя) граница образа f[A] множества А при отображении /.
Очевидно, что —оо является нижней, оо — верхней границей
функции / : М —» Й на любом множестве А С М.
Функция / : М —» Й называется ограниченной сверху (снизу) на
множестве А С М, если она имеет хотя бы одну конечную верхнюю
(нижнюю) границу на множестве А.
Функция f:M—>Й называется ограниченной на множестве Ас М,
если она ограничена на нем сверху и снизу.
Иначе говоря, функция / : М —» Й ограничена на множестве ЛсМ,
если существуют числа if, L Е М такие, что для всех х Е А
выполняются неравенства К < f(x) < L. Можно также сказать, что функция
ограничена на А, если образ этого множества ограничен.
Очевидно, что функция / : М —» Й ограничена на множестве
А С М в том и только в том случае, если существует такое конечное
число L, что для всех х Е А выполняется неравенство \f(x)\ < L.
5.3.2. Точная верхняя граница sup f(A) множества f[A] называется
точной верхней границей функции / на множестве А и обозначается
через sup f(x) либо, короче, через sup/.
хеА А
Точная нижняя граница ini f(A) множества f[A] называется
точной нижней границей функции f на множестве А и обозначается через
inf f(x) либо, короче, через inf /.
хеА А
Согласно определению,
sup f(x) = sup f[A}; inf f(x) = inf f[A].
x£A X^A
5.3.3. Сформулируем признаки точной верхней и точной нижней
границ функции, представляющие собой переформулировки для данной
ситуации соответствующих признаков точной верхней и точной нижней
границ числового множества, заключенных в теореме 4.1.
ф Предложение 5.3. Пусть даны функция f : М —> Й и непустое
множество А С М. Число L Е Й является точной верхней границей
функции f на множестве А в том и только в том случае, если выполнены
следующие условия:
(a) f(x)<L для любого х Е А;

§ 5. Вещественные числовые функции
57
(Ь) для любого р < L существует х Е А такой, что р < f(x).
Число К является точной нижней границей функции / на
множестве А в том и только в том случае, если выполнены следующие условия:
(a7) f(x)>K для любого х Е А;
(bf) для любого q> К найдется х Е А такой, что q > f(x). ф
5.3.4. Отметим-иекоторые свойства точных границ
вещественной функции.
(1) Пусть даны функция / : М —» R и множества А, В С М. Тогда
в случае А С В выполняются неравенства
sup f(x) < sup f(x)\ inf f(x) > inf /(ж).
x£A x£B X$A X^B
Доказательство. Действительно, если А с В, то f[A] с f[B], и
результат вытекает из теоремы 4.2.
(2) Пусть даны множество М и функции f : М —>R и g : М —» Ё.
Если для всех х из множества А С М выполняется неравенство
f(x) < g(x), то
inf f(x) < inf g(x), sup f(x) < s\xpg(x).
xeA xeA X£A xeA
Доказательство. Положим К = inf /(ж). Тогда для всех х Е А
хеА
имеем К < f(x) < g(x). Число К тем самым есть нижняя граница
функции g на множестве А, значит,
К < inf g(x).
xeA
Первое неравенство доказано. Второе доказывается аналогично.
(3) Пусть даны функция f : M —>R и множество А С М. Тогда
inf f(x) = - sup[-/(z)], sup f{x) = - inf [-f(x)].
X^A xeA xeA x^A
Доказательство. Положим р = inf /(ж), pi = — sup[-/(a?)]. Для
xeA xeA
всякого x E А имеем p < /(ж), —f{x) < —p. Таким образом, — р есть
верхняя граница функции —/на множестве А и
sup[-/(z)] < -р,
хеА

58
Гл. 1. Введение в математический анализ
откуда
pi = - sup[-/(ж)] > р. (5.1)
хел
Далее, —р\ = sup [—/(ж)], откуда вытекает, что —f(x) < — pi для
хел
всех х Е А, так что f(x) > р\ для всех х Е А. Таким образом, р\ есть
нижняя граница / на А и, следовательно,
Pl< inf /(я?)=р. (5.2)
Сопоставляя неравенства (5.1) и (5.2), заключаем, что р = р\, и
первое равенство доказано.
Второе равенство получим как следствие первого.
Равенство inf/ = — sup[—/] выполнено для любой функции /. По-
А А
этому оно остается верным, если заменить / на —/. Производя такую
замену, получим
inf\[-f(x)] = -sup f(x),
X^A xeA
откуда
sup/(x) = - mi[-f(x)},
xeA xeA
что и требовалось доказать.
§6. Комплексные числа
Понятие комплексного числа возникло в связи с необходимостью
расширения множества вещественных чисел до такого множества, в
котором можно извлекать квадратный корень из отрицательного числа.
Исторически непосредственным поводом для введения комплексных
чисел послужила знаменитая формула Кардано для решения
кубического уравнения х3 + рх + q — 0. Это уравнение имеет самое большее три
вещественных корня. При этом в том случае, когда указанное уравнение
имеет ровно три вещественных корня, формула Кардано приводит к
выражению, требующему извлечения квадратного корня из
отрицательного числа, и никаким преобразованием формулы Кардано избежать этого
не удается.
6.1. Понятие комплексного числа. Определение и основные
свойства
6.1.1. Пусть М2 — прямое произведение множества Ш на себя, то есть
совокупность всех пар (ж, у) вещественных чисел.

§ 6. Комплексные числа
59
Определим в Ж2 операции сложения и умножения для любых
элементов z = (ж,у), w = (гб,г;) Е М2, полагая
z + w = (х + и^у + v), z -w — (ху — uv,xv + иу).
Множество Ш2 с введенными операциями называется множеством
комплексных чисел и обозначается символом С. Элементы множества С
называются комплексными числами.
6.1.2. Все свойства алгебраических операций на множестве Ш
сохраняются и для алгебраических операций на множестве С, однако теперь
они не носят характера аксиом, а вытекают из определений.
Перечислим свойства операций сложения и умножения
комплексных чисел.
А.1. Для любых z = (#, у), w = (и, v) и t — (г, s) из С
(z + w) + t = z + (w + t).
А.2. Существует число О Е С такое, что для всякого z £ С
z + 0 = 0 + z = z.
А.З. Для всякого z £ С существует число — z £ С такое, что
z + (-z) = 0.
Число — z, удовлетворяющее условиям предложения А.З,
называется противоположным числу z.
А.4. Для любых z и w из С имеем:
z + w = w + z.
М.1. Для любых z = (x,y),w = (u,v) и t = (r, s) из С имеет место
равенство
(z • w) -t = z • (w -t).
M.2. Существует число 1 £ С такое, что для всякого z £ С
1 • Z = Z • 1 = Z.

60
Гл. 1. Введение в математический анализ
М.З. Для любого z Ф 0 из С существует число - такое, что
Z
..1=1.
Z
Число - называется числом, обратным к z.
z
М.4. Для любых z и w из С справедливо равенство
z -w = w • z.
AM (свойство дистрибутивности). Для любых трех чисел z,w и t
из С выполняется равенство:
z - (w + t) = z • w + z -1.
Если z G С, w G С, то число z + (—гн) называется разностью чисел
z и w и обозначается символом г — г/;.
Если г/; ^ 0, то число z— называется частным z uw и обозначается
w
z
символом —-.
W
Произведение произвольных комплексных чисел z и w в
дальнейшем обозначается просто zw.
Докажем перечисленные свойства.
Справедливость свойств А.1, А.З, А.4 и М.4 вытекает сразу из
определений. Для обоснования свойства А.2 легко проверить, что число
0 = (0,0) удовлетворяет требуемым равенствам. При проверке свойства
М.2 достаточно взять 1 = (1,0). /
Проведем несложные вычисления для проверки остальных свойств.
М.1. Пусть z — (#,у); w = (гх, v); t = (r, s). Тогда
zw = (хи — yv, xv + угх), wt = (иг — vs, us + w),
(zw)t = (xur — yvr — xvs — yuS) xus — yvs + xvr + yur);
z(wt) = (xur — xvs — yus — yvr, xus + xvr + yur — yvs).
Сравнивая полученные выражения для (zw)t и z(wt), получаем:
(zw)t = z(wt).
М.З. Пусть z = (ж,у); z Ф 0 = (0,0). Тогда х2 +у2 ф 0. Положим

§ 6. Комплексные числа
61
Тогда
(хх-{-у)у -ху + ху\ ( .
1
и, следовательно, в качестве искомого числа - можно взять ги.
z
AM. Пусть £ = (ж, у), w = (u,v) и £ = (?*>$)• Тогда по определению
w + t = (u + r,v + s) и, значит,
я(ги+ <) = (x(u + r) -y(v + s),x(v + s) + y(u + r)) =
= (хи — yv, xv + уи) + (xr — у5, xs + yr) = zw + zt,
что и требовалось доказать.
ф Предложение 6.1. Число 1, удовлетворяющее условию М.2,
единственно. Число О, удовлетворяющее условию А.2, единственно.
Доказательство. Действительно, пусть числа Iх и 1" таковы,
что 17г = г, 21" = ^ для любого ^ € С. Полагая в первом равенстве
2 = 1", получим: Iх • 1" = 1". Полагая во втором равенстве 2 = 1',
будем иметь: I7 * I77 = I7. Отсюда I7 = I77, что и требовалось доказать.
Аналогично устанавливается единственность числа 0,
удовлетворяющего условию А.2.
Предложение доказано, ф
ф Предложение 6.2. Для всякого z ф О число w такое, что
zw = wz = 1, единственно. Для всякого z £ С число w £ С такое, что
w + z = z + w = 0, единственно.
Доказательство. Предположим, что числа wi и г^2 таковы, что
zwi = 1, W2Z = 1. Тогда
W2 = W2I = W2(2Wi) = (ty^wi =- lwi = гУ1,
что и требовалось доказать.
Аналогично устанавливается единственность числа w такого, что
w + z — z + w = 0.
Предложение доказано, ф
6.1.3. Определим отображение J : Е —> С, полагая для ж £ Е
J(a?) = (ж,0).
Непосредственно проверяется, что для любых ж и у из Е
выполняются равенства:
J(x + y) = J(x) + J{y); J(x-y) = J(x)-J(y); J(0) = О; J(l) = 1.

62
Гл. 1. Введение в математический анализ
Отображение J взаимно однозначно. Будем называть его
каноническим вложением множества 1вС.
Вещественное число х будем отождествлять с комплексным числом
J(x). Иными словами, условимся считать, что комплексное число (я,0)
и вещественное число х представляют собой один и тот же объект.
В дальнейшем число 1 будем обозначать символом 1. Комплексное
число (0,1) обозначается символом г.
Непосредственно проверяется, что имеет место равенство:
i2 = (-l,0) = -l.
Таким образом, уравнение х2 = — 1, которое не имеет решений в R,
оказывается разрешимым в множестве комплексных чисел С.
6.1.4. Пусть z = (х,у). Имеем:
(rr,0) + (0,l)(y,0)-(rr,y).
Комплексные числа (#,0) и (у, 0) отождествляются с
вещественными числами х и у, соответственно, что позволяет записать число
z = (ж, у) следующим образом:
z = х + (0,1)у = х + iy.
Это есть основная форма представления комплексного числа,
которую мы будем использовать в дальнейшем.
6.2. Вещественная и мнимая части комплексного числа.
Модуль. Сопряженное число
6.2.1. Пусть z = х + iy — комплексное число. Число х называется
вещественной частью числа z и обозначается символом Rez.
Число у называется мнимой частью числа z и обозначается Im z.
При записи комплексных чисел вида z = х + гу арифметические
действия над ними можно выполнять как над обычными двучленами,
принимая во внимание, что г2 = — 1.
Пусть z = х + гу. Число х — гу называется сопряженным к z и
обозначается z.
Для комплексного числа z = х + гу полагаем Ы = у/х2 +у2.
Величина \z\ называется модулем комплексного числа z.
Очевидно, что \z\ > 0 для всякого ^ЕСи|^| = 0в том и только в
том случае, когда z = 0.

§ 6. Комплексные числа
63
6.2.2. Отметим некоторые свойства модуля комплексного числа и
операции перехода к сопряженному числу.
(1) Для всякого z G С имеет место равенство:
(Т) = Z. (6.1)
(2) Для любых z\, Z2 G С справедливы равенства:
и
Z\ + %2 — Z\ + Z2,
Z\Z2 = ZlZ2.
\Rez\ < |s|,
|Ims| < \z\.
Действительно, для z G С имеем:
\z\ = yi2 + y2 > vx2 = |ж|
лЛ2 + У2 > Vv* = \у\-
(6.2)
(3) Для всякого z G С
г* = и2. (б.з)
Действительно, для z = x + iy имеем:
zz = (x + iy)(x - iy) = x2 - (iy)2 = x2 + y2.
(4) Для всякого z G С имеют место неравенства:
(6.4)
(5) Для любых двух комплексных чисел z\ и z2 справедливы
соотношения:
\ziz2\ = \zi\\z2\; (6.5)
|*1 + «2|<Ы + Ы. (6-6)

64
Гл. 1. Введение в математический анализ
В самом деле, в силу (6.3),
\Z\Z2\2 = (ziZ2)(ziZ2) = Z1Z2Z1Z2 = Z1Z1Z2Z2 = \zi\2\z2\2,
откуда, очевидно, следует равенство (6.5).
Применяя равенство (6.3), получим:
|*1 + Z2f = (Zi + Z2)(Zi +Z2) = (Zi + Z2)(ZI + 22).
Отсюда
\Z1 + Z2\2 = 2i Zi + 21^2 + ^1^2 + Z2Z2 = kl|2 + Z\ Z2 + Z\Z2 + |22|2.
Заметим, что £112 = ^1(^2) = ^1^2, так что
z\Z2 + Z1Z2 = 2Re(^i^2) € К.
Применяя первое из неравенств (6.4), получаем:
2i^2 + Z1Z2 = 2Re^i^2 < 2|*i||^2|,
откуда
|*i + *2|2 < Nil2 + 2|*i|H + |z2|2 = (\zi\ + \z2\)2.
Неравенство (6.6) доказано.
Из неравенства (6.6) так же, как и в случае вещественных чисел,
выводится, что для любых г, w G С имеют место неравенства:
z\-\w\\ < \z-w\. (6.7)
6.3. Геометрическое представление комплексных чисел
На плоскости зададим декартову ортогональную систему
координат. Пусть О — начало системы координат.
Комплексному числу z = х + iy сопоставим вектор на плоскости,
началом которого служит точка О, а концом — точка А с координатами
(я, у) (см. рис. 7).
Вектор назовем изобраоюением комплексного числа z = х + гу.
Пусть даны комплексные числа z = x + iyjaLW = u + iv,m пусть ОА и
О В — их изображения.

6. Комплексные числа
65
Тогда изображением суммы z + w будет служить вектор ОС =
ОА + ОВ, где сложение векторов определяется известным правилом
параллелограмма (см. рис. 8).
А
у Л .
О х ^
Рис. 7 Рис. 8
Модуль комплексного числа z = х + гу равен длине вектора
который изображает z.
Неравенства (6.6) и (6.7), в силу этого, допускают простое
геометрическое истолкование. А именно, неравенство (6.6) равносильно
утверждению: длина стороны треугольника не превосходит суммы двух
других его сторон, неравенство (6.7) — утверждению: разность длин
двух сторон треугольника не превосходит третьей его стороны.
Операция умножения на комплексное число также допускает
простое геометрическое истолкование.
Пусть дано комплексное число с = a + ib. Будем считать, что с ф 0.
На плоскости зададим декартову ортогональную систему координат.
Произвольное комплексное число z = х + гу отождествим с
точкой (ж, у) на плоскости. Так как с ф 0, в силу установленных свойств
операции умножения комплексных чисел, отображение Рс : z Е С н+ cz
взаимно однозначно отображает множество С на себя. Тем самым
определено некоторое взаимно однозначное отображение плоскости на себя,
которое мы будем обозначать тем же выражением Рс.
Выясним, что представляет собой это преобразование
геометрически (см. рис. 9). Воспользуемся некоторыми результатами
аналитической геометрии.
Сначала рассмотрим случай, когда \с\ = 1. Имеем: с = a + ib и
|с| = у/а2 + Ь2 = 1. Как известно из тригонометрии, для данных а и Ь
существует число (р такое, что 0 < (р < 27Г и выполняются равенства
а = cos <p и Ь = sin (p.

66
Гл. 1. Введение в математический анализ
Рис.9
Геометрический смысл числа <р таков: это есть угол, на
который надо повернуть вектор ei = (1,0), чтобы совместить его с
вектором с, вращая вокруг начала координат О в направлении против часовой
стрелки.
Для произвольного z = х + гу Е С имеем:
Pc(z) = cz = ха — уЬ + г(хЬ + уа).
Тем самым преобразование Рс переводит точку с координатами
(#, у) в точку с координатами (гл,г;), где
и = ха — yb = x cos <p — у sin <p, v = xb + уа = х sin (p + у cos (p. (6.8)
Из курса аналитической геометрии известно, что если w = (гх,г;),
где и is. v выражаются равенствами (6.8), то вектор w получается из
вектора z вращением вокруг начала координат на угол, равный <р, в
направлении против часовой стрелки.
Итак, если \с\ = 1, то преобразование Рс есть вращение плоскости
вокруг начала координат на угол, равный (р.
Пусть г = \с\ ф 1. Положим 7 = -• Тогда
г
Pc(z) = cz = rjz = Pr(P7(^)).

§ 7. Счетные множества
67
Мы видим, что в этом случае преобразование Рс есть результат
последовательного выполнения преобразований Рг и Р7. Так как |7| = 1,
то преобразование Р7, как показано выше, есть вращение плоскости
вокруг начала координат. Осталось выяснить, что представляет собой
преобразование Рг. Если z = 0, то Pr(z) = 0.
Пусть z = x + iy ф 0. Имеем: w = rz = rx + iry. Точки Z = (x, у) и
W = (rx,ry), как легко проверяется, лежат на одном луче, исходящем
из начала координат О, и отношение длин отрезков OZ и OW равно г.
Преобразование плоскости, определенное таким образом,
называется преобразованием подобия относительно точки О с коэффициентом
подобия, равным г.
Таким образом, мы приходим к следующему выводу. Умножение
на комплексное число с ф 0 геометрически сводится к
последовательному выполнению следующих преобразований: сначала плоскость
поворачивается вокруг начала координат О на угол <р, а затем подвергается
преобразованию подобия с коэффициентом г относительно точки О.
Числа г и ср при этом находятся из представления с = г (cosy? + г sirup)
комплексного числа с.
§7. Счетные множества
Одна из основных идей Георга Кантора — создателя теории
множеств — это идея классификации бесконечных множеств по степени их
«обширности». Бесконечные множества могут быть более или менее
обширными. Счетные множества занимают самое низшее место в
иерархии бесконечных множеств, построенной Г. Кантором.
(Приложения вводимого ниже понятия счетного множества будут даны в главе 5:
«Интегральное исчисление для функций одной переменной».)
7.1. Определение счетного множества
7.1.1. Пусть А — произвольное множество. Говорят, что А не более
чем счетно, если существует взаимно однозначное отображение v
множества А в множество натуральных чисел N. Всякое такое отображение
v : А —> N называется нумерацией элементов А.
Число и(х), отвечающее элементу х множества А, называется
номером элемента х в данной нумерации.
Пустое множество 0 также будем считать не более чем счетным.
Множество А не более чем счетно, если каждому его элементу
можно присвоить определенный номер и притом так, что разные элементы

68
Гл. 1. Введение в математический анализ
всегда получают различные номера. При этом не требуется, чтобы
значения этих номеров пробегали подряд все множество N или какой-либо
его отрезок.
Напомним, что множество А называется конечным, если
существует биективное отображение А в отрезок 1П = {1,2,...,п} множества N.
При этом число п называют числом элементов множества А.
Всякое конечное множество, очевидно, не более чем счетно.
Бесконечное не более чем счетное множество называется счетным.
Множество N всех натуральных чисел, очевидно, счетно.
Пусть А — не более чем счетное множество и v : А —> N — его
нумерация.
Отображение и взаимно однозначно и, следовательно, ограничение v
на любое подмножество А также является нумерацией. Отсюда следует,
что любое подмножество не более чем счетного множества не более чем
счетно. В частности, любое подмножество множества N не более чем
счетно.
7.1.2. Докажем некоторые утверждения о сохранении свойства
множества быть не более чем счетным при отображениях. Первое утверждение
таково.
♦ Предложение 7.1. Пусть дано взаимно однозначное отображение
/ : А —> В. Если множество В не более чем счетно, то множество А также
не более чем счетно.
Доказательство. Так как В не более чем счетно, то согласно
определению существует взаимно однозначное отображение \i : В —» N.
Положим v — цо f'. Очевидно, что v есть отображение А в N.
Покажем, что v взаимно однозначно. Действительно, пусть х\ ф
Ф х2, £1,^2 £ А. Тогда ух = f(xi) ф у2 — f(x2), так как / взаимно
однозначно. Отсюда следует, что
v{xi) = /i(yi) ф fi(y2) = v(x2),
и взаимная однозначность v установлена.
Предложение доказано. ♦
7.1.3. Теперь докажем второе утверждение о сохранении не более чем
счетности при отображениях.
♦ Предложение 7.2. Пусть f : А -> В — отображение А на В. Если
А не более чем счетно, то и В не более чем счетно.
Доказательство. Зададим нумерацию v множества А, то есть
взаимно однозначное отображение v : А —> N. Возьмем у € В. Так
как / — отображение А на Б, то множество j~x{y) непусто. Обозначим
через \х(у) наименьший из номеров элементов множества /_1(2/). Этим

7. Счетные множества
69
определено отображение /х : В —> N. Отображение /i взаимно
однозначно. Действительно, если у\ ф уъ, то множества f~1(yi) и /_1(у2) не
имеют общих элементов.
Имеем: /i(yi) = i/(rri), /i(t/2) = 2/(^2), где an G /_1(2/i), а я2 G
G f~1(y2)- Так как множества f~1(yi) и f~1(y2) не имеют общих
элементов, то ал Ф Х2- Так как i/ — взаимно однозначное отображение,
отсюда следует, что u(xi) ф ^(#2), так что fi(yi) Ф /^(уг), и взаимная
однозначность отображения //, установлена.
Предложение доказано. ♦
▼ Следствие. Пусть дано отображение f : А —> Б. Если множество
Е С Ане более чем счетно, то и его образ f(E) есть не более чем счетное
множество.
Для доказательства достаточно заметить, что сужение
отображения / на множество Е есть отображение Е на f(E). ▼
7.1.4. Все бесконечные не более чем счетные множества устроены,
в определенном смысле, одинаково. Справедливость этого утверждения
вытекает из следующей теоремы.
■ Теорема 7.1. Всякое бесконечное подмножество множества N
допускает взаимно однозначное отображение на N.
Доказательство. Пусть М С N — бесконечное множество.
Построим сначала взаимно однозначное отображение множества N на М.
Отображение, обратное к нему, очевидно, и будет искомым.
Обозначим через х\ наименьший элемент множества М.
Предположим, что для некоторого п элементы х\,Х2,..., хп определены. Пусть
Мп — множество, состоящее из всех остальных элементов множества
М. Так как М бесконечно, то Мп непусто.
Обозначим через xn+i наименьший элемент множества Мп. В силу
принципа математической индукции тем самым определена некоторая
последовательность (xn)n£N элементов множества М, то есть
отображение х множества N в М.
Построенное отображение х : N —► М взаимно однозначно.
Действительно, пусть п\ и П2 — произвольные натуральные числа,
причем щ ф П2- Будем считать, что щ < пч- Положим П2 — 1 = п.
Тогда хП1 есть одно из чисел #i,#2, • • • ?#п, а хП2 = xn+\ G Мп и тем
самым Хп2 не равно ни одному из чисел #i,#2,... ,жп. В частности,
Докажем, что х есть отображение N на М.
Допустим, что это не так. Тогда найдется m G М такое, что
m ф хп, каково бы ни было п. Из построения последовательности

70
Гл. 1. Введение в математический анализ
(#n)n€N следует, что т Е Мп при любом п, значит, хп+\ = minMn < m
для всех п. Так как xn+i ф т, то xn+i < т.
Очевидно, что х\ < га, и в силу принципа математической
индукции получаем, что хп < т для всех п.
Отображение х : N —* М, как доказано, взаимно однозначно, и
числа хп все натуральные.
Для всякого п Е N функция fc Е 1п ■-* #& есть взаимно однозначное
отображение 1п в Im. В силу сказанного в п. 4.4.8, отсюда следует, что
п <т для любого п Е N, что противоречит принципу Архимеда.
Итак, допустив, что х не является отображением N на М, мц
приходим к противоречию.
Таким образом, установлено существование взаимно однозначного
отображения N на М, и теорема доказана. ■
Т Следствие 1. Всякое счетное множество допускает взаимно
однозначное отображение на N.
Доказательство. Пусть А — счетное множество. Тогда А
бесконечно и допускает взаимно однозначное отображение v в множество N.
Пусть М — v(A). Очевидно, М есть бесконечное подмножество N и
согласно теореме существует биективное отображение /i : М —* N.
Суперпозиция jttoi/, как нетрудно видеть, и является требуемым
отображением.
Следствие доказано. ▼
Следствие 1 показывает, что элементы счетного множества могут
быть занумерованы так, что их номера будут пробегать все
множество N без пропусков, причем разные элементы будут иметь различные
номера.
▼ / Следствие 2. Для любых двух счетных множеств А и В
существует биективное отображение: <р : А-+ В.
Действительно, пусть А и В суть произвольные счетные
множества. Тогда, в силу следствия 1, существуют взаимно однозначные
отображения а : A-^Nhj8 : В ->N такие, что а(А) = N и /3(B) — N.
Тогда, как нетрудно видеть, отображение tp = (3~г о а : А —► В
биективно, что и требовалось доказать. ▼
Следствие 2 позволяет придать точный смысл утверждению, что
все счетные множества одинаковы. Если множества А и В сч^тны, то
между элементами этих множеств можно установить взаимно
однозначное соответствие так, что каждому элементу А отвечает единственный
элемент множества Б, и каждому элементу В отвечает единственный
элемент А.

§ 7. Счетные множества
71
7.2. Операции над счетными множествами
7.2.1. Опишем некоторую общую схему, полезную при изучении
операций над счетными множествами.
На плоскости зададим декартову ортогональную систему
координат.
Рассмотрим «квадрант»
я > 0; у > 0. (7.1)
Прямыми х = га, у = п, где тип — произвольные натуральные
числа, разобьем его на «квадраты», определяемые неравенствами
га — 1 < х <т; п — 1 <у <п. (7.2)
Разделенный таким образом «квадрант» (7.1), х > 0, у > 0, будем
называть канторовой таблицей и отдельные «квадраты»,
составляющие разбиение, будем именовать клетками канторовой таблицы (см.
рис. 10).
t
т,п
—>-
т-1 т
Рис. 10
Клетку, определенную неравенствами (7.2), будем обозначать
символом Кт,п.
7.2.2. Сформулируем важное утверждение.
■ Лемма 7Л. Множество всех клеток канторовой таблицы счетно.
Доказательство. Определим следующим образом нумерацию
клеток канторовой таблицы. Сопоставим клетке Кш,п натуральное
число
*/(га,п) = (2т -1)2П~\

72
Гл. 1. Введение в математический анализ
Наглядно это означает, что клеткам, образующим самую нижнюю
строку таблицы, в качестве номера присваиваются последовательные
нечетные числа (см. рис. 11).
р
©
©"'
0
©
©'
<й>
®
©2
©
2
©
®
©
®3
©
3
©
®
©
(g)"4
©
4
@
©
© 5
©
5
©
©
©
-6
©
©
6
©J
Ас. //
Клетке каждой следующей строки присваивается номер,
получаемый удвоением номера клетки, расположенной непосредственно под ней.
Докажем, что отображение v : Кт)П н-> (2га — l)2n_1 E N взаимно
однозначно.
Действительно, возьмем две различные клетки Кт1,П1 ж КШ2^П2.
Если п\ ф П2, то числа ^(rai,ni), ^(т2,П2) делятся на разные
степени числа 2 и потому различны.
Если же п\ — П2, то т\ ф Ш2 и, значит, 2mi — 1 ф 2т2 — 1, откуда
^(mi,ni) ^ 1/(ш2,п2).
Таким образом, если клетки Кт1)П1 и Хт2)П2 различны, то и числа
i/(mi,ni) и ^(ш2,П2) различны, так что v есть взаимно однозначное
отображение канторовой таблицы в N.
Можно доказать, что построенное отображение будет
отображением канторовой таблицы на все N. Предоставим сделать это читателю.
Лемма доказана. ■
7.2.3. Применение канторовой таблицы во многих случаях позволяет
придать наглядный характер рассуждениям, посредством которых
доказывается, что те или иные множества не более чем счетны.

§ 7. Счетные множества
73
Пусть дано множество М. Предположим, что каждому элементу
множества М сопоставлена одна или несколько клеток канторовой
таблицы так, что для разных элементов соответствующие им множества
клеток не имеют общих элементов.
Наглядно это можно представить так, что все элементы множества
М вписаны в клетки канторовой таблицы. Один элемент может
вписываться в несколько клеток, но в каждой клетке таблицы должно быть
не более одного элемента множества. Не требуется, чтобы все клетки
канторовой таблицы были заняты элементами множества М.
Пусть Е — множество всех клеток канторовой таблицы, в которых
стоят элементы множества М.
Множество Е не более чем счетно (как подмножество счетного
множества). Сопоставив каждой клетке из Е заключенный в ней элемент
М, получим отображение £наМ.
В силу леммы 7.1, отсюда следует, что М не более чем счетно.
Строение канторовой таблицы во многих случаях облегчает
процесс вписывания в нее элементов множества.
7.2.4. Покажем, как, используя канторову таблицу, доказать,
например, счетность множества всех целых чисел. Запишем в клетки первой
строки канторовой таблицы числа 1,2,3, В первой клетке второй
строки запишем число 0. Наконец, в клетках третьей строки запишем
последовательно числа —1,-2,-3,... (см. рис. 11).
В результате, каждое целое число будет занесено в некоторую
клетку канторовой таблицы.
Сопоставив ему номер этой клетки в построенной выше нумерации
клеток канторовой таблицы, получим взаимно однозначное
отображение Z в N. Тем самым мы доказали, что множество Z является счетным.
7.2.5. Аналогичным образом может быть установлено, что и множество
всех рациональных чисел счетно.
Выведем это утверждение как следствие некоторой общей теоремы.
Пусть (Et)teT — произвольное семейство множеств, где индекс t
пробегает некоторое множество Г. (Это означает, что всякому t Е Т
сопоставлено некоторое множество Et.) Семейство (Et)teT называется
не более чем счетным, если множество индексов Г не более чем счетно.
Объединением семейства множеств (Et)teT называется
совокупность всех объектов ж, каждый из которых принадлежит по крайней
мере одному из множеств Et.
В Теорема 7.2. Объединение любого не более чем счетного
семейства множеств, каждое из которых не более чем счетно, есть не более
чем счетное множество.

74
Гл. 1. Введение в математический анализ
Доказательство. Пусть (Ег)гет — произвольное не более чем
счетное семейство множеств, Е — его объединение.
Зададим произвольно взаимно однозначное отображение v: Т —» N.
Для каждого t e T элементы множества Et разместим последовательно
в клетках строки с номером u(t) канторовой таблицы таким образом,
чтобы никакие два различных элемента множества Et не попали в одну
клетку. Это возможно, поскольку множество Et не более чем счетно.
Разумеется, может оказаться, что при этом будет занята лишь часть
клеток данной строки. В результате, все элементы множества Е
окажутся размещенными в клетках канторовой таблицы.
Пусть N — множество всех клеток канторовой таблицы, занятых
элементами множества Е. Множество N не более чем счетно.
Сопоставив каждой клетке из N записанный в нее элемент х е Е, получим
отображение N на Е. Следовательно, Е не более чем счетно.
Теорема доказана. ■
▼ Следствие. Множество всех рациональных чисел Q счетно.
Действительно, пусть Qn, где п е N, — множество всех чисел х е Q,
z _
представимых в виде х = -, где z e Z.
п
При каждом п е N соответствие — н-> z представляет собой взаимно
п
однозначное отображение множества Qn на Z. В силу предложения 7.1,
существование такого отображения доказывает, что каждое из множеств
Qn не более чем счетно.
Множество Q является объединением множеств Qn, откуда, в силу
теоремы 7.2, следует, что Q не более чем счетно. Так как Q бесконечно,
то Q счетно, что и требовалось доказать. ▼
7.2.6. В связи с полученным результатом, естественно возникает
вопрос: существуют ли бесконечные множества, не являющиеся счетными?
Положительный ответ на этот вопрос дан в главе 2.
■ Теорема 7.3. Произведение конечного числа не более чем счетных
множеств не более чем счетно.
Доказательство. Пусть даны множества
А1,А2,...,Ап, п> 1,
каждое из которых не более чем счетно. Требуется доказать, что
А = Ах х А2х '•- х Ап
есть не более чем счетное множество. Доказательство будем вести
индукцией по п. В случае п — 1 имеем: А = Ai, и результат очевиден.
Предположим, что для некоторого п е N теорема доказана.

Задачи
75
Пусть дана совокупность из п + 1 не более чем счетных множеств
А», г = 1,2,...,п + 1. Для t G An+i обозначим через Et совокупность
всех элементов х\, Х2, •.., #n+i множества А\ х Аг х • • • х An+i, у которых
#n+i — *• Имеем биективное отображение:
(ж1,...,жп) G Ai х А2 х ••• х Ап ь-> (я?1,..-,гсл,*) G #*.
По индукционному допущению множество Ai х Аг х • • • х Ап не
более чем счетно. Отсюда вытекает, что Et не более чем счетно при
каждом t G Ап+ь Очевидно, что
Ai х А2 х ••• х Ап+1 = (J J5t.
В силу теоремы 7.2, отсюда вытекает, что А\ х Аг х • • • х An+i — не
более чем счетное множество.
В силу принципа математической индукции, теорема доказана. ■
▼ Следствие. Для всякого п G N множество всех конечных
последовательностей х = (жьжг,... ,#п) из п рациональных чисел не более
чем счетно.
Действительно, указанное множество есть произведение
Qn = Q х Q х • • • х Q.
4 v '
п
Согласно следствию теоремы 7.2, множество Q не более чем счетно.
Отсюда вытекает, что Qn — не более чем счетное множество, что и
требовалось доказать. ▼
Задачи
1.1. Доказать, что для любых множеств А, Б справедливы равенства
А \ В = А \ (А П В) = (A U Б) \ Б, А\(А\В) = А Г) В.
1.2. Доказать, что для произвольных множеств A, Б, С выполняются
равенства
(А П В) U С = (A U С) П (Б U С), (A U Б) П С = (А П С) U (Б П С).

76
Гл. 1. Введение в математический анализ
1.3. Доказать, что для произвольных множеств А, В, С справедливы
равенства
(AUB)\C=(A\C)U(B\C),
A\(BUC) = (A\B)n(A\C),
А\(ВПС) = (А\В)и(А\С),
А П (В \ С) = (А П В) \ (А П С),
(AUB)\C=(A\C)U(B\ С).
1.4. Дано п множеств А±, А2,..., Ап. Сколько самое большее новых множеств
можно образовать из них, используя операции объединения, пересечения и
взятия разности?
1.5. Дано конечное множество X, имеющее п элементов. Пусть А\, А2,..., А^
— такое семейство подмножеств X, что каждое подмножество X может быть
получено из множеств А\, А2,..., А^ применением теоретико-множественных
операций пересечения, объединения и образования разности.
Найти наименьшее возможное значение к,
1.6. Даны множества Ai, Bi, А2, В2. Доказать равенства:
(Ai х Б1) П (А2 х В2) = (Аг П А2) х (Bi П Б2),
(Аг х Вг) \ (А2 х В2) = [Аг х (Вг \ В2)} U [(Аг \ А2) х (Вг П В2)] =
= [(Лх П Л2) х (Бх \ В2)] U [(Ai \ А2) х JBi].
1.7. Пусть А — конечное множество, п — число его элементов.
Доказать, что число подмножеств множества А, состоящих из т
элементе
тов, где 0 < т < п, равно С™ = — —.
т\(п — ту.
1.8. Пусть п(А) — число элементов конечного множества А.
Доказать, что для любых двух конечных множеств А, В справедливо
равенство п(А U В) = п(А) + п(В) — п(А П В).
Доказать, что для любых трех множеств А, В, С справедливо равенство
п(А U В U С) =
= п(А) + п(В) + п(С) - п(А Г) В)- п(А ПС)- п(В П С) + п(Л ПВПС).
1.9. Пусть дано отображение f : А —* В. Доказать, что для любых двух
множеств Р С В, Q С В справедливы равенства:
ГНр и Q) = Г\Р) и r^Q), Г\р \ Q) = ГЧр) \ f'HQ),
f-1(Pr\Q) = r1(P)nr1(Q)-
1.10. Даны отображение f : х *-+ х2 + рх + q ш интервал (а,(3). Определить
множество /_1((а,/3)).

Задачи
77
1.11. Дано отображение f : А —> В. Доказать, что f(f~1(M)) С М для
всякого М С В.
Привести примеры, показывающие, что равенство /(/""1(М)) = М,
вообще говоря, не верно.
Пусть Е С А. Доказать, что /-1(/(Е)) D Е.
Привести примеры, показывающие, что равенство f"~1(f(E)) = Е,
вообще говоря, не верно.
1.12. Дано отображение / : А —> В. Пусть Ег С А; Еъ С A; Mi С В;
Мъ С В. Доказать, что если Е\ С #2, TO f(Ei) С /(#2); если Mi С Мг, то
Г1{м1)сг1{м2у
1.13. Для произвольной функции у? : А —► R положим:
Ео(<Р) = У_1((05 оо)) = {х е А : <р(х) > 0},
Ei((p) = ^_1((--сх),0)) = {xGi: у>(ж) < 0}.
Пусть даны функции f : А —>Ши д : А —► R. Пусть .F(#) = f{x)g{x).
Доказать равенства
£o(F) = [ВД) П Ео(д)} U [ВД) П Si (<?)];
£i(F) = [ВД) П Ei(д)] U [Ei(f) Л Е0(<?)]
(теоретико-множественная запись правила решения неравенств вида:
f(x) ■ д(х) > 0; f(x) ■ д{х) < 0).
1.14. Пусть даны функции /» : А —* R, i = 1,2,...,». Положим F(x) =
= Л (я) • /2(2;) •... • /n(a:). Доказать, что
Eo(F) = [J [Eei (/1) П Е£2(Л) П • • • П Яе„ (/„)],
£l,£2>*">£n
где каждое из чисел si принимает только значения 0 и 1 и объединение берется
по множеству всех таких комбинаций чисел ei, £2> • • •, £п> сумма которых четна
и Eo(f); Ei(f) имеют тот же смысл, что и в задаче 1.13.
1.15. Пусть А и В — произвольные конечные множества, А имеет п
элементов, В имеет т элементов.
Доказать, что общее число отображений множества А в В равно тп.
1.16. Пусть А и В — конечные множества, п — число элементов
множества А, т > п — число элементов множества В. Определить число взаимно
однозначных отображений множества А в множество В.
1.17. Пусть А — произвольное множество, состоящее из п > к элементов.
Пусть ni > 0, П2 > 0,..., nfc > 0 — такие целые числа, что ni+ri2-\ f-rifc = п.
Доказать, что число отображений / : А —► 1^ таких, что множество
/_1(1) состоит из ni элементов, множество /~*1(2) из П2 элементов и т. д.,
наконец, f~1(k) из п& элементов, равно —-—- -.
ni'712! •• .7lfc!

78
Гл. 1. Введение в математический анализ
1.18. Дано отображение f : А —> В. Доказать, что следующие условия
эквивалентны:
а) / есть взаимно однозначное отображение;
б) J"1 (/(#)) = Е Для любого ЕСА;
в) f(E П М) = f(E) П f(M) для любых Е С А, М С А]
г) f(E) П /(М) = 0 для любой пары множеств Е С А, М С А такой,
что Е П М = 0;
д) /(£ \ М) = /(#) \ /(М) для любой пары множеств Е С А, М С А
такой, что Е Э М.
1.19. Пусть даны множества А, В, С, D и отображения f : А —> В, д : В —± С,
h : С -^ D. Доказать, что если каждая из суперпозиций д о / и h о д есть
взаимно однозначное отображение «на», то и все отображения д, h и / являются
взаимно однозначными отображениями «на».
1.20. Пусть даны произвольные множества А и В и взаимно однозначные
отображения f : А —> В ж д : В —* А.
Доказать, что существуют два подмножества А\, А2 С А и два
подмножества Bi,B2 С £ такие, что В± = /(Аг), А2 = д(В2), AiUA2 = A, jBiUjB2 = Б.
1.21. Пусть п(А) — число элементов конечного множества А.
Доказать следующую общую формулу.
Пусть AuA2,...,A т — конечные множества. Тогда
n(A1UA2U---UAm) = ^(-1)k\ X^ n<<Ail ПА{2 п'"пЛ^к)
fc=l Ll<ii<22.-.<ifc<m
Здесь во внутренней сумме суммирование ведется по всем комбинациям
индексов: zi, г2, •.., г/с, удовлетворяющих условию, стоящему под знаком суммы.
1.22. Пусть А ж В — конечные множества, п — число элементов А, т < п —
число элементов В. Обозначим через А™ число отображений / : А —* В
множества А на В. Тогда A™ = ml.
Вывести формулу, позволяющую вычислять А™ по А^_1? где к < т.
1.23. Доказать, что для любых двух чисел х и у справедливы равенства
тах{ж, у} = -(х + у + \х - у\) = у + {х - у)+ = х + (у - х)+,
тт{ж,2/} = -{х Л-у - \х - у\) = у - (х - у)~ =х- (у - х)~.
1.24. Доказать, что между любыми двумя вещественными числами
содержится иррациональное число.
1.25. Пусть х и у — произвольные вещественные числа. Говорят, что число
z лежит между хну, если либо х < z < у, либо у < z < x. Множество
ЛСМ называется выпуклым, если для любых х, у € А всякая точка z, лежащая
между х ж у также принадлежит А.
Доказать, что всякий отрезок / = (a, b) CM является выпуклым
множеством. _
Доказать, что всякое непустое выпуклое множество в R есть либо
одноточечное множество, либо отрезок.

Задачи
79
1.26. Пусть дано произвольное множество сегментов.
Доказать, что если любые два сегмента, принадлежащие этому
множеству, имеют по крайней мере одну общую точку, то существует число,
принадлежащее каждому сегменту данного множества.
1.27 (принцип разделяющего числа). Пусть А и В — произвольные непустые
подмножества множества R. Предположим, что для всякого х Е А и любого
у Е В выполняется неравенство х < у.
Доказать, что тогда найдется число I Е R такое, что для всякого х Е А
х < I и для всякого у Е В имеет место неравенство у > I.
1.28. Непустое множество АсК называется правым лучом, если для всякого
х Е А любое у > х, также принадлежит А. _
Доказать, что всякий правый луч в множестве Ж есть либо одноточечное
множество {оо}, либо промежуток вида (р, оо], где — оо < р < оо.
1.29. Говорят, что пара множеств (А, В) образует сечение множества М, если
Ш = A U В и для любых х Е А и у Е В выполняется неравенство х < у.
Доказать, что если (А, В) — сечение множества R, то найдется число
р Е М такое, что либо А = (—оо,р], В = (р, оо), либо А = (—оо,р), В = [р, оо).
Замечание. Доказательства утверждений задач 1.25—1.29
существенно опираются на аксиому непрерывности множества всех вещественных
чисел. Каждое из них равносильно аксиоме непрерывности, то есть в качестве
аксиомы непрерывности можно взять любое из этих предложений и вывести из
нее утверждение, принятое нами в качестве аксиомы непрерывности.
Отметим, что задача 1.29 содержит классическую форму аксиомы непрерывности,
которая чаще всего приводится в руководствах по математическому анализу.
1.30. Пусть А С Л£, В С К. — непустые подмножества множества МиА + В =
= {x = y + z\ye A, zeB}.
Доказать, что sup( А + В) = sup A + sup В; inf (А + В) = inf A -f- inf В. При
этом считаем, что — оо + х = — оо для любого ж<ооиоо-Ьж = оо для любого
х > —оо.
1.31. Пусть а Е М и та : М —> R — отображение, определенное следующим
образом: та(х) = х + а.
Доказать, что для любого непустого множества Е С М имеет место
равенство sup та(.Е) = supE + а в том случае, если supE < оо, и равенство
supта(Е) = supE, если sup22 = оо, а также inf та(Е) = inf E + а, если
inf Е > — оо, и inf та(Е) = inf E, если inf E = —оо.
1.32. Зададим функцию ф : Ш —* М, полагая ^(х) =_— х для любого х Е Л£.
Доказать, что для любого множества Е С М имеют место равенства
sup^(E) = —infE, т{ф(Е) = —supE. При этом считаем, что (—1)оо = —оо;
(—1)(—оо) = оо.
1.33. Пусть А — произвольное множество. Доказать, что для любых двух
функций f : А —>М, g : А —>R справедливы неравенства
inf [f(x) + р(я?)] > inf f(x) + inf <?(ж),
xGA xGA x£A
sup[f(x) + 0(e)] < sup /(ж) + sup р(ж).
Здесь сумму справа в случае, если одно из слагаемых равно — оо
(соответственно, оо), следует считать равной —оо (соответственно, оо).

80
Гл. 1. Введение в математический анализ
1.34. Пусть А — произвольное множество.
Доказать, что для всякой функции / : А —► R и любого числа А > 0
справедливы равенства: sup Xf(x) = Asup/(x), inf Xf(x) = A inf f(x).
x€A xeA X$A x£A
1.35. Пусть [x] — целая часть числа x £ Ш, а именно, [х] есть z £ Z такое,
что z < x < z + 1. Величина {x} = x — [x] называется дробной частью числа х.
Возьмем произвольно иррациональное число а и зададим последовательность
(xn)n£N, полагая хп = {па} при всяком п.
Доказать, что inf (хп) = 0, sup(a:n) = 1.
1.36. Дана функция / : [а, Ь] —> Ш. Доказать, что если для любого интервала
(c,d) множество /-1((с, d)) есть интервал, то / монотонна.
1.37. Доказать, что множество всех отрезков [а, 6], где а и 6 — рациональные
числа, счетно.
1.38. На плоскости задана декартова ортогональная система координат.
Доказать, что множество всех точек М, у которых обе координаты х и у
— рациональные числа, не более чем счетно.
1.39. Доказать, что всякое множество попарно не пересекающихся интервалов
в Ш не более чем счетно.
1.40. Построить биективное отображение множества Z в множество N.
1.41. Построить взаимно однозначное отображение отрезка [0,1] на отрезок (0,1].
1.42. Функция / : М —* R такова, что для всякого е > 0 множество значений
х £ М, для которых \f(x)\ > e, не более чем счетно. Доказать, что множество
тех х £ М, для которых f(x) ф 0, не более чем счетно.
1.43. Дана функция / : [0,1] —► М. Предположим, что существует число К < оо
такое, что | YJ /(#)| ^ К для всякого конечного множества М С [0,1].
Докажем
зать, что множество тех ж, для которых f(x) ф0, не более чем счетно.
1.44. Пусть А — счетное подмножество множества Ш. Предположим, что
множество А не имеет ни наименьшего, ни наибольшего элементов, и для любых
ж, у € А таких, что х < у, существует z G А, для которого х < z <y.
Доказать, что тогда существует такая строго возрастающая функция / :
А —* М, что f(A) = Q (Q — множество всех рациональных чисел).
1.45. Пусть Е — произвольное подмножество N. По индукции определим
функцию ve —► К, полагая ^я(1) = 1 при 1 € £ и ^(1) = 0 при 1 ф Е. Если
^е(п) определено для некоторого п £ N, то в случае, когда п + 1 £ Е, пусть
ve{?*> + 1) = »е{п) + 1, а если п + 1 Ф Е, положим 1>е{п + 1) = Ке(п)-
Доказать, что справедливы следующие утверждения:
a) если Е = 0, то ^(п) = 0;
b) если Е есть непустое конечное множество, то ve есть биективное
отображение множества Е в отрезок 1п множества N, где п — число
элементов множества Е;
c) если множество Е бесконечно, то функция ve взаимно однозначно
отображает множество Е на N.

Глава 2
ТЕОРИЯ ПРЕДЕЛА
Г
• Понятия предельной точки множества •
Определения предела и непрерывной функции • Теорема о
предельном переходе в неравенстве • Единственность
предела • Существование предела и асимптотическая
ограниченность функции • Теорема о зажатой
переменной • Операции с бесконечно малыми •
Теоремы о пределах суммы, произведения и частного •
Теоремы о замене переменной под знаком предела •
Теорема о существовании предела у монотонной функции
• Теорема о вложенных отрезках • Понятие
одностороннего предела • Критерий Коши — Больцано
существования конечного предела • Теорема Коши о
промежуточных значениях и ее следствия (теорема о
существовании непрерывной обратной функции) •
Теорема выбора Вейерштрасса • Теорема Вейерштрасса
о наибольшем и наименьшем значениях непрерывной
функции • Теорема Гейне о равномерной
непрерывности • Модуль непрерывности функции •
Критерий Гейне существования предела • Верхний и
нижний пределы последовательности •
_1

82
Гл. 2. Теория предела
§1. Определение и простейшие свойства предела
Понятие предела есть одно из главных средств, с помощью которых
определяется большинство основных объектов, изучаемых в
математическом анализе, в частности, такие как производная функции, сумма
ряда и многие другие.
Мы исследуем здесь понятие предела в простейшей ситуации, когда
речь идет о функциях, определенных на подмножествах множества всех
вещественных чисел R.
Сначала определяется понятие предельной точки для
произвольного множества МсК. Наглядно оно может быть охарактеризовано
следующим образом.
Число pGK есть предельная точка множества М, если М содержит
точки, произвольно близкие к точке р и в то же время с ней не
совпадающие. Всякое число р Е К, например, является предельной точкой
множества Ш.
Предположим, что f(x) есть числовая функция, определенная на
множестве МсК,и пусть р £R есть предельная точка множества М.
Если при приближении точки х к точке р по множеству М величина
f(x) неограниченно приближается к некоторому числу L, то говорят,
что L есть предел f(x) при х, стремящемся к р по множеству М.
Другое важное понятие, которое будет здесь введено, — это понятие
непрерывной функции. Говорят, что функция f(x) непрерывна в точке х
своей области определения, если при малом изменении точки х значение
f(x) изменяется мало.
Исследование общих свойств понятий предела и непрерывной
функции составляет центральную задачу настоящей главы. Далее будут
даны точные определения этих понятий и установлены некоторые их
основные свойства.
1.1. Понятие предельной точки числового множества
1.1.1. Для всякого вещественного числа р Е R определена некоторая
совокупность множеств, называемых окрестностями этого числа.
Если р — конечно, то окрестностью точки р мы будем считать
всякий интервал вида (р — е,р + е), где е > 0 произвольно, е Е R.
Если р = оо, то окрестностью точки р называется всякий
промежуток вида (К, оо], где К конечно. Для точки р = — оо окрестностями
р мы будем считать всевозможные промежутки вида [—oo,.fQ, где К
конечно.

§ 1. Определение и простейшие свойства предела
83
Совокупность всех окрестностей точки р Е Й мы будем обозначать
символом 0(р). Формула U Е 0(р) — это сокращенная запись
высказывания «17 есть окрестность точки р».
■ Лемма 1.1. Пусть р Е Й. Для любого конечного множества
{£/i,172,..., £/т}
окрестностей точки р существует окрестность U этой точки,
содержащаяся в каждом из множеств Щ, г = 1,2,..., га.
Доказательство. Пусть р — конечно. Тогда при каждом г =
= 1,2,... ,га выполнено Ui = (р — Si,p + £i), где Si > 0. Пусть е есть
наименьшее из чисел £i,£2,... ,£m. Очевидно, £ > 0. Положим 17 =
= (р — £,р + в). При каждом г = 1,2, ...,га имеем: £ < ^, откуда
р — 6i <р — е, р + е <р + Si к, значит, 17 С Щ при каждом г.
Множество U — это искомая окрестность.
Пусть р = оо. Тогда 17г = (.fQ, оо] при каждом г = 1,2,..., га. Если
К — это наибольшее из чисел К^ г — 1,2,..., га, то (К, оо] будет той
окрестностью точки р = оо, которая содержится в каждой из данных
окрестностей U%.
Аналогично рассматривается случай р = — оо.
Лемма доказана. ■
1.1.2. Определим понятие предельной точки числового множества.
Пусть дано произвольное множество М СИ.
Число р Е Й называется предельной точкой множества М, если
каждая окрестность U точки р содержит точку х множества М, отличную
от р.
В аннотации к этому параграфу предельная точка числового
множества была охарактеризована как точка, сколь угодно близко к которой
можно найти иные элементы данного множества.
Выражение: «сколь угодно близко к точке р существует число ж,
удовлетворяющее некоторому условию», как видно из данного выше
определения понятия предельной точки, следует трактовать так: «во
всякой окрестности точки р существует элемент ж, удовлетворяющий
этому условию». В данном случае условие, о котором идет речь,
таково: «ж Е М и х ф р».
Условие «ж Е М и х ф р» можно переписать как х Е М \ {р}.
Следовательно, условие: «р есть предельная точка множества М»
эквивалентно условию
(vc/ е 0(р))(3х еи)хем\{Р}

84
Гл. 2. Теория предела
или
(VJ7 еС?(р)) UnM\{p}^0.
Понятие предельной точки множества можно определить не
прибегая к теоретико-множественным представлениям.
Пусть pGK конечно. Окрестностью точки р является всякий
интервал вида (р — <5,р + <5). Утверждение: «# Е (р —<5,р + <5)» равносильно
следующему: «# удовлетворяет неравенствам р — 6 < х < р + <5».
Последнее, в свою очередь, равносильно условию: «точка х удовлетворяет
неравенству \х — р\ < £».
Следовательно, р Е R есть предельная точка множества Мс1в
том и только в том случае, если для всякого 6 > 0 можно указать х £ М
такое, что х ф р и \х — р\ < 6.
Если р = оо, то окрестностями точки р являются промежутки U
вида (if, оо], где — оо < К < оо. Условие х £U равносильно неравенству
х>К.
Окрестностью точки р = — оо является всякий промежуток вида
JJ = [—оо,К), где К Е R. Условие ж Е J7, в данном случае, равносильно
неравенству х < К.
Условие «оо есть предельная точка множества М С R» —
равносильно следующему: для всякого конечного числа К существует
элемент # множества М такой, что К < х < оо.
Условие «—оо есть предельная точка множества М» — равносильно
следующему: для всякого К Е R существует элемент # множества М
такой, что К > х > — оо.
Совокупность всех предельных точек множества М будем
обозначать символом СгтМ. Применяя это обозначение, высказывание: «р
есть предельная точка множества М» сокращенно можно записать так:
«р G CimM».
Пусть дано множество М С R. Предположим, что число р Е R не
является предельной точкой множества М. Тогда найдется окрестность
U точки р, не содержащая элементов множества М, отличных от р.
Действительно, допустим, что такой окрестности у точки р нет. Тогда
всякая окрестность точки р содержит точки множества М, отличные от
р, и, значит, согласно определению, р есть предельная точка множества
М, что противоречит тому, что, согласно предположению, р не является
предельной точкой множества М.
Пусть М С R. Мы получаем, что если р Е М и р ^ CimM, то
найдется окрестность J7 точки р, в которой нет элементов множества М,
отличных от р. Это означает, что в данном случае множество U П М
состоит из единственного элемента — точки р, то есть U П М = {р}.

§ 1. Определение и простейшие свойства предела
85
Если р Е М не является предельной точкой множества М, тор
называется изолированной точкой множества М.
Ш Лемма 1.2. Пусть М и Е — произвольные подмножества Й.
Предположим, что р Е Ж есть предельная точка множества М. Если
Е Э М, то р является предельной точкой также и множества Е.
Доказательство. Пусть р Е СгтМ. Зададим произвольно
окрестность U точки р. Тогда, согласно определению предельной точки,
для всякой окрестности U точки р множество U П (М \ {р}) не пусто и
так как Е э М, то также и U П (Е \ {р}) ф 0, как бы ни была
выбрана окрестность U точки р. Это означает, что р есть предельная точка
множества Е.
Лемма доказана. ■
■ Лемма 1.3. Пусть дано множество Mel. Если число р Е Ш есть
предельная точка множества М, то, какова бы ни была окрестность Uo
точки р, число р является предельной точкой множества G — М DUq.
Доказательство. Пусть выполнены все условия леммы. Пусть
U есть произвольная окрестность точки р. Согласно лемме 1.1, найдется
окрестность Ui точки р такая, что Uo D Ui и U D U±.
Так как, по условию, р есть предельная точка множества М, то
найдется х £ М такое, что х Е Ui и в то же время х ф р. Так как
Ui С Uo, то х Е Uo и, значит, х Е Uo П М = G. Так как Ui С U, то
хеи.
Окрестность U точки р была задана произвольно. Следовательно,
мы получаем, что всякая окрестность U точки р содержит элементы
множества G, отличные от р. По определению, это и означает, что р
есть предельная точка множества G.
Лемма доказана. ■
1.1.3. Докажем предложение, устанавливающее связь понятия
предельной точки с понятиями точной верхней и точной нижней границ
числового множества.
■ Теорема 1.1. Пусть дано непустое множество М С Й и пусть
р = supM. Если р не является элементом М, то р — это предельная
точка М. Аналогично, если р — inf М и р £ М, то р — предельная
точка множества М.
Доказательство. Сначала докажем утверждение теоремы,
относящееся к точной верхней границе множества М.

86
Гл. 2. Теория предела
Пусть М есть непустое множество и р — supM, причем р не
принадлежит М. Так как, по условию, множество М непусто, то
существует хотя бы одно х Е М. Тогда х < р. Поскольку р £ М, то х ф р и,
стало быть, х < р. В частности, отсюда следует, что —оо < р.
Зададим произвольно U Е 0(р). Множество U в случае, когда р
конечно, есть интервал U' = (р — е,р + е), а если р = оо — промежуток
U = (X, оо]. Левый конец промежутка U обозначим символом р'.
В обоих случаях р' < р и, значит, согласно признаку точной верхней
границы, найдется # Е М такое, что р' < х < р. Пусть точка х такова.
Имеем: р' < х < р. Отсюда вытекает, что х Е U. Так как р £ М,
то х ф р.
Таким образом, любая окрестность U точки р содержит элементы
множества М, не совпадающие с точкой р. Согласно определению, это
и означает, что р есть предельная точка множества М.
Утверждение, касающееся точной нижней границы, доказывается
аналогично. Формально, достаточно в рассуждениях, проделанных
выше, надлежащим образом изменить знаки неравенств и заменить «—»
на «+».
Мы предоставляем читателю выполнить эту работу.
Теорема доказана. ■
Напомним, что символ N& означает совокупность всех целых чисел
z > fc, где к — произвольное целое число.
▼ Следствие 1. Число оо есть предельная точка множества N&.
Действительно, как показано в гл. 1, оо = supNfc. Так как оо не
является элементом Nfc, то, в силу теоремы 1.1, отсюда следует, что оо
есть предельная точка множества М&, что и требовалось доказать. ▼
▼ Следствие 2. Если МсК есть отрезок (а, Ь), где a < b, то
совокупность всех предельных точек множества М совпадает с замкнутым
отрезком [а, Ь], то есть
Cim((a,b)) = [а,Ь].
Доказательство. Положим Mq = (а, Ь). Согласно лемме 4.1
главы 1, a — inf Mo, b = sup Mo. Так как a £ Mo и b £ Mo, то, в силу
теоремы 1.1, а и b суть предельные точки Мо. Очевидно, Мо С М.
Тогда, как следует из леммы 1.2, а и b являются предельными точками
множества М.

§ 1. Определение и простейшие свойства предела
87
Пусть а < р <Ь. Применяя доказанное утверждение к интервалам
(а,р) и (р, Ь), получаем, что р есть предельная точка каждого из них и,
стало быть, согласно лемме 1.2, р является предельной точкой М.
Мы доказали, таким образом, что все точки замкнутого отрезка
[а,Ь] являются предельными точками множества М.
Покажем, что других предельных точек множество М не имеет.
Пусть р £ [а, Ь]. Тогда либо р < а, либо р> Ъ.
Рассмотрим случай р < а. Если р = —оо, то пусть С7 = [—оо,а), a
если р — конечно, то пусть U = (р — е,р + е), где е = а — р.
Множество U есть окрестность точки рив обоих случаях а
является правым концом промежутка U. Отсюда видно, что U не содержит
точек множества М.
Таким образом, для данного р существует окрестность U £ 0(р),
не содержащая точек множества М, и, значит, р не является предельной
точкой множества М.
Аналогичным образом устанавливается, что никакое число р > Ъ
не может быть предельной точкой множества М = (а,Ь).
Следствие доказано. ▼
1.2. Определение предела функции на произвольном
подмножестве R
1.2.1. Зададим произвольным образом множество Мс1и функцию
/ : М —► Е. Пусть р есть предельная точка множества М.
Число L ЕШ называется пределом функции f{x) при #,
стремящемся к точке р по множеству М, если выполняется следующее условие:
каково бы ни было число е > 0, найдется окрестность U точки р такая,
что для всякой точки х G М, принадлежащей данной окрестности и
отличной от р, имеет место неравенство \f(x) — L\ < е.
В этом случае говорят также, что f(x) стремится к L, когда х
стремится к р по множеству М, в обозначениях: f(x)—>L при х -* р,
х Е М. Если L £ Ш есть предел функции /(#) при #, стремящемся к
точке р по множеству М, то мы будем писать:
х—*р,х£М
Данное определение символически может быть записано
следующим образом:
х—+р,х€М
& (Ve > 0) (3U е 0(p))(\/x) :{xeUD(M\ {р}) =► \f(x) -L\< e}.

88
Гл. 2. Теория предела
Наглядный смысл приведенного определения таков.
Число L E R есть предел функции f(x) при х, стремящемся к точке
р по множеству М, если при приближении х к точке р по множеству М
значение f(x) неограниченно приближается к L.
Каково бы ни было е > О, разность f(x)—L по модулю будет меньше
этого г для всех х Е М, достаточно близких к точке р и отличных от р.
Точный смысл высказывания «для всех х Е М, достаточно
близких к точке р и отличных от р» таков: существует окрестность U
точки р такая, что условие, о котором идет речь, выполняется для всех
х Е М, принадлежащих U и отличных от р. В нашем случае это
условие \f(x) — L\ < е.
Предположим, что р — конечно. Тогда всякая окрестность U точки
р представляет собой интервал вида (р — <5,р + <5), и условие х Е U
равносильно условию: точка х удовлетворяет неравенству \х — р\ < <5.
В силу сказанного, определение того, что значит, что L Е Ш
является пределом f(x) при х —> р по М для случая, когда р конечно, может
быть представлено в следующей эквивалентной форме.
Каково бы ни было е > О, найдется число 6 > О такое, что для
любого х Е М, отличного отри удовлетворяющего условию \х — р\ < <5,
выполняется неравенство: \f(x) — L\ < е.
Функция / : М —> Ж называется бесконечно малой при х,
стремящемся к р Е Сгт(М) по множеству М, если lim f(x) = 0. Тот
х—+р,х£М
факт, что функция f(x) бесконечно мала при х —> р по М, символически
записывается следующим образом: f(x) = о(1) при х —> р по М.
Переформулируя определение предела применительно к данному
частному случаю, получаем, что функция / является бесконечно малой
при х, стремящемся к р по множеству М, если для всякого е > 0
существует окрестность U точки р такая, что для любого х Е U П (М \ {р})
выполняется неравенство: |/(ж)| < е.
В определении бесконечно малой функции налагается некоторое
условие на абсолютные величины значений функции /. Отсюда ясно,
что f(x) = о(1) при х —> р по множеству М в том и только в том случае,
когда \f(x)\ = о(1) при х —► р по М.
■ Лемма 1.4. Пусть дана вещественная функция f(x),
определенная на множестве М С Ё, я пусть р Е Сгт(М). Число L еШ является
пределом f(x) при х, стремящемся к р по множеству М в том и только
в том случае, если разность f(x) — L есть функция, бесконечно малая
при х, стремящемся к р по множеству М.
Доказательство. Пусть L = lim f(x). Рассмотрим раз-
х—+р,х£М
ность: u{x) = f(x) — L. Зададим произвольно е > 0.

§ 1. Определение и простейшие свойства предела
89
Согласно определению предела, найдется окрестность U точки р
такая, что для любого х Е U П (М \ {р}) выполняется неравенство:
\f(x)-L\<e,
то есть \и(х)\ < е для всех я, принадлежащих [/пМи отличных от р.
В силу произвольности е > О, это означает, что
lim u(x) = О,
то есть функция и(х) является бесконечно малой при х —> р по М.
Обратно, предположим, что гх(х) = о(1) при я —► р по М. Зададим
произвольно е > 0. По нему найдется £7 е 0(р) такое, что для всякого
х е U П М, отличного от р, выполняется неравенство: \и(х)\ < е, то есть
если х eUn(M\ {р}), то |/(ж) - Ц < е.
В силу произвольности е > 0, тем самым установлено, что
£= linlA/f/(x)-
Лемма доказана. ■
1.2.2. Далее нам потребуется понятие бесконечного предела.
Пусть даны множество МсМи его предельная точка р е R.
Будем говорить, что функция / : М —> R имеет равный оо предел
при х —> р по множеству М, если для всякого конечного К е R можно
указать U е О(р) такое, что для любой точки ж е Uf)(M\{p}) выполняется
неравенство: f(x) > К.
Будем говорить, что функция / : М —> R имеет равный — оо предел
при х —> р по множеству М, если функция х \-+ [—f(x)] имеет предел,
равный оо при х —> р.
Обозначения, введенные для случая конечных пределов,
автоматически распространяются на случай предела, равного ±оо.
Докажем предложение, которое позволяет в дальнейшем сводить
случай бесконечных пределов к случаю, когда предел конечен.
Введем некоторые вспомогательные функции R+ и i?_, полагая для
хеш
/ - при х > 1;
К+(х) = < х
[ 1 при х < 1
и R-(x) — R+(—x).
Очевидно, функция R+ убывает, функция i?_ возрастает и для всех
х е R выполнены неравенства 0 < R+{x) < 1, 0 < R-(x) < 1.

90
Гл. 2. Теория предела
■ Лемма 1.5. Пусть даны множество М С К и его предельная
точка р. Для того чтобы функция f, определенная на множестве М, имела
предел, равный оо, при х, стремящемся к р по множеству М,
необходимо и достаточно, чтобы функция i?+[/(#)] имела предел, равный нулю,
при х —> р по М.
Функция f : М —> К имеет предел, равный —оо при х —> р в том и
только в том случае, если lim i?_ [/(#)] = 0.
х—+р,х£М
Доказательство. Необходимость. Пусть
L = lim f{x) = оо.
х—*р,х£М
Зададим произвольно е > 0 и положим К = -.
Согласно определению предела, равного оо, найдется окрестность С7
точки р такая, что для всякого х £ М, отличного от р и принадлежащего
окрестности U, выполняется неравенство: f(x) > К. Отсюда следует,
что для всех таких х имеет место неравенство: 0 < i?+[/(#)] < е.
Действительно, если е > 1, то это верно для всех х, а значит, и для
любого х £ (иг\М\ {р}).
Если е < 1, то из условия f(x) > К == - следует, что /(#) > 1, и,
стало быть, R+[f(x)] = ( г. Тогда из условия /(#) > X вытекает, что
Д+[/(яг)]<е.
Так как J?+[/(#)] — неотрицательно, то для всякого £ > 0
существует окрестность [7 точки р такая, что для любого х € М \ {р},
принадлежащего окрестности U, выполняется неравенство: I-R+[/(#)] | < £-
Согласно определению предела, это и означает, что
lim Д+[/(я?)] = 0.
х—+р,х£М
Предположим, что lim f(x) = — оо. Согласно определению,
х—+р,х£М
lim [—f(x)] = оо и, значит, по доказанному,
0= lim Д+[-/(ж)] = lim Д-[/(ж)].
х—*р,х£М х—+р,х£М
Необходимость условия леммы доказана.
Докажем его достаточность.

§ 1. Определение и простейшие свойства предела
91
Предположим, что имеет место равенство: lim R+[f(x)] = 0.
х—>р,х£М
Требуется доказать, что lim f(x) = оо.
х—>р,х£М
Зададим произвольно число К Е R, и пусть е = 1 при К < 1 и
е = — при Jf > 1.
J\
Очевидно, во всех случаях - > К. Согласно определению предела,
равного нулю, по данному е найдется окрестность U точки р такая, что
для любого х eU П (М \ {р}) выполняется неравенство: Л+[/(ж)] < е.
Возьмем произвольно х Е U П (М \ {р}). Имеем: Д+[/(#)] < е.
Так как е < 1, то из определения функции Д+ следует, что в этом
случае f(x) > 1, и, значит, R+[f(x)} = г. Отсюда получаем, что для
данного ж выполняется неравенство: f(x) > - > К.
Таким образом, для всех х Е UC\M\{p} выполняется неравенство:
/(*) > К.
В силу произвольности К Е М, доказано, что функция f[x) имеет
предел, равный оо при х —> р по М.
Итак,
lim Д+[/(а;)] = 0=* lim /(ж) = оо.
ж—*р,жЕМ ж—>р,жЕМ
Если lim R-[f(x)] = 0, то так как R-[f(x)] — Д+[—/(ж)], из
ж—>р,х£М
доказанного следует, что lim [—/(#)] = оои, значит, согласно опре-
х—*р,х£М
делению предела, равного — оо,
lim f(x) = —оо.
х—>р,х£М
Достаточность условия леммы также установлена.
Лемма доказана. ■
1.2.3. Пусть (хп)П£щ есть числовая последовательность, то есть
функция, областью определения которой является множество 1%. Это
множество Nfc имеет предельную точку оо.
Предел функции х : п Е Nfc ь-> хп при п —► оо по множеству Nfc
называется пределом последовательности (хп)п^к, и обозначается
символом lim xn.
п—*-оо _
Если L Е М есть предел последовательности (#n)neNfc, то мы будем
также говорить, что хп стремится к L при п —> оо.

92
Гл. 2. Теория предела
Последовательность вещественных чисел (хп)п^к называется
сходящейся,, если она имеет конечный предел.
Представим определение предела последовательности в форме, которая
является общепринятой. Справедливо следующее предложение.
■ Лемма 1.6. Пусть дана числовая последовательность (xn)neNk-
Число LGM является пределом этой последовательности в том и только
в том случае, если для всякого е > О можно указать номер n Е Nfc такой,
что при каждом п >п выполняется неравенство: \хп — L\ < е.
Последовательность (xn)n^k имеет предел, равный оо, в том и
только в том случае, если для всякого К < оо существует n E N& такое,
что при каждом п>п выполняется неравенство хп > К.
Доказательство. Пусть L Е (—оо, оо] есть предел данной
последовательности. Выберем произвольно некоторое число. В случае, когда
L — конечно, это число мы обозначим е и потребуем, чтобы
выполнялось неравенство е > 0. Если L = оо, то это число обозначим символом
if и от него будем требовать только, чтобы оно было конечно.
Согласно определению предела, найдется окрестность U точки оо
такая, что для всякого n E U П N& в случае конечного L выполняется
неравенство \хп — L\ < е, в случае L = оо — неравенство хп > К.
Окрестность U есть полуинтервал вида (Н, оо]. Выберем
произвольно n E Nfc такое, что п > Н. Если п > п, то n E U, и, значит, для
этого п выполняются неравенства, требуемые определением предела, то
есть \хп — L\ < е в случае конечного L, и хп > К, если L = оо.
Необходимость условия леммы установлена.
Докажем достаточность. Пусть L конечно.
Предположим, что для всякого е > 0 можно указать номер п такой,
что для любого п>п выполняется неравенство: \хп — L\ < е.
Зададим произвольно е > 0 и найдем соответствующее значение
п Е 1%. Положим U = (п,оо]. Если n E U, то п > п, и, следовательно,
\хп - L\ < е.
Итак, для всякого е > 0 существует окрестность U точки оо такая,
что для любого n £UDNk выполняется неравенство: \хп — L\ < е. Тем
самым доказано, что L есть предел последовательности (#n)neNfc.
В случае L = оо рассуждения аналогичны.
Лемма доказана. ■
1.2.4. Рассмотрим некоторые примеры.
Пример 1. Пусть М есть произвольное подмножество Й и пусть
pGl есть предельная точка М.

§ 1. Определение и простейшие свойства предела
93
Предположим, что функция / : М —> R постоянна на множестве М,
то есть существует число LGl такое, что /(ж) = L для всех ж G М.
Тогда число L и является пределом функции f(x) при х —> р.
Действительно, пусть дано е > 0. Пусть U есть произвольная
окрестность точки р. Для всякого iGM, принадлежащего
окрестности U и отличного от р, \f(x) — L\ = 0 < е. Согласно определению
предела, это означает, что L = lim f{x).
х—*р,х£М
Пример 2. Пусть М — произвольное множество вещественных
чисел, р — предельная точка М. Пусть jm есть отображение вложения
множества Мв1, Jm(x) = х для всякого х G М. Тогда для всякой
точки р G Cim(M) предел lim jm(x) существует и равен р.
х—*р,х£М
Докажем это утверждение. Пусть р G Cim(M) — конечно.
Зададим произвольно е > 0. Положим 6 = е и U = (р — 6,р + 6).
Тогда для всякого х G М \ {р} такого, что х G U, имеет место
неравенство: |^м(ж) — р| = \х — р\ < 6 = е.
В силу произвольности е > 0, р есть предел jm(x) при ж —> р по М.
Пусть р = оо. Зададим произвольно К < оо. Пусть С/ есть
окрестность (К, оо] точки р. Тогда для всякого х G М П С/ выполняется
неравенство: зм{х) — х > К. В силу произвольности К < оо, справедливо
р = оо= lim jm(x).
х—*р,х£М
Пусть р = — оо. Докажем, что в этом случае
lim [-Jm(z)] = оо.
х—*р,х£М
Зададим произвольно К G R и положим С/ = [—оо, —if). Очевидно,
C/G0(-oo).
Для всякого ж Е t/ПМ имеем: jm(x) = х < —К и, значит,
—Jm(х) > К. В силу произвольности К € R этим доказано, что
lim [-Jm(z)] = оо
х—► — оо,жЕМ
и, следовательно,
lim jm(z) = -оо.
Пример 3. Применяя результат примера 2 к случаю, когда М = ЛГ,
получим, что предел последовательности (xn)neN такой, что хп = п для

94
Гл. 2. Теория предела
всех п, равен оо, то есть lim n = оо. Согласно определению, отсюда
п—юо
следует, что lim (—п) = —оо.
п—юо
Воспользуемся результатом леммы 1.5. Имеем: Д+(п) = — для
ть
всех п. На основании леммы 1.5 получаем, что последовательность
( — ) имеет предел, равный нулю, lim — = 0.
1.3. Понятие непрерывной функции
1.3.1. Пусть дана функция / : М -+ М, где Met. Функция /
называется непрерывной в точке р G М„ если выполнено следующее условие:
каково бы ни было е > 0, по нему найдется окрестность С/ точки р такая,
что для любой точки х множества М, принадлежащей окрестности £/,
выполняется неравенство \f(x) — f(p)\ < е.
Это определение может быть записано следующим образом:
(функция / : М —> R непрерывна в точке р G М) Ф>
<* (Ve > 0) {3U G 0(p))(Vrc G С/П M) \f(x) - /(р)| < е.
Говорят, что функция / : М —> R непрерывна, если она непрерывна
в каждой точке множества М.
Понятие непрерывности, как и понятие предела, мы определяем
только для функций с конечными значениями. Это не связано с какими-
либо трудностями принципиального характера, а вызвано только
соображениями простоты изложения.
■ Теорема 1.2. Пусть дано множество М с И и р G М является
предельной точкой множества М. Для того чтобы функция f : М —► R
была непрерывна в точке р, необходимо и достаточно, чтобы ее значение
в этой точке было пределом f(x) при х, стремящемся к р по М.
Доказательство. Пусть р G М есть предельная точка
множества М. Предположим, что функция / непрерывна в точке р G М.
Зададим произвольно е > 0. Согласно определению функции,
непрерывной в точке р, найдется окрестность U точки р такая, что для
всякого х G М, принадлежащего окрестности (7, выполняется
неравенство: \f(x) — f(p)\ < е. В частности, это неравенство выполняется и для
точек х G (U П М) \ {р}, как это требуется определением предела.
Так как е > 0 было выбрано произвольно, то тем самым доказано,
что
/(р)= Нт /(*).

§ 1. Определение и простейшие свойства предела
95
Теперь пусть для функции / : М —► R справедливо соотношение:
f(p)=]imf(x).
х—*р
Зададим произвольно е > 0. По нему найдется окрестность U точки
р такая, что если х Е Un(M\{p}), то \f(x) — f(p)\ < е. Это неравенство
выполняется для всех х Е U П М. Если х ф р, то неравенство верно, в
силу выбора окрестности U. Если же х = р, то \f(x) — f(p)\ = 0 < е.
Так как е > 0 было выбрано произвольно, то тем самым
установлено, что функция / непрерывна в точке р.
Теорема доказана. ■
1.4. Теорема о предельном переходе в неравенстве.
Единственность предела
1.4.1. Доказательство основного результата этого раздела существенно
опирается на следующую лемму.
■ Лемма 1.7. Пусть даны функция f : М —► М и число L Е 1.
Предположим, что
L — lim /(#).
х—*р,х£М
Тогда для любого числа К ф L можно указать окрестность U точки
р такую, что для всякого х Е М, принадлежащего множеству U и
отличного отр, в случае К < L выполняется неравенство К < fix), а в случае
К > L — неравенство К > f(x). (Иначе говоря, если х Е U П (М \ {р}),
то величина f(x) лежит по ту же сторону от К, что и предел
L функции /.)
Доказательство. Пусть L = lim f(x) и К ф L, К Е Ё.
х—*р,х£М
Предположим сначала, что L — конечно. Тогда найдется число
е > 0 такое, что если L < К, то L + е < К, а если L > К, то L — е > К.
Согласно определению предела, найдется окрестность U точки р
такая, что для всех х Е С/ПМ, отличных отр, выполняется неравенство:
\f(x) - L\ < е, то есть L - е < f(x) < L + е для любого х Е U П М,
отличного от р. Отсюда, в силу выбора е > 0, следует, что для всех
таких х в случае К < L выполняется неравенство К < /(#), а если
К > L, то неравенство if > /(ж), и для случая конечного L требуемое
утверждение доказано.
Пусть L = оо и пусть К ф L. Тогда К < L и, значит, согласно
определению предела, равного оо, найдется окрестность U точки р такая,
что для любого х Е U П (М \ {р}) выполняется неравенство: f(x) > К.
Данная окрестность U точки р, очевидно, и есть искомая.

96
Гл. 2. Теория предела
Пусть L = — оо. По определению это означает, что
lim J~/(*)] = °°-
Зададим произвольно К G Ди положим Кг = —К. Согласно
определению предела, равного оо, найдется окрестность U точки р такая,
что для всех х G U П (М \ {р}) выполняется неравенство: —f(x) > К\,
и, значит, f(x) < —К\ = К для всех таких х.
Лемма доказана. ■
Т Следствие 1. Пусть даны произвольное множество М С Ш и
функция f : М —► М. Предположим, что функция f непрерывна в точке
хо G М. Если хо — конечно, то для всякого числа К ф f(xo) найдется
число 6 > О такое, что для всех х G М, для которых \х — хо\ < 8, при
К < f(xo) выполняется неравенство К < f(x), а при К > /(#о) —
неравенство К > f{x).
Если хо = оо, то для любого К ф f(xo) найдется число Н < оо
такое, что если х € М и Н < х, то при К < /(жо) выполняется
неравенство К < fix), а при К > f(xo) — неравенство К > f(x).
Если хо = — оо, то для любого К ф f[xo) можно указать число
if > — оо такое, что если х£Мих>Н,то при К < f(xo) выполняется
неравенство К < /(#), а при К > /(жо) — неравенство К > f{x).
Доказательство» Если хо не является предельной точкой
множества М, то существует окрестность U точки хо такая, что U П М
состоит из одной этой точки. Для всякого х G U П М имеем: f(x) = /(#o)
и, стало быть, для х G UDM выполняется любое неравенство, которому
удовлетворяет f(xo).
Предположим, что хо есть предельная точка множества М.
Согласно теореме 1.2, условие — функция / непрерывна в точке
хо G М — равносильно тому, что f(xo) есть предел функции / по
множеству М. В силу леммы 1.7, для всякого К ф f(xo) можно указать
окрестность U точки р такую, что для любого х G U П М, отличного от
хо, в случае К < f(xo) выполняется неравенство К < fix), а в случае
К > f(xo) — неравенство f(x) < К. В силу выбора К, неравенство
выполняется также и для х = хо.
Осталось заметить, что в случае конечного хо окрестность U
представляет собой интервал (жо — 6, хо + 8), где 6 > 0, для хо — оо
множество U является промежутком вида: (Н, оо], а если хо = — оо, то
Е7 = [-оо,#).
Следствие доказано. Т

§ 1. Определение и простейшие свойства предела
97
▼ Следствие 2. Пусть L € R есть предел числовой
последовательности (xn e M)nGNm. Тогда для всякого К ф L найдется номер n e Nm такой,
что для всякого п>п в случае L > К выполняется неравенство хп > К,
а в случае L < К — неравенство хп < К,
Действительно, пусть выполнены все условия следствия. Согласно
лемме 1.7, найдется окрестность С/ точки оо такая, что для всех n e C/fiNm
в случае L > К выполняется неравенство хп > К, а в случае L < К
— неравенство хп < К. Окрестность С/ есть промежуток вида (Я, оо].
Возьмем произвольно п е С/ П Nm. Если п > п, то n e С/, откуда ясно, что
номер п и есть искомый.
Следствие доказано. ▼
1.4.2. Справедлива следующая
■ Теорема 1.3 (о предельном переходе в неравенстве). Пусть даны
функции f : М —>R и g : М —> R, каждая из которых имеет предел при х,
стремящемся к р по множеству М. (Здесь М с R и р е Cim M.)
Предположим, что существует окрестность С/о точки р такая, что
для всякого х е М, принадлежащего окрестности С/о и отличного от р,
выполняется неравенство: f(x)<g(x). Тогда
lim f{x) < lim o(i).
х—*р,х£М х—>р,х£М
Доказательство. Для упрощения опустим некоторые детали в
обозначении пределов и положим lim f(x) = К, \\mg(x) = L.
Требуется доказать, что К < L. Предположим, напротив, что К > L. Тогда
найдется число Н такое, что К > Н > L.
Поскольку К = lim f(x) и К > Я, то, согласно лемме 1.7, найдется
окрестность C/i точки р такая, что для всякого х е U\ П (М \ {р})
выполняется неравенство: f(x) > Н.
Так как L = \\mg{x) и1<Я, то, применяя лемму 1.7 к функции д,
получим, что существует такая окрестность С/г точки р, что для любого
х е С/г П (М \ {р}) имеет место неравенство: д(х) < Я.
Согласно лемме 1.1, точка р имеет окрестность С/, содержащуюся в
каждой из указанных окрестностей С/о, C/i и С/г. Возьмем произвольно
точку хо € М, принадлежащую окрестности С/ и отличную от р.
Такая точка хо заведомо существует, поскольку р есть предельная точка
множества М. Очевидно, хо G С/о и одновременно хо G C/i и хо € С/г.
Так как #0 € С/о, то f(xQ) < д(х0). С другой стороны, х0 е U\ и, значит,
/Ы > Я.
(1.1)

98
Гл. 2. Теория предела
В то же время х0 е £/25 и потому
д(хо) < Я. (1.2)
Из неравенств (1.1) и (1.2) вытекает, что f(x0) > д{х0). Таким
образом, мы получаем, что одновременно /(#о) < <?(#о) и f(xo) > д(хо).
Допущение, что К > L, приводит нас, следовательно, к
противоречию. Значит, К < L, что и требовалось доказать. ■
▼ Следствие 1. Предположим, что каждая из функций f : М —► R и
р : М —► R имеет предел при ж, стремящемся jsc p по множеству М. Если
f(x) < g(x) для всех х е М, то
x—*p,xGM ж—ф,ж€М
Доказательство очевидно. ▼
т Следствие 2. Всякая вещественная функция, определенная на
множестве М с R, имеет не более одного предела при х, стремящемся
кр£ Cim(M).
Доказательство. Пусть числа К и L таковы, что
К = lim f(x) и L = lim /(#).
х—>р,х£М х-*р,х£М
Так как для всех х е М выполняется неравенство f(x) < /(#), то, в силу
следствия 1, отсюда вытекает, что К < L. С другой стороны, для всех
х е М верно также соотношение f(x) > f(x). Это позволяет заключить,
что К > L.
Таким образом, мы имеем одновременно: К < L и К > L. Значит,
L = К, что и требовалось доказать. ▼
1.5. Существование предела и асимптотическая
ограниченность
Всюду в этом разделе М обозначает подмножество множества R, а
р — это некоторая предельная точка М.
1.5.1. Пусть / есть или вещественная, или комплексная функция,
определенная на множестве М. Говорят, что функция / является
асимптотически ограниченной при х, стремящемся к р по множеству М, если
существуют число К е R и окрестность U точки р такие, что для всякого
х eU Г\(М\ {р}) выполняется неравенство: \f(x)\ < К.

§ 1. Определение и простейшие свойства предела
99
Если функция / удовлетворяет данному условию, то мы будем
писать: f(x) = 0(1) при х —> р, х G М.
Пусть дана числовая последовательность (xn)neNk- Множество N&
имеет предельную точку оо. Если последовательность (хп)п^к является
асимптотически ограниченной при и —> оо, то мы будем говорить, что
эта последовательность асимптотически ограниченная.
Ш Лемма 1.8. Всякая асимптотически ограниченная числовая
последовательность является ограниченной.
Доказательство. Пусть (хп)пет$к есть асимптотически
ограниченная числовая последовательность. Это означает, что найдутся число
К G Ш и окрестность U = (#, оо] точки оо такие, что для всякого номера
n EU выполняется неравенство: \хп\ < К.
Пусть no G Nfc таково, что Н < по. Обозначим через Ко
наибольшее из чисел
\xk\,\xk+i\,. •. ,\хПо\, К.
Возьмем произвольно n G N&.
Если п < по, то \хп\ есть одно из чисел |ж*|, |#fc+i|,..., \хПо\, и,
значит, \хп\ < Ко.
Если же п > по, то п > Н и, стало быть, п G C/flNfc. Следовательно,
|я?п| <К<К0.
Итак, мы показали, что существует число Ко < оо такое, что
\хп\ < ^о при всех п G Nfc. Это и означает, что (#n)neN есть
ограниченная последовательность.
Лемма доказана. ■
1.5.2. Следующая теорема показывает, что понятие асимптотической
ограниченности описывает некоторое свойство функции, имеющей
конечный предел.
■ Теорема 1.4. Пусть дана функция f : М —> R. Если предел
lim /(ж) существует и конечен, то функция f(x) асимптотически
х—+р,х£М
ограничена при х, стремящемся к р по множеству М.
Доказательство. Пусть L = lim f(x) G R. Положим e = 1.
Согласно определению предела, найдется окрестность U точки р такая,
что для любого х G U П (М \ {р}), отличного от р, выполняется
неравенство: \f(x) — L\ < 1.
Для всякого х G М, принадлежащего окрестности С/ и отличного
отр, очевидно, имеем: |/(#)| < \f{x)—L\ + \L\ < \L\ + 1. По определению,
это и означает, что f(x) = 0(1) при х —* р no M.
Теорема доказана. ■

100
Гл. 2. Теория предела
▼ Следствие. Если числовая последовательность сходится, то она
является ограниченной.
Действительно, если последовательность (хп)пе^к имеет конечный
предел, то она, согласно теореме 1.4, является асимптотически
ограниченной и, значит, в силу леммы 1.8, эта последовательность
ограниченная, т
1.6. Теорема о зажатой переменной и ее следствия
Докажем теорему, которая во многих случаях является
эффективным средством для доказательства существования предела функции.
Зададим произвольно множество М с R и его предельную точку р.
Все дальнейшие рассуждения относятся именно к этим множеству и
точке.
Пусть R+(x) есть функция, определенная в п. 1.2.2. Тогда
R+(x) = {l "P" Х^ 1; (1.3)
при х < 1.
{}
Функция Д+ — невозрастающая и 0 < R+(x) < 1 для всех х.
Согласно лемме 1.5, функция / : М -* К имеет равный оо предел при ж,
стремящемся к р по множеству М в том и только в том случае, если
lim А.[/(*)1 = 0.
х—*р,х£М
Ш Теорема 1.5 (теорема о зажатой переменной). Пусть функция f
определена на множестве М. Предположим, что существуют
окрестность С/о точки р и функции и : Мг -> Ж, v : М2 -* R, области определения
которых содержат множество G = U0 П М, такие, что выполнены следу-
ющие условия:
1) для каждого х е G, отличного от р, величина f(x) лежит между
и(х) и v(x) (то есть для всякого х € (G \ {р}) либо u(x) < f(x) < v(x), либо
u(x) > f(x) > v(x));
2) существует число L е R такое, что
L = lim гх(ж) = lim v(x).
a;->p,a;6Mi х—*р,х£М2
Тогда
L = lim /(ж).
х—>р,х£М

§ 1. Определение и простейшие свойства предела
101
Доказательство. Пусть выполнены все условия теоремы.
Рассмотрим сначала случай, когда L — конечно. Зададим
произвольно е > 0. По нему найдутся окрестности Ui и Ui точки р такие,
что для любого х G Mi, отличного отри принадлежащего окрестности
C/i, выполняется \и(х) — L\ < £, а для всякого х G Мг, отличного от р и
принадлежащего С/г, справедливо соотношение: \v(x) — L\ < е.
Согласно лемме 1.1, найдется окрестность U точки р, которая
содержится в каждой из окрестностей (7о, t/i и [/г.
Пусть точка х G М принадлежит указанной окрестности С/, причем
х ф р. Так как U С С/о, то х G С/о, и, значит, х G G. Поскольку U С Ui
и С/ С С/г? то х принадлежит также каждой из окрестностей t/i и [/г.
Отсюда, в силу выбора U\ и С/г, вытекает, что для данного х
выполняются неравенства: L — е < и(х) < L + е m L — е < v(x) < L + е.
Так как х G G, то, согласно условию теоремы, /(ж) лежит между
и(х) и г?(ж), то есть либо u(x) < f(x) < v(x), либо u(x) > f(x) > v(x).
Отсюда следует, что для всякого х G М, удовлетворяющего
условиям х G С/, х ф р, имеют место неравенства: L — е < f(x) < L + £, то
есть |/(ж) — Z/| < £г для каждого ж G С/ П (М \ 0>}).
Число е > 0 было выбрано произвольно. Из доказанного вытекает,
согласно определению предела, что L = lim f(x).
х—+р,х£М
Для случая конечного L теорема доказана.
Рассмотрим случай, когда L — оо. Положим a(x) = R+[u(x)],
/3(х) = R+[v(x)], и пусть <р(х) = Я+[/(ж)].
Так как
lim u{x) = lim v(a;) = 00,
ТО
lim а(ж) = lim /3(ж) = 0.
х—>p,x£Mi x—*p,x£M2
Функция j?+ монотонна. Отсюда следует, что при каждом х G G,
отличном от р, величина <р(ж) лежит между а(х) и /3(ж) и, значит,
lim <р(ж) = 0.
х—*р,х£М
Согласно лемме 1.5 отсюда вытекает, что
lim f(x) = 00.
Рассмотрим случай, когда L == — оо. В этом случае имеем:
lim [—Цж)] = lim [—^(ж)] = оо.
ж—►PjEGM ж—*-р,ж€М

102
Гл. 2. Теория предела
При каждом х £ G, отличном от р, число —f(x) лежит между —и(х)
и — v(x).
По доказанному, отсюда следует, что
и™ [-/(*)] = °°>
ж—»-р,жем
и, значит,
lim f(x) = —оо.
x—>p,xGM
Теорема доказана. ■
¥ Следствие 1 (признак сравнения бесконечной малости функции).
Предположим, что для функции /, определенной на множестве М С Ж,
и предельной точки р множества М существуют окрестность Uq точки р
и функция а(х), определенная на множестве G = М C\Uq, такие, что для
всех х е G выполняются неравенства: О < f(x) < a(x). Если a(x) = o(l)
при х -* р, то также и f(x) = о(1) при х -> р по М.
Данное утверждение непосредственно вытекает из теоремы, если
положить в ней и(х) = 0 и v(x) = a(x). Следствие 1 доказано. Т
т Следствие 2 (признак сравнения существования бесконечного
предела). Пусть функция /, определенная на множестве М, такова, что для
нее существуют окрестность J70 точки р и функция w, определенная на
множестве G = М r\Uo, такие, что f(x) > w(x) для всех х eG.
Если
оо = lim w(x),
х—>р,х£М
TO
оо = lim f(x).
x—>p,xGM
Аналогично, если существуют окрестность J70 точки р и функция w,
определенная на множестве G = М HUq, такие, что f(x) < w(x) для всех
xeG и
—оо = lim w(x),
x—>p,xGM
то
—оо = lim f(x).
х—>р,х£М
Доказательство. Пусть i?+ есть функция, определенная
равенством (1.3). При каждом х eG имеем:
a(x) = R+[w(x)] > R+[f(x)] > 0.

§ 1. Определение и простейшие свойства предела
103
По условию lim w(x) = оо и, значит, согласно лемме 1.5,
х—*р,х£М
lim a(x) = 0.
х—+р,х£М
Отсюда, на основании следствия 1, вытекает, что
lim Д+[/(яО] = 0.
Применяя лемму 1.5 еще раз, получаем:
lim f(x) = оо,
х—+р,х£М
что и требовалось доказать.
Докажем второе утверждение.
Пусть С/о — это окрестность точки р и функция w, определенная
на множестве G = С/о П М, такова, что /(ж) < w(x) для всех х £ G,
отличных от р.
Если lim 'ш(ж) = —оо, то lim [—w(x)] = оо, и для любого
i-»p,i6M ж—^р,жЕМ
ж Е G\ {p} выполняется неравенство: — w(x) < —f(x).
По доказанному, отсюда вытекает, что lim [—/(#)] = оо, и, ста-
х—*р,х£М
ло быть, согласно определению предела, равного —оо,
lim f(x) = —оо.
х—*р,х£М
Следствие 2 доказано. ▼
Следующее предложение показывает, что свойство функции иметь
предел при х, стремящемся к р, и значение этого предела полностью
определяются ее поведением в некоторой окрестности точки р.
▼ Следствие 3 (свойство локальности предела). Пусть даны
множества ЕсШиМсШирЕЖ является предельной точкой каждого
из этих множеств, причем существует окрестность С/о точки р такая,
что С/о П Е — С/о П М. Предположим, что функции f и д,
определенные на множествах Е и М, соответственно, таковы, что для всякого
xeG = UoC\E = Uon M, отличного от р, f(x) = g(x).
Если одна из данных функций имеет предел при х, стремящемся к
р, то и другая имеет предел при х, стремящемся к р, причем значения
этих пределов совпадают.

104
Гл. 2. Теория предела
Доказательство. Пусть выполнены все условия следствия. Для
определенности будем считать, что существует предел
lim д(х) = L.
х-+р,х£Е
Полагаем Mi = M2 = Е и и(х) = v(x) = g(x). Тогда
L = lim и{х) = lim v(x)
ж—>-р,х£М\ x—+p,x£M2
и для всех х £ G, отличных от р, /(ж) лежит между и(х) и v(#).
Таким образом, все условия теоремы 1.5 выполняются и,
следовательно, L = lim f{x). Следствие 3 доказано. Т
х—*р,х£М
Т Следствие 4. Пусть числовые последовательности (xn)n^k и
(Уп)пе^т таковы, что хп = уп, начиная с некоторого номера n = I, I > k
и I > га. Если одна из данных последовательностей имеет предел, то
также и другая последовательность имеет предел, причем значения этих
пределов совпадают.
Доказательство. Пусть U = (J,oo]. Тогда N& П U = Nm П U.
Действительно, если n Е Z принадлежит U, то п > I, и, значит, n > га и
одновременно п > к. Отсюда ясно, что если n G f/flNfc, то одновременно
n Е UnNm. Это означает, что имеет место включение UC\Nk С C/DNm.
Меняя в рассуждениях к и га местами, получим включение С/ П Nm С
С U П Nfc и, значит, С/ П Nfc = С/ П Nm = G.
Для всякого n E G имеет место равенство хп = уп. На множестве
G функции п I—► хп и п I—► уп совпадают.
Доказываемое утверждение, в силу сказанного, есть частный
случай следствия 3. Следствие 4 доказано. Т
Приведем примеры.
Пример 2. Пусть жп = 2П при всяком n E N.
Имеем неравенство Бернулли:
(1 + х)п >1 + пх (1.4)
для любых х > — 1 и n Е N.
Полагая в этом неравенстве ж = 1, получим, что при каждом n Е N
2n = (l + l)n>l + n>n.
(1.5)

§ 1. Определение и простейшие свойства предела
105
Отсюда
2П
для любого п е N.
Как было показано выше,
lim п = оо, lim — = 0.
п—юо п—кх> 77,
Применяя следствия 1 и 2 теоремы 1.5 к последовательностям: (2п)пещ;
(^)n€N' полУчим> с учетом (1.5) и (1.6), что
lim 2n = оо; lim — = 0.
п—юо га—юо 2П
Пример 2. Пусть (nfc)fc€N есть строго возрастающая
последовательность натуральных чисел, так что при каждом к eN имеем Пк е N и
rtk < nfc+i. Докажем, что при каждом к eN имеет место неравенство
пк > к. (1.7)
При к = 1 неравенство (1.7) верно, так как ni e N, а 1 есть
наименьшее из натуральных чисел.
Предположим, что для некоторого к eN неравенство (1.7)
выполняется. По условию, nfc+i > rtk и, значит, Пк+\ — Пк > 0.
Так как rik+i — rtk есть целое число, то Пк+г — rtk > 1, и, следовательно,
ttfc+1 > П* + 1 > fc + 1.
Таким образом, если неравенство (1.7) верно для некоторого fc, то
оно остается верным, если заменить в нем к на к + 1, и, стало быть, в
силу принципа математической индукции, оно верно для всех fceN.
Применяя следствие 2 теоремы 1.5, получаем, что справедливо
следующее утверждение.
ф Предложение 1.1. Всякая строго возрастающая последователь-
ность натуральных чисел имеет предел, равный оо.
Доказательство очевидно. ♦
1.7. Характеристика предельных точек числового множества
Для произвольной точки р е Ш определим некоторую специальную
последовательность ее окрестностей (Un(p))nen.
Если р — конечно, то полагаем Un(p) = [р ,р ч— ) при всяком
\ п п)
neN. Для р = -оо пусть Un(p) = [-оо, -п) для всех n e N. Наконец, в
случае р = оо положим Un(p) = (n, оо] для любого n e N.
<
1 1
7 < ~
п +1 п
(1.6)

106
Гл. 2. Теория предела
Последовательность окрестностей (Un(p))n&i точки р называется
канонической базой точки р £ М.
Справедливо следующее предложение.
■ Лемма 1.9. Пусть р £_ R и (хп G M)neN — числовая
последовательность такая, что xn G Un(p) при каждом п. Тогда р = lim хп-
п—юо
Доказательство, Пусть последовательность (хп)пеъ такова,
что хп G Un(p) при каждом п.
Если р конечно, то Un(p) = (р .рН—). Следовательно, из
V п п)
1 1 1
условия хп G Un(р) вытекает, что р <хп < р+ —, откуда \хп — р\ < —
при всех п.
Имеем: lim — = 0, откуда lim \хп — р\ = 0 и, значит, согласно
п—+оо ТЬ га—юо
лемме 1.4, р = lim жп.
га—юо
Если р — оо, то Un(p) = (п,оо]. Из условия хп G Un(p)
вытекает, что хп > п при каждом п. Последовательность (an)neN, У которой
ап = п при каждом п, имеет предел, равный оо. Отсюда, в силу
следствия 2 теоремы 1.5, получаем lim хп = ос = р.
п—юо
Аналогично рассматривается случай р = — оо.
Лемма доказана. Я
■ Лемма 1.10 (лемма о характеристике предельных точек
числового множества через понятие предела последовательности). Пусть М
есть произвольное непустое подмножество мноясества Ё. Число р € R
является предельной точкой множества М в том и только в том случае,
если существует последовательность (xn)neN точек множества М такая,
что при каждом п число хп конечно, хп фр и р — lim xn.
п—юо
Доказательство. Предположим, что р G CimM. Установим,
что в этом случае существует последовательность точек множества М,
удовлетворяющая всем условиям теоремы.
Пусть (t/n(p)), n = 1,2>..., есть каноническая база точки р.
Согласно определению предельной точки, при каждом n G N
найдется хп G М такое, что хп G Un(p), причем хп ф р.
Мы получаем, таким образом, что существует последовательность
(#n)n£N точек множества М такая, что хп G Un(p) и хп ф р при
каждом п. В силу леммы 1.9, lim xn =р, так что последовательность
га—юо
(^n)neN и есть требуемая.

§ 1. Определение и простейшие свойства предела
107
Предположим, что точка р Е Й такова, что для нее существует
последовательность (#n)neN точек множества М такая, что хп ф р при
каждом пир есть предел этой последовательности.
Пусть р — конечно. Зададим произвольно окрестность U точки р.
Если р — конечно, то U = (р — е,р + ег), где е > 0. Согласно лемме 1.6,
найдется п такое, что если п > п, то \хп — р\ < е. Для всех таких п
имеем хп Е U. Если р = оо, то U = (X, оо], где ЛГ 6 К.
Применяя определение предела в этом случае, получим, что
найдется номер п такой, что для всех п >п будет хп > К и, значит, хп Е U
для любого такого значения к.
Аналогично рассуждаем в случае р = — оо.
Таким образом, любая окрестность U точки р содержит элементы
множества М, отличные от точки р и такие, что хп Е U. Согласно
определению, это и означает, что р есть предельная точка множества М.
Лемма доказана. ■
1.8. ПОНЯТИЯ НЕПРЕРЫВНОСТИ И ПРЕДЕЛА ДЛЯ КОМПЛЕКСНЫХ
ФУНКЦИЙ
Определим понятия предела и непрерывности для функций с
комплексными значениями.
Пусть дано множество М С Й и р Е К есть предельная точка М.
Предположим, что задана функция /, определенная на М и
принимающая значения в множестве всех комплексных чисел С.
Число с Е С называется пределом функции f при ж, стремящемся к
р по множеству М, если выполнено следующее условие:
lim |/(х)-с| = 0.
х—+р,х£М
Комплексная функция / : М -+ С, где М С Й, называется
непрерывной в точке xq Е М, если каждая из вещественных функций Re / и
Im/ непрерывна в этой точке.
Обозначения и терминология, введенные ранее для случая
вещественных функций, автоматически переносятся на случай комплексных
функций.
Отметим, что для комплексных функций понятие бесконечного
предела не определяется.
■ Теорема 1.6. Пусть далы множество М СИ, число р Е СгтМ и
комплексная функция f, определенная на множестве М. Для того чтобы
комплексное число с было пределом функции f(x) при х, стремящемся

108
Гл. 2. Теория предела
к р по множеству М, необходимо и достаточно, чтобы выполнялись
соотношения:
Re с = lim Re f(x), Im с = lim Im f(x).
x—>p,x£M x—rp,x€M
Комплексная функция, определенная на множестве М с R, может
иметь не более одного предела при х, стремящемся к р е Cim(M) по
множеству М.
Если комплексная функция имеет предел при х —> р по множеству
М, то она является асимптотически ограниченной при х -* р по М.
Доказательство. Заметим, что для произвольного
комплексного числа z = р 4- iq, где р е R и g ^ R, справедливы следующие легко
проверяемые неравенства:
bl<N, M<N, N<|p| + |«|. (1.8)
Положим: Re/(x) = м(х), Im/(x) = v(x), a = Re с и Ь = Imc. Применяя
неравенства (1.8), получим, что справедливы неравенства:
\Ф) ~а\< |/(я) - с|, |v(x) - Ь| < |/(х) - с|, (1.9)
|/(х) - с| < \и(х) - a| + |v(x) - Ь|. ' (1.10)
Из соотношений (1.10) следует необходимость условий теоремы.
Докажем их достаточность. Пусть а = limu(x), Ъ = limv(x),
с = a -h гб. Зададим произвольно е > 0. Согласно определению предела,
найдутся f/i Е 0(р) и J72 € 0(р) такие, что если х € J7i П М \ {р}, то
\и(х) - а\ < е/2, а если х е Е/г П М \ {р}, то \v(x) - b\ < е/2. По лемме 1.1
найдется U £ 0(р) такое, что Ui э U и С72 Э I/. Для всякого х € J7nM\{p},
в силу неравенства (1.10), имеем: |/(х) - с\ < е/2 + е/2 = е. Так как е > 0
произвольно, то тем самым доказано, что
lim |/(х)-с|=0,
х—>р,х£М
то есть с = lim /(x).
ж—»р,жем
Пусть ci = lim /(х) и с2 = lim /(х). Тогда из доказанного сле-
х—>р,х€М х-+р,х€М
дует, что
Reci = lim Re/(x), Imci = lim Im/(x),
x-+p,x£M x-+p,x£M
Rec2 = lim Re/(x), Imc2 = lim Im/(x).
x—>p,x£M x—>p,x£M

§ 2. Теоремы об операциях над пределами
109
Как показано выше, вещественная функция может иметь не более
одного предела. Отсюда вытекает, что Reci = Rec2 и Imci = Imc2, и,
значит, ci = С2.
Справедливость утверждения теоремы об асимптотической
ограниченности при х —> р по М функции / : М —» С устанавливается
рассуждениями, дословно повторяющими доказательство теоремы 1.4,
и мы их опускаем.
Теорема доказана. D
§2. Теоремы об операциях над пределами
Основные результаты этого параграфа — теоремы, которые кратко
можно сформулировать так: предел суммы (соответственно,
произведения) двух и более функций, каждая из которых имеет предел, равен
сумме (соответственно, произведению) пределов исходных функцию-
предел частного двух функций равен частному пределов этих функций.
(Последнее утверждение верно лишь при условии, что предел функции,
стоящей в знаменателе, отличен от нуля.)
Другой важный результат, который устанавливается здесь, — это
теоремы о пределе суперпозиции двух функций, каждая из которых
имеет предел.
2.1. Операции с бесконечно малыми
2.1.1. Зададим произвольно непустое множество МсКи его
предельную точку р. Все функции, рассматриваемые здесь, предполагаются
определенными на множестве М и принимающими значения либо в
множестве всех вещественных чисел К, либо в множестве всех комплексных
чисел С. Всякую такую функцию мы будем именовать числовой
функцией, определенной на множестве М.
Напомним, что числовая функция f(x) называется бесконечно
малой при ж->рпо множеству М, если lim f(x) — 0. В этом случае
х—*р,х£М
используется также обозначение: f(x) = о(1) при х —► р, х Е М.
Ш Теорема 2.1. Пусть даны числовые функции fj,j = 1,2,..., га,
определенные на множестве М. Если fj(x) = о(1) при х -* р по
множеству М для каждого j = 1,2,..., га, то также и
Н(Х) + Ь(Х) + • • • + fm(x) = 0(1)
при х —» р по множеству М.

110
Гл. 2. Теория предела
Доказательство. Пусть функции fj, j = 1,2,..., га,
удовлетворяют условиям теоремы. Зададим произвольно е > 0.
Положим 6i = е/га. Тогда ei > 0 и, стало быть, при каждом
j = 1, 2,..., га найдется окрестность Uj точки р такая, что для всякого
х eUj П (М \ {р}) выполняется неравенство: \fj{x)\ < ei.
Согласно лемме 1.1, найдется окрестность U точки р,
содержащаяся в каждой из окрестностей Uj, j = 1,2,..., га. Возьмем произвольно
xGM такое, что х EUих фр. Тогда х Е Uj для любого j = 1,2,..., га
и, значит, для всякого j имеет место неравенство |/^(ж)| < £ь Отсюда
следует, что для любого х EU П (М \ {р}) выполняется неравенство:
\fi(x) + f2(x) + ... + /т(я?)| < |Л(ж)| + \f2(x)\ + • •. + |/т(ж)| < raei = е.
Так как £ > 0 — произвольно, и для выполнения последнего
неравенства требовалось лишь, чтобы х Е М, отличное от р, принадлежало
окрестности U точки р, то тем самым установлено, что
0 = lim{/i(aO + f2(x) + - • • + /m(s)}.
ж—*-р
Теорема доказана. ■
Выше (см. п. 1.5) было введено понятие функции, асимптотически
ограниченной при ж, стремящемся к р по множеству М. Напомним, что,
согласно определению, функция F : М —► С называется асимптотически
ограниченной при ж —► р по М, если существует окрестность U точки р
такая, что функция / является ограниченной на множестве U Г\М\ {р},
то есть можно указать положительную постоянную К < оо, для
которой при любом х Е U П М \ {р} выполняется равенство: \f(x)\ < К.
Тот факт, что функция / удовлетворяет данному условию, сокращенно
записывается следующим образом: f(x) = 0(1) при х -^ р no M.
Согласно теореме 1.4, если вещественная функция / имеет
конечный предел при х —► р по М, то она является асимптотически
ограниченной при х, стремящемся к р по множеству М. В силу теоремы 1.6,
то же самое верно и для функций со значениями в С.
■ Теорема 2.2. Пусть даны числовые функции f и д,
определенные на множестве М. Если функция / является бесконечно малой, а
g — асимптотически ограничена при х —> р, то произведение fg есть
функция, бесконечно малая при х —* р по множеству М.
Доказательство. Пусть выполнены все условия теоремы. Так
как g(x) = O(l) при х —> р, то найдутся окрестность U\ точки р и

§ 2. Теоремы об операциях над пределами
111
число L < оо такие, что для любого х G C/i П (М \ {р}) выполняется
неравенство \д(х)\ < L.
Зададим произвольно е > 0. Пусть ei = e/(L + 1). Так как / есть
бесконечно малая при х —► р функция, то найдется окрестность С/г точки
р такая, что для всякого х G С/г П (М \ {р}) имеет место неравенство:
1/0*01 < еь
Пусть U есть окрестность точки р, содержащаяся в каждой из
окрестностей C/i и С/г.
Возьмем произвольно точку х G С/ П (М \ {р}) такую, что х ф р is.
одновременно х Е U. Так как С/ С ЕЛ., то х G C/i и, значит, для этого
х верно неравенство \д(х)\ < L. Так как Е/ С Е/г, то ж G Е/г, откуда
следует, что для данного х имеет место неравенство:
|/(x)|<ei=e/(L + l).
В результате получаем, что для всякого х G U П М \ {р} выполняется
неравенство:
|/(ЖЖх)|<1^1<е.
Так как е > О было выбрано произвольно, то из доказанного,
согласно определению предела, вытекает, что 0 = lim f(x)g(x), то есть
f(x)g(x) = о(1) при х —► р по множеству М.
Теорема доказана. ■
▼ Следствие 1. Пусть функция g имеет конечный предел, а
функция f является бесконечно малой при х —> р. Тогда
f(x)g(x) = о(1) при х->р.
Действительно, если предел lim g(x) существует и конечен, то, со-
х—*р
гласно теореме 1.3, функция g является асимптотически ограниченной
при х —► р, откуда и вытекает требуемое утверждение. ▼
▼ Следствие 2. Если f(x) = о(1) прл х —> р, то для всякого Л G С
также и Xf(x) = о(1) прл х —> р.
Очевидно — в силу следствия 1. ▼
▼ Следствие 3. Числовая функция f : М —> С, определенная на
множестве Mel, является бесконечно малой при х —> р в том и только
в том случае, если выполняется соотношение
1/0*01 = 0(1)
при х —> р по множеству М.

112
Гл. 2. Теория предела
Доказательство. Пусть дана функция / : М —> С. Определим
по ней новую функцию a : М —> С, полагая о-(ж) = 1, если /(ж) = О,
<r(s) = l^j| при/(*)/(>.
Для всех х выполняются равенства \<т(х)\ = 1 и
*(х)
= 1 и,
значит, функции а и — являются ограниченными. Отсюда вытекает, что
а(ж) = 0(1) и —г^ = 0(1) при х -> р.
<т{х)
Имеем: \f(x)\ = a(x)f(x), /(ж) = —г-г 1/0*01 при всяком х е М. Отсюда
<т[х)
следует, что если одна из функций / и |/| является бесконечно малой при
х —> р, то и другая будет таковой, как произведение бесконечно малой
функции и ограниченной функции.
Следствие доказано. Т
2.2. Теоремы об операциях с пределами. Случай конечных
пределов
Зададим произвольно непустое множество М с R, и пусть р есть
предельная точка М.
Пусть даны числовая функция /, определенная на множестве М, и
число L е С. Положим и(х) = /(ж) — L. Если L является пределом f(x)
при ж, стремящемся к р по множеству М, то и{х) = о(1) при ж->рпоМ.
Обратно, если L е С и функция / : М —> С таковы, что разность
/(ж) - L = u(:r), где и(ж) = о(1) при ж —► р по множеству М, то
L= К™ .,/(*)•
х-+р,х€М
Для вещественных функций справедливость данных утверждений
следует из леммы 1.4, для функций со значениями в С —
непосредственно из определения предела для комплексных функций.
■ Теорема 2.3. Предположим, что числовые функции /ид,
определенные на множестве М, имеют пределы:
lim f(x) = К; lim g(x) = L,
х-+р,х£М х-+р,х£М
причем в случае, если /ид — вещественные функции, эти пределы
конечны. Тогда каждая из функций |/|, / + g и fg также имеет предел
при х —> р. При этом
lim \f(x)\ = \K\; lim[f(x) + g(x)] = К + L; lim f(x)g(x) = KL.
x-+p x-+p x-+p

§ 2. Теоремы об операциях над пределами
113
Если д(х) ф О для всех х е М и L ф О, то также и функция — имеет предел
9
при х —> р. В этом случае
х-+р,хем g[x) L
Доказательство. Пусть функции / и д удовлетворяют условиям
теоремы. Имеем:
f(x) =К + и(х); д(х) = L + v(x),
где и(х) = о(1) и v(x) — о(1) при х -* р.
Для всякого х € М выполняется неравенство:
||/(*)|-|^||<|/(х)-Л-| = |и(х)|.
Согласно следствию 3 теоремы 2.2, функция \и(х)\ является
бесконечно малой при х -+ рпо множеству М. Следствие 1 теоремы о
зажатой переменной (теорема 1.5) позволяет заключить, что
||/(aO|-|lir|| = 0(l)
при х —> р и, значит, \К\ есть предел функции |/| при х —► р.
Имеем:
f(x) + д{х) = K + L + и{х) + v(x).
На основании теоремы 2.1, и(х) + v(x) = о(1) при х —> р, откуда следует,
что
A' + L=lim[/(x)+S(x)]1
ж—>р
и утверждение, касающееся суммы, доказано.
Рассмотрим произведение:
f(x)g(x) = (К + и(х))д(х) = Яр(ж) + и(ж)р(ж) =
= i^i + lifv(x) + и(ж)0(ж) = KL + w(z),
где г^(ж) = Kv(x) + и(ж)р(ж).
Следствия 1 и 2 теоремы 2.2 позволяют теперь заключить, что
Kv(x) = о(1) и и(х)д(х) = о(1) при х —► р. В силу теоремы 2.1, отсюда
следует, что ги(#) = о(1) при ж —> р, и утверждение, касающееся
произведения, доказано.

114
Гл. 2. Теория предела
Предположим, что д(х) ф О для всех х Е М и L ф 0. По
доказанному,
|L|=lim|0(s)|.
х—*р
Так как \L\ > |I/|/2, то, как следует из леммы 1.7, найдется
окрестность U точки р такая, что для всякого х £ U П (М \ {р})
выполняется неравенство: \д(х)\ > \L\/2. Для любого такого #, очевидно,
\1/д(х)\ < 2/\L\. Таким образом, 1/д(х) = 0(1) при ж —>р.
Далее, имеем:
f(x) К _ Lf[x) - ЛСр(я:) _
flf(a?) L Lg(x)
L[K + u{x)\ -K[L + v(x)] ___ 1
г*(ж) —t-v(x)
Ju
Lg(x) g(x)
Теоремы 2.1 и 2.2 позволяют заключить, что
zr
и{х) —^jrv{x) = о(1)
при ж —> р. Так как 1/д(х) == 0(1) при ж —» р, то, в силу теоремы 2.2,
отсюда вытекает, что
при ж —* р, и, значит,
Теорема доказана.
д{х) L
L х->Р д(х)
2.3. Правила замены переменной под знаком предела
Один из основных приемов, применяемых при решении различных
задач математического анализа, — замена переменной. Формально этот
прием состоит в переходе от исходной функции f(x) к суперпозиции
f[<p(t)]. При надлежащем выборе функции <р(£), функция f[<p(t)] может
оказаться устроенной проще, чем f(x) в том смысле, что интересующая
нас задача в результате преобразуется в такую, которую мы уже
умеем решать. Найдя решение этой новой задачи, мы сможем решить и
первоначальную задачу.
Приведем здесь теоремы, на которых основано применение
указанного приема в теории предела.

§ 2. Теоремы об операциях над пределами
115
2.3.1. Предварительно докажем следующее предложение.
■ Лемма 2.1. Пусть даны множество Е С S, его предельная точка
а и вещественная функция х, определенная на множестве Е.
Предположим, что
р = lim x(t).
t-+a,t€E
Тогда для всякой окрестности U точки р можно указать окрестность
V точки а такую, что для всякого t £ Е, отличного от а и
принадлежащего окрестности V, значение функции х в точке t принадлежит
окрестности U.
Доказательство. Пусть выполнены все условия леммы.
Зададим произвольно окрестность U точки р. Предположим сначала, что р
конечно. Тогда U есть интервал (р — е,р + е), где е > 0.
Согласно определению предела, найдется окрестность V точки a
такая, что для всех t £ V П (Е \ {а}) выполняется неравенство:
\x(t)-p\<e
и, значит, x(t) £ U для всех таких t.
В случае р = ±оо требуемое также непосредственно следует из
определения предела. Если р = оо, то окрестность U точки р есть
промежуток вида (К, оо]. Согласно определению предела, равного оо,
найдется окрестность V точки а такая, что для всех t £ V П (Е \ {а})
выполняется неравенство x(t) > К и, следовательно, x(t) G U для всех
таких t.
Если р = —оо, то U = [—оо,-К"), где К > — оо. В этом случае
lim [—x(t)] = оо и, значит, найдется окрестность V точки а такая,
t—*a,t€E
что для всякого t G U П Е, отличного от а, выполняется неравенство:
—x(t) > —К, и, стало быть, x(t) < К, то есть x(t) G U для всех таких t.
Лемма доказана. ■
■ Теорема 2.4 (о непрерывности суперпозиции непрерывных
функций). Пусть даны множества М С М, Е С R, функция f, определенная
на множестве М, и функция х, определенная на множестве Е.
Предположим, что x(t) G М для всех t £ Е и функция х непрерывна в
точке a £ Е. Если функция / непрерывна в точке р = #(£), то функция
f о х : t Е Е *-> f[x(t)] является непрерывной в точке а.
Доказательство. Пусть выполнены все условия теоремы.
Зададим произвольно е > 0. Так как функция х всюду конечна, тор = х(а) —
конечно. Значит, согласно определению функции, непрерывной в точке
р, найдется 6 > 0 такое, что если х £ М и |ж— р| < 6, то |/(#) — f(p)\ < £•

116
Гл. 2. Теория предела
Так как функция #, по условию, непрерывна в точке а е Е и 5 > О, то,
согласно определению непрерывной в точке функции, найдется
окрестность V точки а такая, что для всякого t е E, принадлежащего данной
окрестности V, выполняется неравенство:
\x(t) -p\ = \x(t) - х(а)\ < S.
Возьмем произвольно t е V П Е. Положим х = x(t). Из условий
теоремы следует, что х е М. В силу выбора окрестности V, будем иметь:
\х-р\< S, и, значит, \f(x) - f(p)\ < е.
Так как t е V П Е было выбрано произвольно, то мы, следовательно,
получаем, что для любого t eV ПЕ выполняется неравенство:
\f[x(t))-f[x(a)]\<e.
Число е > 0 было задано произвольно. Мы видим, что для функции fox
выполнены все условия определения непрерывности в точке а.
Теорема доказана. В
▼ Следствие. Пусть даны множество М с М, точка р е М и
множество G с М такое, что р е G. Если функция f : М —> Е непрерывна
в точке р, то функция f\c : х е G *-+ f(x) — ограничение функции f на
множество G — непрерывна в точке р.
Доказательство. Отображение jo • х £ G ь-* х е R непрерывно.
Имеем: f\c = f ° jg- В силу теоремы 2.4, отсюда вытекает
непрерывность отображения f\c — сужения отображения / на множестве G, что
и требовалось доказать, т
2.3.2. Теперь докажем первую теорему о замене переменной под знаком
предела.
■ Теорема 2.5 (первая теорема о пределе сложной функции). Пусть
даны множества М с М, Е с М, функция /, определенная на множестве
М, и функция х, определенная на множестве Е. Пусть а есть предельная
точка множества Е. Предположим, что выполнены следующие условия:
а) x(t) е М для всех t £ Е, и существует предел Km x(t) = р,
t—w,,t£E
причем р G М;
б) функция f непрерывна в точке р.
Тогда сложная функция f[x(t)] имеет предел при t —> а по множеству Е.
При этом
ton /[*(*)]=/(?)•
г—*a,t£b

§ 2. Теоремы об операциях над пределами
117
Доказательство. Пусть выполнены все условия теоремы.
Зададим произвольно е > 0. Так как, по условию, функция / непрерывна
в точке р, то найдется окрестность U точки р такая, что для всякого
х EiU П М выполняется неравенство: \f(x) — f(p)\ < е.
Имеем, по условию, р= lim x(t). В силу леммы 2.1, найдется
t-+a,teE
окрестность V точки а такая, что для всякого t Е V П (Е \ {а}) точка
х = x{t) принадлежит окрестности U.
Окрестность С/, по условию, такова, что для всякого х Е U П М
выполняется неравенство: \f(x) — f(p)\ < е.
В частности, мы получаем, что для всякого t G V П (Е \ {а})
выполняется неравенство: |/[#(£)] — f(p)\ < £•
Так как е > 0 было выбрано произвольно, то тем самым
установлено, что
/(р)= lim /[*(<)].
t—>a,teE
Теорема доказана. ■
Т Следствие. Если функция f', определенная на множестве Met,
непрерывна в точке р Е М, то для всякой последовательности (xn)ne^k
точек множества М, имеющей пределом точку р, выполняется
равенство: f(p) = lim /(жп).
п-*оо
Данное утверждение есть тот частный случай теоремы 2.5, когда
Е = Nfc и a = сю. ▼
2.3.3. Второй результат о замене переменной под знаком предела
дается следующей теоремой 2.6. По сравнению с теоремой 2.5, требования
на функцию f(x) в ней несколько ослаблены. При этом, однако,
требования, налагаемые на x(t), в сравнении с теоремой 2.5, усилены.
■ Теорема 2.6 (вторая теорема о пределе сложной функции). Пусть
даны множество МсК, предельная точка р множества М, множество
Е С R, имеющее предельную точку а, и функции f их, определенные на
множествах: М и Е, соответственно. Предположим, чтор = lim x(t),
t-+a,teE
причем для всех t Е Е, отличных от a, x(t) Е М и р ф x(t). Если
функция f имеет предел при х, стремящемся к р по множеству М, то
функция f[x(t)] имеет предел при t, стремящемся к а по множеству Е.
При этом имеет место равенство:
f[x(t)]= lim /(*).
х-+р,х£М

118
Гл. 2. Теория предела
Доказательство. Предположим, что все условия теоремы
выполнены.
Пусть L — конечно. Зададим произвольно е > 0. Так как, по
условию, L есть предел f(x) при ж, стремящемся к р по множеству М, то
найдется окрестность U точки р такая, что для всякого х е U П М,
отличного от р, выполняется неравенство: \f(x) — L\ < е.
Имеем, по условию,
р= lim x(t).
t->a,teE
В силу леммы 2.1, найдется окрестность V точки а такая, что для всякого
t e Vn(E\{a}) точка х = x(t) принадлежит окрестности J7, причем x(t) ф р.
По условию, x(t) е М для всех t £ Е.
Окрестность U такова, что для всякого х е Un(M\{p}) выполняется
неравенство: \f(x) — L\ < е. В частности, мы получаем, что для всякого
t e E, отличного от а и принадлежащего окрестности V, выполняется
неравенство: |/[#(£)] - Ц < е.
В силу произвольности е > 0, тем самым установлено, что
R+(x) = < х
{ 1
Пусть L = оо. Положим F(x) = Д+[/(#)], где функция Д+ определена
равенствами:
при х > 1;
при х < 1.
Согласно лемме 1.5, lim F(x) = 0. Отсюда, по доказанному, сле-
х—*р,х£М
дует, что lim F[x(t)] = 0. Имеем: F[x(t)] = R+[f[x(t)]]. Применяя лемму
1.5 еще раз, заключаем, что lim f[x(t)] = оо.
t-*a,t£E L J
Если L = lim f(x) = -оо, то lim [-f(x)] = оо, и, значит, по до-
х—>р,х€М х-+р,х€М
казанному,
Отсюда следует, что
t—>a,t£E
AEf[x{t)] = -°°-
Теорема доказана. О
Т Следствие 1. Пусть даны множество М с Е, предельная точка
р множества М и функция /. Предположим, что f имеет предел при х,
стремящемся к р по множеству М, и L e R есть значение этого предела.
Тогда для всякой последовательности (хп)пещ точек множества М,

§ 2. Теоремы об операциях над пределами
119
имеющей пределом точку р и такой, что хп ф Р для всех n E N&, имеет
место равенство: L— lim f(xn).
Данное утверждение есть тот частный случай теоремы 2.6, когда
Е = Nfc и a = оо. ▼
Т Следствие 2. Пусть даны множество МсМ, предельная точка
р множества М и функция f, причем существует предел
L = lim /(ж).
Предположим, что задано подмножество Е множества М такое, что
р является его предельной точкой.
Тогда число L является также пределом f(x) при х, стремящемся
к р по множеству Е, L = lim fix).
х—*р,х£Е
Данное утверждение есть частный случай теоремы 2.6, когда x=je
есть отображение вложения множества Е в М,
je :t Е Е н-> t е М. ▼
▼ Следствие 3 (теорема о пределе подпоследовательности). Если
последовательность (xn)n^k имеет предел, то для всякой
последовательности (z/m)m€Nr элементов множества N& такой, что lim vm = оо,
имеет место равенство: го-юо
lim жп = lim a^.
п—>оо га—юо
Данное предложение есть частный случай теоремы 2.6, получаемый
при М = Nfc, £ = Nr. ▼
2,4, Пределы суммы, произведения и частного. Случай
бесконечных пределов
Зададим произвольно непустое множество МсКи его предельную
точку р. Все функции предполагаются здесь определенными на
множестве М и принимающими значения в 1R.
Пусть Д+ есть функция, определенная на множестве Ж следующим
образом:
( v J - при ж > 1;
Д+(я?) = < х
\ 1 при х < 1.

120
Гл. 2. Теория предела
Функция Д+ — убывающая и 0 < Д+ (х) < 1 для всех х eR.
Согласно лемме 1.5, функция / имеет равный оо предел при ж,
стремящемся к р по множеству М, в том и только в том случае, если
lim R+[f(x)} = 0.
х-+р,х£М
Ш Лемма 2.2. Если функция f : М —> Ж имеет равный ±оо предел
при х —> р, то
Ит|/(аО| = оо. (2.1)
х—*р
Доказательство. Предположим, что функция / имеет равный
сю предел при #, стремящемся к р по множеству М.
В силу леммы 1.7, найдется окрестность U точки р такая, что для
всякого х Е U П (М \ {р}) выполняется неравенство: f(x) > 0. Для
всех таких х будет \f(x)\ = f(x), то есть f(x) = \f(x)\ для любого
х Е С/ПМ, отличного от р. Отсюда, на основании следствия 2 теоремы
о зажатой переменной (теорема 1.5), вытекает, что lim \f(x)\ = оо,
х-+р,х€М
что и требовалось доказать.
Пусть lim f(x) = —сю. Положим: fi(x) = —f{x). Тогда
lim \-f(x)\ = оо
х—*р,х£М
и, значит, по доказанному, lim | — f(x)\ = сю.
Так как | — f(x)\ = |/(я?)|, то тем самым установлено, что
lim |/(z)| = oo
х—+р7х£М
и в этом случае.
Лемма доказана. ■
■ Лемма 2.3. Предположим, что функция f : М —> Ж имеет предел
при х —> р, равный сю. Тогда:
1) для всякого конечного L Е М
lim [/(#)+ L] = оо;
2) для любого конечного L > 0
lim .Л^/О*)] = °°-

§ 2. Теоремы об операциях над пределами
121
Доказательство. Докажем первое утверждение леммы.
Зададим произвольно К < оо и положим К\ = К — L.
Так как К\ < оо, то, как следует из определения предела, равного
оо, найдется окрестность U точки р такая, что для всякого х G М П 17,
отличного от р, выполняется неравенство: К\ < f(x).
Возьмем произвольно х G М такое, что х G J7, причем х ф р. Для
этого х имеем: f (х) + L > Ki + L = К.
Число К ЕШ было взято произвольно. Таким образом, для всякого
К G Ш существует окрестность U точки р такая, что для всякого х G М,
отличного от р и принадлежащего этой окрестности 17, выполняется
неравенство: f(x) + L > К.
Тем самым доказано, что
lim [f(x) + L] = оо.
х—*р,ж£М
Второе утверждение леммы доказывается аналогичным образом.
ту-
Пусть L > 0. Зададим произвольно ХеМи положим ifi = —.
L
Так как К\ < оо, то, согласно определению предела, равного оо,
найдется окрестность U точкир такая, что для любого х G Uf)(M\{p})
выполняется неравенство: К\ < f(x).
Для всякого х G U П (М \ {р}) имеем Lf(x) > LK\ — К.
Число ifGK было взято произвольно. Следовательно, для всякого
К £ Ш существует окрестность U точки р такая, что если х G U П М,
причем х фр,то выполняется неравенство: Lf(x) > К.
В соответствии с определением предела, равного оо, тем самым
установлено, что lim [Lf(x)] = оо.
Лемма доказана. ■
■ Теорема 2.7. Пусть функции /:М—>Мир:М—>R
имеют пределы при х —> р, причем lim f(x) = оо, lim g(x) > — оо.
х—*р,х€М ж—►PjXGM
Тогда
lim [/(ж) + g(x)] = оо.
Ж—►£>
Если lim /(ж) = —оо, a lim #(#) < оо, то
х—►р ж—►р
lim [/(я)+#(#)] = -оо.
х—*р

122
Гл. 2. Теория предела
Доказательство. Рассмотрим только случай, когда предел f(x)
равен +оо. (Случай, когда указанный предел равен -оо, сводится к
этому.)
По условию, lim д(х) > —оо. Пусть L таково, что
х—*р
—оо < L < lim g(x).
х—>р,х£М
Так как lim д{х) > L, то найдется окрестность U точки р такая,
х—>р,х£М
что если х GU ПМ, причем х ф р, то д(х) > L, а значит, и
f(x)+g(x)>f(x) + L.
Согласно лемме 2.3,
lim [f(x) + L] = оо.
х—>р,х£М
Отсюда, в силу признака сравнения для существования
бесконечного предела (следствие 2 теоремы 1.5), вытекает, что
lim \f(x)+g(x)] = оо,
х—>р,х£М
что и требовалось доказать. ■
Пусть L = ±оо и К ф О, К е R. Определим произведение LK, полагая
LK = L при К > О и LK = -L при К < 0.
■ Теорема 2.8. Пусть функции /:М—>Ми#:М->М имеют пределы
при х -> р, причем lim f(x) = ±оо, a lim g(x) ф 0. Тогда произве-
х—>р,х£М х—>р,х£М
дение fg функций f и g имеет предел при х -> р, причем выполняется
равенство:
lim. ., /(*)0(х) = ( 1ш\ л, ^) ( lmV », ^ ) '
х—>р,х£М \х—>р,х£М J \х—>р,х£М J
Доказательство. Предположим, что
lim f(x) = оо; lim g(x) > 0.
х—>р,х£М х—>р,х£М
Общий случай сводится к этому, в силу определения предела,
равного -оо. Работу, связанную с детальным обоснованием соответствующей
редукции, мы предоставляем читателю.

§ 2. Теоремы об операциях над пределами
123
Пусть Л таково, что 0 < Л < lim д(х).
х—+р,х£М
В силу установленных выше свойств предела (лемма 1.7), найдется
окрестность C/i точки р такая, что для любого х G М, принадлежащего
окрестности C/i и отличного от р, выполняется неравенство: д(х) > Л.
Так как lim f(x) = оо, то найдется окрестность С/2 G 0(р) точ-
х—*р,х£М
ки р такая, что f(x) > 0 для любого ж G М, принадлежащего
окрестности U и отличного от р.
Пусть U есть окрестность точки р, содержащаяся в каждой из
окрестностей C/i и С/г. Если точка х € М принадлежит С/ и отлична
от р, то х G C/i и, значит, д(х) > А. Одновременно х G С/г, и потому
/(х)>0.
Принимая во внимание сказанное, заключаем, что для любого
х G М, принадлежащего окрестности С/ и отличного от р, выполняется
неравенство: f(x)g(x) > \f(x).
Согласно лемме 2.3,
lim А/ (х) = оо.
Отсюда, в силу признака сравнения существования бесконечного
предела (следствие 2 теоремы 1.5), получаем
lim f(x)g(x) = 00,
х—*р,х£М
что и требовалось доказать. ■
■ Теорема 2.9. Пусть функция f : М —> Е такова, что /(#) ^ О
для всех х G М. Если lim /(ж) = ±оо, то имеет место равенство:
х—*р,х£М
lim -гт-г = 0.
Если lim /(ж) = 0 и существует такая окрестность С/о точки р, что
х—►£>,#£ М
/(ж) для всех ж G С/ П (М \ {р}) имеет один и тот же знак, то:
а) lim -77-r- = оов случае, когда f(x) > 0 при ж G С/о П М \ {р};
б) lim -77-т- = -оо, если f(x) < 0 при х G С/о П М \ {р}.
ж—►PjXGM /(ж)
Доказательство. Предположим, что lim f(x) = 00 и для
ж—►pjicGM
всех жЕМ будет /(ж) ф 0. В этом случае lim #+[/(#)] = 0.

124
Гл. 2. Теория предела
Из определения предела, равного сю, вытекает, что найдется
окрестность U точки р такая, что для всякого х £ М, отличного от р и
принадлежащего окрестности С/, выполняется неравенство: f(x) > 1. Для
всякого такого х имеем: R+[f(x)] = ( .
J\x)
Таким образом, точка р имеет окрестность U такую, что на
множестве U Л М \ {р} функция г совпадает с некоторой функцией,
f\x)
имеющей предел, равный нулю.
Согласно следствию 3 теоремы 1.5, отсюда следует, что
lim
№
= о.
Предположим, что f(x) ф 0 для всех х и lim f(x) = —оо. Тогда
х—<-р,ж€М
Hm J-/(a;)] = oo
и, значит, по доказанному,
lim
№
= о.
Отсюда также следует, что lim
0.
х—>р,хем f(x)
Докажем утверждение теоремы, относящееся к случаю, когда
функция / при х —> р имеет предел, равный нулю.
Предположим, что f(x) ф 0 для всех х G М. Пусть д(х) =
Найдем окрестность С/о точки р такую, что для всех х £ С/о Л М \ {р}
выполняется неравенство f(x) > 0.
Так как lim f(x) = 0, то найдется окрестность C/i точки р такая,
что для всех х £ С/ Л М, отличных от р, выполняется неравенство:
№ < 1.
Найдем окрестность С/ точки р, содержащуюся в каждой из
окрестностей С/о и C/i.
Возьмем произвольно точку х £ М, принадлежащую окрестности
С/ и отличную от точки р. Тогда х £ С/о и одновременно ж £ C/i.
Отсюда следует, что для данного х выполняются неравенства:
0 < f(x) < 1

§ 3. Признаки существования предела
125
и,значит,
«М = ум > h
Это позволяет заключить, что для всех х £U П М\ {р}
адк*)] = ^У = /(*)•
Таким образом, мы получаем, что для некоторой окрестности U
точки р функция R+[g(x)] на множестве U ПМ\ {р} совпадает с
функцией, имеющей предел, равный нулю.
На основании теоремы о локальности предела (следствие 3
теоремы 1.5), отсюда следует, что
lim R+\g(x)] = 0
х—*р,х£М
и, следовательно,
lim g(x) = lim -7-7-т = оо.
х->р,хбМ х—>р,х£М J\X)
Случай, когда f(x) < О для всех х Е Uo П М, отличных от р, где С/о
— некоторая окрестность точки р, сводится к рассмотренному заменой
/ на -/.
Теорема доказана. ■
§3. Признаки существования предела
В этом параграфе рассматриваются функции, определенные на
подмножествах множества вещественных чисел Е.
Прежде всего, здесь будет доказана теорема о существовании
предела у произвольной монотонной функции, заданной на некотором
подмножестве М. Из этой теоремы, в частности, следует, что всякая
монотонная числовая последовательность имеет предел.
Следствие теоремы — так называемая теорема о вложенных
отрезках. Последняя часто применяется при доказательстве различных
теорем о свойствах множества вещественных чисел, которые далее
неоднократно применяются.
С помощью теоремы о вложенных отрезках доказывается
критерий сходимости Коши — Болъцано, дающий необходимое и достаточное
условия существования конечного предела.

126
Гл. 2. Теория предела
С помощью теоремы о вложенных отрезках доказывается
существование бесконечных несчетных множеств. Оказывается, что всякий
отрезок, например, отрезок [О,1] множества вещественных чисел R, является
несчетным множеством.
В заключительной части параграфа изучаются понятия пределов
слева и справа для функции, определенной на отрезке. Это позволяет
указать некоторую классификацию точек разрыва функции,
определенной на отрезке.
3.1. Теорема о существовании предела монотонной функции
Пусть даны множество АсМи функция / : А -» R. Напомним, что
функция / называется возрастающей, если для любых х±, Х2 € А таких,
что xi < Х2, выполняется неравенство
f(xi) < f(x2).
Если для любых xi, X2 € А таких, что х\ < х2, справедливо неравенство
f(xi) > /Ы,
то функция / называется убывающей.
Пусть xi ижг — два произвольных элемента множества А. Если
/0*i) < /Ы, то ~/{хг) > -/(х2), а если f(Xl) > /(ж2), то -/(хг) < -f(x2).
Отсюда следует, что если функция / является возрастающей, то
функция —/ — убывающая, а если / есть убывающая функция, то —/,
напротив, представляет собой возрастающую функцию.
Для того чтобы установить, что числовая последовательность
монотонна, нет необходимости сравнивать значения ее членов с
произвольными номерами ni,n2 G N&, как показывает следующее утверждение:
♦ Предложение 3.1. Пусть (xn)ne^k есть произвольная
последовательность вещественных чисел. Если для всякого n e Nk выполняется
неравенство xn < rrn+i, то последовательность (хп)п^щк — возрастающая.
Если для всякого n е М^ имеет место неравенство xn > жп+1, то данная
последовательность является убывающей.
В самом деле, пусть последовательность (хп)п^к такова, что при
каждом п справедливо неравенство: xn < xn+i. Зададим произвольно
щ е Nfc и П2 £ Nfc такие, что ni < п2, и положим: га = п2 - щ. Очевидно,
га G N. Подставляя в неравенство хп < хп+\ индексы п — ri\, n = ni + 1,
n = ni + 2 и т. д., наконец, п = щ + га - 1, получим цепочку неравенств:
из которой, очевидно, следует, что хП1 < х,

§ 3. Признаки существования предела
127
Так как щ, П2 E N& такие, что ni < П2, были выбраны произвольно,
то тем самым доказано, что п н-► хп есть возрастающая функция на
множестве N&.
Если для всякого n G Nfe имеет место неравенство: хп > #n+i, то
—Хп < —#n+i для любого n G Nfc. По доказанному, отсюда вытекает,
что последовательность (—хп)пе^к является возрастающей и, значит,
последовательность хп — убывающая.
Предложение доказано. ♦
■ Теорема. 3.1 (о пределе монотонной функции). Пусть даны
множество МсКи вещественная функция f : М —> R, которая определена
и является монотонной на множестве М. Предположим, что q = sup M
есть предельная точка множества М, и пусть М1 = М \ {q}. Тогда
функция f имеет предел при х —> q по множеству М. При этом
lim f(x) = sup /(#),
x^q,x£M x£M'
если f — возрастающая функция, и
если функция f — убывающая.
Аналогично, если р = inf M есть предельная точка множества М,
то функция f имеет предел при х —> р по множеству М. При этом если
М" = М\{р}, то
lim f(x) = inf f(x)
в случае, когда функция f является возрастающей, и
lim f(x) = sup f(x),
х-*р,х£М х£М"
если f — убывающая функция.
Доказательство. Пусть q = sup M является предельной точкой
множества М. Предположим, что функция / — возрастающая.
Положим
L= sup f(x).
хем'
Покажем, что
L = lim f(x).
x—*q,x€M

128
Гл. 2. Теория предела
Очевидно, L > —оо. Рассмотрим сначала случай, когда L конечно.
Зададим произвольно е > 0. Тогда I/ = L — е < L и, значит, в силу
признака точной верхней границы функции (см. теорему 4.1 гл. 1),
найдется х' Е М' такое, что
L-e<f{x')<L. (3.1)
Так как ж' G М', то х' ф q, и, значит, х1 < q.
Построим некоторую окрестность U точки q. Если q = oo, то
полагаем U = (#',оо].
Если же ^ — конечно, то пусть J7 = (# — 5, # + #), где 6 = q — х' > 0.
Очевидно, как в случае q = оо, так и в случае конечного g
окрестность U есть промежуток, левым концом которого является точка х'.
Возьмем произвольно точку х Е U П М, отличную от q. Имеем:
х' < х < q и, значит, для данного х выполняются неравенства L — е <
< /(#') < /(#) < ■£• Отсюда следует, что для всякого х Е U П (М \ {#})
справедливо соотношение: |/(#) — L\ < е.
Итак, мы установили, что каково бы ни было е > 0, по нему
найдется окрестность U точки q такая, что для любого х Е U П (М \ {q})
имеет место неравенство: \f(x) — L\ < s. Согласно определению предела
это означает, что L = lim f(x).
Рассмотрим случай, когда L = оо. (Рассуждения для этого случая
аналогичны проделанным выше.)
Зададим произвольно К Е К. По нему найдется точка ж' Е М
такая, что If < f(xf). По точке ж' строим окрестность i7 точки g
такую, что точка х' является ее левым концом. (Если q конечно, то
U = (q — 8,q + 6), где 6 = q — #'>(), ав случае # = оо полагаем
U = (ж',оо].) Для всех ж Е С/ П (М \ {#}) имеет место неравенство:
/(ж) > X. В силу произвольности К Е М отсюда следует, что
lim /(ж) = L = оо.
Если функция / — убывающая, то функция — / — возрастающая,
и, значит, по доказанному, имеет предел. При этом
lim[-/(s)]= sup [-/(*)].
Отсюда следует, что функция / имеет предел при х —► #, причем
lim f(x) = - sup [~f(x)] = inf f{x).
x-^q хеМ* хвМ'

§ 3. Признаки существования предела
129
Утверждение теоремы 3.1 относительно предела при х —> q — sup M
доказано.
Утверждение теоремы, касающееся предела при х —> р = inf M,
доказывается аналогичными рассуждениями. Необходимо только
надлежащим образом изменить знаки неравенств. Мы предоставляем
читателю разобраться в этом самостоятельно.
Теорема доказана. ■
Числовая последовательность (xn)neNk называется возрастающей
(убывающей), если она представляет собой возрастающую
(соответственно, убывающую) функцию на множестве N&.
Числовая последовательность называется монотонной, если она
либо возрастающая, либо убывающая.
Применяя теорему 3.1 к случаю, когда область определения
функции есть множество N&, получаем следующий результат.
▼ Следствие 1. Если числовая последовательность (xn)neNk
является монотонной, то она имеет предел. При этом если данная
последовательность возрастающая, то
lim xn = sup#n,
а если она является убывающей, то
lim xn = inf xn-
п—юо nGN
Доказательство — очевидно. ▼
▼ Следствие 2. Всякая ограниченная монотонная числовая
последовательность является сходящейся, то есть имеет конечный предел.
Данное утверждение очевидным образом следует из предыдущего,
если заметить, что ограниченность последовательности означает, что
ее точная верхняя и точная нижняя границы суть конечные числа. ▼
Т Следствие 3 (теорема о вложенных отрезках). Пусть дана
последовательность замкнутых отрезков ([an, ftn])neN множества Ш. Если при
каждом п отрезок [ап,Ьп] содержит в себе отрезок [an+i,6n+i],
[a>n, bn] D [an+ijbn+i], то существует точка р Е К, принадлежащая всем
отрезкам последовательности. Если при этом длина Ьп — an
промежутка [ап, Ъп] стремится к нулю при п —* оо, то такая точка р единственна,
причем р = lim an = lim bn.
n—► oo n—*oo

130
Гл. 2. Теория предела
Доказательство. Предположим, что ([an,bn])neN есть
последовательность отрезков, удовлетворяющая всем условиям следствия.
Из включения [an,ftn] D [an+i,bn+i] вытекает, что an < an+i и
bn+i < Ъп.
Таким образом, мы получаем, что последовательность (an)neN
является возрастающей, а последовательность (ftn)neN — убывающей.
Стало быть, в силу следствия 1, существуют пределы:
А = lim an, В = lim bn.
п—юо п-юо
Так как последовательность (an)neN — возрастающая, то ап < А при
любом п, а в силу того, что (ftn)neN есть убывающая
последовательность, В <Ьп при всех п.
Далее, при каждом п Е N имеет место неравенство an < bn.
Отсюда, в силу теоремы о предельном переходе в неравенстве (следствие 1
теоремы 1.3), вытекает, что А < В.
Итак, для данной последовательности отрезков ([an,bn])n£N
существуют такие числа А и В, что при каждом п выполняются неравенства:
ап < А < В < Ьп.
В частности, отсюда видно, что числа А и В — конечны. Любое
число р такое, что А < р < В, очевидно, принадлежит всем отрезкам
[а>п,Ьп].
Если Ьп — а>п —■> 0 при п —>оо, то А = Вир = А = В является
общим пределом последовательностей (an)neN и (ftn)neN.
Следствие доказано. ▼
3.2. Критерий Коши — Больцано существования конечного
предела
Зададим произвольно множество М С 1, имеющее предельную
точку р.
Ш Теорема 3.2 (признак сходимости Коши — Больцано). Для того
чтобы числовая функция f(x), определенная на множестве МсК,
имела конечный предел при х, стремящемся к р Е Cim(M) по множеству
М, необходимо и достаточно, чтобы для всякого е > 0 можно было
указать окрестность U точки р такую, что для любых xi € М и Х2 € М,
принадлежащих окрестности U и отличных от р, выполняется
неравенство:
|/0п)-/Ы1<£.

§ 3. Признаки существования предела
131
Доказательство. Необходимость. Предположим,
что функция f(x) имеет конечный предел при #, стремящемся к р по
множеству М, причем в случае, когда / — вещественная функция, этот
предел конечен. (Напомним, что для комплексных функций понятие
бесконечного предела вообще не определено.)
Пусть L = lim /(ж). Зададим произвольно е > 0. Положим
х-+р,х£М
Si = е/2. Очевидно, е\ > 0.
Согласно определению предела, найдется окрестность U точки р
такая, что для любого х Е М, отличного от р и принадлежащего
окрестности С/, имеет место неравенство: \f(x) — L\ < е/2.
Пусть х±их2 — два произвольных элемента множества UC)M\{p}.
Имеем:
|/Ы - /Ы1 < l/Orx) -l\ + \l- f(X2)\ <| + £=£.
Так как е > 0 было взято произвольно, то необходимость условия
теоремы доказана.
Достаточность. Рассмотрим сначала случай, когда функция
/ является вещественной. Предположим, что для всякого е > 0 можно
указать окрестность U точкир такую, что для любых #i, #2 Е М,
отличных отри принадлежащих окрестности С/, выполняется неравенство:
|/(*1)-/Ы|<£.
Требуется доказать, что данная функция имеет конечный предел
при #, стремящемся к р по множеству М.
Сначала построим число L, которое могло бы считаться
возможным «претендентом на должность предела». После этого наша задача
будет состоять в том, чтобы показать, что этот «претендент»
соответствует указанной «должности».
Построим некоторую специальную последовательность (Vn)neN
окрестностей точки р.
<- 1
Пусть Vn есть окрестность точки р, отвечающая значению е = —-,
2п
то есть такая, что для любых #i,#2 £ Vn П М, отличных от р,
выполняется неравенство:
|/Ы-/(х2)|<^.
Полагаем: Vi = VI. Если для некоторого п 6 N окрестность V^
определена, то пусть Уп+1 есть окрестность точки р, содержащаяся в
каждой из окрестностей Vn и Vn+i.

132
Гл. 2. Теория предела
Последовательность (Vn)neN является убывающей, то есть при
каждом п G N выполняется включение Vn Э Vn+ь При каждом п имеем:
vn с vn.
Положим Gn = VnCiM\ {p}, и пусть
ап = inf /(ж), Ьп = sup /(ж).
При каждом п будет <3n Э Gn+i- В силу известных свойств точной
верхней и точной нижней границ функции, отсюда следует, что при
каждом п имеем ап < an+i и Ьп > Ьп+ь
Возьмем произвольно точку хп Е Gn- Для всякого ж Е С?п
выполняется неравенство:
1/(Ж)_/(Жп)1<±.
Заключаем, что
/(*») - ^ < /(*) < /(*») + ^
для всякого х Е Gn. Отсюда следует, что
<*>п > f(xn) - 77-, Ьп < f(xn) + тг"-
Zn 2п
В частности, мы получаем, что ап и Ъп — конечны.
Имеем неравенства:
-ап < -f(xn) + 5-, Ьп < /(жп) + г-,
складывая которые почленно, получим:
Ьп — ап < —.
п
Отсюда, в частности, следует, что разность Ъп — ап стремится к
нулю при п —> оо.
На основании теоремы о вложенных отрезках (следствие 3
теоремы 3.1), существует вещественное число L такое, что L Е [an,bn] при
всяком п, причем ап —> L и Ьп —> L при п —> оо.
Таким образом, построено некоторое число LGM.

§ 3. Признаки существования предела
133
Докажем, что L — lim /(#)• Зададим произвольно е > 0. Пусть
no G N таково, что — < е. Положим U = Vno. Возьмем произвольно
По
точку х G U П М, отличную от р. Тогда х £ Gno и, следовательно,
«п0 < /(ж) < ЬПо.
Имеем также i Алл < L < bn0. Отсюда следует, что
\f(x) - L\< ЪПо - апо < — < е.
по
В силу произвольности е > 0, тем самым установлено, что
L = lim /(ж).
ж—>-р,ж€М
Таким образом, для случая вещественных функций достаточность
условия теоремы установлена.
Предположим, что / есть комплексная функция. Для любых двух
точек х' и х" множества М имеют место неравенства:
| Re/(*') - Re/(z")| < \f(x') - f(x")\,
\Imf(x') - Imf(x")\ < \f(x') - f(x")\.
Отсюда вытекает, что если функция / удовлетворяет условию теоремы,
то и каждая из вещественных функций Re / и Im / удовлетворяет этому
условию.
В силу доказанного, это позволяет заключить, что пределы
lim Re f(x), lim 1т/(ж)
существуют и конечны, и, значит, функция / имеет предел:
ит /(ж).
х—*р,х£М
Таким образом, достаточность условия теоремы установлена и для
случая, когда функция / комплексная.
Теорема доказана. ■
Т Следствие 1. Для того чтобы числовая последовательность
(#n)neN была сходящейся, необходимо и достаточно, чтобы для всякого

134
Гл. 2. Теория предела
е > О существовал номер п такой, что для любых ni > п и П2 > п
выполняется неравенство: \хП1 — хП2 \ < s.
Доказательство. Необходимость. Пусть
последовательность (#7i)neNfe является сходящейся.
Зададим произвольно е > 0. Согласно теореме, по данному е > 0
найдется окрестность U = (if, оо] точки р = оо такая, что для любых
номеров ni,n2 G ?7 выполняется неравенство: \хП1 — хП2\ < £•
Выберем произвольно n > if, n £ Nfc. Если ni > n и пг > п, то
ni G С/ и пг G С/, и, значит, |жП1 — хП21 < £•
Необходимость установлена.
Докажем достаточность. Предположим, что для всякого
е > 0 можно указать номер п такой, что для любых п\ > п и пг > п
выполняется неравенство: \хП1 — хП2 \ < £•
Зададим произвольно г>0и найдем соответствующее ему
значение п. Положим U — (п,оо].
Множество U есть окрестность точки р = оо. Из условия n € U
вытекает, что п > п, и, следовательно, в силу выбора п, для любых
номеров ni G С/ и пг G ?7 выполняется неравенство: |#П1 — хП2 \ < е.
Таким образом, для последовательности, как функции на
множестве Nfc, выполнены условия теоремы 3.2 и, значит, эта
последовательность имеет конечный предел при п —> оо, то есть является сходящейся.
Следствие 1 доказано. ▼
Другое доказательство достаточности критерия сходимости Коши
— Больцано для последовательности (следствие 1 теоремы 3.2)
приводится в п. 6.2.2 этой главы.
Заметим, что в части, касающейся достаточности, условие
следствия может быть несколько ослаблено. Справедливо следующее пред-
. ложение.
▼ Следствие 2. Если числовая последовательность (хп)пещ
удовлетворяет условию: для всякого £ > 0 можно указать номер п такой,
что для любого n > n выполняется неравенство \хп — х~\ < е, то она
является сходящейся.
Доказательство. Действительно, предположим, что
последовательность (#n)n€Nfe удовлетворяет условию следствия.
Зададим произвольно е > 0. Положим е\ = е/2. Тогда, в силу
предположения, найдется п такое, что если п > п, то \хп — х-\ < ei.
Пусть п\ > h и П2 > п. Тогда
\х<гы - Хп2\ < кщ ~ х-\ + \х- - хП2\ < ei+ei = е.

§ 3. Признаки существования предела
135
Таким образом, для любых п\ > п и П2 > п выполняется
неравенство:
Так как е > О — произвольно, то для данной последовательности
выполняется условие следствия 1, и тем самым доказано, что эта
последовательность является сходящейся.
Следствие 2 доказано. Т
3.3. Критерий Гейне существования предела
Докажем теорему, из которой следует, что понятие предела
функции в общем случае может быть сведено к понятию предела
последовательности.
■ Теорема 3.3 (критерий Гейне существования предела). Пусть
даны множество МсКи его предельная точка р. Предположим, что
числовая функция f, определенная на множестве М, такова, что для всякой
последовательности (xn)neN точек множества М такой, что р = lim xn
п—+оо
ир ф Хп для всех п, последовательность (f(xn))neN имеет предел. Тогда
существует предел: lim f(x).
х—*р,х£М
Замечание. В условиях теоремы областью значений функции
/ может быть как множество М, так и множество всех комплексных
чисел С. В случае, когда функция / — вещественная, допускаются
бесконечные значения предела: lim f(xn).
n—*oo
Доказательство. Пусть выполнены все условия теоремы.
Последующие рассуждения состоят из двух частей.
В первой части мы докажем, что значение предела lim f(xn) не
71—*00
зависит от выбора последовательности (xn)neN, удовлетворяющей всем
требуемым условиям.
Пусть (xn)neN есть последовательность точек множества М такая,
что хп ф р и р = lim хп при каждом п. Согласно условию теоремы,
п—+оо
существует предел: lim f(xn) = L.
п—+оо
Пусть (tn)neN — какая-либо другая последовательность точек
множества М, удовлетворяющая тем же условиям: lim tn = р и tn ф р для
п—+оо
всех п.
В силу условия теоремы, существует предел: lim f(tn) = L1'.
п—юо
Покажем, что L — L'. Для этой цели построим новую
последовательность (^n)nGN, полагая zn — жп, если п — четно, и zn — tn для
нечетного п.

136
Гл. 2. Теория предела
При каждом п точка zn лежит между хп и tn, zn £ М и zn ф р.
Применяя теорему о зажатой переменной (теорема 1.5), заключаем,
что zn стремится к р при п —► оо.
В силу условия теоремы, существует предел: lim f(zn) = L".
п—+оо
Имеем:
L" = lim f(z2n) = lim f(x2n) = lim /(a?n) = £
71—-ЮО П—ЮО 71—ЮО
и точно так же заключаем, что
L" = lim ffan-i) = lim f(t2n-i) = lim /(tn) = Z/.
n—*oo n—+oo n—+oo
Из доказанного вытекает, что Lf = L.
Последовательность (tn) точек множества М \ {р}, сходящаяся к
точке р, была выбрана произвольно.
Мы получаем, таким образом, что если функция / удовлетворяет
всем условиям теоремы, то существует число L такое, что для любой
последовательности (in), п = 1,2,..., точек множества М \ {р}, имеющей
пределом точку р, f(tn) стремится к L при п —> оо.
Вторая часть доказательства теоремы, к которой мы переходим,
состоит в том, чтобы доказать, что полученное число L есть предел
функции f(x) при х —► р по множеству М.
Будем предполагать, что в случае, когда функция / является
вещественной, L — конечно. Зададим произвольно е > 0.
Докажем, что найдется окрестность U точки р такая, что для
всякого х £ М \ {р}, принадлежащего этой окрестности, выполняется
неравенство:
\f(x)-L\<e. (3.2)
Предположим, напротив, что окрестность U точки р,
удовлетворяющая данному условию, не существует. Это означает, что, какова бы
ни была окрестность U точки р, обязательно найдется точка х £ М,
принадлежащая окрестности U и отличная от точки р, для которой
неравенство (3.2) не выполняется, то есть такая, что \f(x) — L\> е.
Пусть (C/n)neN есть последовательность окрестностей точки р,
которая является ее канонической базой. Для всякого п £ N, в силу
сделанного предположения, найдется точка хп Е Un П М, отличная от р,
для которой \f(xn) — L\> е.
Полагая п = 1,2,..., получим последовательность (хп)пеп точек
множества М такую, что при каждом п £ N справедливо хп £ С/п,
хпфр,ж имеет место неравенство: \f(xn) — L\ > е.

§ 3. Признаки существования предела
137
При п —> оо, согласно лемме 1.10, жп-^ри, значит, по доказанному,
/(#п) —> Ь. Переходя в неравенстве |/(жп) —L| > е к пределу при п —> оо,
получим, что 0 > е. Это, однако, противоречит тому, что по условию
£>0.
Итак, допущение, что у точки р нет окрестности такой, что для
всех точек х £ М, принадлежащих этой окрестности и отличных от р,
выполняется неравенство (3.2), приводит к противоречию.
Таким образом, доказано существование окрестности С/,
обладающей тем свойством, что для любого х Е U П (М \ {р}) выполняется
неравенство: \f(x) — L\ <e.
Согласно определению предела, этим установлено, что
L= lim *J(X)'
Рассмотрим случай, когда функция / — вещественная иЬ = ±оо.
Положим F(x) = R+[f(x)] в случае L = оо и F(x) = R+[—/(ж)],
если L = —оо. Тогда для всякой последовательности (#n)n€N точек
множества М \ {р}, имеющей пределом точку р, F(xn) —> 0 при п —* оо.
По доказанному, отсюда вытекает, что 0 = lim F(x). Тем самым
х—>р,х£М
установлено, что L = lim f(x) и в данном случае.
х—+р,х£М
Теорема доказана. ■
3.4. Несчетность множества вещественных чисел Ш
В качестве приложения теоремы о вложенных отрезках
(следствие 3 теоремы 3.1), установим некоторое важное свойство множества
всех вещественных чисел Ш.
Всякий промежуток (а,Ь), где а < Ь, множества вещественных
чисел представляет собой бесконечное множество.
Оказывается, что всякий промежуток в К. имеет существенно
больше элементов, чем множество натуральных чисел N. Говорят, что
промежуток является несчетным множеством.
Этот факт может показаться неожиданным, если вспомнить, что
множество всех рациональных чисел Q, как было показано ранее (см.
главу 1,§7), — счетно. Между тем рациональные числа
достаточно густо располагаются в множестве всех вещественных чисел и,
казалось бы, это множество не должно быть существенно богаче
множества всех рациональных чисел.
■ Теорема 3.4 (теорема о несчетности отрезка в множестве
вещественных чисел). Для любых а, Ь £ R таких, что a < Ь, отрезок [а, Ь] не
является счетным множеством.

138
Гл. 2. Теория предела
Доказательство. Пусть а, Ь El, причем а <Ъ. Предположим,
вопреки доказываемому, что множество [а, ft] — счетно.
Промежуток [а, Ь] представляет собой бесконечное множество и,
значит, на основании следствия 1 теоремы 7.1 главы 1, существует
взаимно однозначное отображение множества [а, ft] на множество всех
натуральных чисел N.
Точку отрезка [a, ft] с номером п обозначим через хп.
Построим, по индукции, некоторую последовательность отрезков
([ttn,bn])nGN.
Счет отрезков удобнее начинать сп = 0. Полагаем [ао,Ьо] = [а, ft].
Предположим, что для некоторого целого п > О отрезок [ап,Ьп]
определен. Разделим его на три равные части точками сп и dn такими,
что ап < сп < dn < bn.
Заметим, что хотя бы один из этих трех отрезков [anjCn], [cn,rfn]
и [dn,ftn] не содержит точку xn+i- Тот из них, для которого это имеет
место (то есть который не содержит точку #n+i), обозначим символом:
[fln+ljftn+l].
Таким образом, по индукции определена последовательность
отрезков ([an,&n])n>o- Из построения следует, что при любом целом п > О
Хп £ [ап,Ьп] и при каждом п будет [ап,Ьп] Э [an+i,bn+i].
В силу следствия 3 теоремы 3.1, найдется число у G И такое, что
у е [an, Ьп) для всех п G N.
В частности, у £ [a, ft] и, значит, в нумерации элементов
промежутка [a,ft], существование которой мы предполагаем, у имеет некоторый
номер.
Пусть у = хПо • Но тогда, как следует из определения промежутка
[ttno?bn0]5 точка у = хПо этому отрезку не принадлежит, то есть
справедливо соотношение: у £ [ano,ftno]-
В то же время у £ [an, bn] для всех п и, в частности, для п = по.
Мы получаем, таким образом, противоречие: с одной стороны,
у £ [ano,ftn0], а с другой — у g [ano,ftno].
Допущение, что промежуток [a, ft] представляет собой счетное
множество, привело нас к противоречию.
Следовательно, [a, ft] не может быть счетным множеством, и
теорема тем самым доказана. ■
3.5. Понятие одностороннего предела и классификация точек
разрыва функции на отрезке
Пусть даны промежуток I = (a,ft) С К и функция f : I —>Ш.

§ 3. Признаки существования предела
139
Возьмем произвольно внутреннюю точку хо промежутка J. Эта
точка разбивает /на два частичных промежутка:
/~ = I П [—оо,жо) и /+=7П(жо,оо]
и является предельной для каждого из них.
Предел функции / по промежутку /~ при х —> хо называется
пределом слева функции / в точке хо и обозначается формулой:
lim /(ж) = /(жо-0).
х—►жо — О
Предел f(x) при ж, стремящемся к хо по промежутку /+,
называется пределом справа функции / в точке хо и обозначается формулой:
lim /(ж) = /(жо + 0).
X —*£С0+0
Пределы слева и справа функции / : / —> К в
произвольной внутренней точке жо промежутка J называются односторонними
пределами функции f в точке хо.
Для величин f(xo + 0) и f(xo — 0) в литературе используются также
обозначения: /|(жо) и /|(жо), соответственно.
Если функция / имеет предел при ж, стремящемся к точке жо, то,
в силу установленных ранее свойств предела (см. следствие 2
теоремы 2.6), ее пределы слева и справа также существуют и равны lim /(ж).
X—+XQ
■ Теорема. 3.5. Пусть дал промежуток I = (а, Ь) С К. Пусть жо —
это произвольная внутренняя точка промежутка I. Если пределы слева
и справа функции f в точке жо существуют и равны между собой, то
функция f имеет предел при ж —» жо по множеству I, равный общему
значению пределов слева и справа функции /.
Доказательство. Пусть выполнены все условия теоремы.
Положим /~ = If] [—оо,жо), /+ = /П (жо, оо]. Пусть L есть общее значение
пределов слева и справа функции / в точке жо.
Предположим сначала, что L — конечно.
Зададим произвольно е > 0. Пусть 6i > 0 таково, что если жЕГ,
причем |ж — жо| < <5i, то выполняется неравенство |/(ж) — L\ < е.
Далее, пусть 62 > 0 таково, что если ж Е /+, причем |ж — жо| < 62,
то |/(ж) - L| < г.
Наименьшее из чисел 6i и <5г обозначим через 6.
Пусть ж £ / \ {жо} таково, что |ж — жо| < <5.

140
Гл. 2. Теория предела
Если х < жо, тоже/ . Так как 6 < <5i, то \х — хо\ < <5i, и, значит,
\f{x)-L\<e.
Если же точка х расположена справа от жо, то х Е /+. Так
как \х — хо\ < 6 < <$2, то и в этом случае \f(x) — L\ < е.
Так как е > 0 было взято произвольно, то тем самым установлено,
что
L = lim f(x).
X—>XQ
Мы предполагали, что число L — конечно. Случай, в котором
L = ±оо, сводится к этому стандартным приемом. Он состоит в том,
чтобы вместо / рассмотреть функцию F : / —> R, определенную
следующим образом: F(x) = R+[f(x)] при L = ос и F(x) = Л_[/(ж)] при
L = —оо.
Рассмотрение всех деталей, относящихся к случаю L = ±оо, мы
предоставляем читателю.
Теорема доказана. ■
Пусть / : М —» R есть функция, область определения которой
содержит интервал Д = (&,13). Пусть р есть произвольная точка
промежутка А.
Если функция / не является непрерывной в точке р, то говорят,
что р есть точка разрыва функции /.
При этом если пределы слева и справа функции / в точке р
существуют и оба конечны, то говорят, что р есть точка разрыва
первого рода. Во всех остальных случаях, то есть если хотя бы один
из этих пределов не существует или существует и
равен ±оо, — точкой разрыва второго рода функции /.
Приведем некоторые примеры.
Пример 1. Для произвольного х £ К положим:
{—1 при х < 0;
0 при х = 0;
1 при х > р.
Как нетрудно видеть,
lim sgn x = —1, lim sgn x = 1.
ж-»-0 ж-»+0
Отсюда ясно, что 0 есть точка разрыва первого рода функции sgn
(см. рис. 1).

§ 3. Признаки существования предела
141
1(
О
S
X
.-;
Рис. 1
Рис.2
Пример 2. Положим:
л*)
■{
1/х при ж^О;
О при х = 0.
Для данной функции / имеем:
lim /(ж) = — оо, lim /(ж) = оо.
х—► —О as—►+()
Точка 0 является, в соответствии с данным здесь определением,
точкой разрыва второго рода функции / (см. рис. 2).
Пример 3. Пусть /
щим образом:
/(*) =
есть функция, определенная следую-
sin ( — ] при х ф 0;
при х = 0.
О
В точке 0 у данной функции / пределы слева и справа не
существуют.
Чтобы доказать, что данная функция / не имеет в точке 0
предела справа, рассмотрим последовательности (хп)пе^ и (yn)neN, где
2 2
Хг,
ПУп =
при каждом п.
4п + 1 4п - 1
Тогда /(#п) = 1 и /(уп) = —1 при всех п £ N и, значит,
lim f(xn) = 1, lim /(j/n) = -1.
Так как эти пределы различны, то предел lim f(x) не
ж—»-+0
существует, что и требовалось доказать.

142
Гл. 2. Теория предела
Аналогично доказывается, что у функции / данного примера
предел слева в точке 0 также не существует (см. рис. 3).
Рис.3
Ш Теорема 3.6. Пусть I — (а,Ь) есть произвольный открытый
промежуток в Ж. Если функция f : I —> Ж монотонна, то она может
иметь только точки разрыва первого рода. При этом если функция / —
возрастающая, то в каждой точке р £ / выполняются неравенства:
/(р - о)< Др) </(р + о). (з.з)
Если f есть убывающая функция, то в каждой точке р Е (а, Ь)
Яр-о)>Яр)>Яр + о). (3.4)
Доказательство. Пусть / есть возрастающая функция.
Возьмем произвольно точку р Е (а, Ь) и положим 1~ = (а,р), /+ = (р, Ь).
Предел f(x) при х —> р по промежутку /"", согласно определению,
данному выше, есть предел слева функции / в точке р.
Аналогично, предел f(x) при х —► р по промежутку /+ есть предел
этой функции справа в точке р.
Из теоремы 3.1 следует, что функция / имеет в точке р пределы
слева и справа.
При этом, так как / есть возрастающая функция, то f(p)
является верхней границей функции / на промежутке /" и ее
нижней границей на промежутке /+. В силу теоремы 3.5, отсюда,
очевидно, вытекают неравенства (3.3).

§4. Теорема о разрешимости уравнения f(x) = h
143
Функция /, по условию, всюду конечна. Тогда
f(p - 0) = sup f(x) > -оо, f(p + 0) = inf f{x) < oo.
xei- *e/+
Принимая во внимание неравенства (3.3), заключаем, что величины
f{p — 0) и f(p + 0) — конечны.
Таким образом, функция / имеет в точке р конечные
пределы слева и справа, что, по определению, и означает, что р есть точка
разрыва первого рода функции /.
В проделанных рассуждениях предполагалось, что функция / —
возрастающая.
Случай, когда / есть убывающая функция, сводится к этому
заменой / на —/.
Теорема доказана. ■
§4. Теорема о разрешимости уравнения f(x) = h
и ее следствия
Предположим, что функция f определена и непрерывна на некотором
промежутке [а, Ь] с R. Если существует число ftel такое, что /(а) < h, a
f(b) > h, то в промежутке [а, Ь] обязательно найдется точка х такая, что
f(x) = h (см. рис. 4).
Наглядно этот результат может быть истолкован так: График
непрерывной функции есть некоторая непрерывная линия на плоскости. Если
один ее конец лежит выше прямой, заданной уравнением у = h, а другой
располагается ниже этой прямой, то данная линия, в силу своей
непрерывности, пересекает эту прямую.
Эти наглядные соображения, однако, не имеют доказательной силы
и, требуется точное доказательство. Таковое и приводится здесь.
В качестве приложения полученного результата доказывается
некоторая теорема о существовании непрерывной обратной функции.
Рис.4

144
Гл. 2. Теория предела
4.1. Теорема Коши о промежуточных значениях
Теорема, устанавливаемая здесь, показывает, что понятие
непрерывной функции отвечает наглядному представлению о непрерывности,
как о сплошной протяженности, не имеющей скачков.
Предварительно докажем следующее вспомогательное
предложение, полезное и само по себе.
■ Лемма 4.1. Пусть М есть непустое подмножество множества Ж и
р есть либо точная верхняя, либо точная нижняя граница множества М.
Тогда найдется последовательность (хп)пе^ точек множества М такая,
что
р = lim хп.
п—юо
Доказательство. Пусть М — непустое множество
вещественных чисел и р есть или его точная нижняя, или его точная верхняя
граница.
Если р не принадлежит множеству М, то, согласно теореме 1.1, р
есть предельная точка множества М, и существование требуемой
последовательности непосредственно вытекает из характеристики
предельных точек множества, которая дается леммой 1.10.
Если же р является элементом множества М, то
последовательность (#n)neN, в которой xn = p для всех п, и будет требуемой.
Лемма доказана. ■
■ Теорема 4.1 (теорема Коши о промежуточных значениях). Пусть
даны промежуток [a,b] С Ш и непрерывная функция /, определенная
на этом промежутке. Если /(а) > 0, a /(b) < 0, то найдется число
£ G (а, Ь] такое, что /(£) = 0 и для всех х G [а, £) имеет место
неравенство: f(x) > 0.
Если функция / такова, что /(а) < 0, a f(b) > 0, то найдется точка
£ G [а, Ь) такая, что /(£) = 0 и f(x) > 0 для всех х G (£, Ь].
Первое доказательство теоремы 4.1. Рассмотрим сначала
случай, когда f(a) > 0 и /(b) < 0. Обозначим через Е множество всех
точек х G (а,Ь] таких, что f(x) < 0. Множество Е непусто, так как,
по условию, Ъ G Е. Пусть £ = infi£. Поскольку Е С (а,Ь], то число a
является нижней границей Е и, следовательно, £ > а.
Согласно лемме 4.1, существует последовательность (xn)neis точек
множества Е такая, что £ = lim xn. Так как функция / непрерыв-
71—ЮО
на, то /(£) = lim f(xn)- При каждом n G N выполняется неравенство
71—ЮО
f(xn) < 0, и, стало быть, согласно теореме о предельном переходе в

§4. Теорема о разрешимости уравнения f(x) = h
145
неравенстве, имеем: /(£) < 0. Так как f(a) > 0, то из доказанного
следует, что а ф £ и, значит, а < £.
Пусть х е [а,£). Тогда х < £. Так как £ = infE, то х ф Е. По
определению, Е — множество всех х € [а, Ь] таких, что f(x) < 0, и, значит,
если х € [а, 6] не принадлежит £", то f(x) > 0. Отсюда вытекает, что для
всех х £ [а, £) выполняется неравенство: /(х) > 0. В силу непрерывности
/, получаем, что /(£) = lim f(x). Таким образом, имеем /(£) < 0 и
одновременно /(£) > 0, то есть /(£) = 0.
Первое утверждение теоремы доказано.
Второе доказывается аналогичным образом. Необходимо только в
проделанных рассуждениях надлежащим образом изменить знаки
неравенств и вместо iniE рассмотреть swpE. (Множество Е определяется
так же, как и в предыдущем случае.) Рассмотрение всех деталей
доказательства в этом случае предоставляется читателю.
Теорема доказана. В
Приведем здесь еще одно доказательство теоремы 4.1. Оно
представляет интерес в том отношении, что в нем содержится процедура для
вычисления корня £ уравнения f(x) = 0, которая может быть
использована для практических целей.
Второе доказательство теоремы 4.1. Пусть даны
промежуток [a,b] с R и непрерывная функция /, определенная на этом
промежутке. Предположим, что f(a) > 0, a /(b) < 0. Докажем сначала, что
при этом условии найдется £ е (а, Ь] такое, что /(£) = 0.
Утверждение теоремы, относящееся к случаю /(а) > 0, /(b) < 0,
доказывается аналогичным образом.
Определим по индукции некоторую последовательность отрезков
([a<n,bn])neNo. Положим а0 = а, &о = Ь.
Предположим, что для некоторого целого п > 0 определен отрезок
[а>п,Ьп] С [а,6], причем f(an) > 0, f(bn) < 0. Положим сп = п п.
В случае f(cn) > 0 пусть an+i = сп, а bn+i = bn. Если же f(cn) < 0, то
пусть an+i = an, bn+i = сп. В обоих случаях имеем:
/(an+i)>0, /(b„+i)<0
и
Ki+b&n+i] С [an,bn] С [a,b].
В силу принципа математической индукции последовательность
отрезков ([ап,Ьп])пещ0 определена.

146
Гл. 2. Теория предела
Из построения последовательности ([ап, bn])n€N0 следует, что при
каждом п е No имеем [an+bbn+i] с [ап,Ьп] и Ьп+1 - ап+1 = п п.
г
Отсюда вытекает, что [ап,6п] с [а, 6] и Ъп — ап — —— при каждом п.
2п
Для всех п е No, по построению, имеем: f(an) > 0 и f(bn) < 0.
По теореме о вложенных отрезках (следствие 3 теоремы 3.1),
существует точка £ е [а, Ь], принадлежащая всем отрезкам данной
последовательности. При п —► оо будет ап —» £ и &п —> £.
По условию, функция / непрерывна и, значит, /(ап) —> /(f) и
ДЫ -+ /(0 при п -> оо.
Применяя теорему о предельном переходе в неравенстве (теорема
1.3), получим: /(О > 0 и /(f) < 0, откуда /(f) = 0.
Имеем: /(а) > 0 и, значит, £Ф а. Следовательно, а < f < Ъ.
Таким образом, установлено, что в промежутке [а, Ь] существуют
точки, в которых функция / обращается в нуль. Теорема 4.1 утверждает,
однако, нечто большее, а именно, — что существует точка f е (а, Ь] такая,
что f(x) > О для всех х € (а, Ъ].
Чтобы доказать это, рассмотрим множество N всех х € [а, Ь] таких,
что f(x) = 0. По доказанному, множество N непусто. Пусть f = inf N.
Тогда точка f и будет искомой. Доказательство этого предоставляется
читателю.
Теорема доказана. ■
т Следствие. Пусть дана непрерывная функция / : [а, Ь] —» R.
Предположим, что число h e R таково, что /(а) < hnh < f(b). Тогда найдется
точка £ такая, что a < £ < Ь, /(f) = Л, и для всех а: € [а, О выполняется
неравенство: h < f{x).
Для доказательства следствия достаточно применить теорему 4.1 к
функции /i(ж) = /(ж) -Л. Т
■ Теорема 4.2. Пусть даны промежуток I = (a,b) с R и функция
/ : I —► R. Если функция / непрерывна, то множество /(/) является либо
промежутком, либо состоит из единственной точки.
Доказательство. Пусть выполнены все условия теоремы.
Положим:
р = inf f(x) = inf /(/), g = sup f(x) = sup /(J).
Тогда р < g. Для всех # € J имеем: р < f(x) < q.
Если р = q, то отсюда следует, что функция / постоянна на
множестве /ив этом случае /(/) есть одноточечное множество.
Предположим, что р < q. Очевидно, что /(/) c\p,q].

§4. Теорема о разрешимости уравнения f(x) = h
147
Теорема будет доказана, если мы покажем, что /(/) D (p,q).
Возьмем произвольно у ЕЖ такое, что р < у < q. В силу признаков
точной верхней и точной нижней границ множества (см. теорему 4.1
главы 1), найдутся точки х\ Е / и Х2 Е / такие, что f{x\) > у, а
/0*2) < У'
Точки ^1 ИЖ2 — различны. Пусть [а,/3] есть отрезок с
концами х\ и #2, то есть либо а — #i, /3 = #2, либо а = #2, /3 = х\.
Очевидно, [а,/3] С /. Функция F : х v-> f(x) — у на концах
промежутка [а,/3] принимает отличные от нуля значения разных знаков.
Следовательно, найдется х Е (а,/3) такое, что ^(#) = 0, то есть
/0*0 = у-
Очевидно, х Е / и, стало быть, у Е /(-О-
Точка у такая, что р < у < q, была взята произвольно. Тогда из
доказанного вытекает, что /(/) Э (p,q)-
Теорема доказана. ■
Говорят, что вещественная функция /, определенная на некотором
промежутке / = (а,Ь), обладает свойством Дарбу, если для любых
уг = f{x\) и ?/2 = /(#2), где х\ и Х2 суть произвольные точки
промежутка /, функция / в промежутке с концами в точках х\ и Х2 принимает
любое значение, лежащее между у\ и у2.
Теорема 4.2, таким образом, утверждает, что всяк ал непрерывная
функция обладает свойством Дарбу.
Обратное, вообще говоря, неверно, как показывает следующий
Пример. Функция
f(x) = lsia{l) при^°;
^ 0 при х — О
не является непрерывной в промежутке [—1,1]. В то же время она, как
нетрудно показать, обладает свойством Дарбу.
4.2. Теорема о существовании непрерывной обратной
функции
■ Лемма 4.2. Пусть I = (а, Ь) — произвольный промежуток в Ж
и f : I —> Е есть монотонная функция. Если множество f(I) является
промежутком, то функция f — непрерывна.
Доказательство. Пусть функция / удовлетворяет условию
леммы. Ограничимся случаем, когда / есть возрастающая функция.
(В случае убывающей функции рассуждения проводятся аналогично.)

148
Гл. 2. Теория предела
Возьмем произвольно точку хо G /. Предположим, что а <
Тогда имеем: f(xo — 0) < /(#о). Докажем, что f(xo — 0) = f(xo).
Xq.
Рис.5
Допустим, напротив, что f(xo — 0) < f{xo). Пусть р = f(xo — 0),
q = f{xo). Положим I\ = [—оо,#о) П J. По теореме о пределе
монотонной функции (теорема 3.1), f(xo — 0) есть точная верхняя граница
функции / на множестве Д. Отсюда следует, что при х G h имеем
/(*)</(*о-0).
Возьмем произвольно значение х G /. Если х > жо, то f(x) >
> f(xo) = q и, значит, f(x) £ (p,q). Если х < хо, то ж G ii и,
следовательно, /(ж) < /(ж0 - 0) = р.
Мы получаем, таким образом, что для любого х G / точка /(ж)
лежит вне интервала (р, д). Множество /(/) имеет как точки,
лежащие слева от этого интервала (таковой будет любая точка
у = /(ж), где ж < #о), так и точки, лежащие справа от
него (например, точка уо = /(#о) лежит справа от данного интервала).
Интервал (f(xo — 0),/(#о)) образует своего рода «дыру» в множестве
/(/). Отсюда следует, что множество /(/) не является промежутком
(см. рис. 5).
Итак, допущение, что f(xo — 0) < /(#о), приводит к противоречию.
Аналогичным образом, в случае хо < Ь, приводится к
противоречию допущение, что /(#о) < /(#о + 0).
Следовательно, если функция / удовлетворяет условиям леммы, то
в каждой точке xq G / левый и правый пределы функции равны
f(xo) и, значит, функция / непрерывна в каждой точке
промежутка /, что и требовалось доказать. ■
Замечание. Условие монотонности в формулировке леммы 4.2
существенно, как видно из указанного в конце предыдущего раздела

§4. Теорема о разрешимости уравнения f(x) = h
149
примера разрывной функции, обладающей свойством Дарбу. Приведем
другой, более простой
Пример (см. рис. 6). Пусть / = [-1,1], /(#) = х + 1 при -1 <
< х < 0, /(0) = 0и f(x) = х — 1 при 0 < х < 1. Здесь функция / имеет
в точке 0 разрыв первого рода. В то же время /(/) = (—1,1), так что
множество /(/) является промежутком.
Рис. б
Функция, построенная в данном примере, не обладает свойством
Дарбу.
Пусть I ж 3 — два произвольных невырожденных промежутка в R.
Будем говорить, что I ж J суть промежутки одного и того же
топологического типа, если они либо оба открытые, либо оба замкнутые,
либо, наконец, оба являются полуоткрытыми.
Далее используется понятие строго монотонной функции.
Приведем определение.
Пусть дано множество А С 1. Функция / : А —» R называется
строго монотонной, если она монотонна и для любых х±,Х2 G А таких,
что х\ ф ж2, всегда f(xi) ф Д#2).
Иначе говоря, функция / : А —» R строго монотонна, если она
монотонна и отображает А в Ё взаимно однозначно.
■ Теорема 4.3 (теорема о непрерывной обратной функции). Пусть
I есть произвольный невырожденный отрезок в Ж, a f : I —» М —
непрерывная строго монотонная функция. Тогда множество J — f(I) есть
отрезок в Ж того же топологического типа, что и отрезок I.
Отображение f — взаимно однозначно, и обратное отображение /_1 является
непрерывной функцией, строго монотонной в том же смысле, что и
исходная функция /.

150
Гл. 2. Теория предела
Доказательство. Пусть функция f : I —*R удовлетворяет всем
условиям теоремы. Из теоремы 4.2 следует, что множество J = /(/)
есть либо отрезок, либо одноточечное множество.
В силу строгой монотонности, функция / не является
тождественно постоянной, поэтому множество J не может быть одноточечным и,
значит, J есть отрезок.
Так как функция / строго монотонна, то при х\ ф Х2 также и
f(xi) ф /(#2), и, значит, / есть взаимно однозначное отображение.
Следовательно, определено обратное отображение: /_1 : J —* /.
Покажем, что функция /_1 монотонна. Предположим, что / есть
возрастающая функция.
Возьмем произвольно точки у± и у2 промежутка J такие, что у\<у2-
Пусть xi = f^iyi), X2 - /_1(2/2). Тогда х\ < х2.
Действительно, допустим, напротив, что х± > Х2. Так как / —
возрастающая функция, то отсюда следует неравенство у\ — f{x\) >
> /(#2) = 2/2, что противоречит условию yi < У2- Это означает, что
xi < Х2. Таким образом, /_1 — это возрастающая функция.
В случае, если / есть убывающая функция, точно так же
устанавливается, что функция 7"1 является убывающей.
Функция g = f"1 отображает промежуток J в / и множество g(J),
очевидно, совпадает с /.
Таким образом, функция g — монотонна и множество g(J) есть
промежуток /. В силу леммы 4.2, отсюда следует, что функция g —
непрерывна.
Для завершения доказательства осталось показать, что /и J суть
промежутки одного и того же топологического типа.
Пусть / = (a,b), J — (с, d). Предположим, что функция /
возрастающая.
Пусть а £ I. Тогда, очевидно, /(а) £ J. Для всякого х G /
выполняется неравенство /(а) < у = f(x) G J. Отсюда следует, что /(а) есть
левый конец промежутка J, то есть /(а) = с. Таким образом, в этом
случае с G J. Следовательно, мы получаем, что если отрезок
/замкнут слева, то и отрезок J является замкнутым слева.
Применяя то же самое рассуждение к функции g = /_1, получим,
что если отрезок J замкнут слева, то и отрезок / является
замкнутым слева.
Таким образом, если один из данных отрезков I is. J замкнут слева,
то и другой будет замкнутым слева. Отсюда следует, что если один
из промежутков I is J является открытым слева, то и другой будет
открытым слева.

§ 5. Основные теоремы о непрерывных функциях
151
Аналогично устанавливается, что если один из отрезков I и J
замкнут справа, то замкнут справа и другой, и, следовательно, если один
из них является открытым справа, то открытым справа будет и другой.
Из доказанного, очевидно, следует, что в рассматриваемом случае
J и J суть отрезки одного и того же топологического типа.
В случае, когда функция / — убывающая, аналогичными
рассуждениями устанавливается, что если один из данных отрезков J и J
содержит свой левый (правый) конец, то другой содержит
свой правый (соответственно, левый) конец. Отсюда нетрудно
заключить, что и в этом случае J и J — отрезки одного и того же
топологического типа.
Теорема доказана. ■
В связи с доказанной теоремой, введем следующее общее понятие.
Пусть дано множество ЛсК. Отображение / : А —► R называется
топологическим, если / — взаимно однозначно и каждое из
отображений / и /-1 — непрерывно.
Множества А,ВсШ называются гомеоморфными, если
существует топологическое отображение / : А —* Е такое, что f(A) = В.
Вместо термина «топологическое отображение» часто употребляется
термин «гомеоморфизм».
Теорема 4.3 устанавливает, что непрерывная, строго возрастающая
функция, определенная на отрезке I множества R, представляет собой
топологическое отображение этого отрезка в множество R.
Из этой теоремы вытекает также, что если промежутки I и J го-
меоморфны, то они принадлежат одному и тому же топологическому
типу. Верно и обратное: если промежутки I и J принадлежат одному
и тому же топологическому типу, то они гомеоморфны.
Последнее утверждение доказывается построением какой-либо
конкретной непрерывной, строго возрастающей функции, отображающей
один из данных промежутков на другой.
§5. Основные теоремы о непрерывных функциях
В этом параграфе устанавливаются некоторые общие свойства
непрерывных функций, определенных на замкнутом отрезке, играющие
фундаментальную роль в дальнейшем изложении.
К числу задач, часто встречающихся в математике и в различных
ее приложениях, относятся задачи на отыскание наименьшего или
наибольшего значения какой-либо величины, представленной как функция
некоторых переменных.

152
Гл. 2. Теория предела
Прежде чем приступить к поиску наибольшего или наименьшего
значения функции и определения того, для каких значений переменных
функция принимает эти значения, полезно знать, имеет ли эта задача
решение или нет. (Выходя на охоту, стоит выяснить сначала, есть ли в
лесу, где мы будем охотиться, нужный нам зверь?)
Здесь устанавливается, что в том частном случае, когда функция
непрерывна, а область ее определения есть замкнутый отрезок, — она
принимает свои наименьшее и наибольшее значения. Задача — найти
наименьшее и наибольшее значения функции в этом случае — заведомо
имеет решение.
Другое свойство непрерывных функций, определенных на
замкнутом отрезке, которое устанавливается здесь, — равномерная
непрерывность.
Согласно определению, функция f непрерывна в точке хо £ М, если
для всякого е > О можно указать 6 > О такое, что если \х — хо\ < 6, то
\f(x) — f(xo)\ < е. Это число 6 > О, в общем случае, зависит не только
от е, но также и от выбора точки хо.
Оказывается, что если область определения функции есть
замкнутый отрезок, а функция / — непрерывна, то можно выбрать 6 не
зависящим от хо.
5.1. Теорема выбора Вейерштрасса
5.1.1. Подпоследовательностью последовательности
(хп)пект (5.1)
называется всякая последовательность вида
(ZnJfcGN, (5.2)
где (nfc)fceN есть строго возрастающая последовательность элементов
множества Nm.
Будем также говорить, что (xnk)kei$ есть подпоследовательность,
которая извлечена из последовательности (#n)neNm.
Наглядно последовательность (5.2) можно представить как
результат следующего построения.
Из последовательности (5.1) вычеркивается часть членов так,
чтобы номера невычеркнутых членов образовывали бесконечное множество.
Затем невычеркнутые члены нумеруются заново в порядке следования
их прежних номеров.

§5. Основные теоремы о непрерывных функциях
153
■ Теорема 5Л (теорема выбора Вейерштрасса). Из всякой
ограниченной числовой последовательности можно извлечь сходящуюся
подпоследовательность.
Доказательство. Пусть {xn)nenrn есть произвольная
ограниченная числовая последовательность. Тогда найдутся числа а и Ъ такие, что
—оо<а<Ь<оои для всех n € Nm выполняются неравенства:
a < хп < Ъ.
Для всякого целого к > О построим некоторый отрезок [ak,bk] и
номер nfc. Полагаем [ао,Ьо] = [&, Ь], щ = га.
Предположим, что для некоторого целого к > О отрезок [ак, bk] и
номер rik определены, причем хПк е [а^,^], и множество значений n € Nm,
для которых точка хп принадлежит отрезку [ak,bk], является
бесконечным. Оба эти условия выполнены в случае к = 0.
Положим
Ск = (ак + 6*0/2.
Если хп € [ак,Ск] для бесконечного множества
значений n e Nm, то полагаем а&+1 = а&, Ък+\ = с*.
Предположим, что хп е [ак,Ск] только для конечного числа номеров
n е Nm. Тогда множество тех п € Nm, для которых хп € [ск,Ьк], является
бесконечным.
Действительно, если бы множество значений п € Nm таких, что xn e
£ [О:, М> также было бы конечным, то промежуток [ак, bk] содержал бы хп
лишь для конечного числа номеров п, что противоречит предположению.
Полагаем в данном случае ak+i = с^ bfc+i = Ък-
Отрезок [afc+i,6fc+i], таким образом, определен. При этом множество
значений n e Nm таких, что xn e [afc+i,bfc+i], является бесконечным.
Поэтому среди тех номеров п € Nm, для которых xn £ [ak+i, bfc+i], есть
номера, большие Пк- Более того, таких номеров — бесконечно много.
Выберем из них, произвольным образом, один и положим п&+1 равным
ему.
В силу принципа математической индукции, описанное построение
определяет некоторую последовательность чисел (пк)кеп и
последовательность отрезков ([ак,Ьк])кещ-
Из определения следует, что пк < nk+i, хПк £ [ак, Ьк], [ак, Ък] Э [afc+i, Ък+i]
и 6fc+i — afc+i = {bk-ak)/2 при каждом к £ N. Отсюда, по индукции,
заключаем, что длина Ък - ак отрезка [ак, Ък] равна {Ъ - а)/2к, и, следовательно,
она стремится к нулю при к —» оо.
По теореме о вложенных отрезках (см. следствие 3 теоремы 3.1),
найдется точка р, принадлежащая всем отрезкам [а^М- При этом
р = lim ак = Ит bk, так как Ък - ак -> 0 при к —> оо.
к—>оо к—>оо

154
Гл. 2. Теория предела
При каждом к EN выполняются неравенства: аи < хПк < Ьк.
Отсюда, в силу теоремы о зажатой переменной (теорема 1.5),
вытекает, что р = lim хПк.
fc—*ОС>
Таким образом, построена подпоследовательность (хПк)кещ
последовательности (#n)neNm, которая является сходящейся.
Теорема доказана. ■
5.1.2. Результат теоремы 5.1 может быть распространен также на
случай неограниченных последовательностей, что вытекает из следующего
утверждения.
▼ Следствие. У всякой числовой последовательности существует
такая ее подпоследовательность, которая имеет предел.
Замечание. В отличие от теоремы 5.1, здесь
ограниченность исходной последовательности не предполагается и существование
сходящейся подпоследовательности не утверждается. (Напомним, что
числовая последовательность называется сходящейся, если она имеет
конечный предел.)
Доказательство следствия. Пусть (#n)neNm — произвольная
числовая последовательность. Если эта последовательность
ограничена, то требуемое утверждение, в силу теоремы 5.1, верно.
Предположим, что числовая последовательность (xn)n€N не
является ограниченной. Тогда либо ее точная верхняя, либо ее точная
нижняя граница — бесконечна.
Для определенности, предположим, что sup xn = оо. Положим
nGNm
т = т. Предположим, что для некоторого к £ N величина п&
определена.
Обозначим через L& наибольшее из чисел хш,хш+1,... ,хПк- Так
как sup xn = оо, то найдется значение n £ Nm, для которого
ВЫПОЛНЯТЬ GNm
ется неравенство xn > Lfc. Из таких значений п выберем, произвольным
образом, одно и полагаем его равным rik+i.
Имеем: хПк+1 > Lk и, значит, rik+i > Пк, ибо для всякого п такого,
что т < п < п/с, согласно определению числа L^, выполняется
неравенство: xn < Lk. В частности, хПк < Lk и, следовательно, хПк < хПк+1.
В силу принципа математической индукции, описанное
построение определяет некоторую подпоследовательность (xnic)keN
последовательности (#n)n€Nm. Эта последовательность является возрастающей
и, значит, она имеет предел. Нетрудно показать, что этот предел равен
оо. Предоставляем читателю доказать это.
Следствие доказано. ▼

§ 5. Основные теоремы о непрерывных функциях
155
5.2. Теорема Вейерштрасса о наибольшем и наименьшем
значениях непрерывной функции
Здесь мы докажем первую основную теорему о непрерывных
функциях на замкнутых промежутках множества R.
Пусть дана функция / : М —> Е.
Если можно указать значение а £ М такое, что для всех х £ М
выполняется неравенство f(x) < /(а), то говорят, что / принимает на
множестве М свое наибольшее значение и а есть тот элемент множества
М, на котором это значение достигается функцией /.
Аналогично, если существует /ЗеМ такое, что /(/3) < f(x) для
всех х Е М, то говорят, что / принимает на множестве М свое
наименьшее значение и /3 есть тот элемент множества М, на котором это
значение достигается функцией /.
■ Теорема 5.2 (теорема Вейерштрасса о наименьшем и
наибольшем значениях). Пусть I = [а, Ь] есть замкнутый отрезок в множестве
R. Тогда всякая непрерывная функция f : [а, Ь] —» М принимает в
промежутке I свои наибольшее и наименьшее значения и является
ограниченной.
Доказательство. Пусть выполнены все условия теоремы.
Положим:
Р = inf /0*0 = inf/(/); q = sup f(x) = sup/(J).
я€[а,Ь] ж€[о,Ь]
Так как функция / всюду конечна, то р < оо, a g > — оо. Положим
—п, если р = —оо;
un = <ь 1
р Н—, если р конечно;
п
п, если q = оо;
t% = ^ 1
</ , если g конечно.
п
При каждом п, в силу критерия точной верхней и точной нижней
границ функции найдутся хп £ / и yn £ / такие, что р < f{xn) < un и
# > /(2/п) > ^п- При п —► оо мы видим, что tin —► р, a vn —► q.
В силу теоремы о зажатой переменной (теорема 1.5),
справедливы соотношения:
р= lim f(xn), q~ lim f(yn)-

156
Гл. 2. Теория предела
В силу теоремы выбора Вейерштрасса (теорема 5.1), у
последовательностей (хп)пея и (2/n)neN существуют, соответственно,
подпоследовательности (хти)ием и (yku)veN, каждая из которых имеет предел.
Пусть
а = lim Хти; /3 = lim уки.
Так как а < жШ1/ < Ь и а < у^ < Ь при каждом и Е N, то, в силу
теоремы о предельном переходе в неравенстве (теорема 1.3), имеют место
неравенства: а<а<Ъжа<Р<Ъ, то есть точки а и /3 принадлежат
замкнутому промежутку [а,Ь].
По условию, функция / — непрерывна. Значит, при v —> оо
выполняются f(xmv) -> /(Of) И /(I/O -> /(/3).
По теореме о пределе подпоследовательности (следствие 3
теоремы 2.6), справедливы соотношения:
р = lim f(xn) = lim /(жт„) = /(а);
g = lim /(y«) = lim /(аъ„) = /(/3).
Таким образом, f(a) = р и /(/3) = д. Так как р есть точная нижняя,
а </ есть точная верхняя границы функции / на множестве [а, Ь], то для
всех х Е [а,Ь] выполняются неравенства р < f(x) < q, то есть
<Ухе[а,Щ) f(a)<f(x)<f(p). (5.3)
Это означает, что в точке а функция / принимает свое наименьшее,
а в точке (5 — свое наибольшее значение на промежутке [а, Ь].
Так как f(a) и /(/3) — конечны, то из соотношений (5.3) следует
ограниченность функции / на промежутке [а, Ь].
Теорема доказана, а
5.3. Понятие равномерно непрерывной функции
Здесь будет установлено, что непрерывные функции, определенные
на замкнутом промежутке, обладают некоторым свойством,
называемым равномерной непрерывностью. Это свойство находит применение
при изучении разных вопросов, касающихся непрерывных функций.
5.3.1. Пусть дано множество icK. Вещественная функция /,
определенная на множестве А, называется равномерно непрерывной на А, если
она удовлетворяет следующему условию: каково бы ни было е > 0, по
нему найдется 6 > О такое, что для любых двух точек х\,хъ множества
А, для которых \х2 — xi\ < 6, справедливо: \f(x2) — Z(#i)| < е.

§ 5. Основные теоремы о непрерывных функциях
157
Приведем некоторую другую характеристику понятия
равномерной непрерывности.
Предварительно введем одно вспомогательное понятие.
Пусть даны множество АсКи функция / : А —► R.
Функция и : [0,/i) —> М, где 0 < /i < оо, называется модулем
непрерывности функции / на множестве А, если она удовлетворяет
следующим условиям:
МС 1) о; есть неотрицательная возрастающая функция;
МС 2) имеет место равенство:
limo;(*) = 0;
МС 3) для любых xi,X2 Е А таких, что \х± — Х2\ < h, выполняется
неравенство:
\f(xi)-f(x2)\<u(\xi-x2\).
Говорят, что функция f : А —* Ш удовлетворяет условию
Липшица, если функция t £ R н-> С£, где С > 0 — постоянная, является ее
модулем непрерывности.
Если функция t £ [0,/i) ь-> СТ*, где Сиа — постоянные, причем
С>0и0<а<1, есть модуль непрерывности функции /, то говорят,
что / удовлетворяет условию Гёлъдера с показателем а.
Существование модуля непрерывности функции есть необходимое
и достаточное условие равномерной непрерывности функции.
Доказательство этого использует конструкцию, которая
применяется также и при доказательстве основного результата о равномерной
непрерывности (теорема 5.3).
Пусть дано множество АсК. Тогда определено множество А2 =
= ЛхА — совокупность всех пар чисел (#, у) таких, что х £ А и у £ А.
Для произвольного t > 0 символом DtA обозначим множество всех
пар (#, у) £ А2 таких, что \х — у\ < t.
Пусть дана функция /, определенная на множестве А. Точную
верхнюю границу величины \f(x) — f(y)\ на множестве DtA обозначим
символом Qf(t), так что
n,(t)= sup \f(x)-f(y)\.
(x,y)eDtA
Для всякого t > 0 имеем: fi/(t) > 0. Очевидно, также fi/(0) = 0.

158
Гл. 2. Теория предела
Определением допускаются значения fi/(t) = оо.
Если t\ > О и £2 > 0 таковы, что 0 < t\ < fe, то Dt±A С Dt2A.
Отсюда, в силу известных нам свойств точной верхней границы, вытекает,
что в этом случае выполняется неравенство
П/(*1) < П/(*2),
так что функция £lf(t) — неубывающая.
Для любых хуу £ А имеет место неравенство:
\№-№\<nf(\x-y\).
Действительно, положим \х — у\ = t. Очевидно, пара (#, у)
принадлежит множеству DtA, отвечающему данному значению £, и, значит,
\f(x)-f(y)\<nf(t) = nf(\x-y\).
Ш Лемма 5.1. Пусть АсМи вещественная функция f определена
на множестве А. Для того чтобы функция f была равномерно
непрерывной на множестве А, необходимо и достаточно, чтобы она имела на
А модуль непрерывности.
Доказательство. Необходимость. Предположим, что
функция / равномерно непрерывна.
Зададим произвольно е > 0. Положим е\ = -.
Согласно определению равномерной непрерывности, найдется 6 > 0
такое, что для любых х,у Е А, для которых \х — у\ < <5, выполняется
неравенство: \f(x) - f(y)\ < ei.
Пусть 0 < t < 6. Если (ж, у) Е DtA, то \х — у\ < t < <5, и, значит, в
силу выбора 6 > 0, имеет место неравенство: \f(x) — f(y)\ < £ь
Пара (х, у) Е DtA была выбрана произвольно и, следовательно,
имеет место соотношение:
П/(*)= sup \f(x)-f(y)\<e1<e.
(x,y)eDtA
Отсюда, в частности, вытекает, что найдется 6о > 0 такое, что
£}/(£) < оо для всех t Е [0,£о) (чтобы найти такое <5о, достаточно взять
6 > 0, отвечающее какому-либо конкретному значению £, например
е = 1010 , и положить 6о = 6).
Далее, в силу произвольности е > 0, из доказанного, очевидно,
вытекает, что
limQf(t) = 0.

§ 5. Основные теоремы о непрерывных функциях
159
Функция Г2/(£), как отмечено выше, — неубывающая и для любых
х,у Е А выполняется неравенство: \f(x) — f(y)\ < Qf(\x — у\)-
Мы видим, что функция Qf(t) удовлетворяет всем условиям
определения модуля непрерывности функции /, и необходимость условия
леммы тем самым установлена.
Докажем достаточность. Предположим, что функция /,
определенная на множестве А С М, имеет модуль непрерывности на
множестве А. Пусть функция и : [О, К) —► М удовлетворяет указанным
выше условиям МС 1-МС 3 определения модуля непрерывности.
Зададим произвольно е > 0. Так как w(t) —> 0 при t —> 0, то
найдется 6 Е [0, К) такое, что 6 > 0, и u(t) < е при 0 < t < 6.
Возьмем произвольно точки £i,£2 Е А, для которых \xi — жг| < 5.
Тогда |/(xi) - /(д?2)| < а;(|ж! - д?2|) < е.
Так как е > 0 — произвольно, то тем самым равномерная
непрерывность функции / установлена.
Лемма доказана. D
Если функция / : А —» R равномерно непрерывна, то она, очевидно,
является непрерывной.
Обратное, вообще говоря, неверно.
Рассмотрим примеры.
Пример 1. Пусть А = [0, сх)) и f(x) = ж2 для всех жЕА.
Предположим, что данная функция равномерно непрерывна. Зададим
произвольно е > 0. Тогда, в силу сделанного предположения, найдется 6 > 0
такое, что если |#i — ггг| < S, то |/(#2) — /(#i)| < е.
Положим t = 6/2. Для всякого х > 0, в силу сделанного
предположения, |/(ж +1) - f(x)\ < е.
Но, как очевидно, f(x +1) - f(x) = 2to +12 —► oo при x —* oo, и тем
самым мы получаем противоречие.
Следовательно, данная функция / не является равномерно
непрерывной.
Пример 2. Пусть А = (0,1] и f(x) = - для всех х £ А. Зададим
произвольно е > 0.
Докажем, что, каково бы ни было 6 > 0, найдутся точки ж, у Е (0,1]
такие, что \х - у\ < 6, а |/(#) - /(у)| > е. Этим будет доказано, что
функция / не является равномерно непрерывной.
Положим:
__ 1 1
хп — j Уп — ; •
п п + е
Имеем, очевидно: \f(xn) - f(yn)\ = £, а \хп - уп\ —> 0 при п —► оо.

160
Гл. 2. Теория предела
Это означает, что для любого S > 0 найдется значение п такое, что
|яп ~Уп\ < £? что и требовалось доказать.
5.3.2. Теперь мы можем доказать основной результат этого раздела —
теорему о равномерной непрерывности непрерывной функции на
ограниченном замкнутом промежутке.
■ Теорема 5.3 (теорема Гейне о равномерной непрерывности).
Всякая непрерывная вещественная функция, определенная на замкнутом
промежутке множества R, является равномерно непрерывной.
Доказательство. Пусть / есть непрерывная функция,
определенная на промежутке [а, Ъ] с R. Полагая А — [а, 6], как было описано
выше, определим по / функцию 0/(t). Имеем:
П,(*) = sup \f(x)-f(y)\.
\x-y\<t
Функция Clf(t) неотрицательна и является неубывающей. Для
любых х,у € [а, Ъ] выполняется неравенство:
1/(*)-/М1<П/(1*-у|).
Теорема будет доказана, если мы покажем, что величина fi/(t)
конечна для всех t и стремится к нулю при t —> 0.
Так как функция /, по условию, непрерывна, то, в силу теоремы 5.2
(теорема Вейерштрасса о наибольшем и наименьшем значениях), она
ограничена, то есть найдется такое конечное число L, что \f(x)\ < L
для всех х е [а,Ъ]. Для любых х,у G [а,Ь] имеем: \f(x) — f(y)\ < |/(а0|+
+|/(2/)| <
Отсюда, очевидно, следует, что £lf(t) < 2L для всех t. Таким образом,
мы получаем, что величина £}/(£) конечна для любого t > 0.
Так как функция Qf(t) — неубывающая, то существует предел:
limfl f(t) = a.
Для всякого n € N
nf(-)= sup \f(x)-f(y)\
и, значит, согласно признаку точной верхней границы функции (см.
главу 1, предложение 5.3), найдется пара хп,уп точек промежутка [а, Ь]
такая, что
\хп уп\ S
п

§ 5. Основные теоремы о непрерывных функциях
161
|/(*«)-/(У»)|>П/(£)-£•
При каждом п имеем:
П/(£)<1/(*»)-/Ы1 + £.
При п —► оо разность хп — уп стремится к нулю. В силу
теоремы выбора Вейерштрасса (теорема 5.1), из последовательности (xn)neN
можно извлечь сходящуюся подпоследовательность.
Пусть (x<nk)keN — эта подпоследовательность и хо € [а,Ь] — ее
предел. По условию, функция / непрерывна в каждой точке промежутка
[а,Ь]. В частности, она непрерывна и в точке хо. При к —* оо имеем
Хпк —» #о, и так как разность #nfe — Упк стремится к нулю при к —» оо,
то также и ynfe —> #о при к —* оо.
В силу непрерывности /, отсюда вытекает, что f(xnk) —» /(#о) и
f(Vnk) -* f(%o) при fc -> оо, и, значит, |/(#nfe) - f(Vnk)\ -* 0 при А; -» оо.
Имеем:
limft/(t) = ton fi/ f—Л .
t->0 J fc-+oo J \Пк/
При каждом fc G N выполняется неравенство:
П/(^)<1/(*«.)-/(^)1 + ^-
Правая часть последнего неравенства, по доказанному, стремится
к нулю при к —► оо, а левая — неотрицательна и, стало быть,
Slf(-) ->0
Vnfe/
при fc —* оо. Отсюда следует, что ton ttf(t) = 0.
Теорема доказана. ■
Из доказанной теоремы вытекает условие, выполнение которого
гарантирует равномерную непрерывность непрерывной функции. А
именно, для этого достаточно, чтобы ее область определения была
замкнутым промежутком множества R.
5.4. Топологические отображения отрезков в множество R
Здесь мы докажем, что утверждение теоремы 4.3 может быть
обращено, а именно, — справедливо следующее предложение.

162
Гл. 2. Теория предела
■ Теорема 5.4. Пусть I = (а, Ь) — произвольный промежуток в
множестве R и / : J —> R — непрерывная функция. Если f представляет
собой взаимно однозначное отображение, то f есть строго монотонная
функция.
Доказательство. Предположим, что функция / : J —> R
удовлетворяет всем условиям теоремы.
Пусть х\,Х2,хг — три произвольные точки промежутка J такие,
ЧТО Х\ <Х2 < Х$.
В силу взаимной однозначности отображения /, числа /(#i), /(#2)
и f(xz) попарно различны.
Докажем, что f{x\) и f(xz) лежат по разные стороны
от /(#2), то есть или f{x\) < /(#2) < /(#з), или f(xi) > /(#2) > /(#з).
Допустим, что это не так. Тогда либо f{x\) < /(#2) и /(#з) <
< /(#2), либо /(#i) > /(з2) и /(#3) > /(а?2).
Пусть у есть в первом случае — наименьшее, а во втором —
наибольшее из чисел f(xi) и /(#з).
Тогда в первом случае: /(#i) < у < /(#2) и /(#з) < У < /(#2), а во
втором: f(xi) > у > f(x2) и /(#з) > у > /(^2).
В силу теоремы 4.1, отсюда вытекает, что найдутся такие точки
£ € [Ж1,ж2] и т/ G [#2,#з], что /(С) = f(r]) = у. Так как у / Д#2), то
£Ф Х2 кг) ф X2i откуда, в частности, следует, что £ < #2 < ?)-
Итак, предположив, что f(xi) и f(xz) лежат по одну сторону от Х2,
мы находим две различные точки £ G [ж1,жз] и г/ € [#1,#з]
такие, что /(£) = /(ту). Последнее противоречит тому, что, по
условию, / — взаимно однозначно.
Таким образом, допущение, что значения f(xi) и f(xz) лежат
по одну сторону от /(#2), приводит к противоречию.
Из доказанного вытекает, что функция / — монотонна на всяком
множестве Ус/, состоящем из трех точек.
Докажем, что / — монотонна на всяком множестве Y С /,
состоящем из четырех точек.
Действительно, пусть Y = {#1,Ж2,#з,#4}, где xi < Х2 < xz < х±.
Пусть f(xi) < /(#2) < /(#з). В силу доказанного, тогда также
и f(x2) < f(xz) < /(#4). Если же f(xi) > f(x2) > /(жз), то f(x2) >
> /(#з) > /(#4), что и требовалось доказать.
Выберем произвольно точки а, /3 из J такие, что a < /3.
Возможны два случая:
1)/(а)</(/9) и 2) f (<*)>№.
Докажем, что в случае 1) функция / является возрастающей, а в
случае 2) — убывающей.

§ 6. Верхний и нижний пределы последовательности
163
Возьмем произвольно Х\,Х2 £ I такие, что х\ < Х2.
Рассмотрим множество Y — {a,/3,xi,X2}> Множество Y имеет не
более четырех элементов и, значит, по доказанному, функция / является
монотонной на множестве Y,
В случае 1) функция / будет, очевидно, возрастающей на
множестве Y и, значит, в этом случае имеет место неравенство: f(xi) < /(#2)-
Так как х\,хъ £ I взяты произвольно, то тем самым доказано, что
в этом случае функция / является возрастающей,
В случае 2) функция / является убывающей на множестве Y и
потому f(xi) > /(#2). В силу того, что х\,Хъ Е J взяты произвольно, мы
получаем, что в этом случае функция / является убывающей.
Теорема доказана. ■
§6. Верхний и нижний пределы
последовательности
Произвольная последовательность вещественных чисел, вообще
говоря, может не иметь предела, В этом параграфе будут рассмотрены
понятия верхнего и нижнего пределов последовательности
вещественных ЧИСеЛ (Жп)пЕ1Чт.
В отличие от обычного предела, верхний и нижний пределы
последовательности существуют всегда.
Некоторые теоремы, в которых используется понятие предела,
можно представить в более общей форме, заменяя в их формулировках
обычный предел либо верхним, либо нижним пределом. Соответствующие
примеры будут приведены позднее,
6.1. Определение и простейшие свойства верхнего и нижнего
пределов
6.1.1. Приведем определение верхнего и нижнего пределов
последовательности.
Пусть дана последовательность вещественных чисел (#n)neNm.
Число К Е R называется нижним числом данной
последовательности, если выполнено следующее условие:
существует номер п такой, что для любого n > n выполняется
неравенство: хп > К.
Будем говорить, что К £ Ж есть верхнее число
последовательности (#n)n€Nm, если существует номер п Е Nm такой, что для всякого
п>п выполняется неравенство: хп < К,

164
Гл. 2. Теория предела
Множество всех нижних чисел последовательности (#n)neNm
обозначим символом N(x). Совокупность всех верхних чисел
последовательности (#n)neNm обозначается символом V(x).
Число — оо является нижним числом любой последовательности
(xn G M)n€Nm. В качестве номера п, существование которого требуется
определением, можно взять любое число n G Nm, например, п = т.
Аналогично, оо является верхним числом для любой
последовательности вещественных чисел (#n)neNm.
Мы видим, в частности, что множества N(x) и V(x) непусты.
■ Лемма 6.1. Пусть дана последовательность (xn)ne^rn, K\ есть
произвольное нижнее, Къ — произвольное верхнее число этой
последовательности. Тогда найдется номер n G Nm такой, что для любого
п>п выполняются неравенства: К\ < хп < К2-
Доказательство. Пусть Кг G N(x), K2 G V(x). Согласно
определению нижнего числа, найдется номер п\ > 0 такой, что если n > ni,
то Хп > Ki.
Далее, согласно определению верхнего числа, найдется пг > О
такое, что если п > П2, то выполняется неравенство: хп < Къ.
Пусть п есть большее из чисел п\ и пг.
Возьмем произвольно п>п. Тогда п > п\ и в то же время п >П2-
Отсюда следует, что для данного п выполняются неравенства: К\ <
< хп < Къ, и, значит, данный номер п и есть требуемый.
Лемма доказана. ■
▼ Следствие. Всякое нижнее число последовательности (#n)n£Nm
является нижней границей множества V(x) всех ее верхних чисел и
любое ее верхнее число является верхней границей множества N(x).
Действительно, возьмем произвольно К G N(x) и К' € V(x).
Тогда, согласно лемме 6.1, найдется n G N такое, что если п > п, то
выполняются неравенства: К < хп < К'. Отсюда, в частности,
следует, что для любых К G N(x) и К' G V(x) имеет место неравенство
К<К'.
Это означает, что К — это нижняя граница множества
V(x), а К' — верхняя граница N(x).
Следствие доказано. ▼
Точная верхняя граница множества всех нижних чисел
последовательности (#n)n€Nm называется нижним пределом этой
последовательности и обозначается символом: Ит хп.
п—+оо

§ 6. Верхний и нижний пределы последовательности
165
Точная нижняя граница множества всех верхних чисел
последовательности (#n)n€Nm называется ее верхним пределом и обозначается
символом: lim xn.
п-юо
Согласно определению верхнего и нижнего пределов, имеем:
lim Xn = sup JV(#); lim xn = inf V(x).
n-oo ' n-*°°
6.1.2. Отметим свойства верхнего и нижнего пределов,
непосредственно вытекающие из определения.
■ Лемма 6.2. Справедливы следующие утверждения.
I. Для всякой последовательности вещественных чисел (xn)neNm
верны неравенства:
lim xn < lim xn.
„_^ п—+оо
П. Для любой последовательности (xn Е M)neNm имеют место
равенства:
lim xn = — lim (—xn)\ Hm хп = — Ит (—#п).
п^оо "-<*> п-+оо п_^00
III. ЕСЛИ
#< lim Хпч
п—юо
то К есть нижнее число последовательности (#n)n€Nm и любое число
К > Ит хп является верхним числом этой последовательности.
п—>оо
Доказательство. Пусть дана последовательность
вещественных ЧИСеЛ (Zn)n<ENm.
Возьмем произвольно К Е N(x). Положим:
/ = lim xn', L = lim #п-
п—»-оо
Согласно следствию леммы 6.1, К есть нижняя граница множества
У (ж), и, значит,
# <infy(rr) = L.
Так как К Е iV(#) взято произвольно, то мы получаем тем самым,
что L есть верхняя граница множества N(x).
Следовательно, sup N(x) = I < L, и справедливость утверждения I,
таким образом, установлена.

166
Гл. 2. Теория предела
Докажем утверждение П. Пусть К есть нижнее число
последовательности (#n)n€Nm. Согласно определению ниоюнего числа, найдется
номер п G Nm такой, что если п > п, то К < хп.
Если п > п, то — хп < —if, и, стало быть, —if является верхним
числом последовательности (—xn)neNm-
Отсюда следует, что
lim (-хп) < -if,
п—юо
и, значит,
— lim (—хп) > if.
п—+оо
Число К G N(x) было взято произвольно. Поэтому из доказанного
заключаем, что
— lim (—хп) > s\xpN(x) = lim xn. (6.1)
п—»-оо
Для всякого К G V(—x) найдется п G Nm такое, что если п > п, то
-хп < if.
Если п>п, то хп > —if, и, значит, —if является нижним
числом последовательности (хп)п^.
Отсюда следует, что
lim хп > —if,
71—* ОО
и, значит,
— lim xn < if.
п—»-оо
Число if G V(—ж) было взято произвольно. Из доказанного поэтому
следует, что
— lim хп < inf V(—ж) = lim (—rcn),
n—юо
и, значит,
lim xn > — linn (—#n). (6-2)
«^^ П—ЮО
n—юо
Из неравенств (6.1) и (6.2) вытекает первое из доказываемых
равенств.
Докажем второе. Последовательность (xn)neN в проделанных
рассуждениях произвольна. Заменяя хп на хп = — хп, получим,
что lim х'п = — lim (—а4), т0 есть Um (—хп) = — lim xn-

§ 6. Верхний и нижний пределы последовательности
167
Отсюда
— lim (—Хп) = Нт #п,
__^. П—+00
П—+00
что и требовалось доказать. Утверждение II доказано.
Докажем утверждение III. Пусть К < I = lim #п. Имеем, по опре-
п—юо
делению:
/ = supiV(#).
В силу признака точной верхней границы функции (теорема 4.1
главы 1), найдется К' Е N(x) такое, что К < К' < I. К' есть нижнее
число последовательности (xn)neNm-
Согласно определению нижнего числа, найдется число п Е Nm
такое, что если п > п, то хп > К' > К. Это и означает, что К есть
нижнее число последовательности (#n)n€Nm-
Аналогично устанавливается, что всякое число К > L = lim xn
п—+оо
является верхним числом последовательности (#n)n€Nm. Утверждение
III установлено.
Лемма доказана. ■
6.2. Критерий существования предела последовательности
6.2.1. Следующая теорема содержит критерий существования предела,
который будет использован в дальнейшем.
■ Теорема 6.1. Для того чтобы последовательность (#n)neNm
имела предел, необходимо и достаточно, чтобы ее верхний и нижний
пределы были равны между собой. Их общее значение и является пределом
последовательности.
Доказательство. Необходимость. Предположим, что
последовательность (xn)ne^m имеет предел при п —> сю. Пусть L есть
значение этого предела.
Докажем, что
lim хп > L. (6.3)
п-юо
Если L = — оо, то это верно. Будем считать, что L > —оо.
Возьмем произвольно Н < L. Следствие 2 леммы 1.7 позволяет
заключить, что найдется п £ Nm такое, что для всякого п > п
выполняется неравенство хп > Н. Это означает, что Н есть нижнее
число последовательности (#n)neNm.
Так как Н < L было взято произвольно, то мы, следовательно,
получаем, что [—oo,L) С N(x).

168
Гл. 2. Теория предела
Отсюда вытекает, что
L = sup[—oo,L) < sup N(x) = lim #n,
n—юо
и неравенство (6.3) доказано.
Докажем, что
lim хп < L. (6.4)
п—*оо
Если L = оо, то это верно.
Пусть L < оо. Зададим произвольно К > L. Согласно следствию 2
леммы 1.7 существует номер п Е Nm такой, что для всякого п > п
выполняется неравенство: К > хп, так что К является верхним
числом последовательности (#n)neNm.
Отсюда вытекает, что V(x) D (L,oo], и, значит,
lim хп = inf V(x) < inf(L, оо] = L,
n—>oo
и неравенство (6.4) доказано.
Таким образом, для данной последовательности
lim хп < L < lim xn. (6.5)
В силу предложения I леммы 6.2 имеет место неравенство:
lim xn > lim xn. (6.6)
п—юо „_^
п—+оо
Из неравенств (6.5) и (6.6), очевидно, следует, что для
последовательности (#n)n€Nm:
lim xn = L = lim #n-
n—юо
Необходимость условия теоремы доказана.
Докажем достаточность. Предположим, что для
последовательности (хп)пеПт верхний и нижний пределы совпадают.
Их общее значение обозначим через L.
Требуется доказать, что L = lim xn-
п—юо

§ 6. Верхний и нижний пределы последовательности
169
Пусть L конечно. Зададим произвольно е > 0. Тогда:
L-e<L<L + e.
В силу предложения III леммы 6.2, отсюда вытекает, что L — е есть
нижнее число данной последовательности, L + е — ее верхнее число. В
силу леммы 6.1 это позволяет заключить, что найдется номер п Е Nm
такой, что при всяком п > п выполняются неравенства: L — е < хп <
< L + е, то есть \хп — L\ < е для всех п>п. Так как е > 0 произвольно,
то тем самым доказано, что L = lim xn-
п—+оо
Пусть L = оо. Возьмем произвольно К G К. Тогда
К < L = lim rcn
п—+оо
и, значит, К есть нижнее число последовательности. Согласно
определению нижнего числа, отсюда вытекает, что найдется номер п G Nm
такой, что для всякого п > п выполняется неравенство: хп > К. Так
как К G R было взято произвольно, то тем самым установлено, что
оо = L = lim жп.
Предположим, что верхний и нижний пределы данной
последовательности равны — оо. Применяя предложение II леммы 6.2, получим,
что верхний и нижний пределы последовательности (—xn)n^Nm равны
оо. Значит, по доказанному lim [—хп] = оо. Отсюда, согласно опреде-
п—юо
лению предела, равного —оо, следует, что lim хп = — оо.
п—юо
Теорема доказана. ■
6.2.2. В качестве приложения теоремы 6.1 приведем новое
доказательство утверждения о числовых последовательностях, содержащееся в
следствии 1 теоремы 3.2 этой главы.
■ Другое доказательство достаточности критерия сходимости
Коши — Болыдано для последовательностей.
Пусть (#n)n€Nm есть произвольная последовательность
вещественных чисел. Предположим, что для всякого е > 0 можно указать номер
п G Nm такой, что для любых ni > п и пч > п выполняется
неравенство: \хП1 — хП21 < £• Требуется доказать, что последовательность
(xn)neN имеет конечный предел.

170
Гл. 2. Теория предела
Пусть / есть нижний, L — верхний пределы данной
последовательности. Зададим произвольно е > 0 и найдем соответствующий ему
номер п £ Nm. Фиксируем произвольно по >п. Тогда для всякого п > п
выполняется неравенство: \хп — хПо \ < е и, значит, хПо —£ < хп < хПо +£
для всех п>п. Это означает, что хПо — е есть нижнее число
последовательности (#n)neNm5 а Хп0 + е — ее верхнее число. Отсюда вытекают
неравенства хпо — е < /, L < хПо + е.
Принимая во внимание, что / < L, получаем: хПо — е <l < L <
< Хп0 + е. Отсюда, в частности, вытекает, что верхний и нижний
пределы данной последовательности конечны. При этом имеют место
неравенства: 0 < L — I < 2е. Так как е > 0 произвольно, отсюда следует,
что / = L и, в силу теоремы 6.1, мы получаем, что данная
последовательность (#n)neNm имеет предел. Предел этот равен общему значению
верхнего и нижнего пределов и, следовательно, конечен, что и
требовалось доказать. ■
6.3. Понятие частичного предела последовательности
6.3.1. Здесь мы установим еще некоторую полезную характеристику
верхнего и нижнего пределов последовательности вещественных чисел.
Число L G М называется частичным пределом числовой
последовательности (#n)n€Nm5 если существует последовательность номеров
(rife £ Nm)fceN такая, что Пк < nk+i при каждом к и L есть предел
последовательности (#nfe)fceN-
■ Лемма. 6.3. Пусть (#n)n€Nm есть произвольная числовая
последовательность и I есть ее нижний предел.
Для всякой окрестности U числа I и любого номера г £ Nm найдется
n £ Nm такое, что п>г и xn €U.
Доказательство. Пусть последовательность (rcn)n€N
удовлетворяет всем условиям леммы.
Если I = оо, то, так как lim xn < lim xn (см. лемму 6.2 вы-
п—>оо
ше), также и верхний предел последовательности равен бесконечности.
Таким образом, в этом случае верхний и нижний пределы
последовательности оба равны оо. В силу теоремы 6.1, отсюда вытекает, что
lim xn = оо.
п—»-оо
Пусть U есть произвольная окрестность точки оо, U представляет
собой промежуток вида (К, оо], где К конечно. Следствие 2 теоремы 1.2
позволяет заключить, что найдется номер n £ Nm такой, что хп > К
для всякого п > п. Для всех таких п имеем: хп £ U. В частности, если
п > г и одновременно п > п, то хп £ U.

§ 6. Верхний и нижний пределы последовательности
171
Теперь рассмотрим случай, когда I < оо. Пусть U есть окрестность
точки / £ Й. Множество U есть некоторый промежуток в множестве Й.
Пусть р есть левый конец этого промежутка, q — его правый конец.
Если I = — оо., то р = I = — оо. В этом случае хп > р для всех
n £ Nm, поскольку мы рассматриваем только такие последовательности,
все члены которых конечны.
Пусть I > —оо. Тогда р — I — £, где £ > 0. Утверждение III
леммы 6.2 позволяет заключить, что найдется V £ ЛГ(ж) такое, что 1-е <
I' < I. Согласно определению нижнего числа, найдется номер п > т
такой, что для всех п > п выполняется неравенство: хп > р. В случае
/ = — оо будем считать п = т.
Пусть задан номер г £ Nm. Положим г = max{r, п}. Докажем, что
найдется n>r,n£ Nm, для которого хп < q. Допустим, напротив, что
такое п не существует. Тогда для всякого номера п > г выполняется
неравенство хп > q- Это по определению означает, что q есть нижнее
число последовательности (#n)n€Nm. Так как I есть точная верхняя
граница множества всех нижних чисел N(x) данной последовательности, то
имеет место неравенство: I > #, что, однако, противоречит тому, что,
по условию, q > I. Итак, допустив, что не существует номер п £ Nm
такой, что п > г, а хп < q, мы приходим к противоречию. Следовательно,
такое п существует.
Пусть п £ Nm таково, что п > г и в то же время хп < q. Из
определения г следует, что п > г. Далее, имеем также: п > п и, значит,
хп> Р- Таким образом, мы получаем, что для данного п выполняются
неравенства: р < хп < q. Отсюда следует, что хп £ U.
Лемма доказана. О
■ Теорема 6.2. Для всякой последовательности вещественных
чисел (хп)п&яш ее верхний и нижний пределы являются ее частичными
пределами.
Доказательство. Пусть I есть нижний предел
последовательности (rCn)n€Nm-
Пусть (Un(l))neN есть последовательность окрестностей точки Z,
образующая ее каноническую базу (см. п. 1.7 этой главы), то есть
Un{l) — [I , И—) в случае, если I конечно, Un(l) — [—оо, — п) в
случае I — —оо и, наконец, Un = (n, оо] для / = оо.
По индукции, определим некоторую строго возрастающую
последовательность номеров (nfc)fceN- В качестве п\ выбираем произвольный
номер п £ Nm такой, что xn £ Ui{l). Таковой существует, в силу
леммы 6.3.

172
Гл. 2. Теория предела
Предположим, что для некоторого к £ N номер Пк определен,
причем хПк £ Uk(l).
Полагаем г = Пк + 1. Согласно лемме 6.3, найдется п £ Nm такое,
что п > г и в то же время жп £ f/fc+i(0- Из таких значений п выберем
произвольным образом одно и полагаем его равным п^+ь
В силу принципа математической индукции, таким образом
определена последовательность (rik)k€N- При этом, как следует из построения,
при каждом к
nfc+l > Пк + 1 > П*,
так что указанная последовательность номеров является строго
возрастающей.
При каждом к имеем: хПк £ Uk(l). Отсюда, как было показано
выше (см. лемму 1.9), вытекает, что I = lim хПк-
Все утверждения, касающиеся верхнего предела, мы выведем из
доказанного, применяя результат, установленный для нижнего предела
к последовательности (j/n)n€N, где уп = —хп при каждом п.
Пусть L есть верхний предел последовательности (хп)пеы-
Тогда К — —L есть нижний предел последовательности (j/n)n€N-
По доказанному существует строго возрастающая последовательность
номеров (пк)ке^ такая, что
К = lim уПк = lim (~хПк),
откуда получаем, что L — lim хПк.
fc—*>oo
Таким образом, установлено, что верхний предел
последовательности вещественных чисел также является ее частичным пределом.
Теорема доказана. О
Из теоремы 6.2, в частности, следует, что у всякой
последовательности вещественных чисел существует подпоследовательность, которая
имеет предел.
Если последовательность (хп)п^ ограничена, —оо < р < хп < Я. <
< оо для всех п, то предел любой ее подпоследовательности, как следует
из теоремы о предельном переходе в неравенстве (теорема 1.3), также
лежит между р и q и, стало быть, — конечен.
Таким образом, мы имеем новое доказательство теоремы выбора
Вейеуштуасса.
6.3.2. Здесь мы докажем теорему, которая позволяет дать некоторое
новое определение верхнего и нижнего пределов последовательности.

§ 6. Верхний и нижний пределы последовательности
173
■ Теорема 6.3. Всякий частичный предел произвольной
последовательности вещественных чисел лежит между ее нижним и верхним
пределами.
Доказательство* Пусть дана последовательность (хп)п^ и
1= lim хп, L= lim xn.
„_^ п—юо
71—-ЮО
Предположим, что К есть частичный предел последовательности
(#n)n€N. По определению, это означает, что существует строго
возрастающая последовательность номеров (rik £ Nm)fceN такая, что К =
= lim хПк.
к—*оо
Возьмем произвольно I/ £ N(x). По нему, согласно определению
нижних чисел последовательности, найдется п £ N такое, что для всех
п>п выполняется неравенство: xn > L'.
При к —> оо будет Пк —* оо, и, значит, найдется номер ко такой,
что для всех к > ко выполняется неравенство: Пк > п. Для всех к > ко
имеет место неравенство: хПк > L'.
На основании теоремы о предельном переходе в неравенстве
(теорема 1.3), отсюда вытекает, что
К = lim Xnk > L'.
к—юо
Так как I/ £ N(x) было взято произвольно, то тем самым доказано,
что К является верхней границей множества N(x) всех нижних чисел
последовательности (хп)пеы и? значит
К > supN(x) = lim xn = L
n—юо
Аналогичными рассуждениями определяется неравенство: К < L.
Теорема доказана. О
Пусть (#n)n€Nm есть произвольная последовательность
вещественных чисел, I — ее нижний, L — ее верхний пределы. Совокупность
всех частичных пределов данной последовательности обозначим
символом А(х). В силу теоремы 6.2, I £ А(х) и L £ Л(ж). В силу теоремы
6.3, для любого К £ А(х) выполняются неравенства: I < К < L. Мы
получаем, таким образом, следующий результат.
♦ Предложение 6Л. Для всякой последовательности
вещественных чисел множество А(х) ее частичных пределов непусто и имеет
наименьший и наибольший элементы. При этом наименьший из частичных

174
Гл. 2. Теория предела
пределов последовательности есть ее нижний предел, а наибольший из
частичных пределов является ее верхним пределом.
Доказательство, в силу теорем 6.2 и 6.3, — очевидно, ф
6,4. Характеристика верхнего и нижнего пределов
последовательности
Докажем теорему, которая дает некоторый способ определения
верхнего и нижнего пределов.
■ Теорема 6.4. Пусть дана последовательность вещественных
чисел (xn)ne^m- Определим по ней последовательности (Dn)n^m и
(Un)ne^my полагая для n G Nm
Dn = inf ж„, Un = sup xv.
Если lim xn = — oo, то Dn = —oo для всех n G Nm.
Если же lim a?n > —oo, то при каждом n £ Nm число Dn — конеч-
n—юо
но, последовательность (Dn)neN является возрастающей и
lim Dn = lim xn-
Если lim xn = oo, то Un = oo для всех n G Nm.
n-+oo
Если же lim xn < oo, то Un конечно при каждом п и
последовать—*<х>
тельность (?7n)n€N является убывающей, причем
lim [/n = lim xn-
П—+00 П—+0О
Доказательство. Введем обозначения
D= lim жп, 17 = lim жп.
n-оо п->°°
Докажем, что для всех п выполняется неравенство: D > £)п. Если
Dn = — oo, то это очевидно. Пусть Dn конечно. Зададим произвольно
е > 0. При каждом v > п имеем: xu > Dn > Dn — £• Мы получаем,
что Dn — е есть нижнее число последовательности (xn)ne^m и> значит,
D > Dn — е. Так как е > О произвольно, отсюда следует, что D > Dn-
Из доказанного, в частности, вытекает, что если D = — оо, то
Dn = —оо для всех п.

§ 6. Верхний и нижний пределы последовательности
175
Если п\ < П2, то Nni D Nn2. В силу известных свойств точной
верхней границы функции, отсюда вытекает, что при каждом п £ Nm
имеют место неравенства: £>n+i > Dn к Un+i < C/n,-
Предположим, что D > — оо.
Зададим произвольно число п Е N и положим Кп = D в случае,
п
если D конечно, и Кп = п, если D = оо. В силу известных нам свойств
нижнего предела, найдется номер no E Nm такой, что при каждом v > no
выполняется неравенство ж^ > Кп. Из определения величины Du
вытекает, что при каждом v > по имеет место неравенство: Du > Кп.
Обозначим через К' наименьшее из чисел жт, жт+1, ..., хПо,Кп.
Число К1 конечно и хп > К' при каждом п. Значит, Dn > К' > —оо
для всех п G Nm. Из определения Dn следует, что при каждом п
выполняется неравенство: Dn < Жп. Следовательно, мы получаем, что £>п
конечно при каждом n G Nm.
Пусть D' = lim Dn. Так как Dn < D при каждом п, то, в силу
п—юо
теоремы о предельном переходе в неравенстве (см. п. 1.4.2, теорема 1.3),
Df < D. (6.7)
Для всякого v > по выполняется неравенство Dv > Кп. Отсюда
вытекает, что имеет место неравенство Кп < D'.
Число п G N было выбрано произвольно. При п —» оо выполняется
Кп —► D. Переходя в неравенстве D1 > Кп к пределу, получаем:
D' > D. (6.8)
Из неравенств (6.7) и (6.8) следует, что D1 = D.
Утверждение теоремы, касающееся нижнего предела, таким
образом, доказано.
Утверждение, относящееся к верхнему пределу, доказывается
аналогично. Необходимо только надлежащим образом изменить знаки
неравенств.
Формально утверждение относительно верхнего предела может
быть выведено из доказанного применением следующих равенств:
inf {—хи} = — sup #i/,
lim {—хп} = - lim {—xn}.
Мы предлагаем читателю проделать все необходимые построения
для этого случая самостоятельно.
Теорема доказана. ■

176
Гл. 2. Теория предела
Задачи
2.1. Даны числовая последовательность (хп)п^ и число LEM.
Предположим, что существует натуральное число г > 2 такое, что для каждого целого
к = 0,1,... г — 1 имеет место равенство: L = lim #nr.+fc.
п—юо
Доказать, что L = lim жп.
п—юо
2.2. Дана числовая последовательность (#n)n€N- Доказать, что если каждая
из последовательностей: (#2n)n€N5 (^2n-i)n€N и (#5n)n€N имеет предел, то
существует также и предел lim xn.
71—ЮО
2.3. Доказать, что если число рЕК есть предельная точка множества
п
A=[JAk,
к=1
где А\,..., Ап С К, то р — предельная точка хотя бы одного из множеств А &,
к = 1,2,... ,п.
2.4. Множество Л СМ таково, что множество СгтА не пусто.
Доказать, что всякая предельная точка множества £ггаА является
предельной точкой множества А.
2.5. Пусть А С К. Доказать, что если множество СгтА конечно, то множество
А не более чем счетно.
2.6. Доказать, что если множество СгтА предельных точек множества А не
более чем счетно, то множество А также не более чем счетно.
2.7. Пусть А есть множество всех чисел х Е R, представимых в виде:
1 1
х — —I ,
п т
где n E N и m E N. Найти множество СгтА всех предельных точек
множества А.
2.8. Пусть А есть множество всех рациональных чисел х таких, что 0 < х < 1.
Доказать, что CimA = [О,1].
2.9. Пусть Е\ есть множество всех чисел вида —, где п Е N. Предполо-
п
жим, что для некоторого к Е N определено множество Ек. Будем обозначать
символом J5fc.fi совокупность всех чисел z вида , где п Е N, а х 6 i£fc.
Найти множество СгтЕ^.
2.10. Найти все предельные точки множества чисел ж, представимых в виде
х = {у/п} (фигурные скобки здесь означают дробную часть числа, стоящего в
скобках; см. задачу 1.19.).
2.11. Пусть (#n)n€N — последовательность вещественных чисел такая, что
хп > 0 для всех п и хп —» 0 при п —» оо. Доказать, что найдется бесконечное
множество значений п Е N таких, что хт < хп при всех т> п.

Задачи
177
2.12. Пусть (xn)n£N и (2/n)n€N — числовые последовательности, определенные
по индукции следующим образом: х\ = а и у\ = Ь, где а и Ъ — произвольные
вещественные числа и при каждом п
2хп +уп жп + 2уп
xn+i = ; Уп+i = •
Доказать, что существует предел lim xn = lim yn, и найти его.
п—юо п—*>оо
2.13. Пусть числа а > О, /3 > 0 таковы, что а + /3 = 1. Определим
последовательности (хп)П£м и (2/n)nGN> гДв Ж1 = a, 2/i = Ь, а и Ь — произвольно
заданные числа и при каждом п £ N
жп+1 = <22?п + /?2/n; 2/n+l = 0хп 4- ОДп-
Доказать, что существует предел lim xn = lim Ул, и найти его.
п—*>оо п—>оо
2.14. Пусть ж есть иррациональное число. Доказать, что для всякого п £ N
существуют целые числа р и q такие, что
V
х
qn
(теорема Дирихле). (Указание: рассмотреть числа {кх}, к = 1, 2,... , n, n
воспользоваться тем, что, по крайней мере, для двух из них абсолютная
ее.ичипаихраэпостинепрееос^ит1-.)
п
2.15. Пусть а — иррациональное число, Е — множество всех чисел х вида:
х — {an},
где n £ N, а фигурные скобки означают дробную часть числа (см. 1.19).
Доказать, что множество CimE совпадает с отрезком [0,1]. (Указание:
воспользоваться результатом предыдущей задачи.)
2.16. Доказать, что существует число А; £ N такое, что если п > к, то
уравнение
-х3 - х2 + 1 = 0
п
имеет три различных вещественных корня. Пусть п > к и хп < уп < zn —
корни данного уравнения.
Доказать, что при п —*• оо будет хп —* — 1, уп —> 1 и zn —* со.
2.17. Пусть #1,Ж2) • • • ->хп — положительные вещественные числа. Доказать,
что
lim I I = тах{Ж1,Ж2,. ..,жп);
р—юо
р-+ — оо V П
, р \ 1/Р
~г хп \ т
= mm\xi,X2, • • •) xnj-

178
Гл. 2. Теория предела
2.18. Исследовать на непрерывность функцию:
/ : х е R ь-> lim \/l + x2n.
n-юо
Построить график функции /.
2.19. Пусть даны числа а > О и Ъ > О, причем а < Ь. Определим
последовательности (#n)nGN и (2/n)n€N> полагая х\ = а, у\ = 6. Если жп и уп определены,
то
2жп2/п хп + 2/п
жп+1 = — 5 2/п+1 = •
Хп ~т Уп £
Доказать, что последовательность хп — возрастающая,
последовательность уп — убывающая и
lim хп = lim уп = va6.
п—юо п—юо
2.20. Доказать, что для всякого ж £ R. существует конечный предел
х2п
lim — = /(ж).
п-*оо 1 + х2п JK J
Исследовать определенную так функцию / на непрерывность в точках
х = ±1.
2.21. Пусть ср : (0, а) —+ R. — строго возрастающая функция такая, что
lim (p(x) = 0. Доказать, что если существует предел
Иш ^2 = J e R, / ^ О,
ж—►О X
то существует также и предел
lim £±<й = 1.
у—о 2/ /
2.22. Доказать, что
«р(-£)=«*мп)
при ж —* 0, каково бы ни было х £ N.
2.23. Пусть х, у и z — произвольные числа. Положим:
pi(x,y,z) :
P2(x,V,z) =
x + y + z
3 '
xy + yz + xz

Задачи
179
рз(х,у,г) = xyz.
Зададим числа а>0,Ь>Оис>0. Определим по ним
последовательности: (a:n)n€N) (2/n)n€N и (zn)nen такие, что х\ = а, у\ = 6, *i = с, и при
каждом п
Жп+i =Р1(^п,2/п,^п);
Р2(хп,Уп,2п)
Уп+1 — *
Zn+l =
Pl(Xn,yn,Zn)
рг{хп,Уп,*п)
P2(Xn,yn,Zn)
Доказать, что последовательности: (#n)n€N> (2/n)n€N и (^n)n6N —
сходящиеся, причем
lim хп = lim уп = lim 2n = Vabc.
п—+оо п—юо п—юо
2.24. Пусть pi (ж, у,^), P2(x,y,z), pz(x,y,z) имеют тот же смысл, что и в
предыдущей задаче. Зададим произвольно числа а > О, 6>0ис>0и
построим последовательности: (хп), (уп) и (zn). Полагаем х\ = а, у\ = 6,
zi = с и если жп, 2/п для некоторого га £ N определены, то
#п+1 = PlyXm yn<izn)]
Уп+1 = yP2{xn,yn,Zn)\
Zn+l = y/ps(Xn,yn,Zn).
Доказать, что последовательности: (хп), (уп) и (zn), га = 1,2,..., —
сходящиеся, причем
lim хп = Ит уп = lim zn.
п—юо п—юо п—юо
2.25. Пусть а?1, а?2» • • • ? #m — произвольные вещественные числа.
Для к = 1,2,..., га положим:
Р&(ЖЪ #2> • • • )%) = "^~£~ ^ Xi1Xx2 • •-Х{к.
1<%1<%2<"'<г}й<т
Суммирование ведется по всем комбинациям индексов п,г2,..., г&, для
которых выполнено условие, указанное под знаком суммы. Величины С^ суть
биномиальные коэффициенты, С^ равно числу слагаемых в сумме справа.
Положим также po(xi,X2, • • •»ж*п) = 1- В частности, имеем:
Ж1 + Ж2 + • • . Жт
Pi(xi,X2,...,xm) = ;
га
Pm(xi,X2,--.,Xm) = Ж1Ж2 ...Жт.

180
Гл. 2. Теория предела
Пусть даны числа а& > 0, к = 1,2,...,т. Определим по ним некоторые
последовательности
0*4 )n€N» fc = 1,2, ...,га,
(1) (2) (™) т^ л- тчт
полагая ж^ ' = ах,ж^ ' = аг,... ,ж^ ' = ат. Если для некоторого п £ N
величины жп ' определены для всех & = 1,2,..., т, то при каждом к
( (1) (2) (т)^
, (1) (2) (т)х'
Pfc — lv^n ?жп ? • • • ? жп )
Жп+1 ""
Доказать, что при каждом к = 1,2,..., т последовательность
/ (*0\
\Хп MGN
является сходящейся, причем
lim хп ' = Ч/х\Х2 ...хт.
п—юо
2.26. Числовая последовательность (хп)пещ определена следующим образом.
Задаются числа а, Ь £ Ш. Полагаем жо = 0, xi = 1. Если для некоторого п
величины хп и жп-1 уже определены, то жп+1 = ажп4-6жп_1. (В случае а = Ь = 1
(жп)пего называется последовательностью Фибоначчи.)
Доказать, что если предел
п—юо Хп
существует и конечен, то он является корнем квадратного уравнения:
Л2 - аХ - Ь = 0.
При каких условиях указанный предел существует и конечен?
2.27. Даны числовые последовательности (жп)п€^, (уп)пеп- Доказать, что
если существуют пределы ж = lim жп, у = lim 2/n (конечные или бесконеч-
п—юо п—юо
ные), то
lim тах{жп,Уп} = тах{ж,у}; lim min{xn,Уп} = тт{ж,2/}.
п—юо п—юо
2.28. Последовательность (жп)п€К такова, что при каждом п
Хп+1 — хп < aqn,
где |д| < 1. Доказать, что предел lim xn существует, причем
п—юо
—со < lim xn < со.
п—юо

Задачи
181
2.29. Пусть (#n)n€N — числовая последовательность. Предположим, что
существуют числа а > 0 и 6 > 0 такие, что при всяком п
-«
#71+1 -%>
(п + 1)"
Доказать, что тогда существует предел lim жп, причем
п—*оо
—оо < lim xn < оо.
71—>00
Доказать, что существует (конечный или бесконечный) предел lim xn-
71—ЮО
2.30. Построить возрастающую последовательность (#n)n€N такую, что
lim хп = оо, и в то же время lim (#n+fc — хп) = О для любого fc E N.
71—ЮО П—+ 00
2.31. Числовая последовательность хп такова, что для всякой строго
возрастающей последовательности натуральных чисел (rik)ke^ разность аПк — а&
стремится к нулю.
Доказать, что эта последовательность является сходящейся.
2.32. Пусть lim хп — lim уш = 0, где хп > 0, уш > 0 для любых п, га 6 N.
71—»оо т—»оо
Доказать, что тогда найдутся последовательности номеров (ns)seN и
(ms)seN такие, что хПз > Ут8 > %s+1 при всех s.
2.33. Последовательность (хп)п^ называется последовательностью с
ограниченным изменением, если существует число М < оо такое, что \х2 — #i| +
+ |#3 — Х2\ + • * * + \хп — xn-i\ < М при любом п.
Доказать, что всякая последовательность с ограниченным изменением
является сходящейся.
Построить последовательность, не являющуюся последовательностью с
ограниченным изменением и имеющую конечный предел.
2.34. Последовательность (#n)n€N называется последовательностью с
ограниченным верхним изменением, если существует число М < оо такое, что
\Х2 - Xi\+ + \хз — Х2\+ Л Ь \хп — £n_i|+ < М.
Доказать, что всякая последовательность с ограниченным верхним
изменением имеет предел, при этом
—оо < lim xn < оо.
71—»<Х)
Доказать, что если для последовательности с ограниченным верхним
изменением
lim xn > оо,
71—><Х)
то (#n)n€N есть последовательность с ограниченным изменением (см. 2.33).
2.35. Последовательность (xn)n£N называется выпуклой, если для всякого
п G N выполняется неравенство
хп - 2жп+1 + хп+2 > 0.

182
Гл. 2. Теория предела
Доказать, что всякая выпуклая последовательность имеет конечный или
бесконечный предел.
2.36. Пусть (#n)n€N — выпуклая последовательность (см. 2.35). Доказать,
что существует конечный или бесконечный предел lim хп/п.
п—юо
2.37. Последовательность (ап)п^ определена следующим образом: а± и а 2 —
данные числа, ап = (an_i 4-an_2)/2 при п > 2. Доказать, что предел lim an
п—»-оо
существует, и найти его.
2.38. Пусть дана последовательность (хп Е R)n^Nfe • Предположим, что для
всякого е > О можно указать L E R такое, что для любого п > L и любого
A; G N выполняется неравенство жп+& — хп > —е.
Доказать, что существует предел limn-*oo яп, причем — оо < lim хп < оо.
71—»-00
2.39. Пусть (xn)n€N — последовательность вещественных чисел такая, что
хп > О для всех п и хп —► 0 при п —* оо.
Доказать, что найдется бесконечное множество значений n G N таких,
что хт < жп при всех т> п.
2.40. Назовем функцию / : [0, оо) —* К. функцией медленного роста, если /
возрастает, lim /(ж) = оо и lim [f(x + 1) — /(#)] = 0.
X—ЮО Ж-ЮО
Доказать, что если / — функция медленного роста, то для всякого h > 0
lim [/(я? + h) - /(я?)] = 0.
X—ЮО
Доказать, что для всякой функции / : [0, оо) —► R медленного роста
предельные точки последовательностей (sin ж/(n))ra€N заполняют весь
отрезок [—1,1].
2.41. Функция / определена в промежутке (0, оо). Пусть Ln = sup /(#).
ж£[п,оо)
Предположим, что существует предел lim f(x) = L.
X—ЮО
Доказать, что Ln —> L при п —*• оо.
2.42. Пусть / : (-1,1) -> R. Пусть
L = sup /(ж); Z = inf f(x);
»€(-l,l) »€(-l,l)
Ln = sup /(ж); Zn = inf f(x).
x€(-l+l/n,l-l/n) »€(-l+l/n,l-l/n)
Доказать, что X/fi —► X/, /72 —► ь при n —► 00.
2.43. Функция / определена на промежутке [—1,1] и непрерывна в точке 0.
Пусть
V п п/
где п Е N. Положим: ап = inf /(ж); /3n = sup f(x).
x€Un xeun
Доказать, что /(0) = lim an = lim /3n.
n—юо n—»-oo
2.44. Функция / : [0, оо) —* [0, оо) такова, что / ограничена в окрестности
точки х = 0 и f(x + у) < f(x) + f(y) для любых х > 0, у > 0.

Задачи
183
,. /0*0
Доказать, что существует предел lim .
х—юо X
2.45. Функции / : [а,&] —► R и р : [а, &] —* К. непрерывны, и одна из них
монотонна. Предположим, что некоторая последовательность (xn)neN
удовлетворяет условию: f(xn+\) = д(хп) для всех п.
Доказать, что если последовательность имеет предельную точку, то
уравнение /(ж) = д{х) имеет решение.
2.46. Доказать, что всякая числовая последовательность имеет монотонную
подпоследовательность.
2.47. (а) Дана числовая последовательность (xn)n€N-
Доказать, что если из любой ее подпоследовательности можно извлечь
сходящуюся подпоследовательность, то последовательность (xn)n€N
ограничена. _
(Ь) Даны число аЕ^и числовая последовательность (xn)riGN-
Доказать, что если из любой ее подпоследовательности можно извлечь
подпоследовательность, пределом которой является число а, то а = lim xn.
п—юо
2.48. Пусть if : [а,&] —> R — непрерывная возрастающая функция, причем
ip(a) > a, ip(b) < Ь. Для произвольного х Е [а, Ь] определим, по индукции,
последовательность (<^n(^))nGN> полагая y>i(x) = ip(x) и ifn+i(x) = ф(фп{х))-
Доказать, что последовательность (<£nO*0)n€N является сходящейся при
любом х Е [а,&].
Доказать, что если ip(x) > ж для всех х Е (а, &), то lim ipn(x) = b, a если
<р(ж) < ж для всех х Е (а, 6), то lim (pn(x) = «•
2.49. Пусть (xn)n€N — числовая последовательность. Зададим произвольно
к Е N. Индукцией по к определим последовательность (АкХп)п^. Именно,
полагаем Aixn = жп+1 — xn. Если последовательность (AkXn)n^ определена,
то Afc+ixn = AfcXn+i — Afc^n.
Доказать, что Д&жп = X/(~*)fc~J^fcXn+.? для всякого &
i=o
Доказать, что если А^хп > О при каждом п, то для любого целого I
такого, что 0 < I < к — 1, существует конечный или бесконечный предел
lim —у.
п—юо 7Г
2.50. Пусть / : R. —► К. — непрерывная функция такая, что
Доказать, что найдется точка х такая, что f(x) = 0.
2.51. Доказать, что если непустое множество А С К не есть отрезок, то
найдется непрерывная функция / : А —* R, принимающая в некоторых точках
множества А значения разных знаков и не обращающаяся в нуль ни в какой
точке множества А.
2.52. Построить пример немонотонного топологического отображения
f : А -+ R, где А С R.
2.53. Функция / : (а,Ь) -+ R строго монотонна. Пусть 22 = /((с, &)) и пусть
у? : J5 —* R есть функция, обратная к /, ip = f"1.
Доказать, что функция ip непрерывна. (Непрерывность функции / не
предполагается!)

184
Гл. 2. Теория предела
2.54. Построить пример непрерывного взаимно однозначного отображения
/ : А —* R, где А С R, такого, что обратное отображение f"1 не является
непрерывным.
2.55. Построить непрерывную функцию / : [0,1] -* R такую, что для всякого
У € /([^» Ч) множество f~1{y) бесконечно и счетно.
2.56. Может ли быть замкнутый отрезок — топологическим образом
открытого отрезка?
Обратно, может ли быть топологическим образом замкнутого отрезка —
открытый отрезок?
2.57. Функция / : [а, Ь] —► R непрерывна.
Что можно сказать о функции /, если известно, что все ее значения
рациональны (иррациональны)?
Какова будет функция /, если все ее значения целые числа?
Какова будет функция /, если множество /([а,&]) не более чем счетно?
2.58. Пусть Г — множество комплексных чисел z таких, что \z\ = 1. Пусть
Г0 = Г\{-1}.
V
Доказать, что отображение z = и 4- iv Е Го •—► взаимно однозначно.
1 + гх
Определить обратное отображение и доказать его непрерывность.
2.59. Доказать, что не существует непрерывного взаимно однозначного
отображения множества R на множество Г (см. 2.58).
Доказать, что не существует непрерывного биективного отображения
отрезка [—1,1] на множество Г.
2.60. Построить топологическое отображение отрезка (а, Ь) на R.
2.61. Пусть / : [а,Ь] —> С — непрерывное отображение такое, что \f(t)\ ф О
для любого t £ [а,Ь].
Доказать, что тогда существует непрерывная функция a(t) такая, что
а(а) = arg f(a) и a(t) = arg f(t) -f 27гга, где т — целое число, для всех t £ [а, Ь].
2.62. Дана функция / : R —► R. Предположим, что / непрерывна и
существуют конечные пределы lim f(x) и lim f{x).
х—юо х—* — оо
Доказать, что / равномерно непрерывна на множестве R.
Доказать, что при этих условиях функция / — ограниченная.
2.63. Даны функции / : [а, Ь] —* R и д : [а, Ь] —* R. Доказать, что если / и д
непрерывны, то функции р = тах{/, д} и q = min{/,p} также непрерывны.
Пусть a>i есть модуль непрерывности /, а>2 — модуль непрерывности р.
Доказать, что функция ш = max{a>i,a>2} является модулем непрерывности для
каждой из функций р и q.
2.64. Пусть / : R —* R — непрерывна. Предположим, что
lim f(x) = lim f(x) = оо.
ж—>oo х—> — оо
Доказать, что функция / ограничена снизу и принимает свое наименьшее
значение.
2.65. Пусть / : R —► R непрерывна. Доказать, что если
lim f(x) = lim f(x) = 0,
ж—+oo x—* — оо
то функция / принимает или наибольшее, или наименьшее значение.

Задачи
185
Привести пример, в котором функция принимала бы только одно из
указанных значений.
2.66. Доказать, что модуль непрерывности uj функции / : [а, Ь] —► R,
построенный при доказательстве теоремы Гейне, обладает следующими свойствами
минимальности:
пусть cji : [0,оо) —► R — любой другой модуль непрерывности функции
/ : [а, Ь] —► R, тогда oj(t) < uj\{t) для всех t £ [0, со).
2.67. Пусть / : R —► R — периодическая функция. Доказать, что если
существует lim f(x), то / постоянна.
х—»оо
2.68. Функция / : [0, со) —► R — равномерно непрерывна на [0, со). Доказать,
что f(x) = 0{х) при х —► со, то есть
(3JST)(3i4)(Va?>i4)|/(a:)|<lfH.
2.69. Функция / : [а, Ь] —► R имеет модулем непрерывности uj : 6 —► A£1+Q!, где
а > 0. Доказать, что функция / — тождественно постоянна в [а, Ь].
2.70. Дана непрерывная функция / : [а, 6] —► JR. Положим для х £ [а,&]
F(a:) = sup /(i); <3(s) = inf /(*).
а<*<ж a<t<z
Доказать, что функции F ж G непрерывны.
Доказать, что если и;[0, со) —► R есть модуль непрерывности функции /,
то о; есть модуль непрерывности каждой из функций F и G.
2.71. Функция / определена на множестве Qq всех рациональных чисел
отрезка [0,1].
Доказать, что для того, чтобы существовала непрерывная функция д,
определенная на всем отрезке [0,1] и такая, что д(х) = f(x) для всех х £ Qo>
необходимо и достаточно, чтобы / была равномерно непрерывна на Qo-
2.72. Построить непрерывную функцию / : [a, b] —► 1R, не монотонную ни на
каком интервале (а,/3) С [а,Ь].
2.73. Пусть Е — произвольное числовое множество. Для х £ Ш положим:
р(х,Е) = inf \x-y\.
уеЕ
Доказать, что функция х —> р(ж., 12) непрерывна.
2.74. Число ж называется двоично рациональным, если ж = р/2т, где /? и га —
целые числа, га > 0. Обозначим совокупность всех двоично рациональных
чисел символом Q2-
Построить взаимно однозначное отображение / : Q —► $2 так, чтобы
функция / была монотонна на Q.
2.75. Пусть даны числовое множество А и точка р £ £гтА
Предположим, что А = В U С, где множества Б и С не пересекаются и р £ CimB,
р £ CimC. Доказать, что если для функции / : А —► IR пределы lim /(ж),
ж—»-р,ж£В
lim f(x) существуют и равны между собой, то существует также и предел
х—*р,х€С
lim f(x).
х—*р,х£А

186
Гл. 2. Теория предела
2.76. Пусть даны множество А, точка р Е Ш и функция / : А —* Ш.
Предположим, что р является левосторонней предельной точкой А. Доказать, что если
для всякой возрастающей последовательности х : N —► А, такой, что хп —> р
при п —► со, хп < /? при всех п, существует предел lim f(xn), то существует
п—юо
предел lim /(ж).
ж—»-р—0,х£А
2.77. Функция / : [а, Ь] —► К. имеет конечный предел в каждой точке отрезка
[а,Ь]. Доказать, что / ограничена на [а, Ь].
2.78. Доказать, что всякая непрерывная функция / : [а, Ь] —► R, которая не
принимает никакое значение более чем два раза, должна принимать некоторое
значение в точности один раз.
2.79. Дана числовая последовательность (#n)neN-
Доказать, что если ее подпоследовательности (#2n)n€N? (#2n-i)
(#3n)neN сходятся, то последовательность (xn)neN сходится.
2.80. Пусть / : [0, оо) —■> R — строго возрастающая непрерывная функция
такая, что /(ж) —* оо при ж —► оо, /~х — обратная функция.
Доказать, что для всякого е > 0 и любого К найдется х > К такое, что
Лж)/-1(а;)>(1-ф2.
2.81. Можно ли для всякого е > 0 построить многочлен Р так, что для всех
х G [1, оо) будет выполняться неравенство \Р(х) — lnx| < el
2.82. Можно ли для всякого е > 0 построить многочлен Р такой, что
\Р(х)-ех\<е
для всех х G (0, оо)?
2.83. Пусть <р : (0, а) —* Ш — непрерывная строго возрастающая функция,
причем (р(х) —> 0 при х —* 0.
Доказать, что если существует предел lim ^^ = I ф 0, то существует
и предел lim , который равен 1/1.
у—о у
2.84. Пусть / : [а, Ь] —► R — непрерывная функция.
Доказать, что если /([а, Ь]) С [а, Ь], то существует точка х Е [а,&] такая,
что /(ж) = х {теорема Шаудера о неподвижной точке в одномерном случае).
2.85. Пусть / : [а, Ь] —► R — непрерывная функция.
Доказать, что если / принимает всякое свое значение не более двух раз,
то отрезок [а,&] можно разбить на конечное (не превосходящее трех) число
отрезков, в каждом из которых функция строго монотонна.
2.86. Функция / : [а, Ь] —> R имеет только точки разрыва первого рода, то есть
такова, что в каждой точке х Е [а, Ь) существует конечный предел f(x -f- 0), a
в каждой точке х Е (а, Ь] существует конечный предел f(x — 0).
Доказать, что множество точек разрыва функции не более чем счетно.
(Указание: сначала установить, что множество точек х Е (а,Ь), в
которых \f(x + 0) — f(x — 0)1 > 1/rn, где т — фиксированное натуральное число,
конечно при всяком т.)
Доказать, что функция / ограничена.
2.87. Функция / : [а, 6] —► R обладает следующим свойством: существует
число К > 0 такое, что для любых х\, Х2 Е [а, Ь]
f(xi)-f(x2)>-K\zi-x2\.
Доказать, что функция / имеет только точки разрыва первого рода.

Глава 3
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
Г
• Понятия показательной, логарифмической и
степенной функций и их свойства • Тригонометрические
функции • Понятие обратной тригонометрической
функции • Общее понятие элементарной функции
• Сравнение поведения показательной,
логарифмической и степенной функций вблизи концов области
определения • Понятие асимптотического соотношения
• Существование и конечность предела: ехр X =
v Л х\п 1- ехрх — 1
= lim ( 1 Н I • Пределы: lim ;
п—>оо \ п/ х—+0 Ж
.. ln(l+s) (i + z)«-l sinz
lim ; lim ; lim .
x-+0 X x-+0 X x-+Q X
• Показательная функция комплексного аргумента
,. eix - 1
• Предел: lim • Гиперболические
х-+0 х
функции •

188
Гл. 3. Элементарные функции
§1. Показательная, логарифмическая и степенная
функции. Некоторые замечательные пределы
Данные ниже определения степенной, показательной и
логарифмической функций и доказательства их основных свойств существенно
опираются на то свойство множества вещественных чисел Ш, которое
выражается аксиомой непрерывности множества R (см. §4 главы 1).
При этом используется не сама аксиома непрерывности, а некоторые
предложения, доказанные в главе 2 с ее помощью, а именно, теорема
о существовании предела у монотонной последовательности и критерий
сходимости Коши — Больцано,
В соответствии со школьным курсом математики, графики
показательной, степенной и логарифмической функций — это некоторые
плавно идущие или, как говорят, гладкие кривые.
Гладкость подразумевает, что малый участок кривой почти
неотличим от прямолинейного отрезка. Степень отличия тем меньше, чем
меньше взятая дуга.
График функции х —» ах проходит через точку (О,1) на плоскости.
Всякая прямая, проходящая через эту точку и не совпадающая с осью
Оу, задается уравнением у = 1 + кх. Неотличимость или почти
неотличимость малой дуги графика показательной функции от отрезка
прямой в данном случае означает, что при х, малом по абсолютной
величине, можно считать приближенно, что ах « 1 + кх, причем
ошибка бесконечно мала по сравнению с \х\ (см. рис. 1).
Рис. 1
Пусть х € Ш — произвольно. Если n G N достаточно велико, так
х
что — мало, то можно считать, что
п
- 1 . кх
п

§ 1. Показательная, логарифмическая и степенная функции
189
и, значит,
Эти соображения наводят на мысль, что ах может быть определено как
предел
Л kx\n
lim 1 + — ,
71 —ЮО \ П /
соответствующий некоторому конкретному значению к.
(кх\п
1 Н ) действительно
71 /
существует и функция переменной х, получаемая таким образом, есть
функция ах.
Будет показано также, как определять коэффициент к, чтобы
получить показательную функцию именно с данным основанием а. Но
предварительно будет рассмотрен предел
lim (l + -V,
П-+00 \ 71/
где жбК. Сначала мы докажем, что этот предел существует и конечен
для всякого жЕЙ. Данный предел обозначается символом ехрх. Тем
самым на множестве R определяется некоторая функция ехр.
Исследуются свойства ехр. В частности, показывается, что ехр
есть непрерывная строго возрастающая функция, отображающая
промежуток (—оо, оо) на интервал (0, оо).
Функция, обратная к ехр, называется натуральным логарифмом и
обозначается символом In. Существование обратной функции следует
из теоремы об обратной функции, доказанной в главе 2 (теорема 4.3J.
С помощью функций ехр и In определяется операция возведения в
степень (х,у) i-» yx. После этого определяются степенная функция и
показательная функция с произвольным основанием a > 0.
1.1. Существование и конечность предела lim (1 + -)
га—>oo \ 71/
В главе 1, п. 4.4.11 было доказано следующее утверждение.
Если и 6 R таково, что 1 + и > 0, то для любого m E N выполняется
неравенство:
(l + u)m > 1 + mu
(неравенство Бернулли).
Знак равенства здесь имеет место только в том случае, когда либо
и = 0, либо m = 1.

190
Гл. 3. Элементарные функции
■ Теорема 1.1. Для всякого a:GK существует конечный предел
lim (l + -Y.
Доказательство. Зададим произвольно жб1, и пусть к 6 N
таково, что х > — к.
Докажем сначала, что последовательность
\\ П) /n€Nfc
является возрастающей.
Для всякого п > к имеем:
1 + £ = n±*>n+i>0>
п п п
Возьмем произвольно п > к и рассмотрим отношение:
Имеем: 1 Н > 0, 1-\— > 0 и, значит,
п + 1 п
i+ ж
^±± > 0.
1+^
П
Далее,
а? хх
14- —— —
1 + £ + i + £ _i (n + i)(» + x)'
П П
Применим неравенство Бернуллщ полагая в нем т = п + 1 и
i/ =
(п + 1)(п + я?)'

§ 1. Показательная, логарифмическая и степенная функции
191
п
п + х п + х
п /
Отсюда
V п) \ i + £ I "\ п)п + х~
и, значит,
п+1
(^^т) *Ю*
при каждом п > к.
Тем самым доказано, что последовательность (1.1) является
возрастающей, и, следовательно, она имеет предел. При этом
—оо <
(1+!)'*л=.(1+!)"- <1Л>
Для завершения доказательства мы должны установить, что
предел (1.2) конечен.
Пусть / G N таково, что х < L Тогда —х > —I.
Заменяя в проделанных рассуждениях х на — х и к на Z, получим,
что последовательность
((-;)")
пещ
является возрастающей.
В частности, при любом п > / имеет место неравенство:
X
Пусть т = тах{&,/}. При каждом п > т имеем: 1-\— > О,
п
х
1 > 0. Далее,
п
('-|)*ю"-И)"*

192
Гл. 3. Элементарные функции
Отсюда следует, что для всех п >т
Л + *У< I < I
и, ста|го быть, в силу (1.3), для всех п > т > к
Л + *У< 1 <00. (1.4)
I J -(l_.y.
Это позволяет заключить, что
lim (l + -Y <- 1 . , <oo, (1.5)
и тем самым теорема полностью доказана. ■
Предел
lim (l + -V
обозначается символом ехр х. (Для величины ехр х мы будем применять
также и другие обозначения, которые будут введены позднее.)
Замечание. Из неравенств (1.3) и (1.4), полученных при
доказательстве теоремы 1.1, вытекает следующая оценка для ехрх:
если к G N, I G N таковы, что — к < х < Z, то величина ехр ж
удовлетворяет неравенствам:
(l + £)'<exp*<—' (!.6)
В силу свойств предела, установленных ранее, для всякого числа fc E R
и любой бесконечно малой последовательности (^n)nGN величина (1 -Mn)fc при
п, стремящемся к бесконечности, стремится к пределу, равному 1.
В связи с этим может возникнуть вопрос, а не будет ли предел, о котором
идет речь в теореме 1.1, равен единице, каково бы ни было х Е R? На это можно
возразить, что в нашем случае показатель степени не является постоянной
величиной и неограниченно растет вместе с номером п. (Мы знаем, что для
любого t > — 1 предел lim (1 + t)n равен оо, если t > 0, и равен нулю, если
п—юо
t < 0.) В случае, который мы рассматриваем, речь идет о пределе величины
о»
(1 + tn)n, где tn = ► 0 при п —► 0.
п

§ 1. Показательная, логарифмическая и степенная функции
193
Но только неравенства (1.5) и (1.6) позволяют заключить, что предел,
существование которого установлено теоремой 1.1, не равен
тождественно 1, а для х > О — конечен и полученная нами функция х »-*• ехр ж
нетривиальна.
х
Так как х > — &, то 1 + — > 0 и, стало быть, в силу неравенства
к
Бернулли,
1 + х,
Ы)>-
откуда заключаем, что для всех х € R.
ехр х > 1 + х, (1-7)
Полагая в неравенстве (1.6) / = 1, получим, что для всякого х < 1
ехр х < . (1-8)
~" 1 — х
При х = О
для всех п, откуда вытекает равенство: ехр(О) = 1.
Величина ехр(1) обозначается символом е.
Полагая в неравенстве (1.5) к = 1, I = 2, находим следующие
границы, между которыми лежит е: 2 < е < 4.
Более узкий промежуток, содержащий число б, можно
установить, выбирая в неравенстве (1.5) при х = 1 достаточно большие
значения & и /.
Полагая, например, к = 2, Z = 6, найдем, что
Л , XV о1 • ^ 1 45656 0
(1+а) =24^^-Г71у = 15625 <3'
-15
откуда 2 < е < 3.
Приближенное значение числа е с ошибкой, меньшей 10
следующее:
6 = 2,718281828459045... .
Для всякого х £ R определено некоторое число ехр х. Тем самым
на множестве R определена функция ехр: a?gRi-> ехр х.
Далее будут установлены некоторые свойства функции ехр,
из которых, в частности, можно будет усмотреть, что функция ехр есть
не что иное, как показательная функция, имеющая основанием число е.

194
Гл. 3. Элементарные функции
1,2. Свойства функции ехр
■ Лемма 1.1. Пусть дана числовая последовательность (zn)n6N«
Если lim zn = 0, то
п—юо \ П /
Доказательство. Так как lim zn = 0, то найдется I E N такое,
п—юо
что при любом п > / выполняется неравенство \zn\ < 1. Для таких п
< 1. При n > Z имеем:
очевидно также, что
п
l + ^>0; 1-^>0; f 1 + fl) Л _ £2.) = 1 _ £^ < 1,
п п \ п / \ n J п2 ~~
откуда
1 + £и<^_. (1.9)
п
Применяя неравенство Берну лли, отсюда заключаем, что при n > Z
будем иметь:
Л + £2.)" > 1 + n£lL = 1 + Zn. Л _ £lLУ > 1 _ n£?L = 1 _ Zn.
Из этих неравенств и (1.9) следует, что при любом п > /
l + £!L<(i+Mn< L < 1
^n
Так как при п —> оо имеем zn —> 0, то, применяя теорему о
зажатой переменной (теорема 1.5 и ее следствия из главы 2), получаем
lim (l + £2.)n = l,
п—юо \ П /
что и требовалось доказать. ■
■ Лемма 1.2. Пусть {хп)п^ есть сходящаяся числовая
последовательность и
a = lim xn.
П—ЮО

§ 1. Показательная, логарифмическая и степенная функции
195
Тогда
lim (14 I = ехр а.
га—>оо \ П /
Доказательство. Пусть k G N таково, что a > — fc. Для п > к
имеем:
1 л- Хп
"*" п _ п + а?п _ 1 , хп-а _ п(жп - а) 1
1 + — n + а ' п + а n + а п*
п
Для п > & полагаем zn = -. Для всех п > к выполняется
"" п + а
равенство:
При п —» сю будет zn -> 0 и, значит, по лемме 1.1, (1 Н—— 1 —> 1
при п —> оо. Далее, lim (1 -\— ) = ехр а и, следовательно,
га —►оо V П/
lim fl + —V = lim fl + -V lim (l + —Y =expa,
ra—>oo \ П / ra—>>oo \ 71/ n-юо \ П /
что и требовалось доказать. ■
■ Теорема 1.2. Для любых х,у 6 R выполняется равенство:
ехр ж ехр у = ехр(ж + у).
Доказательство. Имеем:
ехр ж ехр у = lim (1 Н— ) lim (1 Н— ) =
га—»>оо \ П/ га —юо \ П/
= lim (1 + £±y + fj)*=lim (l + M",
га —оо \ П ??/ / ra-*oo \ П /
где i/n = ж + у + ху/n. При п —> сю выполняется ип —*■ ж + у.
На основании леммы 1.2, отсюда следует, что
ехр ж ехр у = lim (1 Н—— ) = ехр(ж + у),
га-»оо \ П /
и тем самым теорема доказана. ■

196
Гл. 3. Элементарные функции
▼ Следствие 1. Для всякого х £ R. выполняется равенство:
{ехрх}{ехр(—х)} = 1.
Действительно, полагая в теореме 1.2 у = —х, получим:
{ехр#}{ехр(—х)} = ехрО = 1,
что и требовалось доказать. ▼
Т Следствие 2. Для всякого # £ R справедливо ехр ж > 0.
Действительно, следствие 1 позволяет заключить, что ехр х ф 0
для всех х £ R. Далее, по теореме 1.2, имеем:
ехр* = ехр(! + !) = (ехр!)
и, значит, ехр х > 0. Т
Т Следствие 3. Для любого конечного множества чисел х\, #2,...
..., ссп ямеет место равенство:
(ехрan)(ехржг). ..(exp#n) = exp(#i + #2 Н h #n).
Доказательство индукцией поп — очевидно. Т
Из школьного курса математики читателю известно понятие
показательной функции х I—► ах, где а — положительное число, отличное от
единицы.
Определение того, что есть ах для произвольных а>0,а^1иж£М,
которое дается в школьном курсе математики, не опирается на строгую теорию
вещественного числа и потому не может считаться строгим. В числе свойств
«школьной показательной функции» отметим следующее.
Для любых х\ и ж2 имеет место равенство:
аХ1аХ2 =аХ1+Х2.
Полагая ах = /(ж), это равенство можно записать следующим образом:
f(xi)f(x2) = f(x\ +ж2).
В силу теоремы 1.2, это свойство показательных функций имеет место
также и для функции ехр.

§ 1. Показательная, логарифмическая и степенная функции
197
Полагал в следствии 3 х\ = x<i = • • • = хп = х, получим, что для
всякого х £ R справедливо [ехр х]п = ехр пх.
Ш Теорема 1.3. Функция ехр является непрерывной и строго
возрастающей на множестве Ш. При этом
Km ехр х = оо; lim ехр ж = 0.
х—*оо #—*• —со
Доказательство. Для всякого ж £ (—1,1), как было показано
ранее, имеют место неравенства:
1 + х < ехр х < .
1 — х
При ж —> 0 крайние функции в этих неравенствах имеют общий
предел, равный 1, откуда следует, что
lim ехрх = 1.
Для произвольных x,xq £ М имеем:
ехр ж = (ехр#о)(ехр(ж — xq)).
По доказанному,
lim exp(x — xq) = lim ехрх = 1,
х—>х§ х—>0
откуда вытекает, что
lim ехр х = ехр #о.
а:—>-хо
Непрерывность функции ехр тем самым установлена.
Пусть х\,Х2 £ К таковы, что х\ < Х2> Имеем:
ехр #2 = (exp#i)(exp(#2 — xi)) > exp#i(l + #2 — #i) > exp#i.
Тем самым доказано, что ехр есть строго возрастающая
функция. Неравенство ехр х > 1 + х позволяет заключить, что
lim ехр х = оо.
х—»оо

198
Гл. 3. Элементарные функции
Наконец, из неравенств
^ 1
О < ехрх < ,
1 — х
выполняющихся при х < 1, следует, что
lim ехр х = 0.
X—► — ОО
Теорема доказана. Н
На рис. 2 представлен график функции у = ехр х.
Рис.2
Теорема 1.4. Справедливо равенство:
ехр х — 1
lim = 1.
а?—►() £С
Доказательство. При ж £ (-1Д) имеем:
1
Отсюда
и, значит,
при 0 < х < 1 и
при — 1 < х < 0.
1 + х < ехр ж <
х < ехр ее — 1 <
1-я?"
1-я?
1 < ехр х - 1 < 1
X 1-Х
1 > ехр х - 1 > 1
1-я?

§ 1. Показательная, логарифмическая и степенная функции
199
Таким образом, для всех х € ( — 1,1), отличных от 0, отношение
ехр х — 1 .1
лежит между числами 1 и .
х 1-х
Так как
lim 1 = lirn = 1,
х-»0 х-*0 1 — X
то, в силу теоремы о зажатой переменной (теорема 1.5 главы 2),
отсюда вытекает, что
.. ехр х — 1
1 = lim .
х—»0 X
Теорема доказана. В
1.3. Функция натуральный логарифм
Согласно теореме 1.3, функция ехр является непрерывной и строго
возрастающей на множестве всех вещественных чисел R. При этом
lim ехр х = 0; lim ехр х = оо.
х—*• —оо х—юо
По теореме о непрерывной обратной функции (теорема 4.3 главы
2), отсюда вытекает, что функция ехр взаимно однозначно
отображает множество R. на промежуток (0, сю) и имеет непрерывную обратную
функцию.
Функция, обратная к функции ехр, обозначается символом In.
Согласно теореме 4.3 главы 2, областью определения функции In
является промежуток (0,оо). При этом по той же теореме функция In
является непрерывной и строго возрастающей и отображает
промежуток (0, оо) на R.
Согласно определению обратной функции, для х 6 (0, оо) число In x
есть значение у £ R такое, что х = ехр у.
Число у = \пх 6 К такое, что х = ехр у, называется натуральным
логарифмом х.
По определению, если ехр у = х, то у = In x. Отсюда вытекает, что
для всякого х > 0 выполняется равенство:
exp(lncc) = ж, (1-Ю)
и для любого a?GR справедливо соотношение:
1п(ехрж) = х.
(l.ii)

200
Гл. 3. Элементарные функции
Заметим, что так как ехрО = 1, то
In 1 = 0. (1.12)
■ Теорема 1.5. Функция натуральный логарифм непрерывна,
является строго возрастающей в промежутке (0, оо) и обладает
следующими свойствами:
а) для любых х\,х2 € (0, оо)
Хл
\n{xiX2) = lna^i + In £2; In — = lna^i — lna^; (1-13)
X2
б) для всякого x > 0
x-l>lnx>l-i; (1.14)
X
в) справедливо соотношение:
lim!^±£)=l; (1.15)
ж->0 X
г) выполняются равенства:
lim In ж = —оо; lim lnx = 00. (1-16)
я—»0 я—юо
Доказательство. То, что функция In непрерывна и является
строго возрастающей, как было сказано выше, следует из ее определения
и из теоремы о непрерывной обратной функции (теорема 4.3 главы 2).
а) Пусть xi > 0, х2 > 0. Положим lnxi = 3/1, \пх2 = у2> Тогда exp(t/i +
+у2) = (expt/i)(expt/2) = xix2 и, значит, у\ + у2 = ln(xix2), и первое
из равенств (1.13) доказано.
Для доказательства второго равенства заметим, что
Xi
Xi = Х2 ,
х2
откуда
ln#i = In£2 "bin .
Х2
Следовательно,
In— = lna^i — ln^2,
х2

§ 1. Показательная, логарифмическая и степенная функции
201
что и требовалось доказать.
б) Пусть у = In ж. Тогда х = ехру > у + 1 = 1п# + 1, откуда
вытекает первое из неравенств (1.14).
Второе получается из первого, если заметить, что для всякого
х > 0
In х + In - = In 1 = 0
х
и, стало быть, In — = — In x.
а?
1 > In — = — In х^
X X
откуда In x > 1 .
x
в) Заменяя в неравенстве (1.14) х на 1 + #, получим, что при а? > — 1
x>ln(l + *)>l--L- = T^-.
1 + X 1 + X
Отсюда заключаем, что при х > 0 имеем:
а при ж < 0 получим:
1п(1 + х) 1
Ж 1 + Ж
1<1п(1 + х)< 1
1 + а?
Таким образом, при х Е ( —1,оо) отношение — лежит ме-
х
жду 1 и . Так как
1 + х
lim = lim 1 = 1,
х—>0 1 + X х-+0
то, в силу теоремы о заоюатой переменной (глава 2, теорема 1.5),
получаем, что
],ш М1+4 = 1.
х->0 X

202
Гл. 3. Элементарные функции
г) Так как, по доказанному, функция In — монотонна, то
существуют пределы
lim In x = /; lim In x = L.
x—»-0 x—юо
При этом, согласно теореме о пределе монотонной функции
(теорема 3.1 главы 2), предел lim In x равен точной нижней границе
функции In, а предел lim In x равен ее точной верхней границе.
х—*оо
Так как функция In отображает промежуток (0, оо) на все
множество R, то точная нижняя граница функции In равна точной ниоюней
границе множества R, то есть —оо, а точная верхняя граница \пх
равна supR = оо.
На основании теоремы о пределе монотонной функции (теорема 3.1
главы 2), из сказанного вытекает, что
lim In x — inf In x = inf R = —oo,
rr-+0 arG(0,oo)
a
lim In x sup ln# = supR = oo.
ar-*°° rr€(0,oo)
Теорема доказана. ■
На рис. 3 представлен график функции у = In ж.
f
_^^ i
^^ i
>^ i
Ал?. 5
Равенства (1.13) показывают, в частности, что введенная здесь функция
In обладает тем основным свойством логарифмов, которое определило их роль
в истории науки. А именно: применение логарифмов позволяет свести
операции умножения и деления чисел к значительно менее трудоемким операциям
сложения и вычитания. Таблицы логарифмов еще не так давно были одним
из основных инструментов в области приложений математики. (В связи с
развитием вычислительной техники, прикладное значение таблиц логарифмов в
настоящее время утрачено.)
Открытию логарифмов предшествовало такое наблюдение.
Предположим, что мы имеем некоторую геометрическую прогрессию:
а, а , а,... , а ,... .

§ 1. Показательная, логарифмическая и степенная функции
203
Чтобы найти произведение каких-либо двух членов этой прогрессии,
достаточно сложить их номера. Произведение также будет членом данной
прогрессии, и полученная сумма равна номеру этого произведения.
Если а = 2 или а = 10, то данное утверждение можно отнести к числу
математических курьезов, не имеющих серьезного практического значения.
Ведь перемножать степени двойки или десятки в жизни приходится не так уж
часто.
Ситуация радикально меняется, если взять число а достаточно близким
к единице. Тогда числа а71, где п = 1,2,..., будут располагаться на числовой
прямой R достаточно плотно.
Пусть, например, а = 1 Н . Возьмем произвольно число х > 1.
Тогда найдется номер п 6 N такой, что
Положим
V юооо у - - V юооо/
V + юооо у ~Х1'
п+1
Имеем, очевидно:
1 < — < 1 +
хг ~ ЮООО
Отсюда видим, что в представлении чисел х и х\ — в десятичной системе
счисления — первые три знака совпадают, так что х мало отличается от х\.
Если взять геометрическую прогрессию с основанием
1 +
юооо'
то, используя такое ее свойство, что номер произведения двух членов
прогрессии равен сумме их номеров, мы получим способ, позволяющий
определять произведение произвольных двух чисел с тремя верными десятичными
знаками. Пусть даны ж > 1 и г G N, г > 1, и п £ N таково, что
O + ^f <*<(* +9"+1- (1-17)
Используя установленные свойства натурального логарифма, найдем
некоторые оценки для числа п. Так как функция In — возрастающая, то из
последних неравенств следует, что
Имеем:
In (l + -У < \пх < In (l + i)
h(i+i)*=.i.(i+i)
l\n+1

204
Гл. 3. Элементарные функции
lnfi + iV = (n + i)b(i + i).
Полагая в неравенствах (1.14) х = I 1 Н— J, получим:
г \ v) г +1
Если га таково, что выполняются неравенства (1.17), то
га , п
< In ж < -,
г + 1 г
откуда получаем, что г In ж < га < (г + 1)1пж и, значит, га = (г + е)1пж, где
0 < е < 1.
В частности, если г равно 10т, то величина га10~"т, где n определено
неравенствами (1.17), почти равна натуральному логарифму числа х.
1.4. Операция возведения в степень. Степенная функция.
Показательная функция
■ Теорема 1.6. Пусть дано число у > 0. Тогда для всякого п £ N
существует и притом единственное число z > 0 такое, что zn = у.
Тогда
Доказательство. Пусть дано у > 0. Положим: z = ехр ( — In у \.
zn = ехр ( - In у) = ехр(1п у) = у,
так что данное z и есть искомое.
Единственность z следует из того, что функция
х *-* хп является строго возрастающей на промежутке [0,оо), что и
требовалось доказать. ■
Число z > 0 такое, что zn = у, обозначается символом ^у или
символом у л и называется корнем n-и степени п из числа у.
Имеем:
tyy = z = ехр f - In у J.
Пусть х — произвольное рациональное число, х = —, где п 6 N, а
п
m — целое. В этом случае полагаем:
ух = (у»)т.

§ 1. Показательная, логарифмическая и степенная функции
205
Далее,
у п = ехр I — In у
откуда получаем, что
771
г
то есть для всякого рационального числа х
ух = ехр(#1п у).
Таким образом, мы получаем на множестве рациональных
чисел Q функцию жиух. При этом для всякого х Е Q будем иметь:
ух = ехр(#1п у).
Всякое число х £ R является предельной точкой
множества Q и, в силу непрерывности функции ехр, существует предел:
lim exp(t In х) = ехр(х In у).
Значение этого предела и принимается за ух для произвольного
х 6 М, то есть
ух = ехр(ж1п у).
Данное здесь определение того, что есть ух для у > 0 и
произвольного х £ R, повторяет — с необходимыми уточнениями — то
определение, которое обычно приводится в школьном курсе математики.
Отметим, что если у = е = ехр 1, то ух — ех — ехр(#1п е) = ехр х,
В дальнейшем вместо ехр х мы будем применять, как правило,
более короткое обозначение: ех, оставляя запись: «ехр ж» для того случая,
когда х задается каким-либо громоздким выражением, которое неудобно
писать на месте показателя степени.
■ Теорема 1 • 7. Справедливы следующие утверждения:
1) In (ух) = х\пу для всякого у > 0 и любого х G К;
2) y*i . у*2 _ yXi+*2 для любых ^1 G R, ^2 G К и любого у > 0;
3) 2/1* • 2/2* = (2/12/2)* для любых положительных чисел у\ и у2 и
любого х G R;
4) yXl > 0 И (уХ1)Х2 = yXlX2 ДЛЯ ВСЯКОГО у > 0 И ЛЮбыХ Х\ И Х2]
5) Пусть 2/2 > yi > 0. Если х > 0, то у2Х > у\х, а если х < 0? то
2/2* < 2/1 *•
ехр
(-1пИ =ехр(^1пД

206
Гл. 3. Элементарные функции
6) Пусть Х2 > х\. Тогда, для всякого у > 0, если у > 1, то уХ2 > у*1,
а если у < 1, то у*2 < у*1.
7) Пусть х G R отлично от нуля. Тогда
г х . ° ПРИ * > 0;
lim у = <
у—о ^ оо при а? < 0,
lim ух = \
F х . оо лряя>0;
lim у = <
у-юо [ 0 при а? < 0.
8) Яусть у > 0, у ^ 1. Тогда
,. яг , -, еслиу>1;
lim у = <
если у < 1,
I оо,
I 0,
г яг . —7 если у > 1;
lim у = <
*—оо ^ 0, если у < 1.
Доказательство. Предложение 1) непосредственно следует из
определения у* и соотношения ln(exp z) = z.
2) Имеем:
у*1 . у*2 = {exp(a?i In у)} • {ехр(х2 In у)} =
= exp(a?i In у + х2 In у) = exp[(a?i + x2) In у] = у*1**2,
что и требовалось доказать.
3) Пусть у\ > 0, уг > 0. Тогда
yi* • У2Х = [exp(a?lnyi)] • [а?ехр(1пу2)] = [exp(a?lnyi + а?1пу2)] =
= ехр[яln(yi • у2)] = (угУ2)Ху
и предложение 3) доказано.
4) Пусть даны у > 0 и х\,х<ь € R. Имеем: yXl = exp(#i In у) и так
как функция ехр принимает только положительные значения, то,
значит, yXl > 0. По определению
(уа?1Г2=ехр(х21пу{Г1).
Согласно предложению 1), In у*1 = х\ In у. Отсюда
(у*1 У2 = ехр(хгх2 In у) = у*1*2,

§ 1. Показательная, логарифмическая и степенная функции
207
и тем самым доказано утверждение 4).
5) Пусть 2/2 > yi > 0. Тогда In уч > In у\. Таким образом, при х > 0
выполняется х In г/2 > х In у\, а при х < 0 выполняется a? In г/2 < a? In yi.
Отсюда получаем, что если х > 0, то
г/2* = ехр(а?1пу2) > exp(zlnyi) = г/i*,
а в случае, когда а? < 0, будем иметь:
г/2* = ехр(а?1пу2) < exp(a?lnyi) = у\х.
6) Пусть #2 > #i. При г/ > 1 будет In г/ > In 1 = 0 и, следовательно,
ц этом случае #2 In у > х\ In у, откуда
уХ2 = ехр(а?2 In у) > exp(a?i In у) = yXl.
При г/ < 1 имеем In у < In 1 = 0, откуда #2 In у < a?i In у и, значит,
у*2 = ехр(а?2 In у) < exp(a?i In у) = у*1.
7) Имеем: ух = ехр(#1пу). При у —> 0 выполняется In у —► —оо и,
стало быть, в случае, когда х > 0, при у —► 0 будет a? In у —» —оо, а в
случае а? < 0 при у —> 0 будет a? In у —> оо.
Известно, что ехр и —> 0 при г/ —> —оо и ехр и —> оо при г/ —> оо.
Отсюда, на основании второй теоремы о пределе сложной
функции (теорема 2.6, глава 2), все условия которой здесь выполнены,
вытекает, что при у —> 0 величина ух стремится к пределу, равному 0, если
х > 0, и равному оо, если х < 0.
При у —> оо справедливо In у —> оо и, значит, a? In у —> оо, если
х > 0, и a? In у —> —оо, если а? < 0. Отсюда следует, что
^ Г оо при х > 0;
lim у = <
у—оо [ 0 при х < 0.
8) Имеем: у* = ехр(а?1пу). При у > 1 справедливо In у > In 1 = 0,
а при у < 1 выполняется неравенство In у < In 1 = 0. Отсюда следует,
что если у > 1, то при х —► оо будем иметь: ух = ехр(а?1пу) —► оо, а
если у < 1, то при х —> оо будет у* —» 0.
Аналогично доказывается, что при х —> — оо будет у* —► 0 в случае,
когда у > 1, и у* —► оо в случае, когда у < 1.
Теорема доказана. ■

208
Гл. 3. Элементарные функции
Определим некоторый класс функций, называемых степенными.
Степенная функция определяется заданием некоторого числа а,
называемого показателем степенной функции.
Сначала определим понятие степенной функции для случая, когда
показатель а есть целое число.
Пусть а > 0. В этом случае в качестве области определения
функции х н-> х01 берется всё множество R.
Если а = 0, то функцию х н-+ ха считаем тождественно равной 1.
Если а>0, то а 6 N, ив этом случае ха определяется обычным
образом, как произведение а одинаковых множителей, равных х.
Если а < 0 есть целое число, то областью определения функции
х н-» ха служит множество R \ {0}. Для х £ R \ {0} в этом случае
полагаем: Xе* = ——. (Число —а принадлежит N, так что х~а уже
определено.)
Б случае, когда а есть рациональное число вида: — -, где т —
2к + 1
целое, к £ N, областью определения функции х н-+ ха является: при
а > 0 множество R, а при а < 0 — множество R \ {0}.
Для х > 0 величина ха определяется как указано выше, то есть
равенством: ха =exp(aln#).
ТТ /\ ГП
При х < и для a = полагаем:
(1 \ »
-|я|«+1 J
В этом случае считаем, что для а? = 0 будет #* = 0, если a > 0, а
если a < 0, то х01 не определено при х = 0.
Наконец, если показатель а не соответствует ни одному из
рассмотренных случаев, то область определения степенной функции
х н-^ Xе* в случае a > 0 есть промежуток [0, оо). При этом мы
будем считать, что 0е* = 0. Если же a < 0, то областью определения:
функции х н-+ ха является интервал (0, оо).
Функция жи/ непрерывна в каждой точке своей области
определения.
В случае а > 0 она является строго возрастающей
на промежутке [0, оо).
В случае a < 0 функция х ь-» х01 является строго убывающей
на промежутке (0,оо).
Утверждение 6) теоремы 1.7, совместно с теоремой об обратной
функции, позволяет заключить, что степенная функция в случае a > 0

§ 1. Показательная, логарифмическая и степенная функции 209
отображает промежуток [0,оо) на себя, а в случае а < 0 —
отображает на себя промежуток (0,оо).
При этом обратной к функции х н-> ха является функция
х ь-* х^. В частности, полагая а = 2, мы получим, что обратной к
функции a? G [0,оо) —> а?2 является функция ж1'2, то есть а?1'2 = -y/aF.
Полагая а = n 6 N, мы получаем, что обратной к функции
ж ь-* ж71 является функция х н-> а?1'71, то есть >/# = а?1'*1.
■ Теорема 1.8. Справедливо равенство:
lim = а.
rr-*0 a?
Доказательство. В силу следствия 3 теоремы 2.1 (свойство
локальности предела), при вычислении интересующего нас предела можно
рассматривать только значения х > —1. При а? > —1 имеем:
(1 + х)" -1 _ exp[aln(l + a?)]-l ___
X X
_ /exptaKl + ^j-A /aln(l + «)\ ,
~ ^ aln(l + x) ) \ х J ■ (L18)
Так как In есть непрерывная функция, то при х —» 0
a ln(l + х) —> a In 1 = 0.
По доказанному ранее (теорема 1.4), при у —» 0
ехр у - 1 ^
Применяя первую теорему о пределе суперпозиции (теорема 2.5
главы 2), получаем, что
lim exp[aln(l+ *)]-! = ^
х->о aln(l + a?)
В силу утверждения в) теоремы 1.5, второй множитель в правой
части равенства (1.18) стремится к а при х —► 1. Отсюда, переходя в
равенстве (1.18) к пределу при х —> 0, получим
а = hm ,
х-+о a?
что и требовалось доказать. ■

210
Гл. 3. Элементарные функции
Произвольная показательная функция определяется заданием
некоторого положительного вещественного числа а, отличного от 1 и
называемого основанием показательной функции.
Областью определения показательной функции является вся
числовая прямая R. Ее значение в произвольной точке a?6R есть число ах.
Имеем:
ах = ехр(#1па),
откуда следует, что функция х н+ ах непрерывна как
суперпозиция двух непрерывных функций: ехр и х »-» х In а.
Имеем: In е = 1 и, значит, ехр х = ехр(# In е) = ех для любого х G К.
Таким образом, функция ехр представляет собой показательную
функцию с основанием е.
Утверждение 6) теоремы 1.7 позволяет заключить, что функция
х н-» ах является строго возрастающей в случае а > 1 и
строго убывающей при 0 < а < 1.
Как следует из утверждения 8) теоремы 1.7,
Г оо
lim ах = <
г-оо [ 0,
при а > 1;
lim
аг—оо [ 0, если 0 < а < 1,
lim ax = <
Р—»• — ОО I
0 при а > 1;
оо, если 0 < а < 1.
Применяя теорему о непрерывной обратной функции (теорема 4.3
главы 2), получим, что функция х *-* ах отображает числовую прямую
R на промежуток (0,оо).
Функция, обратная к х ь-* ах, обозначается символом loga и
называется логарифмом по основанию а.
Если х 6 (0, оо) и у = loga ж, то, согласно определению обратной
функции (см. главу 1, п. 2.4), имеем:
х = ау = exp(ylna).
Решал это уравнение, получим:
In х = у In a,
откуда
. In а?
log«x=h^-

§ 2. Тригонометрические функции. Понятие элементарной функции 211
Полагая а = е, имеем loge x = In х. Таким образом, натуральный
логарифм есть не что иное, как логарифм с основанием е.
■ Теорема 1.9. Пусть a > О, а ф 1. Тогда: lim = In a.
х—>0 X
Доказательство. Имеем:
ах — 1 ехр(ж In а) — 1 .
= —-— In а.
х х In a
тт Л еХР 2/ "~ 1
При у —> 0, по доказанному, > 1, откуда следует, что
у
> In а при ж —> 0, что и требовалось доказать. ■
х
Теорема 1.9 показывает, что если х мало, то
а — I
« In а,
и, значит, ах приближенно равно 1 + х In а при малых — по абсолютной
величине — значениях х.
Тем самым получен ответ на вопрос: как выбирать число к, чтобы
в случае, когда \х\ мало, можно было считать, что ах gg 1 + кх?
Именно, к есть натуральный логарифм числа In a.
§2. Тригонометрические функции. Общее
понятие элементарной функции
В этом параграфе приводятся определения тригонометрических
функций и перечень их основных свойств. При этом мы опираемся на
ту информацию об этих функциях, которая известна читателю из курса
средней школы. Наша цель, однако, — несколько упорядочить и
систематизировать эти сведения.
Кроме того, мы определим значения некоторых важных пределов, в
которых фигурируют тригонометрические функции. Эти пределы лона-
добятся нам позднее при определении производных тригонометрических
функций.
2.1. Синус, косинус и тангенс
На плоскости Е2 зададим декартпову ортогональную систему ко-
ординат с началом в точке О и осями Ох и Оу (см. рис. 4).

212
Гл. 3. Элементарные функции
(
1.оЛ
Г
^-~
0
В(0,1)
-У
\В'(0,-1)
\ ,.
А(1,0)
Координаты произвольной точки М на плоскости в этой системе
нам удобнее обозначать здесь греческими буквами £ и г) (вместо х и у,
как это делалось выше).
Пусть S означает окружность радиуса, равного 1, с центром в
точке О. Данная окружность определяется уравнением £2 + rj2 = 1, то
есть представляет собой множество всех точек плоскости, координаты
которых удовлетворяют данному уравнению.
Обозначим через А и А* точки окружности S, лежащие на оси О
справа и, соответственно, слева от точки О. Точка А имеет
координаты (1,0), А' — координаты (—1,0).
Пусть В и В' — точки пересечения S с осью Огу, лежащие выше
и, соответственно, ниже точки О.
Часть плоскости, состоящую из всех точек, у которых вторая
координата rj > 0, будем называть верхней полуплоскостью. Множество
точек, для которых rj < 0, — нижней полуплоскостью.
Мы предполагаем, что читатель знаком с понятием длины дуги
окружности и, в частности, с понятием длины окружности.
Предполагается известным также и то, что длина окружности радиуса 1
равна 27Г, где 7г есть число, лежащее в интервале (3,4). Приближенно,
тг = 3,141592654....
Построим некоторое специальное отображение £ множества
вещественных чисел R на единичную окружность S.
Зададим произвольно число х € К.
Предположим сначала, что х лежит в промежутке (—7г,7г]. Если
х = 0, то полагаем £(#) = А.
Пусть х ^ 0. На окружности S построим дугу AM, длина которой
равна |аг|, лежащую в верхней полуплоскости в случае, когда
#>0, в нижней полуплоскости, когда х < 0.

§ 2. Тригонометрические функции. Понятие элементарной функции 213
Конец этой дуги — точку М — и принимаем за С(х)-
В случае, когда х лежит вне отрезка (—7Г, 7г], точка £(#)
определяется следующим образом. Рассмотрим отношение
X + 7Г
Для него найдется целое число к такое, что
Z7T ~
Отсюда следует, что имеют место неравенства
2тгк < х + тг < 2тгк + 2тг
— 7Г < X — 27Г& < 7Г.
Таким образом, число ж — 27Г& лежит в промежутке (—7Г, 7г] и,
значит, определена точка £(ж — 27г&). Полагаем для данного х:
£(х) = С(х - 2тгк).
Этим отображение £ определяется полностью.
Наглядно построенное отображение £ может быть описано
следующим образом (см. рис. 5).
/
/
\
№)\s
А'\
5"
О
^
~х^^
В'
\ И
Г
Рис.5
Представим себе, что по окружности S движется точка в
направлении против часовой стрелки с постоянной скоростью, равной 1,
причем в момент времени х = 0 она совпадает с точкой А.

214
Гл. 3. Элементарные функции
Тогда С(х) означает положение, которое движущаяся точка
занимает в момент времени х.
Можно представить отображение £ иначе, а именно: числовую
прямую R можно рассматривать как бесконечную в оба конца
«нить» нулевой толщины, изготовленную из нерастяжимого
материала. Эту «нить» мысленно будем наматывать на цилиндрический вал,
сечение которого есть окружность S, так, чтобы точка Осовмести-
л а с ь с точкой А.
При этом правая полуось наматывается на окружность S,
вращаясь против часовой стрелки, а левая полуось при
наматывании вращается п о часовой стрелке.
Положение, которое в итоге займет точка #, и есть ((х).
Из определения следует, что
c(f)-n, см-л-, с (-!) = *'.
Отображение £ обладает свойством периодичности, а именно:
для любых х\, Х2 таких, что #2 = #i + 2п, выполняется
равенство: ((х2) = ((xi).
Действительно, найдем целое число к такое, что х\ — 2кж лежит в
промежутке (—7г,7г]. Существование такого к устанавливается
применением следствия теоремы 4.4 п. 4.4.7 главы 1. Из него вытекает, что
существует целое число р такое, что
Для к = 1 — р, как показывают простые вычисления, выполняются
неравенства:
— 7Г < Xl — 2&7Г < 7Г,
что и требовалось доказать.
Тогда, по определению, ((xi) = ((xi — 2kn). Так как Х2 = х\ + 27Г,
то Х2 — 2{к + 1)7г = х\ — 2кж и, значит, Х2 — 2(к + l)w также лежит в
промежутке (—7Г, 7г].
Следовательно, (fa) = С\х2 — 2(к + 1)7г] = ((хг — 2&7г) = C(#i)? что
и требовалось доказать.
Пусть х 6 R. Координата по оси 0% точки £(#) обозначается
символом cos #, а ее координата по оси От) — символом sin x.
Поскольку х € R взято произвольно, то тем самым
определены вещественные функции х ь-> cos #, х *-> sin x. (Это

§ 2. Тригонометрические функции. Понятие элементарной функции 215
*— известные читателю из школьного курса математики
тригонометрические функции — косинус и синус.)
Отношение называется, как известно, тангенсом х и обо-
COS#
значается символом tg x. Величина tg # определена только для
тех #, для которых cos x ф 0.
Отметим некоторые свойства синуса, косинуса и тангенса.
Прежде всего, имеют место равенства:
sin(—7г) = sin 0 = sin 7г = 0;
sinH)=_1; sinf=i;
cos(—7г) = cos 7г = —1; cos 0 = 1;
COS I — — I = COS — = 0.
I 2/ 2
Справедливы также так называемые формулы приведения:
sin(?r — х) = sin х] cos(7r — х) = — cos х]
. /7Г \ /7Г \
sin I — — х 1 = cos ж; cos I — — х 1 = sin x;
sin(—x) = — sin x; cos(—x) = cos x\
sin(# + 7г) = — sin x\ cos(# + 7г) = — cos x.
Для всякого целого п:
sin(x + П7г) = (—l)n sin x; cos(x + пж) = (—l)n cos x.
В частности, полагая п = 2га, где га — целое, получим:
sin(# + 2т7г) = sin x; cos(# + 2т7г) = cos x.
Для всякого х € R, для которого определена величина tg #,
выполняются равенства:
tg(-ff) = -tg ж;
tg (х + 7г) = tg ж.

216
Гл. 3. Элементарные функции
Функция х ь-> sinx является строго возрастающей в
промежутке ——, х и строго убывающей в каждом из
промежутков
6 7Г
Т'~ 2
2'Г
Функция ж ь-* cosx является строго возрастающей в
промежутке [—7г, 0] и строго убывающей в промежутке [0,7г].
Совокупность решений уравнения cos ж = 0 есть множество чисел
7Г
вида: — + Ш7Г, где т — произвольное целое число.
Отсюда вытекает, что область определения функции х ь-> tgx есть
множество всех чисел, которые не могут быть представлены в виде:
7Г
X = — + 7ШГ,
Zi
где m — целое число, то есть область определения функции х \
объединение счетного множества интервалов
tg х есть
(-1
7Г
+ 7ШГ, — + Ш7Г
)■
где m e Ъ.
График функции x^sinx (см. рис. 6) называют синусоидой.
Он состоит из повторяющихся волн — выступов и впадин. При этом
отдельные выступы и впадины получаются друг из друга параллельным
переносом вдоль оси Ох.
*.ъЬег0
Рис.6
Каждый выступ отдельной волны симметричен относительно
прямой, проходящей через его наивысшую точку и параллельной оси Оу.
Аналогичная картина имеет место для впадин волн с той лишь
разницей, что тут берется наинизшая точка отдельной волны. (Относительно
первой волны, отвечающей промежутку [0,7г], это вытекает из равенства
sin(7r — x) = sin я.)

§ 2. Тригонометрические функции. Понятие элементарной функции 217
Участок графика синуса, соответствующий
промежутку [—7г,0] симметричен относительно точки О
участку, соответствующему отрезку [0,7г]. (Этот факт следует из равенства
sin(—x) = —since.)
График косинуса есть та же синусоида, но сдвинутая
влево на — с тем, чтобы вершина первой волны синусоиды
оказалась лежащей на оси Оу.
Функция х н* tg х является строго возрастающей в
/ 7Г ТГч
промежутке {-^^)-
2'2
7Г
Ясно, что sin х —> 1, cos x —> 0 при х —> — и sin х —► —1, cos а: —> О
7Г
при*-*--.
В интервале (—тт?^) косинус положителен. Отсюда вытекает,
что tg х —> оо, когда ж стремится к— слева, и tg # -* —oo при ж,
7Г
стремящемся к — —■ справа.
ли
-ЗлЯ
-v/2
>-
Рис. 7

218
Гл. 3. Элементарные функции
График функции ж н> tgai имеет вид, указанный на
рис. 7, и получается параллельным переносом его ча-
» / 7Г 7Г\
сти, соответствующей промежутку I — —, — 1, на величину тп, где т
— произвольное целое число.
В связи с перечисленными свойствами тригонометрических функций,
введем некоторые общие понятия.
Пусть дано множество А С К. Будем говорить, что А —
симметрично относительно точки О, если для всякого х £ А также и —х £ А.
Функция / : А —> R, где А С К, называется четной (нечетной),
если ее область определения симметрична относительно точки О, и
для всякого х G А выполняется равенство: /(—ж) = f(x)
(соответственно, f(-x) = -f(x)).
Функция х н-> хп, где п — целое число, является четной при
п четном и нечетной, если п — нечетное число.
Множество R, очевидным образом, симметрично
относительно точки 0. Для всякого х £ К имеем:
sin(—х) = — sin X] cos(—#) = cos х,
и, следовательно, синус есть нечетная, а косинус — четная
функции переменной х.
Пусть А С К, А ф 0. Функция / : А —> М называется
периодической, если существует число h ф 0 такое, что для
любого ж G А точки ж — h и ж + h принадлежат А, и имеет место равенство:
f(x + /i) = /(ж). Число й, при этом называется периодом функции f.
Определение периодической функции содержит в себе два условия.
Одно налагается на область определения, а другое — на саму функцию.
Синус и косинус являются периодическими функциями
с периодом, равным 2ж.
Тангенс также есть периодическая функция с периодом,
равным 7Г.
Отметим, что условие, налагаемое на область определения
функции для синуса и косинуса, выполняется автоматически, поскольку
для этих функций она совпадает со всем множеством М.
Проверка того, что область определения тангенса также
удовлетворяет соответствующему условию, — предоставляется читателю.
Приведем некоторые другие соотношения, относящиеся к
тригонометрическим функциям.
Для всякого aiGR имеет место равенство:
sin2 х + cos2 x = 1.

§ 2. Тригонометрические функции. Понятие элементарной функции 219
Для любых #,г/ £ R имеют место соотношения:
cos(# + у) = cos х cos г/ — sin x sin г/;
cos(# — у) = cos ж cos у + sinx sin г/;
sin(# + у) = sin ж cos г/ + cos ж sin у;
sin(# — г/) = sin x cos г/ — cos x sin y;
tg x + tg г/
tg(* + y) =
1 - tg ж tg у
Последнее равенство выполняется для любых ж, 2/, Для которых
каждая из величин, стоящих слева и справа, имеет смысл.
Для любых ж, 2/ £ R имеют место также равенства:
. . о - Х + У х -У
sin ж + sin у = 2 sin —-— cos —-—;
* 2 2
sin а? — sin г/ = 2 cos —-— sin —-—;
Zd Zd
x+y x-y
cos x + cos у = 2 cos —-— cos —-—;
* 2 2
. ж + 2/ . a?-y
cos ж — cos 2/ = —2 sin —-— sin —-—;
y 2 2'
sin(x + y) sin(a?-j/)
tg x + tg у = —^ £. tg x - tg 2/ = — -.
cos ж cos г/ cos x cos 2/
Последние два равенства верны для любых х и 2/, для которых
каждое из выражений, стоящих в них, имеет смысл.
Кроме перечисленных выше тригонометрических функций, иногда
рассматриваются также следующие:
1 1 cos х
sec : х £ R »->• ; cosec :жЕКн — ; ctg :ж6Ми — .
cos x sin ж sin ж
Эти функции называются, соответственно, секансом, косекансом
и котангенсом.
sin з?
2.2. Предел lim
х—*0 X
7Г
■ Лемма 2.1. Для всякого х £ R такого, что 0 < ж < —, имеют
Zd
место неравенства,: sin ж < х < tg ж.
Доказательство. Пусть 0 < ж < 7г/2. На плоскости построим
(см. рис. 8) круг радиуса г > О с центром О.

220
Гл. 3. Элементарные функции
На окружности круга возьмем произвольно точки А и В такие,
что длина кратчайшей из дуг, на которые они разбивают
окружность, равна гх.
Символом АВ будем обозначать именно эту дугу.
В точке А проведем касательную к окружности, и пусть В\ есть
точка, в которой она пересекает прямую ОБ (см. рис. 8).
1
Л
\\
у
V
,в,
! х
\Л
Рис.8
Рассмотрим треугольники Ai = OAJ3, А2 = ОАВ\ и круговой
сектор £ = ОАВ.
Треугольник Ai содержится в круговом секторе Е, который, в свою
очередь, содержится в треугольнике Дг.
Отсюда вытекает, что площади этих трех фигур связаны
неравенствами:
площадь Ai < площадь £ < площадь Дг. (2-1)
Треугольник Ai — равнобедренный, угол при его вершине О равен
х и \ОА\ = \ОВ\ = г.
Треугольник А2 — прямоугольный. При этом угол при его вершине
А прямой, и |AJ3i| = rtg x.
На основании известных из элементарной геометрии выражений
для площадей указанных трех фигур имеем:
2 2
v v
площадь Ai = — sin х; площадь S = -т-я;
V
площадь Д2 = -г- tg х.
Zt
Подставляя данные выражения для площадей в (2.1) и сокращая
положительный множитель г2/2, получаем:
sin х < х < tg ж,
что и требовалось доказать. ■

§ 2. Тригонометрические функции. Понятие элементарной функции 221
▼ Следствие 1. Для всякого х £ \ 77? 77) имеет место
неравенство: |sin#| < \х\.
Действительно, если х > 0, то sin x > 0, и требуемое
неравенство есть непосредственное следствие леммы 2.1. Пусть # < 0. Тогда
sin ж < 0 и |#| = —#, | sin я?| = —sin x = sin(—#), откуда, в силу
леммы 2.1, вновь следует | sin х\ < —х = |а?|, что и требовалось доказать. ▼
▼ Следствие 2. Функция ж ь-> sina;, ж м- cos x и х »-* tg x
непрерывны.
Доказательство. Возьмем произвольно точку xq £ R. Пусть
х £ R таково, что \х — #о| < тг. Применяя соотношения между
тригонометрическими функциями из п. 2.1, получим:
cos
| sin x — sin хо | = 2
| cos ж — cos #o| = 2 Isin
X + #0
2
sin
sin
X
X
—
2
—
2
#0 1
#0
Заметим, что — 1 < sin ж < 1 и — 1 < cos x < 1 для всех х £ R. Так
как \x — #o| < 7Г, то
Ж — #o
7Г
< —• Отсюда получаем неравенства:
| sin ж — sin#o| < |# ~ #o|; | cos ж — cos#o| < \x — a?o |-
Зададим произвольно е > 0 и положим £ = тт{б,7г}.
Для всякого х £ К. такого, что \х — хо\ < 6, будем иметь:
| sin ее — sin#o| < \х — xq\ < £ < е\ | cos ж — cos#o| <\х — х§\ < Ь < е.
В силу произвольности е > 0, тем самым непрерывность
функций sin и cos в точке хо установлена.
Ранее (см. п. 5.3.1 главы 2) было определено понятие равномерно
непрерывной функции. Из доказанного следует, что функции sin x и
cos х равномерно непрерывны на множестве R.
По определению тангенса, имеем:
tg х =
sm#
cos х'
Величина tg # определена для всех х £ R, для которых
cos х ф 0. В каждой точке х £ R, для которой величина tg x имеет

222
Гл. 3. Элементарные функции
смысл, функция tg непрерывна как отношение двух
непрерывных функций.
Следствие 2 доказано. ▼
Неравенства, установленные в лемме 2.1, позволяют найти предел:
.. sin х
km .
х—>Q> X
Докажем, что для всех х £ ( — —, —■ 1, отличных от точки О,
выполняются неравенства:
sin х /Л ЛЧ
1 > > cos х. (2.2)
X
Действительно, пусть х > 0. Согласно лемме 2.1, имеем:
sin х
sin x < х < tg x =
cos ж'
откуда, после очевидных преобразований, получаем, что в этом случае
неравенства (2.2) выполняются.
Пусть х £ ("~7Т?0)- Тогда 0 < —х < 7г/2, sinх = — sin(—#), и в
этом случае
sin х sin(—#) / ч
= —~—r-^; cost— х) = cosx.
х {—х)
Отсюда заключаем, что если х < 0, то
sin(—x) sin х / N
1 > —т-^—г-^ = > cos(— х) = cos ж,
(—ж) ж
так что неравенство (2.1) верно для всех х £ ( — —, — ), отличных
от нуля.
Функция cos непрерывна в точке 0. При этом cos 0 = 1.
Отсюда следует, что cos х —> 1 при х —► 0.
Левая часть неравенства (2.1) есть функция, тождественно
равная 1, и, следовательно, она имеет равный 1 предел при х —» 0.
Применяя теорему о зажатой переменной (теорема 1.5 главы 2), от-
sin х
сюда получаем, что отношение имеет равный 1 предел при х —> 0,
х
то есть
.. sin х
lim = 1,
х-+0 X
что и было нашей целью, сформулированной в начале раздела.

§ 2. Тригонометрические функции. Понятие элементарной функции 223
2.3» Обратные тригонометрические функции
Косинус, синус и тангенс не являются монотонными
функциями в их областях определений. Поэтому понятие обратной
функции для каждой из них лишено смысла.
В то же время оказывается весьма желательным иметь для
тригонометрических функций хотя бы некоторый «суррогат» понятия
обратной функции.
Необходимость в этом возникает, например, при решении
уравнений вида: sin x = у; cos x = у; tg x = у. В связи с этим поступают
следующим образом.
Для каждой из тригонометрических функций выделяется
промежуток, в котором данная функция строго монотонна. Этот промежуток
называется основным.
Для ограничения тригонометрической функции на основном
промежутке определена обратная функция. В результате
возникают три функции, которые называются обратными
тригонометрическими функциями.
Для функции х i-+ sin ж, в качестве основного промежутка,
выбирается отрезок — — ? — • На этом отрезке синус есть строго
возрастающая функция, sin ( — — J = — 1, sin — = 1.
По теореме о непрерывной обратной функции (теорема 4.3,
глава 2), отсюда следует, что ограничение функции х »-* sin x на отрезке
Г 7Г 7Г1
lo"' о" взаимно однозначно отображает этот отрезок на [—1,1] и имеет
непрерывную обратную функцию, которая называется арксинусом. Ее
значение в точке х £ [—1,1] обозначается символом arcsin #.
Согласно определению обратной функции, arcsin x — это число
такое, что sin у = х. Следовательно, имеют место равен-
yfc
ства
Г 7Г 7Г]
Г 2 '2~ J
'.
для любого у €
7Г 7Г
2' 2
arcsin(sin у) = у
sin (arcsin x) = х
для всех х G [—1,1].
Функция х I-* arcsin x непрерывна и строго возрастает
на отрезке [—1,1] (см. рис. 9).

224
Гл. 3. Элементарные функции
Рис. 9
Для функции х ь-» cos х в качестве основного промежутка
выбирается отрезок [0,7г]. Косинус является строго убывающей
функцией на этом отрезке, причем cos 0 = 1; cos 7г = —1.
Функция, обратная к ограничению косинуса на отрезке [0,7г],
обозначается символом arccos x. Она определена на отрезке [—1,1].
Для всякого х G [—1,1] имеем: cos (arccos #) = х и arccos (cos у) = у
для у € [0,7г].
Функция х I-* arccos x непрерывна и строго убывает на
отрезке [—1,1].
Между введенными здесь функциями имеется простая связь.
Пусть х £ [—1,1], у = arccos х. Тогда у £ [0,7г] и, следовательно,
7Г Г 7Г 7Г1 __. . /7Г \
2 " У в L— 2"' 2"J * Имеем: sm \2 ~~У) = COS y = x'
Согласно определению функции arcsin, отсюда вытекает, что
7Г
— — у = arcsin #,
то есть
и, значит,
7Г
— — arccos х = arcsin x
arcsin x + arccos x =
7Г
для всех x G [—1,1].
Для функции х н-» tg ж, в качестве основного, выбирается
промежуток ( — -,-). В этом промежутке данная функция
непрерывна и является строго возрастающей. Заметим, что tg х —» — оо при

§ 2. Тригонометрические функции. Понятие элементарной функции 225
х -^ — — и tg а? —► оо при х —> — . Отсюда ясно, что функция х »—► tg х
отображает промежуток ( — —, — 1 на множество R.
На основании теоремы о непрерывной обратной функции
(теорема 4.3 главы 2), для всякого # € R существует, и притом
единственное, у € (-~*тт? 77) такое, что tg у = х. Это значение у
обозначается символом arctg x (читается: «арктангенс #»). По той же
теореме о непрерывной обратной функции, функция х ь-> arctg #,
определенная в промежутке (—оо, оо) = R, непрерывна и является
строго возрастающей. При этом
lim arctg x = — — ; lim arctg x = —.
2 х—юо ** 2
X—» — ОО
График функции у = arctg ж приведен на рис. 10.
Рис. 10
Выбор основного промежутка, который производится при
построении обратных тригонометрических функций, в какой-то мере, условен.
Кроме требования строгой монотонности функции в этом промежутке,
он определяется соображениями удобства, а также тем условием, что
множество значений функции в основном промежутке должно
совпадать с множеством всех значений рассматриваемой тригонометрической
функции.
В качестве примера применения обратных тригонометрических
функций приведем формулы, дающие общий вид решения уравнений вида
/(#) = &, где / — тригонометрическая функция.
Уравнение sin ж = к не имеет решений, если \к\ > 1. В случае
\к\ < 1 совокупность всех решений этого уравнения есть множество
{х 6 IR.\х = П7г + (—l)n arcsinfc, где п 6 Z}.

226
Гл. 3. Элементарные функции
Совокупность всех решений уравнения cos х = к есть пустое
множество в случае \к\ > 1 и представляет собой множество
{х € Щ х = 2п7г ± arccos к, где п € Z},
если \к\ < 1.
Уравнение tg х = А? разрешимо при всяком fc G R, и совокупность
всех его решений есть множество
{х € R| ж = П7Г + arctg fc, где n £ Z}.
2.4. Показательная функция комплексного аргумента
Целесообразно придать определенное значение величине ехр z для
случая, когда z есть произвольное комплексное число.
Пусть z = х + гу, где ж, у £ R. Тогда мы полагаем
ez = ехр z = e:F(cos у + г sin у).
Если z £ R, то у = 0 и это определение величины ехр z, очевидно,
приводит к тому же значению, что и определение, данное в п. 1.1.
■ Теорема 2Л. Для любых zi, z2 £ С имеет место равенство:
(expzi)(exp2r2) = exp(zi + z2).
Доказательство. Пусть z\ = x\ + гу\, z2 = х2 + гу2. Тогда
ехр z\ = е*1 (cos yi + i sin yi); ехр z2 = e*2 (cos y2 + i sin y2).
Перемножая эти выражения почленно, получим:
(expzi)(exp2r2) =
= еХ1*Х2 [(cos y\ cos y2 — sin yi sin y2) + i(sin yi cos y2 + sin y2 cos y\)] =
= ea?1+a?2(cos(yi + y2) + isin(yi + 2/2)).
Правая часть этого равенства, по определению, равна
exp(zx +2г2),
и теорема тем самым доказана. ■

§ 2. Тригонометрические функции. Понятие элементарной функции 227
sin х
В качестве следствия леммы 2.1 о пределе отношения
х
при х, стремящемся к нулю, получим следующий результат.
eix - 1
■ Теорема 2.2. Функция х eR*-+ при х, стремящемся к О,
х
имеет предел, р&вный i.
Доказательство. Имеем: егх = cos#-Hsin#. Отсюда получаем:
егх — 1 = cos х — 1 + г sin x и, значит,
+ .'^. (2.3)
X
Заметим, что cos х — 1 = —2 sin — и, следовательно,
costf-1 **\ _ ■ * sinf
= -2 s. = -sin-
* "ж ™ 2 £ '
2
Второй множитель справа при х —» 0 стремится к 1, а
первый стремится к 0. Отсюда вытекает, что при ж —* 0:
cos х — 1
Переходя в равенстве (2.3) к пределу при х —> 0, в результате
получим:
.. егх — 1 ... sin ж
lim = г lim = г,
что и требовалось доказать. ■
Отметим, что комплексная функция х € R ь-» ега? = cos а? + г" sin ж
допускает простое геометрическое истолкование.
Именно, воспользуемся описанной в конце главы 1 геометрической
интерпретацией множества комплексных чисел.
На плоскости введем denapmoey ортогональную систему
координат. Комплексное число z = x + iy отождествим с точкой М(х,у)
плоскости, первая координата которой #, вторая — у.
В п. 2.1 определено отображение £ множества R в плоскость. При
каждом х £ R значение С(х) есть точка M(cos#,sin#).
Отсюда ясно, что комплексная функция жие,х совпадает
с этим отображением (.

228
Гл. 3. Элементарные функции
2.5. Общее понятие элементарной функции
Все функции, определенные в этом параграфе, а также любые
функции, которые могут быть получены из них выполнением конечного
числа арифметических действий и образованием суперпозиции, мы будем
называть элементарными.
Приведем точное определение понятия элементарной функции.
Элементарными называются те и только те функции,
определенные на подмножествах множества R, которые можно получить применяя
конечное число раз следующие три п р а в и л а: А, Б и В.
А. Все функции из следующего списка являются элементарными:
1. Функция х н-+ хту где т £ Z, область определения которой в
случае т > 0 есть всё множество R, а в случае т < О есть множество
R\{0}.
2. Функция х н-> х2я+1, где р и q — целые числа, р ф 0; область
Р
определения есть всё множество R в случае > 0 и множество
2q + 1
М\{0},если^у<0.
3. Функция х *-+ ха, где а € R, а не есть число вида, указанного в
предыдущих двух случаях; область определения есть множество [0, оо)
в случае а > 0 и множество (0, оо) — в случае а < 0.
4. Функция х »—► ехр#; область определения— всё множество R.
5. Функция х н-> In х\ область определения— интервал (0,оо).
6. Функция х ь-> cos х] область определения — всё множество R.
7. Функция х ь-> sin x; область определения— всё множество R.
8. Функция х ь-> tg #; область определения — множество всех #,
7Г
отличных от числа вида — + гая*, где т — произвольное целое.
9. Функция х »-► arcsinx; область определения— сегмент [—1,1].
10. Функция х ь-► arccosa?; область определения— сегмент [—1,1].
11. Функция а? ь+ arctg x\ область определения — всё
множество R.
Перечисленные 11 функций называются базисными
элементарными функциями.
Б. Пусть даны множества АсКиВсКи функции / : А —» R,
Я : В -> R.
Предположим, что АП В ф 0. Пусть A, /i — произвольные
вещественные числа.

§ 2. Тригонометрические функции. Понятие элементарной функции 229
Символами/# и А/ + /лд будем обозначать функции,
определенные на множестве А П В следующим образом:
(А/ + рд)(х) = А/(х) + /ifl(ar),
(/*)(*) = /(*М*).
Если существует, по крайней мере, одно значение х Е А П J5
>е, ч
/ / / \
такое, что #(#) ф О, то определим функцию —, полагая ( — 1 (х) =
— f N для всякого ж, для которого а(#) Ф 0.
Область определения функции f/g есть множество всех х £ АП В
таких, что д(х) ф 0.
Если функции / и д — элементарные, то функции А/ + jig, fg и
//#, определенные указанным здесь образом, также являются
элементарными.
В. Пусть /:А—*'!кид:В—±Ш — элементарные функции. Тогда
суперпозиция д о f также считается элементарной функцией.
2.6. Гиперболические функции
Во многих вопросах математического анализа оказываются
полезными некоторые специальные функции, называемые гиперболическими.
Они принадлежат классу элементарных функций и достаточно просто
выражаются через функции, которые мы уже знаем. По своим
алгебраическим свойствам гиперболические функции во многом напоминают
тригонометрические функции.
Для xGK полагаем:
X —X X | —X X —X
б — б б ~Г € б — б
sha? = ; ch# = ; ihx = . (2.4)
2 2 б* + е-* v ;
Определенные так функции sh, ch и th называются, соответственно,
гиперболическим синусом, гиперболическим косинусом и
гиперболическим тангенсом.
Областью определения каждой из них является всё множество М.
Очевидно, эти функции непрерывны. Выражение sh x
читается: «синус гиперболический» х.
Аналогичный способ чтения употребляется для выражений ch x и
th#.

230
Гл. 3. Элементарные функции
Из (2.4) вытекает, что для любого а? € К.
ех = ch х + sh х; е~х = ch x — sh x. (2.5)
Для всякого х £ К имеем:
sh(—х) = — sh #; ch(—х) = ch x; th(—х) = — th ж, (2.6)
так что гиперболические синус и тангенс есть функции нечетные,
a atmeptfoym^ecKJtzu косинус — функция четная.
Отметим некоторые алгебраические соотношения между
гиперболическими функциями.
Из определения гиперболического тангенса очевидно, что
*.-§§. (2.7)
Из равенств (2.5) следует, что для всех х £ R
ch2 х — sh2 x = (ch x + sh #)(ch ж — sh x) = 1. (2-8)
Для гиперболических функций имеют место соотношения,
аналогичные известным представлениям косинуса и синуса суммы и
разности. Именно, для любых х,у £ К.
sh(# + у) = sh х ch у + ch ж sh у; (2-9)
ch(# + у) = ch ж ch у + sh ж sh у. (2.10)
Для доказательства равенств (2.9) и (2.10) воспользуемся тем, что,
по определению:
sh(;r + у) =
е*+у _ e-*-v е*еу _ е-^е-у
2 2
ch(z + у) =
Выражая здесь ех, еу, е""* и е~~у через char, sh#, chy и shy no
формулам (2.5), после очевидных преобразований, получим равенства
(2.9) и (2.10).

§ 2. Тригонометрические функции. Понятие элементарной функции 231
Заменяя у на —у и принимая во внимание (2.6), получим:

232
Гл. 3. Элементарные функции
Из соотношений lim ех = оо, lim ех = О, в силу свойств пре-
х—+оо х—+ — оо
делов, установленных в §4, очевидным образом вытекают следующие
соотношения:
lim sh x = оо; lim sh х = — оо;
х—*оо х—* — оо
lim ch# = lim ch# = oo;
x—+00 x —+ — oo
lim th# = —1; lim th# = l.
На рис. 11 представлены графики гиперболических функций, из
которых видны основные особенности их поведения.
Рис. 11
По аналогии с обратными тригонометрическими функциями, вводятся
обратные гиперболические функции.
1. Функция sh — непрерывна и строго возрастает в промежутке
(—oo,oo) = R, lim sh# = oo, lim sh# = — oo.
x—+oo x—+ — oo
Отсюда следует, что она взаимно однозначно отображает
множество R на себя и, значит, имеет непрерывную обратную функцию.
Последняя обозначается символом Arsh (читается: «ареасинус
гиперболический»).
Функция Arsh — непрерывна и является строго возрастающей.

§ 2. Тригонометрические функции. Понятие элементарной функции 233
Пусть х £ R, у = Arsh x. Согласно определению обратной функции
(гл. 1, п. 2.4), число у есть решение уравнения:
2
Полагая еу = z, получим:
= х.
1 f ^
- ( z 1 = х.
2 V zj
Отсюда z2 — 2xz — 1 = 0. Решая это квадратное уравнение, найдем:
z = #±\/1 + %2- Так как, очевидно, z > 0, то перед корнем здесь должен
быть взят знак «+», и мы получаем: z = еу = х + у/1 + ж2, откуда
у = Arsh ж = 1п(# + у 1 + х2).
2. Функция th взаимно однозначно отображает R на промежуток
(—1,1). Обратная к ней функция обозначается символом Arth
(читается: «ареатангенс гиперболический»).
Решая уравнение
th у = = х.
найдем, что для всякого х £ (—1,1) выполняется равенство:
Arth х = — In .
2 1 -ж
Мы получаем, таким образом, выражение для Arth через другие
известные нам функции.
3. Функция ch не является монотонной во всей своей области
определения. В связи с этим, так же как и в случае тригонометрических
функций, выбирается некоторый промежуток, в котором эта функция
монотонна.
Рассмотрим функцию, обратную к сужению ch на этом промежутке.
В качестве указанного промежутка берется отрезок [0,оо).
Функция ch, как следует из ее свойств, установленных выше, отображает
данный промежуток на промежуток [1,оо).
Функция, обратная к сужению функции ch на отрезке [0,оо),
обозначается символом Arch (читается: «ареакосинус гиперболический»).

234
Гл. 3. Элементарные функции
Для х G [1,оо), согласно определению обратной функции, число
у = Arch а: определяется следующими условиями: 1) у > 0 и 2) ch у = х.
Решая уравнение
. еу + е~у
chy= - = х,
получим: у = 1п(# ± у/х2 — 1). Заметим, что имеет место равенство:
X — \/ X — 1 = —
х + \/х2 — 1
из которого, в частности, вытекает, что при х > 1
О < я - у^2 - 1 < 1-
Это позволяет заключить, что при х > 1
1п(я? - у/я*^1) < 0.
Знак равенства здесь, очевидно, имеет место только в случае х = 1.
Так как, по условию, у > 0, то из доказанного следует, что в
выражении для у перед корнем следует брать знак «+». Окончательно мы
получаем, что Arch х = \п(х + л/х2 — 1) для всех х > 1.
§3. Сравнение поведения элементарных функций
вблизи концов области определения
Функции ехр, ха и lux являются возрастающими на промежутке
(0,оо) и стремятся к оо при х —> оо. При этом, однако, скорости их
роста при х -* оо различны.
Здесь мы описываем сначала некоторую систему понятий,
используемую для сравнения поведения разных функций вблизи предельной
точки множества, на котором они определены.
Затем доказываются теоремы о сравнительном поведении в концах
некоторого промежутка различных элементарных функций,
определенных на этом промежутке.
Результаты этого раздела существенно используются в
дальнейшем в теории рядов, в интегральном исчислении и в других вопросах
математического анализа.

§ 3. Сравнение поведения элементарных функций
235
3.1, Понятие об асимптотических соотношениях
Рассмотрим последовательности ( — ) , ( —- )
Каждая из них является бесконечно малой при п —> оо, как следует
из доказанного выше.
Мы видим, что члены второй последовательности с ростом п
приближаются к нулю быстрее, чем члены первой. Точно так
же, рассматривал последовательности (n)neN, (rc2)neN, (10n)neN? каждая
из которых имеет предел, равный оо, можно заметить, что вторая
последовательность при п —> оо растет быстрее первой, а третья
растет быстрее второй.
Введем понятия, которые позволят придать точный смысл при-
приведенным здесь утверждениям относительно быстроты убывания
или роста рассмотренных последовательностей.
Зададим произвольно множество МсК. Пусть р есть предельная
точка множества М.
Пусть даны функции f : М -± С и д : М -+ С.
Будем говорить, что функция /подчинена д при х —* р по
М (в обозначениях: f(x) = 0(д(х)) при х —» р, х £ М), если
существуют окрестность U точки р и число К < оо такие, что для любого
х £ М, принадлежащего окрестности U и отличного от р, выполняется
неравенство: \f(x)\ < К\д(х)\.
Будем говорить, что функция / : М —» С пренебрежимо,
сравнительно с функцией д : М —» С при #, стремящемся к р по множеству М,
и писать: «/(а?) = о(д(х)) при ж —* р, х £ М», если для всякого е > О
найдется окрестность J7 точки р такая, что для любого х £ М,
принадлежащего окрестности (7 и отличного от р, выполняется неравенство:
\f(x) < е\д(х)\.
Если f(x) = 0[<7(#)] при ж->рпо множеству М, то говорят также,
что порядок роста f при ж —» р не превышает порядка роста д.
Выражение f(x) = о(д(х)) при г(х) -* 0 иногда читается так: «/
бесконечно мала по сравнению с # при ж —» р».
Пусть даны множество М и число р £ Cim(M). Предположим,
что заданы комплексные функции /, #, у>, определенные на М. Тогда
говорят, что справедливо соотношение:
1(х) = д(х) + 0(ф)) (3.1)
при #, стремящемся к р по множеству М, если /(#) — #(#) = 0(<р(х))
при ж^рпо М.

236
Гл. 3. Элементарные функции
Если f(x) — д(х) = о((р(х)) при х -* р по М, то мы будем писать:
f(x) = g(x) + o(<p(x)) (3.2)
при а?-^рпо М.
Соотношения, содержащие знаки О и о, называются
асимптотическими. (Буквы О и о происходят от первой буквы немецкого слова
Ordnung — порядок или английского order, имеющего то же значение.)
Отметим, что с соотношениями, которые рассматриваются здесь,
вообще говоря, нельзя обращаться как с обыкновенными равенствами
без риска ошибиться.
Асимптотические соотношения обычно применяются в следующих
ситуациях.
Предположим, что изучается некоторая достаточно сложная
функция, определенная в промежутке [а, оо), и требуется получить
информацию о том, как она ведет себя при больших значениях х.
Один из способов исследовать поведение /(#), когда х
велико, состоит в том, что для функции / строится другая,
более простая функция д{х), отличающаяся от f(x) тем меньше, чем
больше х.
Наличие соотношений вида (3.1) или (3.2) характеризует
качество такого приближения, указывает, в какой мере величина
д(х) передает информацию о поведении f(x) при больших
значениях х.
Пр&мер. Рассмотрим функцию х i-> л/х2 + а, где а > 0. Она
определена для всех жЕЙ.
Преобразуем выражение у/х2 + а следующим образом: вынесем х
из-под радикала, тогда получим
у/х2 + а = х^1 + ^.
При х —» оо выражение, стоящее под корнем, стремится к 1. Это
позволяет заключить, что при х —* оо величина \Jx2 + а ведет
себя приблизительно как функция х.
Рассмотрим разность: у/х2 + а — х. Имеем:
ух2 + а — х =
2 | 2
х + а — х
у/х2 + а + х у/х2 + а + ;
при х -* оо.

§ 3. Сравнение поведения элементарных функций
237
Следовательно,
ух2 + а — х = о(1)
при х —*■ оо, и, таким образом, справедливо асимптотическое
соотношение:
ух2 + а = х + <>(1) при ж —» оо. (3.3)
Из соотношения (3.3), в частности, следует, что
Ух2 +а _^
при ж —» оо.
Преобразуем, далее, выражение для <\/#2 + я — х. Имеем:
а 1 а
ух2 + а — х =
При х —► оо
ж + V*2+<* я? /^Г+ а
а
2'
1 + -у*2 + а
х
Отсюда
а __ 1 / а а
2"^ " ж \ -, , 1./Г5-ТТ: ~~ 2
лА2 + <* - х - £ = -( —г-^
Выражение в скобках справа стремится к нулю при х —» оо,
и мы, следовательно, получаем:
при ж -^ оо. Отсюда
>/^ = * + £ + °ф- (3-4)
Равенства (3.3) и (3.4) представляют собой некоторые
асимптотические соотношения.

238
Гл. 3. Элементарные функции
Равенство (3.4) дает, очевидно, больше сведений о поведении
функции у/х2 + а при х —» оо, чем равенство (3.3). Из (3.3) следует только,
что разность у/х2 + а — х стремится к нулю при х -» оо.
Равенство (3.4) позволяет заключить, что эта разность
приближенно равна — с ошибкой, бесконечно малой по сравнению
2х
1
с — при х —*• оо.
3.2. Сравнение поведения основных элементарных функций в
концах области определения
■ Теорема. 3.1. Пусть даны числа а, /3 и а такие, что О < a < /3 и
a > 1. Тогда для х £ (0, оо) справедливы следующие соотношения:
lnx = o(xa)y #а = o(ar ), ar = o(ax) при х —*■ оо, (3.5)
а~*=°Ш' ^=о(3)' ^=o(lnDnpif *-*°°* (3-6)
<Г1/Х = о(^), ** = о(ха), х« = o(j^) при х ^ 0. (3.7)
Доказательство. Установим сначала некоторые
вспомогательные неравенства.
Пусть a > 1. Для всякого п £ N при # > 0 имеем:
а" =ехр(*1па) = Uxp^-Y > (l + ^lY >Mxn, (3.8)
где М = f J .
Полагая здесь а = е и заменяя # на In ж, будем иметь:
*>(1)П(1п*У\
откуда получаем, что при всяком х > 1
nz1/n >lna?. (3.9)
Пусть числа а,/? и а удовлетворяют всем условиям теоремы.
Докажем соотношения (3.5), то есть что
lim — = lim 2-г = lim — = 0. (3.10)
х—юо #** х—юо #" х—юо ах

§ 3. Сравнение поведения элементарных функций
239
Найдем n G N такое, что — < а < j3 < п. При любом 7 > О
lim (l/xy) = 0.
х—*оо
Применяя неравенство (3.9), получим, что при х > 1
о<!Е£< п
хос - х(а-1/п) '
In х
откуда следует, что ► и при ж —» оо.
ееа
Далее, имеем:
ее
0
#0 ж^"а
при х —» оо, так как /3 — а > 0.
Наконец, применяя неравенство (3.8), получим, что при х > 0
о<^-<
Я?"
откуда вытекает, что lim — = 0.
Равенства (3.10), таким образом, доказаны, и тем самым
установлено выполнение соотношений (3.5).
Для того чтобы доказать соотношение (3.6), мы должны
установить, что каждое из частных:
а'х ■ — —— — • —
х& ' х& ' ха ' ха ' In х
стремится к 0 при х —» оо. Эти частные равны, соответственно,
а^ ееа In ее
о*"' ж?' "ж^"
и требуемое утверждение справедливо, в силу (3.10).
Соотношения (3.6) доказаны.
Заменяя в равенствах (3.10) ее на — и принимал во внимание, что
ее
► оо при ее —» 0, получим на основании второй теоремы о пределе
х
сложной функции (теорема 2.6, глава 2):
х13 1
lim (-xa In х) = 0, lim — = 0, lim ,, - = 0. (3.11)

240
Гл. 3. Элементарные функции
Далее имеем:
а~1/х
:хр = —
а* х&
ха : - = ха In х.
In х
Отсюда, в силу (3.11), вытекает справедливость также и
соотношений (3.7).
Теорема доказана. ■
На промежутке (0, оо) определены функция In, степенная функция
жи/, где а > 0, и показательная функция х к-* ах, где а > 1. Каждая
из этих функций является строго возрастающей и стремится
к оо при х —► оо.
Соотношения (3.5) теоремы 3.1 позволяют сравнить
поведение этих функций при х —► оо.
Первое из указанных соотношений (3.5) показывает, что при
х —> оо функция In растет медленнее любой степенной функции
жиа;а, где а > 0.
Второе соотношение (3.5) означает, что степенная функция
ха, а > 0, при х -* оо растет тем быстрее, чем больше
ее показатель степени.
Наконец, третье соотношение (3.5) позволяет заключить, что
показательная функция ех при х —» оо растет быстрее любой
степенной.
Функции
1 1
а
In х' #с
где а > 0, а > 1 в промежутке (1, оо), являются строго
убывающими и стремятся к нулю при х —► оо.
Соотношения (3.6) теоремы 3.1 показывают, что функция х »-» а~~х
стремится к нулю быстрее любой степенной
функции х ь-> —, а функция жи — стремится к нулю тем быстрее,
ха ха
чем больше показатель а, а > 0.
Наконец, величина —, каково бы ни было а > 0, при ж -* оо
ха
стремится к нулю быстрее, чем .
In х
Соотношения (3.7) позволяют сделать аналогичные заключения
относительно поведения указанных в нем функций при х —» 0.

§ 4. Дополнительные сведения об элементарных функциях 241
▼ Следствие» Пусть 0 < а < /3, а > 1. Тогда справедливы
следующие асимптотические соотношения: при п, стремящемся к оо, по
множеству N:
Inn = o{na), na = о(п?), na = o(an),
Доказательство» Данное предложение получается
применением теоремы 3.1 к случаю, когда А = (0,оо), р = оо, a (#n)nGN есть
последовательность, для которой хп = п при всех п.
Следствие доказано. ▼
Полученные здесь результаты о поведении показательной,
степенной и логарифмической функций существенно используются при
решении задач о сходимости рядов и интегралов.
§4. Некоторые дополнительные сведения об
элементарных функциях
В этом параграфе рассматриваются два вопроса.
Первый касается определения величины exp z для случая
комплексного z. Для z = х + iy величина ez была определена выше по формуле:
ez = e^cosa? + i sin x). Здесь будет показано, что величина ez может
быть определена также как предел
Km (l + £>f.
п—юо \ П/
Доказывается существование этого предела и устанавливается, что
если z = x + iy, где х, у Е R, то указанный предел равен ex(cosy-\-i sin у),
В частности, получаем:
>/ \ • . т (л i>x
Q{x) = cos x + г sin x = lim ( 1 -\
n—юо \ 71
Последнее равенство может быть использовано для того, чтобы
дать определение основных тригонометрических функций,
опирающееся на строгую теорию вещественных чисел.
В литературе можно найти и другие способы построения
тригонометрических функций, основанные, например, на использовании теории
рядов.
■

242
Гл. 3. Элементарные функции
Следует сказать, что строгая теория тригонометрических функций
— в полном виде при любом способе изложения — оказывается
достаточно громоздкой. В рамках такой теории должно быть доказано, в
частности, что существует число 7Г > 0 такое, что sin 7Г = О и sin x > О
для всех х G (0,7г).
Другой вопрос, который рассматривается здесь, связан со
следующим.
Пусть f есть показательная функция х ь-> ах. Тогда для любых
х, у G К имеет место равенство:
f(x)f(y) = f(x + y).
Это свойство полностью характеризует показательную функцию.
Всякая непрерывная функция f : Ш —» Ж, не равная тождественно
нулю, для которой выполнено указанное соотношение, является
показательной функцией.
Всякая непрерывная функция f : (О, оо) —> Ш такая, что для любых
х > 0, у > 0 выполняется равенство
f(x-y) = f(x) + f(y),
есть функция вида f(x) = С In х, где С Е R, С — постоянная.
Оказывается, что все основные элементарные функции могут быть
охарактеризованы подобного рода свойством. Доказательство этого
приводится далее.
4.1. О ФУНКЦИИ ехр В КОМПЛЕКСНОЙ ПЛОСКОСТИ
4.1.1. В §2 величина ez была определена для произвольного
комплексного числа z = х + iy. Это определение основано на использовании
некоторых свойств тригонометрических функций.
Докажем, что для всякого z G С существует предел
lim (l + -Y
и значение его в точности совпадает с тем значением ez, которое было
указано в п. 2.4 этой главы.
Дальнейший план действий таков. Сначала будет установлено, что
для всякого комплексного числа z существует предел:
lim (l + ^-V .

§ 4. Дополнительные сведения об элементарных функциях 243
Иначе говоря, будет доказано, что у последовательности с общим
/ z\n
членом (1 Н— ) некоторая специальная подпоследовательность имеет
предел. Используя свойства предела этой подпоследовательности, мож-
/ z\n
но доказать и существование предела lim (1 -\— 1 для любого кои-
п—>-оо \ П/
плексного числа z.
Функция Р : С и С называется полиномом степени не выше п,
если существуют комплексные числа co,ci,... ,сп такие, что
п
P{z) = со + c\z Л h cnzn = 22, Ск*к (4-1)
fc=0
для всех z G С. Числа co,ci,... ,сп называются коэффициентами
полинома Р. Коэффициент Со называется его свободным членом. Имеем,
очевидно: со = -Р(О).
Полином Р называется позитивным, если коэффициенты со, с\,...
... ,сп в равенстве (4.1) суть неотрицательные вещественные числа.
■ Лемма 4.1. Если Р есть позитивный полином, то для всякого
комплексного числа z справедливо неравенство:
\P(z)\ < P(\z\).
Доказательство. Пусть
P{z) = со + c\z Н h cnzn,
где со,с\,... сп — неотрицательные вещественные числа. Тогда имеем:
\Р(г)\<Ы + \сг\\г\ + --- + \сп\\2\п.
Так как коэффициенты Ck, к = 0,1,2,...п, суть неотрицательные
вещественные числа, то \ck\ = Ck при каждом к. Отсюда получаем:
\P(z)\<c0+c1\z\ + ... + cn\z\n = P(\z\),
что и требовалось доказать. ■
Нетрудно видеть, что сумма любого числа позитивных полиномов
есть позитивный полином. Произведение двух, а значит, и любого числа
позитивных полиномов также является позитивным полиномом.

244
Гл. 3. Элементарные функции
■ Лемма 4.2. Пусть р и q — произвольные комплексные числа.
Для п 6 N положим dn = 2П. При всяком n E N выполняется равенство:
Pdn ~qdn =(p-q)(p + Я)(Р2 + ?2)--V""1 + q^1) =
= (p-q)Y[(pdk+qdk)-
fc=0
Доказательство легко осуществляется индукцией по п.
Предоставляем читателю подробное проведение необходимых рассуждений. ■
4.1.2. Докажем существование предела некоторой
подпоследовательности последовательности с общим членом Pn(z) = 11 -\— 1 .
/ z \dn
Положим: En(z) = (1 + — 1
■ Лемма 4.3. Пусть п > О — целое число. Тогда для любого k E N
разность En+k(z) — En(z) представляет собой позитивный полином.
Доказательство. При всяком к € N имеем:
En+k(z) - En{z) =
= [JE»+i(*) - En(z)] + [En+2(z) - En+1(z)] + - • •
• • • + [En+k(z) - En+k-i(z)].
Отсюда ясно, что для доказательства леммы достаточно
убедиться, что при всяком целом п > О разность En+i(z) — En(z) является
позитивным полиномом.
Имеем: cJn+i = 2dn. Отсюда получаем, что
-( z Yn+1_|Y z Y]dn-( z *2 Yn
\ dn+i) \ dn+i J \ \ dn 4dn J
Воспользуемся результатом леммы 4.2, полагая в ней
2 / \2
z z (.. . z
dn 4:dn V <k+i '
z
9 = 1 +т-

§ 4. Дополнительные сведения об элементарных функциях 245
Получим:
En+1(z)-En(z) = £p]l
k=0
Каждый множитель справа является позитивным полиномом.
Произведение конечного числа позитивных полиномов (как сказано
выше) есть позитивный полином.
Отсюда вытекает, что разность En+\(z) — En(z) является
позитивным полиномом.
Лемма доказана. ■
■ Лемма 4.4. Для всякого z £ С существует предел:
lim (l + £-) .
Доказательство. Пусть rai, пг Е N, причем п\ < пг. В силу
леммы 4.3, разность En2(z) — Eni(z) является позитивным полиномом.
Отсюда вытекает, что для всякого z £ С выполняется неравенство:
\En2{z) - Eni(z)\ < En2(\z\) - Eni(\z\).
Зададим произвольно z G С. Как доказано в § 1, существует
конечный предел lim ,Бп(|>гг|).
п—юо
Зададим произвольно е > 0. Согласно тсршпершо сходимости Ко-
ши — Болъцано, по нему найдется номер п такой, что для любых п',
n" > n выполняется неравенство: |£n/(|z|) — £n//(|z|)| < е.
Возьмем произвольно n' > п и п" > п.
Пусть П1 есть наименьшее, пг — наибольшее из чисел п' и п".
Имеем, очевидно:
\En,{z) - Enn{z)\ = \En2(z) - Eni(z)\ < En2(\z\) - Eni(\z\) < e.
Так как е > 0 было выбрано произвольно, то тем самым
установлено, что для последовательности (En(z))n^ выполняются условия
признака сходимости Коши — Больцано.
Лемма доказана. ■
/ z \2П
4.1.3. Предел lim (1 + — ) , где z — произвольное комплексное чи-
ело, обозначим символом Е(^).
*л+1
i +
dn
+
+i
('♦£)'

246
Гл. 3. Элементарные функции
Установим некоторые свойства определенной таким образом
функции Е переменной z £ С, которые позволят нам заключить, что
E(z) = expz = ex(cosy + г sin у) для всякого z Е С. (Если z Е R, то
это непосредственно следует из определения E(z).)
Ш Лемма 4.5. Пусть {zn)n^ есть сходящаяся последовательность
комплексных чисел и с = lim zn. Положим:
те—юо
z. = (1 + f)\ c-(i + £)".
Тогда отношение -р^- имеет предел, равный единице.
Доказательство. Пусть с = lim zn = 0. При каждом n Е N
те—»оо
полином
ад = (i + £)"
является позитивным. Имеем: Рп(0) = 1. Отсюда следует, что
свободный член этого полинома равен 1 и разность Pn(z) — 1 есть позитивный
полином. Это позволяет заключить, что \Pn(z) — 1| < Рте(И) — 1 при
всяком z.
В частности, получаем, что для всех п
\Pn{*n)-l\<Pn{\Zn\)-l.
Для случая вещественных числовых последовательностей
утверждение леммы 4.5 верно, как следует из леммы 1.1, то есть
lim [Pn(|z„|)-1] = 0.
те—юо
В силу теоремы о зажатой переменной, из доказанного следует,
что
lim Pn(zn) = 1.
В данном случае Сп = 1 для всех п и, стало быть, для случая с = 0
утверждение леммы верно.
Предположим, что с есть произвольное комплексное число. Пусть
k E N таково, что \с\ < к. Для и > к имеем:
_ -I I n zn — с
1 +
1 +
iZL
71
с
71
=
n + zn
71 + С
=:
1 +
Zn -С
71 + С
71 + С П

§ 4. Дополнительные сведения об элементарных функциях
247
Положим Сп = (zn — с). Для всех п > к имеем равенство:
п + с ~
zn = c„(i + ^-)\
При п —> оо будет £п —» 0 и, значит, по доказанному,
O + ir)"-1
при п —»• оо. Отсюда получаем, что
lim ^- = lim (l + —Y = 1,
те—юо Gn те—*оо \ 71 /
что и требовалось доказать. ■
■ Теорема 4.1. Для любых z\,z<i G С выполняется равенство:
E(*i)E(*2) = E(*i +z2). (4.2)
Доказательство. Теорема доказывается почти дословно так же,
как и в вещественном случае. Пусть, как и ранее, dn = 2П. Имеем:
E(*i)E(*2)= Ит (l + ?r) П lim fa + zr) " =
n-^oo \ Un / те—юо \ (Ln J
-B„(i + a±i + ^)'-=B„(i + b)'-,
те—>>oo \ an an / п-юо \ an /
где un = 2Ti +Z2 + ziZ2/dn. При n —*■ оо будет глте —» zi +Z2. На основании
леммы 4.5, отсюда следует, что
E(zi)E(z2)= lim (l + £)'" (l + f-Y" =
= lim (l + £l+^.)dn=E(Zl + Z2),
те—юо \ an /
и тем самым теорема доказана. ■
▼ Следствие 1. Для любых комплексных чисел z\,zi,.. .,zn
справедливо равенство:
те
Е(гг + 22 + • • • + zn) = Д E(zk).
fe=i

248
Гл. 3. Элементарные функции
Доказательство осуществляется индукцией по п и, ввиду
очевидности, мы его опускаем. ▼
Т Следствие 2. Для любого z £ С и любого п £ N имеет место
равенство: [E(z)]n = Е(гг^г).
Доказательство — очевидно. ▼
■ Лемма 4.6. Для всякого комплексного числа z имеет место
неравенство:
| Е(г) - 1 - z\ < ехр |*| - 1 - \z\.
Доказательство. При всяком n = 2fc, где k £ N, имеем:
Я„(*)-1-* = Я»(*)-Я0(*)-
В силу леммы 4.2, разность #те(>гг) — Eq(z) при п = 2*, где к £ N, есть
позитивный полином. Отсюда получаем, что для всех таких п £ N
\En(z)-l-z\<En(\z\)-l-\z\.
Переходя в этом неравенстве к пределу при п —► оо, получим
требуемое неравенство.
Лемма доказана. ■
Ш Теорема 4.2. Для всякого z £ С имеет место равенство:
Е(*)= Ню (l + fT-
Доказательство. Пусть z £ С. Если z = 0, то доказывать
нечего.
Будем считать, что z ф 0. Положим: zn =п Е ( — ) — 1 . Имеем:
,n-z = n[E(f)-l-f]
Отсюда, применяя лемму 4.6, получаем:
\zn - z\ < n
ехр
(\А\ _ 1 _ Ml
\ n / n J
ехр
= \-<
(ih-J
Hi
n

§ 4. Дополнительные сведения об элементарных функциях
249
Ы
Поскольку —- —> 0 при п —» оо, то
п
ехр
lim
те—юо \Z\
П
■Vt^ 1 = 0.
Отсюда следует, что zn — z —> 0 при п —> оо. Применяя лемму 4.5,
получаем, что
lim
п—+оо
Осталось заметить, что
(1 + Ь)" = вМ
при каждом п и, следовательно,
lim -р— \п = !•
— (, + £)
Из этого равенства вытекает, что
Е(*) = lim (l+£V.
те—юо \ П/
Теорема доказана. ■
Отметим некоторые дальнейшие свойства функции ехр z для
случал, когда z — произвольное комплексное число.
Пусть z = х + и/, z = х — гу — сопряженные числа. Так как все
коэффициенты многочлена Еп суть вещественные числа, отсюда следует,
что
En(z) = En(z)
при всех п. Переходя к пределу при п —► оо, получим:
E(s) = E(z). (4.3)
Из равенств (4.2) и (4.3) далее получаем:
|E(*)|2 = E(*)E(s) = E(z + z) = E(2Rez) = E(Rez)2.

250
Гл. 3. Элементарные функции
Так как (expRez)2 > 0, то, следовательно, будем иметь:
| exp z\ = exp Re z. (4-4)
Из равенства (4.4), в частности, следует, что если z = г#, где жЕК,
то
| exp z\ = | exp ix\ = exp 0 = 1. (4.5)
Справедливо следующее утверждение.
■ Теорема 4.3. Для всякого х £ К имеет место равенство:
Е(г#) = cos х + i sin ж.
Доказательство. Зададим произвольно п £ N и положим
/ х . , х \
zn = n I cos —h« sin 1) . (4.6)
\ п п )
Имеем:
/ X \ X
lim п (cos 11 =0, lim n sin — = а?,
п—юо \ 72 / те—юо 71
откуда заключаем, что
lim zn = ix.
Из равенства (4.6) следует, что
X . , X Zn
cos —Н sin — = 1 Н .
п п п
Отсюда, в силу известных нам свойств функции х ь-> cos х + i sin a?,
вытекает, что
cos
/ ж . . х\п (Л zn\n
х + г sin х = ( cos —h г sin — J = (1 -\ 1 .
V n n/ \ n J
Так как lim zn = ix, отсюда, в силу леммы 4.5 и теоремы 4.2,
те—»оо
вытекает, что
lim (l + ^Y = E(ix),
те—юо \ П /
и, значит,
cos х + i sin a? = E(i#)9
что и требовалось доказать. ■

§ 4. Дополнительные сведения об элементарных функциях
251
▼ Следствие. Для всякого z = x+iy £ С, где х, у £ Ш, выполняется
равенство:
E(z) = ex(cos у + i sin у).
Действительно, по теореме 4.1, Е(# + гу) = Е(#), Е(«у) = ex(cosy+
+г sin у), что и требовалось доказать. Т
Полученный результат дает способ определения функций cos x
и sin ж, основанный на строгой теории вещественного числа. Именно,
эти функции могут быть определены посредством равенств:
cos х — Reexp(ix), sin x = Imexp(ix)
для произвольного х £ R.
Принимая во внимание теорему 4.3, видим, что функции,
определенные таким образом, в точности совпадают с теми косинусом и
синусом, которые известны читателю из школьного курса математики.
4.2. Функциональные уравнения элементарных функций
Докажем, что базисные элементарные функции полностью
характеризуются тем, что эти функции непрерывны и для них выполняются
соотношения, позволяющие выразить значения f(x + у) или f(xy) через
f(x) и /(у). Эти соотношения мы будем называть функциональными
уравнениями базисных элементарных функций.
Далее R+ означает совокупность всех положительных
вещественных чисел, то есть R+ = (0,оо).
Символом S1 обозначается множество всех комплексных чисел z
таких, что \z\ = 1.
■ Теорема 4.4 (функциональное уравнение Коши). Пусть f есть
числовая функция, которая определена, и непрерывна, в отрезке I = (а, 6)
множества Ш, содержащем точку 0. Предположим, что для любых
х, у £ / таких, что х + у £ I, выполняется равенство:
f(x + y) = f(x) + f(y).
Тогда, существует число к £ R такое, что для всех х £ R выполняется
равенство f(x) = kx.
Доказательство. Пусть функция / удовлетворяет условиям
теоремы, / = (а, 6). Тогда a < 0 < 6.
Если х £ / и п £ N таковы, что пх £ /, то f(nx) = п/(ж). При
п = 1 это утверждение тривиальным образом верно.

252
Гл. 3. Элементарные функции
Предположим, что для некоторого п £ N оно доказано.
Пусть х £ / таково, что (п + 1)х £ /. Тогда также их £ /. Имеем:
/[(и + 1)х] = f(nx + x) = f(nx) + f(x).
Согласно предположению, f(nx) = nf(x). Тогда f[(n+l)x] = (n+l)/(x).
В силу принципа математической индукции, данное утверждение
доказано. Для всякого х £ / имеем:
f(x) = f(x + 0) = f(x) + f(0),
откуда заключаем, что /(0) = 0.
Если х £ / таково, что —х £ /, то
0 = /(0) = f(x + (-х)) = f(x) + f(-x),
откуда
/(-*) = -f(x).
Возьмем произвольно h £ / такое, что 0 ф h. Пусть х £ /. Предпо-
т, ЛТ
ложим сначала, что х = —Д, где п £ N, a m — целое число.
п
Докажем в этом случае, что
f(x) = ^f(h). (4.7)
п
Рассмотрим сначала случай т > 1. Очевидно, — £ /. Имеем:
п
Далее,
л»>=/И)=./(!).
откуда
/ (-) = -/(М-
\п/ п
Мы получаем, что
f (ml) = ?'(*>•
V п/ п
так что в случае m > 0 равенство (4.7) доказано.

§ 4. Дополнительные сведения об элементарных функциях
253
Пусть т < 0. Тогда т = —\т\. Точка = 1—г в данном случае,
п \т\
очевидно, принадлежит /. Имеем:
Л») = / (-М;) = М/ (-£) = -М/ (|) - = Л*).
так что равенство (4.7) доказано ив этом случае.
Пусть х Ф 0 — произвольный элемент отрезка (а, 6).
Положим z = —, и пусть (zn),n = 1,2,..., — последовательность
h
рациональных чисел такая, что 0 < \zn\ < \z\ для всех п и zn -^ z при
п —» оо.
При каждом п точка znh лежит на отрезке, концы которого есть
точки О и х (это следует из неравенств 0 < \zn\ < \z\) и, значит, znh £ /
для всех п.
При п —► оо имеем zn/i —► ж и, стало быть, в силу непрерывности
/, при п -* оо будет f(znh) -* /(ж).
При каждом п, по доказанному,
/(*»Л) = *„/(Л) - */(Л) = |/(Л)
при п —► оо.
Таким образом, для всех а? € / выполнено f(x) = кх, где к = .
Теорема доказана. ■
Замечание. Условие непрерывности функции / в доказанной
теореме 4.4 может быть существенно ослаблено. Однако без каких-либо
дополнительных ограничений обойтись нельзя.
Вопрос: существуют ли функции / : / —► R, где / —
промежуток в R, содержащий точку 0, удовлетворяющие функциональному
уравнению f(x + у) = f(x) + f(y) и отличные от функции / : х ь-> кх,
оказывается связанным с некоторыми вопросами оснований
математики.
В рамках той аксиоматики теории множеств, которая в
настоящее время большинством математиков рассматривается как основная,
можно доказать существование функций /, удовлетворяющих условию:
f(x + у) = f(x) + f(y) Для любых ж, у £ R и отличных от функции
f : х »-» kx, где к £ R — постоянная.
Известны, однако, системы аксиом теории множеств, исходя из
которых можно установить отсутствие решений функционального
уравнения Кошщ отличных от линейной функции / : х »-» кх.

254
Гл. 3. Элементарные функции
Результат теоремы 4.4 допускает определенную трактовку
физического содержания.
Предположим, что рассматривается какой-то физический процесс,
происходящий в течение определенного времени. Это может быть
электрический ток в проводнике, горение свечи, течение жидкости в канале,
полет ракеты в космосе и т. д.
Предположим далее, что для каждого промежутка времени [tfi,^]
можно говорить о результате действия данного процесса в течение
этого промежутка. Это может быть, например, количество тепла,
выделившегося на определенном участке проводника, длина отрезка свечи,
сгоревшего за время, прошедшее от момента t\ до момента t2, объем
воды, протекший в канале за то же время, и т. д.
Среди различных процессов могут быть выделены такие, которые
протекают с постоянной интенсивностью. Что это означает, можно,
однако, понимать по-разному.
Во-первых, процесс, имеющий постоянную интенсивность, можно
определить как такой, для которого для любых двух промежутков
времени равной длины результаты действия процесса в течение этих
промежутков всегда одинаковы.
Во-вторых, физический процесс можно считать происходящим с
постоянной интенсивностью, если результат его действия за произвольный
отрезок времени [tfi,^] пропорционален длине этого отрезка, то есть
равен (t2 — ti)k, где к — некоторая постоянная.
При некоторых весьма общих предположениях приведенные два
определения оказываются эквивалентными.
Пусть, например, изучается движение точки по прямой.
На прямой введем систему координат, и пусть x{t) есть координата
точки в момент времени £, где a <t <Ь.
Возьмем произвольно значения t\ и t2, где а < i\ < t2 < Ъ.
Разность x(t2) — x(t\) называется перемещением точки за
промежуток времени [ti,t2].
Говорят, что точка движется равномерно, если для любых
двух различных отрезков времени [fi,^], [^1^2] таких, что t2 — ti =
= t2 — t[, всегда x(t2) — x(h) = x(t2) — x(t[).
Покажем, что если функция х непрерывна и движение, в смысле
данного определения, равномерно, то существует постоянная v
такая, что #(£2) — x(ti) = (^2 — ti)v для любых ti,t2 € [а,Ь].
Положим 6 — а = L Для и £ [0,/] полагаем (р(и) = х(а + и) — х(а).

§ 4. Дополнительные сведения об элементарных функциях 255
Возьмем произвольно и\ Е [О,/], и2 Е [0,/] такие, что и\ + и2 < /, и
пусть *i = а, ^2 = а + ^2, *з = « + ^i + ^2- Имеем:
<р(иг + и2) = x(t3) - x(ti) = x(t3) - x(t2) + x(t2) - x(h).
Так как t3 —h = «i, то я?(*з) — яг(*2) = #(a + ui +^2) — ^(а + иг) = ¥>(ui).
Далее, ж(^) — #(*i) = х(а + -г^) — х(а) = ^(^г), и мы получаем:
<р(иг + и2) = <р(иг) + <р(и2).
Функция <р, очевидно, непрерывна. На основании теоремы 4.4, из
доказанного вытекает, что <р(и) = гш, где v6R — постоянная.
Для любых hjt2 Е [a,6] таких, что tfi < t2, имеем x(t2) — x(ti) =
= ж(а + *2 — *i) — #(а) = <p(h — h) и, следовательно,
x(t2)-x(t!) = (t2 -<i)t>,
что и требовалось доказать. ■
■ Теорема 4,5. Пусть / : R —► R — непрерывная функция, не
равная тождественно нулю и такая, что для любых х\,х2 Е R выполняется
равенство:
/(si + S2) = /(si)/(s2).
Тогда существует постоянная k Е R такая, что для всех а? £ R
выполняется равенство f(x) = efca?.
Доказательство. Пусть функция / удовлетворяет всем
условиям теоремы. Докажем, что тогда /(а?) ^ 0 для всех ж Е R.
Предположим, что нашлась точка хо € R такая, что /(#о) = 0.
Тогда для любого ж Е R будем иметь:
f(x) = /(ж - хо + а?0) = /(ж - xo)f(xo) = 0,
и, следовательно, в этом случае / тождественно равна нулю, вопреки
предположению.
Итак, /(ж) ф 0 для всех х. Для любого х Е R имеем:
л«)-/(|+|) -/(§)/(§) >"•
так как / I — 1 ^0. Таким образом, f(x) > 0 для всех х Е R.

256
Гл. 3. Элементарные функции
Положим F(x) = In f(x). В силу доказанного, функция F
определена и непрерывна при каждом х £ R. Из соотношения f(x + y) = f(x)f(y)
получаем: In f(x + у) = In f(x) + In /(у), то есть F(x + у) = F(x) + F(y).
На основании теоремы 4.4, отсюда получаем, что F(x) = fcx при
любом х^1и, значит, /(ж) = е*х для всех a?GK.
Теорема доказана. ■
■ Теорема 4.6. Пусть f : R+ —► IR — непрерывная функция такая,
что для любых х > 0 и у > О
/(ху) = /(х) + /(у).
Тогда существует постоянная k £ R такая, что для всех ж £ К.
выполняется равенство f(x) = к In ж.
Доказательство. Положим F(#) = /(ex). Тогда для любых
аг,у еШ:
F(x + y) = f{e*ey) = /(О + /(е*) = F(*) + F(y).
Функция F — непрерывна и, значит, по теореме 4.4, F{x) = kx для
всех х £ R.
Имеем далее: f(x) = F(ln ж) для любого х £ R"1*, откуда получаем
/(х) = A? In ж, что и требовалось доказать. ■
■ Теорема 4.7. Пусть / : R+ -> R+ — непрерывная функция такая,
что f(xy) = f(x)f(y) для любых х > О и у > 0. Тогда f(x) = xk, где
k 6R.
Доказательство. Пусть / : М+ —» М+ удовлетворяет всем
условиям теоремы. Тогда f(x) > 0 для всех х £ М+.
Положим F(x) = In /(ж). Тогда F непрерывна и для любых х £ R+
и у £ R+ будем иметь:
F(*y) = F(x) + F(y).
Отсюда, в силу теоремы 4.6, F(x) = klnx и, следовательно, /(а?) =
= exp -F(#) = exp(fe In x) = xfc, что и требовалось доказать. ■
Установим некоторый аналог теоремы 4.5 для случая функций
со значениями в С. Предварительно введем следующее обозначение:
S1 = {х £ С : |z| = 1}.

§ 4. Дополнительные сведения об элементарных функциях
257
■ Теорема 4.8. Пусть £ : R —► S1 С С — непрерывное отображение.
Предположим, что для любых х Е К и у Е R выполняется равенство:
С(* + у) = С(*К(у).
Тогда существует число к Е К такое, что для всех х Е К
£(х) = expifor.
Доказательство. Пусть функция С : М —» S1 удовлетворяет всем
условиям теоремы. Полагая ж = у = 0 в соотношении С(ж+2/) — C(x)((y)i
получаем: £(0) = [С(0)]2- Отсюда вытекает, что £(0) равно или 0, или 1.
Согласно условию теоремы, £(0) (£ S1 и, значит, |С(0)| = 1.
Следовательно, £(0) = 1.
Функция £ непрерывна и, стало быть, найдется 6 > 0 такое, что
при |а?| < 6 выполняется |С(#) — 1| < 1.
Для всякого х Е (-М) будет |Re[C(a?) - 1]| < 1, |1т[С(я?) - 1]| < 1,
откуда Re£(#) — 1 > — 1 и, значит, Re ("(ж) > 0 и |Im£(x)| < 1.
Возьмем произвольно h Е (0,£). Так как Re ((h) > 0, то найдет-
/ 7Г 7Г \
ся А Е ("~77?77) такое, что Re£(/i) = cos A, Im((h) = sin Л, то есть
((h) = eiX. При \х\ < |Л| справедливо \eix - 1| < 1.
Действительно, имеем:
|е*'"-1| = |е,'*||е'*-е-<*| =
= 2|«in§| < 2|sin^| = |е'А - Ц = |С(Л)- 1| < 1.
Положим А? = —, и пусть Со(#) = СООе"***. Тогда |Co(#)| = 1 для
всех х Е М, функция £о непрерывна и для любых х и у справедливо
равенство:
Со(х + у) = С(х + у)е-'*<*+»> = (С(х)е-ая)(С(у)е-г'к3') = Со(*)Со(у).
Имеем: Со(0) = 1, (o(h) = 1. Для доказательства теоремы
достаточно установить, что (о(х) = 1 при всех х.
Докажем сначала, что (о(х) = 1 для любого х = —^-Л, где m —
произвольное целое число, n E N.

258
Гл. 3. Элементарные функции
Отсюда
Предположим, что Со ( 0п_г ) = 1, где п — целое, п > 0. Тогда
Далее,
Со (£) = от,
где и = С ^J, v = ехр (-^г) • Отсюда:
ко (^-) - ll = \uv - 1| < Itio - v\ + |о - 1| = |u - 1| + |v - 1| < 2.
Это неравенство позволяет заключить, что
Со (£) * -1
и, следовательно,
<°ш->
что и требовалось доказать.
Так как Со(^) = 1> то из доказанного вытекает, что Со (—) = 1
для любого целого п > 0. Отсюда получаем, что
*(#)-[*(£)]"='•
Итак, Со (х) = 1 для любого а? = --—.
Пусть теперь х — произвольное вещественное число.
Построим последовательность рациональных чисел (гп)п^ такую,
что hrn —► х при п -> оо и rn = гап/2Рп, где pneN, при каждом п. Так
как функция Со непрерывна, то Со(^) = lim (o(hrn). С другой стороны,
п—*-оо
по доказанному, Со(^п) = 1 при всех п и, значит, lim Co(^n) = 1, то
п—*-оо
есть (о(х) = 1. Поскольку х было взято произвольно, то тем самым
нами установлено, что Со(#) = 1, и, следовательно, С(#) = ег х для всех
х €R.
Теорема доказана. ■

§ 4. Дополнительные сведения об элементарных функциях 259
Результаты этого раздела могут быть переформулированы
еще с другой точки зрения.
Определения.
Пусть G — произвольное непустое множество.
Предположим, что каждой паре (#, у), где х £ G, у £ G, сопоставлен
некоторый третий элемент z = х * у множества G. Иначе говоря,
дано отображение
(#, у) £ G х G у-* х * у £ G.
В этом случае говорят, что на множестве G определена
некоторая бинарная операция *.
Множество G с бинарной операцией * называется группой, если оно
удовлетворяет следующим трем условиям — аксиомам группы:
1) Для любых #, у и z из G
(ж * у) * z = ж * (у * z).
2) Существует элемент е £ G такой, что для любого х £ G
х*е = е*х = х.
3) Для всякого х £ G существует и при том единственный элемент
у £ G такой, что
Группа G называется коммутативной или абелевой, если она
удовлетворяет еще следующему условию.
К) Для любых ж и у из G имеет место равенство:
х * у = у * ж.
Элемент е, существование которого следует из аксиомы 2),
называется нейтральным элементом группы.
Элемент у (существование которого следует из аксиомы 3))
называется обратным к х элементом группы G и обозначается ж""1.
Результат применения бинарной операции в группе к ее элементам
х и у обозначается обычно символом х + у или ху.
Выражение х + у для обозначения бинарной операции обычно
применяется только для коммутативных групп. В этом случае для
той же цели может использоваться также выражение ху.

260
Гл. 3. Элементарные функции
Нейтральный элемент группы называется также единицей или
(в случае, когда группа коммутативна и бинарная операция
обозначается с помощью символа «+») нулевым элементом и обозначается в
первом случае символом 1, а во втором — символом 0.
Пусть G и Н — произвольные группы. Отображение <р : G —» Н
называется гомоморфизмом, если для любых х,у £ G выполняется
соотношение: ср(х * у) = (р(х) * <р(у).
Имеем следующие группы, элементы которых суть числа:
1. Множество всех вещественных чисел R с обычным сложением в
качестве бинарной операции на нем.
2. Множество всех положительных вещественных чисел
М+ = (0,оо)
с обычным умножением в качестве бинарной операции.
3. Множество S1 всех комплексных чисел z, удовлетворяющих
условию \z\ = 1, с обычным умножением в качестве бинарной
операции.
Будем называть данные группы Ш, R+ и S1 основными числовыми
группами.
Пусть G и Н — основные числовые группы, причем G — одна из
групп R или М+.
Гомоморфизм (р : G —► Н называется непрерывным, если он
представляет собой непрерывное отображение.
Используя введенные понятия, мы можем теперь
переформулировать результаты теорем 4.4-4.8 следующим образом.
■ Теорема 4.9. Всякий непрерывный гомоморфизм f : Ш —► Ш есть
функция вида, f : х ь-> кх;
всякий непрерывный гомоморфизм / : R —» R+ есть функция вида,
/х
:xv-+ a ;
всякий непрерывный гомоморфизм / : М+ —► Ш есть функция вида,
f : х ь-> k In x;
всякий непрерывный гомоморфизм f : R+ —» R+ есть функция вида,
f : х ь-> хк, где к £ М;
каьждый непрерывный гомоморфизм f : R —► S есть функция вида,
f:x^ eikx.
Для доказательства теоремы достаточно заметить, что условие, —
что то или иное отображение есть гомоморфизм, — как раз и означает,
что для него выполнено соответствующее функциональное уравнение.

Задачи
261
Задачи
3.1. Пусть (cn)n€N есть числовая последовательность, определенная
следующими условиями: с\ = 0 и если сп определено, то cn+i =
Доказать, что при каждом п выполняются 0 < сп < 1 и lim cn = 1.
п—юо
Положим 5 тг = у 1 — с|.
Доказать, что последовательность (2nsn)n^ — возрастающая и предел
lim 2nsn — конечен.
п—юо
Доказать, что 3 < lim 2п5т2, < 4.
п—»оо
(Указание: рассмотреть последовательность (2ntn)n£N> г^е tn = —•)
сп
Замечание: предел lim 2nsn есть не что иное, как известное
п—юо
число 7г — отношения длины окружности к ее диаметру; чтобы увидеть это,
необходимо только понять геометрический смысл величины 2n sn.
3.2. Пусть а = р/д, где р и q — целые числа, причем 0 < а < 1.
Найти верхний и нижний пределы последовательностей:
({<*n})n€N, (sinan7r)n€N, (cosan7r)7l€N, (tgari7r)n€N,
где {х} означает дробную часть числа (см. задачу 1.19).
Найти верхний и нижний пределы последовательностей, если а —
иррациональное вещественное число.
3.3. Доказать, что предельные точки каждой из последовательностей
(sin(7r\/n))n€N; (sin(7rlnn))n€N; (sin(7rn3/2))7l€N; (sin(7rnlnn))7l€N
заполняют весь отрезок [—1,1].
3.4. Даны функция s:aiGR^ sin ж и множество А.
Доказать, что если р Е R. есть предельная точка множества А, то s(p)
есть предельная точка множества s(A).
3.5. Доказать, что всякая периодическая непрерывная функция / : R —* R
ограничена и принимает свои наибольшее и наименьшее значения.
Доказать, что всякая непрерывная периодическая функция / : R —* R
равномерно непрерывна на R.
3.6. Пусть / : R —► R — непрерывная функция.
Доказать, что если / имеет два периода Т\ > 0 и Тъ > 0 таких, что
отношение Т2/Т1 иррационально, то функция / — постоянна.
Il+Cn

262
Гл. 3. Элементарные функции
3.7. Используя формулы Эйлера, вычислить суммы:
п п
' sinkx.
\ sinkx, —h / coskx, —\- \ р coskx, \ p sin
3.8. Доказать, что для всякого в Е R. последовательность
жта(0) = \ cosA:0
fc=0
не стремится ни к какому конечному пределу при га —► оо.
3.9. Доказать, что ~ = lim J^ cos Дг.
3.10. Доказать, что е""1/* = о(хп) при ж —► 0 для любого га Е N.
3.11. Пусть а > 0, а ф 1 таково, что логарифм с основанием а удовлетворяет
неравенству loga ж < я? — 1. Доказать, что а = е.
3.12. Доказать, что для любого га £ N функция
Тп : х £ [—1,1] к-► cos(ra arccos x)
есть ограничение на отрезке [—1,1] некоторого многочлена степени га (полином
Чебышёва).
3.13. Доказать, что для любого га > 0 функция
1Г.:,б(-1,1)"*4(ПТ1),1теСО"1
VI — ж2
есть ограничение на отрезке (—1,1) некоторого многочлена степени га (полином
Чебышёва второго рода).
3.14. Найти модуль непрерывности функции / : х Е [0, оо) —» жа, где
0 < а < 1.
3.15. Найти модуль непрерывности функции / : х Е [0,1] —► жа, где а > 1.
3.16. Исследовать на непрерывность и выяснить характер точек разрыва
функции
I 0 для рациональных х\
/0*0 = \ .
I sm7ra; для иррациональных х.
3.17. Доказать, что функция / : х к-► 8т|ж|а равномерно непрерывна на R.
при 0 < а < 1 и неравномерно непрерывна на R. при а > 1.
Построить график функции.
3.18. Определить, при каких е функция х н-► ж + esina; осуществляет
топологическое отображение R. на себя.
3.19. Определить, при каких а функция жиж-|- асов-^/ж отображает R на
себя топологически.
3.20. Функция / : [0, h) —► R. такова, что для любых #i #2 Е [0, h) выполняется
неравенство: /(#2) > /(jci)[1 + к(х2 — #i)]5 где к — постоянная.
Доказать, что f(x) = f(0)ekx на промежутке [0, h).

Глава 4
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
Г
• Понятие производной, некоторые ее применения
• Правила дифференцирования функций •
Дифференцирование основных элементарных функций •
Параметризованные кривые • Касательная
параметризованной кривой • Кривая в полярных координатах
• Производные высших порядков • Функции
классов Dn и Сп • Критерии монотонности функции
• Полиномы одной переменной • Формула Тейлора
с остаточным членом в форме Пеано • Метод Ньютона
решения уравнений вида j \х) = 0 • Понятие точки
экстремума дифференцируемой функции • Формула
Лейбница, теорема о произведении функций •
Теорема Ферма • Теоремы Коши и Лагранжа о среднем
значении функций • Правило Лопиталя раскрытия
неопределенностей • Выпуклые функции •
Неравенства Йенсена, Гёльдера, Юнга, Минковского •
Применение дифференциального исчисления к исследованию
функций одной переменной • Приложения
дифференциального исчисления к физике и механике •

264 Гл. 4. Дифференциальное исчисление функций одной переменной
§1. Определение и простейшие свойства
производной
Понятие производной является одним из основных в курсе
математического анализа. Здесь приводятся необходимые определения и
устанавливаются простейшие свойства производной, непосредственно
вытекающие из ее определения.
Основным в дифференциальном исчислении функций одной
переменной является случай, когда область определения изучаемой функции
есть отрезок. Однако рассматривать только функции, определенные на
отрезках множества Ж, было бы неудобно хотя бы потому, что область
определения произвольной элементарной функции может не быть
отрезком и, вообще, может иметь достаточно сложное строение.
Здесь будут описаны основные правила вычисления производных,
базирующиеся на теоремах о дифференцировании суммы, произведения,
частного, суперпозиции двух функций и обратной функции. Вместе со
знанием производных основных элементарных функций, эти правила
дают все, что необходимо для определения производной произвольной
элементарной функции.
1.1. Понятие функции, дифференцируемой в точке.
Определение производной
Сформулируем минимальное условие, которому должно
удовлетворять множество А С М, для того чтобы можно было говорить о
производной для функции, определенной на этом множестве.
Будем говорить, что множество Acl плотно в себе, если каждая
точка х £ А является предельной точкой множества А.
Всякий отрезок в Е представляет собой плотное в себе множество.
♦ Предложение 1.1. Объединение конечного числа множеств,
каждое из которых плотно в себе, есть плотное в себе множество.
Доказательство. Справедливость данного утверждения почти
непосредственно следует из определения и свойств предельных точек,
известных нам.
Действительно, пусть А\, Аъ,..., Ап — числовые множества,
каждое из которых плотно в себе, А — их объединение. Возьмем
произвольно точку х £ А. Точка х принадлежит хотя бы одному из множеств
-гХ1э "2 5 • • • J -An»
Пусть, например, х £ Ak, 1 < к <п. Так как Ак плотно в себе, то
х является предельной точкой множества А*,. Имеем: Ak С А, откуда
следует, что х является предельной точкой также и множества А. Точка

§ 1. Определение производной
265
х £ А была взята произвольно. Следовательно, все точки множества А
являются его предельными точками.
Предложение тем самым доказано. ♦
Определим, что есть производная функции.
Пусть дана функция / : А —> R, где А — плотное в себе
подмножество R. Рассмотрим отношение
т-па)
х — а
где а £ А, х € А.
Предел этого отношения при х, стремящемся к а по множеству А
в случае, если таковой существует, называется производной функции f
в точке а и обозначается одним из следующих выражений:
f'(a) = ^(a) = Df(a).
Согласно данному определению,
f{a) = щи /(ж)-/(0).
х-+а х — а
Предположим, что а есть двусторонняя предельная точка
множества А. В этом случае для функций, определенных на множестве А,
можно говорить о пределах слева и справа при х —> а.
Пусть дана функция / : А —> R. Пределы
//(а)= иш /(ж)-/(а); К(а)= lim MlM, (1Л)
х-*а-0 X - а х-*а+0 X — а
если таковые существуют, называются, соответственно, левой и правой
производными функции f в точке а. Для их обозначения мы будем
применять запись, указанную в равенствах (1.1).
Данными здесь определениями допускаются значения производных,
равные ±оо.
Определим еще одно важное свойство функций, тесно связанное с
понятием производной.
Пусть А есть плотное в себе множество.
Говорят, что функция / : А —> R дифференцируема в точке а £ А,
если существуют число L £ R и функция а : А —> R такие, что а(а) = 0,
а(х) —► 0 при х —> а, и для всех х £ А выполняется равенство:
f(x) = /(а) + L(x - а) + |я - о|а(я?). (1.2)

266 Гл. 4. Дифференциальное исчисление функций одной переменной
Условие дифференцируемости функции / в точке а допускает
следующее наглядное истолкование. В равенстве (1.2) положим х — а = h
и перепишем его следующим образом: /(а + К) — /(а) = Lh + \h\a(a + h).
Разность f(a + h) — f(a) есть приращение, которое получает значение
функции /, когда независимая переменная получает приращение h.
Равенство (1.2) означает, что приращение функции приближенно можно
считать пропорциональным приращению независимой переменной.
Погрешность, которая при этом возникает, бесконечно мала в сравнении с
приращением независимой переменной.
♦ Предложение 1.2. Если функция f дифференцируема в точке
a £ А, то она непрерывна в этой точке.
Действительно, при х —» а правая часть равенства (1.2) стремится
к /(а) и, значит, f(x) —> f(a) при х —> а. Это и означает, что функция /
непрерывна в точке а. ф
■ Теорема 1.1. Пусть icl есть плотное в себе множество. Для
того чтобы функция f : А —► R была дифференцируема в точке a E А,
необходимо и достаточно, чтобы она имела в этой точке конечную
производную. При этом если f дифференцируема в точке a £ А, то
коэффициент L в равенстве (1.2) равен /'(а).
Доказательство. Необходимость. Предположим, что
функция / : А —> R дифференцируема в точке а. Тогда, по определению,
f(x) = f(a) + L(x - a) + \x - a\a(x),
где a(x) —► 0 при x —> ano множеству А и a(a) = 0.
Отсюда получаем, что при всяком х Е А, отличном от а,
fW-fW=L + <r(x)a(x),
х — a
\gr» q\
где <r(x) = ', a(x) = ±1 при любом хфа.
х — а
Функция а является ограниченной и, значит, а(х)а(х) —> 0 при
х —► а. Отсюда вытекает, что
1ь,/М-/Ц=д.
ж—>а X — а
Таким образом, функция / имеет конечную производную в точке а.
При этом /;(а) = L.
Необходимость условия теоремы тем самым установлена.

§ 1. Определение производной
267
Докажем достаточность. Предположим, что функция
/ : А —► Ж имеет в точке a Е А конечную производную. При х ф а
положим:
a(x) = a(x)(j{x)x-_fa{a)-f'(a)y (1.3)
где, как и ранее, при х ф а
\х — а\
<т(х) =
х — а
Положим также а(а) == 0. Очевидно, а(х) —► 0 при х —► а.
Из равенства (1.3), после очевидных преобразований, получаем:
f(x) = f(a) + f'(a)(x -а) + (х- а)а(х)а(х),
f(x) = /(a) + f'(a)(x - а) + \х - а|а(ж). (1.4)
В проделанных рассуждениях предполагалось, что х ф а.
Полученное равенство, очевидно, выполняется также и при х = а.
Равенство (1.4) и есть то представление функции /, которое
требуется по определению дифференцируемой функции.
Мы получаем, таким образом, что функция / дифференцируема в
точке а и достаточность условия теоремы установлена.
Теорема доказана. ■
1.2. Правила дифференцирования
Зададим произвольно плотное в себе множество Ас1и точку
а £ А.
Ш Теорема 1.2. Пусть f:A-^Rng:A-*R суть функции,
дифференцируемые в точке а, Л и /л — вещественные числа. Тогда
функции S = \f + ^gnP = fg также дифференцируемы в этой точке.
При этом выполняются равенства:
S'(a) = \f'(a)+fig'(ayi (1.5)
P'(a) = f'(a)g(a) + f(a)g'(a). (1.6)
Если для всех х Е А выполнено д(х) ф 0, то функция R = — дифферен-
9
цируема в точке а. При этом
, _ f(a)g(a) - f(a)g'(a)
R{a)~ ьйр • (L7)

268 Гл. 4. Дифференциальное исчисление функций одной переменной
Доказательство. Требуется доказать, что каждая из функций
S = А/ + Mff, Р = /5 и (в случае, если #(#) ^ 0 Для всех ж Е А)
Л = — имеет конечную производную в точке а, причем эти производные
9
выражаются равенствами (1.5)—(1.7).
Для любого х Е А, отличного от а, выполняется равенство:
[А/(яр + м(х)] - [Л/(о) + Mg(tt)] = л/(ж)-/(о) + ^д(х)-д(а)
х — а х — a x — a
При ж —► а правая часть этого равенства стремится к конечному
пределу, равному А/' (а) + /лд'(а). Отсюда вытекает, что функция 5 в
точке а дифференцируема, причем ее производная равна Л/7 (а) +/лд,(а).
Далее имеем:
f(x)g(x) - f(a)g(a) = [/(ж) - /(а)]д(ж) + f(a)[g(x) - g(q)] =
ж — а х —• а
= №^Шд{х) + /(ffl)g(£bgW. (L8)
ж - а ж — а
Так как функция <?, согласно условию теоремы 1.2,
дифференцируема в точке а, то она непрерывна в этой точке и, значит,
д(х) —► д(а) при х —» а. При х —► а
№ ~ /(а) - /'(а); g(a:) ~ 9^а) -> </'(«)•
X CL X U
Отсюда следует, что при ж-^апо множеству А правая часть
равенства (1.8) стремится к пределу, равному
f'(a)g(a) + f(a)g\a).
Таким образом, дифференцируемость функции Р = fg в точке а
установлена. Одновременно доказано и неравенство (1.6).
Наконец, имеем:
РГ„Л _ п(п\ - ZM _ £И _ /(s)fl(a) ~ /(a)g(s) _
Щх) Щ*)-д{х) д{а)- д(х)д(а)
= Ц{х) - f(a)]g(a) - f(a)[g(x) - д(а)}
9(х)д(а)

§ 1. Определение производной
269
Отсюда
R(x) - R(a)
х-а д(х)д(а)
Пх)-Па)д(а)-На)9{х)-9(а)
х — а х - а
(1.9)
Функция д дифференцируема и, значит, непрерывна в точке а.
Следовательно, д{х) —► д(а) при х —> а по множеству А.
Так как при х —> а
ж — a v ж — а
то из равенства (1.9) следует, что отношение
Д(др - R(a)
х — а
при х —► а стремится к пределу, равному
/'(a)g(a)-/(%'(«)
[3(a)]2
Теорема доказана. ■
▼ Следствие. Если функция f : А —► R дифференцируема в точке
а £ А, то для любого A Е К функция А/ дифференцируема в точке a € А
и ее производная в этой точке равна А/'(а).
Для доказательства достаточно воспользоваться утверждением
теоремы о дифференцируемости функции 5 = \f + цд, полагая g = f и
/i = 0. ▼
■ Теорема 1.3 (о производной обратной функции). Пусть I есть
промежуток в множестве R и / : J —► К. — непрерывная строго
монотонная функция. Пусть J = f(I), g = /-1 и Ь — произвольная точка J.
Если функция f имеет в точке a = g(b) конечную или бесконечную
производную, то функция g = f~x имеет производную в точке Ь. При
этом если производная /'(а) конечна и отлична от нуля, то производная
д'(Ь) также конечна, причем
9'{ь) = Ш

270 Гл. 4. Дифференциальное исчисление функций одной переменной
если f{a) = 0, то д'(Ъ) = ±оо, где знак «+» следует брать в случае,
когда функция / — возрастающая, а знак «—» — в случае, когда функция
f является убывающей; если /'(о) = ±оо, то д'(Ъ) = 0.
Доказательство. Пусть у ф b есть произвольная точка
множества J. Имеем:
д(у) - д(Ь) _ д(у) - д(Ь) _ m„,,Ai
где
и-/ \ ж - а
я<*> = н*ГЖУ
При у фЬ будет 0(2/) ^ р(Ь) = а, в силу того, что отображение д
взаимно однозначно. При у —► Ъ выполнено д(у) —► р(Ь) = а.
Если f'{a) ф 0, /'(а) ^ ±оо, то при х —► а по /
Я(Ж) *
/'(«)■
Пусть /'(а) = 0. Если функция / — возрастающая, то
Н(х) > 0 для всех х £ I, x ф а.
Если функция / является убывающей, то Н(х) < 0 для всех
х е I, х ф а.
Отсюда следует, что
lim H(x) = оо
в случае, когда функция / является возрастающей, и
lim Н(х) = —оо,
ж—*а
если / — убывающая функция.
Наконец, если /'(а) = ±оо, то
lim H(x) = 0.
х—*а
Мы получаем, что Н(х) имеет конечный или бесконечный предел
при х —► а.

§ 1. Определение производной
271
В силу теоремы о замене переменной под знаком предела, отсюда
вытекает, что существует предел:
lim g(2/)~f(6) = lim H[g(y)] = lim H(x).
y—*b у — 0 у—*Ъ х—+а
Ввиду сказанного выше о пределе функции Н при х —► а, теорема
доказана. ■
■ Теорема. 1.4 (о производной суперпозиции). Пусть А и В суть
плотные в себе множества и функции f:A—>RHg:B^R таковы,
что f(x) Е В при каждом х £ А. Предположим, что функция f является
дифференцируемой в точке a £ А, ад дифференцируема в точке Ь = /(а).
Тогда суперпозиция g о / дифференцируема в точке а. При этом имеет
место равенство:
(9 о /)'(«) = 9'(b)f(a) = g'[f(a)}f'(a).
Доказательство. Так как, по условию, функция g
дифференцируема в точке 6 = /(а), то функция g допускает представление:
9(У) = 9(b) +9(Щу - Ъ)+(3(у)\у - Ь|, (1.10)
где /3(b) = 0 и /3(2/) —► 0 при у —► 6 по множеству Б.
Отсюда получаем:
«tfWl-itfWl = тМ=Ш + с{х)тх)]
х — а ж — а
/(*)-/(<»)
ж — а
, (1-и)
где <т(ж) = —1 при ж < а, <t(#) = 1 при ж > а и <т(а) = 0.
При х —► а имеем /(ж) —* Ь. Отсюда вытекает, что /3[/(#)] —► 0 при
ж —► а. Выражение, стоящее в равенстве (1.11) справа, при х —► а
стремится к пределу, равному g'{b)f'(a).
Тем самым дифференцируемость функции gof в точке а
установлена и доказано, что производная функции выражается формулой (1.10),
указанной в теореме.
Теорема доказана. ■
1.3. Дифференцирование основных элементарных функций
Исследуем вопрос о дифференцируемое™ основных элементарных
функций и найдем выражения для их производных всюду, где эти
производные существуют.

272 Гл. 4. Дифференциальное исчисление функций одной переменной
1. Функция f(x) = С, которая определена и является постоянной на
множестве R, дифференцируема в каждой точке х Е М, и ее производная
тождественно равна нулю.
2. Пусть п — произвольное целое число. Докажем, что функция
х \-> хп дифференцируема в каждой точке своей области определения,
причем имеет место равенство:
D(xn) = nxn~\ (1.12)
Пусть п —1. Возьмем произвольно точку a;Gl. Положим f(x) = х.
Тогда получим:
/(*) ~ /0*0 = \zJL = 1
t — х t — х
для любого f G К. Отсюда, очевидно, следует, что функция х •—> х
дифференцируема для всех жЕ1, причем D(x) = 1 для всех жЕМ.
Предположим, что для некоторого п Е N дифференцируемость
функции жи/в каждой точке а?ЕКи равенство (1.12) доказаны.
Имеем: хп+1 = хп х х и, значит, согласно теореме 1.2, функция
х н-> хп+1 дифференцируема для всех х Е М. При этом имеет место
равенство:
D(xn+1) = D(xn)x + xnD(x) = пхп-гх + хп = (п + 1)яп.
Это есть равенство, получаемое из (1.12), если заменить в нем п
на п +1.
В силу принципа математической индукции, из доказанного
следуют дифференцируемость функции х \-^ хп для любого п Е N при каждом
жЕ1и равенство (1.12).
Пусть п есть неположительное целое число, п < 0. Если ге = 0, то
хп = 1. В этом случае JD(#n) = 0 для всех х Е К. В частности, формула
(1.12) в этом случае верна.
Рассмотрим случай п < 0. Областью определения функции
х \-> хп в этом случае является множество R \ {0}, получаемое из М
исключением точки 0.
Пусть п = —га, где га Е N. Для любого х ф 0
Отсюда следует, что функция х \-► хп для всякого х ф 0 —
дифференцируема тсатс частное двух дифференцируемых функций — функции
х I—► 1 и функции ж н-> #т.

§ 1. Определение производной
273
Применяя правило дифференцирования частного (см. теорему 1.2),
получим:
1 ^ D(l)xm - rax™'1 _m_x n_x
«и-"!?)-
я»2т
Мы видим, что формула (1.12) верна ив этом случае.
3. Покажем, что функция ехр : х н-> ех для всех жЕМ
дифференцируема, причем для всех жб! выполняется равенство:
D(ex) = ex. (1.13)
Возьмем произвольно точку жЕ1. Для всякого t (Е Ш имеем:
е*-е* хе*~х -I
= е .
t — х t — х
При h -» 0
е^-1
Отсюда следует, что отношение
1.
t — x
при t —> х стремится к пределу, равному еж, что и требовалось доказать.
4. Покажем, что функция х \-> lux дифференцируема в каждой
точке х Е (0,оо), причем для любого х > О выполняется равенство
DQnx) = ±. (1.14)
Воспользуемся теоремой о производной обратной функции
(теорема 1.3).
Полагая в этой теореме I = R, J = (0,оо), / = ехр, Z""1 = In,
х = /(у) = еу, получим, что функция In дифференцируема в каждой
точке ж Е (0,оо), причем
z>(tox) = (r')'W = 7iy = s^ = i'
что и требовалось доказать.

274 Гл. 4. Дифференциальное исчисление функций одной переменной
5. Функция жи/, где аЕК, дифференцируема в каждой точке
х > О, причем D(xa) = аха~г для всех х Е (0, оо).
Действительно, для всех х > О имеем: ха = ехр(а\пх). Применим
теорему 1.4, полагая в ней д = ехр и / = a In. Тогда получим, что
функция х \-^ ха дифференцируема для всех х > 0. При этом
D(xa) = (/[/(ж)]/'(ж) = exp(aliix)aD(]iLx) = аха— = ах""1,
что и требовалось доказать.
В случае а > 0 функция F : х \-^ ха определена на замкнутом
слева промежутке [0, оо).
Исследуем вопрос о дифференцируемое™ этой функции в точке 0.
Имеем:
FQe)-F(O) _ «-1
Л — х .
ж-0
Отсюда следует, что для функции F :жиа;а, где а > 0,
выполнены соотношения:
( 0 при а > 1;
F'(0) = < 1 при а = 1;
^ оо при 0 < а < 1.
Полагая а = 1/2, получим, в частности, что функция х ь-> ^/ж
дифференцируема в каждой точке х > 0. При этом имеет место равенство:
2v^'
6. Для а = р/(2<7 + 1), где р и g — целые числа, р, g > 0, функция
F : ж ^ жа определена также для отрицательных значений х.
Покажем, что и в этом случае функция F является
дифференцируемой для всех х ф 0, причем имеет место равенство: F'(x) = аха~г.
Итак, пусть показатель а является рациональным числом
указанного здесь вида и F есть функция х н-> ха.
Докажем, что для всякого х ф 0 функция F в точке ж
дифференцируема, причем F\x) = ах01"1.
Для случая х > 0 это следует из доказанного ранее (см. 5).

§ 1. Определение производной
275
Рассмотрим случай х < 0.
Имеем: F(x) = (—1)а(—х)а. Если х < 0, то у = — ж > 0 и функция
жи/ дифференцируема в точке у. Отсюда следует, что функция F
дифференцируема во всякой точке х < 0. Имеем:
[F(x)]2q+1 = zp.
Дифференцируя обе части этого равенства, получим:
(2ff + l)[F(a:)]2flF'(ar)=lwp"1.
Отсюда
F// \ р X а—1
(#) = — = ах
что и требовалось доказать.
Мы предоставляем читателю рассмотрение вопроса о
дифференцируемое™ функции ха для данного а в точке 0.
7. Рассмотрим показательную функцию х \-+ ах, где а > 0, а ф 1.
Имеем: аж = ехр(#1па).
Таким образом, функция F : ж н-► аж является суперпозицией
функций д = ехр и / : ж и ж1па. Каждая из этих функций определена и
дифференцируема для всех жЕ1.
Имеем: д'(у) = #(у) для всех у 6 R и /'(я) = In а для всех жЕ1.
Отсюда получаем, что для всякого жЕ1 имеет место равенство:
F'{x) = «/'[/(я)]/'^) = »[/(ж)]1па = а*1па,
то есть мы приходим к тому, что D{ax) = аж1па для всех жЕ1.
Полученный результат может служить своего рода свидетельством
«естественности» натуральных логарифмов. Они с неизбежностью
возникают в связи с задачей о дифференцировании произвольной
показательной функции.
8. Найдем производные основных тригонометрических функций.
Зададим произвольно точку жЕ1. Для всякого t ф х имеем:
. х — t
sint — smx x + t sm о
t-x =C08^- -£НГ;
.V-< <115>
cos t - cos x _ . ж +1 sm о
= -2sin- -
t-z 2 s-t

276 Гл. 4. Дифференциальное исчисление функций одной переменной
Функции cos и sin, как было показано выше, непрерывны. Имеет
место равенство:
smx
lim = 1.
ж-+0 X
При t —» х
о • Х~*
2 sin
X + t X + t . *ош——
cos — ► cos ж; sm — > sma;; - ► 1.
2 ' 2 z-t
Отсюда следует, что каждое из отношений, стоящих в равенствах
(1.15), стремится к некоторому конечному пределу при t —> х.
В результате получаем, что функции sin и cos дифференцируемы
для всякого х £ К. При этом D(sinx) = cos ж; D(cosx) = —sin x для
любого жб1.
Рассмотрим функцию
sin х
tgz = .
cos х
Применяя правило дифференцирования частного (см. теорему 1.2,
равенство (1.7)), получаем:
_ /JL ч D (sin x) cos х — sin #jD (cos x) cos2 ж + sin2 x
D(tg x) = —± '- z = 2 •
COS2 X COS2 X
Окончательно
9. Применяя теорему о производной обратной функции (теорема
1.3), найдем производные обратных тригонометрических функций.
Сначала рассмотрим функции х н-> arcsina; ижи arccosa;.
Функция у I-+ sin у отображает промежуток [—7г/2,7г/2] на
промежуток [—1,1], и если — 7г/2 < у < 7г/2, то производная функции у ь-> sin у
в данной точке у отлична от нуля.
Пусть х € (—1,1), у = arcsinz. Тогда —7г/2 < у < 7г/2 и х = siny.
Из теоремы о производной обратной функции следует, что производная
D(arcsina;) определена и конечна для всех х 6 (—1,1), причем

§ 1. Определение производной
277
то есть
D (arcsin х) =
VT=
х<
Аналогичным образом, для х Е (—1,1), полагая у = arccosrc,
получим, что для всякого х Е (—1,1) функция х ь-> arccosa;
дифференцируема, причем
jD(arccosa?) =
D(cosy) sin у д/l - cos2 у л/l-x2'
то есть
JD(arccosx) = —
л/1 - х2'
Последнее равенство может быть получено также из тождества
arccosa; = -- — arcsin ж,
2
доказательство которого мы предоставляем читателю.
Функции х н-» arcsin а; ижи arccosa; имеют производные также и
в точках — 1 и 1. При этом производные функции arcsin в этих точках
равны оо, производные функции arccos равны — оо.
Выведем формулу для производной функции х »-» arctg x.
Мы получаем результат, который нельзя не считать
удивительным: производные функций arcsin а; и arccos а:, определенных чисто
геометрически, есть функции, которые могут быть определены средствами
алгебры без привлечения каких-либо соображений! Для всех жЕ1
имеем:
у = arctg х е (-7г/2,7г/2).
Возьмем произвольно х El. Пусть у = arctg х. Тогда х = tg у.
Теорема 1.3 о производной обратной функции позволяет
заключить, что функция arctg дифференцируема для всех х £Ж. При этом
1 2,
D(arctg х) = —г г = cos у =
D(tgy) * l + tg2y 1 + х2'
Окончательно получаем:
r>(arctga;) = I-^. (1.17)

278 Гл. 4. Дифференциальное исчисление функций одной переменной
§2. Некоторые приложения понятия производной
В этом параграфе рассматриваются примеры, в которых находит
применение понятие производной. Определяется понятие касательной
для кривой, заданной уравнением у = f(x). Вводится понятие
параметризованной кривой, и определяется понятие касательной в точке
параметризованной кривой. Устанавливается некоторое достаточное условие
существования касательной в точке параметризованной кривой.
Рассматриваются различные примеры параметризованных кривых.
Определяется понятие полярной системы координат на плоскости.
Приводятся примеры кривых в полярной системе координат,
устанавливается достаточное условие существования касательной для кривой,
рассматриваемой в полярной системе координат.
Приводятся также примеры физического происхождения, в которых
возникает понятие производной.
2.1. Касательная графика функции
Пусть дана функция / : М -> R. На плоскости введем декартову
ортогональную систему координат. Координаты произвольной точки
Р на плоскости будем обозначать буквами £ и т?.
Рис. 1
Построим график функции f (см. рис. 1). Зададим произвольно
xq е М, и пусть х — любая другая точка множества М. Рассмотрим
точки Р0 = (x0,f(xo)) и Рх = (х,/(х)). Прямая 1Х = Р0РХ, проходящая
через эти точки, называется секущей графика функции f. Эта прямая
не параллельна оси Оу системы координат и не совпадает с ней.
Как известно из аналитической геометрии, прямая 1Х определяется
уравнением вида т? = к(х)(£ — хо) + f(xo), где к(х) есть некоторое число —
угловой коэффициент прямой 1Х.

§ 2. Некоторые приложения понятия производной
279
Прямая 1Х есть множество всех точек Р = (£,Т7), координаты
которых удовлетворяют данному уравнению. В частности, ему
удовлетворяют координаты точки Рх = (#, /(#)).
Отсюда, после простых вычислений, получаем:
к(х) = /(«) - /Ы,
X — Хо
Предположим, что функция / имеет в точке хо конечную
производную, и пусть I есть проходящая через точку Ро прямая, определяемая
уравнением: т\ = f'(xo)(£ - хо) + f(xo).
Пусть /.(1Х,1) означает наименьший угол между прямыми 1Х и I.
Тогда при х —► хо угол Z(ZX, I) стремится к нулю.
Действительно, применяя известные формулы аналитической
геометрии, получаем:
Z(lx,l) = arctg
к(х) - f(x0)
1 + k(x)f'(x0)
При х —> хо имеем к(х) —* /'(#о), откуда следует, что Z(lx,l) —► О
при х —> хо-
Прямая I называется касательной графика функции f в точке Ро =
— (xo,f(xo))- Она представляет собой предельное положение секущей
1Х графика функции /, когда х —» хо.
Точный смысл этого таков: угол между прямыми 1Х и I стремится
к нулю при х —* хо-
2.2. Понятие параметризованной кривой. Касательная к
параметризованной кривой
2.2.1. Напомним некоторые сведения из аналитической геометрии.
На плоскости зададим декартову ортогональную систему
координат. Пусть X — точка на плоскости, имеющая координаты х и у. Будем
писать: X = (#,у).
Буква О далее означает начало системы координат, символы Ох
и Оу означают оси системы координат, Ох есть множество всех точек
X, у которых вторая координата у равна нулю, и аналогично Оу есть
совокупность всех точек вида (0, у).
Напомним, что вектором на плоскости или в пространстве
называется всякая упорядоченная пара точек (X, У). Точка X, первая
компонента пары, называется началом вектора, а точка У, вторая компонента

280 Гл. 4. Дифференциальное исчисление функций одной переменной
пары, называется концом вектора. Вектор, начало которого есть точка
X, а конец — точка У, обозначается символом XY.
Для векторов определяются понятие равенства и операции
сложения векторов и умножения вектора на число. Мы не приводим этих
определений, отсылая читателя к руководствам по аналитической
геометрии.
Для произвольной точки X на плоскости вектор х = ОХ
называется радиус-вектором точки X относительно точки О.
Пусть х есть произвольный вектор на плоскости, х и у —
координаты этого вектора в данной системе координат. В этом случае мы
будем писать: х = (гг,у).
2.2.2. Далее рассматриваются также и некоторые пространственные
объекты. В пространстве зададим декартову ортогональную систему
координат. Пусть О — начало системы координат. Запись X =
= (#1>#2>#з) означает, что X есть точка пространства, имеющая
координаты ал, жгижз. Точку X будем отождествлять с ее радиус-вектором
х = ОХ относительно начала координат. Координаты вектора х,
очевидно, совпадают с соответствующими координатами точки X.
Пусть I — произвольная прямая на плоскости или в пространстве.
Зададим произвольно точки Хо Е / и Х\ Е L такие, что Хо ф Х\, и
пусть z = Х§Х\. Пусть а = OXq есть радиус-вектор точки Хо
относительно точки О.
Произвольная точка X будет принадлежать данной прямой I в том
и только в том случае, если вектор и = ХоХ коллинеарен вектору z, то
есть существует число t Е Е такое, что u = tz. Имеем:
ОХ = Ш"о+Х^Х.
Отсюда следует, что прямая / совпадает с совокупностью
всех точек -X"(t), для которых имеет место равенство:
x(*) = o£(t) = a + zt, (2.1)
где t — произвольное вещественное число.
Обратно, если заданы векторы а и z, причем z ф 0, то множество /
всех точек X(t), радиус-вектор которых x(t) = OX(t) относительно
начала О допускает представление вида (2.1), есть прямая, коллинеарная
вектору z и проходящая через точку А, радиус-вектор которой ОА = а.
Говорят, что (2.1) есть параметрическое представление прямой I.

§ 2. Некоторые приложения понятия производной
281
2.2.3. Чтобы придать точный смысл интуитивному понятию линии
на плоскости или в пространстве, введем понятие параметризованной
кривой.
На плоскости зададим декартову ортогональную систему
координат. Предположим, что всякому значению t из некоторого множества
МСК сопоставлена точка X(t) = (f(t),g(t)) на плоскости.
Будем говорить, что отображение t ь-> X(t) непрерывно, если
каждая из вещественных функций / и # непрерывна на множестве М.
Непрерывное отображение t Е M ь+ X(t) = (f(t),g(t)) называется
параметризованной кривой на плоскости. Переменная t Е M
называется параметром кривой
X(t) = (f(t),g(t)),
множество М — множеством значений параметра. Образ
множества М относительно отображения X называется носителем
параметризованной кривой.
Обычно, говоря о параметризованной кривой, предполагают, что
множество М есть некоторый отрезок множества Ш. Это условие,
однако, может и не выполняться.
Данное определение распространяется на случай обычного
трехмерного (евклидова) пространства практически без изменений.
Будем предполагать, что в пространстве задана декартова
ортогональная система координат.
Пусть М есть произвольное множество в R. Предположим, что
всякому значению t Е M сопоставлена точка X(t) = (f(t),g(t),h(t)) в
пространстве. Отображение X, определенное указанным образом,
называется непрерывным, если вещественные функции /(£), g(t) и h(t)
непрерывны на множестве М.
Всякое непрерывное отображение I : М и I(t) множества М
в пространство называется параметризованной кривой в пространстве.
Переменная t E M называется параметром кривой
X(t) = (f(t),g(t),h(t)),
М — множеством значений параметра. Совокупность всех точек
вида X(t) = (f(t),g(t),h(t)) называется носителем параметризованной
кривой.
Пусть L — произвольное множество на плоскости. Говорят, что
параметризованная кривая X : М —► Ш2 дает параметрическое
представление множества L, если L есть носитель X, то есть L = Х(М).

282 Гл. 4. Дифференциальное исчисление функций одной переменной
Понятие носителя параметризованной кривой может показаться
отвечающим наглядному представлению о кривой как о линии. Движение
кончика карандаша по листу бумаги естественно рассматривать как
параметризованную кривую на плоскости, понимая под X(t) точку, в
которой кончик карандаша в момент времени t касается плоскости
листа. След, зачерчиваемый кончиком карандаша, есть носитель этой
параметризованной кривой.
Следует сказать, что в общем случае носитель параметризованной
кривой может представлять собой множество, достаточно далекое от
наглядных представлений о линии, как показывает следующая теорема.
■ Теорема 2 Л (теорема Пеано). Существует параметризованная
кривая X : [0,1] —> R2 на плоскости, носителем которой является
квадрат [0,1] х [0,1].
Теорема Пеано утверждает, что существует непрерывное
отображение X отрезка [0,1] в плоскость такое, что, когда параметр t
пробегает промежуток [0,1], точка X(t) пробегает все точки квадрата.
Параметризованная кривая, существование которой устанавливает данная
теорема, называется кривой Пеано.
Мы не будем приводить здесь доказательство теоремы Пеано
(теоремы 2.1), поскольку оно достаточно громоздко и требует применения
свойств плоскости, доказательство которых будет дано позднее. В
дальнейшем теорема Пеано не используется.
2.2.4. Пусть А = (а,Ь) есть произвольная точка на плоскости, а = ОА
— ее радиус-вектор, г > 0 — вещественное число.
Рассмотрим параметризованную кривую X(t) = (/(t),p(t)),
где /(£) = а + г cost, g(t) = b + r sint, t G R. Для всякого t £ К имеем:
|x — a| = г, так что точки x(t) лежат на окружности с центром А и
радиусом г. Будем обозначать эту окружность символом S(A,r).
Пусть X = (х,у) есть точка окружности S(A, r). Тогда имеет ме-
/ \2/ *\9 9i-r X — &л V — Ь
сто равенство [х — а) + (у — о) = г . Полагаем а = , р = .
г г
Имеем: а2 + /?2 = 1, и, значит, найдется t 6 R, для которого а = sint,
/? = cost. Для этого t имеем: х = a + rcost = /(£), у = Ь + rsint = g(t).
Точка X G S(A, r) была взята произвольно. Из доказанного поэтому
следует, что, когда t пробегает множество R, точка X(t) обегает всю
данную окружность, не пропуская ни одной ее точки, то есть t »-► X(t)
есть отображение R на 5(А,г).
Будем говорить, что X(t) = (a + rcost,b + r sint) есть
параметризация окружности 5(А,г).

§ 2. Некоторые приложения понятия производной
283
Определим понятие касательной в точке параметризованной кривой.
Пусть Х(£), t Е М, есть параметризованная кривая на плоскости
или в пространстве. Будем предполагать, что множество МсК
является плотным в себе, то есть всякая точка to Е M является его
предельной точкой.
Пусть ti Е М, £2 Е М. Предположим, что точки Х\ = X(ti) и
Хг = Xfo) различны. Обозначим через lx{ti,t2) прямую, проходящую
через эти точки. Определим некоторый вектор z, полагая z = X1X2 в
>
случае £i < £2, а если £2 < £i, то пусть z = Х2Х1. Вектор z будем
называть направляющим вектором секущей lx{t\,t2) параметризованной
кривой X, определенной по точкам Xi = X(ti) ж Х2 — Xfa)-
Введем еще некоторое обозначение. Пусть z есть направляющий
вектор секущей lx(ti,t2) данной параметризованной кривой. Полагаем:
e(*i,*2) = t-tz-
N
Определим понятие предела для вектор-функций. Пусть М С М
— произвольное множество и р есть предельная точка М.
Предположим, что для всякого t E M определен вектор х(£) на плоскости или в
пространстве. В этом случае говорят, что на множестве М
определена вектор-функция х. Вектор а называется пределом вектор-функции
х при t —► р, если lim |x(t) — а| = 0. В этом случае будем писать:
t-*p,t£M
а= lim x(£).
t-*p,teM
Пусть вектор х(£) имеет координаты: (/(£),#(<)), а координаты
вектора а суть числа (гл, v). (Рассматривается случай вектор-функции,
значения которой суть векторы на плоскости.) Тогда вектор а является
пределом х(£) при t —> р в том и только в том случае, если и = lim f(t)
и v = lim g(t). Аналогичное утверждение верно также и в случае
вектор-функций, значения которых суть векторы в пространстве.
Пусть дана параметризованная кривая X : t E М »-► Х(£) на
плоскости или в пространстве. Символом х(£) будем обозначать радиус-вектор
точки X(t) относительно начала, х(£) = OX(t).
Будем говорить, что to Е М есть точка типа NS(X), если
выполнено следующее условие. Существует 6 > 0 такое, что если t E М, причем
|t - t0| < 6 и t ф to, то X(t) ф X(t0).
Пусть to есть точка типа NS(X) та. 6 > 0 таково, что для всякого
t Е М такого, что t ф to и |£ — to| < 6, X(t) ф X(to). Для всякого такого t
определен вектор е(£о, t). Предел вектор-функции t ь-> е(£о, t) при £ —> to,
если таковой существует, называется касательным ортом в точке X(to)

284 Гл. 4. Дифференциальное исчисление функций одной переменной
параметризованной кривой X(t) и обозначается символом tx(to). При
каждом t € М, для которого X(t) ф X(to), длина вектора e(to, t) равна 1.
Отсюда следует, что длина вектора tx(to) также равна 1.
Предел вектор-функции e(to,t) при t —► to слева, если таковой
существует, называется левым касательным ортом в точке X(to)
параметризованной кривой X и обозначается символом tx(to). Предел вектор-
функции e(to,t) при t, стремящемся к to справа, называется правым
касательным ортом в точке X(to) и обозначается символом tx(to).
Говорят, что X(to) есть гладкая точка параметризованной кривой
X, если существует касательный орт tx(to). Если в точке X(to)
существуют левый и правый касательные орты кривой, причем эти орты
совпадают, t^(to) = tx(to), то X(to) есть гладкая точка кривой. В
этом случае tx(to) = tx(^o) = tx(^o)- Если t^(to) ф tx(^o), то говорят,
что X(to) есть угловая точка параметризованной кривой X(t). В том
частном случае, когда tlx(to) = —tx(to), говорят, что X(to) есть точка
возврата параметризованной кривой X(t).
Прямая Z, проходящая через точку X(to) и ко л линеарная вектору
tx(to), называется касательной в точке X(to) параметризованной
кривой X(t).
Ш Теорема 2.2. Пусть X(t), t е М, где МсК — плотное в себе
множество, есть параметризованная кривая на плоскости, X(t) = (/(t),
9(t))-
Тогда если функции f и g дифференцируемы в точке to Е М и
вектор x'(to) = (f'(to)i9f(to)) отличен от нуля, то параметризованная
кривая X(t) имеет касательную в точке X(to) и вектор т—тт—гг является
1х(*о)|
касательным ортом в точке X(to) кривой X(t).
Аналогично, если параметризованная кривая
X(t) = (f(t),g(t),h(t)), teM,
в пространстве такова, что функции f,gnh дифференцируемы в точке
to Е М и вектор х! (to) = (f'(to)^g' (to),fo'(*o)) отличен от нуля, то кривая
(4. \ гт X'(to)
имеет в точке a;(to) касательную. При этом 7—77—п есть касательный
|x'(t0)|
орт в точке X(to) кривой X(t).
Доказательство. Ограничимся случаем плоских кривых. Для
пространственных кривых рассуждения проводятся аналогичным
образом.

§ 2. Некоторые приложения понятия производной
285
Пусть выполнены все условия теоремы. Имеем:
X(t) = (f(t),g(t)), teM.
Пусть x(t) = OX(t) есть радиус-вектор точки X(t) относительно начала
системы координат. Функции f та. д дифференцируемы в точке to и
вектор х7(£о) = (/Ч'о),*/7^))) отличен от нуля.
Из условия х'(£о) ф 0 вытекает, что, по крайней мере, одна из
производных /'(to) и g'(to) отлична от нуля.
Предположим, что /'(to) ф 0. Согласно определению производной,
пи)= ш fMzlM.
t-^t0,t£M t — to
В силу известных нам свойств предела, найдется 6 > 0 такое, что
f(f\ __ f (f \
для если \t — to\ < £, то —— —- ф 0. Отсюда следует, что если
t — to
t ф to таково, что \t — to\ < 6, то /(t) ф /(to), и, значит, для всякого
t £ М такого, что t ф to и \t — to\ < 6, точка X(t) отлична от точки
X(to), так что to есть точка типа NS(X).
Если /'(to) = 0, то g'{to) ф 0 и аналогично заключаем, что
существует 6 > 0 такое, что если 0 < \t — to\ < 6, то g(t) ф #(to), и, значит,
X(t)?X(t0).
Пусть t £ М таково, что 0 < |t—*о| < 6. Положим R(t) =—— ^-^-.
t — to
Для данного t определен вектор e(to,t). Если t > to, то
, v _ x(t) - x{tp)
e(t0't}-|x(t)-x(t0)r (2-2)
Разделив числитель и знаменатель дроби в правой части равенства (2.2)
на t — to > 0, получим, что
««..O-jjgijj- (2-3)
Если t < <о, то
_ xftp) - s(t) ,
^•^"Widj-xwi- (2'4)
Разделив числитель и знаменатель на to — t > 0 и замечая, что
x(t0) - x(t) _ x(t) - x(t0) = д^
to — t t — to

286 Гл. 4. Дифференциальное исчисление функций одной переменной
получим, что и в этом случае верно равенство (2.3).
Мы получаем, что для всякого t Е М такого, что 0 < \t — to| < 8,
справедливо равенство (2.3).
Имеем:
9(t)-g(toY
R(t)
(№-№)
V t - to '
t-t0
При t —► to, в силу условия теоремы, вектор-функция R(t) стремится
к пределу, равному x'(to) = (f'(to),g'(to)) ф 0. Отсюда следует, что
вектор-функция e(to,t) имеет предел при t —> to, равный т—~—~.
Iх v^o)l
Таким образом установлено, что кривая X(t) имеет в точке X(to)
, ,. ч x'(to)
касательный орт, причем имеет место равенство: tx(to) = -,—7—77.
Iх (*о)|
Теорема доказана. ■
2.2.5. Понятия простой дуги и простой замкнутой
кривой.
Символом Р будем здесь обозначать множество, которое есть либо
плоскость, либо пространство.
Множество L на плоскости или в пространстве называется
простой дугой, если существует непрерывная функция х : [а, Ь] —» Р,
которая взаимно однозначно отображает отрезок [а, Ь] на множество L (см.
рис. 2(1)).
Множество С называется простой замкнутой кривой на
плоскости или в пространстве, если существует непрерывное отображение
х : [а,Ь] —> Р, такое, что х([а, Ь]) = С, причем х(а) = х(Ь), и на
полуоткрытом отрезке [а, Ь) отображение х взаимно однозначно (см. рис. 2 (2)).
(2)
(3)
Рис.2

2. Некоторые приложения понятия производной
287
Отрезок, концами которого являются произвольные точки А и В,
АфВ, является простой дугой. Действительно, пусть а = Ol, b = OB
суть радиус-векторы точек А и В относительно начала О. Тогда
функция х(£) = (1 — t)a + tb взаимно однозначно отображает промежуток
[0,1] наЬ = [АВ].
График произвольной непрерывной функции /, определенной на
замкнутом отрезке [а, Ь] множества R, является простой дугой.
Действительно, в этом случае функция х(£) = (£, f(t)) непрерывна и взаимно
однозначно отображает промежуток [a, ft] на график функции /.
Окружность на плоскости может служить примером простой
замкнутой кривой. Действительно, пусть (а, Ь) есть центр окружности,
г — ее радиус. Положим: х(£) = (a+rcost, ft+r sint),t G [0,27г].
Нетрудно видеть, что функция х отображает промежуток [0,27г] на окружность,
х(0) = х(27г), и на промежутке [0,27г] отображение х взаимно
однозначно.
Можно показать, что граница треугольника представляет собой
простую замкнутую кривую.
Стороны произвольного плоского выпуклого многоугольника также
образуют простую замкнутую кривую. На рис. 2 (3) изображены линии,
ни одна из которых не является ни простой дугой, ни простой замкнутой
кривой.
2.2.6. Рассмотрим примеры параметризованных кривых.
Пример 1. Пусть х(£) = а + Ы есть параметризация некоторой
прямой I на плоскости или в пространстве, z ф 0.
Тогда, как следует из теоремы 2.1, параметризованная кривая х(£),
определенная последним равенством, имеет в каждой точке
касательную. Эта касательная совпадает с прямой I.
Пример 2. Пусть х(£) = (f(t),g(t)) есть параметризация
окружности радиуса г > 0 с центром в точке А = (a, ft),
f(t) = a + rcost, g(t) = ft + rsint,
где t G R. Имеем: /'(£) = —rsint и </(*) = rcost. Отсюда следует, что
[/'(<)]2 + W(t)}2 = r2 # о
для всех t. В силу теоремы 2.1, отсюда вытекает, что
параметризованная кривая х(£) = (f(t),g(t)) имеет касательную в каждой точке x(t).
Вектор х'(£) = (—г sin £, r cost) является касательным ортом в точке

288 Гл. 4. Дифференциальное исчисление функций одной переменной
X = x(t). Вектор АХ имеет координаты: (г cost,rsint). Отсюда
вытекает, что (АХ, х'(£)) = —г2 cos t sin t+r2 sin t cos t = О, и, значит, векторы
AX и x'(£) ортогональны. Это позволяет заключить, что касательная
окружности в точке х(£), как и следовало ожидать, ортогональна
радиусу окружности, концом которого является точка х(£).
Пример 3. Предположим, что дана окружность, катящаяся без
скольжения по некоторой прямой. Тогда всякая точка окружности
описывает на плоскости кривую, которая называется циклоидой.
Найдем параметрические уравнения циклоиды.
Будем считать, что прямая, по которой катится окружность,
совпадает с осью Ох. Фиксируем на окружности некоторую точку X,
траекторию которой мы и будем изучать.
X
Рис. 3
Обозначим через г радиус окружности. Пусть H{t) есть точка (£, 0)
оси Ox, C(t) = (t,r) — положение, которое занимает центр окружности
в момент, когда она касается оси Ох в точке H(t), X(t) = (x(t), y(t))
— положение данной точки X, когда катящаяся окружность касается
оси Ох в точке H(t). Для каких-то значений t точка X(t) будет лежать
на оси Ох. Будем считать, что Х(0) лежит на оси Ох и совпадает с
началом системы координат. Этого, очевидно, можно добиться
надлежащим выбором начала системы координат. Вектор z(t) = C(t)X(t)
(см. рис. 3) при качении окружности вращается п о часовой стрелке
и угол, который он составляет со своим начальным положением z(0),
равен (р = —. Длина дуги окружности от точки H(t) до точки X(t)

§ 2. Некоторые приложения понятия производной
289
равна длине отрезка [OH(t)] прямой Ох. Отсюда вытекает, что имеют
место равенства:
x(t) = t — г sin -, у(t) —r — r cos -.
Это и есть искомые параметрические уравнения циклоиды.
2.2.7. Рассмотрим вопрос о существовании касательных у
циклоиды. Имеем:
//.\ -, t Л . 2 t //,\ . * Л . t t
х (t) = 1 — cos - = 2 sin —, v (*) = sin - = 2sm —- cos —-.
w r 2r' y w r 2r 2r
Тогда [rr'(t)]2 + [y7(*)]2 = 4 sin2 —. Отсюда следует, что [x'(t)]2+
+[y'{t)]2 = 0 в том и только в том случае, если — = 7гш, где т —
2г
произвольное целое число, то есть для t = 2ттгг.
Для всех остальных значений t будет [x'(t)]2 + [y'(t)]2 ^Ои, значит,
для этих t циклоида имеет касательную в точке, отвечающей данному
значению t.
Для значений £, таких, что отношение -— не является целым чи-
27Г7*
слом, имеет место неравенство: y(t) > 0.
Отсюда ясно, что точки, в которых [а/^)]2 + Wit)]2 = 0, совпадают
с теми точками на оси Ож, в которых лежит рассматриваемая точка
окружности. (Вопрос о существовании касательных циклоиды в таких
точках будет рассмотрен в § 9 этой главы.)
Кривая, зачерчиваемая произвольной точкой, лежащей на радиусе
окружности, катящейся без скольжения по прямой, называется
трохоидой (см. рис. 4).
Параметрические уравнения трохоиды имеют вид:
x(t) = t — hsin -, y(t) = г — hcos -.
г г
В этих равенствах h есть расстояние до центра окружности точки,
траектория которой рассматривается. Вид трохоиды зависит от того, будет
h > г или h < г.
Верхняя кривая на рис. 4 есть трохоида, соответствующая случаю
h> г. Средняя кривая на рис. 4 есть циклоида. Третья кривая,
изображенная на рис. 4, есть трохоида, получаемая при h < г.
Обоснование того, что циклоида выглядит именно так, как указано
на рис. 4, приводится в § 9 этой главы.

290 Гл. 4. Дифференциальное исчисление функций одной переменной
Рис. 4
2.2.8. Рассмотрим кривые, получаемые при качении одной окружности
по другой окружности.
Пример 4. Предположим, что на плоскости задана некоторая
окружность Г радиуса Я, и рассматривается окружность Д радиуса г,
катящаяся по окружности Г без скольжения.
Зададим произвольно точку X, жестким образом связанную с
окружностью Д. При движении окружности Д точка X описывает на
плоскости некоторую линию.
Заметим, что возможны два случая:
1) Д катится по внешней стороне окружности Г, то есть Д и Г
лежат по разные стороны их общей касательной;
2) Д катится по внутренней стороне Г, то есть данные
окружности лежат по одну сторону от их общей касательной.

§ 2. Некоторые приложения понятия производной
291
Если окружность Д катится по внешней стороне окружности Г, то
траектория точки X в случае, если точка X лежит на самой окружности
Д, называется эпициклоидой, а если X £ Д, то — эпитрохоидой.
Если Д катится по внутренней стороне окружности Г, то в случае,
когда X G Д, траекторию точки X называют гипоциклоидой, а при
X £ Д — гипотрохоидой.
Найдем параметрические уравнения эпициклоиды и эпитрохоиды.
Пусть i? есть радиус окружности Г, г* — радиус Д. Будем считать,
что центр Г совпадает с началом системы координат (см. рис. 5).
Рис. 5
Предположим, что окружность Д катится по Г в направлении
против часовой стрелки. Пусть t есть длина пути, пройденного по
неподвижной окружности точкой H(t) касания данных окружностей,
отсчитываемая от некоторого начального положения.
Пусть X(t) есть положение точки, траектория которой
рассматривается, отвечающее данному t. Для некоторых значений t точка X(t)
попадает на окружность Г.
Будем считать, что это имеет место, в частности, для t = 0, причем
Х(0) = (Я, 0), то есть точка Х(0) лежит на положительной полуоси оси
Ох. Этого можно добиться надлежащим выбором начала отсчета
параметра t и системы координат, в которой производятся все дальнейшие
построения.

292 Гл. 4. Дифференциальное исчисление функций одной переменной
Очевидно, Н(0) = Х(0). Положение центра окружности А,
соответствующее значению £, обозначим через C(t).
Дуга H(0)H(t) окружности Г и дуга H(t)X(t) окружности А имеют
равные длины. Это и означает, что окружность А катится по Г без
скольжения.
Положим u(t) = OC(t), z(t) = C(i)X(t). Радиус-вектор х(£)
точки X(t), очевидно, равен u(t) + z(t). Вектор z(t) может быть получен
следующим образом. Сначала окружности Г и А, взятые в положении,
соответствующем значению t = О, повернем вокруг точки О на угол,
равный t/R, в направлении против часовой стрелки. В результате
такого вращения окружность Г перейдет в себя, а А займет положение,
соответствующее данному t. После этого окружность А поворачиваем
вокруг ее центра, т. е. вокруг точки C(t) на угол - в направлении
против часовой стрелки (см. рис. 5). В результате вектор C(t)H(t)
перейдет в вектор z(t). Вектор z(t) получается из своего начального
положения, соответствующего значению t = 0 как результат двух вращений
— сначала на угол t/R, а затем на угол t/r. Отсюда следует, что со
своим начальным положением он образует угол, равный — + -. Вектор
R г
С(0)Н(0) составляет с положительной полуосью оси Ох угол, равный
7г. Отсюда получаем, что вектор z(t) составляет с указанной полуосью
угол, равный — Н h 7Г и, значит, вектор z(t) имеет координаты:
R Г
u = rcos(! + i+7r)=-rcos(! + J),
V = rsin(l + ^+7r)=-rsin(| + ^).
Для всякого t £ R имеем: OX(t) = u(t) + z(t), откуда следует, что точка
X(t) имеет координаты:
f(t) = (R + r)cosl-rcos(± + i),
t ft t\ ^ >
g(t) = (R + r)sin--rsm^- + -J .
Полученные равенства и есть параметрические уравнения
эпициклоиды. На рис. 6 и 7 представлены примеры эпициклоид. Вид эпици-
v
клоиды существенно зависит от величины отношения —. На рис. 6
XL

§ 2. Некоторые приложения понятия производной
293
- г х
изображена эпициклоида, для которой — = -, на рис. 7 представлена
R о
г 2
эпициклоида, получаемая, когда — = -.
R о
Рис. 6 Рис. 7
Найдем параметрические уравнения гипоциклоиды.
Параметрические уравнения гипоциклоиды мы получим, если
заменим в равенствах (2.5) г на —г. В результате этого будем иметь:
/(*) = (Я " г) cos - + г cos (- - -J ,
g(t) = (Я - r)sin - + rsin (д - -) •
Это и есть параметрические уравнения гипоциклоиды.
Рис. 8 Рис. 9
г 1
На рис. 8 изображена гипоциклоида, для которой — = ~, на рцс. 9
R 3
г 1
— гипоциклоида, получаемая, когда — = -. Кривая, представленная
хг 4
на рис. 9, называется также астроидой.
Найдем параметрические уравнения эпитрохоиды и гипотрохоиды.

294 Гл. 4. Дифференциальное исчисление функций одной переменной
Заменим в выражении для координат вектора z число г на h.
В результате получим параметрические уравнения эпитрохоиды:
/(*) = (R + г) cos -| - hcos (-| + ^ ,
g(t) = (Я + г) Sin | - hsin (| + £) .
(2.6)
Л/г. /0
Л/л 7/
Примеры эпитрохоид представлены на рис. 10 и 11. На рис. 10 —
эпитрохоида, для которой h > г, а на рис. 11 — эпитрохоида,
получаемая при h < г. На обоих рисунках отношение радиуса катящейся
1
окружности к радиусу неподвижной окружности равно -.
Параметрические уравнения гипотрохоиды имеют вид:
/(*) = (R ~ г) cos - + Л cos (- - -) ,
g(t) = (R-r)sin— + hsm[- - -J .
(2.7)
Рис. 12
Рис. 13

§ 2. Некоторые приложения понятия производной
295
г 1
На рис. 12 изображена гипотрохоида, для которой h > г, а — = -,
И 4
г 1
на рис. 13 — гипотрохоида, которая получается при h < г и. — = -.
XL 4
Легко устанавливается, что в каждой точке x(t) эпициклоиды, для
которой |х(£)| > i2, выполняется условие теоремы 2.2 и, значит, в каждой
такой точке она имеет касательную.
Аналогичным образом заключаем, что гипоциклоида имеет
касательную в каждой точке х(£), для которой выполняется неравенство:
|x(t)| < R.
Можно привести и другие примеры кривых, замечательных в том или
ином отношении. Кривые, рассмотренные здесь, сыграли определенную роль
в истории математики. На заре становления дифференциального и
интегрального исчисления они нередко использовались для проверки эффективности
новых математических методов.
Одна из классических задач, при решении которой возникает циклоида,
— задача о линии наискорейшего ската или «брахистохроне»,
сформулированная в 1696 г. Иоганном Бернулли.
Даны точки Р и Q над поверхностью Земли, не лежащие на одной
вертикальной прямой, причем точка Р расположена выше точки Q. Задача состоит
в том, чтобы найти линию, соединяющую Р и Q и такую, что под
действием силы тяжести материальная точка скатится по этой линии из точки Р в
точку Q за кратчайшее время. Решения этой задачи были найдены И.
Бернулли, Я. Бернулли, Г. Лейбницем, И. Ньютоном и Г. Лопиталем. Оказалось,
что искомая кривая есть дуга циклоиды, получаемой качением окружности
по горизонтальной прямой, проходящей через точку Р. Окружность при этом
должна находиться ниже указанной прямой. Ее радиус определяется из
того условия, что циклоида должна проходить через данные точки Р и Q (см.
рис. 14.)
Рис. 14
Задача о брахистохроне в эпоху Ньютона и Бернулли явилась первой из
числа задач, ставших несколько позже объектом исследования для
направления математического анализа, называемого вариационным исчислением.

296 Гл. 4. Дифференциальное исчисление функций одной переменной
Известны и другие механические задачи, решение которых дается дугой
циклоиды.
Эпитрохоиды, так же как и гипотрохоиды, впервые появились в
математике, по-видимому, в связи с геоцентрической системой мира, разработанной
Клавдием Птолемеем (2-й век нашей эры). В этой системе Земля считается
центром мира, вокруг которого вращаются небесные светила. Согласно
Птолемею, движение планет вокруг Земли получается сложением двух движений.
Планета равномерно движется по некоторой окружности (называемой
эпициклом), центр которой, в свою очередь, равномерно перемещается по другой
окружности. В том случае, когда плоскости этих окружностей совпадают,
траектория планеты представляет собой либо эпитрохоиду, либо
гипотрохоиду-
Заметим, что для того, чтобы объяснить все наблюдаемые особенности
движения планет, Птолемей вынужден был вводить эпициклы высших
порядков и следующим образом описывать движение планеты как сумму
движений. Задается несколько окружностей. Планета движется равномерно по
первой, самой маленькой окружности, центр которой равномерно
перемещается по второй окружности, а центр этой последней равномерно движется по
третьей окружности и т. д.
Геоцентрическая система Птолемея, в свое время, имела важное
практическое значение. Она позволяла предсказывать положение небесных светил с
точностью, удовлетворительной для практических целей. Причины, по
которым человечество, в конце концов, отказалось от системы Птолемея, связаны
с тем, что она не отражает истинную структуру солнечной системы, ибо
физически абсурдно считать, что Земля неподвижна, а Солнце, масса которого
превосходит массу Земли в 333000 раз, вращается вокруг нее.
Циклоиды, а также эпициклоиды и гипоциклоиды встречаются также в
различных задачах технического происхождения, например, в задачах о
профиле зацепления зубчатых колес и других им подобных.
Одно из приложений циклоиды, указанных X. Гюйгенсом, связано с
задачей об изохронном маятнике. Пусть дан маятник, то есть груз, подвешенный
вертикально на нити, закрепленной вверху. Если отклонить груз от
положения равновесия и отпустить его, то под действием силы тяжести он начнет
качаться. Период колебаний маятника, то есть время между двумя
последовательными возвращениями груза в его начальное положение, как было замечено
Г. Галилеем, не зависит ни от амплитуды колебаний (то есть от расстояния
между крайними положениями груза), ни от массы колеблющегося груза. В
дальнейшем, однако, было установлено, что установленный Г. Галилеем закон
независимости периода колебаний маятника от амплитуды выполняется лишь
приближенно, с точностью тем большей, чем меньше амплитуда колебаний.
Можно изменить конструкцию маятника, установив ограничители в виде
изогнутых пластин, перпендикулярных плоскости колебаний маятника так, что
когда маятник находится в покое, нить, на которой подвешен груз, проходит
в щели между этими пластинами, а при колебании нить натягивается либо на
одну из ограничивающих пластин, либо на другую. X. Гюйгенс показал, что
если сечение каждого из ограничителей плоскостью колебаний маятника
представляет собой циклоиду, то период колебаний маятника не будет зависеть от
амплитуды, то есть маятник в этом случае будет изохронным.

§ 2. Некоторые приложения понятия производной
297
2.3. Полярная система координат на плоскости. Графики
ФУНКЦИЙ В ПОЛЯРНОЙ СИСТЕМЕ КООРДИНАТ
На плоскости зададим произвольную декартову ортогональную
систему координат.
2.3.1. Пусть С есть отображение произведения I х 1 = I2 на
плоскость, которое произвольной паре чисел (р, <р) £ R2 сопоставляет
точку на плоскости, декартовы ортогональные координаты которой есть
(pcos<p,psin<p).
Отображение £ является отображением R2 на всю плоскость.
Действительно, пусть X = (ж, у) есть произвольная точка на
плоскости. Положим р(Х) = у/х2 +у2. Если X = О, то С(0,<р) = X при
любом <р £ R.
XV
Если X ф О, то р = р(Х) > 0. Положим а = —, /3 = -. Имеем:
Р Р
а2+/32 = 1 и, значит, как было показано в главе 3, найдется число <р £ R
такое, что а = cosy?, /3 = sin (p. Для этого </?, очевидно, имеем:
х = р cos <р, у = р sin <р, (2.8)
то есть X = £(р, <р) для данных р и (р.
Отображение £ мы будем называть полярной системой координат
на плоскости.
Числа р и <р будем называть полярными координатами точки X =
= £(р, <р), причем р называется полярным радиусом, а <р — амплитудой
точки X.
Если X не является началом системы координат, то существует
единственная пара чисел (р, <р) такая, что X = £(р, <р), и
выполняются условия: р>0и0<<р< 27г.
Геометрический смысл величин р и <р в случае р > 0
таков. Число р равно расстоянию точки X до начала системы
координат, (р есть угол, образуемый лучом ОХ с положительной полуосью оси
Ох декартовой системы координат, заданной на плоскости.
Отображение £ не является взаимно однозначным. Опишем все те
значения р и <р, которые являются полярным радиусом и,
соответственно, амплитудой произвольной точки X на плоскости.
Для точки О множество С"1 (О) совпадает с множеством всех точек
(0,<p)£R2.
Для точки X ф О множество С-1(Х) может быть описано
следующим образом.

298 Гл. 4. Дифференциальное исчисление функций одной переменной
Фиксируем произвольно значения р > 0 и <^о, для которых имеют
место равенства (2.8). Тогда любое другое значение <р,
удовлетворяющее (2.8), выражается через <ро посредством равенства ip = <ро + 2га7г,
где т есть целое число.
Если для данных ж и у для некоторых р и <р выполняются равенства
(2.8), то эти равенства будут выполняться также для р\ — —р и для
Из сказанного вытекает, что если ро и (ро — какие-либо
конкретные значения полярного радиуса и амплитуды точки X ф О, то пары
((—1)тро, ^о + Ш7г) образуют совокупность всех значений (р, <р), для
которых £(р, ¥>):= -X"-
Пусть на плоскости задана полярная система координат.
Предположим, что задана функция г : (а, (3) —* R.
Множество К всех точек X на плоскости, у которых полярный
радиус и амплитуда удовлетворяют условиям (р Е {а,,д) и р = г(<р), будем
называть кривой, заданной в полярной системе координат на плоскости
уравнением: р = г(<р).
Множество К есть график функции р = г(ср) относительно
отображения С-
Кривая К называется также графиком функции г : (а,/3) —> R в
полярной системе координат.
2.3.2. Предположим, что кривая на плоскости в полярной системе
координат задается уравнением р = г(<р), ^ Е (а,/3). Подставляя в равенство
(2.6) р = г(<р), получим функции:
#(<р) = г(ф) cos <р, у(ср) = r(cp) sin <р. (2.9)
Тем самым определена параметризованная кривая:
*(<р) = (*(<р)М<р))> <р е <<*,/?}. (2.Ю)
Покажем, что если функция г для некоторого <р Е (ск, /3)
дифференцируема, причем хотя бы одна из величин г(<р) и г'(<р) отлична
от нуля, то параметризованная кривая Х((р), определенная равенствами
(2.9) и (2.10), в точке, отвечающей данному значению <р, имеет
касательную.
Действительно, из равенств (2.9) вытекает, что в этом случае
функции х и у дифференцируемы для данного (р. При этом
х\<р) = r'(ip) cos tp — r((p) sin <p,
у'(<р) = r'(<p) sin <p + r(<p) cos ср.
(2.11)

§ 2. Некоторые приложения понятия производной
299
После простых вычислений, отсюда получаем, что
[x'iv)]2 + [у»]2 = КЫ]2 + Н<р)}2-
Если хотя бы одна из величин г((р) и г'((р) отлична от нуля, то
выражение в правой части этого равенства отлично от нуля и,
следовательно, что вектор t((p) = (%'(<p),y'(ip)) отличен от нуля.
В силу теоремы 2.2 отсюда следует существование
касательной у кривой Х(<р) для всякого <р = <ро, для которого производная
rf((fo) существует, причем, по крайней мере, одно из чисел r(tpo) и rf((po)
отлично от нуля.
Равенства (2.11) дают координаты направляющего вектора
касательной г'(<р) в точке X(ip).
Найдем угол 0, который касательная (r(<p),ip) образует с радиус-
вектором точки в данной системе координат. Декартовы координаты
радиус-вектора х(<р) этой точки суть х(<р) = r(<p) cos (р и y(ip) = r((p) sin (p.
Отсюда получаем выражение для скалярного произведения:
(t(ip),x(<f)) = r(<p)r'(<p) = cos0|r(p)|V[r'M]2 + Kp)]2,
откуда следует, что
cos в = tM =. (2.12)
vVMP + [rM]2
2.3.3. Рассмотрим примеры.
Пример 1'. Пусть r((p) = R = const. Множество всех точек X
на плоскости, полярный радиус которых равен числу J?, представляет
собой окружность радиуса R с центром в точке О — начале координат
на плоскости.
Пример 2'. Пусть г(<р) = к<р, где к > О — постоянная. Кривая,
заданная в полярной системе координат уравнением р = г((р),
называется спиралью Архимеда (см. рис. 15).
Рис. 15

300 Гл. 4. Дифференциальное исчисление функций одной переменной
Часть кривой, соответствующая отрицательным значениям <р,
называется отрицательной ветвью спирали Архимеда, а часть,
отвечающая положительным значениям <р, называется положительной ветвью
спирали Архимеда.
Положительная ветвь спирали Архимеда имеет следующий
механический смысл: это есть траектория точки, движущейся по лучу,
вращающемуся с постоянной скоростью вокруг начала. При этом
предполагается, что точка выходит из начала луча и движется по нему с
постоянной скоростью.
Функция г ((р) в рассматриваемом случае дифференцируема для
всех (р. При этом г'(<р) ф 0 для всех (р.
Отсюда вытекает, что рассматриваемая кривая имеет касательную
в каждой точке, амплитуда (р которой отлична от нуля.
Из равенства (2.12) вытекает, что косинус угла между касательной
спирали Архимеда и радиус-вектором точки равен:
к 1
у/к2 + fc V ~ 1 + <р2'
Спираль Архимеда была введена в связи с задачами о трисекции угла
и о квадратуре круга.
Первая задача состоит в том, чтобы указать способ деления
произвольного угла с помощью циркуля и линейки на три равные части. Еще в XIX-m
веке было показано, что такое построение невозможно.
Вторая задача — построить с помощью циркуля и линейки квадрат,
площадь которого была бы равна площади данного круга. Неразрешимость этой
задачи была установлена в конце XIX-го века.
Если к циркулю и линейке добавить другие инструменты, то обе
задачи решаются, и по большей части достаточно просто — степень простоты
решения зависит от выбора дополнительных инструментов.
Пример 3'. Кривая, задаваемая в полярной системе координат
уравнением р = ek(f, где к ф 0, называется логарифмической спиралью
(см. рис. 16).
х
Рис. 16

§ 2. Некоторые приложения понятия производной
301
В этом случае г((р) = ек(р > 0 для всех pGR. Функция г в данном
случае дифференцируема для всех ^бК. Для этой функции г имеем:
Г'И _ = к (2 13)
Следовательно, в каждой точке логарифмической спирали угол 0,
который касательная спирали образует с радиус-вектором данной
точки, не зависит от выбора этой точки.
2.4. Приложения понятия производной в физике и механике
Применение дифференциального исчисления в самых
разнообразных приложениях математики обычно основано на том, что производная
функции, представляющей собой ту или иную величину, может быть
истолкована как скорость изменения данной величины. Закономерности,
описывающие данный процесс, можно представить в виде равенств,
которым должны удовлетворять функции, выражающие собой разные
характеристики изучаемого явления, и их производные. Такие равенства
именуются дифференциальными уравнениями.
Пример 1". Скорость и ускорение материальной точки.
Предположим, что изучается движение материальной точки по
прямой в течение некоторого промежутка времени I = [а, 6]. На прямой
предполагается заданной некоторая система координат.
Пусть x{t) есть координата точки в момент времени t E I.
Рассмотрим два произвольных момента времени t\ и fo.
Отношение
x(t2) -x(ti)
*2-*l
называют средней скоростью материальной точки за промежуток
времени (ti,*2)-
Предел
lim gft) - a?(*o)
t—>t0 t — to
называется скоростью материальной точки в момент времени to.
Таким образом, в соответствии с данным выше определением,
скорость материальной точки в момент времени to есть просто значение
производной координаты точки на оси, по которой она движется, в
момент времени t = to.
Пусть v(t) есть скорость материальной точки в момент времени t.
Тем самым в промежутке [а, 6] определена некоторая функция v.

302 Гл. 4. Дифференциальное исчисление функций одной переменной
Производная этой функции в момент времени t называется
ускорением материальной точки в этот момент. Ускорение, таким образом,
является производной от функции x'{t) — производной функции x(t).
(Производная от x'(t) называется второй производной от функции x(t)
и обозначается символом x"(t). Обычную производную x'(t) функции
x(t) называют также первой производной функции x(t).)
Скорость и ускорение суть основные механические
характеристики движения материальной точки. Математически, как видно
из сказанного, они характеризуются посредством понятия производной.
Различные задачи о движении материальной точки по прямой тем
самым сводятся к определению функции х по соотношениям, которым
удовлетворяют функции x(t), x'(t) и x"(t).
Пусть, например, изучается движение по прямой
материальной точки массы га, на которую действует сила F(x),
пропорциональная отклонению точки x(t) от начального положения х(0) и
направленная противоположно x(t). Простоты ради, будем считать, что
х(0) = 0. Имеем: F(x) = —/#, где / > 0 — постоянная.
В силу второго закона Ньютона, ускорение точки в момент, когда
ее координата есть #, равно F(x)/m. С другой стороны, ускорение точки
равно x"{t). Следовательно, имеет место равенство:
x"(t) = х.
га
Данное уравнение может быть записано в виде:
x"(t) + \2x(t)=0.
Как будет показано далее (см. п. 4.5.2), в этом случае зависимость
x(t) от t выражается формулой:
x(t) = A cos Xt + В sin At,
где А и В — постоянные.
Рассмотрим более подробно еще один пример.
Пример 2". Явление уадиоактивного уаспада вещества.
Пусть имеется радиоактивное вещество и m(t) есть его масса в
момент времени t.
Рассмотрим малый промежуток времени (£, t + h). Число атомов
вещества, распадающегося за время от t до t + /ь, приближенно
пропорционально h и составляет строго определенный процент от числа атомов
вещества, имеющихся в момент времени t.

§ 3. Производные высших порядков
303
Иначе говоря, приближенно можно записать следующее уравнение:
m(t + h) - m(t) = -khm{t). (2.14)
Так как величина га(£), очевидно, уменьшается с ростом £, то есть
m(t) есть убывающая функция £, то величина к в равенстве (2.14)
положительна. Поделив обе части равенства (2.14) на h и переходя к пределу
при h —► 0, получим дифференциальное уравнение, которому
удовлетворяет функция га:
^(t) = -km(t). (2.15)
Мы получаем, таким образом, пример явления, в котором скорость
изменения некоторой величины (в данном случае, массы
радиоактивного вещества) пропорциональна значению этой величины.
Из равенства (2.15), как будет показано в п. 4.5.2 §4, вытекает
следующая формула зависимости массы радиоактивного вещества от
времени:
m(t) = m0e~kt. (2.16)
Здесь гао = га(0) — масса рассматриваемого радиоактивного вещества
в момент времени t = 0.
При изучении радиоактивных процессов часто указывается
характеристика процесса, называемая периодом полураспада. Это — время,
в течение которого масса вещества уменьшается вдвое.
Период полураспада Т, как следует из (2.16), определяется
равенством:
— кТ 1
6 =2-
Отсюда получаем, что кТ == In 2, и, значит,
, In 2
Т
Используя это равенство, формулу радиоактивного распада
вещества (2.15) можно переписать иначе:
1п21
m(t) = гао ехр
-*т
■1 = ra02"t/T. (2.17)
§3. Производные высших порядков
Предположим, что дана функция /, определенная на некотором
плотном в себе множестве А СШ и дифференцируемая в каждой точке
этого множества. Тогда для каждого х £ А определено число f'(x) и тем
самым на множестве А определена некоторая функция /' — производная
функции f на множестве А.

304 Гл. 4. Дифференциальное исчисление функций одной переменной
Предположим, что функция /', в свою очередь, дифференцируема
в каждой точке данного множества А. Ее производная обозначается
символом /" и называется второй производной функции /. Производная
функции /" называется третьей производной функции /.
Описанный процесс может быть продолжен, и, таким образом, мы
приходим к понятию производной порядка п для произвольного n Е N.
Естественным образом возникают множества функций V71 и Сп.
Первое состоит из всех функций, имеющих во всех точках своей области
определения производную порядка п. Второе состоит из тех функций,
у которых производная порядка п не только существует, но также и
непрерывна. (По традиции тот факт, что функция f принадлежит Dn
или Сп, иногда выражают словами: «f — функция класса Dn или Сп»,
сокращенно: «f Е Dn», соответственно, «f Е Сп».)
Далее устанавливаются некоторые свойства функций указанных
классов. В частности, выводится выражение для производной
порядка п произведения двух функций из Vй.
В заключение для некоторых из основных элементарных функций
приводятся формулы для производных порядка п и некоторые простые
соотношения, связанные с понятием производной порядка п.
3.1. Определение производной высшего порядка
Зададим произвольно плотное в себе множество А С К. Не
оговаривая особо, мы будем предполагать, что все функции, рассматриваемые
в этом разделе, имеют областью определения множество А
Пусть функция / : А —> Е дифференцируема в каждой точке х Е А.
Тогда определена функция /' : А —> Ж — производная функции / на
множестве А.
Предположим, что функция /' имеет производную в точке хо Е А.
Полагаем:
Df\x0) = f"(xo).
Величина /"(#о) называется второй производной функции f в
точке хо. Будем говорить, что функция / дважды дифференцируема в точке
хо, если величина f"{xo) конечна. Для обозначения второй производной
d2f
используется также одно из следующих выражений: -т~2*(яо); D2f(xo).
ах
Если функция / дважды дифференцируема в каждой точке
множества А, то определена функция /" — вторая производная функции /.
Производная функции /" — в случае, если таковая существует,
называется третьей производной функции / и обозначается символом /'" и
т. д.

§ 3. Производные высших порядков
305
Определим общее понятие n-й производной, где п — произвольное
натуральное число.
Первая производная или, что то же самое, — n-я производная
порядка п = 1, — есть обычная производная.
Предположим, что для некоторого п Е N понятие n-й производной
или, что то же самое, производной порядка п определено.
Пусть функция / в каждой точке х Е А имеет конечную
производную порядка п и пусть f^n\x) есть значение этой производной в
произвольной точке х Е А. На множестве А, таким образом, определена
функция f(n\ Производная функции /^ в точке хо Е А, если таковая
существует, называется (п + 1)-й производной функции f в точке хо и
обозначается символом /^п+1^(жо). По определению, имеем:
х—>хо,хеА X — Хо
Будем говорить, что функция / : А —» Е является п-кратно
дифференцируемой в точке хо Е А, если ее n-я производная в точке хо
определена и конечна. Функция / называется п-кратно дифференцируемой
на множестве А, если она п-кратно дифференцируема в каждой точке
х £ А. Для обозначения производной порядка п функции f : А —> Е
dnf
в точке х € А применяются также следующие выражения: —^(ж);
ахп
Dnf{x).
Производные третьего, четвертого, пятого и т. д. порядка
обозначаются также символами: /'", //v, /v, соответственно.
Совокупность всех функций / : А —► Е, п-кратно
дифференцируемых на множестве А, обозначается далее 7?п(А, Е).
Множество всех функций, принадлежащих множеству X>n(A, E) и
таких, что их производная порядка п непрерывна, обозначается Cn(A, E).
Совокупность всех вещественных функций, определенных на
множестве А С Е и непрерывных на А, будем обозначать С (А, Е) или, когда
это не может повлечь недоразумение, просто символом С.
В формулировках различных предложений, касающихся множеств
СП(А,Е), может возникать случай п = 0. Условимся считать, что
множество С°(А,Е) совпадает с классом С(А,Е) непрерывных функций,
определенных на множестве А. Для обозначения множеств функций,
введенных сейчас, будем употреблять более простые выражения Vй и,
соответственно, Сп.

306 Гл. 4. Дифференциальное исчисление функций одной переменной
Если функция / : А —■> Ш принадлежит множеству Vn, то ее
производная порядка п —1 — дифференцируема и, следовательно,
непрерывна в каждой точке х Е А. Это означает, что / принадлежит множеству
Таким образом, если / 6 Vй, то / Е С71"1, то есть имеет место
включение:
Vn С С71"1.
Производные высших порядков определяются как результат
последовательных дифференцирований функций.
Пусть даны натуральные числа пит, причем 1 < т < п.
Результат m-го шага процесса последовательных дифференцирований
есть функция f^ — производная порядка т функции /. Выполнив
еще п — т дифференцирований, получим, с одной стороны,
производную порядка п функции /, а с другой — производную порядка п — т
функции /(т).
Таким образом, существование производной порядка п
автоматически влечет за собой существование всех производных низших
порядков. При этом производная порядка п функции f является
производной порядка п — т функции f^m\
Совокупность всех функций / : А —> М, каждая из которых
принадлежит множеству Vй при любом п, то есть имеет во всех точках
множества А производную порядка п, каково бы ни было п,
обозначается символом: С°°(А,М). Когда недоразумение невозможно, применяется
выражение С°°(А) или просто С°°.
Определим понятие производной произвольного порядка п Е N
для функций с комплексными значениями.
Пусть дана функция / : А -» С, где А есть плотное в себе
подмножество R. Тогда определены вещественные функции и = Re/ и
v = Im/.
Будем говорить, что функция / является n-кратно
дифференцируемой в точке хо Е А, если таковы функции и и v. Полагаем:
Для комплексных функций понятие бесконечной производной не
определяется.
3.2. Производные высших порядков некоторых элементарных
функций
Докажем, что основные элементарные функции принадлежат
классу С°°. Найдем производные порядка п для некоторых из этих функций.
Ограничимся только теми частными случаями, когда указанные
производные допускают простые выражения.

§ 3. Производные высших порядков
307
1. Степенная функция. Пусть дана степенная функция / : х н-> яа,
где a El, D — ее область определения. Строение множества 2)
определяется значением а, как это было описано в п. 1.4 главы 3. В каждой
точке xGD, отличной от точки 0, имеем:
f(x) = ax""1; f"(x) = а(а - 1)ха"2 и т. д.
Индукцией по п легко устанавливается, что функция аи->жа
принадлежит классу Vй на множестве D\{0} при любом п. При этом имеет
место равенство:
/(п)(ж) = а(а - 1)... (а - п + l)*a~n. (3.1)
Если а Е N, то D = R, и в этом случае функция ха = хп является
m-кратно дифференцируемой также и в точке 0, каково бы ни было
га Е N.
Если п Е N, то Dn(xn) = n(n-l)... 1 = п! и Dm(zn) = 0 при га > п.
Таким образом, при п Е N функция ж и-» #п принадлежит клас-
су С°°.
В случае, когда а есть отрицательное целое число,
а = —га, где га Е N, область определения ха = х~т есть множество
М\ {0}. Функция х~т в этом случае принадлежит классу С°°.
В частности, функция жи- принадлежит классу С°°. Для га Е N
х
при каждом n E N имеем:
Dn(x-m) = (~1)пга(га + 1)... га(га + п - 1)аГто-п. (3.2)
Введем еще некоторые обозначения.
Для произвольного целого г > 0 положим: ег(#) = —. Имеем,
очевидно:
гхг"1 хг~х
D[er(x)] = —^ = —— = er.i(a?).
Отсюда вытекает, что справедливы следующие соотношения:
л»М*)] = { ег-4ж) при п * г; (з.з)
^ 0 при п > г.
2. Показательная функция. Пусть дано число a > 0, а ф 1.
Функция х »-*• аж дифференцируема в R всюду, причем 1?(аж) = axlna для
всех х Е R.

308 Гл. 4. Дифференциальное исчисление функций одной переменной
Отсюда, очевидно, следует, что функция х н-> ах является п-кратно
дифференцируемой в R при любом п. При этом
Dn(ax) = ax(\na)n (3.4)
для всех жЕК при любом п. В частности,
Dn(ex) = ex (3.5)
при любом п G N.
Из сказанного следует, что функция х и-» ах принадлежит клас-
суС°°.
3. Логарифм. Для функции х »—► In ж имеем: D(lnx) = — для всех
х
х > 0. Функция жн- принадлежит классу С°° в промежутке (0,оо).
х
Отсюда следует, что функция х ь-> In ж принадлежит классу С°°.
Применяя формулу (3.1) для вычисления производных степенной
функции, получим равенство:
Вп(Ых) = (-1)п-1^^. (3.6)
4. Комплексная показательная функция и тригонометрические
функции. Пусть с = a + ib — произвольное комплексное число.
Рассмотрим комплексную показательную функцию х »—► exp(a + ib)x. Согласно
определению (см. главу 3, п. 2.4), имеем:
ехр(а + ib)x = eax (cos bx + i sin bx).
Отсюда получаем, что
D[exp(a + ib)x] = aeax (cos bx + i sin bx) + beax (— sin bx + i cos bx).
Заметим, что
— sin bx + i cos bx = i(cos bx + % sin bx).
Это позволяет переписать предыдущее равенство следующим образом:
D[exp(a + ib)x) = aeax (cos bx + i sin bx) + ibeax (cos b# + i sin bx),

§ 3. Производные высших порядков
309
то есть
D[exp(a + ib)x] = (a + ib) exp(a + ib)x.
Из этого соотношения индукцией по п, очевидным образом, выводится,
что функция х н-> exp(a + ib)x принадлежит классу Vй при любом п.
При этом
Dn[exp(a + ib)x) = (a + ib)n exp(a + ib)x (3.7)
для всех п.
В частности, справедливо соотношение:
егх = cos ж + г sin ж.
Отсюда следует, что
Dn (cos ж + г sin ж) = Г>п(е*ж) = iV"
при каждом п.
Имеем: г = ехр — и, значит,
Dn(cosx + isinz) = е<ж+2^) = cos (я? + ™) + isin (* + ™) • (3.8)
При каждом п
Dn (cos ж + г sin х) = Dn (cos ж) + iDn (sin ж),
откуда получаем следующие равенства:
Dn(cosx) = cos (x + ™\ ; L>n(sinz) = sin (я? + ^V (3.9)
3.3. Теорема о произведении функций классов Уп к Сп.
Формула Лейбница
Зададим произвольно плотное в себе множество Act. Из
определения производной n-го порядка непосредственно вытекает, что если
функции fj : А —> Ж, j = 1,2,... ,га, принадлежат классу 2?п, то их
сумма также принадлежит данному классу. При этом имеет место
равенство:
(т \ т

310 Гл. 4. Дифференциальное исчисление функций одной переменной
Формальное доказательство (индукцией по п), ввиду его
очевидности, может быть опущено.
■ Теорема 3.1 (о формуле Лейбница для произведения функций).
Если функции f:A—>'RHg:A—>R принадлежат классу Vn (классу,
Сп), то их произведение fg также является функцией класса V71
(соответственно, Сп).
При каждом п = 1,2,... существует система из п +1 натуральных
чисел Сп,Сп,-. -,С% такая, что для любых двух функций f, g класса
Vn выполняется равенство, называемое формулой Лейбница:
п
°ПШ = E Ckn{Dn-kf){Dkg), (3.10)
fc=0
где Dm для га > 1 означает производную порядка m функции и D°f = f,
a D°g = g.
Коэффициенты С* в равенстве (3.10) выражаются формулами:
k _ n! _ п(п - 1)... (п - fc + 1)
°"- fc!(n-fc)! ~ fc!
для любьхх целых кип таких, что 0 < к < п.
Замечание. Числа С\ называются биномиальными
коэффициентами.
Доказательство теоремы. Для п = 1 утверждение теоремы о
принадлежности произведения классу Vй следует из доказанного ранее.
Согласно правилу дифференцирования произведения (теорема 1.2),
D(fg) = (Df)g + fDg,
и равенство (3.10) для п = 1 верно с коэффициентами С? = С\ — 1.
Предположим, что для некоторого п произведение функций / и д,
принадлежащих классу Т>п, есть функция класса Vn, и существует
такая конечная система натуральных чисел С^, к = 0,1,..., п, что для
любых двух функций / и д класса Vй выполняется равенство (3.10).
Пусть / и д — это функции класса Vn+1. Тогда / и д также
принадлежат классу Vй и, стало быть, для них выполняется (3.10).
Для всякого целого к такого, что 0 < к < п, функция Dn~-kf
принадлежит классу Dm, где га = п + 1 — (п — к) = к + 1 > 1, a Dkg —
классу Dr при г = п + 1 — к > 1.

§ 3. Производные высших порядков
311
Таким образом, мы получаем, что если 0 < к < п, то функции
Dn~kf и Dkg одновременно дифференцируемы.
Отсюда следует, что каждое слагаемое C\Dn"hjDkg в правой
части равенства (3.10) в данном случае дифференцируемо и, значит, вся
сумма представляет собой функцию, дифференцируемую на
множестве А, то есть n-я производная произведения fg
дифференцируема на множестве А.
Следовательно, функция fg принадлежит классу Vn+1.
Дифференцируя равенство (3.10) почленно, получим:
п
Dn+1(fg) = ^Ck[(Dn+1-kf)(Dkg) + (Dn~kf)(Dk+1g)} =
fc=0
n n-f-1
= Y^Cn(Dn+1-kf)(Dkg + J2ct1[(Dn+1-kf)(Dkg) =
fc=0 fc=l
n
= C°n(Dn+1f)g + J2(C* + Ct'KD^^f^g) + CZfDn+1g. (3.11)
Отсюда:
n+l
Dn+1(fg) ^^Ck+1(Dn+1-kf)(Dkg), (3.12)
fc=0
где
С£+1 = С£, (%# = <%> CU^Ci + ClT1 при l<fc<n. (3.13)
Таким образом, существует такая конечная последовательность из
п + 2 чисел Сп+ь & = 0,1,..., п, п + 1, что для любых двух функций /
и д класса X>n+1 производная Dn+1(fg) выражается через производные
функций / и д равенством, которое получается, если в (3.10) заменить
п на п + 1. По предположению индукции, коэффициенты Ск — это
натуральные числа.
В силу равенств (3.13), отсюда следует, что числа С^+1 также
являются натуральными.
Если функции / и д принадлежат классу Сп, то, как нетрудно
видеть, в этом случае каждое слагаемое в правой части формулы (3.10)
представляет собой непрерывную функцию.

312 Гл. 4. Дифференциальное исчисление функций одной переменной
Отсюда следует, что производная порядка п функции fg
непрерывна, то есть fg также принадлежит классу Сп.
Для завершения доказательства осталось указать явные значения
для коэффициентов Ск в равенстве (3.10). Мы сделаем это надлежащим
выбором функций / и д.
Пусть 0 < т < п. Положим f{x) = еп-т(х) и д(х) = ет{х). Тогда
хп nf
f(x)g(x) = ———гт—- = -г—ixnr^nix).
(п — т)\т\ \п — т)\т\
Найдем значение производной Dn[f(x)g(x)]. Имеем:
Dn[f(x)g(x)] = nLmMx) = (П П1мтУ (3-14)
\п — т)\т\ \п — т)\т\
При каждом fc > 0 будет:
Dn~~ken-m = 0 при fc < m и Dn~men-m = 1,
Dkem = 0 при fc > m и £>mem = 1.
Отсюда видно, что произведение Dn~ken-mDk em отлично от нуля
для единственного значения fc, а именно, для fc = га. В этом случае
U e<a—m-Ly 6771 = 1.
Таким образом, мы получаем, что в сумме (3.10) слагаемое,
соответствующее значению fc = га, равно С™, а остальные равны нулю.
Отсюда заключаем, что для данных функций / и д имеет место
равенство:
Dn(fg) = С™.
Следовательно, ввиду (3.14),
71 ~~ (п-га)!га!'
что и требовалось доказать. ■
Иной вывод формулы Лейбница (3.10) см. в §6, п. 6.4.
3.4. Теоремы об операциях над функциями классов Vй и Сп
■ Теорема 3.2. Пусть А и В — плотные в себе подмножества Ш и
функции f : A^R, g : В -+R таковы, что f(A) С В. Тогда если f и g
принадлежат классу Vй (классу С71), то их суперпозиция go f является
функцией класса Vй (соответственно, класса Сп).

§ 3. Производные высших порядков
313
Доказательство. Пусть / и д — функции класса V1. По
определению, это означает, что каждая из функций / и д дифференцируема
во всех точках своей области определения.
Отсюда, на основании теоремы о дифференцируемости
суперпозиции (теорема 1.4), вытекает, что функция g о f дифференцируема в
каждой точке х Е А и, значит, h = g о / принадлежит классу V1. При
этом для всех х Е А выполняется равенство:
h'(x)=g'[f(x)]f'(x).
Если / и g принадлежат классу С1, то функции /, /' и д'
непрерывны. Отсюда, в силу равенства
h' = (g'of)f',
следует, что функция h' также непрерывна на множестве А, то есть в
этом случае
h = gofeC\
Для п = 1 требуемое утверждение доказано.
Предположим, что для некоторого п справедливость утверждения
теоремы установлена, и пусть / и д суть функции класса £>n+1 (Cn+1).
Положим h = д о /. Тогда
h' = (g'of)f.
Функции д!, /, /' принадлежат классу V71 (классу Сп).
Так как для данного п, согласно предположению, утверждение
теоремы верно, то д' о / принадлежит классу Vn (соответственно, классу
Сп).
В силу теоремы 3.1, отсюда следует, что произведение (д' о /)/'
есть функция класса Т>п (Сп).
Таким образом, производная функции h = gof принадлежит классу
Vй (Сп) и, значит, функция h принадлежит классу Vn+1 (Cn+1).
По индукции теорема доказана. ■
▼ Следствие. Для всякой функции f : А —» С класса Vn (класса
Сп) такой, что f(x)^0 для всех x G А, функция х »-> , г принадлежит
классу Vn (соответственно, классу Сп).
Доказательство. Сначала рассмотрим случай, когда функция
/ — вещественная. Функция j : у ь-> 1/у, как было показано выше (см.
п. 3.2), принадлежит классу С°° на множестве R \ {0}.

314 Гл. 4. Дифференциальное исчисление функций одной переменной
Предположим, что функция / : А —» R такова, что для всех х G А
справедливо f(x) ф 0. Функция 7°/= 7 определена для всех х G А
и как суперпозиция функций 7 и /> согласно теореме 3.2, принадлежит
тому же классу гладкости, что и функция /.
Пусть / = u + iv есть произвольная комплексная функция, причем
f(x) ф 0 для всех х G А. Тогда
1 __ и v
f и2 + v2 и2 + v2'
Функция и2 + v2 принадлежит классу Vn (Cn) в силу теоремы 3.1,
и и2 + v2 ф 0 для всех х G А. Значит, функция 1/(и2 +v2) принадлежит
классу Vй (Сп).
Применяя теорему 3.1 еще раз, получаем, что функции
и 1 v 1
-=-■—r=ReT, --5-;—^=ImT
и2 + v2 f и2 + v2 f
принадлежат классу Vй (Сп), что и требовалось доказать. ▼
■ Теорема 3.3. Пусть I = (а,Ь) есть произвольный открытый
отрезок в множестве R и функция f : J —» R строго монотонна и
отображает I на интервал J = (р, д). Если / принадлежит классу Vn (классу
Сп) и для всех х G J производная f'{x) отлична от нуля, то обратная
функция g = /-1 принадлежит классу Х>п (соответственно, классу С71).
Доказательство. Рассмотрим сначала случай п = 1.
Предположим, что функция / дифференцируема во всех точках интервала
/, причем f'(x) ф 0 для всех х G /. Тогда, как было доказано ранее
(теорема 1.3), функция g = Z""1 дифференцируема в каждой точке у G J,
то есть если / G Х>х, то также и j 6 D1. При этом
9'(v)=?га
для всех у Е J.
Функция g — непрерывна, и если производная /7 является
непрерывной функцией, то из представления (3.15) производной функции g
вытекает, что функция д' непрерывна.
Таким образом, мы получаем, что если / принадлежит классу С1,
то также и функция д = f"1 принадлежит этому классу.
(3.15)

§ 4. Теоремы о среднем значении
315
Предположим, что для некоторого п утверждение теоремы
доказано, и функция / принадлежит классу Т>п+1. Для всех у £ J выполняется
равенство:
яЪ) = ТШУ
Функция /' принадлежит классу Vй. Так как / £ Сп, то, по
предположения индукции, д ЕСп. В силу теоремы 3.2, /' о д £ Vй.
Так как f'(x) ф О для всех х £ /, то, согласно следствию
теоремы 3.2, можно заключить, что функция
1
принадлежит классу Т>п. Стало быть, д £ £>n+1.
Если / £ Cn+1, то /' £ Сп и, значит, согласно теореме 3.2, в этом
случае /' о д £ Сп, и, следовательно,
1
принадлежит классу Сп, а потому # £ Cn+1.
В силу принципа математической индукции, теорема доказана. ■
Выражения для производных высших порядков суперпозиции и
обратной функции известны. Мы не приводим их, ввиду громоздкости.
Отметим одну простую формулу, которая часто оказывается полезной.
Пусть g(x) = f(ax + Ь), где a G Киб Е 1 — постоянные. Если
функция / принадлежит классу Х>п, то д принадлежит тому же классу
и для всех х выполняется равенство:
g{n)(x) = anfM(ax + b).
Доказательство этого равенства — индукцией по п, ввиду
очевидности, опускается.
§4. Теоремы о среднем значении
В настоящем параграфе доказываются теоремы, позволяющие
получать определенную информацию о поведении функции, заданной на
некотором отрезке, по свойствам ее производной.

316 Гл. 4. Дифференциальное исчисление функций одной переменной
Основными результатами этого раздела являются теоремы Коши и
Лагранжа о среднем значении' (последняя доказывается здесь как
следствие теоремы Коти). Наименование — «теорема о среднем значении»
связано с тем, что каждая из этих теорем утверждает, что в
промежутке, на котором заданы рассматриваемые в теореме функции, существует
число («среднее значение») £, для которого верны определенные
соотношения.
Применение теорем о среднем значении позволяет получать
некоторые оценки приращения функции по границам, между которыми лежит
ее производная.
Доказывается критерий монотонности функции. Мы приводим
здесь две теоремы, устанавливающие необходимые и достаточные
условия монотонности функции на отрезке. Доказательство первой теоремы
опирается на теорему Лагранжа о среднем значении.
Вторая устанавливает достаточное условие монотонности функции,
более общее, чем то, которое дается теоремой о среднем значении. Этот
результат потребуется позднее в главе 5 «Интегральное исчисление
функций одной переменной».
4.1. Точки экстремума функции. Теорема Ферма
Введем понятие точки экстремума функции. В полном объеме оно
будет рассмотрено в § 7. В этом разделе мы докажем одно простое
утверждение о точках экстремума, на которое опираются доказательства
некоторых теорем о дифференцируемых функциях на отрезке.
Пусть даны множество А С К и функция / : А —► R. Пусть
хо Е А есть предельная точка множества А. Точка хо называется
точкой максимума функции /, если точка хо имеет такую окрестность
U = (хо — 6,хо + 6), что для всех х Е U П А выполняется неравенство
f(x) < /(хо).
Говорят, что Хо есть точка минимума функции /, если существует
окрестность U точки xq такая, что для всех х Е U П А выполняется
неравенство f(x) > /(жо).
Точка хо называется точкой экстремума функции /, если хо есть
либо точка минимума, либо точка максимума функции д.
Для обозначения понятий «точка максимума», «точка минимума»
или «точка экстремума» функции иногда применяются термины:
«точка локадбного максимума», соответственно, «точка локального
минимума» и «точка локального экстремума» функции.
Пусть x(t) есть координата в момент времени t € [а,Ь] точки,
движущейся по прямой. Точки экстремума функции х — это те значения t,
в которых направление движения точки меняется.

§ 4. Теоремы о среднем значении
317
Xj Х2
Рис. 17
На рис. 17 х\ есть точка максимума, Х2 — точка минимума
функции, график которой представлен на этом рисунке.
Если хо Е А есть точка минимума функции / : А —► R, то хо
является точкой максимума функции д = —/, и точно так же, если жо
— точка максимума функции /, то Хо есть точка минимума функции д.
Действительно, пусть хо есть точка минимума функции /. Тогда,
согласно определению, найдется окрестность U точки хо такал, что для
всех х Е U Г) А выполняется неравенство: f(x) > /(жо).
Для всех х EU Г) А, очевидно, имеем:
д(х) = -f(x) < -f(x0) = g(xo).
По определению, это означает, что хо есть точка максимума функции
9 = -f-
Аналогично рассуждаем в случае, когда хо есть точка максимума
функции /.
Если функция / : А —> R принимает в точке хо Е А, предельной для
множества А, свое наименьшее (наибольшее) значение на множестве А,
то #о, очевидно, является точкой максимума (минимума) функции /.
Обратное, вообще говоря, неверно, то есть если хо есть
точка максимума (или точка минимума) функции /, то /(#о) может
не быть наибольшим или наименьшим значением функции / на
множестве А.
Пример. Пусть [а,Ь] = [-2.5,2.5] и f(x) = х3 - Зх (см. рис. 18).
Имеем: f(x) + 2 = х3 — Зх + 2 = (х — 1)2(# + 2). Отсюда вытекает, что
f(x) + 2 > 0 для всякого х > —2. Имеем: /(1) + 2 = 0. Мы
получаем, таким образом, что для всех х Е (—2, ос) выполняется неравенство:
f(x) > /(1). Отсюда следует, что х\ = 1 есть точка минимума функции
/. Из равенства: f(x) + 2 = (х — 1)2(# + 2) вытекает, что для всякого

318 Гл. 4. Дифференциальное исчисление функций одной переменной
х < — 2 имеет место неравенство: f(x) < — 2 = /(#i). Отсюда, в
частности, видно, что функция / принимает в промежутке [—2.5,2.5]
значения, меньшие /(1). Это позволяет заключить, что хотя 1 есть точка
минимума функции /, но ее значение в этой точке заведомо не является
наименьшим значением функции / на отрезке [а,Ь] = [—2.5,2.5].
Рис. 18
Пусть функция / определена на промежутке J = (а, Ь) и в каждой
внутренней точке этого промежутка имеет конечную или бесконечную
производную. Установим некоторое необходимое условие, которому
удовлетворяют точки интервала (а,Ь), являющиеся точками экстремума
данной функции.
■ Теорема 4.1 (теорема Ферма). Пусть даны функция / : I —► Ш,
где I = (а,Ь) С М, и некоторая внутренняя точка хо промежутка I.
Предположим, что хо есть точка экстремума функции /. Тогда если /
имеет в точке хо производную, то эта производная равна нулю.
Доказательство. Пусть хо есть точка экстремума функции
/ : J —► R, причем a < хо < Ъ. Предположим, что хо есть точка
максимума /.
Согласно определению точки максимума, найдется окрестность
U = (хо — 8, хо + 6) точки хо такая, что f(x) < f(xo) для всех х Е U Г)1.
Не уменьшая общности, можно считать, что данная окрестность U
содержится в J, поскольку этого всегда можно добиться уменьшением 6.
Для всех х £ U будет f(x) — f(xo) < 0. Имеем: х — хо < 0 при
х < хо и х — хо > 0, если х > жо. Отсюда следует, что для х Е U при
х < хо имеет место неравенство:
/(g)-/Ы
X — Хо
>о,
(4.1)

§ 4. Теоремы о среднем значении 319
а при х > хо выполняется неравенство:
№ - /Ы
X — Хо
По условию, функция / имеет в точке хо производную.
Переходя в неравенствах (4.1) и (4.2) к пределу при х —> хо слева и справа,
соответственно, получим, что
/'Ы > о,
и одновременно
/'Ы < 0.
Отсюда
/W=o,
что и требовалось доказать.
Выше предполагалось, что хо есть точка максимума функции /.
Если же хо есть точка минимума функции /, то хо есть точка
максимума функции д = —/.
Функция д имеет в точке хо производную, так как / имеет
производную в этой точке. При этом
д'(х0) = -f'(x0).
Из доказанного следует, что
д'(х0) = 0
и, значит,
/'Ы = о.
Теорема доказана. ■
4.2. Теоремы Коши и Лагранжа о среднем значении функции
4.2.1. Предварительно докажем теорему, принадлежащую М. Роллю,
которая понадобится нам в дальнейшем.
■ Теорема 4.2 (теорема Ролля). Предположим, что вещественная
функция f определена и непрерывна на сегменте [а, Ь] С R и в каждой
точке х интервала (а, Ь) имеет производную f'(x). Тогда если имеет
место равенство /(а) = f(b), то существует с такое, что a < с < Ъ, и
производная функции f в точке с обращается в нуль.
(4.2)

320 Гл. 4. Дифференциальное исчисление функций одной переменной
Доказательство. Пусть
m= inf f(x); M= sup f(x); Z, =/(а) =/(b).
a<x<b a<x<b
В силу теоремы Вейерштрасса о непрерывной функции, величины т и
М — конечны.
Имеем: т < L < М. Если т — М, то функция / на промежутке
[а,Ь] постоянна, ив качестве с можно взять произвольную точку
интервала (а, Ь).
Предположим, что т < М. По теореме о наименьшем и
наибольшем значениях непрерывной функции найдутся точки с\ Е [а^Ь] и
С2 Е [а, Ь] такие, что /(ci) = га, /(сг) = М. Очевидно, что ci и сг — это
точки экстремума функции /. Так как т ф М, то, по крайней мере,
одна из величин т и М отлична от L.
Пусть с есть та из точек ci и сг, для которой /(с) отлично от L.
Очевидно, сф а, сфЪи, следовательно, а < с < Ь. Из условий теоремы
вытекает, что функция / имеет в точке с производную. Так как с есть
точка экстремума функции /, то, по теореме Ферма (см. теорему 4.1),
/Чс) = 0.
Теорема доказана. ■
▼ Следствие. Пусть / : [а, Ь] —► R, где [а, Ь] С R, — непрерывная
функция, имеющая конечную или бесконечную производную в каждой
точке х G (а, Ь). Тогда если для всех х G (а, Ь) производная f (х) отлична
от нуля, то /(а) Ф f(b).
Доказательство. Действительно, предположим, что функция
/ удовлетворяет всем условиям следствия. Допустим, что /(а) = /(b).
Тогда, согласно теореме Ролля (теорема 4.2), найдется точка с Е (а,Ь)
такая, что /7(с) = 0. Это противоречит тому, что, согласно
условию следствия, f'{x) ф 0 для всех х Е (а,Ь).
Таким образом, допущение, что /(а) = /(b), ведет к
противоречию. Следовательно, должно быть /(а) ^ /(b), что и требовалось
доказать. ▼
■ Теорема 4.3 (теорема Коши о среднем значении). Пусть даны
отрезок [а, Ь] С К и функции / : [а, Ь] —► Е и # : [а, Ь] —► R, которые
определены и непрерывны на этом промежутке. Предположим, что в
каждой точке х интервала (а, Ь) функции f и g дифференцируемы,
причем д'(х) ф 0 для всех х Е (а, Ь). Тогда найдется значение с такое, что
a < с < Ь, и выполняется равенство:
f(b) - /(а) = Г (с)
0(6)-0(e) 0'(с)'

§ 4. Теоремы о среднем значении
321
Замечание 1. В силу следствия теоремы Ролля, д(Ь) — д(а) ф
Ф О и, значит, отношение в левой части равенства, указанного в
формулировке теоремы 4.3 имеет смысл.
Замечание 2. Утверждение теоремы 4.3 имеет следующий
геометрический смысл. Рассмотрим параметризованную кривую и(х) =
= (f(x),g(x)). Пусть А = (/(а),#(а)), В = (f(b),g(b)). В силу следствия
теоремы 4.2, д(Ь) ф д(а), и, значит, точки А и В различны. Теорема
утверждает, что найдется значение с Е (а,Ь) такое, что касательная
параметризованной кривой и(х) в точке и(с) параллельна прямой АВ
(см. рис. 19).
Рис. 19
Доказательство теоремы. Введем вспомогательную
функцию F, полагая для х Е [а, Ь]
F(x) = [/(*) - /(а)][5(Ь) - 5(а)] - [/(6) - /(а)][а(я) - 5(а)].
Функция F на промежутке [a,b] — непрерывна и, как легко
проверяется, F(a) = F(b) = 0.
Функция F — дифференцируема в каждой точке х Е (а, Ь).
Так как F(a) = F(b), то, по теореме Ролля, найдется точка с такая,
что a < с < Ъ и F'{c) = 0. Имеем, очевидно:
0 = F'(c) = f'(c)[g(b) - 9(a)) - g'(c)[f(b) - /(a)].
По условию, д'(с) ф 0. Как было отмечено выше, д{Ь) — д(а) ф 0.
Поделив обе части последнего равенства на gf(c)[g(b) — д(а)],
получим:
/'(с) /(b) - /(a) _
a'(c) 5(b)-5(a)
Теорема доказана. ■

322 Гл. 4. Дифференциальное исчисление функций одной переменной
▼ Следствие 1 (теорема Лагранжа о среднем значении). Пусть дан
промежуток [a,b], где — ос < a < b < оо. Если функция f непрерывна
на замкнутом промежутке [а, Ь] и дифференцируема в каждой точке х
открытого промежутка (а, Ь), то найдется число с такое, что a < с < Ь,
и выполняется равенство:
№-№ = f{c)
Данное предложение есть частный случай теоремы 4.3, получаемый
при д(х) = х. ▼
▼ Следствие 2. Пусть I = [a,b], f : I —> R, g : I —> R —
непрерывные функции, дифференцируемые в интервале (a, b). Предположим,
что производная д'{х) не обращается в нуль в промежутке (a,b), и
существует число К Е R такое, что
п*)>к (т<к
(П
\9'(
д'(х) ' \9'(х)
для всех х G (о, Ь). Тогда имеет место неравенство:
f(b) - /(а) . к
g(b) - g(a)
(соответственно, неравенство:
/W-/(а)
9(b) - g(a)
Доказательство — очевидно. Т
<К).
▼ Следствие 3 (теорема Коши об оценке приращения для
комплексных функций). Пусть f : [a, b] —> С есть комплексная функция,
g : [а, Ь] —» R — вещественная функция. Предположим, что f и g
непрерывны в промежутке [а, Ь] и дифференцируемы в интервале (а, Ь),
причем д'{х) ф О для всех х Е (а, Ь). Если существует постоянная К Е R
такая, что
'/'(*)!
9'{х)
<К

§ 4. Теоремы о среднем значении
323
для всех х G (а,Ь), то
f(b)~f(a)
9(b) - 9(a)
<К.
Доказательство. Пусть выполнены все условия следствия.
Если f(b) — f(a) = 0, то требуемое неравенство, очевидно,
выполняется. Предположим, что f(b) — f(a) ф О, и пусть
a
= № - 7(a)
f(b) -f(a)'
Тогда [/(6) - f(a)]a = \f(b) - f(a)\ и |<к| = 1.
Положим af(x) = и(х) + iv(x), где и — Rea/ и v = Ima/
вещественные функции. Имеем:
\u(x)\<\u'(x) + iv'(x)\ = \f'{x)\
и, следовательно,
то есть
и'(х)
9'(х)
<К,
-К<^<К.
9'(х)
Применяя результат следствия 2 теоремы 4.3, заключаем, что
выполняются неравенства:
_к<и(р)-и(а)
9(b) ~ 9(a)
Далее имеем: af(b) — otf(a) = и(Ъ) — и(а) + i[v(b) — v(a)]. Число
aif(b) — f(a)] = \f(b) — f(a)\ — вещественное и, значит, v(b) — v(a) = О,
откуда следует, что \f(b) — /(a)| = и(Ъ) — и(а).
Таким образом, мы получаем, что
к , \№-Яа)\ ,к
~К< 9(Ь)-9(а) <*'
откуда, очевидно, вытекает искомое неравенство.
Следствие доказано. ▼
4.2.2. Теорема Лагранжа о среднем значении (следствие! теоремы4.3)
допускает простое геометрическое истолкование.

324 Гл. 4. Дифференциальное исчисление функций одной переменной
Построим график данной функции / (см. рис. 20). Отношение
ЯЪ)-Па)
Ь — а
есть угловой коэффициент секущей, соединяющей концы графика
функции.
Рис. 20
Величина /'(с) есть угловой коэффициент касательной графика
функции / в точке М = (с, /(c)).
Равенство
mzm=ric}
о — а
означает, что секущая, соединяющая концы графика функции, и
касательная графика функции в точке М параллельны.
Теорема Лагранжа о среднем значении (следствие 1 теоремы 4.3),
таким образом, означает, что если функция / непрерывна на сегменте
[а,Ь] и дифференцируема во всех точках интервала (а,Ь), то на графике
функции найдется точка, не совпадающая ни с одним из
его концов и такая, что касательная в этой точке параллельна
секущей, соединяющей концы графика функции.
4.3. Теорема Дарбу о производной
Установим здесь одно полезное свойство производной, в некоторых
отношениях аналогичное свойству непрерывных функций, которое
устанавливается теоремой Коши о промежуточных значениях (см.
теорему 4.1 главы 2).
■ Теорема 4.4 (теорема Дарбу о производной). Пусть f есть
произвольная вещественная функция, определенная в промежутке [а, Ь] С М.

§ 4. Теоремы о среднем значении
325
Предположим, что f дифференцируема в каждой точке х Е [а, Ь]. Тогда
если ее производная принимает значения к и1, то она принимает любое
значение, лежащее между к и I.
Доказательство» Пусть функция / удовлетворяет условиям
теоремы. Предположим, что к и / таковы, что к = f'{x\) и I = /'(жг), где
Х\ЖХ2 — некоторые точки промежутка [а,Ь].
Будем считать, что к ф I (в случае к = I — доказывать нечего) и
Х± < Х2.
Пусть h — произвольное число, лежащее между к и /, то есть такое,
что или к < h < I, или к > h > I. Требуется доказать, что найдется
точка xq Е [а,Ь] такая, что /'(жо) = h.
Рассмотрим сначала тот частный случай, когда fe~0Hfc<0<Z.
Так как функция / дифференцируема, то она непрерывна и, значит,
согласно теореме Вейерштрасса (глава 2, теорема 5.2), принимает на
промежутке [ял, Жг] свое наименьшее значение в некоторой точке xq. Эта
точка xq отлична от х\. Действительно, имеем:
k = f'(Xl)= ton MzS<0.
ж-^жх+О X — Х\
Отсюда следует, что при х Е (ял,^), достаточно близком к ал,
f(x) - /(ал) < О
И
/(*) < /(si).
Таким образом, в промежутке [ал,Ж2] есть точки, в которых /
принимает значение, меньшее /(ал), и потому точка, в которой / принимает
свое наименьшее значение в промежутке [ал,Ж2], не может совпадать с
Я?1, #0 Ф ЯЛ-
Точно так же, ввиду того, что
/ = /'(Ж2)= Ит № ~ !М > О
ж-*Ж2-0 X — X2
для х Е (жьжг), достаточно близкого к точке #2, имеем:
f(x)-f(x2) . 0
X — Х2

326 Гл. 4. Дифференциальное исчисление функций одной переменной
Так как х — Х2 < О, то для таких х
f(x)-f(x2)<0,
то есть
f(x) < f(x2).
Таким образом, функция / принимает в промежутке [xi,#2]
значения, меньшие /(жг), и, значит, функция / не может принимать свое
наименьшее значение на промежутке [rci, X2] в точке #2, так что xq ф Х2*
Из доказанного вытекает, что х\ < хо < Х2- В силу теоремы Ферма
(см. теорему 4.1), отсюда вытекает, что /'(жо) = 0.
Для рассмотренного частного случая доказываемое утверждение
верно. Общий случай сводится к этому следующим образом.
Пусть h — произвольное число, лежащее между к и I. Положим
F(x) = cr[f{x) — hx], где а = 1 в случае к < I и а = — 1, если к > I.
Функция F дифференцируема в промежутке [а,Ъ]. Имеем:
F'(Xl)<0<F'(x2).
Применяя доказанное выше к функции F, получим, что найдется
точка хо такая, что F\xq) = 0, то есть a[f'(xo) — ti\ = 0, откуда следует,
что f'(xo) = h.
Теорема доказана. ■
4.4. Критерий монотонности функции
4.4.1. Применение теоремы Лагранжа о среднем значении (следствие 1
теоремы 4.3), как видно из доказательства следующей теоремы,
позволяет получить некоторый критерий монотонности функции.
■ Теорема 4.5. Пусть даны промежуток I = (a,b) и непрерывная
функция f : / -+ R. Предположим, что в каждой внутренней точке
промежутка I функция f дифференцируема. Тогда:
для того чтобы f была возрастающей в промежутке I, необходимо
и достаточно, чтобы для каждой точки х Е (a,b) производная f (x) была
неотрицательна;
для того чтобы функция f была убывающей в I, необходимо и до-
статочно, чтобы ее производная была неположительна в каждой точке
х G (a,b).
Доказательство* Необходимость. Предположим, что
функция / : / —» R является монотонной.

§ 4. Теоремы о среднем значении
327
Возьмем произвольно точку хо Е / такую, что функция /
дифференцируема в этой точке.
Пусть х ф жо, х Е (а, Ь). Если функция / — возрастающая, то при
х < хо выполняются неравенства f(x) — f(xo) < 0 и х — xq < О, а при
х > xq выполняются неравенства f(x) — f(xo) >0иж~жо >0. Ив том,
и в другом случае
/(*) - /Ы > 0.
Х — Хо ~"
Переходя в этом неравенстве к пределу при х —► хо, получим, что
/Чад) > о.
Если функция / — убывающая, то при х < хо справедливы
неравенства f(x) — f(xo) > 0 и ж — жо<0, а при х > xq будет f(x) — f(xo) < 0
и х — хо > 0. Следовательно,
/(x)-/(xo)^0
X — Жо ~~
для любого ж ^ #о- Отсюда следует, что в этом случае f'(xo) < 0.
Точка хо £ I взята произвольно и тем самым доказано, что
производная функции / неотрицательна, если функция / возрастающая,
и неположительна, если функция / — убывающая.
Необходимость условия теоремы установлена.
Докажем достаточность. Предположим, что функция
/ : / —> Ш непрерывна и в каждой точке х Е (а, Ь) дифференцируема.
Пусть £i,2?2 — две произвольные точки промежутка / такие, что
х\ < Х2. Тогда всякая точка х такая, что х\ < х < Х2, принадлежит,
очевидно, интервалу (а, Ь) и, значит, функция / — дифференцируема во
всех точках интервала (#1,2:2).
На основании теоремы Лагранжа о среднем значении (см.
следствие 1 теоремы 4.3), найдется £ такое, что х± < £ < жг, и
f(x2)-f(x1) = f'(t)(x2-x1). (4.3)
Если производная f'{x) во всех точках интервала (а, Ь)
неотрицательна, то из (4.3) следует, что в этом случае /(жг) — /(#i) > 0, откуда
f(xi)<f(x2).
Так как точки х\,Х2 Е / такие, что х\ < #2, взяты произвольно, то
тем самым доказано, что функция / в данном случае является
возрастающей.
Если f'(x) < 0 для всех х Е (а, Ь), то равенство (4.3) позволяет
заключить, что в этом случае f(xi) > /(#2) Для любых х±, X2 € I
таких, что х\ < Х2, то есть функция / является убывающей.

328 Гл. 4. Дифференциальное исчисление функций одной переменной
Достаточность условия теоремы тем самым также установлена.
Теорема доказана. ■
▼ Следствие. Пусть функция / : (а, Ь) —» М непрерывна и
дифференцируема в каждой точке х £ (а, Ь).
1) для того чтобы функция f была строго возрастающей в
промежутке I = (а,Ь), необходимо и достаточно, чтобы ее производная была
неотрицательна и в каждом интервале (а, (3) С I содержалась точка £
такая, что /'(£) > 0;
2) для того чтобы функция f была строго убывающей в I,
необходимо и достаточно, чтобы ее производная была неположительна и во
всяком интервале (а,/3) С / можно было указать точку £ такую, что
/'(0<о.
Доказательство. Необходимость. Предположим, что
функция / : I —> Ш является строго возрастающей. Тогда, согласно
теореме 4.5, ее производная всюду неотрицательна.
Пусть дан произвольный интервал (а,/3) С /. Так как функция /
строго возрастающая, то f(a) < /(/3).
По теореме Лагранжа о среднем значении (следствие 1 теоремы
4.3), найдется точка £ такая, что а < £ < /3, и
/()9)-/(а) = /,(ОС8-а).
Так как f((3) — f(a) > 0, /3 — а > 0, то /'(£) > 0 и, таким образом,
доказано, что в интервале (а, /3) существует точка £ такая, что
/'(О > о.
Если функция / строго убывающая, то точно так же
доказывается, что в любом интервале (а,/3) С / найдется точка £, для которой
/'(£) < 0. Необходимость условия следствия установлена.
Докажем достаточность. Пусть функция / : I —► R
непрерывна в промежутке / = (а, Ъ) и дифференцируема в интервале
(а, &), причем ее производная неотрицательна, и во всяком интервале
(ос,(3) С / имеется точка £ такая, что /'(£) > 0.
Требуется доказать, что функция / является строго
возрастающей. Так как функция f'(x) — неотрицательна, то,
в силу теоремы 4.5, функция / — возрастающая.
Предположим, вопреки доказываемому, что / не является строго
возрастающей. Тогда найдется пара точек х\,хъ Е / такая, что х\ < Х2
и f(xi) = /(#2). Так как / есть возрастающая функция, то для любого
х, лежащего между х± и Х2, имеем:
f(xi) < fix) < S(x2),

§ 4. Теоремы о среднем значении 329
и поскольку f(xi) = /(#2), то /(ж) = f(x\) = /(#2) для всех х G (ж1,#2).
Функция /, таким образом, на отрезке (х\,Х2) постоянна.
Отсюда следует, что f'{x) = О для всех х £ (#1,^2)- Это, однако,
противоречит тому, что, согласно условию, существует точка
£ G (#1,ж2) такая, что /'(£) > 0.
Полученное противоречие доказывает, что если х\ < Х2,
то f(xi) < f(x2), то есть / является строго возрастающей
функцией.
Аналогично устанавливается достаточность условия
того, что функция / — строго убывающая.
Следствие доказано. ▼
4.5. Ослабленный критерий монотонности функции
4.5.1. Далее мы покажем, что условия критерия монотонности
функции, который содержится в теореме 4.4, в некоторых случаях могут быть
ослаблены. (Результат, доказываемый здесь, будет использован далее
при изучении понятия интеграла, см. далее п. 1.3 главы 5.)
Введем некоторую вспомогательную функцию г;, полагая для х £ R
ех 1
п(х) = =
,v } ех + 1 1 + е~х
Так как жи1 + е~х есть строго убывающая функция,
то функция 77 является строго возрастающей.
Имеем: г)(х) —► 0 при х -* —оо и г){х) -+ 1 при х -» оо. Полагаем:
ij(-oo) = 0, г;(оо) = 1. (4.5)
Функция г;, определенная равенствами (4.4) и (4.5), имеет областью
определения множество R и является непрерывной в каждой точке х Е R.
Функция г; дифференцируема в интервале (—оо, оо) = R. При этом для
всех х G R
"'(*) = (^TIF > °' (4,6)
■ Теорема 4.6. Пусть даны промежуток I = (а,Ь) С R и функция
f : J —» R. Предположим, что функция f непрерывна и существует
не более чем счетное множество Е С (а, Ь) такое, что в каждой точке
х б (a,b)\E функция f имеет левую производную. Тогда:
если в каждой точке х £ Е справедливо //(#) > 0, то функция f
является возрастающей;
(4.4)

330 Гл. 4. Дифференциальное исчисление функций одной переменной
если же в каждой точке х £ Е выполняется f[{x) < 0, то / есть
убывающая функция.
Замечание. Утверждение теоремы также остается верным,
если в ее формулировке вместо левой производной рассматривать
правую.
Доказательство теоремы. Докажем, что если производная
fi(x) — неотрицательна при каждом х Е (а,Ь), не принадлежащем Е,
то функция / является возрастающей.
Предположим сначала, что функция / удовлетворяет более
сильному условию, а именно, — в каждой точке х € (a,b) \ E левая
производная //(ж) функции / — не только неотрицательна, но и
отлична от нуля, то есть f[(x) > 0 для всех х Е (a, b) \ E.
Возьмем произвольно точки х\,Х2 Е I такие, что х\ < Х2.
Требуется доказать, что f(x\) < /(#2).
Предположим, напротив, что f(xi) > /(#2). Пусть А = f(E). По
условию, множество Е не более чем счетно. Согласно предложению 7.2
главы 1, для любого отображения образ не более чем счетного
множества всегда есть не более чем счетное множество и, значит, А не более
чем счетно. Пусть числа р и q таковы, что /(#2) < р < q < f{x\).
Согласно теореме 3.4 главы 2, промежуток [р, q] представляет собой
несчетное множество и, значит, найдется, по крайней мере, одно значение
k E [р, #], не принадлежащее А.
Функция ip : х н-> f(x) — к — непрерывна. При этом ip(xi) = f(x\) —
—k>q — k>0,& iji(x2) = /(#2) — к < р — к < 0. По теореме Коти
о разрешимости уравнения f(x) = 0 (теорема 4.1 главы 2), найдется
точка с Е (ж1,Ж2) такая, что ф(с) = 0, и *ф(х) > 0 при х\ < х < с (см.
рис. 21).
(XpfiX;))
(x2,f(x2))
Рис, 21
Имеем: /(с) = к. Точка с не принадлежит множеству £*, ибо в
противном случае точка к была бы элементом множества А = /(!?), что
противоречит выбору к.

§ 4. Теоремы о среднем значении
331
Так как с ^ Е, то функция / имеет в точке с левую производную,
причем, согласно предположению, //(с) > 0.
Имеем: f(x) — f(c) > 0 и я — с < 0 при #i < х < с. Отсюда вытекает,
что для всех х Е [#i, с)
ж — с
Переходя в этом неравенстве к пределу при ж, стремящемся к с
слева, получим: //(с) < 0. Это, однако, противоречит тому,
что, по условию, //(с) > 0.
Итак, допустив, что для данных точек х\,Х2 имеет место
неравенство f(x\) > /(#2), мы пришли к противоречию и, следовательно,
f(xi)<f(x2).
Так как точки х\ и х2 такие, что х\ < Х2, были взяты произвольно,
то тем самым нами доказано, что / является возрастающей
функцией, — пока, однако, только в предположении, что при каждом
жЕ (а,Ь)\Е производная f{(x) отлична от нуля.
Теперь освободимся от этого предположения.
Зададим произвольно t > 0. Положим / = / + tr). В каждой точке
х Е (a,b) \ E функция / имеет левую производную. При этом
Jl(x) = f{(x) + tr][(x) > 0. В силу доказанного, функция / является
возрастающей.
Возьмем произвольно точки х\ Е / и Х2 G / такие, что х\ < х2.
Имеем:
/(si) + гфг) = /On) < ]{х2) = f(x2) + tri(x2). (4.7)
Здесь t > 0 — произвольно. Переходя в (4.7) к пределу
при t —> 0, получаем: f(x\) < /(^2) и тем самым установлено,
что функция / является возрастающей.
Предположим, что //(ж) < 0 для всех х Е (а,&) \ £". Положим
д = —/. Тогда <?г'(ж) = —//(ж) > 0 для всех х Е (а, Ь) \ Е и, значит,
функция р является возрастающей. Отсюда следует, что в
данном случае функция f — —д — убывающая.
Теорема доказана. В
Справедливость замечания, предшествующего доказательству
теоремы, устанавливается применением результата теоремы к функции
д(х) = /(—ж). Мы предоставляем читателю рассмотрение всех деталей.
▼ Следствие 1. Пусть даны промежуток I = (a,b) и непрерывная
функция f : / —> R. Предположим, что существует такое не более чем
счетное множество Е С (а, Ъ) = 7°, что в каждой точке х Е 1° \Е будет
fl(x) = 0. Тогда функция f является постоянной в промежутке I.

332 Гл. 4. Дифференциальное исчисление функций одной переменной
Доказательство. Действительно, пусть / удовлетворяет
условиям следствия. Тогда получим, что для всякой точки х Е 1° \ Е
одновременно //(#) > 0 и f((x) < 0. Значит, согласно
теореме 4.6, функция / является одновременно
возрастающей и убывающей и, следовательно, для любых х\,Х2 Е /
справедливы неравенства: f(x\) < /(#2) и f(xi) > /(#2).
Отсюда следует, что f(xi) = /(#2)- Фиксируем произвольно хо Е I.
Тогда, полагая х\ = ж, #2 = #о, получим, что для всякого ж G /
выполняется равенство f(x) = f(xo). Это и означает, что функция / —
постоянна на множестве I. ▼
▼ Следствие 2. Пусть даны промежуток I = (а, Ь) С Ш и функция
f : I —*• R. Предположим, что функция f непрерывна и существует
не более чем счетное множество Е С (а, Ь) такое, что в каждой точке
х Е (а, Ь) \ J5 функция f имеет левую производную, причем для
всякого х £ Е справедливо //(#) > 0 и для любого интервала (а,/3) С /
существует точка £ Е (а,/5) такая, что £ £ Е и //(£) > 0.
Тогда функция f является строго возрастающей.
Если в каждой точке х £ Е справедливо неравенство f{(x) < 0 и
во всяком интервале (а, /3) С J существует точка £ Е (а, /3) такая, что
£ £ Е и //(£) < 0, то / есть строго убывающая функция.
Доказательство. Предположим, что функция / непрерывна и
для всех ж Е (а, Ь) \ £? (J5 не более чем счетно) fftx) > 0 и во всяком
интервале (а,/3) С I существует £ £ Е такое, что //(£) > 0.
Из теоремы 4.6 следует, что / — возрастающая
функция. Предположим, что / не является строго возрастающей. Тогда
найдутся точки #i,#2 Е / такие, что х\ < Х2 и f(xi) = /(#2)- Для
всякого ж Е (#ь#2) имеем: /(#i) < /(ж) < /(#2) и, значит, функция / в
промежутке {х\,Х2) — постоянна.,
Отсюда вытекает, что ff(x) = 0 для всех х Е (#i,#2)« Это, однако,
противоречит тому, что в интервале (xi, #2), согласно условию,
существует точка £ такая, что //(£) > 0.
Итак, допустив, что функция / не является строго возрастающей,
мы получаем противоречие.
Первое утверждение следствия тем самым доказано.
Второе утверждение доказывается аналогично. ▼
▼ Следствие 3. Если функция f : I —» R непрерывна в промежутке
I = (а, Ь) С R и дифференцируема в интервале (а, Ь) и f'(x) = 0 для всех
х Е (а, Ь), то функция f постоянна на множестве I.
Данное утверждение есть очевидный частный случай каждого из
следствий 1 и 2. ▼

§ 4. Теоремы о среднем значении
333
В качестве примера на приложение теоремы 4.6 приведем
доказательство оценок приращения функции, полученных ранее как следствия
теоремы Коти о среднем значении (см. теорему 4.3).
Ф Предложение 4.1. Пусть I = [а,Ь], / : / —► Е, g : / —► К
— непрерывные функции, каждая из которых имеет в (а, Ь) конечную
левую производную всюду, кроме точек, образующих не более чем счет-
ное множество. Предположим, что производная д[(х) неотрицательна в
промежутке (а, Ъ) и существует число К ЕЕ такое, что
fl(x) < КдЦх) (f{(x) > Кд{(х))
для всех х £ (а, Ь), исключая точки, образующие не более чем счетное
множество. Тогда имеет место неравенство:
f(b)-f(a)<K(g(b)-g(a))
(соответственно, неравенство:
f(b)-f(a)>K(g(b)-g(a)).
Доказательство. Пусть неравенство f'(x) < Kg' (x)
выполняется в основном в промежутке (а, Ь). Тогда функция F : х >-+ f(x) — Kg{x)
непрерывна и F'(x) < 0 в промежутке (а, Ь) в основном.
Отсюда, в силу теоремы 4.6, следует, что функция F является
убывающей в промежутке [а, Ь], и, следовательно, F(a) < -F(b), то есть
/(b) - Kg(b) < /(а) - Kg(a), откуда /(b) - /(а) < Кд(Ь) - Кд{о) и
неравенство, относящееся к случаю, когда //(#) < Кд[(х), доказано.
Второе неравенство доказывается аналогичным образом.
Предложение доказано, ф
4.5.2. Следствие! теоремы4.6 позволяет найти все решения некоторых
дифференциальных уравнений, рассмотренных в п. 2.4 этой главы.
Сначала рассмотрим уравнение:
x'(t) = fcx(t), (4.8)
где к — постоянная. Любая функция x(t) вида x(t) = Aekt, очевидно,
является решением этого уравнения.
Докажем, что других решений данное дифференциальное
уравнение не имеет. Для этого достаточно установить, что если x(t) есть
решение уравнения (4.8), то функция x(t)e~kt является постоянной.

334 Гл. 4. Дифференциальное исчисление функций одной переменной
Итак, пусть функция x(t) определена и непрерывна в промежутке
(а, Ь)с1и дифференцируема в каждой точке интервала (а, Ь).
Рассмотрим вспомогательную функцию y(t) = x{t)e~kt. Имеем:
y'(t) = e~feV(t) - ke-ktx(t) = e-kt[x'(t) - kx(t)] = 0.
Мы получаем, таким образом, что производная функции y(t)
тождественно равна нулю. Следствие 1 теоремы 4.6 позволяет заключить,
что эта функция постоянна в промежутке (а, Ь), и, значит, x(t) = Cekt
для всех t из этого промежутка.
Таким образом, доказано, что если функция x(i) удовлетворяет в
промежутке (а,Ь) дифференциальному уравнению (4.8), то она задается
формулой:
x(t) = Aek\
где А — постоянная. (Полагая x(t) = m(t), A = mo, получим формулу
(2.16) в п. 2.4.)
Пусть функция x(t) определена и непрерывна в промежутке (а, Ь),
имеет вторую производную в каждой точке t G (а, Ь) и удовлетворяет
дифференциальному уравнению:
x"(t) = kz(t), fc#0. (4.9)
Установим общий вид решения этого уравнения. Возможны два
случая: 1) к > 0 и 2) к < 0.
Рассмотрим первый случай. Положим к = Л2. В результате
уравнение принимает вид:
x"(t) = \2x(t).
Нетрудно видеть, что функции chAt и sh\t удовлетворяет
этому уравнению. Отсюда следует, что также и любая функция вида:
АсЪХЬ + BshXt также является решением данного уравнения.
Покажем, что других решений данное уравнение не имеет.
Если x(t) = A ch Xt + В sh At, то x'(t) = \А sh \t + \B ch \t. Из этих
равенств следует, что
АХ = x(t) ch Xt - x'(t) sh At,
BX = - Aa?(t) sh At + x;(t) ch At.

§ 4. Теоремы о среднем значении
335
Предположим теперь, что x(t) есть произвольная функция,
удовлетворяющая уравнению (4.9) в промежутке (а, Ь) для случае к = Л2 > 0.
Введем вспомогательные функции:
u(t) = Xx(t) ch At - x'(t) sh At, v(t) = -\x(t) sh At + x'(t) ch At.
Докажем, что каждая из эти функций тождественно постоянна в
промежутке (a, ft). Имеем:
u(t) = Ax'(t) ch At + A2z(t) sh At - x"(t) sh At - Xx(i) sh At.
Замечая, что x"(t) — kx(t) = A2#(t), после очевидных
преобразований получим, что u'(t) = 0. Отсюда следует, что функция и в
промежутке (а, Ь) — постоянна, и u(t) = С\ G И.
Аналогичным образом устанавливается, что также и v'{t) = 0 для
всех t G (а,Ь), и, значит, v(t) = C2 G К. Решая систему уравнений
Az(t) ch At - x'(t) sh At = Ci,
-Xx(t) sh At + z'(t) ch At = C2
относительно x(t) и #'(t), получим:
x(t) = AchAt + BshAt,
л Ci C2 A r,
где л=—,В = —,ЛиВ — постоянные.
Л Л
Для случая 1) общий вид решения уравнения (4.9), таким образом,
установлен.
Рассмотрим второй случай. Предположим теперь, что х есть
решение уравнения (4.9), соответствующее случаю к = —А2 < 0.
Определим вспомогательные функции u{t) и v(t), полагая:
u(t) = Xx(t) cos At — x(t) sin At, v(t) = Xx(t) sin At + x'(t) cos At.
После простых преобразований получим: u'{t) = 0 и v'{t) = 0 для
всех t G (а, Ь) и, значит, u(t) = С\ G Е и v(t) = C2 G R. Подставляя
сюда выражения для u(t) и v(t) через #(t) и #'(t), получим:
#(t) = Л cos At + В sin At.
Таким образом, нами установлен общий вид решения уравнения
(4.9) также и для случая 2).

336 Гл. 4. Дифференциальное исчисление функций одной переменной
§5. Правила Лопиталя раскрытия
неопределенностей
Пусть даны две функции, каждая из которых имеет равный нулю
предел при х, стремящемся к некоторой точке р. Тогда, как было
показано выше, о пределе частного этих функций при х —► р, вообще говоря,
ничего сказать нельзя.
Пользуясь средствами дифференциального исчисления, в
некоторых случаях, однако, можно показать, что указанное отношение есть
предел, и найти значение этого предела. Здесь приводится теорема,
позволяющая это сделать.
Аналогичные результаты установлены также для случая, когда
каждая из данных функций имеет предел, равный оо.
5.1. Неопределенности типа -
Пусть даны множество АсКи функции /:Л->Ми^:А->Е.
Предположим, что для некоторой точки р G CimA справедливо д(х) ф О
при х G А \ {р}, и выполняются равенства:
lim f(x) = 0; lim g(x) = 0.
х—*р х—►р
Тогда о пределе отношения ; ( при х —► р, как мы знаем (см. п. 2.4
9УХ)
главы 2), ничего сказать нельзя.
Этот предел может вообще не существовать, а если он
существует, то его значение может быть равно любому наперед заданному числу
ffx)
L G И. В этом случае говорят, что отношение ; ( является неопреде-
9УХ)
0
ленностъю типа - при х —► р.
Аналогично, если
lim f(x) = оо; lim g{x) = оо,
х—>р х—►р
то предел отношения : : может не существовать, а если он существу-
ет, то его значением может оказаться любое число. В данном случае
f ( X) ОО
говорят, что отношение ) ( — это неопределенность типа — при
д(х) оо
х —> р.

§ 5. Правила Лопиталя раскрытия неопределенностей
337
Докажем предложения, облегчающие в некоторых случаях отыскание
f(x\
предела отношения ; , когда fix) и д(х) стремятся к 0 или к оо.
9\х)
Ш Теорема. 5.1 (первая теорема Лопиталя). Пусть даны интервал
I = (а, Ь) и пусть р есть один из его концов (то есть р есть либо точка а,
либо точка Ъ). Предположим, что функции /:I^1hj:J->1
дифференцируемы в промежутке I и таковы, что д(х) ф О и д'(х) ф О
для всех х G I и
lim f(x) = lim g{x) — 0.
х—>р х—>р
Если существует предел
х-+р д'(х)
то существует также и предел
limM,
х->р д[х)
причем значения этих пределов равны.
Доказательство. Положим J = (а,Ь) U {р}. Очевидно, что J
есть или промежуток (а, Ь], или промежуток [а, Ь).
Пусть функции / и g удовлетворяют всем условиям теоремы.
Доопределим их, полагая f(p) = g(p) = 0. Тогда функции
/ и g будут непрерывны в точке р.
Пусть К > —оо. Зададим произвольно L < К. По нему найдется
окрестность U точки р такая, что если х £ U П J, то
Пусть ж есть произвольная точка интервала /, принадлежащая
окрестности U. Имеем:
f(x) = fjx) - f(p) = f'(Q
g(x) g(x)-g(p) д'(0'
где ^ лежит между жир.
Очевидно, £ Е С/. Отсюда следует, что
/(«) = /40 . ,
9{х) 9'(0 > *

338 Гл. 4. Дифференциальное исчисление функций одной переменной
Если К = оо, то из доказанного следует, что
lim Щ = оо = К.
х-+р д(х)
Если К < оо, то, рассуждая аналогичным образом, получим, что
для всякого L > К найдется окрестность U точки р такая, что для всех
х eUnJ выполняется неравенство: —7—f < L. Отсюда сразу вытекает,
что если К = —оо, то
х->Р д(х)
Предположим, что К — конечно. Зададим произвольно е > 0. По
доказанному, найдутся окрестности Ui и Ui точки р такие, что для всех
х е Ui П J
fix)
а для всех ж € С/г П J
9{х)
№
>L1 = K-e,
<L2 = K + e.
Пусть U есть окрестность точки р такая, что Ui D U vt U2 D U.
Для всякого х 6 U П J выполняется неравенство:
'М-х
<£.
В силу произвольности £ > 0, и в этом случае получаем, что
№
К= lim
х-+р д(х)'
Теорема доказана.
▼ Следствие 1. Пусть даны отрезок I = (а, Ь), точка хо такая,
что a < хо < Ь, и функции f и д, дифференцируемые на множестве
(а, Ь) \ {хо}, причем f(x) —> 0, #(#) —> 0 при #—►(). Предположим, что
для всякого х Е (а, Ь) \ {xq} будет д(х) ф 0 и д'{х) ф 0, и существует
предел
х-*х0 д'ух)

§ 5. Правила Лопиталя раскрытия неопределенностей
339
Тогда предел
х^х0 д[х)
также существует, и значения этих пределов совпадают.
Доказательство. Предположим, что выполнены все условия
следствия. Применяя результат теоремы 5.1 к каждому из промежутков
(а, хо) и (жо, Ь) и полагая р = жо, получим, что
lim М= lim Щ = к,
х—>х0-о д[х) ж—*>жо+о д[х)
откуда, очевидно, и следует требуемое утверждение — следствие 1. V
Т Следствие 2. Пусть функция f определена и непрерывна в
полуоткрытом промежутке (а, Ь], где Ь — конечно. Если f дифференцируема
в каждой точке х Е (а, Ь) и существует предел lim f'(x) = К, то функция
х—*Ъ
f имеет в точке Ь производную. При этом f'{b) = К.
Если функция f определена и непрерывна в замкнутом слева
промежутке [а, Ь), где a > —оо, в каждой точке х Е (а, Ь) имеет производную
f'(x) и существует предел lim f'{x) = L, то L = f'{a).
ж—►а
Если с Е (а, Ъ) и функция f : (а, Ь) —*• R непрерывна,
дифференцируема при всяком х Е (а, Ь), отличном от с, и существует предел
lim f(x) = М,тоМ = /'(с).
х—>с
Доказательство. Следствие содержит три утверждения.
Докажем первое. Рассмотрим дробь:
/(*)-/(*>)
х — Ь
Числитель и знаменатель этой дроби стремятся к нулю при х —► Ь.
Производная числителя равна /;(ж), производная знаменателя
тождественно равна единице. Отношение производной числителя к производной
знаменателя, следовательно, равно f'(x) и, значит, согласно условию
следствия, имеет предел при х —» Ъ. Значение этого предела равно К.
Применяя теорему 5.1, получаем, что существует предел:
х-+Ъ X — О
то есть К = f'(b).

340 Гл. 4. Дифференциальное исчисление функций одной переменной
Справедливость двух остальных утверждений следствия
устанавливается аналогично.
Следствие 2 доказано. ▼
▼ Следствие 3. Предположим, что вещественная функция f
определена в интервале (а, Ь) и дифференцируема в каждой точке этого
интервала. Производная /' функции f может иметь в (а, Ь) только точки
разрыва второго рода.
Доказательство. Пусть р £ (а, Ь). Согласно условию, функция
/ дифференцируема в точке р и производная f'(p) — конечна.
Предположим, что р есть точка разрыва первого рода функции /'.
Согласно определению точек разрыва первого рода, это означает, что
функция /' имеет в точке р конечные пределы слева и справа. Согласно
следствию 2, имеем:
lim /'(*) = f'(p), lim f'(x) = f'(p).
x—tp—Q x—*р+0
Таким образом, пределы слева и справа функции /' в точке р, —
в случае, если они существуют, — неизбежным образом оказываются
совпадающими с /'(р) и, следовательно, функция /' в этом случае
является непрерывной в точке р. Это противоречит тому, что, согласно
предположению, р есть точка разрыва функции /'.
Итак, допущение, что некоторая точка р Е (а, Ь) является точкой
разрыва первого рода функции /;, приводит к противоречию.
Следствие 3 доказано. ▼
Замечание. Результат теоремы 5.1 не может быть
обращен. Предположим, что функции / : (а, Ь) —> R и g : (а, Ь) —> Ш
дифференцируемы в промежутке / = (а, Ь), р есть одна из точек а и Ь is.
при х —> р выполнено /(ж) —► 0 и д(х) —> 0.
Если известно, что отношение ; ! при х —> р стремится к некото-
рому пределу, то отсюда, вообще говоря, нельзя заключить, что
/'и
отношение , : имеет предел при х —► р.
9\х)
Пример. Пусть / = (0,оо), р = 0. Положим: /(ж) = ж sin—,
д(х) = у/х. Тогда
/(*)_
7Г
= \fxsin > 0 при х —> 0;
р(ж) ж

§ 5. Правила Лопиталя раскрытия неопределенностей
341
/ (х) = sin cos —;
ж ж х
Ч \ 1
2^'
/'(#) л /- . Я" 27Г 7Г
,; ч = 2у/хsin 7= cos ~•
д'ух) х у/х х
При # —» О первое слагаемое справа стремится к нулю,
второе не имеет предела при х —> 0. Отсюда следует, что в данном
случае предел
не существует.
5.2. Неопределенности типа —
оо
■ Теорема 5.2 (вторая теорема Лопиталя). Пусть I = (а,Ь) и р
— один из концов промежутка I, f : I —> R и д : I —> Ш — функции,
дифференцируемые в промежутке I. Предположим, что lim g{x) = ос,
х—+р
причем д(х) ф 0 и д'(х) ф 0 для всех х £ I, и существует предел:
х-+р д'(х)
Тогда существует также и предел
х-+р д(х)
и значения этих пределов совпадают.
Доказательство. Пусть функции / и g удовлетворяют всем
условиям теоремы.
Пусть К > — оо. Зададим произвольно число L < К. Пусть I/
таково, что L < V < К.
Найдем окрестность Ui точки р такую, что для любого х Е Ui П I
выполняется неравенство:
9'{х)

342 Гл. 4. Дифференциальное исчисление функций одной переменной
Выберем произвольно точку t G / П U\. Для произвольного х G /
положим:
g(x)-g(t)
Тогда имеем, очевидно,
f(x) = h(x)\g(x)-g(t)] + f(t),
откуда
№
9{х)
= h(x)
l_iW
+
т
9{х)'
(5.2)
По теореме Коши о среднем значении (теорема 4.3 этой главы),
найдется £, лежащее между t к х и такое, что
Их) - Ш
Будем далее считать, что х лежит между t и р, то есть х G (а, £)
при р = аихЕ (£, Ь) при р = Ь.
Тогда £ G i7i и, значит, в силу выбора £Л, имеем:
По условию теоремы, р(ж) —* оо при ж-»ри, следовательно,
9(t)
lim
ж—*р
1-
9(х)
= 1,
и потому найдется окрестность t/г точки р такая, что если ж G С/г, то
i-^4>o.
Для всякого х € I C\Ui имеем: /i(#) > I/. Отсюда вытекает, что
если одновременно xGf/iflJHxGf^nJjTO
h(x) + Щ>Ь'
\ 9(х
*0+$- *»

§ 5. Правила Лопиталя раскрытия неопределенностей
343
При х —» р правая часть последнего неравенства стремится к пределу,
равному I/ > L. Отсюда следует, что найдется окрестность £/з точки р
такая, что если х Е (7з5 то
+ Щ > L. (5.4)
Пусть U есть окрестность точки р, содержащаяся в каждой из
окрестностей Ui, С/г и t/з. Тогда для всякого х G U П I
выполняются неравенства (5.1), (5.3) и (5.4) одновременно и, значит, для
таких х
№
9&)
>L.
Число L < К было выбрано произвольно. Из доказанного следует
справедливость теоремы для случая, когда К = оо.
Аналогичным образом устанавливается, что если К < оо, то для
любого числа L > К найдется окрестность U точки р такая, что для
всех х G U П J выполняется неравенство:
т<ь.
9(х)
(Формально, данное утверждение может быть получено
применением доказанного к функциям fi(x) = —f(x) и д±(х) = д(х).)
Отсюда вытекает, что утверждение теоремы верно для случая,
когда К = —оо.
Рассмотрим случай, когда К — конечно.
Зададим произвольно е > 0. По доказанному найдутся окрестности
U' и U" точки р такие, что для всех х G U'nl выполняется неравенство:
/ ч > Li = К — е,
9(?)
а для любого х € U" Г\1 имеет место неравенство:
9{х)
<L2 = K + e.
Пусть U — это окрестность точки р, содержащаяся в каждой из
окрестностей U' и U". Для всякого х G U, очевидно, имеем:
«4-х
Ф)
<е.

344 Гл. 4. Дифференциальное исчисление функций одной переменной
Так как е > О было взято произвольно, то тем самым установлено,
что
х-*Р д[х)
Теорема доказана. ■
▼ Следствие. Пусть даны отрезок I = (а, Ь) С R, точка #о £ J и
функции f : I \ {хо} —> R и g : I \ {хо} —» М, дифференцируемые на
множестве I \ {хо}. Предположим, что д(х) —» оо при ж —* #о и р(ж) ^ О
и </(#) т^ О Для любого х Е I \ {хо}. Если существует предел
x-*xq g \х)
то существует также и предел
ж—►жо д{х)
и значения этих пределов совпадают.
Доказательство. Пусть выполнены все условия следствия. К
каждому из промежутков (а,хо) и (хо,Ь) применим результат
теоремы 5.2. Полагая р = жо, получим, что
lim ^Ц-f = lim "Ч-Т =к-
ж-н.жо-о #(#) ж-^жо+о д(х)
Отсюда, очевидно, и следует требуемое утверждение следствия
теоремы 5.2. ▼
§6. Формула Тейлора
В задачах, появляющихся в приложениях математики, часто
возникает необходимость вычислять значения различных вещественных
функций. Непосредственно из определения функции извлечь удобный
способ вычисления ее значений возможно не всегда. Требуется
выполнение только таких операций, которые «умеет» производить
вычислительное устройство, имеющееся в распоряжении исследователя.
В общем случае основной прием для вычисления значений
произвольной функции состоит в том, что для данной функции^/ строится
другая, более простая с точки зрения вычислений функция f, близкая в

§ 6. Формула Тейлора
345
каком-либо смысле к /. Значения функции f принимаются за
приближенные значения исходной функции. В качестве таких приближающих
функций обычно выбираются полиномы.
В этом параграфе изучается конструкция для построения близких
к функции полиномов, основанная на следующем принципе.
Полином Р считается близким порядка п к функции f, если в
некоторой точке хо Е I выполняется равенство f (хо) = Р(хо) и значения всех
производных полинома Р порядка не выше п равны значениям в точке
хо соответствующих производных данной функции. При этом
предполагается, что степень полинома не превосходит п. Такой полином мы
называем полиномом Тейлора порядка п функции f в точке хо.
Далее устанавливаются некоторые оценки разности между
функцией и ее полиномом Тейлора в точке хо. Сначала исследуется поведение
указанной разности при х, стремящемся к хо. Затем выводятся
некоторые представления для разности функции и ее полинома Тейлора,
позволяющие оценить, сколь мала эта разность во всем промежутке, где
определена функция.
Полиномы Тейлора являются эффективным средством для
построения приближенных представлений функций, удобных для вычислений.
6.1. Некоторые сведения о полиномах одной переменной
Функция Р : М —» С называется полиномом степени не выше п,
если существуют комплексные числа ао, сц,..., ап, хотя бы одно из
которых отлично от нуля, такие что для всех жЕК выполняется равенство:
п
Р(х) = ао + сцх Л Ь anxn = V^ а^хк. (6.1)
А:=0
Числа dk, где к = 0,1,..., п, называются коэффициентами
полинома Р. Равенство (6.1) называется каноническим представлением
полинома Р.
Говорят, что степень полинома Р равна п, если коэффициент ап в
равенстве (6.1) отличен от нуля. Степень полинома Р(х) обозначается
символом: degP.
Если Р есть полином степени не выше п и т > п — целое число,
то Р является также полиномом степени не выше га, поскольку, полагая
fln+i = fln+2 = • • * = ат = 0, равенство (6.1) можно записать также в
следующей форме:
т
Р(х) = У~]акхк.
к=0

346 Гл. 4. Дифференциальное исчисление функций одной переменной
Функция, тождественно равная постоянной, отличной от
нуля, является полиномом, степень которого равна нулю.
Функцию Р, тождественно равную нулю, также будем считать
полиномом. В этом случае полагаем: degP = —оо.
Отметим некоторые свойства полиномов.
I. Пусть Pi, P2,..., Рг — произвольные полиномы степени не выше
п. Тогда для любых чисел Ai, Л2,..., Лг функция
AiPi + Л2Р2 + • • + XrPr
есть полином степени, не превосходящей п.
II. Пусть даны полиномы Рг, г = 1,2,... ,т, причем степень Pi не
превосходит щ. Тогда произведение Р1Р2 ... Рш есть полином степени
не выше
п = т + п2 Н Ь nm. (6.2)
Действительно, если хотя бы один из полиномов Pi тождественно
равен нулю, то и все произведение Р1Р2 ... Рт тождественно равно нулю
и, стало быть, есть полином, степень которого равна —оо. В этом случае
и сумма (6.2) равна —оо.
Будем считать, что ни один из полиномов Pi не обращается в нуль
тождественно. Пусть
Pi(x) = аг,о + a>i,ix H h aiynixni, г = 1,2,...,га,
есть каноническое представление полинома Pi.
Перемножая почленно данные представления полиномов Рг,
получим, что их произведение есть сумма конечного числа слагаемых вида
ai,kla2,k2... am,fcmsfcl+fe2+-+fe™,
где ki < щ при всяком г = 1,2,..., т. Каждое из этих слагаемых есть
полином степени не выше п = п\ + п2 + • • • + пт. Отсюда следует,
что их сумма есть полином степени не выше п, что и требовалось
доказать.
III. Пусть Р есть полином степени не выше п, где п > 0. Тогда,
каково бы ни было вещественное число а, полином Р может быть, и
притом единственным способом, представлен в виде:
Р(х) = Ьо + Ъг(х - а) + • • • + Ъп(х - а)п. (6.3)

§ 6. Формула Тейлора
347
Коэффициенты Ы, i = 0,1,... ,п, определяются по точке а € Ш и
полиному Р следующими равенствами:
Ъо = Р(а), Ьк = ^-^-, к = 1,2,..., п. (6.4)
Замечание. Равенство (6.3) называется разложением полинома
Р по степеням х — а.
Доказательство III. Сначала установим существование
представления вида (6.3) для произвольного полинома Р степени не выше п,
где п > 0.
Пусть Р есть полином степени не выше п, п > 0. Зададим
произвольно точку aGM.
Функция t E M^t + o есть полином степени не выше 1. В силу
предложения II, для любого целого га > 0 функция t Е Ки (t + a)m
является полиномом степени не выше га, как произведение га полиномов
не выше первой степени.
п
Пусть Р(х) = ао + а\х -\ Ь апхп = 2_] akXk есть каноническое
к=0
представление полинома Р. Имеем:
п
P(t + а) = а0 + ai(t + а) + • • - + an(t + а)71 = ]Г afc(* + a)fe
fc=0
для всех t Е М, откуда следует, что Pi(t) = P(t+a) есть полином степени
не выше п.
Пусть
п
Pi(t) = J2htk
fc=0
есть его каноническое представление. Полагая
здесь t = х — а и замечая, что Pi (х — а) = -Р(ж), получаем следующие
равенства:
п
Р(х) = ^Ьк(х - а)к = Ьо + Ъг(х - а) + • • • + Ьп(х - а)п
fc=0
для всех x£R, и существование требуемого представления
полинома Р установлено.

348 Гл. 4. Дифференциальное исчисление функций одной переменной
Докажем, что коэффициенты Ьк в (6.3) по данному числу
а Е К для полинома Р определяются единственным образом.
В равенстве (6.3) положим х = а.
Тогда все слагаемые, номера которых больше 0, обратятся в нуль
и мы получим в результате равенство: Р(а) = Ьо. Видим, что
коэффициент Ьо однозначно определяется по полиному Р.
При всяком целом п > О функция жн {х — а)п имеет производные
всех порядков. При этом
Dr{(x - а)т} = | nQ
т(т — 1)... (га — г + 1)(х — а)т г при г < га;
при г > га.
Дифференцируя равенство (6.3) почленно, в силу последнего
равенства, получим, что в случае г > п справедливо Р^г\х) = 0, а при г <п
будем иметь:
п
Р(г)(ж) = ^2 Ькк(к - 1) ...(*- г + 1)(ж - а)к~г.
fc=r
Положим здесь х = а. В этом случае все те слагаемые справа,
номера которых больше г, обратятся в нуль. Отсюда следует, что
P(r)(a) = brr(r-l)...l = r!br,
и,значит,
ь - р(г)^
иг — : .
г!
Таким образом, мы установили, что коэффициенты Ьк в равенстве
(6.3) определяются полиномом Р, как функцией вМ, единственным
образом.
Предложение III доказано.
Подставляя выражения для коэффициентов Ьк, которые даются
равенством (6.4), в (6.3), получим:
fc=0
Под производной нулевого порядка функции в этой записи
понимается сама функция, то есть мы полагаем здесь Р^°\а) = Р(а).
Равенство (6.5) называется формулой Тейлора для полиномов.

§ 6. Формула Тейлора
349
В случае а = О разложение полинома по степеням х — а
превращается в его каноническое представление.
Из доказанного, следовательно, вытекает, что каноническое
представление полинома однозначно определяется полиномом, как
функцией на множестве М, и может быть записано следующим образом:
fc=0
Формула (6.6) называется также формулой Маклорена для
полинома Р(х).
Ш Лемма 6.1. Пусть Р есть полином степени не выше п. Тогда если
Р(х) = о[(х — a)n] при х —♦ а для некоторой точки a Е Е, то полином Р
тождественно равен нулю.
Доказательство проведем индукцией по п.
Пусть п = 0. В этом случае Р(#) = Ао, где Ао Е С. Условие
леммы в данном случае означает, что Р(х) = о(1) при х —» а, то есть
lim Р(я) = 0. Имеем: lim Р(#) = Ао и, значит, Ао = 0 и Р(ж) = 0.
Для случая п = 0 лемма доказана.
Предположим, что для некоторого п > 0 справедливость
утверждения леммы установлена.
Пусть Р есть полином степени не выше п + 1 такой, что Р{х) =
= о[(х — a)n+1] при ж —» а. Пусть
Р(я?) = Ро + Pi (ж - а) + • • • + Вп(х - a)n + Bn+1xn+1 (6.7)
есть разложение Р{х) по степеням х — а.
Равенство (6.7) перепишем следующим образом:
Р(х) = В0 + (х-а)Р1(х),
где Pi (ж) = J5i Н Ь Вп(х — а)п~1 + Bn+i(x — а)п — полином степени
не выше п.
Из условия: «Р(ж) = о[(х—а)п+1] при х -* а» следует, что Р(ж) —♦ 0
при ж —> а и, значит, Ро = Ит Р(х) = 0.
ж—*а
Из предположения, сделанного относительно полинома Р,
вытекает, что Р(х) = (ж — a)Pi(x), где Pi — полином степени не выше п.
Отсюда получаем, что
Р(х) __ Pi (ж)
(ж - a)n+1 (ж - а)п'

350 Гл. 4. Дифференциальное исчисление функций одной переменной
Так как, по условию, Р(х) = о[(х — а)п+1] при х
и, следовательно,
1*т / 4,1
ж-*а (Ж - а)п+1
hm ^—7- = 0,
ж—а (Ж - а)п
то есть Pi (ж) = о[(ж — а)п] при ж —» а.
Так как, по предположению, для полиномов степени не выше п
утверждение леммы верно, то из соотношения Р\(х) = о[(ж — а)п]
при ж —> а следует, что Pi (ж) = 0 и, стало быть, Р(х) = 0.
В силу принципа математической индукции, лемма доказана. ■
6.2. Формула Тейлора с остаточным членом в форме Пеано
Здесь мы докажем, что если функция, определенная на некотором
промежутке, имеет в нем производную порядка п, то вблизи всякой
точки хо этого промежутка f(x) отличается от некоторого полинома
степени не выше п на величину порядка о(\х — хо\п) при х —» xq.
Предварительно докажем следующее предложение.
■ Лемма. 6.2 (лемма об интегрировании асимптотических
соотношений). Пусть I = (p, q) есть произвольный интервал и f : J —> С —
функция, определенная и дифференцируемая в этом интервале.
Предположим, что для некоторой точки a £ J выполняются равенства f(a) = 0
и f'(x) = о[\х — а|л] при ж —» а, где А > 0.
Тогда f(x) = о[|ж — а|л+1] при ж —* а.
Доказательство. Рассмотрим отношение
-Л|А+1#
|ж — а|
(6.8)
Требуется доказать, что при ж ■—► а оно имеет предел, равный 0.
Так как функция / дифференцируема, то она непрерывна в I, и,
значит, при х —* а справедливо f(x) —» /(а) = 0.
Величина \х — a\x+1 также стремится к нулю при х —* а.
Отношение (6.8), таким образом, представляет собой неопределен-
„J.
Применим первую теорему Лопиталя (теорема 5.1 этой главы),
полагая в ней д(х) = \х - о|Л+1. Имеем: <j'(a;) = —(А + 1)|ж - а\х при

§ 6. Формула Тейлора
351
х < а и д'{х) = (Х + 1)\х — а\х при х > а. В силу условия леммы,
получим:
lim £M = _ lim Ш -о
с-*а-0 <7'(ж) ж-*а-0 (Л + 1)|Ж —а|А
ж-
И
lim £M= Um Ш -р.
ж-^а+0 д'\Х) ж-»а+0 (А + 1)|Ж — а|А
Отсюда вытекает, что
В силу первой теоремы Лопиталя, это позволяет заключить, что
Иш _ZH_ = о.
х-*а \х — а|А+1
Лемма доказана. ■
■ Лемма 6.3. Пусть I = (р, д) и функция / : / —» С является п-
кратно дифференцируемой в промежутке I, причем для некоторой точки
а Е I будет f(a) = 0 и при всяком к = 1,2,..., п выполняется /^ (а) = 0.
Тогда f(x) = о[(ж — а)п] при ж —* а.
Доказательство. Лемма доказывается индукцией по п.
Пусть п = 1. Согласно определению того, что значит, что функция
/ дифференцируема в точке а (см. п. 1.1), имеем:
/(#) = /(а) + f(a)(x — a) + o(x — а) при ж —» а.
Отсюда вытекает, что если /(а) = 0 и /'(а) = 0, то f(x) = о(х — а)
при х —► а, так что для п = 1 утверждение леммы верно.
Предположим, что для некоторого n E N лемма доказана
и функция / является (п + 1)-кратно дифференцируемой в
интервале /, причем /(а) = 0 и для всякого fc = l,2,...,n,n + l справедливо
/(fe)H = 0.
Положим F = /'. Функция F — n-кратно дифференцируема в
промежутке /, F(a) = f'(a) = 0 и при каждом fc = 1,2,... ,п выполняется
FW(a) = /(fe+1)(a)=0.
В силу индукционного предположения, F(x) = о[(х—a)n] при ж —► а.
Таким образом, для функции / имеем: /(a) = 0 и f'{x) = F(x) =
= о[(х — a)n] при х —* а. На основании леммы 6.2, из этого вытекает,
что /(ж) = о[(ж — а)п+1] при ж —> а.
Лемма доказана. ■

352 Гл. 4. Дифференциальное исчисление функций одной переменной
Пусть даны интервал I = (p,q) и функция / : J —► С, п-кратно
дифференцируемая в этом интервале.
Возьмем произвольно точку a Е I. Пусть Р есть полином степени не
выше п. Будем называть его полиномом Тейлора порядка п функции f в
точке а, если /(а) = Р(а) и f^k\a) = Р^(а) для всякого к = 1,2,..., п.
Пусть Р есть полином Тейлора порядка п функции f в точке а.
Применяя формулу Тейлора для многочленов (равенство (6.5)
предыдущего раздела), получим, что Р допускает представление:
fc=0
Под производной нулевого порядка функции, как и ранее,
понимается сама функция.
Пусть Р — это полином Тейлора порядка п функции / в точке
ае/=(р,«).
Разность f(x) — Р(#) = Rn{x,a) называется остаточным
членом формулы Тейлора.
Следующая теорема характеризует поведение остаточного члена
формулы Тейлора функции в точке а при х —► а.
Ш Теорема 6.1. Пусть даны промежуток I = (p,q) и функция
/ : I -+ С, n-кратно дифференцируемая в промежутке I. Тогда при
х —► а для всякой точки a € I справедливо асимптотическое
соотношение:
№ = f(a) + !^(x-a) + i^-(x-af + ...
••• + ^!^(ж-°Г + 0[(а;-а)П]-
Перед доказательством отметим следующее.
Замечание!.. Асимптотическое соотношение, устанавливаемое
этой теоремой, называется формулой Тейлора с остаточным членом в
форме Пеано.
Замечание2. Утверждение этой теоремы означает, что если
Р есть полином Тейлора порядка п функции / в точке a Е /, то
f(x) = Р(х) + о[(х — а)п] при х —► а.

§ 6. Формула Тейлора
353
ЗамечаниеЗ. Частный случай формулы Тейлора,
соответствующий значению а = О, называется формулой Маклорена.
Доказательство теоремы. Предположим, что выполнены все
условия теоремы.
Пусть Р есть полином Тейлора порядка п функции / в точке a E I.
Согласно определению полинома Тейлора, это означает, что
степень Р не превосходит n, P(a) = /(а) и при всяком к = 1,2,..., п
выполняется равенство f^k\a) = Р^к\а).
Положим R(x) = f(x) — Р(х). Функция Д, очевидно, n-кратно
дифференцируема в промежутке i*. При этом R(a) = f(a) — Р(а) = 0 и при
каждом к = 1,2,... ,п будет Д(А:)(«) = /(*°И - Р(*°И = 0.
На основании леммы 6.3, отсюда следует, что R(x) = о[(х — а)п]
при х —» а, что и требовалось доказать. ■
■ Теорема 6.2. Пусть даны интервал I = (p, q) и функция f : I —► С.
Предположим, что функция f является п-кратно дифференцируемой в
интервале J. Пусть Р есть полином степени не выше п. Если для
некоторой точки a Е I выполняется соотношение f (х) = Р(х)+о[(х—а)п]
при х —► а, то Р есть полином Тейлора порядка п функции f в точке а.
Доказательство. Пусть функция / и полином Р удовлетворяют
всем условиям теоремы.
Обозначим через Ро полином Тейлора порядка п функции f в точке
а. Тогда, согласно теореме 6.1, f(x) — Ро(х) = о[(х — а)п] при х —> а, то
есть
lim/W-Po(x)=0
ж->а (Ж — а)п
По условию, при х —> а имеем: f(x) — Р(х) = о[(х — а)71]. Это
означает, что
х-^а [X — а)п
Отсюда, очевидно, следует, что при х —> а
Р(х)-Ро(х)
(х - а)п
0.
Разность Р — Ро есть полином степени не выше п и, значит,
согласно лемме 6.1, Р(х) — Ро(х) = 0 и Р(х) = Ро(х).
Теорема доказана. ■

354 Гл. 4. Дифференциальное исчисление функций одной переменной
6.3. Оценки остаточного члена формулы Тейлора
Теорема 6.1 дает некоторую характеристику поведения разности
между функцией и ее полиномом Тейлора порядка п в точке а при х —> а.
Из этой теоремы, однако, невозможно извлечь какую-либо информацию
о величине этой разности на всей области определения функции или хотя
бы в какой-либо фиксированной окрестности точки а. Здесь мы докажем
теоремы, которые позволяют получать информацию такого рода. При
этом приходится налагать на изучаемую функцию требования, более
ограничительные по сравнению с теоремой 6.1.
■ Лемма 6.4 (основная лемма). Пусть даны интервал I = (p,q) и
функция f : I —> С, принадлежащая классу Vn+1 в промежутке I.
Зададим произвольно точку х Е / и положим:
r»w = m - J2 п^г{х ~t)k- (6-9)
fe=0
Тогда функция гп переменной t E I дифференцируема в промежутке I
и для всех t G I имеет место равенство:
rUt) = -L--r^-(x-t)n. (6.10)
Доказательство. Пусть функция / удовлетворяет всем
условиям леммы. Так как, по условию, / G Dn+1, то каждое из слагаемых в
правой части (6.9) дифференцируемо, как функция переменной £.
Дифференцируя выражение для тп почленно, получим:
fc=0 Х
При к > 0 имеем:
i(^-*)--^*-*-m^'
Производная слагаемого в правой части (6.9), соответствующего
значению к = 0, равна f'(t). Отсюда получаем:
fc=0 fe=l V '

§ 6. Формула Тейлора
355
Принимая в первой сумме за индекс суммирования величину г = к +1 и
меняя затем обозначения, получим:
Первая сумма справа отличается от второй единственным
слагаемым, а именно тем, номер которого равен п + 1.
Так как остальные слагаемые входят в первую и во вторую суммы
с разными знаками, то после сокращения подобных членов мы
получим:
f(n+l)(f\
rUt) = -L-T^(x-t)n,
nl
что и требовалось доказать. ■
Основной результат этого раздела сформулируем в двух вариантах:
первый относится к случаю функций со значениями в С, второй
касается вещественных функций.
■ Теорема 6.3. Пусть I = (p,q) и f : I —► С есть функция
класса X>n+1 в промежутке I. Зададим произвольно число А такое, что
1 < А < п + 1, и пусть х и а суть точки из промежутка I. Положим:
5/,»,л(*,а) = sup (1-в)п-Л+1|/(п+1)[а + в(о;-а)]|.
О<0<1
Тогда:
1) имеет место неравенство:
|/(«)-Ё^(—)'
I fc=0
2) в случае, когда f есть вещественная функция, найдется такая
точка в Е (0,1), что
fc=0
Доказательство.
1) (П е р в ы й вариант.) Пусть выполнены все условия
теоремы. Зададим произвольно точку a Е J, и пусть жЕ/.
<
An!
|ж — а|
п+1.

356 Гл. 4. Дифференциальное исчисление функций одной переменной
Если х = а, то доказывать нечего и мы будем считать, что х ф а.
Пусть функция rn ' t *-> rn(t) определена равенством (6.9)
леммы 6.4. Положим g(t) = \х — <|Л, где 1 < Л < п + 1. Так как гп(х) = 0 и
д{х) = 0, то справедливо равенство:
гп(а) _ гп(а) __ гп(х) -гп(а)
\х-а\х ~~ р(а) 9(х)-д(а)
Отношение производных функций гп и д в произвольной точке £,
заключенной между а и ж, то есть такой, что либо а < £ < х, либо
а > £ > х, равно
/(га+1)(0(*-0"
(т\\х - £|*-in! '
где (7 = —1 при ж < а и <т = 1 при х > а.
Положим
# — а
= 0.
Тогда, как легко проверяется, 0 < в < 1.
Имеем: £ = а + в(х — а), ж — £ = (1 — 0)(ж — а) и, значит,
г'п(0 = (1 - 0)п-Л+1/(п+1)[а + g(s = о)](а? - a)n
5'(0 «тА^-а^п!
откуда следует, что
Г'п(0
9'(0
<Wx,a) Л+1
An!
для всякого £, заключенного между х и а.
В силу теорелш Коши об оценке приращения для комплексных
функций (следствие 3 теоремы 4.3), отсюда вытекает, что
гп(а)
\х — а\х
и, следовательно,
гп(х) -гп(а)
д(х) - д(а)
S An! |х a|
\Гп{а)\<^Ь1^Л\х^а^\
Таким образом, для случая комплексных функций все доказано.

§ 6. Формула Тейлора 357
2) (В т о р о й вариант.) Рассмотрим случай, когда / —
это вещественная функция. Тогда, согласно теореме Коши для
вещественных функций (теорема 4.3), найдется £ такое, что если х < а, то
х < £ < а, а если х > а, то х > £ > а л
гп(а) __ гп(х) -гп(а) г'п(£)
\х-а\х g(x)-g(a) ~ #'(0 '
Это означает, что
гп(о) = (1-^)п~Л+1/(п+1)[а + ^(а;-а)]
\х — а\х а\\х — а|Л_1п!
Отсюда получаем:
(х - а)г
(1-0)п-Л+1/(п+1)[а + 0(*-а)] i
гп(а) = * i хп\ '* ~ а|(ж ~ а)
Осталось заметить, что сг|ж — а\ = а; — а, и теорема доказана
полностью. ■
▼ Следствие 1. Пусть функция / : (р, #) —> С является (п + 1)-
кратно дифференцируемой в промежутке I = (р, д). Зададим
произвольно точку a € J и для a; G / положим
Ln(*,a)= sup |/(п+1)[а + 0(*-а)]|.
О<0<1
Тогда имеет место неравенство:
/<«>-£^(—)*
fc=0
Ln(a?,a)|a?--a|w+1
(n + 1)!
Если / — это вещественная функция, то для любого х е I найдется в
такое, что 0 < в < 1, и
/м=е ^ - .)• н- /"t"!:;f;-a)1^ - .>~.
fc=0 V '
Это частный случай теоремы 6.3 при Л = п + 1.
Следствие 1 доказано. ▼

358 Гл. 4. Дифференциальное исчисление функций одной переменной
Т Следствие 2. Пусть функция / : J —► С, где I есть интервал
множества Ж, в каждой точке х Е I имеет производную порядка п + 1.
Для х Е I и a G / положим:
Cf,n(x,a)= sup (l-e)n\fin+1)[a + e(x-a)]l
O<0<1
Тогда имеет место неравенство:
Cn(x,a)\x-a\n+1
/м-Ёф.-.)1
fc=0
П!
Если / есть вещественная функция, то для любых х,а € I найдется
в G (0,1) такое, что
/w = v z^l (, - «с+а-*)•/<•*";«+«—)](. _„г+>.
/С» 7».
fc=0
Данное утверждение — это частный случай теоремы 6.3
при Л = 1.
Следствие 2 доказано. Т
Т Следствие 3. Пусть функция f : I —> С, где J есть интервал
множества Ж, в каждой точке х Е I имеет производную порядка п + 1.
Если для всех х Е I выполняется равенство /^п+1^(#) = 0, то функция
f является полиномом степени не выше п.
Доказательство. Достаточно заметить, что если /
удовлетворяет условию следствия 3, то для любых x,a e I величина Sftn,\(x,a)
равна нулю. Отсюда
fe=0
Следствие 3 доказано. ▼
6,4. Новое доказательство формулы Лейбница
Применяя формулу Тейлора, мы дадим здесь другой вывод формулы
Лейбница (см. §3, п. 3.3) для производной порядка п произведения
функций класса Х>п.

§ 6. Формула Тейлора
359
Пусть / : I —► С есть функция класса Т>п в промежутке I = (a,b).
Предположим, что для некоторой точки хо Е I построен полином Р
степени не выше п такой, что
f(x) = Р(х) + о[(х - хо)п] при х -* жо.
Тогда, согласно теореме 6.2, Р есть полином Тейлора функции f в
точке хо.
Пусть Р(х) = Ьо + Ь±(х — жо) + &2(а; — #о)2 Н \-Ьп(х — хо)п — это
разложение полинома Р по степеням х — хо.
Тогда имеют место равенства:
bo = /(хо), fti = /'Ы,..., п!Ьп = /(П)Ы.
Таким образом, зная полином Р, мы можем найти значения всех
производных порядка не выше п функции / в точке хо.
В качестве примера, иллюстрирующего данное замечание,
приведем здесь другой вывод формулы Лейбница для
производной п-го порядка произведения функций.
Пусть даны промежуток J = (а, Ь) С М и функции /i,/2,... ,/m,
принадлежащие классу Х>п.
Возьмем произвольно точку хо Е I. Согласно теореме 6.1, при
каждом к = 1,2,..., т имеем:
fk(x) = Л(*о) + £§^(я - хо) + ...
• • • + ^^^(ж - жо)п + а*(х)(х - х0)п, (6.11)
где Q:fc(a;) = о(1) при ж —► жо.
Перемножая почленно равенства (6.11), получим равенство, в левой
части которого стоит произведение fi(x)f2(x)... fm{x). Справа будем
иметь сумму (n + 2)m слагаемых.
Правую часть полученного равенства преобразуем следующим
образом. Прежде всего, заметим, что каждое слагаемое этой суммы,
содержащее множитель вида ak(x)(x — хо)п, есть о[(х — хо)п] при х —> хо.
Заметим также, что сумма конечного числа функций, каждая из
которых есть величина порядка о[(х — хо)п] при х —> жо, также является
величиной порядка о[(х — хо)п] при х —► хо-

360 Гл. 4. Дифференциальное исчисление функций одной переменной
С учетом этих замечаний, получим, что F(x) = fi(x)f2(x)... fm(x)
есть сумма всевозможных произведений вида:
h\l2\...lm\ [ 0) ^ '
и величины о[(х — хо)п] при х —> хо-
Теперь заметим, что если h + fo H \- lm > n, то величина,
представленная равенством (6.12), также есть о[(х — хо)п] при х —> xq.
Пусть I > 0 — целое. Сумма всех тех из произведений (6.12), для
которых h + h + • • • + lm = I, равна Ai(x — xo)1, где Ai — некоторое
число.
Принимая во внимание, что если / > п, то Аг(х — хо)1 = о[(х — хо)п]
при х —> #о, получим, в конце концов, при х —► хо равенство:
fi(x)f2(x)... fm(x) = Л0 + Ai(x - я?о) + h An (ж - #o)n + о[(х - ж0)п]-
(6.13)
В силу теоремы 6.2, полином в правой части (6.13) есть полином
Тейлора порядка п функции F = /1/2 ... fm в точке хо и, значит,
при каждом Z = 0,l,2,...,n. В частности, отсюда получаем
Fw(x0) = nlAn.
Осталось заметить, что величина Ап — это сумма
всевозможных произведений
/1а1)(^0)/2(г2)Ы^>/^т)(^0)
h\h\...lm\
где h > 0, h > 0, ..., 1т > 0 — целые, причем h + h H Ь Zm = ft.
И окончательно получаем формулу дляп-й производной
произведения т функций /:
D (hf2...fm)(X0)- X, П! WW.../т! '
(6.14)
где сумма справа берется по множеству всех наборов hyfo,.•• ,1т
неотрицательных целых чисел таких, что l\ + h H Ь /m = ft.

§ 6. Формула Тейлора
361
Установленная ранее (см. п. 3.3 этой главы) формула Лейбница для
производной произведения двух функций — это частный случай
равенства (6.14).
Таким образом, применяя формулу Тейлора, мы получаем новое
доказательство формулы Лейбница для производной n-го порядка
произведения двух функций.
6.5. Метод Ньютона (метод касательных) приближенного
решения уравнений
6.5.1. Задача исследования функции методами дифференциального
исчисления, которая будет рассмотрена подробно в § 9 этой главы, требует
умения определять некоторые характерные точки функции, что во
многих случаях сводится к решению уравнения вида f(x) = 0. Здесь мы
рассмотрим вопрос о численном решении таких уравнений.
Пусть функция /, определенная в некотором промежутке [а, 6],
непрерывна, причем /(а) < 0, a f(b) > 0.
Согласно теореме 4.1 главы 2, уравнение f(x) = 0 имеет, по
крайней мере, одно решение, лежащее в промежутке (а,Ь). Метод
последовательных делений промежутка пополам, описанный во втором
доказательстве теоремы 4.1 главы 2, может быть использован также и для
практических целей как средство приближенного решения уравнения:
f(x) = 0. (6.15)
Пусть дано произвольное число £ Е К.
Говорят, что число жЕК есть приближенное значение £ с
погрешностью, не превосходящей е, если \х — £| < е.
Пусть I есть длина промежутка [а, 6]. После п шагов построения,
содержащегося во втором доказательстве указанной теоремы 4.1
главы 2, мы получим отрезок длины 1п = —, в котором лежит корень
уравнения (6.15). Точки из этого промежутка можно рассматривать
как приближенные значения корня уравнения (6.15) с погрешностью,
не превосходящей ±. Если, например, I = 1, то для того, чтобы полу-
чить приближенное значение решения уравнения (6.15) с погрешностью,
меньшей 10~6, по методу деления пополам (см. второе доказательство
теоремы 4.1 главы 2), требуется выполнить не менее 20 шагов.
Выполнив еще двадцать шагов, получим приближенное значение корня
уравнения с погрепшостью, меньшей 10~12. Появление быстродействующих
электронно-вычислительных машин делает такую скорость вычисления
во многих случаях удовлетворительной.

362 Гл. 4. Дифференциальное исчисление функций одной переменной
Отметим следующее обстоятельство. Для того чтобы
метод деления пополам можно было применить для решения уравнения
f[x) = О, достаточно, чтобы функция / была непрерывна и принимала
значения разных знаков в концах промежутка, в котором она
определена. По-видимому, неизвестен метод, который позволил бы обеспечить
более быструю скорость приближения к корню уравнения f(x) = О при
этих предположениях.
С точки зрения направления математики и математической логики,
называемого конструктивизмом, метод решения уравнения f(x) = О
последовательным делением отрезка пополам не является «полноценным»
алгоритмом. Однако во многих важных случаях данный метод
оказывается вполне эффективным.
Если функция / удовлетворяет более сильным условиям, чем те,
выполнение которых предполагается в методе деления пополам, то
можно указать способы приближенного решения уравнения f(x) = 0, более
эффективные, чем метод деления пополам.
Пусть функция / определена в промежутке [а, Ь] множества Е и
удовлетворяет следующим условиям:
A) Функция / непрерывна и ее значения в концах промежутка [а, Ь]
имеют разные знаки.
B) Функция / принадлежит классу С2.
C) Производные /' и /" в промежутке [а, Ь] всюду отличны от нуля.
Эти предположения могут показаться чрезмерно жесткими. При
этом особенно неприятным представляется требование постоянства
знака производных функции /, содержащееся в условии С). Для
произвольной функции класса С2 ее производные в разных точках ее области
определения могут иметь различные знаки.
Если, однако, решение £ уравнения f(x) = 0 таково, что /'(£) Ф О
и /"(£) Ф О, то в малой окрестности точки £ условия В) и С) будут
выполнены.
Если каким-либо способом (например, тем же способом деления
отрезка пополам) указан некоторый достаточно малый отрезок,
содержащий корень уравнения f(x) = О, то, с большой степенью уверенности,
можно считать, что в этом отрезке условия А), В) и С) выполняются.
Итак, пусть даны отрезок [а, Ь]с1и функция / : [а, Ь] —■> R такая,
что ее значения /(а) и /(b) имеют разные знаки, причем / удовлетворяет
условиям В) и С).
Из этого предположения вытекает, что каждая из функций /' и /"
в промежутке [а, Ь] имеет постоянный знак. Следовательно, функции /
и /' в этом промежутке строго монотонны. Монотонность производной
f'(x) означает, что когда х меняется от а до Ь, угловой коэффициент

§ 6. Формула Тейлора
363
касательной графика функции / в точке (#, /(#)) либо возрастает, либо
убывает. Геометрически это означает, что указанная касательная при
возрастании х в пределах от а до Ь вращается монотонно либо по часовой
стрелке, либо против.
Так как функция / на концах промежутка [а, Ь] принимает
значения разных знаков, то уравнение f(x) = 0 имеет корень, лежащий в
интервале (а, Ь). В силу строгой монотонности функции /, этот корень
единственный. Далее мы будем обозначать его символом £.
Итак, £ есть число из интервала (а, Ь) такое, что /(£) = 0.
В зависимости от того, какой знак имеют производные /' и /"
функции / в данном промежутке [а, Ь], возможны четыре различных
случая:
1)/' >0и/" >0в[о,Ц;
2)/' >0и/" <0в[о,Ц;
3) /' <0и/" >0в [а,Ь];
4)/' <0и/" <0в[о,Ь].
На рис. 22 показано, как выглядит график функции / в каждом из
этих случаев.

364 Гл. 4. Дифференциальное исчисление функций одной переменной
Все эти случаи сводятся к случаю 1), если принять во внимание
следующие соображения.
Пусть fi(x) = /(—re). Знак первой производной функции Д
противоположен знаку первой производной функции /. В то же время знаки
вторых производных функций /i и / совпадают.
Далее, если /2(2) = —/(#)? т<> знаки первой и второй
производных функции /г противоположны знакам соответствующих
производных функции /.
В силу сказанного, комбинируя замену переменной жи-жс
умножением на —1, всегда можно свести общий случай к случаю 1).
По индукции, определим некоторую последовательность (xn)n>N0
точек промежутка [а, Ь]. В качестве хо выбираем произвольную точку
промежутка [а, Ь]. Предположим, что для некоторого п точка хп
определена.
Построим касательную графика функции / в точке
(xn,f(xn)) (см. рис. 22). Эта касательная задается уравнением:
У = f(xn) + (х- xn)f{xn). (6.16)
Так как хп £ [а,Ь], то ff(xn) ф 0, откуда следует, что правая часть
равенства (6.16) обращается в нуль для некоторого х £ М.
Полагаем хп+1 равным тому значению гс, для которого
f(xn) + (X- Xn)f'(xn) = О
Решая это уравнение, получим:
*«+! = /(*»)-7^- (6-18)
Правильный выбор точки хо имеет важное значение для
описываемого построения. Дело в том, что при неудачном выборе хо точка х\
может оказаться лежащей вне промежутка [а, Ь], и построение в этом
случае не может быть продолжено.
Предположим, что функция / такова, что ff(x) > 0 и f"{x) > О
для всех х G [а, Ь], и точка хо выбрана так, чтобы выполнялись условия:
£ < хо < Ь. Можно взять, например, хо = Ъ. Предположим, что хп
определено, причем выполняются неравенства:
£ < хп < Ь. (6.19)
Докажем, что неравенства (6.19) остаются верными, если в
них заменить хп на xn+i-
(6.17)

§ 6. Формула Тейлора
365
Если f(xn) = 0, то хп = £, и в этом случае также и #n+i = £•
Будем считать, что f(xn) > 0. Тогда гсп > £ и из равенства (6.18)
следует, что
Xn+i <хп<Ъ. (6.20)
В силу теоремы Лагранжа о среднем значении (следствие 1
теоремы 4.3 этой главы),
где £ < 6 < хп. Так как вторая производная функции / в промежутке
[а,Ь], согласно предположению, положительна, то функция /' является
строго возрастающей, откуда вытекает, что f'(6) < f(xn).
Так как /(£) = 0, то из равенства (6.21) следует, что
Отсюда, после простых преобразований, получаем:
t . /fen) _
По условию, точка хо выбрана так, что выполняются неравенства
£ < хо < Ь. В силу принципа математической индукции, как следует
из доказанного, последовательность (xn)n>N0 полностью определена. В
силу неравенства (6.20), эта последовательность является убывающей.
Из (6.19) следует, что она ограничена снизу и, значит, согласно
теореме о пределе монотонной функции (см. глава 2, §3, теорема 3.1),
существует конечный предел:
lim хп = £.
71—ЮО
Имеем:
lim #n+i = Ит хп = £.
71—ЮО 71—ЮО
Переходя в равенстве (6.18) к пределу при п —» оо, получим:
1=1-Ж
? ? ту
откуда /(£) = 0 и, следовательно, £ = £.

366 Гл. 4. Дифференциальное исчисление функций одной переменной
Таким образом, построенная последовательность (xn)n>N0 имеет
своим пределом точку £. Тем самым мы получаем некоторый метод
построения приближенных значений корня уравнения f(x) = 0. Этот
метод называется методом Ньютона, по имени его автора, или
методом касательных.
На рис. 21 показано также, как следует выбирать точку хо в каждом
из случаев 1)-4). Геометрически выбор хо определяется следующим
образом.
График функции / — вместе с отрезком оси Ох, соответствующим
значениям х £ [а, ft], и двумя перпендикулярами, опущенными из концов
графика на ось Ох, — определяет два криволинейных треугольника.
У одного из них искривленная сторона такова, что касательные в ее
концах проходят внутри треугольника. У другого треугольника
касательные в концах его искривленной стороны лежат вне этого
треугольника.
В качестве точки хо следует брать тот конец отрезка [a, ft], который
соответствует первому треугольнику.
Аналитически выбор хо определяется следующим правилом.
В качестве точки хо следует выбирать тот из концов отрезка [a, ft], для
которого выполняется неравенство: f(xo)f"(xo) > 0.
Заметим, что как нетрудно усмотреть из геометрических
соображений, — как бы ни была выбрана точка хо, — если точка х\
оказалась лежащей в промежутке [a, ft], то все последующие значения
хп определены, лежат в отрезке [а, ft] и образуют монотонную
последовательность, имеющую пределом корень £ уравнения f(x) = 0.
Оценим скорость приближения хп к пределу £.
Применяя формулу Тейлора второго порядка, получим:
о = НО = /(*„) + (£ - *„)/'(*«) + {i~*n)*'/"(<?).
Отсюда
х fM _ . 2 f" {в)
Левая часть этого равенства есть Яп+ъ и мы получаем:

§ 6. Формула Тейлора
367
Пусть L = sup /"(#), 6 = inf f{x). Тогда
хе[а,Ъ] хе[а,Ъ]
>"«» <А = М<оо.
2f'(xn) - 26
Следовательно, 0 < хп+\ — £ < М{хп — £)2 при каждом п. Заменяя здесь
п на п + 1, получим:
О < Sn+2 - £ < M(sn+i - О2 < ^3(^п - О4-
По индукции устанавливается, что для всякого fcGN имеют место
неравенства:
О < хп+к - £ < М2*-1^ - О2* - (6.22)
Неравенства (6.22) позволяют заключить, что хп с ростом п
достаточно быстро приближается к искомому корню £ уравнения f(x) = 0.
Пусть М > 1. Предположим, п таково, что М(хп — £) < 0,1. Тогда
из неравенств (6.22) вытекает, что
Хп+к~£< М10 <10 >
так что, начиная с данного п, число верных десятичных знаков
приближенного значения хп+к корня уравнения f(x) = 0 при переходе
от к к к + 1 удваивается.
В случае, если М < 1, выбираем хп так, что хп — £ < 0,1. Тогда
получим, что
0 < хп+к - £ < М2*"110-2* < 1(Г2*
для всякого fcGN.
6.5.2. В качестве примера на приложение метода Ньютона для
решения уравнения f(x) = 0 опишем алгоритм для нахождения
приближенного значения квадратного корня из вещественного числа.
Пусть дано число а > 0. Квадратный корень из него есть решение
уравнения: х2 — а = 0.
Применим описанный выше метод, полагая f(x) = х2 — а. Будем
искать решение уравнения х2 — а = 0, лежащее в промежутке (0, оо).
Имеем: /'(#) = 2ж. Для х > 0 имеет место равенство:
/(ж) ж -а 1 / , а\
/'(я) 2ж 2V ж У

368 Гл. 4. Дифференциальное исчисление функций одной переменной
Полагаем хо = 1 + а/2. Очевидно, х% > а, откуда следует, что
хо > у/а.
Пусть хп для некоторого целого п > О определено. Полагаем:
Xn+1 = UXn + — V (6.23)
& \ Хп /
Определенная таким образом последовательность (xn)n>N0 имеет
своим пределом решение уравнения у2 = а.
Метод построения последовательных приближений числа у/а,
определяемый формулой (6.23), называется методом Герона.
6.5.3. В качестве другого примера опишем способ
вычисления обратной величины числа, основанный на использовании метода
Ньютона.
Пусть aEt. Предположим, что а > 0.
Определение обратной величины числа а формально сводится к
решению уравнения:
а - - = 0.
х
Полагая f(x) = а , получим, что равенство (6.18) в рассматри-
х
ваемом случае принимает вид:
1
а
Xn+i = хп г-2- = #п(2 - ажп). (6.24)
Хп
Для приложений существенно то, что в равенстве (6.24) справа мы
имеем выражение, не содержащее операцию деления.
При реализации процесса, основанного на использовании формулы
(6.24), начальное приближение хо выбирается следующим образом.
Пусть га — целое число такое, что
1 г»
i < 2~wa < 1.
Тогда полагают хо = 2~ш. При таком выборе хо имеет место оценка:
1
Хп
а
< 2я0
(I)
2*
Доказательство последнего неравенства предоставляется читателю
в качестве упражнения.
6.5.4. Метод Ньютона иногда применяется в комбинации с другим
методом, известным под названием «метод хоуд». Несколько слов об
этом методе.

§ 7. Точки экстремума дифференцируемой функции
369
Пусть функция /, определенная в промежутке [а, Ь] С R, принимает
в концах этого промежутка значения разных знаков и для нее выполнены
условия А), В) и С), указанные выше.
Пусть (хп)п€щ есть последовательность приближений, полученная
по методу Ньютона. Определим новую последовательность (хп)пеп
следующим образом.
Пусть х[ есть точка пересечения оси Ох с хордой, соединяющей
концы (a,f(a)) и (ft,/(b)) графика функции /. Предположим, что для
некоторого п £ N точка х'п определена, причем точки х'п и хп лежат по
разные стороны точки £ — корня уравнения f(x) = 0.
Точку x'n+i определим как точку, в которой прямая, соединяющая
точки графика функции /, лежащие над точками хп ихп, пересекает
ось Ох.
Если f"{x) > 0 для всех х £ [а, Ь], то любая касательная графика
функции / лежит ниже графика, а любой отрезок, соединяющий
произвольные две точки графика, располагается выше дуги, концами которой
являются эти точки. (Доказательство этих утверждений будет дано в
§ 8 данной главы.) Отсюда вытекает, что точки хп и х'п при каждом п
лежат по разные стороны точки £.
Точно так же можно заключить, что точки хп и х'п лежат по разные
стороны от корня £ уравнения f(x) = 0 и в случае, когда f"(x) < 0 для
всех х G [а, Ь].
Аналитически последовательность (xfn)n^ определяется
посредством соотношений:
/ __ / _ (Жп — Хп)}\Хп)
Xn+l-Xn f{x,n)_f{Xny
Последовательности (xn)neN и (x'n)neN сходятся к корню
£ уравнения /(ж) = 0 с разных сторон. Это дает возможность для
каждого номера п указать конкретную оценку отличия от £
величин хп и х!п, то есть оценить качество приближенных решений
хп и х'п уравнения fix) = 0.
§ 7. Точки экстремума дифференцируемой
функции
В приложениях математики часто возникают задачи, в которых
требуется найти наименьшее или наибольшее значение той или иной
величины. Здесь рассматривается простейший частный случай указанной
общей задачи, а именно, — случай, когда речь идет о функциях одной
переменной. Результаты, которые будут здесь получены, оказываются
полезными также и в других, существенно более общих случаях.

370 Гл. 4. Дифференциальное исчисление функций одной переменной
7.1. Необходимые условия экстремума
Ранее было введено понятие точки экстремума функции.
Напомним его.
Пусть даны плотное в себе множество АсМи функция / : А —» Е.
Точка р G А является точкой максимума функции /, когда можно
указать 6 > 0 такое, что если х G А и \х — р\ < #, то f(x) < /(р). Точка
р G А называется точкой минимума функции /, если можно указать
6 > 0 такое, что для всякого х G А, отстоящего от р на расстояние,
меньшее 5, выполняется неравенство f(x) > /(р).
Говорят, что р G А — это точка экстремума функции /, если
р является или точкой минимума, или точкой максимума /. Также
говорят, что р G А — это точка строгого минимума функции / : А —> М,
когда существует окрестность U = (р — 6,р + 6) точки р такая, что
если х G U П А, причем х ф р, то f(x) > /(p). Аналогично, точка
р G А называется точкой строгого максимума функции / : А —* М,
когда существует окрестность U = (р — 5,р + 6) точки р такая, что если
х eU П А, причем х ф р, то f(x) < /(р).
Пусть даны множество А С М и функция / : А —» Ш. Как было
показано в п. 4.1, если р £ А — это точка минимума функции д = — /,
то р является точкой максимума функции /, а если р — точка максимума
д = — /, то р есть точка минимума /.
Геометрически, — условие: «р G -А есть точка экстремума функции
/ : А —► R» — означает следующее. Построим график функции / (см.
рис. 23). Тогда р является точкой экстремума функции / в том и только
в том случае, если существует 6 > 0 такое, что часть графика функции
/, соответствующая значениям х G -А, для которых \х — хо\ < £, лежит
по одну сторону от горизонтальной прямой у = /(р), а именно,
выше ее, если р есть точка минимума (точки р\ и рг на рис. 23), и
ниже ее, если р есть точка максимума (точка ро на рис. 23.)
Рис. 23

§ 7. Точки экстремума дифференцируемой функции
371
Если функция / : А —» М принимает в точке р € А свое наименьшее
значение, то р есть точка минимума функции /.
Точно так же, если функция / принимает свое наибольшее значение
на множестве А в точке р, то р — это точка максимума функции /.
Таким образом, точки, в которых функция / принимает свои
наименьшее и наибольшее значения, следует искать среди точек
экстремума функции.
Точка строгого минимума (максимума) функции, очевидно,
является ее точкой минимума (соответственно, максимума).
Обратное, вообще говоря, не верно.
Если функция / определена во всех точках некоторой окрестности
точки р и постоянна в этой окрестности (см. рис. 24(1)), то точка р
является одновременно точкой максимума и точкой минимума функции.
В данном случае, очевидно, р не является точкой строгого минимума
или строгого максимума функции.
Г 7Г1 2
Другой пример получаем, полагая fix) = x2 sin — при х ф О и
L х J
/(0) = 0 (рис. 24(2)). Для всех х е R имеем: f(x) > 0 и /(0) = 0.
Отсюда ясно, что 0 есть точка минимума данной функции /. Для
всякого п Е N выполняется / ( — J =0. При п —► оо будет ► 0, откуда
следует, что любая окрестность U точки 0 содержит точку х = — для
п
некоторого п £ N. Таким образом, любая окрестность U точки 0
содержит точку х ф 0, для которой f(x) = 0 и, следовательно, 0 не является
точкой строгого минимума данной функции /.
Р
О)
-7
-.5
01
(2)
Рис. 24
Пусть даны функция /:А->Ми некоторое подмножество В
области определения данной функции. Пусть р 6 JB.
Будем говорить, чтор есть точка максимума (минимума) функции
/ на множестве В, если р есть точка максимума, соответственно, точка
минимума ограничения / функции / на множестве В,
Пусть, например, А = Е, f(x) = x для всех жбМиВ = [-1,1].

372 Гл. 4. Дифференциальное исчисление функций одной переменной
Тогда —1 есть точка минимума данной функции на множестве Б,
1 есть точка максимума функции на этом множестве.
Нетрудно видеть, что на множестве А = Ш рассматриваемая
функция / не имеет точек экстремума.
Заметим, что если р Е А — это точка минимума или максимума
функции /, то, вообще говоря, нельзя утверждать, что
функция / принимает в этой точке свое наименьшее или,
соответственно, наибольшее значение.
Понятие точки экстремума имеет значение и независимо от задачи
о наименьшем и наибольшем значениях функции. Знание этих точек
помогает получить правильное качественное представление о строении
рассматриваемой функции.
Понятие точки экстремума функции может иметь определенный
физический смысл. Пусть, например, /(£) означает координату в момент
времени t некоторой материальной точки, движущейся по прямой, причем
функция / непостоянна ни в каком промежутке времени. Точки
экстремума суть те моменты времени, в которые происходит изменение
направления движения данной материальной точки.
Ранее была доказана теорема Ферма (теорема 4.1),
устанавливающая некоторое необходимое условие для точек экстремума
дифференцируемой функции.
■ Теорема 7.1 (усиленная теорема Ферма). Пусть А СШ есть
плотное в себе множество ир Е А есть точка экстремума функции f : А —» М.
Если / имеет в точке р левую производную fl(p), то fl(p) > 0 в случае,
когда р есть точка максимума /, и fl(p) < О, когда р есть точка
минимума /. В случае, когда функция f имеет в точке р правую производную,
fr(p) < 0, если р — точка максимума функции /, и f'r{p) > 0, если р
является точкой минимума /.
Доказательство. Пусть р есть точка экстремума функции /.
Найдем 6 > О такое, что если х Е А и \х— р\ < 6, то f(x) > /(p), если
р есть точка минимума, а если р — точка максимума, то f(x) < f(p).
Пусть р есть точка максимума функции /, и для всякого х Е А,
такого что \х — р\ < 6, выполняется неравенство f(x) < /(p). Для всех
таких х имеем: f(x) — f(p) < 0. Если х < р, то х — р < 0, а если х > р,
то х — р > 0. Отсюда следует, что если х е А принадлежит интервалу
(р-6,р + 6), то:
в случае, когда х лежит слева от р, имеем
/ад-/ц>0.
X — р

§ 7. Точки экстремума дифференцируемой функции
373
при ж, лежащем справа от р, выполняется неравенство
№ - № < 0
Ж — р
Отсюда, в силу теоремы о предельном переходе в неравенстве (см.
гл. 2, п. 3.4), следует, что:
если функция / имеет в точке х левую производную, то
Siip) > 0;
если в этой точке у функции / существует правая производная,
то/;(р)<о.
Если р — точка минимума функции /, то р есть точка максимума
функции g = — / и, значит, по доказанному, д[{р) > 0 и д'г{р) < 0.
Осталось заметить, что д[{р) = —fl(p) и д'г(р) = — /г(#)> откуда
очевидным образом следует утверждение теоремы, касающееся данного
случая.
Теорема доказана. ■
Точка р Е А С Ш называется стационарной точкой функции
/ : A-+R, если 0 = f(p).
Из теоремы 7.1 можно получить следующую информацию
относительно того, где следует искать точки экстремума функции.
Пусть дана функция / : [а, 6] —» Ж. Предположим, что / имеет
конечное число угловых точек, то есть таких, что
Si(x) Ф Sr(x),
и во всех остальных точках х Е [а, 6] функция / дифференцируема.
Тогда точками экстремума функции / могут быть только точки
одного из следующих видов:
а) угловые точки, в которых левая и правая производные либо
имеют разные знаки, либо одна из них обращается в нуль;
б) стационарные точки функции / в интервале (а, 6), то есть точки
х Е (а,Ь), для которых f'{x) = 0;
в) концы промежутка [а, 6].
Для того чтобы найти точки экстремума функции, определенной на
некотором промежутке, необходимо найти точки указанных трех
категорий.
Если точка х удовлетворяет одному из данных условий а)-в), то
она, вообще говоря, может и не быть точкой экстремума функции.
Если же х есть точка экстремума функции /, то — пока мы не
имеем в своих руках средств, с помощью которых можно было бы узнать,
— является ли х точкой минимума функции / или же х есть точка
максимума /.

374 Гл. 4. Дифференциальное исчисление функций одной переменной
Приведем некоторые примеры.
Пример 1. Рассмотрим функцию жи/, где п > 2 — целое
число. Имеем:
D(xn) = nxn-\
Производная функции х \-> хп обращается в нуль в точке 0.
Если п — четно, то хп > 0 = 0П для всех х Е Ж, откуда следует,
что 0 есть точка минимума функции х \-> хп.
Если же п — нечетно, то хп > 0 при х > 0 и хп < 0 при х < 0.
Отсюда ясно, что 0 не является точкой экстремума функции.
Данный пример показывает, что из того, что в некоторой точке р
производная функции / обращается в нуль, вообще говоря, нельзя
заключить, что р есть точка экстремума функции /.
Приведем еще пример функции, имеющей особенность, не
позволяющую среди точек, где производная функции обращается в нуль,
распознать точки экстремума имеющимися в нашем распоряжении
средствами.
Пример 2. Пусть [а,6] = [—1,1], р = 0. Определим функцию
/(ж), полагая /(0) = 0 и f(x) = x2 sin — при х ф 0. Имеем:
fix) - /(0) . 7Г п
±±-L—±-^-L = x sin ► 0
X X
при х —» 0.
Производная /'(О), таким образом, существует и равна нулю.
Положим:
- 1
Хп~ п + 1/2'
Тогда
f(xn) = Хп8штг (n+ -J = {-l)nx2n
при каждом п. При п —» оо будет жп —» 0, и мы, следовательно,
получаем, что для всякого 6 > 0 найдутся такие ni и П2, что |жщ| < ^5
|жП2| < 5, причем f(xni) > 0 = /(0), а /(жП2) < 0 = /(0).
Это, очевидно, будет иметь место, если гц и пг достаточно велики,
причем п\ — четно, а П2 — нечетно.
Для функции д(х) = [/(ж)]2 имеем д(х) > 0 = д(0) для всех ж^К.
В данном случае 0 есть точка экстремума функции д.
7.2. Достаточные условия экстремума
Здесь мы приведем правила, позволяющие в некоторых
случаях определять точки экстремума функции.

§ 7. Точки экстремума дифференцируемой функции
375
■ Теорема 7.2. Пусть даны плотное в себе множество А С Ш и
функция f : А —► R. Предположим, что множество А содержится в
промежутке [а, оо), причем a E А, и функция f имеет производную
/'(а) ф 0. Если /'(а) > 0, то а есть точка минимума функции f, а
если /'(а) < 0, то а является точкой максимума /.
Аналогично, если А содержится в промежутке (—оо,Ь], Ь Е А, и
существует производная f'{b) ф 0, то в случае f'(b) < 0 величина Ъ есть
точка минимума, а в случае f'{b) > 0 — точка максимума функции /.
Доказательство. Сначала докажем утверждение теоремы,
относящееся к точке а. Предположим, что f'{o) Ф 0. По определению,
/(а)= lim м^ж.
х-+а,х€А X — О,
Отсюда вытекает, что найдется 6 > 0 такое, что для всякого х Е А
такого, что \х — а\ < 6, в случае, когда /'(а) > 0, имеет место неравенство
'<*>-'<•>> о,
х — а
а если /'(а) < 0, то — неравенство
/WzM<0.
х — а
Так как при х > а выполняется неравенство а; — а > 0, отсюда
получаем, что если /'(а) > 0, то для всякого х Е А такого, что \х—а\ < 8,
f(x) > /(а), откуда видно, что а есть точка минимума /.
Если же /'(а) < 0, то для всякого х Е А такого, что \х — а\ < 6,
имеет место неравенство f(x) < /(a). Это позволяет заключить, что в
данном случае а есть точка максимума функции /.
Обоснование утверждения теоремы, относящегося к точке 6,
предоставляется читателю.
Теорема доказана. ■
Т Следствие. Предположим, что область определения функции
f : А —► Ж содержит в себе некоторый интервал (а, /3) и точка р Е (а, /3)
такова, что функция f имеет в этой точке левую и правую производные.
Если f((p) < 0, а fr(p) > 0, тор есть точка минимума функции f, а если
fi(p) > 0, a fr(p) < 0, тор является точкой максимума функции /.
Доказательство. Положим А\ = А П (—оо,р] и Аг — А П [р, оо).
Точка р принадлежит каждому из множеств А\ и Аг.

376 Гл. 4. Дифференциальное исчисление функций одной переменной
Если flip) < 0 и fr(p) > О, то, согласно теореме 7.2, р является
точкой минимума функции / на каждом из множеств А\ и Аг.
Пусть <5i > 0 таково, что если х Е А± и \х — р\ < 5i, то f(x) > /(р),
а 62 > О таково, что для всякого х Е А2, для которого \х — р\ < 62, верно
неравенство: f(x) > /(р).
Пусть 6 есть наименьшее из чисел 8\ и £2.
Возьмем произвольно точку х Е А такую, что \х — р\ < 6. Тогда
\х — р\ < 6i и одновременно \х — р\ < <$2-
Если х < р, то х Е -Ai, а если ж > р, то а; Е Аг.
И в том, и в другом случае, очевидно, имеем: f(x) > /(p). Этим
доказано, что р есть точка минимума функции /.
Доказательство того, что в случае, когда //(р) > 0 и f'r(p) < 0, р
есть точка максимума функции /, осуществляется аналогичным
образом. Требуется только в проделанных выше рассуждениях надлежащим
образом изменить знаки неравенств. Читатель может выполнить эту
работу в качестве упражнения.
Следствие доказано. Т
Условия следствия теоремы 7.2 имеют весьма специальный
характер. Тем не менее в некоторых случаях результат следствия теоремы
7.2 может быть полезен.
■ Теорема 7.3. Предположим, что функция f : (а, Ь) —► R
дифференцируема в каждой точке х G (а,Ь), отличной от точки р, где
a < р < Ь, и непрерывна в точке р.
Если f'{x) < 0 для всех х Е (а,р) и f'(x) > 0 в интервале (р, 6), то
функция f принимает в точке р свое наименьшее значение в промежутке
(а,Ь).
Если f'{x) > 0 при х Е (а,р) и f'(x) < 0 при х Е (р, Ь), то в точке р
функция f принимает свое наибольшее значение в промежутке (а,Ь).
Доказательство. Пусть функция / непрерывна в точке р и
дифференцируема в каждой точке х ф р.
Предположим, что f{x) < 0 при каждом х Е (а,р) и f'(x) > 0 при
хе (р,ь).
Тогда функция / является убывающей в промежутке (а,р\ и,
значит, для всякого х Е (а,р] имеет место неравенство f(x) > /(р).
В промежутке [р, 6) функция / является возрастающей и,
следовательно, для любого х Е [р, Ь) имеет место неравенство /(р) < f{x).
Таким образом, /(р) < f(x) для всех а; Е (а, 6). Это и означает, что
/(р) есть наименьшее значение функции / в промежутке (а, 6).
Рассмотрим случай, когда f'(x) > 0 при х Е (а,р) и /'(ж) < О
при х Е (р, Ь). Положим: /! = —/.

§ 7. Точки экстремума дифференцируемой функции
377
Функция Д, очевидно, непрерывна в точке р, дифференцируема в
каждой точке х Е (а,Ь), отличной от р, f{(x) < 0 в интервале (а,р) и
fi(x) > 0 в интервале (р,Ь).
Применяя доказанное к функции /i, получаем —f(p) = /i(p) <
< /i(a;) = —f(x) для всех ж Е (а,Ь), то есть для всех а; Е (а,Ь) будет
f(x)<f(p).
Таким образом, в данном случае функция / принимает в точке р
свое наибольшее значение в интервале (а, Ь).
Теорема доказана. ■
▼ Следствие. Пусть даны функция f : А —> Ш и точка р Е А такая,
что функция f непрерывна в точке р, и можно указать 6 > О такое, что
интервал (р — 6,р + 6) содержится в А и функция f дифференцируема в
каждом из интервалов (р — 6,р) и (р,р + 6). Тогда:
если производная функции f в интервале (р — 6,р + 6) слева от р
неположительна, а справа от р неотрицательна, то р есть точка минимума
функции /;
если же производная функции f в интервале (р — 8,р + 6) слева
от р неотрицательна, а справа от р неположительна, то р есть точка
максимума функции /.
Доказательство* Действительно, если функция /
удовлетворяет условиям следствия, то значение функции / в точке р является в
одном случае наименьшим, а в другом — наибольшим ее значением в
интервале (р — 6,р + 6).
Отсюда следует, что в первом случае р есть точка минимума, а во
втором — точка максимума функции / на множестве А, что и
требовалось доказать. ▼
7.3. Достаточные условия экстремума для функции, п-кратно
ДИФФЕРЕНЦИРУЕМОЙ В ТОЧКЕ
Приведем характеристики точек экстремума, использующие
производные высших порядков.
■ Лемма 7.1. Пусть дана функция f : (а,Ь) —* R. Предположим,
что для некоторой точки р Е (а, 6) справедливо соотношение:
f(x) = f(p) + A(x-p)n + o[(x-p)n] прих^р, (7.1)
где А ф 0 и п > 1. Тогда: если п — четно, то в случае А > 0 точка
р есть точка строгого минимума функции /, а в случае А < 0 точка р
есть точка строгого максимума функции /; если п — нечетно, то р не
является точкой экстремума /.

378 Гл. 4. Дифференциальное исчисление функций одной переменной
Доказательство. Из формулы (7.1) получаем:
f(x)=f(p) + A(x-p)n[l + P(x)],
где (3(х) —» 0 при х —» р. Отсюда вытекает, что найдется 6 > О такое,
что если \х — р\ < 6, причем х Е (а, 6), то 1 + /3(х) > 0.
Будем считать, что интервал (р—6,р+6) содержится в (а, Ь). Этого,
очевидно, можно добиться, уменьшая 6, если необходимо.
Пусть п — нечетно. Тогда (х — р)п < 0 при х < р и (х — р)п > 0
при х > р.
Отсюда следует, что для всех х из интервала (р — 6,р + 6),
отличных от р, величина f(x) — f(p) = A[l + (3(х)](х — р)п отлична от нуля
и по разные стороны точки р принимает значения различных
знаков. Это позволяет заключить, что функция / сколь угодно близко
от р принимает как значения, большие /(р), так и значения, меньшие
/(р), и, значит, р не может быть ни точкой минимума, ни
точкой максимума функции /.
Рассмотрим случай, когда п — четно.
Тогда (х — р)п > 0 для всех жЕК. При этом если х ф р, то
неравенство строгое. Если х Е (р — 6,р + 6), причем х ф р, то в случае А > 0
выполняется неравенство f(x) > f(p), а если А < 0, то f(x) < f(p).
Это означает, что точка р является точкой строгого минимума
функции / при А > 0, а если А < 0, то р есть точка строгого
максимума функции /.
Лемма доказана. ■
■ Теорема 7Л. Предположим, что функция f : (а, 6) —» R имеет в
промежутке (а, Ь) производную порядка п > 1, и точка р Е (а, Ь) такова,
что fin)(p) фОи f(m)(p) = 0 при m = 1,2,..., п - 1. Тогда:
если п — нечетно, то р не является точкой экстремума функции f;
если жеп — четно, то р есть точка строгого минимума функции f
в случае, когда f^n\p) > 0 и р есть точка строгого максимума /, если
/(п)(р)<о.
Доказательство. В силу теоремы о формуле Тейлора с
остаточным членом в форме Пеано (теорема 6.1, п. 6.2), имеем:
/(*) = E^^(*-P)fc + °K*-P)n] при х-р.
т=0
Принимая во внимание условия теоремы, получаем:
f(x) = f(p) + ^-^-(x-p)n + o[(x-p)n) при х - р.
п!

§ 8. Выпуклые функции
379
Отсюда видно, что для / выполняются все условия леммы 7.1 с
- А f(n)JP)
постоянной А = р-^.
п\
В силу леммы 7.1, отсюда непосредственно следует утверждение
теоремы. В
§8. Выпуклые функции
Здесь будет описан некоторый класс функций, определенных на
промежутках множества Ж, а именно, класс выпуклых функций.
Понятие выпуклой функции имеет геометрическое происхождение.
Концепция выпуклости является одной из фундаментальных в современной
математике.
Основной результат этого раздела — дифференциальный критерий
выпуклости функции.
Из определения выпуклости непосредственно следует соотношение,
называемое неравенством Иенсена. В качестве его следствия мы
получаем некоторые другие полезные неравенства.
8.1. Определение выпуклой функции. Неравенство Йенсена
Пусть / = (а, Ь) есть произвольный промежуток в множестве Ж.
Пусть даны точки х\ и Х2 промежутка I и числа Л > 0 и fi > О такие,
что А+/х = 1. Тогда точка х = Хх\ +11x2 лежит между х\ и Х2 и, значит,
принадлежит промежутку I.
Функция / : / —* Ж называется выпуклой или выпуклой сверху, если
для любых двух точек х\ и Х2 промежутка / и любых двух чисел Л > О
и /л > 0 таких, что Л + /л = 1, выполняется неравенство
/(Ая?1 + 11х2) < Xf(xi) + iif(x2). (8.1)
Если знак равенства здесь имеет место в том и только в том случае,
когда xi — Х2, то функция / называется строго выпуклой или строго
выпуклой сверху.
Функция f : I -> Ж называется вогнутой функцией или, иначе,
выпуклой снизу, если для любых двух точек х\ и Х2 промежутка / и
любых двух чисел Л > 0 и /х > 0 таких, что Л + ц = 1, выполняется
неравенство:
f(Xxi + fix2) > A/On) + /х/(ж2).

380 Гл. 4. Дифференциальное исчисление функций одной переменной
Если знак равенства здесь имеет место в том и только в том случае,
когда хг = #2, то функция / называется строго вогнутой или строго
выпуклой снизу.
Если функция / — вогнутая, то —/ есть выпуклая
функция, и выпуклость функции —/, очевидно, влечет
вогнутость функции /.
В силу этого замечания, анализ вогнутых функций сводится к
изучению выпуклых функций, и далее мы будем рассматривать только
выпуклые функции.
Установим геометрический смысл понятия выпуклой функции.
Сначала определим понятие выпуклого множества на плоскости.
Множество А на плоскости называется выпуклым, если для любых двух
его точек Mi и Мг отрезок [М1М2], соединяющий эти точки, содержится
в множестве А.
Рис. 25 Рис. 26
На рис. 25 мы видим пример выпуклого множества. На
рис. 26 показано некоторое невыпуклое множество.
Такие элементарные геометрические фигуры, как круг,
треугольник, параллелограмм и т. д. — это простейшие
представители класса выпуклых множеств.
Окружность (именно окружность, а не круг!) есть один из
многочисленных примеров невыпуклых множеств.
Кольцо, состоящее из всех точек плоскости, лежащих между
двумя концентричными окружностями разных радиусов, представляет
собой другой пример невыпуклого множества.
Зададим декартову ортогональную систему координат на
плоскости. Точку, координаты которой ж и у, будем обозначать (ж,у).
Пусть дана функция / : (а, 6) —» R. Множество всех точек (ж, у) на
плоскости таких, что х Е I = (а,Ь) и у > /(ж), называется надграфиком
функции /. Обозначим его символом Г+(/).
Множество всех точек (ж, у) таких, что ж Е / и у < /(ж), называется
подграфиком функции /. Обозначим его символом Г~(/).

§ 8. Выпуклые функции
381
Пусть Р есть полоса, состоящая из всех точек плоскости, у
которых координата х принадлежит промежутку I.
Надграфик функции состоит из всех точек М Е Р, лежащих либо
на самом графике функции /, либо выше его (см. рис. 27(1)).
Аналогично, подграфик функции f состоит из всех точек МЕР,
расположенных либо на самом графике, либо ниже его (см.
рис. 27(2)).
(V (2)
Рис. 27
■ Теорема 8.1. Для того чтобы функция f : (a,b) —» R была
выпуклой, необходимо и достаточно, чтобы ее надграфик был выпуклым
множеством.
Доказательство. Напомним, прежде всего, следующий факт,
известный из аналитической геометрии.
Пусть Mi = (#1,3/1) и Мг = (#2,2/2) — Две произвольные точки на
плоскости. Тогда отрезок, соединяющий эти точки, есть
совокупность всех точек М = (х, у) таких, что х = Хх± + /х#2, У = Aj/i +/xj/2, где
числа Л и fi удовлетворяют условиям: А>0, /х>0иА + /х = 1.
Предположим, что функция / — выпукла, и пусть Mi = (#1,3/1) и
Мг = (#2,3/2) — две произвольные точки ее надграфика Г+(/).
Соединим точки Mi и М2 отрезком.
Требуется доказать, что этот отрезок целиком содержится в
множестве Г+(/).
Пусть М = (#,з/) есть произвольная точка отрезка [М1М2]. Тогда
имеем: # = A#i + /х#2, У = А3/1 + /хз/2, где А>0, /х>0иА + /х = 1.
Если А = 0, то М = Мг и, значит, М Е Г+(/). Если /х = 0, то
М = Mi и, стало быть, и в этом случае М G Г+(/).
Будем далее считать, что А > 0 и /л > 0. По условию, #i,#2 € / =
= (а,Ь). Отсюда следует, что # Е (а,Ь).

382 Гл. 4. Дифференциальное исчисление функций одной переменной
Согласно определению надграфика, имеем: у\ > /(#i), У2 > /(#2),
откуда заключаем, что
у = Ayi + цу2 > Xf(xi) + ///(#2).
В силу выпуклости функции /,
A/(m) + fj,f(x2) > /(Am + //rr2) = /(ж).
Следовательно, у > f(x). Этим доказано, что
М = (я,у)ЕГ+(/).
Так как М Е [М1М2] взято произвольно, то мы,
следовательно, получаем, что отрезок [М1М2] содержится в множестве Г+(/).
Тем самым выпуклость множества Г+ (/) установлена.
Предположим теперь, что функция / такова, что ее надграфик
представляет собой выпуклое множество. Докажем, что
тогда функция / является выпуклой.
Возьмем произвольно х\,Х2 £ (а,Ь), и пусть числа А > 0, // > О
таковы, что А + // = 1. Пусть у\ = /(#i), У2 = /(#2).
Точки Mi = (#i,yi) и М2 = (#2,У2) принадлежат надграфику
функции / и, значит, точка М = (ж, у), где rr = Arri + //#2, У = Ayi + //уг,
принадлежит Г+(/), то есть
А/(ял) + м/(а?2) = у > /(ж) = /(Am + //rr2).
Так как rri, гг25 А и /х, удовлетворяющие всем указанным выше
условиям, были взяты произвольно, то тем самым выпуклость функции
/ установлена.
Теорема доказана. ■
■ Теорема 8.2 (о неравенстве Йенсена). Пусть дана выпуклая
функция f : I —> R, где I = (а, Ь). Тогда для любых точек rco, #i, •. •, #п
промежутка J и для любых чисел Аг, г = 0,1,..., п, таких, что Аг > О при
каждом г, и Ао + Ai Н f- An = 1, точка х = Ао#о + А1Ж1H h Апжп
принадлежит промежутку J, причем выполняется неравенство, называемое
неравенством Йенсена:
/(А0жо + Aixi H h XnXn) < X0f(xo) + Ai/(a?i) H h An/(rrn). (8.2)
Если функция f — строго выпуклая, то знак равенства в (8.2) имеет
место в том и только в том случае, когда хо = х\ = • • • = хп.

§ 8. Выпуклые функции
383
Доказательство. Теорема доказывается индукцией по п. Для
п = 1 неравенство Иенсена следует из определения выпуклой функции.
Предположим, что для некоторого п £ N теорема доказана, и пусть
даны точки rco, #i,. • •, хп, #n+i промежутка J и числа А* > 0, г = 0,1,...,
п,п + 1, сумма которых равна единице.
Пусть х = Ао#о + Ai#i + • • • + An#n + An+ia?n+i- Положим А^ =
= An + An+i- Пусть
An Л An+i / . ^
с*=—; /3=——; я? =аягп+)9я?п+1.
Тогда а > О, /3 > 0, а + 0 = 1. Имеем:
ж = Ао#о Н h An_irrn_i + \'п(ахп + /3xn+i) =
= Аожо Н h An-irrn-i + А^а/.
Числа Ао,..., An-i, Ajj все положительны и их сумма, очевидно,
равна 1.
Точка х' принадлежит J. В силу индукционного предположения,
точка х = Ао#оН f-An_i£n--i+A^a/ также принадлежит промежутку J,
причем имеет место неравенство:
/(*) < Ао/Ы + Ai/(m) + ... + \n'f(x'). (8.3)
Согласно индукционному предположению, в случае, если функция
/ строго выпукла ив соотношении (8.3) имеет место
равенство, то жо = • • • = #n-i = х'. В силу выпуклости /, имеем:
f(x) = f(axn + 0Xn+i) < af(xn) + Pf(xn+i)
и, значит,
Kif(x') < \'n(af(xn) + 0f(xn+i)) = Xnf(xn) + An+i/(a?n+i). (8.4)
Подставляя это выражение в правую часть (8.3), получим:
/(Аожо + Airci H h Anrrn + An+i#n+i) <
< Ао/(а?о) + Ai/(rci) H h \nf(xn) + An+i/(zn+i). (8.5)

384 Гл. 4. Дифференциальное исчисление функций одной переменной
Таким образом, установлено, что если (8.2) верно для
некоторого п, то оно остается верным, если п заменить на
п + 1.
В силу принципа математической индукции, неравенство Йенсена
(8.2) доказано.
Предположим, что в соотношении (8.5) имеет место знак равенства.
Тогда, как видно из рассуждений выше, посредством которых получено
(8.5), равенство имеет место в каждом из соотношений (8.3)
и (8.4).
Следовательно, хо = х\ = • • • = х' — в силу предположения
индукции и хп = #п+1 = х' — в силу строгой выпуклости / и, значит,
хо = х\ = • • • = хп = жп+1. Отсюда следует, что знак равенства в (8.5)
имеет место в том и только в том случае, когда все числа xi равны
между собой.
Теорема доказана. ■
8,2, Критерии выпуклости функции
■ Теорема. 8.3. Пусть даны промежуток I = (a,b) и функция
f : I —► R. Предположим, что функция f дифференцируема в I. Если
функция f является выпуклой, то для любых х £ I и р £ / выполняется
неравенство:
m>m+(x-p)f(p). (s.e)
При этом если функция f — строго выпуклая, то при х ф р неравенство
строгое.
Обратно, если функция f — дифференцируема и для любых х £ I
ир £ I выполняется (8.6), то функция f — выпукла. При этом если при
хфр неравенство (8.6) — строгое, то функция f — строго выпуклая.
Перед доказательством отметим следующее.
Замечание. Равенство у — f(p) + (x —p)f'(p) — это уравнение
касательной графика функции f в точке М = (p,f(p)) (см. п. 2.1).
Рис. 28

§ 8. Выпуклые функции
385
Геометрический смысл неравенства (8.6) поэтому
таков (см. рис. 28). График выпуклой функции класса VX{I) (то есть
выпуклой функции, определенной и дифференцируемой в промежутке I)
лежит выше касательной в любой его точке.
Доказательство теоремы. Пусть / : I —> К есть функция
класса Т)х{1). Предположим, что она является выпуклой. Возьмем
произвольно значения ж,р G /.
В случае х = р соотношение (8.6), очевидно, выполняется.
Будем считать, что х ф р. Пусть 0 < А < 1. Тогда 1 — А > 0 и
А + 1 — А = 1. В силу выпуклости функции /, имеем:
Xf(x) + (1 - Л)/(р) > f[Xx + (1 - Х)р] = f\p + Х(х - р)}.
Отсюда
А/(х) > Л/(р) + {/[р + Х(х - р)} - f(p)}.
Разделив обе части этого неравенства на А, получим:
«^/M + ^lf*!-* (8-7)
При А —* 0 будем иметь:
f\p+X(x-p)]-f(p) ,
Х(х-р) Т(Р)-
Переходя в неравенстве (8.7) к пределу при А —► 0, получаем:
f(x)>f(p) + (x-p)f'(p),
и, таким образом, неравенство (8.6) доказано.
Предположим, что функция / строго выпуклая, и пусть х ф р.
Тогда
/(*) + /(!>)
>/(^)>№) + /'(р)(^-р).
2
Отсюда, после очевидных преобразований, получаем:
№>№ + (x-p)f'(p).
Первое утверждение теоремы доказано полностью.

386 Гл. 4. Дифференциальное исчисление функций одной переменной
Теперь предположим, что / есть функция класса Т>г(1) такая, что
для любых х,р £ I выполняется неравенство:
f(x)>f(p) + (x-p)f'(p).
Зададим произвольно точки xi, X2 £ / и числа А > 0 и // > О такие,
что А + /л = 1. Положим р = Xxi + 11x2- Имеем неравенства:
/Ы > Sip) + (xi -p)/'(p); /Ы > № + (X2-P)f'(p). (8.8)
Умножая обе части первого из этих неравенств на А и обе части
второго неравенства на (л и складывая полученные неравенства, в
результате будем иметь:
\f(zi)+i*f(z2) > (A + //)/(p) + [Am+//rr2-(A + //)p]/» = /(p). (8.9)
Так как точки #i Е / и Х2 Е I взяты произвольно, то
выпуклость функции / доказана.
Предположим, что при всяком х ф р выполняется неравенство
f(x) > f(p) + (х — p)f'(p) (неравенство строгое!). Если х\ ф Х2, то
р = \х\ +/IX2 не совпадает ни с одним из чисел х\ и Х2- Значит, в этом
случае каждое из неравенств (8.6) является строгим. Это
позволяет заключить, что (8.9), получаемое отсюда, также строгое.
Теорема доказана. ■
▼ Следствие. Для того чтобы функция / : (а, 6) —► R класса VX{I)
была вогнутой, необходимо и достаточно, чтобы для любых x,p Е /
выполнялось неравенство:
№<f(p) + (x-P)f'(p).
Доказательство. Действительно, данное утверждение
очевидным образом следует из того, что если функция / — вогнутая, то
функция /i = — / является выпуклой.
Обратно, выпуклость Д влечет вогнутость /.
Следствие доказано. ▼
■ Теорема 8.4. Для того чтобы функция / : J = (а, Ь) —► Ж,
принадлежащая классу VX{I), была выпуклой (соответственно, строго
выпуклой), необходимо и достаточно, чтобы ее производная была
возрастающей (соответственно, строго возрастающей) функцией.

§ 8. Выпуклые функции
387
Доказательство. Необходимость. Пусть / : / —► R есть
выпуклая функция, / Е ^"Ч-О-
Возьмем произвольно точки xi,X2 & I такие, что х\ < Х2>
Полагая в неравенстве (8.6) х = #2> а р = #i, получим:
/(%) > /(*l) + (Х2 ~ *l)/'(*l). (A)
Полагая в (8.6) х = ал, а р = #2, прийдем к неравенству:
/Ы > /Ы + (*i - я?2)/#(ад)- (В)
Складывая полученные неравенства почленно и принимая во
внимание, что xi — X2 = — (х2 — xi), будем иметь:
/Ы + /(*i) > /(an) + Дх2) + (х2 - *i)[/'(xi) - f'(x2)}. (С)
Отсюда
0>(x2-x1)[ff(x1)^ff(x2))
и, наконец,
0>/'(яя)-/'Ы,
то есть
/'(а*) > /'(*i)-
Так как точки m,a?2 G J такие, что х\ < Х2, были взяты
произвольно, этим доказано, что функция /' — возрастающая.
Если функция / — строго выпукла, то, согласно теореме 8.3,
каждое из неравенств (А) и (В) — строгое и, значит, неравенство
(С), получаемое из них, также является строгим, то есть
функция /' является строго возрастающей.
Необходимость условия теоремы доказана.
Докажем достаточность. Пусть / есть функция класса V1 (I).
Предположим, что ее производная является возрастающей
функцией. Покажем, что для функции / выполняется условие теоремы 8.3, то
есть для любых ж,рЕ/ справедливо неравенство:
f(x)>f(P) + (x-p)f'{p).
Зададим произвольно точку р£/и для х € I положим:
и(х) = /(ж) - /(р) -{х- p)f'(p).

388 Гл. 4. Дифференциальное исчисление функций одной переменной
Очевидно, и(р) = 0. Функция гл, определенная так, принадлежит
классу VX{I). Для всех х Е /, очевидно, имеем и'(х) = f'{x) — /'(р).
Так как функция /', по условию, возрастающая, то
и'{х) < 0 при х < р и и'(х) > 0 при х > р.
Отсюда следует, что функция и является убывающей — в
промежутке (а,р] и возрастающей — в промежутке [р, Ь).
Пусть х Е /, х ф р. Если х < р, то w(rr) > Цр) = 0, в силу того,
что функция и является убывающей — в промежутке (а,р].
Если же х > р, то 0 = и(р) < и(х), в силу того, что в промежутке
[р, Ь) функция и возрастает.
И в том, и в другом случае мы получаем, что
f(x)>m + (x-p)f(p)-
Так как точка р Е / была выбрана произвольно, то тем самым
доказано, что для функции / выполнено условие теоремы 8.3 и,
следовательно, функция / является выпуклой.
Если производная функции / является строго
возрастающей функцией, то при х < р
u'(x) = f'(x)-f'(p)<0,
а при х > р будет и'{х) > 0. Это позволяет заключить, что функция и
является строго убывающей в промежутке (а,р] и строго
возрастающей в промежутке [р, Ь).
И в том, и в другом случае получаем, что при х ф р
f(x)-f(p)-(x-p)f'(p)>0,
то есть при хфр
f(x)>f(p) + (x-p)f'{p).
На основании теоремы 8.3 отсюда вытекает, что функция /
является строго выпуклой.
Теорема доказана. ■
▼ Следствие 1. Пусть f : I = (a,b) —> R есть функция класса
Т>г(1). Тогда для того чтобы функция f была вогнутой, необходимо и
достаточно, чтобы ее производная f была убывающей функцией.
Доказательство — очевидно. ▼

§ 8. Выпуклые функции
389
▼ Следствие 2. Пусть f : / = (а, 6) —> R есть функция класса
V2(I). Для того чтобы функция f была выпуклой, необходимо и
достаточно, чтобы ее вторая производная f" была неотрицательна во всех
точках интервала (а, Ь).
Функция f является строго выпуклой в том и только в том
случае, если ее вторая производная неотрицательна и во всяком интервале
(а,/3) С / существует точка х, для которой f"(x) > 0.
Данное предложение следует из теоремы 8.4 и критерия
монотонности дифференцируемой функции (см. п. 4.3 этой главы). ▼
Доказанные здесь критерии выпуклости функции
относятся к случаю дифференцируемых функций. В связи
с этим заметим, что произвольная выпуклая функция, вообще говоря,
может быть не дифференцируемой в некоторых точках
промежутка, в котором она определена.
Пример. Функция х Е К »-> \х\ является выпуклой. В точке х = 0
она не имеет производной.
8,3, Основные неравенства анализа
Выписывал явно неравенство (8.1), определяющее условие
выпуклости функции, и неравенство Йенсена для различных конкретных
функций, можно получить большое число полезных неравенств. Для
доказательства выпуклости рассматриваемых функций мы будем
применять результаты предыдущего раздела.
■ Теорема 8.5 (неравенство Коши для среднего арифметического
и среднего геометрического). Пусть даны числа Ai>0, Аг>0, ...,
>о такие, что Ai + A2 + • • • + An = 1. Тогда для любой системы из
п неотрицательных чисел xi,X2,...,xn выполняется неравенство:
Aim + A2rr2 + • • • + XnXn > х\гХ2* .. .жпп. (8.10)
Знак равенства здесь имеет место в том и только в том случае, если
Xi = Х2 = • • • = Хп.
Замечание. Левая часть неравенства (8.10) называется
взвешенным средним арифметическим чисел х\,Х2->-.. ,хп относительно
весов Ai, A2,..., Ап, правая часть неравенства (8.10) называется
взвешенным средним геометрическим арифметических чисел
относительно тех же весов.
Доказательство теоремы. Предположим, что величины А*,
г = 1,2,..., п, удовлетворяют всем условиям теоремы.
Пусть Ж1,яг2, • • - ,жп суть произвольные неотрицательные числа.

390 Гл. 4. Дифференциальное исчисление функций одной переменной
Если хотя бы одно из чисел х% обращается в нуль, то правая часть
неравенства (8.10) обращается в нуль, а левая — неотрицательна, так
что в этом случае (8.10) верно. При этом если не все Xi равны нулю, то
неравенство строгое.
Далее будем предполагать, что xi > 0 для каждого г = 1,2,...,п.
Вторая производная функции х н-+ — In ж равна — и, стало быть,
xz
положительна для всех х > 0. Отсюда вытекает, что эта функция
выпукла (и даже строго выпукла) в интервале (0, оо).
Применяя к функции х ь-» — \пх неравенство Иенсена, получим,
что для любых чисел х\ > 0, Х2 > 0, ..., хп > 0 выполняется
неравенство:
-Ailnrri-A2lnrc2 Anlnrrn > -ln(Aia;i + A2#2H ЬАпяп). (8.11)
Отсюда получаем:
ln(Ai#i + А2Ж2 Н h An#n) > Ai ln#i + A21пгг2 H Ь Ап 1пжп
и далее
Aim + А2ж2 + • • • + ХпХп > х^х^2 .. .Жпп.
Неравенство (8.10) доказано.
Если Xi, г = 1,2,...,п, таковы, что в правой части неравенства
(8.10) имеет место равенство, то в силу строгой выпуклости функции
х ь-» — lnrr, отсюда вытекает, что х\ = Х2 = • • • = хп.
Теорема доказана. ■
▼ Следствие 1 (о неравенстве Юнга). Пусть числа р > 0 и q > 0
таковы, что
1+1=1.
р q
Тогда для любых х ЕМ и у ЕМ выполняется неравенство, называемое
неравенством Юнга:
l£j! + ML > ^ (8.12)
Доказательство. Это есть частный случай
неравенства (8.10) теоремы 8.5, получаемый при п = 2, если взять х\ = |ж|р;
#2 = М9; Ai = -; Л2 = - и заметить, что \ху\ > ху.
р q
Следствие 1 доказано. ▼

§ 8. Выпуклые функции
391
▼ Следствие 2. Для любых двух чисел и > О и v > О справедливо
равенство:
uptp
uv = inf ^- + ^г). (8.13)
t€(0,oo) \ Р qt<* J
Доказательство. Если u = v = О, то доказывать нечего.
Если только одно из чисел и, v равно нулю, то в правой части
равенства (8.13) будем иметь степенную функцию переменной t с
положительным коэффициентом, и ее точная нижняя граница на множестве
(О, оо) равна 0 = uv.
Пусть и > О и v > 0. Применяя неравенство Юнга (8.12) (см.
следствие 1 теоремы 8.5) для х = utny = v/t, получим, что для всякого
t E (0, оо) имеет место неравенство:
uptp vq ^
Н—-~ > uv.
р qt<*
!
_. VP
При t = — имеем:
р qt*
Следовательно, uv есть наименьшее значение, а значит, и точная
ниэюняя граница функции
р qt<*
в интервале (0,оо).
Следствие 2 доказано. ▼
■ Теорема 8.6 (о неравенстве Гёльдера). Пусть даны две
произвольные системы из п вещественных чисел
(Xl, Х2, • • • , Яп); ({/1,2/2, , Уп)
и пусть р>0и^>0 таковы, что
i + i-i.
Р 9

392 Гл. 4. Дифференциальное исчисление функций одной переменной
Тогда имеет место неравенство, называемое неравенством Гёлъдера:
y^^Xiyi
г=1
г=1 / \г=1
(8.14)
Доказательство. Положим:
Зададим произвольно £ > 0. Имеем:
1
П ^ g
9
y^^XiVi
г=1
<£|te<|
*
г=1
Применяя (8.12) к каждому из слагаемых справа, получим:
y]xiVi
i=l
Отсюда для всякого t > 0 будем иметь:
I n i
I *=1 I
и, значит, согласно следствию 2 теоремы 8.6 (см. (8.13)),
XPtP yq
" р ~q№
y^Xiyi
г=1
< inf (w+xi\=XY.
t€(0,oo) \ p tf£9/
Полученное неравенство и есть требуемое.
Теорема доказана. ■
▼ Следствие (о неравенстве Коши — Буняковского). Для любых
двух систем из п вещественных чисел
(Ж1,Ж2,...,Жп); (У1>У2,...,Уп)

§ 8. Выпуклые функции
393
выполняется неравенство:
y^XiVi
г=1
N
5Х.
г=1 \
Е>
г=1
(8.15)
Неравенство (8.15), называемое неравенством Коши — Буняков-
ского, есть частный случай неравенства (8.14) теоремы 8.6,
получаемый, когда р = q = 2. ▼
■ Теорема 8.7 (о неравенстве Минковского). Пусть даны системы
из п вещественных чисел:
(ж1,Ж2,..-,агп), (2/1,2/2,..., 2/п).
Тогда для всякого р>1 имеет место неравенство
$>«+wip < Х>*п + 1>
п ^ р
(8.16)
,г=1
J=l
кг=1
называемое неравенством Минковского.
Доказательство. В случае р = 1 неравенство Минковского
следует из того, что
\Xi+Vi\ < \Xi\ + \yi\
Р
р-1
Тогда g > 1 и
при всех г = 1,2,..., п.
Будем считать, что р > 1. Положим </
i + i-i.
Р Q
Если левая часть неравенства (8.16) равна нулю, то доказывать
нечего. Будем считать, что левая часть (8.16) отлична от нуля. Имеем:
^|Яг+2/г|Р = ^2\Xi+Vi\P 1\Xi+yi\<
г=1
г=1
^^Ixi + Vir'lxil + ^lxi + yir^yil (8.17)
г=1
г=1

394 Гл. 4. Дифференциальное исчисление функций одной переменной
Применяя неравенство Гёлъдера (8.14), получим:
П / П \ q~ / П
5^i*i+i«ip-li*ii< En+^i9(p_1) En
г=1 \г=1
Аналогично
q / П \ р.
г=1 \г=1 / \г=1
Заметим, что q(p — 1) = р.
Заменяя каждую сумму в правой части (8.17) выражением,
стоящим справа в каждом из последних двух неравенств, в результате
получим неравенство:
5>* + 1й|р< l^lxi + yil1
г=1 \г=1
'Л\Р
Сокращая обе части этого неравенства на первый множитель спра-
ва и принимая во внимание, что 1 = -, в результате получим нера-
q p
венство (8.16).
Теорема доказана. ■
8.4. ТОЧКИ ПЕРЕГИБА ФУНКЦИИ
Введем понятие, полезное при выяснении качественных
особенностей строения той или иной функции, а именно, понятие точки перегиба
функции. Приведем определение того, что есть точка перегиба функции,
и установим некоторые критерии, позволяющие в простейших случаях
эти точки находить.
Пусть дана функция / : М —> R, где М С R. Пусть хо € М.
Предположим, что хо есть внутренняя точка множества М, то есть что
существует окрестность U = (хо — 6,хо + 6) точки #о, содержащаяся в
множестве М.
Точка хо € М называется точкой перегиба функции /, если
функция / дифференцируема в точке хо и выполнено следующее условие:
окрестность U = (хо — 6, xq + 6) С М точки хо может быть
выбрала так, что часть графика функции f, соответствующая интервалу
(хо — £,#о)5 лежит по одну сторону касательной графика в точке Хо =

§ 8. Выпуклые функции
395
= (жо, /(#о)), а часть графика, соответствующая интервалу (хо, хо + 6),
расположена по другую сторону касательной.
Наглядно хо есть точка перегиба функции /, если при переходе х
через хо точка X — (х, f(x)) перемещается с одной стороны касательной
графика функции на другую (см. рис. 29).
Формально условие, которому должна удовлетворять точка
перегиба функции, описывается следующим образом.
Точка хо Е М есть точка перегиба функции /, если хо есть
внутренняя точка множества М, функция / дифференцируема в точке Хо и
существует окрестность U = (хо — 8, хо + 8) С М такая, что либо для
всех х Е (хо — 8,хо) выполняется неравенство:
f(x) > /(#о) + f{xo){x - хо),
а для любого х Е (жо,#о + ^) — неравенство:
f(x) < f(x0) + f(x0)(x - хо),
либо для всех х Е (хо — 8,хо) имеет место неравенство:
/0*0 < /(яо) + f{xo){x - хо),
а для всех х Е (жо,#о + 8) — неравенство:
/0*0 > /(zo) + f(xo)(x - хо).
ЬУ
Рис. 29
Укажем некоторые условия, позволяющие находить точйи перегиба
для различных конкретных функций.
■ Теорема 8.8. Пусть f есть вещественная функция, определенная
во всех точках интервала (а,Ь). Предположим, что точка хо Е (а, Ь)

396 Гл. 4. Дифференциальное исчисление функций одной переменной
является точкой перегиба функции /. Если функция f имеет во всех
точках интервала (а, Ь) вторую производную, то f"{xo) = 0.
Доказательство. Пусть функция / удовлетворяет всем
условиям предложения. Положим F(x) = f(x) — f(xo) — f'(xo)(x — xo)- Тогда
F'(x) = f'(x)-f'(x0).
Функция F имеет в интервале (a,b) вторую производную. При этом
F"(x) = fix) для всех х Е (а,Ь).
Имеем: F'{xo) = 0. Если f"(xo) — F"{xo) > 0, то жо есть точка
строгого минимума функции F (см. лемму 7.2 этой главы) и, стало
быть, найдется окрестность U = (хо — 5, хо + 8) С (а, Ь) точки хо
такая, что для любого х G С/, отличного от #о, выполняется неравенство:
F(x) > F(xo) = 0, то есть f(x) > f(xo) + ff(xo)(x — хо) для любого
такого х. Это, очевидно, противоречит тому, что, по условию,
хо есть точка перегиба функции /.
Аналогичным образом из предположения, что f"{xo) < 0, вытекает,
что хо есть точка строгого максимума функции F и, значит,
f(x) < f(x0) + f(x0)(x - хо)
для всех х ф Жо, принадлежащих некоторой окрестности U точки хо-
Это опять-таки противоречит тому, что, по условию, хо есть
точка перегиба функции /.
Теорема доказана. ■
■ Теорема 8.9. Пусть вещественная функция f определена и
дифференцируема во всех точках интервала (а, Ь) С К. Если точка хо G (а, Ь)
является точкой экстремума производной функции f, то хо есть точка
перегиба функции /.
Доказательство. Пусть хо есть точка максимума функции /'.
Будем считать, что f'(x) < f'{xo) для всех х Е (а, Ь).
Это предположение не умаляет общности, поскольку его
выполнения всегда можно добиться, уменьшая, в случае необходимости,
промежуток (а, Ь).
Пусть a < х < хо- По теореме Лагранжа о среднем значении (см.
следствие 1 теоремы 4.3), найдется £ такое, что
/Ы-/(Ж) = /'(О < /'(-о).

§ 8. Выпуклые функции
397
Отсюда получаем, что для всякого х Е (а,#о) выполняется неравенство:
f(x0) - f(x) < f'(xo)(x0 - х)
и, значит,
f(x)>f(x0) + f'(xo)(x-x0)
для всех таких х.
Предположим, что Хо < х < Ь. Применяя теорему Лагранжа о
среднем значении, получим, что
/(ж)-/Ы=/'(0</'Ы,
X — Хо
откуда заключаем, что в этом случае
/(#) < /0&о) + f{xo){x - хо).
Итак, мы получаем, что если производная функции / принимает
в точке хо свое наибольшее значение в интервале (а,Ь), то для всякого
х G (а,хо) выполняется неравенство
f(x) > f(x0) + f'(xo)(x - д:о),
а для всякого х £ (#о,Ь) верно неравенство
f(x)<f(xo) + f'(x0)(x-xo).
Согласно определению, это и означает, что хо есть точка перегиба
функции /.
Случай, когда хо есть точка минимума функции /,
рассматривается аналогично. Формально, он сводится к рассмотренному случаю
заменой функции / на —/.
Теорема доказана. ■
▼ Следствие. Пусть вещественная функция f определена и имеет
вторую производную во всех точках интервала (а, Ь) С М. Если
точка хо Е (а,Ь) такова, что f"{x) в одном из интервалов (а,хо) и (хо,Ь)
— неотрицательна, а в другом — неположительна, то хо есть точка
перегиба функции /.
Доказательство. Действительно, если f"{x) < О для х Е (а,#о)
и f"{x) > О Для х € (жо,Ь), то #о есть точка минимума функции /' в
интервале (а,Ь).

398 Гл. 4. Дифференциальное исчисление функций одной переменной
Если же /"(#) > 0 для х Е (а,жо) и f"{x) < О для х Е (#о,Ь), то хо
есть точка максимума функции /' в интервале (а,Ь).
В силу теоремы 8.9, получаем, что и в том, и в другом случае точка
хо есть точка перегиба функции /.
Следствие доказано. ▼
Замечание. В случае, описанном в следствии теоремы 8.9
выше, функция / устроена следующим образом. В одном из интервалов
(а,хо) и (#о,Ь) она является функцией, выпуклой снизу, а в другом —
функцией, выпуклой сверху (см рис. 30).
Рис. 30
8.5. Критерий выпуклости функции в общем случае
Выше (см. п. 8.2) было установлено необходимое и достаточное
условие выпуклости дифференцируемой функции.
Произвольная выпуклая функция, однако, может не быть
дифференцируемой в некоторых точках своей области определения.
Здесь будет доказан критерий выпуклости функции, не
требующий каких-либо дополнительных предположений относительно самой
функции.
Сначала докажем некоторые неравенства, имеющие простой
геометрический смысл и являющиеся следствием определения выпуклой
функции.
■ Лемма 8.1. Пусть даны промежуток I — (а, Ь) С Ш и функция
/ : / —» R. Для произвольных значений £i,U2 € / таких, что t\ Ф t<i->
положим:
a((l,fe) = /M-ffii)
<2-tl

§ 8. Выпуклые функции
399
Если функция f является выпуклой, то для любых h,t2,ts € / таких,
что t\ < £2 < £3, выполняются неравенства:
a(ti,t2) < a(ti,ts) < oj(t2,t3).
(8.18)
При этом если функция f — строго выпуклая, то каждое из неравенств
(8.18) — строгое.
Доказательство. Пусть / есть выпуклая функция. Зададим
произвольно точки ^15^2,^з Е / такие, что ti < <2 < *з-
Прежде чем перейти к формальному выводу неравенств (8.18),
отметим их геометрический смысл. На плоскости построим
график функции f (см. рис. 31), и пусть А± = (*i,/(*i)); А2 = (t2, /(t2));
A3 = (^з,/(^з)) — точки графика, соответствующие значениям х,
равным ti, ^2 И £з.
Тогда a(ti,t2) есть угловой коэффициент прямой А\Аъ\ а(£1,£з)
— угловой коэффициент прямой А\А$ и, наконец, a(t2,ts) есть угловой
коэффициент прямой А2А3.
Рис. 31
Неравенства (8.18), геометрически, являются очевидным
следствием того факта, что точка Аг располагается ниже прямой A\Az.
Рис. 31 иллюстрирует данное замечание.
Приведем теперь и формальный вывод неравенств (8.18).
Пусть числа ti,*2 и tz удовлетворяют условию леммы 8.1. Найдем
числа А и /i такие, что
А + /i = 1; Ati + /х£з = ^2.

400 Гл. 4. Дифференциальное исчисление функций одной переменной
Эти равенства образуют линейную систему уравнений относительно А
и /i, решая которую, получим:
. _ tz — tl __ #2 — t\
*з — *i' ^з — ti
Очевидно, A > 0 и // > 0. В силу выпуклости /, получаем
неравенство:
A/(*i) + м/(*з) > /(A*i + /х*з) = /(*2). (8.19)
Если функция / строго выпукла, то в (8.19) может быть поставлен
знак «>».
Вычитая из обеих частей неравенства (8.19) величину f{ti) и
принимая во внимание, что А — 1 = — /х, получим:
/*[/(*з) - /(*i)] > /(fe) - /(*i),
то есть
^5^I/(*8) "/(*!)]> /(fa) -/(*l).
Поделив обе части этого неравенства на *2 ~ *i > 0, получим:
а(*1,*з) > a(<i,<2).
Это есть первое из неравенств (8.18).
Вычитая из обеих частей (8.19) величину f{tz) и принимая во
внимание, что /i — 1 = —А, получим:
Отсюда
то есть
A[/(*l)-/(t3)]>/(*2)-/(*3).
A[/(t3)-/(*i)]</(*3)-/(t2),
*3"fa-[/(*8)-/(*l)]</(t8)-/(fa).
is - ti
Поделив обе части этого неравенства на £з — *2, приходим к
неравенству:
<*(*1>*з) < а(«2,*з).
Это есть второе из неравенств (8.18).
Если функция / — строго выпуклая, то все полученные
неравенства — строгие.
Лемма доказана. ■

§ 8. Выпуклые функции
401
■ Лемма 8.2. Пусть даны промежуток I = (а, Ь) С М и функция
/ : J —» R. Если / есть выпуклая функция, то, какова бы ни была точка
р G I, функция dp, определенная соотношением
ж — р
является возрастающей на множестве /° = J \ {р}.
Доказательство. Пусть / : 7 —► R есть выпуклая функция.
Возьмем произвольно точку р £ I. Для всякого ж 6 /° имеем:
dp(x) = а(#,р) = а(р,ж), где «(tijfo) есть величина, определенная в
лемме 8.1.
Пусть a?i ф р, Х2 Ф р таковы, что х\ <Х2- Требуется доказать, что
dp(xi) < dp(x2).
Возможны три случая: А) х± < #2 < р\ В) х\ < р < Х2 и
С) р < хг < Х2- Рассмотрим их последовательно.
A) Пусть х\ < Х2 < р. Полагая в лемме 8.11\ = х\, t2 = Х2 и t$ = р,
получим dp(xi) = а(*1,*з) < а(*2,*з) = dp(#2), то есть dp(a?i) < <2р(яг).
B) Пусть х\ < р < Х2* Полагая в лемме 8.11\ — rci, £2 = р и £з = #2,
получим: dv{x\) = a(ti,fe) < а(*25'з) = ^р(^г), так что и в этом случае:
dp(m) < dv{x2),
C) Рассмотрим случай, когда р < х\ < Х2. Полагая в лемме 8.1
ti = p, t2 = Xi и £з = #2, получим:
dp(si) = a(*i,<2) < а(*1,*з) = dp(^2).
Таким образом, нами установлено, что если rci < #2, то
dp(#i) < ^(аъ),
и тем самым лемма доказана. ■
Замечание. Если функция / — строго выпуклая, то
рассуждения, посредством которых была доказана лемма 8.2, позволяют
заключить, что функция dp является строго возрастающей.
Следующая теорема устанавливает некоторые общие
свойства выпуклых функций.
■ Теорема 8.10. Если функция f : (а, Ь) —► Ш является выпуклой,
то она непрерывна, и в каждой точке х Е (а, Ь) имеет конечные левую и
правую производные. При этом
fi(x) < fr(x) (8.20)
для любого х Е (а, Ь).

402 Гл. 4. Дифференциальное исчисление функций одной переменной
Если хг ИХ2 — две произвольные точки из промежутка (а, Ь) такие,
ЧТО Х\ < Х2, ТО
fr{xi) < Ш ~ ^х') < //(Ж2). (8.21)
Х2 — Х\
Если функция f — строго выпуклая, то каждое из неравенств (8.21)
является строгим.
Доказательство. Положим (а, Ь) = I. Возьмем произвольно
точку р G / и для хфр положим:
X — р
Согласно лемме 8.2, функция d является возрастающей на
множестве /\ {р}.
Зададим произвольно #i,#2 £ I такие, что х\ < р < Х2- Для
всех х G (#1,2:2) \ {р} имеем: d(xi) < d(x) < d(x2), так что функция d
является ограниченной на множестве (ж 1,^2) \ {р}.
Пусть М < оо таково, что \d(x)\ < М для всех х G (#i,#2) \ {р}-
Тогда, очевидно, имеем:
\f(x)-f(p)\<M\x-p\
ДЛЯ ЛЮбОГО X G (#1,Ж2).
В силу теоремы о зажатой переменной (см. теорему 1.5 главы
2), отсюда, очевидно, следует, что f(x) — f(p) —» 0 при х —» р, то есть
/(р) = lim /(ж), и, значит, функция / непрерывна в точке р.
х—*р
Функция d является возрастающей на множестве / \ {р}
и, стало быть, по теореме о существования предела у монотонной
функции (см. §3 главы 2), существуют конечные пределы lim d(x)
х—»р—О
и lim d(x), причем первый предел не превосходит второго.
ж—»-р+0
Очевидно,
lim d(x) = fl(p)
х-+р—0
И
lim d(x) = fr{p),
x—*p+0
так что существование производных, так же как и неравенство
flip) < Ш,
установлены.

§ 8. Выпуклые функции
403
Так как функция dv — возрастающая для всякого р G /, то при
х < р выполняется неравенство:
dp(x) = /(Ж) " f{p) < lim dp(x) = f[(p), (8.22)
ж — р я—р-о
а при х > р — неравенство:
/;(р)= lim dp(z) < dp(x) = /МиЖ. (8.23)
ж—р+о а: — р
Пусть даны произвольные точки х±,Х2 G /, причем жх < Х2-
Полагая в неравенстве (8.22) р = х±, х — Х2, получим первое из
неравенств (8.23). Полагая в (8.22) р = Х2 и х = х\, получаем второе
неравенство.
Если функция / — строго выпуклая, то функция dv является строго
возрастающей. Отсюда нетрудно заключить, что в этом случае в (8.22)
можно всюду поставить знак «О.
Теорема доказана. В
Т Следствие 1. Если функция f : (а,Ь) -» М — выпуклая, то ее
производные // и f'r суть возрастающие функции. Если функция f —
строго выпуклая, то // и fr суть строго возрастающие функции.
Доказательство. Действительно, пусть / : (а, Ь) —» R есть
выпуклая функция. Зададим произвольно точки 0:1,0:2 G (а,Ь) такие, что
х\ < Х2. Тогда
fi(xi) < КЫ) < ПХ1]~{{Х1) < //Ы < Гг{х2). (8.24)
#2 — #1
Отсюда получаем, что //(а*) < //(ж2) и /^(a:i) < /г(жг).
Тем самым доказано, что функции //и /^ — возрастающие.
Если функция / — строго выпукла, то в каждом из двух
внутренних неравенств (8.24) имеет место знак «<». Отсюда следует,
что fl(xi) < //(#2) и fr(xi) < /г(#2), так что в этом случае функции //
и/г — строго возрастающие.
Следствие 1 доказано. ▼
▼ Следствие 2. Пусть f : (а,Ь) —► Ж есть выпуклая функция,
р G (а,Ь). Тогда для всякого числа к такого, что //(р) < k < fr(p),
и любого х G (а, 6) имеет место неравенство:
/(*) >/(*») + (*-?)*• (8-25)

404 Гл. 4. Дифференциальное исчисление функций одной переменной
При этом если функция f — строго выпукла, то при х ф р в (8.25) имеет
место знак «>».
Доказательство. Пусть выполнены все условия следствия.
Возьмем произвольно точку х ф р. Предположим, что х < р.
Полагая в (8.21) х\ = х, Х2 =р, получим:
f{x) ~ f{p) = Mzm < //(р) < k. (8.26)
х—р р — х — v / —
В этом случае х — р < 0, в силу чего из неравенства (8.26) следует, что
f(x)>f(p) + (x-p)b.
Если же х > р, то, полагая в (8.21) х\ — р, Х2 = х, получим
неравенства:
^ь^1 * *«2 *■
ж — р
В этом случае х — р > 0. Умножая обе части последнего неравенства на
х — р, мы снова получаем, что
f(x)>f(p) + (x~p)k.
Таким образом, для любого х Е (а, Ь) выполняется (8.25).
Если функция / — строго выпуклая, то при х фр, как
следует из доказанного ранее, все неравенства являются строгими.
Следствие 2 доказано. ▼
■ Теорема 8.11. Пусть f : (а,Ь) -» R есть непрерывная функция.
Предположим, что функция f в каждой точке х £ (а,Ь) имеет левую
производную.
Если функция fl является возрастающей (соответственно, строго
возрастающей), то f есть выпуклая (соответственно, строго выпуклая)
функция.
Перед доказательством отметим следующее.
Замечание. Теорема остается верной, если левую
производную в ее формулировке заменить правой производной.
Доказательство теоремы. Пусть функция / : (а, Ь) —> R
имеет в каждой точке х Е (а, Ь) левую производную fl(x) и функция
// является возрастающей.

§ 8. Выпуклые функции
405
Зададим произвольно точку х G (а, Ь) и положим
<р(х) = /(ж) - /(р) - fi{p){x-p).
Функция (р9 определенная так, непрерывна ив каждой точке
х G (а, Ь) имеет левую производную. При этом
(pi(x) = fi(x)-fl(p)
для всех х G (а,Ь).
Так как, по условию, функция // — возрастающая, то
<Pi (х) < 0 ПРИ а < х < V и <Pi (х) > 0 ПРИ р < ж < Ь.
Отсюда, согласно теореме 4.6, следует, что функция ip является
убывающей в промежутке (а,р] и возрастающей — в
промежутке [р, Ь).
Возьмем произвольно ж G (а,{). Докажем, что
¥>(*) > ¥>(р) = 0 (8.27)
для всех х G (а, Ь). Действительно, если ж < р, то неравенство (8.27)
верно, — в силу того, что функция <р является убывающей в
промежутке (а,р], а для х > р, — в силу того, что функция ip является
возрастающей в промежутке [р, Ь).
Если функция // — строго возрастающая, то при
х < р выполняется неравенство (р[(х) < 0, а при х > р выполняется
неравенство ip[(x) > 0. Отсюда следует, что в этом случае при х ф р
будет ip(x) > 0 = 4>{р)-
Пусть х\ и Х2 — две произвольные точки промежутка (а, Ь).
Предположим, что А > 0 и // > 0 таковы, что А + // = 1, ир = Хх± + /1x2.
Очевидно, р Е (а,Ь). В силу неравенства (8.27), для всех х G (а, Ь)
имеем:
f(x)>f(p) + fl(p)(x-p).
Отсюда
/(*i) > /(Р) + //(P)(si - Р); /Ы > /(р) + //(Р)(аг2 - Р).
Умножая обе части первого неравенства на А и обе части
второго неравенства на \i и складывая полученные неравенства почленно, в
результате получим:
A/On) + pf{x2) > (А + /х)/(р) + //{p)[A(a?i - р) + д(я?2 - р)] = /(р).

406 Гл. 4. Дифференциальное исчисление функций одной переменной
Так как х\, х2 и Л > 0, /х > 0, Л + /х = 1, взяты произвольно, то тем
самым выпуклость функции / доказана.
Если при х ф р в (8.27) вместо «<» поставить знак «<», то,
повторяя — с необходимыми уточнениями — проделанные рассуждения при
х\ фх2, получим:
A/(#i) + fJ>f(x2) > f(Xxi + \ix2).
Это означает, что если // — строго возрастающая
функция, то функция / — строго выпуклая.
Теорема доказана. ■
§9. Исследование функций методами
дифференциального исчисления
Результаты дифференциального исчисления, установленные в этой
главе, могут быть использованы для изучения строения функций одной
переменной и построения, как говорят, «эскиза графика функции», то
есть чертежа, дающего представление об основных особенностях
строения данной функции.
Знание основных качественных особенностей функции может иметь
существенное значение при решении разного рода задач, в которых эти
функции возникают.
Здесь будут описаны общие правила, которых следует
придерживаться при решении задачи об исследовании функции. Необходимо
отметить, что эта задача требует творческого подхода к делу и, в
отличие от задачи об отыскании производной функции, заданной какой-либо
формулой, не может быть сведена к чисто механическому выполнению
определенных действий.
Предположим, что рассматривается некоторая параметризованная
кривая на плоскости: х(£) = (x(t),y(t)), t G М С М.
Если относительно функций х и у предполагается только, что они
непрерывны, то носителем данной параметризованной кривой может
оказаться, например, квадрат. В общем случае носитель
параметризованной кривой может быть устроен достаточно сложно.
Если, однако, параметризованная кривая х удовлетворяет
определенным условиям регулярности, состоящим в том, что функции х и
у имеют достаточное число производных, то носитель кривой имеет,
как правило, достаточно простое строение, которое может быть
описано имеющимися в нашем распоряжении средствами.

§ 9. Исследование функций методами дифференциального исчисления 407
Развитие математики показало, что в задачах прикладного
происхождения могут возникать достаточно «плохие» функции, например
функции, не имеющие производной ни в одной точке своей области
определения. (Такие функции возникают, например, в теории броуновского
движения.)
Классики математики, трудами которых были созданы
дифференциальное и интегральное исчисления, считали, что хотя математика
допускает существование сколь угодно «плохих» функций (то есть
функций, к которым неприменимы методы дифференциального и
интегрального исчислений), однако функции, возникающие при решении тех или
иных конкретных задач естествознания, обычно устроены достаточно
«хороню».
Так или иначе, математик должен владеть всеми приемами
исследования функций.
9.1. Построение графика функции
9.1.1. Опишем здесь некоторые основные правила, используемые при
исследовании функции. Пусть f(x) есть некоторая элементарная
функция, то есть функция, заданная формулой, которая содержит только
элементарные функции и знаки основных арифметических действий.
Исследование функции включает несколько этапов.
1. Найти область определения функции.
2. В каждом из промежутков, содержащемся в области
определения данной функции, найти все точки разрыва функции и исследовать
поведение функции вблизи концов этого промежутка.
4. Найти характерные точки функции. К числу таковых
относятся точки экстремума функции, точки пересечения графика функции с
осями координат и точки перегиба.
5. Разбить область определения функции на части, в каждой из
которых функция монотонна.
6. Изучить функцию на выпуклость. Это означает, что должно
быть построено разбиение области определения функции на части, в
каждой из которых функция является либо выпуклой сверху, либо
выпуклой снизу.
9.1.2. Рассмотрим некоторые примеры и приведем комментарии
относительно трудностей, которые могут возникнуть при исследовании
функций в соответствии с указанной выше общей схемой.

408 Гл. 4. Дифференциальное исчисление функций одной переменной
1) Описание области определения данной функции. Пусть
функция f(x) является элементарной, то есть задается формулой,
содержащей основные элементарные функции и знаки арифметических
действий. Область определения / есть совокупность всех х £ Е, для
которых данная формула имеет смысл. При этом следует иметь в виду,
что если формула содержит в себе некоторую дробь, знаменатель
которой зависит от #, то функция не определена во всех точках, в которых
знаменатель обращается в нуль.
Выражение, стоящее под знаком квадратного корня, определено
только для тех ж, для которых оно неотрицательно.
Аналогичным образом выражение под знаком логарифма
определено только для тех ж, для которых это выражение положительно.
Функции arcsin и arccos определены только для х £ [— 1,1] и потому
выражения типа arcsin F(#), arccos F(х) имеют смысл только для таких
#, для которых —1 < F(x) < 1.
Отметим одну опасность, которая может встретиться.
Если функция определяется некоторой формулой, то иногда может
оказаться целесообразным упростить эту формулу посредством
определенных преобразований. При этом следует соблюдать известную
осторожность. Дело в том, что области определения функции, заданной
исходной формулой, и функции, заданной преобразованной формулой, могут
не совпадать. Покажем это на следующих примерах 1 и 2.
х — 1
Пример 1. Пусть дана функция / : х н-> —-— -. Разлагая
х — 1
знаменатель на множители, получим: f(x) = -, -г-/ ;тг- Сокра-
[х-\)[х-2)
щая числитель и знаменатель на общий множитель х — 1, получим, что
f[x) = -. Последняя дробь определена для всякого х ф 2.
X Zi
Областью определения исходной функции является, однако, не
множество Е\ {2}, а множество Е\ {1,2}, ибо для х — 1 знаменатель
исходной дроби —г— обращается в нуль и, следовательно, для х = 1
хг — ох + 2
исходная функция / также не определена.
Пример 2. Несмотря на равенство (х — 1) (х+1) = х2 — 1, функции
/ : х к-* \/х — 1у/х + 1 hjixh у/х2 — 1 различны, так как их области
определения не совпадают.
Область определения функции / есть множество всех жЕК, для
которых одновременно х — 1>0и# + 1>0и, очевидно, совпадает с
промежутком [1, оо). В то же время область определения функции #, как
нетрудно видеть, есть множество (—оо, — 1] U [1, оо).

§ 9. Исследование функций методами дифференциального исчисления 409
2) В общем случае область определения функции может
иметь достаточно сложное строение. Предположим, что область
определения интересующей нас функции является объединением некоторого
множества попарно непересекающихся отрезков. Это условие обычно
выполняется, если данная функция не является слишком «плохой».
Пусть задана функция /. Предположим, что интервал (а,Ь)
содержится в области определения функции /.
Первый вопрос, который должен быть рассмотрен, касается
поведения данной функции на промежутке (а, Ь). Прежде всего, необходимо
выяснить, будет ли данная функция непрерывна во всех точках данного
интервала. Если нет, то следует найти точки разрыва функции / и
определить характер разрыва.
Второй вопрос — это поведение функции вблизи концов интервала
(а, 6). В частности, следует установить, существуют ли пределы
lim f(x) is. lim f(x).
x—Ki+0 ж—►£>—О
Для описания поведения функции вблизи концов промежутка полезно
определить следующее понятие асимптоты графика функции.
Пусть функция / определена на промежутке (а, оо) множества R.
Прямая /, заданная уравнением у = kx + l, называется асимптотой
графика функции f в направлении х —► оо, если
f(x) - kx - / -► 0
при х —► оо.
Подобным образом в том случае, когда функция / определена на
промежутке (—оо, а), прямая у = kx+l называется асимптотой графика
функции f в направлении х —► — оо, если f(x) — kx — l-+0 при х —» —оо.
Пусть а — конечно и функция / определена на интервале /, одним
из концов которого является точка а.
Если f(x) —► ±оо при ж, стремящемся к а по интервалу /, то
говорят, что прямая х — а является вертикальной асимптотой графика
данной функции /. При этом если предел f(x) равен оо, то говорят, что
прямая х = а является асимптотой графика функции в направлении
у -> оо.
Если предел f(x) при х —► а равен — оо, то говорят, что
прямая х = а является асимптотой графика функции f в направлении
у-+ -оо.
Если функция /, определенная на промежутке (а, оо), имеет
конечный предел при х —► оо и / есть величина этого предела, то прямая у = I
является асимптотой графика функции f(x).

410 Гл. 4. Дифференциальное исчисление функций одной переменной
Аналогичное заключение верно также в случае, когда функция /
определена на промежутке (—оо,а) и существует конечный предел:
lim f(x) = I.
Из определения асимптоты непосредственно вытекает способ
отыскания асимптот графика функции Л если таковые существуют.
Пусть функция / определена в интервале /, один из концов
которого есть или оо, или — оо. Чтобы найти асимптоту графика функции,
f(x\
следует сначала рассмотреть отношение . Предположим, что это
х
отношение при х —► оо (или при х —» —оо) стремится к конечному
пределу, равному к. Напомним, что асимптотой графика функции может
быть только прямая вида у = кх +1.
Далее следует рассмотреть разность f(x) — kx. Если эта разность
имеет конечный предел при х —► оо (при х —» — оо) и I — значение этого
предела, то прямая у = кх + I является асимптотой графика данной
функции в направлении оо (соответственно, в направлении —оо).
Приведем примеры нахождения асимптот графика функции.
Пример 3. Рассмотрим функцию /:жн -, Областью опреде-
х
ления данной функции является множество R \ {0}. Имеем:
lim f(x) = —оо, lim f(x) = оо,
ж—►—О х—►+()
lim f(x) = 0, lim f(x) = 0.
Отсюда следует, что ось Оу является асимптотой графика данной
функции / как в направлении у —» оо, так и в направлении у —> — оо, а ось
Оя есть асимптота графика функции f(x) как в направлении х —» оо,
так и в направлении ж —► — оо.
Следующие примеры 4 и 5 касаются более тонких ситуаций и
содержат утверждения общего характера.
Пример 4. Пусть f(x) = у/Р(х), где п > 2 — целое число, а
функция Р(х) есть полином степени п,
Р(х) = аохп + aix71'1 H h an_i# + an,
где a0 > 0.

§9. Исследование функций методами дифференциального исчисления 411
При х —» оо
Р(х) а\ an-i . ап
—~г = а0 Н 1 Ь ——г + —■ -> а0.
Т Т X X
Отсюда следует, что найдется число if > 0 такое, что при х > К
Р(х)
будет —— > 0 и, следовательно, Р(ж) > 0 для всех х > К.
хп
fix)
Выясним сначала, существует ли предел lim —*—^. Имеем:
х—»-оо X
М= ?№) = n/ao + £i + ... + ^^ ^
ж V яп V ж яп v
при х —> оо.
Теперь рассмотрим разность f(x)— ^/аЕх. Имеем:
f(x) - fyaox = ^/оож
аож аож2 ао#п
(9.1)
Воспользуемся формулой Тейлора с остаточным членом в форме
Пеано (см. п. 6.2, теорема 6.1). Имеем:
УТ+^=1 +
п 2п2
Положим в этом равенстве:
U П — 1 о / 2\
гл + о(и ) при г* —► 0.
а\ а,2
гл = гЦя) = 1 - Л Ь
аох аохг
ао#п ж Lao clqx
+ ...+
r.n—1
.ао &о# аохт
Очевидно, и{х) = ^ °( ~)' fafa)]2 = °( ~) ПРИ # -* °°- В
результате получим:
1+-^ + _^ + ... + _^ = 1 + ^_ +
аож ао#
а0я"
паох
•G)
при а: —► оо.
Подставляя это выражение в равенство (9.1), получим, что

412 Гл. 4. Дифференциальное исчисление функций одной переменной
при х —» оо. Отсюда следует, что существует конечный предел:
lim [f(x) - tyaox] =
*-~ na^-1/r1.
Из доказанного вытекает, что график рассматриваемой функции
/(#) имеет асимптоту в направлении х —> оо. Таковой является прямая:
у = уа0х +
1-1/тГ
Пример 5. Исследуем поведение при х —» ±оо произвольной
рациональной функции f(x).
Функция f(x) переменной х £Ш называется рациональной, если она
является отношением двух полиномов, то есть
для всех х G R таких, что Q(x) ф 0.
Здесь Р{х) = аохт + а1хт~1^ Vam-ix + am и Q(x) = b0xn+
+bix71^1 Н Ь bn-ix + Ьп, где т, п — натуральные числа, а
коэффициенты ao, ai,..., am_i, am и Ьо, bi,..., bn-i, Ьп суть вещественные числа,
причем ао Ф 0 vs. bo ф 0.
Область определения рациональной функции f(x), заданной
равенством (9.2), есть множество тех жЕК, для которых Q(x) ф 0.
Предположим, что степень т числителя дроби (9.2) не превосходит
степень п ее знаменателя. Предполагая, что х ф О, запишем полиномы
Р(х) и Q(x) в следующей форме:
Р{х) = а0хтР1 (1) , Q(x) = b0xnQ1 Q) ,
где
P1(t) = l + 2lt + ...+ ^tm, Q^^l + ^+... + ^Г.
При £ —► 0 выполнено Pi(t) —> 1, Qi(t) -+ 1 и, значит, найдется 6 > О
такое, что если |£| < 5, то Qi(t) > 0.
Положим: R = -. Если |ж| > Д, то Q(#) ^ 0. Следовательно, функ-
о
ция / определена в каждом из интервалов (—оо, — Д), (Д, оо). Имеем:
Qi(t) Qi(t) -ta{th

§ 9. Исследование функций методами дифференциального исчисления 413
где a(t) стремится к конечному пределу при t —» 0. Полагая здесь t = —,
получим, что
Рг
G)
ттт" = 1 + О [ — ) при х —* ±оо.
Отсюда вытекает, что
f (ял = £М = Qo Pl У = flo + о f 1 ^
при а; —> ±oo. Отметим, что в рассматриваемом случае, то есть в
предположении, что степень числителя дроби (9.2), определяющей
функцию /(ж), меньше степени ее знаменателя, f(x) —> О при х —> оо и при
я —> — оо. Иначе говоря, ось Ох является асимптотой графика функции
f(x) как при х —> оо, так и при х —> —оо.
Рассмотрим случай, когда га > п. Выполняя процедуру
деления с остатком полинома Р{х) на полином Q(rc), получим равенство
P(x) = a(x)Q(x) + H(x),
где а есть полином степени m — n (частное от деления полинома Р(х) на
полином Q(x)), а Н(х) — это полином, степень которого не превосходит
п — 1; Н(х) есть остаток от деления полинома Р(х) на полином Q(x).
Отсюда вытекает, что при \х\ > Д, где R определено, как указано выше,
имеет место равенство:
,(,)_„<,)+!$.
На основании сказанного выше, получаем соотношения
f(x) = а{х) + О I — 1 при х —► ±оо.
Таким образом, для достаточно больших по абсолютной величине
значений х в рассматриваемом случае функция f(x), с точностью до
величин бесконечно малых при |ж| -+ оо, совпадает с некоторым
полиномом а(х) степени га — п. В частности, если п<га<п + 1, то

414 Гл. 4. Дифференциальное исчисление функций одной переменной
степень полинома а(х) не превосходит единицы, и прямая у — а(х), в
соответствии с данным выше определением, является асимптотой
графика рассматриваемой функции f(x) как при х —» оо, так и при
х —> —сю.
9.1.3. При исследовании графика функции необходимо выяснить,
является ли данная функция периодической или нет, и проверить функцию
на четность или нечетность.
Напомним, что функция /, определенная на некотором
подмножестве М множества R, называется периодической, если существует число
Т ф О такое, что при условии х е М точки х — Т vl x + T принадлежат
множеству М и имеет место равенство: f(x + Г) = f(x).
Число Т ф О при этом называется периодом функции /. Для того
чтобы построить график периодической функции, достаточно построить
ее график на отрезке, длина которого равна Т.
График всей функции получается из части,
соответствующей этому отрезку, последовательными сдвигами влево и вправо вдоль
оси Ох.
Функция / : М —> Е называется четной, если для всякого х Е М
верно, что —х Е М, и выполнено равенство: f(x) = f{—x). Говорят,
что / : М —> Ж есть нечетная функция, если для всякого х Е М точка
—х лежит в М, причем f(—x) = —f(x).
Предположим, что функция f четна. Тогда ее график симметричен
относительно оси Оу.
Действительно, пусть X = (х,у) = (x,f(x)) есть точка графика
функции /. Точка X' = (—x,f(x)) симметрична X относительно оси
Оу. Так как, в силу четности функции /, f(x) = f(—x), то X' также
принадлежит графику функции /, что и требовалось доказать.
Допустим, что f есть нечетная функция. Покажем, что
в этом случае ее график симметричен относительно начала
координат.
Действительно, пусть X = (x,f(x)) есть произвольная точка
графика функции /. Тогда точка X', симметричная X относительно
начала координат, имеет координаты: (—x,—f(x)). Так как функция /,
по условию, нечетна, то —f(x) = f(—x), откуда вытекает, что точка
X' = (—х, f(—x)) принадлежит графику функции /. Поскольку точка
X, принадлежащая графику функции /, была выбрана произвольно, то
тем самым установлено, что график данной функции / симметричен
относительно начала координат.
Таким образом, если функция четна или нечетна, то для
построения графика достаточно знать его часть, соответствующую значени-

§9. Исследование функций методами дифференциального исчисления 415
ям х > 0. Остальная часть графика получается, в соответствии со
сказанным выше, простым геометрическим преобразованием: либо
симметрией относительно оси Ог/, либо симметрией относительно начала
координат.
9.1.4. Пусть (а,Ъ) есть интервал, содержащийся в области определения
функции /. Предположим, что вопрос о непрерывности функции на этом
отрезке решен, найдены все точки разрыва функции в этом интервале,
если таковые имеются. Предположим, что функция имеет в данном
интервале конечное число точек разрыва. Эти точки делят промежуток
на конечное число частичных интервалов.
Другой вопрос, который должен быть рассмотрен, — это вопрос о
дифференцируемости функции /. Следует указать все точки, в которых
функция / не дифференцируема. При этом если функция / непрерывна,
но не дифференцируема в некоторой точке х Е (а,Ь), то ее поведение в
этой точке следует изучить более внимательно.
Приведем пример, иллюстрирующий характер особенностей,
которые при этом могут встретиться.
Пример 6. Пусть f(x) = \(х2 - а2)|, где а > 0. Тогда мы будем
иметь: f(x) = \х — а\\х + а\. Функция / дифференцируема в каждой
точке х ф ±а.
Имеем: /(а) = /(—а) = 0, откуда ясно, что для того, чтобы изучить
вопрос о дифференцируемости функции / в точке а, например, следует
1# — ^1 I I хх
рассмотреть отношение -\х + а . Нетрудно видеть, что
х — а
\х — а\. .
hm J -\х + а\ = -2а,
х—ю,-о х — а
\х — а\. .
hm } -\х + а = 2а.
х—>а+0 X — а
Следовательно, мы получаем, что //(а) = —2а, f'r{a) = 2а и,
аналогично, в точке х = —а левая производная функции / равна —2а, а правая
равна 2а. График функции / имеет изломы в точках х = —а иж = а.
Чтобы построить график данной функции, можно применить
следующее дополнительное соображение. Сначала построим график функции
д(х) = х2 — а2. Этот график является параболой, пересекающей ось Ох
в точках А = (—а, 0) и В = (а, 0).

416 Гл. 4. Дифференциальное исчисление функций одной переменной
Рис. 32
График функции / совпадает с графиком функции д на
промежутках (—оо,— а] и [а,сю). Та часть графика функции /, которая
соответствует промежутку [—а,а], получается из дуги [АВ] графика функции
д зеркальным отражением относительно оси Ох (см. рис. 32).
9.1.5. Результаты пунктов 4.4, 4.5 этой главы дают все средства,
необходимые для определения промежутков монотонности функции.
Предположим, что функция / определена на промежутке (а,Ь) и
дифференцируема в каждой точке этого промежутка. В каждом
промежутке [#1,2:2] С (а, Ь), в котором производная /' имеет постоянный знак,
функция / является монотонной. При этом если производная функции
/ неотрицательна в данном промежутке, то / является в промежутке
[#1,2:2] неубывающей, а если f'{x) < О для всех х Е [#1,2:2], то
функция / является невозрастающей в промежутке [#1,2:2]. Справедливость
сказанного вытекает из теоремы 4.5 этой главы.
Исследование функции включает в себя такой важный момент, как
указание некоторых характерных точек функции. К их числу
относятся, во-первых, точки пересечения графика функции с осями координат,
то есть точки (0,/(0)) (это есть точка пересечения графика функции с
осью Оу) и точки #, такие, что /(#) = 0). Нахождение этих точек
требует умения вычислять значения функции и решать уравнение /(#) = 0.
В простейших случаях характерные точки данного типа могут быть
вычислены явно.
В общем случае их нахождение требует применения методов
численного решения уравнений.
Характерными точками функции являются также ее точки
экстремума. Вопрос об определении точек экстремума для функций одной
переменной был достаточно полно рассмотрен в § 7 этой главы и мы не
будем к этому вопросу более возвращаться.

§9. Исследование функций методами дифференциального исчисления 417
Для построения графика функции надо знать не только те ж,
которые являются точками экстремума, но и значения функции для этих х.
К числу характерных точек функции относятся и так называемые
точки перегиба функции. Знание этих точек, во многих случаях, дает
полезную дополнительную информацию о строении изучаемой функции
(см. §8, п. 8.4 этой главы).
9.2. Исследование алгебраических уравнений второй и
третьей степени
Применим методы дифференциального исчисления для
классической задачи исследования алгебраических уравнений второй и третьей
степени.
9.2.1. Уравнения второй степени. Под уравнением второй степени
понимается уравнение вида:
ах2 + Ьх + с = О, (9.3)
где а, Ь и с — вещественные числа, причем а ф 0.
Разделив обе части данного уравнения на а, мы приведем его к виду
х2 +px + q = 0, (9.4)
Ъ с
где р — — и q = —.
а а
Наша цель — установить, каковы должны быть числа р и q для
того, чтобы уравнение (9.4) имело хотя бы одно вещественное решение,
и указать, сколько таких решений будет иметь данное уравнение.
Из школьного курса алгебры читатель знает ответы на все эти
вопросы. Мы покажем, как получить ответ, применяя известные нам
результаты дифференциального исчисления.
Производная функции f(x) = x2 +px + q равна 2х +р. Она
обращать
ется в нуль в точке хо = — -. При этом f'{x) < 0 в интервале (—оо,#о)
и f'(x) > 0 при х G (ж0,оо).
Отсюда вытекает, что функция / является строго убывающей в
промежутке ( —сю, — - и строго возрастающей в промежутке —-, оо).
Это позволяет заключить, что функция f(x) = х2 + рх + q в точке
Р
xq = — — принимает свое наименьшее значение.
Р2
Имеем: f(xo) = q——. Таким образом, справедливо следующее
утверждение.

418 Гл. 4. Дифференциальное исчисление функций одной переменной
■ Теорема 9Л. Пусть дала, функция f : х ь-+ х2 + рх + q. Тогда:
1) если £q — p2 > О, то f(x) > О для всех жЕ1;
2) если 4д—р2 = 0, то функция f обращается в нуль в единственной
р
точке хо = — - и f{x) > О для всякого х ф xq;
3) если Aq — p2 < О, то функция f обращается в нуль в двух точках:
х\ и Х2 таких, что х\ < хо < Х2.
При этом: f(x) > О, если х < х\\ f(x) < О при х\ < х < Х2 и,
наконец, f(x) > 0 при х > Х2-
Доказательство. Положим 4q — р2 = Д. Пусть А > 0. Имеем:
/<».>-«-£-£•
Отсюда получаем, что если Д > 0, то f(x) > f(xo) > 0 для всех жЕК.
Пусть Д = 0. Тогда /(жо) = 0 и f(x) > 0 при х ф хо.
Действительно, пусть х ф хо. Предположим, что х < xq.
Так как функция / в промежутке (—оо,жо] строго убывает, то в
этом случае f(x) > /(#o) = 0.
Если же х > xq, то неравенство 0 = /(жо) < /(#) следует из того,
что функция / строго возрастает в промежутке [#о,оо).
Следовательно, если Д = 0, то уравнение f(x) = 0 имеет
единственное решение х = хо.
Рассмотрим случай Д < 0. Тогда /(жо) = Д/4 < 0. Имеем:
\ XX2
При х —► ±сх) первый множитель справа стремится к пределу,
равному сю, в то время, как множитель, заключенный в скобки, имеет
пределом число 1.
Отсюда вытекает, что предел функции / : х *—► х2 + рх + q при
х —> сю по промежутку (—оо,а;о] равен оо, и, стало быть, найдется
х' G (—оо,а;о] такое, что f{x') > 0.
Точно так же предел f(x) при х, стремящемся к оо по
промежутку [жо,оо), равен оо и, значит, найдется х" G [жо,оо), для которого
Рассмотрим промежуток [д?;,дсо]. Функция / в этом промежутке
непрерывна. Имеем: f(x') > 0, a f(xo) < 0.
В силу теоремы Коши о промежуточных значениях (теорема 4.1
главы 2), отсюда следует, что найдется число х\ такое, что х' < х\ < хо

§ 9. Исследование функций методами дифференциального исчисления 419
и f(xi) = О» Так как функция / в промежутке (—оо,жо] строго убывает,
то f(x) > 0 при х < xi и f(x) < О при х\ < х < xq.
Рассуждая подобным образом, получаем, что найдется Х2 такое,
что жо < ^2 < х" и f(xo) = 0. При этом f(x) < 0 при хо < х < Х2 и
f(x) > 0 При X > Х2-
Теорема полностью доказана. ■
9.2.2. Уравнения третьей степени. Уравнением третьей степени будем
называть всякое уравнение вида:
ах3 + Ьх2 + сх + d = 0, (9.5)
где a,b,c,d — вещественные числа, причем а ф 0.
Разделив обе части уравнения (9.5) на а, его можно привести к
виду:
х3 + рх2 + qx + г = 0. (9.6)
Далее / означает функцию х н-> #3 +рж2 + до + г. Вопрос о
разрешимости уравнения (9.6) сводится к исследованию функции /. Имеем:
х3 +рх2 + qx + г = х3 I 1 + £ + \ + -^
Выражение в скобках в правой части равенства (9.7) при х —> сю, а
также при # —> —оо стремится к пределу, равному 1. Ясно, что х3 —> сю
при # -+ оо, а ж3 —> — сю при # -+ — сю. Отсюда вытекает, что
lim f(x) = —оо, lim f(x) = оо.
X—► — СХ) Ж—*СХ>
В силу свойств пределов, установленных в главе 2, найдется число
i^i G Ш такое, что f(x) < 0 для любого х < Кг, и точно так же можно
указать число JG Е М такое, что если ж > Хг, то /(я) > 0.
Отсюда, в частности, следует, что найдутся числа х' и х" такие,
что f{x') < 0, a f(x") > 0.
Функция / непрерывна и потому, как следует из теоремы Коти о
промежуточных значениях, найдется жЕК, лежащее между х' и х" и
такое, что f(x) = 0.
Таким образом, уравнение третьей степени всегда имеет, по
крайней мере, одно вещественное решение.
Дифференцируя функцию /, получим:
f{x) = 3x2 + 2px + q = 3 [x2 + (2р/3)я? + q/S] .
(9.7)

420 Гл. 4. Дифференциальное исчисление функций одной переменной
Положим: р\ = 2р/3, qi = q/3.
Поведение функции /', как следует из сказанного в предыдущем
разделе, полностью определяется величиной: Ai = Aqi — р\.
Подставляя сюда выражения для р\ и #i, получим: 4#i — р\ = 4#/3 — 4р2/9.
Из соображений удобства, вместо Ai будем рассматривать величину
jD(/) = 3# — р2, отличающуюся от Ai положительным множителем.
Если jD > 0, то также и Ai > 0, и, значит, как показано выше при
рассмотрении полиномов второй степени, функция /' неотрицательна
для всех жЕ1. Она обращается в нуль, самое большее, — в одной
точке. Отсюда следует, что в данном случае функция / является строго
возрастающей. Следовательно, если для функции / имеет место
неравенство: D(f) > 0, то уравнение (9.6) имеет в точности одно решение.
Наша задача теперь — исследовать случай D(.f) < 0.
Итак, пусть D(f) < 0. Имеем: f"{x) = 6х + 2р. Производная /"
обращается в нуль в точке xq = — -. Более того, f"{x) < 0 при х < яо,
о
a f"{x) > 0 при х > хо.
Это показывает, что точка хо имеет существенное значение для
характеристики данной функции /. Именно, функция / является
вогнутой в промежутке (—оо,а;о] и выпуклой в промежутке [жо,оо).
Точка Р графика функции /, соответствующая значению х = хо =
= —р/3, является точкой перегиба кривой у = /(#). Часть этой кривой,
лежащая слева от точки Р, направлена выпуклостью вверх, тогда как
ее часть, расположенная справа от Р, направлена выпуклостью вниз.
Дальнейшие рассуждения существенно упрощаются, если
произвести замену переменной по формуле: х = t + xo = t — p/З. Геометрически
это равносильно преобразованию, состоящему в том, что график
функции / смещается в направлении, параллельном оси Ох так, чтобы его
точка перегиба оказалась лежащей на оси ординат.
Положим: /(t-p/3) =F(t). Тогда
+pf*2-y«+yj + <z*-^+r = *3 + Pt + Q, (9.8)
где
3 ч' * 27 3
Заметим, что коэффициент Р полинома F(t) — f(t — р/3) равен
£)(/)/3. Согласно предположению, D(f) < 0 и, значит, Р < 0.

§ 9. Исследование функций методами дифференциального исчисления 421
Для функции F имеем: F'(t) = 3t2+P. Так как Р < О, то уравнение
F'(£) = 0 имеет два вещественных корня:
*! = -у/-Р/3, t2 = л/~рА
Применяя результаты исследования, проделанного выше, для
полиномов второй степени, заключаем, что F'(t) > 0 при t < *i, F'(t) < О
при *i < t < t2 и, наконец, F'(t) > О при £ > £2.
Отсюда следует, что функция F является возрастающей, причем
строго возрастающей в промежутке (—oo,£i], строго убывающей на
отрезке [ti,*2] и строго возрастающей в промежутке [<2,оо).
Видим, что точка t\ есть точка максимума, a ti — точка
минимума функции F. График функции F показан на рис. 33.
Рис. 33
Найдем значения функции F в ее точках экстремума U и ti.
Получим:
Предположим, что F(t\) > 0. Имеем: lim F(t) = — оо и, значит,
t—*оо
найдется t' < t\ такое, что F(t') < 0.
Отсюда, в силу теоремы Коши о промежуточных значениях
(теорема 4.1 главы 2), следует, что в данном случае уравнение F(t) = 0
имеет, по крайней мере, одно значение, лежащее в промежутке (—oo,ti].

422 Гл. 4. Дифференциальное исчисление функций одной переменной
Так как функция F в этом промежутке является строго
возрастающей, то такое значение t — единственно.
Допустим, что для функции F имеет место неравенство: F(fa) < 0.
Функция F является строго возрастающей в промежутке [fa,oo) и при
t —► оо будет F(t) —> оо. Кроме того, при сделанном допущении
уравнение F(t) = 0 имеет решение, лежащее в промежутке [fa,oo), и такое
решение. единственно.
Если F(ti) < 0, то уравнение F(t) = 0 имеет в точности один
корень.
Справедливость этого легко усматривается геометрически.
Аналитически это также нетрудно показать.
Так как функция F является строго возрастающей в
промежутке (—oo,fa] и строго убывающей в промежутке [*i, *г], отсюда ясно,
что F принимает в точке fa свое наибольшее значение на
промежутке (—oo,fa], и, значит, для всех t £ (—oo,fa] выполняются неравенства
F(t) < F(ti) < 0. Поэтому все корни уравнения F(t) = 0 лежат в
промежутке [fa,oo). В этом промежутке функция F строго возрастает и,
следовательно, уравнение F(t) = 0 имеет в нем не более одного корня,
а, стало быть, в точности один корень.
Предположим, что J1 (fa) > 0. Рассуждая аналогично предыдущему
случаю, получим, что функция F в промежутке [fa,oo) принимает свое
наименьшее значение в точке fa, и, значит, при сделанном
предположении, F(t) > 0 для всех t £ [fa, 00).
В промежутке (—oo,fa] функция F является строго возрастающей
и, следовательно, уравнение F(t) = 0 имеет в точности одно решение.
Теперь рассмотрим случай, когда F(ti) > 0, a F(fa) < 0.
Принимая найденные выше значения для F(ti) и -F(fa), получим,
что данные неравенства равносильны следующим:
Из условия F(ti) > 0, как показано выше, следует, что уравнение
F(t) = 0 имеет, по крайней мере, один корень, лежащий в промежутке
(-oo,fa].
Так как F(fa) > 0 > -F(fa), то, согласно теореме Коши о
промежуточных значениях (теорема 4.1 главы 2), уравнение F(t) = 0 имеет
в промежутке [fa,fa] хотя бы одно решение.
Так как функция F в этом промежутке является строго убывающей,
то это решение единственно.

§ 9. Исследование функций методами дифференциального исчисления 423
Поскольку F(t2) > О, то уравнение F(t) = 0 имеет, и притом только
одно, решение, лежащее в промежутке [£2,00).
Итогом проделанных рассуждений является следующая теорема.
■ Теорема 9.2. Пусть дано уравнение:
f(x) = х3 + рх2 + qx + г = 0.
Пусть величины Р и Q выражаются через р, g, r равенствами (9.8).
Если для величин Р и Q выполняются неравенства (9.9), то
существуют числа х\ и Х2 такие, что —оо < х\ < Х2 < оо, и в каждом из
трех промежутков (—oo,#i], [^1,^2] # [ж 1,00) рассматриваемое
уравнение имеет в точности одно решение.
Если же для Р nQ хотя бы одно из неравенств (9.9) не выполняется,
то уравнение f(x) = 0 имеет единственное решение жЕК.
Доказательство. Числа х\ и Х2 выражаются через указанные
выше значения t± и £2 по формулам: х\ = t\ — р/3, Х2 = £г — р/3.
Решения уравнения f(x) = 0, лежащие в промежутках (—oo,a:i]
и [#1,Ж2], могут совпадать. Очевидно, это будет иметь место в том
и только в том случае, когда f(xi) = 0 и правое из неравенств (9.9)
обращается в равенство.
Решения уравнения /(£) = 0, лежащие в промежутках [^1,^2] и
[#2, оо), также могут совпадать. Это будет в том и только в том случае,
когда левое из неравенств (9.9) обращается в равенство.
Если каждое из неравенств (9.9) является строгим, то все три корня
уравнения f(x) = 0 — различны.
Теорема доказана. ■
9.3. Исследование параметризованных кривых
9.3.1. Рассмотрим задачу о построении носителя плоской
параметризованной кривой.
Если о параметризованной кривой известно только, что она
непрерывна, то носитель плоской параметризованной кривой может
оказаться множеством достаточно сложной природы.
Все сказанное далее относится к случаю параметризованной
кривой:
x(i) = (*(*), у(*)),
где t G (a, ft) и функции х и у имеют производные первого и второго
порядка.

424 Гл. 4. Дифференциальное исчисление функций одной переменной
Построение носителя плоской параметризованной кривой при этих
предположениях состоит из следующих этапов.
1) Первый шаг исследования состоит в том, что область
определения параметризованной кривой разбивается на промежутки, в каждом
из которых либо функция ж, либо функция у строго монотонна.
2) Второй шаг. Предположим, что указан промежуток [а,/?] С (а,Ь)
такой, что, скажем, функция х в этом промежутке строго монотонна и
не является таковой ни на каком промежутке, содержащем [а,/3]. Тогда
функция х отображает этот промежуток на некоторый отрезок [р, q] и,
по теореме об обратной функции (см. теорему 4.3 главы 2), существует
непрерывная обратная функция: £ = х"1 : [р, q] —► [а, /3].
Если функция х во всех точках промежутка (а, Ь) дифференцируема
и ее производная нигде не обращается в нуль, то функция £
дифференцируема в промежутке (р, q).
Подставляя t = £(#) в выражение х(£) = (ж(£),у(£)), получим, что
часть носителя параметризованной кривой, отвечающая
значениям t £ [#,/3], может быть представлена уравнением: у = /(ж), где
/(х) = уК(х)].
3) Дальнейшее исследование этой части носителя сводится, таким
образом, к исследованию функции f(x) и может быть выполнено уже
имеющимися в нашем распоряжении средствами (см. выше п. 9.1).
9.3.2. Приведем формулы, которые могут быть полезными на
заключительной (см. 3)) части исследования носителя
параметризованной кривой.
Дифференцируя равенства #[£(#)] = #, f(x) = у[£(ж)], получим:
х'Ш]?(х) = 1, f{x) = у%Ш'{х). (9.10)
Первое из этих равенств позволяет заключить, что производная
функции £ имеет тот же знак, что и производная функции х.
Из второго равенства следует, что если функция x(t) является
возрастающей в промежутке [а,/3], то для х G [р,?] знак
производной f'{x) совпадает со знаком производной y'(i) в точке
<=£(*).
Если функция х является убывающей в промежутке [а,/3],
то знак производной f'(x) противоположен знаку производной
y\t) в точке t = £(#).
Наконец, если в точке t = £(x) имеет место равенство
y'(t) = 0, то также справедливо и равенство f'{x) = 0.

§ 9. Исследование функций методами дифференциального исчисления 425
Выражение для производной /'(#) во всякой точке ж, для которой
производная £'(х) определена и конечна, может быть представлено в
виде:
f(x) - ^М = № (9 11)
J {Х)~ x>[ttx)] ~ x'{ty ^Л1)
где t = £(ж)-
Приведем формулы для вычисления производных второго
порядка функции fix) = у[£(х)].
Дифференцируя соотношения (9.11), получим:
0 = х"[ах)№'(х)}2 + х'Шх))£"(х),
/"(я) = у"Шх)][?(х)]2 + y'[t(x)]t"(x),
откуда
Г{х) = *ш] М« W^ - №(*№'№]} ■
Заметим, что £'(х) = . , ч.. Тогда последнее равенство можно запи-
x'[£(t)]
сать в следующей форме:
f"(x) = Щ^Щ-з {*'fc WK(*)1 - v'[t(x)W'lt(*)]} ■ (9-12)
Из равенства (9.12) видно, в частности, что знак второй
производной /" в точке х полностью определяется знаком производной x'{t) и
знаком выражения
x'(t)y"(t)-y'(t)x"(t)
в точке t = £(х).
Равенство (9.12) может быть представлено также в следующей
форме:
/"(*) = ^щ, [* WW - y'(t)*"(t)}, (9.13)
где t = £(х). Заметим еще, что при изучении носителя
параметризованной кривой разумно предварительно попытаться упростить данную
параметризованную кривую выбором надлежащей системы координат.
При определении носителя параметризованной кривой полезно
выяснить наличие у данной параметризованной кривой каких-либо
дополнительных геометрических свойств типа симметричности и т. п.

426 Гл. 4. Дифференциальное исчисление функций одной переменной
9.3.3. Рассмотрим некоторые примеры.
Пример 1. Пусть параметризованная кривая определяется
уравнениями:
x(i) = t — г sin -, y(t) = г — г cos -. (9.14)
Данная параметризованная кривая есть циклоида. Обозначим ее
носитель символом Т. Циклоида представляет собой траекторию точки,
лежащей на ободе круглого колеса, катящегося без скольжения по оси
Ох системы координат на плоскости Ж2.
Из равенств (9.14) следует, что для всякого целого п имеют место
равенства: x(t + 2ттг) — x(t) + 2тгпг, y(t + 2тгпг) = y(t). Отсюда видно,
что часть рассматриваемого множества Т, соответствующая значениям
t £ [27гпг, 27г(п + 1)г], получается из той ее части, которая отвечает
значениям параметра t £ [0,2ят], преобразованием (х,у) \—► (х + 2птгг,у),
то есть параллельным переносом вдоль оси Ох на
вектор и = (2п7гг, 0). Поэтому для того чтобы изобразить множество Т,
достаточно нарисовать ту его часть, которая соответствует значениям
параметра t из промежутка [0,2ят].
Последовательными параллельными переносами вдоль оси Ох на
расстояние, равное 2г7г, получим все множество Т.
Допустим, что 0 < t < 2г7г. Имеем:
х (Л) = 1 — cos -
г
и, значит, x'(t) > 0 для всех t. При этом x'(t) > 0 для всех t £ (0,27гг)
и, стало быть, функция х является строго возрастающей.
Имеем: х(0) = 0, х(2тгг) = 2тгг и, следовательно, х отображает
промежуток [0,2тгг] на себя. По теореме об обратной функции (глава 2,
теорема 4.3), существует обратная функция £ = ж-1. Для ж £ [0,27гг]
величина £(ж) есть то значение £ £ [0,27гг], для которого x(t) = х.
Подставляя t = £(х) в (9.14), получим, что дуга кривой Т,
соответствующая отрезку [0,27гг], допускает параметрическое
представление (ж[£(ж)],?/[£(ж)]) = (ж,2/[£(ж)]), то есть эта дуга является графиком
функции f(x) = у[£{х)}.
Функция £ непрерывна в замкнутом промежутке [0,27гг] и
дифференцируема во всех точках интервала (0,27гг). Отсюда следует диф-
ференцируемость функции f(x) в интервале (0,27гг). В силу
равенства (9.11), имеем:

§ 9. Исследование функций методами дифференциального исчисления 427
где t = £(#)• Поскольку x'(t) > 0 для всех t Е (0,2тгг) и
y'(t) = sin-,
г
ТО y'{t) > 0 При 0 < t < 7ГГ И ?/(£) < 0 При 7ГГ <t < 27ГГ.
Пусть теперь ж(7гг) = 7гг. Тогда £(7гг) = кг. Следовательно,
производная функции f(x) положительна для t Е [0, кг) и
отрицательна для t Е (7гг, 2ят].
Отсюда вытекает, что функция f(x) является возрастающей
в промежутке [0,ят] и убывающей в промежутке [7гг, 27гг], а в
точке х — кг принимает свое наибольшее значение. Имеем
также: /(0) = /(2тгг) = 0.
Исследуем функцию fix) на выпуклость.
Согласно формуле (9.13), имеем:
где t — i{x).
Множитель, стоящий перед скобками справа, положителен.
Простые вычисления позволяют заключить, что
x'(t)y"(t) - y'(t)x"(t) = - (cos - - Л.
г у г J
Отсюда следует, что f"{x) < 0 для всех х Е (0,27гг), и, значит,
функция f(x) выпукла снизу.
Дуга циклоиды Т, отвечающая значениям параметра t Е [0,2ят],
таким образом, имеет форму арки, концы которой лежат на оси Ох,
и которая направлена выпуклостью вверх (см. рис. 34). При этом
наивысшая точка этой арки соответствует значению t = тег и имеет
координаты (кг, 2г).
Легко проверяется (мы предоставляем читателю проделать это
самостоятельно), что данная дуга симметрична относительно
вертикальной прямой х = кг. Для этого достаточно установить, что функция
/(ж), графиком которой является рассматриваемая дуга циклоиды,
удовлетворяет тождеству: f(x) = /(27гг — х). Вся циклоида Т в целом
получается сдвигами ее дуги, лежащей над отрезком [0,27гг].

428 Гл. 4. Дифференциальное исчисление функций одной переменной
Имеем:
Рис. 34
Wit)? + iy'(t)}2 = (l - cos I)' + (sin If = 2(l - cos 1).
Отсюда видно, что если параметр £ не является числом вида t = 27гпг,
где п есть целое число, то [ж'(£)]2 + [2/'(£)]2 ф 0, и, значит, в этом случае
циклоида имеет касательную в точке: x(i) = (#(£), у(£)).
Исследуем вопрос о существовании касательной циклоиды в точках,
соответствующих значениям t = 2т:пг.
Из соображений периодичности, достаточно рассмотреть случай
t — 0. Имеем: х(0) — 0, у(0) = 0. Пусть e(t) = e(0,£) есть вектор,
х(£) x(t)
равный 7~7тт в случае t > 0 и равный — т-ттт ПРИ * < 0. Предел e(t)
|x(t)| * - |x(t)|
при £, стремящемся к 0 справа, если таковой существует, есть правый
касательный орт в точке х(0), а предел e(t) при £, стремящемся к 0
слева, есть левый касательный орт в точке х(0) рассматриваемой кривой.
Имеем:
х(£) = It — г sin -, г — г cos - J
t t3 t t*
и t — r sin - = —-=■ + o(t3) при t —> 0, r — r cos - = -—h o(t2) при t —> 0.
r 6r2 r 2r
t2
Отсюда вытекает, что |х(*)| = -—h o(t2) при £ —> 0. В результате
получаем, что если
t > 0, то e(t) = (д- + *(*)> 1 + Ф)) > а Для
t < 0 имеем: e(t) = (- — + o(t), -1 + о(«)) при £ -► 0.
Из сказанного вытекает, что существуют пределы
значении
lim e(t) = (0,1), lim e(t) = (0, -1).
t-*+o t->-o
Это означает, что рассматриваемая кривая имеет в точке х(0) левый и
правый касательные орты.

§ 9. Исследование функций методами дифференциального исчисления 429
При этом tx(0) = (0,-1), a tx(0) = (0,1). Таким образом, левый
и правый касательные циклоиды в точке х(0) = (0,0) коллинеарны оси
ординат и имеют различные направления. Точка х(0), следовательно,
является точкой возврата циклоиды.
Пример 2. Рассмотрим параметризованную кривую на
плоскости:
x(t) = (г-зм4-2г), *е
(9.15)
Функция x(t) = t3 — 3* имеет производные всех порядков в каждой
точке t Е К. Имеем: #'(£) = 3(£2 — 1). Отсюда вытекает, что функция
х является возрастающей в промежутке (—оо, — 1), убывающей в
промежутке (—1,1) и, наконец, в промежутке (1,оо) она является строго
возрастающей. Ясно, что x(t) — 2 при t = — 1, a, x(t) = — 2 при £ = 1.
Из сказанного можно извлечь следующую информацию о
строении рассматриваемой кривой (см. рис. 35).
Построим на плоскости прямые х = —2 и х = 2. Кривая
разбивается на три дуги АВ, ВС и CjD, каждая из которых взаимно однозначно
проектируется на ось Ох. При этом дуга АВ проектируется на
промежуток (—оо,2] и доходит до прямой х = 2 (здесь А следует понимать
как обозначение для части кривой, соответствующее точке — оо).
Рис. 35
Затем кривая меняет направление движения и точка х(£) движется
при изменении t от 1 до —1 в пределах полосы, заключенной между
прямыми ж = — 2и# = 2, описывая дугу ВС. Точка В при этом лежит
на прямой х = 2, С — на прямой х = —2. После этого точка х(£),

430 Гл. 4. Дифференциальное исчисление функций одной переменной
«оттолкнувшись» от прямой х = — 2, описывает дугу CD, однозначно
проектирующуюся на ось Ох и «уходящую в бесконечность». Символ
D означает бесконечно удаленную часть этой дуги кривой.
Функция х является непрерывной и строго возрастающей в
промежутке h = (—оо, —1]. Кроме того, x(t) —> —оо при t —> —оо.
В силу теоремы об обратной функции (см. теорему 4.3 главы 2),
х отображает Д взаимно однозначно на промежуток (—ос, 2).
Пусть £i есть функция, обратная к х на h. По теореме об обратной
функции, отображение £i непрерывно. Для всех t Е (—ос,—1) верно
x'{t) ф 0. Отсюда вытекает, что функция £i дифференцируема для всех
х < 2.
Положим: fi(x) — v(£i(x)). Дуга АВ изучаемой кривой является
графиком функции fi(x). Исследуем функцию Д более детально.
Она дифференцируема во всех точках интервала (—ос, 2). Имеем:
Il[X) x'{ty
где t = £(х). Тогда для t = £(ж) имеет место равенство:
y'(t) _ At3 - 4t _ 4
x'(t) ~ 3t2-3 " 3 '
Отсюда видно, что для всех х Е (—ос, 2) производная функции fi(x)
отрицательна и, значит, функция fi(x) является убывающей на всем
промежутке, где она определена.
Изучим вопрос о дифференцируемости функции fл (х) в точке х — 2.
Заметим, что при х —> 2 — 0 будет fi(x) —► /i(2) = 2/(—1) = — 1? а
4
t = £i(x) —► — 1. Следовательно, Л(ж) —► — - при х —► 2 — 0. Соглас-
но следствию 2 первой теоремы Лопиталя (теорема 5.1 данной главы),
отсюда вытекает, что функция /i в точке х = — 1 имеет производную,
равную -- = lim f[(x).
О х—^2-0
Теперь заметим, что ?/(£) —> оо при £ —> —ос, откуда следует, что
fi(x) —► оо при ж —► —оо. Для достаточно больших по абсолютной
величине значений ж выполняется fi(x) > 0. Так как /i(2) = — 1 < 0,
то функция / обращается в нуль для некоторого х Е (—оо, 2).
Приравнивая y(t) к нулю, получим уравнение: t4 — 2t2 = 0, которое
имеет корни: ti = £2 = 0 и t$ = —л/2, t± = л/2. Из этих корней только

§ 9. Исследование функций методами дифференциального исчисления 431
один принадлежит промежутку (—оо, —1], а именно, £з = — л/2 < — 1.
Имеем:
x{U) = -2>/2 + Зл/2 = у/2,
у/2 < 2 и £i(\/2) = *з = -V2. Тем самым
/i(V2)=yKi(^)]=y(*s) = 0.
Таким образом, функция fi(x) обращается в нуль в точке х = л/2-
Исследуем вопрос о выпуклости функции А (ж). Согласно равенству
(9.13), будем иметь:
/Г(ж) = RM1 И%"(<)" »'(*)*"(*)]'
где t = £i(#). Простое вычисление показывает, что в рассматриваемом
случае:
'"<*> = 9(ЙЛУ <"6>
Отсюда вытекает, что f"(x) > 0 для всех х £ (—ос, 2]. Функция Д,
таким образом, является выпуклой в промежутке (—оо, 2].
Исследуем часть изучаемой кривой, отвечающую значениям:
t £ [—1,1] — 1ч. В этом промежутке функция х является строго
убывающей, х{—1) = 2, х{1) = —2.
По теореме об обратной функции (теорема 4.3, гл. 2),
существует непрерывная функция £2 : [—2,2] -+R, обратная ограничению х на
промежутке [—1,1]. Положим: /2 (х) = у[&(х)]. Имеем:
h{X) ~ x'(t) - 3*'
где t = £2(ж), * £ (—1,1). Видно, что fi(x) < 0 для тех х, для которых
* = £г(0 £ (—1,0), то есть для х £ (0,2), и /г(ж) > 0 для тех ж, для
которых t = £(ж) £ (0,1), то есть для х £ (—2,0).
Из доказанного следует, что функция /2(х) в промежутке [—2,0]
возрастает, ав промежутке [0,2] — убывает ив точке х = 0
принимает свое наибольшее значение.
Ясно, что х = x(t) —> 2 при £ —► — 1, и мы получаем, что произ-
4
водная f'{x) стремится к пределу, равному — - при х —> 2. Отсюда
о
вытекает, что функция /2 дифференцируема в точке х = 2. При этом
/2(2) = -|.

432 Гл. 4. Дифференциальное исчисление функций одной переменной
Вторая производная функции /2 (х) выражается через вторые
производные функций x(t) и y(t) той же формулой, что и производная функции
/i(x). Различие состоит только в том, что значения этих производных
должны браться для t Е (—1,1). По этой причине
f*№ = 9(*2 - 1)'
где t = £2(х). Видим, что функция /г(х) является вогнутой (выпуклой
снизу) на промежутке [—2,2].
Рассмотрим вопрос о том, как расположены ветви изучаемой кривой,
определяемые уравнениями v = f-[(x),x£(—oo,2]4 и y = fa(x),x£[—2,2].
Функция /2(х) —выпукла снизу, функция fi(x) — выпукла сверху, и
производные этих функций в точке х = 2 совпадают. Отсюда
следует, что разность г = /i — /2 есть функция, выпуклая в промежутке
[-2,2], причем г'(2) = 0.
Функция г' является убывающей (и даже строго убывающей) на
промежутке [—2,2]. Следовательно, г'(х) < 0 для всех х Е [—2,2].
Поэтому функция г — строго убывающая и, значит, г(х) > 0 для всех
х G [—2,2], то есть /г(х) < fi(x) для всех х Е [—2,2].
Для завершения исследования кривой необходимо изучить ее
поведение для t G [1,оо). Этого, однако, можно избежать, если
воспользоваться следующим свойством.
Для всякого tGM, очевидно, имеют место равенства: х(—t) = — x(t),
y(—t) — y(t). Отсюда следует, что если точка (х,у) принадлежит
носителю изучаемой кривой, то ему принадлежит также и точка (—ж, у). Это
означает, что рассматриваемая кривая симметрична
относительно оси Оу. Используя этот факт, мы можем построить всю кривую
по той ее части, которая нами уже построена. Кривая выглядит, как
указано на рис. 35. Кривая состоит из двух ветвей, простирающихся в
бесконечность, каждая из которых выпукла сверху, и выпуклой снизу
дуги, соединяющей концы этих бесконечных дуг.
Бесконечные дуги пересекаются в точке с координатой х = 0.
Уравнение x(t) = t3 — 3t = 0 имеет решения: t\ = 0, £2 = —л/3 и £з = л/3-
Очевидно, t\ лежит в промежутке (—1,1), а точка (х(0),у(0)) = (0,0)
лежит на дуге ВС кривой.
Далее, £2 E (—оо, —1) и, значит, точка (ж(^),у(^2)) принадлежит
дуге АВ. Имеем: ж(^) = 0, 2/(^2) = 3. Точка (x(ts),y(ts)) принадлежит
дуге CD, причем x(ts) = 0, y(t$) = 3. Следовательно, бесконечные дуги
АВ is. CD изучаемой кривой (9.15) пересекаются в точке (0,3), лежащей
на оси Оу. Заметим еще, что точки В и С являются точками возврата
этой параметризованной кривой.

Задачи
433
Задачи
4.1. Доказать равенство
*L(bl) = tV™(bX _!-!_ ....IV
<2жп V х J хп+г V 2 nj
4.2. Доказать формулу
4.3. Пусть / : (а, Ь) —> R — трижды дифференцируемая функция.
Предположим, что для всех х £ (а, &) выполнено /(ж) ^ 0 и /'(ж) > 0- Положим:
«(*) = [fix)]-1/2, V(X) = /(a;)[/'(x)]-1/2.,
Доказать равенство:
1 с*2ц _ 1 rf2?;
w dx2 v dx2
4.4. Доказать, что среди всех выпуклых n-угольников, вписанных в
окружность, наибольший периметр имеет правильный n-угольник, наибольшую
площадь ограничивает также правильный п-угольник.
4.5. Исследовать на дифференцируемость функцию / : жи \х — 1| — е^-1'.
4.6. Исследовать на дифференцируемость функцию / : ж ь-► [ж] sin2 7гж, где
[х] — целая часть числа ж, т. е. [ж] — наибольшее целое число у, такое, что
у < ж.
4.7. Пусть р > О — вещественное число. Предположим, что существует число
п Е N такое, что п < р < п + 1.
Доказать, что функция / : ж н-> |ж|р принадлежит классу 2>n(R) и не
принадлежит классу Dn+1(R), когда р не есть четное целое число.
Найти производную Dkf, где 1 < /г < п.
4.8. Доказать, что функция ж н-> cos7T\/^ принадлежит классу С°°.
4.9. Построить функцию / : R —> R класса С1 (класса С2, класса С3, класса
Сп, где п — произвольное натуральное число), такую, что /(ж) = — 1 при
ж < —1, /(ж) = 1 при ж > 1.
4.10. Пусть даны функции / : (а, Ь) —► R и р : (а, Ь) —> R. Положим:
и(ж) = тах{/(ж),р(ж)};
v(x) = тт{/(ж),р(ж)}.
Доказать, что если / и д имеют конечные левую и правую производные
в каждой точке ж Е (а, &), то функции и тя. v также имеют конечные левую и
правую производные в каждой точке ж Е (а, Ь).
4.11. Дана функция / : ж
ные //(ж) и #(ж).
7Г
cos —
ж
Определить левую и правую произвол-

434 Гл. 4. Дифференциальное исчисление функций одной переменной
4.12. Исследовать на дифференцируемость, построить график функции /, оп-
sin ж
ределенной условиями: /(ж) = ——— при х ф 0, /(0) = 1.
\х\
4.13. Функция / определена и дифференцируема при всех ж £ R. Определить,
каким должно быть выбрано 6 > 0, чтобы из неравенства |ж| < 6 следовало,
что |/(ж) — /(0)| < е, если известно, что \f'(x)\ < М при всех ж.
4.14. Доказать следующее правило дифференцирования произвольного числа
множителей:
D(fif2 х • • • х fn) = (Afi)/2 х • • • х fn + /i(Af2) x • • • x fn + ...
n
• • • + /1/2 x • • • x Dfn = ]T /1/2 x •. • x fk-i(Dfk)fk+1 x ... x /n.
4.15. Функция / : (—/,/) —* R принадлежит множеству 2>n[(—1,1)]. Пусть
/(0) = o0, /(m)(0) = am, m = 1, 2,..., n, g(x) = /(ж2).
Найти производные: p'(0), g"(0),... ,g(n\0).
4.16. Построить график и найти производные функций
<ра : х £ R •—> гшп{ж, а},
-0а : ж £ R •—> тах{ж, а},
где а £ R. Найти производные функций (ж — а)+ и (ж — а)~~.
Воспользоваться результатом для того, чтобы выразить (ра(х) и фа(х)
через (ж — а)+ и (ж — а)~.
4.17. Доказать, что функция /:жи (£р|ж — а|)<р(ж), где ср непрерывна в точке
а и (р(а) ф 0, не имеет производной в точке а.
4.18. Построить график функции
,. 1 - х2п
х н+ hm —.
71 —ОО 1 + Ж2П
4.19. Вычислить суммы
п п п п
2_^кхк~1, \^fc2efca:, /J^sinte, y^kcoskx.
fc=l fc=l fc=l fc=l
4.20. Определить суммы
n n n
^2c%kukvn-k, J2ckk2ukvn-k, ^Ckk3ukvn-k.
fe=0 fe=0 fc=0

Задачи
435
4.21. Пусть функции / : (а, Ь) —► R и д : (а, b) —► R принадлежат классу
2>п((а, Ь)). Доказать формулу:
/(»> • р = ^(-l)fcC*D—fc[/ • р«].
fc=0
4.22. Функция / определена в интервале (а — £, а + £) и представима в виде
/(ж) = (ж - a)tp(x).
Какому условию должна удовлетворять функция (р для того, чтобы /
была дифференцируема в точке а?
4.23. Функция / определена равенством /(ж) = (ж — a)nip(x), где ip определена
в некоторой окрестности точки а и имеет там производную порядка (п — 1).
Доказать, что если ip^n~1\x) = о ( 1 при х —> а, то производная
\(ж — а)71-1 J
/^n)(a) существует и найти эту производную.
4.24. Пусть / : (а, Ь) —* R — функция, принадлежащая множеству Dn((a, Ь)),
п
и пусть хо Е (а, 6). Положим Д^/(жо) = ^ (—l)fcC^/(a:oH-A;/i). Доказать, что
fc=o
4.25. Доказать, что если / дифференцируема и п натуральное, то
lim n\f(x+-)-f(x)] =/'(x).
Верно ли, что если для / существует указанный предел, то /
дифференцируема?
4.26. Функция / : [0, оо) —► R определяется из условий: для любого х Е [0, оо)
у = /(ж) есть решение уравнения ур + у = ж (р > 1).
Доказать, что производная /'(ж) — это монотонная функция, причем
/'(ж) —► 0 при ж —► оо.
4.27. Дан многочлен Р : ж н-* жр + axq + Ь, где р и q — натуральные числа,
р > q, а и b — произвольные вещественные числа. Сколько, самое большее,
вещественных корней может иметь многочлен Р?
Указать необходимые и достаточные условия для того, чтобы количество
вещественных корней многочлена было равно этому максимальному числу.
Какие условия необходимы и достаточны, чтобы многочлен Р имел, по
крайней мере, один вещественный корень?
4.28. Доказать, что уравнение 1 — ж Н h • • • + (—1)п— = 0 имеет один
2 п
вещественный корень, если п нечетно, и ни одного, если п четно.

436 Гл. 4. Дифференциальное исчисление функций одной переменной
4.29. Доказать, что полином Р(х) = 14—- Н Н 1 не имеет веще-
1! 2! п\
ственных корней при п четном, и имеет ровно один вещественный корень,
если п нечетно.
4.30. Пусть х G R. Доказать, что если ж > О, тоеж>1 + ж+^--Ь--- + ~у-
при любом п.
Доказать, что если х < 0, то при п четном
г X2 ХП
«■<! + ,+ - + ...+ _,
при п нечетном —
еж > 1 + ж+ — + •••+ —.
2! п!
4.31. Доказать, что функция
ж к* 1пж - С* 1п(ж + 1) + Cl 1п(ж + 2) + • • • + (-1)п 1п(ж + п)
неположительна при всех х > 0, возрастает на полуоси (0, оо) и стремится к
нулю при х —> оо.
4.32. Функция /: (а—£, а+£) —■> R принадлежит множеству функций Сп+2((а—6,
а+ 8)). Имеем по формуле Тейлора с остаточным членом в форме Лагранжа:
f(a + h) = /(a) + f'(a)h + ■■■ + /<л>(а) — + ^п+1Ца + eh)——
п\ (n + 1)!
Доказать, что при ft —> О будет 0 —> 1/(п + 2), если f(n+2\a) ф 0.
4.33. Найти все дифференцируемые функции / : R —> R, для которых число 0
в формуле /(ж + ft) — /(ж) = /&/'(ж + 0ft) не зависит от ft.
4.34. Найти все дифференцируемые функции / : R —► R, для которых число 0
в формуле /(ж + ft) — /(ж) = /г/'(ж + 0ft) не зависит от ж.
4.35. Функция / : [0, оо) —> R принадлежит классу С1 ([0, оо)), и существует
конечный предел lim [/(ж) + /'(#)] == '• Доказать, что при ж —> оо будет
/(*) - I, /'(») -> 0.""°°
4.36. Дана функция F : R —» R, дифференцируемая на R и такая, что |-Р'(ж)| <
< А < 1, А = const, для всех ж > 0 и F(0) > 0. Доказать, что уравнение
-Р(ж) = ж имеет единственный положительный корень. Доказать, что этот
корень есть предел последовательности (хп)п^, где х± = F(0) и жп+1 = F(xn)
при всяком п.
4.37. Для п е N и у G R пусть

Задачи
437
Доказать, что для всякого ж > 1 уравнение Еп(у) = х имеет и при том
единственное решение у = Ln(x). Доказать, что функция Ln является
вогнутой в промежутке [1,оо). Найти предел lim Ln(x).
п—юо
4.38. А. Определим функцию / : R —> R, полагая
ftx\ _ j с * при ж > 0;
о
при ж < 0.
Доказать, что / Е 2>n(R) при любом п Е N.
В. Пусть F : R —> R — непрерывная функция. Предположим, что F
принадлежит классу С°° в каждом из промежутков (—оо, 0) и [0, оо). Показать,
что тогда функция ip : х —► F{e^1/X ) при ж ^ 0, <р(0) = -F(O) принадлежит
классу С°° на всем множестве R.
4.39. Пусть Ж1, Ж2,..., жп — положительны. Для вещественного t ф 0
полагаем
l/t
# £КГ -5- 3!I -+-•••-+- fl!"'. i
= /ж1+4 + -" + жпУ
Доказать, что существует предел lim fi(t) = VJx\X2 •... • жп-
Доказать, что функция /х является возрастающей на R.
4.40. Дана параметризованная кривая X : £ Е [а, Ь] ь-> (ж(£),г/(£)).
Предположим, что функции жиг/ дифференцируемы на [а, Ь] и [ж'(£)]2 + [?/(£)]2 ф 0 для
всех £ E [а, 6].
Доказать, что если касательные во всех точках параметризованной
кривой проходят через одну и ту же точку М[р, q], то кривая лежит на одной
прямой (т. е. существуют числа А, В и С такие, что А2+В2 ф 0 и Ax(t)+By(t)+
+С = 0 для всех t E [а, Ь]).
4.41. Функция / : [а, Ь] —► R дифференцируема на [а, 6]. Оценить разность
df . .
через модуль непрерывности функции — на отрезке [а, б], если известно, что
ах
— непрерывна на [a, о],
аж
4.42. Пусть функция / : (а, &) —> R непрерывна на (а, 6). Предположим, что
существуют непрерывные функции Д : (а,&) —* R и /2(а, Ь) —> R такие, что
для любого £ Е (а, 6)
/(*) = /(<) + (х - «)Д (*) + ^^/2(*) + е(х, *)(* - *)2,
где £(ж, £) —► 0 при ж —* £.

438 Гл. 4. Дифференциальное исчисление функций одной переменной
Доказать, что тогда функция / дважды дифференцируема на (а, Ь) и
df , d2f
— = /1, —о = /2-
ах dxz
4.43. Функция / : [0, оо) —*• R дифференцируема в [0, оо). Доказать, что если
/ \ /0е») Л
существует последовательность (#n)nGN такая, что жп->оои —> 0, то
Жп
найдется последовательность (2/n)nGN такая, что г/п —> оо и f'(yn) —► 0 при
п -^ оо.
4.44. Пусть / : [0, оо) —► R — функция класса Х>г([0, оо)). Доказать, что если
/0е)
► 0 при х —► оо, то найдется такая последовательность точек (жп)пе]^5
что жп —> оо и f^r\xn) —► 0 при п -^ оо.
4.45. Пусть функция / : [0, оо) —* R принадлежит классу 2}Г([0, оо)), где г > 1.
Предположим, что /(р)(х) > О для всех ж G [0, оо). Доказать, что существует
конечный или бесконечный предел lim ——.
х—юо Хг 1
4.46. Функция / : [а, Ь] —► R принадлежит классу Сп([а, Ь]). Оценить разность
fc=0
через модуль непрерывности функции f^n\
4.47. Функция / : [0,оо) —► R дифференцируема и \f'(x)\ < Мж1"6, где
М < оо, 8 > О для всех х G [0, оо). Доказать, что если f(y/n) —► 0 при
п —> оо, то /(ж) —► 0 при ж —► оо.
4.48. Функция / : [0, оо) —» R непрерывна и дифференцируема на [0, оо),
причем /'(ж) ^ 0 для всех ж £ [0, оо). Доказать, что если f(y/n) —* 0 при п —► оо,
то lim /(ж) = 0.
X—ЮО
4.49. Функция / : [0,ft] -* R принадлежит классу 2>n([0, ft]), /(0) = 0 и /(fc)(0) =
0 для всех к = 1,2, ...,п. Доказать, что если А < f(n\x) < В для всех
хп хп
х G [0, ft], то А — < /(ж) < J5—- для любого ж G [0, ft],
п! п!
4.50. Функция / : [0, оо) —* R принадлежит классу ^([О, оо)).
Доказать, что если /'(ж) —> 0 при ж —* оо, то для любого ft > 0 разность
/(ж -Ь ft) — /(ж) —» 0 при ж —^ оо.
4.51. Функция / : [а,Ь] —> R дифференцируема на отрезке [а, Ь]. Пусть
Et = {xE[a,b]\f(x)=t}.
Доказать, что если /'(ж) ^0в каждой точке ж Е ^t, то множество Et
конечно.
4.52. Функция / G l^Qa,^]). Производная /7 монотонна. Доказать, что для
всякого £ G (а, &) найдутся жх и Ж2 такие, что а<Ж1<£<Ж2<&и
/'(£) = *^Ж2) ~ ^^Ж1^
Ж2 ~ Ж1

Задачи
439
4.53. Пусть даны числа xi,a?2,... ,хп G [0,7г]. Доказать, что для любых
п
Ai, Л2,. •., An G (0, оо), таких, что ]Р А^ = 1 выполняется неравенство
г=1
п
sin |
4=1 7 г=1
in I N^ АгЖг ) > У, ^г sin ж*
Доказать, что равенство здесь возможно в том и только том случае, если
х\ = Х2 = * • * = жп.
4.54. Даны числа A>0hAG(0,1). Найти точную нижнюю границу функции
/Л ч А + \х
f : х G (0,оо) ь-+ г—.
хл
Доказать, используя полученный результат, неравенство Коши о среднем
арифметическом и среднем геометрическом.
4.55. Пусть / : (а, Ь) —► R — непрерывная функция. Доказать, что если для
любых 2:1,2:2 € (а, Ь) выполняется неравенство
/Ж1 + ж2\ /(ж!)4-/(ж2)
Т\ 2 )S 2
то функция / выпуклая.
4.56. Пусть fi : (а, Ь) —> R, г = 1,2, ...,п, — выпуклые функции. Положим
f(x) = max{/i(x),..., fn(x)}. Доказать, что функция / выпукла.
4.57. Пусть / : R —► R — выпуклая функция. Доказать, что если / ограничена,
то она постоянна.
Верно ли это утверждение для выпуклых функций, определенных на
произвольном неограниченном промежутке?
4.58. Доказать, что результат предыдущей задачи может быть усилен
следующим образом.
Пусть / : R —» R. — выпуклая функция. Тогда, если
х—*оо X х—► —оо X
то / постоянна.
Верно ли это заключение, когда только один из указанных пределов равен
нулю?
4.59. Пусть / : [Z, оо) —► R — выпуклая функция. Доказать, что существует
конечный или бесконечный предел lim .
х—юо X

440 Гл. 4. Дифференциальное исчисление функций одной переменной
4.60. Пусть дана функция ср : I —► R, где / — промежуток множества R.
Положим /(ж) = sup{atf — ip(t)}. Пусть J — множество тех жЕМ, для кото-
tei
рых f(x) < со. (Функция / : J —► R называется преобразованием Леоюандра
функции (р.)
Доказать, что J либо пусто, либо представляет собой одноточечное
множество, либо некоторый промежуток множества R и / есть выпуклая функция
на множестве J.
Определить функцию / и множество J в следующих случаях:
а) J = R, ?>(*) = £;
б) / = R, уф) = |*|;
в) J=(0,co), yft) = -Vg;
г) I = R, ip(t) = Vt2 + h2, h^O;
n)J = R, *>(*) = ^, P>1;
e)J=[-l,l], V(t) = 0;
ж) / = [-1,1], <p(t) = -Va2-*2;
з) J = R, ip{t) = e*.
Доказать, что если функция <р выпукла, то множество J всегда не пусто,
и справедливо равенство cp(t) = sup{xt — f(x)} для всех t E I.
xeJ
4.61. Доказать, что множество угловых точек выпуклой функции, т. е. точек,
где f[(x) ф fr(x)> не более чем счетно.
4.62. Функция / : (а, Ь) —► R называется логарифмически выпуклой, если
f(x) > 0 для всех х Е (а, Ь) и функция g{x) — In /(ж) выпукла.
Доказать, что если / логарифмически выпукла, то / выпукла.
Доказать, что сумма двух логарифмически выпуклых функций есть
логарифмически выпуклая функция.
4.63. Дана функция / : [а, Ь] —► R. Число у Е R называется экстремальным
значением функции /, если существует точка хо Е [а, Ь] такая, что /(жо) = г/,
и жо есть точка экстремума. Доказать, что множество всех экстремальных
значений функции / не более чем счетно.
4.64. Дана непрерывная функция / : [a, b] —> R. Доказать, что если всякая
точка х Е [а, Ь] является точкой экстремума /, то / постоянна на [а, Ь].
4.65. Пусть функция / : [а, Ь] —► R принадлежит классу С2([а, Ь]).
Предположим, что /(а) = 0, /(b) = 0 и существует точка с Е (а, Ь) такая, что /(с) > 0.
Доказать, что тогда найдется точка £ Е (а, Ь) такая, что /"(£) < 0.
4.66. Функции / : [а, &] —> R и р : [а, 6] —► R непрерывны на [а, Ь] и принадлежат
классу Р((а, &)). Доказать, что тогда найдется точка £ Е (а, 6) такая, что
/(«) /(b)
5(а) Р(Ь)
= (Ь-а)
/(«) /'(О
4.67. Функции /, д и /i определены и непрерывны на отрезке [а,Ь] и
дифференцируемы на отрезке (а, Ь). Доказать, что тогда найдется точка £ Е (а,Ь)
такая, что
f(a) № f'(0
9(a) 9(b) 9'(0
h(a) h(b) h'({)
= 0.

Задачи
441
4.68. Функции f,gnh определены и непрерывны на отрезке [р, q] и дважды
дифференцируемы в (р, q). Пусть а, Ъ и с — три произвольные точки отрезка
\p,q]. Доказать, что тогда найдутся £ и 77, заключенные между наибольшим и
наименьшим из чисел а, бис такие, что
/(a) /(b) /(с)
0(а) 9(b) 9(c)
h(a) h(b) h(c)
-(b-c)(c-a)(a-b)
f(a) f'(0 f"(v)
9(a) 9'(0 9"(V)
h(a) h'(0 h"(V)
4.69. Пусть функция / : (a, b) —► R. дифференцируема в (а, Ь). Доказать, что
если для любой пары точек х± и Х2 из (а, &), где х\ < Ж2, существует
единственная точка £ такая, что х\ < £ < Х2 и /(жг) — /(#i) = /'(0(ж2 — #i), то /
либо строго выпукла, либо строго вогнута на (a, b).
4.70. Функция / : R —» R. дифференцируема на R.
Доказать, что если lim /'(ж) = lim /'(ж) ф О, то найдется точка
X—*• — ОО Ж—ЮО
жо £ К. такая, что /(жо) = 0.
4.71. Функция д определена и имеет непрерывную производную порядка п + 1
всюду на отрезке [—1,1]. Положим f(x) = при х ф 0, /(0) = #'(()).
ж
д(п+1)/0\
Доказать, что существует производная /^п^(0), причем ,рп'(0) = .
п -Ь 1
4.72. Дана функция / : (а, оо) —» М, где а > 1, дифференцируемая на (а, оо).
Известно, что /'(ж) = 0(жЛ;(1пж)т) при ж —► оо, где кит — действительные
числа.
Исследовать асимптотическое поведение функции / при ж —► оо.
Рассмотреть 4 случая:
1) к > 0, т > 0; 2) к > 0, т < 0: 3) fc < 0, т > 0; 4) А; < 0, т < 0.
Что можно сказать об асимптотическом поведении функции / при ж —> оо,
если дано, что /'(ж) = о(жп(1пж)т) при ж —► оо?
4.73. Функция / : (а, Ь) —► R дифференцируема на отрезке (а, 6).
Доказать, что если множество точек, в которых /'(ж) = 0 является
конечным, то для любого t £ М множество jE?t = {ж £ (а,6) | /(ж) =£} конечно.
4.74. Функция / : [0,1] -► R принадлежит классу £>2([0,1]) и /(0) = /(1) = 0.
Доказать, что если /"(ж) < 1 для всех ж £ [0,1], то /(ж) > |ж(ж — 1) для всех
жЕ [0,1].
4.75. Исследовать сходимость при ж —> оо
/(ж) = \ ~(sini/n + sinn/ж).
п<ж
4.76. Последовательность (xn)neN стРоится по следующему закону: х\ = 1,
жп+1 = жп Н при каждом п. Доказать, что —> 1 при
Ж1+Ж2Н \-хп V2inn
п —» оо.
4.77. Дана функция f :< а,Ь >—* R. Число / £ М называется правой (левой)
производной в сильном смысле функции / в точке жо £ (а, &), если для всякого

442 Гл. 4. Дифференциальное исчисление функций одной переменной
-I
<е.
е > О найдется 6 > О такое, что для любых жь Ж2 из промежутка (ж6,жо + ^)
/ / с чч у 1/(ж1)-/(ж2)
(соответственно из промежутка (жо -- о, жо)), Ж1 ^ Ж2,
I Ж1 — Ж2
Доказать, что если / имеет в точке х правую (левую) производную в
сильном смысле, то / непрерывна в некотором интервале (жо, жо + 6)
(соответственно, (жо — £, жо)) и имеет конечный предел lim /(ж) (соответственно,
lim /(*)).
ж—*-жо— О
Доказать, что если / непрерывна в точке жо и I есть правая (левая)
производная в сильном смысле, то I = /£(жо) (I = //(жо)). (Символы fr и f[ здесь
обозначают обычные производные справа и слева).
4.78. Функция / : [а, Ь] —► R называется односторонне гладкой, если /
непрерывна и имеет в каждой точке отрезка < а,Ь > левую и правую производные
в сильном смысле (в точках а и Ь существует, разумеется, лишь одна из этих
двух производных) (см. задачу 4.77).
Показать, что тогда в каждой точке жо Е (а, Ь] имеет место равенство:
//(х0)= lim //(*)= lim J'r{x)
ж—♦жо—0 ж—>*жо— О
и в каждой точке жо Е [а, &) выполняется равенство:
/;(х0)= lim_//(*)= Um /;(*).
ж-^жо+О ж—»-жо— О
Показать, что множество всех точек жо Е [а, &), для которых //(ж) ^ /£(ж)
(/ — односторонне гладкая функция), не более чем счетно. (Указание:
сначала установить, что множество тех ж Е (а,Ь), где //(ж) — f'r(x)\ > —,
1 ' га
га G N — конечно.)
4.79. Доказать, что всякая выпуклая функция / : (а, Ь) —» R является
односторонне гладкой (см. задачу 4.78).
4.80. Показать, что функция / : ж »-> ж2 sin - при ж ^ О, /(0) = 0, дифферен-
ж
цируема в точке 0 и не имеет в этой точке ни левой, ни правой производной в
сильном смысле.

Указатель обозначений
е, 13
А С В, 13
P=>Q, 15
V, 16
3, 16
Ai х А2 х ■ ■ ■ х Ап, 18
>, 28
(а, Ь), 30
[в, Ь],30
[а, 6), 30
0*4'13 М], 30
?'_1 ,. (М),зо
|ж|, 30
В D Л 13 ^ 31
р&д, 14 х-'31
IЛ 2*14 -в»'*.32
ppv,?14 тахл'33
' 15 vain А, 33
sup Д 34
f^£>15 шМ,34
N,38
Z, 39
(Vxex)p, i6 q 39
(3xgx)p, i6 N;j41
1*Л" .„, ,в KeMWN„42
(xn)nenk, 42
Л _ X i=1 Л-, 18 (*n)n=jk,jk+i,..., 42
D(f), 19 (*п),п = *,* + 1,* + 2,...,42
Я(/), 19 (*„), n € Nfc, 42
/:i£An /(x) e B) 19 ВД, 43
idA, 20 W, 43
/-^M], 20 In, 44
PS" £—
R, 26 n
<, 28 П xk, 50
<:5
nil, 51
1/1, 53
/+, 53
/",53

444
Указатель обозначений
С, 59
Rez, 62
Imz, 62
^(р), 83
JZimM, 84
р Е J^imM, 84
/(ж) —> L при ж —> р, ж Е М, 87
L = lim /(ж), 87
f(x) — о(1) при ж —> р по М, 88
lim жп, 91
п—+оо
/(ж0-0), 139
/(ж0 + 0), 139
/Т(*о), 139
/i(*o), 139
lim жп, 164
п—+оо
lim жп, 165
п—+оо
ехрж, 192
е, 193
log ж, 199
cos ж, 214
sin ж, 214
tga:, 215
sin ж
222
Предел lim
х—►О ж
arcsinx, 223
агссовж, 224
arctga:, 225
впж, 229
спж, 229
tha:, 229
Arsh, 232
Arth, 233
Arch, 233
/(ж) = 0(р(ж)) при ж
ж Е М, 235
/(ж) = о(р(ж)) при ж -
ж Е М, 235
/(ж) = д[х) + 0(<р(ж)), 235
/(ж) = д(х) + о{<р{х)), 236
lim (1 + - ) для ж Е С, 241
п—юо \ П )
R+, 251
S1, 251
^■(а), 265
аж
/'(а), 265
£>/(а), 265
//(а), 265
#(а), 265
e(tbt2),283
tx(to), 284
tzx(t0), 284
t^(to), 284
/"(*o), 304
d2f
^(*o), 304
Г>2/(ж0), 304
/(п)(ж), 305
/<п>, 305
з^305
Dnf(x), 305
/'", 305
/iv, 305
/v, 305
@n(A,R), 305
ifn(A,R), 305
^n, 305
^n, 305
^00(A)R), 306
<€co, 306
er(x) = ^-, 307
r!
P»
/~<fc _ n!
un — fc!(n-fc)!
310
n(n-l)...(n-fc+l)
fe! •

Предметный указатель
п дважды факториал, 51
n-кратно дифференцируемая в
точке функция, 305
п-факториал, 51
п-я производная функции, 305
абелева группа — см.
коммутативная группа, 259
абсолютная величина
вещественного числа, 30
абсцисса точки М на плоскости, 55
аксиома непрерывности множества
вещественных чисел, 35
аксиомы алгебраической структуры
множества R, 27
аксиомы порядка в множестве R, 28
амплитуда точки на плоскости, 297
ареакосинус гиперболический, 233
ареасинус гиперболический, 232
ареатангенс гиперболический, 233
арифметический квадратный
корень из числа х > 0, 48
арккосинус, 224
арксинус, 223
арктангенс, 225
асимптота графика функции в
направлении х —► — оо, 409
асимптота графика функции в
направлении х -* оо, 409
асимптотическая характеристика
полинома Тейлора порядка п
функции / в точке а, теорема
о таковой, 353
асимптотически ограниченная при
ж-^рпоМсК функция, 98
астроида, 293
базисные элементарные функции,
228
бесконечно малая при х —» р,
х G М, функция, 88
бесконечные элементы множества
Й, 29
биективное отображение, 21
биномиальные коэффициенты, 310
Вейерштрасса теорема выбора, 153
Вейерштрасса теорема о
наименьшем и наибольшем
значениях, 155
вектор на плоскости или в
пространстве, 279
вектор-функции предел, 283
вертикальная асимптота графика
функции в направлении
у —» —оо, 409
вертикальная асимптота графика
функции в направлении
у -* оо, 409

446
Предметный указатель
верхнее число последовательности
(xnGM)neNm, 163
верхний и нижний пределы —
характеристика посредством
понятия частичного предела,
173
верхний предел последовательности
(хп G R)n€Nm, 165
верхняя граница вещественной
функции, 56
верхняя граница множества
А С R, 33
вещественная функция,
определенная на произвольном
множестве, 52
вещественная часть комплексного
числа, 62
взаимно однозначное отображение,
21
взвешенное среднее арифметическое
чисел, 389
взвешенное среднее геометрическое
чисел, 389
включение множеств, 13
вогнутая функция, 379
возрастающая функция на
множестве А С К, 53
вторая производная функции, 304
вторая теорема Лопиталя, 341
второй основной постулат
аналитической геометрии, 55
выпуклая сверху функция — см.
выпуклая функция, 379
выпуклая снизу функция — см.
вогнутая функция, 379
выпуклая функция, 379
выпуклое множество на плоскости,
380
Гейне теорема о равномерной
непрерывности, 160
Гёльдера неравенство для
сумм, 391
гиперболический косинус, 229
гиперболический синус, 229
гиперболический тангенс, 229
гипотрохоида, 291
гипоциклоида, 291
гладкая точка кривой, 284
гомеоморфность множеств, 151
гомоморфизм групп, 260
график отображения, 25
график функции в полярной
системе координат, 298
группа, 259
Дарбу теорема о производной, 324
декартова ортогональная система
координат на плоскости, 54
дизъюнктные множества, 17
дизъюнкция высказываний, 14
дифференцируемая в точке
функция одной переменной, 265
достаточное условие постоянности
функции в промежутке, 331
достаточное условие существования
касательной, 284
единица группы, 259
единичная точка оси, 53
единственность предела, 98
задача о брахистохроне, 295
замкнутый промежуток в R, 30
знак числа — см. функция sgnx, 32
значение отображения на элементе
множества, 19
импликация высказываний, 15
индуктивное множество, 38
интервал вМ — см. открытый
промежуток в М, 30
инъективное отображение, 21
иррациональное число, 39
Йенсена неравенство, 382

Предметный указатель
447
каноническая база точки р € R, 106
канторова таблица, 71
касательная графика функции, 279
касательной в точке
параметризованной кривой, 284
касательный орт
параметризованной кривой, 283
кванторы, 16
класс функций ^°°(А,Е), 306
классы функций ^n(A,R) и
^n(A,R), 305
коммутативная группа, 259
комплексного числа основная форма
представления, 62
комплексное число, сопряженное
z е С, 62
комплексные числа, 59
комплексных чисел геометрическое
представление, 64
композиция отображений — см.
суперпозиция отображений, 21
конечная вещественная функция, 52
конечное множество, 44
конечные элементы множества
1, 29
концы промежутка, 30
конъюнкция высказываний, 14
координата точки на оси, 54
координаты точки на плоскости, 55
корень п-ой степени из числа
у > 0, 204
косинус, 215
Коши — Больцано критерий
существования конечного
предела, 130
Коши — Больцано признак
сходимости — см. Коши
— Больцано критерий
существования конечного
предела, 130
Коши — Больцано признак
сходимости для
последовательности, 133
Коши — Буняковского неравенство
для сумм, 392
Коши неравенство между средним
арифметическим и средним
геометрическим, 389
Коши теорема о среднем значении,
320
Коши теорема об оценке
приращения для комплексных
функций,322
критерий Гейне для существования
предела, 135
критерий монотонности всюду
дифференцируемой функции,
326
критерий постоянности функции
на отрезке, 332
критерий строгой монотонности
всюду дифференцируемой
функции,328
Лагранжа теорема о среднем
значении, 322
Лейбница формула для производной
порядка п произведения
функций, 310
левое обратное отображение, 22
левый касательный орт
параметризованной кривой, 284
лемма о существовании предела и
локальной ограниченности, 95
лемма об интегрировании
асимптотических соотношений
для функции одной
переменной, 350
логарифмическая спираль, 300
мажоранта множества А С R
— см. верхняя граница
множества А С R, 33
метод Ньютона решения уравнения
f(x) = 0, 366

448
метод касательных решения
уравнения f(x) = О — см.
метод Ньютона, 366
метод хорд приближенного
решения уравнения f(x) = 0,
368
метод деления пополам
приближенного решения
уравнения f(x) = 0, 361
Минковского неравенство, 393
миноранта множества А С R — см.
нижняя граница множества
А С R, 33
мнимая часть комплексного
числа, 62
множество Nfc, 41
множество всех вещественных
чисел Е, 26
множество всех комплексных
чисел С, 59
множество всех рациональных
чисел Q, 39
множество всех целых чисел Z, 39
множество значений отображения,
19
множество натуральных чисел, 38
множество, 12
модуль вещественного числа —
см. абсолютная величина
вещественного числа, 30
модуль комплексного числа, 62
модуль непрерывности функции
на множестве А, 157
монотонная функция на множестве
А С R, 53
монотонные функции, критерий
непрерывности, 147
монотонные функции, теорема о
существовании и величине
предела, 127
надграфик функции, 380
Предметный указатель
наибольший элемент числового
множества, 33
наименьший элемент числового
множества, 33
накрывающее отображение, 20
натуральный логарифм ж, 199
не более чем счетное множество, 67
невозрастающая функция — см.
убывающая функция, 53
нейтральный элемент группы, 259
неопределенность типа ^, 336
неопределенность типа ^, правило
Лопиталя отыскания ее
предела — см. первая теорема
Лопиталя, 337
неопределенность типа Ц, 336
неопределенность типа ~, правило
отыскания ее предела — см.
вторая теорема Лопиталя, 341
непрерывная обратная функция
— теорема существования
в случае функции одной
переменной, 149
непрерывная функция, 94
неравенство Бернулли, 47
несчетность отрезка множества
R, 137
неубывающая функция — см.
возрастающая функция, 53
нечетная функция, 218
нижнее число последовательности
(*neR)neNm,163
нижний предел последовательности
(%ei)n€Nm, 164
нижняя граница вещественной
функции, 56
нижняя граница множества
А С R, 33
номер элемента не более чем
счетного множества в заданной
нумерации, 67
нулевая точка оси, 53

Предметный указатель
449
нулевой элемент коммутативной
группы, 260
нумерация элементов не более чем
счетного множества, 67
о вложенных отрезках, теорема,
129
о зажатой переменной, теорема, 100
о непрерывности суперпозиций
непрерывных функций,
теорема, 115
о пределе сложной функции, вторая
теорема, 117
о пределе сложной функции, первая
теорема, 116
о предельном переходе в
неравенстве, теорема, 97
о произведении бесконечно малой и
асимптотически ограниченной
функций, теорема, 110
о точках разрыва монотонной
функции, теорема, 142
об операциях над функциями,
имеющими бесконечный
предел, теоремы, 121
об операциях над функциями,
имеющими бесконечный
предел, теоремы, 122
об операциях над функциями,
имеющими бесконечный
предел, теоремы, 123
об операциях над функциями,
имеющими конечный предел,
теорема, 112
область определения отображения,
19
образ множества при данном
отображении, 20
обратное отображение, 23
обращение производных в нуль
и порядок малости функции
— случай функции одной
переменной, 351
объединение множеств, 16
ограничение функции
(отображения), 25
ограниченная на множестве А
функция, 56
ограниченная сверху на множестве
А функция, 56
ограниченная снизу на множестве
А функция, 56
ограниченное множество А С R, 33
ограниченное сверху множество, 33
ограниченное снизу множество, 33
ограниченный промежуток в R, 30
односторонние пределы функции,
определенной на отрезке, 139
окрестность числа р Е К, 82
операция возведения в степень, 205
операция сложения комплексных
чисел — геометрическое
истолкование, 65
операция умножения комплексных
чисел — геометрическое
истолкование, 65
ордината точки М на плоскости, 55
ослабленный критерий
монотонности, 329
ослабленный критерий строгой
монотонности функции, 332
основные числовые группы, 260
остаточный член формулы
Тейлора, 352
ось, 53
открытый промежуток в R, 30
отношение порядка в множестве
R, 28
отношение порядка в множестве
R, 29
отображение множества А на
множество В, 20
отображение числовой прямой R
на окружность S, 212
отображение, 19

450
Предметный указатель
отрезок 1п множества N, 44
отрицание высказывания, 15
отрицательная часть
вещественного числа, 31
параметр кривой, 281
параметризованная кривая в
пространстве, 281
параметризованная кривая на
плоскости, 281
параметрическое представление
прямой, 280
Пеано кривая, 282
Пеано теорема, 282
первая производная, 305
первая теорема Лопиталя, 337
первый основной постулат
аналитической геометрии, 54
пересечение множеств, 17
периодическая функция, 218
периодическая функция, её
период, 218
плотное в себе множество
А С R, 264
подграфик функции, 381
подпоследовательность, 152
подпоследовательность,
извлеченная из
последовательности, 152
позитивный полином, 243
показательная функция
комплексного аргумента, 226
полинома каноническое
представление, 345
полинома коэффициенты, 345
полинома разложение по степеням
х — а, 347
полиномом Тейлора порядка п
функции / в точке а, 352
полиномом степени не выше п, 345
полиномы, формула Маклорена
для полиномов, 349
полиномы, формула Тейлора для
полиномов, 348
полный прообраз множества
f-ЦА), 20
положительная часть
вещественного числа, 31
полуоткрытый промежуток в R, 30
полярная система координат на
плоскости, 297
полярный радиус точки на
плоскости, 297
последовательность элементов
множества, 41
постоянное отображение, 20
правила дифференцирования
суммы, произведения и
частного двух функций, 267
правило дифференцирования
обратной функции, 269
правило дифференцирования
сложной функции, 271
правое обратное отображение, 22
правый касательный орт
параметризованной кривой, 284
предел последовательности, 91
предел слева функции,
определенной на отрезке, 139
предел справа функции,
определенной на отрезке, 139
предел функции при ж,
стремящемся к р Е Jfim(M)
по множеству М С К, 87
предел функции при ж,
стремящемся кр Е J£?гга(М)
по множеству М С Й, 89
предел функции при ж,
стремящемся к р £ Jfim(M)
по множеству М С К, 89
предел функции со значениями
в С, 107
предельная точка множества
М С R, 83

Предметный указатель
451
признак сравнения бесконечной
малости функции, 102
признак сравнения существования
бесконечного предела, 102
признак точной верхней (точной
нижней) границы множества
А С R, 35
принцип Архимеда, 40
принцип математической
индукции, 38
продолжение функции
(отображения), 25
производная n-го порядка суммы
га функций, 309
производная в точке функции
/ : А -> R, 265
производная левая функции
/ : А -> R, 265
производная порядка п — см. п-я
производная функции, 305
производная правая функции
/ : А -> R, 265
производные порядка п > 2,
применение к отысканию точек
экстремума, 378
произвольная показательная
функция, 210
промежутки [а, 6], (а, Ь], [а, Ь),
(а,Ь), 30
промежуток в множестве R, 30
промежуточные значения функции,
теорема Коши, 144
прообраз множества при
отображении, 20
простая дуга, 286
простая замкнутая кривая, 286
прямое произведение п множеств
(декартово произведение п
множеств), 18
прямое произведение множеств, 17
пустое множество, 13
равенство множеств, 14
равномерная непрерывность, 156
радиус-вектор точки, 280
разность множеств, 17
распознавание точек экстремума по
поведению производной вблизи
стационарной точки, 376
распознавание точек экстремума
функции в концах области
определения, 375
распознавание точек экстремума
функции среди угловых
точек, 375
расширенное множество
вещественных чисел R, 29
рациональное число, 39
Ролл я теорема, 319
свойство Дарбу, 147
свойство локальности предела, 103
сегмент в! — см. замкнутый
промежуток в R, 30
секущая графика функции, 278
секущая параметризованной
кривой, 283
синус, 215
скорость и ускорение, 301
сложение и умножение
комплексных чисел —
определение, 59
спираль Архимеда, 299
спираль Архимеда, ее
отрицательная ветвь, 300
спираль Архимеда, ее
положительная ветвь, 300
степенная функция, 208
степенная функция, производная
степенной функции, 272, 274
степенной функции показатель, 208
строго вогнутая функция, 380
строго возрастающая функция на
множестве А С R, 53

452
строго выпуклая сверху функция
— см. строго выпуклая
функция, 379
строго выпуклая снизу функция
— см. строго вогнутая
функция, 380
строго выпуклая функция, 379
строго монотонная функция на
множестве А С М, 53
строго убывающая функция на
множестве А С К, 53
сужение функции (отображения)
— см. ограничение функции
(отображения), 25
сумма и произведение двух
конечных вещественных
функций, 52
суперпозиция отображений, 21
существование
подпоследовательности, имеющей предел, 154
существование предела
lim *Z=±, 211
х-+0 х
существование предела
Шп d+f*-1, 209
существование предела
Um ««p*-1, 198
ж—0 х
существование предела
Ит logd+s) 2Ш
х-+0 х
существование предела
lim (l+f) , 190
существование предела
и асимптотическая
ограниченность, 99
существование предела
последовательности, критерий,
167
сходящаяся последовательность, 92
счетное множество, 68
сюръективное отображение, 21
тангенс, 215
Тейлора формула с остаточным*
членом в форме Пеано
Предметный указатель
(случай функции одной
переменной), 352
теорема Лопиталя о
неопределенности вида §, 337
теорема Лопиталя о
неопределенности вида —, 341
теорема о вложенных отрезках, 129
теорема о сумме бесконечно малых
функций, 109
теорема о существовании л/х
для х > 0, 49
теорема об ассоциативности
суперпозиции, 21
тождественно постоянная функция,
ее производная, 272
тождественное отображение, 20
топологическое отображение, 151
точка возврата кривой, 284
точка локального максимума
функции — см. точка
максимума функции, 316
точка локального минимума
функции — см. точка
минимума функции, 316
точка локального экстремума
функции — см. точка
экстремума функции, 316
точка максимума функции, 316
точка минимума функции, 316
точка перегиба функции, 394
точка разрыва второго рода, 140
точка разрыва первого рода, 140
точка экстремума функции, 316
точки экстремума функции,
усиленная теорема Ферма, 372
точная верхняя граница
вещественной функции, 56
точная верхняя граница числового
множества, 34
точная верхняя и точная нижняя
границы числового множества
как пределы, 144

Предметный указатель
453
точная нижняя граница
вещественной функции, 56
точная нижняя граница числового
множества, 34
третья производная функции, 304
тригонометрические функции,
формулы приведения, 215
трохоида, 289
убывающая функция на множестве
А С Й, 53
угловой коэффициент прямой, 278
упорядоченная пара, 17
упорядоченная система из п
элементов, 18
условие Гёльдера с показателем
а, 157
условие Липшица, 157
Ферма теорема, 318
формула Тейлора порядка п
функции класса ^n+1, общая
оценка остаточного члена, 355
функции sin х и cos х, их
производные, 276
функциональное уравнение
Коши, 251
функция arccos ж, ее производная,
276
функция arcsinx, ее производная,
276
функция arctgx, ее производная, 277
функция log х, ее производная, 273
функция sgnx, 32
функция tg#, ее производная, 276
функция аж, ее производная, 275
функция еж, ее производная, 273
функция, 19
функция, непрерывная в точке р, 94
характеристика предельной
точки через понятие предела
последовательности, 106
целая часть числа х 6 К, 43
целое число, 39
циклоида, 288
частичный предел
последовательности (хп € M)n€Nm, 170
частное двух комплексных
чисел, 60
частное двух конечных
вещественных функций, 52
четная функция, 218
число 7г, 212
число е, 193
число элементов конечного
множества, 44
числовая прямая — см. множество
всех вещественных чисел, 26
элементарные функции, 228
элементы множества, 12
эпитрохоида, 291
эпициклоида, 291
Юнга неравенство, 390
явление радиоактивности, 302
явление радиоактивности, период
полураспада, 303

Учебное издание
РЕШЕТНЯК Юрий Григорьевич
КУРС МАТЕМАТИЧЕСКОГО АНАЛИЗА
Часть 1, книга 1
Ответственные редакторы
Шведов Игорь Александрович
Ионин Владимир Кузьмич
Редактор издательства
И. И. Кожанова
Издание подготовлено с использованием макро-пакета Aj^S-T^i.,
разработанного Американским математическим обществом.
This publication was typeset using •АД/fS-'IEX,
the American Mathematical Society's T]eX macro system.
Подписано в печать 30.11.99. Формат 70x100 1/16. Печать офсетная.
Усл.-печ. л. 37. Уч.-изд. л. 28. Тираж 1000 экз. Заказ № 21.
Лицензия ЛР № 065614 от 8 января 1998 г.
Издательство Института математики СО РАН.
630090 Новосибирск, пр. Академика Коптюга, 4
Отпечатано в Редакционно-полиграфическом объединении СО РАСХН
633128 Новосибирская обл., пос. Краснообск