Автор: Колмогоров А.Н.
Теги: алгебра школьная алгебра издательство просвещение учебник для школы
Год: 1975
Текст
АЛГЕБРА
И НАЧАЛА
АНАЛИЗА
УЧЕБНОЕ ПОСОБИЕ
ДЛЯ 9-ГО КЛАССА
СРЕДНЕЙ ШКОЛЫ
под редакцией
А. Н. КОЛМОГОРОВА
Утверждено Министерством
просвещения СССР
МОСКВА «ПРОСВЕЩЕНИЕ» 1975
512 (075)
А45
A. H. КОЛМОГОРОВ,
Б. Е. ВЕЙЦ,
И, Т, ДЕМИДОВ ,
О. С. ИВАШЕВ-МУСАТОВ,
С. И. ШВАРЦБУРД
60601 - 465
103 (03) — 75
инф. письмо
© Издательство «Просвещение», 1975 г.
ОГЛАВЛЕНИЕ
Глава I.
ПРИНЦИП МАТЕМАТИЧЕСКОЙ
ИНДУКЦИИ
§ 1. Принцип математической индукции и его применение
1. Понятия полной и неполной индукций .................. 7
2. Принцип математической индукции ..................... 9
3. Обобщение принципа математической индукции ......... 13
Дополнительные упражнения к главе /.................... 14
Глава II.
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
§ 2. Упорядоченные множества
4. Перестановки. Число перестановок ................... 17
5. Упорядоченные множества и размещения ............... 20
§ 3. Сочетания
6. Число подмножеств конечного множества .............. 22
7. Некоторые свойства числа сочетаний ................. 25
8. Рекуррентная формула для вычисления числа сочетаний. 27
§ 4. Натуральная степень бинома (формула Ньютона)
9. Формула Ньютона. Основные следствия ................ 29
10. Сведения из истории. Применение комбинаторики к теории
вероятностей .......................................... 32
11. Примеры более сложных задач из теории вероятностей . . 34
Дополнительные упражнения к главе II .......... 37
3
Глава III.
ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА,
БЕСКОНЕЧНЫЕ ПОСЛЕДОВА-
ТЕЛЬНОСТИ И ИХ ПРЕДЕЛЫ
§ 5. Действительные числа
12. Вводные замечания ..................................... 40
13. Периодические десятичные дроби ........................ 42
14. Действительные числа ................................ 44
15. Десятичные приближения к действительному числу по не-
достатку и по избытку и арифметические действия с действи-
тельными числами . ........................................ 45
16. Изображение чисел точками координатной прямой ... 48
17. Числовая прямая и числовая плоскость .................. 51
18. Некоторые свойства множества действительных чисел ... 54
§ 6. Бесконечные числовые последовательности. Предел последова-
тельности
19. Бесконечные числовые последовательности ............... 55
20. Геометрическое изображение последовательности и нагляд-
ные представления о пределе последовательности .... 57
21. Определение предела последовательности ................ 60
22. Единственность предела. Сходящиеся и расходящиеся по-
следовательности .......................................... 63
23. lim qn, если | q | < 1 64
я->со
24. Сумма бесконечной геометрической прогрессии при |<?|< 1 65
25. Понятие числового ряда ................................ 67
§ 7. Существование пределов и их вычисление
26. Необходимое условие сходимости ........................ 70
27. Теоремы о пределах .................................... 72
28. Бесконечно малые последовательности ................... 73
29. Примеры вычисления пределов ........................... 75
30. Сравнение роста арифметической и геометрической прогрес-
сий ...................................................... 76
31. Монотонные последовательности ......................... 79
32. Существование предела монотонной и ограниченной после-
довательности ............................................. 81
33. Число л и длина окружности ............................ 84
Дополнительные упражнения к главе 111 87
Глава IV.
ПРЕДЕЛ ФУНКЦИИ
И ПРОИЗВОДНАЯ
§ 8. Первоначальные представления о производной и пределе функции
34. Числовые функции ...................................... 93
35. Изменение функции, ее возрастание и убывание .......... 97
36. Приращение функции .................................... 99
37. Производная как скорость изменения функции ........... 103
38. Непрерывные и разрывные функции. Предел функции . . . 107
39. Теорема о единственности предела ..................... 111
40. Теоремы о пределах ................................... 113
41. Непрерывность рациональных функций ................... 114
4
§ 9. Производная
42. Определение производной .............................. 118
43. Примеры вычисления производных ...................... 119
44. Производная суммы функций ............................ 122
45. Производная произведения функций 123
46. Производная многочлена ............................. 125
47. Производная частного ................................ 126
48. Производная дробно-рациональной функции . . 127
49. Сложная функция ................................... 128
50. Производная сложной функции ......................... 129
Дополнительные упражнения к главе IV ..................... 131
Глава V.
ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ
§ 10. Применение производной к приближенным вычислениям, геомет-
рии и физике
51. Главная часть приращения функции .................. 135
52. Касательная к графику функции ..................... 138
53. Скорость и ускорение .............................. 141
§11. Применение производной к исследованию функций
54. Возрастание и убывание функции .................... 144
55. Критические точки функции, ее максимумы и минимумы 146
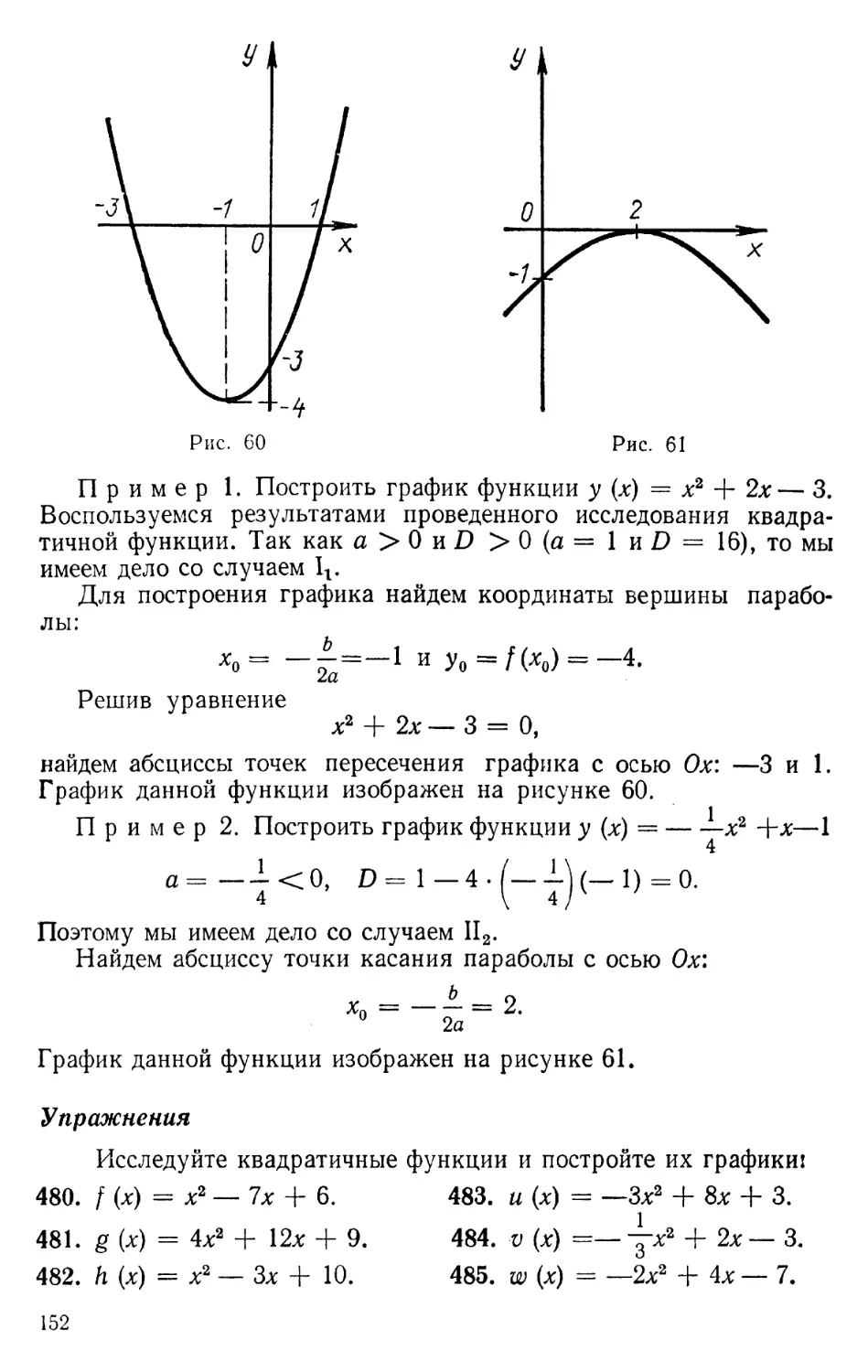
56. Исследование квадратичной функции ................. 150
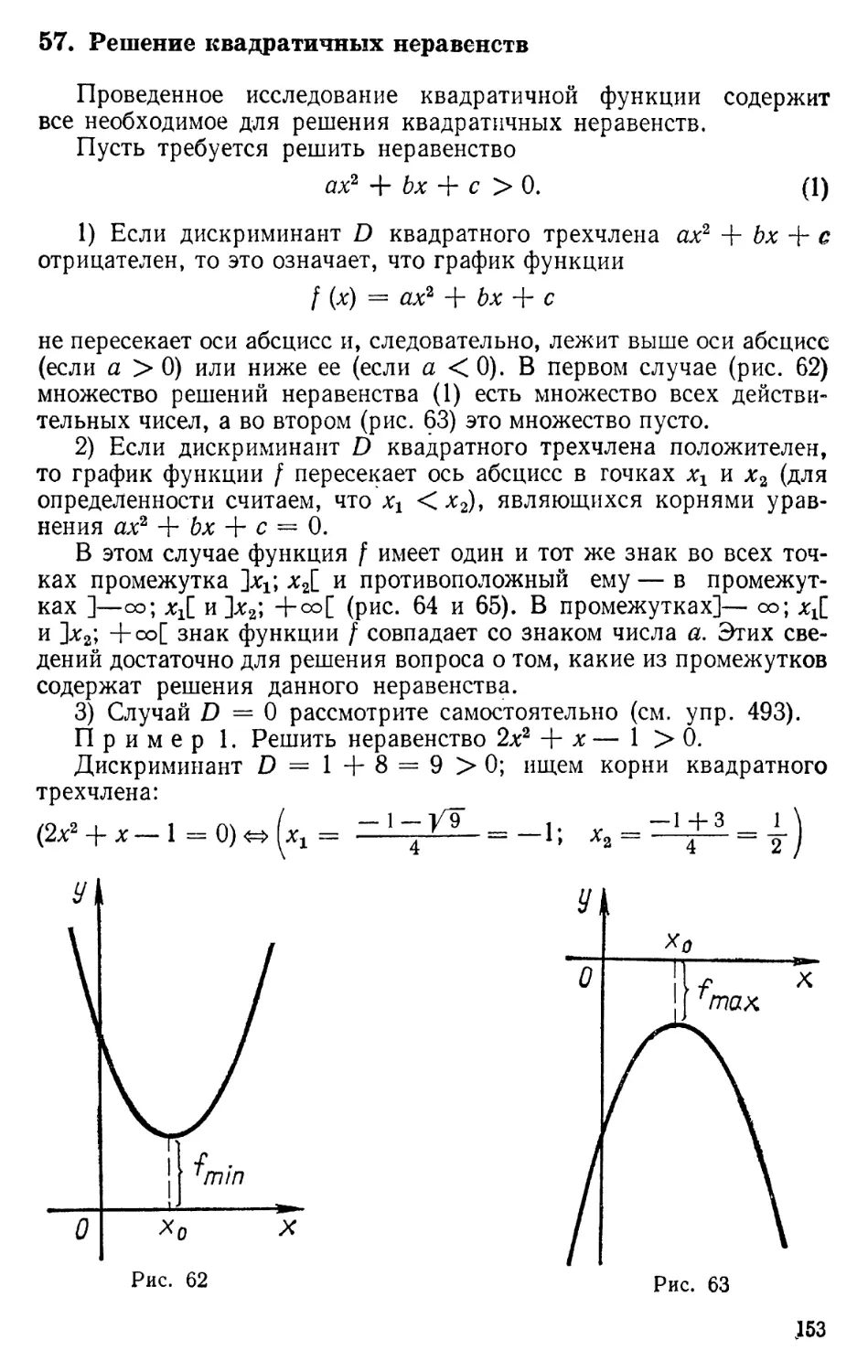
57. Решение квадратичных неравенств ................... 153
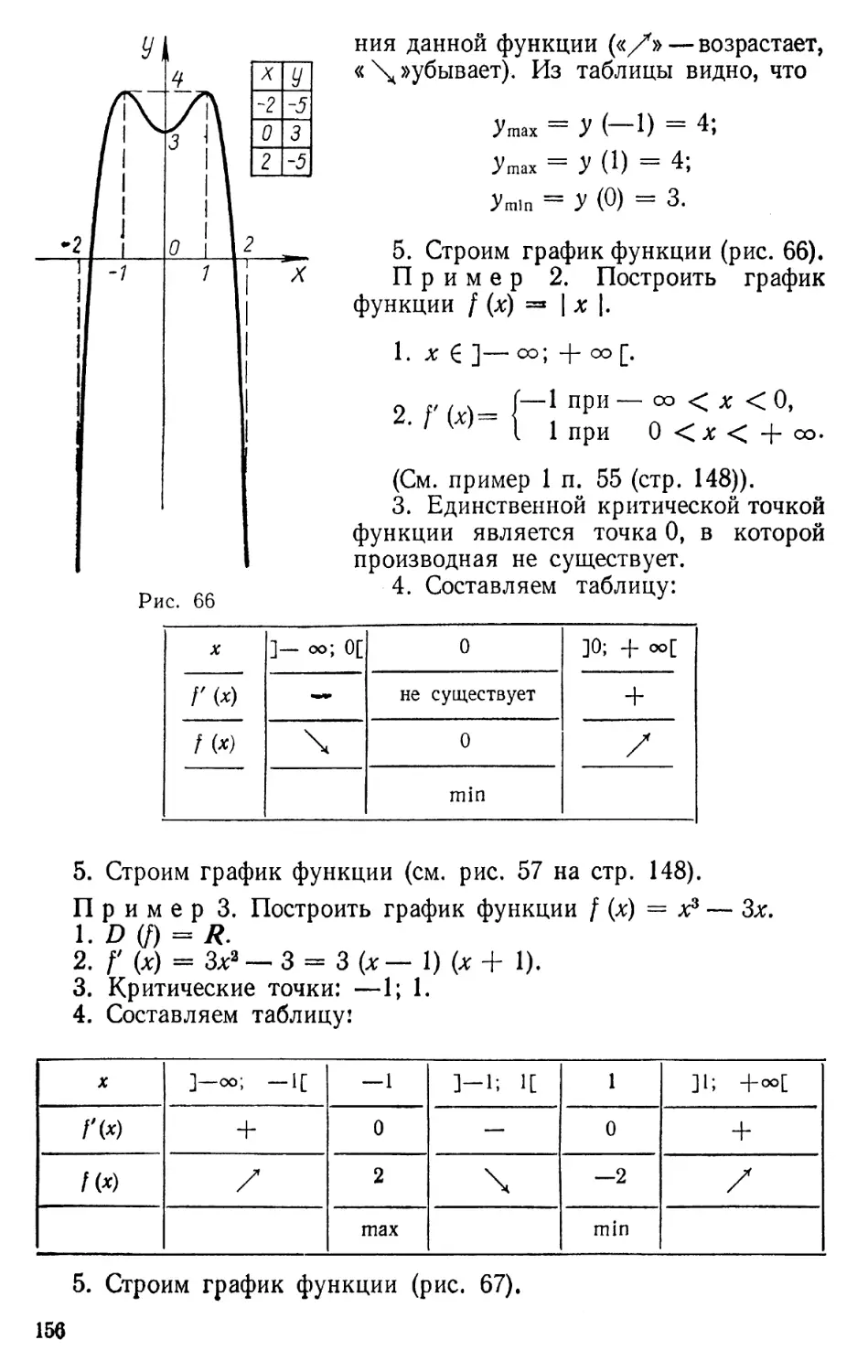
58. Общая схема исследования функций .................. 155
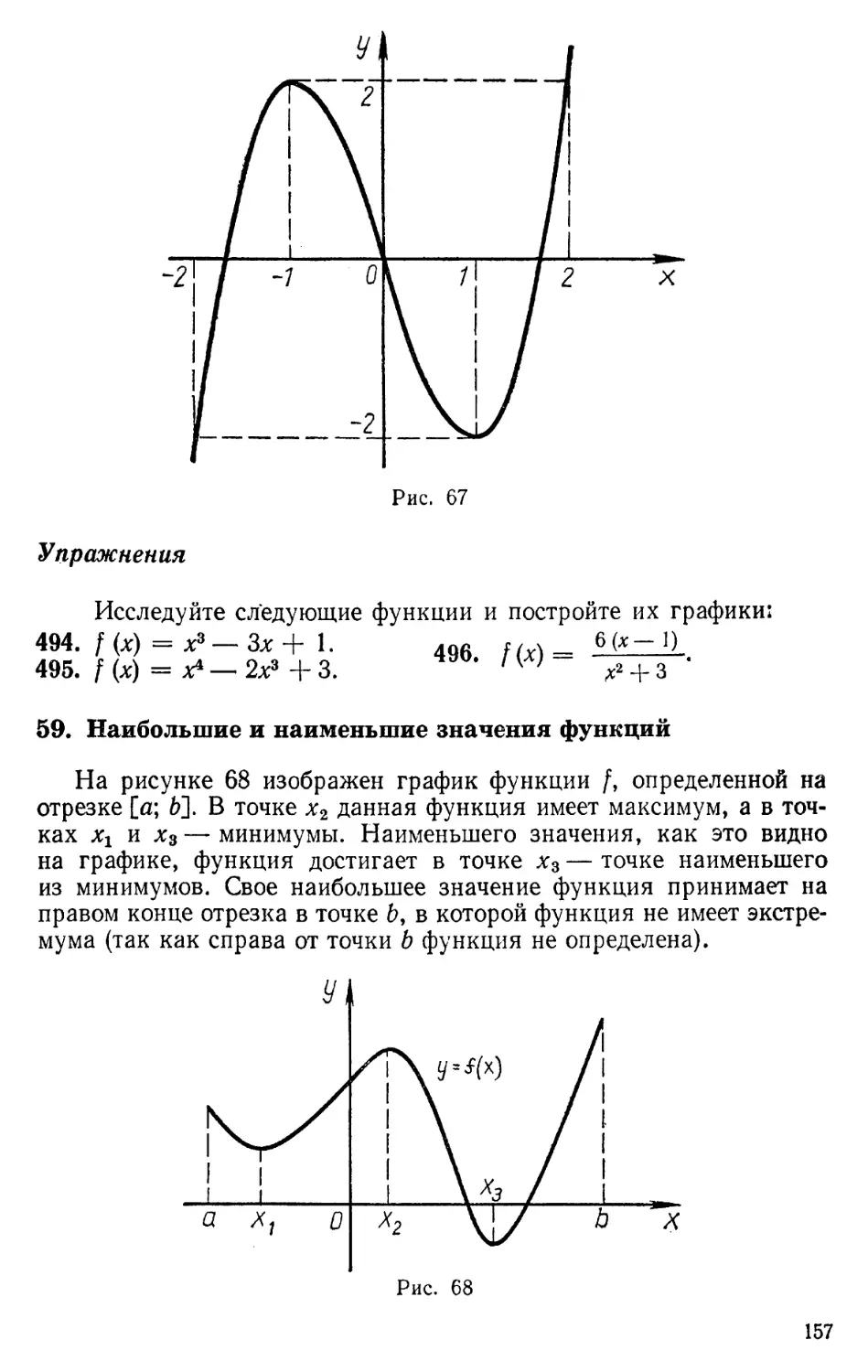
59. Наибольшие и наименьшие значения функций .......... 157
60. Сведения из истории . ............................. 161
Дополнительные упражнения к главе V ................... 162
Глава VI.
ТРИГОНОМЕТРИЧЕСКИЕ
ФУНКЦИИ, ИХ ГРАФИКИ
И ПРОИЗВОДНЫЕ
§ 12. Тригонометрические функции числового аргумента
61. Радианное измерение угловых величин ............... 165
62. Длина дуги и площадь сектора .................... 171
63. Синус и косинус числового аргумента . ........... 172
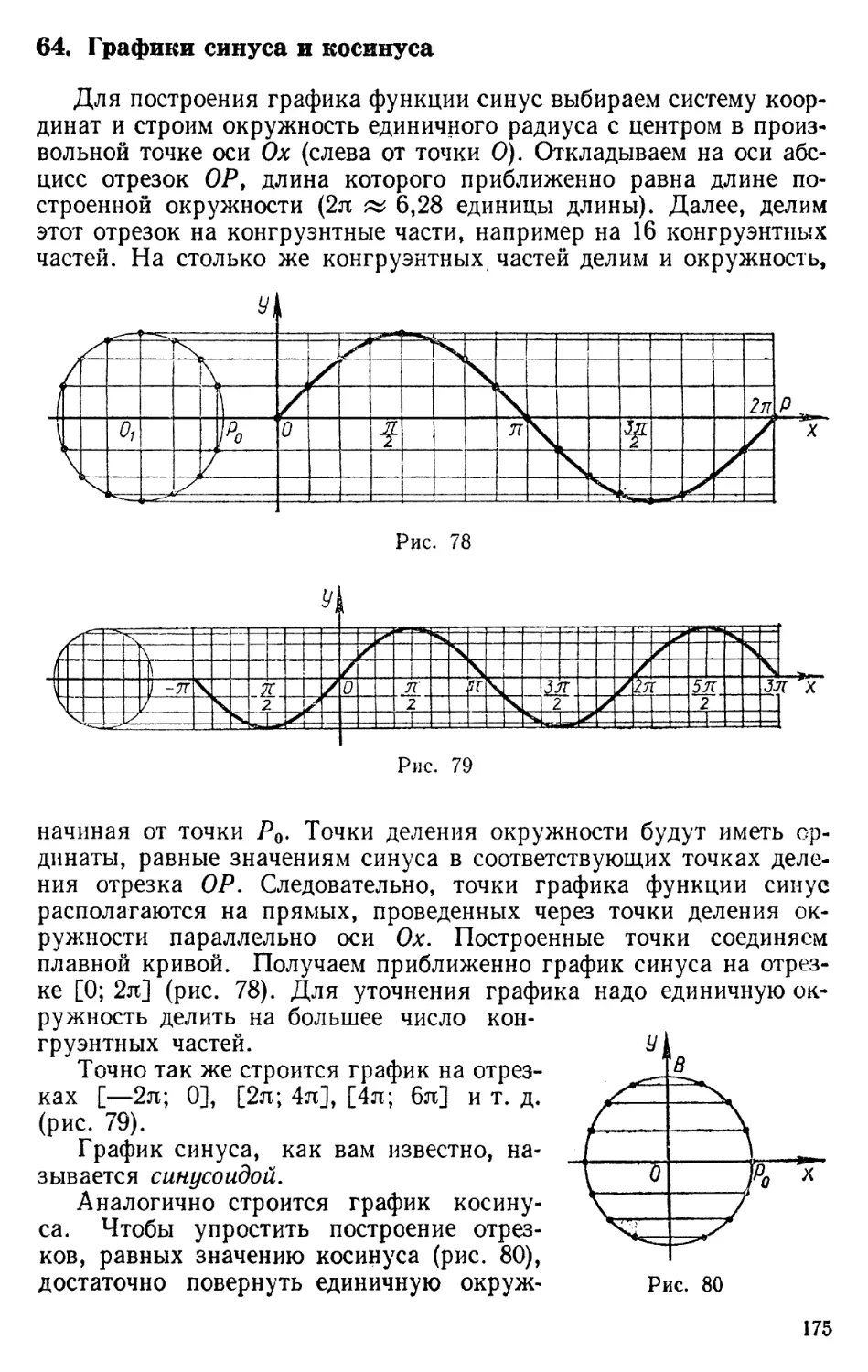
64. Графики синуса и косинуса ......................... 175
65. Тангенс и котангенс числового аргумента ........... 177
66. Таблицы значений тригонометрических функций числового
аргумента .............................................. 179
§ 13. Основные свойства тригонометрических функций
67. Знаки значений тригонометрических функций ............... 181
68. Четные и нечетные тригонометрические функции . . 184
69. Периодичность тригонометрических функций .......... 185
5
§ 14. Формулы сложения и следствия из них
70. Координаты вектора .................................... 188
7k Косинус и синус суммы .................................. 189
72. Тангенс суммы ......................................... 193
73. Тригонометрические функции двойного аргумента .... 194
74. Формулы суммы и разности одноименных тригонометриче-
ских функций.............................................. 196
Дополнительные упражнения к главе VI ...................... 197
Ответы и указания к упражнениям............................ 200
Обозначения, встречающиеся в учебном пособии............... 221
Глава
ПРИНЦИП
МАТЕМАТИЧЕСКОЙ
ИНДУКЦИИ
§ 1.
ПРИНЦИП МАТЕМАТИЧЕСКОЙ
ИНДУКЦИИ И ЕГО ПРИМЕНЕНИЕ
1. Понятия полной и неполной индукций
Индукцией* называют метод рассуждений, ведущий от частных
примеров к некоторому общему выводу. Например, складывая
нечетные числа 1, 3, 5, 7, ..., 2п— 1 при различных значениях пе-
ременной п = 1, 2, 3, ... , получим**:
1 = 1 = I2;
1 + з = 4 = 22;
1 4- з + 5 = 9 = З2;
1 4- 3 + 5 + 7 = 16 = 42;
1 + 3 4- 5 + 7 + 9 = 25 - 52.
Легко заметить, что во всех приведенных примерах сумма пер-
вых нечетных натуральных чисел равна квадрату числа слагаемых.
Напрашивается вывод, что это свойство имеет место при любом
числе слагаемых. Наше предположение (гипотезу) можно сформу-
лировать следующим образом: «Для всех натуральных п справед-
ливо равенство:
1 + 3 + 5 + ... + (2п — 1) = п2». (1)
Таким образом, 5 рассмотренных примеров «навели» нас на
гипотезу, которая, как будет показано ниже, справедлива.
* inductio — латинское слово, означающее «наведение».
** В первой строке стоит «сумма, состоящая из одного слагаемого».
Такое понимание слова «сумма», при котором не исключаются и суммы, со-
стоящие из одного слагаемого, иногда полезно в математике.
7
Рассмотрим еще один пример. Подставляя в квадратный трех-
член
Р (х) = х2 4- х + 41
вместо х натуральные числа 1, 2, 3, 4, 5, найдем:
Р(1) = 43; Р(2) = 47; Р(3) = 53; Р(4) = 61; Р(5) = 71.
Все полученные значения данного трехчлена являются просты-
м и числами. Подставляя вместо х числа 0, —1, —2, —3, —4, по-
лучим: Р (0) = 41; Р (—1) = 41; Р (—2) = 43; Р(—3) = 47; Р (—4) =
= 53. Значения данного трехчлена при указанных значениях пере-
менной х также являются простыми числами.
Возникает гипотеза, что значение трехчлена Р(х) является про-
стым числом при любом целом значении х. Однако высказанная
гипотеза ошибочна, так как, например,
Р(41) = 412 + 41 + 41 = 41 • 43.
Таким образом, один и тот же метод рассуждений приводит в
некоторых случаях к правильному выводу (в первом примере), а
в других— к ошибочному выводу (во втором примере). Так как
при этом методе вывод делается после разбора нескольких
примеров, не охватывающих всех возможных случаев, то этот ме-
тод называется неполной индукцией.
Метод неполной индукции, как мы видим, не приводит к вполне
надежным выводам, но он полезен тем, что позволяет сформулиро-
вать гипотезу, которую потом можно доказать или опровергнуть.
Если же вывод делается на основании разбора всех случаев,
то такой метод рассуждений называют полной индукцией. Ясно,
что такой метод применим, когда число случаев конечно (и не
«слишком велико»).
Приведем несколько примеров применения метода полной индук-
ции.
Пример 1. Доказать, что каждое натуральное число п, удов-
летворяющее неравенству 2 п 15, либо является простым,
либо представляется в виде произведения не более чем трех про-
стых множителей.
Для доказательства рассматриваем каждое из натуральных
чисел от 2 до 15. Числа 2, 3, 5, 7, 11, 13 простые. Числа 4, 6, 9,
10, 14, 15 представляются в виде произведения двух простых мно-
жителей, наконец, числа 8 и 12—в виде произведения трех простых
множителей.
Пример 2. Доказать, что при любых а и Ъ верно неравен-
ство
| а + b |< | а | + | b |. (1)
Для доказательства надо вспомнить, как в разных случаях
определяется модуль суммы, и в каждом из этих случаев устано-
вить справедливость неравенства (1).
8
1) Числа а и b одного знака (оба положительны или оба отри-
цательны). В этом случае
| а + b | = | а | + | b
и (не строгое!) неравенство (1) выполнено.
2) Числа а и b разных знаков (одно положительно, а другое
отрицательно). В этом случае модуль суммы равен разности моду-
лей слагаемых (естественно, что из двух разностей | а | — | b | и
I b | — | а | выбирается неотрицательная). Так как модули сла-
гаемых положительны, то их разность меньше их суммы. Поэтому
и во втором случае
|а + 6|<1«1+Ш,
и неравенство (1) тоже выполнено.
3) Если одно из чисел равно нулю, то обе части неравенства (1)
равны модулю второго числа (независимо от того, является ли
второе число нулем или нет). Поэтому неравенство (1) также вы-
полнено.
Мы разобрали все возможные случаи и установили, что в каж-
дом из них неравенство (1) верно.
Упражнения
1. Докажите, что каждое четное натуральное число п, большее
двух, но меньшее 40, можно представить в виде суммы двух
простых чисел*.
2. Посмотрите в учебнике алгебры VIII класса, как доказывается,
что ах > 0 при а > 0 и х £ Z. Можно ли сказать, что доказатель-
ство проведено методом полной индукции?
2. Принцип математической индукции
Вернемся к равенству
1 + 3 + 5 + ... + (2п — 1) = я2. (1)
Для удобства обозначим через Л(п) равенство (1) для нату-
рального числа п. Тогда истинность Д(1), Л(2), Л(3), Л(4), Л(5)
означает, что равенство (1) истинно при п = 1, п = 2, п = 3,
п — 4, п = 5 (как было показано в начале пункта 1).
Поскольку высказывание Л(5) истинно: 1 + 3 + 54-7 + 9 =
- 5а, то
1+3 + 5 + 7 + 9+ 11 = 52 + 11 = 52 + 2- 5+1 =
= (5 + I)2 = 62,
т. е. истинно высказывание Л(6).
* Математики до сих пор не знают, будет ли это верно для любого чет-
ного натурального числа, большего двух.
9
Таким образом, доказано, что из истинности 4(5) следует ис-
тинность 4(6).
Предложение «из 4(5) следует 4(6)» записывают короче, ис-
пользуя вместо слова «следует» знак е=>: 4(5) ==> 4(6).
Докажем, что A(k) A(k 4- 1). Это означает, что из равен-
ства
1 + 3 + 5 4- ... + (2/г— 1) = /г2
следует равенство
1 4- 3 4- 5 4- ... 4- (2k 4- 1) = (k 4- I)2.
В самом деле,
1 4- 3 4- 5 4- ... 4- (2k — 1) 4- (2k 4- 1) =
= [1 4- 3 4- 5 4- ... 4- (2k — 1)] 4- (2k 4- 1) =
= k* 4- 2k 4- 1 = (k 4- I)2.
Теперь уже ясно, что из 4(6) следует 4(7).
Точно так же из 4(7) следует 4(8), из 4(8) — 4(9) и так
далее. Представляется очевидным, что таким образом можно доб-
раться до любого натурального числа п и доказать для него вы-
сказывание 4(п). Иначе говоря, представляется очевидным, что
предложение 4(п), — о котором известно, что оно верно при п = 1
и что при любом k из A(k) вытекает A(k 4~ 1), — верно при всех
натуральных п. Но при всей наглядности и убедительности ска-
занного мы имеем здесь дело с новым математическим принци-
пом, который принято называть принципом математической индук-
ции.
Сформулируем его:
Если предложение А(п), в котором п—натуральное число,
истинно для п = 1 и из того, что оно истинно для п = k (где k —
любое натуральное число), следует, что оно истинно и для следующего
числа п — k 4- 1, то предложение А(п) истинно для любого нату-
рального числа п.
Принцип математической индукции является одной из а к с и о м
арифметики натуральных чисел, имеющей много
применений в математике. На этом принципе основан метод дока-
зательства, называемый методом математической индукции.
Доказательство методом математической индукции состоит из
двух частей: в первой части доказывают (проверяют) истинность
высказывания 4(1); во второй части предполагают, что А(п) верно
для п = k, и доказывают справедливость предложения А(п) для
п = k 4- 1, Т. е. A(k) A(k 4- 1).
Если обе части доказательства проведены, то на основании
принципа математической индукции предложение А(п) истинно
для любого натурального числа п.
Теперь мы можем считать, что равенство (1) справедливо для
любого натурального числа п, так как оно справедливо для п = 1
и из A(k) следует 4(k 4- 1).
10
Пример 1. Вычислить сумму
_L + _L + _L _|_ 1
1-3 3-5 5-7 (2n —l)(2n + 1)
для любого натурального значения п.
Обозначим эту сумму через Sn. Чтобы догадаться, какова фор-
мула для Snt вычислим несколько первых значений этой суммы
Sb S2, S3, S4, .... Рассмотрев эти числа, сформулируем гипотезу,
а для ее доказательства воспользуемся методом математической
индукции.
S =1-
1 1-3 з’
& = — + Д_ =s, + _!_ = 1 + _!_ = 1.
1-33-5 1 3 • 5 3 3-5 5
S3 = -L+-l_+-L = Sa+ —
1.33.55.7 а 5•7 55.7 7
St = _L + ^_ + _L + _L=s3+-l-==
1.3 3.5 5.7 7.9 3 7 • 9 7 7- 9 9
Рассматривая эти суммы, замечаем, что в числителе стоит номер
искомой суммы, а в знаменателе — второй множитель знаменателя
последнего слагаемого.
Таким образом, возникает гипотеза, что
— 4* — + — 4- • • • 4----------------= —— • (2)
1.3 3.5 5.7 (2п — 1) (2п + 1) 2п + 1
Чтобы доказать истинность равенства (2), воспользуемся мето-
дом математической индукции.
Обозначим через Д(п) равенство (2) для натурального числа п.
1. Д(1) имеет место, так как S, = — =---.
2. Докажем, что A(k) =^> A(k 4- 1):
S* + . = Sk 4----------- = —— 4--------------- =
а 1 й (й + 1)(й+ 3) 2k 4- 1 (2k 4- 1) (2k 4-3)
_ fe (2fe + 3) 4- 1 = (k + 1) (2fe + 1) = fe4-l
(2Й4- 1) (2fe 4-3) ~ (2k + 1) <2* + 3) 2 (fe 4-1)4*1
Обе части доказательства методом математической индукции
проведены. Значит, равенство (2) доказано и
J_ 4. _L + _1_ + + 1 =
1 • 3 3 • 5 5 7 (2п — 1) (2п 4* 1) 2п 4- 1
при любом натуральном значении п.
11
Пример 2. Доказать, что сумма п3 4- 5п делится на 6 при
любом натуральном п.
Обозначим через А (п) предложение «хп = п3 + 5п делится на 6».
Так как xt — 1 4- 5 = 6, то при п = 1 сумма хп делится на 6,
т. е. Д(1) имеет место. Докажем: A(k) => A(k Д- 1), т. е. из «хЛ де-
лится на 6» следует: «хЛ+1 делится на 6».
Действительно,
хА+1= (k + I)3 + 5(k + 1) = k3 + 3k2 4- 3k + 1 + 5k + 5 =
= (k3 + 5k) 4- 3k(k 4- 1) 4- 6 = xh 4- 3k(k 4- 1) 4- 6.
Как видим, xft+1 состоит из трех слагаемых. Первое слагаемое
этой суммы делится на 6 в силу A(k), второе слагаемое также де-
лится на 6, так как произведение k(k 4-1) — число четное (объяс-
ните почему). Следовательно, каждое из трех слагаемых в выраже-
нии для xk+l делится на 6. Значит, и хА+1 делится на 6. Утвержде-
ние доказано.
Пример 3. Доказать, что при h > —1 неравенство
(1 4- h)n > 1 4- nh (3)
верно для любого натурального п*.
1. При п = 1 имеем: 1 4- h = 1 4- h. Одно из соотношений
«>» или «=» имеет место, значит, Д(1) истинно.
2. Докажем, что A(k) => A(k 4- 1).
Умножим обе части неравенства (14- h)fc 1 + kh на 14-^-
Знак неравенства не изменится, так как 1 4- h > 0 ввиду условия
h >— 1. Поэтому имеем:
(1 4- (1 4- kh) (1 4- h) = 1 4- kh 4- h 4- kh2.
Так как kh2 0, то последнее слагаемое можно отбросить.
Получим:
(1 4- h)!:+l > 1 4- (& + l)h.
Обе части доказательства методом математической индукции про-
ведены, и, следовательно, неравенство Бернулли доказано.
Вы познакомились с тремя способами обоснования общих вы-
водов. Первые два из них имеют широкое применение и за преде-
лами математики.
1) Полная индукция приводит к общему выводу на
основе рассмотрения каждого из конечного числа возможных част-
ных случаев. Это вполне надежный метод рассуждений.
2) Неполная индукция приводит лишь к правдопо-
добному выводу на основе рассмотрения достаточно большого
числа случаев. В математике неполная индукция служит лишь для
* Неравенство (3) называется неравенством Бернулли, в честь извест-
ного швейцарского математика Якоба Бернулли (1654—1705).
12
того, чтобы формулировать гипотезы, нуждающиеся затем в настоя-
щем доказательстве или поддающиеся опровержению.
3) Математическая индукция — это специаль-
ный метод доказательства общих высказываний, верных для каж-
дого натурального числа, т. е. высказываний вида: «Для каждого
натурального числа п. верно Д(п)». Этот метод, как и метод полной
индукции, приводит к вполне надежным выводам.
Упражнения
3. Пользуясь методом математической индукции, докажите, что
при любом натуральном значении п истинно равенство:
а) 1+2 + 3+ ... + л = ^п2+1);
б) р + 22 + З2 + ...+ /г2 = п(п +
4. Последовательность (я„) — арифметическая прогрессия. Мето-
дом математической индукции докажите, что
а„ = о, + (л—l)d и S„ = +
5. Последовательность (Ьп) — геометрическая прогрессия. Мето-
дом математической индукции докажите, что
= и з„= (f/¥,1K
q— 1
6. Вычислите сумму
_±_ + _L + _____
1-2 2-3 3-4 ' ‘ ‘ ' п (п + 1) ’
7. Методом математической индукции докажите, что при любом
натуральном п верно равенство:
а) 1 • 2 + 2 • 3 + 3 • 4 + ... + п (п + 1) = "(,г +
б) 1 • 4 + 2 • 7 + 3 • 10 + ... + п (Зл + 1) = п\п + I)2.
8. Докажите, что при любом натуральном п значение выражения
л3 + 11 есть число, кратное 6.
9. Докажите, что при любом натуральном п значение выражения
7п— 1 кратно 6.
3*. Обобщение принципа математической индукции
Иногда предложение А (п) с переменной п при некоторых на-
туральных значениях л ложно или не имеет смысла, но удается
доказать, что предложение А (л) имеет место для всех натураль-
ных л, начиная с л = tn, С другой стороны, иногда А (п) удается
13
доказать не только для натуральных значений п, но и для целых
п, например, начиная с нуля или с какого-нибудь целого отрица-
тельного значения п. В подобных случаях помогает такое обоб-
щение принципа математической индукции:
Если предложение А (п), в котором п — целое число, истин-
но при п=т и из того, что оно истинно для числа n = k, где k—
любое целое число, большее или равное tn, вытекает, что оно
истинно для следующего числа п = k-{- 1, то предложение А (п)
истинно для любого целого значения п^т.
Пример. Найти все натуральные значения п, для которых
выполняется неравенство 2" >п2.
При п = 1 это неравенство выполняется, но при п = 2, 3, 4
получаем соответственно: 22 = 22, 23<32, 24 = 42. Но при п,
большем 4, данное неравенство справедливо. Докажем это.
Если п = 5, то 25 > 52. Докажем, что при k 5 из истинно-
сти высказывания А (/г): 2й >/г2 — следует истинность высказыва-
ния Л(&-|-1): 2/г+) >(&4-1)2. Так как k^5, то /г>1 и k—2>1.
Перемножая почленно последние два неравенства, получаем:
k (/г — 2) > 1, /г2 — 2/г > 1, k2 > 2k 4- 1.
Поэтому
2Й+1 = 2.2й > 2/г2 = k2 + /г2 > k2 4- 2k 4- 1 = (k 4- I)2.
Следовательно, 2й+1> (k 4- I)2.
Упражнения *
10. Пользуясь методом математической индукции, докажите, что
верно неравенство:
а) 2” > п при л > 0 (n С Z);
б) 2“ > 2п 4- 1 при п > 3 (n £ Z).
11. Докажите, что при п^2 верно неравенство
1 4- 4* ••• + °n I I ai I 4" I а21 4* «• + | ап (•
Дополнительные упражнения к главе I
12. Докажите, что при любом значении х верно неравенство
х+ |х| >0. Объясните, в каком месте доказательства при-
меняется полная индукция.
13. Докажите, что значением выражения х2+у2, где x£Z и
y£Z, не может служить число, которое при делении на 4
дает в остатке 3. (Указание. Рассмотрите случаи, когда
значения х и у — четные числа, нечетные числа, одно четное,
а другое нечетное).
14. Докажите, что если ни одно из чисел а и b не кратно 3, то
сумма их квадратов при делении на 3 дает в остатке 2,
14
15. Докажите, что при k С N значение выражения /г5 — k делится
на 30.
16. Методом математической индукции докажите, что при любом
натуральном п верно равенство:
а) 1 + 2 + 22 + ... + 2"-1 = 2"— 1;
б) I3 + 23 + З3 + ... + п3 = "2 (п + 1)2-.
4
17. Пусть последовательность (си) задана рекуррентно:
О ”1“ 2
с. = 2 и сп . . — —-— сп.
X П т Л ' •
Докажите, что
cn = п (п 4- 1).
18. Последовательность (хп) задана рекуррентно:
— 1 и xn + J = хп------5---. Найдите формулу для хп.
П (tl + 1)
19. Пусть последовательность (сп) такова, что сх = 1 и сп+1 =
= сп (п + 1).
Докажите, что эту последовательность можно задать формулой
сп— 1 • 2 • 3 • ... • п.
20. Последовательность (ап) задана рекуррентно:
Задайте эту последовательность формулой n-го члена.
Пользуясь методом математической индукции, докажите спра-
ведливость равенства для любого натурального значения п:
21* а) I2 + З2 + 52 + • • • + (2n — I)2 = п<2га~1Н2,г+ Ч
б) I3 + З3 4- 53 4- ... + (2/г — I)3 = п2 (2п2 — 1).
22.* а) 1 • 2 • 3 4- 2 • 3 • 4 + ... 4- «(и 4- 1) (п 4- 2)
= 7 п (п 4- 1) (п 4- 2) (и 4- 3);
б) I2 —22 4- 32 —42 4-... 4-(—I)""1"2 = (—I)""1
23.* а) — 4- — 4------------Н - - 4--------------- = ——;
1-5 5 9 9-13 (4п — 3) (4п + 1) 4n + 1
' 1-3-5 + 3 5 7 *''*’* (2п — 1) (2п4- 1) (2п + 3) ~~
= «(»+!)
2 (2л + 1) (2л 4- 3) *
15
24*. Докажите, что п прямых, расположенных в одной плоскости,
из которых никакие две не параллельны и никакие три не
проходят через одну точку, делят плоскость на 1 +
частей.
25*. Докажите, что п плоскостей, из которых никакие две не па-
раллельны, никакие три не проходят через одну прямую и
никакие четыре — через одну точку, делят пространство на
6
26*. Докажите, что п окружностей, расположенных на одной
плоскости, делят плоскость не более чем на п2 — п + 2 частей.
Докажите, что при любом натуральном tv.
27. а) 62"-1 + 1 кратно 7;
б) 4" + 15/? — 1 кратно 9.
28. а) 10" + 18ч — 28 кратно 27;
б) 9,н ’ — 8/Z — 9 кратно 16.
29. Методом математической индукции докажите, что при любом
натуральном п имеет место неравенство
2"+2 > 2п + 5.
30. Докажите, что при натуральном п 10 имеет место неравен-
ство
2" > п3.
31. Докажите, что квадрат суммы п чисел, где п > 2, равен сумме
квадратов этих п чисел и всех удвоенных попарных произведе-
ний этих чисел.
Глава
ЭЛЕМЕНТЫ
КОМБИНАТОРИКИ
Часто приходится составлять из конечного числа элементов
различные комбинации и производить подсчет числа всех возмож-
ных комбинаций, составленных по некоторому правилу. Такие за-
дачи получили название комбинаторных, а раздел математики,
занимающийся их решением, называется комбинаторикой. В ком-
бинаторике имеют дело только с конечными множествами. Этот
раздел математики имеет большое значение в теории вероятностей,
теории управляющих систем и вычислительных машин и во мно-
гих других разделах науки и техники. В этой главе вы познакоми-
тесь с некоторыми простейшими комбинаторными задачами.
§ 2.
УПОРЯДОЧЕННЫЕ МНОЖЕСТВА
4. Перестановки. Число перестановок
Тридцать три буквы русского алфавита принято располагать
в таком порядке:
А, Б, В, Г, Д, Е, Ё, Ж, 3, И, Й, К, Л, М, Н, О, П, Р, С, Т, У,
Ф, X, Ц, Ч, Ш, Щ, Ъ, Ы, Ь, Э, Ю, я.
При этом порядке расположения букв буква А является пер-
вой, Б — второй, В — третьей и т, д. вплоть до последней
17
тридцать третьей буквы Я. Можно те же буквы расположить в об-
ратном порядке: первой буквой считать букву Я, второй — Ю
и т. д. вплоть до последней тридцать третьей буквы А. Каждое
расположение наших тридцати трех букв в определенном порядке
называется их перестановкой. Различных перестановок тридцати
трех букв очень много: их число — тридцатисемизначное!
Перестановки можно образовывать из элементов любого ко-
нечного множества. Множество из одного элемента можно упоря-
дочить одним-единственным образом: единственный элемент мно-
жества приходится считать первым. Возьмем множество из двух
элементов, для примера, из двух букв А и Б. Ясно, что их можно
расположить по порядку двумя способами:
АБ или БА.
Три буквы А, Б и В можно расположить по порядку шестью спосо-
бами:
АБВ; АВБ; БАВ; БВА; ВАБ; ВБА.
В комбинаторике установленный в конечном множестве порядок
называют перестановкой его элементов. Число переста-
новок из п элементов обозначают через Рп. Мы нашли, что
Pv = 1, Р2 - 2, Р3 = 6.
Вычислять Рп очень удобно последовательно, пользуясь рекуррент-
ной формулой:
Рп = nPn_v (1)
Докажем ее. Пусть требуется упорядочить множество из п элемен-
тов. Какой-то из этих элементов придется поставить на последнее,
n-е место. Этот элемент можно выбрать п различными способами.
Если он уже выбран, то останется п— 1 элемент. Ими придется
занять первые п — 1 мест. Это можно сделать Pn-i способами (по
смыслу Всего получается пР^ способов упорядочить
множество из п элементов, т. е. Рп = пРп^г.
По формуле (1) последовательно получаем:
Рз = 2 • Л - 2; Р7 = 7 • 720 - 5040;
Рз - 3 • - 6; Рз =8 • 5040 - 40320;
Pi - 4 • Рз = 24; Рз =9 • 40320 = 362880;
р5 - 5 • Р4 = 120; Р1о = 10 • 362880 = 3628800;
р* = 6 • Р5 = 720; Л1 = п • 3628800 = 39916800
Например, 11 гостей можно рассадить по 11 местам за столом
39 916 800 способами.
Из формулы (1) вытекает (см. упр. 19), что, вообще, Рп (число
перестановок из п элементов) равно произведению первых п нату-
ральных чисел:
Рп = 1 • 2 • 3 • ... • п. (2)
18
Для произведения первых п натуральных чисел принято спе-
циальное обозначение: п! (читается ««-факториал»). Пользуясь
этим обозначением, формулу (2) можно записать в виде
Рп = п\ (3)
Для дальнейшего удобно считать, что пустое множество можно
упорядочить только одним способом, т. е. Ро = 1. Тогда форму-
лой (1) можно пользоваться и при п = 1:
Л = 1 • Ро = 1.
Упражнения
32. Из элементов множества А составьте всевозможные перестанов-
ки, если:
а) А = {1}; в) А = {а; 6; с};
б) А = {7; 8}; г) А = {m; п; р; q}.
33. Сколько различных трехцветных флагов с тремя горизонталь-
ными полосами можно получить, если использовать красный,
синий, белый цвета?
34. Докажите формулы:
a) 3)1- = (m+ l)(m + 2)(m + 3);
пг\
б)-----—---- = п(п — 1)...(« — т 2) (« — т + 1) при п>т.
(л — т)!
35. Найдите значение выражения:
а) 8!+9!; 6)10! —II; в)
36. Сократите дробь:
102! ч 6! —51
> Г) •
100! 120
(л — 1)1. . 2fe(2fe— 1)
(л — 3)1’ Г' (2/г) I
37. Выполните действия:
ЯХ 1 _ 1 . м р(р-1)(р-2)(р-3)(р-4)! .
’ п1 (п + 1)1’ } (р-2)!
' (k— 1)! *! * ' ml 1 ''
38. Сколько элементов должно содержать множество, чтобы число
всех перестановок из элементов этого множества было:
а) не больше 1000; б) не меньше 500?
39. Сколькими способами можно составить список из 9 учеников?
40. В пассажирском поезде 14 вагонов. Сколькими способами
можно распределить по вагонам 14 проводников, если за каж-
дым вагоном закрепляется один проводник?
19
41. Из цифр О, 1, 2, 3 составлены всевозможные четырехзначные
числа так, что в каждом числе нет одинаковых цифр. Сколько
получилось чисел?
42. Из цифр. 1, 2, 3, 4, 5 составлены всевозможные пятизначные
числа без повторения цифр. Выясните, сколько среди этих
пятизначных чисел таких, которые:
а) начинаются цифрой 3;
б) не начинаются с цифры 5;
в) начинаются с 54;
г) не начинаются с 543.
5. Упорядоченные множества и размещения
Множество вместе с заданным порядком расположения его эле-
ментов называют упорядоченным множеством. Упо-
рядоченные множества будем записывать, располагая в круглых
скобках его элементы в заданном порядке. Например,
(А; В) и (В; А)
различные упорядоченные множества, которые можно получить из
одного и того же множества {А; В), упорядочивая его двумя спо-
собами. (Напомним, что при записи множества порядок рас-
положения его элементов не существен, т. е. {А; В} = {В; А}.)
Пусть даны четыре буквы А, Б, В, Г. Требуется выделить из
них две буквы, расположив эти две буквы в определенном поряд-
ке. Сколькими способами это можно сделать? Таких способов две-
надцать. В самом деле, первую букву можно выбрать четырьмя
способами, а вторую придется выбирать из оставшихся трех. Вот
эти двенадцать способов:
(А; Б); (А; В); (А; Г);
(Б; А); (Б; В); (Б; Г);
(В; А); (В; Б); (В; Г);
(Г; А); (Г; Б); (Г; В).
В этой задаче мы имели множество из четырех элементов
{А; Б; В; Г} и обнаружили, что из его элементов можно образовать
двенадцать упорядоченных множеств, по два элемента в каждом.
Поставим теперь общую задачу: сколько упорядоченных множеств,
по т элементов в каждом, можно образовать из п элементов?
В комбинаторике конечные упорядоченные множества называют
размещениями. Нашу задачу коротко формулируют так:
«Сколько существует размещений из п по т?»
Число размещений из п по т обозначают А™. Мы уже видели,
что
Al = 12.
20
Легко понять, что
А'п = п. (1)
В самом деле, один элемент из п можно выбрать п способами, а из
этого одного элемента получается одно-единственное упорядочен-
ное множество.
Докажем теперь, что при 1 <1 т < п
+1 = (п-т)А™. (2)
Вместе с формулой (1) эта формула позволит нам вычислять после-
довательно А%, А%, ... , А* . Например,
< = 35,
Л325 = (35 — 1) Л|5 = 35 • 34 = 1190,
= (35 — 2) Ап = 35 • 34 • 33 = 39270.
Так что из 35 учеников класса выбрать старосту, комсорга и физор-
га можно А%5 = 39 270 способами.
Докажем теперь формулу (2). Чтобы распределить tn + 1 эле-
ментов, взятых из данных п элементов, по т + 1 местам, можно
сначала выбрать какие-либо т элементов и разместить их по
первым т местам. Это можно сделать А™ способами. При каждом
из этих способов останется п — т элементов. Любой из них можно
поставить на т + 1-е место. Таким образом, при каждом из А™
заполнений первых т мест получим п — т возможных заполне-
ний (т + 1)-го места. Следовательно, всего их будет
Ап (п — т),
что и требовалось доказать.
Пользуясь формулами (1) и (2), получаем последовательно:
Ап = п, Ап — п(п—1), Ап=п(п— 1)(п — 2),
Ап = п(п— 1)(п — 2)...(п — т+1). (3)
Но произведение пг последовательных убывающих натуральных
чисел от п до (п — tn + 1) равно отношению факториалов чисел п и
п — т (см. задачу 34, б):
п (п — 1) (п — 2)... (п — т 4- 1) =
Поэтому окончательно получаем:
При т = 0 по формуле (4) получаем:
Ло = 1.
21
Это верно: существует только одно пустое множество, оно является
подмножеством любого множества, и мы условились считать, что
оно может быть упорядочено одним-единственным способом. Фор-
мулы (3) и (4) применимы при любых целых тип, удовлетворяю-
щих неравенству
О т п.
Вот таблица значений А™ при п 5.
Заметьте еще, что
Ап = Рп = п\ (5)
Упражнения
43. Покажите, что Ап-1 = Ah = п\
44. Сколькими способами можно выбрать четырех человек на четы-
ре различные должности из девяти кандидатов на эти должно-
сти?
45. В девятом классе 35 учащихся. Они обменялись друг с другом
фотокарточками. Сколько всего было роздано фотокарточек?
46. Из скольких различных предметов можно составить 210 разме-
щений по два элемента в каждом?
47. Найдите п, если А^ = 18 • Д^_2.
48. Какая часть из 107 семизначных телефонных номеров состоит
из семи различных цифр?
§ 3.
СОЧЕТАНИЯ
6. Число подмножеств конечного множества
Рассмотрим все подмножества множества А; Б; В; их восемь:
0 — пустое множество;
{А}, {Б}, {В} — три множества по одному элементу в каждом;
22
{А; Б}, {А; В}, {Б; В} — три множества по два элемента в каж-
дом;
{А; Б; В} — одно множество из трех элементов.
Число подмножеств по т элементов в каждом, содержащихся
в множестве из п элементов, обозначается С™. В комбинаторике
конечные множества называют сочетаниями. Поэтому С™ назы-
вают «числом сочетаний из п по т». Мы видим, что
С3° = 1, С'3 = 3, Сз = 3, = 1
И
Ci + С'з 4- Cl + Сз3 = 8 = 23.
Чтобы вывести формулу для С™, докажем сначала, что
А™ =£% • Рт. (1)
До общего доказательства рассмотрим случай п = 3 и т = 2.
Мы видели, что из трех букв А, Б и В можно образовать С^ = 3
множество по две буквы в каждом. Каждое из этих множеств можно
упорядочить Р2 = 2 способами, что дает 3 • 2 = 6 упорядоченных
множеств. В предыдущем пункте мы видели, что и в самом деле
А23 - 6.
Общее доказательство вполне аналогично. Чтобы образовать
упорядоченное множество, содержащее т элементов из данных п,
надо: а) выделить какие-либо т из этих п элементов, что можно
сделать способами, б) выделенные т элементов упорядочить,
что можно сделать Рт способами. Всего получим С™ • Рт способов
(упорядоченных множеств), т. е.
Ат — С’п . Р
г т*
что и требовалось доказать.
Из формулы (1) получаем:
. р
. гт,
Подставив сюда уже известные нам выражения
получим:
гт __ п\
-- --------— »
ml (п — т)1
что можно записать иначе так:
гт _ п(п—!)...(« — ffl + 1)
П ~ т\
Например,
с|5 = = 35 . 17 . ц = 6545.
6
(2)
(3)
23
Следовательно, в классе с 35 учащимися можно выбрать трех де-
легатов на конференцию 6545 способами (порядок, в котором
они называются, считается несущественным).
Приведем небольшую таблицу значений С™. В самом правом
столбце указаны суммы всех С” с данным п (С% определяются
для значений т, удовлетворяющих условию 0 т п).
Упражнения
49. Составьте все подмножества множества М и найдите их число,
если:
а) М = {1}; б) М = {1; 2}; в) М = {а\ b\ с; d}.
Для случая в) выпишите все подмножества, содержащие: 1) один
элемент; 2) два элемента; 3) три элемента; 4) четыре элемента.
50. Дано множество X = {a; b\ с\ d}. Составьте все подмножества
множества X, которые:
а) не содержат элемент а; б) содержат элемент а.
Сколько подмножеств получилось в случае а) и в случае б)?
51. Сколько подмножеств имеет множество из 6 элементов?
52. Найдите:
a) Cl; в) С4;
б) С}7; г) Cf;
Д) Ct+Cg;
е) Cioo С1оо-
53. Из 20 рабочих нужно выделить 6 для работы на определенном
участке. Сколькими способами это можно сделать?
54. В девятом классе 35 учащихся. Из них нужно избрать 4 делега-
та на конференцию. Сколько имеется возможностей такого
выбора?
55. Сколько можно составить из простых делителей числа 2310
составных чисел, которые содержат только два простых дели-
теля?
56. Сколько можно составить из простых делителей числа 3570
составных чисел, которые содержат только три простых дели-
теля?
24
57. Докажите, что верно равенство:
а) $ + & = (% б) С?о+С?о =
58. Упростите выражение:
ч 2 ^п-1 3 ^-з
а) ----Сп д-1; б) --------С 2/1
п + 1 г 2(2п — 1)
59. Сколько различных плоскостей можно провести через п точек
пространства, из которых никакие четыре не лежат в одной
плоскости, если каждая плоскость проходит через три из дан-
ных точек?
Рассмотрите
а) п = 3;
б) п = 5;
ch.
случаи:
в) п = 6;
г) п = 10.
60. Сколько диагоналей имеет:
а) выпуклый пятиугольник;
б) выпуклый двенадцатиугольник;
в) выпуклый двадцатипятиугольник;
г) выпуклый «-угольник, где п > 3?
61. Сколько человек участвовало в шахматном турнире, если из-
вестно, что каждый участник сыграл с каждым из остальных
по одной партии, а всего было сыграно 210 партий?
62. Сколькими способами можно группу из 15 учащихся разделить
на две группы так, чтобы в одной группе было четыре человека,
а в другой — одиннадцать человек?
7. Некоторые свойства числа сочетаний
Приведенную в предыдущем пункте таблицу значений
можно неограниченно продолжить вниз. Ее строки нумеруются це-
лыми неотрицательными числами п = 0, 1, 2, 3, ... Строка с номе-
ром п состоит из п + 1 числа:
СО 1 z~>2
Пу '->/!» > • • • ?
Таблицу эту принято называть «треугольником Паскаля», в честь
французского математика Б. Паскаля (1623—1662), исследо-
вавшего ее свойства.
В треугольнике Паскаля, выписанном на странице 24, замечаем,
что его строки симметричны: числа, одинаково удаленные от на-
чала и конца строки, равны. Например,
Cl = cl~2 = d = 10.
Оказывается, что правило это имеет общий характер: при любых
п и т (0 п) верно равенство
С™ = СТ”. (1)
25
Доказательство довольно просто:
т! (п — т)! (п — т) I (n — (п — т)) I
Сумма
есть не что иное, как полное число подмножеств множества из п
элементов. Поэтому равенство
Й + с,1, + й + •. • + Ск = 2" (2)
является следствием такой теоремы:
Теорема. Число всех подмножеств множества, состоящего
из п элементов, равно 2п.
Утверждение теоремы верно при п = 0 (пустое множество
имеет единственное подмножество—само себя). Для до-
казательство проведем методом математической индукции.
1) Множество из одного элемента, например множество {а},
имеет два подмножества: пустое множество 0 и само множество
{а}. Следовательно, при п = 1 теорема доказана, так как 21 = 2.
2) Докажем, что A(k) => A(k + 1), т. е. из того, что мно-
жество, состоящее из k элементов, имеет 2й подмножеств (высказы-
вание A(k)), следует, что множество, состоящее из k + 1 элементов,
имеет 2Й+1 подмножеств (высказывание A(k + 1)).
Рассмотрим множество В, содержащее k + 1 элементов:
В = {Ьх\ Ь2, Ьз, ... ; bh+1}.
Пусть множество В' содержит все элементы множества В, кроме
элемента bh+1:
в' = {Ьг, ь2; 63;...; bk}.
По A(k) множество В' имеет 2й подмножеств. Из каждого такого
подмножества образуется новое множество добавлением элемен-
та bk+1. Получили еще 2й подмножеств множества В. Всего получи-
лось 2й 4~ 2й = 2Й+1 подмножеств. На основании принципа математи-
ческой индукции теорема доказана.
Упражнения
63. Вычислите:
а) ей; в) С'М; д) Й};
б) г) е) C?So.
64. Покажите, что истинно равенство:
Сб + + Cl d + С| + Сб5 + cl = 26.
65. Докажите, что справедливо равенство:
а) С5 С5 С5 = Cl 4~ С5 + Cf;
б) Cq 4- Cg 4- Cq = 4- C$ 4" Сб.
26
66. Вычислите
с\ + с? + с? + с?.
67. Учащийся имеет по одной монете достоинством в 1 коп., 2 коп.,
3 коп., 5 коп., 10 коп., 15 коп., 20 коп. Сколькими способами
он может эти монеты разложить в два кармана?
68. Из 10 различных цветков нужно составить букет так, чтобы
в него входило не менее двух цветков. Сколько способов су-
ществует для составления такого букета?
69. Имеется 12 различных конфет. Сколькими способами можно
из них составить набор, если в наборе должно быть четное
число конфет?
8. Рекуррентная формула для вычисления числа сочетаний
Попробуйте сложить два соседних числа в какой-либо строке
треугольника Паскаля. Вы всегда получите число следующей
строки, стоящее под правым слагаемым. Например, складывая
4 и 6 из четвертой строки треугольника Паскаля, приведенного
на странице 24, получим число 10, которое стоит в пятой строке
под числом 6, стоящим в четвертой строке. Оказывается, что при
0 т < п справедлива формула
С? + С”+1 = СД1. (1)
Для доказательства достаточно привести дроби
/и ___ п (п — 1) • . . . • (п — т + 1)
и
£,m-H _ п(п—!)•...•(« — m+l)(n — т)
п 1 • 2 • 3 • ... • т(т+ 1)
к общему знаменателю и сложить:
Ст + Ст+' = (n(n-l).....(n-m+l))(/n+l)
1 • 2 • 3 • . .. • т (т + 1)
(п(п — 1) ... • (n — ffl + 1)) (п — т) _
1 • 2 • 3 • ... • m(m+l)
— п^п — !)••••(« — m 4- 1) рп 4- 1 п — m) _
1 • 2 • 3 • . .. • т(т 4- 1)
— (» + 0 ” (» — 1) • •. • (л — m 4~ 1) __ pm+l
Формула (1) позволяет последовательно заполнять строки тре-
угольника Паскаля, пользуясь тем, что в начале и конце каждой
строки стоят единицы.
27
Приведем здесь каля: первые одиннадцать строк треугольника Пас-
0 1 1 1 1
2 1 2 1
3 1 3 3 1
4 1 4 6 4 1
5 1 5 10 10 5 1
6 1 6 15 20 15 6 1
7 1 7 21 35 35 21 7 1
8 1 8 28 56 70 56 28 8 1
9 1 9 26 84 126 126 84 36 9 1
10 1 10 45 120 210 252 210 120 45 10 1
i
Равенство (1) можно доказать и другим способом, с помощью следую-
щих рассуждений.
Пусть дано множество А = {ai; а2; ... ; ап; ап+1} из п + 1 элементов.
Число его подмножеств, каждое из которых содержит т + 1 элементов,
равно СЙ*- С другой стороны, это число можно подсчитать следующим
образом.
Подмножества множества А, содержащие т 4“ 1 элементов, делятся на
две (не пересекающиеся) группы:
1) содержащие элемент сл+1,
2) не содержащие элемента ая+1
В первой группе столько же подмножеств, сколько подмножеств, со-
держащих по т элементов, имеет множество
А' = {аг, а2; ... ; ап },
состоящее из п элементов. Их число равно С”.
Число же подмножеств второй группы равно числу подмножеств мно-
жества А’, содержащих т 4- 1 элементов, т. е. Поэтому всего у множе-
ства А подмножеств, содержащих т 4- 1 элементов, будет
С™ + С«+‘.
Итак, мы получили для
два разных выражения для
элементов. Следовательно,
множества А, содержащего п 4- 1 элементов,
числа его подмножеств, содержащих tn + 1
гт ।
“г .
Упражнения
70. Докажите, что справедливо равенство:
а) С 4- 2СЙ -}- СЙ2 = СЙ;
б) с„ 4- зей + зся+2 4- ей3 = ей3-
28
§ 4.
НАТУРАЛЬНАЯ СТЕПЕНЬ БИНОМА
(ФОРМУЛА НЬЮТОНА)
9. Формула Ньютона а Основные следствия.
Вам знакомы формулы:
(а + Ь)1 = а + Ь,
(а + 6)2 = а2 + 2аЬ + Ь2,
(а + &)з = а3 + За2Ь + ЗаЬ2 + Ь3.
Нетрудно вычислить, что
(а + Ь)* = а4 + 4а36 + 6а262 + 4а63 + 64,
(а + £>)б = аъ 4- $&ь 4- 10а362 + 10а263 + 5а&4 + Ь5.
Сразу бросается в глаза то обстоятельство, что коэффициенты в
правых частях этих формул равны числам из соответствующей
строки треугольника Паскаля.
Оказывается, что при любом натуральном п верна формула
(а 4- Ь)п = С°ап 4- dnan~'b 4- ... 4- С^ап~тЬт + ... + О", (1)
которая называется формулой Ньютона, в честь английского
физика и математика Исаака Ньютона (1642—1727). Правую
часть равенства (1) называют разложением степени бинома.
Доказательство проведем методом математической, индукции.
Обозначим через Л(п) равенство (1) при данном п.
1) Д(1) верной так как
(а 4- Ь)1 = а 4- b = С3а + С\Ь.
2) Остается показать, что A (k) => A (k 4- 1) при любом натураль-
ном k. Сначала проведем это доказательство на примере k — 3.
Пусть известно, что
(а 4- Ь)3 = da3 4- С\а2Ь 4- dab2 + db3.
Тогда
(а 4- b)* = (da3 + da2b 4- dab2 + db3) (a 4- b) =-•
= da* + da3b 4- da2b 4- dab3 4-
4- da3b 4- da2b 4- dab3 4- db* =
= da* + (Cg + d) a3b 4- (d + C32) a2b2 4- (Cf 4- Оз) ab3 4- db*.
Так как
/>0 । z>0 z>0 I /-Л । />2 z>2 . z>3 ^>3
Ьз = 1 = C4, G3 -j- C3 = C4, C3 4- C3 = C4, C3 -f- C3 = C4,
d = i=d,
то окончательно получаем:
(a 4- b)* = da* 4- C\a3b 4- da2b2 4- dab3 4- db*.
29
При любом натуральном й вычисления проводятся аналогично:
(а + b)k+1 = (С3а* 4- Clak-'b 4- ... 4- C?ak-mbm 4-... 4- Ckbk) X
X (а 4- b) = Cft°aft+1 + C'kakb 4- ... 4- С™+'а*-тЬт+1 4- ... 4- Ckhabk 4-
4- C°kakb 4-... 4- Ckak-mbm+1 4-... 4- Ckh~}abk 4- Chhbk+1 =
= C°hak+' + (C£ + Ci) akb 4- ... 4- № 4- C^’) a^b^ 4- • • • 4-
4- (С*-1 4- Cft abk 4- Chhb^ = C°ft+1a*+1 4- C\^akb 4- ... 4-
4- C^ak-mbm^ 4- . • • + Ckh+\abk 4- СЭД&*+1.
Из 1) и 2), на основании принципа математической индукции,
следует, что предложение А(п) истинно для любого натурального п.
Формула (1) доказана.
Пример 1. (а 4- Ь)7 = а7 4* 7ав6 4~ 21а5Ь2 4- 35а463 4~ 35а364 4-
4- 2W 4- 7аЬ6 4- Ь7.
Коэффициенты С„ формулы Ньютона называют биномиаль-
ными коэффициентами.
Рассмотрим основные следствия из формулы Ньютона.
1°. В разложении (а 4- Ь)п по формуле Ньютона содержится
«4-1 слагаемых. Это видно из равенства (1) (объясните почему).
2°. В формуле Ньютона — равенстве (1) — показатель степени
при а убывает от п до 0, а показатель степени при b возрастает от
О до п. Сумма показателей степеней при а и b в любом слагаемом
разложения равна п — показателю степени бинома.
3°. Биномиальные коэффициенты, равноудаленные от концов
разложения, равны между собой (так как С™ = С“~т).
4°. Биномиальные коэффициенты сначала возрастают, а затем
убывают. Если показатель степени бинома четный, то биномиаль-
ный коэффициент среднего слагаемого разложения наибольший,
если же показатель степени бинома нечетный, то биномиальные
коэффициенты двух средних слагаемых равны между собой и яв-
ляются наибольшими.
5°. Чтобы записать в общем виде слагаемые в равенстве (1),
удобно (k 4- 1)-е слагаемое считать /г-м членом и обозначать его
через Th . Тогда
Tk = Cknan~kbk, 6 = 0, 1,..., п. (2)
Например, То = С^а^Ь0 — первое слагаемое, Т\ = С^ап-16 — вто-
рое слагаемое, Т2 — С»ап~2Ь2 — третье слагаемое.
1 1
Пример 2. Найти четвертый член разложения (г2 4- г3 )12.
Искомый член разложения находим по формуле (2)
1_ 2_ 20
= С12 (г2 )8 (г3 )4 = 495 г3.
80
Пример 3. Найти номер члена разложения (г + г~а)12, не
содержащего z, т. е. содержащего z в нулевой степени.
По формуле (2) находим:
Tk = C?2zl2-ft(z~2)ft = C?2z12-3\
По условию задачи 12 — 3k = 0. Следовательно, k — 4. Таким
образом, это четвертый член разложения.
Пример 4*. Найти номер наибольшего члена в разложении
(1 4- 0,01)1000.
Tk+l _ tfwo • 0,01_ 0,01 . fej (1000 — /г)! _ (1000 —/г)
~ С1000-°.°1А ~ (Л+1)! (ЮОО-fe-l)! “ 100(6 4-1) '
Выясним, при каких fe^±-1>l: 1000~fe ^1ф»&<8—.
г ТА 100(6 4-1) 101
Таким образом, > 1 при k < 8 и ^±-1 < 1 при остальных k,
т. е. при k^-9.
Итак, члены разложения (1 4- 0,01)1000 с возрастанием номера
возрастают вплоть до Тв, а затем убывают. Следовательно, Та —
наибольший член разложения.
Примечание. Не следует забывать о различии между коэф-
фициентом слагаемого разложения и биномиальным коэффициентом
того же слагаемого. Например, в разложении
(2а — 36)4 = 16а4 — 96а36 4- 216а262 — 216а63 4- 8164
коэффициент 3-го слагаемого разложения равен 216, а его биноми-
альный коэффициент равен С2 = 6.
Упражнения
71. Найдите разложение степени бинома:
а) (а 4- &)’; L L
б) (х 4- у)6; Д) (х + У )5;
В) (х у)5; _ е) (х — 2у)в;
г) (Кх — Ку)4; ж) (Зх— 1)7;
з) (1 4- у2)4;
и) (р~2-1)в;
к) (| + 2)>.
72. Найдите два средних члена разложения (а3 — ab)31.
73. Пользуясь формулой Ньютона, докажите, что:
а) сумма всех биномиальных коэффициентов разложения
(а 4- Ъ)а равна 2й;
б) сумма биномиальных коэффициентов, стоящих на четных
местах, равна сумме биномиальных коэффициентов, стоящих
на нечетных местах.
Указания. а) Положите в формуле Ньютона а = 1,
&= 1;
б) положите в формуле Ньютона а = 1, b = —1.
31
10*. Сведения из истории. Применение комбинаторики
к теории вероятностей
Отдельные комбинаторные задачи занимали еще древнегре-
ческих математиков. Но основные факты из области комбинато-
рики, которые теперь входят в курс общеобразовательной сред-
ней школы, были получены математиками XVII и XVIII вв.—
Паскалем, Лейбницем, Якобом Бернулли и другими — в связи с
развитием алгебры и теории вероятностей.
Несомненно, что каждому из вас случалось рассуждать о «ве-
роятности» наступления того или иного события, говорить, что ка-
кое-либо событие «очень вероятно», «мало вероятно», «столь же
вероятно», как некоторое другое событие, и т. п. Теория вероят-
ностей имеет дело с такими ситуациями, когда вероятность
наступления событий допускает точную количественную оценку.
Проще всего ситуации, обладающие известной симметрией. На-
пример, при бросании правильной кубической кости естественно
считать выпадение одного, двух, трех, четырех, пяти или шести
очков одинаково вероятными событиями и приписывать каждому
1 _
из них вероятность—. Так как в трех из этих шести случаев число
очков будет четным, то естественно считать, что вероятность вы-
3 1
падения четного числа очков равна — — — .
Вообще, вероятностью события называют отноше-
ние числа благоприятствующих ему случаев к общему числу
исключающих друг друга случаев.
Рассмотрим некоторые примеры.
Пример 1. В урне лежат 10 одинаковых по форме шаров:
3 белых, 2 черных и 5 красных. Чему равна вероятность того, что
наугад вынутый шар окажется: а) красным; б) не черным?
Так как все 10 шаров одинаковы по форме, то общее число
равновозможных случаев равно десяти (мы можем вынуть лю-
бой из десяти шаров). В задаче а) благоприятных случаев 5 —
по числу красных шаров, т. е. вероятность события равна — = — •
В задаче б) благоприятных случаев 8 — мы можем вынуть лю-
бой из 3 белых и любой из 5 красных шаров. Поэтому искомая
8 4
вероятность равна — = — .
10 5
Пример 2. Имеется пять отрезков: длины 1, 3, 5, 7 и 9 см.
Определить вероятность того, что из трех наудачу взятых отрез-
ков из указанных пяти можно составить треугольник.
Имеется С2, т. е. десять возможностей взять наудачу три от-
резка из данных пяти.
Подсчитаем число случаев, когда из выбранных трех отрезков
можно составить треугольник. Напомним, что треугольник из от-
32
резкое длин a, b, с (a^b^Zc) можно составить тогда и только
тогда, когда с — b < а.
Если длина а наименьшего отрезка равна 1, то треугольник
составить нельзя, так как разность двух нечетных чисел с и b
(cZ>b) больше 1 (таких случаев С^, т. е. 6).
Если длина а наименьшего отрезка равна 3, то треугольник
можно составить, если
b = 5, с — 7 или b = 7, с = 9
(и нельзя, если b — 5, с = 9).
Если длина наименьшего отрезка равна 5, то b == 7 и с = 9, и
в этом случае из выбранных отрезков можно составить тре-
угольник.
Таким образом, из 10 возможных случаев благоприятными
-> 3
являются 3 и искомая вероятность равна —.
Пример 3. Считая 36 возможных исходов бросания двух
костей равновероятностными, найти вероятность выпадения сум-
мы в 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 и 12 очков.
На каждую из шести возможностей выпадения 1, 2, 3, 4, 5 и 6
очков на первой кости имеется столько же возможностей выпа-
дения от 1 до 6 очков на второй кости. Таким образом, всего
имеется 6-6 = 36 разных исходов. По условию задачи эти исхо-
ды равновероятностны. Посчитаем число благоприятных исходов,
например, для суммы в 8 очков.
Сумма в 8 очков может получиться при выпадении 6 очков на
первой и 2 очков на второй, 5 на первой и 3 на второй, 4 на пер-
вой и 4 на второй, 3 на первой и 5 на второй и, наконец, 2 на
первой и 6 на второй, т. е. благоприятных исходов пять. Таким
Л 3
образом, вероятность выпадения суммы в 8 очков равна —.
36
Решения для остальных случаев видны из таблицы:
Число очков Благоприятные исходы Число благоп риятных исх одов Вероятность
2 1 и 1 1 1 26
3 1 и 2; 2 и 1 2 1 18
4 1 и 3; 2 и 2: 3 и 1 3 1 12
5 1 и 4; 2 и 3; 3 и 2; 4 и 1 4 Д 9
6 1 и 5; 2 н 4; 3 и 3; 4 и 2; 5 и 1 5 5 36
7 1 и 6; 2 и 5; 3 и 4; 4 и 3; 5 и 2; 6 и 1 6 1 6
2 Заказ 243
33
Продолжение
Число очков Благоприятные исходы Число благоприятных исходов Вероятность
9 Зи6;4и5;5и4;6иЗ 4 1 9
10 4и6;5и5;6и4 3 £ 12
11 5 и 6; 6 и 5 2 1 18
12 8 и 6 1 1 36
Упражнения*
74. На шести одинаковых карточках написаны буквы А, В, К, М, О
и С. Карточки перемешиваются и раскладываются наугад в
ряд. Какова вероятность, что получилось слово МОСКВА?
75. Из урны, содержащей 5 шаров, занумерованных числами 1, 2, 3,
4, 5, извлекаются наудачу два шара один за другим. Какова
вероятность того, что номера извлеченных шаров идут в по-
рядке возрастания?
76. Из урны, содержащей 5 шаров, занумерованных числами
1, 2, 3, 4, 5, извлекаются наудачу все 5 шаров один за другим.
Какова вероятность того, что номера извлеченных шаров идут
в возрастающем порядке?
77. Из урны, содержащей 5 шаров, занумерованных числами
1, 2, 3, 4, 5, извлекаются наудачу сразу 4 шара. Какова вероят-
ность того, что номера извлеченных шаров нечетны?
78. Библиотечка состоит из 10 различных книг, причем 5 книг
стоят по 4 руб. каждая, 2 книги — по 3 руб. и 3 книги — по
1 руб. Найти вероятность того, что взятые наудачу две книги
стоят 5 руб.
79. На восьми одинаковых карточках написаны числа 2, 4, 6, 7, 8,
11, 12 и 13. Наугад берутся 2 карточки. Определить вероят-
ность того, что образованная из двух полученных чисел дробь
сократима.
11*. Примеры более сложных задач из теории
вероятностей
Пример 1. Еще в XVII в. игроки в кости обнаружили, что
более чем в половине случаев при четырех бросаниях кости хотя
бы раз появляется шестерка. Расчет по правилам теории вероят-
ностей подтверждает это наблюдение. При первом бросании кос-
ти имеется шесть различных возможностей (выпадение 1, 2, 3, 4,
34
5 и 6 очков). Каждая из них разбивается на шесть возможностей
в зависимости от результата второго бросания, что дает 62 = 36
возможностей. При трех бросаниях число различных возможно-
стей будет 63 = 216, а при четырех — 64 = 1296. Но среди этих
1296 случаев, которые естественно считать равновозможными,
будет 54 = 625 таких, где шестерка не появилась ни разу, а в
1296—625 = 671 случае хотя бы один раз из четырех выпадает
шестерка. Значит, вероятность выпадения хотя бы одной шестер-
ки при четырех бросаниях кости равна:
— « 0,52 > ±.
1296 2
Когда секрет был разгадан, один из игроков придумал новый
вариант игры. Так как выпадение при бросании двух костей двух
шестерок казалось ему событием в шесть раз менее вероятным,
чем выпадение шестерки при одном бросании (в этом он был
прав), он сделал вывод, что при 4-6 = 24 бросаниях пары костей
более чем в половине случаев хоть один раз будут появляться
шестерки. Но экспериментальная проверка этого вывода принес-
ла ему разочарование: две шестерки при 24 бросаниях пары кос-
тей появлялись менее чем в половине случаев. Тогда игрок обра-
тился к Паскалю за разъяснениями. Паскаль легко объяснил ка-
жущийся парадокс. При одном бросании двух костей имеется
36 возможностей, из которых только одна соответствует выпаде-
нию двух шестерок. При 24 бросаниях всего получается 3624 воз-
можных случаев, из которых в 3524 случаях ни при одном броса-
нии не выпадает сразу двух шестерок, а в 3624—3524 случаях хотя
бы раз две шестерки появятся вместе в одном броске. Вероят-
ность выпадения хотя бы раз двух шестерок равна *:
3624 3521 * Л5\24 1
—-----— = 1 — р « 0,48 < -.
3624 1зб/ 2
Как видим, вероятность несколько меньше, чем половина.
Пример 2. При приемке массовой продукции производится
выборочный контроль: из партии в 100 изделий выбирается 20 и
при обнаружении в этой выборке хотя бы одного дефектного из-
делия вся партия бракуется (или передается на сплошную про-
верку). В партии имеется 10 дефектных изделий. Какова вероят-
ность, что хотя бы одно дефектное изделие попадает в выборку?
Решение. Число различных способов выбрать 20 изделий из
100 равно числу размещений из 100 по 20:
А 20 1001
100 == --•.
801
Среди этих способов имеется
л 20 90!
^эо = —
__________ 70!
* Проведите расчет с помощью логарифмов.
2*
35
таких, что ни одно дефектное изделие не попало в выборку.
В остальных
Л 20 д20
/1100 — /190
случаях хотя бы одно дефектное изделие будет обнаружено. Со-
ответствующая вероятность равна:
= 1 - 901801 « 0,9049.
л20 100! 701
Л100
Первый пример типичен для начального периода развития
теории вероятностей. Значительная часть разбиравшихся мате-
матиками задач на подсчет вероятностей бралась из области
азартных игр, выигрышных лотерей и т. п. Это объясняется тем,
что при самом изготовлении костей и карт и организации лоте-
рей заботятся о соблюдении «равновозможности» различных ис-
ходов испытания, так что применение определения вероятности
как отношения числа благоприятствующих случаев к общему чис-
лу равновозможных особенно просто. В настоящее время о том
же заботятся и при организации выборочного контроля и выбо-
рочных статистических исследований. Но область применений тео-
рии вероятностей не исчерпывается такого рода ситуациями, где
легко все возможные исходы испытаний разбить на «равновоз-
можные» случаи. Здесь мы лишены возможности рассказать о
том, как определяется вероятность в более общей ситуации.
К началу XX в. комбинаторика считалась в существенном за-
конченной частью математики. Давно сложилась и принятая здесь
специфическая терминология (перестановки, сочетания, разме-
щения и т. п.). В XX в. комбинаторику стали воспринимать как
первую главу теории множеств, занимающуюся конечными мно-
жествами (их подмножествами, отображениями друг от друга
и т. п.), что содействовало более последовательной классифика-
ции комбинаторных задач. В новейшее время роль комбинатори-
ки значительно возросла в связи с разработкой сложных управ-
ляющих и счетно-решающих устройств и развитием «теории ин-
формации». В комбинаторике появилось много новых задач,
которые вновь привлекают внимание математиков.
Упражнения*
80. В урне а белых и Ь черных шаров. Из урны извлекаются два
шара. Найти вероятность того, что оба шара будут белыми.
81. Из 10 билетов выигрышными являются 2. Определить вероят-
ность того, что среди взятых наудачу 5 билетов: а) один вы-
игрышный, б) два выигрышных, в) хотя бы один выигрышный.
82. Из 60 билетов, входящих в экзаменационные билеты, студент
подготовил 50. На экзамене студент должен ответить на 2 би-
36
лета. Какова вероятность того, что студент ответит на оба би-
лета?
83. В шахматном турнире участвуют 16 человек, которые будут
распределены по жребию на две группы по 8 человек в каждой.
Какова вероятность того, что двое наиболее сильных участни-
ков: а) будут играть в одной группе, б) в разных группах?
84. В партии из г изделий k бракованных. Определить вероятность
того, что среди выбранных наудачу для проверки s изделий
ровно / окажутся бракованными.
85. Найдите вероятность того, что при k бросаниях кости все вы-
павшие числа очков будут различны (k = 2, 3, 4, 5, 6).
86*. Пятеро гостей пришли в шляпах. Какова вероятность того,
что, наудачу надевая при расставании шляпу, каждый из них
надел чужую шляпу?
87*. Восемь различных книг расставлены наудачу на одной полке.
Найти вероятность того, что две определенные книги окажутся
рядом.
88*. Докажите, что множество из п элементов можно разбить
--------—------ различными способами на k попарно не пере-
тх\ т21 ... т^\
секающихся (не имеющих общих элементов) подмножеств,
содержащих по mlt ... , mk элементов, где т1 + т2 + ... -h
+ mk = п.
89. Сколькими различными способами можно разбить множество
из десяти элементов на два подмножества из трех элементов
и два подмножества из двух элементов?
Дополнительные упражнения к главе П
90. Решите уравнение:
а) <“ + 2>!.= 72; в) = 2М ;
nl ’ (2п — 3)! (л—2)!
б) (MJIL = 30; г) fel = !2fe! .
' (k — 1)! (k — 4)! (k — 2)!
91. Решите неравенство:
a) С”-1)1 < 72; в) -----------— < ЮОО;
(л — 3)! (n+l)(n+2)
б) (2n~ °- > 420; г) (n~4) > 0,00002.
(2л —3)! (л —3)1
92. Сколько всевозможных пятизначных чисел можно составить
из цифр 0, 1,2, 3, 4, не повторяя цифры в числе?
93. Найдите сумму всех трехзначных чисел, которые можно со-
ставить из цифр 1, 2, 3, не повторяя цифры в числе.
94. Найдите сумму всех четырехзначных чисел, которые можно
составить из цифр 1, 3, 5, 7, не повторяя цифры в числе.
37
©5. Среди перестановок цифр числа 1 234 567 сколько таких, кото-
рые:
а) начинаются с 123;
б) кончаются 123;
в) начинаются с цифр 1, 2, 3, причем эти цифры расположе-
ны в любом порядке и занимают первые три места;
г) начинаются с рядом стоящих цифр 1 и 2?
96. На книжной полке помещается 30 томов. Сколькими способа-
ми их можно расставить, чтобы при этом 1-й и 2-й тома: а) не
стояли рядом; б) стояли рядом?
97. Решите уравнение:
а) С’ = jcJ+2;
б) ЗС?,7' =
98. При каких значениях п
а) С5п < б)
99. Решите неравенство:
а) С* < С3п; в)
б) С27л > CL; г)
2п
В) r n-1
ь2«+1
Сп
ь2п-1
г>п—1
С2п
имеет место неравенство:
С5 *> С4?
Ch—1 и
19 < С19,
Ck—2
15 > С15-
7
“ 13’
_ 9
~ 17'
100. Сколько окружностей можно провести через 10 точек пло-
скости, из которых никакие четыре точки не лежат на одной
окружности и никакие три точки не лежат на одной прямой,
если каждая окружность проходит через три из этих точек?
101*. Докажите, что верно равенство:
Сэ 4- Cio 4- Си 4- ••• 4~ С20 = С21.
102. Сколько различных аккордов можно взять на десяти выбран-
ных клавишах рояля, если каждый аккорд может содержать
от трех до десяти звуков?
103. Собрание из 40 человек избирает председателя, секретаря и
трех членов редакционной комиссии. Сколькими способами
можно выбрать этих пять человек?
104. В подразделении 60 солдат и 5 офицеров. Сколькими способа-
ми можно выделить караул, состоящий из трех солдат и од-
ного офицера?
105. Из 10 юношей, 8 мальчиков и 5 девушек нужно составить шах-
матную команду, в которую входили бы 4 юноши, 1 мальчик
и 2 девушки. Сколькими способами это можно сделать?
106. Имеются т белых шаров и п черных шаров, причем т > п.
Сколькими способами можно все шары разложить в ряд так,
чтобы никакие два черных шара не лежали рядом?
38
107. Из 10 роз и 8 георгин нужно составить букет так, чтобы в нем
были 2 розы и 3 георгина. Сколькими способами можно со-
ставить такой букет?
108. Докажите, что биномиальные коэффициенты, равноудаленные
от концов, равны между собой.
109. В разложении (-^у 4- -/У5) сумма биномиальных коэффи-
циентов, стоящих на четных местах, равна 32. Найдите член,
содержащий у2>8.
ПО. Найдите сумму коэффициентов разложения (5х2 — 4у3)7.
111*. Найдите номер наибольшего члена в разложении:
ч / , 1V00
а) —J- — ;
' \2 2
2 _l _LVC0
ю+цу
112*. Сколько членов разложения (1 + 0,01)10 надо взять, чтобы
определить число (1 + 0,01)10 с точностью до 0,001; до
0,000001?
Глава
ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА,
БЕСКОНЕЧНЫЕ
ПОСЛЕДОВАТЕЛЬНОСТИ
И ИХ ПРЕДЕЛЫ
§ 5.
ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
12. Вводные замечания
1. Представления о числах складывались постепенно под вли-
янием требований практики. С давних пор числа употреблялись:
а) при счете, б) при измерении величин.
Ответ на вопрос «сколько элементов содержит данное конечное
множество?» всегда выражается либо натуральным числом, либо
числом нуль (если множество пусто). Следовательно, множество
Zo= {0; 1; 2; 3; ...}
всех неотрицательных целых чисел обслуживает все потребности
счета.
Иначе обстоит дело при измерении величин. Расстояние между
двумя селениями может равняться 3,5 километра, площадь комна-
ты — 16,45 квадратным метрам и т. п.
При помощи алгоритма деления любое дробное неотрицатель-
ное число — (т 0, п > 0 — целые) превращается в конечную
п
или в бесконечную десятичную дробь:
— = 0,125;
8
- = 3,66666666... .
з
Для единообразия мы будем конечные десятичные дроби дополнять
справа бесконечной последовательностью нулей:
40
1 = 0,12500000... .
8
Целые числа будем тоже дополнять бесконечной последователь-
ностью нулей справа от запятой:
17 = 17,00000... .
Таким образом, мы видим, что любое неотрицательное рациональ-
ное число может быть представлено в виде бесконечной десятичной
дроби:
г = До, «2 «з ••• •
При этом есть целая часть числа г, а
0, cij а% аз...
его дробная часть.
2. Такое же представление годится и для отрицательных рацио-
нальных чисел. Только во избежание йедоразумений целую часть
отрицательного числа надо обозначать чертой (минусом) сверху.
Например, число
мы будем представлять себе записанным в виде
2,500000000... .
Аналогично
—0,789 - 1,21100000...
— 117-1 = — 117,3333... = — 118 + - = 118,66666... .
3 3
Таким образом, любое рациональное число г представляется
в виде бесконечной десятичной дроби:
г = а0, а^аз ... ,
где а0 — целое число, а целые числа ah (k=1,2,3,...) лежат в
пределах
0 < ah <9.
При этом aQ есть целая часть числа г, а дробная часть числа г пред-
ставляется бесконечной десятичной дробью
0, а^аз... .
3. Если целая часть числа х меньше целой части числа у, то
само число х меньше числа у. Если целые части двух чисел равны,
то для их сравнения приходится обращаться к их дробным частям.
Например,
15,30405... < 15,30410... ,
41
так как у этих чисел равны целые части и первые три десятичных
знака после запятой, а четвертый знак после запятой у левого числа
меньше: 0 < 1.
Правило сравнения бесконечных десятичных дро-
бей:
если aft< bk и at = bt при всех i < k.
Заметьте, что это правило применимо при любых знаках целых
частей а0 и bQ. Например,
1,75000... <1,75010... .
Замечание. Записи чисел с отрицательными целыми частями
применяют на практике при вычислениях с помощью логарифмов, где целую
часть числа называют его характеристикой, а дробную — его мантиссой.
В практических вычислениях, конечно, не выписывают бесконечных после-
довательностей нулей справа.
Упражнения
113. Запишите число в виде бесконечной десятичной дроби:
а) 7; б) 12,38; в) -7,935; г) 1; д) -1; е) -1.
4 4 3
114. Сравните числа:
а) 17,586631 и 17,586897;
б) —2,37561 и —2,37571;
в) —0,786 и 0,687;
г) 0,2444444444... и 0,244.
13. Периодические десятичные дроби
В предыдущем пункте мы встретились с десятичными дробями,
у которых начиная с некоторого места все знаки повторяются:
0,12500000... , 3,6666666... . и т. п. Такие десятичные дроби назы-
ваются периодическими.
Определение. Бесконечная десятичная дробь
Оо» а^а^а^...
называется периодической, если существуют такие нату-
ральные числаN up, что
ап+р = ап для всех n N.
Например, 3,6666666... есть периодическая десятичная дробь:
для нее N = 1, р = 1 и а„+1 = ап — 6 для всех n 1. Число
0,12500000... тоже представлено в виде бесконечной периодической
десятичной дроби: здесь N = 4, р — 1 и ая+1 = ап = 0 для всех
л > 4. Число 2,1783838383... . тоже записано в виде бесконечной
42
периодической десятичной дроби: здесь N = 3, р = 2 и ап+2 = ап
для всех п > 3, так как при нечетных п имеем ап = 8, а при чет-
ных — ап = 3. Периодические дроби принято записывать короче:
вместо 3,66666666... пишут -3,(6), вместо 0,1250000000... пишут
0,125(0), вместо 2,17838383838383... пишут 2,17(83). Число, напи-
санное в скобках, называют периодом; 3,(6) читается «три целых
и шесть в периоде», 2,17(83) читается «два с минусом, семнадцать
сотых и восемьдесят три в периоде».
Докажем теперь важную теорему.
Теорема 1. Каждое рациональное число представляется
бесконечной периодической десятичной дробью.
При доказательстве достаточно рассматривать только неотри-
цательные числа, так как десятичные знаки после запятой в пред-
ставлении числа г в виде дроби
«0, а^аз...
совпадают с десятичными знаками дробной части этого числа, а
дробная часть рационального числа есть неотрицательное рацио-
нальное число.
Представление рационального числа в виде десятичной дроби
получается в результате применения алгоритма деления. Рассмотрим
пример. Будем делить 12 на 55:
12 |55
ПО 0,218
-* 100
55
450
440
-> 10
Получив два раза остаток 10, мы можем не вести вычисления даль-
ше: как остатки, так и цифры в частном будут повторяться. По-
этому
^ = 0,2(18).
В общем случае: при делении на произвольное натуральное
число п возможно только п остатков
0, 1, 2, ... , п — 1.
Поэтому какой-либо из них должен повториться после не более
чем п шагов алгоритма.
Замечание. Бесконечные десятичные дроби с нулем в
периоде получаются, если какой-либо остаток в алгоритме деления
оказывается равным нулю. После этого, конечно, идут сплошь
нулевые остатки.
43
Какие же периодические десятичные дроби являются представ-
лениями рациональных чисел? Ответ оказывается простым: лю-
бые, кроме имеющих девятку в периоде.
Теорема 2. Любая периодическая десятичная дробь
не имеющая девятку в периоде, является представлением како-
го-либо рационального числа, получающимся из этого числа в
результате алгоритма деления.
Доказательства этой теоремы мы не даем. Несколько позднее
мы научимся находить по бесконечной периодической десятичной
дроби (за указанным исключением) обыкновенную дробь — , из
п
которой заданная периодическая дробь получается.
Легко понять, почему, например, бесконечная дробь
0,23(9)
не может получиться в результате деления натурального числа пг на нату-
tn
ральное число п. Допустив обратное, мы получили бы, что число г = —
и
должно удовлетворять неравенствам г < 0,24 и г > 0,2399...9 при любом fe.
Но тогда разность ь "знаке в
0,24 — г,
будучи положительной, должна была бы быть меньше
0,24 — 0,2399... 9 = 10’*
. , k знаков
при любом k, что невозможно.
Упражнения
115. Представьте число в виде бесконечной десятичной дроби.
Объясните, почему эта дробь является периодической:
ч 7 -.23 . 3 .29
а) —; б) —; в)---------------; г)----------.
3 ’ 30 7 11
14. Действительные числа
О том, что множество Q рациональных чисел включается в бо-
лее обширное множество R действительных, чисел, уже говорилось
в учебнике седьмого класса. Действительные не рациональные
числа называются иррациональными. В качестве примера такого
иррационального числа в учебнике седьмого класса приводилось
число ]/2. Для него был указан алгоритм построения представляю-
щей его бесконечной десятичной дроби:
/2 = 1,41421356... .
Строгая теория действительных чисел довольно трудна и не
входит в программу средней школы. Но сейчас вы достаточно под-
готовлены для того, чтобы понять в общих чертах, как она может
быть построена.
44
Основной замысел очень прост. Кроме периодических беско-
нечных десятичных дробей, существуют непериодические. Такова,
например, дробь
0,101001000100001000001...
(после первой единицы — один нуль, после второй — два и т. д.).
Мы примем теперь, что каждая непериодическая бесконечная де-
сятичная дробь является представлением некоторого нового числа.
Множество всех этих чисел и есть множество всех иррациональных
чисел. Вместе с рациональными числами иррациональные числа
образуют множество JR всех действительных чисел.
Таким образом, оказывается, что любое действительное число
представляется бесконечной десятичной дробью. Соответствие
х -> а0, аха2а3...
между действительными числами и бесконечными десятичными дро-
бями, не имеющими девять в периоде, взаимно однозначно: каждому
действительному числу х соответствует одна вполне определенная
такая десятичная дробь и каждая такая десятичная дробь является
представлением вполне определенного действительного числа.
Смысл неравенства между действительными числа-
ми определяется приведенным в п. 12 правилом сравнения беско-
нечных десятичных дробей. Для рациональных чисел такое опре-
деление неравенства равносильно известному вам еще из младших
классов.
Остается определить для вновь введенных чисел арифметические
операции сложения и умножения. Понятие о том, как это делается,
будет дано в следующем пункте. Вычитание по-прежнему опреде-
ляется как действие, обратное сложению, а деление — как дейст-
вие, обратное умножению.
Чтобы теория действительных чисел была закончена, надо еще
доказать, что для новых чисел неравенства и арифметические опе-
рации обладают теми же основными свойствами, которые нам извест-
ны для рациональных чисел: если х< у, то при любом z
х + г < у + z
и т. п.
Упражнения
2
116. Укажите рациональные числа среди чисел ——; 5; 4,2; —1,6;
О
]/6; j/2?0; 0,757557555755557... (в последнем числе: после пер-
вой семерки—одна пятерка, после второй — две и т. д.).
Представьте каждое рациональное число в виде отношения
— , где tn С Z и п £ N.
п
117*. Назовите несколько положительных значений переменной а
таких, при которых значение выражения
а) является иррациональным числом;
б) является рациональным числом.
4L
15. Десятичные приближения к действительному числу
по недостатку и по избытку и арифметические
действия с действительными числами
1. Десятичные приближения по недостатку и по избытку с точ-
ностью до 1, до 0,1, до 0,01 и т. д. вводятся хорошо известным вам
способом. Для числа
х = 5,3991...
первые пять из них выписаны в следующей табличке:
5 < х < 5 + 1 - 6;
5,3 <х <5,3 + 0,1 = 5,4;
5,39 < х < 5,39 + 0,01 = 5,4;
5,399 < х < 5,399 + 0,001 = 5,4;
5,3991 < х < 5,3991 + 0,0001 = 5,3992.
Вообще, для числа
х — а$,
приближения с точностью до 10-л имеют вид:
по недостатку: хп = а0,
по избытку: х'л = хп + 10~л.
Замечание. При записи приближений хп и хп мы не пишем нули
справа от значащих цифр. Но, выписав их, можно убедиться в том, что не-
равенства
хп < х < х'п
верны в смысле установленного в п. 12 правила сравнения бесконечных де-
сятичных дробей. Например, по этому правилу действительно
5,3991000... < 5,3991... < 5,3992000...,
каковы бы ни были следующие за данными нам десятичные знаки числа
5,3991...
2. Пусть даны два действительных числа х и у. Для их прибли-
жений по недостатку и по избытку с точностью до 10-л верны не-
равенства
xrt<x<xz't> уя<у<у«.
Если бы х и у были рациональными числами, то из этих неравенств
вытекало бы неравенство
Хп -Ь Ул < X + у < Хп -I- Уп.
Но для действительных чисел, которые могут и не быть рациональ-
ными, нам надо еще определить смысл сложения.
Определение. Суммой действительных чисел х и у
называется такое действительное число г, которое при любом целом
неотрицательном п удовлетворяет неравенству
хп + Уп < г < х'п + Ул-
45
Можно доказать, что такое число существует и притом только
одно. Мы ограничимся тем, что покажем, как это определение сум-
мы позволяет находить ее приближенное значение с хорошей точ-
ностью. Пусть
х = 1,23001... , у = 0,78044... .
В этом примере (независимо от того, каковы дальнейшие десятич-
ные знаки чисел х и у)
х5 + У5 = 2,01045 <х + у<*5 + У5 = 2,01047,
и мы можем написать четыре знака после запятой для суммы:
х + у = 2,0104... .
Менее приятен случай
х = 0,14508... , у = 0,85491... ,
х6 + у. = 0,99999, х'5 + уд = 1,00001,
и мы так и не узнали даже целой части суммы! Тем не менее
(^.+>,) + « +У.;) = 1(ЙС00
2
является приближением к ней с точностью до 10“5:
х + у = 1,00000 ± 0,00001.
3. Вполне аналогично определяется произведение неотри-
цательных действительных чисел.
Определение. Произведением двух неотрица-
тельных действительных чисел х и у называется такое действитель-
ное число z, которое при. любом целом неотрицательном п удовлет-
воряет неравенствам
хпУп < г < х’п уп.
Можно доказать, что такое число существует и только одно.
Если одно или оба числа отрицательны, то при определении их
произведения надо воспользоваться известным вам правилом зна-
ков.
В виде примера оценим квадрат числа
х= 1,4142... .
В этом случае
х4= 1,4142, Х4= 1,4143;
х24 = 1,99996164 < х2 < (х^)2 = 2,00024449.
Мы видим, что квадрат нашего числа х очень близок к числу 2.
Большего нельзя сказать, не зная дальнейших десятичных знаков
числа х. В действительности при надлежащем их выборе мы по-
лучим число, квадрат которого точно равен двум.
47
Упражнения
118. Докажите, что числа 2,6 и 2,7 являются десятичными прибли-
жениями соответственно по недостатку и по избытку числа
У 7 с точностью до 0,1.
119. Найдите десятичные приближения с точностью до 0,1 по не-
достатку и по избытку для числа:
а) 0,2664; б) —1,27; в) 2--; г) ]/ТТ.
6
120. Пусть х— некоторое действительное число, причем
3 < х < 4,
3,6 < х < 3,7,
3,60 < х < 3,61,
3,609 <х < 3,610,
3,6091 < х < 3,6092.
Выпишите четыре первых десятичных знака бесконечной деся-
тичной дроби, которой задается число х.
121. Найдите три первых десятичных приближения по недостатку
и по избытку и первые три десятичных знака числа;
а) Г4: б) “Т в) г) ~ 1/1
122. Известно, что х = 0,5638413... , у = 1,3414825... . Найдите
пять первых десятичных знаков суммы х + у.
123. Известно, что х = 2,1468... , у — 1,5431... . Найдите два пер-
вых десятичных знака произведения х и у.
124. Найдите четыре первые значащие цифры суммы:
a)j + /2; б) 1<2 + ]/5.
125*. Найдите три первых десятичных знака произведения:
а) 1 . /3; б) ]/2 • /5.
16. Изображение чисел точками координатной прямой
1. В геометрии принимают, что расстояние между любыми точ-
ками при выбранной единице измерения выражается неотрицатель-
ным числом. При этом имеются в виду именно действительные не-
отрицательные числа. Если в учебнике для шестого класса гово-
рится просто о числах, то это делается лишь потому, что учащиеся
в шестом классе еще не знают никаких чисел кроме рациональных.
Мы будем считать, что единица измерения расстояний уже вы-
брана, и для простоты будем называть числовое значение расстояния
просто расстоянием. Таким образом, расстояние | АВ | между
точками А и В есть просто неотрицательное действительное число.
48
О Е
—I------1--------1 .....।--------1------1-------1-------1------1_______t_______i________L
-2,5 -2 -1,5 -7 -0,5 0 0,5 1 1,5 2 2,5 J
Рис. 1
Пусть О и Е — точки на прямой и
расстояние | ОЕ | = 1. Каждой точке
М луча ОЕ соответствует неотрицатель-
ное число хм = | ОМ |. Одно из основ-
ных допущений курса геометрии со-
стоит в том, что отображение (рис. 1, 2)
М —* хм
луча на множество /?0 неотрицательных
действительных чисел обратимо: каждо-
му неотрицательному действительному числу х соответствует одна
вполне определенная точка М = М(х), координата которойхм= х.
Доказать это допущение, введенное в курсе геометрии в каче-
стве аксиомы, нельзя, не заменив его каким-либо по существу рав-
носильным допущением.
Полезно, однако, понять его наглядную основу. Будем считать, что
мы умеем строить точки Л4 (х) для неотрицательных чисел, записывающихся
конечными десятичными дробями. Возьмем какое-либо неотрицательное
действительное число
х —
и рассмотрим отрезки
Д„ = [М (х„); М (х'я)]
с концами, имеющими координаты хп и х'п. Отрезок Дя имеет длину 10~л.
Легко понять, что отрезки Дя вложены друг в друга:
Д1 о Д2 Д3 => ... то Дя гэ Дя+1 о ...
Существо нашего допущения заключается в том, что существует одна и толь-
ко одна точка М, принадлежащая всем отрезкам Дя. Она-то и является
точкой М (х) (рис. 3).
2. Точка О делит прямую на два луча: положительный луч ОЕ
и отрицательный луч. Если точка М принадлежит отрицательному
лучу, то ее координатой служит число
хм — — I ОМ | .
Отображение
М хм,
определенное теперь на всей прямой ОЕ, отображает эту прямую
на множество R всех действительных чисел и тоже обратимо: каж-
0~М(0)
х=1,73...
Е=М(1)
Рис. 3
У™ М(2)
т i...—
M(lrf
49
А В
- ---------•-------•----»>
Л4 о хд
Рис. 4
В_________А О
' Z Z *
Рис. 5
О А_______________В
<4 *В
Рис. 6
дому действительному числу х соответ-
ствует одна определенная точка М(х)
прямой ОЕ, имеющая координату
Хм = х.
3. Пусть А и В — две точки коорди-
натной прямой. Расстояние | АВ | вы-
ражается через координаты точек А и
В по формуле
| ЛВ | = | хв — хА | .
Доказательство этой формулы про-
водится рассмотрением всех возможных
случаев взаимного расположения точек
А и В по отношению к начальной
точке О.
Например, если ха < 0 < хв, то точка А принадлежит от-
рицательному лучу координатной прямой, а точка В — положи-
тельному. Точка О лежит на отрезке АВ. Поэтому (рис. 4)
| АВ | = | ОА | + [ ОВ | = —ха + хв = | хв — ха |
(хви—хА положительны). Другие случаи разберите сами (рис. 5, 6).
Упражнения
126. На координатной прямой постройте точки с координатами:
2 з
—;----; —1,6; 0,7. Найдите расстояния между этими точками.
3 4
127. Постройте отрезок длины ]/3; ]/5; ]/б (используйте теорему
Пифагора).
128. Отметьте на координатной прямой точки с координатами:
]/3; — ]АЗ; /5; —/5; /6; — /6?
129. Какие из чисел:
±; 6,4; ]/3; /081; -8; -/5; 0; 27-1
являются: а) целыми, б) дробными, в) рациональными, г) ир-
рациональными?
130. Приведите пример квадратного уравнения, корни которого—'*
иррациональные числа.
131. Рационально или иррационально число:
a) sin а, если а = 0°, 30°, 45°, 60°;
б) cos а, если а = 0°, 309, 45°, 60°;
в) tg а, если а = 0°, 309, 45°, 60°;
г) ctg а, если а = 30°, 45°, 60°, 90°?
132. Какое множество является дополнением:
а) множества целых чисел до множества рациональных чисел;
50
б) множества иррациональных чисел до множества действи-
тельных чисел?
133. Найдите объединение и пересечение множества рациональных
чисел и множества иррациональных чисел.
17. Числовая прямая и числовая плоскость
1. Установленное взаимно однозначное соответствие между
действительными числами х и изображающими их точками Л1(х)
координатной прямой позволяет рассуждать о числах, пользуясь
геометрической терминологией.
Будем считать координатную прямую расположенной горизон-
тально и за положительное направление на ней выберем направле-
ние слева направо. Тогда неравенство х < у обозначает, что точка
М(х) лежит слева от точки М(у). Удобно говорить, что само число х
лежит «левее» числа у. Если х <,z < у, или у < г < х, то говорят
(в обоих случаях), что число z лежит «между» числами х и у. Число
1У — х |,
выражающее расстояние между точками М(х) и М(у), удобно на-
зывать просто «расстоянием между числами х и у».
Само множество R всех действительных чисел называют «число-
вой прямой»*, а его элементы, т. е. числа, — «точками числовой
прямой». Вы уже знакомы с числовыми множествами, называемыми
«промежутками». Перечислим их:
Замкнутый промежуток (или отрезок) с началом а и концом Ь:
[а; Ь] = {х £ R | а х < Ь}.
Открытый промежуток (или интервал) с началом а и концом Ь:
К = {х £ R | а < х < 6}.
Полуоткрытые промежутки'.
Ь] = {х € R I а < х < b}\ [а; &Е = {х С R I а < х < Ь}.
Число b — а называется длиной промежутка.
Бесконечные промежутки (лучи, полупрямые)'.
]а; +°о[ = {х £ R | х > а}; [а; 4-ооЕ = {х € Я | х > а};
]—оо; = {х £ R | х < а}', ]—со; а] = {х £ R | х а}.
С
Числовая прямая'. ]—оо; 4-оо[ = R.
Пример 1. Решить неравенство | х — 7 | 2.
Будем рассматривать выражение | х — 7 | как расстояние меж-
ду точками х и 7. Тогда требование решить неравенство равно-
сильно такому: найти множество точек, расстояние от которых
до точки 7 не превосходит 2.
* Заметьте, что «координатных прямых» много, а «числовая прямая»одна—
множество действительных чисел.
51
* 5 7 9 На единицы от точки 7 удалены точ-
ки 5 и 9 (7 — 2 = 5, 7 + 2 = 9); менее
Рис- 7 чем на 2 единицы — точки, расположен-
ные между ними (рис. 7). Значит, ис-
•---g---- » .о—комое множество решений неравенства
"5 есть отрезок [5; 9].
Рис 8 Пример 2. Решить неравенство
| х + 5 | <1. Данное неравенство рав-
носильно неравенству |х—(—5) |<1.
Решить неравенство |х—(—5) | <1—значит найти множество
точек, расстояние от которых до точки —5 меньше 1. Легко по-
нять, что множество решений этого неравенства есть интервал
]—5 — 1; — 5 + 1[, т. е. ]—6; —4[ (рис. 8).
2. Начиная с младших классов вы пользовались для обозначе-
ния точек плоскости их координатами. Не будем вновь описывать,
каким образом упорядоченной паре чисел (х; у) ставится в соответ-
ствие точка М(х; у) плоскости. Но теперь очевидно, что соответ-
ствие
(х; у) -> М(х; у)
между упорядоченными парами чисел и соответствующими точками
плоскости взаимно однозначно.
Естественно поэтому множество упорядоченных пар действи-
тельных чисел называть числовой плоскостью, а любую упорядочен-
ную пару действительных чисел — точкой числовой плоскости.
Числовую плоскость принято обозначать символом /?2 (читается:
«эр два»). Обычная же геометрическая плоскость с выбранной на
ней системой координат называется координатной плоскостью. Вы
хорошо знаете, что на одной и той же плоскости можно многими
способами выбрать систему координат и, значит, многими способа-
ми изображать точки числовой плоскости, которая сама по себе
при этом не меняется — она остается просто множеством пар дей-
ствительных чисел.
К точкам числовой плоскости можно применять геометрическую
терминологию. Например: множество точек (х; у) С /?2, координаты
которых удовлетворяют уравнению
ах + by + с = О,
в котором хотя бы одно из чисел а или Ь отлично от нуля, называет-
ся прямой.
Множество точек (х; у) С координаты которых удовлетворя-
ют неравенству
х2 + у2 < г2 (г > 0),
изображается в координатной плоскости кругом радиуса г с цент-
ром в начале координат, и поэтому в числовой плоскости это мно-
жество также называется кругом радиуса г с центром в точке (0; 0).
52
Задача. Опишите на геометрическом языке множество:
{(х; у) € R* I (х- 1) (у + 1) = 0}. (1)
Так как
((х — 1) (у + 1) - 0) <=Ф (х — 1 = 0 или у + 1 = 0)
<=> (х = 1 или у = —1),
то данное множество является объединением множеств точек пря-
мых X = 1 и у = —1.
Замечание. Так как в этом учебнике рассматриваются
лишь пары действительных чисел, то множество (1) можно записать
и так:
{(х; у) | (х- 1) (у + 1) = 0},
опуская указание на то, что (х; у) С R2.
Упражнения
134. Закончите доказательство равенства | АВ | = | хй— хл |.
Найдите расстояние между точками координатной прямой:
135. М(1,5) и Л4(—2).
136. Щ—10,3) и Л4(6,2).
137. М(—3,6) и М(0).
138. Л4(—5,7) и М(—7,1).
Найдите множество решений:
139. а) | х | = 5;
140. а) | х — 10 | = 4;
141. а) | х | 5;
б) | х | < 5.
б) | х — 10 |< 4.
б) | х — 10 | > 4.
Запишите в виде уравнения или неравенства предложение с
переменной и укажите множество значений переменной, при
которых это предложение истинно:
142. Расстояние между точками М(х) и Л4(5) координатной прямой
равно 2.
143. Расстояние между точками М(а) и Л1(—1) координатной пря-
мой меньше 3,5.
144. Расстояние между точками М(—4,5) и М(у) не больше 0,2.
145. Расстояние между точками М(—12) и Л1(—Ь) не меньше —.
Опишите на геометрическом языке следующие множества и
изобразите их в координатной плоскости:
146. а) {(х; у) | (х - 2) (у + 3) = 0}; 6) !(х; у)| = о).
147. {(х; у) |х <0, у >-1}.
53
18*. Некоторые свойства множества действительных чисел
Если бы математика ограничилась лишь рациональными числами,
она во многих отношениях была бы беднее содержанием (не су-
ществовало бы «точного» корня квадратного из двух, не каждая
точка координатной прямой имела бы координату и т. д.). Но с
чисто практической точки зрения, как уже отмечалось, измене-
ние не столь велико. На практике можно было бы обойтись даже
не всеми рациональными числами, а лишь теми, которые пред-
ставимы конечными десятичными дробями.
В этом по существу и заключается свойство плотности под-
множества рациональных чисел в множестве всех действитель-
ных чисел. Геометрически это свойство означает, что на любом
отрезке координатной прямой лежит хотя бы одна рацио-
нальная точка (а значит, и бесконечное множество рациональных
точек).
Отвлекаясь от реальных возможностей, можно сказать, что
если в каждой рациональной точке зажечь по фонарику, то на
прямой не окажется никакого темного промежутка, вся прямая
будет светиться. Тем не менее на ней будет спрятано очень мно-
го иррациональных точек. В некотором смысле их даже «боль-
ше», чем рациональных.
Поясним смысл последнего утверждения. Все рациональные
числа можно расположить в виде последовательности: (rj г2; —
...; гп; ...), выписывая несократимые дроби —в порядке возраста-
Q
ния суммы |р|+*7» а при одинаковом значении этой суммы — в
порядке возрастания числителя:
£ ~1 1 —2 ~~1 1 £ —з — 1 _£ 2 —4 —3
Г 1'1' 1 ' 2 ' 2' 1' 1 ' 3 ' 3' 1' 1 ' 2 '
— 2 — 1 j_ 2 — ~5 —1
3 ' 4 ' 4' з' 2’ Т' 1 ' ”5”'
Полученное взаимно однозначное соответствие между множест-
вом всех рациональных чисел и множеством N всех натуральных
чисел показывает, что в известном смысле рациональных чисел
«столько же», сколько и натуральных чисел. Немецкий математик
Г. Кантор в 1874 г. доказал, что «занумеровать» аналогичным
образом множество всех действительных чисел нельзя: какова
бы ни была последовательность (х{; —;*п» •••) действительных
чисел, найдется действительное число х, не являющееся членом
этой последовательности.
Подробнее об этом можно узнать из популярных и научных
книг, посвященных теории бесконечных множеств. Теория мно-
жеств стала складываться в самостоятельную науку и вызвала
всеобщий интерес математиков в конце XIX в., когда в ней поя-
вились интересные и неожиданные результаты, вроде указанных
выше.
54
§ 6.
БЕСКОНЕЧНЫЕ ЧИСЛОВЫЕ
ПОСЛЕДОВАТЕЛЬНОСТИ.
ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
19. Бесконечные числовые последовательности
С бесконечными числовыми последовательностями вы уже по-
знакомились в VIII классе. Это, например, бесконечная геометри-
ческая прогрессия с первым членом 1 и знаменателем 2:
1; 2; 4; 8; 16; ...
В предыдущем параграфе мы рассмотрели еще несколько примеров
числовых последовательностей. С каждым действительным числом
Ct == tZ, ... Дд...
связаны следующие последовательности:
1) десятичных знаков числа а: аг\ а2', а3‘, ... ; а„; ... ;
2) десятичных приближений числа а по недостатку: ах = а,
а2 a, ... , сСд tz, а^а2... tz^, ... ,
3) десятичных приближений числа а по избытку: «/= а, ;
, . 1 , ,1 10
«2 ^1^2 “Г ]Q2’, ••• ; а п #1^2 ... ип “Гдод» ••• •
Задать бесконечную числовую последовательность — это значит
задать соответствие, при котором каждому натуральному числу п
(номеру) соответствует одно и только одно число (член последова-
тельности с номером п). Это соответствие обычно записывают с по-
мощью такой стрелки
п -> ип.
Например, если ип есть десятичное приближение по недостатку
числа 1/2 с точностью до —, то
F 10«
!->«!= 1,4; 2 -> «2 = 1,41; 3 -> w3 = 1,414; ... .
Такое соответствие есть не что иное, как функция, областью
определения которой является множество 2V — {1; 2; 3; ...} всех
натуральных чисел и значения которой принадлежат множеству R
всех действительных чисел.
Определение. Бесконечной числовой по-
следовательностью называется числовая функция, опре-
деленная на множестве N натуральных чисел.
Иначе это определение можно выразить так: числовой последова-
тельностью называется отображение множества N в множестве R.
Так как в этой главе мы будем заниматься лишь бесконечными
числовыми последовательностями, то будем называть их просто
55
последовательностями, опуская прилагательные «бесконечная» и
«числовая».
Как и любую функцию, последовательность можно обозначить
какой-нибудь буквой, например буквой f. Тогда /(1) есть первый
член последовательности, /(2) — второй,..., f(n) — энный член
последовательности. Обычно, однако, члены последовательности
обозначают буквами, снабженными индексами:
Л1) = А; /(2) = А;... ; №>) = А,; ....
Последовательность с л-м членом flt часто обозначают так:
(/i> ••• » fn* •••)
или более коротко: (fn). В последнем обозначении подразумевается,
что переменная п «пробегает» все множество JV; например, геомет-
рическая прогрессия, указанная в начале пункта, л-й член которой
fn = 2я-1, записывается (1; 2; 4; ... ; 2я-1; ...) или (2я-1).
Напомним основные способы задания последовательности.
1. Последовательность может быть задана аналитически при
помощи формулы, указывающей, как по номеру п вычислить член
последовательности хп с этим номером.
Пример!. хп = —!—; п £N.
2п — 1
С помощью этой формулы можно вычислить любой член последо-
вательности, например:
1 1. 1 1.
Xi — --------— 1, Xi о — -------- — —1 ••• •
1 2-1 — 1 10 2-10—1 19
Вместо слов «рассмотрим последовательность (х;1), заданную
формулой хп = » говорят короче: «рассмотрим последо-
1 х 1
вательность хп — -----; п С /V» или просто «х„ =---».
п 2л—1 1 п 2л—1
Пример 2. хп = 5; п £ N.
У этой последовательности все члены совпадают: (5; 5; ...).
Последовательность, у которой все члены совпадают, называется
постоянной последовательностью или просто постоянной.
2. Часто употребляется рекуррентный способ задания последо-
вательности.
Пример 3. Если известно, что a) = 1 и б) при любом
п 1 имеем хл+1 = (л + 1)хм,
то легко найти:
х2 = 2; х3 = 6; х4 = 24; х5 = 120; ... .
Ясно, что условия а) и б) определяют значения хп для любого на-
турального л, т. е. задают бесконечную последовательность. В рас-
сматриваемом случае это хорошо известная вам последовательность
хя = л’.
56
В примере 3 мы имели дело с простейшей схемой рекуррентного опреде-
ления последовательности:
1) указывается первый член последовательности;
2) дается формула, позволяющая по номеру n > 1 и члену последователь-
ности с номером я вычислить член с номером п + 1. Интуитивно достаточно
ясно, что условия 1) и 2) позволяют вычислить любой член последователь-
ности. Строгое доказательство этого утверждения может быть проведено
с помощью принципа математической индукции.
Упражнения
148.
149.
а) Последовательность (хл) задана формулой хп = -2/г
п 4~ 3
Найдите х10, х25, хя+1, хп+1 — хп.
б) Последовательность (Ьп) задана формулой Ьп = —.
3й
Найдите Ь3, Ьь, Ъп+1,
Вычислите первые
а) I +-^;
6) Х„ = 2» + 1;
^п+1
Ьп ’
пять членов последовательности:
в) а„ = 2 + 2;
п
г) Ь,. =
Зп
Для каких членов последовательности (уп) выполняется усло-
вие:
150. уп > 200, если уп — 2п— 5?
151. уп 30, если уп = Зп— 100?
152. Выпишите первые пять членов последовательности и
задайте эту последовательность формулой п-го члена, если:
а) хг = —10, хп+1 = хп + 5, n > 1;
б) Xi = 4, лй+1 = — хп, n > 1.
20. Геометрическое изображение последовательности
и наглядные представления о пределе последовательности
Для геометрического изображения последовательностей поль-
зуются двумя способами.
Первый способ. Так как последовательность (у„) яв-
ляется функцией, то геометрически эту функцию можно изобразить
с помощью ее графика, т. е. множества точек Л4(п; у„) координат-
ной плоскости. Масштабы на осях координат удобно иногда выби-
рать различными.
Второй способ. Члены последовательности изображают-
ся точками координатной прямой, снабженными соответствующими
пометками.
П р и м е р 1. уп = —; n£N.
57
На рисунке 9,а, б сопо-
ставлены оба способа изображе-
ния этой последовательности.
Подчеркнем, что график по-
следовательности состоит из от-
дельных точек, которые изобра-
жены на рисунке 9, а, а тонкие
вертикальные линии проведены
для наглядности и к графику не
относятся.
При обоих способах изобра-
жения видно, что при возраста-
нии номера п члены последова-
тельности подходят все ближе к
нулю.Более того, n-й член этой последовательности уп = — «сколь
п
угодно мало» отличается от нуля, если только его номер п является
«достаточно большим» числом. Этот факт условимся записывать
так: 1
lim — = 0.
П-> оо П
Говорят, что «предел последовательности (уи) равен нулю».
Пример 2. уп = — n^N.
п
(—1)л| 1
—- = -» ТО
п п
Так как [у,г [ =
точно больших п» члены последовательности (ул) также «сколь
угодно мало» отличаются от нуля. Но в отличие от предыдущего
и в этом случае при «доста-
примера члены последовательности подходят к нулю, поочередно
меняя знаки (рис. 10, а, б). И в этом случае
I_ 1 мг
Jim '—= 0.
оо П
Пример 3. уп = ; n£N.
У к На рисунке 11, а, б видно,
• что члены этой последователь-
! т ности при возрастании номера п
О ;! i р 4 *5 д’ «стремятся» к —. Это делается
' ясным, если записать п-й член
• а) последовательности в виде
б)
Рис. 10
Ул 3 3«’
при возрастании номера п второе
слагаемое «стремится к нулю»,
58
-------------------i------------------i । д.
1 2 3 4 x
a)
У/
1 1
поэтому разность------
3 Зп
следующим образом:
0_______________________________________
' У2 № J ‘
5)
Рис. 11
стремится к числу у. Записывают это
г п— 1 1
Jim----- = —.
оо Зп 3
Пример 4. Десятичные приближения по недостатку числа
_ _1_,
" 3'
= 0,3; а2 = 0,33; а3 = 0,333; ... ; ай = 0,33 ... 3; ...
п десятичных
знаков
с возрастанием номера п все меньше отличаются от самого числа
Естественно считать, что предел этой последовательности равен
Вообще, для любого действительного числа а
lim ап = Пт а'п = а.
П_>оо П->оо
Упражнения
Изобразите геометрически (двумя способами) последователь-
ность (ап):
153. а) а„ =-----6; б) ап — ——.
2 п
154. а) ап = (— 1)яп; б) ап = -1 ~K.~~-.U-,
155. Изобразите геометрически каким-либо одним способом после-
довательность (хл). Скажите, существует ли такое число, к
которому «стремится» эта последовательность:
а) хп = п2 + 1; в) хп = 1 4- -;
п
10 ч 5п+(—1)л+1
б) хп = -; г) хя = ——.
п п
69
2/г + З
п
156. Последовательность (ая) задана формулой ап
Найдите расстояние от точки 2 до точки: а) п5; б) а20; в) а100;
г) й1000-
157. Изобразите члены последовательности гп =
точками
2п+ 1
координатной прямой. Чему равен предел этой последова-
тельности? Укажите номера членов последовательности, уда-
ленных от точки 0:
а) менее чем на 0,1; б) менее чем на 0,01.
__ I
158. Изобразите члены последовательности уп =------точками коор-
п
__I
динатной прямой. Как высчитаете, верно ли, что lim ---- = 3?
П_>оо Л
Укажите номера членов последовательности (у,,), которые
удалены от числа 3: а) менее чем на 0,1; б) менее чем на 0,04.
21. Определение предела последовательности
Рассмотрим более подробно третий пример из предыдущего пунк-
та. Какой точный смысл имеет утверждение: «При достаточно
большом п значение выражения уп = ” сколь угодно мало
отличается от —»?
3
Поставим для начала такой вопрос: каким должно быть п, чтобы
модуль разности уп-----был меньше 0,001? Так как
з
1
J _ _
Зп Зп’
то вопрос сводится к тому, чтобы найти, при каких натуральных п
выполнено неравенство
1< 0,001.
Зп
Но это неравенство равносильно неравенству
Зп > 1000,
или неравенству
п > 3331.
3
Получаем, что неравенство
0,001
в»
выполняется для любого
п > п0 = 333.
Если бы вместо 0,001 мы взяли 0,000001, то такими же подсчета-
ми установили, что
у,.— - <0,000001
'п з
при любом
п > nt = 333 333.
Возьмем произвольное положительное число е и спросим себя,
при каких п выполняется неравенство
<*>
Это неравенство равносильно неравенству
Так как нас интересуют только целые п, то ответ на наш вопрос
таков: неравенство (1) выполняется при всех
п > N,
где N — целая часть числа —.
Зе
Разберите сами первый и второй примеры предыдущего пункта
и установите, что в этих случаях для любого положительного числа
е найдется такое натуральное N, что при всех п > N будет выпол-
няться неравенство
|уп — 0|<е.
Дадим определение предела последовательности.
О п р е д е л е н и е. Ч исло а называется пределом последова-
тельности (хп), если для любого положительного числа е найдется
такое натуральное число N, что при всех п > N выполняется нера-
венство
I хп я | < £• (2)
Говорят: «Последовательность (хл) имеет пределом число а» и пи-
шут:
Птхл= а.
в-* оо
О последовательности, имеющей предел, говорят, что она схидится.
Число N (в определении предела последовательности) зависит
как от рассматриваемой последовательности, так и от взятого чис-
ла е.
Докажем, что последовательности (а,2) и (а'и) десятичных при-
ближений числа а сходятся к этому числу:
lim att = lim а'п = а.
n^CQ П-+<Х>
6!
Если а — любое действительное число, (ап) и (а'п) — последова-
тельности его десятичных приближений соответственно по недо-
статку и по избытку, то
, , 1 । ' 1^-1
а,, — а < — и ап — а % —.
1 п 1 юл 1 1 10я
Так как для любого положительного числа найдется натуральное
число N такое, что — < 8 при п > N, то
10я
[сс/; — а|<е и [ — а|<е.
Поэтому
lim а;г = а и lim аг'г — а.
ОО оо
Выясним геометрический смысл понятия предела по-
следовательности. Неравенство (2) равносильно двойному неравен-
ству:
•—8 < хп — а <8
или
а — 8 <хп < а + е.
(3)
Двойное неравенство (3) показывает, что все члены последователь-
ности (хп), сходящейся к числу а, с номерами п > N, т. е. члены
— ,« ..-------- ХЛЧ-1 ’ XN+2’
а попадают в интервал —б; а + е[
Рис. 12 (рис. 12), который называется &-окрест-
ностью точки а.
Таким образом, если число а является пределом последовательно-
сти (хп), то в произвольную (как угодно малую) окрестность точки
а попадают все члены данной последовательности, кроме конечного
их числа.
Упражнения
Докажите, что:
159. a) lim = 1;
П_± оо Л
.. 5п — 2 |-
б) lim------- = 5;
П_> оо И
в) lim —- = 1,5;
Л_>оо Z/Z
г) lim —-— = 0.
П-ч-ОЭ 4“ 1
160. Какой предел имеет последовательность (проведите доказа-
тельство):
а) ап =
5п — 1
2/г
б) »„=
1 з
п2
62
161. Пусть хп = с, где с— некоторое число. Докажите, что Пт хп =
Л->ОО
= С.
162*. Докажите, что число 1 не является пределом последователь-
ности
22. Единственность предела.
Сходящиеся и расходящиеся последовательности
Интуитивно кажется правильным, что последовательность может
иметь только один предел.
Теорема. Если последовательность сходится, то она имеет
только один предел.
Доказательство. Пусть limхп = а, Птхп = Ь.
Из определения предела вытекает, что при любом е > 0 существуют
такие щ и п2, что
I хп — а | < при п > п-l и |хл — 61 < — при п > пг
2 2
Выберем номер п0 большим, чем п1 и п2. Тогда
\х„ — а ] < — и |хп — b 1 < —
и, следовательно,
| а — b | = | (а — хп) + (х ч — &) | < | а — хИо | + 1— Ы <
Мы получили, что неотрицательное число | а — b | меньше любого
положительного числа е. Но этому условию может удовлетворять
только число нуль, т. е. | а — b | = 0, и следовательно, а = Ь.
Итак, возможны только два случая: 1) у последовательности
имеется предел, и тогда он единствен; такие последовательности
называют сходящимися', 2) у последовательности нет предела; такие
последовательности называют расходящимися.
Приведем примеры расходящихся последовательностей.
Пример 1. хп = щ п С N.
Предположим, что последовательность (хп) сходится и имеет
пределом число а. Возьмем е = 1. Тогда по определению предела
существует такой номер пъ что для всех п > щ выполняется не-
равенство | хп — а | < 1, т. е. | п — а | < 1 для всех п > щ. За-
пишем это в виде двойного неравенства:
•—1 < п — а <1
.63
или
а — 1 < п < а 4- 1 для всех п > пг.
Но неравенство п < а + 1 для всех п > пх ложно, так как мно-
жество натуральных чисел неограничено.
Пример 2. хп = (—1)л; п £ N.
Как и в предыдущем примере, доказательство проведем от про-
тивного. Предположим, что последовательность хп сходится к чис-
лу а. Возьмем окрестность ] а— ; а 4--^- [ точки а. Так как длина
этого интервала равна 1, то в него не могут попасть одновременно
точки —1 и 1, поскольку расстояние между ними равно 2. Значит,
вне окрестности ] а—а 4* -[ точки а находится бесконечное
число членов последовательности, и потому число а не может быть
пределом (хп).
Упражнения
163. Докажите, что последовательность (хп) сходится, а (уп) рас-
ходится, если:
= в) у„ = (—1)'Ч-1;
6п
б) = 2 4- г) уп = 2п — 1.
п
23. lim qn, если | q | < 1
о*
Рассмотрим несколько членов последовательности сп =
111 1
1 5 2 25 3125 10 9765625
Мы Видим, что с увеличением номера члена последовательности
его значение неограниченно уменьшается.
Возникает гипотеза, что
lim (—Y*= О-
Покажем, что это действительно так, доказав более общее ут-
верждение.
Теорема. Если | q | < 1, то lim qn = 0.
о*
Доказательство. Если q = 0, то qn = 0 при любом я,
и в этом случае теорема очевидна.
Для случая 0 предварительно установим одно вспомога-
тельное неравенство. Так как по условию теоремы | q | < 1, то
64
----> 1 и ------- можно записать в виде
1<7| Ы
— = 1 4- а, где а > 0.
1<7|
Возводя обе части неравенства в степень п, получим:
- (1 Н- а)'г.
И"
Так как а > 0, то по неравенству Бернулли
—-— — (1 -|- а)" 1 /?а >на.
I 7 Г4
Поэтому
Это и есть нужное нам вспомогательное неравенство.
Вернемся к доказательству теоремы. Мы должны показать, что
для любого е > 0 существует натуральное У, такое, что из п > N
вытекает
| qn — 01 = | q < е.
Выберем У > —. Тогда при п > N
а&
1 .11^
п > —; па > —; — < е
as е па
и в силу (1)
I<7" — 0| = |<7р < — < е,
па
что и требовалось доказать.
Упражнения
164. Укажите такое натуральное число п0 (хотя бы одно), чтобы
при всех п > п0 выполнялось неравенство:
а) (0,3)" <0,01; в) (0,99)" <0,001;
б) (0,7)« <0,01; г) (0,45)" <0,001.
24. Сумма
бесконечной
при|«|<1.
геометрической прогрессии
Пусть последовательность (хп) является геометрической про-
грессией со знаменателем q, где | q | < 1 и xL =£ 0. Тогда сумма
Sn первых п членов этой прогрессии, как известно, вычисляется по
формуле
•
1 —
1 — я ’
3 Заказ 243
65
Так как qn при достаточно больших п становится сколь угодно
малым числом, то естественно предположить, что Sn при возраста-
нии номера п стремится к пределу
а =
1 — q '
Докажем это. Составим модуль разности | Sn — а | :
|$я —«I =
v 1 — яп
Л-i
1 — q i — q
I Xjqn
I 1— q
*i
\—q
= I a | • | q |".
Зададим произвольное положительное число е и посмотрим, при
каких п будет выполняться неравенство
|S„-a | = |о | • I? |" < е. (1)
Это неравенство равносильно неравенству
\Q\n <-~г- (2)
1«1
Так как lim qn = 0, то можно найти такое натуральное п0, что
и-*оо
при всех п > п0 степень | q |rt будет меньше любого наперед задан-
ного положительного числа, в частности числа — . Для всех
1«|
таких п неравенство (1) будет выполняться.
Итак, если знаменатель q геометрической прогрессии удовлетво-
ряет условию |^| <1, то существует, предел суммы п первых чле-
нов этой прогрессии, равный :
1—<7
lim Sn =
П 1—9
(3)
Этот предел называют суммой бесконечной геометрической
прогрессии и часто обозначают буквой S.
Пример. Найти сумму геометрической прогрессии 2;---------;
2 2 \ 1
—;-----; ... . Для этой прогрессии jq = 2; q =---, т. е. | q | =
9 27 у 3
l^i о
= — < 1, и потому ее сумму 5 находим так:
з
S = limS,, = - z2 -п - -; S - -
п^п , / 1 \ 4 2 2
66
Упражнения
165. Найдите сумму бесконечной геометрической прогрессии:
166. Найдите сумму бесконечной геометрической прогрессии (хп),
если известно, что:
. 5 2 5 1
а) q = б) х2 = - q = - -.
О О ч/ ч/
167. Найдите бесконечную геометрическую прогрессию (уп), если
известно, что:
г;
а) У, + у, = 12; 3 = 12,5; б) у, + уа = 0,8; 8 = |.
25*. Понятие числового ряда
Вам известно, что
а^,а.а2 ... а„ = а0 -}- — -f- — + ••• + — •
1 2 п 0 ю ю2 10я
Бесконечную десятичную дробь ao,0ia2Q3'-.-, с помощью которой
представляется число х, хотелось бы тоже понимать как сумму
«о+- + — +—+••• (1)
10 102 lb3 V
бесконечного числа слагаемых. Но мы не знаем, что означают сло-
ва «сумма бесконечного числа слагаемых»,— это надо опреде-
лить. Наводящие соображения для такого определения могут
быть следующими: обозначим через (х„) последовательность де-
сятичных приближений числа х по недостатку. Тогда
хп = а0 + + ... + (2)
п 0 10 Ю2 10я v
В п. 20 было выяснено, что
lim хп = х. (3)
П-+ оо
Поэтому естественно определить сумму бесконечного числа сла-
гаемых (1), используя формулы (2) и (3).
Перейдем к определению понятий, связанных с суммой бес-
конечного числа слагаемых.
Определение. Для заданной числовой последовательно-
сти (хп) выражение
xi “Ь х2 ••• З- хн •••
называют числовым рядом, а хп — п-м членом этого ряда.
3* 67
Определение. Сумма п первых членов ряда называ-
ется п-й частичной су м м о й этого ряда и обозначается
через 8 п:
Sx - - хр,
— X} -|- X-j -}- Хц,
Определение. Если существует предел последовательности
(8:1) частичных сумм ряда, то говорят, что этот ряд сходится,
а указанный предел называется суммой ряда.
Таким образом, равенство (3) означает, что действительное
число а = а, О1 аг ••• является суммой ряда
1. а2
10 10а
«п I
10« '
частичными суммами которого являются десятичные приближе-
ния
ап а, а^а-2
а
£1 j- I 1 ап
10 ' 10* г " 10«
этого числа по недостатку.
Из результатов предыдущего пункта следует, что если зна-
менатель q геометрической прогрессии (хп) удовлетворяет нера-
венству |<?| <1, то ряд
Х1 Х2 ~г ”• Хп Н- ••• »
составленный из членов этой прогрессии, сходится и его сумма
равна ------:
Х1 1“ Х2 + • • ХИ
Рассмотрим примеры.
Пример 1. Найти сумму ряда
Последовательность (а;;), где а„ — (—-j , представляет
собой геометрическую прогрессию, у которой = q =
— — у-. Так как |^| = |— | <1, то ряд сходится и его сумма
2 2
68
Ol
равна —— • Поэтому
1 — q
__ 2
1 \ ~ 3
Пример 2. Записать число 0,(8) в виде обыкновенной дро-
8 8 8
би. Число 0,(8) можно записать в виде ряда-1----1-----!-••• +
' ' г 10 100 1000
+ — +••• , члены которого представляют собой геометрическую
,, . ,8 1
прогрессию (о„), причем = —, q — —.
Этот ряд сходится (]<?| < 1), и его сумма
6, _
равна ——. Отсюда
1— Я
имеем:
0,8 _ 8_
1—0,1 “ 9
0, (8) = - + — + - + —
’ k ' 10 100 10«
Пример 3. Представить дробь 0,2(35) в виде обыкновенной:
0,2(35) = - + + ...\
v 10 \103 105 107 )
В правой части равенства выражение в скобках является чис-
ловым рядом, члены которого представляют геометрическую
, . 35
прогрессию (с„), у которой <\ = —,
сходится:
1
q = —,
100
так что этот ряд
2 35 _ 233
10 + 990 ~ 990
Подобно тому как это сделано в примерах 2 и 3, любую пе-
риодическую десятичную дробь можно обратить в обыкновен-
ную.
0,035
1—0,01
Упражнения
168. Найдите сумму ряда:
а4Ч+^+ -+г» + -;
б) 8 _ ... +(_Г)"+1+ ....
25 125 625 \ 5/
169. Представьте в виде обыкновенной периодическую десятичную
дробь:
а) 0,(5);
б) 3,(27);
в) 0,5(8);
г) 28,10(01).
4
69
170. В равносторонний треугольник, длина стороны которого рав-
на 1 м, вписан другой треугольник так, что его вершины на-
ходятся в серединах сторон первого треугольника. Во второй
треугольник таким же образом вписан третий треугольник,
в него — четвертый и т. д. до бесконечности. Найдите:
а) сумму периметров этих треугольников;
б) сумму площадей этих треугольников.
171. В круг радиуса R вписан квадрат; в квадрат вписан круг;
в этот круг вписан второй квадрат и т. д. до бесконечности.
Найдите сумму площадей всех квадратов.
172. Найдите сумму ряда:
1 — -+ 4 — 1 + - , зная, что |х] > 1.
XX2 \ X)
§ 7.
СУЩЕСТВОВАНИЕ ПРЕДЕЛОВ
И ИХ ВЫЧИСЛЕНИЕ
26. Необходимое условие сходимости
Если последовательность (лп) сходится к числу а, т. е. если
lim хп - а,
П->ОО
то для любого 8 > 0 все ее члены, кроме конечного их числа, по-
падают в 8-окрестность точки а. Если, например, 8 = 1, то за пре-
делами соответствующей окрестности ]а — 1; а + 1[ может ока-
заться лишь конечное число п0 членов
хх, х2, х3, ... , х„о
этой последовательности (рис. 13). Поэтому существуют два числа
т и М такие, что отрезок [/и; А1] содержит уже все члены данной
последовательности: хп £ [т; 7И] для всех п С N.
Таким образом, всякая сходящаяся последовательность обла-
дает следующим свойством: существует отрезок [/п; М], содержа-
щий все члены этой последовательности. Последовательности,
обладающие таким свойством, называют ограниченными.
Определение. Последовательность (хп) называется
ограниченной, если существуют два числа т и М такие,
что для всех п выполняется неравенство
т хп М.
J 4 L
Л/ а-1 а а+1 х2
Рис. 13
70
Мы получили, что из сходимости последовательности следует
ее ограниченность. Это означает, что ограниченность последо-
вательности является необходимым условием сходи-
мости.
Теперь легко понять, почему последовательность хп — п, рас-
смотренная в п. 24, расходится. Дело в том, что эта последователь-
ность не является ограниченной.
Пример 1. Последовательность (xn)= fl; — ; —; ...|
\ 2 3 п )
ограничена.
В самом деле, все члены этой последовательности удовлетворя-
ют неравенству 0 хп 1.
Пример 2. Последовательность хп — ограничена.
п 4* 2
В самом деле, во-первых, хп > 0. Во-вторых,
3/1 г, П ~ Г)
хп =------= 3------< 3.
п 4- 2 п 4~ 2
Следовательно, 0 < хп < 3 для всех п.
п I 1
Пример 3. Последовательность уп —
не
является
ограниченной.
В самом деле, какое бы мы большое число М ни выбрали, су-
ществует натуральное N > ЗМ. При п > N имеем уп > М.
Возникает вопрос, не является ли ограниченность последова-
тельности достаточным условием сходимости. Оказывается, что
ответ на этот вопрос отрицателен. В самом деле, последователь-
ность
(мп) = (—1; 1; —1; 1; ...)
ограничена, так как —1 ип 1. Но эта последовательность,
как это мы видели в п. 23, расходится.
В п. 32 мы увидим, что достаточным условием сходимости бес-
конечной последовательности являются ее ограниченность и моно-
тонность.
Упражнения
173. Существует ли числовой промежуток [а; Ь], где а и b — не-
которые числа, которому принадлежат все члены последова-
тельности:
ч 2/14-1
а) ап = —— ;
п
174. Докажите, что последовательность (ип) является ограничен-
ной, если:
а) ип I — I ,
б) Ьп = (- 2)"?
б) ип=
fl
71
175. Ограничена ли последовательность (уп), если:
а) уп = 2п — 1; в) уп = п2;
б) Уп = ; О Уп = (~ 1)" • «?
27. Теоремы о пределах
Сформулируем три теоремы, облегчающие вычисление пределов.
Докажем одну из них.
Т е о р е м а 1. Если последовательности (хп) и (уп) сходят-
ся, то
lim (хп 4- у„) = lim хп + lim уп.
п-»оо л->со л->оо
При доказательстве этой теоремы используют определение пре-
дела и известное неравенство
|а+6|<|а|+Ш.
Пусть limxn = а и lim уп Ь. Тогда для любого числа е > О
Л->ОО П->00
найдется номер п± такой, что для всех п > выполнено нера-
венство
1ХП-Й|<|, (1)
и найдется номер п2 такой, что для всех п > п2 выполнено неравен-
ство
Наибольшее из чисел П! и п2 обозначим через N. Тогда для любого
n>N выполнено как неравенство (1), так и неравенство (2), и
потому для этих п
I (хп + Уп) — (« + 6) I = I (хп — «) + (Уп — Ь) )<
<|хп — а1+|уп— 6|<-| + | = е.
Поскольку е > 0 было взято произвольным, то этим доказано,
что
lim (хп + уп) = а+ b = limxn + lim yn.
п->оо /1->СО л->оо
Теорема доказана.
Т е о р е м а 2. Если последовательности (хп) и (у п) сходят-
ся, то
1>т(-*пУп) == Cim хп) • (|im Уп)-
Z2-> ОО П-*ОО П->СО
Т е о р е м а 3. Если последовательности (хп) и (у п) сходят-
ся и предел последовательности (у п) отличен от нуля, то
72
л->оо Уп Hmy„
«->oo
Отметим еще следующее часто применяемое при вычислениях
правило.
Следствие теоремы 2. Постоянный множитель можно
выносить за знак предела:
iim(cA\) = с • lim хп, с £ R.
«-►со л->оо
В самом деле, по теореме 2
lim (схп) = lim с • lim хп = с • lim хп.
п^оо п-+<ю П-Н.ОО п^оо
Упражнения
176. Найдите lim(xn4-yn), lim(xn — yn), lim(xnyn) и lim^,
«->oo n-+oo n-+c:> n-+co Уц
если:
a) limxn = l; limyn = 3; 6) limxn =—1; limyn = 5.
«->00 «-►OO «->00 «-►00
177. Известно, что limxn = 0,4; limy,, =0,2.
«-►00 «->00
Найдите:
a) lim5xrt; в) lim (2x„y„ 4-1);
«-►OO «->00
/7r
6) lim (3xn 4- yn)\ r) lim I—* 4- 3
«-►00 n->00 \ yn
178*. Известно, что limxn = a. Докажите, что для любого m
«->00
верно равенство
limxm = atn.
п
«-►00
28*. Бесконечно малые
последовательности
Доказательства многих теорем о пределах и, в частности, тео-
рем 2 и 3 предыдущего пункта существенно облегчаются, если
ввести понятие бесконечно малой последовательности.
Определение. Последовательность называется беско-
нечно малой последовательностью или просто бес-
конечно малой, если ее предел равен нулю.
Иными словами, последовательность (хп) называется бесконеч-
но малой, если для любого числа е > 0 найдется такой номер N,
что при всех п >> N
I ап — 01 = I а« I < е-
73
Пример 1. Последовательность ая= —является бесконеч-
п
но малой, так как
lim — = 0.
«-►СО /I
Пример 2. Так как lim q„ = 0 при | q | <Z 1, то при этом усло-
вии последовательность (q, q2, q3, ...) бесконечно малая.
Теорема 1. Сумма двух бесконечно малых последователь-
ностей является бесконечно малой.
Д о к а з а те л ь.с т в о.Пусть (ая) и (0„) — две бесконечно ма-
лые последовательности. Тогда по теореме 1 предыдущего
пункта
Jim (а„ + р„) = lim ап + lim р„ = 0 + 0 = 0.
«-►00 «-*00 «-*00
А это означает, что последовательность (а„ + р/г) является бес-
конечно малой.
Методом математической индукции можно доказать, что сум-
ма любого конечного числа бесконечно малых является беско-
нечно малой.
Теорема 2. Произведение ограниченной последовательно-
сти на бесконечно малую является бесконечно малой.
Доказательство. Пусть последовательность (ха) ограни-
чена. Тогда существует число М > 0 такое, что для всех п
Если (а„) — бесконечно малая последовательность, то
для любого е > 0 найдется номер N такой, что
I -- 8
0С/г|<- при
всех п > Л\ Но тогда при этих п
I I I %п I ' I ^ti I < М • 8.
А это и означает, что последовательность (а/гхп) является беско-
нечно малой.
С л е д с т в и е. Произведение двух бесконечно малых явля-
ется бесконечно малой.
В самом деле, так как бесконечно малая последовательность
ограничена (всякая сходящаяся последовательность ограничена;
см. п. 26), то сформулированное утверждение следует из теоре-
мы 2. Методом математической индукции можно показать, что
произведение любого конечного числа бесконечно малых есть
бесконечно малая.
Теорема 3. Для того чтобы выполнялось равенство
lim хп = а,
п-^оэ
необходимо и достаточно, чтобы
хп — a -f- а„, где 1ппая = 0.
74
Необходимость. Если lim xtl = а, то
П~+ оо
lim ап = lim (хп — а) = lim хп — lim а — а — а = 0.
и-»-оо Л->ОО Л->00 л->оо
Достаточность. Если lim ап = 0, то
СО
lim хп — lim (а + а/г) = Пш а + lim сс/г = а Ц- 0 = а.
П-+СО Л-*ОО П-+СО п->00
Приведем теперь доказательство теоремы о пределе произ-
ведения (теоремы 2 предыдущего пункта).
Если lim хп = а и lim уп — Ь, то по первой части теоремы 3
л->оо п-*со
для всех п £N
хп — а + , и lim а,г = 0,
Уп = ь + и lim р„ = 0.
Л->00
Перемножив эти равенства, получим:
ХпУп =ab+ (а$п + Ьан + алр,г).
Последовательности (арл), (Ьап), (ая0я) являются бесконечно ма-
лыми, поэтому бесконечно малой является также и их сумма, и,
следовательно, на основании второй части теоремы 3
lim (хпуп) = ab = (limxn) • (lim уп).
п-+со п-*со П-+СО
Аналогично доказывается теорема о пределе частного.
29. Примеры вычисления пределов
Пример 1. Пусть требуется найти
lim 5А±а .
л-»со Зп — 1
Так как числитель и знаменатель представляют собой неограни-
ченные последовательности и, следовательно, пределов не имеют,
то сразу применять теорему о пределе частного нельзя. Разделим
числитель и знаменатель на п (при этом значение дроби не изменит-
ся). Приведем подробную запись вычисления предела:
5п + 2 .. п
lim —!— = lim-----
П->ОО 3n—1 л-»оо1
n
lim 5+—I lim 5 +lim —
n->oo\ П / __ n-*OO n->oo tl _ 5 Ц- 0 _ 5
lim 13— — I lim 3 — lim —
n~>00\ П ) П-+ОЭ n-*co tl
Пример 2.
]im4.±Z_2
Л->ОО П
— 4- lim -—- = 4 • lim fl —= 4.
n->OO П \ П ]
75
Пример 3.
2 5
34-— — —
v 3/i2 + 2п — 5 v п п2
lim-------------= lim --------------
л-*оо 7п2 —11 4“ 3 rt->00 13
Пример 4.
.. 3 — п v п2 п
lim----------= lim------------
П-*ОО П2 “Ь 2/1 — 1 n->00 2 1
п п2
lim (з+А_ 5\
п->-<х> \ П П* /
, / 1 3\
lim 7— — + ~: I
я->оо \ П П*/
-°--0 = 0.
1+0—0
Упражнения
179. С помощью теорем о пределах докажите, что:
а) предел последовательности хп = —1-!— равен 1,5;
п
3__ 4/г2 I п
б) предел последовательности уп=--------—— равен —0,8.
5п2+ 2/г + 6
180. С помощью теорем о пределах найдите предел:
2/1 — 9
в) lim-----------------,
ZI-+OO 3/12 + /I-- 1
(п + 2) (п + 5)
г) lim
м->оо
a) lim ;
л->-оо 3 — 2/1
.. 3 — и + 2/г2
б) lim -------->----;
ге-оо 2 + п — 4/12
181. Найдите пределы:
. .. /2/1— 1 2п2 + 3 \
a) lim-----------------!— ;
л^оо \3/г + 1 Зп2 — 1/
_ .. 72/13 + 5/1— 1 . 3 + 5л\
б) lim -------!-------------!— ;
„_оо\ З/t3 —2/12 3/1—1/
в) lim f -3n
n->oo \5n — 1
г) lim f
n->oo \3/i + 2
• 2n2 + 1 \ .
П2_|_2/1—1/ ’
2/i2 \
n2+ n—1/ '
182. Отрезок AB, длина которого равна а, разделен на п конгруэнт-
ных частей. На каждой из этих частей построен равнобедрен-
ный треугольник с углом
ук ук ук уч при основании, равным 45°.
/ Xz к/ к. Найдите предел периметров
А в Рп получающихся фигур
Рис. 14 (рис. 14) при П-> оо.
30*. Сравнение роста арифметической и геометрической
прогрессий
При помощи неравенства Бернулли можно решить одну очень
интересную задачу. Сравним рост членов положительных ариф-
метической и геометрической прогрессий. Пусть первый член at
и разность d арифметической прогрессии, а также первый член
геометрической прогрессии Ь\ — положительные числа, а ее
знаменатель q больше 1, т. е. ai>0, rf>0, &i>0, q>\.
76
Для того чтобы сравнить
рассмотрим отношение
^/Z 1 1
Ьц 41
скорости роста этих прогрессий,
__ dn
b^q'1
и докажем, что
lim = о,
п->оо &ZJH
Поскольку q > 1, то /^> 1, и потому,
Уq = 1 4- а, где а> 0.
В силу неравенства Бернулли
(уqy= (1 -|- а)'1 1 + па > па.
Следовательно,
q < an+i _ ai + dn _ Qj + dn <7t 4- dn
bn+1 bi ‘ MK?)2" by(na)z
Поскольку правая часть этого неравенства имеет пределом нуль,
то для любого числа 8 > 0 существует такое Л1’, что для всех
п > W
4- dn g
by (па)2
Поэтому для всех п > N
°П+1 _ Q _ А ГН А < П1 4~ dn < £
bn+i bn\i by (па)2
что и требовалось доказать.
В виде примера рассмотрим геометрическую прогрессию
Ьп = (1,00001)". Сначала она возрастает очень медленно, при вы-
числениях с точностью до пяти знаков после запятой:
Ь2= 1,00002; 6ю=1,00010; 6100 = 1,00100; 6юоо= 1,01005.
Тем не менее Ьп при достаточно большом п делается боль-
ше п-го члена любой арифметической прогрессии, например
больше 1000 п.
Для наглядного представления о сравнительном росте членов
арифметической и геометрической прогрессий (рис. 15) на коор-
динатной плоскости изображено несколько точек графиков ариф-
метической прогрессии с общим членом ап= 1 4“2(П'— 1) и гео-
метрической прогрессии с общим членом bn= 2"-1. На рисунке
для лучшей обозримости точки арифметической прогрессии изоб-
ражены на графике линейной функции у = — 1 + 2х, целочис-
ленными значениями которой являются точки прогрессии ап =
= 14~2(п—1), а точки геометрической прогрессии — на гра-
фике показательной функции у = 2'-1, целочисленными значе-
ниями которой являются bn = 2"-1. Видно, что значения первых
77
Рис. 15
членов обеих прогрессий совпадают, а второй и третий члены
арифметической прогрессии больше второго и третьего членов
геометрической прогрессии; все последующие члены геометри-
чёской прогрессии больше соответствующих членов арифметиче-
ской прогрессии.
78
Упражнения
fl р
183*. Докажите, что Нт— = 0 при q > 1 и р > 0.
Указание. Представьте в виде 1 + а, где а > О,
и используйте неравенство Бернулли.
31. Монотонные последовательности
В VIII классе уже были введены понятия убывающей и возрас-
тающей последовательностей. Напомним их определения.
Определение 1. Последовательность (хп) называется
возрастающей, если каждый ее член, начиная со второго,
больше предыдущего, т. е. если для любого п выполняется неравенство
•^п+1 > %п'
Пример!.
0; -; - ; ..
2 3
п п — 1
Так как хп+1 — хп = —-------------
п + 1 п
п (п + 1)
то хп+1 > хп и данная последовательность является возрастающей.
Определение 2. Последовательность (хп) называется
убывающей, если каждый ее член, начиная со второго, меньше
предыдущего, т. е. если для любого п выполняется неравенство
Пример 2. (ул) = (1; 1; 1; ... ; - ; ... \
у 2^ О fl у
- 1 _ 1
Так как уп+1 =----< — = уп, то данная последовательность явля-
п + 1 п
ется убывающей.
В теории пределов полезны также понятия «неубывающих»
и «невозрастающих» последовательностей.
Пример 3. (г„) = (1; 1; -1; -Ь
\ ООО
В последовательности (z^j числа вида
1 \
5 ’ )’
1
------ подряд повто-
2п — 1
ряются дважды.
У этой последовательности каждый член, начиная со второго,
меньше или равен предыдущему: zn+1^ zn. Такие последователь-
ности называются невозрастающими. Заметим, что убывающие
последовательности есть частный случай невозрастающих после-
довательностей.
79
Опр еделенпе 3. Последовательность (хп) называется н е-
возрастающей, если каждый ее член, начиная со второго,
не больше предыдущего, т. е. если для любого п выполняется неравен-
ство
*п+%ir
Определение 4. Последовательность (х„) называется н е-
убывающей, если каждый ее член, начиная со второго, не
меньше предыдущего, т. е. если для любого п выполняется неравен-
ство
Xfl+1^ %П’
Неубывающие и невозрастающие последовательности называют-
ся монотонными последовательностями (в частности, возрастаю-
щие и убывающие последовательности монотонны).
Не всякая последовательность является монотонной. В самом
деле, последовательность
не является монотонной. С другой стороны, мы уже знаем, что эта
последовательность сходится (см. п. 23) и
n->oo tl
Следовательно, условие монотонности не является необходимым
для сходимости последовательности.
Итак, подведем некоторые итоги: ограниченность последователь-
ности является необходимым условием сходимости, монотонность
не является необходимым условием. Совместное же выполнение
обоих условий, как мы увидим в следующем пункте, уже обеспе-
чивает сходимость последовательности.
Замечание. Из определения возрастающей последова-
тельности следует, что для установления возрастания последова-
тельности с положительными членами достаточно установить не-
равенство
-^i-> Г, n6N.
хп
Аналогичные замечания можно сделать относительно других
видов монотонных последовательностей с положительными членами.
Пример. Пусть хп = —— , тогда хп+1 = —.
Поэтому
хя+1 _п + 2 . n-f-l _п (п 2)_____п2 4~ 2п ।
хп ~ п 4- 1 п ~ (п + I)2 ~ п- 4- 2п 4- I
Следовательно, данная последовательность является убывающей.
80-
Упражнения
184. Является ли убывающей или возрастающей последователь-
ность (&„), если:
а) Ьа = 2п2-, в) If;
\ /
б) &„ = 7~«-2; г) Ьп = (-1)^п.
185. Является ли последовательность (ап) возрастающей, убываю-
щей, невозрастающей, неубывающей, если при любом нату-
ральном п верно неравенство:
а) а„+1 — ап> 0; в) ап+1 — ап < 0;
б) а/г+1 — а„ < о; г) ап+1 — ап > 0.
186. Докажите, что последовательность (у„) является монотонной,
если:
ч 2 — 9п Зп + 7
а)у„=—; б)ь. = ^гг5-
187. Докажите, что последовательность (хп) не является монотон-
ной, если:
а) хп = п2 — 12п; б) хп = 4п — п2.
188. Монотонная ли: а) арифметическая прогрессия; б) геометриче-
ская прогрессия? Приведите примеры.
189. Является ли последовательность (с„), все члены которой —
положительные числа, возрастающей, убывающей, невозра-
стающей, неубывающей, если при любом натуральном п верно
неравенство:
а)с2Ш_<1; б)с-^>1; В)^Д<1; г) ^-> 1?
сп сп сп сп
190. Пусть рп — периметр правильного n-угольника, вписанного
в окружность радиуса г. Докажите, что последовательность
Рз, Р«, Pit, P2i, ••• , Р3.2п-1’ •••
является возрастающей.
191. Пусть qn—периметр правильного n-угольника, описанного
около окружности радиуса г. Докажите, что последователь-
ность
<7з, *712» ••• » •••
является убывающей.
32. Существование предела монотонной и ограниченной
последовательности
Теорема Вейерштрасса. Если последовательность
монотонна и ограничена, то она имеет предел.
Доказательство этой теоремы мы не приводим. Отметим лишь, что в
множестве Q рациональных чисел теорема Вейерштрасса не имеет места.
81
В самом деле, десятичные приближения по недостатку хп к числу х
рациональны и образуют монотонную последовательность. Эта последова-
тельность сходится к числу х. Если число иррационально, то в силу теоремы
о единственности предела последовательность (хл) не может иметь рациональ-
ного предела. Например, члены последовательности
Xi = 0,1;
х2 = 0,1001;
х3 = 0,100100001;
хл = 10-1 + 10-2* + 10-3’ + ... 4-
являются десятичными приближениями по недостатку числа а, у которого
единицы стоят на местах с номерами, равными квадратам натуральных чи-
сел, нули — на остальных местах. И поэтому
lim хл = а.
п+<х>
Число а является иррациональным, так как оно является непериодической
бесконечной десятичной дробью. Следовательно, если бы в нашем распоря-
жении имелись лишь рациональные числа, то мы должны были бы сказать,
что последовательность (хл) не имеет предела, хотя она и удовлетворяет
всем условиям теоремы Вейерштрасса:
0 хл 0,2 и хЛ4-1 хл.
В теореме Вейерштрасса сформулированы достаточные условия
существования предела последовательности. Но способ нахожде-
ния этого предела теоремой не указывается. Тем не менее часто
бывает, что одна лишь информация о* существовании предела по-
зволяет его вычислить. С этой точки зрения весьма интересны сле-
дующие примеры. В них мы пользуемся тем, что для любой схо-
дящейся последовательности (хл)
lim хп — НгиХд-х,
И-+ОО П-+СО
поскольку (хл) и (хл_г) это по существу одна и та же последователь-
ность (они отличаются лишь'первым членом и порядком нумерации
членов).
Пример 1. Доказать, что lim qn — 0 при | q | <1.
п->со
Проведем доказательство для положительных q. Последова-
тельность (дп) ограничена, так как 0 < qn < 1, и монотонно
убывает, поскольку qn+1= q - qn <qn. Эта последовательность
удовлетворяет обоим условиям теоремы Вейерштрасса. Поэтому
она имеет предел, обозначим его через а:
lim qn = а .
п->оо
Но
lim qn = lim q • qn~r = q lim qn~x = q • a.
n-j-OO n->co n->co
Из a = q • а вытекает a(l — q) — 0. Так как 1 — q Ф 0, получаем
a = 0.
А это и означает, что lim qn — 0.
л-» co
82
Случай q < 0 сводится к случаю q > 0 (объясните как). Вы
видите, что теорема Вейерштрасса позволила нам обойтись без
выкладок с неравенствами из п. 23.
Пример 2*. Дадим обоснование одного старого способа
приближенного извлечения квадратных корней. Пусть требуется
найти квадратный корень из положительного числа а. В виде пер-
вого приближения возьмем положительное число Х|, квадрат ко-
торого больше а. Тогда Xi будет больше а число — — мень-
ше У а : — < У а < xv
Xi
В виде следующего приближения возьмем
1 / а \
2 ~ 2 ( х, +
а затем определим последовательность (хп) рекуррентно:
__ 1 / а \
*7/4-1 “Z I г %п )•
z \хп /
1) Докажите сами, что всегда
- < У а < хп.
хп
2) Докажите сами, что последовательность (хп) убывающая.
3) Так как при всех п (п 2) а<хп<Х\, то последова-
тельность (хп) ограничена. По теореме Вейерштрасса она имеет
предел. Чтобы его найти, «перейдем к пределу» в равенстве (1),
заметив, что
Птх/г+1 = b’mxrt.
л->оо м->оо
Обозначая этот предел через с, имеем:
1 / а . \
с — — —И с ;
2 \с )
с2 — а = 0;
с =Уа .
4) Отметим, что последовательность (хп) сходится к У а очень
быстро.
Так, при а = 2 и Xi = 2 имеем:
1 X, = — 1 2 2 |'- + 2К- = 1,5; \2 ) 2
1 Хч - — 3 2 /2 . 3\ 17 . Л1с. (з/2 2/ 12 ~ ’
1 , Х4 = — 4 2 1 (— 4- « 1,414216, U7/12 12/ 408
83
Как видите, этот способ прост и очень быстро дает большую точ-
ность: %2 «У 2с точностью до 0,1; %з имеет два верных десятич-
ных знака; Х4 имеет уже пять верных десятичных знаков.
Если провести рассуждения в общем виде, то для разности
Alt = Хп
можно вывести рекуррентную формулу
Л - _____
“+1 +
из которой вытекает, что
т. е. число верных десятичных знаков с каждым шагом приблизи-
тельно удваивается.
Упражнения
192. Истинно ли высказывание:
а) если последовательность не ограничена, то ойа не имеет
предела;
б) если последовательность имеет предел, то она ограничена;
в) если последовательность не монотонна, то она не имеет
предела;
г) если последовательность имеет предел, то она монотонна.
193. Найдите пределы:
а) хп — 2П > б) хп— .
У Казани е. Проверьте условия применимости теоремы
Вейерштрасса и сравните lim х,г и lim хя_х.
п->со п->оо
33. Число л и длина окружности
Еще в V классе вы узнали, что длина окружности единичного
диаметра выражается числом
л = 3,14159...
Длина окружности диаметра d выражается формулой
С = nd. (1)
В учебнике геометрии для VIII класса сказано, что длина окруж-
ности должна быть больше периметра любого правильного вписан-
ного в окружность многоугольника и меньше периметра любого
описанного около нее правильного многоугольника (рис. 16, 17).
84
Это предположение позволяет дать хорошие приближенные
оценки числа л. Еще Архимед установил, что периметр Р9в вписан-
ного в окружность диаметра d правильного девяностошестиуголь-
ника удовлетворяет неравенству
а периметр Q96 описанного правильного девяностошестиугольника
неравенству
0)6 < 3 — d.
Отсюда вытекает (если принять высказанное выше допущение),
что
Из соображений подобия вытекает, что
Ptl = Pnd> Qn = <!nd* (2)
где рп и qn — периметры соответственно вписанных и описан-
ных правильных многоугольников для окружности диаметра d = 1.
Оказывается, что последовательности
Рз, Р4, Рэ’ » Рт ••• »
рз, q^ q&, •••, qtl>
имеют общий предел. Этот предел и есть число л:
л = lim рп = lim qn. (3)
n->oo n->oo
Из равенств (2) и (3) вытекает равенство (1).
Дадим теперь определение длины окружности.
Определение. Длиной окружности называет-
ся предел последовательности периметров правильных вписанных
многоугольников.
85
Доказывать существование и совпадение пределов (3) мы не
будем, но расскажем, как можно воспользоваться для вычисления
л с любой требующейся точностью периметрами
Ре» Pi2> Ри> ••• > Рз-г*’ •••
правильных вписанных в окружность, диаметр которой равен
единице, многоугольников и периметрами
9б» *712» *?24» ••• » *7з'2^’
правильных описанных около окружности, диаметр которой ра-
вен единице, многоугольников, получающихся «удвоением» числа
сторон.
Очевидно, что
Рп ^**л» Яп. nbn, (4)
где ап — сторона правильного вписанного в окружность диаметра
единицы n-угольника и Ьп — стороны правильного описанного
около этой же окружности n-угольника. Для вычисления а.2п по ап
существует формула
= 71^2 — 2]/1^а2 . (5)
Для вычисления Ъп по ап можно воспользоваться формулой
: V1 - '< (6)
Формулы (5), (6) и (4) позволяют последовательно вычислять
a3.2ft и b3.2ft, p3.2ft и q3.2k для любого натурального k, отправ-
ляясь от а6 = 0,5. (7)
Число л есть общий предел:
л = lim p3.2k = lim q3.2k (8)
n->oo n->oo
последовательностей (p3.2*) и (<?3.2ft). Можно показать, что первая
из этих последовательностей монотонно возрастает и ограничена
сверху, а вторая — монотонно убывает и ограничена снизу. По-
этому существование их пределов есть следствие теоремы Вейер-
штрасса. Совпадение их пределов вытекает из формулы
Яп = РпУХ— ап
и того обстоятельства, что ап при п-+ со стремится к нулю.
Приведем в заключение таблицу, которая иллюстрирует при-
ближения p3.2k и q3.2k к числу л:
п 1 Рп 1 I Рп
6 3,00000 3,46414
12 3,10595 3,21554
24 3,13301 3,16005
48 3,13475 3,14665
96 3,14134 3,14284
Для 3072-угольников, вписанных и описанных около окружно-
сти; диаметр которой равен 1, получены уже совсем близкие друг
к другу значения
Рзо72 — 3,141592652...
<7зо72 = 3,141592654...
Упражнения
194. Вычислите с точностью до 0,001 длину окружности, если:
а) г = 2,1000; б) г = 1,2300; в) г = 12,7000; г) г = 3,2785.
195. Вычислите периметр полукруга с точностью до 0,001, если:
а) г = 1,3000; б) г = 3,7000; в) г = 15,2000; г) г = 5,2329.
196. Для окружности радиуса г вычислите длину дуги с централь-
ным углом, равным:
а) 30°; б) 45°; в)‘ 60°; г) 90°; д) 1%
197. Для окружности радиуса г выведите формулу для длины ее
дуги с центральным углом в а градусов.
198. Фигура состоит из объединения двух одинаковых кругов
радиуса г, центры которых находятся на расстоянии г J3.
Найдите периметр этой фигуры.
Дополнительные упражнения к главе III
199. Истинно ли высказывание:
a)5UN; г) Цо е) “МАГ;
б) -]/3CQ; 3^’ ж)]Л7С£;
в) 0,737£Z; Д) з) 1g 36 £ Q ?
200. Докажите, что не существует рационального числа, квадрат
которого равен: а) 7; б) 11.
201. Докажите, что не существует рационального числа, равного:
a) 1g 5; б) 1g 43.
202. Докажите, что числа j/"; У 2 не рациональны.
203. Известно, что 0 — 10,6071246... . Найдите десятичные при-
ближения числа Р по недостатку и по избытку с точностью до
0,1; 0,001; 0,00001.
204. Известно, что:
а) 6,8^ V47 <6,9. Найдите десятичные приближения ]/47
по недостатку и по избытку с точностью до 0,01.
б) 3,6 У 12,96 < 3,7. Найдите десятичные приближения
У 12,96 по недостатку и по избытку с точностью до 0,01.
205. Какие из данных чисел представляются в виде бесконечных
периодических десятичных дробей и какие — в виде беско-
нечных непериодических десятичных дробей:
/2, |,/5, /36, —1 -/3?
/ э 1<э
87
206. Каким является число а, рациональным или иррациональ-
ным, если начиная с некоторого номера все его десятичные при-
ближения по недостатку представляют собой равные дроби?
207. Известно; что а = 3,6711845... Приведите пример действитель-
ного числа, меньшего а; большего а.
208. При каких натуральных значениях п верно неравенство уК < е,
если:
а) £ — 0,0003685... ; б) е - 0,001645...?
209. Докажите, что если г и s— рациональные числа и г < s, то
г+«
число -у- лежит между ними.
210*. Докажите, что если аир — два действительных числа и
а < р, то существует хотя бы одно рациональное число г,
лежащее между ними.
211. Пусть а и Р — иррациональные числа, а а + Р — рациональ-
ное число. Докажите, что числа а—р, а+2Р иррациональны.
212. Докажите, что если а— положительное иррациональное чис-
ло, то Уа — иррациональное число.
Найдите три первых десятичных знака бесконечной десятич-
ной дроби, выражающей число:
213. 3-г |/2. 214. у + |/гЗ. 215. 0,(6) — Кб.
216. 5 V 2. £17. ]£ • КЗ. _ 218^ |/3 •
219. Что больше: К7 + К 10_или КЗ + К19?
220. Докажите, что число КЗ + К5 иррациональное.
221. Докажите, что сумма рационального и иррационального чи-
сел есть число иррациональное.
222. Докажите, что разность рационального и иррационального
чисел есть число иррациональное.
223. Приведите пример двух иррациональных чисел:
а) сумма которых есть число иррациональное;
б) сумма которых есть число рациональное.
224. Пусть а — иррациональное число. Докажите, что число —
а
также иррациональное.
225. Найдите координату точки М координатной прямой, для
которой:
а) | AM | = | ВМ | , если Л(—10,2) и В(0,4);
б) | ВМ | - 2 | AM | , если Л(0) и В(12).
226. Пользуясь теоремой Пифагора, постройте отрезок, длина ко-
торого равна: а) 1^10; б) К14.
227. Решите уравнение или неравенство:
а) |х—2 | = 0,3; г) | 10 — х | < 7;
б) |х + 3 | = 0,1; д) 1 х + 1 | : > 1;
в) | х — 2,5 | 0,5; е) | 8 + х | ; >0,7.
88
228. Решите уравнение:
а) | х + 4 | - | х — 4 | ; б) | х + 2,5 | = | х — 3,3 |.
229. Решите неравенство:
а)|х|>|х—2|; б)|х—5|<|х—1|.
230. Изобразите множество точек координатной плоскости:
а) {(х, у) | х2 4- у2 = 0}; д) {(х, у) | | х | = | у | );
б) {(х, у) | х2 4~ у2 == 9}; е) {(х, у) | | х | 4- х = |у |4-у};
В) {(х, у) |х2 — у2 = 0}; ж) [(х,-у)| _?L =-2-1;
I 1*1 ly|J
г) {(х, у) | (х2 — 4)2 4- у2 = 0}; з) {(х, у) I I х | 4~ I У I
- X 4- у).
231*. Изобразите в координатной плоскости множество точек:
а) {(х, у) |(х-4)(у+ 1) -0};
б) {(х, у) |х2-у2>0};
232.
В) {(X, у) I - 0};
г) {(х, у) | у2 < х2 и | х | < 2};
д) {(х, у) | (х2 - у2) (х2 4- у2 - 1) - 0);
е) {(х, у) | (х2 — у2) (х2 + у2 — 1) < 0}.
Последовательность (хл) задана формулой хп —
___1_
2«-Ь 1
Най-
дите Х3, Xj, X;(^_j, X2rt-|-i, .
хя
233. Подберите формулу /i-го члена конечной последовательности:
з)1; 2 2 . 1 16 ’ 2. 25’ 2 ’ 22 ,3 . ’ 2» ’ 4 . 2* ’ 2. 2> ’
б)4; 2 X 1 1 в) —; —; 3 . 27 ’ 2. 4 . 81 ’ 2. 5 243’ 2. ж) 1; 2 ’ 10 2 . 1 ’ 28’ 4 . 2 . 82 ’ 8 .
’ 3 6 Ч 1 1 9 ’ 1 Г2 ’ 1 15’ 1 . 1 101 ’ 201 ’ V2 / 3' 301 ’
г) —; —; ’ 4 7 10 ’ 13 ’ 16» 3)7: 1 — \ 5 ,); (7. 1 ’ уэ- 1 •
234. Изобразите геометрически (двумя способами) последователь-
ность (м„). Существует ли такое число, к которому стремится
последовательность . 2л + 1 Ю- 2» — 3
3) ~ 2п ’ в) U'^ Зп ;
_ 4п — 1 . U'i ~ Зп ' г) = 2+ ? 11
235. Укажите номера членов последовательности (уя), где уп =
5п — 1 г- \ 1
= ------, которые удалены от точки 5: а) менее чем на — ;
п 3
б) менее чем на 0,001.
2П___з
236. Последовательность (х) задана формулой хп = ----------. При
каких натуральных значениях п выполняется условие:
а) | хп —2 | <0,1; б) |хл-2 | <0,01?
89
237. Последовательность (z„) задана формулой гп = . при
2п
каких натуральных значениях п выполняется условие:
а) | гп~ 1,5 | <0,1; б) |гя-1,5| <0,01?
238. Докажите, что верно равенство:
a) lim —— = 1; б) lim = 2.
п->оо п 4” 1 П->оо П 4“ 1
239. Имеет ли предел последовательность
он равен? (Приведите доказательство.)
240. Докажите, что:
*л=Ш”* Чему
a) lim == О;
п->00 П2+1
б) lim п* = 1;
в) lim ——— = 0;
fl-> OO П44~ 16
г) lim — = 0.
n-*oo nl
241. Известно, что lim xa = а и a < q. Докажите, что почти
n-*-oo
все члены последовательности (х„) меньше q (за исключением,
быть может, конечного числа членов).
242. Известно, что lim хп = а и а > р. Докажите, что почти
Л->ОО
все члены последовательности (х„) (за исключением, быть
может, лишь конечного числа членов) больше р.
243. Докажите, что если lim хп = а, то lim | хп | ~ | а |.
п-*оо п->оо
Указание. Воспользуйтесь неравенством
1 \а |- \Ь | | < |а-b | .
244. Известно, что lim ап = р и lim bn = р. Существует ли
П->00 п->оо
предел последовательности
at\ а2, Ь2, ... ; ап; Ьп\ ... ?
Чему он равен?
245. Найдите значение выражения:
ч 0.(5) . б) 0.1(2) + 0.3(4)
’ 0,(3) ’ ' 0,4(5) —0,2(3)
246. Найдите сумму ряда:
ч 1 . 1 , 1 . , 1 ,
а) Т"2+ ^з + Г. 4 + - + ^77 + - ’
б) 1/"3 4—7s 4“ —7= 4” ••• 4” -— +....
' Y /3 3/3 З"-1
247*. Укажите какие-нибудь значения х, при которых верно ра-
венство:
a) (1 _Х)(1 _хц-х2 — х3 +...+(- l)«-i хп~1 + ...);
90
б) - = 1 + (1 - х) + (1 - х)2 + (1 - х)»-2+ ....
X
248*.Докажите методом математической индукции, что если по-
следовательности (х„), (уи), , (Д) сходятся, то:
a) lim (хп + уп + ... -J- /„) = lim хп + lim уп + ... + lim /л;
П->ОО Zl-j-оо п-*со п->оо
б) lim (хл • уп • ... • /л) = limx„ - lim уп •... • lim/„.
/7->ОО п->оо П->ОО П->00
249*.Пусть lim апЪп = 0 и lim ап — 0. Следует ли отсюда, что
И->ОО П->ОО
lim bn = 0?
П->ОО
250*.Известно, что последовательности (хп) и (уп) расходятся.
Могут ли сходиться последовательности (хп + уп) и (хлу„)?
Приведите примеры.
251*.Известно, что последовательность (хп) сходится, а последо-
вательность (уп) расходится. Могут ли сходиться последова-
тельности <Хп + уп) и (хлул)?
252. Найдите предел:
lim 2л* + 3п*-2л* lim (3n-2)(l-n)(2 + n)
,woo n + 2/l»—2 л5 «->00 2n’4-n2—1
253.
254.
255.
Вычислите
П^оо \ 3 9 27 3я-1 )
Катет а прямоугольного треугольника разделен на п кон-
груэнтных частей и на полученных отрезках построены вписан-
ные прямоугольники (рис. 18). Найдите предел последователь-
ности (Sn) площадей образованных ступенчатых фигур. Ис-
толкуйте геометрически полученный результат.
Найдите «площадь» фигуры, ограниченной параболой у = х2,
отрезком [0; 2] оси абсцисс и прямой х = 2 (рис. 19), как
91
предел площадей ступенчатых фигур, построенных так же,
как и в предыдущем упражнении.
256. Найдите предел:
lim (И- <2 + Зн) <3 — 4/0
л-юо (1 +2п)(3 + 2л)
257. Является ли монотонной последовательность (хя), если:
. 2/1 — 3 2" .
а) хп =------; б)* хп = - ?
И п\ —
258*.Докажите, что последовательность (а„) является возрастаю-
щей, если:
а) аи
2 22
1+1
2“ 32
2п ’
_1^
п2
259. Докажите, что:
а) последовательность хп — ---- является возрастающей;
5/1 2
б) последовательность у — -~п- является убывающей.
5п — 1
260*.При каких коэффициентах а и b последовательность
является возрастающей, убывающей, невозрастаю-
щей, неубывающей?
26Г*.Докажите, что последовательность (цп):
„ - q _2 + ««
1 ’ U,l+1~ 2ип ’
262.
263.
264.
является убывающей.
Пусть ап—сторона правильного n-угольника, вписанного
в окружность радиуса г. Докажите, что последовательность
а4, а8, а16, ... , a2n+i является убывающей.
Пусть Ьп — сторона правильного n-угольника, описанного
около окружности радиуса г. Докажите, что последователь-
ность b3t Ьв, Ь12, ... , bs.2,l~l является убывающей.
Пусть Sn — площадь правильного n-угольника, описанного
около окружности радиуса г. Докажите, что последователь-
ность
^3, ^>6’ ^12» ••• » *^3-2,г ”•
является убывающей.
T^r j ПРЕДЕЛ ФУНКЦИИ
Глава IV И ПРОИЗВОДНАЯ
§ 8.
ПЕРВОНАЧАЛЬНЫЕ
ПРЕДСТАВЛЕНИЯ О ПРОИЗВОДНОЙ
И ПРЕДЕЛЕ ФУНКЦИИ
34. Числовые функции
Мы будем заниматься далее функциями, у которых область оп-
ределения и множество значений состоят из действительных чисел.
Область определения функции f будем обозначать £>(/), а множе-
ство ее значений — E(f).
П р и мер 1. Последовательность
(—1; 1; —1; 1; —1; ...)
есть функция /, определенная формулой
К") = (-1)«
на множестве натуральных чисел. Ее область определения D(f) — N,
а множество значений Е([) = {-И; 1} состоит из двух чисел: —1 и 1.
Пример 2. Формула
Кх) =
задает функцию область опреде-
ления которой есть отрезок [—1; 1]
(рис. 20), а множество значений — отре-
зок [0; 1].
Вообще, числовая функция есть
отображение некоторого подмножества D
множества R на другое подмножество Е
множества R. Множество D называют
областью определения, а множество Е —
множеством значений функции.
93
Пример 3. Отображение
1
х -> —
к
есть функция, для которой областью определения и множеством
значений служит одно и то же множество — множество всех от-
личных от нуля действительных чисел (рис. 21).
Функция f полностью определяется заданием множества пар
(х; /(х)),
где х пробегает все множество £>(/), а /(х) — соответствующие значе-
ния функции.
Множество этих пар можно записать еще таким образом:
{(х-, у) | у = f(x)}.
Очевидно, это подмножество множества /?в, т. е. числовой плоско-
сти. Изображение этого множества на координатной плоскости
есть график функции (см. на рис. 20 и 21 графики функций из при-
меров 2 и 3).
Далеко не всякое множество точек координатной плоскости
является графиком какой-либо функции. Например, множество,
изображенное на рисунке 22, не есть график функции, так как оно
содержит две точки с абсциссой а и разными ординатами и Ь2.
Если бы мы сочли это множество графиком функции, нам пришлось
бы считать, что наша функция имеет при х — а сразу два значения:
у = и у = b2t что противоречит определению понятия функции.
Еще в учебнике для VI класса было сказано, что функции — это част-
ный случай соответствий. Чтобы задать числовое соответствие, для каждого
х указываются все те у, которые соответствуют этому числу х (для некоторых х
таких у может и не быть). Например, формула
х2 + у2 = 1
задает соответствие, в котором каждому х из интервала ]—1; 1[ соответству-
ют два числа:
Ух = V1 — х2 и у2 =— У1 — №,
числу х = 1 и числу х = —1 соответствует одно-единственное число у — О,
94
а числам x, по модулю превышающим единицу, не соответствует ничего.
На рисунке 23 дан график этого соответствия.
Произвольное подмножество множества задает числовое соответст-
вие. В современной математике, стремясь уменьшить число основных мате-
матических понятий, говорят проще: числовое соответствие есть множест-
во пар чисел, т. е. подмножество множества /?2 — числовой плоскости.
С этой точки зрения числовая функция, как частный случай соответ-
ствия, тоже есть множество пар чисел, но уже не произвольное. Числовая
функция есть такое множество f пар .
чисел (х; у), что для любого числа х УI
имеется в этом множестве не более Т
одной пары (х; у) с первым элемен-
том х.
Второе число в этой единствен-
ной паре и есть f (х):
/ (х) = у <=> (х; у) G f.
Например, функция
1
х —
X
есть множество числовых пар вида
I 1 \
х; — •
\ х /
Пример 4. Отображение
х -* [х] (М — целая часть чис-
ла х).
Вспомнив, что на промежут-
ке [и; п 4- If, где п — целое
число, [х]= п, построим график
этой функции (рис. 24). График
состоит из горизонтальных от-
резков, из которых исключены
их правые концы (отмеченные
кружочками).
Пример 5. Отображение
х -*• {х} ({х} — дробная часть
числа х).-
Из определения дробной ча-
сти числа х следует, что
/(х) = х — п для х С [л; п + If.
Таким образом, на каждом
промежутке [л; п + 1[ графи-
ком рассматриваемой функции
служит отрезок прямой, на-
клоненной к оси Ох под углом
45°, из которого исключен пра-
вый конец. Полный график этой
функции состоит из бесконечно-
го числа таких отрезков (рис.
25).
-2 -] 0 1 2 3 х
Рис. 25
95
Упражнения
285. f(x) Х+-. Найдите /(1). /(2), fl Д. /('—') /(-0,5).
266. Уравнение Зу = 5х— 2 определяет функции у = f(x) и
х - g(y). Найдите f(Q), ftl), / (а2 + 1), f(x — 1), g(x),
g(5), g(-3).
267. Изобразите множества и назовите полученные фигуры:
а) {(х; у) | ху = 0); в) {(х; у) | | х | < 1 и | у | < 1};
б) {(х;у) | |х—3 |< 1}; г) {(х; у) | |х-2 | < 1 и
1У + 3 | <1}.
268. Укажите области определения функции /, заданных формула-
ми:
a) f(x) = х — 1; в) fix) =
6) / (х) = х + 3; г) /(х) = .
269. а) у = ; в) g(x) = ]/10х-5;
б) у-4-; г) /(х) = /5-10х.
X + 1
270. Найдите / (—5); / (—7); Д5); /(х); /(/), если /(п) = J//Z4-&H-1.
271. Найдите/(5), f(z), f(u), если: а) Дх)= б) f (r) = lg
г X X “у"
272. Вычислите/( —2); /(0); f(—\ f(—Y, /(1); /(4), если:
\ 2 ] \ 3 /
/м =
—1 при —3 X 5^ 0,
х при 0 < х <1,
1 при 1 х 5.
273. Вычислите /(—2); /(0); /(2); /(3); /(5), если
х2 — х + 1 при | х | 2,
1 при х > 2.
274. В квадрате
со стороной а проведена прямая, параллельная
диагонали. Установите зависимость между
площадью S отсекаемой фигуры и рас-
стоянием х прямой до вершины квадрата
(рис. 26). Найдите область определения
функции х-> S(x). Начертите ее график.
275. Является ли окружность с центром в на-
чале координат графйком какой-либо
функции?
276. Приведите три примера функций, графи-
ки которых симметричны относительно
оси ординат.
96
277. График функции х->Дх) симметричен относительно оси ор-
динат. Запишите это свойство в виде равенства.
278. Приведите три примера функций, графики которых симмет-
ричны относительно начала координат.
279. График функции х->Дх) симметричен относительно начала
координат. Запишите это свойство в виде равенства.
280. Постройте графики функций f, заданных формулами:
a) Дх) = х2; б) Дх) = х3; в) Дх) = —; г) Дх) = х4; д) Дх) = 0.
х
Какие из графиков этих функций симметричны относительно
оси ординат, а какие симметричны относительно начала коор-
динат?
281*. Заданы три функции f, g, h:
f(x) = 1g xa, g(x) = 21g x, h(x) = 21g | x |.
При каких значениях x #= 0 равенства
a) f(x) = g(x); 6) f(x) = Zi(x); e)g(x) = /i(x)
становятся ложными высказываниями, а при каких — истин-
ными?
35. Изменение функции, ее возрастание и убывание
На рисунке 27 изображен график изменения высоты самолета
в течение полета, продолжающегося десять часов (время измеряется
в часах, высота — в километрах). В течение первого часа самолет
набирает высоту, затем в течение трех часов летит на постоянной
высоте, в течение часа вновь набирает высоту, летит на новой по-
стоянной высоте четыре часа, а в течение последнего часа спускает-
ся. Высота h является в этом примере функцией времени /, опре-
4 Заказ 243
97
деленной на промежутке [0; 10], обозначим эту функцию* через
h (/). На промежутке [0; 1] функция возрастает, на промежутке
[1; 4] постоянна, на промежутке [4; 5] вновь возрастает, на проме-
жутке [5; 9] постоянна, на последнем промежутке [9; 10] убывает
до нуля.
Если рассмотреть промежуток [0; 9], то нельзя сказать, что
функция
h = h (0
на этом промежутке все время возрастает. Верно только, что она
на этом промежутке нигде не убывает. Аналогично про поведение
нашей функции на промежутке [5; 10] можно сказать, что она на
этом промежутке нигде не возрастает.
Сформулируем соответствующие этим наглядным соображениям
математические определения.
I. Функция f называется возрастающей на множестве Е, если
для любых х± и х2, принадлежащих множеству Е, из xt < х2 вы-
текает: /(х,) </(х2).
II. Функция f называется убыва-
ющей на множестве Е, если для лю-
бых хг и х2, принадлежащих множест-
ву Е, из Xi < х2 вытекает:
Ж) >f(x2).
Примеры. 1) Функции х х,
х -> х2 (рис. 28) и вообще х -> х" при
любом натуральном нечетном п возра-
стают на всей числовой прямой.
2) Функции х -> х2 и вообще х хп
(рис. 29) при любом натуральном чет-
ном п возрастают на положительной
полупрямой [0; + <*>[ и убывают на от-
рицательной полупрямой ]—оо; 0].
3) {х} (дробная часть х) возраста-
ет на каждом промежутке [/?; п + 1[,
где п — произвольное целое число.
4) Так как последовательность есть не что
иное, как функция хп = /(и), определенная
на множестве натуральных чисел, то естест-
венно думать, что в применении к таким
функциям наши новые определения возрас-
тания и убывания равносильны данным в п.31.
* Заметьте, что в прикладных вопросах,
особенно в том случае, когда независимым пе-
ременным (аргументом) является время, часто
функцию и ее значение обозначают одной и
той же буквой.
98
Это предположение верно. Рассмотрим подробнее случай возрастания.
По новому определению последовательность (хп) возрастает в том и только
в том случае, если при любых натуральных т и п из т < п вытекает:
хт < хп- 0)
Ясно, что в этом случае, в частности при любом натуральном т,
хт < хт+1' (2)
Если неравенства (2) верны при любом натуральном т, как этого требует
определение возрастающей последовательности из п. 31, то из цепочки не-
равенств хт < xmvi< ... < хп получаем при любых т (п > т) неравенство
(О-
Упражнения
Определите промежутки возрастания и убывания функций f:
1
282. f(x) =— Зх+ 2. 290. /(х) = х2.(
283. /(х) = |х — 2|. 291. /(х)=—х2. £
284. /(х)=—-|х2 + 2. 292. f (х) = | х |2 . 1
285. f(x) = (х — 2)2. 293. /(x) = 0,5xJ.
286. f(x) =— (х — З)2. 294. /(х) = 2х.
287. f (х) = —2х2 + 6х —7. 295. / (х) =
288. f(x)= -. X 296. /(х) = |lgx|.
289. /(х)= —— . 297. / (х) — 1g | х).
х
36. Приращение функции
В формуле
У = fix)
переменную х называют независимой переменной (или аргументом
функции). Каждому ее значению из области определения
функции f соответствует определенное значение у = f (х) зависимой
переменной у из множества значений Е ([) функции f* .
Если х и х0 — два значения независимой переменной из D (f),
то разность их х — х0 называется приращением независимой пере-
менной и обозначается через Дх (читается: «дельта икс»).
* Условившись в качестве независимой переменной употреблять букву х,
можно более кратко функцию /, заданную формулой f (х) = у = х® — Зх,
называть «функцией х® — Зх» или «функцией у = г* — Зх». Дальше
мы часто будем пользоваться такими сокращенными оборотами речи.
4* 99
Рис. 30
Таким образом,
Ах = х — х0,
откуда следует, что
х = х0 + Ах.
При этом говорят, что пер-
воначальное значение х0 неза-
висимой переменной «получило
приращение Ах». Вследствие
этого значение функции изме-
нится на величину
f (х)— f (х0) = f (х0 + Ах) — f (х0).
Эта разница между новым значе-
нием функции Дх0+Ах) и перво-
начальным ее значением /(х0) называется приращением функции!
в точке х0 и обозначается символом А/(х0) (читается: «дельта эф
в точке х0»). Так что А/ (х0) = f (х0 + Ах) — f (х0).
Короче А/(х0) называют приращением зависимой переменной
и обозначают через Af или Ау (рис. 30).
Употребляя введенную терминологию, можно следующим обра-
зом переформулировать определения возрастающих и убывающих
функций.
Функция называется возрастающей, если ее приращения в каж-
дой точке х0 положительны при любых положительных прираще-
ниях независимой переменной; убывающей, если ее приращения
в каждой точке х0 отрицательны при любых положительных при-
ращениях независимой переменной. При этом если речь идет о
возрастании или убывании не на всей действительной оси, а только
на некотором ее подмножестве Е, то имеют в виду только прираще-
ния независимой переменной при переходе от точки х0 из этого
множества к точке х из того же множества.
Рассмотрим два примера, которые позволят нам понять основ-
ной замысел важного раздела нашего курса, посвященного началам
дифференциального исчисления (оно составляет главное содержа-
ние этой и следующих глав учебника).
Первый пример будет очень простым. Мы применим новый ме-
тод исследования к функции f(x) — х2. При этом мы узнаем мало
нового об этой функции, но зато поймем основы нового метода.
Второй пример будет интереснее. Исследовать на возрастание
и убывание функцию f (х) = х3 — Зх при помощи тех способов,
которые вы уже знаете, было бы не очень легко. Новый метод позво-
лит это сделать очень просто.
Пример 1. Исследовать на возрастание и убывание функ-
цию
f (х) = х2.
100
Вычислим приращение функции
в точке х'.
Д/ (х) = f (х + Ах) — f (х) = (х +
+ Дх)2 — х2 = 2хДх + (Дх)2.
Если приращение Дх мало по абсолю-
тной величине, то его квадрат будет
еще много меньше. Например, если
Дх = 0,001, то (Дх)2 = 0,000001. По-
этому естественно считать
2хДх
главной частью приращения функ- Рис. 31
ции и надеяться на то, что уже
она одна поможет нам решить вопрос о возрастании или убывании
функции.
Для положительных приращений Дх имеем:
2хДх > 0 при х > 0;
2хДх < 0 при х < 0.
Таким образом, мы снова убедились, что функция х -> х2 дейст-
вительно убывает на отрицательной полуоси и возрастает на поло-
жительной (рис. 31).
Пример 2. Исследовать на возрастание и убывание функ-
цию
f (х) — х3 — Зх.
Вновь вычислим приращение функции в произвольной точке х:
А/ (х) = (х + Дх)3 — 3 (х + Дх) — (х3 — Зх).
Сгруппировав вместе члены с одинаковой степенью приращения
Дх, получим:
Af (х) = (Зх2 — 3) Дх + Зх (Дх)2 + (Дх)3.
Естественно считать здесь главной частью приращения выражение
(Зх2 — 3) Дх.
Тогда если в точке х коэффициент Зх2 —3 > 0, то при достаточно
малых Дх > 0 будет Д/ > 0. Возникает гипотеза: если на интер-
вале Зх2 — 3 > 0, то на этом интервале функция возрастает, а
если Зх2 — 3 < 0 — убывает.
Позднее мы познакомимся с общими положениями, которые
позволят ее обосновать без громоздких вычислений. Остается ис-
следовать, при каких х выражение Зх2 — 3 положительно, а при
каких х— отрицательно. Решая уравнение
Зх2 — 3 = 0,
получаем два корня хх =—1, х2= 1. Выражение Зх2 —3 отри-
цательно в промежутке ]—1; 1[ между этими корнями, а при
х < — 1 и при х > 1 положительно. Следовательно, функция
101
/ (х) — л3 — Зх возрастает в проме-
жутке ]—оо; —1], убывает в про-
межутке [—1; 1] и вновь возрастает
в промежутке [1; +оо[ (рис. 32).
При х — —1 имеем f (—1) = 2. Это
максимальное значение функции в
том смысле, что слева от точки х =
— —1 функция возрастает, а справа
от нее убывает. Аналогично значе-
ние f (4-1) = —2 является минималь-
ным (слева от точки х — —1 функция
убывает, а справа от нее возрастает).
Говорят, что данная функция имеет
в точке х = —1 максимум, а в точке
х = 1 минимум.
Упражнения
298. Для функции у = 2х 4- 5 найдите:
а) х, если х0 = 3 и Дх = 0,2;
б) х, если х0 = 4 и Дх = 0,02;
в) Ду, если х0 = 4 и Дх = 0,1;
г) Ду, если х0 = 7 и Дх = 0,01.
299. Для функции у = х2 найдите:
а) приращение Дх, если х = 2,5 и х0 = 2, и соответствующее
Ду;
б) приращение Дх, если х = 3,9 и х0 = 3,75, и соответствую-
щее Ду.
300. Для функции у = — найдите Ду, если:
х
а) х0 — 9; Дх = 0,06; в) х0 — 5,06, Дх = —0,3;
б) х = 4,02, Дх = 0,02; г) х = 6, Дх = —0,02.
301. Запишите приращение функции в точке х, соответствующее
приращению аргумента Дх, для функций:
а) у = 5 —_3х; в) f (х) = Зх2;
б) у = 2|/х; г) f (х) = 2х — х2.
302. Найдите f (х 4- Л), f (х 4- h) — f (х), ~ №.
h
а) при /(х) — х2; в) при /(х) = ах2 4- bx 4“ G
б) при /(х) = kx 4- b; г) при /(х) = х3.
303. Найдите —*:
2й
а) при f (х) = х2; б) при f (х) = Xs.
304. Найдите /(* + ')-W) + f (*-')
й2
102
а) при f (x) = x2; б) при f (x) = x3.
305. Докажите, что для функции f (х) = kx 4- b
Af (x) = kAx.
306. Найдите главную часть приращения функции
f (х) — ах2 + Ьх 4- с.
37. Производная как скорость изменения функции
Пример. Рассмотрим падение тела, при котором пройденный
путь s как функция времени t задается формулой
s = s(0 = .
Выберем какой-либо момент времени ta и рассмотрим промежуток
времени длительности А/ от момента /0 до момента
t = /0 + АЛ
За этот промежуток времени тело пройдет путь
As = s (0 - s (/„) = i ((t„ + ДО3 - ф = glaM + i (ДО3-
По известному из физики определению отношение
A_s = gt 4- £ м
At & * 2
есть средняя скорость тела на промежутке времени [/0; 4* Л/].
Примем, что g — 9,8, и подсчитаем средние скорости за проме-
жутки времени различной длительности, начинающиеся в момент
времени /0 =. 2.
At 1 0,1 0,01 0,001
As 24,5000 20,0900 19,6490 19,6049
At
Мы видим, что при малых А/ вычисленное значение средней
скорости оказывается очень близким к значению
gt0 = 19,6.
Это значение называют пределом средней скорости при At, стре-
мящемся к нулю, и пишут:
lim .
Д<->0
Мы имеем здесь дело с новым понятием, отличным от понятия
предела последовательности. Точно это новое понятие предела
функции будет определено в п. 38.
103
Естественно, что при любом /0
lim — = - gt0.
Л/-+0 Д/
Из физики вы уже знаете, что
v = gt
есть мгновенная скорость падающего тела в момент времени t.
По аналогии со средней и мгновенной скоростью движущегося
тела средней скоростью изменения функции на промежутке
[х0; х] = [х0; х0 + Ах]
называется отношение приращений функции и независимого пере-
менного:
Л/ (х0) _ f (хр + Дх) — / (х0)
Дх Дх
Предел средней скорости при стремящемся к нулю приращении
независимого переменного
lim = lim (*° + Ах) ~ <*о)
Дх-+0 Дх Дх-»0 Дх
называется скоростью изменения функции в точке х0. Для скоро-
сти изменения функции в точке х0 принято название производная.
Производная от функции f в точке х0 обозначается так что
по определению
f w = lim f + ^-1 W .
Дх-»о Дх
Если считать х0 переменным, то производная оказывается новой
функцией от этого переменного. Сама по себе эта функция обозна-
чается просто
Приведем ряд примеров, оговорившись, что пока наши рассуж-
дения имеют предварительный характер, так как мы не имеем еще
определения предела функции.
Пример 1. Найти производную функции / (х) = kx + b.
(Хо) — k (х0 + Ьх) + b — (йх0 + Ь) = £Ах,
Д/ (х0) = k
Дх
Предел постоянного равен этому постоянному. Поэтому при лю-
бом х0
/'(х0) = k.
Пример 2. Найти производную функции f (х) = ха,
N Uo) = 2х0Ах + (Ах)2,
= 2х0 + Ах.
Дх
104
При Дх, стремящемся к нулю, получаем:
/' (х.) = lim = 2х0.
Ах->о Ах
Сопоставим этот результат с графиком данной функции у = х2
(см. рис. 31 на стр. 101).
На графике видно, что при возрастании х от —со до +сю снача-
ла функция убывает очень быстро, потом все медленнее, до тех пор,
пока ее скорость изменения при х — 0 не обратится в нуль, а по-
том начинает возрастать все быстрее и быстрее. Эти наблюдения
вполне соответствуют полученной формуле для производной,
которую принято записывать так:
(х2)' = 2х.
Пр и м е р 3. Найти производную функции f (х) = х8 — Зх.
Д/ (х) - (Зх2 — 3)Дх + Зх (Дх)2 + (Дх)3,
=3х2 — 3 + ЗхДх + (Дх)2.
Дх
Ясно, что при стремлении Дх к нулю стремится к нулю и сумма
ЗхДх + (Дх)2.
Поэтому
Г (х) - lim = Зх2 — 3.
1 у 7 д^о Дх
Сравните этот результат с полученным при разборе примера 2 из
пункта 36. Вы видите, что знак производной позволил нам опреде-
лить, где функция возрастает, а где
и минимум функции оказы-
вались в тех точках, где произ-
водная равна нулю. Позднее мы
увидим, что обнаруженные зако-
номерности сохраняются в общем
случае. На рисунке 33 изображены
графики функции f (х) = х3 — Зх
и ее производной f (х) = Зх2— 3.
Проследите на этом рисунке, как
соответствуют значения и знак про-
изводной ходу изменения функции.
В заключение первого знаком-
ства с понятием производной ре-
шим такую задачу.
Задача. Из квадратного ли-
ста жести со стороной а надо
она убывает. Максимум
105
изготовить открытую сверху короб-
ку, вырезав по углам (рис. 34) квад-
ратики и загнув образовавшиеся
кромки. Какой должна быть сторо-
на основания коробки, чтобы ее
объем был максимальным?
Обозначим через х сторону осно-
вания коробки. Стороны вырезанных
квадратиков будут равны (а— х), а
объем коробки равен
V(x) = |(а-х)х!.
Л
Надо найти максимальное значение
этой функции в промежутке 0 х^а.
График функции изображен на рисун-
ке 35. Он построен с учетом замеча-
ний, сделанных к примеру 3. Снача-
ла по образцу предшествующих при-
меров найдем:
V (х) = — у х2 + ах.
Приравнивая эту производную ну-
лю, получаем уравнение
— — х2 4- ах ~ О,
2
которое в промежутке ]0; а[ имеет
2 тл
один корень х = — а. Из построен-
3
кого Трафика видно, что максималь-
ное значение объема V получается
2
при х = — а, т. е. вырезать по углам
надо квадратики со сторонами
1 / 2 \ 1
— а-----а] — — а.
2 \ з 6
При этом получится максимально возможный объем коробки:
17 /2 \2 1 2 з
Утак = — а —а=—а.
так \ 3 / 6 27
В систематическом порядке мы вернемся к отысканию максиму-
мов и минимумов функций в п. 55.
106
Упражнения
307. При помощи производной постройте графики следующих
функций:
а) у = х3 — Зх2 — 2; б) у = х4 — 2х2.
308. Из прямоугольного листа картона со сторонами 1 м и 1,6 .и
изготовьте открытую сверху коробку, вырезав квадратики по
углам. Какими должны быть измерения коробки, чтобы ее
объем был наибольшим?
38. Непрерывные н разрывные функции. Предел функции
При вычерчивании графика функции по точкам вам часто сове-
товали провести через нанесенные на бумагу точки «непрерывную
кривую». Но вы познакомились в п. 34 с такими функциями, гра-
фик которых состоит из отдельных отрезков, не примыкающих
друг к другу «непрерывно». Например, функция
/ (х) = {х},
график которой изображен на рисунке 25, на каждом промежутке
[п; п + 1[, где п — целое число, «непрерывно» возрастает, при-
ближаясь к значению единица, но этого значения не достигает, а
в точке х = п 4- 1 внезапно, скачком возвращается к значению
нуль, с которого началось ее постепенное возрастание в точке
х = п.
Эти наблюдения подводят нас к необходимости различать не-
прерывные и разрывные функции. Например, рассмотренная сей-
час функция «дробная часть от х» непрерывна во всех точках х,
кроме целочисленных, в которых она разрывна.
Определение непрерывности функции f в точке х0 можно сфор-
мулировать уже сейчас: функция f называется непрерывной
в точке х0, если при стремлении точки х к точке х0 значение
функции f (х) стремится к значению f (х0). Но это определение
вновь опирается на понятие предела функции. Поэтому мы сначала
познакомимся с понятием предела функции.
Далее, в п. 41, мы узнаем, что любой многочлен является не-
прерывной функцией.
Выясним точный смысл предложения «функция f (х) при х,
стремящемся к а, имеет предел &». Такое предложение мы уже за-
писывали в виде
lim / (х) = Ь,
х-+а
но еще не дали точного определения.
Начнем с очень простого примера. Рассмотрим функцию /, за-
данную равенством
f (х) = 2х -Т 1.
107
I f (*) - 3 I =
На ее графике (рис. 36) мы видим,
что при приближении точки х к точ-
ке а = 1 значения этой функции при-
ближаются к числу b = /(1) = 3.
Естественно считать, что число 3 и
есть предел рассматриваемой функ-
ции при х, стремящемся к числу 1:
lim (2х + 1) = 3. (1)
Каков точный смысл этого утвержде-
ния?
Рассмотрим разность
/(х)_ 3 = (2х+ 1) — 3=2(х — 1).
Ее модуль
| 2 (х—1) | = 2 | х—1 |
есть расстояние между числом f (х) и числом 3. Это расстояние бу-
дет меньше 0,01, если
| х — 1 | < 0,005,
т. е. если х принадлежит интервалу ]0,995; 1,005[.
Если мы пожелаем, чтобы выполнялось другое неравенство
\f(x) — 3 1 <0,0001,
то достаточно будет потребовать, чтобы число х удовлетворяло не-
равенству
| х — 1 | < 0,00005,
т. е. чтобы х принадлежало интервалу ]0,99995; 1,000050-
Вообще, задав произвольное (сколь угодно малое) число е > 0,
мы можем утверждать, что модуль разности f (х) — 3 будет мень-
ше 8, если только
И— 1| <
8
2 '
Существенно здесь только то, что для любого положительного чис-
ла 8 можно выбрать столь малое положительное число д (у нас
д = Л ), что из неравенства
|х — 1 | <д
будет следовать неравенство
|/(X) — 3 | <8.
В этом и заключается смысл высказывания (1).
Определение. Число b называется пределом функции f (х)
при х, стремящемся к а, если для любого положительного числа 8
108
найдется такое положительное
число б, что при всех а,
удовлетворяющих неравенству
| х — а | <6,
будет выполнено неравенство
| f(X) - b | < 8.
Неравенство | х — а | < б
равносильно двойному неравен-
ству
а — б < х < а + б.
При любом положительном 6
интервал ]а — б; а + б[ назы-
Рис. 37
вают окрестностью точки а.
Пользуясь этим названием, определение предела функции мож-
но сформулировать так:
Число b называется пределом f (х) при х, стремящемся к а,
если при любом 8 > 0 существует, такая окрестность точки а, чтО
для любого х^= а из этой окрестности (рис. 37)
\f(x)-b\ <е.
Из определения предела функции видно, что для существования
предела f (х) в точке а необходимо, чтобы функция f (х) была опре-
делена во всех точках некоторой окрестности точки а, кроме, мо-
жет быть, самой точки а.
Оговорка о том, что функция f (х) может не быть определенной в точке
х — а, существенна. Без нее понятие предела нельзя было бы применить
к определению производной по формуле
так как при Дх — О дробь
Af(x)
Дх
lim
Дх->0
А/ (х)
Дх
теряет смысл.
Г (х) =
Пример 1. Докажем, что предел постоянной функции равен
этой же постоянной. В самом деле, если f (х) = k для всех х из
некоторого интервала, содержащего точку а, то для таких х
| f (х) — k | - \k — fe | — 0 < 8,
где 8 — любое положительное число. Таким образом,
lim f (х) = lim k = k.
x->a x-+a
Пример 2. Рассмотрим функцию f (x) = x и докажем, что
lim x - a.
x-+a
В самом деле, если 8 — произвольное положительное число, то,
109
выбрав 6 = 8, получим, что | f (х) — а | — | х — а | < е, как
только | х — а | <6.
Пример 3. Функция
/(*) =
х2 —9
х + 3
определена всюду, за исключением точки х = —3. Докажем, что
эта функция при х, стремящемся к —3, имеет предел, равный—6.
В самом деле, при х #= —3
6) =|х-3 + 6| = |х + 3| = |х-(-3)|.
Следовательно,
х2 - 9
х 3
-(-6)
< е, если | х — (—3) | < в и х#=—3.
Поэтому если для произвольного положительного числа 8 выбрать
б = 8, то при | х — (—3) | < б и х =# —3
х2 —9
х 4*" 3
-(-6)
е,
а это и означает, что
г х2 — 9 с
11Ш ------------------------- =—6.
з х 4~ 3
Пример 4*. Доказать, что lim х2 — 1.
х->1
Доказательство. Требуется доказать, что для любого
положительного числа е найдется такое положительное число б,
что для всех х, удовлетворяющих условиям
| х — 1 | < б и х =# 1, (2)
выполняется неравенство
|х2—1|<е. (3)
Неравенство (3) можно переписать в виде
|х+ 1 | • |х — 1 | <е. (4)
Будем выбирать 6^1. Тогда
|х— 1 | < 1, т. е. —1 <х— 1 < 1.
Прибавляя ко всем частям этого двойного неравенства число 2,
получим:
1 < X + 1 <3.
Следовательно,
I х + 1 | < 3.
Поэтому если рассматривать х, удовлетворяющие неравенству
3 | х — 1 | < 8, (5)
ио
то эти х будут удовлетворять и неравенству (4), а следовательно, и
неравенству (3).
Из неравенства (5) видно, что если б выбрать равным наимень-
шему из двух чисел 1 и то из неравенства (2) будет следовать
неравенство (3).
Последний пример показывает, что находить предел функции
непосредственно на основе определений довольно сложно. На прак-
тике пользуются теоремами о пределах, которые приведены в пп. 40
и 41.
Упражнения
310. lim (5 — Зх) = 4.
-4
312. lim | х | = 0.
х->0
при а > 0.
Докажите следующие равенства, пользуясь определением пре-
дела функции:
309. 1йп(2х) = 6.
Х-»3
311. lim - — 1.
з х_
313. limj/x = У а
х^а
Указание. Воспользуйтесь тем, что
х — а
Ух+Уа ’
39. Теорема о единственности предела
Теорема. Если функция f (х) имеет предел при х, стремя-
щемся к а, то этот предел единствен.
Доказательство. Если lim f (х) = b и lim f (х) =
х-*а х^а
= с, то для любого 8 > 0 найдется такое б > 0 (почему?), что для
всех х^= а, удовлетворяющих неравенству
| х — а I < б,
выполняются сразу два неравенства:
— 6l<f и |/(х) —с| <-|.
Но тогда
<16-/М| + 1 /«-с|< |+ | = 8-
Следовательно, неотрицательное число | Ь — с | меньше любого
положительного. Таким числом может быть только число нуль.
Поэтому | Ъ — с | = 0, Ъ — с — 0, и, следовательно, b — с.
Ill
Таким образом, у данной функции в данной точке может быть
не более одного предела. Покажем на примере, что у функции
f (х) в данной точке х0 может совсем не быть предела, хотя она и
определена всюду. Таким примером послужит функция
f (х) = Сх].
По ее графику (рис. 24) видно, что она разрывна при всех целых
значениях независимой переменной х. Покажем, что не существует
limfx]. Будем доказывать методом от противного. Допустим, что такой
х->1
предел существует и равен а. Тогда или а
1 1
—, или а С —.
2 2
Возь-
мем е = — и покажем, что, вопреки определению предела, в лю-
4
бой окрестности точки 1 найдутся точки х, отличные от 1, для
которых | [х] — а | ^>е.
В случае а > — — это точки х из промежутка [0; 1[.
Для этих точек [х] — 0, и поэтому
|[Х]_а| = |0 —а| = |а|> 1 > 1 = 8.
В случае а — — это точки х из промежутка ]1; 2[.
Для этих точек [х] = 1, и поэтому
[х] — а — 1 — а .
Следовательно,
|[х] — а\ = 11 — а\> 1>1 = 8.
Упражнения
314*. Докажите, что не существует предела функции у = [х] при х,
стремящемся к 3.
315*. Докажите, что не существует предела функции у — {х} при х,
стремящемся к —2.
316. Докажите, что для функции
1 при х > 0,
—1 при х < 0
не существует предела при х, стремящемся к 0.
317. Расскажите, почему функция, график которой изображен на
рисунке 38, при х, стремящемся к 1,5, не имеет предела.
318. Расскажите, почему функция, график которой изоб-
Л2
/« = {
ражен на рисунке 38, при
х, стремящемся к—1, име-
ет предел. Чему равен этот
предел?
319. Расскажите, почему функ-
ция, график которой изоб-
ражен на рисунке 38, прих,
стремящемся к 2,5, имеет
предел. Чему равен этот
предел?
320. Расскажите, почему функ-
ция, график которой изоб-
ражен на рисунке 39, при
х, стремящемся к 1, имеет
предел. Чему равен этот
предел? Чему равно значе-
ние функции при х = 1?
40. Теоремы о пределах
Основные теоремы о преде-
лах функций, облегчающие вы-
числение пределов, аналогичны
соответствующим теоремам о
пределах последовательностей.
А именно, для функций справед-
ливы следующие три теоремы,
связывающие арифметические
операции с переходом к пре-
делу.
Теорема 1. Если при х,
стремящемся к а, существуют
пределы функций f и g, то при
х, стремящемся к а, существует
также и предел их суммы, равный сумме пределов функций f
» g:
lim (/(х) -J- g(x)) = lim f(x)*-f- lim g (x).
x->a x^a x^a
Теорема 2. Если при x, стремящемся к а, существуют преде-
лы функций fug, то прих, стремящемся к а, существует также и
предел их произведения, равный произведению пределов функ-
ций f и g:
lim(/(x) • g(x)) = lim/(x) . lim g(x).
x-+a x-+a x-+a
Теорема 3. Если при x, стремящемся к а, существуют преде-
лы функций fu g, и предел функции g отличен от нуля, то при х,
из
стремящемся к а, существует также предел отношения рав-
ный отношению пределов функций f и g:
limbi’=
х-а g(x)
lim/ (х)
lim g (х)
х-*а
Следствие теоремы 2. Постоянный множитель можно
вынести за знак предела.
В самом деле,
lim (kf (х)) = lim & • Jim f (x) — k • lim f (x).
x-+a x-+a x-*a x-+a
Теоремы 1, 2 и 3 приводятся без доказательства. При помощи
метода математической индукции теорема 1 обобщается на п слагае-
мых, а теорема 2 — на п множителей.
Для доказательства этих теорем вводится понятие бесконечно малой
функции: функция а называется бесконечно малой при х, стремя-
щемся к а (или в точке а), если lim а (х) = 0. Затем доказываются теоремы
х-+а
о бесконечно малых, аналогичные теоремам о бесконечно малых последова-
тельностях, и с их помощью доказываются теоремы о пределах точно так же,
как и в п. 28. Приводить эти доказательства мы не будем.
Упражнения
Вычислите пределы:
321. Iim(|/x — Зх). 322. lim (7 + Зх + х2).
х-->4 х->—2 __
323. lim (х — 5) (х2 + 5х + 25). 324. lim У2х +.! .
х-»5 х-*2 3 + X
325*. Сформулируйте и докажите теоремы о бесконечно малых
аналогично тому, как это сделано в п. 28.
326*. С помощью теорем о бесконечно малых функциях докажите
теоремы о пределах.
41. Непрерывность рациональных функций
Напомним, что любая целая рациональная функция представля-
ется в виде многочлена, любая дробно-рациональная функция —
в виде отношения двух многочленов.
Теоремы предыдущего пункта позволяют вычислять пределы
многочленов, а при некоторых ограничениях и пределы дробно-
рациональных функций. Пусть, например, требуется вычислить
предел
,. Зх2—2
пт--------
х-.3 2х2+ 7
Так как lim х = 3, то по теореме о пределе произведения
х-»3
lim х2 = lim (х • х) = lim х • lim х = 3 • 3 = 9.
х-+3 х-+3 х-»3 х-+3
114
По следствию из этой теоремы
ПтЗх2 = 3 • 9 = 27 и lim2x2 = 2 9 = 18.
х-*3 х->3
По теореме о пределе суммы
lim (Зх2 — 2) = 27 — 2 = 25,
х->3
lim (2х2 + 7) = 18 + 7 = 25.
х-*3
По теореме о пределе частного получаем, наконец:
Зх2—2 25 ,
lim-----— — = 1.
Х-+3 2х2+ 7 25
Но такое непосредственное обращение к теоремам предыдущего
пункта слишком громоздко. Удобнее пользоваться следующими
двумя теоремами.
Теорема 1. Для любого многочлена Р предел Р (х) при
х, стремящемся к х0, равен Р (х0).
Сначала докажем, что при любом натуральном п
LT=х- о)
Доказательство проведем методом математической индукции.
1) При п = 1 имеем: lim х = х0, т. е. утверждение истинно.
2) Предположив, что при некотором п
limxn = xg,
получим
limxn+1 = lim(x't • х) = limxn • Птх = х" • х0 = хп+1.
Х-кХ0 Х-^Ха X-*Xq Х-+Х9 0
Из 1) и 2) по принципу математической индукции заключаем, что
(1) верно при любом натуральном п.
Пользуясь формулой (1), докажем теорему 1. Возьмем произ-
вольный многочлен степени п:
Р (х) == аохл + а^-1 + ... Н- ап^х +ап, где а0 Ф 0.
Вычислим его предел при х, стремящемся к х0:
lim Р (х) = lim (aoxn) 4- lim (atxn-1) 4- ... 4- lim (a„_tx) + lim an =
X-+XQ x-*xq X-+Xq x-*xq
~ ^0^0 M 1 “b ••• 4~ 1^0 4* ~ P (^o)*
По теореме 1 мы можем сразу написать, например,
lim(xs — 4х2 4- 2х — 1) = 23 — 4 • 22 4- 2 • 2 — 1 =— 5.
Х-»2
Любую дробно-рациональную функцию можно записать в виде
Я(х) =
«(*)
где Р(х) и Q(x) — многочлены.
115
Она определена при тех значениях независимой переменной, при
которых знаменатель Q отличен от нуля. По теореме о пределе част-
ного имеем при Q (х0) =И= 0:
lim Р (х)
lim/?(x) = lim = R(x ).
х-х» x-x0Q(x) limQ(x) Q(x0)
Поэтому верна теорема:
Теорема 2. Если число х0 входит в область определения
D(R) дробно-рациональной функции R, то
lim Я (л?) = Я(л?0).
X-+XG
Например:
Uin^-2 =3-3»-2 = h
,.12х’ + 7 2 3> + 7
Замечание. Теоремой 2 нельзя воспользоваться непосред-
ственно при вычислении предела дробно-рациональной функции
в точке, где она не определена. Например, функция
х2 — 1
X — 1
не определена при х — 1. Но заметив, что при х 1
f (х) = (*—»)<*+ О = х + !,
X— 1
мы находим ее предел при х -> 1:
lim "5—- = Пт(х+ 1) = 1 + 1 =2.
х->1 X — 1 х-1
При вычислении пределов мы уже видели, что для ряда функций
выполнено равенство
11ш/(х) = /(а). (2)
х-+а
Далее нам встретятся примеры функций, для которых равенство (2)
не выполнено. Такие функции называются разрывными, а точка а
называется их точкой разрыва. Те же функции, для которых равен-
ство (2) выполнено, называются непрерывными в точке а.
Теперь теоремы 1и2можно сформулировать так: многочлены
непрерывны при всех значениях независимой переменной;
любые рациональные функции непрерывны при всех
значениях независимой переменной, при которых они
определены.
Из теорем о пределах п. 40 следует, что сумма, произведение
или частное непрерывных в данной точке функций есть тоже не-
прерывная функция. Для частного надо еще только проверить,
чтобы знаменатель не обращался в нуль в рассматриваемой точке.
В X классе будет доказано, что функция f (х) = уТх непрерывна
для всех х > 0 при любом п. Отметим, что при п — 2 это дока-
зано в упражнении 313.
116
Упражнения
Найдите пределы:
327. lim (х3 4-2ха — Зх — 4).
1
328. lim 3>, + 2*+' .
х->Г х3 — 2х2 + Зх — 1
329. lim
х->—2 Зх3— 1
330. lim(4xa— 2х+ 1).
331. Пт +?* + \
Хч— 1 X3 4- X2 — 2х
337. Пт 41Т..Х+2 .
хч—2 2х2 4-х — 6
338. Нт —’~2х~
х-»-1 2х2 + X — 1
339. Пт l7* ~ 1 ~2
хч-5 X —5
340. Пт —х~*~3—.
х->—3 /х + 4— 1
341. Пт Ух—2
Х-.8 X—8
342. Пт ———
*-*> Ух—1 ‘ _
343. lim^x + ft-lA; .
й->0 h
344. На рисунках 38—42 при-
ведены графики функций.
332. lim £х-+ 1)(x2.7L.!l,
Хч-2 X3 + X2 + X
333. lim +
, 1 « + 2
2*
334. Пт £+1.
хч—1 х 4-1
335. limx3~8.
Х-.-2 х —2
336*. lim У^~х
х"*° Ух Н-х
У
-
1
0 1 X
Рис. 40
117
Какие из них непрерывны, а какие— разрывны? Укажите точ-
ки разрыва. Укажите значение функции в точке разрыва.
Постройте графики приведенных ниже функций. Укажите, в
каких точках эти функции непрерывны, а в каких — разрывны.
Укажите значение функции в точке разрыва:
345. а) у _ (2 — х при х < 0, ., = (х — 1 при х 0, Z\ V/ J У \ 1
( х при X 0; (I — х при х > 0.
346. а) У _ Г 2х2 при х I» б) у = +3х при х <—I;
у (1 — 2х при х > I; ' у ( —х2 при х —I.
347. а) ( 3 — при X - 3, ® х при х < — ,
у= х 2 « У = •
,х-|-2 при х > — 3; i . i
1 при х> — .
х 2
348. а) _ ( 2 — х при х < I б) /1V , У Ы При х<— I,
11g х при х > I; У = М2'
2 при х >— I.
§ 9.
ПРОИЗВОДНАЯ
42. Определение производной
В п. 37 было сказано, что производная f(x0) функции f в точке
х0 есть предел
Hm = Пт + —/(х0) . j
Дл-+0 Дх Дх->0 Дх
Или словами: производной функции f в точке х0 называется предел
отношения приращения функции f в точке х0 к приращению Дх,
когда это последнее стремится к нулю. Но только теперь, когда
мы выяснили точный смысл понятия предела, это определение
производной приобрело точный смысл.
Например, для того чтобы найти производную функции /, за-
данной формулой
f (х) = х3 — Зх,
в точке х, надо найти предел отношения приращений Д/ и Дх:
= Зх2 — 3 + ЗхДх -И (Дх)2
Дх
при Дх, стремящемся к нулю (см. п. 36). При этом значение х счи-
тается постоянным, а предел ищется при переменном приращении
Дх, стремящемся к нулю. Так как предел постоянной есть сама
эта постоянная, то
lim (Зх2 — 3) = Зх2 — 3,
Дх-.О
118
a
lim(ЗхАх) = 0, lim(At)2 = О,
Дх-*О Дх-.О
и по теореме о пределе суммы получаем, наконец:
f (х) = lim (Зх2 — 3 + ЗхАх + (Ах)2) = Зх2 — 3.
Дх-*0
Придадим определению производной несколько другую форму.
Вспомним, что
Ах - - х — х0 и х. = х0 + Ах.
Тогда отношение приращений функции и переменной х приобретает
вид:
Л/ f (х) —f(x0) (2)
Дх х — х0
Сказать, что приращение Ах стремится к нулю, это то же самое,
что сказать: х стремится к х0. Поэтому определение производной (1)
можно записать в виде
f (х^ = lim = lim . (3)
Дх-.О Дх X—х0
В этом определении х0 считается постоянным и рассматривается
предел отношения (2) при х, стремящемся к х0. Чтобы этот предел
мог быть определен, необходимо, чтобы отношение (2) было опре-
делено для всех х=#х0 из некоторой окрестности точки х0, а для этого
необходимо, чтобы сама функция f была определена в некоторой
окрестности точки х0, включая эту точку. Поэтому функция мо-
жет иметь производную в точке х0, только если функция опреде-
лена во всех точках некоторой окрестности точки х0.
Операция нахождения производной [' от данной функции f назы-
вается дифференцированием этой функции. Название это связано
с тем, что, прежде чем перейти к пределу, составляется отношение
разностей /(х)-/(х0)
X —Хо
а разность на латинском языке обозначается словом differentia.
Функция Д имеющая в каждой точке некоторого промежутка
производную, называется дифференцируемой в этом промежутке.
Упражнения
Вычислить в точке х0 производные следующих функций:
349. Дх) = 2х 4- 3. 350. Дх) = Зх — 5.
43. Примеры вычисления производных
Пользуясь определением, вычислим производные некоторых
функций.
Пример 1. Пусть
f (х) = С = const
119
для всех х из некоторого проме-
с________________________ жутка I. Найдем производную
' ] этой функции:
I I А/(х) = / (х 4- Ах) — / (х) =
I ’ Дх Дх
О 1 7 jT = = — = о.
Дх Дх
Рис 43 Следовательно,
(С)' = lim = lim 0 = 0.
Дх->0 Дх Дж->0
Таким образом, производная постоянной равна нулю
(СУ = 0.
Этот результат и следовало ожидать — если функция не изменяется,
то скорость ее изменения равна нулю (рис.43).
Пример 2. Найдем производную функции f (х) = х:
(х) _ f (х + Дх) — / (х) х 4- Дх —х _ Дх ।
Дх Дх Дх Дх
Следовательно,
/'(х) = lim = lim 1 = 1.
Дх->0 Дх Дх->0
Пишут также: (х)' = 1.
Пример 3. Найдем производную функции g (х) — х2:
Ag(x) = g(x 4- Дх) — g(x) _ (х 4- Ах)2 — х2 = Дх (2х 4- Ьх) = 2х 4- Дх
Дх Дх Дх Дх
Следовательно,
(х2)' = lim Ag = lim (2х 4- Дх) =2х.
Дл->0 Дх Дя->0
В частности, g'(2) = 2-2 = 4; = 2 • 0,5 = 1 и т. п.
Пример 4. Продифференцируем функцию (рис. 44):
. , . _ . _ (— х, если х < 0,
/ (х) — I х I — | если х о.
Пусть х < 0. Выберем Дх настолько малым, чтобы выполнялось
неравенство
х 4- Дх < 0.
Тогда
f (х 4- Дх) = | х 4- Дх | = — (х 4- Дх) = —х — Дх и
Д) __ / (х + Ах) — / (х) _ | х 4- Ах | — I х | — х — Дх — (— х) _
Дх Дх Дх Дх
_ — Дх_____ j
Дх
120
Следовательно, при х < О
(|x|)' = lim = lim (—1)=—1.
Av-»-0 Лх Дх-»0
Аналогично прозеряется, что (|х|)' =
= 1 при х> 0.
При х = 0 данная функция не
имеет производной. В самом деле,
Л/(0) = /(0 + Ax)-/(0) e / (Ах)- = I Ах| _f 1 при Дх > 0,
Дх Ах Ах Ах (-1 при Дх < 0.
Но тогда (см. п. 39, упр. 316) не существует предела
lim , (1)
Ах-+о Ах
а значит, не существует и производной рассматриваемой функции
в точке 0.
Действительно, если допустить, что предел (1) существует и равен чис-
лу Л, то в некоторой окрестности точки 0
А/(0) л
< 1.
В частности, при положительных Дх из этой окрестности
11 — Л| < 1, т. е. —1<1 — Л < 1, или
0 < Л <2.
(2)
Для отрицательных же Дх из этой окрестности |—1 — Л| < 1, т. е. —1 <
< —1 — Л < 1, или
—2 < Л < 0.
Неравенства (2) и (3)
о существовании предела
противоречивы, и, следовательно, наше допущение
(1) неверно.
Итак, существуют функции, не имеющие производных в неко-
торых точках.
Из наших рассмотрений сле-
дует, что производной функции & |
f (*) = I X I
является функция /, опреде-
ленная на всей числовой пря-
мой, за исключением точки 0: ----------------------------*-
0 X
f/ . . ... v [—1 при х<0,
I « = ( |х|) =( ! х>0.
График этой функции изобра-
жен на рисунке 45.
Рис. 45
121
Упражнения
Пользуясь определением производной, найдите производные
следующих функций:
351. h (х) = ах + b в точках: а) 2; б) 4.
352. f (х) = — в точках: а) х; б) 1; в) 4.
353. f (у) = 4у2_ + Зу + 1. Найдите f (х), f (1), f (2), f (5).
354. у(х)=]/х. Найдите у’ (х), у' (1), у'(4).
355. — —Найдите и' (х), и (1), и'(—1), и’ (3).
356. v(x) — ]/бх + 2. Найдите v' (х), о' (1).
357. f (х) = х3. Найдите f (х), f (0), f (2).
358. g (х) = ах2 4- bx + с. Найдите g’ (х), g' (0), g’ (2).
Используя материал п. 37, найдите для функций промежутки
возрастания и убывания, точки максимума и минимума и
изобразите их графики:
359. у = х3 — х. 361. у = х3 — Зх2.
360. у = Зх — х3. 362. у — Зх2 — х3.
44. Производная суммы функций
Пусть и и v — две функции, определенные на одном и том же
промежутке.
Теорема. Производная сумма двух функций равна сумме
их производных, если последние существуют, т. е.
(и (х) 4- v(x))' = и' (х) 4- v' (х).
Доказательство. Обозначим сумму и (х) 4- v (х) через
w (х) и вычислим производную этой функции.
Дш(х) _ йу(х4~Дх) — ш(х) _и (х + Дх) + о (х 4- Дх) — а(х)— о(х) __
Дх
Дх Дх
_ и (х + Дх) — и (х) + v (х + Дх) — v (х) _ Ди . Да
Дх Дх ’
Дх
Следовательно,
Дх-.о Дх дх-»о\Дх
.. Да . .. До , . ,
----- lim — 4- lim — = и ф- и.
Дх-»0 Дх Дх->0 Дх
Теорема доказана.
Замечание. Методом математической индукции можно
доказать, что эта теорема справедлива для любого конечного числа
122
слагаемых:
(щ 4-н2 4- ••• 4" ил)' = и*г + ii 2 + ... 4- и’п .
Упражнения
Пользуясь примерами из п. 43 и упражнениями 352 и 354,
найдите производные следующих функций:
363. a) f (х) - х 4- 5; б) g (х) = х2 4- 3.
364. a) h (х) = х2 4- х\ б) и (х) — х2 4- х 4- 7.
365. a) v (х) — х2 4- — 4- 5; б) у (х) = х24- — 4- ]^х.
X X
366*. Докажите, что производная разности двух функций равна
разности производных этих функций, если последние сущест-
вуют.
45. Производная произведения функций
Лемма. Если функция f имеет производную в точке Xq, то
lim А/ (х0) = 0.
Дх->0
Доказательство.
lim А/ (х.,) = lim • Ах = f' (х0) -0 = 0.
Дх->0 Дх->0 Дх
Из этой леммы следует, что функция /, имеющая производную в точке х0,
непрерывна в этой точке. Действительно, так как
f(x) = f (х0) 4- f (х) - f (ХО) = / (х0) 4- д/ (ХО),
то, вспоминая пояснения к формуле (3) п. 42, имеем:
lim f (х) = lim (f (х0) + Д/ (х0)) = f (х0) + lim Д/ (х0) = f (х0),
х-+х0 Дх->0 Дх->0
что доказывает сделанное утверждение.
Важное замечание. Из леммы следует, что если не-
которая функция f не является непрерывной в точке х0, то она в
этой точке не имеет производной. Обратное же неверно. Функция
может быть непрерывной в точке х0 и тем не менее в этой точке не
иметь производной, как, например, функция / (х) = | х [ непре-
рывна в точке 0, но не имеет в этой точке производной (см. п. 43).
Теорема. Производная произведения двух функций и и
v вычисляется по формуле
(uv)' = u'<v 4- uv'
в предположении, что производные и' и v' существуют.
Эту формулу называют формулой Лейбница.
Доказательство. Обозначим произведение и (х) • v (х)
через w (х) и вычислим производную этой функции. Сначала заме-
тим, что из определения приращения функции
Ан = ц (х 4- Ах) — и (х)
123
следует, что
и (х 4- Дх) = и (х) + Дм,
или короче, обозначив и (х) через и:
и (х + Дх) = « + Дм.
Аналогично
v (х + Дх) = v + До
Тогда
Дао (х) _ а> (х 4- Ах) — ш (х) _и (х 4~ Ах) о (х 4~ Ах) — и (к) у (х)
Дх Дх Дх
__(и 4- Ди) (и + До) — uv
у&и + иДо + Ди До Ди . До . А До
-----!------•------- = V-----U---------I- Дм —.
Дх Дх Дх Дх
Поскольку м = м (х) и v = v (х) есть постоянные множители (при
фиксированном х), а
lim Дм = О
Дх-»-0
в силу леммы (так как функция м дифференцируема), то
(мо) = w = lim — = lim о---------1- и----|-Дм —
Дх->оДх Дх-иО \ Дх Дх Дх/
= lim (и • — 4- lim (и • — 4- lim (Дм • — 'j =
Дх-.О \ Дх/ Дх-0 \ Ах/ Дх-кО\ Дх/
= v • lim — 4- и • lim — 4- lim Дм • lim — =
дх-»оДх Дх-о Ах Дх-»о Дх-оДх
= v • и! 4- м • v 4- 0 • v' = uv' 4- и’и.
П р и м е р 1. ((х 4- 3) (х 4- 15))' = (х + 3)' (х 4- 15) 4- (х 4-
4- 3) (х 4- 15)' = (1 4- 0) • (х 4- 15) 4- (х 4- 3) • (1 4- 0) = 2х 4-
4- 18.
Следствие. Постоянный множитель можно выносить за
знак производной:
В самом деле, применяя теорему к произведению kf (х), где k —
число, получим:
(kf(x))' = (k)'f (х) 4- kf'(x) = 0 • f(x) + kf'(x) =
Пример 2. — зУ= (-Y—0= —(x)'= - .
r \15 / \15/ 15 15
Упражнения
Найдите производные следующих функций, пользуясь выве-
денными в пп. 44 и 45 формулами:
367. а) у (х) = б) h (х) = — - .
5 4
124
368. а) у (х) = 2х — 5; 6)u(x) = 2 —
осп ч 7 ч з , О\ лх / ч (Зх 4-2) (2х — 3)
369. а) у (х)= — х (х — 2); б) и (х) = -—!—у-
370. g (х) = (2х—3) (Зх 4- 1).
371. у(х) = (—х 4- 1W-X — 2У-х4-3\
\5 /\2 Дз /
372. g (х) = (2х — З)3. 373. и (х) = Зх2 (1 — х2).
374. Постройте графики следующих функций:
X >1 2.2
а) у — х 4—; б) у = ха 4—.
х х
46. Производная многочлена
Теорема. Производная степенной функции
х—^х'!
с натуральным показателем п> 1 равна произведению показате-
ля п на степень х ”-1, т. е.
(Л№)' = ПХп~х. (1)
Доказательство проведем методом математической ин-
дукции. При п = 2 формула (1) верна (см. пример 3, п. 43). Пока-
жем, что если формула (1) верна при п = k, то она верна и при
п = k 4- 1. Действительно, по правилу дифференцирования произ-
ведения
(хй+1)' = (xk • х)' = (xk)' • х + х* (х)' — kxh~x • х 4- xk • 1 = (k 4- 1) х*.
Отсюда в силу принципа математической индукции следует, что
формула (1) верна для всех натуральных п > 1.
Из этой теоремы и полученных ранее правил дифференцирова-
ния следует, что многочлен есть всюду дифференцируемая функция.
Действительно,
(аохя 4- а1хп~1 4-... 4- an-ix + ап)' = (Мя)' + (^-^Ч ... 4"
4- («„-1Х)' 4- (ап)' = па.х"-1 4- (п — 1) аххп-2 4-... 4- а„-г
Пример 1. (х10)' = 10х9.
Пример 2. (бх4 4- 4Х3 4- Зх2 4- 2х 4- 1)' — 5 • 4х3 4~ 4-Зх24~
4- 2 • Зх 4- 2 = 20х3 4~ 12х2 4- 6х 4- 2.
Упражнения
Найдите производные следующих функций:
375. a) f (х) = х4; б) g (х) = х3; в) h (х) = (х — 4)4.
376. a) f (х) = 2х5 — Зх4 4- 7х2 — 5х 4- 9.
б) g (х) = 7 — 2х3 4- х4 — Зх9.
125
377. Постройте графики следующих функций:
а) у = х2 (х — 2); б) у = х3 — 6х.
47. Производная частного
Теорема. Если функции и и <о имеют в точке х произ-
водные и если v (х)^0, то в этой точке существует производ-
ная их частного , которая вычисляется по формуле
и \'_ «'о — uv'
V /
Доказательство. Обозначим частное _. через w.
v
Тогда
и (х 4- Ах) и (х)
Дц>(х) w (х + Дх) — w (х) у (х 4~ Ах) v (х)
Дх Дх Дх
и 4- Ди и &и Ди
---------— — V-- — и--
_______________________________________ v + Ду v _ уДи — иДу _ Ах Дх
Дх Дх-у(у+Ду) у(у + Ду)
Согласно лемме п. 45 lim Ди (х) = 0, и потому
Дх~*0
,. Ди .. Ду
v lim — — и lim —
д*->оДх Дх»оДх
Ди Ду
„ — — и —
[ и \ , г Д&у г Дх Дх
— =w -= lim — = lim------------------------
\У/ Дл + оДх Дг->0 у (у + Ду)
v lim (у 4* Ду)
Дх->0
__ vu! — uv' _vu — иг/
v * v v2
Пример !2 + 3xY = (2 + 3xY • (1 - 2х) - (2 4- ЗХ) (1 - 2х)'
Р Р’ V — 2х/ (1—2х)а
= 3(1 — 2х) 4-2 (2 4-Зх) = 7
~ (1—2х)2 ~(1 — 2х)а
Упражнения
378. /<х) = Найдите ГМ. Г (О). /'(О-
379. g (у) = ^=-3. Найдите g' (у), g' (х), g' (0), g' (1).
380. h (/) = —— . Найдите h' (t), h' (0), h' (1).
1 4- 6/
381. p(x)= ax + b. Найдите v' (x), v'(y), v' (0), v' (1).
ex -f- d
126
48. Производная дробно-рациональной функции
Теорема. Производная степенной функции
х-+хп
с целым показателем степени п равна произведению показате-
ля п на степень хп~1, т. е.
(хпУ = пхп~Л (1)
при п > 2 для всех х, а при п 1 для х =/= 0.
Доказательство. При п > 1 формула (1) доказана в п.46.
Если п = 1, то
(х)' = 1 = 1- х1"1
при хУ=0, и, следовательно, теорема справедлива и для п = I.
Формула (1) верна и при п — 0: х° = 1 при х^=0 и (1)' = 0 =
= 0 • х0-1. Если п — целое отрицательное число, то п = —т, где
т — натуральное число. Применяя теорему о производной част-
ного, получим при х =5^ 0:
1 V (1)'хт—(хт)' —тхт-1 т.
_ = и.-----ь— -----------= — тх т 1 — пхп 1.
т / у2т У2П1
Теорема доказана.
В частности,
/1у=(х->у=-1.х-’=-1.
\х/ ха
Итак,
/_1_ у_ _ j_
\Х / X2
Поскольку дробно-рациональная функция представима как
частное двух многочленов, то из предыдущего следует важное ут-
верждение: дробно-рациональная функция дифференцируема во
всей своей области определения.
Пример 1. (х~6)' = —5х~в.
Пример 2. (Зх*—= 12х3+—.
г \ х3 / X4
Формула (1) справедлива для любого рационального показателя
г при х > 0 (это будет доказано в X классе):
(хг)' = гхг-1.
I / —\' 1 —-
В частности, если г = —, то lx2 I =— х 2 (что было найдено в
2 \ / 2
упр. 354, п. 43) и, следовательно,
__1
2/х
127
/ 4 V 1_
Пример 3. (Кх*)'= \-х3 / = у х3 — у Vх (* > 0).
/ 3 \' 5
п л / 1 V I ~2 I 3 ~2 3
Пример 4. = 1х / ——— х =—=
\Ух3) х 2 2 /х5
-------~7=- (X > 0).
2х2 Ух
Упражнения
Найдите производные следующих функций:
382. у(х) = ± 384. g(x) = i.
383. f (х) = - . 385. h (х) = 3 . х~б.
х
386*. При каких п £ Z существует (х")' в точке х — 0 и для каких
п определяется формулой (1)?
387. Постройте графики функций:
а) у = 2х + 4 ; б) у = .
X2 1 + X2
49. Сложная функция
Со сложными функциями вы уже встречались. Например, при
вычислении
h (х) = ]/Т=х2
сначала для данного х вычисляют значение функции /:
f (х) = 1 - х2,
а по этому значению
У = f (х)
находят значение функции:
g (У) = KF-
Функция
h (х) = g (/ (х)) (1)
и есть сложная функция, составленная из функций f и g.
Функции называют иначе отображениями. Отображение, опре-
деляемое формулой (1), называют композицией отображений f и g
и обозначают
h = go f.
Такая терминология в школе употребляется в учебниках геомет-
рии.
Какова область определения сложной функции (1)? Ясно, что
эта область определения D(h) должна входить в область определе-
ния функции /. Без этого по х нельзя определить /(х), что необхо-
128
димо для того, чтобы воспользоваться формулой (1). Но из D(f) в
D(h) войдут только те точки х, для которых f(x) принадлежит
D(g). В нашем примере
f(x)= 1 — х2, g (у) = Xb h (х) = g (f (х)).
Областью определения функции f служит вся числовая прямая R.
Но для того, чтобы Дх) попало в
D (g) = Ro = [0; оо[,
требуется, чтобы выполнялось неравенство
1 — х2 > 0.
А оно будет выполнено только при
х2 < 1,
т. е. при
-1 <х< 1.
Значит, областью определения функции
h (х) = ]/1 — х2
является отрезок [—1; 1].
Упражнения
Найдите области определения функции!
388. y = lg(9 — х2). 392 = 1
389.у = 1ЛТ^. ’8<2 + “> ’
390. y=]/lgx. 393. .
391. у = 1g (2 —Ух). lg(3-x) + l
394. Заданы функции:
/ (х) = 2 — х 4- х2, g (х) = 1g х, h (х) = -1—,
3 — х
запишите: / о g, go f, f о h, ho f, go h, ho g.
395. Представьте функции, заданные в упражнениях 388—393,
как композиции более простых функций.
50. Производная сложной функции
Производная от сложной функции
Л W = g (f (х))
находится по замечательной формуле
К (х) = g' (f (х)) • f (х). (1)
Например, при
f (х) = 1 + х2, g (х) = х100
5 Заказ 243
129
получаем:
h (х) = (1+ х2)100.
Так как
f (х) = 2х, g' (х) = ЮОх",
то
((1 + х2)100)' = 100 (1 + X2)99 2х = 200х (1 + х2)99.
Без формулы (1) нам пришлось бы разложить сотую степень
1 4- х2 по формуле Ньютона и дифференцировать 101 член этого
разложения.
Формулу (1) записывают еще и так:
(g (/ «))' = g' (/ «) /' W. (2)
Строгое доказательство формулы (2) довольно сложно. Его за-
мысел можно пояснить таким нестрогим рассуждением.
Пусть значение х = х0 соответствует
f (*о) = Уо» h (х0) = g (у0) = z0.
Если переменной х придать приращение Ах, то переменная у полу-
чит приращение
Ay = f (х0 4- Дх) — f (х0),
а переменная г — приращение
Az = h (х0 4- Ах) — Л (х0) = g (у0 4- Ay) — g (у0).
Мы ищем
h' (х0) = lim — = lim (— • — = lim — • lim — . (3)
Дх-»оАх Дх-»0 \Ау Ах/ Дх+оАу Дх->.оАх
Значение второго множителя в силу определения производной
известно:
i‘m = f' <хо)- (4)
Дх->о Дх
Чтобы найти значение первого множителя, заметим, что при Ах,
стремящемся к нулю, Ау тоже стремится к нулю. Поэтому
lim Дг = lim = lim е<у» + Ду> ~ я (у‘> = (5)
Дхн-ОАу Ду-иОАу Ду->0 Ау
= ё'(Уо) = g'tf (*о))-
Из (3), (4) и (5) получим:
й' (х0) = lim lim = g' (J (х0)) f (х0).
Дх-»оАу Дх->оАх
Один из недостатков такого вывода заключаете^ в том, что не
учтена возможность обращения в нуль Ау при Ах 0. Недостатки
130
этого вывода устранимы. Формула (1) верна при следующих усло-
виях: 1) функция / имеет производную в точке х0; 2) функция g
имеет производную в точке у0 = f (х0).
Упражнения
Вычислите производные следующих функций:
396. у = (3 — 5х + х2)100. 398. у = (х2 + 7)12.
397. у = Fx6—7х2+9. 399. у = (2 + 5х)л.
400. Из всех цилиндров заданного объема найдите цилиндр с
меньшей полной поверхностью.
Дополнительные упражнения к главе IV
401. Как геометрически изображаются множества:
а) {(х; у) |(х — 2) (у + 3) = 0};
б) {(х; у)|(х2- I)2 + (у2- I)2 = 0);
в) {(х; у)|]х + у 1< 1 и |х —у|<1};
г) | (х; у) - > 1 ;
I X J
[ у2 — X2 )
402. Укажите область определения следующих функций:
а) /(х) = д) /(х)=/Г+Т + —L= ;
у х — 4
в)/(х) = /*** ; ж) Нх) = /х + 1 + /1 —х;
Г) gr(x) = ; з) g(x) =/(1 — х)(1 + 5х).
X2 + X + 1
403. Найдите f(6); f(z); f(u), если
а) ?(/)= ; в) / (0 = /з + //=5;
б) f (/) = ]g^±1 ; г) f(0 = ....
бЗ/-1 ,/w lg(/2—з/—4)
404. В кубе с ребром а проведена плоскость, параллельная
тональной плоскости. Установите зависимость между
наи-
диа-
пло-
5*
131
щадью S(x) сечения и расстоянием
х плоскости до вершины А куба
(рис. 46). Найдите область определе-
ния функции х -> 5(х). Нарисуйте ее
график.
405. Является ли графиком некоторой
функции (какой?) нижняя половина
окружности?
406. В каком случае график функции сим-
метричен относительно осиабсцисс?
407. 3аданы две функции: /(х)=У х(х— 1) и
g (х) = Ух • Ух— 1. Истинно ли ра-
венство f = £?
408. Найдите промежутки возрастания и убывания функций:
1
а) у = (х—I)2 — 3; в) у =—0,5-х3;
б) у = 3 —(х —2)2; г) у = (0,25)*
409. Докажите методом математической индукции, что:
а) функция х -> хп при четном п убывает на полупрямой
]—оо; 0] и возрастает на полупрямой [0; +оо[;
б) функция х -> хп при нечетном п возрастает на всей число-
вой прямой.
410. Докажите, что если Зх2 — 3 0, то главная часть прираще-
ния (Зх2 —' 3) • Дх для функции у — х3 — Зх имеет тот же
знак, что и приращение функции А/ (х), если
। а , 1 । а । Зх2 — 31
Дх < 1 и Дх < -— ---------! .
1 3|х + 1
411. При помощи производной постройте графики следующих функ-
ций:
v4
а) у = х3+ Зх2 4-1; б) у = — -|- — х2.
4 о
412. Докажите равенство, пользуясь определением предела функ-
ции:
lim]/'|x| =0.
ЛГ-.0 Г 1 1
413. Объясните, почему неверно равенство
Ит]/х = 0.
х->0 г
Вычислите пределы:
414. lim?__У"*~3 .
х-»7 х2 — 49
3 — 3 г~~~
416. lim / xA-h — yx > q\
Л->о h v
415. lim—4- "..
1— Ух2 — 8 *
132
417. Докажите, что сумма, произведение и частное непрерывных
в данной точке функций — функции непрерывные. Для част-
ного надо еще проверить, чтобы знаменатель не обращался
в нуль в рассматриваемой точке.
418. f (у) = 2у3 + Зу2 — 2у + 1. Найдите f (х), f (0); f (-1),
Г (-2).
419. f(x) — —x4-f- — х3— — х2— х. Найдите /'(х), f' (0), f' (1).
4 3 2
420. Докажите, что функция g (х) = | х — 1 [ не имеет производ-
ной в точке х = 1.
421. Докажите, что функция f (х) = j/x2 не имеет производной
в точке х = 0.
422. Докажите правило нахождения производной суммы конечного
числа функций.
Найдите производные следующих функций:
423. v (х) = (х2 — 2х + 3) (Зх2 + 2х + 1).
424. f (х) = (ах + b) (сх2 + dx + е).
425. f (у) = (Зу + 1) (у - 3). Найдите f (х), f (0), f' (2).
426. g (и) = би2 (5и3 + 1). Найдите g' (у), g' (0), g' (—1).
427. Докажите правило нахождения производной для произведе-
ния трех функций и, v, w:
(и • v ш)' = и' • v • w + и • v' • w 4- и • v • ш'.
428. Докажите методом математической индукции формулу произ-
водной произведения конечного числа функций.
429. Постройте графики следующих функций:
а) у = ха (х — 2)2; б) у = х3 — Зх2 — 9х;
в) у — х* — 4х2.
430. и(г) = г 5-. Найдите ц'(г), и'(х — 3), ц'(0), и' (1).
1 — Зг
431. /(0=^7?Й-- Найдите /'(/), Г (4), f (1).
432. h(z) = 2г~~ 3 . Найдите К (г), h'(t), /г'(0), —h'(—1).
4 — 5г
433. g(x) Найдите g' (x), g' (4), g'(l).
У *4-2
434. h (u) = u- ~ 2u2 ^"u~~ — . Найдите h' (a).
u6
3 4 5
435. v(x)=---------1--. Чему равно v'(x).
X3 X4 X5
2 3
436. Найдите u'M\, если u(a) = —I— .
a4 a5
133
437. Найдите Ф' (и), если Ф (и) = -7 + Зу-Б-
С/4
438. Постройте график функции у = yGt3 (х — 5).
Вычислите производные следующих функций:
439. У= ~=;
z V2 + X2’
440. у=]/3 —2х.
Постройте графики функций:
441. у = хУ2^х2-, 442. у = + У^х.
443. В пунктах А и В расположены два громкоговорителя, один
из которых ведет передачу в 8 раз громче другого. Найдите
на отрезке АВ место, в котором суммарная громкость наимень-
шая.
444. f (/)= У? —/3 + /а — 1 . Найдите f (/), f (2).
445. g(y) = 1/4^4 • Найдите g' (х), g' (2).
Г у2+ 1
446. А(0 = у? + j. Найдите h' (2).
447. Найдите производную функции У (5х3 — 2х + I)61.
V ПРИМЕНЕНИЕ
ПРОИЗВОДНОЙ
§ 10.
ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ
К ПРИБЛИЖЕННЫМ
ВЫЧИСЛЕНИЯМ, ГЕОМЕТРИИ
И ФИЗИКЕ
51. Главная часть приращения функции
Из определения производной функции f в точке х9
Нт
Дх->0
А/ (*о)
Дх
следует, что для всех достаточно малых Ах
так что
А/ (*о)
Дх
« Г (X.),
М ж [' (х0)Ах.
(1)
Эта формула является основной для простейших приближенных
вычислений.
Пример 1. Выведем приближенную формулу
п /----г—
у х04- Ах
п.--
у х0 4- —5 Ах при х0 =£ 0.
лх0
Рассмотрим функцию f (х) == улх. При х =/= 0
1
1 п
л
л
пх
/' (х) =
V X
135
Поэтому в силу формулы (1)
Д/ (х0) = Vх х0+ Дх — /х^ ж
пх0
. Дх,
откуда следует после переноса Ух0 в правую часть полученного
приближенного равенства, что
Например,
Ух0 4- х « |/х0 + •*—9 • Дх.
пх0
(2)
]/4Д1 = У 4 + 0,01 «У4 + 2 1 _ • 0,01 = 2,0025.
Значение 1^4,01 с девятью знаками после запятой* таково:
]/4/И « 2,002498440.
Смысл приближенного равенства (1) состоит в следующем. Раз-
ность между левой и правой частью этого равенства есть функция
от Дх; обозначим ее через R (Дх).
Тогда
Д/ (х0) = f' (*о) • Дх + Я (Дх), (3)
где функция R (Дх) такая, что
lim = о. (4)
Дх->0 Дх
Действительно,
lim R <Ах> = Нт М — f' (хо) ‘ Ах =а
Дх->-0 Дх Дх-0 Дх
= lim _ f (Х )1 = пт _ f (Х ) = f (х„) _ f (х0) = 0.
дх-+о L Дх J Дх-*о Дх
Если для функции f выполнены равенства (3) и (4), то коротко
говорят, что первое слагаемое в равенстве (3) (т. е. f' (х0)Дх) есть
главная часть приращения функции /, а остаток R (Дх) (второе
слагаемое) есть бесконечно малая по сравнению с Дх (точный смысл
этого предложения записан формулой (4).
Пример 2. Вычислить приближенно, пользуясь формулой
(2): а) у 27,03; б) У1000. По формуле примера 1 имеем:
а) |/27ДЗ »-j/27 + 121 .0,03 = 3 + ^^3,0011;
3 • 27 9
б) ХУ1000 = У210 — 24= 2 1/1 _ 24
=2--------— « 1,995.
26 • 10
* См. способ вычислений, описанный в п. 32.
136
Рис. 47
Упражнения
448. На рисунке 47 (стр. 137) построены графики функций у — Ух,
у = у^х, у = ]/х7 з
а) Найдите по графику значения ]/2, >/3, /"З.
б) Найдите значения ]/^, |/3, У3, пользуясь таблицами.
в) Вычислите приближенные значения },Л3 и у^З, поль-
зуясь формулой (2).
Указание. Воспользуйтесь тем, что 3 = (1,4)’ 4- 0,256
и 3 = (1,3)4 + 0,1439.
г) Сравните полученные результаты.
£
449. Вычислите, пользуясь формулой (2), (8 • З)3 , ^81, у/ 625 ’ 3,
£
484 с точностью до второго десятичного знака.
450. Вычислите с точностью до второго десятичного знака:
1о'е('"Лг), 10*4 ю2,еЧ
Найдите приближенные значения:
451. а) /9^2; б) ^30.
452. а) >/90; б) ^33.
62. Касательная к графику функции
Рассмотрим функцию f и ее график (рис. 48). Если в точке х0
функция f имеет производную, то справедлива формула (3). Пере-
пишем эту формулу, вспомнив, что Дх — х — х0, а Д/ (х0) = f (х) —
— f(*o):
f (х) — / (х0) = f (х0) (х — х0) + R (Дх),
или, обозначив f (х) через у, а
f(x0) через у0:
У = Уо + Г(х0) (х—х0) +
+ Я(Дх). (5)
Здесь х и у есть координа-
ты точки графика функции f.
Если опустить в левой части
уравнения (5) остаток R (Дх),
то получим уравнение прямой
У = У о +f (*о) (х— х0), (6)
где х и у суть координаты точек
этой прямой. Полученная таким
образом прямая называется ка-
сательной к графику функции f
138
в точке х0. Точка Мо = М (х0; у0), через которую проходит и график
функции и касательная, называется точкой касания.
Переписав уравнение касательной (формулу (6)) в виде
У = /' {хй}х + (у0 — f (х0) • х0),
мы получим уравнение прямой с угловым коэффициентом:
k = f (х0) и b = у0 — f (x^Xq.
Таким образом, угловой коэффициент касательной к графику
функции равен производной этой функции, вычисленной в точке
касания.
Пример 1. Написать уравнение касательной к графику
функции х2 в точке х0 = 1.
Так как (х2)' = 2х, то угловой коэффициент касательной
f (х0) = 2х0 = 2 • 1=2. Далее, у0 = f (х0) == I2 = 1. Подставляя
эти значения в уравнение касательной (формула (6)), получаем:
у — 1 + 2 (х— 1), или у = 2х— 1.
Пример 2. Найдите уравнение касательной к параболе у ==
= х2 в точке Л40 = М (х0; х02).
Угловой коэффициент касательной находим так же, как и в
предыдущем примере: f (х0) = 2х0. Тогда, пользуясь уравнением
(6), получаем:
У = х02 + 2х0 (х — х0),
или
у — 2хох — х02.
Это и есть искомое уравнение.
Найдем координаты точки Т пересечения касательной с осью
абсцисс. Если (хх; О)—* координаты точки Т, то 0 = 2хоХ! — х02, и
если х0 =Н= 0, то хг = — х0.
Полученный результат дает способ построения касательной
к параболе в произвольной точ-
ке Af0: достаточно соединить точ-
ку Л40 с точкой Т, делящей
отрезок с концами О и х0 попо-
лам (рис. 49).
Замечание 1. Функция
У а2 — х2 дифференцируема в
интервале ]—а; а[, поэтому в
каждой точке этого интервала
график этой функции имеет ка-
сательную. С другой стороны,
этот график представляет собой
полуокружность, и потому каса-
тельная к этой линии была еще
определена в геометрии. Оказы-
139
вается, что оба определения да-
ют одну и ту же прямую.
Замечание 2. Касатель-
ная к графику функции может
пересекать этот график в другой
точке, в отличие от касательной
к окружности, которая имеет с
окружностью только одну общую
точку. Например, касательная
к графику функции х3 в точке
х0 = ~ (рис. 50) имеет уравне-
ние (проверьте это, проделав
необходимые вычисления):
Однако эта прямая пересекается с графиком функции еще в точке
(—1; —1). Проверьте это самостоятельно.
Замечание 3. Рассмотрим расстояние между точкой графика
функции и точкой касательной к этому графику, имеющими одну и ту же
абсциссу. Из формул (5) и (6)-(см. также рис. 48) видно, что это расстояние
равно |Z? (Дх)|, и потому есть бесконечно малая по сравнению с Дх (при Ах,
стремящемся к нулю). Поскольку для точки Л4(х; / (х)) |Дх| С |Л4Л4О|, то
| R (Дх) |
1Л4Л10|
R (Дх) 1 | Дх |
Дх I ' | ЛШ0| ’
и потому это бесконечно малая функция при Дх, стремящемся к нулю, как
произведение бесконечно малой функции (первый множитель) на ограничен-
ную функцию (второй множитель). Следовательно, рассматриваемое расстоя-
ние есть также и бесконечно малая по сравнению с расстоянием |Л4Мо|,
«когда точка М стремится по графику к точке Моу>. Это уже чисто геометриче-
ская характеристика касательной, надо дать только точное определение
утверждению, заключенному в кавычки, но это выходит за рамки нашего
курса.
Упражнения
453. Найдите уравнения касательных к параболе у = х2 в точках
с абсциссами х — 0, х = —1, х = 1.
з
454. Найдите уравнения касательных к гиперболе у = — в точ-
х
ках с абсциссами х = —1, х = 1.
455. Найдите уравнение касательной к кубической параболе у = Xе
в точке с абсциссой х = 2.
140
53. Скорость и ускорение
Пусть точка движется по прямой и в момент времени I находится
в точке с координатой х (t). Производная функции х от времени
v (/) = х' (/)
есть не что иное, как скорость v нашей точки в момент вре-
мени t.
В применении к задаче о падении тела под действием силы тяже-
сти об этом уже говорилось в п. 37.
Пусть координата точки зависит от времени квадрэтически:
х (0 = pt2 + qt + г, р Ф 0. (1)
Тогда скорость точки выражается формулой
v (/) = у (0 = 2pt + q. (2)
Найдем производную функции о, заданной формулой (2):
а (0 = v' (0 = 2р. (3)
Это не что иное, как скорость изменения скорости в движении, за-
данной формулой (1), т. е. ускорение при этом движении. Мы видим,
что ускорение при движении по квадратическому закону (1) по-
стоянно. Если р > 0, то мы имеем дело с равномерно ускоренным
движением, если же р < 0, то с равномерно замедленным.
Верно и обратное:
Если при движении точки по прямой ускорение постоянно, то
движение управляется квадратичным законом вида (1), где
коэффициент р при t2 есть половина ускорения:
1
р = — а.
н 2
Пусть в начальный момент времени t = 0 координата точки
есть
х0 = х (0) = г,
а скорость v(t) равна
v0 = v (0) = q.
Мы видим, что
Р = 7 а, г = х0, q = и0.
Поэтому уравнение равномерно ускоренного и равномерно замед-
ленного движения (1) можно записать в виде
х(0=-£/2+ + <4)
141
где х0— начальная координата точки, ц,— начальная скорость,
а — ускорение.
Рассмотрим более сложный пример. Тело, брошенное с поверхности
Земли вертикально вверх в начальный момент времени t = 0 со второй кос-
мической скоростью, удаляется от центра Земли по закону
2
*(/) = £>(/ + с)3. (А)
Смысл констант D и с вскоре выяснится. Если R — радиус Земли, то
2_
х (0) - De3 = R. (5)
Это первое соотношение между константами D и с.
Вычисляя первую и вторую производную функции х от времени /, по-
лучаем скорость и ускорение рассматриваемого тела:
1
9 ~ 7
v(l) = x'(t) = -D(t + c) (Б)
и •
2 --
«(/)=р'(0=--ОНс) 3. (В)
На поверхности Земли ускорение равно ускорению силы тяжести со
знаком минус:
2 — —
o(0)=--Dc 3=~g- <6)
Это дает второе соотношение между константами D и с. Из формул (5) и (6)
можно вычислить константы D и с.
Заметьте, что вторая космическая скорость — это скорость тела с0 в
начальный момент времени t = 0:
v^-Dc~~\ (7)
° 3
Из соотношений (5), (6) и (7) можно вычислить зная R и g.
Из уравнений (А) и (В) получаем:
2
а (/) =— k • г2 (/), где ft = gR2 = — D3.
Мы видим, что движение тела подчинено закону тяготения Ньютона:
вызываемое притяжением Земли ускорение тела обратно пропорционально
квадрату его расстояния от центра Земли.
Формула (А) была получена теоретически из закона тяготения Ньютона,
в отличие от формулы Галилея h = —
2
которая была найдена в результате
обработки наблюдений. Но для этого надо уметь по заданной зависимости
между функцией х (/) и ее второй производной х" (/) находить саму функ-
цию х (/). Это уже задача «интегрирования дифференциальных уравнений».
С ней на более простых примерах вы познакомитесь в X классе.
142
Упражнения
456. Человек приближается со скоростью 8 км/ч к подножию баш-
ни высотой 60 м. Какова скорость его приближения к вершине
башни, когда он находится на расстоянии 80 м от ее основа-
ния?
457. Вращение тела вокруг оси совершается по закону
ф (/) = з/2 _ 4/ + 2 (рад).
Найдите угловую скорость со (/) в произвольный момент вре-
мени t и при t = 4 (сек).
458. Маховик, задерживаемый тормозом, за t (сек) поворачивается
на угол ср (t) = 4t — 0,3/2 (рад). Определите: 1) угловую ско-
рость о (/) вращения маховика в момент времени t — 2 (сек);
2) в какой момент времени вращение маховика прекратится.
459. Пусть точка движется прямолинейно по закону
s (/) = 2/3 + t— 1 (ел*).
Найдите:
1) ускорение в момент времени t (сек)\
2) в какой момент времени ускорение будет равно:
а) 1 см/сек2-, б) 2 см/сек^
460. Тело массой 2 кг движется прямолинейно по закону s (f) —
— t2 + t + 1, где s (f) — путь в сантиметрах, t— время
в секундах.
Найдите:
1) действующую силу;
2) кинетическую энергию Е тела через 2 сек после начала
движения.
461. Пусть известно, что для любой точки С стержня АВ, отстоящей
от точки А на расстоянии I (см), масса куска стержня АС опре-
деляется по формуле т (1) — 312 + 5/ (а). Найдите линейную
плотность стержня:
а) в точке I = 10 (cjm); б) в конце В стержня при условии,
что | АВ | = 20 см.
462. Найдите силу F, действующую на материальную точку С мас-
сой т, движущуюся прямолинейно по закону s (t) = 2^ — /2(лс)
при t — 2 (сек). _
463. Точка движется прямолинейно по закону s (t) — Уt. Покажи-
те, что ее ускорение пропорционально кубу скорости.
464. Пусть точка движется прямолинейно по закону s (0 ----/3 +
6
+ З/2 — 5 (время измеряется в секундах, пройденный путь —.
в метрах).
Определите:
а) момент времени /, когда ускорение точки равно нулю;
б) с какой скоростью движется в этот момент точка.
143
§ 11.
ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ
К ИССЛЕДОВАНИЮ ФУНКЦИЙ
54. Возрастание и убывание функции
В нашем курсе производная появилась (в п. 37) как средство
исследования функции. Сейчас мы этим вопросом займемся под-
робнее.
Теорема 1. Если f (х0)>0, то существует такое число
6 >0, что f (х)> f (xQ) для всех х из интервала ]х0; х0 + 6 [ и
f (х) <f (хо) для всех х из интервала ]х0— 6; х0[ (рис. 51).
Коротко эту теорему формулируют так| если f'( х0) > 0, то
функция f возрастает в точке х0. Аналогичное утверждение можно
сформулировать для убывания функции в точке.
Теорема 2. Если Г(х0)<0,то существует такое число
6 > 0, что f (х) < f (х0) для всех х из интервала ]х0; х0+ б [ и
f (х) > f (хо) для всех х из интервала ]х0— 6; х0[ (рис. 52).
Доказательство теоремы 1. Поскольку число
f' (х0) = lim о,
X **► X 0 X Xq
то по определению предела для числа 8 = f' (х0) > 0 существует
такое число 6 > 0, что для всех х =/= х0 и принадлежащих интервалу
]х0 — б; х0 + б[ выполнено неравенство
f W - / Ы _ r w <fw>
X — Xq
откуда следует, что
144
или
(1)
— f (х0) > Q
X — х0
Для всех х из интервала ]х0; х0 + б[ разность х1— х0 >0, и пото-
му для этих х имеем f (х) > f (х0) в силу неравенства (1). Если же
х — любое число из интервала ]х0 — 6; х0[, то х — х0 < 0, и по-
тому для этих х имеем f (х) < f (х0) в силу неравенства (1). Теорема 1
доказана.
Доказательство теоремы 2. Рассмотрим функ-
цию р (х) = —f (х). Поскольку р' (х0) “ —/' (х0) > 0 по условию
теоремы 2, то функция р(х) возрастает в точке х0 в силу теоремы 1.
Следовательно, существует такое число б > 0, что для всех х из
интервала ]х0; х0 + б[ выполнено неравенство
р(х) > р(х0), т. е. — Дх) > —Дх0),
так что для всех х из интервала ]х0; х0 + б[ имеем:
Дх)<Дх0).
А для всех х из интервала ]х0 — б; х0[ выполнено неравенство
р(х) < р(х0), т. е. —Дх) <—Дх0), так что для всех х из интервала
]х0 — б; х0[ имеем:
Кх) > Дх0).
Теорема 2 доказана.
Естественно предположить, что если функция возрастает в
каждой точке некоторого интервала, то она возрастает на этом
интервале.
Сформулируем теорему о достаточном условии возрастания (убы-
вания) функции на интервале.
Теорема 3. Если функция f имеет положительную произ-
водную в каждой точке интервала I, то эта функция f возра-
стает на этом интервале I. Если функция f имеет отрицатель-
ную производную в каждой точке интервала I, то эта функция
f убывает на этом интервале.
Доказательство этой теоремы сложно и не входит в программу.
Замечание. Отметим еще (без доказательства), что если
функция f монотонна на интервале и непрерывна в точках а
и Ь, то она монотонна на отрезке [а; 6].
Пример. Найдем интервалы монотонности и начертим гра-
фик функции
у (х) = х — х3.
Данная функция определена на всей действительной прямой.
Так как
у' (х) = 1 — Зх3,
то у' (х) > 0, если 1 — Зх2 > 0. Решим следующее неравенство:
(Зх2 < 1)4=> /х2 < —^фф6х[< --L'xf------U- <х < “4=1
\ з / \1 уТ / Кз уз/
145
ции (рис.53).
Следовательно, данная функция
и убывает для
возрастает в интервале
’____1_. 1
/Г’ /3"
всех х, удовлетворяющих нера-
венству 1 — Зх2 < 0, т. е. в
промежутках
1 1 Г 1 1 ,
—-------т= и -т=; + оо
J /з[ J/3
D / 1 \
Вычислив значения у
\/3 }
1 / 1 \» 2
= ~7= — ~^= =----7^ И
/Т \/3 / 3/3
строим график функ-
Упражнения
Определите промежутки монотонности следующих функций
465. a) f (х) == Зх + 1;
466. a) f (х) =
X
467. a) v (х) = х2;
468. а) у (х) = 5х2 — Зх + 1;
469. a) h (х) = х3 — 27х;
б) g (х) = —4х + 2.
б) у(х)--^-.
2 — х
б) Их) = (X- I)2.
б) f (х) = х2 — 2х -Ь 5.
б) и (х) — х2 (х — 3).
55. Критические точки функции, ее максимумы
и минимумы
В предыдущем пункте мы видели, что в точке, в которой про-
изводная положительна, функция возрастает, а в точке, в которой
производная отрицательна, функция убывает. Остается рассмот-
реть внутренние точки области определения, в которых производная
функция равна нулю или не существует. Эти точки называются
критическими.
В п. 36 уже упоминались понятия максимума и минимума функ-
ции. Теперь дадим определение этих понятий.
Определение. Точка х0 из области определения функции
f называется точкой минимума этой функции, если найдется такая
^-окрестность ]х0 — б; х0 + б[ точки х0, что для всех х0 из
этой окрестности выполняется неравенство
t W >1W.
146
На рисунке 54 в точках хх
и х3 функция f имеет минимумы.
Определение. Точка
х0 из области определения функ-
ции f называется точкой
максимума этой функции,
если найдется такая Ь-окрест-
ность ]х0 — 6; х0 + б[ точки х0,
что для всех х х0 из этой ок-
рестности выполняется неравен-
ство
/ (х) < / (х0).
На рисунке 54 в точках х2 и х4 функция f имеет максимумы.
Точки минимума и максимума называются точками экстремума
данной функции, а значения функции в этих точках называют
экстремумами функции* .
Замечание. Точки а и & (см. рис. 54) не считаются точками
экстремума функции f, так как у этих точек нет окрестности, це-
ликом входящей в область определения функции.
Покажем, что точки экстремума являются критическими для
данной функции.
Теорема Ферм а**. Если точка ха является точкой экст-
ремума для функции f (х) и в этой точке существует производ-
ная, то она равна нулю: f' (х0)=0.
Доказательство. Для определенности будем считать,
что экстремальная точка х0 есть точка минимума. Проведем дока-
зательство от противного.
Пусть f (х0) #= 0. Тогда возможны два случая: f (х0) > 0 и
Г (Хо) < о.
1. f (х0) >0. По теореме 1 п. 54 (стр. 144) существует такое
б > 0, что для всех х из интервала ]х0 — б; х0[ выполняется нера-
венство f (х) <f(x0). Это неравенство противоречит тому, что
точка х0 есть точка минимума. Полученное противоречие показы-
вает, что неравенство f' (х0) > 0 неверно.
2. f (х0) < 0. По теореме 2 п. 54 (стр. 144) существует такое
б > 0, что для всех х из интервала ]х0; х0 + б[ выполняется нера-
венство f (х) < f (х0). Это неравенство противоречит тому, что точ-
ка х0 есть точка минимума. Полученное противоречие показывает,
что неравенство f (х0) < 0 неверно.
Таким образом, в точке минимума f (х0) не может быть больше
нуля и не может быть меньше нуля. Следовательно, /' (х0) = 0.
* Латинское слово «экстремум» в переводе на русский язык означает «край-
ний».
*♦ Эта теорема впервые доказана французским математиком Франсуа Ферма
(1601 —1665).
147
Точно так же разбирается
случай максимума.
Например, для функции
f (х) = Зх — х8, график которой
изображен на рисунке 55, точкой
минимума является —1, а точ-
кой максимума +1. В этих точ-
ках производная равна нулю:
Г (-1) = 0 и f (+1) = 0.
Подчеркнем, что теорема Фер-
ма есть лишь необходимое усло-
вие существования экстремума:
из того, что производная в точ-
ке обращается в нуль не обяза-
тельно следует, что в этой точ-
ке функция имеет экстремум.
Например, для функции х х3
производная в точке 0 обра-
щается в нуль, а экстремума в
этой точке функция не имеет
(рис. 56).
Мы рассмотрели те критиче-
ские точки, в которых производ-
ная равна нулю. Остается рас-
смотреть критические точки, в
которых производная не суще-
ствует. В этих точках функция
также может иметь или не иметь
экстремума.
Пример 1. Рассмотрим
функцию х-> | х | (рис. 57). В
п. 43 (пример на стр. 121) было
показано, что в точке 0 эта функ-
ция не имеет производной. Зна-
чит, эта точка критическая. По
графику же видно, что в точке 0
эта функция имеет минимум.
Пример 2. Рассмотрим
функцию f(x) = 2х+ |х| (рис. 58).
По графику видно, что в точке 0
эта функция не имеет экстрему-
ма. В этой точке функция не име-
ет и производной. В самом деле
из определения данной функции
имеем: |х|=/(х)—2х. Если пред-
348
положить, что функция f (х) в точке 0 имеет производную, то f (х) —>
— 2х также имеет производную в точке 0, а | х | в точке 0 произ-
водной не имеет. Получается противоречие. Значит, в точке О
эта функция производной не имеет.
Чтобы выяснить, имеет ли функция в данной критической точ-
ке экстремум, пользуются следующими достаточными условиями
существования экстремума.
Теорема 1. Если функция f(x) непрерывна в точке х0,
f'(x)>0 на интервале ]а; х0[ uf(x) < 0 на интервале ]х0; Ь[,
то точка х0 является точкой максимума функции f(x).
В разговоре пользуются упрощенной формулировкой этой тео-
ремы: если в точке х0 производная меняет знак с «плюса» на «ми-
нус», то х0 есть точка максимума.
Доказательство этой теоремы следует из теоремы 3 п. 54 (стр. 145)
и замечания к ней. Действительно, на интервале ]а; х0[ функция
монотонно возрастает. Так как она непрерывна в точке х0, то f (х) <
< f (х0) для всех х из интервала ]а; х0[. На интервале ]х0; Ь[ функ-
ция монотонно убывает. Так как она непрерывна в точке х0, то
f (х) < f (х0) для всех х из ]х0; 6[.
Таким образом, мы получили, что f (х) < f (х0) для всех х ф х0
из интервала £>[, т. е. х0 есть точка максимума функции f (х).
Теорема 2. Если функция f(x) непрерывна в точке х0 и
f'(x)<.0 на интервале ]а; х0[ uf'(x)Z>0 на интервале]х0; &[,то
точка Хо является точкой минимума функции f(x).
В разговоре пользуются упрощенной формулировкой этой тео-
ремы: если в точке х0 производная меняет знак с «минуса» на «плюс»,
то х0 есть точка минимума.
Доказательство этой теоремы следует из теоремы 3 п. 54 (стр. 145)
и замечания к ней. Предоставляем учащимся провести его само-
стоятельно по образцу доказательства теоремы 1.
Рассмотрим, например, функцию Зх— х3 (см. рис. 55). Ее произ-
водная 3 — Зх2 меняет знак с «минуса» на «плюс» в точке —1 и о
«плюса» на «минус» в точке +1. Отсюда следует в силу теорем 1 и 2,
что точка —1 является точкой минимума, точка +1—точкой
максимума.
Упражнения
Найдите критические точки приведенных ниже функций, вы-
яснив, какие из них есть точки максимума, а какие — точки
минимума.
470. a) f(x) = -х2 — Зх;
2
471. а) Л(х) = | +
472. а) и (х) = Зх4 — 4х3;
б) g(x) = х2—-i-x4.
б) у (х) = 2х3+ 6х2 — 18х + 120.
б) V (х) = ]/х.
149
Исследуйте на монотонность и экстремумы следующие функ-
ции. Для функций из упражнений 474, 476, 478 постройте
графики.
473. a) v (х) = 4х2— 6х;
474.
475.
476.
a) s(t) = Vt — 1;
а) /(х)=6х54- 15л4-)- 10х3;
X2
h (%) = —------.
' х2 4* 3
477. у (х) = 2х + 2.
х— 1
б) w (х) — х2 — Зх.
б) и (х) = j/Gc2 (х 0).
б) g(x) = x2(x—12)2.
478. и (х) = (х~2) (8~х) .
X2
479. у(х) =
16
х (4 — х2)
56. Исследование квадратичной функции
Функция f (х) = ах2 + х + с, где а =/= 0, называется квадра-
тичной. Эта функция определена и непрерывна на всей числовой
прямой. Ее производная
f (х) = 2ах + b
существует при всех х £ R и обращается в нуль в единственной
точке
х0 —
b
2а
(1)
Значение функции f в этой точке равно:
х, ч ,/ 6\ Ь2 , . / b\ , fc2,
НО =- f\ — 7 = а • тт + ь ’ — тг Н-с = —— + с =
\ 2а] 4 а2 \ 2а] 4а
Ь2 — 4ас D
4а 4а ’
где D — Ь2 — 4ас есть дискриминант квадратного трехчлена ах2 +
+ Ьх + с. Обозначим f (х0) через у0.
Вспомним, что от знака дискриминанта D зависит наличие и
число корней квадратного трехчлена: при D > 0 трехчлен имеет
два корня:
—b—^D „ у „ — Ь +
у ----L И Л Л -'—
*1 — 2 2а
2а
которые можно записать в виде
Xi = х0 — А и х2 = х0 + Д, где Д =
при D = 0 этот трехчлен имеет один корень:
ь
хп =-----,
0 2а
а при D <. 0 трехчлен не имеет действительных корней.
150
Исследуем знак производной функции f при х =/= х0. Из равен-
ства (1) следует, что b = —2ах0, поэтому производную f можно
представить в виде
У (х) — 2а (х — х0).
Для исследования функции f по знаку производной рассмот-
рим следующие случаи:
1) Если а > 0, то f (х) < 0 при х < х0 и f (х) >0 при х > х0.
Следовательно, функция f убывает в промежутке ]—оо; х0] и
возрастает в промежутке [х0; 4-оо[. В точке х0 функция f принимает
минимальное значение:
fmin = f (*о) = Уо-
2) Если а < 0, то У (х) > 0 при х < х0 и f (х) <0 при х > х0.
Следовательно, функция f возрастает в промежутке ]—оо; х0] и
убывает в промежутке [х0; 4-оо[. В точке х0 функция / принимает
максимальное значение:
fmax f С*-») = Уо-
Каждый из этих двух случаев разбивается на три подслучая
в зависимости от знака дискриминанта D.
Расположение графика функции по отношению к оси абсцисс в
шести подслучаях изображено на рисунке 59.
а> 0 a<0
D>0 -A- Hl
D = 0 X0 ^2 /£ rX ' ' n2
D<0 *0 ^3 , у Л
Рис. 59
151
Рис. 60
Пример 1. Построить график функции у (х) = х2 + 2х — 3.
Воспользуемся результатами проведенного исследования квадра-
тичной функции. Так как а >0 и D > 0 (а = 1 и D = 16), то мы
имеем дело со случаем 1г.
Для построения графика найдем координаты вершины парабо-
лы:
х0= — £=—1 и Уо = /(*о) = —4-
Решив уравнение
х2 + 2х — 3 = 0,
найдем абсциссы точек пересечения графика с осью Ох: —3 и 1.
График данной функции изображен на рисунке 60.
Пример 2. Построить график функции у (х) —---------х2 +х—1
4
а =-----<0, D = 1 — 4 • (— Д (— 1) =0.
4 V 4/
Поэтому мы имеем дело со случаем П2.
Найдем абсциссу точки касания параболы с осью Ох:
График данной функции изображен на рисунке 61.
Упражнения
Исследуйте квадратичные
480. f (х) = х2 — 7х + 6.
481. g (х) = 4ха + 12х + 9.
482. h (х) = х2 — Зх + 10.
функции и постройте их графики!
483. и (х) = —Зх2 + 8х 4- 3.
484. v (х) =— ~х2 + 2х — 3.
485. w (х) = —2х2 + 4х — 7.
152
57. Решение квадратичных неравенств
Проведенное исследование квадратичной функции содержит
все необходимое для решения квадратичных неравенств.
Пусть требуется решить неравенство
ах2 + Ьх + с > 0. (1)
1) Если дискриминант D квадратного трехчлена ах2 + Ьх + с
отрицателен, то это означает, что график функции
f (х) = ах2 + Ьх + с
не пересекает оси абсцисс и, следовательно, лежит выше оси абсцисс
(если а > 0) или ниже ее (если а < 0). В первом случае (рис. 62)
множество решений неравенства (1) есть множество всех действи-
тельных чисел, а во втором (рис. 63) это множество пусто.
2) Если дискриминант D квадратного трехчлена положителен,
то график функции f пересекает ось абсцисс в точках хг и х2 (для
определенности считаем, что хх <х2), являющихся корнями урав-
нения ах2 + Ьх + с = 0.
В этом случае функция f имеет один и тот же знак во всех точ-
ках промежутка ]хх; х2[ и противоположный ему — в промежут-
ках ]—со; хх[ и ]х2; +оо[ (рис. 64 и 65). В промежутках]— оо; х^
и ]х2; +оо[ знак функции / совпадает со знаком числа а. Этих све-
дений достаточно для решения вопроса о том, какие из промежутков
содержат решения данного неравенства.
3) Случай D = 0 рассмотрите самостоятельно (см. упр. 493).
Пример 1. Решить неравенство 2х2 + х — 1 >0.
Дискриминант D = l+ 8 = 9>0; ищем корни квадратного
трехчлена:
Д53
Пусть / (х) = 2х2 + х— 1, тогда / (0) == —1. Следовательно, / (х) <
<0 для х С]—1; 'уЕ и / (х) >0 для хЦ- оо; —1[ Ц ]у; + <»[.
Итак, решениями данного неравенства являются все действи-
тельные числа, удовлетворяющие неравенствам
^•1 1
X < — 1 ИЛИ X > —.
2
Пример 2. Решите неравенство х2 — 4х + 5 0.
Дискриминант D = 16 — 20 = —4 < 0. Положим / (х) —
= х2 — 4х + 5, тогда / (0) = 5 > 0. Следовательно, график функ-
ции / лежит выше оси абсцисс, т. е. / (х) >0 для всех х £ R. По-
этому данное неравенство выполняется на всей числовой прямой.
Пример 3. Докажите, что при х > 1 выполняется неравен-
ство
х3 — Зх + 2 >0.
Пусть / (х) = х3 — Зх + 2. Тогда
/' (х) = Зх2 — 3 = 3 (х2 — 1) >0 при х > 1.
Следовательно, функция возрастает при х > 1, и так как
/ (1) = 1 — 3 + 2 = 0, то / (х) >0 при х > 1.
Упражнения
Решите следующие неравенства:
486. 6х2 — х — 2 > 0.
487. 2ха + 6х + 5 > 0.
488. х2— Зх + 2 > 0.
489. х2 — 2х + 3 <0.
490. 9х2 — Зх — 2 > 0.
491. 2 —х—х2 > 0.
154
492. Докажите, что при х > 0 имеют место следующие неравенства:
а) -у х3 — 2х2 4- х > 0; б) хб — х34- х > 0.
493. Рассмотрите решение неравенства ах2 4- Ьх 4* с > 0 в случае
0 = 0.
58. Общая схема исследования функций
Способ построения графика функции по точкам очень несовер-
шенен: даже вычисление ординат большого числа точек может не
дать верного представления о графике функции, а следовательно,
и о ходе изменения функции.
Если предварительно исследовать функцию на монотонность
и экстремумы, то потребуется значительно меньше точек и построен-
ный по этим точкам график будет точнее отражать ход изменения
функции. Такое исследование удобно проводить по определенному
плану.
1. Находим область определения функции.
2. Находим производную данной функции.
3. Находим критические точки данной функции.
4. Находим промежутки монотонности и экстремумы функции.
5. Строим график функции.
Пример 1. Построить с исследованием график функции у (х)=
= — X4 4- 2х2 4- 3.
1. D (у) = Я.
2. у' (х) = —4Х3 4- 4х = —4х (х — 1) (х 4- 1).
3. Критические точки: 0; 1;—1.
4. Составляем таблицу:
X —оо< X < —1 —1 — 1 < х <0 0 0 < х < 1 1 1 < X < 4-00
/W 4- 0 — 0 4- 0 —
У(*) 4 3 У 4
max min max
В первой строке этой таблицы расположены в порядке возра-
стания критические точки функции и ограниченные ими интерва-
лы. Во второй строке отмечены знаки производной в этих интерва-
лах. В третьей и четвертой строках сделаны выводы о ходе измене-
155
ния данной функции («/*»— возрастает,
«\»убывает). Из таблицы видно, что
Утах У ( D 4,
Утах У (0
У min = У (0) = 3.
5. Строим график функции (рис. 66).
Пример 2. Построить график
функции f (х) =* | х |.
1. х С ]— + 00 [.
2. Г (х)= (-! при--<х<0,
11 При 0 <Х < + ОО.
(См. пример 1 п. 55 (стр. 148)).
3. Единственной критической точкой
функции является точка 0, в которой
производная не существует.
4. Составляем таблицу:
Рис. 66
X ]- оо; 0[ 0 ]0; 4- оо[
Г (X) не существует +
/ (х) х^ 0 у/
min
5. Строим график функции (см. рис. 57 на стр. 148).
Пример 3. Построить график функции f (х) = х3 — Зх.
1. D (f) = /?.
2. f (х) = Зх3 — 3 = 3 (х — 1) (х + 1).
3. Критические точки: —1; 1.
4. Составляем таблицу:
X ]—оо; -1[ —1 ]-1; 1[ 1 Ji; +°о[
f'(x) + 0 — 0 +
/(х) 2 х^ —2
max min
5. Строим график функции (рис. 67).
156
Рис. 67
Упражнения
Исследуйте следующие функции и постройте их графики:
494. f(x) = х3 — Зх + 1.
495. f(x) = xi— 2х3 + 3.
496. /(х)=
X2 + 3
59. Наибольшие и наименьшие значения функций
На рисунке 68 изображен график функции f, определенной на
отрезке [а; Ь]. В точке х2 данная функция имеет максимум, а в точ-
ках хг и х3—минимумы. Наименьшего значения, как это видно
на графике, функция достигает в точке х3 — точке наименьшего
из минимумов. Свое наибольшее значение функция принимает на
правом конце отрезка в точке Ь, в которой функция не имеет экстре-
мума (так как справа от точки b функция не определена).
157
Этот пример иллюстрирует следующее правило.
Для отыскания наименьшего и наибольшего значения функции,
дифференцируемой в данном промежутке, следует найти все кри-
тические точки функции, лежащие внутри промежутка, вычислить
значения функции в этих точках и на концах промежутка и из всех
полученных таким образом чисел выбрать наименьшее и наи-
большее.
Пример 1. Найти наименьшее и наибольшее значения функ-
ции у (х) = 2г3 + Зх2— 1 в следующих промежутках: а) [—2; —0,5];
б) Г-0,5; 1]; в) [1; 3[.
Находим критические точки данной функции. Так как
у' (х) = 6х2 + 6х = 6х (х + 1),
то критических точек две: 0 и —1.
а) В промежутке Г—2; —0,5] лежит лишь одна из критических
точек: х — —1. Так как
у (-2) = -5, у (-1) = 0 и у (-0,5) = -0,5,
то наибольшее значение этой функции достигается в точке —1 и
равно 0, а наименьшее значение — в точке — 2 и равно —5. Ко-
ротко это записывается так:
max у (х) = у (—1) = 0, min у (х) = у (—2) — —5.
[—2; -0,5] [-2; -0,5]
б) у (-0,5) = -0,5; у (0) - -1, у (1) = 4.
Следовательно, min у (х) — —1, max у (х) = 4.
[-0,5; 1] [-0,5; +1]
в) В промежутке [1; 3[ данная функция возрастает. Поэтому
min у (х) = у (1) = 4. Наибольшего значения эта функция не
[1; з[
достигает в промежутке [1; 3[, так как точка 3 не принадлежит
этому промежутку.
Пример 2. Имеется кусок проволоки длиной I {м) (напри-
мер, 80 м). Требуется оградить этой проволокой прямоугольный
участок земли, одна сторона которого примыкает к стене завод-
ского здания, так, чтобы площадь огороженного участка была наи-
большей.
Обозначим длину одной
1-2х
Рис. 69
из сторон участка через х (рис. 69).
Тогда длина смежной стороны равна
I — 2х. В этом случае площадь равна:
S (х) - х (I — 2х) = 1х — 2х2.
Очевидно, 0 х Таким обра-
зом, задача свелась к отысканию наи-
большего значения функции 5 в про-
Гл / 1
межутке 0; — .
I 2.
153
Находим критические точки этой
функции:
S'(x) — I — 4х; I — 4х = 0 при х = —,
\4/ 4 \ 2] 8
а так как S (0) = 0 и SО»тосвсе'
го наибольшего значения функция «S дос-
I
тигает при х = —:
max S(x) = S ~ (л/2)
В частности, при I = 80 (м) max S(x) =
= 800 (м2). 4°J
Пример 3. Дан прямоугольный лист жести 80 X 50 см.
Требуется изготовить открытую сверху коробку наибольшей вме-
стимости, вырезая по углам квадраты и загибая оставшиеся кром-
ки (рис. 70).
Обозначим через х длину стороны вырезаемого квадрата. Лег-
ко видеть, что 0 < х < 25, и объем коробки при этом равен
V (х) = х (80 — 2х) (50 — 2х) = 4х3 — 260х2 + 4000х.
Задача свелась к отысканию наибольшего значения функции V на
отрезке [0; 25]. Так как
V' (х) = 12х2 — 520х + 4000,
то, решая уравнение
12ха — 520х + 4000 = 0,
„ 100 г>
найдем критические точки: х± = ——, х2 = 10. В промежутке
[0; 25] находится лишь одна из них: 10. Так как V (0) — V (25) = 0,
а V (10) >0, то в точке 10 функция V принимает наибольшее
значение, и, вырезая квадраты со стороной 10 (см), мы получим
коробку наибольшего объема:
max V (х) = У(10) = 18 000(cju3).
[0; 25]
Пример 4. Пусть материальная точка движется из точки М в ниж-
ней полуплоскости в точку N верхней полуплоскости так, что в нижней по-
луплоскости ее скорость постоянна и равна ц, а в верхней — о2. По ка-
159
кому пути должна двигаться точка,
чтобы на весь путь затратить мини-
мум времени (рис.71)?
Если vi = у2» то искомый путь
есть отрезок MN. Если же щ =/» v2,
то точка должна двигаться по лома-
ной MON, причем положение точки О
следует определить так, чтобы на путь
М ON было затрачено наименьшее время
Пусть отрезок МО точка проходит за
время /i, a [O7V] — за время /г. Про-
ведем отрезки ММ' ±AT/V', NN' 1M'N'
и введем следующие обозначения:
JAf'OI = х, [MM'l = hi,
INN'I = h2, IM'N'I = I.
Тогда путь MON будет пройден за
время
|ЛЮ1 ] ОЛ7| _ У h\ + х» У h2 +(/-х)« .
" I ----------- —I— .......... I
г>1 v2 Vi 1 va
1 х 1 I — х
Vi У x^ У л|+(/ —x)a ’
f (x) = 0, если
x I — x vr sin a v-.
: —,>Z4 • = —, т. e. если —— = —•
| MO | | NO 1 sin p t>2
В курсе физики вы узнаете, что именно так преломляется луч света при
переходе из одной среды в другую (угол а называется углом падения, а угол
Р — углом преломления). Таким образом, луч света движется по такому пути,
при котором время движения будет наименьшим. В этом и состоит известный
в физике принцип Ферма.
Упражнения
497. Найдите наименьшее и наибольшее значения функции
f (Х) = х4 — 8х2 — 9
в промежутках: а) [—1; 1]; б) [0; 3].
498. Материальная точка совершает прямолинейное движение по
2
закону s (/) = 51 + 2/2---/3, где s (/) — путь (в метрах) и
3
t—время (в секундах). В какой момент времени скорость
движения точки будет наибольшей и какова величина этой
наибольшей скорости?
499. Покажите, что из всех равнобедренных треугольников, впи-
санных в данный круг, наибольшую площадь имеет равносто-
ронний треугольник.
500. Докажите, что из всех прямоугольных треугольников с за-
данной гипотенузой наибольшую площадь имеет равнобедрен-
ный треугольник.
601. Данное положительное число разложить на два слагаемых
так, чтобы их произведение было наибольшим.
160
502. Открытый бак с квадратным основанием должен вмещать
V литров жидкости. При каких размерах на его изготовление
уйдет наименьшее количество материала?
503. Буровая вышка расположена в поле в 9 км от ближайшей
точки шоссе. С буровой надо направить курьера в населен-
ный пункт, расположенный по шоссе в 15 км от упомянутой
точки на шоссе (считаем шоссе прямой линией). Если курьер
на велосипеде проезжал по полю 8 км/ч, а по шоссе 10 км/ч,
то к какой точке шоссе ему надо ехать, чтобы в кратчайшее
время достичь населенного пункта.
60*. Сведения из истории
Переломным пунктом в истории математики был XVII век.
Декарт ввел в употребление метод координат для изучения рас-
положенных в плоскости кривых. Развитие естествознания приве-
ло к необходимости исследования изменения функций, в особен-
ности функций, выражающих зависимость координат движущихся
тел и других физических величин от времени. Производная при-
менялась к нахождению экстремумов функций, к нахождению ка-
сательных к разнообразным линиям и т. п. Первые работы Де-
карта, Паскаля и Ферма уже содержали в себе по существу пра-
вила нахождения производных от любых многочленов.
В настоящее время математическим анализом называют часть
математики, которая изучает дифференциальное и интегральное
исчисление (с элементами интегрального исчисления вы познако-
митесь в X классе). Систематическое учение о производных, диф-
ференциальное исчисление, было развито немецким математи-
ком и философом Г. Лейбницем (164'6—1716) и английским
математиком и основателем современного математического ес-
тествознания И. Ньютоном (1643—1727).
Термин «функция» был введен Лейбницем, но долго под ним
подразумевались лишь функции, заданные каким-либо аналити-
ческим выражением. Во времена Эйлера функции, заданные в
различных частях интервала разными уравнениями, не считались
«настоящими» функциями. Но уже в 1822 г. французский мате-
матик Фурье в своих исследованиях пользовался по существу
самым общим понятием функции, хотя явно и не сформулировал
определение этого понятия.
Современное определение числовой функции, в котором это
понятие освобождалось от способа задания, было дано незави-
симо друг от друга русским математиком Н. И. Лобачевским
в 1834 г. и немецким математиком Л. Дирихле в 1837 г. Основ-
ная идея этих определений заключалась в том, что в понятии
функции не существенно, каким образом каждому х поставлено
в соответствие определенное значение f (х), важно только, чтобы
это соответствие было установлено.
6 Заказ 243
161
Современное же понятие функции с произвольной областью
определения и произвольным множеством значений (не обяза-
тельно числовыми), современная терминология и обозначения
сформировались по существу совсем недавно — в первой поло-
вине текущего столетия.
Наглядный смысл понятия предела функции был ясен мате-
матикам XVII в. Они умели фактически правильно находить пре-
делы. Но строгие определения понятий предела последователь-
ности и предела функции, сохранившиеся до наших дней, были
даны лишь французским математиком О. Коши (1789—1857) и
далеко не сразу были всеми поняты.
Яркие характеристики глубины переворота в математике, про-
исшедшего в XVII в., дали Карл Маркс и Фридрих Энгельс. Эн-
гельс писал: «Поворотным пунктом в математике была декарто-
ва переменная величина. Благодаря этому в математику вошли
движение и диалектика». Но начальный период развития новых
ветвей математики, связанных с понятиями функции, бесконечно
малых величин, пределов и производных, был охарактеризован
Марксом как «мистический».
Лозунгом многих математиков XVIII в. был: «Двигайтесь впе-
ред, и вера в правильность результатов к вам придет».
Только после работ Коши в течение XIX в. начала математи-
ческого анализа получили логическое обоснование. Для этого, в
частности, была необходима строгая теория действительных чи-
сел. А она была развита только во второй половине XIX в. Вей-
ерштрассом, Дедекиндом и Кантором.
Дополнительные упражнения к главе V
504. В какой точке графика функции у = касательная накло-
нена к оси абсцисс под углом в 45°?
505. Найдите способ построения касательной к графику кубиче-
ской параболы у = х3 аналогично примеру 2 (стр. 139).
506. Постройте график какой-нибудь функции, у которой в задан-
ной точке х0:
a) f Uo) = 0 и /' (х0) 0;
б) f (х0) = 0 и f (х0) < 0;
в) f (*о) = 0 и /' (х0) > 0.
Определите промежутки монотонности следующих функций:
507. а) и (х) = б) g (х) = Зх2 + 2х 4- 1.
508. a) f (х) — 2х2 -4- Зх -|- 4; б) g (х) = Зх2 — 2х + 1.
509. a) g(x) — х3-}--i-x2 — 2х —2; б) f (х) = х + —.
3 2 х
510. Исследуйте на монотонность и экстремумы следующие функ-
ции: ______
a)SW=y=-; б) u(t) = В) /М = /г2-Л
162
Исследуйте квадратичные функции и постройте их графики:
511. у = 2х2 + 5х — 3. 514. Н (х) = —х2 + 6х — 9.
512. F (х) = х2 + 8х + 16. 515. f (х) = _2%2 + 5х + 3.
513. Ф (х) = Зх2 + 4х + 2. 516. g (х) = —Зх2 4- 5х — 4.
Решите неравенство:
517. Зх2 — 2х — 1 < 0. 519. х2 — 2х + 1 < 0.
518. 6х2 — х + 2 < 0. 520. -х2 + 2х — 5 > 0.
4
Исследуйте функции и постройте их графики:
521. g (х) = Зх3 — 2х2 + 4. 523. и (х) = х3 — Зх2 + 2.
522. h (х) = Зх4 — Зх2 + 5. 524. w (х) = х3 + х.
525. Найдите наименьшее и наибольшее значения функции g (х) =
= х3— Зх2 + 3 в промежутках: а) [—1; 1]; б) [1; 3].
526. Найдите наименьшее и наибольшее значения функции h (х) =
= Зх3 — 9х2 + 2 в промежутках: а) [—1; 1]; б) [1; 3].
527. Из всех прямоугольников, вписанных в полукруг (одна сто-
рона прямоугольника лежит на диаметре полукруга), найдите
прямоугольник наибольшей площади.
528. Найдите отношение высоты к диаметру конуса, который при
заданном объеме имеет наименьшую боковую поверхность.
529. Кусок проволоки данной длины I нужно согнуть так, чтобы
площадь ограниченного ею прямоугольника была наибольшей.
Какими должны быть размеры прямоугольника?
530. Какой из равнобедренных треугольников с заданным перимет-
ром 2р имеет наибольшую площадь?
531. Представьте число 12 в виде суммы двух положительных сла-
гаемых, произведение которых имело бы наибольшее значение.
532. Представьте число 10 в виде суммы двух положительных сла-
гаемых так, чтобы сумма их квадратов была наименьшей.
533. Число 8 представьте в виде суммы двух положительных сла-
гаемых так, чтобы сумма их кубов была наименьшей.
534. В равнобедренный треугольник с основанием 20 см и высотой
8 см вписан прямоугольник, одна из сторон которого лежит
на основании треугольника. Какова должна быть высота пря-
моугольника, чтобы он имел наибольшую площадь?
535. Найдите число, которое в сумме со своим квадратом дает этой
сумме наименьшее значение.
536. Лодка находится на расстоянии 3 км от ближайшей точки А
берега. Пассажир лодки желает достигнуть села В, находя-
щегося на берегу на расстоянии 5 км от А. Лодка движется со
скоростью 4 км/ч,, а пассажир, выйдя из лодки, может в час
пройти 5 км. К какому пункту берега должна пристать
лодка, чтобы пассажир достиг села В в кратчайшее время?
6*
163
537. Концы отрезка АВ, |ЛВ| = 5 м, скользят по координатным ссям.
Скорость перемещения конца А равна 2 м/сек,. Каков модуль
скорости перемещения конца В в тот момент, когда конец А
находится от начала координат на расстоянии 3 м?
538. Длина вертикально стоящей лестницы равна 5 м. Нижний
конец лестницы начинает скользить с постоянной скоростью
2 м/сек. С какой скоростью опускается в момент времени t верх-
ний конец лестницы, с каким ускорением?
539. Неоднородный стержень АВ имеет длину 12 см. Масса его
части AM растет пропорционально квадрату расстояния
точки М от конца А и равна 10 г при AM — 2 см. Найдите:
1) массу всего стержня АВ и линейную плотность в любой
его точке /И; 2) чему равна линейная плотность стержня
в точках А и В.
540. Тело, масса которого т, движется прямолинейно по закону
S (/) = at2 + р/ + у (а, р, у— постоянные). Докажите, что
сила, действующая на точку, постоянна.
541. Колесо вращается так, что угол поворота пропорционален
квадрату времени. Первый оборот был сделан колесом за
8 сек. Определите угловую скорость колеса через 48 сек после
начала вращения.
542. Тело с высоты 10 м брошено вертикально вверх с начальной
скоростью 40 м/сек. Определите: а) на какой высоте от поверх-
ности земли оно будет через 1 сек-, б) через сколько секунд
тело достигнет наивысшей точки и на каком расстоянии от
земли? (Считать g = 10 м/сек.)
543. Круглый металлический диск расширяется при нагревании
так, что его радиус равномерно увеличивается на 0,01 см/сек,
С какой скоростью увеличивается его площадь в тот момент,
когда его радиус равен 2 см?
544. Лампа подвешена на высоте 12 м над прямой горизонтальной
дорожкой, по которой идет человек, рост которого равен 1,8 м.
С какой скоростью удлиняется его тень, если он удаляется
со скоростью 50 м/мин?
545. Из всех прямоугольников, вписанных в окружность, найдите
прямоугольник наибольшей площади.
ТТТ ТРИГОНОМЕТРИЧЕСКИЕ
Глава VI ФУНКЦИИ, ИХ ГРАФИКИ
---------- И ПРОИЗВОДНЫЕ
§ 12.
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
ЧИСЛОВОГО АРГУМЕНТА
61. Радианное измерение угловых величин
Из курса восьмилетней школы известны различные единицы
измерения угловых величин: прямой угол d*, градус, минута, се-
кунда. Эти единицы связаны между собой равенствами:
d = 90°, 1° = 60', Г = 60",
90 \60/ \60
В этих единицах измеряют величины углов, дуг, поворотов.
На рисунке 72 величина АОВ угла АОВ равна 60°. То же значение
60° имеет угловая величина АВ дуги АВ. ЛуЧ ОА отображается
на луч ОВ при повороте вокруг точки О на 4-60Q, или, что то же
самое, на —300°.
Теперь мы познакомимся еще с одной
единицей измерения угловых величин—
г> 180
радианом. Радиан— это — градусов:
«ГС
1 рад = (—57° 17'45".
\ л /
Целесообразность введения такой еди-
ницы измерения угловых величин мо-
* Строго говоря, d — общая величина
всех прямых углов.
Рис. 72
165
жет быть понята, если заметить, что длина дуги в один градус окруж-
ности радиуса г равна —— г, а длина I дуги в один радиан той же
180
окружности выражается проще:
I = г.
С еще более существенным преимуществом радианной меры угло-
вых величин мы познакомимся позднее.
Радианную меру угловых величин мы будем считать основной
и обозначение рад опускать, т. е. писать просто: d = —, 2d = л,
1° _ 0,01745 и т. д. Так же будем поступать при обозна-
чении поворотов;
R60° = R3.
Поворот на 2л радианов, т. е. на 360°, как мы знаем, есть тождест-
венное отображение:
~ = Е.
При измерении углов поворота в радианах, каково бы ни было
целое п, имеем:
2пп _ ра
Для практического измерения углов в радианной мере может
служить специальный транспортир, на полуокружности которого
отмечены радианы и их десятые части (рис. 73). Разделив каждое
наименьшее деление на 10 конгруэнтных частей, мы получим воз-
можность измерять углы с точностью до 0,01 радиана и т. д.
На рисунке 73 радианные меры углов АОВ, ДОС, AOD, АОЕ
соответственно равны: 0,5; 1,1; 2,0; 2,9.
Пример 1. Выразить в радианной мере величины углов
в 45°, 36®, 135®, 250°, 330°, 360°.
Из определения радиана имеем:
45° = — • 45 = 180 л V’
135° = — • 135 = 180 2л . ~Г’
330° = — . 330 = 180 11л. 6 ’
36° = • 36 = 180 л 5 ’
250° = — • 250 = 180 22л 18
360° = — . 360 = 180 2л
16б
В расчетах часто приходится градусную меру угловых величин
переводить в радианную или наоборот. Чтобы облегчить эту рабо-
ту, составлены специальные таблицы. На странице 168 приведена
часть таблиц из сборника В. М. Брадиса (стр. 61, изд. 1974 г.).
Пример 2. Найти радианную меру угла в 86°38'.
В левом столбце таблицы отыскиваем 86°, затем перемещаемся
по соответствующей строке до столбца таблицы, под которым (или
над которым) написано число минут, ближайшее к 38, т. е. до столб-
ца для 36'. На пересечении указанных строки и столбца находим
радианную меру угла 86°36', к ней надо еще прибавить поправку
на недостающие 2' (см. три последних столбца); получаем:
86°36'« 1,5115
+ 2' -)-6
Ответ: 86°38'» 1,5121"
Пример 3. Найдите градусную меру угла а = 1,5248.
Находим в таблице число, ближайшее к данной радианной мере,
и вычитаем поправку:
1,5254«87°24'
—6 —2'
Ответ: 1,5248^87°22'
Пример 4. Выразите в градусной мере величины углов:
л 2л
е"’ Т’
5л
V’
л
Т’
— —, Зл.
4
Проведем вычисления:
л т _ /180\° л qf.o 2л /180\° 2л юла \ л / 6 3 \ л / 3
5л j Зл 4 Ч80\° 5л _ 205ц я /180\° л 9qo л / 4 ’ 2 \ л / 2 * = _W. _ 135°, Зл = (—Г- Зл = 540°. \ л / 4 \ л /
П р и мер 5. Постройте на единичной окружности (окруж-
ность с центром в начале координат и радиусом г = 1) точку, на
которую отображается единичная точка оси абсцисс Ро при
повороте Ra вокруг центра окружности на угол в а ради-
анов*, л л л л л 2л если а принимает значение: 0, —, —, —, —, -у-,
Зл 5л 7л 5л 4л Зл 5л 7л 11л п • Л • , « "г • • • " " , —— 6 6 4 3 2 3 4 6
* Всюду в этой главе рассматриваются повороты вокруг начальной точки О
на координатной плоскости. Поэтому вместо Rq мы пишем просто Ra.
167
лА\
180/
Радианная мера Arc
А° =
А 0' 6' 12' 18' 24' 30' 36' 42' 48' 54' 1' 2' 3'
70° 1,2217 2235 2252 2270 2287 2305 2322 2339 2357 2374 3 6 9
71° 1,2392 2409 2427 2444 2462 2479 2497 2514 2531 2549 3 6 9
72° 1,2566 2584 2601 2619 2636 2654 2671 2689 2706 2723 3 6 9
73° 1,2741 2758 2776 2793 2811 2828 2846 2863 2881 2898 3 6 9
74° 1,2915 2933 2950 2968 2985 3003 3020 3038 3055 3073 3 6 9
75° 1,3090 3107 3125 3142 3160 3177 3195 3212 3230 3247 3 6 9
76° 1,3265 3282 3299 3317 3334 3352 3369 3387 3404 3422 3 6 9
77° 1,3439 3456 3474 3491 3509 3526 3544 3561 3579 3596 3 6 9
78° 1,3614 3631 3648 3666 3683 3701 3718 3736 3753 3771 3 6 9
79° 1,3788 3806 3823 3840 3858 3875 3893 3910 3928 3945 3 с 9
80° 1,3963 3980 3998 4015 4032 4050 4067 4085 4102 4120 3 6 9
81° 1,4137 4155 4172 4190 4207 4224 4242 4259 4277 4294 3 6 9
82° 1,4312 4329 4347 4364 4382 4399 4416 4434 4451 4469 3 6 9
83° 1,4486 4504 4521 4539 4556 4573 4591 4608 4626 4643 3 6 9
84° 1,4661 4678 4696 4713 4731 4748 4765 4783 4800 4818 3 6 9
85° 1,4835 4853 4870 4888 4905 4923 4940 4957 4975 4992 3 6 9
86° 1,5010 5027 5045 5062 5080 5097 5115 5132 5149 5167 3 6 9
87° 1,5184 5202 5219 5237 5254 5272 5289 5307 5324 5341 3 6 9
88° 1,5359 5376 5394 5411 5429 5446 5464 5481 5499 5516 3 6 9
89° 1,5533 5551 5568 5586 5603 5621 5638 5656 5673 5691 3 6 9
90° 1,5708
0' 6' 12' 18' 24' 30' 36' 42' 48' 54' 1' 2' 3'
А Аге А А Аге А А Аге А А Аге А
1" 0,000 004 848 6" 0,000 029 089 1' 0,000 2909 6' 0,001 7453
2" 0,000 009 696 7" 0,000 033 937 2' 0,000 5818 7' 0,002 0362
3" 0,000 014 544 8" 0,000 038 785 3' 0,000 8727 8' 0,002 3271
4" 0,000 019 393 9" 0,000 043 633 4' 0,001 1636 9' 0,002 6180
5" 0,000 024 241 10" 0,000 048 481 5' 0,001 4544 10' 0,002 9089
Решение дано на рисунке 74.
/?3(ро) = R3’ (Р„) = л, = Л,;
Л
R ЧР0) = Я3»° (Ро) = Рзэо = Р„,
6
А^(Р0) = (Ро) = Р45о = Р^,
4
л
К3 (в,) = R»»° (Р.) = /V = Р
3
/Д(Л,) = ft) = Рю° = Р„.
2
2л
ЯЦР,) = R™° (Р^Рпг = Р^,
3
Зл
R4 ft) = Яю" ft) = Р135о = Р^
4
5л
РЧРВ) = «1И°(Р») = Р«==Р55
6
и т. д.
Мы условились поворот на t ра-
дианов для любого действитель-
ного числа t обозначать через PC
Любому числу t теперь соответст-
вует точка единичной окружности
Pt = R‘ (Ро)-
Поэтому можно сказать, что за-
дано отображение / Pt множес-
тва действительных чисел R на мно-
жество точек единичной окруж-
ности. Так как повороты Pz и р/+2я"
Рис. 75
совпадают, то точка Pt будет соответствовать не только числу t,
но и всем числам вида t + 2лп, где п С Z.
Отображение t-+ Pt можно представить наглядно. Для этого
выберем на прямой х = 1, проходящей через точку Ро, направле-
ние такое же, как на оси Оу, и превратим ее в ось Pot. Затем
представим себе бесконечную нерастяжимую нить, натянутую вдоль
этой оси и закрепленную в точке Ро. Будем оба конца этой нити
«наматывать» на единичную окружность, как это показано на рисун-
ке 75.
Ясно, что точка нити, которая в начальном положении (нить про-
тянута вдоль прямой х = 1) имела ординату t на оси Ро/, после
наматывания попадет в точку Pt единичной окружности, а точки
4С9
прямой, ординаты которых отличаются друг от друга на число,
кратное 2л, наложатся при наматывании на окружность на одну
и ту же точку.
Таким образом, для того чтобы два действительных числа s и t
отображались на одну и ту же точку единичной окружности, не-
обходимо и достаточно, чтобы выполнялось равенство
s — t — 2л л,
где п — некоторое целое число.
Упражнения
546. Определите градусную и радианную меру углов равнобедрен-
ного прямоугольного треугольника, не пользуясь таблицами.
547. Определите градусную и радианную меру углов четырехуголь-
ника, если их величины относятся как 5:9:10:12 (без таб-
лицы) .
548. Найдите угловую скорость диска, вращающегося со скоростью
об
'в радианах в секунду).
549. Вычислите угловую скорость часовой и минутной стрелок
(в радианах в час).
550. С помощью таблиц найдите радианные меры углов по данным
их градусным мерам: а) 25°; б) 50°36'; в) 137°; г) 237Q.
551. С помощью таблиц найдите градусные меры углов по дан-
ным их радианным мерам: а) 0,4853; б) 0,3756; в) 1,3246;
г) 3,1416.
552. Окружность морского компаса делится на 32 конгруэнтные
части, называемые румбами. Выразите один румб в градусной
и радианной мерах.
553. Постройте на координатной плоскости точку, на которую
отображает единичную точку Ро оси абсцисс поворот /?а, если:
а) а = 25°; б) а = —100°; в) а = — ; г) а = — —.
4 4
554. Постройте на единичной окружности точку, на которую ото-
бражается единичная точка Мо оси ординат при повороте
если:
а) а == -j- •+- 2лп; б) а — + 2лп; в) а = 4- 2лл;
г) х — —^4-2лп; п—любое целое число.
555. При повороте около центра О на угол а точка М отображается
на точку ML. Задайте этот же поворот, используя другой
5л
угол поворота, если: а) а = 125°; б) а = —400°; в) а = —;
г) х = —Зл.
170
556. Будут ли повороты Rn и R-180° различны? Какое другое назва-
ние имеют эти повороты?
557. Поворот около центра О на угол 0 отображает точку N на точ-
ку Л\. Задайте этот поворот с помощью всех возможных углов
поворота, если 0 принимает значение:
а) 0 = 40°; в) 0 = -; д) 0 = 2л; ж) 0= 1,5;
6
б) р = — 20°; г)₽=-4; е)₽ = 1; з)₽ = -0,8.
4
558. Найдите а, если:
Зл
а) /Л Rn= RT\ в) R2^ • Rn = Ra;
л л‘
б) R~ 2 • Ra= R”-, г) RT- Ra= R'1.
62. Длина дуги и площадь сектора
Ранее вы узнали, что длина дуги I в 1 радиан равна радиусу г:
I = г.
Поэтому длина дуги в а радианов выразится так:
I = г • а.
Как вы знаете из восьмилетпей школы, площадь сектора, дуга
которого содержит 1°, равна
_____ лг2
CfcK’ “ 360’
а площадь сектора, дуга которого содержит 1 радиан, выражается
проще:
г2
9 -- -—
°сек. — 2 •
Поэтому площадь сектора (рис. 76), дуга которого
радианов, выразится так:
о _ Г2
*^сек. 2 *
Пример 1. Найти длину дуги окружно-
сти радиуса г — 15 см, если дуга содержит
л
— радиана.
Длина дуги I — 15 • — — 5л (см).
Пример 2. Найти
круга радиуса г = 20 см,
Зл
содержит — радиана.
4
Площадь сектора SceK. =
= 150л (см2).
площадь сектора
если дуга сектора
202 Зл
2 ’ 4
содержит а
171
Упражнения
2 jt
559. Угловая величина дуги АВ равна —, а ее радиус г = 3 м.
3
Найдите длину дуги АВ.
5 л
660. Угловая величина дуги CD равна —, а ее длина равна 10 см.
4
Найдите радиус дуги.
Зл
561. Угловая величина дуги MN равна а ее радиус г = 8 м.
Найдите длину дуги.
562. Найдите длину дуги единичной окружности, если радианная
Зл
мера дуги равна —.
4
563. Длина дуги равна 10 см, а ее радиус г = 2 см. Найдите ра-
дианную меру дуги.
564. Найдите площадь сектора радиуса г = 15 см, радианная мера
л
дуги которого равна —.
5
2 л
565. Радианная мера дуги сектора равна —, а радиус г — 30 см.
3
Найдите площадь сектора.
566. Длина дуги сектора равна 20 см, а радиус г = 15 см. Найдите
площадь сектора.
567. Радианная мера дуги равна 2, а площадь сектора равна 256 см2.
Найдите радиус сектора.
568. Радиус сектора г — 5 см, а его площадь равна 75 см2. Найдите
радианную меру дуги сектора.
63. Синус и косинус числового аргумента
Вспомним определение синуса
и косинуса угла а, данное в учеб-
нике геометрии VIII класса. Пово-
рот на угол а вокруг начала
координат отображает единичную
точку Ро оси абсцисс на точку
Ра = RaW,
которая, как и точка Ро, лежит на
единичной окружности (рис. 77).
При этом ордината точки Ра есть
синус угла а, а ее абсцисса— коси-
нус угла а, т. е.
у„ = sin а, х„ — cos а.
* (Л (Л
172
После введения радианного измерения угловых величин мы
установили взаимно однозначное соответствие между множеством
действительных чисел и множеством значений угловых вели-
чин, выраженных в радианной мере. Поэтому можно говорить о
тригонометрических функциях синуса и косинуса числового
аргумента.
Определение. Пусть
= R* (Ро)
есть точка координатной плоскости, получающаяся из единичной
точки оси абсцисс Ро при повороте вокруг начала координат на t
радиан. Ордината yt точки Pt называется синусом числа t,
а абсцисса xt точки Pt называется косинусом числа t, т. е.
xt — cos t, yt = sin t.
Область определения функций синуса и косинуса есть множе-
ство R всех действительных чисел. А так как координаты любой
точки Pt единичной окружности по модулю не превосходят едини-
цы, то множеством значений функций синуса и косинуса является
отрезок [—1; 1].
Так как Pt —М (xt; yt)— точка единичной окружности, то х* +
+ у2 = 1, т. е. справедливо тождество*
cos21 + sin21 — 1. (1)
На рисунке 74 (стр. 169) отмечены точки, соответствующие
числам: 0, —, 6 Л Л Л 2л Зл 5 л 7 л
т ’ Т’ Т’ Т’ 4 ’ , Л, , 6 6
5л 4л Зл 5л 7л 11л о , , 2л.
4 3 ’ 2 ’ 3 ’ 4 6
Составим таблицу значений синуса и косинуса для значений
аргументов, выраженных этими числами.
Ординаты этих точек единичной окружности соответственно
равны
1 /2 /3 < /3 /2 Л _1
’ 2’ 2 ’ 2 ’ ’ 2 ’ 2 ’ 2’ ’ 2’
TZ, — TL, -1, -К1, о,
2 2 2 2 2
* Так как независимую переменную под знаком функции можно обозначить
любой буквой, то тождество (1) можно записать и так:
sin2a cos2a = 1, sin2* cos2* = 1 и т. д.
J73
а абсциссы:
. /З- /2 1 л 1 /Т /3 . Уз
2 2 2 2 2 2 2
_2, о, 1, А 12, I.
2 2 2 2 2
Тем самым получаем таблицу искомых значений синуса и коси-
Упражнения
569. Проверьте справедливость равенства (1) для значений синуса
и косинуса из выше приведенной таблицы.
3 20
570. Найдите значение sin а, если: a) cos а = —; б) cos а = — .
5 29
571. Определите значение cos а, если:
. . 12 .. . 1
a) sin а = —; б) sin а = —.
13 3
Упростите следующие выражения с помощью тождества (1):
572. sin2 а — 1.
573. sin4 а 4- 2 sin2 а cos2 а 4- cos4 а.
574. (sin а 4* cos а)2 4- (sin а — cos а)2.
575. cos2 а — cos4 а 4- sin4 а.
576. sin4 а 4- cos2 а 4- sin2 а • cos2 а.
577. sin4 а — cos4 а — sin2 а 4- cos2 а.
578. .cos.2 а ..
1 — sin2 а
579. 1 ~ 2sin2a.
2 cos2 а — 1
580. ;
sin а cos а
12 1^2"
581. Может ли косинус быть равным: а) 0,67; б) —; в) -—
11
\ / 15э
г) ----?
174
64. Графики синуса и косинуса
Для построения графика функции синус выбираем систему коор-
динат и строим окружность единичного радиуса с центром в произ-
вольной точке оси Ох (слева от точки О). Откладываем на оси абс-
цисс отрезок ОР, длина которого приближенно равна длине по-
строенной окружности (2л « 6,28 единицы длины). Далее, делим
этот отрезок на конгруэнтные части, например на 16 конгруэнтных
частей. На столько же конгруэнтных частей делим и окружность,
начиная от точки Ро. Точки деления окружности будут иметь ор-
динаты, равные значениям синуса в соответствующих точках деле-
ния отрезка ОР. Следовательно, точки графика функции синус
располагаются на прямых, проведенных через точки деления ок-
ружности параллельно оси Ох. Построенные точки соединяем
плавной кривой. Получаем приближенно график синуса на отрез-
ке [0; 2л] (рис. 78). Для уточнения графика надо единичную ок-
ружность делить на большее число кон-
груэнтных частей.
Точно так же строится график на отрез-
ках [—2л; 0], [2л; 4л], [4л; 6л] и т. д.
(рис. 79).
График синуса, как вам известно, на-
зывается синусоидой.
Аналогично строится график косину-
са. Чтобы упростить построение отрез-
ков, равных значению косинуса (рис. 80),
достаточно повернуть единичную окруж-
175
У
ность вокруг центра на 90° и далее поступать так же, как и при
построении синусоиды (рис. 81).
Аналогично строится график косинуса на отрезках [—2л; 0],
[2л; 4л] и т. д. (рис. 82).
График косинуса, как вам известно, называется косинусоидой.
Упражнения
582. На координатной прямой Ох отметьте точки, соответствующие
•< гл л> 3 л jt jt
, 1, л, 2л, —I, —л, —2л, —, —,--------, —,
2 2 2 4
Зл 5л 7л л Зл 5л 7л
I-’ ~ Т’ ~’
583. Отметьте на единичной окружности точки, соот-
ветствующие числам 0, —, л, — и 2л. Определите
4 >77 у 0 1 X Ря! "7 Рис. 83 координаты этих точек. 584. На миллиметровой бумаге построй- те единичную окружность и отметь- те на ней точки, соответствующие л Зл л Зл числам —, —, , . 4 4 4 4 Найдите по рисунку координаты этих точек. 585. На единичной окружности (рис. 83) отмечены точки Ро, Рп ,Р п , Рп. Г —Т Запишите в общем виде числа, ко- торым соответствуют эти точки.
176
586. Постройте на миллиметровой бумаге график функции х sin х,
используя при этом таблицу на странице 174.
587. Запишите, чему равен синус числа: — у , 0, у, л.
588. Постройте на миллиметровой бумаге график функции х -> cos х,
используя для этого таблицу на странице 174.
589. Запишите, чему равен косинус числа: —у, —л,-у-, —2л.
590. Для каких значений аргумента х верно равенство:
a) sin х = 1; в) sin х = —1; д) sin х = 0;
б) cos х = 1; г) cos х = — 1; е) cos х = 0?
65. Тангенс и котангенс числового аргумента
Определение 1. Тангенсом числа а называется
отношение синуса этого числа к его косинусу, т. е.
Определение 2. Котангенсом числа а назы-
вается отношение косинуса этого числа к его синусу, т. е.
j cos а /о\
ctga=-----. (2)
sin а
Из этих определений следует: область определения тангенса
состоит из всех действительных чисел, кроме чисел вида — + лп,
где п = 0, +1, ±2, ... ; область определения котангенса состоит
из всех действительных чисел, кроме чисел вида пп, где п = 0,
±1.....Числа вида + лп и лп не включаются в область опре-
делений соответственно функций тангенса и котангенса, так как
при значениях чисел вида — + лп косинус равен 0, а при значе-
ниях чисел вида ли синус равен 0.
Перемножая почленно равенства (1) и (2), получим:
tg а • ctg а = 1. (3)
Равенство (3) справедливо только для тех значений а, которые
входят в общую часть областей определения тангенса и котангенса,
т. е. для всех действительных чисел, кроме чисел вида
где п = 0;±1; +2; ±3; ... .
177
Часто приходится пользоваться следующими тождествами:
l+tg2a=—(4)
ccs“a v '
1 + ctg2 а = -2-. (5)
sin2 а
Тождество (4) справедливо в области определения тангенса,
т. е. для всех действительных чисел, кроме чисел вида + лп,
где п = 0; ±1; ±2; ... , а тождество (5) — в области определения
котангенса, т. е. для всех действительных чисел, кроме чисел вида
лп, где п = 0; ±1; ±2; ... .
Для доказательства тождества (4) достаточно обе части тожде-
ства sin2 а + cos2 а = 1 разделить на cos2 а, а для доказательства
тождества (5) — на sin 2а.
Синус и косинус, тангенс и котангенс считаются основными
тригонометрическими функциями.
Иногда рассматривают еще две тригонометрические функции — секанс
и косеканс, которые определяются так:
1
sec а =---,
cos а
1
cosec а =--•
sin а
Пользуясь определением секанса и косеканса, формулы (4) и (5) можно за-
писать так:
1 + tg2 а = sec2 а, (4')
1 4- ctg2 а — cosec2 а. (5')
Рассмотрим вектор а длины а = |а|, образующий угол а с положитель-
ным направлением оси абсцисс. Если х и у — координаты этого вектора, то
у х у х а
sin а = —, cos а = —, tg а — —, ctg а = —, sec а =—,
а а х у х
а
cosec а — —.
У
Так как из трех величин а, х и у можно составить только шесть различных
попарных отношений, то становится понятным, почему число основных три-
гонометрических функций равно шести.
Упражнения
591*.Найдите области определения секанса и косеканса.
592. Составьте таблицу значений тангенса и котангенса по образцу
таблицы на стр. 174.
178
Упростите следующие выражения:
593. a) sin a ctg а + cos а; б) —-------------tg2 а — sin2 а.
cos2 а
594. a) sin2 а + cos2a + tg2 а; б) 1 — sin2 u + ctg2 а • sin2 а.
595. (1 4- tg2 a) cos2 а. 597.
v s ' ctga + ctgp
me 1 — sin2 a . . . _AO cos2 a —ctg2 a
596. h tg a • ctg a. 598. ----------5—.
1 — cos2 a sin2 a — tg2 a
Докажите справедливость следующих равенств:
599. sin4 a — cos4 a = sin2 a — cos2 a.
600. sin2 a — sin2 0 = cos2 0 — cos2 a.
601 sin a ________1 4-cos a 1 — 2 sin2 a
1 — cos a sin a 2 cos2 a — 1
603. ctg2 a — cos2 a = ctg2 a • cos2 a.
604. -=2tg2a.
ctg a — sin a cos a
СЛ_ 2 sin2 a — 1 cos2 a — 1 1
1 — 2 cos2 a 1 — sin2 a cos2 a
плп sin2 a sin a 4- cos a . , ~
606.------------------------—-------= sin a + cos a.
sin a— cos a tg2 a — 1
607. ‘+tg“ + y° =tg8a.
1 ctg a -|- ctg2 a
„ЛО 1 — 4 sin2 a • cos2a . o .
608.------------------------------------------= 1 — 2 sin a cos a.
(sin a 4“ cos a)2
609. ° - cos! ° + c°5' g = tg* a.
cos2 a — sin2 a 4- sin4 a
66. Таблицы значений тригонометрических функций
числового аргумента
В «Четырехзначных математических таблицах» В. М. Брадиса
даны таблицы VII, VIII, IX, X для определения значений триго-
нометрических функций углов, выраженных в градусной мере.
Там же приведена таблица XII, отрывок из которой приводится
ниже (см. стр. 180).
По этой таблице можно находить значения синуса, косинуса и
тангенса числового аргумента. Например, sin 2,04 = 0,8919,
cos 2,04 - —0,4522, tg 2,04 = —1,9725.
Упражнения
610. С помощью таблицы XII найдите значения синуса, косинуса
и тангенса чисел: 0,03; 0,30; 0,37; 1; 1,43; 2; 2,15; 3; 3,07.
179
Тригонометрические функции от аргумента в радианах
X sin х cos X tg X X sin x cos t tg X X sin x cos X tgx
1,20 0,9320 0,3624 2,572 1,60 0,9996 —0,0292 —34,233 2,00 0,9093 —0,4161 —2,1850
1,21 9356 3530 650 1,61 9992 0392 —25,495 2,01 9051 4252 1285
1,22 9391 3436 733 1,62 9988 0492 —20,307 2,02 9008 4342 0744
1,23 9425 3342 820 1,63 9982 0592 — 16,871 2,03 8964 4432 0224
1,24 9458 3248 912 1,64 9976 0691 —14,427 2,04 8919 4522 —1,9725
1,25 9490 3153 3,010 1,65 9969 0791 —12,599 2,05 8874 4611 9246
1,26 9521 3058 113 1,66 9960 0891 —11,181 2,06 8827 4699 8784
1,27 9551 2963 224 1,67 9951 0990 — 10,047 2,07 8780 4787 8340
1,28 9580 2867 341 1,68 9940 1090 —9,1208 2,08 8731 4875 7911
1,29 9608 2771 467 1,69 9929 1189 —8,3492 2,09 8682 4962 7498
1,30 0,9636 0,2675 3,602 1,70 0,9917 -0,1288 —7,6966 2,10 0,8632 —0,5048 —1,7098
1,31 9662 2579 747 1,71 9903 1388 -7,1373 2,11 8581 5135 6713
1,32 9687 2482 903 1,72 9889 I486 —6,6524 2,12 8529 5220 6340
1,33 9711 2385 4,072 1,73 9874 1585 —6,2281 2,13 8477 5305 5979
1,34 9735 2288 256 1,74 9857 1684 —5,8535 2,14 8423 5390 5629
1,35 9757 2190 455 1,75 9840 1782 —5,5204 2,15 8369 5474 5290
1,36 9779 2092 673 1,76 9822 1881 —5,2221 2,16 8314 5557 4961
1,37 9799 1994 913 1,77 9802 1979 —4,9534 2,17 8258 5640 4642
<38 9819 1896 5,177 1,78 9782 2077 —4,7101 2,18 8201 5722 4332
1,39 9837 1798 471 1,79 9761 2175 —4,4887 2,19 8143 5804 4031
1,40 0,9854 0,1700 5,798 1,80 0,9738 —0,2272 —4,2863 2,20 0,8085 —0,5885 —1,3738
1,41 9871 1601 6,165 1,81 9715 2369 —4,1005 2,21 8026 5966 3453
1,42 9887 1502 6,581 1,82 9691 2466 -3,9294 2,22 7966 6046 3176
1,43 9901 1403 7,055 1,83 9666 2563 —3,7712 2,23 7905 6125 2906
1,44 9915 1304 7,602 1,84 9640 2660 —3,6245 2,24 7843 6204 2643
1,45 9927 1205 8,238 1,85 9613 2756 —3,4881 2,25 7781 6282 2386
1,46 9939 1106 8,989 1,86 9585 2852 —3,3608 2,26 7717 6359 2136
1,47 9949 1006 9,887 1,87 9556 2948 —3,2419 2,27 7654 6436 1892
1,48 9959 0907 10,983 1,88 9526 3043 —3,1304 2,28 7589 6512 1653
1,49 9967 0807 12,350 1,89 9495 3138 —3,0257 2,29 7523 6588 1420
1,50 0,9975 0,0707 14,10 1,90 0,9463 —0,3233 -2,9271 2,30 0,7457 —0,6663 —1,1192
1,51 9982 0608 16,43 1,91 9430 3327 8341 2,31 7390 6737 0969
1,52 9987 0508 19,67 1,92 9396 3421 7463 2,32 7322 6811 0751
1,53 9992 0408 24,50 1,93 9362 3515 6632 2,33 7254 6883 0538
1,54 9995 0308 32,46 1,94 9326 3609 5843 2,34 7185 6956 0329
1,55 9998 0208 48,08 1,95 9290 3702 5095 2,35 7115 7027 0125
1,56 9999 0108 92,62 1,96 9252 3795 4383 2,36 7044 7098 —0,9924
1,57 1,0000 0008 1256 1,97 9214 3887 3705 2,37 6973 7168 9728
1,58 1,0000 —0,0092 —108,6 1,98 9174 3979 3058 2,38 6901 7237 9535
1,59 0,9998 —0,0192 —52,07 1,99 9134 4070 2441 2,39 6828 7306 9346
X sin х cos x tg X X sin x cos X tg X X sin x cos X tgx
§ 13.
ОСНОВНЫЕ СВОЙСТВА
ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
67. Знаки значений тригонометрических функций
Оси координат Ох, Оу прямоугольной системы координат делят
всю координатную плоскость на четыре части, называемые четвер-
тями или квадрантами. Эти четверти нумеруются против движения
часовой стрелки, как показано на рисунке 84. Единичная окруж-
ность с центром в начале координат тоже делится на четыре чет-
верти, которые нумеруются так же, как и четверти плоскости.
Если точка Ра, изображающая число а, находится на дуге пер-
вой четверти единичной окружности, то мы будем говорить, что
число а находится (лежит) в I четверти. Если а изображается
точкой II четверти единичной окружности, то будем говорить, что
число а находится во II четверти, и т. д. Так, например, число а,
удовлетворяющее одному из неравенств:
о , Зл
— 2л < а <-------,
2
/Л _х
О < а < —,
2
п 5л
2л < а <----,
2
л 9л
4л < а <----
2
ит. д., находится в I четверти. А число р, принадлежащее одному
из интервалов ] — + 2лп; л + 2лп[, где п = 0 ± 1, ±2, ... , на-
2
ходится во II четверти, и т. д.
Если поворот на а градусов с центром в начале координат ото-
бражает точку Ро на точку Ра, принадлежащую, например, IV чет-
верти, то, по аналогии, будем говорить, что1 угол в а градусов на-
ходится также в IV четверти.
О точках (числах) единичной окруж-
ности, принадлежащих осям координат,
будем говорить, что они находятся либо
на положительной, либо на отрицательной
полуоси абсцисс или ординат.
Так как ординаты точек I и II четвер-
тей положительны, а III и IV четвертей
отрицательны, то синусы чисел (углов),
находящихся в I или II четверти, имеют
положительные значения, а синусы чисел
(углов), находящихся в III или IV четвер-
ти, — отрицательные значения. Короче, в
181
Знаки синуса
Рис. 85
I и II четвертях синус положителен, а в III и IV четвертях синус
отрицателен.
Так как абсциссы точек I и IV четвертей положительны, а II и
III четвертей отрицательны, то в I и IV четвертях косинус поло-
жителен, а во II и III четвертях косинус отрицателен.
Знаки синуса и косинуса по четвертям показаны на рисунке 85.
В I и III четвертях знаки синуса и косинуса совпадают, поэтому
тангенс и котангенс в этих четвертях положительны. Во II и IV
четвертях знаки синуса и косинуса противоположны, поэтому
в этих четвертях тангенс и котангенс отрицательны (рис. 86).
Примеры. I} Угол 350° находится в IV четверти, поэтому
sin 350° < 0, cos 350° > 0, tg 350° < 0, ctg 350° < 0.
2) Угол—160° находится в III четверти, поэтому
sin (—160°) < 0, cos (—160°) < 0, tg (—160°) > 0, ctg (—160°) > 0.
3) Число 2,5 находится во II четверти, поэтому
sin 2,5 > 0, cos 2,5 < 0, tg 2,5 < 0, ctg 2,5 < 0.
4) Число (—2,5) находится в III четверти, поэтому
sin (—2,5) < 0, cos (—2,5) < 0, tg (—2,5) > 0, ctg (—2,5) > 0.
5) Найти cos a, tg а и ctg а, если
12 .Зл
известно, что sin а =-----и л<а<—.
13 2
Из равенства cos2 а + sin2 а = 1 полу-
чаем: cos а = ±У 1—sin2 а, что справед-
ливо при любом значении а. Знак в пос-
леднем равенстве выбирается в зависи-
мости от четверти, в которой находит-
ся а. В данном примере число а нахо-
дится в III четверти, поэтому получа-
ем cos а = —У1—sin2 а. Следователь-
но,
182
tga =
sin a 12.
cos a 5 ’
ctg a —
cos a 5
sin a 12
6) Найти sin a, tg a и cos a, если известно, что ctg a = — — и
3
a— число во II четверти.
1 3
Так как tg a • ctg a = 1, то tga =-----=-------.
ctg a 4
Для отыскания sin a и cos a можно воспользоваться тождест-
вами (4), (5) п. 65:
— = 1
cos2a
+ tg2 a = 1 + — = — =$> cos2 a
& 16 16
Так как a—во II четверти, то cos a = —- , a sin a = —.
5 5
Упражнения
611. Определите знаки значений всех тригонометрических функ-
ций следующих углов и чисел: 1) 143°; 2) —243°; 3) 735°;
4) —735; 5) 0,35; 6) —0,5; 7) 5,6; 8) —3,5; 9) 7,3; 10) —7,3.
612. Определите знаки следующих выражений:
1) sin 300° • cos 200°;
2) sin 193° • tg 202°;
3) cos 247° • sin 112°;
4) tg 147° • ctg 293°;
5) cos40°-sin 120°-tg 150°;
6) tg97°«ctg 197°-cos 297°;
7) sin 1000° • cos 840° • tg 375°;
8) sin 3 • cos 5;
9) cos 8 • cos 5 • tg 1;
10) tg 5 • ctg 3 • sin 2;
11) sin (—5)-cos(—3) • tg(—2)-ctg2.
В следующих задачах по данному значению одной из тригоно-
метрических функций sin a, cos a, tg a, ctg a и интервалу,
в котором находится а, найдите значения остальных трех
функций:
613. sin a = —, — < a < л.
13 2
614. cos a = —, — < a < 2л.
5 2
615. tg a = —, л < a < — .
6 40 2
616. ctga=——, — <а<л.
6 15 2
618. cosa =—л<а< —
6 2
619. tg a = —• —, 0 < a «< л.
s 35
620. ctg a = —, 0 < a < —.
s 84 2
621. sin a = 0 < a.< — .
617. sina = — - <а<3л.
3 2
622. tga = —1/3, — <а<2л.
r 2
183
68. Четные и нечетные тригонометрические функции
Определение 1. Функция f называется четной, если
вместе с каждым значением переменной х из области определения f
значение —х также входит в область определения этой функции и
при этом выполняется равенство
f (—х) = f (х),
т. е. для любых противоположных значений переменной х из
области определения [ значения функции f равны.
Например, функция f (х) = х2 четная, так как f(—х) = (—х)2 —
= х2 = f (х) и функция определена на множестве R.
Определение 2. Функция f называется н е ч е т н о й, ес-
ли вместе с каждым значением переменной х из области определе-
ния f значение —х также входит в область определения этой функ-
ции и при этом выполняется равенство
f (-Х) = -/ (X),
т. е. для любых противоположных значений переменной х из
области определения f значения функции f противоположны.
Теорема. Косинус — четная функция, а синус, тангенс и
котангенс — нечетные функции.
Доказательство. Любые два противоположных дейст-
вительных числа а и —а изображаются на единичной окружности
двумя точками Ра и P-а, симметричными относительно оси абс-
цисс (рис. 97). Так как точки Ра и Р_алежат на единичной окруж-
ности с центром в начале координат О, то координатами точки Ра
будут числа cos а и sin а, координатами точки Р_а будут числа
cos (—а) и sin (—а). Из того, что точки Ра и Р_а симметричны от-
носительно оси абсцисс, следует, что их абсциссы совпадают, а
их ординаты противоположны. Поэтому при любом а справедли-
вы равенства
cos (—а) = cos а и sin (—а) = —sin а.
Для тангенса и котангенса имеем:
, , х sin (— а) — sin а ,
tg — а) = —------- =------- = —tg а;
cos (— а) cos а
, . ч cos(—а) cos а ,
ctg (— а) = —------- =----- = — Ctg а.
° v sin (— а) —sin а
Упражнения
623. Докажите, что если число а вхо-
дит в область определения танген-
са, то и —а входит в эту же об-
ласть; если же одно из этих чисел не входит в область оп-
ределения тангенса, то и другое не входит. Докажите то же
самое для котангенса.
624. Докажите, что секанс—четная функция, а косеканс—не-
четная.
Установите, какие из заданных ниже функций являются чет-
ными, какие нечетными, какие не являются ни четными, ни
нечетными:
625. а) / (х) = 1 — cos х; б) g (х) = х — sin х; в) h (х) = х2 cos х.
626. a) F (х) = х3 4- sin х; 627. а) Н (х) = tgx+1 ; v tgx—1 628. а) / (!) = '44^7 1 + sin21 629. a) <jp (a) = cos a • sin a; 630. a) h (y) = sin у • ctg2 y; z*\ /") 1 — COS X 6) G (x) = 1 + COS X л\ /х x 4- sin x 6) y(x) = . . X — sin X /х 1 4- sin a 6) g(a) = -1— . 1 — sin a б) у (₽) = tg ₽ • sin2 ft. 6) F (y) = tg у • ctg3 y.
631. Докажите, что график нечетной функции симметричен относи-
тельно начала координат.
632. Докажите, что график четной функции симметричен относи-
тельно оси ординат.
69. Периодичность тригонометрических функций
Определение. Функция f называется периодиче-
ской, если для нее существует такое число I 0, что при любом х
из области определения функции числа х — I и х + I также при-
надлежат этой области и выполняется равенство
f (х — — f (х) = f {хI).
В этом случае число I называется периодом функции f.
Если число I является периодом функции f, то ее периодами,
как легко видеть, будут также числа nl при любом целом п =£ 0.
Теорема. Функции синус, косинус, тангенс и котангенс
являются периодическими.
Доказательство. Числа а,
а + 2л и а — 2л изображаются одной
и той же точкой единичной окружно-
сти (рис. 88), поэтому если число а при-
надлежит области определения какой-
либо тригонометрической функции, то
и числа а ± 2л также принадлежат об-
ласти определения этой функции и для
них выполняются равенства:
sin (а ± 2л) = sin а, cos(a±2n)=cos а,
tg (а ± 2л) ~ tg в, ctg (а ± 2л) = ctg а.
185
Таким образом, число 2л является периодом указанных функ-
ций.
Особенно важно знать наименьший положительный период функ-
ции* . Пусть /0 — наименьший положительный период функции f.
Можно доказать, что все периоды функции кратны /0, т. е. если
I — любой период, то
I = п • 10,
где п — целое число, не равное 0.
Предположим, что существует период h функции f, такой,
ГА]
.1,.
что
г ие
10
Тогда
т. е. -rti/o < h < (nt +
1)/о.
есть целое число. Положим щ—
f (х) — f (х + h) = f (х h — гик)” и мы получили, что положительное
число h — nilo < /о есть период функции /. Но это противоречит тому, что
10 есть наименьший положительный период функции /. Следовательно, наше пред-
4
положение неверно и — — целое число,
‘о
Докажем, что наименьший положительный период синуса ра-
вен 2л. Из тождества sin (а + /) = sin а при а = 0 получаем
sin I = 0. На единичной окружности (рис. 88) только две точки
имеют ординату, равную нулю: точки Ро и Рп- Наименьшие поло-
жительные числа, изображаемые этими точками, соответственно
равны 2л и л. Из этих чисел число л явно не подходит в качестве
•ГС JT
периода, так как sin — = 1, a sin (— + л) = —1. Следовательно,
2 2
наименьшим положительным периодом может быть только 2л, что
и подтверждается равенством sin (а ± 2л) = sin а для любого а.
Наименьший положительный период косинуса тоже равен 2л.
В самом деле, из тождества cos (а + /) = cos а при а = 0 сле-
дует равенство cos I = cos 0 = 1. Наименьшее положительное
число /, для которого cos I = 1, равно 2л.
Для функций тангенс и котангенс наименьшим положительным
периодом является число л.
В самом деле, при любом значении а числа а и а ± л изобража-
ются точками Р и Q единичной окруж-
ности, симметричными относительно на-
чала координат О (рис. 89), и поэтому
соответственные координаты этих точек
противоположны. Если точка Р имеет
координаты х и у, то координатами точ-
ки Q будут числа (—х) и (—у). Следо-
вательно, cos а = х, sin а = у, cos (а ±
± л) — —х, sin (а±л) = —у и, значит,
* Обычно говорят просто о периоде функции,
понимая под этим наименьший положительный пе-
риод функции, если он существует.
186
tg a = —, ctg a = —, tg (a ± n) = —, ctg (а±л) = —.
X у X у
Если I — положительный период тангенса, Totg I = tg (0 + /) =
— tg О = 0; так как на J0; л[ тангенс нулей не имеет, то / л, т. е.
л есть наименьший положительный период тангенса.
Свойства четности, нечетности и периодичности тригонометриче-
ских функций позволяют упрощать вычисления.
Пример. Пусть надо найти
. 17л „ 17л । 17л 17л
sm — cos —; tg —; ctg —.
з. з ь з з
Находим указанные значения тригонометрических функций
следующим образом:
17 л • /г л\ . / л\ .л 1/"з
sin---= sin 6л------= Sill-----= — sin — __F
3 \ 3 ) \ 3 / 3 2 ’
17л л\ / л\ л 1
cos — = cos 6л---— cos---------== cos — = —;
3 \ 3 J \ 3 J 32
tglZ?^ tgf6n — -'j = tg(— -"j = —tg- = —/3;
S 3 \ 3/ \ з J S 3 r
,17 л , i~l -T \ г 11 1^3
rtg-з =ctgl6n-yJ = ctg(--jJ = -ctg? = --L .
При рассмотрении первых двух примеров был выделен период
синуса и косинуса, т. е. число 3 • 2л = 6л. В последних примерах
выделен период тангенса и котангенса, т. е. число, кратное числу л.
Если угол задан в градусной мере, то периодами синуса и коси-
нуса будут 360° и любое целое, кратное 360°. Для тангенса и ко-
тангенса — целое, кратное 180°.
Примеры. 1) sin(—1125°)——sin 1125°=—sih(360°-3+45°)=
=—sin 45°=— ;
2
2) cos( —1125°) = cos 1125° - cos(360° . 3 4- 45°) = cos45°
3) tg{—1125°) = —tg 1125° = —tg (180° • 6 4- 45°) = —tg 45°= —1.
Упражнения
Используя периодичность тригонометрических функций, за-
пишите значения заданных функций так, чтобы аргумент был
выражен наименьшим положительным числом градусов:
633. sin 485°. 634. cos 1025°. 635. tg 869°.
636. ctg 1743°. 637. sin (—875°). 638. cos(- 1694°).
639. tg(—1759°). 640. ctg (—3953°). 641. cos 3976°.
642. cos (—2305°). 643. tg5729°. 644. ctg 1875°.
645. sin (—5108°). 646. cos (—815°). 647. sin (—4187°).
187
§ 14.
ФОРМУЛЫ СЛОЖЕНИЯ
И СЛЕДСТВИЯ из них
70. Координаты вектора
Пусть на плоскости задана система координат. На осях коор-
динат отложены в положительном направлении отрезки ОЕ и OD
единичной длины (рис. 90). Векторы
i - ОЕ, j — OD
суть координатные векторы. Длина их равна единице:
Для дальнейшего заметим еще, что (рис. 91)
Л л_
r2Ci\=T r4T) = -i.
Повернув* вектор i на угол а, получим вектор
тоже единичной длины. Очевидно, что таким образом получаются
(при надлежащем угле а) все векторы единичной длины. Из рисун-
ка 92 ясно, что
еа = cosa • i + sina • /. (1)
Любой ненулевой вектор а представляется в виде
а = геа,
* В результате поворота Rn вектора О А получается вектор
Ra (ОД) = ORa (А)-
188
где г = | а | — длина вектора «, а еди-
ничный вектор еа имеет то же направ-
ление, что и вектор а (рис. 93). Из ра-
венства (1) получаем:
a=rcosa- f+^sina • j = xj, + у_/.
a a
Множители
%_>=rcosa; y_> = rsina
a a
называются координатами вектора а. Яс-
но, что для вектора а = ОА это не что
иное, как координаты точки А
(рис. 93).
Рис. 93
Упражнения
648. Изобразите на координатной плоскости вектор, координаты
которого равны:
а) 2); б)(-1;3); в) (2; - 1); r)(—1; — 2).
Запишите разложение вектора по координатным векторам i и /.
Л
649. Выразите вектор е в системе координат (/; /), где / = R2 (/),
через координатные векторы i и /, если:
а)7=ЯГ(7); б)е = ЯГ(7); в)7 = Т?л(7); г)Т?7(7).
650. Дан вектор а = ОА с координатами = 2, у^ = 3. Построй-
ся а
те вектор:
а) 6)2«"(J); в) й"Г(а); г) 3^!”(а).
651. Докажите, что совпадают векторы:
а) R* (2а) и 2flr(a); б) Ял(3а) и 3R\a).
71. Косинус и синус суммы
Сделаем сначала два геометрически очевидных замечания.
1) Повернув на угол а вектор k а, где k числовой множитель,
получим вектор Ra (ka) = (a).
2) Повернув на угол а сумму векторов с = a -j- b, получим вектор
Ra (с), равный сумме векторов /?а (а) и R (7).
189
R&(OA+OB}=Ru(OA]+Ra(dB)^OBt
Чтобы убедиться в правильности второго замечания, рассмотрим
векторы ОА = a, OB = b и ОС = с, удовлетворяющие равенству
с = а + 7.
Поворот Ro отобразит параллелограмм ОАСВ на параллело-
грамм OAjC^i (рис. 94). В результате получится:
Ra(a)~OAv Ra(b) = OBlt На(с) = ОСг.
Поэтому
/Г (?) = R“(S + ь) = /Г(а) + Ra(b).
Пользуясь этими замечаниями, в дополнение к установленной в
п. 70 формуле
Ra(i) = cos а. • i + sin a • /, (1)
докажем формулу
Ra (j) = — si*1 a • / 4- cos a-/. (2)
В самом деле,
(Л \ л л
T?2~(7)/l = #T(/?a(7)) = flr(cosa -7 + sin a • / ) =
л л
= cos a- R2 (i) 4- sin a • R2 (j ) = cos a-j 4- sin a • ( —i) =
= —sin a- i 4- cos a-/.
190
Выразим теперь cos (а + р) и sin (а + Р) через косинусы и
синусы углов аир. Для этого заметим, что
еа+р = cos (а 4- Р) • i + sin (а + Р) • j (3)
и, с другой стороны,
е а+р — (г а) — (cos «4 + sin а-j) =
= cos а • ) -j- sin а • R® (/
В силу равенств (1) и (2)
еа+р = cos а (cos Р • i 4- sin Р • /) 4- sin а (—sin Р • i 4-
4- cos Р • /) = (cos а • cos р — sin а • sin Р) • i 4- (sin а • cos P4*
4- cos а • sin P) • /• (4)
Сравнивая равенства (3) и (4), получаем:
cos (а 4* Р) = cos а • cos Р — sin а • sin р; /г\
sin (а 4- Р) = sin а • cos Р 4- cos а • sin р.
Формулы (5) называются формулами косинуса и синуса суммы.
Если в этих формулах заменить Р на —Р и учесть, что cos (—Р) =
= cos Р, a sin (—р) = —sin Р, то получим:
cos (а — Р) = cos а • cos Р 4- sin а • sin Р; /ф
sin (а — р) = sin а • cos Р — cos а • sin р. ' '
Формулы (6) называются формулами косинуса и синуса разности.
Пример. Вычислить sin 15°, cos 15Q, tg 15°, ctg 15Q.
Известно, что
sin 45° = cos 45° = ^-2-, sin 60° — cos 60° =
Для вычисления воспользуемся формулами синуса и косинуса раз-
ности двух углов: 15Q = 60Q— 45°.
sin 15° — sin (60° — 45°) = sin 60D-cos 45° — cos 60° -sin 45° =
= V_3 =
cos 15° — cos (60° — 45°) — cos 60°-cos 45° 4- sin 60°>sin 45° =
tg 15° = = XIE.-.1 = 2 — /3;
cos 15° /У _J_ 1
ctg 15° = Jil+J = 24-/3:
/3—1
Примечание. Для вычисления можно было бы также
воспользоваться равенством 15° — 45° — 30°.
191
Упражнения
652. Найдите значение выражения
cos 43° • cos 17° — sin 43° • sin 17°.
653. Вычислите
sin 56° • cos 34° + cos 56° • sin 34е.
654. Чему равна разность произведений
sin 57° • cos 12°— cos 57° • sin 12°?
655. Вычислите
sin 104° • cos 14° — cos 104° • sin 14°.
656. Найдите значения: sin 75°, cos 75°.
657. Вычислите sin 105°, cos 105°.
658. Докажите истинность равенств:
a) sin-----a = cos a;
\2 У
6) sin + a) = cos a;
659. a) sin (л 4- a) = — sin a;
o) sin I — + al = — cos a;
660. Найдите значение sin (a + P), если
8 Q 4
cos a —-----, cos p = —
17 5
и a в III четверти, а p в IV четверти.
661. Вычислите sin (a—P), если
5 • a 8
cos a =-----, sinP = —
13 r 17
и a в III четверти, а p в I четверти.
662. Чему равно значение sin(a+P), если
5 4
cos a = —, sin Р =----
13 r 5
и a в I четверти, а P в III четверти?
663. Вычислите cos (a + Р), если
9 . о 40
cos a =-----, sm р — —
41 41
и а в III четверти, а Р во II четверти.
в) cos-------a
\2 /
г) COS + 0^ =
в) cos (л 4- a) =
\ /Зя । \
г 1 cos I--1- a 1 =
- sin a;
— sin a.
- cos a;
sin a.
192
sin (а 4~ Р) 4~ sin (а — Р)
sin (а + Р) — sin (а — Р)
cos (а 4~ Р) 4~ cos (а — р)
cos (а 4- Р) — cos (а — Р) *
\ / JT
— 4- а — cos — 4- а
6 / \3
• / \
sin — 4- а 4- cos — 4- а
\6 / \3 /
664. Найдите значение cos (а — 0), если
20 р 7
sin а — —, cos р =-------
29 25
и а и Р во II четверти.
665. Вычислите sin (а—Р), если
15 - о 3
cos а =------, sin р = — —
17 5
и а во II четверти, а р в IV четверти.
Упростите следующие выражения:
666. cos (а + 60°) + cos (а — 60°).
667. sin (а + 60°) 4- sin (а — 60°).
668. cos/— 4-4— cos/——сД 671.
\6 / \б /
669 sin (а — ft) + 2 cos а • Sin Р 672
2 cos а cos р — cos (а — Р)
cos а cos Р — cos (а 4- Р)
670. —;------£---. к-- 673.
ccs (а — Р) — sin а • sin р
Докажите следующие тождества:
674. sin (а + Р) • sin (а — Р) = sin2 а — sin2 р.
675. cos (а 4- Р) • cos (а — Р) = cos2 а — sin2 р.
676. Jin.,(”±PL=tga+tgp. 677. -sin (а ~Р) =tga-tgp.
cos а • cos р cos а • cos р
678. Найдите cos (а 4~ Р) и cos (а — Р), если cos а = cos Р и
sin а = sin р.
72. Тангенс суммы
Из формул (5) п. 71 для косинуса и синуса суммы можно полу-
чить другие важные тригонометрические формулы. Так, для тан-
генса суммы получаем:
. , . о\ sin (а 4- Р) sin а cos р 4- cos а sin Р
а cos (а 4- Р) cos а cos р — sin а sin р
Учитывая область определения для tg (а 4- Р), надо считать, что
ct 4~ Р — 4* где k £ Z-
2
Полученное выражение не удобно для частого употребления
тем, что в нем тангенс суммы выражен через синусы и косинусы.
7 Заказ 243
193
Удобнее пользоваться формулой, в которой тангенс суммы выра-
жается через тангенсы заданных углов аир. Для этой цели разде-
лим числитель и знаменатель полученного выражения (1) на произ-
ведение cos a cos р. При этом предполагается, что cos a cos Р 0.
В результате получаем:
sin a cos р cos а sin Р
f _|_ р\ — cos а cos P cos а cos Р tg а 4- tg р
cos a cos Р_sin а sin Р 1 — tg а- tg р
cos а cos р cos а cos р
Окончательно имеем:
tg(<x + р) = (2)
1 — tg а tg р
В этой формуле а, р и а + р не являются числами вида 4- л/г,
где k £ Z. Если в формуле (2) вместо Р подставить (—Р) и учесть
свойства нечетности тангенса, то получим формулу для тангенса
разности:
tg(<x—(3)
1 4- tg a tg р
Упражнения
679. Вычислите tg 75°, tg 15е.
Указание. Представьте 75° в виде суммы 45° 4- 30®, а 15°
в виде разности 45° — 30°.
680. Вычислите tg (— -f- al если sin a = — и — < a < л.
\3 ) 4 2
681. Вычислите tg (45°— а), если tg a = 7.
682. Найдите tg (х 4- у) и tg (х — у), если tg х — 1,2 и tg у = 0,7.
683. Вычислите:
tg22°4-tg23°
а' 1 — tg22°.tg23°;
684. Докажите тождество:
, л . , 4л
tg — + tg —
8 15 15
, л , 4л
1 — tg — • tg —
8 15 s 15
а) tg 4- a
\ 4
A tg a 4~ tg (45° — a) ।
1 — tg a tg (45°— a)
1 4- tg a .
1 — tg a ’
73. Тригонометрические функции двойного аргумента
Из формул (6) п. 71 можно получить формулы тригонометриче-
ских функций для двойного аргумента. Для этого положим в фор-
мулах (б) Р = а:
194
cos 2a = cos2 a — sin2 a, (1)
sin 2a = 2 sin a cos a, (2)
которые истинны для любого числа a £ R.
Если же выразить правую часть формулы (1) через одну триго-
нометрическую функцию, (синус или косинус), получим формулы:
cos 2a = 1 — 2 sin2 a, (3)
cos 2a = 2 cos2 a— 1. (4)
Эти формулы позволяют выразить sin2 а или cos2 a через cos 2a:
. 2 1 — cos 2 a z[-4
Sin2 a =------------, (5)
2
о 1 + cos 2a
cos2 a =------*-------
2
(6)
Из формулы (2) п. 72, полагая a = 0, можно получить формулу
тангенса двойного аргумента:
tg 2a = (7)
1 — tg2a
В формуле (7) a =/= — -Ь — kt где k £ Zt и a =/= — -|- лиг, где
4 2 2
т С Z.
Упражнения
685. sin a = 0,6; 0
. Tt
a < —.
2
Вычислите sin 2a, cos 2a, tg 2a.
686. cos a -------- и sin a >0.
13
Найдите sin 2a, cos 2a, tg 2a.
687. Докажите, что при 0 < a < -^ имеет место неравенство
sin 2a < 2 sin a.
688. Докажите тождества:
a) sin 15° • cos 15Q = — ; б) 1 — 4sin2 a cos2 a — cos2 2a.
4
Упростите выражение:
689. 2‘е|5° .
I -16*16°
690. 1 — 2 sin2 a + cos 2a.
691. cos 4a + 2 sin2 2a.
692. (cos2 a + 2 sin a cos a — sin2 a)2.
7*
195
74. Формулы суммы и разности одноименных
тригонометрических функций
В дальнейшем изложении нам потребуются формулы для суммы
и разности синусов и косинусов двух углов или чисел.
Для вывода этих формул выпишем равенства
sin (х 4- у) = sin х cos у + cos х sin у. (1)
sin (х — у) = sin х cos у — cos x sin у, (2)
cos (х + у) = cos x cos у — sin x sin y, (3)
cos (х — у) = cos x cos у + sin x sin y, (4)
полученные в предыдущем пункте.
Каковы бы ни были два числа аир, всегда существует и при-
том единственная пара чисел х и у, для которой выполняются ра-
венства:
| х + у = а,
у=р. (5)
Это следует из того, что система уравнений (5) имеет и притом
единственное решение:
Теперь мы можем получить нужные нам формулы.
Складывая почленно равенства (1) и (2), получим:
sin (х + у) + sin (х — у) = 2 sin х cos у.
В последнем равенстве производим замену по формулам (5) и (6)
и получаем формулу для суммы синусов:
sin а sin р = 2 sin —• cos (7)
Вычитая из равенства (1) почленно равенство (2), получим ра-
венство
sin (х + у) — sin (х — у) — 2 cos х • sin у,
которое после замены по формулам (5) и (6) принимает вид:
smа — sin р = 2 cos —• sin (8)
Точно так же из равенств (3) и (4) получим еще два равенства
для суммы и разности косинусов:
cos а -|- cos р = 2 cos • cos —; (9)
cos а — cos р = — 2 sin —— • sm —. (10)
2. 2
196
Иногда, учитывая то, что синус — нечетная функция, последнюю
формулу записывают в виде
о о . а 4- Р . Р — a /tn \
cos а — cos р = 2 sin -у2- sm *-у—. (10a)
Упражнения
693. Докажите формулы (9) и (10).
Преобразуйте в произведения следующие выражения:
694. sin 40° 4- sin 80q.
695. sin 80° — sin 40q
696. cos 50° -h cos 20q.
697. cos 15° — cos 25q.
698. sin 20° + cos 80q.
699. sin 40° — cos 25q.
700.
701.
702.
703.
sin a 4- cos a.
sin a — cos p.
sin a 4* sin P
sin a — sin P’
sin a — cos a
sin a 4* cos a
Докажите следующие тождества:
704. ctg a 4- ctg P =
sin (a -f- P)
sin a • sin p
705. ctg a — ctgP =
sin (P — a)
sin a • sin P
706.
708.
sin a 4- sin 5a ___।
cos a 4- cos 5a
1 4~ cos a 4- cos 2a 4- cos 3a
2 cos2 a 4- cos a — 1
707. sin 100° — sin 40° = cos 70°.
2 cos a.
709. cos2 p — cos2 a = sin (a 4- P) • sin (a — p).
710. sin2 a — cos2 P => —cos (a + P) • cos (a — P).
711.
tg (a 4~ P) — tg a — tg P = | p
tg a • tg (a 4- P)
Дополнительные упражнения к главе VI
Может ли синус быть равным:
712 713 а 4- 714. 7- "° -?
п . /io. a -t- а. У
Упростите выражение:
sinx . cosx
716.------1---------.
cos х 1 4- sin х
717. (3 sin x 4- 2 cos x)2 4- (2sin x — 3 cos x)2.
Докажите тождество:
718. (1 4- tg2 a) (1 — sin2 a) — sin2 a = cos2 a.
719. sin2 a • sin2 P -f- sin2 a • cos2 P 4* cos2 a = 1.
715.
а 4- Ь
197
Упростите выражение:
720. tg2x— sin2x—tg2xsin2x.
Упростите выражение:
721.
1 — cos а
1 4- cos а
1 4- cos а
1 — cos а
722. cos (а 4- Р) • cos (а — Р) 4- sin (а 4- Р) • sin (а — Р).
723 sin (а 4~ Р) — cos а sin Р
cos (а — Р) — sin а sin Р
Докажите тождество:
724. sin (х 4* 45°) = —(sin х 4- cos х).
/2
725. sin 32° cos 15° 4- cos 32° sin 15° = sin 26° cos 21° 4- cos 26° X
Xsin 21°.
726.
727.
sin (P — y) sin (y — a) । sin (a — P) q
cos p cos у cos у cos a cos a cos P
• f \
sin — 4- x — cos — 4 x
\4 \4 .
----7---------(--------7--------Г = tg x-
/ jX \ / ЭТ \ °
sin — + x I + cos — + x I
\ 4 } \ 4 /
728. Дано: tg a = ~ ; tg p = 4 Найдите: tg (a + p); tg (a—p);
4 5
ctg (a 4- P); ctg (a — P).
Докажите тождество:
729.
730.
tg (45° 4~ x) — tg (45° — x)
tg (45° 4- x) 4- tg (45° - x)
= 2 sin x cos x.
fe4<.-tg3a =t ,
1 4- tg 4a tg 3a
Упростите:
731. * 1 + sl-”2_x. .. 733. 2 cos2 — — 1.
(sin x 4* cos x)2 2
-on 10-2 2 'гол 1 —cos 2x4-sin 2x
732. 1—8 sin2 a • cos2 a. 734. ---------—-------.
1 4- cos 2x 4- sin 2x
Докажите тождество:
735. tg2a — tga =
cos 2a
736. 16 cos 20° cos 40° cos 60° cos 80° = 1.
737. cos2 3 + cos2 1 — cos 4 cos 2=1.
198
Представьте в виде произведения:
738. sin2x— sin2 у. 739. tg2a — tg2p.
740. cos x + cos 2x + cos 3x + cos 4x.
741. sin x + sin 2x 4- sin 3x + sin 4x.
Следующие выражения преобразуйте в произведение введе-
нием вспомогательного аргумента (например, 1 = sin — j:
742. 1 sin a. 747. 3 2 cosct. 4
743. KT -ч sin a. & 748. 1 • 2 sin2 a. 4
744. KT . . -к—|- sin a. 749. 1 2 cos2 a. 4
745. — sin 35°. & 750. 3 — tg2 a.
746. 3 . 2 »sin2 a. 751. ]ЛЗ 4- 2 cos a.
4
ОТВЕТЫ И УКАЗАНИЯ
К УПРАЖНЕНИЯМ
Глава I
6 ------. 14. У к а з а н и е. Если число не делится на 3, то его можно
л 4- 1
представить в виде 3ft + 1 или 3k — 1. 18. хп = — . 20. а„ — П .
л п -j- 2
24. Решение. Предварительно следует доказать, что п точек, располо-
женных на прямой, делят ее на п 4- 1 частей. Далее, а) при п = 1 утвержде-
1 • 2
ние справедливо, так как 1 4—~ ~ 2, а одна прямая делит плоскость на
две части; б) пусть утверждение верно для п = k, т. е. k прямых делят плос-
(Ь п
кость на 1 4--------частей. Докажем, что утверждение верно для л = k 4-1-
Выберем одну из k 4~ 1 прямых и будем ее в дальнейшем называть (k 4" 1)-й.
В силу предположения индукции оставшиеся k прямых разделят плоскость
k(k + I)
на 1 4----------частей; (k 4~ 1)-я прямая пересечет k первых в k точках
2
и потому разделится этими точками на k 4" 1 частей. Так как полученные k
точек отличны от точек пересечения k первых прямых между собой, то каж-
дая из этих частей разбивает одну из имевшихся частей плоскости на две
k (k + 1)
части, т. е. к имевшимся 1 4" ------ частям добавится еще k 4" 1. Всего
получим
ft (ft 4-1) (ft 4-1) (ft 4-2)
14----------4- (ft 4- 1) = 1 4-------------- (частей).
25. Р е ш е н и е. а) При л = 1 утверждение справедливо, так как одна плос-
(л4-1)(п24-6—и) (14-1) (I2—14-6)
кость делит пространство на две части и--------------—----------------- =
= 2; б) предположим, что утверждение истинно для л = ft, и докажем его
истинность для л — ft + 1. Выберем одну из плоскостей, тогда, во-первых,
для прямых ее пересечения с остальными ft плоскостями будут выполнены
условия задачи № 24, поэтому выбранная плоскость разделится этими пря-
fe2 4* k 4- 2
мыми на---------
2
частей; во-вторых, в силу предположения индукции остав-
200
. „ (fe+ l)(*2_fe + 6)
шиеся k плоскостей разделят пространство на -------------- частей.
6
Каждая часть выбранной плоскости разделит одну из имевшихся частей иа
две (это обеспечивается условиями задачи). Всего получим
+ 1) (*2_ *+б) b2_|_ft + 2 (fc + 2)(£2+fe+6)
----------ё----+ ~—“-----------------6-------
26. Р е ш е н и е. а) Для п = 1 утверждение истинно, так как одна окруж-
ность делит плоскость на (I2 —• 1 + 2) = 2 части; б) пусть утверждение
истинно для п = k, докажем его истинность для п = k + 1. Выберем одну
из окружностей, тогда, во-первых, она пересечется с каждой из остальных Л
окружностей не более чем в двух точках, во-вторых, оставшиеся k окружно-
стей делят плоскости не более чем на (Z4 — k 4- 2) частей (в силу предполо-
жения индукции). Полученные (не более чем 2k} точки пересечения выбран-
ной окружности с остальными разделят ее не более чем на 2k частей (про-
верьте!), каждая из этих дуг разделит одну из имевшихся частей плоскости
на две. Итак, к имевшимся не более чем А2 — k 4- 2 частям добавится не
более чем 2k частей. Всего получим не более чем k2 — Л4“24*2Л = А*4-
+ k + 2 = (k + I)2 — (k + 1) + 2 частей.
Глава II
32. а) (1); б) (7; 8) и (8; 7). 33. 6. 35. а) 403200; б) 3 628 799;
в) 10 302; г) 5. 36. а) п; б) 1 ; в) (п - 1) (п - 2); г) .
п (п — 1) (2k — 2)!
87- а) T7Z7T > б) Чг; в> р (р - г> / 1 ы •38-а) °’ 2; з; 4> * *
(п, +1)! k\ (tn — k)l
б) n > 6. 39. 9! = 362 880. 40. 14! 41. 18. 42. а) 24; б) 96; в) 6; г) 118.
44. 3024. 45. 1190. 46. 15. 47. {9; 10}. 48. 0,06048. 49. а) 0; {1}; б) 0; {!};
{2}; {1; 2}. 50. а) 8; б) 8. 51. 64. 52. а) 28; б) 17; в) 35; г) 28; д) 6; е) 101.
53. С|о = 38 760. 54. Cf5 = 52 360. 55. Решение. 2310 = 2 • 3 • 5 X
X 7 • 11. Поэтому для решения задачи достаточно определить, сколькими
способами можно из пяти чисел 2, 3, 5, 7, 11 выбрать два. Число таких спо-
собов равно С| = 10. 56. 10. 58. а) п; б) п (п — 1). 59. С3; а) 1; б) 10; в) 20;
г) 120. 60. а) 5; б) 54; в) 275; г) Р е ш е н и е. Из каждом вершины n-уголь-
ника можно провести п — 3 диагоналей; так как вершин п, а каждая диаго-
наль проходит через две вершины, то искомое число равно 0,5п (п — 3).
61. 21. 62. 1365. 63. а) 18; б) 190; в) 1; г) 1000; д) 7770; е) 4950. 65. б) У к а з а-
н и е. = С3; С'6 = С|; С%= С|. 67. 27 = 128. 68. 210 — 1 — 10 =
= 1013. 69. 2047. 71. а) а6 + 6а‘& 4- 15a4Z>2 4- 20а363 4- 15а264 4- баб® 4-
4- Ь*’, б) х5 4- 5х4у 4- 10х3у2 4“ 10х2у3 -г бху4 -|- у5; в) х5 —J>xty 4-
4- 10х3у2 — 10х2у8 4- бху4 — у5; г) х2 — 4х У ху 4- бху — 4у]/ ху 4- У2;
5_ 4_ 1_ 2_ 2_ 1_ 4_ 5_
д) х3 4“ 5х3 у3 4- Юху3 4- Юх3 у 4“ 5х3 у3 4- У3 ; е) х® — 12х®у -|- 60х4у2 —
—ЮОх’у3 4- 240х2у* — 192ху5 4- 64у«; ж) 2187х7 — 5103х® 4- 5103х® -
— 2835х4 4- 945х® — 189х2 4- 21х — 1; з) 1 4- 4у2 4- бу4 4- 4у« 4- у8;
в 1 10 40 80
и) р-12 _ бр-104- — 20/г* 4- 15/г4 — 6/г2 +11к)-¥4-'74-^ + —+
201
8Э
77 0. 78.
72.
5 4 3
Г2
с10
545
354’
Т15= — dfae3Z>15; Т18 = Clfaeli>le. 74. 75. —. 76. — .
1 31 18 31 720 2 120
1
3 ‘
83. а)
79.
Г2
с5
С2
g8
5
14’
7
15’
8
6)-. 84.
са 5 2
80. . 81. а) — ; б) —; в)
С«2+6 9 9
Н ps—I Ah
----------. 85. —. 86. P e ш e и
Г5 6*
7_
9 '
и e.
У
Решим задачу в общем виде, т. е. для любого натурального числа п. 1-й спо-
соб. Общее число способов надеть п шляп на п человек равно числу пе-
рестановок из п элементов. Для подсчета «благоприятных» исходов доста-
точно вычесть из п\ число способов, когда хотя бы один человек на-
дел свою шляпу. Пусть k-и человек надел свою шляпу, тогда остальные
п — 1 человек могут надевать шляпы произвольным образом, т. е. (п— 1)!
способами. Так как число способов одинаково ((п— 1)!) для каждого из п
человек, то всего мы получим п • (п — 1)1 = п\ способов. При этом мы два
раза учли способы, когда два человека надели свои шляпы. Так как число
таких пар равно С^, а оставшиеся п — 2 человек могут надевать шляпы
произвольным образом, то мы должны вычесть из полученного результата
Сд • (л — 2)!. Далее, подсчитаем, сколько раз мы учли способы, когда три
человека надели свои шляпы (пусть это будут А, В и С). На первом шаге мы
учли их три раза (для А, для В, для С), на втором шаге мы их вычли три раза
(для пары А, В, для пары А, С, для пары В, С). Таким образом, нам нужно
добавить (п — 3)! способов для каждой тройки А, В, С, т. е. С3 • (п — 3)1
способов. Возникает гипотеза, что искомое число способов равно
п • (п - 1)1 - С%(п - 2)! 4- С*(п - 3)1 - С*(п - 4)! + ... + (-1)«С«(п-п)1
(мы сначала взяли (п — 1)1 способов для каждого из п человек, за-
тем вычли (п — 2)! способов на каждую пару из п человек, затем
добавили (п — 3)1 способов на каждую тройку из п человек и т. д.).
Докажем, что мы подсчитали каждый способ (т. е. когда хотя бы один
человек надел свою шляпу) ровно один раз. Пусть при выбранном способе
ровно р человек надели свои шляпы. Тогда на первом шаге мы учли этот
способ р (т. е. Ср) раз, на втором вычли раз, на третьем прибавили С^
раз, на четвертом вычли С? раз и т. д. Всего получается Ср— Ср + С3 —.
— С^4- ... способов. Так как
l+^+Cj+C^4-... =С»4-С34-С34-С;+ ...
(см. задачу № 74, б), то написанное выше число равно единице. Таким обра-
зом, число «неблагоприятных» способов равно
п (п - 1)! - С* (п - 2)! + С3 (п - 3)! - С*п (п - 4)1 + ... =
/ 1 1 1,1
" V 21 +31 41 +51
а число благоприятных
nl
202
Итак, искомая вероятность равна
21
— ~~ -4- ••• -4* (~ 1)^ 1
31 4! 51 V '
1
пГ
При п = 5 получаем р = . 2-й способ. Пусть (аг, а2; ... ; — пере-
ои
становка из п элементов (чисел от 1 до п). Назовем перестановку беспоряд-
ком, если щ =£ i, т. е. для всех i = 1, 2, 3, ... , п (на f-м месте стоит число
ai =£ I). Другими словами, в беспорядке ни один элемент не занимает своего
первоначального места. Пусть Dn обозначает число всех беспорядков из п
элементов. Подсчитаем это число. Очевидно, что Dt = 0, D2 = 1. Первое
место в беспорядке может быть занято любым элементом, исключая первый
элемент, т. е. п — 1 элементами. Если первое место займет число k 1, то
все беспорядки можно разбить на две группы в зависимости от того, займет
ли первый элемент &-е место или нет. Если первый элемент займет &-е место,
то число беспорядков в этом случае равно числу беспорядков, образованных
(п — 2) элементами, т. е. Dn_2. Если же первый элемент не будет занимать
fe-ro места, то беспорядки будут такими, что в них элементы 1, 2, ... , k — 1,
k + 1, ... , п занимают места от 2-го до n-го, и, следовательно, их число
равно Dn_t. Таким образом, когда число k занимает первое место, то будем
иметь всего Dn^ + Dn_2 беспорядков. А так как k может принимать
п — 1 различных значений, то всех беспорядков из п элементов будет
(« - 1) (Dn.x + Д„_8).
Для решения задачи в общем виде далее следует убедиться, что формула
для Dn как раз такая, какая была получена при 1-м способе решения. Это
можно сделать, например, методом математической индукции. Для неболь-
ших п, с которыми мы имеем дело, проще вычислить Dn, используя получен-
ную рекуррентную формулу:
D3 = 2(D8 + Di) = 2(1 + 0) = 2;
= 3(D3 + D3) = 3(2 + 1) = 9;
D6 = 4(D, + D3) = 4(9 + 2) = 44.
Следовательно, вероятность того, что 5 гостей наденут каждый чужую шляпу,
D. 44 11 2-7! 1
равна — = — = — « 0,367. 87. --------= —. 88. Решение. Од-
Е 51 120 30 8! 4
но подмножество, содержащее элементов, можно выбрать
способами, из оставшихся п — /пх элементов можно выделить подмно-
жество, содержащее т8 элементов, способами, и т. д. Поэтому
число всех способов выбора k попарно не пересекающихся подмножеств,
удовлетворяющих указанному в задаче условию, равно:
rmt . . rm, . pmk-i _ nl________
я b„_Mi ...
89. 25 200. 90. a) {7}; 6) {5}; в) {3}; г) {6}. 91. a) {3; 4; 5; 6; 7; 8; 9}; б) n
n > 11; в) {0; 1; 2; 3; 4; 5; 6>; r) {5; 6; 7; 8; 9; 10; 11; 12; 13}. 92. 96. 93. 1332.
94. Решение. Каждая из 4 цифр встретится в каждом из десятичных
203
разрядов 6 раз. Поэтому искомая сумма будет равна 6 • 1111 • (Г + 3 +
+ 54-7)= 1111 • 96 = 106 656. 95. а) 24; 6)24; в) 31 • 4! = 144; г) 2 • 5! =
= 240. 96. а) 28 • 291; б) 2 • 29!. 97. а) (3; 14}; б) {5}; в) {19}; г) {17}.
98. а) {5; 6; 7; .8}; б) п € N, п > 9. 99. а) {5; 6; 7}; б) п 6 N, п >;6;
в) k^N, 1 < k < 9; г) {9; 10; 11; 12; 13; 14; 15}. 100. 120. 102. 968.
103. 13 160 160. 104. 171 100. 105. 16 800. 106. Решение. Разместим
сначала белые шары:
*Б * Б *Б «... «Б* .
На п из tn + 1 отмеченных звездочками мест нужно поместить п черных
шаров. По определению числа сочетаний это можно сделать способами.
.107. С^о • = 2520. 109. 20у2’8. ПО. Решение. Положим х2 = у3 = 1.
Тогда при разложении по формуле Ньютона и замены х2 и у3 на 1 мы полу-
чим искомую сумму коэффициентов. Итак, сумма коэффициентов равна
(5 — 4)7 = 1. 111. а) 50; б) 33; в) 10. 112. Решени е. Нужно найти такое i,
чтобы сумма первых i членов- разложения (1 + 0,01)10 отличалась от
числа (1 + 0,01)10 меньше, чем на 0,001, для этого достаточно, чтобы сумма
членов разложения начиная с t-го была меньше 0,001. Решим неравенство
< 0,001, т. е. 2С10 • °>01Л <0,001- Но^Сц) <1000, отсюда 2 cioX
h>i k>i к>3 k>i
X 0,01Л < 103- 10-8 < 0,001 при i > 3, кроме того, 1\ = 0,0045, поэтому
двух членов разложения недостаточно. Аналогично, 2^10 ' 0,01й < 103 X
х 0,01й < 103 • ю-10 < 10-® при i > 5, a Tt = С?о • 10"3 = 0,0000021 >
> 0,000001. Таким образом, в I случае нужно взять три члена разложения
(нулевой, первый, второй), а во II — пять.
Глава III
113. б) 12, 3800... в) 8,065000... 114. а) 17,586631 <17,586897; б) —2,37561 >
> — 2,37571; г) 0,2444444444... > 0,244. 115. а) 2,(3); б) 0,7(6); в) 1,(571428);
_ р ____2 5
г) 3,(36). 116. — - = —; 5 =-; 4,2 =
7 3 3 I
21 —8 0
= —;—1,6=—;0=—. 117. а) 2; 3; 7,1;
5 5 1
1001; б) 4; 9; 1,44; 1024. 119. а) 0,2 <
< 0,2664 < 0,3; б) —1,3 < —1,27 < —1,2;
5 г—
в) 1,1 < 2—< 1,2; г) 3,3 </И < 3,4.
6
3
120. 3,6091... . 121. а) 0,2 < —< 0,3; 0,21с
14
3 3 3
< — < 0,22; 0,214< — < 0,215; — =
14 14 14
10
= 0,214... ; б) — — = —0,333; в) /3 =
3
= 1,732 ... ; г) —/3 =2,267... = —1,732,,..
122. 1,90532... . 123. ху = 3,31... . 124.
204
a) 1,747... ;_б) 3,650... . 125. a) 0,247_.. ;6) 3,162.._. 127. Указание. (уЗ)2=
= 12 + (/2)2; (/5)2 = 12+ 22; (/6)2 = 22+ (/2)2. 130. x2 — x — 1 - 0. 131.
а) рациональное при a— 0° и a = 30°; б) рациональное при a = 0° и a=60°;
в) рациональное при a = 0° и a =45°. 132. а) множество дробных чисел; б) мно-
жество рациональных чисел. 133. /?; 0. 135. 3,5. 136. 16,5. 137. 3,6. 138. 1,4.
139. а) {—5; 5}; б) ]—5; 5[. 140. а) {6; 14}; б) [6; 14]. 141. а)]—оо; — 5](JЕ5;оо[;
б) ] — оо ; 6[ U ] 14; со [. 142. {3; 7}.
143. ]— 4,5; 2,5[. 144. [ — 4,7; — 4,3].
145. ]—оо ; 11—]|)[12- ; со [. 146.
48jul 48
а) Объединение двух прямых; б) пря-
мая с «выколотой» точкой. 147. См.
_ /7=7 Л=2 п=3 , _ /7=4_
-б'~5 -4 -J -2 *-/ 0 1 Та^
рис. 95 (точки оси Оу не принадлежат
21 51
множеству). 148. а) х10= — ; х26= — ;
10 ZO
2/1+ 3 5
Xa+1=^ п + 4; xn+i-^n- (n+ 3)(rt+4);
1 5 п + 1 Ьп+1
1111
•. 149. б) 2—; 4 —; 8 —; 16 —;
' 2 4 8 16
5 5 3 3
. 150. При
Зп
1
32 32 ’ 3’6’9’ 4’5
32 ’
п> 103. 151. При п<43. 152. а) хл= —
— 15 + 5п; б) хп = ( — 1)и+1 • 4. 153.
а) Графики изображены на рис. 96.
154. а) Графики изображены на рис. 97
155. а) Нет; б) да; в) да; г) да. 156.
а) 0,6; б) 0,15; в) 0,03; г) 0,003. 157.
а) л>4; б) п > 49. 158. а) п> И; п>
> 26. 160. а) 2,5; б) 3. 164. а) 42;
2
б) 233; в) 99 000; г) 818. 165. а) 2 — ;
О
б) 2.166. а) 7,5; б) 4,5. 167. а) уп= 10Х
/ 1\п~1 / 1 \«-1
XI— или уп= 15 • — — ;
/ 1 у»-1 2 / 1 \л-1
6)Ь= —т ИЛИУ«=Т‘ Т •
\ 5 / 3 \ 5 )
14 5 3
168. а) — ; б) — . 169 а) — ; б) 3 — ;
' 2 35 9 ' 11
в) F; г) 28;гтз? ,7°- а) 6 м>
' 90 ' 9900
б) ж2. 171. 47?2. 172. .
3 х+ 1
173. а) Да (например, [2; 3]); б) нет.
175. а) Нет; б) да; в) нет;
Рис. 96
/7= J /7=7 /7=2 Л=4
205
г) нет. 176. а) 4; —2; 3; —; б) 4; —6; —5; —0,2. 180. а) —2,5; б) —0,5; в) 0;
3
г) 1. 181. а) 0; б) 2 —; в) 1,2; г) 3—. 182. 0^2. 184. а) Возрастающая; б) убы-
<5 о
вающая; в) нет; г) нет. 185. а) Возрастающая; б) убывающая; в) невозрастаю-
щая; г) неубывающая. 188. а) Да; б) вообще говоря, нет. 189. а) Убывающая;
б) неубывающая; в) невозрастающая; г) возрастающая. 192. а) Да; б) да;
в) нет; г) нет. 193. а) 0; б) 0. 194. а) 13,195; б) 7,728; в) 79,797; г) 20,599.
яг яг яг
195. а) 6,684; б) 19,024; в) 78,152; г) 26,905. 196. а) —; б) —; в) у;
яг яг яга „ 1
о 7; д) 77? ,97- 77 • ,98- Зтлл 199- а>Да; б)иет; в> да; г)нет;
4 1 OU 1 OU О
д) да; е) да; ж) нет; з) нет. 203. 10,6 и 10,7; 10,607 и 10,608;
10,60712 и 10,60713. 204. а) 6,85 и 6,86; б) 3,60 и 3,61. 205. Бесконечными
2 з ________ 1
периодическими десятичными дробями являются числа: — ; у; /36 '; — —
206. Рациональным. 207. 1; 7,3. 208. а) При п > 4; при п > 3. 213. 4,414.
214. 2,160.... 215. —1,782.... 216. 7,071.... 217. 2,449.... 218. 3,872....
219. /7+/10</3+/19. 225. а) М (—4,9); б) М (4) и М (—12). 226. Указа-
ние. а) (/ 10)2 = I2 + З2; б) (/14)2 = (/10)2 + 22. 22 7. а) {1,7; 2,3};
б) {—2,9; -3,1}; в) [2; 3]; г) ]3; 17[; д) ]—оо; — 2[(Л|0; оо[; е)]-оо; -8,7]|J
UC—7,3; оо[. 228. а) {0}; б) {0,4}. 229. а) [1; оо[; б) ]3; оо[. 230. а) Множе-
ство, состоящее из одной точки (начала координат); б) окружность радиуса
3 с центром в начале координат; в) объединение двух прямых (у = х и у =
= —х); г) множество, состоящее из двух точек М (2; 0) и М (—2; 0); е) мно-
жество изображено на рисунке 98; ж) множество изображено на рисунке 99;
з) 1-я координатная четверть. 231. Множества изображены на рисунке 100.
206
232. х3 — —; х5 = — ; хл.ь1= ------ ; x2„+i —-------: ~— — ----------
3 9 ° 33 Л'1 2п+1+ 1 2n+1 2^+Ч-Г хп 2«+Ч-1
1 1 2я"1
233. а)ап = —; 1 <п<5; в)ап= —; 1 < п < 5; ж) ап = —----—— ; 1 <п<4.
п2 Зп 100(/1—1)4- 1
235. а) п >4; б) п > 1001. 236. а) п > 31; б) п > 301. 237. а) п_> 26; б) п >
>251. 239. Да. 244. Да; р. 245. а) 1^-; б) 2,1. 246. а) 1; б) 3 К3„ 247. а) Лю-
3 2
бое х из промежутка ]—1; 1[; б) любое х из промежутка ]0; 2 [. 249. Нет.
(Пример: ап— — ; bn— 1.) 250. Могут. Пример, годный для обоих случаев:
хп = (—1)"; Уп = (—1)я+1. 251. (хп 4- ул) не может сходиться, а (хпуп) мо-
ab 2
жет. 252. а) —1; б) —1,5. 253. 0,75. 254. — . 255. 2—. 256. —3. 257. а) Да;
£ о
б) да. 260. I. При а = 2Ь и b =£ — —• ни для какого натурального п, после-
довательность постоянная (т. е. и невозрастающая и неубывающая). II.
При а — 2Ь > 0 и b £ [—1; 0[ последовательность возрастающая. III. При
а — 26 < 0 и & £ [—1; 0[ последовательность убывающая.
Глава IV
265. /(1) = 2; Ц2) = 2,5; /^=2,5; ; f (— 0,5) =— 2,5.
\ 2 / \ а / а
2 5 5 у 7
266. /(0)=——/ (1) =1; /(а2 4-1)= 7а2 4-1; f(x-l)---—; g(x) =
о о о
Зх 4- 2 2 7
= -----; g (5) = 3 — ; g (— 3) =— — . 267. а) Объединение двух пря-
5 5 5
мых — осей координат; б) открытая полоса (рис. 101); в) квадрат (рис. 102);
г) открытый квадрат. 268. а) б) /?; в) ]—оо; —1] (J[l; оо[;
208
Г) ]—8; — 2CU3—2; 2[(J]2; оо[. 269. а) /?; в) [0,5; оо[. 270. f (—5) = 1;
f (-7) = /Тб; f (5) = /51; f (x) = /х2 + 5x 4- 1; f (/) = //2 + 5/ + 1.
272. f(-2) = -i; 7(0) = -1; = у ; f (y) = y; HD = 1;
f(4)=l. 273. /(-2) = 7; f (0) = 1; f (2) = 3; f (3) = 1; f (5) = 1.
a2 — x2 при 0 < x < ?./?., .—
F 2 D (S) = [0; a/2 ].
274. S(x) = a Vo
(a /2 — x)2 при —L < x < a /2;
275. Нет. 276. f (x) = |x|; f (x) = x2; f (x) = | x | 4* x2. 277. Для каждого x
из области определения функции f точка —х также принадлежит области
определения функции f и f (х) = f (—х). 278. х ->• х; х -> х3; х -> х 4- х7.
279. Для каждого х из области определения функции f точка —х также при-
надлежит области определения функции f и f (х) = —f (—х). 280. а), г) и д)
симметричны относительно оси ординат; б), в) и д) симметричны относительно
начала координат. 281. а) Истинно при х > 0, ложно при х < 0; б) истинно
при всех х 0; в) истинно при х > 0, ложно при х < 0. 282. Функция убы-
вает на всей числовой прямой. 283. Возрастает на [2; со[; убывает на]—оо;
2]. 284. Возрастает на ]—оо; 0], убывает на [0; оо[. 285. Возрастает на [2; оо[;
убывает на ]—оо; 2]. 286. Возрастает на,]—оо; 3]; убывает на [3; оо[. 287.
Возрастает на ]—оо; 1,5]; убывает на [1,5; оо[. 288. Убывает на ]—оо; 0[
и на ]0; оо[. 289. Возрастает на ]—оо; 0[ и на ]0; оо[. 290. Возрастает на
[0; оо[. 291. Убывает на [0; оо[. 292. Возрастает на [0; оо[; убывает на ]—оо;
0]. 293. Возрастает на [0; оо[. 294. Возрастает на ]—со; оо[. 295. Убывает
на ]—оо; оо[. 296. Возрастает на [1; оо[; убывает на ]0; 1]. 297. Возрастает
на ]0; оо[; убывает на ]—оо; 0[ 298. а) 3,2; б) 4,02; в) 0,2; г) 0,02.
1 1
299 .а) Дх=0,5; Ду=2,25; б) Дх=0,15; Ду= 1,1475. 300. а)——— ; б) — — ;
7 1359 804
375 1 2Дх
7 30107 1806 7 ]/х+Дх + /х
г) Дх (2 — 2х — Дх). 302. а) х2 + 2хЛ + ft2; 2xh 4- h2; 2х 4- h; б) kx 4- kh 4-
4* b; kh; k; в) ax2 4“ bx + c 4- 2axh 4- ah2 4- bh; 2axh 4- ah2 4- bh; 2ax 4~ 6 4~
4- ah; r) x3 4- Зх2Л 4-3x/i24- h3; 3x2/i4- 3x/i2 4- h3; 3x2 4- ЗхЛ 4- h2. 303. a) x 4-
4- 4 ; 6) ~ (3x2 4- 3x/i 4- h2). 304. a) 2; 6) 6x. 306. (2ax 4- b)h. 308. Сто-
рона вырезаемого квадратика должна быть равна 0,2 м. 309. Решение.
е
(f (х) — а) = |2х — 6| = 2|х — 3| <8 при |х — 3| < —
т. е. за б можно
взять—. 311. Решение.
2
|/(х) —а| =
< | 34-х | <8
при |х| > 1 и |3 4- х| < 8, первое из этих неравенств будет заведомо верным,
если |3 4~ *1 < 2. Итак, в качестве б можно взять минимальное из чисел 2
И 8. 316. Р е ш е и и е. Покажем, что для е0 = — в произвольной окрестно-
сти точки х = 0 существуют точки, такие, что (х) — а\> г0, каково бы
209
ни было действительное число а. Если а > 0, то для х < 0 ( а такие точки
есть в произвольной d-окрестности точки х ~ 0) имеем:
(х)—а|=| — 1 — а| > 1 >е0,
если же а < 0, то для х > 0 (например, для х = — I:
I/ (х) — а|=|1 — а[ > 1 > е0.
3
321. —10. 322. 5. 323. 0. 324. —. 327. 0. 328. 6. 329. —0,72. 330. 3. 331. —1.
5
9 1
332. —. 333. 0,4. 334. 3. 335. 12. 336. Предел не существует. 337. —.
4 1 1 1
338. — . 339. — . 340. 2. 341. —. 342. 3. 343. —ps. 345. а) у (0) = 0; б) у (0) =
3 4 12 2у х
=• —1. 346. а) у (1) = 2 (рис. 103); б) у (—1) = —1. 347. а) Функция непре-
рывна; б) у (0,5)= 1. 348. а) у (1) = 0 (рис. 104); б) функция непрерывна
(рис. 105). 349. 2. 350. 3. 351. а) а; б) а. 352. а) — ; б) —1; в) — —.
х 16
1 6 2
с. ~ . 355. —----------; —6; — — ; _ 6.
2 Ух 2 4 (х —2)1 2 3
353. 8x4-3; 11; 19; 43. 354. 1 1
356. ——; — . 357. Зх2; 0; 12. 358.
2/Г 2
1 — 11
растает на —оо; т=“| и на
оо функция убывает на
график функции изображен на рисунке 106; х= —у^У~
2ах + Ь\ Ъ\ 4а + Ь. 359. Функция воз-
J______1_*
К§"; /з\|;
точка максиму-
210
ма; х = —точка минимума. 360. Функция возрастает на [—1; 1];
функция убывает на ]—оо; —1] и на [1; оо[; точка х = —1 —точка мини-
мума; точка х = 1 — точка максимума. 361. Функция возрастает на ]—оо; 0]
и на [2; оо[, убывает на [0; 2]; точка х = 0 — точка максимума; точка
х == 2 — точка минимума. 362. Функция возрастает на [0; 2]; функция
убывает на ]—оо; 0] и на [2; оо[; х = 0 —
точка минимума; х = 2 — точка максимума;
график функции изображен на рисунке 107.
363. а) 1; б) 2х. 364. а) 2х + 1; б) 2х + 1.
36S. а) 2х - - ; б) 2х - ~ + ~^= .
х2 х2 2 у х
366. Р еш е н и е. Пусть w(x) = и (х) — v(x).
_ Дш (х) w (х + Ax)— w (х)
Тогда —— =----------------------- =
Дх Дх
и (х 4- Ах) — и (х) — v (х 4- Дх) + v (х)
= ’---------------------------------- =
Дх
и (х + Дх) ц (х) а (х + Л*) — у (х)
Дх Дх
Да Да
— — — — и
Дх Дх
t Да; (х) . (&и Да\ . Да
lira —-— = lim I — — — = hm — —
Ax~>0 Дх Дх->0 \Дх Дх/ Дх->0 Дх
А»
— lim — - и — и,
дх-,0 Дх Рис. 107
211
Рис. 109
13 1 6 12х —5
367. а) — ; б) — — . 368. а) 2; б) — 3- . 369. а) — (х — 1); б) ------------.
о 4 2 5 7
9х2 4- 4 Ох 83
370. 12х —7. 371. ----------------. 372. 6(2х —З)2. 373. 6х— 12х® 374. Гра-
фики изображены на рисунках 108 и 109. 375. а) 4х3; б) Зх2; в) 4( х — 4)3.
378. _ —J------
(1+Зу)2
6/2 + 2/
(1 + 602 ’ ’
376. a) 10x4 — 12x3 + 14x — 5; 6) — 6x2 + 4x® — 27X8.
7 3
-----------; — 7; — 1— .
(1—3x)2 4
ad — be
(°) = —— ПРИ d 0
d2
. 1 7
— 1; — — . 379. —-----------------;
16 (1 - Зу)2
8 ad — be ad — be
— . 381. ------------- ; -----------;
49 (ex + d)2 (cy -f- d)2
380.
вует при d = 0.
и не сущест-
ad — be
v (1) = (7+dF
существует при
при с — d и не
2
с - —d. 382. — — . 383. - 5х-2.
384. —12х“4. 385. —15х-«. 386. Произ-
водная существует при п > 1, опре-
деляется формулой (1) при п > 2.
387. б) График приведен на рисун-
ке 110. 388. 1—3; 3[. 389. [0; 16].
390. [1; оо[.-391. [0; 4[. 392. 1—^2;
— 1CU3— и °°С 393. ]—со; 2,9[U]2,9;
3[. 394. f о g = 2 — 1g х + lg2 х;
212
X
X2
g lg(2 — X 4~ X2); / ой=2_-1-+- " ft = ;
3 — x (3 — x)2 1 4- x — x2
lg X
——;----. 395. Например, для 390: у = f о a
3 — lg x
g °/i = lg---------; h °g =
3 — x
где g (x) = lg x; f (z) = Уz; для 393: у = f о g о <p о ф, где ф (x) = 3 — x;
<р (z) = lg z; g (u) = 1 4- u;
/ (/) = -y . 396. 100(2x — '5)(3 — 5x4- x2)99.
/ _____ х2 I 7
398. (х2 4- 7)11 24х/х + 2 4---1--
5x4— 14x
397. -o ----- .
3/(3x5 — 7x2 4- 9)2
399. 5n (2 4- 5x)”-1 при n
4- 2лгй. Из формулы V — Лг2й выразим h и подставим полученное значение
2V
в выражение для S. Получим S (г) = 2лг2 4----• Приравниваем S'(r) =
1; 5 при п — 1. 400. Решение. S = 2лг2 +
2V з/у
= 4лг — — нулю, получаем V = 2лг®. Убеждаемся, что г =1/ — — точка ми-
г2 V 2л
нимума функции S (г). Далее, V = 2л/-3 = лг2й, откуда h = 2г. 401. а) Объе-
динение двух прямых: х = 2 и у = —3; б) множество из четырех точек:
{(1; 1); (1; —1); (—1; 1); (—1; —1)}; в) квадрат (рис. 111); г) объединение двух
открытых углов (рис. 112); д) окружность с четырьмя «выколотыми» точками.
2
402. а) [—4; 4]; б) х Ех ; в) ]—оо; 1[U]1;2[|J]2; оо[; г) ]—оо; оо[;
и
д) ]4; ооЕ; е) ]-оэ; - 3[; ж) [-1; 1]; з)
1 1
— ; 1 . 403.
5
———; lg —; в) 2; У34- У z— 0;
3z — 1 5 Зи — 1 ' r
Рис. Ill
213
2ах при 0 < х
а/2
2
. _ аУ 2 г— г—
2а (а У 2 —х) при —— < х <а У 2. D (S) =» [0; а У2 ].
Ал
405. Да, у = Ь — УА?2 — (х — а)2, где /? — радиус, а М (а; Ь) — центр
окружности. 406. Если Е (f) = {0}. 407. Нет. 408. а) Возрастает на [1; со[;
убывает на
вает на [0;
— а)2, где R — радиус, а М (а; Ь) — центр
] — оо; 1]; б) возрастает на ]—оо; 2]; убывает на [2; оо[; в) убы-
оо[; г) убывает на ]—оо; со[. 414. — — . 415. 3. 416.
56 Зух2
не существует при х=0. 418. 6х2 4“ 6х — 2; —2; —2; 10.
1 при Дх>0,
—1 при Дх<0, аэта функция не
стремящемся к нулю (см. упр. 316*). 423. 12х® —
• “ : ~; • : '; : ----- - .8. _8; 4>
138. 429. б) График изображен на рисунке ИЗ.
430.---—----; ---—----; 16; 4. 431. / + Ю — 1 ; ; А 432. _---1--
(1 — 3z)2 (10—Зх)2 4//-(/_}_ 1)з 200’8 (4—5г)2
7 . 7 7 5x4-20/7-3.57 И -2i? + 6ы2-12^-20
(4-502’ 16’8f ‘ 2КГ(/74-2)2’64' 9 •
16 25 8 15 20
I- - - - 436. --- 437. - --
х6 х® а4 а® и5
2
рисунке 114. 439. -------
(24- 4*
при Л > 0;
Дет
419. х8 + х2 — х — 1; —1; 0. 420. —
Дх
имеет предела при Дх, стремящемся к нулю (см. упр. 316*). 421
— 12х2 4- 12х 4- 4. 424. Засх2 + 2 (ad 4* bc)x 4- ае 4- bd. 425. 6х — 8; —8; 4.
426. 150у44- 12у; 0; - - - -
16 16
435. —
Сражен
и6
2
х4
на
15
7’
2
440. — — (3 — 2х)
п
438. График изо*
1—л
। п • 441. Гра*
214
фик функции изображен на ри-
сунке 115. 443. На расстоянии
АВ
9
от точки, в которой уста-
новлен более мощный динамик.
4/з _ 9/2 + 2/ 12
444 —=
2//4—/3-|_/2_1’ /11
_ 2х 4
445 —=— —
’/х2—1/(х2+1)3’ 5/15’
445.
.447. 30, 5(15х2 —2)(5х3—
2х + 1)29.5.
Глава V
448. б) 1,414; 1,4423; 1,316; в) 1,4435; 1,316; г) |/"3 вычислен с точностью
до 0,002, а Уз'с точностью до 0,001. 449. 2,89; 4,33; 6,58; 2,63. 450. 14,44;
2,89; 1,73. 451. а) 3,003; б) 3,11. 452. а) 3,083; б) 2,013. 453. у = 0; у =
— —2х — 1; у = 2х — 1. 454. у = —Зх — 6; у = —Зх + 6. 455. у = 12х—
2
,— 16. 456. 6,4 км/ч. 457. Gt— 4(рад/сек); 20 рад/сек. 458. 1) 2,8 рад/сек-, 6 — сек.
О
459. 1) 12/(сл</се№); 2) а) сек-, б) ~ сек. 460. 1) 0,04 н. 461. 65 г/см-, 125г/см.
1 О
464. а) 6 сек', б) 18 м/сек. 465. а) Возрастает на ]—оо; оо[; б) убывает на
]—оо; оо[. 466. а) Убывает на ]—оо; 0[ и на ]0; оо[; б) возрастает на ]—оо; 2[
и на ]2; оо[. 467. а) Возрастает на [0; оо[; убывает на ]—со; 0]; б) воз-
растает на [1; оо[; убывает на ]—оо; 1]. 468. а) Возрастает на [0,3; оо];
убывает на ]—оо; 0,3]; б) возрастает на [1; оо[; убывает на ]—оо; 1].
469. а) Возрастает на]— оо; —3] и на [3; оо[; убывает на [—3; 3]; б) возраста-
ет на ]—оо; 0] и на [2; оо[; убывает на [0; 2]. 470. а) х = 3—точка
минимума; б) х=— 1 и х— 1 —точки максимума; х = 0 — точка минимума.
471. а) х = —3 — точка максимума; х= 3 — точка минимума; б) х=—3—
точка максимума; х=1—точка минимума. 472. а) х=1—точка мини-
мума; х = 0 — критическая точка,
функции; б) функция монотонна.
3
473. а) х = -
4
—точка минимума;
Г3 Г X
— ; оо|, убывает
б) х = 3 — точка
возрастает на
1 31
на I—оо; ~ ;
J 4 J
минимума; возрастает на [3; оо[,
убывает на ]—оо; 3]. 474. а) Фун-
кция возрастает на всей области
определения [1; оо[; б) функция
возрастает на всей области опре-
не являющаяся точкой экстремума
215
ма; возрастает на ]—оо; 0] и на
деления [0; оо[. 475. а) Функция
возрастает на всей числовой пря-
мой; б) х = 0 и х — 12 — точки
минимума, х = 6 — точка макай-
мума; функция возрастает на [12;
* оо[ и на [0; 6], убывает на ]—оо;
0] и на [6; 12]. 476. х =0 — точ-
ка минимума; возрастает на [0;
оо[, убывает на ]—оо; 0]; гра-
фик функции приведен на рисун-
ке 116. 477. х = 0 — точка мак-
симума, х — 2 — точка миниму-
[2; оо[, убывает на [0; 1[ и на ]1; 2].
478. х — 3,2 — точка максимума; возрастает на ]0; 3,2], убывает на ]—оо;
0[ и на [3,2; оо[. 479. х = — —?=. — точка
2
максимума, х = р^==— точка ми-
нимума; возрастает на]—оо;—2[, на —2;
--Д=|, наГ-L; 2[и
/з J |уз L
на ] 2;
оо[; убывает на
2 Г ] 2 '
— 0 и на 0; —~
L /3 [ 1 /3 J
487. ]—оо; оо[. 488. ]—оо; 1[J]2; оо[. 489.
486. —оо;
0. 490.
оо [. 491. [—2; I]. 495. График функции изображен на рисунке 118.
496. х = —1 — точка минимума, х = 3 — точка максимума; возрастает
на [—1; 3], убывает на ]—оо; —1] и на [3; оо[; график функции изобра-
жен на рисунке 117. 497. a) min f (х) = f(—1) = /(1) = — 16; max f (x) =
= f (0) = —9; 6) min f (x) = f (2) - — 25; max f (x) = f (3) = 0. 498. 1 сек\
7 м/сек, 499. Указание. Пусть основание треугольника равно 2а, Дока-
жите, что S2 = Л3 (2R — h), где h — высота треугольника, а 7? — ра-
диус описанного круга. Далее можно искать
максимум функции S (Л), но вычисления
проще, если воспользоваться тем, что пло-
щадь максимальна, когда ее квадрат макси-
мален, и искать максимум квадрата площади.
501. Слагаемые должны быть равными.
502. h : а = 1 : 2, где h — высота, а а —
основание бака. У казакие. Выразите пол-
ную поверхность S бака через а и V (V —
объем) и найдите минимум функции S (а)=
4V
= а2 + —. 503. В точку, удаленную на
3 км от населенного пункта и на 12 км от
ближайшей к буровой вышке точки шоссе.
504. х = 505. Провести прямую через точки
4
216
оо[, убывает на ]—со; —0,75]; б) возрастает на
/2 \
М0(х0; xg) и Л1 — х0; 01. 507. а) Возрастает на ]—оо;— 1[ и на ]—1; оо[; б) воз-
\ О /
растает на Г— —; ооГ, убывает на 1—со; —-~1. 508. а) Возрастает на [—0,75;
L з L J з j
Г1 г х 1 П
з l I з I
509. а) Возрастает на 1— со; —2] и на [1; со[, убывает на [—2; 1]; б) воз-
растает на ]—оо; —1] и на [1; оо[, убывает на [—1; 0[ и на ]0; 1]. 510. a) t =
= 0 — точка максимума; возрастает на ]—оо; 0], убывает на [0; оо[; б) воз-
растает на [1; оо[, убывает на ]—со; —1]; экстремумов нет; в) х = 0 — точка
максимума; возрастает на [—|г|; 0], убывает на [0; |г|]. 517. ]—— ; 1[.
3
518. 0. 519. {1}. 520. ]—оо; —10[|J]2; оо[. 521. х = 0 — точка максимума,
4 г 4 Г
х = — — точка минимума; возрастает на ]—оо; 0[ и на — ; оо , убывает
У I ч/
г 41 11
на 0; — I. 522. х = 0 — точка максимума, х = и х = — —г— — точки
1 1
^=; 0 |и на
минимума; возрастает на
г 1 Г 1
1 у-==; со!; убывает на —оо;
1 '
У2~.
Г 1
и на 0; —т-
. 523. График функции изображен на рисунке 119. 524. Функция
монотонно возрастает. 525. a) gmax = g (0) = 3; gmin = g (— 1) = — Г,
6) gm ах = ё (3) — 3; gmin ~ ё (2) !• 526. a) Amjn ~ h ( 1) — 10;
Ашах = А (0) ~ 2; б) Amin ~ А (2) = 10; Атах = А (3) = 2. 527. Сторона,
лежащая на диаметре, в 2 раза
529. Квадрат со стороной
4
12=
8 =
-0,5.
530. Равносторонний. 531.
=64-6. 532. 10= 5 4- 5. 533.
= 4 4- 4. 534. 4 см. 535. -
536. К точке отрезка АВ, удален-
ной от В на 1 км. 537.
— 4/
м/сек. 538. . =
у 25 —4/2
— 100
, —==, м сек2. 539.
/(25 — 4/2)?
5х г/см; 2) 0 г/см;
|V|=1,5
м/сек;
1) 360 г;
60 г/см.
541. 1,5 об/сек. 542. а) 45 м;
б) 4 сек; 90 м. 543. 0,04л см2!сек.
544. 7,5 м/мин. 545. Квадрат.
больше другой стороны. 528. 1 : у 2.
217
Глава VI
546. 45°; 45°; 90°; —; — ; —. 547. 50°; 90°; 100°; 120°; — ; —; — ; — .
4 4 2 18 2 9 3
548. Юл рад!сек; 549. 2л рад!ч и 120л рад/ч. 550. а) 0,4363; б) 0,8831; в) 2,3911;
г) 4,1364. 551. а) 27°48'21"; б) 21°31'22"; в) 75°53'39"; г) 180°. 552. 11°15'; —«
16
ж 0,1964. 555. Например: а) 485°; б) —40°; в) —135°; г) —5л. 556. Нет; цент-
ральная симметрия. 557. а) 40° + 360°л; л (Z; б) —20° + 360°л, п Е Z;
в) -77 -Ь 2лл, n £ Z; г) — -у- +2ли, п Е Z; д) 2лл, п Е Z; е) 1 + 2лл, л Е -27;
6 4
ж) 1,5 + 2лл, п Е Z; з) —0,8 + 2лл, n Е Z- 558. а) — — ; б) —-; в) 2,5 + л;
4 2
. . л 8 3л
r) —1 — —. 559. 2л м. 560. — см. 561. 12л м. 562. —. 563. 5.
3 л 4
564. 22,5 л см2. 565. 300 л CM2. 566. 150 4 см2. 567. 16 см. 568. 6. 570. а) — или 5
4 21 21 5 5 21<2 о/Г
— —; б) — или — — . 571. а) — или — —; б) —--или — —------ 572.—cos2 а.
5 29 29 13 13 ’ 3 3
573.
1. 574. 2. 575. sin2a. 576. 1. 577.
л
0. 578. 1; а=# — + Лл, л Е Z. 579. 1
Л ли
при а =£ — + —
л £ Z- 580. sin а — cos а при а у= — — 4~ лл, л Е Z.
4
581.
а) Да; б) нет; в) нет; г) да. 585.
JT л
2лл; —2лл; —-----------------[-2лл; л+ 2лл;
2 2
Л
nfZ. 587. —1; 0; 1; 0. 589. 0; —1; 0; 1. 590. а) — + 2лл, л £ Z; б) 2лл,
п
л л
£ Z; в) —-----|-2лл, п £ Z; г) л + 2лл, п £ Z; д) ям, п £ Z; е) — + лл,
2 2
л л
п £ Z. 591. D (sec) = (/] — — + лл;--------------------------h ял[; D (cosec) = [7]лл;
neZ 2 2 ncZ
Л
П(л + 1)[- 593. а) 2 cos a, а ля, л £ Z; б) cos2 a, a #=--------------------h лп, n £ Z.
&
1 Л
594. a) -----------; 6) 2 cos2 a при a =/= л/t, л £ Z 595. 1 при a Ф— + nn,
cos2 a 2
n £ Z. 596. —— при a =# — , n £ Z. 597. tg a-tg P при a, В , n£Z.
sin2 a 2 2
лл 12 5
598. ctg® a при a =A — , n <^Z. 613. cos a =— ; tg a--— —; ctg a —— 2,4.
Z 10 1Z
4 13 9
614. sin a =—— ; tga =— 1— ; ctga=— —. 615. sin a =— — ; cosa= —
5 3 4 41
40 4 15 8
— — ; ctg a = 4— . 616. sin a= — ; cos a —— — ;
41 s 9 17 17
7
tga =— 1— . 617. cosa=
8
= 12L;tga=—-Д=; ctga —— EJL. 618. sin a —— 1—11 ; tga = 1—-1 •,
3 VT 2 65
21’8
5 12 35 L 11 ллл . 84
ctga=^y=-. ®19- sina= — ; cosa=— ctga=—2-. 620. sina = -;
У 11 о/ of 1Z оЭ
cos a= — ; tg a — 6— . 621. cos a = — ; tg a = КЗ; ctg a = . 622. sin a=>
85 13 2 3
i/" q 1 тЛ 3
=— ; cos a = — ; ctg a =— X— . 625. а) Четная; б) нечетная; в) чст-
2 2 3
ная. 626. а) Нечетная; б) четная.
628. а) Четная; б) ни четная,
б) нечетная. 630.
627. а) Ни четная, ни нечетная;
ни нечетная. 629. а) Нечет-
а) Нечетная; б) четная. 633. sin 125°.
640. ctg 7°. 642. cos 145°. 644.
б) четная,
ная;
635. —tg 31°. 637. —sin 155°. 638. cos 106°.
ctg 75°. 646. cos 95°. 648. a) - Г+ 2/; 6) —i + 3j\ в) 2i — j; r) — i' — 2j.
2
649. а) — Г+ 1-L7; в) —7. 652. 0,5. 653. 1. 654. 1CL . 655. 1. 656. sin 75° =
2 2 ' ’ 2
= — (/6 + /Т); cos 75° = — (Кб — К2)- 657. sin 105° = v (Кб' + У2);
4 4 4
n 1 , г- г- 36 140 56
cos 105° = — (К2 — Кб). 660. — —. 661. — —. 662. — —. 663. 1.
4 v 85 221 65
627 13 —
664. —. 665. — 666. cos a. 667. sin a. 668. —КЗ sin a. 669. tg (a + 0).
725 85
670. tga tg 0. 671. tg a < ctg 0. 672. —ctg a ctg 0. 673. КЗ tg a. 678. cos
(a 4* 0) = cos2 a — sin2 a; cos (a — 0) = 1. 679. 2 4* КЗ; 2 — K^
l/'oT a 7 25 t—
680. -L_£l—£_. 681. —0,75. 682. 11- ; —. 683. а) 1; 6) V3. 685. sin 2a=0,96;
K7+3K3 8 92
3 120 119
cos 2a = 0,28; tg 2a = 3— . 686. sin 2a = — — ; cos 2a = — — ;
7 169 169
tg2a==I719‘ 689- Kf- 69°- 2 cos 2a. 691. 1. 692. 1 + sin 4a.
694.K3cos 20°.695. sin20°. 696. 2cos35°cosl5°. 697. 2sin5°sin20°.698. 2sinl5°cos5°.
699. —2sin 12,5°sin 37,5°. 700. K2 cos (a — 45°). 701. 2 sin ” + ~ 90 - x
a —0 + 90° a 4* 0 a — 0
X cos ---------. 702. tg-—ctg-y^. 703. tg(a—45°). 712. Нет. 713. Нет.
1 я 2
715. Да. 716.----. 717. 13. 720. 0 при х —- + лга, п 6 Z. 721. --------. 722.
cos х 2 |sin a|
я 71
cos 20. 723. tg a при 0 =/= — 4~ ЯП, n £ Z. 728. tg (a 4- 0)= — —; tg (a—0)=
Z
1 _ 43 л
= — 77J ctg (a+ 0) = — —; ctg (a—0) = — 83. 731. 1 при x * — — +nn, n € Z.
oo /1 4
я
732. cos 4a. 733. cos x. 734. tg x при x — — + an, n C Z. 738. sin (x 4- y)X
. , v sin (a 4-0) sin (a — 0) . x 5x 5x
X -sill (x — y). 739.-----------------—------------ 740. 4cos— cos x cos — . 741. 4 sin —X
cos2 a cos2 0 2 2 2
219
х 2а 4- л 2а— л „ 2а— л / „
X cos х cos —. 742. 2 sin--------cos------— =2 cos2 ------. 743. 2 sin I 30 —
2 4 4 4 \
a \ I a \ 4а4- л 4a— л
— T I cos 130°H-----I . 744. 2 sin ------ cos ---------. 745. 2 sin 5 cos 40 .
2 / \ 2 ) 8 8
746. sin (60°+a)sin(60°-a). 747. sin (a+30°) sin(a-30°). 748. sin(30°-a)sin (304
. , . 4 sin (60°+c:> sin (60°—a)
+ a). 749. sin (a — 60°) sin (a + 60°). 750. -----1---1-------------
cos2 a
(a \ / a \
— -f-150) cos I——15°).
2 / \ 2 /
ОБОЗНАЧЕНИЯ,
ВСТРЕЧАЮЩИЕСЯ
В УЧЕБНОМ ПОСОБИИ
/V Z — множество всех натуральных чисел — множество всех целых чисел
— множество всех неотрицательных целых чисел
Q — множество всех рациональных чисел
R — множество всех действительных чисел, числовая прямая
R- — числовая плоскость, множество пар (х, у), х Е /?, у С Л
1а; 6] — замкнутый промежуток (отрезок) с началом а и концом bt a <b, b —а —длина этого промежутка (отрезка)
]а; ft[ — открытый промежуток (интервал) с началом а и концом Ь, a <Zb, b —а —длина этого интервала
]j; ft], [а; ft] ]а; + оо], [а; + со], 1 — о°; ft], — полуоткрытые промежутки с началом а и концом Ь, а <ЬУ b —а —длина этого промежутка
] — оо; ft] — бесконечные промежутки, лучи числовой прямой
j — оо; -j- ос — бесконечный промежуток, числовая прямая
=> — знак следования
— знак равносильности
€ — знак принадлежности
п С N — число п принадлежит множеству натуральных чисел
GZ — знак включения множеств
С <= D — множество С включено в множество D, или множество С
есть подмножество множества D, или множество D содер- жит множество С
и — знак объединения множеств
с U D — объединение множеств С и D
{а; — множество, состоящее из элементов а, 6,
(а; ft) — упорядоченная пара
(а; ft; с) — упорядоченная тройка
Если а, Ь, с попарно различные, (а; Ь)(а\ Ь: с) обозначают также упорядоченные множества
nl — п факториал — произведение первых п натуральных чисел
Рп — число перестановок из п элементов
Атп — число размещений из п по т
гт — число сочетаний из п по т
[Л В] — отрезок прямой с концами Ли В
(АВ) — прямая, проходящая через точки А и В
!ЛД| — длина отрезка АВ
АВ — вектор с началом в точке А и концом в точке В
Ы — целая часть числа х
221
{X}
И
(Яд)» (ад).
(/д)
11охл
д-»ео
«1 + ха 4-
— дробная часть числа х
— модуль (абсолютная величина) числа х
— бесконечная последовательность
= а — число а является пределом последовательности (хп)
+ Х„ 4- ... — числовой ряд
f (*) — значение функции f в точке х
D (f) — область определения функции f
E(f) — множество значений функции f
fog — композиция функции f и g, т. е. сложная функция, состав-
ленная из функций f и g. Если h = f о gt то h (х) = f (g (х))
A x — приращение аргумента х
A f (*0), A f — приращение функции f в точке х0
lim l(x) = b — число b является пределом функции f при х, стремящемся к а
f'(x0) — производная функции f в точке х0
ЛАОВ — угол АОВ
AOB — величина угла АОВ
— поворот плоскости (луча, вектора) на угол а вокруг точки О.
Если О — начало координат, то просто: Ra
Андрей Николаевич. Колмогоров,
Борис Ефимович Вейц,
Иван Тимофеевич Демидов |
Олег Сергеевич Ивашев-Мусатов,
Семен Исаакович ШварцБурд
АЛГЕБРА
И НАЧАЛА
АНАЛИЗА
Учебное пособие
для 9 класса
Спец, редакторы
Б. М. Ивлев,
А. Д. Кутасов
Редактор
Г. С. Уманский
Художник переплета
Б. Л. Николаев
Художественный редактор
Е. Н. Карасик
Технический редактор
В. Ф. Коскина
Корректоры
К- А. Иванова,
Г. С. Попкова
Сдано в набор 21/ХП 1974 г. Подписано к печати
11/111 1975 г. 60X90l/i« Бумага тип* № 3. Печ.
л. 14,0. Уч.-изд. л. 12,38. Тираж 3900 тыс» экз.
Заказ № 243.
Ордена Трудового Красного Знамени из-
дательство «Просвещение» Государственного
комитета Совета Министров РСФСР по делам
издательств, полиграфии и книжной торговли
Москва, З’й проезд Марьиной рощи, 41.
Саратовский ордена Трудового Красного'
Знамени полиграфический комбинат Росглав-
полиграфпрома Государственного комитета
Совета Министров РСФСР по делам изда-
тельств, полиграфии и книжной торговли.
Саратов ул. Чернышевского, 59,
Цена 24 коп.