Jean DIEUDONNÉ
ELEMENTS D'ANALYSE
Tome IX
TOPOLOGIE ALGÉBRIQUE
TOPOLOGIE DIFFÉRENTIELLE ÉLÉMENTAIRE
ÉDITIONS
JACQUES GABAY

ÉLÉMENTS D'ANALYSE
TOME IX

Extrait du catalogue
Emil ARTIN
René BAIRE
René BAIRE
Stefan BANACH
Emile BOREL
Emile BOREL
Jean DIEUDONNÉ
Jean DIEUDONNÉ
Jacques DIXMIER
Jacques DIXMIER
Jacques DIXMIER
Pierre DUGAC
Maurice FRÉCHET
Claude GEORGE
Edouard GOURSAT
A. G. GREENHILL
G.-H. HALPHEN
G.-H. HALPHEN
G. H. HARDY
Charles HERMITE
Charles HERMITE
Charles HERMITE
& T. J. STIELTJES
David HILBERT
Camille JORDAN
C. KURATOWSKI
Charles-Jean de
LA VALLÉE POUSSIN
Charles-Jean de
LA VALLÉE POUSSIN
Henri LEBESGUE
Ernst LINDELÔF
Saunders MacLANE
& Garrett BIRKHOFF
Emile PICARD
Frédéric RIESZ
& Béla SZ.-NAGY
Georges VALIRON
Algèbre géométrique
Leçons sur les fonctions discontinues
Théorie des nombres irrationnels, des limites et de la continuité
Théorie des opérations linéaires
Leçons sur la théorie des fonctions
Leçons sur les séries divergentes
Éléments d'Analyse (9 tomes)
Panorama des mathématiques pures. Le choix bourbachique
Les algèbres d'opérateurs dans l'espace hilbertien (Algèbres de von Neumann)
Les C*-algèbres et leurs représentations
Algèbres enveloppantes
Jean Dieudonné, mathématicien complet
Les espaces abstraits
Exercices et problèmes d'intégration
Cours d'Analyse mathématique (3 tomes)
Les fonctions elliptiques et leurs applications
Traité des fonctions elliptiques et de leurs applications (3 tomes)
Œuvres (4 tomes)
Divergent Séries
Cours d'Analyse de l'École Polytechnique
Œuvres (4 tomes)
Correspondance d'Hermite et de Stieltjes
Théorie des corps de nombres algébriques
Cours d'Analyse de l'École Polytechnique (3 tomes)
Topologie I et II
Cours d'Analyse infinitésimale (2 tomes)
Intégrales de Lebesgue. Fonctions d'ensemble. Classes de Baire
Leçons sur l'intégration et la recherche des fonctions primitives
Le calcul des résidus et ses applications à la théorie des fonctions
Algèbre + Solutions développées des exercices
Traité d'Analyse (3 tomes)
Leçons d'Analyse fonctionnelle
Cours d'Analyse mathématique : Équations fonctionnelles. Applications

Jean DIEUDONNÉ
ELEMENTS D'ANALYSE
Tome IX
TOPOLOGIE ALGÉBRIQUE
TOPOLOGIE DIFFÉRENTIELLE ÉLÉMENTAIRE
ÉDITIONS
JACQUES GABAY

© Bordas, 1982
Réimpression autorisée du Tome IX, publié par Gauthier-Villars.
© 2003, 2006 (2e tirage), Éditions Jacques Gabay
Tous droits réservés. Aucun extrait de ce livre ne peut être adapté, traduit ou reproduit, sous
quelque forme ou quelque procédé que ce soit, sans le consentement préalable de l'Éditeur.
ISBN 2-87647-219-8

CAHIERS SCIENTIFIQUES
PUBLIÉS SOUS LA DIRECTION DE M. GASTON JULIA
FASCICULE XLII
ÉLÉMENTS D'ANALYSE
Tome IX
Chapitre XXIV
J. DIEUDONNÉ
Membre de 1 Institut
Ouvrage publié avec le concours du C. N. R. S.
gMilhlfrrYnte

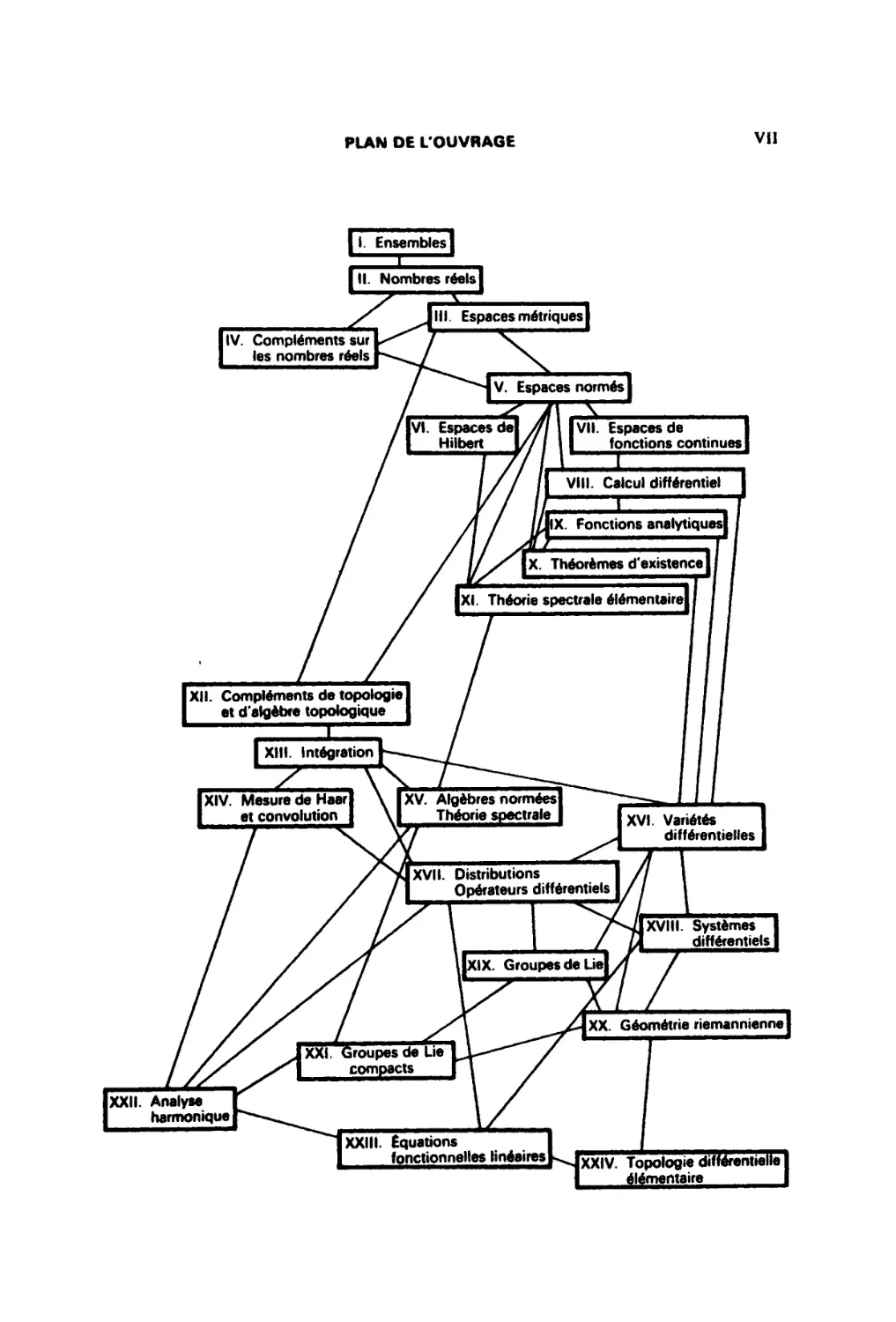
PLAN DE L'OUVRAGE
VII
11. Ensembles I
I II. Nombres réels j
I , A I
IV. Compléments sur
les nombres réels
Espaces métriques |
S À
VI. Espaces del m
Hilbert 1/7 /
VII. Espaces de
fonctions continues
1
VIII. Calcul différentiel
||X. Fonctions analytiquesj
XII. Compléments de topologie
et d'algèbre topologique
XIV. Mesure de Haar
et convolution
Théorèmes d'existence
XI. Théorie spectrale élémentaire
I XIII. Intégration I
XV. Algèbres normées
Théorie spectrale
XVI Variétés
différentielles
XVII. Distributions
Opérateurs différentiels
JXIX. Groupes de Lie]
XVIII. Systèmes
différentiels
IXX. Géométrie riemanniennel
XXI. Groupes de Lie
compacts
XXII. Analyse
harmonique
XXIII. Equations
fonctionnelles linéaires!
1XXIV. Topologie différentielle I
élémentaire I

TABLE DES MATIÈRES
Plan de l'ouvrage ix
Notations xi
Chapitre XXIV
Topologie algébrique
et topologie différentielle élémentaires
Table de résultats sur l'homologie d'espaces particuliers 3
1. Cohomologie et cohomologie à supports compacts d'une variété différentielle. S
2. La formule d'homotopie 10
3. Les suites de Mayer-Vietoris 14
4. Cohomologie des sphères 18
5. Le théorème de Kûnneth 20
6. La dualité de Poincaré 30
7. Cohomologie d'une sous-variété compacte 39
8. Les théorèmes de Brouwer 44
9. Degré d'une application 48
10. Homologie des courants 60
11. Homologie des courants sur une variété orientée 63
12. Régularisation des courants 64
13. L'anneau d'intersection 76
14. La formule de Stokes 88
15. Applications : I. Nombre de racines d'une équation 100
16. Applications: II. Intersections de courbes algébriques sur une surface
algébrique 105
17. Homologie des courants cellulaires 116
18. Subdivisions cellulaires et simpliciales 118
19. Bords des courants simpliciaux 127
20. Chaînes simpliciales formelles et homologie singulière 128
21. Lemmes de subdivision 133
22. Propriétés de l'homologie singulière 138
23. Les théorèmes de de Rham : I. Courants associés à une subdivision simpli-
ciale 154
24. Les théorèmes de de Rham : II. Approximation d'un courant par les
courants d'une subdivision simpliciale 159
25. Les théorèmes de de Rham : III. Prolongement de p-formes 163
26. Les théorèmes de de Rham : IV. Fin de la démonstration 166
27. Structure des modules d'homologie 170
28. Homologie des complexes simpliciaux euclidiens compacts 174

X TABLE DES MATIÈRES
29. La cohomologie singulière 184
30. Structure des groupes de cohomologie 188
31. L'anneau de cohomologie singulière 192
32. Cohomologie singulière des complexes simpliciaux euclidiens compacts . 195
33. Cohomologie singulière d'une variété différentielle 196
34. La cohomologie singulière à supports compacts 210
35. Homologie et cohomologie singulière relatives 211
36. Cohomologie relative et cohomologie à supports compacts 220
37. Excision et suites de Mayer-Vietoris relatives 227
38. Cohomologie des produits de variétés et des espaces fibres 240
39. Suite de Gysin et classe d'Euler 248
40. Cohomologie des grassmanniennes 266
41. Classes de Chern 277
42. Propriétés des classes de Chern 281
43. Classes de Pontrjagin 291
44. Compléments sur les formes différentielles vectorielles et les connexions
principales 295
45. L'homomorphisme de Weil 298
46. Courbure et classes caractéristiques 304
47. Classes de Stiefel-Whitney 313
48. La théorie de Hodge 317
49. La formule d'Atiyah-Bott-Lefschetz 322
50. Applications : I. La formule de Hopf pour les champs de vecteurs ... 331
51. Applications: II. Formules de Bott pour les classes caractéristiques 333
52. Cohomologie des groupes de Lie 341
53. Éléments primitifs 346
Annexe : Compléments d'algèbre (suite) 354
Bibliographie 369
Index 377

NOTATIONS
^p,r(X), ^p,c(X), <fp(X) espace vectoriel des p-formes différentielles de
classe C°° sur une variété X : 24.1.
®p.«(X), 9>p,éX), ®p(X) espace vectoriel des p-formes différentielles de
classe C°° à support compact : 24.1.
^H(X), j^c(X), <g/"(X) algèbre différentielle somme directe des &P{X) : 24.1.
<*iR(X), j^'.cW, j<(X) algèbre différentielle somme directe des S^X): 24.1.
ZP(X), Z'(X) espaces des cocycles (formes fermées) de s/'(X) : 24.1.
BP(X), B"(X) espaces des cobords (formes exactes) de sf'(X) : 24.1.
HP(X), H'(X), HP(X;R) espaces de cohomologie, algèbre de cohomologie
HP(X; C), H'(X; R), H'(X; C) de X : 24.1.
deg a degré d'un élément homogène de H*(X) : 24.1.
a ~ b cup-produit dans H'(X) : 24.1.
bp p-ème nombre de Betti : 24.1.
PX(T) polynôme de Poincaré : 24.1.
X[X) caractéristique d'Euler-Poincaré : 24.1.
Zf(X), Z^X) espaces des cocycles de st'c{X) : 24.1.
B?(X), BXX) espaces des cobords de j<(X) : 24.1.
H£(X), H&X) espaces de cohomologie à supports compacts, algèbre
de cohomologie à supports compacts : 24.1.
E S F espaces vectoriels isomorphes : 24.1.
u*, Hp(m), u* homomorphismes en cohomologie déduits d'une
application u de classe C°° : 24.1.
s/'+(X), s/i(X), H'+(X), H'_(X) sous-espaces invariants par permutation des
deux feuillets d'un revêtement X : 24.1.
lim M„ Jim u„ limites inductives de modules et d'homomorphismes :
24.1, prob. 2.
h
asds intégrale d'une famille lisse de sections : 24.2.
f
Ju
homomorphisme en cohomologie déduit d'une
application continue u d'une variété compacte dans une
variété compacte : 24.2.
homomorphisme de s/\X) *® st'ÇY) dans s/\X x Y) :
24.5.

NOTATIONS
homomorphisme de s/'fiC) g(g> s/j(Y) dans s/'fii x Y) :
24.5.
homomorphisme (de Kùnneth) de H'C(X)g® H^(Y)
dans H^X x Y) : 24.5.
application diagonale x -* (x, x) : 24.5.
p
n-forme différentielle sur Y à valeurs dans /\ (T^X)*)
déduite d'une (p + n)-forme différentielle scalaire co
sur X x Y : 24.5.
intégrale partielle suivant Y d'une (p + n)-forme
différentielle scalaire co sur X x Y : 24.5.
application canonique de HP+"(X x Y) dans Hf(X) :
24.5.
forme bilinéaire canonique sur HP(X) x HJ-P(X) :
24.6.
application de Poincaré de HP(X) dans (HJT'W)* :
24.6.
application canonique H"(X) -> R, classe
fondamentale de cohomologie pour une variété compacte
connexe orientée X de dimension n : 24.6.
signature d'une variété compacte pure orientée : 24.6.
classe de Lefschetz dans H"(X x X) pour une variété
compacte pure orientée X de dimension n : 24.6.
degré d'une application continue /: X -» Y pour
des variétés compactes connexes orientées X, Y
de même dimension : 24.9.
nombre d'entrelacement de deux variétés compactes,
connexes et orientées de R" : 24.9.
espace vectoriel des p-courants de support compact
sur une variété X : 24.10.
somme directe des <?P(X) : 24.10.
espace des cycles de s/'.(X) : 24.10.
espace des bords de s/'.(X) : 24.10.
espaces d'homologie des courants sur X : 24.10.
homomorphisme en homologie des courants déduit
d'une application u de classe C°° : 24.10.
application canonique de H"~P(X) dans H^(X) pour
une variété pure orientée X de dimension n : 24.11.
application canonique de HP(X) dans (HJ^X))* pour
une variété pure orientée X : 24.12.
classe fondamentale d'homologie des courants d'une
variété pure compacte orientée X : 24.12.

NOTATIONS
XIII
produit d'intersection de deux courants : 24.13.
support singulier d'un courant : 24.13.
nombre d'intersection de deux courants de
dimensions complémentaires : 24.13.
intégrale d'une (n — l)-forme ( sur la frontière
régulière d'un ouvert : 24.14.
degré en un point isolé a d'une application / : X -» Y
de classe Cœ, X et Y ayant même dimension : 24.14,
prob. 10.
courant d'intégration le long d'une courbe
algébrique r sur une surface algébrique lisse : 24.16.
classe d'homologie du courant Ir : 24.16.
nombre d'intersection de deux courbes algébriques r\,
T2, ou d'une courbe algébrique T avec elle-même :
24.16.
courant sur X défini par une application s : U -» X
de classe C00, où U est un polyèdre ouvert convexe
relativement compact : 24.17.
sous-espace de S'fii) engendré par les courants
cellulaires : 24.17.
somme directe des <?P(X) : 24.17.
espace des cycles de s/"(X) : 24.17.
espace des bords de sf"(X) : 24.17.
espace d'homologie des courants cellulaires sur X :
24.17.
simplexe standard de dimension n : 24.18.
application linéaire affine de A„ dans un RN : 24.18.
simplexe géométrique de dimension n : 24.18.
première subdivision barycentrique : 24.18.
fc-ième subdivision barycentrique : 24.18.
application linéaire affine (e0 ... ei-, ... ep) de Ap_j
sur la face ¥} de Ap : 24.19.
application s ° Oj : Âp_! -» X : 24.19.
ensemble des simplexes singuliers de dimension p
dans X : 24.20.
A-module de base <tf(Âp; X) : 24.20.
somme directe des SP(X; A) : 24.20.
application A-linéaire de S.(X ; A) dans S.(Y ; A)
définie par une application continue / : X Y :
24.20.

XIV
NOTATIONS
<?(AP; X) ensemble des simplexes singuliers lisses de
dimension p : 24.20.
S^X ; A) A-module de base <?(ÂP ; X) : 24.20.
60 bord (formel) dans S.(X ; A) : 24.20.
ZpiX; A), Z.(X; A) module des cycles dans S.(X; A) : 24.20.
BP(X; A), B.(X ; A) module des bords dans S.(X ; A) : 24.20.
HP(X ; A), H.(X ; A) module d'homologie singulière de X à coefficients
dans A : 24.20.
/*, H.(/) application A-linéaire de H.(X; A) dans H.(Y; A)
correspondant à une application continue/: X -+ Y:
24.20.
ZP°(X; A) module des cycles lisses dans Sp°(X; A) : 24.20.
Bp°(X; A) module des bords lisses dans Sp°(X; A) : 24.20.
HP°(X; A) module d'homologie singulière lisse de X : 24.20.
Cc application « cône de sommet c » : 24.21.
Sd(2), Sdm(z) subdivisions barycentriques d'une chaîne : 24.21.
^(Kp ; X) ensemble des simplexes singuliers de dimension p et
de support contenu dans un ensemble du
recouvrement U : 24.22.
S^(X;A), ZUP{X;A), B^(X;A), H^(X;A) A-module de base tfu(Âp;X), ses
modules de cycles, bords et d'homologie : 24.22.
/•£ application canonique HP(X ; A) -+ Hp(X ; A) :
24.22.
HP(X; A), HP(X; A) sous-modules de Hp(X; A) invariants par
permutation des deux feuillets d'un revêtement X : 24.22.
Lp(<3 ; A) module des ^-chaînes d'une subdivision simpliciale S :
24.24.
St(v) réunion des simplexes d'une subdivision dont v est
un sommet : 24.24.
dim (X) dimension topologique d'un espace séparé X : 24.24,
prob. 6.
Lp(6) espace des /7-courants d'une subdivision ® : 24.25.
s,- courants définis par les simplexes Uf de dimension p
de la subdivision ® : 24.25.
SPCS) ensemble des p-formes différentielles sur X dont le
support ne rencontre aucun simplexe de S de
dimension < p : 24.25.
Lp(® ; A), Lp(® ; A) sous-modules libres supplémentaires dans L^S ; A) :
24.26
L.(S ; A), L!(<5 ; A) somme directe des L/S ; A) (resp. des L^S ; A)) :
24.28.

NOTATIONS
XV
c„ classe fondamentale d'homologie singulière de S„ :
24.28.
SP(X ; G), S'(X ; G) groupes de cochaînes singulières sur X à valeurs
dans G : 24.29.
d0 cobord dans S'(X ; G) : 24.29.
ZP(X ; G), Z"(X ; G) groupe des cocycles de S'(X ; G) : 24.29.
BP(X ; G), B*(X; G) groupe des cobords de S*(X; G) : 24.29.
HP(X ; G), H'(X ; G) groupe de cohomologie singulière de X à coefficients
dans G : 24.29.
Sp(u), Hp(u), u* applications déduites d'une application continue u :
X -» Y : 24.29.
f g, a ~ b cup-produit de cocycles, de classes de cohomologie
singulière : 24.31, 24.35 et 24.37.
c* classe fondamentale de cohomologie singulière de S„ :
24.32.
HDR(X) autre notation pour H'(X) défini en 24.1 : 24.33.
Sp(X ; G), Zf(X ; G), BP(X ; G), HP(X ; G) groupes de cochaînes, cocycles,
cobords et cohomologie singulière à supports
compacts : 24.34.
SpfX.Y; A), S.(X,Y; A) modules quotients S„(X; A)/Sp(Y; A) et
S.(X; A)/S.(Y; A): 24.35
60 bord dans S.(X, Y ; A) : 24.35.
ZP(X, Y ; A), Z.(X, Y ; A) modules de cycles relatifs modulo Y : 24.35.
Bp(X, Y ; A), B.(X, Y ; A) modules de bords relatifs modulo Y : 24.35.
Hp(X, Y; A), H.(X, Y; A) modules d'homologie relative modulo Y : 24.35.
r application canonique Hp(X ; A) -» H^X, Y ; A) :
24.35.
Sp(u), Hp(u), u+ applications canoniques déduites d'une application
continue h : X -» X' telle que w(Y) <= Y' : 24.35.
SP(X, Y; A), S'(X, Y; A) modules de cochaînes relatives modulo Y : 24.3.
ZP(X, Y; A), Z'(X, Y; A) modules de cocycles relatifs modulo Y : 24.35.
Bp(X, Y ; A), B'(X, Y ; A) modules de cobords relatifs modulo Y : 24.35.
HP(X,Y;A), H'(X, Y; A) modules de cohomologie relative de X modulo Y :
24.35.
Hp(u), m* application HP(X', Y' ; A) -* HP(X, Y ; A) déduite
d'une application continue u : X -» X' telle que
«(Y) c Y' : 24.35.
a application canonique HP(X, Y ; A) -♦ HP(X ; A) :
24.35.
°* classe fondamentale de cohomologie de R" modulo
R" - {0} : 24.35.

XVI
NOTATIONS
z^f, c ~u cap-produit d'une chaîne z (resp. d'une classe
d'homologie c) et d'une cochaine / (resp. d'une classe de
cohomologie u) : 24.35, prob. 5.
2X double de l'adhérence d'un ouvert à frontière
régulière : 24.35, prob. 6.
HP(X, Y ; A) module de cohomologie de Cech : 24.37, prob. 18.
catx (Y), cat (X) catégorie de Lusternik-Schnirelmann : 24.37, prob. 23.
ej(£), eJ[E) classe de cohomologie dans HN(B ; A) correspondant
à une classe u de A-orientation pour une fibra-
tion £ = (E, B, n) où E est un fibre vectoriel réel
de rang N : 24.39.
e(Ç), e(E) classe d'Euler d'une fibration orientée £ = (E, B, n) :
24.39.
e2(^), e2(E) classe d'Euler modulo 2 : 24.39.
U,,iP(C) fibre vectoriel canonique sur GB>P(C) : 24.40.
r1 sous-espace de C orthogonal à «6G»iP(Q : 24.40.
UÏJQ fibre des (v, x) où x * 0 est dans i>A : 24.40.
(UBjP(C))o, (UAjP(C))o complémentaires de la section nulle : 24.40.
cf« générateurs de H'(GP+,>P(C);Z) : 24.40.
U„(RX Ui^R), (UA.,(R))0, (U^RJX, fibres sur G.JR) : 24.40.
wp« générateurs de H'(GP+,>P(R) ; F2) : 24.40.
Ê fibre vectoriel de rang N — 1 et de base E0,
complémentaire de la section nulle dans un fibre vectoriel E
de rang N : 24.41.
e(E) classe d'Euler du fibre réel sous-jacent à un fibre
vectoriel complexe E, pour l'orientation canonique :
24.41.
Cj(E), c(E) classes de Chern, classe totale de Chern d'un fibre
vectoriel complexe E : 24.41.
Vt, O espace vectoriel complexe conjugué d'un espace
vectoriel complexe V, sa loi de multiplication par un
scalaire : 24.42.
E1 fibre vectoriel complexe conjugué d'un fibre
vectoriel complexe E : 24.42.
Pj(E), p{E) classes de Pontrjagin, classe totale de Pontrjagin
d'un fibre vectoriel réel E : 24.43.
<fm(M; W) espace des m-formes différentielles vectorielles de
classe C00 sur M, à valeur dans W : 24.44.
<D application de <?m,(M ; x ... x ^mii(M ; Vh) dans
4n1+m2+...+m,.(M î v) déduite d'une application
/j-linéaire O de V, x ... x Vt dans V : 24.44.

NOTATIONS
XVII
FB(J1) 2p-forme différentielle fermée sur B déduite d'une
connexion principale sur un fibre principal X de
base B et de groupe G, et d'une forme p-linéaire F
sur gp invariante par G : 24.45.
Cf(X) classe de cohomologie de F^il) dans H2p(B; R) :
24.45.
I(G) algèbre des formes multilinéaires sur ge invariantes
par G : 24.45.
w/E), w(E) classes de Stiefel-Whitney, classe totale de Stiefel-
Whitney d'un fibre vectoriel réel E : 24.47.
A,- opérateurs de Laplace-Hodge dans un complexe
elliptique : 24.48.
L40, Mjjp = Li° n Ker db Nj? = Lj? n Ker i sous-espaces de la
décomposition canonique de T^Ej) : 24.48.
Ai" valeurs propres > 0 et distinctes de A( : 24.48.
H{n valeurs propres de A( comptées avec leur ordre de
multiplicité : 24.48.
HJ(X) espace des y-formes harmoniques complexes sur la
variété riemannienne X : 24.48.
L((y,)) nombre de Lefschetz d'un endomorphisme
géométrique (jj) d'un complexe elliptique (E(, d,) : 24.49.
Fix (/) ensemble des points fixes de / : X -* X : 24.49.
j(a) indice d'un champ de vecteurs en un point critique
a non dégénéré : 24.50.
Ax, Ax champ de tenseurs de Tj(M) et application de R(M)
dans End (R") associés à un champ de vecteurs X
sur M et à une connexion linéaire C sur M : 24.51.
Fjlftlï) 2(p - réforme différentielle sur une variété
riemannienne compacte orientée M de dimension n,
associée à une application p-linéaire symétrique F
de (so{ri)f dans R : 24.51.
(ZpiM) espace vectoriel des p-formes différentielles de
classe C00 sur M invariantes par l'action du
groupe G : 24.52.
pn projecteur canonique de <?p(M) sur ^(M) : 24.52.
j&q(M), H^(M) somme directe des «^(M) et sa cohomologie : 24.52.
pjfc homomorphisme canonique H*(M) -» HG(M) :24.52.
H+(G) idéal de H'(G), somme directe des HP(G) pour p > 1 :
24.53.
b*(G) sous-algèbre graduée de A 8* constituée par les
formes différentielles biinvariantes : 24.53.
b* sous-algèbre de A 9? isomorphe à b*(G) : 24.53.

XVIII NOTATIONS
FlE0 produit d'une famille de A-modules : Ann. 27.1.
a
E ®A F, E ® F produit tensoriel d'un A-module libre E et d'un
A-module F : Ann. 28.1.
u®v produit tensoriel de deux applications linéaires :
Ann. 28.3.
Z"(E), B"(E), H"(E) modules des cocycles, des cobords, de cohomologie
d'un module différentiel gradué E : Ann. 30.2.
H"(u), u*, H'(u) homomorphisme déduit d'un homomorphisme u de
modules différentiels gradués par passage à la
cohomologie : Ann. 30.3.
ZJ(E), B„(E), H„(E) modules des cycles, des bords et d'homologie d'un
module codifférentiel gradué : Ann. 30.7.
H„(u), u„, H.(u) homomorphisme déduit d'un homomorphisme u de
modules codifférentiels gradués par passage à
l'homologie : Ann. 30.7.
E *<g) F produit tensoriel gauche d'algèbres graduées anti-
commutatives : Ann. 30.9.
Pf (U) pfaffiien d'une matrice alternée U : Ann. 33.1.
rg (E) rang d'un Z-module de type fini : Ann. 34.1.

CHAPITRE XXIV
TOPOLOGIE ALGÉBRIQUE
ET TOPOLOGIE DIFFÉRENTIELLE
ÉLÉMENTAIRES
Le développement de la Topologie algébrique et de la Topologie
différentielle, et les applications de plus en plus fécondes de ces deux théories dans
les questions les plus diverses, sont sans doute les contributions les plus
importantes du xxc siècle aux mathématiques. Le jaillissement ininterrompu de
nouvelles idées depuis 50 ans y est tel qu'il est encore impossible à l'heure actuelle
de concevoir un traité qui couvrirait tous les aspects de ces théories
(nécessairement en une suite de nombreux volumes), et qui ne risquerait pas d'être périmé
au lendemain de sa parution C"). C'est dire que le présent chapitre ne peut
qu'apparaître dérisoire aux yeux des spécialistes ; son but, beaucoup plus modeste, est
d'initier les analystes aux aspects les plus simples de cet immense édifice
topologique, en cherchant à rester aussi proche que possible de l'esprit de l'Analyse,
conformément au plan de ce Traité.
Le caractère élémentaire des matières traitées apparaît dans les
observations suivantes :
1° On s'est graduellement aperçu que la notion fondamentale, en Topologie
algébrique, est celle d'homotopie ; or, il n'en est pratiquement pas question dans
ce chapitre, qui est centré sur la notion, moins importante mais plus accessible,
d'homologie (ou cohomologie).
2° L'étude des outils les plus puissants de la théorie homologique
(puissances de Steenrod, cohomologie des faisceaux, suites spectrales) n'est pas
abordée ; en dehors de l'Algèbre linéaire et multilinéaire, le seul outil de l'Algèbre
homologique utilisé est la suite exacte d'homologie (Ann. 30.7).
3° Comme l'Analyse moderne est l'Analyse sur les variétés différentielles,
ce sont ces dernières et leurs sous-ensembles les plus fréquemment rencontrés
(sous-variétés et leurs complémentaires) qui sont à peu près exclusivement
étudiés, et le but principal est de calculer leur homologie (voir la liste à la fin
de cette Introduction). On a donc éliminé systématiquement toutes les
constructions d'espaces beaucoup plus généraux (espaces de lacets, limites inductives
(*) Voir la Bibliographie de ce chapitre.

2 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
d'espaces, tours de Postnikov, etc.), bien que ce soient elles qui ont permis les
progrès les plus spectaculaires, même dans les questions relatives aux seules
variétés.
Le plan du chapitre consiste à introduire graduellement et naturellement
les notions homologiques en partant des plus simples, et en décrivant au fur et à
mesure les résultats qu'elles permettent d'obtenir. Cela entraine certainement
des longueurs et des redites ; mais du moins n'est-il pas nécessaire d'absorber
150 pages sur les catégories, l'Algèbre homologique et les complexes simpliciaux,
avant de savoir calculer l'homologie des sphères.
Le point de départ est celui même de Riemann et Poincaré, l'idée de
« mesurer » d'une certaine façon le « défaut d'exactitude » des p-formes
différentielles fermées sur une variété autre que R" ; c'est ce qu'on appelle souvent
la cohomologie de de Rham (à coefficients réels). Il est remarquable que, sans
la moindre technique « combinatoire », on puisse immédiatement attacher aux
variétés compactes des invariants cohomologiques indépendants de la structure
différentielle, les calculer pour des variétés telles que Sw T" et PB(R), et obtenir
les célèbres théorèmes de Brouwer qui ont imposé la Topologie algébrique à
l'attention des mathématiciens, le tout en moins de 60 pages (sections 24.1 à 24.9).
Par la dualité canonique entre formes différentielles et courants (17.3),
on déduit aussitôt de la cohomologie de de Rham la notion d'homologie des
courants, ici encore dégagée de conceptions « combinatoires ». En outre, sur
une variété orientée, la régularisation des courants (24.12) permet, comme l'a
montré de Rham, de définir de la façon la plus naturelle l'intersection de deux
courants fermés (et même celle de certains courants non fermés) sans les pénibles
contorsions habituelles de « position générale » (24.13).
La régularisation des courants montre aussi que sur une variété orientée
la cohomologie des formes est en fait duale de l'homologie des courants à support
compact (24.12.10), ce qui est une version de la dualité de Poincaré. Mais il y a
bien d'autres courants intéressants en dehors de ceux qui sont définis par des
formes différentielles (voir par exemple [171] et [222]); ceux qui jouent le plus
grand rôle dans le développement ultérieur de l'homologie sont identifiés à
certains ouverts relativement compacts dans une variété orientée, à savoir ceux
qui ont une frontière dont tous les points sont réguliers (ou tout au moins dans
laquelle les points non réguliers sont sur une sous-variété de codimension > 2).
Cette importance tient au fait que, contrairement à ce qui se passe pour les
courants généraux, où la notion de bord n'a pas d'interprétation géométrique
intuitive, ici le bord d'un tel courant s'identifie à la frontière de l'ouvert considéré,
munie d'une orientation convenable ; c'est ce qu'exprime la formule de Stokes
(24.14.4).
La substance des célèbres théorèmes de de Rham est qu'on peut calculer
l'homologie des courants à l'aide de ces courants particuliers et de leurs images
par des applications de classe C°° (sections 24.23 à 24.26). C'est ici qu'intervient

XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFERENTIELLE ÉLÉMENTAIRES 3
pour la première fois le concept d'homologie singulière où les objets que l'on
combine linéairement en « chaînes » sont les applications continues (ou diffé-
rentiables) d'un « simplexe standard » fixe, et non leurs images, la notion de
« bord » adaptée à cette conception étant imposée par la formule de Stokes (24.20).
L'intérêt de cette manière traditionnelle d'envisager l'homologie est d'une
part qu'elle s'applique à tous les espaces séparés et non plus seulement aux
variétés différentielles; et d'autre part, même pour les variétés, elle conduit à
de nouveaux invariants topologiques qui échappent à la cohomologie des formes
différentielles, grâce à la possibilité d'introduire des « chaînes » à coefficients
entiers (ou plus généralement à coefficients dans un anneau commutatif), et
non plus seulement à coefficients réels. C'est ici naturellement qu'interviennent
les outils classiques de subdivision simpliciale (24.18 et 24.21) et
d'approximation simpliciale (24.24), mais on ne les introduit qu'au fur et à mesure, en tant
que lemmes techniques, et non pour eux-mêmes.
L'homologie singulière donne naissance à son tour à la cohomologie
singulière (sections 24.29 à 24.33), et finalement aux homologies et cohomologies
relatives (sections 24.35 à 24.37). A l'aide de ces outils, on peut alors revenir à
l'objet central du chapitre, la cohomologie des variétés, et explorer quelques-uns
de ses liens avec la théorie des connexions et celle des équations aux dérivées
partielles linéaires : classes caractéristiques et méthode de Chern-Weil
(sections 24.40 à 24.47), théorie de Hodge et formule d'Atiyah-Bott-Lefschetz
(sections 24.48 à 24.51) et enfin cohomologie des groupes de Lie (24.52 et 24.53).
Table de résultats sur Vhomologie d'espaces particuliers.
Cohomologie (de de Rham) : d'une variété rétractile, d'un fibre vectoriel : 24.2.7
d'un revêtement d'une variété : 24.1.4,24.6, prob. 1
et 24.9, prob. 31
de S„ : 24.4.1
de P„(R) : 24.4.2
de R" (à supports compacts) : 24.4.4
de T" : 24.5.5
de la bande de Môbius : 24.5, prob. 2
de la bouteille de Klein : 24.5, prob. 3
du complémentaire d'un tore dans R3 : 24.5,
prob. 4 et 24.7, prob. 2
d'une quadrique projective réelle : 24.5, prob. 7
d'une variété symplectique : 24.6, prob. 4
de X - F (X variété, F ensemble fini) : 24.7.9
d'une somme connexe : 24.7, prob. 1
de T" - T" : 24.7, prob. 4
de S„ — Er (Er homéomorphe à un cube) : 24.8.1
de S„ - Zr (2r homéomorphe à Sr) : 24.8.2

4 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
de R" - D (D ensemble dénombrable) : 24.7,
prob. 6
d'une variété de Stiefel S„jt(R) : 24.39, prob. 6
des groupes compacts SO(n), U(n, C), U(«, H) :
24.50, prob. 1
Homologie singulière : d'un espace rétractile : 24.22.3
de S„ : 24.22.9
d'un bouquet de variétés : 24.22.11
d'un attachement de boules : 24.22.12
de P2(R) : 24.22.13
de P„(C) : 24.22.14
d'un revêtement : 24.22.15
d'un espace lenticulaire : 24.22, prob. 6
de P„(H) : 24.22, prob. 7
de l'espace icosaédral : 24.22, prob. 14
d'un quotient du disque unité : 24.28, prob. 3
d'une variété de Pham : 24.28, prob. 23
d'un éclatement : 24.37, prob. 22
d'un complexe cellulaire : 24.37, prob. 28
Cohomologie singulière : des espaces sans torsion : 24.30.4
de R" (à supports compacts) : 24.36.4
de P„(R) : 24.30.8 et 24.36.5
d'une variété différentielle : 24.33
de X/A (A sous-espace fermé de X contracté en
un point) : 24.36, prob. 3
de SX (suspension de X) : 24.36, prob. 4
d'un demi-espace fermé, du complémentaire dans
un demi-espace fermé d'un ensemble fini : 24.36,
prob. 9
d'un éclatement : 24.37, prob. 22
de SJLQ et SB>ik(H) : 24.38, prob. 7
de S„,2(R) : 24.39, prob. 4
d'une quadrique projective réelle : 24.39, prob. 10
d'une quadrique projective complexe : 24.40,
prob. 4
d'une grassmannienne réelle : 24.43, prob. S
Homologie relative H.(X, X - {x} ; Z) : pour une variété différentielle X :
24.37.5
pour un complexe simplicial
euclidien X : 24.37, prob. 6

1. COHOMOLOGIE ET COHOMOLOGIE A SUPPORTS COMPACTS
5
Cohomologie relative H'(X, X-{x} ;Z): pour une variété différentielle X :
24.35.12 et 24.37.12
Anneau de cohomologie singulière : de P„(R) : 24.36, prob. 2
de P„(C) : 24.40.6
de G,+W(C) : 24.40.8
de P„(R) (à coefficients dans F2) :
24.40.12
de Gp+,iP(R) (à coefficients dans F2) :
24.40.14
de Gp+,iP(R) (à coefficients dans F2):
24.40, prob. 5
de GP+,P(R) (à coefficients dans un
corps) : 24.43, prob. 4
1. Cohomologie et cohomologie à supports compacts d'une variété différentielle.
(24.1.1) Soit X une variété différentielle pure de dimension n. Rappelons que
pour 0 ^ p < n, on note ^p,R(X) (resp. <£p>c(X)) l'espace vectoriel sur R (resp. C)
des p-formes différentielles de classe C00 sur X (resp. l'espace <fPfK(X) ® RC des
p-formes différentielles à valeurs complexes) ; on écrit aussi <^P(X) pour l'un ou
l'autre de ces espaces lorsqu'il n'y a pas de confusion à craindre. On note ^P,R(X)
(resp. ®p,c(X)) ou simplement 0p(X) le sous-espace de £p,B(X) (resp. <?p,c(X)) des
p-formes différentielles de classe C00 à support compact.
Il est clair que, pour le produit extérieur et la différentielle extérieure d
(17.15.2), les sommes directes
^«(X) = 0 *,JX), ^X) = 0 <*p,c(X)
p = 0 p= 0
sont des algèbres différentielles graduées (Ann. 30.8) sur R et C respectivement,
ayant pour élément unité la fonction constante égale à 1 (on les écrira s/\X) si
cela n'entraîne pas confusion). Les sommes directes
<i(X) = ê , <c(x) = è ®p.c(x)
p=0 p = 0
(aussi notées ^(X)) sont des sous-algèbres différentielles graduées (sans élément
unité si X n'est pas compact) et des idéaux bilatères de j/r(X) et -s*c(X)
respectivement.
On peut donc appliquer les définitions de la cohomologie des algèbres

6 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
différentielles graduées (Ann. 30.2). La sous-algèbre graduée Z'(X) des cocycles
de sf'ÇX) est égale à
n
Z'(X) = © ZP(X)
p = 0
où ZP(X) est l'espace vectoriel des p-formes a telles que du = 0 ; on dit aussi
que ces formes sont fermées. L'idéal bilatère gradué B'(X) des cobords de s/\X)
est égal à
n
B'(X) = © BP(X)
p = 0
où BP(X) pour 1 est l'espace vectoriel desp-formes dp, où /? parcourt Sp- t(X) ;
on dit que ces formes sont exactes ; pour p = 0, on pose B°(X) = {0}.
L'algèbre graduée
H'(X)= ©HP(X),
p = 0
ou
HP(X) = ZP(X)/BP(X)
est Valgèbre de cohomologie de X, HP(X) étant appelé le p-ème espace de
cohomologie de X et ses éléments étant dits de degré p ; pour a # 0 dans H'(X), deg(a)
désigne le degré de a ; on pose HP(X) = {0}si/>>nou/><0. Lorsqu'on précise
le corps des scalaires, on écrit H'(X ; R) et HP(X ; R) pour la cohomologie de
jtfHX), H'(X ; Q et HP(X ; Q pour la cohomologie de s/^X) ; on a
Hp(X ; C) = Hp(X ; R) ® ,C.
Dans la suite de ce chapitre, lorsqu'on notera H*(X) la cohomologie de X, il
s'agira toujours de H'(X ; R).
Lorsque a e HP(X), b e H«(X), on note a — b e HP+«(X) le produit de a et b
dans l'algèbre H'(X) et on dit aussi que c'est le cup-produit de a et b ; si a (resp. b)
est la classe de cohomologie de la p-forme a (resp. de la q-forme P),a-^b est la
classe de cohomologie de la (p+q)-îonae a a /S, et l'on a donc b — a=( — l)Ma ^-b.
Lorsque HP(X) est de dimension finie, cette dimension se note bp et s'appelle
le p-ème nombre de Betti de X. Si H*(X) est de dimension finie on appelle polynôme
de Poincaré de X le polynôme
PxCT) = t bpT"
p = 0
et caractéristique d'Euler-Poincaré de X l'entier
x(X)= î(-iybp = PA-n-
p = 0

1. COHOMOLOGIE ET COHOMOLOGIE A SUPPORTS COMPACTS
7
La cohomologie de sf'JiX) s'obtient de même à partir des cocycles à support
compact et des cobords de formes à supports compacts, c'est-à-dire des espaces
Zf(X) - Z"(X) n 9JX), Bf(X) = d{2p+ ,(X)) l
n
cette algèbre de cohomologie est YQX) = 0 Hf(X), où
p = 0
H'(X) = Z'(X)/Bf(X);
on dit que c'est l'algèbre de cohomologie à supports compacts de X ; on a encore
Hf(X) = {0} pour p > n et p < 0. Si X est compacte, H*(X) = H^X).
Remarques (24.1.1.1). — Comme Zf(X) c Z"(X) et Bf(X) <= B"(X), il est
immédiat que l'injection canonique Z'fii) -* Z*(X) donne, par passage aux
quotients, un homomorphisme d'algèbres H'fii) -* H'(X); il n'est en général
ni injectif ni surjectif.
D'autre part, si a e Z'(X) et P e Z^X), alors a a P e Z'£X) ; de même, si
aeZ*(X)et^6B^X),onaa a p e B^X), car si p = dy.onaa a p = ± d{a a y);
enfin, si aeB'(X) et /îeZj(X), on a a a /îeB^X) car si a=dy, on a a a /?= ±d{y a P).
On en déduit que, par passage aux quotients, l'application (a, p) -* a a P
définit sur H*(X) une structure canonique de H'(X)-module gradué.
(24.1.2) Exemples. — I) Pour toute variété différentielle connexe X, l'espace
Z°(X) est de dimension 1, car il est constitué par les fonctions / e <?(X) telles
que df = 0, ce qui entraine que / est constante (16.5.5). Comme B°(X) = {0},
on voit que l'on a H°(X) = R (*), et
H?(X) = R si X est compacte
H°(X) = {0} si X est non compacte.
II) Supposons que X soit réunion d'une famille (XA) d'ouverts non vides
deux à deux disjoints. Pour toute p-forme différentielle oc sur X, chacune des
restrictions a | Xx de a à Xx est une p-forme, et réciproquement, pour toute
famille (aj, où a.x est une p-forme sur X^ il y a une p-forme et une seule a sur X
telle que a | Xx = <xx pour tout A ; en outre, on a dot. \ Xx = daÀ. Ceci montre
que l'espace vectoriel Sp{X) s'identifie à l'espace produit \~\6p{Xx), et ses sous-
espaces Z"(X) et B^X) à nz,,(Xa) et IiB"^) respectivement ; par suite H"(X)
X X
s'identifie canoniquement à nHp(XJ. Comme un ensemble compact ne peut
x
rencontrer qu'un nombre fini d'ouverts XA, on voit de même que ^P(X) s'identifie
(*) L'écriture E s F signifie que les espaces vectoriels E et F sont isomorphes.

8 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
à l'espace somme directe 0 3lÂXk), et par suite Zf(X) à 0 Zf(X x) et BP(X) à
x x
0 WC(XX), de sorte que HP(X) s'identifie canoniquement à 0 HP(XA).
x x
(24.1.3) Soient X, Y deux variétés différentielles pures, et u : X -» Y une
application de classe Cœ. Pour tout entier p > 0, a -* '«(a) est une application linéaire
de <fp(Y) dans <?P(X) (16.20.8), et l'on a d('u(a)) = '«(da) (17.15.3), donc il y a une
application
'« : j*\Y) - jaf(X)
se réduisant à 'u dans chaque sous-espace <?p(Y), et qui est un homomorphisme
d'algèbres différentielles graduées en vertu de (16.20.9.5) (Ann. 30.8). On en
déduit canoniquement un homomorphisme d'algèbres graduées (Ann. 30.8)
u* : H'(Y) - H*(X)
(dont la restriction à HP(Y) est aussi notée Hp(u)) tel que, si a e HP(Y) est la classe
d'une p-forme différentielle fermée a, u*(a) est la classe de 'u(a) dans HP(X).
Si de plus u est une application propre (17.3.7), 'u applique ZP(Y) (resp.
BP(Y)) dans ZP(X) (resp. BP(X)), donc on en déduit encore un homomorphisme
d'algèbres graduées qu'on note
m?:h;(y) - h;(X),
et qui est défini de la même façon.
Pour toute application de classe C00, v : Y -♦ Z, on a [v ° u)* = u* ° v* ;
si u et v sont propres, on a de même (v ° u)* = u* ° v*.
Exemple. — Si Y est réduit à un point, u l'unique application X -» Y,
m* applique H'(Y) = H°(Y) = R sur le sous-espace vectoriel de H°(X) formé
des multiples réels de l'unité (fonctions constantes dans X).
(24.1.4) Cohomologie des variétés non orientables. Soient X0 une variété pure,
X un revêtement à deux feuillets de X0, n : X -> X0 sa projection ; cette
situation se présente en particulier lorsque X0 est connexe et non orientable, et X le
revêtement orientable canonique de X0 (16.21.16). Pour tout z e X, soit s(z) e X
l'unique point distinct de z et tel que 7i(z) = n(s(z)) ; il est clair que s2(z) = z,
et s est un isomorphisme de X sur lui-même (appelé involution canonique de X),
comme on le voit aussitôt en considérant, pour tout z e X, un voisinage ouvert V
de 7t(z) tel que 7t_1(V) soit réunion de deux ouverts disjoints Uj, U2, la
restriction de 7i à L1! (resp. U2) étant un difféomorphisme de U! (resp. U2) sur V.
Pour toute p-forme différentielle a0 sur X0, la p-forme a = '7t(a0) sur X
est telle que < a(z), h2 > = < a0(7t(z)), Tz(7t).hz > pour tout zeX et tout vecteur
tangent ht en ce point ; donc 's(a) = a. Réciproquement, soit a une p-forme

1. COHOMOLOGIE ET COHOMOLOGIE A SUPPORTS COMPACTS
9
différentielle sur X telle que *s(a) = a ; pour tout x e X0, il y a alors un unique
p-covecteur tangent u0{x) en x tel que < a0M, Tz(n).hz > = <a(z), hz> pour
chacun des deux points z e X tels que 7i(z) = x, et il est immédiat (en prenant un
voisinage ouvert V de x défini comme ci-dessus) que la p-forme <x0 sur X0 ainsi
définie est de classe C°° si a l'est.
On voit donc que si sf'+(X) est la sous-algèbre graduée de jtf'(X) formée
des éléments invariants par 's, l'homomorphisme 'n : s/\X0) -» •s&XX) est injec-
tif et a pour image sf'+(X). D'ailleurs, comme ('s)2 = 1 ^{X), sf'(X)=s/'+(X)® st'-(X),
où j/1(X) est l'ensemble des ae j&'{X) tels que 's(a) = — a ; en outre, comme
a\'s(<x)) = 's(da), Z"(X) est somme directe de Z'+(X) = Z'(X) n sf+(X) et de
Z"_(X) = Z*(X) n s/l{X), et B*(X) somme directe de B'+(X) = B'(X) n jS+ÇX)
et de B'_(X) = B'(X) n ^l(X), ce qui entraîne B'(X) n Z'+(X) = B'+(X). On en
conclut que H'(X) = H+(X) © H'_(X), où H'+(X) est la sous-algèbre graduée
de H'(X) formée des classes de cohomologie invariantes par s* et H"_(X) l'espace
vectoriel des classes de cohomologie telles que s*(a) = — a. En outre, 'n applique
Z'(X0) sur Z'+(X) et B'(X0) sur B'+(X), donc l'homomorphisme
(24.1.4.1) ît* : H*(X0) H'(X)
est injectif et applique H'(X0) sur H'+(X). On a un résultat analogue pour la
cohomologie à supports compacts.
1) a) Soient X0 une variété pure, X un revêtement galoisien de X (section 16.28, problème 2)
de groupe G. Pour tout s e G, s* est un automorphisme de l'algèbre de cohomologie H'(X), et
G opère donc dans H'(X) par (s, a) -» s*(a). Si ji : X -» X0 est la projection canonique,
montrer que si G est fini, l'homomorphisme ît* : H'(X0) -► H'(X) est injectif et a pour image la sous-
algèbre de H'(X) formée des éléments invariants par G (remarquer que si r est l'ordre de G,
1 v-,
a - 2. est une projection de si (X) sur la sous-algèbre des formes différentielles
invariantes par G).
b) On suppose G fini et H'(X) de dimension finie bp; si pj^s) est l'application linéaire a -> s*(a)
de H'(X) dans lui-même, montrer que le nombre de Betti b° de X0 est donné par
(utiliser l'orthogonalité des caractères (21.3.2.6)).
2) Soit A un ensemble ordonné filtrant, c'est-à-dire que pour deux éléments quelconques a, p
de A il existe y e A tel que a < y et p ^ y. Étant donné un anneau commutatif A, un système inductif
de A-modules indexé par A est une famille {ma,f,.), où (M,)MA est une famille de A-modules et,
pour tout couple (a, p) tel que a $ p,ft. est un A-homomorphisme de M„ dans M,, et on suppose
que /„ = Id et fyt°f„ =fya si a « p « y.
On appelle limite inductive du système inductif (M„,/;„) et on note M = lim M, le A-module
défini de la façon suivante : si L = ©M, est la somme directe des M. et si l'on identifie chaque M.
PROBLÈMES

10 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFERENTIELLE ÉLÉMENTAIRES
à son image canonique dans L, M = L/N, où N est le sous-module de L engendré par tous les
éléments fpjix,) — x, pour tous les couples (a, p) tels que a < p, et tous les x, e M,.
a) On désigne par /. la restriction à M, de l'homomorphisme canonique L -» M = L/N.
Montrer que pour a < 0, on a /, ° fa = f„ et que M est somme des sous-modules /«(M.).
Montrer que si f£x.) = 0 pour un xa e M«, il existe p > a tel que faix,) — 0.
b) Soit M' un A-module, et pour tout a e A, soit u. : M. -» M' un A-homomorphisme tel
que, pour a < p, on ait u. = ut° fa. Montrer qu'il existe un A-homomorphisme et un seul
u : lim M. M' tel que «« = «»/« pour tout a g A.
c) Soit (m'„fa) un second système inductif ayant même ensemble d'indices, et pour tout a.
soit u, : M, -► Mi un A-homomorphisme, tel que pour a < 0, on ait fa ■> u, = uf °fa. Montrer
qu'il existe un A-homomorphisme u : lim M. -» lim M; et un seul tel que, pour tout «,»»/,=° u„;
on dit que (u.) est un système imfacti/d'homoraorphismes, et u sa limite inductive, qu'on note lim u,.
d) Soient (M., fa), (Mi, fa), (M." fa) trois systèmes inductifs ayant même ensemble d'indices,
et (u.), (rj deux systèmes inductifs d'homomorphismes u. : Mi -» M., va : M. -» Mi' ; montrer
que si chacune des suites Mi * M, MJ est exacte, la suite M' -4 M A M" est exacte,
où M' = lim Mi, M = lim M„ M" = lim m", u = lim m. et v = lim v,.
3) Soit X une variété pure, réunion d'une suite croissante d'ouverts X„. Montrer qu'il existe
un isomorphisme canonique lim H'f(X„) H'^X).
4) Soit U un ouvert de R", tel que H'(U) = {0} pour tout p > 0. Pour un p > 1, soit co
une p-forme différentielle de classe c sur R" telle que dai = 0. Il y a alors une (p - 1 (-forme ot
sur R" telle que co = da, et une (p - Informe p sur U telle que co | U = dp. Montrer qu'il existe
une (p — 2)-forme y sur U telle que p — (a | U) = dy. En déduire un exemple où p ne peut pas se
prolonger en une p-forme continue sur R". Si V est un ouvert tel que V c U, montrer qu'il existe
une (p - Informe x de classe C°° sur R" telle que p | V = x | V et dx = co.
2. La formule d'homotopie.
(24.2.1) Soient X une variété différentielle pure de dimension n, E un fibre
vectoriel de base X. Une famille (tr^, de sections de E au-dessus de X, ayant pour
ensemble d'indices un intervalle ouvert I de R, est dite lisse si l'application
(s, x) -* <t^x) de I x X dans E est de classe C°°. Pour tout xeX, l'application
s -* as(x) de I dans la fibre Ex est de classe C00 et admet donc une dérivée
d
s -» —- (o-jC*)) ; il existe une famille lisse (tr^i de sections de E au-dessus de X
ôs ô
telle que cr'Ax) = —(oJix)) pour (s, x)el x X; en effet, la question étant locale
os
sur X, il suffit de considérer le cas où E = X x F est trivial, l'application
(s, x) -* <t£x) s'écrivant (s, x) -*■ (x, o{s, x)), où a est une application de classe C"
de I x X dans F ; alors (s, x) -* ^- (tr/x)) s'écrit (s, x) -* [x,^- cr(s, x) ), d'où
notre assertion. De même, pour tout intervalle compact [a, b] contenu dans I
(x, ^ o(s, x^j, d'c
îme, pour tout intervalle compact [
xeE, I oJ(x)ds
et tout x e E, I o£x)ds est un vecteur de E„ et il existe une section t de classe C°°
J« p*
de E au-dessus de X telle que x(x) = o&)ds pour tout jc e X ; on est encore

2. LA FORMULE D'HOMOTOPIE
11
ramené au cas où E = X x F et alors t(jc) = ^x, j* a\s, x)dsj, ce qui établit
encore cette assertion ; on écrit t = oyis. Il est clair que ces définitions entraînent
aussitôt la formule *"
,2.1.1) ob — aa = I a'^ds.
(24,
(24.2.2) Considérons en particulier le cas où E = A"T(X)* est le fibre des
p-covecteurs tangents à X, et soit (co,)^, une famille lisse de p-formes différentielles
sur X. Alors (da>s)xl est une famille lisse de (p + Informes différentielles sur X
et Ton a
(24.2.2.1) d^ tojsj = £ (dœ,)ds
En effet, la question est locale sur X ; on peut donc supposer que X est un
ouvert de R" et (par linéarité) que to£x) est somme d'un nombre fini de p-formes
du type /(s, x)dÇil a d?1 a ... a dÇip, et il suffit de prouver notre assertion
pour une de ces formes ; mais alors le premier membre de (24.2.2.1) est égal à
et le second à
t([|(s)^a^a.
l'égalité résulte de la formule de dérivation sous le signe d'intégration.
(24.2.3) Considérons maintenant une variété différentielle pure X de
dimension n et, sur la variété produit I x X, une p-forme différentielle co de classe C°°.
Pour tout sel, notons j, l'application x ~* (s, x) de X dans I x X ; alors la
famille ('j,(o)))Ki de p-formes différentielles sur X est lisse. Pour le voir, on se
ramène encore au cas où X est un ouvert de R", de sorte que co est somme d'un
nombre fini de p-formes qui sont, soit du type
(24.2.3.1) f(s, x)ds a dth a ... a d?'-1
soit du type
(24.2.3.2) gis, x)dth a ... a d?>.
Mais 'jlio) est nulle lorsque co est du premier type, et égale à la p-forme x -* co(s, x)
sur X lorsque co est du second type (16.20.9.2), ce qui établit notre assertion.

12 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
Sous les mêmes hypothèses, soit £ le champ de vecteurs sur I x X tel que
E{s, x) soit le vecteur de composante t,-1(1) dans T,(I) et de composante 0 dans
TJX), quand on identifie T(liX)(I x X) à TJJ) x T^X) (16.6.2) ; il revient au même
de dire que, pour toute fonction (s, x) -» f(s, x) de classe C00 sur I x X, on a
d
(0E.f)(s,x)- — f(s,x) (17.14.1). On a alors, avec les notations de (24.2.1),
os
pour tout intervalle compact [a, b] <= I,
(24.2.3.3) 'Uco) - 'jM = ^We-o¥s .
Vu (24.2.1.1), il suffit en effet de montrer que l'on a
(24.2.3.4) Ctico))'= We-co)
et on peut supposer que co est de l'un des types (24.2.3.1) ou (24.2.3.2). Or, pour
une forme co du type (24.2.3.1), dE.co est du même type en raison de la
relation 6B.(ds) = 0 et du fait que 6E est une dérivation (17.14.7.5), donc les deux
membres de (24.2.3.4) sont nuls. Si au contraire co est du type (24.2.3.2), les
dg
deux membres de (24.2.3.4) sont égaux à — d£,h a ... a d?'.
os
(24.2.4) Rappelons maintenant (17.15.3.4) que l'on a 0E.co = iE.dco + d(iE.co).
Posons
(24.2.4.1) L. co = | 'jJLiE. co)ds
de sorte que pour chaque p, L est une application linéaire de Sp{\ x X) dans
<fp_t(X); d'autre part, le support de i£.co est contenu dans celui de co, donc la
réunion des supports des formes 'jJLiE.a>) pour a ^ s < b est contenue dans
l'adhérence de la projection sur X de Supp(co) n([a,b] x X); il en résulte que L
applique aussi 9)$ x X) dans @p-t(X).
Tenant compte de la formule (24.2.2.1), on peut alors écrire la formule
(24.2.3.3) sous la forme
(24.2.4.2) <jb(co) - 'jJico) = d(L.co) + L.(dco)
(formule de Vhomotopie). On peut dire que cette formule évalue la « variation
par continuité » d'une p-forme différentielle sur X « dépendant d'un paramètre ».
Cette formule va nous permettre de prouver le résultat fondamental
d'invariance par homotopie de la cohomologie :
(24.2.5) Soient X, Y deux variétés différentielles pures, u et v deux applications
de classe C" de X dans Y. Si u et v sont homotopes de classe C00, les homomor-
phismes d'algèbres graduées u* et v* de H"(Y) dans H'(X) sont égaux.

2. LA FORMULE D'HOMOTOPIE
13
Il s'agit de montrer que si a est une p-forme différentielle sur Y telle que
dix = 0, la p-forme '«(a) — ri<a) sur X s'écrit dfi pour une (p - 1)-forme fi. Par
hypothèse, il existe un intervalle ouvert I de R et une application F : I x X -» Y
de classe C00, telle que pour deux nombres a ^ b de I, on ait F(a, x) = u(x) et
F(b, x)=v{x) pour xeX. Avec les notations introduites dans (24.2.3), cela s'écrit
aussi u = F ° j„ et v = F ° j'j, donc si l'on pose co = 'F(a), p-forme sur I x X,
on peut écrire
(24.2.5.1) 'v{a) - '«(a) = 'Mto) - 'Mco) = d(L.co) + L.(dco)
en vertu de la formule de Fhomotopie. Mais on a dot = 'F(da) — 0 (17.15.3.2)
donc p = L.co répond à la question.
Remarque (24.2.6). — Avec les notations précédentes, si l'homotopie F est
propre (ce qui entraîne que u et v le sont), et si la forme a est à support compact,
il en est de même de co, donc de /? = L. co (24.2.4) ; donc les homomorphismes
m* et v* de H'JY) dans H*(X) sont encore égaux.
Exemples (24.2.7). — Prenons X = Y, et supposons que l'application
identique lx soit homotope de classe C°° à l'unique application r : X -» {x0},
où x0eX. Il est clair que pour toute p-forme a sur X telle que p > 1, on a
'r(a) = 0, et que pour toute fonction / e<?(X), 'r(/) = f(x0), donc on déduit
de (24.2.5) que l'on a H"(X) = {0} si p > 1 et H°(X) £ R.
En particulier, ces hypothèses sont vérifiées quand on prend pour X un
ouvert étoile de R", c'est-à-dire tel que les relations x e X, 0 < t ^ 1 entraînent
tx e X ; si g est une application de classe C°° de R dans [0, 1 ] telle que g(t) = 0
pour t < 0 et g(t) = 1 pour t > 1, l'application F(t, x) = g(t)x est une homotopie
de classe C00 de lx sur l'application x -* 0. Le fait qu'on a alors H^X) = {0}
pour p ^ 1 est connu sous le nom de lemme de Poincaré.
Soit E un espace fibre vectoriel de base une variété différentielle pure Y et
de projection n ; on identifie Y à la section nulle de E (16.15.1). Soit X => Y un
ouvert de E tel que la relation hyeX entraîne thyeX pour 0 < t < 1. Alors,
si i : Y -y X est l'injection canonique, l'application i ° n de X dans lui-même
est homotope de classe C°° à l'application identique : en effet, en prenant pour g
une application de R dans [0, 1] définie comme ci-dessus, l'application
F : R x X X définie par F(t, hy) = g(t)hy pour hy e X est une homotopie
de i o 7t dans lx. On a donc n* ° i* = 1h#<x) ; d'autre part, comme n ° i = 1Y, on
a i* on* = 1H.(Y) ; autrement dit, H*(X) s'identifie canoniquement à H'(Y)
(généralisation du lemme de Poincaré).
Remarque (24.2.8). — Soient X, Y deux variétés différentielles pures, X étant
supposée compacte, et soit u : X -» Y une application dont nous supposons
seulement qu'elle est continue. Si d est une distance définissant la topologie de Y,

14 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
il existe e > 0 tel que : 1° il existe une application v : X -» Y de classe C°° telle
que d(u(x), v(x)) < e pour tout x e X ; 2° v est homotope à u ; 3° si t>, : X -♦ Y
est une seconde application de classe C°° vérifiant la condition 1°, alors v et vt
sont homotopes de classe C°° ((16.26.4) et (16.26.6)). Pour toutes les
applications v vérifiant la condition 1°, l'application v* : H'(Y) -* H*(X) est donc la
même ; par définition, on note u* cette application, et il résulte de (16.26.6) que
si m' : X -> Y est une seconde application continue homotope à u, on a u'* = m*.
Supposons aussi Y compacte, et soit w : Y -» Z une application continue ;
si Ui : X -» Y, wl : Y -» Z sont respectivement homotopes à u et w, on voit
aussitôt que w o u est homotope à w, ° «t ; on en conclut que (w <> m)* = u* ° w*.
En particulier, si « : X -> Y est un homéomorphisme et w : Y -» X l'homéo-
morphisme réciproque, u* et w* sont des bijections réciproques, en d'autres
termes H'(X) ne dépend que de la topologie de X, et non de sa structure de variété
différentielle. Nous verrons plus loin qu'il en est de même pour toute variété
pure non compacte (24.27.1).
3. Les suites de Mayer-Vietoris.
(24.3.1) Soient X une variété différentielle pure, U,, U2 deux ouverts non
vides de X tels que U! u U2 = X et que Ut n U2 soit non vide. On note
les injections canoniques. On déduit de ces applications une suite d'applications
linéaires homogènes de degré zéro
(24.3.1.1) 0 j^*(X) j*'(Ui) © s/\U2) ^'(U, nU2) -> 0
de la façon suivante : pour toute forme différentielle coes/'(X), on pose
(243.1.2) u(co) = (%{co), ,i2{co))
et pour tout couple de formes différentielles Oie s/\\Ji), co2 e s/\\J2),
(243.13) vioiu œ2) = '^(«i) - %(oi2).
(24.3.2) Avec ces notations, nous allons montrer que la suite (24.3.1.1) est
1) u est injective : en effet, si u(to) = 0, on a '^(co) = 0 et 'i2(co) = 0, ce qui
signifie que les restrictions de co à et U2 sont nulles, donc co = 0 puisque
X = U, u U2.
2) On a Ker(«;) = Im(u). Comme i, o y, = i2 o y2, il est clair que v ° u — 0,
jx : Uj n U2 -* U
ix : U! -+ X,
j2 :U,nU2 -> U2
i2 : U2 - X
exacte.

3. LES SUITES DE MAYER-VIETORIS
15
donc Im(u) <= Ker(t>). Inversement, supposons que (a>l, co2) e Ker(t)). Cela signifie
que les restrictions de cox et co2 à U2 n U2 sont égales, donc il y a une forme
différentielle unique co sur X telle que 'ii(a>) = eu, et 'i2(co) = co2, ce qui signifie
que (co,, cu2)elm(w).
3) v est surjective. En effet, soit eue^"(U, n U2), et considérons une
partition de l'unité (/i, f2) subordonnée au recouvrement { U,, U2 } de X et formée
de fonctions de classe C°°. La forme différentielle col sur U,, égale à f2co dans
Uj n U2 et à 0 dans U, - (U, n U2) est de classe C°° ; il en est de même de la
forme différentielle co2 sur U2, égale à f^co dans U, nU2 et à 0 dans U2—(U j nll2) ;
puisque fi + f2 = 1, on a bien co = i^a),, — co2).
(24.3.3) Notons dlt d2, dl2etd les différentielles extérieures sur U 2, U2, U, nU2
et X ; il résulte des définitions (24.3.1.2) et (24.3.1.3) que l'on a par (17.15.3.2)
u°d = (d| ®d2)°u, v°(dY ® d2) = d12°v
donc m et d sont des applications linéaires homogènes de degré 0 de modules
différentiels. On en déduit (Ann. 30.3) deux applications linéaires homogènes de
degré 0 :
(243.3.1)
: H'(X) - H'(U,) © H*(U2), »„ : H'(Ui) © H'(U2) - H"(Ui n U2)
et l'exactitude de la suite (24.3.1.1) entraine l'existence d'une application linéaire
homogène de degré + 1
d : H'(U, n U2) - H'(X)
telle que la suite (commençant par 0 ~* H°(X))
(24.3.3.2)
... -* H"(X) H* H"(U,) © H"(U2) 5 H'(U,nU2) -4 HP+1(X) - ...
soit exacte (Ann. 30.5). On dit que c'est la suite de Mayer- Vietoris pour la
cohomologie. Rappelons (loc. cit.) que l'application d est définie de la façon suivante :
si c est la classe de cohomologie d'une p-forme fermée y sur Uj n U2 et y 2 e «^(Uj),
y2 e <?p(U2) deux p-formes telles que y = viyu y2), les formes dyt et dy2 ont même
restriction à U,n U2, donc sont les restrictions d'une même (p + l)-forme
fermée P sur X, et de est la classe de p.
(24.3.4) Soient Y une seconde variété différentielle pure, V,, V2 deux ouverts
non vides de Y tels que Vt u V2 = Y, et h : X -» Y une application de classe C°°
telle que Ji(U,) <= V, et Ji(U2) c V2, de sorte que ^Uj n U2) c V, n V2. Notons

16
XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
hy, h2, hl2 les restrictions de h à Uj, U2 et U! n U2 respectivement ; alors il est
clair que le diagramme
j^'(X) -^U sfÇUi) © ^'(U2) — .0^(11, nU2) - 0
0
•h 'k1e>k2
s^(Wl n V2)
«Y i;y
est commutatif. On en conclut que le diagramme de suites exactes
H'(X) -* HfJJjieHTUa) - Hp(U,nU2) - H'+,(X) - ...
(24.3.4.1)
... - H"(Y) -+ H'(V1)©HI'(V2) - H"^ n V2) H'+1(Y) - ...
est commutatif (Ann. 30.6).
(24.3.5) Soient X une variété différentielle pure, U un ouvert non vide de X,
j : U -* X l'injection canonique. Pour toute p-forme différentielle a de classe C",
à support compact sur U, la p-forme sur X obtenue en prolongeant a par 0 dans
X — U est encore de classe C°° et à support compact ; on a ainsi défini une
application linéaire injective/ : %(U) -*■ ®p(X), et on obtient une application linéaire
injective
/ : j/;(U) -> «X)
se réduisant à / dans chaque sous-espace @J(U), et qui est un homomorphisme
d'algèbres différentielles graduées.
(24.3.6) Reprenons les hypothèses et les notations de (24.3.1) ; utilisant (24.3.5),
on définit une suite d'applications linéaires homogènes de degré 0
(243.6.1) 0 -► j<(U, n U2) ^ J<(Ut) © j<(U2) ^ <(X) 0
de la façon suivante : pour a e .s/c'(Ui n U2), on pose
(24.3.6.2) ^a) = (/1(a),-/2(a))
et pour tout couple de p-formes différentielles ales/^i), 0l2es/c(^2)
(24.3.6.3) uXalt a2) = i^ott) + r2{ct2).
Cette suite est encore exacte. En effet, il est clair que vc est injective, et la
relation °= i2 ° j2 entraîne encore ue°vc = 0, donc Im(i>c) <= Ker(uc). Si
inversement (au a2) e Ker(uc), on a ii(a,) = — f2(<x2) ; cela entraîne que a^x) = 0
dans X — Supp(a2), a.2(x) = 0 dans X — Supp(at) et finalement a,(jc) = - <x2(x)
dans Supp(aj) n Supp(a2); comme Supp(a,) n Supp(a2) est compact et contenu

3. LES SUITES DE MAYER-VIETORIS
17
dans Ut n U2, la forme différentielle a sur U,nU2 égale à at(x) = - a2(x)
dans Suppfa,) n Supp(a2), à 0 ailleurs, est de classe C°° et on a i^a) = (a,, a2),
donc Kerfu,.) <= lm(vc). Enfin, montrons que uc est surjective. Soit (/,, /2) une
partition de l'unité subordonnée au recouvrement { U,, U2} et formée de
fonctions de classe C°°. Pour toute forme différentielle ae^X), /,a et /2a sont
des formes différentielles dont les supports sont compacts et contenus
respectivement dans U, et U2, et l'on a /,a + /2a = a; si ai et a2 sont les restrictions
de fi<x à Ut et de /2a à U2, on a bien a = wc(a„ a2).
(24.3.7) Avec les mêmes notations que dans (24.3.3), on a encore
vc°d12 = (di © d2)o»c, uc°(di © d2) = d ° uc
donc on déduit de vc et uc deux applications linéaires homogènes de degré 0
(24.3.7.1) Vc. : H^U! n U2) H^U,) © H^U2)
«^H^U,)©!^) -> H"(X)
et l'exactitude de la suite (24.3.6.1) entraine l'existence d'une application linéaire
homogène de degré + 1
dc:Hm - HXU,nU2)
telle que la suite (commençant par 0 -+ H°(Ut n U2))
(24.3.7.2)
... - HJflJ, nU2) "S Hf(U,)©H?(U2) Hf(X) ^ Hf+ 1(L\ nU2) - ...
soit exacte. On dit que c'est /a suite de Mayer-Vietoris pour la cohomologie à
supports compacts. L'application dc est définie de la façon suivante : si a est la
classe de cohomologie d'une p-forme fermée a sur X, à support compact, et si
al e^piUj) et a2e^p(U2) sont deux p-formes telles que a = a, + a2) alors
est la classe de cohomologie de dai = — da2, considérées comme (p + 1 (-formes
sur Uj Pi U2.
(24.3.8) Les notations étant celles de (24.3.4), supposons que les applications
ht : U, -* V\ et h2 : U2 ~* V2 soient propres, ce qui entraîne que h et hl2
soient aussi propres; on a alors un diagramme commutatif
0 - 4'(U,nU2) - j<(Ux) © j<(U2) - s/'c(X) - 0
0 - i.'IV.nV,) - j/;(V,)© j<(V2) - <(Y) - 0

18 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
'application (t]0, z) -»• (z/|| z ||, c;0) de U n V dans S„_ t x J - i, ^ est bijec-
tive et de classe C00, et son application réciproque est (z, Ç°) -* (1 -(<^°)2)*z),
qui est donc aussi de classe C00. On en conclut par (24.2.7) que l'on a
HP(U n V) s HP(S„_,) pour tout p > 0. Appliquons alors à U et V la suite
de Mayer-Vietoris (24.3.3.2); elle se décompose en suites exactes
0 - H°(SB) -> R2 -» H^S,.,) - H'(S.) -> 0
et
0 - H^S,.!) - HP+1(S„) - 0 pour p > 1.
Pour n = 1, la première suite exacte donne H'(S,) = R, l'application
et on en déduit un diagramme commutatif de suites exactes (Ann. 30.6)
(24.3.8.1)
... - HflU,nU2) - HJTUOGHflUi) - Hf(X) Hf+,(U,nU2)
| h'u.c **.<-©*5.c « J **J.c
•.. - Hf(Vt n V2) - H'(Vt) © Hf(V2) H?(Y) -» Hf + »(V, n V2) -» ...
4. Cohomologie des sphères.
(24.4.1) Pour tout entier n ^ 1, on a
H°(S„) s H"(S„) s R
H"(SB) = {0 } pour 1 < /> < n - 1 .
En particulier, on voit que pour n > 1, 2a sphère S„ n'est pas rétractile.
Comme S„ est connexe pour n > 1, on a H°(S„) S R (24.1.2), tandis que
pour S0 = { — 1, 1}, on a H°(S0) = R2 (24.1.2). On va raisonner par récurrence
sur n ; avec les notations de (16.2.3), soient U l'ouvert de S„ défini par Ç° >
1
V l'ouvert défini par {° < - ; U et V sont difféomorphes à un disque ouvert
dans R" par projection stéréographique (16.2.3), donc (24.2.7), on a
H°(U) = H°(V) s R
et
H"(U) = H'(V) = {0} pour p > 1.
D'autre part, U n V, défini par - ^ < Ç0 < ^, est difféomorphe àSB-ixJ-^,^|j
en effet, si l'on écrit fé0, z) un point de Sm avec z=(^,..., É"), et (Ç0)2 +1| z 112 = 1,

4. COHOMOLOGIE DES SPHÈRES 19
(24.4.1.1) PSn(T) = 1 + T"
XfS„) = 0 si n est impair
X(S„) = 2 si n est pair .
Remarque (24.4.2). — La n-forme « angle solide » a'"' sur S„ est telle que
a1"' ^ 0 (16.24.9), donc elle ne peut être de la forme dp pour une (n — l)-forme P
(24.4.1.2) |
I
(17.15.5.1); sa classe de cohomologie est donc une base de l'espace H"(S„) de
dimension 1.
(24.4.3) Cohomologie de P„(R). Pour n ^ 1, S„ est un revêtement à deux feuillets
de P„(R) (16.14.10), et on peut donc appliquer à X = S„ et X0 = P„(R) les résultats
de (24.1.4); ici s est l'application x — x. On a donc déjà H°(P,,(R)) s R,
HP(P„(R)) = {0} pour 1 ^p < n - 1. En outre on a 'V») = (- l)n+1o(n)
(16.21.10.2), donc on voit que si n est pair, H"+(S„) = {0}, H"_(S„) s R, et au
contraire, si n est impair, H+(SII) = R, H"_(S,,) = {0} ; on en conclut que
(24 4 3 11 i H"(P"(R)) = {0 } si " est pair
( ' j H"(Pn(R)) ~ R si « est impair .
On notera que pour tout n impair ^ 3, P„(R) et S„ ont même cohomologie
mais ne sont pas homéomorphes, puisque P„(R) n'est pas simplement connexe
(16.28.5). Pour n pair ^ 2, tous les HP(P„(R)) sont nuls pour p > 1, mais P„(R)
n'est pas rétractile puisqu'il n'est pas simplement connexe.
(24.4.4) Cohomologie de R" à supports compacts. Par projection stéréographique,
R" s'identifie à l'ouvert S„ - {e0 } de S„ (16.2.3). Il est clair que ^(S„ - {e0 } )
est un idéal différentiel gradué de l'algèbre différentielle graduée s#'(S„) ; notons 38'
l'algèbre différentielle graduée quotient s/'(Sn)/sfc(Sn - {e0} ), de sorte que
si co -* co est l'homomorphisme canonique de s/'(Sn) sur 08', la différentielle ô
de 38' est telle que <5à> = {dco)~. On a donc une suite exacte
(24.4.4.1) ... - Hf(R") - Hp(S,,) - H"(&') - HP+1(R") - ...
qui va nous permettre de calculer les HP(R") en évaluant d'abord les espaces de
cohomologie de & (cf. (24.35.8)).
R2 -> H°(S0) = R2 ayant un noyau de dimension 1 ; au contraire, pour n > 1,
on a H^Sn-x) s R, donc H^SJ = {0}. La seconde suite exacte montre alors
que HP+1(S„) est isomorphe à H^S,,-!) pour p ^ 1, ce qui achève de prouver
(24.4.1) par récurrence sur n.
Le polynôme de Poincaré et la caractéristique d'Euler-Poincaré des sphères
sont donc donnés pour n > 1, par

20 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
(24.4.5) En premier lieu, H°(âi') est formé des classes / de fonctions /e£(S„)
telles que ôf = 0, c'est-à-dire telles que df = 0 dans un voisinage de e0; cela
entraîne que / est constante dans un voisinage de e0, donc les classes / sont
aussi les classes des constantes, autrement dit on a H°(âf ) s R.
Considérons maintenant, pour p ^ 1, une classe co d'une p-forme
différentielle co de classe C°° sur S„, telle que ôco = 0 ; il y a donc un voisinage ouvert
de e0 dans lequel dco = 0, et on peut supposer que ce voisinage V est difféo-
morphe à R" ; le lemme de Poincaré montre donc qu'il existe sur V une
(p — l)-forme p telle que eu = dfi dans V. Soit / une fonction de <f(S„) égale à 1
dans un voisinage W c V de e0 et de support contenu dans V, et soit a la
(p — l)-forme sur S,, égale à ffi dans V et prolongée par 0 hors de V ; il est clair
que l'on a eu = dot dans W, donc co = ôà ; cela prouve que W(0S') = {0}.
(24.4.6) La suite exacte (24.4.4.1) se décompose donc pour « > 1 en les suites
exactes
0 HC0(R") -v H0(Sn) -» R HCHR") - HHS,,) 0
et
0 -* Hf(R") -*■ HP(S„) -» 0 pour p>2.
Comme H°(R") = {0 } (24.1.2) et H0(S,,) s R, la première suite exacte se réduit
à 0 -► HCHR") -» H^S,) -► 0, et finalement on voit que Hf(R") est isomorphe
à H'fjS,,) pour p > 0, d'où
nAAtn JHP(R") = {0} pour p<n
(24A61) lH«(R«)SR.
Si / e ®(R") est une fonction > 0 non identiquement nulle, on a
f(x)dÇldÇ2 ... d? > 0
L
puisque le support de la mesure de Lebesgue est l'espace R" tout entier; la
«-forme u = /(x)dij1 a dl2 a ... a df" ne peut donc être égale à une forme
exacte du pour une (n - l)-forme a à support compact en vertu de (17.15.5.1) ;
cela montre que la classe de cohomologie de o est une base de H^R").
5. Le théorème de Kiinneth.
(24.5.1) Soient X, Y deux variétés différentielles pures. Considérons la variété
produit X x Y, et soient jix : X x Y -> X, itY : X x Y -» Y les deux
projections. Quels que soient les entiersp^0, q^0, on définit une application bilinéaire
de <?P(X) x <?,(Y) dans t^+^X x Y) par la formule
(24.5.1.1) (a, p) -» Ox(«)) a ('nv(p))

5. LE THÉORÈME DE K.UNNETH
21
et par suite une application linéaire
(24.5.1.2) fcp>, : S^X) ® t^Y) - Sp+q{X x Y)
telle que kpq(a ® P) = ('nx(<x)) a ('ny(p)). Sur l'espace produit tensoriel
•fi^(X) ® ^'(Y), on définit une graduation en prenant, pour tout r > 0
0»r = © (/,(X)®^(Y))
p + q = r
et alors l'application linéaire se réduisant à fcM dans chaque sous-espace
^(X) ® ^Y)
k : j^'(X) ® ^'(Y) - jaT(X x Y)
est une application homogène de degré 0. Considérons sur si'{X) ® s&'(Y) la
structure de produit tensoriel gauche d'algèbres anticommutatives graduées
(Ann. 30.9) ; rappelons qu'elle est définie par la formule
(24.5.1.3) (<x„ ® fiq). (y, ® ôs) = ( - 1H«, a yr) ® (pq a <5s)
pour ape^X), /3,e^Y), yPe£(X), cSse<?s(Y), et qu'on note j**(X) «® jaT(Y)
l'algèbre graduée ainsi définie ; alors l'application
(24.5.1.4) k : j^'(X) "® ^'(Y) jaf'(X x Y)
est un homomorphisme d'algèbres graduées, comme il résulte de la définition
(24.5.1.1).
(24.5.2) Si maintenant on définit un endomorphisme d de s/'(X)g® .s/"(Y)
par la formule
(24.5.2.1) d(ap ® pq) = (dap) ® Pq + ( - l)'(ap ® (dpq))
pour <xp e <?p(X) et /?, e ^(Y), cette application est une antidérivation de degré +1
de cette algèbre graduée ; si f = ap ® Pv m = yr ® «5,, la relation
dK.if) = (dÉ).i| + (- îr^-(dn)
résulte en effet des formules (24.5.1.3) et (24.5.2.1), les deux membres étant égaux à
(- ir(<fap a yr) ® (pq a ôs) + (- ir+r+"r(ap a yr) ® (d/?, a <5s)
+ (- l)"+"(ap a dyr) ® (pq a 55) + (- l)"+"+'+«'(ap a yr) ® (0, a dcS,).
Enfin, on a d2 = 0 dans s/'(X) *® s/'(Y), comme il résulte de (24.5.2.1) et des
relations d2ap = 0, d2pq = 0. On a donc défini sur s/'(X) *® s/'(Y) une structure
d'algèbre différentielle graduée, et la formule (24.5.1.1) ainsi que les règles de la

22 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
dérivation extérieure prouvent aussitôt qu'avec la définition (24.5.2.1),
l'application k est un homomorphisme d'algèbres différentielles graduées.
Notons en outre que si a et P sont des formes différentielles sur X et Y
respectivement, le support de ((7tx(a)) a ('ny(p)) est contenu dans Supp(a) x Supp(/J)
et il est par suite compact lorsque ceux de a et P le sont. Il en résulte que la
restriction de k à J^C'(X)B® .s/c'(Y) est aussi un homomorphisme d'algèbres différentielles
graduées
(24.5.2.2) kc : j<(X) g® <'(Y) -» ^C'(X x Y).
(24.5.3) On déduit de (24.5.2.2) un homomorphisme d'algèbres graduées
(24.5.3.1) k* : H'C(X)K® HC*(Y) - HC'(X x Y)
appelé homomorphisme de Kiinneth. Si u : X -» Xt et v : Y Yj sont deux
applications propres de classe C00, il est clair que le diagramme
j/eÏX)g® j/;(Y) ^ j/e'(X x Y)
<'u)®<'i>)
'(u x „)
<(X,)E® <(YX) ^ <(X, x Yi)
est commutatif, en vertu des relations u ° 7ix = 7tXl ° (m x v)etv°nY = 7tYl ° (u x t)).
On a par suite un diagramme commutatif
h;(X) s® h;(Y) 5 h;(x x y)
(24.5.3.2)
h;(x.) »® h;(yx) ^ h;^ x y,)
(24.5.4) (Théorème de Kùnneth). L'homomorphisme de Kiinneth est bijectif.
La démonstration repose sur trois lemmes préliminaires.
(24.5.4.1) Supposons que X soit réunion d'une famille (X;) d'ouverts non vides
deux à deux disjoints. Si chacun des homomorphismes de Kiinneth
wc(xx) *® h;(Y) -> h;(x, x y)
est bijectif, il en est de même de l'homomorphisme de Kiinneth
hc\x) »® h;(Y) h;(x x y) .
En effet, comme HC*(X) s'identifie canoniquement à ©HJ(XA) (24.1.2), le
x
produit tensoriel HC*(X) ® HC*(Y) s'identifie à ®(HC'(XA) ® HC*(Y)), et de même,
x
comme X x Y est réunion des ouverts disjoints Xx x Y, Hf'(X x Y) s'identifie

5. LE THÉORÈME DE KUNNETH 23
Hf(X x y)
h?+1(w x y)
canoniquement à © Hc"(x,, x Y) ; en outre, la définition (24.5.1.1) montre que
la restriction à chaque Hc'(xa) ® HC'(Y) de l'homomorphisme de Kiinneth
Hc'(x) ® HC'(Y) -> Hc(x x Y) est l'homomorphisme de Kûnneth
h;(xa)®h;(y) - h;(xa x y);
cela prouve le lemme.
(24.5.4.2) Supposons que X soit réunion de deux ouverts non vides U, V, et posons
W = U n V ; si W est non vide et si chacun des homomorphismes de Kiinneth
h;(U) »® h;(Y) - h;(u x y) ,
h;<v) *® h;(Y) h;(v x y) , h;(W) *® h;<y) - h;(w x y>
est bijectif, il en est de même de l'homomorphisme de Kiinneth
h;(X) «® h;(y) - h;<x x y) .
On a en effet les suites exactes (24.3.6.1)
o .<(w) ^C*(U)©^;(V) -» <'(x) - o
et 0 - .<(W x Y) -> <'(U x Y)© j/e'(V x Y) sf'c(X x Y) -► 0 .
Les définitions (24.3.6.2) et (24.3.6.3) des flèches dans ces diagrammes et la
définition de l'homomorphisme kc (24.5.2.2) à partir de l'application (24.5.1.1)
montrent aussitôt qu'on déduit des deux suites exactes précédentes, après avoir
tensorisé la première par s4'c(Y), le diagramme commutatif
0 -> <"(W)"®<(Y) -»
0 » j<(W x Y) >
-» «(u)*® <(Y)) © «(V) »® «Y)) -> <(x) *® <(Y) 0
► «(U x Y)) © «(V x Y)) ► j*c\X x Y) ► 0
On en déduit un diagramme commutatif de suites exactes de cohomologie
... - (he*(w) «® h;(Y))" -» (h;(U) b® h;(Y))" © (h;(V) ^> h;(Y)v ->
1 I
... ► H?(W x Y) ► H'(U x Y) © Hf(V x Y) ►
-> (Hc'(x) "® HC-(Y))' -» (H;(W) «® HC(Y))P+1 ^ ...

24 xxiv. TOPOLOGIE ALGEBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
où les flèches verticales sont les homomorphismes de kiinneth. la conclusion
du lemme résulte alors des hypothèses et du lemme des cinq (ann. 29.4).
(24.5.4.3) Soit sb une base de la topologie de x telle que l'intersection de deux
ensembles de sb appartienne à sb. Si, pour tout ouvert u e sb, l'homomorphisme
de Kùnneth H'C(\J) g® hc'(y) -» h*(u x y) est bijectif, alors l'homomorphisme
de Kiinneth hc'(x)g® hc'(y) hc'(x x y) est bijectif.
soit sb' l'ensemble des réunions finies d'ensembles de sb ; il est clair que
l'intersection de deux ensembles de sb' appartient à sb' et que pour tout ouvert
v e sb', l'homomorphisme de kûnneth hc'(v) «® hc'(y) hc'(v x y) est
bijectif, par récurrence sur le nombre d'ensembles de sb dont v est réunion, et
application de (24.5.4.2) ou (24.5.4.1).
soit maintenant (g;) une suite croissante d'ouverts relativement compacts
de x de réunion égale à x et telle que gj c gitl pour j > 0 (3.18.3). on va
définir une suite (vy) d'ouverts appartenant à sb', telle que v,. Gj — gj_ x et
Y/ n vt = 0 dès que | k — j \ > 1. on prend pour v0 la réunion des ensembles
d'un recouvrement fini de g0 par des ouverts de sb assujettis à la condition que
leurs adhérences soient contenues dans Gi ; et en général on déterminera vy par
récurrence, réunion des ensembles d'un recouvrement fini de — g;_, par des
ouverts de sb, assujettis à la condition que leurs adhérences soient contenues
dans GJ+i et ne rencontrent pas vj_2 <= gj_,.
cela étant, soient u la réunion des v2^ (j' > 0) et u' la réunion des v2j +1
(/ > 0). la construction des v^ et le lemme (24.5.4.1) montrent que les
homomorphismes de kùnneth h;(u)«®h;(y) hc'(u x y) et hc'(u')g® hcïy) hc"(u' x y)
sont bijectifs. d'autre part, u n u' est réunion des ensembles v,- n vj+, pour
j > 0, qui sont deux à deux disjoints par construction et appartiennent à sb' ;
on voit donc de même que l'homomorphisme de kùnneth
h;(u n u') "® hc'(y) - hc'((u n u') x y)
est bijectif. la conclusion résulte alors de (24.5.4.2).
(24.5.4.4) la démonstration du théorème de kùnneth se fait maintenant en
considérant successivement les cas suivants.
a) x = rm, y = r"; alors hc'(x) = h"(x) s r, hc'(y) = h?(y) s r, et
hc"(x x y) = Hr+"(x x y) s r (24.4.6.1). tout revient donc à voir que la
restriction de l'homomorphisme de kûnneth à h"(x) ® hj(y) n'est pas
identiquement nulle. or, soient / e ^(rm) et g e ®(r") deux fonctions à valeurs > 0
et non identiquement nulles, et considérons la m-forme a=/(x)dcj1 a d£1 a ... a dÇm
sur x et la «-forme fi = g{y)dnl a dn2 a ... a dr\n sur y, dont les classes de
cohomologie a e h"(x) et be h"(y) ne sont pas nulles ; comme fcc(a ® fi) est
la (m + «Horme f(x)g{y)dc:i a ... a di)m a dn1 a • • • a dn" sur x x y, sa

5. LE THÉORÈME DE KÙNNETH
25
classe de cohomologie kc^a (g) b) n'est pas nulle (24.4.6), d'où le théorème dans
ce cas.
b) x est un ouvert de r™ et y = r". il y a une base de la topologie de x
formée de pavés ouverts, et l'intersection de deux tels pavés est encore un pavé
ouvert ; comme un pavé ouvert de r" est difféomorphe à r", le théorème résulte
dans ce cas du cas a) et du lemme (24.5.4.3).
c) x est une variété pure de dimension m, y = r". soit 93 l'ensemble des
domaines de définition des cartes de x ; c'est une base de la topologie de x et
l'intersection de deux ensembles de 95 appartient à 93. le théorème résulte donc
de (24.5.4.3) et du cas b).
d) x est une variété pure de dimension m, Y un ouvert de r". il est clair que
les lemmes (24.5.4.1), (24.5.4.2) et (24.5.4.3) sont encore valables quand on y
échange les rôles de x et y. le théorème résulte donc de (24.5.4.3) et du cas c),
en considérant une base de la topologie de y formée de pavés ouverts.
e) Cas général. il résulte de (24.5.4.3) et du cas d), en considérant une
base de la topologie de y formée des domaines de définition des cartes de y.
(24.5.5) si x et y sont deux variétés compactes, on a donc la relation entre les
polynômes de poincaré
(24.5.5.1) PXxy(T) = PxCWT)
et par suite, pour les caractéristiques d'euler-poincaré
(24.5.5.2) *(x x y) = x(x).x(y).
par exemple, le polynôme de poincaré du tore T" est donné par
(24.5.5.3) pT„(T) = (1 + T)"
comme il résulte de (24.5.5.1) par récurrence sur n, en vertu du fait que le
polynôme de poincaré de T est 1 + T (24.4.1.1) ; d'où l'expression bp = (0<p<n)
des nombres de betti de T", et la valeur ^T") = 0 de sa caractéristique d'euler-
poincaré.
Remarques (24.5.6). — (i) soit y0 un point de y ; si i : x -» x x y est
l'application x -» {x, y0), l'application i* : h'(x x y) h'(x)
correspondante est surjective. en effet, pour toute p-forme fermée a sur x de classe c°°,
la p-forme fermée co = 'pr,(a) sur x x y est telle que H{co) — a.
(ii) soit x une variété compacte connexe, et soit ô : x -* (x, x)
l'application diagonale de x dans x x x, qui est de classe c™. considérons l'application
composée
H : h'(x)«(g> h'(x) ^ h'(x xx)ï h'(x)

26 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
qui est évidemment un homomorphisme d'algèbres graduées; montrons que
l'on a
H(a ® b) = a ~ b .
Comme a ® b = (a ® 1X1 ® b), il suffit de le prouver lorsque b = 1 ou a = 1.
Or, si a e HP(X) est la classe de la p-forme différentielle a, k*(a ® 1) est la classe
de la p-forme 'pr,(a), et ô*(k*(a ® 1)) celle de la p-forme 'c5('pr,(a)); mais comme
pr, ° ô est l'identité dans X, on a bien ô*{k*{a ® 1)) = a, et on montre de même
que ô*(k*(l ® b)) = b.
(24.5.7) Lorsque les variétés X et Y sont orientées, on peut définir
canoniquement des applications HC'(X x Y) -+ HC'(X) et HC'(X x Y) - H.ÏY). Soient m
et n les dimensions de X et Y ; ces applications se déduisent, par passage à la
cohomologie, d'applications linéaires
S>P+B(X xY) -» ®JX) et 0,+m(X x Y) - @P(Y)
que nous allons définir.
Considérons une (p + n)-forme différentielle co sur X x Y. Identifiant
T(x,y)(X x Y) au produit TJX) x TJY) (16.6.2), pour tout système (klt k2,..., k„)
de vecteurs tangents dans Tj,(Y), l'application
(hl5..., hp) -» < oix, y), kj a k2 a ... a k„ a hx a h2 a ... a hp >
est une forme p-linéaire alternée sur (TX(X))P, autrement dit un p-covecteur
p
f(x, y, ki, ..., k„) dans /\(TJX)*). Il est clair que l'application
(ki, ..., k„) -> f(x, y, ki, k„)
est n-linéaire alternée ; si on la note cojy), on peut dire que cox est une n-forme
p
différentielle vectorielle sur Y, à valeurs dans A(TX(X)*) (16.20.15). Il est clair
que si co est de classe C (r entier > 0 ou oo), il en est de même de <ox, et que si co
a un support compact, il en est de même de cox. Donc, si co est de classe C et à
support compact, l'intégrale j* cox sur la variété orientée Y est définie (16.24.2)
p
et est un p-covecteur de /\ (T^X)*) ; par suite l'application
(24.5.7.1)
est une p-forme différentielle (scalaire) sur X, dite intégrale partielle de co suivant Y.
(24.5.8) Soit (U, q>, m) une carte de X préservant l'orientation et cherchons

5. LE THÉORÈME DE KÛNNETH 27
l'expression locale correspondante de/^co. Il existe un nombre fini de cartes
(Vj, n) de Y préservant l'orientation telles que les ensembles U x Vf forment
un recouvrement de l'intersection de '(U) et du support de co. Si (g,) est une
partition de l'unité subordonnée au recouvrement formé des Vf et formée de
fonctions de classe C00, on a /co = £/J 8i<°- °n P^ut supposer que <p(U) = rm
et = r" ; l'expression locale de gpi pour la carte (U x Vj, cp x ^r„ m + n)
s'écrit d'une seule manière
(24.5.8.1) Z cKH(x, y)dyK a dx"
K,H
où les cKH sont de classe C dans rm+" et pour chaque x e r™, y -* cKH(x, y) a
un support compact ; le couple (H, K) parcourt l'ensemble des couples de parties
Hcjl,2, ..., m}, K c {1, 2, ...,«} telles que Card(H) + Card(K) = p + n,
et si H = {ij, i2, ..., i,} avec it < i2 < ... < i,, K = {juj2, .. .,jr} avec
ji <j2 < ... <)„ on pose abc" = dxh a «V2 a ... a dx\ dyK=d/1 a dy*1 a ... a dy^.
La définition de (gfi))x montre que son expression locale est
(24.5.8.2) E«KoH(x)e8
H
où K0 = {1, 2, ..., n}, de sorte que H a p éléments,
(24.5.8.3) aKoH(x) = cKoH(x, y)d/ a dy2 a ... a df
p
et ej5 est l'élément de base canonique du dual de f\Rm correspondant à H
(Ann. 14.1). On notera que cela entraine (gfo)x — 0 si les cKoH sont toutes nulles.
L'expression locale dej'gjco est donc
(24.5.8.4) £ (|BncKoH(x, yWy))<^
(p mesure de Lebesgue sur r") puisque les cartes ^, préservent l'orientation.
On en déduit l'expression locale de Y co, et il résulte alors de (13.8.6) que la
r Jy
p-forme/jco est de classe C, et a évidemment un support compact.
(24.5.9) Prouvons maintenant la propriété suivante (pour r ^ 1) :
(24.5.9.1) d(/p(0) =^doi ■

28 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFERENTIELLE ÉLÉMENTAIRES
Posons dcKH = £ DJ<KHdxJ + dYcKH, ou ^Vkh est 1& somme des termes conte-
nant les différentielles dy\ et écrivons dYaKH(x) = £dYcKH a ^yK. On a alors
par définition K
(24.5.9.2) (do), = I (I PU. H)(D/rKoH(x, y)dy' a dy2 a ... a dy") Ww
H V#H /
où, dans la première somme, H parcourt l'ensemble des parties de {1, 2, ..., m}
à p éléments, et p(j, H) = ± 1 ; dans la seconde somme, H' parcourt l'ensemble
des parties de { 1, 2 m}àp+l éléments, et ek = ± 1. Or, pour x fixé,
dYaKH(x) est la différentielle extérieure d'une (n — l)-forme différentielle sur R"
à support compact, donc (17.15.5.1), on a dYaKo_(M H.(x) = 0 pour tout k e K0
et toute partie H' de {1, 2, .... m} à p + 1 éléments; par suite
(24.5.9.3) £ (Ad), = S (l PU. H)(jjDjCKoli(x, yJdMy)^*»
Mais d'autre part, on a, par (13.8.6),
d(£aKo„(x)) = t DjCk^x, yW/4y))dx>
etd(|.)
est donc égale au second membre de (24.5.9.3), ce qui prouve (24.5.9.1).
Il résulte de (24.5.9.1) que l'image de Z'+"(X x Y) (resp. B?+B(X x Y)) par
l'application est contenue dans Zf(X) (resp. Bf(X)) ; par passage aux quotients,
cette application définit donc, pour tout p > 0, une application R-linéaire
canonique
(24.5.9.4) ^* : H?+"(X xY)-> Hf(X).
En échangeant les rôles de X et Y, on définit de même l'intégration partielle
suivant X, et l'application F : H'+m(X x Y) H?(Y).
x Jx
La question est locale sur X, et compte tenu de (17.15.3.2), on peut se borner
au cas où X = R™, Y = R" et co est de la forme (24.5.8.1), d'où
dco = £ dcKH(x, y) a dy* a dx*.
K.H

5. LE THÉORÈME DE KÙNNETH
29
(24.5.10) Quels que soient aeH?(X) et beH*+n{X x Y), on a
(24.5.10.1) (- îy^n&a) - b - a -^b .
Si a est une p-forme de la classe a, et co une (q + n)-forme de la classe b,
il suffit évidemment de montrer que l'on a
(24.5.10.2) ( - 1)""^ '7cx(a) a co = a a j^to.
Avec les notations de (24.5.8), on est ramené à prouver cette relation en
remplaçant co par chacune des formes gjCo, donc lorsque X = rm et Y = r" ; on
peut en outre se limiter au cas où a = f(x)dxL pour une partie L de {1, 2, ..., m}
à p éléments. On voit alors aussitôt, avec les notations de (24.5.9), que les deux
membres de (24.5.10.2) sont égaux à
/(x).I (JBn^(x, y)W^*L a dx".
PROBLÊMES
1) Soient X et Y deux variétés différentielles pures. On déduit de (24.5.1.4) un
homomorphisme d'algèbres graduées
k* : H'(X) «<g> H'(Y) -» H'(X x Y).
Montrer que si l'une des algèbres H*(X), H'(Y) est de dimension finie, l'homomorphisme k*
est bijectif. (Si X et Y sont orientables, utiliser la dualité de Poincaré (24.6.2) ; sinon, se ramener
au cas où X et Y sont orientables à l'aide de (24.1.4)).
Donner un exemple où k* n'est pas bijectif (prendre pour X et Y des variétés ayant chacune
une infinité de composantes connexes).
2) Soit X la bande de Môbius (16.14.10).
a) Montrer que l'on a h°(X) = HC'(X) = H2(X) = { 0 }. (En utilisant le théorème de Kûnneth,
déterminer des formes différentielles dont les classes de cohomologie sont des bases des espaces
de cohomologie à supports compacts de S, x R, revêtement orientable à deux feuillets de X ;
puis appliquer (24.1.4)).
b) Montrer que l'on a H°(X) s R, H'(X) s R et H2(X) = {0 }.
3) Soit X la bouteille de Klein (16.14.10). Montrer que l'on a H°(X) s R, H'(X) s R et
H2(X) = {0} (même méthode que dans le problème 2, St x S, étant ici le revêtement orientable
à deux feuillets de X).
4) Montrer que l'algèbre de cohomologie H*(T") du tore T" est isomorphe à l'algèbre
extérieure A (R").
5) Soit Y un tore de révolution plongé dans R3, et soit X la composante connexe bornée
de R3 - Y. Montrer que l'on a He°(X) = HC'(X) = {0}, Hf2(X) = HC3(X) s R.
6) Soit (E, S., n) une fibration de base la sphère S. (n > 1), de fibre type F. Montrer qu'on a
une suite exacte (commençant par 0 -» H°(E))
-» H'(E) -» H'(F) -» H'-"+l(F) H'+I(E) -

30 xxiv. TOPOLOGIE ALGEBRIQUE ET DIFFERENTIELLE ÉLÉMENTAIRES
(suite exacte de Wang). (Considérer les fibres induits sur les ouverts U et V de (24.4.1). Utiliser
le fait qu'une fibration dont la base est rétractile est trivialisable (raisonner comme dans la
section 16.26, problème 7) ; remarquer que les homomorphismes canoniques
sont injectifs et ont une même image, en utilisant le théorème de Kûnneth).
7) Soient p, q deux entiers ^ 2 ; on désigne par QPi, la quadrique réelle projective, sous-
variété de dimension p + q — 2 dans l'espace projectif P,+,- t(R), définie par l'équation (en
coordonnées homogènes)
a) Montrer que S,-, x S,_, est un revêtement à deux feuillets de Q,,, de sorte que
*i(Q,.„) s Z/2Z.
b) Pour que Q, , soit orientable, il faut et il suffit que p + q soit pair (raisonner comme dans
(16.21.11) et (16.21.12)).
c) Montrer que pour j > 1, Hj(QM) = {0} sauf peut-être pour j = p - 1, j = q - 1 et
j=p+q - 2 ; si p * q. H'- '(Q,,.,) = {0 } si p est impair. H'" l(Q„„) s R si p est pair. H'- '(Q,.,)={0}
si q est impair, H*" '(Q,.,) S R si q est pair, H'*• " J(Q,,,)={0} si p+q est impair, H'+'~ 2(Q,,,)£ R
si p + q est pair ; si p = q, W '(Q,,) = {0} si p est impair, Hp~ '(Q,,) = R2 si p est pair,
HJ'-J(Q,,,)sR.
6. La dualité de poincaré.
(24.6.1) soit x une variété pure orientée de dimension n. pour tout entier p
tel que 0 < p ^ n, toute p-forme o^e^x) et toute (n — p)-forme à support
compact P„-pe&>„-J(X.), la «-forme P„-p a <xp a un support compact, donc est
intégrable, et l'on définit ainsi une forme bilinéaire canonique
sur d?p(X) x ©„_p(x). nous allons considérer la restriction de cette forme aux
formes différentielles fermées; on a alors #(otp, P„-p) = 0 lorsque l'une des
formes différentielles est fermée et l'autre exacte. en effet, supposons d'abord
que dap = 0 et /?b_p = dco„-p.u où coH-p-i est une (n — p - informe à support
compact : on en déduit par (17.15.2.1) que /?„_„ a a, = d(to„-p-i a ap); la
forme co„_p_ j a ap a un support compact, et notre assertion résulte de (17.15.5.1).
de même, si dp„-p = 0 et ap = dcop-„ où cop_, e Sp-i(X), on a
H-(it"'(U)) - H-(«-'(UnV)) et
H^jr-'CV)) -* H"(jr'(UnV))
« + «+...
+ -n -3.. -... -«;♦,-<>.
(24.6.1.1)
/?B_pAap = (- iy-y
APn-p a co,-,);
la forme /?b_d a top-l a encore un support compact, et on conclut de même.
on voit donc que la valeur de p„.p) pour <xpezp(x) et j8b_pez;tp(x)
ne dépend que des classes de cohomologie a e hp(x) et t» e h""p(x) de ap et /?b_p

6. LA DUALITÉ DE POINCARÉ
31
respectivement, et l'on a ainsi défini une forme bilinéaire canonique sur
H"(X) x HT"(X),
(24.
,6.1.2) (a, b) - b(a, b) = j\_p a olp
On peut évidemment écrire B(a, b) = < Dxa, b >, où Dxa est un élément
bien déterminé de l'espace vectoriel (H"~P(X))* dual de H"~P(X), et on a ainsi
défini une application linéaire canonique
(24.6.1.3) Dx : H"(X) -> (H,"""(X))*.
Nous dirons que Dx est l'application de Poincaré, et nous allons prouver
le théorème fondamental de dualité :
(24.6.2) Soit X une variété pure orientée de dimension n. Alors, pour 0 < p ^ n,
l'application de Poincaré (24.6.1.3) est bijective.
Nous désignerons encore par
Dx : H'(X) -> (HC'(X))*
l'application linéaire qui se réduit à l'application de Poincaré dans chacun
des HP(X) ; il s'agit donc de prouver que cette application est bijective. L'outil
principal de la démonstration est l'utilisation des deux suites de Mayer-Vietoris
(24.3.3.2) et (24.3.7.2). Par dualité, on déduit de la seconde de ces suites la suite
exacte des applications linéaires transposées (Ann. 29.6)
... '-5 (htw(Hc-tUi))* e (hrp(u2))*
"s (H.'-'lU.nU,))* ^ (HT'-w
D'autre part, dans la première suite (24.3.3.2), on peut remplacer d par (- l)"~pd
sans modifier l'exactitude de la suite. On a alors le lemme suivant :
(24.6.2.1) Le diagramme de suites exactes
est commutatif.
H'(X)-
Dx
H"(U,) © H'(U2)
(hrp(X))* ^ (HT'(U1))*©(Hr'(U2))!
HfU.nUj)
Hp+ l(X)
Dx
^.(Hï-'C^nUa))* (HT'-w

32 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
Il y a trois commutativités à vérifier :
1° On part de la classe de cohomologie aehp(x) d'une p-forme fermée
ap6Zp(x) et on considère les classes ajehp(uj) et a2ehp(u2) des
restrictions <xpl) et ap2) de <xp à ut et u2 respectivement. On considère d'autre part les
classes bveht'çui) et b1eHnc-p(U1) de (n-p)-fbrmes fermées /jb1jp€Zrp(u1)
et pl22peZ"~p(U2) et on considère ces (n — p)-formes comme prolongées par 0
en des (n — p)-formes sur x = uj u u2. Si b est la classe de p^lp + f?£lp dans
h"_|,(x), il s'agit de voir que l'on a
< dxa, b > = < dula„ *>,> + < DVia2, b2 > .
Mais les définitions de (24.6.1) montrent que cela revient à la relation
f (tfj. + fil,) a ap = f ftl, a ap + f a «p
Jx JUi Ju2
qui est évidente.
2° On part des classes de cohomologie a, € hp(uj), a2 e hp(u2) de p-formes
fermées a.(pl)e Z"(\Jt), ap2) e zp(u2), et on considère la classe ai2 de la p-forme
ap12) = (a^ku! nu2)) - (ap2)|(u, r«u2)) dans hp(u, n u2). On considère
d'autre part la classe fc12eh!"'(u1nu2) d'une (n - p)-forme fermée
py_2>ezt'(u1 n ua) et les classes 6, ehc"-p(u,) et b2eHnc-p(V2) des (n - p)-
formes /yjpezjr^u,) et )3<i2_)pezr''(u2) obtenues en prolongeant fljiy par 0
dans u, et u2 respectivement; il s'agit de voir que
< du.fli, fci > - < dula2, 62 > = < duinl)2a12, b12 > .
Ici encore les définitions montrent que cette relation n'est autre que
f f^l, a O*,» - f fôlp a ap2> = f A«> a «p12»
qui est encore évidente.
3° On part cette fois de la classe de cohomologie c12 6 hp(u, o u2) d'une
p-forme fermée yp12)ezp(uj n u2), qui peut toujours s'écrire comme différence
y»> | (u, n u2) - 7p2) | (u, n u2), où y»> e /^ut)et y<,2>e ^(u2)(24.3.2) ; Ôcl2 est
alors la classe de cohomologie de la (p + l)-forme fermée ap+1 ezp+1(x) telle
que ap+11 uj = dypl) et ap+11u2 = dyp2). On considère d'autre part la classe
beWc~p-\X) d'une (n-p - Informe fermée /*._,_, eZ?-'_1(X) que l'on
écrit ^M-ffVi+ffi!,-,, où ftl,.^!».-,-^) et pv-î,-i6^,-,-i(u2);
dco est la classe de dfiflp-x = - dffilp-u dont le support est contenu dans
ut n u2, et qui est considérée comme une forme tam.p de ^,,_p(uj n u2). Cela
étant, il s'agit de prouver que
(24.6.2.2) (- 1)"-p < dx(acj2), b > = < DVinVlcl2, dcb > .

6. LA DUALITÉ DE POINCARÉ
33
Or, le premier membre est par définition
(24.6.2.3)
Mais on a
(
p-i
p-i
a dyp» = - d(jB.V
a dyf = - d(/?<V
,-lA}i") + (C
^p-i a y]
et comme /Y-p-i et pi2-P-i ont des supports compacts, il résulte de (17.15.5.1)
que le second membre de (24.6.2.3) s'écrit aussi
ce qui n'est autre par définition que le second membre de (24.6.2.2).
On en déduit la conséquence suivante :
(24.6.2.4) Soit 33 une base de la topologie de X telle que l'intersection de deux
ensembles de 93 appartienne à 93. Si, pour tout ouvert U e 93, l'application de
Poincaré Dv est bijective, alors l'application de Poincaré Dx est bijective.
Il résulte de (24.6.2.1) et du lemme des cinq que si les applications Du,, DU2
et DUinU2 sont bijectives, il en est de même de DuluUa. Si 93' est l'ensemble des
réunions finies d'ensembles de 93, il en résulte que pour tout ensemble V e 93',
Dv est bijective, par application de la remarque précédente et récurrence sur le
nombre d'ensembles de 93 dont V est réunion.
Supposons en second lieu que X soit réunion d'une famille (Xx) d'ouverts
non vides deux à deux disjoints. Alors (24.1.2) H'(X) s'identifie
canoniquement à riH'(XA) et HC*(X) à ©HC"(XJ, donc (Ann. 27.3) (HC"(X))* s'identifie
canoniquement à n(Hc'(XA))* ; il résulte immédiatement de la définition de
l'application de Poincaré que Dx s'identifie à l'application (ax) -» (DXjLax) de
IlH'(XA) dans ri(H^(XJ)*. Donc, si les Dx, sont bijectives, il en est de même
x x
de Dx.
Pour terminer de prouver (24.6.2.4), on construit comme dans (24.5.4.3)
une suite (V,) d'ouverts appartenant à 93', telle que X soit réunion des Vj et que
Y;n v* = 0 P°ur \ k-j\>l. Soient U la réunion des V2j 0' > °) et U' la
réunion des V2J+1 (J1 > 0). D'après ce qui précède, les applications de
Poincaré Dy et Du- sont bijectives. D'autre part, U n U' est réunion des V^n VJ+Ï
x
x
x

34 xxiv. TOPOLOGIE ALGEBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
f(x)dçl a di2 a ... a d?, on al 1 a fin = /(x)dçj1 ... d? > 0 ce qui
prouve notre assertion.
b) x est un ouvert de r". il y a une base de la topologie de x formée de
pavés ouverts, et l'intersection de deux tels pavés est encore un pavé ouvert ;
comme un pavé ouvert de r" est difféomorphe à r", le théorème résulte du
cas a) et de (24.6.2.4).
c) Cas général. il suffit d'appliquer (24.6.2.4) et le cas b), en considérant
une base de la topologie de x formée des domaines de définition des cartes de x.
(24.6.3) Si X est une variété pure orientée de dimension n, l'espace hjj(x) a une
dimension égale au nombre de composantes connexes de X (dimension infinie si
l'ensemble de ces composantes est infini).
en effet, il suffit, par (24.1.2) de prouver que si x est connexe, on a hj(x) s r ;
par dualité cela résulte de ce que h°(x) s r.
Remarques. — (24.6.3.1) soit x une variété pure orientée de dimension n ;
l'application linéaire co -* J co de ®„(x) = zj(x) dans r est surjective, car si u
est une n-forme appartenant à l'orientation de x et / e ©(x) une fonction à
valeurs > 0 et non identiquement nulle, on a J fv > 0. d'après (17.15.5.1X le
noyau de cette forme linéaire contient b"(x) = a\%. i(x)). on conclut donc
de (24.6.3) que, pour que x soit connexe, il faut et il suffit que toute n-forme à
support compact a telle que i a = 0 soit de la forme d/3 pour une (n — \)-forme fi à
Jx
support compact. par passage au quotient à partir de l'application linéaire
canonique co —► co, on obtient donc, lorsque x est connexe, une bijection canonique
(24.6.3.2) ix : hj(x) r .
l'élément e\ de h"(x) dont l'image par ix est 1 est appelée la classe fondamentale
lx
pour j > 0, qui sont deux à deux disjoints et appartiennent à 33' ; on voit donc
de même que dunu- est bijective. la conclusion résulte donc de (24.6.2.1) et du
lemme des cinq.
(24.6.2.5) la fin de la démonstration de (24.6.2) se fait en considérant
successivement les cas suivants.
a)x = r"; alors h*(r") = h°(r") s r et h^r") = hj(r") s r ; tout
revient à voir que l'application de poincaré h°(r") -> (h?(r"))* n'est pas nulle.
or, si / e ®(r") est une fonction > 0 non identiquement nulle, et fin la n-forme

6. LA DUALITÉ DE POINCARÉ
35
de cohomologie (ou classe d'orientation) de la variété connexe x, pour
l'orientation choisie sur x. si on change l'orientation de x, la classe fondamentale change
de signe (16.24.4).
par exemple, pour la sphère s„ orientée vers l'extérieur, la classe
fondamentale de cohomologie est celle de la n-forme
V ' g<">
(n + l)7t<"+1)/2
avec les notations de (16.21.10), en vertu de la formule (16.24.9.3).
(24.6.3.3) si x est une variété différentielle telle que l'application identique lx
soit homotope de classe c°° à l'unique application x -> {x0 }, où x0 e x, x est
simplement connexe (16.27.7), donc orientable (16.21.16). il résulte donc de la
dualité de poincaré et de (24.2.7) que si x est de dimension n, on a
(24.6.3.4) hf(x) = {0 } si p * n , h?(x) s r .
(24.6.4) pour toute variété compacte pure X de dimension n, l'algèbre de
cohomologie h"(x) est de dimension finie. Si de plus X est orientable, les nombres de Betti
de X sont tels que bp = bn-p pour 0 < p ^ n.
nous donnerons plus tard (24.29.1 et 24.48.9) deux démonstrations
indépendantes du fait que h'(x) est de dimension finie lorsque x est compacte.
on peut le démontrer ici en invoquant des considérations de théorie des
ensembles. on a H'JX) = h'(x) ; si x est orientable, pour 0 ^ p < n, hp(x) est
isomorphe au dual (h"-p(x))* et h"-p(x) isomorphe au dual (hp(x))*, si bien
que hp(x) est isomorphe à son bidual (hp(x))**. or, on montre que dans un
espace vectoriel de dimension infinie, deux bases ont même cardinal, et que si
un espace vectoriel sur r a une base infinie b, son dual a une base dont le
cardinal est (card r)c»rd(b) ^ 2card<b) > card(b) (théorème d'erdôs-kaplansky,
cf. [13], p. 247); cela exclut qu'un espace vectoriel de dimension infinie puisse
être isomorphe à son bidual. si x n'est pas orientable et si x est le revêtement
orientable à deux feuillets de x, x est compacte et on a vu (24.1.4) que h'(x)
s'identifie à un sous-espace de h'(x), donc est de dimension finie.
(24.6.5) Soit X une variété connexe orientable de dimension n. On a alors
h"(x) s r si x est compacte
h"(x) = {0 } si X est non compacte .
en effet, on a vu que h?(x) est de dimension 1 si x est compacte, et réduit à 0
dans le cas contraire (24.1.2).

36 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFERENTIELLE ÉLÉMENTAIRES
Une variété connexe compacte orientable de dimension ^ 1 n'est donc
jamais rétractile.
Remarque (24.6.6). — Soit X une variété compacte, connexe et orientée ; il
existe alors dans l'orientation de X (16.21.2) une n-forme différentielle v telle
que j* v = 1 ; toutes les n-formes ayant cette propriété ont la même classe de
cohomologie égale à la classe fondamentale de X (24.6.3).
(24.6.7) Soit X une variété compacte pure orientée, de dimension paire n = 2m.
Il résulte de la définition (24.6.1.2) de la forme bilinéaire canonique
(a, b) - B(a, b) = j\xm a pm
que l'on a B(£>, a) = (- l)mB(a, b) dans Hm(X) x HM(X) ; l'application de Poincaré
étant une bijection de Hm(X) sur lui-même, on voit que B est une forme alternée
non dégénérée si m est impair, une forme symétrique non dégénérée si m est pair ;
dans ce dernier cas, la signature de cette forme (différence du nombre r de termes
> 0 et du nombre s de termes < 0 dans la diagonale de la matrice de B par
rapport à une base orthogonale) est aussi appelée la signature de X et notée
Sig(X) ; comme r + s = bm, on a Sig(X) = bm (mod. 2).
(24.6.8) Soit X une variété pure compacte orientée de dimension n. Si n est impair,
on a x(X) = 0. Si n = 2m est pair, on a x(X) = bm (mod. 2) ; si de plus m est impair,
bm et x(X) sont pairs.
Par définition, on a tfX) = î(-l)"bD= £ (- Wbn-, = (- l)"x(X),
p=0 p = 0
d'où la première assertion. Si n = 2m, on peut aussi écrire
x(X) = 2mi(- m, + (- irbH
p = 0
donc x(X) = bm (mod. 2) ; si m est impair, on a vu que la forme B sur Hm(X) x Hm(X)
est alternée non dégénérée, donc la dimension bm de Hm(X) est nécessairement
paire (Ann. 16.1).
Remarque (24.6.9). — L'exemple des espaces projectifs P2b(R) de dimension
paire (24.4.3) montre que la dualité de Poincaré ne peut s'étendre telle quelle
aux variétés non orientables.
(24.6.10) Soit X une variété pure compacte orientée de dimension n, et
considérons l'application linéaire canonique ô* : H"(X x X) -♦ H"(X) correspondant
à l'application diagonale ô : x -» (x, x). Nous allons définir canoniquement

6. LA DUALITÉ DE POINCARÉ
37
une classe de cohomologie /x e H"(X x X) telle que l'on ait, avec les notations
de (24.6.3.2),
(24.6.10.1) W**('x)) = zP0.
caractéristique d'Euler-Poincaré de X. Pour cela, notons que pour 0 s* p ^ n,
l'application de Poincaré définit un isomorphisme d'espaces vectoriels
1 ® Dx : H"(X) ® H"-"(X) ^ H'(X) ® (H'(X))*
et l'on a d'autre part un isomorphisme canonique (Ann. 10.5.5)
H"(X) ® (H"(X))* s» End(H"(X))
d'où, en les composant, un isomorphisme canonique d'espaces vectoriels
ap : H'(X) ® H"-"(X) st End(H"(X)).
De façon précise, si aeH'(X), i>GH"_p(X), oja ® b) est l'endomorphisme
c -f < Dxb, c > a .
On en déduit que
Tr(o> ® b)) = < Dxb, a > - ix(a - b)
en vertu de (24.6.1.2) ; comme a ^ b = ô*(k*(a ® b)) par (24.5.6), on voit
finalement qu'on peut écrire
pour tout w e End(Hp(X)). En appliquant cette formule à l'identité lHi><x)> on
aura donc la formule (24.6.10.1) en prenant
On dit que cette classe de cohomologie dans H"(X x X) est la classe de
Lefschetz de X. Elle peut aussi être caractérisée par la propriété suivante :
(24.6.11) La classe de Lefschetz lx est la seule classe appartenant à H"(X x X)
et telle que, pour tout a e H"(X), on ait
(Dans cette formule, l'intégration partielle est faite suivant le second facteur
de X x X).
Tr(M) = ix(^(fc*(o-;1(«))))
(24.6.10.2)
(24.6.11.1)

38 xxiv. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
il suffira de montrer, plus généralement, que pour p > 0, q ^ 0, a e h*(x)
et ueend(h"(x)), on a
(24.6.11.2)
|V(<r; »(«)) ~ pr.(a) = 0 si q # p
(- \yi fc*(o-;1(«))-pr!(û) = m(c
l jx
(o) si q=p
et de prendre pour u l'application identique de hp(x), ce qui donnera (24.6.11.1)
pour tout a e h'(x) ; l'unicité résulte de ce que ap est un isomorphisme. par
linéarité, on peut se borner au cas où « = ajb (g) c), avec b e hp(x) et c e W'^X).
on a alors par définition k*(b (g) c) ~ prj(a) = pr*{b) ~ prj(c) ~ prj(a) et la
formule (24.5.10.1) donne
^(k*(b <g> c) ~ prî(a)) = (- iy-(fc (prkc) - pr?(a))).
si a (resp. y) est une a-forme (resp. une (n — p)-forme) de la classe a (resp. c),
^ (prj(c) — prj(a)) est la classe de la {q - p)-forme 'pr2(y a a) ; mais il
résulte aussitôt des définitions (24.5.8) que cette forme est nulle si q # p, ce qui
prouve déjà la première relation (24.6.11.2). si q —p, comme y a a=( — 1 )p(" " p,a a y
le premier membre de la seconde formule (24.6.11.2) est égal à
< dxc, a > b = u(a). cqfd.
nous donnerons une autre interprétation de la classe de lefschetz dans
(24.39.25).
PROBLÈMES
1) Soit X0 une variété connexe non orientable de dimension n ; montrer que l'on a
H;(X0) = {0 }. (Soient X le revêtement orientable à deux feuillets de X0, s l'involution
canonique de X ; observer que j renverse l'orientation de X et en déduire que si a est une n-forme à
support compact sur X telle que 's(a) = a on a j" a = 0^.
2) Soit X une variété compacte, connexe et orientable, de dimension n = 4/c divisible par 4 ;
montrer que si Sig(X) <t 0, il n'existe pas de difféomorphisme de X sur elle-même renversant
l'orientation.
3) a) Soient o,, o2 deux n-formes différentielles sur R", de classe C°° et positives pour
l'orientation canonique de R" (16.21.2). On suppose qu'il existe une (n — Informe différentielle a> sur R",
de classe C°° et de support compact, telle que u, — u2 = da>. Montrer qu'il existe un
difféomorphisme u de R" sur lui-même, qui est tel que u(x) = x à l'extérieur d'une boule de rayon assez
grand, et que l'on ait u, = 'u(»2). (Montrer qu'on peut prendre u = (u1, u2, ...,«") tel que uJ(x)=£i
pour j ~& 2).

7. COHOMOLOGIE D'UNE SOUS-VARIÉTÉ COMPACTE
39
b) Soient X une variété compacte, connexe et orientée de dimension n, u, et v2 deux n-formes
différentielles sur X, de classe C°° et appartenant à l'orientation de X. Montrer que si u, et v2 sont
cohomologues, il existe un difféomorphisme u de X sur elle-même tel que v, = 'u(o2) (se ramener
au résultat de a), par une partition de l'unité).
4) Sur une variété pure X, une structure symplectique ou hamiltonienne est définie par la
donnée d'une 2-forme différentielle eu sur X, de classe C", telle que (o(x) soit non dégénérée en
tout point x e X, et qui est fermée. Le fibre cotangent T(M)* d'une variété pure M est muni d'une
structure symplectique canonique définie par la 2-forme — dx^ (17.15.2.4).
a) Montrer qu'une variété munie d'une structure symplectique est de dimension paire et
est orientable.
b) Soit X une variété compacte, connexe, de dimension 2n et munie d'une structure
symplectique définie par une 2-forme eu. Montrer que si a est la classe de eu dans H2(X), les puissances ap
dans l'anneau H'(X) sont toutes # 0 pour p k n.
5) Soient X, Y deux variétés pures compactes et orientées, de dimensions multiples de 4 ;
montrer que si on munit la variété X x Y de l'orientation produit (16.21.5), on a
Sig(X x Y) = Sig(X)Sig(Y).
7. Cohomologie d'une sous-variété compacte.
(24.7.1) Soient X une variété différentielle pure de dimension n, Y une sous-
variété pure compacte de X, de dimension p. Pour tout voisinage ouvert U de Y
dans X, il existe un voisinage ouvert V cr U de Y tel que, si jv : Y -► V est
l'injection canonique, l'homomorphisme j*, : H"(V) -» H"(Y) soit bijectif.
Munissons X d'une structure de variété riemannienne (20.7.13) ; pour tout
xeX et tout vecteur h^eT^M), notons || hx|| sa longueur (20.8.2). Rappelons
qu'on a défini un voisinage ouvert Q de X dans T(X) (X étant identifié à la section
nulle) et l'application exponentielle exp : Q -> X (18.4.3 et 20.16.3).
Considérons le fibre normal N de Y relativement à X, de rang n—p (20.12.2)
et de dimension n, et notons N(e), pour tout e > 0, le voisinage ouvert de Y
dans N formé des vecteurs h, e N tels que || h, || < e. On a le lemme suivant :
(24.7.1.1) // existe un nombre ô > 0 tel que, pour 0 < e < ô, la restriction de
exp à N(e) soit un difféomorphisme de N(e) sur un voisinage ouvert de Y dans X.
En effet, la définition de N montre aussitôt que pour tout y e Y,
l'application linéaire tangente en y à la restriction de exp à N n Cl est une bijection sur
T/X) (18.4.5), donc il y a un voisinage ouvert de y dans N tel que la restriction
de exp à W,. soit un difféomorphisme sur un voisinage ouvert de y dans X (16.5.6).
Il suffit de voir que pour ô assez petit, la restriction de exp à N(<5) est injective. Dans
le cas contraire, il existerait, pour chaque entier m, deux points distincts um, vm
dans N(l/m) tels que exp um = exp vm; comme on peut supposer N(<5) compact
pour ô assez petit, on peut supposer que les suites (um) et (vm) convergent,
nécessairement vers des points y, z de Y ; mais comme par passage à la limite on a
exp(y) = exp(z) et que y = exp(y) et z = exp(z), on aurait y = z, et pour m assez
grand, on aurait um e W,, et vm e W, contrairement au fait que exp est injective
dans W,.

40 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFERENTIELLE ÉLÉMENTAIRES
Cela étant, on peut supposer e assez petit pour que l'image de N(e) par
exp soit un voisinage ouvert V <= U de Y. Si rv : V -♦ Y est la submersion déduite
de la projection n : N(e) -> Y par transport de structure à l'aide de exp, on a
rv ° jv = idY et jv <> rv est homotope à idv (24.2.7), ce qui prouve (24.7.1).
(24.7.2) Pour une distance définissant la topologie de X, soit Um l'ensemble
des x e U dont la distance à Y est < 1/m ; appliquant à chacun des Um le résultat
de (24.7.1), on voit qu'on obtient une suite décroissante (VJ de voisinages ouverts
de Y, telle que f] Vm = Y et que j*,m : H'(VJ H"(Y) soit bijectif pour tout m ;
m
on peut en outre, vu la preuve de (24.7.1), supposer que les « rétractions » rVm
sont toutes restrictions de rVl.
Soient to^ et co2 deux p-formes différentielles définies chacune sur un
voisinage de Y dans X ; comme les Vm forment un système fondamental de voisinages
de Y (3.17.11), il existe un m tel que cot et co2 soient toutes deux définies dans Vm ;
nous dirons qu'elles sont équivalentes s'il existe m telles que coj et co2 aient même
restriction à Vm. Il est immédiat qu'on définit bien ainsi une relation d'équivalence,
dont les classes d'équivalence sont appelées les germes de p-formes différentielles
le long de Y. On définit pour deux germes <bu œ2 la somme + cÔ2 (resp. le
produit Aco, par un scalaire, resp. le produit extérieur w{ a cô2, resp. la
différentielle dcOi) comme le germe d'une forme égale à a>i + co2 (resp. Aco1; resp. coi a co2,
resp. dojj) dans un voisinage où ojt et a>2 sont toutes deux définies ; muni de ces
opérations, il est immédiat que l'ensemble s/'(X, Y) des germes de formes
différentielles est une algèbre différentielle graduée.
On définit alors un homomorphisme u : ^C*(X) -» s/'(X, Y) d'algèbres
différentielles graduées en faisant correspondre à toute forme co€^c'(X) son
germe ta dans s/\X, Y). On a d'autre part une injection canonique
v : <(X - Y) - j/;(X)
faisant correspondre à toute forme de support compact ne rencontrant pas Y
son prolongement par 0 dans Y (24.3.5).
(24.7.3) La suite d'homomorphismes d'algèbres différentielles graduées
(24.7.3.1) 0 <(X - Y) A j/;(X) A j/'(X, Y) 0
est exacte.
Si ta e J2/C'(X - Y), il y a un voisinage Vm qui ne rencontre pas le support
de co, donc co | Vm = 0, ce qui prouve que u ° v = 0. Inversement, si a e .s/c'(X)
est telle que u(ot) = 0, cela signifie que a | Vm = 0 pour un m, et par suite le support
de a est contenu dans X - Vm, donc a e j^c'(X - Y). Enfin, si cô est un germe

7. COHOMOLOGIE D'UNE SOUS-VARIETÉ COMPACTE
41
d'une p-forme différentielle co définie dans un voisinage ouvert w de y, et si /
est une fonction de classe c°° égale à 1 dans un vm et de support compact contenu
dans w, cô est aussi le germe de /co, qui est une forme de st'c{X) quand on la
prolonge par 0 hors de w.
de la suite (24.7.3.1), on déduit donc la suite exacte de cohomologie des
algèbres différentielles graduées (ann. 30.5)
(24.7.3.2) ... ^ hf(x-y) * hcp(x) 4 W(tf\X, y)) - h?+ \X-Y)
(24.7.4) il est clair que si deux formes différentielles définies chacune sur un
voisinage de y dans x ont même germe, elles ont même restriction à y, ce qui
définit un homomorphisme - canonique d'algèbres différentielles graduées
'j : s/\X, y) s/'(Y), et par suite un homomorphisme j* : H'(s/'(X, y)) - h *(y)
des algèbres de cohomologie ; nous allons voir que j* est un isomorphisme.
notons en premier lieu que pour tout m, %m : s/'(W„) -* sf'{Y) se factorise
en s/\W„) -* s/'(X, y) -4 sf\Y), où la première flèche est l'application co -+ cô
faisant correspondre à une forme son germe. on en déduit une factorisation
JZm : htvj - h V(x, y)) 4 h'(y)
en homomorphismes d'algèbres de cohomologie; comme jVm est un
isomorphisme, cela prouve que est surjectif.
soit d'autre part 5 e s/\X, y) un germe tel que dS, = 0 et que |/(5) = dco
pour une forme co e s/'(Y) ; il y a un indice m tel que a soit le germe d'une forme
ae.s/'(vm) telle que da = 0; comme on sait d'autre part (24.7.1) que %m est
surjectif, il existe fi e s/'ÇVm) telle que co = 'jyj.fi), d'où l'on conclut que
'/vm(a — dp) = 0. mais cela signifie que l'image par j'vm de la classe de
cohomologie de a — dfi (qui n'est autre que la classe de a) est nulle. comme j*,m est un
isomorphisme, on en déduit que la classe de a est nulle, donc aussi celle de à,
ce qui prouve que j* est injectif.
on déduit donc de ce résultat et de (24.7.3.2) la suite exacte de cohomologie
(commençant par 0 -» h°(x — y))
(24.7.4.1) ... - hf(x - y) i hf(x) $ h"(y) h?+1(x - y) -> ...
où i : y -* X est l'injection canonique, et d est l'homomorphisme défini de la
façon suivante : si a e h^y), il y a une forme fermée a de classe a qui s'écrit
a = ';'vm(^) pour une forme fi e sfp(Vm), et en multipliant p par une fonction
de ®(vm) égale à 1 dans un voisinage de y, on peut supposer que p e s/p(Wm) ;
on a alors dp e l(Vm - Y) puisque da = 0, et da est la classe dans h?+ *(x - y)
de la restriction à x — y de dp.

42 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
En particulier, on déduit de la suite exacte (24.7.4.1) les corollaires suivants:
(24.7.5) Soit Y une sous-variété différentielle pure compacte de r" de
dimension < n — 1. Alors on a des isomorphismes
IH'(R""Y) = H'"1(Y) P0Uf
(z4. .5. ) | H"(r" - Y) S H"~ *(Y) © r.
Il suffit en effet de prendre X = r" dans la suite (24.7.4.1), puisque
H^r") = {0} pour ; < n et H^r") s r (24.4.6.1).
(24.7.6) Soient X une variété pure de dimension n, Y une sous-variété
différentielle pure compacte de X, de dimension k < n — 1. Alors on a
(24.7.6.1) Hp-Y)sHp) pour fc + 2 < ; < n .
En particulier, si k ^ n — 2 et si X est connexe et orientable, X — Y est connexe.
La relation (24.7.6.1) résulte en effet de la suite exacte (24.7.4.1), puisque
H-*(Y) = {0} pour ; ^ k + 1. La dernière assertion résulte de (24.7.6.1) pour
j = n et de (24.6.3).
(24.7.7) Si Y est «ne variété pure compacte de r", de dimension n — 1, orientable
et ayant r composantes connexes, alors r" — Y a r + 1 composantes connexes.
En effet, H"-'(Y) S H°(Y) = rr par dualité de Poincaré et (24.1.2). La
conclusion résulte de (24.7.5.1) et de (24.6.3).
Remarque (24.7.8). — En fait, l'hypothèse que Y est orientable est inutile,
car on peut montrer qu'une variété compacte pure non orientable de dimension
n — 1 ne peut être plongée dans r" (section 24.37, problème 16).
(24.7.9) Soient X une variété connexe de dimension n > 1, F une partie finie
de r points de X ; alors on a
f H£X — F) = HflX) pour j > 2
(24.7.9.1) | H^X - F) s H^X) © r'-1 si X est compacte
[ HC'(X - F) s H*(X) © rr si X est non compacte.
La première relation est un cas particulier de (24.7.6); les deux autres
résultent de la suite exacte (24.7.4.1)
0 -» HC°(X) - H°(F) -» H^X - F) - HCHX) -+ 0
puisque H°(F) = r', HC°(X) = {0} si X est non compacte et HC°(X) s r si X
est compacte (24.1.2).

7. COHOMOLOGIE D'UNE SOUS-VARIÉTÉ COMPACTE
43
PROBLÊMES
1) Soient X,, X2 deux variétés connexes de dimension n > 2, dont chacune est, soit non
orientable, soit orientable et admettant un difféomorphisme sur elle-même renversant
l'orientation ; la somme connexe X, # X2 est alors définie à un difféomorphisme près (section 16.26,
problème 15).
a) Montrer que pour 2 < p « n - 2, on a H'(X, # X2) s HftX,) © H»(X2) (utiliser
(24.7.9.1)).
b) Montrer que, pour que X, # X2 soit orientable, il faut et il suffit que X, et X2 le soient
(utiliser (24.7.9.1) et le problème 1 de la section 24.6). En déduire que si n à 3, on a
h;-'(X, # x2) s Hr'(X.) © h;-'(x2),
sauf lorsque X, et X2 sont toutes deux non orientables, auquel cas
Hr'(X, # X,)s Hrl(X,)©Hr,(X2)©R.
c) Montrer que si n > 3, on a HC'(X, # X2) S H^X,) © H£'(X2), sauf si X, et X2 sont toutes
deux non compactes, auquel cas on a HC'(X, # X2) s HC'(X,) © H'(X2) © R.
d) On suppose n = 2. Montrer qu'on a H'(X, # X2) S H'(X,) © H'(X2) sauf dans les
cas suivants :
a) Une au moins des variétés X,, X2 est compacte, et toutes deux sont non orientables ;
on a alors
Hcl(X, # X2) s He'(X,) © HC'(X2) © R.
P) Xt et X2 sont non compactes, l'une au moins est orientable ; alors
H£'(X, # X2) s H^X,) © HC'(X2) © R.
y) X, et X2 sont non compactes et non orientables ; alors
XC'(X, # X2) s H^X,) © HC'(X2) © R2 .
e) Déterminer la cohomologie d'une somme connexe X, # X2 # ... # Xk lorsque les Xj
sont l'une des surfaces R2, T2, P2(R) ou le complémentaire d'un point dans P2(R).
2) Soit Y un tore de révolution plongé dans R3, et soit X' la composante connexe non bornée
de R3 - Y. Montrer que l'on a HC°(X') = {0}, HC'(X') s H2(X') = H3(X') s R. (Utiliser le
problème 4 de la section 24.5). Si on considère Y comme plongé dans S3, en déduire la cohomologie
a o
de la composante connexe X' de S3 — Y. Retrouver ce résultat en montrant que X' est difféo-
morphe à la composante connexe bornée de R3 — Y (utiliser une inversion).
3) Montrer que si l'on oriente S._, et S. vers l'extérieur, l'image par l'application
canonique H"" '(S,-,) -* H"(S„) (24.4.1) de la classe fondamentale de S„_, est la classe fondamentale
de S, (avec les notations de (24.4.1), considérer l'application (<J°, z) e/ || z || de U n V sur
S,-, comme composée des deux applications ((°, z) -» ( z/|| z||, i") et pr,, et utiliser la
définition de l'application d donnée dans (24.3.3)).
4) Le plongeaient canonique x -» (x, 0) de R' dans R" = R' x R""p pour p < n définit
par passage aux quotients un plongement canonique T' -> T". Calculer l'algèbre de
cohomologie H^T" - T') et l'algèbre de cohomologie H'(T" - T') (remarquer que
T" — T' = T' x (T""' - {0})).
5) Soit Y une sous-variété compacte de T2, difféomorphe à S, = T. Montrer que, ou bien
T2 - Y est connexe, et alors HC'(T2 - Y) s R, ou bien T2 - Y a deux composantes connexes,
et alors H'(T2 - Y) s R2. Donner des exemples des deux cas. En déduire un exemple d'un ouvert
connexe U dans T2, non homéomorphe à R2 et ayant une frontière régulière homéomorphe à St.

44 xxiv. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
6) Dans R" (n > 2), soit D une partie infinie, discrète et fermée (par exemple un Z' pour
1 < p < n). Montrer que l'espace vectoriel Ht'(R" — D) a une base infinie dénombrable. (Soit (aj
la suite des points de D, et pour chaque m, soit V„ un voisinage ouvert de a„ tel que les V„ soient
deux à deux disjoints. Considérer pour chaque m une fonction /„ 6 @(R") de support dans V„
et égale à 1 dans un voisinage de a„).
7) Soient X une variété compacte, U un ouvert non vide de X. Montrer que l'image de
l'homomorphisme canonique H^U) -> H*(U) (24.1.1.1) est de dimension finie (utiliser le fait que H'(X)
est de dimension finie). En déduire qu'il n'existe aucune variété compacte X contenant un ouvert U,
réunion d'une infinité d'ouverts deux à deux sans point commun et difféomorphes à T" — {0}
pour un n > 2.
8. les théorèmes de brouwer.
(24.8.1) Soient i l'intervalle [0, 1 ] de r, Y le cube produit de r espaces égaux
à i (pour r = 0, on convient que 1° est réduit à un point ). Soit f un homéomorphisme
de Y sur un sous-espace er de S„ pour n > 1. Alors s„ — er n'est pas vide, et l'on a
1 h?(sb
(24.8.u) r™~*!"{»0} pour p<n
1 t«/c £J ^ R
(nous verrons un peu plus loin (24.8.2) que les hypothèses impliquent
nécessairement l'inégalité r < n).
le fait que er ^ sb résulte de ce que Y (donc er) est rétractile, mais non s„
(24.4.1). nous prouverons (24.8.1.1) en plusieurs étapes.
i) pour p = 0, le fait que h^s, - er) = {0} résulte de ce que s„ - er
est un ouvert de s„ dont les composantes connexes sont donc ouvertes dans s„
(3.19.5) et par suite non compactes puisque distinctes de s„ ; on peut donc
appliquer (24.1.2).
ii) pour r = 0, sb - e0, complémentaire d'un point dans s„, est difféo-
morphe à r", donc les relations (24.8.1.1) ne sont autres que (24.4.6.1).
iii) supposons que 1 < p < n et raisonnons par récurrence sur r ^ 1, la
proposition étant donc supposée démontrée pour e,-!. soit a une p-forme
différentielle fermée et de support compact sur l'ouvert non vide s„ - er ; il
s'agit de prouver qu'il existe une (p — informe fi sur s„ — e„ de support compact
et telle que a = dp. pour tout tel, l'application s -* f(t, s) est un
homéomorphisme de sur ep_,(t) = /( {t} x Y~l\ et on a s, - e,_j(t) => sb - er;
donc l'hypothèse de récurrence implique qu'il existe une (p — l)-forme P, sur
s„ — er_!(t), de support compact et telle que a = dp,. en vertu de la continuité
uniforme de / dans Y, il existe par suite un voisinage j, de t dans i tel que
/(j, x i,_1) ne rencontre pas le support de p,. cela étant, il existe un nombre
p > 0 tel que tout intervalle de longueur ^ p contenu dans i soit contenu dans
l'un des intervalles j, (3.16.6). soit m un entier tel que l/m < p, et considérons
L m mj
dans i les intervalles fermés ht = , — pour 1 < k ^ m, et les images

8. LES THÉORÈMES DE BROUWER 45
(24.8.2.1)
h'(s„
hî+1(s„
h;(s„
h;(s„
ErJk = /(Ht x Ir_1) ; ce qui précède montre que pour 1 ^ k < m, il existe une
(p — Informe fik sur S„ - Erk, de support compact et telle que a = dfik. Par
récurrence sur k, il est clair que l'on est ramené à prouver le lemme suivant :
(24.8.1.2) Soient J', J" deux intervalles fermés contenus dans I et tels que
J'n J" = {t}, et soient E' = f(J' x I'"1), E" = f(J" x I'"1). Supposons qu'il
existe deux [p — Informes fi', fi" sur S„ — E', SB — E" respectivement, de supports
compacts et tels que a = dp" = dfl"; alors il existe une (p — 1)-forme fi sur
S„ — (E' u E") de support compact et telle que a = dfi.
Posons U' = S„ - E', U" = S„ - E", de sorte que U' n U" = S„ - (E' u E")
et U'uU" = S, - Er_!(t). On a la suite exacte de Mayer-Vietoris (24.3.7.2)
0 - Hf(U' n U") -» H?(U') 0 Hf(U")
puisque H£-I(S„ - Er_i(r)) = {0} par l'hypothèse de récurrence. Si alors a
est la classe de cohomologie de a dans HP(U' n U"), ses images dans Hf(U')
et Hf(U") sont nulles par hypothèse ; donc a = 0, ce qui prouve le lemme et
démontre les relations (24.8.1.1) pour p < n.
IV) Pour achever la démonstration, il suffit, en vertu de (24.6.3.1), de
montrer que si a est une n-forme de support compact sur S„ — Er telle que j"a = 0,
il existe une (n — Informe fi sur S„ — Er, de support compact et telle que a = dfi.
Le raisonnement est le même que dans III), et on est ramené à prouver le même
énoncé que (24.8.1.2) avec p = n et l'hypothèse j"a = 0; la démonstration est
sans changement, vu qu'on a encore H|!-1(S„ - Er_!(t)) = {0} par III).
CQFD.
Compte tenu de (24.6.3.1), on voit que S„ — Er est toujours connexe.
(24.8.2) Soit f un homéomorphisme de Sr sur un sous-espace L, de Sm pour n ^ 1.
Alors
(i) On a nécessairement r < n, et pour r = n, on a ZB = S„.
(ii) Pour r < n, S„ — Zr n'est pas vide, et l'on a
Zr) = {0} sip<netpïr+l
Ï,)SR si r < n - 2
£r) = R si r^n-2
E„-i)sR2
La sphère Sr étant définie par l'équation (i0)2 + (ej1)2 + ... + («H2 = 1
dans Rr+1, est réunion des deux hémisphères fermés Dr+ et D,-, intersections
de Sr avec les demi-espaces définis respectivement par Ç° ^ 0 et <j° < 0. La

46 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
projection stéréographique de pôle — e0 (resp. e0) (16.2.3) transforme Dr+
(resp. Dr") en la boule fermée B : || x || < 1 dans Rr, et l'application x -* A(x)x,
où A(x) = ( sup | | )/|| x ||, est un homéomorphisme de B sur Ir. Les résultats
de (24.8.1) sont donc applicables en remplaçant Er par D* ou D~. Appliquons
la suite exacte de Mayer-Vietoris (24.3.7.2) aux ouverts Ut - S„ - Dr+ et
U2 = S„ - D", qui sont tels que U1nU2=S,- Zr et Ut u U2 = S, - Zr_ „
en désignant par ZP_, l'image par / de Sr_j = Dr+ n Dr-. En vertu de (24.8.1),
l'hypothèse entraîne que et U2 sont non vides; si l'on suppose de plus que
S„ — Zr est non vide, on a donc les suites exactes
(24.8.2.2) 0 -» H?(S„ - £,_,) - H? +1(S„ - Zr) - 0 pour p^n-2
(24.8.2.3) 0 - HT\S.- Zr_x) -* WC(S„ - Zr) -+ R2 -+ HRS^-E,-,)-.0.
Distinguons deux cas suivant que r < n — 1 ou r = n.
A) Supposons que 0 s% r < n - 1 et prouvons les relations (24.8.2.1) par
récurrence sur r. Pour r = 0, Z0 est formé de deux points, donc S, - Z0 est
difféomorphe à R" — {0}, et les relations (24.8.2.1) ne sont autres que celles
de (24.7.8). Supposons maintenant ces relations vérifiées pour r ^ n — 2 ; la
troisième de ces relations montre que SB — Zr est connexe (24.6.3), donc S„—Zr +,
ne peut être vide : en effet, on a déjà remarqué que S„ - Dr++1 et SB — Dr~+1
sont des ouverts non vides de Sm et si leur intersection était vide, leur réunion
S„ - Zr ne serait pas connexe. On conclut donc de (24.8.2.2) que HP+^S,,- Zr+1)
est isomorphe à HP(S„ — Zr) pour p ^ n — 2 ; l'hypothèse de récurrence montre
alors que les deux premières relations (24.8.2.1) sont vérifiées lorsqu'on y
remplace r par r + 1. Si r ^ n - 3, la relation (24.8.2.3) donne la suite exacte
0 -» H;(S„-Zr+1) - R2 -> R - 0
d'où l'on déduit la troisième relation (24.8.2.1) où r est remplacé par r + 1.
Si au contraire r = n — 2, la relation (24.8.2.3) donne la suite exacte
0 - R - H;(S„ - - R2 R - 0
d'où l'on déduit la quatrième relation (24.8.2.1).
B) Supposons r = n, et raisonnons par l'absurde, en supposant S„ - Z„
non vide. Pour r = n, la suite exacte (24.8.2.3) donnerait une suite exacte
0 -» HC"(S„ - ZJ - R2 - R2 - 0, donc H?(S„ - Z„)={0},
ce qui est absurde (24.6.3) ; on a donc nécessairement S„ = Z„, et cela prouve
aussitôt qu'un homéomorphisme / de Sr sur un sous-espace de S„ ne peut exister
pour r > n.
(24.8.3) (Théorème de Jordan-Brouwer) Soit f un homéomorphisme de S„_i

8. LES THÉORÈMES DE BROUWER
47
sur un sous-espace £„_, de S„, pour n > 1. Alors S„ — a deux composantes
connexes, qui ont toutes deux 'LH-l comme frontière.
Le fait que S„ — !„_! ait deux composantes connexes résulte de la dernière
relation (24.8.2.1) et de (24.6.3). Si Ul3 U2 sont ces composantes, la frontière
de chacun de ces ensembles ouverts est évidemment contenue dans £„_i. Il
reste à voir qu'inversement tout point xel.n-i est point frontière de Uj et U2,
ou encore que tout voisinage ouvert V de x rencontre à la fois et U2. Soit
*' = f~l(x)eS„-i ; comme /_1(v) est un voisinage ouvert de x' dans S„-i,
il existe dans S,-! une boule ouverte B' de centre x" contenue dans /-1(V),
de sorte que son complémentaire C dans SB-i est homéomorphe à I"-1 ;
l'ensemble E„_ i = /(C) c £„_! est donc homéomorphe à I"-1 et B = /(B') est
un voisinage ouvert de x dans I„_,, complémentaire de E„_, et contenu dans V.
Il résulte de (24.8.1.1) que Hnc(SH - E„_t) s R, donc l'ouvert S„ - E,., est
connexe (24.6.3). Soient alors yt e Uu y2 e U2 ; il résulte de (16.26.10) qu'il existe
une application continue g de I dans S„ — E,-! telle que g(Q) = yu g(l) = y2.
Mais comme yt et y2 sont dans des composantes distinctes de S„ — £„_!,
l'ensemble g(l) nï,.! est fermé et non vide (3.19.9). L'ensemble fermég_1(g(I)nSB_,)
dans l'intervalle I est donc fermé non vide ; soient tt et t2 sa borne inférieure et
sa borne supérieure ; comme g(0) = yt e Ub on a g([0, t, [) c et lorsque t
tend vers t^ par valeurs < tx, g(t) tend vers git^eZn-i n V; de même, comme
g(l) = y2eU2, on a gi]t2, 1]) c U2 et lorsque t tend vers t2 par valeurs > t2,
g{t) tend vers g(t2)eI,.,nV,ce qui achève la démonstration.
(24.8.4) Soit f un homéomorphisme de Sn-i sur un sous-espace de R",
pour n ^ 2. Alors R" — a deux composantes connexes, qui ont toutes deux
2Zn-i comme frontière.
En effet, comme R" s'identifie au complémentaire d'un point dans S„, il
suffit de remarquer, avec les notations de (24.8.3), que si x0e\Ju U, - {x0}
est connexe puisque n > 2 (24.7.6).
Comme IB_j est contenu dans une boule fermée de R", dont l'extérieur
est connexe, on voit qu'une des composantes connexes de R" — £„_ i est bornée
et l'autre non.
(24.8.5) (Brouwer) Pour m > n, il n'existe pas d'application continue injective
d'un ouvert non vide de Rm sur un sous-espace de R" (invariance de la dimension).
En effet, en considérant une boule fermée contenue dans l'ouvert en
question, on en déduirait un homéomorphisme deSm_! sur un sous-espace compact
de R" (3.17.12), qui peut être considéré comme sous-espace compact de S„,
distinct de S,, puisque R" s'identifie au complémentaire d'un point dans S,.
Mais cela contredirait (24.8.2) puisque m — 1 > n.

48. XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
(24.8.6) Pour n ^ 2, soit f un homéomorphisme de la boule fermée B„ : || x || < 1
o
de R" sur un sous-espace de R" ; alors l'image par f de la boule ouverte B„ est la
composante connexe bornée de R" — /(S„_i).
Si l'on considère R" comme le complémentaire d'un point x0 dans Sw
l'ouvert S„ - /(B„) est connexe par (24.6.3), puisque B„ est homéomorphe à I" et
par suite Wc{Sn - /(B,)) s R (24.8.1.1); comme x0i /(B„) et que n > 2, on en
déduit que R" - /(B„) est aussi connexe (24.7.6). L'ouvert R" - /(B„) étant non
borné, il est contenu dans la composante connexe non bornée de R" — /(S,,, i) ;
par suite, si A est la composante connexe bornée de R" — /(S„_ t), on a A c /(B,),
et comme /(B„) = /(B,) u f(Sn-i) et que /(B„) n /(S,-,) = 0, cela entraîne
O O o o
A cz f( B„). Mais comme BB est connexe, il en est de même de /( B„), donc A=/( B„)
par définition d'une composante connexe.
(24.8.7) (Brouwer) Pour n ^ 2, soit U un ouvert connexe non vide dans R".
Si f est une application continue injective de U dans R", /(U) est ouvert dans R"
et f est un homéomorphisme de U sur /(U) (invariance du domaine).
Il suffit de montrer que pour tout x 6 U, et tout voisinage V de x dans U,
/(V) est un voisinage de f(x) dans R" ; or, si B est une boule fermée de centre x
contenue dans V, la restriction de / à Best un homéomorphisme sur /(B)(3.17.12),
o
donc /(B) est ouvert dans R" en vertu de (24.8.6).
PROBLÈMES
1) Soient X et Y deux variétés pures de classe C° et de dimension n (section 16.1, problème 2),
/: X -» Y une application continue et localement injective, c'est-à-dire telle que tout xeX
possède un voisinage ouvert tel que la restriction de / à cet ouvert soit injective. Montrer que pour
tout ouvert U c X, /(U) est ouvert dans Y.
2) Soient X, Y deux variétés pures de classe C°, de dimensions respectives m et n.
a) Montrer que si m > n, il n'existe pas d'application continue localement injective
(problème 1) de X dans Y. En particulier, une variété de classe C° ne peut être à la fois de dimension m
et de dimension n.
b) Montrer que si m < n, et si/: X -> Y est une application continue injective de X dans Y,
l'intérieur de /(X) est vide.
9. Degré d'une application.
(24.9.1) Soient X, Y deux variétés différentielles connexes, compactes, orientées
et de même dimension n ; les espaces de cohomologie H"(X) et H"(Y) sont donc
tous deux isomorphes à R (24.6.3). En outre (24.6.3.1) rappelons qu'on a deux
isomorphismes canoniques ix : H"(X) -► R, iY : H"(Y) -* R, déduits par passage

9. DEGRÉ D'UNE APPLICATION
49
aux quotients des applications linéaires ot->Jaet/?-»j/?de 2„{X) et $>„{Y)
dans R. Considérons alors une application / : X -♦ Y de classe C00, et
l'application linéaire correspondante /* : H"(Y) -♦ H"(X) (24.1.3). Il lui correspond
donc une application linéaire de R dans lui-même
(24.9.1.1) ix°f*°iyl - t ^ et.
Le nombre réel c ainsi déterminé est appelé le degré de f et noté deg /. Il résulte
de la définition de /* (24.1.3) et des définitions précédentes de ix et iY que, pour
toute n-forme différentielle co sur Y, de classe C°°, on a
(24.9.1.2) jV(co) = deg /. j\o .
On notera que le degré de / dépend des orientations choisies sur X et Y ;
si l'on remplace l'une de ces orientations par son opposée, deg / change de
signe (16.24.4).
(24.9.2) (i) Si f : X -> Y est un difféomorphisme, on a deg f = + 1 si f
préserve l'orientation, deg f = — l si f renverse l'orientation.
(ii) Si f : X -» Y et g : X -» Y sont homotopes de classe C00, on a
deg / = deg g.
(iii) Soit Z une troisième variété connexe, compacte, orientée et de
dimension n. Pour tout couple d'applications / : X -» Y, g :Y -> Z de classe C°°,
°n ° deg(g°f) = deg g.deg /.
L'assertion (i) résulte de (24.9.1.2) et de (16.24.5.1) ; l'assertion (iii) résulte
de (24.9.1.2) et de ce que '(go f) = 'f °'g; enfin (ii) résulte de la définition du
degré et du théorème d'invariance par homotopie (24.2.5).
(24.9.3) Nous allons voir que le degré d'une application est toujours un entier
(positif ou négatif), en en donnant une autre expression. Pour cela, considérons
une valeur régulière b e Y de / qui existe en vertu du théorème de Sard (16.23.1) ;
en tout point xe f~l(b), f est une submersion, et comme les dimensions de X
et Y sont égales, l'application linéaire tangente TJf) est bijective ; par suite, il
existe un voisinage ouvert connexe Ux de x dans X tel que la restriction de /
à Ux soit un difféomorphisme de Ux sur un voisinage ouvert Vx de b (16.7.4).
Le point x est donc isolé dans f~l(b); l'espace f~l(b) est par suite discret, et
comme il est compact, il est fini (3.16.3). Si f~l(b) n'est pas vide, nous poserons,
pour tout xe f~l(b), e(x) = 4- 1 si la restriction de / à Ux préserve
l'orientation, e(x) = — 1 dans le cas contraire. On a alors le résultat suivant :

50 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
(24.9.4) Soit beY une valeur régulière (16.23) pour r application f ' : X -> Y.
(i) SibtfOQ, o«fldeg/ = 0.
(ii) Si be f(X), et si xx, xr sont les points de f~l(b), on a
(24.9.4.1) deg/= £**,).
(i) Comme /(X) est fermé dans Y, il y a une n-forme co sur Y, de support
dans un voisinage de b ne rencontrant pas /(X) et telle que co # 0. Comme
'/(co) = 0, on a deg / = 0 par (24.9.1.2).
(ii) Pour chaque indice j, soit Uj un voisinage ouvert de x} tel que la
restriction de / àUj soit un difféomorphisme sur un voisinage ouvert f(Uj) de b;
on peut en outre supposer les r ensembles U, deux à deux disjoints. Si A est le
complémentaire de la réunion des U, dans X, /(A) est compact et b$/(A);
il y a donc un voisinage ouvert V de b ne rencontrant pas /(A) et par suite
/-1(V) c \J\Jj. Si l'on prend V contenu dans tous les /(U,), /_1(V) est donc
j
réunion disjointe des Wy = Uy n /-1(V) et la restriction de / à chaque Wj est
un difféomorphisme de W, sur V. Soit co une n-forme de classe C" sur Y, de
support contenu dans V et telle que j* co = 1 ; on a donc par (24.9.1.2)
deg/= f'/(co) = Z f '/(co) ;
Jx j JV/j
mais par (16.24.5.1), on a '/(co) = t{x}) co = e(xj). CQFD.
JV/ Jv
(24.9.5) Exemples. — I) Prenons X = Y = S„ ; on a vu que pour une
transformation orthogonale s e 0(n + 1, R), 's(o) = (det s)a pour la forme angle solide o
(16.20.10) ; on a donc deg s = det s. En particulier, la symétrie x -» — x a un
degré (- 1)"+1.
II) Prenons X = Y = S,, identifié au cercle unité U : | z | = 1 de C ; toute
application / de classe C00 de U dans lui-même s'écrit e" -+ eim, où t e R et ^
est une application de classe C00 de R dans lui-même telle que \p(t + 2n)=ip(t)+2nn
pour un entier n e Z et tout t e R (9.8.1). Pour calculer deg /, on applique la
formule (24.9.1.2) en prenant pour co la 1-forme restriction à U de dz/z, dont
l'image réciproque par l'application <p : t -> e" est idt ; '/(co) a donc pour image
réciproque par (p la forme i^f'(t)dt, et on a co = 2ni, '/"(co) = 2wti, d'où
Ju Ju
deg / = n, qui n'est autre que Yindice j(0 ; y) du chemin t -* défini dans
[0, 2n] (9.8.2).

9. DEGRÉ D'UNE APPLICATION
51
III) Soient f, g deux applications de classe Cœ de S„ dans S„ telles que
fi*)^ — g(x) pour tout xeS„. Montrons que f et g sont homotopes, et par
suite deg / = deg g. En effet, considérons la fonction
Fïtxlr- + (!-*>/(*>
||rg(x) + (l -r)/(x)|f
Comme pour /(x) ?t — g(x) la droite joignant /(x) et g(x) ne passe jamais par
l'origine de R"+1, on voit que F est définie pour tout couple [t, x)e [0, 1] x S„
et est une homotopie de f à g.
En particulier, si /(x) — x pour tout xeS„, on a deg / = 1, et si /(x)#x
pour tout xeSm on a deg / = (— 1)"+1.
IV) Supposons que l'application / : X -> Y ait un degré ^ 0 ; alors
l'homomorphisme canonique /* : H'(Y) H'(X) est injectif. En effet, soit a une
p-forme fermée sur Y telle que la classe de cohomologie de '/(a) soit nulle; il
s'agit de voir qu'il en est de même de la classe de cohomologie a de a. Or, pour
toute (n — p)-forme p sur Y, on a, en appliquant (24.9.1.2) à la n-forme co = a a p,
(24.9.5.1) deg /.J\* a /? = JV(«) a '/(/?)
et comme '/(a) = dy pour une (p — l)-forme y sur X par hypothèse, le second
membre de (24.9.5.1) est nul pour toute forme fermée P ; en effet, co = '/(/?) est
alors une (n — p)-forme fermée sur X, et on a
dy a co = d(y a co) — (— l)p_1y a dco = d(y a co)
puisque dco = 0 ; mais on sait que I d{y a co) = 0 (17.15.5.1). La relation
r Jx
I a a fi = 0 pour toute forme j8eZ"-'(Y) signifie que DYa = 0 (24.6.1) et en
vertu de la dualité de Poincaré (24.6.2), on a bien a = 0.
En particulier, il ne peut exister d'application f de classe C00 de S„ dans
une variété compacte, connexe et orientable X de dimension n, telle que deg / # 0,
que si l'on a H"(X) = {0 } pour 1 s; p < n - 1.
V) Soit X une variété connexe, compacte, orientée et de dimension n.
Montrons que, pour tout entier m e Z, il existe une application f : X -> S„ de
classe C00 telle que deg f = m.
Munissons X d'une orientation, et considérons | m \ points distincts a,,aw
de X puis pour chaque indice 7, un voisinage ouvert U, de dans X tel que les
adhérences U,- soient deux à deux disjointes, et qu'il existe un difféomorphisme gj
de Uj sur R", préservant (resp. renversant) l'orientation si m ^ 0 (resp. m < 0);

52 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
nous supposerons en outre que gjlcij) = 0. Considérons d'autre part la
projection stéréographique q>2 : S„ - { - e0} -* R" de pôle - e0 (16.2.3) ; pour
chaque j, l'application q>2l°g) est donc un difféomorphisme de U, sur S„ - {- e0},
et si nous munissons S„ de l'orientation telle que <p2 préserve les orientations,
chacun des difféomorphismes <p21 ° gj préserve (resp. renverse) l'orientation
si m 5= 0 (resp. m < 0).
On a d'autre part le lemme suivant :
(24.9.5.2) Pour tout voisinage V de e0 dansSm il existe une application \j/ : S„ -» S„
de classe C00, homotope à Videntité, telle que i^(z) = z dans un voisinage de e0
contenu dans V, et i/f(z) = — e0 pour tout zeSB — V.
Si nous appliquons ce lemme à un voisinage V ne contenant pas — e0, on
voit que chacune des applications fj = \j/ ° <p2l o gj de Uj dans S„ est telle que
fj{aj) = e0 et qu'il existe un voisinage Wj de aj tel que Wj <= U, et que fj{x)= —e0
pour xeVj - W,. Il y a donc une application / : X -+ S„ de classe Cœ, qui
coïncide avec fj dans chaque Uj et est égale à — e0 dans X — I [j U71. Comme
/ Heo) = {au a2> • • •> a\m\}. il résulte du choix des gj et de (24.9.4) que l'on
a deg f = m.
Reste à prouver le lemme (24.9.5.2). Il existe e > 0 tel que e < ^ et que,
pour un point z = (Ç°, C1, • • - , C") de SB <= R"+1, la relation £° > 1 - 2s entraîne
z g V ; soit A une application de classe C00 de R dans [0, 1 ], égale à 1 pour t < 1 — 2e,
à 0 pour t ^ 1 — 6 ; on vérifie aussitôt que la fonction
répond à la question (en remplaçant X par sX, où 0 < s ^ 1, on définit l'homo-
topie cherchée).
(24.9.6) Soient X, Y deux variétés différentielles compactes, connexes,
orientées et de même dimension n ; de même que dans (24.2.8), on peut étendre la
définition du degré à une application / : X -> Y supposée seulement continue.
En effet, si d est une distance définissant la topologie de Y, il existe e > 0 tel
qu'il y ait des applications u : X -» Y de classe C00 pour lesquelles d(f (x), u(x)) ^ e
pour tout xeX, et deux quelconques de ces applications sont homotopes de
classe C00 ; le nombre deg u ne dépend donc que de / et on dit encore que c'est
le degré de / noté deg / Si /i : X Y est une seconde application continue
de X dans Y, homotope à / il résulte de (16.26.6) que deg /, = deg / Enfin,
soit Z une variété compacte, connexe, orientée et de dimension n, et soit
g : Y -+ Z une application continue ; si (t, x) -* F(t, x) (resp. (t, y) G(t, y))
(1 - A(C°))z - A(C°)e0
||(1 -A(C°))z-A(C0)eoll

9. DEGRÉ D'UNE APPLICATION
53
est une homotopie de / dans une application u : X -» Y de classe C00 (resp.
de g dans une application v : Y -* Z de classe Cœ), il est clair que
(t, x) -» G(t, F(t, x)) est une homotopie de g° / dans eu, donc on a encore
deg (g o/) = deg g. deg /
On notera aussi que la conclusion de l'exemple III) de (24.9.5) subsiste
sans modification lorsqu'on suppose seulement f et g continues.
(24.9.7) Applications : I. Théorèmes de points fixes.
(24.9.7.1) (Brouwer) (i) Pour toute application continue f de la sphère S„ dans
elle-même telle que deg / # (- l)n+1, il existe xeS„ tel que f(x) = x.
(ii) Pour toute application continue f de la boule fermée B„: ||x|| < 1
de R" dans elle-même, il existe xeB„ tel que /(x) = x.
(i) Compte tenu de (24.9.6), on a déjà vu dans (24.9.5, III) que si /(x) # x
pour tout xeS„, on a deg f = {— 1)"+1.
(ii) Raisonnons par l'absurde en supposant que /(x) ^ x pour tout x e B„ ;
/(x) - x
alors l'application x -» g(x) = -— de B„ dans S„_j serait définie et
Il /(x) — x ||
continue dans B„. Montrons d'abord que la restriction gj :S„^i -» SH-X de g
à S„_i est de degré 0. En effet, l'application (t, y) -» g{ty) de [0, 1] x S„-,
dans S„_! est une homotopie de gx dans l'application constante g0 '■ y -» g(0).
D'autre part, l'application
F:(,,y) <'-»'<>"->
1(1 -<)/(/)-» Il
est définie et continue dans [0, 1] x S„_i ; en effet, pour 0 < t < 1, on a
(1 - f)_1y^B„, et pour t = 0, F(0, y) = gj(y); comme F(l, y) = - y, on
déduirait de (24.9.6) que deg g, = (- 1)"; la contradiction ainsi obtenue prouve la
proposition.
(24.9.7.2) (Brouwer) Pour tout champ de vecteurs continu X sur une sphère S„
de dimension paire, il existe x e SB tel que X(x) = 0.
Supposons le contraire; pour tout xeS„cR"+1, considérons l'espace
tangent TX(S,,) comme plongé canoniquement dans TX(R"+1) (16.8.6), de sorte
que X'(x) - t„(^(x)) est un vecteur 0 de Rn+1, orthogonal au vecteur x
^puisque JW = 0 dans S^. Posons /(x) = X'{x)/\\ X'(x) ||, de sorte
que / est une application continue de S„ dans elle-même telle que (x | /(x)) = 0.
Ceci implique en particulier que /(x) ^ x et f(x) # — x pour tout xeS„;
mais alors (24.9.5, Exemple III), deg / serait à la fois égal à 1 et à ( - 1)"+1 = -1,
ce qui est absurde.

54 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFERENTIELLE ÉLÉMENTAIRES
Par contre, pour n impair, il est facile de définir sur S„ un champ de
vecteurs X de classe C00 tel que X(x) # 0 pour tout xeS„ (problème 21).
(24.9.8) Applications : II. L'intégrale de Kronecker.
Soient X une variété différentielle compacte, connexe, orientée et de
dimension n — 1 ^ 1, et soit / une application de classe C00 de X dans R" - {0}. Sip est
la surjection z -» z/|| z || de R" — {0} sur S„_ u p ° f est donc une application
de classe Cx de X dans Sn-x. Orientons S„_i vers l'extérieur; alors, pour toute
(n — l)-forme différentielle œ sur Sn-U on a d'après (24.9.1.2)
Si nous prenons pour eu la forme « angle solide » <r(" u sur S„_ j (16.24.7), on a
donc pour expression du degré de p ° f l'intégrale de Kronecker
où t(b) est la (n - l)-forme VKct("-1)) sur R" - {0}. Il est facile d'avoir
l'expression explicite de cette forme : en effet, elle est invariante par les
rotations de SO(n, R) et, par définition (16.20.8.3), au point te, de R" - {0} (avec
t > 0) elle a une expression qui peut s'écrire - tg(t)aX2 a dÇ3 a ... a dÇ",
où g est une fonction de classe C00 dans R+ - {0} ; compte tenu de l'expression
de la forme o0 (16.21.10.1), cela s'écrit aussi g(t)a0(t), et comme la forme a0 est
invariante par rotation, on voit que l'on peut écrire t(b)(z) = g(r(z))o-0(z) pour
tout zeR" - {0}, avec r[z) = ( ^(Ç1)2) . D'autre part, comme dtr("-1) = 0
v-1 /
puisque S„_ t est de dimension n — 1, on a aussi dx(n) = 'p(da{n~l)) = 0 ; comme
la définition de tr0 (16.21.10.1) montre que da0 = nv, on a
en utilisant encore la définition de a0. On a donc pour g l'équation différentielle
g'(t) + ng(t)=0, d'oùg(t) = c/f" où c est une constante. Mais sij : S„_ j -+ R" - {0}
est l'injection canonique, p°j est l'application identique de Sn_1; donc
'/(t00) = tr("-1), ce qui implique c = 1. Finalement on a l'expression
(24.9.8.1)
1
(24.9.8.2)
r"(z)
qui donne l'expression explicite de l'intégrale de Kronecker.

9. DEGRÉ D'UNE APPLICATION
55
(24.9.9) Applications : III. Le nombre d'entrelacement.
Soient X, Y deux sous-variétés différentielles compactes, connexes et
orientées dans R". On suppose que X n Y = 0 et que dim X + dim Y = n — 1, de
sorte que X x Y, muni du produit des orientations de X et Y (16.21.5) est une
variété compacte, connexe, orientée, de dimension n — 1. En outre l'hypothèse
X n Y = 0 entraine que
/ : (x, y) y - x
est une application de classe C00 de X x Y dans R" — {0}. Avec les notations
de (24.9.8), le nombre entier
(24.9.9.1) entrel(X, Y) = deg(/> o /)
est appelé le nombre d'entrelacement de X et Y ; il peut donc se calculer par une
intégrale de Kronecker. On a
entrel(Y, X) = (- l)(1+d,mX)<1+dlmY)entrel(X, Y)
comme il résulte de (16.21.5), (24.9.2, (i)) et l'Exemple I de (24.9.5). Soient X', Y'
deux autres sous-variétés de R" telles qu'il existe des homotopies
F : [0, 1 ] x X - R", G : [0, 1 ] x Y - R"
F(0, .) (resp. G(0, .)) étant l'application identique de X (resp. Y), F(l, .) (resp.
G(l, .)) un difféomorphisme de X sur X' (resp. de Y sur Y') préservant
l'orientation; on suppose en outre que l'image de X par F(t, .) ne rencontre pas celle
de Y par G(t, . ) pour aucun t e [0,1 ]. Alors il résulte de (24.9.2, (ii) et (iii)) que
l'on a
entrel(X, Y) - entrel(X', Y').
Exemples (24.9.9.1). — Dans R3, considérons deux courbes X, Y sans point
commun situées dans un même plan ; alors entrel(X, Y) = 0, car l'image de X x Y
par l'application p° f est contenu dans un grand cercle de S2, et par suite p ° f
n'est pas surjective, d'où la conclusion (24.9.4, (i)).
Au contraire, prenons pour X le cercle x\ + x\ — 1 = 0, x3 = 0, pour Y le
cercle (xx - l)2 + x\ — 1, x2 = 0. L'image réciproque par p o f du vecteur
- e, eS2 est réduite au seul point (e,, 0) de X x Y, et le calcul des dérivées
partielles de y — x montre que p ° f est une submersion en ce point ; on a donc
entrel(X, Y) = ± 1 suivant les orientations choisies (24.9.4, (ii)).
Si deux courbes sans point commun X, Y dans R3 sont telles que
entrel(X, Y) # 0, il n'existe donc pas de couple d'homotopies (F, G) du type
décrit plus haut, tel que X' et Y' soient dans un même plan ; mais cette condition
suffisante n'est pas nécessaire.

56 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
PROBLÊMES
1) Soient X une variété pure de dimension n, U un ouvert relativement compact dans X,
/ une application continue de U dans S„, z un point de S. n'appartenant pas à l'image /(Fr(U))
de la frontière (compacte) de U dans X. Montrer qu'il existe une application continue F : X -«S.,
prolongeant/et telle que z n'appartienne pas à F(X — U) ; en outre, si F, : X -> S„ est une seconde
application continue prolongeant / et telle que z n'appartienne pas à F,(X - U), F et F, sont
homotopes. (Soit h un homéomorphisme de S. — { z } sur R". Appliquer le théorème de Tietze-
Urysohn (4.5.1) à la partie fermée Fr(U) de X - U et à l'application h°fàe Fr(U) dans R").
2) Soient U un ouvert de S,,/une application continue de U dans S„. z un point de S.
n'appartenant pas à /(Fr(U)). On pose d(f, U, z) = degF, où F est un prolongement de / à S. tel que
z n'appartienne pas à F(S„ — U) (problème 1); ce nombre ne dépend que de /, U et z et non du
prolongement F choisi.
a) Montrer que si z i /(U), on a d(f, U, z) = 0.
b) Si j : U -+ S, est l'injection canonique, montrer que d(j, U, z) =0 si z i U et d(j, U, z) = 1
si z 6 U.
c) Soient /„, ft deux applications continues de U dans S„ ; on suppose qu'il existe une
homotopie «P ; U x [0, 1 ] -♦ S„ de fQ à /, et que z e S„ n'est pas de la forme <D(x, t) pour un x 6 Fr(U)
et t e [0, 1 ]. Montrer que d(f0, U, z) = d(/„ U, z).
d) Soient f,ft deux applications continues de U dans S, telles que, si S est la distance rieman-
nienne canonique sur S„, on ait ci(/(x),/,(x)) < s pour tout xeU, où e est un nombre tel que
0 < e < jt. Montrer que si z eS„ est tel que ô(f(x), z) > e pour tout x e Fr(U), on a
d(/,U, »)-*/„ U.z).
(Utiliser c), en prenant <t> telle que <b(x, t) appartienne à l'arc de grand cercle < ît joignant f(x)
et/,(*)).
e) Pour toute application continue/de U dans S„, montrer que l'application z -» d(f, U, z)
est constante dans chaque composante connexe de S» — /(Fr(U)). (Comparer d(f, U, z) et
d(r ° /• U, z), où r est une rotation assez voisine de l'identité).
3) Soient U un ouvert de S„, (U;) une suite (finie ou non) d'ouverts deux à deux disjoints
contenus dans U, / une application continue de U dans S., z un point de S. n'appartenant pas
à l'image par /de U - (J U,.
s
a) Montrer que / ~ '(z) n U, = 0 sauf pour un nombre fini de valeurs de j (raisonner par
l'absurde).
b) Montrer que d{f, U, z) = £d(/ Uj, z). (Se ramener au cas où les U; sont en nombre fini,
puis au cas où /est la restriction à U d'une application de classe C°°, en utilisant (16.26.5) ; enfin
se ramener au cas où f''(z) est un ensemble fini, en utilisant le problème 2e)).
4) Soient U un ouvert de S„, / une application continue de U dans S„, (A;) la famille des
composantes connexes de S. - /(Fr(U)) ; on note d(f, U, Aj) la valeur commune des nombres
d(f, U, y) pour y e A; (problème 2 e)). Soit g une application continue de S. dans S., et supposons
que z e S. soit tel que g' '(z) ne rencontre pas /(Fr(U)). On se propose de montrer que l'on a
d(g » /, U, z) = I d(f, U, Aj)d(g, Aj, z).
J
a) Montrer qu'on peut se ramener au cas où g est une application de classe C".
b) Montrer que g" '(z) n A; = 0 sauf pour un nombre fini de valeurs de j.
c) Pour tout j tel que At n g' '(z) / 0, soit V} un voisinage ouvert de Aj o g' '(z) tel que

9. DEGRÉ D'UNE APPLICATION
57
Vj a At. Montrer qu'il existe une application /, de U dans S„ restriction d'une application de
classe C", homotope à /, et telle que pour tout j tel que Aj n g' '(z) # 0, on ait
d(f,U, Aj) = d(fu U,Vj).
d) Montrer qu'il existe y arbitrairement voisin de z, tel que g~'(y) soit contenu dans la
réunion des V,, et que g"'(y) et /"-1(g~l(y)) soient des ensembles finis (utiliser le fait que si E est
l'ensemble des points critiques de / restreint à U, E, l'ensemble des points critiques de g, g(E,)
et #(/(E)) sont négligeables (section 16.22, problème 1 c))).
5) Soit A une partie non vide de R" ; on dit qu'une application <p de A dans R" est admissible
si elle est continue et si l'application x -» cp(x) — x de A dans R" est bornée.
a) Soit h : S, - { •„ } R" la projection stêréographique de pôle e0 (16.2.3), et soit As la
réunion de h''(A) et de {e0}. Montrer que, pour que <p soit admissible, il faut que
l'application /r'°<p°nden~ '(A) dans S. se prolonge en une application continue cps de As dans S. telle
que <ps(eo) = e0.
b) Si A est compact, toute application continue de A dans R" est admissible.
c) Montrer que toute application admissible d'un ensemble fermé A dans R" se prolonge
en une application admissible de R" dans lui-même.
d) Montrer que toute application admissible d'un ensemble fermé A dans R" est propre
(section 17.3.7).
e) Si <f est une application admissible de A c R" dans R" et ip une application admissible
de <p(A) dans R", (/» » <p est une application admissible de A dans R". Si <p est un homéomorphisme
de A sur <p(A), (p~* est admissible.
6) Les notations étant celles du problème S, on suppose A ouvert dans R". Si q> est une
application admissible de A dans R", et si z e R" n'appartient pas à ç>(Fr(A)), le nombre d(cps, h ' '(A), h ' '(z))
est défini (problème 2) ; on pose d(<p, A, z) = d(cps, h~'(A), h-"'(z)).
Soit ç>, une seconde application admissible de A dans R", telle que tPi(x) = <jp(x) dans Fr(A).
Montrer que l'on a d(<pt, A, z) = </(cp, A, z) (utiliser le problème 2 c)).
7) Soient F une partie fermée de R", <p une application admissible de F dans R", \j/ un
prolongement continu de tp en une application admissible de R" dans lui-même. Le nombre d(<ji, D„ z)
est alors défini pour toute composante connexe D, de R" — F et tout point z 4 <P(F). Montrer
qu'il ne dépend pas du prolongement admissible ^ de cp ; on le note d(<p, D,, z). Montrer que
l'application z -+ d{(fi, D,, z) est continue dans R" — <p(F), et ne dépend donc que de la
composante connexe Aj de R" — cp(F) à laquelle appartient z; on écrit alors d{<p, D,, Aj) au lieu de
d(<p, D,, z). Montrer que pour un indice j donné, d(<p, D,, Aj) = 0 sauf pour un nombre fini
de valeurs de i.
8) Soient F une partie fermée de R",/une application admissible de F dans R", g une
application admissible de /(F) dans R", de sorte que g » / est une application admissible de F dans R".
Soit (D,) (resp. (DJ), (D»)) la famille des composantes connexes de R* - F (resp. R" - /(F),
R" — g(/(F))). Montrer (avec les notations du problème 7) que l'on a
d{g°f, D„ Di') = Y.d(f, D„ D'jWg, D,, D»)
J
(utiliser le problème 4).
En particulier, supposons que / soit un homéomorphisme (admissible) de F sur /(F).
Montrer alors que l'ensemble des composantes connexes de R" - F est équipotent à l'ensemble des
composantes connexes de R" - /(F) (généralisation du théorème de Jordan-Brouwer ; si l'on
pose a,j=d(f, D„ DJ), &;=<*(/""', DJ, D(), on a et Y.Pjfl,k = 6Jk; observer qu'il ne
j i
peut y avoir de bijection d'un espace vectoriel de dimension finie sur un espace vectoriel de
dimension infinie).
9) Soient X, Y deux variétés compactes, connexes, orientées, de même dimension. Soit / une
application injective de X dans Y, de classe C". Montrer que deg/ = ± 1, et par suite que / est
bijective. Donner un exemple où X = Y = S, et où/est bijective mais/'1 n'est pas différentiable
en certains points.
10) a) On considère la sphère S3 comme l'ensemble des quaternions de norme 1. Pour tout pe Z,

58 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
/ : z -» z' est une application de classe C°° de S3 dans S3 ; montrer que son degré est égal à p.
(Écrire les points de S3 sous la forme cos <p cos i\i cos 0+ i cos tp cos ^ sin 6+j cos <p sin ^+k sin cp,
et considérer l'image réciproque / " '(z) pour un point z correspondant à cp = 0, iji = 0, 0 diff-
rent de 0 et de n).
b) On identifie le corps des quaternions H ( = R4) au complémentaire du pôle «o de la
projection stéréographique S4 - {e0 } -» R4. Montrer que pour p > 0 l'application z -» z' de H
dans lui-même se prolonge en une application continue g de S4 dans S*, et que l'on a deg g = p.
c) Déduire de b) que pour tout entier p > 1, l'équation a<,x' + a^'"1 + ... + a, = 0
où les »j sont des quaternions et a0 # 0, a au moins une racine dans H.
11) Soit / une application de classe C°° de S. dans S. (pour n > 2) ; si D+ (resp. D") est
l'hémisphère fermé de S„ défini par (° > 0 (resp. £° < 0), montrer que/est homotope à une
application g de S. dans S., de classe C°°, telle que g(D+) soit contenu dans S. - { - «0 } et g(D " ) contenu
dans S„ - { e0 }. Pour cela, on considère deux valeurs régulières distinctes a, b de / ; soient
/_1(a) = {a,, ....a,}, /" '(b) = { b„ ..., b,}. Montrer qu'il existe un difféomorphisme tp
de S, sur elle-même, homotope à l'identité, tel que cp(aj)eS„-D~ (intérieur de D+) pour 1 £j£p
et </>(bt)eS„ - D+ (intérieur de D") pour 1 « k < q ((16.26.10) et (16.26.8)). De même, il existe
un difféomorphisme ^ de S, sur elle-même, homotope à l'identité, tel que ^(a) - e0 et ^(b) = - e0.
Montrer que g = répond à la question.
12) a) Pour tout nombre a tel que 0 < a < 1, soit U, (resp. V„) l'ouvert de S, (pour n ^ 1)
défini par {° > — a (resp. £° < a). Montrer qu'il existe une application 0 de S. dans elle-même,
de classe C°° et homotope à l'identité, se réduisant à l'identité dans un voisinage de «0 et dans un
voisinage de - e0, et telle que 0(U. - D+) <= S._, et 0(V. - D") c S.-!.
b) Soit/une application de classe C" de S, dans S. (pour n > 2). Montrer que/est homotope
à une application h de classe C°° de S. dans S. telle que h(D+) <= D+ et h(D~) <= D", et par suite
HiS.-i) <= S„_ ! (utiliser le problème 11 et montrer que, pour un nombre a < 1 convenable,
l'application 0 définie dans a) est telle que h = 0 ° g répond à la question).
13) Soit / une application de classe C de S. dans S. (pour n ~» 2), telle que /(D*) <= D*
et /(D") c D", d'où f(S,-i) = S.-i ; soit f0 sa restriction à S.-,, application de classe C°° de
S.-, dans S.-t. Montrer que deg/ = deg/0. (Remarquer qu'il existe deux nombres a, b tels que
0 < a < 6 < 1 et que l'on ait /(UJ <= Ut et /(V„) <= Vt. Utiliser le diagramme commutatif de
suites exactes (24.3.4.1) en y prenant X = Y = S., h =/, U, = U„ Vt = U», U, = V„ V2 = Vt.
Utiliser aussi le problème 3 de la section 24.7).
14) a) Soit/une application de classe C°° de S. dans S. (pour n > 2), telle que/(D+) c D+
et /(D") c= D", et soit g une seconde application de S. dans S. ayant les mêmes propriétés.
Montrer que si les restrictions de/et g à S,_, sont égales,/et g sont homotopes (utiliser l'exemple
24.9.5, III).
b) Soient/0, g0 deux applications de classe C de S„_, dans S._,. Montrer que si/0 et g0
sont homotopes, il existe deux applications /, g de S. dans S„ prolongeant respectivement/0 et g0,
telles que/(D+) c D+, g(D+) <= D+,/(D") c D", g(D") c D-, et qui sont homotopes.
15) Soient /, g deux applications de classe Cx de S„ dans S» (pour n > 1). Montrer que si
deg / = deg g, f et g sont homotopes (théorime de H. Hopf}. (Raisonner par récurrence sur n,
en utilisant les problèmes 12 b), 13 et 14. Pour n = 1, utiliser l'exemple 24.9.5, II).
16) a) Soit/une application de classe C de S, dans S. telle que/( - x) / /(x) pour x eS„.
Montrer qu'il existe une application g de classe C°° de S. dans S., homotope à / et telle que
g(— x) = — g(x) pour tout xeS„. (Considérer l'arc de géodésique de longueur < n joignant /(x)
et —/(— x), et le milieu de cet arc).
b) On suppose que /(x) = — /(x) pour tout xeS„. Montrer qu'il existe une application g
de classe C" de S. dans S„ homotope à /, telle que g(— x) = - g(x) pour tout xeS, et que
g(D+) cD*et g(D~) c D". (Reprendre les raisonnements des problèmes 11 et 12 a), mais pour
obtenir des applications tp et 6 telles que <p{- x) = - <p(x) et 0(- x) = - 0(x), raisonner dans
P^R))-
c) Montrer que si / est une application de classe C de S, dans S„ telle que /(-x)5*/(x),
deg / est un nombre impair et par suite / est surjective. (Raisonner par récurrence sur n, en
utilisant a) et b)).
17) Soit/une application de classe C°° de S, dans R". Montrer qu'il existe xeS. tel que

9. DEGRÉ D'UNE APPLICATION
59
/(- x) =/(x) (théorème de Borsuk-Ulam) (considérer R" comme plongé dans S. et utiliser le
problème 16 c)). Généraliser au cas où / est seulement continue.
18) Soit (A,, A2,..., A„+1) un recouvrement de S, constitué par des ensembles fermés.
Montrer qu'il existe un indice j tel que Aj contienne deux points opposés x, — x de S,. (Raisonner
par l'absurde ; si la proposition n'était pas vraie, montrer d'abord que l'intersection
Ai n Aj n ... n A.+i — 0 ;
pour tout j, considérer une application fj de S. dans [0, 1 ], de classe C", telle que //x) = 0 dans Aj
et //x) > 0 dans S, - Aj (cf. section 16.25, problème 2 a)) ; utiliser ensuite le théorème de Borsuk-
Ulam pour obtenir une contradiction) (théorème de Lusternik-Schnirelmann- Borsuk).
19) Soient X, Y deux variétés compactes, connexes, orientées et de même dimension, et
soit / : X -» Y une application de classe C" qui est un difféomorphisme local en tout point.
Montrer que si deg/ = 1, / est un difféomorphisme de X sur Y préservant l'orientation. (Avec
les notations de (24.9.3), montrer que l'on a e(x) = 1 en tout point xeX).
20) Soient X,, Y, (resp. X2, Y2) deux variétés compactes, connexes, orientées et de même
dimension, et soient/, : X, -» Y,,/2 : X2 -» Y2 deux applications de classe C". Montrer que
si on munit X, x X2 et Y! x Y2 des orientations produits (16.21.5), on a deg(/, x /2) = deg A deg /2.
21) Identifiant R2"*2 à C"+1, pour tout point z eS2„+l, on identifie l'espace tangent
T,(S2.+ 1) à un sous-espace de IJfi}'*1) = C+I x C"+1 ; pour tout z eS2,+ i montrer que
X(z) = (z, ii) est un vecteur =A 0 tangent à S2-+1.
22) Soit X un tore de révolution plongé dans R3, image de [0, 2n] x [0, 2n] par l'application
(0, cp) -» ((a + r cos 0) cos cp, (a + r cos 0) sin cp, r sin 0)
où 0 < r < a. Soit Y„ la courbe dans X définie par 0 = mcp, où m est un entier rationnel # 0.
Montrer que toutes les variétés X — Y„ sont diflféomorphes, mais que si m / n, il n'existe pas
d'homotopie de Y„ à Y, à valeurs dans X (cf. section 24.7, problème S). (Calculer le nombre
d'entrelacement de Y„ et du cercle cp -» (a cos cp, a sin cp, 0)).
23) Soit X l'image dans R3 de [0,4rt] x [0,3/4 [ par l'application
(( 0\ ( 0\ e\
(0, r) -♦ III + r cos -I cos 0,1 1 + r cos -I sin 0, r sin -I
sous-variété difféomorphe à la bande de Môbius (16.14.10). On considère sur X les deux courbes
C,, C2 définies par les équations r = - et r = - . Montrer que entrel(C,, C2) = ± 2.
4 2
24) Soit / une immersion de classe C' (16.7.8) de S, dans R2 = C ; si g(s) =/(c"), on pose
"(«'') = ï'(s)/1 «'(s) l> vecteur unitaire tangent à la courbe /(S,) au point f(é") ; d est une application
continue de S, dans lui-même ; on appelle enroulement de fie nombre enroul(/) — deg(t>). Pour
tout difféomorphisme h deS, sur lui-même préservant l'orientation, on a enroul(/4) = enroul(/).
Si/,,/2 sont deux immersions de classe C1 de S, dans R2, on appelle homotopie régulière
de/, à/2 une application F de classe C1 de [0, 1 ] x S, dans R2 telle que F(0, t) = /,((), F(l, t) = /2(t)
et que, pour tout X e [0, 1 ], t -> F(X, t) soit une immersion de S, dans R2. Montrer que, pour que
/, et /2 soient régulièrement homotopes, il faut et il suffit que enroul(/,) = enroul(/2) (théorème
de fVhitney-Graustein). (Pour voir que la condition est suffisante, on peut se ramener au cas où
M**) = £/(«) pour j = 1, 2 avec | g"J(s) \ = 1 pour 0 < s «S 2ji, et gî(0) = g'2(0) ; on peut en outre
supposer que g'J(s) = expfin/s)) où h/0) = 0 et n,(2n) = h2(2n) = 2kn, où k est égal à
l'enroulement commun de/, et/2. Considérer la fonction H(X, s) = exp(i((l - A)h,(s) + h2(s))) pour 0 < X < 1,
f» s f2'
0 < s $ 2tt, et montrer que F(X, s) = I H(A, u)du H(X, u)du définit une homotopie
régulière de /, à /,. J° 2"Jo
25) Soit / une application de classe C°° de S. dans S„. Montrer qu'il existe xeS„ tel que
/(— x) = — /(x) dans les deux cas suivants : 1° n est pair et deg/ # 0 ; 2° deg/est impair.
(Raisonner par l'absurde en se ramenant au cas où /(- x) = /(x) pour tout x comme dans le
problème 16 a)).

60 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFERENTIELLE ÉLÉMENTAIRES
26) On note e0, «i, .... e„ la base canonique de R"+ ', et on identifie R" à l'hyperplan
engendré par e,, e2, ..., •„. Pour tout x eS„, on désigne par D+(x) le demi-espace contenant x,
déterminé par l'hyperplan affine passant par le point ^ e0 et orthogonal à x.
a) Soit X la mesure de Lebesgue dans R". Montrer que pour toute partie intégrable A de R",
la fonction u : x X(A o D+(x)) est continue dans S„ et on a u(x) + m(- x) = /K.A).
b) Soient A,, ..., A. n parties intégrables de R". Montrer qu'il existe dans R" un hyper-
plan affine H tel que si A+ et A " sont les deux demi-espaces déterminés par H dans R", on ait
A(A, n A+) — A(A( nA") pour 1 < i < n ( « théorème du sandwich » ). (Appliquer le théorème de
Borsuk-Ulam (problème 17) en utilisant a)).
27) Soient /0. • • •> /«. " + 1 fonctions continues définies dans R"+1 à valeurs > 0,
homogènes d'un même degré m > 1, et telles que pour chaque indice j, les relations x0 > 0, ..., x. > 0
et fj(xo, x.) = 0 entraînent x„ = xt = ...=*„ = 0. Soit d'autre part || x || une norme
sur R"+ '. Montrer qu'il existe un point x = (x0, ..., x,) de R"+ ', distinct de 0, et de coordonnées
x0 > 0, ..., x. > 0, et un nombre X > 0, tels que l'on ait fj{x) = X || x ||"" lxt pour 0 < y < n.
(Considérer dans P^R) l'ensemble des points de coordonnées homogènes > 0). (Pour m = 1,
comparer au problème 6 de la section 11.1).
28) Soit (ej)l(j(] la base canonique de R3, et soit K une partie compacte non vide de R1
(identifié au sous-espace engendré par e2 et e3) telle que le sous-groupe H du groupe I des iso-
métries de R3 qui laisse K globalement invariant soit fini. On suppose qu'à tout vecteur x e S2
corresponde une partie compacte A(x) du plan d'équation (x | y) = 0 dans R3 orthogonal à x,
telle qu'il existe une isométrie de R3 transformant K en A(x). Cela définit une application x -» s(x)
deS2 dans l'espace homogène I/H ; montrer que cette application ne peut être continue (remarquer
qu'on en déduirait une application continue x -» /(x)deS2danselle-mêmetelleque(x|/(x))=0).
Généraliser.
29) a) Soit K. une partie compacte non vide de R3. On suppose qu'il existe un point a e R3
tel que les intersections de K et de tous les plans passant par a se déduisent de l'une d'elles par une
isométrie de R3. Montrer que chacune de ces intersections est nécessairement une réunion de
cercles concentriques (et éventuellement de leur centre) (utiliser le problème 28, le problème 4
de la section 3.20 et le fait que si un sous-groupe fermé de SO(3) est infini, il contient un tore
maximal).
b) On suppose en outre que K est un ensemble convexe ayant un point intérieur. Montrer
alors que K est une boule euclidienne fermée (considérer les couples de points b, c de K tels que
la distance || b — c || soit égale au diamètre de K, et un plan contenant a, b, c, en utilisant la
section 6.3, problème 2).
30) Démontrer les propriétés analogues à celles du problème 29, en remplaçant les
intersections de K et des plans passant par a, par les projections orthogonales de K sur tous les plans
de R3.
31) Les hypothèses étant celles de la section 24.1, problème 1 b), on suppose de plus que
X est une variété compacte orientée connexe de dimension n.
a) Montrer que pour 0 < p < n, on a
Tr(p^s)) = degs.Tr(p,_p(s-1))
(où on a nécessairement deg s = ± 1).
b) On suppose que X est un revêtement à 2 feuillets de X0 et que X0 est non orientable, de
sorte que G est un groupe à deux éléments {e, s] avec deg .v = — 1. Si l'on pose r, = Tr(p,,(s)),
montrer qu'on a entre les nombres de Betti de X et X0 les relations
b0, + b°m-, = b„ b°p-b°.-, = rp.
10. Homologie des courants.
(24.10.1) Soit X une variété différentielle pure de dimension n. Pour 0 ^ p < n,
nous noterons <fp,t(X) (resp. ^p,c(X)) l'espace vectoriel sur R (resp. Q des p-cou-

10. HOMOLOGIE DES COURANTS
61
rants réels (17.6.1) (resp. desp-courants) de support compact; il peut être considéré
comme espace des formes linéaires continues sur l'espace de Fréchet ^.«(X)
(resp. <?p,c(X)) de toutes les p-formes différentielles réelles (resp. complexes) de
classe C* sur X (17.7.1); on a *'P,C(X) = S'pM <g> ,C = <f;.,(X) © iS'p,JX). Jusqu'à
la section 24.48, nous n'aurons à considérer que des p-formes différentielles
réelles et des p-courants réels, et nous écrirons donc simplement <?p(X) et S'J^X)
au lieu de <fPiB(X) et <yp,«(X).
(24.10.2) Pour 1 < p ^ n et pour tout p-courant T, nous avons défini (17.15.4)
le bord 6T de T comme le (p - 1/-courant tel que, pour toute (p — l)-forme
différentielle a de classe C°° à support compact, on ait
(24.10.2.1) < 6T, oc > = < T, da > .
On dit que T est un cycle (ou est fermé) si 6T = 0.
Si L = SuppfT), on a < T, da > =0 pour toute p-forme a de support compact
ne rencontrant pas L, donc Supp(6T) <= Supp(T). L'application 6 est donc une
application linéaire de S'pÇX) dans S'P-JX); on notera en outre que lorsque T
a un support compact, la formule (24.10.2.1) a encore un sens et est valable pour
toute (p - Informe différentielle a de classe C°°, et non seulement pour celles
de support compact.
On pose par définition 6T = 0 pour tout Q-courant (ou distribution) sur X
(on prend êL j(X) = {0} par convention).
(24.10.3) Pour p ^ 2, on a vu que, pour tout p-courant T, on a 6(6T) = 0
(17.15.4.3), et la convention introduite ci-dessus étend cette formule aux cas
p = 1 et p = 0. On voit donc que, pour l'application bord, l'espace vectoriel
gradué
^'.(X)= ©^(X)
p = 0
est un espace codifférentiel gradué sur C, pour un opérateur différentiel tt de
degré - 1 (Ann. 30.7). On peut donc lui appliquer les définitions de l'homologie
de tels espaces (Ann. 30.7) : le sous-espace gradué Z'.(X) des cycles de sf'.{X)
est égal à
Z'.(X) = © Z'flQ
p = 0
où ZP(X) est l'espace vectoriel des p-courants de support compact tels que 6T=0.
Le sous-espace gradué B'.(X) des bords de sf'.(X) est égal à
B'.(X) = © Bp(X)
p = 0

62 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFERENTIELLE ÉLÉMENTAIRES
où B'JX) est l'espace vectoriel des p-courants T de la forme SS, où S parcourt
£'p+l{X). L'espace vectoriel gradué
H:(X) = ê Hp(X)
p = 0
°U H'JX) = ZJPQ/BJPQ
est l'espace (total) d'homologie de X (pour les courants), Hp(X) étant appelé
le p-ème espace d'homologie de X (pour les courants) ; on pose U'pÇX) = {0}
pour p > n ou p < 0. On dit que deux courants sont homologues si leur différence
est le bord d'un courant.
(24.10.4) Soient X, Y deux variétés différentielles pures, et u : X -* Y une
application de classe C°° ; alors u(T) est défini pour tout p-courant à support
compact T e £'p(X) et est un p-courant à support compact (contenu dans l'image
par u de Supp(T)) sur Y (17.7.1). On a en outre, avec les mêmes notations,
u(6"T) = 6(uÇT)) (17.15.4.2) ; on a donc défini une application
u : tf'JX) - tf'XY)
se réduisant à T -+ u(T) dans chaque espace S'^X) et qui est une application
linéaire homogène d'espaces codifférentiels gradués (Ann. 30.7). On en déduit
canoniquement une application linéaire homogène d'espaces gradués
u„ : Hi(X) H:(Y)
telle que, si a e H'/X) est la classe d'un p-courant T à support compact qui est
un cycle, u„(a) est la classe du cycle uÇT) dans Hp(Y).
En outre, on a un théorème d'invariance par homotopie pour l'homologie
des courants :
(24.10.5) Soient X et Y deux variétés différentielles pures, u et v deux
applications de classe C°° de X dans Y. Si uetv sont homotopes de classe C00, les
applications linéaires homogènes d'espaces gradués «„ et d, de H((X) dans H'.(Y) sont égales.
Il s'agit de voir que si T est un p-courant à support compact sur X tel que
6T = 0, le p-courant w(T) - u(T) sur Y s'écrit 6S pour un (p + l)-courant S sur Y,
à support compact. Gardant les notations de (24.2.4) et (24.2.5), on a, pour
toute p-forme différentielle a de classe C00 sur Y, en vertu de la formule (24.2.5.1),
(24.10.5.1) < m(T), a > — < v(T), a > =
< T, '«(a) - 'm> = < T, d(L.o>) > + < T, L.(dco) >
où co — T(a). Posons LF.a = L.('F(a)) ; pour une homotopie F fixée et pour
chaque p, l'application linéaire LF de ^p(Y) dans rfp_j(X) est continue pour les

11 . HOMOLOGIE DES COURANTS SUR UNE VARIÉTÉ ORIENTÉE
63
topologies d'espace de Fréchet de ces deux espaces. U est immédiat en effet
que a -» 'F(a) est une application linéaire continue de ^/Y) dans 8$ x X),
en vertu de la définition (16.20.9.2) et de (17.1.5). L'application co -* iE.co
de Sfi x X) dans <?p_i(I x X) est continue par (17.2.3) ; si une suite (/?*)
converge vers p dans Sp- t(I x X), la suite des 'jJiPk) converge vers 'jJ(P) dans
iïp-iÇX), uniformément pour se [a, b], et la formule (24.2.4.1) achève de prouver
la continuité de LF. Cette application a donc (pour chaque p) une transposée
'LF : S'p-,(X) tfjJiY), continue pour les topologies faibles (12.15.3), et la
formule (24.10.5.1) s'écrit
< «CD - *T), a > = < 'LF.(6T), a > + < S('LF.T), a >
pour toute p-forme a puisque L{dco) = L('F(da)) = LF.da ; autrement dit
(24.10.5.2) u(T) - v(T) = 'LF.(6T) + 6('LF.T) ;
si 6T = 0, on a donc bien u(T) - v(T) = 6S avec S = 'LF. T.
Remarque (24.10.6). — Supposons que l'homotopie F soit propre (ce qui
entraîne que u et v le sont) ; alors pour tout p-courant T sur X, u(T) et v(T) sont
définis sur Y (17.3.7), et on a encore la formule (24.10.5.1) pour toute p-forme a
à support compact, car L.co et L.(dco) sont à supports compacts (24.2.4). La
suite du raisonnement de (24.10.5) prouve de même l'existence de la transposée
'LF : 2'JCi), et par suite, si 61 = 0, on a encore uÇT) - d(T) = 6S
avec S = 'LF.T.
U. Homologie des courants sur une variété orientée.
(24.11.1) Supposons maintenant que X soit une variété différentielle pure
orientée de dimension n. Pour tout p tel que 0 < p < n, on a alors défini (173.1)
une application linéaire canonique
de l'espace «?„_p(X) des (w - p)-formes différentielles (réelles) de classe C00 dans
l'espace ^X) des p-courants sur X ; par définition, on a
pour toute p-forme a de classe C°° et à support compact sur X ; il est clair que
cette application est injective ; en outre, le diagramme
(24.11.1.1) jp : fi -
(24.11.1.2)
W)
(24.11.1.3) t-iv-">é
^»-p+i(X)
®;-i(X)

64 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
et comme /? a a a un support compact, on a d(fi a a) = 0 (17.15.5.1), ce qui
prouve notre assertion pour p > 0. Pour p = 0, la seconde ligne de (24.11.1.3)
est formée d'espaces réduits à 0, et la commutativité résulte encore de la
définition du bord 6 pour les 0-courants.
Il est clair que Tf est un p-courant d'ordre zéro (17.3.2).
Notons enfin que restreinte à l'espace @n-p{X) des (n - p)-formes
différentielles à support compact, est une application de cet espace dans l'espace <?p(X)
des p-courants à support compact.
(24.11.2) Il résulte aussitôt de la commutativité du diagramme (24.11.1.3)
que l'on a j^^X)) c Z'JX) et jjB^^X)) c B'JX), donc, par passage aux
quotients, on déduit de jp une application linéaire canonique
Dans la section suivante, nous nous proposons de prouver le théorème
suivant :
(24.11.3) (de Rham) Pour toute variété pure orientée X de dimension n,
ï'application linéaire j* est une bijection de H"-D(X) sur H'JX).
12. Régularisation des courants.
(24.12.1) Rappelons que l'espace <fp(R") des p-formes de classe C°° sur R" est
un <?(R")-module libre de rang (J) ayant pour base les p-formes
où H parcourt l'ensemble des parties à p éléments de [1, n] et on a noté
h < h < • • • < 'p les éléments de H rangés dans l'ordre croissant. On notera H'
le complémentaire de H dans [1, n], et on pose
Mais d'autre part (17.15.2.1)
d{fi a a) = (dp) a a + (- l)"-"/? a da
(24.11.2.1) j* : HT"(X) - H'JX).
(24.12.1.1) Ch = a d?* a ... a dp
(24.12.1.2) Ch a Ch- = p(H, W)d? a d? a ... a d?
est commutatif. En effet, pour toute a e 9)p-i(X), on a

12. RÉGULARISATION DES COURANTS
65
avec p(H, H') = ±1. Tout p-courant S sur R" s'écrit alors d'une seule manière,
pour <A)6(3(R")A
(24.12.1.3) Z/hCh - E<S„,/h>
h h
où les SH sont des distributions sur R", et l'application S -» (SH) est un
isomorphisme de l'espace ©^R") des p-courants sur R", muni de la topologie faible,
(")
sur l'espace produit (@'(R"))VP/, où l'espace des distributions ®'(R") est muni
de la topologie faible (17.5.4). Pour que S ait un support compact, il faut et il
suffit que chaque Sh ait un support compact.
(24.12.2) Soit maintenant g une fonction de @(R") ; pour tout courant S e ®p(R"),
on définit le p-courant g * S, convolution de g et de S, comme correspondant
par l'isomorphisme précédent à la famille de distributions (g * Sh). Chacune
des distributions g * Sh étant identifiée à une fonction de classe C00 (17.12.1),
le p-courant g * S est de la forme jJP), où /? est la (n - pyforme de classe C°°
Zp(H', HX^ShKh-.
h
En outre, si, pour toute p-forme à support compact a = Y,/hCh> °n Pose
= E(I*/h)Ch, on a, par (17.12.5.2), H
h
(24.12.2.1) <g.S,<x> = Z<g.S„,JÎ,> = I<SH,|./„> = <S,|.a>.
h h
Dans chaque espace ^R" ; K) (K compact dans R"), a -*■ g * a est une
application linéaire continue de cet espace de Fréchet dans l'espace de Fréchet
®p(R" ; K - V) si Supp(g) est contenu dans l'ouvert relativement compact V ;
l'application S -» g * S de dans lui-même peut donc être considérée
comme transposée de l'application a -» g*a (12.15.4).
(24.12.3) Afin de généraliser la régularisation des courants à une variété
quelconque, il faut d'abord « localiser » la convolution définie ci-dessus. Soit B la
boule ouverte r(x) < 1 dans R" ^avec r(x) = ^S(^J)2^ ^ ; si <I> est un
difféomorphisme de B sur R", "P = 0j)_1 le difféomorphisme réciproque, on peut
transporter par *P la convolution par une fonction de ®(R") : pour toute p-forme a
de support contenu dans B, on définit la p-forme R'g. a de support contenu dans B,
par la formule
(24.12.3.1) R'f. a = '<D(g * '*(«))

66 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
f 0(x, y) =
(24.12.5.1) \ 7
{ 0(x, y) =
= *(^(x)-y) si xe B
si x£B
la fonction 0 est de classe C00 dans R" x R" tout entier.
Tout revient à voir que 0 est de classe C°° au voisinage de tout point (x0, yo)
tel que r(x0) = 1. Or la dérivée D20(x, y) est égale à
- D«P($(x) - y)) = - DWGKx, y))) pour x e B,
à 0 pour x£B. Utilisant (10.9.5) appliqué à l'équation z' = l/(z), où Ufz) = 0
pour z $ B, l/(z) = — D*P(<ï»(z)) pour z e B, il suffit de montrer que la fonction U
est de classe Cœ au voisinage de x0. Or, si l'on écrit p -» cp(p) la fonction
réciproque de r -► rh{r), la relation u = <D(z), avec u = (uJ), z = (zJ), équivaut à
= h(r)zj pour 1 < y ^ n, ou à zJ = (en posant pour abréger r = r(z),
P
<p(p) 1
p = r(u)), et comme p = rh(r), on a = —•. On a donc
p h(r)
w(o) u'u*
D/F'(u) = 5^ + <p'(p)— - cp(p)~
P P P
et c/(p) = l/(r«'(r) + n(r)), d'où, pour les éléments de la matrice I7(z)
ce qui s'écrit explicitement, pour a = fHCH
(24.12.3.2) R'g.(/„C„) = (£,*<- DMWH• ) - y))dy)cH •
(24.12.4) Toutefois, pour la suite du raisonnement, il est nécessaire de pouvoir
étendre l'opérateur R'g à toutes les p-formes de support compact sur R", de façon
que si le support de a ne rencontre pas B, on ait R't. a = a. Pour y parvenir, nous
ferons un choix particulier de 4>, en prenant
(24.12.4.1) <I>(x) = n(r(x))x
avec
(24.12.4.2) h(t) = exp ~ *) P°m 0 < f < 1 •
Nous utiliserons le lemme suivant :
(24.12.5) Si l'on définit dans R" x R" la fonction © par les conditions suivantes :

12. RÉGULARISATION DES COURANTS
67
Il est alors facile de voir par récurrence que, pour z e B, toute dérivée de
multiindice X d'une telle fonction est de la forme
Qa(r,*)
(1 - r)3|A|n(r)
où Qx est une fonction rationnelle en r et les z', définie pour r = 1 et z — x0 ;
la conclusion du lemme résulte donc de ce que (1 — tfh(t) tend vers + oo lorsque
t tend vers 1, quel que soit l'entier k > 0.
(24.12.6) On définit maintenant R'g. a pour toute p-forme a de ®P(RB), en posant
(24.12.6.1) R't. (/„CH) = (£ «( - y)/H(©( •, y)¥y)cH
qui satisfait évidemment aux conditions de (24.12.4). Comme O est continue,
pour tout compact K c R" et tout voisinage compact L de K, il y a un
voisinage symétrique V de 0 dans R" tel que les relations 0(x, y)e K et y e V entraînent
x e L ; par suite, si Supp(a) c K et Supp(g) c V, on a Supp(/?g.a) c L. Comme
0 est de classe C°°, il résulte de (13.8.6) que R'( est alors une application linéaire
continue de l'espace de Fréchet %(R" ; K) dans l'espace de Fréchet ®p(R" ; L).
On peut donc considérer la transposée Rt de R't, application linéaire de ^R")
dans lui-même, continue pour les topologies faibles, et définie par la relation
(24.12.6.2) < Rg. S, a > = < S, R'g. a >
pour tout p-courant S. Avec les notations précédentes, on voit que si le support
de S est contenu dans K, celui de Rg.S est contenu dans L ; si le support de S
est contenu dans B, Rg. S s'écrit jjfi) pour une (n - p)-forme fi de classe Cœ (en
termes imagés, Rg « régularise » les courants de support contenu dans B) ; enfin,
si le support de S ne rencontre pas B, on a Rg.S = S. De plus :
(24.12.7) Supposons que I g(y)dy = 1.
J»-
(i) Pour chaque entier p tel que 0 < p < n, il existe une application linéaire Ag
de l'espace des (p - \)-courants ®P_,(R") dans l'espace des p-courants ^R"),
continue pour les topologies faibles et telle que l'on ait, pour tout p-courant S e ^R"),
(24.12.7.1) Rg.S - S — Ag.(6S) + 6{Ag.S).
(ii) Si S s'écrit jp-i(fi) pour une (n - p + iyforme fi de classe C00, on a
Ag.S = jjy) pour une (n — p)-forme y de classe C°°.
(iii) Si le support de S ne rencontre pas B, Ag.S = 0.
(iv) Avec les notations de (24.12.6), si Supp(S) c K, on o Supp(/ig.S) c L.

68 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
(v) Si (gm) est une suite régularisante (17.1.2), la suite (Agm.S) converge
vers 0 pour la topologie faible de ^(r").
Pour toute p-forme a de classe C00 à support compact, on a
(24.12.7.2) < Rg.S - S, a > = < S, R'g.ct - a > .
Nous allons exprimer autrement la différence R'g.a. — a ; il suffira de
considérer le cas où a=fHCn, autrement dit cc(x)=f^x)dp a dif1 a ... a dp.
Remarquons d'abord que si /SJx) = xjh(x» yKh(x) est une p-forme sur r"
h
dépendant d'un paramètre y e U, où U est un ouvert de r* et \esfH sont de classe C00
dans r" x U, on peut définir l'intégrale j* fiydy pour tout compact K c U,
comme égale à la p-forme £ ^ j" jh(x> Y)dy*jÇtA*) > °n a encore la relation
(24.12.7.3) d /vx) = £ WJdy
comme il résulte de (13.8.6). Puisque g est à support compact et que g( — y)dy — 1,
on peut écrire **
(24.12.7.4) R'g. oc - et = g{ - yX<xy - ct)dy
où ay(x) = fyi&{x, y))ch(x)- Pour évaluer la différence <xy — a, nous allons
utiliser la formule de l'homotopie (24.2.5.1) : on y prend pour u l'application
identique 1B„, pour f l'application x -*■ 0(x, y), et on a une homotopie de u à v
FJs, x) = 0(x, sy)
définie dans [0, 1 ] x r". Avec les notations de (24.2.3) et (24.2.4), il s'agit, en
écrivant coy au lieu de co la forme 'Fy(a), d'exprimer L.coy pour cette p-forme.
On a par définition
cojs, x) = /H(©(x, sy))%(dp) a ... a >FJdp).
Posons y = (f?1, .... n"), 0 = (01, ..., 0") et notons D'j les dérivées par
rapport aux coordonnées de x, D" les dérivées par rapport aux coordonnées
de y ; on a alors, pour 1 ^ i ^ n
n
(24.12.7.5) 'FJdp = e (D;0'(x, syW + rjrD;'0'(x, sy)ds).
r= 1
Pour abréger, posons
(24.12.7.6) Aii5y(x) = t D;0'(x,

12. RÉGULARISATION DES COURANTS
69
et, pour 1 < k ^ p, introduisons les (p — l)-formes
(24.12.7.7) /uMy = Ail>jy a ... /ci^a" ... a AIp>sy
qui ne dépendent pas de fH. Alors, par définition, on a
(i£.coyxs, x) = t (-1)*' 7h(®(x, f)){tt "rD;'®ik(x.
et finalement
(L.coyxx) = £ (~ 1)*"1 ({/h(®(x, sy))mrD;'eik(x, sy))pmy(x)ds).
De la formule de l'homotopie
<xy - a = d(L.coy) 4- L.(dcoy)
et de (24.12.7.4), on tire donc, compte tenu de (24.12.7.3)
(24.12.7.8) R'g.a - a = d(L.coy)g(- y)dy) + £(L.(dcoy))g(- y)dy.
Puisque dcoy = Ty(da), l'expression de L.coy permet d'écrire cette formule
(24.12.7.9) R'g.a-a = d(A't. a) + A'g. (da)
où l'application linéaire A'g est définie par linéarité et par
(24.12.7.10) (A'g.(UH)Yx)
= ^1 ( - 1)*"1 ( >b S(" y)^ Jo /h(0(x, sy)) ( f n'D;'0ik(x, sy)k.sy(x^.
Il résulte aussitôt de (13.8.6) que, dans chaque espace @P(R" ; K) (K compact
dans R"), A'g est une application linéaire continue de cet espace de Fréchet dans
l'espace de Fréchet ^.^R" ; K — V) si Supp(g) c V. On peut donc définir
une application transposée Ag de 3'p-^R") dans ^(R") par la formule
(24.12.7.11) < Ag. S, a > = < S, A'g. a >
pour toute p-forme a à support compact et tout (p — l)-courant S. En vertu de
la formule (24.10.2.1) définissant le bord d'un courant, il est clair que de (24.12.7.9)
on déduit la formule (24.12.7.1), ainsi que la relation Supp(Ag.S) <= Supp(S) — V.
Comme les dérivées D"0'(x, y) sont toutes nulles pour x £ B, on déduit de
(24.12.7.10) que le second membre de cette formule est nul pour x $ B ; par
suite on a Ag. S = 0 si le support de S ne rencontre pas B.

70 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
Supposons que S = jp-i(P) pour une (n — p + l)-forme fi de classe c°° ;
il s'agit de voir que dans la formule
< A,.j,. muH > = <;,_ m ^.(/hCh) > = < t„,/h >
la distribution TH est en fait (identifiée à) une fonction de classe c". Mais comme
<J,-i(0M;UhCh)> = [ P a (X;.(/HCH)),celarésultedelaformule(24.12.7.10):
écrivons en effet
(P a pt.syXx) = ««(x, syW a ... a dÇ"
où uk est de classe c°° ; notons d'autre part que la matrice jacobienne du
difféomorphisme x -> ©(x, sy) est toujours inversible, et égale à l'identité si x £ B ;
le difféomorphisme réciproque z -» S(z, sy) a donc un jacobien J(z, sy)
toujours ?é 0, de classe c00 et égal à 1 pour z £ B. On a alors par la formule du
changement de variables (16.22.1.1)
<TH,/H> = j^MtoMâz
où
I (~ D*"1 f Si- V)dy f ( t »rD;'0'HS^, sy), sy)ut(H(z, sy), sy)| J(z, sy)|\h
t=i Jr" Jo V=i /
fonction qui est de classe c°° en vertu de (13.8.6), ce qui prouve notre assertion.
Enfin, si (gm) est une suite régularisante, le support de gm est contenu dans
une boule de centre 0 et de rayon tendant vers 0 avec 1 /m ; comme gm( — y)dy = 1,
r Jr-
chaque intégrale 1rgJ,— y)dy tend vers 0 avec 1/m; la formule (24.12.7.10)
Jr»
montre donc que A'tm. {/hCh) tend vers 0 dans l'espace de Fréchet 2P-i(R" ; K - V),
et par suite Agm.S tend faiblement vers 0 pour tout p-courant S.
On peut maintenant définir la régularisation des courants à support compact
sur toute variété pure orientée X :
(24.12.8) Soit X une variété différentielle pure orientée de dimension n. Pour
chaque entier p tel que 0 < p < n, il existe une suite (Rm) d'applications linéaires
de l'espace des p-courants à support compact S'J^X) dans lui-même et une suite (Am)
d'applications linéaires de ê'p- ^X) dans «J^X), telles que :
(i) Pour tout p-courant S e ^(X), on a
(24.12.8.1) Rm. S - S = Am. (6S) + 6{Am. S)

12. RÉGULARISATION DES COURANTS
71
et il existe m0 (dépendant de S) tel que pour m > m0 Rm.S s'écrive jjfi), où /? est
une (n — pyforme différentielle de classe C00, à support compact. En outre Rm
et Am sont continues pour les topologies faibles.
(ii) Si S s'écrit jp-i(P) pour une (n — p + l)-forme fi de classe C°°, on a
Am. S = jja) pour une (n — pYforme y de classe C°°.
(iii) Pour tout courant S et tout voisinage U de Supp(S), les supports de R„. S
et de Am. S sont contenus dans U dès que m est assez grand.
(iv) Pour tout courant S, /lm.S tend vers 0 avec l/m pour la topologie faible.
Tout xeX appartient à un domaine V, d'une carte cpx telle que cpjyx) soit
la boule ||z|| < 2 dans R"; soit Ux l'image réciproque par cpx de la boule B : ||z|| < 1.
Le raisonnement de (12.6.1) montre qu'il existe une famille dénombrable (cp,)
de cartes de la forme <pXj, telle que les ouverts Uj correspondants forment un
recouvrement localement fini de X ; on notera V} le domaine de <pp et hje 3>{X)
une fonction de support contenu dans Y, et égale à 1 dans un voisinage de U,.
Pour chaque indice j, posons, en utilisant les notations de (24.12.7), pour tout
p-courant S e <?p(X),
RJtm. S = <pf '(*,„. q>j(hj. S)) + (1 - hj). S, Ahm. S = q>J\Aim. cpj(hj. S))
où (pj{hj.S), courant sur «p/Y,), est identifié à un courant sur R" et son image
par Rgm ou Atm à un courant sur cp/Vj). Il résulte de (24.12.7) que l'on a Rjm. S=S
et AJm.S = 0 pour tout courant dont le support ne rencontre pas U,-; en
particulier AJm.((l — hj).S) = 0 pour tout courant S, et par suite on déduit de
(24.12.7.1) que l'on a
(24.12.8.2) RJjm. S - S = Ahm. (SS) + 6(A^. S).
Posons
«i? = Ki,J*2.n • • • Rj.m et Ag = RUmR2.m ... Rj-UmAh„.
Pour toute partie compacte K de X, il y a un indice j0 tel que Uj ne rencontre
pas K pour tout > j0. Pour tout courant S de support contenu dans K, on a
donc Rg.S = KJi!o).S et A$.S = 0 pour tout j > j0. On peut donc, pour ces
courants, définir Rm.S comme la valeur commune des Ri?.S pour ; > j0, et
oo
Am.S comme la somme £ A$.S puisque cette somme n'a qu'un nombre fini
de termes non nuls. En outre, si K' => K est une seconde partie compacte de X,
les valeurs de Rm.S et de Am.S sont les mêmes, que l'on considère S comme
ayant son support dans K ou dans K'. On a ainsi bien défini les applications
linéaires Rm et Am dans chacun des espaces S'JX), et leur continuité pour les
topologies faibles est immédiate. En outre, on tire de (24.12.8.2), par récurrence,
que
««S - RO-»>.S = Atf.(ffS) + 6(4?.S)

72 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
Rm.T -T = Am(6T) + 6(Am.T)
d'où, en ajoutant membre à membre ces relations, et compte tenu de ce qui
précède, on obtient la relation (24.12.8.1) pour tout courant S à support compact.
Soit (fj) une partition de l'unité subordonnée au recouvrement (Uj) et
formée de fonctions de classe C°° (16.4.1). Gardant les notations précédentes,
Jo
on peut écrire, pour tout courant de support contenu dans K, S = £ /}.S. En
vertu de (24.12.7), pour 1 < ; < jQ il existé un entier nij tel que, pour m> rrij,
le support de (RJ+ 1>mKj+2,m • • • Rjo<m).(fj.S) soit contenu dans Uj. On en déduit
(24.12.6) que Rm.(fj.S) s'écrit jjfi) pour une (n — p)-forme fi de classe Cx et
de support compact. Prenant pour m0 le plus grand des entiers /n,(l < j < j0),
on voit que la même propriété a lieu pour Rm. S dès que m ^ m0.
Les propriétés (ii), (iii) et (iv) sont vraies quand on y remplace Rm et Am
par Rjm et Aim> en vertu de (24.12.7), d'où on déduit aussitôt qu'elles sont aussi
valables pour Rm et Am par définition de ces opérateurs. CQFD.
Remarque (24.12.8.3). — Si on prend les bords des deux membres de
(24.12.8.1), on obtient
6(Rm.S) - 6S = ê(Aa.(6S))
et d'autre part, si l'on applique (24.12.8.1) au (p — l)-courant 6S, on a
Rm.(6S) -6S = 6(Am.(6S))
n
(on considère ici Rm et Am comme des applications de © S'JX) dans lui-même) ;
la comparaison de ces formules montre que D=0
(24.12.8.4) 6(Rm.S) = RJ6S)
et en particulier 6(Rm.S) = 0 si 6S = 0.
(24.12.9) Preuve de (24.11.3).
Montrons d'abord que l'application de H"~P(X) dans H'JX) est surjec-
tive. En effet, soit S un p-courant à support compact qui soit un cycle, c'est-à-dire
que 6S = 0. On déduit alors de (24.12.8.1) que l'on a S = Rm.S - 6{Am.S) et
la classe de S dans HP(X) est égale à celle de Rm.S. Mais pour m assez grand,
R„.S est de la forme jjfi) pour une (n — p)-forme P de classe C°°.
Prouvons ensuite que j*. est injective ; soit donc fi une (n — p)-forme de
classe C00, à support compact, telle que jp(fi) = 6T, où T est un (p + l)-courant
à support compact. On peut écrire

12. RÉGULARISATION DES COURANTS
73
et par suite
6T = 6^m.T)-6^4m.(6T)).
Puisque ST = jp(fi), Am.(6T) = jp+l(— X), où X est une (n — p — l)-forme de
classe C00 à support compact ; d'autre part, on peut supposer m pris assez grand
pour que Rm.T = jp+i(n), où p est une (n — p — l)-forme de classe C00 à
support compact. On déduit donc du diagramme commutatif (24.11.1.3) que
JAfi = ty,+ i& +l*))=JM(- l)"-"^ +/*))). et finalement, puisque jp est
injectif, fi = d(( — 1)"~P(A + p)), ce qui termine la démonstration.
Le théorème de de Rham (24.11.3) et la dualité de Poincaré (24.6.2) entraînent
le théorème de dualité suivant :
(24.12.10) Pour toute variété pure orientée X, il existe pour chaque p > 0 un
isomorphisme canonique
(24.12.10.1) Dx : HP(X) - (H'P(X))*
de Vespace HP(X) sur le dual de l'espace H'JX), tel que, pour toute application
f: X -* Y de classe C00 de X dans une variété pure orientée Y, le diagramme
soit commutatif.
Définissons d'abord l'application linéaire (24.12.10.1) pour une variété
différentielle pure quelconque X (orientable ou non). Pour toute p-forme
différentielle y e <?P(X), le nombre < T, y > est défini pour tout p-courant T à support
compact, et il est clair que T -+ < T, y > est une forme linéaire y sur l'espace
S'JiX) de ces p-courants. Si y est une p-forme fermée, nous désignerons encore
par y la restriction de cette forme linéaire à l'espace Z'JX) des cycles ; si de plus
T = eS est un bord, on a alors < y, T > = < 6S, y > = < S, dy > = 0, donc < y, T >
ne dépend que de la classe d'homologie a e H'JX) de T. En outre, si y = dfi est
un cobord, on a < y, T > = < T, dfi > = < 6T, fi > = 0 puisque T est un cycle ;
autrement dit < y, T > ne dépend aussi que de la classe de cohomologie c de y, et si
on note ce nombre < c, a >, on voit qu'on a défini une forme linéaire c:a -* < c, a >
sur HP(X). L'application Dx : c -» c est l'application canonique (24.12.10.1) de
l'énoncé ; en outre, pour cette application, le diagramme (24.12.10.2) est
commutatif. En effet, si T e Z'JX) a pour classe d'homologie a, et y' e ZP(Y) a pour classe
de cohomologie c', on a
< (/V))~, a > = < '/(/), T > = < y',/(T) > = <c',/,(a) > = < '(/.)(?'), a > .
HP(Y)
(HP(Y))*
(24.12.10.2) '*
HP(X)
(HP(X))*

74 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
Si maintenant X est orientée et de dimension n, il suffit, pour prouver
(24.12.10), de montrer que le diagramme
HP(X) Dx . (Hrp(X))*
mx))*
est commutatif, en vertu de (24.11.3) et (24.6.2). Or, si y e ZP(X) a pour classe
de cohomologie c, et /3eZ"_p(X) a pour classe de cohomologie b, on a
< TpWxc), b > = < Dxc, j*p(b) > = < y, jp(fi) > = £ fi a y = < Dxc, b >
d'après les définitions de Dx, de (24.11.2) et de Dx (24.6.1.3).
Nous montrerons plus tard ((24.30.5) et (24.33.1)) que Dx est encore un
isomorphisme pour une variété non orientable.
Remarque (24.12.10.3). — Soit X une variété pure compacte et orientée,
de dimension n ; alors, pour 0 < p ^ n, on a un isomorphisme canonique
j*p : H"-'(X) - H'P(X)
et comme d'autre part HP(X) est un espace vectoriel de dimension finie, HJ^X)
s'identifie au dual (HP(X))* par l'isomorphisme 'Dx.
En particulier, supposons que X soit connexe, compacte et orientée, de
dimension n ; alors la classe de la fonction constante 1 est une base de l'espace
vectoriel H°(X) (24.1.2) ; son image par j* est donc une base de l'espace
vectoriel Wn(X), qu'on appelle classe fondamentale d'homologie des courants de X,
et qu'on note parfois [X ] ; quand on identifie Hi(X) au dual de H"(X), pour
toute classe de cohomologie c e H"(X), on a donc
(24.12.10.4) <c, [X]>
■I
si y est une n-forme quelconque de la classe c ( [X ] est donc la classe du
«-courant Tvx (173.2), qui est un cycle). En particulier, si e\ est la classe
fondamentale de cohomologie de X (24.6.3.1), qui est une base de H"(X), on a < e$, [X] > = 1,
autrement dit ex et [X] sont des bases duales.
Le théorème de régularisation (24.12.8) entraîne aussi la conséquence
suivante :
(24.12.11) Soit X une variété pure orientée. Pour qu'un p-courant à support
compact T sur X soit de la forme 6S, où S est un(p + l)-courant à support compact,

12. RÉGULARISATION DES COURANTS
75
il faut et il suffit que T soif un cycle et que pour toute p-forme fermée a, on ait
La condition est évidemment nécessaire, puisque < 6S, a > = < S, da > = 0
si a est fermée. Inversement, supposons que 6T = 0 ; comme dans (24.12.9)
on peut alors écrire T = jJP) + gS^où/Jest une(n — p)-forme à support compact
et S, un (p + l)-courant à support compact. Pour toute p-forme fermée a, on a
donc < T, a > = /J a a + < 6St, a >, et on a < 6SU a > = < S„ da > = 0.
f
Si < T, a > =0 pour toute p-forme fermée a, on en déduit que J fi a a = 0
pour ces formes, ce qui signifie encore, avec les notations de (24.6.1), B(a, b) = 0
si a e HP(X) et b e H"~P(X) sont les classes de a et /? respectivement. Cette relation
ayant lieu quel que soit a e HD(X), on en déduit que b — 0 par le théorème de
dualité (24.6.2) et par (Ann. 32.3). Par suite P = dy, où y est une (n — p — Informe
à support compact, et on en tire T = 6((- l)n~pjp+i(y) + Si) par (24.11.1.3).
Remarque (24.12.12). — Soient X une variété pure orientée, Y une sous-
variété pure orientée de X, et soit j : Y -* X l'injection canonique. Si T est un
p-courant sur X, d'ordre 0 et de support compact contenu dans Y, il existe un
unique p-courant T0 sur Y tel que jJJ0) = T. En effet, puisque T est d'ordre 0,
les distributions TH qui interviennent dans chacune de ses expressions locales
(17.5.4) sont des mesures portées par Y ; pour toute p-forme P de classe C00
sur Y, si P° désigne la p-forme discontinue sur X obtenue en prolongeant P
par 0 dans X - Y, < T, p° > est défini et l'application p -> < T, p° > est continue
dans tfp(Y), par définition d'une mesure ; c'est évidemment la distribution T0
cherchée.
Sous les hypothèses précédentes, si T est un cycle, il en est de même de T0.
En effet, toute (p - l)-forme a de classe C00 sur Y est la restriction '/(co) d'une
(p - l)-forme co de classe C00 sur X (16.12.11) ; on a donc
<6T0, a> = <T0, da> = <T0, '&dœ)> = <T, dco> = 0
par hypothèse, d'où 6T0 = 0.
Par contre, si T est un bord sur X, en général T0 n'est pas un bord sur Y.
Toutefois, si l'application canonique j* : H"(X) -> H"(Y) est surjective, alors,
pour tout courant T de support compact et d'ordre 0, qui est un bord sur X,
T0 est un bord sur Y. En effet, T0 est un cycle sur Y, et en vertu de (24.12.11),
il suffit de voir que < T0, a > = 0 pour toute p-forme fermée a sur Y. Mais
l'hypothèse de surjectivité implique que a est cohomologue à une forme ';'(/*), où P est
une p-forme fermée sur X, de classe C°° ; comme T = 6S, où S est un (p + l)-cou-
rant sur X, on a < T0, a > = < T0,'./(/?) > = < T, P > = < 6S, p > = < S, dp > = 0.
Un exemple où j* est surjective est donné par le cas où Y est une sous-
variété compacte d'une variété compacte orientée Z et X un voisinage ouvert
<T,a> = 0.

76 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFERENTIELLE ÉLÉMENTAIRES
assez petit de Y dans Z : on peut en effet supposer Z plongée dans un R" (16.25.1),
et il existe alors un « voisinage tubulaire » V de Y dans R" et une projection n :
V -» Yde classe C00, telle que 7t(y) = y pour y 6 Y (16.25.4). Pour toute p-forme
fermée a sur Y, la p-forme p = Xa) sur V est alors fermée et telle que a soit sa
restriction à Y, et la restriction de P à X = V n Z a les mêmes propriétés, d'où
notre assertion.
PROBLÊME
Soient X, Y deux variétés connexes, compactes et orientées, de même dimension n et/ : X -» Y
une application de classe C°°. Montrer que /,( [X ]) = deg/. [Y ].
13. L'anneau d'intersection.
(24.13.1) Soit X une variété pure orientée de dimension n. Les isomorphismes
canoniques/* (24.11.3) définissent une application linéaire bijective de l'espace vec-
n n
toriel gradué HC'(X)= © H"-p(X) sur l'espace vectoriel gradué H'.(X)= © H'^X),
p = 0 p=0
et l'on peut donc transporter par cette application la structure d'algèbre
graduée de H*(X) (24.1.1) en une structure d'algèbre graduée sur H'(X). La
première de ces structures a été déduite d'une structure d'algèbre graduée sur
s#XX) = © %(X) ; on peut aussi transporter cette dernière par les injections
p=0
canoniques jp (24.11.1.1) en une structure d'algèbre graduée sur la somme directe
des images jJ^-JX)) ; mais il n'y a pas de moyen « raisonnable » d'étendre
cette structure à toute la somme directe © S'fii) des espaces de courants à
p = 0
support compact. Toutefois nous allons voir que dans des cas étendus, il est
possible de définir un « produit » S. T de deux courants qui, lorsque S et T ont
des supports compacts et sont des cycles, donne, par passage au quotient, le
produit sur H'(X) transporté de celui de H'JX).
(24.13.2) Le théorème de régularisation (24.12.8) montre que, dans l'espace S'J^X)
des p-courants à support compact, l'image par l'injection canonique jp (24.11.1)
de l'espace 0„_P(X) des (n — p)-formes différentielles de classe C00 à support
compact est partout dense pour la topologie faible de ^(X). En outre, tout
p-courant T sur X (de support quelconque) peut être approché arbitrairement, pour
la topologie faible de ®P(X), par un p-courant à support compact (par exemple
un courant h.T, où la fonction he@(X) est égale à 1 dans un compact assez
grand) ; on en conclut que jJfy-JX)) est aussi dense dans ^(X) pour la
topologie faible.

13. l'anneau d'intersection
77
Soient p, q deux entiers ^ 0 tels que p + q > n. Pour tout p-courant S
sur X et toute (n — q)-forme différentielle /?e®„_,(X), on a défini le (p+q — n)-
courant S a p (17.3.5) ; lorsque S s'écrit lui-même jj^ct) pour une (n - p)-forme
ote^-pfX), on a jja) a p = jp+^a a /3), car, pour toute (p + q - n)-forme y
de classe C00, on a
O» a 0, y > = <;», /?Ay> = £<XA/JAy = <;p+,(a a fi), y > .
On est donc conduit à considérer ;'p(<x) a /i comme « produit » jJ((x).jq(P), et
par suite, plus généralement, S a /S comme « produit » S .j^P) ; d'où l'idée,
pour définir un produit S. T de S et d'un tj-courant quelconque T, de chercher
s'il est possible de prolonger par continuité au point T l'application jjp) -* S a fi
de ;',(®n_,(X)) dans ©P+,_„(X). Des exemples simples montrent que ce n'est pas
toujours possible (problèmes 1 et 2) ; toutefois, nous allons voir que cette idée
permet de définir un (p + q — «)-courant S.T dans des cas assez étendus.
Nous utiliserons le lemme élémentaire suivant :
(24.13.3) Pour tout p-courant S et toute q-forme différentielle P de classe Cœ
telle que q < p — 1, on a
(24.13.3.1) 6(S a fi) = (- \y{6S a fi-S a dfi).
En effet, pour toute (p — q — l)-forme y de classe C°° et de support compact,
on a
<<r(S a fi), y > = <S a fi, dy > = <S, p a dy > ;
or p a dy — (— l)9(d(p a y) - (dp) a y), donc
<6XS a p), y > = (- 1)*(< S, d(P a y)> - < S, (dp) a y >)
= (-lH<ss,/JAy>-<S Ad/8,y>) = (-l)«(<ssa/J,y>-<S a d/J, y ».
Cela entraîne que si S et ;',(/?) sont des cycles, il en est de même de S .j^P), et
que si en outre un des courants S, j^P) est un bord d'un courant à support compact,
il en est de même de S .jq(P) ; comme en outre, tout p-courant à support compact S
qui est un cycle est homologue à un cycle jp(fi) (24.11.3), on voit que la classe
d'homologie du produit S .jJJS) de deux cycles dans HP+,_„(X) est bien le produit
des classes d'homologie de ces deux cycles pour le produit transporté de celui
de H;(X).
(24.13.4) Nous aurons aussi besoin d'étendre aux courants la notion de
support singulier (17.5.14). Comme l'application jp : én-p(X) -* £2P(X) est
injective, si (WJ est une famille d'ouverts de X telle que la restriction d'un p-courant S
à chaque WA s'écrive jp(PÀ) pour une (n — p)-forme Pxe Sn-p(Wx), les pk sont

78 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
les restrictions aux WA d'une unique (n — p)-forme P de classe C°° sur W = u WA,
x
et la restriction de S à W est égale à jJP). Il y a donc un plus grand ouvert V tel
que la restriction de S à V s'écrive jjp) pour une (n - p)-forme peSn.JW) ;
le complémentaire de V dans X est appelé le support singulier de S et noté
Supp.sing(S). On a évidemment Supp.sing(S) c= Supp(S), et il résulte de la
commutativité du diagramme (24.11.1.3) que l'on a
(24.13.4.1) Supp.sing(§S) c Supp.sing(S).
Enfin, pour toute fonction h e #(X), on a
(24.13.4.2) Supp.sing(n.S) <= Supp.sing(S)
comme il résulte de la définition.
(24.13.5) Si les produits Si. T. et S2.T peuvent se définir par prolongement
continu, il en est de même de (Si + S2).T, qui est alors égal à St .T + S2.T.
Soit (WA) un recouvrement ouvert localement fini de X, et (SA) une famille de
p-courants tels que Supp(SA) <= pour tout A ; alors la somme de S = SX est
X
définie, et si chacun des produits SX.T peut être défini par prolongement continu,
il en est de même de S.T et l'on a S.T = zs^.T. Comme tout p-courant peut
x
toujours s'écrire sous la forme £ $x> ou les WA sont relativement compacts (au
x
moyen d'une partition de l'unité), on voit que pour examiner si un produit S.T
peut être défini par prolongement continu, on peut toujours se ramener au cas
où S a un support compact.
Enfin, soit (hj une partition de l'unité dans X, formée de fonctions de
classe C00. Si chacun des produits S.(hA.T) peut se définir par prolongement
continu, il en est de même de S.T et l'on a S.T = XS.(nA.T) ; cela résulte de
x
la continuité faible de l'application T -»■ nA.T dans ©J(X).
(24.13.6) Soient S un p-courant à support compact, T un q-courant, avec p + q^n.
Si les supports singuliers de S et T ne se rencontrent pas, les (p + q — n)-cou-
rants S.T et T.S peuvent se définir par prolongement continu, et Von a
(24.13.6.1) T.S = (- l)<»-"«»-«>S.T
(24.13.6.2) Supp(S. T) c Supp(S) n SuppfT).
On se ramène aussitôt au cas où T a aussi un support compact. Supposons
d'abord que Supp(S) n SuppfT) = 0 ; comme le tj-courant T peut être approché
arbitrairement par un courant j^P), où P est une (n — <7)-forme dont le support

13. l'anneau d'intersection
79
est contenu dans un voisinage arbitraire de SuppfT), on peut supposer que
Supp(S) n Supp(0) = 0, et alors Saj} = 0 (17.4.3) ; le produit S.T est alors
défini par prolongement continu et est nul.
En second lieu supposons que Supp.sing(S) = 0, donc S = jja) pour
une (n — p)-forme a à support compact. Supposons que le q-courant jq(fi)
tende faiblement vers T ; on a alors S a P = jja) a P = (-l)in~p)i''~9)jq(P) a a
(17.5.2.2), qui tend faiblement vers (- 1)<*-pH»-«)t a ^ et par définition T a a
est le produit T.S ; la proposition est donc prouvée dans ce cas.
Dans le cas général, soient V un voisinage relativement compact de
Supp.sing(S), W un voisinage relativement compact de Supp.singfT) tels que
V n W = 0 ; soit g (resp. h) une fonction de ®(X) de support contenu dans V
(resp. W) et égale à 1 dans un voisinage de Supp.sing(S) (resp. Supp.singfT)).
Écrivons S = g.S + (1 — g).S et T = h.T + (1 - h).T ; il est immédiat que
les supports singuliers de (1 - g).S et (1 — h).T sont vides, et que les supports
de g. S et h. T ne se rencontrent pas ; on est donc ramené aux deux cas précédents,
ce qui achève de prouver (24.13.6).
(24.13.7) En dehors du cas considéré dans (24.13.6), il ne semble pas y avoir
de cas plus généraux où l'on puisse définir intrinsèquement un produit S.T par
prolongement continu : autrement dit, il se peut que pour deux suites (Pk), (P'k)
de (n - q)-formes telles que {jq{pk)) et (jJiPQ) tendent toutes deux faiblement
vers T, les deux suites (S a fik) et (S a P'k) aient chacune une limite, mais que
ces limites soient distinctes (problème 1).
Nous allons voir toutefois qu'on peut donner un procédé linéaire
applicable à tout courant T sur X (mais indépendant de T), permettant d'approcher T
par une suite (/«(/?»)) bien déterminée d'images de (n — qj-formes et de définir S.T
dans des cas plus étendus, de façon à remplir les conditions suivantes :
10 si S et T sont des cycles de Z'(X), il en est de même de S.T, et la classe
d'homologie de S.T dans H,+4-„(X) est égale au produit de celles de S et T pour
la structure d'algèbre définie dans (24.13.1) ;
2° toutefois, le produit S.T garde un sens, sous des conditions assez larges,
même lorsque 6S et 6T ne sont pas nuls, et cela permet souvent de calculer
explicitement le produit des classes d'homologie de deux cycles, en les décomposant
en somme de courants qui ne sont plus des cycles.
(24.13.8) La méthode générale consiste à régulariser localement T, mais sans
exiger de résultats aussi précis que dans (24.12.8). On considère un
recouvrement localement fini (W*) de X par des domaines de cartes (WA, ujx, n) de X,
relativement compacts ; on considère une partition de l'unité (hx) sur X,
subordonnée à (Wj) et formée de fonctions de classe C°°, et les images Tx = *j/x(hx.J\
T, étant un ^-courant sur R", de support compact contenu dans \lfx(V/x). On

80 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
considère ensuite une suite régularisante (gM) sur R", telle que le q-courant
gk,x * ^ ait son support dans faÇ^x) ; il est alors de la forme j^P^x), où /?M est
une (n — gj-forme de classe C°° et de support contenu dans ^(WJ (24.12.2).
Si la suite de (p + q — n)-courants ^(S | a fjk ijt sur R" tend vers une limite
faible, il en est de même de la suite des {p + q — n)-courants S a '^(P^x) sur X ;
si cela a lieu pour tout X et si, pour tout k, on pose Lk.T = J^'^xiPk x)> la suite
x
des (p + q — n)-courants S a Lk.T a aussi une limite faible, puisque le support
d'une (p + q — n)-forme y e i^+g-^X) ne rencontre qu'un nombre fini
d'ouverts Wx. Nous dirons alors que la limite de cette suite est le produit S.T
obtenu par le procédé d'approximation (Lk). Un point essentiel dans cette méthode
est que l'on a
(24.13.8.1) d(Lk.T) = (- l)"-9+1Lk(6T).
En effet, il suffit de montrer que 6(gkX*TJ = gkX*(6TX), ce qui résulte
aussitôt de la formule (24.12.2.1) et du fait que d(gkwk*a) = g\,x*(da) pour
toute p-forme a (17.11.11.1).
(24.13.9) Soient S un p-courant, T un q-courant avec p + q^ n.Sile produit S.T
peut être défini par un procédé d'approximation, et si SetT sont des cycles, S.T est
un cycle. Supposons de plus que S soit un cycle à support compact et T un bord,
ou que S soit le bord d'un courant à support compact et T un cycle ; alors S.T est
bord d'un courant à support compact.
Supposons que 6S = 0 et 6°T = 0 ; il s'agit de montrer que pour toute
{p + q — n — Informe a à support compact, on a < S.T, da > = 0 (on peut
évidemment se borner au cas où p + q — n ^ 1). Posons pk = Lk.T ; d'après
(24.13.8.1) et l'hypothèse, on a df}k = 0, donc d(fik a a) = (- \)qfik a da ; par suite
<S a pk,da} = <S, pk a da> = (- 1)«<S,d(0k a <x)> = (- 1)"{6S,pk a a> = 0;en
passant à la limite, on a bien < S.T, da > = 0. Supposons que ffS = 0, T = §T
et que S ait un support compact ; alors S.T est un cycle à support compact,
et pour montrer que c'est le bord d'un courant à support compact, il suffit de
prouver que < S.T, a > = 0 pour toute (p + q — n)-forme fermée a (de
support quelconque) (24.12.11). Si P'k = Lk.T, on a Lk.1 = (- lV*",+ 1ti/îi, donc
< S, (dp'k) a a > = < S, d(p'k a a) > = < 6S, p'k a a > = 0 puisque da = 0 ; en
passant à la limite, on a bien < S.T, da > = 0. Si S = 6S' où le support de S' est
compact, et 6T = 0, on a < S, pk a a > = < 6S', pk a a > = < S', d(Pk a a)> =0
puisque da = 0 et dpk = 0 ; on en déduit encore que < S.T, a > = 0.
(24.13.10) Sous les hypothèses de (24.13.9), si S et T sont des cycles {à supports
compacts) et si le produit S.T peut être défini par un procédé d'approximation,
la classe d'homologie de S.T est le produit (défini dans (24.13.1)) de la classe
d'homologie de S et de celle de T.

13. l'anneau d'intersection
81
Si S = jp(ot) et T = ;',(/?), où a (resp. p) est une (n - p)-forme fermée (resp.
une (n — c])-forme fermée) à support compact, cela n'est autre que la définition.
Supposons en second lieu que S soit un cycle quelconque et T = y,(/?) ; d'après
(24.12.8.1), on peut écrire S = jp(a) + 6S' pour une (n — p)-forme fermée a
et un (p + l)-courant S', à supports compacts ; comme (^S') .jj^P) est bord d'un
courant à support compact d'après (24.13.9), S.T est homologue à j^.j^P), et
la conclusion résulte de ce que S est homologue à jp(a). Considérons enfin le
cas général ; alors, par (24.12.8.1), on a T = j£P) + 6T\ où P est une (n - q)-
forme fermée et T' un [q + l)-courant, à supports compacts. Par hypothèse,
S. T peut être défini par un procédé d'approximation, et il en est donc de même
de S.(6T'), qui est par suite bord d'un courant à support compact en vertu de
(24.13.9) ; S.T est donc homologue à S.jJiP), et j^P) étant homologue à T, on
est ramené au cas précédent.
(24.13.11) Nous allons d'abord étudier un exemple simple qui nous donnera
de nombreux cas où le produit S.T peut être défini par un procédé
d'approximation. Soient p, q deux entiers tels que p + q > n ; dans l'espace R", nous
écrirons les n coordonnées
Xi, ..., -Xp+,j_m yj, ..., yn—q, Zj, ..., zn~p ,
l'orientation de R" sera prise telle que la «-forme
dx\ a ... a dxp+q-n a dy, a ... a dy„-q a dzt a ... a dzn-p
soit positive. Nous désignerons par Rp (resp. R*, Rp+<~") le sous-espace
vectoriel engendré par les p premiers vecteurs (resp. les p + q — n premiers et les
n — p derniers, resp. les p + q — n premiers) de la base canonique, de sorte
que R'+^'sR'nR'; les orientations sur ces trois sous-espaces sont prises
telles que les formes
dxi a ... a dxp+q-n a dy, a ... a dy„-q,
dx\ a ... a dxp+q-„ a dz\ a ... a dzn_p et dxi a ... a dxp+q-„
soient positives. Nous noterons aussi x, y, z les vecteurs
(*t, ..., x,+(.j6R'+'-", (y, y„_,) et (Zl z„.p).
Soient alors (x, y) -+ A(x, y) une fonction numérique continue définie
dans R", (x,z) -+ B(x, z) une fonction numérique continue définie dans R«,
et considérons sur R" le p-courant S et le tj-courant T définis par
(24.13.11.1) S : a ^ | A.a
(24.13.11.2) T:P B.p

82 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
Alors :
(24.13.12) Le produit S.T peut être défini par un procédé d'approximation, et
est le (p + q — n)-courant
(24.13.12.1) co - \ C.co
où Qx) = A(x, 0)B(x, 0).
Avec les notations de (24.12.1), remarquons d'abord que l'on a < S, ÇH > = 0
sauf pour les p-formes
a =/(x, y,z)dxl a ... a dxp+„-n a dy, a ... a dy._,
pour lesquelles
< S, a > = £a(x, y)/(x, y, O^x, y)
(on note Ar la mesure de Lebesgue sur R') ; de même < T, ÇH > = 0 sauf pour
les q-formes
P = «(x, y, zjtixi a ... a dxp+9-„ a dzx a ... a dzH.p
pour lesquelles
<T,/?>= [ B(x,z)«(x,0,z^x,z).
Soit (hk) une suite régularisante sur R", et calculons la (n — <j)-forme v* te^e
que hk*T =Uyk);on a <hk*T, /}> = <T, fc>/ï>, et
= (£nk(x'-x,y'-y,z'-z)g(x',y',z'^x',y',z')^1 a ... Adv,;
par définition < T, hk * p > = £ yk a p, ce qui donne
(_ 1)(p+«-n)(n-,)^ B(x',i'Mx-x',y,i-i')<i^',i'))^1 a ... a dy.-,.
Par suite, pour une (p + q — «)-forme à support compact
co = u(x, y, zjd*! a ... a <£*■„+,_,

13. l'anneau d'intersection
83
on a, pour < S, yk a co >, l'expression
que l'on peut aussi écrire
(x-x', y, -z')dA,(x', z')
lx-x',y',-z')dXjtx',y',z');
JW*n-» Jb"
par définition d'une suite régularisante, l'intégrale intérieure tend vers
A(x, 0)B(x, 0)«(x, 0, 0) ; la conclusion résulte donc du théorème de
convergence dominée (u étant une fonction de ®(R")).
(24.13.13) Avec les notations précédentes, il est clair que S, T et S.T sont des
courants d'ordre 0 (17.3.2). Pour tout compact K c R", l'espace K)
des r-formes de classe C° à support dans K est un espace de Banach, pour la
norme définie par sup (sup | f^t) \ ) pour une r-forme Y /HCH- Les calculs de
H leK H
(24.13.12) montrent donc que, pour toute (p + q — n)-forme co à support dans K,
on a, pour tout indice k,
|<SAy»,c»>|< sup |A(x,y)|- sup |B(x, T)\Xp+^n(KnR"+"''>y\\co\\.
(24.13.14) Considérons maintenant dans X deux sous-variétés fermées, pures,
orientées Y, Z, de dimensions respectives p, q avec p + q> n. Nous supposerons
que ces variétés se coupent transversalement : cela signifie par définition qu'en
tout point x e Y n Z, les sous-espaces tangents TX(Y) et TJZ), de dimensions
respectives p et q, ont une intersection de dimension p + q — n. Alors Y n Z
est une sous-variété fermée pure, de dimension p + q — n, qui est orientable.
En effet, pour tout x e Y n Z, il y a une carte ^ d'un voisinage ouvert V
de x dans X sur un ouvert ^(V) de R" telle que t/f(x) = 0 et que (en identifiant
l'espace tangent à R" au point 0 à l'espace R" lui-même), les images par Tx(ip)
de TJY) et TJZ) soient respectivement Rp et R* (avec les conventions de (24.13.11)).
Alors, il résulte de (16.8.3.2) que l'on peut supposer que, dans i^(V), i^(Y n V)
(resp. \p(Z n V)) est définie par des équations
z» - • • -, xp+q-n, y,, ..., y„-,) = 0 pour 1 < k < n - p
(resp. y, - Vj{xu xp+q-n, zu ..., z„-p) = 0 pour 1 < j < n - q)
avec duk(0) = 0 pour 1 < A; ^ n -p (resp. dvj(0) = 0 pour 1 < n - q). Comme
le jacobien des n fonctions
x] = xt (1 ^ i p + q — n)
y) = yj - vÂxi> ■ ■ •> xP+q-«> zu ■ ■ ■> 2»-p) (i q)
z» = z» ~ • • •. xp+q-H, y„ ..., y„-,) (1 ^ k < n - p)

84 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
est égal à 1 au point 0, un difféomorphisme d'un voisinage de 0 contenu dans i^(V)
permet de se ramener au cas où
^(Y n V) = MV) n R", tfV n Z) = ^(V) n R«
et alors \j/(Y n Z n V) = ^(V) n Rp+«~", ce qui prouve déjà que Y n Z est une
sous-variété pure de dimension p + q — n.
Pour voir qu'elle est orientable, soient o, p, a des formes différentielles
appartenant respectivement aux orientations de X, Y et Z (en se bornant, comme
on peut toujours le faire, au cas où ces variétés sont connexes). Pour tout xe YnZ,
» p
soit v{x) (resp. r(x), $(x)) le «-vecteur de a TJX) (resp. le p-vecteur de a TJY), le
q-vecteur de a TJZ)) tel que < u(x), v(x) >=1 (resp. < p(x), r(x) > = 1, < <x(x), s(x) >=1).
Comme r(x) (resp. s(x)) est produit de p vecteurs de TJY) (resp. de q vecteurs
p
de TJZ)), on peut l'identifier à un p-vecteur de a TJX) (resp. à un g-vecteur
de a TJX)) ; posons
p'(x) = r(x) J o(x) (resp. o'(x) = s(x) J v(x))
*-p n-q
qui est un («-p)-covecteur de a TJX)* (resp. un (n-qj-covecteur de a TJX)*).
2n-p-q
Alors p'(x) a tr'(x) est un (2n - (p + tj))-covecteur de a TJX)*, et par
suite m(x) = (p'(x) a ct'(x)) j v(x) un (p + q — «)-vecteur de a TJX), et
il résulte aussitôt de (Ann. 15.3.2) que ce (p + q — n)-vecteur est produit de
p + q — n vecteurs formant une base de TJY n Z). Par ailleurs, en utilisant
la carte i//, on voit que la section x -» m(x) est continue dans Y n Z ; si u(x) est
p + q-n
le (p + q — n)-covecteur de a TJY n Z)* tel que < «(x), m(x)> = 1, x -» /4*)
est aussi continue, donc Y n Z est orientable et on a un procédé intrinsèque
pour déduire, des orientations données sur X, Y, Z, une orientation de Y n Z.
Nous supposerons que l'on ait choisi cette orientation.
Soient alors y -♦ A(y) une fonction complexe continue dans Y, z -> B(z)
une fonction complexe continue dans Z, S le p-courant et T le q-courant sur X
définis par
(24.13.14.1) S : a - j^A-a
(24.13.14.2) T : fi - | B/J

13. l'anneau d'intersection
85
(cf. 17.5.2.4). Alors le produit S • T peut être défini par un procédé
d'approximation ; c'est le (p + q — n)-courant
avec t = p(n — p) + q(n — q) ; il ne dépend donc pas du procédé d'approximation.
On prend un recouvrement localement fini de Y n Z par des domaines vx
de cartes ^ de X telles que ^(Y n VA) = ^(V,) n R", kVa(Z n V,) = ^(VJ n R« ;
on peut supposer que les supports de S et T sont contenus dans la réunion des
wx (24.13.6). On peut alors appliquer pour chaque A le résultat de (24.13.12) et
la conclusion en résulte (24.13.8), le signe (— 1)' étant déterminé en utilisant
(Ann. 15.3.2).
Lorsque l'on prend pour A et B la fonction égale à la constante 1, on dit
que les courants S et T sont les courants d'intégration (sur X) définis par Y et Z
et on les note IY et Iz, ou même, par abus de langage, Y et Z ; en vertu de (17.15.5.1),
ce sont des cycles, et le résultat précédent peut s'écrire
(24.13.14.4) Y • Z = ( - 1)'Y n Z
En raison de cet exemple, on dit que l'algèbre graduée H'(X) définie dans
(24.13.1) est l'algèbre d'intersection sur X.
(24.13.15) Supposons X connexe, de sorte qu'il existe une bijection
canonique H"(X) -* R (24.6.3.2), et par suite aussi, par composition avec la
bijection canonique (/S)-1 : Hq(X) -♦ HJ(X), une bijection canonique ix : HÔ(X) -» R;
les définitions (24.6.3.2) et (24.11.1.2) montrent que si ceH0(X) est la classe
d'homologie d'un O-courant (c'est-à-dire une distribution) T à support compact,
on a ,x(c) = <T, 1>.
Supposons que p + q = n ; si S est un p-courant, T un q-courant, et si le
produit S • T peut être défini par un procédé d'approximation, S • T est une
distribution ; si son support est compact, on pose alors
et on dit que (S • T) est le nombre d'intersection de S et T.
Soient alors Y, Z deux sous-variétés pures, fermées, orientées, de X, de
dimensions respectives p et q = n — p, telles que Y et Z se coupent
transversalement en un nombre fini de points { xly ..., xr}. Pour chaque xj, avec les
notations de (24.13.14), il est clair que p(xj) a o(Xj) est proportionnel à v(xj) ; si le
coefficient de proportionnalité est > 0 (resp. < 0), l'orientation de {xj} déduite
de celles de Y et Z par le procédé de (24.13.14) est formé des nombres réels > 0
(resp. < 0). Considérons alors le p-courant S et le (n — p)-courant T définis
en prenant dans (24.13.14) les fonctions continues à support compact A et B
(24.13.14.3) co -» (- 1)'
(24.13.15.1) (ST) = <ST, 1 >

86 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
égales à la constante 1 dans un voisinage de chacun des Xj. Il est immédiat que le
nombre d'intersection (S - T) ne dépend pas des choix de A et B soumis aux
conditions précédentes ; on le note (Y • Z) et on l'appelle le nombre (algébrique)
d'intersection des sous-variétés orientées Y et Z; la formule (24.13.15.1) donne donc
(24.13.15.2) (Y • Z) = £ e(Xj)
j=t
avec e(Xj) = 1 (resp. e(Xj) = - 1) si l'orientation de {Xj} définie ci-dessus est
formée de nombres > 0 (resp. < 0). Il est clair que
(24.13.15.3) (Z • Y) = (- l^'-^Y • Z).
Un cas particulièrement important est celui où X, Y, Z sont des variétés
holomorphes, munies chacune de l'orientation canonique (16.21.13) ; alors il est
immédiat que pour chaque j, l'orientation de {Xj} est formée des nombres > 0,
et par suite que dans ce cas (Y • Z) est le nombre de points de l'intersection Y n Z.
(24.13.16) Bornons-nous toujours au cas où p + q = n ; il se peut que pour
un p-courant S à support compact et un (n — p)-courant T sur X, le produit S • T
ne puisse être défini par un procédé d'approximation, mais que l'on puisse
cependant définir le nombre d'intersection (S • T) par un tel procédé. Il suffit en effet,
avec les notations de (24.13.8), que la suite des nombres < S a Lk • T, 1 > ait une
limite, qui sera alors par définition le nombre d'intersection (S ■ T). Il en est ainsi
en particulier si S est le bord d'un courant à support compact et T un cycle, ou
si S est un cycle et T un bord, et l'on a alors (S • T) = 0. En effet, supposons d'abord
que S = 6S', où S' a un support compact, et 6T = 0 ; alors, si f}k = Lk • T, on a
dpk = 0, et < S a pk, 1 > = < S, pk > = < 6S\ pk > = < S', dpk > = 0 pour tout k.
De même, si 6S — 0 et T = 6T', on peut écrire pk = dp'k, donc
<s, p\> = <s, <*/?;> = < es,&> = o.
On en déduit des cas plus généraux où (S - T) est défini :
(24.13.17) Soient S un p-courant à support compact, T un (n — p)-courant. Si
le support singulier de chacun des courants S, T ne rencontre pas le support
singulier du bord de l'autre (et en particulier si S et T sont des cycles), le nombre
d'intersection (S • T) peut être défini par un procédé d'approximation.
On peut se ramener au cas où le support de T est compact (24.13.6).
Appliquant (24.12.8) à T, on peut écrire T = jn-p(P) + T, + 6T2, où p est une p-forme
de classe C00, le support singulier de Tj est arbitrairement voisin de celui de 6T,
T2 a un support compact et son support singulier est arbitrairement voisin de
celui de T. On peut donc supposer que les supports singuliers de S et de T, ne se
rencontrent pas, et en vertu de (24.13.6), on est ramené à démontrer que le nombre
d'intersection (S-6T2) est défini. On peut de même écrire S=7p(a)+Sj-l-6,S2,

13. l'anneau d'intersection
87
où a est une (n - />)-forme de classe Cœ, S2 a un support compact, et le
support singulier de Si est arbitrairement voisin de celui de 6S ; on peut donc
supposer que les supports singuliers de S, et de 6T2 ne se rencontrent pas.
Finalement, en vertu de (24.13.6), il reste à montrer que le nombre d'intersection
(é"S2 • 6T2) est défini, ce qu'on a vu dans (24.13.16) (avec la valeur 0).
Sous les conditions de (24.13.17), on a encore
(24.13.17.1) (T ■ S) = (- l^-^S • T).
En outre, si S' est un (p + l)-courant tel que le support singulier de CS'
ne rencontre pas celui de T, le produit 6S' ■ T est défini (24.13.6) donc aussi
a fortiori le nombre d'intersection (6S' • T) ; en outre, le nombre d'intersection
(S' • 6T) est alors défini par un procédé d'approximation, et l'on a
(24.13.17.2) (£S'-T) = (S'-rr).
En effet, avec les mêmes notations que dans (24.13.16), on a < S', dfik > = < 6S', fik >,
qui par hypothèse tend vers (6S' ■ T). De la même manière, si T'est un (n — p + 1)-
courant tel que le support singulier de 6T' ne rencontre pas celui de S, le nombre
d'intersection (5S-T') est défini et l'on a
(24.13.17.3) (ffS • T') = (S • 6T).
PROBLÈMES
1) On considère sur R2 les deux 1-courants S, T définis par
< S, UtdXi + u2dx2 > = I 0)dxt
< T, K,d*i + M*i > = "2(0, x2)dx2
pour u,, u2 dans £2(R2). Soit {gk) une suite régularisante sur R, et soit (hk) une suite de fonctions
r 1 0
de S>{R) telles que | /t» | $ 1 et que le support de ht soit contenu dans l'intervalle —, - ; on
L k kj
pose ak = g»(x,)(l - hk(X2))dxi. Montrer que la suite des courants ji(ak) converge vers T dans
S',(R2) pour la topologie faible, mais que, suivant le choix de la suite (hk), la suite des
distributions S a j, converge ou ne converge pas vers une limite dans ®'(R2), et peut converger vers des
limites dépendant de (hk).
2) On considère sur R2 les deux 1-courants S, T définis par
< S, u,dx, + u2dx2 > = u,(0, 0)
< T, utdxi + u2dx2 > = u2(0, 0)
Soit (g») une suite régularisante sur R2. Si l'on pose gk * T = j,(flk), la suite des distributions SaJI,
converge ou ne converge pas vers une limite dans ®'(R2), suivant le choix de la suite régularisante
(gk), et peut converger vers des limites dépendant de (gk).

88 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
14. La formule de Stokes.
(24.14.1) Soient X une variété pure orientée de dimension n, et soit U un ensemble
ouvert dans X ; la frontière régulière Frr(U) de U dans X (23.48.1) est alors une
variété orientable de dimension n — 1. Nous munirons Frr(U) de l'orientation
canonique (ou vers l'intérieur) (23.48.2) si n est pair, de l'orientation opposée
(ou vers l'extérieur) si n est impair. Si (V, i/>, n) est une carte de X en un point
n
régulier x de Fr(U) telle que ^(x) = 0, que ^(V) soit la boule ouverte £ (e?f < p2
n 7=1
et i/<(U n V) la demi-boule définie par £ (£*)2 < P2 et > 0> alors, si l'image
7=1
réciproque de de)1 a de;2 a ... a de? par i// appartient à l'orientation de V
induite par celle de X, l'image réciproque de (— Ifde)1 a de)2 a ... a de)"'1
par la restriction de \}/ à V n Fr(U) appartient à l'orientation de V n Fr(U)
induite par celle de Frr(U).
Étant donnée une (n — Informe différentielle Ç sur X, telle que l'image
réciproque 'j(Ç) par l'injection canonique j : Frr(U) -» X soit intégrable (16.24.2),
nous dirons que Ç est intégrable dans Frr(U) et nous écrirons Ç son intégrale,
f jFrr(U)
au lieu de Avec ces notations, on a le théorème suivant :
JFrr(U)
(24.14.2) Soit C une (n — l)-forme différentielle de classe C1 sur X. Si
l'intersection de U et du support de Ç est compacte et ne contient que des points réguliers
de Fr(U), dÇ est intégrable dans U, Ç est intégrable dans Frr(U), et l'on a
1«-J
Ju jFr
(24.14.2.1) | dÇ = C
jFrr(U)
(formule de Stokes).
Par hypothèse, on peut recouvrir un voisinage compact V de
l'intersection de U et de Supp(() par un nombre fini d'ensembles ouverts relativement
compacts Wt (1 < fe < N) ayant les propriétés suivantes : ou bien Wt est contenu
dans U, ou bien W* contient un point frontière régulier ak de U, et il y a une
carte i//k = (ijfk, ..., i^j) de Wt sur le cube K défini par -1 <<!;'< 1 (l^i*£n),
préservant l'orientation, telle que \pk(ak) = 0 et que U n Wt soit l'ensemble
des z e Wt pour lesquels ^J(z) > 0. Soit (hk) (0 < k < N) une partition de l'unité
de classe C00 subordonnée au recouvrement de X formé des Wk et de QV (avec
Supp(n0) cr QV). Comme le support de dÇ est contenu dans celui de C, son
intersection avec U est compacte ; dÇ est donc intégrable dans U puisqu'elle est de
classe C°, et l'on a d( = H d(hkÇ) ; d'autre part, l'intersection de Supp(Ç)
Ju *=0 Ju
et de Frr(U) étant compacte, Ç est intégrable dans Frr(U) et l'on a de même

14. LA FORMULE DE STOKES
89
N Ç
C = Z ("*£)• Tout revient donc à démontrer la formule de Stokes
Frr(U) * = 0 jFrr(U)
lorsque le support de Ç est contenu dans l'un des W», que nous désignerons
simplement par W. Si W c U, on a d(, = d(, = 0 en vertu de (17.15.5.1) (la
Ju Jx
démonstration de cette relation est valable pour toute forme de classe C1 à
support compact) ; en outre — 0 dans ce cas, d'où (24.14.2.1). Si W contient
un point de Frr(U), nous noterons a ce point, et i// = ..., i]/") la carte
correspondante. On peut alors écrire
V_1(C) = t gMl a ... TCd^X ...Ad?
i=l
où les g( sont des fonctions de classe C1 dans R", dont les supports sont compacts
et contenus dans K ; on a donc
dcr\Q) = (.£ (- ir1 ^f)^1 a dp a ... a dçn
et par suite, puisque i/y préserve l'orientation (16.24.5.1)
(24.14.2.2) £dC = t (- l)'"1 |p^dïdp ...de?
P étant le pavé intersection de K et du demi-espace > 0. D'autre part, la
restriction ty' de \\i à Frr(U) n W est une carte de cet ouvert sur l'intersection K'
de K et de l'hyperplan L? = 0, identifié à R""1. En vertu de la définition de
l'orientation de Frr(U) (24.14.1), l'image par d'une forme ^ 0 de degré n — 1 sur
Frr(U) n W a le signe de (- 1)" sur R""1 (orienté canoniquement). Comme on a
(16.20.8)
V'-1cxo) = .. -, <rm1 a dp a ... a d?-1
on en déduit que
(24.14.2.3) f C = (- I)" \ gj&\ ■.., Om'dp ■ • • d?'1.
JFrr(U) JK'
Pour établir (24.14.2.1), il suffit donc de prouver les deux formules
(24.14.2.4) J ^d^dp ... d? = 0 pourl^i<«-l;
(24.14.2.5) £ j^d^dP ... d? = - j^tf1, ..., «T1, 0)dpd? .. .de?'1.

90 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
l %d?d? ■ ■ ■ d? = j/' jK. % I?' • • m?*? ■ ■ ■ d?~l ■
Mais, pour 0 < t < 1, la forme différentielle
...,c?-l,t)dZlAdt2 a ... Ajr1
sur R" -1 est, au signe près, la dérivée extérieure de la (n — 2)-forme différentielle
atë1,..., «r1, m? a ... âI^a ... a d?-1
dont le support est contenu dans une partie compacte de K'. On a donc, par
(17.15.5.1).
*°' ?~l,t)dtldZ2 ... d?~l =0,
f ^tt1
d'où la formule (24.14.2.4).
Enfin, le théorème de Lebesgue-Fubini montre que
l %d?d? ■■■*?=j^1... £ ^(é\ ...,
= - |k g^1,..<r <WdÉa... d?-1
puisque l'on a par hypothèse gJÉ1,.. 1) = 0. Cela achève de prouver
(24.14.2.5), donc le théorème (24.14.2).
Remarque (24.14.2.6) Pour X = R" avec n = 2 ou n = 3, la formule de Stokes
s'écrit
(formule de Greeri) et
(24.14.2.8) (Pxdx2 a dx* + P2dx3 a dx1 + P3dxl a dx2)
JjFrr(U> fflY^P, ôp2 <5P3\ 2J 3
(formule d'Ostrogradsky) respectivement.
(24.14.3) Nous allons maintenant montrer qu'on peut étendre la formule
Or, en vertu du théorème de Lebesgue-Fubini, pour 1< i^n — 1, on a

14. LA FORMULE DE STOKES
91
de Stokes à des cas plus généraux que celui considéré dans (24.14.2). Soit d0
une n-forme différentielle de classe C°° appartenant à l'orientation de X, de
sorte que toute n-forme différentielle intégrable o sur X s'écrit u = go0, où g est
intégrable pour la mesure utt0 définie par u0 (16.24.2) ; nous poserons
I ■»Il = Wg-H.
g I du,.
cette définition est indépendante de la n-forme u0 choisie dans l'orientation
j*u I au lieu de || o ||, et pour toute partie intégrable A
de X (16.24.2). On écrira
de X, on posera
Jb Ja
iuHIK°
; si B est une partie intégrable de A, on a
Cela étant, nous dirons qu'une partie compacte N de X est
différentiellement négligeable s'il existe une suite (uk) de fonctions de classe C1 sur X, possédant
les propriétés suivantes :
(i) Chaque fonction uk prend ses valeurs dans [0, 1 ] et est égale à 0 dans un
voisinage de N ; en outre, pour tout voisinage V de N, il existe k0 tel que, pour
k ^ k0, uk soit égale à 1 dans QV.
(ii) Pour toute (n — îyforme différentielle ç de classe C° sur X, on a
lim || (duk) a ç || = 0 (relation qui a un sens, car (duk) a ç a un support compact
d'après (i), dès que k est assez grand).
Une suite (uk) ayant les deux propriétés précédentes sera dite suite d'approche
de l'ensemble différentiellement négligeable N.
(24.14.4) Soit ç une (n — l)-forme différentielle de classe C1 sur X, satisfaisant
aux conditions suivantes :
a) L'intersection de U et du support de Ç est compacte, et l'intersection
(compacte) N du support de Ç et de l'ensemble des points non réguliers de Fr(U)
est différentiellement négligeable.
b) C est intégrable dans Frr(U).
On a encore alors la formule de Stokes (24.14.2.1).
Soit en effet (uk) une suite d'approche de N ; pour chaque indice k,
l'intersection de U et du support de la (n — Informe ukÇ ne contient que des points
réguliers de Fr(U) ; on a alors, par (24.14.2.1)
[d(ukQ=[ ukC.
JV jFrrflJ)

92 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
Mais d(ukQ = (duk) a( + u^Ç. Comme lim || (duk) a C II = 0, et
< Il (<*"*) a Cil
on a lim (duk) a C = 0. Il est clair que dÇ est intégrable dans U ; comme
les fonctions uk sont bornées dans leur ensemble, et que uk(z) tend vers 1 en tout
point zg U, le théorème de convergence dominée montre que Um J^ukdC=j^C-
Enfin, uk{z) tend aussi vers 1 en tout point z de Frr(U) ; comme par hypothèse C
est intégrable dans FrifU), le théorème de convergence dominée montre aussi
que lim ukC = C, ce qui prouve le théorème.
*"'00 jFrr<U) jFrrfU)
Pour appliquer (24.14.4), il faut disposer de critères commodes permettant
de reconnaître qu'un ensemble est différentiellement négligeable.
(24.14.5) Si N' et N" sont deux ensembles différentiellement négligeables, il en
est de même de N' u N".
Soient (u'k) et (u'k) des suites d'approche de N' et N" respectivement ; il
suffit de prouver que les uk = ukuk forment une suite d'approche de N' u N".
Il est clair que toute fonction uk est nulle dans un voisinage de N' u N" ; d'autre
part, si, pour un voisinage V de N' u N", on a u'k{z) = 1 dans (JV pour k ^ kx
et uk(z) = 1 dans (Jv pour Jtc ^ k2, on aura uk(z) = 1 dans Cv pour k ^ sup(/ci, fc2)-
Enfin, si C est une (n - l)-forme différentielle de classe C° sur X, on a
(duk) a C = «£((<*«;') a C) + <((du'k) a C)
et comme | u'k \ < 1 et | uk \ < 1, on a
||(duk) a C II ^ Il (^«i) a CI! + Il a C II
d'où lim \\(duk) a Cil = 0.
(24.14.6) Par transport de structure, il est clair que si/est un difféomorphisme
de X sur une variété orientée X', pour que N soit différentiellement négligeable
dans X, il faut et il suffit que /(N) soit différentiellement négligeable dans X'.
En vertu de cette remarque et de (24.14.5), on ramène l'étude des ensembles
différentiellement négligeables au cas où X = R". En effet, toute partie compacte N
d'une variété X de dimension n est réunion d'un nombre fini d'ensembles compacts
dont chacun est contenu dans le domaine d'une carte de X, et il suffit que chacun
de ces ensembles soit différentiellement négligeable pour qu'il en soit ainsi de N.

14. LA FORMULE DE STOKES 93
J h((duk) a Q = t (- D'"1 JteAMÉ1 ■■■de?
^ anCkX{\fk)
où a est une borne supérieure des \gt \ dans V2(N). La condition de l'énoncé
entraine donc bien que (uk) est une suite d'approche pour N.
Prouvons le lemme (24.14.7.1). Soit v une fonction de classe C°° dans R,
à valeurs dans [0, 1 ], égale à 0 pour t ^, à 1 pour t > 1 ; définissons dans R"
la fonction vk de classe C°° par vk(x) = v(k || x || ) ; il est immédiat qu'il y a une
constante Cx ne dépendant que de v et de n, telle que | Dj^ | < pour
et tout entier k. Pour tout m = (m1, ..., m") e Z", on considère la fonction
translatée x -> iv(x et on pose
(24.14.7.2) «Jx) = ru(x--^=)
»» \ fc^/n/
kyfn J k
(d étant la distance euclidienne sur R"). Montrons d'abord que u*(x) = 0 lorsque
■77-. En effet, il y a un m e Z" tel que dix,- _,
4fc V k^fn)
où le produit est étendu à tous les points m e Z" tels que d ( —-=, N j <
\kyjn /
i*(x) = 0 lo
d(x, N) < -- . En effet, il y a un m e Z" tel que d ( x, —— ) < — , donc
\ kjn) 2fe
,/ m \ 1 1 1 / m \ „ ,
d —F, NU- + -<-, et par suite vk\x ■= figure dans le
J 2k 4k k \ k^/nJ
pro-
(24.14.7) Soit N une partie compacte de R", et, pour tout p > 0, soit VJN)
l'ensemble des points de R" dont la distance à N est < p. Si on a lim - A( VJN)) = 0
p-*o p
(où X est la mesure de Lebesgue), N est différentiellement négligeable.
La proposition résultera du lemme suivant :
(24.14.7.1) Pour tout entier k > 1, soit \Jk — V2/lk(N). // existe une fonction uk
de classe C°° dans R", à valeurs dans [0, 1 ], égale à 0 dans un voisinage de N, à 1
dans le complémentaire de \Jk, et telle que || Djt^ || < Ck pour 1 ^ ( < n, où C est
une constante ne dépendant que de n.
Supposons en effet ce lemme prouvé, et soit
C = £ gid? a ... /Td^A ... a de?
i=l
une (n - l)-forme différentielle de classe C° sur R". Pour toute fonction continue h
à support compact et telle que | « | < 1, on a

94 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
duit (24.14.7.2) ; mais comme
m
x —
1
,ona
2k
pour
ce point m, donc uk(x) = 0. En second lieu, si d(x, N) ^ 2/k, alors, pour tout
meZ" tel que vk(x — figure dans le produit (24.14.7.2), on a
d'où vk(x - ~~j=j = et Par smte "*(x) ~ Enfin. P°ur majorer les dérivées
premières de uk en un point x0, on peut supposer qu'on n'a pas uk(x) = 1
identiquement dans un voisinage de x0 c'est-à-dire qu'il y a un m0 e Z" tel que
Xn -
m0
ky/n
< - ; les seuls facteurs
k
qui ne soient pas
nécessairement égaux à 1 dans un voisinage de x0 sont ceux pour lesquels
m
kjr\
1
<k'
ce qui entraine \\m — m0|| < 2y/n; il est clair que cela n'est possible que si
l'une des différences | m1 — mb \ est < 2,/n, donc le nombre des points me Z"
correspondants est < (4[>Jn] + 5f = C2. Une dérivée Dtuk(x0) est donc somme
d'au plus C2 termes dont chacun est produit d'une dérivée Dji^Xo - ~j~/=j
et de facteurs de valeur absolue < 1, d'où |D|«t(x0)| < C2Cjk. CQFD.
(24.14.8) Dans une variété orientée pure X de dimension n, tout ensemble compact N
contenu dans une sous-variété Y de dimension < n — 2 est différentiablement
négligeable.
On peut en effet recouvrir N par un nombre fini de compacts dont chacun
est contenu dans un ouvert Wj, domaine d'une carte transformant Y n V, en
un ouvert de Rp, où p ^ n — 2. Compte tenu de (24.14.5), on peut donc se limiter
au cas où X = R" et Y = R"-2. Avec les notations de (24.14.7), si N est contenu
dans un cube de R"-2 de côté a, VP(N) est contenu dans le produit d'un disque
fermé de rayon p dans R2 et du cube de R"-2 de même centre et de côté 2a, dès
que p < a ; on a donc A(VP(N)) < bp2 où b est une constante indépendante de p,
dès que p est assez petit, et on peut appliquer le critère de (24.14.7).
(24.14.9) On notera que, dans le théorème (24.14.4), la condition b) n'est pas

14. LA FORMULE DE STOKES
95
conséquence de a). Elle sera toutefois conséquence de a) si la frontière de U
est contenue dans la réunion d'un nombrefini de sous-variétés fermées Y, (1 </ < m)
de dimension n — 1 ; en effet, Y, n Frr(U) est alors un ensemble dont
l'intersection avec le support de Ç est relativement compact dans Yj ; comme £ est de
classe C1, elle est intégrable dans cet ensemble, donc aussi dans Frr(U), qui est
par hypothèse réunion des Y/ n FrrfU).
Nous dirons pour abréger qu'un ouvert U c X est stokien s'il vérifie les
deux conditions suivantes :
(i) La frontière de U est contenue dans la réunion d'un nombre fini de sous-
variétés fermées de X, de dimension n — 1.
(ii) L'ensemble des points non réguliers de Fr(U) est contenu dans la réunion
d'un nombre fini de sous-variétés de X de dimension < n — 2.
Il résulte alors de (24.14.4), (24.14.8) et des remarques ci-dessus que la
formule de Stokes est valable pour tout ouvert stokien U de X et toute (n — 1)-
forme Ç de classe C1 surX telle que U n Supp(0 soit compact.
(24.14.10) Tout ouvert dont la frontière est régulière est évidemment stokien,
par exemple toute boule ouverte dans R". Un autre exemple d'ouverts stokiens,
qui va être fondamental dans la suite du chapitre, est fourni par les polyèdres
convexes ouverts de dimension n dans une sous-variété linéaire affine E d'un RN,
de dimension n. On appelle ainsi toute intersection non vide U d'un nombre fini
de demi-espaces ouverts distincts Dk dans E, d'équations fjx) < ak (1 < k </>),
où les fk sont des formes linéaires sur RN, non constantes dans E. En effet, pour
tout point frontière x0 de U, il est clair que l'on a /Jx0) = ak pour un indice k
au moins ; il y a deux cas possibles :
1° Ou bien on a fk(x0) = ak pour un seul indice k ; le point x0 est alors un
point frontière régulier. En effet, par déplacement on se ramène au cas où x0 = 0
dans E = R", fk(x) = — £" dans R" et ak = 0 ; pour p > 0 assez petit, tous les
points de la boule ouverte B : 11 x 11 < p sont tels que /Jx) < ah pour tous les h¥^k,
donc U n B est la demi-boule formée des points de B tels que £" > 0.
2° Ou bien fh(x0) = ah et fk(x0) = ak pour deux indices distincts ; comme
tous les demi-espaces D, sont supposés distincts et que U est non vide, les
deux hyperplans affines de E, d'équations fh(x) = ak et fk(x) = ak sont distincts
et ont une intersection non vide Wu, qui est donc une sous-variété linéaire affine
de E, de dimension n — 2. Ceci prouve que U est un ouvert stokien.
(24.14.11) Les hypothèses et notations étant celles de (24.14.10), supposons
pour simplifier (comme on peut toujours le faire) que E = R" et que 0 e U et
supposons U compact. Alors la frontière régulière Frr(U) est l'ensemble des
points appartenant à un seul hyperplan affine Pt : /Jx) = ak. Nous avons vu
en effet que ces points frontière sont réguliers; ceux qui appartiennent à P*

96 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
satisfont dans cet hyperplan aux relations fh(x) < ah pour h # k, donc leur
ensemble Fk est un polyèdre convexe ouvert dans Pk, de dimension n — 1 ; on dit
que c'est la face de U contenue dans Pk. On observera que certains des hyper-
plans affines Pk figurant dans la définition de U peuvent ne contenir aucune face;
on peut supposer que les Pk contenant une face Fk sont ceux pour lesquels l^k^q.
Montrons que tout point frontière x0 d'un Fk par rapport à Pk n'est pas un point
frontière régulier de U. En effet, il appartient à un Ww avec h ^ k ; si xt e Fk,
le segment d'extrémités x0 et Xj est contenu dans FrfU) ; la demi-droite ouverte A
d'origine x0 et passant par le point x2 symétrique de xt par rapport à x0 est
contenue dans E — D„ par définition, donc dans l'extérieur de U. Il y a par
suite un cône épointé d'axe A et de sommet x0 contenu dans cet extérieur ;
on en conclut qu'il ne peut y avoir de courbe contenue dans Fr(U), passant
par x0 et ayant pour tangente en ce point la droite contenant A ; cela prouve
que x0 n'est pas régulier.
D'autre part, il existe un homéomorphisme de R" sur lui-même transformant U
en la boule fermée ||x || < 1 dans R", et Fr(U) = U — U en la sphère S„_,.
En effet, l'intersection de U et de toute demi-droite d'origine 0 passant par un
point zeSn-l est un segment fermé d'extrémités 0 et un point g(z)eFr(U) tel
que g(z) = t(z)z, où t(z) est le plus petit des p nombres t„>0 tels que fkzePk
pour 1 ^ h < p. Comme th = aj/k(z), il est immédiat que g est continue dans
SH-i, donc un homéomorphisme de S„-i sur Fr(U) (3.17.12); en outre g se
prolonge en un homéomorphisme g0 de R" sur lui-même, défini par g0(0)=0,
go(z) = II* Il gtz/ II* Il ) P°ur z ^ 0 ; il applique la boule ||z || < 1 sur U.
Notons alors que dans R" le complémentaire de la réunion des hyperplans
engendrés par les u {0} (pour les couples (h, k) tels que Ww # 0) est partout
dense (12.16.1). On voit donc que :
a) la réunion des Fk (1 < k < q) est égale à Frr(U), et Fr(U) est la réunion
des Fk ;
b) U est l'intersection des demi-espaces ouverts Dk correspondant aux
seuls Pk contenant les faces de U (1 < k ^ q).
(24.14.12) Gardons les hypothèses et notations de (24.14.11). Pour toute partie
non vide L de {1,2,..., q}, soit VL l'intersection des hyperplans affines Pk
pour les indices k e L ; ces variétés peuvent être vides, et ne sont pas toutes
distinctes en général. Soit £ l'ensemble des parties non vides L de {1,2,.. .,q}
telles que : 1° l'intersection Fr(U) n VL n'est pas vide ; 2° il n'y a pas de partie
L' r> L de {1,2, ..., q } distincte de L et telle que VL. = VL. Il est clair que chaque
point x e Fr(U) appartient à un VL tel que L e fi, et un seul : L est l'ensemble
des indices k tels que fk{x) = ak. D'autre part, si PL est la variété linéaire affine
engendrée par Fr(U) n VL, les points x g Fr(U) qui sont intérieurs à Fr(U) n VL
par rapport à l'espace PL sont ceux de l'intersection de PL avec les demi-espaces

14. LA FORMULE DE STOKES
97
ouverts Dk tels que k$ L et que Dk n PL soit distinct de PL. On voit donc que
Fr(U) est réunion disjointe de polyèdres convexes FL de dimensions < n — 1 ;
on dit que ce sont les facettes de U, celles de dimension n — 1 étant les faces Fk
(1 < k ^ q) ; on dit aussi que U est Tunique facette de dimension n de U. La
frontière de chaque facette FL, relativement à la variété linéaire affine PL (qu'elle
engendre) est réunion disjointe de facettes FL. pour des L'e fi contenant L.
(24.14.13) L'exemple le plus simple de polyèdres convexes est celui des cubes
de dimension n, K. : | — or* | < a (1 < Je ^ n) dans R" ; la frontière
régulière Frr(K) est réunion des 2n faces, cubes de dimension n — 1 définis par
£* = or* ± a, | ÇJ — aJ | < a pour j k, et 1 < k < n. Par récurrence sur n,
on en déduit que Fr(K) est réunion disjointe d'une famille finie de cubes dont les
dimensions varient de 0 à n — 1. De façon précise, pour chaque entier p tel que
0 ^ p ^ n — let chaque partie H de {1, 2,..., n} ayant p éléments, on
considère les 2P cubes de dimension p définis par
Çk = a* ± a pour k e H
| ÇJ - a* | < a pour j £ H.
»-1
Lorsqu'on fait varier p et H, on obtient les £ 2P(P) = 3" - 1 cubes dont la
réunion disjointe est Fr(K). p=0
PROBLÈMES
1) Les notations étant celles de (24.14.1), soit N l'ensemble des points non réguliers de Fr(U) ;
on suppose que N est compact et que pour tout point de N, il y a une carte (V, <p, n) de X en ce
point tel que l'ensemble <p(V n N) c R" vérifie la condition de (24.14.7). Montrer que la formule
de Stokes est encore valable sous les hypothèses suivantes : 1° C est définie et continue dans U — N
et bornée au voisinage de tout point de N ; 2° ( est intégrable dans Frr(U) = Fr(U) — N ; 3° ( est
de classe C1 dans U et d{ est intégrable dans U.
2) On prend pour U le pavé 0 < x < 1, 0<y<l dans R2, et on considère la 1-forme
{ = (xdy — ydx)/{xz + y2), qui est continue dans U — { 0 }, bornée dans Fr(U) — { 0 }, de classe C1
et telle que dr = 0 dans U ; mais on a d( # I C, bien que l'ensemble des points non régu-
*V •'fiku)
liers de Fr(U) soit différentiellement négligeable.
3) On prend pour U le pavé 0 < x < 1, 0<y<l dans R2, et on considère dans
l'intervalle 0 ^ x ^ 1 de R un ensemble fermé rare A de mesure a > 0 (section 13.8, problème 4 a)).
Montrer qu'il existe dans U une fonction f(x, y) telle que 0 </(x, y) < 1, égale à 1 dans A, à 0
— df
dans (0, 1 ] - A, continue en tous les points de U - A, de classe C1 dans U et telle que — > 0
dy
dans U. (On pourra considérer, dans l'ensemble ] - 1,1 ] x [0, + oo [, la fonction égale à 1 pour
y > 1 - x2, égale à 2t - t2 avec t = y/(l - x2) pour 0 < y < 1 - x2).
On considère dans U la forme ( = f(x, y)dx ; montrer que dÇ est intégrable dans U mais
que l'on a \ dÇ # I {.
4) Soit U un ouvert relativement compact dans une variété pure orientée X de dimension n,
tel que Fr(U) soit régulière et connexe. Soit g une application de classe C" de X dans une variété

98 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
compacte, connexe et orientée Y de dimension n — 1. Si /: Fr(U) -» Y est la restriction de g
à Fr(U), montrer que deg / = 0 (utiliser le théorème de Stokes).
5) Dans l'espace C", soit H(x. y) = A(x, y) + iB(x, y) une forme hermitienne positive non
dégénérée, A et B étant sa partie réelle et sa partie imaginaire, de sorte que A est, sur R2", une
forme bilinéaire symétrique positive non dégénérée et B une forme alternée.
a) Soient x, y deux vecteurs tels que A(x, x) = A(y, y) = 1, A(x, y) = 0. Montrer que l'on a
| B(x, y) | < 1, l'égalité ne pouvant avoir lieu que si y = Xx pour un X e C (cf. section 6.2,
problème 3).
b) Soit E un sous-espace vectoriel réel de C", de dimension paire 2k. La restriction de B à E
s'identifie à une 2-forme eu sur E ; notons coA* le produit extérieur de k formes égales à a>. Soit
(e,, ..., e2t) une base orthonormale de E pour la forme A. Montrer que l'on a
| < co*', e, a e2 a ... a *2» > I ^ k !
et que l'égalité a lieu si et seulement si E est un sous-espace vectoriel complexe de C de
dimension k (Ann. 33.1).
6) Sur le fibre tangent à l'espace vectoriel complexe C, on considère la structure
hermitienne (23.27.2) définie par le tenseur covariant complexe d'ordre 2 sur C"
H0 = dzl ® <fz, + dz2 ® dz2 + ... + dz„ ® dzN ;
sa partie réelle est la métrique riemannienne canonique (20.11.2)
g0 = dx, ® dxi + dyt®dyt + ... + dxN ® <fxN + dj^ ® dyN
sur R2N, et sa partie imaginaire s'identifie à la 2-forme sur R2N
fl<> = ~(àZi a dïi + ... + dzN a dzN).
a) Soit M une sous-variété pure de R2N, de dimension paire 2k, supposée orientable, et
soit u, la forme volume canonique sur M correspondant à la métrique riemannienne g induite
sur M par g0 (20.8.6) ; montrer que si il est la 2-forme induite par ilo sur M, on a, pour tout x e M
ifr'(x)
k\
»JL*)
L'égalité ne peut avoir lieu pour tout x € M que si M est une sous-variété holomorphe de C*
(utiliser le problème S) ; dans ce cas, la 2fc-forme 7/",^** est positive lorsqu'on munit M de son
orientation canonique (en utilisant le fait que la forme H„ est invariante par le groupe unitaire SU(N),
se ramener au cas où M est définie par N —(t équations zt+J = //z, zk) pour 1 ^ N — fc,
où les ft sont holomorphes au voisinage de 0 dans C*, et <f/y(0) = 0 pour 1 ^ j ^ N - k).
b) Soient X, X' deux sous-variétés pures de R2N, de même dimension paire 2k et orientables ;
soient U c X, U' c X' deux ouverts relativement compacts ayant même frontière, que l'on
suppose telle que ses points non réguliers forment un ensemble différentiellement négligeable. On
note vol(U) et vol(U') les mesures de U et U' respectivement pour les volumes riemanniens sur X
et X' correspondant aux métriques induites par g0. Montrer que si X est une variété holomorphe,
on a vol(U) < vol(U'), l'égalité ne pouvant avoir lieu que si U' est aussi une variété holomorphe
(inégalité de Wirtinger). (Observer qu'il existe une (2k - Informe Ot sur C telle que il$k = d^,
et utiliser la formule de Stokes).
7) Dans R*. identifié à R' x R*"' pour 2 « p « n - 1, soit Y la sphère S,.,c R', et
soit Z une sous-variété de R" compacte, connexe, orientable de dimension n-p dont
l'intersection avec la boule || x|| < 2 dans R" soit égale à l'intersection Z, de cette boule et de R""'.
On considère Y comme frontière de la boule B : || x || < 1 dans R" et on munit B de l'orientation
canonique de R', Y de l'orientation qui s'en déduit par la règle de (24.14.1), Z de l'orientation qui
coïncide sur Z, avec l'orientation canonique de R""p. Montrer qu'on a alors (B. Z) = 1 pour
le nombre d'intersection (24.13.15). Montrer que l'on a aussi entrel(Y, Z) = 1. (A l'aide du calcul

14. LA FORMULE DE STOKES
99
de l'intégrale de Kronecker, montrer qu'on peut remplacer Z — Zi par l'image de Zt par la
projection stéréographique dont le pôle est un point de 25,-!, image qui est une partie de la sphère
2S..,. On utilisera le fait que si M et N sont deux sous-variétés de R", compactes, connexes,
orientées, séparées par une sphère de R" et telles que dim M+dim N = n — 1, on a entrel(M, N)=0).
8) Soit X une sous-variété pure orientée de R", de dimension p telle que 2 < p ^ n — 1,
et soit U un ouvert relativement compact dans X, tel que Fr(U) soit connexe et régulière. Soit Y
une sous-variété compacte, connexe et orientée de R", de dimension n - p ; on suppose que Y ne
rencontre pas Fr(U), que l'intersection Y n U soit finie et que Y et U se coupent transversalement
en chacun de leurs points d'intersection. Montrer qu'on a alors (U. Y) — entrel(Fr(U), Y).
(Utiliser la formule de Stokes pour le calcul de entrel(Fr(U), Y) par l'intégrale de Kronecker, en
considérant pour chaque point Xj de U n Y un petit voisinage de xt dans U, et en se ramenant de cette
façon au cas considéré dans le problème 7).
9) a) Soit ; : S„_, -> R" - {0 } l'injection canonique pour n ^ 2 ; si c est la classe
fondamentale de cohomologie de S._, (24.6.3.1), b = j*{c) est une base de l'espace H"~'(R" - {0 } ).
Soit p une (n - 1 (-forme fermée sur R" - {0} ; si sa classe de cohomologie est Xb, montrer que
pour toute fonction /6 é(tt"), égale à 0 dans un voisinage de 0 et à 1 hors d'une partie compacte
de R", on a j* df a p = X. (Montrer d'abord que cette intégrale ne dépend pas du choix de /
puis appliquer la formule de Stokes pour une fonction/égale à 1 dans S„_ i).
b) Soit u une application de classe C00 de R" dans lui-même, telle que u(0) = 0 et
u(R" - { 0} ) c R" - { 0 }, de sorte que u définit un endomorphisme u* de H" " l(R" - { 0 } ) ; on
pose u*(b) = (deg0u)b. Si p : z -» z/||x|| est la surjection canonique de R" — (0} sur S..,,
montrer que l'on a deg„u = deg(p » u o j), ce qui prouve que deg0u est un entier.
c) Montrer que si le jacobien J de u au point 0 est # 0, on a deg0u = 1 si J > 0 et deg0u = — 1
si J < 0 (observer qu'il existe un voisinage ouvert U de 0 tel que u | U soit un difféomorphisme de U
sur un voisinage ouvert V de 0).
10) Soient X, Y deux variétés pures orientées de même dimension n > 2, /: X -» Y une
application de classe C". On dit qu'un point a € X est isolé pour f s'il existe un voisinage ouvert U
de a dans X tel que/(x) # f(a) pour x e U - { a }. On peut supposer que U est le domaine d'une
carte (U, (p, n) de X telle que <p(U) = R*, <p(a) = 0, et qu'il existe une carte (V, ^, n) de Y telle que
/(U) c V, ir(V) = R" et <li{f{a)) = 0. On pose alors deg./ = deg0W »/» p"1) (problème 9).
a) Montrer que le nombre deg,/ne dépend pas des choix de U, V, <p, \j/ vérifiant les
conditions précédentes.
b) Si TJif) est une bijection de Ta(X) sur T/(a)(Y), on a deg„/= 1 si T^/) préserve
l'orientation, deg./ = — 1 dans le cas contraire.
c) Soit g : Y Z une application de classe C°° de Y dans une variété pure orientée Z
de dimension n, telle que /(a) soit isolé pour g. Alors a est isolé pour g'Jet l'on a
deg^g ° f) = deg/wg • deg,/
d) Il existe un voisinage compact V, de /(o) contenu dans V et tel que U, = U r\f~ '(V,)
soit un voisinage compact de a contenu dans U. Si v est une fonction de <&(Y) de support contenu
dans V, et égale à 1 dans un voisinage de/(a), v ° (/1 U) est une fonction de @(X) de support contenu
dans U, et égale à 1 dans un voisinage de a. Montrer alors que pour toute (n — Informe p de
classe C" sur Y, on a J 'f(dv a p) = (deg./)J^ dv a p.
e) On suppose que X et Y sont des variétés compactes, connexes et orientées. Montrer
que s'il existe un point y0 e Y tel que/_1(y0) soit un ensemble fini { jc„ ..., x,}, les xj sont isolés
r
pour / et l'on a deg / = X deg, / (utiliser d)).
11) Soit G le groupe des déplacements de l'espace euclidien R", identifié au groupe des
matrices d'ordre n + 1

100 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
où U eSO(n, R), zeR" (identifié à une matrice colonne de type (n, 1)). Soit s0 la symétrie par
rapport à la droite Rej, et a l'automorphisme involutif t -» s0fsô ' de G ; la composante
neutre H0 du sous-groupe H de G formé des éléments invariants par a est le groupe des
déplacements laissant invariante la droite Ret et préservant son orientation ; il s'identifie au groupe
des matrices
/l 0 a\
I 0 V 0 J
\0 0 1/
où aeR et KeSO(n - 1, R). L'espace Dî,, = G/H0 est l'espace homogène symétrique (20.4.3)
des droites orientées de R", de dimension 2(n — 1). Le groupe G s'identifie au fibre des repères
de R" pour sa structure riemannienne canonique (20.11.2), d'après (20.7.9), les repères au-dessus
du point z e R* étant formés des colonnes •, a. de la matrice U ; on peut écrire (section 20.12,
problème S)
M n
1=1 j-i
où les ot et coji sont des 1-formes sur G telles que cj,j + co,, = 0 et qui vérifient les équations de
structure
M H
dffj = — £ Oi,j A Oj, dojfj = — £ tl)u A Cl>w.
J-1 à-1
a) Le groupe G s'identifie aussi au fibre des repères de D',,. pour la H0-structure
correspondant au couple symétrique (G, H0) (20.7.10). Montrer que la fibre de G au-dessus d'une droite
orientée f e Dî,, se compose des repères tels que z e / et que a, soit un vecteur parallèle à I et positif
pour son orientation.
b) Soient / -» R(l), l -» R'(l) deux repères mobiles définis dans un ouvert V de D[. ; si
on les note(z, •,, ..., a„)et(z', a',, .... e',), on a donca't = a, et z' - z =/. où/est une
fonction scalaire de classe C™ dans V. En déduire que l'on a da\R) = da1,"'1, et par suite que la 2-forme
m = mfi a a 2"> + ... + co'/? a of>
est indépendante du repère mobile R considéré, et est par suite une 2-forme de classe C" sur DJ „,
invariante par G. En déduire que u = roM""" est une (2n - 2)-forme ^ 0 et invariante par G,
et par suite que D',. est orientable.
c) Soit / une immersion injective de R dans R", périodique de période 1, de sorte que son
image C est une courbe lisse fermée. Dans le triangle ouvert A c R2, défini par les inégalités
0 < t, < t2 < 1, on considère l'application F qui, à tout couple ((,, t2)e A, fait correspondre
la droite orientée joignant/(rj à f(t2\ le vecteur f(t2) - f(ti) étant positif. Montrer, en utilisant
la formule de Stokes, que l'intégrale I 'F(ro) est égale à la longueur de la courbe C.
■■a
15. Applications : I. Nombre de racines d'une équation.
(24.15.1) Soient X une variété pure orientée de dimension n > 2, U un ouvert
dans X, relativement compact et connexe, dont la frontière est régulière et connexe,
donc est une variété compacte de dimension n — 1. Soit f une application de
classe C°° d'un voisinage ouvert U0 de U dans R". Nous allons voir que sous
certaines conditions on peut évaluer le nombre de solutions de l'équation ffx)=0
dans U à l'aide d'une intégrale.
(24,15.2) Sous les hypothèses de (24.15.1), supposons que 1{x) # 0 pour x e Fr(U),

15. APPLICATIONS : I. NOMBRE DE RACINES D'UNE EQUATION 101
et que 0 soit une valeur régulière (16.23) de t. Alors Vensemble U n f " '(0) est
une partie finie {xu x2, ■ ■ -, x,} de U ; au voisinage de chaque point Xj, f est
un difféomorphisme local, et si p est la surjection z -► z/||z || de R" — {0} sur
S„-,, on a
(24.15.2.1) (- D""1 t «(*/)-deg (po(f| Fr(U)))
où e(xj) = 1 (resp. e(Xj) = — 1) si au voisinage de x}, f préserve (resp. renverse)
l'orientation.
Par définition, les points de f~'(0) sont isolés (16.7.4) ; comme Unf"l(0)
est fermé dans U, si cet ensemble était infini, il aurait un point adhérent dans U,
ne lui appartenant pas ; ce point serait donc dans Fr(U) ; mais en un tel point x0,
on aurait f{x0) = 0 par continuité, contrairement à l'hypothèse. Il existe un
nombre p > 0 assez petit tel que la boule ouverte B de centre 0 et de rayon p
dans R" ne rencontre pas f(Fr(U)), et que f " ^B) contienne la réunion disjointe
de r ouverts Vj (1 < j < r) tels que XjeWj pour toutet que la restriction de f
à Vj soit un difféomorphisme de V; sur B. Pour chaque soit W,- l'intersection
de V, et de f"1Q B^ ; si S est la sphère || z || = ^ p, la restriction de f à FrfW/)
est un difféomorphisme de cette variété sur S.
Cela étant, comme on peut supposer le voisinage U0 de U tel que f ne
s'annule pas dans U0 - U, l'image réciproque '^t'"') (notation de (24.9.8))
est une (n - Informe de classe C00 sur U0 — {xt xr}, qui est fermée puisque
dt<") = 0. On a vu (24.9.8.1) que l'on peut écrire
(24.15.2.2) deg(po(f|Fr(U))) = i- | 'f^).
"n JFrftI)
Appliquons alors à la forme fermée 'Ht'"') la formule de Stokes dans l'ouvert
r
U - ( U Wj), dont la frontière est réunion disjointe des sous-variétés de dimen-
sion n - 1, Fr(U) et Fr(Wj), pour 1 < j ^ r. On a donc, avec les orientations
de Fr(U) et Fr(W;) définies dans (24.14.1)
(24.15.2.3) deg(p » (f | Fr(U))) = t deg(p o
en désignant par fj la restriction de f à FifWj). Or, p ° f, est un difféomorphisme
de Fr(W/) sur Sn-i ; comme SB_! est orientée vers l'extérieur, tandis que Fr(Wj)
est orientée vers l'intérieur si n est pair, vers l'extérieur si n est impair, on voit
que si f préserve (resp. renverse) l'orientation au voisinage de xJt p ° f, préserve
(resp. renverse) l'orientation si n est impair, mais renverse (resp. préserve)
l'orientation si n est pair ; on a donc deg(p » ij) = (— l)"""1^^) (24.9.2) ; cela prouve
(24.15.2.1).

102 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
On noiera que si U n f_1(0) est vide, la formule (24.15.2.1) est encore
valable, le second membre étant égal à 0 en vertu de la formule de Stokes
appliquée à U.
Remarque (24.15.2.4) Le raisonnement précédent s'étend au cas où on ne
suppose plus Fr(U) régulière, mais seulement que l'ensemble des points non
réguliers de Fr(U) est différentiellement négligeable (24.14.3). La formule (24.15.2.1)
est alors remplacée par
(24.15.3) Soient bt et b2 deux valeurs régulières de f, telles qu'il existe un
chemin y : t -+ b(f) défini dans [0, 1 ], à valeurs dans R" - f(Fr(U)), pour lequel
b(0) = bt, b(l) = b2 et b(t) est valeur régulière de f pour tout te [0, 1]. i4/ors
les ensembles f_1(bi) = {xu ..., x,} et f~1(b2) = {yi yr} sont fi™,
Pour montrer que le nombre n(t) d'éléments de f-i(b(t)) est constant, il
suffit de voir qu'il est localement constant (3.19.7). Soit donc t0 € [0, 1 ], et posons
f_1(b(to)) = {ai, • • -, a,} où r = n(t0);'\\ y a donc un voisinage ouvert B0 de b(t0)
dans R"-f(Fr(U)) tel que f-1(Bo) contienne la réunion disjointe de r ouverts
Vj (1 < j < r) tels que a}e Vj pour tout j et que la restriction de f à V, soit un
difféomorphisme sur B0. Cela montre déjà que pour t assez voisin de t0> on a
n(t) ^ n(t0). L'image par f de l'ensemble compact U - ((J y,) est une partie
compacte de R" qui ne contient pas b(t0) ; il y a par suite un voisinage de t0
dans [0, 1 ] dont l'image par b ne rencontre pas f(U — ((J y,)), et on a donc
bien n(t) = n(t0) dans ce voisinage. J
Pour terminer la démonstration, il suffit de remarquer que (x,t) -» f(x)-b(t)
est une homotopie de f — bt à f — b2 et d'utiliser l'invariance du degré par
homotopie (24.9.6).
(24.15.4) La formule (24.15.2.1) est particulièrement intéressante lorsque
tous les e(Xj) sont égaux, le second membre étant alors, au signe près, le nombre
d'éléments de f ~ '(0). Il en est toujours ainsi lorsque/vérifie la condition suivante :
(P) Pour toute carte (V, cp, n) de U dans R" préservant l'orientation, le jaco-
bien de l'expression locale F = focp-1 de f pour cette carte est $s 0.
Cette condition est en particulier toujours vérifiée lorsque n = 2m est pair,
que X est une variété holomorphe de dimension complexe m et f une application
holomorphe de U0 dans C™, X et C" étant munies des orientations canoniques
(24.15.2.5)
ont le même nombre d'éléments et l'on a e{Xj) = £ e(y<).
7=1 7=1
7
(16.21.13).

15. APPLICATIONS : I. NOMBRE DE RACINES D'UNE ÉQUATION
103
Lorsque la condition (P) est vérifiée, on peut préciser le résultat de (24.15.2),
en supposant seulement f_1(0) fini, sans que 0 soit nécessairement une valeur
régulière de f :
(24.15.5) Supposons que f vérifie la condition (P), que f(x) # 0 dans Fr(U),
et que U n f_1(0) = { at, ..., ap } soit fini ; soit V, un voisinage ouvert de a,
dans U (1 <;'</») tel que les soient deux à deux disjoints. Il existe alors un
voisinage ouvert B de 0 dans R" - f(Fr(U)) tel que, pour point be B, f" l(b) soit
contenu dans la réunion des V, ; en outre, pour chaque j, il existe un entier q^ 0
tel que,pour tout b g B qui est valeur régulière de i, le nombre d'éléments de t~ *(b)n V}
soit égal à q}, et on a, en choisissant convenablement l'orientation de Fr(U),
On peut évidemment supposer que la frontière Fr(Vj) est régulière pour
1 < j < p ; par hypothèse on a f(jc) ^ o dans FifV,) ; pour tout point b g R"
n'appartenant pas à Fr(V,) et qui est une valeur régulière de f, il résulte de (24.15.2)
que le nombre de points de f " !(b) n V, est égal à
(avec un choix convenable de l'orientation de Fr(V,)), où fb(x) = f(x) — b.
Il est clair (par (16.20.8.3) et (13.8.6)) que l'intégrale (24.15.5.2) est fonction
continue de b au voisinage de 0 ; comme sa valeur est un entier > 0 lorsque
b est valeur régulière de f, et que l'ensemble des valeurs régulières de f est
partout dense dans R" (16.23.1), cette intégrale est constante et égale à un entier
qj > 0 dans un voisinage de 0. Le fait que f " l(b) soit contenu dans la réunion
des V} pour b voisin de 0 se prouve comme dans (24.15.3), et la formule (24.15.5.1)
s'obtient par application de la formule de Stokes comme dans (24.15.2).
(24.15.6) Il se peut que sous les hypothèses de (24.15.5), on ait qj = 0 pour
tout j, comme le montre l'exemple de l'application [x, y) -> (x2 + y2, 0) de R2
dans lui-même. Dans ce cas, tous les points de U sont critiques. Par contre, si,
aux hypothèses de (24.15.5), on ajoute que dans tout voisinage de chacun des a},
il y a des points non critiques de f (où f est donc un difféomorphisme local),
on a qj > 1 pour tout j. On dit alors que q} est la multiplicité de la racine a-} de
l'équation f(x) — 0, et que le premier membre de (24.15.5.1) est le nombre de
racines de f(x) = 0 dans U, comptées avec leur multiplicité. Ce nombre est le
même pour l'équation f(x) = b, où be B, pourvu que l'ensemble f-1(b) dans U
soit fini.
(24.15.5.1)
(24.15.5.2)
(24.15.7) En particulier, si X est une variété holomorphe de dimension complexe m

104 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
et f une application holomorphe de U0 dans Cm, telle que les points de U ne soient
pas tous critiques, alors les points non critiques forment un ensemble ouvert
partout dense dans U, puisque le jacobien d'une expression locale de f est une
fonction holomorphe. La notion de multiplicité des racines d'une équation f(x)=b
dans U a donc un sens lorsque f-1(b) est fini. Par exemple, si f est l'application
{zu z2) -* {z\, z2) de C2 dans lui-même, la multiplicité de l'unique racine de
f(x) = 0 est égale à 4. Mais il ne faut pas oublier que, dans ces conditions, il peut
exister des points beC" tels que f_1(b) soit infini (section 16.11, problème 3).
PROBLÈMES
1) Soit f une application de classe C" d'un voisinage de la boule || x || $ 1 de R" dans R".
On suppose que pour tout x e S, _ [ on a (x | f (x)) < 0 et que l'ensemble f " '(0) soit fini et formé
de points Xj (1 $ j < r) de la boule || x || < 1. Montrer que l'on a (avec la définition de la
section 24.14, problème 9)
t degll/fl = (- ir
(remarquer que la restriction de f à S,_i est homotope à l'application x -» - x deS„_, sur elle-
même).
2) Dans ce problème, on appellera courbe fermée dans R2 une immersion (non
nécessairement injective) v : R -» R2, périodique et de plus petite période L > 0, telle que || v'(s) || = 1
pour tout s e R. On note n(s) le vecteur orthogonal à v'(s), de longueur 1 et tel que le repère
(v'(s), n(s)) soit direct ; on a alors v"(s) = k(s)n(s), où k(s) est la courbure (de signe quelconque)
au point d'abscisse curviligne s. On note T, la tangente affine (16.8.5) au point d'abscisse
curviligne s, c'est-à-dire la droite affine image de t -* v(s) + tv'(s) (pour t e R).
On appelle point multiple de la courbe un point v(s) tel qu'il existe s'e R tel que s' — s ne
soit pas multiple entier de L et que v(s') = v(s) ; s'il n'existe qu'un seul point s' de cette nature
dans l'intervalle ]s, s + L [, on dit que v(s) est un point double de la courbe, et on dit que c'est un
point double ordinaire si de plus T,- ^ T,.
On appelle tangente multiple une tangente T, telle qu'il existe s" e R tel que s' — s ne soit pas
multiple entier de L et que T,. = T, ; s'il n'existe qu'un seul s'de cette nature dans l'intervalle ]s, s + L [,
on dit que T, est une tangente double, et qu'elle est ordinaire si de plus vfs') # v(s) et k(s)k(s') # 0.
On dit qu'une tangente double ordinaire est externe si n(s) = nf/), et interne si n(s) = — n(s').
On appelle point d'inflexion de la courbe un point v(s) tel que k(s) = 0. On dit qu'il est
ordinaire si de plus fc'(s) # 0.
On considère une courbe fermée dans R2 dont les seuls points multiples sont des points
doubles ordinaires, les seules tangentes multiples des tangentes doubles ordinaires, et qui n'a que
des points d'inflexion ordinaires. On se propose de montrer que l'ensemble N+ des tangentes
doubles externes, l'ensemble N" des tangentes doubles internes, l'ensemble D des points doubles
et l'ensemble I des points d'inflexion, sont finis et que l'on a
1
Card(N+) = Card(N") + Card(D) + - Card(I)
(formule de Fabricius-Bjerre-Halpern).
Pour deux vecteurs u,,u2 de R2, on note det(u,, u2) le déterminant de la matrice ayant
Ui, u2 pour colonnes. On considère l'application de R2 dans R2
w(t, s) = (det(v'(t), v(t) - v(s)), det(v'(s), v(s) - v(t))).
a) L'ensemble des couples (s, t) appartenant à [0, L [ x [0, L [, tels que s / t et w(t, s) = 0

16. APPLICATIONS : II. INTERSECTIONS DE COURBES ALGÉBRIQUES 105
est tel que v(s) soit un point double ou T, une tangente double. Si J(s, t) est le jacobien de w en
un tel point, montrer que l(s, t) > 0 si v(s) est un point double ou si T, est une tangente double
interne, et J(s, t) < 0 si T, est une tangente double externe.
b) Montrer qu'il existe un nombre s > 0 tel que, pour tout te R : 1° la restriction de v
à [t, t + e] soit injective ; 2° la courbure k s'annule pour une valeur au plus dans [t, t + e] ; 3° si
t < s s* t + e, on a (v'(s) | v'(i)) > 0. En déduire que pour t < s ^ t + e, on a w(t, s) # 0 (pour
montrer qu'on ne peut avoir T, = T„ considérer les maxima et minima relatifs de la fonction
(v| n(s)) dans l'intervalle [r, t + «]).
c) Déduire de b) que l'ensemble N* uN" uD est fini, et que si U désigne dans R x R
l'ouvert défini par les relations t0<t<t0 + L, t + e<s<t + L — e, pour un t0 convenable,
l'ensemble w" '(0) ne rencontre pas Fr(U), l'ensemble w" '(0) n U est un ensemble fini { x, xr}
et que l'on a
I e(xj) = 2(Card(N-) + Card(D) - Card(N+)).
j-i
d) On pose
w(r, t + e) , . „
— = h(e2""/L)
l|w(r,r+ <s)||
F
où h est une application déclasse C™ deSt dans Si. Montrer que l'on a £ e(xj) = 2 deg h (utiliser
(24.15.2.5)).
e) On désigne par Q, le quadrant ouvert x, > 0, x2 > 0 de R2, par Q2 le quadrant fermé
*i < 0, x2 > 0, par Qj le quadrant ouvert — Qt, par Q4 le quadrant fermé — Q2. Montrer que
l'on a les propriétés suivantes, si v(r) et v(t + c) ne sont pas points d'inflexion :
1° si w(t, t + e)e Q„ on a k(s) < 0 pour t « s < t + e, et, ou bien w{s, s + e)e Q, pour
tout se [t, t + e], ou bien il existe s0e [t, t + e] tel que w(s, s + e)eQ, pour t < s < s0, et
w(s, s + e) e Q4 pour s„ < s < t + s ;
2° si w(t, t + i)eQ„ on a k(t) < 0, k(t + e) > 0, et, ou bien il existe s0e [t, t + e] tel que
w(s, s + e)eQ4 pour t < s $ s0 et w(s, s + e)eQ3 pour s0 < s < t + £, ou bien il existe s,, s2
dans [r, t + e] tels que w(s, s + e)eQ4 pour t $ « $ s,, w(s, s + e)eQ3 pour s, < s < s2 et
w(s, ! + «)eQi pour s2 < s < t + e ;
3° si w(i, t + e) e Q3, on a k(s) > 0 pour t ^ s ^ t + e, et, ou bien w(s, s + s) e Q3 pour
tout s 6 [t, t + b], ou bien il existe s0 e [t, t + e] tel que w(s, s + s) e Q3 pour t ^ s < s0 et
w(s, s + s) e Q2 pour s0 < s < t + e ;
4" si w(t, t + e) e Q2, on a fc(t) > 0, /c(r + e) < 0, et, ou bien il existe s0 6 [t, t + e ] tel que
w(s, s + e)e Q2 pour t < s < s0 et w(s, s + e)e Q, pour s0 < s < t + e, ou bien il existe slt s2
dans [t, t + «] tels que w(s, s + «)eQ2 pour t < s ^ s,, w(s, s + eJeQj pour st < s < s2 et
w(s, s + «) e Q4 pour s2 < s < t + e.
(Si • est un vecteur orthogonal à v(r+e)- v(t), considérer les maxima et minima de (v(s)| e)
pour se [t, t +'£], en utilisant les conditions de b) sur le nombre c).
f) On peut écrire Me2*1"1-) = e""\ où g est une application de classe C00 de R dans R (9.8.1).
Soient (,<...<(„ les valeurs de t dans [t0, t0 + L] telles que les vtf,) (1 ^ j 4 m) soient les
points d'inflexion. On peut supposer que f0 < t, < t0 + e et que w(r0, l0 + e)eQ«; déduire
alorsdee)queg(t1)e£-^,oj,g(r2)e£-y, - nj,..., g(tjej^-(m - l)rc — ^, - (m - lnj.
Conclure que'2 deg h = - m.
16. Applications : H. Intersections de courbes algébriques sur une surface
algébrique.
A titre d'exemple d'application de la notion de nombre (algébrique)
d'intersection (24.13.15), nous allons étudier les intersections de courbes algébriques

106 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFERENTIELLE ÉLÉMENTAIRES
sur une surface algébrique. Nous admettrons un certain nombre de résultats
élémentaires de géométrie algébrique projective complexe, pour lesquels nous
renvoyons aux problèmes mentionnés dans le texte.
(24.16.1) Par surface algébrique, nous entendrons l'ensemble des points de
l'espace projectif complexe P3(C) dont les coordonnées homogènes (zi, z2, z3, z4)
vérifient une équation de la forme P(zn z2, z3, z4) = 0, où P est un polynôme
homogène irréductible de degré > 0, non identiquement nul. C'est un ensemble
compact Z, dans lequel l'ensemble des points où les 4 dérivées partielles de P
s'annulent simultanément est un ensemble fermé rare S (éventuellement vide)
dont les points sont appelés points singuliers de Z ; son complémentaire Z — S
par rapport à Z est une sous-variété holomorphe de dimension complexe 2 (donc
de dimension réelle 4) de P3(C). On dit que Z est une surface algébrique lisse
si S = 0 ; Z est alors une sous-variété holomorphe compacte de P3(Q (on peut
montrer que toute sous-variété holomorphe compacte de P3(C) de dimension
complexe 2 est une surface algébrique lisse).
(24.16.2) Dans toute cette section, Z désignera une surface algébrique lisse ;
elle est nécessairement connexe (problème 1). Une courbe algébrique sur Z est
une réunion de composantes connexes non réduites à un point de
l'intersection de Z et d'un certain nombre fini de surfaces algébriques (lisses ou non) :
par exemple, sur une quadrique Z, une droite (de l'un des systèmes de
génératrices) est l'intersection de Z et de deux plans passant par cette droite.
Nous admettrons les propriétés suivantes : si T est une courbe algébrique
sur Z, il y a un ensemble fini (éventuellement vide) S de points de T, dits singuliers,
tels que le complémentaire T — S soit une variété holomorphe de dimension
complexe 1 (donc de dimension réelle 2) ; si S est vide, T est une sous-variété
holomorphe compacte de Z, de dimension complexe 1 ; on dit alors que T est
une courbe algébrique lisse. En général, si M est un point singulier de T, il existe
un voisinage ouvert V de M dans Z tel que VnT soit réunion d'un nombre fini
de branches, n'ayant deux à deux en commun que le point M, et dont chacune B
est l'image du disque D : 111 < 1 de C par une application holomorphe
injective u de D dans Z qui, pour un système convenable de coordonnées locales
holomorphes (x, y) dans V (dépendant de B), s'écrit
(24.16.2.1) x(u(t)) = at', y(w(t)) = bt* + ...
où p et q > p sont des entiers premiers entre eux, a et b des nombres complexes ^ 0,
bt* + ... une série entière convergente dans D, et dont bt9 est le premier terme
( « développements de Puiseux », cf. section 23.15, problème 5) ; on notera que
pour tout voisinage fermé W de M dans Z et pour toute branche B c V de T,
le complémentaire B — (B n W) est une variété holomorphe de dimension
complexe 1.

16. APPLICATIONS : II. INTERSECTIONS DE COURBES ALGEBRIQUES 107
(24.16.3) Rappelons (16.21.13) que toute variété holomorphe est munie d'une
orientation canonique ; quand par la suite, nous considérerons une variété
holomorphe comme une variété orientée, c'est toujours de cette orientation
canonique qu'il s'agira, sauf mention expresse du contraire.
Rappelons qu'une courbe algébrique lisse T sur £, munie de son orientation
canonique, définit sur £ un 2-courant d'ordre 0, le courant d'intégration Ir, tel
que, pour toute 2-forme fi de classe C°° sur £, on ait (24.13.14)
On écrira souvent T au lieu de Ir si cela ne crée pas de confusion.
Rappelons que ce 2-courant est un cycle (24.13.14).
(24.16.4) Nous allons voir que ces propriétés peuvent s'étendre à une courbe
algébrique T quelconque sur £. D'après ce qu'on a vu dans (24.16.2), la question
est locale au voisinage d'un point singulier M de T : il s'agit de voir que pour
toute 2-forme jS sur £ et toute branche B de T passant par M, la restriction de p
à la sous-variété (non fermée) B — {M } est intégrable (16.24.2) sur cette variété.
Or, pour le système (x, y) de coordonnées locales holomorphes au point M
considéré dans (24.16.2), la forme fi s'écrit
(24.16.4.1) Ci(x, y)dx a dx + c2(x, y)dx a dy + c3(x, y)dx a dy
où les Cj sont des fonctions bornées de classe Cœ, et tout revient à voir que
lorsqu'on remplace dans cette expression x, y par les fonctions de t définies
dans (24.16.2.1) et x, y par les fonctions de 7 complexes conjuguées, on obtient
une forme différentielle f(t, ~t)dt a dt intégrable dans le disque D : 11 | < 1,
ce qui est immédiat, / étant continue et bornée par la plus grande des bornes
des Cj multipliée par un facteur ne dépendant pas de fi ; cette dernière remarque
montre que la formule (24.16.3.1) définit encore un 2-courant d'ordre 0 sur £,
qu'on appelle encore courant d'intégration défini par la courbe T.
Montrons maintenant que ce courant est encore un cycle, c'est-à-dire que pour
toute 1-forme a de classe C°° sur Z, on a encore da = 0. Soit S = { M,, ..., M,}
l'ensemble des points singuliers de T ; il suffira de montrer qu'il y a une suite
de fonctions vk de classe C°° sur £, à valeurs dans [0,1 ], tendant vers 1 en chaque
point £ autre que les Mj, dont chacune est nulle dans un voisinage de S, et qui
sont telles que I vkda tende vers 0. Comme vkda = d(vka) — (dvk) a a, et que
d(vka) = d(vka) = 0, puisque la restriction de la forme vka à la sous-
(24.16.3.1)
+ c4(x, y)dy a dy + c5(x, y)dx a dy + c6(x, y)dx a dy

108 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFERENTIELLE ÉLÉMENTAIRES
variété T - S a un support compact (17.15.5.1), il suffira de montrer que
jW)Aa
tend vers 0. Supposons d'abord pour simplifier qu'il n'y ait qu'un seul point
singulier M et une seule branche B passant par M, les notations étant celles de
(24.16.2). Soit v une fonction croissante de classe C°° dans [0, + oo [, à valeurs
1 3
dans [0, 1 ], égale à 0 pour 0 < s < - , à 1 pour s ^ - ; on prendra la restriction
4 4
de vk à B égale à v(k \ u~i(z) \ ) pour tout zeB, puis on prolongera vk à Z de sorte
qu'elle soit égale à 1 dans Z — V et à 0 dans un voisinage de M (16.4.3). On a
alors, si p = 1t \,
j* (dvk) a a = | kv\kp)dp a {f(t)dt + gfflt)
où /et g sont continues et bornées dans D. Si l'on pose t = pe'9, cette intégrale
s'écrit
f dO | kv'{
Jo Jo
>'(kp)h(p, 8)pdp
où h est continue et bornée ; elle est donc majorée par C j* kv'(kp)pdp où C
f1 1 °f1
est une constante indépendante de k. Mais I kv'(kp)pdp = - su'(s)ds, puisque
Jo k Jo
v est constante pour s ^ 1 ; cela démontre notre assertion dans ce cas. Dans
le cas général, on définit de la même manière la restriction de vk à chacune des
branches passant par les divers points singuliers, puis on prolonge vk à Z de
sorte qu'elle soit nulle dans un voisinage de S et égale à 1 dans Z - V, où V est
la réunion des voisinages des M} où sont définies les branches considérées (16.4.3)
(cf. problème 12).
(24.16.5) Pour toute courbe algébrique T sur Z, la classe d'homologie du
2-courant Ir est donc définie dans H2(Z) ; on la notera [r], et on dit que c'est la classe
d'homologie de la courbe T. Deux courbes algébriques ayant même classe
d'homologie sont dites homologues. Si r, et T2 sont deux courbes algébriques sur Z
dont l'intersection est un ensemble fini de points, la réunion r\ u T2 est une
courbe algébrique et l'on a Ir,ur2=Ir, + ïr2» et Par su'te IT\ur2]= [^1+ [r2].
En outre, comme les bords de Ir, et Ir2 sont nuls, le nombre d'intersection (In • Ir2)
est toujours défini, même si rt = T2 (24.13.17) ; on dit encore que c'est le nombre
d'intersection des courbes Tt et T2, et on le note (r\ • T2) ; c'est l'image du
produit [r\ ] • [r2 ] des classes d'homologie des deux courbes (élément de H0(Z))
par l'application canonique de H0(Z) dans R (24.13.15); lorsque r!=r2 = r,
on écrit aussi ce nombre (r2). Si rt et T2 ont une intersection finie, dont les points
sont non singuliers sur Tj et sur T2, et si r\ et T2 se coupent transversalement

16. APPLICATIONS : II. INTERSECTIONS DE COURBES ALGEBRIQUES 109
en chacun de ces points (ce qui revient ici à dire que leurs tangentes sont des
droites complexes distinctes) alors (r\ - T2) est égal au nombre de ces points
car on peut remplacer Ir, et Ir2 par les courants a A • a et a -» B • a,
Jr, Jr2
où A et B sont des fonctions de classe C°° seulement assujetties à être égales à 1
au voisinage de chaque point de T, n r2, sans changer le produit
d'intersection In • Ij-j (24.13.15), si bien que l'existence des points singuliers n'intervient pas
sous les hypothèses faites.
Mais nous allons voir des exemples où ces hypothèses ne sont pas
satisfaites et où le nombre d'intersection de deux courbes algébriques peut prendre
des valeurs < 0.
(24.16.6) Pour toute surface algébrique lisse Z dans P3(C), distincte d'un plan,
les courbes algébriques planes intersections de Z et des plans de P3(C) sont toutes
homologues.
On peut montrer que l'hypothèse que Z est lisse entraine qu'un plan de
P3(C) ne peut être tangent à Z qu'en un nombre fini de points (problème 2).
Soient r\ = Zr»H1} T2 = ZnH2 les courbes algébriques intersections
de Z et de deux plans distincts H1( H2. On peut supposer que la droite A,
intersection de H] et H2, n'est pas contenue dans Z. En effet, dans le cas contraire,
on considère un point A de A, un point A, de Ht n'appartenant pas à Z et un
point A2 de H2 n'appartenant pas à Z. Si A, (resp. A2) est la droite passant par
A et A, (resp. A et A2) et H3 le plan contenant A, A, et A2, alors, si l'on a prouvé
que r3 = Z n H3 et T, sont homologues, ainsi que T3 et T2, il en résultera que
r\ et T2 sont homologues.
De la même manière, on peut supposer que Z et A se coupent transversalement.
En effet, s'il n'en est pas ainsi, on prend cette fois un point A de A non situé sur Z,
on considère dans H! (resp. H2) une droite At (resp. A2) non tangente à Tj
(resp. r2), donc coupant Z transversalement. Si H3 est le plan contenant A,
et A2, il suffira encore de prouver que T3 = Z n H3 et Tt sont homologues,
ainsi que T3 et T2, pour avoir établi que r\ et T2 sont homologues.
Soit donc A une droite coupant Z transversalement en N points Aj (1 ^j<N),
où N est le degré de Z ; soit A' une droite de P3(C) ne rencontrant pas A. La
projection p : (JA -> A' qui, à tout point M£ A fait correspondre le point 5
où le plan passant par A et M rencontre A', est une submersion de l'ouvert QA
sur A' ; nous désignerons par Hs le plan contenant s et A, par T, la courbe
algébrique Z n H,. Pour prouver le théorème (24.16.6), il suffira, pour tout s0 e A',
de montrer qu'il existe un voisinage W de s0 dans A' tel que, pour tout s e W,
la courbe Ts soit homologue à rso ; par compacité, on pourra recouvrir A' d'un
nombre fini de tels voisinages, ce qui prouvera que toutes les courbes Fs sont
homologues, en vertu du fait que A' est connexe, étant homéomorphe à S2
(16.11.12).

110 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
Il n'y a qu'un nombre fini de valeurs st, ..., sr de s telles que les plans HtJ
soient tangents à £, et les points de contact BJk de H3J et £ sont en nombre fini
(1 < k < tij). Pour s distinct des sp H, et £ se coupent donc transversalement
le long de r„ et r, est par suite une courbe lisse. Au contraire, si s = Sj, les BkJ
sont les points singuliers de T,y On va alors distinguer deux cas, suivant que
s0 est distinct ou non des s}.
A) r,0 est lisse. Prenons d'abord un voisinage ouvert U de £ dans P3(C)
tel que toute 2-forme fermée de classe C°° sur £ se prolonge en une 2-forme
fermée de classe C00 sur U (24.12.12). On va définir un voisinage ouvert W de s0
dans A' et un voisinage ouvert V c U de rso dans P3(Q, ayant les propriétés
suivantes :
1° W ne contient aucun des Sj (1 <y < r) et, pour tout seW, l'ouvert
L, = Hs n V de H4 contient T, ;
2° pour tout s e W, il existe une homotopie de classe C", F : I x Lj0 -» V
(avec I intervalle ouvert de R contenant [0, 1]) telle que F(0,.) soit l'injection
canonique j0 : L,0 -> V, et que, pour tout tel, F(t,.) soit un difféomorphisme
de Ls„ sur Ly(t) préservant l'orientation, y étant une application de classe C00
de I dans W telle que y(0) = s0 et y(l) = s ;
3° la réunion des ensembles Ta, lorsque s parcourt W, est une partie
compacte K de £ contenue dans V.
Il s'agit de montrer que pour toute 2-forme fermée co de classe C°° sur £,
on a I co = co (24.12.11) ; or co se prolonge en une 2-forme fermée a de
Jr,0 Jr,
classe C00 sur V, et il suffit de montrer qu'en tant que courants sur V, les courants
d'intégration rj0 et F, à support compact sont homologues. Comme L, et V n £
se coupent transversalement dans V pour tout s e W, on peut écrire r,=L, • (Vo£)
en tant que courant d'intégration (24.13.14). Or, les courants d'intégration L,
et LSo sur V sont homologues en raison de l'hypothèse 2° ci-dessus et de (24.10.6);
toutefois, comme V n £ n'est pas compact, on ne peut pas appliquer
directement (24.13.9) pour en déduire que T, et rso sont homologues comme courants
sur V. Mais le raisonnement de (24.13.9) s'applique encore en posant S = V n £,
T = L, — LJo (courants d'intégration). En effet, avec les mêmes notations, le
support des formes P'k est arbitrairement voisin de la réunion L, u L,0, donc
l'intersection du support de /JJ a a et de V n £ est contenue dans un voisinage
compact de K dans V, et par suite < S, d(fi'k a a) > = 0 pour tout k (17.15.5.1),
ce qui entraîne, en passant à la limite, que < S • T, a > = 0, donc ! a = I a
pour toute 2-forme fermée a de classe C00 sur V. •'r*o
Pour définir V ayant les propriétés 1°, 2° et 3° ci-dessus, considérons sur A'
un point v distinct de s0, et qu'on peut supposer non dans U (en remplaçant

16. APPLICATIONS : II. INTERSECTIONS DE COURBES ALGÉBRIQUES 111
éventuellement U par un voisinage plus petit) ; prenons d'autre part une suite
décroissante (m„) de voisinages ouverts de rso dans hso, tels que m„ c u et
que l'intersection des m„ se réduise à rso ; enfin, prenons dans a' une suite
décroissante de voisinages ouverts connexes W„ de s0 telle que l'intersection des W„
se réduise à s0. Soit C„ la réunion des droites projectives complexes joignant v
aux points de m„, et soit D„ la réunion des plans projectifs complexes définis
par A et les points de W„. Il est clair que les ensembles C„ n D„ sont compacts
et que leur intersection est rso ; il existe donc un entier n tel que C, n d, c u.
On prend v = C,nU; comme l'intersection des dmnl est r,0, il existe m > n
tel que DanZ soit contenu dans V ; on prend W = Wm) et il est clair que les
conditions 1° et 3° sont alors satisfaites. Enfin, on a LSo = m,, ; si y est une
application de classe Cœ de I dans W, il suffit de prendre pour F(f, z) le point
d'intersection avec Hy„) de la droite projective complexe joignant vhzeMn pour satis-
b) r,„ n'est pas lisse. La construction de V, w et de l'homotopie f est la
même que dans A). Avec les mêmes notations, pour tout procédé
d'approximation (Lk) et toute 2-forme fermée a sur V, on a < S a (dfi'k), a > = 0 mais rien
ne garantit que cette suite de nombres tend vers la différence a — I a, puisque
HSo et £ ne se coupent plus transversalement. Toutefois, si E est l'ensemble fini
des points de contact Bx, ..., Bm de HSo et de £, on sait que l'application
canonique H2(£ — E) -» H2(£) est bijective (24.7.9) ; par suite, toute 2-forme fermée co
de classe C00 sur £ est cohomologue à une 2-forme fermée m, de classe C00 et
de support ne rencontrant pas E, et on peut donc se borner à prouver que
Il est clair en outre que cox se prolonge en une 2-forme fermée ax sur £ dont le
support ne rencontre pas E (24.12.12). Mais, pour une telle forme ctt fixée, on
peut choisir un procédé d'approximation (Lk) tel que la suite des < S a (dfïk), a, >
converge vers I a, — a, : il suffit, dans la construction de (24.13.8), de
prendre les WA qui contiennent un point de E assez petits pour qu'ils ne
rencontrent pas le support de et u de sorte que leur contribution dans < S a Lk • T, olx >
est nulle et la conclusion résulte de ce que, dans les autres WA, HSo et £ se coupent
transversalement. Ceci achève de prouver (24.16.6).
(24.16.7) Supposons que la surface lisse £ de degré N ^ 2 contienne une droite A :
ce sera par exemple le cas pour une surface d'équation
faire à 2°.
(24.16.7.1) x3P(xu x2, x3) - XjQixt, x2, x3) = 0

112 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFERENTIELLE ÉLÉMENTAIRES
où P et Q sont deux polynômes homogènes de degré N — 1 sans facteur
multiple et sans facteur commun tels que, dans P2(C), les courbes algébriques
(irréductibles ou non) d'équations P = 0 et Q = 0 se coupent transversalement en
tous leurs points d'intersection ; on suppose en outre-qu'aucun de ces points,
ni aucun des points singuliers de la courbe d'équation Q = 0, n'est situé sur la
droite x3 = 0. Calculons le nombre d'intersection (A2) de A avec elle-même.
Pour cela considérons d'abord deux plans distincts H1; H2 passant par A ;
comme ils ne sont pas tangents à A en tous les points de A, l'intersection de H,
(resp. H2) et de A est la réunion de A et d'une courbe algébrique (resp. T2)
de degré N — 1 ; nous admettrons que l'on peut trouver Ht et H2 distincts et
tels que A n T, et A n T2 soient des ensembles de N - 1 points, de sorte que
(A • r\) = (A • T2) = N - 1 (problème 3). Soient d'autre part A' une droite
du plan Hj coupant AuT, en N points distincts, H3 un plan distinct de H,
passant par A' et T3 la courbe algébrique £ n H3. En vertu de (24.16.6), on a
((A + r\) • (A 4- T2)) = ((A + r,) - r3) = N, puisque Aur\ et T3 se coupent
transversalement. Or on a {Yx • T2) = 0 puisque l'intersection r\ n T2 est vide ;
on a donc ((A + Tx) • (A + T2)) = (A2) + 2 (N - 1), d'où
(24.16.7.2) (A2) = 2 - N
qui est toujours < 0, et n'est nul que si £ est une quadrique.
(24.16.8) Le théorème de Bezout dans P2(C). Considérons dans P2(C) deux courbes
algébriques (irréductibles ou non, lisses ou non) r,, T2 d'équations respectives
P(*i, x2, x3) = 0, Q(xt, x2, x3) = 0, où P et Q sont des polynômes homogènes
de degré N, dont chacun n'a aucun facteur multiple, et qui n'ont aucun facteur
commun ; on suppose en outre que T, et T2 se coupent transversalement en
chacun de leurs points d'intersection, et qu'aucun de ceux-ci, ni aucun des points
singuliers de T2, n'est sur la droite d'équation x3 = 0. Alors la surface £ d'équation
(24.16.8.1) XtP(xu x2, x3) - (.v4 - jc3)Q(jci , x2, x3) = 0
dans P3(C) est une surface lisse de degré N + 1. Soient A la droite d'équations
x3 = .v4 = 0 dans P3(C), Ht le plan d'équation x4 - x3 = 0, H2 le plan
d'équation ,x4 = 0 ; £ n Ht est la réunion de A et d'une courbe Y\, £ n H2 la réunion
de A et d'une courbe T'2. Si A est le point de £ de coordonnées (0,0,0,1),
l'application p : (xi, x2, x3, x ) -* (je,, x2, x3) est définie dans £ — {A} et est une
application de classe C00 de £ — ( A } sur P2(C), telle que l'image par p de T[ (resp. T'2) est
T, (resp. T2). Il résulte de (24.11.3) et de (24.7.9) que H'2(£) et H'2(£ - {A} )
sont canoniquement isomorphes. Comme les courbes Y{ et T'2 sont homologues
dans £ (24.16.6), elles le sont aussi dans £ - {A }. Nous allons en déduire que
r\ et Y2 sont homologues dans P2(C). En effet, si /S est une 2-forme fermée sur
P2(C), fi' = 'p{fi) est une 2-forme fermée sur £ — {A} ; comme la restriction

16. APPLICATIONS : II. INTERSECTIONS DE COURBES ALGÉBRIQUES 113
de p à r{ (resp. r2) privée de ses points singuliers est un difféomorphisme de
cette variété sur r\ (resp. T2) privée de ses points singuliers, qui préserve
l'orientation, on a /?' = P et P' = p, et comme T\ et T'2 sont homologues
Jr,' Jr, Jr,' Jr2
dans S — { A }, on en conclut bien que p = p.
kl Jr2
Remarquons maintenant que pour toute courbe algébrique r\ de degré N
dans P2(C), il existe une courbe T2 réunion de N droites distinctes et vérifiant
les conditions mentionnées ci-dessus. Comme par ailleurs deux droites
distinctes de P2(C) sont images l'une de l'autre par un automorphisme de P2(C),
on voit que pour toute courbe algébrique T de degré N dans P2(C), on a
(24.16.8.2) [r] = N[A].
Dîautre part, si A et A' sont deux droites distinctes de P2(C), il est clair que
(A • A') = 1. On voit donc que pour deux courbes algébriques quelconques Y, Y'
de P2(C), de degrés respectifs N et N', on a, en vertu de (24.16.8.2)
(24.16.8.3) (rP) = NN'
(théorème de Bezout); si T et F se coupent transversalement en chacun de
leurs points d'intersection, le nombre de ces points est donc NN'.
PROBLÈMES
1) Dans l'espace projectif complexe P„(C), une hypersurface algébrique est l'ensemble £
des points vérifiant P(x, x„+,) = 0, où P est un polynôme homogène irréductible de degré > 0.
Les points singuliers de £ sont ceux où les n + 1 dérivées premières de P s'annulent
simultanément. Montrer que l'ensemble S des points singuliers est un ensemble fermé rare dans £,
tel que £ - S soit une variété holomorphe connexe de dimension n - 1. (Par une transformation
linéaire, se ramener au cas où, si P est de degré m, il existe dans P un monôme ex" avec c / 0.
Utiliser alors le problème 3 de la section 16.29).
2) Soit £ une hypersurface algébrique lisse dans P„(C), Montrer qu'il ne peut exister d'hyper-
plan complexe H tel que H soit tangent à £ en tous les points d'une variété algébrique de
dimension n — 2. (Se ramener au cas où H est défini par x„+, = 0 et montrer que si l'on écrit l'équation
de £ sous la forme ^B+iQ(x,, ..., xn+l) + R(x,, ..., xn) = 0, un des facteurs irréductibles du
polynôme R serait tel que son carré divise R).
3) Les notations étant celles de (24.16.7), montrer qu'il n'existe qu'un nombre fini de plans H
passant par A et tels que, si l'intersection de £ et de H est réunion de A et d'une courbe T,
l'intersection A n T ait moins de N - 1 points (se ramener au cas où dans P et Q, il y a un monôme
en x2_1 de coefficient # 0).
4) Sous les hypothèses de (24.16.6), montrer que toutes les courbes algébriques planes,
intersections de £ et des plans de P3(C), et qui sont lisses, sont difféomorphes. Avec les notations
employées dans (24.16.6), on peut commencer par montrer que pour tout point M e ri0, il existe
un voisinage ouvert SM de M dans r,0, un voisinage ouvert WM de s0 dans A', et pour tout s e WM,
un difféomorphisme uM, de SM sur un ouvert de r„ préservant l'orientation, de sorte que deux tels
difféomorphismes correspondant à deux points distincts M, M' de r,0 coïncident dans SM n SM..
On pourra utiliser (16.25.1) et (16.25.4) pour définir un voisinage V de r„„ dans £ et une submersion

114 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
surjective x de V sur Tso. Si M n'est pas un des points A,, on remarquera que la restriction à un
voisinage de M dans £ de l'application N -» QKN), w(N)) est un difféomorphisme sur le
produit d'un voisinage de M dans rI0 et d'un voisinage de s0 dans A'. Lorsque M est l'un des points Aj,
on pourra projeter un voisinage de M dans £ sur le plan tangent à £ en M, parallèlement à la droite
complexe A.
5) Soit £ une sous-variété holomorphe fermée de dimension (complexe) m < n - 1 dans
l'espace projectif complexe P»(C), non contenue dans un hyperplan.
a) Soit L une variété linéaire projective de dimension n — m — k (pour un entier le tel que
2 < k < n — m) ne rencontrant pas £. Montrer qu'il existe une variété linéaire projective V = L
de dimension n-m-k+l ne rencontrant pas £ (appliquer le théorème de Sard (16.23.1) à
la projection de £ sur une variété linéaire projective de dimension m + k — 1 à partir de L). En
déduire que par tout point de P.(Q non situé sur £ il passe une variété linéaire projective L0 de
dimension n — m — 1 ne rencontrant pas £.
b) Soit L0 une variété linéaire projective de dimension n-m-1 ne rencontrant pas £, et
soit S l'ensemble des points x e £ tels que la variété linéaire projective de dimension n - m
déterminée par x et L0 ne coupe pas transversalement £ au point x. Montrer qu'il ne peut exister dans S
de point intérieur par rapport à £ (en supposant la variété L0 « à l'infini » et utilisant (16.8.3.2)
et le principe des zéros isolés (9.1.5), montrer que dans le cas contraire il existerait une droite
projective complexe contenue dans £ et rencontrant L0).
En déduire que si M0 est une variété linéaire projective de dimension m né rencontrant pas L0.
l'image de £ par la projection sur M0 à partir de L0 contient un ensemble ouvert non vide dans M0.
En déduire qu'il existe des variétés projectives L de dimension n — m contenant L0 et coupant £
transversalement ; l'ensemble L o £ est fini, et le nombre de ses éléments est le même, quels que
soient L0 et L ayant les propriétés précédentes (utiliser le théorème de Sard et la théorie du degré) ;
on dit que c'est le degré de £. En outre, la projection de £ sur M0 à partir de L0 est surjective (24.9.4),
donc toute variété linéaire projective de dimension n — m rencontre £.
c) Soit L0 une variété linéaire projective de dimension n — m + k, avec 0 < k < m — 2,
qui coupe £ transversalement. Montrer qu'il existe des variétés linéaires projectives L de
dimension n — m + k — 1 contenant L0 et coupant £ transversalement. (Considérer l'ouvert £ n (J L0
de £ et la projection de cet ouvert à partir de L0 sur une variété linéaire projective M0 de
dimension m — k — 1 ne rencontrant pas L0, et montrer que cette application est surjective, en
considérant un voisinage d'un point d'intersection de L0 et de £).
6) Soit £ une sous-variété algébrique lisse de dimension (complexe) m < n - 1 dans P»(C),
non contenue dans un hyperplan.
a) Soit L0 une variété linéaire projective de dimension n — 2, coupant £ transversalement
(problème S c)). Si A est une droite projective ne rencontrant pas L0, montrer que l'ensemble des
points s € A tels que l'hyperplan passant par L0 et s soit tangent à £ est fini. (En vertu du théorème
de Sard, cet ensemble est rare dans A ; montrer d'autre part que son image réciproque dans £
est une sous-variété algébrique (non connexe en général) de £. On pourra pour cela considérer
les points de L0 non dans £ et les points de contact des tangentes issues de ces points à I).
b) Déduire de a) que toutes les sous-variétés de £ de dimension m - 1, intersections de £
par des hyperplans coupant £ transversalement, sont homologues (en tant que courants
d'intégration) (même méthode que dans (24.16.6)).
7) Sous les mêmes hypothèses que dans le problème 6, montrer que les groupes d'homologie
H'2i(£) pour 0 < fc < m ne sont pas réduits à 0. (Si x0 est un point de £, montrer qu'il existe
deux variétés linéaires projectives de dimensions (complexes) n-m + keln — k respectivement,
coupant transversalement £ et passant par x0 ; si V et W sont leurs intersections avec £, on a alors
(V. W) > 0).
8) Le groupe discret Z opère analytiquement, proprement et librement dans C" — {0}
par la loi (m, z) c"z, où c est un nombre réel > 1. La variété des orbites £ = (C - {0 } )/Z
est une variété holomorphe compacte connexe (variété de Hopf) dont C" — {0} est un
revêtement galoisien (section 16.28, problème 4) (revêtement universel si n > 2). Montrer que £ est
difféomorphe à Si x S2a-i ; déduire du problème 7 que pour n > 2, £ n'est pas homéomorphe
à une sous-variété algébrique lisse d'un espace projectif complexe.

16. APPLICATIONS : II. INTERSECTIONS DE COURBES ALGÉBRIQUES 115
9) Dans l'espace C", une variété algébrique affine est définie comme l'ensemble des points
annulant une famille de polynômes de C[T,, ..., T„] ; si V est une telle variété et si C est
considéré comme un ensemble ouvert partout dense dans P.(C), l'adhérence V de V dans P„(C) est
une variété algébrique projective, ensemble des points annulant les polynômes qui définissent V,
rendus homogènes. On admettra qu'il existe dans V un ensemble ouvert partout dense W qui
est une variété holomorphe pure de dimension complexe p < n (que l'on appelle la dimension
de V ou de V), et que le complémentaire V — W est une variété algébrique_projective de
dimension < p [164, p. 151 ] ; on dit que les points de W sont les points lisses de V, et W la partie lisse
de V. Lorsque V est définie par une seule équation (problème 1), on a p = n - 1.
Soit a e V, et pour tout z # a dans V, soit D. , la droite complexe passant par a et z ; le
cône tangent C. à V au point a est par définition la réunion des droites valeurs d'adhérence de
z -» D, , lorsque z tend vers a dans V. Montrer que si p = n — 1 et (pour simplifier) a = 0,
le cône tangent au point a à l'hypersurface V est défini par l'équation Pm(z) = 0, où P„ est le
polynôme homogène de plus petit degré non identiquement nul dans l'équation P(z) = 0 de V.
Supposant toujours p = n - 1, montrer qu'en effectuant au besoin une transformation
unitaire dans l'espace hilbertien usuel C, on peut supposer qu'aucun des axes de coordonnées
de C" n'est parallèle à une droite contenant dans C. ; en déduire qu'il existe un entier N > 0 tel
que tout point d'un quelconque des hyperplans z} = 0 (1 < j < n) soit projection orthogonale
d'au plus N points de V sur cet hyperplan (raisonner par récurrence sur n).
Conclure qu'il existe un nombre M > 0 tel que, pour tout r > 0, le volume riemannien
de l'intersection W n B(a ; r) de W et de la boule de centre a et de rayon r soit tel que
vol(W n B(a ; r)) < Mr2'""'1 (utiliser l'expression du volume riemannien d'une variété
holomorphe de C" donnée par le problème 6 a) de la section 24.14).
10) Les notations étant celles du problème 9, montrer que pour p < n - 1, le cône tangent C.
est une variété algébrique de dimension p. (Raisonner par récurrence sur n — p, en considérant
une hypersurface algébrique S parmi celles dont l'intersection est V, et en lui appliquant le résultat
du problème 9 ; on admettra que la projection orthogonale de V sur un hyperplan de C" est
partout dense dans une variété algébrique de dimension p contenue dans cet hyperplan [164, p. 77],
à laquelle on peut appliquer l'hypothèse de récurrence).
Déduire de ce résultat qu'en effectuant au besoin une transformation unitaire de C", on
peut supposer que l'intersection de C. et d'une quelconque des („",) variétés linéaires affines
passant par a et parallèles aux variétés coordonnées de dimension n — p, est réduite au point a.
(Considérer dans la variété de Stiefel S„,„_,(C) (16.11.6) l'ensemble des systèmes (z^i «*«.-,
tels qu'aucune génératrice de C. ne soit parallèle au sous-espace engendré par les z., et montrer
que c'est un ensemble ouvert partout dense dans Sa>n-p(C)).
On admettra que cela entraîne qu'il existe une boule B0 de centre a dans C" et un entier N > 0
tel que tout point d'une quelconque des variétés coordonnées de dimension p, qui appartient
à la projection orthogonale de B0 sur cette variété, soit projection orthogonale d'au plus N points
de B0nV [164, p. 115).
Conclure qu'il existe un nombre M > 0 tel que, pour tout r > 0 pour lequel B(a ; r) c B0,
le volume riemannien de l'intersection W n B(a ; r) soit tel que vol(W r> B(a ; r)) $ Mr2' (même
méthode que dans le problème 9) (lemme de Le long).
11) Avec les mêmes notations, soit L une variété linéaire affine de R2" de dimension réelle q,
et soit K une partie compacte de L ; soit T(K, r) l'ensemble des points de C" dont la distance à K
est < r. Montrer qu'il existe deux nombres r0 > 0, M > 0, tels que pour r < r0, on ait
vol(W n T(K ; r)) < Mr2'"* (considérer une subdivision cubique de L formée de cubes de côté r ;
appliquer à chaque cube le lemme de Lelong, et noter que le nombre des cubes qui rencontrent K
est majoré par Ar *, où A est une constante).
Généraliser ce résultat au cas où L est une variété différentielle de dimension (réelle) q (se
ramener au cas où il existe un voisinage U de L et un difféomorphisme de U sur un ouvert de C"
transformant L en une partie d'une variété linéaire affine).
Soit U un ouvert de C" tel que dans U la distance p(x) d'un point z à L soit une fonction
de classe C' dans U - (L n U) et que la forme différentielle dp soit bornée dans cet ensemble.
Soit d'autre part / une fonction numérique de classe C" dans R, égale i 0 pour t > 1 et à 1 pour

116 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFERENTIELLE ÉLÉMENTAIRES
t < - . Enfin, soit eu une (2p — 1 (-forme différentielle de classe C°° et de support compact contenu
dans U. Montrer qu'il existe une constante M > 0 telle que, lorsque r tend vers 0, on ait
(observer qu'il y a une partie compacte K de L telle que la forme intégrée soit nulle hors de T(K ; r)).
12) Avec les mêmes notations, on définit par récurrence W, comme étant la partie lisse de
la variété algébrique complémentaire de W,uW, u ... uW,H dans V, avec W0 = W ; c'est
une variété holomorphe de dimension complexe < p — k, et W,+, = 0 (problème 9).
a) Soit a une 2/>-forme différentielle de classe C sur C", de support compact. Montrer
que sa restriction à la variété différentielle W de dimension (réelle) 2p est intégrable (utiliser le
lemme de Lelong). L'application a -» a est encore un 2/>-courant sur C", appelé encore cou-
Jw
rant d'intégration défini par V, et noté Iv ou même V.
b) Soit co une (2p - Informe différentielle de classe C" sur C", de support compact.
Montrer que si le support S de co ne rencontre pas W, on a I dco = 0, en raisonnant par récurrence
Jw
sur k. (Se ramener par une partition de l'unité au cas considéré dans le problème 11, avecq^2p-2k;
noter que par l'hypothèse de récurrence, on a
et utiliser le problème 11 pour montrer que j" *. est arbitrairement petit.)
c) Conclure que le courant d'intégration Iv est un cycle {théorème de Lelong).
17. Homologie des courants cellulaires.
(24.17.1) On a vu dans (24.11.3) que, pour calculer l'homologie H'(X) des
courants à support compact sur une variété pure orientée X, on pouvait se borner
aux courants qui sont images canoniques des formes différentielles à support
compact, pour lesquels le bord se calcule à l'aide de la différentielle extérieure.
Nous allons voir qu'une autre méthode de calcul repose sur la considération
d'une autre sorte de courants, de nature plus « géométrique » que les images
de formes différentielles, et pour lesquels le calcul du bord s'appuie sur la
formule de Stokes.
(24.17.2) Considérons un polyèdre convexe ouvert relativement compact U
dans un espace Rp, ou plus généralement dans une variété linéaire affine E de
dimension p dans un espace RN pour un N > p (24.14.10). Par abus de langage,
nous dirons qu'une application s de U dans une variété différentielle X est de
classe Cœ si elle est la restriction à U d'une application de classe Ç00 d'un
voisinage ouvert V de U (par rapport à E) dans X ; s est donc aussi définie dans Fr(U),
et, d'après ce qu'on a vu dans (24.14.10), sa restriction à chaque face de U est
une application de classe C00 de l'adhérence de ce polyèdre convexe dans X.

17. HOMOLOGIE DES COURANTS CELLULAIRES
117
Supposons X pure, non nécessairement orientable, de dimension n ^ p,
et fixons une orientation sur E, induisant donc canoniquement une orientation
sur l'ouvert U de E. L'application s définit alors canoniquement un p-courant "s
sur X, par la relation
(24.17.2.1) < s, a > =
pour toute p-forme différentielle ae^X), ce qui a un sens puisque 's(a) est
une p-forme différentielle de classe C°° sur V et que U est compact. On peut
encore dire que s est Yimage par s du p-courant T,,^ = TVD (notation de (17.5.1))
sur V (la frontière de U étant négligeable pour toute mesure lebesguienne).
On aura soin de se souvenir de ce que le p-courant s dépend, non seulement
de l'application s, mais de Yorientation choisie sur E; lorsqu'on remplace cette
dernière par l'orientation opposée, le p-courant correspondant à s change de signe.
Chaque face Fk de U (1 < k ^ r) est contenue dans un hyperplan affine Hk
de E, les Hk étant deux à deux distincts et Fk étant l'intersection de U et de Hk.
Si l'on munit chaque Fk de l'orientation déduite de celle de E par la règle précisée
dans (24.14.1), il résulte de la formule de Stokes (24.14.9) que l'on peut écrire,
pour toute (p - l)-forme différentielle /? de classe C00 sur X,
<es,py = <s,dpy = t \ \(P) = £ <h,P>
k=l jFk k=l
en désignant par sk la restriction à Fk de s ; d'où l'expression du bord du
courant s ( formule de Stokes pour les courants cellulaires)
(24.17.2.2) ' 6s = £ sk.
k=l
Si/ : X -» Y est une application de classe C00 de X dans une variété pure Y
de dimension ^ p, il est clair que pour toute application s de U dans X, de
classe C00, f ° s est une application de U dans Y, de classe C°° ; comme, pour
toute p-forme différentielle y de classe C00 sur Y, on a '(/ ° s)(y) = 's('f{y)), on
en déduit que
(24.17.2.3) /(s) = (/os)~.
(24.17.3) Étant donnée une variété pure X de dimension n, pour tout entier p
tel que 0 ^ p ^ n, nous appellerons p-courant cellulaire sur X toute
combinaison linéaire à coefficients réels de p-courants de la forme s, où s est une
application vérifiant les conditions de (24.17.2) (pour un polyèdre U dépendant de 5).
Si / : X -► Y est une application de classe Cœ de X dans une variété pure Y
de dimension ^ p, il résulte de (24.17.2.3) que l'image par / d'un p-courant
cellulaire sur X est un p-courant cellulaire sur Y.

118 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
Les p-courants cellulaires sur x forment un sous-espace vectoriel S'p{X)
de l'espace éf'/X) des p-courants à support compact. En outre, il résulte de
(24.17.2.2) que l'application bord 6 : £'PÇX) ->• <^-,(x) applique SP(X) dans
Sp-i(X). On peut donc considérer, pour l'application bord, l'espace codiffé-
rentiel gradué sur R
^".'(x)= e/;**)
p-u
et lui appliquer la théorie générale (Ann. 30.7) : on considère le sous-espace
gradué Z'.'(X) des cycles de s/7(X), somme directe des z'p'(x), où z£(x) est l'espace
des p-courants cellulaires T tels que 6T = 0, autrement dit
(24.17.3.1) z;(x) = z^x) n fi'p'(X) ;
on considère d'autre part le sous-espace B"(x) des bords de s/"{X), somme
directe des BP(X), où Bp'(x) est l'espace des p-courants de la forme 6T, où T est
un (p + l)-courant cellulaire (avec BH'(x) = {0} ). Il est clair que
(24.17.3.2) B;'(x) c B^x)
et il y a donc une application linéaire canonique HP(X) -* hjxx), où
h;(X) = z;(xvb;(X).
On pose h:'(x)= e h;'(x).
p> o
Les sections suivantes vont introduire de nouvelles notions et de nouveaux
invariants topologiques, qui nous permettront d'interpréter autrement les
espaces vectoriels Hp(x).
18. Subdivisions cellulaires et simpliciales.
(24.18.1) Un des outils essentiels dont nous allons nous servir est la notion
de subdivision cellulaire d'une partie x d'un espace RN. On appelle ainsi un
ensemble S de polyèdres convexes bornés de RN, de dimensions < N (24.14.10),
vérifiant les conditions suivantes :
I) Les polyèdres de 6 sont deux à deux disjoints et leur réunion est X.
II) Toute face d'un polyèdre de S est réunion de polyèdres de S.
III) Toute partie compacte deXne rencontre qu'un nombre fini de polyèdres de ®.
Il résulte de II), par récurrence sur la dimension, que la frontière de tout
polyèdre U e S est réunion de polyèdres de 6, et comme cette frontière est
compacte, elle est réunion finie de polyèdres de S. Si x lui-même est compact
l'ensemble <S est fini ; si x est ouvert, tout point de x possède un voisinage compact

18. SUBDIVISIONS CELLULAIRES ET SIMPLICIALES
119
dans RN, contenu dans X, et ne rencontrant donc qu'un nombre fini de polyèdres
de S ; cela montre que S est au plus dénombrable et est un ensemble localement
fini de parties de X (12.2.3). Il en est de même alors, en vertu de ce qui précède,
de l'ensemble des adhérences dans RN des polyèdres U e S ; si X est ouvert,
toute réunion (finie ou non) de ces adhérences est donc un ensemble fermé dans X,
puisqu'un point de X a un voisinage compact contenu dans X et ne rencontrant
par suite qu'un nombre fini de ces adhérences.
On dit qu'une partie X de RN, munie d'une subdivision cellulaire S, est
un complexe cellulaire euclidien.
Exemples (24.18.1.1) Les facettes d'un polyèdre convexe borné U (l'ensemble U
compris (24.14.12)) forment une subdivision cellulaire de D.
Plus généralement, considérons un tel polyèdre ouvert U de dimension «
dans un espace R", et soient Hu ..., Hp des hyperplans affines distincts
rencontrant U. Alors les composantes connexes de l'intersection W de U et de
l'ouvert complémentaire de H, u H2 u ... u Hp sont des polyèdres convexes
bornés de dimension n et l'ensemble des facettes de tous ces polyèdres est une
subdivision cellulaire de U. La proposition est en effet évidente pour n = 1
et il suffit de raisonner par récurrence sur n : on considère les hyperplans affines
Hi, ..., H'q qui contiennent les faces de U, et pour chaque p < n, les variétés
linéaires affines de dimension n — p intersections d'un certain nombre d'hyper-
plans pris parmi les H, ou H'k ; si Sp est l'ensemble de ces variétés linéaires affines,
on applique l'hypothèse de récurrence à chacun des V e 93p, en considérant les
composantes connexes de l'ensemble ouvert (relativement à V) formé des xeVnU
n'appartenant à aucun hyperplan H; ou H'k autres que ceux contenant V ; lorsque
V parcourt 5BP, ces polyèdres de dimension n — p sont ceux de la subdivision
cellulaire considérée. En effet, en vertu de l'hypothèse de récurrence, il suffit
de remarquer que les faces d'un des polyèdres convexes composante connexe
de W figurent parmi les polyèdres de dimension n - 1 ainsi définis (pour p = 1).
On notera que ceux de ces polyèdres de dimension n — 1 qui sont contenus
dans U sont les faces de deux composantes connexes de W.
(24.18.2) Si S est une subdivision cellulaire d'une partie X de RN, ouverte ou
compacte, à chaque polyèdre convexe U e S de dimension p, qui est un ouvert
dans la variété linéaire affine de dimension p qu'il engendre, il correspond
canoniquement le p-courant Tv sur RN, où iu : U -» RN est l'injection canonique
(24.17.2). Ces p-courants ont l'importante propriété de former une famille libre
dans l'espace vectoriel <?P'(RN) des p-courants cellulaires sur RN, lorsque U
parcourt l'ensemble des polyèdres de S de dimension p. En effet, si x0 est un point
de U, intérieur à U par rapport à la variété linéaire affine engendrée par U,
x0 n'appartient à l'adhérence d'aucun des polyèdres convexes U' ^ U de
dimension p appartenant à 6, cette adhérence étant réunion finie de U' et de polyèdres

120 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
de S de dimensions < p. La réunion de ces adhérences étant fermée, il existe
donc un voisinage ouvert V de x0 dans RN qui ne rencontre aucun polyèdre
U' # U de S, de dimension p. Il en résulte qu'il y a une p-forme réelle a de classe C00
sur RN, de support compact, telle que < ïv, a > 0 et < lv-, a > = 0 pour tout
polyèdre U' # U de <5 de dimension p. Pour le voir, on peut supposer par
déplacement que V n U est un voisinage d'un point de Rp dans ce sous-espace de RN,
et il suffit alors de prendre a = gWdcj1 a de;2 a ... a de)", où g > 0 a son
support dans V.
Cela étant, si l'on a une relation linéaire XAj-îu, = 0 où les Aj- sont réels
i
et les Uj- e ® distincts et de dimension p, on en déduit £ X} < JVjl a > = 0 pour
toute p-forme a de classe C°° sur RN et de support compact, et en choisissant
pour chaque j une p-forme a,- ayant les propriétés décrites ci-dessus, on obtient
Aj- = 0 pour tout j, ce qui prouve notre assertion.
(24.18.3) Les subdivisions cellulaires qui joueront le rôle le plus important
par la suite sont les subdivisions simpliciales, que nous allons définir.
Dans l'espace RB+1, nous noterons e0, e,, ..., e„ les n + 1 vecteurs de
la base canonique, (£ °, £l, ...,£") les coordonnées d'un point x, E„ l'hyperplan
affine d'équation
É° + Ê1 + ...+€" = 1
qui est engendré par les n + 1 points e0, et, ..., e„. On appelle simplexe
standard de dimension n et on note A„ le polyèdre convexe de dimension n dans E„,
défini par les n + 1 inégalités
(24.18.3.1) p > 0, c;1 > 0, ..., <T > 0,
ou encore l'ensemble des combinaisons linéaires pe0 + Zl^i + ■ • • + c;"e»
telles que les soient tous > 0 et que + c;1 + ... +£" = 1. Pour n > 1,
nous fixerons une fois pour toutes une orientation sur A,, par la condition que
la n-forme induite sur A„ par de)1 a dp a ... a dÇ" soit positive (16.21.2).
Pour n = 0, A0 est réduit au seul point e0 = 1 dans R ; on l'oriente par la
condition que les fonctions telles que /(e0) > 0 appartiennent à l'orientation de A0.
(24.18.4) Une application linéaire affine a de E„ dans un RN est entièrement
déterminée par les n + 1 points = ofe,) (0 < j < n), qui peuvent être pris
arbitrairement dans RN ; on a en effet
oiPe0 + Z1^ + ...+ ?en) = cfao + Z^i + • ■ • + <X.
On écrit a = (a0 a, ... a„), et on note Im(a0 a, ... a„) l'image cr(AJ. Lorsque
a est injective (autrement dit, lorsque a0, a,, ...,a„ engendrent une variété

18. subdivisions cellulaires et simpliciales
121
linéaire affine de dimension n), on dit que Im(a0 a, ...»„) est un simplexe
géométrique (ou simplement un simplexe) de dimension n, dont ies a, sont appelés
les sommets. Lorsqu'il en est ainsi, Im(a0 a, ... a„) est un polyèdre convexe
qui a n + 1 faces, égales aux simplexes Im(a0 ... â,- ... a„) pour 0 ^ j < n,
avec la convention d'omission habituelle ; la frontière de Im(a0 a, ... a„) est
réunion disjointe de ses facettes de dimension < n, qui sont les 2"+1 — 2 simplexes
lm(aio afl ... aIp) de dimensions p < « — 1, où l'ensemble H des p + 1 indices
j'o < ii < • • • < ip parcourt l'ensemble des parties de {0, 1, ..., n } autres
que 0 et {0, 1, ..., n }. L'adhérence dans RN d'un simplexe géométrique est
encore appelé simplexe fermé.
On a par définition A„ = Im(e0 et ... e„), et aussi, pour toute permutation n
de l'ensemble {0,1, ..., n}, An=Im(en(0) en(1) ... eH(n)) ; mais on notera que
l'application linéaire affine (eK(0) en(1) ... eB(B)) préserve l'orientation de A„
si la permutation n est paire, et la renverse si n est impaire : cela résulte aussitôt
de (16.21.3) et des propriétés des déterminants (voir 24.19.3).
Une subdivision cellulaire S est dite simpliciale si les polyèdres convexes
de <3 sont des simplexes et si toute face d'un simplexe de S appartient à S. Le
couple formé d'une partie X d'un espace RN et d'une subdivision simpliciale S
de X (ou, par abus de langage, l'ensemble X lui-même) est appelé complexe sim-
plicial euclidien).
Remarques (24.18.4.1) Soit S une subdivision simpliciale de Xc R". Alors
l'intersection des adhérences de deux simplexes distincts U, V de S, de
dimensions p et q, est vide ou est l'adhérence d'une facette commune de U et V (facette
qui est donc un simplexe de S, de dimension < inf(p, q)). En effet, tout point
de U n V appartient à une facette et une seule de U et à une facette et une seule
de V, et comme deux simplexes de S ne peuvent avoir de point commun que
s'ils sont égaux, U n V est réunion de facettes communes à U et V. Supposons
U n V non vide, et soit F une facette commune à U et à V, dont la dimension r
est la plus grande possible. Alors on a U n V = F, car U n V est un ensemble
convexe contenant F ; s'il contenait un sommet commun à U et V et non dans F,
il contiendrait aussi la facette de dimension r + 1 ayant pour sommets ce point
et les sommets de F, ce qui est absurde.
Notons en outre que si X est ouvert dans R", tout simplexe F e S de
dimension n — 1 est une face commune de deux simplexes de ® de dimension n. En
effet, on peut supposer que F <= R"~1 et 0 e F, de sorte qu'il y a une boule ouverte B
de centre 0 contenue dans X et telle que BnR""1 c F. En outre, comme 0
n'appartient à aucun simplexe de S de dimension ^ n — 1 autre que F, on peut
supposer que B ne rencontre aucun de ces simplexes. Soient alors B+ et B" les
intersections de B avec les demi-espaces définis par cj" > 0 et Ç" < 0 ; ce sont
des ouverts connexes ne rencontrant aucun simplexe de S de dimension < n — 1 ;
par définition (24.18.1), il y a donc deux simplexes U, V de dimension n dans <5

122 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFERENTIELLE ÉLÉMENTAIRES
tels que B+ c UetB- <= V. Comme U n V est l'adhérence d'une facette commune
à U et V et qu'elle contient B n F, cette facette commune ne peut être que F.
Notons aussi que si X est ouvert, la réunion des simplexes de 6 de dimension
< n — 1 est un ensemble rare, donc tout point de cet ensemble est adhérent
à un simplexe de 6 de dimension n ; en d'autres termes, tout simplexe de
dimension < n — 1 est une facette d'un simplexe (au moins) de dimension n.
(24.18.5) Pour tout polyèdre convexe borné U c R" de dimension n, il existe
une subdivision simpliciale <S de U (nécessairement finie) telle que U et chacune
de ses facettes soit réunion de simplexes de S.
On construit par récurrence sur p s* n une suite croissante finie (<5P), où
®p est un ensemble fini de simplexes de dimensions < p, deux à deux disjoints,
tels que toute face d'un simplexe de Sp appartienne à Sp et que toute facette
(24.13.12) de U, de dimension < p, soit réunion de simplexes de Sp ; l'ensemble
S = SB sera la subdivision cherchée. On prend pour ®0 l'ensemble des facettes
de U de dimension 0 (réduites à un point) ; supposons ensuite Sp défini (pour
p < n) et définissons ®p+, • Soit F une facette de U de dimension p + 1, et soit b
un point de F; tout point de F distinct de b s'écrit d'une seule manière tx+(1 - t)b
avec 0 < t < letxe Fr(F) (frontière relative à la variété linéaire affine de
dimension p + 1 engendrée par F). On sait (24.13.12) que Fr(F) est réunion disjointe
d'un nombre fini de facettes de U de dimensions < p ; par l'hypothèse de
récurrence, Fr(F) est réunion de simplexes appartenant à Sp. Si Im(a0 a, ... a,)
est l'un de ces simplexes (avec q ^ p), l'ensemble des tx + (1 — t)b pour 0 < t < 1
et x e Im(a0 a, ... a,) est le simplexe Im(b a0 at ... a4), dont les faces sont
Im(a0 a, ... a4) et les simplexes Im(b a0 ... &j ... a,) pour O^j^q. Soit
®n+ ,(F) l'ensemble dont les éléments sont {b} et tous les simplexes Im(b a0 ... a,)
précédents ; il est clair que l'ensemble Sp+1, réunion de <5P et de tous les Sp+ ^F),
où F parcourt l'ensemble des facettes de dimension p + 1 de U, répond à la
question.
Remarque (24.18.5.1) La même méthode s'applique pour définir une
subdivision simpliciale de U à partir d'une subdivision cellulaire ® du type décrit dans
(24.18.1.1), définie par un nombre fini d'hyperplans affines rencontrant U :
il suffit de remplacer les facettes de U par les polyèdres de la subdivision S dans
la construction de (24.18.5).
(24.18.6) Pour tout ouvert borné X de R", il existe une subdivision simpliciale de X.
On va procéder en deux étapes, en construisant d'abord une subdivision
« cubique » de X, c'est-à-dire une subdivision cellulaire formée de cubes de R".
A) Définissons par récurrence des ouverts Xm (m > 0) de R" de la façon

18. SUBDIVISIONS CELLULAIRES ET SIMPLICIALES
123
suivante : X0 = 0, et Xm+, est réunion de Xm et de tous les cubes ouverts de
la forme
(24.18.6.1) Kh,m : 2~mh} < & < 2~m(hj + 1) pour l^j^n
avec h = (hj)e Z", qui sont en outre contenus dans ï'ouvert X — Xm. Il est clair
que Xm+1 est réunion de tous les cubes fermés de côté 2~m dont les sommets
appartiennent à 2~mZ", et qui sont contenus dans X. Nous désignerons par Sm+,
l'ensemble de cubes de dimensions < n formé : 1° des cubes Kh m de dimension n,
contenus dans X - Xm ; 2° pour chacun de ces cubes Khm, de celles des
3" — 1 facettes de Kh m de dimension < n qui en outre sont contenues dans Y
intérieur deXm+l. L'intersection des frontières de deux cubes Khm, Kh.>m est réunion
disjointe de facettes communes à ces deux cubes : en effet, si h = (hj), h' = (h]),
soit J l'ensemble des indices j tels que h} # h'} ; pour que Khm n KhVn soit non
vide, il faut et il suffit que hj = h]\± 1 pour tout j e J ; l'intersection Khm n Kh.m
est alors l'ensemble des x = (£*) tels que 2~mhj < £J < 2~m(hj + 1) pour ji J,
et 2~mhj = ÇJ si h) = h} - 1, 2-"JiJ = & si h) = h} + 1. Une facette de KhilB
et une facette de K„. m sont donc identiques ou ne se rencontrent pas. Donc <3m+1
est un ensemble de cubes deux à deux disjoints, dont aucun ne rencontre
l'intérieur de Xm, ni par suite aucun cube appartenant à un Sj pour j < m. Si
maintenant x est un point de Fr(Xm), il existe un entier k tel que 2 ~ m " *v/n < d(x, R"—X),
donc x est intérieur à Xm+>+et il y a un plus petit entier / tel que 1 < / ^ k + 1
et que x appartienne à un cube de l'ensemble Sm+(. Par compacité, on voit donc
que pour tout m, il existe un entier k tel que Xm soit contenu dans l'intérieur
de Xm+k, et tout compact contenu dans X est contenu dans l'un des Xm. Enfin,
si Xm+1 est contenu dans l'intérieur de Xm+k, tout point frontière d'un cube KKm
contenu dans X — Xm appartient à un cube (et un seul) d'un ensemble Sm+,
avec / < k + 1 ; donc si S est la réunion dans $(R") des ensembles (disjoints) <5m
pour m ^ 1, toute face d'un cube de <S est réunion finie de cubes de 6. Cela
achève de montrer que <s est une subdivision cubique de X.
B) Partant de la subdivision <s précédente, on va construire par récurrence
une suite croissante finie (Sp), où <sp est un ensemble au plus dénombrable de
simplexes de dimensions < p, deux à deux disjoints, tels que : 1° toute face d'un
simplexe de 6P appartient à <5P ; 2° tout cube de ®, de dimension < p, est
réunion d'un nombre fini de simplexes de <3p. L'ensemble 6' = <5„ sera une
subdivision simpliciale de X. On définit <30 comme l'ensemble des cubes de dimension 0
(réduits à un point) appartenant à 6 ; supposons 6P défini pour un p < n, et
définissons Sp+1. Soit K un cube de dimension p + 1 appartenant à © ; on
procède comme dans (24.15.5) en prenant dans K un point b, et en considérant,
pour chaque simplexe Im(a0 a, ... a4) dont Fr(K) est réunion (en vertu de
l'hypothèse de récurrence), le simplexe Im(b a0 a, ... a,). Si Sp+ ,(K) est

124 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
l'ensemble formé de { b} et de tous les simplexes Im(b a0 a, ... a,) précédents,
l'ensemble ®p+1, réunion de ®p et de tous les ®p+ ^K), où K parcourt l'ensemble
des cubes de dimension p + 1 appartenant à ®, répond à la question. CQFD.
Remarque (24.18.6.2). — La construction précédente montre que tout
simplexe de ® de dimension n — 1 est une face d'un simplexe (au moins) de ®.
(24.18.7) Pour tout z> 0, il existe une subdivision simpliciale ® de A„
(nécessairement finie) telle que A„ et chacune de ses facettes soit réunion de simplexes
de ®, que le diamètre de chaque simplexe de ® soit < e, et que ® soit invariante
par toute application linéaire affine (eK(0) e„U) ... en(I1)), où n est une permutation
quelconque de { 0, 1, ..., n }.
Une méthode classique pour former des subdivisions d'un simplexe
invariantes par permutation des sommets est celle des subdivisions barycentriques. On
1
appelle barycentre d'un simplexe Im(a0 a, ... ap) le point (a0+a, +... + ap).
p+\
Considérons un simplexe A = Im(a0 at ... a„) de dimension n, et pour toute
partie H de p + 1 éléments i0 < M < • ■ • < «P de J = {0, 1, ..., n } (avec
O^p^n), notons aH le barycentre —î— (a,0+aj +... +a, )de Im(a, a, ... a,).
p+1 '
Nous allons montrer que l'ensemble ®i(A) de tous les simplexes Im(aHo aHl... aHi|),
où Hqc^c ... cH, est une suite strictement croissante de parties non
vides de J, est une subdivision simpliciale de A, telle que A et chacune de ses
facettes soit réunion de simplexes de S i(A). On dira que ®i(A) est la première
subdivision barycentrique de k; on notera ®i(A) la subdivision de A formée des
simplexes de ®t(A) contenus dans A, et on dira aussi que c'est la première
subdivision barycentrique de A ; il est clair que ®i(A) et ®i(A) sont invariantes par
toute permutation des sommets de A.
Raisonnons par récurrence sur n ; il n'y a rien à démontrer pour n = 0
puisque ®i(A) = {A} dans ce cas. Supposons l'assertion établie pour les
simplexes de dimensions < n — 1. Chacune des facettes de A est alors réunion
disjointe des simplexes de sa première subdivision barycentrique, qui par
définition appartiennent à ®i(A). Considérons le barycentre a., de A. Il est clair
que A est réunion disjointe de {a;} et de tous les simplexes Im(aHo aH| ... aH< a,),
où H0 c: Hj a ... c: H, parcourt l'ensemble des suites strictement croissantes
de parties de J ayant au plus n éléments : en effet, par définition les simplexes
Im(aHo aHl ... aH<) parcourent alors l'ensemble des simplexes de ®t(A) contenus
dans Fr(A).
A partir de ®t(A) on définit par récurrence la k-ième subdivision
barycentrique ®»(A) pour tout entier k > 1 : c'est la réunion dans ^B(A) des premières
subdivisions barycentriques ®i(M), où M parcourt l'ensemble des simplexes de

18. SUBDIVISIONS CELLULAIRES ET SIMPLICIALES
125
la subdivision ®t_,(A). Il est clair que ®*(A) est invariante par toute
permutation des sommets de A. Pour achever de prouver (24.18.7), il suffit de montrer
que pour k assez grand, les diamètres de tous les simplexes de ©k(A) sont < s.
Cela résulte du lemme suivant :
(24.18.7.1) Si Ô(A) désigne le diamètre de A, les simplexes de <5,(A) ont tous un
diamètre < Ô\A).
n + 1
Tout simplexe de 6] (A) est contenu dans un simplexe Im(aHo aHl ... aHn)
de 6i(A) de dimension n, et par permutation des sommets, on peut se borner
au cas où Hj={ 0,1,...,j} pour 0<j'<«. Tout point cf>aHo+c;1aH1 + ... + Ç,*h„
de ce simplexe s'écrit alors r/0a0 + r/'a, + ... + r/"aB, avec
V*-ArÉ' + T-^f*1 + ... +-^-T<r
7+1 7 + 2 n+ ls
pour 0 < j < n. Il suffit de montrer que ce point peut aussi s'écrire
1 -«o + -?-r (C°a0 + C'a, + ... + CX)
n + 1 n+ 1
n + 1
où ^ao + Ç'a, + • • • +C"a«e A. Or il est clair que pour j ^ 1, ÇJ = nj > 0,
n
et que l'on a C + C + • • • +
Ç" = 1 ; d'autre part £° = — (rf - -i-) ;
n \ n + lj
mais on a r,0 = c:0+ + ... + -^-cf > -L^ + d;1 + ... +£")= -L, donc
C°>0. CQFD. 2 " + 1 "+1 " + 1
(24.18.8) (lemme du prisme) Soir <S une subdivision simpliciale de A„, invariante
par toute permutation des sommets de A„ et telle que A„ et chacune de ses facettes
soit réunion de simplexes de S. Alors il existe une subdivision simpliciale <3' du
« prisme » A, x [0, 1 ] telle que :
1° le polyèdre convexe A„ x ]0, 1 [ et chacune de ses facettes soit réunion
de simplexes de ©' ;
2° S' soit invariante par toute application de la forme (eK(0) ... e,(B)) x 1,
de E„ x R sur lui-même pour toute permutation n de {0, 1, ..., n} (nous dirons
pour abréger « invariante par permutation des sommets de A„ » ) ;
3° ©' contienne, d'une part l'ensemble formé de A„ x { 0 } et de ses facettes,
et d'autre part l'ensemble formé des simplexes T x { 1 }, où T parcourt ®.
On va définir par récurrence une suite croissante S'0» ®i > ■.•>€>!■ d'ensembles
de simplexes deux à deux disjoints, les simplexes de <s>4 étant de dimensions < q +1
et tels que : 1° toute face d'un simplexe de S, appartient à S, ; 2° S, est invariant
par toute permutation des sommets de A„ ; 3° les simplexes U x {0}, où U par-

126 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
court l'ensemble des facettes de A, de dimension q, appartiennent à S, ; 4° les
simplexes T x {1}, où T parcourt l'ensemble des simplexes de ® de
dimension q, appartiennent à <S't ; 5° pour chaque facette U de A„ de dimension q,
U x ] 0, 1 [ est réunion de simplexes de <ô'q. L'ensemble S' = <S'H répondra à la
question.
On prend S0 formé des simplexes {e,} x {0}, {} x ]0, 1 [ (0 < j < n)
et{x} x {l},où{x} parcourt l'ensemble des simplexes de dimension 0 de ®.
Supposons S, défini pour un q < n, et considérons une facette U de AB, de
dimension q + 1 ; la frontière de U x ]0,1 [ (par rapport à la variété linéaire affine
qu'il engendre) est réunion disjointe de U x {0}, des U' x {0}, où U' parcourt
l'ensemble des facettes de U de dimension < q, des T x {1}, où T parcourt
l'ensemble des simplexes de 6 dont U est la réunion, et enfin, pour chaque
facette U' de U de dimension < q, des simplexes de <S'q dont U' x ]0, 1 [ est la
réunion ; tous ces simplexes appartiennent à <ô'q par l'hypothèse de récurrence.
On prend alors dans U x ]0, 1 [ le point b = I a^, - ), où est le barycentre
de U ; comme dans (24.18.5), on considère pour chaque simplexe Im(a0 a, ... ar)
de S, dont Fr(U x ]0, 1 [) est la réunion, le simplexe Im(b a0 a, ... ar). On
définit alors ®,+j comme réunion de S,, de l'ensemble des simplexes U x {0},
où U parcourt l'ensemble des facettes de A„ de dimension q + 1, de l'ensemble
des simplexes T x {1}, où T parcourt l'ensemble des simplexes de S de
dimension q + 1, et enfin de l'ensemble de tous les simplexes (à savoir { b} et
Im(b a0 a, ... ar) avec les notations précédentes) en lesquels on a décomposé
chaque U x ]0, 1 [, U parcourant l'ensemble des facettes de dimension q + 1
de A„. On vérifie immédiatement que <5'q+t satisfait aux S conditions énoncées
plus haut. CQFD.
1) Montrer qu'un complexe cellulaire euclidien X c RN est une partie localement fermée
de RN (pour tout point x0 adhérent à X, considérer une suite de points de X tendant vers x0, chaque
point de cette suite appartenant par définition à un polyèdre de S).
2) Soit K une partie compacte de R*. Montrer que pour tout voisinage ouvert U de K dans
R", il existe un complexe simplicial euclidien compact X tel que K c X e U.
3) Soient (Xi, S,), (X2, <52) deux complexes simpliciaux euclidiens compacts, X, et X2
étant des parties d'un même espace RN ; soit mt (resp. m2) la plus grande dimension des simplexes
de S, (resp. ®2). Montrer qu'il existe des subdivisions simpliciales S3, S4, S5 de X, u X2, X, n X2
et de l'adhérence de Xt o Q X2 respectivement ; en outre, les plus grandes dimensions m3, m4, m5
des simplexes de ces subdivisions respectives sont telles que m3 = sup (m,, m2), m4 < inf (m,, m2),
(Pour X, vj X2, observer que cet ensemble est contenu dans la réunion d'un nombre fini
de variétés linéaires affines de dimension m = sup^, m2) et raisonner par récurrence sur m).
4) Soient (X„ S,), (X2, S2) deux complexes simpliciaux euclidiens compacts. Montrer
que si ni! (resp. m2) est la plus grande dimension des simplexes de St (resp. €2), il existe une
subdivision simpliciale de X, x X2 telle que la plus grande dimension de ses simplexes soit m, + m2.
5) Déduire du problème 3 que tout sous-espace compact d'un espace euclidien qui admet
une subdivision cellulaire admet aussi une subdivision simpliciale.
PROBLÈMES

19. BORDS DES COURANTS SIMPLICIAUX
127
19. Bords des courants simpliciaux.
(24.19.1) Il résulte de (24.18.5) que, dans la définition des p-courants cellulaires
(24.17.3), on peut se borner aux combinaisons linéaires à coefficients réels de
p-courants particuliers de la forme s, où s est une application dans X, de classe C00,
de l'adhérence Ap du simplexe standard de dimension p, muni de l'orientation
choisie dans (24.15.2) ; nous dirons qu'un tel courant 3 est un p-courant sim-
plicial.
En effet, soit U c R" un polyèdre convexe borné de dimension p, et soit u
une application de U dans X, de classe C°° ; on va voir que le p-courant u est
combinaison linéaire de p-courants simpliciaux, à coefficients entiers. En effet,
soit ® une subdivision simpliciale de U vérifiant (24.18.5), et soient Ut Ur
ceux des simplexes de <3 qui sont de dimension p, chacun d'eux étant muni de
l'orientation induite par celle de U. Pour chaque U;, il y a une bijection linéaire
affine Vj de Ep sur Rp, transformant Ap en Uj et préservant l'orientation. Pour
toute p-forme a de classe C°° sur X, on a alors I '«(a) = j 'v/'«(a)) par (16.24.5.1).
JVj Ja,
Si l'on pose Sj = u ° Vj pour 1 < j ^ r, on a donc û = £ en raison du fait
qu'un simplexe de dimension < p dans Rp est négligeable pour la mesure de
Lebesgue (16.22).
(24.19.2) On a obtenu dans (24.17.2.2) une expression générale du bord d'un
courant ù lorsque u est une application de classe C°° de U dans X, pour un
polyèdre convexe borné UcR'; elle fait intervenir les restrictions de u aux F*,
où les F* sont les faces de U. Il faut modifier cette formule pour les courants
simpliciaux, puisqu'une face du simplexe standard Ap n'est plus toujours un
simplexe standard. De façon précise, pour chaque face F, = Im(e0 ... ê, ... ep)
de Ap (0<><p), on considère l'application linéaire affine ffj=(e0 ... ê, ... ep),
qui transforme Ap_j en F,, et on note Sj l'application de classe C00 composée
Sj = s ° a} : Ap_ t -♦ X. Avec cette notation, on a le résultat suivant :
(24.19.3) Pour toute application s : Ap -♦ X de classe C00, on a
(24.19.3.1) 6s = £(- l^sj.
j=o
p
Le raisonnement de (24.17.2) montre en effet que 6s = X ± Sj, où il
7 = 0
faut prendre le signe + (resp. le signe — ) si l'application linéaire affine
oj — (Bo ... êj ... ep) préserve (resp. renverse) l'orientation, lorsque Ap_i
est muni de l'orientation précisée dans (24.18.3) et F, de l'orientation définie

128 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
sur Frr(Ap) dans (24.14.1) à partir de l'orientation de Ap. Comme la forme
de;1 a ... a de)p~1 est positive pour l'orientation de A,-,, il s'agit de
déterminer le signe de son image par a} pour l'orientation de Frr(Ap) ; pour j > 0
cette image est la restriction à Fj de la forme to} = de)1 a ... Â~~de)î~a ... a de)p.
Or, soit t le difféomorphisme de Rp+1 échangeant e)J et e)p et laissant invariantes
les coordonnées e)k pour les autres indices ; il renverse l'orientation et transforme
la restriction à Fj de co, en la restriction à Fp de (-If'1'^1 a ... Ade)p~x.
D'autre part, la projection orthogonale n de l'hyperplan Ep sur l'hyperplan
d'équation e)° = 0, identifié à Rp, transforme Ep_ x en Rp~l, et l'image par n de la
restriction à Ep (resp. Ep_,) de la forme de)1 a ... a d e)p (resp. de)1 a ... a de)p~*)
est la restriction de la même forme à Rp (resp. Rp_1). La définition (24.14.1)
montre donc que la restriction à Fp de (-Vfde)1 a ... a de)9'1 appartient
à l'orientation induite par celle de Frr(Ap). Compte tenu du fait que x renverse
l'orientation, on voit que la restriction de (- lycoj à F, appartient à l'orientation
induite par celle de Frr(Ap) ; donc ct, préserve l'orientation si j est pair, et la
renverse si ; est impair. Il reste à considérer le cas j = 0, où l'image par a0 de
de)1 a ... a de)p_1 est la restriction à F0 de de)2 a ... a de)p ; mais comme
dans F0 on a e)° = 0 et e)1 + e)2 + ... + e)p = 1, cette restriction est aussi celle
de — de)2 a ... a de)"'1 a dÇ1 = (- l)""1^1 a de)2 a ... a de)"-1; on peut
alors terminer le raisonnement comme ci-dessus. CQFD.
20. Chaînes simpliciales formelles et homologie singulière.
(24.20.1) La formule (24.19.3.1) amène à introduire de nouvelles notions qui
étendent le champ d'application de l'homologie et conduisent (même pour les
variétés différentielles) à de nouveaux invariants topologiques.
Soit X un espace topologique séparé quelconque, et soit A un anneau
commutatif quelconque (ayant un élément unité). Pour tout entier p > 0, nous
noterons SP(X ; A) le A-module libre des combinaisons linéaires formelles des
applications continues de Ap dans X, dont les éléments sont les familles (AL^s ;X), où
#(AP ; X) est l'ensemble des applications continues de Ap dans X, et A, e A pour
tout s, avec A, = 0 sauf pour un nombre fini de valeurs de s ; l'addition de ces
éléments et la multiplication par un scalaire de A se font « terme à terme ». On
dit que les éléments de Sp(X ; A) sont les p-chaînes simpliciales formelles (ou
p-chaînes singulières, ou simplement p-chaînes) dans X, à coefficients dans A,
et on les note X AjS. Les éléments de ^(Ap ; X) sont appelés simplexes singuliers
s
de dimension p, l'ensemble #(AP ; X) étant donc une base (dite canonique) du
A-module S^X ; A) (on aura soin de ne pas confondre les p-chaînes singulières
avec des applications de Ap dans X, sauf pour les simplexes singuliers).
Le support d'une p-chaîne X AyS est par définition la réunion des ensembles

20. CHAÎNES SIMPLICIALES FORMELLES ET HOMOLOGIE SINGULIÈRE 129
s(Ap) pour tous les s tels que As ^ 0 ; c'est donc un ensemble compact, non vide
sauf pour la chaîne 0. On pose par convention S_ ,(X ; A) = {0} et Sp(0 ; A) = {0}
pour tout p.
Le A-module SP(X ; A) peut être considéré comme le A-module Sp(X ; Z)(g)zA
obtenu par extension des scalaires de Z à A à partir du Z-module libre SP(X ; Z),
puisque ces modules ont une même base (Ann. 28.6) .Pour tout
homomorphisme d'anneaux A' -> A, on a donc un homomorphisme canonique
SP(X ; A') -» SP(X ; A), qui est injectif (resp. surjectif) si l'homomorphisme
A' -» A l'est.
Si / : X -»• Y est une application continue de X dans un espace séparé Y,
f°s est une application continue de Ap dans Y pour tout simplexe singulier
s e <#(AP ; X), autrement dit c'est un simplexe singulier de Y. On définit donc
canoniquement une application A-linéaire Sp(/) de S^X ; A) dans SpfY ; A),
en posant
(24.20.1.1) Sp(/XlAsS) = lAs(/os)
s s
pour tout élément de S^X ; A). Il est clair que si g : Y -* Z est une application
continue de Y dans un espace séparé Z, on a
(24.20.1.2) Sp(go/) = Sp(g)oSp(/)
Si / : X ' -♦ Y est injective, il est clair que s / ° s est une application
injective de #(AP ; X) dans #(AP ; Y), donc Sp(/) est aussi injective ; lorsque X est
un sous-espace de Y et / l'injection canonique, on identifie souvent à l'aide de Sp(/)
le A-module Sp(X ; A) à un sous-module libre de Sp(Y ; A), ayant un
supplémentaire libre.
(24.20.2) Supposons que X soit une variété différentielle pure, de sorte que les
applications de classe C00 de Ap dans X sont définies (24.17.2) et forment un
sous-ensemble <?(AP ; X) de #(AP ; X) ; on note Sp°(X ; A) le sous-A-module libre
de SP(X ; A) ayant pour base <f(Ap ; X), et on dit que ses éléments sont les
p-chaines lisses dans X à coefficients dans A. Pour toute application / : X -» Y
de classe C00, la restriction à Sp°(X ; A) de l'application Sp(/) (24.20.1.1) est une
application A-linéaire de Sp°(X ; A) dans Sp°(Y ; A).
Considérons le cas où A est un sous-anneau de R ; alors, pour toute
application s e <f(Ap ; X), on a défini le p-courant s sur X (24.17.2) ; on en déduit
une application canonique A-linéaire SP°(X ; A) -* <fp(X) notée u -* ù, et définie
par
(24.20.2.1) £Ass XAss.
S S
La remarque élémentaire suivante nous sera utile : supposons que X soit

130 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
une partie compacte ou ouverte d'un R", et soit <5 une subdivision simpliciale
de X ; soit ®p l'ensemble des simplexes de S de dimension p, et pour chacun
d'eux U, soit sv une application linéaire affine bijective de Ap sur U ; alors la
restriction de l'application (24.20.2.1) au sous-A-module formé des
combinaisons linéaires des sv (à coefficients dans A c R) est injective ; cela résulte de
ce que les p-courants su pour UeSp sont linéairement indépendants sur R
(24.18.2). On dira que les p-courants combinaisons linéaires des su sont les
p-courants de la subdivision <5.
(24.20.3) Pour toute application continue s : Ap -* X, l'application composée
Sj- = s°Gj: Ap_t -» X (avec la notation de (24.19.2)) est évidemment continue.
La formule (24.193.1) conduit à définir, pour p ^ 1 et pour tout anneau A,
le bord formel (ou simplement le bord) du simplexe singulier s € "^(A, ; X)
(considéré comme élément de S^X ; A)) comme l'élément de Sp_ ,(X ; A)
(24.20.3.1) 60s = £ (- 1)%
ce qui a un sens puisque — 1 e A ; on étend ensuite 60 en une application A-linéaire
de S/X ; A) dans Sp_ ,(X ; A)
«o(l^ = lAs(S0s)-
Pour p = 0, on pose par convention 60s = 0 pour tout se S0(X ; A).
Deux p-chaînes sont dites homologues si leur différence est un bord d'une
(p + l)-chaîne.
Il résulte aussitôt de cette définition que si X et Y sont des espaces séparés
et / : X -> Y une application continue, le diagramme
S^XjA) -X S,_,(X;A)
(24.203.2) W>1 |*-.(/>
Sp(Y;A) -g-. SP_,(Y;A)
est commutatif.
(24.20.4) La propriété fondamentale du bord formel est que l'on a
(24.20.4.1) 60 o 60 = 0
ou, ce qui revient au même, pour toute application s e ^(Ap ; X)
(24.20.4.2) 60(60s) = 0.
Comme on peut écrire s = s ° lAp, on est ramené, par (24.20.3.2), au cas où s est

20. CHAÎNES SIMPLICIALES FORMELLES ET HOMOLOGIE SINGULIÈRE 131
l'application identique de Ap, et par suite s, = a y II est alors facile de vérifier
(24.20.4.2) par un calcul direct, mais cela est inutile. En effet, on a les deux
propriétés suivantes :
1° Si X ext une variété différentielle pure, 60 applique Sp°(X ; A) dans
S^tXjA).
2° Si de plus A est un sous-anneau de R, le diagramme
S"(X;A) S-_,(X;A)
1-
X) ^'_t(X)
(24.20.4.3)
où les flèches verticales sont les applications canoniques définies dans (24.20.2),
est commutatif en raison de (24.19.3.1). Cela étant, pour p ^ 2, on peut se borner
au cas où A = Z ; l'application identique de Ap est une application de classe Cœ,
et M^oOs,)) est combinaison linéaire à coefficients dans Z des injections
canoniques des facettes de dimension p — 2 de Ap. Comme les (p — 2)-courants
correspondants sont linéairement indépendants sur R (24.20.2), et que l'on a
WCh,)) = 0, on a aussi 60(ê0(llp)) = 0.
(24.20.5) Pour l'application A-linéaire 60, le A-module
S.(X;A) = §nSp(X;A)
p = 0
est donc un A-module codifférentiel gradué, auquel on peut appliquer la théorie
générale (Ann. 30.7) : on considère le sous-module gradué Z.(X ; A) des cycles
de S.(X ; A), somme directe des Zp(X ; A), où Zp(X ; A) est le A-module des
p-chaînes u e S,(X ; A) telles que 60u = 0 ; on considère d'autre part le sous-
module B.(X ; A) des bords de S.(X ; A), somme directe des Bp(X ; A), où Bp(X; A)
est le module des p-chaînes de la forme 60v, où v est une (p + l)-chaîne. On définit
alors le A-module gradué
H.(X; A)= 0 Hp(X ; A)
p=0
où
HP(X;A) = ZP(X;A)/BP(X;A)
est appelé le p-ème A-module d'homologie singulière de l'espace topologique X ;
H.(X ; A) est le module (total) d'homologie singulière de X. On a H.(0 ; A)={0 }.
Pour tout homomorphisme d'anneaux A' -» A il est immédiat que le
diagramme
SP(X;A') S„^(X;A')
I I
SpfXjA) —+ SP_,(X; A)

132 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
est commutatif ; l'image de Z^X ; A') (resp. Bp(X ; A')) dans Sp(X ; A) est donc
contenue dans ZP(X ; A) (resp. Bp(X ; A)) et on obtient, par passage aux
quotients, un homomorphisme canonique de A'-modules
(24.20.5.1) HP(X ; A') -* HP(X ; A)
qui en général n'est ni injectif ni surjectif lorsque A' -» A l'est.
Si X et Y sont deux espaces séparés,/:X -» Y une application continue,
les applications A-linéaires Sp(/) (24.20.1.1) définissent une application A-linéaire
homogène de A-modules codifférentiels gradués
S.(/):S.(X; A) - S .(Y ; A)
en vertu de la commutativité du diagramme (24.20.3.2). On en déduit donc
canoniquement une application A-linéaire homogène de A-modules gradués
^:H.(X; A) -> H.(Y;A)
(aussi notée H.(/)) telle que, si a e Hp(X ; A) est la classe d'homologie d'unp-cycle
u e ZP(X ; A), f+(a) est la classe d'homologie de S^/X")- Si g : Y -* Z est une
application continue de Y dans un espace séparé Z, on a (g ° f)„ = g+° f+.
(24.20.6) Supposons que X soit une variété différentielle pure et A un sous-
anneau de R. On définit les sous-A-modules de Sp^X ; A) notés Zp°(X ; A) et
Bp (X ; A) comme étant respectivement l'intersection ZJ^X ; A) n Sp°(X ; A) et
l'image par 60 de Sp+ t(X ; A) ; il est clair que Bp°(X ; A) est un sous-A-module
de BP(X ; A). On définit alors les A-modules
Hp°(X;A) = Zp0(X;A)/Bp°(X;A)
et il est clair qu'on a une application A-linéaire canonique
(24.20.6.1) HP°(X ; A) - HP(X ; A).
D'autre part, il résulte de la commutativité des diagrammes (24.20.4.3) que
l'application canonique u -* u de Sp°(X ; A) dans ^P(X) applique Zp°(X ; A)
dans ZP(X) et BP°(X ; A) dans BP(X) ; par passage aux quotients, on en déduit
une application A-linéaire canonique
(24.20.6.2) HP°(X ; A) -» HP(X),
et par composition avec l'application HP(X) -> H'pÇX), une application A-linéaire
canonique
(24.20.6.3) HP°(X ; A) H'^X).
On va démontrer dans les sections suivantes que, dans ces conditions,

21. LEMMES DE SUBDIVISION
133
(24.20.6.1) est un isomorphisme et que, pour A = R, l'application canonique
H;(X ; R) -» HP(X)
est un isomorphisme (théorèmes de de Rham). Par contre, on verra des exemples
de variétés pour lesquelles on a, pour un entier p > 0, Hp° (X ; R) = 0 mais
Hp°(X ; Z) 9& 0 (24.22.12).
21. Lemmes de subdivision.
(24.21.1) Nous aurons besoin de quelques lemmes sur les p-chaînes dans un
espace RN. Par définition, deux applications linéaires affines (a0 a, ... ap)
et (b0 b, ... bp) ne sont égales que si a^b, pour O^y'^p; les (a0 a, ... ap)
où (a^osçjssp parcourt l'ensemble (RN)P+1 de toutes les suites de p + 1 points
de RN, forment donc une base d'un sous-Z-module SP(RN; Z) du Z-module
SP(RN ; Z) des p-chaînes dans RN. Cela étant, considérons un point quelconque
ceRN; on définit une application Z-linéaire Ce : SP(RN; Z) -» SP+1(RN; Z)
( « cône » de sommet c) en posant
(24.21.1.1) Cc(a0 a, ... ap) = (c a0 a, ... ap)
pour toute suite (aj)0Sj^p de points de RN. Pour tout p ^ 1, on a
(24.21.1.2) 60(C«(z)) = z - Ce(6V) pour tout z e SP(RN ; Z)
11 suffit en effet de le prouver pour z=(a0 a, ... ap), et cela résulte de la
définition (24.20.3.1). On notera aussi que pour toute application linéaire affine f
de RN dans lui-même, on a
(24.21.1.3) Sp+ df*Cc(z)) = C/(C)(SP(/Xz))
car cela est évident lorsque z = (a0 at ... ap).
(24.21.2) Pour tout p > 0, il existe une application Z-linéaire Sd de SP(RN ; Z)
dans lui-même, ayant les propriétés suivantes :
(i) Si A = Im(a0 a1 ... ap) est un simplexe de dimension p, et si (Th)lihir
est la suite des simplexes distincts de dimension p appartenant à la subdivision
barycentrique S^A), on a
(24.21.2.1) Sd(a0 a, ... ap) = t e„(^ a?» ... a?')
où £„ = ± 1 et In^ao" a'*' ... ap*') = TB pour 1 < h ^ r. En outre, on a, dans
l'espace des p-courants <fp'(RN)
(24.21.2.2) (Sd(a0 a, ... ap))~ = iA

134 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFERENTIELLE ÉLÉMENTAIRES
où iA : A -» RN est l'injection canonique, A étant muni de l'orientation image
de celle de Ap par l'application (a0 a, ... ap).
(ii) Pour tout z e Sp(RN ; Z), on a
(24.21.2.3) S0(Sd(z)) = Sd(60z).
(iii) Pour toute application linéaire affine f de RN dans lui-même, on a
(24.21.2.4) Sp(/XSd(z)) = Sd^/X*)) pour tout z e S'^R" ; Z).
On raisonne par récurrence sur p : en prenant Sd(z) = z dans S0(RN ; Z),
on vérifie trivialement les conditions de l'énoncé. Supposons Sd défini dans
tous les S,(RN ; Z) pour q < p et vérifiant ces conditions. On pose alors, pour
toute application linéaire affine (a0 at ... ap)
(24.21.2.5) Sd(a0 at ... ap) = Cb(Sd(60(a0 at ... ap)))
en désignant par b l'image par (a0 a, ... ap) du barycentre de Ap. Comme
p
6°0(a0 a, ... ap) = £ (- iy(a0 a, ... àj ... ap), l'hypothèse de récurrence
montre que lorsque A = Im(a0 a, ... ap) est de dimension p, Sd(6>0(a0 a, ... ap))
est somme, avec des coefficients ± 1, de termes de la forme (c0 c, ... cp_ t),
où Im(c0 Ci ... cp_,) parcourt la famille des simplexes de dimension p - 1
de ®i(A) contenus dans Fr(A); mais alors Im(b c0 ct ... cp-t) parcourt la
famille des Tj, (24.18.7), ce qui prouve la première assertion de (i).
r
Notons en second lieu que l'on a JA = X hh lorsque chaque TB est muni
de l'orientation induite par celle de A (on dira pour abréger que T. a « la même »
orientation que A), puisque la réunion des T„ a un complémentaire par
rapport à A qui est négligeable, étant réunion finie de parties de sous-variétés de
dimensions < p. Compte tenu de l'indépendance linéaire des ïTh (24.18.2),
la relation (24.21.2.2) signifie donc que eh = 1 si l'orientation image de celle
de Ap par (a(ô*' a'*' ... a(p ') est la même que celle de A, eh = - 1 dans le cas
contraire.
Supposons alors que e(c0 ct ... cp_!), avece = ± 1, soit un des termes
de l'expression de Sd(a0 ... àj ... ap). Par l'hypothèse de récurrence, on a
(Sd(a0 ... àj ... ap))~ = lFj, où Fj = Im(a0 ... âj ... ap) est muni de
l'orientation image de celle de Ap-! par (a0 ... â,- ... ap). D'après ce qui précède,
l'orientation image de celle de Ap par (b c0 ... cp_,) est la même que l'image
de celle de Ap par (b a0 ... àj... ap) si e = 1, et est l'opposée dans le cas contraire.
Or, l'application linéaire affine qui laisse invariants les a* d'indice k ^ j, et
transforme b en a;, préserve l'orientation, car b et aj sont d'un même côté de
l'hyperplan affine engendré par F,-; donc on peut dans l'assertion précédente

21. LEMMES DE SUBDIVISION
135
remplacer (b a0 ... â,... ap) par (a, ao ... a,-... ap)=(aj a0 ... a,-, aJ+1 ... ap);
mais l'image de l'orientation de Ap par cette application est la même que celle
de A si j est pair, opposée si j est impair. On voit donc finalement que l'image
de l'orientation de Ap par (b c0 ... cp_,) est la même que celle de A si ( — iye= 1,
opposée si (- l)Je = — 1, ce qui prouve (24.21.2.2).
Pour démontrer (24.21.2.3), on se ramène au cas où z — (a0 at ... ap)
et on raisonne par récurrence sur p. Par (24.21.2.5) et (24.21.1.1), on a
6>0(Sd(z)) = 60(Cb(Sd(t?0z))) = Sd«?0z) - Cb(6>0(Sd(6V)))
et par l'hypothèse de récurrence, 60(Sd(6'0z)) = Sd{60(60z)) = 0, d'où (24.21.2.5).
Enfin, pour (24.21.2.4), on est encore ramené au cas où z=(a0 at ... ap)
et la conclusion résulte de (24.21.2.5), de (24.21.1.2) et de la commutativité du
diagramme (24.30.3.2).
(24.21.3) Par récurrence sur m > 1, on voit que l'application itérée Sdm de
SP(RN; Z) dans lui-même a des propriétés analogues : si (T|,)1$k$r est cette fois
la suite des simplexes distincts de dimension p appartenant à ©m(A), on a
(24.21.3.1) . Sdm(a0 a, ... ap)= £ £B(a<0» a?» ... a<p*>)
où eh = ± 1 et Im(a0*) a'*' ... a**') = T, pour tout h ; en outre, on a
(24.21.3.2) (Sdm(a0 a, ... ap))~ = ÏA,
(24.21.3.3) 60(Sdm(z)) = Sdm(60z)
ainsi que
(24.21.3.4) Sp(/XSdm(z)) = Sd^S^z))
pour z e Sp(RN ; Z) et toute application linéaire affine f de RN dans lui-même.
(24.21.3.5) On peut définir plus généralement, pour tout espace topologique
séparé X, et tout anneau commutatif A, une application A-linéaire Sdm de Sp(X; A)
dans lui-même, qui pour X = RN et A = Z, a une restriction à SP(RN ; Z) égale
à l'application définie dans (24.21.3). Il suffit de remarquer que pour toute
application continue s : Ap -* X, on peut écrire s = Sp(s)(lAp), et de poser
Sdm(s) = Sp(sXSdm(lAj,)). Avec cette définition on voit aussitôt que les
relations (24.21.3.3) et (24.21.3.4) sont encore valables.
(24.21.4) En vertu de (24.21.3.4), l'évaluation de la différence Sdm(z) - z se
déduit du cas particulier où s=(e0 e, ... ep) = lAp par définition des p-chaînes.
Cette évaluation va résulter (cf. 24.22.7.2) d'un lemme un peu plus général, où
nous considérerons, non plus la subdivision barycentrique Sffl(Ap), mais une

136 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
subdivision simpliciale S de Ap, soumise à la seule condition d'être invariante
par permutation des sommets de Ap (24.18.7). Pour une telle subdivision, la
chaîne Sdm(lAj>) se généralise de la façon suivante : si (TB)|^B<r est encore la
suite des simplexes distincts de dimension p appartenant à S, et si
T„ = Im(a(0M a'*» ... ap*») pour tout h, on pose
où les ek = ± 1 sont choisis de telle sorte que l'on ait pour les courants
correspondants
Considérons d'autre part la « translatée » de cette chaine dans Ep x R
qui correspond à la subdivision de la « face supérieure » du « prisme » Ap x [0, 1 ],
déduite de S par translation. Nous associerons à la subdivision S la
subdivision simpliciale correspondante S' de ce prisme vérifiant les conditions de
(24.18.8). Pour chaque face Uj = Im(e0 ... ê, ... ep) de Ap (0 ^ j < p), les
simplexes appartenant à 6' et contenus dans U, x [0, 1] forment une
subdivision simpliciale de cet ensemble, que nous noterons SJ.
Si c est le barycentre de Ap et b = I c, - I, les simplexes de dimension p + 1
appartenant à S' sont de la forme Im(b a0 at ... ap), où T = Im(a0 a, ... ap)
est un des simplexes de dimension p contenus dans Fr(Ap x ]0, 1 [) ; nous les
noterons Im(b T) pour abréger. Ces simplexes sont donc de trois types :
1° le simplexe A' = Im(b Ap) ;
2° les simplexes A'h =Im(b Vn),où (V„)1<B^r est la suite finie des simplexes
T„ x {1}, T„ parcourant la suite des simplexes de dimension p de la
subdivision S;
3° les simplexes Ajk=Im(b Tjk) où, pour chaque j tel que 0</'^p, (1}*),
est la suite finie des simplexes de dimension p de la subdivision SJ-. Vu
l'invariance de S' par permutation des sommets de Ap, on peut en outre supposer
vérifiée la condition suivante : posant, comme dans (24.16.2), oJ=(e0 ... êj... ep)
et <rj = (Tj x 1R, bijection linéaire affine de E,,-, x R sur la variété linéaire affine
engendrée par Uj x ]0, 1 [, on a, pour tout indice k tel que K k ^ q
R(1a„)= IeM)»ï,,...aj?
(24.21.4.1) (R(lAp))~ = rAp.
r
R(1a, x {1} )= Z 1)(a«*>, 1) ... (a<*>, 1))
(24.21.4.2) Tjk = o'io\-\%k))
quels que soient i et /'.

21. LEMMES DE SUBDIVISION
137
(24.21.5) Définissons maintenant des bijections linéaires affines p', p'k (1 </i<r)
et p'jk (0 ^ j^ p, 1 < k < q) de Ap+I sur les simplexes A', A'h et A'„
respectivement, et des bijections linéaires affines de Ap sur leurs faces respectives. Pour
les faces des simplexes précédents qui sont contenues dans P = Ap x ]0,1 [, on prend
arbitrairement une bijection linéaire affine de Ap sur chacune de ces faces. Pour
la face Ap de A', on prend comme bijection l'application identique lAp, puis
p' = Cb(lAp) = (b e0 e, ... ep). Pour une face TB x {1}, on prend pour
bijection ph: Ap - T„x {1} l'application ((■£>, 1) (a'*», 1)... (ap*>, 1)), puis p'h=Cb(ph).
Alors, si ek = 1 (resp. ek = — 1), les images par p' et p'h de l'orientation de Ap+1
sont opposées (resp. les mêmes) : en effet, les images de l'orientation de Ap+1
par p'h et par (b (e0,1)... (ep, 1)) sont alors les mêmes (resp. opposées) comme
on l'a vu dans la preuve de (24.21.2); mais la bijection (b (e0, 1) ... (ep, 1))
est composée de l'application (x, t) -* (x, 1 — t) (qui renverse l'orientation)
et de p'.
Finalement, pour chaque j tel que 0 ^ ; < p, munissons UJ = U; x ]0, 1 [
d'une orientation telle que, pour toute bijection (a0 a, ... ap) de Ap sur un
simplexe de Sj, préservant l'orientation, les images par la bijection (b a0 a, ... ap)
et par p' de l'orientation de Ap+, soient opposées. Pour chacun des simplexes T0k
de dimension p de ©ô, on prend alors une bijection p0k = (a0 a, ... ap) qui
préserve l'orientation ; puis, compte tenu de (24.21.4.2), pour 1 < j < p, on
prend pJk = a]]° a'0~l ° p0k (1 ^ k ^ q), de sorte que pour deux indices
quelconques i, j, on a
(24.21.5.1) pJk = a'ja(r'i-iopik (1 ^ k ^ q) ;
enfin, on prend p'Jk = Cb(pJk). En vertu de (24.13.1), les orientations choisies
sur les M] sont, ou bien toutes induites par celle de Frr(P), ou bien toutes opposées
à cette dernière ; par suite, les images par p' et p'Jk de l'orientation de Ap+1 sont
opposées (resp. les mêmes) lorsque pjk préserve (resp. renverse) l'orientation.
Or, on a vu dans (24.16.3) que o} préserve (resp. renverse) l'orientation si j est pair
(reste impair) ; il en est donc de même de o), et par suite pJk préserve (resp. renverse)
l'orientation si j est pair (resp. impair), en vertu de (24.21.5.1).
Nous pouvons maintenant énoncer le « lemme des chaînes prismatiques » :
(24.21.6) Avec les définitions de (24.21.5), si l'on pose, dans SP+1(EP x R; Z)
(25.21.6.1) 0' = t ehp'k -p'+ t t(- 1)%
h=l k=l j=0
on a, dans SP(EP x R; Z),
(24.21.6.2) 6o0' = R(lAp x {1} ) - lAp + £ £ (- iyPjk.

138 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
En effet, dans l'espace des courants S'p+ j(Ep x R), on a
h=l *=1 j = 0
et ce courant n'est autre que le courant iP où iP : P -> Ep x R est l'injection
canonique, et où l'on munit P de l'orientation opposée à l'image par p' de l'orientation de
Ap+, ; en vertu de (24.14.2), cela résulte en effet de la discussion sur les
orientations faites dans (24.21.5) et du choix des signes dans (24.21.6.1). La formule
de Stokes pour les courants cellulaires (24.17.2.2) montre que 6lP est somme de
courants portés par Fr(P). Or, l'application à 0' de l'opérateur £0 donne, par
définition, et vu les expressions de p', p'k et p'jk, le second membre de (24.21.6.2)
augmenté d'une combinaison linéaire à coefficients entiers de bijections de Ap
sur les simplexes de dimension p appartenant à S' et contenus dans P. Mais nous
venons de voir que par l'application canonique Sp\Ep x R ; Z) -> ^P(EP x R),
l'image de cette combinaison linéaire est nulle; elle est donc nulle elle-même,
en raison de l'injectivité de l'application canonique z -» z, restreinte aux chaînes
combinaisons linéaires des Sy, pour UeS' (24.20.2.1). CQFD.
Remarques (24.21.6.3). — (i) Ce qui précède s'applique aussi lorsque m = 0,
la subdivision barycentrique « d'ordre 0 » étant par définition la subdivision
simpliciale formée de Ap et de ses facettes.
(ii) Pour tout anneau commutatif A, les formules de (24.21.6) sont inchangées
lorsqu'on y remplace tous les éléments de Sp+ ,(Ep x R ; Z) (resp. Sp(Ep x R ; Z))
qui y figurent par leurs images canoniques dans
Sp+ !(EP x R ; A) (resp. SP(EP x R ; A)).
22. Propriétés de l'homologie singulière.
(24.22.1) Comme on doit s'y attendre en vertu de (24.11.3), les propriétés de
l'homologie singulière pour les espaces topologiques séparés sont tout à fait
analogues à celles de la cohomologie à support compacts pour les variétés
différentielles orientées, mais doivent naturellement être démontrées indépendamment.
On a la propriété fondamentale d'invariance par homotopie de l'homologie
singulière :
(24.22.2) Soient X, Y deux espaces topologiques séparés, f et g deux
applications continues de X dans Y. Si f et g sont homotopes (16.25.1), les applications
A-linéaires Hjif) et H^g) de H^X ; A) dans Hp(Y ; A) sont égales pour tout p ^ 0.
Cela résultera du lemme suivant :
(24.22.2.1) // existe une application A-linéaire hp : SpfX; A) -» SP+1(Y; A) et
une application A-linéaire h'p-x : Sp_i(X; A) -» S/Y; A) telles que
(24.22.2.2) S^g) - SJLf) = «0 ° *, + *J -1 - «o •

22. PROPRIETES DE L'HOMOLOGIE SINGULIÈRE
139
On en conclura en effet que pour tout p-cycle z e Zp(X ; A), on a
s,(irXz) - s^/Xz) = w)
donc, si c est la classe d'homologie de z, Hp(gXc) = Hp(/Xc).
Pour prouver le lemme, partons d'une application continue F : X x I -♦ Y,
où I = [0, 1], telle que F(x, 0) = f(x) et F(x, 1) = g(x) pour tout xeX. On va
appliquer le lemme des chaînes prismatiques (24.21.6) en prenant pour 6
la subdivision barycentrique d'ordre 0 (24.21.6J) formée de Ap et de ses
facettes; dans (24.21.6.2), R(lAp x {1}) doit être remplacé par l'application
Pi = ((eo, 1) («i > 1) • • • («P, !))• Pour tout 2 = Z A(S) dans S^fX ; A), où les Xt e A
et chaque s, est une application continue de Ap dans X, on a, par définition
Sp(/Xz) = E>l,Fo(s, x l„)olv Sp(gXz) = lAJFo(s1xlR)oPl.
Prenons la valeur de l'application linéaire ]ÇA|Sp(Fo(s( x 1,)) en chacun
des deux membres de (24.21.6.2); en utilisant la commutativité du diagramme
(24.20.3.2), on obtient
SpfcrXz) - SpUXz)
= «od A,Sp+ t(F o (s, x 1„)K0')) - Z I (- l)jXiF o (S| x 1E) o Pjk.
I k.l j = 0
Le premier terme du second membre s'écrit bien 60(hp(z)), avec
MZv,) = Za,sp+1(Fo(sjx ikw).
Pour définir de même fip_,, remarquons, avec les notations de (24.21.5),
que pour tout indice k tel que l^k^q, on a pf»(x)=(o-,(yit(x)), t,(x)) pour tout
x e Ap, y* étant une application linéaire affine de Ep dans Ep_ t et f, une
application linéaire affine de Ep dans R ; le point essentiel est que pour tout autre indice j
tel que 0 < j < p, on a pJk{x) = (cr/y.fx)), tt(x)) avec les mânes applications y,
et tt, en vertu du choix (24.21.5.1) des pJk. Nous allons voir que si l'on pose,
pour tout élément u = Z UX de Sp_ ,(X ; A), où les p, e A et chaque s£ est une
a
application continue de Ap-t dans X,
(24.22.2.3) - ,(«) = Z ^«F o ((s; o yk) x t.)
l'application A-linéaire /ip_, de Sp_ j(X ; A) dans Sp(Y ; A) répond à la question.
En effet, on a 60z = Z(— iyA|S,°o> qu'on peut écrire Z/*X, où les s'a
l.j a

140 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
sont distinctes et, pour chaque a, ua = Z(— l)JÀ.h la somme étant étendue aux
couples (/, j) tels que s, ° Oj = s'„. Or, on a par définition
{S, X 1R) o p]k = (S, X 1„) o ((oj o yt) X tk) = (s, o ffj o yk) X tk
et par suite
I ( - l)jXtF ° (s, x 1R) o p = £ ( - ° ((«i » ^ o yk) x tt)
= I mJ" • (« « y.) x g = - cqfd.
Exemples (24.22.3). — Pour tout espace topologique séparé rétractile X
(même définition que dans (16.27.7)), on a
SA
{0 } si p > 1.
Il suffit en effet, en vertu de (24.22.2), de le démontrer lorsque X est réduit
à un seul point x0- Or, dans ce cas, pour chaque p ^ 0, la seule application de
Ap dans X est l'application constante cp égale à x0 dans Ap, et on a par
définition (24.20.3.1) 60cp = 0 si p est pair, 60cp = cp-x si p est impair; par suite
Zp(X ; A) = Acp si p est pair, ZJ^X ; A) = {0} si p est impair, BP(X ; A) = {0}
si p est impair ou p = 0, BP(X ; A) = Acp si p est pair et > 0 ; d'où (24.22.3.1).
(24.22.4) Soit X une variété différentielle connexe; on a alors
(24.22.4.1) H0(X ; A) s A.
Par définition, on a en effet S0(X ; A) = Z0(X ; A), et comme une base de
ce A-module libre est formée des applications {e0} -» x pour un x e X
arbitraire, on peut identifier Z0(X ; A) au A-module des combinaisons linéaires
formelles Yj A* de points de X, à coefficients dans A (ou, ce qui revient au même,
xeX
au A-module A(X> des familles (Xx)xeX d'éléments de A telles que Xx = 0 sauf pour
un nombre fini de xeX (Ann. 1.5)). En outre, pour toute application continue
s : Âx -* X, 60s s'identifie à la différence s(ei) - s(e0), et si x0, x sont deux points
quelconques de X, il existe toujours une application continue s : At -* X telle
que s[et) = x et s(e0) = x0 (16.26.10) ; on en conclut que les combinaisons
linéaires x — x0, pour x e X - {xQ }, forment une base de B0(X ; A). Il est clair
alors que le sous-module Ax0 est supplémentaire de B0(X ; A) dans Z0(X ; A),
d'où (24.22.4.1).
Si Y est un espace topologique séparé non vide quelconque, Z0(Y ; A)
s'identifie encore au A-module des combinaisons linéaires formelles Z Xyy des points
yeY
de Y à coefficients dans A, et comme B0(Y ; A) est engendré par certaines des
différences yL — y2 dans ce module, on peut en tout cas dire que pour toute

22. PROPRIÉTÉS DE L'HOMOLOGIE SINGULIÈRE
141
combinaison £ A.yy appartenant à B0(Y ; A), on a £ Xy = 0. On conclut de là
yeY ye\
que pour toute application continue / : X -+ Y d'une variété différentielle
connexe X dans un espace topologique séparé quelconque Y, l'application
fm : H0(X ; A) -» H0(Y ; A) est injective, car l'image par S0(/) de Xx0 est X f(x0),
qui ne peut donc être dans B0(Y ; A) que si X = 0.
(24.22.5) Dans un espace topologique séparé X, soit (X„)œA une famille d'ouverts
deux à deux disjoints, dont la réunion est X. Toute application continue s : Ap -* X
a donc son image contenue dans un des sous-espaces Xa puisque Ap est connexe
(3.19.7) ; elle peut par suite s'identifier canoniquement à une application continue
de Ap dans Xa, et Sp(X ; A) s'identifie donc canoniquement à la somme directe
© Sp(X„ ; A). Avec cette identification, Z.(X ; A) s'identifie canoniquement à
© Zp(X„ ; A) et BP(X ; A) à © Bp(Xa ; A), car S0s est combinaison linéaire de
aeA œA
simplexes singuliers qui prennent leurs valeurs dans le même X„ que s ; on en
conclut que HP(X ; A) s'identifie canoniquement à © Hp(Xa ; A) pour tout p ^ 0.
aeA
(24.22.6) Soit U = (Ua)œA un recouvrement ouvert quelconque d'un espace
séparé X. Pour tout entier p > 0, désignons par U(ÂP ; X) l'ensemble des
applications continues de Ap dans X dont l'image est contenue dans un ensemble de II ;
c'est une partie de <€(AP ; X), et elle forme donc la base d'un sous-A-module (libre)
S"(X ; A) de SP(X ; A) ; en outre, la définition de 60 (24.20.3.1) montre que si
s e u(Âp ; A), on a 60s e SJJ_ ,(X ; A). L'ensemble Zp"(X ; A) (resp. B)|(X ; A)) des
éléments u e S"(X ; A) tels que 60u — 0 (resp. pour lesquels il existe v e S"+ j(X ; A)
tels que u = 60v) est donc un sous-A-module de ZP(X ; A) (resp. de BP(X ; A)) ;
on en déduit, par passage aux quotients, une application A-linéaire canonique
(24.22.6.1) rup : HPU(X ; A) - HP(X ; A)
où l'on a posé H^(X ; A) = Z)|(X ; A)/B)J(X ; A).
(24.22.7) L'application r" est bijective pour tout p ^ 0.
Il faut prouver deux choses : I) pour tout cycle z e Zp(X ; A), il existe un
cycle z' e Z{J(X ; A) tel que z' - z e Bp(X ; A) ; II) pour tout bord v = 60z, où
veZ^(X;A), il existe z'eS"+ ,(X; A) tel que v = 60z\
Preuve de I). Soit z = Z A(s,, où chaque s, est une application continue
1=1
de Ap dans X. Pour chaque /, les ensembles s," '(U,) forment un recouvrement
ouvert de l'espace compact Ap, donc il existe un nombre e > 0 tel que toute
boule fermée de rayon e dans Ap soit contenue dans l'intersection de n ensembles
«i- '(U.,) pour un choix convenable des indices a, (1 ^ / < n) (3.16.6). Consi-

142 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
dérons une subdivision barycentrique S de Ap d'ordre m assez élevé pour que
les diamètres des simplexes de S soient tous < £ (24.18.7), et à partir de cette
subdivision, considérons la subdivision S' de Ap x [0, 1] et les bijections de
Ap+, et Ap sur les simplexes de S', définies dans (24.21.5). Désignant par pr, la
première projection dans Ep x R, il est clair que l'on a prx o Stf"^^ x {1 })=Sd",(lA|>);
on va montrer que la p-chaine
(24.22.7.1) z' = Sd"(z) = . £ A,s, o Sd"(l J
1=1
qui, par construction, appartient à SP(X ; A), répond à la question.
Cela résultera du lemme plus général suivant :
(24.22.7.2) // existe une application A-linéaire hp : S/X; A) -» SP+,(X;A)
et une application A-linéaire h'f-y : Sp_!(X; A) -* SP(X; A) telles que
(24.22.7.3) SdM - 1 = 60 o hp + h'p. ,.«0.
On en conclura en effet que z' — z — 60(npiz)\ et z' sera un p-cycle vérifiant
la propriété de I).
On procède comme dans la preuve de (24.22.2.1) en prenant pour toute
p-chaîne z = Z^/S», la valeur de l'application linéaire Z^/Sisi ° pr,) en chacun
i i
des deux membres de (24.21.6.2) (où R est remplacé par Sdm) ; en utilisant la
commutativité du diagramme (24.20.3.2), il vient
Sd"(z) - z = ê-0(E A,SP+ !(s, o pr^fl')) - Z ( - l)JUs, o pr, o Pjk).
I k,J,l
Le premier terme du second membre s'écrit bien 6Q(hp{z)), avec
Ml>W = EA.sp+1(Sioprix0').
Pour définir de même hp-u on pose, pour tout élément u = Z/V« de
Sp_ t(X ; A), où les ua sont dans A et chaque s'„ est une application continue
de Ap_! dans X,
(24.22.7.4) - - I M o yk)
k,x
avec les mêmes notations que dans la preuve de (24.22.2.1). On écrit 60z = Z M«si
a
où les s. sont distinctes et, pour chaque a, p„ = Z ( - l)^,, la somme étant étendue
aux couples {l,j) tels que s, ° Oj = s'a. On a par définition
«i°pri °Pjk = S/0Pfi °((^°y*) x f4) = s,oct;oyk

22. PROPRIÉTÉS DE L'HOMOLOGIE SINGULIÈRE
143
donc
w.i M CQFD.
On notera que ces définitions montrent que si z appartient à Z"(X ; A),
Mz) appartient à Sp+ ,(X ; A), le support de s, ° pr, étant contenu dans celui de s,.
Preuve de II). — Gardant les mêmes notations, mais remplaçant p par p+1,
prenons z' = Sdm(z), qui appartient à S"+ i(X ; A) ; en vertu de (24.21.3.3), on a
60(z' — z) = Sd"o — d ; mais comme par hypothèse v appartient déjà à Z"(X; A),
il en est de même de Sdmv pour tout m, et en outre, en appliquant le résultat de I)
à v, on voit que Sdmt; - v = 60w, où w appartient à S"+ t(X ; A), en vertu du fait
que v appartient à Z"(X ; A). On a donc finalement v = 60(z' — w), ce qui achève
de prouver II).
(24.22.8) On va déduire de (24.22.7) une suite exacte de Mayer- Vietoris analogue
à (24.3.7.2). On considère un recouvrement ouvert U de X formé de deux ouverts
non vides Ult U2 tels que Ui n U2 soit non vide. On définit une suite
d'applications A-linéaires de modules codifièrentiels gradués
(24.22.8.1) 0 - S?(U, nU2;A)A SV(UX ; A)©S?(U2 ; A) A SV(X ; A) -» 0
de la façon suivante : pour z = Z A|Sj, où les s^àp) sont contenus dans Ut n U2,
on pose 1
(24.22.8.2) v(z) = (z, -z),
où z est identifié à ses images canoniques dans Sp(Ui ; A) et S"(U2 ; A) ; et pour
tout couple de p-chaînes zt eSjftUt ; A), z2 e S"(U2 ; A), on pose
(24.22.8.3) u(z„ z2) = z, + z2,
z, et z2 étant identifiées à leurs images canoniques dans S"(X; A).
La suite (24.22.8.1) est encore exacte, et la vérification de ce fait est ici
immédiate, la surjectivité de u résultant de la définition du recouvrement U. En outre,
on a v(60z) = (ë0z, - 60z) et u(60zu 60z2) — 6'0(z1 + z2), donc on déduit de d et u
deux applications linéaires homogènes de degré 0
». : H.U(U, n U2 ; A) -» H.MJ, ; A) 0 H.U(U2 ; A)
u, : HflUi ; A) 0 H.U(U2 ; A) - H»(X ; A)
et l'exactitude de la suite (24.22.8.1) entraîne l'existence d'une application linéaire
homogène de degré — 1
du : H"(X; A) - H^nU^A)

144 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
telle que la suite (se terminant par H"(X ; A) -► 0)
... - Hj^nU^A) X HjfU, ; A) © H»|
H«(U2;A) -
,(U, n U2 ; A) -
soit exacte. L'application du est définie de la façon suivante (Ann. 30.4) : si z est
la classe d'homologie d'un p-cycle zeZ"(X ; A) et si l'on écrit z = z, + z2 avec
Z{ e SjftUi ; A) et z2 e S"(U2 ; A), de sorte que 60zï = - 60z2, alors 60zi = - $oz2
est un (p - l)-cycle de SpL^Uj n U2; A), et dnz est sa classe d'homologie.
Notons maintenant que par définition de U, on a S. (U! ; A) = S ."(Ut ; A),
S.(U2; A) = S.U(U2; A) et S.(UinU2; A) = S.u(UlnU2; A); par suite H.u(Ui; A),
H"(U2 ; A) et HÎ*(Ui n U2 ; A) sont respectivement identiques à H.(U1 ; A),
H.(U2 ; A) et H.(U1nU2;A); utilisant l'isomorphisme canonique rp1 (24216.1),
on obtient donc une suite exacte (se terminant par H0(X ; A) -> 0)
(24.22.8.4) ... -» Hp(Ui n U2 ; A) Z Hp(Uj ; A) © Hp(U2 ; A) ->
où d = du°(rPl) 1 ; on dit que c'est la suite de Mayer-Vietoris pour rhomologie
singulière.
(24.22.9) Exemple : homologie singulière des sphères.
Pour tout anneau commutatif A, et tout entier n > 1, on a
Comme S„ est une variété différentielle connexe pour n > 1, on a H0(S„ ; A) s A
par (24.22.4), tandis que pour S0 = { -1, 1} on a H0(S0;A)sA2 (24.22.3 et
24.22.5). Les ouverts U et V étant définis comme dans (24.4.1), il résulte du
raisonnement de (24.4.1) et de (24.22.4) que l'on a (pour n S* 1) H0(U ; A) s H0(V ; A)s A
et Hp(U ; A) = HP(V ; A) = {0} pour/7 > 1, ainsi que Hp(Un V ; A) ~ Hp(S„_ t ; A)
pour tout p 2* 0. La suite de Mayer-Vietoris pour le recouvrement (U, V) de S„
se décompose alors en suites exactes
La seconde suite exacte montre d'abord que HP(S„ ; A) = {0} pour p> n,
car ce A-module est égal à Hp_„(S0 ; A) = {0} d'après (24.22.3) et (24.22.5).
Pour 2 ^ p < n, cette même suite exacte ramène la détermination des HP(S,,; A)
au cas/? = 1. Si n > 1, U n V est connexe ainsi que U et V, et par suite, si a e Un V,
les classes a, â, et a~2 de a dans H0(U n V ; A), H0(U ; A) et H0(V ; A) forment
* Hp(X;A) -i HJI_1(UlnUa;A)
(24.22.9.1)
et
0 - H^jA) -i H0(UnV;A) £ H0(U; A) © H0(V; A)
0 Hp(S„; A) -S. Hp_!(SB_, ; A) -> 0 pour/? S* 2etn > 1.

22. PROPRIÉTÉS DE L'HOMOLOGIE SINGULIÈRE
145
des bases respectives de ces A-modules libres (24.22.4), et est l'application
injectiveAâ (Xàu - Xâ2),donc¥ll(Sn; A) = {0}.Sin = 1,U n
Vadeuxcomposantes connexes, U et V sont connexes ; soient a, b deux points contenus dans
des composantes connexes différentes de U n V ; les classes d'homologie a et b
de ces points forment alors une base de H0(U n V ; A), et d'autre part a et b
appartiennent, dans H0(U ; A) (resp. H„(V ; A)) à la même classe ô, (resp. a2).
On en conclut que v+ est l'application Xa + ub -> ((X + u)a~u - (X + u)â2),
et son noyau (qui est l'image de d) est donc le A-module des Xa + ub pour lesquels
X + u = 0 ; comme ce sous-module est libre et a pour base â - b, cela montre
que HjfSj ; A) s A. CQFD.
(24.22.10) Dans un espace topologique séparé X, on dit qu'un sous-espace Y
est un rétracte par homotopie de X s'il existe une application continue
F : X x [0, 1 ] -> X (dite rétraction par homotopie de X sur Y) ayant les
propriétés suivantes :
1) F(x, 0) = x pour tout xeX;
2) F(y, t) = y pour tout y e Y et pour 0 < t 1 ;
3) F(x, l)e Y pour tout jceX.
Alors, si i : Y -» X est l'injection canonique, i+ : H.(Y, A) -» H.(X, A)
est un isomorphisme de A- modules gradués pour tout anneau commutatif A.
En effet, posons r(x) = F(x, 1), r étant considéré comme application de X dans Y;
les conditions 2) et 3) entraînent que l'on a r ° i = 1Y. D'autre part, les
applications i o r et lx de X dans lui-même sont homotopes, car on a F(x, 0) = x
et F{x, 1) = i(K*)) Pour tout * e X. On en conclut que et l'application
r+ : H.(X, A) H.(Y, A) sont telles que o r# et ° sont les applications
identiques, d'où notre assertion. Par exemple, nous avons prouvé dans (24.7.2)
que, pour toute sous-variété compacte Y d'une variété différentielle X, il existe
une suite décroissante (UJ de voisinages de Y dans X, formant un système
fondamental de voisinages de Y, et telle que Y soit rétracte par homotopie de
chacun des Um.
(24.22.11) Exemple : homologie des bouquets de variétés. — On appelle
bouquet de variétés différentielles un espace topologique séparé X réunion de sous-
espaces fermés X,, ..., Xr ayant un seul point commun, et tels que chaque Xj
soit homéomorphe à une variété différentielle (les dimensions des X; n'étant pas
nécessairement les mêmes). Considérons d'abord le cas où X est réunion de
deux tels espaces Xt, X2, et soit a leur point commun. Il y a dans X, (j = 1, 2)
un voisinage ouvert V, de a tel que {a} soit un rétracte par homotopie de V}
dans Xj. Si Uj = V, u X2 et U2 = V2 u Xi, on en conclut que U,, U2 sont des
ouverts dans X, que X2 est rétracte par homotopie de U! et X, rétracte par
homotopie de U2 ; enfin, {a} est rétracte par homotopie de Ui n U2 = Vt u V2.
Dans la suite de Mayer-Vietoris (24.22.8.4) pour Ul5 U2 et X = U, u U2,

146 XXIV. topologie algébrique et différentielle élémentaires
on peut donc remplacer H^U, n U2 ; A) par 0 pour p > 0, par A pour p = 0,
et Hp(U, ; A) (resp. Hp(U2 ; A)) par Hp(X2 ; A) (resp. Hp(X, ; A)) ; on a donc déjà
(24.22.11.1) H^X; A) s ; A)©H,(X2;A) pourp^2.
En outre, si Xt et X2 sont connexes (donc aussi X), le raisonnement de (24.22.4)
montre que H„(X ; A) s A et que l'application
est injective; la relation (24.22.11.1) est donc valable pour tout p > 1.
Par récurrence, on voit que si X est un bouquet de variétés connexes
Xj, ..., Xr, on a
(24.22.11.2) Hfit ; A) s H^X. ; A) © H,(X2 ; A) © ... © H„(Xr ; A)
pour tout p > 1, et H0(X ; A) s A.
(24.22.12) Exemple : attachement de boules. — Soit D„ la boule fermée || z ||< 1
dans R" (où n ^ 2), / : D„ -+ X une application continue de D„ dans un espace
métrisable X, telle que la restriction de / à la boule ouverte D„ ; ||z|| < 1,
intérieur de Dm soit un homéomorphisme de D„ sur un ouvert V de X. Cela
entraîne que /(SB_i) c X — V : en effet, si l'on avait /(z)e V pour un point
zeS,-!, comme par hypothèse il existe z'eD, tel que /(z') = /(z), pour tout
point ZjeD. arbitrairement voisin de z, il y aurait un point ileD,
arbitrairement voisin de z' et tel que /(zj) = f(z\), ce qui contredirait Finjectivité de /
dans D„. On dit alors que X est obtenu par attachement de D„ à Y = X - V
au moyen de f.
Soient B la boule ouverte ||z || < - dans R", U! = /(B) qui est un ouvert
de X homéomorphe à B, et U2 l'ouvert complémentaire du point /(O) dans
X ; (U,, U2) est donc un recouvrement ouvert de X. Montrons en outre que Y est
un rétracte par homotopie de U2 dans X ; il suffit de définir F(x, t) pour x e U2
et 0 < t ^ 1 de la façon suivante : F{x, t) — x pour x e Y et tout t ; si x = /(ru)
avec 0<r< 1 et u6S„-i, F(x, t) =f([\ — t)ru + tu). Le seul point à vérifier
est la continuité de F en un point (x0, tQ) lorsque x0 = /(u0) avec UoeS,,-! ;
si (xm) est une suite de points de X tendant vers x0 et (tm) une suite de points de [0,1 ]
tendant vers t0, on peut se borner au cas où xm = /(rmuj avec 0 < rm < 1 et
umeSn_,. Par compacité et extraction de suites, on peut supposer que (um) a
une limite u0 dans S„_, et (rm) une limite r0 dans [0, 1 ] ; le fait que la restriction
de / à D, est un homéomorphisme sur V entraîne nécessairement que r0 = 1
et/(u0)=x0 ; alors F(xM, tm) =/((! - tm)rMum+tmuJ tend bien vers/(u0) - F(x0> t0).
Enfin, Uj n U2 est homéomorphe à B — {0}, donc/(-S,-! 1, homéo-
HodJ, n U2 ; A) - H0(U, ; A) © H0(U2 ; A)
O
o

22. PROPRIÉTÉS DE L'HOMOLOGIE SINGULIÈRE
147
morphe à S„_i, est un rétracte par homotopie de Uj n U2. Dans la suite de
Mayer-Vietoris (24.22.8.4), on peut donc remplacer H^Uj ; A) par 0 sauf pour
p = 0, où HoflJx ; A) = A, HP(U2 ; A) par HP(Y ; A), et enfin n U2 ; A)
par 0 sauf pour p = 0 ou p = n — 1, où il faut le remplacer par A. On obtient
alors les résultats suivants, compte tenu du fait que, U, n U2 étant une variété
connexe, l'application H0(Ui n U2 ; A) -+ H0(U, ; A) © H0(U2 ; A) est
injective (24.22.4) :
a) Pour n ^ 2, l ^ p ^ n — \ ou p> n, V application
(24.22.12.1) j„ : HJY ; A) - H/X; A)
(où j : Y -» X est l'injection canonique) est bijective.
b) On a une suite exacte
(24.22.12.2) 0 -» H„(Y; A) h H„(X ; A) -i A s H^S,-, ; A) -
£ H._1(Y;A) ^ H.-iPCjA) - 0.
Remarque (24.22.12.3). — Dans la description précédente de X, on remplace
souvent D„ par un espace Z homéomorphe à D„, et on dit alors que X est obtenu
par attachement de Z à Y au moyen de f.
(24.22.13) Exemple : homologie singulière du plan projectif P2(R).
On sait (16.14.10) que S2 est un revêtement à deux feuillets de P2(R) ; soit
jt : S2 P2(R) la projection canonique, deux points distincts x, y de S2 ayant
même image par n si et seulement si y = - x. Soit /la restriction de n à
l'hémisphère fermé D2 de S2 défini par x3 > 0, homéomorphe à D2 par projection
orthogonale osur R2 ; il est clair que /(Dj) = P2(R) et que la restriction de /
à l'intérieur D2 (homéomorphe à D2) est un homéomorphisme sur son image V,
qui est l'ouvert de P2(R) complémentaire de /(Si) = PX(R). Comme Pi(R) est
homéomorphe à S, (16.11.12), on déduit donc de (24.22.12) appliqué à X = P2(R)
et Y = Pt(R) que l'on a Hp(X ; A) = 0 pour p > 3, ainsi qu'une suite exacte
0 -> H2(P2(R); A) - A S Hfà ; A) £ H,(P,(R); A) - Ht(P2(R); A) -* 0
et tout revient à déterminer l'application /*. Considérons pour cela l'applica-
tiong:£ -* ^deS, = U sur lui-même; elle se factorise en S ! Pj(R) Si,
où h est un difféomorphisme, et en identifiant Pi(R) et St au moyen de h, on peut,
dans la suite exacte précédente, remplacer Pt(R) par St et f+ par gm. Rappelons
(24.22.9) que le A-module Hi(S, ; A) a pour base la classe z0 du cycle
fondamental z0 : te0 + (1 - t)et -» e2"", et montrons que l'on a gjz0) — 2z0, ou,
ce qui revient au même, que S^gXzo) — 2z0 est un bord. Or, on vérifie aussitôt
que l'on peut écrire 2z0 = Si(gXSd(z0)), et en vertu du lemme (24.22.7.3), Sd(z0) - Zo
est un bord puisque z0 est un cycle.

148 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
Le noyau de l'application gt est donc Vannulâteur n de l'idéal 2A dans
l'anneau A, et son image est 2Az0 dans le A-module libre H^Sj ; A) = Az0, donc
(24.22.13.1)
H0(P2(R);A)s A
H,(P2(R);A)syV2A
[ H2(P2(R);A)Sn
(24.22.14) Exemple : homologie singulière des espaces projectifs complexes P„(C).
Rappelons (16.11.12) que Pt(C) est homéomorphe à S2 ; nous allons
déterminer l'homologie singulière de P„(C) en partant de ce résultat, par récurrence sur n.
Utilisons pour cela le fait que S2n+1 est un fibre principal de base P„(C) et de
groupe structural U (16.14.10); soit n : S2n+l -* P»(C) la projection canonique
de ce fibre, qui fait correspondre au point z = (zj)1$j$B+ldeS2ll+1 (vérifiant donc
n+l
la relation £ I zj I2 = 1) Ie point n(z) de coordonnées homogènes zlt ..., zn+1.
L'hémisphère fermé D2„ de S2n formé des points zeS2B+1 tels que zB+1 soit
réel et > 0 est homéomorphe à la boule fermée D2„ dans C" = R2" (par
projection de C"+1 sur C") et la restriction f de n à D2n est encore surjective ; en outre
la restriction de / à l'intérieur D2„ de D2„ par rapport à S2lt est un homéomor-
O
phisme de D2n sur l'ouvert V de P„(Q des points de (n + l)-ème coordonnée
homogène zn+l #0, identifié à C". Le complémentaire de V dans P„(C) s'identifie
à Pa-^C), le complémentaire de D2„ dans D2n est S2„_i, et la restriction de /
à S2„ _ ! est la projection canonique. On peut donc appliquer (24.22.12) à X=P„(C),
Y = PB_,(C) et /; on obtient des isomorphismes
(24.22.14.1) Hp(PB(C);A)sHp(P,,_1(C);A) pour l^p<2n-l et p>2n
et une suite exacte
(24.22.14.2) 0 - H2B(PB_1(C);A) - H2B(P„(C);A) -* A -
- H2b_i(Pb-i(C); A) ^ H2lI_1(P1j(Q;A) - 0
Il est alors facile de conclure par récurrence sur n que
f Hp(P„(C);A)s
(24-22'14-3) |hp(Pb(C);A) =
S A pour p = 0, 2, 4, ..., 2n
0 pour les autres valeurs de p > 0.
En effet, ces relations sont vraies pour n = 1 ; en les supposant vraies pour
n - 1, on déduit de la suite exacte (24.22.14.2) que H^-i^C); A) = 0 et
H2ll(PB(C) ; A) S A, et les valeurs de HP(P„(C) ; A) pour les autres entiers p > 1
s'obtiennent à partir de (24.22.14.1); enfin, comme P„(C) est connexe,
H0(PB(C);A)s A.
Remarque (24.22.15). —
Soient X0 une variété différentielle pure, X un revê-

22. PROPRIÉTÉS DE L'HOMOLOGIE SINGULIÈRE
149
tement à deux feuillets de X0, n : X -»• X0 sa projection, s l'isomorphisme de X
sur lui-même qui échange les deux feuillets de X (24.1.4). Pour tout xeX0, il
existe un voisinage ouvert Vx de x dans X0 tel que n~ '(V*) soit réunion disjointe
de deux ouverts V'x, V", la restriction de n à chacun de ces ouverts étant un
difféomorphisme sur Vx (16.12.4.1) ; nous désignerons par U le recouvrement ouvert
de X formé des W'x et VJ' (x parcourant X0) ; en vertu de (24.22.7), on peut
calculer l'homologie singulière de X (resp. X0) à partir du A-module S"(X ; A)
(resp. du A-module S"°(X0 ; A), où U0 est le recouvrement ouvert de X0 formé
des V,). Supposons que dans l'anneau A, pour tout élément a il existe un élément fi
et un seul tel que 2fi = a ^on l'écrira ^ <x^ ; alors tout élément z e S"(X ; A) s'écrit
z = ^(z + Sp(sXz)) + ^(z - Sp(sXz)), et S{J(X; A) est donc somme directe des
deux sous-modules Sp et Sp formés respectivement des z e S"(X ; A) tels que
Sp(sXz) = z et Sp(sXz) = - z. Il est clair que l'application Sp(7t) est nulle dans S~ ;
sa restriction à Sp est une bijection de ce A-module sur SP°(X0 ; A) ; en effet,
pour toute //--chaîne y = £ Aj/i, où Ai e A et chaque fx est une application continue
de Ap dans un ensemble Vx de U0, il existe pour chaque / deux applications
continues/,', f" bien déterminées de Ap dans VJ et V" respectivement, telles que
/, = n o f{ = n ° f," ; donc, si l'on pose z = £ i X^fî + f"), z est le seul élément
de Sp tel que SpfaXz) = y (car on peut évidemment supposer que les/, sont deux
à deux distinctes). En vertu de la commutativité du diagramme (24.20.3.2),
on en déduit, par passage aux quotients, que Hp(X ; A) est somme directe de
deux sous-modules Hp(X;A) et H~(X;A) caractérisés respectivement par
les relations Hp(s)(c) = c et Hp(s)(c) = - c, et que Hp(7c) est une bijection de Hp"(X ; A)
sur HP(X0 ; A).
PROBLÈMES
1) On dit qu'un espace séparé X est un rétracte de voisinage si pour tout espace métrisable Y
et toute application continue/d'un sous-espace fermé B de Y dans X, il existe un voisinage U de B
dans Y et une application continue de U dans X prolongeant /.
a) Toute partie ouverte d'un rétracte de voisinage est un rétracte de voisinage. Tout
produit fini de rétractes de voisinage est un rétracte de voisinage.
b) Montrer que toute partie ouverte non vide d'un espace R" est un rétracte de voisinage
(utiliser le théorème de Tietze-Urysohn (4.5.1)).
c) Si X est un sous-espace d'un espace métrisable Y et si X est un rétracte de voisinage,
il existe un voisinage ouvert U de X dans Y et une application continue r : U -» X telle que r(x) = x
pour tout x 6 X.
d) Soient X un espace métrisable qui est un rétracte de voisinage, et A un sous-espace fermé
de X qui est aussi un rétracte de voisinage. Soit U un voisinage ouvert de A dans X et r : U -> A
une application continue de U dans A telle que r[x) = x pour tout xe A (voir c)). Montrer qu'il
existe un voisinage ouvert V c U de A tel que si r' : V -» A est la restriction de r, et i : A V
l'injection canonique, i o r' et lv sont homotopes, autrement dit, A est rétracte par homotopie de V.

150 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
(Considérer dans U x [0, 1 ] la partie fermée W = (U x { 0} ) u (A x [0, 1 ]) u (U x {1} ) et
utiliser le fait que U est un rétracte de voisinage pour définir la rétraction par homotopie de V
sur A comme restriction d'une application continue d'un voisinage de W dans U x [0, 1 ]).
e) Soit X un espace métrisable qui est un rétracte de voisinage, et soient Y un espace
métrisable, B un sous-espace fermé de Y,/une application continue de B dans X. Montrer que s'il existe
une application continue g de Y dans X telle que f soit homotope à la restriction de g à B, alors
il existe une application continue de Y dans X qui prolonge / (Dans l'espace produit Y x [0, 1 ],
considérer l'ensemble fermé (B x [0,1 ])u(Y x { 0}) et une application continue F de cet ensemble
dans X, telle que F( v, 1) = f(y) pour y e B et F(y, 0) = g(y) pour y € Y. Utiliser le fait que X est
un rétracte de voisinage et le théorème de Tietze-Urysohn (4.5.1).)
2) Montrer qu'une variété topologique (16.1.6) compacte est un rétracte de voisinage
(généraliser (16.25.1) aux variétés topologiques).
3) Soit X le sous-espace compact de R2 formé des couples (x, y) tels que 0 ^ jc < 1 et y = 0,
et des couples (x, y) tels que x = 0 ou x = 1/n et 0 ^ y < 1 (n entier > 0 arbitraire) (« espace
peigne »). Montrer que X est rétractile mais n'est pas un rétracte de voisinage (considérer X comme
sous-espace de R2 et utiliser le problème 1 c)).
4) Soient X un espace métrisable et séparable, a un point de X. L'espace &JX, a) qui sert à
définir le groupe d'homotopie n„(X, a) (section 16.30, problème 3) peut s'identifier avec le sous-
espace de f(Am X) formé des applications continues de A, dans X qui sont égales à a en tout point
de Fr(AJ; soit [s] la classe d'une telle application s dans le groupe ji,(X, a). Montrer que dans
ce groupe, le produit [s' ]■ [s"] de deux éléments s'obtient de la manière suivante : on note a'
l'application linéaire affine ^e0 e, ... e„_, -(en.t + et a" l'application linéaire affine
^e0 e, ... - (e,-., + e„) e„^; alors on considère l'application continue égale à s'°a'~l dans
Im(<r') et à s" » a"'1 dans Im(<r") ; sa classe est [s'] ■ [s"].
a) Soient r', t" deux éléments homotopes de ^„_,(X, a). Montrer qu'il existe une
application continue de A, dans X, égale à r' ° «r, dans la face F,, à t" ° at dans la face F,, et égale à a dans
les autres faces de A..
b) On note a, l'élément de d»„(X, a) égal à a en tout point de A„. Montrer que pour
tout s e ^,(X, a), on a 60s = 0 si n est impair et 60s = a._, si n est pair.
c) Si deux éléments s', s" de &(X, a) sont homotopes (par une homotopie F telle que F(x, t)=a
pour te [0, 1 ] et x e Fr(AJ) montrer que s' - s" est un bord appartenant à BJIX ; Z) (appliquer a)
à s' et s", en construisant l'application continue de A„+, dans X à l'aide de l'homotopie F).
d) Soient s', s" deux éléments de ^.(X, a) et s l'élément de ^.(X, a) construit plus haut dont
la classe dans n„(X, a) est [s' ] ■ [s" ]. Montrer que si n est impair s' + s" - s est un bord de B„(X ; Z)
et si n est pair (s' - a.) + (s" - o.) - {s — a,) est un bord de B,(X ; Z) (utiliser a)).
e) Pour tout s e P„(X, a), la classe de s dans H.(X ; Z) si n est impair, la classe de s — a,
dans H„(X ; Z) si n est pair, ne dépend que de la classe [s] de s dans 7t„(X, a) (utiliser c)) ; en déduire
un homomorphisme canonique (dit homomorphisme de Hurewicz) de n„(X, a) dans H.(X ; Z)
(utiliser d)). Pour n > 2, cet homomorphisme n'est en général ni injectif ni surjectif (section 16 J0,
problème 9 c)).
S) Soit X un espace métrisable, séparable et connexe par arcs (section 16.27, problème 1),
et soit aeX. Pour tout x e X, on désigne par y(x) un chemin Ax -» X tel que y(.x)(*o) = « et
yW(ei) = x.
a) Soit z = £ X,f, un 1-cycle de Z,(X ; Z), les X, appartenant donc à Z. Pour tout I, on pose
i
si = ï(M*o))fiy(M*i))~l 1u' appartient à d*i(X, a). Montrer que dans l'application canonique
de Ki(X, a) dans H,(X ; Z) (problème 4), l'image de \~[ [s, ]1' est la classe d'homologie de z.
i
b) Soit z un élément de #MX, a) qui est un 1-bord de Bt(X ; Z) ; on peut donc écrire
Z = Z^(//0 - fil + fl2Ï

22. PROPRIÉTÉS DE L'HOMOLOGIE SINGULIÈRE
151
où les X, appartiennent à Z, et les fh (j = 0, 1, 2) sont des simplexes singuliers de dimension 1
tels que /,0(«0) = fn(*i), fn(*o) = ii2(«o). = fio(*i)- On pose
s» = r(/io(*o))v(/«o(«i))" '. si. = l</it(«o))/i.y(/«(«i))" ' . *u = W//2(eo))/l2V(/l2(«lM" '
qui sont des éléments de d*i(X, a); montrer que l'élément [s,0]- [s„ ]~1 • [sl2] de «,(X, a] est
l'élément neutre. Montrer que l'image de [z] dans le groupe quotient n,(X, a)/S(îï,(X, a)) de jti(X, a)
par son groupe des commutateurs, est égale au produit des images dans ce groupe quotient des
éléments [sl0]", [s„]~x', [i|2]*', et en conclure que [z] appartient au groupe des commutateurs
B(it,{X, a)).
c) Déduire de a) et b) que l'homomorphisme de Hurewicz de 7t,(X, a) dans H,(X; Z)
(problème 4) est surjectif et que son noyau est S(jt,(X, a)), de sorte que H,(X; Z) est isomorphe à
k,(X, a)/0(*,(X, a)).
6) On considère la sphère S3 comme la sous-variété de C2 définie par | z, |2 + | z2 |2 = 1.
Si p, a sont deux entiers tels que 1 ^ q < p et quepetq soient étrangers, le groupe cyclique G = Z/pZ
opère différentiablement et librement dans S3 par l'action (fc, (z,,z2)) -» (o/z,, ûj**z2), où
tu = exp(2ni/p). Alors l'espace des orbites L(p, 4) = S3/G est une variété connexe compacte
(appelée espace lenticulaire) dont S3 est un revêtement ; soit h : S3 -» L(p, q) la projection
canonique (section 16.28, problème 4). On pose X0 = { Ml, 0)}, X, = /i(S,), où St est l'ensemble
des (zi, z2)eS3 tels que z2 = 0, X2 = h(D2), où D2 est l'ensemble des points (zt, z2) de S3 tels
que | z, | O, *, - (1 - | », I2)*.
a) Montrer que X, est obtenu par attachement de I = [- 1, 1 ] à X0 au moyen de
fi : 6 -* h{e""tp) ; X2 est obtenu par attachement de B : | z | < 1 à X, au moyen de f2 :
z -» h(z, (1 - | z I2)1) ; Hp, q) est obtenu par attachement de B x I à X2 au moyen de
h:(z,6) - -Iz|2)*)-
b) Déduire de a) que H0(L(p, a); Z) s Z, H,(L0», a); Z) S Z//>Z, H2(L(p, a); Z) = { 0 },
H3(Mp,a); Z)s Z.
7) Montrer que H,(P.(H); A) s A pour /> = 0,4 4n, et H^H) ; A) = {0 } pour
les autres valeurs de p.
8) a) Soient X un espace topologique, R une relation d'équivalence dans X, jr : X -» X/R
l'application canonique. Montrer que l'ensemble des parties V de X/R telles que n' '(V) soit ouvert
dans X est une topologie sur X/R, dite topologie quotient ; X/R, muni de cette topologie, est appelé
l'espace quotient de X par la relation R, et n est une application continue de X sur X/R.
b) On suppose que X est compact métrisable, et que la relation d'équivalence R est fermée,
c'est-à-dire que pour toute partie fermée K de X, rt'\n(K)) est fermé. On dit qu'une partie A de X
est saturée pour R si A = n~l{it(A)), autrement dit si A est réunion de classes d'équivalence
suivant R. Montrer que pour toute partie fermée saturée K de X et tout voisinage ouvert U de K,
il existe un voisinage ouvert W c U de K qui est saturé.
c) Sous les hypothèses de b), montrer que la topologie de X/R admet une base dénombrable.
(Soit (U„) une base dénombrable de la topologie de X. Pour tout z e X/R et tout voisinage V de z
dans X/R, recouvrir n'\z) par un nombre fini d'ouverts U„k contenus dans n~'(V) et utiliser b)).
d) Montrer que sous les hypothèses de b), pour tout couple (F, V) formé d'une partie fermée F
de X/R et d'un voisinage ouvert V de F, il existe une application continue de X/R dans [0, 1 ]
prenant la valeur 1 dans F et la valeur 0 dans le complémentaire de V (raisonner comme dans
le problème S de la section 12.10).
e) Déduire de c) et d) que X/R est un espace compact métrisable (raisonner comme dans le
problème S de la section 12.10).
9) Les notations étant celles de (24.22.12), soit R0 une relation d'équivalence fermée dans S„
R la relation d'équivalence dans D. dont les classes d'équivalence sont celles de R0 et les ensembles
{ x } pour x e D. ; X = DJR est alors un espace compact métrisable (problème 8), et si n : D. -> X
est l'application canonique, X est obtenu par attachement de D. à Y - n(S„) = SJK0 au moyen de n.
Montrer qu'il y a des relations d'équivalence fermées R0 dans S, telles que Y = S,/R0 soit
homéomorphe à une sphère SN pour un N arbitrairement grand, et en déduire qu'il existe des
espaces compacts métrisables X dans lesquels existe un ouvert partout dense homéomorphe

152 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
à R2, mais pour lesquels hWX ; Z) n'est pas réduit à 0 (utiliser le problème 3 de la section 4.2).
10) Dans R", soit Y, la réunion des p + 1 boules || x - 3Jce, || 4 1 pour 0 < k $ p. On
considère dans Y, la relation d'équivalence R dont les classes d'équivalence sont les ensembles { x}
pour x intérieur à Y,, et les ensembles {x, x + 3e,, ..., x + 3/>«,} où x parcourt la sphère
|| x ||=1. Montrer que pour l'espace quotient métrisable X,=Y^/R (problème 8), on a H^X,; Z)s Z,
H/X,; Z) = {0} pour 1 « ; < n - 1 et j > n, et H„(X,; Z) s Z' (utiliser (24.22.12)).
11) Dans R2, soit A. le cercle
1 1
— e! = - pour n > 1, et soit X l'ensemble compact
n n
réunion des A„ pour n à 1 (« pendentif hawaïen » ). Montrer que H,(X; Z) est isomorphe à
Hj(X; Z) © Z, et en déduire que H,(X ; Z) n'est pas un Z-module de type fini (remarquer que
si X' est la réunion des A, pour n > 2, X' est homéomorphe à X, et utiliser (24.22.12)).
12) Soit X un espace séparé et connexe par arcs, tel en outre que H^X ; Z) = {0}. Montrer
que si A et B sont deux ensembles fermés non vides et disjoints dans X, tels que X — A et X — B
soient connexes par arcs, alors X — (A u B) est connexe par arcs. (Utiliser la suite exacte de Mayer-
Vietoris).
13) Soit X un espace vérifiant les propriétés du problème 12, et qui est en outre localement
connexe par arcs (section 16.27, problème 1).
a) Soit (UJ une famille infinie d'ouverts de X, deux à deux disjoints. Montrer que si un
point n'appartenant à aucun des U, est adhérent à leur réunion, il est adhérent à la réunion des
frontières des U„.
b) Soient A et B deux fermés sans point commun dans X. Soit (U„) une famille de
composantes connexes de X - A, et soit A' l'adhérence de la réunion de A et des U, ; montrer que si B'
est le complémentaire dans B de la réunion des ensembles B n U„, A' et B' sont deux fermés sans
point commun (utiliser a)).
c) Soient A et B deux fermés sans point commun dans X. Montrer que si x et y sont deux points
de X qui appartiennent à une même composante connexe de X — A et à une même composante
connexe de X — B, ils appartiennent à une même composante connexe de X — (A u B) (utiliser b)
et le problème 12).
d) Si A est un ensemble fermé dans X et connexe, toute composante connexe de X - A
a une frontière connexe. (Considérer d'abord le cas où X — A est connexe. Si Fr(X — A) était
réunion de deux fermés non vides M, N, montrer que l'intérieur A de A serait non vide et qu'une
au moins de ses composantes connexes aurait une frontière rencontrant à la fois M et N ; en déduire
qu'il existerait un point x 6 M et deux points y' 6 X - A et y" e A assez voisins de x, qui
appartiendraient à une même composante connexe de X — M ; conclure alors à l'aide de c). Lorsque
X — A n'est pas connexe, pour une composante connexe C de cet ensemble, montrer d'abord que
X — C est connexe).
e) Soient A et B deux ensembles fermés connexes dans X, distincts de X, tels que X = AuB.
Montrer que A n B est connexe. (Si C est une composante connexe de X - A ou de X — B,
montrer que si A n B était réunion de deux fermés non vides M et N, la frontière de C serait contenue
dans M ou dans N, en utilisant d) ; en conclure que X ne serait pas connexe).
f) Soit A un ensemble fermé dans X. Si Ct et C2 sont deux composantes connexes non vides
distinctes de X — A, et si elles ont même frontière B, montrer que B est connexe (utiliser c)).
(Théorèmes de Phragmen-Brouwer).
Donner un exemple de variété connexe X telle que H,(X; Z) # 0 et où les propriétés
précédentes sont en défaut.
14) Soit G le groupe produit 9l4 x { - 1, 1 }4 d'ordre 192 ; il opère dans l'espace R* de la
façon suivante : si s = (n, («,, e2, eit e4)) où les Bj sont égaux à 1 ou — 1, s.(xj) — (EjXn.,U)).
a) Dans le corps des quaternions H, identifié à R4, on considère les trois quaternions 1,
ji 1 / 3n\ 1
q = cos - — - ii + I cos — Jj et r = - (1 + i + j + k). Montrer que la réunion des orbites de 1, q, r
pour l'action du groupe G est un sous-groupe I0 d'ordre 120 de la sphère S3, groupe multiplicatif
/ n 3n
des quaternions de norme 1. I Utiliser le fait que cos - et cos — sont les deux racines de
l'équation 4z2 - 2z

22. PROPRIÉTÉS DE L'HOMOLOGIE SINGULIÈRE
153
b) On identifie R3 à l'espace des quaternions purs z = x,i + xj + x3k, qui sont ceux tels
que z = - z. Pour tout quaternion t = a + r, avec a e R et r # 0 un quaternion pur,
l'application u, : z -» tzt~1 est une rotation dans R3, dont l'axe est la droite D joignant 0 et r, et dont
0 IMI
l'angle 6 > 0 (pour une orientation convenable de D) est tel que tg - = si a ^ 0 et 6 = n
2 a
si a = 0. L'image I du groupe I0 par l'homomorphisme t -> u, est un sous-groupe d'ordre 60
2b
de SO(3), isomorphe au quotient de I0 par le groupe { — 1,1 } ; il contient 6 rotations de —,
2n 5
10 rotations de — et 15 rotations de n (groupe de l'icosaèdre). Ces dernières se répartissent en
S systèmes formés chacun de 3 rotations de n dont les axes constituent un trièdre trirectangle ;
soit X l'ensemble de ces S trièdres.
c) Le groupe I permute entre eux les trièdres de ï et l'opérateur neutre est le seul qui laisse
invariant (globalement) chacun de ces S trièdres. En déduire que I0 est isomorphe au groupe
simple alterné 31, (remarquer que 9t„ est le seul sous-groupe d'indice 2 du groupe symétrique S„,
pour tout m >'2). Montrer que I0 est égal à son groupe des commutateurs (observer que — 1
est un commutateur).
d) Conclure de c) qu'il existe une variété orientable compacte, connexe X de dimension 3,
telle que H0(X ; Z) s H3(X ; Z) s Z, et H,(X ; Z) s H2(X ; Z) = {0 }, mais *,(X) s I0 ( « espace
icosaédral »; utiliser l'exercice S ainsi que la dualité de Poincaré (section 24.37, problème 12)).
15) Traiter comme dans le problème 14 le cas où on remplace q par --^=(1 + i); la réunion
des orbites de 1, q, r pour l'action de G est alors un groupe C0 d'ordre 48 dont le quotient C par
{ - 1, 1} ( « groupe du cube » ) est isomorphe au groupe symétrique S4. On peut montrer qu'en
dehors des groupes cycliques et des groupes diédraux les seuls sous-groupes finis deSO(3) sont
les sous-groupes de I ou de C ou leurs conjugués.
16) Soient M une variété différentielle pure de dimension n, f une fonction numérique
de classe C", dans M, a < b deux nombres réels tels que l'image réciproque /"'([a, b]) soit
compacte et contienne un seul point critique x0 de / ; on suppose en outre que x0 est non dégénéré
(section 16.5, problème 4) et que Yindice de Morse de / au point x0 (section 16.5, problème 3)
soit égal à k. On peut supposer que f(x0) = 0, de sorte qu'il existe un système de coordonnées
locales (ult ..., w.) au point x0 tel que l'expression locale correspondante de / soit
F(«i "») = - «î - • • • - ul + + • • • + ul
(section 16.5, problème 4). On pose, dans R", pour u = (u,, ..., u„),
Q,(u) = u\ + ... + u\, Q2(u) = u2+1 + ... + ul.
a) Soit e > 0 assez petit pour que l'image dans R" du domaine U de la carte considérée
contienne la boule || u || < (2c)1. Soit m une fonction de classe C°° définie dans R et telle que
m(0) > s, m(t) = 0 pour t > 2e, - 1 < tri(t) < 0 pour tout t e R.
Soit g la fonction de classe C" définie dans M, égale à / dans M — U, et dont l'expression locale
dans U est définie par
G(u) = F(u) - m(Q.(ii) + 2Q,(u)) = - Q,(u) + Q2(u) - m(Q,(u) + 2Q2(u)).
Montrer que l'ensemble des points x e M tels que f(x) < e est identique à l'ensemble où g(x) $ s,
et que x0 est le seul point critique de g dans f~l([a, b]).
b) On note M, (resp. N,) l'ensemble des x e M tels que f(x) $ t (resp. g(x) < t). Montrer
qu'il existe dans M une rétraction par homotopie de M, sur N-, (observer que g n'a pas de point
critique dans l'ensemble g'l([— e, e]); utiliser a) et la section 20.8, problème 5).
c) Soit Al'«anse», adhérence dans M deg"'([a, - é]) - M_„desortequeN_, = M_,uA.
Soit d'autre part D la partie de U définie par les relations Q,(u) < c, Q2(u) = 0. Montrer que l'on

154 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
a D c A, et qu'il existe dans M-, u A une rétraction par homotopie (x, t) -» h(x, ()deM_,uA
sur M.,uD. (Définir l'expression locale de h par
("i t) -» («i "*» 0«» + i «K». 0«„)
où (p est une fonction numérique convenablement choisie).
d) Conclure qu'il existe dans M une rétraction par homotopie de M, sur un espace
homéomorphe à l'espace obtenu par attachement à M., d'une boule de dimension k.
e) Généraliser au cas où il y a dans f~l( [a, b]) un nombre fini de points critiques non
dégénérés tels que les valeurs de / en ces points soient égales.
23. Les théorèmes de de Rham : I. Courants associés à une subdivision
simpliciale.
(24.23.1) Reprenons les notations de (24.20.6). Nous nous proposons de
montrer en premier lieu que, pour toute variété pure X de dimension n, l'application
canonique
(24.23.1.1) H»(X;R) -» ItyX)
définie dans (24.20.6.3), est un isomorphisme pour tout entier p ^ 0.
Il suffit de prouver les deux propositions suivantes :
(24.23.2) Tout p-courant à support compact sur X qui est un cycle est homologue
à Vimage canonique d'un cycle de Z"(X ; R).
(24.23.3) Si un cycle de Zp°(X ; R) a pour image canonique dans Z'pÇX) un
p-courant qui est un bord, il appartient à Bp°(X ; R).
(24.23.4) Les démonstrations de ces propositions occupent cette section (pour
(24.23.2)) et les trois suivantes (pour (24.23.3)) et comportent un assez grand
nombre d'étapes.
(24.23.4.1) A) Réduction de (24.23.2) au cas où X est un ouvert borné de R".
Supposons (24.23.2) établi lorsque X est un ouvert borné de R". Soient X
une variété pure quelconque de dimension n, S un p-courant à support compact
sur X tel que 6S = 0. On peut supposer qu'un voisinage ouvert relativement
compact V de Supp(S) est une sous-variété d'un RN (16.25.1), et il y a alors un
voisinage ouvert relativement compact W de V dans RN et une submersion n :
W -» V de classe C00 ayant les propriétés de (16.25.4). Soit j : V W
l'injection canonique, de sorte que j(S) est un p-courant à support compact sur W qui
est un cycle, et qui est par hypothèse homologue au courant c, image canonique
d'un p-cycle c e S, (W ; R) ; comme jt(j(S)) = S, S est homologue au p-courant
n(c), image canonique du p-cycle SD(7tXc).

23. LES THÉORÈMES DE DE RHAM : I.
155
(24.23.4.2) B) Courants associés à une subdivision simpliciale.
On suppose à partir de maintenant que X est un ouvert borné de R", et on
désigne par S une subdivision simpliciale de X (24.18.6) ; rangeons en une suite
(Uj) les simplexes (de toutes les dimensions < n) de 6, et pour chaque U( de
dimension p, soit s, =(a0 at ... ap) une application linéaire affine bijective
de Ap sur Ut, dont le choix est arbitraire pour p < n, et, pour p = n, soumis
à la seule restriction que s, préserve l'orientation lorsque Uj est muni de
l'orientation induite par celle de R". Si U, est de dimension p, et si ht : Uj -* R" est
l'injection canonique, on a s( e /(Ap ; X) et le p-courant s, sur X est donné par
la relation
(24.23.4.3) <sif(i>=['hm
JVi
pour toute forme différentielle fi de classe C°° sur X.
Avec les mêmes notations, rappelons que, pour toute q-forme différentielle a
de classe C00 sur X, telle que q < p, on a défini (173.5) le (p — q)-courant s, a a
sur X par la formule
(24.23.4.4) < sf a o, y > = < s„ a a y > = 'fc/a a y)
pour toute (p — q)-forme y de classe C* ; nous dirons que Sj a a est un (p — q)-
courant de type [p, q), et que tout r-courant sur X combinaison linéaire de
courants de type (r + k, k) (pour un entier k variable ^ n — r) est un courant associé
à la subdivision S. Un tel courant est donc de la forme £ s< a ot<, où les U, sont
i
de dimension > r et, pour chaque i, aj est une fc-forme de classe C°° sur X, avec
k = dim(Uj) — r ; en outre, la relation Z Sj a <Xj = 0 équivaut au fait que 'hfai) = 0
pour tout i. '
En effet, comme Z < A a<» V > == Z
i i
de classe C00 sur X, si 'hfai) = 0 pour tout i, on a bien Z h a a, = 0. Inversement,
supposons que Z $ a a( = 0, et soit r + k la plus grande dimension des U(
i
pour lesquels af 0. On voit comme dans (24.18.2) que pour tout i tel que
dim(Uf) = r + k, il y a une r-forme y de classe C00 dont le support est compact
et rencontre Uj, mais ne rencontre aucun des simplexes U, d'indice j ^ i; on a
alors £ '/»,(aj) a 'h^y) = 0, et comme cela doit avoir lieu pour toutes les r-formes y
ayant la propriété précédente, on voit comme dans (24.18.2) que cela entraîne
'fj^a,) = 0. On est alors ramené au même problème où k est remplacé par k - 1,
et il suffit de raisonner par récurrence descendante sur k ^ 0.
La notion de p-courant associé à la subdivision S généralise celle de p-cou-
i'/jj(<Xj) a '/ij(y) pour toute r-forme y

156 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
rant de la subdivision S (24.20.2) : ces derniers ne sont autres que les courants
associés à S, combinaisons linéaires de courants de type (p, 0) st a a, = a,Sj,
où les at sont des constantes.
(24.23.4.5) Le bord d'un courant associé à S est encore un courant associé à S.
Pour le voir, notons d'abord que, de façon générale, pour tout p-courant T
et toute g-forme a de classe C00, avec q ^ p, on a
(24.23.4.6) 6TT a a) = (- 1)«(6T) a a + (- 1)«+ lT a (da).
En effet, pour toute (p — q — l)-forme fi de classe C°° et de support compact,
on a
<*(T a «),/»> = <T a a,dfi} = <T,a a dfi}
et il suffit de remplacer dans cette relation a a dfi par sa valeur
(- l)«d(a a + l)9+1(da) a fi
(17.15.2.1) pour obtenir la formule (24.23.4.6). En particulier, on a donc
(24.23.4.7) «(s, a a) = (- l)"{6st) a a + (- 1)*+1 s, a (da)
et comme 6st est une somme £ ± ou les U4 sont des simplexes de dimen-
k
sion p — 1 de S (24.17.2.2), cela prouve notre assertion, et de façon plus précise,
6(Sj a a) est somme de courants de type (p — 1, q) et d'un courant de type [p,q + 1),
dont les supports sont contenus dans Uj.
Cela étant, soit a une (n — p)-forme de classe C°° et de support compact
sur X ; avec les notations de (24.11.1), jj^a) est un p-courant de support compact
sur X ; montrons qu'on a, avec les notations précédentes,
(24.23.4.8) jjfl) = I s, a a
iel
où I est l'ensemble fini des indices tels que le simplexe fermé Uj soit de dimension n
et rencontre le support de a.
En effet, pour toute p-forme fi de classe C00 sur X, on a, par définition
(24.11.1.2), <7p(a), fi y = a a /?, et comme le support de a a fi est contenu
Jx f f
dans la réunion F des simplexes fermés Uf pour i e I, on a J a a fi = J a a fi.
Mais F est réunion des simplexes (ouverts) Uj pour i e I, deux à deux disjoints,
et de simplexes de <S de dimensions < n — 1, qui sont négligeables pour la
mesure de Lebesgue (16.22) ; on a donc « a^=m aAÔ;en raison du
JF tel Ju,

23. LES THÉORÈMES DE DE RHAM : I.
157
choix des orientations pour la définition des simplexes singuliers st pour i e I,
on a aAj8 = <si,aA^) = (ïjAa)^); cela prouve (24.23.4.8).
Ju,
(24.23.4.9) C) Fin de la preuve de (24.23.2).
Comme l'ouvert XcR' est une variété orientée, il résulte de (24.11.3)
que pour prouver que tout p-courant à support compact qui est un cycle est
homologue à un p-courant image canonique d'une p-chaîne lisse, on peut se
borner au cas des p-courants de la forme ^(oc), où a est une (n — p)-forme fermée
de classe C°° à support compact. Si maintenant on tient compte de (24.23.4.8),
on voit que cette assertion sera conséquence de la proposition suivante :
(24.23.4.10) Tout p-courant T associé d S et tel que 6T = 0 est homologue à
un p-courant de la subdivision S.
Soit T = Z «i a a„ où, pour chaque indice i e J, Uf est un simplexe de
ieJ
dimension p + k et oc( une fc-forme # 0, avec k < n — p ; soit / la plus grande
valeur de ces entiers k. On peut écrire T = E sf a dt + £ sf a af, où J' est
ieJ' isJ"
l'ensemble des indices i e J tels que Uj soit de dimension p + l et J" = J — J'.
Le bord 6T est, d'après (24.23.4.7), somme de (- 1)'+1 £ Sj a (d<xf) et de cou-
ieJ'
rants de type (p + k — 1, k) avec k < /. La relation 6T = 0 implique donc la
relation 'h^dctt) = 0 pour tout i e J'.
Raisonnons alors par récurrence sur /. Si / = 0, on a J" = 0 ; les a; sont
des fonctions de <^(X), et dire que 'h^dcti) = 0 signifie que la restriction de a,- à Uj
a une différentielle nulle, donc est constante puisque Uf est connexe;
l'assertion (24.23.4.10) est donc prouvée dans ce cas.
Pour terminer le raisonnement, il suffira de prouver le lemme suivant :
(24.23.4.11) Soit V un ouvert étoile de R', considéré comme plongé dans R" (avec
n > l), et soit h : V R" l'injection canonique. Si a est une l-forme différentielle
sur R", de classe Cœ, telle que 'h(da) = 0, il existe une (l — \\-forme différentielle j8
sur R", de classe C00, telle que %dfl - a) = 0.
En effet, une fois ce lemme prouvé, il en résulte que pour chaque indice i e J',
il existe une (/ — l)-forme différentielle f}t sur X telle que 'hldfit — a() = 0 ;
posons Ti = Yj Si a Par construction, T — (— 1),+16T1 est associé à la
subdivision S et est somme de courants de type (p + k, k) avec k < / — 1. Comme
g(T - (— l)'+1o"ri) = 0, on peut appliquer l'hypothèse de récurrence pour
prouver (24.23.4.10), et par suite (24.23.2).

158 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
Reste à démontrer le lemme. Considérons d'abord le cas où / = n, et posons
F(s, x) = sx pour se R et xe R" ; comme F(0, x) = 0 et F(l, x) = x, on peut
exprimer a à l'aide de la formule de l'homotopie (24.2.5.1), en posant co = 'F(a) :
a = d(L.co) + L.(dco)
et tout revient à démontrer que l'on a 'h(L ■ (dco)) = 0. Si
da = I/hW^'1 a dp a ... a dp"
h
(avec H = {iu i2, ..., il+l } ), la forme dco = 'F(da) s'écrit
dco(s, x) = Z^+lUsx)dP a ... a dp"
h
1+1
+ Is'MsxiY (-if-'Pds A dp A . . . Ad£'^A ... A dp")
h Jk= 1
et par suite (avec les notations de (24.2.4))
(L.(dû))Xx)
= l(JW„(SX)ds^Z (-if^PdP A ... <dp>A ... A dp*').
Cela étant, l'hypothèse lh(da) = 0 signifie que pour toute partie H de / + 1
éléments de [1, n], on a f^x) = 0 pour x e V ; mais comme V est étoile, on a aussi
/h(sx) = 0 pour xeVetO<s< 1; donc (L. (dco))(x) = 0 pour x e V et la forme
P = L.co vérifie les conditions du lemme.
Passons au cas général où / < n ; soient n : R" -» R' la projection canonique,
et i : R' -* R" l'injection canonique. En vertu de ce qui précède, appliqué à la
/-forme différentielle at = %a) sur R', il y a une (/- l)-forme différentielle pl sur R'
telle que 'Mdp\ — at) = 0, où ht : V R' est l'injection canonique. Alors
la (/ — lyforme p = 'it(Pi) répond à la question. En effet, on a h = i <> l»1, et n ° i
est l'identité dans R'; comme dp='Tt(dPi), on a ,h(dp)=%('i(,Tt(dpl)))=,hl(dpl),
et '/«(a)='/j1('i(a))=,/j1(al), donc 'h(dp-a)='hl(dpi-al)=0.
Remarque (24.23.4.12). — Les raisonnements précédents montrent que si
T est un p-courant sur X, qui est un cycle, et si V est un voisinage ouvert
relativement compact (dans X) de SuppfT), alors T est homologue à un p-courant
de la subdivision S, dont le support est contenu dans la réunion des U,, où Uf
parcourt l'ensemble fini des simplexes de <5 qui rencontrent V. On peut en effet
supposer que T est homologue à un courant jj^a), où a est une (n — p)-forme
fermée dont le support est contenu dans V (24.12.8).

24. LES THÉORÈMES DE DE RHAM : II.
159
24. Les théorèmes de de Rham : II. Approximation d'un courant par les
courants d'une subdivision simpliciale.
(24.24.1) A) Réduction de (24.23.3) au cas où X est un ouvert borné de R".
Supposons (24.23.3) établi lorsque X est un ouvert borné de R". Soient X
une variété pure quelconque de dimension n, S un p-courant cellulaire sur X,
image canonique d'un p-cycle lisse z e Zp°(X ; R), et supposons que l'on ait S=6T,
où T est un (p + l)-courant sur X à support compact. On peut supposer qu'un
voisinage ouvert relativement compact V de Supp(S) u Supp(T) est une sous-
variété d'un RN (16.25.1), et il y a alors un voisinage ouvert relativement compact W
de V dans RN et une submersion n : W -> V de classe C00 ayant les propriétés
de (16.25.4). Soit j : V -> W l'injection canonique, de sorte que j(S) est le
p-courant sur W image canonique de SpO'Xz), Qui est encore un p-cycle lisse; on a
d'autre part )(S) = 6{j(T)), donc il y a par hypothèse une (p + l)-chaîne lisse
w e S"+ ,(W ; R) telle que ;(S) = 6R, où R = w est le (p + l)-courant sur W image
canonique de w ; comme 7t(/(S)) = S, on a S = ^(R)) = ô^R)), et it{R) est le
(p + l)-courant sur W image canonique de la (p + l)-chaîne lisse Sp+ i(jtXw).
(24.24.2) On suppose à partir de maintenant que X est un ouvert borné de R".
Nous considérons une subdivision simpliciale <3 de X, dont nous supposerons
les sommets (simplexes de dimension 0 de 6) rangés en une suite (ck)k& j ; pour
chaque simplexe U; de S, de dimension p, soient k0 < fcx < ... < kp les indices
de ses sommets rangés par ordre croissant; nous poserons s,=(cto ctl ... ckp).
Pour tout p > 0 et tout anneau commutatif A, nous désignerons par L„(® ; A)
le sous-A-module de Sp°(X ; A) ayant pour base les éléments (v0 v, ... vp),
où (Vj)0«j«p est une suite formée dep + 1 sommets, non nécessairement distincts,
d'un même simplexe de ® ; on dira que Lp(6 ; A) est le A-module des p-chaînes
de la subdivision ® (à coefficients dans A).
Pour toute p-chaine z e Lp(® ; R), z est un p-courant de la subdivision S :
il suffit en effet de le montrer pour z =(v0 v, ... vp). Or, si les Vj sont deux à
deux distincts, z est égal à ± s,, où U; est le simplexe de S ayant v0, vt, ..., vp
pour sommets ; et dans le cas contraire, onaz = 0, car la restriction d'une p-forme
à une variété linéaire affine de dimension < p — 1 est nulle.
La preuve de (24.23.3) comporte alors trois étapes principales :
B) Pour toute p-chaîne lisse z e Zp°(X ; R) (donc telle que 60z — 0), il existe
une p-chaîne z' e Lp(<5; R) et une (p + Xychaîne lisse u telles que z' — z = ë0u.
C) Si ze Lp(® ; R) est telle qu'il existe un (p + ïycourant T sur X à support
compact pour lequel z = 6T, alors il existe une (p + l)-chaîne W6LP+1(S; R)
telle que z = 6w.
D) Si zeLp(<3; R) est telle que 60z = 0 et qu'il existe une (p 4- \)-chaîne

160 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFERENTIELLE ÉLÉMENTAIRES
w e Lp+ j(® ; R) telle que z = 6w, alors il existe une (p + \)-chaîne u e Lp+ j(S; R)
telle que z = 60w.
Cette section est consacrée à la preuve de B).
(24.24.3) Réduction au cas où les supports des simplexes singuliers figurant dans z
sont assez petits.
Pour tout sommet v d'un simplexe de S (autrement dit, un simplexe de
dimension 0 de S), nous noterons St(v) la réunion des simplexes de S (en nombre
fini) dont v est un sommet (ou, ce qui revient au même, les simplexes auxquels
v est adhérent). L'ensemble St(v) est le complémentaire de la réunion des
adhérences dans X des simplexes de S dont v n'est pas un sommet ; puisque l'ensemble
de ces adhérences est localement fini (24.18.1), cette réunion est fermée dans X
(12.6), et par suite St(v) est un voisinage ouvert de v, et l'ensemble des St(v),
où v parcourt l'ensemble des sommets des simplexes de S, est un recouvrement
ouvert de X. En outre, si v,, v2, ..., vk sont des sommets de simplexes de S,
deux à deux distincts et tels que l'intersection des St(vj) pour 1 < j < k soit
non vide, il y a par définition un simplexe de S au moins dont vt, ..., vk sont
des sommets (puisque les simplexes de <5 sont deux à deux disjoints) ; par suite
V =Im(v! v2 ... v*) est un simplexe de dimension k — 1 de S (ce qui montre
que k < n + 1), et l'intersection des St(vj) est la réunion des simplexes dont
l'adhérence contient V (ou, ce qui revient au même, ceux dont V est une facette).
r
Soit z = Z XJi, et soit K son support, réunion des/i(Ap). Il y a un nombre
1=1
fini v1; ..., v, de sommets de simplexes de S tels que les ouverts de St(vk)
pour 1 < k < q forment un recouvrement ouvert de K ; il y a par suite un nombre
p > 0 tel que toute boule de rayon p et de centre dans K soit contenue dans un
des St(v*) (3.16.6). On a vu dans la preuve de (24.22.7) qu'il existe une subdivision
barycentrique de Ap d'ordre m assez élevé pour que la p-chaîne z" = Sdm(z)
soit combinaison linéaire de simplexes singuliers dont chacun a un support
de diamètre < p, et la preuve de (24.22.7.3) montre (puisque S0z = 0) que
z" — z = 60w, où w est une (p + l)-chaîne lisse. Pour prouver l'assertion B),
on peut donc remplacer z par z".
(24.24.4) Approximation simpliciale d'un p-cycle par un p-cycle de S.
r
Nous supposons donc que z = £ X,f, est tel que chacun des ensembles
1=1
f,(Âp) ait un diamètre < p. Posons ./Xe,) = z.n pour 0 < j < p et 1 ^ / ^ r et
soit (bj la famille des points aj7 distincts pour tous les couples (j, I). Pour chaque a
il existe un sommet v^(a) d'un simplexe de 6 tel que la boule de centre b. et de
rayon p soit contenue dans St(v^(ct)) (on peut prendre pour v^(a) le premier
sommet ck tel que St(c*) ait cette propriété). Pour chaque /, et pour 0 < j> ^ p, soit

24. LES THÉORÈMES DE DE RHAM : II. 161
^ l'indice tel que_a.j, = bv et soit g, le simplexe singulier (v^,,, v^(ai) ... v^,,);
par définition, /,(AP) est contenu dans l'intersection des ouverts St(v^(aj)) pour
0 < j < p, donc les p + 1 sommets vWaj) pour 0 < j < p sont des sommets
(non nécessairement distincts) d'un simplexe de <5 de dimension ^ p; par suite
r
z' = Y ï-iSi est une p-chaîne de L_(<5 ; R). Nous allons voir que z' répond aux
i=i
conditions de B).
Pour cela, considérons, pour chaque indice l ^ r, l'application F, du « prisme »
Ap x [0, 1 ] dans R" définie par
F,(x,t) = (l -t)m + tg/ix);
elle prend ses valeurs dans X, car chaque point de MAp) appartient à un
simplexe de © dont g/iAp) est une facette ; en outre, l'hypothèse sur/, et la définition
de gt montrent que F, est de classe C°°.
Avec les mêmes notations que dans la preuve de (24.22.2) on peut écrire
r r
z = L A,F, o 1A z' = Y ^|F, ° pi
1=1 1=1
et on a donc, en prenant pour chacun des deux membres de (24.21.6.2) la valeur
r
de l'application linéaire Y ^/Sp(F,)
1=1
z' - z = 60u-Y Y (- w,oPjl
k,l j = 0
f
avec u = Y ^iSp+1(F,X6"). Comme u est une {p + l)-chaîne lisse, il suffit de
1=1
montrer que la relation 60z = 0 entraîne que
I i (- l)%F,°pJk = 0.
k.l j=0
Or, soit (H„) la partition de l'ensemble des couples (j, I) formée des ensembles
où l'application (j, /) -* /, ° o, prend chacune de ses valeurs distinctes. Comme
$oz = Z(_ l)J^r(/[0 °j)> la relation 60z = 0 signifie que pour chacun des indices p,
on a Y (— 1)"% = 0- Mais, avec les notations de la preuve de (24.22.2.1), on a
Fi ° pjk = (i - t»X/i ° ° y») + t*(#i ° o-j ° yt)
et il suffit de voir que si (i, /) et {j, V) sont deux couples tels que /, o at = /,. ° ffj,
on a aussi g, ° ff; = gc ° ffj ; mais par définition g, o o-j ne dépend que des valeurs
de /, ° o-j aux sommets de Ap_i, ce qui établit notre assertion.

162 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
PROBLÈMES
1) Soit <s une subdivision simpliciale de A,, telle que toute facette de Ap soit réunion de
simplexes de S. Pour tout x 6 Ar on note F(x) la facette de A, à laquelle appartient x. On considère
une application / de l'ensemble des sommets des simplexes de ® dans l'ensemble { «0, e,, ...,•,}
des sommets de A,, telle que pour tout sommet v d'un simplexe de S, on ait /(v) e F(v). Montrer
qu'il existe un simplexe Im(v0 v, ... v„) de S de dimension p tel que Im(/(v0) /(v,)... /(v,)) = A,
(lemme de Sperner). (Pour tout simplexe singulier (v0 vt ... vt) où k < p et les v; sont les sommets
d'un simplexe de S de dimension k, on pose /i((v0 Vi ... v»)~) = (/(v0) /(v,)... /(Vj))~, qui
est donc un /c-courant ; on définit ensuite fk par linéarité dans l'espace vectoriel des fc-courants
de la subdivision ©. Pour k = p, fp((v0 v, ... v,)") est toujours égal à ± lAj ou à 0. Montrer
que l'on a 6fk(z) = /t.,(cîz) pour tout /c-courant z de la subdivision S; en raisonnant par
récurrence sur p, montrer que pour le p-courant lip, qui est un courant de la subdivision S, on a
2) Soient X un espace compact métrique, F,, F2, ..., Fr des parties fermées de X. Montrer
qu'il existe un nombre a > 0 tel que pour toute partie J de { 1, 2 r] et tout ensemble M de
diamètre < a tel que M n Fj / 0 pour tout je J, on a M n f]Fj * 0. (Soient J„ (1 < k < s)
J"
les parties de { 1, 2, ..., r} telles que [ ] F, = 0; pour chaque k, il existe un nombre ak tel que
tout ensemble M de diamètre < ok soit contenu dans le complémentaire d'un des F, avec j e Jk
(3.16.6). Montrer qu'on peut prendre a = inf <rk.)
3) Soient A0, A,, ..., A, p + 1 parties compactes de la variété linéaire affine engendrée
par A, dans R,+ 1, formant un recouvrement de Ar On suppose en outre que pour toute partie
J = {;'o,7i j,} àe {0,1 p}, on a
Im(ejoe7l ... e,,) <= Ajo w Ah u ... u A,,.
Montrer que A„n A, n ... n Ap # 0. (Soit S une subdivision simpliciale de Ap telle que toute
facette de Ap soit réunion de simplexes de S. Montrer qu'on peut définir une application / de
l'ensemble des sommets de 3 dans {0, 1, ..., p } telle que, pour tout sommet v de S, on ait
e/(», e F(v) et v e A/(>l. En utilisant le problème 1, montrer qu'il existe un simplexe Im(v0 v, ... vp)
de S, de dimension p, tel que Im(v0 v, ... vp) n Ay * 0 pour 0 < < p. Conclure à l'aide du
problème 2).
4) Soient A0, A1( ..., Ap p + 1 parties compactes de la variété linéaire affine engendrée
par Ap dans R**1, formant un recouvrement de Ap. On suppose en outre que, si F0, F,, ..., Fp
sont les faces de A,, on a A^ n F, = 0 pour 0 < < p. Montrer que l'on aAonA,n...r»Ap#0
(se ramener au problème 3).
5) Montrer qu'il existe un nombre a > 0 tel que, pour tout recouvrement fini
91 = { A„ A2, ..., A„} de A, formé d'ensembles compacts de diamètre < <r, il existe au moins
un point xe A, appartenant à p + 1 des ensembles A,- (lemme de Lebesgue). (En utilisant le
problème 2, montrer qu'on peut d'abord supposer a assez petit pour que, si F0, F,, ..., Fp sont les
faces de Ap alors pour tour Aj, il existe au moins une face Fk telle que Aj n Fk = 0. Pour chaque
indice k tel que 0 < k < p, soit 9tk l'ensemble des Aj tels que At n Fk ^ 0 pour h < k et
Aj n Fk = 0. Soit B4 la réunion des Aj appartenant à 9l4. Montrer que B0 n B, n ... n Bp ? 0
en utilisant le problème 4.)
6) Soit X un espace compact métrisable. On appelle ordre d'un recouvrement ouvert fini 9?
de X le plus grand nombre p tel qu'il existe un point de X appartenant à p + 1 ensembles de 91.
Soit n(9t) la borne inférieure des ordres des recouvrements ouverts finis de X qui sont plus fins
que 9t. On appelle dimension topologique de X la borne supérieure (finie ou + oo) des entiers n(9i)
lorsque 9t parcourt l'ensemble des recouvrements ouverts finis de X. Si aucune confusion n'en
résulte, on dit aussi « dimension » au lieu de « dimension topologique » et on note cette dimension
dim(X). Pour tout sous-espace fermé Y de X, on a dim(Y) < dim(X).
Si Y est un espace localement compact métrisable et séparable, on appelle dimension topo-

25. LES THÉORÈMES DE DE RHAM : Ul.
163
logique (ou simplement dimension) de Y la borne supérieure des dimensions des sous-espaces
compacts de Y.
a) Soit («j)i<j<. la base canonique de R"; pour 1 < m < n, on identifie R" au sous-espace
vectoriel de R" ayant pour base e, e„. On définit par récurrence sur m un recouvrement
S. de R" formé de cubes fermés, de la façon suivante. Le recouvrement g, est formé des intervalles
{p, p + 1 ] de R, avec peZ. On pose ensuite, pour m > 2
1 1 1
m m — 1 2
et on désigne par I, l'ensemble des (•„ pour p ^ t < p + 1, avec p e Z. Le recouvrement est
formé des cubes C + I2p, où C parcourt 5„_, et p e Z, et des cubes C + u„ + I2j>+1, où C parcourt
, et p e Z. Montrer que tout point de R" appartient à m + 1 cubes de S, au plus.
b) Déduire de a) et du problème S ci-dessus que la dimension topologique de R" est égale
àn.
c) Soit X l'espace compact métrisable produit d'une infinité dénombrable de facteurs égaux
à l'intervalle [0, 1 ] de R. Montrer que X est de dimension topologique +oo.
25. Les théorèmes de de Rham : III. Prolongements de p-formes.
(24.25.1) Cette section est consacrée à la preuve de C) (24.24.2). Soit Lp(2>)
l'espace vectoriel (sur R) des p-courants de la subdivision S, qui a donc pour
base l'ensemble des s{ pour les simplexes U, de 6 de dimension p ; nous
noterons Ip l'ensemble des indices i correspondants. On a vu que Lp(S) est l'image
de Lp(6 ; R) par l'application linéaire z -* z. Désignons d'autre part par <%<»)
l'ensemble des p-formes différentielles de classe C00 sur X, dont le support ne
rencontre aucun simplexe de ® de dimension < p. Pour toute p-forme a e <fp(S),
2 -> < a, 2 > est une forme linéaire sur Lp(6), autrement dit un élément 7t(a)
du dual Lp(2>)* de cet espace vectoriel; nous allons d'abord voir que
l'application linéaire n : SJJS) -* Lp(<5)* est surjective.
Il s'agit de prouver que lorsqu'on se donne arbitrairement une famille (a,)^
de nombres réels, il existe une p-forme a e <£p(6) telle que < a, % > = at pour
tout ielp. Pour cela, il suffit de prendre une famille (V,)iel|) d'ouverts non vides
deux à deux disjoints dans X, tels que V, rencontre le simplexe U{, mais aucun des
simplexes U, de dimension < p, ni aucun des simplexes Uy de dimension p
distincts de Uj : une telle famille existe toujours, parce que les U; forment une famille
localement finie et qu'aucun d'eux ne rencontre Uj, ce qui permet de définir
les Vj par récurrence (en rangeant les indices i e Ip en une suite) ; on peut en outre
supposer que la famille (Vj) est localement finie. On considère ensuite, pour
tout i e Ip, une p-forme af de classe C00 et de support contenu dans V( et
rencontrant U,, telle que < aj, st > = at. Par construction, on a < aj, Sj > = 0 pour
les indices j e Ip distincts de i, et la somme a = X ai est définie et est une p-forme
répondant à la question. telp
(24.25.2) Soit Bp(®) le sous-espace vectoriel de Lp(<3) formé des bords des
(p + l)-courants de la subdivision ®, image par 6 de Lp+1(®). Pour prouver C),

164 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
il s'agit de voir que si zeLp(<5 ; R) est telle que z = ffT pour un (p + l)-courant T
à support compact sur X, on a zeBp(<5). Pour cela, soit B°(S) l'orthogonal
de ce sous-espace dans le dual Lp(S)*, sous-espace des formes linéaires s'annu-
lant dans Bp(S) ; il suffit de montrer que pour toute forme linéaire /e B°(S),
on a /(z) = 0 (Ann. 32.3). Soit z = £ Aj?;; soit J l'ensemble fini des indices i
tels que A,- =t 0, et pour tout i e J, posons f(st) = at. Notre assertion sera prouvée
si l'on montre qu'il existe une p-forme p e SpifS) ayant les propriétés suivantes :
1° dp = 0; 2° pour tout ie J, < P, ~s( > = a,.
En effet, on aura alors < p, z > = < P, ffT > = < dp, T > = 0, donc
0 = IVi=/(2).
ï
(24.25.3) Pour définir P, considérons une p-forme a e 4^(5) telle que ;t(a) = /
L'hypothèse que / appartient à B°(S) entraine que pour tout simplexe U, de 8,
de dimension p -(- 1, on a
(24.25.3.1) < da, s, > = < a, ff s,, > = /(ff s,) = 0.
Pour tout entier q tel quep^q^n, désignons par X, la réunion des simplexes
de S de dimension < q, qui est une partie fermée de X ; on a X„ = X. Nous allons
définir par récurrence une suite de p-formes de classe C°°, Pp+i, Pp+2> ■ ■ •> Pm
telles que :
1° Pp+k est définie dans un voisinage ouvert de Xp+k, et dpp+k = 0 ;
2° Pp+k+i coïncide avec Pp+k dans un voisinage ouvert de Xp+k;
3° la restriction de Pp+1 à Xp est égale à celle de a.
Il est clair alors que P = P„ répondra aux conditions de (24.25.2).
(24.25.4) La construction des pp+k repose sur les propriétés de prolongement
suivantes :
(AriJ) Soit U un simplexe euclidien de dimension s ^ 1 dans R", et soit œ0
une r-forme de classe Cœ définie dans un voisinage dans R" de la réunion Fr(U)
des adhérences des faces de U. On suppose que dcoQ = 0, et si de plus r = s — 1,
on suppose que < œ0, 6ÎV > = 0 [iv étant l'injection canonique de U dans R").
Alors il existe une r-forme fermée œ de classe C°° définie dans un voisinage de U
et égale à co0 dans un voisinage de Fr(U).
(Br>J) Soit U un simplexe euclidien de dimension s ^ 1 dans R", et soit co une
(r + lyforme de classe C00 définie dans un voisinage de U. Soit Ç0 une r-forme
de classe C00 définie dans un voisinage de Fr(U). On suppose que dc)0 = co dans
un voisinage dt?Fr(U), et si de plus r = s — l, on suppose que ( Ç0, 6iv > = < co, ïv >.
Alors il existe une r-forme t] dé classe C00 définie dans un voisinage de U, telle que
dÇ = co dans un voisinage de U et égale à Ç0 dans un voisinage de Fr(U).

25. LES THÉORÈMES DE DE RHAM : III.
165
Supposons ces propriétés établies et définissons d'abord PP+l. Pour tout
simplexe Uj de 6 de dimension p, soient Ej la variété linéaire affine qu'il engendre,
et Cj(pj) le « tube » formé des points de R" à distance < Pj de Ej. Soit a0 la p-forme
(nécessairement fermée) restriction de a à la variété de dimension p réunion des
simplexes Uj de dimension p de <3. Si a$ est la restriction de <x0 à Uj, et
7tj : Cjipj) -* Ej la projection orthogonale, on peut considérer a$ comme une
p-forme sur Ej puisque son support ne rencontre pas la frontière de Uj, et on en
déduit donc une p-forme fermée 'n^o^) sur C/pj). Si on prend les pj assez petits,
les supports des formes 'itj(a$) ne se rencontrent pas, et si V est le voisinage
de Xp réunion des Cj(pj), il y a une p-forme fip de classe C00 définie dans V et
égale à 'nj(a.{f) dans chaque C,(pj). Cette forme est fermée, et il résulte de (24.25.3.1)
que l'on a < /Sp, 6ÏVj > = 0 pour chaque simplexe Uj de dimension p de ®. On
applique alors (ApP+,) à chaque simplexe Uj de dimension p + 1 de S avec
to0 = fip, et on obtient une p-forme fermée fi^X i de classe C00, définie dans un
voisinage W, de Uj et coïncidant avec fip dans un voisinage de Fr(Uj). Mais
comme chaque simplexe de S de dimension p n'est adhérent qu'à un nombre
fini de simplexes de dimension p + 1, on peut, en remplaçant les W, par des
voisinages plus petits, faire en sorte que deux p-formes /3p+i, (ip+i coïncident
dans l'intersection Wj n Wt, quels que soient j et k ; les fâX i sont donc les
restrictions d'une p-forme fermée fip+l définie dans un voisinage de Xp+1.
On suppose ensuite fip+h définie pour un h ^ 1 et on définit /Sp+B +1 en
procédant de la même manière : on applique (APtP+h+1) à chaque simplexe Uj de
dimension p + h + 1 de ®, avec co0 = fip+h, et on obtient une p-forme fermée
1 de classe C00, définie dans un voisinage Wj de Uj et coïncidant avec fip+h
dans un voisinage de Fr(Uj). On remplace ensuite éventuellement les Wj par des
voisinages plus petits, de sorte que les /fp+B+i soient restrictions d'une même
p-forme fermée fip+h+1 définie dans un voisinage de Xp+h+Pour h — n — p — 1,
on obtiendra ainsi la forme p = fiH voulue.
(24.25.5) Il reste à prouver les propriétés (Ar5) et (Brs). Nous procéderons par
récurrence sur r, en trois étapes :
I) Preuve de (A0iI) pour tout s.
II) Preuve que (Arj) pour tout s entraine (Brs) pour tout s.
III) Preuve que (Brs) pour tout s entraîne (Ar+ls) pour tout s.
Étape I). — Ici co0 est une fonction, et dire que dco0 = 0 signifie qu'elle
est constante dans toute partie connexe de son domaine de définition. Comme
Fr(U) est connexe si s ^ 2, on peut supposer que co0 est définie dans un voisinage
connexe de Fr(U) et prendre alors œ égale à la même constante dans un
voisinage de U. Si s = 1, on a U =Im(b0 bj) pour deux points distincts ; l'hypothèse
entraine que a)0(b,) - £o0(b0) = 0, et on prend co égale à co0(b0) = ojoibi) dans
un voisinage de U.

166 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
(24.26.1.1) o^S ; A)) c L,_ ,(S ; A)
_Étape II). — On peut supposer co définie dans un voisinage convexe
de U, et il résulte du lemme de Poincaré (24.2.6) qu'il existe une r-forme ^ de
classe C°° définie dans le même voisinage et telle que dÇl = co. La forme r/0 = Ç0 — É i
est donc définie et fermée dans un voisinage de Fr(U). Si s ^ r + 1, il résulte
de (Ar>,) qu'il existe une r-forme fermée t] définie dans un voisinage de U et
égale à t]Q dans un voisinage de Fr(U), et la r-forme e) — e;x + t] est donc telle
que de; = co dans un voisinage de U, et égale à Ç0 dans un voisinage de FifU).
Cette conclusion est encore valable lorsque s = r + 1, car on a alors
< «o, 6ÎV > = < U 6ÏV > - < £„ §ïv > = < co, Jv > - < dt;u ïv > = 0
en vertu de l'hypothèse, et (Ar>1.+1) est donc applicable.
Étape III). — Soit U = Im(b0 bt ... bs), et considérons les faces
F, = Im(b0 ... b, ... b5)
de U pour 0 < j < s ; si V/e) est l'ensemble des points de R" dont la distance
à Fj est <e, on peut supposer que co0 est définie dans la réunion des V/e) pour
0 < j < s. On vérifie aussitôt que la réunion W0 des V,(e) pour 1 < j < s est un
ensemble ouvert étoile par rapport à b0 pris comme origine (24.2.7) ; le lemme
de Poincaré montre donc qu'il existe une r-forme Ç0 de classe C* dans W0 et
telle que dÇQ = co0 dans cet ensemble. Si s # r + 2, en remplaçant
éventuellement 8 par un nombre plus petit, on déduit de (BriJ_ t), appliqué au simplexe F0
et à la forme Ç0 définie dans le voisinage W0 n V0(e) de Fr(F0), qu'il existe une
r-forme ^ de classe C00 définie dans V0(e) et telle que dc)i = co0 dans ce voisinage
et £i = £o dans W0 n V0(e). Il existe alors une r-forme Z de classe C00 dans un
voisinage de U et coïncidant avec {0 dans W0 et avec ^ dans V0(e) (16.4.3); il
suffit de prendre co= de; dans ce voisinage pour répondre à la question. La conclu-
s
sion est encore valable lorsque s=r+2 ; on peut en effet écrire Sïv — ïF = £ (—1)TF
(24.193), et ce (s — l)-courant T a donc son support dans W0 et est tel que
6T = — 6iFo. Par suite, on a
< £o, SÎFo > = - < £0> 6T > = - < dÇ0, T > = - < o>0,6ÏU > + <to0, ïFo > = <tu0, Îf0 >
en vertu de l'hypothèse, si bien que (Br-r+1) est encore applicable.
26. Les théorèmes de de Rham : IV. Fin de la démonstration.
(24.26.1) Reprenons les notations de (24.24.2) ; remarquons tout d'abord que
l'on a

26. LES THÉORÈMES DE DE RHAM : IV.
167
par définition de 60 (24.20.3.1). Il est clair d'autre part que
(24.26.1.2) L„(S ; A) = L,(® ; A) 0 L'p'(® ; A)
où LJX® ; A) est le sous-module libre ayant pour base les s, correspondant aux
simplexes U, de S de dimension p, et Lp'(® ; A) est le sous-module libre ayant
une base formée :
1° des (v0 V! ... vp), où la suite (v,) a au moins deux termes égaux ;
2° des éléments st — e„jr(Sj), où Sj=(cko ctl ... ctp) est un des éléments
de la base de Lp(<5 ; A), n une permutation de {0, 1, ...,/»} distincte de
l'identité, e, sa signature, et on a posé
rt(S() = (<*„,„, c^(l) ... ckMp)).
Si p > n, on a donc Lp(<3 ; A) = {0}, et une base de LP'(S ; A) = Lp(® ; A) est
formée des (v0 v, ... vp), où les v, sont des sommets d'un même simplexe de <3,
la suite (v,-) ayant ici nécessairement au moins deux termes égaux.
Lorsque A c R et p < w, l'indépendance linéaire des courants §j, où st
parcourt la base de LP(S ; A) (24.18.2), montre que la restriction à Lp(® ; A) de
l'application linéaire z -► z est injective et a pour image le A-module ayant
pour base les p-courants s( ; d'autre part, la restriction de z -» z à LP(S ; A)
est nulle. En effet, cela résulte de (24.24.2) lorsque z = (v0Vi ... vp) avec deux
des Vj égaux, et de (24.17.2) et (24.18.4) lorsque z = s{ — £,7t(s,). On voit donc
que Lp(® ; A) est le noyau de l'application z -» z de Lp(® ; A) dans ê'J^X).
On en déduit que pour tout p ^ 0 et tout anneau commutatif A, on a
(24.26.1.3) 60(U;(<5 ; A)) c L^'_ t(® ; A).
En effet, d'après les définitions de 60 et de Lp(® ; A), il suffit de prouver cette
relation pour A = Z <= R ; mais cela résulte alors de la remarque précédente
et de la commutativité du diagramme (24.20.4.3).
(24.26.2) Pour prouver l'assertion D) de (24.24.2), on peut, en remplaçant z
par z - S0w, supposer que z = 0, c'est-à-dire que z e Lp(<3 ; R), et il s'agit donc
de voir que tous les cycles de Lp(<5 ; R) sont des bords de chaînes de Lp+ ; R).
Cela va résulter de la proposition plus générale suivante :
(24.26.3) Soit A un anneau commutatif. Pour chaque p ^ 0, soit fp l'application
linéaire de Lp(® ; A) dans lui-même, nulle dans Lp(® ; A) et telle que f^z) = z
dans Lp(® ; A). Alors, pour chaque p > 0, il existe une application linéaire hp
de L/®; A) dans Lp+1(S; A) telle que Von ait, pour tout zeLp(®; A),
(24.26.3.1) z - ffr) = /ip_ iftfoz) + <f0(Mz))

168 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
est un isomorphisme pour tout p ^ 0.
et que, pour tout simplexe singulier s e Lp(© ; A), le support de /ip(s) soit contenu
dans celui de s.
Cette propriété entraîne en effet que si z e Lp(<5 ; A) et si 60z = 0, on a
z = <?0(yz)).
Notons d'abord que, pour tout z e Lp(<5 ; A), on a
(24.26.3.2) 6U/,(z)) = /,-i(M-
En effet, si z e Lp(® ; A), on a aussi 60z e Lp_ t(<3 ; A) en vertu de la
définition de 60 et de la définition des st au moyen de l'ordre pris sur l'ensemble des
sommets de S, d'où (24.26.3.2) dans ce cas ; si au contraire z e Lp(® ; A), les
deux membres de (24.26.3.2) sont nuls en vertu de (24.26.1.3).
On définit les hp par récurrence sur p. Il est clair qu'on satisfait à (24.26.3.1)
pour p = 0 en prenant h0(z) = 0 dans L0(S ; A), puisque f0{z) = z dans L0(<5 ; A)
(L_!(<»; A) étant posé égal à {0}). Supposons les hj définies pour j<p; il
suffit de définir /ip(z) pour tout simplexe singulier z =(v0 vt ... vp), où (v^) est
une suite de p + 1 sommets d'un même simplexe de S. Posons
y = z - fp(z) - hp-i{60z);
comme fjiz) = 0 ou /p(z) = e%n{z) pour une permutation n, il résulte de
l'hypothèse de récurrence que le support de y est contenu dans celui de z. Montrons
que l'on a 60y = 0. En effet, d'après la relation (24.26.3.2), on a
6Qy = 60z - fp-i(60z) - ^(/ip.^éV))
et en vertu de (24.26.3.1) appliqué en remplaçant p par p - 1 et z par 60z, cette
expression est égale à /ip_2(6,o(°3oz)) = 0- Considérons alors l'application « cône
de sommet v0 » (24.21.1.1) ; il suffira de poser /ip(z) = Cwo(y). En effet, le support
de hp(z) est alors contenu dans celui de z, et d'après (24.21.1.2), on a y = 60{CV0{y)),
ce qui s'écrit z - fp{z) - rip_ i{60z) = 60{hp(z)).
Ceci termine la preuve de (24.23.3) et établit par suite que
l'homomorphisme de de Rham (24.23.1.1) est un isomorphisme.
Remarque (24.26.3.3). — La proposition (24.26.3) s'applique sans
modification lorsque © est une subdivision simpliciale d'un ensemble fermé dans R".
Prouvons maintenant le complément (24.20.6.1) annoncé au théorème de
de Rham.
(24.26.4) Soit A un anneau commutatif; pour toute variété différentielle pure X
de dimension n, l'application canonique
(24.26.4.1) H;(X ; A) -» HP(X ; A)

26. LES THÉORÈMES DE DE RHAM : IV.
169
Il s'agit de prouver que :
I) pour tout cycle z e Z„(X ; A), il existe un cycle lisse z' 6 Zp°(X ; A) tel
que z' - z e BP(X ; A) ;
II) pour tout u = 60z, où ue Zp°(X ; A) et z e Sp+ X(X ; A), il existe
z' e Sp°+ /(X ; A) tel que w = 60z'.
Les méthodes sont très analogues à celles utilisées ci-dessus dans les preuves
de (24.23.2) et (24.23.3), et nous n'entrerons pas dans tous les détails du
raisonnement.
Preuve de I). — On se ramène d'abord au cas où X est un ouvert de R" en
procédant comme dans (24.23.4.1), dont on garde les notations : Sp(JXz) est un
p-cycle dans W, donc il existe par hypothèse un p-cycle lisse z" dans W tel que
z" - SpfJX2) = 60u, où u est une (p + l)-chaîne dans W ; on en conclut que
SpfrXz") - z = MSp+ifaX")). et Sp(tcXz") est un p-cycle lisse dans X.
Supposant donc que X est un ouvert de R", on considère, comme dans
(24.24.3), dont on conserve les notations, une subdivision simpliciale 6 de X ;
en remplaçant z par Sdm(z) pour m assez grand (qui est un cycle homologue à z),
on peut supposer que z = Z-t,/,, où chaque /, est un simplexe singulier (non
i _
nécessairement lisse) tel que /((AP) soit contenu dans au moins un des ouverts
St( v,), et les A, appartiennent à A. On en déduit comme dans (24.24.4) un p-cycle
lisse z' — Y.A-i8i de la subdivision <5, et, pour chaque /, une application F( de
i
Ap x [0, 1 ] dans X, qui ici est seulement continue en général ; mais le
raisonnement de (24.24.4) s'applique encore et montre que z' — z = S0u, où m est une
(p + l)-chaîne (non nécessairement lisse).
Preuve de II). — On commence encore par se ramener au cas où X est un
ouvert de R" : avec les notations de (24.23.4.1), on a SpfjX") = $0(Sp+i(Mz))>
donc il existe par hypothèse une (p + l)-chaîne lisse z" dans W telle que
SpOX") = 60z", d'où u = <>o(Sp+1(7tXz")), et Sp+1(ttXz") est une (p + l)-chaîne
lisse dans X.
Supposant donc que X est un ouvert de R", on considère encore comme
dans (24.24.3), avec les mêmes notations, une subdivision simpliciale ® de X ;
on observe d'abord que si u est un p-cycle lisse dans X, il résulte de (24.24.4)
qu'il y a un p-cycle u" de S (donc lisse par définition) à coefficients dans A, tel
que u" - u — ffow, où w est une (p + l)-chaîne lisse ; on peut donc remplacer u
par u", autrement dit supposer que u est un cycle de la subdivision S. La preuve
de (24.22.7.2) montre que Sdm(m) - u est le bord d'une (p -I- l)-chaîne lisse,
donc on peut remplacer u par Sdm(u) ; en outre, on a Sdm(u) = ^(Sd^z)), donc
on peut supposer que z = Yhfi, où chaque simplexe singulier /, est tel que
_ j
fi(Ap) soit contenu dans une boule contenue dans X. On a alors
« = <?0z = L(- mAfi°Oi);

170 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
si (HJ est la partition de l'ensemble des couples formée des parties dans
chacune desquelles l'application -+ fi°aj prend chacune de ses valeurs
distinctes, on a E ( — 1)% = 0 lorsque ft ° a, ri est pas une application linéaire
(UIeH,
affine, puisque u est un cycle de la subdivision <3. Posons ./j(e,) = a^, et pour
chaque indice /, considérons l'application linéaire affine &=(al0 a(1 ... a,p)
de Ap dans R", qui est telle par construction queg,(Ap) soit encore contenu dans X.
On a alors g,»aj = fi°ctj sauf lorsque /,<>a} n'est pas une application linéaire
affine. Par suite, si z' = £ai£i> il résulte de ce qui précède que l'on a encore
i
u = S0f, ce qui achève de prouver (24.26.4).
Remarque (24.26.5). — Soient X, Y deux variétés différentielles pures,
h : X -+ Y une application de classe C00. On en déduit canoniquement, pour
tout p ^ 0, une application A-linéaire hm : Hp°(X ; A) -♦ Hp°(Y ; A) de la même
manière que dans (24.20.5), et il résulte des définitions que les diagrammes
H/X; R) - H,»(X; R) - HP'(X) HP(X)
(24.26.5.1) "*| ** **J *'|
HP(Y;R) +- HP(Y; R) -+ H;'(Y) HP(X)
où les flèches horizontales sont les applications canoniques, sont commutatifs.
27. Structure des modules d'homologie.
Les résultats précédents et leurs méthodes de démonstration entraînent
les corollaires suivants :
(24.27.1) Pour toute variété différentielle pure X de dimension n :
(i) L'espace H'(X) d'homologie des courants sur X ne dépend que de la
topologie de X et non de sa structure de variété différentielle.
(ii) Si X est compacte (resp. quelconque), chaque Z-module H^X ; Z) admet
un système générateur fini (resp. fini ou dénombrable).
(iii) Pour tout p > n, on a H^X ; Z) = { 0 } .
L'assertion (i) est une conséquence évidente des théorèmes de de Rham,
puisque H.(X ; R) ne dépend que de la topologie de X. Si X est compacte, on peut
supposer que X tout entière est une sous-variété d'un RN, et considérer un
voisinage ouvert relativement compact W de X dans RN et une submersion i:W->X
de classe C°° ayant les propriétés de (16.25.4). Soit 6 une subdivision simpliciale
de W, et soit ®' la partie finie de S formée des simplexes de S rencontrant X
et de leurs facettes; si v,, ..., vr sont les sommets (simplexes de dimension 0)
de <5', l'ensemble S" formé des simplexes de € ayant un de leurs sommets en

27. STRUCTURE DES MODULES D'HOMOLOGIE
171
un des v,, et de leurs facettes, est encore fini. Les ouverts St( v7) forment un
recouvrement de X, et les raisonnements de (24.24.3) et (24.24.4) montrent que si
; : X -» W est l'injection canonique, pour tout p-cycle z de ZP(X ; Z), il existe
un p-cycle (à coefficients entiers) z' de la subdivision ©" homologue à SpOXz)>
et par suite SptrcXz') est homologue à z. Mais l'ensemble des p-chaînes à
coefficients entiers de la subdivision 6" est un Z-module de type fini, donc il en est
de même de son sous-module formé des cycles, de l'image de ce sous-module
par S pin), et de HP(X ; Z) qui est un quotient de cette image.
Si maintenant X est une variété pure quelconque, il existe une suite
croissante d'ouverts relativement compacts V, de X telle que X soit réunion des V,-
(3.18.3), et tout p-cycle de ZpÇX ; Z) a son support contenu dans l'un des V,-.
Appliquant à chaque V, le raisonnement fait ci-dessus pour une variété compacte,
on voit que pour chaque j, il existe un nombre fini de cycles de ZP(X ; Z) tels
que tout p-cycle de ZJiX ; Z) de support contenu dans soit homologue à une
combinaison linéaire de ces cycles à coefficients entiers. Cela montre que HP(X ; Z),
admet un système générateur fini ou dénombrable.
Enfin, pour prouver que si p > n, tout p-cycle de ZJ(X ; Z) est un bord,
on se ramène par les mêmes méthodes à prouver qu'il en est ainsi pour tout
cycle de L^S ; Z), où 6 est une subdivision simpliciale d'un ouvert de R". Mais
(avec les notations de (24.26.1)), on a alors Lp(© ; Z)= Lp(© ; Z), et la conclusion
résulte de (24.26.3).
(24.27.2) On montre en Algèbre homologique comment, pour tout espace
topologique séparé X, la donnée des Z-modules HP(X ; Z) et Hp_ t(X ; Z)
détermine Hp(X; A) pour tout anneau commutatif A [160]. Nous nous bornerons
à le voir dans deux cas particuliers.
(24.27.3) Soit X un espace topologique séparé. Si Hp(X ; Z) et Hp_ j(X ; Z) sont
des Z-modules libres, rhomomorphisme canonique ((24.20.5) et (Ann. 28.6))
(24.27.3.1) Hp(X ; Z) <g> ZA -> HJ(X ; A)
est bijectif pour tout anneau commutatif A.
Comme les SJJL ; Z) sont des Z-modules libres, cela résulte de (Ann. 31.4).
Remarque (24.27.3.2). — Sous les hypothèses de (24.27.3), si de plus
l'homomorphisme canonique Z -+ A est injectif, H^X ; Z) s'identifie canoniquement
à un sous-Z-module de Hp(X ; A).
On dit qu'un espace séparé X est sans torsion si tous les modules
d'homologie Hp(X ; Z) sont libres ; il en est ainsi des espaces rétractiles, des sphères,
des espaces projectifs complexes, des bouquets de variétés sans torsion ((24.22.3),

172 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
(24.22.9), (24.22.11), (24.22.14)). Pour un espace sans torsion X, tous les Hp(X ; A)
sont donc des A-modules libres, et si l'homomorphisme Z -» A est injectif,
chaque Hp(X ; Z) est un sous-Z-module de HP(X ; A).
(24.27.4) En second lieu, nous allons considérer le cas où X est une variété
différentielle pure compacte de dimension n, et voir comment HP(X ; A) s'exprime
explicitement à l'aide de HP(X ; Z) et de Hp-^X; Z).
Montrons d'abord que pour tout entier p tel que 0 < p < n, il existe un
sous-Z-module libre de type fini Ep de Sp(X ; Z) (avec Ep = {0} pour p < 0
ou p > n) tel que si on pose Fp = Ep o ZjÇX ; Z) et Gp = Fp n BP(X ; Z), on ait
Gp = 60(EP+1) et Hp(X; Z) s Fp/Gp. En effet, utilisant les définitions et
notations de (24.27.1), on prend pour E0 l'image par S0(îi) du Z-module des 0-chaînes
de la subdivision ®" ; puis, en supposant Ep (et par suite aussi Fp et Gp) défini
par récurrence, on prend pour Ep+1 le sous-Z-module de Sp+j(X; Z) engendré
par :
1° l'image par Sp+1(7t) du Z-module des (p + l)-cycles de ®" (qui est de
type fini) ; 2° un ensemble (fini) de (p + l)-chaines dont les images par §0
constituent un système générateur de G,. Comme tout cycle de Zp(X ; Z) est alors
homologue à un cycle de Fp (24.27.1), HP(X ; Z) est canoniquement isomorphe
à (Fp + BP(X ; Zfl/B^X ; Z), c'est-à-dire à F^F, n BP(X ; Z)) = Fp/Gp.
Comme tout sous-Z-module de Ep est libre de type fini (Ann. 26.2), Ep/Fp,
isomorphe à Gp_ u est libre, et par suite (Ann. 29.2) Fp admet dans Ep un Z-module
libre supplémentaire F£, la restriction de §0 à F'p étant une bijection de ce Z-module
sur Gp_ t. On sait (Ann. 26.3) qu'il existe une base de Fp
n(p) n(p) n(p) n(p) j,p) „(p)
"1 , • • •> "r > "r+1, • ■ •> "r + s, "r + s+l> • • •> "r + s + r
telle que Gp ait pour base
„(P) „(P) n{p)n(p) «<P>n<P)
où a(ip), ..., <4P) sont des entiers > 0 différents de 1, dont chacun divise le suivant.
On a donc
(24.27.4.1) Hp(X ; Z) = (Z/afZ) © ... © (Z/a<p)Z) © Z'.
De même, il y a une base de Fp_t
«1 , • ■ •> "u > "u+l > • • •> "u + i; » "u + w+l> • • •> "u + u + w
telle que Gp-1 ait pour base
"1 ,•••,"« , wl "u+l at> "u + «

27. STRUCTURE DES MODULES D'HOMOLOGIE
173
où o/f~l), ..., aj,"-1' sont des entiers > 0 différents de 1, dont chacun divise
le suivant, de sorte que
(24.27.4.2) Hp_ t(X ; Z) s (Z/a(f ~ 1JZ) © ... © (Z/«Jf- 1(Z) © Zw.
En outre, on peut prendre une base de Fp
n'lP) n'(P) n'(P) fl'(p)
«1 , • • -j "u , "«+ 1> • • •> uu+v
telle que l'on ait
(24.27.4.3) e?oaf> = a1,"- »>, ..., S0a'u(f) = 11
La formule (24.27.4.1) montre que les nombres s, t et les a^p) ne dépendent que
de la topologie de la variété compacte X, et non des choix de Ep, Fp, Gp et des
choix de bases dans ces Z-modules (Ann. 26.4).
(24.27.5) Cela étant, il résulte aussi de (24.27.1) que pour tout anneau
commutatif A, tout cycle de Zp(X ; A) est homologue à un cycle de Ep ® ZA, et tout
cycle de Ep ® ZA qui est un bord est aussi un bord d'une chaîne de Ep+1 (g) ZA ;
donc, pour calculer Hp(X ; A), il faut considérer le A-module libre Ep ® ZA, et
faire le quotient du noyau de l'application S0 de Ep ® ZA dans Ep_i ® ZA par
l'image de l'application 60 de Ep+ j <g) ZA dans Ep ® ZA. D'après les choix de
bases faits dans (24.27.4), l'image de Ep+ j ® ZA par S0 est somme directe des
A-modules
\af\ Afl<">, AaV"^!, ..., Aa^fl»,.
D'autre part, le noyau de 60 dans Ep ® ZA est somme directe de Fp ® ZA
et du noyau de 60 dans Fp ® ZA (Ann. 31.3) ; si nf~l) est l'idéal de A annulateur
de l'idéal Aaf'^, ce dernier noyau est somme directe des nf'^a'^j pour 1
On obtient donc la règle suivante donnant H^X ; A) à partir des expressions
(24.27.4.1) et (24.27.4.2) :
(24.27.6) Le A-module d'homologie singulière HP(X, A) de X à coefficients dans
un anneau commutatif A est donné à partir des expressions de Hp(X ; Z) et
Hp_,(X;Z)/>ar
(24.27.6.1)
HP(X ; A) S (A/a1/" A) © ... © (A/a<p)A) ©A' © nf~u © ... © n?"1}
ou nf~l) est l'idéal annulateur de l'idéal otf'^A dans A (1 <y ^ v).
Cela entraîne les corollaires suivants :
(24.27.7) (i) Si K est un corps de caractéristique 0, Hp(X ; K) est un K-espace
vectoriel de dimension t.

174 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
28. Homologie des complexes simpliciaux euclidiens compacts.
(24.28.1) Rappelons (24.18.4) qu'un complexe simplicial euclidien compact
est un sous-espace compact X d'un espace RN, muni d'une subdivision
simpliciale ® (nécessairement finie). Gardant les notations de (24.26), il résulte de
(24.26.3.2) et (24.263.3) que L'.(® ; Z)= © Lp(® ; Z) est un sous-module codiffè-
rentielgradué du module codifférentiel gradué S.(X ; Z); nous noterons H.(® ; Z)
son homologie (Ann. 30.7).
(24.28.2) Vinjection canonique f : L'.(® ; Z) -» S.(X ; Z) donne un
isomorphisme f+ : H.(® ; Z) -♦ H.(X ; Z) en homologie.
Soit n la plus grande dimension des simplexes de ®, et soit d le nombre
des simplexes de ® de dimension n ; nous prouverons la proposition par
récurrence sur n, et, pour chaque n, par récurrence sur d. Le résultat est évident pour
n = 0, car on a alors L„(® ; Z) = S0(X ; Z) = S.(X ; Z). _
Considérons donc un simplexe L^e® de dimension n; alors Xt = U,,
X2 = X — Ui et X3 = X, n X2 = Fr(U,) (frontière par rapport à la variété
linéaire affine engendrée par U,) sont des complexes simpliciaux euclidiens
compacts, pour les simplexes de ® qu'ils contiennent. La subdivision simpliciale
®! <= ® de Xj est formée de Ut et de ses facettes de dimension < n ; la
subdivision simpliciale ®2 c ® de X2 est formée de tous les simplexes de ® autres
que Ut ; enfin la subdivision simpliciale S3 = S, n ®2 de X3 est formée des
facettes de U! de dimension < n. L'hypothèse de récurrence entraine donc que
la proposition est vraie pour ®2 et X2, ainsi que pour ®3 et X3 ; montrons qu'elle
est vraie aussi pour ®t et X,. En effet, soient c0, cu ..., cB les sommets de U!
rangés dans l'ordre choisi ; alors L'J[<Si ; Z) est formé des multiples entiers de
s, =(c0 ct ... c„), et L'JiSi ; Z) = Lp(<53 ; Z) pour p < n. Ceci montre déjà
que les homomorphismes H^®! ; Z) -» H^X, ; Z) sont bijectifs pourp^n-2 :
en effet, on a alors Hp(®t ; Z) = Hp(63 ; Z), et les homomorphismes
(ii) Si K est un corps de caractéristique q > 0, Hp(X ; K) est un ^.-espace
vectoriel de dimension s1 + t + v', ou s' est le nombre des entiers a/' divisibles
par q, et v' le nombre des entiers ctf~l) divisibles par q.
En effet, si K est de caractéristique 0, on a aK = K pour tout entier a # 0 ;
si K est de caractéristique q > 0, K/aK = {0} sauf si q divise ce, auquel cas
K/aK = K, et l'annulateur de aK est {0} sauf si q divise a, auquel cas cet
annulateur est K.
Nous verrons plus loin que l'entier t est le p-ème nombre de Betti (24.1.1)
de X (24.33.2).

28. HOMOLOGIE DES COMPLEXES SIMPLICIAUX EUCLIDIENS COMPACTS 175
Hp(®3 ; Z) -* HJIX3 ; Z) sont bijectifs par l'hypothèse de récurrence ; en outre
H^X, ; Z) = HP(X3 ; Z) pour p < n — 2, puisque Xt est rétractile, et que X3
est homéomorphe à la sphère S„_ t, d'où notre assertion.
Pour/» = n - 1,H,_ ,(®3 ; Z) = L'„-^ ; Z) n Z„_ ,(X3 ; Z) £ Z par
récurrence; SQst appartient à Li_!(®3 ; Z) n Z,,_1(X3 ; Z), donc est un multiple
entier d'un générateur de ce Z-module monogène ; mais comme £0Si est somme
de simplexes de ®3 de dimension n — 1 avec des coefficients ± 1, 6°0Si est
nécessairement un générateur lui-même ; cela montre que
L;_,(®, ; Z) n Z„_ .(X» ; Z) = L;_ 1(61 ; Z) n B._ X(X, ; Z),
donc H„_ t(®! ; Z) = {0} = H,. ,(Xt ; Z). Enfin, comme 6Vi * 0,
L;(®1;Z)nZH(X1;Z)= {0},
d'où HB(®1;Z) = {0} = HB(X1;Z).
Nous allons maintenant définir dans X un voisinage ouvert V\ de Xt et un
voisinage ouvert V2 de X2, tels que Xu X2 et X3 soient des rétractes par
homotopie (24.22.10) de V2 et Vt n V2 respectivement. Alors les homomorphismes
composés
H.(®, ; Z) - H.(X, ; Z) * H.^ ; Z),
H.(®2;Z) -* H.(X2;Z)^H.(V2;Z)
Ct H.(®3 ; Z) H.(X3 ; Z) * H^V, n V2 ; Z)
sont des isomorphismes par l'hypothèse de récurrence. Cela étant, on a un
diagramme commutatif de suites exactes
0 -+ U(®3 ; Z) - L:(®! ; Z) © U(®2 ; Z) -.. L'.(® ; Z) - 0
1 I !
0 -+ Sîf(V, n V2 ; Z) - S?(Vt ; Z) © SÏ(V2 ; Z) - S?(X ; Z) - 0
où la seconde ligne est la suite (24.22.8.1) pour le recouvrement ouvert U=(V,, V2)
de X, et les flèches verticales sont les injections canoniques ; l'exactitude de la
première ligne provient du fait que ®3 = ®t n ®2 et ® = ®t u ®2. On déduit
de là en homologie un diagramme commutatif de suites exactes, que l'on peut
écrire, en raison de la suite exacte de Mayer-Vietoris (24.22.8.4) et des choix
de Vj et V2
... - Hp(®3 ; Z) - Hp(®t ; Z) © HJL<52 ; Z) -» H,(® ; Z) - Hp_ t(®3 ; Z) -» ...
I 111
... Hp(X3 ; Z) - H^X, ; Z) © HfiL2 ; Z) - HJ£ ; Z) -» Hp_ j(X3 ; Z) -» ...
donc la proposition (24.28.2) résulte de l'hypothèse de récurrence et du lemme
des cinq.

176 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFERENTIELLE ÉLÉMENTAIRES
U reste donc à définir Vx et V2. Pour Vt nous prendrons la réunion de \Jt
et des simplexes de 8 dont l'adhérence rencontre \Jr ; pour V2 le complémentaire
dans X du barycentre b de U,. Il est immédiat que V2 est un voisinage ouvert
de X2 dans X, et on définit une rétraction par homotopie F2 de V2 sur X2 en
prenant F2(x, t) = x pour x e X2) et
F2(sy + (1 - s)b, t) = ty + (1 - t*sy + (1 - s)b)
pour 0<s<l,0<f^lety6 Fr(Ui).
Comme X — Vx est la réunion des adhérences des simplexes de S dont
l'adhérence ne rencontre pas U,, X — V, est fermé, donc V, est un voisinage
ouvert de Xt dans X. Pour définir une rétraction par homotopie Fj de V! sur X,,
il suffit de la définir dans U x [0, 1] pour tout simplexe U <£ U, de S dont
l'adhérence rencontre \Jt. En fait, on va définir canoniquement une application
continue Fw de U x [0,1 ] dans Vt qui se prolonge par continuité à (Un Vt) x [0,1 ]
de telle façon que, si U' est une facette de U dont l'adhérence rencontre U! et
n'est pas contenue dans Uu la restriction de Fv (prolongée) à U' soit égale à Fv..
Il en résultera que l'application Ft de Vj x [0, 1 ] dans V, telle que Ft(x, t) = x
pour x e Ui et que Fi coïncide avec Fu dans U x [0, 1 ] pour chaque simplexe
U dp U! de S dont l'adhérence rencontre U,, est continue; le fait que ce soit
une rétraction par homotopie sur Xt = L1! résultera de la construction des Fv.
Pour faire cette construction, on peut supposer que U = Am, que
UnU, = Im(e0 et ... ep)
pour un p < m, et que U n Vt = W est l'ensemble des
x = <f e0 + ... + {'e, + £p+1ep+1 + ... + Émeme Âm
(donc tels que les & soient ^ 0 et f° + + ... + Zm = 1) pour lesquels un
au moins des & tels que 0 < y < p est > 0. On pose alors
y(x) = (£°e0 + ... + £'ep)/(ê° + {» + ...+<*),
point qui appartient àUnU,, et F,j(x, t) = ty(x) + (1 - t)x pour tout xe W;
la vérification des conditions imposées aux Fu est immédiate.
Enfin, pour définir une rétraction par homotopie F3 de Vt n V2 sur X3,
il suffit de prendre F3(x, t) = x pour x e X3, F3(x, t) = F2(x, t) pour x e V2 - X2
et F3(x, t) = F^x, t) pour x e V, - X^ CQFD.
Remarque (24.28.2.1). — Il résulte de (24.26.1.3) et (24.26.3) que tout cycle
de Lp(S ; Z) est homologue à un cycle de Lp(6 ; Z), et que si un cycle de L^S ; Z)
est un bord de LP(S ; Z), il est aussi un bord de L^S ; Z) ; l'injection canonique
L'.(® ; Z) -> L.(S ; Z) donne donc un isomorphisme en homologie, et on peut
dans (24.28.2) remplacer L'.(S ; Z) par L.(® ; Z).

28. HOMOLOGIE DES COMPLEXES SIMPLICIAUX EUCLIDIENS COMPACTS 177
(24.28.3) Application : Classe fondamentale d'homologie de S„. Le Z-module
H„(S„ ; Z) est monogène ; nous allons en définir un générateur canonique c„
appelé classe fondamentale d'homologie singulière de S„. Il est commode pour
cela de remplacer S„ par le « cube creux » A„ défini dans R"+1 par l'équation
| x \n = 1, où, pour x = <J°e0 + Ç1el + ... + t?e„ on pose | x |œ = sup \tV I ;
la « projection centrale » x -> x/| x \x est un homéomorphisme de S„ sur A„
dont l'homéomorphisme réciproque est x ~* x/|| x||. Nous allons définir un
n-cycle y„ sur AB dont la classe d'homologie est une base de HB(A„ ; Z).
Pour cela, soit T l'ensemble des couples ((e0, £1, ..., £„), a), où les sont
égaux à 1 ou à - 1, et a est une permutation de l'ensemble {0, 1, ..., n} (T a
donc 2"+1(n + 1) ! éléments). Pour tout y — ((e0, ..., e„), a)e T, et tout indice i
tel que 0 < i < n, posons
aj1 = eoe<r(0) + 6leir(l) + • • • + £ieo(i)
(centre d'une facette de A„ de dimension n — i). Alors les simplexes
Im(a& aï ... aj)
et leurs facettes forment une subdivision simpliciale <3 de A„, et les « cônes »
correspondants de sommet 0
lm(0 aj a? ... a?)
et leurs facettes une subdivision simpliciale <50 du « pavé » Bn+1 défini par
| x I.» < 1. On le voit par récurrence sur n : en effet, S et S0 sont invariantes
par toute permutation des vecteurs e,- de la base canonique de R" +1 ; l'adhérence
de la face de A„ dans l'hyperplan Ç° = 1 s'obtient par la translation e0 à partir
de B„ ; enfin les simplexes de <ô contenus dans cette face proviennent de la
subdivision simpliciale de B„ par la translation e0.
Pour tout y = ((e0, e,, ..., £„), <r)e T, considérons le (n + l)-simplexe
singulier (0 »y0 aï ... aj), et posons r\a = 1 si cette application linéaire affine de AB+x
dans R"+t préserve l'orientation (R"+1 étant muni de son orientation
canonique (16.21.4)), r\a — — 1 sinon. Nous allons voir que la (n -t- l)-chaîne sur B..+1
(24.28.3.1) xn+1 = 1^0 aj aï ... an)
a pour bord le n-cycle
(24.28.3.2) yB= E^a0aï ... aj)
sur A„, et que la classe d'homologie de ce n-cycle est un générateur de H„(AB ; Z).
Pour prouver que Sqx„+i = y„ il suffit, par définition du bord, de vérifier

178 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
que dans l'expression de 6Vcn+1, les simplexes singuliers dans lesquels 0 est un
sommet se détruisent. On peut le faire directement, mais c'est inutile ; en effet,
si iBn+l est l'injection canonique de BB+i dans R"+1, on a rBntI = xB+1 dans
^+1(R"+1) en raison du choix des r\„ (24.19.1X et SÏBntl est somme de courants
portés par A„ (24.17.2.2); Pinjectivité de l'application canonique (24.20.2.1)
montre donc, comme dans (24.21.6), que l'expression de 60xH+l ne peut contenir
de simplexes singuliers dont le support rencontre l'intérieur de BB+1.
Ordonnons maintenant l'ensemble des sommets de <5 de façon que af < a}'
si i < j, quels que soient y et y' ; alors, avec les notations de (24.26), le n-cycle y„
appartient à L„(S ; Z). Utilisant (24.28.1), la classe d'homologie de y„ est un
multiple entier d'un générateur de H„(S ; Z) ; mais comme dans y„ les coefficients
des simplexes singuliers (formant la base de LB(6 ; Z)) sont ± 1, cette classe
d'homologie est elle-même un générateur de H„(® ; Z) ; c'est son image c„ dans
H^A, ; Z) ou dans H„(S„ ; Z) qu'on appelle la classe fondamentale d'homologie
singulière.
Remarque (24.28.4). — Comme H„(S„ ; R) = H„(SB ; Z) ® ZR (24.27.3),
H„(SB ; Z) s'identifie à un sous-Z-module du R-espace vectoriel HB(S„ ; R) ; la
restriction à H„(SB ; Z) de l'isomorphisme de de Rham H.(SB ; R) H,(SB)
est donc injective. Nous allons voir que l'image de la classe fondamentale
c„ e H^S, ; Z) par cette injection est la classe (- 1)"[SB], où [S„] est la classe
fondamentale de l'homologie des courants (24.12.10.3). En effet, de la relation
éV^+i = y„ on déduit, dans ^'(R""1"1) la relation 6xn+l = y„; de la formule
de Stokes pour les courants cellulaires (24.17.2.2), on déduit que si Fy est la
o
face de BB+1 contenant Uy = Im(aj; aï ... aï), le courant aï ... aj)~ est
l'image dans (?B'(R"+1) du n-courant fUy sur Fy (iVy : Uy -+ F, étant l'injection
canonique) par l'injection canonique Fy -* R"+1, lorsqu'on munit Ty de
l'orientation vers l'intérieur de B„+, si n est impair et de l'orientation vers l'extérieur
de B„+i si n est pair (24.14.1). L'image par la projection x -» x/|| x || du
courant y„ est donc le n-courant sur S„ (orientée vers l'extérieur) qui correspond
(17.5.1.1) à la fonction constante — 1 si n est impair et à la fonction constante 1
si n est pair.
PROBLÊMES
1) On appelle complexe simplicial abstrait (fini) un couple (A, €>0) formé d'un ensemble
fini A (dont les éléments sont appelés les sommets du complexe), et d'une partie ®0 de 3HA), telle
que si X e ®0 et Y <= X, alors YeS0; les éléments non vides de S0 sont appelés les simplexes
abstraits du complexe ; pour X e ®0 non vide, Card(X) — 1 est appelé la dimension de X ; on peut
supposer que A est l'ensemble des simplexes de dimension 0.
Soient X un complexe simplicial euclidien compact, S sa subdivision simpliciale, A l'ensemble
de ses sommets ; à tout simplexe euclidien U e S, on fait correspondre la partie I0(U) de A formée
des sommets de U ; si S0 est l'ensemble formé de l'ensemble vide et des £0(U), où U parcourt S,
le couple (A, €0) est un complexe simplicial abstrait, dit associé à (X, S).

28. HOMOLOGIE DES COMPLEXES SIMPLICIAUX EUCLIDIENS COMPACTS 179
Inversement, soit (A, ®0) un complexe simplicial abstrait non vide, et soit N + 1 le nombre
de ses sommets ; on identifie A à l'ensemble des entiers j tels que 0 < j < N. On associe à (A, ®0)
le sous-espace X de AN formé des points x — ({°, ..., £N) vérifiant la condition suivante :
l'ensemble des indices j tels que {■* > 0 appartient à @0. Pour tout Z e ®0 non vide, soit £(Z)
l'ensemble des x e X pour lesquels les indices j tels que (J > 0 sont exactement les éléments de Z ;
montrer que HZ) est un simplexe euclidien, que lorsque Z parcourt ®0 - { 0 }. les E(Z) forment
une subdivision simpliciale S de X, X étant un complexe simplicial euclidien compact pour la
subdivision 6 ; enfin (A, ®0) est associé à (X, S). On dit que (X, S) est la réalisation canonique
de (A, ®„).
On dit qu'un complexe simplicial euclidien compact (X, 6) auquel est associé un complexe
abstrait (A, ®0) est une réalisation de (A, ®„). Tout complexe simplicial abstrait (fini) admet donc
une réalisation ; montrer que toutes les réalisations d'un même complexe simplicial abstrait sont
homéomorphes.
2) Soit (X, S) un complexe simplicial euclidien compact. Dans l'ensemble Sx®, soit 91
le graphe d'une relation d'équivalence telle que, si (U, V) e 91, U et V sont des simplexes de même
dimension. Pour tout couple (U, V) e 91 on suppose en outre donnée une bijection hvv de U sur V
qui_est une application linéaire affine, se prolongeant donc en une application linéaire affine
de U sur V, encore notée hvy. On suppose que :
1° pour tout UeS, hvv est l'identité;
2° si (U, V) e 91 et (V, W) e 91, fcuw == fcvw ° fcuv ;
3° si U' est une face de U, de sorte que fc0v(U') = V est une face de V, on a (U', V) e 91
et Vy est la restriction de huy à U'.
Pour tout x 6 X, soit F(x) le simplexe (unique) de ® contenant x. On définit sur X une
relation de graphe Rx tel que (x, y) e Rx si le couple (F(x), F(y)) e 91 et si y = /iF(a)>F(y)(x). Montrer
que Rx est le graphe d'une relation d'équivalence fermée sur X (section 24.22, problème 8) ; on se
propose de montrer que X/Rx est homéomorphe à un complexe simplicial euclidien compact.
a) Soit n : X -» X/Rx l'application canonique. On suppose d'abord que Rx vérifie les
conditions suivantes :
a) Deux sommets distincts d'un même simplexe de @ ne sont pas équivalents pour Rx.
P) Si U = Im(a0a, ... a,) et V = Im(b„ b, ... b,) sont deux simplexes de ® tels que
(aj, bj) e Rx pour 0 « j < p, alors (U, V) e 91.
Soit alors (A, ®0) le complexe simplicial abstrait associé à (X, ®) ; soit A' = n(A) et soit ®ô
l'ensemble des parties n(Z) de A', où Z parcourt S0 ; montrer que X/Rx est homéomorphe à une
réalisation du complexe simplicial abstrait (A', ®J>).
b) Si l'on remplace la subdivision @ par Sd2(S), montrer que pour la relation
d'équivalence Rx- les conditions a) et p) sont vérifiées pour Sd2(3).
3) a) Dans le cercle U : | z | = 1, soit 91 l'ensemble des m arcs ouverts Lk définis par
2kn 2(fc + 1)ji
— < 9 < pour z=e, avec 0</t<m-l. On considère une partition { 51,, 9l2, ..., 91» }
m nx
de 91 en h parties non vides, 9L, comportant ms éléments de sorte que m = mt + m2 + ... + mt.
Soient pour tout j, Cj un élément de 91,, pt et qt deux entiers » 0 tels que p} > 1, pj + qt = mj.
On définit dans U une relation d'équivalence R0 de la façon suivante : les points exp(2fcni/m)
(0 ^ k ^ m - 1) forment une classe d'équivalence. Pour chaque j, soient CJ" = Cp Cj2', .... C{/'\
Cff'+l\ ..., cy'+,j) les éléments de 91^ et pour tout xeC„ soit K0(x) l'ensemble formé de x,
des pj - 1 points déduits de x par les rotations transformant C, en les Cj" pour 2 < / ^ pj, et
des qj points déduits de x par les symétries transformant Ct en les C}" pour p} + 1 < 1 < pj + qj.
Les classes d'équivalence autres que celle des points exp(2fcjti/m) sont les R0(x) pour xeCj, 1
Soit R la relation d'équivalence dans le disque fermé D : | z | ^ 1, dont les classes
d'équivalence sont celles de R0 et les ensembles { z } pour | z | < 1. Montrer que l'espace X = D/R est
homéomorphe à un complexe euclidien compact (utiliser le problème 2).
b) Soient n, = \pt — qj\, d le plus grand commun diviseur de n,, .... nh si ces nombres
ne sont pas tous nuls. Montrer que l'on a H0(X ; Z) s Z, H,(X ; Z) s Z* et H2(X ; Z) S Z si tous
les nj sont nuls, H,(X; Z) s Z*-1 0(Z/dZ) et H2(X; Z) = {0} dans le cas contraire (consi-

180 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
dérer X comme obtenu par attachement d'un disque à l'espace Gh bouquet de h cercles ((24.22.11)
et (24.22.12))).
c) On considère le cas où m = 4, h = 2, Sli est formé des arcs L0 et L2, 4l2 des arcs Lt et L3,
P\ = <li = Pi = I2 — 1- Montrer que X est alors homéomorphe au tore T2.
d) On prend m = 5, h = 3, 91, formé des arcs L„ et L2> 812 des arcs L, et L4, 213 du seul
arc L3, p, = q, = p2 = g2 = p3 = 1. Montrer que X est alors homéomorphe au complémentaire
dans T2 d'un voisinage ouvert d'un point, homéomorphe à R2.
e) On prend m = 4g pour un entier g > 1 et h = 2g ; pour 0 ^ j ^ g - 1, on prend
9I2j+, = { L4> L4;+2 }, 9l2j+2 = { L4J+ „ L4J+3 }, tous les pt et qt égaux à 1. Montrer que X est
homéomorphe à la somme connexe (16.26, problème 15) de g surfaces T2 (raisonner par récurrence
sur g en utilisant c) et d)).
4) On dit qu'un espace compact métrisable X est triangulable s'il est homéomorphe à un
complexe simplicial euclidien compact (Y, S); les images par un homéomorphisme de Y sur X
des simplexes de S forment une triangulation de X et on dit que ces images sont les simplexes
(curvilignes) de la triangulation. Montrer que pour qu'un espace compact X soit triangulable, il faut et
il suffit qu'il existe un complexe simplicial abstrait (A, ®0) et pour tout Z e ®0 de dimension j
un simplexe singulier sz : A, -* X qui soit une application injective, avec les propriétés suivantes :
1° les images sz(A,) sont deux à deux disjointes ; 2° la réunion de ces images est X ; 3° si Z' c Z
est de dimension - 1, sz. = sz ° o-, pour un i ^ j (Considérer une réalisation de (A, S0))-
5) Soit (X, S) un complexe simplicial euclidien compact. Montrer que pour toute partie
finie F de X, il existe une subdivision S' de S telle que tous les points de F soient des sommets
de S'.
6) Dans le plan projectif complexe P2(C), on considère une courbe algébrique
irréductible X définie par une équation
/ + a,(x, z)/"1 + ... -(- a„(jt, z) = 0
en coordonnées homogènes, le polynôme du premier membre étant irréductible ; soit A(x, z) son
discriminant, S l'ensemble fini des points (x, z) 6 P,(C) tels que A(x, z) = 0. On se propose de
montrer que X est triangulable (problème 4).
a) On peut supposer que le point à l'infini (1, 0) de Pt(C) n'est pas dans S. Pour tout point
{x, y, z) e X, on pose f(x, y, z) = (x, z). Pour tout point s = (x, z) <f S, il existe un voisinage ouvert V,
de s dans Pt(Q tel que /"'(V,) soit réunion disjointe de n ouverts U^ tels que la restriction de /
à U'j) soit un difféomorphisme de Uj/' sur V, pour 1 <y < n. Pour tout point s 6 S, f~\s) est
formé de m points distincts t,, ..., tm avec m < n; il existe un voisinage ouvert V, dans P,(C)
tel que /"'(V.) soit réunion de p < m ouverts U£" dont deux quelconques ne peuvent avoir en
commun qu'un des points tk ; pour chaque j, il existe une application holomorphe bijective du
disque | u | < 1 de C sur U£" de la forme u -► (u", au*' + ..., 1) où pt > 1, qj > 1 est premier
à pj (section 23.15, problème 5).
b) Déduire de a) qu'il existe une triangulation de Pi(C), dont les points de S sont des
sommets et qui est telle que pour tout simplexe Z de cette triangulation, autre qu'un point de S, / " '(Z)
soit réunion disjointe de n ensembles Zk dans X tels que la restriction de / à chacun des Zk soit
un difféomorphisme de Zk sur Z (recouvrir P,(C) par un nombre fini d'ouverts V, et utiliser le
problème S pour former une triangulation de Pt(C) dont chaque simplexe est contenu dans un de
ces ouverts).
c) Montrer que les Zk et les points de /_1(S) forment la triangulation cherchée de X (*).
7) a) Soit (X, 6) un complexe simplicial euclidien compact contenu dans un RN. On suppose
qu'il existe un voisinage ouvert V de X dans RN et une application continue r :V -* X telle que
r(x) = x pour tout x 6 X. Si U c X est un simplexe de S ouvert dans X (ce qui revient à dire qu'il
n'est pas une facette d'un autre simplexe de S), montrer qu'il existe un voisinage ouvert W de
X - U et une application continue r" de W dans X - U telle que r'(x) = x pour tout x e X - U.
(*) On montre que toute variété différentielle compacte est triangulable [222 ], ainsi que toute
intersection d'hypersurfaces algébriques (lisses ou non) dans un espace projectif complexe [175].

28. HOMOLOGIE DES COMPLEXES SIMPLICIAUX EUCLIDIENS COMPACTS 181
(Observer que dans U, il y a un voisinage ouvert T de Fr(U) et une application continue r" de T
dans Fr(U) telle que r"(x) = x dans Fr(U).)
b) Déduire de a) que tout complexe simplicial euclidien compact est un rétracte de voisinage
(section 24.22. problème 1). (C'est évident pour Ap; partir de Ap et appliquer a) par récurrence, en
utilisant le problème 1 pour voir qu'on peut obtenir ainsi tout complexe simplicial euclidien
compact).
8) Soient (X, <5) un complexe simplicial euclidien compact, F une partie fermée de X. Soit U
un simplexe de ® tel que ; 1° aucun simplexe de <3 dont U est une facette et qui est distinct de U
ne contient de point de F ; 2° F n U ^ U. Montrer qu'il existe alors une application continue /
de F dans X telle que /(x) = x en tous les points de F n'appartenant à aucun simplexe de S dont U
est une facette, et que /(F n U) soit contenu dans la frontière de U.
9) Soit (X, S) un complexe simplicial euclidien compact. Si n est la plus grande des
dimensions des simplexes de <5, montrer que la dimension topologique (section 24.24, problème 6)
de X est égale à n. (Si X c RN, projeter orthogonalement X sur un sous-espace vectoriel V de RN
de dimension n, tel que la projection sur V d'une quelconque des variétés linéaires engendrées
par les simplexes de ® soit injective).
10) Soient X, Y deux espaces compacts métriques, d, d'les distances sur X et Y.
a) Étant donné un nombre e > 0, on dit qu'une application continue / de X dans Y est
une e-application si pour tout y6 Y, le diamètre de /"'(y) est < e. Montrer qu'il existe alors
ô>0 tel que l'image réciproque par / de tout ensemble de diamètre <S dans Y ait un diamètre <e.
b) Montrer que si Y est de dimension topologique n et si, pour tout e > 0, il existe une
E-application continue de X dans Y, la dimension topologique de X est < n.
11) Soient X un espace compact métrisable, (U.)MA un recouvrement ouvert fini de X.
Soit ®0 la partie de Ç(A) formée des ensembles H c A tels que l'intersection des U« pour a e H
soit non vide. Le couple (A, <s0) est un complexe simplicial abstrait, qu'on appelle le nerf du
recouvrement (U.) ; la réalisation canonique (N, S) de (A, S0) (problème 1) est appelée le nerf
euclidien de (U.).
a) Soit (/J.«A une partition continue de l'unité subordonnée au recouvrement (U,), et soit f
l'application x -» (f^x))„K de X dans RA ; montrer que f est une application continue de X dans
le nerf euclidien N de (U„) ; en outre, si les U, ont tous un diamètre < e, / est une £-application
(problème 10).
b) Déduire de a) et des problèmes 9 et 10 que pour que X ait une dimension < n, il faut et
il suffit que pour tout e > 0, il existe une E-application de X dans un complexe simplicial euclidien
compact de dimension 4 n.
c) Déduire de b) que si X et Y sont deux espaces compacts métrisables, on a
dim(X x Y) « dim(X) + dim(Y),
l'égalité ayant lieu si X et Y sont des complexes simpliciaux euclidiens compacts.
12) Soient X un espace compact métrisable, (P, S) un complexe simplicial euclidien compact
de dimension topologique n contenu dans un RN, g une application continue de X dans P, / une
application continue de X dans la frontière Y du simplexe A„+, par rapport à la variété linéaire E
de R"+2 qu'il engendre.
a) Pour toute application cp de l'ensemble des sommets de S dans l'ensemble des sommets
de A.+ 1, il existe une application continue 0 de P dans Y et une seule qui prolonge <p et est telle
que la restriction de <I> à un simplexe U de € soit une application linéaire affine de U dans une
facette de
b) Montrer qu'il existe une application <p de l'ensemble des sommets d'une subdivision
barycentrique ®m convenable de S dans l'ensemble des sommets de A„+, telle que, si <J> est
l'application correspondante de P dans Y, / et O ° g soient homotopes. (Prendre m assez grand pour
que, pour tout simplexe U de ®„, f(g~ '(U)) soit contenu dans un des ensembles St( v4), où les vt
sont les sommets de AI+1.)
13) Soit X un espace compact métrisable de dimension topologique < n. Montrer que
toute application continue / d'un sous-espace fermé A de X dans S„ peut être prolongée en une

182 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
application continue de X dans S.. (Utiliser le problème 1 e) de la section 24.22, et les problèmes 11b)
et 12 ci-dessus).
14) Soient X un espace compact métrisable, A une partie fermée de X, / une application
continue de A dans S.. Montrer que si l'espace localement compact X — A est de dimension
topologique < n, / peut être prolongée en une application continue de X dans S,. (Utiliser le
fait que S„ est un rétracte de voisinage, et le problème 13).
15) Soit X un espace compact métrisable. On suppose que toute application continue d'une
partie fermée quelconque de X dans S, se prolonge en une application continue de X dans S..
Montrer que toute application continue d'une partie fermée de X dans S,+ 1 se prolonge en une
application continue de X dans S„+,. (Soit f une application continue d'une partie fermée A de X
dansSa+1,et soit B = /"'(SJ. La restriction g de / à B se prolonge en une application continue h
de X dans S.. Montrer que / et la restriction de h à A sont homotopes et utiliser le problème 1 e)
de la section 24.22).
16) Soit X un espace compact métrisable de dimension topologique finie. On suppose que
toute application continue d'une partie fermée quelconque de X dans S. se prolonge en une
application continue de X dans S,.
a) Soit / une «-application de X dans un complexe simplicial euclidien compact (P, S)
de dimension N > n, et soit 6 > 0 tel que l'image réciproque par / de tout ensemble de diamètre < 5
dans P ait un diamètre < e. Soit <3m une subdivision barycentrique de S telle que les simplexes
de S„ aient un diamètre < ô. Si U est un simplexe de S„ de dimension N, montrer qu'il existe
une application continue g de X dans P qui est une e-appUcation, coïncide avec / dans le
complémentaire de /~'(U) et est telle que g-1(U) - 0. (Appliquer le problème 15 à la partie fermée
/" '(FifU)) de X, en remplaçant n par N - 1 et S. par Fr(U)).
b) Déduire de a) que la dimension topologique de X est < n.
c) Conclure que, pour qu'un espace compact métrisable X ait une dimension topologique < n,
il faut et il suffit que toute application continue d'une partie fermée quelconque de X dans S. se
prolonge en une application continue de X dans S..
17) Soit A un sous-espace fermé d'un espace localement compact X, métrisable et séparable.
Montrer que si dim(A) < n et dim(X - A) < n, on a dim(X) s? n. (Se ramener au cas où X est
compact, et utiliser les problèmes 16 c) et 14 ci-dessus).
En déduire que si X est réunion finie de sous-espaces fermés de dimension topologique < n,
on a dim(X) < n.
18) Soit X un espace localement compact métrisable et séparable; pour tout xeX, on
appelle dimension de X au point x la borne inférieure (finie ou + oo) des dimensions topologiques
des voisinages compacts de x dans X. La dimension topologique de X est la borne supérieure des
dimensions aux points de X. On appelle noyau d'ordre n de X l'ensemble des points de X où la
dimension est > n.
a) Montrer que si dim(X) > n, le noyau d'ordre n de X est un sous-espace fermé non vide
dont la dimension en chacun de ses points est > n. (Si N est le noyau d'ordre n de X et V un
voisinage compact de x e N dans X, observer que V n QN est de dimension < n — 1 et utiliser
le problème 17 ci-dessus).
b) Si X est réunion d'une suite de sous-espaces fermés X, de dimension < n, montrer que
dim(X) < n. (Si l'on avait dim(X) > n, le noyau N d'ordre n + 1 ne serait pas vide ; en déduire
que N n X, contiendrait un point intérieur à N pour un indice i au moins et par suite qu'on aurait
dim(X,) > n + 1.)
c) Déduire de b) que si X est une variété différentielle pure de dimension n (au sens de
(16.1.5)), la dimension topologique de X est égale à n.
19) Soit X un espace compact métrisable de dimension topologique < n, et soient A, B
deux sous-espaces fermés non vides sans point commun dans X. Si d est une distance définissant
la topologie de X, soit a = d(A, B) > 0.
a) Soit 91 un recouvrement ouvert fini de X dont les ensembles ont un diamètre < a/2 et
dont le nerf euclidien (N, S) (problème 11) soit de dimension < n. Soit / une application continue
de X dans N définie par le procédé du problème 11 a). Soient Pt la réunion des simplexes de S
dont l'adhérence rencontre /(A), Q la réunion des facettes de ces simplexes dont l'adhérence ne

28. HOMOLOGIE DES COMPLEXES SIMPLICIAUX EUCLIDIENS COMPACTS 183
rencontre pas /(A), P2 la réunion des autres simplexes de S. Montrer que /"'(Pi) et f'\P2)
sont ouverts, et que les traces sur /"'(Q) des ensembles de 91 forment un recouvrement dont le
nerf est de dimension < n — 1.
b) Déduire de a) qu'il existe deux ensembles ouverts A', B' contenant respectivement A
et B, dont les adhérences ne se rencontrent pas, et un recouvrement ouvert 91' de X plus fin que 91,
tel que les traces sur X — (A' u B') des ensembles de 9t' forment un recouvrement dont le nerf est
de dimension < n - 1. (Utiliser (12.6.2) et considérer un voisinage fermé assez petit de f'l{Q)).
c) Conclure qu'il existe un ensemble fermé C c X, de dimension < n - 1, et qui sépare A
et B, c'est-à-dire que X — C est réunion de deux ouverts sans point commun contenant
respectivement A et B (appliquer b) à une suite de recouvrements (91.) de X tels que le maximum des diamètres
des ensembles de 91. tende assez vite vers 0).
20) Soit X un espace compact métrisable ayant la propriété suivante : deux points distincts
de X peuvent être séparés (problème 19) par un ensemble fermé de dimension < n — 1. Tout
point de X possède alors un système fondamental de voisinages ouverts dont la frontière est de
dimension < n — 1.
a) Soit 9t un recouvrement ouvert fini de X. Montrer qu'il existe un recouvrement ouvert
fini 91' plus fin que 9t et tel que la réunion F des frontières des ensembles de 91' ait une
dimension < n - 1. Montrer ensuite qu'il existe un recouvrement fini 91, de F par des ensembles ouverts
dans X, dont chacun est contenu dans un ensemble de 91', et dont le nerf est de dimension < n - 1.
En déduire un recouvrement ouvert fini 91" de X tout entier, plus fin que 91' et dont le nerf est de
dimension < n (on pourra utiliser (12.6.2) et procéder par récurrence en rangeant les ensembles
de 9)' en une suite finie).
b) Conclure que l'espace X est de dimension < n.
21) Montrer que pour qu'une partie fermée X de R* soit de dimension topologique n, il
faut et il suffit qu'elle ait un intérieur non vide. (Se ramener au cas où X est compact, donc contenu
dans un simplexe P assez grand. Pour prouver que la condition est nécessaire, raisonner par
l'absurde en considérant une subdivision simpliciale S de P, dont les simplexes sont
arbitrairement petits, et utiliser le problème 8 et le problème 10 pour montrer que X serait de
dimension < n - 1).
22) Soient (X, S) un complexe simplicial euclidien contenu dans un espace RN, et soit T
un sous-groupe commutatif de GL(N, R) qui transforme tout simplexe de 6 en un simplexe de S.
Soit (Y, Z) un sous-complexe de (X, €>), c'est-à-dire que l'on a Z c S pour ce complexe
simplicial ; supposons en outre que tout simplexe de ® soit l'image par une application de T d'un
simplexe de I.
a) On suppose que pour un entier p > 1, on ait HP(Y ; A) = { 0 } pour tour anneau
commutatif A. Montrer alors que l'on a HP(X ; Z) = { 0 }. (Remarquer que toute chaîne de la
subdivision S peut s'écrire comme chaîne de la subdivision Z à coefficients dans l'algèbre de groupe ZIT-],
de sorte que L,(® ; Z) est muni d'une structure de Z[r]-module, dont les simplexes singuliers
de L,(X; Z) forment un système générateur; si a est l'idéal de Z[r] annulateur d'un simplexe
singulier de LJLZ ; Z), écrire que H,(Y ; Z [rj/o) = {0}.)
b) On suppose que Y est un simplexe euclidien fermé de dimension n, Z étant formé de ses
facettes. Montrer que si n est l'intersection des idéaux de Z[r] annulateurs des n + 1 faces de Y,
H,(X ; Z) = {0 } pour 1 < p < n — 1, et H.(X ; Z) est isomorphe au Z-module n/m, où m est
■'annulateur de Y.
23) Dans l'espace C+1 où on note z0, z„ ..., z, les coordonnées, on appelle variété de
Pham une partie V = V(v0, v, v.) définie par une équation de la forme
z"0° + z\> + ... + z'K-= l
où les Vj sont des entiers > 2 (0 < j $ n) ; c'est une sous-variété holomorphe de C+ \ de
dimension (réelle) 2n (16.8.9). Soit T le sous-groupe commutatif de GL(n + 1, C) engendré par les
n + 1 rotations
r} : (z0 Zj-i> z> Zj+i *„) — Uo, ■ ■ •. z,_„ e2""'Zj, zJ+„ ..., z,)
pour 0 < j < n.

184 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
a) Pour tout z = (z0, z„ ..., z.)eC"+\on pose 3ti = (£z0, 3tzu #z„). Soit H
l'hyperplan complexe d'équation z0 + z, + ... + z, = 1 ; alors l'application (z, t) -» tâtz + (1 — t)z
de H x [0,1] dans H est une rétraction par homotopie de H dans H n R"+1. Montrerd'autre
part qu'on définit une rétraction par homotopie F de H n R"+1 sur le simplexe fermé A„ de la
m
façon suivante : soit x = Y, *j*j un point de H n R"+1 n'appartenant pas à A„ de sorte que
. J-o
S Xj = 1, mais il y a une partie non vide J de {0, 1 n } formée des indices tels que xt < 0 ;
on pose alors F(x, t) = (1 - OZ*/»/ + (1 - ' + ( '/X*. ) }£■*»•» Pour 0 < t < 1. Par compo-
Jml \ \ kil //uj _
sition, on définit donc une rétraction par homotopie G de H dans A,. _
b) Montrer qu'il existe une rétraction par homotopie G0 de V sur g_1(A«) telle que
g(G0(z, t)) = G(g{z), t). (En projetant G(z, t) sur chacun des facteurs de C"+ ', se ramener à montrer
que pour une rétraction par homotopie G; de C sur l'intervalle [0, 1] de R, il y a une rétraction
par homotopie G} de C sur l'image réciproque de [0, 1 ] par l'application g}: z -* z"' telle que
g/Gfc, t)) = G/g/z), t).)
c) Montrer que g '(A.) est homéomorphe au complexe simplicial euclidien X réunion
de A„ et de ses transformés par les éléments de T. En utilisant le problème 22, conclure que
r
H^X; Z) = {0} pour p * 0 et p # n, et que H„(V; Z) est isomorphe à Z* où p = \~\ (v, - 1)
J-o
(montrer que les n-cycles de X sont les multiples a. la„, où a parcourt l'idéal principal de Z[r]
engendré par (1 — r0Xl — r,) ... (1 — r„)) (théorème de Pham).
29. La cohomologie singulière.
(24.29.1) Soit X un espace topologique séparé. Pour tout groupe commutatif
(écrit additivement) G, on appelle p-cochaînes singulières surXà valeurs dans G
les homomorphismes du groupe commutatif S/X ; Z) des p-chaînes singulières
sur X (à coefficients entiers) dans le groupe commutatif G. Elles forment donc
un groupe commutatif
(24.29.1.1) S"(X ; G) = Hom(Sp(X ; Z), G).
Si G est le groupe additif d'un anneau commutatif A, on écrit SP(X ; A) au
lieu de SP(X; G); il est clair que SP(X; A) est un A-module, le produit af d'un
élément aeA et d'une p-cochaîne / étant la p-cochaîne z -» oc/(z); SP(X; A)
n'est donc autre que le A-module dual (SP(X ; A))* du A-module SP(X ; A) des
p-chaînes singulières.
Pour chaque p ^ 0, le bord formel 60 est un homomorphisme du groupe
SP(X ; Z) dans le groupe SP_ X(X ; Z) ; il lui correspond canoniquement un
homomorphisme
(24.29.1.2) d0 : Sp" *(X ; G) -> SP(X ; G)
égal à Hom(£0, 1g)> et Qui est donc défini par
(24.29.1.3) (d0/Xz) = /(M
pour tout z e SP(X ; Z) et toute / e Sp X(X ; G) ; on dit que d0f est le cobord

29. LA COHOMOLOGIE SINGULIÈRE
185
de la cochaîne singulière / Pour un anneau commutatif A, d0 est identifié au
transposé du bord formel 60, considéré comme application A-linéaire du
A-module SP(X ; A) dans le A-module Sp_ i(X ; A).
La définition du bord formel (24.20.3.1) donne pour le cobord d0
l'expression
(24.29.1.4) (d0/X*) = t ( - ° oj)
pour tout simplexe singulier s e #(AP ; X) et toute cochaîne / e Sp_ '(X ; G).
U est clair que d0°d0 = 0, et par suite la somme directe
S*(X;G) = ©SP(X;G)
pjsu
est un groupe différentiel gradué, auquel on peut appliquer les définitions
générales concernant la cohomologie (Ann. 30.2). Le sous-groupe gradué Z*(X ; G)
des cocycles de S'(X ; G) est la somme directe
Z'(X;G)= ©ZP(X;G)
p^O
où ZP(X ; G) est le groupe des p-cochaînes / telles que d0f = 0. Le sous-groupe
gradué B'(X ; G) des cobords de S"(X ; G) est la somme directe
B"(X;G)= ©BP(X;G)
où BP(X ; G) est le sous-groupe de Zp (X ; G) formé des />-cochaînes d0g, où g
parcourt Sp_ X(X ; G). Le groupe gradué H'(X; G) = © HP(X; G), où
HP(X ; G) = ZP(X ; G)/BP(X ; G)
est appelé le groupe (total) de cohomologie singulière de X à coefficients dans G,
HP(X ; G) étant le p-ème groupe de cohomologie singulière de X à coefficients
dans G. Pour un anneau commutatif A, HP(X ; A) est un A-module. On a
évidemment H'(0; A) = {0}.
Exemples (24.29.2). — Comme on a convenu de poser S_j(X;Z) = {0}
(24.20.1), on a aussi S_1(X; Z) = {0}. Comme S0(X ; Z) s'identifie au groupe Z(X)
des combinaisons linéaires formelles des points de X à coefficients entiers,
S°(X ; G) s'identifie au groupe Gx de toutes les applications de X dans G ; le
sous-groupe B°(X ; G) est réduit à 0, et H°(X ; G) = Z°(X ; G) est le sous-groupe
de Gx formé des applications f :X -* G telles que f(x) = /(y) pour tous
les couples de points x, y de X qui peuvent être joints par un chemin. En
particulier, si X est une variété différentielle connexe, les seules fonctions ayant cette
propriété sont les constantes (16.26.10), donc
(24.29.2.1) H°(X ; G) s G .

186 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
Soit (Xa)aeA une famille d'ouverts deux à deux disjoints dans un espace
séparé X, telle que X soit la réunion des Xa. Comme SP(X ; A) s'identifie à la
somme directe © SP(X„ ; A) (24.22.5), SP(X ; A) s'identifie au module produit
aeA
PI SP(X„ ; A) (Ann. 27.3) ; on voit aussitôt que pour que / e SP(X ; A) soit un
«A
cocycle (resp. un cobord), il faut et il suffit que chacune des composantes de f
sur les Sp(Xa ; A) le soit. Donc HP(X ; A) s'identifie au A-module produit
FI HP(X„ ; A), pour tout p > 0.
œA
(24.29.3) Soient X, Y deux espaces séparés, u : X -+ Y une application
continue; on a vu (24.20.1) qu'elle définit canoniquement un homomorphisme de
Z-modules
SJM-.SJXiZ) - S^YjZ);
il lui correspond canoniquement un homomorphisme
(24.29.3.1) Sp(u) : SP(Y ; G) -* SP(X ; G)
égal à Hom(Sp(«), 1G) et qui est donc défini par
(24.29.3.2) (Sp(hX/)Xz) = /(S,(«X*))
pour tout z e Sp(X ; Z) et toute / e SP(Y ; G). Si v est une application continue
de Y dans un espace séparé Z, on a Sp(u °u) = Sp(u) ° Sp(u). Si G est le groupe
additif d'un anneau commutatif A, Sp(u) est une application A-linéaire.
La commutativité du diagramme (24.20.3.2) entraîne que le diagramme
« transposé »
Sp(Y;G) ^ Sp+1(Y;G)
(24.293.3) s'iu> s"*Hu)
Sp(X;G) To Sp+X(X;G)
est aussi commutatif. L'image de ZP(Y ; G) par Sp(u) est donc contenue dans
ZP(X ; G) et l'image de BP(Y ; G) est contenue dans BP(X ; G) ; par passage aux
quotients, on en déduit donc un homomorphisme canonique de groupes commu-
tatifs
u* : HP(Y ; G) HP(X ; G)
qu'on note aussi Hp(u) si des confusions sont à craindre. Pour toute application
continue v : Y Z, on a Hp(i; ° u) = Hp(m) ° Hp(t;).
La propriété d'invariance par homotopie (24.22.2) se « transpose » pour la
cohomologie singulière :

29. LA COHOMOLOGIE SINGULIÈRE
187
(24.29.4) Soient X, Y deux espaces séparés, u et v deux applications continues
de X dans Y. Si u et v sont homotopes, les homomorphismes Hp(u) et Hp{v) de
HP(Y ; G) dans HP(X ; G) sont égaux.
En effet, avec les notations de (24.22.2.1), si l'on pose (pour A = Z)
h" = Homt/j,..,, 1G) : SP(Y; G) -+ Sp~l(X; G),
on déduit de (24.22.2.2) la relation
S'{v) - S"(u) = hp+1 o d0 + d0 ° h"
et par suite, si c est la classe de cohomologie de / e ZP(Y ; G), on a
Hp(v\c) - Hp(uXc)
puisque d0f = 0.
(24.29.5) Soient G, G' deux groupes commutatifs, h ; G -* G' un
homomorphisme de groupes. Pour tout espace séparé X, on en déduit un
homomorphisme de groupes gradués :
qui à toute p-cochaine / 6 SP(X ; G) fait correspondre la p-cochaine
h° f e SP(X ; G'). Il est immédiat que le diagramme
est commutatif, et par suite hm un homomorphisme de groupes différentiels
gradués, d'où l'on déduit un homomorphisme
/»«:H'(X;G) -> H'(X;G')
de groupes gradués (Ann. 30.3).
Si X, Y sont deux espaces séparés, u : X -» Y une application continue,
on vérifie aussitôt que le diagramme
hp+1 = Hom(/v la) : Sp+ X(Y ; G) - SP(X ; G),
et
A„ = Homih.ixx» h) : S'(X ; G) -. S'(X ; G')
S'(X;G) ^ S*(X;G)
S*(X;G0 sj S'(X;G')
S'(Y;G) ^ S*(Y;G')
S'(X;G) £ S'(X;G')

188 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
est commutatif, et on en déduit un diagramme commutatif d'applications de
groupes gradués
H"(Y;G) ^ H'(Y;G')
(24.29.5.1) H("»J H(u)
H'(X;G) v H'(X;G')
On notera que si h est injectif (resp. surjectif), il n'en est pas de même de h+
en général.
PROBLÈMES
1) Soit X un espace séparé tel que H.(X; Z) soit un Z-module libre gradué de type fini.
Montrer que H'(X; G) est canoniquement isomorphe à H'(X;Z)®ZG. Donner un exemple
où cette propriété est en défaut, bien que H.(X; Z) soit un Z-module libre.
2) Soit 0 -♦ G' -4 G A G" -► 0 une suite exacte de groupes commutatifs. Montrer
qu'on a une suite exacte de cohomologie.
... -» H'(X;G') ^ H'(X;G) S H'(X;G") 4 H'+1(X;G')
débutant par 0 -» H°(X ; G') ; l'application d se définit comme suit. Si /" est un p-cocycle de
Z'(X ; G"i on peut l'écrire /" = p\f\où / est une p-cochaîne de S'(X ; G) ; on a d0f = M.fi
où /' est une (p + l)-cochaîne de S'+l(X; G'); l'opérateur d fait correspondre à la classe de
cohomologie de /" celle de f.
30. Structure des groupes de cohomologie.
(24.30.1) Soit X un espace séparé. La définition (24.29.1.3) de d0 montre que
les p-cocycles / e ZP(X ; G) sont exactement les homomorphismes de SP(X ; Z)
dans G qui s'annulent dans Bp(X ; Z). D'autre part, si / = d0g, où g g S"~ \X ; G),
d0g s'annule dans Zp(X ; Z), donc est entièrement déterminé par sa restriction
à un Z-module libre Ep supplémentaire de Zp(X ; Z) dans Sp(X ; Z) (Ann. 31.2).
Comme §0 est un isomorphisme de Ep sur Bp_ ,(X ; Z), on voit que les cobords
/ e BP(X ; G) ne sont autres que les cochaînes de la forme g ° ô^, où g est un
homomorphisme de Bp_ t(X ; Z) dans G qui peut se prolonger en un homomorphisme
de Zp_ t(X ; Z) dans G ; cela entraîne en effet que g peut aussi se prolonger en
une (p - l)-cochaîne, puisque ZP_!(X;Z) admet un supplémentaire Ep_j
dansS,_I(X;Z).
Rappelons (Ann. 31.5) que cette description permet de définir un
homomorphisme canonique
(24.30.1.1) H"(X ; G) Hom(Hp(X ; Z), G)
et de prouver la proposition suivante (Ann. 31.6) :
(24.30.2) L'homomorphisme (24.30.1.1) est toujours surjectif; si Hp_ ,(X ; Z)
est un Z-module libre, l'homomorphisme (2430.1.1) est bijectif.

30. STRUCTURE DES GROUPES DE COHOMOLOGIE
189
Remarque (24.30.3). — Il résulte des définitions précédentes que si X, Y
sont deux espaces séparés, et u : X -> Y une application continue, le diagramme
est commutatif.
Exemples (24.30.4). — Lorsque X est un espace séparé sans torsion (24.27.3.2),
on a donc HP(X ; A) ^ (HP(X ; A))* pour tout p^Oet tout anneau commutatif A.
En outre, si X et Y sont deux espaces sans torsion, et u : X -> Y une application
continue, il résulte de (24.30.3.1) que l'on a Hp(u) = 'Hp(«), transposée de Hp(«).
Si de plus HP(X ; Z) est de type fini (donc isomorphe à un Z'), HP(X ; A) est
canoniquement isomorphe à HP(X ; Z) (g) ZA (donc à A') ; lorsque l'homomorphisme
canonique Z -+ A est injectif, HP(X ; Z) s'identifie alors canoniquement à un
sous-Z-module de HP(X ; A) savoir l'ensemble des classes de cohomologie des
p-cocycles de ZP(X ; A) qui prennent des valeurs entières pour les simplexes
singuliers.
(24.30.5) Si A est un corps commutatif, l'homomorphisme canonique
est bijectif, pour tout espace séparé X et tout p ^ 0.
C'est un cas particulier de (Ann. 32.4).
(24.30.6) Considérons maintenant le cas où X est une variété différentielle
pure compacte de dimension n. Nous allons reprendre les constructions des
Z-modules Ep, Fp, Gp et F, faites dans (24.27.4) de manière à avoir les propriétés
additionnelles suivantes :
1° Gp = F, n B/X ; Z) admet un supplémentaire Gp dans BP(X ; Z) ;
2° Fp, sous-module libre de Ep supplémentaire de Fp = Ep n Zp(X ; Z), est
contenu dans le supplémentaire libre E'„ de ZP(X ; Z) dans Sp(X ; Z) (24.30.1)
et admet un supplémentaire Fp dans Ep.
En effet, dans la construction de Ep, pour p = 0, désignons par E'ô l'image
par S0(n) du Z-module des 0-chaînes de la subdivision 6" de (24.27.1) ; alors
Eq o B0(X ; Z) est un Z-module de type fini du Z-module libre B0(X ; Z), donc
est engendré par des combinaisons linéaires d'une partie finie d'une base de
B0(X ; Z) ; le sous-module G0 de B0(X ; Z) engendré par cette partie finie admet
donc un supplémentaire G'0 dans B0(X ; Z) ; on prend E0 = Eô' + G0, et comme
Z0(X;Z) - S0(X;Z), on a ici F0 = E0, E0 = Fé = Fg = {0}.
Supposons ensuite Ep (donc Fp et Gp) définis et satisfaisant aux conditions 1°
Hp(Y;G) - Hom(Hp(Y;Z),G)
(24.30.3.1)
Hp(X ; G) - Hom(Hp(X ; Z), G)
(24.30.5.1) HP(X ; A) (Hp(X ; A))*

190 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
et 2° ci-dessus, et soit E'p+l l'image par Sp+1(7t) du Z-module des (p + l)-cycles
de <5", qui est un sous-module de type fini de Zp+ t(X ; Z) ; on voit comme plus
haut qu'il existe un sous-module libre de type fini Gp+1 de BP+1(X; Z),
contenant Ep+ ! n Bp+ i(X ; Z) et admettant un supplémentaire Gp+ ! dans BP+ i(X ; Z).
D'autre part, comme 6*0 est une bijection de Ep+ 2 sur BpfX ; Z), Fp+j = ôô '(G,,)
est un sous-module de Ep+1 admettant un supplémentaire Fp'+i dans Ep+1.
On prend alors Ep+1 = Ep+1 + Gp+, + Fp+ u et il est immédiat que les
conditions 1° et 2° ci-dessus sont vérifiées.
Avec ces choix des Ep, nous allons voir que, pour tout anneau
commutatif A, on peut, dans la description de HP(X ; A) donnée dans (24.30.1) remplacer
les Z-modules Sp(X ; Z), Zp(X ; Z), Bp(X ; Z) et E'p par Ep, Fp, Gp et F'p
respectivement.
Pour le voir, montrons d'abord que si / est une p-cochaîne qui est nulle
dans Zp(X ; Z) et dans F'^ alors / est un cobord. En effet, comme Gp_ x = 60(F'P),
la restriction de / à Ep peut s'écrire g ° 60, où g est un homomorphisme de
Bp_ i(X ; Z) dans A qui est nul dans Gp_, ; en raison des relations
Zp_,(X;Z) = Fp_1 + B,_,(X;Z) et G,., = F,.,nB,.,(X;Z)1
g se prolonge à Zp_ t(X ; Z) en prenant la valeur 0 dans Fp_ t ; d'où notre
assertion par (24.30.1).
Cela montre que tout p-cocycle / est cohomologue à un p-cocycle qui est
nul dans F, ; comme un tel cocycle est nul dans Bp.^X; Z) il est entièrement
déterminé par ses valeurs dans Ep = Fp © F'r Inversement, un homomorphisme
de Ep dans A qui est nul dans Gp se prolonge à Zp(X ; Z) en prenant la valeur 0
dans Bp(X ; Z), puis à Sp(X ; Z) en prenant la valeur 0 dans Fp. Il y a donc
correspondance biunivoque entre les p-cocycles / nuls dans F'p et les
homomorphismes f0 de Ep dans A, nuls dans Gp, qui en sont les restrictions. En outre,
pour qu'un tel homomorphisme f0 soit restriction d'un p-cobord g o ô0, où g est
un homomorphisme de Bp-t(X; Z) dans A, nul dans Gp_, et qui peut se
prolonger à Zp_ i(X ; Z), il est nécessaire que f0 = g0 ° 60, où g0 est un
homomorphisme de Gp_ t dans A, qui peut se prolonger en un homomorphisme g'0 de
Fp_! dans A. Mais inversement, un tel homomorphisme g0 se prolonge d'une
seule manière en un homomorphisme g de Bp_ ,(X ; Z) dans A, nul dans Gp_ t ;
puis g se prolonge d'une seule manière en un homomorphisme g' de Zp_ t(X ; Z)
dans A égal agi dans Fp_i, en raison des relations ZP_!(X ; Z) = FP_1 +Bp_i(X ; Z)
et Gp_! = Fp_! nBp_i(X;Z); ceci achève de prouver notre assertion.
(24.30.7) La possibilité de calculer H"(X ; Z) à partir de Ep, Fp, G, et F; permet
de déterminer entièrement ce Z-module à partir de Hp(X;Z) et Hp_i(X;Z).
En effet, partons pour cela des bases de Fp et Fp_! décrites dans (24.27.4). Le
A-module Hom(Ep, A) a pour base la base duale de celle de Ep, formée des fj

30. STRUCTURE DES GROUPES DE COHOMOLOGIE
191
(1 < y < r + s -I- t) et des j? (1 < k < u + d) tels que /j(ay>) = 1, jfK") = 1,
les valeurs de f} (resp. j£') aux autres éléments de la base de Ep étant nulles. Le
sous-module de Hom(Ep) A) formé des homomorphismes s'annulant dans Gp
est donc déterminé par la condition que, dans un tel homomorphisme, le
coefficient de fj pour 1 < j < r est 0, et le coefficient de fr+J pour 1 < j < s appartient
à l'annulateur ny** de l'idéal Aa'/P) dans A. D'autre part, le sous-module de
Hom(Ep) A) formé des homomorphismes qui s'écrivent g0 ° §0, où g0 est un
homomorphisme de Gp_ x dans A qui peut se prolonger à Fp_ i, est déterminé
par la condition que, dans un tel homomorphisme, le coefficient de fj pour
1 < j < r + s + t est 0, et le coefficient de //+« P0"1- 1 appartient à
l'idéal Aa,p_1) de A. On obtient donc la règle suivante :
(24.30.8) Le A-module de cohomologie singulière de X à coefficients dans un
anneau commutatif A est donné à partir des expressions (24.27.4.1) et (24.27.4.2)
deH,J[X;Z)et H,_»(X;Z)par
(24.30.8.1) H"(X; A)s(A/a(1|,"1)A)© ... ©(A/a(„p-l»A)©A'©n'i'»© ... ©n<p>
où ny** est l'idéal annulateur de a^'A dans l'anneau A pour 1 < j < s.
Ici encore, les notions plus avancées d'Algèbre homologique permettent
de voir que la donnée des Z-modules Hp(X ; Z) et Hp_ t(X ; Z) détermine
entièrement H"(X; A) pour tout espace séparé X et tout anneau commutatif A [160].
Exemple : cohomologie de P2(R) (24.30.8.2). — La règle (24.30.8.1) et la
détermination des HP(P2(R) ; Z) faite dans (24.22.13.1) montre que l'on a
H°(P2(R);A)S A,
(24.30.8.3) H'(P2(R) ; A) = n, annulateur de 2A dans A,
H2(P2(R);A)£ A/2A
Remarque (24.30.8.4). — Les formules (24.27.4.1), (24.27.4.2) et (24.30.8.1)
montrent qu'inversement, la connaissance des groupes HP(X ; Z) et Hp+ l(X ; Z)
pour une variété pure compacte X détermine explicitement le groupe
d'homologie H^XîZ).
PROBLÈMES
1) Les hypothèses et notations étant celles de (24.24.2) et (24.28.1), on note I l'intervalle [1, N ]
des indices des sommets ct de la subdivision S ; les simplexes singuliers formant la base de L'.(€> ; Z)
peuvent alors se noter sK = (ckl ctj ... ckp), où kt < k2 < ... < k, sont les éléments d'une
partie K de I. A l'injection canonique / : L'.(<3; Z) -> S.(X; Z) correspond par transposition
une surjection '/:S*(X;Z) -» (L'.(S;Z))*; (L'.(S;Z))* est un Z-module différentiel gradué,
dont le cobord d0 est donné, pour tout élément / e (LJ^S ; Z))*, par la formule
k-0

192 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
si K est formé des indices i0 < ii < ... < »',+ ,. L'application '/ donne un isomorphisme en
cohomologie.
2) La suite exacte de Z-modules
0 -» Z J> Z A z/2Z 0
où « 2 » désigne la multiplication par 2 dans Z, donne une suite exacte de cohomologie (section
24.29, problème 2)
... -» H'(X;Z) h H'(X;Z) ^ H'(X;F,) A H'+1(X;Z)
où fl est appelé l'homomorphisme de Bockstein. Si X est une variété compacte, ou un complexe
simplicial euclidien compact, les modules de cohomologie sont de type fini ; avec les notations
de (24.30.8), montrer que l'image de fi est l'ensemble des éléments de Hp+ '(X ; Z) d'ordre 2 et que
la dimension de cet espace vectoriel (sur F2) est égal au nombre des a/' qui sont divisibles par 2.
31. L'anneau de cohomologie singulière.
(24.31.1) Soient X un espace séparé, A un anneau commutatif. Pour tout
couple d'entiers p ^ 0, q > 0, on définit une application A-bilinéaire (f,g) -* f—g
(appelée cup-produit de / et g) de SP(X ; A) x S«(X ; A) dans SP+«(X ; A). Notons a'„
l'application linéaire affine (e0 et ... ep) de Ap dans Ap+4, et o'q l'application
linéaire affine (ep ep+1 ... ep+,) de A, dans Ap+,. On pose alors, pour tout
simplexe singulier se%(Ap+q; X),
(24.31.1.1) < / ~ g, s > = < / s o a'p >< g, s o < >
et on étend / —g en une p-cochaîne de SP+,(X; A) par linéarité.
Par linéarité, ces applications bilinéaires SP(X ; A) x S«(X ; A) -* SP+«(X ; A)
définissent sur S"(X ; A) = 0 SP(X ; A) une multiplication, qui fait de ce A-module
p»0
une A-algèbre graduée. On vérifie aussitôt que pour / e SP(X ; A), g e S«(X ; A),
h e Sr(X ; A), on a (/-g)-h = /~(g~«), autrement dit S'(X ; A) est une
algèbre associative; elle admet comme élément unité la 0-cochaîne identifiée
à l'application constante de X dans A égale à 1 (24.29.2).
On vérifie sur la définition que pour toute application continue m de X
dans un espace séparé Y, on a, pour / e SP(Y ; A), g e S*(Y ; A),
(24.31.1.2) Sp+«(«)(/ ~g) = (Sp(«)(/)) ~ (S"(u)(g))
autrement dit les Sp(w) définissent un homomorphisme souvent noté «*, de Valgèbre
graduée S'(Y ; A) dans Y algèbre graduée S'(X ; A).
(24.31.2) Montrons maintenant qu'avec les mêmes notations, on a
(24.31.2.1) d0(f - g) = (d0/) ~g + (-Wf~(dog).

31 . L'ANNEAU DE COHOMOLOGIE SINGULIÈRE
193
En effet, pour tout simplexe singulier se<#(Ap+,+ 1, X), on a
<dM~g),s> = <f~g, 60s} = " t \~ lY<f,s°°j°cr'p><g, soffj.oo-;'>
où comme d'ordinaire ctj = (e0 ... ê, ... 6,+,+!) pour 0 + q + 1.
Or
ap + k°<?q
Posons
p'p+,=(e0e, ... ep+1), Pp = (e0ei ... ep),
applications linéaires affines de Ap+1 et Ap respectivement dans Ap+,+ i, et
Pq = (ep + 1 ep+2 • ■ • ep + $+l) , Pq+ 1 = (ep ep+1 ••■•p+«+l)>
applications linéaires affines de A, et A,+ 1 respectivement dans Ap+,+ 1. Avec
ces notations, on peut écrire
p
I(- l)J</,soff.off;><g)Soff.o0--> =
J=0 (</Ms°Pp+,)>-(- iY+l<f,s°P;».<g,Sopz>
et de même
Z (- 1)* < / « ° 0"p + k 0 0-p >< g, S o ffp + l o aj' > =
1=1 </sop,>.(<ft Ms°p;'+i)>-<f,5op;'>).
Comme </, 630(sopp+,)> = <d0/,Sopp+1> et <g, 60(sop^+l)> = (d0g,s°p'q\l >,
cela prouve (2431.2.1).
La formule (24.31.2.1) montre donc que S'(X ; A) est une algèbre
différentielle graduée pour l'application cobord ; Z'(X ; A) = © ZP(X ; A) est donc
p»0
une sous-algèbre graduée de S'(X;A), et B'(X;A) = ©BP(X;A) un idéal
p£0
bilatère gradué de Z'(X ; A). Par passage au quotient, on définit par suite sur
H'(X ; A) = © HP(X ; A) une structure d'algèbre graduée, dite algèbre de cohomo-
p20
logie singulière de X, à coefficients dans A, où la multiplication est encore appelée
cup-produit et notée a ~ b. En outre, il résulte de (24.29.3.3) et (24.31.2.1) que
pour toute application continue m de X dans itn espace séparé Y, H'(«) est un
homomorphisme d'algèbres graduées de H "(Y; A) dans H'(X; A).
(e0 ... ëj ... ep+1)
(e0 ... ep)
(ep+1 ... Cp+4+1)
bp+*
• ep+«+1)
pour j^p,
pour j ^ p + 1,
pour j ^p,
pour k ^ 1.

194 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
(24.31.3) L'algèbre graduée H'(X;A) est anticommutative, c'est-à-dire que,
pour ap e H"(X ; A) et bq e H«(X ; A), on a
(24.31.3.1) bq ~ at = (- \y»ap ~ bq .
Pour chaque p > 0, définissons un endomorphisme xp de SP(X ; A) de la
façon suivante : pour tout simplexe singulier s e ^(Ap, X), on pose
(24.31.3.2) tp(s) = t]^ o (ep ep_, ... e, e0)
avec
(24.31.3.3) t]p = (- iy<'+1)/2(
et on définit ensuite xp dans S^X ; A) par linéarité. On a alors, pour toute chaine
zeSJ(X;A),
(24.31.3.4) 60(xp(z)) = xp-l(60z).
En effet, il s'agit de voir que l'on a
p p
fpE(- iys°(e„ ... êp-j ... eo) = i|rlI(- iy-Js°(ep ... êp_j ... e0)
et cela résulte de ce que la différence
fpjp + 1) , A fpjp ~ 1) , A
est paire.
Par transposition, on déduit de xp un endomorphisme 'xp de SP(X ; A).
Montrons que, si / e SP(X ; A) et g e S«(X ; A) on a
(24.31.3.5) 'xp+q(f ~ g) = ( - ir C^g)) ~ Cx^f)).
En effet, soit se(é(Âp+q, X) un simplexe singulier; on a
< W/ ~*)» s > = < / -s, Ws) >
= '/P+,</—«,s°(ep+,ep+,_1 ... e0)>.
Or, on peut écrire
s°(ep+, ... e0)°(e0 ... ep) = s°(ep+, ... e,) = tf^s ° a';)
s°(ep+, ... e0)°(ep ... ep+,) = s°(e, ... e0) = n,x^s°a'q)
donc
< / ~ g. tp+^s) > = V,,f,p+, < g, o a'q) >< /, Tp(s ° o-p') >

32. cohomologie singulière des complexes simpliciaux euclidiens 195
32. Cohomologie singulière des complexes simpliciaux euclidiens compacts.
(24.32.1) Soient X un complexe simplicial euclidien compact dans un espace RN,
S la subdivision simpliciale qui le définit (24.18.4). Avec les notations de (24.26),
on a vu (24.28.2) que l'injection canonique / : L'.(S ; Z) S.(X ; Z) donne un
isomorphisme en homologie ; comme L'.(S ; Z) admet dans S.(X ; Z) un
supplémentaire libre, il en résulte que l'homomorphisme transposé
'/:S*(X;Z) -» (L'.(®:Z))*
donne un isomorphisme en cohomologie H"(X; Z) -* H*(S; Z) (Ann. 31.8). On
et la relation (24.31.3.5) résulte de la définition (24.31.1.1) et du fait que
—2— + —2— 2 =p(p+i)+q<q+l)+pq
a la même parité que pq.
Pour prouver (24.31.3.1), il suffit donc, en vertu de (24.31.3.5), de montrer
que pour tout p > 0, tout cocycle f e ZP(X ; A) est cohomologue à 'x^f). Par
transposition, cela résultera du lemme suivant :
(24.31.3.6) Pour tout p > 0, il existe une application A-linéaire hp de Sp(X ; A)
dans Sp+ t(X ; A) telle que Von ait, pour toute z e Sp(X ; A)
(24.31.3.7) z - t/z) = hp_ ^éV) + ^o(Vz))
et que, pour tout simplexe singulier s e ^(Ap, X), le support de h^s) soit contenu
dans celui de s.
En effet, on en déduira, pour toute cochaîne / 6 SP(X ; A),
r-'xp(/) = ^o(Vi(/)) + 'v^o/)
et si d0f = 0, on en conclura que / — 'xj^f) est un cobord.
Pour prouver (24.31.3.6), on procède par récurrence sur p comme dans
(24.26.3). Pour p = 0, on prend h0(z) = 0, puisque x0(z) — z. Supposons les hj
définies pour j <p ; il suffit de définir hp(s) pour tout simplexe singulier s e ^(Ap, X).
Posons . . , ,
y = s - tp(s) -
par définition de x^s) (24.31.3.2) et en vertu de l'hypothèse de récurrence, le
support de y est contenu dans celui de s. On voit comme dans (24.26.3) que
60y = 0. Mais y peut être considéré comme un p-cycle singulier dans l'espace
rétractile s(Ap), donc il existe une (p + l)chaîne singulière w de support contenu
dans s(Ap) telle que y = 60w (24.223) ; il suffit alors de poser /ip(s) = w.

196 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
peut donc calculer la cohomologie de X en calculant H "(S; Z); on observera
pour cela que, si (sf) est la suite finie des simplexes de S, qui constitue une base
de L'.(S ; Z), le Z-module dual (L'.(S ; Z))* a pour base la base (s,*) duale de (sf)
définie par les conditions < sf, Sj > = ôtj.
(24.32.2) Exemple: classe fondamentale de cohomologie singulière de S„(n>l).
Pour calculer la cohomologie singulière de Sm on peut remplacer S„ par
le « cube creux » A„ (24.28.3). Avec les notations de (24.28.3), il est immédiat
que st = (e0 e0 + et ... e0 + et + ... + e„) est xm élément de la base de
L'„(<5; Z); vu la définition de l'orientation de A„+,(24.18.3), le coefficient de st
dans l'expression (24.28.3.2) de y„ est égal à 1. Si est l'élément correspondant
de la base duale de (L^(S ; Z))*, la classe de cohomologie c* du n-cocycle s* est
une base du Z-module H"(<5 ; Z) = Z, car on a < s?, y„ > = 1 par définition de ym
et on sait que H"(A,, ; Z) s'identifie au dual de H^A,, ; Z) (24.30.4). On dit que
l'image de c* dans H"(S„ ; Z), que l'on note encore c*, est la classe fondamentale
de cohomologie singulière de S„.
En vertu de (24.28.2.1), l'injection canonique y':L.(<5;Z) -» S.(X;Z)
donne aussi un isomorphisme en homologie, donc 'f : S'(X ; Z) -» (L.(S; Z))*
donne un isomorphisme en cohomologie ; on peut donc prolonger s? (d'une infinité
de manière) en un n-cocycle de Z"(A,, ; Z) nul dans L"(S ; Z).
33. Cohomologie singulière d'une variété différentielle.
(24.33.1) Soit X une variété différentielle pure de dimension n ; désignons
provisoirement par Hf)R(X) les espaces vectoriels de cohomologie sur le corps R,
définis dans (24.1.1) (et notés alors HP(X)). On a une application linéaire canonique
(24.33.1.1) h(p) : Hf>R(X) - H"(X; R)
pour tout p ^ 0, le second membre étant le p-ème espace de cohomologie
singulière de X à coefficients dans R. En effet, on a défini, dans la preuve de (24.12.10)
une application R-linéaire canonique
(24.33.1.2) H&R(X) - (HJ(X))*.
Il suffit de définir hiv) comme l'application linéaire composée
H&R(X) - (H,(X))* - (HP(X;R))* - H"(X;R)
où la première flèche est (24.33.1.2), la seconde le transposé de l'isomorphisme
de de Rham HP(X ; R) -»• H'„{X) (composé de (24.23.1.1) et de l'isomorphisme
réciproque de (24.26.4.1)), et enfin la troisième est l'isomorphisme réciproque
de (24.30.5.1) pour A = R.

33. COHOMOLOGIE SINGULIÈRE D'UNE VARIÉTÉ DIFFÉRENTIELLE 197
On peut expliciter h(p) de la façon suivante. Soit a une p-forme différentielle
de classe C00 sur X ; elle définit une forme linéaire
(24.33.1.3) htiXa) : z -> < a, z >
sur l'espace vectoriel Sp°(X ; R) des p-chaînes lisses sur X à coefficients réels
(24.20.2) ; si dix = 0, on a < a, z > = 0 pour tout p-bord lisse z = §0w, puisqu'alors
z = 6iv (24.20.4.3). Si maintenant a e HgR(X) est la classe de cohomologie d'une
p-forme fermée a, et si c e Hp(X ; R), il y a un p-cycle lisse z dont c est la classe
d'homologie, et l'on a (en identifiant H"(X ; R) à (Hp(X ; R))*)
(24.33.1.4) < hSp)(a), c > = < Hg\<t\ z > = < a, z > .
En outre, il résulte de la commutativité des diagrammes (24.12.10.2),
(24.30.3.1) et (par transposition) (24.26.5.1) que, pour toute application u :X -* Y
de classe C00, le diagramme
Hf>R(Y) ► H"(Y;R)
(24.33.1.5) "&»«">[ ( HP<">
H&R(X) ► HP(X;R)
(où Hf>R(u) est la flèche définie dans (24.1.3)) est commutatif.
(24.33.2) Pour toute variété pure X et tout p ^ 0, l'application linéaire (24.33.1.1)
est bijective.
En effet, si X est orientable, cela résulte de (24.12.10) et de la définition
de hip). Si X n'est pas orientable, considérons son revêtement orientable
canonique X à deux feuillets, et l'automorphisme s de X qui échange les deux
feuillets (24.1.4). On sait (24.1.4) que Hf>R(X) est somme directe des sous-espaces
propres et Hp de HgR(s) pour les valeurs propres 1 et — 1 ; de même, il résulte
par transposition de (24.22.15) que HP(X ; R) est somme directe des sous-espaces
propres H'.f et H'f de Hp(s) pour les valeurs propres 1 et - 1. Le diagramme
(24.33.1.5) appliqué à l'automorphisme s de X montre que l'isomorphisme
H&R(X) -> HP(X ; R) applique sur H'+p. D'autre part, si n : X -y X est
l'application canonique, on sait que HgR(7t) applique HgR(X) sur (24.1.4),
et (par transposition) que Hp(7t) applique HP(X ; R) sur H'f (24.22.15) ; la
conclusion résulte du diagramme (24.33.1.5) appliqué à n.
En raison de l'isomorphisme (24.33.1.1), il n'y a pas d'inconvénient à utiliser
la notation HP(X) indifféremment pour Hf^X) et HP(X ; R).
(24.33.3) Remarques. — (i) Lorsque X est une variété pure sans torsion (24.27.3.2),
chaque Z-module HP(X ; Z) s'identifie donc au sous-module de l'espace
vectoriel Hf)R(X) formé des classes de cohomologie des p-formes différentielles a
telles que < a, s > soit un entier pour tout simplexe singulier lisse s.

198 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFERENTIELLE ÉLÉMENTAIRES
(ii) En particulier, pour X = S„, il résulte de l'identification faite dans
(24.28.4) de la classe fondamentale c„ d'homologie singulière de S, avec ( - Vf [S, ],
que la classe fondamentale c* de cohomologie singulière de S, s'identifie à ( - l)"e£
où e£ est la classe fondamentale de cohomologie définie dans (24.6.3.1).
(iii) Soit u une application continue de S„ dans elle-même ; alors l'endo-
morphisme H"(«) de H"(SB ; Z) est rhomothétie de rapport deg u (24.9.6). En
effet, en raison de (16.26.6) et (24.29.4), on peut se borner au cas où u est de
classe C00. Comme H^S,, ; Z) est isomorphe à Z, Fendomorphisme HJu) de
HJiSn ; Z) est une homothétie de rapport c e Z, donc il en est de même de l'endo-
morphisme H"(m) de H"(S,, ; A) pour tout anneau A, en vertu de (24.30.2) et
(24.303.1). L'assertion résulte donc de ce que, dans le diagramme (2433.1.5),
les flèches horizontales sont des isomorphismes, et HDR(u) est l'homothétie de
rapport deg u (24.9.1.1).
(2433.4) Si l'on note HDR(X) l'algèbre de cohomologie (sur R) ©Hfc^X)
définie dans (24.1.1), les applications linéaires canoniques hlp) définissent un
isomorphisme d'espaces vectoriels gradués
(24.33.4.1) h : HDR(X) -* H\X ; R).
Nous allons prouver le résultat plus précis :
(24.33.5) L'application h est un isomorphisme d'algèbres graduées.
En d'autres termes, si a 6 Hf»(X) et b e Hr>R(X), on a
(24.33.5.1) h(a~b) = Ha) - h{b).
Soit a 6 Z'(X) (resp. /? e Z«(X)) une p-forme (resp. q-forme) fermée dont a
(resp. b) soit la classe de cohomologie, et soit ceHp+q(X; R). D'après la
définition (2433.1.3) de h et la définition (2431.1.1) du cup-produit dans H*(X ; R),
il s'agit de montrer qu'il existe un (p + q)-cycle lisse z = £aisi (où les s, sont des
simplexes singuliers) dont c est la classe d'homologie, pour lequel on ait
(24.33.5.2) < a a /U > = lA, < a, (si ° o-p)~ > • < (»i0 <)~ > •
i
On notera que chacun des deux membres de (24.33.5.2) ne dépend pas du
choix du (p + q)-cycle lisse z dans la classe c, en vertu de la formule (24.31.2.1),
et du fait que a a P est une (p + q)-foTme fermée et que «{^(a) htyif}) est un
cocycle.
La démonstration nécessite un assez grand nombre d'étapes.
A) Réduction au cas ou X est un ouvert borné dans R".
Supposons (24.33.5.2) établi lorsque X est un ouvert borné de R", et prouvons

33. COHOMOLOGIE SINGULIÈRE D'UNE VARIÉTÉ DIFFÉRENTIELLE 199
cette égalité en général. Avec les notations précédentes, on peut supposer qu'un
voisinage ouvert relativement compact V du support de z est une sous-variété
d'un RN (16.25.1), et il y a alors un voisinage ouvert relativement compact W
de V dans RN et une submersion n : W -» V de classe C00 ayant les propriétés
de (16.25.4). Par hypothèse, on peut appliquer (24.33.5.2) en remplaçant a et fi
par 'n(a) et 'n{fi\ et z par Sp+JJiz), où j : V -* W est l'injection canonique.
On a (Sp+JjHz))~ =/z) et 'jt(a) a ln(fi) = y» a fi), donc
< 'm a 'm, {S,+M*))~ > = < '«(« A A 7(5) > = < « a fi, z >
puisque 7t°j=lv (17.3.7). D'autre part, Sp+,(/Xsi)°a'P — Sp(/Xsi°a'P) donc
< 'n(a), (Sp+,(j)(Si) ° o-;)~ > = < '*(a), j((s, o ffp)~) > = < a, (s, ° o-p)~ > par le même
raisonnement, et on a de même < 'it(fi), (Sp+^/X*i) ° o"«)~ > = < ft («i0 ff'«')~ > »
donc on obtient bien la relation (24.33.5.2).
On suppose donc désormais que X est un ouvert borné de R".
B) Réduction au cas où z est un (p + q)-cycle d'une subdivision simpliciale <5
de X. En vertu de la remarque préliminaire, il suffit de remarquer que tout
(p -t- q)-cycle lisse dans X est homologue à un (p + q)-cycle lisse d'une telle
subdivision (24.24.2, B)).
C) Formation d'une suite de cycles homologues à z et dont les simplexes
singuliers qui y figurent ont des supports arbitrairement petits.
Pour un simplexe géométrique A = Im(a0 at ... ap) de dimension p dans
un espace R" de dimension n > p, nous noterons volp(A) la mesure de Lebesgue
dans Rp d'une image u(A), où u est un déplacement de R" tel que u(A) c RP ; ce
nombre en effet ne dépend pas du déplacement u choisi puisque la mesure de
Lebesgue est invariante par déplacement (14.3.9).
Nous nous proposons de définir, pour chaque entier fe > 1, un (p+q)-cyc\e
zk = Y.ukmskm homologue à z, où les simplexes singuliers s^, sont affines et ont
m
pour supports des simplexes géométriques d'une subdivision simpliciale <Zk d'un
voisinage fermé Xk du support de z contenu dans X ; nous imposons en outre
les trois propriétés suivantes :
I) Le diamètre 5(5^,(5,+,)) «S 2"*.
II) Il y a une constante C > 0 indépendante de k et telle que
ZI A» I volp+^s)[m(Âp+,)) < C .
m
Ul) U y a une constante C > 0 indépendante de k, telle que, pour tout
simplexe singulier skm de dimension p + q et toute écriture de s^Ap^,) sous la
forme Im(a0a, ... ap+4), on ait
volptfmtao ai ... ap)). vol^Im(ap ap+1 ... ap+,))
^ C'.volp+,(Im(a0 at ... ap+,))

200 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFERENTIELLE ÉLÉMENTAIRES
(cette troisième condition empêche de prendre pour les zk les subdivisions
barycentriques Sd*(z)).
Pour tout entier h ^ 1, nous définirons d'abord une subdivision cellulaire
(£h de Ap+,. Pour cela, on considère les (p + q + 1X2* — 1) hyperplans affines
de Rp+,+ 1 définis par les équations
tV = m/2* pour 1 < u < 2* - 1 et O^j ^p + q
et les intersections de ces hyperplans affines avec l'hyperplan affine Ep+, engendré
par Ap+,, d'équation £° + Ç1 + ... + t?*9 = 1. Ces intersections définissent
une subdivision cellulaire de Ap+Î (24.18.1.1) dont tous les polyèdres ont un
diamètre ^ (p + q + 1)*2~* ; en outre ceux de ces polyèdres qui sont de
dimension p + q sont les intersections d'au plus 3(/> + q + 1) demi-espaces, donc le
nombre de leurs facettes est borné par un nombre Nt indépendant de h. A partir
de (£'h, on définit une subdivision simpliciale <5'k de Ap+, par la méthode de
(24.18.5.1), en prenant, pour former les simplexes de cette subdivision, les bary-
centres des polyèdres de Cette définition entraîne aussitôt que <B'k est invariante
par permutation des sommets de Ap+r et est formée de simplexes de diamètre
^ (P + 1 + 1)*2-*. En outre, le nombre des simplexes fermés de dimension
p + q dont l'adhérence d'un polyèdre de dimension p + q de d.'h est la réunion,
est borné par un nombre N2 indépendant de h. Majorons le nombre N(n) des
simplexes de dimension p + q de S), ; il est au plus égal à N2N'(li), où N'(h)
est le nombre des polyèdres de d'h de dimension p + q. Or ces derniers sont les
intersections non vides de Ep+, avec les cubes
Ku,h : 2-"uj < Z> < 2-\uj + 1) pour 0^j^p + q
où u = (uj)eZp+q+x. Ceux de ces cubes qui coupent Ep+, sont deux à deux
disjoints et contenus dans le polyèdre défini par
e > o, é1 > o,..., > o
1 - iP + q + 1)2"* < P + P + ■ ■ ■ + < 1 + (P + q + 1)2_*.
En vertu de (14.3.10.2), le volume de ce polyèdre est
(\+{p + g+ l)2-Y+"+1 - (1 - (/> + g + l)2-*)p+«+1
(p + q+l)i
et on a donc N'(h) < Vll/2_(p+,+1)*, d'où l'on déduit qu'il existe une constante C,
indépendante de h et telle que
(24.33.5.3) N(/i) ^ C^"*'»*.
Associons à la subdivision S* la (p + g)-chaîne R/,(lApt,) définie dans

33. COHOMOLOGIE SINGULIÈRE D'UNE VARIÉTÉ DIFFÉRENTIELLE 201
(24.21.4). Si le (p + g)-cycle z s'écrit z = XA,s,, où les simplexes singuliers st
i
sont deux à deux distincts, la (p + q)-chaîne
(24.33.5.4) zi = EA,s, oRfc(lAp+,)
i
est un cycle homologue à z ; la démonstration est identique à celle de (24.22.7.2),
où il faut seulement remplacer Sdm par Rh, l'application du lemme des chaînes
prismatiques (24.21.6) étant justifiée par le fait que la subdivision 6k est invariante
par permutation des sommets de Ap+,. Si l'on écrit
N(A)
(24.33.5.5) z' = I lAra(S;,
1 m= 1
où, pour chaque i, smi est l'application linéaire affine composée de st et d'un des
termes de Ri,(1ap+,). on a Aml = ± A,, et par suite
(24.33.5.6) E I Am, I < N(/.)£ | A, K C22<"+«>*
m.l I
où C2 est indépendant de h. Le support de zJ, est le même que celui de z ; enfin, le
diamètre de s'ml(Ap+q) est majoré par le produit d'un diamètre d'un simplexe
de SJ, de dimension p + q et d'un nombre ne dépendant que de l'application
linéaire affine s, ; il y a donc une constante C3 indépendante de h, telle que l'on
ait
(24.33.5.7) ô(sUàP+q))^C32-".
Définissons maintenant les subdivisions Sk. On considère la subdivision
cubique de R" formée des cubes
Ku> : 2~kuj < ZJ < 2-k(Uj + 1)
pour 1 < j15$ n et u = (Uj)eZ", et de leurs facettes; on considère ensuite la
réunion Xk des cubes fermés Kuk contenus dans X, et on définit la subdivision
simpliciale <3k à partir de la subdivision cubique précédente de Xk, par la méthode
de (24.18.5.1), en prenant, pour former les simplexes de cette subdivision, les
harycentres des facettes des cubes KuJt. La propriété fondamentale de cette
subdivision est que tout simplexe de dimension r < n de <Zk est homothétique
dans le rapport 2~k d'un des simplexes de la subdivision du cube unité
Ko.o : 0 < < 1 (1 ^ j ^ n). Il en résulte en particulier qu'il existe une
constante C4 indépendante de k tel que le volume de tout simplexe de dimension r
de <Zk soit ^ C42-r\ puisque le nombre des simplexes de la subdivision de K0 0
est fini et indépendant de k. Nous nous bornerons aux entiers k > k0, où k0 est
pris tel que le diamètre y/n.2~ko des cubes K,,.^ soit plus petit que la distance

202 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
du support de z à R" — X ; alors l'intérieur de Xk est un voisinage du support
de z, car tout point de ce support rencontre un cube fermé KUit+2 contenu dans X
et est donc intérieur à un cube Ku-jk contenu dans X.
Il y a un nombre fini de sommets vt, ..., v, de simplexes de <5k tels que
les ouverts St(v,) (24.24.3) forment un recouvrement ouvert du support de z ;
montrons qu'il y a un nombre p0 indépendant de k tel que toute boule de rayon
Po.2~k et de centre dans le support de z soit contenue dans un des St(y,) au
moins. Il suffit en effet de prendre un nombre px tel que toute boule de rayon px
et de centre dans un cube Kuto soit contenue dans un des ouverts St(w,), où w,
parcourt l'ensemble des sommets des simplexes de contenus dans un cube
K„',to-2 auquel KUiJko est intérieur; une homothétie de rapport 2~k+ko montre
que l'on peut prendre p0 = pt .2*°. On peut d'ailleurs remplacer p0 par n'importe
quel nombre de ]0, p0 [ ; pour la commodité des calculs, nous supposerons qu'on
ait remplacé p0 par p < p0 tel que C3/p == 2V pour un entier v > 0.
Cela étant, pour tout entier k > k0, déterminons l'entier h par la condition
C3.2_* = p.2-*, ce qui donne h = k + v. Alors, chaque simplexe singulier s„,
figurant dans l'expression de z'h est tel que
La méthode d'approximation simpliciale de (24.24.4) associe à chaque s'ml un
simplexe singulier sm, = (vJo ... Vjp+q), où les Vj sont des sommets (non
nécessairement distincts) d'un même simplexe de <Sk, et si l'on pose
zk — Z Am|Sm| ,
m.l
zk est un (p + q)-cycle lisse homologue à zfc, donc à z. Les trois conditions I), II), III)
sont alors remplies: c'est évident pour I) par (2433.5.7) et par construction, et
pour III) parce que cette condition est invariante par homothétie. Enfin, on a,
en vertu de (24.33.5.6)
El^milvolp+^ni(Â,+,)) *S C2.2<'+«>\C4.2-<'+«* = C2Q2<'+«'»
m.l
ce qui prouve la propriété II).
D) Réduction aux cycles alternés.
Nous utiliserons les notations et les résultats de (24.26.1). On peut écrire
d'une seule manière zk = z'k + z'k, où z'ke L'p+q(<àk ; R) et z'k eL'p+q(<5k; R),
et par suite 0 = S0zk = 60z'k + S0zk ; mais on a vu dans (24.26.1) que
60z'keVp+<l-x(<5k \ R) et S°zk eLp'+,_x(<5k; R); on en conclut que 60z'k = 0 et
S0z'k = 0. Mais en vertu de (24.26.3), cela entraîne que z'k est un bord, donc z'k est
homologue à zk. En remplaçant zk par zi, on peut donc supposer que zk=Y,^kmskm
m
est combinaison linéaire de simplexes singuliers affines dont les images sont des

33. COHOMOLOGIE SINGULIÈRE D'UNE VARIÉTÉ DIFFÉRENTIELLE 203
simplexes de <s>k de dimension p + q. Comme le passage de zk à z'k consistait à
permuter les sommets des sml dont les images sont de dimension p + q (en
changeant au besoin le signe de XmL) et à supprimer les autres, la condition II) est
encore vérifiée pour z'k.
Posons maintenant ar+q(s)= -— Eê„ji(s) pour tout seLp+q(<Sk;R),
(p+q+l)\ k
n parcourant le groupe des permutations de {0, 1, ..., p + q}, et soit
«p + «(Z*) = Z^kmap + ^Sto,) •
m
Nous allons voir que ap+q{zk) est encore un (p + q}-cycle lisse homologue à zk,
donc à z. Cela résultera du lemme suivant :
(24.33.5.8) Pour toute subdivision simpliciale S d'un ouvert (ou fermé) de R",
et tout r > 0, il existe une application R-linéaire h, de M S ; R) dans Lr+1(<5 ; R)
telle que l'on ait, pour tout z e Lr(<3 ; R),
(24.33.5.9) z - ar(z) = /»,_ ,(6V) + 60{hJ(z))
et que, pour tout simplexe singulier s e L^S ; R), le support de hr(s) soit contenu
dans celui de s.
Montrons d'abord que l'on a
(24.33.5.10) 6<AaAs)) = ar_ tfos)
pour tout simplexe singulier s e L4® ; R) ; il suffit évidemment de le voir lorsque
s = (e0 e! ... er) = lAp. Pour cela, notons que pour tout ie { 0, 1, ..., r} et
toute permutation rc, de l'ensemble {0, 1, ..., r} — {i}, le terme
* = (•«!«» • • • •«,((- 1) •«,«+ 1) • • • e«,<r))
figure dans (r + 1) ! ar-,{S0s) avec le coefficient (— l)'e«,(r + 1); il figure r + l
fois dans (r + 1) ! 6'0(ar(s)) avec les coefficients (— lVe», pour les r + 1
permutations n de {0, 1, ..., r} telles que l'on ait n{j) — i et que la suite
(jt(0), 7t(l), ..., n{j - 1), n(j + 1), ..., 7t(r))
soit la même que la suite (n^O), ...,nfa — 1), n^i + 1), ..., n,{r)). On peut
voir directement que ces r + 1 coefficients (— l^e, sont tous égaux à (— l)%t,
mais c'est inutile, car il suffit de remarquer que, pour les courants correspondants
sur R", on a (e„7t(s))~ = s et eXtl = (e0 ex ... e,_t ei+l ... er)~ ; on a
(6>0(ar(s))~ = 6s = (ar-iiSos))", et l'égalité n'aurait pas lieu si certains des
(- iye„ avaient un signe opposé à celui de (— lYent.
On raisonne ensuite comme dans (24.26.3) en définissant les hr par récur-

204 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFERENTIELLE ÉLÉMENTAIRES
rence sur r. On prend h0(z) = 0 dans L0(S ; R), ce qui vérifie (24.33.5.9) pour
r = 0 puisque a0(z) = z. On pose ensuite, pour un simplexe singulier
z = (v0 v, ... vr)eL,(6;R),
et l'hypothèse de récurrence assure que le support de y est contenu dans celui
de z. On voit ensuite que 60y = 0, et on pose nr(z) = Cwo(y), ce qui entraîne
que le support de hr(z) est contenu dans celui de z, et que y = S0{Cvo(y)), d'où
z - aJiz) = /Jr-!(M + <?0(A(z)).
Il est clair que si on remplace zk par ap+q(zk), les conditions I), II) et III) sont
encore remplies par ap+,(zk).
E) Réduction au cas de formes différentielles constantes.
Comme la différence des deux membres de (2433.5.2), lorsqu'on remplace z
par zk = Z ukmskm vérifiant I), II) et III), ne dépend pas de k, on va montrer que.
pour tout e > 0, il existe k tel que cette différence soit en valeur absolue au plus
égale à e, ce qui achèvera la démonstration de (24.33.5).
Pour toute r-forme différentielle y = X/hM^*", où H parcourt l'ensemble
h
des parties de r entiers jj < i2 < ... < ir de {1, 2, ..., n }, on a posé
dx" = dp a dp a ... a dp et fH est une fonction de classe C00, on pose,
pour toute partie E de R", | y |E = sup (sup | /H(x) I )• H existe alors une
constante Cr telle que, pour toute r-forme différentielle y de classe C°° et tout simplexe
géométrique A de dimension r dans R", on ait
car cela résulte des définitions et du fait que les éléments d'une matrice
orthogonale ont tous une valeur absolue ^ 1. Nous dirons d'autre part qu'une forme y
est constante si les fH sont constantes. Cela étant, posons A^ = 5^,(5,+,). Il
existe un entier k tel que, en désignant par a**"0 et /f1*"0 des formes constantes,
égales respectivement à a et en un point de A^, on ait
y = z - ar(z) - nr_,(50z)
m
h
(24.33.5.11)
|a-a(
\Akm^e et \P-Fm>\Akm*e
l<« a fi, zt> - TjinioP* a p"\ ~Skm}\
<eCCp+q(\0L\Xl + |j8|Xl).

33. COHOMOLOGIE SINGULIÈRE D'UNE VARIÉTÉ DIFFÉRENTIELLE 205
| < or, (skm o a'py > < P, (skm » <r > - < «(km), (skm ° a'p)~ > < ^m), (5ta » <)~ > I
< eC'C,C,( | a |Akm + | fi |AkJvolp+^Akm)
I *ukm < a, (Skm o a'pT ><fi, {skm o a'qT >
- 2>ta < a(bn). (sta « o'p)~ >< /*»»>, (sta o <r»)~ > I < eC'CCpC,( | a |Xl +1 fi |Xl).
F) Fin de la démonstration.
On voit donc qu'on est finalement ramené à prouver la proposition
suivante :
(24.33.5.12) La relation (24.33.5.2) a lieu lorsque net fi sont des formes
différentielles constantes, et z — £e,,7r(s), où s = (e0 et ... ep+q) et n parcourt l'ensemble
des permutations de { 0, 1, ..., p + q }.
Il suffit évidemment de prouver (24.33.5.12) pour a = dxH et P = dx",
où H est une partie de p éléments et K une partie de q éléments de
I = {0, 1, ..., p + q}. D'une façon générale, si L est une partie de r éléments
»! < i2 < ... < ir de I, et tM = (eJoBjt ... ejr) un simplexe singulier affine
dont les sommets sont distincts (donc de dimension r) on ne peut avoir
<dx1-, tM> # 0 que si M = {j0Ji, ■ ■ - Jr} contient L, auquel cas M - L est
réduit à un seul élément. On ne peut donc avoir
que si H n K est vide ou réduit à un seul élément, qui est alors nécessairement
rt(p), puisque c'est le seul élément commun aux ensembles { n(0), 7t(l), .... n(p)}
et {n(p), n(p + 1), ..., n(p + q)}. Distinguons ces deux cas.
I) H n K = 0. On peut alors supposer que H = { 1, 2, ..., p } et
K = {/> + 1, .. .,p + q}, donc, par définition de l'orientation de Ap+q (24.18.3),
on a, en vertu de (24.17.2.1)
et par définition (16.24.2), cette intégrale est la mesure de Lebesgue de l'ensemble
défini dans Rp+4 par les relations
^^0, p >0, ...,£'+«>0, ^ + p + ... + p+"^l
mesure qui vaut \/(p + q)\ (14.3.10.2). En outre, on a (eKit{s))~ = s pour toute
permutation n de I, donc
et par suite, de nouveau en vertu de la condition II)
m
< dx", (n{s) o a'p)~ > . < dx*, (n(s) ° <)~ > * 0
< dx" a dx*, z > = (p + q + !)!/(/> + q)\ = p + q + 1.
De même, il résulte de (24.33.5.11) et de la condition III) que l'on a

206 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
D'autre part, le produit <dx", (ji(s)°ffp)~ >. <dxx, (n(s)ooq)~ > ne peut
être / o que si l'on a, ou bien {7t(0), 7t(l), ..., ix{p) } = { 0, 1, ...,/»} et
{jrt», 7t(/» + 1), ..., n(p + q)} = {j-, p + 1, ...,p + q) pour un j tel que
0 <y <p, ou bien {nfO), 7i(l), ..., tc(/>) } = {/> + fc, 1, 2, ..., p} pour un k tel
que 1 < k < et {n{p), iip + 1), ..., iAjp + q)} = {0, p + 1, ..., p + q}.
I a) Dans le premier cas, on a nécessairement n(p) = j, la restriction de
n à {0, 1, ..., p — 1} est une bijection arbitraire sur {0, 1, ..., p} — {j} et
la restriction de n à {p + 1, ...,/» + g} une permutation arbitraire de cet
ensemble. Soit n0 celle de ces permutations pour laquelle la suite (tc(0), ...,n{p + q))
est
(0, 1 j - hp,j+ 1, ...,p- l,j,p+ 1, ...,/> +g),
de sorte que e„0 = - 1, (7t0(s) ° a'p)~ = - (e0 e, ... ep)~ et
(tt0(s) o o-J')~ = (e, ep+1 ... ep+,)~ .
On en déduit comme ci-dessus que
< dx", (7to(s) » a'pT > = - l/p !, < dx", (7t0(s) o o-;')~ > = Vq !
et par suite
£„„ < dx», (n0(s) o <r'p)~ > . < dx*, (7i0(s) » <)~ > = Vp\q\ ■
Toutes les autres permutations n à considérer peuvent s'écrire 7tv7t0, où 7t'
est une permutation laissant invariants j, p + 1, ..., p + q et n" une permutation
laissant invariants 0, 1, ..., p ; on a donc e„ = ex-8b»eko ; d'autre part
(n{s) o <t'p)~ = (7i'(7t0(s) » o-p))~ = Mio(s) ° ff'P)~
(n» ° <)~ = (7r"(7r0(s) o ✓,'))- = eAnois) » <)~ ;
donc, pour toutes les permutations n considérées (pour une valeur donnée de j),
les produits e» < dx", (ji(s) » o'p)~ > . < d;**, (ji(s) ° o^')~ > sont tous égaux à
l/p\q\; leur somme est donc égale à 1.
I b) Dans le second cas, on a nécessairement n{p) = p + k, la restriction
de n à {0, 1, ..., p — 1} est une bijection arbitraire sur {1, 2, ..., p} et la
restriction de n à {p + 1, ...,/» + g} une bijection arbitraire sur
{0,p + 1, ■..,/> + «} - {/> + *}•
Soit cette fois jc0 celle de ces permutations n pour laquelle la suite (7i(0),7t(/> + q))
est
(p, 1,2, -1, />+k, p+1,p+k -1,0, p+k +1,p+q)
de sorte que £„„ = 1, (nQ{s) ° ap)~ = - (ep+t e, ... ep)~ et
(t0(s)°O~ = - («o •,+!•• • ep+,)~ •

33. COHOMOLOGIE SINGULIÈRE D'UNE VARIÉTÉ DIFFÉRENTIELLE 207
On voit alors comme dans le cas I a) que tous les produits
ËK < dx», m o o'Pr >. < dx*, m o aqr >,
pour une valeur donnée de k, sont égaux à 1/plql, et leur somme est donc encore
égale à 1.
Enfin, il faut donner p + 1 valeurs à j et q valeurs à k ; le second membre
de (24.33.5.2) est donc égal à p + q + 1 et l'égalité des deux membres est vérifiée
dans ce cas.
II) H n K a un seul élément. On peut supposer que H = { 1,2, ...,/»}
et K = {p,p + 1, ..., p + q - 1}; on a dx" a dx* = 0 et le premier membre
de (24.33.5.2) est nul. Le produit < dx", (n(s) ° tr'p)~ > . < dx*, (n(s) ° a'9T > ne
peut être # 0 que si l'on a, ou bien {7t(0), 7t(l), ..., ix(p)} = {0, 1 p} et
{ <P\ HP + 1), • • -, <P + q)} = {p, P + 1, ...,p + q}, ou bien
{TtfO), 71(1), ...,7rtj>)} = {p + q, 1, 2 p}
et {Tt/.p), 7t(/> + 1) n(p + q)} = {0, p, p + 1, ..., p + g - 1}. Dans tous
les cas 7t(p) = p.
II a) La restriction de n à {0, 1, 2, ..., p — 1} est une permutation
arbitraire de cet ensemble et la restriction denk{p + 1, + une permutation
arbitraire de cet ensemble. Si jx est l'identité, on a e„ = 1, (n(s)o o'p)~~ = (e0 et... ep)~
et (?t(s) o o-£)~ = (ep ep+, ... ep+,)~, d'où l'on déduit
e, < dx", (n{s) o a'p)~ > . < dx*, (lis) o <)~ > ~ - l/p!«!.
Toutes les autres permutations n à considérer sont alors les permutations n'n",
où n' laisse invariants p, p + 1, ..., p + q et n" laisse invariants 0, 1, ..., p ;
on voit comme dans I a) que pour toutes ces permutations le produit
a, < dx", (n(s)o a'p)~ > . < dx*, (n(s)c o-;')~ > = - l/p\q\,
et la somme de ces produits est donc — 1.
II b) La restriction de n à {0, 1, ..., p - 1} est une bijection arbitraire de
cet ensemble sur {p+q, 1,2, .. .,p-1} et la restriction de n à {p +1,.. -,p + q}
une bijection arbitraire de cet ensemble sur {0, p -i- 1, ..., p + q — 1}. Soit
jt0 celle de ces permutations n pour laquelle la suite (7t(0), ..., n(p + q)) est
(p + q, 1, ..., p - 1, p, p + 1, ..., p + q - 1, 0), de sorte que e,0 = - 1,
(7i0(s) ° ffp)~ = (op+,e, ... ep)~ et (ti0(s) ° <)~ = (epep+1 ... ep+,_t e0)~. On
a donc cette fois
< dx", (n0(s) o o'p)~ > = 1/p !, < dx*, (n0(s) oa'-)~)=- \/q \
d'où
£n0 < dx", (n0(s) o a'p)~ > . < dx", (nQ(s) ° aqT > = Wql ■
Les autres permutations n à considérer s'écrivent n = n'n"n0, où n' est une

208 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFERENTIELLE ÉLÉMENTAIRES
permutation laissant invariants 0, p, p + 1 p + q — 1 et n" une
permutation laissant invariants 1, ...,p- 1,p,p + q — 1. Le même raisonnement
que ci-dessus montre que pour toutes ces permutations, on a encore
eB < dx», (7i(s) o a'p)~ > . < dx*, (11(5) o o-;')" > = 1/p ! q !
et la somme de ces produits est donc 1. On vérifie ainsi que le second membre
de (24.33.5.2) est 0, ce qui achève la preuve de (24.33.5).
PROBLÈMES
1) Soit X une variété différentielle compacte et connexe de dimension n. Pour toute p-forme
différentielle a sur X, à valeurs complexes, de classe C°° et fermée, on appelle période de a tout
nombre < a, z >, où z est un p-cycle lisse sur X à coefficients dans Z ; les périodes de a forment
un Z-module Q(a) <= C engendré par br éléments au plus, où bp est le p-ème nombre de Betti de X.
Pour que a soit de la forme dp où p est une (p — Informe, il faut et il suffit que A(a) soit réduit à 0.
2) Soit X une variété différentielle compacte et connexe. On note L'(X ; Q l'ensemble des
1-formes différentielles co sur X, à valeurs complexes, de la forme co = df/f, où / est une application
de classe C° de X dans C*. C'est un sous-groupe additif de l'espace vectoriel Z'(X ; C) des 1-formes
fermées à valeurs complexes, et il contient l'espace vectoriel B'(X ; C) des 1-formes à valeurs
complexes qui sont des cobords.
a) Montrer que toute forme coe L'(X; C) est cohomologue à une forme dg/g où g est une
application de classe C°° de X dans le cercle unité U.
b) Montrer que pour qu'une 1-forme co appartenant à Z'(X ; C) appartienne à L'(X ; C),
il faut et il suffit que son groupe des périodes (problème 1) fl(co) soit contenu dans 2niZ. (Pour
voir que la condition est nécessaire, utiliser a) en considérant l'image réciproque de co sur le
revêtement universel de X. Pour voir que la condition est suffisante montrer d'abord que si y est un
chemin C1 par morceaux dans X, d'origine a et d'extrémité x, le nombre expl eu I ne dépend que
de a et jc.) ^' '
c) Soienty„y2>.. .,ytl des 1-cycles risses dont les classes d'homologie dans Ht(X; Z) forment
une base d'un Z-module libre supplémentaire du Z-module de torsion de Ht(X; Z). Il existe
alors bi 1-formes fermées oij à valeurs réelles telles que I a)j -7 2nôJk pour 1 < /, k ^ fc, ; les
formes ico; forment alors une base d'un Z-module supplémentaire de B'(X; Q dans L'(X; C).
d) On suppose qu'il existe sur X une 1-forme fermée eu à valeurs réelles, telle que eu(x) / 0
pour tout xeX. On peut alors écrire eu = Y.cj<»} + df, où les Cj sont des constantes réelles non
j
toutes nulles et / une fonction réelle de classe C°° dans X. Montrer qu'il existe alors une 1-forme
fermée co' à valeurs réelles telle que co'(x) ï 0 pour tout x e X et que ico' appartienne à Ll(X ; C).
(Se ramener par continuité au cas où les c, sont rationnels). En déduire qu'il existe une submersion
de X sur le cercle unité U, et par suite que X est difféomorphe à un espace fibre de base U
(section 20.8, problème 4).
3) Soit X une variété différentielle compacte et connexe de dimension n. On suppose que
l'application canonique de l'algèbre extérieure A H'(X ; R) dans l'algèbre de cohomologie H'(X ; R)
qui prolonge l'injection canonique H'(X;R) -» H'(X;R) est un isomorphisme d'algèbres.
Montrer qu'il existe une application / : X -» T" déclassée telle que/* : H'(T"; R) -> H'(X;R)
soit un isomorphisme d'algèbres (utiliser la base de H'(X ; R) définie dans le problème 2 c)).
4) Soient X un espace compact métrisable, (X,)icl un recouvrement fini de X formé d'ensembles
fermés, 92 l'ensemble des parties J de I telles que X, = (~)Xt soit non vide. On suppose que pour
i.j
tout J e 91, Xj est contenu dans un ensemble ouvert Uj dont chacun est rétracte par homotopie
d'un espace R", et que lorsque J 6 91, J'e 91 et J = J', on a V, <= U,..

33. COHOMOLOGIE SINGULIÈRE D'UNE VARIÉTÉ DIFFÉRENTIELLE 209
a) Pour toute partie 91' de 9), soit Y(9t') la réunion des ensembles X, x X, x [0, 1 ] pour
J e 91', sous-espace compact de X x X x [0,1 ]. Supposons que pour un J0 e 91, XJo x X,0 x [0,1 ]
ne soit pas contenu dans Y(9l'), mais que X, x X, x [0, 1 j soit contenu dans Y(9l') pour tout
J e 91 tel que J => J0 et J ^ J0. Soit F une application continue de Y(9l') dans X, ayant les propriétés
suivantes : pour J 6 91', x e Xj, y e Xj, on a F(x, y, t) e V, et F{x, x, t) =» x pour t e [0, 1 ], F{x, y, 0)=x
et F(x, y, 1) = y. Montrer qu'il existe une application continue G de Y(9l' u { J0 }) dans X,
coïncidant avec F dans Y(9l') n (X,0 x X,0 x [0, 1 ]), telle que GLx, y, t) e U,0, G(x, x, t) = x, G(x, y, 0)=x
et G(x, y, 1) = y pour x e X,0, y e X,0 et te [0, 1 ], et enfin que G(x, y, t) e U,. pour tout J' 6 91
lorsque x, y sont dans X,0 ri Xj. et t e [0, 1 ].
b) Déduire de a) qu'il existe une application continue F de Y(9l) dans X telle que, pour
toute partie J e 91, et pour x e XJt ye X,, on ait F(x, y, t) e V, et F(x, x, t) = x pour t e [0,1 ],
F(x. y, 0) = x et F(x, y, 1) = y. (Procéder par récurrence descendante sur le nombre d'éléments
de Je 91).
c) Soient /, g deux applications continues d'un espace topologique E dans X telles que
pour tout z e E, il existe i e I tel que f(z) e X, et g(z) e X,. Montrer que / et g sont homotopes.
5) Soient X un espace compact métrisable, (U,),6| un recouvrement ouvert fini de X, S0 la
partie de S|$(l) formée des ensembles H c I tels que l'intersection UH = Ç\M, soit non vide, (N, S)
teH
le nerf euclidien du recouvrement (U,) (section 24.28, problème 11). Toutes les applications / de X
dans N e R1, définies par le procédé de la section 24.28, problème 11 a), sont homotopes.
a) On suppose que, pour toute partie J e S0, U, est rétractile (16.27.7), de sorte que toute
application continue dans Uj de la frontière d'un simplexe A, se prolonge par continuité en une
application de Ap dans U,. Pour toute partie Je S0, soit Z(J) le simplexe euclidien correspondant
de la subdivision <5 (section 24.28, problème 1); pour toute suite strictement croissante
J0 c J, c ... c Jm de parties de S0> soit 2(J0, J, Jm) le simplexe euclidien de la subdivision
barycentrique de I(JJ correspondant à cette suite (24.18.7). Montrer qu'il existe une application
continue g de N dans X telle que g(Z(J0, Ji, • • -, JJ) <= U,0 pour toute suite strictement croissante
J0 <= J, c ... c im de parties de S0, et que deux telles applications sont homotopes. (Définir g
sur les simplexes des subdivisions barycentriques des £(J) par récurrence sur la dimension de ces
simplexes).
b) Pour chaque i e I, soit F, <= U, l'ensemble compact réunion des ensembles g(X(J0, J i Jm))
pour toutes les suites strictement croissantes telles que i e J0. Il existe un recouvrement ouvert
(V()(,i de X tel que F, c V, et V, c U, pour tout ie I. Soit (/))„, une partition continue de l'unité
subordonnée au recouvrement (V,),6l et telle que fix) > 0 pour tout x e F,. Soit f : x -* (Mx))i€l
l'application correspondante de X dans N (section 24.28, problème 11).
Si (v,)te, est la famille des sommets des simplexes de S, et si, pour tout z = (z,)w dans N,
on pose <pfa) = inl(z„ /te(z))), montrer que cp(z) = £cPi(z) > 0 pour tout z e N, et que les fonctions
i
Jijtz) = c/>((z)/cp(z) forment une partition continue de l'unité subordonnée au recouvrement ouvert
de N formé des St(v,). Conclure que l'application z -» (/i|(z))i., de N dans N est, d'une part
homotope à l'application identique, d'autre part homotope à l'application / «g.
c) On suppose de plus que chaque Uj est rétracte par homotopie d'un espace R™. Pour un
point x e X, soit J l'ensemble des i e I tels que fix) > 0. Montrer que x et g(f{x)) appartiennent
tous deux à V,, et en déduire que g « f est homotope à l'application identique de X (utiliser le
problème 4). Conclure que X et N ont même type d'homotopie (section 16.26, problème 2) et par
suite que, pour tout anneau commutatif A, les anneaux de cohomologie H'(X; A) et H'(N; A)
sont isomorphes.
d) Si X est une variété différentielle pure compacte, il existe un recouvrement ouvert fini
U = (Uj),,, de X satisfaisant aux conditions de a) et c), et par suite X et le nerf euclidien N de ce
recouvrement ont même type d'homotopie (utiliser (18.5.4) et (20.17.5)).
6) Soient X une variété différentielle pure compacte, I un intervalle fini de N, U = (U,)le,
un recouvrement ouvert de X, satisfaisant aux conditions a) et c) du problème S ci-dessus. On
conserve les notations du problème S, et on note e, pour i e I les sommets du complexe simplicial
euclidien N.
a) On note (f'(U) l'ensemble ZSo des applications de l'ensemble ®0 dans Z, qui est en
correspondance biunivoque avec le Z-module différentiel gradué (L'.(<3 ; Z))* (notation du problème

210 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
de la section 24.30) : à une partie KeS0 on fait correspondre l'élément si de la base duale de
la base {s,)H9k> de L'.(S ; Z). On transporte à <£"(U) la structure de Z-module différentiel gradué
de (L'.(<3 ; Z))* ; en désignant par g : N -» X l'application continue définie dans le problème S a),
on a alors une application Z-linéaire composée
r„ : S'(X; Z) jh» S'(N; Z) y (L'.(® ; Z))* a» Œ'(U)
telle que, pour Je ®0 et ueS"(X; Z\ on ait
<r^u\ J> = <«,g = s,>.
L'application ru donne alors un isomorphisme r* en cohomologie, indépendant du choix de
l'application g vérifiant les conditions du problème S a). En outre, si I, est une partie de I telle que la
sous-famille U, = (U,),.,, soit encore un recouvrement de X, on a rg, = rj.
b) Soit X' une seconde variété pure compacte, et soit h: X' -* X une application de classe C" ;
les ensembles JT'fUi) pour ieI forment alors un recouvrement ouvert /T'(U) de X', et il existe
un recouvrement ouvert U' = (UJ-),..,. ayant les mêmes propriétés que U, et plus fin que fc"'(U);
il y a par suite une application t : I' -» I telle que U[. <= U„n pour tout i' e I'. On déduit
canoniquement de t une application Z-linéaire 't : Œ'(U) -► Œ'(U') qui est un homomorphisme de
degré 0 de Z-modules différentiels gradués, et donne donc un homomorphisme
t* : H "(11) -» H'(U')
pour leurs modules de cohomologie. Montrer que le diagramme
H'(X;Z) % H'(U)
II* r"
H'(X'; Z) -* H'(U')
est commutatif ; en particulier, si X' = X et si h est l'identité, t* est une bijection.
34. La cohomologie singulière à supports compacts.
(24.34.1) Soit X un espace séparé ; on dit qu'une p-cochaîne / e SP(X ; G)
est à support compact s'il existe une partie compacte K de X telle que /(z) = 0
pour toute p-chaîne z e Sp(X ; Z) dont le support ne rencontre pas K ; on note
Sf(X ; G) l'ensemble de ces cochaînes, qui est évidemment un sous-groupe de
SP(X ; G). Si / est une p-cochaîne à support compact, la (p + l)-cochaîne d0f
est aussi à support compact, car si le support de z e Sp+t(X ; Z) ne rencontre pas K,
il en est de même du support de 60z, donc (d0/Xz) = /(*>oz) = 0- La restriction
de d0 au groupe gradué SC"(X ; G) = © Sf(X ; G) en fait donc un groupe diffé-
rentiel gradué, dont la cohomologie se définit à partir des cocycles à support
compact et des cobords de cochaînes à support compact, c'est-à-dire les groupes
Z?(X;G) = Z'(X;G)nS'(X;G), Bf(X;G) = d0(Sf-1(X;G)) ;
le groupe gradué HC'(X;G)= ©H?(X;G), où
p^O
Hf(X;G) = Z?(X;G)/B?(X;G),

35. HOMOLOGIE ET COHOMOLOGIE SINGULIÈRE RELATIVES
211
est appelé le groupe de cohomologie à supports compacts de X à coefficients dans G ;
si X est compact, on a évidemment HC'(X; G) = H'(X; G).
(24.34.2) Exemples. — Si X est une variété différentielle connexe, on a vu que
Z°(X ; G) s'identifie au groupe des applications constantes de X dans G (24.29.2).
Si X est non compacte, la seule application constante de X dans G de support
compact est 0, donc on a alors H°(X ; G) = {0}.
Soit X un espace séparé localement connexe, et soit (X„)aeA une famille
d'ouverts deux à deux disjoints de X, de réunion X. Comme un ensemble compact
K c X ne peut rencontrer qu'un nombre fini de X„ SP(X ; G) est isomorphe à
la somme directe des SP(X„ ; G) ; donc HP(X ; G) s'identifie à la somme directe
desHP(Xa;G).
(24.34.3) Si A est un anneau commutatif, il résulte aussitôt de la
définition (24.31.1.1) du cup-produit que, pour cette multiplication, SC'(X; A) est une
sous-algèbre différentielle graduée de S'(X ; A) qui est associative mais n'admet
pas d'élément unité si X n'est pas compact. On en déduit sur HC'(X ; A) une structure
d'algèbre graduée, qu'on appelle Yalgèbre de cohomologie à supports compacts
de X, à coefficients dans A. Le même raisonnement que dans (24.31.3) montre
que cette algèbre est anticommutative : le seul point à vérifier, avec les notations
de (24.31.3.6), est que, pour une cochaîne à support compact / e SP(X ; A),
'hp{f) est aussi à support compact; mais, par définition, pour tout simplexe
singulier seSp+ ,(X; A), on a < 'hp(f), s> = < /, /ip(s) > ; comme le support de
hJLs) est contenu dans celui de s; on voit que si < / z > = 0 pour toute p-chaîne z
dont le support ne rencontre pas un ensemble compact K, on aura aussi
< 'hjif), y > = 0 pour toute (p + l)-chaîne y dont le support ne rencontre pas K.
35. Homologie et cohomologie singulière relatives.
(24.35.1) Soient X un espace topologique séparé, Y un sous-espace de X. Pour
tout p *s 0, on a vu (24.20.1) que, si j : Y -» X est l'injection canonique, Sp(/)
est injective et identifie donc SP(Y ; A) à un sous-A-module de SP(X ; A), formé
des p-chaînes dont le support est contenu dans Y. Comme le bord d'une telle chaîne
a aussi son support dans Y, l'application A-linéaire 60 : Sp(X ; A) -* SP_!(X ; A)
applique SP(Y ; A) dans Sp_ ^Y ; A) et définit par suite, par passage aux quotients,
une application A-linéaire
(24.35.1.1) 6o : SP(X ; A)/SP(Y ; A) - Sp_ t(X ; A)/Sp_ t(Y ; A) ;
il est clair que l'on a 60 <> 60 = 0, et l'on a donc défini sur
S.(X, Y ; A) = © (S/X ; A)/SP(Y ; A))

212 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
une structure de A-module codifférentiel gradué ; on a par suite des A-modules
d'homologie Hp(X, Y ; A) correspondants (Ann. 30.7) ; on dit que lyX, Y ; A)
est le p-ème module d'homologie relative de X modulo Y, à coefficients dans A.
On peut décrire ces modules de la façon suivante : si ZJX, Y ; A) est l'image
réciproque dans SpfX ; A) du noyau de l'application (24.35.1.1) et BplX, Y ; A)
l'image réciproque dans S^X; A) de l'image 60(SP+1(X; A)/SP+1(Y; A)),
H^X, Y; A) est isomorphe au quotient Z^X, Y; AJ/B^X, Y ; A). La définition
de 60 montre que ZfX, Y ; A) est le sous-module des p-chaînes de SJLX ; A)
dont le bord a son support dans Y ; on dit encore que ce sont les p-cycles relatifs
modulo Y. De même B^X, Y ; A) est le sous-module des p-chaînes homologues
à une p-chaîne dont le support est dans Y ; on dit que ce sont les p-bords relatifs
modulo Y. Si Y = 0, on a H.(X, Y ; A) = H.(X ; A) ; si Y = X, H.(X, X ; A) = {0}.
(24.35.2) Exemple. — Soient X une variété différentielle connexe, Y une partie
non vide de X ; alors on a
(24.35.2.1) H0(X, Y ; A) = {0}.
En effet, si xQ e Y, pour tout point x e X, il existe un simplexe singulier s : At -* X
tel que s^) = x et s(e0) = x0 (16.26.10), donc, dans S0(X ; A) = Z0(X ; A),
identifié au A-module des combinaisons linéaires formelles des points de X
(24.22.4), tout point xeX est homologue à x0, et par suite
B0(X, Y ; A) = Z0(X, Y ; A) = Z0(X ; A).
(24.35.3) Les définitions précédentes montrent que dans la suite exacte
(24.35.3.1) 0 -» S.(Y ; A) -► S.(X ; A) -+ S.(X, Y ; A) - 0
les applications canoniques sont des homomqrphismes de modules codifférentiels
gradués. On en déduit donc (Ann. 30.5) une suite exacte d'homologie relative
(24.35.3.2)
... - Hp(Y; A) ^lyXjA) A H./X.YjA) 4 Hp_t(Y;A)
se terminant par H0(X, Y ; A) -+ 0. L'application r fait correspondre à la classe
d'homologie d'un p-cycle z (ou classe d'homologie « absolue ») sa classe
d'homologie relative quand z est considéré comme p-cycle relatif modulo Y.
L'application d est définie comme suit : si c est la classe d'homologie relative d'un p-cycle
relatif z, ë0z a son support dans Y, et comme 60(60z) = 0, c'est un (p - l)-cycle
de Y; de est la classe d'homologie de 60z dans HP_!(Y; A).
(24.35.4) Soit u : X -» X' une application continue de X dans un espace
séparé X', et soit Y' un sous-espace de X' tel que uÇY) c Y'. L'application linéaire

35. HOMOLOGIE ET COHOMOLOGIE SINGULIÈRE RELATIVES 213
S.(u)
S.(u)| S.(u)|
0 - S.(Y' ; A) -+ S.(X' ; A) ->• S.(X' ; A)/S.(Y' ; A) - 0
on en déduit (Ann. 30.6) un diagramme commutatif pour les suites exactes
d'homologie relative
(24.35.4.1)
... - H,(Y;A) -» lyXjA) - H,(X,Y;A) - H,_,(Y;A)
H,(u)| H,<u)| Hp(«)| Hp-i(u)
... - H^Y'jA) - H/X'jA) - H/X'.Y'jA) - H^^Y'jA)
Remarque (2435.4.2). — Si HP(X)Y;Z) et HP_1(X,Y;Z) sont des
Z-modules libres, on a un isomorphisme canonique
H^YjZ)®^ - HpfX, Y ; A)
pour tout anneau commutatif A (Ann. 31.4).
(24.35.5) Avec les notations de (24.35.1), l'application
Sp(j) : SP(X ; A) -* SP(Y ; A)
est surjective : en effet, comme la base canonique de SP(Y ; Z) est une partie de
la base canonique de SpfX ; Z), SP(Y ; Z) admet un supplémentaire dans Sp(X; Z),
et toute p-cochaîne sur Y peut donc se prolonger en une p-cochaîne sur X. Si
l'on note SP(X, Y ; A) le noyau <?~. S'(/) c'est-à-dire l'ensemble des cochaînes
de SP(X ; A) qui s'annulent sur tout p-simplexe singulier de Y (dites p-cochaînes
relatives modulo Y), on a donc une suite exacte
(24.35.5.1) 0 - S'(X, Y ; A) - S'(X; A)-^ S'(Y ; A) -* 0
où S*(X, Y ; A) = © SP(X, Y ; A) est un idéal gradué de S'(X ; A).
p*0
On peut encore dire que cette suite exacte s'obtient par transposition à
S.(«) : S.(X ; A) -► S.(X' ; A) applique alors S.(Y ; A) dans S.(Y' ; A), et définit
donc par passage aux quotients une application linéaire
S.(X ; A)/S.(Y ; A) - S.(X' ; A)/S.(Y' ; A),
que nous noterons encore S.(u). Il est immédiat que l'image de Zp(X, Y ; A)
(resp. B,(X, Y ; A)) par S» est contenue dans ZP(X', Y' ; A) (resp. B^X', Y' ; A)) ;
donc on déduit de S/u) par passage aux quotients une application linéaire
Hplw) : Hp(X, Y ; A) -» Hp(X', Y' ; A) aussi notée «„. Comme on a un diagramme
commutatif
0 - S.(Y;A) - S.(X;A) - S.(X; A)/S.(Y; A) - 0

214 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
partir de la suite exacte scindée de A-modules libres gradués (24.35.3.1), S '(X, Y ; A)
étant donc le dual gradué du A-module libre gradué
S.(X, Y ; A) = S.(X ; A)/S.(Y ; A).
Comme S'(j) est un homomorphisme d'algèbres différentielles graduées,
S'(X, Y ; A), pour la restriction à ce module gradué de la différentielle d0 de
S'(X ; A), est un module différentiel gradué, dont on désigne par HP(X, Y ; A)
les modules de cohomologie correspondants ; on dit que HP(X, Y ; A) est le
p-ème module de cohomologie relative de X modulo Y, à coefficients dans A. C'est
donc le quotient ZP(X, Y ; A)/B"(X, Y ; A), où ZP(X, Y ; A) est le sous-module
de ZP(X ; A) formé des p-cocycles sur X qui sont nuls sur tout p-simplexe singulier
de Y (dits p-cocycles relatifs modulo Y), et BP(X, Y ; A) le sous-module des cobords
des (p — Yy-cochaînes nulles sur tout (p — l)-simplexe singulier de Y (dits p-cobords
relatifs modulo Y). Si Y = 0, H'(X, Y ; A) = H'(X ; A). Si Y = X, H'(X, Y; A)={0 }.
(24.35.6) Exemples. — Si X est une variété différentielle connexe et Y une partie
non vide de X, on a
(24.35.6.1) H°(X, Y ; A) = {0}.
En effet, Z°(X ; A) s'identifie au A-module des applications X -► A constantes
dans X (24.29.2), et celles qui sont nulles dans Y se réduisent à 0.
Soit (X„)a6A une famille d'ouverts deux à deux disjoints dans un espace
séparé X, telle que X soit réunion des X„. Si l'on pose Ya = Y n X„ pour tout
a g A, ZP(X, Y ; A) s'identifie au A-module produit lî[Zp(Xa, Y. ; A) et BP(X, Y ; A)
a
au A-module produit riBp(Xa, Y„; A); donc HP(X, Y ; A) s'identifie au module
a
produit llHp(Xa, Y„; A) (Ann. 27.3).
a
(24.35.7) Comme SP(X ; Z)/SP(Y ; Z) est un Z-module libre et que la restriction
de d0 à SP(X, Y ; A) peut être considérée comme le transposé de
l'homomorphisme 60, il résulte de (Ann. 31.6) que l'on a un homomorphisme canonique
(24.35.7.1) Hp(X, Y ; A) (Hp(X, Y ; A))*
que cet homomorphisme est toujours surjectif et qu'il est bijectif lorsque A est
un corps, ou lorsque Hp-i(X, Y; Z) est un Z-module libre.
(24.35.8) Comme les applications de la suite (24.35.5.1) sont des
homomorphismes de A-modules différentiels gradués, on en déduit une suite exacte de
cohomologie relative
(24.35.8.1)
... - HP(X, Y ; A) A HP(X;A) 4 HP(Y;A) A HP+1(X, Y ; A) -» ...

35. HOMOLOGIE ET COHOMOLOGIE SINGULIÈRE RELATIVES 215
débutant par 0 -+ H°(X, Y ; A). L'application a fait correspondre à la classe
de cohomologie d'un p-cocycle « relatif » modulo Y la classe de cohomologie
de ce p-cocycle considéré comme élément de ZP(X ; A) (ou p-cocycle « absolu »).
L'application ô est définie comme suit : si c est la classe de cohomologie d'un
p-cocycle g sur Y, g se prolonge en une p-cochaîne / sur X, et d0f est nulle sur
les (p + l)-simplexes singuliers de Y; comme d0{dof) = 0, d0f est un (p + 1)-
cocycle sur X, donc appartient à Zp+ '(X, Y ; A), et de est sa classe de cohomologie
« relative ».
(24.35.9) Soit u : X -> X' une application continue de X dans un espace
séparé X', et soit Y' un sous-espace de X' tel que h(Y) c Y'. Alors l'image par
S"(w) : S*(X' ; A) -> S'(X ; A) de S*(X', Y' ; A) est contenue dans S'(X, Y ; A),
comme il résulte de la définition de S*(u) (24.29.3.1); en outre, l'image de
Zp(X', Y'; A) (resp. BP(X', Y'; A)) par Sp(«) est contenue dans ZP(X, Y ; A)
(resp. BP(X, Y ; A)), donc on déduit de Sp(u) par passage aux quotients une
application linéaire Hp(u) : HP(X', Y' ; A) HP(X, Y ; A) (aussi notée m*). Comme
on a un diagramme commutatif de suites exactes
0
S*(X', Y'; A) S"(X';A) - S*(Y';A)
S<u)
S-(u)
S(«)
0 S'(X, Y; A) -* S'(X;A) S'(Y;A)
0
0
on en déduit un diagramme commutatif pour les suites exactes de cohomologie
relatives
(24.35.9.1)
... -> Hp(X', Y' ; A)
HP(u)
... -+ Hp(X,Y;A)
Hp+1(X', Y'; A)
H" + 1(u)j
Hp(X;A) - Hp(Y;A) HP+1(X, Y ; A)
HP(X' ; A)
H»(u)
Hp(Y' ; A)
Soit i? : X -» X' une seconde application continue telle que u(Y) <= Y', et
supposons que u et v soient homotopes par une homotopie F : X x [0, 1 ] -> X'
telle que F(y, t) e Y' pour tout y e Y et tout t e [0, 1 ]. Alors les applications Hp(«)
et Hp(u) de HP(X', Y' ; A) dans HP(X, Y ; A) sont égales : cela résulte de (24.29.4),
de la suite exacte de cohomologie (24.35.9.1) et du lemme des cinq (Ann. 29.4).
(24.35.10) Comme S'(X, Y ; A) est une sous-algèbre différentielle graduée de
S"(X ; A), le cup-produit définit, en vertu de (24.31.2.1), une structure d'algèbre
graduée sur H'(X, Y ; A), par passage au quotient. Cette algèbre est encore
anticommutative : en effet, avec les notations de (24.31.3), tp applique S^(Y ; A)
dans lui-même, donc donne par passage aux quotients un endomorphisme xp
de Sp(X ; A)/Sp(Y ; A), puis par transposition un endomorphisme 'fp de SP(X, Y ; A).

216 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFERENTIELLE ÉLÉMENTAIRES
Comme on a encore 60(V2)) = ïP-i(fioz) P°ur tout z e SP(X ; A)/Sp(Y ; A), le
raisonnement de (24.31.3) s'applique tel quel à H'(X, Y ; A), en observant que,
dans le lemme (24.31.3.6), h„ applique S/Y; A) dans SP+1(Y; A).
Il est immédiat que dans la suite exacte de cohomologie (24.35.8.1), les
applications a et j* sont des homomorphismes d'algèbres graduées, mais il rien
est pas de même des homomorphismes d de A-modules.
En outre, sous les hypothèses de (24.35.9), les
définissent un homomorphisme noté u* ou H \u) de Y algèbre graduée H '(X', Y' ; A)
dans Valgèbre graduée H*(X, Y ; A).
Remarquons enfin que les définitions et résultats de (24.29.5) se généralisent
à la cohomologie relative : pour tout homomorphisme d'anneaux h : A -* A',
on a un homomorphisme d'algèbres graduées «„ :H"(X, Y; A) -» H'(X,Y;A'),
et sous les hypothèses de (24.35.9), un diagramme commutatif
H-(X,Y;A) - H'(X,Y;A')
(24.35.11) On a vu en outre que S'(X, Y ; A) est un idéal bilatère gradué de
l'algèbre graduée S'(X ; A) ; la formule (24.31.2.1) entraine que si / e Z'(X ; A)
et geZ"(X, Y; A) (resp. geB'fX, Y; A)), on a /~geZ'(X, Y; A) (resp.
/ ~ g e B'(X, Y ; A)) ; de même, si / e B'(X ; A) et g e Z'(X, Y ; A), on a
Par passage aux quotients, on déduit donc du cup-produit une application
bilinéaire (dite encore cup-produit) (x, y) -» x^y de H'(X; A) x H'(X, Y; A)
dans H"(X, Y ; A) ; elle fait de H'(X, Y ; A) un module à gauche gradué sur l'anneau
gradué H'(X ; A). On notera que si x, y sont tous deux dans H'(X, Y ; A), on a
avec les notations de (24.35.8.1)
(24.35.11.1) a(x)~y = x~y
où au premier membre il s'agit sur H'(X, Y ; A) de sa structure de H'(X ; A)-
module et au second de sa structure d'algèbre (24.35.10) : en effet, pour deux
cocycles relatifs /, g, le cocycle relatif / — g est le même, que l'on considère f
comme cocycle « relatif » ou comme cocycle « absolu ».
Sous les hypothèses de (24.35.9), il résulte du fait que S'(«) est un
homomorphisme d'algèbres différentielles graduées, que pour x e H'(X' ; A) et
yeH*(X\ Y'; A), on a
W(u) : H"(X', Y' ; A) - H"(X, Y ; A)
H'(X', Y' ; A) *4 H'(X', Y' ; A')
(24.35.10.1)
/~geB'(X,Y;A).
(24.35.11.2) u*(x - y) = u*(x) - u*(y).

35. HOMOLOGIE ET COHOMOLOGIE SINGULIÈRE RELATIVES
217
(24.35.12) Exemple. — Pour tout entier n > 1, on a
(24.35.12.1)
HP(R-,R"-{0}; A) = {0} si p # n
H„(R", R" — {0} ; A) = A.
En effet, pour tout p > 2, dans la suite exacte d'homologie relative
H^R"; A) - H/R", R" - {0} ; A) - H,_,(R" - { 0 } ; A) -> H^tR"; A)
les termes extrêmes sont nuls (24.22.3.1), et SB_! est un rétracte par homotopie
de R" - {0}, donc H,_^R" - {0} ; A) s Hp_t(SB_i ; A); compte tenu de
(24.22.9), cela prouve (24.35.12.1) pour p > 2. Pour p = 1 et n > 2, R" - {0}
est connexe, donc l'application canonique H0(R" — {0} ; A) -» H0(R" ; A)
est injective (24.22.4), et on a par suite H^R", R" - {0} ; A) = {0}. Enfin,
pour p = n = l,R-{0}a deux composantes connexes R% et — R\, et chacune
des applications HQ(R\ ; A) -» H„(R ; A), H0(- Rî ; A) H0(R ; A) est
bijective, en vertu de (24.22.4), (24.35.2.1) et (24.35.3.2) ; le noyau Hj(R, R - {0} ; A)
de l'application canonique H0(R — {0} ; A) -♦ H0(R ; A) s A est donc
isomorphe à A. Le cas p = 0 a déjà été traité (24.35.2.1).
Comme tous les Z-modules H^R", R" — {0} ; Z) sont libres,
l'homomorphisme (24.35.7.1) est bijectif pour X = R" et Y = R" - { 0 }, donc
Remarque (24.35.13). — Soit u un automorphisme de l'espace vectoriel R" ;
alors l'automorphisme m* de H"(R", R" - {0} ; Z) est l'identité si det(w) > 0,
et la symétrie z -* — z dans le cas contraire. Pour le voir, notons d'abord que,
dans GL(n, R), u est homotope à une transformation orthogonale : en effet, il
résulte de (21.17.6), restreint aux matrices réelles, qu'on peut écrire u = e* ° w,
où w est une transformation orthogonale et h un endomorphisme de R", et notre
assertion en résulte en considérant les automorphismes e** ° w, pour 0 < s < 1.
On peut donc se borner au cas où w est une transformation orthogonale, et on a
alors deg w = det w (24.9.5). La conclusion résulte alors de (24.33.3, (ii)) et du
diagramme (24.35.9.1) appliqué à w.
Remarque (24.35.14). — Pour n ^ 2, on appelle classe fondamentale de
cohomologie de R" modulo R" - {0} le générateur e* de H"(R", R" - {0} ; Z),
image de la classe fondamentale c*_t de cohomologie de A„_j (24.32.2) par la
bijection canonique
(24.35.12.2)
H"(R", R" - { 0 } ; A) = { 0 } si p / n
H"(R", R" — { 0} ; A) S A.
H"-1i
•(A._i;Z) ^ H"_1(R" - {0}; Z) A H"(R", R" — {0};Z)
où n : R" - {0} -t AB_X est la projection x -»• x/\x\

218 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
Avec la définition (24.28.3.1) de la n-chaîne xn) la relation ë0x„ = y„-i
montre que x„ est un n-cycle relatif sur R" modulo R" — {0}, dont la classe
d'homologie relative est une base de HB(R", R" - ( 0} ; Z) (24.35.3.2). Les
n-cocycles relatifs ayant e* comme classe de cohomologie relative sont donc ceux
dont la valeur pour le n-cycle relatif x„ est égale à 1, puisque H"(R", R" — {0} ; Z)
s'identifie au dual de HB(R", R" - {0 } ; Z).
Pour définir un tel n-cocycle relatif /„, partons du (n — l)-cocycle noté sf
dans (24.32.2) (où il faut remplacer n par n — 1) ; il prend la valeur 1 pour le
simplexe singulier sx et la valeur 0 pour tous les autres (n — l)-simplexes singuliers
(a0 ... a^_!) de ®, ainsi que dans L"-^® ; Z). Prolongeons (arbitrairement)
s? en un (n - l)-cocycle g„-x eZn_1(A„_i ; Z), puis posons /B_t =gB_1ojr,
dont la classe de cohomologie dans H"_1(R" - {0} ; Z) est 7t*(c*-i)- Par
définition de l'homomorphisme d (24.35.8), e* = ô[n*(c*-,)) est la classe du n-cocycle
relatif /„ = d0/B'_i, où /„'_! est la (n — l)-cochaîne sur R" obtenue en
prolongeant f'„- ! par 0 pour tous les (n — l)-simplexes singuliers de R", dont le support
n'est pas contenu dans R" — {0}. On vérifie alors aussitôt que la valeur de /„
pour le n-simplexe singulier
(0eoeo + ex ... e0 + et + ... + e„_i)
est égale à 1, et que sa valeur est 0 pour les autres simplexes singuliers
(0 a0 aï ... a„_ x) de ®0, ainsi que dans LB'(®0 ; Z). On a donc bien < f„ xn > = 1,
donc la classe de cohomologie relative de fn est e*.
Pour n = 1, on définit e\ comme l'image canonique de l'élément de
H°(S0 ; Z) identifié à la fonction égale à 1 au point -(- 1, à 0 au point - 1 ; il
vérifie encore les mêmes propriétés.
Notons que, si l'on pose, pour 0 < k ^ n,
(24.35.14.1) x<*> = S r,M aï ... «ï 0 aj[ +1 ... «D
l'élément z = xn — (— 1)*+1jcb*) appartient à LB(®0; Z), donc on a
</-x?)> = (-l>*+1.
PROBLÈMES
1) Soient X un espace séparé, Y un sous-espace de X. Si deux des Z-modules H.(X; Z),
H.(X; Z), H.(X, Y; Z) sont de type fini, il en est de même du troisième. On pose alors
JC(X) = K - iyrg(H/X ; Z)), jf(X, Y) = £( - D^H/X, Y ; Z))
J J
(« caractéristiques d'Euler-Poincaré » de X et de X relativement à Y). Montrer que
X(X) = Z(Y) + Z(X,Y).

35. HOMOLOGIE ET COHOMOLOGIE SINGULIÈRE RELATIVES
219
2) Soient X un espace séparé, X' un sous-espace de X, X" un sous-espace de X'.
a) Définir une suite exacte d'homologie relative
... - H^X', X" ; A) - H,(X, X" ; A) - H^X, X' ; A) -» H,_,(X', X" ; A) - ...
et une suite exacte de cohomologie relative
... - H'(X, X' ; A) - H'(X, X" ; A) - H'(X', X" ; A) - H'+ '(X, X' ; A) - ...
b) On suppose que A est un corps. Alors, si pour tout p > 0, HjlX, X' ; A) et H,(X', X" ; A)
sont de dimension finie, Hp(X, X" ; A) est de dimension finie et l'on a
dim(H,(X, X" ; A)) « dim(H,(X, X' ; A)) + dim(H,(X', X" ; A)).
Si de plus Hp(X, X' ; A) = {0} et H,(X', X" ; A) = {0 } pour p assez grand, et si l'on pose
Z(X, X' ; A) = Ë (- l)'dim(H,(X, X'; A)) et de même pour Z(X', X" ; A) et Z(X, X"; A), on a
X(X, X" ; A) ='^X, X' ; A) + Z(X', X" ; A).
3) Soient X une variété différentielle pure, Y une sous-variété fermée de X. Pour tout entier
p > 0, on note 6P(X, Y) le sous-espace de S^X) formé des p-formes nulles dans Y, s4'(X, Y) l'algèbre
graduée somme directe des 3P(X, Y) ; cette algèbre est stable par la différentiation extérieure,
et on peut donc définir sa cohomologie Hqr(X, Y). Définir un isomorphisme canonique
Hd„(X,Y) - H'(X, Y; R)
(montrer l'existence d'une suite exacte de cohomologie pour les Hftn(X), HgR(Y) et HgR(X, Y) ;
utiliser (24.33.2) et le lemme des cinq).
4) Soient X un espace séparé, Y un sous-espace de X.
a) Montrer que si l'injection canonique j : Y -» X est une équivalence d'homotopie
(section 16.26, problème 2), on a H^X, Y ; A) = 0 et H^X, Y ; A) = 0 pour tout p > 0.
b) On suppose qu'il existe une application continue / : X -» Y telle que f(y) = y pour
tout y e Y. Montrer que dans la suite exacte d'homologie relative (24.35.3.2), j, est injective, r est
surjective et que H^X ; A) est isomorphe à la somme directe H,(Y ; A) © HJ(X, Y ; A) pour
tout p. Dans la suite exacte de cohomologie relative (24.35.8.1), j* est surjective, a est injective
et H"(X ; A) est isomorphe à la somme directe H"(Y ; A) © H'(X, Y ; A) pour tout p (observer
que » est l'identité, ainsi que j* o /*).
c) On suppose qu'il existe une application continue F de X x [0, 1] dans X telle que
F(x, 0) = x pour tout x 6 X, et que f : x -* F(x, 1) soit une application de X dans Y. Montrer
que dans la suite exacte d'homologie relative (24.35.3.2),y, est surjective, d est injective, et Hjy ; A)
est isomorphe à la somme directe H^X ; A) © Hp+ t(X, Y ; A) pour tout p. Dans la suite exacte
de cohomologie relative (24.35.8.1), j* est injective, d est surjective et H'(Y ; A) est isomorphe à
la somme directe HP(X ; A) © HP(X, Y ; A) pour tout p (observer que jm « /„ est l'identité, ainsi
que /* -j*).
5) Soient X un espace séparé, A un anneau commutatif. Avec les notations de (24.31.1),
pour tout simplexe singulier se¥(A,+,; X) et toute cochaîne / eSp(X; A), on pose
s~/ = </s°a,>(s°<)
et on définit ainsi par linéarité une application A-bilinéaire(z, /) -» z~-f de S,+^X; A) x SP(X; A)
dans S,(X ; A), appelée cap-produit.
a) Montrer que pour toute q-cochaine g e S'(X ; A), on a
<z~/,g> = <z,/~g>.
b) Si zeS,+,+r(X; A), /eS*(X; A), geS<(X; A), on a
z~(/~g) = (z~/)~g
en d'autres termes, S.(X ; A) est un S'(X ; \)-module à droite pour le cap-produit.

220 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
c) Montrer que l'on a, pour zeS,+^X; A), feS'(X; A)
«o(z - /) - ( - l)'««0z) -z- (d0/)) •
En déduire, par passage aux quotients, une application A-bilinéaire (c, u) -» c — u de
H,+^X; A) x H'(X; A) dans HJX; A) telle que l'on ait
<c~u,t>> = <c, u — u>.
d) Montrer que, pour toute application continue / : X -» Y, on a
H,(/X« - (H'(/Xu))) = (Hp^/Xa)) ^ u
pour a e H,+^X ; A) et u e H'(Y ; A).
e) Montrer que par restriction, le cap-produit définit des applications A-bilinéaires
H,+f(X, A; A) x H'(X, A ; A) - H^X; A)
H,+4(X, A ; A) x H'(X ; A) - H^X, A ; A)
pour toute partie A de X.
1) Montrer que pour toute classe a e H,,+^X, A ; A), le diagramme
H'(X, A ; A) - H'(X;A)
H^X;A) - H^X, A; A)
où les flèches horizontales sont les homomorphismes canoniques, est commutatif.
6) Soient Y une variété pure de dimension n, U un ouvert non vide dans Y dont la frontière
est régulière, et X = U. On considère dans l'espace topologique Y x [0, 1 ] le sous-espace produit
X x [0, 1 ] ; sa frontière dans Y x [0, 1 ] est réunion de X x {0 }, X x { 1} et Fr(X) x [0, 1 ] ;
on dit que cette frontière est le double de X et on le note 2X.
a) Définir sur 2X une structure de variété différentielle qui induise sur U et Fr(X) les structures
différentielles données. (Considérer sur Y une structure de variété riemanienne ; avec les notations
de (23.48.4), considérer en un point (x, 0) de FrfX) x { 0}, l'application de V x ] — a, a [ dans
2X égale à (x, t) -» exp(tn(x)) pour t > 0 et à (x, t) -» (x, - t) pour t < 0).
b) Montrer que si Y est orientable, pour une orientation donnée sur Y il existe une
orientation sur 2X qui induit sur U l'orientation donnée.
c) Montrer que si X est compact on a *(2X) = 2g(X) — x(Fr(X)). (Considérer les ouverts
V, = (X x {0 }) u (Fr(X) x [0, 10 et V2 = (X x {1}) u (Fr(X) x ]0, 1 ]) et utiliser la suite
exacte de Mayer-Vietoris).
d) Si Y est orientable et si X est compact, montrer que x(FY(X)) est pair. En déduire que
P2a(R), P2.(C) et P2,(H) ne peuvent être frontières d'ouverts dans une variété orientable dont la
dimension surpasse la leur d'une unité.
36. Cohomologie relative et cohomologie à supports compacts.
(24.36.1) Soient X un espace compact métrisable, Y un sous-espace fermé
de X distinct de X. Pour tout voisinage ouvert V de Y dans X et tout p > 0, le
module ZP(X, V ; A) est un sous-module de Zf(X - Y ; A), car X - V est compact,
et tout p-cocycle dont la valeur, pour tout simplexe singulier de support contenu
dans V, est nulle, appartient évidemment à Zf(X - Y ; A). Pour la même raison,
on a BP(X, V ; A) c Bf(X — Y ; A) ; par passage aux quotients, on obtient donc
une application A-linéaire canonique
(24.36.1.1) H'(X, V ; A) H?(X - Y ; A).

36. COHOMOLOGIE RELATIVE ET COHOMOLOGIE A SUPPORTS COMPACTS 221
On peut ajouter que lorsque V parcourt l'ensemble des voisinages ouverts
de Y, la réunion des images des applications (24.36.1.1) est HP(X — Y ; A) tout
entier. En effet, si / est un p-cocycle de Zf(X — Y ; A), il y a un compact K cr X—Y
tel que / s'annule en tous les simplexes singuliers dont le support ne rencontre
pas K, ce qui signifie que / e ZP(X, X - K ; A).
On déduit de ces remarques la proposition suivante :
(24.36.2) Soient X un espace compact métrisable, Y un sous-espace fermé de X
distinct de X. On suppose qu'il existe un système fondamental dénombrable
décroissant (Vm) de voisinages ouverts de Y dans X tel que Y soit un rétracte par homotopie
(24.22.10) de chacun des Vm. On a alors une suite exacte de cohomologie
(24.36.2.1)
... -* Hf(X - Y; A) A HP(X; A) £ HP(Y; A) À H?+1(X - Y; A) -+ ...
débutant par 0 -+ H°(X - Y ; A).
En effet, pour m < n, il résulte de (24.35.9.1) que l'on a un diagramme
commutatif de suites exactes
(24.36.2.2)
HP(X;A) -> Hp(Vm;A) - H'+^X, Vm; A) -
HP(X;A) - HP(V„;A) -» Hp+X(X, V„ ; A) -
HP+1(X;A) - H'+1(Vm;A)
Id
- Hp+1(
(X;A) - H"+1(VB;A)
où jm : V„ -* Vm est l'injection canonique. L'hypothèse entraîne que chaque
application y*, : Hp(Vm ; A) H^V, ; A) est bijective, car si j„ : Y -» VB et
jm : Y -♦ Vm sont les injections canoniques, jZ et j* sont bijectives (24.22.10),
donc il en est de même de j*„, puisque f* = j* ° j*„. Le lemme des cinq entraîne
donc que chacune des applications canoniques HP(X, Vm ; A) -+ HP(X, V„ ; A)
est bijective. Mais en composant cette application avec l'application canonique
(24.36.1.1) HP(X, V„; A) Hf(X - Y; A), on obtient l'application canonique
HP(X, Vm ; A) -+ HP(X - Y ; A) ; on voit donc que toutes les images dans
HP(X - Y ; A) des applications canoniques HP(X, Vm ; A) HP(X - Y ; A) sont
égales, et en vertu de ce qu'on a vu dans (24.36.1), elles sont toutes égales à
HP(X — Y ; A). Il reste à voir que les applications surjectives
Hp(X,Vm;A) Hcp(X-Y;A)
sont aussi injectives. Or, si / e ZP(X, Vm ; A) est un cobord de BP(X — Y ; A),
il est de la forme dog, où g est une (p — l)-cochaîne dont le support (compact)

222 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFERENTIELLE ÉLÉMENTAIRES
ne rencontre pas Y ; il y a donc un n ^ m tel que ce support ne rencontre pas
V„ ((12.6.2) et (3.17.11)), donc / eBp(X, V„ ; A), et le fait que l'application )*,
est bijective entraine que / e BP(X, Vm ; A), ce qui achève de prouver que les
applications canoniques HP(X, Vm ; A) -» Hf(X — Y ; A) sont bijectives. On
peut donc, dans la suite exacte de cohomologie relative pour X et son sous-
espace Vm, remplacer Hp(Vm ; A) par HP(Y ; A) et HP(X, Vm ; A) par H P(X - Y ; A),
d'où la suite (24.36.2.1). Dans cette suite, j : Y -♦ X est l'injection canonique ;
l'application a fait correspondre à la classe de cohomologie dans HP(X - Y ; A)
d'un p-cocycle à support compact la classe de cohomologie de ce même cocycle
considéré comme élément de ZP(X ; A). Enfin, pour définir l'application d, on
part de la classe de cohomologie c d'un p-cocycle / de Y ; on considère d'abord
le p-cocycle g de Vm qui correspond à / par la rétraction de Vm sur Y ; on prolonge g
(arbitrairement) en une p-cochaîne h sur X, et d0h est un (p + l)-cocycle à support
compact sur X — Y; de est sa classe de cohomologie dans HP+1(X — Y; A).
En vertu de ce qui a été prouvé dans (24.7.1), la proposition (24.36.2) est
applicable à toute variété différentielle pure compacte X et toute sous-variété
fermée Y de X.
Remarque (24.36.2.3). — Si, dans le diagramme (24.36.2.2), on remplace
VH par Y dans la seconde ligne, jm étant remplacé par jm, on voit que HP(X, Y ; A)
est isomorphe à HP(X — Y ; A).
(24.36.3) Supposons remplies les hypothèses de (24.36.2), et soit u : X' -» X
une application continue d'un espace compact X' dans X ; posons Y' = u~ '(Y)
et Vm = m_1(Vm) et supposons en outre que Y' soit un rétracte par homotopie
de chacun des Vm. Alors, dans le diagramme commutatif de suites exactes (24.35.9.1)
... - Hp(X;A) -» Hp(VM;A) -> Hp+1(X,Vm;A) _
Hp(X' ; A) - Hp(Vm; A) - HP+1(X', Vm; A)
-> Hp+1(X;A) Hp+1(Vm;A) -
-» Hp+1(X';A) -> Hp+1(Vm;A)
on peut remplacer Hp(Vm ; A) (resp. Hp(Vm ; A)) par HP(Y ; A) (resp. HP(Y' ; A))
et Hp(X, Vm ; A) (resp. HP(X', Vm ; A)) par HP(X - Y ; A) (resp. HP(X' - Y' ; A)) ;
on obtient donc un diagramme commutatif de suites exactes de cohomologie
(24.36.3.1)
... HP(X-Y;A) -» Hp(X;A) -* HP(Y;A) HP+1(X-Y;A) -» ...
HCP(X' - Y' ; A) -» Hp(X' ; A) - HP(Y' ; A) - H?+ \X' - Y' ; A)

36. COHOMOLOGIE RELATIVE ET COHOMOLOGIE A SUPPORTS COMPACTS 223
WKAn I Hf(R";A) = {(
Appliquons en effet la suite exacte de cohomologie (24.36.2.1) à X = S„
et au sous-espace Y réduit à un point x0 ; pour p > 2, on a donc une suite exacte
0 = H'-»({ x0 } ; A) - HflR"; A) - HP(S„ ; A) - H'({ x0 } ; A) = 0
autrement dit Hf(R" ; A) s HP(S„ ; A), et d'après (24.22.9.1) et (24.30.4), cela
prouve (24.36.4.1) pour p > 2. On sait déjà (24.34.2) que H?(R" ; A) = {0} ; on a
donc une suite exacte
0 -> H°(S„;A) H0({x0};A) -» H^îA) - H'fS^A) 0
Comme H°(S„ ; A) s'identifie au module des fonctions constantes dans S„ (24.29.2),
et que toute fonction sur {x0} se prolonge en une fonction constante sur S„,
l'application canonique H°(SB ; A) -* H°({ x0 } ; A) est surjective, ce qui prouve
que Hcl(R" ; A) s Hl{Sn ; A) et achève de démontrer (24.36.4.1).
(24.36.5) Exemple : cohomologie de P„(R). Nous allons voir que
0 pour p > n et pour p pair et 2 ^ p ^ n
Z/2Z pour p impair et l ^p ^ n — 1
Z pour p = 0, et p = n lorsque n est impair
0 pour p > net pour p impair etl<p<n—1
Z/2Z pour p pair et 2 < p < n
Z pour p = 0, et p = n lorsque n est impair
(24.36.5.1) Hp(P„(R);Z)s
(24.36.5.2) H"(P„(R);Z)S
Rappelons (24.30.8) que chacun de ces résultats entraîne l'autre; nous
prouverons (24.36.5.2) en raisonnant par récurrence sur n. La proposition est
évidente pour n = 1, puisque PX(R) est homéomorphe à Sx, et pour n — 2 elle
résulte de (24.30.8.3) ; nous la supposerons démontrée pour n ^ 2m et nous la
prouverons successivement pour n — 2m + 1 et n = 2m + 2.
I) n = 2m + 1. On applique la suite exacte de cohomologie (24.36.2.1)
à X = P„(R) et Y = Pn_!(R); comme P„_!(R) est un hyperplan de l'espace
projectif P„(R), X - Y est identifié à R". Pour p < n - 1 ou p > n, on a donc
une suite exacte
(24.36.5.3) 0 H"(P,,(R); Z) -> H"(PB_X(R); Z) - 0
où les flèches verticales proviennent canoniquement de u et de ses restrictions
à Y' et X' - Y'.
(24.36.4) Exemple : cohomologie à supports compacts de R". Nous allons voir que,
pour tout n > 0
= { 0} pour p ^ n

224 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
en vertu de (24.36.4.1) ; reste à déterminer H^p^R) ; Z) pour p = n - 1 et
p = n. On a la suite exacte
(24.36.5.4)
o - H"_1(Pn(R); z) - h--Hp„-,(R);Z) -+ h?(r-;z) - H"(PB(R);Z) - o
et par l'hypothèse de récurrence, H"-1(PB-i(R); Z) ^ Z/2Z; l'image de ce
module dans HJ!(R" ; Z) s Z ne peut être que {0}, donc H" -; Z) £ Z/2Z,
et H"(P„(R) ; Z) S Z, ce qui prouve (24.36.5.2) pour n = 2m + 1. Toutefois,
en vue de la preuve de (24.36.5.2) pour n = 2m + 2, nous avons besoin de préciser
l'application jt* : HB(P„(R); Z) H"(SB ; Z) pour n = 2m + I.oùtt. :S„ FJJBL)
est l'application canonique.
Pour cela, montrons qu'on peut appliquer le diagramme (24.36.3.1) à
X = pM(R), X' = Sm à l'application n et à Y = P^iR), Y' = SB_!. Écrivons
les points de S„ sous la forme x = y cos 0 + e0 sin 0 avec y e S„_, et
n „ te
-2^2;
71
pour tout 0O tel que 0 < 0O < - , soit V'(0O) l'ouvert de S„ défini par - 0O < 0<0O;
en considérant la fonction F(y, 0, t) = y cos td + e0 sin t6 pour yeS,,-!,
— 0O < 0 < et 0 < ' ^ 1> on v°it °.ue S„_ i est rétracte par homotopie de
V'(0O) ; en outre, on a F(- y, - 0, t) = - F(y, 0, t), donc, si V(0O) = 7t(V'(0o))
dans p.(R), p„ _ i{R) est rétracte par homotopie de V(0O), et on a V'(0O)=n " 1(V(0O)).
Soit U (resp. V) l'ouvert de SB formé des (y, 0) tels que 0 < 0 ^ ^ ^resp. - ^ < 0 < 0^ ;
l'application de (24.36.3.1) donne le diagramme commutatif de suites exactes
0 - H-HPjfJDîZ) - H-1(P._1(R);Z) -
(24.36.5.5) "j
0 ►H"-1(SB_1;Z) -»
*—► hj(R" ; Z) s ► H"(PB(R) ; Z) -+ 0
-y H?(U ; Z) 0 H"(V ; Z) H"(SB ; Z) - 0
Les restrictions de n à U et à V sont des homéomorphismes de ces espaces
sur X - Y = R"; si b„ est un générateur de HJtfR"; Z), on a 7t*(6B) = (b'm bB),
où oB (resp. b„') est un générateur de H^U ; Z) (resp. hj(V ; Z)). Si s est l'homéo-
morphisme x -» — x de S„ sur elle-même, on a deg s = 1 puisque n est impair
(24.9.5) ; d'autre part, la restriction de s à U est un homéomorphisme de U sur V

36. COHOMOLOGIE RELATIVE ET COHOMOLOGIE A SUPPORTS COMPACTS 225
tel que 7t | U = (rt | V) o (s | U), et par suite b'n' = s*(b'H). Or, on déduit de (24.36.3.1)
un diagramme commutatif de suites exactes
(24.36.5.6)
0 - H"-1(SÉ_1;Z) - H;(U;Z)0Hc"(V;Z) A H"(S„;Z) 0
0 - H"" »(&,_, ; Z) - H"(V ; Z) © HRU; Z) H"(S„; Z) - 0
Si cB est un générateur de H"(SB ; Z) s Z, on a s*(c„) = c'„ (24.33.3, (ii)) ;
par suite, si a(b'„) = Xc'm on a aussi a(b") = Xc'n ; comme a est surjectif, cela n'est
possible que si X = ± 1 ; en remplaçant au besoin c'„ par — c'm on peut supposer
que X = 1. On a par suite a(7t*(bB)) = 2cn = n*(a(bn)). Mais c„ = a(b„) est un
générateur de H"(PB(R) ; Z), donc on voit que 7t*(cB) = 2c'n.
II) n = 2m + 2. On a encore la suite exacte (24.36.5.3) pour p < n — 1
ou p > n, et les diagrammes commutatifs (24.36.5.5) et (24.36.5.6), mais cette
fois deg s = - 1 ; donc, si a(b'„) = Xc'n, on a a(bB) = — AcB ; en choisissant c'n
convenablement, on peut supposer que X = 1, et le noyau de l'application
a : HC"(U ; Z) © HC"(V ; Z) ^ H"(SB ; Z)
est donc engendré par (b'„ b'i). Par suite, on peut prendre le générateur cB_,
de H"-1(SB-1 ; Z) tel que ô(cB_,) = (b; bB') = 7t*(bB). Mais on a vu dans le cas I)
qu'il y a un générateur cH-t de H"_1(P»-i(R); Z) tel que n*(c„-i) = 2cB_1.
Ceci montre déjà que l'homomorphisme n* : H"- 1(PB_ ,(R) ; Z) -» H"-'(S»- j ; Z)
est injectif, donc H"-1(P„(R); Z) = {0} en vertu de (24.36.5.5). En outre, on a
n^c,-,)) = 2{b'm Kl donc d(cB_i) = 2bB; on conclut alors de (24.36.5.5)
que H"(P„(R); Z) s Z/2Z, ce qui achève de prouver (24.36.5.2).
1) Pour 0 < m < n, déterminer les groupes de cohomologie H^(P^R) - P„(R); Z).
(Raisonner par récurrence sur n — m, en utilisant la suite exacte de la section 24.35, problème 2).
2) Déterminer la structure de l'anneau de cohomologie H'(P„(R) ; Z) et montrer en particulier
que pour p, q pairs et p + q < n, l'application (a, b) -» a — b de H'(P^R) ; Z) x H'(P^R) ; Z)
dans H'+,(P,(R); Z) est surjective (considérer l'application canonique
et utiliser (24.40.12) et la suite exacte de la section 24.30, problème 2, correspondant à la suite
exacte 0 -> Z -» Z -> Z/2Z -. 0).
3) Soient X un espace compact métrisable, A une partie fermée de X, ayant un système
dénombrable de voisinages (VJ tel que A soit rétracte par homotopie de chaque Vm. Soit X/A
l'espace quotient de X par la relation d'équivalence dont les classes sont A et les ensembles { x },
où x parcourt X - A (section 24.22, problème 8 et section 12.5, problème 10). Montrer qu'on a
H'(X/A ; Z) s Hf(X - A ; Z) pour p > 1, et H°(X/A ; Z) s H?(X - A ; Z) © Z.
PROBLÈMES
H'(P^R);Z) - H'(P^R);F2)

226 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
4) Soit X un espace compact métrisable. Dans l'espace X x [0, 1 ], on considère la relation
d'équivalence dont les classes sont X x { 0}, X x {1} et les ensembles {(x, t)}, où x parcourt X
et t l'intervalle ouvert ]0, 1 [. On dit que l'espace quotient de X x [0, 1 ] par cette relation est
la suspension de X et on le note SX. Montrer que l'on a H°(SX ; Z) s Z, et H'(SX ; Z) s H'" l(X; Z)
pour p > 1.
5) Soit Y un espace séparé tel que le Z-module H.(Y ; Z) soit de type fini. Montrer que si X
est obtenu par attachement à Y d'une boule D„ on a pour les caractéristiques d'Euler-Poincaré
la relation
z(X) = z(y) + (- 1)".
6) Soit X un espace séparé ayant la propriété suivante : il existe une suite (Yj)0<j<m de sous-
espaces fermés de X tels que Y0 soit réduit à <x0 points, que YJ+, se déduise de Yj par attachement
d'une boule (de dimension quelconque) pour 0 ^ j < m — 1, et que X = Y„. Si l'on a ainsi attaché
en tout a, boules de dimension q, pour 1 $ q $ N, montrer que
Z(X)= i (-!)'«,•
l'O
7) Soit X une partie compacte d'un espace RN admettant une subdivision cellulaire
(section 28.14). Si, dans cette subdivision, le nombre des polyèdres convexes de dimension q est a,
pour 0 ïS <j < N, montrer que l'on a
n
Z(X) = s (- iy«, (formule d'Euler).
En déduire que si X c: R™ et Y <= R" sont des sous-espaces compacts admettant chacun une
subdivision cellulaire, X x Y c R1"-1-" admet une subdivision cellulaire et l'on a x(X x Y) = *(X)x(Y).
8) On appelle complexe cellulaire (fini) un espace compact X obtenu par le procédé du
problème 6, avec les conditions supplémentaires suivantes :
1 ° Si Y j +1 est obtenu par attachement de D,, à Y j au moyen de fj +1, la suite des dimensions n t
est croissante (mais non nécessairement strictement croissante).
2° L'ensemble /}+i(S,,,-i) ne rencontre aucun des ensembles A+i(D.k) (qu'on appelle
encore les cellules de X) pour les indices k < j tels que nk = n,.
Un complexe simplicial euclidien est un cas particulier de complexe cellulaire.
On suppose X connexe par arcs, et on considère un C°-revêtement X' de X (section 16.25,
problème 8), connexe par arcs et à d feuillets, et sa projection n : X' -» X.
a) Soit x0eX; il appartient à un ensemble fj+l(i)ni) pour une seule valeur de j. Soient
xi (1 < h < d) les points distincts de x~'(x0). Montrer qu'il existe d applications continues
Sj+i.» : D», -» X' telles que g)+uk(fj~+\(xo)) = xi pour 1 < h < 4, et que y°gJ+i,k = /}+,- Les
d images £,+ sont deux à deux disjointes, et la restriction de gJ+ lJt à D./ est un
homéomorphisme de ce disque sur son image dans X'.
b) Déduire de a) que X' est un complexe cellulaire et que l'on a
Z(X') = <fz(X).
9) a) Soit X le demi-espace fermé défini par c;" > 0 dans R" ; montrer que H?(X ; Z) = {0}
pour tout p > 0.
b) Si F est une partie finie de q éléments dans X, montrer que HC'(X - F ; Z) s Z*
et Hf(X - F ; Z) = { 0 } pour p > 2.
c) Soit Y le sous-espace fermé de R" défini par 0 < i" < 1 ; montrer que H;(Y ; Z) s Z, et
Hf(Y ; Z) = {0} pour p ■£ n. (Considérer X et Y comme des sous-espaces ouverts d'une boule
fermée).
10) Soit X un espace localement compact métrisable et séparable, et soit (K.) une suite
croissante de compacts tels que X soit réunion des intérieurs des K„ (3.18.3). Pour m < n on a
alors un homomorphisme canonique H^X, X — K„; A) -» H'(X, X — K, ; A), et les

37. EXCISION ET SUITE DE MAYER-VIETORIS RELATIVE
227
HP(X, X - K, ; A) forment un système inductif pour ces homomorphismes (section 24.1,
problème 2). On a d'autre part pour tout n un homomorphisme canonique
H'(X, X - K„; A) -» H?(X; A);
montrer que ces homomorphismes définissent par passage à la limite inductive un isomorphisme
canonique
limH'tX, X - K„ ; A) =t Hf(X ; A).
11) Soit X le bouquet des deux variétés P2(R) et S3 (24.22.11). Montrer que l'anneau de
cohomologie H*(X ; Z) est isomorphe à l'anneau de cohomologie H'(P3(R) ; Z), mais que l'anneau
de cohomologie H'(X; F2) n'est pas isomorphe à l'anneau de cohomologie H'(P3(R); F2).
37. Excision et suite de Mayer-Vietoris relative.
(24.37.1) Soient X un espace séparé, Xu X2 deux sous-espaces de X. Pour tout
anneau commutatif A, S.(Xj ; A) et S.(X2 ; A) sont des sous-A-modules
différentiels gradués de S.(X; A); donc il en est de même de S .(Xi ; A) + S.(X2 ; A)
et de S.(Xi n X2 ; A) = S.{XX ; A) n S.(X2 ; A), et on a une suite exacte
(24.37.1.1)
0 - S.(Xj n X2 ; A) A S.^ ; A) © S.(X2 ; A) A S.^ ; A) + S.(X2 ; A) -» 0
avec v(z) = (z, — z) et u(zx, z2) = zx + z2 (cf. (24.22.8)).
De l'injection canonique h : Xx -> Xt u X2 et de sa restriction X, n X2 -+ X2,
on déduit des inclusions canoniques
S.(/i) : S.(Xi ; A) S.^ ; A) + S.(X2 ; A) A S.(X,uX2;A)
S.(«) : S.(X, n X2 ; A) -* S.(X2 ; A)
d'où des homomorphismes de modules différentiels gradués quotients, formant
un diagramme commutatif
S.(X, ; A)/S.(Xj n X2 ; A) À (S.(Xi ; A) + S.(X2 ; A))/S.(X2 ; A)
(24.37.1.2) y^j
S.(X, u X2 ; A)/S.(X2 ; A)
(24.37.2) Les propriétés suivantes sont équivalentes :
(i) L'injection j : S.(X, ; A) + S.(X2 ; A) -» S.(Xj u X2 ; A) donne un iso-
morphisnïe j^ en homologie (Ann. 30.3).
(ii) L'homomorphisme
e : S.(X! ; A)/S.(X, n X2 ; A) - S.(Xt u X2 ; A)/S.(X2 ; A)
donne un isomorphisme e^ = H.(h) : H.(X,, X,nX2; A) H.{XXuX2,X2; A)
en homologie (la définition de H.(h) étant celle de (24.35.4)).

228 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
Comme S.(X! n X2 ; A) = S.(Xi ; A) n S.(X2 ; A), rhomomorphisme i, dans
le diagramme (24.37.1.2), est bijectif, et est donc un isomorphisme ; par suite,
il revient au même de dire que e„ est un isomorphisme ou que j„ est un
isomorphisme. Tout revient donc à voir que si j\ est un isomorphisme, il en est de même
de et réciproquement. Or on a le diagramme commutatif de suites exactes
0 - S.(X2 ; A) -» S.(Xj ; A) + S.(X2 ; A) -
w j
0 - S.(X2 ; A) ► S.(X! u X2 ; A) -
- (S.(X! ; A) + S.(X2 ; A))/S.(X2 ; A) 0
1
► S.(Xi u X2 ; A)/S.(X2 ; A) > 0
et la conclusion résulte de (Ann. 30.6) et du lemme des cinq.
Lorsque les propriétés équivalentes de (24.37.2) sont satisfaites pour tout
anneau commutatif A, on dit que (Xt, X2) est un couple excisif de sous-espaces
deX.
(24.37.3) Tout couple (Xt, X2) de sous-espaces ouverts de X est excisif.
Ce n'est autre que le cas particulier de (24.22.7) que l'on a utilisé dans (24.22.8)
en prenant le recouvrement U de Xt u X2 formé de Xt et X2 ; dans ce cas
l'application définie dans (24.22.6) n'est autre que /„.
(24.37.4) Soient U un ouvert de X, A un fermé de X tels que AcU; alors
rhomomorphisme canonique d'homologie relative (cf. (24.35.4.1))
(24.37.4.1) h,. : H.(X - A, U - A ; A) - H.(X, U ; A)
déduit de l'injection canonique h : X - A -* X (24.35.4) est bijectif (théorème
d'excision).
En effet, si l'on pose Xt = U, X2=X—A, on a Xt u X2 = X, Xx n X2 = U—A ;
l'homomorphisme (24.37.4.1) n'est autre que l'homomorphisme e+ de (24.37.2),
et il est bijectif en vertu de (24.37.3).
Exemple (24.37.5). — Pour toute variété différentielle pure X de dimension
n > 1, et tout point x e X, on a
nAV*n i Hp(X,X-{x};A) = {0} pour/>#«
(24'37-5-1) tHB(X,X-{*};A)^A

37. EXCISION ET SUITE DE MAYER-VIETORIS RELATIVE
229
En effet, soit V un voisinage ouvert de x homéomorphe à R"; on peut
appliquer (24.37.4) en remplaçant U par X - {x} et A par X - V ; en vertu
de (24.35.12.1), on a donc
Hp(X, X — {x} ; A) s HP(V, V — {x} ; A) S H^R", R" — {0} ; A),
et il suffit d'appliquer (24.35.12.1).
Le fait que pour un couple excisif l'injection j de (24.37.2) donne un
isomorphisme en homologie permet d'étendre la suite exacte de Mayer-Vietoris
(24.22.8.4) à tout couple excisif (Xj, X2). Mais on a un résultat plus général
faisant intervenir l'homologie relative :
(24.37.6) Dans un espace séparé X, soient Xu X2, Ah A2 quatre ensembles tels
que Ai c Xu A2 <= X2, et que les couples (Xt, X2) et (Au A2) soient tous deux
excisif s. On a alors une suite exacte d'homologie relative
(24.37.6.1)
... -> HP(X, n Xa, A, o A2 ; A) - H^, A, ; A) © HP(X2, A2 ; A) -
- H/Xj u X2, Ai u A2 ; A) -» H^X, n X2, A, n A2 ; A) -» ...
se terminant par H0(Xi u X2, At u A2 ; A) -> 0 (suite exacte de Mayer-Vietoris
pour l'homologie relative).
La démonstration résulte des deux propriétés suivantes :
I) La suite de A-modules codifférentiels gradués
(24.37.6.2) 0 -> S.(Xt n X2 ; A)/S.(A, n A2 ; A) -»
- (S.(X, ; A)/S.(A, ; A)) © (S.(X2 ; A)/S.(A2 ; A)) ->
- (S.(Xt ; A) + S.(X2 ; A))/(S.(A, ; A) + S.(A2 ; A)) - 0
est exacte.
II) L'homomorphisme de modules codifférentiels gradués
(24.37.6.3) (S.(X, ; A) + S.(X2 ; A))/(S.(A! ; A) + S.(A2 ; A))
S.(X, u X2 ; A)/S.(A, u A2 ; A)
donne un isomorphisme en homologie.
En effet, on peut appliquer la suite exacte d'homologie à la suite exacte de
modules codifférentiels gradués de I), puis, grâce à II), remplacer dans la suite
obtenue, les modules d'homologie de (S.^ ; A)+S.(X2 ; A))/(S.(Ai ; A)+S.(A2 ; A))
par ceux de S.(Xj u X2 ; AyS.fA, u A2 ; A), ce qui donne (24.37.6).

230 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFERENTIELLE ÉLÉMENTAIRES
Pour prouver I), il suffit de remarquer que, dans le diagramme commutatif
G
(où l'on omet A pour simplifier, et l'on écrit — pour G/H)
H
0 0 0
1 l i
0 - S.(Ai n A2) - S^Aj) © S.(A2) -» S.(A,) + S.(A2) - 0
(24.37.6.4) o s#(Xl n x2) - S.(Xi) © S.(X2) - S.^) + S.(X2) 0
ï i ï
^ S.(Xt n X2) ^ SJXi) _^ S.(Xt) -f S.(X2) ^
"* S.(A! n A2) S.(Ai)W S.(A2) ~* S.(A,) + S.(A2)
1 1 i
0 0 0
les colonnes sont exactes ainsi que les deux premières lignes (Ann. 29.3).
Pour prouver II), on note que dans le diagramme commutatif de suites
exactes
0 - S.(Ai) + S.(A2) S.(X,) + S.(X2) -*
(24.37.6.5) | |
0 > S.(Aj u A2) > S.(Xi u X2) -»
- (S.fXJ + S.(X2))/(S.(A,) + S.(A2))-+0
i
► S.(Xi u X2)/S.(Ai u A2) ► 0
les deux premières flèches verticales donnent par hypothèse des isomorphismes
en homologie ; il en est alors de même de la troisième par (Ann. 30.6) et le lemme
des cinq.
(24.37.7) Comme les trois modules gradués figurant dans la suite exacte
(2437.1.1) sont des modules libres gradués, cette suite est scindée (Ann. 29.2)
et la suite des homomorphismes transposés de duals gradués
0 - (S.(Xt ; A) + S.(X2 ; A))* -> S'(X, ; A)©S'(X2; A) - S'fX.nX, ; A) - 0
est exacte et scindée. D'autre part, la suite exacte (24.35.3.1) est aussi scindée,
donc S*(X, Y ; A) = (S.(X ; A)/S.(Y ; A))*, comme on l'a vu (24.35.5). Enfin,
rappelons que si A. = (A„) et B. = (B„) sont deux Z-modules codifférentiels
libres gradués tels que A„ c= B„ et que A„ ait un supplémentaire libre dans B„
pour tout n, et si l'injection u : A. -* B. donne un isomorphisme en homologie,
alors l'homomorphisme Hom(w, 1) : Hom(B„ A) -•> Hom(A„ A) de A-modules
différentiels gradués donne un isomorphisme en cohomologie (Ann. 31.8).

37. EXCISION ET SUITE DE MAYER-VIETORIS RELATIVE 231
De ces remarques, on déduit d'abord que si (Xu X2) est un couple excisif,
les homomorphismes de A-modules différentiels gradués
•j : S'(X, u X2 ; A) - (S^X, ; A) + S.(X2 ; A))*
'e : S*(X, u X2, X2 ; A) - S'(X„ X,nX2; A)
donnent des isomorphismes en cohomologie, le second n'étant autre que
l'homomorphisme H'(/i) = h* correspondant à l'injection h : X, -+ X,uX2 (24.35.9).
En particulier, on a un isomorphisme d'excision en cohomologie :
(24.37.8) Soient U un ouvert de X, A un fermé de X tel que AcU; alors
l'homomorphisme de cohomologie relative:
(24.37.8.1) h* : H'(X, U ; A) - H'(X - A, U — A ; A)
déduit de l'injection canonique h : X — A -» X (24.35.9) est bijectif.
En second lieu, on a une suite exacte de Mayer- Vietoris pour la cohomologie
relative :
(24.37.9) Dans un espace séparé X, soient Xu X2, Al5 A2 quatre ensembles tels
que A, c Xj, A2 c X2, et que les couples (X,, X2) et (A1( A2) soient tous deux
excisifs. On a alors une suite exacte de cohomologie relative
(24.37.9.1) ... -* H"(X,uX2, A,uA2 ; A) A W(XU A, ; A)©H"(X2, A2 ; A) -
A H"(X, n X2, A, n A2 ; A) A W+\XX u X2, A,uA2;A) -> ...
débutant par 0 -* H°(Xj u X2, At u A2 ; A).
La méthode de démonstration est la même que pour (24.37.6); on doit
établir que :
I) La suite de A-modules différentiels gradués
0 - ((S.(X! ; A) + S.(X2 ; A))/(S.(A, ; A) + S.(A2 ; A)))* -
- S'(Xlt Aj ; A) © S'(X2, A2 ; A) -* S*(X, n X2, At n A2 ; A) -» 0
est exacte.
II) L'homomorphisme de modules différentiels gradués
S*(X, u X2, Ai u A2 ; A) -* ((S.(X, ; A) + S.(X2 ; A))/(S.(At ; A) + S.(A2; A)))*
donne un isomorphisme en cohomologie.
Pour I), on remarque que dans le diagramme (24.37.6.4) de suites exactes,
comme elles sont formées de modules libres, elles sont toutes scindées (Ann.29.2) ;
il suffit alors de prendre la suite des homomorphismes transposés de duals
gradués de (24.37.6.2). Pour II), on note de même que les suites exactes dans
(24.37.6.5) sont formées de modules libres, donc on a un diagramme commutatif

232 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFERENTIELLE ÉLÉMENTAIRES
de suites exactes en prenant les homomorphismes transposés de duals gradués ;
on conclut alors de la même manière en utilisant le fait que les homomorphismes
donnent des isomorphismes en cohomologie, par hypothèse (24.37.7).
(24.37.10) Dans la suite exacte (24.37.9.1), l'homomorphisme u provient par
passage à la cohomologie relative (24.35.9) des injections canoniques
Xt -+ Xt u X2 et X2 -+ Xj u X2 : de façon précise, si c est la classe de
cohomologie relative d'un p-cocycle relatif g sur X, u X2, modulo A,uA2, u(c) est le
couple (ci, — c2), où Ci (resp. c2) est la classe de cohomologie relative modulo Aj
(resp. A2) de la restriction gt de g k Xt (resp. de la restriction g2 de g à X2). De
même, l'homomorphisme v provient par passage à la cohomologie relative
des injections canoniques Xt nX2 -> Xt et X1nX2 -* X2 : de façon précise,
si {bi, b2) est un couple formé de la classe bt (resp. b2) de cohomologie relative
modulo At (resp. A2) d'un p-cocycle relatif ht (resp. h2) sur Xt (resp. X2), u(b1, b2)
est la somme des classes de cohomologie relative modulo A, n A2 des restrictions
de /?! et h2 à Xt n X2. Enfin, ô se définit comme suit : si a est la classe de
cohomologie relative d'unp-cocycle relatif / surX] n X2, modulo A ! r> A2, on prolonge /
en une forme linéaire fi sur le A-module
da est la classe de cohomologie relative de d0fu en identifiant canoniquement
la cohomologie de S'(Xt u X2, A, u A2 ; A) et celle de
((S.(X! ; A) + S.(X2 ; A))/(S.(A, ; A) + S.(A2 ; A)))*.
(24.37.11) Faisant At = A2 = 0 dans (24.37.9), on obtient la suite exacte
de Mayer-Vietoris en cohomologie, qui s'applique par exemple lorsque Xi et
X2 sont ouverts dans X (24.37.3).
Exemple (24.37.12). — Pour toute variété différentielle pure X de dimension
w > 1, tout point xeX et tout anneau commutatif A, on a
La preuve est la même que dans (24.37.5), en montrant que pour un voisinage
ouvert V de x homéomorphe à R", on a, par l'isomorphisme d'excision (24.37.8.1)
S'fXj u X2 ; A) -» (S.(X, ; A) + S.(X2 ; A))*
S*(A, u A2 ; A) -+ (S.(A, ; A) + S.(A2 ; A))*
(S/Xi ; A) + SP(X2 ; A))/(SP(A! ; A) + SP(A2 ; A)) ;
(24.37.12.1)
pour p # n
H"(X, X - {x}; A) s H"(V, V - {x}; A) s H'(R", R" - {0}; A).

37. EXCISION ET SUITE DE MAYER-VIETORIS RELATIVE
233
Nous allons considérer plus particulièrement le cas où X est une variété
compacte, connexe et orientée, et où on prend A = R. De la suite exacte de
cohomologie relative (24.35.8.1), on tire en particulier la suite exacte
H"(X, X- {x};R) A H"(X;R) - H"(X - (*};R).
Vu l'identification de H'(X; R) et de HDR(X), on a H"(X; R) s R et
H"(X - {x} ; R) = {0} par dualité de Poincaré et (24.1.2), et par suite
l'application a : H"(X, X - {x} ; R) -> H"(X ; R) est bijective. Nous allons montrer
que l'image par l'application composée
H"(R", R" - { 0 } ; R) A~ H"(X, X - { x} ; R) A H"(X; R)
de la classe fondamentale de cohomologie relative e* (24.35.14) est la classe
fondamentale de cohomologie e\ de X (24.6.3), pourvu qu'on prenne le
difféomorphisme cp : V -* R" tel que cp(x) = 0 de sorte qu'il préserve l'orientation.
En effet, si B est l'image par cp du cube | x |œ < 1 dans R", et si z est la n-chaîne
cp o xn de support B (notation de (24.28.3.1)), cp*{e*) est la classe de cohomologie
relative d'un n-cocycle relatif / tel que < f, z > = 1. Comme on a vu que tous
les n-cocycles relatifs ayant cette propriété sont cohomologues, la définition de
l'isomorphisme d'excision (24.37.7) montre que l'image de cp*(eï) dans
H"(X, X — {x} ; R) est la classe de cohomologie relative d'un n-cocycle relatif g
tel que < g, z > = 1 (lorsque z est considéré comme une n-chaine dans X), et
< g, z' > = 0 pour les n-chaines z' dont le support est contenu dans X — {x}.
Or, pour le calcul de l'homologie de X, on peut se borner à ne considérer que les
chaînes définies dans (24.27.4) à partir d'un plongement de X dans un espace RN ;
et ce plongement (16.25.1) peut être choisi de sorte que les seuls simplexes
singuliers que l'on a à considérer dans cette méthode et dont le support est contenu
dans X — {x}, aient en fait un support contenu dans X — B (il suffit dans (16.25.1)
de considérer les cartes, autres que cp, ayant un domaine qui ne rencontre pas
B, ce qui est toujours possible). Alors g (en tant que cocycle « absolu ») est cohomo-
logue à un cocycle identifié à une n-forme différentielle y de classe C00 sur X,
de support contenu dans B ; comme en outre I y = 1, la classe de cohomologie
de y est bien e%. *'B
On notera que cela prouve en outre que l'image de cp*(e*) dans
H"(X, X — {x} ; R) par l'isomorphisme d'excision est indépendante du choix
de cp et de V, puisque a(e*) = e$.
Remarque (24.37.13). — Les cup-produits définis dans (24.35.10) et (24.35.11)
sont des cas particuliers d'une définition plus générale. Soient Au A2 deux sous-
espaces d'un espace topologique séparé X, formant un couple excisif (24.37.1).
Pour tout couple d'entiers p > 0, q > 0, on peut alors définir une application

234 XXIV. topologie algebrique et differentielle élémentaires
PROBLÊMES
1) a) Soient X un espace séparé, A, U deux parties de X telles que A <= U. Soient
z 6 S,(X — A ; A), z' e S^U ; A), ïv, e S,+ ,(X - A ; A), w2 e S,+ ^U ; A) tels que z - z' = e^w, + w2) ;
montrer que z e Z,(X — A, U — A ; A).
b) Soit Y une partie de X. Montrer que si z e Z,(X, Y ; A), on a Sdm(z) - z e B^X, Y ; A)
(généraliser le raisonnement de (24.22.7.2)).
c) Déduire de a) et b) que si A est contenu dans l'intérieur de U, l'application canonique
H.(X — A, U — A; A) -<• H.(X, U; A) est bijective (considérer le recouvrement ouvert de X
o
formé de X - A et de U et raisonner comme dans (24.22.7)).
d) Montrer que si X,, X2 sont deux parties de X telles que la réunion des intérieurs de X]
et X2 soit égale à X, le couple (Xt, X2) est excisif.
2
2) Soit X la partie de R2 définie par les relations \x \ < —, - 1 < y < 2, et soit C sa fron-
tière dans R2. Soit U l'ouvert de R2 contenu dans X et formé des (x, y) tels que x = 0,1 < y < 2,
2 1 —
ou 0 < | x | < —, sin - < y < 2. On pose F = X - U, fermé dans X, B = U n F, frontière de F
3tt x
et A = F - B, intérieur de F.
a) Montrer que l'image d'un 1-simplexe singulier contenue dans B est ou bien contenue
dans le segment D des points (x, y) tels que x = 0, | y \ 1, ou bien contenue dans B - D. En
déduire que l'on a H0(B ; Z) S Z © Z et H,(B ; Z) = {0 }.
b) Montrer que C est un rétracte par homotopie de F, et en déduire que H2(X, F ; Z) S Z.
c) Montrer que H2(X - A, F - A ; Z) = {0}, bien que A <= F ; autrement dit, F et X - A
ne forment pas un couple excisif.
3) Soit X un espace métrisable qui est un rétracte de voisinage (section 24.22, problème 1)
et soit F un sous-espace fermé de X qui est aussi un rétracte de voisinage. Montrer que pour toute
partie A de F, l'homomorphisme canonique H.(X — A, F - A; A) -* H.(X, F; A) est bijectif,
autrement dit, (X - A, F) est un couple excisif. (Utiliser le fait que F est rétracte par homotopie
d'un voisinage ouvert de F dans X (section 24.22, problème 1), le problème 1 ci-dessus et le
diagramme (24.35.4.1)). En particulier, on peut prendre pour X et F des variétés différentielles
compactes (section 24.22, problème 2) ou des complexes euclidiens compacts (section 24.28, problème 7).
A-bilinéaire (cu c2) -» t?i •— c2 de HP(X, At ; A) x H*(X, A2 ; A) dans
HP+«(X, A,uA2; A). En effet, soient /, e Sp(X, Aj ; A), f2 e S«(X, A2 ; A) des
cocycles relatifs de classes cu c2 respectivement ; alors, en vertu de la définition
(24.31.1.1), le (/»+cj)-cocycle fx^f2 s'annule dans Sp+,( A, ; A)etdansSp+,(A2 ; A),
et appartient donc à (SP+,(X; \)/(Sp+q{Al ; A) + SP+,(A2; A)))*. Mais comme
(At, A2) est un couple excisif, on a vu dans la preuve de (24.37.9) que la
cohomologie de (S.(X; A)/(S.(A! ; A) + S.(A2; A)))* est canoniquement isomorphe à
celle de S"(X, At u A2 ; A); par passage au quotient, fx ^ f2 donne donc une
classe de cohomologie identifiée à un élément de Hp+qÇX., A,uA2; A).
Il résulte de cette définition que si a„ : HP(X, A! ; A) -> H"(X;A),
a, ; H«(X, A2; A) - H«(X; A) et ap+, : H'+«(X, A,uA2;A) -» H"+%X; A)
sont les applications canoniques (24.35.8), on a
(24.37.13.1) ap+,(c! - c2) = a^cj ~ a,(c2),
le produit du second membre étant pris dans l'anneau de cohomologie H'(X ; A).

37. EXCISION ET SUITE DE MAYER-VIETORIS RELATIVE
235
4) Soient X un espace métrisable, A, B, C trois parties fermées de X, telles que X = A u B
et A n B c C. On suppose que X, A, B, C, A u C et B w C sont des rétractes de voisinage. Montrer
que pour tout r>0, Hr(X, C ; A) est isomorphe à la somme directe H'(A, AnC ; A)©H'(B, BnC ; A).
(Considérer le diagramme commutatif
où les flèches sont les applications canoniques).
5) a) Soit X un espace séparé, localement connexe par arcs (section 16.27, problème 1).
Soit x un point de X admettant un voisinage ouvert rétractile V. Montrer que pour p > 2,
H^X, X - { x } ; Z) est isomorphe à H,_ ,(V - { x } ; Z) ; si V - { x } a q composantes connexes
par arcs, H,(X, X - { x } ; Z) est isomorphe à Z*"1.
b) On suppose que (X, ©) est un complexe simplicial euclidien compact (24.18.4). Pour
tout x € X, soit <3„ l'ensemble des simplexes de la subdivision S auxquels x est adhérent, et soit C,
la réunion des facettes des simplexes de ®„ auxquelles x n'est pas adhérent. Montrer que pour
p>2, H,(X, X - { x } ; Z) est isomorphe à H,. ,(C, ; Z) et Hj(X, X - { x } ; Z) est isomorphe
à Z'"', si C, a q composantes connexes.
c) Les hypothèses étant celles de b), soit n > 2 la plus grande des dimensions des simplexes
de ®. Si le simplexe de ® contenant x est de dimension n, on a H„(X, X — { x} ; Z) = Z,
Hp(X, X - { x } ; Z) = { 0} pour p ± n. Si le simplexe de ® contenant x est de dimension n — 1,
on a H,(X, X - { x } ; Z) = {0 } pour p # n et H„(X, X - { x} ; Z) S Z'"1 si x est adhérent
à r > 1 simplexes de ® de dimension n ; si x n'est adhérent à aucun simplexe de ® de dimension n,
on a H,(X, X - { x } ; Z) = {0 } pour p * n - 1 et H._,(X, X - { x } ; Z) s Z.
6) Les hypothèses et notations étant celles du problème 5, pour tout ouvert U de X, soit i(U)
le plus grand entier i tel que H^X, X - { y} ; Z) / {0 } pour un point au moins y e U ; et pour
tout xeX, soit i(x) la borne inférieure des entiers i(V) lorsque V parcourt l'ensemble des
voisinages ouverts de x dans X. Montrer que i(x) est le plus grand entier j tel que x soit adhérent à
un simplexe de ® de dimension j.
7) On appelle pseudovariété (compacte) un espace homéomorphe à un complexe simplicial
euclidien compact (X, ®) vérifiant les propriétés suivantes :
(PV 1) Si n est la plus grande des dimensions des simplexes de S, tout point de X est adhérent
à au moins un simplexe de dimension n de S (autrement dit, i(x) =- n (problème S) pour tout
(PV 2) Tout simplexe de S de dimension n — 1 est une face de deux simplexes de ® de
dimension n.
(PV 3) Si A„ A2 sont deux simplexes de ® de dimension n, il existe une suite (Bj)0<;<r de
simplexes de S de dimension n telle que B0 — A,, B, — A2 et que pour 0 j < r — 1, B, et Bj+,
aient une face commune.
On peut montrer que toute variété différentielle compacte et connexe est une
pseudovariété [205], Un bouquet de sphères de même dimension n > 2 est connexe et vérifie les
propriétés (PV 1) et (PV 2) mais n'est pas une pseudovariété.
a) Donner un exemple de pseudovariété, avec n > 2, dans laquelle il existe un point x et
un voisinage ouvert connexe V de x dans X tels que V — {x } ne soit pas connexe.
b) Montrer que la suspension (section 24.36, problème 4) d'une pseudovariété est une
pseudovariêté. En déduire un exemple de pseudovariété avec n > 3, telle que pour tout x e X,
on ait H^X, X - { x } ; Z) s Z mais H.-i(X, X - {x} ; Z) # {0 } (comparer au problème 6).
c) Soient A„ ..., Am les simplexes de <5 de dimension n. On dit que X est orientable s'il
existe sur chaque Aj une orientation telle que pour tout simplexe de S de dimension n — 1, les
orientations déduites sur ce simplexe de celles des deux simplexes de dimension n dont il est la
face, soient opposées. Montrer que si X est orientable, on a H.(X ; Z) S Z, et si X est non
orientable, H„(X; Z) = {0} (utiliser (24.28.2)); dans tous les cas on a HJX; F2) £ F2.
H'(X, B u C; A) -* H'(X, C; A) - Hr(B u C, C; A)
H'(X, A u C ; A)
xeX).

236 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFERENTIELLE ÉLÉMENTAIRES
8) Soient X un espace localement compact, métrisable et séparable, U, V deux ouverts
de X tels que U n V soit non vide. Définir canoniquement une suite exacte de Mayer-Vietoris
pour la cohomologie singulière à support compact
... - Hf(UuV;A) - HJ(U; A)®Hf(V; A) - Hf(UnV;A) -» H?+1(UuV;A)- ...
(Soit (K.) (resp. (L,)) une suite croissante de compacts telle que U (resp. V) soit réunion des
intérieurs des K, (resp. L.). Considérer les suites de Mayer-Vietoris pour la cohomologie relative
... - H'(UuV,(U-KJu(V-Lj;A) - H'(U, U - K. ; A) 0 H'(V, V - L„ ; A) -.
-» H'(U n V, (U - K,)n(V - L,); A) H'*'(Uu V, (U - K.) u(V - L,); A) ...
et passer à la limite (cf. section 24.1, problème 2 et section 24.36, problème 10)).
9) a) Soit X une variété différentielle orientée pure de dimension n. Pour tout x e X, montrer
qu'il existe un unique générateur p.x de H^X, X — {x } ; Z) ayant la propriété suivante : pour
toute carte cp de X au point x, définie dans un voisinage ouvert V de x, telle que <p(x) = 0, <p(V) = R"
et que <p préserve l'orientation, l'image de p„ par l'homomorphisme composé
HJ.X,X-{x};Z) H/V, V - (x};Z) * H^R", R-- {0} ; Z)
est la classe e, d'homologie relative du n-cycle x, défini dans (24.28.3.1).
b) Montrer que pour tout x e X, il existe un voisinage compact U de x dans X, et une classe
Hv e H«(X, X — U ; Z) tels que, pour tout y e U, l'image par l'application canonique
$:H.(X,X-U;Z) - H.(X, X - {y } ; Z)
de pv soit égale à pr (Observer que pour tout voisinage ouvert W de x dans X qui est le domaine
d'une carte cp telle que <p(x) = 0 et cp(W) = R*, il existe un voisinage ouvert V de x contenu dans W
et tel que l'homomorphisme canonique HJW, W — V ; Z) -» H^W, W — { y } ; Z) soit bijectif
pour tout y e V, en utilisant 24.35.9).
10) Soit X une variété différentielle pure de dimension n, et soit K une partie compacte
non vide de X. On se propose de prouver la propriété suivante :
P(K) Si une classe a e H.(X, X — K ; Z) est telle que pour tout x e K, l'image de a par
l'application canonique H^X, X - K ; Z) -» H^X, X - {x} ; Z) est nulle, alors a = 0.
On pourra procéder de la façon suivante :
a) Si deux compacts K1( K2 de X sont tels que P(Kt), P(K2) et P(K, n K2) sont vraies,
alors P(Ki i_i K2) est vraie.
p) P(K) est vraie lorsque X = R" et K est un produit d'intervalles compacts de R
(éventuellement réduits à un point) (utiliser 24.35.9).
y) P(K) est vraie lorsque X = R* (on peut supposer que a est la classe d'homologie relative
d'un cycle dont le support ne rencontre pas un voisinage compact N de K ; recouvrir alors K
par un nombre fini de pavés compacts contenus dans N et utiliser a) et fi)).
ô) X est quelconque, K est contenu dans un ensemble ouvert homéomorphe à R".
Appliquer enfin a) pour conclure.
11) Soit X une variété différentielle orientée pure de dimension n. Montrer que, pour tout
compact K e X, il existe une classe et une seule (dite fondamentale) pxx e HJiX, X - K ; Z)
telle que, pour tout x e K, l'image de nXiK par l'homomorphisme canonique y* (problème 9) soit
égale à fix. (L'unicité de /ux,k résulte du problème 10. Pour prouver l'existence de /jx,k>
considérer K comme réunion d'un nombre fini de compacts assez petits ; puis utiliser le problème 9
et la suite de Mayer-Vietoris relative (24.37.6)).
Si K' est un compact contenu dans K, l'image de /uxk par l'application canonique
H^X, X - K ; Z) -> H^X, X - K' ; Z) est /ix,K..
Lorsque X est une variété compacte, pure et orientée, on pose p.x = /<x,x> Qui appartient
à H„(X ; Z). Montrer que si de plus X est connexe, l'image canonique de p.x dans tïJX ; R), identifié
à l'espace vectoriel H'JiX) de l'homologie des courants, est la classe fondamentale [X] d'homologie
des courants.

37. EXCISION ET SUITE DE MAYER-VIETORIS RELATIVE
237
12) Soit X une variété différentielle orientée pure de dimension n. Pour tout p tel que
0 < p < n, on définit un homomorphisme
DX:H?(X;Z) - H.-^XjZ)
de la façon suivante. On considère une suite croissante (Km) de compacts telle que X soit réunion
des intérieurs des K„ (3.18.3) ; pour chaque K„, soit i»x,Km e H„(X, X - K„ ; Z) la classe
fondamentale (problème 11), et soit z„ un cycle relatif dont la classe est /ux,Km. Pour chaque p-cocycle
à support compact / e Zf(X ; Z), la classe du cap-produit zm^ f dans H„_,,(X ; Z) (section 24.35,
problème S) est la même pour tous les entiers m assez grands, et ne dépend que de la classe c At f
dans H?(X ; Z) ; c'est cette classe que l'on note Dxc.
Montrer que Dx est un isomorphisme (dualité de Poincaré). (Procéder comme dans 24.6.2,
en utilisant le problème 8 et la suite exacte d'homologie relative de Mayer-Vietoris (24.37.6)).
En particulier, si X est une variété compacte, connexe et orientée de dimension n, on a
HfX-Z) SZ.
13) Pour une variété différentielle pure X quelconque, de dimension n, définir de même,
pour tout compact K c X, une classe fondamentale /ux>K 6 H»(X, X — K. ; F2) et des isomorphismes
de « dualité »
H?(X; F,) - H„.,(X; F2).
14) Soient X une variété différentielle orientée, compacte, pure de dimension n, et Y un
sous-espace fermé de X vérifiant les hypothèses de (24.36.2). Les HP(V„ ; Z) forment alors un
système inductif.
a) Montrer que les homomorphismes H'(Vn ; Z) -» H'(Y ; Z) définissent par passage à la
limite inductive un isomorphisme canonique
lim H'(V„;Z) =* H'(Y;Z).
m
b) Pour tout m, l'homomorphisme canonique Hjym Vm — Y ; Z) -» H„(X, X — Y ; Z)
est bijectif; soit /jy.» l'image réciproque de la classe p.y (problème 11) par cet isomorphisme. On
considère l'homomorphisme c -» /jy.» — c de HfV,, ; Z) dans H.-^y., Vm — Y ; Z) (section 24.35,
problème 5 e)), qui, composé avec l'isomorphisme H.-^V^ V„ — Y; Z) 2* H„_,(X, X — Y; Z),
donne un homomorphisme H'(V„; Z) -» H,_p(X, X - Y; Z); ces homomorphismes définissent
par passage à la limite inductive un homomorphisme
DY : H'(Y; Z) - H..JIX, X - Y; Z).
Montrer que DY est bijectif (dualité d'Alexander). (Utiliser le diagramme
Hf(X - Y;Z) ► H'(X;Z) ► H'(Y;Z) ► Hf + 1(X - Y;Z) ► ...
Dx | Dv Dx - v |
H..,(X-Y;Z) - H..^X;Z) -» H.-^X, X - Y; Z) - H..,.,(X - Y ; Z) - ...
et la dualité de Poincaré).
15) Pour une variété différentielle compacte pure quelconque de dimension n, définir de
même des isomorphismes de « dualité »
DY:H'(Y;F2) st H..^X, X - Y ; FJ.
16) Soit Y un sous-espace compact de R" qui est un rétracte de voisinage (section 24.22,
problème 1).
a) Montrer que pour p ï n — 1, on a un isomorphisme canonique
H'(Y;Z) st H._,.,(R"- Y;Z)
et que si R" - Y a q composantes connexes, on a H"" '(Y ; Z) £ Z* -1 (considérer Y comme sous-
espace de S.).

238 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
b) On a les mêmes propriétés en remplaçant Z par F2. En conclure que si Y est une variété
compacte pure de dimension n - 1, Y a q - 1 composantes connexes (observer que H0(Y ; F2)
est isomorphe à H""'(Y; F2)).
c) Montrer qu'il n'existe aucune sous-variété compacte pure Y de R", de dimension n — 1
et qui soit non orientable. (Observer que les rangs des Z-modules (non nécessairement libres)
H„_ ,(Y ; Z) et H"" '(Y ; Z) sont égaux et d'autre part que si Y a k composantes connexes, le rang
de H""'(Y; Z) est < k, en utilisant le problème 1 de la section 24.7; conclure une contradiction
à l'aide de a) et b)).
17) Soient Y une variété pure de dimension n, U un ouvert non vide relativement compact
dont la frontière dans Y est régulière, et X = U. Montrer que H'(X ; Z) est canoniquement
isomorphe à H„_,(X, Fr(X); Z) (utiliser les ouverts V, et V2 introduits dans la section 24.35,
problème 6, pour montrer que H.-^X, Fr(X) ; Z) est isomorphe à H„.P(2X, 2X - X ; Z)).
18) Soient YcX deux parties compactes d'un espace R", et soient (V„), (UJ deux systèmes
fondamentaux de voisinages de Y et X respectivement, tels que V„ c U„ pour tout m. Pour tout
anneau commutatif A, les A-modules de cohomologie H'(U„, V„ ; A) forment un système inductif
pour les homomorphismes canoniques ; on note H'(X, Y ; A) leur limite inductive et on dit que
c'est le A-module de cohomologie de £ech de X relativement à Y. En particulier, on a
H'(X, Y; A) = {0} pour p > n (*).
a) Examiner si les propriétés de la cohomologie singulière sont encore valables pour la
cohomologie de Cech.
b) Montrer que pour toute partie compacte Y de R", on a un isomorphisme de dualité
H'(Y; Z) - H.-p.JR" - Y; Z) pour p # n - 1.
c) La limite inductive des homomorphismes canoniques H'(U„Y.;A) -> H'(X, Y; A)
est un homomorphisme canonique H'(X, Y; A) -» H'(X, Y; A).
19) On considère l'espace compact X (« pendentif hawaïen ») défini dans la section 24.22,
problème 11.
a) Pour chaque n, l'homomorphisme canonique H'(X; Z) -» H'(A.; Z) est surjectif.
b) Pour chaque n, soit c. e H'(A, ; Z). Montrer qu'il existe une classe de cohomologie
c e H'(X ; Z) dont l'image dans chaque H'(A, ; Z) soit égale à c„. (Construire d'abord par
récurrence un 1-cocycle z. e Z'(B. ; Z), où B, est le sous-espace réunion des Am pour m < n, tel que z,
soit restriction de z, pour p < q, et que l'image de la classe de cohomologie de z, dans H-(A„ ; Z)
soit égale à c„ pour tout m < n. Montrer qu'il existe un 1-cocycle zeZ'(X; Z) prolongeant tous
les z„, en remarquant qu'on peut prendre la valeur de z égale à 0 sur tous les bords 60s, où s est
un 2-simplexe singulier dont le support rencontre une infinité d'ensembles A„ — {0} ).
c) Déduire de b) que l'homomorphisme canonique fi-(X;Z) -» H'(X;Z) n'est pas
surjectif (montrer que si c appartient à l'image de fi'fX; Z), l'image de c dans H'(A.; Z) est nulle
sauf pour un nombre fini de valeurs de n).
20) Soit B le sous-espace compact de R2 défini dans le problème 2 de la section 24.37.
Montrer que l'on a H'(B; Z) S Z, et par suite que l'homomorphisme H'(B; Z) -» H'(B; Z) n'est
pas injectif.
21) Soit X une variété différentielle pure connexe de dimension n > 2, et soit a un point
de X. Montrer que pour p ^ n — 2, on a
H/X-{«);Z)ïH^X;Z) et H'(X - { a } ; Z) s H'(X; Z)
ainsi que deux suites exactes
0 - H,(X-{a};Z) - H^X;Z) - Z - H._ ,(X - {a} ; Z) -. H„-,(X;Z) - 0
0 - H"-'(X;Z) H"-'(X - {a} ; Z) -» Z -» H"(X;Z) - H"(X - {a} ; Z) - 0
(*) Par contre, il y a des ensembles fermés dans des espaces R" tels qu'une infinité de groupes
d'homologie singulière de ces espaces soient # {0} (cf. [154]).

37. EXCISION ET SUITE DE MAYER-VIETORIS RELATIVE
239
22) Soit X une variété différentielle pure connexe de dimension n > 2, et soit a un point
de X. On note Y la variété obtenue à partir de X par éclatement du point a (section 16.11,
problème 3). Montrer que pour p < n — 2, on a
H,(Y ; Z) = H,(X ; Z) © H^P.. ,(R) ; Z)
et que l'on a une suite exacte
0 -» HJ[X - {a} ; Z) - H.(Y; Z) - Z -
- H.^X-fal-ZïeH.-.tP.-.W-Z) -. H.-,(Y;Z) - 0
23) Soit X un espace séparé ; on dit qu'un sous-espace non vide A de X est déformable (dans X)
en un point si l'injection canonique j : A -» X est homotope à une application constante x -» a
de A dans X ; autrement dit, s'il existe une application continue / : A x [0, 1 ] -» X telle que
f(x, 0) = a et f(x,l) = x pour tout x e A ; tout sous-espace B <= A non vide est alors aussi
déformable en un point.
On dit qu'un sous-espace Y de X est de catégorie (de Lusternik-Schnirelmann) finie dans X
s'il est réunion finie de sous-espaces déformables chacun (dans X) en un point ; le plus petit nombre
de tels sous-espaces dont Y soit la réunion est appelé la catégorie de Y dans X et noté catx(Y) ;
on pose cat(X) = catxfX). Si Y n'est pas de catégorie finie dans X, on pose catx(Y) — + oo.
a) Si Y ci Z sont deux sous-espaces non vides de X, on a catx(Y) < catx(Z) ; en particulier,
si X est rétractile, on a catx(Y) = 1 pour tout Y c X.
b) On a cat(S„) = 2 pour tout n » 0.
c) Si Y, Z sont deux sous-espaces non vides de X, catx(Y uZ)$ catx(Y) + catx(Z). Si X est
connexe par arcs et si de plus Y n Z = 0, catx(Y u Z) = sup(catx(Y), catx(Z)).
24) Soient X une variété différentielle pure, A une partie compacte de X déformable en
un point, de sorte qu'il existe une application continue / :A x [0,1] -» X telle que/(x,0) = aeX,
f(x, 1) = x pour tout x e A. Montrer qu'il existe un voisinage ouvert U de A dans X tel que U
soit déformable en un point. (Si B est l'ensemble compact image de /, on peut supposer qu'il existe
un voisinage ouvert relativement compact V de B dans X qui soit plongé dans un espace RN (16.25.1).
Prolonger alors / en une application continue g de V x [0, 1 ] dans RN (4.5.1), telle que g(x, 0)=a
et gix, 1) = x pour jceV; puis utiliser (16.25.4)).
25) Soient X une variété différentielle pure, A une partie relativement compacte de X, et
(U,)j.i un recouvrement ouvert de A dans X tel que chacun des sous-espaces U, soit déformable
en un point dans X. Pour toute partie J de I, on pose V, = f]\Jh et on suppose que V, = 0 pour
taJ
toute partie J de I ayant n + 2 éléments. Montrer alors que catx(A) n + 1. (Considérer la
réunion B des Vj pour Card(J) = n + 1 et remarquer que si B n'est pas vide, on a catx(B) = 1 ; raisonner
ensuite par récurrence sur n en considérant A n QB).
26) Déduire du problème 25 que, pour toute partie compacte A d'une variété différentielle
pure X, on a catx(A) < dim(A) + 1, ou dim(A) est la dimension topologique (section 24.22,
problème 6) de A.
27) a) Soient X un espace séparé, Y un sous-espace de X déformable en un point dans X.
Montrer que, pour tout p > 1, l'application canonique HP(X, Y; A) -* H'(X; A) est surjective
pour tout anneau commutatif A (utiliser (24.29.4)).
b) Montrer que si X est une variété différentielle pure compacte telle que cat(X) = n, le
cup-produit dans H'(X; A) de n éléments dont chacun appartient à un Hr(X; A) avec p > 1
(p dépendant de l'élément considéré) est nul. (Utiliser a) et la relation (24.37.13.1) en se ramenant,
à l'aide du problème 24, à un recouvrement de X par des ensembles ouverts déformables en un
point dans X).
c) Montrer que cat(T") = n + 1 et cat(P^R)) = n + 1 en utilisant b) et le problème 26,
ainsi que (24.40.12).
28) Soit X un complexe cellulaire (section 24.36, problème 8) de dimension n. Pour tout
p $ n, on désigne par Xp la réunion des Y; de dimension < p.
a) Pour tout anneau commutatif A, montrer que HjiXr X,_, ; A) = {0} pour i ï p, et

240 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
38. Cohomologie des produits de variétés et des espaces fibres.
(24.38.1) Soient X une variété différentielle pure de dimension m, Y une variété
différentielle pure de dimension n, Y0 un ouvert (éventuellement vide) de Y, A un
anneau commutatif. On suppose que chacun des A-modules HP(Y, Y0 ; A) de
cohomologie relative est libre de type fini. /{ existe alors un isomorphisme canonique
kx : H'(X ; A) ® AH'(Y, Y0 ; A) - HÏX x Y, X x Y0 ; A) de A-modules gra-
dués„tel que pour a e HP(X ; A) et b e H«(Y, Y0 ; A), on ait
(24.38.1.1) kx(a ®b) = prf(a) - prf(b) g Hp+*(X x Y, X x Y0 ; A).
Dans cet énoncé, prt et pr2 sont les deux projections de X x Y, de sorte que
pr?(a)eHp(X x Y ; A) ; comme pr2(X x Y0) c Y0, on a prJ(b)gh«(X x Y, X x Y0 ; A) ;
le cup-produit est celui défini dans (24.35.11).
Ce résultat est un cas particulier du théorème de Kiinneth général relatif
à la cohomologie singulière d'un produit d'espaces, que nous ne démontrerons
pas (voir [160]). Nous allons procéder par étapes comme dans la preuve de
(24.5.4).
I) X = R". Identifions Y et Y0 à {0} x Y et {0} x Y0 respectivement ;
Hp(xp, Xp_, ; A) s A', où r est le nombre des entiers nt égaux à p. (Soit S un ensemble fini dont
l'intersection avec chacune des « cellules » pour ns = p est réduite à un point ; montrer
que H^X,, Xp_, ; A) = H,<X,, X, - S; A) en remarquant que X,-i est un rétracte par
homotopie de X, — S. Si E est la réunion des fj+ i(Dmj) pour les nt = p, on a
H,(X„ X, - S; A) s HKE, E - S; A)).
b) Déduire de a) que H,(XP ; A) est nul pour i > p et isomorphe à H^X ; A) pour i < p.
c) On pose C^X) = HpiXp Xp_, ; A); la suite exacte d'homologie de la section 24.35,
problème 2, définit une application canonique b : CyX) -» C,_i(X) tel que b«b = 0, de sorte
que les C,(X) forment un A-module codifférentiel gradué. Montrer que Ker(fc) = h^xp, xp_2 ; A)
et que le p-ème module d'homologie de C.(X) est isomorphe à HP(XP+1) Xp_2; A) (utiliser la
section 24.35, problème 2, pour les triplets (X,, Xp_,, X,_2) et (Xp+1, Xp, X,_2)). Conclure à
l'aide de b) que HP{XP+,, X,_2 ; A) est isomorphe à H,(XP+, ; A), donc à HP(X ; A).
d) Démontrer les résultats analogues pour la cohomologie d'un complexe cellulaire.
29) Avec les hypothèses et notations de la section 24.22, problème 16, montrer que l'on a
H,(M„ M_, ; A) = {0} pour p » 1 et p / K et H^M,, M_, ; A) s A. (Utiliser (24.7.1.1) et le
théorème d'excision (24.37.4)).
30) Soit M une variété pure compacte de dimension n, et soit / une fonction numérique
de classe C°° dans M, n'ayant qu'un nombre fini de points critiques, qui sont tous non dégénérés.
Soit ck le nombre de ces points dont l'indice de Morse (section 16.5, problème 3) est égal à k. Si bk
est le fc-ème nombre de Betti de M, prouver les inégalités de Morse bk < ck pour 0 < k < n, ainsi
que la relation x(M) = c0 — cx + c2 — ■ ■ ■ + (— l)"c,. (Si vt, ..., vm sont les valeurs de / aux
points critiques, considérer des nombres aj (0 £j m) tels que
a0 < vi < ai < »2 < ... < am-i < vm < am.
Utiliser la section 20.8, problème S, la section 24.22, problème 16, la section 24.35, problème 2
et le problème 29 ci-dessus).

38. COHOMOLOGIE DES PRODUITS DE VARIETES ET DES ESPACES FIBRES 241
alors Y (resp. Y0) est un rétracte par homotopie de X x Y (resp. X x Y0). Le
diagramme commutatif (24.35.9.1) de suites exactes
... > H"(Y ; A) > H'(Y0 ; A) > Hp+ '(Y, Y0 ; A) ►
prî | prî prî j
... -y HP(X x Y; A) -> HP(X x Y0; A) - HP+1(X x Y, X x Y0; A) -
> Hp+ l(Y ; A) ► HP+1(Y0 ; A) ► ...
p'îj P'!
- HP+1(X x Y; A) - HP+1(X x Y0; A) - ...
et le lemme des cinq montrent donc que prj : H'(Y, Y0 ; A) ->■ H'(X x Y, X x Y0 ; A)
est un isomorphisme de A-modules gradués. Par ailleurs, comme HP(R" ; A)={0}
pour p > 1, et que H°(RM ; A) s'identifie à l'espace des applications constantes
de Rm dans A, l'application kx est la composée
A <g) AH'(Y, Y0 ; A) H"(Y, Y0 ; A) 3 H*(X x Y, X x Y0 ; A)
où la première flèche est l'application canonique (Ann. 28.2).
II) X est réunion finie de pavés ouverts de R". On raisonne par récurrence
sur le nombre de ces pavés, et on est ramené à prouver le lemme suivant :
(24.38.1.2) Soient U, V deux ouverts d'une variété pure X de dimension m; si
les applications canoniques kv, kv et kVnV (lorsque UnV#0) sont bijectives,
il en est de même de fcUuV-
Le lemme est immédiat lorsque U n V # 0, compte tenu de la description
des cochaînes sur un espace non connexe (24.29.2). Supposons donc U n V 0,
et posons pour simplifier MP(X) = © (H«(X ; A) (g) AHr(Y, Y0 ; A)) et
« + r = p
NP(X) = HP(X x Y, X x Y0 ; A). Nous allons voir qu'on a alors un diagramme
commutatif de suites exactes
... MP(U) © MP(V) -> Mp(UnV) Mp+1(UuV)
NP(U)©NP(V) -> Np(UnV) -» Np+1(UuV) -»•
MP+1(U)©MP+1(V) M'+1(UnV) - ...
*u$kv | Ikunv |
-> Np+ l(U) © Np+ l(V) -* Np+1(UnV) - ...
Dans ce diagramme, la ligne inférieure n'est autre que la suite de Mayer-Vietoris
(24.37.9) où l'on prend Xt = U x Y, X2 = V x Y, A, = U x Y0, A2 = V x Y0.
Pour obtenir la ligne supérieure, on considère la suite de Mayer-Vietoris (24.37.9)
ku©*v

242 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
où l'on fait Xt = U, X2 = V, At = A2 = 0, et on la prolonge aux exposants
négatifs par des zéros ; on la tensorise ensuite successivement par les n + 1 modules
libres Hr(Y, Y0 ; A) pour 0 ^ r < n, ce qui donne n + 1 suites exactes (Ann. 29.5)
et on fait ensuite la somme directe de ces n + 1 suites, ce qui donne encore une
suite exacte quand on regroupe les modules pour lesquels q + r est le même.
Reste à prouver la commutativité du diagramme ; vérifions par exemple celle de
H«(UnV; A)<g>AH'(Y, Y0; A) -2t±. H,+1(UuV; A)(g>AH'(Y, Y0; A)
H«+r((UnV) x Y, (UnV) x Y0; A) H«+r+1((UuV) x Y, (UuV) x Y0; A)
Soient donc a e H*(U n V ; A), b e Hr(Y, Y0 ; A), classes de cocycles / g
respectivement. On considère une forme linéaire /i sur S,(U ; A) + S^V ; A) qui
prolonge /, et da est la classe de cohomologie de d0/i> de sorte que kVuV(da ® b)
est la classe de cohomologie relative de ((d0/"i)opr1)--'(g°pr2); d'autre part
/tUnV(fl <g> b) est la classe de cohomologie relative de (fi ° pr,) — (g ° pr2) ; comme
d0(f\ ° pri) - (dofi) ° Pfi et d0(g ° pr2) = (d0g) o pr2 = 0, l'égalité
ôXkVny/(a ® b)) = kVuV(da ® b)
résulte donc de la formule (24.31.2.1).
On vérifie plus simplement encore les autres commutativités. Pour prouver
(24.38.1.2), il suffit alors d'appliquer le lemme des cinq.
III) X est un ouvert de Rm. Comme dans (24.5.4.3), on écrit X comme réunion
d'une suite croissante d'ouverts V, (j > 0) dont chacun est réunion finie de pavés
ouverts, et tels que V} n Vk = 0 pour | k — j | > 1 ; on désigne par U la réunion
des V2j U ^ 0). par U' la réunion des \2j+1 0' ^ 0)> de sorte que X = U u U',
U est réunion des V2J, deux à deux disjoints, U' réunion des V2^+1, deux à deux
disjoints, et enfin U n U' est réunion des \2J n W2J+ u deux à deux disjoints.
Dans ce cas, (24.38.1) résulte donc du lemme (24.38.1.2) appliqué à U et U',
et du lemme suivant :
(24.38.1.3) Si X est réunion d'une famille (UJ d'ouverts non vides deux à deux
disjoints et si chacune des applications feU(i est bijective, il en est de même de kx.
En effet, H"(X;A) s'identifie au produit \~[ H \Ua; A), donc, puisque
CL
H*(Y, Y0 ; A) est un module libre de type fini, H*(X ; A) ® AH'(Y, Y0 ; A)
s'identifie au produit Yl (H°(U« ; A) <g> AH*(Y, Y0 ; A)) (Ann. 28.5). De même,
a
H'(X x Y, X x Y0 ; A) s'identifie canoniquement au produit
nH*(U. xY,U,x Y0;A)
en vertu de (24.35.6) ; le lemme en résulte aussitôt.

38. COHOMOLOGIE DES PRODUITS DE VARIÉTÉS ET DES ESPACES FIBRES 243
IV) Cas général. — Il résulte de III) et du lemme (24.38.1.2) que le théorème
est vrai lorsque X est réunion d'un nombre fini de domaines de cartes. Dans
le cas général, on écrit X comme réunion d'une suite d'ouverts V^ dont chacun
est réunion finie de domaines de cartes, et tels que V, n Vt = 0 pour | k—j | > 1 ;
on termine alors le raisonnement comme dans III), en utilisant le lemme (24.38.1.3).
CQFD.
(24.38.2) Remarque. — Les structures d'algèbres anticommutatives graduées
de H'(X; A) et de H'(Y, Y0; A) ((24.31.2) et (24.35.10)) permettent de définir
sur le A-module H'(X; A) (g) AH'(Y, Y0; A) la structure de produit tensoriel
gauche de ces algèbres (Ann. 30.9). Pour cette structure, kx est un isomorphisme
d'algèbres graduées de H*(X ; A) *® AH"(Y, Y0 ; A) sur H*(X x Y, X x Y0 ; A).
Il suffit en effet pour le voir de raisonner comme dans (24.5.2), en remplaçant
j*'{X) (resp. jtf'(Y)) par S'(X; A) (resp. S'(Y, Y„; A)), le produit extérieur par
le cup-produit et la dérivée extérieure d par d0.
(24.38.3) Soit — (X, B, 7t) une fibration pour laquelle B est une variété
différentielle pure de dimension m et toutes les fibres sont difféomorphes à une même
variété différentielle pure F de dimension n. Soit X0 un ouvert de X qui est vide
ou est tel que (X0, B, n | X0) soit encore une fibration ; de façon plus précise,
nous supposons qu'il existe un ouvert F0 (éventuellement vide) dans F tel que,
pour tout b e B, il existe un voisinage ouvert U de b dans B et un difféomorphisme
<p : U x F -+ 7t_1(U) tel Que 7t(<p{y> 0) = y pour y e U et t e F, et que
(p(U x F0) = 7t-1(U)nX0.
Pour tout beB, il existe alors un difféomorphisme jb : F -*■ n~l(b) = X0
tel que jb(F0) = XbnX0; bien entendu ce difféomorphisme n'est pas unique en
général.
(24.38.4) (Leray-G. Hirsch) Les hypothèses et notations étant celles de (24.38.3),
soit A un anneau commutatif, et supposons en outre que:
1° chacun des A-modules HP(F, F0; A) est libre de type fini;
2° pour chaque entier p > 0, il existe dans HP(X, X0 ; A) une famille
(api, ap,rJ telle que, pour tout beB, les éléments ft(apl), .. .,jt(ap<rp) (où
jb est considéré comme une injection de F dans X) forment une base (dépendant
du choix de jb) du A-module HP(F, F0 ; A).
Alors, lorsqu'on considère H"(X, X0;A) comme un H"(B; A)-module par
l'action
(24.38.4.1) (c, a) -» 7t*(c)-a
(le cup-produit étant celui qui définit la structure de H'(X ; A)-module sur
H'(X, X0 ; A) (24J5.11)), ce module est libre et a pour base la famille
i.apk)l*k*rp,l*p*ir

244 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
La démonstration procède encore en plusieurs étapes.
I) Cas où B est connexe, X = B x F et X0 = B x F0. Avec les notations
de (24.38.1), le A-module kû 1{H'(X, X0; A)) est somme directe des A-modules
H"(B ; A) ® AH"(F, F0 ; A) pour O^p^metO^q^n. Il suffira de montrer
que, pour 0 < q < n, il existe une base (a'qh)lik^rii de H*(F, F0; A) telle que
(24.38.4.2) prf (a'qk) -= aqh pour 1 < h < rq.
On va prouver l'existence des a'qh par récurrence sur q. Notons que, pour q = 0,
H°(B ; A) s'identifie canoniquement à A puisque B est connexe (24.29.2),
l'application kB : H°(B ; A) ® AH°(F, F0 ; A) -> H°(X, X0 ; A) s'identifiant à
l'isomorphisme k® a' -* X prj(a')- H existe donc des éléments bien déterminés a'0k
(1 < h < r„) de H°(F, F0 ; A) tels que pr2(aôn) = <*oi> ! comme on peut supposer
que pr2 °jb est l'identité de F, on a a'0h = ^(pr^aô*)) = jîiaoh), et par hypothèse
les a'0h forment donc une base de H°(F, F0 ; A).
Supposons maintenant démontrée l'existence des bases {a'ik) pour i < q.
Comme kB \Hq(X, X0 ; A)) est somme directe des H'(B ; A) ® AH«~'(F, F0 ; A)
pour 0 i < q, et que H°(B ; A) s'identifie canoniquement à A, on peut écrire,
pour 1 < h ^ rq,
où les a'qh e H*(F, F0 ; A) et les cik, e H'(B ; A) pour 1 ^ i < q et 1 < / < r{ sont
bien déterminés. Par suite
Utilisons maintenant le fait que pr2 ° jb est l'identité de F, et que pr, ° jb
applique F sur l'espace { b} réduit à un point ; pour i ^ 1, on a donc y?(prî(ciB,)) = 0,
et comme y'f(prî(a^)) = a'qh, on a Jt(aqh) = a'qh puisque est un homomorphisme
d'algèbres; l'hypothèse entraîne donc que (a'qk)lsih^r<i est une base du A-module
H*(F, F0 ; A), ce qui achève de prouver (24.38.4) dans ce cas.
II) B est quelconque, 'X = B x F et X0 = B x F0. Soit (B.) la famille des
composantes connexes de B, et pour chaque a, soit i„ : Ba -» B l'injection
canonique ; si on pose d$ = i*(apk) pour l</c<rp,0</><m,on poseyj(apt) =jtltfl)
pour tout b e B„ où jbtt est l'application jb considérée comme injection de F dans
En vertu du cas I) appliqué à chaque B,, à l'espace fibre X„ = n~ '(B») et à
l'ouvert X0a = X0nX„ chacun des H"(X., X0«; A) est un H'(B„; A)-module
libre ayant pour base la famille (aj5?). Comme H'(X, X0 ; A) s'identifie au A-module
produit nH'(Xa, X0„ ; A), de façon que chacun des apk s'identifie à la famille (a^)
«_1(BJ.
a

38. COHOMOLOGIE DES PRODUITS DE VARIÉTÉS ET DES ESPACES FIBRES 245
gtr
«fJiv
NS(U)©NS(V) -+ N'(UnV) Ns+1(UuV) -
MS+1(U)©MS+1(V) - Ms+1(UnV)
•♦• I
gunv
NS+1(U)©NS+1(V) - Ns+I(UnV)
(24.35.6), et que H'(B; A) s'identifie à la A-algèbre produit nH'(Ba; A), on
a
conclut que (apk) est une base du H'(B ; A)-module H'(X, X0 ; A).
III) Cas général. — Pour tout ouvert U c B, notons Xu l'espace fibre n" *(U)
de base U, nv sa projection ; si iu : Xv -* X est l'injection canonique, posons
Opk = 'ufap*) Pour l^k^r^O^p^m. Pour tout entier s tel que 0 s < m + n,
posons pour abréger
m
MS(U) = © (H"(U ; A))r- - ' (avec (H"(U ; A))r* - - = {0} si s - p < 0))
p = 0
NS(U) = H5(X,j, Xu n X0 ; A)
et définissons une application A-linéaire gû : MS(U) -» NS(U), en posant, pour
0 <p < m et pour tout élément (cph)lihirt_pe(tlp(\J; A)Y'~P
gU(cph)i ^r,.p) = L n*(cPk) - fl-p.» ■
Il s'agit de montrer que pour U = B, chacune des g% est bijective. En vertu
de II), les gfj sont bijectives lorsque U est un voisinage ouvert d'un point beB
vérifiant les conditions de (24.38.3) ; on dira pour abréger que ces ouverts sont
distingués. Il est clair que tout ouvert non vide contenu dans un ouvert distingué
est distingué. Partant de là, on procède comme dans (24.5.4) et (24.38.1), en
établissant d'abord les deux lemmes suivants :
(24.38.4.3) Si U est une réunion d'une famille (UJ d'ouverts deux à deux
disjoints et si les gû« sont bijectives, il en est de même des gfj.
En effet, M5(U) s'identifie au produit U M^U J et NS(U) au produit fl NS(UJ,
a a
chaque a^k s'identifiant à la famille (aty) ; gt- s'identifie alors à la famille
d'applications (guj, d'où la conclusion.
(24.38.4.4) Si U, V sont deux ouverts tels que les g^, gy et gûnv soient bijectives,
il en est de même des gûuv-
En vertu de (24.38.4.3), on peut se limiter au cas ou U n V # 0. On a alors
un diagramme commutatif de suites exactes
... - MS(U) © MS(V) - MS(U nV)-. Ms+ '(U u V) -

246 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
Dans ce diagramme, la ligne inférieure est la suite exacte de Mayer-Vietoris
(24.37.9.1) pour les couples d'ouverts (Xu, Xv) et (Xu n X0, Xv n X0) ; la ligne
supérieure est la somme directe de r0 + rt + ... + r„ suites exactes de Mayer-
Vietoris pour le couple (U, V) (24.37.11), prolongées aux exposants négatifs
par des zéros, et où l'on regroupe les termes correspondant à une même valeur
de s (en notant que r(J+1)_(p+1) = r5_p). Prouvons la commutativité des carrés
contenant les homomorphismes d ; il s'agit de montrer que l'on a
En effet, soit d'une part u un (s - p)-cocycle relatif sur X, modulo X0, dont
a,-ph est la classe de cohomologie relative; soit d'autre part v un p-cocycle
sur U n V, dont cph est la classe de cohomologie ; alors
e = n^nV{cph)^a^j,
est la classe de cohomologie relative du s-cocycle relatif {v ° n) — (u | XUnV)-
Pour former de, on prolonge v en une forme linéaire t»! sur Sp(U ; A) + S/V ; A),
et on peut alors prolonger (f ° 7t) ~ (m | XUnV) en la forme linéaire (t^ 07c)-- uu
où ut est la restriction de u à
(S.-ptXu; A) + S.-ptXv ; AMS^Xu n X0 ; A) + S5_,(XV n X0 ; A));
comme d0u est un cobord relatif, do((t>! 07c)-— «|) et ((d0t>i)°7t)-'U1 ont même
classe de cohomologie relative (24.31.2.1), égale à 7tUuv(3cpS) ^a^Pih. La
vérification des autres commutativités est analogue et plus simple, et il suffit pour
conclure la preuve du lemme d'appliquer le lemme des cinq.
Ces lemmes étant établis, on prouve successivement que les gû sont bijectives
dans les trois cas suivants :
A) U est réunion finie d'ouverts distingués. On raisonne par récurrence sur
le nombre t de ces ouverts, et on applique le lemme (24.38.4.4) au cas où U est
réunion de t — 1 ouverts distingués, V un ouvert distingué, si U n V # 0, et
le lemme (24.38.4.3) si U n V = 0.
B) U est réunion d'une famille (UJ d'ouverts disjoints, chaque Ua étant
réunion finie d'ouverts distingués. On applique le lemme (24.38.4.3).
C) U = B. Comme dans (24.5.4.3), on écrit B comme réunion d'une suite (V,)
d'ouverts, dont chacun est réunion finie d'ouverts distingués, et telle que
V} n Vt = 0 si | k — j \ > 1 ; on termine le raisonnement comme dans (24.38.1),
en appliquant les lemmes (24.38.4J) et (24.38.4.4). CQFD.
PROBLÊMES
1) On considère les deux variétés X = P3(R) x S2, V = P2(R) x S3. Montrer que pour tout
n > 1, les groupes d'homotopie 7t,(X) et ji„(Y) sont isomorphes (utiliser la section 16.30, problème 7);
par contre, montrer que H„(X ; Z) n'est pas isomorphe à H„(Y ; Z) pour 2 n ^ S.

38. COHOMOLOGIE DES PRODUITS DE VARIETES ET DES ESPACES FIBRES 247
2) On considère les deux variétés X = S2 x S4, Y = P3(C). Montrer que pour tout n > 0,
les groupes d'homologie H„(X ; Z) et H„(Y ; Z) sont isomorphes. Mais montrer que n4(Y) = {0}
(considérer S7 comme espace fibre principal de base P3(C) (16.14.10) et utiliser la section 16.30,
problème 6), tandis que n4(X) n'est pas réduit à l'élément neutre (utiliser la section 16.30,
problème 9 b)).
3) Soient X = S, x S2, et Y le bouquet des trois sphères S„ S2, S3. Montrer que H'(X ; Z)
et H'(Y ; Z) sont isomorphes à Z pour 0 < p < 3 ; mais si a est un générateur de Hl(X ; Z) et
b un générateur de H2(X ; Z), on a a ~ b * 0, tandis que si a' est un générateur de H'(Y ; Z) et
b' un générateur de H2(Y ; Z), on a a' b' = 0, de sorte que les anneaux de cohomologie H*(X ; Z)
et H'(Y ; Z) ne sont pas isomorphes.
4) Soient X et Y deux variétés pures, A un anneau commutatif. Montrer que si chacun
des A-modules de cohomologie à supports compacts H'(Y ; A) est libre de type fini, il existe un
isomorphisme canonique
HC'(X ; A) «® AHJ(Y ; A) X HC"(X x Y ; A).
(Procéder comme dans (24.5.4)).
5) Dans ce problème, A désigne un corps commutatif.
a) Soient X, Y deux variétés différentielles pures. Montrer que pour p > 0, q > 0, il existe
une application bilinéaire et une seule (u, a) -> u/adeH'+,(X x Y; A) x H,(Y ; A) dans H'{X ; A)
ayant la propriété suivante : pour v e H'(X ; A) et w e H*(Y ; A), on a (prj(t)) — prj(w))/(i = < w, a > v.
En déduire que si s 6 H'(X ; A), on a (prf(s) ~ u)/a = s ~ (m/û).
b) Soient weH'tX x Y; A), weH'(X; A), w e H*(Y ; A), aeH,(Y; A) avec q «S p et q « s.
Montrer que l'on a
(prî(u) ~ prj(w) ~ u)/a - ( - l)«>-+'\v ~ (u/(a - w)))
(cf. section 24.35, problème S).
c) Supposons X et Y compactes, connexes et orientées, et A = R. Si Y est de dimension n,
montrer que pour tout ue H'+"(X x Y ; R), on a k/[Y] = ^ u (notation de 24.5.9.4)).
6) Soit (E, S„, n)une fibration de base la sphère S, (n> 1), de fibre type F, et soient b un point
de S„, ib : F -» Ek un difféomorphisme. Montrer que pour tout anneau commutatif A, on a une
suite exacte (commençant par 0 -> H°(E ; A))
... H'(E;A) $ H'(F;A) HP""+1(F; A) HP+1(E;A) - ...
(suite de Wang). (Généraliser la méthode de la section 24.5, problème 6; on utilisera (24.38.1)
et le lemme élémentaire d'algèbre suivant : si u, : M, -» N, u2 : M2 -> N sont deux bijections
de A-modules, et u = u, + u2 : M, © M2 -» N, M, 0 M2 est somme directe de Ker(u) et d'un
A-module isomorphe à M, et M2).
7) a) Montrer qu'il existe une fibration (S.^C), S2„_i, n) sur la variété de Stiefel S„i4(C)
(16.11.6) dont la fibre est difféomorphe à S,_, ^-^C), pour n>2et2<k^n. (Utiliser le fait
que S„,k(C) est isomorphe à U(n)/U(n - k), ainsi que (16.14.9)).
b) Montrer que H'(S„it(C); Z) est un Z-module libre, et que, pour 1 < v < k, il existe dans
H2(.+»-*)-i(S|it(Q;Z) un eiément Xj # 0 tel que l'algèbre H'(S.t(C);Z) soit isomorphe à
k
l'algèbre extérieure du Z-module libre ®Zx,. (Raisonner par récurrence sur k. Déduire de la
V- 1
suite exacte de Wang (problème 6) que pour 1 < v < k — 1,
,...H2,.+.-.,-I(S<t(C);Z) _ H2<" + -«-'(S._I,4.1(C);Z)
est bijectif. Si y, y4-, sont les éléments de H"(S.-,t_,(C); Z) tels que cette algèbre soit
k-l
isomorphe à l'algèbre extérieure de © Zy„ montrer que les éléments xv = (i*)"'(y») sont indé-
V» 1
pendants du point b. Appliquer ensuite le théorème de Leray-Hirsch (24.38.4) et prendre

248 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
x, = Jt*(cî,_i), ou cf.-! est la classe fondamentale de cohomologie singulière de S2„-i (24.32.2).
Pour voir que x, — x» = 0 utiliser l'anticommutativité de H'(S„i()(C) ; Z) et le fait que cette algèbre
est un Z-module libre).
c) Énoncer et démontrer les résultats correspondants pour S„it(H).
8) Les hypothèses étant celles de (24.38.4), on suppose que A est un corps commutatif.
Montrer que H.(X, X0; A) est un A-espace vectoriel canoniquement isomorphe au produit
tensoriel H.(B ; A) ® AH.(F, F„ ; A) ; si l'on identifie ce produit tensoriel à H.(X, X„;A), alors,
pour b e H.(B ; A), / e H.(F, F0 ; A), u e H'(B ; A), v e H'(F, F0 ; A), on a
< «•(«) — è<8»/> = <«,6>.<», / >.
39. Suite de Gysin et classe d'Euler.
(24.39.1) Soient B une variété pure de dimension m, E un espace fibre vectoriel
réel de rang N et de base B, tc : E -+ B sa projection ; soit E0 l'ouvert de E,
complémentaire de la section nulle de E (16.15.1). La fibration t] = (E, B, 7t) et
l'ouvert E0 vérifient alors les conditions de (24.38.3), avec F=RN et F0 = RN - {0}.
On a vu (24.35.12.2) que pour tout anneau commutatif A,
HP(RN, RN - {0} ; A) = {0} si p ± N,
et HN(RN, RN - {0} ; A) s A; la condition 1° du théorème de Leray-Hirsch
(24.38.4) est donc remplie par la fibration c\. Pour que la condition 2° soit
satisfaite, il faut et il suffit qu'il existe dans HN(E, E0 ; A) un élément u tel que, pour
tout b e B,jb(u) soit un générateur du A-module monogène HN(RN, RN — {0} ; A).
Lorsqu'il en est ainsi, on dit que la fibration £, est A-orientable, et chacun des
éléments u ayant la propriété précédente est appelé classe de A-orientation de Ç.
On aura soin de ne pas confondre cette notion avec celle d'orientation de la
variété différentielle E (16.21.1) ; par exemple, si le fibre vectoriel E est triviali-
sable, la fibration £ est toujours A-orientable en vertu de (24.38.1), tandis que la
variété E n'est orientable que si B l'est (16.21.9.3).
Si la fibration t; est A-orientable, il résulte du théorème de Leray-Hirsch
que, pour toute classe de A-orientation u de £ et tout entier p e Z, l'application
A-linéaire
(24.39.1.1) % : c -» «*(c)wM
est un isomorphisme de HP(B ; A) sur HP+N(E, E0 ; A) (en convenant comme
d'ordinaire de remplacer par {0} les modules de cohomologie de dimension < 0).
(24.39.2) Écrivons maintenant, pour E et E0, la suite exacte de cohomologie
relative (24.35.8.1).
(24.39.2.1)
... -> Hr(E, E0 ; A) A H'(E;A) £ H'(E0;A) À H'+1(E,E0;A) -» ...

39. SUITE DE CYSIN ET CLASSE D'EULER
249
où i : E0 -» E est l'injection canonique et a l'application faisant correspondre
à la classe de cohomologie relative d'un cocycle relatif sa classe de cohomologie
« absolue ». Notons en outre que B, identifié à la section nulle de E, est un rétracte
par homotopie de E (24.2.7), et par suite l'application n* : H'(B ; A) -> H'(E ; A)
est bijective et a pour réciproque l'application « section nulle »
O* : H*(E; A) -. H"(B; A).
Utilisant ces isomorphismes et les isomorphismes (24.39.1.1), on obtient le
résultat suivant :
(24.39.3) Soient E un espace fibre vectoriel réel de rang N, de base B et de
projection w, tel que la fibration £ — (E, B, 7t) soit A-orientable. Alors, pour toute
classe u de A-orientation, on a une suite exacte
(24.39.3.1)
... - HP(B ; A) HP+N(B ; A) 3 HP+N(E0 ; A) ^ Hp+ i{B ; A) -» ...
débutant par 0 -» H ~N(B ; A); dans cette suite, n0 = n ° i: E0 -> B est la
projection canonique, ^-eAÇ) est l'application c -» c^-ej£), avec ej£)=0*(a(«))e HN(B ; A),
et = <b~1 o d (suite exacte de Gysin). (On écrit aussi e„(E) pour eJ(Q).
En effet, l'application HP(B ; A) -» HP+N(B ; A) qui figure dans cette suite
est par définition la composée
Hp(B ; A) % Hp+N(E, E0 ; A) A HP+N(E ; A) £ HP+N(B ; A)
qui s'écrit donc c -» 0*(a(7t*(c) — «)) ; mais par définition (24.35.11)
a(n*(c) - m) = 7t*(c) - a(u), donc 0*(a{n*(c) - m))=0*(rc*(c) - a(«))=c-0*(a(u)).
Pour appliquer (24.39.3), il importe d'obtenir des critères de A-orientabilité.
(24.39.4) Pour tout espace fibre vectoriel réel E de rang N sur une variété pure B,
la fibration Ç = (E, B, 7t) est ¥2-orientable et il existe dans HN(E, E0 ; F2) une
seule classe de ¥2-orientation.
La preuve suit la même marche que dans (24.38.4).
I) Cas ùù E = B x RN, E0 = B x(RN-{0}). Comme HN(RN, RN-{0} ; F2)
est un ensemble à deux éléments 0 et v, il résulte de (24.38.1) que l'application
c -» prf(c)~u, où u=prf(v), est un isomorphisme de H°(B; F2) sur HN(E, E0 ; F2).
Si (BJ est la famille des composantes connexes de B, un élément c e H°(B ; F2)
s'identifie à la famille (c„) de ses restrictions aux B„ et comme H°(Ba ; F2) est
identifié à F2, on ne peut avoir que ca = 0 ou c„ = 1 ; mais pour un b e B„ on ne
peut avoir 7Î(prî(c) — u) = 1 que si c„ = 1, ce qui montre que u est l'unique
classe de F2-orientation de E.

250 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
II) Disons qu'un ouvert U c B a la propriété P(U) si l'énoncé (24.39.4)
est vrai pour la fibration Çv induite par <Z sur 7t-1(U), et si de plus
Hp(tT '(U), «~ \U) n E0 ; F2) = {0} pour p< N.
Il résulte de I) et de (24.38.1) que P(U) est vraie si E est trivialisable au-dessus de U.
Le même raisonnement que dans (2438.4) ramène à prouver les deux lemmes
suivants :
(24.39.4.1) Si U est réunion d'une famille (UJ d'ouverts deux à deux disjoints
et si P(UJ est vraie pour tout a, alors P(U) est vraie.
Cest immédiat en ce qui concerne la nullité des modules de
cohomologie en dimension < N (24.35.6) ; d'autre part, si u„ est un élément de
HN(7TJ(UJ, n~X(UJn E0; F2) et si « = (uj, dire que jt(u) # 0 pour tout bel]
équivaut à dire que yia)*(«) ^ 0 pour tout a et tout b e U„ ou fb} est l'injection jb
considérée comme appliquant RN sur n~l(b) considérée comme fibre de n~ *(UJ-
(24.39.4.2) Si U, V sont deux ouverts de B tels que U n V # 0 et si P(U), P(V)
et P(U n V) sont vraies, il en est de même de P(U u V).
En effet, posons Mp(U)=Hp(7t_1(U), 7t-1(U)^Eo; F2)- La suite exacte de
Mayer-Vietoris M'_1(UnV) -► Mp(UuV) -» MP(U)©MP(V) pour /><N montre
que l'on a MP(U u V) = {0}. Pour p = N, on a la suite exacte de Mayer-
Vietoris
0 MN(U u V) A MN(U) © MN(V) -4 MN(U n V).
Soient u, v les uniques classes de F2-orientation pour les fibrations Çv et £v
respectivement ; par hypothèse, leurs restrictions à 7t_1(U n V) sont toutes deux égales
à l'unique classe de F2-orientation de <*UnV ; donc, par définition de g (24.37.10),
on a g(u, — v) = 0 ; mais cela signifie que (u, — v) appartient à l'image de /
et comme / est injective, il existe une unique classe w e MN(U u V) dont les
restrictions à 7t_1(U) et Jt-1(V) soient respectivement u et i;; c'est donc l'unique
classe de F2-orientation de ^uuV. -
(24.39.5) La notion de variété orientable définie dans (16.21.1) se généralise
de la façon suivante : avec les notations de (24.39.1), rappelons que si
cp : U x RN -+ n-1(U), cp' : U' x RN -» 7t-1(U') sont deux applications repères
de E, et si U n U' =t 0, le difféomorphisme de transition de cp' à cp s'écrit (16.15.1.1)
(24.39.5.1) (x, t) (x, ^(x).t)
où x -y A(x) est une application de classe C00 de U x U' dans GL(N, R). On
a alors la proposition suivante qui généralise (16.21.1) :
(24.39.6) Les propriétés suivantes sont équivalentes:

39. SUITE DE CYSIN ET CLASSE D'EULER
251
n
a) /f existe une section continue w de /\ E au-dessus de B telle que w(x)^0
pour tout xeB.
b) // existe un recouvrement ouvert U de B tel que, pour tout U e U, le fibre E
soit trivialisable au-dessus de U, et que, pour U, U' dans U et U n U' 0, le
difféomorphisme de transition (24.39.5.1) soit tel que det(A(x)) > 0 pour tout
xeUnU'.
Lorsque E est le fibre cotangent T(B)*, on retrouve la proposition (16.21.1)
dont nous calquons la démonstration. Montrons d'abord que a) entraîne b).
On prend un recouvrement ouvert U de B dont tous les éléments sont connexes ;
si cp : (y, et1, ..., <JN) -» c^s^y) + ... -I- -fs-^y) est une application repère
de E au-dessus de U (16.15.1), la restriction de w à U s'écrit
y -+ WufyXs^y) a ... a s,jty))
où Wu est une application continue de U dans R ; comme par hypothèse wlXy)^0
dans U et que U est connexe, on peut (en changeant au besoin st de signe) supposer
que wu(y) > 0 dans U (3.19.8). Si alors U, U' sont dans U et tels que U n U' # 0,
on a Wu(y) = àet(A(y))wv.(y) pour tout yeU n U'.
Inversement, pour prouver que b) entraîne a), on peut, en remplaçant U par
un recouvrement ouvert plus fin, supposer que U est une famille localement
finie (Ut) au plus dénombrable, avec, pour chaque k, une application repère
(y, S1 P) - Zi*lk(y)+ ... +£n«n*(y).
Soit (fk) une partition de l'unité sur B, subordonnée à (UJ et formée de fonctions
de classe C°° ; si l'on pose wk(x:)=0 pour jcgUto et wk(x)=fk(.x)slk(x) a ... a sNk(x)
n
pour x e Uk, wk est une section continue de A E au-dessus de B. Comme tout
x e B admet un voisinage ne rencontrant qu'un nombre fini des Uk, la somme
n
w = Ywk est définie et est une section continue de f\ E au-dessus de B ; il
k
reste à voir que w(x) # 0 pour tout xeB. Soient h0,hu ..., hm les indices k
tels que x e Uk. Par hypothèse, pour chaque j tel que 1 < j ^ m, on peut écrire
»i.*/*) a ... a sNthj(x) = gj(x)sliho(x) a ... a sKho(x) avec gj(x) > 0; donc
••• a sKko(x);
comme les fk(x) sont ^ 0 et que /*0(x) + Z fh,(x) = 1, un au moins des fhl{x)
pour 0 < i ^ m est > 0, ce qui entraine bien w(x) # 0.
(2439.7) Nous dirons que la fibration e\ - (E, B, n) est orientable si les pro-

252 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFERENTIELLE ÉLÉMENTAIRES
priétés équivalentes de (24.39.6) sont vérifiées. Si E est trivialisable, il est clair
que Ç est orientable. Pour une fibration orientable t), on définit une relation d'équi-
N
valence entre les sections continues de A E au-dessus de B qui sont # 0 en tout
point : deux telles sections wuw2 sont équivalentes si, en posant Wj(x)=l{x)w2{x),
le scalaire X{x) est > 0 en tout point xeB. Les classes d'équivalence pour cette
relation sont appelées orientations de c\, et le couple formé de <!; et d'une de ses
orientations est appelé une fibration orientée. Si w appartient à une orientation,
on dit que — w appartient à l'orientation opposée. La donnée d'une orientation
de £ définit sur chaque espace vectoriel E„ fibre de E au point xeB, une
orientation, celle définie par le N-vecteur w(x), où w est une quelconque des sections
N
continues de AE appartenant à l'orientation considérée.
On notera encore ici qu'une fibration t\ peut être non orientable, bien que
la variété E soit orientable (section 16.21, problème 4).
Il est clair que dire qu'une variété pure X de dimension n est orientable
signifie que la fibration (T(X), X, ox) est orientable ; le choix d'une orientation
sur X, c'est-à-dire d'une n-forme v telle que o(x) # 0 en tout point, détermine
canoniquement une orientation de (T(X), X, ox), par le choix d'une section w
n
de AT(X) telle que <o(x), w(x)} = 1 pour tout xeX.
(24.39.8) Si E est un espace fibre vectoriel complexe de base B et de rang
complexe N, et EK le fibre vectoriel réel de rang 2N sous-jacent à E (16.15.1), la
fibration c; = (ER, B, 7t) est orientable et possède une orientation canonique. En effet,
on peut ne considérer que des applications repères de E (et non de Eg), de sorte
que dans (24.39.5.1), A{x) est un endomorphisme de CN ; on sait alors (16.21.13.2)
que lorsque A(x) est considéré comme endomorphisme de R2N, il est tel que
det(i4(x)) > 0. La construction de la section w faite dans (24.39.6) en n'utilisant
que des applications repères de E montre alors que toutes les sections ainsi
construites sont équivalentes ; leur classe est Yorientation canonique de t) (ou de E).
(24.39.9) Les filtrations orientables sont A-orientables pour tout anneau
commutatif A. Pour énoncer ce résultat (qui généralise (24.39.4)) d'une façon plus précise,
rappelons que nous avons défini dans HN(RN, RN — {0} ; Z) un générateur
privilégié e&, appelé classe fondamentale de cohomologie de RN modulo RN — {0}
(24.35.14); pour tout anneau commutatif A, l'image canonique de ejj dans
HN(RN, RN - { 0 } ; A) = HN(RN, RN - { 0} ; Z) <g> ZA est encore appelée classe
fondamentale de cohomologie de RN modulo RN — { 0}, à coefficients dans A
et notée aussi
Si une fibration vectorielle t% = (E, B, n) est orientée, pour tout b e B on
restreint le choix des injections jb : RN ->• E (24.38.3) à celles qui sont telles
que, pour la base canonique {ek)likiN de RN, y^i) a ... a jb(eN) soit produit

39. SUITE DE CYSIN ET CLASSE D'EULER
253
de w(b) par un scalaire > 0, pour toute section w appartenant à l'orientation
de cl (autrement dit, considérée comme une bijection de RN sur E,,, préserve
V orientation).
Si j'b est une seconde injection ayant cette propriété, il est clair que fb = jb ° A(b),
où l'endomorphisme A(b) de RN est tel que det(.4(b)) > 0 ; comme Fendomor-
phisme {A(b))* de HN(RN, RN - {0} ; Z) est alors l'identité (24.35.13), on&fb*=fg.
Ces points étant précisés :
(24.39.10) Soit i = (E, B, 7t) une fibration vectorielle orientée de rang N. Pour
tout anneau commutatif A, i/ existe dans HN(E, E0 ; A) une et une seule classe
de A-orientation u telle que,pour tout beB, jf(u) soit la classe fondamentale de
cohomologie relative dans HN(RN, RN - {0} ; A).
Il suffit de reprendre point par point la preuve de (24.39.4), en remplaçant
partout « l'unique classe de F2-orientation » par « l'unique classe de
A-orientation dont les images par les applications jf soient égales à la classe fondamentale
de cohomologie relative ». On dit encore que u est la classe de A-orientation
canonique dans HN(E, E0 ; A) ; lorsqu'on remplace l'orientation de t; par
l'orientation opposée, u change de signe.
Remarque (24.39.10.1). — Il résulte de la commutativité du diagramme
(24.35.10.1) et de la définition de la classe fondamentale de cohomologie de RN
modulo RN - {0}, à coefficients dans A, que l'image canonique de la classe
de Z-orientation canonique par l'homomorphisme canonique
HN(E,E0;Z) - HN(E, E0 ; A)
est la classe de A-orientation canonique.
(24.39.11) Sous les hypothèses de (24.39.10) et avec les mêmes notations, on
appelle classe d'Euler de la fibration orientée £ = (E, B, n) et on note e{Jl) ou
e(E) Vêlement de HN(B ; Z) noté e^cl) dans (24.39.3), où u est la classe de
Z-orientation canonique de £. Il résulte de cette définition que lorsqu'on remplace
l'orientation de cl par l'orientation opposée, e(cl) change de signe.
Pour tout anneau commutatif A, l'image de e(ct) par l'homomorphisme
canonique HN(B ; Z) -* HN(B ; A) est l'élément ev{Ç) où v est la classe de
A-orientation canonique ; on dit encore que c'est la classe d'Euler à coefficients dans A
(classe d'Euler réelle si A = R) de cl ou de E.
S'il existe un B-isomorphisme (16.12) g d'une fibration orientée <^'=(E', B, n')
sur une fibration orientée £ = (E, B, n), qui préserve l'orientation, on a e(cl') = e(cl)
pour leurs classes d'Euler. En effet, pour tout beB, on peut supposer que les
injections jb : RN -> E et fb : RN -*■ E' sont telles que jb = g°j'b, donc
j'*(g*(u)) = Jt(u) pour la classe u de Z-orientation canonique de £, ce qui, par

254 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
(24.39.10), montre que g*(u) est la classe de Z-orientation canonique de Ç' ;
comme a(g*(u)) = £*(«(«)) et n'* = g*° n*, on a
««O = (it'*)-\g*(a(u))) = (7i*)-Ha(«)) - etf).
Une définition équivalente de e(€) est la suivante : en désignant par <DU
l'isomorphisme HN(B ; Z) H2N(E, E0; Z) de (24.39.1.1), on a
(2439.11.1) e(£) = ôjr ^u - u).
En effet, on a par définition e(Ç) = (jr*)_1(a(u)), donc <b^ei<l)) = a(u)~u ;
mais d'après (24.35.11.1), on a a(u) ^ u = m — u dans l'algèbre H*(E, E0;Z).
On déduit de cette formule le corollaire suivant :
(24.39.12) Si le rang N de E est impair, on a 2e(<t) = 0 dans le Z-module HN(B ; Z).
En effet, l'algèbre H"(E, E0 ; Z) est anticommutative (2435.10), donc
uu = (— I)1*2!*^u, et par suite 2(u^- u) = 0.
(24.39.13) Si E admet au-dessus de B une section continue qui est / 0 en tout
point, on a e{Ç) = 0.
L'hypothèse revient à dire qu'il existe une section continue / : B -* E0
de l'espace fibre E0, ou encore que l'application composée
B A E0 A E A B
(où i : E0 -» E est l'injection canonique) est l'identité. Par suite l'application
composée correspondante
HN(B ; Z) * HN(E ; Z) £ HN(E0 ; Z) C HN(B ; Z)
est aussi l'identité ; mais on a 7t*(e(^)) = a(u), et i*(a(u)) = 0 en vertu de
l'exactitude de la suite (24.39.2.1) ; donc e(£) = 0.
(24.39.14) Soit f : B' -» B «ne application de classe C00 d'une variété pure B'
dans une variété pure B, et soit E un /ïbre vectoriel de rang N et de base B, dont
la fibration t] = (E, B, n) est orientable. Alors la fibration £' = (/*(E), B', n')
N
est orientable; si w est une section de /\E appartenant à une orientation de Ç
et si w' = /*(w), w' appartient à une orientation de Ç'; lorsqu'on munit i et £'
de ces orientations, on a la relation entre les classes d'Euler
(24.39.14.1) e(/*(E)) = /*(e(E)).
N
Si w est une section continue de f\E au-dessus de B, qui est # 0 en tout
N
point, son image réciproque f*(w) s'identifie à une section continue de /\f*(E)
(16.19.3), évidemment # 0 en tout point de B', d'où la première assertion. Posons

39. SUITE DE CYSIN ET CLASSE D'EULER
255
E' = /*(E), et soit g : E' -» E le morphisme canonique (16.19), dont la
restriction à B' est /, quand on identifie B (resp. B') à la section nulle de E (resp. E') ;
soit Eé = g~ 1{E0), complémentaire de B' dans E'. En vertu du choix des
orientations de cl et c;', on peut prendre jfm = g o jb, pour tout b' e B' (24.39.9) ; donc
Jtis*(«)) = j}(b'iu) est la classe fondamentale de cohomologie relative de
HN(RN, RN - {0} ; Z) ; u' = g*(u) est par suite la classe de Z-orientation
canonique de E'. La proposition résulte alors de la définition de la classe d'Euler
et des diagrammes commutatifs (24.35.9.1)
HN(E,E0;Z) A HN(E;Z) £ HN(B;Z)
HN(E',E0;Z) ? HN(E';Z) r. HN(B';Z)
La propriété la plus importante des classes d'Euler est la suivante :
(24.39.15) Soient B une variété pure, E', E" deux fibres vectoriels réels de base B
et de rangs respectifs N', N". Si les fibrations de E' et E" sont orientables, il en
est de même de celle de E = E' © E", et si w' (resp. w") est une section continue
w / N" \
partout 0 de /\E' I resp. AE" J, w = w' ® w" est une section continue par-
N' + N" \ /
tout # 0 de A E. Lorsqu'on munit les fibrations de E', E" et E des orientations
définies respectivement par w', w" et w, on a, pour les classes d'Euler, la relation
(24.39.15.1) e(E' © E") = e(E') - e(E").
N' + N" /N' \ /N" \
Notons d'abord que A E s'identifie canoniquement à I AE'I ® I AE" )
N' / N" \
(Ann. 30.9) ; donc, si w' (resp. w") est une section continue de AE' I resp. AE" )
N' + N"
au-dessus de B, partout ± 0, w' ® w" est une section continue de A E,
partout # 0, ce qui montre que la fibration de E est orientable. Identifiant B aux
sections nulles des fibres vectoriels considérés, notons E'0, E'ô et E0 les
complémentaires respectifs de B dans E', E" et E. Rappelons (16.16.1) que l'on a des
B-morphismes injectifs canoniques i' : E' -* E, i" : E" -» E, et des B-mor-
phismes surjectifs canoniques p' : E -* E', p" : E -» E". Le même
raisonnement que (24.2.7) montre que i' ° p' (resp. i" o p") est homotope à l'identité ; si
i'0 : E'0 -+ E-E", : E'ô -* E—E' sont les restrictions de i' et i",p'0 : E-E" -» E'Q,
p'ô : E - E' -» Eo les restrictions de p' et p", ï0 ° p'0 et i'ô ° p'ô sont de même
homotopes à l'identité. Il résulte alors de (24.35.9.1) et du lemme des cinq que
les homomorphismes canoniques
p'* : H'(E',E0;Z) - H'(E,E-E";Z), p"* : H'(E",Erj;Z) - H'(E,E-E';Z)

256 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
sont bijectifs. Soient alors u' e hN'(E', E'0 ; z), u" e hN"(E", ES* ; z) les classes de
z-orientation canoniques de E' et E", et considérons leurs images
p'*{u')e hN(E, E - E"; z) et p"*(u")e hn (E, E - E' ; z);
comme E — E' et E — E" sont des ouverts dans E, ils forment un couple excisif
(24.37.3) et leur réunion est E0 ; le cup-produit p'*(u') — p"*(u") est donc défini
et est un élément de hN+N"(E, E0 ; z) (24.37.13). Si u est la classe de
z-orientation canonique de E, nous allons voir que l'on a
(24.39.15.2) u = p'*(u') ~p"*(u").
Il suffit de montrer que pour tout beB, l'élément jl*(p'*(u')^p"*{u")) est la
classe fondamentale de cohomologie dans hn'+n"(Rn'+n", Rn+n" - {0} ;z).
Or, en vertu de la définition (24.37.12) et de (24.31.1.2)
;?(/>'*(«')-/>"*(«")) = Jt(p'>'))~JÎ(p"*(u")).
Soient «' : RN'+N" -> RN', n" : RN'+N" -► RN" les projections canoniques; on
peut supposer choisies les injections j'b : RN' -» E', j'b' : RN" -> E" de sorte
que p' °jb = j'b o n', p" °jb = fb' » n", donc
Jt(p'*(u'))~jt(p"*(u")) = n'*0T(u')) -*"*(/?*(""))•
Mais par hypothèse j'*(u') = e$.,j'b'*(u") = eS», classes fondamentales de
cohomologie. On est donc ramené à prouver (24.39.15.2) lorsque B est réduite à un seul
point, ce que nous supposerons désormais.
Soient /N. et /N» les cocycles définis dans (24.35.14), dont les classes de
cohomologie relatives sont e& et ; le (N' -l- N")-cocycle F=(/N. ° n') ^(fN-° n")
est un cocycle du z-module différentiel
(24.39.15.3) (S.(RN'+N" ; z)/(S.(RN'+N" - RN" ; z) + S.(RN'+N" - RN' ; z)))* ;
il s'agit de montrer que sa classe de cohomologie correspondante est l'image
de e*N<+N» Par l'isomorphisme déduit en cohomologie (24.37.6.3) de l'application
canonique
S'(RN'+N", RN'+N"-{0};z) -
-+ (S.(RN'+N" ; z)/(S.(RN'+N" - RN" ; z) + S.(RN'+N" - RN' ; z))*
où l'on utilise le fait que RN'+N" - {0} = (RN+N" - RN")u(RN +N' - RN) et
que les deux ensembles du second membre sont ouverts. Le fait que l'on obtienne
un isomorphisme en cohomologie à partir de cette application implique qu'il
existe un (N' + N")-cocycle g dans S'(RN'+N", RN'+N" - {0} ; z) et une
(N' + N" - l)-cochaîne h dans le Z-module différentiel (24.39.15.3) tels que
F = g + d0h. Il s'agit de montrer que la classe de cohomologie de g est eN.+N» ;

39. SUITE DE CYSIN ET CLASSE D'EULER
257
avec les notations de (24.35.14), il suffit pour cela de voir que < g, xN.+N- > = 1.
Or on a < d0h, xN.+N» > = < h, 60*n'+n" > = < k vn'+n"-i > (notations de
(24.28.3)), et par définition le support de chacun des simplexes singuliers figurant
dans yN.+N»-i est contenu, soit dans RN'+N" - RN", soit dans RN'+N" - RN';
comme par définition h s'annule pour tous ces simplexes singuliers, il reste à
prouver que < F, xN.+N» > = 1, et en vertu de (24.35.14), il est équivalent de
montrer que < F, x$.'lN.. > = (- 1)N'+
Or, considérons un simplexe singulier (cf. (24.28.3))
S = (eoeff(0) e0e<r<0) + elea(l) • • • £0eo(0) + • • • + £n'- le<r(n'- 1) u
e0e«r(0) + • • • + ên'e<r(n') • • • £0e<r(0) + • • • + £n'+n"-le<r(n'+n"-l))
qui figure dans xff'+n-- Par définition (24.31.1.1), on a
<F,s> = </N, s'X/N-, 5">
où l'on a posé
s' = (e07c'(e„(o)) • • • eoTt^o)) + ... + eN.-^'K^.-^O)
s" = (0 e0it"(eal0)) + • ■ • + ên^"(e0(N.,)
. . . 807l"(eB(0)) + . . . + £n'+n" -'(e<»(n'+n"-l))) •
On a tout d'abord < F, s > = 0 si l'un des vecteurs Jt'(eff(J)) = 0 pour un
indice j tel que 0 < j < N' — 1, car alors deux au moins des sommets du simplexe
singulier s' sont égaux, et on a donc < /N-, s' > = 0 (24.35.14) ; tous les effU) pour
0 < j < N' - 1 doivent donc être dans RN', et alors (24.35.14) le seul simplexe
singulier s' pour lequel < /N-, s' > # 0 est
s' = (e0 e0 + e, ... e0 + et + ... + eN._|0),
pour lequel < /N-, s'} = (- 1)N+1. On n'a donc à considérer que les
permutations a pour lesquelles tjfj) = j pour 0 ^ j ^ N' - 1, ce qui entraîne que les eff(t)
sont dans RN" pour N' < < N' + N" - 1. Mais (24.35.14) le seul simplexe
singulier s" pour lequel < /N», s" > ^ 0 est alors
s" = (0 eN. eN< + eN- + i ... eN- 4- ... + eN. + N"_i),
et pour ce dernier < /N-, s" > = 1. Ceci achève de prouver (24.39.15).
(24.39.16) Pour un espace fibre vectoriel réel E de rang N (de fibration
orientable ou non) sur une variété pure B, on appelle de même classe d'Euler modulo 2
de E (ou de la fibration c) = (E, B, n)) et on note e2(E) ou e2(É) l'élément de
HN(B ; F2) noté ej£) dans (24.39.3), où u est la classe de F2-orientation dans
HN(E, E0 ; F2) (24.39.4). Les propositions (24.39.11.1), (24.39.13), (24.39.14) et
(24.39.15) sont encore valables lorsqu'on y remplace e par e2 ; il suffit en effet
de remplacer partout Z par F2 dans les démonstrations, qui autrement sont

258 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
inchangées. Lorsque E est orientée, e2(E) coïncide avec la classe d'Euler à
coefficients dans F2 définie dans (24.39.11).
(24.39.17) Soient B une variété pure compacte, E un fibre vectoriel réel de rang N
sur B, tel que la fibration { = (E, B, n) soit orientable. Alors le Z-module H'(E0 ; Z)
est de type fini, et les Z-modules de type fini lm(ii*) et Coken^S) sont tels que
(2439.17.1) rgflmfxg)) = rgfCokerfcS)) = i rg(H'(E0 ; Z)).
Comme, dans la suite de Gysin (24.393.1), HP+N(B ; Z) et HP+1(B ; Z) sont
de type fini (24.27.1), il en est de même de l'image de HP+N(B ; Z) et de celle de
HP+N(E0;Z), qui est un sous-module de HP+1(B;Z); mais cette dernière est
isomorphe au conoyau de 7t$ : HP+N(B ; Z) HP+N(E0 ; Z), donc HP+N(E0 ; Z)
est de type fini, et il en est de même de H'(E0 ; Z), puisque les HP(B ; Z) sont nuls
pour p assez grand. Si l'on considère l'homomorphisme
~e(c;):H-(B;Z) - H*(B;Z),
la suite de Gysin montre aussi que l'on a Im(7tJ) s Coker(—• e(H)), et
CokerfcS)^ Ker(~ <*£)) ;
d'autre part rg(Coker(~ e(ê))) = rg(Ker(~ <?(£))) (Ann. 34.4), et
rg(Im(*8)) + rgfCokerfag)) = rg(H*(E0 ; Z))
(Ann. 34.3), d'où la conclusion.
(24.39.18) On voit de même que pour un fibre vectoriel E (de fibration
orientable ou non) sur une variété pure compacte B, le F2-espace vectoriel H'(E0 ; F2)
est de dimension finie, et que l'on a, pour les dimensions des F2-espaces
vectoriels Imfng) et Coke^g),
(24.39.18.1) dimflmfrcg)) = dim(Coker(7tg)) = ^ dim(H'(E0 ; F2)).
Application : classe d'Euler d'un fibre normal et classe de Lefschetz.
(24.39.19) Soient X une variété riemannienne pure de dimension n, Y une sous-
variété pure compacte de X, de dimension p, N le fibre normal de Y relatif à X
(20.12.2), N0 l'ouvert de N complémentaire de la section nulle (identifiée à Y).
// existe alors un isomorphisme canonique H'(X, X - Y ; A) ^ H*(N, N0 ; A).
On a vu (24.7.1.1) que si N(e) désigne le voisinage ouvert de Y dans N formé
des vecteurs h,, tels que || hy || < e, la restriction de l'exponentielle de X à N(e)

39. SUITE DE CYSIN ET CLASSE D'EULER
259
est un difféomorphisme sur un voisinage ouvert V£ de Y dans X pour e assez
petit ; on a donc un isomorphisme d'excision (24.37.7)
puisque la réunion des ouverts X — Y et V£ est X et leur intersection \t — Y.
D'autre part, l'application exponentielle définit, par transport de structure, un
isomorphisme H'(V„ Ve - Y; A) ^ H'(N(e), N(e) - Y; A); enfin, comme la
réunion des ouverts N - Y = N0 et N(e) est N et leur intersection N(e) — Y,
on a encore un isomorphisme d'excision H*(N(e), N(e) — Y ; A) s* H*(N, N0 ; A).
Le fait que l'isomorphisme composé ne dépend pas du choix de e résulte de ce
que, pour n < e, l'isomorphisme H'(X, X - Y ; A) =i V, - Y ; A) est
composé des isomorphismes d'excision
et de la propriété analogue dans N.
Supposons maintenant que le fibre normal N soit orienté, et soit u sa classe
de A-orientation (24.39.10); elle est donc l'image d'une classe de cohomologie
relative bien déterminée
(24.39.19.1) «Y G H"""(X, X - Y ; A).
(24.39.20) Supposons le fibre normal N orienté, et soit j : Y -»• X l'injection
canonique; alors l'image de la classe uY por l'homomorphisme composé
(24.39.20.1) H"-'(X, X - Y ; A) A H"-p(X ; A) 4 H"-p(Y ; A)
est la classe de cohomologie ejjti).
Gardons les notations de la preuve de (24.39.19); on voit aussitôt que
l'application f : hv -* exp(———| est un difféomorphisme de N sur V„
Vi+ 11 M/
qui laisse fixes les points de Y ; on a donc un diagramme commutatif
où O : Y -» N est la section nulle de N, et / la même application considérée
comme injection de Y dans V£. On a d'autre part un autre diagramme
d'applications linéaires
H'(X, X - Y; A) si H^V., Ve — Y ; A)
H'(X, X - Y; A) * H-(V„ V, - Y; A) * H'fV, V, - Y; A)
H"-"(N, N0; A) -a-» H"-'(N; A) % H"~P(Y; A)
H"-'^ Ve - Y ; A) -+ H"-'(Ve; A) -+ H"~P(Y; A)
H-'tV., Vt — Y ; A) A H"-'(Vt; A) S H""P(Y; A)
H""P(X, X — Y; A) ? H-p(X;A) y H"-p(Y;A)

260 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
où i : Wc -* X et j : Y -» X sont les injections canoniques et ia flèche verticale
de gauche l'isomorphisme d'excision ; il est clair que le carré de droite est
commutatif, et la commutativité du carré de gauche est une conséquence de (24.35.9.1).
Compte tenu de la définition eu(N) = 0*(a(«)) (24.39.3), la proposition
résulte de la commutativité des deux diagrammes précédents.
(24.39.21) Soit X une variété riemannienne pure de dimension n; si g est la
métrique riemannienne de X, on définit canoniquement une métrique
riemannienne g2 sur la variété produit X x X de la façon suivante. Pour tout point
(x, y) e X x X, l'espace tangent T<Jtjy)(X x X) s'identifie canoniquement à
TX(X) x Tj,(X) ; si hu kt sont des vecteurs de T^X), h2, k2 des vecteurs de T/X),
on pose
(24.39.21.1)
< Ei(x, y), (hlf h2) ® (klt k2) > = < g(x), ht ® k, > + < g(y), h2 ® k2 >
et le fait que g2 est une métrique riemannienne se vérifie aussitôt.
Nous allons considérer dans la variété riemannienne X x X ainsi définie
la sous-variété fermée diagonale A(X); rappelons (16.8.13) que l'application
diagonale ô : x -» {x, x) est un difféomorphisme de X sur A(X). En outre :
(24.39.22) // existe un isomorphisme canonique (ô, p) du fibre tangent T(X)
sur le fibre normal N de A(X) relatif à X x X.
En effet, un vecteur tangent (hu h2) à X x X au point (x, x) est tangent
à A(X) si et seulement si hj = h2 ; d'après (24.39.21.1), un vecteur (h,, h2) de
T(*,x)(X x X) est donc normal à A(X) si et seulement si (ht + h21 k) = 0 pour
tout keTx(X), c'est-à-dire si hi = — h2. L'isomorphisme canonique de l'énoncé
est donc défini en prenant p(hx) = (- h,, hx) pour tout h^eT^X); la définition
des fibres tangents (16.15.4) montre en effet aussitôt que p est de classe C00.
Ceci entraine en particulier que le fibre normal N est orientable si et
seulement si la fibration (T(X), X, Ox) est orientable, c'est-à-dire si la variété X est
orientable.
(24.39.23) Nous allons nous restreindre maintenant au cas où X est une variété
compacte, connexe et orientée de dimension n, et où A = R. Nous orienterons
le fibre normal N de A(X) dans X x X par transport de structure de l'orientation
de T(X) à l'aide de l'isomorphisme canonique (ô, p) ; on a donc dans H"(N, N0 ; R)
une classe de R-orientation u bien déterminée, et il lui correspond dans
H"(X x X, X x X - A(X) ; R)
une classe de cohomologie bien déterminée uA(X) par (24.39.19).

39. SUITE DE CYSIN ET CLASSE D'EULER
261
(24.39.24) Sous les hypothèses de (24.39.23), pour tout x e X, soit ix
l'application y -» (x, y) de X dans X x X. Alors on a
(24.39.24.1) iî(uA(X)) = e*x
dans H"(X, X - { x } ; R) (24.37.12).
On va utiliser (24.39.19) en remplaçant X par X x X et Y par A(X). Notons
d'abord que l'exponentielle de la variété riemannienne X x X n'est autre que
l'application (h1; h2) -» (exp^), exp(h2)) où au second membre l'exponentielle
est celle de X. Cela résulte aussitôt de la définition (24.39.21.1) et du fait que
si x -> (eî(x), ..., e^(x)) est un repère mobile de X au voisinage de x0 et
y -+ (e'/( y), • • •, e^'( y)) un repère mobile de X au voisinage de y0, alors
(x, y) -* (e\(x), ..., e'n(x), e"(y), ..., e'J(y)) est un repère mobile de X x X
au voisinage de (x0) yo) ; l'expression locale (20.9.6) de la connexion de Levi-
Civita sur X x X à partir de la métrique g2 et l'équation en coordonnées locales
des géodésiques (18.6.1.3) montrent alors aussitôt que toute géodésique de
X x X est de la forme t -» (vi(t), t>2(t)), où ( -» v^t) et t -» v2{t) sont des
géodésiques de X, ce qui établit notre assertion.
Les voisinages N(e) de A(X) dans N et V£ de A(X) dans X x X étant définis
comme dans la preuve de (24.39.19), soient u' et uA(X) les images de u et uA(X)
dans H"(N(e), N(e) - A(X) ; R) et H"(V£> V£ - A(X); R) par les isomorphismes
d'excision, de sorte que exp*(uA(X)) = u' (l'exponentielle étant celle de X x X).
Soit7(xx) une isométrie linéaire de R" sur la fibre N(XiX) de N au point (x, x),
préservant l'orientation ; si j(xx) est considérée comme une injection de R" dans N,
on a par définition j^>x)(u) = e*, classe fondamentale de cohomologie relative
dans H"(R", R" - {0} ; R) (24.39.10); par suite jfXtX)(u') = e'*, image de e* par
l'isomorphisme d'excision dans H"(B0 B£ — {0 } ; R), où B£ est la boule ouverte
de centre 0 et de rayon e dans R", puisque y(x,x)(B£) est l'intersection
N(x,x)>£ = N(XiX) n N(e).
En vertu de (24.37.12), et en tenant compte des isomorphismes d'excision,
il suffira de montrer qu'il existe un difféomorphisme i/> de B£ sur un voisinage
ouvert W£ de x dans X, préservant l'orientation, et pour lequel on a
<A*('Î("W) = C
ix étant ici l'application y (x, y) de W£ dans V£.
Or, on a défini dans (24.39.22) une bijection linéaire px : hx -* ( — hx, hx)
de l'espace tangent TX(X) sur N(xx) préservant l'orientation; l'image par p'1
de N(XiX)i£ est la boule ouverte Tx,c/j2: Il hx || < e/,/2 dans TX(X). On peut
supposer e assez petit pour que l'application expx (où l'exponentielle est celle de X)

262 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
soit un difféomorphisme de TXie/yj sur un voisinage ouvert We de x dans X (18.4.6).
Nous allons montrer que l'application composée
^:Be^N(x.x/^Tx,^'3wt
qui préserve l'orientation, répond à là question.
Notons exp(xx) la restriction à N(XiX) de l'application exponentielle de X xX;
il suffira de voir que les applications i//* » i* et jfXiX) ° exp* = jfXfX) » exp(* iX) sont
égales ; vu la définition de cela va résulter de ce que les applications exp(xx)
et ix » expx o p~1 de N(xxM dans Ve sont homotopes par une homotopie fixant x
(24.35.9). Or, d'après les remarques du début, ces applications s'écrivent
respectivement
k - (exPx( - px" '(k)), exPx(p; »(k))) et k -» (x, exPx(p; '(k))) ;
l'application (k, t) -» (exp^- tp;1(k)).expx(p;:1(k)))deN(x>x),t x [0, l]dansV4
fournit l'homotopie cherchée. CQFD.
(24.39.25) Sous les hypothèses de (24.39.23), l'image canonique a(uA(X)) dans
H"(X x X ; R) est la classe de Lefschetz lx (24.6.10).
Nous allons vérifier pour cette classe de cohomologie la propriété (24.6.11)
qui caractérise la classe de Lefschetz. En premier lieu, on a le diagramme
commutatif
H"(X x X, X x X - A(X); R) A H"(X x X; R)
«I !•
H"(X, X - {x} ; R) --► H"(X; R)
(24.35.9.1) ; comme on a vu (24.37.12.1) que l'image a(e%) est la classe
fondamentale de cohomologie ex de X, on a «î(a(uA(X))) = ex par (24.39.24.1). On va
d'abord déduire de ce résultat que l'on a, avec les notations de (24.5.9)
(24.39.25.1) £a(uA(X)) = 1,
élément unité de H°(X ; R) (l'intégrale partielle étant prise suivant le second
facteur de X x X). En effet, soit co une n-forme différentielle de classe C°° sur
X x X, dont la classe de cohomologie est a(uMX)). Avec les notations de (24.5.8),
il est immédiat que dans l'expression locale de co, les seuls termes qui donnent
une contribution ^ o dans J g,co sont les termes en dx, y)dyl a ... a dy",
c'est-à-dire ceux de la n-forme 'ix(co), et on a ^ co^(x) = j* 'ij^co) ; mais la
relation ix(o(uA(X))) = ex signifie que cette dernière intégrale est égale à 1 (24.63),
d'où la formule (24.39.25.1).

39. SUITE DE CYSIN ET CLASSE D'EULER
263
Pour vérifier la propriété (24.6.11), il suffira de prouver le lemme suivant :
(24.39.25.2) Pour toute classe de cohomologie c e HP(X ; R), on a
(24.39.25.3) a(»A(X)) ~ prftc) = a[uMX)) ~ pr*(c).
En effet, il résulte de (24.5.10.1) que Ton a
Pour prouver le lemme (24.39.25.2), notons que si j : V£ -♦ X x X
(notations de (24.39.24)) est l'injection canonique, l'isomorphisme d'excision
est tel que j*(b ~ ma(x)) = j*(b) — u'A(X) en vertu de (24.35.11.2), pour toute classe
de cohomologie b e HP(X x X ; R). Appliquant ceci à b = pr*(c) et b = prf (c),
on voit qu'il suffit de montrer que y*(pr*(c)) = /"*(prf(c)), et pour cela il suffit
de voir que les applications prj °j et pr2 ° j de V£ dans X sont homotopes par
une homotopie laissant fixes les points de A(X) (24.35.9). En prenant e assez
petit et utilisant le difféomorphisme de N(e) sur V, donné par l'exponentielle
de X x X, puis le difféomorphisme p de T(X) sur N (24.39.22), on est ramené,
par transport de structure, à montrer que les deux applications k -+ exp(k),
k -» exp( — k) d'un voisinage U de X dans T(X) sont homotopes par une
homotopie fixant les points de X (exp étant ici l'exponentielle de X). Mais l'application
(k, t) -* expftk) de U x [— 1, 1] dans X est évidemment une telle
homotopie. CQFD.
Ce résultat entraine le corollaire suivant :
(24.39.26) (i) Pour toute variété pure compacte, connexe et orientée X de
dimension n, la classe d'Euler réelle e(T(X)) du fibre tangent T(X) dans H"(X ; R) est
donnée par
où ô : x -* [x, x) est l'application diagonale et lx la classe de Lefschetz de X.
en vertu de (24.39.25.1), d'où
f : H"+p(X x X, X x X - AfX); R) - H"+p(V£, V£ - A(X); R)
(24.39.26.1) e(T(X)) = ô*{lx)
(ii) On a
(24.39.26.2) < efT(X)), [X] > = jrfX)

264 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFERENTIELLE ÉLÉMENTAIRES
caractéristique d'Euler-Poincaré de X (ce qui justifie le nom de « classe d'Euler »).
La formule (24.39.26.2) est conséquence immédiate de (24.39.26.1) et de la
définition (24.6.10.1) de la classe de Lefschetz. Il suffit donc de prouver (i).
Si h : A(X) -» X x X est l'injection canonique, il résulte de (24.39.20) que
l'on a /i*(/"x) = 0*(a(w)) pour la classe d'orientation u de N. Mais en vertu de
(24.39.22), on a un diagramme commutatif
H"(N, N0 ; R) -—► H"(N ; R) SL, H"(A(X) ; R)
H"(T(X), T(X) — X ; R) -+ H"(T(X) ; R) ^ H"(X ; R)
où les flèches verticales sont bijectives; p*(u) est donc la classe d'orientation
de T(X), et comme O*(o(p*(u))) est par définition la classe d'Euler e(T(X)) (24.39.3),
on obtient la formule (24.39.26.1).
PROBLÈMES
1) Soit X une variété compacte, connexe, non orientable et de dimension n.
a) Généraliser les résultats de (24.37.12) et (24.39.24) à la variété X, pour la cohomologie
à coefficients dans F2.
b) Généraliser le lemme (24.39.25.2) à toute classe de cohomologie c e H'(X ; F2).
c) Si px est la classe fondamentale d'homologie dans H,(X ; F2) (section 24.37, problème 13),
déduire de a) et b) que pour toute classe de cohomologie c e H'(X ; F2), on a (a(ua(X)) — prjc)/^x = c
(notation de la section 24.38, problème S).
2) Les hypothèses et notations sont celles du problème 1.
a) Soit (bi)liiir une base de H'(X; F2), réunion de bases des H'(X; F2). Montrer que l'on
r
peut écrire a(uA(X)) = Z pr*(bi)w prJVi). ou pour chaque i, si fc, e H'(X ; F2), on a c, e H" " "(X ; F2),
et < fc, - c„ ux > = 1. < bt - cj, Hx > = 0 si j * i.
b) Généraliser la proposition (24.39.20) aux variétés non orientables, et en déduire que la
r
classe d'Euler e2(T(X)) = S bt - c„ et que < e2(T(X)), nx > est le reste de z(X) modulo 2.
i = i
c) Montrer que l'inverse de l'isomorphisme de dualité défini dans la section 24.37,
problème 13 est l'homomorphisme z -» a(uA(X))/z.
d) Énoncer et démontrer les résultats analogues pour les variétés compactes orientées et
l'homologie et cohomologie singulière à coefficients dans un corps quelconque A.
3) On dit qu'une C°-fibration (section 16.25, problème 8) est une fibration en boules (resp.
en sphères) si dans la définition ((16.12.1), où les variétés différentielles sont remplacées par des
espaces topologiques et les difféomorphismes par des homéomorphismes) la « fibre type » F est
une boule fermée (resp. une sphère) dans un espace euclidien R" ; l'espace X est alors appelé espace
fibre en boules (resp. en sphères).
a) Soit (X, B, 71) une fibration en boules, F étant la boule || x|| < 1 dans R". Pour tout
b e B et tout voisinage ouvert U de b dans B pour lequel il existe un homéomorphisme
q> : U x F -► n' '(U) tel que n(<p{y, t)) = y, montrer que l'image de la sphèreS„_ [ part -» (p{b, t)
est une partie fermée X° de la fibre X^, qui est indépendante du voisinage U de b et de l'homéomor-
phisme tp choisis (utiliser la section 24.37, problème 6). Si X° est la réunion des fibres X? pour
beB, (X°, B, iz| X°) est une fibration en sphères.

39. SUITE DE CYSIN ET CLASSE D'EULER
265
b) Inversement, soit (Y, B, n0) une fibration en sphères, F étant la sphère S„_,. Dans l'espace
Y x [0, 1 ], on considère la relation d'équivalence dont les classes sont les ensembles {(y, t)}
pour t # 0 et les ensembles Yt x {0} pour beB. Soit X l'espace quotient de Y x [0, 1 ] par
cette relation ; si x est la classe de (y, r) dans X, n0(y) ne dépend que de x, et si on le note n(x),
(X, B, n) est une fibration en boules, telle que la fibration en sphères correspondante (X°, B, n | X°)
définie dans a) soit B-isomorphe à (Y, B, n0).
c) Définir, pour un anneau commutatif A, la notion de fibre en sphères A-orientable, et
pour un tel fibre (Y, B, n0), dont les fibres sont homéomorphes à S„_i, établir une suite exacte
de Gysin
... - H'(B;A) - H'+"(B;A) - H'+"(Y;A) - H'+1(B;A) - .
d) Soit E un espace fibre vectoriel réel de rang n et de base une variété différentielle B,
n : E -> B sa projection. On munit E d'une structure euclidienne (définie comme la structure
hermitienne sur un fibre vectoriel complexe dans 23.27.3), et on désigne par Y la sous-variété
de E formée des vecteurs ueE, tels que || u || = 1, b parcourant B. Alors Y est un espace fibre
en sphères, qui est A-orientable si et seulement si (E, B, ji) est A-orientable, et on a
H*(Y;A)sH*(E0;A).
4) a) Soit Y2ll-3 le fibre en sphères canoniquement déduit (section 20.9, problème 3 e))
du fibre tangent à la sphère S„_, munie de sa structure riemannienne usuelle. Montrer que, si n
est la projection Y2„-3 -+ S..,, l'application h -> (n(h), t^^h)) est un difféomorphisme de
Y2„-3 sur la variété de Stiefel S„-2(R). En particulier, Y3 est difféomorphe au groupe SO(3).
b) Déduire de a) que, pour n > 3 :
a) Si n = 2m est pair, H'(S,,2(R) ; Z) = { 0}, sauf pour p = 0, 2m - 2, 2m - 1, 4m - 3,
où H'(S,;(R);Z)ïZ; l'algèbre H'(S„ 2(R) ; Z) est isomorphe au produit tensoriel gauche
H'tS^-.-Z)"® H-(S2„_2;Z).
P) Si n = 2m + 1 est impair, H'(S„i2(R) ; Z) = {0} sauf pour p = 0, 2m et 4m - 1 ; on a
H°(S„i2(R) ; Z) = H4"-'(S„.2(R); Z) = Z, et H2"(S,,2(R) ; Z) s Z/2Z. (Utiliser la suite de Gysin,
et le fait que la classe d'Euler de T(S„_,) est 0 si n est pair et 2cJ_ t si n est impair (24.39.26) ; pour
la structure d'algèbre, utiliser le théorème de Leray-Hirsch).
5) Soit (X, B, k) une fibration pour laquelle X et B sont des variétés différentielles
orientables pures, toutes les fibres étant difféomorphes à une même variété différentielle connexe F,
et on suppose que pour un anneau commutatif A, l'algèbre H'(F; A) soit isomorphe à H'(S„; A).
Montrer que H'(X; A) est une algèbre isomorphe à H'(B; A) '® AH'(F; A). (Raisonner comme
dans (24.39.10) pour appliquer le théorème de Leray-Hirsch). Par contre, si X est un revêtement
orientable connexe à deux feuillets d'une variété orientable connexe B, lorsque (X, B, n) est
considéré comme une fibration en sphères de dimension 0, cette fibration n'est jamais Z-orientable.
6) Montrer que le polynôme de Poincaré de la variété de Stiefel S. „(R) est donné par les
formules suivantes :
i
sin = 2m, k = 21 + 1 < n, P(S„ ^R)) = (1 + X2"" ') FI (1+ X*1"-*'-l) ;
i >-»
si n = 2m + 1, k = 2/ < n, P(S„ 4(R)) = J/I d + X4"-4J+3) ;
j=l i-i
sin = 2m, k = 2l<n, P(S„ t(R)) = (1 + X2"-2X1 + X2""l)fl (1 + X4™-4j-l);
sin = 2m+l, k = 21 + 1 < n, PfS.^R)) = (1 + X2""2) u (1 + X4-"4' + 3).
(Raisonner par récurrence sur k < n ; si n - k est impair, considérer S„it(R) comme fibre sur
S„,t-2(R) de fibre S,-t+2-2(R), et utiliser les problèmes 4 et 5; si n - k est pair, considérer S„,j(R)
comme fibre en sphères sur S„,t - ,(R) et utiliser le problème S ; on tiendra compte de la section 16.21,
problème 1).
7) Soit i = (E, B, n) une fibration orientée telle que 2e(i) # 0 dans HN(B ; Z). Montrer
qu'il ne peut exister de sous-espace fibre vectoriel F de E de rang impair tel que la fibration (F, B, ji)
soit orientable.

266 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFERENTIELLE ÉLÉMENTAIRES
8) Si X est une sous-variété différentielle pure compacte de R", et N son fibre normal, montrer
que l'on a e(N) = 0 si X est orientable, e2(N) = 0 sinon.
9) Soit X un revêtement connexe à deux feuillets d'une variété connexe B ; montrer que
dans la suite exacte de Gysin (problème 3), l'homomorphisme 1 -» e de H°(B ; F2) dans H'(B ; F2)
est nécessairement injectif.
10) Montrer que la cohomologie H'(QM ; F2) de la quadrique réelle projective (section 24.5,
problème 7), pour p > q, est donnée par :
a) si p>q, H'(Qr.,; F2)sF2 pour 0^/<?-l et pour p-l çj^p+q-2, HJ(Q,.,; F2)={0}
pour q < j < p - 2 ;
b) si p=q, HJ(Q,,, ; F2)=F2 pour 0 *j <p - 2 et p <J «S 2p - 2, et H'" '(QM ; F2) s F|.(Utiliser
le fait que Q,,, est un revêtement connexe à deux feuillets de la variété P, - ,(R) x P,. ,(R) ; montrer
qu'avec les notations du problème 9, et en identifiant H'(P,_i(R) x P^.^R); F2) à
H"(PP. ,(R) ; F2) ® H"(P,_ ,(R) ; F2),
on a e = c,_, ® 1 + 1 ® c€-„ où ct est le générateur de l'algèbre H'fjyR); F2) (24.40.12)).
11) Sous les hypothèses de (24.39.3), on suppose en outre que A est un corps, que B est
compacte et orientée, et que la fibration i est orientable, de sorte que E est une variété orientable.
On appelle encore classes fondamentales à coefficients dans A les images canoniques dans les
espaces d'homologie à coefficients dans A des classes fondamentales définies dans la section 24.37,
problème 11. Montrer que la classe fondamentale /iEiB s'identifie (section 24.38, problème 8) au
produit tensoriel p.B ® eN, où eN est la classe fondamentale d'homologie relative dans
H^R", RN - {0} ; A), classe du N-cycle relatif noté xN dans (24.28.3.1), lorsqu'on prend sur E
une orientation convenable.
En déduire que si u est la classe de A-orientation choisie pour {, on a
J*e.b -u = Un
(section 24.35, problème S).
12) Soient X une variété compacte pure orientée de dimension n, Y une sous-variété compacte
pure orientée de X de dimension p, telles que le fibre normal N de Y relatif i X soit orientable.
Avec les notations de (24.39.20), montrer que pour une orientation convenable de N, on a
Dx(a(uY)) = Mx "~ o(«y) = 7»(My)- (Utiliser la commutativité du diagramme
HJX ; A) ® AH-'(X, X - Y ; A) '^i HJiX, X - Y ; A) ® AH"-'(X, X - Y ; A)
i»« | |«
HJX ; A) ® AH"-'(X ; A) ► H^X ; A)
et le problème 11).
Énoncer et démontrer les résultats analogues pour des variétés non nécessairement
orientables avec A = F2.
40. Cohomologie des grassmanniennes.
(24.40.1) Pour 1 < p < n, l'étude de la cohomologie de la grassmannienne
G„iP(C) des sous-espaces vectoriels complexes de C de dimension p (16.11.9),
peut se faire à l'aide de certains fibres vectoriels canoniquement attachés à
GB>P(C), auxquels on applique la suite de Gysin (24.39.3.1).
Dans ce qui suit, nous supposerons l'espace C" muni du produit scalaire
canonique {x | y) = X Considérons le fibre vectoriel complexe trivial
E = G„,P(C) x C" de base GBiP(C) et de rang n, et soit UBjP(C) la partie de E

40. COHOMOLOGIE DES GRASSMANNIENNES
267
formée des couples (v, x), où v e G„JC) et x est un vecteur du sous-espace v de C.
Montrons d'abord que UB>P(C) est un sous-espace fibre vectoriel de E, de rang p.
Pour cela, pour toute partie J de {1, 2, ..., n}, nous désignerons par CJ
le sous-espace vectoriel de C" ayant pour base les éléments e,- de la base
canonique de C" tels que jeJ, et nous noterons J' le complémentaire de J. On sait
(16.11.10) que pour toute partie J de {1, 2, ..., n} ayant p éléments, l'ensemble V,
des sous-espaces v e G,,<P(C) tels que v n Cy = {0} (v étant donc
supplémentaire de CJ') est un ouvert de G,iP(C) et que les Vj forment un recouvrement de
GB>P(C). Pour tout ve Vj et tout je], soit = e, + E»;*** l'unique vecteur
kel'
de v qui se projette sur e, dans CJ. Si, pour k e V, on pose sk(v) = e,, les n
sections tj (pour je5) et sk (pour keJ') forment un repère de E au-dessus de V,
(16.15.1) ; comme les p vecteurs s/i>) pour jeJ forment une base du sous-espace v,
pour tout ueVj, notre assertion est démontrée (16.17.1). On dit que U„>P(C)
est le fibre vectoriel canonique (ou tautologique) sur GaiP(C).
(24.40.2) Pour tout sous-espace veG„iP{C), soit t>i6GBI1_p(C) le sous-espace
vectoriel (complexe) orthogonal à v (pour le produit scalaire canonique).
L'application co : v -* v1 est évidemment une bijection de G„èP(C) sur GB|l,_p(C);
montrons que c'est un difféomorphisme. Pour toute partie J de p éléments de
{ 1, 2, ..., n }, tout v e V,, tel que tj(v) = e; -I- £ njk*k P°ur jei, et tout indice
keV, il existe un unique vecteur ek + ZC/*«j se projetant sur e* dans CJ' et
orthogonal à v ; en effet, on voit aussitôt que les relations + £ tjk*j I *n(v)j=0
pour tout h e J se réduisent à Cjk = - ïjk- Autrement dit, pour tout k e J', on a
*k(vx) — e* — Y.fjjkej> ce qui montre que la restriction de co à V, est un difféo-
morphisme de V, sur V,., d'où notre assertion.
(24.40.3) Soit maintenant U^pjC) la partie de E formée des couples (u, x\
où v e GBp(C) et x est un vecteur de C" orthogonal à v. Nous allons voir que
UB>P(C) est un sous-espace fibre vectoriel (complexe) de E isomorphe à a)*(U,,iB_p(C)).
En effet, par définition (16.12.8), co*{Ki„^p(C)) est la sous-variété de
G»>P(C) x G^-pfC) x C"
formée des triplets (v, v1, x) tels que xe»1. La projection de co*(Ulljl,_p(C))
dans E = G„,P(C) x C" est un difféomorphisme, car la projection sur Gnp(Q
du graphe de co dans GBp(Q x G^-^C) est un difféomorphisme (16.8.13);
cela définit un isomorphisme de l'espace fibre to*(UIIil,_p(C)) sur l'espace
fibre Uj^C).
(24.40.4) Pour tout ve G.,P(C) et tout x # 0 dans v, l'orthogonal (Cx)1 n v

268 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
de la droite Cx dans v est un sous-espace vectoriel complexe de dimensionp — 1.
Notons (U„P(C))0 et (U^P(C))0 les complémentaires de la section nulle dans les
fibres vectoriels Un>p(C) et Uj^C). Alors l'application
(24.40.4.1) / : (t>, x) ((Cx)1 n », x)
est un difféomorphisme de (UBjP(C))0 sur (U1,,-i(C))0. En effet, c'est évidemment
une bijection, dont la bijection réciproque est
(24.40.4.2) /"1 : (w, x) - (Cx + w, x).
Il suffit de montrer que l'application (w, x) -» Cx + w de (U;l;p_1(C))o dans
G„iP(C) et l'application (v, x) -> (Cx)1 n v de (U„iP(C))o dans G^^fC) sont
de classe C00. En ce qui concerne la première, rappelons que GBp(C) peut être
identifiée à l'image, par l'application canonique p : j\(C) — {0} -*■ P( j\{C)
(qui est de classe C00) de l'ensemble des p-vecteurs décomposantes ^
non nuls. Soit n0 : (U„LiP_1(C))o -» GB>P_1(C) la projection canonique, et
considérons une partie J de p — 1 éléments it < i2 < ... < ip-i de { 1, 2, ..., n} ;
alors la restriction de l'application (w, x) Cx + w à nô '(Vj) s'écrit
(24.40.4.3) (w, x) ^ p(x a ttl(w) a ... a sip.,(w)).
Or, si s,(w) = e, + Z'/*ek Pour 76J> on P6"1 écrire x = X «^(V"), et le
calcul des sk(wL) fait dans (24.40.2) montre que les composantes du p-vecteur
x a s,-,(w) a ... a s.p.^vv) sont des polynômes à coefficients entiers par
rapport aux nJk, rjjk et aux ; cela montre bien que (24.40.4.3) est de classe Cœ.
Le même raisonnement montre que (v, x) -+ (Cx)1 n v est de classe C00, car
on peut écrire (Cx)1 n v = (Cx + u1)1, et on a vu dans (24.40.2) que v -* v1
est un difféomorphisme ; donc (v, x) -> (v1, x) est un difféomorphisme de
(24.40.5) Nous allons utiliser les constructions précédentes pour étudier la
cohomologie de G„iP(C), en procédant par récurrence sur p. Pour p = 1, on a
GM(C) = P„-i(C), et nous avons déjà déterminé le Z-module H'(P„(C);Z)
((24.22.14) et (24.30.8)) : on a H*(P,,(Q ; Z) = {0} sauf si k est pair et tel que
0 ^ k < 2n, et alors Hk(P»(C) ; Z) s Z. On peut aller plus loin et déterminer
l'anneau de cohomologie H'(P„(C);Z); pour cela, nous noterons e la classe
d'Euler (24.39.11) du fibre vectoriel réel F de rang 2, sous-jacent au fibre
canonique (complexe) UB+1>1(C), la fibration correspondante étant canoniquement
orientée (24.39.8); on a donc e e H2(P„(Q ; Z).
p
X| a Xj a ... a Xp
(IMQo sur {VÏ„-P(C))0.

40. COHOMOLOGIE DES GRASSMANNIENNES
269
(24.40.6) L'anneau de cohomologie H'(P„(C); Z) est engendré par e, et est
isomorphe à l'anneau quotient Z[T]/(T"+1).
Par définition (24.40.1), (UB+u(C))o est le sous-espace de P„(C) x (C+1 - {0} )
formé des couples (v, x) avec x e v ; la projection g : (v, x) -*■ x est une bijection
de (U„+ i,i(C))o sur C+1 - {0}, dont la bijection réciproque est x -* (p(x), x),
où p : C +1 - {0} -»• PB(C) est l'application canonique ; il est clair que g et g"1
sont de classe Cœ, donc g est un difféomorphisme, et par suite
H"(F0;Z)sH,(Sa.+ l;Z).
La suite exacte de Gysin (24.39.3.1)
H*+1(F0;Z) - H*(PB(C);Z) =f H*+2(Pn(C); Z) 3 Ht+2(F0;Z)
pour 0 < k < 2n — 2, a donc ses termes extrêmes nuls, d'où aussitôt la
proposition, H2k(PB(C) ; Z) ayant pour générateur e"k pour 1 ^ k ^ n.
(24.40.7) Posons n = p + q, et notons M et N les fibres vectoriels réels sous-
jacents à UP+,P(C) et Up+,p_i(C) respectivement; les fibrations correspondant
à ces fibres vectoriels complexes sont munies de l'orientation canonique (24.39.8).
Les rangs de M et N étant égaux à 2p et 2{q + 1) respectivement, on a les suites
de Gysin
(24.40.7.1)
... - H*(G,+W(C);Z) Hi+2'(Gp+,iP(C);Z) $ H*+2"(M0;Z) -»
- H*+1(GP+,,P(C);Z)
(24.40.7.2) ... - H*(GP+Ï>P_ X(Q ; Z) ^ H*+2<«+ ''(G,*,.,. ,(C) ; Z) -
il Hk+2<«+1»(N0;Z) -» H^HG^^-^QjZ)
où a : M0 -» Gp+,iP(C) et 0 : N0 -» Gp+,iP_1(C) sont les projections.
Faisant k = — 2p, — 2p + 1, ..., — 2 dans la première suite, on voit que
les applications a* : HJ{Gp+9iP(C) ; Z) -»• HJ(M0;Z) sont des isomorphismes
pour 0 < y < 2p — 2. Rappelons d'autre part (24.40.4) qu'on a un
difféomorphisme canonique / : M0 -+ N0. On peut alors énoncer le résultat suivant :
(24.40.8) (i) Les Z-modules HJ(Gp+ïiP(C) ; Z) sont libres pour tout j.
(ii) Pour chaque indice j tel que 1 ^j ^ p, il existe, dans H2j(Gp+,p(C) ; Z),
un élément cp'q tel que les cf", pour 1 ^j^p, engendrent (avec l'élément unité)
l'anneau de cohomologie H'(Gp+qp(C); Z). En outre, on a
(24.40.8.1) cp« = e(M) ;
(24.40.8.2) a*(cj'*) = /*(/3*(cJT1-4+1)) pour 1 < j ^ p - 1.
En particulier H2-/+1(GP+,P(C); Z) = { 0 } pour tout j.

270 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
Raisonnons par récurrence sur p ; pour p = 1, la proposition résulte de
(24.40.6). Considérons les homomorphismes de Z-modules gradués
H"(GF+M(C) ; Z) 22? H-(G,+M(C) ; Z) £ H-(M0 ; Z)
H\G,+„-iiQlZ) ^ H^G^^.^OjZ) 4 H'(N0;Z)
et supposons le théorème prouvé pour Gp+,jP_1(C). Comme H'(Gp+,iP_1(C); Z)
est un Z-module libre gradué, il en est de même de son sous-module Ker(— e(N)),
et par suite aussi de Coker(/?*), qui lui est isomorphe en vertu de (24.40.7.2);
on a donc (Ann. 29.2) un isomorphisme
H *(N0 ; Z) s lm(p*) © CokerO?*)
et puisque /* est un isomorphisme, on a de même
H"(M0 ; Z) s Im(/* = p*) © CokerfJ* o p*),
puisque Coker(/* ° /?*) est libre. Définissons alors les éléments cj* pour 1 ^j^p
par les formules (24.40.8.1) et (24.40.8.2), ce qui est licite puisque, pour 1 ^j^p-1,
a* : H2-*(Gp+,jP(C) ; Z) -> H2J{M0 ; Z) est bijectif. Par l'hypothèse de récurrence,
les éléments P*(cp~l,q+l) engendrent le sous-anneau Im(/J*); le sous-anneau
Im(a*) de H'(M0;Z), qui contient les éléments a*(cf«) =/*(/9*(cp_1,,+ 1))
pour K/</>-l, contient donc Im(/* »/?*). Appliquons maintenant (24.39.17.1)
aux deux suites (24.40.7.1) et (24.40.7.2); on en tire les relations
rg(Im(a*)) - A rg(H-(M0 ; Z)) = i rgfH'CNo ; Z)) = rg(Im(/* o /?♦)).
Si le Z-module Im(a*) était distinct de son sous-module Im(/* ° P*), le quotient
Im(a*)/Im(/*°P*) serait donc un Z-module de torsion; mais c'est un sous-
module du Z-module libre Coker(/* o p*\ donc ce sous-module est nul (Ann. 26.2),
on a Im(a*) = Im(/* o p*) et Coker(a*) s Cokert,/* ° 0*) est /iore.
Le Z-module Ker(— e(M)), qui est isomorphe à Cokeifa*) d'après (24.40.7.1)
est donc libre. On en conclut que H"(GP+,>P(C) ; Z) est aussi libre : en effet, dans
le cas contraire, il existerait dans ce Z-module gradué de type fini un élément
z ^ 0 appartenant à un Hj(Gp+,iP(C); Z) non libre et tel qu'il n'existe aucun
élément ayant ces propriétés dans les H*(Gp+4iP(C); Z) pour k > f. On aurait
donc z — é(M) = 0, puisque z~e(M) appartient à HJ+2p(Gp+,iP(C); Z) et n'est
évidemment pas libre; mais cela est contradictoire, car on en conclurait que
z 6 Ker(— e(M)), qui est libre.
On a donc prouvé l'assertion (i). On a en outre montré que pour tout j—k+2p,
tout élément de HJ(Gp+q<p(C) ; Z) est somme d'un polynôme à coefficients entiers

40. COHOMOLOGIE DES GRASSMANNIENNES
271
par rapport aux cf■* d'indice i ^ p — 1, et d'un élément de Ker(a*). Pour en
déduire l'assertion (ii), c'est-à-dire que tout élément de H-,(GP+,P(C); Z) est
égal à un polynôme à coefficients entiers par rapport à tous les cf,q, raisonnons
par récurrence sur / La proposition est évidente pour j < 2p — 2, puisque le
noyau de a* dans HJ(GP+4P(C); Z) est alors réduit à 0; mais si elle est vraie
pour un indice j, elle l'est aussi pour j + 2p : en effet le sous-module Ker(a*)
de H-/+2p(Gp+,p(C); Z) est égal à l'image de HJ(Gp+qp(Ç); Z) par l'application
z -» z^e(M) de HJ(Gp+4P(C); Z), et la conclusion résulte de la définition
de cppq. CQFD.
(24.40.9) Disons qu'un polynôme de ZrTj, T2, ..., Tp] est isobare de poids j
s'il est combinaison linéaire de monômes Ti'T22 ... Tpp tels que
2vt + 4v2 + ... + 2pvp = j.
Comme cf1* e H2i(Gp+,>p(C) ; Z), il résulte de (24.40.8) que tout élément de
Hj(Gp+,iP(C) ; Z) est égal à un polynôme isobare de poids j par rapport à
cf* ..., c™. L'exemple de P„(C) (24.40.6), où e"1 = 0 pourj > n, montre qu'un
tel polynôme n'est pas unique en général. Toutefois :
(24.40.10) (i) Pour tout indice j tel que j < q, on a une suite exacte canonique
(24.40.10.1) 0 -> H2"-"»(GP+,>P(C);Z) ^ H^G^fC) ; Z) -
A H24G,+,.,_,.(C);Z) 0
(ii) Le seul polynôme PeZ[Ti, ...,Tp] isobare de poids 2/< 2q tel que
P(cr, ci*, cppq) = 0 est P = 0.
(i) Il résulte de (24.40.7.2) que pour k < - 2, l'application
0.:H*+2<,+ i>(Gp+^_i(C);Z) _ Hk+2««+1>(N0;Z)
est bijective ; compte tenu du fait que les modules de cohomologie de GP+,P(C)
sont nuls en dimension impaire, on déduit donc la suite exacte (24.40.10.1) de
(24.40.7.1), avec A = (/* » p*)~1 o a*.
(ii) La proposition résultant de (24.40.6) pour p = 1, nous raisonnerons
par récurrence sur p, puis, pour chaque p, par récurrence sur j < q, la
proposition étant évidente pour j = 0. Le polynôme P peut s'écrire
P^, ....VO + T^CTi, ...,TP),
où P, est de poids 2j et P2 de poids 2(j — p). En vertu de la suite exacte (24.40.10.1),
on a ^(cr, cfîj) = 0 puisque P2(cf-« cpp,q) e H2{J~p)(Gp+qp(C) ; Z)
et que cp,q ~ P2(cf•*, ..., cp,q) appartient donc à Ker(A) ; en vertu de la
définition de X et de (24.40.8.2), on a Pi(cÇ~1,«+1, ..., cpZ\-q+ J) = 0, a*, p* et /* étant

272 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
des homomorphismes d'algèbres. L'hypothèse de récurrence sur p entraine
donc Pj = 0. D'autre part, comme l'application ~ cj-* est injective par (24.40.10.1X
on conclut de la relation c^P^c?/' cp-«)=0 que l'on a P2(c?/« cj«)=0;
comme P2 est de poids HJ — p), l'hypothèse de récurrence sur j entraine P2 = 0.
CQFD.
(24.40.11) Tous les raisonnements faits de (24.40.1) à (24.40.4) peuvent se
répéter en changeant uniquement C en R et le produit scalaire en £ €V- Nous
allons les utiliser pour étudier la cohomologie de G„iP(R) à coefficients dans F2,
en procédant par récurrence sur p. Pour p — 1, on pourrait déterminer
directement le F2-espace vectoriel H*(P„(R) ; F2) à partir de (24.36.5), en utilisant le
passage de l'homologie à coefficients dans Z à la cohomologie à coefficients
dans F2 (24.30.8). Mais on peut directement déterminer Vanneau de cohomologie
H'(P„(R) ; F2) en raisonnant comme dans (24.40.5) ; on considère la classe d'Euler
e2 modulo 2 du fibre vectoriel réel de rang 1, F = UB+1 t(R); on a donc
e2eH1(Pn{R); F2).
(24.40.12) L'algèbre de cohomologie H'(P,,(R); F2) est engendrée par e2, et est
isomorphe à l'algèbre quotient F2[T]/(T"+1).
Avec les mêmes notations que dans (24.40.5), on voit que F0 est difféo-
morphe à R"+1 - {0}, donc H'(F0 ; F2) = H*(S,,; F2). Cette fois, la suite de
Gysin
(24.40.12.1)
H*(F0; F2) -> tffJPtfR); F2) 3? H*+1(P„(R); F2) 3 H*+1(F„; F2),
a ses termes extrêmes nuls pour 1 ^ k < n — 2. Pour k = 0, le début de la suite
de Gysin donne une suite exacte
0 - H0(P„(R); F2) - H°(F0; F2) -» H0(P,,(R); F2) -
^ H^RJîF,) - H^Fq ; F2)
où les 3 premiers termes sont égaux à F2, donc — e2 est injectif; si n > 2, le dernier
terme est nul, donc — e2 est aussi surjectif ; si n = 1, H°(Pi(R) ; F2) et H^P^R) ; F2)
sont isomorphes à F2, donc — e2 est encore bijectif. Pour k = n — 1, on a la suite
exacte
0 - H"-HPB(R); F2) ^ H"(P„(R); F2) *-X H"(F0; F2) H"(P,,(R); F2) - 0
donc ~ e2 est injectif, et par suite H"(P„(R) ; F2) * 0 ; comme H"(F0 ; F2) s F2,
cela montre que H"(P„(R) ; F2) s F2, donc ~ e2 est bijectif, et cela achève la
démonstration.

40. COHOMOLOGIE DES GRASSMANNIENNES 273
(24.40.13) Posons encore n = p + q, M = Up+,,P(R) et N = U^+^-^R),
fibres vectoriels réels de rangs p et q + 1 respectivement. Écrivons les suites de
Gysin pour M et N :
(24.40.13.1) ... - H*(GP+,,P(R); F2) ^ H*+'(Gp+ï>p(R); F2) -
£ H*+'(Mo; F2) Ht+1(GP+,,P(R); F2) - ...
(24.40.13.2) ... ^ H*(GP+,,P_ ,(R) ; F2) ~-^> H*+«+ '(Gp^.p- ,(R) ; F2) -
5 Ht+«+1(N0;F2) - H'^G^^R)^)
où a : M0 -► GP+,P(R) et fi : N0 -» Gp+^.^R) sont les projections.
La proposition correspondant à (24.40.8) est la suivante :
(24.40.14) Pour chaque indice j tel que 1 < j < p, il existe dans H^Gp+^R) ; F2)
un élément wp,q tel que les wp,q, pour 1 < j < p, engendrent (avec l'élément unité)
l'algèbre de cohomologie H'(GP+4P(R); F2). En outre, on a
(24.40.14.1) wp-« = e2(M) ;
(24.40.14.2) «*(>?•«) = f*(P*(wp-l-q+t)) pour 1 <p - 1
où f : M0 -► N0 est le difféomorphisme canonique (24.40.4).
On procède encore par récurrence sur p, car pour p = 1 la proposition
résulte de (24.40.12). On considère encore les homomorphismes de F2-espaces
vectoriels
(24.40.14.3) H'(Gp+,>p(R);F2) ^ H'(GP+,,P(R); F2)^H'(M0; F2)
H'(Gp+,,p_i(R); F2) =228 H'(GP+,,P_1(R);F2) « H'(N0 ; F2)
Si l'on fait k = — p, — p + \, 2 dans (24.40.13.1), on voit que les
applications a* : HJ(GP+4P(R); F2) -» HJ(M0; F2) sont des isomorphismes pour
0 < j < p — 2 ; par contre, pour k = - 1, on peut seulement déduire de
(24.40.13.1) que a* : H'-l(G,+9,J(R)i F2) H'-^Mo; F2) est injectif.
On peut alors définir les éléments wp,q par la formule (24.40.14.2) pour
1 ^ j < p - 2, mais pour pouvoir aussi le faire pour j = p — 1, il faut prouver
le lemme suivant :
(24.40.14.4) L'image par f*°fi* de H'-^Gp+^-^R); F2) est contenue dans
l'image par a* de Hp~ *(G,+f>f(R) ; F2).
Supposons ce lemme démontré; alors, par l'hypothèse de récurrence, les
éléments /3*(w*-1,«+1) engendrent la sous-algèbre Im(/?*) de H'(N0; F2) et la
sous-algèbre Im(a*) de H*(M0 ; F2), qui contient les et*(wp-q) pour 1 < j < p — 1,

274 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
contient donc Im(/* ° fi*). Mais par (24.39.18.1) appliqué aux deux suites
(24.40.13.1) et (24.40.13.2), on a
dim(Im(a*)) = i dim(H'(M0 ; F2)) = A dim(H*(N0 ; F2)) = dim(Im(/* o fi*))
d'où l'on conclut que Im(a*) = Im(/* ° /?*). On voit donc que, pour tout j=k+p,
tout élément de HJ(GP+,P(R); F2) est somme d'un polynôme à coefficients
dans F2 par rapport aux wf•* d'indice i < p — 1, et d'un élément de Ker(a*).
Pour montrer que tout élément de HJ(Gp+,iP(R); F2) est égal à un polynôme
par rapport à tous les wf'9, raisonnons par récurrence sur j. L'assertion est
évidente pour j < p — 1, puisque le noyau de a* dans HJ(GP+,P(R); F2) est alors
réduit à 0 ; mais si elle est vraie pour un indice j, elle l'est aussi pour j + p, car le
sous-module Ker(a*) de HJ+p(Gp+,tP(R); F2) est égal à l'image par l'application
z -» z~e2(M) de HJ(Gp+,iP(R); F2), et la conclusion résulte de la définition
de w™.
Reste donc à démontrer (24.40.14.4); par définition de la suite de Gysin
(24.39.3.1), cela équivaut à montrer que l'application composée
Hp_1(Gp+,,p_i(R); F2) £ H"-'(No; F2) £ H'"1^; F2) A H"(M, M0; F2)
est nulle. Or, considérons un point ve Gp+(,iP(R) et l'injection correspondante
j„ : Rp -» M dans la fibre de M au point v. Le diagramme (24.35.9.1) des suites
exactes de cohomologie relative donne le diagramme commutatif
H'~'(M,,; F2) e- ► H"(M, M0; F2)
31
H'-HR' - {0 } ; f H'(R', R" - { 0 } ; F2)
Dans ce diagramme, la flèche horizontale du bas est un isomorphisme pour
p > 2 (24.35.8.1), et il en est de même de la seconde flèche verticale, en raison
de (24.39.4) appliqué au fibre vectoriel M, compte tenu du fait que GP+,P(R)
est connexe (16.11.9), donc H°(Gp+1JjP(R); F2) s F2. On est donc ramené à prouver
que l'application composée
W-l(Gp+ll,p.i(R);¥2) ^ H'-l(N0;F2) C H'" •(Mo ; Fa)->
£ H'-^R" - {0} ; F2)
est nulle. Or, l'application composée fi o f o jv fait correspondre à un vecteur
x ^ 0 de Rp — {0}, où Rp est identifié par jtt au sous-espace vectoriel v = M„
de R*"**, le sous-espace (Rx)1 orthogonal à Rx dans v, élément de Gp+^p-^R).
Comme (Rx)1 ne dépend que de Rx, on peut écrire /? ° / °jv = g ° p, où
p:R"- {0} - Pp_!(R)

40. COHOMOLOGIE DES GRASSMANNIENNES
275
est l'application canonique, et g : PP_!(R) -» Gp+ïp_i(R) est une application
continue (24.40.4 et 16.10.4). Comme j* ° /* ° 0* = p* ° g*, on voit que (24.40.14.4)
sera prouvé pour p ^ 3 si nous montrons que l'application
p* : H'-'(Pp-i(R); F2) -> H'-»(R' - {0} ; F2)
est nulle pour p ^ 3. Or, p* : H"(Pp_t(R); F2) H"(R" - {0} ; F2) est un
homomorphisme de ¥2-algèbres, et H°(PP_ ,(R) ; F2) est engendrée par un élément
ejeH'fPp-tfR); F2) (24.40.12); H'-1^-^); F2) a donc une base formée de
l'élément e?-1 ; mais p*(e2)eHl(Rp - {0} ; F2) s H^Sp-t ; F2) est nul pour
p > 3, donc p*(ef,~l) = 0. Pour p = 2, p* est au contraire bijectif et ce
raisonnement ne s'applique plus, mais nous allons voir qu'on a alors g* = 0. En effet,
on a G,+21(R) = P,+ 1(R) et g est composé de l'injection canonique
i:Pm - P,+ 1(R)
déduite par passage aux quotients de l'injection canonique
i0:R2 - {0} - R"2 - {0},
et du difféomorphisme Rx -> (Rx)1 de Pt(R) sur lui-même; il suffit donc de
montrer que j* = 0. Or, on a le diagramme commutatif
H*(P<+ ,(R) ; F2) —H^R) ; F2)
Hl(R«+2 - {0};F2) ^ HW-iOjîFj)
et comme H^R'*2 - { 0 } ; F2) s H^S^+i ; F2) = 0 pour q ^ 1 et que la
seconde flèche verticale du diagramme est bijective, on a bien i* = 0. CQFD.
(24.40.15) Disons ici qu'un polynôme de F2[T,, T2, ...,TP] est isobare de
poids j s'il est combinaison linéaire de monômes Tj'T22 ... Tp" tels que
vi + 2v2 + ... + pvp =/ Comme wf*e H,'(Gp+,ip(R) ; F2), il résulte de (24.40.14)
que tout élément de Hj(Gp+qJR) ; F2) est égal à un polynôme isobare de poids j
par rapport à wÇ", ..., wp'9. On a la proposition correspondant à (24.40.10) :
(24.40.16) (i) Pour tout indice j tel que j < q, on a une suite exacte canonique
(24.40.16.1) 0 -» HJ-'(Gp+,,p(R); F2) ^ H\Gp+qJR) ; F2) -
A H\Gp+q,p^(R);¥2) -> 0
(ii) Le seul polynôme PeF2rTÎ, ...,TP] isobare de poids j<q tel que
P(wÇ'«, wf,-9, wp-9) = 0 est P = 0.

276 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFERENTIELLE ÉLÉMENTAIRES
Il résulte de (24.40.13.2) que, pour k < - 2, l'application
fi* : H'+^HG,*,,,-^R); F2) -> H*+«+1(N0; F2)
est bijective. Comme on a vu dans la preuve de (24.40.14) que l'on a
Im(a*) = Im(/*o/3*),
on en déduit que pour j ^ q — 1, l'application
a* : HJ(Gp+qiP{R); F2) - H\M0; F2)
est surjective; de la suite exacte de Gysin
H7-1(Gp+,,p(R); F2) A H^HMo; F2) -+ H^"(Gp+,!P(R); F2) -
^ HJ(Gp+,jR);F2)
on tire alors que pour y < g — 1, l'application
H^"(Gp+,iP(R); F2) H^(GP+,,P(R); F2)
est injective. On a donc bien la suite exacte (24.40.16.1), avec X = (/* ° /?*)"1 ° a*.
Le raisonnement prouvant (ii) reproduit alors exactement celui de (24.40.10, (ii))
en remplaçant la suite exacte (24.40.10.1) par (24.40.16.1).
PROBLÈMES
1) Pour m < n, on identifie R" au sous-espace vectoriel de R" engendré par les m premiers
vecteurs de la base canonique (ej)1<iS. de R". On désigne par H, le demi-espace ouvert de R"
formé des points dont la n-ème coordonnée est > 0.
a) Pour p < n, on appelle symbole de Schubert d'ordre p toute suite a = (<r/)i<j«, d'entiers
tels que \^ol<o1< ... <<r,<n. On note e(o) l'ensemble des sous-espaces vectoriels XeG„,,(R)
tels que l'on ait
dim(X n R") = i, dim(X n R*""1) = i — 1 pour 1 < i < p.
Il revient au même de dire que X doit avoir une base (x,, x2, ..., x,) telle que x,e H„, pour
1 « i « p.
Montrer que si Xee{a), il existe une base orthonormale unique (x,, x2 x„) de X telle
que x,- e H», pour 1 s* i < p.
2) Avec les notations du problème 1, soit B(<x) l'ensemble des systèmes orthonormaux
(xi, ..., xp) dans la variété de Stiefel S. P(R) (16.11.9) tels que l'on ait x,e H„ pour 1 ^ i < p.
On a (•„,, e,,, e.r)eB(o).
a) Étant donnés deux vecteurs u, v de R" tels que || u || = || v || = 1 et v * - u, il existe
une rotation et une seule R(u, v)eSO(n) qui transforme u en v et laisse fixes les vecteurs
orthogonaux à u et à v. L'application (x, u, v) -» R(u, v). x est continue pour x e R", || u || = Il v || = 1
et u # - v. En outre, si u et v appartiennent à R* pour k < n, R(u, v). x - x appartient à R1
pour tout x e R".
b) Pour tout point (x„ x2, ..., xp)e B(ct), on considère la rotation
R(x„ x2, ..., x,) = R(ea(>, x„)o R(e„,.„ x,.,)» ... o R(e„i, x,) aussi notée R)

41 . CLASSES DE CHERN
277
qui est telle que R. e„, — x, pour 1 < i < p. Soit <rp+, tel que ap < (xp+, < n, et soit D l'ensemble
des vecteurs u e H„f. , tels que || u || = 1 et qui sont orthogonaux aux «„ pour 1 =S i $ p. Montrer
que l'application
f : ((x„ .... x,), u) (x„ .... x,, R(x, xp). u)
est un homéomorphisme de B(<r) x D sur B(<t'), où a' = (u,, ..., a,, <rp+1). En déduire que
B(o) est homéomorphe à une boule fermée dans un espace de dimension
(«r, - 1) + (a, - 2) + ... + (a, - p),
et B(a) à l'intérieur de cette boule (raisonner par récurrence sur p).
c) Soit n : S„-P(R) -» G„>P(R) la projection canonique (16.11.9). Montrer que la restriction
de n à B(<r) est un homéomorphisme de B(a) sur e(a) (remarquer que si (X, x,) appartient
à Wâ) - B((t), son image par ir ne peut appartenir i e(a)).
d) Déduire de c) que G„iP(R) est un complexe cellulaire (section 24.36, problème 8) dont
les cellules sont les e(&). Montrer que le nombre de ces cellules de dimension r est égal au
nombre d(r) des suites croissantes Ui, <i2< ... <i,<n— p telles que s<p et i1 + i2+ . ■. +i, = r.
e) Montrer que la dimension de Hr(Gp+,iP(R) ; F2) est égale à d\r) pour r < q, et que
Hr(Gp+,tP(R); Z) est un Z-module de rang < a\r) pour tout r. (Utiliser d) ainsi que (24.40.15),
en faisant correspondre à toute suite d'entiers > 0 tels que v, + 2v2 + ... + pv, = r la suite
des entiers
V vp + vr-i' • • -, v, + v,_, + . . . + v, .
On appliquera les résultats de la section 24.37, problème 28.)
3) Énoncer et démontrer les énoncés relatifs aux grassmanniennes G„tP(C) et Ga>p(H)
correspondant à ceux des problèmes 1 et 2 (il faut prendre pour H„ l'ensemble des points de C" (resp. H")
dont la n-ème coordonnée est un nombre réel > 0). En utilisant le problème 28 de la section 24.37,
montrer que pour tout r, Hr(Gp+,>p(C); Z) (resp. Hr(Gp+,iP(H); Z)) est un Z-module libre, qui
est nul si r n'est pas multiple de 2 (resp. de 4) et de rang d(r/2) (resp. d(r/4)) sinon. (Observer que
les « cellules » ont toutes une dimension divisible par 2 (resp. 4)).
4) a) Soit Q la quadrique complexe non dégénérée de dimension complexe n — 1 dans
P^C), définie par l'équation Cj + îî + • • • + Cî = 0. Montrer que Q est difféomorphe à la grass-
manienne Gî+t,2(R) des plans orientés de R" + 1 (section 16.21, problème 1) (décomposer les Çt en
partie réelle et partie imaginaire).
b) La variété de Stiefel S„+1,2(R) peut être considérée comme fibre en cercles, de base
Gâ+i,2(R). En déduire que :
a) Si n = 2m est pair, H'(Q ; K) = {0} pour p impair et tout corps K, et H"(Q ; K) s K
pour p pair tel que 0 < p < 4m - 2 et tout corps K (utiliser la section 24.39, problème 4 et la
suite de Gysin).
P) Si n = 2m + 1 est impair, H'(Q ; Z) = { 0} pour p impair, H'(Q ; Z) s Z pour p pair
tel que 0 ^ p ^ 4m et p / 2m, H2"(Q ; Z) S Z2 (même méthode).
5) Montrer que H'(GJ+M(R); F2) = {0} et que pour chaque indice j tel que 2 < p,
il existe dans HJ(G,+<il^R); F2) un élément w'f" tel que les w'/" pour 2 < j ^ p engendrent (avec
l'élément unité) l'algèbre de cohomologie H'(GP+,P(R); F2) et que le seul polynôme isobare de
poids j <q tel que P(w'/'', ..., w'/q) = 0 soit P = 0. (Pour voir que Hl(G,+f-p(R); F2) = 0,
considérer Gp+,iP(R) comme un fibre sur GP+,P(R) auquel on peut appliquer la suite de Gysin
pour les fibres en sphères de dimension 0 (section 24.39, problèmes 3 et 9) ; pour les autres
assertions, raisonner par récurrence sur p comme dans (24.40.14) en utilisant le problème 4).
41. Classes de Chern.
(24.41.1) Soient B une variété pure, E un espace fibre vectoriel complexe de
rang (complexe) N et de base B. Nous allons décrire un procédé faisant corres-

278 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
pondre canoniquement à E un espace fibre vectoriel complexe Ê, de rang N — 1
et de base l'ouvert E0 de E, complémentaire de la section nulle dans E. Considérons
d'abord le fibre vectoriel E © E sur B (16.16.1), et soit pi : E © E E
l'application telle que px(ux © vx) = ux pour tout point ux © vx d'une fibre (E © E)x
de E © E ; (E © E, E, pt) est alors un fibre vectoriel complexe de rang N sur la
base E ; en effet la question étant locale sur B, on peut supposer E trivial ; alors
E © E s'identifie à (B x CN) x CN et E à B x C1^,/», étant la première projection.
Soit H = pï 1(E0) le fibre induit par ce fibre vectoriel sur l'ouvert E0 de E (16.12.9),
et considérons, pour tout x e B, le sous-ensemble Fx de (E © E)x formé des vecteurs
ux © tux, où ux # 0 dans Ex et t e C ; la réunion F des Fx lorsque x parcourt B
est un sous-fibré vectoriel complexe de rang 1 de H. En effet, on peut encore se
borner au cas où E est trivial, de sorte que H s'identifie à (B x (CN - {0})) x CN ;
pour 1 <N, soit V,- l'ouvert de CN - {0} formé des points z = (z1, z2,zN)eCN
tels que zJ ^ 0. On définit alors dans B x V, des sections de classe C°° de H
au-dessus de cet ouvert en posant s/jc, u) = u et s^x, u) = ek pour k ^ j (en
désignant par eeN les vecteurs de la base canonique de CN); en raison
de la définition de V,-, les N sections sk (1 ^ k < N) forment un repère de H
au-dessus de B x V, (16.15.1); d'autre part, pour tout xeB et tout uxeV/)
l'ensemble des ux © tu„ pour t e C, est un sous-espace vectoriel complexe de
dimension 1 de H(XUx), et sj(x, ux) = ux en est une base ; cela prouve que F est
un sous-fibré vectoriel de H (16.17.1) de rang (complexe) 1. On définit alors
le fibre E au-dessus de E0 comme le quotient H/F (16.17.2) de rang (complexe)
N — 1. Cette définition étant canonique, on déduit canoniquement de tout
B-isomorphisme g : E -»• E' de fibres vectoriels complexes un isomorphisme
(g, g) de Ê sur le fibre Ê' : posant gt(ux © vx) = g(ux) © g(vx), (g, g,) est un
isomorphisme de H sur le fibre analogue H' de base E'0, et l'image de F par cet
isomorphisme est le sous-fibré F' de H' défini de façon analogue ; par passage
aux quotients, on en déduit un isomorphisme (g, g) de H/F sur H'/F'.
(24.41.2) Supposons choisie sur E une structure hermitienne (23.27.2). On
définit alors une structure hermitienne sur le fibre H au-dessus de E0 en prenant
pour produit scalaire hermitien dans la fibre HUx
(ux© vx|ux©vi') = (vx|vi').
On définit un E0-morphisme du fibre H dans le fibre trivial E0 x C au-dessus
de E0, en faisant correspondre à ux © vx le couple (ux, (vx | ux)) ; par définition
de E0, ce morphisme est surjectif, donc son noyau K est un sous-fibré vectoriel
de H de base E0 et de rang complexe N — 1 (16.17.5), dont la fibre en ux est le
sous-espace de HUx orthogonal (pour la structure hermitienne) à la droite
(complexe) FUx. Si maintenant, pour tout point ux © vx e HUx, on désigne par
Puji^x © vi) 'a projection orthogonale de ce point dans l'hyperplan complexe KUx,

41 . CLASSES DE CHERN
279
l'application ux © vx -+ pUx(ux © vx) est un E0-morphisme de fibres vectoriels
de H sur K, comme on le voit aussitôt en se restreignant (avec les notations
de (24.41.1)) à un ouvert de E0 de la forme B x V, (lorsque E est supposé trivial,
ce à quoi on peut toujours se ramener). Cet E0-morphisme a pour noyau le fibre F,
donc K est isomorphe à H/F (16.17.5), et on pourra donc identifier E = H/F à
K dans les raisonnements.
(24.41.3) Désignons par e(E) la classe d'Euler du fibre vectoriel réel sous-jacent
à E, muni de l'orientation canonique (24.39.8). La suite exacte de Gysin (24.39.3.1)
appliquée à ce fibre vectoriel réel
... - Hp(B;Z) H'+2N(B;Z) 4 H*+2N(E0 ; Z) -+ HP+1(B;Z) - ...
montre que n* : H2<N~''(B; Z) H2(N_i)(E0 ; Z) est un isomorphisme pour
1 ^ i < N (qui correspond à - 2N < p < — 2). Cela permet, au moyen de la
construction de (24.41.1), de définir, par récurrence sur N, les classes de Chern
d'un fibre vectoriel complexe E de rang N et de base B : ce sont N éléments
(24.41.3.1) Cj(E) e H2'(B ; Z) pour 1 ^ i < N
définis comme suit. Pour i = N, cJE) est la classe d'Euler e(E) 6 H2N(B ; Z)
(24.39.11). Pour 1 ^ i < N, on considère le fibre vectoriel complexe E de base E0
et de rang N — 1, construit dans (24.41.1), et on pose
(24.41.3.2) c,(E) = (n%)~ \c,{È)) pour 1 < i < N - 1
ce qui a un sens puisque 7tJ est une bijection de H2'(B ; Z) sur H2'(E0 ; Z). Il
est commode de poser Cj(E) = Opouri > N,c0(E) = 1 (élément unité de H'(B;Z));
on appelle classe totale de Chern de E l'élément
(24.41.3.3) c(E) = 1 + c,(E) + ... + cN(E) = J ct{E)
i = 0
de l'anneau H'(B ; Z).
Pour tout anneau commutatif A, on appelle encore classes de Chern de E
à valeurs dans H'(B; A) les images canoniques (24.29.5) des classes de Chern
c,i(E)e H2*(B ; Z) par l'homomorphisme H2*(B ;.Z) H2*(B ; A) correspondant
à l'homomorphisme canonique Z -» A.
(24.41.4) Soit f : B' -* B une application de classe C°° d'une variété pure
B' dans B ; on a alors, pour 1 < i ^ N,
(24.41.4.1) /*(c,<E)) = c,</*(E)).
On raisonne par récurrence sur N ; pour i = N, la relation (24.41.4.1)
n'est autre que la relation (24.39.14.1) entre les classes d'Euler des fibres réels

280 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
sous-jacents à E et à E' = /*(E) : il suffit de remarquer que si w est une section
appartenant à l'orientation canonique de £ = (E, B, n), f*{w) appartient à
l'orientation canonique de /*(£), comme le montrent les constructions de (24.39.6)
et (24.39.8). Pour i < N, considérons le morphisme canonique (/ /') de /*(<!;)
dans £ (16.12.8), de sorte que /' est une application de classe C°° de la variété E'
dans E. Il est clair que sa restriction f0' à E'0 (complémentaire de la section nulle
de E') applique E0 dans E0 ; comme le diagramme
est commutatif, il suffira, en vertu de la définition (24.41.3.2) et de l'hypothèse
de récurrence, de montrer que l'on a
(24.41.4.2) Ë' = /o*(Ê)
avec les notations de (24.41.1). Si F est le fibre de rang 1 sur E0 défini dans (24.41.1)
et F' le fibre analogue sur E0, il suffira de montrer que F' = /ô*(F), en vertu
de (16.19.3) et de l'existence d'un supplémentaire d'un sous-fibré vectoriel (16.173).
Or, pour tout x" e B', fx. : Ex. ~* E/(x.( est une bijection linéaire (16.19) ; donc
l'image réciproque par fx. de Fy,,.) est le sous-ensemble de (E' © E')*- formé
des vecteurs u'x. © tu'x. pour t e C et u'x. # 0 dans E'x., c'est-à-dire F'x..
(24.41.4.3) Si g : E' -» E est un B-isomorphisme de fibres vectoriels complexes,
g préserve l'orientation canonique des fibres vectoriels réels sous-jacents ; on a
donc e(E') = e(E) (24.39.11) ; d'autre part, on a vu (24.41.1) qu'on déduit
canoniquement de g un isomorphisme (g, g) de E' sur E ; en factorisant g en
Ë' -» g*(Ë) -» Ë (16.19.1), on déduit de (24.41.4), par récurrence sur N, que
l'on a c(E') = c(E).
(24.41.5) Exemple : classes de Chern des grassmanniennes complexes. On a
obtenu dans (24.40.8) un système de générateurs cp'q de l'anneau de cohomologie
H'(GP+,>P(C); Z) d'une grassmannienne complexe. Ces éléments ne sont autres
que des classes de Chern ; de façon précise :
(24.41.5.1) On a c'y* = Cj<UF+w(Ç)) pour l^j^p.
Pour j = p, la proposition résulte de la définition (24.41.3) de cp{Up+<lJÇ))
et de la formule (24.40.8.1). Pour j < p, raisonnons par récurrence sur p, en
reprenant les notations de (24.40.7) ; vu (24.41.4) et la relation (24.40.8.2) définissant
les cp'q pour j ^ p — 1, il suffit de montrer que le difféomorphisme / : M0 -» N0
est tel que /*(N) est isomorphe à M ; nous construirons ici M et N en utilisant
EJ, ^ E0

42. PROPRIÉTÉS DES CLASSES DE CHERN
281
(24.41.2) les structures hermitiennes sur M et N définies par le produit scalaire
canonique sur Cp+q (24.40.1). Il résulte en effet des définitions que, pour tout
point (v, x) € M0, la fibre M(„>K) est l'ensemble des triplets (v, x, y), où y parcourt
le sous-espace (Cx)1 n v des vecteurs de v orthogonaux à x. D'autre part, pour
tout point (w, x') e N0, où x' e w1, la fibre N(w est l'ensemble des triplets
(w, x', z), où z parcourt le sous-espace w. Comme f((v, x)) = ((Cx)1 n v, x)
et que f est un difféomorphisme de M0 sur N0, on voit que si l'on pose
g((r,x),y) = (((Cx)1nt;,x),y),
(/, g) est un isomorphisme de M sur N, d'où l'on conclut que /*(N) et M sont
isomorphes (16.19.1).
PROBLÈMES
1) Les notations étant celles de (24.40.6), soit Y une sous-variété projective linéaire de P„(C),
de dimension (complexe) p. Si j : Y -» P„(C) est l'injection canonique, montrer que l'on a
«* = (- WV).
2) Soit Y une sous-variété holomorphe fermée de dimension complexe p ^ n - 1 dans
P.(C).
a) Avec les notations de (24.39.20), montrer que l'on a a(uv) = (- \f~'d.e"~r, où d est
le degré de Y (section 24.16, problème 5) (section 24.39, problème 12).
b) On suppose que Y est une hypersurface (p = n — 1 ). Montrer que l'on a pour la classe totale
de Chern de T(Y)
c(T(Y))=y*((l -e)"+1/(l - d.e))
(se rappeler que e"+1 =0).
42. Propriétés des classes de Chern.
(24.42.1) Nous allons voir que l'on peut définir les classes de Chern d'un fibre
vectoriel complexe quelconque de base une variété pure compacte, à l'aide des
classes de Chern cp,« des grassmanniennes complexes. Cela va résulter de (24.41.4)
et de la proposition suivante :
(24.42.2) Soient B une variété pure compacte, E un fibre vectoriel complexe
de base B, de projection n et de rang complexe p. Il existe alors une application f
de classe Cœ de B dans une grassmannienne Gp+q P(C) telle que E soit B-isomorphe
au fibre /*(UP+,>P(C)).
Il existe un recouvrement fini (VJ)1<i^m de B formé d'ouverts trivialisants
pour E ; pour chaque indice y, il y a donc un difféomorphisme
hj:n-l(\j) -.VjxC,
réciproque d'une application repère au-dessus de V, (16.15.1). Soit (W^^,,

282 XXIV. topologie algebrique et différentielle élémentaires
un recouvrement ouvert de B tel que W,- <= Vj pour tout j (12.6.2), et pour chaque j,
soit gj une fonction de classe C" sur B à valeurs dans [0, 1 ], égale à 1 dans VY,
et de support contenu dans V, (16.4.2). Pour tout u e E, posons
j» = g/7i(u))pr2(h,{u))
si u en~l{Wj) et //(u) = 0 sinon ; il est clair que ff est une application de classe
C00 de E dans Cp, dont la restriction à toute fibre n~ï(x) est C-linéaire. Définissons
alors l'application /' de E dans Cmp par
/'(u) = (/», /i*(u), ..., /») ;
la restriction de /' à toute fibre n~1{x) est une bijection C-linéaire sur un sous-
espace vectoriel de dimension p de Cmp, car x appartient à un des W, au moins,
donc, si ux ^ 0 est un vecteur de n~ 1(x), on a f'j{ux) # 0 par construction, ce
qui montre que /' est injective dans 7i-1(x). Posons ensuite, pour tout xeB,
f(x) = f'(n~l(x))e Gmpp(C), et montrons que (/ /') est un morphisme du fibre
vectoriel E dans Umpp(C). Il suffit évidemment pour cela de voir que / est une
application de classe C00 ; or /' est évidemment de classe C00, et si n' est la
projection de Umpp(C) sur GmPiP(C), on a n' ° f = f °n; donc / ° n est de classe C00,
et il en est par suite de même de / puisque n est une submersion surjective (16.7.7).
Pour terminer la démonstration il suffit d'invoquer (16.19.1), puisque la restriction
de /' à la fibre Ex est une bijection sur la fibre de Umpp(C) au point f(x).
Remarque (24.42.2.1). — Dans l'énoncé de (24.42.2), on peut prendre q
aussi grand qu'on veut, car on peut prendre m arbitrairement grand (en répétant
par exemple un nombre quelconque de fois un des ensembles V,).
(24.42.3) Soient B une variété pure compacte, E' et E" deux fibres vectoriels
complexes de base B et de rang constant. On a alors, pour les classes totales de
Chern, la relation
(24.42.3.1) c(E' © E") = c(E') ~ c(E")
(produit dans l'anneau de cohomologie H'(B ; Z) ; comme les classes de Chern
appartiennent à des modules de cohomologie de dimension paire, l'ordre des
facteurs du second membre n'a pas d'importance).
Nous prouverons d'abord un cas particulier de (24.42.3.1) (valable pour
toute variété pure B) :
(24.42.3.2) Si le fibre E" est trivialisable et de rang constant, on a
(24.42.3.3) c(E' © E") = c(E').
On peut supposer que E" = B x C\ et il suffit évidemment de raisonner

42. PROPRIÉTÉS DES CLASSES DE CHERN
283
par récurrence sur k, donc on peut se borner au cas k = 1. Notons d'abord que
s : x -* (x, 1) est une section de classe C°° de E" = Bx C(etparsuitedeE'©E")
au-dessus de B, qui est partout ^ 0, donc (24.39.13), on a e{E' © E") = 0, c'est-
à-dire cn+i(E' © E") = cn+1(E') = 0, si n est le rang de E'. La construction
de (24.41.1) appliquée à E' © E" donne ici pour ensemble Hx l'ensemble des
(ux © (x, t')) © (vx © (x, f")), avec d'une part ux # 0 dans E'x ou t' # 0 dans C,
de l'autre vx e E'x et t" e C ; la fibre F(Xil) est la partie de Hx formée des éléments
(x, 1)© f(x, 1) où teC. Pour xeB et uxeE'„ posons s'(ux) = ux©(x, 1); il
est immédiat que (s, s') est un morphisme du fibre vectoriel E' de base B, dans
le fibre vectoriel H de base (E' © E")o, et en composant avec ce morphisme
le morphisme canonique H -+ H/F, on obtient un morphisme (s, /') de E'
dans (E' © E")~ ; comme s'(E'x) (ensemble des ux © (x, 1) pour ux e E'x) et F(xl)
sont des sous-espaces supplémentaires dans la fibre H(x>1) de H, la restriction
f'x de /' à E'x est une bijection sur la fibre de (E' © E")~ au point s(x), ce qui
entraîne (16.19.1) que E' est isomorphe à s*((E' © E")~); par suite, en raison
de (24.41.4),
s*(cf((E' © E")~)) = Cj(E') pour 1 < i < n.
Mais, par définition, pour ces valeurs de i, on a c,{(E' © E")~) = n*(c,iE' © E")),
où 7t0 est la projection E' © E" -» B (24.41.3.2) ; comme n0 ° s est l'identité
de B, on obtient bien c^E' © E") = c,<E') pour 1 ^ i ^ n.
En second lieu, prouvons le résultat suivant :
(24.42.3.4) Pour tout couple d'entiers m > 0, n > 0, il existe un polynôme et
un seul Pm„eZ[Si, ..., Sm, Tj, ..., T„] en m + n indéterminées, somme de
polynômes isobares en les S, et en les T) {au sens de (24.40.9)) de poids < 2(m + n),
tel que pour toute variété pure compacte B et tout couple de fibres vectoriels
complexes E', E" de base B, où E' est de rang m et E" de rang n, on ait, dans Falgèbre
H|B;Z),
(24.42.3.5) c(E' © E") = PmB(Cl(E') cm(E'), Cl(E") c„(E")).
En vertu de (24.42.2), il existe un entier q > m + n et deux applications
/ : B -» Gm+,m(C), g : B -* G,,+,iB(C) telles que E' soit isomorphe à
/*(Um+(l)m(C)) et E" isomorphe à g*(UB+,„(C)). Considérons l'espace produit
(compact) X = Gm+,m(C) x GB+,!B(C) et sur cet espace les deux fibres
E„,,, = prftUm+,,m(C)) et = pr*(UB+,,B(C)).
En vertu de (24.41.4) et (24.41.5), on a c,{E'mJ = pr*(c?•«) pour 1 «S i < m et
Cj(EB',) = prî(cJ-«) pour 1 < j < n. Or on sait (24.40.8) que les (?•« (resp. c)A)
engendrent l'anneau de cohomologie de Gm+,m(C) (resp. GB+,„(C)); en vertu

284 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
de (2438.1), les produits c^E^,) ~ c/EBi,) engendrent donc l'anneau H'(X; Z),
et par suite il existe un polynôme
Pm,n,«eZ[Si, ..., Sm, Ti, ..., T„]
tel que
c(e;,,© e;:,) = pm>Bic1(EB1,,) cje;,,), Cl(EH\q\ ....Cb(Eb',,)).
En outre, si l'on décompose Pm,n>4 en ses composants isobares par rapport aux
S{ et aux Tj, on peut supposer ces polynômes nuls sauf ceux de poids < %m + n) ;
comme H'(X ; Z) est isomorphe (24.38.1) à H "(G,,+,,M(Q; Z) <g> ZH'(GB+,,B(C);Z)
et que l'on a pris q > m + n, ces polynômes sont uniquement déterminés en vertu
de (24.40.10, (ii)). Si alors on pose h = (/, g) : B -» X, on a par définition, à
isomorphie près, E' = h*(E'm>q) et E" = n*(E,',,), donc E' © E" = «"(E,,., © EB>,),
et par suite
c(E' © E") = KME'), cm(E'), c,(E"), .... c„(E")).
Il reste à voir que le polynôme PmBi, est en fait indépendant de l'entier q>m+n
choisi. Soit donc q' > m + n un second entier, et posons
X' = Gm+,.m(C) x GB+,%B(C).
Il existe un entier q" > supfô, q1) et des applications de classe C00,
fi ■ X Gm+,»>in(C), gi : X -+ GH+q..^C),
f2 : X' -+ Gm+,.,m(Q, g2 : X' GB+,~,B(C),
telles que E„,jV E„'v E'mA., EB',. soient respectivement isomorphes à /î(Um+,.. m(C)),
^Ï(UB+,».B(C)), /!(UM+,...M(C)), g*(UB+,..>B(C)). On a donc
Pm.n.^CttE,,,,), .... cB(EB',,)) = Pm,B,,4c1(EBI>,) Cfl(EB',,)).
Mais en vertu de (24.38.1) et (24.40.10, (ii)), cela entraîne PmiBi, = Pm,Bf," ; de la
même manière on voit que P„,„^ = Pm,ii,«"> donc Pm>B,,- = Pm>„,,, et cela démontre
(24.42.3.4).
(24.42.3.6) Il reste à prouver que l'on a
(24.42.3.7) P., - (1 + St + ... + SJ(1 + Tt + ... + TJ.
Nous raisonnerons par récurrence sur m et n ; pour m = n = 0, la formule
est évidente, un fibre vectoriel de rang 0 sur B s'identifiant à B, et pour un tel
fibre la classe totale de Chern se réduit à 1. Supposons donc que Pm_ 1>B et PmiB_ x
soient donnés par (24.42.3.7) où l'on remplace m par m — 1 et n par n — 1
respectivement. Considérons alors, sur la base Y = GB,_1+,m_1(Q x G.+^Q (avec

42. PROPRIÉTÉS DES CLASSES DE CHERN
285
q>m + n) le fibre vectoriel E'm-l<q © E„', © E, où E = Y x C est le fibre
trivial de rang 1 ; on a donc
ciEm-Uq(BKq®E)
= P^c^E;-!.,© E) cM(E^_,,,@ E), c,(E,'.,), ..., c„(EB'.,)).
D'après (24.42.3.2), cela s'écrit aussi
dE'm-Uq®eb',,) = p^c^e;^.,) cm_1(E;_1>4),o,c,(e;'.,), ...,cb(e;',,)).
Mais par l'hypothèse de récurrence et l'unicité des polynômes P^,, cela entraine
P^S,, ..., Sm_1( 0, T„ ..., TB) = Si + ... + S._iXl + T» + ... + TJ.
Cela signifie que le polynôme
p»«(S, S*, 1*! TJ - (1 + S» + ... + SmXl + Ti + ... +
est divisible par Sm ; échangeant les rôles de m et n, on voit que ce même polynôme
est divisible par TB ; il est donc divisible par SmTm autrement dit on a
P.JS,, ..., Sm, T„ ..., T„) = (1 + St + ... + SJ(1 + Ti + ... + TJ+RS^T.
où R est un polynôme ; mais comme Pmil est somme de polynômes isobares de
poids < 2(m + n), R est nécessairement un entier r. On a donc en particulier
cm+(1(E' © E") = (1 + rJcJEO-c.XE'OîmaiscommecJE'Xc^E'Oetc+^E'©^)
sont les classes d'Euler de E', E" et E' © E", et prennent toutes trois des valeurs
# 0 pour certains fibres vectoriels (par exemple EJ,,, et EJ', sur X), il résulte de
(24.39.15.1) que r = 0. CQFD.
(24.42.4) Si V est un espace vectoriel complexe, on définit sur V une structure
d'espace vectoriel complexe différente, dite conjuguée de la structure donnée,
en conservant dans V la même addition, mais en définissant une nouvelle
multiplication (k, z) -* XQ z par les scalaires A e C en posant k Q z = kz ; on notera
Vr l'espace vectoriel complexe ainsi défini ; V et V1 ont le même espace vectoriel
réel sous-jacent, noté VR. Si {e1( ..., eN} est une base de V sur C, c'est aussi
une base de Vf sur C, et on définit une bijection C-linéaire cp de V sur Vf en
posant <jo(C,e, + ... + ÇNeN) = Cie, + ... + Ci^n. puisque = Cj O ey par
définition; cp transforme donc la suite (eu je,, e2, ie2, ..., eN, ieN), base de
Vt, en (elt — ieu e2, — ie2, ..., eN, — ieN); par définition de l'orientation
canonique d'un espace vectoriel complexe (16.21.13), on voit donc que cp préserve
l'orientation canonique de VR si N est pair, et la renverse si N est impair.
Considérons maintenant un espace fibre vectoriel complexe E de rang N,
de base B et de projection n. Si l'on munit chaque fibre n~ 1(x) de E de la structure
d'espace vectoriel complexe conjuguée, on obtient encore un fibre vectoriel

286 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
complexe Ef, dit conjugué de E. En effet, soit U un ouvert de B au-dessus duquel
existe un repère
«A : (y, Ci, • • -, CN) -» CiSilv) + • • • + Cn*nO0,
difféomorphisme de U x CN sur 7t-1(U). Alors l'application
^' : (y, Ci. • • - , Cn) - Ct$i(y) + ... + Cn»n(y)
est évidemment encore un difféomorphisme de U x CN sur rc_1(U), et pour
chaque yeU, ^ (y, ■) est une bijection C-linéaire de CN sur l'espace vectoriel
complexe (n_1(y))t, ce qui prouve notre assertion (16.15.1). Si l'on remarque
que les 2N sections su isu ..., sN, isN forment un repère du fibre vectoriel
réel ER sous-jacent à E et à Et, et les 2N sections slt — islt ..., sN, — isN un
autre repère de ER, on voit que Vorientation canonique de E (24.39.8) est la même
que celle de si N est pair, et Vopposée de Vorientation canonique de Ef si N
est impair.
On déduit de ces remarques la proposition suivante :
(24.42.5) Pour tout fibre vectoriel complexe E de base B, les classes de Chern
du fibre conjugué E1 sont données par
(24.42.5.1) ck(Ef) = (- l)*c*(E) pour tout k^l.
On raisonne encore par récurrence sur le rang n de E. Comme on sait que
la classe d'Euler d'une fibration orientée change de signe quand on remplace
l'orientation par son opposée (24.39.11), on a bien c„(Ef) = (- l)"cB(E) d'après
(24.42.4). D'autre part, on a évidemment (E © E)f = Ef © E * ; la construction
de (24.41.1) faite sur Ef donne comme fibre de rang n sur E0 le fibre H1, et comme
sous-fibré de rang 1 de Ht le fibre F* : en effet, avec les notations de (24.41.1),
pour ux e E0, l'ensemble des ux © (t Q ux) e H(x Ux) est égal à F(x „x) (puisque
f O ux = fux) et on a s O (ux © (r O ux)) = ux © ((st) Q ux) pour tout s e C.
On a donc (E*)~ = (E)1 ; l'hypothèse de récurrence montre que
ck((E*)~) = (- l)*ct(Ê) pour 1 < fc < n - 1,
d'où Ct(Ef ) = (nô 1)*(ct((E *)~)) = ( - lfck(E) par définition des classes de Chern.
(24.42.6) Les classes de Chern du dual E* = Hom(E, B x C) (16.16.3) d'un
fibre vectoriel complexe E sont égales à celles du conjugué Ef.
Il suffit de montrer que E* est isomorphe à E*. On peut supposer que E
est muni d'une structure hermitienne (23.27.2) ; pour tout x e B et tout ux e E,,
soit ûx la forme linéaire vx -> (vx | ux) sur Ex ; l'application ux -» ûx est une
bijection de Ex sur (E*)x (6.3.2) et l'on a (Aux)~ = Xû„ donc ux -» ûx est une
bijection C-linéaire de (Ef )x sur (E*)x ; il est clair que ces applications définissent
un isomorphisme de Ef sur E*.

42. PROPRIÉTÉS DES CLASSES DE CHERN
287
(24.42.7) Exemple : classes de Chern du fibre tangent à P„(C). — Les notations
étant celles de (24.40.1) et (24.40.2), nous prouverons d'abord les résultats
préliminaires suivants :
(24.42.7.1) (i) Le fibre vectoriel complexe End(UB+ i,i(C)) est trivialisable.
(ii) Le fibre tangent complexe T(P„(C)) est canoniquement isomorphe à
E = Hom(U.+ 1>1(C), Ui+lil(Q).
(i) Il suffit de remarquer que, si / est la section de End(Un+1>i(C)) au-dessus
de P„(C) telle que i(v) soit l'application identique de t; pour toute droite v e P„(C),
I est une section de classe C00 formant un repère du fibre vectoriel End(U,,+ ltt(C))
de rang 1 au-dessus de P„(C) tout entier.
(ii) La fibre de E = Hom(U„ +,,i(C), ttl(C)) au point v e P„(C) est l'espace
vectoriel Hom(u, v1). Pour tout xeu — {0}, et tout u„e Hom(i>, v1), le couple
(x, u„(x)) est un point de l'espace tangent à C+1 — { 0 } au point x.
Si n : C+1 - {0} -» P„(C) est la projection canonique, Tx(7t)(x, u„(x)) est
un vecteur tangent à P„(C) au point v = 7t(x), qui ne dépend que de u„ ; en effet,
pour tout tèC, on a u„(tx) = tu„(x) et Tt(tx) = 7t(x) = v, donc, pour heC+1,
T,x(7t) • (tx, th) = Tx(îr) • (x, h) (16.5.4.1), et en particulier
Ttx(n) ■ (tx, uJLtx)) = TJjt) ■ (x, uj(x».
Posons g(u„) = Tx(7t) • (x, u„(x)) pour un x quelconque dans v — {0} ; g est
donc une application de E dans T(P„(C)), dont la restriction à une fibre quelconque
E„ = Hom(t), t>x) est une bijection C-linéaire sur l'espace tangent T^PB(C)) au
point v; en effet, n, restreinte à l'hyperplan affine x + uxcCn+1 — {0} pour
un x e v — {0}, est de rang n au point x, donc h -» Tx(ît) • (x, h) est une bijection
C-linéaire de v1 sur T„(P„(C)), et de même l'application qui à tout hev1 fait
correspondre l'homomorphisme u„ tel que u„(x) = h est une bijection C-linéaire
de v1 sur Hom(i;, v1).
Reste à voir que g est de classe C00, ce qui est une propriété locale sur P„(C).
Pour 1 < y ^ n + 1, soit V,- l'ouvert de P„(C) formé des points de coordonnées
homogènes (Ç1, C2, • • •, Cn+ x) telles que (j # 0 ; on va montrer que g est de classe
C00 dans 7t£ 1(VJ) ; on peut supposer pour simplifier que j = n + 1. On peut
prendre alors C1, ...,(," pour coordonnées locales dans Vn+t du point v de
coordonnées homogènes C1, 1; la section v -* sn+1(v) de Un+11(C)
n
au-dessus de VB+1, d'expression locale (£' Ç") -* eB+1 + X C*©*, forme
un repère de UB+ i,i(C) au-dessus de VB+1( et les sections v -* sk{v) de UB+ i,i(C)
au-dessus de VB+1 d'expressions locales (C1, ...,£") -* ek - 1 (1 < k < n)
forment un repère de UB+1>1(C) au-dessus de VB+1. Si l'on définit les sections
v -» uk(v) de E au-dessus de V,,+1 par la condition que uk{v). sn+1(v) — s^v)
pour 1 ^ k < n, elles forment un repère de E au-dessus de VB+1. Cela étant,

288 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
un calcul immédiat montre que la restriction de n à l'hyperplan affine
n
x + v1 c C"+1 — {0} fait correspondre au point x + £ w^s^u) de cet
hyperplan le point de P„(C) de coordonnées homogènes *=1
C1 + I1 £" + »"
i _ £cy i - Xcy
*=i *=i
L'application linéaire h -* Tx(7t).(x, h) de v^ sur T(PB(C)) est donc
î«*«*(«0 - «C1, -...CM»1. ...,1"))
k= 1
en identifiant T,,(PB(C)) à jtJxC" pour i>eVB+1; par suite, l'application g,
restreinte à «ë1(Xi+i) est
tffatP) - (K1. ....CM»1 «"))
ce qui achève de prouver (24.42.7.1).
(24.42.7.2) La classe totale de Chern tfT(P„(C))) du fibre tangent à P„(C) est
égale à (1 - c1(UB+1,1(C))y,+ l dans l'anneau H'(P.(C); Z).
Notons que par définition, le fibre somme directe UB+lil(C)© UjJ+^C)
est le fibre trivial L = P„(Q x C"+1 de rang n + 1 ; le fibre
M = Hom(U.+lfl(0, UB+ltl(Q © U^iQ)
est donc isomorphe à (n + l).Hom(UB+ lfl(C), P„(C) x C) = (n + 1).(UB+ M(Q)* ;
mais par (24.42.7.1, (i)) M est isomorphe à E © End(UB+,i(Q), donc aussi à
E © (P„(C) x Q. On en conclut que c(E) = c(M) par (24.42.3.2), donc
c(E) = c((n + l).(UB+lil(Qn = (1 - c,(U.+lil(Q)r+l
par (24.42.6), (24.42.5) et (24.42.3). La proposition résulte donc de l'isomorphie
de E et de T(PB(Q) (24.42.7.1, (ii)).
(24.42.7.3) (i) La classe d'Euler ei\J2,i(C)) est égale à — eJl(C), opposée de la
classe fondamentale de cohomologie de Pt(C) muni de son orientation canonique
(24.6.3).
(ii) Pour une orientation sur la sphère S2, la classe d'Euler c(T(S2)) du fibre
tangent T(S2) muni de l'orientation correspondante (24.39.7) est le double 2e|2
de la classe fondamentale de cohomologie de la variété orientée S2.

42. PROPRIÉTÉS DES CLASSES DE CHERN
289
(i) On a en effet e(T(P,(C))) = - 2e(U21(C)) en vertu de (24.42.7.2); mais
on a vu (24.39.26.2) que l'on a < e(T(P,(C))), [Pi(Q]> = jrfPjXQ) = 2, d'où
notre assertion en vertu de la définition de efl(C) (24.12.10.4).
(ii) Il existe un difféomorphisme / de Pi(C) sur S2 (16.11.12); s'il préserve
(resp. renverse) l'orientation, son application linéaire tangente T(/) préserve
(resp. renverse l'orientation), donc /* transforme e(T(S2)) en e(T(Pi(Q)) (resp.
— e(T(Pi(C)))) ; mais /* transforme aussi c|, en e*l{C) (resp. — e*.l(C)) d'après
(16.24.5.1) ; d'où la conclusion.
1) a) Pour un fibre vectoriel complexe E de rang (complexe) n, de base une variété
différentielle pure B et de projection n, généraliser la définition du fibre projectif P(E) de base B, donnée
dans la section 16.19, problème 9, pour les fibres vectoriels réels. Si p : P(E) -» B est la projection
de ce fibre, on définit le fibre vectoriel canonique LE(1) de rang 1 sur P(E) comme l'ensemble des
couples (z, u) e P(E) x E tels que p\z) = n(u) et que, ou bien u = 0 dans E^,,, ou bien z = p(u),
où p est l'application canonique de E0 = E - 0(B) sur P(E). Pour tout b e B, soit jb un
isomorphisme d'espace vectoriel de C" sur Eto et soit j'b l'application rendant commutatif le diagramme
Alors le fibre vectoriel image réciproque j'*(LJ,l)) (où j'b est considéré comme injection de
P„_i(C) dans P(E)) est isomorphe au fibre canonique U„4(C) (24.40.1).
b) Soit aE la classe de Chern c,(LE(l))e H2(P(E); Z). Montrer que H-(P(E); Z) est un
H'(B; Z)-module libre ayant une base formée des éléments 1, oE, al a"E~' (appliquer le
théorème de Leray-Hirsch en utilisant a)).
2) a) Avec les notations du problème 1, L^l) est un sous-fibré vectoriel complexe de rang 1
dans le fibre vectoriel image réciproque p*(E) de base P(E) et de rang n ; il existe donc un
supplémentaire de Lb(1) dans p*(E), de rang n - i (16.17.3).
b) Montrer qu'il existe une variété pure B, et une application / : Bt -> B de classe C°°
telle que le fibre image réciproque /*(E) soit isomorphe à une somme directe L, © L2 © ... © L„
de n fibres vectoriels de base Bt et de rang 1, et que l'application f* : H'(B; Z) -> H*(B, ; Z)
soit injective. (Raisonner par récurrence sur n, en utilisant a) et le problème 1). Si B est compacte,
on peut prendre B, compacte, et on a alors c(/*(E)) = (1 + C|(Li)Xl + ct(L2)).. .(1 + ct(LN)).
On dit que / est une application de décomposition pour le fibre E.
3) Soient X une variété pure compacte, L un fibre en droites complexes de base X (fibre
complexe de rang complexe 1). Soit d'autre part U - (U,),,, un recouvrement ouvert de X ayant
les propriétés mentionnées dans la section 24.33, problème 6, et tel que L soit trivialisable au-dessus
de chacun des U(.
a) Ayant choisi pour chaque i e I une application repère <p, pour L (16.15.1) pour tout couple
(i, j) d'éléments distincts de I tels que U, n U, ne soit pas vide, on a un difféomorphisme de
transition
de (U, n Uj) x C dans lui-même, où C*; est une application de classe C" de U, n U, dans C*.
On a Cj, = r-\ et si i, j, k sont trois éléments distincts de I tels que U, n Uj n U, / 0, on a
CifijkCu = 1 dans cet ensemble.
Dans chaque ensemble ouvert simplement connexe U, n U( ^ 0 avec i < j, on désigne
par log,jC,j une fonction continue telle que expOog,/,/*)) = (,/jc) pour tout x e U( n Vj ; une telle
PROBLÈMES
C"-{0} h (E0)k
P._,(C) y (P(E))t
(x, z) - (x, C,/x)z)

290 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFERENTIELLE ÉLÉMENTAIRES
fonction n'est définie qu'à un multiple entier de 2ni près (16.28.9). Montrer que pour trois indices
i < j < k de I tels que Us n U, n Uk # 0, la fonction
x - ^(Io&jCijM + l°gj»W*) + log»,CnW)
est constante dans U( n Uj n Uk et est égale à un entier positif ou négatif cljk ; en outre les c,jk
définissent un 2-cocycle de <E2(U). Prouver de plus que : 1° la classe de cohomologie e(U) de ce
cocycle ne dépend pas du choix des logarithmes ; 2° elle ne dépend pas du choix des applications
repères <p,. Enfin, montrer que la classe de cohomologie e'(L) = (r{)' '(e(U)) dans H2(X ; Z)
(notations de la section 24.33, problème 6) ne dépend pas du recouvrement U considéré.
b) Soient f : X' -» X une application de classe C°°, où X' est une variété pure compacte,
et L' = /*(L) l'image réciproque du fibre en droites complexes L. Montrer que l'on a
/ V(L)) = e'(L') dans H2(X' ; Z) (utiliser la section 24.33, problème 6).
4) On se propose de montrer que la classe de cohomologie e'(L) définie dans le problème 3
est la classe d'Euler e(L) du fibre en droites complexes L.
a) Montrer qu'on peut se ramener au cas où X = P^C) et L = U.+ i,i(C) (utiliser le
problème 3 b) et 24.42.2)). On a alors e'(L) = c„e(L), où c„ est un entier.
b) Montrer que c, est indépendant de n (considérer l'injection canonique de P„(C) dans
P,(C) pour m < n).
c) Pour n = 1, calculer «'(L) à l'aide d'un recouvrement U de Pi(C) (identifié à la réunion
de C et du point oo) formé de : 1° trois disques ouverts de centres respectifs 1, exp(2ni/3), exp(4iti/3)
et de rayon 2 ; 2° du complémentaire du disque fermé de centre 0 et de rayon 2. (Utiliser 24.42.7.3)).
5) Dans ce problème, les classes de Chern considérées sont les classes de Chern rationnelles,
à valeurs dans H'(B ; Q) pour une variété compacte pure B.
a) Soit E un fibre vectoriel complexe de base B et de rang n. Montrer qu'il existe dans
H*(B; Q) un élément bien déterminé ch(E), appelé caractère de Chern de E, ayant la propriété
suivante : pour toute application de décomposition (problème 2) / : B, -> B du fibre E, tel que
/*(E) soit isomorphe à L, © L2 © ... © L„ où les L, sont des fibres complexes de rang 1, on a
/•(chtE)) = exp(c1(L1)) + exp(ei(L2)) + ... + exptc^L.))
°° 1
(l'exponentielle exp(z) = £ — z™ est définie dans l'algèbre H'^ ; Q) puisque tout zeH+(Bl ; Q)
est nilpotent). m-om\
b) Montrer que, pour deux fibres vectoriels Et, E2 de base B et de rangs constants, on a
ch(E, © E2) = ch(E,) + ch(E2)
ch(E, ® E2) = ch(E,)~ch(E2).
(A l'aide du problème 2, se ramener au cas où E, et E2 sont de rang 1. Pour la seconde formule,
utiliser le calcul de la classe d'Euler décrit dans le problème 3).
6) Montrer que le fibre tangent T(P.(C)) n'est pas isomorphe au fibre conjugué.
7) a) Une partition d'un entier le > 0 est une suite décroissante I = { a, ^ a2 > ... > a„ }
d'entiers > 0 tels que k = a, + a2 + ... + a„. Pour N > It et toute permutation a de {1,2,.... N },
on pose Tm = T#„T%>... TJ,™, dans Z[Ti, ..., TN]; il existe alors un polynôme unique à
coefficients entiers M, en le indéterminées, indépendant de N > le et tel que
Z T"11' = MjiSt, ..., St)
où St est le y-ème polynôme symétrique élémentaire Z T», ... Thj.
*l <*2 <••• <*J
b) Soient B une variété pure compacte, E un fibre vectoriel complexe de base B et de rang
complexe n. Pour tout le > 0 et toute partition I de le, on note M](E) la classe de cohomologie
M^c^E), ..., ct(E)) dans H2*(B ; Z). Montrer que si Et et E2 sont deux fibres vectoriels complexes
de base B, on a
MI(E1©E2) = IM^-M^E,)
J.K

43. CLASSES DE PONTRJAGIN
291
la somme étant étendue aux couples de partitions J = {a1^a2>■■■>ap}, K = {^,>/?2>.
tels que les p + q entiers a, et /Sk, ordonnés par ordre décroissant, forment une partition (notée JK)
égale à I.
8) a) Soit B une variété holomorphe compacte connexe, de dimension complexe n. Pour
toute partition 1 de n, on note M^B) l'entier
< M,(T(B)), pa >
où hb est 'a classe fondamentale d'homologie de B (section 24.37, problème 11). En particulier,
on note M„(B) l'entier M,(B) correspondant à la partition { n } de n à un seul élément. Montrer
que l'on a M,(P.(C)) =(- l)"(n + 1).
b) Si B est produit de deux variétés holomorphes compactes connexes B,, B2 de dimensions
respectives n, et n2, on a
M,(B) = X M^B.JM,,^)
iiii-i
où I, parcourt les partitions de n„ I2 celles de n2, soumises à la condition I,I2 = 1. En particulier,
si ni > 1 et n2 > 1, on a M„(B) = 0. L'espace projectif P^C) n'est donc pas isomorphe au produit
de deux variétés holomorphes de dimension complexe > 1.
43. Classes de Pontrjagin.
(24.43.1) Soient B une variété pure, E un espace fibre vectoriel réel de rang N
et de base B, et considérons son complexifié E(q = E (g) (B x C) (16.18.5), espace
fibre vectoriel complexe de rang (complexe) N.
Si (E(C))B est le fibre vectoriel réel sous-jacent au fibre vectoriel complexe
E(C) (16.15.1), il est clair que si, pour tout ux e E, on pose f(ux) = ux ® 1 et
j"(ux) = ux (g) i, / et /' sont des morphismes injectifs de E dans (E(C))n, et par
définition, (E(C))R est isomorphe à /(E) © /'(E).
(24.43.2) Le fibre vectoriel complexe E(C) est canoniquement isomorphe à son
conjugué (E(C))f (24.42.4).
En effet, soit u : (x, ç) -* {x, 1) l'automorphisme « conjugaison » du fibre
vectoriel réel trivial B x C ; alors / = 1E (g) u est un automorphisme du fibre
vectoriel réel E (g) (B x C). Pour toute section s de E, de classe C00, au-dessus
d'un ouvert U de B, et pour tout £ e C, on a fv(s (g) £) = s (g) w ; vu la définition
de la structure de fibre vectoriel complexe de (E^,)* (24.42.4), cela prouve que
/ est un isomorphisme de fibres vectoriels complexes de E(C) sur (E(C))1.
(24.43.3) On déduit de ce qui précède et de (24.42.5) que l'on a, pour 1 < k s* N,
(24.43.3.1) c,(E(C)) = (- l)*ck(E(C)),
autrement dit, dans les groupes de cohomologie H2'(B ; Z) pour k impair, les
classes de Chern ck(E(C)) sont des éléments d'ordre 2 ou l'élément 0.
Pour tout entier j ^ 1, on appelle classe de Pontrjagin d'indice j du fibre
vectoriel réel E et on note pfE) l'élément (— iyc2j(E(C)), qui appartient donc à

292 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFERENTIELLE ÉLÉMENTAIRES
H4j(B ; Z) ; on appelle classe totale de Pontrjagin de E l'élément de l'anneau
H-(B;Z)
(24.43.3.2) p(E) = 1 + Pl(E) + ...+ />[N/2](E) = £/>/£).
Les propriétés des classes de Chern entraînent les propriétés suivantes des
classes de Pontrjagin :
(24.43.4) (i) Si f : B' -» B est une application de classe C00 d'une variété pure
B' dans B, on a, pour tout fibre vectoriel réel E de rang N et de base B,
(24.43.4.1) f*(p}(E)) = p0*{E)) pour 1 < j < N/2.
(ii) Si F est un fibre vectoriel réel trivialisable et de rang constant, on a
(24.43.4.2) /HE ©F) = /*E).
(iii) Si B est compacte et si E', E" sont deux fibres vectoriels réels de base B
et de rang constant, on a
(24.43.4.3) 2/KE' © E") = 2p{E') ~ p(E").
En effet, (i) résulte de (24.41.4) appliqué à E(C) et de ce que /*(E(C)) est
isomorphe à (/*(E))(C) (16.19.3) ; (ii) résulte de ce que (E © F)(C) est isomorphe à
E(o © F(o et de (24.42.3.2) ; enfin (iii) résulte de (24.42.3.1) appliqué à E('C) et
E,c), qui donne
c2k{{E' © E")(C)) = Z cXE^c/Efo).
i+j = 2k
Multipliant les deux membres par 2 et tenant compte de ce que les classes ch{E[C))
et cB(E(c)) sont nulles ou d'ordre 2 pour h impair, il reste
2c2k((E' © E")(C)) = 2 Z cdE'MEfo) ;
i + j=k
en multipliant les deux membres par (— 1)* = (— 1)'(— iy, il vient
2A(E' © E") = 2 E p.<E'HE")
i+j-k
pour tout k, ce qui équivaut à (24.43.4.3).
Exemple (24.43.4.4). — Sur la sphère Sm hypersurface plongée dans R"+1,
le fibre normal N (20.12.2) est trivialisable, l'application x -* x~ 1(x) étant une
section de classe C°° partout / 0 au-dessus de S„ de ce fibre de rang 1 (16.5.2.1) ;
comme T(SB) © N est la restriction à Sn du fibre trivial T(R"+1), on a
p(T(SJ © N) = 1, donc p(T(SJ) = 1, les classes Pn(T(SB)) sont toutes nulles pour
k ^ 1.

43. CLASSES DE PONTRJAGIN 293
(24.43.5) Considérons maintenant un fibre vectoriel complexe E de rang
(complexe) N et de base B, et le fibre vectoriel réel sous-jacent ER de rang 2N
(16.15.1) ; on peut alors former le fibre vectoriel complexe (E^C) de rang (complexe)
2N.
(24.43.6) Le fibre vectoriel complexe (EB)(C) est canoniquement isomorphe à la
somme directe E © Et.
Avec les notations de (24.43.1), posons, pour tout ux e E,
g(ux) = f(ux) - j"{iux), h(ux) = /(u J + /'(iux).
Il est clair que g et h sont des morphismes injectifs de E„ dans ((E„)(C))R. En outre,
on a i/(ux) = /'(ux), y"(ux) = - /(ux) par définition de (E^c,, donc
g(iux) =/(iux) + /'(ux) = y'(ux) - y"(iux) = ig(ux)
' h(iux) =/(iux) -/'(ux) = - i/(ux) - y"(iux) = - ih(»x).
Par suite, les images £(Er) et /i(Er) sont des fibres vectoriels complexes, g est un
isomorphisme de E sur g(E) et h un isomorphisme de Ef sur h(E). On a
/("*) = \ fe("x) + h(ux)) et /'(iux) = X- (/j(ux) - g(ux)),
donc (ER)(C), qui est somme de /(E) et de /'(E), est somme de g(E) et de h(E).
D'autre part, la relation g(ux) = h(vx) équivaut à
/(ux)-/(vx)=/'(iux)+/'(ivx);
mais (E^o est somme directe de /(E) et /'(E), et les applications / et /' sont
injectives, donc la relation précédente entraîne ux = vx et iux = — ivx, et par
suite ux = vx = 0 ; on en conclut que (E^m est somme directe de g(E) et de h(E).
(24.43.7) Pour tout fibre vectoriel complexe E de rang N et de base B, les classes
de Pontrjagin du fibre réel sous-jacent EB de rang 2N sont données par la formule
(24.43.7.1) 1 - Pl(ER) + p2(EK) -...+(- ifp^EJ
= (1 - ct(E) + c2(E) -...+(- 1)%(E)X1 + Cl(E) + ... + Cn(E)) .
On a en effet cflE^o) = c(E © Ef ) d'après (24.43.6), et il résulte de (24.42.3.1)
et de (24.42.5) que c(E © Ef) est égale au second membre de (24.43.7.1); mais
tous les termes de ce produit appartiennent à des groupes de cohomologie de
dimensions multiples de 4 ; donc les classes cl((E„)(C)) sont nulles pour k impair,
et comme c2k((E^C)) = (- l)Vk(ER), on a bien l'égalité (24.43.7.1).
(24.43.8) Exemple : classes de Pontrjagin du fibre tangent à P„(C). Il résulte de

294 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
(24.42.7.2) que l'on a ^(TïPJC))) = (- 1)'
en posant a=c1(UB+M(C)).
On en déduit que pour E = T(P„(C)j, le second membre de (24.43.7.1) est égal à
(1 - a)B+1(l + a)n+1 = (1 - a2)"+1, d'où
(24.43.9) Soit E un fibre vectoriel réel orienté de base B et de rang pair 2N ;
alors la classe de Pontrjagin pN(E) est égale au carré de la classe d'Euler e\E)
dans ranneau H*(B ; Z).
En effet, (E(C))B est somme directe de E et de iE ; si l'on prend sur iE
l'orientation transportée de celle de E par le B-isomorphisme u -> iu, puis sur E © iE
l'orientation définie dans (24.39.15), on a e(E © iE) = e(E) ~ e\iE) = (e(E))2
puisque E et iE sont isomorphes avec préservation de l'orientation ((24.39.15)
et (24.39.11)). Mais l'orientation canonique de E(C) n'est pas nécessairement la
précédente : de façon précise, si s,, $2, ..., s2N est une suite directe de sections de
E au-dessus d'un ouvert de B, la suite slt isj, s2, is2 s2N, is2N est directe
pour l'orientation canonique de E(C), tandis que la suite s,, s2, ...,s2N,
ist, is2 is2N est directe pour l'orientation de E © iE définie ci-dessus ; les
deux orientations sont donc les mêmes ou sont opposées suivant que
est pair ou impair, c'est-à-dire finalement suivant que N est pair ou impair. Mais
on a />n(E) = (— 1)nc2n(E(C)) = (— l)Ne(E(C)) (24.41.3), où l'on a pris sur E(C)
l'orientation canonique ; on en conclut par (24.39.11) que /»N(E) = (e(E))2.
Remarque (24.43.9.1). — On notera que, par définition, les classes de
Pontrjagin d'un fibre vectoriel réel orienté sont indépendantes de l'orientation
choisie, contrairement à la classe d'Euler.
1) Montrer que si M est une hypersurface orientable dans R"+1, on a pt(t(M)) = 0 pour
tout k > 1.
2) a) Généraliser aux classes de Pontrjagin les résultats de la section 24.42, problème 7.
b) Soit B une variété pure compacte orientable de dimension n = 4k. Pour toute partition I
de k, on note M|(B) l'entier < M,(t(B)), Hb ) où /jb est la classe fondamentale d'homologie de B,
et M^t(B)) est la classe de cohomologie définie dans a) à l'aide des classes de Pontrjagin de t(B).
Montrer que si B est difféomorphe à la frontière (régulière) d'un ouvert dans une variété connexe
compacte et orientable, de dimension 4k + 1, on a M|(B) = 0 pour toute partition I de k (utiliser
le théorème de Stokes en observant qu'on peut identifier les classes de Pontrjagin réelles à des
classes de cohomologie de formes différentielles fermées).
c) Déduire de b) qu'il n'existe pas d'ouvert connexe dans une variété connexe compacte
et orientable, dont la frontière soit difféomorphe à une réunion disjointe de sous-variétés identiques
à P2»(C) pour un entier k > 1.
(24.43.8.1)
pour 1 < k < n/2.
(2N - 1) + (2N - 2) + ... + 1 = N(2N - 1)
PROBLÈMES

44. COMPLÉMENTS SUR LES FORMES DIFFÉRENTIELLES VECTORIELLES 295
3) On définit comme dans la section 24.40 un fibre vectoriel canonique U„+11(H), de rang
réel 4, ayant pour base l'espace projectif quaternionien P„(H). En considérant le corps C comme
identifié au sous-corps de H engendré par 1 et i, U„+ i,i(H) est muni d'une structure de fibre vectoriel
complexe de rang (complexe) 2, noté E.
a) Montrer que si u est la classe d'Euler du fibre vectoriel réel Ea de rang 4 sous-jacent à E,
l'anneau de cohomologie H'(P^H); Z) est engendré par u, et est isomorphe à Z[T]/(T"+1) (même
méthode que dans 24.40.6).
b) Déduire de a) que la classe de Pontrjagin p,{EK) — — 2u ^ 0.
c) En prenant n = 1, conclure que pour tout entier pair 2k eZ, il existe un fibre vectoriel
réel F de base S4 et de rang 4 tel que Pi(F) = 2ku (utiliser le fait qu'il existe des applications
/ : S4 S„ de classe C°° et de degré arbitraire (24.9.5)).
4) On considère la grassmannienne Gp+,iP(R) des sous-espaces vectoriels orientés de
dimension p dans R'** comme un revêtement à deux feuillets de GP+,,P(R), et on note n :
n : GP+,,P(R) - GP+,,P(R)
la projection canonique ; soit UP+,,P(R) = 7i*(Up+,iP(R)), fibre canonique de rang p sur Gp+,iP(R).
a) Montrer que ce fibre est orientable.
b) Soit K un corps de caractéristique # 2 ; on note e la classe d'Euler à valeurs dans K de
U'p+,iP(R) muni d'une orientation, et pk la classe de Pontrjagin d'indice k < {p/2] à valeurs dans
K de UP+,,P(R). Montrer que, si q > 2p :
a) sip = 2»i est pair, tout élément de HJ(GJ+,iP(R) ; K) pour j < q s'écrit d'une seule manière
comme polynôme isobare à coefficients dans K par rapport à e et pup2, ...,pm-1 ;
/?) si p = 2m + 1 est impair, tout élément de HJ(G'p+,iP(R); K) pour j < q s'écrit d'une
seule manière comme polynôme isobare à coefficients dans K par rapport kpl,p1 pm.
(Noter que si p est impair, on a e = 0, et d'autre part que GJ+1-,(R) est difféomorphe à la
sphère S, ; procéder par récurrence sur p en suivant la même méthode que dans 24.40.8).
c) Déduire de b) que tout élément de HJ(Gp+,i()(R) ; K) pour j < q s'écrit d'une seule manière
comme polynôme isobare à coefficients dans K par rapport aux classes de Pontrjagin de UP+,,P(R)
à valeurs dans K (utiliser 24.22.15).
5) a) Montrer que pour j < q, tout élément de torsion d'un Z-module H;(Gp4, P(R); Z)
est d'ordre 2. (Raisonner par récurrence sur p en utilisant les suites exactes de Gysin de (24.40.13)
et les suites analogues pour la cohomologie à coefficients dans Z ; utiliser également le problème 2
de la section 24.30).
b) En déduire que, pour j < q, tout Z-module de cohomologie H-'(Gp+,iP(R) ; Z) est somme
directe d'un certain nombre d) de Z-modules isomorphes à F2 et d'un certain nombre r^de Z-modules
isomorphes à Z ; en outre ces nombres vérifient les relations suivantes
rt = dim(HJ(Gp+„p(R) ; Q)), d, + rj + dJ+, = dim(H>(Gp + ,.p(R) ; F2|
et sont calculables explicitement à l'aide du problème 4 c) et de 24.40.14 et 24.40.16.
44. Compléments sur les formes différentielles vectorielles et les connexions
principales.
(24.44.1) Les définitions de (16.20.15) se généralisent comme suit. Soient
Vi, ..., V„, V des espaces vectoriels réels (resp. complexes) de dimension finie,
et soit
(D : Vi x V2 x ... x VB -» V
une application h-linéaire. D'autre part, soit M une variété différentielle (resp.
holomorphe) pure ; pour tout entier m ^ 0 et tout espace vectoriel réel (resp.
complexe) W de dimension finie, notons SJM ; W) l'espace vectoriel des m-formes

296 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFERENTIELLE ÉLÉMENTAIRES
(24.44.3) De la définition (24.44.1.1), on déduit aussitôt la formule donnant
différentielles vectorielles de classe C°° sur M, à valeurs dans W (16.20.15). Quels
que soient les entiers positifs mlt ..., mh, il existe une application h-linéaire
unique notée
4» : /mi(M; Vt) x SmiQA; V2) x ... x «fmh(M; V„) - £mi+mi+...+mh(M; V)
telle que l'on ait
(24.44.1.1) •d>nIalll, £a2.-2a2l-2 L«kh"*h)
il h ih
= Z an, A a2i2 a ... a a2)j awJ
<1.12 l'h
quels que soient les vecteurs aWk e Vk et les mk-formes akjk réelles (resp. complexes)
pourl < fe ^ h. Il suffit en effet de définir l'application <ï> par la formule (24.44.1.1)
lorsque chaque famille (aW|t) est une base de V, pour 1 < k < h ; la formule
générale (24.44.1.1) s'en déduit par linéarité.
Cette définition généralise (16.20.15.7). Une définition équivalente
généralisant (16.20.15.5) consiste à dire que pour des formes
©x e Smi(U ; Vj), ...,©» 6 £mh(M ; V»),
la valeur de la (mi + m2 + ■.. + mB)-forme différentielle <ÏKo),, u>2, ...,©„)
pour une famille (ut, ..., umi+m2+...+„,,) de vecteurs tangents en un point xe M
est donnée (avec les notations de (Ann. 12.2)) par
(24.44.1.2) — 1 -«WcMxJ.Oi! umi),
<ù2(x) (u
» Umi+ ...+«»)))•
(24.44.2) Considérons en particulier le cas où O est le crochet (x, y) -» [x, y]
dans une algèbre de Lie réelle (resp. complexe) g. Alors si (resp. a>2) est une
mi-forme différentielle (resp. m2-forme différentielle) de classe C°° sur M, à
valeurs dans g, [iou to2] est une (m^ + m2)-forme différentielle sur M à valeurs
dans g, et il résulte de (24.44.1.1) que l'on a
(24.44.2.1) [<o2) ©!] = (- l)mimî+1 K, ©21 ■
En outre, si co3 est une m3-forme différentielle de classe C00 sur M, à valeurs
dans g, on a l'identité de Jacobi
(24.44.2.2) ( - 1P"" K, [a>2, «3 ] ] + ( - ipmi [co2, [<o3, a>x ] ]
+ (- ipmj[«>3, [«i, c»a]] = 0.

44. COMPLÉMENTS SUR LES FORMES DIFFÉRENTIELLES VECTORIELLES 297
la différentielle extérieure de la (mi + m2 + ... + ms)-forme Q>(tùu w2, • • - .«o»)
à valeurs dans V (17.15.8) :
(24.44.3.1) d(<U(«>i> ©2 ©*))
n
= Z(- + "'+"^,«(œi, ....©j-i, dWj, nJ+t, ...,©„)•
D'autre part, si / : M' -> M est une application de classe C00 (resp.
holomorphe) d'une variété différentielle (resp. holomorphe) pure M' dans M, on a
(24.44.3.2) '/(<Wa>i, ...,©.)) = «K'/K), • • •, '/K))
en raison de (16.20.15.4).
(24.44.4) Soient B une variété différentielle pure, X un espace fibre principal
de base B et de groupe G (16.14.2). Soient B' une seconde variété différentielle
pure, / : B' -+ B une application de classe Cœ, X' = B' x BX le fibre principal
de base B' et de groupe G, image réciproque de X par / (16.14.6), et soit u : X' -» X
le morphisme canonique correspondant à / (16.12.8).
Supposons donnée sur X une connexion principale P (20.2.2), et soit tu la
1-forme différentielle de la connexion P (20.2.3.4), définie sur X et à valeurs
dans l'algèbre de Lie ge. Montrons que sur X' la 1-forme différentielle ©'='u(©),
image réciproque de ©, est encore la 1-forme d'une connexion principale P"
sur X'. Appliquons pour cela les critères de (20.2.5) ; par définition, pour tout
r'b.eX'b. et tout se G, u(r'b..s) - rb.s, en posant b = f(b') et rb = w(r£.) (16.14.6).
Cela entraîne d'une part Trii,.s(w).(h'.s) = (T,fc,(u).h').s pour tout h'eTri>.(X'),
et par suite co'(r'b-.s). W = <a(rb.s).(ÇTrb{u).h').s), ce qui prouve que co' vérifie
la condition (20.2.5.1). D'autre part, pour tout vecteur v e ge, en posant
Z'M-) = r'b-.v, on a par définition ((16.10.1) et (19.3.7)), Z'Jlj',,.) = liprb). v, donc
«'(rM.ZCWO = a{rb).(Trh{u).Z'v(r'b.))
= <a(r6).((Trfc.(«).T>r,.)).v) = e*rb).ZJrb) = v
en raison de la relation o,b = w ° orf>, qui découle de la définition de ox : s -* x.s
(19.3.7).
On dit que la connexion principale P* est l'image réciproque par f de la
connexion principale P ; de l'équation de structure (20.3.3.1)
(24.44.4.1) dm = - ^ [©,©] + il
(où le facteur ^ provient de la définition (24.44.2) de [©, ©], qui diffère de la

298 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
convention faite dans (16.20.15.8)), et de (24.44.3.2), il résulte que la courbure
de la connexion P' est donnée par
(24.44.4.2) ft' = 'u(ft)
en fonction de la courbure ft de P.
45. L'homomorphisme de Weil.
(24.45.1) Soit G un groupe de Lie réel (resp. complexe) ; rappelons que G opère
à gauche sur son algèbre de Lie ge par (s, u) -* Ad(s). u. Il opère donc à gauche
(19.1.2.2) sur l'espace vectoriel des applications p-linéaires de gf. dans un espace
vectoriel réel (resp. complexe) V par la formule
(24.45.1.1) (s.FXxl x2, ..., Xp) = F{Ad(s-l).xu ..., AdCs"1)^,)
Pour xu ..., x, fixés, on déduit de (19.11.2) et du fait que F est p-linéaire, que
la différentielle au point e (16.5.7) de l'application s -* (s.F)(xu ..., xp) de
G dans V est donnée par
p
h -» £ F(x!, ..., Xy_lf [h, Xj], Xj+1, ..., Xp).
j= i
En particulier, si F est une application p-linéaire invariante par G, on a, pour
tout vecteur yege,
p
(24.45.1.2) £ F(x!, ..., Xj-j, [y, x,-], xJ+1, ..., xp) = 0
j= i
quels que soient les Xj e ge (on peut montrer que réciproquement, si cette
condition est vérifiée et si G est connexe, F est invariante par G ; il suffit de raisonner
comme dans (19.8.11)).
Si alors, pour 1 < j ^ p, toj est une rrij-forme différentielle de classe C00 à
valeurs dans g^ et <a une m-forme différentielle de classe C°° à valeurs dans g„
(toutes ces formes étant définies sur une même variété pure M), on a, pour une
application p-linéaire F de gf dans V, invariante par G,
(24.45.1.3) £(- l)T*-' + -+"i-'>F(<o1, ...,»,_!, [iù,iOj],<aJ+l, ...,œp) = 0.
7=1
Remarque (24.45.1.4). — On obtient des formes p-linéaires symétriques F
sur g£ par le procédé suivant, appelé polarisation : on part d'un polynôme x -» P(x)
homogène de degré p sur ge, par quoi on entend une fonction polynôme à
coefficients réels (resp. complexes) par rapport aux coordonnées de x pour une base
quelconque de ge; alors (tlf t2, tp) -» P(t1x1 + t2x2 + ... + tpxp), pour

45. l'homomorphisme de weil
299
des Xj e ge quelconques, est une fonction polynôme homogène de degré p sur
Rp (resp. Cp) ; si on note p ! F(x1( x2, ..., xp) le coefficient du monôme tit2... îp
dans ce polynôme, F est une forme p-linéaire symétrique sur gp, dite polarisation
de P, et l'on a P(x) = F(x, x, ..., x). Si P est invariant par G (c'est-à-dire que
P(Ad(s ~1 ). x) = P(x) pour tout s e G), F est aussi invariante par G.
(24.45.2) Soient B une variété différentielle pure, X un espace fibre principal
de base B et de groupe G, P une connexion principale sur X, dont co est la 1-forme
différentielle à valeurs dans ge. Si ft est la forme de courbure de la connexion P,
2-forme différentielle à valeurs dans ge, on a, en différentiant l'équation de
structure (24.44.4.1) et substituant dans le résultat la valeur de dco donnée par
(24.44.4.1)
(24.45.2.1) dil = ^([ft, to] - [co, ft]) = [ft, co] = - [co, ft]
compte tenu de (24.44.3.1) et du fait que [co, [co, co]] = 0 en vertu de l'identité
de Jacobi (24.44.2.2) ; la relation (24.45.2.1) n'est qu'une autre manière d'écrire
l'identité de Bianchi (20.3.4).
De ce résultat et de (24.45.1.3), on déduit le résultat fondamental suivant :
(24.45.3) Pour toute connexion principale P sur X et toute forme p-linéaire F
sur gp, invariante par G, la 2p-forme différentielle scalaire F(ft, ft, ..., ft) (où
ft est la forme de courbure de P) est invariante pour Faction à droite de G sur
2
/\T(X) ; en outre, cette forme est fermée.
En effet, la formule (24.44.1.2) montre que pour tout reX la valeur de
F(ft, ft, ..., ft) pour le 2p-vecteur h, a h2 a ... a h2p, où les h, sont des
vecteurs de T^X), est donnée par
(24.45.3.1) l^flf/Mli, a h2), ..., iK/Mhj,., a h2p))).
Mais ft étant invariante par G (20.3.2), on a, pour tout s e G,
fl(r.s).(li2i-_1.s a h2j.s) = Ad^Mftf.rMh,,-, a h2j))
donc la valeur de F(ft, ft, ..., ft) pour le 2p-vecteur
(h,.s) a (h2.s) a ... a (h2p, s)
est encore donnée par (24.45.3.1), en vertu de l'invariance de F (24.45.1.1). Pour
voir que F(ft, ft, ..., ft) est fermée, appliquons (24.44.3.1), où toutes les formes
ut j sont égales à ft, donc tous les m, à 2, ce qui donne
d(F(ft, ft, ..., ft)) = £ F(ft, ..., ft, dft, ft, ..., ft).

300 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
On remplace ensuite dil par sa valeur — [ta, II] déduite de (24.45.2.1); il suffit
enfin d'appliquer (24.45.1.3) avec m = 1 et les ms égaux à 2, pour obtenir
wa ...,n)) = a
(24.45.4) Les hypothèses étant les mêmes que dans (24.45.3), nous allons voir
qu'à partir de la 2/?-forme différentielle fermée F(Î2, il, ..., il) sur X, on peut
définir de façon canonique une 2/>forme différentielle fermée FB(iï) sur B. Il
suffit évidemment de définir la restriction de cette forme à tout ouvert UcB
trivialisant pour X. Il existe alors au-dessus de U une section R de X, de classe C00,
et on prend
FB(fl) - 'R(F(ft, il, ..., il)) = F('R(ft), 'R(ft) 'R(ft))
((16.20.15.4) et (16.20.9.5)) qui est bien une 2/>-forme fermée (17.15.3.2). Il suffit
de vérifier que cette forme est indépendante de la section R choisie. En effet,
toute autre section R' de classe C00 de X au-dessus de U est de la forme
b -* R(b). s(b), où s est une application de classe C°° de U dans le groupe de Lie G;
comme il est une 2-forme invariante par G (20.3.2), on a, quels que soient les
vecteurs h, k de TR(i)(X),
il(R(b).s(b)).(h.s(b) a k.s(b)) = Ad(s"l(b)).(ft(R(b)).(h a k)).
Or, pour deux vecteurs tangents u, v de Tb{B), on a
'R(iW).(u a v) = «(RWJ.CLURM a Tt(R).v),
'RW).(u a v) = (T^RO-ii a Tj,(R'). v).
Mais Tt(R'). u = CWR). u). s(b) + R(b). (T„(s). u)
= ÇTb(R).u).s(b) + RW.Wr'.iTAs).»))
et le second terme est un vecteur vertical au point R'(b) ; comme la forme il est
horizontale (20.3.2), on a
ft(fi'(t)).fri(R').uatl(R').y) =
= il(R(b)-s(b)).((Tb(R)M).s{b) a (T,(R).v).s(b))
= Ad(s{b)-l).(m(b)).(TÀ'i)-» a T6(R).v))
d ou finalement
(24.45.4.1) 'R'(il){b).(u a v) = Ad(s(o)-1).('R(ftXfc)-(u a v)).
Cela étant, la valeur de FB(iï) pour un 2p-vecteur ut a u2 a ... a u2p où les
Uj sont des vecteurs de Tn(B), est donnée, en vertu de (24.45.3.1) par
l«FCA(ilX&).(ui a u2), ...,'R(ftXt)-(u2p-i a u2p))).
Mais si dans cette formule on remplace R par R', il résulte de (24.45.4.1) et de

45. l'homomorphisme de weil
301
l'invariance de F (24.45.1.1) que l'expression obtenue est la même, d'où notre
assertion.
(24.45.5) Soit G un groupe de Lie réel (resp. complexe). Les notations et
hypothèses étant celles de (24.45.3), la classe de cohomologie de la 2p-forme fermée
FB(il) dans H2p(B ; R) (resp. H2p(B ; C)) est indépendante de la connexion P
choisie sur X.
Soient P0, Pi deux connexions principales sur X, co0, cot les 1-formes de
connexion correspondantes, Sl0, fti les 2-formes de courbure correspondantes.
Considérons la variété B' = B x I, où I est un intervalle ouvert de R contenant
[0, 1 ] ; soit X' = prJ(X) l'image réciproque par la première projection du fibre
principal X (16.14.6) ; si ît : X -* B est la projection canonique, X' s'identifie
au produit X x I et la projection X' -» B' à (r, t) -» (n{r), t), car l'application
(r, (7t(r), t)) -» (r, t) est un isomorphisme de fibres principaux de X' = X x BB'
sur X x I (cf. (23.6.1)). Avec cette identification, to0 = 'pri(coo) et to', = 'prifco,)
sont les formes de connexion de deux connexions sur X' = X x I (24.44.4).
Montrons que la 1-forme sur X'
co' : (r, t) -» t(ù\{r) + (1 - t)co0(r)
est encore la 1-forme d'une connexion principale P' sur X', en vérifiant les
conditions de (20.2.5). En effet, l'espace tangent T(M)(X') s'identifie à XfX) x R ; l'action
du groupe G sur cet espace tangent est alors donnée par (h, x).s = (h.s, x).
On a donc, pour tout vecteur tangent (h, x) e T(l.j()(X')
co'(r, t).(h, x) = t©!(r).h + (1 - t)e>0{r).h
et d'autre part le champ de vecteurs verticaux transporté de Xu (19.3.3) par l'action
de G est (r, t) (Zu(r), 0) (19.3.7). La vérification des conditions (20.2.5.1) et
(20.2.5.2) est alors immédiate.
Considérons maintenant les deux applications i0 : b -» (b, 0)etil : b -» (b, 1)
de B dans B'; comme pr, ° i0 et pr, o jj sont égales à l'identité de B, on a
X = i*(X') = i*(X') et les morphismes de X dans X' correspondant à i0 et it
sont j0:r -» (r, 0) et ji'.r -* (r, 1). En raison de la définition de co', on a
t»o = î/ot40') et ©i = 'y'iC*9') ! si est la 2-forme de courbure de la connexion F
sur X', on a donc ft0 = 7o(ft') et = 'j^il') (24.44.4.2). Posons
<D0=F(ft0,ft0,...,n0), *i=F(n1,n1,...,n1) et cp'=F(n',ft',...,n'),
qui sont des 2p-formes fermées ; on a il0 = %(t~l') et = 'Ji(Sl') et il résulte de
la formule de l'homotopie (24.2.4.2) que O0 et et, sont cohomologues. Nous allons
montrer de façon plus précise que l'on a
(24.45.5.1) <D, - <D0 = dE

302 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
où S est une (2p — l)-forme de classe C00 sur X, invariante par G. En effet, la
formule (24.2.4.1) donne pour expression de E
(24.45.5.2) 3 = J %{iEV)du
où ju est l'injection r -* (r, u) de X dans X'. Il suffit évidemment de voir que
iE.<t>' est invariante pour l'action de G sur X'. Or il en est ainsi de <P' ; d'autre
part, toute 2/>-forme différentielle de classe C00 sur X' s'écrit d'une seule manière
y = ctu a du + /?„
où, pour chaque u e I, r -» aB(r) et r -» fij^r) sont respectivement une {2p - 1)-
forme et une 2/>-forme sur X. Tout 2/»-vecteur décomposable de AT<r,„)(X') s'écrit
z = (h„ X-j) A (h2, X2) A ... A (h2p) x2p)
2p
= (hx a h2 a . . . a h2p, 0) + Z (hi a ... a h; a ... a h2py xj)
j= 1
pour des vecteurs h,eTr(X)et des nombres réels Xj-, on a donc
< "Ar, «), z > = < Pu(r), ht a h2 a ... a h2p >
+ Z < a^)» h, a ... a h, a ... a h2. > x,
j=i
et comme les Xj sont arbitraires, la définition de l'action de G sur X' montre
que si y est invariante par G, il en est de même de aM et jSu pour tout « e I. Comme
on vérifie aussitôt que iE.y est la forme (r, u) -* ajr), cela achève de prouver
que S est invariante par G.
Si maintenant R est une section de classe C00 de X au-dessus d'un ouvert U
de B, le même raisonnement que dans (24.45.4) montre que 'R(H) est une (2p — 1)-
forme sur U indépendante du choix de R ; de cette unicité résulte aussitôt qu'il
existe sur B une (2p — l)-forme SB de classe Cœ telle que, pour toute section R
de classe Cœ de X au-dessus d'un ouvert U de B, 'R(S) soit la restriction de SB
à U. Vu la définition de FB(ft) (24.45.4), on a
FatOi) - FB(ft0) = dEB
ce qui achève de prouver (24.45.5).
Nous noterons Cf(X) la classe de cohomologie de FB(1Î) dans H2p(B ; R)
(resp. H2p(B ; C)), pour toute connexion principale p sur X, dont il est la forme
de courbure.
(24.45.6) Soient B, B' deux variétés pures, f : B' -* B une application de classe

45. l'homomorphisme de weil
303
C00, X un espace fibre principal de base B, X' = /*(X) son image réciproque par f.
Alors, pour toute forme p-linéaire F sur g£ invariante par G, on a
(24.45.6.1) Cp(/*(X)) = f*(CF(X)) ■
En effet, considérons sur X une connexion principale P, dont ft est la forme
de courbure ; soit g : X' -» X le morphisme canonique correspondant à /,
et prenons sur X' la connexion principale P* image réciproque de P par g (24.44.4),
de sorte que sa forme de courbure est 12' = 'g(il). Il suffit de montrer que l'on a
F„.(ft') = '/(FB(ft)) (24.1.3). Or, soit R une section de classe C00 de X au-dessus
d'un ouvert U de B, et considérons la section R' = f*(R) de X' au-dessus de
f~ '(U), image réciproque de R par f (16.12.8), de sorte que l'on a g ° R' = R ° /.
On a ¥(il', il' il') ='g(¥(il, il il)), d'où, au-dessus de /-1(U),
FB.(ft') = 'R'(F(ft', il', ., il')) = 'R'('g(F(ft, il,.., il)))
= !/ÏR(F(ft, a ••.,"))) = '/(FB(ft)) • CQFD.
(24.45.7) Si F, est une forme />-linéaire réelle (resp. complexe) sur gj, F2 une
forme ^-linéaire réelle (resp. complexe) sur q% il est clair que l'application
(24.45.7.1) F : (x„ ..., xp+,) F,(x1, ..., xp)F2(xp+1, ..., xp+,)
est une forme (p + q)-linéaire réelle (resp. complexe) sur gf+q ; elle est invariante
par G lorsque Ft et F2 le sont. Lorsqu'il en est ainsi, il est clair qu'avec les
hypothèses et notations de (24.45.3), on a
F(li, il, ..., il) = Fi(ft, il, ..., il) a F2(ft, ft, ..., ft)
donc aussi, en vertu de la définition (24.45.4)
FB(ft) = F1B(ft) a F2B(ft)
et par suite, dans l'algèbre de cohomologie H"(B; R) (resp. H'(B; C))
(24.45.7.2) Cf(X) = cFl(X) ~ cFj(X).
Notons I(G) l'ensemble des formes multilinéaires réelles (resp. complexes) sur
l'algèbre de Lie ge de G qui sont invariantes par G; l'application (24.45.7.1)
définit sur I(G) une structure d'algèbre associative sur R (resp. Q. La formule
(24.45.7.2) signifie donc que l'application
(24.45.7.3) F ^ Cp(X)
est un homomorphisme de r algèbre I(G) dans V algèbre de cohomologie H"(B; R)
(resp. H'(B ; C)). On dit que (24.45.7.3) est l'homomorphisme de Weil correspondant
à l'espace fibre principal X, de base B et de groupe G.

304 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
PROBLÈME
Sous les hypothèses de (24.45.3), supposons que F soit une forme p-linéaire symétrique
déduite par polarisation d'un polynôme invariant de degré p sur g,. Pour tout t tel que 0 < t < 1,
o>, = <o0 + t(o), — co0) est une 1-forme de connexion sur X, dont on note ft, la 2-forme de courbure.
Montrer que l'on peut prendre, dans (24.45.5.2)
(calculer la dérivée de r -> F(il„ il,, ..., ft,) et l'exprimer à l'aide de la différentielle extérieure
</(F(», -e»0, O,, ...,ft,)).
46. Courbure et classes caractéristiques.
Les résultats de la section 24.45 vont nous permettre de donner des méthodes
de calcul des classes de Chern, de Pontrjagin et d'Euler utilisant la courbure
de certaines connexions.
(24.46.1) I. Calcul des classes de Chern. — Soit E un fibre vectoriel complexe
de rang (complexe) N, ayant pour base une variété pure B. Rappelons la façon
dont on lui associe canoniquement un fibre principal X(E) de base B et de groupe
GL(N, Q, en prenant X(E) = Isom(B x CN, E) (20.1.1) ; la fibre (X(E))t en un
point beB est l'ensemble des isomorphismes de CN sur l'espace vectoriel Ej,
et l'action de GL(N, C) sur X(E) est donnée par {ub, s) -*■ ub ° s pour tout
isomorphisme ub de CN sur Eb.
Soit / : B' -+ B une application de classe C00 d'une variété pure B' dans
B, et soit E' = /*(E) l'image réciproque de E par / ; on a alors
à isomorphisme canonique près. En effet, le fibre trivial B' x CN est
canoniquement isomorphe à /*(B x CN) par l'application
et d'autre part, /*(Hom(B x CN, E)) est canoniquement B'-isomorphe à
Hom(/*(B x CN), /*(E)) (16.19.3), l'isomorphisme transformant évidemment
/*(Isom(B x CN, E)) en Isom(/*(B x CN), /*(E)); d'où notre assertion.
(24.46.2) A toute forme p-linéaire F sur (g!(N, C)f, invariante par GL(N, C),
on peut donc associer une classe de cohomologie Cp(X(E)) appartenant à H2p(B ; Q
par le procédé de (24.45.5). Or gI(N, C) s'identifie à l'algèbre de Lie M^Q des
matrices carrées d'ordre N à éléments dans C, l'action de GL(N, C) sur Mn(C)
(24.46.1.1) X(/*(E)) = /*(X(E))
(b',t) - (b',(f(b'),t));
étant
(S, X) - sxs-1.
(19.11.2.4) Pour définir des formes p-linéaires sur M^C) invariantes par
GL(N, C), il suffit donc de définir des polynômes à une indéterminée PeC[T]

46. COURBURE ET CLASSES CARACTÉRISTIQUES
305
tels que P(SXS~ ') = P(A") pour toute matrice X e M^C) et toute matrice
inversible S e GL(N, C), et de déduire de chacun d'eux une forme multilinéaire
invariante par G, par polarisation (24.45.1.4). Or, on obtient immédiatement de tels
polynômes en considérant le déterminant caractéristique
(24.46.2.1) det^t/N - ~ X^j = fN + rN_ ^(X) + ... + a^X)
car le premier membre ne change pas quand on remplace X par SXS~l, donc
il en est de même des coefficients Oj(X) du second membre. Si F,- est la forme
>linéaire déduite par polarisation du polynôme oJ(X) homogène de degré j
par rapport aux éléments de X, on obtient donc ainsi N classes de cohomologie
(24.46.2.2) c'j(E) = cF/X(E)) e H2J(B ; C) pour 1 ^ j < N.
La construction des 2/'-formes Fj^il) sur B dont les c'j[E) sont les classes de
cohomologie s'explicite ici de la façon suivante. On part de N2 1-formes différentielles
cow de classe C00 sur B, à valeurs complexes. On considère, un recouvrement
fini (UA) de B par des ouverts au-dessus de chacun desquels existe une section Rx
de classe C00 du fibre principal X(E); il existe alors, en vertu de (20.3.5), une
1-forrrie de connexion tox et une seule sur n~ \UX) (n étant la projection X(E) -► B)
telle que 'R(coA) soit la restriction à U* de la forme m = (coBt) à valeurs dans
Mn(C). Si (fx) est une partition de l'unité subordonnée à (U^) et formée de fonctions
de classe C00, co = ^Jifx°n).iox est une 1-forme de connexion sur X(E), et on
a
prend pour il la 2-forme de courbure de cette connexion. La forme Fp(ll) est
alors définie de la façon suivante : on pose
n
fy* = dcOhK + I(ohl a COlk
1=1
et on a
(24.46.2.3) F,B(ll) = (^iY £
(où les déterminants se développent comme d'ordinaire, le produit de deux
formes étant le produit extérieur ; l'ordre des facteurs est sans importance puisqu'il
s'agit de 2-formes).
(24.46.3) Soit / : B' -* B une application de classe C00 d'une variété pure B'
dans B ; on a alors
(24.46.3.1) C//*(E)) = /•(£#£)).
Cela résulte en effet de (24.46.1.1) et (24.45.6.1).
ft*i«i ft*in2 • • •

306 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
(24.46.4) Nous nous proposons de montrer que pour une variété pure compacte B,
on a
(24.46.4.1) c'j{E) = c/E) pour 1 < j < N
où le second membre est l'image canonique dans H2j(B ; C) de la classe de Chern
c/E) (qui est un élément de H2-'(B ; Z)). Compte tenu de la définition des classes
de Chern pour les variétés compactes (24.42.2), et des relations (24.41.4.1) et
(24.46.3.1), on voit qu'on peut se borner à prouver (24.46.4.1) pour B = G,+NN(Q
et E = U,+NN(Q pour q grand (auquel cas on peut d'ailleurs remplacer c/E)
par c/E) puisque G,+N)N(Q est sans torsion et qu'on peut donc identifier H'(B ; Z)
à un sous-Z-module de H*(B ; Q). Nous distinguerons plusieurs cas.
(24.46.5) A) Cas N = 1 ; alors ^(E) = e(E), classe d'Euler du fibre réel de
rang 2 sous-jacent à E, muni de l'orientation canonique de E. Comme H2(P^C) ; C)
est de dimension 1 sur C, on a nécessairement
c'i(U,+1,1(Q) = a.c1(U,+ 1,1(C))
où aeC (puisque c^Ug+^^C)) # 0), et la remarque de (24.46.4) montre que
pour tout fibre vectoriel complexe E de rang 1 sur P^C), on a encore
c'1(E) = a.c1(E)
la constante a ne dépendant ni de q ni de E ; pour voir que a = 1, on peut se borner
à un seul cas particulier. Prenons q = 1, de sorte que Pi(C) est difféomorphe
à S2. Orientons S2 vers l'extérieur et prenons pour E le fibre tangent T(S2) muni
de l'orientation correspondante; si on munit S2 de sa structure riemannienne
usuelle, E est canoniquement muni (comme d'ailleurs le fibre tangent de toute
surface riemannienne orientée) d'une structure de fibre vectoriel complexe :
pour tout vecteur tangent hx e Tx(S2), ihx est l'unique vecteur de même longueur
que hx, orthogonal à hx et tel que le 2-vecteur hx a ihx soit > 0. Prenons comme
connexion sur X(E) la connexion principale de Levi-Civita de S2, considérée
comme connexion sur un fibre principal de groupe C" ; si (e,, e2) est un repère
orthonormal direct de la variété riemannienne S2, on a e2 = i«i d'après ce qui
précède, donc (20.10.9.5), la 1-forme correspondant à cette connexion et au
repère formé de la seule section et est — ico12 ; la 2-forme de courbure
correspondante est donc - iQ12 = — iv, où v est la forme volume canonique (20.8.6.4)
de la variété riemannienne S2 ; cela résulte de (20.10.9.7), puisque la courbure
gaussienne est égale à 1. D'où la valeur de la 2-forme FB(ft) = ^- v ; on en conclut
que pour l'orientation prise sur S2, FB(iî) = 2, et la classe de cohomologie
Js2
de FB(ft) est 2e*2 ; mais d'après (24.42.7.3), cette classe est bien égale à e(E) = ct(E).

46. COURBURE ET CLASSES CARACTÉRISTIQUES
307
(24.46.6) B) Comme second cas, prenons B = (Pm(C))N pour un m > 1 ; si
l'on note pr,- la projection de B sur le j'-ème facteur Pm(C), on considère sur B
les N fibres vectoriels complexes de rang 1, Ej — pr*(Um+lii(C)) et le fibre de
rang N
E = Ei © E2 © ... © EN.
Si eeH2(PJC); Z) est la classe d'Euler de Um+11(C), la classe d'Euler c^Ej)
est ej = pr*(e*), et l'on a donc, pour la classe de Chern totale de E (24.42.3)
(24.46.6.1) c(E) = (1 + eiKl + e2)... (1 + <?N).
Considérons sur le fibre principal X(Um+ til(C)) une 1-forme de connexion co
(à valeurs dans C); si pj : X{Ej) -* X(Um+i_1(C)) est le morphisme canonique,
posons coj = 'pjlco), qui est une 1-forme de connexion sur X(Ej), à valeurs dans C
((24.44.4) et (24.46.1)) ; si ilj est la 2-forme de courbure de cette connexion sur
X(Ej), il résulte du cas A) que e} = cx{E}) est la classe de cohomologie de la 2-forme
fermée FB(Q;) sur B ; si R, est une section de classe C00 de X(E;) au-dessus d'un
ouvert U de B, rappelons que la valeur de FB(£2^) en un point de U est
^-'w (24.46.2.3).
Cela étant, on vérifie immédiatement par les critères (20.2.5) que la 1-forme
sur X(E) à valeurs dans qI(N, C) = MN(C)
co = Diag(a>i, co2 coN)
est la 1-forme d'une connexion sur X(E), dont la forme de courbure est
ft = Diag(n1,£i2 ftN).
Or, à partir de sections Rj de X(Ej) au-dessus de U pour 1 ^7 ^ N, on définit
une section b -* (Ri(b), ..., R^ip)) de X(E). La formule (24.46.2.3) donne alors,
pour 1 < 7 ^ N,
FjbCO) = (^r) S '*/.,("/.,) a 'Rk2(Qh2) a ... a 'Rnj(ftBj.)
\27ll /h,<(i2<...<lij
et la classe de cohomologie de cette forme est donc, en vertu de (24.46.6.1),
Z e», e„2 ... ek = c/E).
*J <*2<...<*j
(24.46.7) C) Avec les hypothèses et notations de B), rappelons maintenant
((24.40.6) et (24.38.1)) que l'homomorphisme d'algèbres qui, à chaque
indéterminée T, fait correspondre ej (1 < j < N), est un isomorphisme de l'algèbre
C[TU T2, ..., TN]/((Tr+1) + (TT1) + • • • + (TT'))

308 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
sur l'algèbre de cohomologie H'ftPJC))*; C). Cela montre que si l'on prend
m + 1 > N, le seul polynôme PeCrj!, T2 TN] de degré < N pour lequel
P(eu e2 eN) = 0 est P = 0.
Fixons donc un entier m > N — 1 ; pour un entier q assez grand, il existe
une application / : B -+ G,+NN(C) de classe C°° telle que E soit B-isomorphe
au fibre /*(U,+N>N(C)) (24.42.2); on a par suite (24.41.5.1)
(24.46.7.1) c/E) = /*(c?'N) pour 1 ^ j < N.
Prenons sur X (U,+NiN(C)) une connexion principale P à l'aide de laquelle nous
définissons (24.46.2) les éléments cF/X(U,+NiN(C))) = c'jq'N appartenant à
H2j(G,+N>N(C); C) pour 1 < / < N. Si q > N, «'résulte de (24.40.10, (ii)) qu'il
existe un unique polynôme QJ>Ne C[Ti, T2, ..., TN] isobare de poids 2j, tel que
cr = qj.m-"> 4-n, ...,4N)-
Prenons alors sur X(E) la connexion principale image réciproque de P par /.
Il résulte de (24.46.3.1) que l'on a
Cj(E) = f *(c'j>-") = Q^c^E), c2(E), .... cJUE))
compte tenu de (24.46.7.1). Comme on a vu dans B) que c'/E) = c/E), on en
conclut que le polynôme isobare de poids 2j en les indéterminées S»,
Sj - Qj,n(Si, S2, ..., Sj), prend la valeur 0 lorsqu'on y remplace chaque Sk
par c*(E) pour 1 < k ^ / En vertu de (24.46.6.1), cela signifie encore que, si
P(Ti, ..., TN) est le polynôme obtenu en remplaçant dans Sj- - QjiN(Si, .... Sj),
chaque S* par le « polynôme symétrique élémentaire » £ TBl TB2 ... TBt
(l|<*2<...<*k
pour 1 < k <_/, on a P^, e2, ..., eN) = 0; mais comme P est de degré < N,
on a nécessairement P = 0, et le théorème des fonctions symétriques entraine
que Sj = Qjd$i> S2, ..., S;) et par suite c'f-N = cJ,N pour 1 < j < N. CQFD.
(24.46.8) II. Calcul des classes de Pontrjagin. — Pour tout fibre vectoriel réel E
de rang N ayant pour base une variété pure B, on peut reprendre les raisonnements
de (24.46.1) et (24.46.2) pour définir un fibre principal X(E) de base B et de groupe
GL(N, R) ; il suffit de remplacer partout C par R. Pour obtenir des formes multi-
linéaires sur MN(R) invariantes par GL(N, R), on considère ici le déterminant
caractéristique
(24.46.8.1) det^t/N - ^-X^j = f* + t^W*) + ... + o^X)
et en désignant par F, la forme y-linéaire déduite par polarisation du
polynôme o}(X) homogène de degré j, on obtient N classes de cohomologie
(24.46.8.2) c'/E) = cFj(X(E)) e H2J(B ; R) pour 1 < j < N.

46. COURBURE ET CLASSES CARACTÉRISTIQUES
309
L'expression de F^ft) s'obtient comme dans (24.46.2) en remplaçant les tow
par des 1-formes à valeurs réelles, et on a
(24.46.8.3) FjB(iï) = f-i-Y £
\ In) a,<*2<..<*
'*2*i
ft
*l*2
*2*2
ft,
*2«j
ft
Cette fois, lorsque B est une variété pure compacte, on a
f c'2Jk+1(E) = 0
( A) lc2t(E) = /5t(E)6H^(B;r)
où pk(E) est l'image canonique dans H**(B ; r) de la classe de Pontrjagin pk(E\
élément de H4*(B ; Z). Pour le voir, considérons le fibre vectoriel complexe E(C),
de rang complexe N; pour calculer les classes de Chern c/E(C)), en utilisant
(24.46.4.1), on peut prendre les mêmes 1-formes cou que ci-dessus, considérées
comme des 1-formes à valeurs complexes. Lorsqu'on considère H*(B ; r) comme
sous-espace vectoriel (sur r) de H"(B ; C), la classe de cohomologie de la 2/'-forme
définie par (24.46.8.3) est donc ivcJ<E(C)). Mais on a vu (24.43.3) que pour j=2k+1,
la classe de Chern c2k+1(E(C)) est un élément d'ordre 2 (ou est égale à 0) dans
H2(2*+1)(B; Z); son image canonique dans H2(2t+1)(B; C) est donc toujours 0.
Pour j = 2k, la classe de cohomologie ijCj(E(C)) = (— l)*c2n(E(C)) = p^E) par
définition (24.43.3).
(24.46.9) III. Calcul des classes d'Euler. —Soit E un fibre vectoriel réel orienté
de rang N ayant pour base une variété pure B. On définit comme dans (23.27.2)
une structure riemannienne sur E ; c'est par définition une section g de classe Cœ
du fibre Hom(E (g) RE, r) telle que, pour tout xeB, l'application r-bjlinéaire
(ht, h2) -*■ g(x).(hi ® h2) soit un produit scalaire euclidien sur Ex; l'existence
de telles structures se prouve comme dans (20.7.13), et on écrit (h, | h2), ou
simplement (h, | h2) le produit scalaire g(x).(h1 (g) h2) dans Ex. Si E' est un second
fibre vectoriel réel orienté de rang N et de base B, muni d'une structure
riemannienne g', un isomorphisme riemannien direct f : E -» E' est un B-isomorphisme
préservant l'orientation et tel que (/Jh^ \ /c(h2))g. = (ht | h2), quels que soient
xeB et les vecteurs hx, h2 de Ex.
Sur le fibre trivial B x rn, on définit une structure riemannienne canonique
en prenant ((x, h^Kx, h2)) = (h! | h2), où le second membre est le produit
scalaire canonique. Soit alors X0(E) la partie du fibre vectoriel
X(E) = Isom(B x rn, E)

310 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
formée des isomorphismes riemanniens directs de B x RN sur E. Ici le groupe
spécial orthogonal SO(N) opère sur X0(E) par (mj, s) -* ub°s pour tout se SO(N)
et tout isomorphisme ub de l'espace euclidien RN sur l'espace euclidien Eb
préservant l'orientation. En se ramenant au cas où E est trivial, on voit comme
dans (20.1.1) que X0(E) est un fibre principal de base B et de groupe SO(N).
Soit / : B' -+ B une application de classe C00 d'une variété pure B' dans B ;
sur E' = /*(E), on définit une structure riemannienne image réciproque par f
de celle de E en prenant la section g' de Hom(E' <g> BE', R) telle que, pour tout
x'eB'
g'(x'Uh\ (g) h'2) = g(/(x')).(/'(hi) (g) f'(h>2))
pour deux vecteurs h\, h2 de E'x-, f : E' -* E étant le morphisme canonique.
On vérifie alors comme dans (24.46.1) que l'on a
(24.46.9.1) X0(/*(E))=/*(X0(E))
à isomorphisme canonique près.
(24.46.10) L'algèbre de Lie so(N) du groupe SO(N) est la sous-algèbre de
Lie de Mm(R) formée des matrices alternées (19.4.3), l'action de SO(N) sur so(N)
étant encore
(S, X) -► SXS'1 .
Nous supposerons à partir de maintenant que le rang N est un nombre pair 2m.
On sait (Ann. 33.1) qu'on définit alors sur so(2m) un polynôme X -* Pi(X) de
degré m, invariant par SO(2m) : si X = (x^) avec xkh — — xhk, on a
(24.46.10.1) Pf(X) = E eKhxhiklxh2kl ... x„^m
(h.k)
où les couples de suites h = (hu h2, .... hj, k = (klt k2, ..., km) parcourent
l'ensemble défini par les conditions que l'ensemble {hlt kiy h2, k2, ..., hm> km}
est égal à {1, 2, ..., 2m} et que l'on a hj < kj pour 1 < j < m ; le nombre ehk
est + 1 ou — 1 suivant que la permutation de {1, 2, ..., 2m} qui applique
chaque hj sur 2j — 1 et chaque k} sur 2j est paire ou impaire.
On définit alors sur X0(E) une 1-forme de connexion ta à valeurs dans so(2m)
en prenant arbitrairement sur B m(2m — 1) 1-formes co^ à valeurs réelles pour
1 < h < k < 2m, en posant cokh = — co^ pour k < h et en « remontant » la
1-forme m = (co^) à valeurs dans so(2m) en une 1-forme tu sur le fibre principal
X0(E) au moyen d'une partition de l'unité et de repères mobiles, comme dans
(24.46.2). Posant alors
2m
&hk = dco^ + E 03hl a Oilk
1=1

46. COURBURE ET CLASSES CARACTÉRISTIQUES
311
on considère la 2m-forme sur B
(24.46.10.2) FmB(ft) = (±\ lefcjA,*, a Cl„2k2 a ... a Qhmkm
\2n/ (h.k)
qui donne donc la classe de cohomologie
(24.46.10.3) , e'2JE) = cFm(X0(E)) e H2m(B ; R).
(24.46.11) Nous allons montrer que l'on a, pour une variété pure compacte B,
(24.46.11.1) e'2m(E) = ~e(E)
où le second membre est l'image canonique dans H2m(B ; R) de la classe d'Euler
eiE) e H2m(B ; Z) du fibre vectoriel orienté E.
Or, on sait que pour toute matrice alternée X d'ordre 2m, on a
(PÎ{X))2 = det(X) (Ann. 33.3). L'homomorphisme de Weil et la comparaison
des formules (24.46.8.3) et (24.46.10.2) montrent, compte tenu de (24.46.8.4),
que l'on a, dans l'anneau H'(B; R)
(e'2m(E))2 = pm(E)
et l'on a vu (24.43.9) que l'on a pJE) = (e(E))2.
Pour prouver que e'2JE) = è(E), il suffit de le faire lorsque B = Gq+2m2m(C)
et E = U,+2lI),2in(Q« mum de l'orientation canonique. C'est en effet une
conséquence de (24.39.14), (24.46.9.1) et du raisonnement de (24.42.2), où il faut
seulement prendre pour les h} des isomorphismes de fibres vectoriels réels orientés.
Comme on peut supposer q > Am, de la relation (e2m(E) — e(E)Xe2m(E) -I- e{E))—0
dans H'(B ; R) (24.40.10, (ii)), on déduit que e2m(E) = ± e(E). Cela entraîne
alors que pour toute variété compacte pure B et tout fibre réel orienté E de base B
et de rang 2m, on a e'2m(E) = ± e(E), le signe étant indépendant du choix de B
et E. U suffit donc de déterminer ce signe sur un seul exemple. On procède comme
dans (24.46.6) : on prend B = (S2)m où S2 est orientée vers l'extérieur et on prend
sur B le produit des orientations des facteurs (16.21.5). On prend sur B la structure
riemannienne produit des structures riemanniennes des facteurs, le produit
scalaire étant donc (en identifiant E = T(B) à (T(S2))m)
((h'„ b2 | (hî, Wj, WJ) = (hi | hï) + ... + {Wm | IO.
On peut alors ne considérer que des repères orthonormaux (e,, e2, ..., e2J
sur B tels que pour 1 ^m, (e2j_1, e2J) se projette sur le y'-ème facteur de
T(B) en un repère orthonormal duy'-ème facteur S2. Si m2j-l>2j est la 1-forme de
la connexion de Levi-Civita de ce facteur, relative au repère projeté de (e2j-_ u e2j\

312 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
et co2j-i.2j son image réciproque dans B, il résulte aussitôt de (20.6.6.3) que la
1-forme à valeurs dans so(2m)
/
0
Cû12
0
0 ..
0
-col2
0
0
0 ..
0
0
0
0
W34 ..
0
0
0
0 ..
0
0
0
0
0 ..
0
0
0
0
0 ..
■ -w2m
0
0
0
0
\
w2m- 1,2m
0
est la 1-forme de la connexion de Levi-Civita relative au repère (et, e2, ..., e2m).
Si l'on pose dco2j_127- = fi2j_li2;, la 2m-forme (24.46.10.2) est donc ici
1 \m
-J Q12 a Q34 a
a n
2m- 1,2b
Mais Q2j_12j est l'image réciproque de la forme volume canonique o, duy'-ème
facteur S2 (20.10.9.7) ; on a donc
i^-(s)fl(]>)-
Comme d'autre part la classe d'Euler de T(S2) est 2e*2, où e|2 est la classe
fondamentale de cohomologie de S2, on a e(E) = 2me%, où e% est la classe fondamentale
de cohomologie de B ; on a donc bien e'2m(E) = e(E).
Ceci entraine comme corollaire :
(24.46.12) Soit B une variété riemannienne compacte, connexe et orientée, de
dimension paire 2m. Soient E le fibre tangent à B, X0(E) le fibre principal
correspondant, de groupe SO(2m) (24.46.9), SI la 2-forme sur X0(E), à valeurs dans so(2m),
qui est la forme de courbure de la connexion de Levi-Civita de B. Si FmB(ïl) est
la 2m-forme sur B définie à partir de SI par la formule (24.46.10.2), on a
(24.46.12.1) jV^ft) = m
caractéristique d'Euler-Poincaré de B {formule de Gauss-Bonnet).
C'est une conséquence de (24.39.26.2) et du fait que la classe de cohomologie
de FmB(ft) est la classe d'Euler de E.
Lorsque m = 1, FmB(12) se réduit à — u, où K est la courbure gaussienne et
2n

47. CLASSES DE STIEFEL-WHITNEY
313
v la forme volume canonique (20.10.9), d'où la formule de Gauss-Bonnet classique
pour les surfaces
a) Soient M une variété différentielle pure de dimension n, a- -> Lx un champ de/^-directions
(18.8.5) sur M qui est complètement intégrable. Les L, pour xe M sont alors les fibres d'un sous-
espace fibre vectoriel L du fibre tangent T(M) (18.8.1). Montrer qu'on peut définir une connexion
sur le fibre vectoriel quotient T(M)/L telle que, pour tout x e M, si le champ y ~> Ly est défini
au voisinage de x par un système de Pfaff coj = 0(1 ^j^,n—p), les (n — p)2 formes de connexion
correspondant à un repère mobile défini au voisinage de x (20.6.5) soient des combinaisons linéaires
des Wj. (Se ramener au cas où localement M est un produit (18.14.3)).
b) On suppose M compacte. Montrer que sous les hypothèses de a), les classes de Pontrjagin
Pj(T(M)/L) sont nulles pour k > l(n — p) (observer que les formes de courbure de la connexion
considérée dans a) appartiennent localement à l'idéal engendré par les co,) (théorème de Bott).
47. Classes de Stiefel-Whitney.
(24.47.1) Soient B une variété pure, E un espace fibre vectoriel réel de rang N
et de base B {orientable ou non). La construction de (24.41.1) peut être répétée
en changeant partout C en R et fibres vectoriels complexes en fibres vectoriels
réels ; elle associe donc canoniquement à E un espace fibre vectoriel réel Ë de
rang N - 1 et de base l'ouvert E0 de E, complémentaire de la section nulle.
On peut aussi, comme dans (24.41.2), définir É (à isomorphie près) à l'aide d'une
structure riemannienne (24.46.9) sur E.
(24.47.2) Soit alors e2{E) e HN(B ; F2) la classe d'Euler modulo 2 du fibre E
(24.39.16). On a la suite exacte de Gysin (24.39.3.1) pour A = F2
... H"(B; F2) ^ Hp+N(B; F2) ^ HP+N(E0;F2) -> HP+1(B;F2) -+ ...
qui montre que n% : HN_i(B; F2) -» HN_i(E0; F2) est un isomorphisme pour
2 ^ i ^ N (correspondant à - N < p < - 2) et est injectif pour i = 1. Pour
pouvoir transférer la définition des classes de Chern donnée dans (24.41.3),
nous avons en outre besoin du lemme suivant :
(24.47.2.1) Pour N ^ 2 la classe d'Euler e2{È)e HN_1(E0 ; F2) appartient à
l'image de H"-l{B; F2) par Ttg.
Compte tenu de la définition de l'application dans la suite exacte de
Gysin, il suffit de montrer la propriété suivante :
(24.46.12.2)
PROBLÈME
(24.47.2.2) L'image de e2(E) e HN_1i
HN-»(E0; F2) -+ HN(E
'(E,E0;F2)
(E0 ; F2) par l'application d :
est nulle.

314 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
On raisonne comme dans (24.40.14.4), en prenant un point beB et en
considérant le diagramme commutatif extrait de (24.35.9.1)
HN-i(Eo ; F2) ? ► HN(E, E0 ; F2)
(24.47.2.3) Ji Ji
hn-i(rn _ { q }. f2) hn(rn Rn _ I o } ; F2)
Supposons d'abord B connexe. Alors, dans ce diagramme, la flèche
horizontale du bas est un isomorphisme pour N ^ 2 (24.35.8.1), et il en est de même de
la seconde flèche verticale en raison de (24.39.4) et du fait que H°(B ; F2) s F2.
Il suffit donc de prouver que j*(e2(È)) = 0. Compte tenu de (24.41.4.2), qui est
valable sans modification pour les fibres vectoriels réels, et de (24.39.14), qui
est valable pour les classes d'Euler modulo 2, on voit qu'on est ramené à prouver
que e2(E) = 0 lorsque B est réduit à un seul point. On a alors E = RN, E0 = RN - {0} ;
avec les notations de (24.41.1), H = (RN — {0}) x RN, et en prenant sur RN
le produit scalaire usuel, on voit que pour tout vecteur u 6 RN - {0}, la fibre
Eu est l'hyperplan affine passant par u et orthogonal à u. Autrement dit, si
p : RN — {0} -» SN_t est la projection canonique x -» x/||x||, on a
E = p^iSfi-i)), et en utilisant de nouveau (24.39.14), il reste à voir que
^(TfSrj-,)) = 0. Mais le raisonnement de (24.43.4.4), joint aux propriétés
(24.39.13) et (24.39.15.1), valables pour les classes d'Euler modulo 2, prouve
cette relation.
Lorsque B n'est pas connexe, on répète le raisonnement précédent pour
chaque composante connexe de B.
(24.47.3) On peut maintenant procéder comme dans (24.41.3) par récurrence
sur N, pour définir les classes de Stiefel-Whitney d'un fibre vectoriel réel E de
rang N et de base B : ce sont N éléments
(24.47.3.1) w,<E) e H'(B ; F2) pour 1 < i «S N
définis comme suit. Pour i = N, w^E) est la classe d'Euler modulo 2
e2(E)eHN(B; F2). Pour 1 ^ i < N, on considère le fibre vectoriel Ê de base E0
et de rang N — 1 et on pose
(24.47.3.2) w,<E) = (k8)-1(w<(Ê)) pour 1 < i < N - 1
ce qui a un sens puisque N > 2 et qu'on a vu que 7tg est injectif et que les w^Ë)
pour 1 < i ^ N — 1 appartiennent à son image. On pose encore Wj(E) = 0
pour i > N, w0(E) = 1, et on appelle classe totale de Stiefel-rVhitney l'élément
(24.47.3.3) w(E) = 1 + Wl(E) + ... + w^E) = £ w,<E)
1 = 0
de l'algèbre H"(B ; F2).

47. CLASSES DE STIEFEL-WHITNEY
315
On a pour les classes de Stiefel-Whitney les propriétés analogues à celles
de classes de Chern :
(24.47.4) (i) Soit f : B' -» B une application de classe C00 d'une variété pure B'
dans B ; on a alors, pour 1 ^ i < N,
(24.47.4.1) /*ME)) = wrf/*(E)).
(ii) Si E, et E2 sont deux/îbrés vectoriels réels de base B oui sont B-isomorphes,
on a wiEi) = vv(E2).
(iii) Soient E', E" deux yîbr^s vectoriels réels de base B et de rang constant ;
si E" est trivialisable, on a
(24.47.4.2) w(E' © E") = w(E').
(iv) Soient B une variété pure compacte, E', E" deux fibres vectoriels réels
de base B et de rang constant ; alors
(24.47.4.3) w(E' © E") = w(E') ~ w(E").
(v) Pour le fibre canonique UP+4>P(R) de base la grassmannienne Gp+,tP(R),
on a w/Up+,iP(R)) = wj* (24.40.14). '
Les preuves de (i) et (ii) sont celles de (24.41.4) et (24.41.4.3) où on remplace
C par R ; la preuve de (iii) se déduit de même de celle de (24.42.3.2). La
démonstration de (v) se fait par récurrence sur p comme celle de (24.41.5.1) en remplaçant
(24.40.8) par (24.40.10) ; enfin, pour prouver (iv), on utilise la version de (24.42.2)
adaptée aux fibres vectoriels réels et on raisonne comme dans (24.42.3), en utilisant
(24.40.16, (ii)) au lieu de (24.40.10, (ii)).
(24.47.5) Pour tout fibre vectoriel réel E de rang constant sur une variété pure B,
les classes de Stiefel-Whitney du dual E* = Hom(E, B x R) (16.16.3) sont égales
à celles de E.
En effet, le raisonnement de (24.42.6) où on remplace la structure
hermitienne par une structure riemannienne et C par R, montre que E* est isomorphe
à E.
(24.47.6) Exemple : classes de Stiefel- Whitney du fibre tangent à p„(R). L'analogue
de (24.42.7.2) est ici la relation
(24.47.6.1) wcrip^R))) = (1 + vv1(Ull+iil(R)))B+1
dans l'algèbre h'(p„(R); f2).
La démonstration est calquée sur celle de (24.42.7), en remplaçant C par R
et le produit scalaire hermitien par le produit scalaire euclidien.

316 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
PROBLÈMES
1) Soient B une variété différentielle pure compacte, E un fibre vectoriel réel de base B et
de rang N. Montrer que s'il existe k sections de E de classe C°°, linéairement indépendantes, on a
w„(E) = 0 pour m > N — k (remarquer que E est somme directe d'un sous-fibré vectoriel de rang
N - k et d'un fibre vectoriel trivialisable).
2) Soient B une variété pure compacte, E un fibre vectoriel réel de base B et de rang N ;
comme les éléments de l'algèbre de cohomologie H'(B; F2) sont nilpotents, la classe de Stiefel-
Whitney totale vv(E) admet dans cette algèbre un inverse 1 + w,(E) + ... + w^E) + ..., où
î*i(E) e H*(B ; F2).
a) Montrer que
w.(U„i+1,1(R)) = K(U.+ 1.1(R))V
b) Si B est de dimension n et s'il existe une immersion de B dans R"+\ montrer que l'on a
w/i"(B)) = Opoury > le (considérer l'image réciproque par l'immersion considérée du fibre T(R"+*)).
c) Déduire de b) que si n = 2' et s'il existe une immersion de P„(R) dans R"+\ on a
nécessairement k > 2r — 1.
3) Montrer que l'espace projectif P„(R) ne peut être une variété parallélisable (section 16.15,
problème 1) que si n + 1 est une puissance de 2.
4) a) Montrer que pour qu'il existe dans le fibre tangent T(P«(R)) un sous-espace fibre vectoriel
de rang 1, il faut et il suffit que n soit impair.
b) Montrer que pour n = 4 ou n = 6, il n'existe pas de sous-espace fibre vectoriel de rang 2
dansT(P„(R)).
5) On pose Wj = w/Up+,>p(R)) pour 1 s£ j < p, wt = wt(Up+,„(R)) pour 1 < k < q. Montrer
que l'on a (1 + w, + ... + w„)(l + w, + ... + wq) = 1.
6) a) Étendre le résultat de (24.39.20) au cas où le fibre normal N n'est pas nécessairement
orientable, avec A = F2.
b) Déduire de a) que si une variété pure compacte B de dimension n est plongée dans R"+\
on a nécessairement M>k(T(B)) = 0. En particulier, si n = 2' et si P„(R) peut être plongé dans R"+t,
on a nécessairement k > 2' (comparer au problème 2 c)).
7) Soient E„ E2 deux fibres vectoriels réels de base une variété pure compacte B, et de rangs
respectifs m et n. Montrer que l'on a
w(E, ® E2) = P^w^E,) wJE,), w,(E2), .... w,(E2))
où P„,»(Si, ..., S„, Si, ..., Si) est un polynôme en m + n indéterminées à coefficients dans F2,
indépendant de B, Ex et E2 et caractérisé par la propriété suivante : si l'on remplace chaque S;
par la y'-ème « fonction symétrique élémentaire » de m indéterminées T, (1 sï i < m) et chaque
Si par la k-ème « fonction symétrique élémentaire » de n indéterminées T,' (1 < 1 < n), on a
m m
p„.,(s„ ..., s„, s; sy = n Ild + t, + t/)
i-i i-i
(procéder comme dans le problème 5 de la section 24.42).
8) Soient B une variété pure compacte, E un fibre vectoriel réel orientable de base B. Montrer
que w,(E) = 0. (Généraliser (24.42.2) en remplaçant Gp+tP(C) par la grassmannienne Gp+,tP(R)
des sous-espaces vectoriels orientés, et UP+,,,(C) par Up+,iP(R) (section 24.43, problème 4) ; utiliser
ensuite la section 24.40, problème S).
9) Soit E un fibre vectoriel complexe sur une variété pure compacte B. Montrer que pour
le fibre réel sous-jacent Eg on a w2J+ X(E^ = 0, et que w2J(Bm) est l'image de la classe de Chern c/E)
par l'homomorphisme canonique H2-'(B ; Z) H^B ; F2).

48. LA THÉORIE DE HODGE
317
48. La théorie de Hodge.
(24.48.1) Nous allons voir que pour une variété différentielle compacte la
cohomologie à coefficients complexes peut s'interpréter à l'aide de la théorie des
opérateurs elliptiques hermitiens sur la variété (23.35).
Soit X une variété différentielle pure compacte de dimension n > 0, et
considérons une suite finie (Ej)0$,<N d'espaces fibres vectoriels complexes de
base B. Supposons en outre donné, pour chaque indice i tel que 0 < i ^ N — 1,
un opérateur pseudo-différentiel d'ordre m > 0, dt : Ej -> Ei+1. Comme X est
compacte, les composés di+1 °dj : E,- -» Ej+2 sont définis (23.27.8). Nous
supposerons que pour 1 < i s* N - 1, on a
(24.48.1.1) diodj-^O.
Chaque opérateur dt définit une application linéaire continue (encore
notée d,) de l'espace de Fréchet r(Ef) dans l'espace de Fréchet r(Ei+i) (23.26.6),
et la condition (24.48.1) signifie encore que la suite d'espaces vectoriels complexes
et d'applications linéaires
définit sur la somme directe de ces espaces vectoriels une structure d'espace
différentiel gradué. Nous allons voir comment sous certaines hypothèses on peut
en calculer la cohomologie.
(24.48.2) Nous allons supposer en outre que chacun des opérateurs d, admet
un symbole principal at (23.29.4). Pour tout x e X et tout covecteur tangent non
nul bJeT^X)*, at{h*) est donc une application linéaire de (E,)x dans (Et+l)„
et d'après (24.48.1.1), on a oi+i(h*) ° o,{h*) = 0. Nous ferons l'hypothèse
supplémentaire que, pour tout xeX et tout covecteur tangent h* # 0, la suite
(24.48.2.1) 0 (E0)x (E,), - ... (EN_,)* (EN)X - 0
est exacte. On dit alors que la suite des d, est un complexe elliptique d'opérateurs
pseudo-différentiels d'ordre m.
Lorsque N = 1 et E0 = Ei, la notion de complexe elliptique coïncide avec
celle d'opérateur elliptique ayant un symbole principal de type bijectif (23.30.3).
L'exemple le plus important de complexe elliptique est formé par les fibres
vectoriels E, = ( /\T(X)* j , complexités des fibres vectoriels des j-covecteurs
tangents à X (17.3.1), les opérateurs ds étant d'ordre 1 et égaux à la différentielle
extérieure (0 < j < n) ; ils vérifient évidemment (17.15.2) la condition (24.48.1.1),
et on dit que la suite des d} est le complexe de de Rham de X, On a vu (23.29.10)
(24.48.1.2) r(E0) * r(E.) 4 ... r(EN_i) r(EN)

318 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
(24.48.3) Considérons un complexe elliptique (E,, d,) et munissons chacun
des E( d'une structure hermitienne (23.27.2). Prenons d'autre part sur X une
mesure lebesguienne v, de sorte que chacun des espaces vectoriels T(E,) est muni
d'une structure d'espace préhilbertien (23.27.3), partout dense dans l'espace
hilbertien fL2(E() des classes de sections de carré intégrable au-dessus de X
(23.31.1). A chacun des opérateurs pseudo-différentiels dt ; E, -» Ej+1
correspond alors son adjoint df ; E,+1 -» Eh qui est un opérateur pseudo-différentiel
d'ordre m (23.27.4), admettant un symbole principal af tel que, pour tout x e X
et tout h* ^ 0 dans TX(X)*, a*(h*), application linéaire de (Ei+1)x dans (Ej)„
soit l'adjointe de «((hj) (23.29.8). On définit alors pour 0 ^ i < N un opérateur
pseudo-différentiel d'ordre 2m de Ej dans lui-même
(24.48.3.1) Aj = d* ° dj + dj _ j ° d*_ j
qu'on appelle opérateur de Laplace-Hodge (ou laplacien de Hodge) sur Ef (on
convient que d_! = 0 et dN = 0).
Exemple (24.48.3.2). — Pour le complexe de De Rham (24.48.1), supposons X
J
orientée et munie d'une métrique riemannienne et prenons sur chaque /\T(X)*
la structure riemannienne correspondante (20.8.4.3), que l'on complexifie comme
d'ordinaire en une structure hermitienne sur Ej. Calculons explicitement A0,
qui est ici égal à d% ° d0, puisque d_t = 0. Pour deux fonctions réelles /, g de
classe C°° sur X, on a donc
(A0/1 g) = f (df I dg)v = [ (grad /1 grad g)o = j (0grad/.g)u
avec les notations de (23.30.12). Mais, pour tout champ de vecteurs Z de classe Cœ
sur X, on peut écrire
(ez.g)v = ez.(gv) - g{ez.u)
et comme d{go) = 0, on a, par (17.15.3.4)
6z.(gv) = d(iz.(gv));
que crj(h*) est l'application linéaire z* -* 2ni.h* a zJ; or, si l'on prend dans
T^X)* une base dont h* # 0 est l'un des vecteurs, et les bases correspondantes
dans les puissances extérieures (Ann. 13.3), on voit aussitôt que la relation
h* a z* — 0 pour un j-covecteur zJ équivaut à l'existence d'un (j —
l)-covecteur u* tel que z* = a u* ; cela prouve l'exactitude de la suite (24.48.2.1),
donc le complexe de de Rham est elliptique.

48. la théorie de hodge
319
mais on a j" doc = 0 pour toute (n - l)-forme a sur X (17.15.5.1) ; par suite
|(0gr.d/•£)»= - | lK<U./») = ~ f S(div(grad /))„
Jx Jx Jx
par définition de la divergence (23.30.12), d'où finalement A0 = — A, où A est
le laplacien de Beltrami (23.30.12.8).
(24.48.4) Les opérateurs A, sont elliptiques hermitiens positifs et admettent des
symboles principaux de type bijectif (23.30.3).
Comme pour toute section s e r(Ef), on a
(24.48.4.1) (A,s| $) = (d,s|d,$) + (df_l$\d*-l*)>0,
il n'y a à prouver que la dernière assertion. Pour un x e X et un covecteur
bJeT^X)* non nul, posons pour simplifier Ut = a^hj) et L7,_t = <*,_,(h*),
de sorte que le symbole principal de A, prend, pour le covecteur h*, la valeur
UfUj + Ui-iUf-x ; il suffit évidemment de prouver que cet endomorphisme
de (E,)x est injectif (Ann. 4.19) ; mais on a, pour ux e (Ej)x,
((Uf U, + U,_ ! Uf. i). ux | ux) = (17,. ux 1U,. ux) + (Ut-, • x | Vf. x. x)
et le premier membre ne peut donc être nul que si l'on a à la fois ux = 0
et Uf- !. ux = 0 ; mais la seconde relation signifie que l'on a (ux | Ut-j. vx) = 0
pour tout vecteur vx elE^L.. Or on a Ker Ut = Im [7j_i d'après (24.48.2.1),
et cela entraine (ux | ux) = 0 et finalement ux = 0.
(24.48.5) Comme X est compacte, les résultats de (23.35.2) sont applicables
à chacun des opérateurs A(. L'espace hilbertien rL2(Ej) est somme hilbertienne
de Ker Af et d'une suite infinie (Ljt'))k=li2,... de sous-espaces de dimension finie;
Ker Aj et chacun des Lx" est contenu dans r(E,), et il existe une suite strictement
croissante < A(20 < ... < A»0 < ... de nombres > 0 telle que dans chacun
des Li°, on ait Aj.i = Ax°s.
Il résulte immédiatement de la définition (24.48.3.1) de Af et des relations
djodj-, = 0 et dj*-! °dj* = 0 (qui se déduit de la précédente en passant aux
adjoints (23.27.8.1)) que l'on a
(24.48.5.1) djA, = djd(*dj = Ai+,dj, A,d* = dj*djd? = d*Aj+, .
On en déduit les résultats suivants :
(24.48.6) (i) On a Ker A, = (Ker dj) n (Ker d*_,).

320 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
(ii) Pour tout k ^ 1, Lki} est somme directe de deux sous-espaces orthogonaux
Mg> = U'> n Ker d, et N," = Lj.0 n Ker d*_ ^ dont l'un ou Vautre peut être
réduit à 0.
(iii) On a N,° ï 0 si et seulement s'il existe k' tel que Xlki.+ l)=Xki\ et alors
d,-(N«0) = M£+1) = dfiJV) et d.INjp est une similitude de rapport ± (A,0)* de
Ni0 sur Mi^1». On a * 0 si et seulement s'il existe k" tel que Xp» = Aj»
et a/ors d*_^Mj0) = Nk'~l) = df.^Lj.0), er df. 11 M,° est une similitude de rapport
±(Xki))i deMkl) surNi'-r1».
(iv) L'adhérence de Ker d, dans rL2(E,) est somme hilbertienne de Ker Af
et des M," pour k ^ 1, et l'adhérence de Im d,-! est somme hilbertienne des M£°
pour k ^ 1. L'adhérence de Ker d*_! est somme hilbertienne de Ker A( et des
Njppowr fc ^ 1, et l'adhérence de lia df est somme hilbertienne des Nj0 pour k^l.
(v) rL2(E,) est somme hilbertienne de Ker Aj; de T adhérence de Im dj_i et
de l'adhérence de Im df.
On a, pour deux sections s, s' de r(E,),
(24.48.6.1) (A($ | s') = (d(s | dfs') + {df., s | df_, s')
ce qui montre que si s6(Ker d() n (Ker df-J, on a A(s = 0; la réciproque
résulte de (24.48.4.1). Supposons que Mj° soit distinct de L," et soit Ni(0 le
supplémentaire orthogonal de M£° dans LJ.0 ; la restriction de d, à Ni(() est donc injective
et di(N£w) = di(U"). Pour tout seN«(,), on a A,s = Ajps, donc d'après (24.48.5.1),
Ai+1(dj$) = A£.°djS, et comme par hypothèse d,s # 0 pour $#0 dans Ni(i),
cela n'est possible que si d,(Ni(i)) est contenu dans un des sous-espaces
propres L#+ " et si Ai'.+1) = 4° (Ann. 32.7). Pour toute s'e 1), on a alors, d'après
(24.48.5.1) A,{dfs') = X^dfs', donc d*(l#+l)) c L.0. En particulier, pour s e N?",
on a di(dfdiS - Xkl)s) = 0, autrement dit
(24.48.6.2) dfd.s = A,"s -I- s"
où s" 6 Mj.°. Mais pour toute s'e L#+ n et toute s" e M[°, on a
(dfs'|s") = ($'|djs") = 0,
donc d*(L#+1)) c N?'»; en outre, il résulte de (24.48.6.2) que dfdiS = Af's, donc
N£(i) = d*(Lj.'+1)) et la restriction de df à dj(N£(i)) est une bijection de ce sous-
espace sur N£(0. D'autre part, cela entraîne que N£(i) est contenu dans Ker df. u
et comme (Ker df. t) n Mj." = 0 d'après (i), on a nécessairement Wkw = Nj.".
Si s, s' sont dans N»°, la relation (24.48.6.1) montre que
4i)(«|s') = W$|dis')
ce qui montre que la restriction de dt à N," est une similitude de rapport ± (A,0)*
sur son image.

48. LA THÉORIE DE HODGE
321
On prouve de la même façon que si Ni" est distinct de LJ.'1, Mk° est le
supplémentaire orthogonal de Ni0 dans U°, que d*_ i(M,0) = df_ ^U0) est contenu
dans un des sous-espaces Lp1}, ce qui entraine Xp » = A»0, et d,_ xd*_, s = XK()s
pour t e Mi°, la restriction de d*_ x à MK° étant une similitude de rapport ±
sur son image. Les autres assertions de (24.48.6) découlent aussitôt de là.
(24.48.7) Désignons par Pt le projecteur orthogonal de rL2(Ej) sur son sous-
espace Ker Aj de dimension finie ; c'est un opérateur intégral (sections 23.3
et 23.4) dont le noyau est la section de E- [x] E,
(24.48.7.1) h, = £ (»v "j) 13 U,
où (Uj)iijini est une base orthonormale de Ker A,- (notations de 23.35.6). Il
est clair que Ht est une section de classe C00, et par suite P( est un opérateur
régularisant de E, dans lui-même (23.28.11).
(24.48.8) // existe pour chaque i e [0, N ] un opérateur linéaire continu
Qf:r(Ei+1) - r(E;)
pour les topologies d'espaces de Fréchet (avec Q-t = 0 et QN = 0) tel que
l'application identique dans l'espace r(E() s'écrive
(24.48.8.1) lr(Ei, = Pi + d,_ lQi-, + QA .
Avec les notations de (24.48.6), on définit un opérateur continu Gt de rL2(Ef)
dans lui-même en prenant Gj égal à 0 dans Ker A,, et à l'homothétie de
rapport (A,0)-1 dans chaque L«° (k > 1); cela résulte de (15.10.8.1). Si (un°) est une
base hilbertienne de rL2(E,) réunion de bases hilbertiennes de Ker A, et des L,1',
et si les unl) pour n ^ nt forment la base de Ker Aj, on peut écrire de façon
équivalente
(24.48.8.2) Gj.s = I -L (s | u<")u<"
»>»- hn
où (/iR°) est la suite des valeurs propres (i. e. Ajiij,0 = u^u^) de A{. Il résulte du
fait que la suite (pB°) tend vers + oo et de (23.35.12, (iv)) que si $ e r(Ej), on a
aussi Gj.sefXEj); de la continuité de Gf pour la topologie de f^E,) et de
(23.9.2.2), il résulte donc que G, est un endomorphisme continu de l'espace de
Fréchet r(E(). Nous allons voir que l'opérateur continu
(24.48.8.3) Qt = Gfdf
répond à la question. Comme la somme directe de Ker Aj et des LK° est dense
dans T(Ej) (2335.12, (v)), il suffit par continuité de vérifier que les deux membres

322 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
de (24.48.8.1) prennent la même valeur dans Ker A, et dans chacun des Lj'1.
La vérification est immédiate dans Ker A{, puisqu'alors P(.s = s, d,s = 0 et
df-ls = 0. Dans Lk'\ on a Pt.s = 0; si ssMf, on a d,s = 0 et on a vu dans
la preuve de (24.48.6) que d£_ ,df_ t s = 4°*; en outre, si s # 0, on a vu que
df-iSeLp» avec 4-r1' = 4"> donc on a bien dj-^ôf-!. s) = s. Enfin, si
seNjp, on a df_is = 0 et d*d,s = 4°s, donc Q,.(d,i) = s. CQFD.
Si, pour l'espace différentiel gradué (24.48.1.2), on pose Z(Ef) = Ker d„
B(E,) = Im dj-j et H(E.) = Z(Ej)/B(Ei), on a Ker A, <= Z(E,) et le résultat de
(24.48.8) entraîne comme corollaire :
(24.48.9) (théorème de Hodge) L'application canonique Ker A, -» H(E,) est
bijective, et H(E,) est donc de dimension finie.
(24.48.10) Pour le complexe de De Rham (24.48.2), où l'on prend sur les
(f\T(X)* J les structures hermitiennes déduites d'une même métrique rieman-
V /(c)
nienne sur X (20.8.4.3), les y-formes différentielles vérifiant A/x = 0 sont appelées
les j-formes harmoniques (et pour j = 0, les fonctions harmoniques) sur la variété
riemannienne X. On a alors, par définition (24.1.1), H(E;) = Hj(X ; C); l'espace
Ker Aj des y-formes harmoniques se note aussi HJ(X), et le théorème de Hodge
montre que l'application canonique H\X) -* H\X ; C) est bijective, ce qui
signifie encore que dans toute classe de cohomologie des j-formes sur X, il existe
une et une seule j-forme harmonique (dépendant naturellement de la métrique
riemannienne choisie sur X). On notera que cela donne une autre preuve du fait
que pour une variété compacte X, les espaces de cohomologie H^X) sont de
dimension finie (24.6.4). Inversement, comme on sait que si X est connexe H°(X)
est formé des fonctions constantes (24.1.2), on voit que sur une variété
riemannienne compacte et connexe, les seules fonctions harmoniques sont les constantes,
ce qui résulte aussi du principe du maximum (23.61.2).
49. La formule d'Atiyah-Bott-Lefschetz.
(24.49.1) Soient E, F deux fibres vectoriels complexes ayant une même base X
de dimension n. Un morphisme (f, g) de E dans F, où / n'est pas bijective, ne
permet pas en général de faire correspondre à une section de E une section de F.
Par contre, supposons qu'on se soit donné une application / : X -> X de
classe C°° et un X-morphisme (1, M) de l'image réciproque /*(E) dans F. Alors,
à toute section s de E au-dessus de X on peut d'abord faire correspondre la
section image réciproque /*($) : x -*■ (x, $(/(*))) de /*(E), puis la section
y($) : x -> M(x).[f*(s)(x)) de F. Il est clair que si s est de classe C", il en est
de même de y(s) ; nous dirons que l'application C-linéaire y : T(E) -» T(F)
est l'homomorphisme défini par le couple (y^ M). Il résulte de (17.1.5) que cet

49. LA FORMULE D'ATIYAH-BOTT-LEFSCHETZ
323
homomorphisme est continu pour les topologies d'espace de Fréchet de T(E)
et T(F).
(24.49.2) Considérons maintenant d'une part une application / : X -♦ X de
classe C00, et de l'autre un complexe elliptique (Ej, dj)0^n de fibres vectoriels
complexes de base X (24.48.2), les d, étant ici des opérateurs différentiels de même
ordre m > 1. Supposons donné, pour tout ie [0, N], un X-morphisme
Mr.flfid - e,,
et soit ft : r(E,) -♦ r(Ef) l'endomorphisme d'espace vectoriel défini par le
couple (/, Mt). On dit que la famille (y,)0«i«n est 1111 endomorphisme géométrique
du complexe elliptique (Ej, dt) si le diagramme
r(E0) 4 r(Et) ^ ... - rfjEN-j r(EN)
70 71 | 7n-
r(E0) To r(Et) Ti ... - r(EN_t) ^ r(EN)
est commutatif, c'est-à-dire si
(24.49.2.1) d,_, o yi_ j = yf o ^_, pour 1 < i < N .
Il résulte aussitôt de ces relations que l'on a, avec les notations de (24.48.8),
Vj(Z(Ej)) c Z(E,) et y,-(B(Ei)) <= B(E,), donc, par passage aux quotients, on déduit
de yt un endomorphisme
(24.49.2.2) y? : H(E.) -» H(E<)
de l'espace de dimension /mie H(Ef). La trace de cet endomorphisme est donc
définie; on appelle nombre de Lefschetz de l'endomorphisme géométrique (y,)
le nombre
(24.49.2.3) U(yà) = i (- 1)' Tr(y?)
i = 0
et il s'agit d'évaluer ce nombre moyennant certaines hypothèses sur
l'application / et les morphismes M(. On notera que lorsque / et les Ms sont les
applications identiques, les yt sont les applications identiques, et le nombre de Lefschetz
s'écrit
(24.49.2.4) Xm) = i (- 1)' dim(H(E()) ;
i = 0
lorsque (Ej, dt) est le complexe de de Rham (24.48.2), ce nombre n'est autre que
la caractéristique d'Euler-Poincaré de X (24.1.1); aussi dit-on en général que
X((E,)) est la caractéristique d'Euler-Poincaré du complexe elliptique (E,, dj).

324 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
Lorsque N = 1, E0 = Et = E, de sorte qu'il ne s'agit que d'un seul opérateur
elliptique P : E -» E ayant un symbole de type bijectif, la caractéristique d'Euler-
Poincaré s'écrit
ind(P) = dim Ker P — dim Ker P*
et s'appelle Vindice de P.
(24.49.3) Les notations étant celles de la section (24.48), considérons pour
chaque ie [0, N], la base orthonormale {uf)iiJint de Ker(A,). Il résulte de
(24.48.8.1) et de (24.49.2.1) que l'on a
(24.49.3.1) yt{uf) - PMu^emù pour K/^n,
puisque dtuf = 0. Si cl(u) désigne la classe de ueKer(À,) dans l'espace H(Ef),
on peut donc écrire
(24.49.3.2) yf(cl«)) = t (vM0) I «i0) cl«'>)
k= 1
et comme les classes des uf forment une base de H(E,), on a l'expression de
la trace de yf
(24.49.3.3) Tr(y*) = f (y,<uf) | uf)
k=l
qui va nous servir à évaluer le nombre de Lefschetz. Si y\ est la restriction de y{
au sous-espace Ker At de dimension finie, la formule précédente s'écrit aussi
(24.49.3.4) Tr(y*) = Tr(Pf o y<) = Tr(y,. o Pt)
ce qui a un sens, puisque yt ° Pt est un endomorphisme de rang fini (donc somme
d'un nombre fini d'endomorphismes de rang 1) de l'espace vectoriel r(Ef) (cf.
(22.9.4), note de bas de page).
(24.49.4) Nous allons approcher l'opérateur de projection Pt par un opérateur
régularisant dépendant d'un paramètre réel, à l'aide de la théorie des équations
paraboliques (23.64). Nous considérons l'équation d'évolution pour les
sections de Ej
ds
(24.49.4.1) — + AjS = 0
à laquelle on peut appliquer la théorie de (23.64), car on a vu dans (24.48.4)
que le symbole principal de A( a toutes ses valeurs propres réelles et > 0, d'où
notre assertion (23.63.3). Pour toute section v e r(E(), il existe une section continue
et une seule (t, x) -*■ s(t, jc) de [0, + oo[x Ef au-dessus de [0, +oo[x X, de

49. la formule d'atiyah-bott-lefschetz 325
classe C°° dans ]0, + oo [ x X, vérifiant (24.49.4.1) pour t > 0 et se réduisant
à v pour t = 0. Pour t > 0, on peut écrire
(24.49.4.2) «t, x) = [Ut)- vX*)
où K,{t) est un opérateur régularisant de E, dans lui-même ; et pour tout t > 0,
on a
(24.49.4.3) s(t, x) = £ exp( - uft) (v | u<'K>
n
(notations de (24.48.8)), où la série est absolument convergente et convergente
dans l'espace de Fréchet r(E() pour t ^ 0 (23.35.12).
(24.49.5) Si l'on désigne par v0 la projection orthogonale de v sur Ker à.h
par vk sa projection orthogonale sur L,0 (notation de (24.48.5)), la relation
(24.49.4.3) s'écrit encore
*(',*)= Z exp(-Aj^v.
Jk»0
en convenant que A50 = 0. On a donc P(. f(t, x) = v0, ce qui s'écrit aussi
(24.49.5.1) K,{t) o P, = P, (0 < i ^ N)
pour tout t > 0. D'autre part, comme d, est une application continue de r(E,)
dans r(Ei+i), on a, compte tenu de (24.48.6),
d,Wt,x))= Z expC-Ar^K-v*
ce qui, pour t > 0, s'écrit encore
(24.49.5.2) d, » K,(t) = Ki+1(t) o dt (0 < f < N - 1).
Posons, pour 0 ^ i ^ N — 1 et pour t > 0
(24.49.5.3) Sj(t) = K1<t)o(2J
qui est un opérateur régularisant de r(Ej+i) dans r(E(). En effet, compte tenu
de la définition (24.48.8.3) de Qb et de (23.27.8), il suffit de montrer que K,(t) ° Gt
est un opérateur régularisant de r(Ef) dans lui-même. Or, Gt est égal à son adjoint,
et G, o (Kj(t))* est régularisant en vertu du critère (23.28.10) et de la continuité
de G, ; donc K,{t) o G, est aussi régularisant.
On déduit alors de (24.48.8.1), (24.49.5.1) et (24.49.5.2) que l'on peut écrire,
pour t > 0,
(24.49.5.4) Pj = K^t) - d(_ 1Si_ ,(t) - S£t)di

326 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
et par suite, en raison de (24.49.2.1)
y, o Pf = y. o Kit) - d,_ ifo. ! o $,-&)) - (y, o S,{t))di.
Le critère (23.28.10) montre que les opérateurs y( ° S,<t) sont régularisants. On
peut donc (23.4.11) prendre les traces des opérateurs des deux membres de
l'équation précédente, et compte tenu de la relation (23.28.13.1), il vient
(24.49.5.5) Tr(y, ° P,) = T^y, o K#)) - Ti(d,_ ,(y,_ t o Sf_ ,(t)))-Tr(d,<y,- » S# )))
et en utilisant (24.49.3.4), on obtient pour expression du nombre de Lefschetz
(24.49.5.6) U(yd) = I (- 1)' Tifa o
les autres termes des seconds membres de (24.49.5.5) pour 0 ^ i < N se
détruisant deux à deux. Le second membre de (24.49.5.6) est donc indépendant de t>0.
(24.49.6) Lorsque N = 1, E0 = Et = Eet que y0 et Vi sont l'identité, P : E -» E
étant un opérateur différentiel elliptique d'ordre m > 1, on a À0 = P*P et
At = PP*. Si u e T(E) est une fonction propre de A0 correspondant à une valeur
propre p / 0, on a (PP*)P. u = P .(pu) = uP. u, autrement dit (comme P. u # 0
puisque P*P. u = pu ^ 0) P. u est fonction propre de PP* pour la même valeur
propre. On peut échanger dans cette remarque les rôles de P et P* ; si on observe
en outre que pour tout v6 T(E), on a (P. u | P. v) = (P*P. u | v) = p(u | v), on
voit que dans les décompositions en somme hilbertienne de rL2(E)
Ker A0 © 0 Vk0), Ker Ax © © L,1»
on a Ker A0 = Ker P, Ker At = Ker P*, et P(Vk0)) = L»1', P*(Li1') = U°> pour
tout /c ^ 1. On sait (23.64.4.4) que pour les deux opérateurs régularisants K0(t)
et Ki(t), on a, pour t > 0 voisin de 0, des développements asymptotiques
Tr(K0(t)) ~ a.nrni2m + a.n+lrln-l)l2m+... +a0 + ai'1/2m+ •. •
TrtKjtt)) ~ b.nrni2m+b-n+lr^-l)i2m+... +b0+b1tll2m+ ...
Comme Tr(K0(t)) — TiiKt(t)) doit être indépendant de t, on a nécessairement
Oj = bj pour j 0, et par suite
(24.49.6.1) ind(P) = a0 - b0 .
Cette formule sert de point de départ au calcul de l'indice de P au moyen
de la formule d'Atiyah-Singer [206].
(24.49.7) Nous allons maintenant particulariser les endomorphismes yt. En
premier lieu, nous supposerons que l'ensemble Fïx(/) des points x e X tels que

49. LA FORMULE D'ATIYAH-BOTT-LEFSCHETZ
327
f(x) = x est fini. Pour un point aeFix(/), l'application linéaire tangente Ta(/)
est un endomorphisme de l'espace tangent Ta(X) ; nous supposerons que pour
tout a e Fix(/) cet endomorphisme n'a aucune valeur propre égale à 1 ; il revient
au même de dire que
(24.49.7.1) det(/„ - Ta(/)) # 0 pour tout a e Fix(/),
ou /„ est l'identité dans T^X).
Dans ces conditions, nous allons calculer explicitement chacun des termes
Trfj, ° K,{t)) pour t > 0, puis nous ferons tendre t vers 0 dans la formule (24.49.5.6)
pour obtenir le nombre de Lefschetz en fonction des y,.
(24.49.8) Ce calcul va utiliser un recouvrement ouvert assez fin de X permettant
de calculer la section noyau correspondant à K&t) suivant la méthode donnée
dans (23.63). On part tout d'abord d'un recouvrement ouvert fini (WA) de X
formé de domaines de cartes de X et tel que WA u Wu soit trivialisant pour Et
pour tout couple (A, u) (23.3.2). Soient a,, a2, ..., a, les points de Fix(/); si a>
est contenu dans un W2 et si (WA, tpx, n) est une carte telle que <px{aj) — 0. ii
existe un voisinage ouvert Wj[ <= W2 de a, tel que /(Wj) c W2; en raison de
l'hypothèse (24.49.7.1) et du théorème des fonctions implicites, il existe une
boule ouverte B7 <= R" de centre 0 et de rayon assez petit, et une application
de classe C°°, z' -» ujz') de B; dans cpx(W'x) telle que
(24.49.8.1) uj(z') - tpx(f(<pl l(Uj(ï)))) = z'
pour z' e Bj ; on a uj(0) = 0, u} est injective et u/(Bj) est un voisinage de 0 dans R".
On peut en outre supposer les Bj assez petites pour que les ouverts UJ^ïHm/Bj))
dans X soient deux à deux sans point commun (1 < j! ^ r).
(24.49.9) Pour la construction du recouvrement ouvert de X dont nous avons
besoin, on peut supposer que l'ensemble des indices a des ouverts Ua de ce
recouvrement est un intervalle de N d'origine 1. On fixe d'abord les ouverts Lf, pour
1 ^ j < r : on les prend tels que <px(\Jj) soit une boule ouverte de centre 0 contenue
dans Uj(Bj), puis on prend pour la carte ^ un multiple scalaire de la
restriction cox|U, tel que ^(Uf) contienne la boule fermée B'(0; 1); on pose comme
dans (23.63.5) V, = ^_1(B(°; ^) et on Pose WJ = ^_1(B(0; J)) ' Si d CSt
une distance définissant la topologie de X, il existe par définition un nombre p>0
r
tel que l'on ait d(x, f{x)) > p pour tout xeX - U V- ; on prend alors les Ua
pour a > r + 1 contenus dans X - U Vj, de diamètre < p et formant un recou-
j
vrement de X — [j Vj. Les cartes ^„ et les ouverts V, pour a ^ r + 1 se définissent
j
alors comme dans (23.633) (par application de (12.6.2)).

328 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
(24.49.10) Notons £,{t) l'opérateur de E( dans lui-même correspondant à
l'opérateur Af et au recouvrement (UJ comme l'opérateur £(t) défini dans
(23.63.5.3) correspond à l'opérateur — Q. Remarquons d'abord que pour
calculer Trtjj o Kfa)) (qui est indépendant de t > 0), il suffit de calculer Tr(y, ° Efa))
et de prendre sa limite pour t tendant vers 0. Cela résulte du fait que, dans la
formule (23.64.1.1), la section noyau correspondant à l'opérateur K(t) — E(t)
tend uniformément vers 0 lorsque t tend vers 0 : on l'a vu en effet dans (23.63.11, C))
et dans la démonstration de (23.64.2).
(24.49.11) Pour poursuivre le calcul, il faut d'abord, pour un opérateur
régularisant L de Ej dans lui-même, défini par une section noyau (y, x) -» L(y, x)
appartenant à T(E' [x] E,), expliciter la section noyau définissant l'opérateur
régularisant yt ° L. Notons pour cela qu'on a en premier lieu une application
1 x / de classe Cœ de X x X dans lui-même, et que l'on peut donc considérer
le fibre vectoriel image réciproque (1 x f)*{E\ |x] E,) = EJ [x| /*(E.) de base X x X.
En second lieu, le X-morphisme (1, Mt) de f*(Et) dans E,- définit canoniquement
un (X x X)-morphisme (1, / 0 M;) de E| fxj /*(E() dans E{ S E, ((16.16.1) et
(16.19.1)). Alors (24.49.1) le couple (1 x / / [x] Mt) définit une application
C-linéaire y, : T(EJ SE,) -+ T(E| S E,), et la section noyau définissant ytoL
est égale a y,{L). Il suffit en effet (23.4.8) de le vérifier lorsque la section noyau L
a la forme particulière (23.4.7.1), et c'est alors une conséquence immédiate des
définitions.
(24.49.12) Pour calculer Tifj,- ° £,•(£)), on commence par décomposer
l'opérateur £,{t) selon le recouvrement (UJ par la formule (23.63.5.2) correspondante
pour les sections noyaux
(24.49.12.1) Ej(t, x, y) = IE Jt, x, y),
a
et on est ramené à calculer chacun des nombres Tr(y; o £ Jt)). Mais pour tous
les a ^ r + 1, ces nombres sont nuls. En effet, en raison du choix des U„ pour
a 2* r + 1 (24.49.9), pour tout x e Ua, on a f(x) e U., donc (23.63.5.1) la section
(1 x /)*(Eja) de E'i [x] /*(Ef) est nulle, ce qui prouve notre assertion.
(24.49.13) Reste donc le calcul de chacun des nombres Tr(yjo£Jt)) pour
Uj<r. L'expression locale fj de / pour la carte fibrée correspondant à la
carte xfij est une application de classe C00 de B(0 ; 1) dans R", telle que //(O) = 0 ;
en outre, en vertu du choix de Uj (24.49.8), x' -* x' — //(x') est un
difféomorphisme de B(0; 1) sur un ouvert de R". D'autre part l'expression locale du
X-morphisme M, est une application x' -> Mj/x') de B(0 ; 1) dans MJC), de

49. LA FORMULE D'ATIYAH-BOTT-LEFSCHETZ
329
classe C00. Il résulte alors de (24.49.11) et de (23.63.5.1) que l'expression locale
de la section noyau y^jEtj) définissant l'opérateur y, o E^t) est
(t, x', y') - g(x', y')M|/x^£exp(to,.(y', + 2ni(ff(x') - y' | £)/N)dÉ
où g est une fonction de ®(R2n) telle que g(0, 0) = 1 et dont le support est contenu
dans B(0 ; 1) x B{0 ; 1), et a/y', Ç) est une matrice d'ordre N vérifiant les
conditions de (23.62.4).
Cela étant, il résulte de (23.4.11) que l'on a
= f dx'ï rI(x')Tr(M;j(x').exp(taJ.(x', Ç) + 2niifj'(x') - x' | £)/NM
Jan Jh"
où ri(x') = g(x', x') a son support dans B(0 ; 1) ; on peut par suite étendre la
première intégrale à R" tout entier. Soit V l'image de B(0 ; 1) par le
difféomorphisme x' -» x' - //(x'), et soit z' -» Vj(z') le difféomorphisme réciproque.
Comme z' -» h(vj(z')) est de classe Cœ et a son support dans V, on peut la
prolonger par 0 hors de V, et en appliquant la formule du changement de variables
(16.22.1.1), écrire
Ti(y(o£y(t))
= L^'L'l(t''(Z')) 'J(Z) ' Tr(M'A(*0)-exp(fo>j(z'), 0 - 2**1' | £)/NM
où J(z') est le jacobien de v}- au point z'. Comme z' -» h(Vj(z')) est une fonction
à support compact, le raisonnement fait pour l'intégrale (23.62.10.8) s'applique
à l'intégrale intérieure dans la formule précédente, et montre que cette intégrale
tend vers la transformée de F ourler de la fonction z' -* h(Vj(z')) | J(z') | Trf.My^fz')))
dans l'espace Sf(R") lorsque t tend vers 0. La formule de réciprocité de Fourier
montre donc que l'on a
lim Tr(7i o £y(0) = A(0) | J(0) | Tr(MÎ/0)).
Mais /i(0) = 1, J(0) est l'inverse du jacobien de x' -* x' — //(x') au point x' = 0,
et comme fj'(0) = 0, ce dernier est égal à det(J„ — Taj(f)). Enfin, la fibre de /*(E.)
au point a} s'identifie à celle de E, puisque f(aj) = aj, et M fa) est donc un
endomorphisme de cette fibre, donc Tr(My(0)) = Tr(M fa)). On obtient donc
finalement le théorème suivant :
(24.49.13) L'application f :X -* X et les X-morphismes M{ : /*(E() -» E(

330 XXIV. TOPOLOGIE ALGÉBRIQUE BT DIFFÉRENTIELLE ÉLÉMENTAIRES
étant supposés satisfaire à la relation de commutation (24.49.2.1) et aux
hypothèses de (24.49.7), on a
(24.49.13.1) L((y,.)) = £ £ ( - 1)' Tr(Mj(a)) | det(/„ - TJJ)) \ ~1
i = 0 aeFixf/)
(formule d'Atiyah-Bott).
(24.49.14) Considérons en particulier le cas où (Ej, df) est le complexe de
de Rham (24.48.2) ; pour chaque indice i tel que 0 ^ i < n, il correspond alors
canoniquement à toute application / : X X de classe C00, un X-morphisme
M( : /*(Ej) -* E( tel que, pour chaque xeX, (Mt)x soit l'application linéaire
composée
i
(24.49.14.1) {f*(Et))x =» {Edm » (E,)x
où vx est l'application canonique de (16.12.8, (ii)) (cf. (16.20.7)). L'endomorphisme
y, : r(E.) -► T(Ej) défini par le couple (/, M,) (24.49.2) n'est donc autre que
l'application a '/(a) définie dans (16.20.9) et (16.20.15) ; la relation de
commutativité (24.49.2.1) pour les yt est alors conséquence immédiate de la relation
d('u(a)) = 'M(da) de (17.15.3.2). En outre, comme H(E.) = H'(X ; C),
l'endomorphisme yf n'est autre que l'endomorphisme H'(/) défini dans (24.1.3).
D'autre part, si a e Fix(/) et si l'on pose A = Ta(f), endomorphisme de T^X),
on a
TiMfl)) = Tr^ÂCTi/)) ® lc) = Tr(ÀW))
d'après (24.49.14.1). On est donc amené, dans la formule d'Atiyah-Bott, à évaluer
l'expression £ (— l)'Tr^A(^))- Mais, pour tout teR, on a
n /n-k \
(24.49.14.2) det(t/„ + A) = I **Tr ( A (A) J
car (en identifiant A avec sa matrice par rapport à une base de T^X)) il est
immédiat que le coefficient de t* au second membre est la somme des mineurs
principaux AHH, où H parcourt l'ensemble des parties de n—k éléments de {1,2,...,«};
i
la formule (24.49.14.2) résulte donc de l'expression de la matrice /\(A) donnée
dans (Ann. 13.4.1). Faisant t = - 1 dans (24.49.14.2), on déduit donc de la
formule d'Atiyah-Bott que :
(24.49.15) Soif / : X -* X une application de classe C00 telle que Fix(/) soit

50. APPLICATIONS : I. FORMULES DE HOPF
331
fini et que pour tout a e Fix(/), le déterminant det(In — Ta(f)) soit non nul. Alors
on a
(24.49.15.1) t (- l)'Tr(H'(/)) = £ sgn(det(/„ - Uf)))
1 = 0 aeFix(/)
(formule de Lefschetz).
50. Applications : I. Formule de Hopf pour les champs de vecteurs.
(24.50.1) Soient M une variété différentielle pure compacte de dimension n,
et soit X un champ de vecteurs sur M de classe C°°. Un point a e M tel que X(a)=0
est appelé point critique de X. Considérons en un tel point a l'expression locale
de X pour une carte locale de M au point a appliquant a sur 0 e R" ; elle est de
la forme y -» (y, G(y)), où y e V, voisinage ouvert de 0, et y -* G(y) est une
application de classe C00 de V dans R" ; l'hypothèse que a est point critique signifie
que G(0) = 0. On dit que a est un point critique non dégénéré si la dérivée DG(0)
est une matrice inversible dans M„(R). Cette notion ne dépend pas de la carte
locale choisie : en effet, si y -» (y, G,(y)) est l'expression locale de X pour une
autre carte locale au point a, on a G,(y) = 4(y).G(y), où y -* .4(y) est une
application de classe C°° d'un voisinage de 0 dans le groupe GL(n, R) des matrices
inversibles (16.15.4). Par suite la dérivée de G, est
h -» (D>l(y).h).G(y)-f-/l(y).(DG(y).h),
donc DGx(0) = /4(0)oDG(0), ce qui prouve notre assertion.
Il résulte du théorème des fonctions implicites que si a est un point critique
non dégénéré de X, alors, avec les notations précédentes, G est un
difféomorphisme d'un voisinage de 0 dans R" sur un voisinage de 0 dans R", et par suite a
est isolé dans l'ensemble des points critiques.
(24.50.2) Supposons maintenant la variété M orientée ; alors, si a est un point
critique non dégénéré de X et si l'on n'utilise que des cartes locales au point a
qui préservent l'orientation (R" étant canoniquement orienté), le signe de
det(DG(0)) dans (24.50.1) ne dépend pas de la carte locale choisie : en effet, avec
les mêmes notations, on a dettDG^O)) = det(/l(0))det(DG(0)), et det(4(0)) > 0
en vertu de (16.21.3), d'où notre assertion. On peut donc définir Yindice j(a)
de X au point critique non dégénéré a par la formule
(24.50.2.1) j(a) = sgn(det(DG(0)))
pour une carte locale quelconque de M au point a. Si l'on remplace
l'orientation de M par l'orientation opposée, j(a) est multiplié par (— 1)".

332 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
Avec ces notations, on a le théorème suivant :
(24.50.3) Soit M une variété différentielle pure compacte orientée de
dimension n, et soit X un champ de vecteurs sur M de classe C00, n'admettant que des
points critiques non dégénérés (nécessairement en nombre fini) au a2, ...,ar.
Alors on a
(24.50.3.1) tK) + Âa2) + ■■■+ yR) = (- l)"x(M)
(formule de H. Hopf J. (Si n est impair on a jj(M) = 0 (24.6.8), donc on peut
supprimer le facteur ( — 1Y1 dans le second membre de (24.50.3.1)).
Pour cela, considérons la coulée (x, t) -* Fx(x, 0 du champ X (18.2.2),
qui ici est définie dans M x R tout entier (18.2.11), et posons g,{x) = F^fx, t)
pour t > 0. Nous allons voir que (24.50.3) se ramène à l'application de la formule
de Lefschetz (24.49.15.1) pour t > 0 assez voisin de 0 ; cela résultera du lemme
suivant :
(24.50.3.2) // existe un nombre a > 0 tel que pour 0 < t < a, les seuls points
fixes de l'application g, soient les points critiques aua2 ar et que Von ait
às\(lB — Taj(g,)) # 0 en chacun de ces points.
Supposons en effet ce lemme établi. Il est clair que (x, s) -* Fx(x, s) pour
0 < s < t est une homotopie de l'application identique 1M à g, ; donc (24.2.5)
les endomorphismes H'(gt) sont les applications identiques, et le premier membre
de (24.49.15.1) appliqué à g, est par suite la caractéristique d'Euler-Poincaré x(M).
D'autre part, en prenant une carte locale de M en un point ak, l'expression locale
deTait(g,)est
(24.50.3.3) I„ + tDG(0) + tW(t)
d'après (18.2.14.4), W(t) étant une matrice qui tend vers 0 lorsque t tend vers 0 ;
le signe de det(/,, — Taj{g,)) est donc celui de ( — 1)" det(DG(0)) dès que f est assez
petit, autrement dit il est égal à (— l)"j(ak); le second membre de (24.49.15.1)
est par suite égal à (- l)"(j(ai) + ... +Mr)\ ce qui achève de prouver la
formule de H. Hopf.
Reste donc à établir le lemme (24.50.3.2). Raisonnons par l'absurde, en
supposant qu'il existe une suite (tk) de nombres > 0 tendant vers 0 et une suite (xk)
de points de M distincts des points critiques, tels que F^x*, £*) = xk ; par
compacité, on peut supposer que la suite (xk) a une limite a e M. Montrons d'abord
que a est nécessairement un point critique de X ; en effet on a aussi Fx(xk, mktk)=xk
pour toute suite d'entiers (mk), par (18.2.3.2). Comme on peut choisir les mk de
façon que la suite (mktk) tende vers n'importe quel nombre réel, on a Fx(a, t) = a
pour tout t e R, ce qui signifie que X(a) = 0. Supposons donc que a — ; notons

51. APPLICATIONS : II. FORMULES DE BOTT
333
alors que par définition l'application linéaire tangente TXk(Fx(., mktk)) laisse
invariant le vecteur X{xk) # 0, autrement dit a une valeur propre égale à 1. Par
passage à la limite il en est donc de même de Tttj(gt) pour tout t > 0 ; mais d'après
l'expression locale (24.50.3.3), cela entraînerait det(DG(0)) = 0, contrairement
à l'hypothèse. La même expression locale montre que det(J„ — Taj(g,)) ^ 0
pour t assez voisin de 0.
Remarque (24.50.4). — La formule de Hopf montre que les seules variétés
compactes pures orientées M sur lesquelles il peut exister des champs de vecteurs
sans point critique sont celles pour lesquelles x(M) = 0.
51. Applications : II. Formules de Bott pour les classes caractéristiques.
(24.51.1) Soit M une variété pure compacte de dimension n, C une connexion
linéaire sur M (17.18.1). Soit d'autre part X un champ de vecteurs de classe C00
sur M ; la coulée (x, t) -* Fx(x, t) de ce champ est alors définie dans M x R
tout entier (18.2.11), et pour tout teR, h, : x -* Fx(x, t) est un difféomorphisme
de M sur elle-même, tel que = h, ° ht. = ht. ° h, (18.2.11). Nous dirons que
le champ X est un automorphisme infinitésimal de la connexion C si les difféo-
morphismes h, laissent C invariante.
(24.51.2) Soient X un automorphisme infinitésimal de la connexion C. Pour tout
champ de vecteurs Y sur X de classe Cœ, on a
(24.51.2.1) 0xoVv- VrofJx = V[X,n.
Pour tout champ de vecteurs Z de classe C°° sur M, posons
Z,(x) = Thtah-,).Ah,{x))
de sorte que l'on a (18.2.14.2)
(24.51.2.2) (0x.Z)(x) = jt (Z,(x))(=0 .
Calculons f9x.(Vy.Z) à l'aide de cette formule. L'hypothèse que h, laisse
invariante la connexion C entraîne, par transport de structure, que l'on a
(Vy.Z),W = (Vvt(x).Zt)(x),
et par linéarité
rWy.zux) - (Vy.zxx)) = (V,-1(y,<x)_yw).z,x*) + (Vy(x,.(r Hz, - z»x*).
Mais en vertu de (24.51.2.2), lorsque t tend vers 0, le premier terme du second
membre tend vers (Vflx.y.Z)(x) = (V[X yj.Z)(x), et le second terme tend vers

334 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
(Vy. (6X. Z)){x). Comme le premier membre tend vers (dx. (Vy. Z))(x), cela démontre
(24.51.2.1).
(24.51.3) Si X est un champ de vecteurs quelconque sur M, de classe C°°,
l'application R-linéaire Y -* 6X. Y— Vx. Y est aussi ^(M)-linéaire, autrement dit
Ojcif Y) - Vx(f Y) = f(0x.Y-VX.Y)pour toute fonction réelle / de classe Cœ ;
cela résulte des expressions (17.14.4.2) de Ox.{fY) et (17.18.1.4) de Vx.(fY).
On peut donc écrire cette application Y -» Ax. Y, où Ax est une section de
classe C°° au-dessus de M du fibre End(T(X)) = T(X)* ® T(X), ou encore un
champ de tenseurs de (f* (M).
Soient R(M) le fibre des repères de M (20.1.1) et P la connexion principale
sur R(M) associée à la connexion linéaire C (20.5.2) ; au champ de tenseurs Ax
correspond canoniquement une application Ax de R(M) dans Vespace End(R"),
de classe C00, définie par la formule
(24.51.3.1) Ax(rx) = rx"1 o A^x) <> rx
pour tout repère rx : R" -*■ TX(M) de la fibre R(M)X. Montrons que pour tout
vecteur tangent hxeTx(M), on a
(24.51.3.2) Vhx. Ax = rx o (DAx(rx). rel(hx)) o rx"1
ou D est la différentielle extérieure covariante relative à la connexion
principale P (20.3.2) et rel(hx) le relèvement horizontal de hx au point rx (20.2.2). En
effet, il résulte de (17.18.2) que pour tout champ de vecteurs Z de classe C00
sur M, on a
(24.51.3.3) (Vhx. AX).Z = Vhx.(4x.Z) - A^.^.Z).
Posons *P(rx) = r~1. Z(x) de sorte que *P est une application de R(M)
dans R", et 0(rx) = Ax(rx).*(rx), autre application de R(M) dans R"; la
formule (20.5.3.4) appliquée à ces deux fonctions, donne
V.Z=rx.(0rel(hx).»P)
Vhx.(a*.Z) = rx.(0rel(hx).<I^
et comme par définition (20.3.2.1) on a 9„litix).Ax = Z)/4x(rx).rel(hx), la formule
(24.51.3.2) résulte des deux précédentes et de (24.51.3.3).
(24.51.4) Supposons que X soit un automorphisme infinitésimal de C. Avec les
notations de (24.51.3), on a
(24.51.4.1) DAX = irel(X).ft
où rel(-Y) est le relèvement horizontal du champ X dans R(M) (20.2.2) et SI la
2-forme de courbure de la connexion principale P (20.3.2.2).

51. APPLICATIONS : IL FORMULES DE BOTT
335
En effet, pour tout couple de champs de vecteurs Y, Z sur M, de classe Cœ,
il résulte de (24.51.3.3), en remplaçant Ax par sa définition, que l'on a
(Vy. AX).Z = VY.(AX.Z) - Ax.(Vy.Z)
= Vy.(6x.Z - VX.Z) - 9x.(Wr.Z) + Vx.(Vr.Z).
En vertu de (24.51.2.1) et de (17.20.4.1), cette dernière expression n'est
autre que (r. (X a Y)). Z, où r est la courbure (17.20.5) de la connexion linéaire C.
Mais on déduit de (20.6.6.8) et (20.6.6.10) que l'on a
rix).(hx a kx) = rxo(ft(rx).(rel(hx) a rel(kj)) o r;1
pour deux vecteurs tangents hx, kx de T^M). Comparant à (24.51.3.2) et
utilisant le fait que il est une forme horizontale (20.3.2) et la définition du produit
intérieur (16.18.4.5), on obtient (24.51.4.1).
(24.51.5) Supposons maintenant que la variété compacte M soit munie d'une
structure riemannienne, et prenons pour C la connexion de Levi-Civita
correspondante. Alors, avec les notations de (24.51.1), on dit que le champ de vecteurs X
est une isométrie infinitésimale si, pour tout f e R, le difféomorphisme h, est une
isométrie de M ; il est clair alors que X est aussi un automorphisme infinitésimal
de la connexion C (en fait, si M est connexe et orientée, on peut montrer que
la réciproque est vraie ; cf. section 20.10, problème 8).
Il résulte de cette définition que, si g est la métrique de M, la formule
(18.2.14.8) appliqué au champ de tenseurs g, montre que
(24.51.5.1) 0x.g = O.
Cela entraine, pour le champ de tenseurs Ax :
(24.51.6) Si X est une isométrie infinitésimale de la variété riemannienne
compacte M, on a, pour deux champs de vecteurs Y, Z de classe C00 sur M,
(24.51.6.1) ( Ax. Y | Z) + (Y | Ax. Z) = 0
En effet, il résulte des propriétés de la dérivée de Lie (17.14.7) et de la
relation (24.51.5.1), que l'on a
(24.51.6.2) 6X.(Y |Z) = (6X.Y \Z) + (Y \dx.Z).
Mais on a aussi (20.9.5.3)
6X.(Y\Z) = (VX.Y\Z) + (Y\VX.Z),
et il suffit de retrancher membre à membre les deux relations précédentes pour
avoir (24.51.6.1).

336 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
(24.51.7) Soit S(M) <= R(M) le fibre des repères orthonormaux sur M, de
groupe 0(n), correspondant à la métrique g sur M (20.7.6) ; si X est une isométrie
infinitésimale, notons encore Ax la restriction à S(M) de la fonction Ax définie
par (24.51.3.1). Comme tout rxeS(M)x est une isométrie de R" sur T*(M), il
résulte de (24.51.6.1) que la fonction Ax prend ses valeurs dans l'algèbre de Lie
so(n) du groupe Ofn), formée des matrices antisymétriques d'ordre n (19.4.3J).
Nous nous proposons de montrer que lorsqu'il existe une isométrie
infinitésimale X sur M qui a la propriété de n'avoir qu'un nombre fini de points critiques
non dégénérés (24.50.1), alors il est possible de généraliser la formule de Hopf
(24.50.3) pour obtenir, à l'aide du tenseur ax, certaines classes de
cohomologie Cp(S(M)) (24.45.5).
(24.51.8) Considérons une application p-linéaire symétrique F de (so(n)Y
dans R. Pour tout entier r tel que 0 < r ^ p, on peut définir (24.44.1)
où SI est la 2-forme de courbure (sur S(M)) de la connexion principale de Levi-
Civita ; c'est une 2(p — réforme différentielle scalaire sur S(M). Comme DSI = 0
en vertu de l'identité de Bianchi (20.3.4), on a, en appliquant (24.51.4.1) et la
propriété d'antidérivation du produit intérieur (16.18.4.9)
(24.51.8.2) DF(r,(ft) = irel(X).F<r-1)(n) pour 1 < r < p
et DF(0>(Q) = 0.
Bornons-nous au cas où la variété riemannienne compacte M est orientée,
et ajoutons aux hypothèses précédentes que F est invariante par le groupeSO(n).
On peut alors, comme dans (24.45.4), définir canoniquement une 2{p - r)-forme
différentielle Fjjftft) sur la variété M. Soit en effet U un ouvert de M au-dessus
duquel est défini un repère orthonormal direct R = (et, ..., e,), section de S(M)
de classe C°°. Pour tout x e U, posons
(24.51.8.3) Af\x) = AjMA) = «(*)"1 ° 0 **(*)
ainsi que SliR) = 'R(îl). Alors la 2(p - réforme
est indépendante du choix du repère R au-dessus de U, comme il résulte de
l'hypothèse sur F, de l'expression (24.51.8.3) et de la formule (24.45.4.1).
Montrons maintenant que l'on a, pour les formes différentielles scalaires
F$(£l) sur M, les relations
(24.51.8.5) dFjftfl) = ix.F$rl\n) pour 1 s? r < p
(24.51.8.1) F<"(fl) = T JF(^, Ax, l1, SI)
(24.51.8.4) F&XSl) = 'R(F(r)(ft)) =

51. APPLICATIONS : II. FORMULES DE BOTT
337
et dFtfXtl) = 0. Si, pour simplifier, on pose m = 2{p - r), a = F(r)(ft) et
a(*> = 'R(a) notre assertion résultera de (24.51.8.2) et des relations
(24.51.8.6) daw = 'R(Da) pour 1 < r < p
(24.51.8.7) ix.«iH) = 'R(W)-a) pour 0<r<j»-l.
Pour prouver (24.51.8.6), considérons, en un point x e U, m + 1 vecteurs
tangents h,, hm+1 linéairement indépendants, et m + 1 champs de
vecteurs Xj, Xm+i définis dans un voisinage V c U de x et tels que Xj{x) = h,
pour 1 < j < m + 1 ; comme a est indépendante du repère R choisi, on peut
toujours supposer en outre que les champs de vecteurs R(y) -» T^RJ.X/y)
sur R(V) transportés des À", se prolongent en des champs de vecteurs Xj sur
S(M) tels que Xj(R(x)) = rel(h,) pour 1 < j < m + 1.
On a
< daw(x), h, a h2 a ... a hm+ ! > = < da("U Xt(x) a . . . a Xm+jM > .
Or, par transport de structure au moyen de R considéré comme difféomorphisme
de V sur R(V), on a <daw, ^a...a Xm+l > = < da, X\ a ... a X'm+l >
dans R(V), et la valeur du second membre au point R(x) n'est autre que
<do(R(x)),rel(h1) a ... a rel(hm+1)>
= <DWM), Tj,(R). hj a ... a T,(R). hn+, > ,
ce qui prouve (24.51.8.6). D'autre part, on a, par définition (16.18.4.5)
<(i*.a<">Xx), ht a ... a hn_,>
- < mx)l TJLR).XM a TMK a ... a Tx(R). hm_! >
et comme a est horizontale et m ^ 1, on peut dans le second membre remplacer
Tx(R).X(x) par re\(X(x)), ce qui donne l'expression
< (W>•<*)(«(*))- TXR). h, a ... a T^R). h.., >
d'où l'on déduit (24.51.8.7).
(24.51.9) Ces préliminaires étant posés, nous supposerons que la variété
riemannienne compacte M est connexe, orientée et de dimension paire 2m. Nous
supposerons de plus qu'il existe sur M une isométrie infinitésimale X telle qu'elle
n'a qu'un nombre fini de points critiques non dégénérés (24.50.1) au ..., ar. En
un de ces points ap on a VX(aj).Y = 0 puisque X(àj) = 0 (17.17.2.2), donc
Ax(aj). Y(aj) = (6X. Y){a}); notons pour simplifier Lj l'endomorphisme A^aj)
de l'espace vectoriel TafM); pour le produit scalaire sur Taj(M), on a donc
Lj = — Lj. Si on prolonge canoniquement le produit scalaire euclidien sur
Taj(M) en un produit scalaire hermitien sur son complexifié (Taj(M))(C), le prolon-

338 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
gement canonique de L, en un endomorphisme C-linéaire (que nous notons
encore Lj) est donc tel que (iLj)* = iLj, autrement dit iLj est hermitien ; en outre,
si c est la conjugaison x -f iy -* x — iy dans (Tay(M))(C), L} commute avec c,
donc si z est un vecteur propre de iLj pour la valeur propre (réelle) u, c(z) est
un vecteur propre de iLj pour la valeur propre — u. Observons d'autre part
que l'hypothèse que a, est un point critique non dégénéré pour X entraine,
en vertu de (17.14.3.2), que pour une base convenable de T0J(M), L, a pour matrice
celle qui a été notée — DG(0) dans (24.50.1), donc L} est inversible. On conclut
de ces remarques qu'il y a dans (TflJ(M))(C) une base orthonormale (b*)^,^*
telle que Lj-.b2._i = ipkb2k.u b2k = cfb^-.,) et L;.b2k = - iukb2k, où les uk
sont des nombres > 0; comme les vecteurs b2Jk_i + b2t et i(b2lk_1 — b2k) sont
orthogonaux et appartiennent à T„ IM), on voit finalement qu'il existe dans Ta>(M)
une base orthonormale (cl)1^t^2m telle que l'on ait
(24.51.9.1) Lj. c__-i = ukc2k , Lj.c2k = - ^c^-j pour 1 ^ k =$m.
Nous poserons
(24.51.9.2) det(r/2m-i-L,-)
= ft (t2 + ^A2) = t2m + ^t2"-2 + ...+ a2m(aj).
Posons d'autre part
(24.51.9.3) T(a,) = (iJ"pf(L,.)
qui est égal à a2u2 ... um.
Enfin, notons pour abréger pk(M) et e(M) les classes de Pontrjagin réelles
et la classe d'Euler du fibre orienté T(M). Avec ces notations, on a le résultat
suivant :
(24.51.10) (Bott) Soient M une variété riemannienne compacte, connexe et
orientée, X une isométrie infinitésimale de M, champ de vecteurs n'ayant qu'un
nombre fini de points critiques au a2 a„ qui sont non dégénérés. Alors, pour
tout système d'entiers >0,(a!,a2,.. .,a.h,p)telsque2(al+2a2+ ... +hak)+fim=m
(ce qui implique fi = 0 ou j8 = 1), on a [avec les notations de (24.51.9))
(24.51.10.1) <pl(Mr,j92(Mr • • • pJWeWY, [M ] >
= I ^(a/W*/1 • • • ^(fl/Ma/-1 •
Notons que pour P = 1, les ak étant nécessairement nuls, cette formule se
réduit à la formule de Hopf (24.50.3.1), car les formules (24.51.9.1) montrent
qu'en chacun des points l'indice de X est égal à + 1.

51. APPLICATIONS : II. FORMULES DE BOTT 339
D'après (24.46.8) et (24.46.11), et compte tenu de l'homomorphisme de
Weil (24.45.7), le polynôme homogène de degré m
p(z) = <r2(zr<r4(zr • • • o-2,(zr^i-)mpf(Z))
sur l'algèbre de Lie so(2m), est tel que, si F est sa polarisation, le premier
membre de (24.51.10.1) est égal à FM(_Î), où il est la forme de courbure de la con-
Jm
nexion de Levi-Civita de M. Pour évaluer cette intégrale, on va :
1° construire une (2m — l)-forme différentielle A sur l'ouvert
M' = M - {au a2 ar)
telle que l'on ait FJft) | M' = dA ;
2° appliquer la formule de Stokes (24.14.2) à l'ouvert U~ complémentaire
dans M de la réunion de boules fermées (pour une distance convenable) de
centres a,, a2, ■ ■ ■, a, et de rayon e ;
3° faire tendre e vers 0.
Pour définir la forme A, considérons d'abord sur M' la 1-forme
différentielle y telle que, pour tout h^eTJM), on ait
(24.51.10.2) y(hx) = (X(x) | hx)/\\ X(x)\\2.
En premier lieu, montrons que l'on a 6x.y = 0. En effet, pour tout champ
de vecteurs Y de classe C00 sur M', on a (17.14.7.7)
(24.51.10.3) < 0X. y, Y> + < y, 6X. Y> = 6X. < y, Y> .
Mais il résulte de (24.51.6.2) que l'on a dx.\\X ||2=0 et 6X.{X | Y)=(X | [X, Y]),
donc 6X. <y, Y} = (X | [X, Y])/\\ X ||2 = < y, 0X.Y> , donc il résulte de
(24.51.10.3) que < 6x.y, Y> = 0.
En second lieu, on a les relations
(24.51.10.4) ix.y = l, ix.dy = 0.
En effet, la première résulte de la définition (24.51.10.2); d'autre part,
utilisant le fait que 0X = ix ° d + d ° ix (17.15.3.4), la seconde relation (24.51.10.4)
résulte de la première et de ce que 8X. y = 0.
Utilisant (24.51.10.4) et (24.51.8.5) et le fait que ix et d sont des
antidérivations, on obtient, pour 0 ^ r ^ m - 1,
(24.51.10.5) ix.d(y a (dy)Ar a Fïî+1)(ft))
= M(dyr(r+1) a FT "(ft) - y a (dy)- a dFT »(Q))
= (dyr<'+1> a (ix.FS+1Xn)) - (dy)- a (ix.FÏÏ>(ft)).

340 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
Il résulte alors de ces formules que la (2m — Informe
m- 1
(24.51.10.6) X — — Z (y a (dy)Ar a Fft+1)(__))
r = 0
répond à la question. En effet, on a
ix.dX = - (dyy a (f_.F8*(n)) + ix.FtfXSl)
et comme, d'après (24.51.8.1), F$\il) = FJCl) et que
(24.51.10.7) F») = F(Aix\ A^, A&)
pour tout repère mobile R, est une fonction scalaire, il reste
«*.(dA-FM(ft)) = 0.
Or, en tout point x e M', on a X(x) / 0, donc tout 2m-vecteur tangent en x
peut s'écrire X(x) a zx pour un (2m — l)-vecteur tangent zx. La relation
précédente entraîne donc bien dk = FJil) dans M'.
(24.51.11) Pour définir l'ensemble ouvert U_ nous supposons choisie au
voisinage de chaque point a, une carte ÇVj,cpj, 2m) telle que <pj(a}) = 0 et que
l'expression locale de la métrique de M pour cette carte soit une matrice symétrique (g**)
d'ordre 2m, qui au point 0 = cpjiaj) se réduit à la matrice unité. Si x -> (x, G(x))
est l'expression locale du champ X pour cette carte, on a vu (24.51.9) qu'on peut
en outre supposer que la matrice — DG(0) est telle que — DG(0).e2*-i = nke2k
et - DG(0).e2ik = - uke2k-i pour 1 s* k ^ m. On voit alors aussitôt sur la
définition (24.51.10.2) que l'expression locale y de y pour la carte précédente
est telle que
(m \ m
Z Hkixik-i + x22k))y = Z y-kix2kdx2k.l -Xu-idxaJ+ll x||2yi
k=1 / k=ï
où || x H est la norme euclidienne, et yx une forme différentielle continue au
voisinage de 0. Par le changement de variables
y2k = ukx2k , )>2k-l = ukx2k-l
on a une nouvelle expression locale de y (encore notée y) telle que
(24.51.11.2) ||y||2y = f -(y2kdy2k-i - y^-M + ||y||2yi
*=i uk
d'où
(24.51.11.3) ||y ||2dy = Z -dy2k a dy2k^ + ||y ||2£
*=i uk

52. COHOMOLOGIE DES GROUPES DE LIE
341
où i est une 2-forme continue au voisinage de 0. Pour e assez petit, désignons
par Bt(aj) l'image réciproque par ^ de la boule || y || < e de R2m, et par Se(a,)
sa frontière, image réciproque par cpj de la sphère || y || = e. On prend
naturellement e assez petit pour que les ensembles Be(a,) soient deux à deux disjoints
et Uc est alors le complémentaire de la réunion des Be(Oj) pour 1 < j < r. On
déduit alors de la formule de Stokes que
(24.51.11.4) f FJft) = t f A
Ju, J = 1 Js«(0j)
chaque frontière S£(a,) étant orientée vers l'extérieur (24.14.1).
(24.51.12) Vu l'expression (24.51.10.6) de A, l'étude de l'intégrale A repose
Js«(aj)
sur l'étude de chacune des (2r -f Informes y a (dy)Ar au voisinage de 0, compte
tenu du fait que l'expression locale de Fft+ l){ïl) est continue au voisinage de 0.
Or, il résulte aussitôt de (24.51.11.2) et (24.51.11.3) que l'on peut écrire
y a(dyr = ||y||-(2'+V
où n est une (2r + l)-f°rme continue au voisinage de 0. Comme la mesure de la
sphère ||y|| = e est proportionnelle à e2m_1, on voit que dans l'intégrale tous
les termes de (24.51.10.6) donnent des nombres tendant vers 0 avec s, sauf le
dernier. Dans celui-ci, FJ[,m)(__) est la fonction scalaire (24.51.10.7), dont
l'expression locale tend vers P(Lj) lorsque x tend vers 0. On est donc ramené à évaluer
l'intégrale - (y a (dy)A<m-1));ilestclair,en vertu des formules (24.51.11.2)
Jlly||=*
et (24.51.11.3), que lorsque e tend vers 0, cette intégrale tend vers C/(pip2 • • • um)>
où C est une constante indépendante de a, et de la fonction F. On a donc démontré
la formule (24.51.10.1), à cela près que le second membre est multiplié par la
constante C. Mais nous avons observé plus haut que pour fi = 1, la formule
se réduit à la formule de Hopf, donc on a C = 1. CQFD.
52. Cohomologie des groupes de Lie.
(24.52.1) Nous nous proposons de montrer comment l'on peut calculer la
cohomologie H'(G ; R) d'un groupe de Lie compact et connexe G à l'aide de
son algèbre de Lie Comme on peut montrer que tout groupe de Lie connexe
est difféomorphe au produit d'un groupe compact connexe et d'un espace Rm
(section 21.23, problème 8), cette méthode permet donc en principe le calcul de
la cohomologie à coefficients réels de tout groupe de Lie.
Nous identifierons canoniquement H "(M ; R) (pour toute variété différen-

342 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
tielle M) à l'algèbre de cohomologie H'(M) définie à partir des formes
différentielles (24.1.1), en vertu de (24.33.5).
(24.52.2) Soit G un groupe de Lie compact connexe de dimension n. Soit M
une variété différentielle sur laquelle G opère différentiablement à droite ; nous
noterons (x, s) -* m{x, s) — x.s l'action de G sur M. Le groupe G opère donc
équilinéairement sur chaque espace _yM) (resp. _2p(M)) des p-formes
différentielles réelles de classe C00 (resp. à support compact) (19.1.9) ; on notera (co, s)-*to.s
(ou S(s)a)) cette action. On notera «^(M) (resp. _?°(M)) le sous-espace vectoriel
des p-formes invariantes par cette action.
Rappelons (19.16.4) qu'il existe sur G une n-forme invariante à gauche fi,
qui détermine sur G une orientation pour laquelle j* îî = 1. Comme G est
compact, pour toute p-forme différentielle oce_*p(M), l'intégrale partielle
suivant G
(24.52.2.1) pn(a) = J 'pr2(Q) a 'm(a)
est définie (24.5.7) et est une p-forme de classe C00 sur M (24.5.8).
(24.52.3) L'application pn est un projecteur de ~°p(M) sur «^(M), transformant
formes fermées (resp. exactes) en formes fermées (resp. exactes), et tel que pour
toute p-forme fermée a, pa(<x) et a. soient cohomologues.
Pour tout xe M, on peut écrire, en vertu de (24.5.8),
/>nM*) = £a(x.s)ds
où s -» oc(jc.s) est une application de classe C00 de G dans l'espace vectoriel
p
/\TJM)*, et l'intégration est prise pour la mesure de Haar déduite de Q (qui
est d'ailleurs aussi invariante à droite puisque G est compact (14.3.3)). On a
donc, pour tout teG
(ô(t)pn(a)X*) = ^a((x.t).s)ds =Pn(aXx)
en raison de l'invariance de la mesure de Haar, autrement dit pja) e £f(M).
Si l'on suppose que l'on a déjà a e SfifA), ona«(j:.s)- a(x) pour tout x e M et
tout se G, donc p„(a) = a puisque la mesure de Haar a une masse totale 1.
Ceci prouve que pn est un projecteur. Comme £2 est une n-forme, on a dfi = 0,
donc d(*pr2(Q)) = 0 et d('pr2(Q) a 'm(a)) = (- l)B('pr2(fi) a 'm(da)); il résulte
donc de (24.5.9.1) que l'on a d(pn(a)) = (- lY'pJda). Ceci démontre les deux
premières parties de la proposition.

52. COHOMOLOGIE DES GROUPES DE LIE 343
(24.52.3.1) UO = | ('pr2(û>) a t)
où co est une n-forme sur G telle que co = 1, et i une p-forme sur M x G.
On a alors le lemme suivant : •'G
(24.52.3.2) Pour tout point b e G, soit jb l'application x -» (x, b) de M dans
M x G. // existe deux applications linéaires Kx : <fp(M x G) -» (fp_,(M) et
X2: _*p+i(M x G) -» <?P(M) t./tes que /'on ait, pour toute forme £,<eSp(M. x G)
(24.52.3.3) UÉ) - %(£) = d(Kl.O + K2.d^.
Notons d'abord que si cox est une seconde n-forme sur G telle que j* c_i = 1,
il existe une (n - l)-forme Çe/.-^G) telle que co - cox - d£ puisque G est
connexe (24.6.3.1). On déduit alors de (24.5.9.1) que l'on a
d(|G(*pr2(C) a Qj = £CPT2(0> - »i) a 0 + (- lV'j^WO a d£)
ce qui s'écrit aussi
(24.52.3.4) UO - L_,(0 - d(£(«pr_(0 a + (- l^CpraK) a d£).
Soit U un voisinage ouvert de b dans G difféomorphe à une boule ouverte
de R". Comme l'application identique de U est homotope à l'application s -* b
par une homotopie de classe C°°, l'application identique de M x U est homotope
à l'application jb » pr, de M x U sur M x {b} par une homotopie de classe C00.
Prenons alors pour to1 une n-forme de support contenu dans U et telle que I col = l;
jv
la formule de l'homotopie (24.2.4.2) montre que pour toute p-forme £ de classe C°°
sur M x U on a
- S = àlh .0 + L .dt
où L est une application linéaire de s/'(M x U) dans lui-même de degré — 1.
Si on tient compte du fait que pour toute p-forme a sur M, on a I_,('pr1(a)) = a
en raison de (24.5.10.2), et de (24.5.9.1), on voit que
(24.52.3.5) 'JM) - __,«[) = d(IMl(L.« | M x U))) + I_,(L.«|Mx U))
pour toute p-forme t de classe C°° sur M x G (on utilise le fait que le support
Pour prouver la dernière assertion, nous étudierons plus généralement les
intégrales partielles

344 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
de 'pr2(û>,) est contenu dans M x U). En retranchant membre à membre
(24.52.3.4) et (24.52.3.5), on obtient (24.52.3.3), avec
K,.£ = £cpra(0 a 0 - I„,(L.« | M x U)),
K2.r, = (- l)"£('pr2(0 An) - I_,(L.(i, | M x U)).
Appliquons maintenant le lemme (24.52.3.2) àa» = fî,b = eetà^ = 'm(a)
pour une p-forme fermée a sur M ; on obtient
pJa)-a = d(lC1.'m(a))
ce qui achève de prouver (24.52.3).
(24.52.4) Il est clair que, pour le produit extérieur et la différentielle
extérieure, la somme directe j/g(M) des éf(M) est une algèbre différentielle graduée
dont nous désignerons par HG(M) l'algèbre de cohomologie. Il résulte de (24.52.3)
que, par passage aux quotients, on déduit de pa un homomorphisme d'algèbres
graduées p*î : H "(M) -» HG(M), et en outre :
(2432.5) U homomorphisme p*, : H "(M) -* HG(M) est bijectif (pour un groupe
de Lie G compact et connexe).
(24.52.6) Soit G un groupe de Lie compact, connexe et de dimension n. Alors
G x G est un groupe de Lie compact, connexe et de dimension 2n, et il opère
différentiablement à droite sur G par l'action
(x, (s, t)) -* s~lxt.
Il résulte donc de (24.523) que l'on a un isomorphisme canonique
p„:H'(G) _* HGXG(G).
L'algèbre différentielle s/qxG(G) consiste ici en les formes différentielles
extérieures sur G invariantes à la fois à gauche et à droite, qu'on appelle encore
biinvariantes. L'espace vectoriel des 1-formes différentielles invariantes à gauche
s'identifie à l'espace dual q* de l'algèbre de Lie g des champs de vecteurs invariants
à gauche (19.163) ; comme a -» a(e) est une bijection de l'espace des p-formes
invariantes à gauche sur l'espace des p-covecteurs tangents au point e (19.2.2),
p
l'espace des p-formes invariantes à gauche s'identifie à A_*> et ^_xg(G) n'est
p
autre que le sous-espace de A 9* consistant en les p-formes qui sont aussi
invariantes à droite. Or on les caractérise de la façon suivante :

52. COHOMOLOGIE DES GROUPES DE LIE
345
(24.52.7) Pour qu'une p-forme a e /\q* soit invariante à droite, il faut et il suffit
que 6X • a = 0 pour tout champ de vecteurs X e g ; cela entraîne da = 0.
Comme a est déjà invariante à gauche, dire qu'elle est invariante à droite
équivaut à dire que s. a., s'1 = a pour tout s e G ; cela signifie que pour p vecteurs
tangents h,, ..., hp en un point x, on a
< o^sjcs-1), s. hi .s'1 a ... as. h-.s"1 > = < x(x), hj a h2 a ... a hp >.
Comme on peut écrire h,- = x.Uj avec U/_ge = TJG), l'invariance à gauche
de a montre que la relation précédente équivaut à
(24.52.7.1) < a(e), Ad(s). ut a ... a Ad(s). up > = < a(e), u, a ... a up >,
ce qui signifie que le premier membre est une fonction de s constante dans G,
quels que soient ut, ..., up. Cela entraine que la différentielle de cette fonction est
nulle. Remplaçant s par exp(^u) pour uege et «JeR, on obtient en particulier,
en prenant la dérivée par rapport à ^ au point <f = 0 et utilisant (19.11.2.2), la
relation
p
(24.52.7.2) Y <<*(«)> u, a ... a uhl a [u, uj a uj+1 a ... a up> = 0.
j= i
Vu l'invariance à gauche de a, cela entraîne que pour p + 1 champs de
vecteurs X0, Xu ..., Xp sur G invariants à gauche, on a
(24.52.7.3) t <«, *i a ... a Xj.x a [X0, X}] a Xj+1 a ... a!,)=0
D'autre part, chacune des fonctions < a, X0 a ... a X} a ... a Xp > est
invariante à gauche, donc constante. La formule (17.14.7.7) montre donc que
6X. a = 0 pour tout champ de vecteurs X e g, et la formule (17.15.3.5) montre
que da = 0.
Inversement, si &x. a = 0 pour tout champ de vecteurs X e g, la formule
(17.14.7.7) montre que l'on a la relation (24.52.7.3) pour tous les champs de
vecteurs X0, Xx Xp dans g, et par suite la relation (24.52.7.2) quels que
soient u, u,, updans g„. Comme Ad(exp(£ + w)u)=Ad(exp(<!;u))°Ad(exp(Hii)),
la relation (24.52.7.2) où on remplace chaque Uj par Ad(exp(nu)). Uj, montre
que la relation (2432.7.1) est vraie pour s appartenant à un sous-groupe à un
paramètre quelconque de G, image de R par n -» exp^u); par (19.9.15) et la
relation Ad(st) = Ad(s) ° Ad(t), on déduit qu'elle est encore vraie pour tous les
points s d'un voisinage de e dans G ; enfin comme G est connexe, la relation est
vraie pour tout s e G en vertu de (12.8.8).
(24.52.8) Le fait que da = 0 pour toute forme différentielle extérieure biinva-

346 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
riante entraîne que dans le calcul de la cohomologie H'G x G(G), toutes les cochaines
sont des cocycles et tous les cobords sont nuls ; autrement dit :
(24.52.9) L'isomorphisme p[\ est un isomorphisme de Valgèbre graduée H'(G)
sur Valgèbre graduée b*(G) des formes différentielles extérieures biinvariantes.
On notera que la condition (24.52.7.2) est satisfaite pour tous les vecteurs
u, uup de ge lorsqu'elle l'est pour les vecteurs d'une base de ge. La
connaissance de la table de multiplication de cette base détermine donc un système
p
d'équations linéaires (24.52.7.2) caractérisant les vecteurs <x(e)e/\Q*, et par
suite l'espace vectoriel HP(G).
53. Éléments primitifs.
(24.53.1) Soit G un groupe de Lie compact connexe, de dimension n. Rappelons
(24.5.4) que l'homomorphisme de Kûnneth H'(G)g® H*(G) -> H "(G x G) est
un isomorphisme d'algèbres graduées anticommutatives ; dans ce qui suit nous
identifierons H'(G x G) à H'(G) *® H'(G) par cet isomorphisme.
L'application m : (s, t) -» st de G x G dans G étant de classe C°°, elle
définit canoniquement un homomorphisme d'algèbres graduées
(24.53.1.1) m* : H'(G) -» H*(G x G)
que nous considérons donc comme un homomorphisme H'(G) -► H'(G)* (g) H'(G),
et qu'on appelle comultiplication ; il transforme l'élément unité 1 e H°(G) s R
de H'(G) en l'élément unité 1 ® 1 de H "(G) *® H*(G).
Nous noterons H+(G) la somme directe des HP(G) pour p ^ 1, qui est
un idéal gradué de l'algèbre H'(G), de sorte que H'(G) = R. 1 © H+(G), et
H'(G x G) = R.(l (g) 1) © (H+(G) ® 1) © (1 ® H+(G)) © (H+(G) ® H+(G)).
Pour tout x e HP(G) où p > 1, on a donc
(24.53.1.2) m*(x) = m^x) ® 1 + 1 ® m2(x) + £ yk ® zk
k
où mx{x) et m2{x) appartiennent à HP(G), les yk et zk (qui ne sont pas
uniquement déterminés par x) sont tels que deg yk > 1, deg zk > 1 et deg yk + deg zk—p.
(24.53.2) Les applications de classe C", j\ : s -* (s, e) et j2 : s -* (e, s) de G
dans G x G sont telles que m ojt = m °j2 = id ; elles donnent donc des
homomorphismes d'algèbres graduées
ft : H\G x G) -* H'(G) et jt : H"(G x G) -» H'(G)
telles que ff °m* =j*°m* = id. D'autre part, on a pri ° jt = pr2 ° j2 = id, donc

53. ÉLÉMENTS PRIMITIFS
347
Ji ° Prî = J* ° Pr* = «d, et pr2(/i(s)) = pr,0'2(s) = e, doncy* ° pr$ etjï ° pr* sont
nuls dans H+(G) et l'identité dans H°(G). Pour deux éléments y, z de H+(G),
puisque y (g) z est identifié à pr*(y) ~ pr*(z), on a donc j*(y®z) =j%(y <g> z) = 0 ;
appliquant cette remarque à (24.53.1.2) on obtient my{x) = m2(x) = x pour
xgH+(G).
(24.53.3) Nous allons voir que les propriétés précédentes permettent déjà à
elles seules de prouver qu'il existe un sous-espace vectoriel gradué E de H "(G)
tel que l'algèbre H'(G) soit isomorphe à V algèbre extérieure AE.
De façon précise, considérons l'idéal gradué H+(G)2 engendré par les
produits de deux éléments quelconques de H+(G), et soit Ep un sous-espace
vectoriel de HP(G) supplémentaire de HP(G) n H+(G)2, pour tout p > 1. Nous
allons montrer que Ep = {0} si p est pair, et que le sous-espace E, somme (directe)
de R. 1 et des Ep pour p impair, répond à la question.
Considérons pour cela une base de E formée de 1 et de la réunion de bases
des Ep pour p ^ 1 ; nous la rangerons en une suite 1, xu x2, ..., xm telle que
deg(Xj) ^ deg(xJ+1) pour tout indice j < m. Il suffira de prouver la proposition
suivante (où le cup-produit dans H'(G) est simplement noté xy) :
(24.53.4) Tous les xk sont de degrés impairs, et l'unité et les produits xjlxh ... xjh
pour toutes les suites d'indices jx < j2 < ... <jh^m forment une base de
l'espace vectoriel H'(G).
L'isomorphie de l'algèbre H'(G) et de l'algèbre extérieure AE résultera
en effet de la définition de cette dernière (Ann. 13.5) et de ce que x2 = 0 et
XjXk — - xkXj en raison de l'anticommutativité de H'(G) et de ce que les degrés
des xk sont impairs.
Nous allons prouver par récurrence sur k ^ m la propriété suivante :
(Pt) Si xke HP(G), p est impair, les produits xhxJ2 ... xih pour toutes les suites
strictement croissantes d'indices ^ k sont linéairement indépendants, et l'espace
vectoriel engendré par 1 et par ces produits contient les H*(G) pour q < p.
En effet, (PJ entraînera (24.53.4).
Supposons donc prouvée (Pk-i) (pour k = 1, cela veut dire qu'on ne fait
aucune hypothèse). Cette hypothèse entraîne que l'ensemble des combinaisons
linéaires de 1 et des produits xhxJ2 ... xjh pour toutes les suites strictement
croissantes d'indices < k - 1 est une sous-algèbre graduée Bk-l de H'(G), dont
les éléments précédents forment une base. Nous désignerons par ak_, l'idéal
gradué de H'(G) engendré par Bt_, n H+(G). Notons d'abord que xk$ak-l ;
r
sinon on aurait une relation de la forme xk = £ Cjxl, où les c} sont chacun pro-
j = 0
duit d'un élément de Bt_, r> H+(G) et d'un élément de H'(G) ; pour des raisons

348 XXIV. TOPOLOGIE ALGEBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
de degré, cela impliquerait xk = c0, donc, ou bien x,eBt_,, ou bien xk serait
produit de deux éléments de degrés > 0 ; mais ces deux éventualités sont exclues
par définition des Ep.
Montrons d'abord que p est impair; remarquons pour cela que, puisque
H'(G) est de dimension finie, on a x\ = 0 pour r assez grand. Nous allons montrer
qu'une telle relation serait impossible si p était pair. Plus généralement, consi-
r
dérons toutes les relations de la forme Z bjx{ = 0 pour des bJeBk.l tels que
b, =t 0, et parmi celles-là une dont le degré r > 1 est le plus petit possible. Notons
maintenant qu'en raison de la formule (2433.1.2) et de (24.53.2), l'hypothèse (Pt_,)
entraine les relations
(24.53.4.1) m*{xk) s xk ® 1 + 1 ® xk mod. H'(G) ® ot_,
(24.53.4.2) m*(xj) = xy ® 1 mod. H'(G) ® , pour j<k
et par suite
(24.53.4.3) m*(b) = b ® 1 mod. H'(G) ® o,_ j pour tout b e Bt_,.
On aurait donc
0 = m*( t bjxi] = Z (b, ® l)(xk ® 1 + 1 ® xtf mod. H'(G) ® ot_ t
= (jt Jbj4~ ') ® ** + Z Cj ® x, mod. H'(G) ® a,_,
avec des Cj€H'(G); pour des raisons de degré, cela entraînerait aussi
0 = ^ __ jbjx{~ *) ® xk mod. H'(G) ® a,_ t
et comme x^a*-!, on en déduirait que Y,jbjx{ 1 = 0- Mais en raison du
choix des by, cela n'est pas possible si r > 1, et pour r = 1 cela entraînerait bx =0
contrairement à l'hypothèse.
En second lieu, montrons que les produits xh ... xjh pour les suites
d'indices < k strictement croissantes sont linéairement indépendants ; cela équivaut,
vu (P,-i), à prouver qu'il ne peut avoir de relation bQ + biXt = 0 avec b0, bt
dans Bt_x et non tous deux nuls; mais c'est ce qui résulte du même calcul que
ci-dessus avec r = 1. Enfin la dernière assertion de (Pk) résulte de (P»-i) si
xk-i eHp(G); sinon, Bk.1 contient par hypothèse les H*(G) pour q < p - 1,
ainsi que Ep_,, donc, par définition, il contient aussi HP_1(G). CQFD.

53. ÉLÉMENTS PRIMITIFS
349
(24.53.5) Le résultat précédent est susceptible de vastes généralisations, en y
remplaçant G par ce qu'on appelle des H-espaces (cf. section 16.30, problème 1
et [178]). Mais pour les groupes de Lie compacts connexes, on peut beaucoup
préciser la proposition (24.53.4). En premier lieu :
(2433.6) (E. Cartan) La dimension de l'espace vectoriel E est égale au rang l
(21.7.7.2) du groupe G.
Il suffit évidemment de montrer que
(24.53.6.1) dim(H'(G)) = 2'.
Cela s'exprime aussi en disant que, si PG(X) est le polynôme de Poincaré
de G (24.1.1), on a PG(1) = 2'. Pour le voir, nous allons donner une expression
intégrale de ce polynôme :
(24.53.6.2) Le polynôme de Poincaré d'un groupe de Lie compact connexe G
est donné par la formule
(24.53.6.3) PG(X) = | det(Ad(s) + X. I)dmG(s)
où mG est la mesure de Haar de masse totale 1.
En effet, on a vu (24.52.7) que les p-formes différentielles biinvariantes
p
sur G sont celles dont la valeur en e est un p-covecteur de a 9* invariant par
p
les automorphismes /\('Ad(s)) pour se G; la dimension bp = dim(Hp(G)) de
l'espace de ces p-covecteurs est donc la multiplicité de la représentation triviale
p
de G dans la représentation s -* /\('Ad(s)) ; par suite ((21.4.4.1) et (21.3.2.6))
(24.53.6.4) bp = |otr(â ('Ad(s)))dmG(S) = j^â (Ad^m^s).
Il suffit alors de remarquer que pour tout endomorphisme U d'un espace
vectoriel réel F de dimension r, on a
(24.53.6.5) det(U + X./r) =
comme on le voit aussitôt en considérant U comme une matrice complexe et
en prenant une matrice inversible Q à éléments complexes telle que QUQ'1
soit triangulaire (Ann. 6.10).
Notons maintenant que det(Ad(s) + X./) est une fonction centrale sur G,

350 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
puisque Adfusw-1) = Ad(«)Ad(s)Ad(«)_1. Par suite, si T est un tore maximal
de G, la formule d'intégration de Weyl (21.15.4.2) montre que
(24.53.6.6) PG(X) = (Card(W))"1 j" det(Ad(t) + X. /) | A(t) l'dm^t).
Or, si l'on prend dans ge une base formée d'une base de t et des éléments ya et za
définis dans (21.8.3.1), il résulte de (21.8.3.3) que l'on a
(24.53.6.7) det(Ad(t) + X./) = (X + 1)' fi (X + e-"U))(X + e"<»)
aeS+
(en écrivant a(exp(u)) au lieu de a(u) pour u e t (21.13.6)). Comme
i m i2 = n i -112 = n (-*» - ix--**» - d ,
xeS + aeS +
on peut écrire
Il (X + .««XX + _"■») | A(t) |2 = I ap(X]e^
somme étendue aux poids de T (21.13.6), où les ap(X) sont des polynômes ; on
tire alors de (24.53.6.6) que
(24.53.6.8) PG(X) = (Card(W))-1a0(XXX + 1)'
d'où PG(l)=(Card(W))-1a0(l)2'. Mais si l'on écrit de même | A(f) |2 = Y.cpe«'\
peP
on a Card(W) = c0 (21.15.4), donc tout revient à voir que a0(l) = c0. Mais
on a
la^l)^ = FI (1 ~ e2ai,\\ - e-2ttit)) = Icpe2p">
peP aeS+ peP
et en particulier a0(l) = c0.
(24.53.7) Nous allons maintenant voir que, pour un groupe de Lie compact
connexe G, il y a une manière canonique de choisir les sous-espaces vectoriels Ep
introduits dans (24.53.3).
Remarquons d'abord pour cela que, d'après (24.52.9), l'algèbre graduée H'(G)
s'identifie à la sous-algèbre graduée b*(G) de l'algèbre extérieure A g* constituée
par les formes différentielles extérieures biinvariantes ; l'algèbre A g* peut aussi
être identifiée à l'algèbre extérieure A g* de l'espace dual de l'algèbre de Lie ge
de G, et b*(G) à la sous-algèbre graduée correspondante b* de A g* ; nous
supposerons faite cette identification dans ce qui suit. L'algèbre b* peut encore
être définie comme la sous-algèbre des éléments de A g* invariants par les auto-
morphismes 'Ad(s) de g*, pour tout s e G. De façon plus précise, le sous-espace b*(l,)
formé des p-covecteurs appartenant à b* est le sous-espace des invariants de

53. ÉLÉMENTS PRIMITIFS 351
P A -
Ag? pour la représentation linéaire s -»• A('Ad(s) ') du groupe G dans l'espace
p
vectoriel /\a*.
(24.53.8) Faisons maintenant intervenir le fait que l'on a aussi une
représentation linéaire canonique s -+ Ad(s) de G dans l'algèbre de Lie g~ d'où, pour
p
chaque p < n, on déduit une représentation linéaire canonique s -» /\ (Ad(s))
p
de G dans l'espace vectoriel AôV C*n sait (21.4.3) qu'il y a sur ge un produit
scalaire invariant par l'action (s, u) -♦ Ad(s). u de G sur ge ; il revient au même
de dire qu'il y a une bijection linéaire cp : ge -* g* telle que l'on ait
(24.53.8.1) 'Ad(s~ Ad(s)
pour tout se G, le produit scalaire étant (u | v) = < u, <p(v) >. On déduit de cp
un isomorphisme d'algèbres graduées A cp : A ge -» A g*, d'où sur A ge un
produit scalaire prolongeant celui de Qe, défini par (z | w) = < z, ( A <j?Xw) >, et de
même sur A g* un produit scalaire tel que (z* | w*) = <(Aç>)-1(z*), w* >.
p
Cela étant, désignons par blep) le sous-espace de A 9e formé des invariants
p
par A(Ad(s)) pour tout se G, qui est donc défini intrinsèquement; il résulte
aussitôt de (24.53.8.1) que l'on a
(24.53.8.2) (K^ib^^b*^.
Soit be+ (resp. b*+) l'idéal de l'algèbre be (resp. b*) somme directe des blep)
(resp. b*(p)) pour p > 1, supplémentaire de R.l dans cette algèbre; notons oe
(resp. o*) le carré de cet idéal, engendré par les produits de deux éléments de b*
(resp. b*+) ; il est clair que l'on a ( A cp)iae) = a*, donc aussi
(24.53.8.3) ^Â<p)K r\ blp)) = o* n b*ip) pour tout p > 1.
Le sous-espace b*(p) de b* est alors somme directe de a* n b*<p) et de son
orthogonal pour le produit scalaire défini ci-dessus ; mais ce dernier n'est autre
p
que Yorthogonal (ae n b|.p))0 de oe n b<,p) pour la dualité canonique entre A 9»
p
et A 9* (Ann. 9.6), et est donc défini intrinsèquement. On voit par suite qu'on
peut prendre Ep = (ae n bip))° (avec l'identification canonique de H'(G) et de b*).
(24.53.9) On peut caractériser autrement le sous-espace E de H "(G) ainsi
défini. Notons e*, ef, ..., e,* les éléments de base de E notés xu x2 xt

352 XXIV. TOPOLOGIE ALGÉBRIQUE ET DIFFÉRENTIELLE ÉLÉMENTAIRES
dans la construction de (24.53.4), et pour toute partie J de p éléments jt <J2<-<jP
de {1, 2, ...,/}, posons e* = e*, a ef2 a ... a ejp, de sorte que les 2'
éléments e* (pour toutes les parties J de {1, 2, ...,/} ) forment une base de b*.
Nous désignerons par (ej la base duale dans de sorte que les ej tels que
Card(J) ^ 2 et deg(ej) = p forment une base de ae n bjp>, par construction de E~
Notons m la multiplication dans l'algèbre b„ considérée comme une application
linéaire de b„ ® be dans de sorte que m(u<g>v)=UAv; comme la dualité
entre be et b* définit canoniquement une dualité entre be cg> be et b* <g> b*
(Ann. 10.5.4), la transposée 'm est une application linéaire de b* dans b* (g) b*.
Cela étant, montrons que les éléments de E sont les éléments u* e b* tels que
(24.53.9.1) 'm(u*) = u* <g> 1 + 1 ® u*.
En effet, prouvons d'abord que les e* vérifient (24.53.9.1) pour 1 < j «S /.
On peut écrire
(24.53.9.2) 'm(ef) = ef (g) 1 + 1 ® ef + Zc^et (g) e*.
où la somme est étendue à tous les couples (K, L) tels que deg eg > 1, deg ef, > 1,
deg eÊ + deg e_ = deg e*. Or, par construction de E, on a < ef, eK a eL > = 0,
ce qui s'écrit < ef, m(eK ® eL) > = < 'm(ef), eK ® eL > = 0 ; si l'on substitue
à 'm{ef) sa valeur (24.53.9.2), on obtient bien cKL = 0.
D'autre part, 'm est un homomorphisme d'algèbres de b* dans le produit
tensoriel gauche b* g(g> b*, d'où l'on déduit aussitôt que pour toute partie J de
{1, 2, ...,/} telle que Card(J) > 2, on a
'Me?)= I e*:®eî
KoL = J
et par suite, pour deux parties distinctes J, J', aucun produit tensoriel figurant
dans l'expression de 'm(ef) ne figure dans celle de 'm(ef.). Cela prouve qu'aucun
élément de b* n'appartenant pas à E ne peut satisfaire (24.53.9.1). Revenant à
l'algèbre de cohomologie H'(G) et aux notations de (24.53.4), on voit qu'on a
prouvé le résultat suivant :
(24.53.10) L'algèbre de cohomologie H '(G) d'un groupe de Lie compact connexe G
est isomorphe à l'algèbre extérieure du sous-espace vectoriel E de H*(G), de
dimension l, formé des éléments zeH'(G) tels que
(24.53.10.1) m*(z) = z ® 1 + 1 ® z
appelés éléments primitifs de H "(G); ces éléments sont tous de degrés impairs.
Il est possible de déterminer explicitement les dimensions des espaces Ep
pour tous les groupes compacts semi-simples [155].

53. ÉLÉMENTS PRIMITIFS
353
PROBLÈMES
1) Montrer que les polynômes de Poincaré des groupes unitaires et orthogonaux sont
donnés par les formules suivantes
pU(..c,(T)= fl(l +T«-»)
pu«..h,(t)= 0(1 +t*>-»)
j-» __,
PicWT) - 0 + T2-')!! (1 + T*'"'). pW2_+1)(T) - fî(l + T4-'"1)
J-i 7-»
(utiliser la section 24.38, problème 7 et la section 24.39, problème 6).
2) a) Pour tout point zeP„_,(C), on note X, l'endomorphisme de C" de rang 1,
x - (x|a)a/||-||',
où • e C" — {0} est tel que z soit son image canonique dans P.. ,(C), (x | y) étant le produit
scalaire hilbertien usuel ; X, ne dépend pas du choix du représentant a de z, et est autoadjoint positif.
b) On considère l'application g : (t, z) -» exp(2itUX,) de [0,1 ] x P._ ,(C) dans le groupe U(n)
(21.17.6). Si SP„-!(C) est la suspension de Pa-i(C) (section 24.36, problème 4), montrer que g
se factorise en
10, 1] x P..,(C) A SP.-,(C) 4 U(«)
où ji est l'application canonique, et / est un homéomorphisme de SP„_,(C) sur son image.
c) Soit (e,), la base canonique de C". On note B,, pour K/c<n, la partie de /(SP,_ ,(C))
formée des Y tels que Y.*j = pour k + 1 <y < n; on note B0 l'ensemble réduit à l'élément
neutre /„. Montrer que hk — Bk_, est homéomorphe à R""'.
d) Pour toute suite k = (fc,, k2, ..., kk) strictement décroissante d'entiers de [1, n] on
pose CK = (B4, - Bt,.,)(Bt] - B,,-,) ... (Bth — Bt>_,) dans le groupe U(n). Montrer que U(n)
est ainsi décrit comme un complexe cellulaire (section 24.36, problème 7) dont B0 et les Ck sont
t
les cellules, Ck étant de dimension ii (2fc/ — 1). (Utiliser la diagonalisation des matrices unitaires).
j-i
3) Soit p : U(n) -» U(n)/U(n — m) l'application canonique de U(n) sur la variété de Stiefel
S„,m(C) (U(n — m) étant identifié au sous-groupe de U(n) laissant fixes les e, pour n-m + U^n).
On conserve les notations du problème 2.
a) Montrer que pour les suites k formées d'entiers appartenant à [n — m + 1, n], p est
un homéomorphisme de Ck sur p(Ck) et que S.,„(C) est un complexe cellulaire dont p(B0) et les p(Ch)
correspondant aux suites précédentes sont les cellules.
b) Soit A0 la cellule p(Ch) pour la suite k = (n, n — 1, ..., n — m + 1), qui est un ensemble
ouvert partout dense dans Sn_JÇ), homéomorphe à R"2""J. Soient C, (2. • ■ •> d w nombres
complexes distincts de valeur absolue 1, distincts de 1. Montrer que A0 et les m ensembles ouverts
(J"1A0 forment un recouvrement de S, _(C). (Si Y i A0, montrer que Y = p(X), où pour un indice j
au moins, rtX n'a pas de valeur propre égale à 1, et par suite pi(jX) e A0).
c) Conclure de b) que cat(S. „(C)) = m + 1 (utiliser la section 24.37, problème 27, ainsi
que 24.S3.6).

ANNEXE (suite)
COMPLÉMENTS D'ALGÈBRE
27. Produits infinis de modules.
(Ann. 27.1) Soient A un anneau commutatif, (E„)„, une famille quelconque de A-modules.
L'ensemble produit y[E, est alors muni canoniquement d'une structure de A-module, pour
Ml
laquelle („J + (y,) = (x, + y,) et X(xa) = (Xx,) pour tout X e A ; la somme directe © E. (Ann. 1.5)
est un sous-module de ce produit, qui lui est égal lorsque I est fini. **'
Pour tout a e I, soit F. un sous-module de E« ; alors \~[ F, est un sous-module de y] E«.
Ml Ml
(Ann. 27.2) Soient (MJ„„ (N.).,, deux familles de A-modules ayant même ensemble d'indices,
et pour tout a € I, soit : M. -» N. une application linéaire. Alors l'application
/ = (A) : (*«) - (fM)
est une application linéaire de n M. dans F] N«. Il résulte aussitôt de cette définition que l'on a
Ml «I
Ker(/) = fi Ker(/J, Im(/) = FJ Im(/J .
Ml Ml
En particulier, si (Ea)„, est une famille de A-modules, et si pour tout a e I, F, est un sous-module
de E_ on a un isomorphisme canonique
(Ann. 27.2.1) (u^ltuf) * u(EJFJ
\Ml // \Ml / Ml
obtenu en appliquant ce qui précède aux applications canoniques E. -> EJF,.
(Ann. 27.3) Soient (E„)Ml une famille de A-modules, F un A-module. On a alors un isomorphisme
canonique
(Ann. 27.3.1) Hom(©E„ F] ylHom(E„ F)
\ Ml / Ml
qui fait correspondre à toute application linéaire u : © E„ -> F, la famille (u °y'J, oùy. : E« -» © E,
Ml f»i
est l'injection canonique ; cela résulte aussitôt de (Ann. 3.1). En particulier, le dual I © E, )
s'identifie canoniquement au produit II E?.
Ml
(Ann. 27.4) Lorsque A n'est pas un corps, il faut noter que (contrairement aux sommes directes),
un produit infini de A-modules libres n'est pas nécessairement un A-module libre. Par exemple,
on peut montrer que le Z-module ZN n'est pas libre [3, chap. 7].
28. Produits tensoriels de modules.
(Ann. 28.1) Soient A un anneau commutatif, E un A-module libre (de type fini ou non), F un
A-module quelconque. Pour deux éléments quelconques x e E, y e F, on définit une
application A-linéaire du dual E* dans F par
(Ann. 28.1.1) x* -> <x,x*>y

28. PRODUITS TENSORIELS DE MODULES
355
que l'on note x ® y ; on note E ® AF ou simplement E (g) F le sous-A-module de Hom(E*, F)
engendré par les éléments x ® y, et on dit que x ® y est le produit tensoriel de x et y et E ® F le
produit tensoriel de E et de F.
(Ann. 28.2) Soit (e.)ul une base de E ; alors tout élément de E ® F se met d'une seule manière
sous la forme £(e. ® yj, où (y„)_,, est une famille d'éléments de F nuls sauf pour un nombre fini
xel
d'indices. En effet il est clair que l'application (x, y) -» jc ® y de E x F dans E ® F est bilinéaire;
comme x = y.Z,e„ on a x ® y = £(e, ® <J.y). D'autre part, si £(e« ® y») = 0, cela signifie
Ml Ml Ml
que l'application linéaire
x* - I<e., Jc*>y«
Ml
est nulle ; mais si ef est la forme linéaire sur E telle que < e„ ef > = ô.f, l'hypothèse entraîne que
t.6.ty. — 0, c'est-à-dire yr — 0 pour tout fiel.
«i
Pour chaque a e I, y -* ea ® y est donc un isomorphisme de F sur un sous-module F,
de E ® F, et E ® F est somme directe des F.. En particulier A ® AF s'identifie à F par
l'application y -» 1 ® y.
Si F, est un sous-module de F, il est clair que l'ensemble des sommes £e. ® y. où les y.
Ml
appartiennent à F1( est un sous-module de E ® F isomorphe à E ® F,, avec lequel on l'identifie
généralement.
Si F est somme directe d'une famille (FA)isL de sous-modules, ce qui précède montre que
E ® F s'identifie i la somme directe de la famille de sous-modules E ® F,,. Plus particulièrement,
si F est un A-module libre et si (/à).ul est une base de F, les éléments e, ® fÀ forment une base
de E ® F, de sorte que dans ce cas particulier la définition de E ® F coïncide, à un isomorphisme
canonique près, avec celle donnée dans (Ann. 20) pour le produit tensoriel de deux espaces vectoriels.
(Ann. 28.3) Soient Ei un A-module libre, F, un A-module, u : E E, et i> : F -» F, deux
applications A-linéaires; alors il existe une application A-linéaire unique m>:E®F -> E,®F,
telle que
(Ann. 28.3.1) w(x ® y) = u(x) ® v(y)
pour tout couple (x, y) e E x F. En effet, en considérant la transposée 'u ; EJ -» E*, on définit
une application A-linéaire
(Ami. 28.3.2) wa : / v ° / ° 'u
de Hom(E*, F) dans Hom(Ef, F,), et si / = x ® y, w0(x ® y) est l'application linéaire
„î - s( < x, 'u(xî) > y) = < u(x), *î > v(y)
ce qui montre que la restriction w de w0 à E ® F répond à la question. L'application w s'appelle
produit tensoriel des applications linéaires u et v et se note encore u ® v si cela n'entraîne pas
confusion.
(Ann. 28.4) En particulier, si on prend pour u l'application identique 1E, l'application lE®r
est telle que
(1e 0 v)(Z(e« ® yj) = le. ® «(yj .
\u| / Ml
Cela montre aussitôt que l'on a
(Ann. 28.4.1) Im(lE ® v) = E ® Im(v), Ker(le ® v) = E ® Ker(t>).

356
ANNEXES
(Ann. 28.5) Soient E un A-module libre de type fini, (FJll une famille de A-modules. Alors il
y a un isomorphisme canonique de E ® I II F* ) sur le produit H(E <S) FJ, qui à tout produit
tensoriel x ® (yj fait correspondre la famille (x ® yj^. U suffit pour le voir de considérer une
base (finie) (e,)! (iim de E, de sorte que les éléments de E ® ^ij s'écrivent d'une seule manière
m / m \
Z (ei ® (ynï) ; il est immédiat qu'en lui faisant correspondre la famille ( Z (*i ® yu) ) on
définit l'isomorphisme cherché. Le résultat cesse d'être exact lorsque E est libre mais a une base
infinie.
(Ann. 28.6) Soient B un anneau commutatif, <p : A -» B un homomorphisme d'anneau qui
fait de B une A-algèbre. Si E est un A-module libre, on peut considérer le produit tensoriel E ® AB
en considérant B comme un A-module. On munit cet ensemble d'une structure unique de B-module
telle que p\x ® X) = x ® (pX) pour x e E et X, p dans B. En effet, si (ej„, est une base de E, de
sorte que tout élément de E ® AB s'écrit d'une seule manière Z*« ® il suffit de définir
/i(Ze„®-u = He.®(pX.)
\<Ml / Ml
pour répondre à la question. Il est clair que (e.® l)Ml est une base du B-module E ® AB.
Soit maintenant F un B-module, qu'on peut considérer comme un A-module par restriction
des scalaires ; alors, si u : E -» F est une application A-linéaire, il existe une application B-linéaire
et une seule v : E ® AB -> F telle que v(x ® p) = p.u(x) ; avec les mêmes notations que ci-dessus,
on définit v par v[ Ze, ® X. ) = Z^««(0-
29. suites exactes.
(Ann. 29.1) Soient A un anneau commutatif, I un intervalle (fini ou infini) de Z, (E„)M, une suite
de A-modules, et pour chaque n 6 I distinct de l'extrémité de I (lorsque celle-ci est finie), soit
/» : E. -» E„+1 une application A-linéaire; on dit que ces applications forment une suite exacte
si l'on a
(Ann. 29.1.1) Im(/J = Ker(/.+ 1)
sauf si n + 1 est l'extrémité de I. Les suites de A-modules et d'applications linéaires définies comme
ci-dessus pour un intervalle I de Z se notent d'ordinaire (qu'elles soient exactes ou non)
(Ann. 29.1.2) ... - E. - E.+ 1 — E.+J — E.+3 - ...
où l'on fait figurer plusieurs des modules de la suite. Une suite exacte à S termes de la forme
(Ann. 29.13) O-E^F-fcG-O
est dite suite exacte courte, et dire qu'une telle suite est exacte signifie que / est injective, g
surjective et G isomorphe à F//(E).
Dire que la suite (Ann. 29.1.2) est exacte équivaut à dire que /.+ , » fm = 0 pour tout n, et
que chacune des suites courtes
0 -* Ker/. - E. Ker/,+ I - 0
est exacte.
On dit qu'une suite exacte courte (Ann. 29.1.3) est scindée si le sous-module /(E) de F admet
un supplémentaire Gj dans F; la restriction de g à G, est alors une bijection de G] sur G, et F
est donc isomorphe à la somme directe E © G.

29. SUITES EXACTES
357
(Ann. 29.2) Si, dans une suite exacte courte (Ann. 29.1.3), G est un K-module libre, la suite est
scindée.
En effet, soit (e„)«i une base de G ; comme g est surjective, il existe alors une famille (a.)„,
d'éléments de F telle que g(a„) = ea pour tout a e I (1.4.5), et il est clair que cette famille est libre ;
elle engendre donc un sous-module G, de F dont elle est une base. Pour tout xeF, on a
g(x) = £ A,e. pour une famille de scalaires (A.), donc g\ x — t.X.a. 1=0, ce qui signifie que
Ul \ Ml /
x - \ZXaaae /(E), ou encore que F = Gt + /(E); en outre, la restriction de g à G, est un iso-
ul
morphisme de G| sur G, donc G( n /(E) = G, n Ker(g) = { 0}, ce qui prouve que F est somme
directe de G] et de /(E).
(Ann. 29.3) Dans un diagramme commutatif d'applications linéaires
0 0 0
1 i i
0 -» E F G - 0
|. |. |.
(Ann. 29.3.1) 0 -» E' F' G' - 0
I' I' I'
0 - E" F" G" -> 0
i i i
0 0 0
on suppose que les lignes verticales et les deux premières lignes horizontales sont des suites exactes ;
alors il en est de même de la troisième.
Comme w' ° g' = g" ° v' et que w' est surjective, il en est de même de g". En second lieu,
montrons que Im /" c Ker g". Soit x" e E" ; comme u' est surjective, il existe x' e E' tel que
x" = u'(x'), donc f'(x") = /"(u'(x')) == v'(f(x% et g"(f"(x"))^g"(v'(f(x'))) = w'(g'(/-'(x')))=0.
Montrons ensuite qu'inversement Ker g" c Im /". Soit y" 6 F" tel que g"(y") = 0. Comme v'
est surjective, il existe y'eF' tel que y" = t>'(y')), donc g"(v'(/)) = «''(g'(y')) = 0, et comme
Ker w' = Im w, il existe zeG tel que g'(y') = w(z). Comme g est surjective, il existe yeF tel
quez = g(y),doncg'(/) = w(g(y)) = g'M y)), autrement dit y' - tO)eKerg'. Mais Ker g'= Im/',
donc il existe x'eE' tel que y' = v(y) + f'(x'), et par suite y" = v'{f'{x')) = /"(u'(x'))-
Enfin, prouvons que /" est injective. Soit x" e E" tel que /"(x") = 0 ; comme u' est
surjective, il existe x' e E' tel que x" = u'(x'), donc 0 = f"(u'(x')) = »'(/'(*')). et comme Ker t)' = Im v,
il existe yeF tel que /'(x') = v(y). On a alors 0 = g'(f (x')) = g'My)) = w(g(y)) et comme w
est injective, g(y) = 0. Mais comme Ker g = Im / il existe xeE tel que y = f(x), donc
/'(x*) = K/ix)) = /'(u(x)), et comme /' est injective, x! = u(x), d'où finalement x" = u'(u(x)) = 0.
(Ann. 29.4) (lemme des cinq) Dans un diagramme commutatif d'applications linéaires
Eft . p /' . p /3 . p f' . p
1 ► C. 2 ► —3 * li4 * L 5
(Ann. 29.4.1) "' j ">[ "J| j "'j
p. -rr F> -n- p3 -ir F* ir F*
on suppose que les deux lignes sont exactes, et que Ui,u2, u4 et u5 sont bijectives. Alors u3 est bijective.
Montrons d'abord que u3 est surjective. Soit y3 6 F3 ; il existe x4 6 E4 tel que g3(y3) = u4(x4),
donc g4(u4(x4)) = 0, ou encore u5(/4(x4)) = 0, d'où /4(x4) = 0. U existe donc x3 e E3 tel que
x* = f3(.x3), donc g3(u3(-x3)) = g3(y3)- Comme Ker g3 = Im g2, il existe y2 e F2 tel que
y3 ~ u3(x3) = g2(y2\ et il existe x2eE2 tel que y2 = u2(x2), d'où g2(y2) = u3(f2(x2)), et
finalement y3 = u3(x3 + /2(x2)).
Montrons en second lieu que u3 est injective. Soit x3 e E3 tel que u3(x3) = 0 ; on a donc

358 ANNEXES
30. cohomologie d'un module différentiel gradué.
(Ann. 30.1) Soit A un anneau commutatif. Un A-module gradué est la somme directe E d'une
famille (EJ^ de A-modules ; les éléments de E„ sont dits de degré n. Un homomorphisme homogène
de degré 0 (ou simplement un homomorphisme) d'un A-module gradué E = © E. dans un A-module
mZ
gradué F = © F, est une application A-linéaire u : E -» F telle que u(E J c F. pour tout n e Z.
mZ
Le dual gradué d'un A-module gradué E = © E, est la somme directe des duals EJ pour
mZ
n e Z ; c'est donc un A-module gradué si l'on considère les éléments de E* comme étant de degré - n ;
s'il y a une infinité de E, non réduits à 0, on notera que le dual gradué de E est distinct du dual E*
(Ann. 27.3).
(Ann. 30.2) On appelle A-module différentiel gradué la donnée d'un A-module gradué E = © E„
Ml
et pour chaque n d'une application A-linéaire dn : E. -* E„+1, telles que pour tout net, on ait
(Ann. 30.2.1) d.+ 1 «d, = 0
ce qui s'écrit encore Im d. <= Ker d,+ 1;on dit aussi que les d, constituent un opérateur différentiel
de degré 1. En général la suite des applications </„ n'est pas exacte ; on pose
(Ann. 30.2.2) Z" = Ker d., B" = Im </,_,
(notés aussi Z"(E) et B"(E)) et on dit que les éléments de Z" (resp. B") sont les cocycles (resp. les
cobords) de degré n. Le A-module
(Ann. 30.2.3) H" = Z"/B"
0 = g3(u3{x3)) = ut(f3(x3)), donc f3(x3) = 0. Il existe par suite x2 e E2 tel que x3 = /2(x2), donc
0 = "3(72(^2)) = gi(u2(x2)). Il existe alors y, e Fj tel que u2(x2) = gi(yi), et il existe x, e E, tel
que y, = u^x,) ; alors u2(x2) = gdu^Xi)) = u2(/i(xi)), d'où x2 = /,(x,) et finalement
*3 = A(/l(Xl)) = 0.
(Ann. 29.5) Soient E un A-module libre, et
■• - F- 7. f»*> /tt. f"+* /t, f-»
une suite exacte. Alors il résulte aussitôt de (Ann. 28.4.1) que la suite
••• - e®f« iïîti E ® F«+i .litt, e®f-> û57t, e®f"' - •••
est exacte.
(Ann. 29.6) Supposons que les applications linéaires /„ : E. -» E„+1 forment une suite exacte,
et considérons les applications linéaires transposées (Ann. 9.3) '/„ : EJ+1 -> E*. Si l'on pose
F„ = Et„_i et = g-„-u on a gm+l °g„ = 0 pour ne — I, mais en général les g» ne forment
pas nécessairement une suite exacte. Toutefois, si l'on considère une suite exacte courte scindée
(Ann. 29.1.2), la suite
0 G* F* '-i E* -» 0
est exacte et scindée. Cela résulte aussitôt de (Ann. 27.3) appliqué à une somme directe de deux
modules.
Plus généralement, pour tout A-module L, la suite
0 -» Hom(G, L) - Hom(F, L) -» Hom(E, L) 0
est alors exacte et scindée.

30. cohomologie d'un module differentiel gradué
359
(note aussi h"(e)) est appelé le module de cohomologie de degré n de e ; ces modules « mesurent »
en quelque sorte le « défaut d'exactitude » de la suite des d,. On note h' (ou h'(e)) le A-module
gradué somme directe des H" pour n e Z.
(Ann. 30.3) Soient e = © e„ e' = © e; deux A-modules différentiels gradués, (d.) et (d'J les
nZ jmZ
applications linéaires qui les définissent. Un homomorphisme u : e -» E' de A-modules
différentiels gradués est un homomorphisme de A-modules gradués tel que, si u, : E, -* E'm est la
restriction de u à e„ on ait, pour tout n e Z
(Ann. 30.3.1) u.+ 1 «d. = d'.'U.
ce qu'on exprime encore en disant que le diagramme
e. e;
est commutatif. Il résulte de ces conditions que l'on a
uJFim = Z"(E'), ^B"(E)) e B"(E') ;
par passage aux quotients on obtient donc des homomorphismes pour les modules de cohomologie
(Ann. 30.3.2) H"(u) : H"(E) - H"(E')
qu'on note aussi u* ; les H"(u) définissent un homomorphisme de modules gradués
H'(u): H'(E) - H'(E'),
aussi noté u*. Si v : E' -» E" est un second homomorphisme de A-modules différentiels gradués,
on a
(Ann. 30.3.3) H'(p ° u) = H» » H'(u).
On dit que H'(u) est l'homomorphisme déduit de u par passage à la cohomologie.
(Ann. 30.4) Supposons maintenant qu'on ait une suite exacte courte d'homomorphismes de
modules différentiels gradués
(Ann. 30.4.1) 0 E' a E a E" -» 0
définis respectivement par les suites d'applications linéaires (d.) et (d,'); il revient au même
de dire qu'on a pour chaque n une suite exacte courte d'applications linéaires
(Ann. 30.4.2) 0 -. Ei 5 E, 5 E," -. 0
avec les conditions dm°u„ = u.+, °d'm et d'I ° v, = vm+l° d,. On déduit donc déjà de ces données
deux suites d'applications linéaires
H» : H"(E;) - H"(E.), W(v) : H"(E.) - H"(E;')
telles que H"(u) ° H"(u) = 0. En outre, nous allons voir qu'on peut définir pour chaque n e Z une
application A-linéaire
(Ann. 30.4.3) d,: H"(E;') - H"+,(E;).
Considérons en effet un élément c'i e H"(E?), image d'un n-cocycle z'i e Z"(Ei'). Il existe
un z.eE. tel que z'i = »^zj, et on a 0 = d'i(vJ,zK)) = t).+ l(^z.)), donc il existe z;+l eE;+I tel
qued^zj = «,+ 1(zi+i)-

360
ANNEXES
Montrons en premier lieu que z'„+, est un cocycle : en effet on a
donc d;+i(zi+1) = 0 puisque u.+2 est injective. Nous allons voir que la classe , eH"+1(E')
de z'm+, est bien déterminée par c?. En effet, en premier lieu z, n'est déterminé qu'à l'addition prés
d'un élément uj<.y'm) pour un y'meE'm; mais on a dji.uji.y'j) = u,+ 1(d',+ 1(y'^), donc quand on
remplace z. par z. + u^yi), z»+i est remplacé par z£+I + <£+,(yy, et c;+, n'est pas changée.
En second lieu, soit yi' un cobord de B"(Ei'). soit y" = «f".,(y"_,); si y,eE. est tel que
.v" = f^y.). on peut écrire v,(y,) = d'J.,(y„_,)) pour uny„_„eE._„donc t>.(y.) = ».(</,-1)).
ou encore y„ = d.-,(y._,) + uJi/,) pour un yleE;. Mais alors <Uy.) = ^u^yl)) = u.+ ,(y;)),
et quand on remplace zi' par Z? + y?, zi+1 est remplacé par zi+, + rfi+i(yi), donc c; + 1 n'est
pas changé.
U est immédiat que l'application c'î -* ôj^c'i) = C.+ , ainsi définie est A-linéaire.
(Ann. 30.5) Nous pouvons maintenant énoncer le théorème fondamental suivant.
Pour toute suite exacte courte (Ann. 30.4.1) de A-modules différentiels gradués, la suite infinie
(Ann. 30.5.1) ... - H"(E') H"(E) H-%2 HfE") ^ H"+l(E') -. ...
est exacte (suite exacte de cohomologie).
On sait déjà que Im(H"(u)) <= Ker(H"(v)) ; il reste 5 relations à vérifier.
1) Ker(H"(u)) <= Im(H"(«)). Soit c, e Ker(H"(t>)), classe d'un n-cocycle z. e Z"(E) ; il existe donc
z;'_,eE;'_, tel que w^zj = d,'.,(zi'_,), puis v^E,., tel que z;'_, =»,_,(z,_l); par suite
vjizj = ««(<(.-et z. = d.-^z,.,) + uJLz'J pour un zJeE; Comme 0 = d^zj, on a
0 = dJluAz'J)) = u. + l(d',+ l(z',)), donc d;+,(z;) = 0, z', est un cocycle, et c, = H"(uXc;), où c; est
la classe de z'm.
2) Im(H"(i;)) <= Ker(da). Cest immédiat en raison de la définition de d, : si z,' = d,(z.), où z,
est un cocycle, on a, avec les notations de (Ann. 30.4), u.+ ,(z;+1) = 0, donc zi+1 =0.
3) Kerfd.) c Im(H"(e)). En effet, avec les notations de (Ann. 30.4), si d,(c';) = 0, cela signifie
que l'élément z;+1 est de la forme d'Jiz',) pour un z'meE',; donc d^zj = u.+ .WMzl)) = dMz',)\
autrement dit z, - u„(zi) e Z"(E). Par suite z'i = i).(zj = u.(z, — u.(zi )) appartient à vJ[Z"(E)), ce
qui montre que c'i = H"(v)(cJ, où c, est la classe de z„ — u„(zi).
4) Im(5„) c Ker(H"+,(«)). Toujours avec les mêmes notations, onaen effet u.tl(z'm+1)=dJiz.),
ce qui montre que H*+I(«Kci+i) = 0.
5) Ker(H"+1(«)) <= Im(ô,). En effet, soit c',+ l e H"+l(E') tel que pour un élément z;+1 de
classe c'n + l, on ait um+l(z',+ l) = dJiz.) pour un z. € E. ; en premier lieu z» = vj(zn) est un cocycle,
car on a d'ï(z'f) — d"(vj^z^)) = vm+i(d,(z.)) = vM+l(u,+1(z,+1)) = 0 ; la définition de d. prouve ensuite
que l'on a ci+, = djic"\ où est la classe du cocycle z?.
(Ann. 30.6) Supposons maintenant qu'on ait un diagramme commutatif d'homomorphismes de
modules différentiels gradués
où les deux lignes horizontales sont exactes. Alors, on a, pour les suites exactes de cohomologie
correspondant à ces deux lignes, le diagramme commutatif
0 E' —ï-» E E" -» 0
(Ann. 30.6.1)
0 - F' ► F ► F" - 0
... - H"(E')
H"(E") -^-* H"+,(E') - ...
(Ann. 30.6.2)
... - H"(F') ► H"(F) ► H"(F") ► H"+1(F') - ...
V ' H»(r) v ' H"(») *. '

30. COHOMOLOGIE D'UN MODULE DIFFÉRENTIEL GRADUÉ
361
Comme / ° u = r ° /' et /"»i) = s«/ona
HV) . H"(u) = mr) ° H"(/') et H"(f") . H"(t>) = H"(s). H"(/) ;
reste à montrer que l'on a
(Ann. 30.6.3) 3.. H"(/") = H"+ '(/') o Ô,.
Or, en gardant toujours les notations de (Ann. 30.4), on a par hypothèse f"(z") = fi'(vj[z„)) = «.(/.(z„)X
et d„(/.(r.)) = /»+,(d,(:.)) = /.+ i(«»+,U';+1)) = r.+ i(/:+1(z;+,)). Mais H"(/")(0 est la classe
du cocycle /„"(z") et par construction d„(H"(/"')(c")) est la classe du cocycle /,'+ ,{zi+,), c'est-à-dire
H"+'(/'Xe;+1) = H"+1(/'K5,(c;')).
(Ann. 30.7) Une théorie équivalente à la précédente est celle des A-modules codifférentiels gradués :
on se donne encore un A-module gradué E = © E„, mais, pour chaque n, une application A-linéaire
mZ
d, : E„ -» E._,, avec, pour tout neZ, la condition
(Ann. 30.7.1) °d, = 0 ( « opérateur différentiel de degré - 1 » ).
Il suffit en effet de poser EJ = E_, et d'n = d-, pour retrouver la notion de A-module
différentiel gradué. Mais dans les applications il est commode d'utiliser une autre terminologie ; on
pose
Z, = Ker d,, B„ = Im<l, + ,
et on dit que les éléments de Z„ (resp. BJ sont les cycles (resp. les bords) de degré n. Le A-module
H. = ZJB.
est alors appelé le module d'homologie de degré n. On écrira H„(u), H.(u) ou u, au lieu de H"(u),
H'(u) et u*, et la suite exacte correspondant à (Ann. 30.5.1) par le changement d'indexation sera
dite suite exacte d'homologie.
(Ann. 30.8) Rappelons (Ann. 18.1) qu'une A-algèbre graduée associative est un A-module gradué
E = © E„ où E. = {0} pour n < 0 (on écrira donc E = © E. ], dans lequel est défini une
mZ \ «3>0 /
multiplication associative telle que
(Ann. 30.8.1) E,E, c Ep+, pour p > 0 et q > 0 .
On dit qu'une A-algèbre graduée E est une A-algèbre différentielle graduée si E est un A-module
différentiel gradué pour lequel les applications A-linéaires d„:E, -> E„+1 ont en outre la
propriété d'être des anti-dérivations de degré 1 (Ann. 18.4) ; autrement dit, pour xp e E,, x, e Ev on a
(Ann. 30.8.2) d,+,(xpx,) = (d^x,))*, + (- l)'x^x,)).
Il résulte aussitôt de cette relation que l'on a
(Ann. 30.8.3) Z'Z« c Z'+', B'Z« + Z'B* c B'+«
pour p > 0 et q > 0. On en déduit que l'application (x,, x,) -> XpX, de Z' x Z* dans Z,+' est
compatible avec les relations d'équivalence x, - x't e Bp et x, — x\ e B,, et donne donc par
passage aux quotients une application bilinéaire (cp, c,) -» c„cq de Hp x H* dans H*+*. Ces
applications définissent donc une structure d'algèbre graduée sur la somme directe H' = © H", et il
■ »o
est clair que la multiplication dans cette algèbre est associative; on dit que l'algèbre graduée H'
est l'algèbre de cohomologie de l'algèbre différentielle graduée E.
Un homomorphisme u : E -> E' de A-algèbres différentielles graduées est un homomorphisme
de A-modules différentiels gradués qui en même temps est un homomorphisme d'algèbres. Il
est immédiat alors que H*(u) est un homomorphisme d'algèbres.

362
ANNEXES
(Ann. 30.9) Soient E = © E., F = ©F, deux A-modules gradués, et supposons que chacun
meZ ncZ
des E. soit libre. Alors les produits tensoriels E, ® F, sont définis, et E ® F est somme directe de
ses sous-modules E, ® F, (Ann. 28.2). Pour tout n € Z, soit G. la somme directe des modules
E, ® F, pour p + q — n ; on définit alors une structure de A-module gradué sur E ® F en prenant
pour module des éléments de degré n le sous-module G„ pour tout n e Z.
Supposons que E et F soient deux algèbres graduées associatives, et anticommutatives, c'est-
à-dire que si xp et x, sont des éléments d'une de ces algèbres, homogènes de degré p, q
respectivement, on a
(Ann. 30.9.1) x.xr = (- l)"%x,
(c'est le cas par exemple pour les algèbres extérieures (Ann. 13.2.2)). On peut alors définir sur
le A-module E ® F une structure d'algèbre graduée associative et anticommutative, en définissant
les produits par les relations
(Ann. 30.9.2) (x„ ® y,X*, ® y.) = ( - W*,*,) ® (y,y.) ;
la vérification de ces assertions est immédiate. On note E *® F cette algèbre graduée et on dit
que c'est le produit tensoriel gauche des algèbres graduées anticommutatives E et F.
Par exemple, si M est un A-module libre de type fini, somme directe de deux-sous-modules
libres N, P, on voit aussitôt, en prenant des bases dans N et P (dont la réunion est une base de M)
que l'algèbre extérieure a M est isomorphe au produit tensoriel gauche ( a N) *® ( a P).
(Ann. 30.10) Supposons maintenant que E et F soient des A-modules différentiels gradués,
définis par des applications linéaires d, : E, -» E„+i, d', : F, -» F.+ 1, et supposons en outre
que les E. soient libres. Alors on peut définir sur E ® F une structure de A-module différentiel
gradué : pour définir les applications d" : G, -* G„+ „ il suffit de le faire dans chacun des modules
E, ® F, pour p + q - n. On prend pour x„ e E,, y, e F,
(Ann. 30.10.1) d';+t(xt ® y,) = (d,(x,)) ® y, + ( - 1)% ® (d'^y,)).
La vérification des relations
d;+q+1°d';+, = o
est immédiate.
Si en outre E et F sont des algèbres différentielles graduées anticommutatives, on vérifie
que la définition (Ann. 30.10.1) définit sur le produit tensoriel gauche E "® F une structure d'algèbre
différentielle graduée.
31. Homologie et cohomologie d'un Z-module codifférentiel gradué libre.
(Ann. 31.1) On a vu (Ann. 26.2) que tout sous-module d'un Z-module libre de type fini est
lui-même libre. La démonstration s'adapte aussitôt au cas où le Z-module libre L considéré a
une base dénombrable (a„)MN (la seule différence étant que les a* e L*, définis par < am, a* > = <$„«,
ne forment plus une base de L*). En fait, pour tout Z-module libre L, tout sous-module de L est
libre; nous admettrons ce résultat (voir [3, chap. 7] pour la démonstration, qui est encore une
adaptation de la précédente, mais il faut « bien ordonner » la base de L).
(Ann. 31.2) Un A-module gradué E = © E. est dit module gradué libre si chacun des A-modules E.
■aZ
est libre. Pour un Z-module codifférentiel gradué libre E, l'homologie présente des particularités
importantes. En effet, pour tout n e Z, le Z-module B. des bords et le Z-module Z, des cycles sont
des sous-modules du Z-module libre E„ donc sont libres par (Ann. 31.1). Mais on a une suite
exacte courte

31 . HOMOLOGIE ET COHOMOLOGIE D'UN Z-MODULE CODIFFÉRENTIEL 363
donc cette suite est scindée (Ann. 29.2); autrement dit, Z„+1 (qui est libre) admet un
supplémentaire F,+1 (lui aussi libre) dans E„+I, la restriction de d,+ l à Fa+1 étant une bijection sur B„.
(Ann. 31.3) Soit E = ©E. un Z-module codifférentiel gradué libre; pour tout Z-module G,
«i
on peut définir sur E ® G = ©(E. ® G) (Ann. 28.2) une structure de Z-module codifférentiel,
mZ
en prenant les d, ® 1G comme applications Z-linéaires E, ® G -» E„_,®G. Pour tout n,
E, ® G est alors somme directe de Z, ® G et de F. ® G; l'application d. ® 1G est nulle dans
Z. ® G, et est une surjection de F. ® G sur B._ ,(E ® G) ; mais il faut prendre garde qu'en général
B„_ i(E) n'a pas de supplémentaire dans E„_et que la restriction de d.® 1G a un noyau Z'm dans
F. ® G, non réduit à 0 ; de sorte que l'on peut écrire
(Ann. 31.3.1) Z^E ® G) = (ZJE) ® G) © ZJ.
(Ann. 31.4) Sous les conditions générales de (Ann. 31.3), montrons maintenant que si H,(E)
et H._,(E) sont des Z-modules libres, alors H«(E ® G) est isomorphe à HJE) ® G.
En effet, l'hypothèse que H, = H«(E) est libre entraine que la suite exacte
0 -» B„ Z„ -» H, -» 0
est scindée, autrement dit B. admet un supplémentaire (libre) L. dans Z„ et par suite un
supplémentaire (libre) F, © L, dans E,. Mais alors l'image B^E ® G) de E.+ , ® G par d„+1 ® 1G
s'identifie à B. ® G, qui admet un supplémentaire identifié à L. ® G dans Z, ® G ; mais en vertu
de (Ann. 31.3.1), ce supplémentaire n'est pas nécessairement isomorphe à H.(E ® G).
Toutefois, si on suppose de plus que H„_ ,(E) est libre, il en résulte cette fois que B„_ ,(E ® G)
s'identifie à B,. ,(E) ® G, et que d, ® 1G est une bijection de F. ® G sur B._ ,(E) ® G ; avec les
notations précédentes, on a donc Z'm = {0 }, Z.(E ® G) = Z^E) ® G, et L. ® G s'identifie à
HJf) ® G, ce qui achève la démonstration.
(Ann. 31.5) Pour tout A-module codifférentiel gradué E = © E„ et tout A-module G, on définit
canoniquement sur le A-module gradué "*z
E' = © Hom(Em G)
jmZ
une structure de A-module différentiel gradué, en prenant pour applications linéaires définissant
cette structure les applications
Hom(d,+ 1, 1G) : /„
de Hom(E„ G) dans Hom(E.+,, G) ; désignons par H'(E ; G) le A-module de cohomologie
correspondant. Nous nous bornerons, en ce qui concerne les relations entre H.(E) et H'(E; G), à la
proposition suivante :
(Ann. 31.6) Soit E = © E. un Z-module codifférentiel gradué libre ; il existe pour tout n une
mZ
application Z-linéaire surjective canonique
(Ann. 31.6.1) H"(E ; G) -» Hom(H^E), G) ;
si de plus H,_,(E) est libre, l'application précédente est bijective.
Les définitions précédentes montrent qu'on peut caractériser les cocycles et les cobords
de E' de la façon suivante :
1) l'ensemble Z"(E') des n-cocycles est formé des applications linéaires fm de E. dans G
qui s'annulent dans BJE);
2) l'ensemble B"(E') des n-cobords est formé des applications linéaires f,-1"d„ où
e HomfE.-!, G); elles s'annulent dans ZJE), mais une application Z-linéaire de E. dans G
qui s'annule dans Z^E) n'est pas nécessairement un cobord.

364
ANNEXES
L'application (Ann. 31.6.1) s'obtient en faisant correspondre à un n-cocycle fm sa
restriction à Z^E), qui s'annule dans B^E) et donne donc par passage au quotient une application linéaire
de H„(E) - Z.(E)/B^E) dans G ; si /. est un cobord, sa restriction à Z.(E) est nulle, donc on définit
bien ainsi une application Z-linéaire de H'(E') = Z"(E')/B"(E') dans Hom(H„(E), G). Enfin cette
application est surjective, car Z„(E) admet un supplémentaire F. dans E. (Ann. 31.2), et toute
application Z-linéaire de Z^E) dans G qui s'annule dans BJ.E) se prolonge en une application
Z-linéaire de E. dans G (par exemple en lui donnant la valeur 0 dans F.).
Supposons maintenant que H._j(E) soit un Z-module libre; alors on a vu (Ann. 31.4) que
B.-i(E) admet un supplémentaire F._, © L._, dans E„-,. Si un n-cocycle f, est nul dans Z^E),
sa restriction à F. peut s'écrire g.-1 ° à„ où g„_, est une application linéaire de B„_ t(E) dans G ;
mais ici g„_i peut se prolonger en une application linéaire de E._, dans G, donc
/« = /■-■ °àneB"(E'), et on a ainsi prouvé que l'application (Ann. 31.6.1) est bijective.
(Ann. 31.7) Considérons maintenant deux Z-modules codifférentiels gradués libres E = © Em
mZ
F = © F„ tels que E, c F. et que E. admette dans F. un supplémentaire libre. Supposons que
mZ
l'injection canonique j : E -» F soit un homomorphisme de modules codifférentiels gradués.
Si l'on pose E' = ffi Hom(E, G), F' = © Hom(F, G), on déduit de j une application Z-linéaire
mZ jmZ
/ = Hom(/, 10) : F' - E'
qui est un homomorphisme de Z-modules différentiels gradués.
(Ann. 31.8) Sous les hypothèses de (Ann. 31.7), si H.(j) : H.(E) -> H.(F) est un isomorphisme,
alors H'O") : H'(F') H'(E') est un isomorphisme.
L'hypothèse signifie que pour tout n e Z, on a
(Ann. 31.8.1) ZJ& + Bj(F) = Zffi), ZJft n Bj(F) - B«(E)
et en outre on a évidemment Z,(E) = E„ n Z«(F).
Nous allons en déduire que B^E) admet un supplémentaire libre dans B^F), qui sera aussi
un supplémentaire de ZJ(E) dans Z^F), puisque Z.(F)/Z^E) et B.(F)/BJE) sont canoniquement
isomorphes d'après (Ann. 31.8.1). On a en effet un diagramme commutatif
0 0 0
0 ► ZJ.E) ► E. —B,-,(E) > 0
0 ► Zj(F) ► F. —i-. B._,(F) » 0
1 i i
0 - Z.(F)/Z^E) -. FJE. - B._1(F)/B._I(E) 0
I i i
0 0 0
dans lequel les colonnes et les deux premières lignes sont exactes; la troisième ligne est donc
exacte (Ann. 29.3). Comme FJE, est libre, il en est de même de son sous-module Z«(F)/Z.(E),
isomorphe à B^F)/B,(E), d'où notre assertion (Ann. 29.2). En outre, comme B._,(F)/B._,(E)
est libre, E„ + ZJ[F) admet dans F. un supplémentaire (Ann. 29.2). Finalement on voit qu'on
peut écrire F, = E„ © L„ © M„ où L„ est supplémentaire de B„(E) dans B,(F).
Cela étant, montrons d'abord que H"(/) est surjective. Soit /„ e Z'(E'), c'est-à-dire une
application linéaire de E„ dans G nulle dans B.(E) ; on la prolonge en une application linéaire
de F. dans G, nulle dans L. © M„ donc nulle dans B^F), et cette application est donc dans Z*(F').
Prouvons enfin que H"(/) est injective. Soit donc g, e Z"(F') telle que la restriction de g,
à E» appartienne à B"(E'), autrement dit soit de la forme /,_ i « d„ où f, est une application linéaire

33. LE PLAFFIEN
365
de E._, dans G. D'après ce qu'on a vu plus haut, la restriction de d, à M. est une bijection sur L._,.
Prolongeons alors /„_, en une application linéaire g.-1 de F,_, dans G, égale à g, » d,"1 dans L„_,
et arbitraire dans M._, ; il est clair que l'on aura g, = g,-t°d„ donc g„eB"(F'). CQFD.
32. Compléments sur les espaces vectoriels.
(Ann. 32.1) On a vu (Ann. 4.5) que si E est un espace vectoriel et V un sous-espace vectoriel
tel que E soit engendré par V et une famille finie (x,)l(lta de vecteurs, il existe une sous-
famille (x,J, <t<r qui est une base d'un supplémentaire de V dans E. Une variante de la
démonstration consiste à supprimer, par récurrence, de la famille (x,)1(i(m les vecteurs qui sont
combinaisons linéaires des précédents et de vecteurs de V ; les vecteurs restants sont les xik. Ce procédé
s'applique sans modification lorsque E est engendré par V et une suite infinie (x.) de vecteurs.
En fait, lorsque E est engendré par V et une famille quelconque (x„)hA de vecteurs, il existe une
sous-famille (x,),,i de (x,).,A qui constitue une base d'un supplémentaire de V dans E ; nous
admettrons ce résultat (voir [3, chap. 2] pour la démonstration, qu'on peut présenter comme une
adaptation de la précédente, en « bien ordonnant » A).
(Ann. 32.2) De ce qui précède, on déduit que tout système générateur d'un espace vectoriel
quelconque E contient une base de E, et que tout sous-espace vectoriel de E admet un
supplémentaire dans E ; tout système libre dans E est contenu dans une base de E. Enfin, on peut
montrer [3] que deux bases de E sont toujours équipotentes.
(Ann. 32.3) Si E est un espace vectoriel quelconque, V un sous-espace vectoriel de E, W un
supplémentaire de V,p : E -» Vet<j:E -> W les projections canoniques, l'identité x=p\x)+q(x)
donne par transposition l'identité x* = 'p(x*) + 'q(x*) pour tout x* e E*, donc E* est somme
des sous-espaces '/HE*) et 'q(Em); cette somme est directe, car si 'piy*) = 'q{z*), pour xe V, donc
x = p(x) et q(x) - 0, on a 0 = < x, 'q(z*) > = < x, 'p(y*) >, et de même pour x 6 W, donc x - q{x)
et p(x) = 0,0 - < x, *p(y*) > = < x, 'q{z*) >, donc 'p(y*) = 'tfz*) = 0. En outre, on a V° = '(j(W*)
et W° = 'p(V*); on en déduit que
(Ann. 32.3.1) (V0)0 = V
car si x i V, y *= x - p(x) e W n'est pas nul, donc peut être pris comme élément d'une base de W,
et il existe par suite y* e W* tel que < y, y* > = 1, ce qui entraine 1 = < x -p(x), 'q{y*) > = < x, 'q{ y*) >,
donc x*(V°)°.
(Ann. 32.4) Pour les espaces vectoriels toutes les suites exactes courtes sont scindées. Ce fait,
et le fait que tout espace vectoriel est libre, entraînent que tout ce qui a été dit dans (Ann. 31) sur
l'homologie et la cohomologie pour, les Z-modules libres est valable sans modification quand on
remplace partout « Z-module libre » par « espace vectoriel » les conditions restrictives de (Ann. 31.4)
et (Ann. 31.6) étant sans objet puisque vérifiées d'elles-mêmes.
33. Le pfaffien.
(Ann. 33.1) Soient K un corps commutatif de caractéristique 0, E un espace vectoriel sur K
de dimension paire 2m, B une forme bilinéaire alternée sur E x E (Ann. 16.1); si (ei)1<l<2m est
une base de E, (e*), flflm la base duale de E*, on peut donc écrire
B - Z «0«f a ej = \ Z auef a ej
où (a,j) est une matrice alternée d'ordre 2m, c'est-à-dire telle que aJt = — au (on identifie B à un
2 2m
bivecteur de ae*). Il est clair que la puissance extérieure m-ème BA" est un 2m-vecteur de ae*.

366
ANNEXES
donc de la forme o.e* a e* a ... a efm-, a e}„, a étant un scalaire que nous allons calculer.
Par définition, B*" est somme de tous les termes
«.,«,«.,., • • • «.„*,.< a el a et, a et, a ... a etm a eîm
pour toutes les suites d'indices telles que hj < kj pour 1 < j < m. Un tel terme est nul s'il y figure
deux ef égaux, c'est-à-dire si l'ensemble { hlt fc,, .. .,hm fc„ } est distinct de {1, 2 2m }.
En outre, si dans le produit précédent on échange simultanément e£ et cfr(l d'une part, ef. et ef,.,
d'autre part, le produit ne change pas ; il ne change donc pas pour toute permutation effectuée
sur les couples (hu ..., (hm, kj. Considérons alors les ensembles (et non les suites)
S = {(h„ >£(), ..., (hm kj } de couples (hj, kj) tels que 1 < hj < kj < 2m pour 1 < j < m ; soit y
l'ensemble de ces couples. Pour tout S e Sf, posons
1* «(S) = 0 si {/>„ fc, hm km } # {1, 2, ..., 2m } ;
2° dans le cas contraire, c(S) = 1 ou e(S) = — 1 suivant que la permutation de { 1,2 2m }
qui applique chaque ht sur lj — 1 et chaque kt sur 2j est paire ou impaire.
Avec ces notations, on a donc
(Ann. 33.1.1) BA" = m! £ <S)( u «A* a eî a ... a «J. .
s> y \l«.«)«S /
On dit que l'élément de K
(Ann. 33.1.2) Pf((«tt)) = Z e(S)( fi «J
est le pfaffien de la matrice alternée U = (au).
(Ann. 33.2) Pour toute matrice alternée U d'ordre 2m sur K et toute matrice carrée inversible P
d'ordre 2m sur K, on a
(Ann. 33.2.1) Pf('P. U.P) = (det P)P((U).
En effet, posons P = (/}„), U - (a(J) et soit B la forme bilinéaire alternée sur E x E ayant pour
matrice U par rapport à la base (et) ; considérons d'autre part 'P comme la matrice, par rapport
à la base (ef), d'un endomorphisme / de E* ; alors la forme bilinéaire alternée ayant pour matrice
'P. V.P est identifiée au bivecteur ^A/^(B). car elle est égale par définition à
1 „
- L PiAifisfi* a e* .
2
U résulte des définitions (Ann. 13.4 et 13.5) que l'application Af de l'algèbre extérieure A E*
r r
dans elle-même, égale à f\f dans chaque AE*, est un endomorphisme pour la structure d'algèbre
de A E* et que l'on a
((Â/)(B)y"-(A/)(B*"';
2m 2m
mais l'application f\f est l'homothétie de rapport det(/) dans A E*, donc il résulte de (Ann. 33.1.1)
que l'on a
m ! Pf('P.l/.P) = m!(det P)Pf(U).
(Ann. 33.3) Pour toute matrice alternée U d'ordre 2m sur K, on a
(Ann. 33.3.1) det U = (Pf(l/))2 .
Comme det('P.U.P) = (det P)2(det U), il suffit, en vertu de (Ann. 33.2), de prouver la

34. COMPLÉMENTS SUR LES Z-MODULES DE TYPE FINI
367
relation (Ann. 33.3.1) pour la matrice 'P.U.P avec un choix convenable de la matrice
inversible P. Or (Ann. 16.1), on peut toujours trouver une telle matrice telle que 'P.U.P soit la matrice
d'une forme
B = e? a e\ + e* a ej + ... + e*r_, a e\r.
Mais il est immédiat en vertu des définitions que pour cette forme on a Pf(C) = det(f) ■= 0
si r < m et Pf(l/) » det(l/) = 1 si r = m.
34. Compléments sur les Z-modules de type fini.
(Ann. 34.1) Rappelons (Ann. 26.4) qu'un Z-module de type fini E est somme directe de son
sous-module de torsion T, formé des xe E pour lesquels il y a un entier n ^ 0 tel que n.x = 0,
et d'un Z-module libre ; le nombre d'éléments d'une base du module libre E/T est appelé le rang
de E et noté rg(E).
(Ann. 34.2) Soient E un Z-module de type fini, F un sous-module de E ; alors on a
(Ann. 34.2.1) rg(F) + fg(E/F) = rg(E).
Notons d'abord que si G est un Z-module de type fini et H un sous-module de son sous-
module de torsion, on a rg(G) = rg(G/H) par définition. Soit alors T le sous-module de torsion
de E. Comme (T+F)/F est un sous-module du module de torsion de E/F, on a rg(E/F)=rg(E/(T+F));
d'autre part, (T + F)/T est isomorphe à F/(T n F), donc rg(F) = rg((T + F)/T). Si E' = E/T,
F' = (T + F)/T, on a donc rg(F') = rg(F), rg(E'/F') = rg(E/F) et rg(E') = rg(E). On est donc
ramené à prouver (Ann. 34.2.1) lorsque E est libre et F un sous-module de E, qui est donc aussi
libre (Ann. 26.2); la proposition est alors conséquence du théorème des facteurs invariants
(Ann. 26.3).
(Ann. 34.3) Soient E, F deux Z-modules de type fini, et u : E -» F une application Z-linéaire.
Alors on a
(Ann. 34.3.1) rg(Im u) + rg(Coker u) = rg(F).
Il suffit en effet d'appliquer (Ann. 34.2.1) à F et à son sous-module Im u.
(Ann. 34.4) Soient maintenant E un Z-module de type fini, et u : E -> E un endomorphisme
de E. Alors on a
(Ann. 34.4.1) rg(Ker u) = rg(Coker u).
En effet, E/Ker u est isomorphe à Im u, donc d'après (Ann. 34.2.1)
rg(Ker u) + rg(Im u) = rg(E).
Mais d'autre part (Ann. 34.3.1)
rg(Im u) + rg(Coker u) = rg(E).
La comparaison de ces deux relations donne (Ann. 34.4.1).

bibliographie
Volume I
[I] Ahlfors, L., Complex Analysa, McGraw-Hill, New York, 1963.
[2] Bachmann, H., Transfinite Zahlen. Ergebnisse der Math., Neue Folge, Heft 1, Springer,
Berlin, 19SS.
[3] Bourbaki, N., « Éléments de Mathématique : Théorie des Ensembles » (nouvelle éd.),
Hermann, Paris, 1970.
[4] Bourbaki, N., « Éléments de Mathématique : Algèbre » (nouvelle éd.), Chap. 1-3,
Hermann, Paris, 1970; Chap. 4-7 (nouvelle éd.), Masson, Paris, 1981.
[5] Bourbaki, N., « Éléments de Mathématique : Topologie générale » (nouvelle éd.),
Chap. 1-4, Hermann, Paris, 1971 ; Chap. 5-10, Hermann, Paris, 1974.
[6] Bourbaki, N., « Éléments de Mathématique : Espaces vectoriels topologiques »
(nouvelle éd.), Chap. 1-5, Masson, Paris, 1981.
[7] Cartan, H., Séminaire de l'École Normale Supérieure, 1951-52 : Fonctions analytiques et
faisceaux analytiques.
[8] Cartan, H., Théorie élémentaire des fonctions analytiques. Hermann, Paris, 1961.
[9] Coddinoton, E. and Lbvinson, B., Theory of ordinary différential équations. McGraw-Hill,
New York. 1955.
[10] Courant, R. und Hilbbrt, D., Methoden der mathemalischen Physik, I (2* éd.). Berlin,
Springer, 1931.
[II] Halmos, P., Finite dimensional vector spaces (2* éd.). D. Van Nostrand, New York, 1958.
[12] Ince, E., Ordinary differential équations. Dover Publ., New York, 1949.
[13] Jacobson, N., Lectures in abstract algebra : II, Linear algebra. D. Van Nostrand, New York,
1953.
[14] Kamkb, E„ Differenlialgteichungen reeller Funktionen. Akad. Verlag, Leipzig, 1930.
[15] K.bllby, J., General topology. D. Van Nostrand, New York, 1955.
[16] Landau, E., Foundalions of Analysis. Chelsea, New York, 1951.
[17] Sprinoer, G., Introduction to Riemann surfaces. Addison-Wesley, Reading, Mass., 1957.
[18] Weil, A., « Introduction à l'étude des variété* kahlériennes ». Actual. Scient. Ind., n* 1267.
Hermann, Paris, 1958.
[19] Weyl, H., Dit Idée der Riemannschen Floche (3' éd.). Teubner, Stuttgart, 1955.
Volume II
[20] Akhiezer, N., The classical moment problem. Oliver and Boyd, Edinburgh-London, 1965.
[21] Arnold, V et Avez, A., Théorie ergodique des systèmes dynamiques. Gauthier-Villars, Paris,
1967.
[22] Bourbaki, N., « Élément* de mathématique : Livre VI, Intégration ». Actual. Scient. Ind.,
Chap. I-IV, n« 1175 (2* éd.), Chap. V, n» 1244 (2« éd.), Chap. VII-VIII, n» 1306.
Hermann, Paris, 1963-67.
[23] Bourbaki, N., « Éléments de mathématique : Théories spectrales », Chap. I-II. Actual.
Scient. Ind., n* 1332. Hermann, Paris, 1967.
[24] Dixmibr, j., Les algèbres d'opérateurs dans l'espace hitbertien. Gauthier-Villars, Paris, 1957.
[25] Dixmier, J., Les C*-algèbres et leurs représentations. Gauthier-Villars, Paris, 1964.

370
BIBLIOGRAPHIE
[26] Dunford, N. and Schwartz, J., Linear operators. Part. II : Spectral theory. Interscience,
New York-London, 1963.
[27] Hadwioer, H., Vorlesungen iiber Inhall, Oberftàche und Isoperimetrie. Springer, Berlin, 19S7.
[28] Halmos, P., « Lectures on ergodic theory », Math. Soc. of Japon, 1956.
[29] Hoffman, K.., Banach spaces of analytic functions, New York, 1962.
[30] Jacobs, K., « Neuere Metboden und Ergebnisse der Ergodentheorie ». Ergebnisse der Math.,
Neue Folge, Heft 29. Springer, Berlin, 1960.
[31] Kaczmarz, S. und Steinhaus, H., Théorie der Orthogonalreihen. New York, 1951.
[32] K.ato, T., Perturbation theory for linear operators. Springer, Berlin, 1966.
[33] Montgomery, D. and Zippin, L., Topological transformation groups. Interscience, New York,
1955.
[34] Naimark, M., Normed rings. P. Nordhoff, Groningen, 1959.
[35] Rickart, C, General theory of Banach algebras. D. Van Nostrand, New York, 1960.
[36] Weil, A., Adeles and algebraic groups. The Institute for advanced Study, Princeton, 1961.
Volume III
[37] Abraham, R., Foundations of mechanics. W. A. Benjamin, New York, 1967.
[38] Cartan, H., Séminaire de l École Normale Supérieure, 1949-50 : Homotopie ; espaces fibres.
[39] Chern, S. S., Complex manifolds (Textos de matematica, n* 5, Univ. do Recife, 1959).
[40] Gublfand, I. M. et Shilov, G. E., Les distributions, vol. 1 et 2. Dunod, Paris, 1962.
[41] Gunnino, R., Lectures on Riemann surfaces. Princeton Univ. Press, 1966.
[42] Gunnino, R., Lectures on vector bundles over Riemann surfaces. Princeton Univ. Press, 1967.
[43] Hu, S. T., Homotopy theory. Académie Press, New York, 1959.
[44] Husemoller, D., Fibre bundles. McGraw-Hill, New York, 1966.
[45] Kobayashi, S. and Nomizu, K.., Foundations of différential geometry, vol. I, Interscience,
New York, 1963 ; vol. II, Interscience, New York, 1969.
[46] Lano, S., Introduction to differentiable manifolds. Interscience, New York, 1962.
[47] Porteous, I. R., Topological geometry. Van Nostrand, New York, 1969.
[48] Schwartz, L., Théorie des distributions (nouv. éd.). Hermann, Paris, 1966.
[49] Steenrod, N., The topology of fibre bundles. Princeton Univ. Press, 1951.
[50] Sternbbrg, S., Lectures on differential geometry. Prentice-Hall, Englewood Cliffs, 1964.
Volume IV
[51] Abraham, R. and Robbin, J., Transversal mappings and fiows. W. A. Benjamin, New York,
1967.
[52] Berger, M., Lectures on geodesics in Riemannian geometry. Tata Institute of fundamental
research, Bombay, 1965.
[53] Carathbodory, C, Calculus of variations and partial differential équations of the firsl order,
2 vol., Holden-Day, 1965.
[54] Cartan, E., Œuvres complètes, 6 vol., Paris, Gauthier-Villars, 1952-1955.
[55] Cartan, E., Leçons sur la théorie des espaces à connexion projective. Gauthier-Villars, Paris,
1937.
[56] Cartan, E., La théorie des groupes finis et continus et la géométrie différentielle traitées par
la méthode du repère mobile. Gauthier-Villars, Paris, 1937.
[57] Cartan, E., Les systèmes différentiels extérieurs et leurs applications géométriques. Hermann,
Paris, 1945.
[58] Gelfand, I. and Fomin, S., Calculus of variations. Prentice Hall, 1963.
[59] Godbillon, C, Géométrie différentielle et mécanique analytique. Hermann, Paris, 1969.
[60] Gromoll, D., K.ungenbero, W. und Meyer, W., Riemannsche Géométrie im Grossen,
Lecture Notes in Mathematics n" 55. Springer, Berlin, 1968.

BIBLIOGRAPHIE
371
[61] Guggenheimer, H., Differential geometry. McGraw Hill, 1963.
[62] Helgason, S., Differential geometry and symmetric spaces. Académie Press, New York, 1962.
[63] Hermann, R., Differential geometry and the calculus of variations. Académie Press, New York,
1968.
[64] Hochschild, G., La structure des groupes de Lie. Dunod, Paris, 1968.
[65] Kxôtzlbr, R., Mehrdimensionale Variâtionsrechnung. Birkhâuser, Bâle, 1970.
[66] Loos, O., Symmetric spaces, 2 vol., W. A. Benjamin, New York, 1969.
[67] Milnor, J., Morse theory. Princeton University Press, Princeton, 1963.
[68] Morrey, C, Multiple intégrais in the calculus of variations. Springer, Berlin, 1966.
[69] Reeb, G., Sur les variétés feuilletées. Hermann, Paris, 1952.
[70] Rund, H., The differential geometry of Finsler spaces. Springer, Berlin, 1959.
[71] Schirokow, P. und Schirokow, A., Affine Différentialgeometrie. Teubner, Leipzig, 1962.
[72] Serre, J. P., Lie algebras and Lie groups. W. A. Benjamin, New York, 1965.
[73] Wolf, J., Spaces of constant curvature. McGraw Hill, 1967.
Volumes V et VI
[74] Algebraic groups and discontinuous subgroups (Proceedings of Symposia in Pure Mathe-
matics, vol. IX), American Math. Soc., Providence, 1966.
[75] Bellman, R., A brief introduction to thêta functions. H oit, Rinehart and Winston, New York,
1961.
[76] Bernât, P. et al.. Représentations des groupes de Lie résolubles (Monographies de la Soc.
math, de France, n" 4), Dunod, Paris, 1972.
[77] Borel, A., Linear algebraic groups, Benjamin, New York-Amsterdam, 1969.
[78] Borel, A., Introduction aux groupes arithmétiques, Hermann, Paris, 1969.
[79] Bourbaki, N., Éléments de Mathématique, Groupes et algèbres de Lie. Actual. Scient. Ind.,
Chap. I, n* 1285, Chap. II-III, n» 1349, Chap. IV-V-V1, n° 1337, Hermann, Paris. 1960-
1972.
[80] Carter, R., Simple groups of Lie type, Wiley, New York, 1972.
[81] Chbvalley, C, Classification des groupes de Lie algébriques, 2 vol., Séminaire de l'École
Normale Supérieure 1956-58, Paris (Secr. math., 11, Rue P.-Curie).
[82] Conférence on Harmonie Analysis (Collège Park, 1971), Lecture Notes in math., n° 266,
Springer, Berlin-Heidelberg-New York, 1972.
[83] Edwards, R., Fourier Séries, 2 vol., Holt, Rinehart and Winston, New York, 1967.
[84] Gunnino, R., Lectures on modular forms, Princeton Univ. Press, 1962.
[85] Hausner, M., Schwartz, J., Lie groups. Lie algebras, Gordon Breach, New York, 1968.
[86] Igusa, J., Thêta functions, Springer, Berlin-Heidelberg-New York, 1972.
[87] ICahane, J.-P., Salem, R., Ensembles parfaits et séries trigonométriques, Hermann, Paris, 1963.
[88] Katznelson, Y., An introduction to harmonie analysis, Wiley, New York, 1968.
[89] Kawata, T., Fourier analysis in probability theory. Académie Press, New York, 1972.
[90] Meyer, Y., Trois problèmes sur les sommes trigonométriques, Astérisque, n" 1, 1973.
[91] Miller, W., Lie theory and spécial functions, Académie Press, New York, 1968.
[92] Pukansky, L., Leçons sur les représentations des groupes (Monographies de la Soc. math.
de France, n* 2), Dunod, Paris, 1967.
[93] Rudin, W., Fourier analysis on groups, Interscience, New York, 1968.
[94] Sbrrb, J.-P., Cours d'arithmétique (Collection SUP), Presses Univ. de France, Paris, 1970.
[95] Stein, E., Wbiss, G., Introduction to Fourier analysis on Euclidean spaces, Princeton Univ.
Press, 1971.
(96) Vilenkin, N., Fonctions spéciales et théorie de la représentation des groupes, Dunod, Paris, 1969.
[97] Warner, G., Harmonie analysis on semi-simple Lie groups, vol. I et II, Springer,
Berlin-Heidelberg-New York, 1972.
[98] Weil, A., Basic number theory, Springer, Berlin-Heidelberg-New York, 1967.
[99] Zygmund, A., Trigonométrie séries, 2* éd., 2 vol., Cambridge Univ. Press, 1968.

372
BIBLIOGRAPHIE
Volumes VII et VIII
[100] Abbott, M., An introduction to the method of characteristics, Thames and Hudson,
London, 1966.
[101] Agmon, S., Lectures on elliptic boundary value problems, Van Nostrand, Princeton, 1965.
[102] Bateman, H., Partial differential équations of mathematical physics, Cambridge Univ.
Press, 1952.
[103] Bers, L., John, F., Schechter, M., Partial differential équations, Interscience, New York,
1964.
[104] Bitsadze, A., Equations of the mixed type, Pergamon, Oxford, 1954.
[105] Brelot, M., Éléments de la théorie classique au potentiel. Centre de Doc. Univ., Paris,
1969.
[106] Brelot, M., Lectures on potential theory, Tata Institute of fundamental research,
Bombay, 1967.
[107] Carslaw, H., Jaeger, J., Conduction of heat in solids, Clarendon Press, Oxford, 1948.
[108] Courant, R., Dirichlet's principle, conformai mapping and minimal surfaces. Interscience,
New York, 1950.
[109] Courant, R., Hilbert, D., Methods of mathematical physics, vol. II, Interscience,
New York, 1962.
[110] Duff, G., Naylor, D., Differential équations of applied mathematics, Wiley, New York,
1966.
[111] Duistermaat, J., Fourier intégral operators, Courant Inst. of Math. Sciences, New York
University, New York, 1973.
[112] Duistermaat, J., Guillemin, V., The spectrum of positive elliptic operators and periodic
bicharacteristics, Inventiones Math., 29 (1975), p. 39-79.
[113] Eidel'man, S., Parabolic équations, North Holland, Amsterdam, 1969.
[114] El'sgol'c, L., Norkin, S., Introduction to the theory and applications of differential
équations with deviating arguments. Académie Press, New York, 1973.
[115] Ewing, W., Jardetzky, W., Press, F., Elastic waves in layered média, McGraw Hill,
New York, 1957.
[116] Fourier intégral operators and partial differential équations, Lecture Notes in Math.,
n" 459, Springer, Berlin-Heidelberg-New York, 1975.
[117] Friedman, A., Generalized functions and partial différentiel équations, Prentice Hall,
Englewood Cliffs, 1963.
[118] Friedman, A., Partial differential équations, Holt, Winston and Rinehart, New York, 1969.
[119] Friedman, A., Partial differential équations of parabolic type, Prentice Hall, Englewood
Cliffs, 1964.
[120] Fuglede, B., Finely harmonie functions, Lecture Notes in Math., n° 289, Springer,
Berlin-Heidelberg-New York, 1972.
[121] GaraBEDIAn, P., Partial differential équations, Wiley, New York, 1964.
[122] Gilbert, R., Function theoretic methods in partial differential équations. Académie Press,
New York, 1969.
[123] Gilbert, R., Constructive methods for elliptic équations, Lecture Notes in Math., n° 365,
Springer, Berlin-Heidelberg-New York, 1974.
[124] Hûrmandbr, L., Linear partial differential operators, Springer, Berlin-Gôttingen-Heidel-
berg, 1964.
[125] Hôrmander, L., On the existence and the regularity of solutions of linear pseudo-
differential équations, L'Enseignement math., (2), 17 (1971), p. 99-163.
[126] John, F., Plane waves and spherical means, Interscience, New York, 1955.
[127] Koshlyakov, N., Smirnov, M., Gliner, E., Differential équations of mathematical
physics, North Holland, Amsterdam, 1964.
[128] Lax, P., Phillips, R., Scattering theory, Académie Press, New York, 1967.
[129] Lions, J. L., Équations différentielles opérationnelles et problèmes aux limites, Springer,
Berlin-Gôttingen-Heidelberg, 1961.

BIBLIOGRAPHIE
373
[130] Lions, J. L., Magenes, E., Problèmes aux limites non homogènes et applications, 3 vol.,
Dunod, Paris, 1968.
[131] Maslov, V., Théorie des perturbations et méthodes asymptotiques, Dunod, Paris, 1972.
[132] Meyer, P. A., Probabilités et potentiel, Hermann, Paris, 1966.
[133] Mikhlin, S., Mathematical physics, an advanced course, North Holland, Amsterdam,
1970.
[134] Mizohata, S., The theory of partial differential équations, Cambridge Univ. Press, 1973.
[135] Noble, B., Methods based on the Wiener-Hopf techniques, Pergamon Press, London, 1958.
[136] Polva, G., Szego, G., Isoperimetric inequalities in mathematical physics (Ann. of Math.
Studies. n° 27) Princeton Univ. Press, 1951.
[137] Potential theory, Centro Internazionale matematico estivo, 1° Ciclo, Cremonese, Roma, 1969.
[138] Protter, M., Weinberger, H., Maximum principles in differential équations, Prentice
Hall, Englewood Cliffs, 1967.
[139] Rasulov, M., Methods of contour intégration, North Holland, Amsterdam, 1967.
[140] Reed, M., Simon, B., Methods of modem mathematical physics, 4 vol., Académie Press,
New York, 1972-79.
[141] Schechter, M., Spectra of partial differential équations, North Holland, Amsterdam,
1971.
[142] Simader, C, On Dirichlet's boundary value problem, Lecture Notes in Math., n° 268,
Springer, Berlin-Heidelberg-New York, 1972.
[143] Simon, B., Quantum méchantes for Hamiltonians defined as quadratic forms, Princeton
Univ. Press, 1971.
[144] Taylor, M., Pseudo-differential operators, Lecture Notes in Math., n* 416, Springer,
Berlin-Heidelberg-New York, 1974.
[145] Tikhonov, A., Samarskii, A., Equations of mathematical physics, Pergamon Press,
London, 1963.
[146] Trêves, F., Linear partial differential équations with constant coefficients, Gordon and
Breach, New York, 1966.
[147] Trêves, F., Basic linear partial differential équations. Académie Press, New York, 1975.
[148] Vladimirov, V., Equations of mathematical physics, M. Dekker, New York, 1971.
Volume IX
[149] Adams, J. F., Algebraic topology. A student's guide, London, Math. Soc. Lecture
Notes séries, n° 4, Cambridge Univ. Press, 1972.
[150] Adams, J. F., Infinité loop spaces (Ann of Math. Studies, n" 90), Princeton Univ. Press,
1978.
[151] Adams, J. F., Stable homotopy and generalized homology, Univ. of Chicago Press,
1974.
[152] Algebraic Topology (Proceedings of Symposia in Pure Mathematics, vol. XXII),
American Math. Soc., Providence, 1971.
[153] Algebraic and géométrie topology (Proceedings of Symposia in Pure Mathematics,
vol. XXXII et XXXIII), American Math. Soc., Providence, 1976.
[154] Barrait, M., Milnor, J., An example of anomalous singular homology, Proc. Amer.
Math. Soc, 13 (1962), p. 293-297.
[155] Borel, A., Topology of Lie groups and characteristic classes, Bull. Amer. Math. Soc,
61 (1955), p. 397-432.
[156] Borel, A. et al., Seminar on transformation groups (Ann. of Math. Studies, n° 46),
Princeton Univ. Press, 1960.
[157] Bott, R., Gitler, S., James, I. M., Lectures on algebraic and differential topology,
Lecture Notes in Math., n° 279, Springer, Berlin-Heidelberg-New York, 1972.
[158] Bousfield, A., Kan, D., Homotopy limits, complétions and localizations, Lecture
Notes in Math., n° 304, Springer, Berlin-Heidelberg-New York, 1972.
[159] Browder, W., Surgery on simply connectée manifolds, Ergebnisse der Math., Neue Folge,
Heft 65, Springer, Berlin-Heidelberg-New York, 1972.

374
BIBLIOGRAPHIE
160] Cartan, H. Eilenberg. S., Homological algebra, Princeton Univ. Press. 1956.
161] Conner, P., Lectures on the action of a finite group, Lecture Notes in Math., n° 73,
Springer, Berlin-Heidelberg-New York, 1968.
162] Cooke, G., Finnby, R., Homology of cell complexes, Princeton Univ. Press, 1967.
163] Croweix, R., Fox, R., Introduction to knot theory, Ginn, Boston, 1963.
164] Dibudonne, J., Cours de géométrie algébrique, vol. 2 (Collection SUP), Presses Univ.
de France, Paris, 1974.
165] Differential topology, Foliations and Gelfand-Fuks cohomology (ed. P. Schweitzer),
Lecture Notes in Math., n° 652, Springer, Berlin-Heidelberg-New York, 1978.
166] Dupont, J. L., Curvature and characteristic classes, Lecture Notes in Math., n° 640,
Springer, Berlin-Heidelberg-New York, 1978.
167] Dydak, J., Segal, J., Shape theory, Lecture Notes in Math., n° 688, Springer, Berlin-
Heidelberg-New York, 1978.
168] Eckmann, B., Homotopie et cohomologie, Presses Univ., Montréal, 1965.
169] Eells, J., Singularises of smooth maps, Gordon and Breach, New York-London-
Paris, 1967.
170] Eilenberg, S., Steenrod, N., Foundations of algebraic topology, Princeton Univ. Press,
1952.
171] Fédérer, H., Géométrie measure theory, Springer, Berlin-Heidelberg-New York, 1969.
172] Géométrie applications of homotopy theory (ed. M. Barratt and M. Mahowald),
Lecture Notes in Math., n™ 657-658, Springer, Berlin-Heidelberg-New York, 1978.
173] Godement, R., Topologie algébrique et théorie des faisceaux, Hermann, Paris, 1958.
174] Gray, B., Homotopy theory, Académie Press, New York, 1975.
175] Griffiths, P., Harris, J., Algebraic geometry, Wiley, New York, 1978.
176] Hilton, P., Mislin, G., Roitberg, J., Localization of nilpotent groups and spaces
(Notas de Mat., n" 55), North Holland, Amsterdam, 1975.
177] Hirsch, M., Differential topology, Springer, Berlin-Heidelberg-New York.
178] H-spaces (ed. F. Sigrist), Lecture Notes in Math., n° 196, Springer, Berlin-Heidelberg-
New York, 1971.
179] HsiANG, W. Y., Cohomology theory of topological transformation groups, Ergebnisse
der Math., Neue Folge, Heft 85, Springer, Berlin-Heidelberg-New York, 1975.
180] Hudson, J. F. P., Piecewise linear topology, Benjamin, New York-Amsterdam, 1969.
181] Husaini, S., The topology of classical groups and related topics, Gordon and Breach,
New York-London-Paris, 1969.
182] Hwa, R., Teplitz, L., Homology and Feynman intégrais. Benjamin, New
York-Amsterdam, 1966.
183] James, I. M., The topology of Stiefel manifolds, London Math. Soc. Lecture Notes
séries, n° 24, Cambridge Univ. Press, 1976.
184] Kamber. F., Tondeur, P., Foliated bundles and characteristic classes, Lecture Notes
in Math., n" 493, Springer, Berlin-Heidelberg-New York, 1975.
185] Karoubi, M., K-theory, Springer-Heidelberg-New York, 1978.
186] Kirby, R., Siebenmann, L., Foundational essays on topological manifolds, smoothings
and triangulations, Princeton Univ. Press, 1977.
187] Knots, groups and 3-manifolds (ed. Neuwirth) (Ann. of Math. Studies, n" 84),
Princeton Univ. Press, 1975.
188] Lamotke, K., Semisimpliziale algebraische Topologie, Springer, Berlin-Heidelberg-
New-York, 1968.
189] Landell, A., Weingram, S., The topology of CW-complexes, Van Nostrand, New York,
1969.
190] Laudenbach, F., Topologie de la dimension 3, Astérisque, n° 12.
191] Lefschetz, S., Applications of algebraic topology, Springer, Berlin-Heidelberg-New York,
1975.
192] Lehmann, D., Théorie homotopique des formes différentielles, Astérique, n° 45.
193] Lemaire, J. M., Algèbres connexes et homologie des espaces de lacets, Lecture Notes
in Math., n° 422, Springer, Berlin-Heidelberg-New York, 1974.
[194] Lloyd, N., Degree theory, Cambridge tracts, n" 73, Cambridge Univ. Press, 1978.

BIBLIOGRAPHIE
375
Manifolds Tokyo, 1973, Proc. of a Conférence, Tokyo Univ. Press, 1975.
Massey, W., Homology and cohomology theory, Dekker, New York, 1978.
May, J. P., Simplicial objects in algebraic geometry. Van Nostrand, New York, 1967.
May, J. P., The geometry of iterated loop spaces, Lecture Notes in Math., n" 271,
Springer, Berlin-Heidelberg-New York, 1972.
Milnor, }., Lectures on the h-cobordism theorem, Princeton Univ. Press, 1965.
Milnor, J., Stasheff, J., Characteristic classes (Ann. of Math. Studies, n° 76), Princeton
Univ. Press, 1974.
No vi ko v, S., The methods of algebraic topology from the viewpoint of cobordism
théories, hvest. Akad. Nauk SSSR, 31 (1967), p. 855-961.
Penrose, R., Techniques of differential topology in Relativity (CBMS Régional Conf.
Séries in applied Math., n° 7), SIAM, Philadelphia, 1972.
Rushing, T. B., Topological embeddings, Académie Press, New York, 1973.
Sbgal, G., New developments in topology, London Math. Soc. Lecture Notes séries,
n" 11, Cambridge Univ. Press, 1974.
Seifert, H., Threlfall, W., Lehrbuch der Topologie, Teubner, Leipzig-Berlin, 1934.
Shanahan, P., The Atiyah-Singer index theorem, Lecture Notes in Math., n° 638,
Springer, Berlin-Heidelberg-New York, 1978.
Spanier, E., Algebraic topology, McGraw Hill, New York, 1966.
Stallings, J., Group theory and 3-dimensional manifolds, Yale Univ. Press, New Haven,
1971.
Steenrod, N., Epstein, D., Cohomology opérations (Ann. of Math. Studies, n" 50),
Princeton Univ. Press, 1962.
Stong, R., Notes on cobordism theory, Princeton Univ. Press, 1968.
Switzer, R., Algebraic topology, homotopy and homology, Springer, Berlin-Heidelberg-
New York, 1975.
Toda, H., Composition methods in homotopy groups of sphères (Ann. of Math. Studies,
n° 49), Princeton Univ. Press, 1962.
Toda, H., A survey of homotopy theory, Advances in Math., 10 (1973), p. 417-455.
Topology of low-dimensional manifolds (ed. R. Fenn), Lecture Notes in Math., n° 722,
Springer, Berlin-Heidelberg-New York, 1979.
Topology of manifolds, Proc. of a conférence at Univ. of Georgia in 1969, Markham,
Chicago. 1970.
Wall, C. T. C, Surgery on compact manifolds. Académie Press, New York, 1970.
Wells, R., Differential analysis on complex manifolds, Prentice-Hall, Englewood Cliffs,
N. J., 1973.
Wells, R., Complex manifolds and mathematical physics, Bull. Amer. Math. Soc. 1
(New Séries), (1979), p. 297-336.
Wmtehead, G., Eléments of homotopy theory, Springer, Berlin-Heidelberg-New York,
1978.
Whitehead, G., Generalized homology théories, Trans. Amer. Math. Soc, 102 (1962),
p. 227-283.
Whitehead, G., Récent advances in homotopy theory (CBMS Régional Conf. Séries
in math., n° 5), Amer. math. Soc, Providence, 1970.
Whitney, H., Géométrie intégration theory, Princeton Univ. Press, 1957.
Wu-Wen-Tsun, Sur les espaces fibres, Actual Scient. Ind., n° 1183, Hermann, Paris,
1952.

INDEX
A
Alexander (dualité d') : 24.37, prob. 14.
Algèbre de cohomologie des formes
différentielles, algèbre de cohomologie des formes
différentielles à support compact : 24.1.
Algèbre de cohomologie d'une algèbre
différentielle graduée : Ann. 30.8.
Algèbre de cohomologie singulière : 24.31.
Algèbre de cohomologie singulière à support
compact : 24.34.
Algèbre de cohomologie singulière relative :
24.35.
Algèbre différentielle graduée : Ann. 30,8.
Algèbre d'intersection : 24.13.
Algèbre graduée anticommutative : Ann. 30.9.
e-application : 24.28, prob. 10.
Atiyah-Bott (formule d') : 24.29.
Attachement de boules : 24.22.
Automorphisme infinitésimal d'une
connexion : 24.51.
B
Barycentre d'un simplexe : 24.18.
Betti (nombre de) : 24.1.
Bezout (théorème de) : 24.16.
Bockstein (homomorphisme de) 24.30,
prob. 2.
Bord : Ann. 30.7.
Bord d'un courant : 24.10.
Bord (formel) d'une chaîne : 24.20.
Bord relatif d'une chaîne : 24.35.
Borsuk-Ulam (théorème de) : 24.9, prob. 17.
Bott (formules de) : 24.51.
Bott (théorème de) : 24.46, problème.
Bouquet de variétés : 24.22.
C
Cap-produit : 24.35, prob. 5.
Caractéristique d'Euler-Poincaré d'une
variété : 24.1.
Caractéristique d'Euler-Poincaré d'un
complexe elliptique : 24.49.
Catégorie de Lusternik-Schnirelmann : 24.37,
prob. 23.
Chaîne d'une subdivision simpliciable : 24.24.
Chaîne simpliciale (formelle), chaîne
singulière : 24.20.
Chaînes homologues : 24.20.
Chaînes prismatiques (lemme des) : 24.21.
Classe de Chern, classe totale de Chern : 24.41.
Classe d'Euler : 24.39.
Classe de A-orientation, classe de
A-orientation canonique : 24.39.
Classe de Lefschetz : 24.6.
Classe de Pontrjagin, classe totale de
Pontrjagin : 24.43.
Classe de Stiefel-Whitney, classe totale de
Stiefel-Whitney : 24.47.
Classe d'homologie d'une courbe algébrique
sur une surface algébrique lisse : 24.16.
Classe fondamentale d'homologie des courants
sur une variété compacte orientée : 24.11.
Classe fondamentale d'homologie singulière
de S.: 24.28.
Classe fondamentale de cohomologie
singulière de S„ : 24.31.
Classe fondamentale de cohomologie relative
de R" modulo R" - { 0 } : 24.35.
Classe fondamentale de cohomologie d'une
variété compacte connexe orientée, classe
d'orientation : 24.6.
Cobord : 24.29 et Ann. 30.2.
Cobord relatif : 24.35.
Cochaîne singulière : 24.29.
Cochaîne à support compact : 24.34.
Cocycle : 24.29 et Ann. 30.2.
Cocycle relatif : 24.35.
Cohomologie singulière : 24.29.
Cohomologie singulière relative : 24.35.
Cohomologie de Cech : 24.37, prob. 18.
Complexe cellulaire : 24.36, prob. 7.
Complexe cellulaire euclidien : 24.18.
Complexe de de Rham : 24.48.
Complexe elliptique : 24.48.
Complexe simplicial abstrait : 24.28, prob. 1.
Complexe simplicial abstrait associé à un
complexe simplicial euclidien 24.28,
prob. 1.
Complexe simplicial euclidien (fini) : 24.18.
Cône de sommet c : 24.21.

378
INDEX
Conjugué d'un espace vectoriel complexe,
d'un espace fibre vectoriel complexe : 24.42.
Couple excisif : 24.37.
Courant associé à une subdivision simpliciale,
courant de type (p, q) : 24.23.
Courant cellulaire : 24.17.
Courant d'intégration : 24.13 et 24.16.
Courant d'une subdivision simpliciale : 24.20.
Courant simplicial : 24.19.
Cube creux : 24.28.
Cup-produit : 24.1, 24.31, 24.35 et 24.37.
Cycle : Ann. 30.7, 24.20 et 24.10.
Cycle relatif : 24.35.
D
Degré d'une application continue : 24.9.
De Rham (théorèmes de) : 24.11 et 24.20.
Différentiellement négligeable (ensemble) :
24.14.
Dimension d'un simplexe abstrait : 24.24,
prob. 1.
Dimension topologique : 24.24, prob. 6.
Dimension en un point : 24.28, prob. 18.
Double de l'adhérence d'un ouvert : 24.35,
prob. 6.
Dual gradué d'un module gradué : Ann.
30.1.
E
Elément primitif : 24.53.
Endomorphisme géométrique d'un complexe
elliptique : 24.49.
Enroulement d'une courbe plane : 24.9, prob.
24.
Ensemble séparant deux ensembles : 24.28,
prob. 19.
Espace icosaédral : 24.22, prob. 14.
Espace lenticulaire : 24,22, prob. 6.
Espace peigne : 24.22, prob. 3.
Espace quotient : 24.22, prob. 8.
Espace sans torsion : 24.27.
Espace triangulable : 24.28, prob. 4.
Euler (formule d') : 24.36, prob. 7.
Exacte (forme différentielle) : 24.1.
Excision (théorème d') : 24.37.
F
Fabricius-Bjerre-Halpern (théorème de)
24.15, prob. 2.
Faces, facettes d'un polyèdre convexe : 24.14.
Fermé (courant) : 24.10.
Fermée (forme différentielle) : 24.1.
Fibration orientable, orientée, A-orientable :
24.39.
Fibration en boules, en sphères : 24.39,
prob. 13.
Fibre canomique sur une grassmannienne :
24,40.
Formes différentielles biinvariantes : 24.52.
Formes différentielles harmoniques : 24.48.
G
Gauss-Bonnet (formule de) : 24.46.
Germe d'une forme différentielle : 24.7.
Green (formule de) : 24.14.
Groupe de cohomologie singulière : 24.29.
Groupe de l'icosaèdre : 24.22, prob. 14.
Groupe du cube : 24.22, prob. 15.
Gysin (suite exacte de) : 24.39 et 24.39,
prob. 3.
H
Hodge (théorème de) : 24.48.
Homologie singulière : 24.20.
Homologie singulière relative : 24.35.
Homologues (courants) : 24.10.
Homomorphisme homogène de degré 0 :
Ann. 30.1.
Homomorphisme de A-module différentiel
gradué : Ann. 30.3.
Homomorphisme d'algèbres différentielles
graduées : Ann. 30.8.
Homotopie régulière : 24.9, prob. 24.
Hopf (formule de) : 24.50.
Hopf (théorème de) sur le degré : 24.9,
prob. 15.
Hurewicz (homomorphisme de) 24.22,
prob. 4.
I
Image réciproque d'une connexion : 24.44.
Image réciproque d'une structure
riemannienne : 24.46.
Indice d'un opérateur elliptique : 24.49.
Indice d'un champ de vecteurs en un point
critique non dégénéré : 24.50.
Inégalités de Morse : 24.37, prob. 30.
Intégration partielle d'une forme
différentielle : 24.5.
Involution canonique dans un revêtement à
deux feuillets : 24.1.
Isométrie infinitésimale d'un espace
riemannien : 24.51.
K
Kronecker (intégrale de) : 24.9.
Kùnneth (théorème de) : 24.5 et 24.38.

INDEX
379
L
Phragmen-Brouwer (théorèmes de) : 24.22,
prob. 13.
Poincaré (dualité de) : 24.6 et 24.37, prob. 12.
Poincaré (lemme de) : 24.2.
Poincaré (polynôme de) : 24.1.
Point critique, point critique non dégénéré
d'un champ de vecteurs : 24.50.
Point singulier : 24.16.
Polarisation d'un polynôme homogène
24.45.
Polyèdre convexe ouvert : 24.14.
Polynôme isobare : 24.40.
Prisme ((lemme du) : 24.18.
Produit de deux courants : 24.13.
Produit tensoriel de deux modules : Ann. 28.1.
Produit tensoriel de deux applications
linéaires : Ann. 28.4.
Produit tensoriel gauche d'algèbres graduées :
Ann. 30.9.
R
Réalisation, réalisation canonique d'un
complexe simplicial abstrait : 24.28, prob. 1.
Rétracte de voisinage : 24.22, prob. 1.
Rétracte par homotopie, rétraction par
homotopie : 24.22.
S
Sandwich (théorème du) : 24.9, prob. 26.
Schubert (symbole de) : 24.40, prob. 1.
Signature d'une variété compacte : 24.6.
Simplexe abstrait : 24.24, prob. 1.
Simplexe fermé : 24.18.
Simplexe géométrique : 24.18.
Simplexe singulier : 24.20.
Simplexe standard : 24.18.
Sommet d'un simplexe géométrique : 24.18.
Sous-espace déformable en un point : 24.37,
prob. 23.
Sous-module de torsion : Ann. 34.1.
Sperner (lemme de) : 24.24, prob. 1.
Stokes (formule de) : 24.14 et 24.17.
Stokien (ouvert) : 24.14.
Subdivision cellulaire : 24.18.
Subdivision simpliciale : 24.18.
Subdivisions barycentriques : 24.18.
Suite d'approche : 24.14.
Suite exacte, suite exacte courte : Ann. 29.1.
Suite exacte de cohomologie : Ann. 30.5.
Suite exacte de cohomologie relative : 24.35.
Suite exacte d'homologie relative : 24.35.
Suite exacte scindée : Ann. 29.1.
Support d'un simplexe singulier : 24.20.
Support singulier d'un courant : 24.13.
Laplace-Hodge (opérateur de), Laplacien
de Hodge : 24.48.
Lebesgue (lemme de) : 24.24, prob. 5.
Lemme des cinq : Ann. 29.4.
Lefschetz (formule de) : 24.49.
Lefschetz (nombre de) : 24.49.
Lelong (théorème de) : 24.16, prob. 12.
Leray-Hirsch (théorème de) : 24.38.
Localement injective (application) : 24.8,
prob. 1.
Lusternik-Schnirelmann-Borsuk (théorème de):
24.9, prob. 18.
M
Mayer-Vietoris (suite exacte de) : 24.3, 24.22
et 24.37.
Module codifférentiel gradué : Ann. 30.7.
Module de cohomologie : Ann. 30.3.
Module d'homologie : Ann. 30.7.
Module différentiel gradué : Ann. 30.2.
Module gradué : Ann. 30.1.
Module gradué libre : Ann. 31.1.
Multiplicité d'une racine : 24.15.
N
Nerf, nerf euclidien d'un recouvrement ouvert
fini : 24.28, prob. 10.
Nombre d'entrelacement de deux
sous-variétés : 24.9.
Nombre d'intersection de deux courants,
de deux sous-variétés : 24.13.
Nombre d'intersection de deux courbes
algébriques : 24.16.
Noyau d'ordre n d'un espace : 24.28, prob. 18.
O
Ordre d'un recouvrement ouvert fini : 24.24,
prob. 6.
Orientation canonique : 24.39.
Orientation d'une fibration : 24.39.
Orientations opposées : 24.39.
Ostrogradsky (formule d') : 24.14.
P
Pendentif hawaïen : 24.22, prob. 11.
Pfaffien : Ann. 33.1.
Pham (variété de) : 24.28, prob. 23.

380 l*
Surface algébrique, surface algébrique lisse :
24.16.
Suspension d'un espace topologique : 24.36,
prob. 4.
T
Topologie quotient : 24.22, prob. 8.
Triangulation : 24.28, prob. 4.
W
Wang (suite exacte de) : 24.S, prob. 6 et 24.38,
prob. 6.
Whitney-Graustein (théorème de) : 24.9;
prob. 24.
Wirtinger (inégalité de) : 24.14, prob. 6.
Achevé d'imprimer par Coriet Numérique en juillet 2006 - 14110 Condé-sur-Noireau
N° d'Imprimeur : 32958 - Dépôt légal : juillet 2006 - Imprimé en France

p
Mi
EDITIONS
JACQUES GABAY
Niels Henrik ABEL
• Œuvres complètes (2 tomes)
suivies par :
- Niels Henrik Abel - Sa vie et son action
scientifique,
par C.-A. BJERKNES
Jean d'ALEMBERT
• Traité de Dynamique
André-Marie AMPÈRE
• Théorie mathématique des phénomènes
électrodynamiques
Paul APPELL
• Traité de Mécanique rationnelle (5 tomes en 3 vol.)
EmilARTIN
• Algèbre géométrique
Louis BACHELIER
• Théorie de la spéculation
suivie par
- Théorie mathématique du jeu
• Calcul des probabilités
• Le Jeu, la Chance et le Hasard
René BAIRE
• Leçons sur les fonctions discontinues
• Théorie des nombres irrationnels, des limites et de
la continuité
W. W. Rouse BALL
• Histoire des mathématiques
• Récréations mathématiques et problèmes
des temps anciens et modernes
Stefan BANACH
• Théorie des opérations linéaires
Paul BARBARIN
• La Géométrie non euclidienne
Edmond BAUER
• Introduction à la théorie des groupes
et à ses applications à la physique quantique
Richard BECKER
• Théorie des électrons
Joseph BERTRAND
• Calcul des probabilités
Niels BOHR
• La théorie atomique et la description des
phénomènes
Marcel BOLL
• La chance et les jeux de hasard
Ludwig BOLTZMANN
• Leçons sur la théorie des gaz
Emile BOREL
• Leçons sur la théorie des fonctions
• Leçons sur les séries divergentes
Emile BOREL & André CHERON
• Théorie mathématique du bridge à la portée de tous
suivie par
- Applications de la théorie des probabilités aux
jeux de hasard, par Emile BOREL & Jean VILLE
- Valeur pratique et philosophie des probabilités, par
Emile BOREL
Z.I. BOREVITCH & I.R. CHAFAREVITCH
• Théorie des nombres
MaxBORN
• La Théorie de la Relativité d'Einstein et ses bases
physiques
Pierre BOUTROUX
• L'idéal scientifique des mathématiciens
dans l'antiquité et dans les temps modernes
Ed. BRAHY
• Exercices méthodiques de calcul différentiel et
intégral
Léon BRILLOUIN
• Les tenseurs en mécanique et en élasticité
• La science et la théorie de l'information
Louis de BROGLIE
• Ondes et mouvements
• Éléments de théorie des quanta et de mécanique
ondulatoire
Georg CANTOR
• Sur les fondements de la théorie des ensembles
transfinis
Lazare CARNOT
• Réflexions sur la métaphysique du calcul
infinitésimal
Sadi CARNOT
• Réflexions sur la puissance motrice du feu
Élie CARTAN
• Leçons sur la géométrie des espaces de Riemann
• Leçons sur la géométrie projective complexe
suivie par
- La théorie des groupes finis et continus et la
géométrie différentielle traitées par la méthode du repère
mobile
- Leçons sur la théorie des espaces à connexion
projective
Augustin-Louis CAUCHY
• Analyse algébrique
Michel CHASLES
• Aperçu historique sur l'origine et le
développement des méthodes en géométrie
• La dualité et l'homographie
• Traité de géométrie supérieure
• Traité des sections coniques
• Les trois livres de porismes d'Euclide
• Rapport sur les progrès de la géométrie
Jean CHAZY
• La Théorie de la Relativité et la Mécanique céleste
Alexis-Claude CLAIRAUT
• Éléments de géométrie
Emile CLAPEYRON
• Mémoire sur la puissance motrice de la chaleur
Rudolph CLAUS1US
• Théorie mécanique de la chaleur
H. COMMISSAIRE & G. CAGNAC
• Cours de Mathématiques spéciales (3 tomes)

Antoine-Nicolas de CONDORCET
• Essai sur l'application de l'analyse à la probabilité
des décisions rendues à la pluralité des voix
Gaspard-Gustave CORIOLIS
• Théorie mathématique des effets du jeu de billard
suivie des deux célèbres Mémoires
- Sur le principe des forces vives dans les
mouvements relatifs des machines
- Sur les équations du mouvement relatif des
systèmes de corps
H.S.M. COXETER & S.L. GREITZER
• Redécouvrons la géométrie
Gaston DARBOUX
• Leçons sur la théorie générale des surfaces et les
applications géométriques du calcul infinitésimal
suivies par
- Leçons sur les systèmes orthogonaux et les
coordonnées curvilignes
- Principes de géométrie analytique (3 titres en 3
volumes)
Maurice DAUMAS
• Les instruments scientifiques aux XVII' et XVIII'
siècles
Jean-Baptiste DELAMBRE
• Histoire de l'astronomie ancienne
• Histoire de l'astronomie au moyen-âge
• Histoire de l'astronomie moderne
• Histoire de l'astronomie au dix-huitième siècle
R. DELTHEIL & D. CAIRE
• Géométrie et Compléments
G. DEMARTRES
• Cours de géométrie infinitésimale
Arnaud DENJOY
• L'énumération transfinie
• Leçons sur le calcul des coefficients d'une série
trigonométrique
• Mémoire sur la dérivation et son calcul inverse
René DESCARTES
• La Géométrie
Jean DIEUDONNÉ
• Panorama des mathématiques pures - Le choix
bqurbachique
• Éléments d'Analyse (9 tomes)
F. DINGELDEY & E. FABRY
• Coniques et Systèmes de coniques
(extr. Encycl. se. math.)
Paul A.M. DIRAC
• Les principes de la Mécanique quantique
Jacques DIXMIER
• Les algèbres d'opérateurs dans l'espace hilbertien
(Algèbres de von Neumann)
• Les C*-algèbres et leurs représentations
• Algèbres enveloppantes
Paul DU BOIS-REYMOND
• Théorie générale des fonctions
Pierre DUGAC
• Jean Dieudonné, mathématicien complet
(Collection "Plus de Lumière")
René DUGAS
• Histoire de la Mécanique
Pierre DUHEM
• Traité d'Énergétique ou de Thermodynamique
générale
• L'origine de la Statique
(Collection "Plus de Lumière")
Jean-Baptiste DUMAS
• Leçons sur la philosophie chimique
Ernest DUPORCQ
• Premiers principes de géométrie moderne
Paul DUPUY
• La vie d'Évarisle Galois
Albert EINSTEIN
Ouvrages séparés :
• Sur l'Électrodynamique des corps en mouvement
• La Théorie de la Relativité restreinte et généralisée
(traduction J. Rouvière)
• Quatre conférences sur la Théorie de la Relativité
• Lettres à Maurice Solovine
Recueil de 7 textes :
• Sur l'Électrodynamique des corps en mouvement
suivi par
- L'Éther et la Théorie de la Relativité
- La Géométrie et l'Expérience
- Quatre conférences sur la Théorie de la Relativité
- Théorie de la Gravitation généralisée
- Sur le Problème cosmologique
- Théorie relativiste du champ non symétrique
ENCYCLOPÉDIE DES SCIENCES
MATHÉMATIQUES PURES ET APPLIQUÉES
Tout ce qui a paru de l'édition française rédigée et
publiée d'après l'édition allemande sous la direction
de
Jules MOLK
• Arithmétique et Algèbre
• Analyse
• Géométrie
• Mécanique
• Physique
• Géodésie et Géophysique
• Astronomie
• Table des matières
Federigo ENRIQUES
• Leçons de géométrie projective
• Principes de la géométrie
(extr. Encycl. se. math.)
EUCLIDE
• Les Œuvres d'Euclide
en grec, en latin et en français, par F. Peyrard
F.G.-M. (Frère GABRIEL-MARIE)
• Exercices de géométrie
comprenant l'exposé des méthodes et 1550 figures
• Géométrie descriptive - Éléments et Exercices
comprenant l'exposé des méthodes et 1680 figures
• Trigonométrie - Éléments, Compléments et
Exercices
comprenant l'exposé des méthodes et les solutions
de 875 exercices et problèmes
G. FANO & É. CARTAN
• La théorie des groupes continus et la géométrie
(extr. Encycl. se. math.)
Pierre FERMAT
• Précis des Œuvres mathématiques et de
l'Arithmétique de Diophante, par Emile Brassinne

J. FITZ-PATRICK
• Exercices d'arithmétique
Joseph FOURIER
• Théorie analytique de la chaleur
Maurice FRÉCHET
• Les espaces abstraits
Maurice FRÉCHET & Ky FAN
• Introduction à la topologie combinatoire
Évariste GALOIS
• Œuvres mathématiques, publiées par Joseph
Liouville
suivies par
- Influence de Galois sur le développement des
mathématiques, par Sophus Lie
• Œuvres mathématiques, publiées par Emile Picard
suivies par
- Manuscrits et papiers inédits de Galois, publiés par
Jules Tannery
• Écrits et mémoires mathématiques
Édition critique intégrale publiée par Robert
Bourgne et Jean-Pierre Azra
Préface de Jean Dieudonné
George GAMOW
• Trente années qui ébranlèrent la physique
Histoire de la théorie quantique
Félix K. GANTMACHER
• Théorie des matrices
Cari Friedrich GAUSS
• Recherches arithmétiques
Claude GEORGE
• Exercices et problèmes d'intégration
Denis GERLL & Georges GIRARD
• Les Olympiades internationales de mathématiques
Josiah-Willard GIBBS
• Équilibre des systèmes chimiques
Lucien GODEAUX
• Les Géométries
Edouard GOURSAT
• Cours d'Analyse mathématique (3 tomes)
Alfred George GREENHILL
• Les fonctions elliptiques et leurs applications
Edouard GRIMAUX
• Lavoisier, 1743-1794
d'après sa correspondance, ses manuscrits, ses
papiers de famille et d'autres documents inédits
Jacques HADAMARD
• Leçons de géométrie élémentaire (2 tomes)
• Essai sur la psychologie de l'invention dans
le domaine mathématique
suivi par :
- L'Invention mathématique, par Henri POINCARÉ
Paul R. HALMOS
• Introduction à la théorie des ensembles
Georges-Henri HALPHEN
• Traité des fonctions elliptiques et de leurs
applications (3 tomes)
• Œuvres (4 tomes)
G.H. HARDY
• Divergent Séries (en anglais)
Werner HEISENBERG
• Les principes physiques de la théorie des quanta
Hermann von HELMHOLTZ
• Optique physiologique (2 tomes)
• Théorie physiologique de la musique
Charles HERMITE
• Cours d'Analyse de l'École Polytechnique
• Œuvres (4 tomes)
Charles HERMITE & Thomas Jan STIELTJES
• Correspondance d'Hermite et de Stieltjes
David HILBERT
• Les fondements de la géométrie
• Théorie des corps de nombres algébriques
• Sur les problèmes futurs des mathématiques
(Les 23 Problèmes)
Camille JORDAN
• Traité des substitutions et des équations
algébriques
• Cours d'Analyse de l'École Polytechnique (3 tomes)
E. JOUFFRET
• Traité élémentaire de géométrie à quatre
dimensions
suivi des
- Mélanges de géométrie à quatre dimensions
Emile JOUGUET
• Lectures de Mécanique
Erich KAMKE
• Théorie des ensembles
Stephen C. KLEENE
• Logique mathématique
Félix KLEIN
• Le programme d'Erlangen
A. KNESER, E. ZERMELO,
H. HAHN & M. LECAT
• Calcul des variations
(extr. Encycl. se. math.)
Casimir KURATOWSKI
• Topologie I et II
Jean LADRIÈRE
• Les limitations internes des formalismes
Étude sur la signification du théorème de Gôdel et
des théorèmes apparentés dans la théorie des
fondements des mathématiques
Joseph-Louis LAGRANGE
• Mécanique analytique (Édition originale)
Œuvres
• 1.1 à VII - Mémoires et Pièces diverses
• t. VIII - Résolution des équations numériques
• t. IX - Théorie des fonctions analytiques
• t. X - Leçons sur le calcul des fonctions
• t. XI et XII - Mécanique analytique (4' édition)
avec des Notes de J. BERTRAND et G. DARBOUX
• t. XIII et XIV - Correspondance
Trajan LALESCO
• La géométrie du triangle
Gabriel LAMÉ
• Leçons sur la théorie mathématique de l'élasticité
des corps solides
Pierre-Simon LAPLACE
Œuvres
• t. I à V - Traité de Mécanique céleste

• t. VI - Exposition du Système du Monde
• t. VII - Théorie analytique des probabilités (2 vol.)
Le premier volume contient le célèbre
"Essai philosophique sur les probabilités"
Max von LAUE
• La Théorie de la Relativité (2 tomes)
Charles-Jean de LA VALLÉE POUSSIN
• Cours d'Analyse infinitésimale (2 tomes)
• Intégrales de Lebesgue. Fonctions d'ensemble.
Classes de Baire
Antoine-Laurent LAVOISIER
• Traité élémentaire de chimie
Henri LEBESGUE
• Les coniques
• Leçons sur les constructions géométriques
• Leçons sur l'intégration et la recherche des
fonctions primitives
C. LEBOSSÉ & C. HÉMERY
• Géométrie (classe de Mathématiques)
Adrien-Marie LEGENDRE
• Théorie des nombres
Tullio LEVI-CIVITA
• Caractéristiques des systèmes différentiels
et propagation des ondes
Paul LÉVY
• Calcul des probabilités
• Processus stochastiques et mouvement brownien
• Théorie de l'addition des variables aléatoires
Alexandre LIAPOUNOFF
• Problème général de la stabilité du mouvement
André LICHNEROWICZ
• Éléments de calcul tensoriel
Ernst L1NDELÔF
• Le calcul des résidus et ses applications à la
théorie des fonctions
Hendrik-Antoon LORENTZ
• The Theory of Electrons and its Applications to the
Phenomena of Light and Radiant Heat (en anglais)
Edouard LUCAS
• Théorie des nombres
Nicolas LUSIN
• Leçons sur les ensembles analytiques et leurs
applications
suivi du Mémoire
- Sur les fonctions représentables analytiquement,
par Henri LEBESGUE
Ernst MACH
• La Mécanique
Exposé historique et critique de son développement
Saunders MacLANE & Garrett BIRKHOFF
• Algèbre
suivie par
- Solutions développées des exercices
Jean MANDEL
• Cours de Mécanique des milieux continus
James Clerk MAXWELL
• Traité d'Électricité et de Magnétisme (2 tomes)
• La Chaleur
Emile MEYERSON
• La déduction relativiste
Charles MICHEL
• Compléments de géométrie moderne
suivie par les solutions des questions proposées
- Exercices de géométrie moderne, de Julien LEMAIRE
et par
- Les correspondances algébriques, de Gaston SIN-
G1ER
Gaston MILHAUD
• Descartes savant
Jules MOLK
• voir ENCYCLOPÉDIE DES SCIENCES
MATHÉMATIQUES PURES ET APPLIQUÉES
Gaspard MONGE
• Géométrie descriptive
Jean Etienne MONTUCLA
• Histoire des Mathématiques (4 tomes)
Henri NAVIER
• Résumé des Leçons de Mécanique données à
l'École Polytechnique
John von NEUMANN
• Les fondements mathématiques de la Mécanique
quantique
Isaac NEWTON
• Principes mathématiques de la philosophie naturelle
(2 tomes)
Niels NIELSEN
• Traité élémentaire des nombres de Bernoulli
R. NOGUÈS
• Théorème de Fermât. Son histoire
Paul PAINLEVÉ
• Les axiomes de la Mécanique
Georges PAPELIER
• Éléments de trigonométrie sphérique
• Exercices de géométrie moderne, précédés de
l'exposé élémentaire des principales théories
l'ouvrage comprend :
1. Géométrie dirigée
2. Transversales
3. Division et faisceau harmonique
4. Pôles, polaires, plans polaires, dans le cercle et la
sphère
5. Rapport anharmonique
6. Inversion
7. Homographie
8. Involution
9. Géométrie projective. Application aux coniques
D.P. PARENT
• Exercices de théorie des nombres
Julius PETERSEN
• Méthodes et théories pour la résolution des
problèmes de constructions géométriques
Emile PICARD
• Traité d'Analyse (3 tomes)
Max PLANCK
• Électromagnétisme
Joseph PLATEAU
• Recherches expérimentales et théoriques sur les
figures d'équilibre d'une masse liquide sans
pesanteur (2 tomes)
Johann Christian POGGENDORFF
• Histoire de la Physique

Henri POINCARÉ
• Théorie mathématique de la lumière
• Électricité et Optique
• Thermodynamique
• Leçons de Mécanique céleste
• La Mécanique nouvelle (Théorie de la Relativité)
• Théorie du potentiel newtonien
• Théorie des tourbillons
• Figures d'équilibre d'une masse fluide
• Calcul des probabilités
• Mémoire sur les courbes définies par une équation
différentielle
suivi par
- Sur les propriétés des fonctions définies par les
équations aux différences partielles (Thèse)
- Note sur les propriétés des fonctions définies par
les équations différentielles
et par Ch. BRIOT et J.-Cl. BOUQUET
- Etude des fonctions d'une variable imaginaire
- Recherches sur les propriétés des fonctions
définies par des équations différentielles
- Mémoire sur l'intégration des équations
différentielles au moyen des fonctions elliptiques
Œuvres
• t. 1 - Équations différentielles
• t. 2 - Équations différentielles
(Fonctions fuchsiennes)
• t. 3 - Équations différentielles.
Théorie des fonctions
• t. 4 - Théorie des fonctions
• t. 5 - Algèbre. Arithmétique
• t. 6 - Géométrie. Analysis situs (Topologie)
• t. 7 - Masses fluides en rotation.
Principes de Mécanique analytique.
Problème des trois corps
• t. 8 - Mécanique céleste. Astronomie
• t. 9 - Physique
• t. 10 - Physique
• t. 11 - Mémoires divers
suivis par
- Le Livre du Centenaire
Siméon-Denis POISSON
• Recherches sur la probabilité des jugements
en matière criminelle et en matière civile
George POLYA
• Comment poser et résoudre un problème
Jean-Victor PONCELET
• Traité des propriétés projectives des figures
Ilya PRIGOGINE
• Introduction à la thermodynamique des processus
irréversibles
A. PRINGSHEIM, G. FABER & J. MOLK
• Analyse algébrique
(extr. Encycl. se. math.)
Alfred RÉNYI
• Calcul des probabilités
avec un appendice sur la théorie de l'information
Bernhard RIEMANN
• Œuvres mathématiques
Frédéric RIESZ & Béla SZ.-NAGY
• Leçons d'Analyse fonctionnelle
Vasco RONCHI
• Histoire de la lumière
Eugène ROUCHÉ
& Charles de COMBEROUSSE
• Traité de géométrie
A. SCHŒNFLIES & R. BAIRE
• Théorie des ensembles
(extr. Encycl. se. math.)
A. SCHŒNFLIES & A. TRESSE
• Géométrie projective
(extr. Encycl. se. math.)
Erwin SCHRÔDINGER
• Mémoires sur la Mécanique ondulatoire
Joseph-Alfred SERRET
• Cours d'Algèbre supérieure (2 tomes)
• Traité de trigonométrie rectiligne et sphérique
Waclaw SIERPINSKI
• 250 problèmes de théorie élémentaire des nombres
• Leçons sur les nombres transfinis
Jean-Marie SOURIAU
• Calcul linéaire
avec la solution détaillée des exercices
O. STAUDE & A. GRÉVY
• Quadriques
(extr. Encycl. se. math.)
E. STUDY & É. CARTAN
• Nombres complexes
(extr. Encycl. se. math.)
Paul TANNERY
• Pour l'histoire de la science hellène
• La géométrie grecque
• Recherches sur l'histoire de l'astronomie ancienne
• Mémoires scientifiques (17 tomes)
P.L. TCHEBYCHEF
• Œuvres (2 tomes)
Francisco Gomes TEIXEIRA
• Traité des courbes spéciales remarquables planes
et gauches (3 tomes)
François-Félix TISSERAND
• Traité de Mécanique céleste (4 tomes)
suivi des
- Leçons sur la détermination des orbites
Georges VALIRON
• Cours d'Analyse malhématique :
Équations fonctionnelles. Applications
Gustave VERRIEST
• Leçons sur la théorie des équations selon Galois,
précédées d'une introduction à la théorie des groupes
suivies par
- Évariste Galois et la théorie des équations
algébriques
Henri VILLAT
• Mécanique des fluides
• Leçons sur la théorie des tourbillons
• Leçons sur les fluides visqueux
Vito VOLTERRA
• Leçons sur la théorie mathématique de la lutte pour
la vie
A. VOSS, E. COSSERAT & F. COSSERAT
• Principes de la Mécanique rationnelle
(extr. Encycl. se. math.)
A VOSS & J. MOLK
• Calcul différentiel
(extr. Encycl. se. math.)

Jean DIEUDONNÉ
1906 - 1992
ÉLÉMENTS D'ANALYSE
Tome 9 - Chapitre XXIV
TOPOLOGIE ALGÉBRIQUE
TOPOLOGIE DIFFÉRENTIELLE ÉLÉMENTAIRE
Le but de ce chapitre est d'initier les analystes aux premiers rudiments de la Topologie
algébrique et de la Topologie différentielle, deux des domaines les plus actifs des
recherches modernes. Conformément à l'esprit de 1' "Analyse globale" qui est celui de ce
Traité, c'est la cohomologie des variétés différentielles et des espaces fibres qui est au
centre de ce chapitre, ainsi que ses relations les plus élémentaires avec les structures
additionnelles portées par les variétés, telles que connexions ou structures de groupes.
Lorsqu'on se borne à la cohomologie à coefficients réels ou complexes, on y accède
immédiatement à l'aide des formes différentielles, sans les moindres préliminaires
"combinatoires", et en n'utilisant comme outil algébrique que la suite exacte de
cohomologie.
Toutefois c'est présenter une image incomplète de la théorie que de se limiter à la
cohomologie à coefficients réels. Aussi, après avoir donné les propriétés essentielles de
cette dernière, on aborde également la théorie de l'homologie singulière, en la mettant,
comme de Rham, en rapport avec l'homologie des courants (duale de la cohomologie sur
une variété orientée), la jonction se faisant par la formule de Stokes ; mais on se limite aux
notions combinatoires strictement indispensables pour permettre le calcul de l'homologie
des variétés différentielles les plus fréquemment rencontrées.
ÉDITIONS JACQUES GABAY
151 bis, rue Saint-Jacques - 75005 Paris (France)
Tél. : +33 (0)1 43 54 64 64 - Fax : +33 (0)1 43 54 87 00
E-mail : infos@gabay.com
www.gabay.com
ISBN 2-87647-219-8
9 "782876"472198'
61 €