Задачи по математической физике - Боголюбов А.В., Кравцов В.В.

Глава I. Метод разделения переменных. Разложение по собственным функциям задачи Штурма-Лиувилля
§3. Разложение по собственным функциям для эллиптического уравнения
§4. Метод интегрального преобразования Фурье
§2. Одномерный случай: периодические граничные условия
§4. Собственные функции прямоугольного параллелепипеда
§6. Собственные функции кругового сектора
§7. Собственные функции кругового кольца
§8. Собственные функции кругового кольцевого сектора
§10. Собственные функции цилиндрического сектора
§11. Собственные функции кругового тора прямоугольного сечения
§12. Собственные функции сектора кругового тора прямоугольного сечения
§13. Собственные функции шара
§15. Задачи на собственные функции для уравнения Шрёдингера
§16. Задачи для самостоятельного решения
Глава III. Краевые задачи для уравнения Лапласа
§2. Краевые задачи для уравнения Лапласа внутри круга
§3. Краевые задачи для уравнения Лапласа вне круга
§4. Краевые задачи для уравнения Лапласа в круговом кольце
§5. Краевые задачи для уравнения Лапласа в круговом секторе
§6. Краевые задачи для уравнения Лапласа в кольцевом секторе
§7. Краевые задачи для уравнения Лапласа в прямоугольнике
§8. Краевые задачи для уравнения Лапласа в прямоугольном параллелепипеде
§9. Краевые задачи для уравнения Лапласа в круговом цилиндре
§10. Частные решения уравнения Лапласа в сферической системе координат
§11. Краевые задачи для уравнения Лапласа в шаре
§12. Краевые задачи для уравнения Лапласа вне шара
§13. Краевые задачи для уравнения Лапласа в шаровом слое
§14. Задачи для самостоятельного решения
Глава IV. Функция Грина оператора Лапласа
Глава V. Задачи для уравнения теплопроводности
§2. Задачи для уравнения теплопроводности в ограниченной области с неоднородными граничными условиями
§3. Задачи для уравнения теплопроводности на бесконечной прямой
§4. Задачи для уравнения теплопроводности на полубесконечной прямой
2. Задачи для уравнения теплопроводности на полубесконечной прямой с неоднородными граничными условиями
§5. Задачи для уравнения теплопроводности в пространстве
Глава VI. Задачи для уравнения колебаний
§2. Задачи для уравнения колебаний в ограниченной области с неоднородными граничными условиями
§3. Задачи для уравнения колебаний на бесконечной прямой
§4. Задачи для уравнения колебаний на полупрямой
2. Начально-краевые задачи для уравнения колебаний на полупрямой с неоднородными граничными условиями
§5. Задачи для уравнения колебаний на плоскости и в пространстве
Глава VII. Краевые задачи для уравнения Гельмгольца
$§2. Краевые задачи для уравнения $\Delta u + k^2 u = 0$ внутри круга$
$§3. Краевые задачи для уравнения $\Delta u + k^2 u = 0$ вне круга$
$§4. Краевые задачи для уравнения $\Delta u + k^2 u = 0$ в круговом кольце$
$§5. Краевые задачи для уравнения $\Delta u - k^2 u = 0$ внутри круга$
$§6. Краевые задачи для уравнения $\Delta u - k^2 u = 0$ вне круга$
$§7. Краевые задачи для уравнения $\Delta u - k^2 u = 0$ в круговом кольце$
§8. Частные решения уравнения Гельмгольца в сферической системе координат
$§9. Краевые задачи для уравнения $\Delta u + k^2 u = 0$ внутри шара$
$§10. Краевые задачи для уравнения $\Delta u + k^2 u = 0$ вне шара$
$§11. Краевые задачи для уравнения $\Delta u + k^2 u = 0$ в шаровом слое$
$§12. Краевые задачи для уравнения $\Delta u - k^2 u = 0$ внутри шара §13. Краевые задачи для уравнения $\Delta u - k^2 u = 0$ вне шара$
$§14. Краевые задачи для уравнения $\Delta u - k^2 u = 0$ в шаровом слое$
§15. Примеры решения краевых задач для уравнения Гельмгольца
§2. Теоремы сложения для цилиндрических функций
§4. Некоторые интегралы, содержащие цилиндрические функции
$§2. Краевые задачи для уравнения $\Delta u + k^2 u = 0$ внутри круга$
$§3. Краевые задачи для уравнения $\Delta u + k^2 u = 0$ вне круга$
$§4. Краевые задачи для уравнения $\Delta u + k^2 u = 0$ в круговом кольце$
$§5. Краевые задачи для уравнения $\Delta u - k^2 u = 0$ внутри круга$ $§6. Краевые задачи для уравнения $\Delta u - k^2 u = 0$ вне круга$ $§7. Краевые задачи для уравнения $\Delta u - k^2 u = 0$ в круговом кольце$ §8. Частные решения уравнения Гельмгольца в сферической системе координат
$§9. Краевые задачи для уравнения $\Delta u + k^2 u = 0$ внутри шара$ $§10. Краевые задачи для уравнения $\Delta u + k^2 u = 0$ вне шара$ $§11. Краевые задачи для уравнения $\Delta u + k^2 u = 0$ в шаровом слое$
$§12. Краевые задачи для уравнения $\Delta u - k^2 u = 0$ внутри шара §13. Краевые задачи для уравнения $\Delta u - k^2 u = 0$ вне шара$ $§14. Краевые задачи для уравнения $\Delta u - k^2 u = 0$ в шаровом слое$ §15. Примеры решения краевых задач для уравнения Гельмгольца
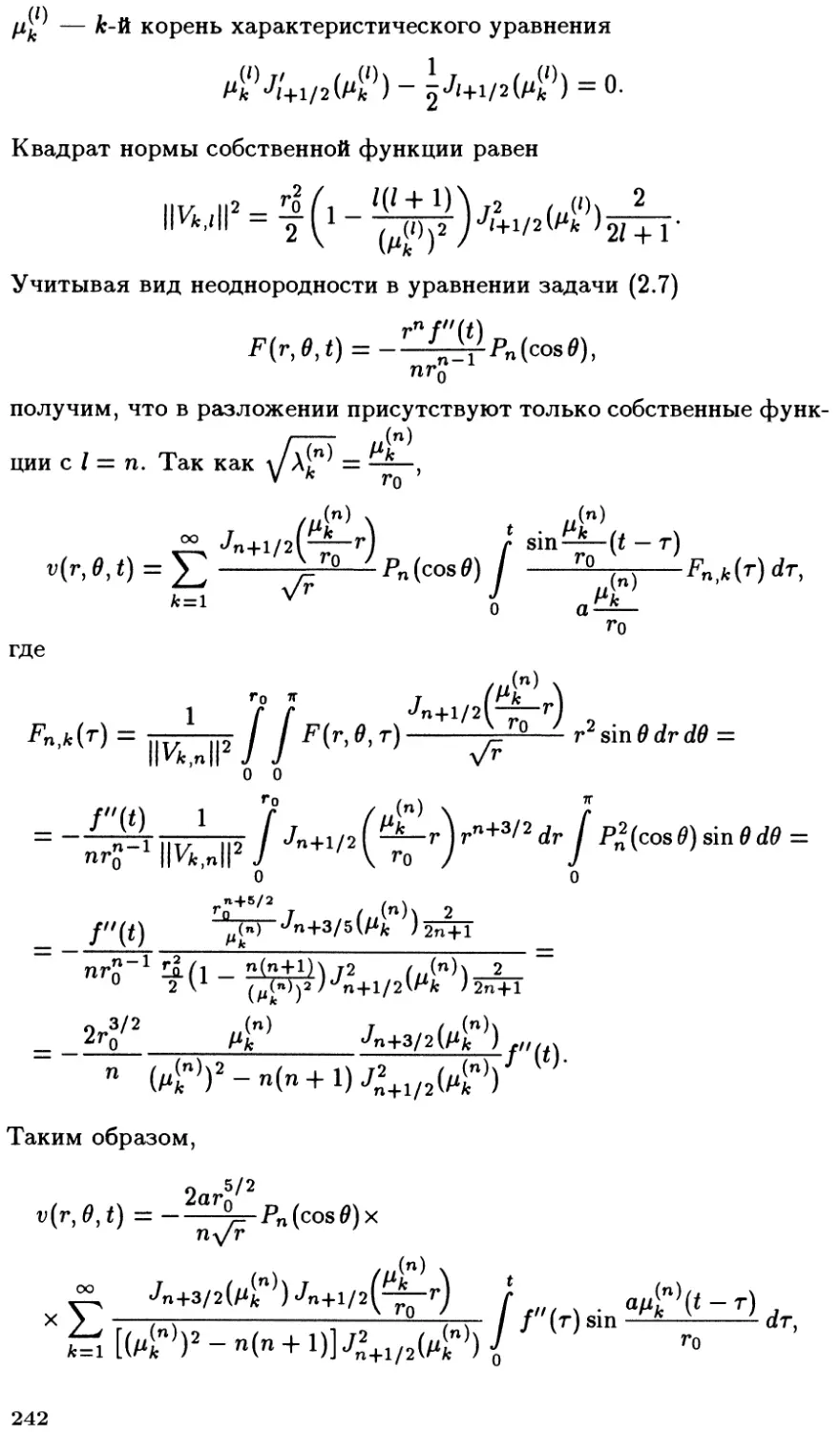
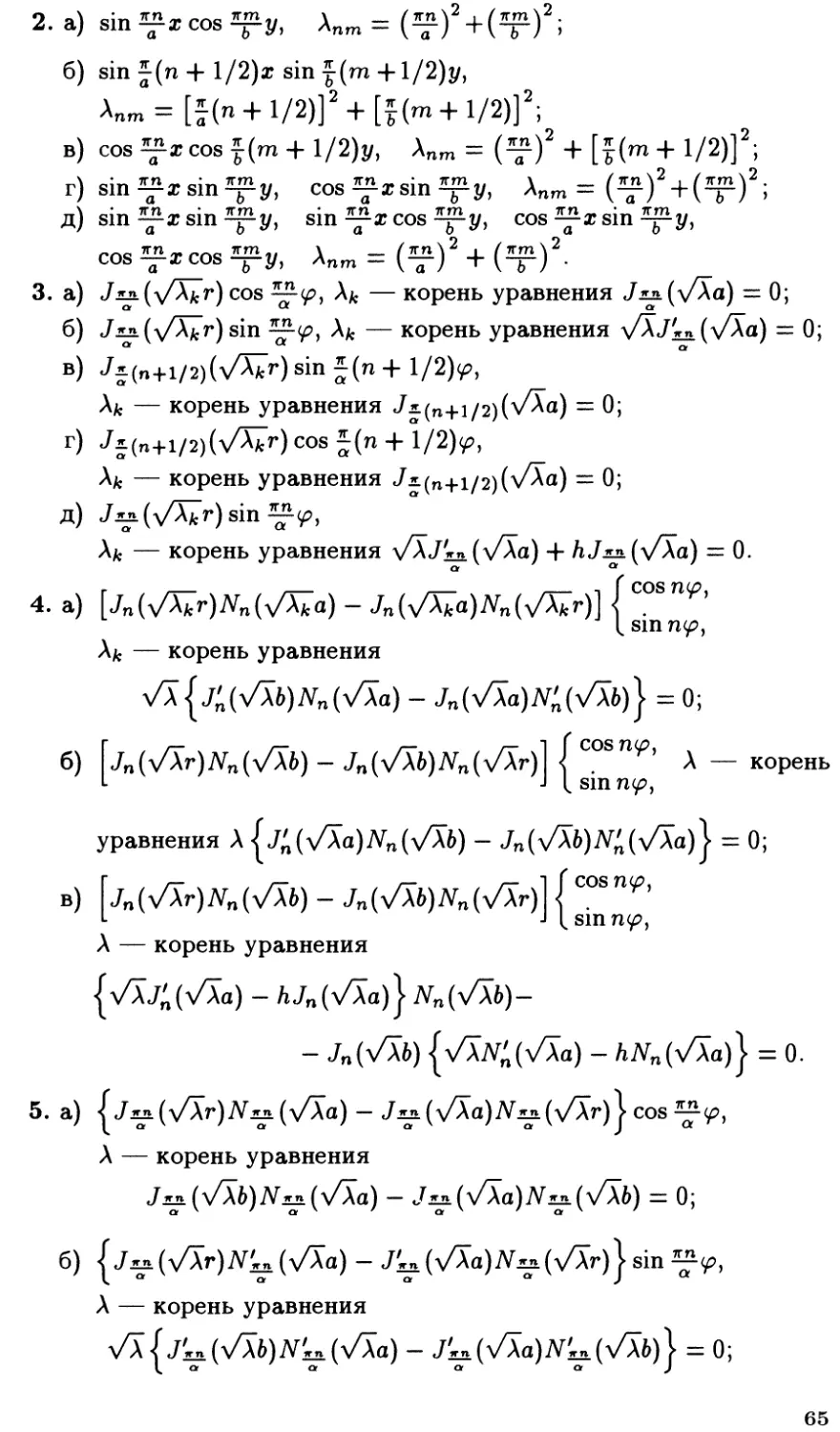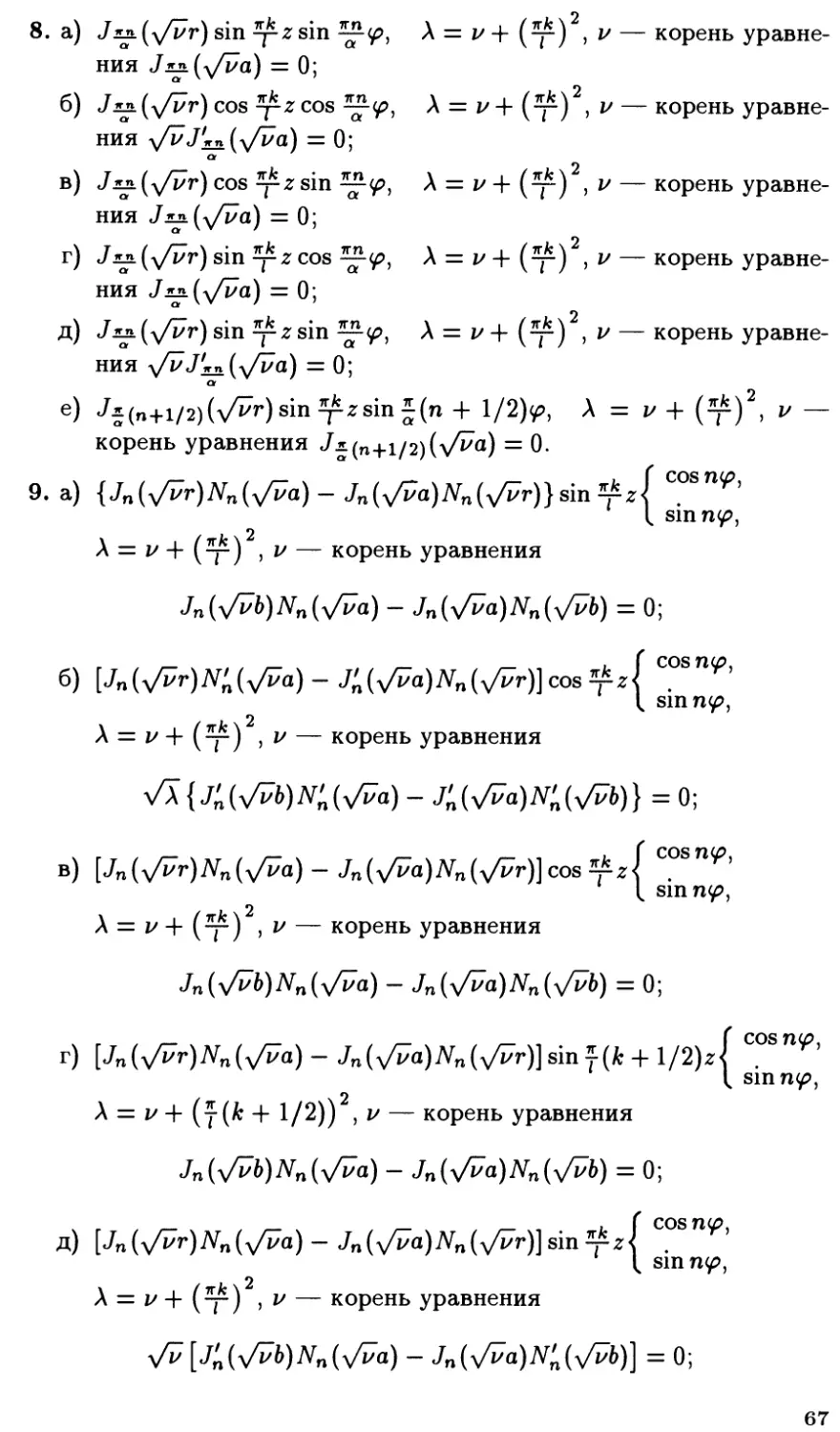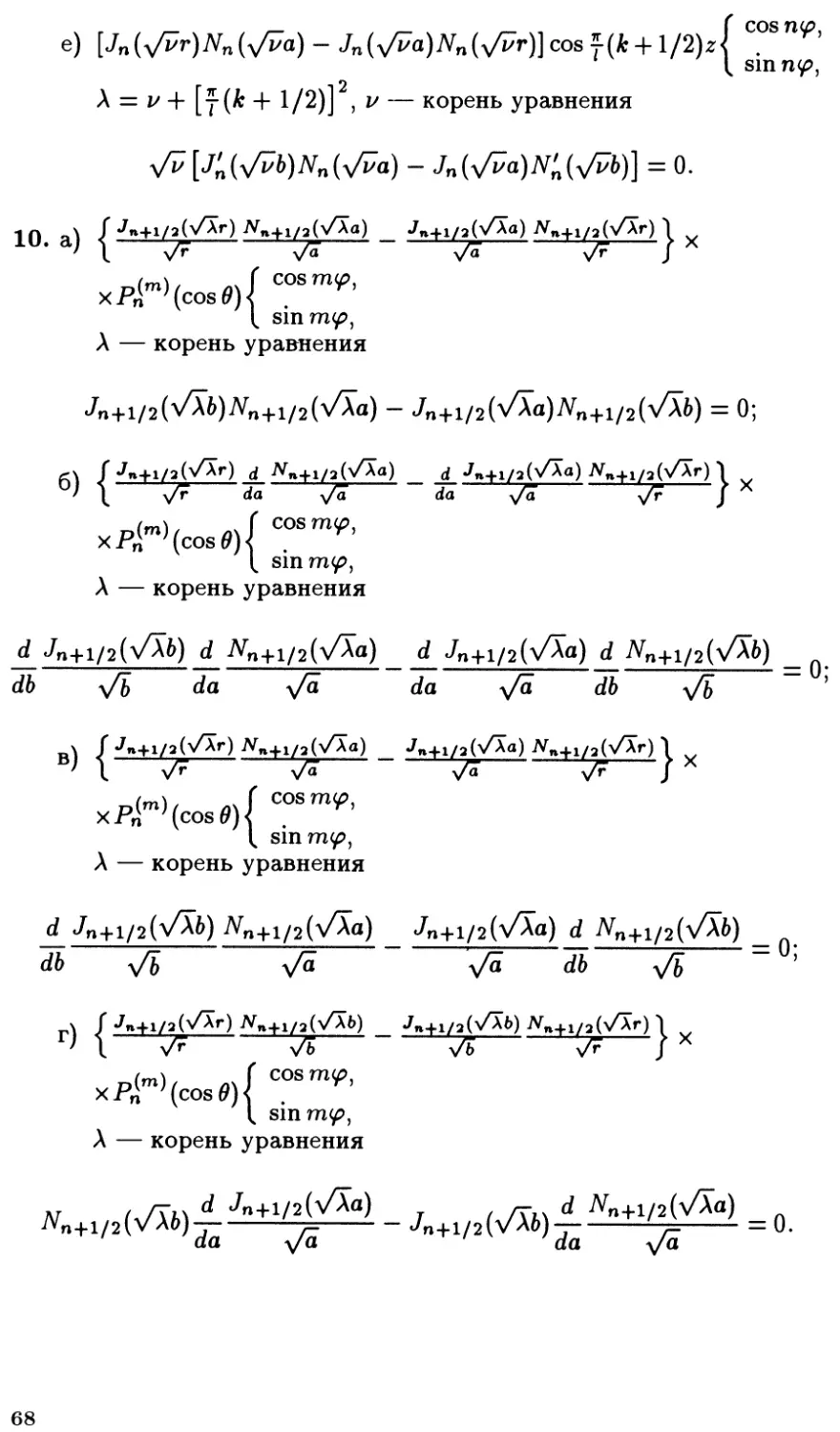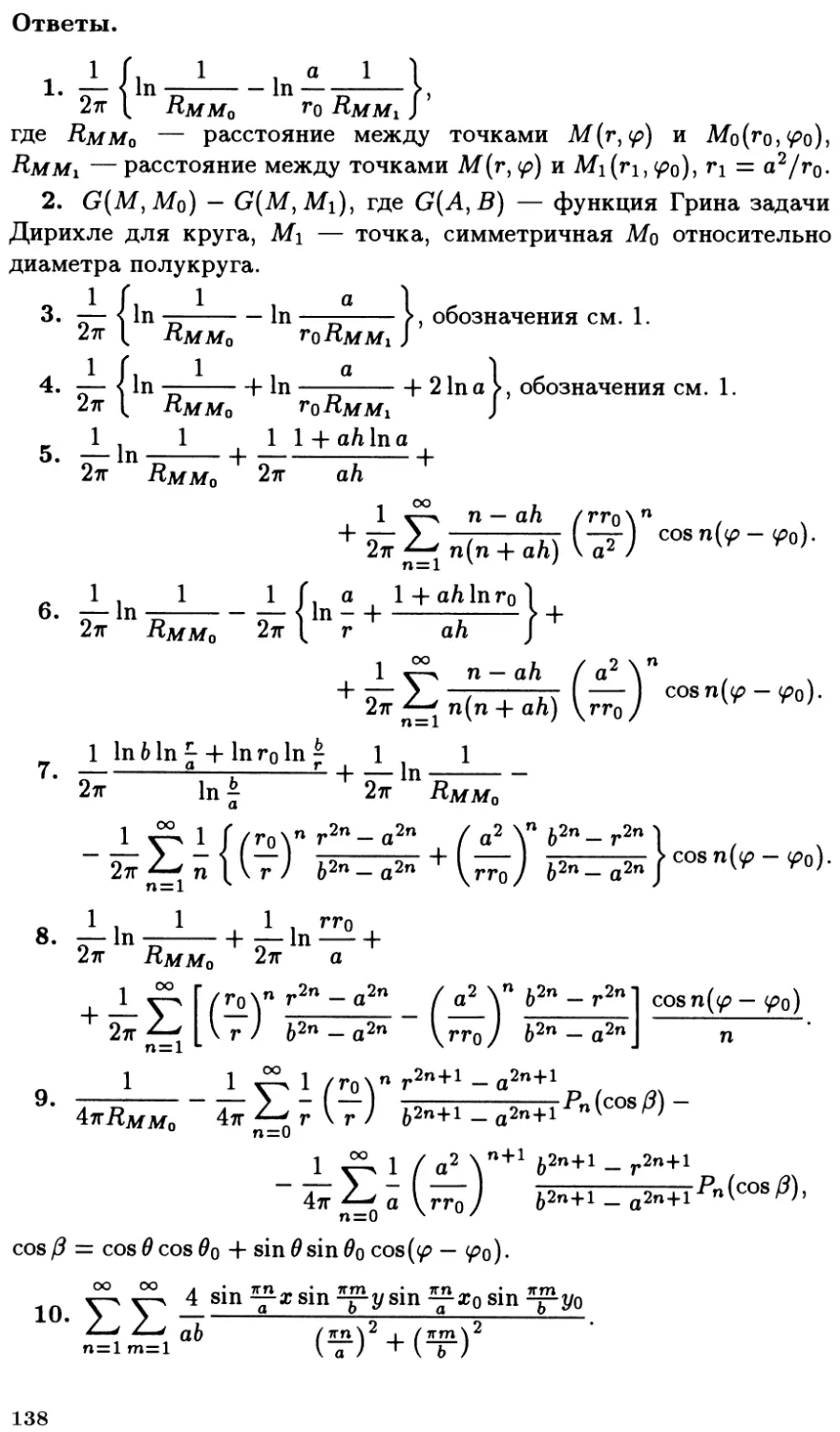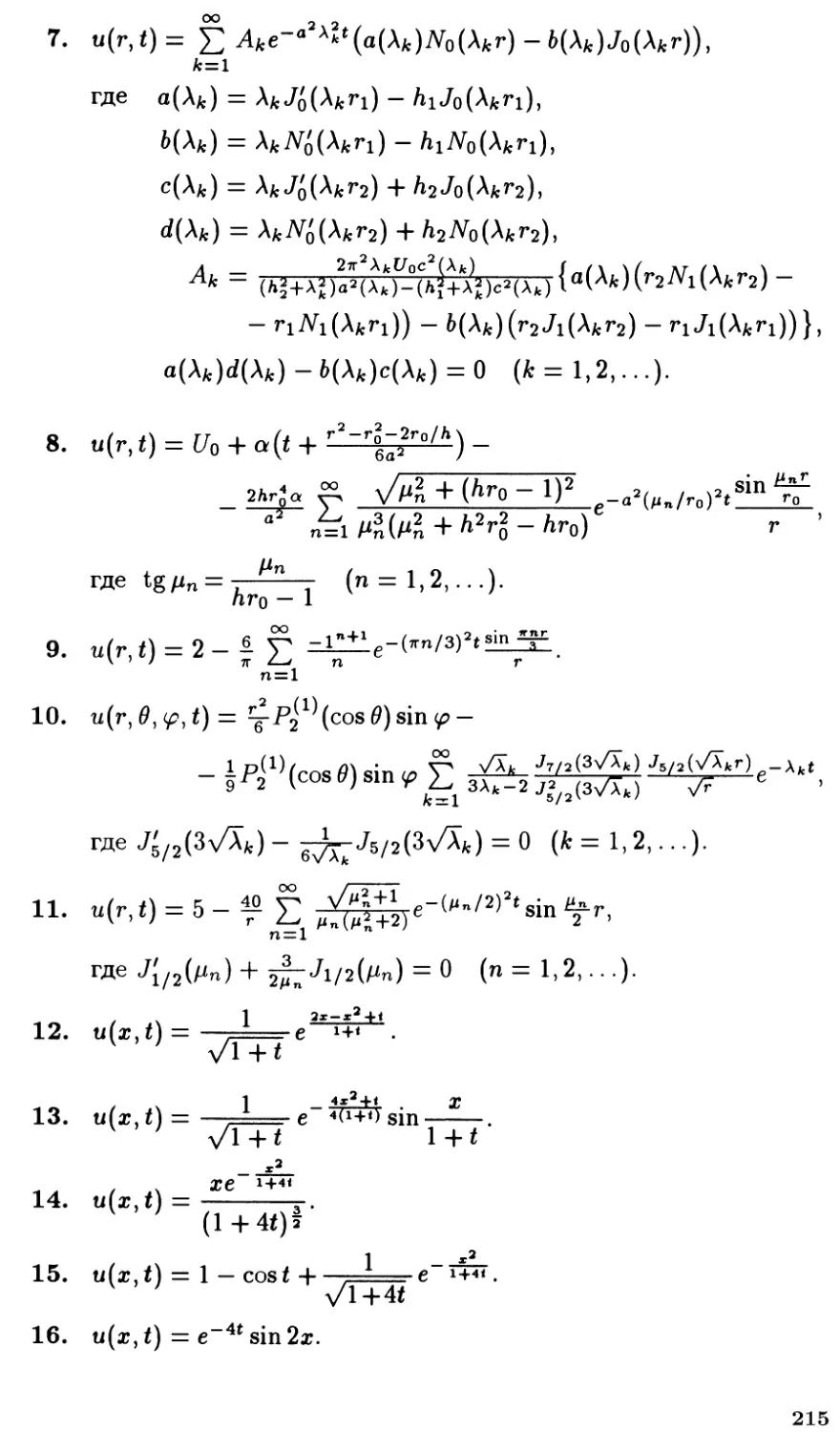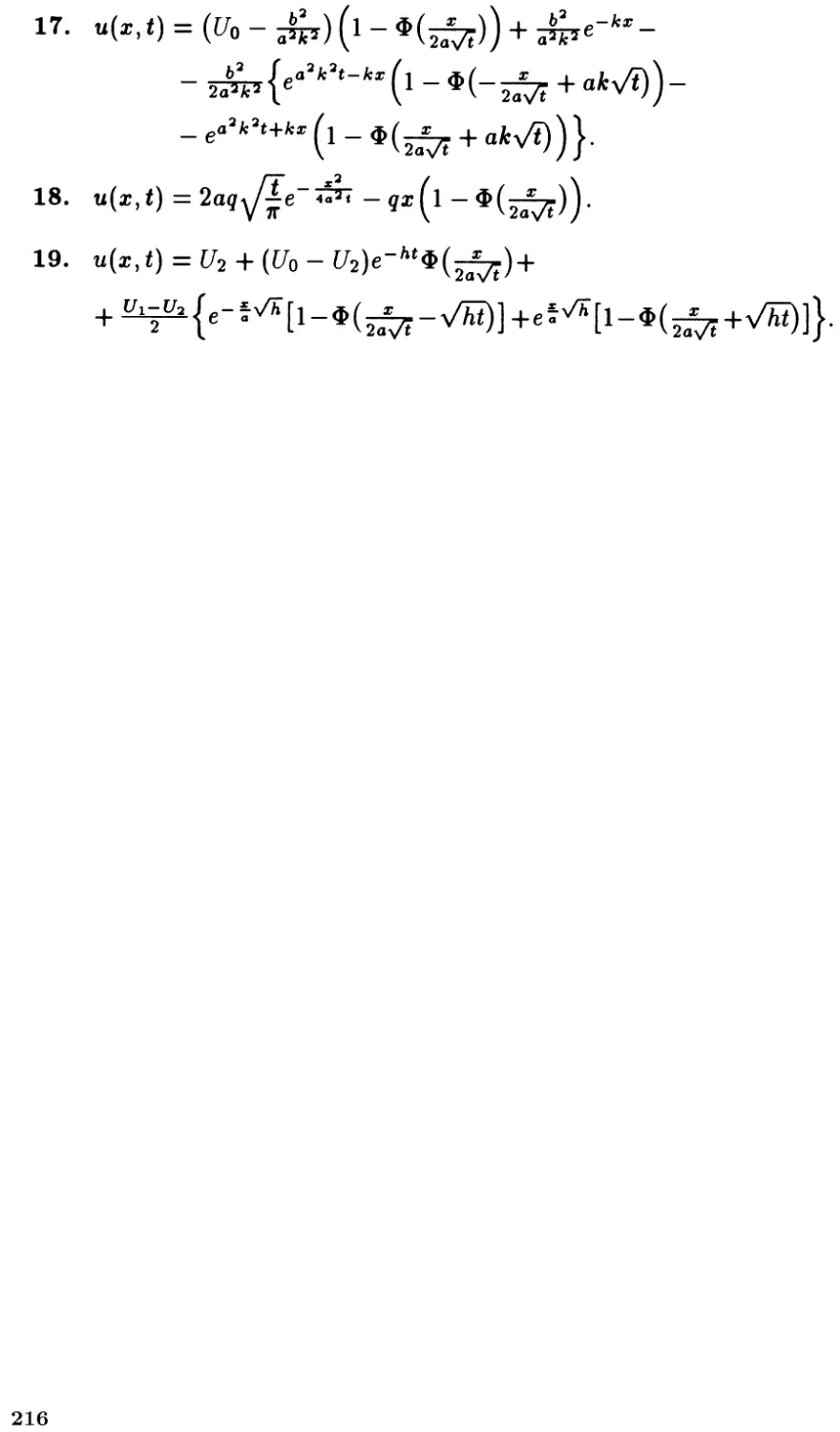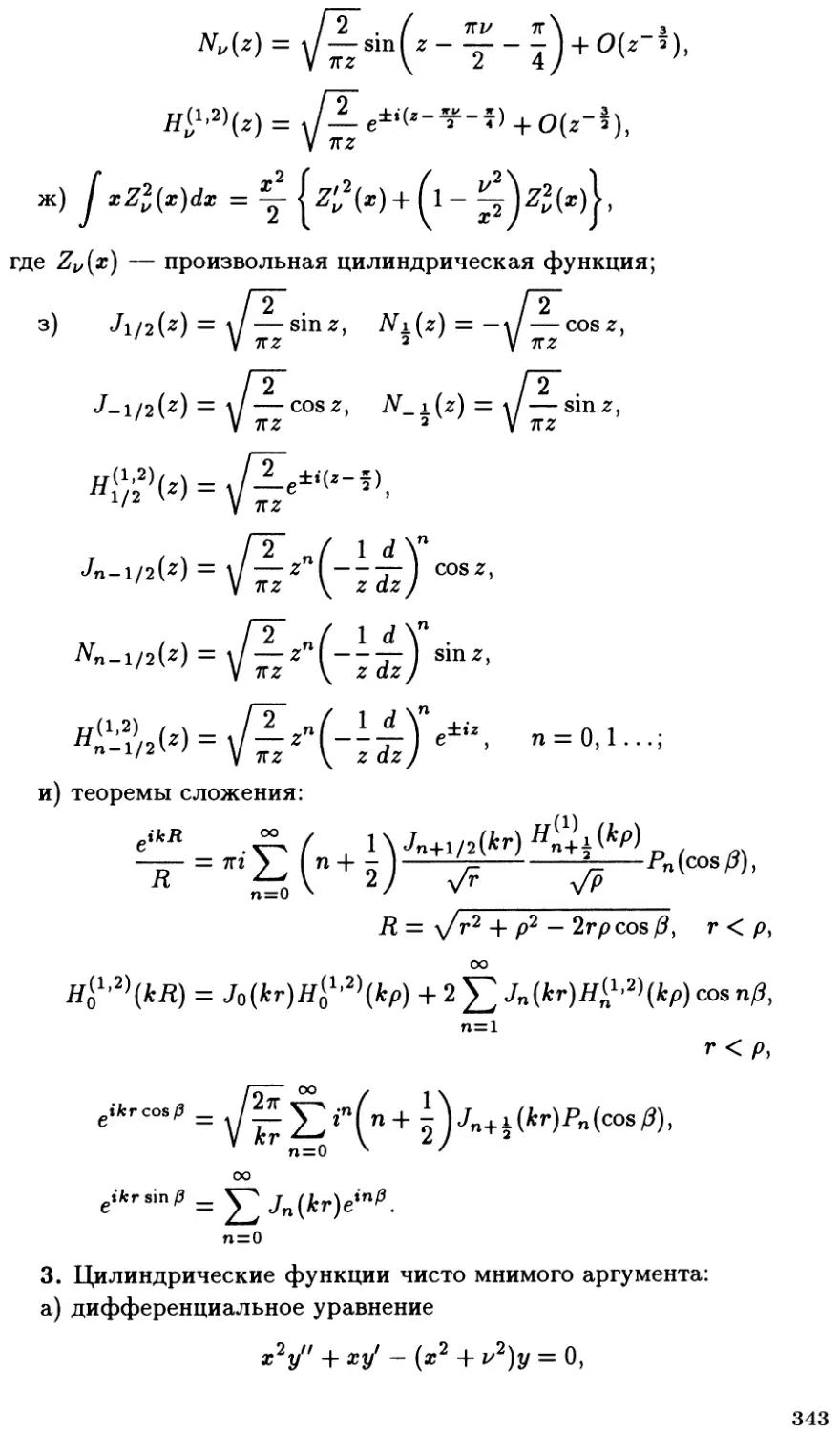Автор: Боголюбов А.В. Кравцов В.В.
Теги: физика математика математическая физика
ISBN: 211-03373-6
Год: 1998
Похожие
Сборник заданий по специальным курсам высшей математематики
Сборник задач по уравнениям математической физики
Сборник задач по математической физике
Дифференциальные уравнения в частных производных математической физики. Часть 2
Текст
                    А.Н. Боголюбов,
В. В. Кравцов
ЗАДАЧИ
ПО МАТЕМАТИЧЕСКОЙ
ФИЗИКЕ
ПОД РЕДАКЦИЕЙ А.Г. СВЕШНИКОВА
Рекомендовано Министерством общего и профес-
профессионального образования Российской Федерации в
качестве учебного пособия для студентов высших учебных
заведений, обучающихся по направлениям «Физика» и
«Прикладная математика и информатика»
Издательство
Московского
университета
1998

УДК 530.145
ББК 22.311
Б74
Рецензенты:
кафедра высшей математики N 1
Московского института электронной техники,
профессор С.Я. Секерж-Зенькович
Федеральная целевая программа
книгоиздания России
Боголюбов А.Н., Кравцов В.В.
Задачи по математической физике: Учеб. пособие.— М.:
Изд-во МГУ, 1998. — 350с.
ISBN 211-03373-6
В учебном пособии рассматриваются основные методы решения
краевых и начально-краевых задач для линейных дифференци-
дифференциальных уравнений в частных производных второго порядка. Рас-
Рассматриваются метод разделения переменных, метод интегрального
преобразования Фурье, метод отражения, метод распространяю-
распространяющихся волн и др. Приводятся минимальные теоретические сведе-
сведения, используемые при решении задач этими методами. Даются
подробные примеры решения конкретных задач и приводятся за-
задачи с ответами для самостоятельного решения.
Для студентов физических специальностей университетов.
УДК 530.145
ББК 22.311
ISBN 5-211-03373-6	© Боголюбов А.Н., Кравцов В.В.,
1998 г.

ОГЛАВЛЕНИЕ
Предисловие .................................................... 7
Глава I. Метод разделения переменных. Разложение по соб-
собственным функциям задачи Штурма-Лиувилля ....... 8
§ 1. Однородные граничные условия .................. 8
§ 2. Неоднородные граничные условия ................ 14
§ 3. Разложение по собственным функциям для элли-
эллиптического уравнения ............................. 15
§ 4. Метод интегрального преобразования Фурье ..... 17
Глава П. Задача Штурма-Лиувилля ........................... 23
§ 1. Одномерный случай: отрезок...................... 24
§ 2. Одномерный случай: периодические граничные ус-
условия .............................................. 29
§ 3. Собственные функции прямоугольника ........... 30
§ 4. Собственные функции прямоугольного параллеле-
параллелепипеда ............................................. 32
§ 5. Собственные функции круга ...................... 33
§ 6. Собственные функции кругового сектора ......... 37
§ 7. Собственные функции кругового кольца .......... 39
§ 8. Собственные функции кругового кольцевого секто-
сектора ................................................. 43
§ 9. Собственные функции цилиндра .................. 44
§ 10. Собственные функции цилиндрического сектора . 46
§ 11. Собственные функции кругового тора прямоуголь-
прямоугольного сечения ....................................... 47
§ 12. Собственные функции сектора кругового тора пря-
прямоугольного сечения .............................. 48
§ 13. Собственные функции шара .......... ............ 48
§ 14. Собственные функции шарового слоя ............. 52
§ 15. Задачи на собственные функции для уравнения
Шредингера ....................................... 55
§ 16. Задачи для самостоятельного решения ........... 62

Глава III. Краевые задачи для уравнения Лапласа............ 69
§ 1. Частные решения уравнения Лапласа в полярной
системе координат ................................. 71
§ 2. Краевые задачи для уравнения Лапласа внутри
круга .............................................. 73
§ 3. Краевые задачи для уравнения Лапласа вне круга 74
§ 4. Краевые задачи для уравнения Лапласа в круго-
круговом кольце ........................................ 75
§ 5. Краевые задачи для уравнения Лапласа в круго-
круговом секторе ........................................ 83
§ 6. Краевые задачи для уравнения Лапласа в кольце-
кольцевом секторе ........................................ 84
§ 7. Краевые задачи для уравнения Лапласа в прямо-
прямоугольнике .......................................... 86
§ 8. Краевые задачи для уравнения Лапласа в прямо-
прямоугольном параллелепипеде ........................ 90
§ 9. Краевые задачи для уравнения Лапласа в круго-
круговом цилиндре...................................... 95
§ 10. Частные решения уравнения Лапласа в сфериче-
сферической системе координат ........................... 106
§ 11. Краевые задачи для уравнения Лапласа в шаре .. 107
§ 12. Краевые задачи для уравнения Лапласа вне шара 108
§ 13. Краевые задачи для уравнения Лапласа в шаро-
шаровом слое .......................................... 109
§ 14. Задачи для самостоятельного решения ........... 116
Глава IV. Функция Грина оператора Лапласа .................. 123
Глава V. Задачи для уравнения теплопроводности ............. 140
§ 1. Задачи для уравнения теплопроводности в ограни-
ограниченной области с однородными граничными усло-
условиями .............................................. 141
§ 2. Задачи для уравнения теплопроводности в огра-
ограниченной области с неоднородными граничными
условиями ......................................... 157
§ 3. Задачи для уравнения теплопроводности на беско-
бесконечной прямой .................................... 169
§ 4. Задачи для уравнения теплопроводности на полу-
полубесконечной прямой ............................... 177

1. Задачи для уравнения теплопроводности на
полубесконечной прямой с однородными гра-
граничными условиями ......................... 178
2. Задачи для уравнения теплопроводности на
полубесконечной прямой с неоднородными
граничными условиями ...................... 186
3. Примеры решения задач .................... 196
§ 5. Задачи для уравнения теплопроводности в про-
пространстве .......................................... 201
§ 6. Задачи для самостоятельного решения ........... 211
Глава VI. Задачи для уравнения колебаний .................... 217
§ 1. Задачи для уравнения колебаний в ограниченной
области с однородными граничными условиями .. 218
§ 2. Задачи для уравнения колебаний в ограниченной
области с неоднородными граничными условиями 237
§ 3. Задачи для уравнения колебаний на бесконечной
прямой ............................................ 244
§ 4. Задачи для уравнения колебаний на полупрямой 255
1. Начально-краевые задачи для уравнения ко-
колебаний на полупрямой с однородными гра-
граничными условиями ......................... 255
2. Начально-краевые задачи для уравнения ко-
колебаний на полупрямой с неоднородными гра-
граничными условиями ......................... 266
§ 5. Задачи для уравнения колебаний на плоскости и в
пространстве ...................................... 274
§ 6. Задачи для самостоятельного решения ........... 283
Глава VII. Краевые задачи для уравнения Гельмгольца ....... 288
§ 1. Частные решения уравнения Гельмгольца в поляр-
полярной системе координат ............................ 288
§ 2. Краевые задачи для уравнения Дг/4-&2г/ — О внутри
круга .............................................. 291
§ 3. Краевые задачи для уравнения Ди + k2u — О вне
круга .............................................. 293
§ 4. Краевые задачи для уравнения Au + k2u — О в кру-
круговом кольце ...................................... 295

§ 5. Краевые задачи для уравнения Дu — k2u = 0 вну-
внутри круга .......................................... 297
§ 6. Краевые задачи для уравнения Дu — k2u = 0 вне
круга .............................................. 298
§ 7. Краевые задачи для уравнения Дu — k2u = 0 в кру-
круговом кольце ...................................... 299
§ 8. Частные решения уравнения Гельмгольца в сфери-
сферической системе координат ......................... 300
§ 9. Краевые задачи для уравнения Дu + k2u = 0 вну-
внутри шара .......................................... 303
§ 10. Краевые задачи для уравнения Дu + k2u = 0 вне
шара ............................................... 304
§11. Краевые задачи для уравнения Дu + k2u = 0 в ша-
шаровом слое ......................................... 305
§ 12. Краевые задачи для уравнения Дu — k2u = 0 вну-
внутри шара .......................................... 308
§ 13. Краевые задачи для уравнения Дu — k2u = 0 вне
шара ............................................... 308
§ 14. Краевые задачи для уравнения Дu — k2u = 0 в ша-
шаровом слое ......................................... 309
§ 15. Примеры решения краевых задач для уравнения
Гельмгольца ....................................... 310
§ 16. Задачи для самостоятельного решения ...........	317
Приложение ....................................................	320
§ 1. Формула сложения для сферических функций ...	320
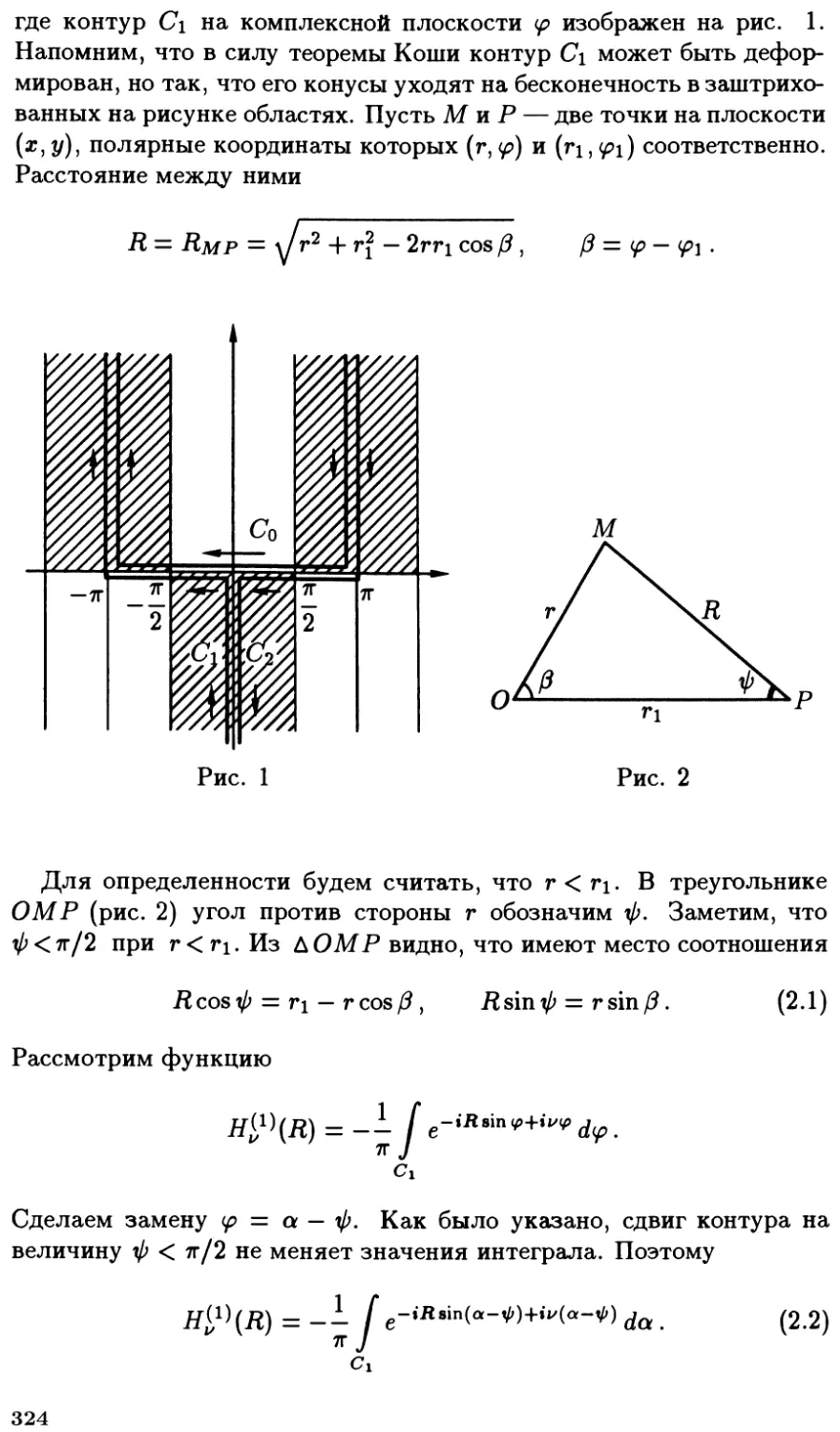
§ 2. Теоремы сложения для цилиндрических функций	323
§ 3. Суммирование некоторых рядов .................. 329
§ 4. Некоторые интегралы, содержащие цилиндричес-
цилиндрические функции ...................................... 333
§ 5. Справочный материал ............................. 338
Литература ..................................................... 349

ПРЕДИСЛОВИЕ
Настоящая книга является естественным дополнением пособия
А.Г.Свешникова, А.Н.Боголюбова, В.В.Кравцова «Лекции по ма-
математической физике». Ее основная цель - помочь студентам при-
приобрести необходимые практические навыки исследования математи-
математических моделей физических явлений, являющихся краевыми или
начально-краевыми задачами для линейных дифференциальных
уравнений в частных производных второго порядка. С этой целью
каждая глава пособия построена следующим образом. В начале ка-
каждого параграфа главы приводятся необходимые минимальные све-
сведения теоретического характера, используемые для решения данного
типа задач. Затем эти методы демонстрируются в работе, для чего
даются примеры решения конкретных задач. В конце главы приво-
приводятся задачи с ответами для самостоятельного решения.
Содержание пособия полностью соответствует курсу «Методы ма-
математической физики», читаемому на физическом факультете МГУ.
Пособие написано на основе более чем двадцатилетнего опыта препо-
преподавания на физическом факультете Московского университета. Оно
рассчитано в первую очередь на студентов физических специально-
специальностей университетов, но будет полезно и студентам инженерных специ-
специальностей и лицам, занимающимся математической физикой и при-
прикладной математикой.
Авторы выражают свою глубокую благодарность заведующему ка-
кафедрой ВМ-1 Московского государственного института электронной
техники (ТУ) профессору А.С. Поспелову, профессорам А.В. Ефи-
Ефимову, А.С. Ильинскому и С.Я. Секерж-Зеньковичу, взявшим на себя
труд ознакомиться с рукописью и сделавшим ряд ценных замечаний.

Глава 1
МЕТОД РАЗДЕЛЕНИЯ
ПЕРЕМЕННЫХ. РАЗЛОЖЕНИЕ
ПО СОБСТВЕННЫМ ФУНКЦИЯМ
ЗАДАЧИ ШТУРМА-ЛИУВИЛЛЯ
Метод разделения переменных, или метод Фурье, является одним
из самых старых и распространенных методов аналитического реше-
решения краевых задач математической физики. Он состоит в построении
решения в виде ряда по собственным функциям соответствующей за-
задачи Штурма-Лиувилля.
В настоящем пособии метод разделения переменных рассматрива-
рассматривается на примере решения краевых задач для уравнения
где
Lu = div(k(M) grad и) — q(M)u,
Pt[u} =
p(M),k(M),q(M) — функции переменной М в области D, ограни-
ограниченной замкнутой поверхностью 5, a,-(t) — функции переменной
t € [О, Т]. Уравнение рассматривается в области П = D * (О, Т).
Заметим, что при m = 2 это уравнение гиперболического типа, при
m = 1 — параболического типа, при m = 0 — эллиптического типа.
В случае m = 0 область Q отождествляется с областью D.
В § 1 и 2 настоящей главы рассматривается начально-краевая (сме-
(смешанная) задача для уравнений гиперболического или параболическо-
параболического типов, а в § 3 — краевая задача для уравнения эллиптического
типа. § 4 посвящен использованию интегрального преобразования
Фурье для решения начальных и начально-краевых задач в неогра-
неограниченных областях.
§ 1. ОДНОРОДНЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
Рассмотрим начально-краевую задачу с однородными граничными

условиями
pPt [и] = Lu + /(М, t) в П,	A-1)
= о, м+ |/?|/о,	A.2)
dv.
адп
dhu
5
fc = 0,l,...,m-l.	A.3)
t=o
Пусть {An}i° и {fn(Af)}i° — полные системы собственных зна-
значений и ортонормированных собственных функций соответствующей
задачи Штурма-Лиувилля:
Lvn + \npvn = 0 в D,
a^ + 0vn = 0,	A4)
дп s
Напомним основные определения и свойства собственных функций и
собственных значений.
Пусть D — конечная область, ограниченная замкнутой поверхно-
поверхностью S (на плоскости — замкнутой кривой С). Пусть в области D
задан эллиптический оператор Lu :
Lu = div(k(M) gradu) — q(M)u.
Определение. Те значения параметра А, при которых существует
нетривиальное решение краевой задачи
Lv + \pv = 0 в D,
где P[v] = а|^ +/?v, n — внешняя к области D нормаль к поверхности
5, \а\ + \/3\ ф 0, называются собственными значениями оператора
L в области D, а соответствующие им нетривиальные решения —
собственными функциями.
Перечислим основные свойства собственных значений и собствен-
собственных функций.
1. Существует бесконечное множество собственных значений
{Ап} и собственных функций {vn(M)}] собственные значения
при увеличении номера ?г неограниченно возрастают. Каждо-
Каждому собственному значению соответствует лишь конечное чи-
число линейно независимых собственных функций, т.е. ранг всех
собственных значений конечен.

В дальнейшем будем считать, что в последовательности
{Ап} каждое собственное значение повторяется столько раз,
каков его ранг.
2. При q > О собственные значения задачи Дирихле (а = О,
/3=1) положительны:
Ап > 0 при всех п.
3. Собственные функции ортогональны между собой в области
D с весом р(М) :
j vn(M)vm(M)p(M)dV = О, п ф т.
D
4. Теорема разложимости Стеклова. Произвольная дважды не-
непрерывно дифференцируемая в D функция ДМ), удовлетво-
удовлетворяющая однородному граничному условию, разлагается в аб-
абсолютно и равномерно сходящийся ряд по собственным функ-
функциям данной краевой задачи:
ДМ) = f;/ntln(M),	/п = тгрр ffvnPdV.
п=0 " я" ?
Заметим, что собственные функции представляют собой
собственные колебания, которые могут существовать в данной
области (отрезке, мембране или объеме) без подвода энергии
бесконечно долго.
Решение начально-краевой задачи A.!)-(!.3) будем искать в виде
разложения в ряд по собственным функциям задачи A.4):
A.5)
коэффициенты которого un(t) зависят от переменной t. Чтобы опре-
определить коэффициенты un(t), подставим ряд A.5) в уравнение A.1)
(предполагая, что ряд можно почленно дифференцировать нужное
число раз). Получим
00	00
? P^Pt(un} = ^ un(t)Lvn + ДМ, t).	A.6)
n=l	n=l
Поскольку Lvn = — An/wn, то, умножив A.6) на v^(M) и проинте-
проинтегрировав по области Д получим, в силу ортогональности системы
К(м)}
PtK] + Avii,, =/,,(*), i/= 1,2,... ,00,

где
D
Отметим, что здесь /t/(t) отличается от коэффициента Фурье в раз-
разложении /(М, t) в ряд по ортонормированной с весом р(М) системе
{vn(M)}> еслир(М) ? 1.
Домножив начальные условия A.3) на pvl/(M) и проинтегрировав
по области D, получим начальные условия для функций u^(t):
= 0,l,...,m-1, i/ = 1,2,..., oo,
t=0
где
A.7)
Таким образом, для определения коэффициентов и„A) при ка-
каждом I/ = 1, 2, . . . , оо получаем задачу Коши
*,, = /„(*),
A.8)
A.9)
t=o
Уравнение A.8) есть обыкновенное линейное дифференциальное
уравнение ш-го порядка. Его общее решение может быть записано
в виде
ш-1
*
/ /C(t,r)—
am(T
A.10)
где yj — произвольные постоянные, i/jtl — фундамен-
фундаментальная система решений, K^(t,r) — импульсная функция Коши*)
для уравнения A.8). Будем считать, что фундаментальная система
Tuj(t) выбрана так, что она удовлетворяет начальным условиям
dk
т
lv
t=o
j = k,
*' См.: Тихонов А.Н., Васильева А.Б., Свешников А.Г. Дифференциальные
уравнения. М.: Наука, 1985.

Подставляя A.10) в начальные условия A.9) и учитывая, что инте-
интегральное слагаемое в A.10) удовлетворяет нулевым начальным усло-
условиям, получим
cvj = (w)v.	(i.ii)
Итак, решение задачи (!.!)-( 1.3) имеет вид A.5), где функции un(t)
определяются формулами A.10), A.11) и A.7).
Выпишем выражения решений для уравнения теплопроводности и
уравнения колебаний.
Для уравнения теплопроводности с постоянными коэффициентами
Следовательно, уравнение A.8) имеет вид
+ АИ1„ = /„(*).	A.12)
Общее решение однородного уравнения:
«„(*) = ае"'А"',
Импульсная функция Коши
Kv(t,r) = Kv(i - г) = е-аЗА"('-т).
Поэтому общее решение уравнения A.12) записывается в виде
«„(<) =
Таким образом, решение начально-краевой задачи для уравнения те-
теплопроводности с однородным граничным условием
) в О,	A.13)
ос— -\- 0и\ — 0, сИ -}- ш ^ 0	A.14)
дп
u\t=o = ф(М)	A-15)
может быть записано в виде
u(M,t) =
A.16)

где {Ап} и {^„(m)} — собственные значения и собственные функции
задачи Штурма-Лиувилля
—
on
+ \v = 0 в Д
= 0, v(M) ?
fn(T) =
A.17)
Заметим, что первый ряд в A.16) представляет решение однород-
однородного уравнения с заданным начальным условием, второй — решение
неоднородного уравнения с нулевым начальным условием.
Для уравнения колебаний с постоянными коэффициентами
Pt[u} =
Уравнение A.8) принимает вид
A.18)
Общее решение однородного уравнения:
импульсная функция Коши:
Поэтому общее решение уравнения A.18) записывается в виде
/2 f
„ = (!/„.
Таким образом, решение начально-краевой задачи для уравнения ко-
колебаний с однородным граничным условием
titt =
= 0,
о,

может быть записано в виде
u(M,t) =
A.19)
где {Лп} и {vn(M)} — собственные значения и собственные функции
задачи A.17),
Первый ряд в A.19) дает решение однородного уравнения с заданны-
заданными начальными условиями, второй — решение неоднородного урав-
уравнения с нулевыми начальными условиями.
§ 2. НЕОДНОРОДНЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
Решение начально-краевой задачи с неоднородным граничным
условием можно свести к случаю, рассмотренному в предыдущем па-
параграфе.
Действительно, рассмотрим задачу с неоднородным граничным
условием
pPt[u] = Lu,
0ti „
а— + /3и
dtk
= 0, fc = 0,l,...,m- 1.
B.1)
B.2)
B.3)
t=0
Решение этой задачи будем искать в виде
и =
где I/(M, t) — новая неизвестная функция, а функция V(M, t) выбра-
выбрана так, чтобы она удовлетворяла неоднородному граничному усло-
условию B.2):

и обладала нужным числом непрерывных производных по М и t.
Тогда для функции U(M,t) получаем задачу
PPt[U] = LU + f(M,t) вП,
dku
dtk
dkv
t=o
dtk
, k = О,1,..., m— 1,
t=o
где /(M, ?) = Z/F — />Р*[У]. Эта задача рассмотрена в § 1.
§ 3. РАЗЛОЖЕНИЕ ПО
СОБСТВЕННЫМ ФУНКЦИЯМ ДЛЯ
ЭЛЛИПТИЧЕСКОГО УРАВНЕНИЯ
Решение внутренней краевой задачи для эллиптического уравне-
уравнения также может быть построено в виде ряда по собственным функ-
функциям соответствующей задачи Штурма- Л иу БИЛЛЯ.
Рассмотрим краевую задачу для неоднородного уравнения
Lu + cu = -f в D	C.1)
с однородным граничным условием
af^ + /Ns = 0, M + lfl^O,	C.2)
где
Lu = div(k grad и) — qu, с — const .
Пусть {An}?° и {vn(M)}i° — системы собственных значений и ор-
тонормированных собственных функций следующей задачи Штурма-
Лиувилля:
Lv + Xv = О в Д
а^+/?и|5=0, Н + |/?|^0,	C.3)
v(M) ф 0.
Заметим, что собственные функции этой задачи ортогональны с ве-
весом р = 1 .
Решение задачи C.1), C,2) может быть разложено в ряд по соб-
собственным функциям задачи C.3):
C.4)
г>=1

причем для коэффициентов ап имеем формулу
an=fu(M)vn(M)dV.
D
Коэффициенты ап разложения C.4) определим энергетическим ме-
методом. Для этого уравнение C.1) домножим на vn(M) и проинтегри-
проинтегрируем по области D :
vnLu dV + с ( vnudV = - I fvn dV.
D	D D
Используя вторую формулу Грина и учитывая однородные гранич-
граничные условия, получим
(Ая - с)ап = /п, п = 1, 2,..., оо,	C.5)
где /п = fD fvn dV.
Из соотношения C.5) вытекают следующие утверждения.
1. Пусть с ф \п при всех п = 1, 2,..., оо. Тогда
ап = -———, п = 1, 2,..., оо
Ап - с
и решение принимает вид
n=l
В этом случае решение единственно.
2. Пусть при п = п0, Ая* = с, * = I, 2,... ,р, где р = rang АЯо. Если
хотя бы одно /п0 ^ 0, то соотношение C.5) при п = п0 теряет смысл.
Это означает, что в этом случае (/п0 ф 0) задача C.1), C.2) решения
не имеет. Если же все Д0 = 0, то все коэффициенты ап, кроме апо
определяются однозначно:
/п	,
ап — ————, п +• HO,
Ап - с
коэффициент апо неопределен, и решение принимает вид
«= Е ^

где р = ran&Ano , Vn0 (М) — собственные функции, соответствующие
(k}
собственному значению ЛПо, а,п0 ~~ произвольные постоянные. В этом
случае решение существует, но не единственно.
Таким образом, при с = ХПо необходимым условием разрешимости
задачи C.1), C.2) является выполнение равенств
т.е. правая часть f(M) должна быть ортогональна всем собственным
функциям, соответствующим собственному значению Л„0. Это усло-
условие является также и достаточным условием разрешимости задачи
C-1), C,2).
Общую краевую задачу (с неоднородным граничным условием)
для эллиптического уравнения аналогично тому, как это сделано в
§ 2, можно свести к задаче C.1), C.2).
Этот метод используется для построения в виде ряда функции
Грина для внутренних краевых задач, о чем несколько подробнее
сказано в гл. III.
§ 4. МЕТОД ИНТЕГРАЛЬНОГО
ПРЕОБРАЗОВАНИЯ ФУРЬЕ
При решении начально-краевых задач для уравнений гиперболи-
гиперболического и параболического типов с постоянными по пространствен-
пространственным переменным коэффициентами в неограниченной области можно
использовать различные интегральные преобразования. Рассмотрим
одномерную начально-краевую задачу на бесконечной прямой:
Pt[tl] = !!
-00<Х<00, t>0,
D.1)
D.2)
t=o
где оператор Pt имеет вид
i=0
Будем искать ограниченные решения этой задачи.
Рассмотрим прежде всего задачу Штурма-Лиувилля, соответству-
соответствующую задаче D.1), D.2): найти значения параметра А, при котором
уравнение
Xй + XX = О

на всей оси — оо < х < оо имеет ненулевые ограниченные решения.
Легко видеть, что ограниченные решения существуют при любом нео-
неотрицательном А и имеют вид
Х± (х) = Ce±ix , С = const .	D.3)
При А < 0 решения будут неограниченными. Таким образом, рассма-
рассматриваемая задача Штурма- Л иувилля имеет непрерывный спектр:
любое неотрицательное число А является собственным значением, ко-
которому соответствуют две линейно независимые собственные функ-
функции D.3).
Положим А = //2, где ц действительно. Тогда
D.4)
Собственные функции D.3) можно отнормировать «на E-функцию»:
,	D.5)
где 6(/3) — E-функция Дирака, а черта означает знак комплексного
сопряжения. Такая нормировка обычно применяется для собствен-
собственных функций непрерывного спектра.
Используя известное разложение <$-функции в интеграл Фурье
находим значение нормировочного коэффициента
Таким образом, нормированные собственные функции имеют вид
Теперь будем искать решение исходной задачи D.1), D.2) в виде
интегрального разложения по нормированным собственным функци-
функциям D.6):
00
)e"»dp.	D.7)

Представление решения в виде D.7) соответствует его разложению
в тригонометрический интеграл Фурье, ядром которого является соб-
собственная функция Х+(х) = -jL-ettAX . Функция U называется образом
Фурье функции и, которая называется оригиналом.
Чтобы из соотношения D.7) выразить U(ii,i) через г/(х,?), умно-
умножим обе части равенства D.7) на Х*(х) и проинтегрируем по х от
-оо до со. Учитывая нормировку D.5), получаем
D.8)
Соотношения D.7) и D.8) называются интегральными преобразо-
преобразованиями Фурье. При этом переход от оригинала к образу по формуле
D.8) называется прямым преобразованием Фурье, а переход от образа
к оригиналу по формуле D.7) — обратным преобразованием Фурье.
Для существования преобразования Фурье функции вещественно-
вещественного переменного /(х) достаточно, чтобы функция /(х) была непрерыв-
непрерывна всюду, кроме, быть может, конечного числа точек разрыва первого
ряда, а интеграл
00
' |/(*)| А*
сходился.
В дальнейшем будем предполагать, что функция u(x,t) вместе со
своими производными до второго порядка достаточно быстро убывает
при х -> ±оо.
Получим задачу в пространстве образов для определения U(ii,i).
Умножим уравнение D.1) на Х+(х) и проинтегрируем по х от —оо до
+оо:
/ .——«[.]*. -?. / .-"•.„(.,,)*+-?; / .--/*.
Проинтегрируем первый интеграл в правой части формулы два
раза по частям, учитывая, что в силу предположения о поведении
функции и и ее частных производных на бесконечности подстановки
на ±оо обратятся в нуль. Учитывая, что
оо
-±= j e-i>"Pt(<U]dx=Pt[U(n,t)],

и обозначая
1 Г
-,0 = -7= /
Л/27Г У
— оо
получаем уравнение для функции
1,0» < > О-
,=1
Аналогичным образом из начальных условий D.2) получаем началь-
начальные условия для функции [/(//, 0:
dkU
dtk t=0
где
Таким образом, для определения функции C/(//,t) получаем сле-
следующую задачу Коши:
dk U
dtk
)<™+SU = F, 00,	D.9)
* = 0,l,...,m-l,	D.10)
t=0
в которой // является параметром. Решение этой задачи Коши было
рассмотрено в § 1. Определив функцию [/(//, t), решение исходной
задачи D.1), D,2) получим с помощью формулы D.7).
Аналогичным образом можно использовать интегральное преобра-
преобразование Фурье для решения задач на полу бесконечной прямой х > 0.
В качестве ядра интегрального преобразования Фурье на полупрямой
х > 0 нужно брать собственную функцию соответствующей задачи
Штурма-Л иу вилл я. Таким образом, в случае граничного условия
Дирихле используется синус-преобразование Фурье, при котором пе-
переход от оригинала f(x) к изображению F^(X) осуществляется по
формуле
i— °°
Л/'
= - f(x)sm\xdx,

а обратный переход — по формуле
.—— 00
f(x) = J- f F^(X)smXxdX.
Ядро синус-преобразования Фурье К(х,Х) = \l^smXx является ре-
решением уравнения Xй + Х2Х = О и удовлетворяет однородному гра-
граничному условию Дирихле К@,Х) = 0.
В случае граничного условия Неймана используется косинус-пре-
косинус-преобразование Фурье, при котором формулы прямого и обратного пре-
преобразований имеют соответственно вид
.—— 00
р(°)(Х) = J- I f(x)cos\xdx
Ядро косинус-преобразования Фурье К = -v/|-cosAx является реше-
решением уравнения X11 + Х2Х = 0, удовлетворяющим однородному гра-
граничному условию Неймана при х = 0.
Применяются интегральные преобразования Фурье и с более слож-
сложными ядрами. Например, в случае граничного условия третьего рода
их — hu\x=Q =0, h = const > О,
используется преобразование с ядром
К(х,\) =
для которого формулы прямого и обратного преобразований имеют
вид
F(A) =
/(*) =

Мы рассмотрим применение интегрального преобразования Фурье
к одномерным задачам. Аналогично используется интегральное пре-
преобразование Фурье в случае многих пространственных переменных.
Причем в многомерном случае можно производить преобразование
Фурье по части пространственных переменных, получая в результате
дифференциальное уравнение в пространственной области меньшей
размерности.
Кроме интегрального преобразования Фурье при решении началь-
начально-краевых задач для уравнений гиперболического и параболическо-
параболического типов в неограниченной области используются и другие интеграль-
интегральные преобразования. Например, если коэффициенты а,- оператора
Pt[u] являются постоянными, удобно использовать интегральное пре-
преобразование Лапласа*).
*' См.: Свешников А.Г., Тихонов А.Н. Теория функций комплексной перемен-
переменной. М.: Наука, 1979.

Глава 2
ЗАДАЧА ШТУРМА-ЛИУВИЛЛЯ
Как было показано в гл. I, если известны полные наборы собствен-
собственных значений и собственных функций данной области для соответ-
соответствующей краевой задачи, то решение начально-краевой задачи для
уравнений гиперболического и параболического типов и краевой за-
задачи для эллиптического уравнения может быть построено в виде
ряда.
В настоящей главе построены собственные функции и собственные
значения оператора Лапласа для основных канонических областей
(отрезок, прямоугольник, прямоугольный параллелепипед, круг,
круговой сектор, круговое кольцо, сектор кругового кольца, прямой
круговой цилиндр и его сектор, круговой тор прямоугольного сечения
и его сектор, шар, шаровой слой).
Напомним еще раз, что задача Штурма-Лиувилля для оператора
Лапласа имеет следующий вид (р(М) = 1):
Р[и]| =0, и?0,
!••>
где Р[и] = а|^--}-/?г/, п — внешняя к области D нормаль к поверхности
S, \а\ + \/3\ -ф О (всюду в дальнейшем предполагается, что а и /? —
постоянные) .
Заметим, что собственные значения Ап оператора Lu = Дг/ + сг/,
где с = const, получаются из собственных значений Ап оператора
Лапласа для соответствующей краевой задачи в результате сдвига
на величину —с:
Ап = Ап — с.
При решении задачи Штурма-Лиувилля с граничными условиями
Дирихле (а = 0, /3=1) для оператора с постоянными коэффициен-
коэффициентами
Lu = Аи + biux + 62% + bsuz + си
удобно сделать замену неизвестной функции
и = ехр (--

Тогда задача
Lu + At/ = 0 в Д
ti|s = 0, г/^0
переходит в следующую задачу для функции v
собственные значения которой выражаются через собственные зна-
значения оператора Лапласа.
Перейдем к рассмотрению задачи Штурма-Лиувилля для опера-
оператора Лапласа (Lu = Дм, р = 1) в конкретных областях.
§ 1. ОДНОМЕРНЫЙ СЛУЧАЙ: ОТРЕЗОК
В одномерном случае рассмотрим общую схему нахождения соб-
собственных функций и собственных значений следующей задачи Штур-
Штурма-Лиувилля:
— (k(x)-^j -qy + \py = Q, О < х < /, A.1)
I*0,	A.2)
=/ = о, |а2| + IAI Ф о.	A.3)
Обозначим через {t/i(z, A), 2/2(^5 А)} фундаментальную систему реше-
решений уравнения A.1). Фундаментальные решения у\ и t/2 зависят от А
как от параметра. Общее решение уравнения A.1) можно записать в
виде
А).	A-4)
Подставляя A.4) в граничные условия A.2), A.3), получим
)} = 0,
A.5)
Соотношения A.5) представляют собой однородную систему линей-
линейных алгебраических уравнений относительно С\ и С2. Эта система

имеет ненулевое решение только в том случае, когда ее определитель
равен нулю:
<*iyi@,A)-/?i!/i@,A) aivKO.AJ-fti&fO.A)
,A) + /?2yi(/,A) а2У2(/,А)+/?2У2(/,А) ~ °'	(L6)
Соотношение A.6) представляет собой уравнение для определения
собственных значений Л. Это уравнение называется дисперсионным.
Пусть {Лп} — корни уравнения A.6). Каждому Лп соответствует
ненулевое решение уравнения A.5) и, следовательно, ненулевое ре-
решение уравнения A.1), представимое в виде A.4).
Выше был рассмотрен общий алгоритм построения собственных
значений и собственных функций. В ряде случаев его можно упро-
упростить. Пусть фундаментальная система уравнения A.1) выбрана так,
что на одном из концов отрезка, например при х = О, функции yi(x, Л)
и т/2 (я> А) удовлетворяют граничным условиям
Тогда, подставляя A.4) в граничное условие A.2), сразу находим
С2 = 0. Следовательно, собственная функция, согласно A.4), должна
представляться в виде
у(х) = Ciyi(s,A).
Подстановка в граничное условие A.3) дает дисперсионное уравнение
для Л :
i) = (*. Л) + Ят(*. А)|ж=( = о.
Рассмотрим теперь частный случай Ly = у". В этом случае общее
решение A.4) может быть записано в виде
у(х) = Ci cos л/Ах + С2 sin л/Ах, (p=l).	A.7)
Коэффициенты С\ и Съ определяются из системы
-а2л/Л sin V\l + /?2 cos л/Л/} +	A.8)
= 0.
Уравнение A.6) имеет вид
А/?2) tg л/А/ = лД(«1/?2 + /?i«2).	A.9)

Легко убедиться (например, графическим методом), что уравнение
A.9) имеет бесконечное счетное множество корней {Ап}?°. Для ка-
каждого корня Ап находим ненулевое решение системы A.8):
Ci=	C2= A.10)
где С — произвольная постоянная, отличная от нуля (С ф 0). Вели-
Величина
Nn = \\yn\\ =
представляет собой норму собственной функции. Если постоянная
выбрана так, что Nn = 1, то собственные функции уп(х] будут орто-
нормированными .
Итак, ненормированные собственные функции задачи Штурма-
Лиувилля
«И/ - АУ|«О = 0. «21/ + Ау|«/ - О
можно записать в виде
Уп(х)=	A.11)
при этом
Ы12 =	A.12)
где Ап — корни уравнения A.9).
Формулу A.11) для собственной функции можно привести к виду
уп(х) = з
где величина Sn определяется соотношениями
с
cos *n =
Уравнение A.9) имеет нулевое решение АО = 0. Ему будет соответ-
соответствовать ненулевая функция уо(#), определяемая A.11), если /?i = О
и /?2 = 0, и эта функция равна 1. Следовательно, при А0 = 0 ||уо||2 = I-

Выделим частные случаи.
1. Граничные условия: у@) = уA) = О (c*i = а2 = 0, ft = ft = 1),
/ \ • Л — \ /тгпч2 .. ||2 /
уп(х) = 8ш^Апх, An=(^— J , ||уп||2 = ~,
п= 1,2, ...,оо.
2. Граничные условия: t/@) = t/(/) = 0, (e*i = с*2 = 1, ft = ft = 0),
yn(x)=cos^/\^xy Ап = (™j , ||yn||2 = -A+Ляо),
n = 0, l,...,oo.
Заметим, что в этом случае существует нулевое собственное значение
АО = 0, которому соответствует собственная функция уо(х) = 1.
3. Граничные условия: у@) = t/(/) = О (e*i = /32 = 0, $\ — а2 = 1),
4. Граничные условия: t/@) = y(l) = 0, (/?i = «2 = 0, /?2 = «1 = 1),
n = 0, 1, . .. ,оо.
5. Граничные условия: у@) = 0, yf + Л2у|а._/ = 0 (ai = 0, /?i = 1,
«2 = 1, /?2 = Л2),
^я, ||Уп||2=
2(А„ + hi)'
Л„ — корни уравнения
6. Граничные условия: t/@) = 0, t/(/) + /i2y(/) = 0 (ft = 0, аг = 1,
«2 = 1, /?2 = Л2),
уя(«) = cos v/A^x, ||yn||2 = - + 2/Ал^Л2» я = 1,2,..., оо,

An — корни уравнения
7. Граничные условия: t/@) — ftiy(O) = 0, y(l) = О (c*i = 1, /3\ =
уп(х) = smy/\^(l-x), ||yn||2 =
2(А„ + Л?)'
An — корни уравнения
8. Граничные условия: t/@) — /iiy(O) = 0, t/(/) = 0 (ai = 1, /?i = /ii,
«2 = 1, A = 0),
yn(x) = cos^\(l-x), ||yn||2 =
2
2(ЛП + /i2) ?
Лп — корни уравнения
9. Граничные условия: t/@) - /iiy(O), j/(i) + /i2y(/) = 0 (ori = 1,
yn(x) =
Лп — корни уравнения
Заметим, что в этом случае собственную функцию можно записать
также в виде
где Ап — корни уравнения

§ 2. ОДНОМЕРНЫЙ СЛУЧАЙ:
ПЕРИОДИЧЕСКИЕ ГРАНИЧНЫЕ УСЛОВИЯ
Рассмотрим задачу Штурма- Л иувилля на отрезке [0, /] с условием
периодичности
у" + Ау = 0, 0<х</,	B.1)
у(х) = у(х + /) при любом х Е [0, /],
У(*) * 0.	B.2)
Условия периодичности B.2) можно заменить граничными условиями
Общее решение уравнения B.1):
у(х) = Ci cos л/А/ + С2 sin л/А/	B.3)
подставим в условия B.2):
Ci cos л/А(х + /) + С2 sin л/А(х + /) = Ci sin л/Az Н- С2 cos л/Ах.
Воспользовавшись линейной независимостью функций cos\/Ax и
sin\/Ax, отсюда получим
( Ci(cos\/A/ - 1) + CismVXl = 0,
| -Ci sin \/А/ -f C2(cos \/Л/ ~ 1) = 0.
Система B.4) имеет ненулевое решение только при условии
cos л/А/ — 1 sin v\l
— sin л/Л/ cos л/Л/ — 1
или
cos л/Л/ = 1.
Отсюда находим Лп = (^j11) , п = 0, 1, 2, . . . , оо.
При найденных значениях Лп система B.4) имеет два линейно не-
независимых ненулевых решения:
Подставляя B.5) в B.3), находим собственные функции
= cos ^х, Ух = sn

Заметим, что собственному значению АО = 0 соответствует одна соб-
собственная функция уо(х) = 1, в то время как все ненулевые собствен-
собственные значения Лп имеют ранг, равный двум.
Таким образом, задача B.1), B.2) с периодическими граничными
условиями имеет следующие наборы собственных значений и соб-
собственных функций:
B.6)
B.7)
= -, п= 1,2,...,оо.
Г cosnx
= 2тг An = rr, yn(x) = < . , уо = I-
t smnx
§ 3. СОБСТВЕННЫЕ ФУНКЦИИ
ПРЯМОУГОЛЬНИКА
Рассмотрим задачу Штурма-Лиувилля для оператора Лапласа в
прямоугольнике:
и = 0, 0<х<а, 0<у<6,	C.1)
Pi(u) = aig - /3lU\x=Q = 0, Р2(и) = a2g + fru\x=a = 0, C.2)
Ps(n) = «з~ ^ /%u|=0 = 0, Р4(и) = a4 + /?4u|=fe = 0, C.3)
где а,-, fa — постоянные, причем |а,-| + |/?,-| ^ 0.
Задачу (ЗЛ)-(З.З) будем решать методом разделения переменных.
Найдем ненулевые решения уравнения C.1), представимые в виде
*0.	C.4)
Подставляя C.4) в уравнение C.1) и разделяя переменные, получим
Х"(х) Y"(y)
Т?Г = ~Ты"
Следовательно, для функции Х(х) и У (у) получаем одномерные за-
задачи Штурма-Лиувилля для отрезка:
X" + цХ = 0, 0 < х < а,

{У" + vY = О, 0 < у < 6,
где I/ = Л — р. Решив каждую из этих задач, собственные функции
задачи C.1)-C.3) найдем согласно A.11), а собственные значения А
вычислим по формуле А = ц + v.
Таким образом, справедливо следующее утверждение: собствен-
собственные функции оператора Лапласа для прямоугольника равны про-
произведению собственных функций по каждой переменной с соответ-
соответствующими граничными условиями ипт — Xn(x)Ym(y)y а собствен-
собственные значения равны сумме собственных значений одномерных задач
АПГП = Цп "Г "т*
В качестве примера приведем собственные функции и собственные
значения для задач Дирихле и Неймана:
а) задача Дирихле и\с = О, где С — контур прямоугольника:
, ч . тгп тгга
Мпт(я, У) = Sin —— XSin -7-У,
а	о
.	/тгп\2 /тгтх2
Апт = ^— J + (^—— J , п,т=1,2, ...,
II ii9 и . Я1 ••«> II . 7Г^ по &Ь
\\Unm\\2 = || Sin —— Х||2 || Sin ——— у||2 = -.
б) задача Неймана |^|с = 0, где п — внешняя нормаль к контуру
прямоугольника:
ТГП	7ГТП
=cos —
а
\
nm =	" ' n,m = 0,l,2,...,
Собственные функции и собственные значения для других граничных
условий легко выписать, используя результаты § 1.
Рассмотрим также задачу Штурма-Лиувилля для оператора Lu =
Aw -f Ь\их + Ь^иу + си Fi, 62 ) с — постоянные) в прямоугольнике:
Ди Н- 6iux + Ь2иу Н- си Н- Хи = 0, 0 < х < а, 0 < у < 6, C.5)
и|с = 0,	C.6)
где С — граница прямоугольника.

Как было указано ранее, удобно ввести новую неизвестную функ-
функцию v(x, у) следующим соотношением:
u = e-*(b>x+b^v(x,y).	C.7)
Тогда для функции v получаем задачу
Дг; + fjtv = О, 0 < х < а, 0 < у < 6,
Ь4-Ь
где введено обозначение ^ = Л + с — *^ а , решение которой только
что было рассмотрено.
Следовательно, собственные значения и собственные функции за-
задачи C.5), C.6) имеют вид
= е
тгп . тгга
—х sin -7-
а	о
1„о ,-
причем при с < On = 1,2,..., m = 1,2,..., а при с > 0 начальные
значения пит выбираются так, чтобы Anm > 0.
При граничных условиях второго и третьего рода рассмотрение
проводится аналогично, следует только при замене C.7) преобразо-
преобразовать и граничное условие.
§ 4. СОБСТВЕННЫЕ ФУНКЦИИ
ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА
Задача Штурма-Лиувилля для оператора Лапласа в прямоуголь-
прямоугольном параллелепипеде имеет вид
tH-Au = 0, 0<x<a, 0<y<6, 0<z<c,
Pi(ti) = «1— - fan
f\
= 0,
= 0,
= 0,
ar=a
= 0,
у=Ь
= 0,
= 0,
г=с
* = 1,2,. ..,6.
a,-, fa = const, |о,-| + |А|^
Используя результаты § 3, легко показать, что собственные функ-
функции и собственные значения для прямоугольного параллелепипеда
имеют вид
unmk(x,y,z) = Xn(x)Ym(y)Zk(z),

где (Хя(х),/1я), (Ут(у),1>т), (Zk(z),*k) — собственные функции и
собственные значения соответствующих одномерных задач Штурма-
Лиувилля по каждой переменной. На доказательстве этого утвер-
утверждения мы не останавливаемся, поскольку оно полностью аналогич-
аналогично приведенному в § 3.
§ 5. СОБСТВЕННЫЕ ФУНКЦИИ КРУГА
Рассмотрим задачу Штурма-Лиувилля для круга Ка:
Ди + Аи = 0, (х,у)€Ка,	E.1)
Введем полярную систему координат (г, (р) с началом в центре круга
Ка. Напомним, что оператор Лапласа в полярной системе координат
равен
1	Q / Q >
I О f OU
U=rdr\1
Собственную функцию будем искать в виде
и(г, (р} = Н(г}Ф((р) ^ 0.	E-3)
Уравнение E.1) запишем в полярной системе координат, подставим в
него E.3) и разделим переменные. Получим
Я(г)
Поскольку собственная функция должна быть периодической по (р с
периодом 2тг, то для Ф получаем задачу Штурма- Лиувилля
ф" + */ф = 0, 0 < (р < 2тг,
Ф(^) =Ф(<р + 2тг),
решение которой имеет вид (см. § 2)
„ = „„ = „>,	E.5)
п = 0, 1,2, . . .,оо.
При каждом I/ = п2 получаем задачу для R(r):
d (dR
dr \ dr
\ ^ (Лг2 _ ^R = Q^ Q<r<a	E б)
J

Функция R должна удовлетворять граничному условию
a™+CR = 0 |a| + |/?|^0,
dr	r=a
вытекающему из E.2), и естественному условию ограниченности при
г = 0:
; оо,
поскольку г = 0 является особой точкой уравнения E.6). Следова-
Следовательно, для определения R(r) получается задача Штурма-Лиувилля
г2Д" + гД' + (Аг2 - n2)R = О, 0 < г < а,	E.7)
a^ + /3R = 0, \а\+\/3\?0, E.8)
dr	г-а
|Я@)|<оо, Д(г)^0.	E.9)
Уравнение E.7) заменой х = r^/\ приводится к уравнению Бесселя
n-го порядка:
Поэтому общее решение уравнения E.7) можно записать в виде
Д(г) = Rn(r) =
Учитывая неограниченность функции 7Vn(\/Ar) при г -> 0 и условие
E.9), находим С% = 0. Будем считать С\ = 1, поскольку собствен-
собственная функция определяется с точностью до числового множителя, ко-
который определяется из условия нормировки. Поэтому собственная
функция задачи E.7)-E.9) имеет вид
Д»(г) = 7п(л/Аг).	E.10)
Подставляя E.10) в граничное условие E.8), получим дисперсионное
уравнение для определения собственных значений А:
aVXJ'n(VXa) + pJn(V\a) = 0,	E.11)
где штрих обозначает производную функции Бесселя по полному ар-
аргументу. Обозначим ц = л/А а. Тогда собственные функции и соб-
собственные значения задачи E.7)-E.9) можно записать в виде

где ц^' — fc-й корень уравнения
/,)+ /За Jn(/i) = О,	E.13)
при фиксированном п = 0, 1, 2, . . .
Таким образом, собственные функции круга имеют вид
p)=	E.14)
71 = 0,1,2,.. ., fc = l,2,...,
/»(")\2
а собственные значения равны Аг' = ( -?— I .
V а )
Найдем норму собственной функции E.14):
E.15)
Поскольку норма Фп (Фп = cos п(р или Фп = sin п(р) известна, остается
найти ||Jn||.
Чтобы найти || Jn||, вычислим интеграл
где Zv(x) — произвольная цилиндрическая функция.
Имеем
Используя уравнение Бесселя
х2^' + xZ'v + (х2 - i?}Zv = О,
находим
= -х2^' - xZ'v + v^Zv = -x-(zZ?) + V*ZV.

Поэтому
Итак
Zl(x)xdx=	E.16)
/
Полученная формула позволяет вычислить квадрат нормы функции
Бесселя для соответствующей краевой задачи:
\\Jn\\2 =
E.17)
Рассмотрим теперь первую, вторую и третью краевые задачи отдель-
отдельно.
Для задачи Дирихле (а = О, /3 = 1) собственные значения опреде-
определяются (согласно E.13)) из уравнения
Следовательно,
\\Jn\\l =	E.18)
Для задачи Неймана (а = 1, /3 = 0) собственные значения опреде-
определяются из уравнения
Следовательно,
\\Jn\\l =	E.19)

Для третьей краевой задачи (а = 1, /3 = h) собственные значения
определяются из уравнения
Следовательно ,
Шз =
E.20)
\\Jn\\l =	E.21)
Формула E.20) удобна для вычислений при малых Л (Л -> 0), а фор-
формула E.21) — при больших Л (Л — >• оо). Непосредственно видно, что
при Л — >• 0 формула E.20) переходит в E.19), а при Л — >• оо E.21)
переходит в E.18).
§ 6. СОБСТВЕННЫЕ ФУНКЦИИ
КРУГОВОГО СЕКТОРА
Пусть D — круговой сектор: 0<г<а,0<^><а;С — граница
области D. Задача Штурма-Лиувилля имеет вид
Au + Au = 0 BjD,	F.1)
|о0| + |/ЗЬ| ^ 0,	F.2)
|/?i|*0,	F.3)
|/%|,40,	F.4)
где n — единичная нормаль (внешняя) к С, с*о, Аь <*ъ /?ъ <*2, /?2 =
const.
Представляя функцию и в виде
подставляя ее в (б.1)-F.4) и разделяя переменные, получим отдельно
задачи для R(r) и
г2 Я" -h rR' -h (Ar2 - i/2)E = 0, 0 < г < a,	F.5)
*) = *o^ + A*U.=°.
|Д@)|<оо, Д(г)^0.	(б.б)

ф" + i/Ф = О, 0 < <f < а,	F.7)
0 = 0,
а = 0, F.8)
0.
Задача F.7), F.8) есть задача Штурма-Лиувилля для отрезка, рас-
рассмотренная в § 2. Ее собственные значения i/n и собственные функции
Фп(^>) определяются формулами B.6) и B.7).
Задача для R(r) также рассмотрена ранее (см. § 5). Ограниченное
решение уравнения F.5) имеет вид
Л(г) = Л„ (г) = СЛ,. (ч/Аг).	F.9)
Подставляя F.9) в граничное условие F.6), получаем уравнение для
определения собственного значения А:
ay/XJvn(V\a) + pJvn(V\a) = О,	F.10)
где штрих обозначает производную функции Бесселя по полному ар-
аргументу. Таким образом, решение задачи F.5), F.6) можно записать
в виде
где /4 — fc-й корень уравнения
(р) = 0	F.11)
при фиксированном п. Квадрат нормы функции Rn(r) выражается
формулами E.18)-E.21) (в зависимости от типа краевой задачи), в
которых п следует заменить на i/n .
Итак, собственные функции задачи Штурма-Лиувилля для кру-
кругового сектора имеют вид
где функции Фп(^) определяются формулой B.7), а собственные зна-
значения А^ ^ = f ?h — } , где /*Jt — корни уравнения F.11).

§ 7. СОБСТВЕННЫЕ ФУНКЦИИ
КРУГОВОГО КОЛЬЦА
Перейдем к вычислению собственных функций кругового кольца.
Пусть D — круговое кольцо: а<г<6,0<^><2тг. Рассмотрим
задачу Штурма-Лиувилля
Аи + \и = 0 в Д	G.1)
Представляя решение в виде м(г, (р) = Н(г)Ф((р), подставляя в
уравнение G.1) и разделяя переменные, получаем задачи для функ-
функций R и Ф:
г2R" + rR' + (Аг2 - i/2)R = О, 0 < г < 6,	G.4)
e = 0,	G.5)
ь = 0	G.6)
ф" + t/ф = 0, 0 < (р < 2тг,	G.7)
= Ф(<р + 2тг) при любом (р. G.8)
Задача G.7), G.8) решена в § 2. Ее собственные значения i/ и соб-
собственные функции Ф соответственно равны
п	( cos п(р
v = Vn = n\ Ф = Ф„(^) = { . Y ,	G.9)
t sm nif>
Общее решение уравнения G.4) при v = n2 имеет вид
Д(г) = dJn(V\r) + C2Nn(V\r).	G.10)
Подставляя G.10) в граничные условия G.5), G.6), получим
Г CMMVXa)] + С^ШчЪа)} = О,

где
^y/Xa) - /?iJn(\/Aa),
n(\/Aa)] и P2[Nn(\/A&)] определяются аналогичным образом. Си-
Система G.11) относительно С\ и С*2 имеет ненулевое решение, если ее
определитель равен нулю:
( '
При выполнении условия G.12) из системы G.11) находим
GЛЗ)
Подставляя G.13) в G.11) и выбирая С\ = Pi[Nn(V\a)], ненулевое
решение задачи G.4)-G.б) запишем в виде
R(r) = Rn(r) = Jn(VAr)P![7Vn(VAa)] - ^(VXrJP^J^VAa)] G.14)
или, учитывая G.12), в виде
G.15)
Значение А = А^ определяется из уравнения G.12) при каждом фик-
фиксированном п = 0,1,...
Подсчитаем квадрат нормы Rn(r):
||Лп||2 =
Для этого воспользуемся формулой (см. E.16))
ь

где Zl(\i\r) — любое решение уравнения Бесселя:
Итак,
|2 _
Поскольку
Rn(V\b) =
(напомним, что штрих обозначает производную по полному аргумен-
аргументу)
тгуАа

где H^[Jn> АГП] — якобиан функции Jn(x) и Nn(я), равный —-, получим
G.16)
Таким образом, собственные функции кругового кольца можно запи-
записать в виде
где Лп(у А?П г) определяется формулой G.14) или G.15), а собствен-
собственные значения А^ есть корни уравнения G.12):
Выделим отдельно случаи граничных условий первого и второго
рода. Пусть на обеих границах (г = а, г — Ь) выполняются граничные
условия Дирихле (c*i = 0, а2 = 0, /?i = — 1, /?2 = 1)
Тогда
G.17)
где А = А?П^ есть fc-й корень уравнения
G.18)
2 _
G.19)
В случае граничных условий Неймана на обеих границах (e*i =
«2 =!,& =02=0)
ди
дг
дг
= 0,
г=6
G.20)

где
А = А!П) — k-Л
корень уравнения
= 0,
над =
2 _
G.21)
G.22)
Заметим, что в этом случае уравнение G.21) имеет нулевой корень
(Л = 0), т.е. существует нулевое собственное значение. Написанные
выражения для собственных функций справедливы при Л ф 0. Ну-
Нулевому собственному значению соответствует собственная функция,
равная единице.
§ 8. СОБСТВЕННЫЕ ФУНКЦИИ
КРУГОВОГО КОЛЬЦЕВОГО СЕКТОРА
Пусть D — круговой кольцевой сектор: а<г<6,0<^><а.
Соответствующая задача Штурма-Лиувилля имеет вид
Ди + Хи = 0 в jD,
Pl(«) = C
Рз(«) = с
Рз(«) = о
Р4(«) = а
1^0, |а
ri— -/?i«
GГ
ди
от
, ди
ди
4^— + /?4«
c/v?
= 0,
г=а
= о,
г=6
= 0,
= 0,
tl + lftl^O, i=l,2,3,4.
(8.1)
(8.2)
(8.3)
(8.4)
(8.5)
Представляя решение в виде
и =
и разделяя переменные, получаем задачу Штурма-Лиувилля для
отрезка 0 < <р < а :
ф" + j/Ф = О,
= 0, Р4(Ф)
= 0
(8.6)

и задачу Штурма-Лиувилля на отрезке для оператора Бесселя:
г2Д" + гД' + (Аг2 - 1/)Д = 0, а < г < 6,
= 0, Р2(Д)
г=а
= 0,	(8.7)
Г=6
каждая из которых была подробно рассмотрена выше (см. § 1 и 7).
Следовательно, собственные функции кругового кольцевого сектора
имеют вид
где
(8.8)
Фп(?)=	(8.9)
где i/n — n-й корень уравнения (см. § 1, A.8) и A.11))
(a3a4v - /?3/?4) tg V^a = >/Я<*з/?4 + /?з<*4),	(8.10)
А = А? — k-u корень уравнения
(8.11)
Явные выражения для Фп для всех возможных случаев граничных
условий при <р = 0 и <р = а выписаны в § 1.
§ 9. СОБСТВЕННЫЕ ФУНКЦИИ ЦИЛИНДРА
Рассмотрим задачу Штурма- Лиувилля для прямого кругового ци-
цилиндра. Введем цилиндрическую систему координат (г, ^>, z) с нача-
началом в центре нижнего основания цилиндра и осью z, направленной
вдоль оси цилиндра. Напомним, что оператор Лапласа в цилиндри-
цилиндрической системе координат имеет вид
—— ,

где Д2 — оператор Лапласа на плоскости. Задача Штурма-Лиувил-
ля имеет вид
Ди + Аи = О, 0<r<a, 0<^>< 2тг, 0 < z < /, (9.1)
ди
Решение будем строить методом разделения переменных, отделяя пе-
переменную z:
u(r, <р, z) = v(r, (p)Z(z).	(9.4)
Подставляя (9.4) в уравнение (9.1), записанное в цилиндрической си-
системе координат, и разделяя переменные, получим
ади
= 0, (9.2)
г=а
ди
*=о ' *dz
= 0. (9.3)
А2г> + Аг> _ Z" (z)
v(r,<f>) ~ Z(z) ~
(9.5)
С учетом граничных условий (9.2), (9.3) для определения v и Z имеем
следующие задачи Штурма-Лиувилля:
Г z" + i/z = o,
0<z</,
A2v -f xv = 0,
О < г < a, 0 < у < 2тг,
где x = A — i/,
Первая задача есть задача определения собственных функций и
собственных значений отрезка, вторая — задача определения соб-
собственных функций и собственных значений круга. Первая решена в
§ 1, вторая — в § 5.
Следовательно, собственные функции цилиндра имеют вид
а собственные значения вычисляются по формуле
= х(п) + i/m,

где х^ — собственные значения круга при граничных условиях
(9.2), Zm(z) и i/m — собственные функции и собственные значения
соответственно отрезка при граничных условиях (9.3).
§ 10. СОБСТВЕННЫЕ ФУНКЦИИ
ЦИЛИНДРИЧЕСКОГО СЕКТОРА
Пусть D — сектор конечного кругового цилиндра: 0 < г < а,
0< у>< а, 0 < z< /.
Задача Штурма-Лиувилля имеет вид
и = 0 вД	A0.1)
а=0, A0.2)
= 0,	A0.4)
0, A0.5)
0,	A0.6)
ti(r, р, z) ф 0, Н + | ft) ± 0, i = 2,..., 6.
Как и в предыдущем пункте, решение ищем в виде
.	A0.7)
Подставляя A0.7) в A0.1)-A0.б) и разделяя переменные, получаем
для функции Z(z) задачу Штурма-Лиувилля для отрезка:
f Z" + aZ = 0, 0 < z < /,
l = 0,	A0.8)
а для функции v(r, (p) — задачу Штурма-Лиувилля для кругового
сектора:
( Av + ЯУ = 0, 0 < г < а, 0 < <р < а,

где х = Л — <т.
Задача A0.8) рассмотрена в § 1, задача A0.9) — в § 6. Следова-
Следовательно, собственные функции цилиндрического сектора имеют вид
, <f>)Zm(z),
где Rnk(r, (p) — собственные функции кругового сектора 0 < г < а,
О < <р < а, Zm(z) — собственные функции отрезка 0 < z < /, а
собственные значения
= Mnk "т
где xnk и ат — собственные значения кругового сектора и отрезка
соответственно .
§ 11. СОБСТВЕННЫЕ ФУНКЦИИ КРУГОВОГО
ТОРА ПРЯМОУГОЛЬНОГО СЕЧЕНИЯ
Пусть D — круговой тор прямоугольного сечения: а < г < 6,
О < (р < 2тг, 0 < z < /. Задача Штурма- Лиувилля имеет вид
' Аи + \и = 0 в
.г , ди л
k u(r, ^>, z) = ti(r, (p + 2тг, z) при любом (р.
Решая ее так же, как соответствующую задачу для цилиндра (см.
§ 10), получим, что собственная функция представима в виде
где vnk (г, (р) — собственные функции кругового кольца а < г < 6,
О < (р < 2тг, Zm(z) — собственные функции отрезка 0 < z < /, которые
построены в § 7 и 1, а собственные значения
~T
где xn/j и (Тт — собственные значения кругового кольца и отрезка
соответственно.

§ 12. СОБСТВЕННЫЕ ФУНКЦИИ СЕКТОРА
КРУГОВОГО ТОРА ПРЯМОУГОЛЬНОГО СЕЧЕНИЯ
Пусть D — сектор кругового тора прямоугольного сечения: а <
<6,0<^><a,0<z</. Рассмотрим задачу Штурма- Л иу вил ля
Ди + Au = 0 в Д
= 0, Ръ[и}= <*2~^ + /?2"
= 0,
г=Ь
= 0,
= 0,
z=0
= 0,
= о,
.,6.
Решая эту задачу аналогично тому, как это сделано для случая ци-
цилиндрического сектора (см. §11), получим, что собственные функции
представимы в виде
где vnk(r, (р) — собственные функции кольцевого сектора a < г < 6,
О < <р < а, построенные в § 8, Zm(z) — собственные функции отрезка
О < z < /, построенные в § 1, а собственные значения
А =
где xnk и (тт — собственные значения кольцевого сектора и отрезка
соответственно .
§ 13. СОБСТВЕННЫЕ ФУНКЦИИ ШАРА
Теперь построим собственные функции шара Ка. Введем сфери-
сферическую систему координат (г, 0, <р)у 0 < г < а, 0 < в < тг, 0 < <р < 2тг
с началом в центре шара. Оператор Лапласа в сферической системе
имеет вид
Дм =
где &вц>и — сферический оператор Лапласа, равный

Рассмотрим задачу Штурма-Лиувилля для шара:
Дм + Хи = О, М ? Ка,	A^-1)
dU . Я	П MQ9\
ая^ + ^ =°>	A3-2)
Г = <2
т^^О.
Решение строим методом разделения переменных, отделяя радиаль-
радиальную переменную г:
u = R(r)v(e,vJQ.	A3.3)
Подставляя A3.3) в уравнение A3.1), записанное в сферической си-
системе координат, и разделяя переменные, получим
A3.4)
l ^
Я(г)
Собственные функции должны быть ограничены в Ка и периодичны
по (р с периодом 2тг. Поэтому из A3.4) для функции v получаем
задачу Штурма-Лиувилля
+ At; = О, 0 < в < тг, 0 < у < 2тг,
собственными функциями которой являются сферические функции:
„ = Vnm (в, <р) = У„(т) (в, у) = Р^ (cos
sm my?,
а собственные значения равны
/i = /in = n(n+l),
n = 0, 1, . . .,00, m = 0, 1, . . .,n.
Для каждого р, = n(n -f 1) из A3.4) получаем уравнение для R(z):
решение которого должно удовлетворять согласно A3.2) граничному
условию при г = а:
=0

и естественному условию ограниченности при г = 0:
оо.
С помощью замены
R =
задача для R приводится к следующей задаче Штурма-Лиувилля:
г V + гу' + [Аг2 - п + 1 'ly = 0,	A3.6)
=0,	A3.7)
а
|у@)| < гс.	A3.8)
Общее решение уравнения A3.6) имеет вид
У =
Учитывая поведение функций Неймана в нуле и условие ограничен-
ограниченности A3.8), находим
С2 = 0.
Будем считать С\ = 1. Для определения А из A3.7) получаем диспе-
дисперсионное уравнение
= 0.
Пусть р, = ал/А. Тогда функцию R(r) можно записать в виде
71 = 0,1,..., fc=l,2,...,
где ц? — fc-й корень уравнения
= 0	A3.9)
при фиксированном п = 0, 1, . . .

Таким образом, собственная функция шара имеет вид
Unfcm (Г, !/,?) =	A3.10)
71 = 0,1,..., fc=l,2,...,
а собственные значения равны
где /4"	— корни уравнения A3.9).
Видно, что каждому собственному значению \nk соответствуют
2п+1 линейно независимых собственных функций (rangAn^ = 2n-f 1).
Найдем норму собственных функций:
Значение ||УП ||2 определяется формулой
где ет
=С:
Вычислим
A3.11)
(использована формула E.17)).
Рассмотрим, как и для круга, отдельно первую, вторую и третью
краевые задачи.
Для задачи Дирихле (а = О, 0=1) собственные значения опреде-
определяются уравнением

Поэтому
A3.12)
Для задачи Неймана (а = 1, C = 0) собственные значения опреде-
определяются уравнением
= 0.
Следовательно,
A3.13)
Для третьей краевой задачи (а = 1, /3 = Л) собственные значения Л
определяются уравнением
= 0, Л =
Выражение для квадрата нормы, так же как и для круга, для третьей
краевой задачи можно записать по-разному:
2
A3.14)
ИЛИ
•Лг+1/2
A3.15)
Формула A3.14) удобна при малых, а формула A3.15) — при больших
Л.
§ 14. СОБСТВЕННЫЕ ФУНКЦИИ ШАРОВОГО СЛОЯ
Рассмотрим задачу Штурма- Лиувилля для шарового слоя D
(а < г < 6):
Д« + Л« = 0 в D,
Л[«]=*1ТГГ-А« =0,
«(г,*,?)? о, Ы
= 0,
г=6
О, i=l,2.
A4.1)
A4.2)
A4.3)

Записывая решение в виде
подставляя в уравнение A4.1) и разделяя переменные, получим за-
задачу Штурма-Лиувилля для функции v@,(p) на сфере г = а:
+ xv = 0, 0<0<тг, 0<^><2тг,
0=0 < °°>
A4.4)
dR
lrfr
и задачу Штурма-Лиувилля для функции R(r) на отрезке а < г < 6:
Д=0,	A4.5)
- О,	A4.6)
= О,	A4.7)
г=Ь
Собственными функциями задачи A4.4) являются сферические
функции
а собственные значения равны
х = хп = п(п 4-1), п = О,1,..., m = 0,1,.. . ,п.
Общее решение уравнения A4.5) при х = п(п 4- 1) имеет вид
A4.8)
-ti/ — wi	у— г ^<г /—
Подставляя A4.8) в граничные условия A4.6), A4.7), получим
/
A4.9)

где
pi(A,a) =
gi(A,a) =
Приравнивая нулю определитель системы A4.9), получаем дисперси-
дисперсионное уравнение для определения А
Pi(A,a) _ gi (A, a)
й(А,6)
Из A4.9) имеем
r _
02 — —
тт —— г.
gi(A,a)
Полагая Ci = gi(A, a), собственную функцию запишем согласно A4.8)
в виде
Я=	A4.11)
или, учитывая A4.10), в виде
Д=	A4.12)
Таким образом, собственные функции шарового слоя можно записать
в виде
n = 0,l,..., m = 0,l,...,n, 4=1,2,...,
A4.13)
где А = Ад.п ' ' — fc-й корень уравнения A4.10) при каждом фикси-
фиксированном п.

Вычислим квадрат нормы собственной функции:
A4.14)
Квадрат нормы функции Rnk вычисляется так же, как в § 7. Окон-
Окончательная формула имеет вид
A4.15)
§ 15. ЗАДАЧИ НА СОБСТВЕННЫЕ ФУНКЦИИ
ДЛЯ УРАВНЕНИЯ ШРЕДИНГЕРА
Как уже ранее отмечалось, собственные функции с физической
точки зрения представляют собой те виды установившихся колеба-
колебаний, которые в данной области могут существовать без «подкачки»
энергии извне.
В квантовой механике задачи Штурма-Лиувилля возникают при
вычислении уровней энергии стационарных состояний частицы в не-
некотором силовом поле. Стационарное состояние частицы, находя-
находящейся в поле потенциальных сил, описывается стационарным урав-
уравнением Шредингера
= 0,	A5.1)
где h — постоянная Планка; ц — масса частицы, U(m) — ее по-
потенциальная энергия в силовом поле, ф — волновая функция. В
этом уравнении Е — полная энергия частицы — играет роль соб-
собственного значения, подлежащего определению. Непосредственный

физический смысл имеет не сама волновая функция *ф, а величина
!, которая истолковывается в статистическом духе: выражение
представляет собой вероятность пребывания частицы в
элементарном объеме dxdydz в точке (x,t/, z) пространства. В со-
соответствии с этим нормировка собственных функций к единице, ко-
которая неоднократно использовалась ранее в целях математической
простоты, теперь приобретает иной смысл и имеет фундаментальное
значение.
Условие нормировки
00
^dxdydz = 1	A5.2)
означает, что частица находится в какой-либо точке пространства и
вероятность найти частицу где-нибудь в пространстве равна единице
(достоверное событие). Условие нормировки A5.2) налагает также
определенные условия на убывание волновой функции на бесконеч-
бесконечности.
Таким образом, задача состоит в определении тех значений па-
параметра Е (уровней энергии), при которых уравнение A5.1) имеет
неправильное решение, удовлетворяющее условию A5.2).
Рассмотрим несколько простейших задач.
1. Гармонический осциллятор.
Уравнение Шредингера для линейного гармонического осциллято-
осциллятора имеет вид
где ш — собственная частота (циклическая) осциллятора. Условие
нормировки имеет вид
00
: 1.	A5.4)
Итак, задача состоит в определении собственных значений Е и соб-
собственных функций ф уравнения A5.3), удовлетворяющих условию
A5.4). Введя безразмерные переменные
f=— х /А Л= —
XQ '	У ЦШ ' fa '
?
перепишем уравнение A5.3) в виде
^ + (А-^ = 0.	A5.5)

Условие нормировки принимает вид
00
/
-.
XQ
Уравнение A5.5) есть уравнение для функции Эрмита*) (см. также
приложение § 5), которое имеет ненулевое решение, интегрируемое с
квадратом на всей оси х, лишь при
и это решение имеет вид
где Нп(х) — многочлен Эрмита, ||ЯП|| — его норма, причем
ЦЯ„||2 =
Используя условие нормировки, находим С:
С =
Возвращаясь к старым переменным, получаем следующие собствен-
собственные функции и собственные значения:
Еп=	п = 0,1,2,...
Число п, определяющее номер уровня энергии, называется главным
квантовым числом. В низшем квантовом состоянии при п = 0 энергия
осциллятора отлична от нуля и равна
Е0 =
*' См. Никифоров А.Ф., Уваров В.Б. Специальные функции математической
физики. М.: Наука, 1984.

2. Вычисление уровней энергии ротатора со свободной
осью.
Ротатором называется частица, вращающаяся на одном и том же
расстоянии вокруг неподвижного центра в пространстве.
Поскольку потенциальная энергия U ротатора сохраняет одно и
тоже значение при всех положениях вращающейся частицы, то можно
считать U = 0. Поэтому уравнение Шредингера для ротатора имеет
вид
= 0.	A5.6)
Введя сферическую систему (г, 0, р) с началом координат в неподвиж-
неподвижном центре и учитывая, что для ротатора
= 0,
из A5.6) получаем уравнение
AV> = 0,	A5.7)
где Л = 2/Е"/Й2, / = /ir2 — момент инерции.
Таким образом, приходим к задаче на собственные значения для
уравнения A5.7) с естественным условием ограниченности и услови-
условием нормировки:
= 1.
Собственные значения сферического оператора Лапласа являются
(см. § 13)
Ап = п(п+ 1), п = О, 1,...,
а нормированные собственные функции имеют вид
1 Q' n = 0,1,2,..., го = 0,1,2,....п, РГ\х}-
присоединенные функции Лежандра. Отсюда получаем формулу для
квантованных значений энергии ротатора:
Заметим, что каждый уровень имеет Bп+1)-кратное вырождение, т.е.
ему соответствует 2п +1 линейно независимая собственная функция.

3. Математическая модель водородоподобного атома —
движение электрона в кулоновском поле ядра.
В атоме водорода электрон находится в электростатическом поле
ядра (протона), так что потенциал U имеет вид
где г — расстояние электрона от ядра, —е — заряд электрона, е —
заряд ядра.
Уравнение Шредингера имеет вид
A5.8)
Будем искать отрицательные значения Е (уровни энергии), при ко-
которых существует непрерывное во всем пространстве решение напи-
написанного уравнения, удовлетворяющее условию нормировки:
A5.9)
Введем сферическую систему координат (г, 0, <р) с началом в ядре
и будем искать решение уравнения A5.8) в виде
tf(r,ff,p) = fl(r)v(ff,p).	A5.10)
Подставляя A5.10) в A5.8) и разделяя переменные, получим уравне-
уравнения для R и v:
,15.,!)
г dr	2 2 v '
г; + xt; = О,	A5.12)
где ж — параметр разделения.
Уравнение A5.12) вместе с условием ограниченности при в = 0 и
в = тг и периодичности по ф с периодом 2тг дают задачу Штурма-
Лиувилля для сферического оператора Лапласа, собственными зна-
значениями которой являются
х=х,=/(/+1), / = 0,1,2,...,

а собственными функциями будут сферические функции
/ = 0,1,2,..., m = 0,l, ...,/.
Рассмотрим теперь уравнение A5.11) для Л (г). Перейдем к без-
безразмерным переменным: р = ?, е = Jj^, где а = -^7, ?"о = ^рг = V*
при этом будем помнить, что определяются отрицательные уровни
энергии, т.е. е < 0. Уравнение A5.11) принимает вид
Л = 0.
Введя новую неизвестную функцию у соотношением
R =
получим уравнение
= 0,	A5.13)
где а = 2/ + 1 .
Сделав замену переменной х = р\/—%е (е < 0), приведем уравне-
уравнение A5.13) к стандартному виду:
= 0,	A5.14)
где А =
Уравнение A5.14) есть уравнение обобщенных функций Лагерра*).
Оно имеет интегрируемое с квадратом на [0, оо) решение при
А = АПг = пг +	, пг = 0,1,2 ...,
и это решение имеет вид
y(«) = «?e-f4ep)(«),	A5.15)
*' См. Никифоров А.Ф., Уваров В.Б. Специальные функции математической
физики. М.: Наука, 1984.

где Lnr (я) — обобщенный полином Лаггера.
Поскольку а = 21 + 1 (I = О, 1, . . . ),
а + 1
АПг = пг + — — = пг + / + 1 = п, п = 1, 2, . . .
Целое число п называется главным квантовым числом. пг — ради-
радиальным квантовым числом, / — азимутальным квантовым числом.
Уровни энергии (отрицательные) определяются из соотношения
А = АПг = ,——- - п, п = 1, 2, . . . ,
V — 2е
откуда
Они зависят только от главного квантового числа п.
Возвращаясь к старым переменным, собственные функции запи-
запишем в виде
Фп1т =
A5.16)
где коэффициент С определяется из условия нормировки A5.9). Под-
Подставляя A5.16) в A5.9), найдем С:
С =
где со = 2 и ст = 1, m ^ 0. Число m (т = 0, 1, 2, ...,/) называется
магнитным квантовым числом.
Так как пг всегда неотрицательно (пг = О, 1, 2, . . . ), при фиксиро-
фиксированном п в силу соотношения
п = пг + / + 1
квантовое число / не может быть больше п— 1 (/ = 0,1,2,...,п— 1).
Поэтому при определенном значении главного квантового числа п
число / может принимать п значений (/ = 0, 1, . . . , п — 1), а каждому
значению / соответствует 2/ + 1 значений т. Отсюда следует, что
заданному энергетическому уровню ?"п, т.е. заданному значению п,
соответствует
п-1
+ 1) = 1 + 3 + 5 + - - - + Bп - 1) = п
2
/=о

различных собственных функций. Таким образом, каждый энергети-
энергетический уровень имеет вырождение кратности п2.
Итак, нами найдены отрицательные уровни энергии. Особенно-
Особенностью уравнения A5.8) является то, что всякое положительное чи-
число Е является собственным значением уравнения A5.8), т.е. это
уравнение имеет непрерывный спектр положительных собственных
значений. Исследование этого случая выходит за рамки настоящего
пособия, и его можно найти в специальной литературе.
§ 16. ЗАДАЧИ ДЛЯ
САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Найти собственные значения и собственные функции отрезка
—/ < х < I при граничных условиях:
а) «(-/) = «(/) = 0;
6) ?<-!) = ?A)=0;
в) «(-О = ?@ = 0;
г) ?(-0=«@ = 0.
2. Решить задачу Штурма-Лиувилля для прямоугольника 0 <
<х<а,0<у<6с граничными условиями:
__	__ л l/U. | __ t/Ц
*=0 ~ Wl*=a ~ ' 9y ly=0 ~ "^
у=ь
= 0;
— П
~
= — I —О —\ —
o ~ дх 1*=в "" ' ду ly=o ~ Н
г) по переменной х — периодические граничные условия с пери-
периодом а
д) периодические граничные условия по обеим переменным: по
х — с периодом а, по у — с периодом 6.
3. Решить задачу Штурма-Лиувилля для кругового сектора 0 <
<г<а,0<<р<ас граничными условиями:
ч I	* ди _ ди
ди\
= и
ди

f\
4. Решить задачу Штурма-Лиувилля для кругового кольца а <
<г<6, 0 < <р < 2тг с граничными условиями:
б) i| =tl|	о;
' 9г1г=а	1г=Ь
в) т~ + /ш|г=а = 0, и|г=ь = 0, Л = const.
5. Решить задачу Штурма- Л иувилля для кольцевого сектора а <
< г < 6, 0 < <р < а с граничными условиями:
\ I	I л ди I 9u I л
а) Ulr=« = «1г=6 = °' 0^=0 = ^L=a = °;
е\ ди |	9l? | л I I л
б) ^Г1г=а = fr\r=b = °- «1^=0 = «U« = О?
л
В) Wlr=a = 1г=Ь = °' WUo = ^1^=а = °^
6. Решить задачу Штурма-Лиувилля для прямоугольного парал-
параллелепипеда 0<?<a,0<y<6,0<z<cc граничными условиями:
а) и г=0 = «L=o = 0, -?
1у=Ь
ди
z=o
ди
y=0,y=fe
= 0;
z=0,z=c
= 0;
в) — 15 = О, S — полная поверхность параллелепипеда;
_ ди\	_ n I _ п
0,х=а - дп 1у=0,у=Ь ~ U> Ul*=0,*=c ~ Uj
д) -^ -|- AtiL = 0, 5 — поверхность параллелепипеда, п — внеш-
дп |<ь
няя нормаль, h = const.
7. Решить задачу Штурма-Лиувилля для прямого кругового ци-
цилиндра 0<r<a, 0<^<2тг,0<г</с граничными условиями:
ди	ди
f\ ди | п -^
б) — 15 = 0, 5 — полная поверхность цилиндра;
ч l?|
г) :

8. Решить задачу Штурма-Лиувилля для сектора прямого кру-
кругового цилиндра: 0<r<a,0<<p<a,0<z</c граничными
условиями:
а) u\s = О, 5 — полная поверхность;
6) — = О, S — полная поверхность;
с/ /i «ь
-)<«, = о, «u,=. = °. lu=i=°;
Г) Ulr=a = °. fljf Uo,*,=a = °' Ulz=0,2=l = °'
л
Д)	=°' Uo,=a = 0> UL=02=<=°:
9. Решить задачу Штурма- Л иувилля для прямого кругового то-
тора прямоугольного сечения: a<r<6, 0<<р< 2тг, 0 < z < I с
граничными условиями:
а) условия Дирихле;
б) условия Неймана;
Ur=a
10. Решить задачу Штурма-Лиувилля для шаровой оболочки a <
< г < 6 с граничными условиями:
а) и\ = и\ , = 0;
' lr=a	1г=Ь '
| - | - п-
дг 1г=а ~ 9г 1г=Ь "" '
= « .=о.
r=a	lr=fr
Ответы.
б)	cos^(*
в)	sin [§(n
г)	со8[§(п+1/2)(* + /)], А„ = [§(п+1/2)]2, « = 0,1,2,.

2. a) sin *px cos spy, \nm = (^J + (*f J ;
6) sin |(n + 1/2)* sin f (m +l/2)y,
в) cos^xcos?(m+l/2)y, Anm = (^J + [f (m+ 1/2)]2;
r) sin *px sin 2f y, cos ^x sin 2f y, Anm = (^J + (*f f ;
д) sin 22-x sin ^t/, sin ^xcos ^jp-y, cos ^x sin ™y,
3. а) «/.^(л/А^У) cos ~L^>, A^ — корень уравнения J*ji(\f\a) = 0;
6) Jia (>/A^r) sin ~L^, Afc — корень уравнения \/AJ5rn (\/Aa) = 0;
B) Ji(n + l/2)(>AfeO sin J(n + V2)^
Ajt — корень уравнения «7л.(п+1/2)(>/Аа) = 0;
г) Ji(n+i/2)(\/A/>)cos J(n + l/2)^,
A^ — корень уравнения «/i(n-i-i/2)(v/Aa) = 0;
д) J^(v^r)sin^,
\k — корень уравнения л/AJ^n (\/Aa) -f /iJ^a(\/Aa) = 0.
4. a) [jn(
A^ — корень уравнения
V\{j^b)Nn(V\a) - Jn(x/Aa)^(x/A6)} = 0;
6) [jn(\/ArOVn(x/A6) - Jn(x/A6OVn(v/Ar)l ( С°8П^' А - корень
L	J t sm n^>,
уравнения A j^
А — корень уравнения
5. a) j^(
A — корень уравнения
= 0;
6)
A — корень уравнения
= 0;

в)
A — корень уравнения
г)
корень уравнения
д)
х Arj(
А — корень уравнения
= 0;
= 0;
= 0.
6. а) sin *p*sin *f ycos f z, A = (^
6) sin ^x cos 2-2/ sin fz, A=(^J+BfJ+(fJ;
в) cos ^x cos 2ft/ cos fz, A=(^J+(^fJ+(fJ;
r) cos^xcos^ysinfz, A=(^J + BfJ + (^J;
д) sin(>/ATa; + <$i) s'm(^/\^y + (J2) sin(v/A~3Z + J3), A = AI + A2 + A3,
А„ (v = 1, 2, 3) — корень уравнения tg \Д]Х = /fffi., /i = a,
__ V A|/-f-/l
/2 = 6, /3 = С, С08*„ =	L, Sinrf, = --, t,= 1,2,3.
7. a) Jm(\/^r) cos ^г<	' A = i/ 4- (^r) , i' — корень урав-
L s
нения
6)
= 0;
' A = i/+ f2^-) , i/ — корень урав-
v l
нения
в)
) — 0;
'
2 , i/ — корень уравне-
*
ния
r)
корень уравнения
Д) ^т(л/^г) cos
sm тп<р
корень уравнения Jm(<^va) = 0.
A = i/+ (f(*
— 0;
' A = i/ + [f (t

8. a)
6)
в)
г)
д)
e)
9. a)
sin ^-z sin ^<p, Л = i/ + (^) , i/ — корень уравне-
уравнения J«jL(y/va) = 0;
J.ZL2: (\/^) cos ^z cos ?2-^>, Л = i/ 4- (^y1) , i' — корень уравне-
уравнения ^3'™(^/па) = 0;
Ot
«/-^(-y/i/r) cos ^?z sin ^r-<?>, A = i/ + (:5p) , v — корень уравне-
уравнения Jiu(x/i7a) = 0;
J*j!L(y/vr} sin zjs-z cos ^<р, A = i/ 4- (^y1) , ^ — корень уравне-
уравнения Jin(x/J7a) = 0;
J*jL(y/vr) sin ^zsin •Z^L^), A = i/ H- (^r) , i/ — корень уравне-
уравнения ^J'™(^fva) = 0;
корень уравнения Js.(n+\ii)(\/va) = 0.
, A = v + (^), v
A = i/ + (^) ,j/ — корень уравнения
= 0;
6)
cosn^'
— корень уравнения
в)
COS П<?>,
sin n<?>,
A = i/ + (^) ,J/ — корень уравнения
г) [Jn
smi(k + 1/2)
A = j/ + (j(k + 1/2)) , j/ — корень уравнения
Nn(Vtb) = 0;
srnny»,
д) [Jn
cos n<?>,
sin n<?>,
-j^ ,^ — корень уравнения

Г cos n^>,
e) [Jn(yvr)Nn(yva) — Jn(v^a)^n(v^r)]cos т(^Н" l/tyz{
{ siring,
A = i/ + [ j(k 4- 1/2)] , i' — корень уравнения
= 0.
)• aj s ——~7"———"^ *>"—— — —' */"———* r~—— r x
(т\ /	ч Г COS m^)
x PAm) (cos (9) j
A — корень уравнения
-Jn+i/2(V\a)Nn+l/2(VXb) = Q-
fl _ d •y«+i/a(/Ag) J
da	ya
A — корень уравнения
d Л+1/2(у/АЬ) d Nn+l/2(V\a) d </n+i/2(VAa) d Nn+l/2(V\b) = Q
db ^/b da	^/a da ^a db ^b
Г ^+i/a(>/Ar) ^n4.1/3(%Aa) Jn+i/3(>/Aa) ^4.j/a(>/Ar) 1
\	77 ^T >A ^ J
A — корень уравнения
d Л
л/а
~
COS m^>,
sm m^>,
A — корень уравнения
= o.

Глава 3
КРАЕВЫЕ ЗАДАЧИ
ДЛЯ УРАВНЕНИЯ ЛАПЛАСА
Уравнение Лапласа является простейшим уравнением эллиптиче-
эллиптического типа. При изучении краевых задач для уравнения Лапласа
следует различать внутренние и внешние краевые задачи. Гранич-
Граничные условия вытекают из существа той физической задачи, матема-
математической моделью которой является краевая задача для уравнения
Лапласа. Наиболее часто встречаются граничные условия первого
(задача Дирихле), второго (задача Неймана) или третьего рода.
Пусть D — конечная область, ограниченная замкнутой поверхно-
поверхностью (на плоскости — кривой) Ляпунова 5.
Классическим решением внутренней задачи Дирихле будем назы-
называть функцию г/(М), непрерывную в замкнутой области 5, удовле-
удовлетворяющую в открытой области D уравнению Лапласа и принима-
принимающую на поверхности S заданные значения: г/|5 = f(P)\s. Клас-
Классическим решением внутренней второй или третьей краевой задачи
будем называть функцию г/(М), непрерывную вместе с первыми про-
производными в замкнутой области 5, удовлетворяющую в открытой
области D уравнению Лапласа и удовлетворяющую на поверхности
S заданным граничным условиям второго или третьего рода.
Классическое решение внутренней задачи Дирихле
и внутренней третьей краевой задачи
ди
fa
Ди = 0в?>, ^ + /ш = f(P)\s,
где п — внешняя по отношению к области D нормаль к поверхно-
поверхности 5, h(P) > О, Л(Р)^0, единственно. Решение внутренней задачи
Неймана
Ли=0вД Д=
существует лишь при условии
f(P)dS = О

(это условие необходимое и достаточное) и определено с точностью
до произвольного постоянного слагаемого.
Для выделения единственного решения внешней краевой задачи
следует поставить дополнительное условие, описывающее поведение
искомой функции на бесконечности. Для уравнения Лапласа таким
условием является требование, чтобы решение было регулярно на
бесконечности. При этом понятие функции, регулярной на бесконеч-
бесконечности, в двумерном (плоском) и трехмерном случаях формулируется
по-разному. В трехмерном случае функция и называется регулярной
на бесконечности, если существует такая постоянная А > О, что вне
некоторой сферы 5Го (г > TQ) имеют место неравенства
А
г '
На плоскости функция и называется регулярной на бесконечности,
если она на бесконечности имеет конечный предел.
В трехмерном случае для гармонической функции требование
и i4 0 при г —>• оо
эквивалентно требованию регулярности на бесконечности.
В трехмерном случае решения первой, второй и третьей краевых
задач, регулярные на бесконечности, единственны (для третьей кра-
краевой задачи
^. + hus = f(P)\s
при h(P) > О, если п — внешняя по отношению к области De нормаль
к поверхности 5).
На плоскости опять выделяется внешняя задача Неймана, реше-
решение которой существует не всегда, а если существует — то не един-
единственно и определяется с точностью до произвольного постоянного
слагаемого.
Для решения краевых задач для уравнения Лапласа используют-
используются различные методы (метод разделения переменных, метод функ-
функции Грина, метод интегральных уравнений, вариационные методы,
численные методы и др.). В настоящем пособии рассматриваются
метод разделения переменных и метод функции Грина.
Рассмотрим метод разделения переменных решения краевых задач
для уравнения Лапласа. Этот метод применим в том случае, когда
граница области совпадает с координатной поверхностью (или состо-
состоит из частей координатных поверхностей) криволинейной системы
координат, которая допускает разделение переменных в уравнении
Лапласа.

В настоящей главе будут рассмотрены краевые задачи для урав-
уравнения Лапласа в круге и вне круга, в круговом кольце, в круговом
и кольцевом секторах, в прямоугольнике, прямоугольном паралле-
параллелепипеде и прямом круговом цилиндре, в цилиндрическом секторе,
в круговом торе прямоугольного сечения и его секторе, в шаре, вне
шара и в шаровом слое.
§ 1. ЧАСТНЫЕ РЕШЕНИЯ УРАВНЕНИЯ
ЛАПЛАСА В ПОЛЯРНОЙ СИСТЕМЕ КООРДИНАТ
Введем полярную систему координат (г, (р) и построим частные
решения уравнения Лапласа
1 д ( ди\ 1 д2и А
At/ = -д- I Г-^- + ~2^-2 =0,
г дг \ дг) г2 д<р2
представимые в виде
ti(r, <р) = Д
Для этого искомый вид решения подставляем в уравнение Лапласа
и разделяем переменные:
Л(г) -
Отсюда получаем отдельно уравнения для R(r) и Ф (<?>). Рассмотрим
сначала уравнение для Ф (<?>):
ф" + АФ = 0.
Будем считать, что переменная (р изменяется от 0 до 2тг (случай, ко-
когда переменная (р изменяется в меньшей области: 0 < (р < а < 2тг,
соответствует решению уравнения Лапласа в секторе и будет рас-
рассмотрен в § 5). Если 0 < (р < 2тг, то решение (в силу непрерывности)
должно быть периодично по (р с периодом 2 тт. Следовательно, для
определения функции Ф(<?>) получаем одномерную задачу Штурма-
Лиувилля с условиями периодичности
ф" -|- АФ = 0, 0 < v? < 2тг,
+ 2тг) = Ф(<р) при любом <р,
Эта задача имеет решение (см. гл. II, § 2)
А = А„=п2, п = 0,1,...,оо.
sm

Из A.1) с учетом найденных значений Лп получаем уравнение для
Я(г):
г2Я" + гЯ'-п2Я = 0.
Это уравнение Эйлера*', и общее решение его может быть записано
в виде
Я = Я„ (г) = drn + С2г-" , п ? О,
Следовательно, построены следующие серии частных решений урав-
уравнения Лапласа:
Эти решения ограничены при г — » 0 и неограничены на бесконечно-
бесконечности. Общее решение уравнения Лапласа в круге 0 < г < а записыва-
записывается в виде разложения по этим решениям:
А
A.3)
Эти решения ограничены на бесконечности и неограничены при г —>• 0.
Они используются при решении уравнения Лапласа вне круга. Об-
Общее решение уравнения Лапласа вне круга (г > а), ограниченное на
бесконечности, может быть записано в виде
A.5)
n=l
в) Третья серия решений

неограничена как при г — » 0 , так и при г — >• оо . Она используется
при решении уравнения Лапласа в круговом кольце а < г < Ь.
§ 2. КРАЕВЫЕ ЗАДАЧИ ДЛЯ
УРАВНЕНИЯ ЛАПЛАСА ВНУТРИ КРУГА
Рассмотрим краевую задачу для уравнения Лапласа внутри круга
0<г <а:
Дг/ = 0 вкругеО<г<а,	B.1)
РМ = *^ + /Н-=« = /(*>), Н+|/?|^0. B.2)
Решение этой краевой задачи можно записать в виде разложения
A.3), коэффициенты которого определяются из граничного условия
B.2). Но вычисления оказываются проще, если решение задачи B.1),
B.2) записать в виде
гп
T —— {Ап cos П(Р + Вп si
). Подставляя B.3) в граничное условие B.2), получаем
А	°°
,п cos пр + Вп si
п = 1
Следовательно, Ап и Вп есть коэффициенты Фурье функции
по системе тригонометрических функций {cosn<?>, sinn^>}, которые
вычисляются по формулам
2тг	2тг
An = $ f f(<f>) cos npdp,	Bn = I / f((p) sin nipdip,
о	о
n = 0,	1, 2,...
Выпишем отдельно решения первой, второй и третьей краевых за-
задач для уравнения Лапласа в круге.
1. Задача Дирихле: и\г-а —
i / ^ \ i |.* ——— --т " —™—** '"rjm	V "/
n = l
2. Задача Неймана: |^|г=в = /(<?>),
ln cos n^> + Bn sin n^>) -h C,	B.6)

где С — произвольная постоянная. Напомним, что решение внутрен-
внутренней задачи Неймана существует только при условии
27Г
//(*>)<*?> =
О
(это условие необходимое и достаточное) и определяется с точностью
до произвольной постоянной.
3. Третья краевая задача: — + hu
= f(v), Л = const,
дг
B.7)
Коэффициенты в разложениях B.5)-B.7) определяются по форму-
формулам B.4).
Остановимся кратко на вопросе о сходимости рядов B.5)-B.7).
Если граничная функция f((f>] абсолютно интегрируема, то ее ко-
коэффициенты Фурье, по крайней мере, ограничены, и, как видно из
структуры указанных рядов, эти ряды будут в любой внутренней
точке круга (г < а) сходиться не хуже, чем геометрическая прогрес-
прогрессия со знаменателем q = г/а. При увеличении гладкости функции
/(<р) сходимость указанных рядов улучшается. На получении стро-
строгих оценок скорости сходимости мы здесь не останавливаемся.
§ 3. КРАЕВЫЕ ЗАДАЧИ ДЛЯ
УРАВНЕНИЯ ЛАПЛАСА ВНЕ КРУГА
Рассмотрим теперь внешнюю краевую задачу
Дг/ = 0 вне круга (г > а),
Р[и] = а-тг~ — /Зи = /(<?>),
ОГ	г=а
г/ регулярна на бесконечности.
Напомним, что в двумерном случае регулярность на бесконечности
означает, что функция г/ имеет конечный предел при г —>> оо.
Решение этой задачи можно записать в виде разложения A.5). Но,
как и для внутренней задачи, решение удобнее представить в виде
г/(г, <р) =
C.1)

(при /3^0). Коэффициенты Ап и Вп определяются из граничного
условия и вычисляются по формулам
п = 0, 1, 2,...	C.2)
Вп =
Отдельно выпишем решения первой, второй и третьей краевых задач
вне круга.
1. Задача Дирихле: «I = f(<p) (а = О, /3 = — 1),
и =	C.3)
2. Задача Неймана: -z-
(а = 1, /? = <)),
дг
C.4)
где С — произвольная постоянная. Опять напомним, что на плоско-
плоскости внешняя задача Неймана разрешима лишь при условии
2тг
Са	О
и ее решение определяется с точностью до постоянного слагаемого.
3. Третья краевая задача: тт- — hu
or
и =	C.5)
Коэффициенты Ап и Вп в разложениях C.3)-C.5) являются коэф-
коэффициентами Фурье функции /(<р) и вычисляются по формулам C.2).
§ 4. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ
ЛАПЛАСА В КРУГОВОМ КОЛЬЦЕ
Разберем теперь решение краевой задачи для уравнения Лапласа
внутри кругового кольца.

Рассмотрим сначала задачу Дирихле
Дг/ = 0 в кольце а < г < 6,	D.1)
D.2)
Решение этой задачи можно записать в виде разложения по частным
решениям A.6). Но вычисления значительно упрощаются, если при
каждом п построить систему фундаментальных решений {Д}» (г),
•Rn (Г)} уравнения
г2Д" + гД'-п2Д = 0,	D.3)
удовлетворяющих граничным условиям
Поскольку общее решение уравнения D.3) имеет вид
R = С\ + Съ In г	при п = О,
R = Cirn + C2r~n при п ф О,
мы, подбирая коэффициенты С\ и Съ, легко построим нужные реше-
решения. Они определяются с точностью до числового множителя, и их
можно взять, например, в виде
п	2n
Построив функции Д^а и Дп , получаем систему частных решений
уравнения Лапласа:
«S'>(r,y) = hij, 4*'('.»>) = bj,	D.4)
ограниченных внутри кольца и удовлетворяющих граничным усло-
условиям
п(па)\г=а = 0, г4ь)|г=ь = 0.	D.5)
Заметим, что

Теперь решение краевой задачи D.1), D.2) можно записать в виде
разложения по этим частным решениям:
D.6)
Подставляя D.6) в граничное условие при г = а и учитывая D.5),
получаем
Отсюда находим С„ и ?>„ :
С„ =
D.7)
А,=
Аналогичным образом, подставляя D.6) в граничное условие при
г = 6, находим коэффициенты ^4П и Вп:
D.8)
Таким образом, построив предварительно радиальные функции
Rn (r) и Rn '(r), удовлетворяющие нужным однородным граничным
условиям при г = а и г = 6, нам удалось «развязать» граничные
условия, заданные при г = а и при г = 6.
Аналогичным образом можно поступать и при решении других
краевых задач для уравнения Лапласа внутри кольца.
При построении радиальных функций Rn (r) для граничных усло-
условий второго рода следует иметь в виду, что при п = 0 не существует
двух линейно независимых решений уравнения D.3), одно из кото-
которых удовлетворяет условию
?(«)
IP
dr
dR},
dr

Обоим этим условиям удовлетворяет одно и то же решение Ro(r) — 1.
При п ф О нужную пару фундаментальных решений образуют функ-
функции
2п
,2n.
•• x '	*»71 '• л ' *»П
Поэтому решение задачи Неймана внутри кольца а < г < Ь:
Дг/ =
Or
удобно записывать в виде ряда
г/(г, v?) =
в кольце,
г=Ь
D.9)
коэффициенты которого определяются из граничных условий по
формулам D.7), D.8) при п -ф. О, коэффициент Со равен
С0 =
D.10)
a const — произвольная постоянная. Равенство D.10) противоречия
при произвольных функциях f\((p) и /2(<?>) не содержит, поскольку
оно соответствует условию разрешимости задачи Неймана
= 0.
Рассмотрим вопрос о сходимости полученных рядов. Рассмотрим,
для примера, ряд D.6). Поскольку при а < г < 6

ряды в D.6) сходятся внутри кольца а < г < Ь не хуже, чем геометри-
геометрические прогрессии. При увеличении гладкости граничных функций
f\((p) и fi((p) скорость сходимости увеличивается.
Рассмотрим примеры решения задач.
1. Внутри круга решить краевую задачу
Дг/ = 0, 0<г<а, 0 < <р < 2тт,
,	тг-р
и|„. = -J--
Решение. Общее решение задачи Дирихле внутри круга можно за-
записать в виде
и =
Коэффициенты ряда определяются из граничного условия по фор-
формулам
Вп =
Следовательно,
г/(г,<р) =
2. Внутри кольца а < г < Ь решить краевую задачу
Or
= sin 2<p, u\r=b = 1 + cos (p.
r—a
Решение. Радиальные решения, удовлетворяющие однородному
граничному условию при г = а, имеют вид

а удовлетворяющие однородному граничному условию при г = Ь —
Поэтому решение поставленной задачи можно записать в виде
Подставляя в граничное условие при г = а, получим
= sin 2<p.
Отсюда находим
Сп = О, п = О, 1,..., D2 = 1, Dn = О, п ф 2.
Подставляя общий вид решения в граничное условие при г = 6, по-
получим
= 14- cos (p.
Отсюда
АО = 2, AI = 1, Лг = 0, п ± О, 1, Вп = 0, п = 1, 2,...
Следовательно,
г/(г, v?) =
3. Для задачи Дирихле внутри круга:
Аг/ = 0 в круге 0 < г < а,
г/г=а =

вывести формулу Пуассона
J_ J (a2-r2)f(a)da
2тг J а2 + г2 — 2ar cos(<p — а)
о
Решение. Решение задачи Дирихле в круге может быть записано в
виде ряда
и=	D.11)
коэффициенты которого определяются формулами
Ап =
Вп =
Подставляя значения Ап и Вп в D.11) и меняя порядок суммирования
и интегрирования, получим
Поскольку (см. приложение, § 3) при - < 1
можем записать
При непрерывной функции /(<?>) формула Пуассона дает классиче-
классическое решение задачи Дирихле в круге.
4. Построить интегральную формулу, аналогичную формуле Пу-
Пуассона, для решения внутренней задачи Неймана для круга.

Решение. Рассмотрим внутреннюю задачу Неймана для круга:
Аг/ = 0 в круге 0 < г < а,
ди
Считаем, что задача разрешима, т.е.
= 0.
Решение поставленной задачи можно записать в виде ряда
и =
коэффициенты которого определяются формулами
Подставим значения Лп и Вп в ряд и поменяем порядок интегриро-
интегрирования и суммирования:
г/(г, v?) =
Поскольку при \t\ < 1 (см. приложение, § 3)
можем записать
г/(г, (р] =	-h const.

Эта формула дает решение внутренней задачи Неймана для круга
(она аналогична формуле Пуассона для задачи Дирихле внутри кру-
га).
§ 5. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ
ЛАПЛАСА В КРУГОВОМ СЕКТОРЕ
Аналогичным образом можно решать краевые задачи внутри кру-
кругового сектора @<г<а,0<<?><с*)и кольцевого сектора (а < г < 6,
О < (р < а) при условии, что граничные условия на лучах (р = О и
(р = а однородные.
Действительно, рассмотрим краевую задачу внутри кругового сек-
сектора:
Дг/ = 0, 0<г<а, 0 < <р < а,	E.1)
E.2)
= 0,	E.3)
Рз[и] = а3—- - /?3г/
г> г т	ди
Р4[и] = C*4^-
= 0,	E.4)
M+IA-I^O, i = 3,4.
Сначала найдем частные решения вида
E.5)
Подставляя E.5) в уравнение Лапласа и разделяя переменные, по-
получаем для определения Ф(<р) задачу Штурма- Л иувилля на отрезке
Ф" + АФ = 0, 0 < v? < «,
о = 0,	E.6)
и задачу для определения R(r):
г2 Я" + г R' - XR = 0, 0 < г < а, |Л@)| < оо .	E.7)
Задача E.6) решена в гл. II, § 1. Ограниченное при г = 0 решение
уравнения E.7) имеет вид
Д(г) = CV^, С = const .

Таким образом, построено семейство частных решений уравнения Ла-
Лапласа, ограниченное при г = 0:
ЧП(Г,Р)=	11 = 1,2,..., E.8)
где Фп(^) и Ап > О — собственные функции и собственные значе-
значения задачи E.6) для отрезка 0 < (р < а. Поэтому общее решение
уравнения Лапласа внутри кругового сектора можно записать в виде
г/(г, v?) =
а коэффициенты Сп определяются из граничного условия E.2):
= /и,
E.9)
С„ =
E.10)
Если граничное условие при г = а есть условие третьего рода
то общее решение уравнения Лапласа удобно записать в виде
ti(r,p) =	E.11)
Тогда коэффициенты Сп будут также определяться формулой E.10).
При этом нужно проявлять осмотрительность при решении второй
краевой задачи (задачи Неймана), поскольку она имеет решение не
всегда и ее решение, если оно существует, не единственно.
§ 6. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ
ЛАПЛАСА В КОЛЬЦЕВОМ СЕКТОРЕ
Рассмотрим теперь краевую задачу для уравнения Лапласа вну-
внутри кольцевого сектора (а < г < 6, 0 < (р < а) с однородными гра-
граничными условиями на лучах <р = О и <р = а:
Аг/ = 0, а < г < 6, 0 < (р < а,	F.1)
F.2)
_
, 1 = 1,2,3,4.
F.3)

Семейство частных решений уравнения Лапласа, аналогичное D.4),
удобное для решения поставленной задачи, можно записать в виде
п=1, 2,...,оо,
F.4)
/ \	/I \
где Rn (r) и Rn (r) — решения уравнения
г2Л" + rR' - АД = О,
удовлетворяющие граничным условиям
Pi(R(na)] =
dr
Р2[д(ь>]=а2^_ + /?2Д<Ь)
F.5)
= 0,
г=а
= о,
г=Ь
F.6)
F.7)
d
а Фп (<?>) и Лп — собственные функции и собственные значения задачи
E.6). Общее решение уравнения F.5) имеет вид
R = Cir + С2
R= Ci -hC2lnr
при Л ф О,
приА-0.
Построение решений RJ? и Rn , удовлетворяющих условиям F.6)
и F.7) соответственно, труда не составляет. Например, для задачи
Дирихле (а\ = &ъ = О, /?i = — 1, /?2 = 1) эти решения можно записать
в виде
при Ап ф О,
при АО = 0.
Таким образом, общее решение уравнения Лапласа внутри кольце-
кольцевого сектора можно записать в виде
F.8)

при этом если все Л„ ^ 0, то АО = Во = 0. Коэффициенты А„ и В„
определяются из граничных условий F.2):
Вп =
В том случае, когда граничные условия на лучах (р = О и (р = а не-
неоднородные, для решения соответствующей задачи можно либо сде-
сделать замену неизвестной функции, либо записать решение, используя
функцию Грина.
§ 7. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ
ЛАПЛАСА В ПРЯМОУГОЛЬНИКЕ
Краевые задачи для уравнения Лапласа в прямоугольнике также
могут быть решены методом разделения переменных. Для опреде-
определенности рассмотрим задачу Дирихле
Дг/ = 0, 0 < х < а, 0 < у < 6,
г/у=о =
иу=ь =
G.1)
G.2)
G.3)
Задачу G.1)-G.3) разобьем на две задачи, каждая из которых имеет
однородные граничные условия по одной из переменных. Пусть
где г/i и г/2 есть решения следующих задач в прямоугольнике:
Аг/1 =0,	( Аг/2 = О,
Каждую из этих задач будем называть стандартной. Рассмотрим
стандартную задачу для функции и\(х, у). Построим сначала реше-
решения уравнения Лапласа, представимые в виде
G.4)

и удовлетворяющие однородным граничным условиям по ж:
ti|*=o = ti|a.=« = 0.	G.5)
Подставляя G.4) в уравнение Лапласа и разделяя переменные,
получим
"	"_
G'6)
Отсюда получаем отдельные уравнения для Х(х) и У (у). Поскольку
по переменной х должны выполняться однородные граничные усло-
условия G.5), для определения функции Х(х) имеем одномерную задачу
Шту рма- Л иу ви л ля :
Х" + ХХ =0, 0<х<а,
Х@) = Х(а) = О, *(*)#),
решение которой имеет вид (см. гл. II, § 1)
Х=Хп(х)=вт—х, А=А„ = (— V, п=1,2,...
а	V а /
Учитывая найденное значение Ап, получаем из G.6) уравнение для
Y(y):
У"-АПУ = 0, 0<y<b.	G.7)
Общее решение этого уравнения можно записать в виде
Но такая запись неудобна для дальнейшего. Гораздо удобнее фунда-
фундаментальную систему {Ух , У^} решений уравнения G.7) выбрать так,
чтобы функция У! удовлетворяла однородному граничному условию
при у = 0:
а функция УЬ(у) — однородному граничному условию при у = Ь:
Уз F) = 0.
Такими решениями являются
Ух (у) = eh™ у, У3(у)=вЬ™F-у).
Общее решение уравнения G.7) удобно записать в виде
У = С\ sh —у + С2 sh —F - у) .
а	а

Таким образом, построены следующие системы частных решений
уравнения Лапласа:
«„(*,») =	G-8)
«п (*,»)=	G-9)
Теперь решение задачи для функции MI (x, у) запишем в виде разло-
разложения по этим частным решениям:
ui(x,y) =
G.10)
Подставляя G.10) в граничное условие при у = 0 , получаем
откуда видно, что Вп есть коэффициенты Фурье функции ^i(x) по
системе собственных функций {sin ^р-ж}?0 . Они вычисляются по фор-
формулам
Вп =	G.11)
Подставляя G.10) в граничное условие при у = 6, получим
= Ф2(Х),
откуда
An =	G.12)
Таким образом, решение стандартной задачи для функции и\(х> у)
дается разложением G.10), коэффициенты которого определяются
формулами G.11) и G.12).
Аналогичным образом решается стандартная задача для функции
г/2(х, у) . Решение ее имеет вид
«2(«,У) =	G.13)

где
Dn =	Cn =
Итак, решение задачи G.1)-G.3) имеет вид
где функции г/i и г/2 определяются формулами G.10) и G.13) соот-
соответственно.
Таким же образом может быть решена краевая задача для урав-
уравнения Лапласа в прямоугольнике с другими граничными условиями.
Осторожность нужно проявлять при решении задачи Неймана, по-
поскольку при редукции ее к стандартным задачам может появиться
задача, которая не имеет решения, в то время как решение исходной
задачи существует. В этом случае исходную задачу заменой неизвест-
неизвестной функции можно свести к задаче для неоднородного уравнения с
однородными граничными условиями. Схема решения такой задачи
изложена в гл. I, § 3.
Теперь обсудим характер сходимости полученных рядов.
В качестве примера рассмотрим разложение, полученное для ре-
решения первой стандартной задачи:
G.14)
где Ап = (—•) , а коэффициенты Ап и Вп определяются формулами
G.12) и G.11).
Если ф\(х] и г/>2(х) абсолютно интегрируемы на @, а) , то коэффи-
коэффициенты АП и Вп ограничены:
\Ап | < С, \Вп | < С при всех п .
Поэтому общий член первого ряда при п — »• оо имеет следующий
характер :
Отсюда видно, что во внутренних точках прямоугольника ряд схо-
сходится экспоненциально. Более того, если Ь/а ^> 1, при малых у (т.е.

вблизи основания прямоугольника у = 0) уже первый член ряда име-
имеет порядок ехр(— тгб/а). Коэффициенты Ап определяются функцией
^(х), заданной на другой стороне (у = Ь) прямоугольника. Следо-
Следовательно, в этом случае влияние граничных условий, заданных при
у = 6, на решение при малых у невелико и при вычислении можно
ограничиться одним- двумя членами ряда.
Аналогичный характер имеют члены второго ряда в G.14), но они
малы при b/а ^> 1, когда у близко к 6.
При увеличении гладкости функций ф\ и V>2 сходимость рядов ста-
становится еще более быстрой.
§ 8. КРАЕВЫЕ ЗАДАЧИ ДЛЯ
УРАВНЕНИЯ ЛАПЛАСА В
ПРЯМОУГОЛЬНОМ ПАРАЛЛЕЛЕПИПЕДЕ
Общая краевая задача для уравнения Лапласа может быть разби-
разбита на три стандартных. Стандартной задачей в данном случае назы-
называется задача, в которой неоднородные граничные условия заданы на
двух параллельных сторонах («основаниях»), а на остальной части
поверхности («боковой поверхности») граничные условия нулевые.
Например, рассмотрим стандартную задачу
Ди = 0, 0<х<а,	0<у<6, 0<z</i, (8.1)
U\Z=Q = (pi(x,y),	(8.2)
u\z=h = Ы*>2/Ь	(8.3)
РМ|*=о,*=а = 0,	(8.4)
y=0, y-b
где Р[и] — оператор, соответствующий граничному условию третьего
рода.
Для решения этой задачи сначала находим частные решения урав-
уравнения Лапласа, представимые в виде
(заметим, что отделена та переменная, по которой заданы неоднород-
неоднородные граничные условия) . Подставляя в уравнение Лапласа и разде-
разделяя переменные, получаем
v(x,y) - Z(z)
Отсюда
Д2т; + At; = 0, 0 < х < а, 0 < у < 6,
яг=0, яг=а —
у=0, у=6

Z"(z)-XZ(z) = Q, 0<z<h.	(8.6)
Задача (8.5) есть задача Штурма-Лиувилля для прямоугольника,
рассмотренная в гл. II, § 3. Пусть {un(#>y)}i° и {^n)i° — ее соб-
собственные функции и собственные значения соответственно. Общее
решение уравнения (8.6) удобно записать в виде
Z(z) =	А, В = const.
Таким образом, частные решения уравнения Лапласа имеют вид
un(ж, у, z) =
Теперь решение задачи (8.1)-(8.4) запишем в виде разложения по
этим частным решениям:
ii(x 11 z} —	(8 7}
UV ' с/' / —	V /
коэффициенты Ап и Вп которого определяются из граничных усло-
условий (8.2), (8.3):
Ап =	(8.8)
Вп =	(8.9)
Заметим, что функции Z(z) взяты в виде, удобном при решении зада-
задачи с граничными условиями Дирихле по переменной z. При гранич-
граничных условиях по z другого типа нужно соответствующим образом
выбирать фундаментальную систему решений уравнения (8.6), так,
чтобы «развязать» вычисление коэффициентов Ап и Вп •
Аналогичным образом решаются две другие стандартные задачи с
неоднородными граничными условиями по переменным х и у.
Легко видеть, что полученные ряды имеют тот же характер схо-
сходимости, что и для решения задачи в прямоугольнике (см. § 7).
Рассмотрим несколько примеров решения задач.
1. Найти распределение потенциала внутри куба с ребром а, одна
грань которого z = 0 поддерживается под постоянным потенциалом
17о, а остальные грани заземлены.

Решение. Для потенциала и имеем следующую краевую задачу:
Ди = 0, 0 < ж < а, 0 < у < а, 0<z<a,
U\X=Q = U\x-a = U\y=Q = U\y=a = 0 .
Решение этой задачи имеет вид
и =
где vn k (я, у) — собственные функции квадрата с граничным условием
Дирихле
, ч . тгп . 7Г&
vnk(x,y) = sm — ж sin — у,
a	a
n,k = 1, 2, ...,oo.
Вычислим коэффициенты An k и Вп k :
Ank = 0, n, *= 1, 2,...,oo.
Следовательно,
и =
2. Найти стационарное распределение температуры внутри па-
параллелепипеда 0<x<a,0<y<b,0<z<c,y которого на грани
х = 0 поддерживается температура, равная Ayz, грани z = 0 и z = с
находятся при нулевой температуре, а остальные грани теплоизоли-
рованы, А = const.

Решение. Стационарная температура и(х,у, z) определяется как
решение следующей краевой задачи:
Ди = 0, 0<ж<а, 0<у<6, 0<z<c,
u\x=Q = Ayz , ti|,_0 = u\z=c = 0 ,
ди\	ди 6
дх \х=а ду у=о ду
у=Ь
= 0.
Решение этой задачи следует искать в виде разложения по собствен-
собственным функциям прямоугольника 0<y<b,0<z<cc граничными
условиями
Ч*=о = Ч*=с = 0,
ди_\ =ди_\ _0
ду\у=о ду\у=ь
Они имеют вид
, ч	7ГП 7ГШ
Vnm(y,*) = cos -—у sm——z, n = 0, 1, 2,..., m= 15 2,...
о	с
По переменной ж заданы граничные условия первого рода при х = О
и второго рода при х = а. Поэтому решение задачи можно записать
в виде
и =
Поскольку -?—
их
— О , Апт = 0 при всех пит. Используя гранич-
граничное условие при х = 0 , получаем
= Ayz.
Отсюда

Так как
можем записать
т = 1, 2, ... ,00.
Следовательно, стационарное распределение температуры имеет вид
и =
3. Найти стационарное распределение температуры внутри куба,
две грани которого при z — О и z — а теплоизолированы, а на осталь-
остальных поддерживается постоянная температура TQ .
Решение. Стационарная температура и является решением крае-
краевой задачи
Дм = 0 в кубе,
3z
z=Q
dz
= 0,
U\x=Q - U\x=a - U\y=Q = U\y=a =

Поскольку при z — О и z — а заданы однородные граничные условия
второго рода
— I = —I = О
dz\z=Q dz\z=a	'
а граничные условия на остальной части поверхности куба от z не
зависят, и решение задачи от переменной z зависеть не будет:
и = и(х, у).
Поэтому трехмерная задача вырождается в двумерную:
~5~? + "о~Т - О в квадрате 0 < ж, у < а ,
ox* oyz
Ч*=0 = U\x=a = и\у=0 = и\у=а = Т0 •
Эту задачу можно далее решать методом разделения переменных,
как это изложено в § 7. Но совершенно очевидно, что решением этой
задачи является и = TQ .
Итак, стационарная температура данного куба постоянная и равна
То-
Заметим, что решение этой задачи сразу можно было выписать
«из физических соображений»: на боковых гранях поддерживается
постоянная температура TQ , а две другие грани теплоизолированы.
Следовательно, внутри куба будет сохраняться та же температура
Т0.
Следует всегда учитывать, что если непосредственная проверка
показывает, что каким-то образом «угаданная» или построенная «из
физических соображений» функция действительно является реше-
решением поставленной задачи, то другого решения эта задача иметь не
может в силу теоремы единственности.
§ 9. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ
ЛАПЛАСА В КРУГОВОМ ЦИЛИНДРЕ
Решение краевой задачи для уравнения Лапласа внутри прямого
кругового цилиндра @<г<а,0<^>< 2тг, 0 < z < h) проводится по
той же схеме, что и для прямоугольного параллелепипеда.
Для примера рассмотрим задачу Дирихле
Ди = 0, 0<г<а, 0<<р<2тт, 0 < z < Л,	(9.1)
),	<9-2)
), (9.3)

Полную задачу (9.1)-(9.4) разобьем на две стандартные:
Д« = 0, 0 < г < а, О < V < 2тг, 0 < z < h,	(9.5)
«lr=. = °'	(9-6)
«L=o = /i M'	(9.7)
«\,=h = Mr,v)	(9-8)
Д« = 0, 0 < г < а, 0 < v < 2тг, 0 < z < h,	(9.9)
«|r=e = /(?,*), (9-10)
Рассмотрим каждую из этих задач. Начнем с задачи (9.5)-(9.8).
Найдем частные решения уравнения Лапласа, представимые в виде
г/(г, у, z] — v(r, <f>)Z(z) ф О	(9.12)
и удовлетворяющие однородному граничному условию
«U. = °-
Подставляя (9.12) в уравнение Лапласа и разделяя переменные, по-
получим
A2t; _ Z" _
~ = ~"Y = ~X'
Отсюда, как и для параллелепипеда, получаем задачи для v(r, <p) и
Z(z):
A2t; + At; = 0, 0 < г < а, 0 < <р < 2тг,	(9.13)
Z" - XZ = 0, 0 < z < h.	(9.14)
Задача (9.13) есть задача Штурма-Лиувилля для круга. Ее собствен-
собственные функции равны
( cos п^>,
\ sinn^>,

а собственные значения А^ есть корни уравнения
= 0, п = 0,1,2>...> fc=l,2,...,oo.
Общее решение уравнения (9.14) запишем в виде (удобном для реше-
решения задачи Дирихле по переменной z]
Z(z} =
Таким образом, система частных решений имеет вид
,v, z) =
n = 0,l,..., k= 1,2,... ,00.	(9.15)
Решение задачи (9.5)-(9.8) ищем в виде разложения по этим частным
решениям:
(9.16)
Коэффициенты Ank, Bnk, Cnk, Dnk определяются из граничных усло-
условий (9.7), (9.8):
Cnk =
Dnk =

Замечание 1. Для задачи Дирихле все собственные значения
Mr > 0- При решении задачи Неймана появляется собственное зна-
значение Л = 0. Если Л = 0, то уравнение (9.14) принимает вид
Z" = 0.
Его общее решение:
Z(z) =A + Bz.
Поэтому в системе частных решений для задачи Неймана удобно вы-
выделить решение
UQ = AQ + BQZ,
соответствующее нулевому собственному значению.
Замечание 2. Изложенный метод решения непосредственно перено-
переносится на краевую задачу внутри прямого цилиндра произвольного
поперечного сечения, если на боковой поверхности такого цилиндра
выполняется нулевое граничное условие (первого, второго или тре-
третьего рода).
Замечание 3. Сходимость полученных рядов аналогична сходимости
рядов, появляющихся при решении задач в прямоугольном паралле-
параллелепипеде.
Рассмотрим теперь задачу (9.9)-(9.11). Для ее решения следует
построить систему частных решений уравнения Лапласа, представи-
мых в виде
u(r,p,z) = v(r,p)Z(z)i?0	(9.17)
и удовлетворяющих однородному граничному условию
Подставляя (9.17) в уравнение Лапласа и разделяя переменные, как
это делалось ранее, задачи для Z(z) и u(r, (p) удобно записать в виде
Z" + XZ = О, 0 < z < Л,
z(o) = z(h) = о, z(z) $ о,	(9Л8)
-Аи = 0, 0<г<а, 0<<р<2тг.	(9.19)
Задача (9.18) есть задача Штурма- Лиувилля для отрезка. Ее соб-
собственные значения и собственные функции имеют вид
k = ~

Частные решения уравнения (9.19) также найдем методом разделе-
разделения переменных. Пусть
Подставляя в уравнение (9.19) и разделяя переменные, получим
Отсюда получаем задачу для определения
ф" + j/ф = 0, 0 < v? < 2тг,
~
(9 2(Л
= Ф(у> + 2тг)	V ' ;
и задачу для определения R(r):
г2Я" + rtf - (Лг2 + I/) Д = О, 0 < г < а,	(9.21)
|Д@)| < оо. (9.22)
Задача (9.20) есть задача Штурма- Лиувилля для отрезка с перио-
периодическими граничными условиями. Ее собственные значения и соб-
собственные функции равны
п = 0, 1, ... ,оо.
Уравнение (9.21) есть уравнение функций Бесселя с чисто мнимым
аргументом. Его общее решение имеет вид
Д(г) = Ci/n(\/Ar) + С2#п(\/Аг),
где /п(я) — функция Инфельда, Кп(х] — функция Макдональда.
Условие ограниченности (9.22) дает
Следовательно, система частных решений (9.17) имеет вид
Un/c(r,<p,z) =
(9.23)
(L \ 2
^-J , n = 0,l,..., *=l,2I...,oo.

Решение краевой задачи (9.9)-(9.11) ищем в виде разложения по си-
системе (9.23):
(9.24)
коэффициенты которого определяются из граничного условия (9.10):
где
Таким образом, решение задачи (9.1)-(9.4) представлено в виде
и = г/1 + г/2,
где г/1 — решение стандартной задачи (9.5)-(9.8), определенное фор-
формулой (9.16), г/2 — решение стандартной задачи (9.9)-(9.11), данное
формулой (9.24).
Замечание 1. Решение краевой задачи с другими граничными усло-
условиями проводится по такой же схеме. При этом, как было указано
ранее, следует учитывать возможность появления нулевого собствен-
собственного значения.
Замечание 2. При решении задачи (9.9)-(9.11) внутри тора прямо-
прямоугольного сечения изменится только функция R(r). В этом случае
она будет иметь вид
R =
Замечание 3. Если по переменной z на обоих концах отрезка [О, Л]
(т.е. и при z = О, и при z = Л) задано нулевое граничное условие
, ди
второго рода ( д—
z=0
ди
= 0 и ^-
dz
z=h
= 0), а граничная функция на

боковой поверхности цилиндра не зависит от переменной z, то и ре-
решение краевой задачи для уравнения Лапласа внутри цилиндра не
зависит от z. В этом случае задача вырождается в краевую зада-
задачу для уравнения Лапласа на плоскости в области, представляющей
поперечное сечение данного цилиндра.
Отдельно рассмотрим краевую задачу с нулевыми граничными
условиями второго рода по переменной z:
Дг/ = 0 в цилиндре D,	(9.25)
ди
ди
2=0
(9.26)
(9.27)
В этом случае при разделении переменных по z получаем задачу
Штурма-Лиувилля
Z" + XZ = О, 0 < z < Л,
Z'@) = Z'(h) = О,
ад Ф о,
которая имеет следующее решение:
* /**у	*k
Xk=\ — \ , Zk(z) =cos— z,
k = 0,1,2,... ,00.
Заметим, что при k = О АО = О, ZQ(Z) = 1.
Для функции v(r,<p) получаем уравнение
Д2г; - Av = 0.	(9.28)
При Л/с ф 0 (т.е. при k = 1,2,...) оно имеет следующие частные
решения , ограниченные при г = 0:
„ = 0,1,2,...
При k = О АО = О и уравнение (9.28) переходит в уравнение Лапласа
Д2г; = 0, которое имеет следующие частные решения, ограниченные
при г = 0:
Гсозш,,	]0о
[^ s

Следовательно, частные решения уравнения Лапласа в цилиндре,
представимые в виде
u = v(r,(f>)Z(z)
и удовлетворяющие однородному граничному условию второго рода
= о,
ди
dz
z=0
ди
dz
z=h
имеют вид
cos пу>,
sin n^>,
COS П^>,
sin n<p,
Поэтому решение краевой задачи (9.25)-(9.27) можно представить в
виде суммы двух рядов:
(9.29)
коэффициенты которых определяются из граничного условия (9.27)
и имеют вид
где
N2 =
Рассмотрим несколько примеров решения задач.
1. Найти электростатический потенциал внутри кругового цилин-
цилиндра радиуса а, основания которого z = 0 и z = h заземлены, а на
боковой поверхности поддерживается потенциал cos 2v?.

Решение. Для электростатического потенциала и имеем следую-
следующую краевую задачу внутри цилиндра:
Дг/ = 0 в цилиндре,
Общее решение поставленной задачи имеет вид
и =
Поскольку граничное условие содержит только cos2<p,
Ank = О при п ф 2,
= 0 при всех п и k.
Следовательно, решение можно записать в виде
и =
Коэффициенты АЫ определяются из граничного условия по формуле
Итак, решение поставленной задачи имеет вид
и =
2. Найти распределение потенциала внутри прямого кругового ци-
цилиндра радиуса а, на торцах которого задано нулевое электрическое
поле, а на боковой поверхности поддерживается потенциал, равный
С/о =const.

Решение. Электростатический потенциал и является решением
следующей краевой задачи:
Дг/ = 0 в цилиндре,
ди
_
dz
= 0,
г=0 и
«lr=a = U°Z-
В данном случае решение от переменной <р не зависит и может быть
записано в виде
и =
Коэффициенты Ako определяются из граничного условия по форму-
формулам
Итак, данная задача имеет решение
и =
3. Решить уравнение Лапласа внутри сектора кругового цилиндра
О < г < а, 0 < V7 < f> 0 < z < h с граничными условиями
Решение. Поскольку при z = 0 задано нулевое граничное условие,
то решение поставленной задачи можно записать в виде
и =
где А^^ — корни уравнения «/4п(\/А^4п^а) = 0.

Заметим, что разложение решения проводится по собственным
функциям задачи Дирихле для сектора с углом раствора а = J,
которые имеют вид
>, п = 0,1,... , k = 1,2,...
Коэффициенты ряда определяются из граничного условия при z = h
и равны
Следовательно,
и =
4. Решить уравнение Лапласа внутри тора прямоугольного сече-
сечения: я < г < &, 0 < V7 < 2тг, 0 < z < h с граничными условиями
ди
dz
г=0
ди
dz
= 0,
z=ft
Решение. Граничные условия при z = 0 и z = h являются одно-
однородными граничными условиями второго рода, а при г = а и г = Ь
граничные функции не зависят от z. Поэтому данная задача выро-
вырождается в краевую задачу для уравнения Лапласа внутри кольца
а < г < Ь:
Д2г/ = 0, а < г < 6, 0 < <р < 2тг

решение которой может быть записано в виде (см. D.6))
и =
Из граничных условий находим
Вп=0, п=1,2,...,
Ап = 0, п ф 3,
Следовательно,
б3 г6 - а6 о
г/ = -=• Tfi —— г- cos 3<р.
г3 6е - а6
§ 10. ЧАСТНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ЛАПЛАСА
В СФЕРИЧЕСКОЙ СИСТЕМЕ КООРДИНАТ
Для построения решений краевой задачи для уравнения Лапласа в
шаре, вне шара и в шаровом слое необходимы специальные решения,
называемые шаровыми функциями. Поэтому сначала построим эти
решения.
Введем сферическую систему координат (г, в,р). Найдем решения
уравнения Лапласа, пред ставимые в виде
Подставляя искомый вид решения в уравнение Лапласа и разделяя
переменные, получим
= А,
где
— сферический оператор Лапласа. Отсюда получаем краевую зада-
задачу для определения v@,(f>):
0<0<тг, 0<<р<2тг,
(юл)

и уравнение для функции R(r):
r2R" + 2rR'-\R = Q.	A0.2)
Задача A0.1) есть задача Штурма- Л иу БИЛЛЯ для сферического опе-
оператора Лапласа, собственные значения и собственные функции кото-
которой имеют вид
А = А„ = п(п + 1), v = vnm = pW(cos
n = 0,1,..., oo, m = 0,1,..., n, где Рп (х) — присоединенные
функции Лежандра.
Общее решение уравнения A0.2) при А = п(п + 1) имеет вид
R(r) = С1Гп + С2г~(п+1\
Таким образом, построены два семейства решений уравнения Лапла-
Лапласа:
Функции первого семейства ограничены при г = 0, функции второго
семейства — при г — > оо.
§ 11. КРАЕВЫЕ ЗАДАЧИ ДЛЯ
УРАВНЕНИЯ ЛАПЛАСА В ШАРЕ
Теперь перейдем к решению краевой задачи для уравнения Ла-
Лапласа внутри шара:
Дм = 0 в шаре @ < г < а)
Р1[«] = а!|Н+/?1и|г=в = /(*,?), M + IAI^O. A1.1)
Решение этой задачи (поскольку оно ограничено при г = 0) будем
строить в виде ряда по шаровым функциям:
«=	A1.2)
коэффициенты которого определяются из граничного условия:
А —
-^nm —
A1.3)
Впт =
A1.4)

где
В том случае, если решается задача Неймана, следует иметь в
виду, что решение существует лишь при условии
= 0
и определяется с точностью до постоянного слагаемого. Поэтому
суммирование в A1.2) начинается с п = 1, а коэффициент AQQ оста-
остается произвольным.
Если граничное условие A1.1) не зависит от угла (р, т.е. имеет вид
то и решение соответствующей краевой задачи не будет зависеть от
(р (имеет осевую симметрию) и может быть записано в виде
и=	A1.6)
где
Ап =	A1.7)
Выражение A1.6) получается из A1.2), если учесть, что
AnQ = АП > Апт — -&пт — U При 771 ^р U.
§ 12. КРАЕВЫЕ ЗАДАЧИ ДЛЯ
УРАВНЕНИЯ ЛАПЛАСА ВНЕ ШАРА
Решение внешней краевой задачи:
Дг/ = 0 вне шара (г > а)
и =3 0 при г -> оо

представляется в виде ряда
и =
A2.2)
коэффициенты которого определяются из граничного условия и да-
даются формулами A1.3).
§ 13. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ
ЛАПЛАСА В ШАРОВОМ СЛОЕ
При решении краевой задачи внутри шарового слоя (а < г < Ь)
используются оба семейства решений A0.3). При этом удобно вна-
вначале построить из них две другие серии решений аналогично тому,
как это сделано при решении уравнения Лапласа в круговом кольце.
Для определенности рассмотрим задачу Дирихле в шаровом слое:
Дг/ = 0, а < г < 6,
ti|r=« = /i@,p),	A3.1)
Построим сначала решение уравнения A0.2) при Л = п(п + 1), удо-
удовлетворяющее однородному граничному условию при г = а. Таким
решением является функция
Аналогично строится решение, удовлетворяющее однородному усло-
условию Дирихле при г = Ь:
_ Г2п+!
Таким образом, получаем семейство решений уравнения Лапласа,
удовлетворяющих однородному условию Дирихле при г = а:
unm(r>0>V>) =	A3-2)
и семейство решений, удовлетворяющих однородному условию при
г = Ь:
(Ь} / л \	(л о о\
U^ ' (Г. С/. (О]	= AO.OJ
ПТП \ > > г /	\/

Решение краевой задачи A3.1) теперь можно представить в виде раз-
разложения по семействам решений A3.2) и A3.3) и записать следующим
образом:
и =
A3.4)
Коэффициенты Апт и Впт определяются из граничного условия при
г = 6, а коэффициенты Спт и Dnm — из граничного условия при
г = а. Формулы для коэффициентов аналогичны формулам A1.3),
A1.4).
При решении задачи с другими граничными условиями следу-
следует предварительно построить семейство решений, удовлетворяющих
нужному однородному граничному условию при г = а, и семейство
решений, удовлетворяющих однородному условию при г = Ъ. Напри-
Например, решения, удовлетворяющие граничному условию
ди
дг
можно взять в виде
(в)	(п+1)Г2" + па
Тп Чг) = ————— 1 ————— > п = 0, 1, . . .
Рассмотрим теперь примеры решения задач.
1. Найти искажение однородного электрического поля ЕО при по-
помещении в него идеально проводящего шара радиуса а.
Решение. Электростатический потенциал и вне шара представим в
виде
U = UQ + 17,
где щ — потенциал поля ЕО, г; — потенциал, связанный с присутстви-
присутствием шара. Введем сферическую систему координат (г, 0, (р) с началом
в центре шара и осью z, направленной вдоль поля EQ. Тогда
UQ = —EQZ = — ЕоГСОзв.
На границе шара (при г = а) полное электростатическое поле Е =
= — grad и удовлетворяет условию
[п,Е]|г=а = [ег,Е]|р=в = - [er)grad(«0 + »)]|r=a = 0.

Отсюда
1 д
r=a r sin в
или
(постоянная считается равной нулю, поскольку потенциал опреде-
определен с точностью до const). Следовательно, для функции v получаем
внешнюю задачу:
Дг; = 0 вне шара,
v\_a = — г/о|Г=а = Еоасозв, v =3 0 при г -> оо.
Решение этой задачи не зависит от переменной (р. Поэтому его можно
записать в виде
Р„(С080).
п=0
Из граничного условия, учитывая, что cos# = P\ (cos 0), находим
Следовательно,
3	3
v = E0^Pi(cos9) = ЕО \
г	г
а искажение электрического поля
о
Е = — gradi; = ?to-gBcos^er
Потенциал полного поля вне шара равен
о
U = UQ + V = —Еъ\Г — —— JCOS0.
2. Найти электростатический потенциал внутри сферы, верхняя
половина которой @ < в < ^) заряжена до потешщала С/о, а нижняя
(| < в < тг) заземлена, С/о = const.
Решение. Для потенциала и внутри сферы получаем задачу
Ди = 0 внутри сферы;
9
ч- г<<«>

Решение этой задачи имеет аксиальную симметрию (не зависит от <р)
и может быть записано в виде
и =
Коэффициенты Ап определяются из граничного условия по формуле
1
2n + 1 f „/лч , лч . л ,л rr 2n + 1 / „ , ч ,
Ап = ———— / f(Q)Pn(cosv)sin 0a0 = с/о——— / Pn(x}dx.
'*	f\ I J \ / '* \ I ^^ U л I '* V /
27	2 У
о	о
Вычислим написанный интеграл. Прежде всего заметим, что при
четных п ^ О
1	-Hi
У Рп(х) dx = i / Pn(x) dx = 0.
О	-1
При п = О
1	1
f Pn(x)dx= fdx = l.
о	о
Пусть п = 2k + 1. Используем формулу
Поэтому
1
P2k+i(*)dx =
Поскольку
получим
о
Следовательно,
1
tP2k+i(x)dx =
= О,

и решение имеет вид
и =
3. Определить электростатический потенциал внутри шаровой
оболочки а < г < 6, внешняя поверхность которой заземлена, а вну-
внутренняя заряжена до потенциала
Решение. Потенциал и является решением следующей краевой за-
задачи для уравнения Лапласа внутри шаровой оболочки:
Дк = 0, а < г < 6,
u\r_a = ?/о sin 0 sin ^?,
«1г=Ь = °'
Поскольку граничное условие при г = b нулевое, то решение поста-
поставленной задачи можно записать в виде
и =
где
Учитывая, что sin в sin (р = Р± ^(cos0)sin^>, из граничных условий
сразу находим
Апт = О при всех пит,
Ви = ?/о, Впт = 0 при и ф 1, т ф 1.
Поэтому решение имеет вид
и =
4. Аналогичным образом решаются и более сложные задачи, в
которых дополнительные условия имеют вид "условий сопряжения".
Рассмотрим следующую задачу. Диэлектрический шар с диэлек-
диэлектрической постоянной е\ находится во внешнем однородном постоян-
постоянном электрическом поле EQ. Определить искажение внешнего поля,

вызываемое шаром, если внешняя среда — однородный диэлектрик
с диэлектрической постоянной ?2.
Решение. Введем сферическую систему координат (г, 0, <р) с нача-
началом в центре шара и осью z, направленной вдоль электрического
поля EQ. Пусть UQ — потенциал, создающий внешнее поле Е0:
Н~^
OZ
UQ = —EQZ = —
Обозначим через и\ потенциал электрического поля внутри шара, а
потенциал вне шара представим в виде UQ + и2, где и2 — искаже-
искажение внешнего поля, связанное с наличием диэлектрического шара.
Функция и\ гармонична в шаре:
Atii = 0 при 0 < г < а,	A3.5)
а функция U2 удовлетворяет уравнению Лапласа вне шара:
Ди2 = 0 при г > а.	A3.6)
На поверхности шара (г = а) должны выполняться условия непре-
непрерывности тангенциальных составляющих электрического поля и нор-
нормальных составляющих индукции D = ?Е. Поскольку
EI = - grad tii , Е2 = ЕО - grad ti2,
Din = ?2I?2r,
эти условия принимают вид
дг
= ?2
дг
A3.7)
A3.8)
Кроме того, функция и2 должна быть регулярна на бесконечности:
ti2 =4 0 при г -> оо.	A3.9)
Таким образом, для определения потенциалов и\ и t/2 получена
задача A3.5)-A3.9). Заметим, что роль граничных условий в этой
задаче играют условия сопряжения A3.7), A3.8) на поверхности шара
(при г = а).

Решим задачу A3.5)-A3.9). Сразу отметим, что рассматриваемая
задача имеет осевую симметрию. Следовательно, функции и\ и и^
зависят только от переменных г и 9.
Функция t/i(r, в) удовлетворяет уравнению Лапласа внутри шара.
Следовательно, она может быть представлена в виде
tii =	A3.10)
где Ап — коэффициенты, подлежащие определению.
Функция u2(r, 0) удовлетворяет уравнению Лапласа вне шара и
регулярна на бесконечности. Поэтому ее можно представить в виде
ti2=	A3.11)
где Сп — коэффициенты. Выражения A3.10) и A3.11) учитывают
осевую симметрию функций и\ и и?>.
Коэффициенты Ап и Сп определяются из условий сопряжения
A3.7), A3.8). Подставляя A3.10) и A3.11) в условия сопряжения,
получим
A3.12)
A3.13)
Из A3.12) и A3.13), приравнивая коэффициенты в обеих частях ра-
равенств при полиномах Рп (cos в) одного порядка, получим
-o,
а2-
" = 2,3,..
— ,
2
-j
eiAnnan-1 = -?2Cn-, n = 2, 3, . . .

Отсюда находим
?2 ~
?1 +
Следовательно,
262
Поэтому искажение внешнего поля, вносимое диэлектрическим ша-
шаром, равно
2
2 = — ——— - — ?"о-
е\ + ^^2 ^
§ 14. ЗАДАЧИ ДЛЯ
САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Решить краевую задачу для уравнения Лапласа внутри круга
О < г < а> 0 < v? < 2тг со следующими граничными условиями:
z\ ди	л • з
6) -т— = 4 sm <p:
дг г=а
в) «I = 32(sin6 v + cos6 <p);
' ir=a	v ' i /'
г) &И + и\ =sm -hcos4
2. Решить краевую задачу для уравнения Лапласа вне круга:
г>а, 0<^<2тгсо следующими граничными условиями:
а) «|r=a = 8cosV;
е-\ ди
6> я!
г)
;
|	Г 1, 0<у><7Г,
и = <
1г=а 1-1, тг < ^ < 2тг.
3. Решить краевую задачу для уравнения Лапласа внутри секто-
сектора: 0<r<a, 0<ip<aco следующими граничными условиями:
а) uUo = ul=* = °. ulr=a = Ч>(* - <РУ>

б) «I „ = о, 2й-
' ^=°	д<р
в)
г)
ди
ди
<р=0
<?=•=•
= „1^ = 0, |н
= 0, ti| _ = 1 4- cos 4^>;
4. Решить краевую задачу для уравнения Лапласа в кольце:
а < г < Ь, 0 < (р < 2тг со следующими граничными условиями:
а) и\ = О, и\ = sir/л-1-^ ™°2 у
' 1г=а	1г=о
б) ё =
cos
в)	«I = 1, ^
'	1г=а ' Я».
Г)	^
= 2 sin2 (p\
г=Ь
9t/
= cos^?.
r=b
5. Решить краевую задачу для уравнения Лапласа внутри коль-
кольцевого сектора: а<г<6, 0 < (р < а со следующими граничными
условиями:
Ur=a =
иг=ь =
ди_
d(f>
= °. UL=0 =
6. Решить краевую задачу для уравнения Лапласа в прямоуголь-
прямоугольнике: 0<х<а, 0<у<6со следующими граничными условиями:
ч ди
дх
х=0
б) «|„„ = g
дх
Зтгу
/ 1о?=0 ~~ '	\х=а ~~ ОА ' Я-1/
у=о
= ti .=0;
1у=Ь	'
г^
Г) 5х
д) дГ
x=0
= sin5y, t/| _Q=cosz, t/| _^ = cos3x;
dx
ди
у=о
= 1.
7. Решить краевую задачу для уравнения Лапласа в прямоуголь-
прямоугольном параллелепипеде: 0 < z < а, 0 < у < 6, 0 < z < с со следую-

щими граничными условиями:
\ I	I л ди
а) ii^fiU^O,
у=о
ди
ду
и\ _ = sin x cos у, и\ _ = sin 2x cos 2t/;
Ь=о
б) и\ п = и\ п = и\ п = О, и\ = и\ ,=и\ = 1;
' \х=0	lt/=0 12=0 ' \х=а ly=o \z—c '
ч ди
B)
ди
_
"ду
с=я	У
у=о
у=Ь
8. Найти стационарное распределение температуры внутри прямо-
прямоугольного параллелепипеда, два основания которого (z = О и z = с)
теплоизолированы, а на остальной поверхности поддерживается по-
постоянная температура TQ.
9. Решить краевую задачу для уравнения Лапласа внутри пря-
прямого кругового цилиндра 0<г<а, 0 < z <h со следующими гра-
граничными условиями:
a) «|r=a=cosV, «L=o = ul»=fc=°;
= 0;
z=ft
В) И1г=а =zsinV, «|,=0 =
= 0.
10. Решить краевую задачу для уравнения Лапласа внутри прямо-
прямого цилиндра высоты Д, в основании которого лежит круговой сектор
О < г < а, 0 < (р < а со следующими граничными условиями:
ди
а) и n = ti =0, ti =1, ^
' \(р=0	1у>=тг ' lr=a ' flz
z=0
ди
dz
= 0;
z=h
ди
г) i
ди
11.) Решить краевую задачу для уравнения Лапласа внутри пря-
прямого кругового тора прямоугольного сечения: а<г<6, 0<v?< 2тг,
О < z < h со следующими граничными условиями:
ди	л I
б) и\ = 1, til ,=sin7rz. til n = 0, til ,=0;
1 \r=a	' lr=6 ' \z=0 ' 1г=1 '

в) t/l = cos2v?,
' \r—a	r>
fo
dz
z=Q
dz
= 0.
z-h
12. Решить краевую задачу для сектора прямого кругового тора
прямоугольного сечения: a<r<6, Q<(p<a,Q<z<hco
следующими граничными условиями:
а) и\ = и\ ,=0, и\ = и\ = О, и\ п = г sin у?,
1 \г=а	\г=Ь ' 1^>=0 1<?=тг ' 1,г=0 Г)
-ч I
б) и\г=а =
ди
дг
г=Ь
= 0,
«I _„ =
= 0;
в)
ди
z=h
г=Ь
ftl
дг
«1„* = 2-
13. Найти стационарное распределение температуры внутри пря-
прямого цилиндра произвольного поперечного сечения, боковая поверх-
поверхность которого теплоизолирована, на нижнем основании (z = 0) под-
поддерживается постоянная температура Т\, на верхнем (z = h) — по-
постоянная температура Т%.
14. Решить внутреннюю задачу Дирихле для шара @ < г < а) с
граничными условиями:
а) u\r_a = cos0 + cos2 0;
б) и\ = 1 + sin0cosv?;
' lr=a	r>
в) u\r=a = sin20+ 15sin20cos0cos2y?;
r) u |r=a = 1 + sin в cos в sin (p -h sin5 в cos 5y?.
15. Решить внутреннюю задачу Неймана для шара @ < г < а) с
граничными условиями:
ч ди
а)
б)
в)
ди
дг
ди
дг
= cosO;
= sin3 в sin 3<p + sin в cos <p;
16. Решить внутреннюю третью краевую задачу для шара
(О < г < а) с граничными условиями:
г\
а) 7Г "*" ^Hr=a = s^n2 ^'
б) -^— -|- Лм|г_ = sin 0 sin ^> -h sin 0 cos 0 cos ^>, h = const;
= const;
|r=a = 1 + sin70cos7<?>, Д = const.

17. Решить внешнюю задачу Дирихле для шара (г > а) с гранич-
граничными условиями, указанными в задаче 14.
18. Решить внешнюю задачу Неймана для шара (г > а) с гранич-
граничными условиями, указанными в задаче 15.
19. Решить уравнение Лапласа внутри шарового слоя (а < г < 6)
с граничными условиями:
а) ti|r=e = °> u\r=b = cos3ei
б) u\r=a=
= 0, «r=l
г=а
г=а
-cos30 9l
=а C°S ' 5,
^ = 15 sin3 ^ sin 3^>;
, -^ = 3 sin ^ cos ^ cos v?;
9r r=b
= sin2 ^cos2v?.
Г r=fe
Ответы.
б)
в)
г)
2. а)
б)
в)
г)
3. а)
б)
в)
г)
4. а)
б)
в)
г)
5. а)
б)

в)
г)
6. а)
б)
в)
г)
д)
7. а)
б)
б)
— Ar-й корень уравнения
в)
где — корень уравнения
г)
10. а)
б)
в)
где — корень уравнения

г)
где — корень уравнения
— корень уравнения
13.
14. а)
б)
в)
г)
15. а)
б)
в)
16. а)
б)
в)
17. а)
б)
в)
г)
18. а)
б)
в)
19. а)
б)
в)
г)
д)

Глава 4
ФУНКЦИЯ ГРИНА
ОПЕРАТОРА ЛАПЛАСА
В предыдущих главах рассматривался метод разделения перемен-
переменных для решения краевой задачи для уравнения Лапласа. Реше-
Решение краевой задачи можно представить в интегральной форме через
соответствующую функцию Грина. В этом параграфе рассмотрены
примеры построения функции Грина оператора Лапласа.
Сначала напомним основные теоретические положения.
Определение. Функция Gi(M, MQ) называется функцией Грина
оператора Лапласа для внутренней задачи Дирихле в области JD,
если она удовлетворяет условиям:
1) Gi(M, MQ)= —-——+ v, где v — гармоническая всюду в D
функция;
2)
Если поверхность 5 является поверхностью Ляпунова, то функция
Грина существует и единственна, а решение краевой задачи
Ди = -F в Д
определяется формулой
и(М) =
Функция Грина для внутренней третьей краевой задачи определя-
определяется аналогично.
Для внутренней задачи Неймана функция Грина определяется не-
несколько иначе.
Определение. Функция Съ(М, MQ) называется функцией Грина
внутренней задачи Неймана в области D, если она удовлетворяет
условиям:
1) G2(M, MQ) = — - —— + v, где v — гармоническая всюду в D
функция;

dG
дп
•м
1
2) -—	=— —, где So — площадь поверхности 5, п — еди-
SQ
ничная нормаль к поверхности 5, внешняя по отношению к
области D.
Так определенная функция Грина Gz(M, MQ) неоднозначна. Она
определена с точностью до постоянной (зависящей от точки MQ). Для
определения этой постоянной на функцию Съ(М, М0) можно нало-
наложить условие
= 0.
Решение краевой задачи
Ли = 0 в D]
^1 -f
dn\s J
при выполнении условия разрешимости $s f dS = О определяется
формулой
и(М)=	A.1)
где С — произвольная постоянная. Если условие разрешимости не
выполнено, то формула A.1) дает решение задачи
Ди = 0 в D\
fa
дп s~~
В двумерном случае (на плоскости) для внутренних краевых задач
функция Грина определяется аналогично с заменой фундаменталь-
фундаментального решения ~д на фундаментальное решение уравнения Лапласа
на плоскости: ^- In -^—.
zw MMMO
Перейдем к внешним задачам.
В трехмерном случае функция Грина определяется единообразно
для всех трех внешних краевых задач. Внешняя задача Неймана
в трехмерном случае имеет единственное решение и осложнений не
вызывает. Для примера напомним определение функции Грина для
внешней задачи Дирихле.
Определение. Функция G(M, MQ) называется функцией Грина
внешней задачи Дирихле, если она удовлетворяет условиям:
1) G(M, М0) = —————+ v, где v — гармоническая всюду в De
функция;

2)
3) G(M, M0) =10 при M -> oo.
Аналогичным образом определяется функция Грина для других
внешних краевых задач в трехмерном случае.
Рассмотрим теперь примеры построения функции Грина для неко-
некоторых областей.
Примеры.
1. Функция Грина задачи Дирихле для шара. Для построения
функции Грина задачи Дирихле для шара
GI =
достаточно найти гармоническую функцию v, которая определяется
как решение краевой задачи:
Дг; = О в шаре 0 < г < а,
"
Для решения этой задачи введем сферическую систему координат
(г, 0, (р) с началом в центре шара, а ось z проведем через точку MQ.
Тогда полюс функции Грина — точка MQ — будет иметь координаты
(го, 0, 0), 0 < г о < а. Поскольку граничное условие не зависит от угла
<р, и решение задачи A.2) от <р зависеть не будет. Поэтому решение
задачи A.2) можно представить в виде ряда
v =
коэффициенты Ап которого определяются из граничного условия.
Разложим функцию ~——— в ряд по полиномам Лежандра:
1
RMMO
(использовано выражение для производящей функции полиномов Ле-
Лежандра, см. приложение, § 5). Следовательно,

Отсюда находим
Таким образом, функция v имеет вид
v =
Используя опять же выражение для производящей функции полино-
полиномов Лежандра, полученный ряд можно просуммировать.
Пусть TI = а2/г0. Точка M(ri, 0,0) есть точка, сопряженная точке
MO относительно сферы г = а. Тогда
v =
где RI =
М и MI. Поскольку п/а = а/го,
расстояние между точками
V =
Следовательно, функция Грина имеет вид
G(M,M0) =
2. Функция Грина внутренней задачи Неймана для шара. Функция
Грина внутренней задачи Неймана представима в виде
G2(M,M0)=	A.3)
где v есть решение следующей краевой задачи:
Дг; = 0 в шаре,
~дп s ~
Введем сферическую систему координат (г, 0, (р) с началом в центре
шара. Ось z проведем через точку MQ. Тогда задача для v принимает
вид
= 0, 0<г<а,
_
дг
4тг дг RMMO
4тга2'

Решение этой задачи не зависит от угла (р и может быть записано в
виде
v =
A.4)
ПОСКОЛЬКУ При Г > Т*о
1 _
RMMQ
получим
д 1
дг RMMO
Подставляя найденное разложение в граничное условие, получим
^г=а~
Отсюда находим
Ап =
Следовательно, функция v имеет вид
11 = 1,2,.
v =
A.5)
где АО — произвольная постоянная. Преобразуем выражение A.5):
v =
Пусть т*1 = а2/г0. Тогда (r/ri < 1):

где RI = Нммг = \/r2 + rJ-2rriCos0, MI = (гьО,0) — точка, со-
сопряженная точке MO относительно сферы г = а,
(см. приложение, § 3). Следовательно,
v =
const.
Таким образом, функция Грина внутренней задачи Неймана для ша-
шара имеет вид
G2 =
При г = а
RI
+ const. A.6)
Поэтому решение краевой задачи
+ const.
ди
дг
может быть записано в виде
= 0,
где
RMMQ =
cos /? = cos в cos OQ + sin в sin во cos(y? — y?o)-
Эта формула называется формулой Неймана.

3. Функция Грина внешней задачи Неймана для шара. Для по-
построения функции Грина внешней задачи Неймана для шара доста-
достаточно решить задачу
Ли = 0 вне шара,
_
дп
v =} 0 на бесконечности.
A.7)
В сферической системе координат (г, 0, <р), начало которой распо-
расположено в центре сферы, а ось z проходит через точку MQ, решение
задачи A.7) (учитывая ее осевую симметрию) можно записать в виде
v =
При г < г0
1
6 1
дп RMMO
Подставляя в граничное условие, получим
dv
дг
Отсюда находим
= О, Ап =
Следовательно,
v =

Полученные ряды можно просуммировать (см. приложение § 3).
Пусть TI = а2/го. Тогда (г\/г < 1):
где RI = RMM! =	, М = (гьО,0) — точка, со-
сопряженная точке MO относительно сферы г = а. Следовательно,
получаем
v =
Таким образом, функция Грина внешней задачи Неймана для ша-
шара имеет вид
где
cos /3 = cos в cos #o + sin 0 sin OQ cos(y? — y?o) •
Получим теперь формулу для решения задачи Неймана вне шара:
At/ = 0, г > а,
л~ =-fF>V>)'
or _

Поскольку
G\
\r—a
получаем
A.8)
R =
Формула A.8) называется формулой Бьеркнеса.
4. Функция Грина для полупространства. Для полупространства
z > 0 функция Грина для задачи Дирихле и для задачи Неймана
строится методом электростатического отображения и имеет вид*)
Gi,2(M,M0) =
причем знак «—» берется для задачи Дирихле, знак «+» — для за-
задачи Неймана, М = (х,у, z), М0 = (ЖО,УО,*О), М\ = (XQ^Q.-ZQ).
5. Если известны собственные функции оператора Лапласа для
данной области, то функция Грина может быть построена в виде ря-
ряда.
Рассмотрим этот метод построения функции Грина на примере
внутренней задачи Дирихле для уравнения Лапласа.
Функция Грина оператора Лапласа для внутренней задачи Дири-
Дирихле есть решение следующей краевой задачи:
Ati = -J(M,Mo) в Д	A.9)
ti|5 = 0, A.10)
где ?(М, MO) — дельта-функция.
Пусть {An}f° и {vn(M)}?° — полные наборы собственных значений
и собственных функций оператора Лапласа для задачи Дирихле в
области D:
Дг; + Аг; = 0 в Д
4с = О, Н| = 1.
*' См.: Свешников А.Г., Боголюбов А.Н., Кравцов В.В. Лекции по математи-
математической физике. М.: Изд-во МГУ, 1993.

Решение задачи A.9), A.10) будем искать в виде ряда по собствен-
собственным функциям vn(M):
и(М)=	A.11)
Поскольку
подставляя A.11) в уравнение A.9), получим
Учитывая, что при всех п Ап / 0, отсюда получаем
ап =
Следовательно, функция Грина G(M, MQ) согласно A.11) имеет
вид
G(M,M0)=	A.12)
Аналогичный вид имеет функция Грина для третьей краевой задачи.
Рассмотрим подробнее случай второй краевой задачи (задачи Ней-
Неймана). Пусть {Ап}о° и {г>п(М)}о° — полные системы собственных
значений и собственных функп|ий задачи Неймана
Дг; + \v = 0 в Д
dv
дп
= о,
s
причем Ап / 0 при п=1,...,оо, Ао = 0, нулевому собственному
значению соответствует нормированная собственная функция
где V — объем области D.
Рассмотрим ряд, аналогичный A.12):
0=	A.13)

Функция G, как легко проверить подстановкой, является решением
следующей краевой задачи:
ДС = -S(M, MQ) + в D,
d_G_
дп
= 0.
A.14)
A.15)
Функция G согласно определению функцией Грина оператора Лапла-
Лапласа для внутренней задачи Неймана не является. Ее можно предста-
представить в виде
G=	A.16)
где w есть решение краевой задачи
= — в Д
dw
A.17)
A.18)
Легко проверить, что условие разрешимости уравнений Пуассона с
граничным условием Неймана
для краевой задачи A.17), A.18) выполнено.
Функцию G, определенную соотношениями A.14), A.15), или A.13),
или A.1б)-A.18), также можно использовать для построения реше-
решения внутренней задачи Неймана для уравнения Лапласа
Дгх = 0 в Д -
дп
= 0.
Действительно, применяя формулу Грина, получим
и(М0) =

Заметим, что согласно A.13) функция G(M, MQ) симметрична отно-
относительно своих аргументов и удовлетворяет условию
= 0.
6. Функция Грина оператора Лапласа для задачи Дирихле в од-
носвязной области на плоскости может быть построена методом кон-
конформного отображения. Это делается следующим образом. Если
функция w = /(ZQ,Z) осуществляет конформное отображение обла-
области D плоскости z на внутренность единичного круга \w\ < 1 плоско-
плоскости w так, что точка ZQ 6 D переходит в центр w = 0 этого круга, то
функция
является функцией Грина оператора Лапласа задачи Дирихле в
области D.
Приведем простейшие примеры.
Построим этим методом функцию Грина для полуплоскости:
—оо < х < оо, у > 0. Функция
/(*<>,*) =
где ZQ — точка, комплексно сопряженная ZQ, отображает верхнюю
полуплоскость (у > 0) на единичный круг, причем точка ZQ переходит
в центр круга. Следовательно, функция Грина имеет вид
G(M,M<>) =
Решение краевой задачи для уравнения Лапласа в верхней полуплос-
полуплоскости (у > 0) с граничным условием
« =
имеет вид
и(х,у) =
Рассмотрим конкретный случай: f(x) = cosx. Тогда
и(х,у) =

Этот интеграл вычислим при помощи теории вычетов, используя
лемму Жордана*)
Следовательно,
гх(х, у) = е~у cos ж.
В качестве второго примера построим функцию Грина задачи Ди-
Дирихле для полосы —оо < х < + оо, 0 < у < тт.
Функция wi = ez осуществляет отображение плоскости z на плос-
плоскость wi так, что прямые у = С плоскости z (О < С < 2тг) переходят в
лучи arg wi = С на плоскости wi. Поэтому полоса 0 < у < тг плоско-
плоскости z отображается на верхнюю полуплоскость (Im wi > 0) плоскости
wi. Точка ZQ переходит в точку wj = ez°. Функция
w =
отображает верхнюю полуплоскость плоскости wi на единичный круг
\w\ < 1 на плоскости w, причем wj переходит в центр w = О этого
круга.
Следовательно, функция, осуществляющая конформное отображе-
отображение указанной полосы на единичный круг так, что ZQ переходит в
центр круга, имеет вид
/(*<>,*) =
Поскольку
\е*-е*°\ =
где z = х + iy, ZQ = XQ + jj/o, функцию Грина можно записать в виде
G(M, Mo) =
A.19)
*) См.: Свешников А.Г., Тихонов А.Н. Теория функций комплексной перемен-
переменной. М.: Наука, 1979.

Решение задачи Дирихле в полосе
Дг/ = 0, -оо < х < + оо, 0<у<тг,
Чу=о = /i(*)> и\у=„ = Мх)
может быть записано в виде
«(*,»)=	A-20)
(эту формулу предлагаем читателю получить самостоятельно, ис-
используя явное выражение A.19) для функции Грина).
Рассмотрим пример, когда
/!(*)= О,
Ых) =
Из формулы A.20) получаем
и(х,у) =
A.21)
Из формулы A.21) видно, что
lim и(х.у) =
а?-++оо
lim u(x,y) =
Х-+ — 00
Можно получить и более точное поведение решения при х -» ±оо.
Поскольку

при х -> —оо (е~х -> + oo)
Следовательно, при х -> — оо
и(х,у)
При х-»+оо е = е"* —>• 0, поэтому, разложив arctg ?^°^y по фор-
формуле Тейлора и сохранив первые члены, получим
Следовательно, при х —>• + оо
и(х,у)
Задачи для самостоятельного решения.
1. Построить функцию Грина внутренней задачи Дирихле для
круга.
2. Построить функцию Грина внутренней 'задачи Дирихле для
полукруга.
3. Построить функцию Грина внешней задачи Дирихле для круга.
4. Построить функцию Грина внутренней задачи Неймана для
круга.
5. Построить функцию Грина внутренней третьей краевой задачи
для круга (|р + hu\r=a = 0, h = const).
6. Построить функцию Грина внешней третьей краевой задачи
для круга (|*г — hu\r_a = О, h = const).
7. Построить функцию Грина задачи Дирихле для кольца
(а <г < Ь).
8. Построить функцию Грина для кольца при первом краевом
условии на внутренней границе (г = а) и втором — на внешней
(г = 6).
9. Построить функцию Грина задачи Дирихле для шаровой обо-
оболочки (а < г < Ь).
10. Построить функцию Грина задачи Дирихле для прямоуголь-
прямоугольника @ < х < а, 0 < у <Ь).
11. Построить функцию Грина внутренней задачи Дирихле для
полушара (х2 + у2 + z2 = a2, z > 0).

Ответы.
1.
где RMMO — расстояние между точками М(г, (р) и МО(ГО,<РО)>
RMMI — расстояние между точками М(г, (р) и M\(r\, <?>о), ri = ^2/^о-
2. G(M,MO) — G(M, MI), где G(A,B) — функция Грина задачи
Дирихле для круга, MI — точка, симметричная MQ относительно
диаметра полукруга.
3.	обозначения см. 1.
4.	обозначения см. 1.
5.
6.
7.
10.

11. G(M, Mo) - G(M, M0*), где G(A, В) — функция Грина задачи
Дирихле для шара, М<* — точка, симметричная точке MQ относи-
относительно плоскости z = 0.

Глава 5
ЗАДАЧИ ДЛЯ УРАВНЕНИЯ
ТЕПЛОПРОВОДНОСТИ
В этой главе рассматриваются начально-краевые задачи для урав-
уравнения теплопроводности с постоянными коэффициентами в ограни-
ограниченной и неограниченной областях простейшего вида.
Уравнение теплопроводности чаще всего возникает при изучении
распространения тепла и диффузии, при определенных предположе-
предположениях оно также появляется в задачах дифракции и распространения
волн различной природы.
Для выделения единственного решения уравнения теплопроводно-
теплопроводности в конечной области ?>, ограниченной замкнутой поверхностью 5,
следует задать начальное и граничное условия. Граничные условия
определяются физической постановкой задачи. В линейных задачах
(которые и рассматриваются) чаще всего используются граничные
условия первого, второго и третьего рода. Полная постановка зада-
задачи имеет вид
ut = а2Дгх + /(М, *), М G Д t > О,
где n — внешняя по отношению к области D нормаль к поверхности
5.
Классическим решением начально-краевой задачи для уравнения
теплопроводности называется функция и(М, t), непрерывная вме-
вместе с первыми производными по М в замкнутом цилиндре Qoo =
D x [0,oo), имеющая непрерывные производные первого порядка по
t и второго порядка по М в открытом цилиндре Q^ , удовлетворяю-
удовлетворяющая в QOQ уравнению теплопроводности, начальному и граничному
условиям.
Необходимым условием существования классического решения на-
начально-краевой задачи для уравнения теплопроводности является
согласование начального и граничного условий
), P€S.

Для уравнения теплопроводности в ограниченной области спра-
справедлив принцип максимума: любое непрерывное в замкнутой области
D х [О, Т] решение однородного уравнения теплопроводности
щ = а2Дгх
достигает своих максимального и минимального значений либо на
поверхности 5, либо в начальный момент времени t = 0.
Начально-краевая задача с граничными условиями первого, вто-
второго и третьего рода (третья краевая задача |^ + hu\s = ц при h > 0)
имеет единственное классическое решение.
Задачи для уравнения теплопроводности в неограниченной обла-
области будут рассмотрены позже.
Как было указано в гл. I, решение общей начально-краевой задачи
может быть представлено в виде суммы
где t/i(M, t) — решение неоднородного уравнения с однородным гра-
граничным условием
), мед <>о,
a t/2(M, t) — решение с неоднородным граничным условием
-^ = а2Дг/2, МЕД * >0,
§ 1. ЗАДАЧИ ДЛЯ УРАВНЕНИЯ
ТЕПЛОПРОВОДНОСТИ В ОГРАНИЧЕННОЙ
ОБЛАСТИ С ОДНОРОДНЫМИ
ГРАНИЧНЫМИ УСЛОВИЯМИ
Рассмотрим начально-краевую задачу с однородными граничными
условиями
ut = а2Дг/ + /(M,t), МЕД t>0,

Как было показано в гл. I, решение этой задачи можно представить
в виде разложения
u(M,t) =
коэффициенты и„ (t) которого являются решениями задачи Коши
е\
-?- + a2Anun = /n(*), t > О, tin@) = ря, п = 1,2,... ,00,
где {vn(M)})° и {An}f° — собственные функции и собственные значе-
значения соответствующей задачи Штурма-Лиувилля для оператора Ла-
Лапласа,
/»(<) =	A-2)
V» =	A-3)
Решение задачи Коши для ип (t) можно записать в виде
«„(«) =	A.4)
где Kn(t — г) = е~а л«(*-т) — импульсная функция Коши.
Таким образом, решение начально-краевой задачи с однородными
граничными условиями можно записать в виде
u(M,t) =
A.5)
где значения (рп и /п(т) определяются формулами A.2), A.3). Лег-
Легко видеть, что первое слагаемое в A.5) представляет решение одно-
однородного уравнения с однородным граничным и заданным начальным
условием, а второе слагаемое — решение неоднородного уравнения с
нулевыми дополнительными условиями.
Рассмотрим примеры решения задач.
1. Решить задачу для уравнения теплопроводности на отрезке
0< х< I:
tit = а?ихх, 0 < х < /, t > О,
и|,=0 = и|,=| = 0,
Ч=о = *('-*)•

Решение. Граничные условия — однородные условия Дирихле.
Поэтому решение будет представлено в виде разложения по собствен-
собственным функциям отрезка с граничными условиями Дирихле, которые
имеют вид (см. гл. II, § 1)
/ ч . к™
vn(x) = sm—ж, п = 1,2, ...,оо.
Поскольку уравнение однородное, решение задачи можно записать в
виде
u(x,t) =
где
=2{,-иг>={°' "=»+»• *.,.,,.
1^4, n = 2fc+l,
Следовательно,
Обратим внимание на то обстоятельство, что полученный ряд тем
быстрее сходится, чем больше t, так что при достаточно больших t
можно ограничиться несколькими первыми членами ряда. Кроме то-
того, видно, что скорость сходимости ряда зависит от скорости нараста-
нарастания собственных значений с увеличением индекса, т.е. от размеров
области. Это обстоятельство характерно и для более сложных рядов,
дающих решение уравнения теплопроводности.
2. Решить задачу для уравнения теплопроводности внутри круга
0<г<г0:
ut = а2 Дм,
Решение. Поскольку уравнение однородное, решение записывается
в виде

где vn (г, (p) — собственные функции круга с граничным условием
Дирихле. Они имеют вид
«>п(г,р)=	k =1,2,..., п = 0,1,...,
где А?П' есть решение уравнения «Ли у AJj,n' г0 ] = 0. Поэтому решение
удобнее записать в развернутом виде:
и =
Коэффициенты Ank и Bnk определяются из начального условия
Отсюда сразу получаем
Bnk = О при всех п = 0, 1,..., * = 1,2,...,оо,
Ank = О прип/2, k= 1,2,..., оо,
Следовательно,
и =
3. Решить задачу для неоднородного уравнения внутри круга
О < г< г0:
ut = а2Ди + At,

Решение. Уравнение теплопроводности решается внутри круга с
однородными условиями Дирихле. Следовательно, разложение нуж-
нужно вести по собственным функциям задачи Дирихле для круга, ко-
которые имеют вид (см. гл. II, § 5)
<p)=	n = 0,1,...,оо, 4=1,2,...,
Лп)
где Xk являются корнями уравнения
= 0.
Начальное условие нулевое, правая часть уравнения At не зависит
от угла (р. Следовательно, решение тоже не зависит от угла (р и
записывается в виде
ti(r,*) =
где Uk(t) есть решение задачи Коши
, 00,
=о = °-
а Д определяется соотношением
Решение задачи для Uk(t) имеет вид
Uk(t) =
Следовательно,
и =

4. Решить задачу об остывании шара радиуса г0, на границе ко-
которого поддерживается нулевая температура, а в начальный момент
распределение температуры в шаре равно Arsin0sin<p, (A = const).
Решение. Пусть u(r, 0, (p,t) — температура в точке (г, 0, (р) в мо-
момент времени t. Тогда процесс остывания шара описывается началь-
начально-краевой задачей
щ = а2 Дм в шаре 0 < г < TO, t > О,
ti|t=0 = Ar sin в sin (p.
Поскольку собственные функции задачи Дирихле для шара имеют
вид (см. гл. II, § 13)
k= 1,2,..., oo, n = 0,1,2,..., oo, m = 0, l,...,n,
где A? ' — корень уравнения
= 0,
решение задачи удобно записать в развернутом виде (в виде тройного
ряда):
и =
Коэффициенты А^пт и В^пт определяются из начального условия
= Arsm0smy>.
Так как sin в sin (р = Р± '(cos в) sin <p, отсюда сразу получаем
Aknm = 0 при всех fc, n, m,
= 0 при всех Аг, п ф 1, т / 1,

а для определения коэффициента Bkii (k = 1, 2, . . . ) получаем соот-
соотношение
откуда
t=l,2,
Следовательно,
Учитывая вид начального условия
(начальное условие уже разложено по сферическим функциям), ре-
решение поставленной задачи можно сразу искать в виде разложения
и =
коэффициенты которого определяются из начального условия.
5. Найти температуру прямого однородного бесконечного стержня
прямоугольного сечения, внутри которого имеются равномерно рас-
распределенные тепловые источники постоянной мощности. Боковая по-
поверхность стержня теплоизолирована, а начальная температура рав-
равна нулю.
Решение. Пусть м(ж,г/, t) — температура в точке (ж, у) в момент
времени t (в силу однородности стержня зависимости от продольной

координаты z нет). Для функции и получаем следующую начально-
краевую задачу в прямоугольнике 0<ж</1,0<у</2:
ut = a2 Ди + g, 0<x</i, 0<t/</2 (q = const),
«Uo = О,
ди - _ ди | _ <9м - _ ди | _
fo U=0 ~ foTl*=/i ~ 5^'У=0 ~ 5Г/ 'у='а ""
Решение этой задачи строится в виде ряда по собственным функциям
задачи Неймана для прямоугольника, которые имеют вид
7ГП	7ГШ
1, cos —ж cos -—t/, n,m= 1,2,...,оо.
«1	«2
Выделена собственная функция, равная 1, соответствующая нулево-
нулевому собственному значению. Остальные собственные значения равны
Anm =	n,m = 1,2,...
Решение задачи имеет вид
где unm(t) (n, m = 0,1,...) есть решение задачи Коши
dunm
dt
— /nm> ^лт|е=0 — О,
где
fnm =
g, n = 0, m = О,
О, n/0, m/0.
Следовательно, отличной от нуля будет только функция г*оо@> ко~
торая является решением задачи
= д> и0о(о) = о (АОО = О).

Отсюда
Таким образом, распределение температуры не зависит от координат
х и у и имеет вид
Замечание 1. Решение (т.е. температура стержня) нарастает по вре-
времени. Этого следовало ожидать из физических соображений, по-
поскольку источники постоянной мощности действуют в области с те-
плоизолированной границей, отвода тепла из которой нет. Это и при-
приводит к неограниченному росту температуры со временем.
Замечание 2. Рассматриваемую задачу можно было решить быстрее
и проще, если учесть следующие соображения. Граничные усло-
условия — это однородные условия второго рода, а правая часть урав-
уравнения от пространственных координат не зависит. Естественно, воз-
возникает предположение, что и само решение и не будет зависеть от
координат х и у: и = u(t). Тогда для u(t) сразу получается задача
"* = *> Ч=о = °>
решение которой и = qt. Таким образом, найдено решение исход-
исходной задачи, зависящее только от t. В силу теоремы единственности
другого решения исходной задачи нет.
6. Однородное тело, ограниченное замкнутой поверхностью 5, в
начальный момент имело постоянную температуру То. Поверхность
тела теплоизолирована. Найти температуру тела в любой момент
времени.
Решение. Для температуры тела ti(M, t) получаем следующую за-
задачу:
щ = а2 Дм в D при t > О,
«Lo= To, ?fls = 0.
Получим решение этой задачи из физических соображений, предо-
предоставляя читателю возможность получить его изложенной выше ме-
методикой разложения в ряд по собственным функциям. Поскольку
поверхность тела теплоизолирована, то нет отвода тепла из области
D. Следовательно, постоянная температура тела будет оставаться
неизменной:

7. Найти температуру однородного стержня длины /, если его бо-
боковая поверхность теплоизолирована, начальная температура равна
нулю и температура концов поддерживается равной нулю. Вдоль
стержня распределены источники тепла с плотностью
где а — вещественный параметр.
Решение. Начально-краевая задача, моделирующая описанный в
условии задачи процесс, имеет вид
щ = а2ихх + eatx(l-x), 0< ж < /, t > О,
4=0 = 0'
4=о = 4=1 =°-
Решение задачи записывается с помощью формулы A.5), в которой
в силу однородности начальных условий (рп = О (п = 1,2,...).
Собственные функции отрезка в случае граничных условий Дирихле
имеют вид (см. гл. II, § 1)
/ ч	• 7ГП
vn(x) = sm— ж, п = 1,2,...,
причем квадрат нормы равен ||v||2 = ?.
Таким образом, из формул A.5) и A.2) получаем
!!(*,*) =
Вычисляя интегралы в правой части последней формулы:
получим окончательный ответ:

Из последней формулы вытекает, что при а < 0 температура тела
при t -> + оо стремится к нулю. При а > О температура стержня при
t — > + оо зависит от времени по такому же закону, что и плотность
распределенных источников тепла (система выходит на стационар-
стационарный режим) :
lim e-atu(x,t) =
t-Ц-оо	V '
8. Найти температуру однородного стержня длины /, если его бо-
боковая поверхность теплоизолирована, начальная температура равна
нулю и температура концов поддерживается равной нулю. В стерж-
стержне действует сосредоточенный источник тепла мощности Q, располо-
расположенный в точке XQ.
Решение. С помощью понятия E-функции начально-краевую зада-
задачу можно поставить следующим образом:
ut — а2ихх + — 6(х- ж0), 0<ж</, t > О,
ср
где с — удельная теплоемкость, р — линейная плотность, а2 = — ,
где k — коэффициент теплопроводности.
Данная задача отличается от предыдущей только видом неодно-
неоднородности уравнения
ср
С помощью формул A.5) и A.2) решение записывается в виде
Используя свойство J-функции, получим окончательный ответ:
9. Решить задачу об остывании однородного круглого цилиндра
Qr°>1 радиуса г о и высоты /. Поверхность цилиндра теплоизолирова-
на, а начальная температура равна
,B) v	0^

2
где А — некоторая постоянная, ц\} — первый корень уравнения
AM = о.
Решение. Поскольку поверхность цилиндра теплоизолирована, по-
поток тепла через нее равен нулю, а так как поток тепла через поверх-
поверхность пропорционален нормальной производной от температуры, в
результате получаем однородные граничные условия Неймана.
Начально-краевая задача, моделирующая процесс остывания ци-
цилиндра, имеет, таким образом, следующий вид:
ut = а2Ди, М G Qr°\ t > О,
B)	о
—~г) cos2<pcos -у*»
ди. _ ди. _ди. _
дг 1г=г0 - U' Qz 1ж=0 - Qz \z=l ~ U'
Согласно формуле A.5) решение задачи записывается в виде раз-
разложения в ряд по собственным функциям цилиндра (см. гл. II, § 9):
Для определения коэффициентов разложения воспользуемся началь-
начальным условием
Сравнивая коэффициенты в обеих частях последнего равенства,
получим
^122 = 1,
= 0, п/2, т/2, fc = 2,3,...,

откуда следует окончательный ответ:
10. Рассмотреть процесс остывания шарового слоя ri < г < г2,
на внутренней и внешней поверхностях которого происходит конвек-
тивный теплообмен со средой, имеющей нулевую температуру. На-
Начальная температура шара является линейной функцией радиуса:
/(г) = Аг.
Решение. Начально-краевая задача имеет следующий вид:
-•'+• -<-<•>• •>«•
поскольку в силу условия задачи температура шарового слоя явля-
является функцией радиуса и времени: и = u(r,t).
Для решения поставленной начально-краевой задачи возможны
два подхода. Во-первых, можно воспользоваться разложением ре-
решения по собственным функциям шарового слоя, рассмотренным в
гл. II, § 14. При этом в силу сферической симметрии рассматривае-
рассматриваемой задачи в разложении будут участвовать только цилиндрические
функции Бесселя J\ii(\f\r) и Неймана ЛГ1/2(л/Аг), которые выража-
выражаются через элементарные функции согласно формулам
/ 2
Ni,2(x) = J — cosx.
V 7ГХ
Во-вторых, можно свести поставленную задачу к рассмотренной в
гл. II, § 1 задаче для отрезка. Мы используем второй путь, предла-
предлагая читателю в качестве упражнения решить ту же задачу первым
способом.
Введем функцию v(r, t) = ru(r,t). Для нее получается следующая

начально-краевая задача:
г1<г<г2)
Л
=0.
г=г2
Согласно формуле A.5) решение этой задачи можно записать в виде
ряда
v(r,t) =
где Лп(г) и Лп — собственные функции и собственные значения за-
задачи Штурма-Лиувилля
Д" + АД = 0, ri < г < г2,
г=п
.
Г2/ 1г=г2
Сравнивая эту задачу с задачей Штурма-Лиувилля, рассмотрен-
рассмотренной в гл. II, § 1, видим, что, для того чтобы использовать форму-
формулы гл. II , в них необходимо положить c*i = #2 = 1, /?i = ^i + ;r~,
/?2 = /i2 — т", I = TI — ri, x = r — ri. Тогда из формулы A.11) гл. II
будет следовать выражение для собственных функций
Эти собственные функции не являются нормированными. Выраже-
Выражение для квадрата нормы имеет вид (см. гл. II, § 1)

Собственное значение Лп есть n-й корень характеристического урав-
уравнения, получающегося из уравнения A.9) гл. II:
!-Г1)=	A.6)
Собственные функции Rn(r) можно записать более компактно
(см. гл. II), полагая
sin i/n =
A.7)
COS l/n =
так что
i/n = arctg-——V-
Собственная функция будет иметь вид
Rn(r) = sin \/\^(r — ri) + vn\ .
Таким образом, для функции v(r, t) получается разложение
Для определения коэффициентов разложения воспользуемся началь-
начальным условием
v(r,0} =
откуда для коэффициентов Сп получается формула
Сп =
Интеграл в правой части формулы легко вычисляется двукратным
интегрированием по частям:

Для дальнейших преобразований воспользуемся формулами A.6) и
A.7). Имеем
Sn
COS \А(г2 - ri) +
1/nJ =
откуда
Используя A.6), получим
Аналогично из формулы A.7) следует, что
С помощью двух последних формул выражение для интеграла можно
привести к следующему виду:
Таким образом, для коэффициентов разложения получаем формулу
Сп =

Решение исходной задачи u(r,i) имеет следующий вид:
где
ЦД»1Г =
2 _
Лп — n-й корень уравнения
§ 2. ЗАДАЧИ ДЛЯ УРАВНЕНИЯ
ТЕПЛОПРОВОДНОСТИ В ОГРАНИЧЕННОЙ
ОБЛАСТИ С НЕОДНОРОДНЫМИ
ГРАНИЧНЫМИ УСЛОВИЯМИ
Рассмотрим теперь начально-краевую задачу для уравнения те-
теплопроводности с неоднородным граничным условием
ut = a2 Aw
«|t=o = 0,
ди л
в D,
О,
W
Общая схема решения таких задач, как это указано в гл.1, состоит
в следующем. Вместо функции u(M,t) вводится новая неизвестная
функция v(M, t) соотношением
где функция w(M} i) выбрана так, что она удовлетворяет заданному
граничному условию
dw „

Для функции v(M, t) получается следующая задача:
), МеД О О,
dn "
где /(M, t) = a2Aw — wt. Решение этой задачи рассмотрено в преды-
предыдущем параграфе.
Таким образом, основным является выбор функции w(M, ?), ко-
которая должна быть достаточно гладкой и удовлетворять заданному
граничному условию. Этими требованиями функция w(M, t) опреде-
определяется неоднозначно. Появившейся свободой выбора w(M} t) следует
распорядиться так, чтобы задача B.1) для v(M, t) оказалась возмож-
возможно более простой.
Чаще всего функцию w(M, t) выбирают гармонической по про-
пространственной переменной, т.е. как решение краевой задачи
= О в Д
dw
а-о— Ч- pw
B.2)
в которой переменная t рассматривается как параметр. При таком
выборе функции w следует проявлять осторожность при решении за-
задачи с граничным условием Неймана, поскольку задача B.2) может
не иметь решения. Тогда функцию w нужно выбрать как-то иначе.
Рассмотрим примеры решения задач с неоднородным граничным
условием.
1. Решить уравнение теплопроводности на отрезке 0 < х < I:
ti|t=o = 0,
u\x=Q = A, u\x=i — В , Л, В = const.
Решение. В данном случае функцию w удобно выбрать как реше-
решение задачи
wxx = 0 , 0 < х < I ,
Функция w зависит только от ж и имеет вид
w = w(x) = —-—х + А .

Пусть и = v + w. Для функции v(x, t) получаем задачу
vt = a2vxx , 0 < х < /, t > О,
i	/ ч В~А
v\t=o = -w(x) = -—-—х- Л,
vU=o = v|*=/ =0.
Решение этой задачи имеет вид
v(x,t) =
где
сп =	п=1,2,,
Следовательно,
2. Найти процесс нагревания однородного бесконечного прямого
кругового стержня радиуса TO , на поверхности которого поддержи-
поддерживается температура TO cos (p sin wt. Начальная температура стержня
нулевая.
Решение. Пусть и — температура стержня. Функция и будет за-
зависеть только от г, (р и ty и для нее получается начально-краевая
задача для уравнения теплопроводности в круге:
ие = а2Ди, 0 < г < г0 , 0<у?<2тт, *>0,
ti|t=o = 0,
г/|г=Го = TO cos (p sin wt, TO = const.
Пусть u(M, t) = v(M,t) + w(M)sinu;<, a функцию w(M) выберем как
решение задачи Дирихле для уравнения Лапласа:
Дм = 0 в круге 0 < г < г0 ,
Hr=r0 = TO cos у?.

Решение этой задачи имеет вид
w = То — cos (р.
7*0
Для функции v(r, у?, t) получается задача
vt = a2At; — TQO; — cosy?cosutf,
ro
v|t=o = 0 , v\r=ro = О .
Решение этой задачи, учитывая структуру правой части уравнения,
можно записать в виде
v =
где \k — корень уравнения Л(лД^г0) = 0, k = 1, 2, ... Функция
Uk(t) есть решение следующей задачи Коши:
duk
—— +
^|t=o = 0, k= 1,2, ...,сю,
где
t=l,2,...,oo.
Решая задачу Коши, найдем
uk(t) =
Следовательно,
и =
где коэффициенты Д заданы формулой B.3).

3. Найти распределение температуры в однородном бесконечном
прямом круговом цилиндре радиуса TQ, на поверхности которого за-
задан постоянный тепловой поток. Начальная температура равна ну-
нулю.
Решение. Для температуры и получается начально-краевая зада-
задача внутри круга с неоднородным граничным условием Неймана
ut = a2 Aw
в круге 0 < г < r0, t > О,
Зи
-г-
дг
= q = const .
В данном случае функцию w нельзя выбрать как решение уравнения
Лапласа в круге с граничным условием
dw
Г=Г0
поскольку такая задача решения не имеет. Выберем функцию w в
виде
w=
и сделаем замену
dw
—
Г=Г0
Для функции v(r,(p,t) получается следующая начально-краевая за-
задача:
2 л	2«2
Vt = а Ли + ——q , 0 < г < TO , ? > 0,
я	B-4)
_ Г1	OV _ V 7
Решение этой задачи будем строить в виде разложения в ряд по соб-
собственным функциям задачи Неймана для уравнения Лапласа в кру-
круге, которые имеют вид
где \ь — &-й корень уравнения J'n (v/A^n' TO) = 0, причем нулево-
нулевому корню Ад = 0 соответствует собственная функция, равная 1.
Поскольку правая часть уравнения и начальное условие не зависят

от угла у?, в разложении будут присутствовать только собственные
функции, также не зависящие от (р :
Итак, решение задачи B.4) записывается в виде
где Ak(t) определяются при каждом k = О,1,2,... как решение зада-
задачи Коши
Ak\t=o =
где
/о =	Л =
Вычислим Д и (pk'*
в силу ортогональности собственных функций, соответствующих раз-
различным собственным значениям,
так как
Для вычисления интеграла, входящего в формулу для у?^, восполь-
воспользуемся соотношением (см. приложение, § 4, п = 0)

Тогда получим
поскольку
= 0.
Так как
Ш* =
запишем
4>ъ =	k Ф 0 •
Таким образом, коэффициент АО(Г) является решением задачи
и равен
A0(t) =
Остальные коэффициенты Ak(t) ,k -ф. О, являются решением задачи
dAk .
dt
00,
Они равны
Ak(t):
Следовательно,
v =

Решение исходной задачи имеет вид
и = w + v =
4. Найти распределение температуры в однородном шаре радиуса
г0, если начальная температура шара равна нулю, а на поверхности
задан тепловой поток kP% (cos 9) sin у?, где k — коэффициент тепло-
теплопроводности.
Решение. Введя сферическую систему координат, центр которой
совпадает с центром шара Кг°, для температуры шара u(M, t) =
= и(г, 9, у?, t) получим следующую начально-краевую задачу:
М Е Кг° , * > О,
Г=Го
= Р2 ' (cos 0) sin у? .
Функция в правой части граничного условия есть сферическая функ-
функция У2A)@, <р) = P2A)(cos0)sinv>.
Будем искать решение начально-краевой задачи в виде суммы и =
= v+w, причем в качестве функции w выберем решение задачи Ней-
Неймана для уравнения Лапласа в шаре:
Ди; = 0 , М G Кг° ,
~ = P2A)(cos0)sinv?.
Г=Го
Заметим, что для этой задачи выполняется необходимое условие
разрешимости
Решение задачи Неймана имеет вид
w =

где С — произвольная постоянная. Положим С = 0.
Для функции v(M, t) получается начально-краевая задача для од-
однородного уравнения с неоднородным начальным и однородным гра-
граничным условиями
V\t=Q =
т =«•
ОГ г=г0
Решение этой задачи запишем в виде ряда A.5), где /п(т) = 0, ра-
радиальные собственные функции имеют вид Rk(r) =	, а
\k (k = 1,2,...) — корни характеристического уравнения
= 0
(см. гл. II, § 13),
V =
Выражение для квадрата нормы собственной функции дается фор-
формулой
2
\\Rk\\2 =
Для определения коэффициентов разложения Ak (fc = 1,2,...) вос-
воспользуемся начальным условием для функции v(M, t):
что дает следующее выражение:

Отсюда
Таким образом, для функции v(M, t) получаем выражение
и окончательно имеем
где А/с — fc-й корень уравнения
= 0.
5. Найти распределение температуры в однородном шаре радиуса
г0, если начальная температура шара равна С/о, а внутрь шара через
его поверхность подается постоянный тепловой поток q.
Решение. Введем сферическую систему координат, центр которой
совпадает с центром шара. В силу условий задачи температура шара
будет функцией радиуса и времени и = w(r, ?), для которой получа-
получается следующая начально-краевая задача:
щ = а2 Дг/, 0 < г < г0 , t> О ,
i	тт 1 ди
u\t=Q = С/о , k-
где k — коэффициент теплопроводности.
Будем искать решение в виде и = v(r,t) + u>(r,?), где функцию
w(r, t) выберем следующим образом:

Заметим, что в отличие от предыдущей задачи функцию w нельзя вы-
выбирать как решение задачи Неймана для уравнения Лапласа в шаре
/?г°, поскольку для этой задачи не будет выполняться необходимое
условие разрешимости
При любой функции f(t) функция w(r, t) удовлетворяет гранично-
граничному условию задачи. Для функции v(r, t) получается неоднородное
уравнение
Подберем функцию f(t) так, чтобы выражение в круглых скобках
было равно нулю. Получим f(t) =	t -f С , где постоянную С
определим ниже. Итак,
w(r,t) =
Начальное условие для функции v(r, t) имеет вид
v|t=o =
Полагая С = (/о, получим v\ _ =
В результате для функции v(r, t) получается начально-краевая за-
задача для однородного уравнения с неоднородным начальным и одно-
однородным граничным условиями
= ° 1-519+Г-5Г? • 0<r<r0,
= 0.
dv_
дг
Г=Г0
Введя функцию V(r, t) = rv(r, t), получим для нее начально-краевую
задачу на отрезке
Vt = a2Vrr, 0<r<r0, О О,
v\ =-<?- ^-Ivi ^о
l*=o 2krQ ' 5r r0 I'-^o

Решение этой задачи будем искать в виде разложения по собственным
функциям задачи Штурма-Лиувилля
R" + XR = О , 0 < г < г0 ,
Я| =0, R'-—R\ = 0,
|г=0	' Го |г=г0 '
рассмотренной в гл. П.
Система собственных функций имеет вид {г, sin\A^r}, причем
собственной функции Ro(r) = г соответствует собственное значение
АО = 0, а собственные значения An , n = 1,2, . . ., соответствующие
собственным функциям Rn(r) = sin\/A^r, являются решением транс-
трансцендентного уравнения
(n = 1,2,...).
Воспользовавшись формулой A.5), получим
V(r,t) =
Из начального условия для функции V(r, t) определим коэффициен-
коэффициенты разложения:
П=о =
откуда
С0 =
Сп =
При вычислении коэффициентов Сп (п = 1,2,...) мы воспользова-
воспользовались трансцендентным уравнением для собственных значений и вы-
выражением для квадрата нормы:

Таким образом, для функции V(r, t) получается выражение
V(r,t) = -
откуда получим
и = w+ -V =
г
где Лп — n-й корень уравнения tgV%To =
§ 3. ЗАДАЧИ ДЛЯ УРАВНЕНИЯ
ТЕПЛОПРОВОДНОСТИ НА
БЕСКОНЕЧНОЙ ПРЯМОЙ
Рассмотрим начальную задачу на бесконечной прямой Ж1 для
уравнения теплопроводности с постоянными коэффициентами. Вве-
Введем обозначения О, = Ж1 х @,-foo) , ft = Ж1 х [0,-foo) . Начальная
задача ставится следующим образом:
Ut = a2uxx + f(x,t), (я,*) €П,
u(x,Q) = <p(x) ж ЕМ1.	( ' '
Классическим решением задачи C.1) для уравнения теплопровод-
теплопроводности на бесконечной прямой называется функция u(x,t), непрерыв-
непрерывная в замкнутой области Q, имеющая непрерывные поизводные пер-
первого порядка по t и второго порядка по ж в открытой области Q,
удовлетворяющая в Q уравнению теплопроводности и при t -> 0 на-
начальному условию.
Если функция <р(х) непрерывна и ограничена в М1, а функция
f(x,t) непрерывна по совокупности аргументов и ограничена в Q, то
задача C.1) имеет единственное классическое решение.
В случае менее гладких функций (р(х) и f(x,t) задача C.1) может
иметь обобщенное решение.
Для решения начальной задачи C.1) удобно использовать метод
интегрального преобразования Фурье. Общая схема применения ме-
метода интегрального преобразования Фурье к решению начальных за-
задач на бесконечной прямой приведена в гл. I.
В качестве примера в данном параграфе с помощью преобразова-
преобразования Фурье рассмотрим задачу для уравнения теплопроводности на
бесконечной прямой и запишем для ее решения формулу Пуассона.

Для решения задачи C.1) применим преобразование Фурье с ядром
e~tXx. Обозначим через U(\,t), F(\,t) и Ф(А) образы Фурье функций
u(x,t), f(x,t) и tf>(x) соответственно
U(\,t) =
F(\,t) =
Ф(А) =
Будем предполагать, что выполняются условия существования инте-
интеграла Фурье (это заведомо выполнимо для классического решения
задачи C.1)) и что функция u(x,t) и ее частные производные доста-
достаточно быстро стремятся к нулю при х -> ±оо. Предположим также,
что интеграл для U(\,i) можно дифференцировать по переменной t
под знаком интеграла.
Умножим уравнение теплопроводности и начальное условие на
-Д-е~'Л* и проинтегрируем по х от —оо до + оо. Проинтегрировав
затем полученный в правой части интеграл дважды по частям и учи-
учитывая, что подстановки на ±оо обратятся в нуль, получим следую-
следующую задачу Коши в пространстве образов:
Ut + a2A2!7 = F, t >0 ,
U\t=o = Ф(А).
Решение этой задачи записывается с помощью импульсной функции
в следующем виде:
U(\,t) =
Подставим выражения для образов Фурье F(A, t) и Ф(А) и вернемся
к оригиналу, используя формулу обратного преобразования Фурье.

Меняя порядок интегрирования, получим
u(x,t) =
Обозначим
G(x,t,t)
Используя интеграл*^
будем иметь
G(x,t,t)=	C.2)
Функция G(x,?, ?), определяемая формулой C.2), называется фунда-
фундаментальным решением уравнения теплопроводности на бесконечной
прямой.
Итак, решение задачи C.1) представляется формулой
«(*,<) =	C.3)
Отметим, что в силу линейности задачи C.1) решение C.3) предста-
представляет сумму решений двух задач. Функция
C.4)
*' См.: Свешников А.Г., Боголюбов А.И., Кравцов В.В. Лекции по математиче-
математической физике. М.: Иэд-во МГУ, 1993.

дает решение начальной задачи для неоднородного уравнения тепло-
теплопроводности с однородным начальным условием (<р(х) = 0), а функ-
функция
u(x,t)=	C.5)
— решение задачи для однородного уравнения теплопроводности
(f(x,t) = 0) с неоднородным начальным условием. Интеграл C.5)
называется интегралом Пуассона.
Рассмотрим примеры решения начальных задач для уравнения те-
теплопроводности на бесконечной прямой.
1. Решить задачу об остывании однородного бесконечного стерж-
стержня, если тепловой режим определяется кусочно-постоянной началь-
начальной функцией следующего вида:
Г
= <
\
ГЬ х<0,
Г2, х > 0.
Начальной задачей, описывающей процесс остывания стержня, явля-
является задача для однородного уравнения теплопроводности
Решение. Воспользуемся формулой C.5) и сделаем замену z =
«(*,*) =
Учтем теперь, что имеет место формула (интеграл Пуассона)

и введем функцию ошибок
ФН =	C.6)
Очевидно, Ф@) = О, Ф(+оо) = 1. Легко показать, что функция Ф^)
нечетная:
Отсюда Ф(—оо) = — 1.
С помощью функции ошибок Ф ответ задачи можно записать в виде
«(*,*) =	C-7)
Отметим, что начальная функция <р(х) не является непрерывной, а
претерпевает разрыв в точке х = 0. В этом случае решение задачи
Коши, представимое интегралом Пуассона C.5), уже не будет клас-
классическим, а имеет особую точку х = 0. Проанализируем поведение
решения задачи Коши для уравнения теплопроводности в особой точ-
точке, используя формулу C.7).
Пусть х > 0. Тогда, переходя к пределу при t -> 0, получим, что
2^- -> +оо, *(з^т?) -» 1 и limt_>0,*>ouOM) = Т2. Пусть х < 0.
Тогда -?j- -» -оо, Ф(-?7-) -» -1 и limt-+otX<QU = 7\. Перейдем в
Zdyl	4Uv "
формуле C.7) к пределу сначала при х -> 0, а затем при t -> 0. В
результате будем иметь lim^o,х-+ou(xit) = *^ 2. Из приведенных
рассуждений вытекает, что значение решения задачи Коши в особой
точке х = 0 в начальный момент времени t = 0 зависит от способа
перехода к пределу:
Более того, если рассмотреть одновременный переход к пределу при
х —> 0, t —? 0 вдоль кривой г~7" = w> где w G М1, то с помощью
формулы C.7) получим
= W

и при w ? Ж1 получим любое значение, заключенное в пределах от
Т\ до Тз, поскольку — 1 < Ф(ги) < 1.
Можно показать, что если функция <р(х) — кусочно-непрерывная
и ограниченная на прямой ж ? Ж1 функция с конечным числом точек
разрыва, то формула C.7) определяет решение однородного урав-
уравнения теплопроводности при х ? Ж1, t ? (О,Т], ограниченное при
t ? [О, Т] и непрерывно примыкающее к функции <р(х) в точках ее
непрерывности.
2. Решить задачу Коши для однородного уравнения теплопровод-
теплопроводности:
ut = -ихх , х ? Ж1, * > О,
Решение. Воспользуемся формулой C.5) при а = |:
u(x,t) =
Для выполнения интеграла в правой части формулы рассмотрим ин-
интеграл
Имеем
откуда, обозначая
s =
получим
Таким образом,
«(*,*)=	C.8)

Заметим, что в отличие от предыдущей задачи начальная функция
(р(х) = е~х sin x является непрерывной всюду на бесконечной прямой
Ж1. Формула C.8) представляет собой классическое решение задачи,
непрерывно примыкающее к начальной функции:
limu(x,t) =
3. Найти процесс изменения температуры однородного бесконеч-
бесконечного стержня с равномерно распределенными источниками, мощ-
мощность которых изменяется во времени по закону f(t) = sint. На-
2
чальная температура стержня равна (р(х] = е~х .
Решение. Процесс изменения температуры стержня описывается
следующей начальной задачей:
ut = a2uxx+ sin*, zEM1, t > О,
Ее решение дается формулой C.3):
u(x,t) =
где G(x, ?, t) =	— фундаментальное решение уравнения
теплопроводности .
Подсчитаем интеграл
Поскольку
получаем

где обозначено
s =
Посчитаем второй интеграл. Положив s = 2aJ*-T' ^Удем иметь
/2 =
Таким образом окончательно получим
u(x,t] =
4. Решить задачу Коши для уравнения параболического типа на
бесконечной прямой:
ut = а2ихх -Ati, x Е Ж1 , t > О,
где h > 0 — некоторая постоянная.
Решение. Сделаем замену функции
Тогда
ut = -hu -f e~htvt
и для функции v(x,t) получается следующая задача Коши:
vt = a2vxx ,
x G M1 , t > О,
Решение этой задачи записывается формулой C.5):
v(x,t) =

откуда следует выражение для решения исходной задачи:
ti(x,*)=	C.9)
Задачи 1 и 2 моделируют процесс остывания бесконечного стержня
с теплоизолированной поверхностью, нагретого до начальной темпе-
температуры (р(х). Задача 4 моделирует процесс остывания бесконечного
стержня, нагретого до температуры <?>(х), если через боковую поверх-
поверхность стержня происходит теплообмен по закону Ньютона с внешней
средой, температура которой равна нулю (h > О — коэффициент те-
теплообмена). Из формулы C.9) следует, что чем больше ft, тем скорее
происходит процесс остывания. Случай ft = 0 соответствует тепло-
изолированной боковой стенке.
§ 4. ЗАДАЧИ ДЛЯ УРАВНЕНИЯ
ТЕПЛОПРОВОДНОСТИ НА
ПОЛУБЕСКОНЕЧНОЙ ПРЯМОЙ
Рассмотрим начально-краевую задачу на полубесконечной прямой
Ж ЕЕ{0<х<+оо} для уравнения теплопроводности с постоянными
коэффициентами. Введем обозначения fi+ ЕЕ М х [0,-foo), fi+ =
Ж+ х @,-foo), где М+ = {0 < х < +оо}. Начально-краевая задача
с граничными условиями первого, второго и третьего рода ставится
следующим образом:
щ = а2ихх + /(х,Г), (х,*) € П+ ,	D.1)
*|t=o = ?(*)> *е!+, D.2)
<*|? + /Н=о = М*), *>0,	D.3)
где Н + \/3\ ± 0.
Классическим решением начально-краевой задачи D.1)-D.3) называ-
называется функция м(х,?), непрерывная вместе с первыми производными
по х в замкнутой области U+, имеющая непрерывные производные
первого порядка по t и второго порядка по х в открытой области fi+,
удовлетворяющая в fi+ уравнению теплопроводности, начальному и
граничному условиям.
Заметим, что в случае граничных условий первого рода (а =
О, /? = 1) непрерывной дифференцируемости u(x,t) по х в замкну-
замкнутой области fi+ не требуется, достаточно непрерывности w(x, t) в fi+.

Классическое решение задачи D.1)-D.3) может существовать лишь
при выполнении условия согласования начального и граничного усло-
условий
В силу линейности задачи D.1)-D.3) можно провести ее редукцию
и представить решение u(x,t) задачи D.1)-D.3) в виде суммы двух
функций u(x,t) = Ui(x,t) + U2(x,t),rRe ui(x,t) — решение задачи для
неоднородного уравнения с неоднородным начальным и однородным
граничным условиями, м2(х,?) — решение задачи для однородно-
однородного уравнения с однородным начальным и неоднородным граничным
условиями.
Одним из методов решения начально-краевой задачи для урав-
уравнения теплопроводности на полубесконечной прямой в случае одно-
однородных граничных условий является метод продолжения начальных
данных. В п. 1 настоящего параграфа этот метод рассмотрен для
случая линейного однородного граничного условия общего вида и
проиллюстрирован на примере решения начально-краевых задач с
однородными граничными условиями первого, второго и третьего ро-
рода.
Эффективным методом решения начально-краевых задач для
уравнения теплопроводности на полупрямой является метод инте-
интегрального преобразования Фурье, общие принципы применения ко-
которого изложены в гл. I, § 4. В настоящем параграфе рассматривает-
рассматривается применение метода интегрального преобразования Фурье на полу-
полупрямой к уравнению теплопроводности в случае граничных условий
первого, второго и третьего рода.
1. Задачи для уравнения теплопроводности на полу беско-
бесконечной прямой с однородными граничными условиями.
Начально-краевая задача для уравнения теплопроводности на по-
полубесконечной прямой с однородным граничным условием может
быть решена с помощью интегрального преобразования Фурье с со-
соответствующим образом подобранным ядром, аналогично тому как
это делается в случае неоднородного граничного условия (см. п. 2).
Однако в случае линейного однородного граничного условия общего
вида более физически наглядным является метод продолжения на-
начального условия, при использовании которого оказывается полез-
полезной следующая
Лемма*). Пусть функция ф(х] определена на бесконечной прямой
Ж1, имеет на ней ограниченные производные до N-ro порядка вклю-
*' См.: Свешников А.Г., Боголюбов А.Н., Кравцов В.В. Лекции по математиче-
математической физике. М.: Изд-во МГУ, 1993.

чительно, и линейная комбинация
Ф(х) =	D.4)
где а/с = const, k = О,1,..., нечетна относительно точки х — 0. Тогда
функция
n(x,t)=	D.5)
удовлетворяет условию
= 0.	D.6)
Сформулированная лемма позволяет указать следующий способ
решения начально-краевой задачи для однородного уравнения тепло-
теплопроводности с заданным начальным условием и однородным линей-
линейным граничным условием общего вида:
ut = a2uxx, (ж,*)еП+>	D.7)
и(*,0) = У>(*), *el+, D.8)
= 0, t > 0.	D.9)
Продолжим функцию <?>(х), заданную при х ? М , на всю действи-
действительную ось х, построив функцию <?>(х), которая удовлетворяет усло-
условиям
—+
<?>(х) ЕЕ <р(х) при х ? М ,
при х G М
и непрерывна вместе с производными до JV-ro порядка включительно
на всей оси.
Теперь решим задачу Коши на бесконечной прямой
-1
DЛО)

Согласно лемме функция U(x,i) удовлетворяет граничному условию
при х = 0 задачи D.7)-D.9) и, следовательно, при х ? М u(x,t) =
= ?/(#,?), т.е. решение задачи D.10) при х?М является решением
задачи D.7)-D.9).
Приведем примеры применения метода продолжения для решения
начально-краевых задач для уравнений параболического типа.
1. Рассмотрим начально-краевую задачу для уравнения теплопро-
теплопроводности на полубесконечной прямой для однородного граничного
условия Дирихле
ti(*,0) = ?(*),	DЛ1)
ti@,*) = 0.
Применим доказанную лемму. Имеем а$ = 1, а /с = 0, k = 1, 2, . . . , JV.
Следовательно, функции <р(х) и Ф(х) совпадают и согласно лемме
функцию (р(х) нужно продолжить нечетным образом. Положим
ф(х) =	D.12)
Теперь решение задачи D.11) можно записать в виде интеграла Пуас-
Пуассона C.5):
где
— фундаментальное решение C.2).
Используя формулу D.12), решение задачи D.11) запишем через
функцию <р(х):
Сделав во втором интеграле в правой части формулы замену ? на
—?, получим
u(x,t) =
D.13)

Функция
Gi (*,?,<) =	D-14)
является функцией Грина задачи Дирихле для уравнения теплопро-
теплопроводности на полупрямой.
Из формул D.13) и D.14) следует, что решение задачи D.11) имеет
вид
u(x,t)=	D.15)
Интеграл D.15) называется интегралом Пуассона. Функция, опре-
определенная интегралом Пуассона, удовлетворяет однородному уравне-
уравнению теплопроводности при х ? М+ , t > 0, ограничена в области
х ? М , ? > 0, и в случае ограниченной кусочно-непрерывной функ-
функции <р(х) непрерывно примыкает при t -> 0 к функции <р(х) в точках
ее непрерывности. Это имеет место и в случае несогласования на-
начальных и граничных условий: <?>@) ф 0. При этом граничное усло-
условие м@,?) = 0 выполняется только при t > 0.
Из формулы D.15) вытекает физический смысл функции G(x, ?,t)*\
Функция GI(X,?,?) дает значение температуры в точке х полубеско-
полубесконечного стержня в момент времени t > 0, если в начальный момент
t = О в точке х = ? > 0 мгновенно выделяется количество тепла,
равное ср = р, а граничное сечение х = О все время поддерживается
при нулевой температуре, для чего в точку х = — ? нужно поместить
мгновенный точечный отрицательный источник.
2. Рассмотрим начально-краевую задачу для уравнения теплопро-
теплопроводности на полубесконечной прямой для однородного граничного
условия Неймана
ut = a2uxx, х,*ЕЖ+,
=<
дх х=о
Применим лемму. Имеем OQ = 0, а\ = 1, а/с = 0, k = 2,3, . . ., N.
Следовательно, Ф(х) = ф'(х] и, согласно лемме, функцию (р'(х] нуж-
нужно продолжить нечетным образом. Поскольку производная четной
функции есть нечетная функция, отсюда вытекает, что функцию (р(х]
нужно продолжить четно. Положим
(*)>	*>°> х.17ч
DЛ7)
*' См.: Свешников А.Г., Боголюбов А.Н., Кравцов В.В. Лекции по математиче-
математической физике. М.: Изд-во МГУ, 1993.

Тогда решение задачи D.16) можно записать в виде
и(М) =	D.18)
где функция G(x,?,t) определяется формулой C.2).
Запишем решение задачи через функцию (р(х]. Используя форму-
формулы D.17), D.18), будем иметь
Сделав во втором интеграле в правой части формулы замену ? на
—?, получим
м(*,0 =
D.19)
Функция
60=	D-2°)
является функцией Грина задачи Неймана для уравнения теплопро-
теплопроводности на полупрямой. Из формул D.19) и D.20) вытекает, что
решение задачи D.16) имеет вид
«(*,*)=	D.21)
Интеграл D.21) называется интегралом Пуассона. Когда функция
(р(х) непрерывна при х ? М и выполнены условия согласования
<p'(Q) = 0, формула D.21) определяет классическое решение задачи
D.16). Если же эти условия не выполнены, функция u(x,t) удовле-
удовлетворяет однородному уравнению теплопроводности при х ? М+, t > О,
ограничена при х ? М , t > О и непрерывно примыкает при t -> 0 к
функции (р(х] только в точках ее непрерывности. Причем, если не
выполнены условия согласования, граничное условие выполняется
лишь при t > 0.
3. Рассмотрим начально- краевую задачу для уравнения теплопро-
теплопроводности на полубесконечной прямой для однородного граничного

условия третьего рода:
ti(*,0) = ?>(*),	D22)
г\	\ '
— — hu = О (Л = const).
дх	*=о
Предположим, что функция (р(х} удовлетворяет условию согласова-
согласования начального и граничного условий
Применим доказанную лемму. Для задачи D.22) получаем ао =
= — Л, ai = l, а/с = 0, Аг = 2,3, .. .,JV. Следовательно, Ф(х) = <р'(х)-}кр(х)
и согласно лемме функцию (р'(х] — h(p(x] нужно продолжить на
отрицательную полуось нечетным образом. Таким образом, функция
ф'(х] — Л^(х), где ф(х] — продолжение (р(х) на всю ось х — будет
нечетной.
Очевидно, ф(х] = (р(х] при х > 0.
Для определения функции ф(х] при х < 0 получим задачу Коши
= /(х), х<0,
где правая часть уравнения имеет вид
(штрих есть производная по полному аргументу).
Решение задачи можно записать с помощью импульсной функции
<р(х) =
Итак, функция ф(х) имеет вид
Из леммы вытекает, что решение задачи D.22) можно записать в виде
интеграла Пуассона C.5)

где функция G(x,?, J) определяется формулой C.2).
Запишем решение задачи D.22) через функцию (р(х):
Преобразуем второй и третий интегралы в правой части формулы.
Во втором интеграле сделаем замену ? на — ?:
В третьем интеграле заменим z на — z и ? на — ?
Положив rj = ? — z, будем иметь

В результате получаем следующее выражение для решения исходной
задачи:
Обозначив
запишем решение в виде
«(*,<) =
Функция
Сз(*,?,<) =
D.23)
является функцией Грина третьей краевой задачи для уравнения
теплопроводности на полупрямой.
Преобразуем интеграл в формуле D.23). Выделяя в показателе
экспоненты полный квадрат и полагая
z =
получаем

Таким образом, из формулы D.23) следует
D.24)
где Gi(x,?,i) — функция Грина второй краевой задачи для урав-
уравнения теплопроводности на полупрямой, определяемая формулой
D.20).
Заметим, что функцию Грина Сз(х,?,?) можно записать в следу-
следующем виде:
Эта формула имеет простой физический смысл: для удовлетворения
граничному условию третьего рода нужно в точку х = — ? поместить
источник, равный источнику, находящемуся в точке х = ?, и, кроме
того, добавить на отрицательной части действительной оси от — оо до
— ? непрерывно распределенные источники, мощность которых экспо-
экспоненциально стремится к нулю при rj -> — оо.
2. Задачи для уравнения теплопроводности на полу беско-
бесконечной прямой с неоднородными граничными условиями.
Рассмотрим применение метода интегрального преобразования Фу-
Фурье к решению начально-краевых задач для уравнения теплопровод-
теплопроводности на полубесконечной прямой с неоднородным граничным усло-
условием.
1. Начально-краевая задача для однородного уравнения тепло-
теплопроводности на полупрямой с граничным условием первого рода:
ut = a2uxx, zEK+, t> О,
ti(x,0) = 0, zel*,	D.25)
Будем предполагать, что выполняются условия существования инте-
интеграла Фурье и что функция u(x,t) и ее частные производные доста-
достаточно быстро стремятся к нулю при х — > -foo. Используем синус-
преобразование Фурье с ядром sin Ах (см. гл. I, § 4). Обозначим образ
Фурье функции u(x,i) через U(\,t):
U(\,t) =

Будем также предполагать, что выполнены условия возможности
дифференцирования интеграла для t/(A, t) no t под знаком интегра-
интеграла.
Умножим уравнение задачи D.25) на \1 — sin Ax и проинтегрируем
по х от 0 до -f оо:
Проинтегрируем интеграл в правой части два раза по частям, учи-
учитывая граничное условие при х = 0:
Принимая во внимание начальное условие, получаем следующую на-
начальную задачу в пространстве образов:
Ut + a2X2U=	t>0 t/(A,0) = 0.
Решение этой задачи можно записать с помощью импульсной функ-
функции:
U(X,t) =
Для возвращения к оригиналу w(x, t) используем формулу обратного
синус-преобразования Фурье:
ti(M) =
Проинтегрируем внутренний интеграл по частям:

и учтем, что (см. § 3)
В результате получаем
м(х,0 =	D.26)
Заметим, что формулу D.26), выражающую решение задачи D.25),
можно переписать следующим образом:
и(х,0 =	D-27)
где функция
W(x,t) =
является решением вспомогательной начально-краевой задачи
Wt = a2Wxx, XER+, *>0,
W(x,Q) = Q, W(Q,t) = 1.
Интеграл D.27) носит название интеграла Дюамеля.
Приведенный пример является частным случаем общего метода
решения данного класса линейных начально-краевых задач, извест-
известного под названием принципа Дюамеля. Дадим его формальную схе-
схему для достаточно общего случая.
Пусть требуется построить решение следующей начально-краевой
задачи:
Pt(u(x, t)] = Lf[u(x, 0], 0 < x < /, 00,
дпи
—— (х,0) = 0, n = 0,l,...,m-l,

где Pt — линейный дифференциальный оператор, содержащий част-
частные производные по t до порядка m, Lx — линейный дифференци-
дифференциальный оператор второго порядка по переменной х.
Решение ищется на отрезке [0,/], включая и случай / = -foe. Гра-
Граничное условие при х = I обеспечивает единственность решения за-
задачи, N — оператор граничного условия.
Согласно принципу Дюамеля, решением поставленной задачи яв-
является интеграл Дюамеля
и(М)=	D.28)
где функция W(x, t) в свою очередь определена как решение исходной
начально-краевой задачи для частного случая граничного условия
= 1:
= Lf[W],
dnW
= 1, N[W(l,t)]=Q.
Чтобы проверить справедливость высказанного утверждения, вос-
воспользовавшись очевидным соотношением
f _ .
__(М- г) = --_(*,* -г)
и вычисляя интеграл по частям, получим в предположении существо-
существования производной функции
u(x,t) =
D.29)
Подстановка на верхнем пределе равна нулю в силу начального усло-
условия W(x,Q) = 0. Дифференцируя формулу D.29), получим
дпи
—— =	n = 0,l,2,...,m.

Аналогично
—— -
д^~	"*' '
Из полученных соотношений в силу линейности уравнения следует,
что интеграл Дюамеля D.28) удовлетворяет исходному однородному
уравнению при 0<х</,?>0. Выполнения нулевых начальных и
однородного граничного условий при х = I также очевидно. Остается
проверить выполнение неоднородного граничного условия при х = 0.
В силу граничного условия W(Q, t) = I имеем
2. Начально-краевая задача для однородного уравнения тепло-
теплопроводности на полупрямой с граничным условием второго рода:
-•'-«^о, хеж ,	D_30)
ди_
дх
= i/@, t > о.
Аналогично тому как это было сделано в случае граничного усло-
условия Дирихле, задачу D.30) можно решить, применяя интегральное
косинус-преобразование Фурье с ядром cos Ах. Предлагаем читателю
проделать эту работу самостоятельно.
Мы построим решение данной задачи, исходя из физических со-
соображений, а затем проверим удовлетворение им требуемым услови-
условиям. Граничное условие означает, что задан поток тепла, втекающего
в стержень через сечение х = 0, причем плотность потока, в силу
закона Ньютона, определяется выражением
-Artiar@,0 = -М0>
где k — коэффициент теплопроводности, связанный с коэффици-
коэффициентом температуропроводности а2 соотношением k = а1 р. Поэто-
Поэтому в силу принципа суперпозиции, воспользовавшись выражением

для функции Грина С2(я,?,0 D.20) полуограниченного стержня при
? = 0, можно записать решение поставленной задачи в виде
Очевидно, что это выражение удовлетворяет в области Q+ однород-
однородному уравнению и нулевым начальным условиям. Проверим выпол-
выполнение граничного условия
ux(x,t) =
Сделав в данном интеграле замену переменной интегрирования
а =	<% =
получим
ux(x,t) =
откуда, переходя к пределу при х — > 0, находим
lim ux(x.t) =
На строгом обосновании проведенных здесь формальных рассмотре-
рассмотрении останавливаться не будем.
Аналогичным образом на физическом уровне строгости можно по-
получить формулу D.26) для граничной задачи Дирихле.
3. Начально-краевая задача для однородного уравнения тепло-
теплопроводности на полупрямой с граничным условием третьего рода:
ti(«,0)=0, *ЕК*,	D-31)
их — hu\_ Q = —h(p(t), h = const, t > 0.

Будем предполагать, что выполняются условия существования инте-
интеграла Фурье и что функция u(x,t) и ее частные производные доста-
достаточно быстро стремятся к нулю при х -> + оо. Используем преобра-
преобразование Фурье с ядром
К(х,Х) =	D.32)
и обозначим образ Фурье функции u(x,t) через t/(A,t):
U(X,t) =	D.33)
Напомним, что общие принципы выбора ядра интегрального пре-
преобразования Фурье для решения начально-краевых задач на полу-
полупрямой изложены в гл. I, § 4. В частности, нетрудно убедиться, что
ядро D.32) является ограниченным решением уравнения Кхх+Х2К =
= О, удовлетворяющим однородному граничному условию третьего
рода
Kf(Q,X)-hK(Q,X) = Q.
Предположим, что для интеграла D.33) выполнены условия воз-
возможности дифференцирования по параметру t.
Умножим обе части уравнения задачи D.31) на K(x,t) и проинте-
проинтегрируем по х от 0 до -foo:
Проинтегрируем правую часть уравнения два раза по частям и учтем
граничное условие при х = О задачи D.31):
Учитывая начальное условие задачи D.31), получим начальную за-
задачу для образа Фурье [/(A, t):
Ut + a2X2U=	*>0,

Решение начальной задачи запишем с помощью импульсной функции
U(X,t) =
Чтобы из пространства образов вернуться в пространство оригина-
оригиналов, воспользуемся формулой обратного интегрального преобразова-
преобразования Фурье с ядром К(х, А):
Внутренний интеграл в правой части последней формулы запишем в
виде суммы трех интегралов:
Получим необходимые для дальнейших преобразований формулы
D.34) и D.35).
а) Вычислим интеграл
Продифференцируем интеграл 1\ по параметру а:
da

поскольку
Учитывая, что /i(-foo) = 0, получим для /i(a) следующую задачу
Коши:
Решение задачи Коши записывается с помощью импульсной функции
следующим образом:
/1 =
Преобразуем интеграл

Поскольку /i = —y/neh a/, окончательно получим
б) Используя формулу D.34), вычислим интеграл
/2 =
Поскольку
/2 =
получаем
/2 =
Используя формулы D.34), D.35) и формулу
получим

Таким образом, окончательное выражение для решения начально-
краевой задачи D.31) имеет вид
«(*,*) =
D.36)
С помощью введенной в § 3 функции ошибок (см. C.6)) ответ можно
записать следующим образом:
С физической точки зрения функция it (я, ?), определяемая формулой
D.36), представляет собой температуру в точке х в момент време-
времени t полубесконечного стержня без источников тепла, если на конце
стержня х = О происходит теплообмен с внешней средой, температура
которой определяется заданной функцией <p(t). Начальная темпера-
температура стержня равна нулю. При Л = 0 получается граничное условие
Неймана, которое соответствует заданному в точке х = О нулево-
нулевому тепловому потоку. Температура стержня остается равной нулю.
Случай (p(i) = 0 соответствует теплообмену с внешней средой ну-
нулевой температуры. Из формулы D.36) вытекает, что температура
стержня в этом случае остается равной нулю.
3. Примеры решения задач
Рассмотрим примеры решения начально-краевых задач для урав-
уравнения теплопроводности на полупрямой.
1. Рассмотреть процесс остывания полу бесконечного стержня, на-
начальная температура которого постоянная, а конец поддерживается
при нулевой температуре.
Решение. Процесс остывания стержня описывается следующей на-
начально-краевой задачей:
ti@,*) = 0.

Воспользуемся формулой D.15), положив в ней (p(t) = UQ = const:
«(*,*) =	D.37)
где
Сделаем в интеграле Д замену s = .В результате получим
/1 =
где Ф(о>) — функция ошибок — определяется формулой C.6).
Аналогично с помощью замены s = ?Ц* интеграл /2 можно при-
привести к виду
В результате получим
«(*,*) =
Отметим, что начальные и граничные условия рассматриваемой за-
задачи не являются согласованными (<р@) ^0). На полупрямой Ж+
функция <р(х) = UQ не имеет точек разрыва, Поэтому при х ? Ж+
функция u(x,t) непрерывно примыкает к <р(х): limit = [/о, посколь-
ку lim^^^-c» Ф(и;) = 1. Предельное значений при t —> 0 в точке х = О
зависит от способа перехода к пределу (ср. с п. 1 § 3). Если сна-
сначала перейти к пределу по t, а затем по х, получим lim и = UQ .
Если сначала перейти к пределу по х, а затем по t, будем иметь
lim и = 0. Одновременный переход к пределу при х —> 0+0, t —> О
вдоль кривой —S- = w, где w > 0, дает любое значение, заключенное
между нулем и UQ.

В точках полупрямой Е+ температура и(х, t), равная UQ при t = О,
плавно спадает к нулю при t -> + оо.
2. Решить задачу об остывании полу бесконечного стержня, если
тепловой поток через конец х = 0 равен нулю, а начальная темпера-
температура определяется кусочно-постоянной функцией
Решение. Начально-краевая задача, моделирующая процесс осты-
остывания стержня, имеет вид
ut = а2ихх, х€К+, *>0,
где функция <p(t) определяется формулой D.38). Воспользуемся фор-
формулой D.21). Имеем
«(*,*) =
где
/1 =	/2 =
Сделав в интеграле Д замену s = |""^, перепишем его в виде
где Ф(г#) — функция ошибок C.6).
Интеграл /2 с помощью замены s = 4-^ может быть преобразован
к следующему виду:
/2 =
В результате получим
«(*,<)=	D.39)

3. Рассмотреть процесс остывания полу бесконечного стержня, на
конце х = 0 которого происходит теплообмен с внешней средой ну-
нулевой температуры. Начальная температура стержня постоянная и
равна TQ.
Решение. Начально-краевая задача, моделирующая процесс осты-
остывания стержня, имеет следующий вид:
ut = а?ихх, х > 0, t > О,
Воспользуемся формулой D.23), положив в ней (р(х) = TQ:
«(*,«) =
D.40)
Подсчитаем внутренний интеграл в формуле D.40). Имеем
Таким образом, положив s =	, получим
D.41)
После подстановки D.41) в формулу D.40) необходимо подсчитать
интеграл

Проинтегрируем интеграл / по частям:
D.42)
Покажем, что верхняя подстановка в формуле D.42) равна нулю. В
самом деле
Так как
запишем
D.43)
Подсчитаем интегралы 1\ и /2. Имеем
D.44)
/2 =
D.45)

где использована замена s =
2a
Подсчитаем, наконец, два первых интеграла в формуле D.40). С
помощью замены s = j*/- получаем
2ayt
/3 =
D.46)
где использована нечетность функции Ф(ги).
Аналогично, положив s = г-Ц=, будем иметь
/4 =	D.47)
Подставляя D.43)-D.47) в формулу D.40), получим
!!(*,*) =
§ 5. ЗАДАЧИ ДЛЯ УРАВНЕНИЯ
ТЕПЛОПРОВОДНОСТИ В ПРОСТРАНСТВЕ
Рассмотрим начальную задачу для уравнения теплопроводности с
постоянными коэффициентами в трехмерном пространстве Ж3. Вве-
Введем обозначения
Q3 ЕЕ Ж3 х @, T]={(Myt): M <Е Ж3,* 6@, Г]}.
й3 ЕЕ Ж3 х [О, Т].
Начальная задача для уравнения теплопроводности в простран-
пространстве (задача Коши) ставится следующим образом:
, М€К3,
где А — трехмерный оператор Лапласа.

Классическим решением начальной задачи для уравнения тепло-
теплопроводности называется функция w(M, J), определенная и непрерыв-
непрерывная вместе со вторыми производными по координатам и первой про-
производной по t в области Пз) удовлетворяющая в этой области уравне-
уравнению теплопроводности, непрерывная по координатам и по t в области
QS и удовлетворяющая начальному условию.
Если (р(М) непрерывная и ограниченная в М3 функция, то началь-
начальная задача для уравнения теплопроводности имеет единственное ре-
решение.
Фундаментальным решением G(M, Q,t) задачи Коши для уравне-
уравнения теплопроводности щ = а2 Дм называется такое его решение в
области Пз) которое:
1) удовлетворяет начальному условию
2) непрерывно всюду в замкнутой области Q3) кроме точки (Q, 0) ,
т.е. при М ф Q и t -ф. 0.
При построении фундаментального решения в пространстве весь-
весьма полезной оказывается следующая
Лемма. *) Если в задаче Коши
щ = а2 Дм, (М, t) € Q3, ti(Af , 0) = у?(М)
начальная функция <f>(M) представима в виде
то решением этой задачи будет функция
где HI (x, t), u2(y, t), 1/3B, t) — решения соответствующих одномерных
задач Коши:
, у ЕЖ1, 00,
, zGl1, <> 0,
*' См.: Свешников Л.Г., Боголюбов А.И., Кравцов В.В. Лекции по математиче-
математической физике. М.: Изд-во МГУ, 1993.

Аналогичным образом ставится начальная задача для уравнения
теплопроводности в двумерном случае. При этом имеет место лемма,
аналогичная лемме, сформулированной для трехмерного случая.
С помощью сформулированной леммы легко построить фундамен-
фундаментальное решение уравнения теплопроводности в пространстве R3. В
трехмерном случае дельта-функцию 6(М, Q) можно представить в ви-
виде произведения:
где М = (х, у, z), Q = (?, 77, С)- Поэтому, поскольку фундаментальное
решение G(M, Qyt) является решением уравнения теплопроводности
в ИЗ) удовлетворяющим начальному условию G(M, ф>0) = (J(M, Q),
применяя лемму и воспользовавшись формулой для фундаменталь-
фундаментального решения уравнения теплопроводности на прямой (см. C.2)), по-
получим
Аналогично получается выражение для фундаментального решения
уравнения теплопроводности на плоскости:
Gn(M,Q,t) =
Зная фундаментальное решение, можно аналогично одномерному
случаю выписать формулу для решения начальной задачи для неод-
неоднородного уравнения теплопроводности с неоднородным начальным
условием в трехмерном случае:
u(M,t) =
E.1)
Аналогичная формула в двухмерном случае имеет вид
u(M,t) =
E.2)
В качестве примера рассмотрим решения следующих задач.
1. Решить задачу для неоднородного уравнения теплопроводности
на плоскости
щ =4Д2гх + е~<со8(х + у), (х,у) ЕМ2, * >0,

Решение. Воспользуемся формулой E.2), положив в ней а = 2:
и =
Используя формулу
cos(? -f rj) = cos ? cos rj — sin ? sin 77,
запишем два внутренних интеграла в виде
где
/1 =
/з =
/4 =
— х
Рассмотрим интеграл 1\. Сделаем замену s = —==• Тогда
4\Д — т
где

/12 =
Поскольку подынтегральная функция в интеграле /12 нечетная, /12 =
= 0. А так как подынтегральная функция в интеграле /ц четная,
получим (см. § 4)
/11 =
Учитывая формулы для 1\ и Гц, получим
Поскольку интеграл /2 аналогичен интегралу 1\ ,
Рассмотрим интеграл /з. Используя ту же замену, получим
где
/31 =
/32 =
Таким образом,
/ =е~4^~
Аналогично
/ =е~4^~
Используя формулы для интегралов /i, /2, /3, /4, получим

и окончательно:
u(xyyyt) =
Заметим, что начальная функция у?(х,у, z) может быть растущей
с ограниченной степенью роста, т.е. найдутся такие положительные
постоянные 6 и N, что \(р(х,у, z)\ < Neb^. Рассмотрим пример, в
котором начальная функция является функцией с ограниченной сте-
степенью роста.
2. Решить задачу Коши для уравнения теплопроводности в трех-
трехмерном пространстве
г/е = Дг/, (z,y,z)eE3, t> О,
г/(х, у, z,0) = е~х sh3ycos5z.
Решение. Воспользовавшись формулой E.1), запишем решение в
виде (учтем, что а = 1)
и =
Интеграл в правой части может быть записан в виде произведения
трех интегралов:
/2 =
Учитывая, что

запишем интеграл 1\ следующим образом:
/1 =
Сделав в последнем интеграле замену
s =
получим после несложных преобразований
Для вычисления интеграла /2 учтем, что sh3i? = ^e3f? — |e 3f?, и
представим его в виде
/2 = /21 - /22,
где
/22 =
В интеграле /2i сделаем замену s = —j=- и перепишем его в виде
Учитывая, что s2 — 6\/ts = (s — 3\ДJ — 9J, окончательно получим
/21 =
С помощью аналогичной замены интеграл /22 запишем следующим
образом:
/22 =

Из формул ДЛЯ /2, /21, /22 ПОЛуЧИМ
/2 = e9tsh3t/.
Рассмотрим, наконец, интеграл /з. Сделав замену s — ^Fjr, будем
иметь
поскольку
= 0.
Окончательный ответ имеет вид
Сфомулированная лемма была использована для построения ре-
решения (функции Грина) в неограниченном пространстве. Ее можно
было использовать и для решения рассмотренных примеров.
Заметим, что эта лемма справедлива не только в неограниченном
пространстве, а допускает обобщения на более сложные случаи. Ис-
Исследуем этот вопрос более подробно.
Рассмотрим цилиндрическую область D = {(я, у) ? <т, z\ < z < 22},
причем как плоская область сг может быть неограниченной, так и z\
и Z2 могут быть равны —оо и -hoc соответственно.
Пусть функция v(x,t/, t) удовлетворяет в области сг однородному
уравнению теплопроводности
щ = а2Д2г;,

заданному начальному условию
и однородному первому, второму или третьему граничному условию
на границе С области ст. Пусть функция u$(z, t) удовлетворяет на
отрезке z\ < z < z^ однородному уравнению теплопроводности
_
dt ~ a
заданному начальному условию
U3\t=o - РЗ^
и однородному граничному условию первого, второго или третьего
рода при z = z\ и z — Z2-
Тогда функция г/(х, у, , z, t) = v(x, у, *)г/з(г, 0 в области D удовле-
удовлетворяет однородному уравнению теплопроводности
ut =
начальному условию
и однородному граничному условию на границе области D.
Справедливость этого утверждения устанавливается непосредст-
непосредственной проверкой.
Если плоская область сг вырождается в отрезок, например х\ <
х < #2, причем xi и #2 могут быть равны —оо и +оо соответственно,
а функция <р(х, у) не зависит от переменной у:
то получаем соответствующее утверждение на плоскости (х, z).
Эти утверждения обобщают ранее сформулированную лемму. Они
используются для построений функций Грина для уравнения тепло-
теплопроводности с постоянными коэффициентами в указанных цилиндри-
цилиндрических областях, поскольку функция Грина может быть определена
как решение однородного уравнения теплопроводности в D, удовле-
удовлетворяющее однородному граничному условию на границе области D
и начальному условию следующего вида:

Рассмотрим примеры построения указанным способом функции
Грина для уравнения теплопроводности.
1. Построить функцию Грина уравнения теплопроводности для
плоского слоя: — oo<x,y<oo,0<z</, если на граничных плоско-
плоскостях (z = О и z = I) заданы однородные граничные условия Дирихле.
Решение. Функция Грина G(M,Q,i), М = (х,у, z), Q = (?,??, С)
согласно сформулированным утверждениям будет равна
G(M, Q, t) = G0(x, ?, *)G0(y, i?, t)Gi(z, C, *)>
где
— фундаментальное решение (функция Грина) на бесконечной пря-
прямой, Gi(z,C, t) — функция Грина уравнения теплопроводности для
отрезка 0 < z < I с граничными условиями Дирихле при z = О и
z = l.
Функция GI(Z, С, J) может быть записана в виде ряда по собствен-
собственным функциям соответствующей задачи Штурма-Лиувилля:
Таким образом,
G(M,Q,t) =
2. Построить функцию Грина для бесконечного цилиндра попе-
поперечного сечения <т, если на боковой поверхности цилиндра заданы
однородные граничные условия Дирихле.
Решение. Функция Грина G(M, z,Q,C>0> M=(x,y), Q = (?,rj) име-
имеет вид
G(M, z, Q, С, t) = GQ(z, С, *)Gi (M, Q, О,
где
G\(M, Q, <) — функция Грина задачи Дирихле для уравнения тепло-
теплопроводности в области ст. Функция Gi(M, Q,t) может быть записана
в виде
ос
Gi (M,Q,t)=^ e-'^-'vn (M)vn (Q),
n=l

где {vn(M))i° — ортонормированные собственные функции задачи
Дирихле для оператора Лапласа в области <т, {An}J° — соответству-
соответствующие им собственные значения.
Таким образом,
G(M,z,Q,{,t) =
3. Построить функцию Грина для четверти пространства: 0 <
< х, у < оо, — оо < z < оо. На координатных плоскостях х = 0 и у = О
заданы однородные граничные условия Неймана.
Решение. Функция Грина G(M,Q,*), M=(z,y, z), Q= (?,??, С)
имеет вид
где
— функция Грина уравнения теплопроводности задачи Неймана на
полупрямой.
Следовательно,
G(M,Q,<) =
§ 6. ЗАДАЧИ ДЛЯ
САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Решить начально-краевую задачу на отрезке:
ut = uxx, x€ @,5), te @,-hoc),
г/(х,0) = 0, ж €[0,5],
u@,e) = 2*, tiE,t) = 0, t€[0,+oo).

2. Решить начально-краевую задачу на единичном отрезке:
«» = «,*, «е @,1), <€@,+оо),
«(*,0)=1, * 6@,1),
u@,t) = 2, u(l,<) = 3, <е[0,+оо).
3. Решить начально-краевую задачу на единичном отрезке:
«» = «.., х €@,1), «6 @, +оо),
«(*,<)) = 0, *€[0,1],
и@,*) = 3A-е-'), «s + u = 0, * = 1, *€[0,+оо).
4. Решить начально-краевую задачу в единичном круге:
«( = Д«, г €@,1), р€[0,2тг], <€(о,
u(r)v?,0) = rsin^, г €[0,1], ?€[0,2тг]
u(l,y>,t) = 0, у>€[0,2я-], <€[0,+оо).
5. Решить начально-краевую задачу в круге:
ut = Au, г €@,5), р€[0,2тг], «б(о,
«(г,у>,0) = 0, г€[0,5), р б [0,2ir|,
иE,у>,<) = 8, уе[0,2тг], «б[0,+оо).
6. Решить начально-краевую задачу в круге:
«е = а2Ди, г€@,г0), у>€[0,2я-], <е@,+оо),
u(r,<p,Q) = Uo, r€[0,r0), ^€[0,2тг],
at-u), у>€[0,27г], *е[0,+оо).
7. Решить начально-краевую задачу в круговом кольце:
«( = а2Ди, r€(n,ra), р€[0,2тг], <€(
u(r,<p,0) = U0, r€(ri,r2), ^€[0,2тг],
,<p,t) = 0, <р € [0,2я-],
,?>,<) = 0, <€[0,+оо).
8. Решить начально-краевую задачу в шаре:
tit = а.2Ди, М € Kr° , t€ @, +оо),
u(M,Q) = U0, M€Kr°,
at-u), <€[0,+oo).

9. Решить начально-краевую задачу в шаре:
ut = Дм, М е К3, t е @, -hoc),
м(М,0) = 1, Me К3,
Чг=з=2> t€[0,+oo).
10. Решить начально-краевую задачу в шаре:
ut = Дм, ме к3, *е(о,+оо),
м(М,0) = 0, МеК3,
мг|г=3 = P2A)(cos0)sin^>.
11. Решить начально-краевую задачу в шаре:
ut = Дм, ме к2, *е(о,+оо),
м(м,о) = о, ме к2,
K + ti)|r=2=5, *G[0,+oo).
12. Решить начальную задачу на бесконечной прямой:
ut = \uxx, хек1, *е(о,+оо),
ti(x,0) = e2*-*3, xGM1.
13. Решить начальную задачу на бесконечной прямой:
ut = \uxx, xGM1, t€@,+oo),
-3, x GM1.
14. Решить начальную задачу на бесконечной прямой:
М^М**, XGM1, t€@,+0o),
u(x,Q) = xe~x\ x GM1.
15. Решить начальную задачу на бесконечной прямой:
ut = uxx + sint, хЕЖ1, t€@,-hoo),
м(х,0) = е-*2, хЕЖ1.
16. Решить начальную задачу на бесконечной прямой:
щ = ихх, хеЖ1, t€@,+oo),
м(х,0) = sin2x, хЕЖ1.

17. Решить начально- краевую задачу на полупрямой:
Ut = a2uxx-b2e-kx, fc>0, zEK+, *G@,+oo),
ti(x,0) = 0, z€t+,
ti@,*) = l/o, t€@,+oo).
18. Решить начально- краевую задачу на полупрямой:
ut = a2uxx, хеЖ+
ti(x,o) = o, xei+
ti*((M) = -0, t€(
19. Решить начально-краевую задачу на полупрямой:
11@,0 = 1/0, <€@,+оо).
Ответы.
1.
2.
3.
4.
где
5.
где
6.
где

7. ti(r,
где
8.
где
9. u(r,*)
10. u(r,0,
где
11. u(r,*)
где
12.	u(z,*)
13.	ti(«,*)
14.	ti(a?,t)
15. ti(a?,*)
16. ti«,<

17.
18. u(x,t) =
19. u(x,t) =

Глава 6
ЗАДАЧИ ДЛЯ УРАВНЕНИЯ
КОЛЕБАНИЙ
Уравнения в частных производных второго порядка гиперболиче-
гиперболического типа используются при рассмотрении колебательных процес-
процессов различного вида. В данной главе изучаются методы решения
начально-краевых задач для уравнения колебаний с постоянными
коэффициентами в основных областях, как ограниченных, так и не-
неограниченных.
Пусть задана ограниченная область D с кусочно-гладкой границей
S. Начально-краевая задача для уравнения колебаний в области D
заключается в определении в цилиндре Qoo = D x [0, оо) функции
г/(М, ?), удовлетворяющей уравнению колебаний, двум начальным и
граничному условиям:
ti« = «2 Ли + f(M, t) , (M, t) е Qoo ,
N + 101*0,
где n — внешняя по отношению к области D нормаль к поверхности
S.
Поставленная начально-краевая задача является математической
моделью процесса колебаний объема D в отсутствие сопротивления
под действием внешней силы, распределенной в пространстве и вре-
времени с плотностью /?(М)/(М, ?), где р(М) — плотность тела D, с
заданными начальными условиями и режимом на границе.
Классическим решением начально-краевой задачи для уравнения
колебаний называется функция г/(М, t), непрерывная вместе с первы-
первыми производными в замкнутом цилиндре Qoo > имеющая непрерывные
производные второго порядка в открытом цилиндре Qoo , удовлетво-
удовлетворяющая в Qoo уравнению, двум начальным условиям и граничному
условию.
Если граничное условие является условием Дирихле (а — 0), то
непрерывность первых производных по М в замкнутом цилиндре не
требуется.

Начально-краевая задача с граничными условиями первого, вто-
второго и третьего рода (третья краевая задача |~+/ш|5 = //(Р, ?), Р G S
при h > 0) имеет единственное классическое решение.
Для существования классического решения необходимо (но недо-
недостаточно) выполнения условия согласования начальных и граничного
условий следующего вида:
Если функции /(М, i), <р(М), ф(М), р(Р, t) удовлетворяют опреде-
определенным условиям гладкости, то начально-краевая задача имеет клас-
классическое решение, в случае меньшей гладкости задача может иметь
обобщенное решение.
Начально-краевые задачи для уравнения колебаний в неограни-
неограниченной области будут рассмотрены ниже.
Как было показано в гл. I, можно провести редукцию общей на-
начально-краевой задачи и представить ее решение в виде суммы
ti(AM)=tii(AM) + ti2(AM),
где t/i(M, t) — решение неоднородного уравнения с неоднородными
начальными и однородным граничным условиями
г/т = а2 Дг/1 + /(М, t) , (М, t) <Е Qoo ,
а г/2(М, t) — решение однородного уравнения с однородными началь-
начальными и неоднородными граничными условиями
(M,t) GQoo,
§ 1. ЗАДАЧИ ДЛЯ УРАВНЕНИЯ КОЛЕБАНИЙ
В ОГРАНИЧЕННОЙ ОБЛАСТИ С
ОДНОРОДНЫМИ ГРАНИЧНЫМИ УСЛОВИЯМИ
Рассмотрим начально-краевую задачу с однородными граничными
условиями
м« = а2Дг/ + /(Af,*). (AM) G Qoo,
A.1)
а, /3 = const.

Решение этой задачи, как было показано в гл. I, можно представить
в виде разложения
коэффициенты un(<) которого являются решениями задачи Коши
< + а2 А„ «„=/„(<), <>0,
«п@) = у>„, <@)=Vn, п=1,2,...,
где {vn(M)}™ и {An}J° — собственные функции и собственные значе-
значения соответствующей задачи Штурма- Лиувилля для оператора Ла-
Лапласа
/„(О =	A.2)
V* = A.3)
— коэффициенты Фурье разложения функций f(M,t), <р(М), if>(M)
по системе собственных функций
К112 =
— квадрат нормы собственной функции.
Решение задачи Коши для функции un(t) записывается в виде
«„(О =
где Kn(t — т) —	— импульсная функция*).
*^ См.: Тихонов А.Н., Васильева А.Б., Свешников А.Г. Дифференциальные
уравнения. М.: Наука, 1985.

Таким образом, решение начально-краевой задачи для уравнения
колебаний в случае однородных граничных условий записывается в
следующем виде:
u(M,t) =
+	A-4)
где значения /п(т), (рп и фп определяются формулами A.2) и A.3).
Первое слагаемое в формуле A.4) представляет собой решение на-
начально-краевой задачи для однородного уравнения колебаний с не-
неоднородными начальными и однородными граничными условиями,
а второе слагаемое — решение начально-краевой задачи для неодно-
неоднородного уравнения колебаний с однородными начальными и однород-
однородным граничным условиями.
Пусть функция f(M,i) имеет вид f(M)<	>. Физически это
соответствует процессу колебаний объема D под действием периоди-
периодической силы, распределенной с плотностью p(M)f(M)l >.
I COS (м Т \
Предположим, сопротивление отсутствует, в начальный момент
тело находилось в состоянии покоя и его граница остается неподвиж-
неподвижной в процессе колебаний. Начально-краевая задача, моделирующая
процесс таких колебаний, ставится следующим образом (для опреде-
определенности рассмотрим случай синусоидальной зависимости от време-
времени):
utt = a2 Ati + f(M) sin сЛ , (М, *)€#«>,
4=0 = °' 4=0 = °' U\S = °'
Решение этой задачи представляется формулой A.4) при (рп = фп =
О, которую мы запишем следующим образом:
u(M,t) =
где
A.5)

Отсюда сразу видно, что если /По = 0, то uno(t) = 0. Поэтому если
f(M) ортогональна к собственной функции vno(M), то гармоника но-
номера по в объеме D не возбуждается, какова бы ни была частота
внешней силы.
Введем обозначение: u>n = а^/Х^. Величины u>n являются собст-
собственными частотами области D. Вычислим un(t):
tin @ =
Если и> ф и>п, то
«п@ =
Если о; = u>n, то применяя правило Лопиталя*), получим
«„(<) =
Таким образом, коэффициент uno(t) номера по будет неограниченно
нарастать со временем (линейно по t) только в том случае, когда
и> = и>По и fn0 ^0. В этом случае наступает явление резонанса.
Итак, решение исходной задачи имеет вид:
а) если и ф и>п при всех п— 1,2,..., то
ti(AM)=	A.6)
где /п задано соотношением A.5);
б) если и> — и>По, то
u(Af,0 =
A.7)
значение /По также определено формулой A.5).
Еще раз подчеркнем, что для наступления резонанса, т.е. неогра-
неограниченного нарастания колебаний со временем под действием внешней
*) См.: Ильин В.А., Позпяк Э.Г. Основы математического анализа. Ч. 1. М.:
Наука, 1982.

периодической силы /(M)sinu^, необходимо выполнение двух усло-
условий:
w = о;По = ах/Л^", и /Яо ± 0.
Рассмотрим примеры решения начально-краевых задач для урав-
уравнения колебаний в ограниченных областях.
1. Решить начально-краевую задачу для уравнения колебаний на
отрезке 0 < х < I:
I =0 и \ =sin— г/1 =til
Решение. Граничными условиями являются однородные гранич-
граничные условия Дирихле. Поэтому собственными функциями в разло-
разложении A.4) будут собственные функции отрезка с граничными усло-
условиями Дирихле (см. гл. II, § 1)
Vn(x) = sin -у- х, п=1,2,...,
с квадратом нормы
IKII2 = \.
Собственные значения имеют вид
х /тгп\2	л 0
Ап = {—J , п= 1,2,....
Согласно формуле A.4) общее решение начально-краевой задачи
на отрезке [0,/] с однородными граничными условиями Дирихле для
неоднородного уравнения колебаний с неоднородными начальными
условиями имеет вид
A.8)
где, что следует из формул A.2) и A.3), имеем
A.9)

Поскольку первое начальное условие однородное, (рп = О, а из одно-
однородности уравнения следует, что fn(t) = 0. В результате из формул
A.8) и A.9) получим
где
Таким образом,
Отметим, что решение задачи представляется в виде одного члена
ряда. Это связано с тем, что в качестве второго начального условия
выбрана собственная функция ф(х) = v^(x) = sin ^p, поэтому в силу
ортогональности системы собственных функций все коэффициенты
фп, кроме коэффициента ^2> равны нулю.
2. Решить начально-краевую задачу для неоднородного уравнения
колебаний на отрезке 0 < х < I:
им = а2ихх+Ае~*8т—, 0<х<1, t > О,
Решение. Воспользуемся формулой A.8), в которой в силу одно-
однородности начальных условий <рп =0, фп =0, а собственными функ-
функциями и собственными значениями являются собственные функции
и значения задачи Дирихле на отрезке
vn(x)=	n=l,2,...,
где согласно A.9)

Следовательно,
Отметим, что, как и в задаче 1, решение представляется одним
членом ряда с п = 1. Это объясняется тем, что зависимость от ко-
координаты х в неоднородности уравнения задается собственной функ-
.	. ттх
цией v\(x) = sin—.
3. Найти процесс колебаний однородной ненагруженной струны
длины / с закрепленными концами, если начальная скорость струны
равна нулю, а начальное отклонение имеет вид
<?(*) =
Решение. Пусть в положении равновесия струна расположена
вдоль оси х между точками х = 0 и х = I. Поскольку по условию
струна однородная, то ее линейная плотность постоянна р(х) = р0,
а в силу того, что рассматриваются малые колебания, постоянным
остается натяжение TQ.
Начально-краевая задача, описывающая процесс колебаний сво-
свободной струны с закрепленными концами, ставится следующим обра-
образом:
Решение поставленной задачи записывается с помощью формулы
/\	/ч f / \ л / \ • ^"^ \ /7Г71\2
A.8), в которой ^п = 0, /п(т) = 0, vn(x) = sin — ж, An=f— J ,
ll I (9	'
IKH2=2;
<Pn =

Таким образом,
где u>n = пап/1 — собственные частоты струны.
Отметим, что в выражении для u(x,i) исчезают слагаемые, для
. тгп
которых sin — XQ= О, т.е. отсутствуют обертоны, для которых точка
х = XQ является узлом.
Энергия струны равна сумме энергий гармоник. Подсчитаем энер-
энергию n-й гармоники. Выражение для нее имеет следующий вид:
un(x,t) =
Энергия n-й гармоники струны состоит из двух слагаемых: кинети-
кинетической энергии
тт'(кинетич) __.
и потенциальной энергии
тт'(потенц) __
В процессе колебаний струны происходит постоянная перекачка
энергии из потенциальной в кинетическую, причем сумма потенци-
потенциальной и кинетической энергий остается постоянной. При этом, ко-
когда кинетическая энергия n-й гармоники достигает максимального

значения (струна проходит положение равновесия), ее потенциаль-
потенциальная энергия обращается в нуль, и, наоборот, когда потенциальная
энергия n-й гармоники достигает максимального значения (струна
находится в одном из крайних положений) , ее кинетическая энергия
обращается в нуль. Поэтому
где М = pol — масса струны.
Из последней формулы вытекает, что энергия обертонов, для ко-
.
торых выполнено условие sin — ~ — = О, равна нулю.
4. Решить задачу о малых поперечных колебаниях круглой мем-
мембраны Ur° радиуса г о с закрепленным краем, если начальное откло-
отклонение точек мембраны задано функцией г«о(г, <?>) = А — cos ^, где А —
некоторая постоянная, а начальные скорости равны нулю.
Решение. Начально-краевая задача, описывающая процесс коле-
колебаний мембраны имеет следующий вид:
=0 = °>	г=г0=°-
Здесь Ur° — круг радиуса г0 , Cr° — окружность радиуса г0 .
Ищем решение в виде разложения по собственным функциям за-
задачи Дирихле для круга Ur°. Собственные функции и собственные
значения имеют вид (см. гл. II, § 5)
где /4"' — корень номера k уравнения Jn(p-) = 0.
Квадрат нормы собственных функций равен

Формула A.4) для общего решения начально-краевой задачи в кру-
круге для неоднородного уравнения колебаний с неоднородными началь-
начальными условиями и однородными граничными условиями Дирихле за-
записывается следующим образом:
A.10)
Формулы для коэффициентов разложения следуют из формул A.2),
A.3) и имеют следующий вид:
*?> =
Заметим, что индексы с и s соответствуют коэффициентам разложе-
разложения по косинусам и синусам.
Поскольку в нашем случае f(M,i) == 0 и Ф(М) == 0, из формулы
A.10) получим
и =
Вычисляя коэффициенты, найдем
Ф'^О при

Подставляя коэффициенты в разложение решения, получаем окон-
окончательный ответ:
где р>ь (* = 1> 2, . . , ) — корни уравнения
5. Найти колебания круглой мембраны радиуса TQ с закреплен-
закрепленным краем в среде без сопротивления, вызванные равномерно рас-
распределенным давлением р = ро sinu>?, приложенным к одной стороне
мембраны.
Решение. Решение задачи, описывающей процесс колебаний мем-
мембраны:
utt = a2&u+— sinu;*, М Е [7Г°, t > О,
Ч=о = °' Ч=о = °' 4=г„=°'
где р — поверхностная плотность мембраны — дается формулами
A.5)—A.7), где vn(M) — собственные функции круга в случае гра-
граничных условий Дирихле. Эти функции имеют вид (см. гл. II, § 5)
где IL? — корень номера k уравнения Jn(n) = 0.
Квадрат нормы собственных функций равен
Рассмотрим нерезонансный случай, когда частота вынуждающей
силы и не совпадает с собственной частотой и^п' = ац^ /TQ круга
Ur°: и ф ^k • В этом случае решение дается формулой A.6), прини-
принимающей для круга вид
и =

где коэффициенты /?* и /?„ вычисляются по формулам, получаю-
получающимся из формулы A.5):
f(c) _
Jkn —
f~w _
/fcn —
где по условию задачи /(г, <р) = — .
Учитывая ортогональность системы тригонометрических функ-
функций на отрезке [0,2тг], получаем /?п /fen = О, ПРИ & = 1,2,..., п =
= 1,2,....
Обозначим /Q? = Д, /4 ' = щ<- Вычисляя интеграл, находим
Л =
Таким образом, в нерезонансном случае
и =
В резонансном случае при и = w^0 = а//^0/го решение записывается
в следующем виде, вытекающем из формулы A.7):
и =
Таким образом, при отсутствии сопротивления в случае совпа-
совпадения частоты вынуждающей силы с собственной частотой мембра-
мембраны наступает явление резонанса, при котором амплитуда колебаний
мембраны растет линейно по времени.
6. Найти поперечные колебания круглой мембраны Ur° радиу-
радиуса г0 с закрепленным краем, вызванные сосредоточенным ударом,
нормальным к поверхности мембраны, передавшим мембране в точ-
точке (ri, <pi), где 0 < г\ < го, — импульс К.

Решение. Рассмотрим два способа решения задачи.
Первый способ. Будем считать, что импульс К равномерно распре-
распределяется в момент t = 0 по элементарной площадке Дет = {(pi < (р <
(р\ + Д<р, ri < г < ri + Дг}. Начально-краевая задача, моделирующая
процесс колебаний мембраны, имеет вид
меиг°,
й\ =0,
lt=o '
щ
t=o
1г=г0
где р — поверхностная плотность мембраны. Поскольку
площадь малого участка Д(т, ргхДгД^ — его масса.
Решение начально-краевой задачи с "размазанным" по площадке
Дет импульсом К записывается с помощью формулы A.10):
и =
где р.^ — Аг-й корень уравнения
Для вычисления коэффициентов разложения воспользуемся фор-
формулой A.11):
где
Применяя теорему о среднем*) к интегралу в правой части формулы,
получаем:
*' См.: Ильин В.Л., Позпяк Э.Г. Основы математического анализа. Ч. 1. М.:
Наука, 1982.

где ri < г* < ri 4- Ar, (p\ < <p* < (p\ +
Перейдем к пределу при Дг—> 0 и Д<р —> 0 и обозначим предельные
(с)
значения коэффициентов через ф^:
Таким образом, решение исходной задачи можно получить как пре-
предел решения u(r, <p, t) при Дг —» 0 и Д<^> -> 0:
Подставив в последний ряд выражения для коэффициентов
^п, получим окончательный ответ:
Второй способ. Воспользуемся при постановке задачи дельта-
функцией. Тогда начально-краевая задача записывается следующим
образом:
=0 =
u, ME [7го,
'
TS
u*t=o= —
ul =0
1г=г0
Решение этой задачи согласно формуле A.10) имеет вид
и =
где //^ — корень номера k уравнения Jn(n) == О, А^ =

Коэффициенты разложения подсчитаем по формуле A.11):
Г 2, n = 0,
где („ - i
v '	f
Подставляя коэффициенты разложения в ряд, получаем ответ, ко-
который, естественно, совпадает с ответом, полученным первым спосо-
способом.
7. Решить начально-краевую задачу для уравнения колебаний в
прямом круговом цилиндре Ql>r° радиуса TO и высоты /:
5,,гр = ,
где 81)Г° — полная поверхность цилиндра, С — некоторая постоян-
постоянная.
Решение. Собственные функции и собственные значения цилиндра
в случае граничных условий Дирихле имеют следующий вид (см.
гл. II, § 9):
где Ць — корень номера k уравнения Jm(fi) = 0.
Квадрат нормы собственных функций выражается формулой
Решение задачи записывается с помощью формулы A.4), которая
в данном случае принимает следующий вид:

A.12)
где согласно формулам A.2) и A.3)
A.13)
Индексами с и s как обычно обозначены коэффициенты разложения
при косинусах и синусах соответственно.
В силу ортогональности тригонометрической системы на отрезке
[0,2тг] получим
тг, m = 1,
О, m^l,
= 0 при всех m = 0,1,.
Следовательно, <p*kmn = О, <pckmn = О при m ^ 1.
Поскольку
учитывая выражение для квадрата нормы, получаем
Решение начально-краевой задачи имеет вид
и =

8. Решить начально-краевую задачу в шаре Кг° радиуса
1 М € 7Г°, t> О,
где А — некоторая постоянная.
Решение. Решение ищем в виде разложения по собственным функ-
функциям шара с граничными условиями Дирихле. Собственные функции
и собственные значения имеют вид (см. гл. I, § 13)
Vknm =
(п + 1/2)	, „
где ц^ ' — Аг-й корень уравнения
= 0.
Квадрат нормы собственных функций равен
Из формулы A.4) вытекает формула для решения рассматривае-
рассматриваемой задачи:
A.14)
Формулы для коэффициентов разложения следуют из формул A.2)
и A.3) и имеют вид

A.15)
Так как cos в = Pj (cos 0), учитывая ортогональность системы при-
присоединенных функций Лежандра на отрезке [0, тг] и ортогональность
тригонометрической системы на отрезке [0,2тг], получаем из формул
A.5):
Япт = ° ПРИ ВС6Х *» П> т> Япт = 0 При П ф 1, Ш ± О,
Яю =
и окончательный ответ имеет вид
и =
9. Сферический сосуд с газом в течение длительного времени дви-
двигался равномерно со скоростью v, а затем в момент t = О мгновенно
остановился и остался неподвижным. Найти возникшие вследствие
этого колебания газа в сосуде.
Решение. Введем сферическую систему координат, совместив ее
центр с центром сосуда и направив ось 0 = О вдоль движения со-
сосуда при t < 0. В этом случае потенциал скоростей частиц газа и
не зависит от угла (р\ и = м(г, 0,/). Для него получается следующая
начально-краевая задача:
utt = a2Aw, 0 < г < TO, t > О,
Решение начально-краевой задачи будем искать в виде разложения
A.14) по собственным функциям шара, имеющим вид (см. гл. II, § 13)
Vknm =
где /4 — Ar-й корень характеристического уравнения
= 0.

При этом, поскольку функция г* (г, 0, г) не зависит от <р, в разложе-
разложении присутствуют собственные функции с индексом m = 0. А так
как cos 9 = PI(COS#), в разложении присутствуют только собствен-
собственные функции с индексом п = 1. Поэтому решение и можно искать в
виде и = u>{r, /)cos#, причем для функции u>(r, t) получается разло-
разложение
где ць — *-й корень характеристического уравнения
= 0.
Из начальных условий для функции w(r, 0,t) следуют начальные
условия для функции о; (г, t):
4=0 = W' <Ч=0 = °'
которые используются для определения коэффициентов разложения
Ak и Bk (k = 1, 2, . . . ). Из второго начального условия получаем
Bk = 0, 4=1,2,. ..,00.
Первое начальное условие дает
откуда
Ak =
где квадрат нормы радиальной собственной функции
Rk =
с учетом характеристического уравнения равен
1|Д*112 =
Таким образом,
Ak=	jfc = l,2,...,

Решение исходной задачи имеет вид
§ 2. ЗАДАЧИ ДЛЯ УРАВНЕНИЯ КОЛЕБАНИЙ
В ОГРАНИЧЕННОЙ ОБЛАСТИ С
НЕОДНОРОДНЫМИ ГРАНИЧНЫМИ УСЛОВИЯМИ
Начально-краевая задача для однородного уравнения колебаний
с однородными начальными и неоднородным граничным условиями
имеет вид
utt = а2Ди, (M,t) eQoo = Dx (О, +оо),
u(Af,0) = 0, tit(M,0) = 0, MeD = DUS,
a%± + pu = ii(P,t), PES, *E[0,+oo),
an
|a| + |/?| 7*0, a,/? = const.
Общая схема решения таких задач, как указано в гл. I, заключается
в следующем. Решение задачи ищется в виде
u(M,t) = v(M,t)+u;(M,t),
где v(M, t) — новая неизвестная функция, а функция ги(М, /) выбира-
выбирается так, чтобы она удовлетворяла заданному граничному условию
Для функции v(M , /) получается следующая начально-краевая зада-
задача:
vtt = av
w(M,0) = -г^(М,0), wt(M,0) = -w;t(M,0), M
a|^ + /?v = 0, P€ 5,
где f(M,t) = а2Дгу(М, /) — ги«(М,/). Решение этой задачи было рас-
рассмотрено в предыдущем параграфе.

Функция w(M,t) определяется неоднозначно. Поэтому ее нужно
стремиться выбрать так, чтобы уравнение для функции v(M, t) имело
наиболее простой вид. Удобно в качестве ги(М, t) выбирать гармони-
гармоническую функцию по пространственной переменной М, зависящую от
параметра t:
Aw = О, М Е Д
, Р€5, *€[0,оо).	BЛ)
Однако в случае граничного условия Неймана задача B.1) может не
иметь решения. В этом случае функцию w(M,t) нужно выбирать
другим образом.
Рассмотрим примеры решения конкретных задач с неоднородными
граничными условиями.
1. Решить начально-краевую задачу для уравнения колебаний на
отрезке с неоднородным граничным условием
utt = uxx, «€@,4), *е@,+оо),
u(*,0)=sin2^, «€[0,4],	B.2)
tit(*,0) = 0, ti@,f) = 0, tiD,f) = 1, t € [0, +00).
Решение. Будем искать решение задачи B.2) в виде суммы
u(x,t) = v(x,t) + w(x,t),
где в качестве w(x) выберем функцию w(x) — —. Легко видеть, что
так выбранная функция w(x) удовлетворяет граничным условиям
задачи B.2).
Для функции v(x,t) получается следующая начально-краевая за-
задача:
vtt = vxx, a: €@,4), t€@,+oo),
V(x,0)-sin2^-|, «€[0,4],	B.3)
«t(«,0) = 0, w@,t) = 0, wD,f) =0, te [0, +00).
Решение задачи B.3) можно выписать сразу, используя формулы
A.8) и A.9):
v(x,t) =
где

7ГП
Итак,
= — (А: = 1,2,...)
Следовательно, решение задачи B.2) имеет вид
2. Решить начально-краевую задачу для уравнения колебаний на
отрезке с неоднородными граничными условиями
utt = ихх, х € @, тг), t € @, +оо),
ti(a?,0) = 0, tit (ж, 0) = sin ж, а?€[0,тг],	B.4)
ti@,t) = t2, tiGr,t) = /3, t G [0, +оо).
Решение. Будем снова искать решение задачи B.4) в виде суммы
u(x,i) = v(x,t) -f гу(х,/),
где функцию w(x,t) выберем в виде
w(x,t) =
Функция w(xyt) удовлетворяет обоим граничным условиям задачи
B.4). Для функции v(x,t) получается начально-краевая задача для
неоднородного уравнения колебаний:
vtt=	s€@,7r), /€@,-foo),
ф,0) = 0, vt(x,Q) = sin ж, х е [0,тг],	B-5^
v@,t) = 0, vGr,t)=0, t€[0,-hoo).
С помощью формул A.8), A.9) решение задачи B.5) записывается
следующим образом:
v(x,t) =

где
Таким образом,
v(x,t) =
и, следовательно, решение задачи B.4) имеет вид
3. Найти колебания газа в сферическом сосуде радиуса TQ, вы-
вызванные малыми колебаниями его стенки, начавшимися с момента
t = О, если скорости частиц стенки направлены по радиусам сосуда и
равны Рп (cos #)/(*), где /@) = /'(О) = 0, п > 0. Рассмотреть случай
Решение. Введем сферическую систему координат, совместив ее
начало с центром сосуда. В силу условия задачи потенциал скоростей
и частиц газа не зависит от угла (р и для него получится следующая
начально-краевая задача:
utt = а2 ДГ|*н, г € @, г0), в € @, тг), t е @, +оо),
ti(r,fl,0) = 0, tit(r,fl,0) = 0, г€[0,г0], «€[0,7г],	B.6)
Мго,М) = ^п (сое
где

Будем искать решение задачи B.6) в виде суммы
где в качестве функции w(r, 0,t) выберем произведение шаровой
функции rnYn (в,<р) = rnPn(cos0) на функцию f(t) с коэффициен-
коэффициентом С:
Коэффициент С определим из граничного условия при г = г0:
uvfahM) = Cnr$-lPn(coB0)f(t) = Ря(сов0)/(*),
откуда
С=—L-
nr
0
Функция гу(г, 0,t) при п > 0 является решением краевой задачи при
te [0,+оо):
Дг,^ = 0, г 6@,1-0), 0б@,тг),
и;г(г0,М) - Ря (сое *)/(*), 0 G [0,тг].
Для функции v(r, 0,t) получается начально-краевая задача для не-
неоднородного уравнения колебаний с однородными начальными и гра-
граничными условиями:
rn fit)
vtt = а2Дг,^ - n_YPn(cos0),
пг0
rG@,r0), 0Е@,тг), *Е@,+оо),
v(r,0,0) = —— ?ггРп(совв)/@) = 0,	B.7)
пг0
t»t(r,fl,0) = —— ^Pn(cos0)/'@) = 0, г€[0,го], в€[0,1г],
пг0
vr(r0,e,t) = Q, ffe[0,ir], <€[0,+сю).
Решение задачи B.7) записывается с помощью формул A.14), A.15).
Собственными функциями являются собственные функции шара, ко-
которые при отсутствии зависимости от угла <р имеют вид (см. гл. II,
§13)
V*,iM)=	(* = 1,2,..., / = 0,1,...),

pk ' — Ar-й корень характеристического уравнения
= 0.
Квадрат нормы собственной функции равен
IKill2 =
Учитывая вид неоднородности в уравнении задачи B.7)
F(r,e,t) =
получим, что в разложении присутствуют только собственные функ-
функции с I = п. Так как
где
Таким образом,
v(r,e,t) =

и ответ задачи B.6) имеет вид
B.8)
где
= 0 (*=1,2,...).
В случае f(t) = At2, n = 3 имеем /"(*) = 2Л и, вычисляя интеграл,
получим
4. Найти колебания газа в сферическом сосуде радиуса г0, вызван-
вызванные гармоническими колебаниями его стенки, начавшимися в момент
времени t = 0. Скорости частиц стенки направлены по радиусам со-
сосуда, а величина скоростей равна A cos в sin u>t.
Решение. Воспользуемся формулой B.8) решения предыдущей за-
задачи, учитывая, что cos в = PI(COS#), и положив п = 1, ^k = /4 >
= Asinutt. Подсчитаем интеграл
1 =
Поскольку
можем записать

Таким образом, решение задачи имеет вид
u(r,0,t) =
B.9)
Из формулы B.9) вытекает, что если частота внешнего воздействия
совпадает с собственной частотой сферического сосуда (w = u>k0 =
= afAkQ), то возникает явление резонанса. Переходя в формуле B.9)
к пределу при ш —> ш^0 получим
Таким образом, как это следует из последней формулы, при резо-
резонансе в отсутствие поглощения амплитуда растет линейным образом
с течением времени.
§ 3. ЗАДАЧИ ДЛЯ УРАВНЕНИЯ
КОЛЕБАНИЙ НА БЕСКОНЕЧНОЙ ПРЯМОЙ
Начальная задача (задача Коши) для уравнения колебаний на бес-
бесконечной прямой К1 с постоянными коэффициентами заключается в
определении в области О = К1 х [0, ос) функции u(x,i), удовлетворя-
удовлетворяющей уравнению колебаний и двум начальным условиям:
utt = а2ихх + /(*,*), (х, t) € П = Ж1 х @, оо),

%=o = V?(x)' Н=о = ^ж)'	(ЗЛ)
Классическим решением задачи с начальными условиями называ-
называется функция t/(x,tf), непрерывная вместе со своими первыми произ-
производными по t в замкнутой области Q, имеющая непрерывные произ-
производные второго порядка в открытой области Q, удовлетворяющая в
Q уравнению колебаний и при t — > 0 начальным условиям.
Если функция <р(х) дважды непрерывно дифференцируема, функ-
функция ф(х) непрерывно дифференцируема на бесконечной прямой М1, а
функция f(x,t) непрерывно дифференцируема в области Q, то клас-
классическое решение задачи C.1) существует и единственно.
В случае меньшей гладкости функций у>(х), ф(х) и f(x,t) началь-
начальная задача C.1) может иметь обобщенное решение.
Учитывая линейность задачи C.1), можно провести ее редукцию и
представить решение u(x,t) в виде суммы решений двух задач:
u(x,t) = t/i(z,*) + u2(z,*),
где i/i (x, t) — решение начальной задачи для однородного уравнения
колебаний с неоднородными начальными условиями, u^(x,t) — ре-
решение начальной задачи для неоднородного уравнения колебаний с
однородными начальными условиями.
Для решения начальной задачи для уравнения колебаний на бес-
бесконечной прямой эффективно использовать метод интегрального пре-
преобразования Фурье. Общая схема применения интегрального пре-
преобразования Фурье для решения начальной задачи на бесконечной
прямой дана в гл. I, § 4. Здесь приведены примеры решения задач
для уравнения колебаний на бесконечной прямой методом интеграль-
интегрального преобразования Фурье.
1. Рассмотрим начальную задачу для однородного уравнения ко-
колебаний на бесконечной прямой:
utt = а2ихх, (x,t)
и
t=o
t=0
C-2)
Применим преобразование Фурье с ядром e~lXx и обозначим через
t/(A,tf), Ф(А) и Ф(А) образы Фурье функций t/(x,tf), y>(x) и ф(х) соот-
соответственно:
U(\,t) =
Ф(А) =

Ф(А) =
Предположим, что выполнены условия существования интеграла
Фурье (это заведомо выполнено для классического решения задачи)
и что функция u(x,t) и ее частные призводные достаточно быстро
стремятся к нулю при х —> ±оо. Предположим также, что интеграл
для U(\,i) можно дифференцировать по переменной t под знаком
интеграла.
Умножая уравнение колебаний и начальные условия на ~тх%е~гХх
и интегрируя по х от —оо до +оо, получим для функции С/(А,/), за-
зависящей от параметра А, задачу Коши:
U@) = Ф, U'@) = Ф,
решение которой имеет вид
U(\,t) =
Воспользовавшись формулой обратного преобразования Фурье (см.
гл.1, § 4), возвратимся от изображения U(X,t) к оригиналу u(x,t):
«(*,<) =
где
/1 =
/2 =
Рассмотрим интеграл 1\. Используя выражение для Ф(А), получим

Используя формулу
cosaXt =
и известное интегральное представление дельта-функции*)
*(*) =
интеграл в фигурных скобках преобразуем следующим образом:
С помощью последней формулы получим
Перейдем к интегралу /2. Подставляя в него выражение для Ф(А),
будем иметь
/2 =
Для вычисления внутреннего интеграла воспользуемся формулой
|, при \Ь\ < 1,
= f, при |6| = 1,	C.3)
О, при |6| > 1,
которую несложно получить, вычисляя интеграл в левой части с по-
помощью вычетов**).
*' См.: Владимиров B.C. Уравнения математической физики. М.: Наука, 1988.
**' См.: Свешников А.Г., Тихонов А.И. Теория функций комплексной перемен-
переменной. М.: Наука, 1979.

Вводя замену z = а А/, получим
Таким образом,
-,
7Г
2'
0,
при
при
при
х-(
at
*-?
а/
z-f
а/
/2 =
C.4)
Используя выражения для интегралов 1\ и /2, получаем окончатель-
окончательный ответ:
u(x,t) =
C.5)
Полученное выражение C.5) для решения задачи C.1) носит назва-
название формулы Даламбера.
Формула Даламбера C.5) получена нами с помощью метода ин-
интегрального преобразования Фурье. Из нее следуют единственность,
устойчивость и существование решения задачи C.1)*).
При этом решение представляется в виде суперпозиции двух бегу-
бегущих волн:
и(х, t) = fi(x + at) + h(x - at),
где fi(x + at) — правая бегущая волна:
C.6)
и /2 (х — at) — левая бегущая волна:
h(x-at} =
*) См.: Свешников А.Г., Боголюбов А.И., Кравцов В.В. Лекции по математиче-
математической физике. М.: Изд-во МГУ, 1993.

Можно было сразу искать решение задачи C.1) в виде C.6). Та-
Такой подход к решению задачи носит название метода распространя-
распространяющихся волн, или метода Даламбера. Рассмотрим его подробней.
Предположим, что существует классическое решение задачи C.1).
Преобразуем однородное уравнение колебаний к каноническому виду,
содержащему смешанную производную. Характеристическое уравне-
уравнение для однородного уравнения колебаний имеет вид
(dxJ - a2(dtJ = О
и распадается на два уравнения:
dx - a dt = О, dx + a dt = 0.
Характеристиками являются два семейства прямых:
х — at = С\ , х 4- at = Сч .
Сделаем замену переменных
? — х + at, 77 = х — at.
В переменных ? и г] однородное уравнение колебаний принимает вид
UD = 0,	C.7)
где
Общим интегралом уравнения C.7) является функция
Отсюда вытекает, что общим интегралом однородного уравнения ко-
колебаний будет функция
и(х, у) =fi(x + at) + h(x - at).	C.8)
Таким образом, функция C.8) удовлетворяет уравнению задачи C.1)
и всякое его решение представимо в виде C.8). Если функции fi(x +
+at) и /2B — at) дважды непрерывно дифференцируемы, то формула
C.8) дает классическое решение однородного уравнения колебаний.
Функции /1 и /2 определяются из начальных условий задачи C.1).
Подставляя C.8) в начальные условия, получим

где штрих означает производную по полному аргументу. Обозначая
аргументы функций f\ и /2 через С и интегрируя второе из равенств,
будем иметь
/l(C) + /2(C) =
/1@-/2(С) =
где Со и С — некоторые постоянные.
Складывая и вычитая два последних равенства, получим
/2@ =
и после подстановки /i(C) и /2 (С) в формулу C.8) придем к формуле
Даламбера C.5).
Метод распространяющихся волн используется не только для ре-
решения задач на неограниченной прямой, но на полупрямой и на отрез-
отрезке. В следующем параграфе приведены примеры построения решений
начально-краевых задач для уравнения колебаний на полупрямой.
2. Рассмотрим задачу для неоднородного уравнения колебаний на
бесконечной прямой с однородными начальными условиями
=о = °'	=о = °-
Для решения задачи применим преобразование Фурье с ядром
е~|Ааг, обозначив через U(\,t) и F(\,t) образы Фурье функций u(x,t)
и f(x,t) соответственно:
U(\,t) =

Сделаем те же предположения, что и в случае задачи 1. Умножив
уравнение колебаний на "ТТ"'** и интегрируя по х от — оо до ос,
получим с учетом начальных условий следующую задачу Коши в
пространстве образов:
t/(A,0) = 0, [7t(A,0) = 0.
Решение задачи выписывается с помощью импульсной функции
Подставим в интеграл выражение для F(A, г) и используем формулу
обратного преобразования Фурье (см. гл. I, § 4)
u(x,t) =
Для вычисления внутреннего интеграла в фигурных скобках вос-
воспользуемся формулой C.4). В результате будем иметь
при
7Г
= 2", при
О, при
a(t - г)
a(t - т)
a(t-r)
= 1,
Подставляя это выражение в фигурные скобки, получим окончатель-
окончательный ответ
«(«,0 =
C.10)

Из формул C.5) и C.9) следует формула для решение задачи C.1)
для неоднородного уравнения колебаний на бесконечной прямой с
неоднородными начальными условиями:
+	C.11)
Рассмотрим теперь задачу Коши для несколько более сложного
уравнения гиперболического типа.
3. Решить следующую задачу:
utt = а2ихх — с2и, —оо < х < оо, t > О,
«lt=o = ?(*)• 4=o = V-(*).	C-12)
Решение. Для решения этой задачи используем преобразование
Фурье. Пусть
U(\,t) =
Применяя к уравнению и начальным условиям преобразование Фу-
Фурье, аналогично тому как это сделано в предыдущих задачах, полу-
получаем задачу Коши для образа U(\,t):
Utt + (a2A2 + c2)U = О, * >0,
^ l=o = *(*)• Ч=о = »(*)•	(ЗЛЗ)
где
Ф(А) =
Ф(А) =
Решение задачи C.13) имеет вид
U(\,t) =

Для определения функции u(x,i) используем обратное преобразова-
преобразование Фурье
Введем обозначения
Преобразуем выражение для г/2 (#,?)• Подставляя явное выражение
для W(A), получаем
Для дальнейших преобразований используем формулу*)
Согласно этой формуле
Поэтому
г/2 =
*' См., например: Градилтейн И.С., Рыэюик И.М. Таблицы интегралов, сумм,
рядов и произведений. М.: Наука, 1971.

Поскольку
можем записать
г/2 =
Заметим, что
Поэтому решение можно записать в виде
u(x,t) =
Вычислив производную в первом слагаемом, получим
C.14)

Заметим, что при с = 0 написанная формула переходит в формулу
Даламбера.
§ 4. ЗАДАЧИ ДЛЯ УРАВНЕНИЯ
КОЛЕБАНИЙ НА ПОЛУПРЯМОЙ
Начально-краевая задача для уравнений колебаний на полубеско-
полубесконечной прямой х > О с граничными условиями первого, второго и
третьего рода ставится следующим образом:
где |а| + \/3\ ф 0. При а = 0, /3 = 1 получается задача Дирихле, при
а = 1, /3 = О — задача Неймана, при а ф О, /3 ф О — третья краевая
задача.
Классическим решением начально-краевой задачи для неоднород-
неоднородного уравнения колебаний на полуограниченной прямой называется
функция u(x,i), непрерывная вместе с первыми производными в за-
замкнутой области Q+ = М+ х [0, оо), имеющая непрерывные производ-
производные второго порядка в открытой области ?2+, удовлетворяющая в Q+
уравнению колебаний, начальным и граничному условиям.
Классическое решение начально-краевой задачи может существо-
существовать лишь при выполнении условий согласования начальных и гра-
граничных условий
а<р'@) + /Jp@) = /i@), aV-'(O) + ДО@) = /i'@).
В силу линейности начально-краевой задачи можно провести ее
редукцию и представить решение u(x,i) в виде суммы и = и\ 4- ^2>
где t/i(x, t) — решение задачи с однородными граничными условиями
и U2(x,t) — решение задачи для однородного уравнения с однород-
однородными начальными и неоднородными граничными условиями. Редук-
Редукцию можно продолжить и представить функцию и\(х, t) в виде суммы
двух функций — решений начально-краевых задач для однородного
и неоднородного уравнений.
1. Начально-краевые задачи для уравнения колебаний на
полупрямой с однородными граничными условиями.
При решении начально-краевых задач на полупрямой для уравне-
уравнения колебаний с однородными граничными условиями используют-
используются различные методы: метод интегрального преобразования Фурье,

метод распространяющихся волн, метод продолжения и др. В следу-
следующем пункте, посвященном решению начально-краевых задач с не-
неоднородными граничными условиями, рассматривается применение
метода интегрального преобразования Фурье и метода распростра-
распространяющихся волн. В настоящем пункте излагаются основные положе-
положения метода продолжения, весьма удобного и эффективного в случае
однородных граничных условий.
Для изложения основных положений метода продолжения нам по-
понадобится следующая лемма.
Лемма. Пусть функции ф(х}, ф(х) и f(x,t) определены при —оо <
< х<оо, ? > О, имеют ограниченные производные по х до N-ro поряд-
порядка, а линейные комбинации
Ф(х) =	9(х) =
где а/с = const, k = 0,1,...,АГ, нечетные относительно точки х = 0.
Тогда функция
u(x,t) =
D.1)
удовлетворяет условию
= 0.	D.2)
Доказательство. Рассмотрим линейную комбинацию из производ-
производных функции u(x,t), сделав в интегралах формулы D.1) замену ?
на ? + х:
+
D.3)

Учтем, что
подставим эти выражения в последнюю формулу и заменим в инте-
интегралах ? на ? — х:
Положив х = О, получим
+	D.4)
поскольку функции Ф(я), Ф(ж) и F(x1t) по аргументу х являются
нечетными. •
Приведенная лемма позволяет сформулировать следующий метод
решения начально-краевых задач для уравнения колебаний на полу-
полупрямой в случае однородных граничных условий.
Пусть необходимо решить следующую начально-краевую задачу:
utt = а2ихх + /(ж, *), 0 < х < оо, t > О,
ti(x,0) = ^(x), щ(х,0) = ф(хI
D.5)
= 0.
Продолжим функции <р(х), ф(х] и f(x,t) на отрицательную полуось
х < 0 так, чтобы функции
D.6)
F(x,t) =

где (р(х], ф(х], f(x,i) — продолжения соответственно функций (р(х],
ф(х), f(X)i) на всю прямую я, были нечетными.
Покажем, что функция
+
при х > О является решением задачи D.5).
В самом деле, функция п(я, t) удовлетворяет неоднородному урав-
уравнению колебаний на бесконечной прямой — оо < х < оо (см. § 3) и,
следовательно, на полупрямой х > 0, поскольку f(x,t) = f(x,t) при
х > 0. Функция u(x,t) удовлетворяет начальным условиям задачи
D.5), поскольку (р(х) = <р(я), ф(х) = ф(х) при х > 0. И наконец,
функция u(x,t) удовлетворяет граничному условию задачи D.5) в
силу леммы. Таким образом,
Приведем примеры использования метода продолжения для реше-
решения начально-краевых задач.
1. Рассмотрим начально-краевую задачу для однородного уравне-
уравнения колебаний на полупрямой с однородными граничным условием
Дирихле
utt = a2uxxi х > 0, t > О,
ti(*,0) = ?(*), tit(*,0) = V(*)> "(<М) = 0.	( ' J
Воспользуемся леммой. Поскольку для граничного условия Ди-
Дирихле коэффициенты в формуле D.2) имеют вид OQ = 1, а* = О,
k = 1,2,...,ЛГ, будем иметь Ф(ж) = <?(я), ^(ж) = ф(х], и, для того
чтобы решение задачи D.8) можно было бы представить в виде D.1),
функции <р(х) и ф(х) нужно продолжить на отрицательную полуось
нечетным образом:
ф(х) =	ф(х) = D.9)
Перепишем формулу D.1) при f(x,t) = 0:
«(*,<)=	D.10)

выразив функции (риф через функции (риф соответственно по
формулам D.9). Если выполнены условия х + at > х — at > 0, то
(р(х ± at) = (р(х ± а*), ф(х ± at) = ф(х ± at). Если х — at < О, то
<р(х — at) = —(p(at — х) и ф(х — at) = —^(at — х). Поэтому формула
для решения задачи принимает вид
«(*,*) =	D.11)
Последнюю формулу можно переписать в более компактном виде:
u(x,t) =
*>0, ж>0,
где sgn(z) — сигнум-функция Кронекера, определяемая следующим
образом:
1, если z > О,
sgn(z) = 0, если z - О,
— 1, если z < 0.
2. Рассмотрим начально-краевую задачу для однородного уравне-
уравнения колебаний на полупрямой с однородными граничным условием
Неймана
../_ Л\ _ ,-/— Ч	.. /_ Л\ _ _/./_\ .. /Л а\ _ Л V '
Снова воспользуемся леммой. Для граничного условия Неймана
коэффициенты в формуле D.2) равны а$ = 0, ai = 1, а/с = 0, k_= 2,
3,..., N. Поэтому согласно формуле D.6) Ф(ж) = <р'(я), Ф(х) = ф'(х),
и, для того чтобы решение задачи D.12) можно было бы предста-
представить в виде формулы Даламбера D.10), функции (р'(х) и ^'(х) нужно

продолжить на отрицательную полуось х < 0 нечетным образом. По-
Поскольку производная четной функции есть функция нечетная, функ-
функции (р(х) и ф(х) следует продолжить на отрицательную полуось чет-
четным образом:
<р(х) =	ф(х) =
Записывая решение задачи D.12) в виде D.10) и переходя от функций
ф и ф к функциям (риф аналогично тому, как это было сделано в
случае граничных условий Дирихле, получим ответ:
«(*,*) =
D.13)
который можно записать более компактно:
!!(*,*) =
3. Рассмотрим на полупрямой начально-краевую задачу для од-
однородного уравнения колебаний с однородным граничным условием
третьего рода:
utt = a2uxx, х > О, t > О,
ii(*,0) = *>(*), ММ) = V>(*),	D.14)
ux @, t) - /ш@, 0 = 0, Л = const .
Применим доказанную лемму. Для задачи D.14) получаем а0 = —Л,
GI = 1, а* = 0, k = 2,3, . . . ,N. Следовательно, согласно формуле

D.6) Ф(х) — (р1 — h(p, Ф(ж) = ф1 — ftV>, где <р(я), ф(х) — продолже-
продолжение на отрицательную полуось функций <р(х) и ф(х] соответственно.
Согласно лемме функции (р(х] и 'ф(х) нужно продолжить так, чтобы
функции Ф(ж) и Ф(ж) были нечетными. Тогда решение задачи D.14)
можно записать в виде формулы Даламбера D.10):
u(x,t) =
Построим функции ф(х) и ф(х). Очевидно, <р(х) = <р(х), ф(х) = ф(х)
при х > 0.
Для определения функции ф(х) при х < 0 получим задачу Коши
D.15)
где правая часть уравнения имеет вид
/(х) = V(~*) +
(штрих есть производная по полному аргументу) .
Решение задачи D.15) выписывается с помощью импульсной функ-
функции следующим образом:
Таким образом, функция <р(х] имеет вид
Для определения функции ф(х) на отрицательной полуоси полу-
получаем задачу Коши, аналогичную задаче D.15):
$(x)-h$(x)=g(x), Ж О,
где д(х) = —i/j'(—x) + hi/j(—x) (штрих обозначает производную по пол-
полному аргументу).

Следовательно, функция ij>(x) имеет вид

Таким образом, решение задачи D.14) имеет следующий вид:
D.18)
4. Рассмотрим начально-краевую задачу для неоднородного урав-
уравнения колебаний на полупрямой с однородными начальными услови-
условиями и однородным граничным условием Дирихле
utt = c?uxx + f(x,t], *>0, *>0,
D.19)
ti(x,0) = 0, ti,(*,0) = 0, ti@,*) = 0.
Воспользуемся леммой. Аналогично задаче D.8), для того чтобы ре-
решение задачи D.19) можно было представить в виде D.1), функцию
f(x,t) нужно продолжить на отрицательную полуось нечетным обра-
образом:
/(*,«) =
Рассмотрим формулу D.1) при <?>(х) = О и ф(х) = 0:
u(x,t) =
Выразив функцию f(x,t) через f(x,t), получим:
«(*,*) =

Полученную формулу можно записать в более компактном виде:
п(х,г)=	D.20)
5. Рассмотрим начально-краевую задачу для неоднородного урав-
уравнения колебаний на полупрямой с однородными начальными услови-
условиями и однородным граничным условием Неймана
u(*,0) = 0, M*»0) = 0, ttr@,<) = 0.
Воспользуемся леммой. Аналогично задаче D.12) продолжим функ-
функцию f(x,i) на отрицательную полуось четным образом:
/>,<) =
и запишем формулу D.1) при <f>(x) = 0 и ф(х) = О
«(*,<) =
Выразив функцию /(х, <) через /(х, <), запишем решение задачи D.21)
в виде следующей формулы:
«(*,*) =
D.22)
6. Решить начально-краевую задачу для уравнения колебаний на
полуограниченной прямой с граничными условиями третьего рода:
utt = a2Uxx, x > 0, t > 0,
и(*,0)=	D.23)

Решение. Задача D.23) совпадает с задачей D.14) при ф(х) = 0.
_	У»
Воспользуемся формулой D.18). Пусть 0 < t <-. Тогда
u(x,t) =
D.24)
X	X ~h I
Пусть — < t < ———, тогда 0 < at — x <l и согласно D.18) и D.23)
и(*,*) =	D.25)
Вычислим интеграл, сделав в нем замену z —> — z:
Используя формулу
D.26)
которую легко получить двухкратным интегрированием по частям,
получаем
!!(*,*) =
Пусть, наконец, х~*~ <t < оо. Тогда в силу D.18) и D.23) решение
a
снова записывается в виде D.25), где интеграл с помощью замены
приводится к виду

поскольку <p(z) = О при I < z < at — х.
Используя снова формулу D.26), получаем
и окончательно
Объединив все три случая, можно записать ответ задачи D.23) сле-
следующим образом:
«(*,<) =
2. Начально-краевые задачи для уравнения колебаний на
полупрямой с неоднородными граничными условиями.
Для решения начально-краевой задачи для уравнения гипербо-
гиперболического типа на полупрямой в случае неоднородных граничных
условий рассмотрим метод интегрального преобразования Фурье и
метод распространяющихся волн. Общая схема метода интегрально-
интегрального преобразования приведена в гл. I, § 4. Общая схема применения
метода распространяющихся волн изложена в предыдущем парагра-
параграфе. В данном пункте рассмотрены конкретные примеры решения
начально-краевых задач для уравнения гиперболического типа на
полупрямой с неоднородными граничными условиями методом ин-
интегрального преобразования Фурье и методом распространяющихся
волн.
1. Рассмотрим начально-краевую задачу для однородного уравне-
уравнения колебаний на полупрямой с неоднородным граничным условием
Дирихле
ин = а?ихх, х>0, *>0,
ti(*,0) = 0, tit(*,0) = 0, ti((M)	'

а) Решим задачу D.27) методом интегрального преобразования
Фурье. Применим синус-преобразование Фурье с ядром К(х1у) =
П)
— \j — sinAx. Обозначим через [/(А, 2) синус-образ Фурье функции
u(x,t).
Предположим, что выполнены условия существования интеграла
Фурье, функция u(x,i) и ее частные производные достаточно быстро
стремятся к нулю при х —> оо, а интеграл для U(\,t) можно диффе-
дифференцировать под знаком интеграла по переменной t.
Умножим обе части однородного уравнения колебаний на J— sin Аж
и проинтегрируем по ж от 0 до оо:
Проинтегрируем интеграл в правой части, учитывая граничное усло-
условие задачи D.27):
Отсюда, учитывая однородные начальные условия задачи D.27), по-
получаем следующую задачу Коши в пространстве образов:
, О О,
t/(A,0) = 0, C/t(A,0) = 0.
Решение этой задачи легко выписывается с помощью импульсной
функции
U(\,t) =
С помощью формулы обратного преобразования Фурье вернемся в
пространство оригиналов:
u(x,t) =

Используя формулу
получаем
Поскольку разложение (J-функции в интеграл Фурье имеет вид
получаем
Так как 0 < т < t, при х > О
= 0.
Отсюда
«(*,*) =
D.28)
б) Теперь решим задачу D.27) методом распространяющихся волн.
Так как в силу однородности уравнения и начальных условий зада-
задачи D.27) единственной причиной возмущения является определенный
функцией fi(t) краевой режим, решение можно искать в виде правой
бегущей волны:

где / — некоторая достаточно гладкая функция. Для определения
вида функции / воспользуемся начальными и граничными условия-
условиями задачи. Из первого начального условия получим
u(s,0) = f(x) = 0, при х>0.
Тогда второе начальное условие также выполняется:
ut(x, 0) = -a/'(s), при х > 0.
Используя граничное условие, доопределим функцию f(x) на отри-
отрицательной полуоси:
Таким образом, обозначив аргумент функции / через z, получим
/(*)=
и, подставив z = х — а?, окончательно найдем
Мы снова получаем формулу D.28).
Отметим, что формула D.28) имеет простой физический смысл.
Для точки полупрямой, расположенной от конца х = О на расстоянии
ж, для моментов времени t < х/а возмущение равно нулю, поскольку
в силу конечности скорости распространения возмущение не успевает
достичь этой точки. При t > х/а возмущение, заданное на конце
х = О и представляющее собой правую бегущую волну, доходит в
эту точку. Форма профиля возмущения определяется функцией цA)
граничного условия задачи D.23).
2. Рассмотрим начально-краевую задачу для однородного уравне-
уравнения колебаний на полубесконечной прямой с неоднородным гранич-
граничным условием Неймана
ик = а?ихх, s>0, *>0,
ti(*,0) = 0, tit(*>0) = 0, ti,@, *) = !/(*).	(* }
Для решения задачи применим косинус-преобразование Фурье с
ядром К(х,Х) = \1 =- cosXx. Обозначим через U(\,t) косинус-образ
Фурье функции u(x,t):
U(\,t) =

Сделаем те же предположения, что и при решении задачи D.27).
Умножая обе части однородного уравнения колебаний на \1 — cos \х и
интегрируя по х от 0 до оо, используя граничные и начальные усло-
условия задачи, получаем задачу Коши в пространстве образов:
=-a\P !/(<),
V 7Г
+ eaAatf =-a3 \/::"(<)> <>0,
U(\,0)=Q, t/t(A,0) = 0.
Решение задачи Коши записывается с помощью импульсной функции
следующим образом:
U(X,t) =
Применив обратное преобразование Фурье, получим выражение
для решения u(x,t) начально-краевой задачи D.29):
Используя формулу
и интеграл Дирихле

Учитывая, что 0 < т < J, с помощью последней формулы получаем
X
= 7Г При Т < t — -
= 0 при т > t — —.
Подставляя эту формулу для u(x,t), окончательно находим
tiOM)=	D.30)
Замечания. Мы решили задачу D.29) методом интегрального пре-
преобразования Фурье. Совершенно аналогично тому, как это было сде-
сделано при решении задачи D.27), задачу D.29) можно было решить
методом распространяющихся волн. В качестве упражнения читате-
читателю предлагается получить формулу D.30) этим методом.
Физический смысл формулы D.30) аналогичен физическому смы-
смыслу формулы D.28) для граничных условий Дирихле: до точек по-
полупрямой, расположенных на расстоянии я, возмущение за время
t < х/а не успевает дойти.
Задача D.29) является математической моделью задачи о малых
продольных колебаниях упругого полубесконечного стержня. С фи-
физической точки зрения граничное условие второго рода означает, что
к концу х = 0 приложена заданная сила f(t) = k(Q)v(t), где fc@) —
значение коэффициента упругости в точке х = 0. Пусть теперь за-
заданная сила действует на конце стержня х = 0 в течение конечного
промежутка времени (^1,^2)? где t\ > 0, т.е. функция v(t) является
финитной:
"(*) =
Тогда из формулы D.30) следует, что
«(*,<) =

Из этой формулы вытекает, что в моменты времени t < ti + -
возмущение в точке х равно нулю, т.е. в эти моменты времени вли-
влияние в точке х граничного условия не сказывается: возмущение не
х
успевает дойти до точки х. В момент времени t = ti + - в точке
х возникает возмущение, которое зависит от t до момента времени
X	X
t = Г2 + —. Начиная с момента времени t = i^ + — в точке х устана-
устанавливается возмущение, не зависящее от времени, — система выходит
на стационарный режим.
Пусть теперь на конце х — О стержня задана гармоническая сила
v(t) = Acosut. Поскольку
формула D.30) дает
Таким образом, как это следует из последней формулы, в точке х
х
стержня, начиная с момента времени t = - возникают колебания с
частотой и.
3. Рассмотрим начально-краевую задачу для однородного уравне-
уравнения колебаний на полуограниченной прямой с неоднородным гранич-
граничным условием третьего рода:
utt = а?ихх, х > О, t > О,
и(х, 0) = 0, щ(х, 0) = 0, ii,@, t) - Ati@, t) = i/(*),
где h — некоторая постоянная.
Решим задачу D.31) методом распространяющихся волн. Как и
в случае граничных условий Дирихле D.27), в силу однородности
уравнения и начальных условий задачи D.31) будем искать решение
в виде правой бегущей волны
где / — некоторая достаточно гладкая функция. Из первого началь-
начального условия получаем, что
и(х, 0) = f(x) = О при я>0,

при этом второе начальное условие также выполняется:
ut(x, 0) = -af(x) = О при х > 0.
Подставляя функцию f(x — at) в граничное условие задачи D.31),
получим обыкновенное дифференциальное уравнение
где штрих обозначает производную по полному аргументу.
Сделав замену z = —at и учитывая, что /@) = 0, получаем на-
начальную задачу для функции f(z):
Л*) -*/(*)="(-?),
Решение этой задачи с помощью функции Коши записывается следу-
следующим образом:
f(z) =	z<0.
Сделаем в последнем интеграле замену ? = — — , в результате чего
получим
/(*) =
Подставляя в последней формуле z = х — at, получим окончательный
ответ:
«(*,*)=	D.32)
Заметим, что, положив в формуле D.32) Л = 0, мы получим фор-
формулу D.30) для решения начально-краевой задачи для однородно-
однородного уравнения колебаний на полупрямой с неоднородным граничным
условием Неймана.
Мы решили задачу D.31) методом распространяющихся волн. Ис-
Используя интегральное преобразование Фурье с ядром
R(x,\) =

можно получить формулу D.32) методом интегральных преобразо-
преобразований. Читателю рекомендуется проделать это в качестве полезного
упражнения.
§ 5. ЗАДАЧИ ДЛЯ УРАВНЕНИЯ КОЛЕБАНИЙ
НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
В предыдущих параграфах широко использовалось интегральное
преобразование Фурье для решения пространственно-одномерных за-
задач для уравнения колебаний. В этом параграфе рассмотрим приме-
применение преобразования Фурье для решения задачи Коши для уравне-
уравнения колебаний на плоскости и в неограниченном пространстве.
Как указывалось ранее (гл. I, § 4), при решении пространственно-
многомерных задач можно поступать по-разному. Можно применять
многомерное преобразование Фурье сразу по всем пространственным
переменным. В результате этого для образа Фурье получается од-
одномерная задача Коши по переменной ?, содержащая столько пара-
параметров, сколько было пространственных переменных. Для получе-
получения оригинала, т.е. решения исходной задачи, используется обратное
многомерное преобразование Фурье.
Возможен и несколько иной способ. Интегральное преобразова-
преобразование Фурье применяется не по всем переменным, а только по части
из них, например только по одной из пространственных переменных.
Тогда для образа Фурье получается задача для уравнения в частных
производных (а не обыкновенное дифференциальное уравнение, как
в первом способе), но в пространственной области меньшей размер-
размерности.
Рассмотрим оба этих способа решения двумерных и трехмерных
(по пространственным переменным) задач.
Начнем с задачи Коши для уравнения колебаний на неограничен-
неограниченной плоскости, которая ставится следующим образом:
utt = а2 Д2и, -оо < х, у < +оо, t > О,
E.1)
Эту задачу решим обоими указанными выше способами.
Сначала используем преобразование Фурье по части простран-
пространственных переменных. В данном случае используем преобразование
Фурье по переменной у. Обозначим через С/(х, A, t) образ Фурье функ-
функции и(х,у, z) по переменной у:
U(x,X,t) =

Применив преобразование Фурье по переменной у к задаче E.1) ана-
аналогично тому, как это делалось в предыдущих параграфах, получим
задачу для функции U(x,\,t):
Utt = a2Uxx - а2Л2С/, -оо < х < оо, t > О,
где
Ф(*,А) =
Для функции U(x,\,t) получена задача Коши для одномерного
уравнения гиперболического типа, в которой Л входит как параметр.
Эта задача рассмотрена в предыдущем параграфе, и ее решение удоб-
удобно записать в виде
E.2)
Чтобы получить решение задачи E.1), используем обратное преобра-
преобразование Фурье
где
Преобразуем выражение для иъ(х, у, t). Подставляя явное выражение
для Ф(?, Л) и заменяя порядок интегрирования, получаем

Поскольку (см. приложение, § 4 D.3))
,y, t) принимает вид
E.3)
Повторный интеграл в формуле E.3) представляет собой интеграл
на плоскости (?, ?/), взятый по кругу:
т.е. по кругу K%f с центром в точке М (ж, у) радиуса at. Поэтому
Выражение для функции и\(х, у, i) может быть теперь выписано сра-
сразу:
Таким образом, решение задачи E.1) имеет вид
u(x,y,t) =

+	E.4)
Полученная формула E.4) является формулой Пуассона для неогра-
неограниченной плоскости.
Теперь мы решим ту же задачу E.1), используя двумерное пре-
преобразование Фурье. Обозначим через С/(А,/^, J) двумерное преобразо-
преобразование Фурье функции и(я,у, t) по переменным х и у:
Применив к задаче E.1) двумерное преобразование Фурье с ядром
получим
где
Решение задачи E.5) для С/(А,/^, J) можно записать в виде
Используя обратное преобразование Фурье, находим

= HI + U2	E.6)
Преобразуем выражение для иъ(х,у,t). Подставив явное выражение
для Ф(Л,/i) и изменив порядок интегрирования, получим
E.7)
Вычислим внутренний интеграл по Л и /i. Введем векторы
Тогда
А(я — О + А*(У — rj) = rp= rpcosa,
где а — угол между г и р, г =
На плоскости (A,/i) введем полярные координаты (р, а):
(заметим, что угол а отсчитывается от вектора г).
Внутренний интеграл по А и р, в формуле E.7) принимает вид
Поскольку
(использовано интегральное представление функции Бесселя JQ(X))
и

(см. приложение, формулаD.4)), то выражение для интеграла / при-
принимает вид
Подставляя найденное значение интеграла в E.7), получаем
где K%f — круг радиуса at с центром в точке М(ж, у). Поскольку
выражение E.6) дает формулу Пуассона
Рассмотрим теперь задачу Коши для уравнения колебаний в неогра-
неограниченном пространстве:
utt = а2 Дг/, —оо < ж, у, z < оо, t > О,
E.8)
t=o	lt=o ' '
Для решения этой задачи применим тройное преобразование Фу-
Фурье по пространственным переменным. Используем общепринятую
в физике векторную запись тройного преобразования Фурье. Пусть
г = {я, у, z}, s = {Л, /i, i/}. Обозначим через G(Л, /i, i/, ?) = G(s, ?) образ
Фурье функции и(х, у, z, *) = t/(r, ^):
где использованы обозначения: dr = dxdydz, а интеграл вычисляет-
вычисляется по всему трехмерному пространству.

Применяя к задаче E.8) тройное преобразование Фурье с ядром
получим аналогично предыдущему, задачу Коши для функции G(s, t):
—2" + а2(А2 + у? + v*)U = О, t > О,
^ Lo =
4=0 =
где
Решение задачи E.9) можно записать в виде
U(s,t) =
Используя обратное тройное преобразование Фурье, находим к(г, t):
u(r,t) =
Выражение для к (г, t) запишем в виде
u = ui(r,t) + u2(r,t),
где

Поскольку, как и в предыдущей задаче,
щ =	E.10)
достаточно вычислить интеграл, входящий в выражение для t/2(r,?)-
Подставив явное выражение для \P(s) и изменив порядок интегриро-
интегрирования, получим
112=	E.11)
Для вычисления внутреннего интеграла введем сферическую си-
систему координат (s, а, /3) с полярной осью вдоль вектора г — р. Тогда
Л = s cos a sin /3, ц = s sin a sin /?, v — s cos /?,
(r — p)s = |r — p|scos/?,
\r-p\ =
Внутренний интеграл принимает вид
Выполнив интегрирование по углам а и /3, получим
Поскольку

запишем
Подставляя найденное значение интеграла в E.11), получаем
г/2 =
Поскольку |г — р\ + at > 0 при t > 0, остается интеграл по сфере
или
Таким образом
гдеМ =(a?,y,z),P = K,fj,C),
RMP = |г - р\ -
S%f — сфера радиуса at с центром в точке М, уравнение этой сферы
имеет вид
(x-tf + (y-4J + (z-tf = (at)*.
Согласно E.10)
Следовательно, решение задачи Коши для уравнения колебаний в
неограниченном пространстве имеет вид
u(M,t) =

Как известно, эта формула называется формулой Пуассона*). В
том случае, когда <р(Р) трижды непрерывно дифференцируема, а
ф(Р) — дважды непрерывно дифференцируема, формула Пуассона
дает классическое решение задачи E.8).
Формулу Пуассона в трехмерном случае можно также получить,
применяя преобразование Фурье по части пространственных пере-
переменных. Мы рекомендуем читателям проделать это самостоятельно
в качестве полезного упражнения.
§ 6. ЗАДАЧИ ДЛЯ
САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Решить начально-краевую задачу на отрезке:
utt = а2ихх, х Е @, тг), t Е @, -hoc),
t/(z,0) = x, ut(«,0)=l, *€@,ir),
u,@,0 = 0, ti,(M) = 0, t E @, +oo).
2. Решить начально-краевую задачу на отрезке:
= uxx, a?€@,4), t€@,+oo),
«€[0,2],
«€[2,4],
tit(«,0) = 0, «€[0,4],
n@,t) = 0, МО, 0 = 0, *E[0,+oo).
(!«,
«•••>-{ i-1..
3. Решить начально-краевую задачу на отрезке:
«u = 4uxj;-|-e~tsinx) z€@,rr), t€@,+oo),
u(*,0) = 0, «t(*,0) = 0, *€[0,ir],
«@, t) = 0, u(rr, <) = 0, t € [0, +00).
4. Решить начально-краевую задачу на единичном отрезке:
и„ = а2ихх + хе-*, *€@,1), <€@,+оо),
«(х,0) = 0, ut(*,0) = 0, *6[0,-1],
*' См.: Свешников А.Г., Боголюбов А.И., Кравцов В.В. Лекции по математиче-
математической физике. М.: Изд-во МГУ, 1993.

5. Решить начально-краевую задачу на отрезке:
utt = uxt, ж€@,гг), *€@,+оо),
«(ж,0) = 8т2|ж, «t(*,0) = 0, ж€@,гг),
««@,0 = 0, u(ir,0 = jS <€[0,+oo).
6. Решить начально-краевую задачу на отрезке:
«« = «„, х €@,3), <€@,+оо),
u(*,0) = 0, ut(ar,0) = 0, *6 @,3),
«@,0 = 0, uC,*) = *. *€[0,+оо).
7. Решить начально-краевую задачу на единичном отрезке:
«« = «**, же @,1), *е(о,+оо),
«(ж,0) = ж+1, «4(*,0) = 0, ж €@,1),
«@,0 = « + 1, u(l,0 = «s + 2, <€[0,+oo).
8. Решить начально-краевую задачу в прямоугольнике:
ы„ = а2Д«, *€@,/i), у€@,/3), <е@,+оо),
и(ж,у,0) = 0, же[0,/!], »€[0,/3],
«t(i, У, 0) = ^1жу(/1 - ж) (/2 - у),
«(О, у, 0 = «(/1, У, 0 = 0, У€[0,/а],
«(ж, 0, 0 = и(ж, /2,0 = 0, * € [0, /i], t € [0, +оо).
9. Решить начально-краевую задачу в круге:
и« = Д«, г €@,3), 4p€[0,2ir], <e@,+oo),
«t(r,p,o) = o, re (о,з], v?e[o,27r],
uC,v?,0 = 0, V€[0,2rr], t6[0,+oo),
10. Решить начально-краевую задачу в шаре Кт° :
и„ = а2Ди, М € Kr°, t € @, +оо),
u(M,0) = 0, ut(M,0) = 0, M€Kr°,
ur|r=ro = 4<2P,j2)(cos0)cos2?>, t € [0, +оо).
11. Решить начально-краевую задачу в шаровом слое:
«„ = а2Д«, r€(ri,r2), fl€[0,jr], <р€[0,2тг], <€@,+оо),
, «f(M,0) = 0, r€[ri,r2], ^€[0,тг],

12. Решить начальную задачу на бесконечной прямой:
utt = Жихх + ж*, ж ЕМ1, *Е@,+оо),
г/(ж,0) = 0, г/*(ж,0) = 0, ж ЕМ1.
13. Решить начальную задачу на бесконечной прямой:
titt = uara. + 6, xEK1, *Е@,+оо),
г/(ж,0) = ж2, tit (я, 0) = 4*, ж ЕМ1.
14. Решить начальную задачу на бесконечной прямой:
utt = ихх + ж*, ж ЕМ1, *Е@,+оо),
г/(ж,0) = ж2, г/,(ж,0) = ж, ж ЕМ1.
15. Решить начальную задачу на бесконечной прямой:
utt = ихх + 8шж, ж ЕМ1, ^E(
ut(x,Q) = Q ж ЕМ1.
16. Решить начальную задачу на бесконечной прямой:
titt = 11^ + 6*, ж ЕМ1, <G@,+oo),
г/(ж,0) = 0, t/t(x,0) = ж + cosx, ж ЕМ1.
17. Решить начальную задачу на бесконечной прямой:
utt = 9uxx+smx, ж ЕМ1, *Е@,+оо),
г/(ж,0) = 1, tit(a?,0)=l, ж ЕМ1.
18. Решить начально-краевую задачу на полупрямой:
fitt = 4fiw?, жЕМ+, t€@,+oo),
ii(a?,0) = 0, wt(*,0) = 0, ж Е М+,
г/@,0 = Ssinwt, ^ Е @, -hoc).
19. Решить начально-краевую задачу на полупрямой:
utt = a2uxx+smx, жЕМ+, tG(
ti(a?,0) = 0, tit(«,0) = 0, жЕМ+,
ii@,t) = 0, tG[0,+oo).

Ответы.
i.	«(*,<) =
2.	«(*,<) =
3.	u(x,t) =
4.	«(*,«) =
5.	u(x,t) =
6.	«(*,<) =
7.	«(*,«) =
8.	u(x,y,t) =
9.
10.
где	=0 (A = 1,2,...)-
11. u(r,0,t) =
где

12.	u(x,t) =
13.	ti(M) =
14.	u(x,t) =
15.	ti(a?,<) =
16.	u(z,*) =
17.	ti(M) =
18.	ti(a?,<) =
19.	tia?,t =

Глава 7
КРАЕВЫЕ ЗАДАЧИ ДЛЯ
УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
В этой главе рассматривается метод разделения переменных для
решения краевых задач для уравнения Гельмгольца. В случае двух
переменных изучаются краевые задачи внутри круга, вне круга и в
круговом кольце, а в пространстве — внутри шара, вне шара и ша-
шаровом слое. Методика решения краевых задач для уравнения Гель-
Гельмгольца имеет много общего с методикой решения задач для уравне-
уравнения Лапласа, рассмотренной в гл. III. Поэтому сначала рассмотрим
частные решения уравнения Гельмгольца в полярных и сферических
координатах, а затем будем из них строить решения краевых задач в
соответствующих областях.
§ 1. ЧАСТНЫЕ РЕШЕНИЯ
УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА В
ПОЛЯРНОЙ СИСТЕМЕ КООРДИНАТ
Рассмотрим уравнение Гельмгольца
Дг/ + сг/ = 0, с = const	A.1)
в полярной системе координат (г, (р) и построим его решения, пред-
ставимые в виде
г/(г,^) = Я(г)Ф(^).	A.2)
Подставляя A.2) в уравнение A.1) и разделяя переменные, получим
Отсюда получаем уравнение для функции R(r):
= 0	A.3)
и уравнение для функции Ф(<р):
Ф" 4- АФ = 0.

Поскольку переменная (р — циклическая, функция Ф должна быть
периодической с периодом 2 тт. Следовательно, для определения
получена задача Штурма- Лиувилля с периодическим условием
ф" + АФ = 0, 0 < v < 2тг,
Ф(<?> 4- 2тг) = Ф(<?>) при любом (р,
ФЫ ф о,
рассмотренная в гл. И, § 2. Ее решения имеют вид
( cos п<,
Подставляя найденное значение Лп в A.3), получаем
г2Я" + rRf + (сг2 - n2)R = 0.
Рассмотрим теперь отдельно случаи с > 0 и с < 0. Пусть с = k2 > 0.
Общее решение уравнения
г2 Л" -f rR' + (k2r2-n2)R=Q
можно записать в виде
R = Rn(r) = dJn(kr) + C2Nn(kr)
или в виде
R = Rn(r) =
где Jn(^), Nn(x), Яп (ж), Hj?\x) — функции Бесселя, Неймана, Хан-
келя первого и второго рода n-го порядка соответственно.
Таким образом, при с = k2 уравнение Гельмгольца
имеет следующие серии решений:

A.7)
{cos n<?>,
ограничены при г = 0, решения A.5)-A.7)
sin n(f>
при г — >• 0 неограничены. При г — >• ос решения
удовлетворяют условиям излучения вида
1
а решения
удовлетворяют условиям излучения вида
—
Рассмотрим теперь случай с = — х2 < 0. Общее решение уравнения
можно записать в виде
где /п (ж) и Кп (х) — функции Инфельда и Макдональда n-го порядка
соответственно. Следовательно, уравнение
Дн - х2г/ = О
на плоскости имеет следующие серии решений:
co
.
s
cosn<p,	( cosn<p,
sm n<p, •- x , ^ sm n^}
причем решения

ограничены при г = О и неограниченно возрастают при г —> оо, а
решения
неограничены при г —> О и равномерно стремятся к нулю при г -^ оо.
§ 2. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ
Дг/ -f k2u = О ВНУТРИ КРУГА
Построив частные решения уравнения Гельмгольца в полярной си-
системе координат, перейдем к рассмотрению краевых задач.
Начнем с краевой задачи внутри круга:
Au + k2u = Q в круге 0 < г < а,	B.1)
ди
a^L + ри = /(<?>), |а|+|/?|/О, а,/? = const. B.2)
иГ	г=а
Решение этой задачи будем строить в виде ряда по частным решениям
A.4), ограниченным при г = 0:
ti(r,p)=	B.3)
коэффициенты которого определяются из граничного условия B.2).
Подставляя B.3) в граничное условие B.2) и разлагая функцию f((p)
в тригонометрический ряд, получим
Д,	B.4)
В„	B.5)
где /п и /п — коэффициенты Фурье функции
B.6)
Если при всех п = 0, 1, . . . , оо

то из B.4) и B.5) все коэффициенты Ап и Вп определяются одно-
однозначно, и решение B.3) имеет вид
и =
B.7)
В этом случае решение краевой задачи B.1), B.2) существует и един-
единственно.
Если akJ'n(ka) -f /3Jn(ka) = О при п = по, то соотношения
= /#,	B-8)
= /# B-9)
непротиворечивы лишь при условии /по = /по = 0. Если же хотя
бы один из коэффициентов /по и /по отличен от нуля, то соотноше-
соотношения B.8), B.9) противоречивы, и исходная краевая задача B.1), B.2)
решения не имеет.
Условие
эквивалентно условию: fc2 является собственным значением следую-
следующей задачи Штурма- Лиувилля для круга:
Дг/ + Хи = О в круге 0 < г < а,
«?+*u=o. »*«;	B10)
При ЭТОМ fc2 = Am •
Таким образом, если k2 является собственным значением опе-
оператора Лапласа для круга, то краевая задача B.1), B.2) либо не
имеет решения, либо решение существует, но неединственно. Если
|/по l + 1/по I Ф 0) то решения краевой задачи B.1), B.2) не существует.
Если /по = /по = 0) то из соотношений B.4), B.5) все коэффициенты
Ап и Вп при п ф п0 определяются однозначно, а коэффициенты АПо
и ВПо остаются произвольными. Поэтому решение краевой задачи в
этом случае имеет вид
и =
B.11)
где АПо и ВПо — произвольные постоянные.

§ 3. КРАЕВЫЕ ЗАДАЧИ ДЛЯ
УРАВНЕНИЯ Дг/ + k2u = О ВНЕ КРУГА
Для выделения единственного решения внешней краевой задачи
для уравнения Дг/ + k2u — О на бесконечности нужно поставить до-
дополнительное условие — условие излучения, выделяющее уходящую
волну. На плоскости условие излучения имеет вид либо
^-гЪ/=о(=) при г ->оо,	C.1)
дг
iku — oi—р) при г -> оо.	C.2)
\Vr/
либо
ди
дг
И то и другое условие выделяет единственное решение, но эти реше-
решения различны.
Рассмотрим, например, следующую задачу вне круга:
Дг/ + Аг2г/ = 0 г > а,
оо.
—— — iku = o\ —7= 1 при
дг	\y/rj
Решение поставленной задачи следует искать в виде разложения в
ряд по системе решений A.6), удовлетворяющих данному условию
излучения:
и =	C.3)
Заметим, что kaHn (ka) — /ЗНп (ka) ф 0 при действительных Ага,
а и /3 при всех п = 0,1,...,оо. Подстановка в граничное условие
позволяет определить коэффициенты Ап и Вп:
Ап =
А0 =	C.4)
В„ =

rt	I i/rv ui —— \s i /— i лх|^гжл. f /•' OO.
9r
Решение краевой задачи с условием на бесконечности вида C.2)
выражается через решения A.7). Например, краевая задача
Дм + k2u = 0 вне круга: г > а,
«L. = /(*>)•
ди	1
имеет решение
и =
где /п°^ и /п выражаются через граничную функцию f((p) форму-
формулами C.4).
Внешние задачи для уравнения Дг/ + k2u = 0 обычно называются
задачами дифракции. Они появляются при излучении распростране-
распространения и рассеяния волн различной природы.
Остановимся на вопросе сходимости полученных рядов. В каче-
качестве примера возьмем разложение
II =	C.5)
где коэффициенты Ап и Вп определяются формулами C.4).
При изучении поведения функций Яп (а?) при п -> оо следует
учесть, что формула
п > 0	C.6)
определяет поведение функции Ханкеля не только при малых ж, но
описывает поведение Щ (х) и в том случае, когда п > ж, т.е. при
фиксированном аргументе х и п -> оо (на доказательстве этого утвер-
утверждения мы не останавливаемся, отсылая читателя к специальной ли-
литературе, где можно найти более тонкие оценки*)). Отсюда следует,
что
при п —> оо.	C.7)
Эта оценка обеспечивает сходимость ряда C.5) всюду вне круга (при
г> а).
*) См.: Ватсон Г.Н. Теория бесселевых функций. Ч. I, П. М.: ИЛ, 1949.

Но при вычислении суммы ряда C.5) следует иметь в виду следую-
следующее обстоятельство. Оценка C.7) справедлива при п ^> kr. Поэтому
при ka ^> 1 большое количество начальных членов ряда C.5) име-
имеют одинаковый порядок (их число ~ [Агг]), и члены ряда начинают
существенно убывать при п > kr. Это приводит к тому, что при вы-
вычислении ряда C.5) приходится суммировать большое число членов
ряда, что вызывает определенные трудности. Условие ka > 1 соот-
соответствует тому случаю, когда длина волны А, связанная с волновым
числом соотношением k = 2тг/А, мала по сравнению с радиусом круга
а: а/ А ^> 1. В этом случае часто используются специальные методы
суммирования соответствующих рядов.
В противоположном случае ka <& 1 при суммировании ряда C.5)
трудностей не возникает, и можно ограничиться несколькими первы-
первыми членами ряда.
Аналогичный характер сходимости имеют ряды и для других за-
задач дифракции (в том числе и трехмерных).
§ 4. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ
Аи + k2u = О В КРУГОВОМ КОЛЬЦЕ
Пусть D — круговое кольцо: а<г<6, 0 < <р < 2тг. Рассмотрим
краевую задачу Дирихле
&u + k2u = Q в Д	D.1)
Ч=ь = лм.	D-3)
Построенные ранее системы частных решений A.4)-A.7) ограничены
в D. Для решения поставленной задачи удобнее использовать систе-
системы действительных решений

где
= Jn(kr)Nn(ka) - Jn(ka)Nn(kr),
= Jn(kr)Nn(kb) - Jn(kb)Nn(kr),
Решение краевой задачи D.1)-D.3) будем искать в виде
и =
D.6)
Подставляя D.6) в граничное условие D.2) и разлагая /i(<p) в триго-
тригонометрический ряд, получим, учитывая, что /% = 0, соотношения
Сп = №, Dn = f?,	D.7)
где /1„ и f$ — коэффициенты Фурье функции /i(^). Аналогичным
образом из граничного условия D.3) получаем
А,=/?, *» = /?,	D.8)
/2п и /2п — коэффициенты Фурье функции /2(<р).
Разрешимость краевой задачи D.1)-D.3) исследуется аналогично
тому, как это сделано в § 2, поэтому здесь не будем проводить по-
подробный анализ (который читатель легко может провести самостоя-
самостоятельно), а укажем лишь окончательный результат.
Если &2 не является собственным значением задачи Штурма-
Лиувилля для кольца
Дг/ + Аг/ = 0 в Д
то /^а)F) Ф 0 и Д^Ь)(а) / О ПРИ всех п = 0, 1, . . . , ос, все коэффи-
коэффициенты An, 5n, Cn, J9n однозначно определяются из D.7) и D.8).
Краевая задача D.1)-D.3) имеет и при этом единственное решение,
которое представляется формулой
и =

+	D.10)
Если k2 является собственным значением задачи D.9), то краевая за-
задача D.1)-D.3) либо не имеет решения, либо решение существует, но
неединственно. В этом случае при некотором целом значении п = по
Если хотя бы один из коэффициентов Фурье Дуо , /}*'о , f$o и f$Q не
равен нулю, то исходная краевая задача D.1)-D.3) не имеет решения.
Условием разрешимости при k2 = Am является требование
f (С) _ f(8) _ f(c) _ f(S) _ п
Jln0 "" 'Ino ~~ J2n0 — J2n0 — и'
Решение при этом имеет вид
и =
где АПо, ?По, СПо и Dno — произвольные постоянные.
Аналогичным образом решаются и другие краевые задачи для
уравнения Дг/ + k2u = О внутри кругового кольца.
§ 5. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ
Дг/ - >с2и = О ВНУТРИ КРУГА
Краевые задачи для уравнения Дг/—>с2и = 0 несколько проще, чем
краевые задачи для уравнения Дг/ + k2u = 0. Это связано с тем, что
при достаточно гладких (непрерывных) граничных функциях первая,
вторая и третья (при h > 0) задачи всегда имеют единственное реше-
решение.
Рассмотрим внутреннюю задачу Дирихле для круга
Дг/ - у^и - 0, 0<г<а,

Решение этой задачи будем искать в виде ряда по частным решениям
A.8), ограниченным при г = 0:
и =
E.1)
Подставляя E.1) в граничное условие и разлагая f(p) в тригономе-
тригонометрический ряд, сразу находим коэффициенты
Ап =	п = 1,2,...,оо,
E.2)
Вп =
Аналогичным образом решаются вторая и третья задачи. Напри-
Например, третья краевая задача
Дг/ - х2г/ = 0, 0<г<а,
5г/ ,
1Г- + hu
дг
h — const > 0,
иг	г—а
имеет решение
и =
+	E.3)
где коэффициенты Ап и Вп определяются формулами E.2). При
Л = 0 формула E.3) дает решение задачи Неймана.
§ 6. КРАЕВЫЕ ЗАДАЧИ ДЛЯ
УРАВНЕНИЯ Дг/ - х2и = О ВНЕ КРУГА
Для выделения единственного решения данной краевой задачи для
уравнения Дг/ — х2г/ = 0 следует поставить дополнительное условие
равномерного стремления решения к нулю на бесконечности.
Рассмотрим внешнюю краевую задачу для круга
Дг/-х2г/ = 0, г > а,

ди
a7--/3u\r=a=0, H+|/?|^0, а>0, /? > О,
or
и =? 0 при г -> оо.
Решение этой задачи строится в виде ряда по частным решениям
A.9), удовлетворяющим условиям на бесконечности:
и =
F.1)
коэффициенты которого находятся из граничного условия и опреде-
определяются формулами E.2).
§ 7. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ
Дг/ - у^и = О В КРУГОВОМ КОЛЬЦЕ
Пусть D — круговое кольцо: а < г < 6, 0 < <р < 2тг. Рассмотрим
задачу
Дг/ - х2и = О в D,
Для облегчения определения коэффициентов разложения из систем
частных решений A.8) и A.9) построим две другие системы решений,
одна из которых удовлетворяет нулевому граничному решению при
г = а, другая — при г = Ь. Таковыми являются системы решений
где
причем Я„ (а)=0, Дп F) = 0. Решение исходной задачи будем
искать в виде
и =

Подставляя в граничное условие, сразу определяем коэффициенты
А _ АС) D _ AS) г _ АС) п __ As)
^п — /2п ' **п — /2п » °n — /in ) un — /in )
где Д„ , /}*' — коэффициенты Фурье функции Л(<р),
/2я\ /2^ — коэффициенты Фурье функции h(<{>).
Аналогичным образом строятся решения других краевых задач
для уравнения Дг/ — к2 г/ = 0 внутри кругового кольца.
§ 8. ЧАСТНЫЕ РЕШЕНИЯ
УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА В
СФЕРИЧЕСКОЙ СИСТЕМЕ КООРДИНАТ
Для того чтобы построить решения краевых задач для уравнения
Гельмгольца внутри шара, вне шара и в шаровом слое, построим ме-
методом разделения частные решения уравнения Гельмгольца
Дг/ + си = О, с = const
в сферической системе координат (г, в, (f>), представимые в виде
Подставляя искомый вид решения в уравнение Гельмгольца и разде-
разделяя переменные, получим
= А,
где A0<j>v — сферический оператор Лапласа. Отсюда получаем урав-
уравнение для R(r):
= 0	(8.1)
и уравнение для функции v@, <p)\
+ Xv = 0.	(8.2)
Решение уравнения (8.2) должно быть периодичным по (р с периодом
2тг и ограниченным при в = 0 и в = тт. Это дает задачу Штурма-
Лиувилля
+ Av = 0, 0<0<тг, 0<<р<2тг,

v@, (p + 2тг) = v@, (p) при всех в и (р,
|v@,v?)| < 00, КТГ,Р)| < °°)
*(М?0.
Собственными значениями этой задачи являются А = Ап = п(п + 1),
п = 0,1,...,оо,а собственными функциями — сферические функции
Г„(т) (*,?») =
причем rangAn = 2п + 1.
Рассмотрим уравнение (8.1) при А = п(п + 1):
= 0.	(8.3)
Введем новую функцию соотношением
Д(г) =
Тогда уравнение (8.3) примет вид
rV + ту1 + [сг2 - (n + 1/2J] у = 0.	(8.4)
Рассмотрим отдельно случаи: с > 0 и с < 0. Пусть с = k2 > 0.
Тогда общее решение уравнения (8.4) можно записать в виде
У =
или в виде
У =
где Jn+i/2(*)> #n+i/2(*)> Я^1/2(ж), Я^1/2(ж) — функции Бес-
Бесселя, Неймана, Ханкеля первого и второго рода порядка (п + 1/2)
соответственно.
Таким образом, для уравнения
Дг/ + А:2г/ = О
построены четыре серии частных решений:
(8.5)

П.
n = 0, 1, ... ,00, m = 0, 1, .. .,n.
Решения
(8.6)
ограничены при г = О, решения остальных трех серий неограничены
при г —>• 0.
Решения
удовлетворяет условию излучения в виде
— гки^Ь = о I - 1 при г —>• оо
г»	«"* ^nm — I
дг	пт \г
а решения
удовлетворяют при г -» оо условию
При с = —х2 < 0 уравнение (8.3) имеет вид
г2у" + rj/ - [xV + (n + 1/2J] у = 0.
Его общее решение
у = Ci/n+1/2(xr)
где /п-ы/2(ж) и Ап+1/2(я) — функции Инфельда и Макдональда по-
порядка (п + 1/2) соответственно.
Следовательно, для уравнения
Ди — х2и = О
построены две серии частных решений:

п = О, 1, . . .,оо, т = О, 1, . ..,п.
Решения
-1=/п+1/2(хг)Уп(т)@^)	(8.7)
ограничены при г = О и неограниченно возрастают при г -> со, а
решения
n+1r)yn"(M	(8.8)
равномерно стремятся к нулю при г -> оо и неограничены при г -> 0.
§ 9. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ
Дг/ + k2u = О ВНУТРИ ШАРА
Решение краевых задач для уравнения Гельмгольца в трехмерном
случае проводится полностью аналогично тому, как это сделано в
двумерном случае. Поэтому в этом и последующих параграфах бу-
будут приведены окончательные результаты без подробных выкладок
и объяснений.
Начнем обзор результатов с внутренней краевой задачи для шара.
Рассмотрим краевую задачу
Дг/ -f k2u = О в шаре 0 < г < а,
Решение этой задачи представляется в виде разложения по частным
решениям, ограниченным при г = 0:
и —
Коэффициенты Апгп и Впт определяются из граничного условия.
Разложим функцию /@, (р) в ряд по сферическим функциям:
где
f(c) -
Jnm —
(9.1)

2тг тг
#Л = ^2 / f №<*)pW(cos/3)smmasm(]d(]da, (9.2)
2 о о
Nl = ||P^m)(cos/?)||2||cosma||2, ЛГ2 = ||P^m)(cos/?)||2||sinma||2 .
Если k2 не совпадает ни с одним собственным значением задачи
Штурма-Лиувилля внутри шара:
Дг; + \v = 0 в шаре 0 < г < а,
PM|r=a = o, ,*о,	(9'3)
то все коэффициенты Апт и Впт определяются однозначно, и реше-
решение имеет вид
и =
Если Аг2 = AJ ' , где AJn °' — собственное значение задачи (9.3), т.е.
корень уравнения
и все /пот = 0 и /пот = 0, то решение существует, но неединственно
и имеет следующий вид:
и —
где АПот и ВПот — произвольные постоянные.
Если при Аг2 = А}ПО^ хотя бы один из коэфф]
отличен от нуля, то поставленная задача решения не имеет.
Если при k2 = А}П°^ хотя бы один из коэффициентов /пот и /пот
§ 10. КРАЕВЫЕ ЗАДАЧИ ДЛЯ
УРАВНЕНИЯ Дг/ + k2u = О ВНЕ ШАРА
Для выделения единственного решения внешней краевой задачи
для уравнения Дг/ 4- k2u = 0 на бесконечности ставится дополнитель-
дополнительное условие — условие излучения, выделяющее уходящую волну. В
трехмерном случае условие излучения записывается либо в виде
ди	(\\
—— — гки = о[ — ) при
дг	\г)
00,

либо в виде
•тг- -f iku = o-j при г -> оо .
or	* - '
И то и другое условие на бесконечности выделяет единственное ре-
решение внешней краевой задачи, но эти решения различны. При до-
достаточно гладких граничных функциях решения внешних задач для
шара всегда существуют и единственны.
Решение задачи
Дг/ -f k2u = 0 вне шара г > а,
ди .,	/Л
—— — гки = о [ - ] при
дг	\rj
СХ)
имеет вид
и =
(юл)
где /nm и /nm определяются формулами (9.1), (9.2).
Чтобы получить решение краевой задачи с другим условием на
бесконечности
—- -f iku = о ( - ) при г -too,
or	\rj
нужно в формуле A0.1) функции Ханкеля первого рода
/\
заменить функциями Ханкеля второго рода
§ 11. КРАБВЫБ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ
Дг/ -f k2u = 0 В ШАРОВОМ СЛОЕ
Краевая задача для уравнения Дг/ -f k2u = 0 внутри шарового
слоя рассматривается так же, как соответствующая краевая задача
внутри кругового кольца, разобранная в § 4.
Рассмотрим задачу
Дг/ -f k2u = 0 в слое а < г < 6,	A1.1)
= /1@, Р), Ы + IfrI ± о,

A1.3)
Для того чтобы развязать граничные условия, заданные при г = а
и при г = 6, удобно построить две серии частных решений уравне-
уравнения Дг/ -f k2u = О так, что все решения одной серии удовлетворяют
однородному граничному условию при г = а, а все решения второй
серии — однородному граничному условию при г = Ь. Этот при-
прием уже неоднократно использовался в предыдущих параграфах (см.,
например, § 4).
Итак, используя решение (8.5), построим решения, удовлетворяю-
удовлетворяющие граничному условию
г=а
= 0.
Эти решения можно взять в виде
где
, a) =
(штрих, как обычно, обозначает производную по полному аргументу).
Аналогично строим вторую серию решений гД (г, 0, <р), удовлетво-
удовлетворяющих однородному граничному условию при г = Ь:
Они имеют вид
sin m(p,
где

Теперь решение краевой задачи A1.1)-A1.3) запишем в виде разло-
разложения по этим решениям:
и =
Коэффициенты Апт и Впт определяются из граничного условия при
г — 6, коэффициенты СПт и Dnm — из граничного условия при г = а.
Далее приводим только окончательные результаты без подробных
объяснений и выкладок.
Если k2 не является собственным значением соответствующей за-
задачи Штурма-Лиувилля для шарового слоя, то все коэффициенты
определяются однозначно из граничных условий, и решение имеет
вид
и =
ГДе /lnm> /Inm И /2nm> /2nm — Коэффициенты Фурье фуНКЦИЙ /Х@, V?)
и /2@, ^>) соответственно при разложении их по системе сферических
функций. Формулы для их вычисления аналогичны формулам (9.1),
(9.2).
Если k2 = Апо, где ^по — собственное значение соответствующей
задачи Штурма-Лиувилля для шарового слоя, и хотя бы один из
коэффициентов /^от, /^от, /??от, f$om отличен от нуля, то поста-
поставленная задача (!!.!)-A1.3) решения не имеет.
Если *» = АЙ и все коэффициенты /?>em, fftam, f?om, fgam
обращаются в нуль, то решение существует, но неединственно. Оно
имеет вид
и =

где Ат и Вт — произвольные коэффициенты. (Заметим, что при
k2 = АПО функции Rno (r) и Rnc, (г) становятся линейно зависимыми.)
§ 12. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ
Дг/ - х2г/ = О ВНУТРИ ШАРА
Как и в двумерном случае, внутренние краевые задачи (первая,
вторая и третья при h > 0) для уравнения Дг/ — х2г/ = 0 имеют
единственное решение. Выпишем эти решения.
Рассмотрим задачу внутри шара
Дг/ — х2г/ = 0 в шаре 0 < г < а,
Решение этой задачи представляется в виде разложения по частным
решениям (8.7), ограниченным при г = О, и может быть записано в
виде
и =
где /nm и /nm — коэффициенты Фурье функции /@, (р) по системе
сферических функций, вычисляемые по формулам (9.1), (9.2).
§ 13. КРАЕВЫЕ ЗАДАЧИ ДЛЯ
УРАВНЕНИЯ Дг/ - х2г/ = О ВНЕ ШАРА
Для выделения единственного решения внешней краевой задачи
для уравнения Дг/ — х2г/ = 0 на бесконечности ставится дополни-
дополнительное условие:
г/ =4 0 при г -> оо .
Приведем решение внешней краевой задачи для шара.
Рассмотрим задачу
Дг/ — х2г/ = 0 вне шара: г > а,
™ = «?-/*•„. = /('.*),

и z4 0 при г -> оо.
Решение этой задачи строится в виде разложения по частным реше-
решениям (8.8), удовлетворяющим условиям на бесконечности, и имеет
вид
где /пт и /nm определяются формулами (9.1), (9.2).
§ 14. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ
Дг/ - х2г/ = О В ШАРОВОМ СЛОЕ
Рассмотрим краевую задачу
Дг/ — х2г/ = 0 в шаровом слое а < г < 6,
= /1 (*,?»),
GГ	|г=о
Для решения этой задачи сначала построим частные решения урав-
уравнения Дг/ — х2г/ = 0 аналогично тому, как это сделано в § 11.
Пусть
где
Функции г/n (г, ^, ^) есть частные решения уравнения Дг/ — х2г/ = О,
удовлетворяющие граничному условию
= 0.

Аналогичным образом строим функции Un ' :
где
Функции г/n (г, 0,(р) удовлетворяют однородному граничному усло-
условию при г = 6:
= 0.
Решение поставленной краевой задачи может быть получено в виде
(все необходимые вычисления читатель легко может проделать само-
самостоятельно)
и =
гДе /inm» /inm и /2nm> /2nli ~ коэффициенты Фурье функций Д и
/2 соответственно по системе сферических функций.
§ 15. ПРИМЕРЫ РЕШЕНИЯ КРАЕВЫХ
ЗАДАЧ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
Рассмотрим некоторые примеры решения краевых задач для урав-
уравнения Гельмгольца.
1. Внутри круга г < а решить задачу
Ди- х2и = О,
ti|r=a = |sinp|.
Общее решение задачи Дирихле для данного уравнения имеет вид
ti(r, v?) =

Определяем коэффициенты Ап и Вп:
А0 =
А„ =
так как подынтегральная функция нечетна. Следовательно,
и =
ИЛИ
и =
2. Решить вне круга задачу
Д« — и = О, г > а,
Эй.
дгг=а
и =3 0 при г -> оо .
Общее решение задачи Неймана для этого уравнения вне круга
можно записать в виде
= sin4
В данном случае коэффициенты разложения проще определить не
путем вычисления соответствующих интегралов, а разлагая гранич-
граничную функцию sin4 (p\
sin4 (p =

Подставляя общее решение в граничное условие, получаем
ди
дг
Отсюда сразу находим
Л - 3	А - l A -1
8 '	2 ' 8 '
все остальные коэффициенты равны нулю. Следовательно, решение
имеет вид
и =
На примере решения этой задачи отметим, что если граничная функ-
функция задана в виде ряда Фурье, то решение задачи выписывается сра-
сразу, без вычисления каких-либо интегралов.
3. Внутри круга единичного радиуса решить задачу
Дг/ + №\ = О, 0<г < 1,
и\г-а = sin (p + cos2 (p ,
где Hi — первый ненулевой корень уравнения
= 0.
Общее решение написанного уравнения внутри круга имеет вид
\2
о
В данном случае Аг = р\' совпадает с собственным значением зада-
задачи Штурма-Лиувилля внутри единичного круга. Поэтому для суще-
существования решения необходимо отсутствие третьей гармоники Фурье
в граничной функции. Так как

(третья гармоника отсутствует), решение рассматриваемой задачи
существует, но неединственно. Решение имеет вид
и =
где АЗ и Вз — произвольные постоянные.
4. Построить функцию Грина задачи Дирихле для оператора
Дг/ + k2u
вне сферы.
Функция Грина имеет вид
G=	A5.1)
где v есть решение задачи
Дг> + k2v = О вне сферы: г > а,
A5.2)
.,
— — гАтг> =	при г -> ос .
от
Для решения этой задачи введем сферическую систему координат
(г, 0, (р) с началом в центре сферы и осью г, проходящей через точку
MQ. Тогда точка MQ имеет координаты (го, 0, 0) и
Решение задачи A5.2) имеет вид
v(r,0,<f>)=	A5.3)
Здесь учтено, что в выбранной системе координат решение задачи
A5.2) имеет осевую симметрию, т.е. не зависит от угла (р. Коэффи-
Коэффициенты разложения Ап определяются из граничного условия
V\r=a =

Для определения коэффициентов Ап воспользуемся теоремой сложе-
сложения (см. приложение, § 2)
Подставляя написанное разложение в граничное условие, получаем
Отсюда сразу находим коэффициенты Ап:
Ап=	п = 0,1,... A5.4)
Подставляя коэффициенты Ап в A5.3), получаем решение
v =
A5.5)
а функция Грина определяется формулой A5.1).
Функцию Грина можно записать в произвольной сферической си-
системе координат с началом в центре сферы. Пусть М = (г, 0,^>),
М0 = (г0,0о,^о). Тогда
cos/3 =
G =
A5.6)
а выражение для Рп (cos /?) может быть записано по теореме сложения
(см. приложение, § 1)
Pn(cos/?) = Pn(cos0)Pn(cos00) +

Рассмотренная задача о построении функции Грина имеет про-
простой физический смысл: сферическая волна с центром в точке М0
падает на абсолютно мягкую сферу. Первое слагаемое в формуле
A5.6) представляет потенциал скоростей точечного источника, рас-
расположенного в точке MO и создающего сферическую волну, второе
слагаемое — потенциал скоростей рассеянной сферой волны (дифра-
(дифрагированная волна). Поэтому эта задача называется также задачей о
дифракции сферической волны на абсолютно мягкой сфере.
5. Рассмотрим задачу дифракции плоской волны на абсолютно
жесткой сфере.
Пусть плоская волна, потенциал скоростей которой имеет вид e%kz,
падает на абсолютно твердую сферу радиуса а. Найти полное вол-
волновое поле вне сферы.
Потенциал скоростей полного волнового поля U вне сферы пред-
представим в виде
U = eikz + г/,
где и — потенциал скоростей рассеянного сферой тела.
Введем сферическую систему координат (г,0,^>) с началом в цен-
центре сферы и ось z — вдоль направления распространения плоской
волны. Будем считать, что плоская волна e%kz распространяется в
направлении, противоположном положительному направлению оси z
(т.е. волна падает на "северный" полюс сферы). Тем самым предпо-
предполагается временная зависимость elwt. Граничное условие на поверх-
поверхности абсолютно твердой (непроницаемой) сферы имеет вид
(n,gradCOIs = ——
= 0.
Следовательно, для определения рассеянного поля и получаем кра-
краевую задачу
Дг/ + k2u = 0 при г > а,
дг
'•COS в
A5.7)
ди	f\\
^ + iku = o (-J при
Г -> ОС
(вид условия излучения выбран исходя из временной зависимости
е*"*).

Задача A5.7) имеет осевую симметрию. Следовательно, ее реше-
решение не зависит от <р и может быть записано в виде
ti=	A5.8)
Прежде чем подставить общее решение A5.8) в граничное условие,
разложим плоскую волну etkrcose по полиномам Лежандра, исполь-
использовав вырожденную теорему сложения (см. приложение, § 2)
A5.9)
Подставляя теперь A5.8) и A5.9) в граничное условие, получим
Отсюда находим коэффициенты Ап:
Подставляя найденные коэффициенты Ап в A5.8), получаем рассе-
рассеянное поле в виде
и =
6. Внутри сферы г < а решить задачу
Ди - и = О,
til e = cos 29 + sin 9 sin (p.
Общее решение внутренней задачи Дирихле для этого уравнения
имеет вид
и =

Чтобы определить коэффициенты, нужно граничную функцию раз-
разложить по сферическим функциям. Из граничного условия сразу
видно, что отличны от нуля будут только коэффициенты AnQ и Bni.
Теперь cos 29 разложим по полиномам Лежандра Pn(cos0), a sin в —
по присоединенным функциям Рп (cos в):
4	1
cos 29 = 2cos20 - 1 = -P2(cos0) - -P0(cos0),
о	о
Следовательно, AQQ = — ^, AW = |, Вц = 1, все остальные коэффи-
коэффициенты равны нулю.
Таким образом решение имеет вид
и =
7. Вне сферы г > а решить задачу
Дг/ + г/ = О,
ди . /Г,
-5- - ги = о - при г -4 оо.
Поскольку
cos 9 = PI (cos 9) , sin2 9 cos 2<p = -P2B) (cos 9) cos 2<p ,
«5
решение поставленной задачи имеет вид
и =
§ 16. ЗАДАЧИ ДЛЯ
САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Решить внутри круга г < а задачу
Дм — х2м = О,
ltr=a = Sgn^,	— Я" < < 7Г.

2. Решить вне круга г > а задачу
U\r=a = \<P\ ,	— Я" < (f> < 7Г,
ди	( 1 \
—- + г'Агм = о -т= , г -> oo .
<9r	\v*v
3. Построить функцию Грина внутренней задачи Дирихле для
оператора Ам — х2и внутри круга.
4. Построить функцию Грина задачи Неймана для оператора
Aw — х2и внутри круга.
5. Построить функцию Грина задачи Дирихле для оператора
Ам — х2и вне круга.
6. Построить функцию Грина задачи Неймана для оператора
Ам — >с2и вне круга.
7. Решить двумерную задачу дифракции плоской волны на абсо-
абсолютно жесткой окружности.
8. Построить функцию Грина задачи Дирихле для оператора
Ам + k2u вне круга для условий на бесконечности:
О	/ 1 \ О /1\
\ ди	( I \ ^ ди ( I \
а) _ zku = о \ \ j б) — + iku = о I —р I.
9. Решить плоскую задачу дифракции волны от точечного источ-
источника на абсолютно жесткой окружности с условиями на бесконечно-
бесконечности:
\ ди ( I \	ди
а) —- - iku = о -7= ;	б) — + iku =
дг \л/г/	дг
10. Построить функцию Грина задачи Неймана для оператора
Дм + k2u вне сферы с условиями на бесконечности:
ч ди ..	/1\ ч 9м
a) __lAtl = 0^J; б) ^ + «'*и =
Ответы.
1.
2.
3.

о\
р
р
00
р

ПРИЛОЖЕНИЕ
При применении специальных функций для решения краевых за-
задач часто используются формулы, которые обычно называются фор-
формулами сложения. В этом приложении выведены формулы сложения
для сферических функций и простейшие формулы сложения для ци-
цилиндрических функций.
§ 1. ФОРМУЛА СЛОЖЕНИЯ
ДЛЯ СФЕРИЧЕСКИХ ФУНКЦИЙ
Сферические функции
Р(т) (cos О) cos пир , Р(т) (cos О) sin пир ,
являются собственными функциями следующей задачи Штурма-
Лиувилля:
v + AV = 0, 0<0<тг, 0<<р<2тг,
v(9, (р + 2тг) = v(9, (р) при всех в и <р,
К0,у>)| < оо, HTT,V?)| <оо,
соответствующими собственному значению А = An = n(n-hl), причем
rang An = 2n+ 1. Сферическая гармоника Уп (^, v?) есть линейная ком-
комбинация собственных функций этой задачи, соответствующих одному
собственному значению Ап :
У„ (*,?) =
Пусть М@, (р) и Mi(#i,<pi) — две точки на единичной сфере,
cos /3 = cos 9 cos #i + sin в sin #1 cos(<p — <pi) .
Угол /? есть угол между радиусами, проведенными в точки М и MI.

Рассмотрим функцию
uk = rkPk(cos/3).
По переменным (г, 0, (р) она удовлетворяет уравнению Лапласа. От-
Отсюда вытекает, что Р/с (cos/?) есть сферическая гармоника, соответ-
соответствующая собственному значению А/с = k(k + 1). Собственные функ-
функции, соответствующие различным собственным значениям, ортого-
ортогональны между собой. Следовательно,
= 0 прип^Аг.	A.1)
Пусть Sa — сфера радиуса а с центром в начале координат. Согласно
третьей формуле Грина
г"У„ =	A.2)
На сфере 5а:
—r"Y
dnr Yn
Используя разложения производящей функции для полиномов Ле-
жандра, получим
RMP
Поэтому
Подставляя найденные значения в формулу A.2), получим
г»У„ (*,?) =
A.3)

Учитывая условие ортогональности A.1), из A.3) находим
Yn@,v)=	A.4)
Пусть /(#, V?) — произвольная функция, интегрируемая с квадратом
на единичной сфере: / ? L2Ei), где Si — сфера единичного радиуса.
Она может быть разложена в ряд по сферическим функциям:
A.5)
где Yn(9,(f>) — сферическая гармоника. Коэффициенты разложения
определяются формулами
в -	(L6>
-Опт —
•** пт —
Умножая соотношение
на Pn(cos^) и интегрируя по единичной сфере по переменным @х, <р'),
получим, учитывая A.4):
"	A.7)
cos/? =

Поскольку
A.8)
подставляя в A.8) значения коэффициентов Апт и #пт, определен-
определенных формулами A.6), получим
A.9)
Вычитая A.7) и A.9), получим соотношение
= 0,
справедливое для любой функции / € LI (S\ ) . В силу произвольности
функции /(в, <f>) отсюда следует
A.10)
где cos /3 = cos в cos в1 + sin в sin в' cos(<p — <р') •
Формула AЛО) обычно называется теоремой сложения для сфери-
сферических функций.
§ 2. ТЕОРЕМЫ СЛОЖЕНИЯ
ДЛЯ ЦИЛИНДРИЧЕСКИХ ФУНКЦИЙ
Рассмотрим теперь простейшие теоремы сложения для цилиндри-
цилиндрических функций, которые наиболее часто встречаются в приложени-
приложениях.
Для функции Ханкеля Н^(х) справедливо интегральное предста-
представление Зоммерфельда

где контур Ci на комплексной плоскости <р изображен на рис. 1.
Напомним, что в силу теоремы Коши контур С\ может быть дефор-
деформирован, но так, что его конусы уходят на бесконечность в заштрихо-
заштрихованных на рисунке областях. Пусть М и Р — две точки на плоскости
(я, у), полярные координаты которых (г, <р) и (ri, <pi) соответственно.
Расстояние между ними
R = RMP =
Для определенности будем считать, что г < ri. В треугольнике
ОМР (рис. 2) угол против стороны г обозначим ф. Заметим, что
/2 при г < г\. Из Л ОМР видно, что имеют место соотношения
— г\ — rcos/?, Нзтф — rsin/?.	B.1)
Рассмотрим функцию
Сделаем замену (р = а — ф. Как было указано, сдвиг контура на
величину ф < тг/2 не меняет значения интеграла. Поэтому
Hll)(R) =	B.2)

Так как
in(a — ф) = R sin a cos ф — R cos a sin ф =
— sin OL(T\ — т cos /3) — г cos a sin /3 = r\ sin a — r sin(a + /?) ,
из B.2) получаем
H^(R)e^=	B.3)
Воспользуемся разложением плоской волны в ряд по функциям Бес-
Бесселя
e%r sm(a+p) _	/24)
Подставляя разложение B.4) в B.3) и меняя порядок суммирования
и интегрирования, получим
Так при замене г на Агг, г\ на Arri, R на kR углы /3 и ф не меняются,
полученное соотношение можно записать в виде
r<n. B.5)
Соотношение B.5) называется теоремой сложения Графа. При i/ = О
соотношение B.5) принимает вид
B.6)
г < ri
и представляет собой разложение цилиндрической волны с центром
в точке Р по цилиндрическим волнам с центром в точке О.

Выделяя действительную часть, из B.6) находим
JQ(kR) =
Это соотношение справедливо при любых г и г\.
Заметим, что соотношение B.6) справедливо и при комплексных
значениях Л, г, ri и ф, связанных между собой соотношениями
B.1) при условии |г| < |ri|.
Теперь выведем другую теорему сложения позволяющую получить
разложение сферической волны. Функция
B.7)
где R = у/г2 + r\ — 2rr*i cos/?, является решением уравнения Гельм-
гольца
удовлетворяющем условию излучения на бесконечности
—- — ги = о \ - }	при г ->> оо .
or \г/
Следовательно,, при TI > г она может быть представлена в виде раз-
разложения по частным решениям уравнения Гельмгольца
г < п .	B.8)
Коэффициенты an не зависят от г и /?. Определим коэффициенты
an. Из B.8) имеем

Воспользовавшись явным представлением полиномов Лежандра по
формуле Родрига, получим
Полученный интеграл п раз проинтегрируем по частям, учитывая,
что все внеинтегральные подстановки обратятся в нуль. Поэтому
Поскольку для произвольной функции
д	rndv
можем записать
Используя формулу
1 d Zy(x)
х dx xv
справедливую для любой цилиндрической функции Zv(x) (см. § 5),
получим
Следовательно,
B.9)
Теперь обе части равенства B.9) разделим на гп и перейдем к пределу
при г —^ со, учитывая при этом, что ап от г не зависит. Так как

из B.9) получаем
ап =
Поскольку
получаем
ап =	B.10)
Подставляя найденное значение ап в B.8) и учитывая B.7), получаем
B.11)
Заменяя г на Arr, TI на Arri, перепишем соотношение B.11) в виде
B.12)
R =	г < п .
Соотношение B.12) является частным случаем теоремы сложения Ге-
генбауэра.
Представляет интерес предельная форма теоремы сложения, по-
получающаяся из B.12) при г\ —> оо.Имеем
Поэтому из B.12) получим
B.13)

или, заменяя /? на тг — /?:
Соотношения B.13) и B.14) дают разложение плоской волны по сфе-
сферическим волнам.
В заключение приведем без вывода полную теорему сложения Ге-
генбауэра
,2
BЛ
(*Д)" ~
где Zl/(x) — произвольная цилиндрическая функция порядка i/,
С?(х) — полином Гегенбауэра, R — ^/r2 + г I — 2rri cos /?, г < TI,
i/ > — ^. В этом случае, когда Zv(x] = Jv (я), ограничение г < TI из-
излишне. Доказательство этой формулы можно провести аналогично
тому, как это сделано в данном параграфе при i/ = \.
Аналогичные формулы можно получить и для функций Бесселя
чисто мнимого аргумента. Используя соотношения
М*) =
Kv(x) =
получаем из формул B.6) и B.12), считая k = in:
Ко (хД) =
B.16)
=	Г < Г1,
B.17)
где R —
Эти соотношения используются при построении в виде рядов функ-
функций Грина оператора Дг/ — х2г/.
§ 3. СУММИРОВАНИЕ НЕКОТОРЫХ РЯДОВ
Рассмотрим суммирование некоторых рядов, которые встречаются
при решении краевых задач для уравнения Лапласа.

Для любого комплексного д, такого, что \q\ < 1, справедливо соот-
соотношение
Подставляя q — tettp, где t действительно и \t\ < 1, и разделяя дей-
действительную и мнимую части, получим
Используя C.1), находим
Соотношение C.2) проинтегрируем по (р:
- 1пA - 2* cos (р + 12) + С =
Подставляя сюда t = 0 и используя разложение
определяем постоянную С:
С=0.
Следовательно ,
ln(l-2*cosv? + 12)=	C.4)
Формула C.4) позволяет построить разложение фундаментального
решения уравнения Лапласа на плоскости в тригонометрический
ряд. Действительно, пусть t = го/г < 1. Тогда из C.4) получаем:
< Г.

В трехмерном случае разложение фундаментального решения урав-
уравнения Лапласа 1/R по полиномам Лежандра получается из формулы
C.5)
которая представляет собой определение производящей функции для
полиномов Лежандра. Отсюда сразу имеем
C.6)
Теперь рассмотрим следующие два ряда:
которые встречаются при построении функции Грина для внутренней
и внешней задач Неймана для уравнения Лапласа в случае сферы.
Для вычисления суммы первого ряда обе части разложения
разделим на t и проинтегрируем по t:
Отсюда
Для вычисления интеграла воспользуемся подстановкой Эйлера
Тогда

Следовательно,
Для определения С подставим t = 0. Получим
С =
Таким образом,
|t| < 1. C.7)
Аналогичным образом вычисляется второй ряд:
Для вычисления суммы этого ряда разложение C.5) проинтегрируем
по t. Получим
Для вычисления интеграла опять используем подстановку Эйлера
У =
Получим
Следовательно,
Подставляя сюда t — О, находим С — — 1пA — х). Таким образом,
C.8)

В приложениях достаточно часто встречается следующий ряд:
§ 4. НЕКОТОРЫЕ ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ
ЦИЛИНДРИЧЕСКИЕ ФУНКЦИИ
Рассмотрим несколько определенных интегралов, содержащих ци-
цилиндрические функции. Эти примеры интересны и сами по себе (т.е.
как конкретные интегралы) и поучительны с методической точки
зрения.
1. В качестве первого примера рассмотрим интеграл
Для вычисления этого интеграла воспользуемся интегральным пред-
представлением функции Бесселя
Получим

поскольку
= 0
в силу нечетности подынтегральной функции. Таким образом,
D.1)
Поскольку
из D.1) получим
D.2)
Полагая в D.1) и D.2) а — гш и разделяя действительную и мнимую
части, получаем ряд полезных формул:
D.3)
D.4)
D.5)
2. В качестве второго примера вычислим интеграл Вебера
(а>0, 6>0,

Для его вычисления воспользуемся разложением функции Бесселя
Jv(bx) в степенной ряд. Получим
Поскольку
имеем
Таким образом,
D.6)
3. Рассмотрим теперь часто встречающийся в приложениях инте-
интеграл Сонина-Гегенбауэра
Для вычисления этого интеграла удобно использовать интегральное
представление функции Макдональда
Kv(z) =	D.7)
Сначала преобразуем D.7), сделав замену ^еи — i. Получим
К„(х)=	D.8)

Теперь воспользуемся представлением D.8) для вычисления интег-
интеграла Сонина-Гегенбауэра
(используется интеграл Вебера D.6))
Таким образом,
D.9)
Получим из формулы D.9) ряд следствий. Пусть р, — 1/2. Так как
можем записать

D.10)
При z/ = 0 из D.10) получим
D.11)
Если учесть, что при z/ > 0 и z —>• О
D.12)
и в формуле D.10) при z/ + | > 0 перейти к пределу при у —>• 0, то
получим
D.13)
Формула D.13) является обобщением D.1). Если в D.9) перейти к
пределу при а —>• 0 и учесть поведение функции K^(z) при z —>• 0, то
найдем
D.14)
Отсюда при z/ = 0, ц — | получаем
А при z/ = 0, у — \ из D.14) находим
4. Остановимся также на двух неопределенных интегралах, содер-
содержащих функции Бесселя, которые часто встречаются при решении
различных задач.
Интеграл f x^+l Jl/(x) dx вычисляется путем использования фор-
формулы

Отсюда сразу получаем
Рассмотрим второй интеграл
Для вычисления этого интеграла используем рекуррентную формулу
Л(х) = Л+2(ж) + 2^+1(ж).
Получим
Если воспользоваться другой рекуррентной формулой
и выразить «Л/+з(я) и Jv+i(x) через Jl/^i(x) и «/^(х), получим
Аналогичным образом можно вычислять и другие интегралы вида
х) dx при целом k.
§ 5. СПРАВОЧНЫЙ МАТЕРИАЛ
I. Формулы векторного анализа
1. div(ua) = udiva-h a grad u.
2. grad(ut;) = и grad v + v grad u.
3. rot(ua) = urota-h [gradu,a].
4. div[a,b] = brota — arotb.
5. rot[a,b] = (b, V)a- (a, V)b + adivb - bdiva.
6. grad(a,b) = (b, V)a+ (a, V)b+ [b,rota] + [a,rotb].
7. rot rot a = grad div a — V2a.
8. rot grad и — 0.
9. div rot a = 0.

Дифференциальные операции в криволинейных ортогональных ко-
координатах
Пусть (xi,x2,x3) — ортогональные криволинейные координаты,
GI , е2, е3 — единичные векторы этой системы координат, hi, Л2, /13 —
коэффициенты Ламе.
1. grad и —
2. diva =
3. rota =
4. Ди = div grad и —
5. rota =
Частные случаи
1. Декартовы прямоугольные координаты (я, t/, z)
hi = h2 — Лз = 1,
grad и —
diva =
rota =
2. Цилиндрические координаты (г, у?, z)
/ij = hr = 1, Л2 = hy> = r,

z — z,
grad и —
diva =
rota =
3. Сферические координаты (г, 0,у?):
hi = hr = 1, /12 = Л0 = r, /13 = Лу> = rsin0,
x = r sin 0 cosy?, у = rsinflsiny?, z = rcos0,
grad и —
diva =
rota =
II. Специальные функции
1. Гамма-функция Эйлера:
a)T(z)=	Rez>0;
в) асимптотическое представление при х — } оо:
Г(ж+1)=	х>0,
п! «	п >• 1 (формула Стирлинга).

2. Цилиндрические функции:
а) уравнение Бесселя
Любая пара из следующих функций: < «Л/ (я), NV(X), Н^'(х), Н„'(х) \
образует фундаментальную систему решений уравнения Бесселя при
любых z/. Наиболее удобно общее решение уравнения Бесселя запи-
записывать в виде
или
Определитель Вронского
7TZ
7TZ '
2 sin тп/
W[Jv(z),J-v(z)} = -
7TZ
б) Jy(z) =
Поведение при х —} 0 (х > 0):
в) соотношения между различными цилиндрическими функциями:

г) рекуррентные соотношения и формулы дифференцирования:
(\ i\
где Zv(z) — любая из функций Jl^(z)^Nl/(z)^Hl ' (z)\
д) интегральное представление:
(Co,Ci, С2 — см. рис. 1 на с. 324)
Jn(z) =
е) асимптотическое представление при z —>• оо:

ж)
где Zv(x) — произвольная цилиндрическая функция;
з)
и) теоремы сложения:
R =
3. Цилиндрические функции чисто мнимого аргумента:
а) дифференциальное уравнение

общее решение: у(х) = C\Iv(x) +
определитель Вронского: W[Il/(x)JKl^(x)] = — —;
х
б) /„(z) = rvJv(iz), Kv(z) = e*
в) /„(z) =
поведение при х —)• 0 (х > 0):
интегральное представление:
г) рекуррентные соотношения и формулы дифференцирования:
д)

е) асимптотическое представление:
/„(*) =
Кп(х) =
ж) теоремы сложения:
4. Полиномы Лежандра:
а) дифференциальное уравнение
?[„_ ,.,4] +«„+,„,_ О,
б) формула Родрига
в) рекуррентные соотношения
(n + l)Pn+i(*) - Bп + 1)*Р„(я) + nPn-i(z) = О,
г) ||Рп(х)||2 =
д) Pn(-x) = (-l)nPn(x),
Р„A) = 1, Р„(-1) = (-!)",
P2n+i@) = О,
е) производящая функция:

ж) Ро(х) = 1,
cos в = PI (cos 9) , cos2 0=1 P2(cos 9) +
cos3 в = f P3(cos0) + fp^
5	5
5. Присоединенные функции Лежандра:
а) дифференциальное уравнение
в) Ит)(*)||2 =
г) теорема сложения
Pn(cos/?) =
где cos /3 = cos 0 cos 0х + sin 9 sin 07 cos(y?
д) P1A)(cos0) = sin0,
P2A)(cos0) = 3sin0cos0,
P2B)(cos0) = 3sin20,
D(i), лч . .15cos20-3
P^ ;(cos0) = sm0———————,
L
P^\cosO) = 15 sin2 в cos в,
P3C)(cos0) = 15 sin3 в,
Pjn)(coe*) =	ein'4

6. Сферические функции:
а) дифференциальное уравнение
+ n(n+l)v = 0, 0<0<тг,
б)
в)
где
smy?,
sn у?,
7. Полиномы Лагерра:
а) дифференциальное уравнение (х > 0) :
ИЛИ
XI/' + («+!-*)!/+ (А- ?+1) у = 0;
б) формула Родрига
в) ||Ua)(x)||2 =
г) 4в) (*) = !,

д) производящая функция
е) функция Лагерра
дифференциальное уравнение
d ( dy\ Л х ^2
d
где А = п + ^2~*
8. Полиномы Эрмита:
а) дифференциальное уравнение
, ,~	,|| ——— ^'=0, -00 < X < +00,
ах L dx]
или
у" - 2ху' + 2пу = 0,	-оо < х < +оо;
б) формула Родрига
Я„(х) =
в) ||Я„(х)||2 =
г) Я0(х) = 1,	Я!(х) = 2х,
Я2(х) = 4х2 - 2,	Я3(х) = 8х3 - 12х,
Я4(х) = 16х4 - 48х2 + 12;
д) производящая функция
е) функции Эрмита
MX) =
дифференциальное уравнение
у" + (Л - х2)у = 0, -оо < х < +оо,
где А = 2п+1.

Литература
1. Тихонов А.Н., Самарский А. А. Уравнения математической фи-
физики. М.: Наука, 1966.
2. Будак Б.М., Самарский А.А., Тихонов А.Н. Сборник задач по
математической физике. 1956.
3. Кошляков Н.С., Глинер Э.Б., Смирнов М.М. Уравнения в част-
частных производных математической физики. М.: Физматгиз, 1962.
4. Никифоров А.Ф., Уваров В.Б. Специальные функции матема-
математической физики. М.: Наука, 1984.
5. Владимиров B.C., Михайлов В.П., Вашарин А.А., Каримова
Х.Х., Сидоров Ю.В., Шабунин М.И. Сборник задач по уравнениям
математической физики. М.: Наука, 1974.
6. Бицадзе А.В., Калиниченко Д.Ф. Сборник задач по уравнениям
математической физики. М.: Наука, 1985.
7. Свешников А.Г., Боголюбов А.Н., Кравцов В.В. Лекции по ма-
математической физике. М.: Изд-во МГУ, 1993.
8. Лебедев Н.Н. Специальные функции и их приложение. Гос.
издательство физ-мат. лит-ры, 1963.
9. Бейтман Г., Эрдейи А. Высшие трансцендентные функции.
Т. 1-3. М.: Наука, 1965-1967.

Учебное издание
Боголюбов Александр Николаевич,
Кравцов Владимир Владимирович
ЗАДАЧИ ПО МАТЕМАТИЧЕСКОЙ ФИЗИКЕ
Редактор Р.А. Бунатян
Художественный редактор Ю.М. Добряпская
Технический редактор Г.Д. Колоскова
Корректоры И.А. Мушникова, Т.С. Милякова
Изд. лиц. № 040414 от 18.04.97 г.
Подписано в печать 10.08.98.
Формат 60x90 1/16. Бумага офсетная № 1
Офсетная печать.
Усл. печ. л. 22,0. Уч.-изд. л. 17,69.
Тираж 3000 экз. Заказ 169
Изд. № 5628.
Оригинал-макет подготовлен К. Е.Панкратьевым
с использованием издательской системы TeX
в ЛВМ механико-математического факультета МГУ.
Ордена "Знак Почета"
издательство Московского университета.
103009, Москва, ул. Б. Никитская, 5/7.
Отпечатано в Производственно-издательском комбинате ВИНИТИ,
140010, Люберцы, Октябрьский пр. 403.
тел. 554-21-86