Текст
A. WEBSTER und G. SZEGO
P ARTIELLE
DIFFERENTIALGLEICHUNGEN
DER MATHEMATISCHEN
PHYSIK
TEUBNER IN LEIPZIG UND BERLIN
1ЙЗС
А. ВЕБСТЕР и Г. СЕГЕ
В k- 6
'П
ДИФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
В ЧАСТНЫХ ПРОИЗВОДНЫХ
МАТЕМАТИЧЕСКОЙ /
ФИЗИКИ /
i
часть вторая
ПЕРЕВОД С НЕМЕЦКОГО
И. С. ГРАДШТЕЙНА
ПОД РЕДАКЦИЕЙ
проф. В. В. СТЕПАНОВА
ГОСУДАРСТВЕННОЕ ТЕХНИКО-ТЕОРЕТИЧЕСКОЕ ИЗДАТЕЛЬСТВО
Москва 1934 Ленинград
Т. 21-5-2 (4)
® з
' *
\ v '. ffi®/
Редакционную работу по этой книге провел Г. А. Сухомлинов. Издание оформила В. Ф-
Зазульская. Корректуру держала 3. В. Смирнова. Наблюдал за выпуском В. П. Морев.
Рукопись сдана в производство 26/VIII 1933 г. Листы подписаны к печати 11/II 1934 г.
Книга вышла в свет в марте 1934 г. в количестве 10 000 экз. на бумаге формата 62х941/16.
Печатных знаков в листе 50 112, листов 20. Заказ № 183 ГТТИ. Уполномоченный Глав-
лита В 77257.
Набрано и сматрицировано в 1-й Образцовой типографии ОГИЗа РСФСР^треста «Поли-
графкнига», Москва, Валовая, 28.
Отпечатано в 16-й типографии треста «Полиграфкнига», Москва, Трехпрудный пер., 9.
Оглавление
1 Глава пятая
§
§
§
§
§
§
§
§
§
§
§
§
§
§
§
§
§
§
§
§
Формула Грина. Потенциал. Краевые задачи
50. Теорема Гаусса...........................................
51. Поле ньютонова тяготения ................................
52. Формулы Грина.......................................
53. Ньютонов потенциал................................• . . . .
54. Уравнение Пуассона ....... ..............................
55. Логарифмический потенциал . . ...........................
56. Потенциал простого слоя ......................
57. Потенциал двойного слоя.........................
58. Формулы Фредгольма....................•..................
59. Теорема Грина.....................................
60. Задача Дирихле............................•..............
61. Волновое уравнение в трехмерном пространстве ............
62. Волновой потенциал. Принцип Гюйгенса ..............
63. Неоднородное волновое уравнение .........................
64. Теорема Бельтрами........................................
65. Уравнение колебаний ................................
66 Функция Грина .................................... • . .
67. Примеры (полупространство ,и сфера) ..... ...............
68. Вынужденные колебания. Интегральные уравнения............
69. Бесконечные области......................................
Стр.
7
9
12
13
16
26
27
33
36
38
41
44
46
55
59
61
64
74
Глава шестая
V Интегрирование диференциальных уравнений в частных произ-
водных по методу Римана-Вольтерра
§ 70. Задача Коши. Характеристики............................... 80
§ 71. . Линейные уравнения. Формула Грина ........................ 86
§ 72. !Уравнеияя эллиптического типа ............................ 90
§ 73. Уравнения гиперболического типа............................ 92
§ 74. Телеграфное уравнение...................................... 98
§ 75. Неоднородное волновое уравнение.............................101
§ 76. Уравнения с п переменными................................. 105
§ 77. Формула Грина и характеристики, в n-мерном пространстве.....111
§ 78. Применение метода Вольтерра к волновому уравнению...........116
§ 79. Применение метода Вольтерра к дифереициальному уравнению затуха-
ющих пространственных волн....................................... 125
§ 80. Метод Адамара. Фундаментальные решения .....................129
§ 81. Волна разрывов.......................................... 133
§ 82. Разрывы первого порядка (волны удара) ......................135
§ 83. Разрывы второго порядка (волны ускорения) ..................139
§ 84. Теорема Гюгонио о скорости .................................141
§ 85. Одномерное распространение газа. Характеристики..............142
Глава седьмая
Шаровые функции, функции Бесселя и Ламе
§ 86. Определение шаровых функций..................................148
§ 87. Задача Дирихле для шара................................... 151
§ 88. Представление шаровых функций в форме, данной Максвеллом . . . 152
§ 89. Зональные шаровые функции................... -.............154
§ 90. Ортогональные координаты...................................... —
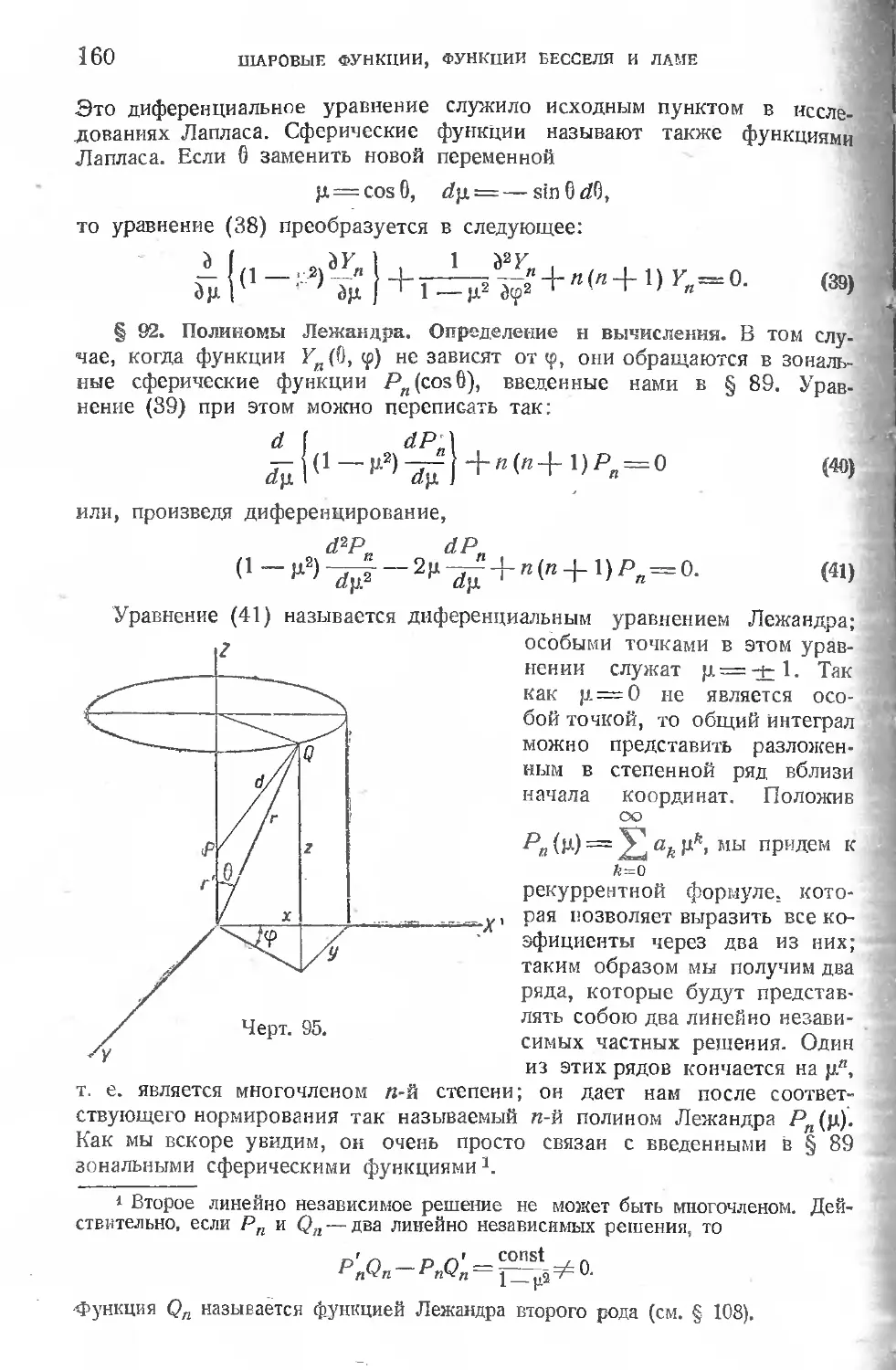
§ 91. Шаровые функции в полярных координатах.................... 158
6
ОГЛАВЛЕНИЕ
§ 92. Полиномы Лежандра. Определение и вычисления................ 160
§ 93. Полиномы Лежандра. Различные их представления................163
§ 94. Соотношения между полиномами Лежандра........................168
§ 95. Присоединенные функции Лежандра............................. 169
§ 96. Сферические функции .........................................172
§ 97. Интегральные соотношения................................... 174
§ 98. Разложение в ряды по сферическим функциям ...................176
§ 99. Сходимость рядов Лапласа.....................................178
§ 100. Бесселевы функции.......................................... 18©
§ 101. Уравнение Бесселя.......................................... 184
§ 102. Выражение бесселевых функций с помощью определенных интегралов 189
§ 103. Цилиндрические координаты.................................. 192
§ 104. Эллиптические координаты.....................................194
§ 105. Диференциальное уравнение Ламе ............................ 197
§ 106. Разложение в ряды по функциям Ламе.......................... 204
§ 107. Связь между функциями Ламе и сферическими функциями.........207
§ 108. Эллипсоиды вращения........................................ 209
Глава восьмая
Приложения сферических, цилиндрических функций и функций
Ламе
§ 109. Притяжение материальною окружностью..........................215
§ НО. Потенциал материального круга и кругового тока...............216
§ 111. Потенциал сферического слоя................................ 217
§ 112. Потенциал любого тела...................................... 218
§ 113. Применения к гидродинамике................................. 226
§ 114. Однородное уравнение колебаний в двумерном пространстве .... 224
§ 115. Колебания круглой пластинки..................................227
§ 116. Однородное уравнение колебаний в трехмерном пространстве .... 229
§ 117. Распространение сферических волн.............................234
§ 118. Колебания эллипсоида вращения.............................. 236
§ 119. Теорема сложения К. Неймана для бесселевых функций ...... 238
§ 120. Асимптотическое представление бесселевых функций.............240
§ 121. Вычисление некоторых интегралов.......................... 242
§ 122. Потенциал масс, распределение которых обладает круговой симметрией 247
§ 123. Формулы Бельтрами для симметрических потенциалов .......... 249
Глава девятая
Интегральные уравнения
§ 124. Интегральные уравнения краевых задач....................... 258
§ 125. Алгебраическая задача........................................259
§ 126. Трансцендентная задача................................ ... . 263
§ 127. Формула Фредгольма....................................... 268
§-128. Метод итерации .................................•............269
§ 129. Фундаментальные числа и фундаментальные функции..............272
§ 130. Теорема Гильберта........................................... 277
§ 131. Разложение в ряд по фундаментальным функциям.................279
Приложение
§ 1. Функции комплексного переменного.............................281
§ 2. Применение теории вычетов к решению линейных диференциальных
уравнений с постоянными коэфициентами............................. 292
§ 3. Линейные диференциальные уравнения в комплексной области . . . 298
Указатель................................................. 317
ГЛАВА ПЯТАЯ
Формула Грина* Потенциал* Краевые задачи
§ 50. Теорема Гаусса. Исследования, которыми мы будем заниматься
в этой главе, основаны главным образом на так называемой формуле
Грина \ которая устанавливает связь между интегралом, взятым по
объему, и интегралом, взятым по поверхности. Эту формулу Грина мы
выведем в § 52, исходя из теоремы Гаусса, с которой мы уже ознако-
мились в § 8, т. I. Вернемся теперь к этой теореме.
Пусть W представляет собою функцию от х, у, z, имеющую непре-
рывные частные производные по всем этим переменным в некоторой
области т, а также на поверхности S, ограничивающей эту область.
Мы при этом предполагаем, что поверхность 5 состоит из конечного
числа частей, в каждой из которых нормаль изменяется непрерывно, и
что прямые, параллельные координатным осям, пересекают поверхность
6’ не более чем в р точках, где р — некоторое вполне определенное ко-
нечное число. В таком случае интеграл
Ж.. А А
— dx dy dz, (1)
взятый по объему т, существует и притом
Чтобы вычислить этот интеграл, рассмотрим элемент тела, объем
которого равен dx = dxdydz. Этот элемент принадлежит цилиндру
с осью, параллельной оси Ох, и с основанием dy dz. Пусть абсциссами
точек пересечения одного из ребер цилиндра с поверхностью 5 служат
•*1» X2t • • • >
причем индексы соответствуют порядку следования точек пересечения
(черт. 68). В таком случае
J +•••+ w2n-v2n^
где
W4=W(x„ у, z).
(2)
1 G. Green, An Essay on the Application of Mathematical Analysis to the
Theories of Electricity and Magnetism, Math. Papers, стр. 23. Nottingham, 1828.
ФОРМУЛА ГРИНА. ПОТЕНЦИАЛ. КРАЕВЫЕ ЗАДАЧИ
Таким образом
Ц dy dz (nz2 - wi + - Ж3 +... -I- 172„ - Win_A). (3)
Циливдр с основанием dy dz и образующей, параллельной оси Ox,
вырезает на поверхности нашего тела ряд элементарных площадок: dSlt
dS2, ... При движении в направлении возрастающих х мы будем под-
ходить к этим площадкам то извне тела, то изнутри его, смотря по
тому, будет ли v нечетным или четным. Проекция любой площадки
dS на плоскость yz равна dydz. Пусть пл, nz>... служат внутренними
нормалями к соответствующим элементам dSv
ности в точках пересечения этой поверхности
В таком случае
dS, cos (п.,х) = dy dz
dS2, ... нашей поверх-
образующими цилиндра.
(4)
при V— 5, 3,... , 2п— 1 и
— dSv cos (п.,х) = dy dz
(5)
при v~2, 4, ... , 2/г; следовательно,
РР 2п
17, cos (п.,х) dS,,.
(6)
Разобьем весь объем - на конечное число частей с помощью цилин-
дров, образующие которых параллельны оси Ох. Возьмем такую после-
довательность этих разбиений, у которой проекции элементов dS4 на
плоскость yz стремятся к нулю. Совокупность всех элементарных пло-
щадок в каждом разбиении заполняет всю поверхность 5, таким обра-
зом в пределе мы получим интеграл
J = — g w cos (пх) dS, (7}
ПОЛЕ ньютонова ТЯГОТЕНИЯ
У
распространенный на всю поверхность Заменяя х через у и г, мы
аналогичным образом получим:
repair, Г Г.,,. , . .„
Ill — dz = — \ | IF cos (пх) dS,
ini
ж
j lTcos(«y)<iS, (8)
A=-j J W cos (nz) dS.
Применим первое из этих равенств к функции X, второе — к Y, а
третье—к Z и сложим результаты. Мы получим:
= — { -’Г cos (пх) -f- Ycos (пу) -}- Z cos (nz) I dS.
(9)
Особенно большое применение в математической физике имеет эта
формула в том случае, когда функции X, Y, Z являются компонентами
некоторой вектор-функции А, т. е. когда
А = Х, A=Y, A„ = Z.
X у
Подинтегральная функция правой части формулы (9) в этом случае
совпадает с компонентой вектора А, взятой по направлению внутренней
нормали п, т. е. с Ап, следовательно, интеграл (9) представляет поток
вектора А сквозь поверхность Подинтегральная функция в левой ча-
сти этой формулы
ЙХ 1 йу ЙД
(10)
представляет собой (см. т. I, § 7) дивергенцию вектора. Итак, формулу
(9) можно переписать в следующем виде:
Формула (10) выражает теорему Гаусса, доказанную в § 8 т. I.
Теорема эта справедлива во всех случаях, когда поверхность 5, ограни-
чивающую объем т, можно разбить на конечное число частей, в каждой
из которых нормаль изменяется непрерывно. Из теоремы Гаусса, как
это было указано в § 8, следует, что интеграл по объему, стоящий
в левой части формулы (10), положителен, если вектор А во всех точ-
ках поверхности 5" направлен наружу. Если последнее условие выпол-
няется внутри некоторой области для любой сколь угодно малой
поверхности, то во всей области div А положительна.
§ 51. Поле ньютонова тяготения. Если дивергенция какого-либо век-
тора в некоторой области тождественно равна нулю, то поток вектора
сквозь любую замкнутую поверхность, лежащую внутри этой области,
равен нулю; теорема, обратная этой, также справедлива. Вектор, дивер-
10
ФОРМУЛА ГРИНА. ПОТЕНЦИАЛ. КРАЕВЫЕ ЗАДАЧИ
генция которого равна нулю, называется соленоидальным (см. т. I, §7).
Примером такого вектора может служить плотность стационарного по-
тока тепла или электричества (см. т. 1, § 10).
Другим примером является поле сил, действующих по закону ньюто-
нова тяготения. Согласно закону Ньютона две массы т и т', на-
ходящиеся в точках Q и Р, притягивают друг друга с силою F, на-
правленною по прямой PQ, соединяющей точки Р и Q, и равною
тт'
где г есть расстояние между точками Р и Q, а у — множитель пропор-
циональности (уф>0). Если я/=1, то силу F называют напряженностью
в точке Р поля, вызванного массой т. По тому же закону действуют
друг на друга и две электрические массы; но электрические массы при-
тягиваются, если они имеют противоположные знаки; если же их знаки
одинаковы, то они по тому же закону отталкиваются (закон Кулона).
В случае действия сил притяжения напряженность поля F представ-
ляет собою вектор, направленный из переменной точки Р в точку Q.
Вычислим величину его внутреннего потока сквозь поверхность 5* сферы,
в центре которой находится масса т.
Мы имеем:
(II)
причем направление вектора F совпадает с направлением внутренней
нормали к поверхности. Чтобы вычислить этот интеграл, разобьем по-
верхность сферы на элементарные площадки dS и построим опираю-
щиеся на них конусы с вершинами в точке с массою т.
Обозначим через </о> телесный угол такого конуса, т. е. проекцию
площадки dS на сферу с радиусом, равным единице.
Тогда
dS=r2 dti>,
и следовательно,
jj Fa dS — \rn da = 4тг(т, (12)
т. e. величина этого интеграла не зависит от размеров сферы. Если
сила F — отталкивающая, то в правой части формулы будем иметь
— 4ттулг.
Вычислим теперь величину внутреннего потока вектора F сквозь
любую замкнутую поверхность с кусочно-непрерывной кривизной. По-
строим сферу радиуса г с центром в точке с массою т (черт. 69).
Обозначим через dY проекцию элемента поверхности dS на эту сферу.
В таком случае d^ — ^VdS cos (nr), где п означает направление внут-
ренней нормали к поверхности dS, а радиус г предполагается направ-
ленным к центру. Знак -ф- или — перед этим выражением выбирается,
•смотря по тому, встречает ли радиус-вектор, направленный в точку
ПОЛЕ НЬЮТОНОВА ТЯГОТЕНИЯ
11
с массою т, поверхность 5 извне или изнутри. Мы предполагаем, что
каждый такой радиус-вектор встречает поверхность S конечное число
раз. Как и раньше,
1 аЪ = г1 da,
и следовательно,
Рп dS— | F [ cos (Fn) dS= | F [ cos (rn) dS—A^ i F | db — ± у/и da. (13j
Знаки в этой формуле взяты в предположении притягивающей силы;
если же силы отталкивающие, то знаки надо изменить иа обратные.
Если т лежит внутри поверхности S, то всякий луч, исходящий из
этой точки, пересекает поверхность 5 нечетное число раз. Таким обра-
зом в каждом направлении останется один лишний элемент с верхним
знаком. Но сукЫа элементов da поверхности сферы единичного радиуса
равна 4п, а потому поток вектора сквозь поверхность 6 также равен
4тг. Если же точка т лежит вне поверхности S, то число точек пере-
сечения этой поверхности с лучом, исходящим из точки т, всегда бу-
Черт. 69. Черт. 70.
дет четным (черт. 70). Сумма элементов поверхности (13), взятых
в каком-либо направлении, будет в этом случае равна нулю, и поток
вектора сквозь поверхность S также равен нулю. Таким образом поле
вектора F во всякой области, не содержащей точки т, безвихревое
Наконец, если точка т лежит на поверхности 5, то число точек пере-
сечения опять окажется нечетным. Но в этом случае вместо 4тг надо
брать поверхность полусферы единичного радиуса; мы в результате
получим, что поток вектора равен 2ттут, при том, конечно, условии,
что к поверхности 5 в точке т можно провести касательную плоскость.
При рассмотрении отталкивающих сил выражения 4тту/и и 2тгу/тг надо
брать с обратным знаком. Этот результат принадлежит Гауссу.
При у = 1, т — 1 интеграл
„ ЕС cos (rn) dS
где г—расстояние от точек поверхности до данной точки Q. Рассмат-
риваемый интеграл (14) как функция от точки Q имеет разрыв на
поверхности S, причем значение этого интеграла на самой поверхности
отличается от обоих предельных значений:
й —0, или 2п, или 4тг, (15)
смотря по тому, лежит ли точка Q вне поверхности 5, на этой поверх-
ности или же внутри нее. При этом, конечно, предполагается, что
12
ФОРМУЛА ГРИНА. ПОТЕНЦИАЛ. КРАЕВЫЕ ЗАДАЧИ
поверхность б1 удовлетворяет вышеуказанным условиям, а направления
нормали п и радиуса г выбраны, как было описано раньше. Стоящий
под знаком интеграла элемент и весь интеграл можно геометрически
рассматривать как телесный угол, под которым из точки Q видны соот-
ветственно элемент dS и поверхность S.
На основании теоремы Гаусса дивергенция безвихревого вектора
в любой области, не содержащей точек, имеющих массу, должна быть
равна нулю, т. е. divF = 0. Это положение можно, конечно, доказать
непосредственно. Для простоты предположим, что начало координат
перенесено в материальную точку, в которой находится масса т. В та-
ком случае, если положительное направление г совпадает с направлением
увеличения расстояния от т (т. е. если за положительное направление
г мы выберем направление, противоположное указанному раньше), и
если вектор F представляет отталкивающую силу, то
г2 —х2 -4-у2 4-г2, г^-—х,
йх
ЙГ х ЙГ у . , ЙГ Z . .
— — cos(rx), — = —= cos (гу), — = — = cos(rx);
йх г ' ' Ъу г Ъг г
с т , х Х с- т t X У
Fy=4-zos{ry)^m — ;
„ т ! X Z
F*=4 >
Таким образом действительно
div F — y/n
§ 52. Формулы Грина. Если применить
вихревому вектору А = grad V, т. е. если
теорему Гаусса (10) к
положить
без-
то получится
Л=’-. л,=’Л
х йх у Ъу я йх
(16)
При этом предполагается, что функция V имеет непрерывные част-
ные производные второго порядка, и что нормаль к поверхности на-
правлена внутрь. Эта формула носит название теоремы о градиенте-
она указывает на зависимость, существующую между градиентом и опе-
ратором Лапласа. Формулу (16) можно распространить и на тот случай,
когда вторая производная от функции кусочно-непрерывна.
НЬЮТОНОВ ПОТЕНЦИАЛ
13
Применим теорему Гаусса к более широкому классу векторов вила:
А = U grad V,
т. е. положим
я W я ГЛУ я ..5V
А=г7—; A=U — ; A=U—~
х Ъх у Ъу 2 Ъг
[см. § 7, (66)]; при этом предполагается, что функция U имеет кусочно -
непрерывные производные первого порядка, а функция V—кусочно-не-
прерывные производные второго порядка. Мы имеем;
я- A==f7p2lZ !_। 5/7 ~1JU 577 5И=
div А— О йд.2 -Ь । й,.2 ) + йх -bdj, -Га2. йг —
= 77ДЕ + Д(77, V).
Последнее выражение представляет собою скалярное произведение
градиентов функций U и V [см. § 5,(35)]. Таким образом мы получим
Щ{С/ Д V+ Д (77, V)}йт=-jp(grad V)ndS=-
U^dS,
(17)
откуда
(18)
Эта формула называется первой формулой Грина. Если производные
второго порядка как функции U, так и функции V кусочно-непре-
рывны, то U и V можно в этой формуле поменять местами, т. е.
Д(Д,Е)г/т-=-
(19)
Вычитая формулу (19) из (18), мы придем к так называемой вто-
рой формуле Грина-
(20)
С помощью этих формул можно некоторые интегралы по объему
заменить соответствующими интегралами по поверхности.
§ 53. Ньютонов потенциал. Вернемся снова к ньютонову потенциалу.
Пусть в точке Q(S, »], С) находится отталкивающая масса иг (источник),
и пусть Р(х, у, д)— какая-либо отличная от Q точка (точка прило-
жения сил). В таком случае, если г — длина вектора, соединяющего точки
Q и Р, то
г2 = (х - SF+ (у - 4- (д - О2,
5г г- 5г 5г _
г — — х—S, г — =у — Ti, r—=z—
Ъх Ъу ‘ iiz
14
ФОРМУЛА ГРИНА. ПОТЕНЦИАЛ. КРАЕВЫЕ ЗАДАЧИ
Направляющие косинусы этого вектора суть:
х-------------------£ Ъг . . У—Т| Sr
cos(rx) = —~==^> cos(ry)— r — Ъу,
cos (rz) — --------------- = . (21)
Г gZ
Компоненты ньютоновского поля потенциала равны:
с т тЪг „ т . . тЪг
^=УДО5(«Н'-2й-, Fy=l~^os(iy} = l-^,
„ т , у т l-rA
= <22)
Если ввести функцию
го эти компоненты можно
будет записать так:
г; _ SV __ йР
Fy Y йу ’ Fg У йа ’
(23)
F = —
г. е. в этом случае
Следовательно, поле тяготения — безвихревое. Функция V называется
потенциалом этого поля. Диференцируя последнее равенство, мы
получим:
divF= — уДР = 0, (24)
т. е. поле тяготения также соленоидально, и потенциал его удовлетво-
ряет уравнению Лапласа. Функцию, которая в некоторой области имеет
непрерывные частные производные второго порядка и удовлетворяет
уравнению Лапласа, называют в этой области гармонической. Гармони-
ческая функция V, не равная постоянному числу внутри области своего
©пределения, не может ни в одной точке иметь относительный макси-
мум или относительный минимум. Доказательство этой теоремы будет
дано в § 59.
Рассмотрим конечное число материальных точек с массами /к1,
т2, ...» и пусть соответствующие им потенциалы будут:
mi и —т*
У V п } • • • 9
Г1 Г2
где гг, г2, ... суть расстояния точки приложения сил Р от материаль-
ных точек Q2, ... , обладающих массами mlt т2, ... Отдельные
силы имеют в этом случае компоненты:
„ й^ _ av2>
НЬЮТОНОВ ПОТЕНЦИАЛ
15
а потому компоненты результирующей силы суть:
—+ И Т- Л- (33)
Положим:
-1+-24-..., (26>
Ч 12
I тогда компоненты результирующей силы опять получаются из общего
' - потенциала V с помощью диференцирования. Таким образом и в этом-
случае изучаемое векторное поле с точностью до постоянного множи-
теля — у равно градиенту потенциала V. Потенциал V является опять-
таки функцией гармонической в любой области, не содержащей мате-
риальных точек Qj, Q2, ...
Если, наконец, вместо конечного числа дискретных материальных
точек рассматривать непрерывное распределение притягивающих масс,
то сумму (26) надо будет заменить интегралом
Через г в этой формуле обозначено расстояние от точки Р до
точки Q, в которой находится масса dm. Интегрирование распростра-
нено на ту часть пространства,' в которой находятся массы. Предполо-
жим, что эта часть пространства ограничена поверхностью с кусочно-
непрерывной нормалью, а точка Р лежит вне этой поверхности.
Если существует функция точки р, удовлетворяющая уравнению
dm = $ dz, то р называется плотностью распределения масс. В дальней-
шем мы будем предполагать, что р кусочно-непрерывна. Пусть £, 4, £ —
координаты точки Q, а х, у, z — координаты точки Р. В таком случае
dm = р (£, iq, £) dx. dTq d.Z.,
Г* = (x — S)2 + (y — 4)2 + (z — C)2,
и таким образом
Vp=ж,, л m ——r. (2S)
-JJ {(x-S)’ + tv-4)>+(2-C)42
При этом точка P лежит вне области интегрирования. Обозначим
через R расстояние точки Р от какой-либо неизменной точки, напри-
мер от начала координат. Если точка Р стремится к бесконечности, то
произведение RV стремится к М, где = представляет собою
всю притягивающую массу. Таким образом для достаточно больших
М
значений R мы имеем приближенно У== — .
R
Функция V вне области, занятой массами, допускает производные
любого порядка. Сила поля, как и в предыдущем случае, равна гра-
диенту от V, умноженному на —у. Производные от функции V полу-
чаются с помощью диференцирования правой части формулы (28) под
знаком интеграла.
16
ФОРМУЛА ГРИНА. ПОТЕНЦИАЛ. КРАЕВЫЕ ЗАЦАЧИ
Например:
УУ ГГГ [3(Х —S)2 —r2]
—Г- °"
’J
Таким образом вне области, занятой массами, функция V удовл
творяет уравнению Лапласа, т. е. является гармонической функцией.
Вне этой области функция V не может иметь ни относительного мак-
симума, ни относительного минимума. Поле сил является в этом случае
безвихревым и соленоидальным, подобно полю плотности потока стацио-
нарного теплового тока. Что же в этом поле соответствует источнику
тепла? Ответу на этот вопрос посвящен следующий параграф.
§ 54. Уравнение Пуассона, а) До сих пор мы рассматривали потен-
циал (27) только в точках, находящихся вне области, занятой массами.
Интегралы (27) и (29) сохраняют, однако, смысл и в том случае, когда
точка Р находится внутри этой области, т. е. когда подинтегральное
выражение в точке Р обращается в бесконечность. В этом случае мы
имеем дело с так называемым несобственным интегралом (см. т. I, при-
ложения, § 2); исключив из области интегрирования некоторую окрест-
ность точки Р, мы найдем, что интеграл, распространенный на осталь-
ную область, стремится к вполне определенному пределу, когда исклю-
чаемая окрестность стягивается к точке Р. Рассматриваемый интеграл
сходится в этом смысле, и притом равномерно, если только плотность
р кусочно-непрерывна.
Действительно, так как функция р (х, у, z) кусочно-непрерывна вну-
три некоторого объема V, то она имеет максимальное значение р
в объеме V, принимаемое ею внутри или на границе одной из обла-
стей ее непрерывности, на которые распадается область, обладающая
этим объемом. Поэтому
и при исследовании равномерной сходимости интегралов
Ж" Ж
мы можем ограничиться случаем постоянной плотности р.“
Рассмотрим сначала последовательность L интегралов (27'), взятых
по объемам шаров ss, s3, ... , радиусы которых стремятся к нулю,
а центры находятся в точке Р. Введя полярные координаты г, 0, ср и
выразив с их помощью элемент объема di — г2 sin 0 drd§ dy, легко по-
казать, что интегралы (27') становятся меньше любого заранее задан-
ного числа, коль скоро диаметр шара vn взят достаточно малым.
Возьмем теперь последовательность X интегралов (27'), взятых по
объемам аа, а2, а3,_ областей, ограниченным произвольно выбран-
ными замкнутыми поверхностями, при условии, что диаметры ’ этих
областей стремятся к нулю, и что точка Р находится внутри каждой из
них. Сопоставим теперь последовательность X с последовательностью
штегралов, взятых по объемам шаров х,, s2, ss,..., диаметр каждого
которых равен диаметру совпадающей с ним по номеру замкнутой
ч'ласти о, и докажем, что
Я!"-®"-
sn °п
Обозначим через 2Я совокупность точек, лежащих внутри сп и вне
sn, и через Sn — совокупность точек, лежащих внутри sB и вне ая Так
как
1 1 „ V
-— — в области 2,
г
— — в области S„,
г ап
где ап~радиус шара хя, то
ГНИ*
и, следовательно,
что и доказывает справедливость неравенства (27а). Следовательно, для
области V можно указать такой диаметр S, что разность двух интегра-
лов, взятых по области И, из которой исключены соответственно две
области произвольной формы, окружающие точку Р и по диаметру
своему меньшие 5, по своей абсолютной величине меньше е, причем
величина 8 зависит только от области V, но не от положения точки Р.
В доказанном факте и состоит равномерная сходимость интегралов (27f).
Чтобы доказать равномерную сходимость интеграла
<я!
V
поступают аналогично предыдущему, помня при этом, что (х—
и, следовательно,
V V
1 Диаметром области называется верхняя граница расстояний между любыми
двумя точками этой области.
Г)
£ Вебстер. вДиФерендиальные уоавнения.
18
ФОРМУЛА ГРИНА, потенциал, краевые задачи
Так как имафал (29) сходите, и формально получен как
производная от (27), то о» Р»« производной, т. е. ранен -
/см т I приложения, § 3).
(LM- 1. и _2_ tytz) имеет непрерывные частные производные по х,у, z,
^СЛИ и^области, занятой массами, функция V имеет еще и вторые
частные производные, причем эти частные производные непрерывны.
В самом деле, запишем первую производную следующим образом:
□ —р(х, у, z)x— £ Г Г С х — £
/ ----—dT-p(x, у,
Диферендируя формально первый член этого выражения, получим:
{p(S’ч’ р(х> у'S(x —~dT'
Гц
Черт- 70а.
Эти интегралы сходятся равномерно по х, у, z. Для первого интеграла
очевидно; справедливость этого утверждения относительно второго
ин°е°пала следует из неравенства | р (£, rb Q — р (х, у, z) |< const г.
Далее, область интегрирования второго
ЙИ
интеграла в выражении для -— мы дополним
до сферы. Интеграл, распространенный на
дополняющую часть, имеет производные лю-
бого порядка вблизи точки Р(х, у, z) (т. е.
вблизи точки, лежащей вне области интегри-
рования). Мы дальше докажем, что интеграл,
соответствующий шару (производная потен-
циала однородного шара), также имеет не-
прерывные производные. Следовательно, по-
тенциал И имеет непрерывные производные
по всем переменным внутри области, занятой
массами.
Итак нам осталось только вычислить потенциал однородной сферы
Пусть р=1. Потенциал V в точке Р зависит, оче-
но тольК0 от Расстояния го точки Р от центра сферы (см. черт. 70а)
И Равгн
г2 sin 6 clrclh d<p 9. С С г2 sin 0 dr dO
V==V(r0) — J J j j/’r2-f-r2—2rr0cosO J J ]/r2-f-r2 -2rr0cosO
0 0 J 0 0
УРАВНЕНИЕ ПУАССОНА
19
r2dr 4тг/?3 1
г0 ~ 3 г0 '
Таким образом для r0 sg R
Гц R , „.
Г r2dr Г r2dr 4п / г® \
----|-4тг\---= -г2 4-2п(/?2_Л2) = 21Г (/?2 — 4
J r0 J г 3 d ° \ 3 /
О г0
и для r0^R
У=4тг
Очевидно теперь, что потенциал V внутри данной сферы действи-
тельно имеет непрерывную вторую производную Ч
Ь) Согласно доказанной в § 51 теореме, поток сквозь замкнутую по-
верхность 5, вызванный отталкивающей массой т, равен либо нулю,
либо — 4тгу/и, смотря по тому, находится ли масса т внутри поверхно-
сти 5 или вне ее. Аналогично этому для потока, вызванного конечным
числом отталкивающих масс, каждая из которых расположена внутри
поверхности S и ни одна не находится на самой поверхности, мы по-
лучаем следующее выражение:
FadS=— у (3)
Суммирование в этом выражении распространяется на все массы,
лежащие внутри поверхности S. Если массы занимают некоторый объем
непрерывно и их плотность представляет собою функцию, имеющую
непрерывные производные первого порядка, то Ът надо заменить dm,
а интегрирование распространить на объем, расположенный внутри
поверхности S:
(Вне области расположения масс надо положить р = 0.) Согласно!
теореме о градиенте (16)
VdT=4rrffipdT’ (зз)
* Исчерпывающее доказательство этих и дальнейших теорем из теории
потенциала читатель может найти в работе Е. Schmidt, Beme'kung zur Poten-
tiaitheorie, Schwarz-Festschrift, 1914, стр. 365—383. Перисе доказательство непре-
рывности второй производной было дано Риманом и основывалось на непрерыв-
ности плотности р. Это доказательство можно найти в книге Н. Н. ШЩллера,
Теория потенциальной функции и обозрение ее приложений к вопросам физики,
Киев 1885. Доказательство той же теоремы было дано Хельдером (Holder) при
гораздо более слабом требовании относительно функции р, а именно при условии
(называемом условием Хельдера) что | р (г, у, г) — р (;, д, С I < const-r^ где а > О
и r=PQ. Об этой и о дальнейших теоремах, касающихся теории потенциала
в современном освещении, см. О. Kellog, Foundations of potential-theory,
Springer, 1929.
2*
20 ФОРМУЛА ГРИНА. ПОТЕНЦИАЛ. КРАЕВЫЕ ЗАДАЧИ
Таким образом
Jjj’(AV+4Trp)dT = 0,
а так как это равенство справедливо ддя любой области, то
(34)
(35)
Мы пришли к так называемому уравнению Пуассона. Оно показывает,
что концентрация—ДИ потенциала V в любой точке равна плотно-
сти в этой точке, умноженной на 4тг. Таким образом в точке, в кото-
рой при заданном распределении масс р=ДО, концентрация Д И 0;
следовательно, дивергенция поля в этой точке отлична от нуля. Такие
точки соответствуют источникам тепла.
Электростатические заряды действуют по закону Кулона, совершенно
аналогичному закону Ньютона. Таким образом уравнение Пуассона ука-
зывает на соотношение, существующее между электрической плотностью
и потенциалом (см. т. I, § 10).
Вывод, к которому мы пришли, можно сформулировать так: реше-
нием диференциального уравнения
&V . Й2И . Й2И . л . . п
служит функция
v = f С С р(М. Qdtdydt
JJj A-t)2 + (J-4)2-|-A-O2'
Функция р в этом выражении представляет кусочно-непрерывную функ-
цию координат материальной точки Q. Вне области, занятой массами,
это решение V имеет производные любых порядков; таким образом гра-
диент от V представляет собою непрерывную во всем пространстве век-
тор-функцию, векторные линии которой вне области распределения
масс не имеют особых точек.
с) Благодаря уравнению Пуассона, потенциал масс в некоторых
определенных случаях симметричного их распределения может быть вы-
числен очень просто. Предположим, например, что V есть функция
только расстояния от некоторой определенной точки. Это имеет место
в том случае, когда плотность р зависит только от расстояния г(когда|
имеет место шаровая симметрия распределения масс). Исходя из этого
предположения, мы вычислим оператор Лапласа ДИ сразу для любого
числа переменных, чем мы и воспользуемся в дальнейшем. Итак,
пусть И^=И(г), где
= (X, - Ец)2 + (X, - у2 +... к _ у*.
В таком случае
йг___х„ —. й2г __ 1______Av — S,)2
ЙХ„ Г ’ Йх2 Г г2
ЙИ__йИйд. Й2И /?2У/йг\2 dV й2г
ЙХ„ ЙГ ЙХУ ’ ЙХ2 ЙГ2 \ЙХ7 / г dr Йх2
УРАВНЕНИЕ ПУАССОНА
21
и следовательно,
п п п
(36)
d2V n—\dV 1 d
dr2 ' r dr
гп~г dr
п-1
В рассматриваемом нами случае п — 3; таким
распределения масс удовлетворяется уравнение
образом вне области
г2 dr \ dr
(37)
Интегрируя это уравнение, мы получим:
„dV dV с
г2—-—с;
dr dr г2
Вторичное интегрирование даст нам:
dV\
dr ) '
Так как V при г—> оо обращается в нуль, то cf = 0. Согласно сде-
ланному раньше замечанию, постоянная — с равна всей массе М. Таким
образом мы видим, что при шаровой симметрии распределения масс
влияние, оказываемое ими на точки, которые находятся вне занятой
ими области, таково же, как если бы вся масса М была сосредоточен-
ной в центре симметрии. Далее, напряженность поля в направлении г
ЙР /И
равна - — =------ .
5г г2
В точках внутри области, занятой массами,
г2 dr
= — 4пр (г).
(38)
Интегрируя, мы получим:
r2p (г) dr.
Рассмотрим в частности равномерное (однородное) распределение масс
внутри шара радиуса R, т. е. предположим, что р (г) = const — р для
r<^R (см. также выше раздел а). В таком случае
2 dV 4п
г Тг—з
22
ФОРМУЛА ГРИНА. ПОТЕНЦИАЛ. КРАЕВЫЕ ЗАДАЧИ
и, следовательно, напряженность поля в направлении радиуса г равна
dV 4тг
Рг»
dr 3
т. е. прямо пропорциональна расстоянию от центра. На поверхности
шара, т. е. при r = R, это значение непрерывно переходит в значение
напряженности поля вне шара, так как для r^> R при г—>R
__М 4тг/?3р
йг г2 3 R2
Для г <ZR интегрирование даст нам
V=C — |-тгрА
Так как потенциал V на поверхности шара должен быть непрерывен,
то С=2тгр/?2. Этот результат совпадает с результатом, полученным
нами раньше непосредственно.
d) Материальную точку Q массы т можно аппроксимировать, рас-
сматривая последовательность распределения масс, в которых плотность р
равна нулю или равномерно стремится к нулю во всякой области, не
содержащей некоторой окрестности и точки (Q; эта окрестность и неогра-
ниченно стягивается к точке Q, а распространенный на нее инте-
грал р dz стремится при этом к т. Это значит, что массу т можно,
например, аппроксимировать с помощью шаров с центром в точке Q,
радиусом г, стремящимся к нулю, и неограниченно возрастающей плот-
Зт „
ностыо р = . Таким образом вне шара в каждом члене последова-
тельности плотность равна нулю, а масса каждого из шаров равна еди-
нице. В этом случае плотность р является кусочно-непрерывной. Иногда
полезно представить себе, что массы распределены по всему простран-
ству, а их плотность сходна с зубцевидной функцией, введенной нами
в § 35 (т. I). Можно, например, положить
}1.т „гл V-m -„г
р = ——е~или р — —-е .
г 3 г 4ТГГ2
2тг2 г2
Как легко подсчитать, эта функция при р.—>оо удовлетворяет нашим
требованиям. С помощью такого рода предельного перехода можно фор-
мулу (12) получить из (31).
Рассмотрим распределение масс вдоль какой-либо кривой, т. е. пре-
дельный случай такого распределения масс, при котором вся или почти
вся масса занимает объем трубки, со стремящимся к нулю поперечным
сечением то. В таком случае dt — dwdl и dS=dl ds, где dl — элемент
длины образующей трубки, a ds — периметр поперечного сечения, плот-
ность р при этом повсюду вне кривой стремится к нулю, и, кроме того,
существует предел,
УРАВНЕНИЕ ПУАССОНА
23
где интеграл распространен на любое поперечное сечение трубки, орто-
гональное данной кривой. Этот предел р мы называем линейной плотно-
стью и определяем потенциал с помощью формулы:
(39)
через dl в этой формуле обозначен элемент дуги данной кривой. При
этом предполагается, что изменение касательной к данной кривой про-
исходит кусочно-непрерывно.
Чтобы получить в этом случае формулы, аналогичные (31) и (33),
рассмотрим сначала случай непрерывного распределения масс по оси Oz
с плотностью ? = p(z). Потенциал в точке, находящейся в плоскости
z=z0 на расстоянии е от оси Oz, равен
оо
__С Р (О (40)
. ~J /(С—VH-e8’
—оо
В плоскости z = 0 проводим окружность с центром в начале координат
и радиусом, равным е. Производная по нормали к этой окружности
равна
ЙИ р(№
•-—• ~ р. 1 —1-----
ЙЛ \ 3.*
J (£2-Н2)2
— оо
а интеграл вдоль этой окружности равен
\ йл \ з.
— ОО
Легко заметить, что предел этого выражения при е—>0 равен
Ит2тге2р(0) ( ---——д-=4тгр(0).
J (С2 4-е2)2
—оо
В случае общей кривой, для которой имеет место формула (39), мы
получаем аналогичным путем:
,. Гйи
lim I —-ds= 4тгр.
J йл г
(41)
Интеграл этот надо взять по окружности, опоясывающей данную кривую
и лежащей в нормальной к ней плоскости. Радиус этой окружности дол-
жен при этом смениться к нулю.
Предположим, что массы равномерно распределены вдоль некоторой
бесконечной прямой, например вдоль оси Oz. Если массы равномерно
24
ФОРМУЛА ГРИНА. ПОТЕНЦИАЛ. КРАЕВЫЕ ЗАДАЧИ
распределены на очень большом интервале то потен-
циал V для точек с небольшими значениями апликаты z почти не зави-
сит от этих значений z. Действительно, если обозначить через г рас-
стояние от точки Р до оси Oz (прямой, вдоль которой расположены
действующие массы), то потенциал масс в точке Р будет равен
+н г___________
С р d£ , Н—z~i-vr2 + (H— z)2
V= | -- - ---р log------------------
—н
= р log (Я~7-Ц- + (^ - ^)2) {H^-z 4- + (ТУфг)2) =
= 2P!og у 4-2р!оё/74-
Первые два слагаемых от z не зависят; последнее же слагаемое для до-
статочно малых по отношению к Н значений z достаточно мало отли-
чается от
2Р106{1+|/1 + ^}.
т. е. весь потенциал в этом случае почти не зависит от г. Если из рас-
сматриваемого потенциала вычесть 2р log(l+ |/2)/7, т. е. величину, не
зависящую от положения точки Р, и затем перейти к пределу при Н—> оо,
то мы получим 2р log — . Это показывает, что потенциал точки отно-
сительно масс, равномерно распределенных на бесконечной прямой, за-
висит только от расстояния точки Р от этой прямой и является лога-
рифмическим потенциалом (см. пример дальше и нижеследующий
параграф).
Точно так же в случае цилиндрического распределения масс между
плоскостями z = — Н и z — Н потенциал точки, апликата которой до-
статочно мала по сравнению с Н, почти не зависит от Н. Заметим для
доказательства, что плотность р в этом случае является функцией только
х и у. Тогда потенциал равен
v = Г Г f p(g, T))rfgrf^c ;=s
JjJ /(5 — x)2 -j-(j]— j)a4-(S— *)2
H
— П P (£» *1) I " ;----- _ .
J J J V - X)2 + (»j —j)2 4- (C - Ф
3 —H
Тройной интеграл взят по объему цилиндра,’ занимаемого массами,
УРАВНЕНИЕ ПУАССОНА
25
а двойной интеграл — по площади (ограничекной) основания этого ци-
линдра. Согласно только что доказанному
н
dt,_________________________________
/(5 — Л-)2 -ф (1) — у)2 -НС — *)2
— н
для достаточно малых z почти не зависит от г, и в этом случае после
вычитания величины, не зависящей от положения точки Р, и перехода
к пределу мы получим потенциал бесконечного цилиндра V, удовлетво-
ряющий уравнению
—+—О,
т, е. наша задача переходит в двумерную. Предположим, кроме того,
что плотность р зависит только от расстояния г точки от оси Oz (та-
кое распределение плотности имело место и при ранее рассмотренном
линейном распределении), т. е. что плотность обладает симметрией вра-
щения. Для точек, лежащих вне области, занятой массами, мы получаем.
1 d ! dV'
----(л —
г dr. I dr
(12)
Две последовательно проведенные интеграции дают:
dV dV С
г ~г- —С,
dr dr г
I7=Clogr-|-C'.
Таким образом силовое поле обратно пропорционально первой степени
расстояния от начальной точки, сам же потенциал прямо пропорцио-
нален логарифму расстояния и на бесконечно большом расстоянии от
масс становится бесконечно большим. Внутри области, занятой массами,
гр (г) dr,
при постоянной плотности р это дает
= — 2ттрг, V=C" — тгрл2.
Для того чтобы поле на границе r=R было непрерывно, необходима,
чтобы С— — 2тгр/?2 =—2рю, где со обозначает площадь круга ра-
диуса R. Таким образом „поток“ в данном случае равен
Й1/
— ds — 2п I pR ds = 4тт2А'яр — 4тгр(о.
(43)
Этот результат вполне согласуется с формулой (41).
26
ФОРМУЛА ГРИНА. ПОТЕНЦИАЛ. КРАЕВЫЕ ЗАДАЧИ
§ 55. Логарифмический потенциал. Выражение
V =— т log r=т log —
(44)
можно рассматривать (см. предыдущий параграф), как потенциал дву-
мерного пиля, напряженность которого обратно пропорциональна первой
степени расстояния. Компоненты этой силы представляют собою частные
производные от V по соответствующим переменным. Кроме того, функ-
ция V для г^> 0 удовлетворяет уравнению Лапласа в двух измерениях
Д1/=
Й2Г
а*2"
= о.
Выражение (44) называют логарифмическим потенциалом материальной
точки массы т. Логарифмический потенциал для непрерывного распре-
деления масс на плоскости получается аналогично тому, как был по-
лучен потенциал для трехмерного пространства (28). Полагая, что эле-
мент массы dm = р dS, где dS означает элемент плоскости, а р = р (£, jj) —
кусочно-непрерывная функция, представляющая собою плотность, мы ло-
гарифмический потенциал плоскостного распределения масс определим так:
где
Vp=V(x,y) =
р (Е, »]) log у dS,
(44')
r2 = (x —£)2-}-(j —т])2.
Относительно логарифмического потенциала справедлив целый ряд тео-
рем, анало! ичных соответствующим теоремам ньютонова потенциала. Они
основываются на некоторых теоремах об интегралах, которые соответ-
ствуют доказанным уже нами теоремам для трехмерного пространства.
Так, формула для логарифмического потенциала, аналогичная фор-
муле (15) § 51, получается, как и в трехмерном случае, путем вычисле-
ния потока сквозь замкнутую кривую вектора F, направленного к неко-
торой постоянной точке Q и равного—, где г — расстояние [до этой
точки. Если г направлено к точке Q, то
n С г- f cos (т) ds . f Л , f ,
2=1 Fds — I ----------'------=4- I —= 4- \ лГ<р, (45)
J J r J r J
где t/X = rr?<p, a dy-—угол, под которым элемент дуги ds виден из
точки Q (ср. с аналогичными обозначениями в §51). Таким образом
этот интеграл равен нулю или 2тг, смотря по тому, лежит ли точка Q
вне кривой или внутри ее; если в качестве точки Q выбрать одну нз
тех точек кривой, в которых имеется касательная, то интеграл будет ра-
вен тг \ Этот факт записывайся так:
2е = 0; 2^ = тг; 2г. = 2тг. (46)
* Из рассмотрения исключаются угловые точки контура; последнее утвержде-
ние неприменимо также к точкам возврата.
ПОТЕНЦИАЛ ПРОСТОГО слоя
27
Условия, которым должна удовлетворять кривая, аналогичны тем, кото-
рым подчинена поверхность в случае трехмерного пространства. Таким
образом в двумерном пространстве множитель 2тг играет ту же роль,
что множитель 4тг в случае ньютонова потенциала. Теорема Гаусса о
дивергенции, теорема о градиенте и обе формулы Грина для плоскости
принимают следующий вид:
При этом контур, аналогично поверхности для трехмерного простран-
ства, должен состоять из конечного числа частей с непрерывно меняю-
щейся нормалью и должен пересекаться с любой прямой, параллельною
одной из координатных осей, не более чем р раз, где р—вполне опре-
деленное число. Функции U и V должны иметь кусочно-непрерывные
вторые производные Г С помощью этих трех теорем и при соответ-
ствующих предположениях относительно выражения (44') нужно, анало-
гично предыдущему, доказать справедливость уравнения Пуассона:
ЙХ2 ' й>2
2пр.
(49)
§ 56. Потенциал простого слоя, а) Вернемся снова к трехмерному
пространству и рассмотрим тот случай, когда массы распределены на
замкнутой или незамкнутой поверхности S. Этот случай можно, анало-
гично предыдущему, рассматривать как
предел непрерывного распрезе-
ления масс плотности р в пространстве, причем эта плотность во всякой
области вне данной поверхности равна или стремится к нулю, а инте-
грал у р dn, распространенный на часть нормали, продолженной в обе
стороны от поверхности, в каждой точке этой поверхности имеет предел а.
Назовем этот предел а поверхностной плотностью. Пусть, кроме того, на-
правление нормали к поверхности 5 и по‘ ерхностная плотность а являются
кусочно-непрерывными функциями. Определим потенциал V такого слоя
равенством
adS
(50)
где dS обозначает элемент поверхности Этот потенциал V предста-
вляет собою функцию гармоническую повсюду вне поверхности 61. 1
1 Теорему Гаусса (47) легко получить из теоремы Стокса, доказанной
в § 16 т. I.
Если точка Р, на которую действуют силы, лежит на поверхности 3",
то подинтегральное выражение в формуле (50) в точке Р становится
бесконечным, и -этот интеграл, как и в случае потенциала сплошного
тела, обращается в несобственный интеграл. Чтобы найти значение этого
интеграла, надо удалить небольшую часть поверхности, окружающую
точку Р, и вычислить предел потенциала всей остальной поверхности
в точке Р в предположении, что удаляемая часть,
вается к точке Р. Оказывается, что
сти а потенциал (50) в эгом случае
повсюду непрерывную функцию. Для
сначала, введя полярные координаты
уменьшаясь, стяги-
для кусочно-непрерывной плотно-
существует и представляет собою
доказательства этою предложения
и заметив, что dS=rdrdw, убе-
ждаются в том, что интеграл
распространенный на площадь
круга, сходится (г — расстояние от центра этого круга). Затем доказы-
вают, что в том случае, когда плотность имеет непрерывные производ-
ные, а кривизна поверхности S’ представляет собою кусочно-непрерыв-
ную функцию, то первые производные от потенциала V при прибли-
жении к поверхности S’ как извне, так и изнутри, равномерно стремятся
к вполне определенным непрерывным функциям Ч Однако предельные
функции, получающиеся при приближении к поверхности S’ извне и из-
нутри, вообще говоря, не совпадают друг с другом (см. § 58).
В частности эти производные при приближении к поверхности 5
ЙУ
-—, -— , —— можно инте-
йх йу Йг
грировать по любой замкнутой поверхности, заключающей внутри часть
ЙУ
поверхности, несущей массы. Интегрируя — по такой поверхности, мы
on
формулах (31) и (32), получим 4тг ЭД с dS, где инте-
йи йи
останутся ограниченными, так что функции -— —
точно так же, как и в
грал распространен на часть поверхности S, заключенную внутри за-
мкнутой поверхности.
Рассмотрим теперь произвольно взятую часть S поверхности 5. Возь-
мем два куска поверхностей «S’j и <S’g, которые отстоят одна от дру-
гой на расстоянии dn, между которыми заключена часть 2, и которые
мало отличаются от 2. Добавив к S', и S2 соответствующим образом
подобранную полоску s, площадь которой стремится к нулю при при-
ближении dn к нулю, мы можем совокупность Sj, S2, s рассматривать
как замкнутую поверхность. Рассмотрим интеграл
, распростра-
ненный на эту замкнутую поверхность. Часть этого интеграла, соответ-
ствующая поверхности s, при предельном переходе dn к нулю обра-
щается в нуль, а потому согласно предыдущему замечанию
1 См. цитированную в § 54 статью Е. Schmidt, § 3.
ПОТЕНЦИАЛ ПРОСТОГО слоя
29
в этой формуле через пА и п, обозначены направления нормалей к по-
верхностям Sj и S2, обращенных в сторону поверхности S. Интеграл,
стоящий в правой части этой формулы, распространяется на часть по-
верхности В пределе dS1 и dS2 можно заменить через dS, производ-
ные, стоящие в подинтегральной функции, — их пределами, и, таким
образом (что можно доказать вполне строго), получится:
(W+^_
JJ \йя, йи2
dS=0.
(51)
Так как эта формула справедлива для любой части S поверхности S, то
на всей поверхности должна выполняться равенство
ЙИ . ЙИ л
Г-----к — = 4то.
Й/Z-J 1 йи2
(52)
Эта формула является уравнением Пуассона для поверхностного слоя.
В случае замкнутой поверхности 5 мы можем предположить, что
лежит внутри 5, a S2 вне S. (Если 5 представляет собой незамкнутую
поверхность, то выбор внутренней и внешней стороны 5 совершенно
произволен.) В таком случае направление внутренней нормали п к по-
верхности £ совпадает с направлением внутренней нормали «2 к поверх-
е rv (*V\ l*V\
ности о2. Обозначим через [ I и I — I пределы производных от V,
\ oft / j \ оП I е
взятых по внутренней^нормали к 5 и получающихся при приближении
к поверхности S соответственно изнутри и извне. Мы тогда будем
иметь:
йу_ _/йи\ ЙИ_/ЙИ\
Й/Zj \й«//’ й«2 \ЙЯ //
Формулу (52) можно теперь переписать так:
(53)
Таким образом производная по нормали, взятая во вполне определен-
ном направлении, при переходе через поверхность 5’ делает скачок,
величина которого равна поверхностной плотности, умноженной на 4ТГ1.
(При переходе из внешней стороны поверхности на ее внутреннюю сто-
рону эта производная уменьшается на 4пс.) Этот факт был обнаружен
Кулоном для электрического потенциала.
Ь) Исследуем в виде примера равномерное распределение масс в пло-
скости yz. В виде приближения рассмотрим очень большой квадрат
— Н^у Н, —z Н, в центре которого находится начало ко-
ординат. Для достаточно малых у и z потенциал почти не зависит от_у
и z. Доказательство этого можно провести аналогично тому, как было
1 См. вышецитированную статью Е. Schmidt, § 3.
30
ФОРМУЛА ГРИНА. ПОТЕНЦИАЛ. КРАЕВЫЕ ЗАДАЧИ
доказано, что потенциал бесконечно большого стержня почти не зави.
сит от конечных смещений точки приложения при которых ее расстоя!
ние ог стержня остается неизменным (см. § 54, d). Для доказательства
в данном случае придется рассматривать двойной интеграл1
н н
f С ___________dr^d?_________
J J j/x2 -j-(4 —J02-H£ — *)2’
— Н — п
* Доказательство того факта, что этот двойной интеграл почти не зависит!
от у и г, можно обосновать его симметрией относительно пар у и г.
Мы имеем:
НН Н __________________________________
С Г d-t} d? = f log 2 + 1^ + <T| —J)2 -I- (- — z}2
x2 д- (4 — J? — (C — *)2 J —(H+z)+Vx^ + (f|— >2) -t- q
H
- f + 4/7 log H+
— н
4 {о+^/(1+в)’+(^)+й) + I
Первые два слагаемых от z не зависят. Чтобы исследовать зависимость от z j
последних слагаемых, заметим, что входящие в подинтегральную функцию лога- J
рифмы при | ~ 1 могут заключаться внутри промежутков
Ы2=2в)М1лд+/I
и следовательно, их можно представить в виде:
причем | <f | < 2 для всех значений | | < 1, | | <2 1 и достаточно малых г.
Поэтому эти два логарифма можно разложить по степеням в равномерно
сходящиеся ряды:
(V)’ й}=^+л-д+^ё+--
'°s{2 + ’ [-Д. Стг) ’ 7р\}=л‘-а‘Т1 + ^№ + '“’
где Лс, Ait Аа
. / Л — J \2 х2
..—функции от \-j^) и
ПОТЕНЦИАЛ ПРОСТОГО слоя
31
й2и
случае к — , т. е. наша задача
дх“
от пластинки, т. е. при х^>й,
который выражается через элементарные функции. Потенциал весьма
мало зависит от у и z также и в том случае, когда массы заполняют
тонкую пластинку,- толщиною в 2/г, средней поверхностью которой слу-
жит рассмотренный нами квадрат. При этом предполагается, что плот-
ность р = р (х) не зависит от у и z. Выражение Д V для небольших
значений у и z приближается в этом
переходит в одномерную. Итак, справа
йх* 2 ’ йх ’
Направление поля перпендикулярно к пластинке; напряженность поля
постоянна; потенциал представляет собою линейную функцию от х.
Внутри пластинки, т. е. при —h<^x<^h,
— = -4ТГр(х).
(54)
Если плотность р постоянна, то
ЙИ л л
-— = — 4тг » р ах -= — 4тгрх;
vx J г
о
Так как производная :
при х> h сила поля -
при X < ' — h, т. е.
ЙИ
— при x = h непрерывна, то С — — 4тгрЛ, т. е.
ЙИ л , п
= —4тгрл. Аналогично этому мы получим, что
й(/'
слева от пластинки,—= 4пр/г. Постоянная Cf
остается неопределенной. Итак, при прохождении через пластинку про-
ЙИ
изводная — делает скачок на 4тгр-2/г. Если р будет принимать после-
довательность значений (как мы объясняли в § 56, а), при которой про-
изведение р-2/г стремится к а, то в пределе мы получим скачок
производной потенциала, а именно 2тгр.
z
При сложении этих рядов члены с первыми степенями -р сократятся. Инте-
грируя полученную сумму, мы замечаем, что коэфициенты при различных сте-
2
пенях — могут оказаться бесконечно большими, порядка не выше первого отно-
сительно Н, так как все коэфициенты подинтегрального ряда содержат л лишь
в виде степеней отношения . Будучи умножены на
, где они дают
слагаемые, порядок малости котгрых по крайней мере равен т, е. последние
два слагаемые, а следовательно, и весь исследуемый нами двойной интеграл
почти не зависят от г. Но, как уже было сказано, этот интеграл симметричен
относительно и С, г, следовательно он должен быть почти независим и от у.
32
ФОРМУЛА ГРИНА. ПОТЕНЦИАЛ. КРАЕВЫЕ ЗАДАЧИ
В проведенном нами вычислении мы пренебрегали производными
от V по у и по z. Однако же результат можно получить с помощьц
вполне строгого вывода. Вычислим
для этого потенциал однородного
круга радиуса R в точке Р, лежа,
щей на перпендикуляре, восстав,
ленном в центре этого круга (черт. 71),
Затем заставим радиус круга бес-
конечно увеличиваться. Введем для
круга полярные координаты И и <р'.
Тогда dS — ddddu>'. Обозначим те.
перь через х расстояние точки Р от
центра круга и предположим, что
поверхностная плотность а постоянна. Тогда, так как г=У х2 то
СС adS Г г’dr1
2 тгр ()/х2/?2 — х). (55)
о
Следовательно, сила поля равна
x2-f-/?2
1
ЙУ
При х—»со как V, так и — обращаются в нуль (черт. 72). Поле
«с обеих сторон круга симметрично. При неограниченном увеличении
у
Черт. 72.
потенциал V также бесконечно возрастает, а напряженность поля —-
йх
стремится к постоянному значению — 2тго 1, — результат, полученный
нами уже ранее.
---------- йу
» Чтобы получить напряженность поля ——, мы для перехода к пределу вы-
ЙХ
читаем из потенциала постоянную величину и ищем предел производной от
функции:
У. = 2ка (УX* + № — х) — 2гесЛ? = 2то - . — ---=
V^+R^ + x+R
2
— — 2глс
2 ’
л'г/?-гГ
и затем производную от предела потенциала Упри /?-+оо заменяем пределом
производной от Уо равным — (Нт У.) =— 2г.о (ср. S 54. d)
<1г г '
ПОТЕНЦИАЛ ДВОЙНОГО слоя
33
в заключение вычислим потенциал масс, равномерно распределен-
ных на поверхности шара радиуса /?. Поверхностную плотность этого
шара обозначим через а. В таком случае вне шара (см. § 54)
/14 4тг/?2а йВ 4тг/?2а
у— г;
у, следовательно,
Внутри шара
I*V\ л
I — | — 4то.
\ ЙИ / е
Ав=о, 1/=~ + С\
г '
Так как потенциал V в начале координат конечен, то С должно быть
равно нулю. Таким образом потенциал внутри шара постоянен, и
ЙВ
Итак, скачок — на поверхности шара действительно равен 4тга.
§ 57, Потенциал двойного слоя. Рассмотрим потенциал диполя, со-
стоящего из двух масс т и — т, расположенных на расстоянии ds
друг от друга. Потенциал точки Р,
расстояния которой от двух точек с
противоположными массами суть гг и г2
(черт. 73), равен
т т г, — г,
V—---------= т ------1.
П Г2 Г1Г2
Обозначим через 0 угол между осью
диполя, направленной из точки с отрицательной массой к точке с
положительной массой, и прямою, соединяющей середину расстояния
между массами с точкой Р. Для достаточно малых значений г2 — гг имеем:
и, следовательно,
г2 — гг = ds cos 6
mds cos О
Если масса т возрастает, а расстояние ds одновременно убывает, при-
чем это изменение происходит так, что „момент" т ds стремится к опре-
деленному пределу, т. е.
Нш (т ds) — М
при ds—>0, то в результате этого предельного перехода потенциал
получает следующее значение:
/И
V~~2 cosO. (56)
« Вебстер, Ди^ерепциаяьные уравнения.
34
ФОРМУЛА ГРИНА ПОТЕНЦИАЛ. КРАЕВЫЕ ЗАДАЧИ
Величину М мы называем моментом диполя. Считая ds направленным
по оси диполя, точку Р неподвижной, a Q переменной, имеем:
dr —— ds cos 0, — = — cosO,
dS
и следовательно,
d —
M dr M cos О
г2 ds
(57)
Таким образом потенциал I/ зависит не только от длины отрезка PQ,
но и от его направления. Вблизи положительного конца диполя потен-
циал положителен, а вблизи отрицательного отрицателен. Такого рода
поле производит, например, небольшой магнит: его приближенно можно
заменить двумя равными, но противоположными по знаку массами
(полюсами).
Определение двойного слоя замкнутой или незамкнутой поверхно-
сти S основано на понятии диполя. Под двойным слоем мы понимаем
такое распределение диполей по поверхности, при котором оси дипо-
лей совпадают с ее нормалями. Массы диполей определяют как бы два
простых слоя, причем поверхностная плотность одной из них равна с?,
а другой —а. Первую из них мы принимаем за „внутреннюю" поверх-
ность нашего двойного слоя, а вторую — за „внешнюю" поверхность.
Направление оси диполя совпадает в таком случае с направлением внут-
ренней нормали. Если расстояние между этими поверхностями обозна-
чить через dn, то момент элементарного диполя есть dM — a dn dS, а
его потенциал в силу (57) есть
d —
dW—adndS-~.
d/Z
Момент на единицу площади при dn—>0, т. е. величину litn з dn — гх,
мы называем плотностью данного двойного слоя. Потенциал двойного
слоя определяется интегралом
z -г—- dS,
дП
причем через п обозначена внутренняя нормаль. В случае постоянной
плотности х мы имеем:
(59)
В этой формуле множитель при х равен углу fi (см. § 51), под кото-
рым данной двойной слой виден из точки/3. В противоположность § 51
в данном случае радиус г целесообразно направить в ту сторону, в ко-
ПОТЕНЦИАЛ ДВОЙНОГО СЛОЯ
35
торую расстояния от точки Р возрастают. Благодаря этому угол о лта
положительной внутренней) стороны двойного слоя положителен а для
отрицательном (внешней стороны отрицателен. Если поверхность ”
замкнута, то внутри ее Г=4та. а вне ее Г=0 Таким пл °
тенциал W при прохождении через двойной слой претерпевает разоив'
Производная по нормали в противоположность потенция™ п Р Р
хождении сквозь двойной слой остается непрерывной (см. нижеГтХ’
образом соотношения в этом случае как раз обратны тем XooJe мы
имели в случае простого слоя, когда потенциал был непрерывен а его
производная по нормали претерпевала на поверхности разрыв.
Непрерывность производной по нормали можно наглядно представить
следующим образом. Производная —— при прохождении сквозь слой а
о/7
в направлении внутренней нормали
на 4тг<7, а при прохождении сквозь
чину. Таким образом при прохож-
дении сквозь двойной слой она дей-
ствительно должна остаться непре-
рывной (черт. 74). С помощью ана-
логичного рассуждения можно уяс-
нить также и скачок потенциала W.
Пусть 1'2' представляет собою часть
нормали, направленную изнутри во-
вне и соединяющую между собою
поверхности а и — <з. Введя обозна-
чение, аналогичное тому, которым ь
й.Ч
-j 4то.
г
возрастает согласно формуле (53)
слой — о убывает на ту же вели
пользовались в § 56, найдем, что
мы
от
Первое слагаемое левой части представляет собою предел, который
получим при приближении к поверхности с изнутри. Интегрируя
2' до 1', т. е. в направлении положительной нормали, мы будем иметь:
J to
2'
dn.
Так как limafifzz —х, то в результате предельного перехода мы получим,
что
Wj — 1Г2 = 4та. (60)
Эта формула представляет собою обобщение результата, найденного
нами для случая х=1.
Резюмируя, можно сказать, что потенциал двойного слоя, при про-
хождении через этот слой в некоторой точке делает скачок, равный
плотности в точке N, умноженной иа 4л. Производная по нормали при
прохождении сквозь слой остается непрерывной. Более строгое и точное
3*
gg ФОРМУЛА ГРИНА. ПОТЕНЦИАЛ. КРАЕВЫЕ ЗАДАЧИ
исследование показывает, что х должно иметь кусочно-непрерывнЛ
вторые производные, а поверхность S должна иметь кусочно-непрерыЖ
нуга кривизну1.
§ 58. Формулы Фредгольма. Полученные нами выше свойства потев
циала W можно также найти другим методом. Удалим небольшой кус®
поверхности .9, по которой распределены массы, и предположим, ч®
точка, на которую действуют массы, находится на этой части поверхности!
Потенциал остальной части поверхности и его частные производные пер!
вогр порядка непрерывны в этой точке. Удаленный кусок поверхности!
мы можем взять столь малым, чтобы потенциал и производные потец.1
циала этого куска весьма мало отличались от потенциала плоского!
кружка и его производных, которые можно вычислить непосредственно.
Таким образом подтверждается справедливость предыдущей теорем!
для всего данного распределения масс.
В случае кружка выясняется, что потенциал W (рассматриваемый кап
несобственный интеграл или, геометрически, как угол зрения) имеет!
смысл также на самой поверхности, и что он равен 2тсх, где х ест|
поверхностная плотность, которую мы предполагаем постоянной. Это]
факт остается справедливым и для более общего случая произвольно^
поверхности S с кусочно-непрерывной кривизной, при условии, чт<
в данной точке можно провести касательную плоскость; относительна
функции х предполагают, что она обладает кусочно-непрерывными вто-
рыми частными производными. Если потенциал двойного слоя для точки
на поверхности 5 обозначить через W, то окажется, что
Wt = 2т + W; We = — 2т -J- W,
где через Wt и We обозначены пределы, получающиеся при прибли-1
жении к поверхности 5 соответственно изнутри и извне; таким образом j
Запишем эти равенства полностью:
(61)
W'(W{ + We) = \\m~ds.
£ .f„I еП,
(62)
В правой части этих формул стоят несобственные интегралы.
1 См. Е. Schmidt, вышеприведенная статья, § 2 и 4..
ФОРМУЛЫ ФРЕДГОЛЬМА
37
Аналогичные равенства имеют место и для производной по нормали
от потенциала V простого слоя. Относительно ограничений, которые
надо наложить на функцию и на поверхность в этом случае, см. § 56, а.
Продиференцируем формально несобственный интеграл
со
rPQ
(точка Р лежит на
мали, проведенной
поверхности S) по направлению пр внутренней нор-
в точке Р. Мы получим:
f С / 1 \ Г f сп cos ф
PQ
(63)
где ф— угол между нормалью в точке Р и отрезком PQ (Q пробегает
всю поверхность S). Это выражение отличается от потенциала двойного
слоя с тою же плотностью
3
3«Q
только тем, что угол ф заменен здесь углом ш между нормалью в точке Q
и отрезком QP (черт. 75). Если точку Q выбрать достаточно близко
л созф
к точке Р, то отношение -------- сколь угодно мало отличается от — 1
cos и
(черт. 76). Поэтому интеграл
(63), распространенный иа до-
статочно малую окрестность
точки Р, отличается сколь угод-
но мало от
Йап cos to
Если к этому потенциалу двой-
ного слоя приложить преды-
0
Черт. 75. Черт. 76.
дущие результаты, то окажется,
что формула (63) имеет смысл как несобственный интеграл также и для
точки, лежащей на самой поверхности. Следовательно,
(£),=-МР-^
(£).=МГ-^
Формулы (52) и (60) относятся к числу классических формул, а их
приложение — формулы (64) и (61)—были получены в последнее время:
go ФОРМУЛА ГРИНА. ПОТЕНЦИАЛ. КРАЕВЫЕ ЗАДАЧИ
ио
они появились впервые в статье Фредгольма в 1900 г. На них основано
сведение граничных задач теории потенциала к интегральным уравнениям.
Предыдущие определения и теоремы легко распространяются на ло-
гарифмический потенциал масс, распределенных вдоль замкнутой плоской
кривой. В этом случае — надо заменить через log —, а множитель 4тт
уменьшить в два раза. Формулы (61) и (64) переходят при этом
§ 59. Теорема Грина. Мы покажем сейчас, что потенциальную функ-
цию можно при очень общих предположениях свести к потенциалу
простого или двойного слоя. Это утверждение основано на одной
теореме интегрального исчисления, имеющей большое значение в теории
диференциальных уравнений математической физики: мы будем в даль-
нейшем называть эту теорему теоремой Грина.
Обозначим через г расстояние от переменной до некоторой по-
стоянной точки Р. Как известно, функция U=— при любом значе-
нии r=^=Q удовлетворяет уравнению Лапласа.
Пусть V — потенциал масс, распределение которых может быть за-
дано совершенно произвольно, Наложим на это распределение масс
такие ограничения, при которых потенциал V имеет кусочно-непре-
рывные вторые производные. Применим вторую формулу Грина к функ-
циям U и V. Точка Р, служащая началом отсчета для расстояний г,
не должна при этом входить в область интегрирования. Рассмотрим
область т, граница которой не проходит через точку Р. Если точка Р
лежит внутри этой области то мы исключим ее из области интегри-
рования вместе с окружающей ее сферой 2 радиуса е. При интегриро-
вании к поверхности 5 добавляют при этом поверхность X. Внутри S
и вне 2
а потому
s -i-s
У дул.
66)
ТЕОРЕМА ГРИНА
39
Нормали к обеим поверхностям направлены внутрь области интегриро-
л й д
вания. На поверхности 1 сферы — =— , а потому, если мы обозна-
дп дГ
чим через Vs потенциал на поверхности S, а через da— телесный угол, те
— da
dr
1
Если радиус е будем приближать к нулю, то последний интеграл
также будет стремиться к нулю, так как — ограничено, а первый
дг
интеграл в силу соотношения lim К, — Ур будет иметь пределом
е—>0
причем интеграл по объему в левой части равенства есть несобствен-
ный интеграл. Определяя отсюда Ур, получим:
Это ч есть искомая теорема Грина. Если точка Р лежит вне области т,
то левая часть этой формулы обращается в нуль. Теорема Грина пока-
зывает, что функция, имеющая непрерывные вторые производные внутри
замкнутой поверхности .S’, вполне определена в каждой точке про-
странства, ограниченного этой поверхностью, если известны:
1.
3.
„Концентрация" — Д V
Значение функции У в
Значение производной
в каждой точке внутри поверхности,
каждой точке на этой поверхности.
по нормали — в каждой точке этой
dn
поверхности.
В частности, если V есть функция гармоническая внутри поверх-
о т,
ности Л, то она вполне определяется значениями V и — на поверх-
ности.
40
ФОРМУЛА ГРИИА. ПОТЕНЦИАЛ. КРАЕВЫЕ ЗАДАЧИ
Пусть V— гармоническая внутри поверхности функция. Применим
формулу (69) к сфере s с центром в точке Р. Тогда на поверхности з
мы будем иметь:
Л а- ,
г Г 1
---------- —----------== — = const.
ЧП----------ЙГ Г2
Подставив это выражение в формулу (69) и воспользовавшись фор-
мулами (16) и (67), мы получим в результате теорему о среднем зна-
чении гармонической функции: .
Отсюда мы можем заключить, что гармоническая функция ни в одной
из точек области т не имеет ни относительного максимума, ни отно-
сительного минимума. Единственное исключение представляет собою
тот случай, когда I/ постоянна и равна 1/р на всей сфере, а следова-
тельно, и в некоторой окрестности точки Р. В этом случае, как легко
показать, V постоянна во всей области т. Таким образом мы доказали
свойство гармонической функции, касающееся максимума и минимума,
о котором у нас была уже речь в § 53.
Вернемся снова к потенциалу. Обозначим через р плотность упомя-
нутого в начале параграфа распределения масс, потенциал которых
равен V. Согласно § 54, Ь потенциал удовлетворяет уравнению Пуассона
Л V — — 4тгр,
а потому второй член
вить в следующем виде:
в правой части формулы (69) можно предста
Это выражение равно потенциалу
верхности Поэтому первый член
интегралов по поверхности
масс, расположенных внутри по-
в этом выражении, т. е. разность
будет представлять потенциал масс, лежащих вне поверхности 5. Эти
два интеграла можно рассматривать как потенциалы соответственно
двойного и простого слоя. Плотность масс двойного слоя есть
х=- V,
ТТ
а плотность простого слоя
1 ЙИ
с = — - —.
4тт in
ЗАДАЧА ДИРИХЛЕ
41
Резюмируем полученные нами результаты: потенциал масс, лежащих
вне поверхности 3, можно для всех точек, лежащих внутри этой по-
верхности, .заменить двумя потенциалами, из которых один соответ-
ствует простому слою, распределенному по поверхности 5”, а второй —
двойному слою. Это представление особенно удобно, когда внутри по-
верхности 3 нет масс, т. е. когда потенциал V представляет собою
функцию гармоническую внутри
Если поверхность 5 есть поверхность уровня потенциала V, т. е.
если на этой поверхности V = const, то, как это следует из теоремы
Гаусса, потенциал двойного слоя дает постоянное слагаемое.
Формула (69) остается справедливой также и в том случае, когда
требуется определить функцию V вне поверхности 3. В таком случае
она кроме указанных условий должна удовлетворять еще и следующему:
при г —»оо должны выполняться неравенства
аг аг| л
|И<7’
где 7И^>0 есть некоторое постоянное число. Точка Р лежит в этом слу-
чае вне поверхности и нормаль к поверхности должна быть обращена
наружу. Чтобы доказать справедливость формулы (69) и в этом случае,
применяют ее к области, ограниченной поверхностью 5 и сферой боль-
шого радиуса. Легко при этом показать, что часть потенциала, соот-
ветствующая сфере, стремится к нулю, когда радиус этой сферы беско-
нечно возрастает. Далее, оказывается, что в этом случае потенциал
масс, лежащих внутри поверхности, можно заменить для точек, лежа-
щих вне этой поверхности, потенциалом простого и двойного слоя.
Заметим, что указанное выше распределение масс на поверх-
ности, которое внутри поверхности 3 равносильно действию внешних,
масс, определяется отнюдь не однозначно. Оно в значительной степени
зависит также от масс, лежащих внутри поверхности 3, которые можно,
конечно, как угодно менять, не изменяя при этом действия внешних масс1.
60. Задача Дирихле. Решение диференциального уравнения в частных
производных, содержит, вообще говоря, как это было показано в гл. II,
произвольные функции. Эти последние определяются так называемыми
начальными условиями, т. е. заданием искомой функции и некоторого
числа ее производных для некоторого определенного значения незави-
симого переменного (т. е. на некоторой плоскости). Например, для вол.-
нового уравнения в одномерном пространстве,
е2и й2и
— — -------
й/2 йх2 ’
рассмотренного нами в § 26, начальными условиями являются:
и — F (л)
^ = G(x)
при t— 0.
* J. Larmor, On the mathematical expression of the principle of Huygens,
Proc. Lond. Math. Soc., серия 2, т. I, cip. 1, 1903.
42
ФОРМУЛА ГРИНА. ПОТЕНЦИАЛ. КРАЕВЫЕ ЗАДАЧИ
Для уравнения Лапласа
й2у й2у й2у
йх2 йу2 ”* йг2
соответствующие условия запишутся так:
V — F(y, z)
^L — G(y,z)
дх
при
Согласно теореме Коши-Ковалевской (см. § 23), этому заданию при
соответствующих предположениях (аналитичность функций F и О) всегда
отвечает некоторое решение (по крайней мере, ,,itn kleinen", т. е. в не-
которой достаточно малой области вблизи плоскости х — а).
Этим условиям, в которых задаются значения (функции и произ-
водных) в плоскости f — О или х = а, можно противопоставить другой
вид заданий, так называемые краевые условия, при которых значения
задаются на замкнутом многообразии, например, в случае потенциаль-
ного уравнения в трехмерном пространстве, на замкнутой поверхности.
Особенно важны те краевые условия, при которых на граничной по-
,, aiz
верхности задаются значения V или -—.
йл
Формула Грина для функции, удовлетворяющей уравнению Лапласа
йу
йи
dS,
(78)
дает нам представление функции V внутри замкнутой поверхности, если
известны значения V и — на границе. Однако и функция V и ее
й/г
производная не могут быть заданы произвольно, независимо друг от
друга; простое рассуждение показывает, что гармоническая функция
вполне определяется своими значениями на поверхности, причем тем
гу
самым в каждой точке определяется градиент, т. е. . В самом деле,
допустим, что существуют две функции У, и У2, гармонические внутри
поверхности 5 и имеющие на поверхности одинаковые значения. В та-
ком случае У3—У, = U также представляет собою внутри поверх-
ности 6" гармоническую функцию, значение которой повсюду на поверх-
ности равно нулю. Согласно доказанному в § 59 свойству максимума
и минимума функция U должна повсюду внутри поверхности S обра-
титься в нуль, и следовательно, У7 — V2.
Тот же факт можно доказать еще иначе, исходя из формулы Грина.
Положим в этой формуле V=U. Тогда
l№dS —
Ъп
(71)
ЗАДАЧА ДИРИХЛЕ
43
Так как Д77=О внутри поверхности S, а на самой поверхности
U^O, то оба интеграла, стоящие в правой части этой формулы, обра-
щаются в нуль. Отсюда следует, что подинтегральная функция левой
части формулы (71) тождественно равна нулю и, следовательно, в ка-
ждой точке внутри поверхности S
dU_ й£__йи_о
ЙХ ду dz '
т.'е. 77= const. Но, так как U—0 на поверхности 5, то 77=0 повсюду
внутри поверхности 5.
Аналогичные рассуждения показывают, что доказанную только что
теорему можно распространить и на пространство, лежащее вне по-
верхности 5, если только функция V при г—»оо удовлетворяет до-
полнительным условиям, указанным в § 59. Вопроса о том, при каких
условиях существует гармоническая внутри (или вне) поверхности S
функция, которая принимала бы на поверхности S заданные непрерыв-
ные значения, мы здесь рассматривать не будем. Этот вопрос был ре-
шен в утвердительном смысле Дирихле с помощью принципа, носящего
его имя. Однако доказательство, данное Дирихле, было, как показал
Вейерштрасс, не безупречно; строго провести принцип Дирихле удалось
только Гильберту1. Задачу о нахождении гармонической функции по
заданным ее значениям на границе называют задачей Дирихле (или пер-
вой краевой задачей теории потенциала). Задача Неймана (Neumann) или
вторая краевая задача состоит в определении гармонической функции
внутри поверхности 5, когда на самой повсрхности заданы значения не
самой функции V, а ее производной по нормали —-. Однозначность
дп
ее решения (с точностью до постоянного слагаемого) доказывается с по-
мощью формулы (71), так же как и в случае задачи Дирихле; первый
из интегралов is правой части этой формулы при задаче Неймана обра-
щается в нуль благодаря второму множителю подинтегрального выра-
жения. С задачей Неймана мы встречаемся, например, в гидродинамике
при определении безвихревого потока несжимаемой жидкости внутри
замкнутой поверхности, когда заданы компоненты скорости по нормали
(т. е. производные по нормали потенциала скорости) во всякой точке
на границе. На основании теоремы о градиенте, заданные на границе
ЙН
значения — должны удовлетворять условию:
Вместо значений V или можно задать на границе значение их
линейной комбинации:
(Л<0).
1 R i е tn a n n - W е b е г, т. 1, стр. 539 и 584.
44 ФОРМУЛА ГРИНА. ПОТЕНЦИАЛ. КРАЕВЫЕ ЗАДАЧИ
Определение гармонической функции по этим условиям на границе, так
называемая третья краевая задача, встречается, например, в теории
теплопроводности.
Мы оставляем пока задачу Дирихле и возвращаемся к волновому
уравнению. Мы покажем сейчас, как решение этого уравнения, найден-
ное нами методом Коши (§ 44, т. I), получить иным способом.
§ 61. Волновое уравнение в трехмерном пространстве. К исследова-
нию диференциального уравнения распространения волн (т. I, § 12)
Э = а2Д<р (а>0) (72)
можно, как было уже упомянуто, подойти с двух точек зрения. Можно
й<р . ,
задать начальные значения ср и при г = £0, как мы это и сделали
в § 44 (т. I), а можно задать граничные значения функции и на какой-
либо замкнутой поверхности, аналогично тому, как мы это делали при
исследовании диференциального уравнения Лапласа. Мы дадим сейчас
новый способ решения первой начальной задачи.
Применим теорему о градиенте к волновому уравнению и будем
интегрировать по объему сферы с центром в точке Р и радиусом,
равным г. Так как г при интегрировании по частям является величиной
постоянной, то мы будем иметь:
(73)
da, как всегда, означает элементарный телесный угол. Введем в левую
часть этого равенства полярные координаты; мы получим:
(OF2 dr.
(74)
Диференцируя это равенство и равенство (73) по г и приравнивая по-
лученные производные, мы найдем:
(75)
В обе части этого равенства входит среднее значение
со = ~ ( Г со da = ~ И и cfco
‘ 4-rrJJ • 4TcJj‘r
функции ср на поверхности сферы радиуса г с центром в точке Р (зна-
чения функции ср на поверхности сферы мы обозначили через <рг).
ВОЛНОВОЕ УРАВНЕНИЕ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ
45
Таким образом
или после деления на г
2й2<р 2 г ЙГ \ ЙГ / ’ (7>')
й2 (г<р) _ йг2 2й2(лр) W • (76)
Функция г<р, рассматриваемая как функция от г и t, удовлетворяет вол-
новому уравнению в одномерном пространстве. Решение этого уравне-
ния, как известно (т. I, § 26), имеет вид:
rw =/} (at 4- г) 4-/2 (at — г), (77)
где /[ (£) и /2(£)—две произвольные функции. При г—>0 имеем:
0 =/i(c0 4-4 (по-
следовательно, для любого значения И
/,(£)=—А (£)=/(£)
и
r^—f(at-\-f) — f(at — г). (77')
Постараемся, исходя из найденного выражения для ср, определить
значение функции ср в точке Р. Продиференцируем с этой целью послед-
нее равенство по г.
и найдем предел
ф 4. r Af —f (at 4- r) (at — r)
оГ
последнего выражения при г—>0. Так как ср, как легко
определения, непрерывно при г—>0, а ~ ограничено,
ЙГ
(78)
усмотреть из его
то в результате предельного перехода мы будем иметь:
(<Д=о = 2/ (at).
Но этот предел должен совпадать с значением <р в точке Р, а потому
<рр = 2/'(с0.
Правую часть этого равенства легко можно выразить через начальные
значения функции. Действительно, складывая равенства
А. (Г!р) (at г) 4-/' (at — г),
(79)
(8С)
(78)
т Аг) (at ~
мы получим: ('А) = 2/ (at + 0- (82)
ФОРМУЛА ГРИНА. ПОТЕНЦИАЛ. КРАЕВЫЕ ЗАДАЧИ
ЭТО равенство переходит в следующее:
(™) + у у (/•?)] = 2/' (г).
О/ и- оГ f—Q
(83)
Подставим сюда вместо <р его выражение через двойной интеграл:
2/'(r) = ~ (Т + т~ И V • (84)
L^‘ \4lTJJ / 4™Ш Jr=0
Если заданные начальные значения суть
(р = Л(х, у, z)
Г! 1
^- = G(x,_y, z)
при t = 0,
то
2f' (Г) (Г И FrA + И <M«>] . (85)
Если положить r—at и принять во внимание формулу (80), то
последнее выражение перепишется так:
f я [w (°' Н '«+* П|о) de ] ’
или полностью:
= t F(x-\-ata, y-j-atfl, z -f- aty -j- j
~ J Q (x -J- ata, у -|- at$, z at-fl da,
(66)
(86')
где x, у, z — координаты точки P, а точка a, f>, у пробегает поверхность
сферы единичного радиуса. Это выражение совпадает с решением Пуас-
сона (86) и (87), которое мы нашли, следуя методу Коши (§ 44, т. 1).
Метод, приведенный нами теперь, в принципе принадлежит Лиувиллю'.
§ 62. Волновой потенциал Принцип Гюйгенса: а) Постараемся для
1
волнового уравнения найти аналог частному решению — уравнения
Лапласа. Предположим для этого, что у зависит только от г и от I.
Е таком случае волновое уравнение согласно формуле (75') примет
вид: .
й^2 ЙГ
1 J. Lionville, Deux memoires de Poisson, Journal de Math., серия 2,
т. 1, стр. 1—6, 8156.
ВОЛНОВОЙ ПОТЕНЦИАЛ. ПРИНЦИП ГЮЙГЕНСА
©сновании (77') мы найдем частное решение:
fit—
\ а
4 =----------- •
(S7)
Здесь г есть расстояние до неизменной точки Р, a )— произвольная
функция. В точке Р волновое уравнение, конечно, не выполняется.
Точку Р, которая такие волны посылает симметрично во все сто-
роны, называют источником. Источник можно себе практически пред-
ставить в виде небольшого шарика, который то расширяется, то сжи-
мается (воздух, который то выталкивается из устья органной трубы,
то втягивается туда, является источником такого рода). По аналогии
с потенциалом Ньютона — функцию и, представленную формулой (87),
называют волновым потенциалом, а иногда также запаздывающим по-
тенциалом, так как это можно рассматривать, как ньютонов потен-
циал массы f(t), действие которого на расстоянии г наступает с за-
позданием, так как оно распространяется со скоростью а. Волна (87)
ведет себя во всех точках, равноотстоящих от источника, одинаково,
почему она и называется сферической волной.
В соответствии с ньютоновым потенциалом масс, заполняющих не-
который объем или распределенных по некоторой поверхности, можно»
построить также и волновые потенциалы:
где точка Е, Гц С в первом случае пробегает некоторый объем, а во
втором случае—поверхность; г представляет собою расстояние между
точками х, у, z и Е, эд, С а функции р и о заданы.
Можно, далее, рассмотреть бнполь, состоящий из двух источников
f(t} и —f(t) (двойной источник), отстоящих один от другого на рас-
стоянии ds. Пусть при этом f(t) зависит от ds так, что существует
lim ds-f(t) — F(t). Тогда соответствующий волновой потенциал будет
ds~>0
равен (обозначения те же, что и в § 57):
Есл-и функция F имеет непрерывную вторую производную, то вы-
ражение в фигурных скобках, стоящее в правой части равенства, для
небольших значений г можно с точностью до бесконечно малых зто-
48 ФОРМУЛА ГРИНА. ПОТЕНЦИАЛ. КРАЕВЫЕ ЗАДАЧИ
рого порядка заменить через F(t). Таким образом для формулы (90) мы
получаем приближенное выражение.
Такой двойной источник можно себе представить конкретно в виде движу,
щейся взад и вперед частицы, впереди которой происходит сжатие воздуха,
а позади—разрежение.
Наконец, на основании формулы (90) можно, как и в случае потен-
циала Ньютона, определить двойной слой источников (или распределе-
ние двойных источников):
8
символ -г—
оп
имеет в этой формуле следующее значение:
(91)
8
8л
= 7.1 7], С, t
1
ar
т. e. при диференцировании по нормали переменным надо считать
только четвертый аргумент.
Функции (88), (89) и (91) вне области интегрирования удовлетво-
ряют волновому уравнению. Две первые из них непрерывны во всем про-
странстве, между тем как (91) на поверхности интегрирования делает
скачок, величина которого равна 4тгх (S, ig, С, t)\ это легко получается
из найденного нами ранее приближенного значения волнового потен-
циала двойного источника; при этом надо принять во внимание фор-
мулу (60). Мы видим, также, что при х>0 выражение (91) больше
с той стороны поверхности, с которой находятся положительные концы
диполей.
Ь) Вычислим теперь поток простейшего волнового потенциала (87)
•сквозь замкнутую поверхность 5. Мы имеем:
(92)
Этот поток в противоположность потоку обычного потенциала ме-
няется при переходе от одной поверхности к другой (жидкость
ВОЛНОВОЙ ПОТЕНЦИАЛ. ПРИНЦИП ГЮЙГЕНСА
49
/•жимаема). Выражение (92) для небольшой сферы, центром которой слу-
жит источник, равно (п обозначает внутреннюю нормаль):
а при г—>U
Величина f(t) играет в данном случае роль массы т; она называется
мощностью источника. Если поверхностью интеграции служит сфера,
центр которой не совпадает с источником, то при стремлении радиуса
к нулю поток в пределе обращается в нуль.
Этот результат можно обобщить. Если проделать такие же вычис-
ления с выражениями (88) и (89), то получится аналог уравнения
Пуассона (35) или уравнения (53). Так, для выражения (89) мы будем
иметь:
м) - U '• 'J- <и'
Таким образом производная волнового потенциала (89) по нормали при
переходе через поверхность интеграции делает скачок.
с) Эта аналогия с потенциалом Ньютона может быть проведена еще
дальше. В соответствии с исследованиями § 59 можно, например, по-
казать, что волновой потенциал при любом расположении источников
в пространстве не изменится внутри замкнутой поверхности 5, если
источники, лежащие вне этой поверхности, заменить простым слоем
источников с плотностью
(S3)
(л — внутренняя нормаль) и двойным слоем с плотностью
•Z (В, 7], С, t) = -L (р (В, 7], С t). (94)
Это следует из того, что функция <р, имеющая непрерывные частные
производные второго порядка и удовлетворяющая внутри поверх-
ности S волновому уравнению, в каждой точке Р внутри поверхностиS
имеет значение:
(95)
где г — расстояние от точки £, 7], ?, описывающей поверхность S, до
£ точки Р.
ФОРМУЛА ГРИНА. ПОТЕНЦИАЛ. КРАЕВЫЕ ЗАДАЧИ
Уравнение (95), которое является аналогом формулы Грина (70),
получается из (69) при
V=tp I х, у, z, t-—
где г—расстояние от постоянной точки Р, лежащей внутри 5. Действи-
тельно, легко показать, что в силу (93) и (94) для всякой точки S, гр
лежащей на поверхности S, имеет место равенство:
1 ( й7~ 1 йУ^ с’ *-~т) &
4тг Ъп г in I г ' 8л J г
1 1 /е р ? Г \ ЙГ
+ 2^
и что для всякой точки у, х, z, лежащей внутри Р,
A TZ А 2 ( ЙГ . ЙГ , йг\ 1 1
Д V = Д Т - + - н- — j + Д г.
^Аргументы производных от и, встречающихся в последней формуле,
г \
суть х, у, z, t — основании волнового уравнения имеем
. 1
Д<р = «2 далее> ПРИ V=logr мы в силу (18) получаем:
fl — (s, J], С, t---) dS=
J J г ‘Ч 1 a J im
Ж й log г Й1о§г <Jlogr\
^xt Ъх Ъу йг )dx 1
! 1 ССС /Slogr>r . Slog г йг . Slog Г йг\ , ССГ л <
+«Ш +^г »г) д logrA.
©тсюда и получается формула (95).
Введя обозначение
й!
А р 1 I г 1 Й<Р йл
0(2, Ч>?>0=------> +Т-;----------(98)
; йл т йл ar Ъп
(аргументы функции ср и ее производных суть £, 4, С, 0> формулу (95)
можно переписать в следующем виде:
(97)
НЕОДНОРОДНОЕ ВОЛНОВОЕ УРАВНЕНИЕ
51
йч>
входит также и производная — , но можно доказать,
й<с
и вполне определяются заданием начальных значе-
ЭТо равенство выражает принадлежащую Кирхгофу1 аналитическую
формулировку принципа Гюйгенса (Huygens), играющего основную роль
в оптике. Этот принцип состоит в следующем: если известны значе-
ния nJ в определенный момент времени на некоторой замкнутой
поверхности S’, то можно вычислить значения, которые имеет функция щ
в любой момент времени в любой точке внутри поверхности S. Хотя
В формулу (97)
что как так
й<р
ний ? и
Рассмотрим
служит сфера с радиусом г и с центром в точке Р. В этом случае
й
== — —, а потому
йл й/"
, л_ 1 । У । 1 __ 1 й(го) । 1 й<д
’ ’ г йг ' г2 'аг й/ г2 йг 'аг й/
тот частный случай, когда поверхностью интеграции
причем при диференцировании по г и по t надо рассматривать как
функцию от В, Т), С и t и в полученной таким образом производной t
заменить через t---Наконец, если положить г—at, то получится.
причем начальные значения подинтегральной функции надо брать на
сфере, описанной около точки/3 радиусом г —at-, это выражение совпадает
с решением Пуассона. Формулу (97) называют формулой Кирхгофа.
§ 63 Неоднородное волновое уравнение. Найдем теперь диференци
альное уравнение, аналогичное уравнению Пуассона, которому удовле
творяет волновой потенциал (интеграция распространяется на заданную
область):
1 G. Kirchhoff, Zur Theorie der Lichtstrahlen, Sitzber. d. k. Akad. d. Wis-
sensch. zu Berlin, стр. 641, 1882; Wied. Ann., t. 18, стр. 663, 1883; Ges. Abb
Nachtrag, стр. 22, 1891.
4*
ФОРМУЛА ГРИНА. ПОТЕНЦИАЛ. КРАЕВЫЕ ЗАДАЧИ
52
В § 62 было показано, что этот интеграл в любой точке, лежащей вне
области расположения источников, удовлетворяет уравнению
о<р=Дф-^^=о. (72)
Если же точка Р находится внутри области интегрирования, то под.
интегральная функция обращается в этой точке в бесконечность, а ин-
теграл (99) становится несобственным. В этом случае опишем около Р,
как около центра, небольшую сферу 2 и обозначим потенциал источ-
ников, лежащих внутри этой сферы, через ср'. Потенциал источников,
находящихся в остальной части области интегрирования, удовлетворяет
уравнению (72), а потому нам остается найти только диференциальное
уравнение для функции ср'.
Представим ср' в следующем виде:
причем оба интеграла распространяются на объем сферы 2. Если
р (Е, jj, С, t) имеет непрерывную производную по t, то подинтегральное
выражение в первом интеграле остается конечным при г—>0; также
конечными остаются при соответствующих предположениях оператор
Лапласа и производные по времени от первого интеграла. Таким обра-
зом величина оператора Q для первого интеграла стремится к нулю
вместе с радиусом сферы 2. Второй интеграл представляет собою обыч-
ный потенциал, для которого оператор Лапласа равен — 4пр (х, у, z, /),
Шдгр Лт
обращается в нуль вместе
с радиусом сферы 2. Итак, в результате указанного предельного пере-
хода мы получим:
□ ср= Д ср —= —4ттр(х, у, z, t).
(101)
Диференциальное уравнение (101) имеет большое значение в теории
электромагнетизма, так как оно определяет распространение скалярного
и векторного потенциалов (т. I, § 17). Исследованию этого уравне-
ния посвящены работы Л. Лоренца, Рэлея, X. А. Лоренца, Бельтрами
(Beltrami) и Пуанкаре. Имея в виду значение этого уравнения, мы да-
дим другой вывод последней теоремы, основанный на теореме Бельтрами.
§ 64. Теорема Бельтрами. Рассмотрим интеграл
U{x, у, z)
ч, С, г) (к,
(102)
где
^=(х-Е)Я-(х-ч)2+(^-02; ....
0Л
теорема бельтрами
53
распространенный на некоторый объем. Предположим, что область ин-
тегрирования удовлетворяет условиям, указанным в § 50, и что функ-
ция f в этой области при г/>0 имеет непрерывные частные производ-
ные второго порядка, а точка х, у, z лежит внутри этой области.
Пусть, кроме того, существует предел
limr2/r(E, *1» г)-
>->0
Будем обозначать частные производные от f индексами: /, ...,
j ..........При этом, например, полная производная от f по Е за-
пишется так:
=4 (Е, ч, С, Г) (Е, 7], С, Г) ж (103)
В таком случае
Применим теорему о дивергенции:
/cos (пх) dS,
(105)
причем второй интеграл взят по поверхности 5, ограничивающей дан-
ную область. Продиференцируем это выражение вторично:
cos (пх) dS—
,, J
cos (rx) dr — I l fr cos (rx) cos (nx) dS; J
(106)
при этом предполагаем, что вектор г направлен от точки х, у, z
к точке Е, 7], С Найдем производную в направлении г от /ДЕ, tj, £, г).
Ъг
В силу (103) и так как =cos(rx),
ОЧ
C0S Л-frr COS (гу),
V^^+ArCOSO'-)- (107>
о<.
и следовательно,
й/ й/_ , . . й/ . . й/г )
d. = cos (rx) —r cos (ry) 4- —r cos (rz) =
йг йг; йт] й; j, (108^
=/rt cos (rx) cos (ry) +/Л cos (rz) -\-frr, J
54
ФОРМУЛА ГРИНА. ПОТЕНЦИАЛ. КРАЕВЫЕ ЗАДАЧИ
Написав по
их и приняв
аналогии с (106) вторые производные по у и z, сложив
во внимание соотношение
cos (ух) cos (их) -f- cos (yy) cos (ny) -f- cos (rz) cos (nz) — cos (г/г), (109)
мы получим:
ffl(--S)-
dS.
(110)
После небольших преобразований последнюю формулу можно
писать так:
пере-
fr cos (г/г) dS.
(Ш)
Под знаком первого интеграла стоит вторая частная производная от rf.
Введя в подинтегральную функцию второго интеграла полярные коор-
динаты с полюсом в точке х, у, z (di — г1 2 dr dw), мы можем этот
последний переписать в следующем виде:
о
Так как г^1ы = — dScos(m), то
А JJ j (//)„ у + 4тт lira (г%). (113)
Эта формула представляет уравнение Пуассона, обобщенное Бельтрами
Если положить
/(Е, Ч, С, г) °,
то мы будем иметь:
(^=о, /.=-£, г%=-р.
Наложив на интеграл
соответствующие ограничения, мы снова придем к уравнению Пуассона:
Д V=— 4пр.
Пусть, далее,
р(э Ч>
/(Е, ч. С, г) = -^---------;
1 Е. Beltrami, Sull’espressione analitica del principio di Huygens, Atti ctei
Lincei, т. 1, стр. 99—108, 1892; Opere matematiche, t. 4, стр. 499—509, особенно
стр. 504. > > к
УРАВНЕНИЕ КОЛЕБАНИЙ
55
тогда
(//) = —
а2 Ы2 ’
Jr ait г
Таким образом функция
Щх, у, z, t) —
dx
удовлетворяет уравнению
asp dx 1 i2U
---------4пр = ——----------4лР-
д/2 г 1 az it2
(! 14)
(ИЗ)
Последнее равенство представляет собою не что иное, как неоднород-
ное волновое уравнение (101).
§ 65. Уравнение колебаний. Другой метод исследования неоднород-
ного волнового уравнения
□ <р -[- 4пР (х> У< z, t) — 0 (101)
основан на интегральной теореме Фурье (т. I, § 43). Мы можем при
существующих допущениях представить р как функцию от t следующим
образом:
со
Р(0 = ^ р (а) е'х da d\. (113)
— со
Предположим, что искомая функция <р также имеет вид:
со
<р(^) = А jj'?(«)e') K<-t~a'> dadk. (117)
—со
Предположим, далее, что функцию и; можно диференцировать дважды
по х, у, z и t, тогда
со
~ = — A Jj* <р (а) 12ел <,-к) da dk.
—со
Диференциальное уравнение (101) после подстановки в него этих вы-
ражений принимает вид:
со
(А А А ? (а) “1“ 4пР (а)| еа da dk—0. (118)
— со ;
Функции <р и р зависят, кроме t и а, еще от х, у, z. Уравнение (118)
удовлетворяется, если равенство
Д ср-|-k2w4тгр — 0 (119)
56
ФОРМУЛА ГРИНА. ПОТЕНЦИАЛ. КРАЕВЫЕ ЗАДАЧИ
выполняется тождественно относительно я. Уравнение (119) мы будем
называть неоднородным уравнением колебаний; оно получается из не-
однородного волнового уравнения, если в этом последнем положить
— tf cos It, р = р cos "kt,
где <р и р завися.' только от пространственных координат (ср.
с исследованием того же уравнения в одномерном пространстве в § 34
т. 1). При k = 0 уравнение (119) переходит в уравнение Пуассона.
Однородное уравнение вида (119), т. е. уравнение
A U-\-k4J=0, (120)
было особенно подробно изучено \ К его исследованиям мы и перейдем
сейчас.
Найдем сначала решение уравнения (120), зависящее только от г.
Если U зависит только от г, то (см. § 52, с)
Это линейное диференниальное уравнение можно переписать в следую-
щем виде:
агг 1
Откуда следует, что
Ur— Ae(kr-f- Be~ikr или A cos kr-j- В sin kr,
где А и В — постоянные. Таким образом мы получаем частные решения:
cos Ar sin/гг eikr . e~lkr
-----, --- — или , -.
г г-----------------------------г г
1 g~ikr
Аналогом — здесь служит функция ---------; она при г—>0 стремится
к бесконечности, как а при г—>-оо обращается в нуль.
С помощью этого частного решения можно построить интеграл
(7(х, у, z) = j j Р(^’ ^^e~‘kr dz, (122)
распространяющийся на некоторый объем. Эта функция во всех точках,
лежащих вне области интегрирования, удовлетворяет диференциальному
уравнению (120). Чтобы найти диференциальное уравнение, которому
удовлетворяет функция (122) для точек, лежащих внутри области инте-
грирования, применим доказанную в предыдущем параграфе теорему
1 См. F. Р о с k е 1 s, Ober die partielle Differentialgleichung A и -f- №u = 0
und deren Auftreten in der mathematischen Physik, Leipzig, Teubner, 1891.
уравнение КОЛЕБАНИЙ
57-
Бельтрами к функции
При этом
(rf)^ — — k2pe±ikr, r2fr — pe—ikr (Д; ikr — 1) —> — p,
и мы в результате получаем:
A U = ~ k2U — 4ттр,
т. е. интеграл (122) удовлетворяет неоднородному уравнению колеба-
ний (И9).
Пусть функция р зависит не только от координат Е, С, но еще
и от параметра а; заменим, кроме того, k через Тогда
а \ а )
функция
а
---dx (123)
Шр («, и, Ц а)е
- ——г
при любом значении а будет представлять решение уравнения (119).
Подставив это выражение <р(а) в формулу (117), мы получим:
ТОО Д. (/=£= — я)
<р (0 = jj da Л j J J p(S’a)re--------------dx. (1-24)
—oo
Так как [см. (116)]
оо
1 ГГ A(z±: — — я) / „
— И p(S, 1), ч, а)е а й'аЛ, —р —
-оо
то
Таким образом мы найденное уже выше решение неоднородного
волнового уравнения получили из решения (122) неоднородного уравне-
ния колебаний Т
Доказанные нами в § 62 теоремы относительно волнового уравне-
ния справедливы, конечно, и для уравнения колебаний; этот частный
случай особенно прост, так как в уравнение в этом случае не входит
время. Если функция U представляет собою решение уравнения (120),
то формула (95) преобразуется, например, следующим образом: пола-
гают в ней <р = Ue,u и делят обе части равенства на В результате
1 См. Rayleigh, т. II, стр. 104.
58
ФОРМУЛА ГРИНА. ПОТЕНЦИАЛ. КРАЕВЫЕ ЗАДАЧИ
получается:
1 ГГас/е-'*''
dS-\-±-
1 4п
£7—
Ъп
dS.
(126)
Этот же результат можно, конечно, получить и непосредственно, при-
g-ikr г 1 ~]
лагая теорему Грина к функциям Un и --------- (вместо —, ср. (69) I.
Можно в формуле (126) e~tkr заменить через созЛг; заменять e~lkr через
. , _ „ , sin&r п
sin kr не имеет смысла. Действительно, функция —-— при г—»и не
имеет особой точки, а потому левая часть формулы (126) обратилась бы
при такой замене в нуль и не дала бы значений функции U.
В двумерном пространстве, когда расположение масс обладает кру-
говой симметрией, однородное уравнение колебаний принимает следую-
щий вид:
15 + —? + ^ = 0. (127)
г дг
Это диференциальное уравнение Бесселя (см. § 101). Одно из его ре-
шений J0(kr), так называемая функция Бесселя первого рода, является
правильной при г=0, решение же (функция Бесселя второго рода)
Y0(kr) при г—>0 стремится к бесконечности, как log г. Аналогично ло-
гарифмическому потенциалу можно построить интеграл
и=
dS,
(128)
распространенный на плоскую область. При соответствующих ограниче
ниях относительно р удовлетворяется диференциальное уравнение
^+^+£2£7=-2np <129)
йх:2 1 йу2 1
(неоднородное уравнение колебаний в двумерном пространстве).
sin kr cos kr
Функции Jo (kr) и Уо (kr) играют в данном случае роль —~ и -—,
Формуле (126) при этом соответствует следующая:
<1зот
интегрирование в данном случае производится по границе заданной
области.
Заметим, наконец, что проведенный нами в этом параграфе метод
исследования волнового уравнения в трехмерном пространстве не рас-
пространяется на случай двумерного пространства (см. т. I, § 49), так
1 , /, г \
как там не существует аналога частного решения —/ 11 — I. Про-
изведение -найденной нами только что функции Y0(kr) на е1?1 нельзя
ФУНКЦИЯ ГРИНА
-59
представить как функцию только от г—at (а — const), между тем как
ее аналог в трехмерном пространстве этим свойством, характеризующим
g—lkr Q-ik{r-at)
распространяющиеся волны, обладает; а именно: eipt—~~---7-----’
§ 66. Функция Грина. Мы возвращаемся опять к уравнению Лапласа
и ставим своей задачей обобщить на случай трехмерного пространства
функцию Грина, определенную в § 3-5, т. I для одного измерения,
В этом последнем случае функция Грина была определена, как оешение
d2y л
диференциального уравнения -^—^=0, обращающееся в нуль на кон-
цах некоторого вполне определенного интервала, первая производная
которого в заданной внутри этого интервала точке Е делает скачок.
По аналогии с этим для некоторой (основной) области трехмерного
пространства, ограниченной поверхностью 6’, мы определяем функцию
Грина G относительно точки Q (Е, rt, Q (источника) следующими
условиями:
а) функция Грина G повсюду, исключая точку Q, удовлетворяет
уравнению Лапласа Д6 = 0;
Ь) на поверхности 5 она обращается в нуль;
с) в точке Q она стремится к бесконечности, как ——, т. е.
Дб = 0, Os = 0, G~—1—
(131)
где <o — правильная гармоническая по всей основной области
Аналогия со сказанным в § 35 бросается в глаза. Уравнению
соответствует Д G— 0; уравнению (163) §134—неоднородное уравне-
ние колебаний
функция.
Й = 0
dx2
At7+^=-/.
Зубцевидную функцию / в трехмерном пространстве можно определить
как функцию, значения которой повсюду, исключая небольшой окруж-
ности L с центром в точке Q, очень малы, и которая внутри окруж-
ности L обращается в бесконечность так, что j^/r?T=l (ср. § 54).
Формулам (176) и (177) § 35 соответствуют
(здесь интегрирование распространяется на сферу, описанную около Q
радиусом, равным е) и
Udz =
lim
e —>0
fdx=\.
Функция Грина G также обладает этими свойствами (k = 0). О такой
функции U мы говорим, что она имеет в точке Q источник (^мощностью,
60
ФОРМУЛА ГРИНА.
ПОТЕНЦИАЛ. КРАЕВЫЕ ЗАДАЧИ
равною единице. Это определение аналогично определению, данному I
формулой (175) в § 35. В этом смысле уравнения (31), (41) и т. п. '
определяют существование источников. Речь идет здесь, очевидно, об
обобщении понятия источника тепла или источника потока жидкости.
Определенную таким образом функцию Грина, однозначность кото-
рой следует из сказанного в § 60, мы будем обозначать через
G (х, у, z; G, 1], Q
или просто через GPq. Физически ее можно интерпретировать как ста-
ционарное распределение температуры в теле, ограниченном поверхно-
стью 5, в том случае, когда в точке Q находится тепловой источник,
мощность которого равна единице, а на поверхности 5 все время под-
держивается температура нуль. Функцию Грина можно представить и
„ 1
в виде потенциала, возбужденного электрическим зарядом, равным —
4тг
электрических единиц, в то время как поверхность S заземлена, т. е.
когда потенциал на ней поддерживается все время равным нулю. Функ-
ция <о в этом случае означает потенциал заряда, индуцированного точкой
Q на поверхности S, так называемый слой Грина.
Можно доказать, что, если переменить роли точек Р и Q, то
функция Грина в трехмерном пространстве, как н в одномерном, остается
неизменной: действительно, пусть G и G' являются двумя функциями
Грина, источники которых находятся в точках Q и Q', так что
g=gpo = t~---bw> g>~gpq,=t~—Ьи'’ О32)
Q 4ttppq v 4nrPQ.
причем со и со'— функции гармонические во всей основной области. При-
меним формулу Грина [§ 52 (20)] к функциям О и О' в области, по-
лученной из основной исключением точек Q и Q1, окружив эти точки
небольшими сферами. Таким образом границей области интегрирования
будут служить кроме поверхности 5 еще и две построенные нами
сферы. Так как функции G и G' в этой области суть гармонические
функции, то
Cf (G — О' dS= 0. (133)
JJ \ Эга Ъп)
Так как на поверхности 5 функции G и G1 обращаются в нуль, то
останутся только интегралы по сферам. Но так как функция G' внутри
сферы с центром в точке Q гармоническая, то на этой сфере
слагаемое входящее в состав функции G, постоянно на этой
сфере, функцию же со приближенно можно также считать постоянной
на этой сфере. Таким образом, когда радиус сферы, центром которой
служит точка Q, стремится к нулю, то первый член левой части фор-
ПРИМЕРЫ (полупространство и сфера)
61
мулы (133) также обращается в нуль. Так как jj —dS=l, то вто-
рой член этой формулы, после применения рассуждения, приведенного
в заключении к формуле (67), в пределе дает G'(Q) = Gqq<. С по-
мощью аналогичных рассуждений находим, что предел этого интеграла,
распространенного на поверхность сферы- с центром в точке Q', равен
Q (Q') = — Gq'q. Следовательно,
Gq'q. (134)
Если переместить источник тепла из точки Q в Q', то в точке Q после
этого образуется температура, которая раньше была в точке Q', при
этом, конечно, предполагается, что на поверхности S температура все
время равна нулю. (Теорема о взаимной переместимости источника
тепла и точки, на которую источник действует.)
Применим, наконец, формулу Грина (20) к функции Грина и функ-
ции G, удовлетворяющей уравнению Пуассона:
A Дх, у, z). (135)
При этом окружим источник функции G (который мы отныне будем
обозначать буквой Р) небольшою сферой. В таком случае
j (О А V- V А О) dx =- j j j GJ dx =
Так как Gs = 0, то отсюда, как и в (67), получается:
(137)
Особенно важное значение имеет тот случай, когда /=0. В этом
случае V является гармонической внутри 5 функцией,
чается следующая формула 1:
н для нее полу-
(138)
Эта формула сводит решение проблемы Дирихле к отысканию функции
Грина для любого положения источника Q. Мы видим, таким образом,
что первая краевая задача сводится к своему частному случаю — к вы-
числению функции Грина. Последняя задача равносильна определению
функции си, т. е. вычислению гармонической функции, краевые значе-
1
ния которой суть —4^7'
§ 67. Примеры (полупространство и сфера). Вычислим функцию Грина
для бесконечной области пространства, лежащей по одну сторону
i При этом предполагается, что кривизна поверхности
ком случае производная по нормали от функции Грина
также непрерывна.
S непрерывна. В та-
на этой поверхности
62
ФОРМУЛА ГРИНА. ПОТЕНЦИАЛ. КРАЕВЫЕ ЗАДАЧИ
от плоскости S' (полупространства). Обозначим через а расстояние
точки Р от плоскости S', и пусть' Р
лежащей по ту же
и Р относительно
соответственно от
1
есть отражение точки Р в этой
плоскости (черт. 77). Пусть, да-
лее, г и / будут расстояния какой-
либо точки,
сторону, что
плоскости S,
точек Р и Р. В таком случае -
4 i
в заданном полупространстве яв-
ляется правильной гармонической
функцией; на плоскости S она совпадает с —. Таким образом выражение
G=4L_1
4тг г г'
(139)
обладает всеми свойствами, характеризующими функцию Грина. Если
векторы г и г1 направлены соответственно от точек Р и р' к точке
своего пересечения, то на поверхности S имеем:
__ II cos (яг) . cos(w/)\ 1 coscp
йя )s 4тг \ г2 п г2 / 2тс г2 ’
где <р — угол между радиусом г и нормалью к плоскости, направленной
внутрь. Таким образом равенство
<«>
дает решение задачи Дирихле для той части полупространства, в кото-
рой лежит точка Р. Выражение (139) допускает простую интерпретацию.
Представим себе, что в точке Р находится положительный электриче-
ский заряд, равный единице, а в точ-
ке Р такой же отрицательный заряд; s'" \ w
в таком случае потенциал на плоско- / '
сти S равен нулю. Предположим те- / /rL >
перь, что плоскость S’ электропроводка I —р-----—i=,r—----
и соединена с землей. Если заряд Р \ Р *
удалить, то электричество, индуциро- \ /
ванное зарядом Р на плоскости S, бу-
так действовать на часть простран- .. „
ства, лежащую слева от S, как если бы
заряд Р оставался на своем месте. Заряд Р называют электрическим
отражением заряда Р. Название это основано на аналогии с зритель-
ным отражением, при котором зеркало S действует точно так же, как
если бы в точке Р был помещен такой же объект, как и в Р.
Этот же метод исследования без труда переносится и на сферу..
Пусть Р радиус сферы, внутри которой на расстоянии а от центра
находится источник Р, и пусть 0 <я<7? (черт. 78). Соединим центр О
ПРИМЕРЫ (полупространство и сфера)
63
с точкой Р лучом ОР и на этом луче выберем точку Р, отстоящую
от точки О на расстоянии Ь, где b удовлетворяет уравнению ^b~R2.
Мы говорим, что каждая из этих точек получена из другой точки путем
инверсии относительно данной сферы. Если 714 какая-либо точка на по-
верхности сферы, то треугольники ОМР и ОМР подобны, так как
в точке О у них общий угол, а прилежащие стороны пропорциональны:
Таким образом, если через г и г' мы вообще обозначаем
расстояния какой-либо точки от Р и Р’, то для точек, лежащих на по-
верхности сферы, мы будем иметь:
d__^,
г а’ г ad
Так как внутри сферы — представляет гармоническую функцию, то
функцией Грина в данном случае будет выражение:
1 _ R _1
г а г'
(141}
G==T~
4тг
(142)
Ее производная по нормали равна:
йо_ _1/_2_йг./?_1_йН\
й/z 4тг \ г2 дп а г'2Ъп)
cos (nr) Р cos (rn')
г2 a d2
(143)
причем векторы гиг' направлены соответственно в точки Р и Р
[в противоположность формуле (139)]. Из треугольников ОМР и
ОМР' мы находим:
а2 = 7?2 г2 — 2/?r cos (nr),
b2 = P2-\-r'2— 2pd cos (nd),
(144)
так что
ЙО
й/Z
а2 — (Р2 г2) Р Ь2 — (^2-ф
2RP a 2Rd3
4п |
Пользуясь формулой (141) и равенством ab = R2,
можно так упростить:
(145)
последнее выражение
Следовательно,
К
ЙО __R2 — a2
Ъп MtRP
R2 — г2
4тгА?
(146
Введем полярные координаты
направлением радиуса-вектора
этом «/5 = /?2 sin О dbd'f, и
и 2-
и обозначим через
переменной точки
у угол между ОР и
интегрирования. При
о о
т//,, л I (/?2 —a2) sinGr/Orfo
V (Р, 0, <р)---------------------р
(Р2 G2 — 2Ра cos у)2
(147),
64 ФОРМУЛА ГРИНА. ПОТЕНЦИАЛ. КРАЕВЫЕ ЗАДАЧИ
Мы получили так называемый интеграл Пуассона. Можно непосредственно
доказать, что для любой заданной на границе непрерывной функции
V(R О ф) этот интеграл при «</? представляет собою гармоническую
функцию, а при «—* R обращается в V’.
Логарифмическому потенциалу соответствует интеграл Пуассона
.следующего вида:
1 Г /?2— с2
VP = о" 1 V-----------------оо-----Ж 048)
2тг J R^-j-a2-—2/?rcosv ’
о
§ 68. Вынужденные колебания. Интегральные уравнения, а) Рассмо-
трим снова уравнение Пуассона (135). Пусть функция V на погранич-
ной поверхности 5 обращается в нуль, а /—любая кусочно-непрерыв-
ная функция. В таком случае из формулы (137) следует, что
Vp== (149)
В этой формуле V есть функция, представленная при помощи источ-
ников [см. т. I, § 35 (189)]. Обратно, определенная таким образом
функция должна в любой точке поверхности S обращаться в нуль, так
как этим свойством обладает функция GPq. Функция GPq представляет
температуру, возбужденную источником с мощностью, равною единице,
а потому этот интеграл можно интерпретировать как температуру, вы-
званную источниками, плотность распределения которых равна /.
Обобщением уравнения Пуассона служит неоднородное волновое
уравнение
□ <р-|-4тгр(х, у, z, t) = Д ср — ^-^-j-4irp = 0. (150)
Его можно рассматривать, как диференциальное уравнение вынужденных
колебаний, соответствующих волновому уравнению. Будем его сначала
изучать при краевом условии и = 0.
Положим, как мы это сделали в § 65,
ф = U cos pt, 4пр ==/cos pt,
Tjye. U и f зависят только от пространственных координат, и кроме
того, U на пограничной поверхности обращается в нуль. В таком
Р
случае, полагая ——а, имеем:
Д U^k4J=—f. (151)
Мы получили в трехмерном пространстве уравнение, аналогичное (163)
§ 34. Это уравнение, разобранное нами уже в § 65, можно рассма-
тривать так же, как обобщение (135).
Уравнение (151) можно свести к интегральному уравнению, анало-
гично тому, как мы это сделали в § 36 т. I с уравнением (163).
« См. R i е m а п n-W е b е г, т. I, стр. 575.
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
65
Из уравнения (151) следует:
GU dt~—
U
(152)
причем из основной области исключена небольшая сфера радиуса е,
окружающая источник Р. Из рассуждений, аналогичных проведенным
нами при выводе формул (69), (133) и (137), мы получаем:
Gp -f- k? UqGPq diQ — J/q^pq •
(153)
Интегралы здесь надо брать по всей основной области. Полагая Fp = Д У fcfipQ — X, (154)
мы получаем: X Uq@pq — Fp- (155)
Таким образом мы действительно пришли к линейному интегральному
уравнению для (7, обладающему симметрическим ядром Gpq [см. т. I,
§ 36 (202)]. Функция, определяемая равенством (154), представлена
при помощи источников.
Если F—0, то мы приходим к однородному интегральному уравнению
(156)
которое имеет решения, не обращающиеся тождественно в нуль, только
при некоторых исключительных значениях X — при так называемых фун-
даментальных числах. Эти решения называются фундаментальными
функциями. Фундаментальные функции зависят только от заданной обла-
сти (и от краевых условий) и определяют колебания, которые возможны
в данной области при заданном краевом условии U=Q.
Фундаментальные функции ип, соответствующие фундаментальным
числам Хв, удовлетворяют диференциальному уравнению [в уравнении
(151) надо соответственно положить /= 0]:
A«„+Vn=° <157)
и исчезают на границе области; их можно нормировать так, чтобы
t?n dx — 1.
(153)
Применим формулу Грина (20) к двум фундаментальным функциям и и нт:
j J] К А ип — «п А ч1п) =Д ( и« ds ^ °’
' 5 Вебстео. Л иЛе погашал ьные гпавпения.
G6
ФОРМУЛА ГРИНА. ПОТЕНЦИАЛ.
КРАЕВЫЕ ЗАДАЧИ
ентальные функции на поверхности S обращаются в нуль,
так как стороны, они удовлетворяют уравнениям:
Так как, с ДРУ1
А«Я4АВЯ=°> А«,д + >л=о,
ТО
да
(«,« А «п — А ит) dt=(кт — у
да
ЕАЙ=°>
(159)
т. е.
ипит^=°
(160)
и, следовательно, функции ип и ит ортогональны, если только
Это свойство фундаментальных функций можно также доказать, исходя
из интегрального уравнения (см. т. I, § 35). Фундаментальные числа 1
как и в случае одномерного пространства, действительны. Всякую
функцию U, имеющую непрерывные вторые производные и обращаю-
щуюся в нуль на поверхности S', можно, как это доказывается в теории
интегральных уравнений\ разложить в равномерно сходящийся ряд
по фундаментальным функциям:
оо
(161)
п=1
Коэфициенты этого ряда получаются, как и в § 38, т. I (228), умноже-
нием на ип и интегрированием:
с-=даи°“А-
(162)
В частности, если в качестве функции U взять ядро Ор(?, то в силу (156)
(163)
«„(Q)
так что еп =——• Мы приходим, таким образом, к билинейному ряду
Q Un(P)Un(Q)
PQ К
(164)
п=1
Справедливость этой формулы подлежит еще доказательству, так как
функция G при P—Q не удовлетворяет условию непрерывности, ко-
торому мы подчинили функцию (J.
При соответствующих условиях сходимости этот ряд, как и в § 36
и 38, т. I, дает нам решение (151) в явном виде. Мы хотим здесь на-
метить ход этого доказательства.
* См. D. Hilbert, Grundziige einer allgemeinen Theorie der Integral-
gleichungen, стр. 63—64, Leipzig, Teubner, 1912.
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
67
Разложим заданную функцию / и неизвестную функцию U в ряд
фундаментальных функций:
сю оо ССС С С г*
и=ЕсЛ> ап=j065)
Подставив эти выражения в уравнение (151), мы получим;
сю сю
СП (А «п + Ч) + Е апип = °>
л=1 п—1
(166)
или на основании формулы (157)
сю
Еко-—и+««} «„=о-
К = 1
Следовательно, сп
п
и мы получаем:
(167)
[ср. т. I, § 38 (222)]. Далее, точно так же, как и в гл. III, доказы-
вается, что этот ряд удовлетворяет интегральному уравнению (155) (ре-
шение Э. Шмидта). Действительно, из определения функции F и фор-
мулы (156) следует, что
,,ю’
п=1 п=1
таким образом в силу формулы (167)
что и доказывает справедливость последнего утверждения. Из формулы
(168) и (169) получается решение Э. Шмидта:
00 СТР
п~\
(170)
Прежде чем перейти к другим краевым условиям, заметим, что про-
стая физическая интерпретация краевого условия U—0 или ип — 0,
как колебания воздуха, невозможна. Действитель-но, если U представ-
5*
68
ФОРМУЛА ГРИНА. ПОТЕНЦИАЛ. КРАЕВЫЕ ЗАДАЧИ
ляет потенциал скорости, то на границе обращается в нуль нс [у
а —. Иные соотношения имеют место в одномерном пространстве.
Там сгущение s = — (и — смещение) удовлетворяет волновому урав-
нению, причем сгущение обращается в нуль у открытого конца трубы.
Аналогичное краевое условие для поверхности, ограничивающей трехмер-
ное пространство, непосредственно неосуществимо; оно осуществляется
лишь у краев двумерной пластинки, в случае узкого пространства между
двумя параллельными, близко друг к другу лежащими пластинками
когда колебания параллельны пластинкам, а пространство у краев пла-
стинки остается открытым.
Ь) В случае краевого условия — =0 получить решения интересую-
оП
щих нас уравнений с помощью определенной выше функции Грина
невозможно (ср. т. I, § 39), так как условия [обозначения те же, что
и в формуле (131)]
ДО=
MJ
~дП
= 0, G = —1--------Н<0,
.$ 4nrPQ
которым должна была бы в этом случае удовлетворять функция Грина,
содержат противоречия. Действительно, так как
то
3G
что противоречит краевому условию — = 0. (Температура, возбуждае-
дП
мая тепловым источником при отсутствии теплового потока, не остается
стационарной, а монотонно возрастает.) Поэтому функцию Грина G
в этом случае определяют следующими равенствами:
ДО = «,
G = ---------|-ш,
(171)
где to — функция, имеющая непрерывные вторые производные, а — по-
стоянная, которая определяется следующим образом [ср. т. I, § 39 (236)
и далее]. Интегрируют Д G по основной области, из которой исключают
источник, окружив его небольшой сферой 2. В результате получается:
где ~ означает объем. Но интеграл, взятый по поверхности 2, равен
единице, между тем как тот же интеграл по поверхности S обращается
ВЫНУЖСЕННЫЕ КОЛЕБАНИЯ. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
69
в нуль. Следовательно, „плотность источников" а отрицательна и по
своей абсолютной величине равна значению объема т; она выбрана
так, чтобы все тепло, исходящее из источника с мощностью единица,
поглощалось, и чтобы никакое тепло не проходило сквозь границы
области. Введенная нами таким образом функция G содержит про-
извольную постоянную, определением которой мы сейчас и займемся.
Если решение U диференциального уравнения
Д(7-|-Ш=0
О ъи п
удовлетворяет на поверхности л краевому условию — =0,
то
или
О,
(172)
(173)
т. е. среднее значение функции U в заданной области обращается
в нуль. Каждая фундаментальная функция данной краевой задачи обла-
дает этим свойством.
Введенная нами функция Грина окажется симметричной, если соответ-
ствующим образом определить произвольную постоянную. Если ее вы-
брать так, чтобы функция G удовлетворяла уравнению (173), то полу-
чится [обозначения те же, что и в формуле (133)]:
с
и-----G
Ъп
(G' Д G— G Д G') dx —
(174)
Отсюда, как и раньше, получается свойство симметрии для функции G.
Пусть функция U служит решением диференциального уравнения
ДК+Ш=-/.
В таком случае, так как Д G = а, то
f JJ(G Д U— UД G)\GUdx = Udx (175)
(точка Р, конечно, окружена сферой и исключена из области интегри-
рования), а отсюда, как и раньше, получается;
-Я ("“-О 4 jjj
Последний член представляет собою среднее значение U функции U
на ссновной области. Так как ~ и на поверхности S’ обращаются
дП
70
ФОРМУЛА [ТИНА. ПОТЕНЦИАЛ. КРАЕВЫЕ ЗАДАЧИ
в нуль, то по умножении на — 1 мы получим уравнение, которое отли-
чается от (155) только тем, что в левой его части стоит Up—U
вместо Up. Но теперь вместо уравнения (173) мы имеем:
так что U обращается в нуль, если то же имеет место для соответству-
ющего среднего значения f функции /. При данном краевом условии
решение исследуемого диференциального уравнения может быть разло-
жено в ряд фундаментальных функций только в том случае, когда / = 0.
Если функция удовлетворяет условию (173), то она может быть пред-
ставлена при помощи источников. (Тот же метод в одномерном простран-
стве приводит к интегральному уравнению для открытой трубы.)
Рассмотрим, наконец, как и в § 40, т. I, функцию Грина Г, удовле-
творяющую диференциальному уравнению
ДГ4-АГ = 0, (176)
(А— заданная, отличная от нуля постоянная) при краевых условиях:
ЪГ
Г—0 и — =0. При втором условии Г представляет потенциал ско-
рости источника звука с мощностью, равной единице, сосредоточен-
ного в одной точке и окруженного твердой стеной. Симметричности
функции Г в акустике и оптике соответствует закон обратимости, со-
гласно которому, не нарушая общего эффекта, можно поменять местами
источник и точку, в которой наблюдается явление.
При краевом условии G — Г—О функция Г удовлетворяет условиям,
соответствующим условиям (131), при этом, конечно, роль уравнения
Лапласа играет уравнение (176). Применим [ср. т. I, § 40 (292)] фор-
мулу Грина к функциям
Так как
11 @PQ0 U — грд^
Ш(гас-°лг)л=1Я
Q Г dt,
(177)
То, окружив источники Qj и Q2 небольшими сферами и перейдя затем
к пределу при стремлении радиусов этих сфер к нулю, мы получим:
/’ол - Сол = И °рп грп dt. (178)
Эта формула соответствует (294) гл. III. Отсюда на основании фор-
мул (156), (164) и (170) мы находим для решающего ядра [ср. т. I,
§ 40 (300)] выражение:
MB®-
п=1 п
с) Наконец, в качестве примера разберем вынужденные колебания
прямоугольной мембраны, в частности колебания мембраны с закре-
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
71
пленными краями. Для нормальных смещений и на краях мембраны мы
имеем и = 0. Геометрически наглядное представление функции Грина G
рлсг нам форма мембраны, если ее оттянуть острым стержнем перпен-
дикулярно к ее плоскости так, чтобы вблизи места приложения стержня
мембрана приняла вид конуса. Геометрическое представление функции Г
дает нам эта мембрана, когда оттянутая точка колеблется.
Диференциальное уравнение колеблющейся мембраны мы уже нашли
в § 12, т. I; здесь мы дадим другой вывод того же уравнения, основан-
ный на свойствах функции Грина.
Пусть мембрана в состоянии покоя находится в плоскости х, у, нор-
мальное смещение равно и, а напряжение, т. е. сила, действующая по
перпендикулярному направлению единицы длины, равна т. На элемент
края ds части мембраны, ограниченной небольшою
, ~ди
перпендикулярно к плоскости х, у сила т ds —, где
4 дП
кривою, действует
п— внешняя нор-
маль этой кривой. В
венств (48), V—u]:
двумерном случае мы имеем
[см. первое из ра-
так что, если а означает поверхностную плотность, то
Отсюда мы получаем диференциальное уравнение колебаний мембраны:
Ъ2и
№
Чтобы найти стоячие волны, положим и — UeW^U—функция отх и _у);
если
Р и
— обозначить через к, то
с
йх2 йу2 ‘
k2U=0.
(180)
Найдем теперь решения, которые имеют вид U = X (х) Y (_у). Под-
ставив это выражение U в (180), мы придем к уравнению
1Ж । 1 Й2У
X йх2 ' У йу2 +
&2 = 0,
(181)
в котором каждый член должен представлять собою постоянную, т. е. по-
лучим два диференциальных уравнения:
d2X d2Y
±Г?_|_^х=0, ^4-r2y=0, q2-\-r2 = k2. (182)
72
ФОРМУЛА ГРИНА. ПОТЕНЦИАЛ. КРАЕВЫЕ ЗАДАЧИ
Решения этих уравнений имеют вид:
X=A cos qx -ф- В sin qx, Y — C cos ry D sin ry. (183)
На границе 77=0. Если мембрана ограничена прямыми х = 0, х~а
у = 0, у = Ъ, причем й^>0, 7>^>0, то
A = C=v), sin qa — sin rb — 0, q — —, r= — (ma n—целые числа).
Таким образом фундаментальные функции и фундаментальные числа
имеют следующие значения:
M™ = sin
ттгх . firry
-----sin—-
a b
(184)
\ =№ = Tts
mn mn
m2 n2 \
+ T2) ’
Ptnn ^mn
где man — любые, отличные от нуля целые числа. Общим решением
этого уравнения, служит
оо оо
г, VI VI - тг-х - ™гх , , , , „
L Sln_T~SIn-y + 085)
m=ln=l
Определение постоянных на основании начальных значений приво-
дит нас к разложению произвольной функции, обращающейся в нуль
на краях прямоугольника, в двойной ряд Фурье:
оо оо
г, ч VI VI » - ткх . тгх
Лх'у)==ЪЪ sln—sin — • (,86>
m=l n = l
Каждому значению частоты соответствует только конечное
2гг
число пар т, п, так как для всех этих пар выражение
т2 . п2 №
должно иметь одно и то же значение. Найдем теперь условия, при ко-
торых собственные 1 колебания являются гармоническими, т. е. их ча-
стоты находятся в рациональном отношении. При т—п=\ имеем:
Это самая низкая частота. При т — п получается:
1 To-есть вызванные фундаментальными функциями.
73
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
т. е. последовательность гармонических обертонов. Естественно является
вопрос, существуют ли еще и другие гармонические последовательности
Если отношение частот, соответствующих парам чисел т, п и т, п’._
рационально и равно h'.h1, то должно быть
1 1т2 п1\ 1 /т'2 । и'й\
h2 ^2 ] — #2 ’
ИЛИ, иначе,
h,2m2 — h2nt2 h2 rt2 -— Л'2 п2
а2 " '
Следовательно, либо — —рациональное число, либо обе части этого
равенства обращаются в нуль, и таким образом,
т2 h2 п2 т т!
tri!2 h!2 и’2’ п г! ’
Положим сначала, что — не рационально, так что имеет место
о2
последнее соотношение. Мы получаем в таком случае обобщение рассмот-
ренного нами частного случая. ’ Если т и п—числа взаимно простые,
и если положить
т =qm, rt — qn,
где q принимает значения натурального ряда 1, 2, 3, ..., то получится
последовательность гармонических обертонов. Если числа тип заме-
нить другой парой взаимно простых чисел, то получится другая после-
довательность гармонических обертонов, все члены которой отличаются
от членов предыдущей последовательности.
Иная картина получается, когда отношение а2 и Ь2 рационально.
Рассмснрим, например, квадратную мембрану, для которой а = Ь. В та-
ком случае уравнению
a2k2
те2
при заданном k могут удовлетворять различные значения тип. Мы по-
лучаем, таким образом, различные фундаментальные функции, соответ-
ствующие одному и тому же фундаментальному числу ’.
Узловым точкам в одномерном пространстве в данном случае соответ-
ствуют узловые линии. При колебании мембраны, определенном фунда-
ментальной функцией и образуются п — I узловых линий, параллель-
ных оси Ох, и т—1 узловых линий, параллельных оси Су, не считая
краев мембраны. Для колебаний, получающихся как линейная функция
собственных колебаний мембраны, закон, указывающий местоположение
и форму узловых линий, может, конечно, оказаться очень сложным.
1 См. указанною в § 65 книгу Pockcls’a, стр. 79.
74
ФОРМУЛА ГРИНА. ПОТЕНЦИАЛ. КРАЕВЫЕ ЗАДАЧИ
Рассмотрим, например, колебание, составленное из двух членов:
. тгх . 2тгу . , . 2 тех . тгу
и = Д12 sin — sin —— + Д21 sin-------sin — • (Ь87)
CL CL CL CL
Узловые точки удовлетворяют в этом случае уравнению
пх . пу ( тгу , „ тгх \
sin — sin — I А,„ cos-----Ь A,, cos — =0,
а а \ a а ]
и, таким образом, кроме краев мембраны узловой линией служит еще
и кривая
к 1TV ТТЛ"
Аг cos + Ai cos — = °- (188)
Вообще, если и и и'—два собственные колебания мембраны, принад-
лежащие одному и тому же фундаментальному числу, то колебание
Аи ф Д'и' (Л и А'— постоянные) принадлежит тому же фундаменталь-
ному числу, и узловые линии этого последнего проходят через точки
пересечения узловых линий колебаний и и и1.
Нормируя фундаментальные функции
^n = AMsin—sin-y-,
т. е. приравнивая единице интеграл их квадрата, мы получаем:
а ь
. , m-пх . ntty , . . я
sin2 --sin2 axdy=l, Л„„ =
а b
££
а b
(189)
о о
Билинейная формула в данном случае принимает вид:
„ тях /ту . ттс, , ятги
00 00 sin sin—-sin-—- sin ——i
VI VI a. b a b
(190)
тг2
а решающим ядром служит
оо оо
rrmx rmy . mt . m
sin----sin —— sin----sin ——
a b a b
(191)
m l я=1
и2
—\
Соответствующее решающее ядро в одномерном пространстве было
дано формулой (300) в § 40, т. I.
В трехмерном пространстве можно аналогичным образом исследо-
вать задачу о колебаниях воздуха в прямоугольном параллелепипеде.
§ 69. Бесконечные области. Когда основная область простирается
в бесконечность, то возникают новые трудности, которые были под
БЕ КОНЕЧНЫЕ ОВЛАСТИ
75
робно изучены Зоммерфельдом С Мы ограничимся здесь кратким изло-
жением его исследований.
а) В § 60 мы показали, что потенциальная функция, правильная
в некоторой конечной области и обращающаяся в нуль на границе этой
области, тождественно равна нулю. Иначе обстоит дело с функцией,
удовлетворяющей однородному колебательному уравнению,
Д и -f- k1 2tt — O.
)],ля этого уравнения существуют отдельные дискретные значения k2,
так называемые фундаментальные числа, при которых решения этого
уравнения не обращаются тождественно в нуль, хотя на границе области
эти решения обращаются в нуль. Разница между уравнением потенциала
и уравнением колебаний проявляется также и в других вопросах, на-
пример, в вопросе о вынужденных колебаниях. Решение уравнения Пуа-
ссона Ди = —/можно, согласно формуле (69), получить путем инте-
грирования из плотности источников, а именно:
Это решение определяется однозначно, если потребовать, чтобы и
в бесконечности надлежащим образом обращалось в нуль. В частности,
решение, при котором в конечной части пространства источники отсутст-
вуют, и которое в бесконечности обращается (надлежащим образом)
в нуль, сводится к нулю тождественно. Наоборот, решения неодно-
родного уравнения колебаний
A u-]rk2u = — f,
когда основная область простирается в бесконечность, не определяется
однозначно заданием источников и условием и = 0 в бесконечности.
А именно: для всякого отличного от нуля значения № существуют ре-
шения однородного уравнения, обращающиеся в бесконечности в нуль,
в конечной части плоскости не имеющие источников, которые все же
/ sin kr \ „
не равны тождественно нулю I например —-—I. Благодаря этому всегда
можно на решения неоднородного уравнения наложить решения соответ-
ствующего однородного уравнения, т. е. фундаментальные функции.
Следовательно, в такого рода бесконечных областях на решение однород-
ного или неоднородного колебательного уравнения надо в бесконечности
наложить еще особое ограничение для того, чтобы обеспечить однознач-
ность. При этих ограничениях уже не появятся никакие „фундаменталь-
ные функции".
Обратимся сначала к решению этого вопроса в одномерном про-
странстве, например к колебаниям струны. Мы видели, что для закреплен-
1 A. Sommerfeld, Die Greensche Funktion der Schwingungsgleichung,
Jahresbericht der deutschen Mathematiker-Vereinigung, t. 21 (1913), стр. 309—353,
см. особенно стр. 326. Надо заметить, что Зоммерфельд буквой G обозначает
вторую функцию Грина, которую мы обозначаем через Г.
76
ФОРМУЛА ГРИНА. ПОТЕНЦИАЛ. КРАЕВЫЕ ЗАДАЧИ
ной на концах струны длины / фундаментальные числа равны &п2 = | — j
(л— целое число). Эти фундаментальные числа неограниченно возра-
стают или, что то же, их обратные величины, которые в данном случае
прямо пропорциональны квадрату длины волны, стремятся к нулю:
спектр разрывен. Разность корней квадратных из двух последовательных
тг
фундаментальных значений постоянна и равна . Если I неограни-
ченно возрастает, то эта разность стремится к нулю, фундаментальные
числа лежат близко друг к другу, приближаясь к непрерывному спектру.
Благодаря этому при I—-> оо получается такая картина, как если бы
любое число А2 могло служить фундаментальным числом. (Действительно,
sin kx для любого значения k представляет стоячую волну.) Заметим,
что билинейная формула [т. I, § 37 (211)] для функции Грина К(х, £)
при этом предельном переходе перейдет в интеграл Фурье. С другой
стороны, при /—>оо функция Грина, согласно формуле (116) § 32, т. I,
стремится к
ГМ-1 t "р“
Is при х и,
а такого рода функция не может быть представлена интегралом Фурье,
так как она в бесконечном интервале не интегрируема.
Однако к вопросу о существовании для бесконечной основной области
фундаментальных функций и фундаментальных чисел можно подойти и
с другой точки зрения. Выше, в случае трехмерного пространства, мы
исследовали решения волнового уравнения и установили, что они рас-
пространяются в бесконечность в виде запаздывающих потенциалов; при
этом не возникают ни явления резонанса, ни периодические гармониче-
ские колебания. Это снова говорит за то, что невозможно выделить
некоторые определенные колебания для всего бесконечного пространства,
а потому бесцельно в этом случае искать какие-либо фундаментальные функ-
ции. Следующие небольшие рассуждения согласуют эти два предположения.
Мы нашли, что диференциальное уравнение
d2ti
dx2
-J- &и ~ О,
имеет решения
cos kx, sin kx или e lkx, etkx,
которые ограничены при всех значениях х: когда х стремится к беско-
нечности, они продолжают колебаться (осциллировать).
Умножив каждое из двух первых решений на cos nt и на sin nt, мы
получим следующие решения волнового уравнения:
cos nt cos kx, sin nt cos kx, cos nt sin kx, sin nt sin kx,
которые все представляют собою стоячие волны. Помножив последние
два решения на elnt, мы получим:
^i{nt-kx} gUnt+kx) *
БЕСКОНЕЧНЫЕ ОБЛАСТИ
77
Действительная часть этих функций представляет распространяющиеся
волны, которые либо уходят в бесконечность, либо приходят из бес-
конечности; надлежащим образом подобранная комбинация этих волн
дает опять стоячие волны. В трехмерном пространстве мы имеем со-
ответственно уравнение:
Ди-}- k2u = 0.
Его решения:
coskr stnkr e~ikr ethr
-----, или , -,
г г-------------------------г-г
найденные нами уже раньше, дают стоячие волны:
cos nt cos kr sin nt cos kr cos nt sin kr sin nt sin kr
из которых первые два имеют источники при г — 0; они вызывают вы-
нужденные колебания. Два других решения не имеют источников и пред-
ставляют свободные колебания. С помощью решений, представленных
в виде показательных функций, мы можем построить распространяю-
щиеся волны:
(«г ~ kr) gUnt+kr)
Действительная часть первого из этих решений представляет так щ
зываемые расходящиеся волны, а действительная часть второго — сходя-
я
щиеся волны. (Сферы с постоянной фазой г —+ —-1 -ф- const при t—>оо
/v
сходягся соответственно к -ф- оо или к —оо .) Надлежащим образом со-
ставленные комбинации этих волн снова дают стоячие волны. Но между
тем как приходящие из бесконечности и теряющиеся в источниках волны
математически так же возможны, как и расходящиеся волны, физически
такие (т. е. приходящие из бесконечности) волны неосуществимы и по-
этому фактически, когда область распространения колебаний прости-
рается в бесконечность, стоячих-волн и фундаментальных функций в
том же смысле, что и в конечной части пространства, не существует.
Зоммерфельд для бесконечных областей вводит добавочное „условие
излучения". Это условие для трехмерного пространства выражается так:
для двумерного:
и для одномерного:
(К этому добавляется еще
мерного пространства состоит
„условие конечности", которое для трех-
в том, что произведение ги должно быть
78
ФОРМУЛА ГРИНА. ПОТЕНЦИАЛ. КРАЕВЫЕ ЗАДАЧИ
ограничено.) Это условие в случае трехмерного пространства выпол-
няется для расходящихся волн. При этих условиях Зоммерфельд дал
теорию волн в бесконечном пространстве, которую по своей завершен-
ности можно сравнить с теорией волн в конечных областях. В частности,
он показал, что при выполнении „условия излучения“ существование
фундаментальных функций невозможно и что при этом решение как
однородного, так и неоднородного колебательного уравнения опреде-
ляется однозначно. Построение функции Грина в бесконечной области при
выполнении этих условий аналогично ее построению в конечной области.
Ь) Вернемся снова к одномерному пространству. Пусть основной
областью служит бесконечная прямая. Функцией Грина для диферен-
циального уравнения £\и-\-k2u = 0 при мы назовем решение,
которое в заданной точке х — £- обладает источником с мощностью,
равной единице, и удовлетворяет условию излучения.
Заметим, что функция
| Ae~ih^x~® при
Л ( В elk (*-5) при х £,
(Л и В — постоянные)
удовлетворяет как диференциальному уравнению, так и условию излу-
чения; так как в точке х — £ находится источник с мощностью, равной
единице, то
и следовательно,
Таким образом функция в данном случае имеет вид:
f e-ik(x-(.)
pix g)------ ) 2гЙ
4ik
при
при
(192)
Ее можно выразить одной формулой с помощью интеграла
1 Г
----Ф------------ Г Е’ = Я J <“>
Черт. 79. причем комплексная переменная инте-
грации z, пробегая действительную
ось от — оо до -|- оо , огибает точки — k и -ф- k, первую справа, а вто-
рую слева, описывая около них небольшие полуокружности, как это по-
казано на черт. 79. Докажем это. Пусть сначала х — £ Ээ 0. Будем при
этом интегрировать по границе области I (черт. 80). Положим
2 = г (cos 0 -j- i sin 9).
БЕСКОНЕЧНЫЕ ОБЛАСТИ
79
g таком случае абсолютная величина числителя равна e~rsinвели-
чина меньшая единицы, когда г—> оо, а О^б^тг. Следовательно,,
интеграл по большой полуокружности стремится ______
и нулю, когда радиус этой полуокружности не- т' х
ограниченно возрастает. Такие же соотношения / | \
имеют место в нижней области II при х — £ sS 0. /____. . , гх ।
Подинтегральное выражение в конечной части пло- Г О'*-”
скости имеет только два полюса z = kuz = — k, \ II
вычеты которых суть х. /
eik(x-F.) е- Ik(х-it
~~2k~ 11 2k Черт-80-
Эти полюсы находятся соответственно в областях II и I. Применяв
теорему о вычетах Коши к / области (см. приложение, § 1, е), мы после
указанного предельного перехода будем иметь:
el{x-V>z г
g2__fe2 = <194)
Аналогично
1 р et U-t) z
2тг Z2^k2dz==1-.
1 elk (x-i)
2k
(x sZ £)o
(195)
Эти равенства и доказывают справедливость сделанного нами утвер-
ждения. Формула (193) является аналогом билинейной формулы в форме
комплексного интеграла. При этом в силу бесконечности основной области
нам пришлось принять во внимание условие излучения.
По аналогии с задачей, разобранной нами в § 40, гл. III, рассмо-
трим функцию Грина для области, уходящей в бесконечность только
в одну сторону, т. е. в области от х===0 до х— оо , и потребуем
при этом, чтобы при х —0 эта функция обращалась в пуль. Мы полу-
чим эту функцию из (193), если отнимем от нее возмущение, вызы-
ваемое таким же источником, находящимся в точке х—— £, т. е.
1 Г />/u-5)Z ы (.v + ')z
Н(х, £)=Г(х, S) — Г (*, — £)—— I --------—---—----- dz,
ZTT I Z2 К4
(196
причем путь интегрирования остается прежним. Если показательные
функции заменить тригонометрическими, то члены, содержащие синусы,
вследствие симметрии кривой интегрирования обратятся в нуль, и мы
получим:
,,, 1 fcos (х — tyz— cos (х 4- £) z . 1 Esinzx sin zz ,
H(x,$=—\-----------------—-—!— dz = — \ —5-------— dz. П971
ZTTj Z2--k2 It j z2— k- 1 '
Мы получим полную аналогию формулы (300) § 40, т. I. Зоммер-
фельд, далее, вычисляет фундаментальные числа для области —
принимая во внимание условия излучения на концах х — -I- /. и пока-
зывает, что для больших значений I все эти числа являются комплекс
ными, как этого и можно было ожидать из предыдущего.
ГЛАВА ШЕСТАЯ
Интегрирование диференциальных уравнений в частных
производных по методу Римана-Вольтерра
§ 70. Задача Коши. Характеристики. В гл. III мы особенно подробно
•остановились на одном частном случае задачи Коши, а именно на ди»
ференциальном уравнении второго порядка с двумя независимыми пере-
менными:
Ъ2и й2и__
^'“йх2""
(волновом уравнении в одном измерении) при начальных условиях:
и — F(x)
М=°{х)
при /=0.
С другой стороны, в гл. V мы рассмотрели различного рода
«раевые задачи для диференциальных уравнений в частных производ-
ных; там было доказано (см. § 60), что для диференциального уравне-
ния Лапласа
Ук й2^
йх2 ' йу2
или
й2И й2И й2Л
ЙХ2 ' ЙУ2
йп
нельзя одновременно задать значения и и — на замкнутой кривой, служа-
щей границей области, так как искомая функция однозначно определяется
краевыми значениями и (задача Дирихле) или — (задача Неймана) ’.
6/Z
В этой главе мы постараемся найти причину этого основного раз-
личия между задачей Коши и задачей Дирихле-Неймана. Методически
мы будем при этом опираться на данное Риманом обобщение функции
Грина, которым в течение последних тридцати лет пользовались в своих
исследованиях Вольтерра (Volterra) и другие ученые и которое стало
важнейшим вспомогательным средством теории диференциальных уравне-
ний в частных производных. Эта формула может быть распространена
на любое число независимых переменных; все же мы ради простоты
ограничимся уравнениями с двумя независимыми переменными, т. е. за-
дачами в плоскости. Результаты, которые мы при этом получим, ле:ко
затем обобщить на любое число измерений.
J Во втором случае с точностью до постоянного слагаемого.
ЗАДАЧА КОШИ. ХАРАКТЕРИСТИКИ
81
Мы будем исходить из уравнения с двумя независимыми перемен-
ными, линейного относительно производных второго порядка,
. й2« . _ „ У и й2Ц I Ъи Ъи\
А —Л-2В —- -фС — = F х, у, и, — , — , (1)
йх2 йхйу 1 йу2 \ йх йу/
где А, В, С и F суть заданные аналитические функции,
три зависят только от х и у, а последняя от х, у, и,
смотрим, можно ли на какой-либо кривой произвольно
причем первые
йм йп „
— , —. По-
ЙХ iy
задать значе-
Йм „
ния и и —. Если рассматривать х, у, и как прямоугольные коорди-
<73
наты, то этот вопрос равносилен следующей геометрической задаче:
через заданную пространственную кривую провести такую интегральную
поверхность, касательная плоскость к которой в каждой точке кривой
имела бы заданное положение. Пусть будет
/(х, у)=:0
(2)
уравнение проекции этой кривой па плоскость ху, мы предполагаем,
что эта проекция является аналитической кривой. Если координаты то-
чек этой проекции представить как аналитические функции параметра t-.
x — x(t) и _y=y(f) (х'2+У2>0), то после подстановки этих вы-
ражений в уравнение (2) левая его часть тождественно обращается в нуль.
Направляющие косинусы нормали к кривой (2) пропорциональны
«И
ЙХ
и —, направляющие же косинусы касательной пропорциональны х' [t]
i>y
и у'(0- Установим положительное направление на кривой (2) и тем
самым определим вектор касательной: положим, далее, что параметриче-
ское представление кривой нами выбрано так, что при увеличении пара-
метра t точка перемещается по кривой в положительном направлении.
Наконец, выберем положительное направление нормали влево от кривой
так, чтобы вектор касательной занимал по отношению к вектору нор-
мали такое же положение, какое занимает положительное направление
оси Ох по отношению к положительному направлению оси Оу. [Если
уравнение (2) представляет замкнутую кривую, и если положительное
направление на этой кривой выбрано против движения часовой стрелки,
то нормаль при этом окажется направленной внутрь области, ограни-
ченной кривою (2).] В таком случае
COS (Ях)
(3)
Краевые значения можно записать также в виде функций
ti--F(t), ^- = G(t) (предполагается, что функции F и G
сП
от i:
также
Вебстер, Диференцналг.ные уравнения.
82
ИНТЕГРИРОВАНИЕ ДИФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
аналитические); таким образом на кривой
du Ъи , . Ъи , ...
= +V111 =-F
cos (пх) + -у cos (пу) — - -- 1 - -- f —
т йх ' йу 1/>24-у'2\ йх
==G(/); (4)
x' = x’(t) ку'—y'lt) сугъ в данном случае заданные функции от t,
ёи
и оба уравнения линейны относительно —
быть определены однозначно, так как детерминант
<'и
и —; последние могут
—у х'
(5)
не обращается в нуль. Таким образом мы можем вычислить на кривой
значения обеих частных производных от и. Эти значения равны:
йи ... йи
Дальнейшее диференцирование дает нам:
й2и dx й2и dy_________________________ г
йх2 dt ' ёх ёу dt ’
й2« dx й2и dy ,
йхйу dt' tsy^dt ’’
(6)
т. е. два линейных уравнения относительно
д2и ~Уи Уи
второго порядка -——, —К ним в
йх2 йх йу йу2
ния присоединим заданное диференциальное
л^и 1 2В 1
йх2 1 йхйу 1 Сйу2
трех частных производных
качестве третьего уравне-
уравнение
О)
В таком случае вторые частные производные определяются также одно-
значно, если только детерминант
dx
dt ’
О,
А,
dy
dt ’
dx
dt ’
2B,
dy
~dt
dxdy
dt dt
(7)
О
— с
r/y\2
dt)
не обращается в нуль. Продолжая эти вычисления дальше, мы найдем
все частные производные от и на кривой, при условии, конечно, что
выражение (7) не равно нулю. В силу этого функцию и можно разло-
ЗАДАЧА КОШИ. ХАРАКТЕРИСТИКИ
83
я<ить в ряд Тейлора. Внутри своего круга сходимости этот ряд пред-
ставляет аналитическую функцию, удовлетворяющую данному диферен-
циальному уравнению и данным условиям на кривой. Радиус сходимости
полученного нами, таким образом, ряда Тейлора отличен от нуля; тео-
рема эта может быть доказана с помощью метода мажорант Ч
Этот метод теряет, однако, силу, если вдоль заданной кривой выра-
жение (7) обращается в нуль, т, е. если
С dx2 — 2В dx dy -|- A dy2 — 0. (8)
Это условие можно рассматривать как обыкновенное диференциальное
уравнение первого порядка и второй степени, которое определяет на
плоскости ху два семейства кривых; эти кривые называются харак-
теристиками диференциального уравнения (1). Таким образом, если
кривая (2) является характеристикой, поставленная нами задача указан-
ным методом не может быть решена.
Разложим правую часть уравнения (8) на линейные множители.
Если А =7^=0, то
{A dy — (В —j— / В2 — AC) dx} {Ady—(B— V В2 —AC) dx} =0, (3)
если же Л = 0, то
dx(Cdx—2Bdy)~0. (S')
Если дискриминант этого уравнения В2—АС^>0, то множители в вы-
ражении (9) действительны, и уравнение (1) называется гиперболиче-
ским. Если В2 — АС<^0, то эти множители, а следовательно, и ха-
рактеристики являются мнимыми, и уравнение называется эллиптическим.
Если, наконец, В2 — ЛС=0, то характеристики сливаются, а уравнение
называется параболическим. Мы даем здесь ту же классификацию, что
и в § 25, с той только разницей, что в § 25 мы ограничились уравне-
ниями с постоянными коэфициентами. Эта классификация относится,
конечно, к определенным точкам плоскости ху, и при переходе от одной
точки к другой класс уравнения может меняться.
Однако, чтобы получить более ясное представление о тех свой-
ствах характеристик, которым они обязаны своими названиями, мы
подойдем к определению этих кривых с несколько иной точки зрения.
Пусть f(x, у)=0 является интегралом диференциального уравнения (8).
Это последнее в силу равенства
^dy = 0
дх ду
эквивалентно следующему уравнению:
(ie>
Мы получили уравнение в частные производных первого порядка, ха-
1 См. J. Horn, Partielle Differentialgteichungen, 2-е изд, Berlin. W. de Gruyter,
1929, а также для всей настоящей главы J. Hadamar d, Lectures on Cauchy's
problem in linear partial differential equations. New Haven, Yale Univ. Press, 1923.
I*
84
ИНТЕГРИРОВАНИЕ ДИФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
рактеристики которого, согласно определению характеристик, данному
в § 24 (45), определяются из уравнений
1 dx 1 dy dz dp dq
Лр-^-Bq^lL Iip-\-Cq '^ ==~~J(==~T (U>
IX и Y—частные производные функции (10) соответственно по х и по у]
dy
Легко показать, что для — из уравнения (11) получается то же выра-,
жение, что и из уравнений (8) или (9). Таким образом характеристики
уравнения второго порядка (1) суть не что иное, как проекции на плос-
кость ху характеристик Коши уравнения (10).
Понятие характеристик наводит нас на такую замену переменных,
при которой урав^ние (1) может быть приведено к нормальному виду
(ср. § 25). Введем вместо х,у новые независимые переменные Е и г]. Тогда
Ъи ЙИ йЕ . ЙИ ЙГ] ЙИ ЙИ йЕ ЙИ ЙГ]
ЙХ йЕ ЙХ ЙГ) ЙХ ’ йу йЕ йу ' ЙГ) йу
Й2И й2П /йЕ \2 | 2 Й2И йЕ Й1] , Й2И/ЙГ] \2 , ЙИ й2Е . ЙИ й2Г)
ЙХ2 йЕ2 \ЙХ / ‘ йЕ ЙГ] ЙХ ЙХ 1 ЙГ]2 \ЙХ / йЕ йх2 ЙГ] Йх2 ’
й2И__й2И /йЕ \2 2 дЕ ЙГ]
й? йЕ2 \йу/ йЕ йг] йу йу
- Й2Н/ЙГ] \2 , ЙИ й2Е . ЙИ й2Г]
' ЙГ]2 \ йу / "Г” йЕ йу2 ЙГ] йу2 ’
(12)
й2н ___й2ийЕ йг; , й2и
йх ду йЕ2 йх Й у ЙЕ ЙГ
Й2ИЙГ] ЙГ]
ЙГ]2ЙХ йу
ЙИ й2Е . йн й2Г|
йЕ йх йу ЙГ] Йх йу ’
Подставим эти выражения в уравнение (1); мы получим:
Й2И
йЕ2
й2и Г
йЕ ЙГ] |
Гйг]2 I
. йЕ йг]
йх йх
йЕ ЙГ]
йу йу
(13)
вгг “Ьс(
ЙХ йу \
йЕ ЙГ] ЙГ] йЕ
йх йу ' йх йу
ЙГ] ЙГ]
йх йу 1
Функция F в этой формуле зависит
ции и и ее частных производных по
этом, что
от Е и г;, а также
Е и г]. Мы предполагаем при
от
фукк-
д(Е, г])
й (х, у)
йЕ йЕ
йх ’ йу
ЙГ] ЙГ]
йх ’ йу
¥=0,
т. е. что преобразования, связывающие х, у и Е, г;, взаимно однозначна
(по крайней мере в достаточно малой области). Рассмотрим эти пре-
образования отдельно для каждого типа уравнений.
J
1
ЗАДАЧА КОШИ. ХАРАКТЕРИСТИКИ
85
Пусть для диференциального уравнения гиперболического типа урав-
нения характеристик суть:
<р(х, у) = const, ф (х, _у) = const.
Эти два семейства кривых действительны и отличны друг от друга,
далее, функции ш и ф удовлетворяют уравнению (10), так что, если по-
е , . , , . . а2м Ъ2и
дожить 6 = <р(х, у) и Г| = ф (х, у), то коэфициенты при 7g» и — обра-
щаются в нуль. Пусть, кроме того, коэфициенты А и С оба одновре-
менно не равны тождественно нулю [иначе данное уравнение имело бы
уже
При
с самого начала вид (14)], например, пусть Ау^О. Коэфициент
д2и
—в уравнении (13) можно переписать в следующем виде:
л И —-LI № 4_Ъ №. J_1 М
А I + 11 а> Цах ау/ + \ах + ау/ \а* ау)
где
_в-1-]/'в2—ас _ аср. а<р___аЕ.аЕ
a ix ’ ау ах ’ ау ’
\ —
в — |/в2 — ас аф аф а^ а^
а ах ау ах' ау ’
При этом Wj, и ф и функциональный детерминант от Е и т( по х и у,
равный (к2 — Xj) ф ф отличны от нуля. Таким образом коэфициент
а2и
приаЩ равеи а£ат, дс-в2
ау ау а •
Если \равнение
вид:
(13) разделить на этот коэфициент,
I г- ай \
° >1> й> ~ •
а; ат, \ as /
то
оно примет
(14)
Это нормальный вид гиперболического уравнения с двумя независимыми
переменными.
Для диференциальных уравнений эллиптического типа мы полагаем:
- ~г Z71 = ? (*> У}^ £ — Щ ~ Ф (х> У)’
Рассмотренный нами прежде функциональный детерминант будет
в этом случае равен ().2 — \)с?^Ф_р7^0 (обозначения остаются преж-
ние). Так как функция и удовлетворяет уравнению (10), то
86
ИНТЕГРИРОВАНИЕ ДИФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Приравнивая в
отдельно нулю,
эфициенты при
этом уравнении действительную и мнимую части
й2И
мы найдем, что коэфициент при -=— равен нулю, а ко-
йч dJ]
й£2 И
й2И
jnf2 суть
, АС—В\/.г,
Таким образом
уравнение (13) сводится в этом случае к следующему:
й2гг . й2И‘______
йч2 "^ЙТ)2
„ й« йг/ \
Н, Гр «, rj-, — .
ЙЧ ЙТ| /
(15)
Это нормальный вид уравнений эллиптического типа.
Если, наконец, данное уравнение параболического типа, то оба се-
мейства кривых <р(х, у) = const и ф(х, у) = const совпадают. В этом
случае мы полагаем (ф3,г/-0)
£ — X, Z] = ф (х, у).
д2и
Коэфициент при опять обращается в нуль, а коэфициент при
о Й2И .ЙГ; , п ЙТ1 „„ „
2-z— оавен А— + В — ; однако в силу условия В2 — АС=О послед-
й£йТ) ЙХ ду
ний коэфициент, так же как и выражение (10), обращается в нуль. Так
, й2« .
как коэфициент при , т. е. А, отличен от нуля, то мы приходим
йЕг
к следующему нормальному виду уравнения параболического типа:
й2и (
й»=° Е’ ’
и,
ди йгг\
й£ ’ Й7] / ‘
(16)
В том случае, когда коэфициенты А, В, С постоянны, эта замена пере-
менных приводит нас к эйлеровым преобразованиям, которыми мы
уже пользовались в § 25.
Примером уравнений эллиптического типа является разобранное уже
нами уравнение Лапласа, примером уравнений гиперболического типа —
волновое уравнение и, наконец, примером уравнения параболического
типа — уравнение теплопроводности Фурье.
§ 71. Линейные уравнения. Формула Грина. Общее линейное дифе-
ренциальное уравнение второго порядка имеет вид:
ЙХ2 йхйу йу2 Йх ду
где коэфициенты А, В, С, D, Е, F зависят только от х и у. Помно-
жим линейный оператор £(и) на функцию г» и проинтегрируем полу-
ченное произведение по области, ограниченной замкнутою кривою С.
Относительно кривой С мы делаем в данном случае те же допущения,
что и при доказательстве теоремы Гаусса на плоскости [см. § 55 (77)].
ЛИНЕЙНЫЕ УРАВНЕНИЯ. ФОРМУЛА ГРИНА
87
Кроме того, предполагается, что коэфициенты в выражении (17) имеют
непрерывные производные второго порядка.
Интеграл мы преобразуем по теореме Гаусса, на которую мы только
что сослались; пусть п означает направление внутренней нормали,
ds— элемент дуги граничной кривой С. Интегрируя первый член ука-
занного произведения по х, мы получим:
Й. й2и Г . йи . . , (Т йи й(Лг»)
Av dx2 dX аУ ~ йх C°S ds — j I йх — х dX
и аналогичным образом
ГГйи й(Аг») . С й(Лг') / \ т С С .
JJ ^^Tdxdy==-J и— dxdy.
Таким образом окончательно
я й2и , ,
Av ; — dx dy =
йх2
йг» йи \ . йА
и ------v — |—1— иг» -
йх йх / 1 йх
dx dy.
Подобным же образом преобразуем третий член
_ й2и
Cv —- dx dy =
dy2
-J- иг» — J cos (ny) ds -|-
(T ^2(Сг») . .
J J u~^dxdy'
(18)
(19)
Второй член мы разбиваем на две части. Интегрируя сначала по х,
мы найдем:
Йо й2и Гь йи . ГГйий(Вг»)
Bv -—- dxdy= — \ Bv — cos (пх) ds — И---1-— dx dy;
йхйу J dy J J ду йх x’
затем интегрируем по у:
CCdud(Bv) f d(Bv) f .. ff Й2(ВИ)Л
1 I r-<—- dxdy— — i и —-—- cos (и v) ds — И и — dx dy
йх x J йх л x' J J йхйу x
и, таким образом, получаем:
й2и (То/ / Л I t .1
Bvdxdydxdy=\ ^с°5(иу)—w^cos(nx) J+и»- cos(пу) I
.(Т й2(£к») ,
(20)
88
ИНТЕГРИРОВАНИЕ ДИФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
С другой стороны, ввиду симметричности второго члена относительно х
и у, мы можем их поменять местами, т. е.
п д2и . г
Bv----dx dy—
йхду
> <*и . .
и — cos {пх)—V—cos {пу)
. ъв
-4- uv— cos
1 йу
{пх) Jefs-]-
4!
a2 (Bv)
и —-----dx dy.
дхду
Члены с производными первого порядка мы интегрируем только по
©дному разу:
D wv ebs {пх) ds —
*(Dv)
и-----dxdy,
дх
f Г „ йи f Cf5 (£М л j
IJ £ г» — dxdy = — I Ewv cos {ny) ds — \ J a ——— dx dy.
(22)
Собрав вместе найденные нами результаты интегрирования отдель-
ных членов, мы придем к следующему уравнению:
{vL {и) — аЛЦя)} dxdy=^{uP(v) — vP{u) -f- uv R} ds, (23)
где
M{v)==-^+2-^ + ^-----ax----^r+Fy==
ах2+ йха_у + сау2+2йх\ах+ау 2™ +
йу\йх 1 йу 2 J ' \ ЙХ2 ' Ъхду ' йу2 <SX ду 1 )'
(24)
Оператор M называется сопряженным по отношению к оператору L.
Через Р мы обозначили линейный оператор:
. й® . „5«\ . . . / „ а« . „а«\ t г
^+%)“s(“,+(Bs+S5;)c°s('v') w
и через R так называемую присоединенную функцию:
п /ая . дв \ , ч . ив . ас \
R={>i+°Г“ <”•” + ( S+- Е) “s^>-
Заметим, что оператор М однозначно определяется данным оператором L,
между тем как Р и R зависят еще и от кривой Cv Если равенства
D ъв ас
йх ' Ъу ’ йх ' йу
(27)
выполняются тождественно, то операторы L и М совпадают, а присое-
диненная функция R обращается в нуль. В этом случае говорят, что
ЛИНЕЙНЫЕ УРАВНЕНИЯ. ФОРМУЛА ГРИНА
88
уравнение сопряжено самому себе. В частности, мы имеем такое урав-
нение, когда все коэфициенты постоянны, и О = Е — 0. На основании
условий (27) мы можем написать самосопряженное уравнение в следую-
щем виде:
й ( йи . „ йк \ , й / D й« , йп \ ,
— л-—рв- -К— в— + с — 4-Уи=о. (28>
ЙХ \ ЙХ Й.У / йу \ ЙХ 1 йу /
Линейный оператор Р имеет особенно важное значение. Чтобы вы-
яснить его значение, определим направление > уравнениями:
A cos (их) В cos (пу) == Л cos (vx),
В cos (пх) В cos (пу) = Л cos (уу),
Л2 = (Л2 -ф- В2) cos2 (пх) 2В (A -j- С) cos (пх) cos (пу) 4-
4- (В2 4~ С2) cos2 (пу); Л > 0.
Теперь этот оператор можно переписать в следующем виде:
Г,, . » /ЙМ , , . ЙИ , \ . йм ,
Р (и) — Л | — cos (у х) -I cos (уу) = Л — , (ЗОу
\ЙХ • йу ) ЙУ
ЙК
где — есть производная от и в направлении у. Луч, имеющий направ-
ление р, называется конормалью. Построение конормали вытекает очень
просто из следующих соображений. Заменим в выражении (10) (харак-
теристической функции)
Ф
{-2В^^4-С
йх йу
й/\2
йУ /
(35)
й/ У
производные — и -х- переменными Ли Ун приравняем
оХ иу
выражение единице:
Ф (X, У) = ЛЛ2 4- 2BXY + СУ2 = 1.
полученное
(32)
Это уравнение (32) представляет собою кривую второго порядка, центр
которой находится в начале координат1. Положив X —pcos (пх),
y=pcos(ny), где р— соответствующим образом подобранный множитель
пропорциональности, мы можем уравнения (29) переписать в следую-
щем виде:
cos (ух)_cos (> у)
йФ йФ ’
йл Гу
(33).
Отсюда становится ясным построение конормали. На кривой (32) опре-
деляют точку, радиус-вектор (т. е. отрезок, соединяющий точку с цент-
1 Коэфициенты А, В, С должны быть вычислены при значениях х, у, z в той
точке кривой /=0, в которой строится копормаль Таким образом при изменении
точки х, у на кривой f=6 изменяется также и форма конического сечения (32).
Если квадратичная фор,, ч Ф отрицательна при всех значениях переменных х и у,
то в правой части уравнения (32) надо взять — 1 вместо 1
90
ИНТЕГРИРОВАНИЕ ДИФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
ром) которой параллелен нормали п к данной кривой; нормаль (перпен-
дикуляр, опущенный из центра на касательную) в найденной нами на
кривой (32) точке и дает нам направление конормали (черт. 81, 82).
Уравнение (9) показывает, что направление асимптоты кривой второго
порядка (32) совпадает с направлением касательных к характеристикам,
проходящим через соответствующую точку кривой /=0.
Вернемся снова к уравнению (23); пользуясь введенными нами обо-
значениями, ее можно переписать в следующем виде:
Ц {vL(u)~ uM(v)} dxdy = \ ^s’
Эта формула представляет собой обобщение на случай двух измерений
обычной [см. § 40 (278)] одномерной функции Грина. Например, для
диференциального уравнения Лапласа мы имеем:
L(u)=M(u) = /\u, А = С=1, B = D = E = F=0,
А=1, у = п, Ф(А’,У) = А'2ф У2, /? = 0, (35)
и формула (34) приводит нас к найденной нами уже в § 52 формуле (20).
§ 72. Уравнения эллиптического типа. Нормальным видом линейных
уравнений эллиптического типа служит
L (и) = Ди 4- а -4- b 4- cti = 0,
1 ЙХ ’ Ъу 1
а уравнением, сопряженным данному, является
,.. , . й (av) й (bv) . .
Л4 (v) ~ Av-------—------4---k cv = 0.
Йх йу
(38)
(37)
Мы предполагаем, что коэфициенты а, Ь, с обладают непрерывными
производными второго порядка в области К, ограниченной аналитиче-
скою кривою С. Характеристическая функция Ф(АГ, У) та же, что и
в уравнении Лапласа, а конормаль совпадает с обычной нормалью.
Мы уже несколько раз указывали на значение, которое имеет для
уравнения Лапласа в двумерном пространстве Гастное решение, зави-
сящее только от г, а именно log/'. Для волнового уравнения в двумер-
УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
91
ном пространстве мы нашли аналогичное по своему характеру решение
(см. § 65), именно функцию J0(kr) вида:
Z71ogr-|-V, (38)
где U—U(x,у) и V—V(x,y)— аналитические функции (см. § 101).
Относительно эллиптического уравнения в общем виде (36) можно
также показать1, что для заданной внутри данной области К точки
Е, существует фундаментальное решение, которое обладает следующими
свойствами:
а) Оно имеет вид (38) (г—расстояние от точки %, /]), где U и V
имеют внутри области К непрерывные производные второго порядка,
и U(Z.,rl) = — 1.
Ь) Повсюду внутри области К, исключая точку 5, zj, оно удовле-
творяет диференциальному уравнению (37).
Обозначим такое фундаментальное решение буквой и. Описав около
точки к] малую окружность, применим к остальной области формулу
Грина (34), как мы это уже делали в § 59, и совершим, далее, предель-
ный переход при г = 0. Так как
/? = —{ a cos (пх) -ф- b cos (яу)}, v = /z, А=1,
то в результате предельного перехода мы получим:
2пи (£, Т|) = —
v L (и) dx dy —
>и й®
v --и-—[a cos (пх) -+- b cos (иу)]
oft o/Z
Эта формула представляет собою обобщение формулы Грина (69) из
§ 59.
Если функция и удовлетворяет диференциальному уравнению Г(«) = 0,
то формула (39) дает возможность вычислить значение и в какой-
либо точке £, г; внутри области К, с помощью интеграла, содержащего
йи . _ _
значения и и — только на границе области — на кривой С. Однако,
бп
как и в случае уравнения Лапласа, эти два краевые условия не незави-
симы друг от друга. Их зависимость вытекает из доказанного Гильбер-
том существования так называемой функции Грина О(£, •/], х,у), т. е.
фундаментального решения, которое кроме указанных выше условий а
и b должно удовлетворять еще и следующему условию:
с) На кривой С, ограничивающей область К, функция 0 = 0.
Действительно, если в формуле (39) в качестве v взять функцию
Грина О (S, гр х, у), то, как и в уравнении Лапласа [см, § 66 (138)],
= X’y}ds-
(40)
ГЛ „ ЙИ
dro равенство и доказывает зависимость значений и и — на данной
дп
1 См. D. Hilbert, Grundztige einer allgcmeinen Theorie der lineuen Integ-
ralgleichungen, гл. 8, стр. 60 и гл. 9, стр. 70, Leipzig, Teubner, 1912.
92
ИНТЕГРИРОВАНИЕ ДИФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
кривой. На основании формулы (34) можно также показать, что функ-
ция Грина /7(Е, Гр х, у) для сопряженного уравнения /И (&)-—О связана
с функцией G (£, т;; х, _у) равенством
Я(5, ч, Ч') = С(Е', г/; Е, У]). (45)
Это равенство соответствует равенству (134) из § 66.
§ 73. Уравнения гиперболического типа. Нормальный вид уравнения
гиперболического типа и уравнения сопряженного есть
. , . Ъ-и . ди , ди
L {и) ~ г-— + а — 4- Л — -f- с« = 0, (42)
ЙХ д_у йх йу
д2® d(av) d(bv)
М (-и) = —------------------------- 4- cv — 0.
ЙХ йу Йх ду
(43)
Для уравнений гиперболического типа мы будем рассматривать фун-
даментальные решения с особыми точками вдоль характеристик вместо
решений с изолированной особой точкой, введенных для уравнений
эллиптического типа. Уравнение характеристик в случае (42) имеет
вид dxdy —0, а самими характеристиками служат прямые х = const и
у — const, параллельные координатным осям. Мы должны искать решения и,
как и значения —, на данной кривой С за-
Ъп
1
i
значения которых, так же
На основании (25), (26) и
даны; мы при этом предполагаем, что ка-
сательная к кривой С непрерывна, что
каждая из характеристик пересекает кри-
вую не более одного раза и, наконец,
что кривая С не касается ни одной из
характеристик.
Возьмем точку Q с координатами £
и У|; предположим для определенности,
что взятая нами точка лежит ниже кри-
вой С. Применим формулу Грина (23) или
(34) к области, ограниченной двумя ха-
рактеристиками, проведенными через точ-
ку Q, и отрезком АВ, отсекаемым от
кривой этими характеристиками (черт.83).
(29)
Л = с=о, £ = Л = 1,
, 1 (дЧ ... ди \
р («) = 2“ cos {пх) ф- — cos (пу) J,
R — — [a cos (пх) cos («У.)] •
Далее, при данной ориентировке граничной кривой и нормали на AQ
cos (их) —0, cos(ny) —1, ds— dx;
на QB
cos (пх) = — 1, cos (пу) = 0, ds — dy.
УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА
93
Наконец, формула (29) дает cos (пу) = cos (vx) и cos(«x) = cos(vy),
т. е. вектор v получается как отражение вектора п в прямой х~у.
Поэтому в силу формул (23) и (34) мы имеем:
Проинтегрируем по частям члены, содержащие производные от и в двух
первых интегралах:
(45)
„Функцию Грина“ G(S, tjjx, у) по Риману определяют в этом случае
следующими условиями: внутри указанной выше области интегрирования
она должна быть решением сопряженного уравнения М. (v) == 0; на отрез-
ке AQ характеристики у — т] она должна удовлетворять уравнению:
bG = 0, (46)
на отрезке QB характеристики х=£ она должна удовлетворять
уравнению:
а~— aG = 0
(47)
и, наконец, в точке Q она должна быть равна единице. В таком слу-
чае, если L(u) = 0, то
в(И)=|((«О)л + («О)в]-Ь
в
a cos (пх) b cos (пу) I uG ds.
(48)
94
ИНТЕГРИРОВАНИЕ ДИФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ
точке Q через значения
йи /
— на кривой С. I Если
G/ф \
Эта формула выражает значение функции и в
этой функции и ее производной по нормали
функция и задана на кривой, то тем самым заданы и значения ее про-
изводной по направлению касательной; с помощью этой производной
йи
и производной по нормали — можно определить значение производной
Ли \
от и по любому направлению, в том числе и — . 1
oV /
Интегрируя вдоль характеристик х = Е, у=т\, мы получаем:
5
1 ЙО
О дХ
й1огО ,, , „ (
——=b(x, 7j), logG = — J
х.
dx,
1 *2
в лу
Й102С
тг==‘,('’л
У
log G = j а (Е, у) dy,
ч
J aii,y)dy
G=e ''
(49)
Определение функции и на основании ее" значений на кривой С сведено
тем самым к определению функции G1. Если а = Ь = О, то функ-
ция О вдоль характеристик постоянна и равна единице.
В качестве примера рассмотрим уравнение колебаний струны:
й2и „ й2«
--- —~ /7- —
йГ2 йх2
(а/>0 и постоянно).
G — e
Введем новую переменную у — at. Тогда рассматриваемое диференциаль-
ное уравнение перейдет в самосопряженное уравнение:
й* 2и й2и
L(u) == 0.
йх2 йу2
(50)
Уравнение (50) можно исследовать и непосредственно, не приводя его пред-
варительно к нормальному виду2. Уравнение характеристик dx2 — dy2 = 0
* Это последнее можно сделать, например, способом последовательного при-
ближешГя. См. § 4 в книге J. Horn, на которую была ссылка в § 70.
2 Приведение этого уравнения к нормальному виду гораздо скорее приво-
дит нас к его решению, чем применение формулы Грина. Действительно, в ре-
й2и
зультате приведения этого уравнения к нормальному виду получается: —— = 0
о? ОТ}
[ср. § 25 J)], а отсюда легко найти решение (53).
УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА
определяет два семейства прямых, которые образуют углы
динатными осями. Для уравнения (50)
4=1, В = 0, С = —1, А —1,
Р(и)cos (их)--COS (ну), Р = 0,
в 45° с коор-
далее (черт. 84), на AQ
dx = dy, cos (пх) = ~= , cos (пу) =
ds = — У 2 dx — — ]/ 2 dy,
на BQ
dx— — dy, cos (nx) = — cos («>) = — —,
Черт. 84.
ds = j/~2 dy - — У 2 dx.
Вектор v получается в силу формул cos (пх) = cos (vx), cos (лу) = cos (vy),
путем отражения вектора п в оси Ох. В результате применения в обла-
сти ABQ формул (23) или (34) к функциям и и V, для которых L (и) = 0
и (v) — 0, мы получим:
(Первые два интеграла суть криволинейные, знаки dx и -dy выбирают
в соответствии с выбором положительного направления на кривой, по
которой интегрируют.) Так как а — Ь = 0, то функция О вдоль харак-
теристик оказывается тождественно равной единице, и, следовательно,
в качестве функции С мы можем просто выбрать v=l. В таком случае
a Q в
f (ill , , ill , \ ( fill , . ill , \ ( ill ,
« — dx 4- — dy\ — I I — dx - - — dy\ — 4 — ds — 0, (52)
J \dx iy ) J V* qy / J dv
Q В A
выполнив интегрирование, мы получим:
в'
А
(53)
ИНТЕГРИРОВАНИЕ ДИФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
94
Возьмем, в частности, в качестве кривой АВ прямую _у = 0;
•при at=y = Q
г,,.., Ъи Ъи 1 йи 1 ч
« = Г(х), — — = — = —— = —G(x).
й> йу О а
и пусть)
*
Если координаты Q суть
,x = Z— >j и x = G4-J], а
Е и j), то абсциссами точек А и В являются
потому
Н71
2и(Е, q) = F(E—7])4-F(E-|-q)-|-y j O(x)dx, (54)i
или
x-\-at
U===Y [f(x—аО+^(х + ^) + у j G(x)rfxj.' (55)
х—at
Это решение совпадает с решением Даламбера [см. § 26 (27)]. Реше-
ния (53) и (55) показывают, как значения и в точках А и В, „распро-
страняясь" вдоль характеристик, „доходят" до точки Q.
. Преимущества этого метода заключаются в том, что он дает нам
возможность кроме найденного нами частного
решения получить реше-
ние для любой начальной кривой АВ.
Такая кривая соответствует некоторой
заданной зависимости между х и у (или
что то же, между х и г); начальные усло-
вия означают, таким образом, для неко-
торой точки струны, проекция которой
движется по оси Ох по данному закону,
й«
заданные значения и и — во все время ее
движения. В качестве примера рассмотрим»
на струне точку, проекция которой дви-
жется с постоянной скоростью, причем
отношение этой скорости к скорости
волны а равно р, где 0< < 1. Кривая С
в этом случае обращается в прямую
x — $y = $at (черт. 85). Проведя через точку Q(E, rj обе характери-
стики, мы найдем координаты точек пересечения, а именно
1-М’
в ( —(т 4- Е) \
D fi-i-У’ 1 + р I •
Чтобы можно было теперь применить выведенные нами формулы (51)
и (52), заметим, что последовательность точек QAB противоположна
той последовательности точек, для которой эти формулы выведены.
УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА
97
Следовательно, направление нормали при интегрировании вдоль QA и
направление пути интегрирования при интегрировании вдоль QB в дан-
ном случае противоположны соответствующим направлениям для указан-
ных формул, и поэтому в данном случае первые два интеграла в этих
формулах должны быть с противоположными знаками. Далее, так как на АВ
1 в
cos (пх) = - . , cos (пу) = - F , ds ~ -4- R2 dy,
/1 + р2 /1 + р
то
(56)
Предельный случай (2 = 0 соответствует неподвижной точке; мы
в этом случае снова получим формулу (54), но х и у в ней будут
заменены друг другом.
Полученный результат можно преобразовать следующим образом,
пользуясь начальными данными. Пусть
u—F(y)
t“x = G(y)
при х = fi_y.
Мы имеем:
v-=F'(y)-$G(y)'
и следовательно,
ч + Е
1 + ₽
2« (Е, тО = F (+ F + J {(1 - ₽е) О (у) -|-рд' (у)} dy. (57)
i-₽
Выполнив интегрирование в последнем члене, мы получим:
л+-
1 + ₽
2К(£,Ч)=(14-₽)д[^') +(1-Р) (1 - № I G(y)dy, (58)
\* 1 "гР/ \* Р/ J
>>—<
1 - ₽
1 Чтобы получить это, надо продиференцировать равенство и J) = F(y),
и принять во внимание, что их($у, у) = G (у).
1 Вебстер, Диференпиаиьпьге уравнения.
98
ИНТЕГРИРОВАНИЕ ДИФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
или в обычных обозначениях:
1 + ₽
= + + J G(ai)dt. (59)
i — —
__а
1-₽
Исследуем, например, действие источника звука
ту , который перемещается со скоростью Ва:
2п
F [at) = О, G (at) — cos pt.
В
имеющего часто-
этом случае мы получим:
(60)
т. е. получим две волны, которые распространяются с тою же ско-
ростью, что и источник звука, причем частота волны, распространяю-
щейся направо (т. е. направление распространения которой совпадает
с направлением перемещения источника), увеличивается в отношении
1:(1—р), а частота волны, распространяющейся в противоположном
направлении, уменьшается в отношении 1:(1-|~Р)- Это явление носиг
название принципа Допплера (Doppler). Благодаря этому принципу
можно с помощью спектроскопа вычислить скорость звезд; для этого
определяют изменение длины волн спектральных линий при приближе-
нии и удалении звезды. Если начальные условия суть F(at} = caspt,
G(at) — Q [при изучении источников звука мы встречаемся чаще всего
« -
именно с этой задачей, так как смещение s —— — удовлетворяет
оХ
волновому уравнению и при движении остается постоянным, см. § 12
(П5)], то частота волн приближающегося источника увеличивается
в отношении 1:(1—-[3), а частота волн удаляющегося источника умень-
шается в отношении 1 :(1 —Р). Примером может служить изменение
высоты тона свистка движущегося поезда.
§ 74. Телеграфное уравнение. В качестве второго примера рассмот-
рим телеграфное уравнение. В § 46 было показано, что, введя с по-
мощью множителя е а новую неизвестную функцию, телеграфное
уравнение можно свести к уравнению
а2н
aF
а2
Ъ2и
аТ2
(61)
где z — пространственная координата. Преобразования
х = (г at), y = ^-(z— at) (62)
ТЕЛЕГРАФНОЕ УРАВНЕНИЕ
99
приводят уравнение (61) к нормальному виду:
L (и) ~ + — = 0.
ЪхЪу 4
(63)
Это последнее уравнение можно проинтегрировать по методу Римана1.
Характеристиками для уравнения (63), как и для уравнения (42),
служат прямые х= const и у — const, а „функция Грина" для этого
' уравнения принимает на характеристиках постоянное значение. На харак-
теристиках, проходящих через точку Q(E, rj) функция <р = (х—&)(у—Jj)
обращается тождественно в нуль. Постараемся теперь найти функцию
(7= С?(ф>), зависящую только от <р, для которой 0(0)= 1, и которая
удовлетворяет самосопряженному уравнению (63). Мы имеем:
йО dCd'f dG
Ъх dy ix dy 'У 1
i2G _dG.d2G __ dO J2 О
<5x1)у dy "I- dy2 dy2 '
Подставим эти выражения в уравнение (63):
d2G . dG . О п
# dy2 dy 4
(63)
Мы пришли к обыкновенному линейному диференииальному уравнению.
С помощью замены переменных
,, dG 1 dO
<s=<!)2, dy = 2фс/ф,
* ‘ ‘ 1 2d) йф
d2G
dw2
1
1 !±_d?G____
4ф \ ф б/ф2 фйг/ф /
мы приведем уравнение (65) к виду:
d2O \dG
й?ф2 ‘ ф б/ф '
0 = 0.
(66)
Полученное нами уравнение есть не что иное, как уравнение Бесселя
[см. § 100 (14)]. Решение его О = 70(ф) при ф = 0 обращается в едини-
цу. Следовательно, на основании формулы (48)
в
2и(В, ч) = («0)л-|-(«0)в4-
А
(67)
1 См. Р. du Bois Reymond, Uber lineare partielle Differentialgleichungen
zweiter Ordnung, Journal ffir Math., t. 104, стр. 241 (1889); Ё. Picard, Sur
1’equation aux derivees partielles qui se rencontre dans la theorie de la propagation de
I’electricite, Comptes Rendus, t, 118, стр. 116 (1894).
7*
W0
ИНТЕГРИРОВАНИЕ ДИФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
где
Начальной
(черт. 86).
правлении
O=J0(/(x-E) (>-Ч)).
кривой пусть, как и раньше, служит t — О, т. е. х =
Тогда на этой кривой, при заданном положительном
:У
на-
cos (пх) = — cos (пу) — cos (уу) =
1
= — cos (ух) =
—= = — dx—— dy,
/ 2
йи
йу
ЙО
ЙУ
ЙИ
/2 \?х
1
йи\
W
йО йО
ЙО dO, . ЙО dG.
j7=^<x“£)’
или, так как на АВ имеем х—у, то
йО 1 ,е rfO
— —Ъ' - " т/) , Сл = Ов=Оо=1.
йу 2 ' dy А v
Следовательно,
clx.
(38)
в
в
Ч) I и ХГ
*' 1 /7т
1
/ 2 \rfx Ъу
в
Вернемся к старым независимым переменным z и t. Пусть коорди-
натами точки Q служат Сити пусть
u~f(z)
ЙИ / ч
it=/M
Мы
имеем:
при / = 0.
ь
>=— (Z— at)>
q = -^^ — ax)
и
для
для
А:
В:
x—y=q, t — 0, z=Z— ах,
х=у = £(, t^O, z = ^-j-aT.
ТЕЛЕГРАФНОЕ УРАВНЕНИЕ
101
Далее,
й« b /Ъи . <to\ йм , (Ъи й/Д
— =— I-----I —== и I----I
~dz а \йх &у) Ы \Ьх Ъу/
У~ 4 = 7 {г — Z — a(t — т)},
S —ч = 2&т,
Ь2
^ = (х-^)(у-^=-2{{х — ^-а2(1-тУ}г
G=J0 (/ <?) = Л { 7 /(г —С)2-а2(г?-т)2| ,
dG_J'(} (l<f-p)
df~~ 2/й
Полагая, наконец, t — 0 и принимая во внимание, что при этом
dx——dz, мы сможем формулу (68) переписать в следующем виде;
[ А ,__ ]
1 Ат С ^ -К^)2-^2
«(?> т) = т{/(£ - ат) 7/(S 7 ат)} - - у (г)—dz +
+ iz f g(?) Jо 17- /(2—S)2 —а2т2j
I I CL
t, — ат
dz.
(69)
Эта формула совпадает с (146) § 46, в чем легко убедиться путем за-
1 Г~ ~с
мены т, z, а, b через х, t, а, —^=, j/----------[При этой замене
|/ а Г а
получается, собственно говоря, не формула (146), а ее частный вид при
b—Q (обозначения § 46); однако формулу (146) в общем виде легко
можно вывести как следствие из этого частного вида; см. в § 46 фор-
мулу (127).] При Ь = 0 (обозначения § 74) из формулы (69) полу---<
чается (55).
102
ИНТЕГРИРОВАНИЕ ДИФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
§ 75. Неоднородное волновое уравнение. В заключение применим,
как это сделал Абрагам1, наш метод к неоднородному волновому урав-
нению в трехмерном пространстве [§ 17 (195); § 63 (101)]:
□ <р = Д(р — -LL? = — 4тгр(х, у, z, t),
q = f(x,y, z)
У, z)
ol
при t = 0.
(70)
Мы вводим, как и в случае однородного уравнения (р = 0, см. § 61
и 62), среднее значение <р функции на сфере радиуса г с центром
s точке Q:
й2(гср) „а2(гср) . [
dw>— здесь телесный угол. Как и в § 61 [см. (76)]:
и = -Д- С С ад d's>,
или, заменяя лр через и:
1 52« й2к , „ СГ ,
^-^2—= «0=/- р(0 dw. (71)
Таким образом мы пришли к линейному диференциальному уравне-
нию второго порядка относительно и, как функции двух независимых
переменных г и t. Перейдем теперь к обычным обозначениям, положив
г = х и at=y [эти х и у не следует смешивать с х и у, входящими
в уравнение (70)]. Тогда последнее уравнение перепишется так:
L(u) =
ЙХ2
у)-
(72)
Мы пришли к уравнению гиперболического типа, которое, в отличие
от разобранных нами до сих пор, имеет правую часть. С помощью вновь
принятых независимых переменных краевые условия запишутся так:
—С =/=(/-) = Л(х), (73)
при у~0;
fgda ~ G(r) = G (х), (74)
йу а Й7 4 па J } 7
здесь г=х>0. Правые части формул (71), (73) и (74) представляют
1 М. Abraham, Sopra un applicazione del metodo di Riemann alia integra-
zione delle equazioni differenziali della teoria degli elettroni, Atti dei Lincei, серия 5,
т 14, (1905), стр. 7. — Далее, Theorie der Elektnzitat, т. II, Elekfromagnetische Theo-
rieder Strahlung, стр. 40, Leipzig, Teubner, 1905.
НЕОДНОРОДНОЕ ВОЛНОВОЕ УРАВНЕНИЕ
103
средние значения функций р, /, g на сфере радиуса г, с центром
г
в точке Q, умноженные соответственно на г, г и — .
Применим формулу Грина (34), которая в данном случае принимает
вид:
--V
причем интегрирование производится по треугольнику АВР
стороны которого РА и РВ являются ха-
рактеристиками данного уравнения. Распро-
страним область определения функций Р (х).
G (х), у(х,у), ограниченную положитель-
ными значениями х, на его отрицательные
значения. Потребуем для этого, чтобы все
эти функции были нечетными [F (—х) =
= —F(x)]. Пусть координаты точки Р
суть Е и jj, тогда абсциссы А и В соот-
ветственно равны С —'/) и Е -|-7j. Пусть и будет решением уравнения (72),
(черт. 87),
я v --= 1, так что
£ (и) = — 1 (х, у), L (v) = 0.
Применяя те же рассуждения, что и при выводе формул (53) и (54), мы
получим:
в
2ир — иА иБ -ф- J G (х) dxf dx dy,
A
ИЛИ
54-4
2и (E, jj) = F(E -ф- J]) -ф F(E— rj) -ф- f G (x) dx -ф-
5-4
(75)
Интеграл по треугольнику ACD (черт. 87) обращается в нуль; далее
54-ч* 54pi 5—4 54-4 4—5 4-Н
У G (х) dx ~ = I — J ~ ^х‘
5—ij О ООО о—£
(76)
Разделим обе части уравнения (75) на Е, т. е. на некоторое значение
радиуса г, мы получим:
- и(Е, и) /=(ч+5) —F(n—Е) . И'' , J , 1 Г Г , , ,
¥ "— g — 2% 2? ] J 2E ) )
4-5 BP CD
Предел этого выражения при Е—представляет собою искомое
значение функции (р в точке Q. В последнем интеграле по площади
значением этого, интеграла по площади треугольника DBD' (черт. 88)
104
ИНТЕГРИРОВАНИЕ ДИФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
можно пренебречь, так как площадь этого треугольника равна £2. Чтобы
оценить значение этого интеграла по площадп DD’PC, введем новые
переменные
х' =у х, у' =у — х,
после чего этот интеграл примет вид:
1 Г (' (xf — у' х' 4-у'\ . , ,
aJr'-5-’ -Г-)"'0'-
Так как
Ч — £ х' -С Е,
то при предельном переходе по $—>4_®> последний интеграл можно
заменить следующим:
Т)
£ I \ ]
Таким образом
(^h->o — (ч) 4-G (’1) + jx(*> >]—X)rfX. (78)
о
Из формул (73) и (74) в силу равенства — следует:
р<ч>=й [I ( J J J J Г=1)=«/
(79)
В этих интегралах надо брать значения функций f и g на сфере с ра-
диусом, равным at, и с центром в точке Q. Далее,
X (Л at) =
р (t) d(D,
у.()., Jj— Х) = Х
da,
(80)
причем надо взять значения р на сфере радиуса X с центром в точке Q-
Поэтому интеграл в формуле (78)
УРАВНЕНИЯ С П ПЕРЕМЕННЫМИ
105
можно рассматривать как интеграл по объему, причем 1 есть радиус-
вектор. Так как элемент объема
с/т = Х2 d).da,
то
ч —х)<а=
точка с координатами £, »j, С пробегает при этом всю внутренность
шара с радиусом, равным at, и центром в точке Q.
Перейдя снова к обычным координатам, мы получим формулу Кирх-
гофа Лоренца:
1 й
4тт й£
do -4-
J , t
=о г/ы У 4- —
(81>
В двух первых членах этой суммы надо взять начальные значения на
поверхности сферы с центром в точке Q и радиусом, равным at. Они да-
дут уже несколько раз полученное нами пуассоново решение однород-
ного волнового уравнения. Третий член совпадает с волновым потен-
циалом Лоренца (Loientz), с которым мы уже встретились в § 63 (99).
§ 76. Уравнения с и переменными. Пусть нам дано однородное ли-
нейное диференциальное уравнение второго порядка общего вида с п
независимыми переменными Хр’ х2, ... , хп:
п п п
и=1-,=1 1 v=l
Спрашивается, можно ли независимо друг от друга задать краевые
йи
значения и и — на гиперповерхности
дп
/(Xj, х2, ... , хп) — 0, (83)
т. е. на многообразии л-мерного пространства, зависящем от п — 1
независимых переменных. Предположим, что координаты точек поверх-
нести (83), а также начальные значения и и — представлены,
о/2
как и в
§ 70, в виде функций п—1 параметров^, t2, ... , tn_v т. е. пусть на
гиперповерхности (83)
Х1---Х1 (^1> • • • > ^-1)> • • • > Хп-Хп^1> ^2’ • • • >
и — tz,.., tn_l), — G (^, t2, . . . , (84)
106
ИНТЕГРИРОВАНИЕ ДИФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
причем функции хп х2, ... , хп тождественно удовлетворяют уравнению
'83). Введем для краткости обозначения:
й/ йхр йи й2и
й^^^’ Й^^^” йх^=А’ ё^^^Р^=Р^‘ (85>
Найдя полный диференциал функции /(х.^ х2, ...,ха), получим:
[1 = 14=1
Так как диференциалы dt, суть независимые ^переменные, то
РП ”1+^21 П2 + • • • +^ОЛЯ = °»
Р12 П1 + Р22 П2 + • • • + Рп^п = °>
Р1, п-1 "1 + Р2, п-1 П2 4- . • . + Рп,п-1 = °- (86)
’Определим из этих п— 1 уравнения отношения п чисел ttv. Мы будем
/иметь:
(S7)
где £>, обозначает детерминант (и—1)-го порядка, который получается
.из матрицы коэфициентов Р вычеркиванием у-го столбца и умноже-
нием на (—1)'+". Мы предполагаем при этом, что среди п чисел Dv
D2, ... , Dn хотя бы одно отлично ог нуля. Заметим, что детерминанты
D, равны, с точностью до знака, функциональным детерминантам
.ж,, х2, ... , xv_j, xv+1, ... , хп по tv t2, ..., ta_y.
Из выражения полного диференциала
п—I п п—1
du = dF= dt, = J] р* dt, (88)
v=l |л=1 v=I
«вытекают /2—1 уравнений:
PiiPi 4* Р21Рг 4- ’ • А-РщРп^^Г »
Ot-j
Л/7
Р12 Р1 + Р22Р2 + • • • 4- Рп2Рп=^ •
Р1, п-1 Р1 4" Р2, я-1 Р2 4“ • • • 4" Рп, п-1Рп~> (89)
, ЙИ
® которым в качестве л-го добавляется уравнение, определяющее —:
cos (zzXj) рг 4- cos (лх2) р2 -f- ... cos (пхп) рв — G. (90)
УРАВНЕНИЯ С П ПЕРЕМЕННЫМИ
107
дез уравнения (83) следует:
e2!gxL) = co!gs)= ^=eo!l»ie) = o
УУ -тч У -л
<U2 Ъх2 ~дха
а из (87) получаются:
cos(/zx,) = poZ\.
Таким образом разложение детерминанта уравнения (86) и (90) по эле-
ментам последней строки будет иметь вид:
ра(р2 4-Я24-...4-^) (92)
[ср. (5)]. Так как коэфициенты Р[Ы зависят только от поверхности (83),
то Д на поверхности (83) вполне определяются начальными значениями
р и G. Вычисленные таким образом значения д на поверхности (83)
мы обозначим через д.
Найдем таким же образом значения вторых производных. Для этого
поступим с р, так, как мы раньше поступали с и; мы получим:
Р11 Р.1 + Р.2 +-----И Рп1 Р.п= »
Р1гРл + Р22.Р^Л~-'’ A-PraPvr^-^- > I -93.
Р1, п-1 Рл 4" Р2, п-1 Р.2 + • • • + Р„, п-1 Р.п^^^ •
Из этой системы п — 1 уравнения нельзя однозначно определить п
неизвестных дп д2, ... , дя: одно из них может быть выбрано про-
извольно.
Для того чтобы вычисляемые нами производные второго порядка
имели более симметричный вид, присоединим к уравнениям (93) сле-
дующее:
Й1А1 -Ь «2^2 + • • • + апР.п = V (94)
В этом уравнении коэфициенты аг, а2, ... , ап суть некоторые выбран-
ные числа, а \ — произвольный параметр. В таком случае д можн®
выразить в виде линейных функций от
Числа аь мы подбираем таким образом, чтобы детерминант
Рц Рц ’ • • Рщ
Рц Р22 ' • • Рп2
D= Р1, п-1 р ^2, л-1 ’ • • Рп, п-1
а1 «2 ап
(95)
108
ИНТЕГРИРОВАНИЕ ДИФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
не обратился в нуль. В таком случае
+ A. + ... + о„., +1, Ot, (9S)
(Ц=1, 2.....и),
где суть миноры, принадлежащие р.-му столбцу детерминанта D, а
£)ц имеет здесь то же значение, что и в формуле (87).
Если во всех этих преобразованиях вместо ру брать pv, причем зна-
чения ak оставить прежними, то получится:
^Р,. ^Ри. ^Р.,
Dp^ = ^ Dn+^Dv+ • • • + ъГ~ + \Л, (97)
I 2 tt — 1
(v=l, 2, ... , n),
причем определение остается прежнее. Заметим, что правые части
формул (96) и (97) линейны относительно ак, и что р представляет
собою линейную однородную функцию правых частей формул (96) и
(97). (Аналогичное утверждение справедливо и относительно р^,.)
Но р^ — р^, и это равенство должно иметь своим следствием опре-
деленные зависимости между параметрами Хг Х2, ... , Хп. Действительно,
уравнения (96) и (97) имеют вид:
= + (98)
где — известные функции. Отсюда следует, что для любых значе-
ний р. И V
D„ DU.
+ \ p=?vli + K-^' • (99)
Мы предположили, что среди детерминантов Dv по крайней мере
один отличен от нуля; пусть это будет £>vl. Заменив в формуле (99) v
через v' и определив Хр, мы найдем, что для всех значений р.:
+ 2,..., п), (100)
где Q— известные функции. Таким образом параметры }.п
можно представить в виде линейных функций одного параметра. Под-
ставляя это значение X в (98), мы получим:
Ху D О
Ррт—ООО
Приняв во внимание соотношения (87) и введя обозначение
Ху 1
О.,' Dp2 ~
УРАВНЕНИЯ С П ПЕРЕМЕННЫМИ 109
можно этот последний результат переписать так:
о°3>
где р,°\— известные функции.
Подставим найденные нами значения р в уравнение (82):
х Е xhv Е р*+Fu=°- (1м)
|Л = 1 V = 1 {4 = 1 v=l V= I
Мы получили уравнение, из которого можно определить 1 и тем самым
вполне определить вторые производные. Подобным же образом можно
определить и производные высших порядков. Этот метод, однако,
нельзя применить к гиперповерхности (83), если
п п
ф=£ о°5)
!*=Iv=l
. т. е. если
уул О_0
• (,06)
Это диференциальное уравнение первого порядка можно рассматри-
вать, как обобщение уравнения (10); оно определяет характеристики
в «-мерном пространстве, которые представляют собою многообразия
(«—1)-го измерения.
Будем ttv рассматривать, как координаты «-мерного пространства;
тогда поверхность, представленная уравнением (105), будет конусом.
Таким образом, если гиперповерхность f(xy, х2, ... , хп) удовлетворяет
уравнению (106), и если коэфициенты Л|И этого уравнения постоянны,
то проведенные через любую точку пространства нормали ко всем та-
ким поверхностям, проходящим через эту точку, лежат на конусе; дей-
ствительно, направляющие косинусы cos(«xj пропорциональны тгч. Если
коэфициенты А не постоянны, то каждой точке хг, х2, ... , хп соот-
ветствует свой особый конус, вершину которого мы поместим в этой
точке. Плоскости, перпендикулярные образующим такого конуса, оги-
бают второй конус, который мы назовем характеристическим кону-
сом' каждая характеристическая гиперповерхность в каждой своей точке
касается соответствующего характеристического конуса. Функция Ф,
стоящая в левой части уравнения (105), называется характеристической
функцией.
Согласно определению характеристик Коши, данному в § 24 (см. 45'),
уравнения характеристик диференциального уравнения (106) суть:
_й?х2 _dxn dz г/тг-j (,07*
йФ йФ ЙФ 0 ЙФ = ЙФ
Й1Т2 Ч ЙЛ*2 Ч Ч
ПС ИНТЕГРИРОВАНИЕ ДИФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
[ср, § 70 (11)]. Проинтегрируем эти уравнения при начальных уело-''
виях -п\ = тг^°1 (v = 1, 2, ... , п) и при условии, что
п п
ф«Е л($ 4°’ п'0) = °* (1о8)
р.=1 » = !
где верхние индексы указывают на то, что точка х®\ х^\ ... , х'О)
является определенною начальною точкою. В результате мы получим не-
которые одномерные многообразия, т. е. кривые, которые согласно
Адамару, называют бихарактеристиками уравнения (82) Ч Совокуп-
Черт. 89.
ность бихарактеристик, проходящих через не-
которую точку xf°>, х®\ ... , х^\ образует ги-
перповерхность Г, для которой точка
х<® ... , является конической (особой) точ-
кой (черт. 89); мы назовем эту поверхность ко-
ноидом. Если коэфициенты Л постоянны, то
коноид совпадает с характеристическим ко-
нусом.
Если мы в какой-либо точке х^\ ...,
х'У будем рассматривать функцию
п п
Ф = V1 V4 Л (°) тг тг
Р-1 Р-
н=11=1
(109)
то при этом могут представиться три возможности:
1) Форма Ф определенная2 *, в этом случае конус характеристик и
коноид мнимы, и уравнение называется эллиптическим.
2) Форма Ф неопределенна, но ее детерминант
А1 Аг
А1 Аз
А,
А я
А„ А„ ... А „
л, ла п.п
1 При этом интегрировании возникает особая трудность, заключающаяся
в том, что уравнения (107) в силу условия (108) как раз в точке х^\
не удовлетворяют условию, необходимому для существования интеграла дифе-
ренциального уравнения. См. стр. 83 и далее в книге Адамара, на которую была
сделана ссылка в § 70.
2 Определенная форма сохраняет знак для всех систем значений независи-
мых переменных; кроме того, при изменении переменных в действительной обла-
сти она обращается в нуль только в том случае, когда все переменные обраща-
ются в нуль; пример: ха + 2ху/ +2_р2=(хфу)2+ >s. Наоборот, формы ху или
х2—_у2 меняют свой знак, при изменении х и у в действительной области. Такие
формы называются неопределенными. С помощью соответствующего линейного
преобразования форму, зависящую от п переменных, можно перевести в сумму
не более п квадратов линейных форм (ср. § 29). Если детерминант какой-либо
формы равен нулю, то эту форму можно преобразован) в сумму квадратов, со-
держащую менее п слагаемых. Обратная теорема также справедлива.
ФОРМУЛА ГРИНА
ПТ
отличен от нуля; конус характеристик действителен, а уравнение
называется гиперболическим.
3) Указанный детерминант равен нулю; тогда уравнение назы-
вается параболическим. Сказанное является, конечно, обобщением на
«-мерное пространство классификации § 70, касавшейся уравнений с
двумя независимыми переменными.
§ 77. Формула Грина и характеристики в «-мерном пространстве. Вы-
ведем теперь в «-мерном пространстве аналог формулы Грина. Чтобы
определить сопряженное уравнение в «-мерном пространстве, применим
прием, которым мы пользовались при выводе формулы (20). Проинте-
грируем по частям сначала по Х|Л, а затем по xv следующий «-кратный
интеграл, распространенный на внутренность замкнутой гиперповерхно-
сти S (АЦЧ=АЧ11):
Д1Г„ vcos («х„)dS—
*' йх., 1
cos («xj ? dS j*
------— dx, dx, ... dx„ ==
ЙХ ЙХ 1 3 "
[A »
(«— 1)-кратные интеграла надо взять по поверхности S.
Левая часть этой формулы симметрична относительно х и х„, а
потому в окончательном результате можно х^ и xv поменять местами;
полусумма правой части (110) и вновь полученного выражения дает
нам симметрическое выражение результата интегрирования по частям
левой части (110)
112
ИНТЕГРИРОВАНИЕ ДИФЕРЕНЦИXПЬНЫХ УРАВНЕНИЙ
Для членов, содержащих производные первого порядка, интеграция
•по частям дает:
Суммируя все такие члены, мы приходим к формуле Грина:
2 ••• dXn^=
(112)
я—1
Сопряженный оператор М в данном случае равен:
далее,
frill! v
|A = 1 V = 1 V=1
ЛИ,СО8(ЯХУ) —
(ИЗ)
(114)
n n
|1=1 V = 1
si, наконец, присоединенной функцией является
cos (пх>).
(115>
Определим положительное число Л и направление v равенствами:
п
^^cosffixJ^A^^^^Acos^) (g = l, 2, , п), (116)
i=i
ФОРМУЛА ГРИНА
113
При этом
(117)
jVlu можем теперь написать:
п
Sdu , . , ди
В = 1
(118)
Луч, имеющий направление у, называется конормалью, Построение
«опормали в «-мерном пространстве аналогично ее построению в дву-
мерном. С этой целью наряду с уравнением (106) конуса нормалей
к характеристическим гиперповерхностям рассмотрим поверхность вто-
рого порядка [см. сноску к формуле (72) § 71];
п п
|J-=1 v = l
Направляющие косинусы нормалей к этой поверхности пропорцио-
нальны п
1 ёФ
2
(119)
Если положить = cos (ихр) (р=1, 2,..., п), то правая часть
в последней формуле окажется равной A cos (ух^). Таким образом ко-
нормаль у к поверхности S ^совпадает с направлением нормали к по-
верхности Ф=1 в той точке этой поверхности, радиус-вектор которой
параллелен п. Далее, из уравнений (107) мы заключаем, что конормаль
имеет то же направление, что и проходящая через ту же точку биха-
рактеристика; действительно, направляющие косинусы касательной
dx
к бихарактеристике равны и, таким образом, пропорциональны
ёФ
-— или,
ч
является
ются ее.
Итак,
вид:
ёФ
что то же, Следовательно, если гиперповерхность S
<’АР.
характеристической гиперповерхностью, то конормали каса-
в обозначениях (116) формула Грина принимает следующий
vL (и) — иМ (ц) } dxx dx2 ... dxa =
п
. / dv ди
А « ------V —
(112')
n—1
8 в е в о е ер$ йиференцнальные уравнения.
114
ИНТЕГРИРОВАНИЕ ДИФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Формула (112') охватывает все рассмотренные нами до сих пор слу- £
чаи формулы Грина [§ 40, (278); § 52, (20); § 71, (34)]; мы покажем, J
что в известных случаях формула дает возможность выразить при по- <
мощи соответствующим образом подобранного решения v сопряженного ]
уравнения Л4(©) = 0 любое решение заданного уравнения £(и) = о ]
через значения функции и ее производной по направлению конормали
на поверхности 5. Однако если поверхность S является характеристи-I
ческой гиперповерхностью, то значения и на S определяют также и I
значения производной от и по направлению конормали, так как конор-
мали в этом случае касаются поверхности S.
Если имеют место равенства:
п
(о=>.оа»
v= 1
то присоединенная функция 7? обращается в нуль, и уравнение £ (и) = 0
называется самосопряженным. Его можно тогда записать в следующем
виде:
<121)
Вольтерра обобщил изложенный в § 72 метод Римана и показал,
как с помощью формулы (112') найти решение задачи Коши. Укажем
„ Ъи
на ход его рассуждений. Пусть заданы значения и и — на поверхно-
сти S. Чтобы найти значения и в точке Q, лежащей вне поверхности Л‘,
построим коноид характеристик Г с вершиной в Q; этот коноид пере-
секает поверхность S по замкнутому
(п — 2)-мерному многообразию а (см.
черт. 90, в котором я = 3; на этом чертеже
многообразие а представляет собою кри-
вую). Мы предполагаем, далее, что суще-
ствует конечная область, ограниченная по-
верхностями У и Г, и применяем к этой
области формулу (112'); при этом надо, ко-
нечно, (я—1)-кратные интегралы брать
по поверхностям У и Г.
Так как коноид является характе-
ристической поверхностью, то (я— I)-
кратные интегралы можно на нем преобразовать, интегрируя по 41-
стям [ср. (44)]. Действительно, мы видели, что коноид образуется
семейством бихарактеристик, проходящих через точку Q, и что направ-
ление конормали в каждой точке коноида совпадает с направлением
бихарактеристики. Обозначим длину дуги бихарактеристики через s,
причем за начало отсчета выберем точку Q. Эту длину s в силу (107)
ФОРМУЛА ГРИНА
115
можно выразить через параметр t\
Выразим теперь все точки коноида через п— 1 параметров tx, ts, f
и s; элемент поверхности коноида выразится при этом так:
dS—A(s, L, t ________ t Adsdtdt ... dt „.
'Li, — X Z П — a
В силу формулы (118) и равенства dy — ds (и—1)-кратный интеграл
из (112'), распространенный на поверхности Г, можно переписать так:
/ А (« <- — + и®/? I Adsdt, ... dt„ ».
I \ ds dS/ 1 j 1
(122)
п—-1
Интегрируя по частям второй член по переменному s, мы найдем
(123)
причем в (п — 2)-кратный интеграл надо подставить разность значений
в точках многообразия о и в точке Q. Аналогом функции Римана G
(из § 73) в данном случае является решение сопряженного уравнения
— удовлетворяющее вдоль бихарактеристики диференциальному
уравнению:
ds \ A ds ‘ /
(12!)
Это условие соответствует уравнениям (46) и (47) (в тех уравнениях
к=А— 1); вследствие этого условия второй член в уравнении (123)
обращается в нуль.
Представление значения функции и в точке Q с помощью интеграла
вида (48) в общем случае невозможно; но и можно вычислить, зная
его значения на части поверхности 6', ограниченной многообразием а.
Эти значения „распространяются" вдоль бихарактеристик в точке Q;
бихарактеристики соответствуют световым лучам (см. § 75). Как это
распространение происходит в отдельных случаях, лучше всего выяс-
нится на примерах.
116
ИНТЕГРИРОВАНИЕ ДИФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
§ 78. Применение метода Вольтерра к волновому уравнению, а) Рас- 4
смотрим, как это сделал Вольтерра г, волновое уравнение в двумерном 1
пространстве — следующего вида:
1 й2^ й?п й2и . , п
(«>»>•
Чтобы упростить его, положим at — z и б]®сем вместо f(x, у, cr^z) |
писать опять /(х, у, z). Тогда
... _ й2и , й2п й2и . j
Т(п)=Пи^ —-+ —=_/(х, у, z). (125) Д
Так как коэфициенты этого уравнения постоянны, то оно является само-
сопряженным, /? — О, а характеристической функцией служит:
—Z2. (126) J
Характеристическим конусом служит круговой конус, у которого угол I
между высотой и образующей равен 45°.
Для конормали имеем:
cos (vx) = cos (пх), cos (vy) — cos (ny), cos (yz) — — cos (nz), A = — 1,
т. e. конормаль является отражением нормали в плоскости ху (черт 90).
ЙИ г, г.
Пусть и и — заданы на поверхности S. Чтооы найти значение и в точке
сП
Q(E, J], О вне поверхности S, построим обращенный отверстием вниз
характеристический конус с вершиной в точке Q. Мы предполагаем при
этом, что существует односвязная область, ограниченная конусом Г и
поверхностью .S'; в таком случае конус Г пересекается с поверхностью
по вполне определенной кривой (черт. 90). В каждой точке конуса Г
конормаль лежит на поверхности этого конуса. Таким образом решение
v уравнения L(v) — 0, которое на конусе Г обращается в постоянное,
ЙФ
удовлетворяет на этом конусе уравнению — = 0.
Уравнение (112') принимает в данном случае следующий вид:
s
(127)
Положим:
йб
йх'
х' = х— Е, у'—у — rt, z' — z---с,
/«=х'24-у2, 6=^-,
z'x? д х'
йб 1
й^'~ Г ’
JO ==_ <У=_
ЙУ /* °r2 ’
йО__ z'
йг —“r2 •
(128)
V
1 V. V о 11 е г г a, Sur les vibrations des corps dastiques isotropes, Acta Mathe-
matica, t. 18, стр. 161—232 (1894).
ПРИМЕНЕНИЕ МЕТОДА ВОЛЬТЕРРА К ВОЛНОВОМУ УРАВНЕНИЮ
117
Уравнение характеристического конуса Г в таком случае будет 6 — — 1,
Внутри этого конуса 6<^—1. Постараемся найти решение 17(6), которое
на конусе обращается в нуль и зависит только от 6. Мы имеем:
dv йб __ о dv х' di?______dv йб____ „ dvy* йт?_____dv 1 'j
jP' <Z6Sx' rf6rs’ йУ </6йУ <Z6r2’ iz' d§ r ’ I
^v <„ dv \ x'2 1 2x'2\
йх'2 dS) < dG/7^ ~6rf6 r4 ) ’
й2-» 6 d L&V2 1 2У2\ (128’)
ЙУ2 { dOj r* ^6 ^r2 r4 J ’
d2V d2v 1
dz'2 d(i2 r2
я следовательно,
£(®>=-7^(02~1)^ + e^}==O- (129>
Решением этого обыкновенного диференциального уравнения служит
i? = logfjA)2—1 — 6 j = log (1/^ — 1 — • (130)
Но v (—1) = 0 и lim v — оо при z1 ^=G. Таким образом прямая г=0,
Z-5-0
т. е. прямая, проходящая через точку Q параллельно оси Oz, является
для нашего решения особой линией. При интегрировании мы исключаем
эту прямую, окружая ее тонким цилиндром Се радиуса s. Поверхность,
по которой мы будем интегрировать, должна заключать в себе также
и цилиндр Се.
При таком выборе функции v подинтегральное выражение в левой
части формулы (127) обращается в силу (125) в vL(u) =— vf\ первый
интеграл справа в этой формуле (127) надо распространить на
а второй интеграл обращается в нуль, т. е. эта формула обращается
б следующую:
(131)
Если через ш мы обозначим азимут, то на цилиндре Cs мы будем иметь
dS— edydz, и, следовательно,
ИЪи ССйп , ,
v — dS — 11 — v s dy> dz. (132)
Се Се
Когда е->0, то slogs, а вместе с ним и интеграл (132) также стре-
мятся к нулю. Далее на цилиндре CG
ЙТ? Й17 йт» 2? d z’ , „
.— — — ’ — .. ~ . (133)
ЙУ йг йб г2 г2 р U2 — 1 г)/z'2 — г2
118 ИНТЕГРИРОВАНИЕ ДИФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Так при возрастании г (т. е. при возрастании 9) и убывает, то выраже- *
ние (133) должно быть отрицательным, а так как z' <^0 вдоль С, то j
квадратный радикал надо взять с положительным знаком. Далее, для не- I
больших значений в функция и. на С'6 зависит только от z. Если принять |
еще во внимание, что lim j/г'1 2 — е2 =— z' = t^— z^>0, то окажется, что I
е-»0
Г
С
Через zs обозначено здесь значение z в точке пересечения особой пря-
мой г—0 с поверхностью S. Итак,
с
2тг J и (С, IQ, z)dz — (и J (135)
г5 5
Эта формула дает нам значение
щей через точку Q параллельно
по С, мы найдем:
интеграла от и вдоль прямой, проходя-
оси Oz. Диференцируя это равенство
2тги(?, ЧД) = А
(136)
Можно проверить непосредственно, что это выражение является иско-
мым решением. Однако это доказательство сопряжено с значительными
трудностями, так как при диференцировании меняется, очевидно, поло-
жение конуса Г. Доказательство это было проведено полностью д’Аде-
маром Ч
Поучительно сравнить этот результат с решением уравнения Пуа-
ссона эллиптического типа:
Д«=-f(x,y, z). (137)
Согласно формуле Грина мы в данном случае имеем [см. § 59, (63)]:
г2 = (х - Е)2 + (J - г()2 + (z - О2,
а со равно либо единице, либо нулю, смотря по тому, лежит ли точка
с, Г|, £ внутри области интегрирования или вне ее. Проинтегрируем обе
части (138) по а затем продиференцируем по тому же переменному.
1 R. d’A d h ё m а г, Sur une classe d'equations aux derivees partielies du second
ordre, du type hyperbolique a 3 ou 4 variables independantes. Journal de Math., се-
рия 5, т. 10 (1904), стр. 131. Ср. также Les equations aux derivdes partielles a ca-
racteristiques reelles (Paris, Gauthier-Villars, 1907).
)
ПРИМЕНЕНИЕ МЕТОДА ВОЛЬТЕРРА К ВОЛНОВОМУ УРАВНЕНИЮ
119
Так как С входит только в — и в — — , то после этих двух операций
формула (138) примет следующий вид:
('3S>
где
f =log I—-в /~.—i^_1 - 1= ср. (1 да)
Jr 1 г (^—S)2-h(> — Xj)2 /(X—S)2j-(>—J])2 /
С другой стороны, если мы в. формуле (137) z заменим через й, то
диференциальное уравнение (137) перейдет в следующее
й2а Ъ2и Ъ2и
+ □«=—f(x,y,z), (141)
йх2 ду2 iz2
т. е. в уравнение (125). Функциям, после замены z и С через iz и и
отбрасывания постоянной интегрирования log I принимает следующий вид:
<?’ iog{|/(x_£()2_[_^_Jj)a 1 + (142)
т. е. преобразуется в v, а выражение
совпадает с (136). Сравнение (139) с (143) показывает, что при пере-
ходе от уравнения (137) к (141) производная по нормали переходит
в производную по направлению конормали, а расстояние г переходит
в „псевдорасстояние"
г'2 ~\/~(z— £)2-ф (х— Е)2 + (у — т))2>
и что множитель 4тг надо заменить множителем 2тг. В первом случае
поверхность, по которой интегрируют, остается одной и тою же при
всех значениях В, ц, Z, во втором она меняется при изменении положения
точки S, 1], Разница в том, что в уравнениях эллиптического типазначе-
„ йи
ниями и на замкнутой поверхности определяются уже значения , между
тем как в уравнениях гиперболического типа и значения и и значе-
йи
ния — можно задать произвольно и независимо друг от друга.
ctl'
Возьмем в качестве поверхности S’ плоскость t = 0) т. е. пло
скость z = 0,—это соответствует обычным начальным условиям—и
рассмотрим полупространство £4>0. Направление конормали будет при
этом противоположно направлению оси Oz, и
й(?'_ йф'_ 1
й> Ъг И
120
ИНТЕГРИРОВАНИЕ ДИФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Выражение (136), при /=0, примет вид:
и
., ,___________________= as 4- {
JJV (*— —(x—S)2—\У — *i)2
_______ i____________^_dS I
V(z— £)2 —(x —£)2— (y— r^Zz j
(144)
(Второй член был формально продиференцирован по изменение поло-
жения конуса при диференцировании не оказывает в данном случае ни-
какого В1ИЯНИЯ.) Мы пришли таким образом к решению Пуассона-Пар-
севаля, найденному нами в § 49, (188).
Ь) Применим метод Вольтерра к волновому уравнению в трехмерном
пространстве:
,, . _ й2и . й2и . й2и й2и
/(х, у, z, t}.
(145)
Можно х, у, z, t рассматривать как координаты точек четырехмерного
пространства. Характеристической функцией является
Ф -т X2 4- Xs ф Z2 — Т2, (143)
так что за характеристический конус можно снова принять круговой
конус с углом в 45° между образующей и высотой. Формула Грина
в данном случае дает:
{г»1(и)—aL(v)} dxdydzdt —
dS,
(147)
где
cos (vx) = cos (их), cos (yy) - = cos (ny), cos (vz) = cos (nz)„
cos (vt) = — cos (nt).
Интегрирование в левой части распространяется на четырехмерную
область, а в правой — на трехмерную границу этой области. Мы пред-
« йи
полагаем, что заданы значения и и — на поверхности 5, т. е. на трех-
мерном многообразии. Вычислим значение решения в точке Q(S, Т], С, т),
лежащей вне поверхности S. Относительно S и Q мы делаем предполо-
жение, аналогичное предположениям в трехмерном случае.
Положим опять:
х' = х — 5, у'—у — г' — z — С, f = t— Ts
^ = л:'2 + У2 + ^2, 6 = — ,
йб ____ . х' йб______________ , У йО___________ _ z' йО_____________ 1
йх’ Г2 ’ йУ г2 ’ йх’ г2 ’ й? г j
(148)
ПРИМЕНЕНИЕ МЕТОДА ВОЛЬТЕРРА К ВОЛНОВОМУ УРАВНЕНИЮ 121
И постараемся сначала найти решение решения v (6), зависящее только-
от нуля. Как и в (128'),
d2f __ /~dv\x's ,dv/l 2х'2\
~ ' 7^)’
й2® __„ d I dv\y'2 dv / 1 2у'2\
йу2'~“и<Д) Vd6/7^~”d0d)’
f z'2 / 1 2z'2\ (149'
te'2 “°rf6 Vrf6/ r* °cZO \ r2 r4 J ’
S2W 1 d2v
Следовательно,
T, 62 — 1 d2v
откуда
ЯП2=°> v = c® + b.
Для того чтобы функция v на конусе Г, т. е. при 6 = —1, обраща-
лась в нуль, необходимо, чтобы’ — а -|- Ь = 0. Поэтому мы можем по-
ложить:
t— 6
Эта функция при /у-0 и г—>0 имеет особенность.
По аналогии с предыдущим, построим гиперцилиндр Се, определяй
ный условием г= е; проекцией этого цилиндра в трехмерное простран-
ство х, у, z служит малый шар. Применим формулы (147) к области...
ограниченной гиперповерхностями S, Г и Ct. Имеем на Св:
Эг» йг» t-— ~
Sv Sr г2 ’
dS=г2 dm dt,
где dm — телесный угол. Вычислим предел соответствующего интеграла-
по поверхности, при е—>0:
= 4тг j (т — t) и (£, г;, С, t) dt,
(151>
122
ИНТ ГРИГОЧАНИЕ ДИФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
где значение ts аналогично значению zs. Подставив это выражение
s формулу (147), найдем:
4п
dv 36
U dft 3v
t — т
%
f___\
---------[- 1 I f dx dy dz dt,
- ЧШ
36 30 , . . 38 , . , 38 . . 36
Sv “ Vxcos +37 cos +37cos {nz) - xcos (nt) =
6 lx? . , . y' . , . / , Л cos(fiZ)
=-----7 — cos (пх) -f- — COS (ny) + — cos (nz) ---— =
T — t , cos («/)
= --^- cos(nr) — —--.
Дпференцируя равенство (153) по т, имеем:
4тт I и (Е, ц,
Jt —/ . .
и <—5— cos (яг) —
I r
(152)
(153)
(154)
г I !
s
— dS == J у dx dy dz dt.
^Найденное равенство (154) снова продиференцируем пот; мы получим:
Ж
4пи(Е, Tj, c, T)= —
и
1 Эи
3v
т — t , cos (л/)]
—— cos (nr)---------------- 6 —
r J
dS + зт J J ~ dx dy dz dt.
(155)
T
7=0
Черт. 91.
Эта формула представляет собою обоб-
щение формулы Кирхгофа - Лоренца
[см. § 75, (81)]. Чтобы получить эту
последнюю из (155), возьмем в каче-
стве гиперповерхности S часть гиперпло-
скости t — G, ограниченную замкнутой
поверхностью F трехмерного простран-
ства, и гиперцилиндр С, образующие
которого параллельны оси Ot, а нап-
равляющей служит двумерная поверхность
з (черт. 91). На гиперплоскости / = 0
имеем:
cos (пх) = cos (/z_y) = cos (nz) — О,
cos (nt) — 1,
cos (vx) — cos (vy) = cos (va) = 0, cos (>t) = — 1,
ПРИМЕНЕНИЕ МЕТОДА ВОЛЬТЕРРА К ВОЛНОВОМУ УРАВНЕНИЮ
123
а на гиперцилиндре С:
cos(yx) — cos(nx), cos(vy) = cos(/iy), cos(vz) = cos(nx),
cos (vf) = cos (nt) — 0, dS=dt da;
,da означает элемент поверхности F. Второй из интегралов в (155) при-
нимает таким образом следующий вид:
2
йг .
о
1 Ъи
— — da
Г дП
так как первый член в левой части этого выражения, представляющий
собою интеграл, распространенный на область, лежащую внутри а, от т
не зависит. (В интеграл по поверхности, стоящий в правой части этого
равенства, входит производная по нормали: чтобы получить ее, надо
при постоянном t вычислить производную по нормали от и (х, у, х, t)
и в полученное выражение подставить / — т — г.) Точно так же:
(157)
Первый интеграл, стоящий в правой части, от т не зависит, а потому
его производная равна нулю. Далее,
т — г Т— г
- J (т— i) и (х, у, z, t) dt — ru (х, у, x,i — г) и (х, у, х, t)dt, (158)
о о
и следовательно,
da =
с С J t
о
у, z,t —г) cos (nr) I
Г ' |
и (х, у, Z, Т-----г) COS (/2/j ,
------- ас —
8 и (х, у, х,т— г)
.2
da
S
Символ имеет в данном случае то же значение, что и
on
в уравне-
нии (95) § 62. Кроме того, надо принять во внимание, что cos(/7r)=—.
124
ИНТЕГРИРОВАНИЕ ДИФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Аналогично этому для четырехкратного интеграла имеем:
dx dy dz = j ff Лх Лу iz.
(160)
о
Подставив преобразованные интегралы из (156), (159) и (160)
мы получим:
в (155),
4nw(G, j;, С, т) = г-—- dxdydz—
С 1 йи(х, j, z,x~r) da
и (х, у, Z, т — г)
da.
(161)
Ъп
Эта формула представляет собою соединение формул Кирхгофа [§ 62,
(95)] и Лоренпа [§ 63, (99)]. Этот вывод формулы Кирхгофа-Лоренца
принадлежит Тедоне \
В случае трехмерного волнового уравнения легко показать, что би-
характеристики соответствуют световым лучам. Уравнением характери-
стических гиперповерхностей диференциального уравнения (145) служит:
rvy.
\йх/
(162)
Полный интеграл этого уравнения (см. § 23)
(563)
содержит четыре произвольные постоянные. Уравнение /=0 в про-
странстве х, у, z представляет плоскую волну, распространяющуюся со
скоростью, равною единице; дейст ви-
тельно, ее расстояние от начала равно
Черт. 92.
]/ г- -j- nil il -|- n‘l1 — c
У t~ +• -j - n'1
Пересечению гиперплоскостей /=0
и t—t0 соответствует
плоской волны в момент
щий интеграл уравнения
общая волна, является
гиперповерхностей /= 0;
ресечение с гиперплоскостью
дает нам положение общей волны
в момент t0 (черт. 92). Гиперпло-
скость f=0 касается огибающей S
точка касания плоской волны с общей
положение
t = t0. Об-
(162), т. е.
огибающею
а0— ее пе-
вдоль характеристики, так что
волной перемещается вдоль бихарактеристики, а это как раз и является
1 О. Те done, Sulla dimostrazione della formola che rappresenta analiticamente
il principlo di Huygfaens. Atti. del Lincei, серия 5, т. 5f (1896), стр. 357.
ПРИМЕНЕНИЕ МЕТОДА ВОЛЬТЕРРА К ДИФЕРЕНЦИАЛЬНОМУ УРАВНЕНИЮ 125
определением светового луча. Мы можем, кроме того, рассматривать
волну, представленную характеристической поверхностью S, как оги-
бающую всех тех характеристических коноидов, вершины которых ле-
экат на а0, т. е. на пересечении поверхности S с гиперплоскостью
t = Каждый коноид представляет собою волну, исходящую из одной
точки. Этому построению волны соответствует общеизвестное графиче-
ское представление принципа Гюйгенса.
§ 79. Применение метода Вольтерра к дифереициальному уравнению
затухающих пространственных волн. Телеграфное уравнение, т. е. ди-
ференциальное уравнение электрических волн в электропроводящей
среде [см. §17, (190), то же в приведенном виде см. § 46, (128), а
также §74,(61)] может быть обобщено на /z-мерное пространство:
й2и , й2н . <й2ы й2и , _
й^ + й4 + и=0' {,64)
В этом общем виде оно было исследовано Кулоном и Тедоне *. При
k—О получается уравнение незатухающих волн, которое мы уже
разобрали при я=1, 2, 3. Мы теперь наметим некоторые обобщения для
любого значения п, а затем перейдем к исследованию волн при k-/=()
и л==3.
_ <^и
Зададимся значениями и и — на некоторой части поверхности 5 и
ofl
постараемся найти значение и в точке Q (2,, 2 , т). Относи-
тельно S и Q мы делаем предположения, аналогичные тем, которые
были сделаны в предыдущих параграфах. Положим:
4 = *, —2j, х’2=х2 — в2, ... , < = — Вй, = т;
=(X -Л)2-н*2 - У2 + • • • + —U2=+4 + • • • + Ч2
и определим сначала решение и, зависящее только от г и t. На осно-
вании § 54 (36) в этом случае диференциальное уравнение преобра-
зуется так:
Ъ-и , п — 1 йи й2ы , , „
чтН------->—^ + /еи=°-
йг2 Г йг ЙГ2
Целесообразно положить « = (/ — т)х<р. В таком случае
= X (/— т)х-1<р-j-(/— т) J ,
s-4).-l)(^4-2<p4-2).(/--Trx4+(/-T)’g.
о?
1 I. С о u 1 о n, Sur I’intdsration des equations aux derivees partielles du second
ordre. These, Paris 1902. О. T e d о n e, Sulla integrazione deil’equazione delle onde
smorzate col metodo delle caratteristiche. Atti del Lined, серия 5, т. 22, (1913),
стр. 757. Sull’ integrazione delle equaz’onl a derivate parziali, linear! ed a coefdcienn
costantl del second’ordine. Там иге, серия 5, т. 23 (19 4), стр. 145.
126
Интегрирование лиференциальных уравнений
Наше уравнение принимает при этом следующий вид:
d2tp d2tp . п—1 dtp 2). dtp / „ ). О-—1)\
» + (*’—<|65>
Положим, как и ранее,
г г
и поставим себе задачей найти решение, которое на характеристиче-
ском конусе
X2 + X2 + •. - -}-Х2 — 7'2= о
принимало бы постоянное г2==/г2(/'2 —г2), ^>0 4 значение и имело Имеем: бы форму (р = -п(0)/(4, где
d£__J_ d/' — г ’ dr ~~ Т2 6 й20 -О ~ г ’ d/'2^ 0. d29 _ 2t'2 dr2 г3 _26 ’ /-2 ’
iz k2l' iz k"r df' Z ’ dr Z ’ d2^ t, /1 k2f2\ v'*=k (7-75-)=- 1 _u»!\ = dr2 Цг 1 z3 ) Подстановка tp==,w(0)/(г) в уравнение (165) k^r2 zs ’ k^t'2 дает: 4 ’ 4 (166)
я Р2/ | п- 1 У______I 2
|dr2 d£2 ‘ Г dr t — Т df ” j”1” | dr dr d/ d£ J
J ! n—1 —4 I______0
' |dr2 d/2 ' Г dr t — T d/ (t — T)2 J
(167)
В силу (166)
Если теперь
нулю, то мы
выражение, стоящее во второй скобке, обращается в нуль,
первую и последнюю скобки приравнять в отдельности
получим два обыкновенных диференпиальных уравнения:
d2f п-]-2Ы/
dz2 ' z dz
(168)
»44<з-»>’-|)ж-‘АА=о- (iral
Первое из этих уравнений связано с уравнениями
Бесселя (§ 101); ре-
шением его служит функция
Ж
2 "Г "
^ + Х
Z 2
1 В рассмотренном ранее случае <р имело вид »(0).
ПРИМЕНЕНИЕ МЕТОДА ВОЛЬТЕРРА К ДИФЕРЕНЦИАЛЬНОМУ УРАВНЕНИЮ 127
где Д(д)— функция Бесселя для мнимого аргумента:
(z \? + 2й
__ I
2 '
Liki(v±k)i
(170)'
В дальнейшем мы ограничим наше исследование только случаем /2 = 3.
Для 7 мы возьмем сначала значение нуль. При этих условиях урав
d^v
пение (169) обращается в -^- = 0. Решение, обращающееся в нуль на
характеристическом конусе 0 = — 1 [ср. предыдущие параграфы].,,
имеет вид:
= е 4-1=^=1 4-1.
1 г 1
Таким образом искомым решением уравнений (165) и (164) является
«о—
z
(171>
Если придать 1 значение единица, то уравнение (169) примет вид:
(1)2-1)
d^O
d№
2 dv
0 d§
Решением этого уравнения, обращающимся в нуль при 6= — 1, служит
tf-(6 + 1)2
U
f .__ *1»
Заменяя 6 его значением Ь=--------------. мы получаем второе частное ре-
шение уравнения (164):
t — т
Z/j = г
2 Л (4
д2
(17 :>
Теперь мы можем в формулу (147) подставить вместо v сначала zz0,.
а затем и zzr Левая часть равенства обратится при этом в нуль, в пра-
вой же части стоит интеграл, распространенный на гиперповерхность, на.
ЙИ
которой заданы значения и и —, на характеристический конус Г и на
гиперцилиндр Се, радиус е которого стремится к нулю. Обе функции
uQ и и, на характеристическом конусе обращаются в нуль, а на цилиндре
являются бесконечно большими того же порядка, что и —. При вы-
числении интеграла по Се надо помнить, что и() представляет собою
128
ИНТЕГРИРОВАНИЕ ДИФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Ф (г, t) ,
функцию вида 1 —и чт0 у имеет частные производные любого
•порядка по обеим переменным; таким образом
1 . 1 йФ
ЙГ Г2 т 1 Г дг
(173)
Следовательно, при предельном переходе по е—>0, как и в (151),
•остается только первый член. Далее,
где —телесный угол. При г = е—>0 имеем: z — — kf — k(x — t)
.{при этом т ^>/), а потому в результате предельного перехода по-
лучаем:
^ \ «(£, э], С, — t)]dt-
fx> }
is имеет в данном случае то же значение, что и в § 78. Если бы вме-
сто и0 мы в (147) подставили uv то, действуя точно так же после пре-
дельного перехода, мы бы нашли:
4тг Г
fs
Все эти преобразования приводят нас к формулам, аналогичным (152):.
(С, ч, с, ^_ф0)
U (М> U) Z2 [k {X- /)] dt = A jjj (« - u. dS=<^.
ts s
(174)
Функции, стоящие в правой части этого равенства, надо считать изве-
стными, так как они могут быть вычислены на основании данных за-
дачи. Они содержат начальные значения и и . По своему строению
-формулы (174) сходны с (135) и (152), однако формула (174) несколько
сложнее, так как множителем при и в них стоит не единица, как
® (135), и не т— t, как в (152), а бесселевы функций. Таким образом
для и мы получаем два интегральных уравнения вида:
X
K(x£)f(Z) dZ = (f (х)
х0
МЕТОД АДАМАРА. ФУНДАМЕНТАЛЬНЫЕ РЕШЕНИЯ
129
[/< и <р — известные функции, /—неизвестная, ср. § 40, (288), а также
гл. IX]. в котором одним из пределов интеграции служит переменная
величина. Такие интегральные уравнения называются уравнениями
Вольтерра.
В данном случае, когда мы имеем дело с двумя уравнениями Воль-
терра, можно получить решение, как показал Тедоне, и без применения
теории интегральных уравнений. Действительно, согласно определению
(170) [ср. § 100, (18)]
= (z), 2—^ = /2(2)-[-Zo(2).
Далее, (0) = Z2 (0) = 0, так что при диференцировании (174) по т оста-
ются только члены, содержащие производные подинтегральной функции.
Итак, мы имеем:
^2 = С zz (£, »], Z, t) k^-dt =
йт J йт
А
(175)
Вторичное диференцирование в силу равенства Zo (0) = 1 дает:
2 Й2ФО
k
ЙФ
ЙТ
(176)
На основании этой формулы нетрудно показать, что в данном слу-
чае, как и в одномерном пространстве, остается „след“ волны.
§ ЬО. Метод Адамара. Фундаментальные решения. Адамар в целом
ряде замечательных работ 1 распространил метод интегрирования Римана
на общие линейные диференциальные уравнения гиперболического типа.
Здесь мы вкратце изложим ход его рассуждений, отослав читателей,
интересующихся подробностями, к указанным работам.
Мы видели, какое большое значение имеют функциональные реше-
1
ния — (в трехмерном пространстве) и log г (в двумерном) для исследо-
вания уравнения Лапласа — уравнения эллиптического типа — и как
с помощью этих решений и формулы Грина мы можем получить реше-
ния краевых задач. Мы показали также, как формально можно перехо-
* Recherches sur les solutions fondamentales et 1’intfegration des Equations linfe-
aires aux deiivces partielles. Ann. ГЕс. Norm. Sup. t. 21 (1904), стр. 535, т. 22 (1905),
стр. 101. Les p obie.nes aux limites dans la thfeorie des fequatio s aux derivees p>r-
tielles. Journal de Physique, t. 6 (1907), стр. 202. Thfeorie des equations aux derivees
partielles lineaires hyp₽rboliques et du prob.feme de Cauchy, Acta Mathemitica, t. 31
(1908), стр. 333, наконец, см. также книгу, на которую была ссылка в § 70 .Lec-
tures on Cauchy’s problem”...
9 B a fi era n. ТТтгЛ>ат1АппэтАлтАииа гпаппапттл.
130
ИНТЕГРИРОВАНИЕ ДИФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
дить от уравнений эллиптического типа к гиперболическим и точно так
же формально от решения одних к решению других. Мы, однако, уста-
новили, что между этими двумя решениями существует также и корен-
ное различие. Для уравнений эллиптического типа мы не можем совер-
шенно произвольно задать на замкнутой пограничной поверхности
краевые значения как искомой функции, так и ее производной по нор-
мали. В случае уравнений гиперболического типа многообразие, огра-
ничивающее область, незамкнуто, и можно произвольно задать на нем
как значения самой функции, так и значения ее производной в направ-
лении конормали. Характеристический коноид в этом случае действите-
лен, и им пользуются при применении формулы Грина. Но аналогичный
подход к решению задачи в случае уравнений гиперболического типа
и испбльзование в качестве фундаментальных решений и log/, где
/ — псевдорасстояние между точками х, у, г и £, j), Z, оказывается не-
возможным. Действительно, это решение на характеристическом коноиде
обращается в бесконечность. На этом основании Вольтерра вместо этих
функций пользуется их интегралом по £ [ср. (130) и (142)] и прихо-
дит, таким образом, к интегралу искомого решения по Z (135). Явная
форма решения Вольтерра [т. е. решение Пуассона-Парсеваля (188) §49]
показывает, что трудности заложены в самой природе этих вопросов:
формальное диференцирование этих интегралов приводит к интегралам,
которые на характеристическом коноиде не имеют смысла.
Выясним теперь на основании одного простого соображения, каким
образом Адамар преодолел эти затруднения. Пусть а<^Ь, 0<^а<^1.
Интеграл
ь
(dx
(b — х)^ ’
а
очевидно, в таком случае расходится. Точно так же расходится, вообще
говоря, и интеграл
ь
fA (х) dx
~ {Ь-х)1*”-'
а
(177)
где А (х) — непрерывная функция. Однако, если А (х) имеет "эпрерыв-
ную производную или если даже она только удовлетворяет условию
Липшица
| А (&) — А (х) | const ] b — х |,
то можно найти такое постоянное число В, чтобы предел
11 ш
х -ьЪ
X
f А (х) dx ! В
J (f> —x)1+e‘T"(f> —х)“
(177>
МЕТОД АДАМАРА. ФУНДАМЕНТАЛЬНЫЕ РЕШЕНИЯ
131
существовал. Действительно, выражение в квадратных скобках можно
переписать в следующем виде:
Г A (x) — A(b) A(b)[ 1 1 \ В
J (Ь — х)1+а Х а \(6— х)а (Ь — а)°- / ' (Ь — х)° ‘ (178)
а
Первое подинтегралыюе выражение интегрируемо, так как
бесконечно малое того же порядка, что и b — х. Если
числитель его
В подобрать
так, чтобы
^>-В = 0,
а
то выражение (178) при х—>Ь стремится к
ь
А(х} — А (Ь)
{Ь — х)1+“
МУ
а(Ь — а)а’
(179)
Адамар называет выражение (179) конечной частью (177) и
его так:
__ .
f А (х) dx
J (Ь — хУ+а'
а
обозначает
(180)
Это понятие можно обобщить еще дальше. Можно сначала принять,
что показатель знаменателя в выражении (177) равен р-)-а, где р —
целое положительное число, а А (х) имеет непрерывные производные
всех порядков вплоть до р-го включительно. В этом случае в добавляе-
мом в формуле (177') слагаемом постоянное В надо заменить много-
членом (п—1)-й степени, подобрав соответствующим образом коэфи-
циенты этого последнего. Дальнейшие обобщения касаются /z-кратных
интегралов; их можно аналогичным образом сделать конечными, доба-
вив к ним соответствующие (и— 1)-кратные интегралы. Эти понятия
в методе Адамара играют очень существенную роль.
Рассмотрим, например, волновое уравнение в двумерном пространстве:
й2« . й2и й2м________________
iu2-^2-’
к которому мы раньше (см. § 78, а) применили метод Вольтерра. По-
ложим:
/< = (Z — Q2 - (X — В)2 — (у — Ч)2.
1 --
Как легко видеть, =К 2 представляет собою решение нашего урав-
132 ИНТЕГРИРОВАНИЕ ДИФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
нения. Подставим это решение в формулу Грина (127), т. е. пусть Л
_ 1
v = K 2 . Так как, согласно § 78, а
А ж cos (пх) Д -4- cos (пу) -cos (nz),
Sv ' ' dx 1 dy Zz
TO
A ——
— = К 2 { cos (nx) (5 — x) -f- COS (ny) (>] —y) -|- cos (nz) (C — z)},
и мы таким образом получим:
{cos(/zx)(E—x)+cos(ny)(-r[—y)+cos(nz)(H,—z)} dS. (181)
tf2
_ 3
Так как К 2 в вершине конуса обращается в бесконечность, то
эту вершину надо исключить, окружив ее небольшой сферой. Выбрав
соответствующим образом область интегрирования, мы после нескольких
предельных переходов, на которых мы не будем останавливаться,
приходим к формуле:
2пи(В, щ, ?) =
—у { cos (пх)$—x)-|-cos(/zy)(j] —_y)-f-cos (nz)(Z—z)}
К2
dS,
причем интеграл в правой части этой формулы надо понимать так же,
1
как и (177). В данном случае а== —, а верхнему пределу b соответствует
пересечение данной поверхности с характеристическим конусом /С=0.
Интегрирование надо распространить на вырезанную характеристическим
конусом часть данной поверхности. Интеграл по конусу надо отбросить.
Справедливость сказанного выясняется в указанной выше работе Ада-
мара, помещенной в Acta Mathematica.
Выберем, например, в качестве начальной поверхности плоскость
2 = 0 и введем полярные координаты:
х — (• —rcostp, у — j]=rsin(p; dS=rdrdy.
Конечная часть искомого интеграла в таком случае равна [ср. (179)]:
С 2.т С 2г
SC и (г) dr dy С С Z {и (г) — и (?)} rdrdy
(?-rf J J (C2-^
оо о о
2г
и (?) dy.
(182)
ВОЛНА РАЗРЫВОВ
133
Пои этом и (£-J-rcos tp, j)-|~rs,ntP, 0) мы сокращенно обозначили
а (г). Итак, мы получим решение задачи Коши в следующем виде:
С 2к 2л
rdrdtp-[- I и (ty dtp.
через
2п« (2, Ч, 0 =
[ 1 дИ :{и(г)—ио}
3
|/<2 (^2_Г2)2
(183)
о о
о
Подобным же образом можно поступить и в общем случае, причем
случай четного числа независимых переменных значительно сложнее ра-
зобранного нами в общих чертах случая нечетного числа переменных.
Подробнее с этим вопросом можно ознакомиться в указанной нами
литературе.
§ 81. Волна разрывов. При выводе волнового уравнения в § 12 мы
ограничились рассмотрением только очень малых смещений, благодаря
этому волновое уравнение оказалось линейным. Однако, как показывает
опыт, смещения отдельных частиц при распространении звуковой волны
в действительности не бесконечно малы. Более того, ряд опытов пока-
зывает, что как плотность, так и скорость или ускорение имеют раз-
рывы в пространстве и во времени, и что эти разрывы распространяются
подобно волнам. Начало теоретической разработки этих явлений было
положено Риманом и Гюгонио1. Мы ограничимся только общим очер-
ком их идей. Подробное изложение этого вопроса можно найти в книге
Адамара „Lemons sur la propagation des ondes“ (Paris, 1903).
Простейшим примером, указывающим на существование волн раз-
рывов, может служить заключенный в трубу газ, которому мы сообщаем
движение с помощью толчка. Возьмем, например, цилиндрическую трубу,
на которую в точках х—0 и х=/ помешены подвижные поршни.
Обозначим через и смещение частиц воздуха. При указанных выше
(§ 12) предположениях имеет место уравнение:
д2и „ й2и
--- __
М2 дх2’
Если в какой-либо момент t — t0 задать положение и скорость частиц
воздуха: u = F(x) и ^~i — G(x), то, диференцируя по х, мы найдем
для ускорения в тот же момент t0 уравнение:
г^и
а2
— a2F"(x).
Однако
движение поршней можно задать независимо от начального их положе-
ния, а потому действительное ускорение частиц воздуха будет, вообще
говоря, отличаться от ускорения, найденного на основании волнового
уравнения. В точках соприкосновения воздуха с поршнями ускорение
1 В. R i е m a n n, Uber die Fortpflanzung ebener Luftwellen von endlicher Schwin-
gungsweite, Abh. KOnigl. Ges. der Wiss. Gottingen, t. 8 (1860); H. Hugoniot, Sur
la propagation du mouvement dans les corps, Journal de i’Ecole Polytechnique,
t. 57, стр. 15 (1887); M&noire sur la propagation du mouvement dans un iluide in-
ddfini, Journal de Math., t. 3-4 (1887). Гюгонио был артиллерийским офицером; на
эти исследования его натолкнули задачи внутренней балистики.
134
ИНТЕГРИРОВАНИЕ ДИФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
имеет разрыв, который при движении поршней распространяется волно-
образно. Даже в случае закрепленных концов, который мы особенно
подробно разобрали, приходящая волна не вполне совпадает с теорети-
чески вычисленной: ее ускорение, теоретически сводящееся к нулю, в
действительности может не равняться нулю. Бывают также случаи, когда
на некоторых поверхностях претерпевает разрыв не ускорение, а ско-
рость или плотность. Так, движение снаряда, скорость которого превос-
ходит скорость звука, сопровождается скачкообразным изменением в плот-
ности воздуха, так называемой волной удара (onde de choc, Stosswelley,
это изменение плотности можно показать и экспериментально, благодаря
изменению показателя преломления
/7 вблизи снаряда; это изменение наб-
/ / \ \ людают с помощью электрической
/ X. искры (черт. 93). Внезапное уплотне-
/ X. ние воздуха вблизи орудия, из кото-
/ X. рого выстрелили, может произвести
/ ____ X. значительный механический эффект.
/ / \ X. Раньше чем математически фор-
/ \ мулировать эти вопросы, вернемся
/ \ опять к основным уравнениям гидро-
динамики. В дальнейшем мы будем
Черт. 93. пользоваться так называемыми урав-
нениями Лагранжа, а не уравнениями
Эйлера, найденными нами в § 12. Начнем наше исследование с вывода
уравнений Лагранжа. Обозначим через х, у, z координаты некоторой
определенной частицы жидкости. Когда жидкость течет, эти координаты
с течением времени меняются. Самую частицу можно характеризовать
с помощью трех параметров а, Ъ, с; в качестве таких параметров можно
взять, например, прямоугольные или криволинейные (см. § 90) коорди-
наты точки в момент t = 0. Таким образом
х~х(а, Ь, с, t), y=y(a,b,c,f), z = z(a, b, c, t).
Изменяя a, b, с при заданном t, мы получаем координаты всех точек
пространства, занимаемых частицами жидкости в определенный момент;
изменяя t при заданных значениях а, Ь, с, мы найдем все те положения,
которые принимает данная частица жидкости при своем движении. При
задании движения данной частицы (а, Ь, с постоянны) мы будем поль-
зоваться символами обыкновенных производных; в прочих же случаях
мы будем писать частные производные. Таким образом компонентами
скорости служат
dx dy dz
т> = — . v = - — . ч> = —
х dt' у dt ’ г dt '
а компонентами ускорения
d?x dzy d2z
~d&' ~diJ'
РАЗРЫВЫ ПЕРВОГО ПОРЯДКА (ВОЛНЫ УЛАРА)
135
Эти последние заменяют четыре члена в левых частях уравнений (106) § 12.
Уравнения гидродинамики принимают при этом следующий вид:
d?x __F — _F __L*P ^L — f —— (184)
dt* x p Ъх’ dt* » ply’ dt* * p 1 1
где p — плотность, a p— давление. Эти три уравнения можно заменить
одним векторным:
d2r _ 1 .
(185)
г здесь — радиус-вектор движущейся частицы.
Чтобы получить уравнение сплошности, рассмотрим часть жидкости,
которая вначале занимает прямоугольный параллелепипед, координаты
двух противоположных вершин ков рого суть а, Ь, с и a -j- da. b -|- db,
с ^\ dc. Через бесконечно малый промежуток времени dt точка а,Ь,с
переходит в х, у, z, а сам параллелепипед претерпевает бесконечно ма-
лую деформацию: ребро da, параллельное оси Ох, переходит в отрезок,
проекции которого приближенно равны
йх , йу йг
•—da, ~db, —de.
йа йо йс
То же происходит и с двумя другими ребрами. В силу формулы (15) § 3
объем измененного параллелепипеда р^вен
ЙХ йг
ia йа йсг
ЙХ йу йг
ib db йГ da db de.
ЙС йу йг
йх йс йс
Так как масса параллелепипеда постоянна, то его плотность обратно про-
порциональна объему. Таким образом мы получаем уравнение сплошности:
ЙХ ЙХ ЙХ
йа дЬ йс
C0 = ^°- йу йу йу_
Р На ЙЙ йс
йг йг йг
йа йс
(185)
р0 здесь постоянно; со мы будем называть отношением объемных рас-
(0 -
ширений, а ——удельным объемом.
§ 82. Разрывы первого порядка (волны удара). Проследим за движе-
нием частицы, которая вначале находилась на поверхности F(a. b, с) = 0.
Пусть (р — функция точки, заданная во всем пространстве. Введем еле-
138
ИНТЕГРИРОВАНИЕ ДИФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
дующее обозначение: если какая-либо функция при приближении к неко-
торой точке поверхности с двух противоположных сторон этой поверх-
ности стремится к пределам и <Ь2, то мы будем писать оф = ф2— ф .
Например, если функции у непрерывная, то tp] = <р2 и о(р —0.
Предположим, кроме того, что функция ср по обе стороны поверх-
ности диференцируема, но производные с различных сторон поверх-
ности могут и не совпадать между собой. Рассмотрим смещение, касатель-
ное к поверхности; для него
dm = d« “А ф~ v1 de,
Т1 Ъа 1 db 1 5с
dcp2 = da ф- db -ф-de.
Т2 5а 1 ЪЬ 1 5с
(187)
На поверхности <р1 = <р2, а потому
к 5с
= 0,
т. е.
° 5а
dc = O,
ЪЬ ' 5с
где da, db, de связаны соотношением
5F . 5F 5F
—- da А- — db4-~ dc=0.
5a 56 1 5c
„ 5» ^5» .5'д
Следовательно, вектор, компоненты которого о , о^-, о — , перпенди-
кулярен к поверхности. Этот вектор даст величину скачка градиента tp.
Мы имеем:
. . 1 5F , . 1 5F , v 1 5F
cos (пх) = — — , cos (пу) = -у- —, cos (nz) = — — ,
Л 5а h ЪЬ ' ' Л 5с
h2~
/г>0,
и следовательно,
t.5^ . 1 5F
г*г
1 5F
-=ХС05(/^) = ф^,
de h de
(188)
где 1 — множитель пропорциональности. В векторной форме эти
ства равносильны следующему:
8 V tP==^ni>
равен»
(188')
где \7<р [см. § 4, (23)] означает градиент <р, а есть единичный вектор
в направлении нормали к поверхности F=0.
разрывы первого порядка (волны удара) 137
Сказанное может быть применено к каждой из трех компонент
X, у, z непрерывной во всем пространстве вектор-функции D, которая
имеет производные по обе стороны от поверхности А=0. Множителю к
соответствуют здесь три множителя Нх, Ну, Hz, которые можно считать
компонентами вектора Н. В таком случае
. ЙХ „ . . ЙХ . . ЙХ
S — = Н cos (пх), ё —=Н cos (пу), ё — = Н cos (nz); da •* ^b x ' dc х \
ё == Ну cos (пх), ё^ = Ну cos (пу), ё~~ = Ну cos (nz); . (189)
8<f-^^4cos(ny), ^=Hecos(nz). ОС* Ov
Если через А обозначим вектор, имеющий произвольное направление^
то эти девять уравнений можно заменить одним векторным уравнением:
^(VD)A = n1HA. (190)
Равносильность уравнений (189'» и (190) легко можно проверить, придав,
вектору А последовательно наг равления осей Ох, Оу, Oz.
Если первые производные радиуса-вектора D на искомой поверхности,
претерпевают разрыв, между тем как сам радиус-вектор D на этой по-
верхности непрерывен, то в этом случае Адамар называет уравнения
(189) й (190)условиями тождественности. В этом случаемы говорим,
что движение жидкости претерпевает разрыв первого рода. Условия
тождественности вполне определяются заданием вектора Н во всех точ-
ках поверхности.
При выводе этих условий существенно, что носителями разрывов
являются одни и те же частицы жидкости. Может, однако, случиться,
что разрывы будут происходить на поверхности, меняющейся с тече-
нием времени в пространстве а, Ь, с. В этом последнем случае должны
быть удовлетворены условия, которые Гюгонио назвал условиями кине-
матической совместности. Пусть F(a, Ъ, с, О — 0—меняющаяся с тече-
нием времени поверхность в трехмерном пространстве, которая является
геометрическим местом разрывов. Можно, однако, считать, аналогично'
тому, как мы делали раньше, что это уравнение представляет собою
неизменную поверхность в четырехмерном пространстве a, b, с, t (гипер-
поверхность). Возьмем функцию со= tp (a, b, с, t), непрерывную во всем-
пространстве и имеющую односторонние производные по обе стороны
от вышеуказанной поверхности, опять имеем:
(191>
1 da 1 db 1 de 1 dt
для всякого смещения, для которого
dF, I I , Й^^ „
to da+db db + й? dc + ¥ dt=°- (I92>
Отсюда мы, как и раньше, заключаем, что четырехмерный градиент
138
ИНТЕГРИРОВАНИЕ ДИФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
три прохождении сквозь поверхность делает скачок в направлении
«нормали. При соответствующем значении 1 удовлетворяются равенства:
gd'f __ 1 йГ _________1_йГ ^йср____)^йГ
йа h ia' ib h ib ' йс h йс ’ й/ h W ’
тде h имеет указанное выше значение. Применим эти преобразования
к непрерывной вектор-функции от а, Ь, с, t. Мы получим уравнения
(189), к которым необходимо
.dx HiF
о________________— _х_____
dt h it ’
прибавить еще и следующие:
jiy^iF
° dt h it ’
dz HiF
g_____«
dt h й/ *
(189а)
Если х, у, z
компоненты
направлению
смещения, то уравнения (189a) дают нам
своему
очень
суть компоненты
скорости; это — вектор, совпадающий по
1 йГ
равный — — Н. Множитель при Н имеет
h dt
Пусть будет dn путь, который проходит
скачка
простое значение.
Г (a, Ь, с, t) = 0 в пространстве а, Ь, с за время dt. Тогда
Ja = rf«cos(/zr), db = dncos (ny), de = dn cos (nz);
волна
с Н и
но мы имеем:
ЙГ , , л ЙГ , , . ЙГ . , .
— —Acos(«x), — — htoslny), — = h cos (nz),
ia ib ic
а потому
1 йF dn д
lt^i~dt~ ’
(193)
т. е. этот множитель равен скорости распространения разрывов в про-
странстве а, Ь, с. Таким образом разрыв первого рода вполне опреде-
ляется одним вектором Н и одним скаляром 0, которые удовлетворяют
двенадцати уравнениям (189) и (189а). Разрыв первого рода называется
продольным или поперечным, если Н является нормальным вектором или
вектором касательным.
Величина 0 дает нам скорость распространения волны разрыва отно-
сительно часгиц жидкости Абсолютную скорость этой волны относи-
тельно неподвижной системы координат мы получим, если вернемся
к координатам х, у, z. Пусть уравнение волны будет
Ф(х, у, z, t) = 0.
Тогда, так же как и в (193), мы найдем, что скорость смещения равна:
йФ
Т=--------1________- (194)
Отсюда можно вычислить разрывы скорости распространения 0 на иско-
мой волне. Пусть 5 (черт. 94) представляет собою положение волны
РАЗРЫВЫ ВТОРОГО ПОРЯДКА (волны ускорения)
139
в момент t, a S' — ее положение в момент t dt. Рассмотрим цилиндр,
заключенный между двумя поверхностями, поперечным сечением кото-
рого служит элемент dS, а образующие в
каждой своей точке нормальны соответствую-
щей поверхности .S’. Высота этого цилиндра
равна Т dt, а его объем Тdt dS. Пусть он
неподвижен в пространстве, и пусть в мо-
мент t он находится на стороне 2 поверхности
разрыва; пусть, кроме того, плотность заклю-
ченной в этом цилиндре жидкости равна р2.
В момент t-\-dt он окажется на стороне /,
и притом плотность наполняющей его жид-
кости станет равной рг Приращение массы
составляет таким образом (ра — р2) Тdt dS.
Это приращение должно быть равно массе
жидкости, которая в течение того же вре-
мени dt проникла в цилиндр. Обозначим
через г» и vn* скорости потока в направ-
лении, нормальном к сторонам 1 и 2. Через
конец / в цилиндр втекает масса py^dtdS,
а через конец 2 вытекает масса p,yn*dtdS. Таким образом
(Pi — Рг) TdtdS= (pyni — p2vj dtdS
Pi(r—VJ = P2(7'—
Но разность Т—есть не что иное, как скорость распростра-
нения волны разрыва относительно жидкости на стороне /; аналогичное
значение имеет и разность Т—г'л, = б2- Следовательно,
Pi®i ~Рг®2-
(195)
если только
Таким образом
§ 83. Разрывы второго порядка (волны ускорения). Пусть все произ-
водные первого порядка некоторой функции непрерывны, но зато про-
изводные второго порядка имеют на некоторой поверхности F(a, b, с,) —О
„ дк
разрывы. Если производную — подвергнуть таким же преобразованиям,
да.
каким мы в предыдущем параграфе подвергали функцию и>, то в ре-
зультате диференцнрования вдоль поверхности F(a, b, с) —0 мы получим:
s й2х . . й2х „ й2х
8 —- da -j- § ——— db -j— о -—— de = О,
йа2 й«й& йайс
ЙЛ , . ЙЛ . ЙГ
-— det, —I— —- db -4— -— de О
йа 1 db 1 йс
^й2х . й2х й2х
о — с---------- о------
йа2 й« db___ да дс
If ~' dF dF~ '
да db дс
140
ИНТЕГРИРОВАНИЕ ДИФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
ЙХ ЙХ
Для и аналогичным образом получается*
аЬ оС
8 й2х -Й2Х й2х
да дЬ db2 db дС
- =ТГ— чг- ~ И Т* Л
dF dF dF
da db de
Эти уравнения, как легко видеть, равносильны следующим:
й^х_/^/йгу —
°йа2“ h2[da ) ’ ° db2~ h*\db ) ’ йс2 ~ Л2 U J ’
й2х __HxdFdF . й2х _H^dFdF „ й2х _HxdFdF
da db h2 da db ’ db de h2 db de * ° Йе da h2 de da ' 19®^
Такие же уравнения имеют место для у и z, с той только разницей,
что в них вместо Нх входят соответственно Ну и Нг. Таким образом
искомый разрыв вполне определяется вектором Н.
Вычислим скачки, которые делают производные по переменным
dx dv dz _
a,b,c от компонент скорости —, —, —. Так как, согласно предпо-
’ dt dt dt
dx
ложению, § — ==0, то, как и в (189), находим:
. d dx Н dF
о-----— - - -
da dt h да
Й dx Н' dF й dx Н' dF
S-----= g-------
db dt h. db de dt h de
d dytfdF d dy FfdF
________ J, _ _______________
da dt h da ’ db dt h db ’
Й dy FfdF
0 — и T. Д.
de dt h de
(197)
Вектор H' с компонентами 7/, H’y, H'g опять однозначно характе-
ризует разрывы. Ускорения дают нам третий вектор Н". Однако эти
векторы не независимы друг от друга: их связывают друг с другом условия
кинематической совместности. Чтобы найти эти последние, предположим
опять-таки, что функция F зависит от a, b, с, t. В таком случае
dF
da
dF
db '
dF
de
ЙЛ"
dt
И мы получаем, как и раньше:
.й2х й dx
da2 ° da dt
~dF'"= dF ’
da dt
ТЕОРЕМА ГЮГОНИО О СКОРО'ТИ
141
Отсюда в силу (193), (196) и (197) следует:
Н ЛЕ
Н‘у=—<'НУ <™>
Таким образом вектор Н' имеет то же направление, что и вектор Н, и полу-
чается путем умножения этого последнего на отрицательную скорость.
Аналогично этому для третьего вектора Н" имеем:
Н"х-=~^ (199)
таким образом Н" получается из Н' гак же, как Н' из Н. Из трех век-
торов Н, Н’ и Н" первый и третий направлены в одну и ту же сторону,
а второй в противоположную; абсолютные величины этих векторов
составляют геометрическую прогрессию с знаменателем 6 (скорость
распространения волны относительно жидкости).
На основании формул (189) можно вычислить скачок, который де-
лает дивергенция непрерывного на заданной поверхности вектора D
(с компонентами х, у, z), которая имеет на этой поверхности разрыв
первого рода. Диагональные элементы в формулах (189) дают:
§divD —о
йх йу . йз\
йа ' ЪЬ йг /
Hxcos (пх) -|- Ну cos (пу)-\-Нг cos (nz) = Нп.
Например, из (189) в соответствии с уравнениями (197) следует, что
в волне второго порядка дивергенция скорости, которая сама предпо-
лагается непрерывной, образует скачок:
о div v = Нп. (200)
§ 84. Теорема Гюгонио о скорости. Скорость распространения волн
ускорения можно вычислить на основании очень важной теоремы Гю-
гонио с помощью так называемых уравнений динамической совместимости,
не прибегая к интегрированию уравнений движения. В § 12 мы при-
няли, что давление р = о (р) пропорционально плотности р. При невы-
полнении этого условия и' (р) перестает быть постоянной, и уравнения
движения (184) приобретают усложненную форму:
d2x
dt*
Применим
(внешние
рыв ними)
х * w йх ’ dt2 У ‘ w йу ’
Й1оцр
(201)
эти
силы
Тогда
уравнения к поверхности разрыва второго порядка
и ср' (р) предполагаются на этой поверхности непре-
= —(Р) S V log р.
(202)
Для скалярной функции logp условия тождественности дают:
S Vlogp^hlp
(203)
142 ИНТЕГРИРОВАНИЕ ДИФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
а из меня условий кинематической совместимости для производных по вр«- получается: »•
Множитель X в (203) и (204) имеет одно и то же значение, а 6 озна-
чает искомую скорость. Перепишем уравнение сплошности [ср. значение двух первых членов в [см. § 12, (107)] в следующем виде § 8, (77)]:
^logp_ dt — div v. (203)
Отсюда находим скачок g<Z1ogp_ dt — S div v, (206)
или на основании (200) rflogp * dt = (207)
Сравнивая полученное выражение с формулой (204), находим, что при 6^=0:
-ч-
Подставив это значение X в (203), получаем:
S V IogP =4’ Чп1- <208>
Таким образом из (202), в силу (199), получается:
62Н' = ср' (р) 7/nr (209)
Это векторное уравнение показывает, что при 6 =7= 0 вектор Н' направ-
лен по нормали, и что мы при этом имеем дело с продольным разры-
вом, который распространяется со скоростью
o=j/W)=]/ <210>
При 0 = 0 и Hn = Q разрыв становится поперечным, стационарным и все
время связан с одними и теми же частицами. Уравнение (210) представ-
ляет собою знаменитую формулу Лапласа для скорости звука; она согла-
суется с результатами, найденными нами для небольших амплитуд (см.
§ 26; скорость а пропорциональна Ут). Мы видим, таким образом, что,
вообще говоря, скорость изменяется с изменением плотности.
§ 85. Одномерное движение газа. Характеристики. Распространение
волн в каком-либо определенном направлении (например движение газа
в цилиндре параллельно оси цилиндра) было особенно подробно иссле-
довано Гюгонио и Риманом. Пусть будет и смещение в направлении
ОДНОМЕРНОЕ ДВИЖЕНИЕ ГАЗА. ХАРАКТЕРИСТИКИ
143'
оси цилиндра (оси Ох), и пусть оно удовлетворяет общему диферен-
циальному уравнению в частных производных второго порядка:
й2п . й2« . й2«
—- -П 2В —— -4- С = F х, t, и,
йх' 1 <1х й гй<2 \
й«
ЙХ’
й«\
й/ ) ’
(211)
где А, В, Си F—аналитические функции. Рассмотрим поверхность с раз-
рывом второго порядка. Пусть движение с одной стороны этой по-
верхности представляется интегралом а с другой—интегралом и2.
Чтобы эти движения переходили одно в другое, должны выполняться
условия совместности Гюгонио. На поверхности разрыва мы имеем:
г«=о, г^=о.
йх й/
Уравнениями совместности служат:
й2и , . j. й2п ,, _ j. й2« , . _й2п _
ss?‘/*+!W‘“=0’ sw‘,x+s^-°- (212>
Оба интеграла должны удовлетворять уравнению (211), у которого
в правой части стоит непрерывная функция. Поэтому
А2ВЪ = 0.
йх2 1 йхй/ #/2
Мы получили три
разрешены только в
в нуль, т. е. когда
dx dt
0 dx
А 2В
уравнения для трех скачков, которые могут быть
том случае, когда их детерминант" обращается
о
dt = Сdx2—2B dx dtAdt2 — 0.
С
(
(213)
уже нами получено в начале главы [см. (8)]; оно
й«\ г> „
-т ). Разрыв, имеющий место у произ-
ot /
Это уравнение было
представляет собою уравнение характеристик.
Мы видим, таким образом, что волны ускорения распространяются
вдоль характеристик. Это свойство волн ускорения вполне определяет
характеристики. Действительно, мы уже говорили, что, если и рас-
сматривать как функцию х и t, то характеристики могут быть опреде-
лены как проекции тех линий, вдоль которых интегральные поверхности
соприкасаются между собою. В случае разрыва второго порядка орди-
наты и и касательные плоскости непрерывны, bu~bp = bq = Q (р и q
обозначают производные — и
оХ
водных второго порядка, показывает, что обе поверхности имеют раз-
личную кривизну.
При изучении различных вопросов акустики и оптики в предыдущих
главах мы предполагали все втемя, что смещения бесконечно малы. Мы
хотим показать сейчас, что если отказаться от этого предположения,
то знакомое нам волновое уравнение надо будет заменить нелинейным
уравнением. Понятие характеристики можно почти без труда перенести
144
ИНТЕГРИРОВАНИЕ ДИФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
на такие нелинейные уравнения, в частности на уравнения вида ([)
или (211), в которых коэфициенты зависят кроме х и t еще от р и q,
В общем случае характеристики зависят также и от интегральных по-
верхностей, в противоположность рассмотренным нами до сих пор ли-
нейным уравнениям, характеристики которых вполне определяются са-
мим диференциальчым уравнением.
Вернемся к обозначению Лагранжа. Уравнением непрерывности (186)
для одномерного пространства служит:
dx
й«’
ш = Р°.:
Р
так что волновое уравнение в этом
(ср. (184) и (201)]:
й2Х , , , й log О
случае принимает следующий вид
где
<И“)
<р‘(р) й<0
<0 ЙХ
<рг (р)
(214)
со2
, , . й2Х
Ъх
как — входит в коэ-
й«
Это уравнение действительно нелинейное, так
й2х
фициент при Независимыми переменными в этом уравнении явля-
ются а и t, а неизвестной функцией х. Уравнением характеристик со-
гласно (213) служит:
(215)
оно дает нам скорость распространения.
Будем, как это делал Гюгонио, брать производные вдоль характе-
ристик, рассматривая а как функцию от t, определяемую уравнением
(215). Мы получим:
d [ йх\ й2х ( й2х da
dt \йа / dtda da2dt ’
d /йх\ й2х й2х da
dt \ Й/ J dt2 ' dtda dt ’
Исключив из этих двух уравнений —— , мы будем иметь:
of са
d (dx\ da d (dx\ _й2х (da\2d2x
dt \ dt J dt dt \йа / й/2 J da2'
\ в
— I . Правая часть при этом
обратится в нуль вследствие (214), и мы получим:
1217)
dt\dtjdtdt\da) 17
ОДНОМЕРНОЕ ДВИЖЕНИЕ ГАЗА. ХАРАКТЕРИСТИКИ
145
Мы полагаем для краткости:
/4>(<o)rf<o=x(®),
{Х»}2 = Ф(Ч
так что уравнение характеристик (215) принимает вид:
da I г, х , ,(^х\
3f=±)!(«»=±X'(J-).
(218)
Таким образом мы получаем два семейства характеристик. Уравнение (217)
преобразуется теперь в следующее:
d /дх\, /дх \ d (dx\
dt \dt) — * / dt \ да /
(219)
Эти два уравнения легко интегрируются: первый член в них вдоль
характеристик представляет собою полную производную по переменной t.
Таким образом
(220)
причем £ остается постоянным вдоль характеристик первого семейства, а
j; остается постоянным вдоль характеристик второго семейства. Если $
и г; принять за новые независимые переменные, то уравнение (214) можно
преобразовать к нормальному виду; при этом получится уравнение ги-
перболического типа (14), которое можно интегрировать по методу
Римана. Фактически метод Римана, изложенный в § 73, изобретен именно
для этой цели.
Мы не будем здесь останавливаться на этих несколько длинных вы
числениях. Покажем только, что полученные нами интегралы удовлетво-
ряют уравнению (214). Действительно, диференцируя (220), мы найдем, что
<1/2 "т" / dt да ’
<~Рх , рх \ <У2х______
dt да / <5а2
Исключая из полученных уравнений у’, мы приходим обратно к урав-
нению (214).
Уравнения (220) допускают очень простую геометрическую интер
претацию. Они показывают, что интегральные поверхности суть разги-
Q бающиеся поверхности (в случае малых колебаний они являются цилин-
дрическими поверхностями). Разгибающиеся поверхности образуются,
как известно, касательными к пространственной кривой. Разгибающиеся
поверхности можно без складок и растяжений развернуть на плоскости.
Читатель, незнакомый с такими поверхностями, может составить себе
о них представление, вырезав кусок бумаги вдоль кривой (которая
Лю В е б с т е п. Лийеюеиииальные уря.впапшт.
146
ИНТЕГРИРОВАНИЕ ДИФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
должна пересечь конец бумаги), начертив касательные к кривой и за-
тем подняв один край бумаги так, чтобы кривая скрутилась. Ее каса-
тельные останутся при этом прямыми, а кривая превратится в так
называемое ребро возврата развертывающейся поверхности. Заметим
при этом, что можно взять два куска бумаги, скрепленные между собою
вдоль ребра возврата гибкими зажимами так, что при изгибании оба
куска отделяются друг от доуга, и мы видим, что поверхность состоит
из двух листов: один из этих листов состоит из полукасательных, про
веденных к ребру возврата в одну сторону, другой — из касательных,
проведенных в другую сторону. Легко заметить, что касательные плос-
кости соприкасаются с развертывающимися поверхностями не в одной
точке, а вдоль прямых, именно, вдоль касательных к ребру возврата.
Разгибающаяся поверхность, подобно цилиндрической поверхности, имеет
только со 1 касательных поверхностей. Вдоль касательной к ребру воз-
врата направляющиеся косинусы нормалей постоянны. Таким образом и
йх йх
р = — и q — — можно представить как функции одного только па-
оГ о(1
раметра, или, что то же, между ними имеется соотношение, не завися-
щее от координат. Каждое из уравнений (220) можно рассматривать
как такого рода соотношение, так что интегральные поверхности в дан-
ном случае действительно представляют собою разгибающиеся поверх-
ности.
Пусть по одну сторону одного из подвижных поршней а — 0 воз»
йх
дух находится в покое. В таком случае на этой стороне — — 0. Пусть,
О*
йх 1
кроме того, — = 1; движение, приходящее с другой стороны, должно
ЙЛ
удовлетворять условию совместности
Х(П,
(221)
причем надо положить ё = у(1). Физически это означает, что скорость
частиц воздуха зависит только от плотности. Движение распространяется
со скоростью звука в пространстве, в котором воздух находится в покое.
Проведем через какую-нибудь неподвижную точку, например через
начало координат, плоскости, параллельные касательным плоскостям
разгибающейся поверхности (220). Построенные нами плоскости огибают
конус, образующие которого параллельны касательным к ребру воз-
врата. Для всех интегральных поверхностей получается таким образом
один и тот же конус, так как характеризующая его связь р и q задана
уравнением (221). С помощью этого конуса можно определить, как мы
сейчас покажем, интегральную поверхность, которая представляет волну
ускорения, соответствующую вполне определенному движению поршня
а = 0. Пусть это движение задано кривою x=f(f) в плоскости « = 0.
Каждая касательная к кривой x—f(t) должна лежать в касательной
плоскости к интегральной поверхности, проходящей через эту кривую.
Таким образом плоскость я —0 надо вращать около этой касательной
ОДНОМЕРНОЕ ДВИЖЕНИЕ ГАЗА, ХАРАКТЕРИСТИКИ
147
до тех пор, пока она не станет параллельной некоторой касательной
плоскости построенного нами конуса (см. черт. 30); соответствующая
образующая конуса даст нам при этом образующую разгибающейся
поверхности, проходящую через данную точку, и тем самым искомая
поверхность будет построена.
Движение, очевидно, будет иметь особенность на ребре возврата
интегральной поверхности. На ребре возврата пересекаются две беско-
нечно близкие касательные к поверхности, так что на этой кривой из
двух волн, распространяющихся с различной скоростью, ндна перего-
няет другую. Подобрав соответствующим образом ускорение поршня,
можно ребро возврата свести к одной точке; интегральная поверхность
перейдет при этом в вышеупомянутый конус, а все волны в определен-
ный момент встретятся в одной точке. При этом плотность внезапно
резко изменится, или, что то же, давление сделает резкий скачок. Та-
кой, носящий характер удара разрыв в волне ускорения носит название
явления Римана-Гюгонио. Практически осуществить его с помощью
указанных поршней довольно трудно, так ка(с для этого понадобились
бы очень большие ускорения. Вией (Vieille)1 сделал наблюдения над
волнами, возникающими при сжигании взрывчатых веществ; результаты
этих наблюдений очень хорошо совпали с теоретически вычисленными.
Мы не можем здесь задерживаться- на этих очень важных вопросах.
Укажем здесь только на недавнюю работу Лова (А. Е. Н. Love) и
Пиддака (Е. В. Pidduck)2 *, в которой обобщаются результаты Римана
Гюгонио и получаются некоторые новые результаты, имеющие значение
в балистике.
1 Comptes Rendus, Paris, т. 126, 127, 129, 130 (1898—1900).
. 8 On Lagrangue’s ballistic problems, Philosophical Transactions of the Royai!
iSociety of London, серия А, т. 222, стр. 168—226 (1922).
ГЛАВА СЕДЬМАЯ
Шаровые функции, функции Бесселя и Ламе
§ 8в. Определение шаровых функций. Вернемся снова к уравнению
Лапласа и задаче Дирихле. В главе V мы указали общий подход к ре-
шению этой задачи для любой граничной поверхности (§ 60) и дали
полное решение только для случая, когда эти поверхности — бесконеч-
ная плоскость или сфера (§ 67). Сейчас мы подробно рассмотрим тот
случай, когда заданной поверхностью является сфера. Решение задачи
в этом случае дается с помощью особых функций, так называемых
шаровых функций.
Шаровой функцией V — Vа мы называем однородный многочлен от
х, у, z, представляющий собою гармоническую функцию. Таким обра-
зом шаровая функция должна одновременно удовлетворять двум урав-
нениям:
ДУ=0, (1)
3V
z — — nV
iz
(2)
(уравнению Лапласа и условию однородности Эйлера), где п есть сте-
пень этого многочлена; п называется степенью шаровой функции. Оче-
видно,
Vo == const,
Уг — ах -ф- by cz, (3)
где а, Ь, с — постоянные,’суть все шаровые функции нулевого и первого
порядка. Однородный многочлен 2-й степени
ах2 -ф- by2 -ф- cz2 4- dxy -ф- eyz -|- fzx
удовлетворяет уравнению Д V — 0 в том и только в том случае, когда
а потому
V2 — а (х2 — z2) -ф- b {у2 — z2) -ф- dxy 4- eyz 4- fzx. (4)
Таким образом существует пять линейно независимых шаровых функ-
ций 2-й степени:
х2— z2, у2 — z2, yz, zx, ху.
Шаровая функция 2-й степени в общем виде получается из этих функ-
ций путем умножения их на произвольные постоянные и сложения по-
лученных произведений.
Рассмотрим, далее, однородный многочлен 3-й степени
ах3 4- bys 4* cz3 4~ dx2y 4- ex2z -ф- fy2x -ф- gy2z 4- hz2x 4~ kz2y -ф- Ixyz. /
ОПРЕДЕЛЕНИЕ ШАРОВЫХ ФУНКЦИЙ
149
Если он удовлетворяет уравнению Лапласа, то
6 (ах -}- by cz} + 2<Zy 4 2ez -j- 2fx -f- 2gz -f- 2.hx 2ky = 0.
Отсюда следуют уравнения:
6a 4 2/-J“2^ = 0»
6&4-2<Z-|-2A = 0,
6c -4 2e 4- 2g~ 0,
или
ь=--1(^4-k), c — l(c+^).
Следовательно, общий вид шаровой функции 3-й степени следующий:
V3=^ [х2у------i-jA Ц-е (x2z-------i-г3) (У*х — -1 х3) -4
4£ (у2г------^-z3) -4Л (z2x-----i-x3) 4-А (z2y-----। bxyz.
\ & / \ & / \ о ]
Легко видеть, что семь функций, входящих в это выражение, линейно
независимы, а потому функция У3 в общем виде содержит семь про-
извольных постоянных.
Общий вид однородного многочлена л-й степени от х, у, z есть
ая,о х“ + а»-з,о + «„-2,0 хП~2У2 +
+ ««-!,! z + «„-2,1 хп~*уг4-
+ аЛ-2,2Л"“2^ +
4- йоо^ 4“
4-«мУ‘-1г 4-
4- а02 yn~s z2 4-
' этот многочлен содержит 1 4 2 4 3 4* • • • 4~я 4“ 1 ~ (л-|- Ч(я 4" 2)
членов. Сумма его вторых производных представляет собою однород-
ный многочлен (п — 2)-й степени, содержащий п (п—1) членов. Так
как последний многочлен должен тождественно обращаться в нуль, то
все коэфициенты в нем должны быть равны нулю, т. е. коэфициенты
шаровой функции л-й степени должны удовлетворять ~^п(п—1) усло-
виям 4 таким образом 2л-)-1 коэфициентов шаровой функции л-й
степени могут быть выбраны произвольно.
, п л (и — 1) х
’ Легко также показать, что эти —- соотношения должны быть ли-
нейно независимы.
150
ШАРОВЫЕ ФУНКЦИИ, ФУНКЦИИ БЕССЕЛЯ И ЛАМЕ
Введем теперь пространственные полярные координаты г, 6, ср, где
г—расстояние от начала координат, 6—расстояние от полюса, а —
географическая долгота. Мы имеем:
X ----- rsin 6 COS Ф, _y = rsinO sin ср, z~ г cos 6. (6)
В однородном многочлене Vn общий множитель гп можно вынести
за скобки; мы тогда получим:
ГЯ®/«УЯ(О, <р). (7)
Функция Ул(<р, 6) определена на сфере единичного радиуса. Она
называется сферической1 функцией п-й степени. Уравнению Ул(<р, О) = 0
геометрически соответствует конус, пересечение которого со сферой
единичного радиуса представляет вполне определенную сферическую кри-
вую. Кривые 0) —const имеют также большое значение; например
У2 = —-^х-— const представляет сферический эллипс.
Пусть Vn — шаровая функция /г-й степени; покажем, что функция
r-2n-i также удовлетворяет уравнению Лапласа. Возьмем какие-либо
две функции и, v, дважды диференцируемые по х, у, z. Мы имеем:
й2(от) . ди dv . й2п
йх2 йх2 йх дх ' йх2 '
(8)
Заменим х сначала через у, затем через z и просуммируем полученные
таким образом уравнения. Результат этой операции в обозначениях § 52
запишется так:
Д(«, ф) = «Д®4-2Д(«, v)-\-v[\u. (9)
Положим и^гт. Тогда
-—- — тгт 1 — = тгт гх.
дх дх
m(m_2)гт-*х2, *10)
Д(гт) = Зшгт-2—т(т — 2) rm~2 = m (т 1) гт~2..
Если V есть шаровая функция /г-й степени, то в силу уравнений (1)
и (2), которым эта функция удовлетворяет, мы имеем:
д(^Уп) = л.тД1/п + т(/гг + 1)гте-2Рл-Н )
4- 2тгт~2 (х 4~ 2 ) =
1 \ йх 1 йу йг /
__лт-2 ут (m-j- 1) -j- 2тп] Vn. J
1 Согласно терминологии, установившейся в последнее время в топологии,
мы будем называть сферой поверхность шара. В соответстеи и с 8ти$ и введены
шаровые (Kugelfunktionen) и сферические функции (Kugelflachenfunktio nen). (.Ред.)
ЗАДАЧА ДИРИХЛЕ ДЛЯ ШАРА
151
При т=—(2л—1) последнее выражение обращается в нуль, чем
и доказывается наше утверждение.
у есть однородная функция /г-й степени, а потому /— (2«+D у^
является также однородной функцией степени —(я-)-1). Этот вывод
показывает, кроме того, что Уп и У суть единственные функ-
ции, удовлетворяющие одновременно уравнениям (1) и (2) [для второй
из них п в уравнении (2) надо заменить через —(n-|~ 1)]- Таким обра-
зом любой шаровой функции Vn соответствует другая вполне опреде-
ленная функция степени —(«-|- 1), именно функция
V_(n+1) = ^(2f!+l) У„(6, ?).
На любой сфере, имеющей центр в начале координат, эти две функции
отличаются друг от друга только постоянным множителем. Если п>0,
то Vn обращается в нуль при г—0 и становится бесконечным при
г—»оо, a V_( г), напротив, обращается в нуль при г—>оо и стано-
вится бесконечным при г—► 0.
§ 87. Задача Дирихле для шара. С помощью сферических функций
можно решить до конца задачу Дирихле для шара. Эта задача сводится
к нахождению функции V — V (г, 6, ш), которая при r<^R удовлетво
ряет уравнению ДУ = 0, а при г—>2? переходит в заданную непре-
рывную функцию У = Уо (0, <р). Если функция Уо (0, <р) разлагается
в ряд сферических функций, сходящийся повсюду на сфере радиуса
единица,
Vs=Ko(0, <р)+ PJ0, <р)4-У2(0, <Р)-|_... + Ул(6, (12)
то ряд
(13)
удовлетворяет поставленным нами требованиям. Действительно, он схо-
1
днтся.
так как —
R
¥ и при
г—переходит в
Ц)1-
Кроме того, как легко видеть, при r<^R этот ряд можно последова-
тельно диференцировать сколь угодно раз; так как каждый член этой
суммы является гармонической функцией, то тем же свойством обладает
и вся сумма.
Та же задача для пространства, лежащего вне сферы, может быть
сформулирована и разрешена аналогичным образом; при этом надо
только добавить условия, указанные в конце § 59 для г—> оо. Реше-
нием в этом случае является:
Каждый член этого ряда представляет собою гармоническую функцию
и стремится к нулю при г—> оо. Ряд сходится при г>/?.
1 Это является следствием так называемой теоремы Абеля о непрерывности,
см. Riemann-Weber, I, стр. 151.
152
ШАРОВЫЕ ФУНКЦИИ, ФУНКЦИИ БЕССЕЛЯ И ЛАМЕ
§ 88. Представление шаровых функций в форме, данной Максвеллом.
Меняя последовательность диференцирования, мы найдем, что произвол-
пая любого порядка от гармонической функции является также функцией
гармонической. Например, для производных первого порядка
Д^=^Д v=o.
Производная k-ro порядка от шаровой функции
dkV
(*=«+₽+?)
есть также шаровая функция степени п — k. Так как
ровой функцией степени —1, то
й*(—)
\ г }
является ша-
Пусть — некоторое направление, направляющие косинусы которого
постоянны и равны I, т, п. Тогда
й , й . й , й
— = I -—|- т -—I- п —- .
й/tj йх 1 iy 1 Й£
Согласно предыдущему замечанию
й / 1 \ 1 ,, .
5/,; (7 Г”
— шаровая функция степени — 2, а
й / 1 \
rS W ( ~г / = — (1х + ту +
— шаровая функция 1-й степени. Если это последнее выражение помно-
жить на произвольную постоянную А, то получится функция:
которая зависит от трех произвольных постоянных А, I, т (так как
/24-т2Н-/г2=1), т. е. представляет собою шаровую функцию 1-й
степени в общем виде.
Шаровые функции = У_г и — у_3 имеют очень про-
стое значение. Первая из них служит ньютоновым потенциалом мате-
риальной точки т, а вторая— потенциалом диполя с моментом M1 = md1
(где d1 представляет собою стремящееся к нулю расстояние между ма-
териальными точками т и — т) и с направлением /г2 (см. § 57).
Возьмем два диполя, имеющие один и тот же момент и одно и
то же направление hr Пусть d2 — длина, а /г2— направление соедини-
ПРЕДСТАВЛЕНИЕ ШАРОВЫХ ФУНКЦИЙ В ФОРМЕ, ДАННОЙ МАКСВЕЛЛОМ 153
ющего их середины отрезка. Их потенциал, если только существует
ду8 = 1пп Мг<12, стремится при <Z2—>0 к пределу
Это выражение
Таким образом
«4" 1:
представляет собою шаровую функцию степени—3.
мы приходим к потенциалу мультиполя любой степени
„ л й а а /1 \
-(л+1) — A^hz г ) ‘ ’
Здесь hlt h2,... , hn — произвольно
произвольная постоянная. Выражение
заданные направления, а А —
а /м
й/гД г)
У„ = Аг**г
_й__й_
a/?j а/?2
(15)
является шаровой функцией n-й степени, как это следует из замечания,
сделанного в § 86. Можно доказать, что выражения (14) и (15) пред-
ставляют общий вид шаровых функций, и что направления hlt h2,____, Л
вполне определяются (с точностью до знака) функцией 1 V. Это пред-
ставление шаровых функций принадлежит Максвеллу. Направления
/гр h2, ... , hn называют осями шаровых функций. Так как каждое на-
правление определяется двумя постоянными, то вместе с А полу-
чаем 2n -|- 1 постоянных, т. е. указанное выше число произвольных по-
стоянных, входящих в общее выражение сферической функции степени п.
Примеры:
,, л з 3 ( 1 \ л J / Ч Ц I 3 I И I 3 ( 1 М
V — Аг* — — = Лг3 I — — -j- т — — -4- п — — —
1 й/z \ г } | йх \ г / 1 Ъу \ г J 1 Ъг \ г
. . ( 1х ту nz\ .,
= Аг(——72 j = — А и* + тУ + nz^
(т9 Зт2у2 3l2xy 3n2yz\ (
73 Я* у *"
ln2 3n2zz 3l2xz 3m2yz\ 1
» 1 у ^-3 ^'*1 j I
(xs-^y^^-z2) -f- 3 (l^x^m^y2-]-n,n2zs) -|-
4- 3 (т2п2 -j- m2nj)yz 4* 3 (пг12 ) zx -J- 3 (l^m2 4* l2m^ xy }.
i См. Курант P. и Гильберт Д., Методы математической физики,
изд. ГТТИ (1933), стр. 489-496.
154 ШАРОВЫЕ ФУНКЦИИ, ФУНКЦИИ БЕССЕЛЯ И ЛАМЕ
Коэфициенты в этих выражениях, конечно, удовлетворяют условиям
^ + ^24- «2=!, Z24-/W2_|_n2==L
§ 89. Зональные шаровые функции. Особенно большое значение
имеет тот частный вид шаровых функций, для которого все оси имеют
одно и то же направление. Пусть это направление совпадает с направ-
лением одной из координатных осей, например оси Oz. В таком случае
Эю выражение, очевидно, является многочленом относительно г и z.
Соответствующая ему сферическая функция
5я / 1
п izn\ г
представляет собою многочлен относительно — = cos(rz). Для всякого
значения и многочлен определен однозначно с точностью до постоянного
множителя; его называют полиномом Лежандра Pn[cos(r, z)]=/3B(£).
Постоянная А определяется из условия Рп(1)=1 (см. § 92). Можно
доказать (см. § 93), что корни уравнения />я($) = 0 действительны,
отличны друг от друга и заключены между —1 и 1. Этим корням
соответствуют и круговых конусов, у которых углы между образующей
и высотой равны арккосинусам этих корней. Они вырезывают на сфере
единичного радиуса п параллельных друг другу кругов, которые делят
поверхность всей сферы на зоны; отсюда полиномы [cos (rz)] и по-
лучили название зональных сферических функций. Соответствующие им
шаровые функции называются зональными шаровыми функциями.
§ 90. Ортогональные координаты. В дальнейшем нам понадобится
преобразовать уравнения Лапласа в полярные координаты. Эту задачу
можно рассматривать как частный случай преобразования уравнения
Лапласа из прямоугольных координат в любые ортогональные. Перей-
дем теперь к решению этой более общей задачи.
Пусть даны три функции: р3 (jc, у, г), р2(х, у, z), р3(х, у, z); урав-
нение р., = const представляет, вообще говоря, поверхность; совокуп-
ность двух таких уравнений представляет кривую, принадлежащую обеим
поверхностям, т. е. линию их пересечения, а три таких уравнения
представляют, вообще говоря, одну точку — точку пересечения этих
поверхностей. Таким образом три значения функций рр р2, р3 при
известных допущениях однозначно определяют положение точки в про-
странстве; назовем их криволинейными координатами этой точки. При-
мером криволинейных координат могут служить полярные координаты
з пространстве: ,_________.
р1==1/^+Р+г2 = Г1
Z А
р2 — arccos — — и,
р3 = агс:ё-^=^.
(16)
ОРТОГОНАЛЬНЫЕ КООРДИНАТЫ
155
Поверхности уровня рд = const, р2 = const,
координатными поверхностями. Направляющие
верхности pj = const суть:
pg = const называются
косинусы нормали к по-
где
. . 1 Эр, , . 1 йр.
. . 1 др,
cos (n, z) = т- — ,
4 /г, йг
/гч = I grad pj ,
Таким образом, например, мы имеем:
^7-= cos (tijх) cos (t^y) 4- cos (nrz) ^ = hlt (17)
о ft j ол dy cZ
а потому расстояние между двумя соседними поверхностями рд = const
есть . Аналогичные формулы имеют место и для dn„ и для dn3.
«1
Особенное значение имеет тот случай, когда в каждой точке про-
странства каждая из ’трех координатных поверхностей перпендикулярна
двум другим координатным поверхностям. В этом случае мы говорим,
что поверхности рд—const, р2 = const, р3 —const образуют трижды
ортогональную систему. Приведенная выше в качестве примера система
полярных координат является трижды ортогональной.
Условия ортогональности суть:
др2 др3 . йр2 йр3 йра dp3 Q
Ъх Ъх ' йу Ъу ' йг йг ’
йрз йрг . йр3 йрд . йрд Йр1
йх йх ' йу/ йу/ йг йг
(18)
йр2 йр2 । дрд йр2 ! йрд йр2 ' Q
йх йх йу/ <>у 1 йг йх
Диференцируя рп р2, р3 и деля полученный результат соответственно
на hv h2, h3, мы найдем:
rfpj _ dn. 1
Ад \йх > йу/ у 1 йг } ’
<7р9 /?2 dn2 1 dx dy 4- dz) , \йх 1 йу/ 1 йг /
^Р8 ^3 dn3 1 /г3 РЬ dx 4- JPs rfy 4- Й-Ез dz) . \йх 1 йу/ йг / ’
(W)
Девять коэфициентов при dx, dy, dz суть девять направляющих
косинусов взаимно перпендикулярных направлений п2, п2, п3. Согласно
§ 3 (7) эти выражения совпадают с проекциями на направление соот-
ветствующей нормали тех векторов, проекции которых на координатные
156
ШАРОВЫЕ ФУНКЦИИ, ФУНКЦИИ БЕССЕЛЯ И ЛАМЕ
оси суть dx, dy, dz' следовательно, dny, dn2, dna суть компоненты
линейного элемента ds в новой системе координат. Таким образом
. <> Л 2 1 Л 2 I Л 2 I ^2 I
ds* = dx*-\-dy*-}- dz* —(20)
представляет собою однородную квадратичную форму dp1, dp2, rfp3.
Те же результаты можно получить и непосредственно. Предположим,
что х, у, z выражены через рп р2, р3. Тогда
rf*=?-idft + ЙХ . ^РзЧ" О?2 Йх ,
‘О’ЧЛ4" ъ+ йу/ . <>1, f1'
йг , йг , . йг ,
<Г ^Р2 + ^Рз-
Подставив эти значения в выражения для dplt dp2, dps, мы получим:
(22)
Приравнивая коэфициенты при dp1 в обеих частях
находим:
йрд йл- йр} йу/ . йр2 йг__
йх йpj ‘ йу/ йр1г^ йг йр2
Аналогичные уравнения имеют место и для р2 и
в формуле (22) коэфициенты при </р2, получаем:
йрг йх Йр5 йу/ йрд йг
йх йр2 йу/ йр2 ' йг йр2
Путем круговой перестановки р2, р2, р3 получаем
уравнения.
Перепишем уравнение (23) в следующем виде:
этого равенства,
(23)
р3. Приравнивая
(24)
два аналогичных
h . Л^Рл_
//j йх 1 йр2 ' h-y йу/
4,х+ lift te
йр! 1 Aj йг *йр2
1.
Отсюда в силу (24) и таких же уравнений для р2 и р3 находим:
= = 1^’ = »,^ о = 1. 2,3),
Л, йх ’йр, Л, йу/ йр, Л, йг ’йр,
ОРТОГОНАЛЬНЫе КООРДИНАТЫ
157
или, иными словами: девять направляющих косинусов
вить в следующем виде:
можно
предста-
(v=1,2, 8).
’Jp, ip, ’ip.
Приравнивая сумму их квадратов единице, мы получаем:
(25)
Образовав сумму квадратов выражений для dx, dy, dz из (21) и
воспользовавшись условиями ортогональности:
йх Ъх , йу йу , йг йг
йр^йр", йр^йр^'!"й^йр7
(2S)
Итак, мы пришли к формуле (20) путем непосредственных вычис-
лений.
Преобразование оператора Лапласа к ортогональным координатам
основано на теореме Гаусса (см. § 50)
Шш''4А=’ЧР"Л!-
где А-—произвольный вектор, а п — внутренняя нормаль замкнутой
поверхности интегрирования. Вместо компонент Ах, Ау, А^ вектора А
в прямоугольной системе, мы возьмем компоненты Др А2, А3 того же
вектора в системе взаимно перпендикулярных нормалей к координатным
поверхностям р. — const, р2 ~ const, р3 =$= const. Положительное направ-
ление нормалей должно при этом соответствовать возрастающим значе-
ниям pj, р2, р3. Проектируя на нормаль п к поверхности S, мы имеем:
Аа = Д1 cos («nJ А3 cos (nn2) -j- Д3 cos (nns).
(25)
Разделим весь объем рядом поверхностей уровня pj и р2 на элемен-
тарные криволинейные призмы. Для каждого элемента, вырезанного та-
кой призмой из поверхности S, имеем:
± dScos [ntij) = t
7z3
и следовательно,
- jj Л, = (A) 41 dh rfp,. (28)
158
ШАРОВЫЕ ФУНКЦИИ, ФУНКЦИИ БЕССЕЛЯ И ЛАМЕ
Переход от двойного интеграла к тройному сделан на основании
тех же соображений, что в § 50 при таком же переходе в прямоуголь-
ной системе координат. Преобразуя точно так же два других интеграла,
мы получим:
Так как эта формула справедлива для любого объема, то
, , , [ <1 ( А-, । 3 / А„ \ . й / Ач \ 1
d1vA = ftjrt2/?3 1 — Нгт- Д--— -f-— —5- В . (30)
[3pj \h2n3/ йр2 5р3 \h1h2/ I
Если вектор А безвихревой, то его можно рассматривать как гра-
диент потенциала У; в таком случае
л ЙУ , ЙУ л ЙУ , ЙУ . йу , йу
А, = — — п, — , A„=—~h2~, A3-~-~h„-—
1 й/Zj 1 Йр, ^п2 Й Р2 ЙП3 3 й р3
(31)
а равенство (30) принимает вид;
А У----А ^3
(32)
Эта формула, как и равенство (27), были найдены Ламе (Lame)1
с помощью очень длинных непосредственных вычислений.
§ 91. Шаровые функции в полярных координатах. В случае поляр-
ных координат имеем: pj — r—расстояние от начала координат, р2 —0—
расстояние от полюса, р3 — ср— географическая долгота;
X — rsinOcostp, _у= rsin 6 sin ш, z = rcos(p. (33)
Поверхности уровня рг — const представляют собою сферы, нормали
к которым совпадают с направлением радиуса, так что dti-l=drl,
й, —1. Поверхности уровня р2 = const являются конусами с углом рас-
твора 6, причем dn2 = rd§, h2 — ~. Поверхности уровня р3 = const
суть плоскости, проходящие через ось Oz, причем rf/z3 = rsinOifa;
k3 = sj- q . Эти результаты можно вычислить из (25). Следовательно.
А ,, 1 I д / 2 I й ( • й » / 1 ЙУ\1
А У = -^—7. { — ( A Sin 6 — 4- -7- I sin 6 -Т- 1 -4- — ---I —
AsinO (йг \ йг / йО \ йО / йш \sin6йср / /
Й2У _____1____1 Э2У
ЙГ2 ‘ Г Йг Г251п0й6 \Sin йб ) 'г2 sin2 0 йи2
1 Journal de 1’Ecole Pclyt., т. 14, стр. 191—288 (183 i).
(34)
ШАРОВЫЕ ФУНКЦИИ В ПОЛЯРНЫХ КООРДИНАТАХ
15»
Мы ищем решение уравнения Лапласа, являющееся произведением
двух функций: одной, зависящей только от г, и другой, зависящей от?
О и ш, т. е. решение, имеющее вид V = R(r) У(0, <р). Поэтому
d2R v . 2 dR R 5 / . m R &Y
dr2 + r dr 1 ^'r2sinOaO \S’n%9 ) + r2sin20 a?2 — °- <35>
Пусть V 0. Умножая
на
RY'
получаем:
11 a / . i 1 ^Y. . M2 2rdR\
Y Sin6a6 \ in йб / ' Zsin20a^2 \7? dr2 * R dr J
Так как левая часть этого равенства зависит только от 0 и <р, а
правая только от г, то каждая' из них должна быть равна постоянному,
которое обозначим через с. Итак, R должно удовлетворять диференцп-
альному уравнению:
dr2 1 г dr г2
(37)
положим:
которое при г=0 имеет особую точку. Чтобы решить его,
оо
и следовательно
ft-2 = 0,
й=—оо
Итак, решение этого уравнения не обращается тождественно в нуль
только в том случае, когда существуют такие значения, для которых
/г(jfe —J—1) —= О. Поэтому необходимо, чтобы было с = —п(п-\-
где п — целое число. Если для данного значения k коэфициент
то, как это следует из последнего уравнения,
/г(&+1) — w(r4-1)=0,
(k — п) (k -ф- п ф- 1) — 0.
Это означает, что либо k = n, либо k =— (п ф~ 1), и таким обра-
зом функции ги и г_(п+1) удовлетворяют уравнению (37); они образуют,
очевидно, фундаментальную систему (см. ч. I, приложения, § 5). От-
сюда следует, что определяемые уравнением (7) сферические функции
К=Уп(0, <р) удовлетворяют уравнению:
1 л / i \2 у
S9»(stoeTr) + ffi?55p’’ + "<" + 1>r«=0- <33>
160
ШАРОВЫЕ ФУНКЦИИ, ФУНКЦИИ БЕССЕЛЯ И ЛАМЕ
Это диференциальное уравнение служило исходным пунктом в иссле-
дованиях Лапласа. Сферические функции называют также функциями
Лапласа. Если 0 заменить новой переменной
p,=cos6, djj. = — sinGrfO,
то уравнение (38) преобразуется в следующее:
ч ( чу 1 42 у
Fg I" - * + ГЯЗ v” + »'» +1 > r- “ °- <»>
§ 92. Полиномы Лежандра. Определение н вычисления. В том слу-
чае, когда функции 1^(0, <р) не зависят от <р, они обращаются в зональ-
ные сферические функции Pn(cos6), введенные нами в § 89. Урав-
нение (39) при этом можно переписать так;
d ( dPn\
или, произведя диференцирование,
d?p dp
(1~^^“2иЖ+"(" + 1)/’п==0- (41)
Уравнение (41) называется диференциальным уравнением Лежандра;
особыми точками в этом урав-
нении служат p = -tl. Так
как р.= 0 не является осо-
бой точкой, то общий интеграл
можно представить разложен-
ным в степенной ряд вблизи
начала координат. Положив
сю
P„(jji) = ^aftpft, мы придем к
й=О
рекуррентной формуле, кото-
, рая позволяет выразить все ко-
эфициенты через два из них;
таким образом мы получим два
ряда, которые будут представ-
лять собою два линейно незави-
симых частных решения. Один
из этих рядов кончается на р.я,
т. е. является многочленом я-й степени; он дает нам после соответ-
ствующего нормирования так называемый п-й полином Лежандра Р„(р).
Как мы вскоре увидим, он очень просто связан с введенными в § 89
зональными сферическими функциями К
1 Второе линейно независимое решение не может быть многочленом. Дей-
ствительно, если Рп и Q/t — два линейно независимых решения, то
р' п р О' — ——- =£ 0
‘п"г1 ‘пЧп—|___2 7= О.
•Функция Qn называется функцией Лежандра второго рода (см. § 108).
ПОЛИНОМЫ ЛЕЖАНДРА
161
Для того чтобы представить Ра (;х) в явном виде, разложим обрат-
ную величину — расстояния d переменной точки Q от неподвижной
точки Р в ряд по сферическим функциям. Заметим при этом, что
является гармонической функцией прямоугольных координат точки Q.
Точку Р мы выберем на оси Oz на расстоянии г’ от начала коорди-
нат, и пусть полярными координатами точки Q будут г, 6, ф. Из спе-
циального выбора точки Р следует, что получающиеся при этом сфе-
рические функции все являются зональными функциями. Мы имеем
(черт. 95):
d2 = г2 г'2— 2ц/г', р = созО,
1 -- -1
— = {r2-|-r'2—2ц/-т’} 2 == [х2-р>2 -|- (z— Д)2] 2. (42)
Разложим это выражение в ряд Тейлора, рассматривая его как функ-
цию от z:
где согласно определению, данному в § 89,
(я=1, 2, 3, ...).
Постоянная А оставалась до сих пор неопределенной. Выберем теперь
для нее значение: Л—(—1)пп! При 1 имеем:
d г
так что Рп(1) = 1 для любого п.
162
ШАРОВЫЕ ФУНКЦИИ, ФУНКЦИИ БЕССЕЛЯ И ЛАМЕ
Чтобы представить Рп в виде многочлена от р, разложим
1
в биномиальный ряд:
оо Р-ч-й-Л
г _VI2 2 2 \ 2 х /(о r' V ( r' V
k\ v~г) Vх—27/ '
k=0
Раскроем последний множитель по биному Ньютона:
(45)
I r'V viz 1xfcft(ft —1)... (ft —ft4-l) ,
О*—,) ——* Ы «
й=0
и подставим полученное выражение в (45). Мы будем иметь:
оо оо _L.JL.A f-L I /г_______________Y
А—О й=0
Объединив члены, для которых k-]-h — n, и заметив, что
1-3-5 ... (2л — 1)(2п)!
nl 2пл! ’
мы получим:
Рп = Ра(ц):=г=
(2п)! Г„п_ «(«-I) п(п-1)(П-2)(П-3) _ 1 _
2«(л!)21И 2-(2л— 1)^ ‘2.4-(2л—1)(2л —3)' * ’ * J ~
[-1
_ V (- 1)------(2д - 2v>!____
— 2j 2«v!(n — у)!(л — 2v)!' "
Отсюда ясно, что Рп(у.) является четной или нечетной функцией, смотря
по тому, четно или нечетно число л.
Пять первых полиномов Лежандра суть:
ЗД) = 1.
Л (н) = н»
ЗД)=4(5н3 — Зц),
Л(н) =у(35р4-ЗОр2 4-3),
=у(63»хБ-70|13+ 15р).
ПОЛИНОМЫ ЛЕЖАНДРА. РАЗЛИЧНЫЕ ИХ ПРЕДСТАВЛЕНИЯ 163
Из формулы (44) следует, что полиномы Лежандра можно определить
как коэфициенты разложения
_ 1
(1 — 2ац -j- а2) 2
в степенной ряд по степеням а:
(1—2а|л-}-а2) 2=Р0(|1)4-Р1(|1)а4-Р2(ц)а2+...
...Н-Ри(ц)ап+... (48)
Функцию (48) называют производящей функцией полиномов Лежандра.
§ 93. Полиномы Лежандра. Различные их представления, а) Разло-
жим бином (Н2-1)" по формуле бинома
(и2 —1)«=р2«—пр 2«-2 -(п2~Н2П-4 — • • .
и продиференцируем его п раз. Мы получим:
^_(И2_ 1)п=2л(2я—1)... (n+l)^ —
— я(2и — 2)(2и — 3)—...(я—1) |1в-2+ ..(49)
или
_1_ (ц2 1 \и_ Г..И П(П 1) „я-2 1 1 — Р („) (50)
2«л! kpn{! ' 2«(л!)2|/ 1-2.(2л— 1)И + '”J "’М ?
Это представление полиномов Лежандра принадлежит Родригу (Rodri-
gues) \ Из формулы Родрига следует, что между — 1 и 1 заключено
п корней уравнения Рп(р) = 0. Действительно, между двумя последова-
тельными корнями функции у лежит, по крайней мере, один корень
производной у'; a (ps—1)" имеет и-кратные корни при р = 1 и при
р ——1. Легко также заметить, что все корни многочлена Р„(р\,
отличны друг от друга.
Производящую функцию полиномов Лежандра можно записать е сле-
дующем виде:
— — —— со
(1 — 2aji-|-а2) 2 = (1 - а^) 2 (1 — ae~iS) 2^^pkMa„^
п=0
=[,+1«л+444в!сМ+14441^+-]х
x[i+i£K-+i44«^+i44.i^--+...]=
V 1.3.5. ..(2k— 1) mVI 1-3-5...(2Л—1) „ _
=S—яй—“ ‘ Е—м—-“м"- w
ft=o й=о
‘ Corresp. sur I’Ecole Polytechnique, т. 3, стр. 361—385 (1814—1816).
11*
164 ШАРОВЫЕ ФУНКЦИИ, ФУНКЦИИ БЕССЕЛЯ И ЛАМЕ
Перемножив два последних ряда, собрав вместе коэфициенты при
ап — /г /г) и приравняв их суммы полиномам Лежандра, получим:
1-3-5 ... (2fe—1)-1-3-5 ... (2я —2fe—1) №
2*/s!2"-ft (п — k)\
(52)
Объединив попарно члены, для которых k — p, с членами, для кото-
рых k = n—р, мы можем эту сумму переписать так:
1-3-5 ... (2р-1)-1-3-5 ... (2д — 2р—1)
2nj»! — р)\
2 cos (п — 2р) 6.
_ п
При этом, в случае четного п, член, для которого р — —,
надо умно-
жить на —. Итак, окончательно мы имеем:
п , „1-3-5... (2и— 1) f . 1 - л ,
<COS 6)32 ' 2-4-6..» 2л |C0S + Г(2^=Т) C0S -2>9 +
, 1-3-д-(/г —1) 1
~^1-2-(2л — 1)(2л— 3) 4)0-|-. . -|
^при п четном последний член этой суммы умножается на
. В этом
виде полиномы Лежандра были получены Лапласом и Лежандром.
Ь) Рассмотрим интеграл
( d<x>
J А — iB costa’
о
(54)
где А и В — постоянные, причем Д^>0. Мы имеем:
71 1*
.__ .Г *Ло । -п С coswdto
“ А J 42 4-В2 cos2 <0 1 J Д2 4-В2 cos2 io' (55)
о о
Второй интеграл равен нулю, так как подинтегральная функция изме-
лит свой знак, если to заменить через it—to. Следовательно,
dts>
j—_ д______________
J А2-\-В2 cos2 to ’
о
(58)
или [см. ч. I, приложения, § 4, (27')] (при Д^>0)
]/42 + В2*
Конечно, при отрицательном А
/д24 В2*
ПОЛИНОМЫ ЛЕЖАНД?.:. РАЗЛИЧНЫЕ ИХ ПРЕДСТАВЛЕНИЯ
165
Положив
Л = 1 — ау, В= а /1 — у2 (0<а<1, — l<p.sSl),
из формулы (57) находим:
It
Г da> it , %
\ ------— —===.. (58)
J 1 — а (у i'у 1 — у2 cos са) у 1 — 2ct;а -]- а2
о ______
Абсолютная величина а(у--|-— у2 costa) при наших предположе-
ниях равна --------------
а у у.2 sin2 со cos2 и а < 1,
а потому ряд оо
--------------7-- ------= V ан (у -Т z |/1 — у2 cos со)” (59)
1 — — у2 cos2 <а) Li
равномерно сходится для любого значения to. Из этой последней фор-
мулы в силу (48) и (58) мы получаем:
It
Рп (у) = — J (уф- i j/1 — у2 cos2 to)" day. (60)
о
Это представление /’„(у) в виде интеграла принадлежит Лапласу. Фор-
мула эта, как оказывается, справедлива при любом значении у. (Знак
перед радикалом, входящим в подинтегральную функцию, может быть
взят произвольно.)
Так как
| у -ф- i 1 — у2 cos (о | =)/ у2 sin2 to -ф- cos2 са 1,
то для всех у между — 1 и 1 справедливо неравенство:
о
Это неравенство переходит в равенство только при у = +1 и zz^>0.
(То же неравенство получится из формулы (53), если принять во вни-
мание, что коэфициенты при всех членах, содержащих косинусы, по-
ложительны.) Положим теперь
Л = ау—1, В = а^1— у2,
предполагая при этом, что 1 у > 0 и ау^>1. Из (57) следует:
1 __ 1 Г d®
)/1—2ауф-а2 п J (ау—1) — ia j/1 — у2costa
о
7t
1 Г day
( а (у — zj/ 1 — у3 cos со) I 1-(у — zj/ 1 — у2 costa)
о
166
ШАРОВЫЕ ФУНКЦИИ, ФУНКЦИИ БЕССЕЛЯ И ЛАМЕ
Но При Ct> 1
, __I ОО
__- 1/ ц 1\2 VI 1
(1-2^ + а2) 2== i_2A+ ря()л) (48f)
и» \ и» и»
n=0
И
___________1___________
a (p — i У1 — p2 cos <o)
Разложение обеих сторон равенства (61) по степеням дает:
dm
(р — У1 — ц2 cos со)п +1
о
(62)
Если (о мы заменим через тг — со, то придем к формуле:
It
dm
(р -ф- iI]/ 1 —р2 cos co)n +1 ’
о
(63)
которая впервые была получена Якоби (Jacobi) Ч Она оказывается спра-
ведливой при любых положительных р.
с) В качестве приложения формулы (60) покажем, что при — 1 <^р<4
Иш Рп(р) = 0.
П->ОО
Мы имеем:
« яг
] р _______ ] Р П
| Ра (р) | 11 р i УI — р2 cos со |" dm ~—I (р2 sin2 co-]-cos2 со)2 dm. (64)
о о
тг
Пусть е — заданное положительное число, меньшее — . Представим по-
&
следний интеграл в виде суммы интегралов
Так как подинтегральная функция в этом интеграле меньше единицы,
то
е s
р ” Г
I (р2 sin2 со -ф- cos2 со) 2 dm I dm = s,
о о
ЯГ
и точно так же У <^е. В среднем интеграле заменим подинтегральное
71-----------------6
1 Journal fiir Math., т. 26, стр. 81—87 (1843).
ПОЛИНОМЫ ЛЕЖАНДРА. РАЗЛИЧНЫЕ ИХ ПРЕДСТАВЛЕНИЯ
167
выражение его наибольшим значением:
С IL —
I {1 — (1 —р2) sin2<o} 2 da < (тт — 2s) {1 — (1 — р2) sin2 е} 2.
е
Следовательно,
Ос тг____9g ”
\Pa(v) I <V + {1 - о -^2) sin2£}2
Выбрав е постоянным и сколь угодно малым, мы в силу предельного
соотношения
п
lim {1—(1—p2)sin2s} 2=0
п->оо
можем затем взять настолько большое п, что второе слагаемое будет
сколь угодно малым, а потому для достаточно больших значений п
абсолютная величина Р (р) действительно сколь угодно мала.
Более точную оценку этого убывания дает приближенная формула
Лапласа
Р (cos0) — ]/ —rlcos (и 4-4-) 6 — 4"
" |/ nTzsinO-l [\ / 4 J J
где sn стремится к нулю при п—>оо. Здесь предполагается 0<^6<^n:.
d) Другое выражение для полиномов Р (р), имеющее большое зна-
чение, получается из (60) введением новых независимых переменных.
Положим при — 1 р 1
р-ф z]Z 1 —p2cos(o;
тогда
dz == — i j/1 — p2 sin to da,
(5 — p.)2 , . s , (5 — p)2 1— 2£p-H2
1 — p2 1 1 — p2 1 — p2
(l-2pe-]-£2)2
Мы имеем:
(>. —iKl—
J (1— 2p^4-£2)2
Здесь путем интегрирования служит прямолинейный отрезок, соединяю-
щий оба предела интеграции; пределы эти лежат на окружности ра-
диуса, равного единице. Согласно теореме Коши (см. ч. И, приложения,
168 ШАРОВЫЕ ФУНКЦИИ, ФУНКЦИИ БЕССЕЛЯ И ЛАМЕ
§ 1), можно заменить этот путь дугой окружности радиуса единица,
соединяющей эти точки. Полагая
Z = dt — iety dy, cos6 = fi;
1 — 2 jiS-f- E2 = 1 — (<?л -f- e“ze) e*? -j- e2Z^=:e^ — (e/e -j- e~K)},
мы находим:
P„(cos6) = ^ I
—e
{2(cos<p—cos 6)} 2
Так как мнимая часть в этом интеграле равна нулю, то
о
Г ( I 1 \ л
I cos ! п -4- — I и «и
2 I \ 1 2 ) т т
рп (cos 6) = — 1--------------2 • (68)
{2(cos(p—cost))}2
Заменив одновременно 0 через тг — 6 и ф через тг—6, мы получим но-
вую формулу:
It 1
2 С sin (« + у) 'И'?
Рп (cos 6) = — \ -------------Т • (66')
{2(cos6 — cos®)}2
Это — интегралы Дирихле-Мел ер а
§ 94. Соотношения между полиномами Лежандра. Возьмем произво-
дящую функцию:
(1 — 2ац 4- а2) ~ = У апРп (р), (48)
п=0
продиференцируем ее по а:
__з 00
01 — а) (1 — 2ар+а2) 2 = У,па?-'Рп (р), (67)
л=0
умножим результат на 1—2ац-j- а2:
(Р- — а) У апРп (Р-) = (1 — 2ар + а2) У па*-' Рп (р)
п=О л=0
и приравняем коэфициенты при а” в обеих частях равенства. Мы
получим:
Vpn (м) — Рп-А (н) =(«+’) Рп+х (н) — 2/гц рп (J1) -4- (п — 1) /эй_1 (д),
1 G. L. Dirichlet, Journal fur Math., т. II, стр. 35 (1837): F. G. Me ti-
le г, Math. Ann., t. 5, стр. 141 (1872).
ПРИСОЕДИНЕННЫЕ ФУНКЦИИ ЛЕЖАНДРА
169
или
(п + 1) Рп+1 (р) — (2я + 1) рРп (р) + л/^ (р) = 0 (л =1, 2, 3, ...), (68}
а при п — О
Pj (р) — рРо(р) = О.
Эта рекуррентная формула дает возможность последовательно и при-
том весьма просто вычислять полиномы Лежандра.
Продиференцируем теперь производящую функцию по р:
3
п=^0
(67'|
и результат опять помножим на 1—2ар-|- а2, мы будем иметь:
оо оо
а]П а«Ря(р) = (1 — 2ар + а2)]П а«^.
/2—0 П=0
Из этого уравнения мы находим:
rfp tiP riP
/3 (fX)==^±l+Er«=i_2p?p („=1,2,3,...). (69),
" dll 1 dp. dp ' 7 J
Далее, из (67) и (67f) получается:
oo сю
(Р — a) J] ап
п=0 п=о
и следовательно,
dP dP
^=пР^ («=1,2,3,...). (7ф
Vv JX.-------------------------------------------JX
dP
Исключим член из формул (69) и (70). Мы получим:
dРцл-i __dPn-i
dp. dp
(2„4-1)Рй(р)
(п = 1, 2, 3, ...). (71)
Эта формула остается справедливой и при п — 0, если только поло-
жить Рч = 0.
Подставив вместо п числа 0,1,2,..., п и сложив полученные та-
ким образом равенства, мы найдем:
dP d Р
ро (Н) + ЗЛ (р) ф 5Р2 (р) +... + (2л + 1) Ра(р) = -^±3 + . (71а)
U IA U IA
§ 95. Присоединенные функции Лежандра. Полиномы Лежандра мы
сначала определили в гл. Ill как решения линейного диференциального
уравнения (319), § 40; в § 92 мы исходили из того же диференцизль-
ного уравнения. На основании этого уравнения легко убедиться, что.
170
ШАРОВЫЕ ФУНКЦИИ, ФУНКЦИИ БЕССЕЛЯ И ЛАМЕ
функции Ря(ф) образуют ортогональную систему. Для этого в формуле
Грина для одномерного пространства [§ 40, (278)] надо положить
р(х)=1 — х2, д(х)=0, и = Рт, v^Pn, р. = х,
а = —1, b— 1.
Мы получим:
1 1
1п{п+\)~т («4-1)] J Рт (И)Р„(ц)^=(1 _ц2) [РпР'т- РтР^} = о. (72)
-1 . -1
Таким образом, действительно, если « не равно п, то
1
^Рт (Ю рп (м) dp. = 0. (73)
—1
Наряду с полиномами Лежандра играют большую роль и присоединен-
ные функции Лежандра. Присоединенные функции /г-го порядка ц
я-й степени определяются уравнением
Г1. , , 9^dkPn ьс, dkР„(cos6)
= (74)
Непосредственное диференцирование дает:
P!l =------------(1 _ ~2
п Чап\(п — k}P
_ („_^)(га_fe—Г) 2
' 2(2я—1) Ц
(п— k)(n — k—1)(я— k — 2) (и— k — 3) "1
2.4Ч2Я_ 1)(2я —3) — • • • J •
(73)
Покажем теперь, что справедливо следующее обобщение формулы (73):
7^(|х)^в0 (т^п).
(76)
С этой целью вычислим интеграл
Ф (т, и, k) = Ф (k) ~-
dv‘
(77)
После (k—1)-кратного диференцирования диференциального уравнения
+ (41)
«ы имеем:
dk+ip dkp dk^P
(1 - м2) - My. —n + (n 4- k) (n - k 4- 1) = 0. (78)
ПРИСОЕДИНЕННЫЕ ФУНКЦИИ ЛЕЖАНДРА
171
Умножим обе части этого равенства на (1 —р2)
^]=- <” +‘И’- *+»(1 - »')*-’ .
выражение (77) проинтегрируем по частям:
Г dk~yPmd
J
dk~yP dkP ,,
dk~^Pn
(79)
(80)
и заметим, что выражение под знаком подстановки обращается в нуль.
В результате из диференциального уравнения (79) получается:
Ф (k) — (п 4- k) (я— &-|-1)Ф(/г—1), (81)
т. е.
ф (k) = (п -}- k) (п — k 4- 1) (я -j- k — 1) (я — k 4- 2) Ф (k — 2) =
=(и _ 1) („ _ k+2)... (я 4- k) ф (0)ф (°)-
\п R).
д так как Ф(0) совпадает с левой частью (73), то отсюда следует,
что Ф(&) равно нулю при т=^п. Дальше, в § 97, мы покажем, что
1
Ф (0) = J [Рп (g)]2 dv. = > (82)
—1
и, таким образом, в силу последнего равенства
— 1
При k — О получаем отсюда (82).
Найдем, наконец, диференциальное уравнение, которому удовлетво-
ряют присоединенные функции Лежандра Pk(v)- Мы имеем:
dPk kdk^P l_1dkP
d2Pk ldk+zP„ L_xdk+^P
-d^~
Г --1 1^21 dkPn
- A(l-g2)2 -&(A-2)g2(l—g2)2' —Д!,
и следовательно,
d2 Pk d Pk
— JI2)2
ifjJL2
rfk+2 tP + lp
... k2v2 \dkPn\
(84)
1 -— v2
172 ШАРОВЫЕ ФУНКЦИИ, ФУНКЦИИ БЕССЕЛЯ И ЛАМЕ
Диференцируя уравнения Лежандра k раз, получаем:
Wft+2D dktlP dkP
а потому правую часть в уравнении (84) можно заменить следующим
выражением:
А
(1-g2)2
I 1 Н J
dhpn== ь*
dp.k 1 — p2 ” *
Таким образом присоединенные функции Лежандра удовлетворяют ди-
ференциальному уравнению
^2/э» dPk /г2 1
§ 96. Сферические функции. Вернемся снова к диференциальному
уравнению Лапласа
1 ((1 - р2)4Ч + «(«+ n уп = ° (P- = cos 0) (39)
йр ( йр ] 1 1 — Р2 йад2
и будем искать частное решение вида Yn (0, <р) = 0 (0) Ф (ад). Подставим
в уравнение это произведение и полученное выражение разделим на
Уп
1 — р2 ’
в результате мы будем иметь:
1______..г d ( d&}
*1 срф
Ф 6?<р2’
(87)
Обе части уравнения равняются одному и тому же постоянному. Обо-
значим это последнее через А2. Уравнение (87) равносильно следующим
двум обыкновенным диференциальным уравнениям:
+А2ф = 0, (88)
«ад2
А|(1_;12}^1+/г(/г+1)0=г^_ (89)
dp. Р ' 6?pj * 1 1 — р2
Решением первого служит:
Ф — A cos kw В sin k<f.
Для того чтобы Yn на сфере единичного радиуса было однозначно, Ф
должно иметь период 2тт, а потому k должно быть целым числом. Мы
можем, кроме того, предположить, что /sJSsO. Тогда, как видно из
сравнения уравнений (86) и (89), можно взять & = Рк, n^k. Таким
образом мы получаем следующие частные решения уравнения (39):
dkP dkP
cos/гад sinfc0 ——, sin /сад sir? 6 ——~ (k — 0, 1, 2, ...,«),
• dp.k T dp.k
СФЕРИЧЕСКИЕ ФУНКЦИИ
173
или полностью
k — 0:
fe=l:
Ра>
cos и sin 0, sin и sin 6
dp. v dp
<Р р iP P
k—2: cos2w sin2 0 - ", sin 2» sin2 0--,
dp2 Y dp2
dnP dnP
k=n: cos raw sin” 0 ——-, sin n'o sin” 0--
T dp? ‘ dpn
Эти полиномы не равны тождественно нулю при k п, так как сте-
пень полинома Р^ в точности равна п.
Каждая из функций
, . ,,r<dkP„ Лк р
cos faf sin” 0 , sin sinfe 0
обращается в нуль при 0 — 0, 0=тг, если &^>0, а также при п — k
других значений 0, которые получаются из п — k корней уравне-ния
dkPn
dpk
Этим последним корням соответствуют на сфере п—k парал-
лелей. Кроме того, указанные функции обращаются в нуль (&^>0),
если cos/s<f = 0, т. е. при
тг Зтг 2k — 1
¥ = 2k ’ 2k ’ ” ’ ’ 2k П’
и если sin ktf — 0, т. е. при
тг
k ’
2тг
~k’
k— 1
k
ф = О,
Этим значениям tp соответствуют k меридианов. Итак, рассматриваемые
сферические функции обращаются в нуль на k меридианах, которые
образуют между собою равные углы, и нал — k
параллелях. Эти параллели и меридианы делят
сферу на сферические четырехугольники. От-
сюда рассматриваемые нами функции и полу-
чили свое название тессеральных (tesseral har-
monics) функций1 степени п и типа k. При
dnP
k~n мы имеем — const, и параллели от-
сутствуют; при /г—0, т. е. в случае полиномов
Лежандра Pre(cosO), отсутствуют меридианы.
Эти 2п -j-1 сферических функций линей-
но независимы. Общий вид сферической
Черт. 95а.
J Tessera (латинск. яз.) — четырехугольная плиточка, употребляющаяся в каче-
стве мозаичного материала.
174 ШАРОВЫЕ ФУНКЦИИ, ФУНКЦИИ БЕССЕЛЯ И ЛАМЕ
функции п-й степени следующий1 *:
п
(6, <?) = S C0S Sin k^> Sin* 9 (90)
й=О
Коэфициенты ЛяЛ, и ВяА., как мы увидим в § 98, определяются одно-
значно.
§ 97. Интегральные соотношения. Вспомним формулу Грина [см
§ 52, (20)]
U и V здесь — две правильные гармонические внутри замкнутой по-
верхности 5 функции, п — внутренняя нормаль.
За поверхность 5 мы возьмем теперь сферу с центром в начале
координат и радиусом, равным г, и положим:
Va=^Yn$, V= Vm==rmym{bj ^);
Yn <9» <р). Ym (9 • <?)• (92)
Мы получим:
(т — п) JJ YmYndS= 0, (93)
т. е. при т-ф п
(91)
Следовательно, функции Ym н Yn на поверхности сферы единичного
радиуса взаимно ортогональны.
Если обе функции Yn и Ym — зональные, т. е. если Г„(0, ф) =
= /’„(cos6) = Рп (р) и Ym (0, <р) ~Рт (g), то, так как при r== 1
6?5=sin0 db dq,
мы получаем:
7t
2irJ Рт (cos 0) Рп (cos 0) sin 0 d0 == 0, (95)
,0
ИЛИ
1
J Pm№ Pn(V-) dy.=O.
—i
Это равенство было нами получено раньше из диференциального урав-
нения Лагранжа.
1 Доказательство см., например, yRiemann-Weber, т. 1, стр. 576. Там же
имеются и другие представления сферических функций.
ИНТЕГРАЛЬНЫЕ СООТНОШЕНИЯ
175
Воспользуемся теперь другой формулой Грина [см. § 60, (70)]
2_м/
d йл
мы распространяем на сферу, определенную выше;
от неподвижной точки Р, не лежащей на
Vp=
dS,
(96)
обозначает расстояние
ере; нормаль направлена внутрь сферы. Мы имеем (см. черт. 95):
1
~d
со
(44)
п=0
здесь г'<^г и p = cos(r/''). Положим в формуле (96)
(mS^O— целое число), в таком случае
к 2л pj,
V = rmYm(0, и)
РМ
V”=и) )
о о
п—<1
(97)
т
77=0
Р„ (р.Й a2 sin 0 гЙ
Пусть г’, 6', ср' будут полярными координатами точки Р; тогда
VP~-=r'mYm(fi, ср). С правой стороны в формуле (97) стоит бесконечный
степенной ряд, расположенный по степеням г'; козфицнентами этого
ряда служат определенные интегралы, взятые по сфере единичного ра-
диуса. Так как равенство (97) выполняется тождественно для всех зна-
чений г' г, то мы можем приравнять коэфициенты при одинаковых
степенях в правой и левой части. Мы таким образом получим’
J j ут (8 > <?) РП (Р) sin 8 dV = 0 (98)
О о
при а при т~п
[ j уп (8> Т) Рп W sin 6 dcp = 2^-1 Yn (9', ср'). (99)
о о
Воспользуемся известной формулой сферической тригонометрии
ц = cos (rr1) = cos 0 cos 9' -[-sin 9 sin 9' cos (cp — cp’)
н подставим это значение ц в последнее равенство, положив 9 = 0 и
Ya(9, ср) = Рп(cos 9). Так как Рп (1) = 1, то это преобразование даст нам:
1
J \Рп (Н)12 dV- ~ 2П-^\ ’
—1
формулу, которой мы пользовались уже выше (82) без доказательства.
176
ШАРОВЫЕ ФУНКЦИИ, ФУНКЦИИ БЕССЕЛЯ И ЛАМЕ
§ 98. Разложение в ряды по сферическим функциям. Интегральные
выражения (98) и (99) дают нам возможность вычислить коэфициенты
разложения функции /(6, (р) в ряд по сферическим функциям в пред,
положении, что такое разложение возможно, и что ряд сходится равно-
мерно. Пусть
/(б, гр) = г0 (б, <р) -f- уг (0, <р) + y2 (0, <р) 4-... 4- Yn (0, ср) 4-... (100)
Умножим обе части этого равенства на Рп (р) sin 0 dA dy и проинтегри-
руем по поверхности сферы единичного радиуса. Все члены ряда, исклю-
чая га-го, обратятся при этом в нуль, а л-й член даст нам:
к 2тс
J j J (6, т) рп 04 sin 6 М d4 = g-2? ! Yn (е'> ’А
о о
р.=cos 0 cos 0f 4~ sin 0 sin 0' cos (<p — tpr). (101)
Разложение (100) называют рядом Лапласа для функции /(0, <р)
(ср. § 87). Ряд этот соответствует в пространстве ряду Фурье для функ-
ции, заданной на окружности (ср. § 42). Мы получаем л-й член этого
разложения в какой-либо точке Р(0', <р'), вычислив зональные сферические
функции с полюсом в точке Р, умножив значение этих функций в пе-
ременной точке на сфере единичного радиуса на соответствующее зна-
2л 4-1
чение функции / и на ——— и проинтегрировав полученное выраже-
ние по поверхности всей сферы. Указанный нами способ вычисления коэ-
фициентов характерен вообще для вычисления коэфициентов разложения
произвольной функции в ряд по фундаментальным функциям (ср. § 33).
Отдельные члены этого разложения в силу формулы (30) можно вы-
разить через присоединенные функции Лежандра. Положим:
п
Yn (0, у) == У (Ank cos ky 4-Bak sin й(р) Л» (p) (p = cos 0),
kS
t. e.
co co n
/(о, <р) у Yn (0, ?)-X X ^Ankcos *<?+Bnksin kv) pn t102)
«=0 n=0&=0
и вычислим коэфициенты А и В. Умножая обе части равенств (102) на
cos/гср, интегрируя и принимая во внимание равенства
Л р (0
I cos &р sin ly dy = 0, 1 cos ky cos lydy—- n
о о 2ir
при
при й = />0
при k^=l — Q
(103)
мы находим:
оо
EV4^04
я=0
2л
/(0, tp) cos ky dy
Oo = 2; lk = 1 при k 0). (104)
РАЗЛОЖЕНИЕ В РЯДЫ ПО СФЕРИЧЕСКИМ ФУНКЦИЯМ
177
Если обе части этого равенства снова умножить на Р*(р), то останется
только один член
1 2я
(л 4- k)l 2Х.тг f f
(wZ.'^)t "2и -f- 1 J J C0S dv~ dV' (105)
— i о
так как [см. (76) и (83)]
С f °
I ркт (М) рка (t>) dP- = । (» + *)>
—1 (. (л —й)1
при m^n
2
---г при
-H
Итак, окончательно:
A _ 2«+*
«* (в А)! 2Хйтг
я 2я
J J/(0, <?)cos (cos 6) sin 6 d?) dtp,
о 0
(1®8)
и аналогично:
_______(л — /г)! 2л -J- 1
пк (л -)- k)l 2Xj.Tr
я 2л
J J/(0> <p) sin ktpP1^ (cos 0) sin 0 r/0 dtp.
о 0
(107)
Мы, таким образом, получаем:
п Г /
я 2n
J J/(0,^)cos^P*(cos0)sIn0d0<fy-f-
COS ktp'
, о 0
пК Li (n±k)\ 2Х*п
ktp' /(6, ф) sin (cos 6) sin 6 dG dtp } P* (cos 6').
co /_
To же после небольшого преобразования можно переписать так:
Гя(0', «?') =
fe=0
= C [X ^^[^V'^(0’'p)/’»(Cose)Pn(cos6’)cos&((p-<p,)sinOrfOd<f.
0 0 Ы) k
Сравнение этого результата с формулой (101) дает:
Рп { cos 6 cos 0' sin 0 sin 6' cos (<p — </)} 3=3
n
=£ (cos 9) (cos t},) cos •
fe=0
(108)
(W9)
(ПО)
Слева в этой формуле стоит сферическая функция, зависящая от двух
пар переменных 0, <р и 0', ip' и симметричная относительно них; сумма,
стоящая в правой части в этом равенстве, представляет эту функцию
12 Вебстер, Дифереициапьные ураененвя.
178
ШАРОВЫЕ ФУНКЦИИ, ФУНКЦИИ БЕССЕЛЯ И ЛАМЕ
с помощью 2/г 4- 1 сферических функций от 0, <р и 6', определенных,
в § 96. Формула (ПО) называется теоремой сложения сферических
функций
§ 99. Сходимость рядов Лапласа. Докажем теперь, что, при соответ-
ствующих допущениях ряды, найденные нами для разложения функ-
ции /(0, <р), сходятся. Итак, согласно (101) мы полагаем:
п 2гс
tp) (р) sin 0 d0 dtp; (Ш)
требуется доказать, что
Нт S„=/(6', tp').
я->оо
Первые попытки доказать эту тео-
рему были сделаны Лапласом и Пуас-
соном; первые строгие доказательства
были даны Дирихле и О. Бонне2. До-
казательство, к изложению которого
мы приступаем, принадлежит Дарбу3.
Выберем новые сферические коор-
динаты у, ф таким образом, чтобы точ-
ка Р (0', <р') оказалась новым полюсом
сферы (черт. 96). Положим при этом,
что /(0, <р) — Р(у, ф). В таком случае
п гс 2«
5/г = ^г^ j ^^(У’ U-PvfcosYJsinydydu. (112)
\=0 0 о
Среднее значение функции F на параллели у обозначим через Ф(у) = Ф(р),
т. е. положим
2гс
j F (у, Ф) = Ф (у) = (ц). (ИЗ)
Тогда °
п 1
sn = | lIf (ц) Л (Д) d}i. =
v=0 — 1
Г
= у j [Ро (м) + ЗЛ (Д) + 5Р2 (р) + ... 4- (2п 4- 1) рп (р)] ф (р) dp.
—1
1 Legendre, Calc. Int, т. II, стр. 262—269.
. 2 G. L. Dirichlet, Journal fur Math., t. 17, стр. 35—57 (1837); О. Bon-
net, Journal de Math., t. 17 (1852), стр. 265—300.
з Journal de Math., серия 2, т. 19 (1874), стр. 1—18.
сходимость рядов Лапласа
179
В силу (71а)
это равенство можно преобразовать так:
f (Sir+S’) м
(114)
Положим, кроме того, что функция ф(ц) между —1 и 1 имеет
непрерывные частные производные. Тогда мы можем применить интегри-
рование по частям, которое даст нам:
5в = ^-[Ф(р)(Ря+1
+ Л)]
i 1
~2~ j ^n+1
-1 -1
W + (115)
Так как в силу (48)
^яП)=Ря+1(1)=1; ^(--i)=-P„+1(-i)=(-i)n,
то подстановка в первый член значения р.——1 дает нуль, и мы по-
лучим ;
5И=Ф (1) - у J 1Л+1 (р) + Рп (Р)) Ч" (р) <*Р-
—1
Пусть |Ч?' (р.) |<М в интервале —в таком случае второй
член по своей абсолютной величине меньше
1
м С
-2 J 1РП+1(Р) + ^Й(Р)|^Р- (115а)
-1
Далее, в силу неравенства Шварца1 мы имеем:
таким образом выражение (115а) при п—юо стремится к нулю. Сле-
довательно,
lim Sa = ф (1) = Ф (0) = /(О', </).
я-»оо
i Неравенством Шварца называется следующее неравенство:
ь ь
f №(*) J [/ (х)]2 dx J [g(x)Pdx,
а а
причем предполагается, что функции f(x) и g(x) непрерывны в конечном
интервале.
12*
180
ШАРОВЫЕ ФУНКЦИИ, ФУНКЦИИ БЕССЕЛЯ И ЛАМЕ
Сходимость рядов Лапласа можно доказать и при более общем до-
пущении, а именно полагая, что определенная нами выше функция ф (g)
удовлетворяет условию Дирихле х.
§ 100. Бесселевы функции, а) Для определения функций Бесселя раз-
ложим выражение
i у-/-*)
Z=e2
в степенной ряд по целым,
переменного t. Так как
Xt 00
е2;
ft=0
положительным и отрицательным
степеням
xt—_
2 .
оо
л=о
е
М ’
то
оо оо
й=ОЛ=О
Z =
k+h tfi-h
ММ'
(2)
Положим k — h = n (откуда k = h-[- п и k h = 2h-\- п). Объединяя
члены с одинаковыми степенями t, мы можем переписать этот ряд в
таком виде:
(v \ 2Л-1-Д
_ j ОО
п=—оо л=о и=— ос
где через
/ у \ 2ч
v=0
обозначена так называемая бесселева функция н-го порядка. При
—1, —2, —3... суммирование надо начать от v = — п и про-
должить до бесконечности.
Функция Z называется производящей функцией для Jn (х) [ср. § 92,
(48)]. Таким образом J„(x\ для всех целочисленных значений п вполне
определена. Независимое переменное х может принимать любые как
действительные, так и комплексные значения.
Ь) Выпишем полностью сумму, стоящую в правой части формулы (3):
Z = Jo (х) + Ц (х) + (х) + ... +1~(х) + V_2 (х) -j- .. .
Заменим теперь t через —<-1. Так как Z при этом не изменит своей
величины, то можно написать:
z_ ,/о {х} _ г-i71 {х} _ц г-яj2 {х} _|_... _ tJ{х) г27_г w . (5)
1 Подробное изложение теории шаровых функций и полиномов Лежандра
можно найти в книге Е. Heine, Handbuch der Kugelfunktionen, т. I и II, 2-е изд,
Berlin, Reimer (1878 и 1881).
БЕССЕЛЕВЫ ФУНКЦИИ
181
Приравняв коэфициенты при одинаковых степенях t, мы получим:
W=*(-iyj_nW- (6)
Мы видим, таким образом, что при п целом Jn (х) и J_п (х) отличаются
друг от друга только постоянным множителем (что можно получить
также и из предыдущего их определения). Легко видеть, что
,T(/-rl)I=JcW+72W(/2Jr/-2)+AW(/4n+ii.
.. •+Л (X) (i - /"’) 4-J3 (X) (/3 - /-3) + . . .
или, заменив t через e*f, где <р— действительное число,
eixsin<p __ Jq 2J2 (х) cos 2tp -|~ 2-Л (*)cos 4tp 4~ • • 1
... -f~ i [2Jj (x) sin <f -}- 2J3 (x) sin 3tp 4~_1 • >
Правую часть этого равенства можно рассматривать как результат раз-
ложения в ряд Фурье функции от ср, стоящей в левой части этого ра-
венства. Пусть х действительно; тогда, приравняв отдельно действитель-
ные и отдельно мнимые части, стоящие по разные стороны знака ра-
венства, мы данное равенство разобьем на два ему равносильных:
cos (х sin <р) = Jo (х) 4~ 2 Jz (х) cos 2tp -[“ 2 (х) cos 4ср 4~ •
sin (х sin <р) = 2Jj (х) sin tp 4~ 4J3 (х) sin 3tp 4* • • »
а потому
JZtl (х) 2= -i- j cos (x sin tp) cos 2в<р dip,
о
Я
n+I (x)=^-i-sin (xsin tp)sin (2и-|~ 1) tp d<f.
о
О)
(Ю)
Заменив переменное <p в формуле (9) переменным tp 4~ -н- > мы будем иметь:
cos (х cos <р) = Jo (х) — 2 J2 (х) cos 2<р -]- 2 Ji (х) cos 4tp — ... , 1
sin (x sin tp) == 2/j (x) — 2J3 (x) cos 3<p -f- ... J
Отсюда можно также найти выражение Jn(x) через интегралы.
с) Согласно определению
х _ оо со
*>=7о {Х) + tnjn(x) + £ (_ 1)я/-ч (х).
Й=г1 Л=1
Заменим в этом равенстве t через
„ х __ оо оо
п=1 л=1
182
ШАРОВЫЕ ФУНКЦИИ, ФУНКЦИИ БЕССЕЛЯ И ЛАМЕ
и перемножим оба эти равенства. Результат умножения можно записать
в следующем виде:
оо оо
Я=1
Так как относительно t это равенство представляет собою тождество, то
4 = °> A_n = Q (« = 1,2, 3,...)
и, в частности,
4=1 =4 W+^ W+24 (х)+..
(12)
Для действительных значений х все встречающиеся здесь величины
действительны; так как все слагаемые положительны, то Jo (х) по абсо-
лютной величине .остается меньше единицы, a JT (х), J2(x) ...
меньше —7=, когда х изменяется в действительной области.
/2
d) Диференцируя производящую функцию Z по х и по t, мы по-
лучаем:
— —tf t-i)Z
йх 2 1 ’ ' йх2 4 ( ' Z’
ZZ__ । ^Z _~х2
й/ “ 2 е- J z’ й/2 — 4
Таким образом функция Z удовлетворяет следующему уравнению в
частных производных:
2^z . йz *2z ,ъг . л
ЙХ2 1 йх й/2 й£ 1
(13)
и в силу равенства (3):
п
S'" S+4"+<'*-
;я= —ос
Отсюда находим, что для всякого значения п
d^Jn 1 dJ / »2\
dx2 * x dx x2J
4=o.
(14)
Это уравнение называется диференциальным уравнением Бесселя, а функ-
ция Jn(x) является его интегралом.
е) Производная от производящей функции Z по t равна;
оо
yd+C^Z^JJ^fx),
«=—ОС
БЕССЕЛЕВЫ ФУНКЦИИ
183
ИЛИ ОО
т(1+/_2) Stn Jn {х)=S ntn~v« (х)- 03)
Я= —ОО —ОО
Приравнивая коэфициенты при £”-1, мы получаем:
У K-i (*) +4+1W]• (16)
с помощью этой формулы можно вычислить Jn+1 (х), если известны
Jn(x) И J^x).
Взяв производную ОТ Z ПО X
оо оо
<п>
п=—оо п~— оо
мы, аналогично предыдущему, получим:
у [Л-1 ~Jn+. == • (18)
С помощью дальнейшего диференцирования и повторного применения
этой формулы можно все производные от J„(x) линейно выразить че-
рез J„(x) различных порядков. Для я —О мы получаем:
= 08')
f) Уравнения (16) и (18) можно рассматривать как функциональные
уравнения; п при этом может принимать любое (не обязательно целое)
значение Любое решение Jn(x) = Cn(x) этих уравнений называется ци-
линдрической функцией. Можно доказать, что цилиндрическая функция
всегда удовлетворяет уравнению Бесселя (14). Действительно, склады-
вая (16) и (18) и вычитая одно из другого, мы получаем:
=- т с«w+с« - (х) i {хПС">=хпс^ (,9)
или
= — сп (х) — Ся+1 (х) — ЛЦ = — ^±1. (20)
dx х "' ' n+1' ’ dx \x ) xn
Продиференцируем равенство (20):
Д (J I Д dCn + 1
dx2 x2 n'x dx dx
dC
и подставим в полученное выражение вместо его значение из (20),
184
ШАРОВЫЕ ФУНКЦИИ, ФУНКЦИИ БЕССЕЛЯ И ЛАМЕ
а вместо
dCn+i
dx
его значение, которое получается из формулы (19), если
мы в ней п заменим через п -j- 1. Мы найдем:
Преобразовав это уравнение с помощью формулы (20), мы придем, на-
конец, к уравнению:
*4 .
dx2 х dx
(21)
т. е. к уравнению Бесселя.
§ 101. Уравнение Бесселя, а) Исследованию уравнения Бесселя мы
предпошлем некоторые сведения из теории функции Г.
Функция Г для любых комплексных значений z (z —1, —2, —3,...)
определяется равенством:
Г (z -k-1)=П (z) — lim ——,— J % * * * Я--—=--пг. (22)
л-»оо(14-г)(2 4-г)(3-|-г)... (и + дг)
О существовании этого предела мы заключаем из сходимости ряда
оо
п = 2
п | , п \
-j---pzlog-----J.
-4-z п — \
г.
Сходимость же этого ряда основана на том, что при п —> оо функция
имеет порядок малости Ряд сходится равномерно во всякой области,
не содержащей точек — 1, — 2, — 3, .. . Определенная таким обра-
зом функция П (z) является правильной, аналитической повсюду, за
исключением точек, которым соответствуют целые отрицательные z;
в этих последних функция II (z) обращается в бесконечность первого
порядка. Кроме того, эта функция удовлетворяет функциональному урав-
нению
П (z)=zTi.(z — 1), (23)
а так как П(0) = 1, то
П(л) = л! (д=1, 2, 3...).
Вычислим
2
2
2
2
П
1-2-3...я | 2-4-6...2» |
3 £ 2л -j- 1 " Д^З-5-7... (2/г-Ь1)Я ’
2 '2 2
УРАВНЕНИЕ БЕССЕЛЯ
185
/ 1\ 1-2-3. ,.п 2-4-6...2л -4
П — -тг = hm т—г—е-----------i« = I'm т Q g--п----ттп
\ 2 / п—>оо 1 3 5 2л 1 л—»оо1 - 3- 5.. .(2л 1)
2 "У*2 2
Перемножив эти два выражения,
мы в силу формулы Валлиса получим
и/1\п/ И г 22-42-62... (2л)2 тг
^2j \ 2 / 32-52-72... (2л— 1)2(2л4-1) 2’
и следовательно, так как П
то
\2 ) 2
Введем обозначение:
_ tflogll (z) _ П'(г)
dz ~’П(г)*
Из (23) следует, что
Ф(*+1) = Ф(г) + * ,
2 1
т, е.
Ф(1)=Ф(0) + у,
ф(2) = Ф(0)+-|-Н-|,
(24)
(25)
(25')
Ф(л) = Ф(0) + 1- + |+...1.
Кроме того, мы имеем:
log II (z) — lim {log 2 -|- log 3 -}- ... -f- log л z log n — log (1 -j- z) —
n->oo
— log(2 + *)~ •.. — log (л “( z)},
а потому
,'(’,=s1°gn w=“” {|<’г“-(гр+2Тт+зр+-+^1))-
Отсюда мы опять-таки можем получить формулу (25').
В частности,
Определенное таким образом число С=0,577215665... называется эйле-
ровой константой.
1 См. Riemann-Weber, т. 1, стр. 169.
186 ШАРСВЫЕ ФУНКЦИИ, ФУНКЦИИ БЕССЕЛЯ И ЛАМЕ
Посмотрим, нельзя ли решение у = С(х) уравнения Бесселя (21)
представить в виде произведения степенного ряда по х на х в некото-
рой степени р:
оо
У = х? 7^ 0)‘ (26)
л=о
Значение степени р мы определим потом. Чтобы ответить на поставлен-
ный нами вопрос, найдем первую и вторую производные от у по х\
оо
s=’E(₽+4‘,*x’“'1’
k-Q
оо
§=2(р++k~!) a^k~2
k=j
и подставим полученные выражения, а также ряд для у в уравнение (21).
Мы получим:
оо
£fiJ[(p4-A)(p_|-/e- 1)4-р4-А-л®]л₽+*-24-^}== 0. (27)
Приравнивая нулю коэфициенты при отдельных степенях х, мы прихо-
дим к рекуррентной формуле:
(р4-а4-«)(р4-*—«)йл4-«*-2=о. (23)
Это уравнение будет иметь смысл также при й = 0 и при k—\, если
положить л_2 = л_1 = 0. А так как ао^О, то
(Р-«)(?+«) = 0, (28')
т. е. р=л или р=—п. Возьмем первое из этих значений. Тогда
* k(2n-\-k)'
откуда
д __________ао п _________ ае _________________ао_______
2~ 22(«4-l)’ 4 4(2л-|-4) 24»2! (л1) (и2) ’ ‘ ”
а все ак с нечетными индексами равны нулю. Положим
1
й°“2«П(л)’
тогда в силу (23)
п (-1)*
2* 2л+2*.А:!П(л4-А)’
УРАВНЕНИЕ БЕССЕЛЯ
187
и мы получаем решение:
ОО (_ 1)й
n+2k
(29)
у La А1П(я4-А)
tbO
Это так называемая бесселева функция первого рода. Для целочислен-
ных п она совпадает с функцией, определенной формулой (4). При п
целом и отрицательном нужно а{
нулю. Формула (29)
1
считать равным
Если п заменить
выражение
продолжает
нулю при v
через —я,
k=0
!oi й2> • • • » й2п-2 положить равными
в этом случае сохранять силу, если
целом отрицательном.
то для нецелочисленных значений п
—n+2k
А!П(— k)
(30)
также будет представлять собою частный интеграл; легко при этом за-
метить, что Jn(x) и J _п(х) в этом случае линейно независимы.
При п целом положительном первые п членов степенного ряда
обращаются в нуль; если положить k — n-\-p, то, как и в (6), имеем:
S(v \П + 2р
Д,1
9 /
(п4-/?)!П(р) = 1
р=0
(31)
Таким образом оба эти решения линейно зависимы. Из общей теории
линейных диференциальных уравнений (см. ч. I, приложения, § 5) сле-
дует, что в этом случае существует еще и другой интеграл, линейно
не зависящий от Jn(x). Этот последний мы и найдем сейчас с помощью
предельного перехода.
Дадим п значение, не равное целому числу. В таком случае функция
(Х) НйГТгп[C0S W ~
(32)
является решением диференциального уравнения (21). Когда п стремится
к целому числу, эта функция становится неопределенной. Предел ее
в этом случае мы найдем, диференцируя числителя и знаменателя по п.
Мы имеем:
(v \л + 2й
— I
(у \n+2k
у)
=Jn W 10g 2“ — А! II (л k) '
А=0
(33)
188 ШАРОВЫЕ ФУНКЦИИ, ФУНКЦИИ БЕССЕЛЯ И ЛАМЕ
_ dJ „ (х)
Аналогичным образом мы вычислим также —, и если п 0 це-
лочисленно, то в некоторые члены соответствующей суммы войдет
ф(г)
дробь утт-р У которой аргумент есть целое отрицательное число z =_.у
11
(у—1, 2, 3, ... ); чтобы определить предел этой дроби при z—>•—.у
(числитель и знаменатель ее стремятся к бесконечности, когда у стре-
мится к целому положительному числу), преобразуем ее в силу (23) и
(25) так:
П(г) IlCer-j-l)
Принимая во внимание, что
п'0>=1-
й подставляя в полученную формулу у= 1, 2, 3, ... , получаем:
ф(— у)
=3—2=-------(-у+ 1)(-v + 2)... (—!) = (— l)vll(v—1),
т. е. при п^О
( у \ —Д +
k=n
+<-^Ч=2(т)^'
k=0
Итак, при п целом формула (32) переходит в пределе в следующую:
ттY (х) = —— (— 1)« ,
nV ' in ' 7 in
или на основании (31)
(v \п + 2А
= -2—д(„+/), {'!-(«+*)+Ч'(Ч} -
п—1
S(n------k---1)! / X \ ~«+8*
k\ \ 2~J
й=0
(34)
1 При и = 0 последний член отпадает.
ВЫРАЖЕНИЕ БЕССЕЛЕВЫХ ФУНКЦИЙ
189
В силу (25') и (25") то же можно записать несколько иначе:
Определенная нами таким образом функция называется функцией
Бесселя второго рода. Мы уже пользовались ею при к —0 в § 65.
Упомянем, наконец, о бесселевых функциях третьего рода (функциях
Ганкеля). Они определяются равенством
H\{x)=^Jn{x)-\-iYn(x), Hl(x)=Jn(x) — iYn(x) (я—целое и я^О) (35)
и играют большую роль при изучении колебательных явлений.
§ 102. Выражение бесселевых функций с помощью определенных
интегралов. Полагая в формуле (7) /зе'?, мы имеем:
оо
6?“siH<P == £ Jn (х) е1пч.
Умножим полученное равенство на и проинтегрируем:
Но
2тс 2к
fOO г»
eixein<pg-{-m<p __ £ Jn (х) 1
6 «=- ОО J
0 при q целом,
2п при q~0,
q^
а потому
2тс
2тгУя (х) =
о
(37)
Так как для действительных значений х функция Jn (х) действительна, то
2п т-
1 С 1 г
Jn (х) = — I cos (х sin <р — я!р) dy == — I cos (х sin у — пу) dy. (38)
о о
В этом виде Бессель и ввел функции Jn (х) г. Отсюда легко также по-
лучить формулы (10).
1 „Untersuchungen des Theils der planetarischen Storungen, welcher aus der
Bewegung der Sonne entsteht", Berliner Abh. (1824).
190 ШАРОВЫЕ ФУНКЦИИ, ФУНКЦИИ БЕССЕЛЯ И ЛАМЕ
Другое выражение бесселевых функций, имеющее также большое
применение, мы найдем, вычисляя интегралы:
1р ч = J sin2P <р cos2? dy (р, q 0 =— целые числа). (39)
о
Интегрирование по частям дает:
sin2*’*1 fp cos2^-1 *p
9 ~ 2/7-f- 1
л 2g—1 (
О 2/7 -f- 1 J
о
sin2^*1) щ cos2(?~-0 и tZ<p =
г 9<7_____1
j sin2? <₽ (1 — cos2 <₽) cos2<?"1> <p dy == ?~1 ~
0
и следовательно (q^--1),
i <
p>9 2(p-\-q) P’9-1 ’
Аналогичным образом
eos^sl^-i,, '+^lf w.„ d
P>Q 2^4-1 2^+1 J f f Y
о
71
= f cos2?<₽ (1 — sin2tp)sin2^-« <pdy = -—^1 ^°-г>?“
1 J £4~V 1
0
t. e. (p 1)
2p~ 1
T —____________ I I
lP,q 2(p-f-^) P-1»0’ '
Применяя q раз подряд рекуррентную формулу (40), мы получаем:
_ (2</—1)(2<7 —3)...3-1
Р>9 2(p + q)-2(p-^q—\)...2(p-\-\)P>0'
Точно таким же образом из (41) получается:
(2/7—1)(2/7-3)... 3-1
Р’° 2/7-2(/7—1) ... 4-2 °’0’
т. е.
_1-3.5 ... (2q— 1). 1-3-5 ... (2/7—1)
<р,9— 2-4-6... 2(/7-j-^) °’0*
ВЫРАЖЕНИЕ БЕССЕЛЕВЫХ ФУНКЦИЙ
191
Но
г
4), о ~ = тс,
о
а потому (2р)!(2?)!тг
ч ~ 2Ш>+^р\д\ (/> + ?)! ‘
Из этой формулы следует:
(V \ 2/г
— 1
2 /
~(2л)Г ТГ] 1“ *Г (2ft) I ’ а<Р " ft!(ft 4-л)! ’
о
И таким образом,
(v \
т)
J” W = Ъ ft! (л 4-ft)! =
k=0
(xcos ?)%
(2ft)! ?
ХП______ 1 f Sin2»
1-3-5 ... (2л—1)^J
о
<p cos (x cos <p) dtp.
(42)
Наконец, полагая costp = x’, мы найдем:
xn 1 С —-
.(з^-ПТУ1-2’* 2 zmx‘dz-
— 1
(43)
До сих пор мы предполагали, что п не принимает целых отрица
тельных значений. Однако формула (38) справедлива при всех значе-
ниях п, а (43), если знаменатель в ней заменить через ]/п2“П I п--— 1,
справедлива при л^> — —. Если
2л —1
2
целое число, то интеграл (43)
может быть вычислен с помощью элементарных методов, и тогда функция
Уя(х) выражается через элементарные функции. Этот частный случай
встречается, например, в теории сферических волн (см. §116). Конечно,
эти функции можно получить и с помощью разложения в ряд бесселе-
вых функций, воспользовавшись при этом известным уже нам значе-
нием П —) . Эти вычисления особенно упрощаются, если пользоваться
уравнением (16), вычислив предварительно J\(x) и J3 (х). Таким образом
2 "2
192
ШАРОВЫЕ ФУНКЦИИ, ФУНКЦИИ БЕССЕЛЯ И ЛАМЕ
Также очень легко получается следующий ряд:
п
(л + у) (л+>—*)
2-4 ..
..(и—v-M) 1
2v (ix}‘
(44')
Укажем, наконец, формулу для приближенного вычисления бесселе-
вых функций при больших значениях аргумента; именно для любого п
при х—>оо имеет место равенство:
Погрешность е(х) имеет тот же порядок, что и х 2. При
— 2 ’
эта формула следует непосредственно из вышеприведен-
ных (44); к этой формуле в случае целых значений п мы еще вернемся
(см. § 120).
Отсюда следует, что функция Jn(x) имеет бесчисленное множество
действительных корней.
§ 101. Цилиндрические координаты. Наряду с пространственными
полярными координатами большое значение имеют цилиндрические ко-
ординаты; цилиндрическими координатами называют числа г, р, <р, опре-
деляющие положение какой-либо точки Р в пространстве; первая из
них z представляет собою третью прямоугольную координату этой
точки, а две другие — обычные полярные координаты проекции точки Р
на плоскость ху. Простые геометрические соображения показывают, что
квадрат линейных элементов имеет выражение
ds2= rfp2 —р2 cZ'p2 —|- dz2,
ЦИЛИНДРИЧЕСКИЕ КООРДИНАТЫ
198
так что в силу § 30, (20)
йр = йг=1, й?=1
отсюда, на основании формулы (32) того же параграфа, имеем:
уу . 1 av i w , уу
ар2 р ар ' р2 а<р2 аг2
(45)
Чтобы найти новые частные решения уравнения Лапласа, разделим
переменные, как мы это уже делали в § 91. Итак, полагаем
y=Z(z)/?(p)®(¥).
Подставляя это выражение в уравнение Лапласа и деля обе части на V
(при Уу^О), получаем:
1 d2R 1 dR 1 1 ^2Ф 1 tPZ ч
R dp2 ' pR dp “г p2 Ф dy2 + Z dz2~Q' (43J
Соображения, аналогичные изложенным в § 91, указывают на то, что
последний член равен постоянному й2, т. е.
d27
—2-й^==0 (46)
И
. Wxl^5_0
R d? + R dt +“ ₽ ' Ф d^ “°’ ,47)
Также и в этом уравнении последний член представляет собою постоян-
ное; полагая его равным —л2, находим, что
^+“!ф=° (48)
И ^+£«+(4,_4)^=0. dp2 р dp \ р2) (49)
Итак, в результате разделения переменных мы пришли к трем обыкно-
венным диференциальным уравнениям. Общими решениями двух пер-
вых— (46) и (48)—служат:
Z — A ch kz -|- В sh kz, Ф = С cos пр -J- D sin ntf.
При этом п должно быть целым числом. Положим сначала йу40. Если
ввести новое независимое переменное х~k'j», то уравнение (49) перей-
дет в уравнение Бесселя:
d2R t I dR / п2\
dx2 х dx *" \ x2/
7? = 0,
13 b.s«. e p, Нифвреяци»пьн« урмн«вив
194
ШАРОВЫЕ ФУНКЦИИ, ФУНКЦИИ БЕССЕЛЯ И ЛАМЕ
следовательно,
(Ар) 4-ГПи(йр).
Положим теперь А —0. Тогда Z~A-]~Bz, а уравнение (49) при-
мет вид:
d2R. 1 dR п2
dp2± p dp p2^
Общим решением этого нового уравнения служит:
R = Ера -j- Fp ~п.
(При п — 0 мы получаем: Ф — C-\-Dq, а при га=А = 0 оказывается
Flogp.)
Итак, мы получили следующие частные решения уравнения Лапласа:
V Е Еch kz + sh kz> cos №? + DnIl sin n<f) (Enb Jn (Ap) +
+ Vfi(Ap)). ’ (30)
Суммирование распространяется на любые значения k и на любые цело-
численные значения п. При бесконечном количестве слагаемых надо
ввести соответствующие допущения, обеспечивающие сходимость этою
ряда. При А = 0 и га —О надо принять во внимание замечания, сделан-
ные выше.
С диференциальным выражением (45) мы уже встретились в теории
потенциала (см. § 54) в частном случае, когда V зависело только от р
(круговая симметрия) Ч
§ 104. Эллиптические координаты. Третьим видом ортогональных ко-
ординат, имеющих большое значение, являются так называемые эллип-
тические координаты. При определении этих координат исходят из се-
мейства поверхностей:
<г2 £-2
-2П——h-гт-^1- (51)
« 2 р + р ~Г Р
где р — параметр. Это уравнение представляет поверхность второго по-
рядка с центром в начале координат. Полуосями этой поверхности
служат:
с2 р, j/>2-|-p, )/ с2 р.
Мы предположим
а2 ~^> Ь2 с2
и ограничим выбор значений р интервалом —с2<^р<^оо. Фокусы глав-
ных сечений лежат на оси Ох на расстояниях
)/а2 — Ь2, а2 — с2
< Дальнейший материал о бесселевых функциях можно найти в обширной
работе G. N. W a t s о n, A treatise on the theory of Bessel functions, Cambridge,
University Press, 1922.
ЭЛЛИПТИЧЕСКИЕ КООРДИНАТЫ
195
от центра и на оси Оу на расстоянии
j/б2 — £2
от центра. Таким образом положение фокусов не зависит от пара-
метра р, т. е. уравнение (51) представляет ссфокусные поверхности.
Если —с2 <Ср <С°° , т0 все члены в уравнении (51) положительны,
и это уравнение представляет эллипсоид. Если — &2<4р<^—с2, то ДЕа
~ первых члена положительны, а третий отрицателен (в сечении z — О по-
лучается эллипс, а в сечениях у~~0 и х = 0 — гиперболы), мы имеем
дело с однополостным гиперболоидом. Наконец, если —«2<^р<^ё2,
то положителен только первый член (в сечениях j —О и z—О полу-
чаются гиперболы, а сечение х = 0 мнимо), и уравнение (51) предста-
. вляет двуполостный гиперболоид.
Придадим х, у, z некоторые значения. Тогда уравнение (51) можно
рассматривать как кубическое уравнение относительно р. Положим:
F ' а2 -|- р Ь2 р с2 -ф- р
Яр) = («2 + р) (Ь2 4- р) (С2 4- р).
(52)
(53)
Тогда произведение /(р) F(p)
при р— — а2 равно х2(а2— Ь2)(а2— с2),
при р = — Ь2 равно —.у2 (я2 — b2)(b2— с2),
при р = —с2 равно z2(a2—c2)(b2— с2),
т. е. существуют три различных значения, удовлетворяющие уравнению
/(р) F (р) = 0. Обозначим их через Ji, V. Эти три значения опреде-
I лягот положение точки х, у, z [см. ниже (56)] и называются эллипти-
ческими координатами этой точки. Мы имеем:
*2 _J'2 । _г2 _ i
О2-|-)Л £2_l_y I C2j_y— *>
•(/2 y2
________I__i____I—-—1
a2 -4 g 1 £>2-|-|x~ c2-j- ji
v2 4)2 y2
- — -- J________[--——= 1
a2 -f- v ~ b2 v c2 -j- v
oo — c2,
---C2 ------------b2,
— b2~y> v 5-— a2.
(54)
i
j Следовательно, через каждую точку х, у, z пространства проходи-
t одна и только одна из указанных выше поверхностей. Выразим прямо*
угольные координаты х, у, z через эллиптические ji, >. Заметим для
этого, что многочлен третьей степени /(р) /7(р) обращается в нуль при
р=Х, ji, v, а следовательно,
F(n\ xZ J_ у2 4- z2 — 1 -- — (Р —(р — МИр —у)
— а2_|_р I 62_|_р’Гс2_|_р (О2+р)(&2+р)(с2-]-р) ‘
(55)
196
ШАРОВЫЕ ФУНКЦИИ, ФУНКЦИИ БЕССЕЛЯ И ЛАМЕ
Помножим обе части этого тождества на й2-|-р и положим затем4
р = — а2. Мы получим:
2 (я2 -4- 1) (я2 -I- (а2 у) (а2 — Ь2) (а2 — с2)
Точно так же находим:
У (Ь2 — с2) (7>2 — а2) ’ 9 (c24-l)(c2 + p)(c2 + v) (с2 — а2) (с2 — Ь2) ’ j * (56)
Таким образом эллиптические координаты определяют декартовы
координаты с точностью до знака. Заданной системе значений х, у, z
соответствуют восемь различных точек, каждая из которых является зер-
кальным отражением в координатных плоскостях трех других.
Докажем, что координатные поверхности образуют ортогональную
систему. Образуем для этого последовательно разности каждых двух
из уравнений (54). Мы получим:
х2 -1 L -4 Z2 1 = 0,
(р.—V) (а2-|-р)(а2-}-у) (62-i-n)(ft24-v) (c2+g)(c2-|-v)
(>-» L у2 j Z2 •==0, (57)
(а2-[-у)(й2-(-1) (624-v)(62-j-l) (С2 + У) (с2 + 1)
(1—р) X2 L У2 1- = 0.
(a2-f-l)(a2+p) (Й2 + Х)(62_|_)Л) (с2 4-1) {с2 4- ц)
С другой стороны, диференцирование уравнений (56) дает нам:
2х йх (я2+ al (а2— ц)(а24-у) Ъ2)(а2 — с2) X2 a2 -f-1 И Т. Д.,
откуда <х 1 X ах 1 X ах 1 X
ai 2 а2-|-1 ’ а^ ' 2 а24-р’ а> 2 а2 4-у’
ау 1 У ау 1 У ау 1 У
ах 2 62-|-Г дЦ 2 й24-р’ av 2 ъ2 у
аг 1 Z аг 1 'У дг 1 у
ах 2 с2 4-1’ ац ” 2 с24-ц’ а> 2 C24~V '
(58)
Пользуясь этими равенствами, мы можем уравнения (57) переписать
так:
ag ' ag от 1 ag от ' 14 ’
(59)
т. е. [см. (90) и (26)] поверхности 1 = const, g = const, у = const попарно
ортогональны и, следовательно, образуют трижды ортогональную систему.
(диференциальное уравнение ламе
197
Вычислим теперь ДИ. Для этого продиференцируем (55) по р:
х2 . У . -г2 (р~>)(р~-|*)(р —у) ( 1
(?+рР + О2 + р)а"г(с2-I- р)2 (а2 + р)(&2+р)(с2+р) I р—х
____L_ । _J_________L_ । _>______L.I
p_]_G2~p—p p_j_^2~p — V ?~t-c2J
(60)
и положим последовательно p = l, p, v. Мы получим:
х2 . ja . г2 (). — р)(1—у) (a2-t-i)2 1 (62 + ))2 1 (с2-р)2 /(1) х2 , У2 = (р—у)(р —1) (а2-|-р)2 (624-р)2 (c2 + p)a== /(Р) ’ х2 . у2 Z2 (у —).) (у — р) (а2 у)2 * (й2 -|- у)2 (с2 -f- у)2 /(у) Из формулы (25) § 90 в силу равенств (50) и (61) мы имеем: 1 _ 1 ( X2 у2 Z2 1 (1— р)(1—V) ^“4 Ца2 + 1)2 1 (Й2Н-Х)2( 1 (c2 + ))2j 4/(Х) й2 = 4 (1-р)(1-у)’ й2 — 4 (62) и- (р — У)(р — )) ^2 = 4 V (y_X)(v—р)’ и
/(И)/(у)
. , . _ 8/—/(M/(m)/(v) h,_ __ hl ^v—p
^^“(p —у)(у-1)(1-р)’ ЙД МД 2
и т. д. 1
Таким образом окончательно
_hhh и (А*П 1 2 (A^AIJA^U
— I a й) / йр йр } ~ йу \йД йу ] J
4]//())/(р)/(у) у—р ) Д-
(р—v)(v —))()—р) [|//(р)/(у) й) V ' ЙМ
— у й / г— ЙИ\ . р —). й .//-ТГДЙГХ!
~//(у)/(Ь) йр \ йр/ v /(Х)/(р) йу \ ЙУ/J
(63)
§ 105. Диференциальное уравнение Ламе, а) Положим
d\
7Ж
= da,
dji
/Тод
dv
-=dY.
(64)
-4
* Из (63) непосредственно следует, что выбор знака в произведении
не имеет значения.
198
ШАРОВЫЕ ФУНКЦИИ, ФУНКЦИИ БЕССЕЛЯ И ЛАМЕ
Тогда 1, ц, v будут эллиптическими функциями новых аргумен-
тов а, у, и мы будем иметь:
4 Г й2П Й2У й2У1
A v—Тм(»-МL(>~rtg+ <|л ~ J' (8S)
Уравнение Лапласа примет при этом следующий вид:
й2У d2V й2П
(v~H)^ + (^-v)^+(g-X)-2-^0. (66)
Постараемся теперь найти решение вида V — L(a) Nft). Под-
ставив это выражение в уравнение (66), мы получим:
v — ji d2L . ). — v гГ2Л! , g — 1 d2N
L ^I2 + 1 ~N~ df~U’ ( ’
т. e. уравнение вида
(v— g) <p(l) -|- (). — v) <p (g) 4- (g — X) <p (v) = 0.
Это уравнение будет удовлетворено, если в качестве <р(и) взять ли-
нейную функцию от и. Положим поэтому y(u) — gu-\-h, где g и h —
две постоянные. Таким образом приходим к обыкновенным диферен-
циальным уравнениям:
d2L
= +
“I
(68)
т. е. каждая из функций L, /И, N удовлетворяет одному и тому же ди-
ференциальному уравнению. Уравнение
t/ч
(69)
в котором эллиптическая функция Х(£) определяется уравнением
(Й )2 =/w={ft2+Х) {Ь2+Х) (с2+Х)’ (70)
называется диференциальным уравнением Ламе. При любом значении
постоянных g и h интегралы этого уравнения дают нам решения
уравнения Лапласа. Однако особенно важны те значения параметров
g и h, при которых решения имеют вид многочленов или других
простых функций от 1.
Так как dr^ dx\ d'l,
d£~~di dz~~V/WA’
d2j] d\ d
d&^d^A
(owt)л (//<!) 4) •
ДИФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ЛАМЕ
199
то уравнение Ламе можно переписать в следующем виде:
S + Т z' <Х) Й -(gl + h} Ч-°- (71)
Это линейное диференциальное уравнение, сходное по своей форме
с уравнениями Лежандра и Бесселя. Оно имеет на конечном расстоянии
три особые точки
1=— а2, —Ь2, —с2
и, кроме того, еще особую точку при 1—оо. Разделим обе части
этого уравнения на /(1):
j_ 1 f 1 | 1 1 I____О __________+ Л о га)
2 \«2+^^2+^2+*M («2+w2+W2 + m'
Для особой точки — а2 имеем определяющее фундаментальное
уравнение (см. ч. II, приложения, § 3, d):
r(r—1) + 4=°»
корни которого суть г=0, . Таким образом решением является либо
степенной ряд относительно «2-|-1, либо такой же ряд, умноженный
на )/а2-ф~1 (решения в окрестностях особых точек —Ь2 и —с2 имеют
аналогичный характер).
Перепишем уравнение (70) в виде:
itiW2
V'i=\dU =/^-^ + ^2 + ^ + С- <70>
А = a2 -J- Ь2 -ф- с2. В — Ь2с2 -ф- с2а2 -ф- a2b2, С = а2Ь2с2
и продиференцируем по £; мы получим:
2ХТ=^=/(Х)У,
так что
& £ &
1 г---
У" = (X) у = (31 + Л) //(1),
Л
*IV=y {/"W'2+/'W" } =
(72а)
{/"(W)WW}- I
Последовательные производные суть попеременно то много-
члены от 1, то такие же многочлены, умноженные на )//(!), смотря по
тому, четно или нечетно п. Двойное диференцирование постоянно уве-
200
ШАРОВЫЕ ФУНКЦИИ, ФУНКЦИИ БЕССЕЛЯ И ЛАМЕ
личивает степень многочлена на единицу. Степень 1<2л> равна л 4*1,
между тем как [/(!)] 2 1< * является многочленом степени п. Линей»
иая комбинация производных только четного или только нечетного
порядка
У _ \(п-2) а^п~6) 4-... (72b)
представляет собою многочлен степени — от 1, если п — число четное,
к _____________________з ____
и многочлен степени —, умноженный на ]/~/(1), если п нечетно. Об-
£1
_ 1 п , \ л —3
ратно, всякий многочлен по А степени — [п четно) или степени ———
Л
умноженный на j// (1) (п нечетно), можно всегда представить в виде (72b).
Такого рода функцию (при соответствующих значениях g и h), удо-
влетворяющую диференциальному уравнению (72), называют функцией
Ламе (первого рода). Представляют интерес, кроме этих двух типов,
еще и те решения уравнения (72), которые получаются путем умноже-
ния многочленов на выражения
|/^Н;
/(^-H)(c2-t-k), /(с24-1)(«24-1), /(а2-|-1)(&2 + 1).
Такие произведения также носят название функций Ламе (первого
рода). Таким образом, если обозначить через Р(1) многочлен, то эти
функции напишутся так:
1. Р(1),
2. ]/ (а2 +1) Р (1), /б24-1Р(1), /^Р1Р(1),
з. /(62+D (c2-j-i)P(i), /(с2+1) (а24-1) Р(1), /(л2+1) (&24-1) р(1),
4. У (а24-1)(й24-1) (с2 4-1) Р (1).
Соответственно этому различают четыре типа функций Ламе. Если сте-
пень Р(1) равна р, то порядок функции Ламе по определению соответ-
ственно равен 2р, 2р 4- 1, 2р 4- 2, '2р 3. Таким образом при п четном
существуют только функции типа 1 и 3, а при п нечетном — только типа
2 и 4. Функцию Ламе л-го порядка мы коротко будем обозначать через
£я(1). Линейно независимых функций Ln (1) существует 2п-\-\.
Ь) Рассмотрим сначала тот случай, к01да п четно. Будем искать ре-
шения у уравнения (72), имеющего
п
вид многочлена степени —,
т. е.
п
2
c*v
A=0
ДИФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ЛАМЕ
201
Подставим это выражение в уравнение
/(1)й+4/'(Х)й~(^+,г)7]==о’
(71)
которое в раскрытой форме имеет следующий вид:
(13-|-Л^ + ВХ+С)
Э+(|р+^+|)Й-^+ЧЧ=о.
Мы получим:
л
2
У сJa (а — 1) {i*+i+а\*++с>№} +
А=о L
{о Rif
— 4- а\* 4- % I*-* — g\^ 4- h\k
А £ I I
(73)
Так как все члены этого многочлена, в том числе и старший член
(п \ 3 п
Т-Ч + у’г'-^
должны обращаться в нуль, то
п (п 4- 1)
§г— 5—
если только Сп =^0. Приравнивая нулю коэфициенты при )л+1,
У
полу-
чаем рекуррентную формулу:
ск ^2~Ь gj + ck+i | (* + l)2^ — h j 4-
+^2{(й4-2)(^4-П4-^}^ + ^з^ + 2)(а + 3)=о->
(74)
Формула
n i i
эта представляет — 4~1 равенств
/j
A=0, 1, 3,
каждое из которых линейно относительно h. Исключив из них ck, мы
п , ,
получим уравнение степени — -ь 1 относительно п. Можно показать, что
2
п
все корни этого уравнения действительны и отличны друг от друга С
„ п
Соответственно этому мы получаем — 1 решений, имеющих вид
многочленов.
Положим, далее,
*) См. Е. Т. Whittaker and G. N. Watsоn, A course of modern analysis,
4-е изд., Cambridge, University Press (1927), гл. XXIII.
202
ШАРОВЫЕ ФУНКЦИИ, ФУНКЦИИ БЕССЕЛЯ И ЛАМЕ
где £ — многочлен от к степени ———
можно показать, что в таком
случае h удовлетворяет уравнению степени —. Поэтому решений этого
Зл
типа имеется --- ,
А!
ниями, составляет
п । ,
что, совместно с ранее полученными i ' реше-
2л -|- 1 решений искомого вида. Итак, для п четного
Зл
функций Ламе 1-го типа и — функций 3-го типа.
существует ——
Перейдем теперь к случаю нечетного л. Положим сначала
ч=/7(Х)С=х'с,
р п — з ..
где Q — многочлен степени —-—. Мы имеем:
____Р)" I у
dZ~- + dV
и в силу (69)
Если ввести X, как новое независимое переменное, то получается:
d^_dZ d^_di.
dt Л ’ dt2 A A2'
Формула (72a) даст нам:
:х'(з14-л)+з^х'(-|-х2+А-(-4)+^1'(хз+^г+5х+с)=
CLk \ Z Z / UK
или
(ХЗ +ЛХ2 + БХ+ С)^ 4- з(|-Х2 + ДХ + в) ^-+С(ЗХ+Д-^Х-Л)=О. (75)
Clkr \ Z / Clk
Будем теперь искать решение этого
. п — 3
члена от X степени —-—. Аналогично
коэфициент при старшем члене в (75),
к — 5,9 л — 3 , „
— +т—+г-^=°-
уравнения, имеющее вид много-
предыдущему, приравнивая нулю
мы получим:
л — 3
~~2
т. е‘., как и прежде,
л (я 4-1)
g 4
Приравняв нулю коэфициенты при остальных степенях X, мы полу-
rz — 3 л — 1
чим еще —-— равенств, т. е. всею ———
Л е
равенств, -эти равенства да-
ДИФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ЛАМЕ
203
дут нач уравнение той же степени относительно h, а каждое решение
этого уравнения даст нам соответствующий многочлен.
В этом случае существуют решения вида
п—1
где S — многочлен степени —-— • Мы имеем:
^= — ---J=,
dk dk 1 2|/a24-l
d*rt d^r^-' , 1 C
— = — yas4-H---------л----; --r -.
A2 A2 Ap4z2-j-l 4jZ(a2-f-k>a
Подставив эти выражения в диференциальное уравнение Ламе и раз-
делив обе части на о2 -j- X, мы получим:
/ rf2c d? 1 £ \
<»+А*+ н+о +j __ +
+ 2 ,Ц<А+2(а2-Н/ \ 4 Х +
или по умножении на я2-]-!: .
(1+(13+л12+в}.+С) 4-
4- р+л12 -j- bi -}- с+(1+с2) 12+Л1+в
г Хз + Л12 + В1+С . з л. в
+ |_ 4(14-й2) + 4 ' + 2 4
_(Ф М)1Н) (14-й2)] с=о.
> (76)
Подставив сюда
чим, аналогично
и, следовательно,
р 1 п —1
вместо <, многочлен от 1 степени —-—, мы полу-
п 4- 1
предыдущему, уравнение —;—
/г-р 1
2
степени относительно h
различных значений h. Заменяя множитель
}/«2 -j-1 множителями /г>24-1, /с24-1, мы получим аналогичные
3
решения. Всего мы получим, таким образом, — (и 4" 1) решений; эти
решения вместе с ранее найденными дают нам 2п 1 решений иско-
й п — 1 ,
мого вида. 1аким образом при нечетном п мы имеем —-— функций
Ламе типа 4 и — (и 4*1) функций типа 2.
204
ШАРОВЫЕ ФУНКЦИИ, ФУНКЦИИ БЕССЕЛЯ И ЛАМЕ
с) При линейном преобразовании
+ Ч №
f(k) переходит снова в многочлен 3-й степени. Соответствующим выбо-
ром /0 и ty мы можем обратить в нуль коэфициент при %>* 2, т. е. сумму
корней преобразованного многочлена. Для этого необходимо взять
£2_|_ с2
Полагая, далее, = 4, мы получим для /(X) так называемую нор-
мальную форму Вейерштрасса; при этом перейдет в вейерштрассову
функцию от £ Если мы в этом выражении независимое переменное
обозначим через и (вместо Е), то уравнение (70) перепишется так:
(^(и))2==(^) =4^з— g^ — gs,
ле g2 и g3 — две постоянные. Уравнение Ламе (69) примет при этом вид;
^2— te'!?(«) + й'}ч = 0.
Так называемые инварианты g3 и gz можно легко выразить через
а2, Ь2, с2. Далее, ^ — 4^, h'—gt^-^-h. Это преобразование не вносит
существенных изменений в предыдущие исследования; однако благодаря
использованию теории эллиптических функций вычисления в этом слу-
чае принимают гораздо более изящный вид 2.
§ 106. Разложение в ряды по функциям Ламе. Пусть Ln (X) — функ-
ция Ламе /2-го порядка. Согласно сказанному в § 105а, функция
V = Ln(k)Ln(iJ.)Ln(v)
удовлетворяет диференциальному уравнению Лапласа. Если вместо (X)
мы последовательно подставим все линейно независимые функции Ламе
и-го порядка Z?(fe=l,2, ..., 2п-]-1), то мы найдем 2га —j—1 решений
диференциального уравнения Лапласа, называемых произведениями Ламе
л-го порядка. Покажем, что эти произведения в прямоугольной системе
координат х, у, z представляют собою многочлены /г-й степени.
Действительно, пусть
Р(Х) = (а1—Х)(а2—X)... (ор — X).
* См. Riemann -Weber, т. I, гл. Ill, стр. 136.
2 Д 1ференциальное уравнение Ламе было систематически исследовано Эрми-
том; см., например, Ch. Hermite, Sur quelques applications des fonctions elhp-
tiques, Paris, Gauthier-Villars (1885). Дальнейшая литература C. Jordan, Cours
p’Analyse, t. Ill (2-е изд., 1896), стр. 290; G. H. Halp hen, Traite des fonctions
aliptiques. т II, стр. 457 (1888); H. Burkhardt, Elliptische Funktionen, стр. 342
(11899). Наконец, упомянем книгу Whittaker and Watson (стр. 392), на кото-
рую мы ссылались уже раньше.
РАЗЛОЖЕНИЕ В РЯДЫ ПО ФУНКЦИЯМ ЛАМЕ
205
На основании (55) мы имеем:
р .
w(i—
ft=l '
Далее, из (56) следует:
X2
y2 z2
£2 + a*—
]/а2-|-1 //z2 -|- |1 j/~a2~j-v= / (а2 — 62) (а2 — с2) х,
так что вышеуказанным типам 1, 2, 3, 4 соответствуют следующие про-
изведения Ламе:
1.
2.
3.
4.
Q;
xQ, yQ, zQ;
yzQ, zxQ, xyQ;
xyzQ.
Здесь Q представляет собою многочлен степени р от х2, у2, z2, и, таким
образом, эти произведения являются многочленами степени 2p, 2р-}-1,
2р Ц- 2 и 2р -|- 3.
Определенные, таким образом, 2п -1-1 произведений Ламе /г-го по-
рядка обладают свойством ортогональности, благодаря которому оказы-
вается возможным функцию, произвольно заданную на поверхности эллип-
соида из семейства (51), разложить в ряд по этим произведениям.
Пусть Lf^4y) — Lm(y) и 1Ур(у)=Ьп(у) будут две функции Ламе
соответственно т-го и /г-го порядка, соответствующие двум определен-
ным решениям h* и h" уравнений, которые были выведены в предыдущем
параграфе. Эти функции удовлетворяют диференциальным уравнениям:
dL-
2 dy ’
f..d2Ln /(P) dLn
JW dy2 2 dy
'т
4
[ (77)
.„ = 0.
4
Помножим первое из этих уравнений на
из одного произведения другое и разделим найденную таким образом
разность на ]//(Р)- В результате мы получим:
/Д/жкЛ
LmLn
Л„, а второе на Lm, вычтем
(78)
'n_j tn \ j ==
dy n dyJ J
_ -4-1)—a (a-4-1)} — -4-ti— Л" .
f/(p) L n 4
Интегрируя это равенство, находим:
щ(т-}-1) —/г(л+1) Г Lm(y)Ln(y) _ ГL„(y}Ln(y) =
J /ЛИ) J //(И)
//(И) jjf
4
Pi
(79)
206
ШАРОВЫЕ ФУНКЦИИ, ФУНКЦИИ БЕССЕЛЯ И ЛАМЕ
и аналогично:
т(/и^!) — »(/?-4-1) Г L„(v)Ln(v) _ С Lm(v}Ln(v)
4 J КЖ J /Ж
vi ’i
\ т dv п dv
Область интегрирования мы выбираем таким образом, что точка с эл-
липтическими координатами X, ц, v, где X > — с2 и равно некоторому
вполне определенному числу, пробегает поверхность эллипсоида
х2 . V2. , z2
а2Ф-х~г (81) 1
Выражения, стоящие в правых частях формул (79) и (80), обра-
щаются в результате подстановки в нуль, так как ра, у? и у2.
служат корнями многочленов /(р) и /(у). Перенесем члены
И»
(й’—й") ( dy
р-1
и
(й’ — й") С Jp
J //(JX)
в правую часть и перемножим накрест полученные таким образом ра-
венства. Если найденный результат мы перенесем в левую часть равен-
ства, то мы будем иметь:
P-а
tA \т (т +1) — п (п + 1)] f f dy dv = 0.
. 4 J J F/(H)/(v)
P-1 V1
Если m=fc n и h'=£h’\ to
Г f (P) (>) Ln (и) Ln (у) (у — V)
В-----------»-----------------d^,=0- <ffl)
Интегрирование происходит по всей поверхности эллипсоида (81).
Это равенство выражает условие ортогональности произведений Ламе
или функций Lm(y) Lm(v) (это последнее произведение соответствует
сферическим функциям). Выберем постоянные Antt так, чтобы ряд
оо ?«+1
Е (83)
СВЯЗЬ МЕЖДУ ФУНКЦИЯМИ ЛАМЕ
207
сходился и допускал двукратное почленное диференцирование. В таком слу-
чае этот ряд должен удовлетворять уравнению Лапласа и на поверхности
у2 ч|2 л»2
—+ —Ч- —= 1.
а2' Ь2 ' с2
т е. при 1=0, обращаться в заданную функцию Р (у, у), если
только коэфициенты AnkZ.W(0) = Cnk выбраны так, что
ОО 2я-|-1
ЕЕ CnhL^(y)L^^.F(y, у). (34)
п=0А=1
Определение коэфициентов Сп}; производится обычным способом: ряд
(84) умножают на
W (>) (у. ~ V) [/(JT)/(V)F ~
и интегрируют по всей поверхности эллипсоида. Таким образом
И/7(р., у) (р) Z.W (у) (р. — у)
----------------г ------------------------dy.d\
_______________________________//(H)/(v)- ,п„.
ГГ£№(р)2£^(у)2(р — V) j
\ I--------= — —-------dy dv
J J V7(li)/(v)
С помощью ряда (83) проблема Дирихле может быть решена для
эллипсоида, подобно тому как эта же проблема для сферы была ре-
шена с помощью рядов сферических функций (§ 87 и § 98).
§ 107. Связь между функциями Лаке и сферическими функциями.
Если мы будем точку х, _у, z удалять в бесконечность таким образом,
что первая эллиптическая кЬордпната неограниченно возрастет, а две
другие координаты р. и у сохраняют постоянное значение, то при этом
выявится связь между произведениями Ламе и шаровыми функциями.
Так, как
X2 V2 ?2
=1 ’ (81)
то угловые координаты ср и 6 можно ввести с помощью равенств
х = а2 1 sin 6 cos ср,
у =]/b2 1 sin 8 sin ср,
(86)
В таком случае в силу (56) мы будем иметь:
sin 0 cos ср =
Ь2)(а2— с2) ’
sin 6 sin ср =
cos
(b2— с2) ib2— а2) ’
(с2-|- ц)(с2 -|- у)
(с2 — я2) (с2 — Ь2)'
(87)
208 ШАРОВЫЕ ФУНКЦИИ, ФУНКЦИИ БЕССЕЛЯ И ЛАМЕ
Следовательно, при вышеуказанном предельном переходе 6 и
остаются неизменными. Из формул (86) следует:
Ха-^-уа~1- Za
hm -------------------— 1. (88)
Х-»оо *
Далее, из уравнений, аналогичных (81) и служащих для определе-
ния р. и V [или из (87)], следует:
(sin 0 cos <р)2. (sin 6 sin <р)2 (cos6)2_
«2-|-Р- c2+J*— ’ ,
(sin 6 cos <р)2 . (sin 6 sin <p)2 (cos 6)2 ' ' '
aa-j-v * 62-{-v '
п
Разделим произведение Ламе V= 1!% (к) (р) L[^ (у) на X2 и пе-
рейдем к пределу при X—юс. Результат будет равен, с точностью до
постоянного множителя, L(^' (v). С другой стороны, V является гар-
моническим многочленом л-й степени от прямоугольных координат
х, j, z, следовательно,
V V
lira lim----------------------7 (00)
WOOX2 ^°°(X2_|_J2_|_^2)2
представляет собою сферическую функцию л-й степени. Таким образом
функции
А(*)(р)£(*>(у) (*=1,2,..., 2«4-l)
при переходе к координатам 6, и преобразуются в сферические функции
и-го порядка. Эти функции линейно независимы. Действительно; из
формулы (85) следует, что равенство
2« + 1
^q^(p)£^(y) = 0, (91)
fc=l
в котором Ск— постоянные коэфициенты, обращается в тождество
в том и только в том случае, когда все эти коэфициенты Ск равны
нулю. Таким образом любую сферическую функцию л-го порядка Кя (И, <р)
можно представить в виде линейной функции указанных произведений:
2л +1
Yn <6> ?) = Ё D'n}L(И) (>). (92)
k=i
Произвольная функция, которую на поверхности можно разложить в ряд
по сферическим функциям (см. § 99), разлагается также по произве-
дениям L(^(n) Lf^(v). Если этот факт сопоставить со сказанным в пре-
дыдущем параграфе, то окажется, что довольно большое число фун-
кций можно разложить в ряд по произведениям Ламе.
ЭЛЛИПСОИДЫ ВРАЩЕНИЯ
209
§ 108. Эллипсоиды вращения. В случае эллипсоидов вращения дифе-
ренциальное уравнение Ламе значительно упрощается. Так как этот
частный случай в приложениях теории играет очень большую роль, то
мы его разберем непосредственно.
Рассмотрим предварительно функцию V, которая зависит только от
цилиндрических координат z и р = х1 2 -]-у2 и не зависит от угла и.
Вместо z и р введем новые координаты и и V, определяемые равенством
z -}- гр — ф (и -ф- г'г»), (93)
причем предполагается, что ф (w) (где та» = гг ф- г-п) в некоторой области
комплексной плоскости w является правильной аналитической функцией;
вблизи точки w= ггф-гм, в которой ф'(та)^0, можно обратно та рас-
сматривать как аналитическую функцию от z ф- гр ф и и v являются орто-
гональными координатами на плоскости, так как (см. ч. II, приложение, § 16)
йгг йи йгг 5г»
= г- = — г-. (94)
fiz йр йр Ъг
На основании сказанного в § 103 имеем:
ds2 — dz2 ф- г/р2 ф- р2 г/»2 — ] фг (и ф- йг) |2 (du2 ф- dv2) -ф- р2 г/<р2,
а потому [§ 90, (20)]
/?2 —— 2 —, _ . . . . .. ..
® | ф’(гг-^гг») | 2 ’
(95)
далее, как и в § 103, —.
Но V не зависит от <р, а потому в силу
§ 90, (32)
Если предположить V= L (и) М (у) и подставить в последнее выра-
жение вместо V это произведение, то уравнение Д У=0 перейдет
в следующее:
1 й / dL\ . 1 й / dM \ .
£ йгг V г/гг) "J-/И йг» V г/п ) "
Если в формуле (93) выбрать ф(та) так, чтобы р приняло вит
/(гг)^(г»), то это уравнение примет следующую форму:
1 d
Lf(u) du\ U du)
1___£
Mg(v) dv
= 0,
(98)
1 Cm. L. Bieberbach, LehrbuchderFunktionentheorie, т. I, 3-еизд.,стр. 195,
.. Leipzig, Teubner (1930).
14 Вебсиер, йиференциапьные уравнения.
210
ШАРОВЫЕ ФУНКЦИИ, ФУНКЦИИ БЕССЕЛЯ И ЛАМЕ
т. е. мы получим диференциальное уравнение в частных производных,
которое распадается на следующие два обыкновенных:
du2'fdu'CL
dv2 1 g dv
(99)
где через с обозначена некоторая постоянная.
Если, например, функцию ф(та) определить"равенством
z -ф- /р — cos (и -j- М — cos « ch «г — г sin и ch v,
z~cosuchv, p=—-sin asht»,
то указанные требования будут выполнены. Исключив из этих
иий сначала и, а затем V, мы получим:
г2 р2 _______j z2 р2 _____j
ch2 v sh2 v * cos2 и sin2 и
(100)
урав;.е-
(101)
Кривые г» —const и и = const суть соответственно эллипсы и гиперболы
на плоскости гр. Так как ch2 г» — sh2 v — cos2 и 4- sin2 и — 1, то все эти
кривые имеют^рбщие фокусы — 1 и 1. Если положить р2 = х24~у2, то
уравнения (101) будут представлять соответственно эллипсоиды враще-
ния и двуполостные гиперболоиды вращения. Так как ch2t»^> sh2t», то
эллипсоиды будут удлиненными. Сохраняя обозначения § 104, мы
будем иметь:
х2 у/24-г2______________________ х2 y24~z2
С’ «24~3 I" ^24~^ ' a2-|-V
(102)
причем в данном случае а2 — b2= 1. Если в уравнениях (102) мы за-
меним х, у, z соответственно через г, х, у и полученные таким образом
равенства сравним с (101), то окажется, что
ch v — а2 4-1, shf = ]//>24-X, ]
cos и = l/й2 4~ v, Zsina = l/£24~v, I
j (
, «1 . . dv
dv — —— --------=, idu = —-r- ..........,
2 ]/ (a24-1) (b2 4-1) 2/(a2-|-y)(624-y) J
так что эллиптические функции в данном случае вырождаются в круговые.
Далее,
| sin (и 4- iv) |2 — sin2 и ch2 v cos2 и sh2 v =
=ch2 v (1 — cos2 u) 4- cos2 и (ch2 v — 1) = ch2 v — cos2 и — ). — v, (104)
следовательно, — равно разности двух эллиптических координат. Кроме
того, в этом случае f(u)~ — sin и, g(v) =shf, а потому диферен-
ЭЛЛИПСОИДЫ ВРАЩЕНИЯ
211
(103)
диальное уравнение (99) в рассматриваемом случае имеет следующий вид:
d2L . х dL
d2M . х, dM
-y-z-4-cth® ——
dv2 dv
Положим, кроме того,
с714 = 0.
p=—У(1 — ч2)(£2-1),
тогда
dL dL .
—=— -j- sin w,
du dц
d2L dL
du2 d-ц
d2L
drf
d2L dL dL . r
sin2 и----- cos и — cig и sin и — -4- cL = 0,
drf d-ц d-ц 1
(106)
-<И. „ <11
11
так что наше уравнение переходит в уравнение Лежандра [см. § 92, (41)].
При с = и(/г-[- 1), где /г^О есть целое число, решением этого уравнения
служит функция, ограниченная в интервале —именно и-й
полином Лежандра Рп (rj. Таким образом
z-='Pk(4):=:x-p„(C0SK);
для М получается то же уравнение, что и для L, а потому можно по-
ложить М — Рп (G). Итак, мы получаем следующее решение дифереи-
циального уравнения Лапласа A V—0:
оо
V = XAnPn^Pn^), (107)
л—0
где коэфициенты Ап — постоянные. При этом £ 5== 1, — 1 J] 1.
Исходя из этого решения, можно решать различные краевые задачи для
растянутого эллипсоида вращения.
Если исследованию подлежит сжатый эллипсоид вращения, то функ-
цию ф определяют равенством:
р -|- iz= ch (»-ф- г«) = ch v cos и i sh v sin и,
p = cos и ch t» = |/(l —82) (1 — nj2), E = sh®, 7i— sin«, (1€8)
z =. sin и sh v=
и тогда
p2 I Z2 P2 I „ V 1
ch2 v + sh2 v ~ 1 -4- S2 + S2 “'1 (ЭЛЛИПе)’ i
~ V il§9)
p p z^ I
cos2 и sin2 и 1 1 — -ц2 ц2 j
14*
212
ШАРОВЫЕ ФУНКЦИИ, ФУНКЦИИ БЕССЕЛЯ И ЛАМЕ
Полагая f{u) — cos и и g(v) = chv, имеем:
d*L . dL . n
d?M , „ dM „ л
-4-th®-;----------с/И==0.
dv2 1 dv
(ИО)
После преобразований, аналогичных приведенным в формуле
получаем:
(106),
функ-
(Ш)
Как и раньше, находим, что L — Pn(q) при е = л («-}-1);
ция М удовлетворяет в данном случае уравнению
и следовательно, М~ Рп(£). Таким образом в этом случае дифереД
циальному уравнению Д Й удовлетворяет функция
оо
(П2)
п=о
причем —1<S<1. Из этого ре-
дело с краевыми задачами на сжатом
g—юо имеют особенность, т. е. теряют
многочленом, имеет полюс при В = оо .
(коэфициенты Ап постоянны),
шения исходят, когда имеют
эллипсоиде вращения.
Решения (107) и (112) «три
«мысл, так как P„(G), будучи
Чтобы решать задачи, которые относятся к внешнему по отношению
к эллипсоиду пространству, рассмотрим другие решения диференциаль-
ного уравнения Лежандра. Эти решения заменяют затем в выражениях
(107) и (112) функции Р„(В) и Рп(&).
Пусть и j;2 будут вообще два независимых решения линейного
диференциального уравнения второго порядка, т. е. пусть
(ИЗ)
где P, Q, P — непрерывные функции. Исключая в этих уравнениях
третий член, найдем:
рк ^51
dp 4
или иначе (в предположении, что Р=^0)
d
___
I 41
= 0,
d, ( dti. dt\„ \
ЭЛЛИПСОИДЫ ВРАЩЕНИЯ
213
Интегрируя, находим:
105(4.^--
и ^51-
42 dl 41 dS
(В и С—постоянные). Наконец, разделив на —<q2 и проинтегрировав
вторично, получим:
d (%, \ С
•—— I I - —-___Q
d \41 / 41
с .
tj2 = Cfy I rjj_ 2 e J dt. -|- const. (114)
В случае диференциального уравнения Лежандра
Q 2g 1 1 Г Q , 1
Р~1— В2 1—В 14-Г —10gEZ^2>
1
е “ 1—£2’
Если положить т)1 = Ря(£), то при соответствующем выборе постоян-
ного интегрирования мы получаем для второго решения выражение:
оо
Qn (S) == Рп Ф j [Рй^)]2(£2„1) • 0
Полученные решения носят название функций Лежандра второго рода.
Эти функции в известном смысле аналогичны бесселевым функциям вт©-
рого рода. При $—»оо функции Лежандра второго рода обращаются
в нуль, а при g = + 1 они имеют логарифмическую особенность. Вычис-
лим для примера Q0(B)h Q1 (В); так как Ро (£)==!, Р1(^) = ^, то
оо
„ /е. Г <£ 1,54-1
Qo(£) J£2—1 2 10gE — 1»
£
с©
П/Pl —сС 1 fl 5+1 1
Qi®—1) — 2 еlogg_ 1 Е
(не)
Вообще
Qe(5)=|^(B)log^±|4
214
ШАРОВЫЕ ФУНКЦИИ, ФУНКЦИИ БЕССЕЛЯ И ЛАМЕ
гае невыписанные члены представляют собою линейную функцию по'
линомов Лежандра более низкого порядка. Этими формулами поль"
зуются при решении проблемы Дирихле для пространства, находящегося
вне растянутого эллипсоида вращения. В этом случае решение дифе-
ренциального уравнения Д У=0 пишется так:
оо
п=0
(107г)
(Лв— постоянные). При решении аналогичной задачи для сжатого эл-
липсоида пользуются функциями При] этом log+ * надо
2 5--1
заменить через arcctg В, а решение принимает вид:
оо
^=Елл(ч)^(В),
п=0
(112)
гае
<70 (В)=arcctg В, 91(B) — 1—В arcctg 6 и т. д.
Функции qn (В) удовлетворяют диференциальному уравнению (Ш) и
имеют вид:
Qn $ =Рп (У arcctg В 4- ...,
гае Ря Д,(Й), а невыписанные члены представляют собою мно- I
гочлен степени п — 1 г.
1 См. Н. Lamb, Lehrbuch der Hydrodynamik, Leipzig, Teubner (1907), crp. 168*
ГЛАВА ВОСЬМАЯ
Приложения сферических, цилиндрических функций
и функций Ламе
§ 109. Притяжение материальной окружностью. С помощью шаровых
функций можно решать целый ряд задач теории потенциала. Вычислим
сначала потенциал однородной проволоки, согнутой в форме окруж-
ности радиуса а, с линейной плотностью S, оказывающей притяжение
по закону Ньютона; масса этой проволоки очевидно равна ш = 2паЗ.
Если плоскость, в которой лежит проволока, принять за плоскость
ху, а ось симметрии проволоки — за ось Oz, то потенциал в точке,
лежащей на оси симметрии на расстоянии z от плоскости проволоки,
выразится так:
1 1
Таким образом при jzKa
а\ 2 а2 2-4а4
1-3-5.,.(2л—1)^ ,
1-4-6... 2/г а2я +
(2)
а при | z | > а
mL 1 а2 1•3•а4
zf 2? + 2-4^4
1-3-5... (2я — 1) а2" ,
2-4-6... 2/г -гм +
Искомый потенциал должен быть симметричен относительно оси Oz,
а потому его можно представить в виде ряда
г *2 »й
при г<^а и
А у А (0) + А А (0) + Л гт (0) + • • - + А 77г ЗД+. • • ©
п, и г^>а. Если притягиваемая точка лежит на оси г, то r—z, 6 — 0,
так что (см. § 92) Рп—\ (» = 0, 1, 2, 3,...). Приравнивая коэфн-
циенты в формулах (2) и (4) [или (3) и (5)], мы найдем:
Л2л= - (— 1)а 1 - ~5-' 'д’ -2" п, Л, 1==0 (12 = 0,1,2,
2л а v ' 2.4-6... 2/г 2я+1
216 ПРИЛОЖЕНИЯ СФЕРИЧЕСКИХ, ЦИЛИНДРИЧЕСКИХ ФУНКЦИЙ И ФУНКЦИЙ ЛАМЕ
Таким образом окончательно
W7 ( 1 в»4
У=— Ро(0) — 7Г~2
а I ° 2 а2 3 1 2 • 4 л4 4
1.3-5...(2л-1)^
••• । ( > 2.4-6... 2л а2« Р2П W + •
при г<^а и
V = — (0) — 4- ~ Р2 (6) -f
I U ' * 4} ' * I
1 а3 „ /Гч . 1-3 а4 .
2" г2 * 2 w/ + 2.4 ri Pi (®)
l-3-5...(2n-l)^ 1
2.4-6...2л —
(6)
(7)
при г>а.
§ 110. Потенциал материального круга и кругового тока. Пользуясь
потенциалом проволоки, вычисленным в предыдущем параграфе, можно
с помощью интегрирования найти потенциал однородного диска [ср.
§ 56, (55)]. Обозначив поверхностную плотность через а, мы най-
дем, что потенциал притягиваемой точки, лежащей на оси Oz, на рас-
стоянии z от начала координат, равен:
а 2л
Н!да=2го<да-г>’
т. е.
V — 2то | — z 4~ а
1 z3
2 «з
1-1 г4
2« 4«4
1-1.3^6
^2.4-бл6
при z<^a,
[ /1 й2
У=2па -г + И1+-^
1-1 а4
2-4^4
1-1-За6
^2-4-б.г6
(8)
(9)
1
при z^>a.
Таким образом мы находим, что для точек вне оси
v=2то Lp0(0) - ГР. (6)4-у р2 (6) -Р4(6) 4-'
5Рб(6)~-”} при'<й.
+ •••} ^г>а’
(W)
(И)
ПОТЕНЦИАЛ СФЕРИЧЕСКОГО СЛОЯ
217
По тому же методу можно вычислить потенциал двойного слоя
какого-либо диска (согласно закону Ампера, этот последний совпадает
с потенциалом однородного кругового тока). Из определения IF [см. § 57,
(58)] следует, что его значение на оси равно производной по нормали
от V; таким образом, если через 7. обозначить поверхностную плот-
ность, то
lF=2w. (1 — -- 2
\ у а2 z2
Отсюда следует, что
{z [ 1 z^ 1 • 3 z^ \ 1
1----(1—4" О-ЗГ Т + • • • I f при г<а, (12)
а\ 2 а2 1 2-4 а4 1 /
[ ( 1 я2
№=2тс 1 — 1 —
I \ 2 г2
1-За4 1-3-5 а® (
2-4г* 2-4-бг6 ’
при.г^> а, (13)
и, как и раньше,
^=2тгх(1 - ^/’1^ + т5Рз(0)-|4у5РБ(0)+...) при г<а, (14)
^=2пх (1 Р. (6) + Ра (6) + ±6РБ (6) ) при г>а. (15)
Эти формулы имеют большое применение в теории электромагне~
тизма.
§ 111. Потенциал сферического слоя. Определим теперь потенциал
тонкого шарового слоя г=а, на котором поверхностная плотность о
задана как функция географических координат 6, ср. Пусть эта плот-
ность допускает разложение по сферическим функциям, т. е. пусть
®=Ш)4Л(И+МШ..-КМ+... Об)
Потенциал внутри сферы можно разложить по шаровым функциям
(см. § 87):
к=4г;+л1-г;+л,ггц-... + л„-г;+... т
Ряд, представляющий разложение потенциала вне сферы, имеет вид:
a cfl пЗ лп+1
у—в°-К+в,^+в1~г;+...+в„‘‘~г+... («,
Так как потенциал на поверхности сферы г=а непрерывен, то
должны выполняться равенства: Ап = Вп, Y' = У" (п — 0,1,2, ...). Кроме
того, на поверхности сферы должно выполняться уравнение Пуассона
[см. § 56, (53)]:
/ау\ /ап\
7— I Н” = 4ТО, (19)
\ Ъп ]е \Ъп ]t ' л
218 ПРИЛОЖЕНИЯ СФЕРИЧЕСКИХ, ЦИЛИНДРИЧЕСКИХ ФУНКЦИЙ И ФУНКЦИЙ ЛАМЕ
а потому
Отсюда следует, что
А'‘У'~2п-^-1 Yt”
и таким образом
2тг f1 . ]
У = Г«(6’ ПРЙ Г<а’
±4 4тг ап+2 I
—i~7 ПРИ г^>а’
^"£2/г-4-1 r°+1 р
я=0 1 )
Пользуясь формулой (44) § 92, можно выразить следующим образом
потенциал любой точки, лежащей вне сферы:
”2* QQ
v==т j J ° {S Рп (g)}sin 0 '=
О 0 я=0
2 р р ОО оо и
=7-] Гт(6, ?)2?rp»(,x)sln6d0^-
О О т=0 и=0
Если это выражение для потенциала сравнить с (2Г), то мы снова
получим формулу:
тг 2п
j j ут (6, <р) рп (И)sin 6 d4
о о
п-----Т Ут (вГ> ф') или О,
2т -J-1 mV ’
(22)
смотря по тому, будет ли т — п или т^п. С этой формулой мы
уже встречались в § 97 [см. (98) и (99)].
§ 112. Потенциал любого тела. Потенциал любого ограниченного
тела, находящегося на достаточно большом расстоянии от масс, может
быть разложен в ряд по сферическим функциям. Пусть точка Р’ с коор-
динатами х', у', z' пробегает все точки, в которых сосредоточены массы,
точка Р с координатами х, у, z — любая точка, находящаяся вне тела,
р — плотность, d — расстояние РР'. Пусть, кроме того, начало коор-
динат находится в точке О, и пусть ОР=г и ОР' — г1. Мы покажем,
что если г больше максимального значения /, равного /?, то
ПОТЕНЦИАЛ ЛЮБОГО ТЕЛА
219
Действительно, в силу (44) § 92 мы имеем:
llf Н Н® И» 1
причем
. пп on ХХ' 4~УУ -\~ZZ'
JA = COS (POP') =----1---------- ,
так что имеет место разложение (23), в котором
(24)
В силу доказанного в § 93 неравенства | Рп (р.) | 1 (— 1 ==с р=с 1)
произведение R~aYn при р кусочно-непрерывном ограничено, а потому
ряд (23) сходится при r>R. Мы имеем:
= = /’2(g)=4-(3g8—I),
,n , . , хх' -4- уу' -j- zz'
г'Ру (м) = г И — ~г ,
1 [ 3 (хх1-)-уу' -4- zz')2— r'2r2
’2 (Н) 2 (-----------------------------
Таким образом первые три члена разложения V дают нам:
V JJJ pdx'dy’ dz> + ^
р х' dx' dy dz' 4-
р .г' dx? dy' dz'^ (25)
2^5 JJ { 3 (x2x>2-j~y2y'2 + z2^2 4~ 2лгл/уУ 4" 2уУ 4" %zz'xxP) —
Коэфициент при , очевидно, равен массе тела М. Интегралы, входя-
1
щие в коэфициенты при —- , соответственно равны произведению массы
на соответствующие координаты центра тяжести; если начало коорди-
нат поместить в центре тяжести, то эти интегралы обратятся в нуль.
Последующие интегралы можно рассматривать как моменты инерции
и центробежные моменты инерции данного тела относительно коорди-*
натных осей. Напомним, что момент инерции тела относительно задан-
ной оси определяется как интеграл произведения элемента массы на
220 ПРИЛОЖЕНИЯ СФЕРИЧЕСКИХ, ЦИЛИНДРИЧЕСКИХ ФУНКЦИЙ И ФУНКЦИЙ ЛАМЕ
квадрат расстояния тела от оси. Моменты инерции тела относительно
координатных осей суть:
А = JJJ р (У2 z’2') dx', В=JJJ р (zn -|- х'2) йт',
c^JJJp^+yw.
Под центробежными моментами инерции относительно осей понимают
интегралы:
D = JJJ рУг'йт', Е — JJJ р г'х'йт', F= JJJp x'y'dx'.
Совместим начало координат с центром тяжести тела. Координатные
оси мы берем так, чтобы центробежные моменты инерции обратились
в нуль; как доказывается в механике, такой выбор осей всегда возмо-
жен Ч В таком случае начальные члены разложения потенциала V
представятся в следующем виде:
М 1 (B + C-2A^ + (C + A-2B)yZ + (A+B-2C)z*
1/= - + -----------------------------------------+•.. (26)
Таким образом тело на большом расстоянии действует приближенно
так, как материальная точка с массой, равной массе тела, помещенная
в его центре тяжести (ср. с действием однородного шара, см. § 54).
Выписанные нами два члена разложения потенциала в большинстве во-
просов небесной механики достаточно точно представляют величину
потенциала.
Таким же способом можно найти разложение в ряд телесного маг-
нита, т. е. тела, каждый элемент которого представляет собою диполь
(см. § 57). Момент, отнесенный к единице объема тела, представляет
собою вполне определенный вектор; обозначив компоненты этого век-
тора через 1Х, 1у, /г и сохранив в отношении остальных величин прежние
обозначения, мы аналогично предыдущему найдем:
dx'dy'd'z1. (<2Т)
Легко видеть, что здесь отсутствуют члены порядка —, и что член,
в который входит , можно рассматривать как потенциал одного диполя.
§ 113. Применения к гидродинамике, а) С помощью сферических
функций можно решить задачу Неймана, формулированную в § 60, для
пространства, лежащего внутри или вне сферы. К задаче Неймана для
пространства, лежащего вне сферы, сводится также и следующая за-
1 Е. Л. Николаи, Лекции по теоретической механике, ГТТИ, (1932), ч. Ш»
выпуск 2, § 105, стр. 130 и далее.
ПРИМЕНЕНИЯ К ГИДРОДИНАМИКЕ
221
дача гидродинамики. Задана скорость жидкости в направлении нормали к
поверхности сферы; жидкость простирается в бесконечность, где ее
скорость равна нулю. Найти закон движения этой жидкости.
Предположим, что жидкость несжимаема. Тогда ее скорость пред-
ставляет собою соленоидальный вектор. Пусть он имеет потенциал
скоростей, равный ср. Функция ср удовлетворяет уравнению Лапласа.
Представим скорость, т. е. нормальную производную от потенциала
скорости ср на сфере г=а, в виде ряда сферических функций и
перейдем к вычислению ср, аналогично тому, как мы это сделали в
§111. Пусть при г^=а
= Го+ ^4- Т2+ ... + ... (28)
Будем искать решение, которое вне сферы (г^> а) представляется рядом:
?=а40+А$4-^4-...+А,Д4-... (2S)
Для этого решения
2Л2-фзл24-... 4-(«4-1)л„^ф-24- ...j, (зо)
а потому
Ап = -^Т (« = 0,1,2,...). (31)
Итак, наще решение имеет следующий вид:
7 Г,+г,+зл г,+...+V.+...). (32)
Простой, но очень важный пример представляет случай, когда шар
радиуса а перемещается с постоянной скоростью v по прямой, парал-
лельной оси Oz, в направлении возрастающих z. Пусть жидкость вна-
чале находится в покое. Через 6 обозначим, как это обычно делается,
угол между радиусом-вектором какой-либо точки на шаре и осью Oz.
Мы имеем на сфере:
—1 = — v cos 0. (33)
аг
Правая часть в этой формуле равна —vP^cosO). Следовательно, ре-
шением в этом .примере служит функция1
= у —cos6. (34)
Таким образом действие шара сводится к действию диполя с мо-
1 ч
ментом — ws, помещенного в центре шара; вследствие движения шара
1 G. G. Stokes, Math, and Phys. Papers, т. I, стр. 17.
222 ПРИЛОЖЕНИЯ СФЕРИЧЕСКИХ, цилиндрических функций и ФУНКЦИЙ ЛАМ-J
возникает поток, линии тока которого совпадают с силовыми линиями j
ноля, возникающего под действием диполя.
Движение эллипсоида вращения в жидкости можно исследовать с по- 1
мощью эллиптических координат, введенных в § 108. Рассмотрим слу-
чай растянутого эллипсоида, перемещающегося с постоянной скоростью у
в направлении своей оси (оси Oz); при решении этой задачи целесо-
образно эллипсоид считать неподвижным, а к скорости потока доба-
вить — v. Согласно § 108,(107') мы можем предположить, что решение
этой задачи имеет следующий вид:
— ^=AP1(ri) Q^) — vz = A(35) I
где $ и 1) представляют собою эллиптические координаты. На поверх-
ности эллипсоида ($—$0) мы имеем:
Отсюда в силу § 118, (116) следует1:
. У У
2 '°Ч- 1 + 1-g
b) Обобщим предыдущие примеры на потоки, обладающие осевой
симметрией. Скорость потока зависит в этом случае только от двух
переменных: расстояния р от оси вращения и координаты z, отсчиты-
ваемой в направлении оси. В этом случае кроме потенциала скорости tp
следует ввести еще и другую функцию, так называемую функцию тока ф,
которая определяется следующим образом: пусть АВ—дуга кривой,
лежащая в меридиональной плоскости, проходящей через ось Oz; рас-
смотрим полосу, которая образуется при повороте кривой АВ вокруг
осн Oz на угол db. Масса жидкости, протекающая сквозь эту полосу,
очевидно, равна
в
I у„р db ds = db \ р ds, (37)
J J
А
где у означает вектор скорости, а п — направление нормали к кривой АВ.
Жидкость, по нашему предположению, несжимаема, а потому эта масса
для всех кривых, соединяющих точки А и В, должна быть одинакова,
и следовательно, подинтегральная функция в последнем интеграле должна
представлять собою полный диференци ал. Так как в меридиональной
плоскости, в которой лежит дуга АВ, прямоугольными координатами
1 См. A. G. Webster und W. Fischer, Tables of the zonal spherical
harmonic of the second kind Qt (z) and Q^z). Proceedings of the National Aca-
demy of Scienses, т. V (1919), стр. 79—82.
ПРИМЕНЕНИЯ К ГИДРОДИНАМИКЕ
223
служат р = ]/х2 У2 и г. то должна существовать функция ф от р
и z, для которой имеет место равенство:
(38)
Определенная этим равенством (с точностью до аддитивной постоян-
ной) функция ф называется функцией тока. Мы имеем [см. § 70, (3)]:
так что Следовательно, dz cos (пр) — — cos (ds, z) = — , f (W cos (nz) — cos (ds, p) = ~, J 'Йи йф \ / ЙФ йф \ ^-cos(np)4-^cos(n2r)jzZs = p | — ^-dz-^dpj. (40) ЙФ йф йф йф й7=рйТ’ й7“рйГ <41>
Кривые ф = const являются линиями тока; они ортогональны к экви-
потенциальным кривым.
Обозначив через ds2 и ds2 два произвольные взаимно перпендику-
лярные направления, мы в силу (38) будем иметь:
йф 5d> ЙФ й<!>
р — = —- и — р — = — .
й^ й$2 г й$2 iSj
(42)
Если мы введем новые ортогональные координаты и и v, анало-
гично тому, как это было сделано в § 108, в формулах (100) и (108),
то мы получим;
йф _ йф йф ________ йф
рйлй~йл/ ?Ъпъ~Ъпи'
« . du , ,dv
А так как dn„ = ~r , dn—d--~, то
h ° h
йф______йф йср йф,
Р й/z йт? ’ Р йи Йй ’
(43)
ншример, для эллиптических координат, соответствующих сплюснутому
эллипсоиду, мы получим [см. § 108, (108)]:
<-<4
Полагая [ер. § 108, (112')]:
224 ПРИЛОЖЕНИЯ СФЕРИЧЕСКИХ, цилиндрических функций и функций ламе
мы получим:
g = Л (1 _ Ч2) /7 {ч) qa (£), = _ А (1 4-$*) рп (Ч) q'n (5). (45)
В силу уравнения Лежандра имеем:
₽.W—«*—Ч*>П<Ч>Ь
мы, таким образом, находим (с точностью до аддитивной постоянной):
П'-П- р'п + Е2) ?' ® (л-1,2,3,...). (46)
п\п~г I)
В простейшем случае при п — 0 эта формула теряет смысл. Легко,
однако, убедиться, что при л = 0 функции
<p = ZP0(j])^0(S) = ^arcctgS, ф = Д1] (47)
удовлетворяют уравнениям (44). Эти функции соответствуют потоку
сквозь круглое отверстие в бесконечной плоскости. В силу § 108 (109) при
z—0 мы имеем i) = j/l—р2 , и следовательно, скорость точек пло-
скости, лежащих внутри указанного отверстия, в силу (41) равна
_й<р_____1 йф __ А
р йр ~ |/1 -- рз'
Эта скорость на краях отверстия при р = 1 становится бесконечной.
К тому же решению мы приходим, определяя распределение электри-
чества на круглом диске.
§ 114. Однородное уравнение колебаний в двумерном пространстве.
Все рассмотренные нами до сих пор приложения специальных функций,
введенных в гл. VII, относились только к уравнению Лапласа. Перейдем
теперь к волновому уравнению:
^ = а2Д« (а>0), (48)
аналог которого в одномерном пространстве был нами подробно разоб-
ран в гл. III. Фундаментальными функциями в этом уравнении при про-
стейших краевых условиях служили синусы н косинусы; это уравнение
являлось исходным пунктом для целого ряда проблем^ касающихся фун-
даментальных функций. Далее, в гл. IV и V мы исследовали это урав-
нение в двумерном и трехмерном пространствах и выяснили связь его
с теорией интегральных уравнений. Однако фундаментальные функции
в явном виде были нами получены только для прямоугольника (§ 68).
Мы хотим теперь решить ту же задачу для круга и шара.
ОДНОРОДНОЕ УРАВНЕНИЕ КОЛЕБАНИЙ В ДВУМЕРНОМ ПРОСТРАНСТВЕ 225
Начнем с уравнения в двумерном пространстве (уравнение в трех-
мерном пространстве будет рассмотрено нами в § 116). Полагая
(/) U(x, у) и рассуждая так же, как и в § 33, (128), мы найдем:
гАЬ
^+^ = 0’
Д(7-|-А2(/ = 0 (k=-^>o\. (5й)
Уравнение (50) мы будем называть однородным уравнением колеба-
ний в двумерном пространстве. К этому уравнению приводят нас сле-
дующие вопросы:
а) Колебания круглой мембраны.
Ь) Колебание газа внутри тонкого слоя, ограниченного двумя плос-
костями и перпендикулярным к этим плоскостям прямым круговым
цилиндром.
с) Колебания жидкости в цилиндрическом сосуде с плоским дном(§ 12).
Уравнение (50) в полярных координатах перепишется так [см. § 103,
(45)]:
й207 , ЙО/ J_ d4J
йр2 ‘ Р Йр р2 й'р2
0.
(51)
Полагая 07 —/? (р) Ф (tp) и разделяя тем самым переменные, мы по-
лучим [см. § 103, (48), (49)]:
™+_L®+(6.H^o
пр2 1 р ар \ р2 /
(53)
Решением первого из этих уравнений служит Acosva>-f-Z^sinvtp,
где Av н —произвольные постоянные; v при этом должно быть це-
лым, для того чтобы функция Ф была периодической. Введя нсцое
переменное x=kp, мы второе уравнение приведем к уравнению Бес-
селя. Таким образом мы находим функцию
Ц — (A cos Vai -|- Ву sin v<p) Jy (Ар), (54)
которая служит одним из решений уравнения (50).
Рассмотрим, например, колебания зажатой круглой мембраны; для
этой мембраны и = 0 при р=1, где р отсчитывается от центра мем-
браны, а I означает ее радиус Таким образом для собственного коле-
бания
Jv(A/) = 0. (55)
Это уравнение определяет фундаментальные числа. Если через
(ц=0, 1, 2,...) обозначить расположенные в порядке возрастания
15 Вебстер, Диференциальвые уравнения.
226 ПРИЛОЖЕНИЯ СФЕРИЧЕСКИХ, ЦИЛИНДРИЧЕСКИХ ФУНКЦИЙ И ФУНКЦИЙ ЛАМВ
положительные корни уравнения (55)\ то фундаментальные функции
запишутся так:
Л Р) cos vw, J„(A6) р) sin vp. (56)
Теперь в силу формулы (49) мы можем предположить, что колеба-
ние и имеет следующий вид:
оо оо
*=ES /„(&£) р) (^cos vtp ~г s'n V(p)cos 4~
p.=0 v=0
oo oo
-j- 22 22 (C^) cos vp DW sin y<p) sin abW t.
p.=0 v=0
Коэфициенты ДО), С-4 и £X9 в этом выражении определяются из
начальных условий:
«==/(р> ф)
^=А(р» ч»)
при р<7, t~ 0.
Это приводит нас к разложению произвольных функций /(р, щ) и
", (р, и) по фундаментальным функциям. Рассмотрим, например, разло-
жение первой из них в такой ряд:
оо оо
/(р. ®) = У, X Р) C0S V'f + Sin VC?)- ®)
р.=0 v=0
Чтобы вычислить коэфициенты этого ряда, заметим, что фундаменталь-
ные функции ортогональны на круге р=С/ (элемент его поверхности
равен pdpdw). Это основано кроме известного интегрального свойства
тригонометрических функций еще и на равенстве
?. 0 пРи М Р1
(58)
являющемся условием ортогональности для функций Бесселя. Последнее
равенство при р. =/= р.г получается из диференциального уравнения Бес-
селя [см. § 40, (307) и далее]. При |/= р’ мы находим сначала, что
левая часть (58) равна:
У РМ’ОРЧ-р-да) (-59)
\ JJ- /
1 Отаоситеаыао существования этих корней см. заключительное замечание
в § 102 и Rieraann-Weber, т. I, гл. VIII, стр. 337.
КОЛЕБАНИЯ КРУГЛОЙ ПЛАСТИНКИ
227
а отсюда уже в силу граничного условия (55) получается (58)Е Коэфн-
циенты ряда (57) можно, таким образом, получить, умножая этот ряд
на фундаментальные функции и интегрируя в области р=С/; исследо-
вание вынужденных колебаний производится по образцу вычислений,
проведенных в гл. III.
Легко дать физическое представление для колебаний, соответствую-
щих различным фундаментальным функциям:
ы —УД/?(')р)coscos(у, р = 0, 1, 2,...),
и = Jv(^Wp)sinycpcostt^)/ (v = 1, 2, 3, ... ; g=0, 1, 2,...).
При у —0 смещение во всех точках, равноотстоящих от центра, одина-
ково; получающиеся при этом узловые линии имеют форму окружно-
стей. При наименьшем 2 из фундаментальных значений A —fe<°> колеба-
ния в каждой точке мембраны направлены в одну сторону. При V —О,
р 0 мембрану можно разделить с помощью концентрических окруж-
ностей, радиусы которых вычисляются при помощи фундаментальных,
чисел, так что все точки одной и той же окружности колеблются в од-
ном и том же направлении, и направлен! е колебаний меняется при
переходе от одной окружности к другой. Таким образом общие кар-
тины колебаний мембраны и струны аналогичны. Однако частоты при
колебаниях мембраны не гармоничны, а пропорциональны корням 1№.
При v^>0 узловыми линиями кроме окружности служат также некото-
рые радиусы. Таким образом мембрана делится узловыми линиями на
конечное число кольцевых секторов. Направление колебаний в каждом
секторе остается все время одинаковым; в двух соседних секторах эта
колебание имеет противоположные направления.
Если мембрана имеет форму кругового кольца, у которого закреп-
лен внутренний край, то в решение задачи входят также и вторые ре-
шения Yv (/гр) диференциального уравнения Бесселя, а фундаментальные
функции принимают совершенно иной вид.
§ 115. Колебания круглой пластинки. При исследовании круглой
пластинки надо в следующие рассуждения внести изменения, аналогич-
ные тем, которые мы внесли в § 41 при переходе от струны к стер-
жню. Диференциальное уравнение колебания пластинки
<«>°) (W
представляет собою уравнение четвертого порядка. Входящий в это
* Ортогональность фундаментальных функций можно вывести также и не-
посредственно из уравнения в частных производных (50), как это сделано
выводе формул (159) и (160) в § 68.
’В данном случае мы имеем < ... (см. Rayleigh, Scien-
tific Papers, т. VI, стр. 1), так что № > вообще говоря, является наименьшим и&
фундаментальных чисел.
16*
228 ПРИЛОЖЕНИЯ СФЕРИЧЕСКИХ, ЦИЛИНДРИЧЕСКИХ ФУНКЦИЙ И ФУНКЦИЙ ЛАМЕ
уравнение оператор ДА, и был нами определен в § 14. Разделим
переменные, для чего положим и — ф (/) U (х, у). Тогда
^| + «2Ф = °. (61)
/ /Z2 \
АА^— k^U=Q 1^ = -). (62)
Последнее уравнение можно записать так:
(А + ^2)(А — A2)zv=o, (63)
или в полярных координатах:
А.+-±+ £+4!) (*+1»+1 д. _ (И)
Vp“ р др р-* д<р2 / vp2 р др р2 dtp2 / *
Это последнее уравнение распадается на два следующих:
i2U 1 д'7 , 1 д2(7
Р др р2 д'.р2 р/г2£7= 0,
1 д(7 1 д®А (65)
гр2 Р2 др р2 д*2 0.
Каждое решение уравнения (64) или (65) удовлетворяет уравнению
(62). Уравнение (65) получается из уравнения (64) при замене k через
М [в случае стержня ср. § 41, (328)]. С этими уравнениями мы можем
яо тупить так же, как и с (51). Если пластинка имеет форму полного
круга, а не кольца, то решения К,(А:р) и КД/4р) отпадают, так как
яри р—>0 они обращаются в бесконечность (см. § 114).
Дальнейшие свойства фундаментальных функций зависят, как и в
случае стержня, от краевых условий. Мы рассмотрим здесь только тот
случай, когда край пластинки зажат, как в фонографе или в телефоне.
Если при этом ограничиться случаем круговой симметрии, то окажется, что
U=AJ0(kp)-\-BIQ(kp), (66)
вде /0(х) = Jo (ix). Краевыми условиями в этом случае являются:
т. е. AJ0 (ka) BI0 (ka) = О,
Д70 (ka) BIQ (ka) = 0. (68)
Для частот мы получаем при этом трансцендентное уравнение
J0(ka)I^(ka)— 1о(ка)^(ка) = О. (631)
1 Это уравнение имеет бесконечное число действительных корней. Действи-
тслыю (см. Riemann-Weber, т. I, гл. IX, стр. 356):
•4 (х) Г'о (х) — 4 (х) Jq (*) = l/S' [sin х ф е (х)],
причем порядок малости функции е(х) при х~—^оотот же, что и функции — •
ОДНОРОДНОЕ УРАВНЕНИЕ КОЛЕБАНИЙ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ 229
Первые пять корней этого уравнения суть1:
£«=3,19; 6,306; 9,425; 12,56; 15,71.
§ 116. Однородное уравнение колебаний в трехмерном пространстве.
К пространственному аналогу диференциального уравнения (50) приво-
дит нас ряд физических задач, как, например:
а) Охлаждение шара.
Ь) Колебания воздуха в полом шаре.
В обоих случаях определяют сначала, как мы это делали раньше,,
фундаментальные функции (собственные колебания), соответствующие
заданным начальным условиям. Искомое состояние температуры или ко-
лебаний представляется, далее, в виде бесконечного ряда по фундамен-
тальным функциям; его коэфициенты вычисляются из начальных условий.
При решении первой задачи мы будем исходить из уравнения теп-
лопроводности Фурье:
гд—с2Ди- (69>
Предположим, что при t = 0 внутри данного шара г<^а температура
известна и что температура на поверхности этого шара поддерживается
все время постоянной, т. е. что
м = 0 при r=a,
u=f(r, 0, <р) при г<^а, / = 0. (70)
Положим:
1 dT с2
-T^-V^v—k^ (75>
тогда
Т=Ае~^‘, ДУ4-£2П=0, (71а)
т. е. мы получаем для V однородное уравнение колебаний в трехмер-
ном пространстве.
Во второй задаче уравнением колебаний воздуха служит
(S9’>
Приравнивая U~T(t) V(r, 0, ср), мы, аналогично предыдущему, найдем:
7'= A cos ckt -|- В sin cki, /\ V-j- k2V=0. (71bji
Будем теперь искать решение уравнения колебания, имеющее вид
V = /?(r) К(0, <р). Как и в § 91 (36), мы получим:
1 । । 1 (г2 d2R . 2r dR . \ 4
=---- 775 ~Г — 3----(- «2л2 — const (72J
у \Й02 ' йО 1 sin20 W J \R2 dr2 ' к dr ' I '
1 См. Е. Jahnke-F. Em de, Funklionentafeln mit Formein und Kurven. Leip-
zig, Teubner (1923), стр. 160.
230 ПРИЛОЖЕНИЯ СФЕРИЧЕСКИХ, ЦИЛИНДРИЧЕСКИХ ФУНКЦИЙ И функций ЛАМЕ
Если постоянному в правой части этой формулы мы дадим значение
— Я (л 4-1) (я — целое положительное число), то в качестве У=Уп(в,(^)
может служить сферическая функция л-го порядка, а /? = /?л(г) должно
удовлетворять диференциальному уравнению
d2R 2 dR j
dr2 г dr [
л (л 4- 1)
г2
R=0.
Положим R~rmz, тогда
dR
dr
dz
dr 1
d^z dz
-^4= ^'-44- — 4- m (m — 1) гт~2г.
dr2 dr2 1 dr
В таком случае для z получится уравнение:
d2z 2(m4-l) dz , — n(n 1) 1
~— ar +1-------------------+ k \Z=Q-
Наконец,положим 2 (m-j- 1)=1, m =-i- и введем обозначение
— л(л4-1)=; — s2; = » x~kr.
Наше уравнение примет теперь следующий вид:
d2z . 1 dz . /, s2 \
j—s 4—5—И1— ~? 1-2 = 0,
dx2 ' x dx \ x2 j •
T. e. перейдет в уравнение Бесселя частного вица, а именно: s в нем
равно половине нечетного числа. Функции Бесселя в этом случае выра-
жаются через элементарные функции (см’. § 102 и ниже). Таким обра-
зом мы получаем частное решение в следующем виде:
1 9
Чтобы окончательно определить фундаментальные функции, надо вос-
пользоваться еще краевыми условиями. В первой задаче согласно (70)
на сфере г=а поддерживается постоянная температура, равная нулю,
а потому
J ! (ka) — 0. (76)
л+т
Положительные корни fe = fe(£'(/« = 0, 1, 2,...) этого уравнения опре-
деляют фундаментальные значения. Во второй задаче мы первое из
уравнений (70) можем заменить условием, что поверхность сферы твер-
ОДНОРОДНОЕ УРАВНЕНИЕ КОЛЕБАНИЙ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ 231
дая (эт0 условие соответствует закрепленной мембране). Для всех зна-
чений t мы должны иметь
-1 =0,
Н=С'
и, следовательно,
d ( 1
1 (kr)
r=a
(¥7)
Корни этого уравнения дают нам фундаментальные значения
(т = 0, 1, 2, ...)Ч
Для первой задачи будем теперь искать решение, имеющее вид:
со со
т Yn^
п=0 т=0 1 2
а для второй задачи — решение вида:
сю о© __
+ (ТО)
л=0/и=0 2
Для определения
условиями:
коэфициентов этих рядов воспользуемся начальными
u=^f(r, 6, tp)
6, <₽)
при r<^a, t = 0.
(SO)
Вопрос таким образом и в этом случае сводится к разложению произ-
вольной функции в ряд по фундаментальным функциям, т. е. в ряд вида:
оо оо
/(г, 6, <Р) = -^У У ^>^(6.
V гЫ в+2
л=0 m=0
(81)
Коэфициенты этого ряда легко определить, если предположить, что ряд
сходится равномерно. С этой целью обе части равенства (81) надо по-
множить на Ри (cos у) sin 0 tZO (Zip, где у — расстояние по сфере между
точками 1, 0, <р и 1, О', <р', и проинтегрировать по поверхности сфе;ы
единичного радиуса. В результате этих двух действий все члены ряда,
исключая л-го, обратятся в нуль [см. §97, (98) и (99)], и мы получим:
СЮ « 2п
е’ <f)^osy)sin6rfOdy. (82)
m=0 л о
* Существование бесконечного числа действительных корней уравнения (77)
следует из заключения в конце § 102 и теоремы Ролля: между двумя корнями
уравнения у = 0 находится всегда корень уравнения у' = 0.
232 ПРИЛОЖЕНИЯ СФЕРИЧЕСКИХ, ЦИЛИНДРИЧЕСКИХ ФУНКЦИЙ И ФУНКЦИЙ ЛАМЕ
Далее, мы должны при данном значении п разложить произвольную
функцию j/г f(r, 6, <р) в ряд вида:
оо
/(Г, о, <₽) = £ CW J ± г), (83)
т— 0 2
где пробегает все значения положительных корней уравнений (76)
и (77). Для определения коэфициентов С^ = С^(6, <р) пользуются
условиями ортогональности
а
\J ^r)J i(k^,r)rdr — G при т=£т!, (84)
J ”+2 ”+2
О
которые имеют место как для ряда (78), так и для ряда (79). Доказа-
тельство этих условий ортогональности аналогично доказательству фор-
мулы (58). Легко также вычислить значение этого интеграла при т~т\
Таким образом мы найдем:
о 3
f л2/(л, О, <р) J L(k^r)dr
Л о
(6, <₽) = °—----------------------. (83)
1 W$r)}*rdr
Й "+'2
Подставив эти значения коэфициентов в (83) и (82), мы получим:
оо
<Р')£^М , (^)л)==
т=0 2
ОО
~ ] Jn+- С<^ Рп (C0S Sin 6 88
m=0 О 0
Приравняв в этой формуле соответствующие члены, найдем:
71 2я
Yn (6'« <?') = j j Ст} (6> <?) Рп (COS Y) Sin 6 db dy. (87)
О о
Особенно просто выражаются колебания сферы, если и является
функцией только расстояния. В этом случае п=6, и мы имеем:
г г . / 2 . 1 г ,, , Л 2 sin/гл
Ji(x) = ]/ —sinx, Ji (kr)=l/------------------, (88)
7 У Ttx У Г ~2 у Ttk г
и уравнением, определяющим частоты для краевого условия, (77) служит
tg ka = ka. (89)
ОДНОРОДНОЕ УРАВНЕНИЕ КОЛЕБАНИЙ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ 233
График функции tgx показывает, что это уравнение имеет бесчислен-
ное множество корней. Так как длина волны 1 равна то числа
— представляют отношение диаметра шара к длине волны (с=1).
я
kct k а
Первые шесть значений —~_т________ 2, 3, 4, 5, 6) суть1 2:
тс п
1,4303; 2,4590; 3,4709; 4,4747; 5,4818; 6,4844.
(90)
Следующие по степени сложности колебания сферы соответствуют
п=Л. Так как У не зависит от <р, то это колебание происходит в ме-
ридиональных плоскостях. Мы имеем:
/2 Zsinx \
—---------cosx ) .
тгх\ х J
(91)
Таким образом уравнением, определяющим частоты, в этом случае
является:
2ka
(92)
Наименьший
корень —— в этом случае равен 4
0,6626,
(93)
т, е. он несколько меньше половины наименьшего из указанных выше
отношений. Это число (93) вообще является наименьшим из возможных
отношений такого рода, возникающих при колебании сферы 3. Колеба-
ния воздуха в этом случае в известной мере сходны с колебаниями
воздуха в трубе.
С частным решением (88) уравнения колебаний мы уже встретились
в § 65. Остальные полученные нами здесь решения (75) могут быть
получены с помощью очень простого алгорифма; в частности с по-
мощью этого алгорифма мы можем вновь найти формулы, приведенные
нами уже в конце § 102. Чтобы ввести этот алгорифм, положим в урав
нении (74) т—п, в таком случае V— гаУп(Ь, w)г = гпУп(Ь, y)zn',
если мы, кроме того, еще положим kr — х, то мы получим для гп дифе-
ренциальное уравнение
g"+~-L,^+^=o. <М>
Мы утверждаем, что две последовательные функции z связаны соотно-
шением:
Rayleigh, т. I, стр. 334.
2 R а у 1 е i g h, т. II, стр. 232.
3 Дока >а ельство этого факта мною получено благодаря содействию.
Г. Н. Уотсона. (II имечаиие редактора немецкого издания.)
‘234 ПРИЛОЖЕНИЯ СФЕРИЧЕСКИХ, ЦИЛИНДРИЧЕСКИХ функций И ФУНКЦИЙ ЛАМЕ
Действительно, если мы подставим
dZn
dx
XZn + V
dx2
2«+i
dzn+i
dx
(ЙЗ)
•в уравнение (94) и продиференцируем полученное равенство, то в ре-
зультате получится уравнение:
I 2 (/? —|— 2) dzn+l I z _f)
dx2 -Г x dx n+1
жоторое совпадает с (94) при замене в этом последнем п на я-|- 1.
При я —О уравнение (94) принимает следующий вид:
d2z0 . 2 . dz0 ______
dx2 ' х dx ' 0
(97)
Решениями уравнения (97) служат (см. § 65)
cos х sinx elx e~tx
----, или — , -
XX------------------------XX
После я-кратного применения формулы (95) мы получим следующие
фешения уравнения (94):
1
°п (*)
1 JVsinx
1-3 ... (2.ч-|-1)
Нп(х)
1-3 ... (2л—1)/,
2 (2/1-)- 3) ~ 2 • 4 (2п 3) (2п -j- 5) (98)
COS X
х2 х4
2(1 —2.4) + 2-4(1 —2я)(3 — 2/г)
Нас интересуют
конечными; т. е.
только те решения, которые при х —> 0 остаются
только Gn{x). Легко показать, что
/~ И — / п4-—\
Н*)-
.Например:
G0(x)
sinx
G1(x)
sinx cosx
x3 x2 ’
„ . . / 3 1 \ . 3cosx
°2 (x)= "7-----J Sln x ~
2 \xs x3/ x4
(см. § 102).
§ 117. Распространение сферических волн. Распространяющиеся волны
выражаются с помощью тех решений волнового уравнения (69г), кото-
рые имеют вид:
и = (/-) Yn (6, <p),
(100)
РАСПРОСТРАНЕНИЕ СФЕРИЧЕСКИХ волн
235
причем v(r) при г—> оо стремится к нулю. Если это выражение для и
сравнить с выражением в § 116, то окажется, что
ck—p и R = e~ikrv(r).
Положим —ikr—x. Тогда уравнение (73) примет вид:
f'k !Л(В+П|п п
dx2 -Г х dx I “Г" х2 /
или, та.; как R = exv, то
+2 (1 +-L) — _1-(1
dx2^ \ x)dx^\x
(101)
(102)
X2 1
Найдем решение последнего уравнения, имеющее вид ряда
оо
V— У, а,х’- (ЮЗ)
v=-ОО
Подставив этот ряд в уравнение (102), мы получим:
оо
У, K{v(v—l)-|-2v — л (tz-}-1)}2vav_j]xv“2 = 0 (104)
•>=—со
и придем к рекуррентной формуле:
т. е.
п у) (w+v-f-i) п
V~1 2у
(105®
л (л 4- D
9 а-1’
(п 4- 2) (п — 1) (л-j-1) (и 4-2) 4 (я—В
й-з 2?2 а-2~ 2-4 й-п
(п -1-3) (п — 2)
а~*~ 2-3 а~3~~
(й —j—1) (*2—{—2) (л—3) п (и— 1) (п — 2)
= 2^44———— а
Так как п—целое число, то эти коэфициенты, начиная с некоторого,
обращаются в нуль. Если предположить еще ао = ап — О, то все а*,
для которых v^>0, обращаются в нуль, и мы получим решение в виде
полинома:
1 /, л(«4-1) 1 (я—1) п (л-|- 1) (п 4 2) *
Т-' ==---( 1------------- -I------------------------
х \ 2х ' 2-4х2
(л-2) (д—!)...(» +3) 1-2.3...2л
3-4-6хЗ -Г----Г1 ) 2.4-6 ... 2пха'
(I0S)
236 ПРИЛОЖЕНИЯ СФЕРИЧЕСКИХ, ЦИЛИНДРИЧЕСКИХ ФУНКЦИЙ И ФУНКЦИЙ ЛАМЕ
Вернемся к прежним переменным, заменив х через —ikr. Тогда1
п (п. 4-1) . (п—1' п(п + 1) (п -J- 2)
2ikr
e-lkr
L rvff
p-lkr
ikr
2 • 4 (ikr)2
(i07)
Сравнение этого выражения с § 102 (44г) показывает, что ряды,
хараК1еригующие функцию f„(x), и функции Ганкеля Н i (х) совпадают
я+т
с точностью до постоянного множителя. Функции fn(x) можно полу-
чить с помощью формулы
e~xfn<x)
x"+1
(-1)”
1 d\ne~x
х dx) х
(107')
аналогично тому, как это было сделано в § 116, (98) для функций Gn(x)‘
Итак, искомое решение имеет следующий вид:
оо
W pi (р* — ^")
г”(6, <?)—~г—о°»)
п=0
Члену, в котором п = 0, соответствует рассмотренная нами уже в
§ 65 симметрическая волна
ei(pt — kr}
и = -—у— . (109)
Такие колебания могут быть вызваны сферой, которая попеременно
то растягивается^ то сжимается, подобно пульсирующим шарам, которые
были изучены К. А. Бьеркнесом 1 2 3 *.
При п = 1
и = — 幑-М f 1 -J- _L V (110)
г \ 1 ikr]
Эта функция представляет действие диполя (ср. с задачей о движе-
нии шара в несжимаемой жидкости, рассмотренной в § 113). Это дей-
ствие диполя можно, например, получить при колебании шара между
двумя точками. Воздух при этом течет от одной стороны шара к другой.
При /г=2 функция и прегставляет колебания камертона. Камертон
соответствует двум диполям; поток воздуха попеременно направлен то
в г внешнее пространство, то вовнутрь к середине камертона 8.
§ 118. Колебания эллипсоида вращения. В случае осевой симметрии
уравнение колебаний принимает согласно § 108, (96) следующий вид:
= 0.
(ИО
1 О. G. Stokes, On the communication of vibration-; from a vibrating body
to a gas. Pnii. Trans, of the Riyal Soc., t. 158, стр. 451 (1868).
2 V Bjerknes, Die hydrodynamishen FernkrSfte, Le pzig, Earth (1900).
3 Об этом и ряде аналогичных вопросов см. Lord Rayleigh, Theory of
Sound, книга, на которую мы не раз ссылались.
КОЛЕБАНИЯ ЭЛЛИПСОИДА ВРАЩЕНИЯ
237
Положим р = f (и) g(v) и V=L(u)M(v). Тогда
1 d ( dL\ 1 d I , dM \ , A2 „ „
Lfyu) du V “ <fK/”^Mg(®) dv )rf®) ^№~0, (,12)
т. e. h~2 представляет собою сумму двух функций, каждая из которых
зависит только от и или только от V. Положим, как эт<> было уже
сделано в указанном месте для случая растянутого эллипсоида,
f(u) = —sin и, g(v)~ ch®,
тек что согласно § 108, (104)
— — ch2® — cos2 и
h2
Уравнение (112) преобразуется тогда в следующее:
+ ) + fe2(ch2^—COS2«)=0. (ИЗ)
L\du2 1 du] ' M\dv2 1 dv / 1 ' '
Это уравнение равносильно двум следующим:
d2L di
~ J_ ctg и । {с — k2 cos2 и) L = 0,
du2 ' du '
dM
4- cth v ~z-1- (k2 ch2®— С) M — 0, (114)
dv2 dv' '
где через С обозначено некоторое постоянное.
Перейдем к эллиптическим координатам £• = ch®, j)=cosw. Тогда
эти уравнения перейдут в следующие:
d2I di
(£2_1)^+2^Т+(^2_с)7и==о- ci5)
Преобразуем теперь первое уравнение, полагая С— k2 > к Мы получим:
~ - ^~2 ~ + ( k2 + , ) L = °,
rflj2 1 —Т| ЙГ] 1 \ 1 1 Т|2/
(116)
Второе уравнение можно преобразовать точно таким способом. Это
уравнение было исследовано Р. С. Маклореном и '1. Аг,рагамом
Абрагам пришел к этой задаче при изучении электрических волн ко-
торые распространяются эллипсоидальным источником Б )лее подробное
изложение этого вопроса выходит за пределы этой книги.
< R. С. Maclaurin, On the solnt'ons of the eyrtoi (r2 + xS)f —0 ii
ell p ic co rd nate and their p'n sic il аррГcationTra.isac i ы I the Cainnri !xe hint.
Soc., t. 17, стр. 41—108 (1898); M Ab ra haul, Ober ei i де, re Schw n unsjsp o-
b.emen au.tretende, Diffeie.i t aigleichun en, Mr:th. Ann., т. F2. стр. 81—112 (1899).
238 приложения сферических, цилиндрических функций и функций Ламе
§ 119. Теорема сложения К. Неймана для бесселевых функций. Из
| 103 следует, что функция вида
V — uJnO-r) cosп<^,
п X
(И7)
где г, <р, z — цилиндрические координаты (в этой главе мы будем пи-
сать г вместо р), удовлетворяет диференциальному уравнению Лапласа.
Можно ожидать, что справедлива и обратная теорема: при достаточно
общих предположениях можно данную гармоническую функцию пред-
ставить в виде ряда (117). Пусть будет <о расстояние переменной точки
в плоскости ху с координатами г, <р, 0 от точки г', 0, 0. Мы имеем:
о2 = г2 -|- /2 — 2rr' cos w.
Перенося начало координат в точку г', 0, 0, мы убеждаемся, что
выражение
е~1г J0(k(£>) — e~^ Jo {lj/r2 -|- r'2 — 2/z'cos<p}
удовлетворяет уравнению Лапласа. Естественно поэтому ожидать, что
это выражение можно представить в виде ряда (117), т. е. что
оо
(^w)== У, ^пе~}г Jn 0-Г) cos nw,
п=0
или в силу симметрии
оо
Л) (М =" У anJn (М Jn (^') c°s «ф, (118)
п=0
где ап зависит только от п. Это равенство действительно имеет место,
и коэфициенты ряда, стоящего в его правой части, определяются одно-
значно. Если положить г' = 0, то все члены ряда (118), исключая пер-
вый, обратятся в нуль, а так как при этом ш = то «0 = 1. Заметим,
что достаточно доказать справедливость равенства (118) при 1=1.
Перейдем к этому доказательству. Заменив в формуле (8) § 100
71
if через —, мы получим:
оо
eir ч> = Jo (г) + 2 £ inJn (г) cos я<р, (119)
м, следовательно,
оо
efr«>s(<p-e)_ уо(г)_|_ 2 Уя (/-) (cos /?ф cos вб 4- sin в'д sin лб). (120)
' Я = 1
Умножая это равенство на cos/ztp (при тг^> 1) и интегрируя, мы
найдем:
eir eos (Т - 6) со§ _ 2то-Л j* до cos (12*)
ТЕОРЕМА СЛОЖЕНИЯ К. НЕЙМАНА ДЛЯ БЕССЕЛЕВЫХ ФУНКЦИЙ 230'
Далее, интегрируя по 6, имеем:
2я 2п 2г
J. С е -ir’ “S о Jfj I eir cos (? - °) cos nw dy = in Jn (r) I e ~ir’cos 6 cos «6 J6. (122)
2TtJ J ‘ J
О о 0
Применив к правой части этого равенства формулу (121), найдем:
2.x 2п
1 С г
— I е -ir' cos 6 jg I eir cos (<? - 0) cos Л(? j^ — 2lTJn (r) Jn (!23)
о 0
Изменим в правой части порядок интегрирования; получим:
2it 2.
~ f cos пи dw I e': cos (<p - 6) - r' css 6] jg _ 2tt j (Z) j ttJ\
ZTt 1**1 n n
о b
В интеграле по 0 сделаем теперь следующую подста ювку:
rcoscp — d — a, rsin<p==f»;
мы получим:
2г 21
р г г____
| ei (a cos О + b sin 6) Jfj __ ei Va* + ft* cos (9 - «) J (g _ a) =2п./0 (j/a2 ft2) =
e b
= 2тг Jo (У r* -f d" — 2rd cos =. 2k Jo (o>) I a = arctg — ) . (125)
В результате получится:
2к
J0((o)cos«w</<p = 2Jn(r) Jn(rr) (« = 1,2,3,...) (126)
о
Следовательно, все коэфициенты «я(л^>0) равны двум, т. е.
оо
4 (“)=J (r) Jo (') 4 (/J)cos лт>
Л = 1
о2 = л2 J2 — 2rd cos w. (127):
Это равенство называют теоремой сложения К. Неймана
При <р = 0 и при 'р --= тг из этой теоремы как следствия получаются
следующие равенства:
оо
Л (/• - '’)=4 (r) Jo (''') + 2 2, Л (/') Jn ('’)> С й)
Я = 1
оо
jo (г+Н=/0 (г) jo (И) + 2 £ (-1Г 4 (г) 4 (И). (129)
___________Л=1
* С. Neumann, Theorie der Besselschen Funktionen, стр. 59—65, Leirzig
>Ж). 1 ь'
2-40 ПРИЛОЖЕНИЯ СФЕРИЧЕСКИХ, ЦИЛИНДРИЧЕСКИХ ФУНКЦИЙ И ФУНКЦИЙ ЛАМЕ
Далее, теорему сложения можно записать еще следующим образом:
2*
Д С -4 (М d4 =* -4 (И -4 (И1 Озо)
ZTl I
6
2к
~ С Jo (ко) cos л<с = JnQx) J„(V') (л= 1, 2, 3, ...). (131)
zn j
о
Но мы имеем:
й» , й<0
© — = г — г cos и, © — — rr sin св. (132)
йл т й'д ‘ ’
'Проди!еренцируем равенство (127) по г, и, приняв во внимание,
что J'0{x) = — Jx{x) [см. § 100, (18')], заменим в полученном выраже-
нии г через ),л и И через V. В результате мы получим, что при 1^>0
J оо
— (ко) (кг) Jo (И + 2 ия (V) Jn(V) cos «<р, (133)
л=1
т. е.
2к
1 f J, (ко) cos
2тг ] со
о
Диференцируя равенство (127) по ср, мы будем иметь:
оо
— X A Q,(?L гИ sin <р = — 2 nJn (к) Jn (кН) sin пу, (135)
Л=1
т. е. при ~ку^0
2я
1 ГД (Хи) . _ Д (V) J, О./)
^-Vsin8^^—W-2’ <136>
о
§ 120. Асимптотическое представление бесселевых функций. Из (121)
легко получается упомянутая уже в § 102 приближенная формула для
бесселевых функций Jn(r)(n—-целое число) при больших значениях
аргумента г. Действительно из (121) при 6 = 0 следует
2п к
1 Г . 1 г
И (л) = — I e" cos f cos пу dy — —- 1 e'rcos T cos ^37^
о о
Заменим cos<р через х. Тогда функция cosпу перейдет в многочлен Тп(х)
(полином Чебышева), причем
Т0(х) — 1, T-^xj — x, 7’2(х) = 2х2 —1, 7’8(х) = 4х3—Зх и т. д. (138)
АСИМПТОТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ БЕССЕЛЕВЫХ ФУНКЦИЙ
241
Так как Тп(—х)=(—1)"Гв(х), то мы имеем:
Jn <r} = * l-A eirx dx =
ТС J |/ 1 ---------X2
-1
тг J ]/1 — х2 тг ) /1-х2
о 'о
Так как cos лер при <р = 0 равен единице, то 7'n(l)= 1. Разложе
нием в строку Тейлора мы убеждаемся, что функция
£(*) =
/1Н--"17
1
/2
(140)
имеет нуль первого порядка при х=1; следовательно, функция
/(*) =
W
У 1 — х2
1___1_
/ 2 /Т-х
имеет нуль порядка — при х=1. Поэтому производная f (х) хотя и
1
обращается в бесконечность, но так, что |/r (х) | dx имеет смысл. Мы
о
можем применить к этой функции утверждение (Г) § 42 (см. соответ-
ствующую сноску). Таким образом, заменяя первый член суммы в урав-
нении (139) выражением
i~« Г eirx J i~netr Ce~lrx , e1 (rCe~ix , v
—t= \ r - dx =-— I —— dx =-—— 1 —— dx, (141)
it /2 J /1 —x тг/2 j / x it / 2 J / x
ooo
мы при г—>oo делаем ошибку порядка — . Последний интеграл в (141)
при г—> оо сходится, и притом
оо
Г е~1х Г тт -- г-
I -~-dx = (l —1)1/ — = е 4/л \ (142)
.1 ух V 2
< Для вычисления этого интеграла можно воспользоваться формулой
оо
2 е—ax'dx = ~fy^
о
[т. 1, приложения, § 4, (20')]. заменив в ней х через /х и положив я = I. Полу-
оо
Г е1*
чающийся при этом несобственный интеграл J dx сходится, как это сле«
о
1 /тс _ __in
дует из (142'), ипритом, так как -у==.^е 4 ? то предел его равен У к е
16 Вебстер. ДиференциальЕые уравнения.
242 ПРИЛОЖЕНИЯ СФЕРИЧЕСКИХ, цилиндрических функций и функций ламе
Далее, интегрируя по частям при г’ г, мы получим:
(142)
Отсюда мы можем заключить, что порядок малости функции
где порядок малости s (г) при г—► сю есть — Ч
Из сходимости интеграла (142) следует сходимость интегралов
оо сю
( Jn(ax) cos bxdx, J Jn (ax) sinbxdx (145)
с 0
при условии, что я>0, и аЬ. Эти интегралы можно выразить
через элементарные функции, что и будет сделано в следующем пара-
1рафе.
§ 121. Вычисление некоторых интегралов. Вычислим интегралы
оо
e~zxJn(ax) cos bxdx^ Рп, (146)
е
сю
e~zxJn (ах) sin bx dx^ Qn (147)
о
при условии, что х:^>0, а>0, Положим для этого8
сю
j e~^~^xJn(ax)dx. (148)
о
_ £
1 В действительности порядок малости е(г) равен г 2. См. Rlemann-We*
b е г, т. I, стр. 354.
2 О дальнейшем ем. указанную в §123 работу Beltrami, стр. 499.
ВЫЧИСЛЕНИЕ НЕКОТОРЫХ ИНТЕГРАЛОВ
243-
Из (119) при (р действительной вытекает, что
оо
e;arcosT _ Jo (ах) 2 у injn (ах) cos Л!р>
«1=1
(149)
ОО
e-{z-ib-ia^^x= Jo (ах) e-(z-.ib)x 2 ^2 ia cos nyJn (ax) e~^x. (150)
«=1
Таким образом, интегрируя по x от 0 до — оо, мы получим:
оо
8_a2focoSy=₽«+«?.+2 S <₽»+iftJ с“ "f
Я=1
Выражение, стоящее в левой части этого равенства, имеет вид:
___L—_
1 — 2а cos <f -f- а2 ’
Исключая из этих двух равенств fi, мы получим:
а2 — 2а^—^4-1=0,
ia
так что
ia
а= ,
у «24-(2 — z£)a4~2— ib
р__
V°2 4- (*—ib)2 4“ z—ib
(<M)
(152)
(153)
(154)
(155)
Произведение корней уравнения (154) равно единице, а потому абсо-
лютная величина одного из них меньше единицы, а другого больше
единицы Ч Выберем значение радикала
/ a24-(z — ib)2^Z~ iB
(156)
так, чтобы [а| С 1. При а—>0, Z и В, очевидно, стремятся к z и Ь.
Из (156) следует:
а2 4-г2— b2 = Z2 — В2, zb = ZB.
(157)
Второе из этих равенств показывает, что Z и В имеют один и тот же
знак. Мы утверждаем, что | а | < 1, если только Z и В не отрица-
тельны. Действительно,
z2Z>2_^8
Т2 ~~В2~
В2 — а2 4~ Д2 — Ь2,
* Абсолютная величина обоих корней не может быть равна единице; действи-
тельно, в этом случае они имели бы вид eh и e~h, и их сумма была бы дейст-
вительна, т. е. я должно было бы быть равно нулю.
16*
244 ПРИЛОЖЕНИЯ СФЕРИЧЕСКИХ, цилиндрических функций и функций ламе
и таким образом,
Z — ~^/ — (l^(a2 z2— b2)24z2b2(a2-f- z2— b2)) (158)
и
В=|/ (l/(a2-j-z2 — b2)2 -j- 4z2b2—(a2-\-z2— b2)). (159)
Согласно условию, эти корни должны быть взяты с положительным зна-
ком. Равенство
а2 z2 — b2—Z2—В2 (160)
можно записать еще и так:
(z Z)2 (b ц_ в)2 = a2 -j- 2 (В2 4- z2 4- zZ 4- ЬВ). (131)
Из этого последнего равенства следует, что
(z4-Z)24-(Z>4-/?)2>a2. (162)
Приняв во внимание равенства (155) и (156), мы действительно полу-
чим |а|<4.
Разложим теперь выражение (152) по степеням а:
ft _ _ Р___________1 —а2 __
1 — 2а cos у 4~ а2 1 — я21 — 2а cos ср 4* я2
1 [> /1 4- . 1 4- ае~1?\
~~ 2 1 — а2 \ 1 — ае*? *" 1 — ае-'®/
— —£—- (1 4- 2а cos <р 4~ 2а2 cos 2<р 4“ • • • 4“ 2а" cos пу 4~ ... )• (163)
Из (153) следует:
1 — а2 2 14- а2 ia
—=т—(г-‘)' °’
а потому в силу (155)
Е _ _ 1
1—а2 l^a2-j-(z—ib)2'
и следовательно,
оо
-------------= 1 11 4- 2 У ал cos пу ). (165)
z — ib — ia cos у у a2-j-(z — ib)n \ /
Сравнивая последнее равенство с (151), мы находим:
пп
г + iQn) = V ~-MS ’
У а2 4- (z — ib)2
ВЫЧИСЛЕНИЕ НЕКОТОРЫХ ИНТЕГРАЛОВ
245
т. е.
/э • I I а \п
" l/a1 2-r(z— ib)2 a2 -|- (z—ib)2-\-z—ib)
_ ________1_______(V a2 -f- (z — ib)2 — (z — ib)
j/ a2 -f- (z— ib)2 \ a .
(166)
где __________
/a24-(z— ib)2=Z--iB, B^O.
Так, для /г = О и п—1 мы имеем:
Ро + »<Зо = ^-Цд, (167)
Пусть а=^Ь. Тогда при z—>0
J {|а2-й2|+(я2_й2)}>
В = Л/ у {\a2-—b2\—(a2 — b2)},
и таким образом
Z — — Ь2, В = 0 при b < а, )
Z = 0, В=]/Ь2— а2 при b'^>a. J
Из сказанного вытекают следующие важные формулы
оо
С Jn(ax) cos bx dx = *
J ]/a2 — b2
о
oo
\ Jo (ах) sin bxdx — 0
о
oo
J Jj (ax) cos bx dx — -i
0
oo
\ J, (ax) sin bx dx — -r- - -
J a^a2— b2
u
приа^-fe, (170)
1 При выводе этих формул надо пользоваться непрерывностью интегра-
лов (146) и (147) при г 5г 0 (см. приложенье т. 1, §4, е).
246 ПРИЛОЖЕНИЯ СФЕРИЧЕСКИХ, ЦИЛИНДРИЧЕСКИХ ФУНКЦИЙ И ФУНКЦИЙ ЛАМЕ
оо
Jo (ах) cos hxdx=G
о
1
I J0(ax) sin bxdx-----—_________
j/ b2 — а2
о
оо
1 J, (ах) cos bx dx — — I1
J а \
0
oo
J1 (ax) sin bx dx = 0
о
b '
\/'b2—a2
Первые два равенства в обеих группах формул носят название разрыв-
ных интегралов ВебераЧ Все интегралы (170) расходятся при a = ftj>0.
Положим теперь х^>0, а>0, Ь — 0. Из (167) следует:
оо
i e"zV0 (ах)--г- ... ,
О
1
(171)
а из (168):
С е ZXJ1 (ах) dx=— I 1
J а \
о
При z—>0, «=1 в силу (171)
оо
Z
2-4-2-2
(172)
1.
(173)
о
[Сходимость этого интеграла следует из сходимости интеграла (142).]
Диференцируя (171) по z, мы получаем:
оо
1 е~гх xJ0 (ах) dx=---—----у ,
о (а«-Н^)2
же равенство по а и принимая во внимание, что
[см. § 100, (18')], находим:
оо
е~гхх (ах) dx
о
(174)
диференцируя то
Л) (•*) == А (*•)
а
з •
(175)
1 Н. Weber, Journal fiir Math., т. 75, 1873, стр. 77.
ПОТЕНЦИАЛ МАСС
247
Эту последнюю формулу можно также получить, диференцируя (172) по z.
Интегрируя (171) по z от 0 до z, мы будем иметь:
оо ______
f 1е~гх , . z 4- ]/а2 4- д2
I----—---Jo (ах) dx = log ——----—— . I176)
о
Интегрирование (172) по z от z до оо дает нам:
оо г——
f J, (ах) ]/ а2 4- г2 — z t ч
--> dx~------—------. 077)
J х а
о
Сопоставляя эти две формулы, мы приходам при z—>0 к формуле
оо
f Л (ах) ,
l x ~ dx=l. (178)
о
§ 122. Потенциал масс, распределение которых обладает круговой
симметрией. В § 109 мы вычислили потенциал окружности, на которой
равномерно распределены массы. Функция должна, очевидно, обладать
в этом случае круговой симметрией, т. е. в цилиндрических координа-
тах она должна быть независимой от угла. Пусть плотность равняется
а радиус окружности равен а. Тогда значение функции V в точке г, z
(г — расстояние точки от оси симметрии, ^-—расстояние от плоскости
круга) выразится так:
В силу (171) это равенство можно переписать в таком виде:
2* ОО OO 2it
и таким ад J 1 (w^) = ад j e~ztdt j Jo (art) dy, 0 0 0 0 образом в силу (130) оо V = 2тагй j e-zt Jo (rf) Jo (at) dt. 0 (180) (181)
Введем ниями: „функцию тока" <Ь, которую мы определили в § ИЗ йф_ ЙУ _ ЙУ йг йг ’ й-г йг ‘ уравне- но
248 ПРИЛОЖЕНИЯ СФЕРИЧЕСКИХ, цилиндрических функций и функций ламе
Принимая во внимание равенство [см. § 100, (19)]
[•* А (*)] - xJ0 (х), (182)
мы в результате небольших вычислений находим:
оо
ф = — 2па8г J e~zt Jr (rt) Jo (at) dt. (183)
о
Вычислим, пользуясь формулой (181), потенциал однородного диска
с радиусом а и с постоянной плотностью с. Обозначим множитель при 8
в правой части формулы (181) через тогда искомый потенциал вы-
разится так:
а а СЮ
V— а Vada=2то J ada J e~zt Jo (rt) Jo (at)dt. (184)
о oo
В силу (182)
a
d [atJ.. (at}) x r , ,ч С r , , «Л (at} ,
—-J--------— atJ0 (at), 1 aJo (at) da = —L------, (182')
CL ICLLI 1 L
0
а потому
сю
Г e~zt
V = 2naa I JQ (rt) {at) dto (185)
D
Функцией тока в данном случае служит
сю
Г e~zl
ф = — 2тшы I -у- \ (rt) (at) dt. (186)
о
Отсюда легко получить также и потенциал двойного слоя диска
г^а, а именно:
оо
W— — = 2пах \ (rt) Jr (zt) dt, ( 87)
0
где X — плотность двойного слоя. В данном случае:
оо
ф = — 2ттахг j" e~zt Jr (rt) (at) dt. (188)
о
Две последние формулы представляют нам также потенциал и функцию
тока кругового электрического тока.
ФОРМУЛЫ БЕЛЬТРАМИ ДЛЯ СИММЕТРИЧЕСКИХ ПОТЕНЦИАЛОВ
249
§ 123. Формулы Бельтрами для симметрических потенциалов. Бельт-
рами изучил потенциалы тел вращения и значительно обобщил фор-
мулы § 122 Ч
а) Согласно §103 функция
У = J0(rt) (189)
служит решением уравнения Лапласа, а функция
ф — Are~xt J'o (rt) = — Are~xt Jr (rt)
является соответствующей функцией тока. Функции
V —Aext J0(rt), 1
ф = — Arezt J'o (rt) = Arext (rt) j
(190)
(190')
можно интерпретировать при z<^0 аналогичным образом. Функцию V,
определенную этими равенствами во всем пространстве (кроме z=0),
можно рассматривать как потенциал масс, находящихся в плоскости
г=0. Вычислив поверхностную плотность h — h(r) этих масс из урав-
нения (53) § 56
kJ ~ U? =4AtJa(rt)^^h, (191).
\ oZ у—о у oZ / о
мы найдем:
At
h(r) = ~J0(rt). (192)
Таким образом для массы, лежащей внутри круга радиуса г, мы имеем
выражение: r г
т (г) — 2тт h (г) г dr--At rJQ (rt) dr — ArJy (rt). (193)
о 0
Умножая обе части равенств (189), (190) и (192) на произвольную
функцию (t) и интегрируя, мы найдем, что если плотность распреде-
ления обладает круговой симметрией и равна
оо
а (г) = ~ I (rt) (t) t dt, (194)
^Tt J
b
то потенциалом и функцией тока соответственно являются:
оо
V = j e~zt JQ (rt) ср (t) dt. (195)
о
oo
ф = — r e~zt (rt) <p (t) dt. (196)
___________ о
1 E. Beltrami, Sulla teorladelle funzlonl potenziali simmetrkhe,Memorie della.
Accademia delle scienze dell’Istituto dl Bologna, серия 4, т. 2, стр. 461—505 (18:51).
250 ПРИЛОЖЕНИЯ СФЕРИЧЕСКИХ, ЦИЛИНДРИЧЕСКИХ ФУНКЦИЙ И ФУНКЦИЙ ЛАМЕ
При этом предполагается, что z>0. Если z<^0, то z надо заменить
через —z к изменить знак в формуле (196). Равенство (194) можно
рассматривать как интегральное уравнение первого рода относительно
функции tp(^) при заданной а {г).
Ь) Функция y(t) определяется через а (г) однозначно повсюду, где
эта последняя функция непрерывна. Пусть z^>0. Из (195) следует, что
непрерывная функция (t) однозначно определяется (поскольку она
существует) функцией V 1. Для окружности радиуса а, плотность кото-
рой равна единице, формулы (181) и (183), дающие потенциал, напи-
шутся так:
V (а) — 2па j e~zt Jo (rt) Jo (at} dt, (197)
о
и
oo
• w (a) = — 2тгаг J e~zt Jx (rt) Jo (at) dt. (198)
о
Легко заметить, что эти формулы получаются из (195) и (196) при
, ср (t) = 2iraJ0 (at). (199)
Таким образом для любого распределения масс, плотность которого а (а)
обладает круговой симметрией, мы имеем:
оо оо
V — v (a) a (a) da, ф = J и> (a) a (a) da, (200)
о о
или, при выполнении соответствующих условий о сходимости интеграла,
оо оо
V == 2п j e~zt Jo (rt) dt J JQ (zt) a (a) a da, (201)
о о
и
oo oo
ф = — 2nr J e~zt J у (rt) dt Jo (at) a (a) a da. (202)
о о
Из сравнения этих формул с (195) и (196) следует, что в данном случае
оо
<р (t) = 2тт J Jo (at) a (a) a da, (203)
____________ о
> Это утверждение основано на известной теореме Лерха (Lerch). Если функ-
ция / (х) удовлетворяет уравнениям
1
f (х) хп dx — 0 (п — 0, 1, 2,...),
о
то / (х) = 0 тождественно.
ФОРМУЛЫ БЕЛЬТРАМИ ДЛЯ СИММЕТРИЧЕСКИХ ПОТЕНЦИАЛОВ
251
таким образом ср (t) выражается через а (г). Равенство (203) является
решением интегрального уравнения (194), и обратно: если равенство (^03)
рассматривать как интегральное уравнение относительно а (а), то фор-
мула (194) даст нам решение этого уравнения. Объединяя обе фор-
мулы, мы получим:
оо оо
ср (t) = Jo (st) s ds j* Jo (sr) rf (r) dr,
о 0
oo oo
a (r) = j* Jo (sr) s ds j" Jo (st) ta (t) dt.
о о
(204)
Эта теорема, принадлежащая Ганкелю1, сходна с интегральной теоре-
мой Фурье [см. § 43, (52)]. Она безусловно справедлива, когда интеграл
оо
J Ч*(г) V^dr
о
существует, если функция ср (г) повсюду непрерывна и в каждом конеч-
ном интервале удовлетворяет условиям Дирихле (см. § 42, с).
Рассмотрим в частности диск радиуса а; для этого диска ср(г) = 0
при и
оо а
о (г) = J Jo (sr) s ds Jo (st) ta (t) dt. (205)
о 0
Покажем теперь, как определить функцию V из ее значений при z=0
[обозначим эти значения через V(r)]. Из (195) следует, что при z—>0
оо
V (г) = J Jo (rt) ср (t) dt. (206)
о
если только этот интеграл сходится. Уравнение (206) того же вида,
что и (194), и получается из этого последнего, если 2то заменить че-
рез V, а ttf (t) -—через ср (t). Равенство (203) переходит в данном случае
в следующее:
оо
= (207)
о
Подставив это выражение в уравнения (195) и (196), мы получим:
ос сю
V = J J e~zt Jo (rt) Jo (st) V (s) st ds dt, (208)
о 0
1 H. H а n k e 1, Bestimnite Integrate mit Zylinderfunktionen, Math., Ann., t. 8,
стр. 453—470 (1875).
252 приложения сферических, цилиндрических функций и функций ламе
и сооо
ф = — г e~zt (rt) Jo (st) V (s) st ds dt. (209)
о 0
В качестве примера снова рассмотрим диск радиуса а, для кото-
рого а(г) = О при г^>а. В силу (203)
а
у (г) = 2п J Jo (rt) a (t) t dt. (210)
о
Так, при а(г) = 1
<f (г) = 2л j” Л, (rt) t dt = 2п« . (211)
"о
Подставив это выражение в (196), мы снова получим (185).
с) Ограничимся в дальнейшем частным случаем диска и положим,
что потенциал В (г) задан только для значений г<^а. Докажем, что
плотность а (г) и функция (t) определяются при этом однозначно.
Действительно, если бы одному и тому же потенциалу соответствовали
две различные функции плотности, то разность этих последних соот-
ветствовала бы распределению масс, потенциал которых при г <Za равен
нулю. Если применить теорему о максимуме и минимуме потенциала
к области, ограниченной диском и большой сферой, то окажется, что
потенциал тождественно равен нулю. Но в таком случае в силу (207)
ср(г)=О, а в силу (194) также и a(zj = O.
Согласно нашему предположению
оо
а(г)=т^^J0(rt)y(f)tdt= 0 при г~^>а. (194')
о
Пусть г<^а и М(г) — масса кругового кольца, ограниченного окруж-
ностями радиусов г и а. Мы имеем:
а
zW(r) = 2nj <j(r)rdr, М(а) = Ъ, (212)
- = -2пгоИ, (213)
Отсюда в силу (203) следует:
J0(rt) — dr= — M(r)J0(rt)
оГ
М (г) J-l (rt) dr—
=M(0)—t I M (r) Jj (rt) dr.
(214)
0
.УЛЫ БЕЛЬТРАМИ ДЛЯ СИММЕТРИЧЕСКИХ ПОТЕНЦИАЛОВ
253
Введем ->'нкцию ^(г)> для которой
а
М (г) — ( , /7 (())__ Q (215)
J р S2 — г2
т
(что такая функция существует, мы покажем ниже). В таком случае мы
должны иметь:
М (0) = F’ (s) ds = F (а),
о
и на основании (214)
а а
г / 1 i С z / J.X .1 С (s) s ds
if (t) = F (a) — t I J3 (rt) dr \ -—_ - =
J J |/ s2 — r2
0 r
a s
= F(a) — t ( F’ (s) s ds C - dr. (216)
J J V s2 — r2
о о
Последний интеграл по г можно выразить с помощью элементарных
тг
функций. Именно из формулы (140) §46 при <р = — следует:
п 2
sinr=-^-J J0(rsin 6) sin6dO==rJ Jo (r sin 6) sin 0 db.
о 0
Интегрируя no z, мы отсюда в силу (182) получим:
2
1 —cosr=r J (rsin 6)
о
То же можно записать несколько иначе.
(2П)
s 2
Г Л (rt) Г г Z J. • m 1 — COS st
I ? dr = I (st sin 6) rfO —--------------. (218)
J J/ s2 — r2 .) st
о 0
Таким образом для y(t) окончательно получится следующее выражение:
и а
tp (t) = F(a) (cos st — 1) F’ (s) ds = C F' (s) cos st ds. (219)
о о
254 ПРИЛОЖЕНИЯ СФЕРИЧЕСКИХ, цилиндрических ФУНКЦИЙ к
ЧКЦИЙ ЛАМЕ
Интегрируя по частям, получим:
а а
а С Г
<р (t) = F (s) cos st t\F (s) sin st dt — F (a) cos att\F (s) sin st ds. (^
о о
Таким образом наша задача сводится к определению функции
Ниже мы покажем, что в формуле (215) можно положить
2 С V(s)sds
тс J — в2
о
(221)
Воспользуемся сейчас этим фактом, приняв его пока без доказатель-
ства. Сделаем в (221) замену переменных
га——sds=tdt
и проднфереицируем полученное равенство
Г
2L F (г) = I V (|/ г2 '— Z2) dt (222)
о
по г; мы будем иметь:
О о
Подставив это выражение в формулу (219), мы получим:
2V(0)sinaf , 2 Г , Г П'Ы ,
и (?) = ----------1 г cos rt dr I ’— ds, (224)
Y к t kJ J /ra —««
о e
т. e. выразим <p (t) в явном виде через V (г).
d) Для доказательства формулы (221) заметим сначала, что функ-
ции F(r) и с (г) определяются однозначно через y(t), а сама функция
(t) определена однозначно, если равенства (206) при и (196)
[причем о (г) — 0] при г^>а имеют место. Докажем сначала, что вы-
ражение (221) удовлетворяет уравнениям:
оо оо в 1
Jj0 (rt) <р (/) dt — р0 (rt) dt '(s) cos stds*= V (г) при r < a, I
0 8 0 • (225)
oo o© a
2na(r)= ( J0(rt)ty(t)dt= \.J0(rt)t dt F1 (s) cos st ds = 0 при r^> a.
й 0 0
ФОРМУЛЫ ВЕЛЬТРАМИ ДЛЯ СИММЕТРИЧЕСКИХ ПОТЕНЦИАЛОВ 255
Изменим в правой части первого из этих равенств порядок инте-
грирования, т. е. представим ее в виде:
а оо
F' (s) ds J Jo (rt) cos st di. (226)
6 о
Так как согласно формуле (170)
оо г 1
Г г___._при г"^>з,
1 Л) (r0 cos dt^= < )/ г1 2 * — s2
о (о при r<^s,
то выражение (226), в котором г<^а, будет равно
р F' (s) ds
J /г2—as’
о
(227)
Определим функцию F(r) равенством (221). Тогда
(228)
(229)
Для выполнения диференцирования в левой части этого равенства по-
ступим так же, как при выводе формулы (223), и примем во внимание,
что F(0) = 0. Мы получим:
С F'(f)dt~ ....
Г \ : = (г),
(2301
что вполне согласуется с первым из равенств (225)а.
Проводя такое же вычисление в случае г>а, мы
логичному результату:
приходим к ана-
(231)
с так называемыми
Е. Hellinger и
J V f2—ts
__________ о
1 Уравнения (221) и (229) тождественны по существу
формулами обращения Абеля. См. в энциклопедии статью
0. Т о е р 1 i t z, на которую мы уже ссылались в § 124, стр. 1350.
256 ПРИЛОЖЕНИЯ СФЕРИЧЕСКИХ, ЦИЛИНДРИЧЕСКИХ ФУНКЦИЙ И ФУНКЦИЙ ЛАМЕ
В силу (221)
мы отсюда находим:
a t
2 р dt d р V (s) sds
ТЕ J |/r2 — t2 dt J t2— s2
о о
(232)
Эта формула выражает потенциал вне данного диска через потенциал
внутри этого диска.
Нам надо еще доказать справедливость второй формулы из (225).
В силу (182) § 124 левая часть этой формулы, умноженная наг, равна
производной по г от
ОО а
г (rt) dt § F' (s) cos st ds. (233)
о 0
Но мы имеем;
ОО а ОО a
(rt) dt F’ (s) cos st ds = J F' (s) ds J J, (rt) cos st dt. (234)
oo 0 0
Так как в силу (170)
оо | 1
С г
\ J. (rt) cos st dt — 5 1 / t
i | 7(‘-F=.
то выражение (234) при r^>a оказывается равным
a
— I F' (s) ds = —— .
r J r
0
(235)
Это последнее выражение после умножения на г становится постоянным,
чем и доказывается наше утверждение. При г>а выражение (234) равно
lj>'(s)ds+-lj(l
О Г
F1(s)ds=^-
г
1 С/7' (s) s ds
rjl/s2 — г2
(23G)
В силу равенства
оо
2тгга (г)=~ {г j (rt) <р (t) dt
о
мы из (236) получаем, что
. d С F' (s) sds
2nra(r) =-------- 1 - .
dr J у s2 — r2
(237)
(?3S)
Этот результат вполне согласуется с формулами (213) и (215).
ФОРМУЛЫ БЕЛЬТРАМИ ДЛЯ СИММЕТРИЧЕСКИХ ПОТЕНЦИАЛОВ
257
Применим формулу (224) к
случае
случаю V— const =1 (г<^а).
2 sin at
тг t
и
оо
.. 1 2 С ~--1 , , л Sinctf ,,
V= — 1 е -* Jn (rt) —-— dt,
ТГ J ° t
0
oo
। 2r Г sin at J.
Ф=~7 e~* Jr (rt) —i- dt,
К J I
0
OO
ч If 11
c(rp--— I __________
K2J _° ТГ2 j/fi2 —r
0
2<- 9 _______
F(r) = —, M(r) = — l/a2 — r2.
ТГ ТГ
В этом
(239)
(240)
Эти формулы дают потенциал, а также изученные выше функции заря-
женного электричеством электропроводящего диска.
Положим в (203)
а(г)==1 при г<^а-, с(г) = 0 при
Тогда
а
(г) = 2тг Jo (rt) t dt — 2тш ^’Г- . (241)
о
и
oo
V — 2raz e ~zi Jo (rt) (at) . (242)
о
Это выражение совпадает с (185), если в
В силу (194) мы имеем:
последнем положить g=1.
G(r) =
ОО
а Jo (rt) (at) dt —
о
1 при r<C.a
0 при г>аг.
(243)
1 Н. Weber, Journal fiir Math., т. 75, стр. 80, (1873).
Вебстер, Диференциаяьные уравнения
ГЛАВА ДЕВЯТАЯ
Интегральные уравнения
§ 124. Интегральные уравнения для краевых задач. Теория инте-
гральных уравнений возникла в результате изучения краевых задач
в математической физике, и в частности при изучении первой краевой
задачи в теории потенциала. Как мы видели в § 69, первая задача (за-
дача Дирихле) состоит в отыскании такого решения уравнения Лап-
ласа, которое было бы правильным внутри области, ограниченной за-
данной поверхностью 5, а на самой поверхности принимало бы данные
непрерывные значения.
Обозначим через W—Wp следующий потенциал двойного слоя
лде Р—точка, лежащая внутри области, ограниченной поверхностью 5.
Обозначим через Q переменную точку, которая при интегрировании
пробегает поверхность 6', и через — угол между внутренней нормалью
к поверхности в точке Q и вектором ОР, направленным из О в Р, а
расстояние между точками Р и О — через r~rPQ. При соответствую-
щих допущениях относительно поверхности 5 и плотности а, потен-
циал W будет существовать также и в том случае, когда точка Р на-
ходится на поверхности S. В § 58 было показано, что потенциал W
при прохождении точки Р через поверхность S претерпевает разрыв,
а именно, если мы через Wt обозначим предел, к которому стремится
потенциал при приближении точки Р к поверхности 5 изнутри, через
We— предел при приближении извне, а через W—значение интеграла (1)
на поверхности, то окажется, что
Wt — W = 2тга, |
W— И7е=2по. / (2)
Задача Дирихле была обобщена Карлом Нейманом я Пуанкаре сле-
дующим образом. Требуется найти двойной слой, который удовлетво-
рял бы краевому условию
у We)-(Г,+ We)^Vs, (3)
где 1 — постоянный параметр, a — заданная на поверхности 5 не-
прерывная функция. При 1—1 мы имеем:
АЛГЕБРАИЧГ СКАЯ ЗАДАЧА
259
и функция We является решением задачи Дирихле для внешней обла-
сти; при 1 ——1 получаем I/s, и обобщенная задача сводится
к задаче Дирихле для внутренней области.
С помощью равенств (2) можно записать условия (3) так:
2то — \W=VS, (4)
или на основании (1),
1 СГ cos и V-
° —o’ И с~2 (5)
2п J J г1 2 2тг
Зададим положение точки Р на поверхности 51 криволинейными ко-
ординатами и и V, а положение переменной точки Q — координатами
и‘ и v'. Тогда
. > 1 ГС , , „ cos (И, V, и' v') 1 ,,,
0(К’г')“2^ЦС(Ы’г,) —----------------dSQ=2iv(u’ (6)
V в этом равенстве есть заданная функция от и и v, а о—неизвест-
ная функция, которую надо определить из функционального уравне-
ния (ь). Мы здесь рассмотрим только аналог этого ураьнения в одно-
мерном пространстве;результаты, полученные в одномерном пространстве,
легко затем перенести на двумерный случай. Известную функцию обо-
значим через /(s), а неизвестную через <р ($). Соответствующее уравне-
ние в одномерном пространстве в таком случае будет иметь вид:
1
($) — X J /< (s, 0 <р (0 dt—f (•?), (7)
о
где /(($, t) — заданная функция двух переменных. Такое уравнение Гиль-
берт (Hilbert) назвал интегральным уравнением второго рода. К этому
уравнению мы пришли уже в § 35,(202) при рассмотрении совершенно
других вопросов. Функция 7<(s, t) называется ядром-, она определяет ха-
рактер всего интегрального уравнения.
Решением уравнения (7) сначала занимался Фредгольм (Fredholm)Д
Гильберт в пяти статьях и в своей книге дал новое обоснование теории
интегральных уравнений и существенно ее продолжил 2.
§ 125. Алгебраическая задача. Мы предполагаем, что как ядро К (s, t)
интегрального уравнения, так и функция /(>) непрерывны. Кроме того,
пусть ядро является симметрической функцией3 * s:
K(s, = s).
1 Ofersigt af Kongl. Svenska Vetenskaps. Akad., Forh.T. 57, стр. 39—46 (1900).
Comptes Rendus, Paris, t. 134. стр. 219—222, стр. 1561 —1564 (1902) Acta Mathe-
matica, t. 27, стр. 365—390. 1903.
2 Gottinger Nachcichten 190 ;—1910. Далее: Grundziige einer allgemeinen Theorie
der linearen Integralgleichungen, Leipzig 1912. Дальнейшая литература см. статью
в энциклопедии Е. Hellinger und О. Toeplitz, Integralgleichungen und Glei-
chungen mit unendlih vielen Unbekannten, т. Il, 3 Heft 9, стр. 1335—1601, осо-
бенно стр. 1338—1339 (1927).
s Значительная часть тео.ем, которые будут доказаны дальше, справедлива
и для несимметрических ядер.
17*
260
ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
Метод, которым мы будем решать интегральное уравнение (7),< сводится
к рассмотрению трансцендентных задач как предельного случая задач
алгебраических. Этот метод принадлежит Гильберту. Разобьем проме-
жуток ин!егрирования Osg/sCl на п равных частей, каждая из кото-
. 1
рых имеет длину о =—, и заменим интеграл суммой
/(S) = ф ($) —
— 18 (К (S, §) (р (8) -I-. Д’(s, 2§) :р (2S) + ... 4- К (s, пл} ср (nb)) . (3)
Потребуем теперь, чтобы наше равенство выполнялось только в точках
деления; в таком случае мы получаем уравнения:
/(8) = ср (8) —
—18 (/<(8, 6) ср(8) 4- К (8, 28) ср(28) 4-... 4-Д'(8, я8) ср (я8)),
/(28) = <р (28) —
— 18 (К(28, 8) <р (8) 4- Д'(28, 28) и (28)4- - • • + К (28, /г8) <р («8)),
/(«8) = <р (/?8)—
—18 (/<(«8, 8) <р (8) 4- ЛГ(я8, 28) <р (28) 4~ ... 4- К (nl, пЪ) ср (я8) ).
(9)
Введем сокращенное обозначение:
?8), 4=/(^8), <рр=<р(/?8)
и положим 18 = — = /.
и
В таком случае наши равенства перепишутся так:
A —— ^(^11?! +^2'Р2+ ••• +^jn'₽n)> )
А — % —1 (^23 ¥1 + ^га’-Рг 4" • • • +
Л = <F„ —1 + *А®2 4- • • • + Кпп^„>-
В этих равенствах числа / и даны, а требуется найти п неизвест-
ных ср. Найдя эти значения, мы сделаем предельный переход, неогра-
ниченно увеличивая п.
Детерминант системы НО), который войдет знаменателем в выраже-
ния для ш, равен { р. § 30, (80)]
!--^и -1КАп
-1КгЛ -11^ ... 1 -1К„„
АЛГЕБРАИЧЕСКАЯ 3 УДАЧА
261
Так как Kpq — Kqp, то этот детерминант симметричен, и его можно рас-
сматривать как детерминант квадратичной формы.
х\ + + 02)
Введем следующие сокращенные обозначения:
1<ху• • +ta-
р=1?=1
/fXj = А’п-'i "4" -^i2x2 Ч~ • • • ~r ^inxn >
%Х2 — “Ь ^22Х2 4~ • • • “Ь ^2пХп ’
(13)
«Хп ^1йх1 4“ ^п2Х2 4~ • • • 4" ^ппХп ’
[X.J] = Х}уг + Х2у2 + • • • 4- ХпУп
Тегерь мы можем сказать, что d (/) является детерминантом формы
[х, х] — 1Кхх.
При п — 3 уравнение </(/) —О совпадает с уравнением, определяющим
три оси поверхности второго порядка. Как при /г==3, так и в общем
случае все корни уравнения </(/)== О действительны (см. § 28)
Для решения системы линейных уравнений (10) введем еще следую-
щий детерминант:
0 Х1 х2 Хп
У1 1-/.^ 1^12 • “ • -1К1п
У2 1—^22 •• ~1к2„
Уп ~1Кп2 ... ^-1Кпп
(14)
Этот детерминант получается путем окаймления d (/) величинами х
и у; он остается неизменным, если системы х1, хг, ..., хп и
у2, у2, ...,у„ поменять местами. Детерминант, получающийся при
замене ур через
Кур=Кр1у,+Кр2У2+...+Крпуа (Р^1,2,..„П),
мы будем обозначать символом
D
I,
х \
Ку)'
Мы имеем:
[-,J] х2 ... Хп
0 1-^п -Z/<2I ...
[x,y}d(l) = 0 ^21 1-/^2 ... ~1К2п
0 — ... ^-1Кт
(15)
262
ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
Сложим детерминант (15) с детерминантом Z)^Z, —
от (15) только первым столбцом; мы получим:
отличающимся
[*>У1 х2 ... Хп
У1 1-/7бп — 1К12 ... -1^п
у2 ^21 1 1К22 • • • (16)
Уп ~1КП1 ~^й2 ••• 1~lf(nn
Помножим (/2-4- 1)-й столбец (/2=1,2,..., и) на ур и вычтем все по-
лученные произведения из 1-го столбца. Величина детерминанта при
этом остается неизменной, а 1-й столбец будет состоять из элементов:
О,
«Ch,
/*>2,
Следовательно, образованная нами сумма детерминантов равна ID
(17)
т, е. мы получаем тождество:
справедливое при всех значениях
Л-1 I » • ’ • ’ Хп ’ • • • • > Уп »
Запишем систему уравнений (10) следующим сокращенным образом:
fp = — 1Кур (р=1,2........п). (18)
Умножив р-& уравнение на ур и сложив все полученные таким образом
уравнения, мы придем к линейной форме:
= - W-y]. (19)
Наша задача сводится к тому, чтобы найти форму
[<р, у!=<рл + <р2л + • • • + f„yn, (2°)
которая обращала бы равенство (19) в тождество; коэфициенты этой
формы суть искомые значения , ср2...сря. Так как Kpq = Kqp, та
в силу (13) имеем:
[^,у] = [Т,А>]. (21)
Отсюда следует, что уравнение (19) равносильно следующему:
ТРАНСЦЕНДЕНТНАЯ ЗА7АЧА
263
Этому уравнению удовлетворяет форма
D
d(l)
(23)
Действительно,
к равенству
подставив эту форму в уравнение (22), мы придем
D
^4~Ж
(24)
которое в силу (17) является тождеством. При этом предполагается.
конечно, что d (1)^=0. Итак, если I
d(Z) = O, то 0 Л
1 У1
Уг ^21
Уп -^п1
не является корнем уравнения;. ^
А • • • fn
^12 • • • -iKin
... ~*in • (25)
-ZM„2 ...
Коэфициенты при ур в этой линейной форме дают нам искомые зна-
чения (fj, <р2, ..., <рв.
§ 126. Трансцендентная задача. Перейдем теперь к пределу при
п —> оо . Разложим детерминант
d(Z) = i-z/cn -^2! (^12 • • • ^ln 1 ZM22 ... ZM2fi (H)
-lKni ...
по степеням I. Мы получим:
d (Z) = 1 — d21+d2P — ... 4- (— 1)« dnla, (26)
+^22 + • • • A-^nn >
V13
^81 ^33
^22 ^23
^32 ^33
(27)
причем вторая из этих сумм состоит из I ) слагаемых. Обозначим во.
обще через dh сумму всех главных детерминантов /г-го порядка, тогда
^PiPi ^р.р»
К к
Р*Р1
КргРЪ
Kptfh
KphPi Kphpi • • • Крт
(28)
264
ИНТЕГРАЛЬНЫЙ УРАВНЕНИЯ
причем А <р2 , А , рг, ...,ph=\, 2, п. Последняя
I п \ п(п — ।) - • (п — h 4- 1)
сумма состоит из I I =-------------—---------- слагаемых.
Воспользуемся теоремой Адамара, которая утверждает, что детер-
минант л-го порядка, элементы которого по своей абсолютной вели-
п
чине меньше /С, не превосходит п 2Кп Ч Следовательно 2, если
]К(s, то
h
(п \ А 2 /
, (29)
т. е.
(30)
Так как — = /, то
п
1
lim = 1 lim ^11+^2+ •" dsA,
П->ОО П-5ОО к ’J
I)
limZ2t/2 = — lim
Л-s-OO я-JOO
Kpp Kpq 1 1
v кл™ = x2 г г
Li П* 2! J J
К (Ml) (sTss) I
^(V1)^(S2^)I
dsA ds2.
При последнем суммировании индексы р и q принимают независимо
друг от друга весь ряд целочисленных значений от 1 до п. Вообще
при любом постоянном значении h мы имеем:
11га ^==§й’
/г->оо п
где
/С (Sp s-j) К (s^j s2) о . о K(s-y, sh)
К (52’ S2^ * * • К (52’ Sh)
dsy ds2... dsh. (31)
/С (5 Sj) К s^} .. „ К (s/i, Sh)
1 Bull, sciences math., серия 2, т. 17, стр. 240—245 (1893). Непосредственная
оценка детерминанта в развернутом виде дает менее точную и для наших це-
лей
недостаточную верхнюю границу.
2 Из формулы
А2
^ = 1 + й + 2Г + ...+йг+...>
№
hl
следует
eh h2
h2
ТРАНСЦЕНДЕНТНАЯ ЗАДАЧА
265
Далее, легко показать, что —j при возрастании п сходится равно-
мерно в конечной области значений 1 к степенному ряду
S(X) = 1 + (32)
т. е. что
lim d j — § W- (33)
„ * \ *
Доказательство этого положения основано на том, что <71— 1, будучи
представлено в виде степенного ряда по в силу неравенства (30)
имеет в качестве мажоранты ряд
этот ряд сходится при всяком значении 1, так как отношение его
(й -|- 1)-го члена к й-му, равное
YeK
й ’
[ 1 \ 2 г_____
стремится к нулю при h —> оо.
Разложим, далее, детерминант D (/, j по степеням I:
При постоянном й мы для
хр — х(рЪ), Ур=У(рЪ) (р=\,2, п)
иу($)— произвольно выбранные непрерывные функции] имеем:
У (sh)^-(sh^si)^(sh^ ^2)’ • sh)
266
ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
-Ряд
также сходится для всех значений 1; коэфициенты этого ряда содержат
произвольные функции x(s) и y(s). Мы имеем:
.. 1 „ / X х \ х\
lim — D I —, ] = Д (1, . (33')
л-»оо П \п у } у ]
Нам надо будет совершить в тождестве
d (I) k, J] + D (l, - /D (/, = О (17)
соответствующий предельный переход, для чего предварительно преобра-
зуем последний его член. Согласно определению
+ + •• • Л-^рпУп
h
а потому, если — стремится к s, то
lim —У-У-= \K(s,t)y(t)dt.
П-*ОО П J
О
Разделим равенство (17) на п. Мы получим:
(13)
(37)
lim
->oo«a
J (38)
и
Но функции Дл линейно зависят от y(s). Поэтому мы можем написать:
lim — D
п-юо п
у (t) dt.
y(s}=K(s,f)
(39)
'Подинтегральное выражение в правой части этого равенства представ-
ляет собою функцию только от t, так как s выпадает при вычисле-
нии Д; таким образом равенство (17), после деления его на л и пре-
дельного перехода при п—>оо, дает:
•8(l)^(s)y(s)tZs +
о
1
о
I у (t)dt = Ъ.
У/ Jy(s)=K(j,/)
(40)
Это равенство при любых непрерывных функциях x(s) и у (я) выпол-
няется тождественно относительно л.
ТРАНСЦЕНДЕНТНАЯ ЗАДАЧА
267
Положим х (г) = K(s, г), y(s) = K(r, t). Тогда, обозначая перемен-
ную интеграции через г, мы можем первый и третий члены переписать
в следующем виде:
1
- И * А к ) - 5 ().) К (х, о] К (г, f) dr. (41)
JL \ У\?)/ ж(р)=ки,р) -I
у (рЖ (р. О
Если для краткости ввести обозначения
Д(Х;М) = х[д[х, -b^)K(s,t), (42)
I \ У V)/ Ж(Г)=К(#1Г)
Х(г)=К(г,0
то сумма крайних и средний член тождества (40) примут соответ-
ственно вид
1
— J Л О'! s> г) К (г, f) dr,
о
А-{§(Х)Л'(х,/) + Д(Х;х,/)}, (43)
а равенство (40) перепишется так:
1
ё (X) K(s, t) -4- Д (X; s, t) — X j Д (X; S, г) К (г, t) dr= 0. (44)
о
Разделим это равенство на S(X) и положим
(45)
Тогда
г
К (s, t) = Г (s, t) - X j Г (s, г) К (г, t) dr. (46)
о
Функции Д (1; s, t) и Г(з, t) симметричны относительно s и Z; они за-
висят от параметра 1, а Г(з, t) представляет собою частное от деле-
ния двух повсюду сходящихся степенных рядов по 1.
Равенство (46) симметрично относительно K(s,t) и r(s,t); относи-
тельно s, t и X оно представляет собою тождество [ср. § 40, (294)].
Функция Г (s, t} называется разрешающим ядром или резольвентой.
Для интегрального уравнения
1
f(s) = <о (s) — X j К (s, t) <р (t) dt (7)
о
268
ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
разрешающее ядро дает решение в следующем виде:
1
t)f(t)dt.
о
(47)
Правильность этого утверждения проверяется путем непосредственной
подстановки выражения (47) в (7).
Полученный нами результат можно интерпретировать еще следую-
щим образом. Введем операторы SK и SL:
1
SK'i (s) — <р (s) —).(s, t) tp (t) dt,
b
i
SLtp (s) — tp (s) —). J L (s, t) tp (t) di. (48)
о
Тогда интегральное уравнение (7) запишется в виде:
(*) =AS),
а символ
1
SL SKy> (s) = tp (s) —). J К {s, t) tp (t) di —
о
i Г 1
— 1J L (s, r) dr <p (r) — 1J К (r, t) <p (t) dt
0 L O
(49)
(50)
будет обозначать новую операцию, которую можно представить также
и в следующем виде:
Sctp (s) = ср ($) —1 С С (s, t) tp (t) dt, (51)
о
причем j
C (s, t) = к (s, t) L (s, t) — ). J L (s, г) К (r, t) dr. (52)
о
Если положить L(s, t) = r(s, t), то в силу (46) мы будем иметь:
C(s, t) = 0,
S£ <p (у) = SLf (s) = Sc <p (s) = tp (s). (53)
Это последнее равенство совпадает с (47).
§ 127. Формулы Фредгольма. Согласно определению [см. (42), (36),
(35), (32), (31)]
Z\(W) =
0 К (s4, s4) К (s4, &>) -.. К (s4. sh)
К (s4, t) К (s4, s4) К (s4, л2) ...К (s4,
К (з2. 0 A' -51) К (s2, sa)... К ($2> sh)
dsids^.-ds^—
К (sh, t) К (sft, s4) К (s/,, s2) • • • К (sh, sh)
МЕТОД ИТЕРАЦИЙ
269
оо
MCspSj) /<(Sj, s2) ... M(s4, s/;)
M(s2, st) M(s.>,s2) ... M(s2, sA)
ds ^ds^ dsh——
h=0
K(sh,s^ K{sh,Si) ... /<(«Й,5Й)
/<(s. 0 K(s, s4) ... K(s, sh)
К (St, t) K(sit sj) ... M(s}, s/;)
ds^ds^ ... dsh (5)
Л=1 о 0
К(sh> f) К(sh,s4) ... К (sh, sh)
слагаемое надо положить равным единице).
(при h = 0 предпоследнее
Таким образом можно написать:
- Д (1; s, t) = Ао (s, t) -1A (s, 0 + ^4(s,O-...+
+ *)+•••> (55)
где
4>(s, 0 =
е
K(s, f) K(s, sJ...K(s, sj
К (st, t) К Gm, «О ... К (s4, sn)
ds। ds^ « « • ds^
о о
1 1
i i
о о
К (sn. 0 К (sniSj) • • • К (sn, S„)
(n= 1, 2, 3
(56)
Положим в этой формуле s = f = sn^1 и проинтегрируем по
до 1. Мы получим:
s«+i
от 0
1
Ап*1= (АА s)ds;
о
(57)
срез An в этой формуле обозначены коэфициенты ряда
> I2
«().) = !- -1JA+ 2!
-Г~Ап> =
определяемые формулой (31). Наконец, из (55) и (58) следует
гчЧ-?8® = ’
0(1)
(58)
(59)
I Д (1; 5, s) ds.
о
Эти формулы принадлежат Фредгольму.
§ 123. Метод итераций. Мы видели [см. (45)], что разрешающее ядро
можно представить в виде частного от деления двух степенных рядов
по 1. Вычисление коэфициентов этих степенных рядов, сводящееся к
i вычислению многократных интегралов, вообще говоря, оказывается на-
столько сложным, что для практического решения интегральных урав-
нений этот метод едва ли годится. Для достаточно малых значений ).
решение может быть выражено непосредственно с помощью степенных
рядов, которые получаются следующим образом.
270
ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
Под символом 5 будем понимать оператор
1
SF(s, = l ( r(s, r)K(r, t) dr.
0
В таком случае из (46) следует
М(у,/) = (1 — S}F(s,t).
Будем искать теперь разложение r(s,t) в ряд следующего вида:
Г($, t) = (1 — К (s, t) = (1 4- 54- S24- ... + Sn ...)K(s, t),
мы полагаем при этом:
i
SK(s, K(s, f)K(r, t) dr=lKs (s, t),
t)
1
S?K(s, t)^S ^SK{st)^\SK2(s, t)=}?^K(s,r)K(r,t)dr=\?K&(s,t),
0
(во>
(61)
(62)
Snf<(S, = (S,t)
Как легко показать, ряд (61) сходится при достаточно малых
нпях 1. Далее, мы действительно убеждаемся в том, что
значе-
(1-5) (14-54-52 4-... -\-S^...)K(s,t)^K(s, t).
Функция
и 1
...Kir^tjdr^ ...drn (63)
00 6
называется n-м повторным ядром или /г-й итерацией ядра К (у, t).
Таким образом [/4 (у, 0 — K(s, /)]:
Г (у, /) = А4 (у, t) 4- \К2 (у, /) 4- ^<s (s, t) + •.. + (у, t) 4-... (64)
Этот ряд сходится, если |Х| меньше абсолютной величины наимень-
шего корня уравнения § (1) == 0. Выразим теперь Д (X; s,t) и S (X)
через повторные ядра. Мы имеем:
= j Д (X; У, у) ds. (59)
° t
это равенство на 3 (X),
(К)
С4Л I
G
МЕТОД ИТЕРАЦИЙ
271
и пользуясь разложением в ряд (64), мы получаем:
d log S ().)
ill 1
₽= У?<1(з,з)б/з4-Х р^з, 3)1/3 4-Х2 JKs (s, s) ds4-... 4-Xя J/Ся+1 (s, s) ds -f-... =
= ai + аа^ + йз)2 + • • • + an+ • • •» C66)
где
i
«„=J^„(3, s)ds. (57)
0
Интегрируя, мы получим отсюда log 8 (1). Подставив вместо 8 (X) сте-
пенной ряд (58), мы найдем, что
~8ЧХ)=А-1д2+^л3-... + ЦР-плй+1+...,
и, следовательно, ряд (66) можно представить в виде частного:
. 1 Л I К л
А ~тт А + 77 Аъ — • • •
ai + а2 * + аз12 + • • • =------х2------• (68)
1 ~ТГ 2Г А —•••
Умножим обе части этого равенства на знаменатель правой части:
«1 + (й2 — ai А)1+(«з — а2 А+^^г)*2 +
(, а, А9 а, АД,. , , А, . Л„,„ Л.,„ ,
— а3 + • • • = Ai — ip + «j,- ^2 — gj-X3 +..., (69)?
и приравняем коэфициенты при одинаковых степенях X в полученном
равенстве. Мы будем иметь:
Л1 и Oj ,
ai А ^2 а2 ’
й а, Л„ , Л.
агА ~2Г+2Тказ>
. а2Л„ а.А„ А.
---2Г+-3. 41”'1*- Р”
272
ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
Отсюда мы находим, что
а, п — 1 0 0 0 ... О
Cj п — 2 О О_____О
«3 а2 а± п — 3 0... О
ап-1 йи-2 йп-3 .............1
ап ап—-\ ап-2............ ” а1
Подставив ряды (55) и (58) в уравнение (44)1
(X )3 \
1 — у А1 + 2] А2 ~~ Ifj Аз “Г" • • ’ j ~
= Ао (S, о - у А (*> t) + V, Аг &
JL 1
1
— ^A'(r, t) po (s, r) ~yAi (s> r) + 4i A A r}— ... j dr
b
(71)
(72)
и приравняв коэфициенты при одинаковых степенях X, мы получим:
AnK(s,t) = Aa{s, 0+«J 0 {г, t) Ап_г (s, г) dr. (73)
Отсюда методом полной индукции находим: /<, ($, г) п 0 0 0 ... 0 0 /<2 (s,i) аг п — 1 0 0 ... 0 0 /<3 (у, t) а2 аг п — 2 0 ... 0 0
A0(S,t) = K(s,ty,All(s,t)= Kn(s,t) . , «г в • * в • в А в | я е <3 ® (71)
(я= 1, 2, 3, ...).
§ 129. Фундаментальные числа и фундаментальные функции. Рас-
смотрим теперь тот случай, когда \ является корнем уравнения 6(1) = 0.
В силу симметричности ядра относительно р и q (К =К9р) корни
детерминанта
_^32... -1К1п
1!\_ 1 ^23 * • • ^2л
(Н)
л Относительно этих формул см. J. Р1 е m е 1 j, Monatshefte fiir Math, und
Physik, t. 15, стр. 93—124 (1904).
ФУНДАМЕНТАЛЬНЫЕ ЧИСЛА И ФУНДАМЕНТАЛЬНЫЕ ФУНКЦИИ
273
действительны; пусть эти корни, расположенные в возрастающий ряд, суть
/(D, /(2),
Пусть, далее, d21 (Z), d22 (Z), ..., dan (/) суть миноры, соответствующие
диагональным элементам.
Найдем производную d! (Г). Для этого следует диференцировать по-
следовательно отдельные строки детерминанта и полученные в резуль-
тате диференцирования детерминанты сложить, т. е.
-/Си /<12 •• • -
~//<2Т 1— 1К22... -ж2п
-/^1 ~1КПЛ...
1-^11 ~1«1п
/<21 — к22... -
-/^1 ^-1Кап
(75)
Если мы эту сумму умножим на I и прибавим к полученному произведе-
нию <Zn (Z) -j- d22 (Z) -f- • - • -f~ dBtl (l), то мы,- очевидно, получим nd (l), т. e.
(0 + ^22 (Z) + - • + U) = V) - W- (76)
Положим Z=Z(ft). В таком случае
du (IW) + d22 (Z(«) -j- ... -I- dnn = — d' (IW). (77)
Если Z(ft) является простым корнем, то d1 (Z(ft)) =^=0; следовательно, не
все миноры d (№) обращаются в нуль. Таким образом система урав-
нений
% — (7<и ¥1 4“ /<!>% + . - -|-= 0»
% - (^21% + /<22% + • • • + /<2в%) = 0,
%-+ <2% 4- *. + /<„„%) = 0 (78)
наверное имеет решения
¥1 = 'Р(?’» % = (?2Й)> • • • ’ Vn — ¥« (78)
среди которых хотя бы одно отлично от нуля. Числа (79) определены
однозначно с точностью до коэфициента пропорциональности. Можно
сказать, что система (78) соответствует функциональному уравнению
I
(s) = l АГ (s, Z) щ (Z) <ZZ = 0 (80)
о
в том же смысле, в каком система (10) соответствует уравнению (7).
Уравнение (80) называют однородным интегральным уравнением
[см. § 38, (215)].
18 в е б с т е р, Диференциальные уравнения
274
ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
Покажем, что каждому корню уравнения о(1) соответствует непре-
• рывная, не обращающаяся тождественно в нуль функция <р(й) (у), удо-
влетворяющая уравнению (80), т. е. имеет место равенство
1
f
щ(/г) (s)=\lh> j K(s, t) (t) dt. (SO')
о
Числа JJ11, 1(2),... называются фундаментальными числами _ или
собственными значениями, а соответствующие им функции а(1> (s),
u/2)(s), ...— фундаментальными или собственными функциями ядра
f\(s, t). Из (80г) непосредственно следует (ср. § 38), что две фунда-
ментальные функции ш(/0 {s) и <р(*) ($р соответствующие различным
фундаментальным числам, взаимно ортогональны, т. е. что
1
(s) (s) ds — 0. (3i)
о
При этом доказательстве мы снова будем исходить из тождества
d (/) [х, у] -Р D 11, Х ) — ID 11, Х j -- 0. (17)
\ У ) \ Ку)
Положим в этом тождестве 1=1<К>. Тогда
D //Ю, = IW D | /О), Х . (S2)
* \ У/ \ Ку)
В обеих сторонах этого уравнения стоят линейные формы от
_Pj ,_у9 , ..., у„ , коэфициенты которых дают нам решения однородного
уравнения (78). Следовательно, линейная форма
[щ(*), _у] = уМу^ _|_ ^Ui)ys _р . _ _ _|_ ц;(g3)
входит множителем в левую часть уравнения (82). Так как равенство
(82) симметрично относительно хр и у , то
D ( Х \ =СП/Й>, х] Г®(Й),У1,
,\ у/ ‘
где С—постоянная. Отсюда следует, что, -умножив <р<й) на соответ-
ствующую постоянную, —- а такая операция, очевидно, допустима, —-
мы получим: / ,.\
D //(»>, ~ j =Ч- [,.(*), х] ^(Л), у]. (85)
Развертывая детерминант и приравнивая коэфициенты при произ-
ведениях х^у^, х2у2, ..., хпуп, мы получаем:
(/(^>) = zp d22 (IW) = =р ^02, dnn (/<Ч) = др ?(Ч2. (85)
Следовательно,
dn (IW) -L- d22 (IW) 4- ... + dan (/(й!) = Др [с/л\ е/л)]. (30)
ФУНДАМЕНТАЛЬНЫЕ ЧИСЛА И ФУНДАМЕНТАЛЬНЫЕ ФУНКЦИИ 275
Левая часть (86) в силу формулы (77) равна —l\h> d
D (IW,
\______yj_
№ d' (№)
(Уй), Jf] [<р(й), _y]
ф<й|]
а потому
(87)
Перейдем к аналогичным исследованиям в трансцендентной задаче.
Пусть
Х(1), V2\ .... Vй), ...
будут нули функции о (к), расположенные в возрастающем порядке:,
для простоты мы исключим из рассмотрения кратные нули. Легко в та-
ком случае показать \ что все эти нули действительны и, далее, что
limzz/(1) = V* 1), lim zz/(2) = Vs), ..., ИтдАй) = Vft), ... ’ (38)
п^>ОО п^>СО п—> со
Кроме того, 7 й) при заданном h и достаточно большом п должно быть
простым нулем функции d{l). Положим в формуле (44) k = k(,iJ; тогда
вследствие симметричности K(s,t) и Д (X; s, t) мы будет иметь:
1
А (Vй1; s, s0) = №> J К (s, t) Д (Vй); г, s0) dr,
о
где s0—произвольная постоянная. Функция <р(й) (в) = Д(Х(й); s, s0) удо-
влетворяет, таким образом, однородному интегральному уравнению (80').
Далее, так как, согласно (50),
1
j А (Vй); s, s) ds =£- с,
о
то мы можем определить s0 так, чтобы Д(к(й’; s0, л())Д0, т. е.
чтобы ($) не обращалась тождественно в нуль. Тем самым мы до-
казали существование фундаментальной функции, соответствующей
фундаментальному числу.
Из (84) вообще следует, что любая система значений
А’ А’ А’А <V=A2, - •» «)
удовлетворяет равенству
D (D (/<й’, = D (D (I™, .
\ У/ \ У') \ *7 \ У/
Переходя к пределу при п—>со, в силу (88) и (33’) получим аналогичное
тождество для Д ^к(й’, , которое в силу (42) можно переписать так:
Д (Vй’; s,t) Д (Vй); s', f) = Д (Vй); s, s') Д Q<ft); t, t').
При s'=:^ = s0 отсюда получается:
Д (Vй); S, t) = С®(й) (S) wW (t),
i Cm. Hilbert, Grundziige..., § 13.
18*
I ,
276
ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
где С—постоянная. Умножив, как и раньше, (s) на соответствую
4цую постоянную, мы последнее равенство сможем переписать так:
1(Л) д (>,(*); s, t) = ± ?(ft) (5) ®(й) (0- ОЗ)
В силу (59) отсюда следует
1
(X(ft)) —+ J (s)^ ds
о
A : s, t) _ (s) (/)
У (Х‘й>) “ —
(31)
2
ds
Q
Пусть x (s) и у (s) — две функции, непрерывные в интервале О “С $ -С I;
«юложим, как и в (87), хр — х (/?§), Ур=у(рЬ). Тогда в силу (33')
lim -- D
п->оо п
(im х\=д Л<й),
\ у) \ У/
lim /<*) d' ((<«) о' (Uft)).
»->ОО
Левая часть этого равенства после деления на п и предельного пере-
хода при п —»оо окажется равной
).<*) o'().('O) “
Чтобы получить аналог формулы (87), положим в уравнении (40)
= Мы получим:
1
I (д y(t}dt. (92)
к У! Л V ЛЬ(Г)=К(М)
Переставив x(s) й у (s), мы получаем:
1
(-’Л (д (}Sh) I х (S) ds.
\ У) Ji V ЯЬ(,)=К(^)
Положим теперь у (г) — К {г, i). На основании (42) мы будем иметь:
1
|д(^Л)» —==Vft> 1 | A I x(s)ds =
I \ у' J ytr^K^f) JI V у/ j x(r)=?<(r,s)
>(-)=/< (GO
^Уд(*(й);М);ф)А?'.
О
ТЕОРЕМА ГИЛЬБЕРТА
277
Подставив
найдем:
это выражение в формулу (92), мы на основании
(89)
У.
=1(й) j j Д (№> ;s,t)x (s)y (t) ds dt =
и 0
I I щ W (s) tpW (/) x (s)у (Z) ds dt,
о 0
т. е.
1
и в силу
Д ^)(й), = + j <Р(Й) (s) x(s)ds J щ(й) (s) у (s) ds,
о о
(90)
1
(ЭЗ)
Итак, мы
)<*) & QS'1))
(Э4)
2 .
,ds
.Й ' '
видим, что при заданном значении h из (87) следует
I mW (S) x(s) ds[ (s)y(s) ds
1 [ttW, x] [ср(/г),у] g g
[<?№,</*)] - J
(95)
as
§ 130. Теорема Гильберта. Мы можем теперь распространить теорему
о преобразовании квадратичной формы в сумму квадратов (см. § 29)
на трансцендентный случай.
(«V \
I, | является многочленом (п— 1)-й степени от Z, тс
У )
разложение на простейшие дроби при условии, что все нули d(l) суть
простые, дает
d(i,x\ d(iw,x\ , d{i^\x\
\ У)_ \ У ’ 1 , \ У 1 1 ।
d{l) d! (ZU)) /21/(1) "Г </>(/(2j) / — /и) 1
d(zw,x'| л
... + -3_____J_
~ z/f(/W) / — /(«)’
(98)
или в силу (87)
d[i x
\ ’ у) [</!), X] [щ(1), У] (ZU)) [(f)(2), X] [<p<2), y] Z(2>
d (/) ~ ' [<f)U), ф(1)] / —./U)‘"1 [ф(2), щ(2)] / — Z<2)
x] y] Z(")
[(f)(«), ф(«)] I — /(»)
(97)
278
ИНТЕГРАЛ1 НЫЕ УРАВНЕНИЯ
Это равенство представляет собою тождество относительно I, х и у.
При 1 = 0 в силу (17) мы имеем:
£>(°,*)=-[х, у], d(0) = l
и, таким образом, находим
г V1 = XI Гф(1), j] F/2), *] [ф(2), j] .
L,JJ [<p(1\ <p(i'] [<p(2). <p(2’] +'”' fS8J
[щйУ, x] [и(й), y]
Заменим в этом равенстве у через Ку. На основании (21) [и, Ку] =
= [АГи, _у], а на основании (78) <pft=/(Л> 7<<р; поэтому
Кху_.г^ у1_Гх W4J,] [<р<2>, х][фЧ Л ,
Аху — LKX, JJ — IX, Ку\ — jCQjyi), /(2> ^(2)^ "Ь---
' I te(n)’ ^(Л)’ Р)Э»
---/(“) (р<л)] ' '
При х=у отсюда получаем каноническое представление квадратичной
формы в виде суммы квадратов: а
Кхх = вП)’ *1* ^(2?’ । । ^(В) 9’ x]2 гад
/(1) [(pH), и(1)] ' /(2)|^(2)1 (р(2)]‘Г ••• Т-/(л) [щ(я)1 щ(«)]' ' ’
В результате предельного перехода по п—>со уравнение (99) пре-
образуется в следующее:
1 1
м ^(1) (s) x(s)ds t?(1) (s)^(s)ds
JJ К (s, t) x (s)y (t) ds dt =-----5-------T---------5-----------------[-
eo (pd) (s)j ds
9
1 1
J cp(2) (sj x(s) ds j (s)у (s) ds
_l------2-----------------2--------------------[_ ... (ioi)
J (<P(2) (s)j2 ds
u
Двойной интеграл, стоящий в левой части этого равенства, есть предел
двойной суммы, стоящей в левой части равенства (100), разделенной на
РАЗЛОЖЕНИЕ В РЯД ПО ФУНДАМЕНТАЛЬНЫМ ФУНКЦИЯМ 279
к2 при п—>со; при этом предельном переходе в правой части равен-
ства (99) надо воспользоваться формулой (95). Положим:
1
(<Р> (у))2ЙУ=1.
о
тогда
(102)>
При мы, как и раньше, имеем:
ф(,г) (у) ф(й) (s) ds = О
*Ь
(103)
Функции ф(й) (у) называются нормированными фундаментальными функ-
циями. В силу (91) мы имеем:
: ~ 0 = Ф'"’ W Ф(Й> И" <104>
Равенство (101) можно переписать в следуюте*м виде:
1
f<(S>
о о
ОО 1 '1
t) X (s)y (t) ds dt — JTJ ^ф (*) (у) X (y) ds (у) у (у) ds. (105)
л =i о о
Эта формула является основной теоремой теории Гильберта.
§ 131. Разложение в ряд по фундаментальным функциям. Особенно
важно применение теоремы Гильберта к разложению произвольной фун
кции в ряд по фундаментальным функциям ядра. Пусть х (у) — непрерыв
мая функция, и пусть
1
f (г) = К (у , t) К (г, t)x(s)dsdt. (103’
о
Применяя дважды формулу (80'), мы получим-
1 11 1
j / (л) ф О) (г) dr~ J J К (у, t) х (у) ds dt j К (г, t) ф(/г) (/-) dr
о оо е
1
= (lip Ф!й) х ds- (ло°
о
280
ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
Если в формуле (105) по ложить у (t) — К (г, t), то ее левая часть
обратится в /(г), и мы получим:
оо Г С
/(г) = <pW(s)x(s) ds Г$(*)(s)K{r, s) ds. (1С8)
л=1 о о
При помощи формулы (80’) мы находим отсюда:
со 1
f(r) - V 1 Ф(й) (s)х ($) ds, (W
й=1 О
и тем самым получаем искомое разложение в ряд:
оо
f (г) = сн ф(й) W- (40)
Н=1
Коэфициенты этого ряда в силу (107) равны
1
ch — 1 /(г) <!> (й> (г) dr, (Ш>
* J
о
т. е. имеют выражение, аналогичное выражению для коэфициентов
в обычном ряде Фурье. Как показали Гильберт и Э. Шмидт 1, разло-
жения в ряды (ПО) и (111) сохраняют силу и в том случае, когда/(г)
можно представить в виде
1
/(г) = К {г, t) х (/) dt, (JOS')
и
где х (t) — непрерывная функция.
Метод исследования интегральных уравнений, который был изложен
в этой главе, в основном принадлежит Гильберту. Подробное изложе-
ние этих вопросов читатель найдет в работах Гильберта, на которые
мы уже не раз ссылались. Примеры на приложение общей теории инте-
гральных уравнений читатель найдет в гл. III и V.
• См. D. Hilbert, Grandzfige..., стр. 24.
Приложение
§ 1. Функции комплексного нерегленного. а) Комплексные числам
Как известно, действительные числа представляют точками на прямой;
при этом расстояние, измеренное в положительном или в отрицательном
направлении от начальной точки до какой-либо точки, дает нам число,
соответствующее этой точке.
Для комплексного числа z = a-\- ib, где а и Ь—два любых действи-
тельных числа, надо найти новое представление. Так как а и Ъ могут
независимо друг от друга принимать всю систему действительных зна-
чений, то вместе они образуют двумерное многообразие значений.
Естественно поэтому представить эти числа в виде точек плоскости, у
которых абсцисса и ордината в некоторой определенной прямоугольной
системе координат равна соответственно а и Ь\ при таком представле-
нии комплексных чисел каждой точке плоскости соответствует вполне
определенное комплексное число, и всякому комплексному числу вполне
определенная точка плоскости.
Другое представление комплексных чисел получается с помощью
векторов. Комплексному числу z — a-\-ib относят вектор, соединяющий
начало координат с точкой а, Ь, или вектор, получающийся параллель-
ным перенесением указанного вектора; в последнем случае начало век-
тора не фиксировано.
Пусть z — х -|- iy есть комплексное число, которому на координат-
ной плоскости соответствует точка с прямоугольными координатами
х и у. Введем полярные координаты
х — г cos и, _у —rsina,
в таком случае
z~r (cos и -}- г sin<р) — relf.
Длину г—|г| называют абсолютной величиной комплексного числа
z, а угол <р—аргументом этого числа. Мы имеем: |zI = j/xs-j-j2 * и
u—-arctg—
Сумма двух комплексных чисел гг~аг-\-1Ьг и z2 = а2 -ф- ib.
т. е. число
zi ~f ~2 = Й1 + й2 4“г (^1 Ч~ ^й)>
определяется как диагональ параллелограма, стороны которого равны
1^1 и |г2| и составляют с осью углы, соответственно равные аргумен-
1 Последняя формула недостаточно точно определяет значение аргумента,
так как аргумент должен быть определен с точностью до кратного 2я, а арктан-
генс определен с точностью до кратного л.
282
ПРИЛОЖЕНИЕ
там чисел. zA и z2 (черт. 97). При указанном выше векторном пред-
ставлении комплексных чисел сложение этих последних тождественно
-слохсению векторов (§ 3, т. I).
Следовательно,
lzj±zsi^lzjl~^iz2l. (3)
.Легко убедиться, что абсолютная величина произведения zAz2 дол-
жна быть равна произведению абсолютных величин этих чисел, а аргу-
мент произведения равен сумме аргументов J, иными словами, если
гг — a, -j- = /-j (cos -j- i sin Wj) — r^1,
z2 = a2 -(- ib2 = r2 (cos -j- i sin <p2) — г2е1'ъ,
'“TO
2^2 = r1/-2e'('P4+'f2» = rAr2 {cos (rp, -j- ш2) 4~ гsin (¥1 + } -
.Аргумент действительного числа равен 0 или тс, а аргумент чиста
, тс
мнимого равен 4г-- - Комплексное число равно нулю в том и только
1^1г в том случае, когда равны нулю и его действитель-
ная и его мнимая части (т. е. обе его координаты).
/у Последнее условие равносильно обращению в нуль абсо-
/ \i лютной величины этого мнимого числа. Аргумент ком-
/ ,/ плексного числа, равного нулю, неопределен. Мы гово-
I / / рим, что переменное комплексное число уходит в
бесконечность, если его абсолютная величина неогра-
0 ниченно возрастает; аргумент комплексного числа может
Черт 07 при этом меняться как угодно. Говорят об единствен-
ной бесконечно удаленной точке г—оо, абсолютная
величина которой равна со, тогда как ее аргумент (как и аргумент
точки г=0) неопределен.
•Изменение денегвительного переменного сопоставляют обыкновенно
с движением точки на прямой; по аналогии с этим изменение ком-
плексного переменного сопоставляют с движением точки в плоскости.
Ь) Аналитические функции. Любая комплексная функция комплекс-
ного переменного z — x-\-iy, или, что то же, любая комплексная
функция двух действительных переменных х и у распадается всегда
на действительную и мнимую части, и (х, у) и v^x, _у), каждая из
которых является действительной функцией двух действительных пере-
менных х, у:
f(z) — и (х, у) 4- iv (х, у). (2)
Таким образом комплексная функция одного комплексного переменного
/равносильна двум функциям двух действительных переменных.
Общеизвестное представление функциональной связи двух действи-
тельных переменных с помощью абсцисс и ординат невозможно в ком-
плексной области, так как в этом случае как значения независимого
переменного, так и значения функции образуют многообразие двух
измерений. Представление комплексной функции с помощью поверхно-
* Аргумент комплексного числа, отличного от нуля, определен однозначно,
чоИечио, только mod 2п.
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
283
сти, расстилающейся над комплексной плоскостью, также невозможно,
так как перпендикулярные к комплексной области ординаты не могут
одновременно представлять и действительную и мнимую части
функции 1.
При общепринятой интерпретации комплексной функции комплек-
сного переменного пользуются двумя плоскостями, представляя в одной
из этих плоскостей независимую переменную г — х-ф/у как точку с пря-
моугольными координатами х и у, а в другой—функцию w— f(z)
как точку с координатами и u v. Соотношение можно пред-
ставщь себе как „отображение" одной из этих плоскостей на другую,
отображение, при котором каждой точке z первой плоскости соответ-
ствует вполне определенная точка vd второй плоскости. При движении
точки z передвигается также и ее „образ" —точка тек Если, в частности,
точка z при своем движении описывает непрерывную кривую, то сбраз
этой последней получается как вполне определенное множество, кото-
рое, вообще говоря, не является непрерывной кривой 2.
Говорят, что функция /(г) непрерывна в точке г0, если любому
сколь угодно малому положительному числу а можно поставить в соот-
ветствие такое положительное число ё, что все значения z, удовлетво-
ряющие неравенству —z0|<^&, удовлетворяют также неравенству
|/(г)-/.(г0)|<г.
Если для функции /(г) это условие выполняется во всякой точке
некоторой области В, то говорят, что эта функция непрерывна в
области В. При этом всякая непрерывная в области В кривая при
01 о сражении w=/(z) переходит в непрерывную кривую. Если кривая
в плоскости z замкнута, то замкнута также и соответствующая ей кри-
вая в плоскости w.
Рассмотрим, далее, функцию /(г), компоненты которой и (х, у) и
v(x, _у) имеют непрерывные производные от х и у. Сравним произволь-
ное изменение dz — dx -ф i dy независимого переменного с соответству-
ющим изменением df(z) функции. Абсолютная величина вектора dz
будет при этом | dz | == dx'1 -ф dy-, а его аргумент равен arctg .
Абсолютная величина вектора
df(z} = d (и -ф iv) = du -ф i dv
есть
| df(z) | = du2 -ф dv2 ,
1 На перпендикуляре к каждой точке z-плоскости можно отложить два от-
резка, длины которых соответствовали бы значениям функций и и v. Таким
образом мы получили бы две поверхности, которые в своей совокупности вполне
характеризуют функцию /(z).
2 Другая важная интерпретация функциональной зависимости между двумя
комплексными переменными может быть осуществлена с помощью векторного
поля; эта интерпретация получается, если каждой точке z z-плоскости отнести
вектор, определяемый значением функции / (z) в этой точке и имеющий свое
начало в точке z.
284
ПРИЛОЖЕНИЕ
а аргумент этого вектора равен arctg —. Далее, с точностью до слагае-
мого, которое и после деления на \dz\ стремится к нулю, мы имеем:
, йи , . й« ,
du = — dx -4- — dy,
йх йу
, й® . й® ,
dv = — dx -4- — dy,
йх йу
J . ЙИ f ЙИ . . [ йи , , й® , 1
rf/«=^+<^=5^+^ + 1|-dx + -^j ,
и таким образом,
~ёи
df du-\-idv ~Ъх
dz dx-\-idy
Ъи (
, йи , . . |'й®
Г г~ dy-\- i — <
йу | Йх
dx -j- i dy
1+(&
Г df r-
Следовательно, в общем случае зависит
dz
изменения z. Однако если выполнено условие
/йи । — V1______\
\йх ”т’ йх j ’ \й.у ”* <У
. йи йи йи , _ЙЧ7
I ---— — — —I —
ЙХ ЙХ ЙУ йу ’
dy
от —, т. е. от направления
г,
т. е. если
й® ЙИ
ЙХ йу ’ ЙХ
Ъи
*У'
(3)
rf/ dy
то — не зависит от — , ив этом случае можно говорить о вполне
их
определенной производной f (z) в точке z, зависящей только от функции
/ (г) и от точки z, аналогично тому как это имеет место в действитель-
ной области. Если условие < 3) выполняется в каждой точке G, то говорят,
что f(z) является правильной аналитической функцией в области G.
Примерами аналитических функций могут служить: степенная функ-
ция zn (и — целое положительное число); линейная комбинация таких
функций с любыми комплексными коэфициентами, т. е. полином от г;
сумма бесконечного ряда таких степенных функций, т. е. степенной
ряд, при условии, что этот ряд сходится в некотором круге, содержа-
щем область G [см. раздел ,,е“]. Например, степенной ряд
гу О'2 tyfl
1 + 1Г + 2Г+"-
представляет правильную аналитическую во всей плоскости функцию.
функции комплексного переменного 285
t
Абсолютная величина степенной функции Zn равна абсолютной ве-
личине г, возведенной в n-ю степень', а аргумент этой функции равен
аргументу 2, умноженному на п. Если |г| = 1, то точки zn при любом
значении z и любом целом положительном п лежат на окружности еди-’
яичного радиуса.
с) Особые точки. Пусть
z — х -j- iy = г (cos <р -|~ i sin ф) — rfo
— отличное от нуля комплексное число.. Если аргумент ф увеличить на
2тг, то z останется неизменным, так что мы можем написать:
g -—
при k целом Итак, если п — целое положительное число, то все числа
± 1_ f(9+2fcO 1г , 2£тг\ ,
zn—гп е п =rnl cost-------------------) —л sin (-З——!---11, (?)
( \ п п / 1 \ П ‘ И / ]
будучи возведены в п-ю степень, дадут нам z. Среди указанных
чисел имеются только п различных чисел, которые получаются при
k—1, 2,..., п. Эти числа называются корнями л-й степени из 2; все
1
они имеют одну и ту же абсолютную величину, равную гп .
В соответствии с этой многозначностью корня, когда z описывает
£
некоторую кривую, функция zn описывает п кривых. Если z при своем
изменении пробегает замкнутую кривую, не заключающую внутри нуле-
£
вой точки, то каждая ветвь zn представляет собой замкнутую кри-
1
вую. При этом надо исходить из произвольно взятого значения zn и
£
при дальнейшем движении точки z выбирать то значение zn , которое
непрерывно связано с выбранным нами (или ранее вычисленным) зна-
£
чением zn. Но если комплексное число z описывает некоторую кри-
вую, заключающую внутри себя нулевую точку, то аргумент его уве-
- 2тг
личивается на 2тг, а аргумент zn на —, и ее образ при л~>1 не
1 п
будет замкнутою кривою. Функция zn является простейшим примером
1
неоднозначной функции. В нулевой точке все значения zn совпадают;
эта точка называется критической точкой или точкой разветвле-
ния функции. В этом же смысле а является точкой разветвления
1
функции (z— а)'1-
Так как ,
z — rel{'<,+JK’x> (k — целое число),
то логарифмическая функция, определенная формулой
log z — log г -j- ito -|- 2 km, (5)
'286
ПРИЛОЖЕНИЕ
имеет бесчисленное множество значений, которые отличаются друг от -
друга числами кратными 2ш. Если z при своем изменении делает один
полный оборот в положительном направлении вокруг начала координат,
то к начальному значению log г прибавляется 2та; таким образом
1 ' '
начало координат является точкой разветвления. Функция zn служила нам
примером конечно-многозначной функции; log г служит примером бес-
конечно-многозначной функции. Если р—.произвольное число, то zP
определяют равенством'zp — ePlo°z. ' ~
Пусть f (г)—функция однозначная и правильная во всех точках некоторой
области, за исключением точки z = а\пусть, далее, при приближении к точ-
ке а функция/(г) стремится к бесконечности (например, f{z) = —-1 .
\ z — al
Точка а называется ‘полюсом функции /(г). Функцию f(z') в окрестно-
сти полюса. z=a можно всегда представить в виде f(z)~ (z — a)~ng{z],
где п — целое положительное число, а^(г)— функция правильная в неко-
торой окрестности z = a. Число п называют порядком полюса. Функция
однозначная и правильная в некоторой области, за исключением конеч-
кого или бесконечного числа полюсов, называется мероморфнощ точ-
ками накопления- полюсов мероморфной функции могут служить только
точки, принадлежащие к границе области. Простейшим примером меро-
морфной функции служит рациональная функция.
• • 1
Иначе ведет себя вблизи точки г = 0 функция es. Когда z прибли- <,
жается вдоль положительной действйтельной оси к нулевой точке,
1
то е'Л стремится к -j-oo, а когда z приближается' к той же точке
1 ,•
вдоль отрицательной действительной оси, то ez стремится к нулю.
Таким образом функция при z —0 не имеет никакого предела. Мы пока- ;
жем, что эта функция в любой сколь угодно малой окрестности нуле-
вой. точки принимает бесконечное число раз любое' заранее заданное ...
значение (за исключением нуля). Действительно, пусть
а±$=еР+%
— произвольное отличное от нуля комплексное число. В таком случае
2. 1
ez =е^+г-У— ip,
если только
1 1 dl
—r~r—P -4- + x4-iy=— --------------------, ’йЯ
I I
где /г — целое число. Отсюда следует, что
71
х== • Р, v~, — fe + 2^) . . , Я
Рл ф ($~t~ 2Атг)2 ’ Р2 ид {Q 2Атг)2 ’
ФУНКЦИИ КОМПЛЕКСНОГО ПЕР МЕННОГО 28/
Выбрав достаточно большое значение k, мы можем-|х| и |_у’, а тем
самым и jz| сделать сколь угодно малыми, откуда и вытекает наше-
. утверждение. Точку'z = О' мы называем существенно особой точкой
I
..- функции ez .
d) Интегралы в комплексной области. Определим сначала ком-1
, плексный интеграл
z
f{z) dz - (g£
, от непрерывной функции f(z) комплексного переменного z; интегриро-
вание надо при этом произвести по заданной спрямляемой кривой, со-
единяющей точки z0 и Z. Отметим -теперь на этой кривой точки-=
zD, z1}^z2, . . zn_1, zr,-=Z и образуем сумму:
п
ч=1
Можно показать, что эта сумма будет стремиться к вполне опреде-
ленному пределу, когда максимум расстояний -|г_,— следующих
друг за другом точек стремится к нулю1. В . таком случае, так. как:
f{z) = и -f- iv, то 1 .
го) {dx + z^)=C(n dx —:v dy) —J— i (о dx -j- a. dy). *
Интеграл этот, вообще говоря, зависит от вида кривой, соединяю-
щей точки zQ и Z. Однако в некоторых случаях, имеющих особо важ-
ное значение, величина интеграла не зависит от вила этой кривой.
. Действительно мы знаем, что криволинейный интеграл
^(Pdx Q dy),
У) и Q(x. у) суть две заданные функции, имеющие непре-
рывные производные, не зависит от пути интеграции в том и толььо-
в том случае, когда функции р{х, у) и Q.(x, у) удовлетворяют
тсловню * * s
Ру
iy ~~Их
Если применить эту теорему к первому из двух интегралов, лагощи:::
в сумме „
\f(z) dz,
1 Привалов И. И., Введение в теорию функций- комплексного перемет-
ного, стр. 95 11932).
s Это следует,, например, из доказанной в §. 16г ь. I. теоремы Стокса, осо-
бенно из формулы (167).
“288
ПРИЛОЖЕНИЕ
то условие (37) напишется так:
5и J V
by йх'
(3')
Применение той же теоремы ко второму из указанных интегралов дает
дъ ди
by йх'
(3")
Оба эти условия совпадают с условием, характеризующим f(z) — и -|- га
как аналитическую функцию. Мы видим, таким образом, что внутри
области, где аналитическая функция f(z) является правильной, значение
интеграла
I f(z) dz
Ъ г
совершенно не зависит от пути интегрирования. Это свойство инте-
грала можно выразить еще и так: интеграл аналитической функ-
ции, взятый по какой угодно замкнутой кривой, всегда равен нулю-
(теорема Коши)
Попробуем обобщить эту теорему на мероморфные
функции. Рассмотрим сначала функцию zn при п целом.
Если и^О, то это по-сюду правильная функция; если
/z<2 0, то эта функция имеет полюс в точке z=0. Вы-
числим интеграл \ zn dz, распространенный на замкнутую
спрямляемую кривую, окружающую нулевую точку. Пусть
переменная точка, описывающая эту кривую, движется в
положительном направлении. Заметим, что этот интеграл
не зависит от пути интегрирования, т. е. что интегралы,
распространенные на две различные кривые С и С1 ука-
занного вида, равны между собой. Действительно, рассмотрим инте-
грал от zrl вдоль кривой и по направлению, указанному на черт. 98.
Точки Р, Р' и Q, Q' могут быть при этом выбраны сколь угодно
близко друг другу. Так как функция в области, лежащей внутри кри-
вей (на чертеже эта область заштрихована), правильная, то рассматри-
ваемый нами интеграл должен быть равен нулю, т. е.
Q' р
С Р' С' Q
Будем теперь точку Р' неограниченно приближать к точке Р, а
точку Q' к точке Q. При этом вследствие непрерывности функции f(z)
Черт. 98.
1 При таком выводе теоремы Коши необходимо, чтобы f (г) была непре-
рывна. В действительности теорему Коши можно доказать при гораздо меньшем
допущении, а именно при допущении одного только существования /'(г). См.
Э. Г у р с а. Курс математического анализа, т. 2, ч. I и вышеуказанную книгу
•Привалова.
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
289
в рассматриваемой области, из которой исключена особая точка, вели-
Q' Q
чина интеграла ( будет стремиться к \ . В пределе, когда точки Р* и Q'
Р р
совпадут с точками Р и Q, сумма этих двух интегралов обратится
в нуль, и мы будем иметь:
f(z)dz=^f(z)dz. (7)
с С'
В качестве кривой С можно, в частности, взять окружность, описанную
около начала координат радиусом, равным р. В таком случае
2'=pez<f, л” = p”e/"'f, dz = peividif,
где р —постоянная. Таким образом
При — 1
sin(zz-[- 1)<рб?<р =
2а
— г cos (zz-j- 1) <р
э
2т
Выражение в скобках для всех целочисленных п обращается в нуль.
При п = — 1
О
%
,, f&z
независимо от величины р. Интеграл 1 — можно также рассматривать
1
как определение log z [ср. (5)]; отсюда мы опять-таки можем заключить,
что logz возрастает на 2та всякий раз, как точка z делает один раз
оборот вокруг точки разветвления г = 0.
„ С dz
1очно так же можно доказать, что интеграл I-------- , распростра-
; ненный иа спрямляемую кривую, окружающую один раз в положитель-
I ном направлении точку 2—<2, равен 2та. Для этого надо положить
I z — а— где р — постоянная.
Напомним, наконец, одно следствие из теоремы Коши. Пусть f(z)
в некоторой области — аналитическая функция и а — точка этой обла-
сти. Вычислим интеграл I —----dz, распространенный на замкнутую
19 Вебстер, Диференциальвые уравнения
И
290
ПРИЛОЖЕНИЕ
спрямляемую кривую С, лежащую в заданной области и окружающую
точку а. Этот интеграл равен сумме
/(«)
dz । f/(z)~Да)
z — а^~ , z— а
dz,
в которой оба интеграла распространены на окружность k с центром
в точке а. Первое слагаемое в этой сумме равно 2п//(а); выбрав радиус
р окружности k достаточно малым, можно сделать [f(z) — f(a) мень-
шей любого заранее заданного положи 1ельного е, а потому второй инте-
грал по абсолютной величине меньше ер"1 2тгр — 2пе. Таким образом
мы имеем:
/(«)
1
2та
С f(z)
] z — а
с
dz.
(9)
Эта формула называется интегральной формулой Коши.
е) Для дальнейшего нам надо будет воспользоваться одним очень
важным следствием из интегральной формулы Коши. Из формулы (9)
мы заключаем, что функция f[z} внутри области, ограничен ой кривой С,
имеет производные любого порядка. Эти производные получаются из
формулы (9) путем формального диференцирования по а. Понимая
д;:ференцируемость функции в том смысле, в каком это было указано
в разделе „Ь“, мы из существования первой производной функции f(z)
можем заключить о существовании у этой функции производных всех
порядков.
Пусть Дг) — правильная аналитическая функция в некоторой области,
содержащей точку z = a. Обозначим через k окружность радиуча г
с центром в точке а, которая лежит всецело в области, где функция
f (z) является правильной. Если — внутренняя точка окружности k, то
Дг0) = f -^-dz,
2га J г — z0
f (го) = Г dz,
° 2ш J (z — z0)2
(Ю)
/W(20) =
д! Г f<z)
2га j (г—г0)л+1 Z'
причем все эти интегралы распространяются на окружность k. Первое
из этих равенств представляет не что иное, как равенство (9); остальные
равенства получены из*первого формальным диференцированием по Zq.
Заменяя в первой из этих формул —-— равною ей конечною строкой
г~го
z — z0 z — a—(z0 ~ a) z — а (г—а)2
। (го-а]П I рп~~a\"+1 1
" ’ "И (z — о)ль1 ' — a) z — z0 ’
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
291
мы получим строку
I-------az
\ z — а
k
_(£0 — а)»
2то
го~йГ /(г)
+ 2та ](г —а)2
k
\(z—a)n^dzJrRn'
k
'(11)
остаточный член которой равен
/? * f
® 2га ] z—z0
fzn — а
\ z— а
л+1
dz.
(12)
Обозначим через /И максимум |/(z)| на окружности k, и пусть
Тогда
к0—а|=р<г.
1 м
2пг— р
и, следовательно,
1ип/?я=0.
я-»оо
Таким образом f (z0) можно разложить в ряд по целым положитель-
ным степеням а0—а, если только zG лежит внутри вышеуказанного
круга k. Коэфициент при (z0 — а/1 равен
1 Г /к) ^_/(я)и
2ш J (z— a)n+1 п\ ’
k
так что
/к)=/(«)4-к— —/у Ч- -. .4-к—а)п—+ ... (13)
Этот ряд формально совпадает с обыкновенным рядом Тейлора. Он
сходится внутри наибольшего круга, лежащего внутри области, в кото-
рой функция f(z) является правильной, и притом равномерно сходится
внутри каждого круга, концентрического указанному и лежащего вну-
три его. Наибольший круг, описанный около точки, внутри которого
степенной ряд (13) сходится, называется кругом сходимости. Из сказан-
ного следует, что круг сходимости простирается по крайней мере до гра-
ницы области, в которой функция остается правильной аналитической.
Из выведенного ранее разложения функции следует, что функция
/ (z'j, имеющая в точке а полюс л-го порядка, может быть представлена
в следующем виде:
л л Л
Ж = —-I- —4- ... 4- + A (z _ а) 4-
(z — а)п (z — а)п 11 ' z — а ' 01 1' ' '
1 О4)
+л (,-«)»+...-л-.« (г“ »)+ !•
19*
292
ПРИЛОЖЕНИЕ
Степенной ряд, стоящий в скобках, сходится р вномерно в некото-
рой окрестности точки а. Распространим интеграл \^f(z)dz на кривую,
описанную около полюса а в положительном направлении. Тогда все инте-
гралы Av (z — c)v dz обратятся в нуль; исключение будет представлять
только интеграл
dz
----= ^1А „
z — а -1
<1
где A_i—коэфициент при (z — а)~г в разложении f(z). Этот коэфи-
циент называют (интегральным) вычетом функции f(z) в точке z = а,
которая впрочем может быть не только плюсом, но также сущест-
венно особой точкой. В последнем случае в окрестности точки z~a
вместо ряда (14) мы будем иметь так называемый ряд Лорана:
оо
/(*)=]£ 4 04')
п=—оо
который представляет разложение функции f(z) в ряд как по положитель-
ным, так и отрицательным степеням z — а. Вычет точки, в которой функ-
ция является правильной, равен нулю. Если функция /(г) на замкнутой
спрямляемой кривой С правильная, а внутри кривой однозначная и за
исключением конечного числа полюсов или существенно особых точек
правильная, то интеграл от f(z), взятый в положительном направлении
вдоль кривой С, равен 2тгг, умноженному на сумму вычетов в особых
точках внутри кривой С. Аналогичное утверждение справедливо и в том
случае, когда граница области, в которой задана функция /(г), состоит
из нескольких кривых.
§ 2. Применение теории вычетов к решению линейных диференци-
альных уравнений с постоянными коэфициентами. Интегральная фор-
мула Коши и теорема об интегральных вычетах дает нам возможность
представить решение линейного диференциального уравнения
dny . rf”-1 . . dy , „ , ,
-j—ф~ —^.y ф-.. .ф- a —\-a y = 0 (15)
dxn 1 dxK 1 1 1 °-’ dx ' n-? '
с постоянными коэфициентами в вице формулы, охватывающей одно-
временно как случай неравных корней, так и случай кратных корней
характеристического уравнения
F(z)=zn JrajZa 1 ф-а^-гф- ... -j-an_1Z-[-an = 0. (16)
Пусть корнями этого характеристического уравнения служат s1, s2, ... , sn,
т. е. пусть
F (£)=(£ — $i)(z—s2) ... (z —sa). (16')
Предположим сначала, что эти корни различны. Общим решением дифе-
ренциального уравнения (15) в таком случае будет
ф-____ф-сяе®«* (Cj, с2, ... , сп — постоянные числа).
ПРИМЕНЕНИЕ ТЕОРИИ ВЫЧЕТОВ
293
Пусть замкнутая кривая L ограничивает область, внутри которой лежат
все корни sk. Положим, далее,
О I ^2
Z---Sj ' Z — s2
С г, _P(Z)
Z — Sn F^'
(17)
где P(z)— многочлен (и — 1)-й степени. Согласно теореме
тральных вычетах, интеграл
-—г I егх dz
2тгг J F\z)
L
об инте-
(18)
Р(г)
равен сумме вычетов функции --------- ezx во всех полюсах z — sk, т. е. равен
/• (z)
сумме che-i-x, так что
1 СР(г)
2тп ] F (г)
(18)
Как известно, для любого многочлена (л—1)-й степени P[z) можно
определить постоянные cv с2, ... , сп таким образом, чтобы равенство
(17) выполнялось. Следовательно, интеграл (18), где P{z} обозначает
произвольный многочлен (л—1)-й степени, представляет общее реше-
ние диференцнального уравнения с постоянными коэфициентами (15)
Полученный нами результат распространяется также на общий слу-
чай, когда характеристическое уравнение (16) может иметь кратные
корни. Пусть j,, $2, ... будут отличными друг от друга корнями урав-
нения (16) и пусть их кратность соответственно равна р3, jt2, ...
В таком случае для любого заданного многочлена P(z} степени (л—1)
мы можем написать:
_ %. . аг-1 , , qi
~F\z) (z — Г(г— sjni-i “Г ••• z — sx r
‘ (z-S2}^~P(z----52X2-1 ' " ' z----Sg
где а, P, ...—некоторые постоянные, определяемые этим тождеством.
Обратно, если а, ...— некоторые произвольно выбранные постоянные,
то тождество (17') определяет многочлен (л—1)-й степени P(z). Далее,
имеем'
Г 1г___S )2 1
~ezx=eSk х ~ х= eSk х I 1 (z — sk) x -|----—xz ... I.
Умножая выражение (17') на егх, получим для коэфициентов —-— ,
Р(г) „ . z~sk
т. е. для вычетов —— еzx в точках z = sb, выражение вида.
F(a) *
esk х h2 — + h3 — 4- ... 4- - J = РА (X) х,
’294
ПРИЛОЖЕНИЕ
где Pk (х) — многочлен степени —I. Соответствующим выбором по-
линома P(z) можно, очевидно, достичь того, чтобы все Pk(x) тождест-
венно обращались в нуль за исключением одного, а этот последний
совпадал бы с заранее заданным многочленом (р.А—1)-й степени. Таким
образом все случаи общего решения заданного диференциального урав-
нения получаются в виде интеграла (18), в котором Р(z)— произвольный
многочлен (п — 1)-й степени.
Аналогичное выражение решения диференциального уравнения с по-
мощью интеграла можно получить и для неоднородного диференциаль-
ного уравнения
~г „ 4* ci-i • • • 4~ апУ 33 (2®)
ахп 1 J dx.n 1 in-' ' '> ' '
где ал, а2, ..
мы положим
ап — постоянные, Т(х} — аналитическая функция. Если
£(z)e™ ,
dz
F(x)
(21)
и подставим это значение у в левую часть уравнения (20), то окажется,
что
1 Г (za 4- а3гп~г + •••+«„) ?• (z} ezx dz
‘2,-tti J F(z)
. I G (z) e*x dz.
Таким образом мы должны определить функцию G (z) и интегральную
кривую так, чтобы
~ ^(z)ezxdz = T(x).
(22)
Мы рассмотрим здесь только тот частный случай (особенно важный для
приложений), когда Т (х) = Р (х) е}х, причем
р (X) = «0 + «1X + 4- ... + amxm
-—данный многочлен от х. Положим:
(у) — I _________Ь . . I J___________Pw-
z-— X (z — * ‘ (z — ),)m+1
(23)
(24)
Постоянные р0, р,, ...,рга мы определим потом. В качестве пути инте-
грирования мы выберем окружность k, описанную около полюса z=L
Согласно примененной уже нами раньше теореме об интегрыьных
вычетах, искомый интеграл равен коэфициенту при (г-—I)-1 в разло-
жении
Z(z\ezx—Г₽° I I -4- IFl+fe ^)2х2
^4-^2-Ь • •+(г_хГ+1] р-Нг-Ь) *+------------------2f—+
т. е. равен
ПРИМЕНЕНИЕ ТЕОРИИ ВЫЧЕТОВ
2У5
Это по следнее выражение будет равно Т (х), если положить
₽о = а<ь = ₽2 = 2!а2, .... L = <25)
Соответствующее решение
1
У
Ъ(г)е*х ,
2тп J F (г)
k
G (<2^) (Fx
можно рассматривать как вычет в полюсе z = \ где
е /~\__ ао_____|_ ai 1 2! g-g i_ _|_______ат
1 ' z — X (z— I)2"1- (z— Z)'; ! (г — л)пг+1
(26)
(24')
Пусть 1 будет р-кратным корнем F(z) ('p^sO). В таком случае X
является (/и ф-р4~ 1)"кРатным полюсом подинтегральпого выражения.
Далее, мы имеем:
4г=<44+ • • •++’«+г> <*->>+ • • •
е™ = еи [ ! (z _ X) х . j ,
и, следовательно, искомый вычет имеет вид:
eXjc (полином (тц)-й степени) .
Так как функции ех*х* (/г —О, 1,_, р— 1) удовлетворяют соответ-
ствующему однородному диференциальному уравнению, то решение
получается в виде произведения x^Q (х) е,х, где Q(x)— многочлен той
же степени, что и Р (х). Напомним, что решение, такого вида получается
в случае, если 1 (х) — Р(х) ех* и если X есть р-кратный корень харак-
теристического уравнения F(z) = 0 (конечно р, в частности, может
быть равно нулю).
Изложенный способ решения неоднородных диференциальных уравне-
ний может быть распространен и на тот случай, когда Т(х) представ-
ляет собой сумму конечного числа функций вида P(x)eXjc или вида
Р(х)созух, P(x)sinyx, где Р(х)— некоторый многочлен. В этом слу-
чае задачу решают для каждого слагаемого в отдельности, и получен-
ные таким образом решения складывают.
Так как вид xvQ(x)Px вышеуказанных решений известен заранее,
то соответствующие уравнения можно решать и по методу неопреде-
ленных коэфициентов.
Пример 1.
d2v I 2
—- + try = cos тх.
dx2 1
296
ПРИЛОЖЕНИЕ
При т* 2 * *=£п“ мы находим решение непосредственно, исходя из предпо-
ложения Л cos/их. Это решение имеет вид:
1
У = --------г cos тх.
п2— т1
Пусть теперь т — п, п=^=0. Мы имеем:
ginx 1 e-inx
cos пх —--------------------------4;-----.
Положим сначала
glflX
ТтМ—2-, 1 = г‘л-
В данном случае
F (z) — z2 га2, Sj = in, s2 = — in,
так что является простым корнем уравнения (р.= 1). Мы имеем:
5(2:) — ———
' 2 (г — ту
1 _ 1
F (г) (г — in) (z 4- in)
= (гLin) I(2Z«)-1 — (2ш)-2(z — in) 4~ (2zra)-s (z — zra)2 ,
= einx |"! (г _ Z/z) X 4- _ in)2 .
£ (z) егх
Вычет — в точке z — in равен
elnx Г Х_______1_ 1
|_4ш 2(2in)2]’
так что
/ V 1 \
v — einx /--I-------\
\ 4/га ~ 8га2 /
При Х = $, мы имеем:
2 / V 1 \
y = e~inx[--------1-----] .
\ 47га ~ 8га2 /
Складывая, мы получаем отсюда частное решение:
X 1
У—?Г sin/zx-4-~—COS/2X.
2га 1 4га2
Второй член решения удовлетворяет соответствующему однородному
уравнению. Общим решением в этом случае служит
х sin пх
у— сг cos пх 4* с2 s*n пх Н-о----- (ci и с2 — постоянные числа).
Пример 2. Рассмотрим уравнение
d2y . dy 9
-у о- 4- « + nty = a cos тх,
dx2 1 dx 1
ПРИМЕНЕНИЕ ТЕОРИИ ВЫЧЕТОВ
297
где k, а, т, п — действительные числа. Мы имеем:
a cos ж—“ (е1тх
Л/
F(z) — z2 -j- kz /Z2,
(— /гi V4л2 — A2),
s2 = — (— k—iV 4и2 — A2).
Здесь im и —im не являются корнями уравнения p(z} — 0 (кроме
того случая, когда k — О и п2~т2, ср. пример 1), и таким образом
в обоих случаях р = 0. Следовательно, мы можем предположить, что
решение имеет вид:
у = A cos тх В sin тх.
В таком случае
— т (— A sin тх 4- В cos тх),
dx 1
— т2 (A cos тх В sin тх),
— т2 (A cos тх В sin тх) km (— A sin тх -|- В cos тх) Ц-
-|- п2 (4 cos тх В sin тх)-= a cos тх,
(п2 — т2) ЛЦ- kmB — a, (и2—т2), В — kmA = 0.
Следовательно,
д2------------------------------------- т2
- ________________ £2
k'-in-1 -f- (п2 — т2У ’
km
№т2 -j- (п2 — т2)2 й'
если только знаменатель этих выражений не обращается в нуль \ Таким
образом
/ 4/г2 — /г2 , У 4п2 — Ь* ) .
у = е 2 < с1 cos —— --------х~тс2 sin--------2----х |
+ {(л2 — т2) cos тх + km sin тх} •
1 k2m2 -f- (п2 — т2)2 1 1 1
1 Это может случиться либо, когда k = 0 и m^ — rfi (ср. пример 1), либо,
когда т = п — 0. В последнем случае данное уравнение с помощью подстановки
сводится к уравнению 1-го порядка.
298
ПРИЛОЖЕНИЕ
Последнее выражение в фигурных скобках можно заменить произведе-
нием D cos(тх — а), причем
а (п2 — т2)
П COS CL =--------------------------
k2m‘+ (п2 — т2)2
_ . akm
Взта=-^ „---------—,
k2m2 -j- (n2 — m2)2
km
tga= —-----j,
n2 — m2
]/ k2m2 -L (n2 — m2)2
§ 3. Линейные диференциальные уравнения в комплексной области,
а) Пусть коэфициенты линейного однородного диференциального урав-
нения
dau , . . , du , , . _ , „
PT)
представляют собою аналитические функции. Мы покажем, что решения
этого уравнения также являются аналитическими функциями, которые
могут иметь особенности только в точках, являющихся особыми для
коэфициентов этого уравнения. Как известно, решение диференциаль-
ного уравнения (27) однозначно определяется заданием начальных условий
du < dn^u . ..
х —х0, и — и0, — — —мо ’
•если только коэфициенты ру (х), р2 (х), ... , рп (х) являются правиль-
ными в точке х = х0. Особые точки решения, определенного этими
условиями, оказываются, таким образом, независимыми от начальных
условий (т. е. от постоянных и0, и'о____ и^‘ ~ 9).
В нелинейных диференциальных уравнениях особые точки решения
могут зависеть от начальных условий. Например, интегралом диферен-
циального уравнения
служит
и2 — х2—с = и2 — х^,
т. е.
И=Ух2-)-^ — х2.
Эта функция многозначна; ее критические точки
x = ±j/x2 — и-,
очевидно, зависят от и0,
ЛИНЕЙНЫЕ ДИФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 299
Для доказательства высказанного нами утверждения перепишем
уравнение (27) в следующем виде:
dnu dn~xu
dxn~~P1 dx^ ~"‘~Рп (*) м-
Рассмотрим интеграл и в окрестности точки х = в которой все
коэфициенты являются правильными. Последовательно диференцируя по-
следнее уравнение, мы покажем, что функция и имеет производные
любых порядков. При этом значения производных любого порядка
при х=а
[dku \
\dxk }х=а
(А = 0, 1, 2, ... )
можно выразить через п — 1 первых производных, а именно:
dn*Au _ dnu t , ч dn~'lu
~dxn+A~~~~PA dx"~'P^Pz’ dx^~A~'P‘2' Ps' dxn~z~~ ’
dn+2u
dx"+2
d^4i dnu
Pa dxn^A dxn
С помощью этих производных можно разложить функцию и в окрест-
ности точки х = а в степенной ряд; остается только показать, что этот
ряд сходится в любом круге с центром в х = а, не содержащем осо-
бых точек коэфициентов.
С этой целью соавним наше диференциальное уравнение со сле-
дующим: d^ * /л d^ , м
dxn j х—a dxn~A х — а™' 28
г г
Здесь г есть положительное число, меньшее, чем наименьшее из рас-
стояний от точки а до особых точек функций ру (х), р2(х), ... , рп(х),
а М — максимум абсолютных величин этих функций на указанном
круге Если начальные значения w, w', ... , wf,l~L> выбрать положи-
тельными и большими, чем абсолютные величины соответствующих на-
чальных значений и, и', ... , иАп~г>, то легко показать, что
I («)| ®(’) (а) при v = n, «4-1,...
Таким образом ряд, в который разлагается функция w в окрестности
точки х—а, является мажорантной по отношению к разложению функ-
ции и, и повсюду, где сходится первый ряд, сходится также и второй.
х — а
Положим —-— — z. Тогда определенному выше кругу в плоско-
сти х соответствует в плоскости z круг радиуса, равного единице.
JHanie диференциальное уравнение после такой замены независимых не-
пременных принимает вид:
v ’ dzn dzn~A 1 dzn~2 1 1 ' '
300
ПРИЛОЖЕНИЕ
Начальные значения
I dim\ fdn~'l'w\
W°’ \dz)o’’" \dzn^1)0
суть заданные положительные числа. Напишем
+ + + «//"+••• + йя+**”+й+--’ , (30)
где а0, йп ... , йи_1 получаются из этих начальных значений умножением
1 1 1
на 1, ту, ----— и, следовательно, также положительны.
1’ 2! (п— 1)!
Подставив этот ряд в уравнение (29') и приравняв коэфициенты при
одинаковых степенях z, мы будем иметь:
(д-Ь А) («+*—1)... (£-Н)я„+л—
— (дф- k — 1) (zz-j- /fe — 2) ...
_|_ (л 4- k — 2) ... (k 4- 1) /Иг2йп+й_2 4- ... 4- Mr^a»
или
(д+^)(д-|-А-1).. .(^+1)«я+л, = (Л1г+Л)(«+^—1).. .(А+1)«й+й_1+... (31)
Отсюда следует, что все коэфициенты в ряду (30) положительны; кроме
того, если М выбрано настолько большим, что Мг^>п, то каждый
последующий коэфициент больше предыдущего. Действительно,
= Mr + k 4 . i
an+k--L " + /е "Г («H-/г) (л 4-A — 1)й„+й_1
а так как все члены в правой части равенства положительны, то правая
Air -4- k „
часть -^> 1. Правая часть последнего равенства состоит из ко-
нечного числа п слагаемых. Так как 1, то второй член при
йп + /г-1
k —»оо стремится к нулю. Легко видеть, что то же утверждение при-
менимо и к остальным слагаемым. Первый же член стремится к еди-
нице, а потому
litn -Л+*_=1. (32)
й-»оо йп+*-1
В разложении im в ряд отношение д-го члена к предыдущему по своей
абсолютной величине стремится, таким образом, к |г|, так что этот ряд
сходится при | z | <Z 1, т. е. при | х— а\<г. То же можно сказать и
о разложении в ряд функции и.
Ь) Исследуем поведение интеграла линейного диференциального
уравнения вблизи изолированной особой точки х — а. Предположим
при этим, что коэфициенты в окрестности этой точки однозначны.
Пусть интегралы _у2, ... , уп являются фундаментальной системой
решений. Если переменная х описывает окружности около точки, то
решения этой системы переходят в другие решения Yv Y2, ... , Yn;
ЛИНЕЙНЫЕ ДИФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
301
эти последние также составляют фундаментальную систему. Действи-
тельно, если бы между Е,, У2, ... , Yn существовала какая-нибудь ли-
нейная. зависимость, то эта зависимость должна была бы остаться и
в том случае, когда х описало бы около точки а окружность в проти-
воположном направлении, иными словами, то же линейное соотношение
должно было бы связывать и решения у2, у2, ...,уп, что противоре-
чит определению фундаментальной системы.
Новые функции У,, У2,_____ Yn выражаются через решения фунда-
ментальной системы jAp_у2, ... ,у линейно с помощью постоянных ко-
эфициентов:
4 = йпЛ А ЗД А • • +
у2 = Й21Л А Й22Л А • • А Й2Л
(33)
Yn---йл1Л А ЙЯ23/2+ • • • А аппУп- .
Из существования этих равенств мы постараемся сделать некоторые за-
ключения о форме заданных интегралов. Предпошлем нашему исследо-
ванию следующее замечание. Когда переменная точка обходит особую
точку х~а по окружности один раз в положительном направлении, то
в случае многозначных функций простейшего типа
(х — й)х =
функция умножается на постоянную. Действительно, в результате такого
обхода аргумент переходит в tp —J— 2тг, а наша функция в следующую:
^Xg>J(!p + 2it) _ е2гЛ — ау.
Указанная постоянная равна, таким образом, Если 1 не является
целым числом, то этот множитель отличен от единицы. Если X —
целое число, то функция однозначна.
Будем теперь искать такое решение
к=А АлА • • • А АпУп (Я
. ташего диференциального уравнения, которое обладает тем же свойством,
т. е. после того как независимое переменное один раз обходт. ючку
а в положительном направлении, это решение обращается в функцию
t^A^AA^A-.-AAA, 05)
{причем U= (аи, где со — некоторый постоянный множитель. Пусть при
[этом yh и Уй имеют указанные выше значения. Мы требуем, таким
{образом, чтобы
А (апУ1 A Й12 Л А • • • А Й1ЯУП) А
А А (Й21Л А йггЛ А • - А Й2«Л) А
А А (йптЛ А йи2Л А • • • А апп л) —
—® (АгУ1 А АчУ^ А • • • А
г. е. чтобы функции ук были связаны между собою однородным линей-
ным соотношением. Вследствие линейной независимости этих последних
302
ПРИЛОЖЕНИЕ
все коэфициенты при ук должны обращаться в нуль, так что
А (ап — ®) + А°21 + А«31 + • • • + Апа,л = °»
AfiJ2 + А (°22 ®) + Аа32 4" • • • Апач& — °> (36)
АЙ1л +А°2п4~ Аазя +" • • 4~ А (аяп — w) = о* .
Если не все Ак равны нулю, то эта система однородных уравнений мо-
жет иметь место только в том случае, когда удовлетворяется характе-
ристическое уравнение'.
ац 10 Й21 . . . Д.
F(<o) =
й12 Й22 W • * an2
(37)
а1п а2п • • • апп W
Мы получаем, таким образом, для множителя со уравнение д-й степени.
Пусть со,, со2, ... , соп будут корнями этого уравнения. Если один из
этих корней подставить в систему (36), то можно будет определить со-
отношения между Ак, и, таким образом, искомое решение и будет
найдено. Если все корни со^ различны, то мы найдем этим способом п
интегралов «р и2,____,ип, обладающих указанным выше свойством, и мы
будем, таким образом, иметь:
= I (33>
Un = Vn- j
Эти решения и,, и2, ... , ип образуют фундаментальную систему. Чтобы
доказать это, предположим противоположное, т. е. предположим, что
можно найти такие отличные от нуля постоянные cv с2, ... , са, что
qiZj -J- с2и2 + спип — 0.
После того как переменная точка один раз обходит вокруг особой
точки, получается:
С1Ю1И1 + С2С02И2 4“ • • 4“ CrPnUn
После того как переменная точка два раза обхозит особую точку —
+ С2“Ч А--------F са^пип = 0,
и, наконец, после (п—1)-го обхода,
^“^Ч4- C2W2“Ч 4~ 4-Ч = °-
Так как скик не обращаются все тождественно в нуль, то должно иметь
место равенство
“1 “2 • • •
= 0.
СО?-1 (О"--1 ... со"~1
12 П
Однако это равенство невозможно, так как иА отличны друг от друга.
ЛИНЕЙНЫЕ ДИФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 303
Функции и* можно представить так, чтобы их особенность в точке
х=д стала наглядной. Функция (х—а)'1, согласно сделанному нами
раньше замечанию, при обходе около особой точки умножается на
е2к/г, т_ е> на ш •
1 1
ri=s2irfl0g®1’ e2rfr,= ®J- (39)
Следовательно, функция (х— а)~Г1ил остается при обходе точки х~а
неизменной; она представляет собою однозначную в окрестности точки а
функцию, для которой сама точка а служит либо правильной точкой,
либо полюсом, либо существенно особой точкой. В таком случае
= (х — a)ri (х) (40)
и аналогично
и2 = (х —с)г’<р2(х),
ип = {х—аУ^п(х).
Можно при этом (х) разложить в ряд Лорана (см. приложение § 1,с)..
Покажем теперь еще, что характеристическое уравнение (37) не за-
висит от выбора фундаментальной системы Js, ... ,уа, т. е. является
инвариантом заданного уравнения. С этой целью рассмотрим другую
фундаментальную систему
®2, ... , ®в.
Пусть
Vn = ^глУ1 + + • • + dnnPn-
После того как переменная точка опин раз обходит точку х = д, все
уь переходят в Yk, а следовательно, в
У1 + ^2 У2 + • • • + пУп = 1, 2, . . . , П).
Пусть, далее,
vk = ькУ\ "Г + • • • + ЬЛ (/г 1 - 2, ... , л).
Если в последние два равенства подставить вместо У и v их выраже-
ния через у2, ... ,уп, то получится:
’°k1 (аТ1У1 -\-а12У2 + • • • 4" dlny^ 4~
4“ bk2 (а2гУ1 + ^22^2 4~ • • + агпУп) 4"
+ ЬЬя (атУ'1 4~ ап2У2 + • • 4- аппУп) =
—djti (аиУ14- йз2Л 4- • • • + ainyJ 4"
4* df!2 (а21У1 4~ а22>2 4- • . . 4- а2иЛ) 4-
4- dkn (ап1У1 4” ЙП2>2 4“ • • • 4~ аппУп)-
304
ПРИЛОЖЕНИЕ
Коэфициентом при у служит
акАр~\~ bh2d2p~Y bkrdnp =
= йкЛ.р + diaa2p 4- • • • + dpnanp = ckp'
Характеристическим уравнением для у будет
ап —о «21 апУ
—— «12 «22 ® • • • ап2 = 0,
«1Я а2п ' • • о о о • апп~ “
а для v
*ц —® ^21 ••• bni
Q (о) — ^12 ^22 ® • • •
Ь, Ъ2п
^12 • • • dtn
d22 ‘ • • d2n
Умножим детерминант
dns----di
по строкам на F(w) и по столбцам на G(w). Мы будем соответствен-
но иметь:
СП ^11® C12 ^12® • • • С1я— dlnW
DF(w) = С21 d21(a С22 d22a • • • С2п d2n® Сп1 dn\® Сп2 dn4a • • • С„п dnn(i>
С11 «12 ^12® • • • с1а — d"lnK>
DG (w)== С21 d21® С22 d22® • • • С2п d2a^ •
СЯ1 — dnia С„2 — ап2® •СПГ~ dn,^
Пусть в линейном соотношении, выражающем интеграл
_у2, • • • > Уп> коэфициент при у* отличен от нуля. Тогда
Так как D^O, то из этих равенств и следует наше утверждение.
Если не все корни характеристического уравнения/?(со; = О отличны
друг от друга, то некоторые из определенных выше uk совпадают друг
с другом. "
через уп
функции
У 2-
У2
(41)
Л
ЛИНЕЙНЫЕ ДИФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
305
образуют фундаментальную систему, детерминант которой
А11 А12 Аз •••Ал
0 1 0 ... 0
0 0 1 ... 0 —Ат
0 0 0 ... 1
отличен от нуля. После одного обхода около точки х = а
функции
Ц = <о1и1,
*2 ~ $21ит + $22X2 + • • • + $гЛ’
Y'i == $31И2 + $ЗгЛ + • • • + $ЗлЛ’
получаются
(42)
Yn — $„т и1 + РлаЛ + • • • + $ппУп- ,
Характеристическое уравнение в этом случае будет:
в В в
(0^ „ (J) г 21
0 $22 $32 • • " $Л2
F((o) = 0 $23 $33 ® • $я2
0 $2л $3л •••$««— ®
$22 ® $32 • • • $«2
$23 $33 Ш • • • $Н3
= (“1 ~ ®)
(37)
$2?г
$3л ••• $ПЯ —®
Если ш2 является корнем функции F(wi}, то <о1 удовлетворяет также и
уравнению
$22 ® $32 • • • $Я2
$23 $33 ® • • $яЗ _______О
$2л $3я • • • $ЛЛ ®
Следовательно, можно определить числа Вг, Bs, ..
удовлетворялись уравнения
Вп так, чтобы
($22 ®1) В2 + $32fi3 + • • • + $п2Вп — °’
$23^2 + ($33 - ®Т) В3 + . • • + $лЗ Рп =°.
$2лА + $3?А + • • • +($ал-®1)^ = 0-
20 Ве/ст в р, Диференциальные уравнения
ЗС6
ПРИЛОЖЕНИЕ
Если мы теперь положим:
М2 — В^2 + ВзУз 4- • • • + ВпУа’
то окажется, что после одного обхода
ц=ад+ад+...впк„==
= В2 (^21К1+₽2аУ24“- • • 4* ₽?Л) + ез(₽3}И14^^325?2+- • •4'₽ЗлЛ)4~ • • •
= (Ргт^г 4- РзА 4" • • • + ₽И1 Br) ui 4~ “1 (ВзУз 4~'ВзУз 4~ • • •-¥впУа)~
C02^fZj —|— WjZ^2.
Повторяя это рассуждение X раз, где X означает кратность корня
мы получим интегралы иг, и2, ... , которые при одном обходе около
точки а обращаются в следующие функции:
Ц = CDjW-p
i?2 = WgjZZj -|- W-jZZg,
С73 = w3iKi ~h W32M2 4“ wiM3»
........................................ I
*4=“>.i ui 4- 4- • • • 4- “A- J
(43)
Обозначим кратность отличных друг от друга корней уравнения (37)
через Xj, ).2, .... Хст. Можно образовать такие группы по Х7, Х2, ... ,\я
интегралов, что интегралы одной и той же группы при одном обходе
вокруг а преобразуются вышеуказанным способом.
Постараемся теперь представить функции uk в окрестности особой
точки а. Для этого рассмотрим сначала корень Wj, кратность которого
равна X. Пусть соответствующие интегралы будут и1( и2, , ик. Как
и в случае простых корней, мы имеем;
Чт. = (х — а)г^п (х),
причем функция <рп (х) однозначна в окрестности точки а, а следова-
тельно, разложима в ряд Лорана. Второй из интегралов, соответству-
ющих ю1( а именно и2, после одного обхода переходит в
772 = w2jKj -f- WjTz2,
так что
^4 ----- - 21 I
U~ Wj ' иг ‘
„ , . и9 , (091
Таким ооразом функция — при одном обходе увеличивается на —.
ЛИНЕЙНЫЕ ДИФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
307
Тем же свойством обладает, очевидно, и функция
log (х -4- а).
Зтасо, 6' 1 '
Поэтому разность
11-^
в окрестности точки а является однозначной функцией и, следовательно,
«2 = зЭю M110g ~
Функция
иА (х — а)~’Xf(x) = tp21 (х)
точно так же однозначна в окрестности точки а. Таким образом
и2 = (х~ а?* {ср2, (х) 4- <р22 (х) log (х — а)},
[73 — со31 п3
'1“з,
U3_____ С031 С0. 5 , 11^
COj ' COj CZj ZZj
где <р21 (х) и tp22 (х) — однозначные функции, а ср22 (х) отличается от
tp31 (х) только постоянным множителем. Для третьей функции и3 мы
имеем:
Положив
мы найдем, что
Ц со3 2тасо2 е' ' иг 04
— =-~L- log (x — a) 4-/(x),
иг 2ric0j e' ’ 1 J' 7
<о„, . со.
со.
Отсюда следует, что — в окрестности точки а ведет себя, как функция
и3
но = k [log (х — а)]2 + ф (х) log (х — а)
[А = const, ф(х) — однозначная функция], а эта функция при одном
обходе около точки а переходит в
W=k [log (х—а) 2т]2 -[- ф (х) [log (х — а) 2т] —
= k {log (х — а)} 2-|-4таЛ log (х — а) — 4тг2А ф (х) log(x—а)-|-2таф (х) =
= W -}~ 4то‘А log (х — a) -J- 2тг/ф (х) — 4тг2А.
20*
308
ПРИЛОЖЕНИЕ
Поэтому, если мы положим:
— 4т#&, -4-—/(х) -4-4п2&== 2таф (х),
2тасо2 ©j 1 со/' ’ 1 т' '
то функция
и„
— ---W
иг
будет однозначна, и следовательно,
«3 = (Х — аУ1 { Ч>31 + Ч>32 10ё (* — «)+ %3 1оё2 (* — «)}•
Аналогично этому мы найдем:
= (х — аУ' { Тм + Фхз 1о£ (*—-«) +
+ Тхз 1оё2 — а) + »• • + ?>./. 1оёх-1 (- — а)} • (44)
Здесь все функции <р в окрестности точки х — а однозначны; власт-
ности, можно найти систему интегралов иг, и2, ... , ик, имеющую ука-
занный ранее вид, и притом такую, что функции <pvl(х), <pv_12(*)» - ,
входящие в эту систему, отличаются только постоянным множителем
(v—1, 2, ... , X)1. Каждому из остальных корней со2, ... соответствует
своя система интегралов.
При замене точки х~а бесконечно удаленною точкой сделанные
выводы в основном остаются в силе и только несколько видоизменяются.
с) Мы называем точку х = а несущественно особой точкой инте-
грала и диференциального уравнения (27) [или вообще функции вида
(44)], если и после умножения на соответствующую степень х — а
остается конечным при х—>а (аналогичное определение имеет место
при х—>оо). Несущественно особой точкой является, например, полюс
функции или точка, в которой функция правильна. Функция, которая в
окрестности точки х~а однозначна, а при х = д имеет существенно
особую точку (т. е. точку, в которой ряд Лорана для этой функции
имеет бесконечно большое число отрицательных степеней), этим свойством
не обладает. Функция (х — a)?[log(x— а)]? при р^>0и произвольном q
стремится к нулю, когда х—>а\ поэтому интегралы (44) имеют несу-
щественно особую точку в том и только в том случае, когда функция ср
имеет только конечное число отрицательных степеней х — а. В этом
случае двучлен (х — а)г с наименьшею степенью г можно вынести за
скобки и представить интеграл в следующем виде:
и =(х—ayt^-HcpjlogGt — fi)-j-c>2Iog2(x—а) -[-... + <pfrlogfe(x —а)]. (45)
При этом функции <р0, ... , cpk в некоторой окрестности точки х = а
являются правильными аналитическими функциями, а при х = а не все
обращаются в нуль. Порядок величины функции (х — а)~ги вблизи
точки х — а в этом случае тот же, что и функции logz(x—а) (х^/г),
умноженной на постоянную. Мы говорим в этом случае, что и принад-
лежит показателю г.
* См., например, F. Н о г п, Gewohnliche Difierentialgleichungen beliebiger Ord-
nttng, стр. 130; Leipzig, Goschen (1905).
ЛИНЕЙНЫЕ ДИФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
309
Если для интеграла и точка х=а является несущественно особой,
то то же имеет место для его производной:
и' = г (х — а)'-1 [<р0 + <Pi log (х — а) + ... + % log* (х — а)]
4“ (х — a)r [<Pq -j- log {х — а) + ... + log* (х — д) 4-
. <Pi ^felog*-1^ —Д)~|
' x — a'”'* (x — a) J
= (x — ay-1 [rep0 -j- nft log (x — д) 4- ... 4- 1оё* U ~’й) 4~
4- (x — д) 4- (x — a) <p' log (x — a) 4- ... 4~ (x — a) <p’ft log* (x — д) 4“
4- <Pi 4- • • • 4-log*-1 (x—a)].
Эта производная, очевидно, принадлежит показателю г — 1 (исключая
тот случай, когда г—О, и и при приближении к а остается конечным),
так как при г 0 из одновременного обращения в нуль при х = а
функций
*То 4- <Р1. 4- 2tP2« • • • > 'Ъ-i +
следует обращение в нуль при х — а также и функций <р0, <р3, ... ,<pfr
(при г= 0 следует обращение в нуль только <р3, <р2, ... , Произ-
ведение двух несущественно особых функций представляет собой опять-
таки несущественно особую функцию.
Является вопрос, какими должны быть коэфициенты диференциаль-
ного уравнения (27) для того, чтобы решения его имели только несу-
щественно особые точки. Чтобы ответить на этот вопрос, выразим коэ-
фициенты через интегралы uv и2, , ип. Имеем:
_ р1К(п-1) — р2Ц«-2) — ... — pji^,
и.М — ... —рпи2,
UW ^—p^-i) — р2 ti^-Ъ —... —Рпап.
Отсюда
IF.
р — _Д-*: (46)
где
U&~2) . . .
K(n-1) д(л~2) . . . И
n n n
a Wk есть детерминант, который получается из W путем замены элемен-
тов /г-го столбца производными Ц"), и^\ ... , и^1. После одного об-
хода около особой точки х = а система и^, и2, ... , ип преобразуется
в новую систему, которая связана с первоначальною системою линейной
подстановкой с постоянными коэфициентами. Детерминанты W и Wk
3 10 ПРИЛОЖЕНИЕ
при этом умножаются на детерминант линейного преобразования, а
IF
отношение — остается неизменным. Отсюда следует однозначность
'"'k
коэфициентов pk, которую мы предположили с самого начала. Кроме того,
отсюда мы можем вывести еще следующее заключение. Если п линейно
независимых функций и2> ...,ип при обходе точки а линейно пре-
образуются, причем коэфициенты этого преобразования постоянны, а
детерминант отличен от нуля, то в окрестности точки а эти функции
можно рассматривать как решение линейного однородного диферен-
циального уравнения с однозначными коэфициентами.
Если полученное для и выражение (45) подставить в равенство (46),
то логарифмы отпадают; кроме того, в выражении для pk может войти
только конечное число отрицательных степеней х — а; отсюда следует,
что точка х — а является либо правильной точкой, либо полюсом. Мы
покажем, что порядок этого полюса не выше k.
Положим u=Tz, где 8—новая неизвестная функция, которую мы
определим потом, и которая имеет вид:
Т=(х — a)₽[e04-Cj(x — а)4-с2(х — а)2. ..] = (* — a)^g(x) (со=£О).
Так как
du dTt dZ
ax dx 1 dx
dku _ dkT^ . hdk~lT
dxk dxk ' dxk~1
k(k— \)dk~2T
2 dxk~2
? +
то наше уравнение примет вид:
dn^ da~i£
+ r+(»~ g5+... +?,7«_0.
Разделим это уравнение на Т:
dnZ
dxn
dn~^ ,
rfx"”1 1
. /п(п — 1)Г . . .. Г . \dn-% . . .
daS . dn~4 . dn~^ . . . л
(48)
311
ЛИНЕЙНЫЕ ДИФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Если интегралы первоначального уравнения при х — а имеют не-
существенно особую точку, то таков же будет характер интегралов
и нового уравнения, так как
„и и Г1 । > , , п
£==Т = (^=^ [+ й) + С2(^~«)2+ ... ].
Но порядок полюса функции
Г_______1_
Т х — а
£(*)]
у//
в точке х — а не выше первого, порядок полюса функции — не выше
второго и т. д. Поэтому, если при х— а порядок полюса коэфициентов qk
уравнения (48) (А=1, 2, ...,«) не выше k, то порядок полюсов коэфи-
циентов рь при х — а также не выше k.
Выше мы нашли, что всегда существует решение п1 = (х—а)'ирп(х),
не содержащее логарифма. Этот интеграл при х = а имеет несуще-
ственно особую точку и может быть выбран в качестве функции Т.
Преобразованное уравнение (48) имеет в этом случае решение 2=1,
так что в этом уравнении отсутствует член, содержащий 2, т. е. для
него qn=b. Это уравнение имеет вид:
d'b dn~^ ^2_
dxa 1 dx"-1 dx
(48')
Если положить — = 2', то 2' будет удовлетворять диференциальному
уравнению (п—1)-го порядка, интегралы которого представляют собою
производные предыдущих интегралов и потому при х — а имеют несу-
щественно особую точку.
Если мы, таким образом, примем, что наше утверждение доказано
для уравнений (zz — 1)-го порядка, то окажется, что х — а является
полюсом не выше /г-го порядка для qb, и тем самым наше утверждение
будет доказано для Нам остается теперь еще доказать, что наша
теорема справедлива при д=1, т. е. для уравнения
.
Положим
и — (х — а)Р [с0 -|- с1 (х — a)-j-c2(x — а)2 =
==(х — a)Pg (х) fg (а) — са=£ 0];
тогда
— р = “’= Е
и х — a' g(x) ’
312
ПРИЛОЖЕНИЕ
Отсюда следует, что рг при х = а имеет полюс не выше первого
порядка.
Итак, линейное диференциальное уравнение, интеграл которого
при х = а имеет несущественно особую точку, должно иметь следую-
щий вид:
d’4i sp2(x) dn-*u spjjc) _
dxrl'~ x— adxn~1'(x—a~}2 dxn~2' "' ' (x—a)nU '
(49)
где (x), $]32 (x), ... , (x) суть правильные аналитические функции
в окрестности точки х — а. Справедливо также обратное положение:
для всех интегралов диференциального уравнения вида (49) точка х = а
является несущественно особой. Доказательство этого предложения ана-
логично предыдущему. При полной индукции, т. е. при обратном пе-
реходе к уравнению (48'), мы используем существование одного реше-
ния заданного уравнения, которое при х—а имеет несущественно
особую точку. Мы докажем это дальше в разделе d). Справед-
ливость нашего утверждения для п = 1 доказывается непосредственно
Из равенства
^-; + Ро+М*—«) + ₽2(*—й)2+ •••
следует:
И = е?1о8(-« —°) + Го + 71 (х — а) + у2(х — o)s+ __
= (х — а)₽[с0 + сг (х — a) -J- с2 (х — с)2 -J-...].
Если число особых точек заданного диференциального уравнения
конечно, и для всех особых точек alt av ..., лежащих в конечной
части плоскости, имеет место указанное только что свойство, то это
уравнение должно иметь вид:
dnu SPj (х) dn~'iu $Р2 (х) dn~2u . I _
dxn ф (х) dxn~1 [ф (х)]2 dxn~2 [ф (х)]л ~
где (х), $]32(х), ..., $]Зя(х)—правильные во всей конечной части
плоскости функции, а
ф(х) = (х —flj)(X — а2) ,..(x — aft).
(51)
Если бесконечно удаленная точка х = оо также является несуще-
ственно особой точкой интегралов, то для интегралов диференциаль-
ного уравнения, в которое преобразуется данное уравнение путем
подстановки х—-^~, точка t — О должна быть несущественно особой.
313
ЛИНЕЙНЫЕ ДИФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Левая часть уравнения (27) после этой подстановки принимает
вид:
dnu . ,
. I dn~ru
dn~2u
. /2«-3^""2И I I
1 1“ dtn-i + dtn~2 + • • • J
ip [p.n-4da~2u . Bdn~2u 1
| d7«“2 21 dtn~* ^ • • • j
dnu d4"1
=tin + (W-1 +рГ2) +
dn~2n
+ (*O2^“2 + зд^Н/у2"4) + • • •»
где eM — некоторые числовые коэфициенты. Деля это уравнение на t'in,
мы получим:
। | —01 I Pi 1 &п *и । I g02 । &T1P1 । Pz 1 dn su .
dtn "Г" I t 72 j dtn~i ( 72 * ts f4 I dttl-z I"
dnu dn~Au dn~2u .
“~dF + 9’ ~dt^ q‘idi^'r ” ’ -rLlnU'
(52')
где
„ ___еОЬ I ei,k-lPl I
Lik £й+1 T
Г /2Й-
Если интегралы при 7=0 имеют несущественно особую точку, то
qh при 7 = 0 могут иметь полюс порядка не выше й, т. е. выражение
> I е1,к-1Р1 1 g2,^-2A | | Рк
Ок г t ti т tk
при 7=0 должно оставаться конечным. Отсюда следует, что для каж-
дого k дробь останется конечной при 7—г-0, т. е. для каждого k
произведение p^ch останется конечным при х—>оо. Таким образом
.W(-4
[ф U)]ft ’
где^(х) — целая функция, которая при х—»оо растет не быстрее, чем
степенная функция. Следовательно, должен быть многочленом. Сте-
пень знаменателя указанной дроби равна mk, а потому степень числи-
теля не выше (т—\)k.
Резюмируем сказанное. Интегралы линейного диференциального урав-
нения (27) в том и только в том случае являются несущественно
314
ПРИЛОЖЕНИЕ
особыми в каждой особой точке, включая х —оо, когда уравнение
имеет вид:
d"u *р2(х) ап~*и I , фй(х)
dx’1 ' ф (х) dxtl~1‘~ [ф (х)]2 dxn~^ ‘ [ф (х)]" U '
При этом
ф(х) = (х — аг)(х — а2) ... (х — ат), (51)
где о1, а2, ... , ат — отличные друг от друга и лежащие в конечной
части плоскости особые точки, а числители $]Зл(х) представляют собой
многочлены степени Совокупность уравнений этого рода на-
зывают классом Фукса (Fuchs) однородных линейных диференциаль-
ных уравнений.
d) Нахождение решения. Рассмотрим снова диференциальное
уравнение:
d“u ^(x)d”-i« $Р2(х) da~^u , фя(х)
dxa Tx-a dxn~y ‘(x — a)2 dxn~*'r (x — a)n u~v>
где $Дх)— правильные в окрестности х = а функции. Постараемся
•найти выражение интеграла
и = {х — a)r[co + ciU — «)4-с2(х —a)2+ •••] (со^°) (54)
в явном виде.
Применим снова подстановку /т= 7Ф, где G — новая неизвестная, а
Т—функция, которую мы потом определим соответствующим образом.
Мы имеем:
dttZ dtt~^ , J«~2G . , .
dxn * Q1 dx”-1 + ^2 jj^-2 + • • • +
причем qk на основании предыдущих вычислений равно
Гл\ TW ,д nT^x) fn_2\T^ QMx)
k) T \/e—V Т х — а ‘ —2/ Т (х — а)2 1
k
<^>.2........«>.
v=0
Положим
Т— (х — а)г,
Т’=г(х — ау~\ Tn=zr(r— 1) (х — а)г~\
T^ = \f\(x — a)r-m,
tn
«причем через [г] мы обозначим здесь произведение г {г—1) ... (г—т)
о
а [г] = 1.
ЛИНЕЙНЫЕ ДИФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
315
Мы имеем:
й и(х-«)-*+1^+
( Zи\ /я - 1 \ 1 Z/2 — 9\ —2
= (x - a) (J И + [k _ ]) И (X) + (k _ 2) № W + • • •
••• + (ЛТЙ)иФ*(-«)} (A=l, 2,... , л).
Новое уравнение можно поэтому переписать так:
, О2(х) d-^ , £>„(*)
dxn ‘x—adxa~1~r~(x — a)2dxn~2' * ’" (x—a)n ' '
где функции
£W=(Z) й + (feZj)H w+
+ (J Z 2) иЧ W+...+(” 7 k) Й (x)=
k
= r~У! 7-------k(rZi7g---Vi W; №) =1
(n — k)l (r—k-]-v)l(k— v)l 4 °
правильны при x = a. Это уравнение имеет решение
Е — с0 4- сг (х — а) 4- с2 (х — д)2 4~ ...
Если умножить обе части уравнения (56) на (х — а)п и совершить
предельный переход при х—то вследствие правильности функции
&п(х) мы в пределе получим
Но Е (д)=со^0, а потому необходимо, чтобы было £}ге(<т)=0. Таким
образом мы приходим к равенству
/ц\ п /п 1 \ я— 1 /„ 9\л-2
(л) И + U _;) и 5-₽1 («) + (л-2) И ?р2 («) 4-. •. = 0.
Так как
то это равенство можно переписать в следующем виде:
ф(г) = г(г_1)(г—2)...(е —л4-1)4-г(г—1)... (г — л4-2)5р1(«)4-
4-г(Г-л + 3).ф2(а)Ч-...-Ж(«) = 0, (57)
т. е. показатель г интеграла и удовлетворяет алгебраическому уравне-
нию л-го порядка. Это последнее зависит только от л и от значений
316
ПРИЛОЖЕНИЕ
функций 5|'л(х), ф2 (х), ... , при х = а. Согласно Фуксу это
уравнение называют определяющим фундаментальным уравнением,
принадлежащим особой точке х = а.
Эти показатели можно, конечно, определить и из выведенного выше
характеристического уравнения (27). Но в то время как определяющее
фундаментальное уравнение можно определить непосредственно из коэ-
фициентов диференциального уравнения и притом очень просто, соста-
вление характеристического уравнения требует предварительно знания
какой-либо фундаментальной системы решений. Показатели г связаны
с корнями <о характеристического уравнения равенствами:
Эти равенства связывают между собой корни уравнений F(w) — 0 и
Ф (г) = 0. Если корень г уравнения Ф (г) = 0 многократный, или если
два корня уравнения ф(г) = 0 отличаются друг от друга на целое
число, то среди корней уравнения 7'(w) = 0 имеются кратные, и су-
ществуют интегралы вида (44). (Наличие в этом выражении логарифмов
не обязательно.)
После того как найдено г, мы можем для функции (х—а)~ги вы-
числить коэфициенты формального разложения в степенной ряд. Схо-
димость этого ряда доказывается, как и для правильной точки, путем
сравнения данного уравнения с „ мажорантным “ дпференциальным
уравнением.
Указатель
Абелева формула обращения 255
— теорема непрерывности 151
Абрагам 102, 237
Адамар 83, 110, 118, 129
Адамара теорема о детерминанте 264
Алгебраическая задача 259
Алгорифм решения уравнений 233
Ампера закон 217
Аргумент комплексного числа 281
Бельтрами теорема 52, 242, 249
Беркнес 236
Бесселя уравнение 58, 99, 184, 193
225 230
— функция 58, 126, 180, 189, 240
Бибербах 209
Билинейная форма 74
Биномиальный ряд 162
Биполь (двойной источник) 47
Бихарактеристика 110
Бонне 178
Баллиса формула 185
Вебер 257
Вебера разрывные интегралы 246
Вебстер 222
Вектор 13
Вейерштрасса функция 204
Вией 147
„Внешняя" и „внутренняя" поверх-
ность двойного слоя 34
Волны стоячие 76
— разрывов 183
— расходящиеся и сходящиеся 77
— удара 134, 135
— ускорения 139
Волновое уравнение 44, 116, 120
--- неоднородное 51, 102
Волновой потенциал 146
Вольтерра метод 80, 114, 116, 125
— уравнение 129
Вынужденные колебания 64
Вычет 292
Ганкеля функция 189, 236
— теорема 251
Гармонические колебания 72
— обертоны 73
— функции 14, 61, 152
ГаУ147 теоРема ° Дивергенции 9, 27,
Геллингер 255
Географическая долгота 158
Гейне 180
Гидродинамики задача 220
Гильберт 43, 66, 91, 259, 275, 280
Гильберта теорема 277
Гиперболическое уравнение 85, 96
Гиперплоскость 124
Г иперповерхность 109
Гиперцилнндр 127
Грина слой 60
— теорема 39
— формулы 13, 27, 90, 113
— функция 59, 63, 68, 70, 76, 91
Гурса 238
Гюгонио 133, 142
— теорема о скорости 141
Гюйгенса принцип 51, 125
Давление 135
Даламбер 96
Дарбу 178
Детерминант 260, 304
Диаметр области 17
Дивергенция вектора 9
Диполя потенциал 33, 48, 220
Дирихле 178
— задача 41, 151, 258
— интеграл 168
Диск 251
Допплера принцип 98
Жидкости движение 219
— колебания 225
Закон обратимости в акустике и оп-
тике 70
Зоммерфельда исследование 75
Зональные шаровые функции 154
Излучения условие 77
Интеграл Дирихле-Меллера 168
— комплексный 79, 287
— несобственный 37, 241, 242
— полный 124
Интегральное уравнение 65, 128, 2о8
318
УКАЗАТЕЛЬ
Интегральное уравнение однородное
273
Источник волны 47
— звука 98
— тепла 16
Итерация 269
Камертон 236
Кирхгофа формула 50, 122
Кинетической совместности условие
137, 143
Колебания газа 74, 225, 229
— круглой пластинки 227
— • струны 75, 94
— собственные 72, 225
— сферы 232
— прямоугольный мембраны 70
— круглой мембраны 225
Колебаний уравнение 55, 75, 224, 229
Компоненты вектор-функции 9
— ньютоновского поля 14
Конечная часть 131
Конечности условие 77
Коноид 110
Коиормаль 89, 113
Конус характеристический 109
Концентрация потенциала 20, 39
Коши-Ковалевской теорема 42
Коши задача 80, 183
— интегральная формула 290
— теорема 288
Краевые условия 42
Кратные корни 295
Кривая спрямляемая 189
Круговое кольцо 227, 252
Круговая симметрия 58
Кулон 10, 20
Кулона исследование 125
Ламб 214
Лагранжа уравнение 134
Ламе диференциальное уравнение 198
— произведения 204
— функции 200
Лапласа ряд 176
— уравнение 26, 42, 80, 172
— формула для скорости звука 142
— функции 160
Лежандра полиномы 154, 162
— присоединенные функции 170
— уравнение 160, 211, 224
— функции второго рода 213
Лерха теорема 250
Линии особые 117
— тока 223
— узловые 73, 227
Линейное диференциальное уравне-
ние 292
--------в комплексной области 298
— уравнение 86
Линейный оператор 88
Липшица условие 130
Лиувилля метод 46
Лова 147
Лорана ряд 303
Лоренц 52, 105, 122
Ма клорен 237
Максвелла представление шаровых
функций 152
Меллер 168
Мембрана круглая 225
— прямоугольная 70
Метод итераций 269
— мажорант 83
— Римана 99
Мероморфная функция 286
Многочлен однородный 148
Момент инерции 219
Мощность источника 49
Направляющие косинусы 14, 152, 155
Напряженность поля 10
Неймана задача 43, 220, 258
— теорема сложения 238
Николаи 220
Норм нрование фундаме нтал ьных
функций 74, 279
Ньютонов потенциал 13, 152
Ньютоново поле тяготения 9
Области бесконечные 74
Однородный многочлен 148
Однородности условие 148
Оператор 88, 228, 268
Определяющее фундаментальное урав-
нение 315
Ортогональные координаты 209, 223
Ортогональные функции 226
Особая линия 117
Особые точки 285
Отношение объемных расширений 135
Охлаждение шара 229'
Параболическое уравнение 86
Пиддакк 147
Плимели 272
Плотность источников 68, 75
— масс двойного слоя 40
— — простого слоя 40
Поверхностная плотность 27
Поверхности уровня 155
Поккельс 56
Поле ньютонова тяготения 9
— силовое 25
Полиномы Лежандра 154, 162
Полюс функции 286
Полупространство 61
Порядок полюса 286
УКАЗАТЕЛЬ
319-
Потенциал 14, 215, 247
— логарифмический 26
— простого слоя 27
— двойного слоя 34, 258
— любого тела 218
— материального круга 216
Потенциал сферического слоя 217
— электропроводящего диска 256
Поток волнового потенциала 48
— сквозь поверхность 10, 19
Привалов И. И. 287
Притяжение материальной окружно-
стью 215
Пуассона интеграл 64
— уравнение 20, 27, 29, 40, 54, 61,
75, 118, 217
Пуассона-Парсеваля решение 120
Разложение в ряды по сферическим
функциям 176, 217
— — — по функциям Ламе 204
— — — по фундаментальным
функциям 231
— в степенные ряды 291
Распределение масс 22
Разрывы продольные и поперечные 138
Реймонд д, Б. 99
Резольвента 267
Релэй 52, 57, 104
Риман 133, 142
Римана определение функции Грина 98
Родрих 163
Ряд биномиальный 162
— Лапласа 176
— Тейлора 291
Самосопряженное уравнение 114
Скорость абсолютная 138
— распределения разрывов 138
„След" волны 129
Соленоидальный вектор 221
Сопряженный оператор 88
Софокусные поверхности 195
Спектр фундаментальных чисел 76
Спектроскоп 98
Сплошности уравнение 135
Среднее значение функции 69
Стоячие волны 76
Сферическая волна 47, 234
— функция 150, 177, 230
Сферический эллипс 150
Сходимость рядов Лапласа 178
Тедоне 124, 125, 129
Телеграфное уравнение 98, 125
Телефон 228
Теорема Адамара 264
— о взаимной переместительности
источника тепла и точки 61
— о градиенте 12, 27
Теорема сложения Неймана 238
— о среднем значении 40
Тессеральные функции 173
Тождественности условие 137, 141
Точка особая 285
— существенно особая 287
— несущественно особая 308
Трансцендентная задача 263
Угол телесный 128
Удельный объем 135
Узловые линии 31, 227
Уравнение гиперболическое 85, 92,111
— волновое 44, 116, 120
— вынужденных колебаний 64
— динамической совместимости 141
— колебаний 55, 75, 224, 229
— Ламе 198
— Лежандра 160
— линейное 86
— параболическое 86, 111
— самосопряженное 89
— с многими переменными 105
— сплошности 135
— телеграфное 98
— эллиптическое 86, 90, 110
Условие Дирихле 251
— излучения 77
— кинетической совместности 137„
143
— конечности 77
— Липшица 130
— однородности (Эйлера) 148
— тождественности 137, 141
Фишер 222
Фонограф 228
Форма квадратическая 260
— линейная 262
— определенная НО
Фредгольм 37, 259, 268
Фукса класс 313
Фундаментальные уравнения 199
— функции 65, 224, 226, 274, 300
— числа 65, 75, 225, 274
Функции аналитические 282
— Вейерштрасса 204
— Гамма 184
— гармонические 14, 61, 152
— зональные шаровые 154
— Ламе 200
— Лежандра 170, 176
— непрерывные 283
— плотности масс 15
— присоединенные 88, 112
— производящие 163, 182
— симметрические 259
— сферические 150, 177, 230'
— тессеральные 173
— тока 223, 247
320
УКАЗАТЕЛЬ
ф Н:*ии шаровые 148
— эллиптические 198
функциональные уравнения 183
Фурье двойной ряд 72
— интеграл 76
— интегральная теорема 55
Характеристики 83, 142
Характеристическое уравнение 302
Хорн 83, 308
Центробежные моменты инерции 220
Цилиндрические координаты 192, 238
— функции 183
Часть конечная 131
Чебышева полиномы 240
Числа комплексные 281
— фундаментальные 65, 75, 225, 274
Шара охлаждение 229
Шаровые функции 148
Шварца неравенство 178
Шмидта Э. решение интегрального
уравнения 67, 280
Эквипотенциальные кривые 223
Электромагнетизм 214
Электрическое отражение заряда f62
Эллиптические координаты 194, 102
237
— функции 198
Эллиптическое уравнение 86, 90
Эллипсоиды вращения 209, 222, 236
Эйлера константа 185
Явление Римана-Гюгонио 147
Ядро интегрального уравнения 259
— разрешающее 257
— решающее 70, 74
Якоби 166
Янке-Емде 229