Автор: Кушнір І.
Теги: тригонометрія видавництво факт доведення тотожностей і нерівностей розв’язання рівнянь обчислення виразів
ISBN: 966-359-135-8
Год: 2006
Текст
ІСААК Кушнір
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
Київ • 2006
УДК 514.116(076.1)
ББК 22.151.0я7 К 96
ISBN 966-359-135-8
© І. Кушнір, 2006 © Дизайн, макет.
«Факт», 2006
ПЕРЕДМОВА
Запропонована 101 задача фактично охоплює весь практикум зі шкільної тригонометрії: доведення тотожностей і нерівностей, розв’язання рівнянь, обчислення виразів.
Розбираючи приклад за прикладом, ви зможете не тільки перевірити себе в застосуванні теоретичних знань, але й збагатити арсенал прийомів розв’язання задач, які зазвичай постійно зустрічаються на іспитах до найпрестижніших вузів.
Сто однією задачею не закінчиться ваше спілкування з цією популярною частиною математики, але вивчена книга надасть З
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
вам упевненості під час контрольної роботи та іспиту, а окремі приклади подарують і естетичну насолоду.. Це і є метою автора та видавництва.
і. ДОВЕДЕННЯ ТОТОЖНОСТЕЙ
Задача 1. Довести, що
sin* 2a + tg2a-l 2 —2 —2 7 = t≡ a∙
cos a-ctg a + 1
Доведення
Винесемо у чисельнику sin2 а, в знамент нику cos2 a:
N>l
∙2ι 1 1
sin a 1 + — —
< cos a sin a?
2 1 1 1
cos a 1 — + ——
I sin a cos a
= tg2α.
5
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
№ 2 Задача 2. Довести, що
tg3α ctg3a 1 4, 3 ,
, + 5 : = tg a + ctg а.
sm a cos a sin a cos а
Доведення
Зауважимо, що
? = tg a + ctg a. cos a sin a
Тоді
tg3a 1 ι ctg3a ^^∙ 2 ∙ ' 2
sin a cosa sin a cos a
= tga
f 1 2
V cos a
= tg a ∙ tg2a + ctg a ∙ ctg2a = tg3a + ctg3a.
n* з Задача 3. Довести тотожність:
sina + sinβ + sinγ-sin(a + β + γ) = λ . a + β . β + γ . a + γ
=4 sin sin -—- sin -.
2 2 2
6
і. Доведення тотожностей
Доведення
Маємо
sinα + sinβ+sinγ-sin(a + β+γ) =
_ . a + β a-β. = 2 sm cos 4
2 2
sinγ-sin(a + β+γ) =
π . a + β a-β =2 sin cos +
2 2
_ . -a-β a + β + 2γ
+2 sin -cos - =
2 2
o . a + βf a-β a + β+2γ^
2 lk 2 2 J
к . a + βf π . a + β+2γ + a-βλ∖
2 I 22 }
f . a-β-a-β-2γ^
I 2-2 )
λ . a + β . a + γ . β+γ =4 sin sin sin -—-
2 2 2
7
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
n>4 Задача 4. Довести, що
tg(α -β) + tg(β -у)+tg(γ - а) = = tg(a -β)tg(β -γ)tg(γ - а).
Доведення
Зауважимо, що з формули
tg(a±βb-⅛2±⅛β,
V p' l + tgatgβ
випливає, що
tg a + tg β = tg(a + β)(l - tg a tg β), Маємо
tg(a -β ÷ β -γ)(l - tg(a -β)tg(β -у))
+tg(γ-a) =
= tg(γ - a)(-l + tg(a -β)tg(β -у) +1) = tg(γ - a)tg(a -β)tg(β -у).
n> s Задача 5. Довести, що
tg2 a tg(30o-a) + tg2 a tg(60o-a) + +tg(60o-a)tg(30o-a)=1.
8
і. Доведення тотожностей
Доведення
Використаємо формулу з попередньої задачі. Позначимо А — ліву частину тотожності: A = tg2α(tg(30o-α) + tg(60o-a)) + +tg(60o-a)tg(30o-a) =
= tg 2 a tg(30o-a+60o-a) × × (1 - tg(30o-a)tg(60o-a)) + +tg(60o-a)tg(30o-a) =
= tg2a ctg2a(l-tg(30o-a)tg(60o-a)) + +tg(60o-a)tg(30o-a) = 1.
Задача 6. Довести тотожність
№6
ctga-tga-2tg2a =4ctg4a.
Доведення
Маємо
ctga-tga-2tg2a =
2 • 2
cos a—sin a _
2tg2a =
cosa ∙ sin a
2cos2a 2sin2a sin2a cos2a
9
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
2(cos22 α - sin2 2 a) sin2a∙cos2a
4cos4a λ i a
= = 4ctg 4a.
sin4a
Зверніть увагу на формулу, яка була доведена «по ходу»:
ctg a-tg a =2ctg2a.
№ 7 Задача 7. Довести тотожність sin8a + cos8a+4sin2acos2a = = 1 + 2 sin4 a cos4 a.
Доведення
Маємо
sin8a + cos8a+4sin2acos2a = = (sin4 a + cos4 a)2 -2 sin4 a cos4 a + +4sin2acos2a =
= ((sin2a + cos2a)2 -2 sin2 a cos2 a) -2 sin4 a cos4 a + 4 sin2 a cos2 a =
10
і. Доведення тотожностей
= (1 -2 sin2 α cos2 a)2 -
-2 sin4acos4a+4sin2acos2a =
= l-4sin2acos2a+4sin4 a cos4 a-
-2 sin4 acos4 a+4sin2acos2a =
= 1+2 sin4 a cos4 a.
Задача 8. Довести, що ns 8
sin5 a =-sina——sin3a + - sin5a.
8 16 16
Доведення
sin5 a = sin a sin4 a =
= sina
1 + cos4a
= -sina l-2cos2a +
4 I
1 .
tf к z
1 . (з 1
= -sina —2cos2a + -cos4a
4 2
11
101 задача з тригонометрії
-sinα—(sin3a
8 4v
= -sina—sin3a + -sina + 8 4 4
1 . _ 1 • о
+—sin 5 a sm3a =
16 16
5 . 5 . 0 1 . ,
= - sin a sm3on— sm5a.
8 16 16
№ 9 Задача 9. Довести тотожність
i cos2a + sin2a
tg 4a + cos 4a = rτr-∙
cos2a-sm2a
Доведення
Розглянемо ліву частину тотожності: л 1 tg4a + — =
cos4a
sin4a 1 1 + sin4a
= 1
cos4a cos4a cos4a
12
і. Доведення тотожностей
71
1 + cos —4α
V )
cos4a
ґп А
2 cos* 2 —2 a
U J
cos4a
Доведемо, що цьому дробу дорівнює права частина тотожності:
π J π п
. ^ cos2a + cos —2a cos2a + sm2a 12
cos2a-sin2a ∏ (π o А
cos2a-cos —2 а
∖2 J
2 cos-cos —2 а
4 \4 )
o . π . (π n А
2 sin-sin —2 а
4 U J
оґ 71
2 cos2 —2 а
И )
sinf--4a'
Ь )
(тг А
2 cos2 —2 а
И )
cos4a
Задана тотожність доведена.
13
2. СПРОСТИТИ...
№10
Задача 1. Спростити
sin2 β - cos2(α - β) + 2 cos a cosβ cos(a - β).
Розв’язання
Застосуємо формулу «пониження степеня»:
l-cos2β , оХ
—-+cos(a - β) ×
× (-cos(a -β) + 2 cos a cosβ) =
l-cos2β , oλ
= —- + cos(a - β) ×
× (-cosa cosβ - sin a sinβ + 2 cos a cosβ) =
= J—cos2β + cos(a cos(a + β) =
14
2. Спростити...
1—cos2β + l(c0s2 α + cos2β) = = — (1 + cos2 a) = cos2 a.
Відповідь: cos2 a.
Задача 2. Спростити
№11
sina +
sin a J
+ cosa +
4 cosa >
Розв’язання
Розкривши дужки, отримаємо . 2 1 π 2 1 sin a + ■ + 2 + cos a + . +
sin a cos a
+2 -tg2a-ctg2a =
= sin2 a + cos2 a+4 +
+(1 + tg2a) +(1 + ctg2a) - -tg2a-ctg2a =1+4 + 2 =7.
Відповідь: 7.
15
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
№ 12 Задача 3. Спростити
ctg2α tg4a 6
• 2 "Г 2 "*^ 2 ’
sm a cos a cos a
∕ 1 tg2a
ksin2a cos2 a,
Розв’язання
Маємо
cos2 a sin4 a 6 4 4sin2a
—∑- ÷ —r- + —5— + —5— ÷ —4— sin a cos a cos a sin a cos a
1
= 7 7-×
sin a cos a
× (cos8 a + sin8 a+6 cos4 a sin4 a +
+4cos6asin2a+4cos2asin6a) =
(sin2 a + cos2 a)4 1
sin4 a cos6 a sin4 a cos6 a
d 1
Відповідь: —3 7—.
sin a cos a
16
2. Спростити...
Задача 4. Спростити № із
sin2 4α+4 sin4 2 α-4 sin2 2 α cos2 2 а
4 - sin2 4α -4 sin2 2 а
Розв’язання
Маємо
sin24α+4sin42α-4sin22αcos22α _
4 - sin2 4a -4 sin2 2 a
(sin4a)2+4sin42a-4sin22acos22a _ (4 -4 sin2 2 a) -(sin4a)2
(2sin2acos2a)2 +4sin4 2a -4sin22acos2 2a 4^1 -sin22a)-(2sin 2acos2a)^
4sin22acos22a+4sin42a-4sin22acos22a 4cos22a-4sin22acos22a
4sin42a _ sin4 2 а
4cos22a(l-sin22a) cos2 2 a cos2 2 а
sin4 2 а cos4 2 а
= tg42a.
Відповідь: tg42a.
2-6-1991
17
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
n, 14 Задача 5. Спростити
0 -4( sin4 α + cos4 α-sin6 α-cos6 α)) 1 -1.
Розв’язання
Розкладемо спочатку на множники вираз у внутрішніх дужках. Дістанемо:
1 -4(sin4 α + cos4 а - sin6 а - cos6 а) =
= 1 -4^sin4 а(1 - sin2 а) + cos4 α(l -cos2 а)) =
= 1 -4(sin4 а cos2 а + cos4 а sin2 а) =
= l-4sin2αcos2α(sin2α + cos2α) =
= 1-4 sin2 a cos2 а =1-(2 sin a cos а)2 =
= l-sin22a =cos22a.
Отже, заданий вираз дорівнює
1 1 l-cos22a tr 2n
—5 1 = з = tg 2 а.
cos 2a cos 2 а
Відповідь: tg22a.
18
2. Спростити...
Задача 6. Спростити до is
cos(α -β+γ) + cos(β+у -а) -
-cos(a + β -γ) - cos(a + β+у).
Розв’язання
Маємо
(cos(a -β + у) + cos(β + у - а)) -
-(cos(a + β - у) + cos(a + β + у)) =
n a-β+γ÷β+γ-a
2
a-β+γ-β-γ+a
× cos —-—-—
2
^ a+β-γ+a+β+γ
2
a÷β-γ-a-β-γ
× cos — —- =
2
= 2 cosγcos(a -β) -2 cos(a + β)cosγ =
= 2 cosγ(cos(a -β) - cos(a + β)) =
=4 sin a sin βcosy.
Відповідь: 4 sin a sinβcosy.
19
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
№ їв Задача 7. Спростити
r 4tg2α(l-tg22α)
2 sin 2 a + √3 sin4a -> —÷.
sin8a(l + tg22a)
Розв’язання
Позначимо заданий вираз як А. Маємо sin22a l-tg22a _ cos22a _ l + tg22a і ι sin22a cos22a cos22a-sin22a = cos22a — _ cos4a.
cos22a + sin22a cos22 a
Далі, враховуючи формулу
2tgf smx = —,
l + tg2∣
дістанемо, що
2tg2a . л —≡-— = sm4a.
l + tg22a
20
2. Спростити...
Отримуємо
. , . /т . λ 2sin4acos4a
А = 1 - cos4a + √3 sm4a
sin 8 a
= T3sin4α-cos4α =2 —sin4a—cos4a , 2 2
= 2
( . . π л ∙
sm4a cos— cos4a sin—
= 2 sin
(Λ 4a —
I 6 6j
I 6 J
7Γ
Відповідь: 2 sin 4a —
21
з. ЧИСЛОВІ РІВНОСТІ
n» 17 Задача 1. Довести, що
sinl0o coslO°
Доведення
Враховуючи, що 7з = tg 60°, нерівність, яку ми доводимо, запишемо у вигляді:
1 sin60o λ =4. sin 10o cos600cosl00
Перетворимо ліву частину: cos600cosl00-sin600sinl00 _ sin 10o∙cos60o∙ cosl 0° _ cos70o _4sin20°_4 ^ -sin20o~ ' sin20° 2 2
22
З- Числові рівності
Задача 2. Довести, що tg20o+4sin20o=73. №18
Доведення
♦ 'їло л • оло sin200+4sin200cos200
tg 20o+4 sm20o=
cos20o
sin20o+2sin40o _ sin20o+sin40o+sin40o cos20o cos20o
2sin300cosl00+cos500 _ cosl00+cos500 cos20o cos20o
_ 2 cos300∙cos200 _ cos20o
Задача 3. Довести, що
№19
√33-16√3 sin80o =1 + 8 sinl0o.
Доведення
Маємо
(1 + 8 sin 10o)2 = 1 +16 sin 10o+64 sin210o=
= l + 32(sin300∙sinl00-cos200+l) = = 33 + 32(sin300∙sinl00-cos(300-100)) = = 33 + 32(-cos30°∙cosl 0o) = 33 -16>/3 sin80o.
23
101-ЗАДАЧА З ТРИГОНОМЕТРІЇ
N»20
Задача 4. Довести, що
tg7o30'=√6 + √2-√3-2.
Доведення
1 ∕l + cos30o
2
tg7W=≥⅛-ї sinl5°
l-cos30o
2
Але
√3
2
2
2
2
= √8+4√3 =2√2 + √3, тобто tg 7o30' = >/б + л/2 ->/3 -2.
24
З- Числові рівності
Задача 5. Довести, що № 21
tg 20o+tg 40o+tg 80o= 8 sin40o+л/З.
Доведення
Маємо
tg 20o+tg 40o+tg 80o-tg 60o=
sin60o sin20o = 1 =
cos200cos400 cos800cos600
sin600cos800 λ .no z14
= +4 cost 0o. (1)
cos200cos400cos800
Використаємо дуже важливу формулу:
4cosαcos(600-a)cos(600+a) = cos3a. (2)
Звідси
cos200∙cos400∙cos800= і, 8
тому вираз (1) набуде вигляду:
8sin600sinl00+4cosl00=
=4(cos50°-cos700+cosl00) =
=4(sin40o+2 sin40osin30o) =8sin40o.
Отже,
tg 20o+tg 40o+tg 80o= 8 sin40o+T3.
25
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
№ 22 Задача 6. Довести, що
sin 36o ∙ sin 72o=-.
4
Доведення
sin 36o ∙ sin 72 o= √sin236o∙ sin272o =
= у √(1 - cos 72 o)(l - cosl44o) =
= і λ∕1 - cos 72 o-cosl 44o+ cos 72 o ∙ cosl 44o =
=—Jl-2cos36o ∙ cosl080+cos720 ∙ cosl44o =
2 v
=—Jl + 2 cos36o ∙ cos72 o-cos72 o ∙ cos36o =
2 *
= jλ∕1 + cos36o∙ cos72°.
Доведемо, що
cos36o∙cos72o= і
4
Справді, домножимо і розділимо ліву частину на 4 sin 36°.
26
3. Числові рівності
Маємо:
->zn 2 ∙2sin36o∙ cos36o∙ cos72o
cos36o ∙ cos 72°= —— =
4sm36o
_ 2 ∙ sin 72o ∙ cos72 o _ sin!44o _ 4sin36o 4sin36o 4
Отже, повертаючись до заданої рівності, дістанемо:
sin 36o ∙ sin 72 o= - Ji +- = 2 V 4 4
що і треба було довести.
Задача 7. Довести, що № гз
tg210o+tg250o+tg270o=9.
Доведення
Враховуючи, що , 1 1 + tg а=—J—, cos а
ліва частина рівності дорівнює
1 ι 1 ι 1 3 cos210o cos2 50o cos270o
27
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
Використаємо формулу (2) із задачі 5: cosl00cos500cos700=icos300=-. 4 8
Звідси ліва частина заданої рівності набуде вигляду:
— Г cos2 50ocos2 70o+ cos2 70ocos210o+
З l +cos2100cos2500] -3 =
= — [(1 - cos80o)(l - cos40o) +
+(1 - cos40o)(l + cos20o) + +(1 + cos20o)(l -cos80o)]-3 =
= т^[3 -2(cos400+cos800-cos200) +
+cos800cos400-cos400cos200- -cos200cos800]-3.
Оскільки
cos800cos400-cos200cos800-cos400cos200= = cos800(cos400-cos200) -i(cos600+cos200) =
28
З- Числові рівності
1 (1
= cos800(cos400-cos200) cos!60o
2^2
= cos800(cos400-cos200) 2 cos2 80o+1
2\2
= cos800(cos400-cos200+ cos80o) —.
то, враховуючи рівність cos400-cos200+ cos80o=
= 2 cos600cos200-cos200=0,
дістанемо
1А/ -5λ
tg210o+tg250o+tg270o=- 3-- -3=9.
4
Задача 8. Довести, шо
№ 24
Зте л . 2π /тт tg — +4sm— = √11.
11 11
Доведення
Доведемо рівносильну рівність
2 З ТЕ і > 2 2 ТЕ л З ТЕ . 2 ТЕ ∣ • л tg— + 16sm— + 8tg—sin 1.1 =0.
11 11 11 11
29
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
Домножимо її на cos2 ⅛ Дістанемо
. 23π o . 3π . 2π 3π
sin — + 8 sin—sin—cos— +
11 11 11 11
+16sin2-cos2 — -llcos2- =0,
11 11 11
звідси
1 lo 23π o . 3π . 2π 3π 1-12 cos— + 8sιn—sm—cos— +
11 11 11 11
4πY1 6π^ +4 1-cos— l÷cos—
=0,
тобто
1 -б( 1 + cos—
I ∏J
. . 6π . 2π +4sιn—sin— + 11 11
λ( ∖ 4πYι 6πA n +4 1-cos— 1 + cos— =0,
або _ r 6π n 4π _ 8π -5-6 cos— + 2 cos 2 cos— +
11 11 11
. λ 6π . 4π λ 4π 6π λ
+4+4 cos 4 cos 4 cos—cos— =0,
11 11 11 11
30
3. Числові рівності
отримаємо
, ~ 6π n 4π ~ 8π -1-2 cos 2 cos 2 cos
11 11 11
n 10π ~ 2π λ
-2 cos 2 cos— =0,
11 11
що рівносильно тотожності
2π 4π 6π 8π 10π 1
cos— + cos— + cos— + cos— + cos— = —.
11 11 11 11 11 2
Для її доведення домножимо обидві частини на 2 sin—. Маємо:
π . 3π . 3π . 5π . 5π
-sin— + sin sin— + sin sin +
11 11 11 11 11
. 7π . 7π . 9π . 9π
_ . . . llπ
+ sin sin — + sin sin— + sin
11 11 11 11 11 π = -sm-,
11
що є очевидною тотожністю.
31
4. ОБЧИСЛИТИ...
№25
Задача 1. Обчислити
2 cos400-cos200 sin20o
Розв’язання
2 cos400-cos200 _ cos400+(cos400-cos200) sin20o sin20o
_ cos40o-2 sin30osin 10° _ sin 20° cos400-sinl00 sin50o-sinl0o
sin20o
sin20o
2sin200cos300 sin20o
= 2cos30o=73.
Відповідь: √3.
32
4. Обчислити...
Задача 2. Обчислити № ге
(sinx + cosx)3 + 2(sinx-cosx) (sin х -cosx)3 - 7(sin х + cosx)
при tgx =0,6.
Розв'язання
Домножимо на «тригонометричну одиницю». Маємо:
(sin X + cos x)3 + 2(sin х - cos x)( sin2 x + cos2 x)
(sin x - cosx)3 - 7(sin x + cosx)(sin2 x + cos2 x)
Поділимо чисельник та знаменник на cos3 х. Дістанемо вираз
(tg х +1)3 + 2(tg х -l)(tg2x +1)
(tg х - І)3 - 7(tg х +1)( tg2x +1) ’
який при tg х =0,6 дорівнює 3,008 _ 47 15,296 " 239’
d∙ . 47
Відповідь: .
239
3-6-1991
33
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
№27
Задача 3. Обчислити
1
+ π sin— 15
. 2π sm— 15
. 4π
sin— 15
1 8π* 15
Маємо
Розв'язання
π sin— 15
. 4π sin— 15
1
1
1
π . 4π -sin— + sm—
15 15
π . 4π sin—sm—
15 15
. π . π λ γz Zπ 4 cos— sin — 4√3 cos—
6 10 5
π 1 n π і cos 2 cos—1
5 2 5
Аналогічно,
1 1 4>∕3cos-
і і _ 5
. 2π+ . 8π o 2π 1
sin— sin— 2 cos— + 1
15 15 5
34
4. Обчислити...
Таким чином,
2π cos— 5
π COS-
5
2cos--l 2 cos— + 1
5 5
2 cos2 — + cos—+2 cos2 - - cos- =4√3 -—- ½-=—— =
. 7t 2 7C л 7t ∕⅛ 2 7C і
4 cos-cos— + 2 cos—2 cos 1
5 5 5 5
2-2 cos--cos—'1
=4√3 ≡ *Λ=
. 7C 21L z‰ 7L * 2 71 1
4 cos-cos— + 2 cos—2 cos 1
5 5 5 5
Враховуючи, що
(довести!) помічаємо, що π 2π 1
cos—cos— = —.
5 5 2
Таким чином, заданий вираз дорівнює 4л/3.
Відповідь: 4л/3.
з*
35
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
№ 28 Задача 4. Обчислити
tg 9o-tg 63 o+tg 8 Γ-tg 27°.
Розв’язання
Маємо
tg9o-tg63o÷tg81o-tg27o= =(tg 9o÷ tg 8 lo) -(tg 63o+ tg 27o) = sin90o sin90o
cos90cos810
і
cos63ocos27°
1
cos9osin9o
sin27ocos27o
2
2
2 cos9osin9o
2 sin27ocos27o
2
2
sinl80
sin 54°
_ 2(sin54,
3-sinl8o) _
sinl 8o∙sin54o
2∙2sinl8o∙cos36o 4cos36o
sinl8o∙sin54o sin54o
Відповідь: 4.
36
4- Обчислити...
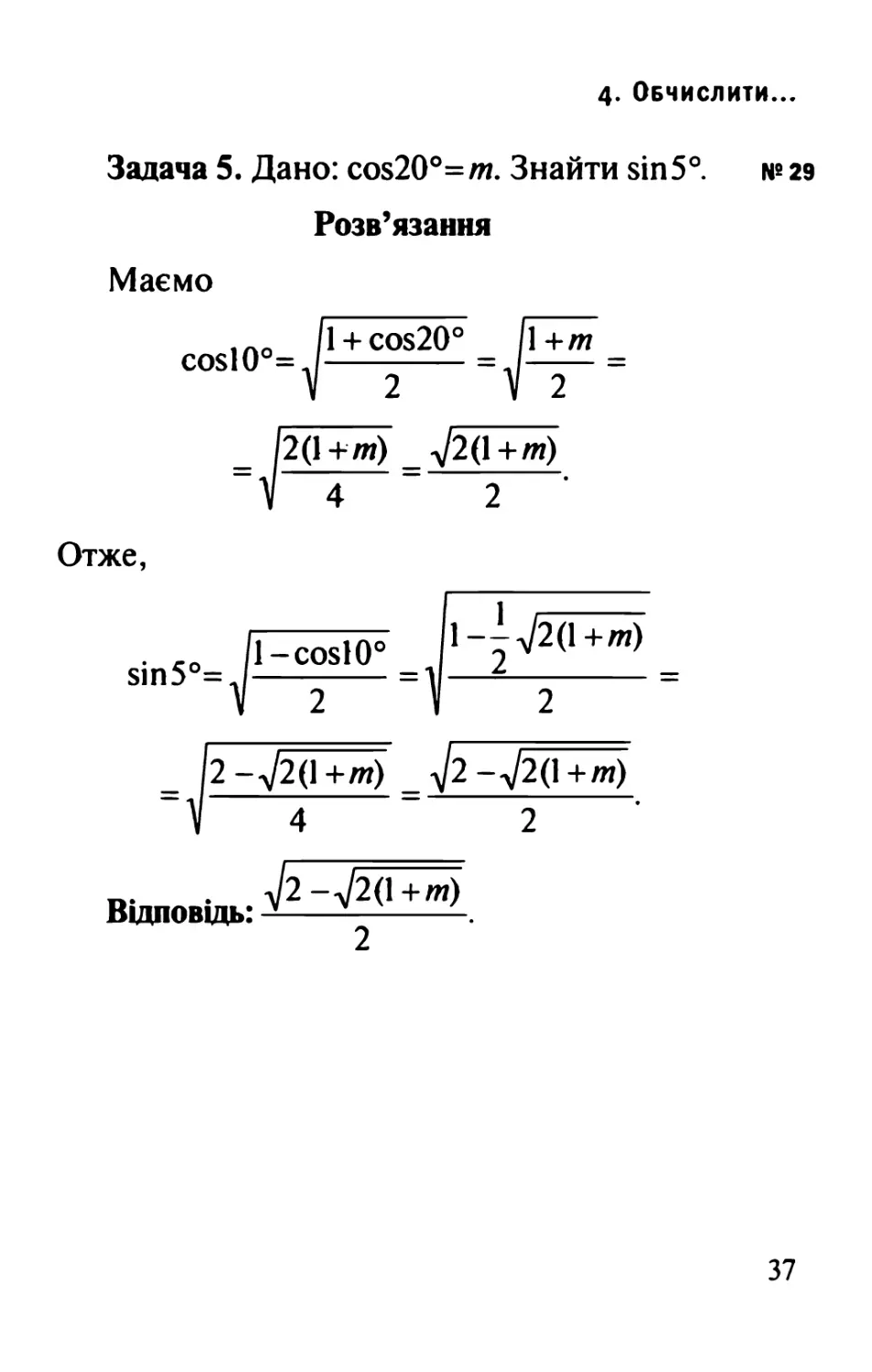
Задача 5. Дано: cos20o=т. Знайти sin50. № 29
Розв’язання
Маємо
iλo 11 + cos20o 11 +т
V 2 V 2
_ ∣2(l+m) _у/2(1+т)
У 4 " 2 ’
Отже,
. „ ∕l-cosl0o )∙-p20+^
sιn5o= =1 —÷ =
V 2 ї 2
= ⅛-√2(l+m) = √2-√2(l+∕n)
V 4 ^ 2
. √2-√2(l+m)
Відповідь: 2.
2
37
5. УМОВНІ РІВНОСТІ
м» зо Задача 1. Довести, що коли
х = a cosα sinβ, у = a sin a sinβ, z = a cosβ,
2 2 1 ">
то х +y +z =a^.
Доведення
Маємо 2 2 2
x+y+z- = я2 cos2 asin2β+ a2 sin2 asin2β + a2 cos2β = = а2 sin2 β( cos2 a + sin2 a) + +a2cos2β = a2sin2β + a2cos2β = a2.
38
5. Умовні рівності
Задача 2. Обчислити № зі
(l + tgα)(l + tgβ),
n π якщо α + β = —.
Розв’язання
Скористаємося співвідношенням
tgα + tgβ = tg(α + β)(l-tgα tgβ).
Маємо
(l÷tgaχi + tgβ) =
= 1 + tg β+tg a + tg a tg β =
= l + tg(a + β)(l-tga tgβ) + tga tgβ =
= l + tg-j(l-tga tgβ) + tga tgβ = 2.
Відповідь: 2.
Задача 3. Величини a, β, γ утворюють №32 арифметичну прогресію. Довести, що
sin a-sin γ cosγ-cosa
= ctgβ,
39
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
Доведення
За властивістю членів арифметичної про- гресп β= .Тоді
* a+γ . a-γ
2 cos f-sm
sma-smγ _ 2 2
cosγ-cosa^2sina + γsina-γ 2 2
= Ctg^y^- = Ctgβ,
n> зз Задача 4. Довести, шо коли tgatgβ = l, то sin2a=sin2β і cos2a =-cos2β, Доведення Маємо
sin a sin β = cosa cosβ, cos(a + β) =0.
Отже, sin2a-sin2β = 2sin(a-β)cos(a + β) =0, cos2 a + cos2β = 2 cos(a -β) cos(a + β) = 0.
5. Умовні рівності
Задача 5. Довести, що коли № 34
α + β+γ =2π, то
cos2 a + cos2 β + cos2 γ -2 cosa ∙ cosβ ∙ cosγ = 1.
Доведення
Маємо
cosγ = cos(2 π - (a + β)) = cos(a + β), звідки
cos2 a + cos2β + cos2γ -2 cosa cosβ ∙ cosγ =
_ 1 + cos2a +1 + cos2β
^ 2 +
+cosγ(cosγ -2 cos a ∙ cosβ) =
= 1 + cos(a + β)cos(a -β) +
+cos(a + β)(cos(a + β) -2 cosa ∙ cosβ) =
=1 + cos(a + β)cos(a -β) +
+cos(a ÷ β)(-cosa ∙ cosβ - sin a ∙ sin β) =
= 1 + cos(a + β)cos(a -β) - -cos(a + β)cos(a -β) = 1, що й треба було довести.
41
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
Я
n* 35 Задача 6. Довести, що коли a + β+γ =
sin2α + sin2β + sin2γ + 2sinα ∙ sinβ∙ sinγ =1
то
Доведення
sin2a + sin2β + sin2γ + 2sina ∙ sinβ∙ sinγ =
_ 1 - cos2 а +1 - cos2 β
" 2 +
+sin γ(sin γ + 2 sin a ∙ sin β) =
= 1 - cos(a + β) cos(a -β) +
+cos(a + β)(cos(a + β) + 2 sin a ∙ sin β) = = 1 -cos(a + β)cos(a -β) +
+ cos(a + β)(cosa ∙ cosβ + sin a ∙ sinβ) = = 1 - cos(a + β) cos(a -β) + +cos(a + β) cos(a - β) = 1,
шо й треба було довести.
42
6. ДОВЕДЕННЯ НЕРІВНОСТЕЙ
Задача 1. Довести нерівність № зв
0>4< sin4α +rE∞4α <од 1 + sin α 1 + cos а
Доведення
Враховуючи рівність
sin4 а + cos4 а =
= (sin2 а + cos2 а)2 -2 sin2 а cos2 а =
= l-2sin2αcos2 а,
дістанемо
sin4 a ι cos4 а 2 _
1 + sin4 а 1 + cos4 а 5
43
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
З sin4 α + 3 cos4 a + 8 sin4 a cos4 a -2 5(1 + sin4 a)(l + cos4 a) _ 1 -6 sin2 a cos2 a + 8 sin4 a cos4 a _ 5(1 + sin4 a)(l + cos4 a) (1 -4sin2 a cos2 a)(l -2 sin2 a cos2 a) 5(1 + sin4 a)(l + cos4 a) (1 -sin22a)(sin4 a + cos4 a 5(1 + sin4 a)(l + cos4 a)
Аналогічно, sin4 a cos4 a I 1 + sin4 a 1 ÷ cos4 a 2 sin4 a + cos4 a + 3sin4 a cos4 a -1 2(1 + sin4 a)(l + cos4 a) -2 sin2 a cos2 a + 3 sin4 a cos4 a 2(1 + sin4 a)(l + cos4 a)
• 2 2 j ∙ 2 ^> ι
sin a cos a -sin acos^a-l (l + sin4a)(l + cos4 a)
44
6. Доведення нерівностей
оскільки
3.2 2 3 . 2-л -х 3 .
—sin αcos a =-sm 2a ≤- <1.
2 8 8
Задача 2. Довести, що при будь-якому a №37 має місце нерівність
4sin3a + 5 ≥4cos2a + 5sina.
Доведення
Виразивши sin За і cos2a через sin а (див., зокрема, розділ 8 цієї книги) і позначивши sin a = у, отримаємо
4(3j'-4∕) + 5>4-8∕ + 5y, 16∕-8∕-7y-l<0.
Оскільки
16y3 -8y2 -7y -1 =(y -l)(4y +1)2,
то, враховуючи, що у = sin а, тобто у-1 ≤0, дістанемо
16y3-8y2-7y-l ≤0, що доводить задану нерівність.
45
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
№38
№ 39
Задача 3. Довести, що при всіх припустимих значеннях a
sina + tga >θ
cosa + ctga
Доведення
Помножимо чисельник і знаменник лівої частини нерівності на добуток sinα ∙cosα ≠0, отримаємо
sin2acosa÷sin2a 2 1 + cosa — = tg a- ; . sin a cos a + cos a l + sιna
Так як tga≠O, то tg2a>0; 1 + cosa > 0 і
1 + sina >0, такяксоза >-lisina >-l.
Задача 4. Довести, що cos(sinx) > sin(cosx).
Доведення
Маємо
cos(sinx
-cosx
46
6. Доведення нерівностей
^ . 1 π
= 2sιn + sιnx-cosx
2І2
×sιn
— sin х-COS X
×
π
П ∙ 1 π ∕T ∙ π
= 2 sin + √2 sin x —
×
2 2
f I ( _
1 π
×sm
2 2
π
— 7C
2 < — (1,41 <1,57) і так як
∣sinα∣ ≤1 i∣cosα∣≤l, то О < —÷72 sinΓx--
2 I 4j
< π,
2 cos
<π,
звідки і випливає потрібна нерівність, так як при таких аргументах обидва синуси у добутках додатні.
47
101 ЗАДАЧА з тригонометрії
№40
Задача 5. Довести, що коли
А А О А
0<α<-, 0<β<-, 0<γ<-,
2 2 2
то нерівності
tga tgβ + tgβtgγ + tgγ tga <1
та
O<a+β+γ<^
рівносильні.
Доведення
За заданих обмежень нерівність
рівносильна нерівності
1 l-tgatgβ tg(a + β) tga + tgβ
(боО <γτa^-(a + β) <у).
48
6. Доведення нерівностей
Помножимо обидві частини нерівності
. l-tgα∙tgβ tgγ<
tg a + tg β
на додатний при заданих обмеженнях вираз
tg a + tg β∙ Маємо рівносильну нерівність
tgγ(tga + tgβ) <1 -tg a tgβ,
або
tga∙tgβ+tgβ∙tgγ + tgγ∙tga <1,
що і потрібно було довести.
Задача 6. Довести № 41
tglo+tg2o+tg3o+...+tg44o>44(V2 -1).
Доведення
Якщо0 < a < х <45°, то
tg(x - a) + tg(x + а) =
_ sin2x
cos2 xcos2 a - sin2 xsin2 а
2sinxcosx
> з =2tgx,
cos х
оскільки 0 < cos2 xcos2 a -sin2 xsin2 a < cos2 х.
4-6-1991
49
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
Тому
tglo+tg44o>2tg-,
Хг
45°
tg2°+tg43°>2tg-,
45° tg22°+tg23o>2tg--,
звідки
tglo+tg2o+tg3o+...+tg44o>
.. 45° лл sin45o >44 tg— =44
Б 2 l + cos45o
=44(√2-1).
50
7. НЕЗАЛЕЖНІ
Задача 1. Довести, що коли cos α sin а ~a~ ~Г
№42
то вираз A = αcos2α+∕>sin2α не залежить ні від а, ні від/>.
Доведення
o b sina ~
З умови випливає, що — = . Тому
a cos a
( b ∖
A=a cos2a + -sin2a =
I a J
( λ1 sina . π
= a cos2a + sin 2 a =
∖ cosa >
4*
51
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
cos2 α cosa + sm2 a sin a = a
cos a
cos(2a-a)
= a —— l = a,
cos a
тобто А залежить лише від a.
№ 43 Задача 2. Довести, шо вираз
. π ^ sin —2 a
, πn π rjrx
не залежить від a (a ≠ — + —, п ∈ Z).
2 12
Доведення
Заданий вираз позначимо А. Маємо
. -cos2a +л/З sin2a А = 7 ; = • І π п sin —2 a
-2 -cos2a
2
√3 . _
— sιn2a 2
. π ~ sin —2 a
52
7∙ Незалежні
-2 sin —-2α ∖6 √ _ о
• і π sin —2a
Задача 3. Довести, шо вираз № 44
4 sin3 a cos3a+4cos3 a sin За - 3 sin4a не залежить від a.
Доведення
Можна використати формулу потрійного кута, але ми просто понизимо степінь 4sin3acos3a+4cos3asin3a-3sin4a =
=2(1 - cos2 a)sin a cos3a +
+2(1 + cos2a)cosasin3a-3sin4a =
= 2(sin acos3a + cosa sin3a) -
-2 cos2 a(sin a cos3a - cos a sin 3 а) - -З sin 4а =
= 2 sin4a + 2 cos2 a ∙ sin2 а -3 sin4a =
= - sin4a + sin4a = 0, звідки випливає твердження задачі.
53
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
и» 45 Задача 4. Довести, що вираз
cos2 φ + cos2(α + φ) -2 cosa cosφcos(a + φ) не залежить від φ.
Доведення
Об’єднавши другий і третій члени, винесемо за дужки
cos(a + φ) = cosa cosφ - sin a sin φ, Маємо
cos2 φ -(cosa cosφ - sin a sin φ) ×
× (cosa cosφ + sin a sin φ),
або
cos2 φ - cos2 a cos2 φ + sin2 a sin2 φ =
= cos2 φ(l - cos2 a) + sin2 a sin2 φ =
2 ∙ 2 ∙ 2 ∙ 2
= cos φsm a + sιn asm φ =
= sin2 a(cos2 φ + sin2 φ) = sin2 a,
а це означає, що заданий вираз не залежить ВІД ф.
54
7« Незалежні
Задача 5. Довести, що коли р — стале, то nmb функція
„ v pcos3α-cos3α psin3a + sin3a
/(а) + :
cosa sin а
також є сталою.
Доведення
Використаємо формули (див. наступний розділ)
cos3x =4cos3x-3cosx,
sin3x =3sinx-4sin3x
Маємо
∕(α) =
cos a
р sin3 a + 3 sin a -4 sin3 a _ sin a cos а sin а( р sin2 а -4 sin2 а + 3) sin а
55
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
= pcos2α-4∞s2α+3 + psin2α-4sin2α + 3 = = p(cos2a + sin2a)-4(cos2a÷sin2a) + 6 =
= ∕j-4 + 6 =p+2, звідки випливає твердження задачі.
56
8. ПОТРІЙНИЙ КУТ
Задача 1. Довести, що № 47
8cos318o=5tg54°
Доведення
Понизимо степінь «куб»:
2 cos54°+6cosl8°-5tg 54°=0,
1 ÷ cosl 08 o+3(cos 72 0+ cos36 o) - 5 sin 54°=0,
l + 2sinl8o-2sin54o=0, !-4sinl80cos360=0, 4sinl8ocosl8ocos36° θ
cos!8o
ςin72o
1sιn∕z =0, cosl8o=sin72o
cosl8o
що очевидно.
57
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
n> 48 Задача 2. Довести
tg55o∙tg65o∙tg 75o=tg85o.
Доведення
Помножимо обидві частини нерівності, яку доводимо, на tg 5o= ctg 85° і скористаємося формулою
tg За = tg α ∙ tg(60o-α)tg(60o÷α).
Тоді
tg5o∙tg55o∙tg65o∙tg 75°=
= tg 15 o∙tg 75o= ctg 75o∙tg 750= 1.
n> 49 Задача 3. Обчислити
tg 9o÷ tg 8 lo-(tg 27o+ tg 63o)^l + tg 15o+ tg 750.
Розв’язання
Маємо
tg 9o+ tg 8 lo= tg 9o+ ctg 9°;
tg 27o+ tg 63o= tg 27o+ ctg 27°;
tgl5o+tg75o=tgl5o+ctgl5o.
Оскільки
1 2
tg a + ctg a = = ——,
sin a cos a sin 2 a
58
8. Потрійний кут
то, позначивши заданий вираз через/1, маємо: λ 2 sin54o 2 sin!8o 2 sin 30° sin(318°), 1 sin 18° 2
Використовуючи формулу sin Зх = 3 sin х -4sin3 х, отримуємо λ 2 3sinl8o-4sin318o л А +4 =
sinl8o 2 4sin418o-3sin218o+4 . +4. 2sinl8o
Доведемо, що
sinl8°=^- 4
Запишемо очевидну тотожність sin54o= cos36° і застосуємо формули потрійного та подвійного кутів:
3sinl8o-4sin318o=l-2sin218o
59
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
Позначимо sinl8o= х (0 < х < 1) і розв’яжемо рівняння
4x3 -2х2 -Зх + 1 =0.
Маємо:
4x3 -4x2 + 2x2 -2x-x + l =0;
(*-l)(4√ +2x-l) =0.
Корені х, =1 та х, — <0 не підходять,
4
отже, sin 18o= x3 = * є(0;1).
Тоді
4sin418o-3sin218o+4 =
60
8. Потрійний кут
Звідси
4∙2∙-
4
8
Відповідь:
8
Задача 4. Довести, що
tg(60o+a) - tg(60o-a) + tg a = 3tg 3a.
Доведення
Скористаємося формулою t 0 3tga-tg3a tg3a=-= ≤—.
1 -3tg2a
Перетворимо ліву частину заданої тожності:
tg 60°+tg a tg 60o-tg a ÷ tg Cl = l-tg60otga l + tg60otga
№50
то-
3+tgα √3-tga * —∣=^ γ=b— + tg a =
-√3tga l+√3tga
61
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
+ tg α)ζl + √3tg a) l-3tg2a
(у/З - tg a)ζl - л/З tg a) + tga
l-3tg2a
= (l-3tg2a) ,[73+3tga + tga + V3tg2a- -√3 + tg a - √f3tg2a + 3tg a + tg a -3tg3a] = 9tg<z-3tgia 3(3tga-tgia)
l-3tg⅛ l-3tg2a B
N>51
Задача 5. Довести
tg a + tg(a + 20o) + +tg(a +40o) +... +tg(a + 160o) = 9tg 9a.
Доведення
Тричі застосуємо попередню тотожність: tg a + tg(a +60o) + tg(a + 120o) = 3tg 3a; tg(a + 20o) + tg(a + 80o) + tg(a + 140o) = = 3 tg(3a + 60°);
62
8. Потрійний кут
tg(α +40o) + tg(a + 100o) + tg(a +160°) = = 3tg(3a + 120o).
Додавши всі три записані тотожності, отримаємо
tga + tg(a + 20o) + +tg(a+40o)+...+ tg(a + 160o) = = 3(tg За + tg(3a+60o) + tg(3a +120°)) = =9tg9a.
Задача 6. Обчислити № 52
sinl2o∙sin24o∙sin48o∙sin84o.
Розв’язання
Скористаємося вже знайомою формулою sin За =4sinasin(60o-a)sin(60o+a), звідки
sin3a sin а = .
4 sin(60o-a) sin(60o+a)
Нехай а =12°. Тоді
. loo sin36o sin 12 °= .
4sin48osin 72°
63
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
Нехай а =24°. Тоді
. пло sin72o sm24o=
4sin360sin84
Маємо
sinl2o∙sin24o∙sin48o∙sin84o= sin36o sin 72° X 4sin48o∙sin72o 4sin36o∙sin84o
× sin48o∙sin84o=—.
16
Відповідь: —.
16
№ S3 Задача 7. Довести
tg620o-33tg420o+27tg220o-3 =0.
Доведення
Маємо
√3 = tg 60°= tg(3 -20”) = 3tg20°~tg3^.
v 7 l-3tg220o
Звідси випливає, що 9tg220o-6tg420o+tg620o = l-6tg220o+9tg420o
64
8. Потрійний кут
атому
tg620o-33tg420o+27tg220o-3 =0, що і треба було довести.
Задача 8. Довести тотожність № 54
8 cos4 α+4cos3α-8cos2α-3cosα + l =
« 7a a = 2 cos—cos—.
2 2
Доведення
(8cos4 a-8cos2a) + (4cos3a-3cosa) + l =
= 8 cos2 a(-sin2 a) + cos3a +1 =
= -2 sin22a + l + cos3a = cos4a + cos3a =
π 7a a = 2 cos—cos—, 2 2
що і треба було довести.
5-6-1991
65
9. ВИКЛЮЧИТИ...
№55 Задача 1. Виключити кути з системи рів- ностей
cos(x-y) =с
< sin x +sin у = а. cosx + cosy =b
Розв’язання
Підвівши друге і третє рівняння у квадрат і додавши їх, отримаємо
ζsin2x + cos2x) +
+2 (sin х sin у + cos х cos у) +
+(sin2y + cos2y) = a2 + b2.
66
9. Виключити...
Використовуючи першу рівність, отримаємо
2+2c = 02 + ∕Λ
Задача 2. Виключити а з системи
№ 56
∖
tg
+ α
<8
J
rπ
∖
tg
—
-a
<8
√
=т
= п
Розв’язання
З очевидної тотожності
π
— + а
8
))
знаходимо
[/д 48
t π ( π
tg - + α +tg —а
18 J 18
1-tg
(π
λ
f π
—
+ a
tg
—
<8
)
<8
-а
або
т + п , =1, т + п + ти = 1 1-гил
5*
67
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
№ 57 Задача 3. Виключити кут а з системи рівнянь
х =2cosα
у =2sina
Розв’язання
Піднесемо обидва рівняння до квадрату та додамо. Враховуючи тотожність sin2 a + cos2 a = 1,
дістанемо
x2 + y2 =4cos2 a +4sin2 a =4.
№ 58 Задача 4. Виключити t з рівностей и =10cos3', v =10sin3'.
Розв’язання
Маємо
lgw = cos3r, lgv = sin3r.
Піднесемо обидві частини обох рівнянь . 2 .
у степінь — і додамо результати:
2 2
lg hi + lg3v = cos2r + sin2 г = 1.
68
9- Виключити...
Задача 5. Виключити t з системи рівнянь № 59 х = tfcos3z + 3α coszsin2z у = αsin3z + 3αcos2zsinz
Розв’язання
Склавши і віднявши почленно задані рівняння, отримаємо
х-у = α(cosz-si∏z)3.
З рівності (1) знаходимо
Іх + у
S1∏Z + COSZ = З
N а
а з рівності (2)
cosz-sinz =з/—- N а
З рівностей (3) і (4) маємо
(cosz-sinz)2 = з
69
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
Додавши ці рівності, отримаємо
+ 2 cos2
= 2 sin
№ бо Задача 6. Виключити х, якщо
sin'x cos’х sinx cosx + — = a> j— + —τ~=b. cosx sιnx COS X sin X
Розв’язання
Маємо
sin4 х + cos4 x , sin4x + cos4x a , b =
sin x cos x sin3 x cos5 x
Тоді
Q ∙ 2 ’
— =sιn xcos^x, sιnx∙cosx = b
Знову використаємо формулу sin4x + cos4x = = 1 -2 sin2 х cos2 х.
70
g. Виключити...
Маємо
1 -2 sin2 х cos2 х a =
sin x cos x
Отже, остаточно, a4ab =b-2a.
Задача 7. Виключити а і φ з системи: № бі
pcos2a + ^cos2φ = 1
< pctg2a + gctg2φ = 1 .
∕>sina = <7 sin φ
Розв’язання
Запишемо першу рівність системи у вигляді pζl -sin2a) + (∕ζl -sin2φ) = 1, або psin2a + <7sin2φ = р + q -1.
Підвівши третю рівність до квадрату, отримаємо систему двох рівностей відносно ве- • 2 • • 2
личин sin а і sin φ
f p sin2 a + (/sin2 φ = p ÷ q -1
I p sin a = q^ sin φ
71
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
Оскільки за умовою sinφ ≠ 0 і sinα ≠ 0, то, з третього рівняння заданої системи випливає, шо р ≠ 0, q ≠ 0.
Тоді система (1) рівносильна такій q(P + tf)si∏і 2 φ = p(p + q -І) p(p + q) sin2 a = q(p + q -1)
Звідси легко бачити, що р + q ≠ 0, р + q ≠ 1.
Отже,
. 2 p(p + q-ty . 2 φ>+^-i)
sin φ = —k- -j-, sin a = -k- -А
q(p+q) p(p + q)
Переписавши тепер другу рівність заданої системи у вигляді
і підставляючи знайдені значення sin2φ і
sin2 а, після перетворень отримаємо (p2-q2)2 =-pq∙
72
іо. п — ДОДАНКІВ, п— СПІВМНОЖНИКІВ
Задача 1. Довести, що №62
α x а а tg — ∙ secα + tg—sec— + 2 4 2
a a i а а +tg— sec— +...+tg—sec г =
8 4 2" 2
= tga-tgΛ
(Нагадаємо, що secx =—!—.) cosx
73
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
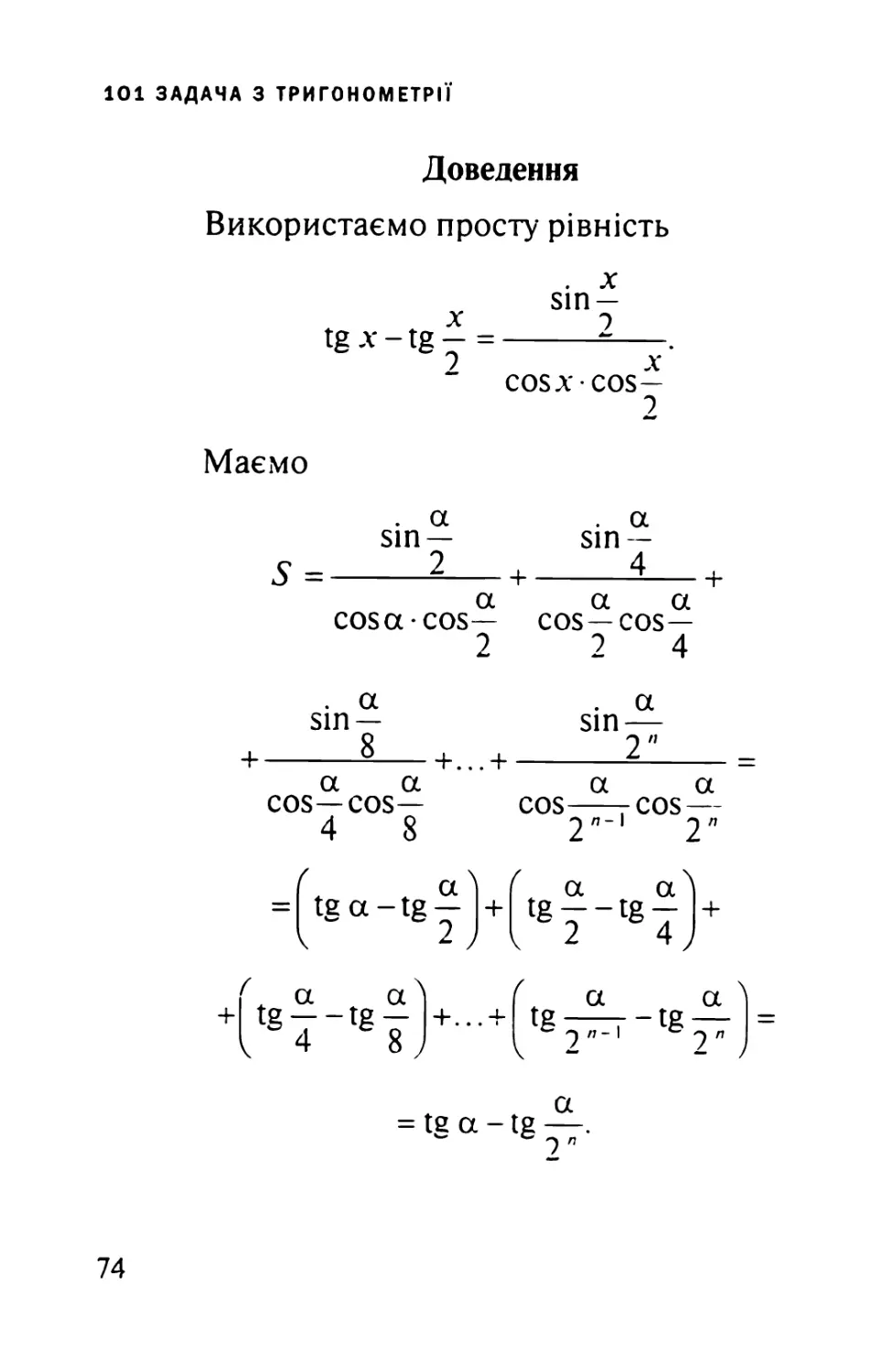
Доведення
Використаємо просту рівність . х sin —
X ?
tg∙v^tg7=
COSXCOS—
2
Маємо
. а sin —
2
. а sin¬
а
cosα∙cos-
2
ce а
cos—cos—
2 4
. а sin —
8
а а
cos—cos—
4 8
. а sin — 2"
а а
cos rcos—
2n -1 2n
а а
r-lg —
j п-І у n
= tg а - tg —.
2”
74
10. Л - ДОДАНКІВ, п - СПІВМНОЖНИКІВ
Задача 2. Довести, що № вз
S =-!s-sin420α + -i-sin42la + 40 4і
+-!∑-sin422a+...+ -sin42"a =
42 4"
= sιn a r sin 2 a.
4"+1
Доведення
Напишемо ряд очевидних рівностей:
1.4 1 • 2 1 , п
—sm a=-sin a — sin 2a;
40 40 4
J-sin42a =-ζsin22a —ζsin222a∙, 4 4 42
-ζsin422a =-ζ-sin222a--Lsin,23aj
42 42 4’
— sin4 2 "a = —sin22"a—^-i-sin22z,+ la.
4« 4n 4"λ,
Додавши цю w + 1 рівність, отримаємо
5= sin* a -sin 2 a.
4∏÷ I
75
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
н® 64 Задача 3. Обчислити суму
S = arctg і + arctg -+...+ arctg !—5∙.
З 7 1 + и + и
Розв’язання
Має місце формула (доведіть!)
1 (£ + 1)-* arctg = arctg v z 7 =
1 + к + к l+(k + l)k
= arctg(Λ +1) - arctg к. (*)
Скориставшись формулою (*), запишемо:
1 2-1
arctg - = arctg = arctg 2 - arctg 1;
З 1 + 2∙1
1 3-2
arctg - = arctg = arctg 3 - arctg 2;
7 l + 3∙2
arctg 7 = arctg(w +1) - arctg n.
↑ + n + n
Додамо отримані рівності:
S = arctg(w +1) - arctg 1 = arctg(∕ι +1) -
π
4
Відповідь: arctg(w ÷ 1) -
π
4
76
10. n - ДОДАНКІВ, Л - СПІВМНОЖНИКІВ
Задача 4. Обчислити без таблиць і каль- №65 кулятора
. π . 3π . 5π . 31π sin—sin—sin—...sin
64 64 64 64
Розв’язання
Перетворимо добутки пар множників, рів- новіддалених від кінців даного добутку: π . 31π π π 1 . π
sin—sin — = sin—cos— = - sin —. 64 64 64 . 64 2 32
Аналогічно можна перетворити кожну пару з інших вказаних множників. Тоді отримаємо: 1 . π . 3π . π∙15 — sin—sin—... sin =
28 32 32 32
28
28
1 . π . 3π . 7π
— sin—∙sm—...sin =
16 16 16
24
28
24
1 . π . 3π
— sin—∙ sin =
22 8 8
28
24
1 1 . π √2 -•-•sin- =—-. 22 2 4 2 6
»• . √2
Відповідь: —ir.
216
77
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
№ 66
Задача 5. Довести, що
_ . _A. sm2 a
cosa∙cos2a∙cos4a∙...∙cos2 a=-1-.
2sina
Доведення
При доведенні цієї тотожності скористаємося рівностями
2sinα∙cosα sin2a cos a = = ;
2 sin a 2 sin a
_ sin4a
cos2 a = ;
2sin2a
. sin8a
cos4a = ;
2 sin4a
^k sin2*+la cos2 a = —,
2sin2*a
що і доводить твердження задачі.
№ 67
Задача 6. Обчислити без допомоги таблиць і калькулятора
sin60∙sinl2 o∙sinl 8o∙sin24o∙... ∙sin84o.
78
10. n - ДОДАНКІВ, Л - СПІВМНОЖНИКІВ
Розв’язання
Використаємо формулу sin3α =4sinasin(60o-a)sin(60o+a).
Позначимо шукану величину через х, маємо:
1 л/З 4sin6osin54osiπ66o
х = ×
2 2 4
4sin 12osin48osin72o 4sin 18osin42osin780
X ×
4 4
4sin24osin36osm84o
× =
4
= ^sinl 8osin36osin54osin 72 o=
2 ∣o
= ^sinl80sin360cos360cosl80=
2 ∣o
_ -х/з sin36o sin72o _
~21° 2 2 ^
л/З cos360-cosl080 ~2τy 2 "
= y^-(cos36o+ sin 18°).
79
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
Оскільки sin!8o=
(с. 59), то
cos36o= 1 -2 sin218o=
Отже,
№ 68 Задача 7. Довести, що якщо числа xl, х„ складають арифметичну прогресію із різницею d, то
cos X. cos х> cosx7cosx, cosxn ∣cosxn
J 2 L J Л — І П
_ tg xn -tg χ∣ sind
Доведення
Маємо
4 a sin(x,. -xk 1) sin<y
tg xk - tg xk 1 = =
COS X, cos X,. _. COS X. COS X. _ 1
Λ ¼ I ⅛ Λ I
80
10. п — ДОДАНКІВ, п - СПІВМНОЖНИКІВ
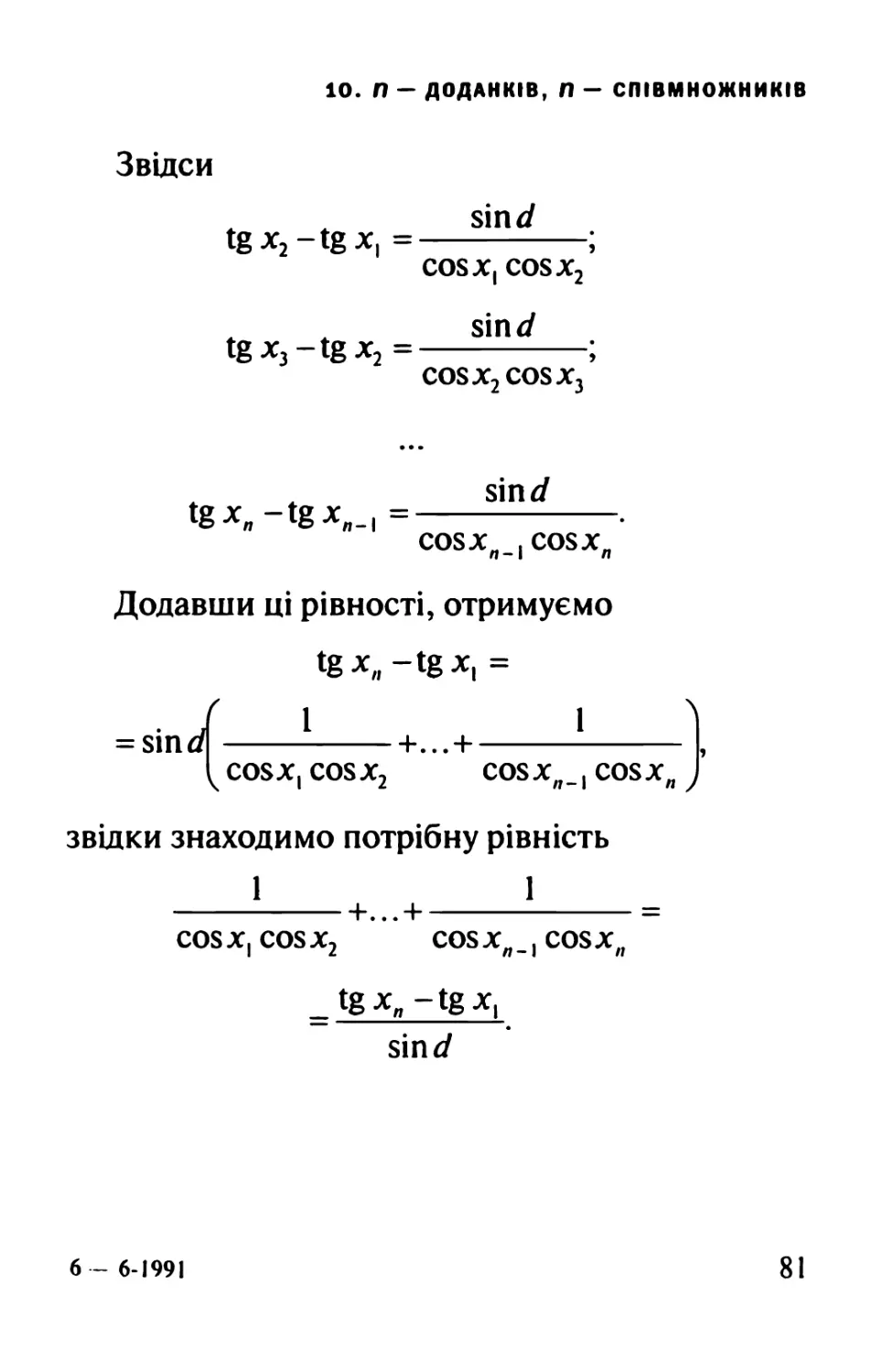
Звідси
ж sin d
tg x2 - tg xl = ;
cosx1 cosx2
_ . Si∏<∕
tg x3 - tg x2 = ;
cosx2cosx3
tgxn-tgxn,
sin J
cosx„ ,cosx„ n - і л
Додавши ці рівності, отримуємо
tgx,,-tgx1 =
= sind
∣4cosxl cosx2
cosxn.l cosx„)
звідки знаходимо потрібну рівність
cosxlcosx2 cosxzl.1 cosx,, ^tgxn-tgxl sin d
6 - 6-1991
81
її. РОЗВ’ЯЗАТИ РІВНЯННЯ
№ 69 Задача 1. Розв’язати рівняння (sin х + cosx)>∣2 = tg х + ctg х.
Розв’язання
Перетворимо рівняння:
(sin х + cosx)λ∕2 = .
v sinxcosx
Зробимо заміну sinx + cosx=Z;
отримаємо
82
її. Розв'язати рівняння
звідки
√2∕-√2∕-2 =0,
(r - √Γ)(√2z2 + 2/ + √2 ) = 0, t=41,
отже,
sinx + cosx = V2;
х = ^ + 2kπi к ∈ Z.
Відповідь: х =- + 2kπ, к ∈ Z.
4
Задача 2. Розв’язати рівняння
0 ∙ √3 1
8 sin х = +
cosx sinx
Розв’язання
Маємо
8sin2xcosx = 73sinx + cosx; 4sin2xsinx = >/3 sinx + cosx;
№70
6*
83
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
cos х-cos 3 х =—sinx + -cosx;
2 2
cos3x- —cosx 2
√3
—sinx =0;
2
cos3x -cos(60o+x) =0;
2 sin(2x + 30o)sin(x -30o) =0; xl = -15o+90ow, n ∈ Z, x2 = 30o+180%, к ∈Z∙ Відповідь: x∣ = -15o+90oλ, n ∈ Z, x2=30o+180%Λ ∈Z.
№ 7i Задача З (М ГУ, 1965). Розв’язати рівняння
cosx + cosy - cos(x + у) = —∙
Розв’язання
Задане рівняння перетворюється на рівняння
4 cos2 x + ^- -4 cosx — cos +1=0,
2 2 2
84
її. Розв'язати рівняння
а це рівняння запишемо у вигляді:
fn х+у Х~У] . 2*-y n 2cos --cos—- +sιn —-=0.
І 2 2 ) 2
Це рівняння рівносильне системі
• Х~У Л sin — =0
2
З другого рівняння:
х - у = 2kπ, або у = х-2kπ, к е Z.
Підставимо у перше рівняння, отримаємо
Звідси
cosx = —; х = ±- + 2πn, п є Z.
2 З
В результаті
Відповідь: х = ±- + 2πn,
85
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
№ 72 Задача 4. Розв’язати рівняння sin(πcosx) = cos(πsinx)∙ Розв’язання
Маємо
. π sin —πsmx
= sin(πcosx),
. (тс sin —πsιnx
І2
-sin(πcosx) =0,
π
—πsιnx + πcosx 2 cos ×
2
—πsinx-πcosx × sin- = 0.
2
Таким чином,
1) або
πcosx + --πsinx = π+2πΛ,⅛ ∈Z,
2
звідки
4& + І
cosx - sin х = —-—.
86
її. Розв'язати рівняння
Отже,
Єдиним цілим розв’язком нерівності
4Л + 1
є к =0. Таким чином,
xl =2πn±arccos—7= —, п ∈ ¾
1 2√2 4
2) або π _ ,
πcosx — + πsmx =2πκ.
2
Розв’яжемо це рівняння
Знову к =0. Тому
87
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
№73
x,=2πm± arccos—j= + —, т ∈ Z.
2 2√2 4
1 я
Відповідь: x1 =2πn ± arccos^-∕= , п ∈ Z;
х, = 2 πm + arccos—ζ= + —, т ∈ Z. 2 2√2 4
Задача 5. Розв’язати рівняння 4sin3x-sinx + cosx =0.
Розв’язання
Скористаємося «тригонометричною одиницею»:
1 = sin2 х + cos2 х.
Тоді
sin х = sin3 х + cos2 xsin X,
• 2 З
cosx = cosxsm X + COS X,
і задане рівняння перепишеться у вигляді: З sin3 х + sin2 xcosx -
-sin х cos2 x + cos3 X = 0,
отримали однорідне рівняння відносно sin X і cosx. Оскільки cosx ≠ 0 (перевірте!), то задане 88
її. Розв’язати рівняння
рівняння можна розділити на cos3 х, і поклавши у = tg х, отримаємо
3y3 + у2 -у+ 1 =0,
яке еквівалентне рівнянню
(y + l)(3y2-2y÷l) =0.
Звідси
у = -1, х = + тік, к ∈ Z.
4
7Г
Відповідь: х = — + тік, кєі.
4
Задача 6. Розв’яжіть рівняння № 74
26sin2x2 + 12 cos2x + 5sin2x =13.
Розв’язання
Враховуючи, шо
12cos2x + 5sin2x =
Ґ12 5 λ
113 13 J
вводимо допоміжний кут γ, такий що n 12 . * 5
cos2γ=-, sιn2γ = -.
89
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
Задане рівняння еквівалентне рівнянню
2 sin2(x2) + cos(2x -2γ) = 1.
Звідси
1 - cos(2 x2) + cos(2 х-2γ) = 1, cosζ2x2)-cos(2x-2γ) =0, 2sinζx2 + x-γ)sin(x-γ-x2) =0.
Отже,
x2 + x-γ = kπ,k ∈Z
або
x-γ-x2 = nπ, неї.
n. • -l±Jl+4γ+4Λπ , rjt
Відповідь: x1 2 = , кед
2
1± Jl -4γ-4wπ
¾ 4 = —’ n є Z’
^ 12 . n 5
де cos2γ = —, sι∏2γ = —.
90
12. РОЗВ’ЯЗАТИ НЕРІВНІСТЬ
Задача 1. Розв’язати нерівність cos(sin х) < 0. Розв’язання
№ 75
Оскільки
ріп И.| 1 ,
a cosφ > 0 при ∣φ∣ < - , то задана нерівність роз-
в’язків не має.
Відповідь: х ∈ 0.
Задача 2. Розв’язати нерівність № 76
∣sinx∣ > ∣COSX∣.
91
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
Розв’язання
Задана нерівність рівносильна такій: sin2 х > cos2 х, звідси
cos2 х - sin2 х < 0, cos2 х < О, тобто
—+ 2πw<2x< — + 2πn, л ∈ Z,
π Jπ rπ
- + πn<x< — + πn,n <= ⅞.
4 4
(71 Зті і
Відповідь: х ∈ — + πιτ,— + πn , л ∈ Z.
№77
Задача 3. Розв’язати нерівність
cos22x cos2x
≥3tgx.
Розв’язання
cos22x 3sinx>θ.
cos2x cosx cos22x-3sinxcosx
cos2x
92
12. Розв'язати нерівність
COS^X
Ця нерівність еквівалентна системі
2sin22x+3sin2x-2 ≤0 cos2 х ≠ 0
звідки
2J
cosx ≠0
а оскільки sin2 х + 2 > 0 при всіх х, то f . o 1
sm2x ≤-
2, cosx ≠0
-- + 2πk ≤2x ≤- + 2πk. к ∈ Z
6 6
π 7
х ≠ — ÷ πn, п ∈ Z
t 2
Відповідь: х є
93
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
№ 78 Задача 4. Розв’яжіть нерівність
sinx-cosx
Розв’язання
Область припустимих значень визначається співвідношенням sinx ≠ cosx, тобто
Маємо
Л т
х ≠ — + πn, п ∈ Z.
4
(1)
або
звідки
пк < х< — + πki к ∈ Z.
4 6
(2)
Розв’язуючи спільно (1) і (2), отримаємо розв’язки заданої нерівності.
(л 5л А
Відповідь: х ∈ — + πk∖— + πk ,k ∈ Z.
И
94
12. Розв’язати нерівність
Задача 5. Розв’язати нерівність * 79
cos3 xcos3x - sin3 xsin3x > ∣. О
Розв’язання
Використовуючи формулу потрійного кута,
маємо
(cos3x + 3cosx)cos3x- -(3sinx-sin3x)si∏3x > р
або
sin23x + cos23x +
z . „ . x 5
+3(cos3xcosx-sιn3xsmx) >—,
або
5 л 1
1 + 3 cos4x > —; cos4x > —, 2 2
звідки
—-+2πn <4x <- + 2πn, п ∈ Z.
3 3
( π πn π πn А σ7
Відповідь: x∈ —iτ∑^ + v ,n e
І 12 2 12 2 у
95
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
№ so Задача 6. Розв’язати нерівність 7sinx + √cosx > 1.
Розв’язання
Оскільки sinx >0 і cosx >0, то задана нерівність рівносильна такій:
sinx + cosx + 2√sinxcosx >1. (1)
Оскільки sin х ≥ 0 і cosx > 0, то
0≤x≤j. (2)
Використаємо вже добре знайому нам рівність:
/Т ∙ I π
smx + cosx = √2 sin х + — .
З (2) маємо:
π
π 3π
Тоді з графіка функції у = sin х випливає, що
π
• і π ї . π sin х + — >sιn — =sιn
r2,
тобто
sinx + cosx ≥1.
96
12. Розв’язати нерівність
Причому рівність досягається тільки на межах інтервалу, тобто при sinx =0 або cosx =0.
Отже, строга нерівність в (1) можлива лише, якщо
COSX > 0
я Відповідь: х ∈ 2πrr,- + 2πn , л е Z.
І 2 J
Задача 7. Розв’язати нерівність
Розв’язання
Задана нерівність рівносильна такій: tg2x-tg х < sinx,
або
sinx . Л smx <0, cos2xcosx
або
sin x(l - cos2 х cos х) cos2xcosx
№81
(1)
1/4 7 — 6-1991
97
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
Ясно, ЩО
1 -cos2xcosx ≥0, причому рівність можлива тільки якщо cosx = cos2x =1,
тобто при
х =2πn, neZ.
Отже, з (1) випливає, що х ≠ 2πn, п ∈ Z і sinx θ tgx < θ cos2xcosx ’ cos2x
Використаємо формули
cos2x =
l-tg2x
l + tg2χ,
tg2x
2tgx "l-tg2χ,
тоді
tgx(l + tg2x) l-tg2x
tgx l-tg2x
<0,
-⅛<o
1 —tg2x
tg2x<0. (2)
Зазначимо, що і умови з області визначення заданої нерівності cosx≠0, cos2x≠0,
і умова х ≠ 2 πn, п ∈ Z враховані в нерівності (2).
98
12. Розв’язати нерівність
Отже,
71
— + πk <2x <πk, к ∈Z.
2
Відповідь: х ∈
π
4
πk тік У
Гт]
, к ∈Z.
99
13. РОЗВ’ЯЗАТИ СИСТЕМУ РІВНЯНЬ
№ 82
Задача 1. Розв’язати систему рівнянь:
sinх = √2 sin у tgx=√3tgy
Розв’язання
Маємо
sinx д siny.
cosx cosy
cosx cosy
sin y(y∣2 cosy -√3 cosx
100
13∙ Розв’язати систему рівнянь
а) sin у =0; у = πkik ∈ Z.
Підставляємо у перше рівняння: sinx =0; х = πn, п ∈ Z. Отже,
x1 = πn, yl =πk, k,neZ.
б) 72 cosy-73cosx =0.
Маємо
л/2 cosy = л/з cosx.
Піднесемо це рівняння та перше рівняння заданої системи до квадрату та додамо:
2 cos2 у + 2 sin2 у = 3 cos2 х + sin2 х,
, √2
2 cos x = l, cosx = ±—.
2
Тоді, відповідно,
cosy =±—.
Відповідь: (пп; πty, (±+ 2 кп; ± + 2 πk , ґ Зтг 5π А
+- + 2πn',+- + 2πk , k,n≡Z.
4 6 /
7*
101
1О1 ЗАДАЧА З ТРИГОНОМЕТРІЇ
№ аз Задача 2. Розв’язати систему рівнянь
sin2 x = sin у
< sin2y = sinz,
• 2
sin z = sιnx
Λe0≤x≤π,0≤y≤π,0≤z≤π,
Розв’язання
Маємо
sin2 х ≤ sin х, sin2 у ≤ sin у, sin2 х ≤ sin г
звідси
sin у ≤ sinx, sin г ≤ sin у, sinx ≤ sin г
Таким чином,
sinx = siny = sinz∙
Отже, ґ • 2 sin x = sιnx
• 2
< sin у = sin у,
sin2z = sinz
sinx(sinx-l) =0
« siny(siny-l)=O.
sinz(sinz-l) =0
102
13- Розв'язати систему рівнянь
Остаточно маємо:
sinx =0
< sin у =0 si∏z =0
sinx=l
або piny=l.
sinz =1
Відповідь: (πk^πk2,πk3), kj e%t,i = 1, 2, 3;
-+2π∕p-+2π∕2^+2π∕3
∣2 і’2 2>2
>
Задача З (МГУ, 1967). Розв’язати систему в» м tg2x÷ctg2x=2sin2y sin2y + cos2z = l
Розв’язання
Оскільки
tg2x + ctg2x ≥2tgxctgx=2,
2 sin2 у ≤2,
то перша рівність заданої системи можлива тільки, якщо
tg2x=l sin2 у =1
103
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
Тоді з другого рівняння заданої системи випливає, що cos2z =0.
Отже, маємо
tgx = ±l
< cosy =0.
cosz =0 ч
. π kπ π π
Відповідь: х = — + —, у =- + nπ,z = -+m‰
4 2 2 2
ΛjW,∕∏∈Z∙
№ 85 Задача 4. Розв’язати систему
'tgxl + 3ctgxl = 2tgx2
tgx2 + 3ctgx2 =2tgx3
tgx,,.1 + 3ctgxn., =2tgxw tgxn+3ctgxn =2tgx∣
Розв’язання
Ясно, uιotgxλ ≠0(Λ =1,...,λ).
Якщо, наприклад, tgx1 >0, то ctgxl >0 і з першого рівняння маємо, що tgx2 >0. Так само покажемо, що tg хк >0 (A =1,...,∕∣).
104
13- Розв’язати систему рівнянь
Якщо ж tgx1 <0, то, аналогічно, tgxλ <0 (к = l,...,w).
У першому випадку для всіх к = 1,..., п
tgxj+-≥2Jtg¾-=2√3. tg xk N tg χk
Тоді для всіхЛ
tgxl>√3, — ≤√3. (1)
tgxt
У другому випадку для всіх к = 1 п
tgxλ +
З tgxt
= -2√3
і для всіхЛ =1,...,λ
tg xk < -√3,
— > -√3. (2)
tgxs
Додамо всі рівняння заданої системи:
tg х, + tg x2 +... + tg xn =
3 3 З
= + +...+ .
tg *l tg x2 tg xn
В обох випадках остання рівність можлива тільки коли в (1) або (2) є знаки рівності.
105
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
Маємо:
π
xk = — + πml
,*
_ π або хк = — + πntk,
mk ∈¾ k=∖i...in.
Відповідь: xk = ±— + πmk, mk ∈ Z, к = 1,
106
14. ТРИГОНОМЕТРІЯ
КУТІВ ТРИКУТНИКА
Задача 1. Довести, що для кутів будь-якого * ββ трикутника ABC виконується рівність А В С
sin A + sin-β+sinC =4cos— cos—cos—. 2 2 2
Доведення
Враховуючи, що
В+С 2
. А sin— = cos 2
(оскільки А + В+С = π), то
107
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
sinΛ + sin2f+sinC =
, . A A π . В+С _В-С = 2 sin—cos— + 2 sin cos——
2 2 2 2
= 2 cos— cos + cos—-
21 2 2
л в с
=4 cos—cos—cos—,
2 2 2
що й треба було довести. Зауважимо, що цей
факт випливає також і із задачі 3 розділу 1.
№87
Задача 2. Довести, що для кутів будь-якого трикутника ABC має місце співвідношення А В С ABC ctg — + ctg - + ctg - = ctg—ctg—ctg Л х. Z Z Z X-
Доведення
Враховуючи, що
А+В 1r С tg———=ctg-
та
A t В t tg — + tg- = tg
X> Xι
2tg2,
2
108
ід. Тригонометрія кутів трикутника
маємо
Л В С ctg — + ctg- + ctg- =
Z X
А , в
1 1 С tg 2 +tg2
— ÷ -g+ctg 1=-jπ ,g2 tg- tgytg-
l + 5Y1 . A В}
/4, В tgItgI
А
+ ctg- =
tg
+ Ctgy =
В . А
А
= ctg-∙ctg-ctg- l-tg-rg- + tg-tg-
2 2 2 \ 22 Z Z
2 ~ 2
2
2
2
/4 В t .
= ctg- ctg- ∙ctg -,
it L
що й треба було довести.
Задача 3. Довести, шо коли кути трикут- N«88 ника ABC задовольняють рівності
, .А . В С . ЗА . ЗВ ЗС n
З sin—sin—cos— + sιn—sin—-cos— =0,
2 2 2 2 2 2
то сторони трикутника пов’язані залежністю a,+b1=c,.
109
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
Доведення
Маємо
С π А+В ЗС 3π 3(Л+Д)
2 2 2 ’ 2 ^2 2
тому
cos— = sin 2
ЗС cos— = -sin 2
cos
2
= sιn-
2
3(A+B) . ЗС
cos— l = -sin .
2 2
Враховуючи ці співвідношення, отримуємо
„ . А . В С . ЗА . ЗВ ЗС
3sm—sm—cos— + sm—sin—cos— =
2 2 2 2 2 2
A-В Λ + cos cos
2 2
cos—+ 2
+— cos 2
-cos 2
3C cos =
2
2
2
A-В . A+B . C СЇ cos sm sin—cos— +
2 2 2 2 J
3(A-B) . 3(A+B) . 3C ЗСЇ -ς l sm — l + sin—cos
2 2 2 2 )
+ cos
2
110
14- Тригонометрія кутів трикутника
÷i(-sin3Λ -sin3B+sin3C),
Враховуючи умову задачі, маємо З sin А + 3 sinZ? -3 sinC - -sin3Λ-sin3B +sin3C =0,
звідки
2(sin A + sin Л -sinC) +(sin А -sin3 А) + +(sinB-sin35)- (sinC — si∩3C) =0, або
sinΛ(l-cos2Λ) +
+sinB(l -cos2B)-sinC(l-cos2C) =0. Тому
sin3 A + sin35 = sin3C.
Оскільки
sin',=⅛ sin2,=⅛ sinc=⅛
то a3 + b3 = с3, що й треба було довести.
111
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
№ 89
Задача 4. Довести, що коли сторони а, Ь, с трикутника складають арифметичну про- А , В С
гресію, то ctg—, ctg—, ctg — також склада- 2 2 2
ють арифметичну прогресію.
Доведення
Оскільки сторони трикутника складають арифметичну прогресію, то a-b=b-c. Тоді за теоремою синусів отримаємо
sin А - sin2? = sin2? - sinC.
Звідси
o . A-В A+B o .
2 sin cos = 2 sin
2
—cos
2 2
2
Отже, . (А В sin
π-C
cos
2 2 J 2
. (В C і π-A
= sιn cos ;
I 2 2 J 2
( . A В A . B∖ . C
sin—cos—cos—sin— sin—=
V 2 2 2 2) 2
( . В C В . C}
sin—cos—cos—sin—
<22 2 2 J
sin—.
2
112
ід. Тригонометрія кутів трикутника
Розділивши обидві частини останньої рів- . А . В . С
ності на sin у sin у sin у, отримаємо
В АС В ctg--ctg- = ctg--ctg-,
Z> X* Х> X»
шо й треба було довести.
Задача 5. Довести, шо коли між кутами №90 трикутника ABC існує залежність
(sin Л + sin5 + sinC)(sinJ + sin2f-sinC) =
= 3 sin A sin В, то ZC =60°.
2
І 2
. А + В × 2 sin
Доведення
Маємо sinC = sin(Λ + Л). Отже,
(sinΛ + sinZ7 + sinC)(sin∕l + sinZ?-sinC) = ∕∖ . А+В A-В o . А+В А+В' = 2 sin cos + 2 sin cos
2 2
A —В ^ . A + В cos 2 sin cos
2 2 2 2
λ . ^A+B( 2 √4-J? % A + B^
=4 sin cos cos
2 2 2 J
×
113
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
= 2 cos2 —(1 + cos(Λ -В) -1 - cos(Λ + #)) =
=2 cos2 ∙ 2 sin A sin# = 4sin A sin#cos2 —.
2 2
Таким чином, задана залежність набуває вигляду
4sin A sin# cos2 — = 3 sin A sin#,
або, так як sin A ≠ 0, sin# ≠ О, 4cos2-=3.
2
Отже,
COSy = — (кут -— гострий),
тоді С =60°, що й треба було довести.
№ 91 Задача 6. Для того, щоб один з кутів три¬
кутника ABC дорівнював 36° або 108°, необхідно і достатньо, щоб виконувалася рівність: sin5Λ + sin5# + sin5C =0.
Довести.
114
ід. Тригонометрія кутів трикутника
Доведення
sin5Λ+ sin5B + sin5C =
0 . 5А 5Λ o . 5(B + C) 5(B-C)
= 2 sin—cos— + 2 sin — lcos— l -
2 2 2 2
o . 5A 5 A 5(180o-√l) 5(B-C)
= 2 sin—cos— + 2 sin — l cos-λ =
2 2 2 2
0 . 5Λ 5A n . <icλo 5√∩ Kb~c) = 2 sin—cos— + 2 sin 450o cos- =
2 2 lk 2 J 2
n . 5Λ 5A π 5A 5(B-C)
= 2 sin—cos— + 2 cos—cos-δ l =
2 2 2 2
n 5Af . 5A 4β"c)A
= 2 cos— sin— + cos- '- -
2 I 2 2 J
5A( . 5zlono zd z,4∖ 5B-5C∖
= 2 cos— sin—(180o-(5+C)) + cos
2 к 2 2 J
∕
sin 450o ∖
n 5A
= 2 cos—
2
5(B+C)} 5B-5C}
— l +cos
2 2
z 7 z √
n 5z4f = 2 cos—
2 I
5Я+5С cos
2
a 5A 5B 5C
=4 cos—cos—cos—.
2 2 2
115
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
Отже, рівність з умови виконується тоді і тільки тоді, коли
5А 5В 5С n
cos—cos—cos— =0, 2 2 2
тобто коли
5А λ λ 5В ^ ei 5С Л cos—=0 або cos—=0 або cos—=0.
2 2 2
Звідси випливає, що один з кутів дорівнює - або —, що й треба було довести.
№92 Задача 7. Довести, що коли a, β та γ — кути трикутника, то
. a . β . γ . 1 sin—sin—sin- ≤-.
2 2 2 8
Доведення
Маємо
. α . β . γ sin—sin—sin— =
2 2 2
a-β a+β
cos -cos —
2 2
sin— = 2
116
14. Тригонометрія кутів трикутника
a-β π-γ]. γ cos --cos sm— =
2 J 2
2
α-β . γ . 2Y -smj—sm -
2 2
cos 2
a-β . γ 1 2a - β
sin——cos - -+
2 2 8 2
—sin — +—cos 2 2 2
2«-р_
+-cos 8 2
. γ 1 a-βV sin——cos -
2 2 2 J
1 2 a-β
-cos -
8 2
J 2a-β^l ≤-cos—- ≤-
8 2 8
що й треба було довести.
8 —6-1991
117
15. АРКУСИ
№93
Задача 1. Довести, шо при х ∈ [-1; 1]
π arcsιn х + arccosx = —.
2
Доведення
Запишемо потрібну тотожність у вигляді π
arcsιn х =—arccosx.
Оскільки
0 ≤ arccosx ≤ π,
π . . π
— ≤ arcsιn х ≤ -
2 2
то
π π . π
— ≤ — arccosx ≤-
2 2 2
118
15* Аркуси
і маємо, що
sin(arcsin х) = х, • (π z λ
sin —arccosx = cos(arccosx) =
Отже, тотожність справедлива.
Задача 2. Довести, що коли х <0, то . π . 1 arctg х = ÷ arctg —.
2 х
Доведення
Доведемо спочатку, що при х <0
№94
arctg — = arcctg х - π,
(1)
(71
Дійсно, якщо х <0, то arcctgх є —;к . Отже,
π π
( Л і arcctgx-π∈ —;0 ⊂ —
І 2 J І
ку
тобто обидві частини в (1) належать проміж- π π 2’2
У = tgχ.
— проміжку монотонності функції
8*
119
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
Тому досить довести, що
tg arctg— = tg(arcctgx-π)∙
Аналогічно попередній задачі можна показати, що
π arctg х+arcctg х = —.
Отже, маємо
= ctg(arctgx)
1 Г П
= —= tg arctg— .
х I χ√
Таким чином, рівність (1) доведена. Застосувавши (2) до рівності (1), дістанемо потрібну тотожність.
№ 95 Задача 3. Обчислити суму
arctg 2 + arctg 3.
120
15. Аркуси
Розв’язання
Пропонуємо довести самостійно, що якщо х > 0, у > 0, то
х 1-ху arctg х + arctg у = arcctg .
х + у
(Порада: порахувати котангенси від обох частин). Отже, тоді
1 6 3 тс
arctg 2 + arctg 3 = arcctg = π - arcctgl = —.
5 4
d. . 3π
Відповідь: —.
4
Задача 4. Розв’язати рівняння
_ . π π2
2 arcsmx = — + .
З 9arcsinx
№96
Розв’язання
Позначимо arcsinx = у. Тоді
_ π π2 2у =- + —,
З 9/
18y2 -3πy-π2 =0,
121
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
ЗВІДКИ
π _ π у = — або у = --
Маємо
π . π √3
або
arcsinx = , х = sin =
6 \ 67
. √3 л 1
Відповідь: х = — або х = —.
2 2
№ 97 Задача 5. Розв’язати нерівність
arccosfx2-3x+2) _
Розв’язання
Зауважимо, що
arccosz ≥0
при ∣z∣ ≤1, причому рівність можлива тільки при z = 1.
122
15. Аркуси
Тому задана нерівність рівносильна такій системі
8x2-10x + 3 >0
< x2-3x + 2≥-l.
х2 -Зх + 2 <1
Отже,
8x2-10x + 3>0 x2-3x + 3>0 . x2-3x + l <0
Дискримінант другої нерівності від’ємний, а тому вона справедлива при всіх х.
З першої нерівності маємо:
X є
η
U
гз ї
-i+∞ .
2j
И )
А з третьої —
Відповідь: х ∈
123
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
№ 98 Задача 6. Розв’язати нерівність
arctg 4x > arccos(l - х).
Розв’язання
Помітимо, що 1 - х > 0, бо якщо 1 - х ≤ 0, то
При l-x>O обидві частини нерівності належать інтервалу Оскільки косинус на цьому інтервалі спадає, то
причому 1-х ≤1. Разом з 1-х >0 отримаємо 0 ≤x <1.
Оскільки
отримаємо систему нерівностей
0 ≤x <1
124
15. Аркуси
Ця нерівність не має розв’язків (доведіть це самостійно!).
Відповідь: х ∈ 0.
Задача 7. Обчислити sin(arcctg(-2)), * 99
Розв’язання
де a = arcctg2 ∈l 0; j
Оскільки
arcctg(-2) = π - arcctg 2,
то
sin(arcctg(-2)) = sin(π - arcctg 2) = = sin(arcctg 2) = sin α,
J
Маємо
sin2 a = 5—
1 + ctg a
(
Оскільки a ∈ 0; — , то
sin a =-τ=
√5
Відповідь:
125
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
№ іоо Задача 8. Довести, що сума
arcsin х + 3arccosx + arcsin^2 xVl-x2)
2 1
не залежить від х, якщо х < 2
Доведення
Нехай arcsinx = у. Тоді sin у = х. Далі, sin2 у = 2 sin у cosy = 2 x^∖-x2 (поясніть самостійно, чому не виникає «±» перед коренем). Звідси
2у = (-1)* arcsin^2χy∣↑-x2^ ÷ Aπ, к ∈ Z.
А 2 1
Але з умови х < — випливає, що
тоді
отже, к =0. Тому
2 arcsin х = 2 у = arcsin( 2 х ∙ Vl-x2
126
15- Аркуси
Тому
arcsinx+3arccosx + arcsin
о/ • \ 3π
= 3(arcsιnx + arccosx) = —, що й доводить твердження задачі.
Задача 9. Чому дорівнює arcsin(sin х)?
Розв’язання
N»101
Так як
π . х . π
— ≤ arcsιn( sin X) ≤ —, 2 v 7 2
π π
ТО якщо — ≤ х ≤ —, то 2 2
arcsin(sinx) = x.
n 71 З
Якщо - ≤ х ≤—π, то
2 2
arcsin(sin х) = arcsin(sin(π - x)) = π - х,
π π
так як в цьому випадку <π-x≤-.
127
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
ст Зл 5л
Якщо ж, наприклад, — ≤ х < —, то 2 2
arcsin(sin х) = arcsin(sin( х -2 π)) = х -2 л,
л ~ л
тому що — ≤x-2π≤- 2 2
Загальна формула, очевидно, має такий вигляд:
л _ , л ~ , якщохє — + 2πk'i- + 2πk ,то 2 2
arcsin(sin х) = х -2 тік, л π
тому що — ≤ X-2πk ≤ 2 2
якщохє - + 2πk',— + 2πk ,то 2 2
arcsin(sin х) = -х + л+2 πk, тому що-- ≤-x + π+2πk <-.
2 2
128
ЗМІСТ
Передмова З
1. Доведення тотожностей 5
2. Спростити 14
3. Числові рівності 22
4. Обчислити 32
5. Умовні рівності 38
6. Доведення нерівностей 43
7. Незалежні 31
8. Потрійний кут 37
101 ЗАДАЧА З ТРИГОНОМЕТРІЇ
9. Виключити 66
10. п — доданків, п—співмножників . . . 73
11. Розв’язати рівняння 82
12. Розв’язати нерівність 91
13. Розв’язати систему рівнянь 100
14. Тригонометрія кутів трикутника ... 107
15. Аркуси 118
Кушнір, Ісаак
К 96 101 задача з тригонометрії. — К.: Факт,
2006.- 132 с.
ISBN 966-359-135-8
Запропонована 101 задача охоплює весь практикум зі шкільної тригонометрії: доведення тотожностей і нерівностей, розв’язання рівнянь, обчислення виразів. Розбираючи приклад за прикладом, читач зможе не тільки перевірити себе в застосуванні теоретичних знань, але й збагатити арсенал прийомів розв’язання задач, які зазвичай постійно зустрічаються на іспитах до най- престижніших вузів.
УДК 514.116(076.1)
ББК22.151.0я7
Науково-методичне видання
Ісаак КУШНІР
101 задача З ТРИГОНОМЕТРІЇ
Редактор Леонід Фінкельштейн Технічний редактор Оксана Кравцова Коректор Дарія ІНарговська Макетування обкладинки Інокентія Вирового Верстка та макетування Дмитра Фінкельштейна
Здано до виробництва 15.08.2006. Підписано до друку 10.11.2006. Формат 60x84 1/32. Папір офсетний № 1. Гарнітура «Ньютон». Друк офсетний. Ум. друк. арк. 3,85. Обл.-вид. арк. 4,2. Наклад 3000 прим. Зам. № 6-1991
ТОВ «Видавництво „Факт"» 04080, Україна, Київ-80, а/с 76 Реєстраційне свідоцтво ДК№ 1284 від 19.03.2003 Тел./факс: (044) 287 1882, 287 1886 E-mail: ofTice@fact.kiev.ua Відділ збуту: (044) 463 6887 E-mail: sbyt@fact.kiev.ua www.fact.kiev.ua
Надруковано з готових форм на ЗАТ «ВІПОЛ» 03151, Київ, вул. Волинська, 60 Свідоцтво про внесення до Державного реєстру серія ДК № 752 від 27.12.2001