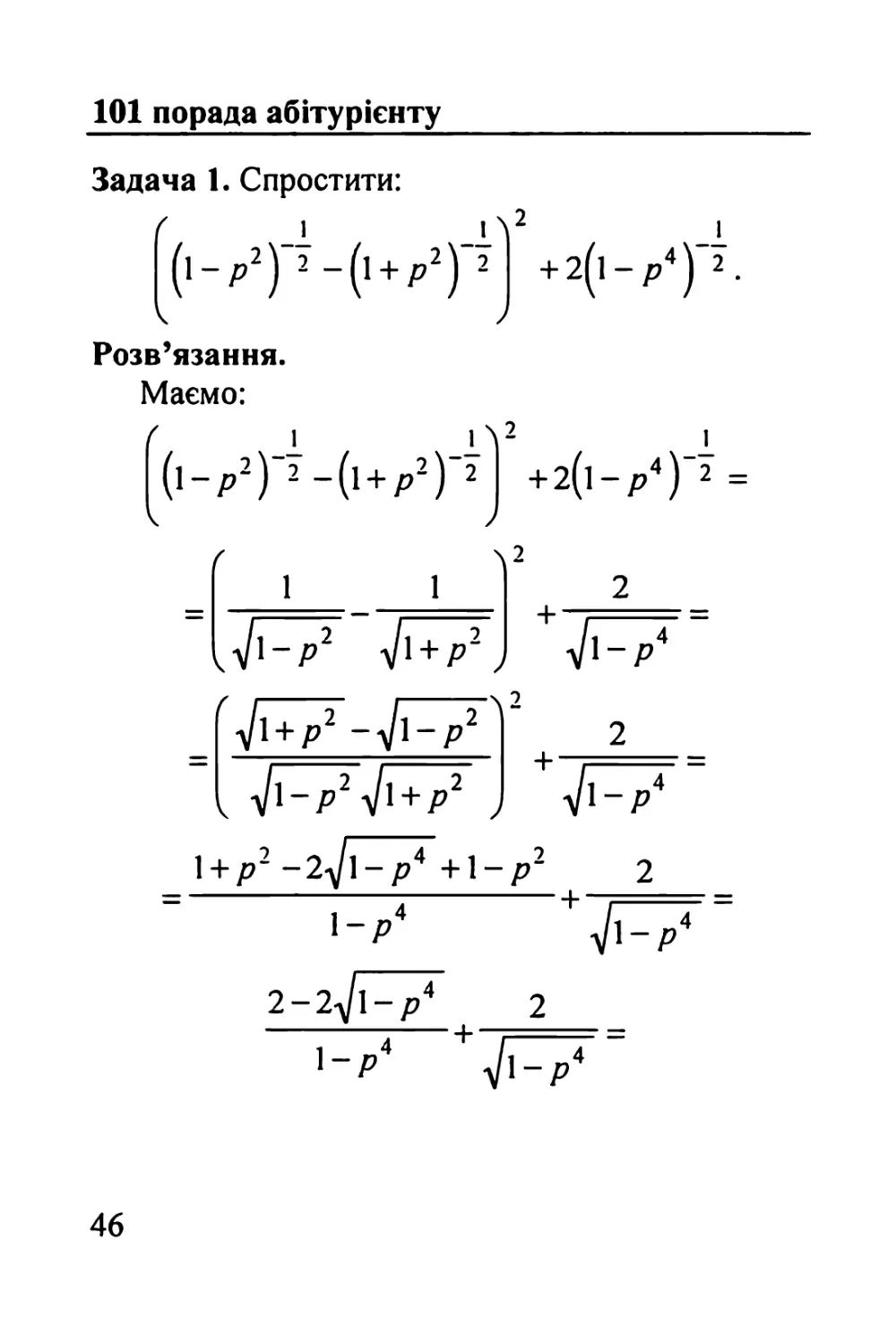i∣
І. Кушнір Λ. ФІНКЕЛЬШТЕЙН
Математика
У ПРИКЛАДАХ і задачах


Ісаак КУШНІР Леонід ФІНКЕЛЬШТЕЙН
МАТЕМАТИКА
В ЗАДАЧАХ
І ПРИКЛАДАХ
101
ПОРАДА
АБІТУ РІЄ НТУ
Київ*2004


ББК 22.1я729
К 96
ISBN 966-7274-91-8 © Кушнір I. A.,
Фінкельштейн JI. ∏., 2004 © Дизайн, макет «Факт», 2004


ПЕРЕДМОВА
З якого б класу Ви не почали готуватися до вступного іспиту з математики, підготовка має іти послідовно. Стосовно теорії Вам допоможе єдина програма для вступників. А як бути з задачами? Мета нашого посібника — допомогти абітурієнтам правильно організувати самостійну роботу саме під час розв’язання задач. Обрана нами форма дозволяє виділити головний момент у кожному з розглядуваних питань. Це в першу чергу стосується основних методів і спеціальних прийомів розв’язання задач, поділу задач на типи як за умовою, так і за методами розв’язання. Саме тому кожна з рекомендацій підтверджується задачами з розв’язаннями.
Таким чином, розв’язавши більш ніж двісті ключових задач, Ви здійсните «розвідку боєм» матеріалу для вступників. І в яке б питання Ви тепер не заглиблювалися — початок покладений — наші ПОРАДИ допоможуть зорієнтуватися в морі задач як з алгебри, так і з геометрії.
З


Ми впевнені, що поради охоплюють не тільки весь курс шкільної математики, але й питання, що виходять за його межі, коли справа стосується розв’язання задач. Ми намагались іти шляхом від простого до складного, щоб абітурієнт, в першу чергу, не робив помилок у задачах першого ступеня складності (такі помилки називаються «грубими»). Основою високої техніки розв’язання є розв’язання саме тих задач, які так детально розібрані в кожній з ПОРАД. Лише оволодівши такою технікою Ви зможете імпровізувати в задачах підвищеної складності, які в наших ПОРАДАХ також враховані.
Не гайте жодної хвилини!
Як кажуть, екзамени вже «на носі»!
Сміливо відкривайте першу сторінку!
4


І. Числа
І.ЧИСЛА
W1
Перевірте, чи пам ’ятаєте Ви типи чисел, які вивчають у школі.
• Числа 1, 2, З,л,які використовують при лічбі, називаються натуральними (множина цих чисел позначається буквою N).
• Сукупність чисел 0, ±1, ±2, ±3, ... утворює множину цілих чисел (позначається — Z).
• Парні числа — числа, які діляться на 2 без остачі, тобто числа вигляду т = 2k, kε Z .
• Непарні числа — числа, які не діляться на 2. тобто числа вигляду I = 2n- 1, п ∈ Z.
• Нуль парне число.
• Натуральне число, яке не дорівнює одиниці, називається простим, якщо воно ділиться тільки на себе і на одиницю.
• Натуральне число, яке не дорівнює одиниці і не є простим, називається складеним.
5


101 порада абітурієнту
« . . m
• Раціональні числа — числа вигляду —, де
п
т ∈ Z , п ∈ N (множина цих чисел позначається буквою QsJ.
• Ірраціональні числа — це числа, які можна зобразити у вигляді нескінченного неперіодичного десяткового дробу.
• Числа раціональні та ірраціональні називають дійсними числами (множина цих чисел позначається буквою R).
W 2
a⅛e потрап у дроби»
За пораду ми взяли німецьке прислів’я, аналогічне нашому виразу «не потрап у халепу».
Перевірте, чи гарно Ви володієте технікою розв’язання задач з дробами.
Для цього розв’яжіть приклади на наступній сторінці:


І. Числа
5 2 „ 5 2 2 —
1) 8 3 14
і \ \ Я
З —+ 4,375 :19 —
J 9 43 450 113 ’ 495
n 17 Відповідь: 2 —.
21
2)
Відповідь: 1.
Якщо Ви не знаєте, як перетворити нескінченний періодичний Нескінченний десятковий дріб на
пе іодичний то повторіть
* формулу суми членів
нескінченно спадної геометричної прогресії: „ "і
де ил перший член прогресії, q її знаменник.
7


101 порада абітурієнту
Приклад: перетворити на звичайний дріб 0,(4).
Розв’язання.
10 100 1000
10 _ 4
_J_ 9
" 10
Відповідь: 0, (4) = —.
Рекомендуємо для перетворення нескінченного періодичного десяткового дробу на звичайний скористатися таким способом:
Приклад: перетворити на звичайний дріб
Розв’язання.
Нехай тоді отже,
х = 0,4(13) = 0,4131313...» 100x = 41,313131..., ЮОх-х = 41,313131...-0,4131313..., λλ .λ Л 409 99х = 40,9, х = .
990 409
Відповідь: 0,4(13) = .
990
звідси
8


І. Числа
W 4
Задачі про чис/іа
Частіше на усному, рідше на письмовому екзамені зустрічаються задачі «на числа». Рекомендуємо звернути увагу на деякі їхні типи.
Задача 1. Доведіть, що сума трьох послідовно взятих чисел ділиться на три.
Доведення.
Нехай п ∈ N. Маємо
п + п + 1 + п + 2 = Зп. + 3 = 3(л + 1), що доводить твердження задачі.
Задача 2. Доведіть, що добуток двох останніх цифр квадрата цілого двозначного числа— парне число.
Доведення.
Маємо:
(10α + Z>)2 = 100α2 + 20αZ> + ∕Λ
Сума 100a2 +20ab має парне число десятків.
Перевіримо, чи може дати у2 число, яке 9


101 порада абітурієнту
закінчується двома непарними цифрами. Це неможливо, тому що
І2 = 1, З2 = 9, 52 = 25, 72 = 49, 92 = 81.
Задача 3. Розв’яжіть в цілих числах рівняння: Юх + у = (x + y )2. *
Розв’язання.
Маємо: 10x + y = x2 + 2xy + y2, (1)
або x2 -2(5-y)x-y + у2 = 0, звідки x = 5-y±y∣25-9y .
Оскільки число х повинно бути цілим, то необхідно, щоб різниця 25-9у була квадратом натурального числа; ця різниця може бути квадратом тільки при у = 0 і у = 1.
Нехай у = 0. Тоді з (1) випливає, що x∣ = 10, Х2 ~ 0.
Нехай тепер у = 1. Тоді з (1) випливає, що Хз = 8, х4 = 0.
Відповідь:
х = 10
у = 0’
х = 0 iτ = 0'
х = 8 jx = 0
у = 1 ’ [ у = 1
♦
Рівняння, розв’язки яких знаходяться в цілих числах. називають діофантовими рівняннями.
10


І. Числа
W 5
Радимо в задачах про числа «залишити місце»
Задачі задачам на подільність.
на подільність
Рекомендуємо повторити:
основні ознаки подільності, що таке спільний дільник, спільне кратне, найбільший спільний дільник (НСД), найменше спільне кратне (НСК).
Будь яке число, що ділить націло кожне з чисел a↑, «2 ,..., ak > називається їхнім спільним дільником. Найбільше з чисел, які ділять націло кожне з чисел aι, a2, ..., ak, називається їхнім найбільшим спільним дільником.
Будь яке число, що ділиться на кожне з чисел b↑, b2, .... bk називається їх спільним кратним. Найменше додатне спільне кратне називається найменшим спільним кратним.


101 порада абітурієнту
Задача 1. Доведіть, що при будь-якому цілому п число n(n2 + 5) ділиться на 6.
Доведення.
Маємо
n(n2 + 5) = n(n2 - 1 + 6) = n(n - 1)(л + 1) + 6п. Оскільки добуток трьох послідовних цілих чисел кратний 6, тобто
n(n - l)(n + 1) = 6к, де kE∕Z,, то n(n - l)(n + 1) + 6п = 6(к + л), отже ділиться націло на 6.
Задача 2. Доведіть, що число p2 - 1 ділиться на 24, якщо р — просте число і р ≥ 5 .
Доведення.
Маємо p2 - 1 = (р - 1)( р + 1). Числа (р - 1) і (р + 1) — парні, оскільки р — непарне число. З двох послідовних парних чисел одне ділиться на 2, друге — на 4, тому p2 - 1 ділиться на 8. Крім того, (р - 1) або (р + 1) ділиться на 3, оскільки ці числа разом з р є трьома послідовними цілими числами, а р на 3 за умовою не ділиться. Звідси випливає, що p2 - 1 ділиться на 24.
12


І. Числа
W 6
A6cojιwmud величина чис/іа
Поняття «абсолютна величина числа» або «модуль» є одним з основних у курсі алгебри та «абітурієнтської математики».
Немає жодного розділу, в якому б не було задач на модуль. При їх розв’язанні варто дотримуватися декількох принципів.
Перший (означення):
а, якщо a ≥ О -а, якщо α< O.
к
Другий (найпростіші властивості):
1) ∣a∣≥<⅛
2) ∖a∖≥a∙,
3) ∣-α∣ = ∣α∣.
із


101 порада абітурієнту
Третій:
У процесі навчання розв’язанню задач з модулем варто пам’ятати, що розглядаються щонайменше два випадки, коли підмодульний вираз більше нуля (не мен- ше) і коли не більше нуля (менше),
Задача 1. Розв’язати рівняння: ∣x-8∣ = 10. Розв’язання.
1) Нехай x-8>0 (x≠8). Тоді ∣x-8∣ = = х-8, і рівняння набуває вигляду: х - 8 = 10, х= 18.
2) Нехай x-8<0. Тоді ∣x-8∣ =-(х-8), і рівняння набуває вигляду: 8 - х = 10, х = -2.
Відповідь: {-2;18}.
Задача 2. Розв’язати рівняння: |х - 5∣ = 2х -18. Розв’язання.
Очевидно, що рівняння може мати корені при х > 9 . Тоді |х - 5∣ = х - 5. отже x-5 = 2x-18, х = 13.
Відповідь: х = 13 .
14


І. Числа
Задача 3. Побудувати графіки функцій:
Розв’язання
15


101 порада абітурієнту
II. АЛГЕБРАЇЧНІ ПЕРЕТВОРЕННЯ
7Ґро типи
Оскільки на іспиті зустрічаються перетворення алгебраїчних виразів, варто знати їх
алгебраїчний
класифікацію.
виразів
Алгебраїчним виразом називається вираз, що складається з чисел (позначених буквами або цифрами) за допомогою алгебраїчних дій (додавання, віднімання, множення, ділення, піднесення до степеня та добування кореня).
Два алгебраїчних вирази А і В зі знаком « = » між ними утворюють рівність:
А = В.
Рівність, яка справедлива для всіх допустимих значень букв, що входять до неї, називається тотожністю.
16


IL Алгебраїчні перетворення
Рівність, яка справедлива не для всіх допустимих значень букв, що входять до неї, називається рівнянням.
Перехід від алгебраїчного виразу А до тотожного йому алгебраїчного виразу В називається тотожним перетворенням виразу А.
Алгебраїчні вирази поділяються на раціональні та ірраціональні.
Алгебраїчний вираз називається раціональним відносно деякої величини, що входить у цей вираз, якщо над цією величиною виконуються тільки дії додавання, віднімання, множення, ділення та піднесення до цілого степеня.
Алгебраїчний вираз називається ірраціональним відносно деякої величини, що входить до цього виразу, якщо він містить цю величину під знаком кореня (радикала).
Наприклад, 3 + 5х — х2, —* раціо-
2 x*+y-7
√^> і ^> ^∖Γ~ . >/ Г
x"+l, y~y∣x+yy∣x' ір¬
раціональні вирази відносно х.
2-4-636
17


101 порада абітурієнту
8
Φopjuyjιu отороченою JHHffζeHHJL
До формул цього типу ми рекомендуємо, крім відомих: [a±b^2=a2,±2ab+b2i (α±Λ)3= ±b? +3al{a+b}, a3+b^=(a+b⅛a2+ab+b2∖ \ / віднести формулу
(a + b + c)1 =a2 + b2 +c2 +2ab + 2ac + 2bc
і 	так звану «чудову тотожність»: a3 + b3 + c3 - 3abc =
= (α + b + c)(fl2 + b2 + c2 - 2ab - 2ac - 2bc).
Сама назва формул говорить про їхнє призначення— «скорочено множити». Додамо, що з їхньою допомогою сума або різниця подається у вигляді добутку.
Радимо в тотожних перетвореннях застосовувати винесення спільного множни- ка та спосіб групування,
18


II. Алгебраїчні перетворення
Задача 1. Довести «чудову тотожність».
Доведення.
α3 +b3 + c3 -3abc =
= (α3 + a2b + a2 c^+(b3 +b2a + b2c∣ + (з э 2 > ∖ ∕ ^> і ^> і \ с +c~a + c b∖-∖a~Ь + а~c+ abc∖- -(b2a + b2c + abcj - {c2 a + c2b + abcj =
= a~ [a + b ÷ с) + b~ (<7 + Ь + с) +
+ c2 (a + b + с) - a(ab + ас + Ьс) -
-b(ab + ac+bc)- c(ab + ас+Ьс) =
= [a + b + c)(a2 +b2 +c2^-(a + b + c)(ab + ac+bc) = = (tf + 6 + c)(α2 +b2 +c2 - ab- ac-bc∖
Задача 2. Розкласти на два множники,
b а а b сума яких дорівнює —+ — . b а
Розв’язання.
. a b a2-b2 (a + b}(a-b) Оскільки = = , то
b a ab ab
2*
19


101 порада абітурієнту
а Ь а + Ь . а-Ь
розкладається на множники і
Ь а а b
... . а Ь .
(їх сума дорівнює — + —
Ь а
. а + Ь а-Ь
Відповідь: , —-—.
а Ь
Задача 3. Розкласти на множники х3 - Зх - 2.
Розв’язання.
Маємо:
A=x3 -3x-2 = (x3-x)-(2x + 2) = = x(x + 1 )(x - 1) - 2(x + 1) = (х + 1 )(x2 - х - 2).
Оскільки
х2 - х - 2 = (х + 1) (х - 2),
то А = (х + 1 )2 (х - 2).
Відповідь: xj - Зх - 2 = (х + 1 )2 (х - 2).
Тїро пропорції
Радимо звернути увагу на похідні пропорції, які є наслідками даної ... а с пропорції -r = ~rf и саме: Ь а
20


II, Алгебраїчні перетворення
a+b c+d. а _ с , b d ' a+b c+d' d^∖^b c~∖^d
а-b c-d
і деякі інші
Задача 1. Довести, що коли
a∖ a^> a3 aιι
— = —— = —- = = — , ТО
¼ b2 b3 bn
П] + +...+ 67yz сі і a*) a- ап
b∖ + b2 +...+bl1 b∖ b2 b3 bll
Доведення.
аі ( \
Позначимо — = k (1 ≤ і ≤ п). Тоді
a∖ = kb↑; a2 = kb2; a3 = kb3:.. .∖an≈ kb,,.
Додамо ліві та праві частини рівностей:
÷ u2 ^f^ cι2 ÷ ... + cιa = k(bі + b2 + b3 + . . . + bn),
звідки дістанемо, що
671+^2 +•••+ al1 _ _ ci∖ _ cι2 _ а3 _ _ Ωn
b∖ + b2 +...+bf1 b∖ b2 b3 bll
21


101 порада абітурієнту
Це співвідношення називається рядом рівних відношень.
Задача 2. Довести, що
/ \ п n I " І і n
αkY cιaι +c2a2 + ■ ■ ■ +ctak
,bι J c∣b" +C2l>2 + . . . +ca6⅛
ЯКЩО
£l_£2__£l_ ⅜
Z>∣ b2 b3 bk
а Ci, c2,..., ск— довільні числа, не рівні нулю.
Доведення.
З даної пропорції одержуємо:
л W II
c∖a} c2a2 _ ckak
C∣6∣ c2^2 ck^fk
Звідси, користуючись рядом рівних відношень, одержимо, що
Л . Л . І л
c∣α1 +c2<72 ÷ ∙ ∙ ∙ ">*ci,⅜ к
cχb" +c2b2 + . . . +ckbk
що і треба було довести.
22


II. Алгебраїчні перетворення
ιy 1 о
СпрощеннJL раціональний виразів
Ці приклади вимагають зосередженості й уваги. їх часто виконують «ланцюжком».
Радимо пам’ятати, що іноді доцільно розв’язувати ці приклади по діях. Радимо не забувати застосовувати формули скороченого множення.
Задача 1. Спростити вираз:
9c 1f с 12с2-9с 9 ї
(3-c)2 27-c3 c2+3c + 9j
Розв’язання.
1Ч с 12с2 -9с 9
1) + —+ -: =
с-3 27-c^ c~ ÷3c + 9
-c(c2 +Зс+9І+12с2 -9c+9(3-c) 27-с3
23


101 порада абітурієнту
_ -c3+9c2 -27с+ 27 _ (З-с)3 _ (3-с)2 27-c3 “ 27-c3 ~ c2 + 3c+9 ’
(3-с)2 c2+3c + 9
c2 + 3c + 9 (3 —с)2
_ 9c c2 +3c÷9
3) - —=
(3-c)2 (3-с)2
_-c2+6c-9 _ (3-c)~ _ J (3-с)2
Відповідь: -1.
Задача 2. Спростити:
а —5 4(α+l) r 9а л + 4
6-Зс a2 + 4a kcr2-16 а2-4а) при а > 4 .
Розв’язання.
α-5+4(α + l) r 9а а+ 4 _
6”3я α^+4αlα^-16 а“-4а>
_ 5-а 4(α + l) / 9а а + 4
3(α-2) α(α + 4) k(α-4)(tz + 4) a(a-4)^
24


II. Алгебраїчні перетворення
а-5 4(α+l) 9a2-(α + 4)2 _
3(α-2) σ(tf÷4) α(α-4)(α + 4) а-5 4(α + l) (За-я-4)(3<7 + я + 4)
3(α-2) α(π + 4) α(α-4)(α + 4)
5-а 4(α + l)α(α-4)(α+4)
3{a - 2) a(a + 4)2(α - 2)4(α + 1)
_ 5-а а-4 _10-2я + Зя-12_І ^ 3(α-2) 2(a-2) ~ 6(a-2) ~б’
. 1
Відповідь : —.
11
УJlLO0Hi momox(Hθcmi
Рекомендуємо розглянути тотожності, що справедливі за деяких умов, так звані умовні тотожності.
Навіть найпростіші з них вимагають для доведення певних навичок, оскільки введення додаткових умов вимагає розв’язувати задачу в двох напрямках: виконувати алгебраїчні пере25


101 порада абітурієнту
творення та «озиратися», щоб вчасно скористатися цими умовами.
Задача 1. Показати, що з рівності
a2 + b2 + c2 - ab + ac+Ьс випливає, що a = b = с.
Доведення.
Помножимо обидві частини рівності на 2. Маємо:
l(a2 +b2 + c2^ = 2(ab + ac+bc),
2^a2 + b2 +c2 -ab-ac-bcj = 0,
a2 -2ab + b2 +a2 -2ac+c2 +b2 -2bc+c2 = 0,
(a-b)2 + (α-c)2 + (6-c)2 =0, що можливо тоді і тільки тоді, коли a = b = с.
Задача 2. Показати, що при непарному п з рівності
випливає рівність
26


II. Алгебраїчні перетворення
Доведення.
Маємо:
(x + y)(x + z)(y + z)
. . (переконайтеся!) = 0,
xyz[x + у + Z) звідси
(x + ^)(x + z)(^ + z) = 0. (І)
Аналогічно, перетворюючи задану в умові рівність, одержуємо, що необхідно довести, що при непарному п з рівності (1) випливає рівність (х" + у" )(x', + z" )(∕' + z" ) = 0. (2)
Дійсно, нехай у + z = 0, тоді у = -z, тому yn +zn = у" - у” = 0 . Отже, (2) має місце, а тому й рівність, яку треба довести, також справедлива.
27


101 порада абітурієнту
W12
Корінь
Перш ніж вчитися виконувати алгебраїчні перетворення виразів, які містять корені, п-оіо степені варто, в першу чергу, повторити теорію.
Необхідно розуміти різницю між поняттями
кореня та арифметичного кореня.
Коренем н-ого степеня (// 2) з числа а називається число, и-ий степінь якого дорівнює а.
Арифметичним коренем /1-ОГО степеня (∕∕ ∈ N) з невід’ємного числа а називається невід’ємне число, л-ий степінь якого дорівнює а.
Позначення: '∙∖[a .
Арифметичний корінь /1-ого степеня з від’ємного числа а визначений у випадку непарного п. Тоді, за домовленістю покладають
28


П. Алгебраїчні перетворення
Звертаємо увагу читачів на те, що
Мають місце співвідношення:
• 'l[a = (a ≥ 0) — основна властивість
кореня.
Зауважимо, що
29


101 порада абітурієнту
Задача. Спростити вираз
⅛ ~ b∖ ' 2 > ПРИ У > 0.
V а - 2ab + b
Розв’язання.
Маємо:
(a.JZΞΞZ=⅛∕Σ= ya~-2ab + b~ ∣6z-^,∣
якщо a>b
= не має змісту,
якщо a = b якщо a<b.
ПО 1 з
Знищенні ірраціонаjιrb ності 6 знауиенни^у (HUCejlbHUty) Позбутися ірраціональності у знаменнику (чисельнику) дробу популярна серія задач, які звичайно пропонують на усному іспиті
з математики.
ЗО


II. Алгебраїчні перетворення
До того ж, як елемент розв’язання, цей вид задач присутній не тільки в тотожних перетвореннях виразів, а й в розв’язаннях рівнянь і нерівностей.
Задача 1. Позбутися ірраціональності у знаменнику (чисельнику) дробу:
31


101 порада абітурієнту
Задача 2. Позбутися ірраціональності у знамен-
32


II. Алгебраїчні перетворення
4a+<Jb~4c Ja+4b~4c
(√7+√*)2-(√^)2 (a + fe-c) + 2√^⅛
(a + b - c)^ - 4ab
4) Вказівка: застосувати «чудову тотожність» (див. ПОРАДУ 8).
З _ 4-636
33


101 порада абітурієнту
∣y 14
Mθ∂yj1∕b
і карені
Серед великої кількості задач і прикладів з коренями найбільш цікавими є ті, в яких явно чи неявно «прихована» рівність л/х2 = М (рідше 2y∣x2n =∣X∣Λ
Зазвичай перетворення такого виразу зводиться до виділення повного квадрату двох чисел або алгебраїчних виразів,
Задача 1.Спростити: √x-2√x-1 .
Розв’язання.
Задача 2. Спростити:
∕α-√x ∕α + √x / 16 V—Т + V—r ~ уі~— ’ yα + √x yα-√x У а -х
якщо х = 4(а -1) .
34


II. Алгебраїчні перетворення
Розв’язання.
х + 4
Виразимо а через х: а = , і підставивши
4
в даний вираз, дістанемо:
W-*
2х + 8 16 х-4
|х - 4∣ |.х -4∣ |л -4∣
Ще зауважимо, що
х > 4, якщо а > 2
і
х < 4, якщо 1 ≤ а < 2.
Відповідь: 2 , якщо а > 2; -2 , якщо 1 ≤ а < 2.
з*
35


101 порада абітурієнту
Радимо звернути увагу на співвідношення, які були використані при розв’язанні:
для всіх a ib
Задача 3. Спростити вираз:
Розв’язання.
Очевидно, що х ≥ 2; х ≠ 4. Маємо:
^x-2y∕2x-4 +'∖∣x + 2y∕2x-4
36


II. Алгебраїчні перетворення
y∣x2 -8x +16
якщо 2 ≤ х < 4
2√2
4-х’
2√x-2
Відповідь:
,якщо х>4.
lW15
Ці задачі аналогічні задачам на спрощення раціональних виразів»
Спрощення ірраціональ ни^ виразів
І тут ми радимо розв’язувати приклади по діях і «ланцюжком», виділяючи «головний
вузол» прикладу.
37


101 порада абітурієнту
Задача 1. Спростити вираз:
Розв’язання.
= 7χ(7χ-ι)(χ+Vχ+1);
Відповідь: х-1.
Задача 2. Спростити:
Розв’язання.
1) 71-x2 +x-l=71+x∙71-x-(l-x) =
= Vi + x ∙y∕∖-x -(71 - х) = л/\-х ■ (√1 + л -л/1 -л);
38


II. Алгебраїчні перетворення
Відповідь: -1.
39


101 порада абітурієнту
У16
Φopjuyjιa «спадного pa∂uf(ajιa>>
Вираз вигляду ^a±4b іноді називають «складним радикалом». Радимо його запам’ятати, тому що він може допомогти побачити, де заховано «точний квадрат».
Секрет тут у тому, що потрібно перевірити, чи є вираз М = а2 -Ь точним квадратом
(а ,9, 25, (а ± Ь) тощо) чи ні. Якщо так, то «складний радикал» спрощується за формулою:
40


IL Алгебраїчні перетворення
Задача 1. Спростити: √α+2√α-1.
Розв’язання.
Запишемо даний в умові вираз у вигляді, що розглядається:
М - а~ -4а+ 4 = (а-2)2, тоді
Задача 2. Довести, що
√4√2+2√6 =V18+V2.
Доведення.
Покладемо 4√2 = а; 24 = Ь. Маємо:
√4√2+2√6 =
41


101 порада абітурієнту
∣4√2+√32-24 ∕4√2-√32-24
2 V 2 = √3^ + T√2 = V18 + V2.
W17
9ІҐотоя(ні перетворенню з щ/бічни/ии ^оренююш
Рекомендуємо, виконуючи тотожні перетворення виразів з кубічними коренями, використовувати формулу
(α±⅛)3 =α3 ±⅛3 +3ab *(α±⅛),l
Наявність у лівій частині рівності виразу а + Ь дозволяє спростити розв’язання задачи
Задача 1. Довести, що
42


IL Алгебраїчні перетворення
Доведення.
Позначимо Z = ⅛∣9 + VδO + ⅛∣9 - д/80. Потрібно довести, що Z = 3. Маємо:
Z3 =9 + √80+9-√80 + 3V81-80∙Z.
Отже,
Z3 = 18 + 3Z; Z3-3Z2 +3Z2 -9Z + 6Z-18 = 0;
(Z-3)(Z2 +3Z + 6) = 0; Z = 3.
Задача 2. Дано: tfx + tfy + ⅛J∑ = 0. Довести, що (х + у + z)3 = 21xy∑.
Доведення.
Маємо: y[x + ⅛∕y = -⅛[z. Піднесемо до куба обидві частини рівності, одержимо:
x +y + 31Jxy(tfx +V7)=-zi
звідси
х + у + z = -3^∕xy(Vx + V7);
X + у + z = -3∙}∕xy(- Vz);
звідки
(x + ^ + z)3 =27xyz.
43


101 порада абітурієнту
Задача 3. Довести, що —= = 2 - √3.
V26-15√3
Доведення.
Маємо:
7-4√3 4-4√3+3
V2'6-∣5√3 V≡-12√3 +18-3√3
(2-√3)2 (2-√3)2
~⅛-J5), ^ U-√3) ~2 3'
18
'Bi∂'ejU.HUU та дробовий пощізни^
На усному іспиті з математики абітурієнт іноді «доводить», що
«Розглянемо частку
N =a1∙.ai=-. а
44


II. Алгебраїчні перетворення
З іншого боку —
2 3 1-3 -І
а : а = а = а .
Отже, 1 1 а~' =~ (???)». а
Доведення здається логічним, але є... помилковим!
а 1 = 37 за означенням, а
Отже,
a0 = 1, a ≠ 0.
cΓ,' = —, де a ≠ 0, п ∈ N. а
р_
a4 =-∖Jap , де a≥0, {/?,<?} cN, q≥2.
a q = , де a>0, {p,<∕}cN, q ≥ 2.
л
Дії над степенями з нульовим, від’ємним та дробовим показником аналогічні діям над степенями з натуральним показником.
45


101 порада абітурієнту
Задача 1. Спростити:
r 1 _iV _і
(l-p2) з-(1 + P2) 2 +2(l-√)2.
І )
Розв’язання.
Маємо:
46


II. Алгебраїчні перетворення
Відповідь
1-р
Задача 2. Спростити:
т2
п2)
п2
• ∕w + - к п)
Розв’язання
n~m -m2n ∙nm~n
n2"∙mn-n, Λm2п2
т-п
2 2 т п
m2 √
mn+m -n,n-3n
2ιιι-2n •
mn + n, -nm~3"
Відповідь:
2т - 2п
47


101 порада абітурієнту
lW19
Розкласти на множники — означає зобразити алгебраїчну суму у Розпадання на jιiHθ^HUfQi
вигляді добутку. При розкладанні на множники
використовують:
1) винесення спільного множника за дужки;
2) групування;
3) формули скороченого множення.
Задача 1. Розкласти на множники x1° + x3 + 1.
Розв’язання.
Маємо
xl0+x5 + l = (x,0+x9+x8)-(x9 + x8 + x7) + + (x7 + x6 + x5)-(x6 + x5 + x4) + (x5 + χ4 +λ'3)-
48


IL Алгебраїчні перетворення
4/2 Л з ( 7 ,∖
-x* ∙(x +x+1J + λ√ ∙(x^ +x+1)-
Задача 2. Розкласти на множники
Розв’язання.
Маємо
7 2 2 7 7 7
= x~y-x z+y z-xy~ +xz~-yz~ =
2 2.2 2.2 2 .
= x у-х z+y z-xy +xz -yz +x)^-xyz =
( 2 2.2\ 2.2._2
= ∖xy∑-xy -x∑+xy)-yz +y z+x2Γ -xyz =
4-4-636
49


101 порада абітурієнту
У 20
JIθ∂ijlbHWTIVb JlLHOlO4JieHiβ. <JT⅛opejua (Безу
При розкладанні многочленів на множники, розв’язуванні рівнянь доводиться ділити многочлен на многочлен.
Поділити многочлен Р(х) на многочлен S(x) з остачею означає зобразити многочлен Р(х) у вигляді:
P(x) = S(x) Q(x) + R(x), де Q(x) і R(x) многочлени, причому степінь R(x) меньша за степінь S(x).
Ділення многочленів виконується аналогічно діленню багатоцифрових чисел. Застосовується правило «ділення кутом». Перш за все, всі доданки в діленому й дільнику записують у порядку зменшення степенів х. Подальші обчислення виконуються так, як показано в прикладі.
50


II. Алгебраїчні перетворення
Приклад:
2х4 + х3 - 10x2 - 7х + 3
2x4 +6x3 +4х2
х2 + Зх + 2 2x2 - 5х +1
-5x3 - 14x2-Їх
-5x3-15x2-10x
х2 ÷ Зх+З
х2 + Зх + 2
І
Отже,
2x4 ÷x3 - 10x2 -7x + 3 = (x2 +3x + 2^2x2 -5x + 1)+ і.
Теорема Безу, Остача від ділення Jr многочлена Р(х) на двочлен X — а S λ дорівнює Р(л).
Відмітимо два важливих наслідки з теореми Безу:
• Якщо а — корінь многочлена, то многочлен ділиться нах - а без остачі.
4*
51


101 порада абітурієнту
• Якщо многочлен ділиться над - а без остачі, то а—корінь многочлена.
Задача. При яких значеннях т многочлен х3 + y3 +∑3 +mxy∑ ділиться без остачі на x + y + ∑f>
Розв’язання.
За теоремою Безу остача від ділення много- 3 3 3
члена х +y +∑ +mxy∑ на x + y + ∑ дорівнює значенню цього многочлена при x = -y-∑, тобто
R = (-y-z)3 +y3 +∑3 +
+ m∙(-y-∑)-y∑ = -(m + 3)-(y2∑ + y∑2). Якщо т + 3 = 0, то R = 0, звідки т = -3. Відповідь: т = -3.
52


III. Рівняння
III. 	РІВНЯННЯ
21 уіінійні
fJTapajuemp
Лінійним рівнянням називається рівняння вигляду ах + b = Q, деа, b задані числа, причому a ≠ 0.
Це рівняння має єдиний розв’язок: x = -b.
а
Лінійні рівняння розв’язують навіть малята: 2х + 5 = 7. Але варто в рівнянні з’явитися букві, як ми грізно називаємо його — «рівнянням з параметром»: ах = 1.
Що ж таке параметрі
Параметр — це величина, що входить до формул і виразів, значення якої є сталим у межах розглядуваної задачі, але може змінитися при переході до іншої задачі.
53


101 порада абітурієнту
У рівнянні буквені величини, які входять до нього за умовою задачі, можуть бути нерівноправними. Одні величини можуть приймати всі свої допустимі значення — це параметри. Інші величини називають невідомими.
Розв’язати рівняння з параметром а — означає, що для кожного припустимого а потрібно знайти всі значення невідомої, які задовольняють це рівняння.
Задача 1. Розв’язати рівняння: ах + b = ex + d.
Розв’язання.
Маємо (a-c}x-d-b, отже:
н Л d-b
1) якщо а - с ≠ 0, то х = ;
а-с
2) якщо α-c = 0,i d-b≠O, то рівняння не має розв’язків;
3) 	якщо a-c=d-b = 0, то коренями рівняння будуть всі дійсні числа
Задача 2. Розв’язати рівняння b2x+ 1 = 2 + b + х .
54


III. Рівняння
Розв’язання.
Маємо (b2 -l)x = b +1. Звідси якщо b2 ≠ 1, тобто b ≠ 1 і b ≠ -1, то початкове рівняння має 1 єдиним розв язок х = .
Ь- 1
Якщо b = 1, то рівняння не має розв’язків, оскільки Ox ≠ 2.
Якщо b = -1, тох—довільне дійсне число.
V 22
Що nunςe jιιemo∂ інтервалів у розв'язанні задач з уаодуяялш
Радимо читачу пам’ятати, що існує декілька «методів інтервалів». Чимось вони схожі, але відрізняються об’єктом дослідження.
У даному випадку ми розглянемо рівняння першого степеня з декількома
55


101 порада абітурієнту
модулями, а також графіки функцій з декількома модулями,
Задача 1. Розв’язати рівняння:
Розв’язання.
1. Знайдемо значення х, при якому кожен з підмодульних виразів рівний нулю:
х - 2 = 0, х = 2; х - 3 = 0, х = 3;
2х + 8 = 0, х = -4.
2. Розташуємо ці «підмодульні корені» на числовій вісі:
Розв’язуємо рівняння на кожному інтервалі:
• х ∈ (- ∞,-4). На цій множині
х - 2 < 0, х - 3 < 0, 2х + 8 < 0 .
Дане рівняння набуде вигляду:
2-x-x + 3 + 2x + 8 = 9, 13 = 9?!
Отже, на розглядуваному інтервалі коренів немає.
56


III. Рівняння
• x ∈ [- 4;2). На цій множині
х -2 < 0, х - 3 < 0, 2х + 8 > 0.
Дане рівняння набуде вигляду: 2-x-x + 3-2x-8 = 9.
- 4х = 12, х = -3.
— З ∈ [— 4;2), отже х = -3 — розв’язок.
• х є [2;3). На цій множині
х - 2 > 0, х - 3 < 0, 2х + 8 > 0.
Дане рівняння набуде вигляду:
х - 2 - х + 3 - 2х - 8 = 9,
- 2х = 16, х = -8 —
сторонній корінь.
• х ∈ [3,∙+∞). На цій множині
x-2>0, x-3>0, 2x + 8>0.
Дане рівняння набуде вигляду:
x-2 + x-3-2x-8 = 9, -13 = 9?!
Отже, на розглядуваному інтервалі коренів немає.
Відповідь: х = -3 .
57


101 порада абітурієнту
Задача 2. Побудувати графік функції у = ∣χ-ι∣-k+ι∣.
Розв’язання.
у23 квадратне. piβHJlHHJi.
Φopjuyjιa
ax2 + bx + с =
= a(x - x↑)(x - хт)
Мабуть, немає абітурієнта, який би не знав, як розв’язувати квадратне рівняння і що таке дискримінант.
58


III. Рівняння
Нагадаємо читачу доведення формули коренів квадратного рівняння ах2 + Ьх + с = 0 (a ≠ 0).
Маємо:
( 2 - Ь
( b}
2
( b}
2 >
с
= а
х +2 х +
- —
—
—
+ —
t 2a
а)
b2 - 4ac c . _ ,7 . ч
, або (£> = b~ -4ас)
4α
2α,
v=0∙
звідки
2α,
2а
= 0, або
b у/Р
2а 2а
b JD
— н
2а 2а
= 0:
, б) х2 =
59


101 порада абітурієнту
Зауважимо, що:
якщо D = 0 , то квадратне рівняння має один b
корінь X = ,
2а
якщо D < 0, то квадратне рівняння не має дійсних коренів.
Рівняння вигляду χ2 + рх + q = 0 (1) називається зведеним квадратним рівнянням.
Доведемо формулу: х2 +px + q = (х - хі)( х - Х2), де Х1 І Х2 корені рівняння (1).
Якщо D > 0, то рівняння (1) має два кореня: р J~D р /Б , ×2=-~-~> D = p~-4q.
60


III. Рівняння
Зауважимо, що
ax2 + bx + с =a(x-x∖ )(x-x2)∙
24
<JJtfeope∕ua iBiema
Це теорема, яка встановлює зв’язок між коренями многочлена f(x) (алгебраїчного рівняння/(х) - 0) та його коефіцієнтами.
Нехай x∣,x2,...,xw—корені рівняння α0x"+α1x"~l + ... + α,,.∣x + an = 0.
61


101 порада абітурієнту
Теорема Вієта для квадратного рівняння:
Нехай x1, х2 — корені рівняння ах2 + Ьх + с = 0.
⅛> т , c
К. Тоді Xi+Xι =—, X∣Λ½ = —. ->i∙ ~ а ~ а
Справедлива й теорема, обернена до теореми Вієта (наведемо її для зведеного квадратного рівняння):
Якщо числа x∣,x2 такі, що Xl+.r2=-p> X∣X2 =^> то вони є коренями рівняння x~ + рх + q = 0.
62


III. Рівняння
Зверніть увагу на задачу, яка є ключем до розв’язання багатьох задач,* Задача. Не розв’язуючи квадратного рівняння ax2 + bx + с = 0,
знайти (виразити через коефіцієнти рівняння):
1) 	x∣ -х2; 2) X∖ + xj; 3) х2 -х2:
4) Х\ +х%; 5) x∣3 -х2; 6) x↑ + х2; 7)xj, -х2.
Розв’язання.
* Такі задачі назвемо задачами-теоремами.
63


101 порада абітурієнту
64


III. Рівняння
Задача. При якому значенні параметра а різниця коренів рівняння
2х2 — (a + 2)x + (2а - 1) = 0 дорівнює квадрату їхнього добутку. Розв’язання.
Маємо (див. перший пункт попередньої задачі) ∕ ∖2 fα + 2λ∣2 2α-l α2-12α + 12
= — -4 — = 4 ■
Далі,
2α-l x∣x2 = ~•
Будемо вимагати, щоб
a2-l2a + 12 (2a-∖∖2
4 “I 2 J
Тоді
а~ - 12α +12 = (2α-1)2;
За218а-11 = 0;
а = 1, а = -3 —.
8
d. . α З
Відповідь: а = 1, а = -3—.
8
5-4-636
65


101 порада абітурієнту
Jlapajiienip у ζβa∂pamHθjuy piβκjLHκi
Якщо у квадратному рівнянні хоча б один з коефіцієнтів або вільний член замінено буквою, то маємо квадратне рівняння з параметром.
Розв’язуючи таке рівняння потрібно врахувати, що якщо перший коефіцієнт дорівнює нулю (а = 0), то рівняння +bx + c = to перетворюється («вироджується») в лінійне.
Умова Z)≥0 є необхідною і достатньою для існування коренів рівняння.
Необхідною і достатньою умовою рівності коренів є умова D = 0.
Розв’язуючи нерівність Z><0, знаходять, при яких значеннях параметра рівняння не має дійсних коренів.
66


III. Рівняння
Задача 1. Розв’язати рівняння відносно*:
ах2 = Ь.
Розв’язання.
1) Якщо а = 0, b = 0, то х ∈ R;
2) якщо а = 0, b ≠ 0, то розв’язків немає;
3) якщо a ≠ 0, b = 0, то х = 0;
4) якщо ab < 0, то розв’язків немає;
5) якщо ab > 0, то х = -∙^^ •
Задача 2. При яких значеннях параметра а
і ,
х~ — ах +1 рівняння = 0 має єдиний розв’язок?
х + 3
Розв’язання.
Дане рівняння має єдиний розв’язок, якщо дискримінант чисельника дорівнює нулю (тоді а = ±2), або якщо
х2 - ах + 1 = (х + 3)(x - b).
о , 1 . ю
В останньому випадку b = і а = —.
10
Відповідь: а = +2 ; а = —.
5*
67


101 порада абітурієнту
Ірраціональні
рівняння
Розглянемо рівняння, яке містить невідому під знаком кореня (радикала).
При розв’язанні ірраціональних рівнянь, зазвичай, «звільнюються» від радикалів шляхом піднесення обох частин рівняння до квадрата або до якогось іншого степеня. Оскільки при цьому, взагалі кажучи, одержується рівняння, не рівносильне початковому, одержані значення невідомої потрібно перевірити підстановкою в початкове рівняння.
Задача 1. Розв’язати рівняння: л/х-2 —. 1 ■ = √2x-6.
√x-2
Розв’язання.
Очевидно, х ≠ 2. Помножимо обидві частини рівняння на7х-2 і піднесемо до квадрату.
68


III. Рівняння
Одержимо (х - З)2 = (х - 2)(2x - б), звідки x2-4x + 3 = 0, х = 1 або х = 3. Перевірка показує, що х = І — сторонній корінь.
Відповідь: х = 3 .
Задача 2. Розв’язати рівняння:
Vx + V2x -3 = ^12(x- 1).
Розв’язання.
Піднесемо рівняння до кубу:
Зх - 3 + 3 + 3^x(2x - 3) (Vx + ^2х-з) = 12(х - 1). Двочлен, який стоїть у дужках у лівій частині, замінимо правою частиною даного рівняння (добро, вони рівні). Але! Така заміна може призвести до появи сторонніх коренів. Тому буде потрібна перевірка. Маємо:
3^x(2x - 3) ♦ ^12(x -1) = 12(х - 1).
Піднесемо це рівняння до кубу:
4x∙(2x-3)∙(-v-1) = 9(x-1)3; х = 1 або х = 3.
Перевірка показує, що обидва кореня задовольняють рівняння.
Відповідь: х = 3, х = 1.
69


101 порада абітурієнту
W 27
^OtD3 ірраціонаjib ни^ piβκjiHb
Областю допустимих значень (ОДЗ) рівняння f∖ (х) =Д (х) називається множина всіх значень аргументу, при яких обидві частини рівності мають зміст.
Ще раз зауважимо, що головна мета в розв’язанні рівнянь знайти корені.
Якщо Ви знайдете ОДЗ, але не знайдете корені, то екзаменатор не зарахує розв’язок. Якщо ж Ви вірно знайдете корені, не знаходячи ОДЗ, то рівняння вважається розв’язаним.
Між іншим, ОДЗ може бути корисною не тільки для відкидання сторонніх коренів (тут також потрібно бути обережним: сторонній корінь може належати ОДЗ), але й для знаходження коренів.
70


ПІ. Рівняння
Задача 1. Розв’язати рівняння:
V2x-4 + =Vx + 6 = 2 - ^2-x.
Розв’язання.
Знайдемо ОДЗ:
2x-4≥0
2-х ≥ 0
Розв’язок можливий, якщо х = 2. Перевірка показує, що х = 2 — корінь рівняння.
Відповідь: х = 2.
Задача 2. Розв’язати рівняння:
Розв’язання.
Знайдемо ОДЗ:
х + Vx2 -16 - 6 ≥ 0
х + 4 ≥ 0 x-4≥0
х2 -16≥0
Піднесемо обидві частини рівняння до квадрата:
∕ l ∖2 Z І ч
2x + -vx2-16∣ -25| x + √x2 - 16 ]+ 72 = 0,
71


101 порада абітурієнту
звідси
-16 = —
2
145
36 .
x + √x -16=8 Lx = :>
145 Л 1 145
<4—, отже, х = — не підходить за
36 3 36
ОДЗ. Перевірка показує, що х = 5 — корінь рівняння.
Відповідь: х = 5.
Радимо пам’ятати основні методи розв’язання ірраціональних рівнянь.
ну 28
9Tpo ju,etno∂u розв'язання ірраціоналъ ни% рівнянь
Про один з них (піднесення до степеня) ми вже говорили. Ніби на противагу йому існує прийом: виділення повного квадрату (тут доречно пригадати формулу «складного радикала» ПОРАДА 16).
72


III. Рівняння
Задача 1. Розв’язати рівняння:
д/х + 3-4л/х-1 + -∖∕*÷8-6-∖∕x- 1 = І .
Розв’язання.
Маємо: х + 3-4λ∕x- 1 = х-1 -4л/х- 1 + 4 = (л/х-1 -2) ;
х + 8 - 6д/х -1 = х -1 - 6л/х - 1 + 9 = (л/х - 1 ~ з) .
Отже, дане рівняння рівносильне рівнянню:
Розв’язуючи його методом інтервалів, одержимо 5≤x≤ 10.
Відповідь: 5 ≤ х ≤ 10.
К г,
Г Звертаємо увагу на досить поширений метод заміни.
Задача 2. Розв’язати рівняння:
∣2x + 2 І х+ 2 _ 7
V х + 2 V2x + 2 12
Розв’язання.
Зробимо заміну ∣2x + 2 _ >
V x÷2 '
73


101 порада абітурієнту
тоді 2х + 2 _ 1 х + 2 ∑
і рівняння після перетворень матиме вигляд: 12z2 -7z-12 = 0, звідси
4 c z = — або 2
3
9
: = - — —сторонній корінь.
Тоді
∣2x + 2 4
J =-, х = 7.
V х + 2 3
Відповідь: х = 7.
ГІ ще один прийом зведення до систем рівнянь.
Задача 3. Розв’язати рівняння:
Vδ-x+Vδ9 + x =5.
Розв’язання.
Покладемо 8-x = <24 і 89 + x = Z>4. Одержимо систему рівнянь:
а + Ь = 5
a4 + b4 = 97'
74


III. Рівняння
Оскільки
a4 +b4 = (я2 + b2 J -2ab =
∕∕ ∖2 ∖2 9 9
= Hα + Z>) -2abj -2a~b~, то одержимо рівняння
(25-2ab)2 -2a2b2 = 97. звідки
ab = 6 або ab = 44, тобто
а + 6 = 5 a + b = 5
, або і
ab = 6 ab = 44
Друга система несумісна, перша система має два розв’язки: а = 2; b = 3 або а = 3; b = 2 . Отже, х = -8 або х = -73.
Відповідь: х ∈ {-8,-73}.
75


101 порада абітурієнту
IV. 	НЕРІВНОСТІ
Уіінійні нерівності. 9∖∕[o∂yjιrb. JTapajucmp
Лінійною нерівністю називається нерівність одного з видів ax>b, ах <Ь, ах ≥b, ax≤b.
Якщо в лінійну нерівність «закрався» модуль, то корисно пам’ятати важливе співвідношення:
;-A)U(/?;
76


IV. Нерівності
Задача 1. Розв’язати нерівність
Розв’язання.
Відповідь: x∈0.
Задача 2. Знайти найбільше ціле число, що задовольняє нерівність:
2x +1 Зх - 1 ,
> 1.
З 2
Розв’язання.
Маємо
2(2x + l)-3(3x-l)-6>0,
звідки
c , , 1
-5х > 1, або х < —,
5
отже, найбільше ціле х, що задовольняє дану нерівність, дорівнює -1 .
Відповідь: -1 .
77


101 порада абітурієнту
Задача 3. Розв’язати нерівність ∣2x - 3∣ ≤ 2.
Розв’язання.
Нерівність рівносильна подвійній нерівності -2≤2x-3≤2, або l≤2x≤5, звідки 0,5 ≤ х ≤ 2,5 .
Відповідь: хє[0,5; 2,5].
Задача 4. Розв’язати нерівності:
1) ах > 3; 2) ах > -3.
Відповідь: 1) Якщо а > 0, то х > —; а
З якщо а < 0, то х < —;
а
якщо а = 0, то х ∈ 0.
ЛХ п Л З
2) Якщо а > 0, то х > —; а
якщо а < 0 , то х < ;
а
якщо а = 0, то х є R.
78


IV, Нерівності
∣y зо
квадратні
нерівності
Як завжди, почнемо з найпростіших, наприклад, х < 3. Ця нерівність рівносильна нерівності Іх| < л/З або -√3 <х<д/З.
2
Ось інша нерівність: х > 5.
Вона рівносильна нерівності
м
>л/5або
х ∈ (- ∞j-√5 j U (Vδ; ∞).
Звичайно, ці нерівності можна розв’язати методом інтервалів («змійкою»). Наприклад,
X2 < 3 або (х-д/з j∙(x +>/з)< 0, x∈(-√3i√3∣
Перейдемо до розв’язання квадратних нерівностей в залежності від D.
79


101 порада абітурієнту
Геометрична
a)D>0.
Розв’язати нерівність: ?г2 _ і 0
6)D = 0.
У цьому випадку в квадратному тричлені ax2 +bx + c
X∣ = х2
і він перетворюється на повний квадрат
α(x - xj) (х, = x1
Тому квадратна нерівність 7 ,
істинна при а > 0 і при всіх х, крім xi.
80


IV. Нерівності
Розв’язати нерівність: Xі -2x + 1 >0.
Розв’язання.
(x-l)i>0,
отже,
b)D<0.
Тут нам хотілося б поставити знак оклику (!) Увага! Не порівнюйте цей випадок з рівнянням! Рівняння при D < 0 не має розв’язків, а не- рівність може мати; Та ще и усю числову вісь (х ∈ R)! Потрібно, щоб знак першого коефіцієнта співпадав зі знаком нерівності Розв’язати нерівність: у 1
Xі -Λ∙ + 10>0. І 7
Розв’язання. λ**s
D = l-40 = -39<0. 10
отже, — ►
λ-∈R.
6 — 4-636
81


101 порада абітурієнту
У 31
Cucmejuu нерівностей
Розглянемо спочатку систему двох нерівностей першого степеня з однією невідомою.
Звичайні операції з кожною з нерівностей не викликають ускладнень. Помил- ки бувають у записі загальної відповіді
Задача 1. Розв’язати систему нерівностей:
14 _ л
—х +12 < 0
5
9--x<14
І 5
Розв’язання.
Перетворимо систему:
7 25’
отже, X ∈
Відповідь: хе -
12,5;-4
2
82


IV. Нерівності
Рекомендуємо як вправу наступну задачу: Задача 2. При якому значенні а системи нерівностей
не мають розв’язків?
Відповідь: 1) a ≥ 4; 2) ні при якому;
3) а>5; 4) a≤2.
Інтерес до систем нерівностей посилюється ще й тим, що часто розв’язання нерівності зводиться до розв’язання систем нерівностей. Задача З (Обережно! Параметр!).
Розв’язати нерівність:
а
х-1
Розв’язання.
Перетворимо задану нерівність:
Одержана нерівність рівносильна сукупності двох систем нерівностей:
x-(a +1) > 0
х -1 > 0
(*)
або
x-(α+ 1) < 0 х - 1 < 0
(**).
6*
83


101 порада абітурієнту
х > а +1
х < 1
Розглянемо (♦):
. Очевидно, що
система має розв’язок при а + 1 < 1, тобто при а < 0. Отже, при а < 0 х є (1 + а\ 1).
Розглянемо (**):
х < а + 1 \х>1
Очевидно, що
система має розв’язок при а + 1 > 1, тобто при а > 0. При а > 0 тільки друга система сумісна, й її розв’язками є значення хе(1; 1+а). При а = 0 задана нерівність розв’язків не має.
Відповідь: якщо a>Q, то хє(1; 1 + а); якщо а < 0, то х є (1 + а', 1); якщо а = 0, то х є 0 .
У 32
Ірраціональні нерівності
Ми навмисно розглядаємо ірраціональні нерівності після систем нерівностей тому, що розв’язання ірраціональних нерівностей зводиться до розв’язання рівносильної сукупності систем раціональних нерівностей.
84


IV. Нерівності
Рекомендуємо пам’ятати, що
то
то
2
Задача 1. Розв’язати нерівність -∖M - х • Розв’язання.
Дана нерівність рівносильна системі
ЗВІДКИ ’
або «
Відповідь: х ∈ (3;4].
85


101 порада абітурієнту
Задача 2. Розв’язати нерівність
Розв’язання.
51 - 2х - х2 ≥ 0 l-x<0
86


IV. Нерівності
fDoβe∂eHκjb нерівностей
До цих пір ми розв’язували нерівності різних типів, тобто шукали значення букви (невідомої), при якому задана нерівність була б вірною.
Але існують нерівності, вірні при всіх допустимих значеннях букв. Такі нерівності називають тотожними.
Вони не розв’язуються, а доводяться!
Рекомендуємо найбільш популярний спосіб: шляхом рівносильних перетворень дана нерівність зводиться до очевидної. наприклад: A1 ≥ 0.
Задача 1. Довести, що при довільних а і b „2 , і , » 2 л
Доведення.
Маємо: a2+ab + b2
а + —Ь 2
4
що вірно (рівність досягається при a = b = 0).
87


101 порада абітурієнту
Задача 2. Довести, що при а > 0, b ≥ 0 справед- . . а + Ь /—-
лива нерівність —-— ≥ √αo .
Доведення.
Маємо:
(рівність — при α = Z>).
Задача 3. Довести, що при довільних a,b,c a1 +b2 +c1 ≥ ab + ac+bc.
Доведення.
Маємо:
a2 +b2 +c2 -ab-ac-bc =
= ~(2a2 +2b2 + 2c2 -2ab-2ac-2bc] =
= у [(а - b)2 + (b-c)2 + (а - c)2j ≥ 0 (рівність — при a = b = с).
Задача 4. Довести, що при довільних значеннях х має місце нерівність:
x'0-√+√-√+l>0 .
88


IV. Нерівності
Доведення.
Маємо:
— що очевидно.
Γ∣βhΛf[3 34 Серед різноманітних * JQp способів доведення
Нерівність
Ноші
нерівностей, спосіб доведення за допомогою нерівності Коші посідає особливе місце, в першу чергу, завдяки ефективності його застосування.
Мова йде про нерівність
названу на честь французького математика Коші (1789-1857 рр.).
89


101 порада абітурієнту
_ , . 671 ÷ 67 т і
Для и = 2 нерівність —! -≥y∣a∣a2 нами
2
вже доводилась (див. ПОРАДУ 33).
«Перлиною» нерівностей є доведення
нерівності Коші для п = 3:
Радимо звернути на неї увагу.
Вже початок є таємничим і романтичним! Доведемо («чомусь!») нерівність Коші для чотирьох членів:
⅛67∣ + 67-> + 67β + 67д і
 ≥ √α∣ ∙ a1 ∙ α3 ■ a4.
Маємо:
90


IV. Нерівності
Тепер для доведення нерівності Коші для /1 = 3 візьмемо чотири (!!!) числа: λ∣ + a-> + cι⅛
a∖>a2>a3∙>
і 	застосуємо до них доведену нами нерівність Коші для чотирьох членів.
Маємо:
звідки
z \ 4
<7∣ + ∏2 +
к з >
≥ ala2a3,
отже,
А тепер покажемо застосування нерівності Коші,
91


101 порада абітурієнту
Задача (авторська). Довести нерівність n^m-∖ + m>ln-∖ ≤ пт.
Доведення.
Очевидно, що т ≥ 1, п ≥ 1. Маємо:
г( т-1 +1 пт
ny∣∖m -1) • 1 ≤ п = — (1)
г, ^r~ п - 1 + 1 пт т^(п -1) • 1 ≤ т - = —- (2).
Додамо ліві й праві частини (1) і (2), одержимо n∙y∣m- 1 + m-Jn-∖ ≤ пт.
Знак рівності буде при т = 2, п = 2.
92


V. Системи рівнянь
V. 	СИСТЕМИ РІВНЯНЬ
Систеβiu рівнянь першою степеня. 7Tapajιιemp
Система двох лінійних рівнянь з двома невідомими має вигляд: aλx + b↑y = cx a2x+b2y = c2
Розв’язувати такі системи неважко, набагато цікавіше їх досліджувати, якщо хоча б в одному з рівнянь є параметр.
Рекомендуємо звернути увагу:
Система (1):
• має єдиний розв’язок тоді і тільки тоді, коли fL≠Δ-∙ α2 ⅛2
• має нескінченну множину розв’язків тоді і a∖ b∖ cι
тільки тоді, коли —- = — = —;
a2 b1 с2
93


101 порада абітурієнту
• не має розв’язків тоді і тільки тоді, коли
a2 с2
Задача. При яких значеннях параметра а система рівнянь
ах - 4y = а +1
2х + (я + 6)j> = а + З
буде несумісною?
Розв’язання.
Маємо:
а -4 а +1
— = ≠ .
2 	а + 6 а + 3
Звідси
а2 + 6а + 8 = 0
• ; а = -4.
a2 + a-2 ≠ 0
Таким чином, при а--4 дана система не має розв’язків.
Відповідь: α = -4.
94


V. Системи рівнянь
ІЇгуїіншні систедш piβHjLH∙b
Якщо одне з рівнянь системи лінійне, а інше — другого степеня, то з лінійного рівняння виражають одну невідому через іншу і підставляють у друге рівняння. Якщо система складається з
однорідних рівнянь, то заміна у = tx
зводить систему до квадратного ф. рівняння,
УГЯкщо система не змінюється при взаємній заміні невідомих (х на у і у на х), то така система називається симетричною й розв’язується заміною х +y = u, ху -t,
Задача 1. Розв’язати систему рівнянь
3-∕ =7
95


101 порада абітурієнту
Розв’язання.
Ліву частину другого рівняння розкладемо на
множники:
х-у = 1
( ∖( ^> ^> \ -,, ∖x^JzΛx^ + χy+y~ ) = 7
звідси
х-у = 1
<
(x-y)[(x-у)2 + 3xyj = 7
Підставимох-у = 1 з першого рівняння у друге:
звідки*
х-у = 1 [х-у - і
1 + Зху = 7 ’ ху = 2
х = 2 (х = —1
1 або
Ly = l ∖y = -2
Відповідь: >
x = 2 ∫x = -l
У = 1 ’ 1У = ’
Далі може бути використана теорема, обернена теоремі Вієта.
96


V. Системи рівнянь
Задача 2. Розв’язати систему рівнянь ху + х + у = 11 x2y + xy2 = ЗО Розв’язання.
Покладемо
х + у = и, xy = t.
Тоді система рівнянь набуде вигляду: u + t = 11
' ut = ЗО ’
звідки маємо, що
и = 5, і = 6 або и = 6, / = 5.
Тоді
х + у = 6 або ху = 5
х + у = 5 ху = 6
Розв’язуючи кожну з одержаних систем за теоремою, оберненою до теореми Вієта, знайдемо чотири пари розв’язків заданої системи.
х = 5
/ = 1
х = 1
у = 5
х = 2
7 = 3
Відповідь:
х = 3
y = 2,
7 — 4.636
97


101 порада абітурієнту
∣y 37
Cucmejuu ірраціоналъ hu⅛ рібнушь
Якщо Ви розв’язуєте системи рівнянь з квадратними, кубічними і т. д. коренями, то після різноманітних перетворень, замін вони зводяться до розв’язання систем раціональних рівнянь.
Задача 1. Розв’язати систему рівнянь 3y∣4x + 2 у - 5y∣2x - у = 2 l-y∣4x + 2y +y∣2x-y = 32
Розв’язання.
Позначимо y∣4x + 2y = a, -y]2x-y = b.
Тоді дана система рівнянь набуде вигляду: '3α-56 = 2 7α + 26 = 32 ’
98


V. Системи рівнянь
звідки а = 4 , b = 2. Переходячи до невідомих х і І4х + 2у = 16 у, одержуємо систему рівнянь { ,
|2х - у = 4 яка має розв’язки: х = 3; у = 2.
Відповідь
х = З
7 = 2
Задача 2. Розв’язати систему рівнянь
∣4x + у2 = 4
Розв’язання.
Очевидно, що
Піднесемо ліву та праву частини першого рівняння системи до квадрата:
Після повторного піднесення до квадрата (х ≤ 2 (♦*)), одержимо
7*
99


101 порада абітурієнту
Таким чином, маємо систему рівнянь 4x-∕ -4 = 0 4x+y~ =4
розв’язуючи яку, остаточно одержимо [х = 1 \у = 0
х = 1
Λ = θ'
Відповідь:
Систе/іш
Щоб навчитися розв’язувати системи рівнянь з трьома невідомими, необхідно
рівнлкъ скористатися загальною, з mpιbojua ajιe дуже корисною невід о juujιιu порадою: ПРАКТИКА, ПРАКТИКА, практика!
У таких системах зосереджено весь арсенал методів розв’язання систем рівнянь:
100


V. Системи рівнянь
заміни, комбінація одного чи двох рівнянь з третім, зведення до рівняння третього степеня (теорема Вієта для кубічного рівняння)...
Якщо рівняння
∕3 +at2 + bt + с = 0 має корені X, у, z, то, як відомо, вони повинні задовольняти співвідношення:
Вірне й обернене: х, у, z, що задовольняють цій системі, можна розглядати як корені рівняння
∕3 +at2 +bt + c = Q.
Задача 1. Розв’язати систему рівнянь х + у + z = 0 ∙x2 +∕ +z2 =38. xyz = ЗО
101


101 порада абітурієнту
Розв’язання.
Піднесемо перше рівняння до квадрата
Xі +y2 + z1 + 2xy + 2xz + 2yz = 0;
враховуючи друге рівняння системи, одержимо:
38 + 2(xy + xz + yz) = 0.
Таким чином, маємо систему рівнянь:
х + у + Z = 0
’ ху + xz + yz = -19, хуг = ЗО
розв’язання якої зводиться до знаходження коренів рівняння
t3— 19/ —30 = 0.
Це рівняння має три корені:
/1 = —2; І2 — 5; ~3,
звідки дістанемо відповідь.
х = -2
х = -2
х = 5
Відповідь:
У = 5 , '
У = -з, ‘
У = 2 ,
z = -3
z = 5
z = -3
х = 5
х = -3
х = -3
У = -з, '
У = 5 > '
j, = -2.
z = 2
2 =-2
z = 5
102


V. Системи рівнянь
Задача 2. Розв’язати систему рівнянь Λy = z2
<x + y + z- 7 x2 +y2 +z2 = 21 Розв’язання.
Маємо
х + у = 7-z, звідки
х2 + 2xy + y2 = 49- I4z + z2 ,
але 2 , 2 пі 2 2
х + у =2∖- z , xy = z ,
а тому одержимо
21 -z2 +2z2 =49- 14z + z2 , звідки z = 2.
{х + у = 5
, тобто ху = 4
Відповідь:
103


101 порада абітурієнту
VI. 	ПРОГРЕСІЇ
Задач і рекомендацій на одну з найдавніших тем шкільної математики достатньо.
Яриф^етична та геометрична прогресії
Ми нагадаємо різні формули арифметичної (позначається « — ») та геометричної (позначається <<^^>>) прогресій, а Вам радимо звернути увагу на їхні основні властивості, які називаються характеристичними.
Не прогайте таку пораду: якщо в умові задачі фігурують обидві прогресії} то позначення потрібно вводити за допомогою членів геометричної прогресії.
Отже, почнемо...
104


VI. Прогресії
АРИФМЕТИЧНА ПРОГРЕСІЯ
Формула загального члена .
an =a↑ +iZ(w-l), де d—різниця.
Сума п членів .
(α1 +all )п
S"= 2 •
Характеристичні вла-
СТИВОСТІ ^J∙ .
1) Довільний член арифметичної прогресії (крім першого) дорівнює півсумі рівно- віддалених від нього членів:
ГЕОМЕТРИЧНА ПРОГРЕСІЯ
Формула загального
члена ∙^∙.
⅛ = b↑qn~x,
де q—знаменник.
Сума п членів .
і (і „п\
M1~<7 j
" 1-? '
Характеристичні властивості .
1) Квадрат довільного члена геометричної прогресії (крім першого) дорівнює добутку рівновіддалених від нього членів:
⅛2 =⅛-l⅛÷∣∙
105


101 порада абітурієнту
При к = 1
an-∖ + ⅛1 a"~ 2
2) У скінченній арифметичній прогресії суми членів, рівновідда- лених від її кінців, рівні між собою і дорівнюють сумі крайніх членів:
A+47=¾+4h=∙∙∙= =⅝+⅛÷n=2°l+rf∙ «-•)•
2) У скінченній геометричній прогресії добутки членів, рівно- віддалених від її кінців, рівні між собою і дорівнюють добутку крайніх членів:
⅛1 -bn =b, ∙bn-2 =...= = ⅛ ∙⅛-*+ι = *∣V'^'∙
Задача 1. Написати перші три члени арифметичної прогресії, в якій сума довільного числа членів задана формулою S„ = 7п2 -5п.
Розв’язання.
Нехай п = 1. Тоді 5∣ = a1 = 2. При п = 2 маємо S1=α1+α2=18. Отже, α2=18-α∣ = = 18-2 = 16, а різниця прогресії б/= 16-2 = = 14, отже, перші три члени будуть: 2, 16, ЗО. Відповідь: 2, 16, ЗО.
106


VI. Прогресії
Задача 2. Довести, що якщо числа , ,
Ь + с с + а
1 * 2/22
утворюють v, то числа а , о , с та- Ь + а
кож утворюють .
Розв’язання.
Враховуючи умову, маємо 1 1 = J 1
с + а b + c b +а с + а’
або
Ь+с-с-а _ с+а-Ь-а
(c + a)∙ (b + c) (b + a)∙(c + а)’
або (b - а) - (а + Ь) = (Ь + с) - (с - а),
λ2 . „2 _ і 2 2 2 / 2 /2 и -г С
тобто Ь -а — с -b . Ь = ,
2
а це означає, що твердження задачі доведено.
Задача 3. Чотири числа складають-^. Якщо від них відняти відповідно 2; 6; 7; 2, то одержимо числа, які утворюють . Знайти ці числа.
107


101 порада абітурієнту
Розв’язання.
Користуючись ПОРАДОЮ 39, позначимо невідомі числа як члени . Нехай перше з чисел, яке утворює буде Ь, а знаменник прогресії— qi тоді друге число буде bq, третє — bq2 і четверте — bq3. 3 умови випливає, що числа b + 2; bq + 6; bq1 +7; bq3 +2 утворюють Остання умова виконується, якщо
(bq+б) • 2 = bq2 + 7+b+2
(bq~ +7^∙2 = bq3+2+bq+6
або
звідси
2bq-bq2 -Ь =-З
<
2bq1 —bq3 -bq = -6 ’
2bq-bcf^ -Ь = -З q(^2bq-bql -b) = -6
Поділивши друге рівняння системи на перше, одержимо q - 2. Тоді b = 3 . Отже, 3; 6; 12; 24 — шукані числа.
Відповідь: 3; 6; 12; 24.
108


VII. Логарифми. Логарифмічні рівняння...
VII. ЛОГАРИФМИ. ЛОГАРИФМІЧНІ РІВНЯННЯ ТА НЕРІВНОСТІ
У 40
J[θldpuφjlLU
Впевнені, що Ви знайомі з означенням і властивостями логарифмів.
Ми радимо звернути увагу на основну логарифмічну тотожність: ½u^n=N (л>0; a≠∖', Λf>O) як «предка» багатьох формул із логарифмами.
⅛ Розглянемо одну з головних груп формул: логарифми з різними основами.
109


101 порада абітурієнту
Якщо
Λ>O,α≠l,x>O,7V>O,7V ≠ 1,
Λ>O,δ≠l,∕ι≠O,σΛ≠l,c>l,
то
ЇХ. »r 1 • -х lθg∕,2V
1) log л = ; 2) log л = ;
logfvα 6β log* а
3) 1о8Л=И„Л”;4) 1θg8^ = 1 + 10≡α* ;
5)α⅛c = c⅛a. Доведення.
1) Маємо: al0%a ” = N. Прологарифмуємо обидві частини рівності за основою N:
logα/V-log^ α = logjv 2V, і х, 1
отже, logσ N = .
logy7 а
2) Маємо: a^a^≈ N. Прологарифмуємо обидві частини рівності за основою b (b > 0, b ≠ 1):
logα N ∙ logz, a = logz, W, або logo N = уё/> N-.
log/, а
ПО


VII. Логарифми. Логарифмічні рівняння...
3) Маємо: an^a = Nn. Прологарифмує- мо обидві частини рівності за основою а” (αn > 0, an ≠ 1): logα N ∙ loga„ an = Iogα,, Nn, таким чином, logfl N = logα∏ Nn.
λ . , ж, log„ N logn N
4) Оскільки logfljfc N = — = —— ,
∣ogtz ак 1 + logα к то твердження задачі доведено.
5) Вказівка: прологарифмуйте спочатку за основою а, потім — за Ь.
Якщо Ви познайомилися із запропонованими формулами, рекомендуємо звернути увагу на серію задач на знаходження логарифмів, що відрізняються один від одного основою та степенем.
Деякі з таких задач потребують кмітливості і знання властивостей чисел.


101 порада абітурієнту
Задача 1. Дано: log∣2 27 = а. Знайти log6 16. Розв’язання.
Маємо:
logp 27 = 3 log p 3 = -—- = а.
log3 4 +1
Тоді log4 3 = ——. 5-а
З 	іншого боку, log6 16 = 21og64 =
2 4 12-4α
1 2log4 3 + 1 3-а
lθg43 + -
o. . 12-4α
Відповідь: .
3-<7
Задача 2. Дано: log5 4 = a; log5 3 = b . Знайти
Розв’язання.
2 	~ o∙ ∙ a + b Відповідь:
2
а + Ь
2
2
112


VII. Логарифми. Логарифмічні рівняння...
Звертаємо увагу читача на серію задач на логарифми: «Що більше?».
При їх розв’язанні радимо не робити громіздких перетворень, а користуватися порівнянням чисел.
з 4
Задача 1. Що більше ∣og52 чи cos у ?
Розв’язання.
З 	одного боку
,°δ5 ~ ∣og2 5 > log2 22л/ї 2√2 4* ’
• з 4 з тг ∙^2^
а з іншого — cos — < cos — = — .Тому
5 4 4
log5 2 >cosj -.
Задача 2. Що більше log4 26 чи log6 17 ?
Розв’язання.
Маємо:
log4 26 > log4 16 = 2, a log6 17 < log6 36 = 2.
Отже, log4 26 > log6 17 .
8 — 4-636
113


101 порада абітурієнту
Задача 3. Що більше log2 5 чи log3 4 +1 ?
Розв’язання.
Доведемо, що
Iog2 5 - log3 4 > 1.
Це співвідношення рівносильне співвідношенню 5 4
log2 5-2 > log3 4 -1, або log2 - > log3 -,
тобто необхідно довести, що
,°g27 4
3
з
Скористаємося тотожністю log* с log* а
'' . ∙ 1 4
и очевидною нерівністю log2 3 > —. Отже,
Нам залишилося перевірити, що
З
( 5 V 4
— > , або що 125•9 >1024 .
U√ з
Таким чином, Iog2 5 > log3 4 + І.
114


VII. Логарифми. Логарифмічні рівняння...
≡41
jTθζajHUI(θβi рівняння
Рівняння називається показниковим, якщо невідома входить до показників степенів сталих основ.
Радимо виділити два основні методи розв’язання показникових рівнянь:
• метод прирівнювання показників, тобто зведення заданого рівняння до вигляду
∕W g(x) а = а Ж'
а потім — до вигляду Дх) = g(x)', д 1
• метод введення нової змінної (заміна).
Звертаємо увагу! Врахуйте, що ах > 0, а > 0, a ≠ 1, що важливо при відсіканні сторонніх коренів.
Розв’язання.
Очевидно, що х > 0 . Маємо:
8*
115


101 порада абітурієнту
5
7ς √∑-4
5vx =5 , звідки
Відповідь: х = 25.
Задача 2. Розв’язати рівняння
4x-2∙14∙v =3∙49x.
Розв’язання.
Поділимо обидві частини рівняння на 4х.
Одержимо:
1-2- —
<49
або 1-2- —
49
Позначимо
= y∙ Тоді l-2y = 3y2, у = - або у = -1 — не підходить.
о - ,1
Відповідь: χ = log_ -.
1 З
2
116


VII. Логарифми. Логарифмічні рівняння...
Задача 3. Розв’язати рівняння
27х - 13∙9x + 13∙3x+l-27 = 0.
Розв’язання.
Маємо: 33x-13∙32x+39∙3x-27 = 0, звідки
(зх - з) • (з2х -10 • 3х + 9^ = 0, тобто (3х - з) • (зх -1) • (3х - 9) = 0, а отже,
3 х =3 Γx = ∣
3x = 1 , X = 0 . 3x = 9 x = 2
Відповідь: х є {0;1;2.}
Щоб розв’язати рівняння вигляду ιθ⅞zω=ioga∕2u)
у 42
оіариф/нічні
рівняння необхідно:
1) розв’язати рівняння ∕1 (х) = ∕2(x) і
2) серед знайдених коренів відібрати ті, які задовольняють нерівностям ∕1 (х) > 0 і /2 (х) > 0.
117


101 порада абітурієнту
< J^ Увага! 7Ї корені рівняння, -/Ж fi (х) = /2 (*)> Щ° залишилися,
є сторонніми для вихідного рівняння. Радимо виділити два основні методи розв’язання логарифмічних рівнянь (аналогічно показниковим рівнянням):
• метод, що полягає у зведенні рівняння до вигляду logo /] (х) = logσ ∕2 W, a потім — до вигляду /і(х) = /2(х);
• метод введення нової змінної.
Задача 1. Розв’язати рівняння log∣-r3-log1-x2-0,5 = 0.
Розв’язання.
[l-x>0 їх< 1 З Л _
°Д3: її ^і’1 л• Маємо 1°g∣-x Т = 0>5> l-x≠l ∣x≠0 2
З і 5
— = √1 -х , звідки х = — (належить до ОДЗ).
Відповідь: х = — .
4
118


VII. Логарифми. Логарифмічні рівняння...
Задача 2. Розв’язати рівняння
lg(x + l,5) = -lgx •
Розв’язання.
fx + l,5> 0
, х > 0. Маємо після потен-
ОДЗ:
[х > 0 ціювання lg(x + l,5)x = 0 маємо x2 + l,5x -1 = 0,
х = — або х = -2 — не підходить за ОДЗ.
Відповідь: х = —.
2
Задача 3. Розв’язати рівняння
3√log3 х - log3 (Зх) -1 = 0.
Розв’язання.
ОДЗ:
log3 х - 3√log3 х +2 = 0.
Нехай λ∕log3 х = /, тоді t2 - 3/ + 2 = 0, / = 1 або t = 2. Отже λ∕log3 х = 1 або -λ∕log3 х = 2 , звідси х = 3 або х = 81.
Відповідь: х ∈ {3; 81}.
119


101 порада абітурієнту
Лої^азниі^рві
та уюгарифjuiκκi piβHjLHKji з «родзинкою»
Пропонується звернути увагу на задачі підвищеної складності, при розв’язанні яких застосовується нестандартний прийом, їх ми називаємо
«задачами з “родзинкою”».
Задача 1. Розв’язати рівняння
Розв’язання.
Помітимо, що
√9-4√5 ∙√9 + 4√5 = 1.
Нехай
Маємо:
z + - = 18, z2-18z + l = 0, z = 9±4√5.
7
120


VIL Логарифми. Логарифмічні рівняння...
Відповідь: X ∈ {2;-2}.
Задача 2. Розв’язати рівняння x,g7 + 7,g* =98.
Розв’язання.
Помітимо, що xlg7=7lg*. Таким чином, дане в умові рівняння можна записати у вигляді 2∙7lg* =98, або 7,gx = 49 , lgx = 2 ,х = 100 .
Відповідь: х = 100.
Задача 3. Розв’язати рівняння ∣°g,χ log х
З +х 3 =
162 •
Розв’язання.
Маємо: т1о£з x =f√0g3 xV0g∙3 * = √0⅛3 x .
•А» I ∙z І —/
Підставимо одержаний вираз у вихідне рівняння,
121


101 порада абітурієнту
log;* 9
дістанемо 2-З =162» або log3x = 4,
звідки log3 х = 2 або log3 х = -2.
л 1
Відповідь: х = 9; х = —.
9
Задача 4. Розв’язати рівняння
,, , .2 l(m+√e<"'-"j
(lglgx) = - ТТТТ' ⅛l<‰ '0
⅛(m-√÷+">
при т > |л|.
Розв’язання.
Зрозуміло, що
ти - л > 0, w + и > 0, х > 0, x≠l.
Обчислимо підкореневий вираз. Нехай
. (m+n)'et",-") .
А (т-л)'е("'+,,) '
Тоді
lg A = lg(∕w - п) lg(∕n + w) - lg(∕w + п) lg(w - п).
Отже,
А = \.
122


VIL Логарифми. Логарифмічні рівняння...
Маємо:
/ \2 1 / \2
(klglgx} =-∣g-, (IglgxJ = lglgx, lg X
lglgx = 0 lgx = l х = 10
lg∣gx = 1 ’ [lgx = 10’ [χ=10lo'
Відповідь: х ∈ (1О;1О10}.
Задача 5. Розв’язати рівняння
ig(x2) ⅛(χ3) ⅛(χ4)
(lgx)2 (lgx)3 (lgx)4
Розв’язання.
Рівняння може мати розв’язок, якщо
lgx > 1 • (*)
Маємо
2 3 4 5
⅛χ + Λ V+Λ V+6 V +'■ ■ ^8, (1)
1⅛λ (IgxJ (ιlgxJ (lgx)
Поділимо обидві частини рівняння на lgx :
123


101 порада абітурієнту
Віднімемо (2) від (1). одержимо:
1 1 1 o 10
г + г + r + ...= 8--— • (lgx)" (lgx) (lgx) ⅛*
У лівій частині рівняння стоїть сума нескінченно спадної геометричної прогресії зі знамен- 1 • ником . Тоді
lgx
1
/ \2
l- = 8^i⅛ ’ (8⅛*->θ)∙(⅛*-l)=',
1 lgχ
81g2x -181gx + 9 = 0.
Розв’язуючи останнє рівняння відносно Igx,
З З
одержимо lgx = - або lgx=- — сторонній
2 ^1
корінь (див. (*)). Тоді
з
х = 102 = 1000.
Відповідь: х = 1000.
124


VIL Логарифми. Логарифмічні рівняння
44
tjTdpa.juemp у показникових, і jιoιapuφ^іічни^ piβujiHHjut
Як тільки в рівнянні з’являється параметр, його «рейтинг» зростає. Ми радимо починати з простих рівнянь з параметром:
] у Найпростіше показникове рівняння
з 	параметром: ах - с, де а > 0, a ≠ 1.
2) Найпростіше логарифмічне рівняння з параметром: logtf х = с, де а > 0, a ≠ 1.
1) При с > 0 це рівняння має єдиний розв’язок
х = logα с, при с ≤ 0 —розв’язків немає.
2) При с ∈ ]К рівняння має
єдиний розв’язок—х = ас.
Задача 1. При яких значеннях параметра а рів- х—2 х— 2
няння 3∙4 +27 = α + α∙4 ^ має розв’язок?
Розв’язання.
Перепишемо задане рівняння у вигляді:
125


101 порада абітурієнту
„ х-2 .χ-2 r, а —27
3∙4 - а • 4 = а - 27, або 4 ^ = .
3-а
Маємо ——— > 0 або 3<а <27 (*). Далі, на 3-а
множині (*):
9 а-27 а-27
Iog4 4’ - = log4 , х-2 = log4 ,
а-27
x = 2 + log4 — .
3-а
При інших значеннях а розв’язків немає.
Відповідь: при а є (3;27).
Задача 2. Знайти кількість коренів рівняння 2xlgx = 3-αlgx в залежності від значення параметра а.
Розв’язання.
Запишемо задане рівняння у вигляді
lgx = і розглянемо графіки функцій, що
2х + а
стоять у лівій і правій частині останнього рівняння при а<0 (мал. 1), при а = 0 (мал. 2), при а > 0 (мал. 3):
126


VIL Логарифми. Логарифмічні рівняння.».
Отже, при а < 0 дане в умові рівняння має два корені, при а = 0 рівняння має один корінь,


101 порада абітурієнту
також один корінь рівняння має у випадку, коли a>Q.
Відповідь: при а < 0 —два корені;
при a ≥ 0 —один корінь.
У 45 fJIo∣(a3κuιςpβi jιoιapuφуиічні нерівності
та
Одразу відмітимо, що при розв’язанні показникових і логарифмічних нерівностей необхідно: по-перше, розв’язати нерівності, які визначають ОДЗ;
по-друге, звернути увагу на зміну знака
при переході від логарифмічної чи показникової нерівності до раціональної чи ірраціональної нерівності.
*Taκi нерівності називаються трансцендентними.
128


VII. Логарифми. Логарифмічні рівняння...
Отже,
НЕХАЙ
ax>ay, а > 0, a ≠ 1.
ТОДІ:
(а > 1) =» (х > j>);
(θ<α<l)=⅛(x<∕).
НЕХАЙ
logfl х > logo у, а > 0, a ≠ 1, х > 0, у > 0. ТОДІ:
(α>l)=>(x>y), (0 < а < 1) => (х < у).
Задача 1. Розв’язати нерівність
бх-І
Розв’язання.
_ . _ _ 1 , 6х -1
Оскільки 0,2 = — < 1, то
5 3-х
Відповідь: х є
Задача 2. Знайти найменше ціле х, що задовольняє нерівність: 22x -15∙llx < 11х -15∙22x+3.
9-4-636
129


101 порада абітурієнту
Розв’язання.
Маємо 22λ' + 120∙22x < 11х +15-1 Iх, або 121∙22x < 16-1 Iх. Поділивши обидві частини нерівності на 121-16, маємо 22x-4 <llx-2, або 4χ-2<Hχ~2 поділивши обидві частини
нерівності на 4 х-2 (4 х-2 > 0), одержимо
(1∏x~2
— >1 звідки x-2>0, х>2.
Найменшим цілим числом, яке задовольняє дану в умові нерівність, є число 3.
Відповідь: 3.
Задача 3. Розв’язати нерівність
log0 3 - 3) > lθβo,з (*2 + 4) •
Розв’язання.
Дана в умові нерівність рівносильна системі нерівностей
3x-8>0
Зх-8 < Xі +4
, отже,
х2 - Зх + 12 > 0
Відповідь: x∈
130


VIL Логарифми. Логарифмічні рівняння.
Задача 4. Розв’язати нерівність log*2-3 729 > 3. Розв’язання.
Оскільки 729 = 93, то дану нерівність можна записати так:
l°gχ2-3 93 > 3, або lθgχ2~3 9 > 1.
Ця нерівність рівносильна сукупності двох систем нерівностей:
х2 -3>0 x2-3<l
х2 - 3 > 9, звідси
х2 -3>1
х2 -3<9
x∈0
(х + 2)(х - 2) > 0
(x + √12)(x-√i2)<0
х < -2
тоді
Відповідь: х ∈ (-712; -2)U(2; J∖2).
9*
131


101 порада абітурієнту
VIII. ФОРМУЛИ ТРИГОНОМЕТРІЇ.
ТРИГОНОМЕТРИЧНІ ТОТОЖНОСТІ ТА ПЕРЕТВОРЕННЯ
Хто не знає, що при довільних sin2 + cos2 = 1
триіоноβiernpu4Ha тото^ість
Проте ми рекомендуємо абітурієнтам поставитися до цієї тотожності досить серйозно. І справа не тільки в тому, що з неї ми одержуємо тотожності:
l + tg2α = sec2α
1 + ctg2α = cosec2α
sec а = ;
cosα^
( 1 cosec а =
l sin а
132


VΠL Формули тригонометрії.
За допомогою основної тригонометричної тотожності доводяться найважливіші співвідношення, які неодноразово використовуються при розв’язанні різноманітних задач:
Дано: sin a + cos а = т.
Знайти: 1) sinacosa; 2)sina-cosa;
3) 	sin3 a ± cos3 а ; 4) sin4 a + cos4 a,
5) sin6 α±cos6 a.
Розв’язання.
1) 	Маємо: sin α + cos а = т. Піднесемо обидві частини рівності до квадрата:
sin2 α + 2sinαcosα + cos2 а = т2,
m2 - 1 звідки sin α cosα = = А.
2
2) (sin а-cosа)2 = (sinα + cosα)2 -4sinαcosα,
а тому sin а - cos a = +y∣m2 -4А = В.
3) sin3 a ± cos3 а =
= (sin a ± cos a) ∙ (sin2 а т sin a cos a + cos2 а), а отже, sin3 α + cos3 а = /и(1 - А);
sin3 а-cos3 а = В(1 + Л).
133


101 порада абітурієнту
sin4 a + cos4 а =
= (sin2 α + cos2 α)2 -2sin2 αcos2 a = 1 -2А.
(\3 / \3
sin2 α I ±(cos2cπ =
sm a ± cos а I ∙ (sin a + cos a + sin" a cos' а
отже, sin6 a + cos6 а = 1 - ЗА2,
sin6 а - cos6 а = тв(\ - А2).
Задача. Довести тотожність:
sm α + cos а -1 _ 2
sin6 а + cos6 а -1 З
Доведення.
sin a + cos а -1 _
sin6 <x + cos6 а -1
_ 1-2 sin2 а cos2 a-↑ _ - 2 _ 2
l-3sin2 αcos2 а-1 ^3 З
134


VIII. Формули тригонометрії.
Г Для тих читачів, які підглядають у таблицю, щоб знайти, наприклад, Формули sta(180o-α) зведенню a6o ctg(270 0 + х)
рекомендуємо два правила: № 1. СПОЧАТКУ знак!
Наприклад,
sin( 180 0 - а)—друга чверть — знак «+», ctg(270 °+,г) — четверта чверть—знак «-».
І № 2. НЕБЕЗПЕЧНІ КУТНІ ∣900±α, 2700^±α —
X функція змінюється!
А саме:
135


101 порада абітурієнту
Приклад 1: sin(27Oo - а).
СПОЧАТКУ знак! III чверть —«-». НЕБЕЗПЕЧНИЙ КУТІ sin(27Oo - а) = -cosor.
Приклад 2: tg^360° - β).
IV чверть — «-». КУТ НЕ Є небезпечним!
ФУНКЦІЯ НЕ змінюється! Отже, tg^36Oo - β ) = -tg β.
136


VIII. Формули тригонометрії,».
Рекомендується звернути увагу на такі співвідношення:
sin(450 ± a) = cos(450 + а);
⅝tg(450 ± а) = ctg(450 + а);
sin(6Oo ± а) = cos(300 + а);
s іп(з Oo ± a) = cos(600 + а);
sin(l 50° + а) = cos(300 - а).
Вони легко доводяться за допомогою формул зведення. Наприклад:
sin(450 + a) = sin^9Oo - (450 - а)) =
= cos(450 - а);
sin0 50° + а) = sin(l 80° - (зо0 - a =
= sin(300 - а).
137


101 порада абітурієнту
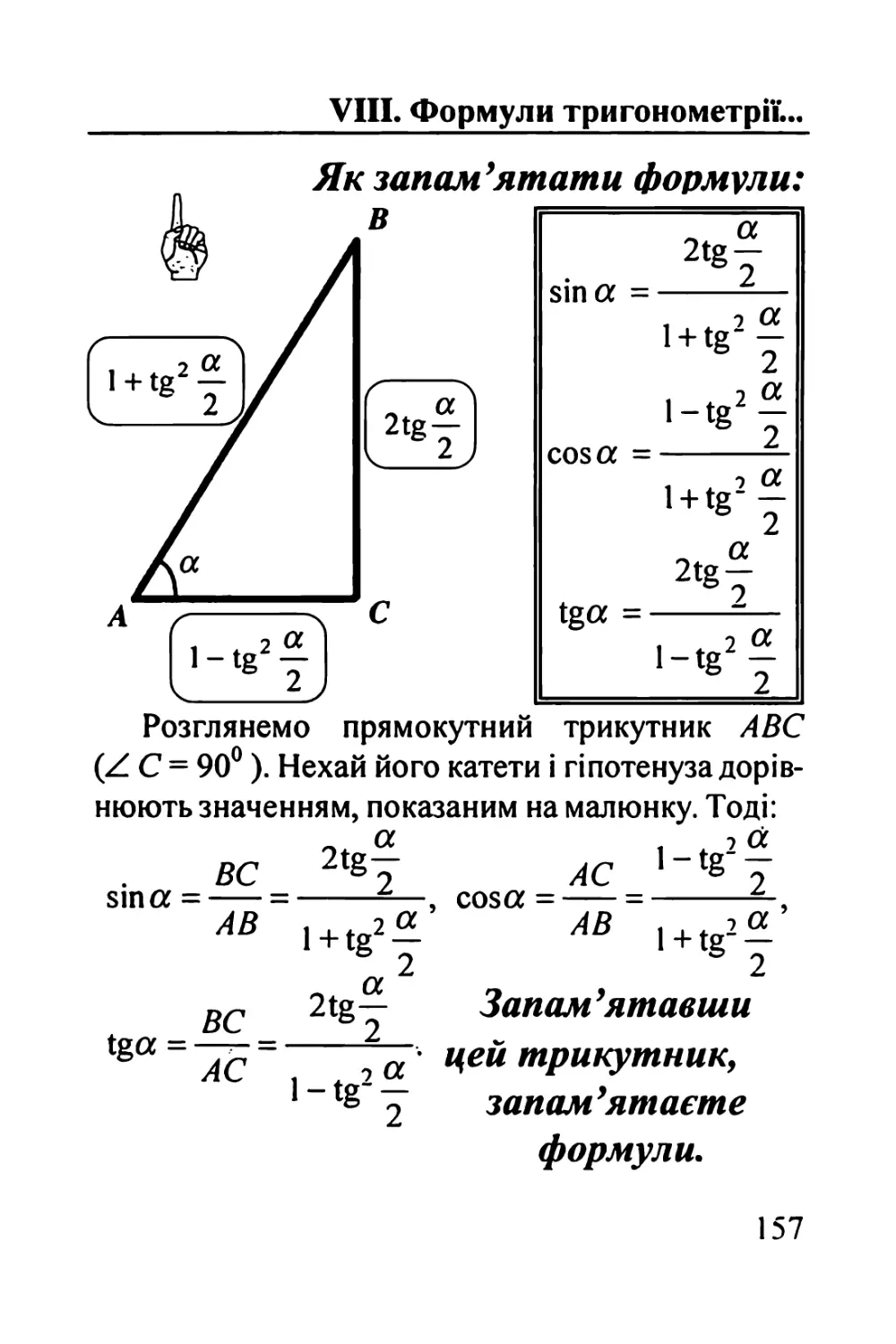
АО Рекомендуємо в задачах^ *'j де аргументами
тригонометричних Φθpjuyjiu функцій є кути додавання Д a, a +β, 2a, 2β,
застосовувати співвідношення a =(α +β)-βt, 2a =(α +β)-(β -а).
Задача 1. Якщо sin a = A sin(a + β), то
tg(α+∕5) = ^- v , cosp - А
Довести.
Доведення.
Оскільки a =(α +β)-β, то sin( (а +Д) - Д) = A sin(α + Д ), або sin(α+Д)созД-cos(α +β)sinβ = = A sin(c∣f + Д).
Ділення на cos(α + Д) ≠ 0 дає
tg(α +β)cosβ -s∖nβ =Atg(a +Д), „„ • / Л\ зіпД
звідки tg(a + Д) = —- •
5v ' cosβ - А
138


VIII. Формули тригонометрії...
Задача 2. Спростити
sin a + sin β cos(α + β).
Розв’язання.
sin a + sin β cos(α + β) =
= sin((α + β)-/3)+sinβ cos(α + β) = = sin(α+β)cosβ - sinβ cos(α + β) + + sinβ cos(α+β) = sin(α+β)cosβ.
Відповідь: sin(α +β )cosβ.
9Tρo φoρjuyjιy cyjuu тангенсів
Відомо, що a±β)= tg«±tg/?. l÷tgαtgβ
Рекомендуємо запам’ятати
співвідношення, що випливає з цієї
, формули:
∕ tgα±tgβ = tg(α ±0)∙(l + tgα tgβ).
139


101 порада абітурієнту
В ефективності цієї формули можна переконатися, розв’язуючи запропоновані задачи.
Задача 1. Довести тотожність
tgα tg/3 +(tgα +tg∕3 )ctg(α + β) = 1.
Доведення.
tgα tgβ + (tgα + tgβ) ctg(α + β) = = tgα tgβ + tg(α + β )(1 - tgα tgβ )ctg(α + β) =
=tgα tgβ +1 - tgα tgβ = 1.
Задача 2. Довести тотожність
tg(α +β)- tgα - tgβ = tg(α + β)tga tgβ.
Доведення.
tg(α+β)-tgα -tgβ = = tg(α +β)-tg(α ÷β)(l-tgα tgβ) =
= tg(α +β)(l-l + tgα tgβ) = tg(α +β)tgα tgβ.
Задача 3. Довести, що якщо AiB,C — кути непрямокутного трикутника, то
tg A + tg В + tg C= tg A tg В tg С.
140


VIII. Формули тригонометрії.,.
Доведення.
tgA + tgB + tgC=tg∕4 + tg(B + Q(l -tgBtgQ =
= tgΛ + tg(18Oo-Λ)(l-tgβtgθ =
= tg∕4-tg∕4 (1 -tgZJtgQ =
= tg/4(1-1 + tgZJtgC) = tg∕4 tg5tgC.
Дійсно:
1) l-2sιn a =sιn-α+cos^α-
- 2 sin1  2 a = cos2 а - sin2 a = cos2α;
2) sin(450 + a )sin(450 - а) =
= cos^450 + a )sin(450 - а) =
= — sin(9Oo - а 1 = —cos2α.
2 \ '2
141


101 порада абітурієнту
Саме за допомогою формул подвійного аргументу в тригонометрії виконується «згортання».
Задача 1. Довести, що sin 180 cos 360=- .
4
Доведення.
Помножимо і поділимо ліву частину рівності, що доводиться, на 2 cos 18°:
• і ©о ozrθ 2 cos 180 sin 180 cos36° sin 18 - cos 36 = =
2cosl80
_ 2sin360 cos360 _ sin720 _ 1
4cosl80 4cosl80 4
Задача 2. Довести, що
π 2π 3π 4π
cos—cos—cos—cos—×
15 15 15 15
5π 6π 7π
×cos—cos—cos— = 15 15 15
Доведення.
У лівій частині рівності можна виділити два добутки, які легко обчислюються «згортанням»:
142


VΠL Формули тригонометрії.»
,4 π 2π 4π 7π 1) cos—cos—cos—cos— = 15 15 15 15
1 λ . π π 2π
2 sin—cos—cos— × -)cinπ 15 15 15
2 sin —
15
4π ( ⅛π∖
×cos—cosπ =
15 ∖ 15 J
1
2 sin —
15
. 2π 2π 4π 8π • sin—cos—cos— cos—
15 15 15 15
4sin—
15
. 4π 4π 8π
•sin—cos—cos— = 15 15 15
8 sin —
15
. 8π 8π sin—cos— =
15 15
. 16π sin
15 __
1, . π
16 sin —
15
,. . π 16sιn —
15
. π sin— 1
15 1 .
., ■ jt 16' 16sιn —
15
143


101 порада абітурієнту
λ . 3π 3π 6π
o r 2 sin — cos—cos—
oλ 3π 6π 15 15 15
2) cos—cos — = — -
15 15
_ . 3π
2 sin —
15
• ґ ЗяЛ sin π
І 15J _
„ . 6π 6π
2 sin — cos—
15 15
. . 3π 4 sin —
15
. 12τr sm
15
Λ ∙ 3π 4 sin — 15
. 3π sm —  15_ = . λ . 3π 4 sin — 15
Таким чином, ліва частина дорівнює
. 3π
4 sin —
15
даної рівності
1 1 5π  cos— = 16 4 15
що й треба було довести.
144


VIII. Формули тригонометрії...
У 51
Φopjuyjιu половинного аргументу
Рекомендуємо користуватися формулами половинного аргументу у вигляді
. 2 a
l + cosα = 2 cos —;
2
1 о ∙ -> a
l-cosα = 2sιn~ —.
2
О l∣∣∣))) «КОЖЕН МІНУС ДАЄ СИНУС»
' (приказка)
Використовуючи формули половинного аргументу, одержимо:
l-sinα
1 + sinα
«Серцем» багатьох тригонометричних прикладів є тотожність:
l + sinα  =tg cos а
'a π λ∣
12 1 4 /
10-4-636
145


101 порада абітурієнту
Рекомендуємо запам’ятати її, а також звернути увагу на спосіб доведення:
l + sinα l + cos(900-α)
∞sα sin(900 -а)
2cos2f450--1
: І 2 )
o ∙ (л<о α∏ ∕zico сЛ
2 sin 45 cos 45
I 2) ∖ 2)
<∏ оЛ (а л /Л 45 =tg — + 45° z√ < z √
Задача. Довести тотожність
∙(1-sin 2a) = cos2α .
Доведення.
146


VIII. Формули тригонометрії...
. •>
sin"
= 2 sin
= 2 sin
= sin —∖-2a I = cos2α.
10*
147


101 порада абітурієнту
W 52
cmeneκjL називають «бойовими формулами тригонометрії», тому що вони легко «розправляються» з квадратами функцій sinx та cos х.
Формули
.за І - cosα sin — =
2 2
2 а 1 + cosα cos — =
2 2
Дійсно, «клас» абітурієнта (і просто учня) можна зразу встановити за тим, як він перетворює на добуток різницю квадратів, наприклад, sin2 a -cos2 β
Звичайно учень розкладає цей вираз на множники:
(sinα -cosβ)∙(sinα + cosβ),
потім перетворює cos β на sin β і т. д.
148


VIII. Формули тригонометрії.
Подивіться на дію бойових формул:
2 2 _ l-cos2α l+cos2β
sin а - cos р = т =
2 2
cos2α + cos2β / \ /
1 = -cost а + В і-cost а -
Отже, радимо: якщо є квадрати синусів або косинусів будь-яких аргументів знижуйте степінь\\\
Задача. Довести тотожність
sin2(α -3Oo) + sin2(а + ЗО0)-sin2 а = 0,5.
Доведення.
sin2 (а - 30°)+sin2 (а + 30°) - sin2 а =
1 - cos(2α - 60°) +1 - cos(2α + 60°) -1 + cos2α
= 2
1 - 2 cos2αcos600 + cos2α 1 - cos2α+cos2α
= 0,5.
2
2
149


101 порада абітурієнту
«ТІеретборити на добуто^! »
Такий заголовок чи умову Ви можете побачити у багатьох задачниках та циклах задач з тригонометрії.
Вивчіть «головні вузли»
ВОНИ ПЕРЕД ВАМИ.
Отже, перетворити на добуток:
1) 	sinα +cos/3; 2) tg1  2α -tg2/3; 3) 3-4sin2 а;
4) 	tgα +ctgβ ; 5) 1 + 2 sin а; 6) 1-tga;
7) sin2 a -sin2 Д; 8) І + л/2 cosa; 9) 3-V3tgα.
1) sinα+cosβ = sinα+sin(9Oo-Д) =
α+9Oo-β α-9Oo+0 = 2 sin - cos т .
2 2
2) tgα + ctgβ = tgα + tg(9Oo - β) =
sin(α + 90° - β) cos(α - β)
^ cosαcos(900 -β)~ cos a sin β '
150


VIIL Формули тригонометрії...
-14 э -> l-cos2α -l + cos2β
3) 	sin2 a -sin2 β =
sin
cos2 a cos2 β
1 + 2 sin а - 2 — + sin а = 2^sin 30° + sin a ) =
„ . 30°+ct 30°-ct
= 2 sin cos
2 2
6)
l + √2 cosα =√2
/2 —+ coset 2
∣ri π
2 cos—I-coset
= 2y∣2 cos
f π ay J+2^>
cos
J^2^>
151


101 порада абітурієнту
3-4sin2α =
2я
1 - cos 1 + cos2α
2
2π cos2α-cos—
= 4 sin
sin
π VyS>-VyS>OL
4
cosα
152


VIII. Формули тригонометрії.
Задача. Перетворити на добуток
1 + sin α +cosα.
Розв’язання.
Радимо прослідкувати, які з «головних вузлів» використовуються при розв’язанні.
Маємо:
l+sinα +cosα = (l + cosα) + sinα =
Л 2 а ^ . а а = 2 cos —+2sιn-cos—= 2 2 2
а
^ а а . а] 2 cos— cos—+sιn —
2∖ 2 2J
a
2 cos— sin
2
π
— а
Л а . я 2
= 4 cos—sin — cos—
2 4 2
π а
= 2V2 cos — cos∣
2 ∖4
Відповідь: 2>∕2cos-cos
2 Д
π а
153


101 порада абітурієнту
У 54 Φopjuyjιu потрійною кута
Рекомендуємо запам’ятати та вміти виводити такі формули:
(1) sin За = 3 sin а -4 sin3 а;
(2) cos3α = 4cos3 a-3cosa;
(3) tg3α =
3tgα -tg3α l-3tg1  2α
(4) sin За =4 sin а sin^6Oo-αjsin^6θo+а
(5) cos За = 4 cos a cos(600 - a)cos(600 + а
(6) 	tg3a = tga tg^6Oo -a)tg^6Oo +а).
Формули (1) - (3) слугують для зниження степеня; формули (4) - (6) допомагають «розправлятися» з нестандартними перетвореннями.
Доведемо формули (1 к (31 (4):
(1) sin За = sin(2a + а) = = sin2acosa +cos2asina = 154


УШ. Формули тригонометрії...
= 4sina
= 2sinαcos2 ce + (cos2 a -sin2 α)since = = 2since (1 - sin2 ce) + (l -2sin2 ce)sinα = = 2since-2sin3α + since -2sin3α =
= 3sinα-4sin3 a;
. x tg2ce ÷ tgce
(3) 	tg3a = tg(2a + a) = — —=
v ' 5 k 7 1-tg2atga
2tgce
+ tsa з
1-tg ce 3tga - tg^ a
l-3tg2a i
1-tg a
(4) 	sin За = 3 sin a - 4 sin3 a =
—- sin2 cel = 4 sin ce(sin2 60° - sin2 a 4 J V
л . l-cosl200 -l + cos2a
= 4 sin a
2
= 2 sin a (cos2ce - cos 120°) = = 4sinasin∣6Oo -ce∣sin(6Oo +a).
155


101 порада абітурієнту
Задача. Обчислити без таблиць та мікрокалькулятора sin 180.
Розв’язання.
Враховуючи, що
sin2∙180 = sin 360 = cos 540 = cos3∙180, застосуємо формули подвійного та потрійного аргументу. Одержимо
2∙sin 180 ∙cosl80 = 4∙cos3180 -3∙cosl80 . Оскільки sin 180 ≠ 0, то
2 ∙ sin 180 = 4 ∙ cos2 18° - 3 = 4(l - sin2 180 ) - З,
4 	sin2 180 + 2 sin 180 -1 = 0, звідки
η∩nα∏3 55 Формули
ч ІДИ тригі
Тїорада, .Мій ціни неуиа !
які виражають тригонометричні функції через тангенс половинного аргументу, знати корисно,
але нелегко запам’ятати.
156


VΠL Формули тригонометрії.
Розглянемо прямокутний трикутник ABC (Z-C = 90°). Нехай його катети і гіпотенуза дорівнюють значенням, показаним на малюнку. Тоді:
вс sin а = ■
АВ
^ а , 7 сх
2⅛y ac 1-tg-y
= —, cos а = = —,
l÷tg2" АВ l÷tg2"
а2 2
ВС ts°l = АС =
2tg— Запам’ятавши
. 2
a • цей трикутник,
1 “tg у запам ’ятаєте
формули.
157


101 порада абітурієнту
У 56
Знаходженню тригоно- _/иетричних
Суми
51 = sinα + sin2α +... +sinnα,
52 = cos α +cos2α +...+ c0s∕7α відомі в практикумі
з тригонометрії.
Іноді вони зустрічаються під час доведення тотожностей або обчислення декількох доданків.
У будь-якому випадку ми радимо: якщо вимагається знайти суму синусів або косинусів, аргументи яких складають арифметичну прогресію, то для знаходження суми в обох випадках потрібно кожен доданок помножити
о ∙ d
(і поділити) на 2s,ny , де d
різниця
прогресії.
Задача 1. Знайти
S,2 =cosα +cos2α +cos3α +...+ cos∕70t.
158


VIII. Формули тригонометрії.
Розв’язання.
. а а а
2S-> sin — = 2 sin — cosα +2 sin — cos2α +
2 2 2 2
+ 2 sin — cos3α + ... + 2sin — coswα = 2 2
. За . a . 5a .За = sin sin — + sin sin — +
2 2 2 2
. la . 5a . (2fl+l)α . (2w-l)α + sin —-— sin — +... + sin sin
2 2 2 2
. a . (2«+l)a φ na (λ + 1)<z = - sin — + sin = 2 sin — cos .
2 2 2 2
. na (w + l)α sin—cos
Відповідь: So = —.
. a sin— 2
Розглянемо інший тип сум:
Задача 2. Знайти суму
tgα + 2tg2α + 4tg4α+.. .+2" tg2" а .
Розв’язання.
Застосуємо формулу:
ctgα - tgα = 2ctg2 а.
159


101 порада абітурієнту
Звідси tgα = ctgα - 2ctg2 а . Маємо:
tgα+2tg2α+4tg4α+.. .+2" tg2" а = = ctgα - 2ctg2α+2(ctg2α - 2ctg4α) +
+4(ctg4α - 2ctg8α)+.. .+2" (ctg2" а - 2ctg2"+1 а) =
= ctgα - 2ctg2α+2ctg2α - 4ctg4α +
+4ctg4α - 8ctg8α+...+2"ctg2"а - 2w+1 ctg2"+, а =
= ctgα-2"+,ctg2"+,α.
Відповідь: ctgα - 2"+1 ctg2"+, а.
у57
JllpUZOHO- jιtenιpu4κi (руннії ζymiβ
Існує велика серія тригонометричних задач, об’єднаних умовою: сума трьох кутів дорівнює 180°. Якщо Ви будете
три^утнищі знайомі з розв’язаннями
деяких таких задач, то, ми впевнені,
що й інші приклади серії не будуть для Вас важкими.
160


VΠL Формули тригонометрії...
Отже, А, В, С кути трикутника. Довести, що
β4 . j . n . „ λ А В C
1) sin A + sm B + sιnC = 4 cos—cos—cos—;
2 2 2
. . . . a . b c
2) sin A + sin В - sin C = 4 sin — sin — cos—;
2 2 2
,4 А В C ABC
3) ctg—+ctg— + ctg—= ctg—ctg—ctg—;
2 2 2 2 2 2
4) 	sin2Λ + sin2B + sin2C = 4sin Λ sin В sin C;
5) cos 2 A + cos 2В + cos 2C = -1 - 4 cos A cos В cos C;
6) cos2 ∕4 + cos2 B + cos2 C= 1-2cosAcosBcosC;
7) sin2 Λ + sin2 B + sin2 C = 2 + 2cosΛcosBcosC÷
θ4 А В AC В C ,
8)tg-tg—÷tg-tg— + tg-tg— = 1.
2 2 2 2 2 2
Доведемо деякі з наведених тотожностей.
1) 	Оскільки А + В + С = 180°, то
. А + В . 180°
sin = sin
2 2
Тому
= sin 90°
= cos—.
2
2J
sin A + sin В + sin С = 2 sin cos
2 2
11-4-636
161


101 порада абітурієнту
n . С С „ С( А-В А + В + 2 sin—cos— = 2 cos— cos + cos
2 2 2 V 2 2
л ABC = 4 cos—cos—cos—;
2 2 2
,4 A В Cl
3)ctg- + ctg- + ctg- = —- £ t ^* tg7
ι
в tg7
tg7+tg7
A В C(, A В A B∖
= ctg-ctg—ctg— 1-tg—tg—+tg-tg—
2 2 2∖4 22 22y
ABC ctg—ctg —ctg—.
2 2 2
162


VIII. Формули тригонометрії.
∣y 58 tKPjιeιςu,ijι триюно- juempu4κu^ задач з «родзинкою»
Серед великої кількості тригонометричних вправ на спрощення виразів, доведення тотожностей, обчислення існують особливі, найцікавіші задачи
Радимо не просто ознайомитися з ними, але й запам’ятати, тому що часто «ерудиція перемагає інтуїцію».
1) Обчислити
lgtg3Oo - lgtg310 - lgtg320 ∙ ...∙ Igtg6θo .
2) Довести, що tg210° + tg25Oo + tg2 70° = 9 .
3) Обчислити ctg7Oo +4cos700 .
Л/_ π 2π Зп
4) Обчислити tgy ∙ tg—∙ tg— •
5) Довести, що ctgα - tgα - 2tg2α = 4ctg4α .
163


101 порада абітурієнту
6) Довести, що tg550 ∙ tg650 ∙ tg750 = ctg850 .
7) Довести, що tg360 ∙ tg720 = √5 .
8) Розкласти на множники 2√3 + √5 -1.
9) Довести, що tg610° + tg65Oo + tg67Oo = 433 .
10) Знайти суму
cosec2α + cosec4α +...+cosec2"α.
Розв’яжемо запропоновані задачі:
1) Оскільки tg 450 = 1, lg 1 = 0, то даний добуток дорівнює нулю.
Відповідь: 0.
2)
tg2100+ tg25Oo+tg27Oo =
<cos210°
< cos2 70°
2 спО J ∖cos 50 )
cos2 50° cos2 70° cos210° cos2 50° cos2 70° cos210° cos2 70° cos210° cos2 50° cos2 70° cos210° cos2500
cos 10 cos 50 cos 70
164


VIII. Формули тригонометрії...
(і - cos80° )(1 - cos 40°) = 4 * Л l - +
4 cos 1 Oo cos(600 -1 Oo ) cos(600 +1 Oo
(1-cos400Vl+ cos200)
+ 4*T ∕ ∖ ∕ ∖∖2- +
14 cos 1 Oo cos(600 - 1 Oo ) cos(600 + 1 Oo )j
(1 + cos 20° Y1 - cos 80°)
+ 4 ’ ~∕ ~∕ ∖ ^∕ “ ^
∣4 cos 1 Oo cos(600 -10o) cos(600 +10o H
У знаменнику дробу формула потрійного кута «справа-наліво», тому
^4 cos 1 Oo cos^600 - 1 Oo ) cos(600 - 10°)) =
2 aλo З = cos з0 = —.
4
Чисельник дробу після розкриття дужок і пере-
9 .
творень дорівнює —. Тоді
4
tg210° + tg25Oo +tg27Oo = 4∙-.--3 = 9,
4 4
що і треба було довести.
165


101 порада абітурієнту
„ х ™о л ™о cos 70°+4 cos 70° sin 70° 3) ctg70υ + 4 cos 70υ = =
sin 70°
_ sin2Oo +2sin4Oo _ 2cosl00 sin3Oo +sin4Oo _ sin7Oo sin7Oo
_ cosl00 +sin4Oo _ sin8Oo +sin4Oo _ sin7Oo sin7Oo
2sin6Oo cos200 „ √3 z- cos200 2
Відповідь: д/з .
4) 	Маємо
π 2π
3π cos—∙cos cos— =
о ∙ π 8sιn-
. „ . π π 2π 3π ∙4∙2∙sm--cos—∙cos cos— =
о ∙ π
8 sm —
_ _ . 2π 2π 3π • 2 ∙ 2 ∙ sin — cos cos — =
166


VIII. Формули тригонометрії.,.
1 ^ . 4π ( 4π
2∙ sin -cos— 8sin- * 7 < 7-
-1
8sin-
7
. 8π •sin —
2π . 2 3π  sin — =
л ∙ 2 7Γ . 2 8∙sιn —∙sιn
7
7
7
∕
2πΛ
∩ 4τ∩
(л ⅛π∖
= 1 - cos
■ ∙
1-cos—
• 1-cos—
к
7 J
I 7 )
I 7 )
2π
z
Xπ 6π
2π
-cos
-cos-
cos—
+ cos cos
7
7 7
7
4π
4τr 6ττ 2π 6π
+ cos cos— + cos cos
7 7 7 7
2π 4π 6π
-cos cos cos— =
7 7 7
, 2π 4π 6π = 1 - cos cos cos— +
7 7 7
1 ( 6π 2π IOπ
+ — cos—+cos— + cos +
2(4 7 7 7
167


101 порада абітурієнту
2π 8π 4π А
+ cos— + cos— + cos— -
7 7 7 )
2π 3π π
-cos cos cos— =
7 7 7
, π 2π 3π 7
= 1-cos—-cos cos— = —.
7 7 7 8
Тоді
QQ op cr?
1 1 *4j
"q ∣
(TO
1 1 lo
II ∞∣iη 00 1 —
II
Відповідь: √7 .
5) Скористаємося вже відомою нам формулою (див. с. 159):
ctgα - tgα - 2tg2α = 2ctg2α - 2tg2α = 4ctg4α .
6) Маємо
tg550 ∙tg650 ∙tg750 =
= ctg50 ■ tg50 ∙tg550 ∙tg650 ∙ tg750 =
див. ПОРАДУ 54, формула 6
= ctg850 ∙tg!50 ∙ctg!50 =ctg850.
168


VIII. Формули тригонометрії...
7) 	sin 180 = 1 + (див. с. 156), тоді
4
,o0 √10 + 2√5 „ ,<,0 √5-l
cos 18 = ; tgl8 = . =.
4 √10 + 2√5
Отже,
tg360∙tg720 =tg(2∙180)∙ctgl80 =
2∙ tgl80∙ctgl80 2
l-tg2180 1 5-2√5 + l
10 + 2√5
2(10 + 2√5) 4√5(√5 + l)
4 + 4√5 4(√5 + l)
8) 	Знову скористаємося рівністю
Маємо
= 4(sin60° + sin 180) = 8sin390 ∙cos210.
169


101 порада абітурієнту
9) 	Скористаємося «чудовою тотожністю» (див. ПОРАДУ 8). Маємо
tg6100+tg65Oo+tg67Oo =
= (tg2100+tg25Oo+tg27Oo)× див. формулу 2
× (tg41 Oo + tg4 50° + tg4 70° - tg210° ♦ tg2 50° -
- tg21 Oo - tg2 70° - tg2 50° ∙ tg2 70°) +
+ 3∙tg210° ∙tg25Oo ∙tg27Oo =
= 9 ∙ ((tg21 Oo + tg2 5Oo ÷ tg2 70° )2 -
-3∙tg2lOo∙tg25Oo- -3∙tg2100 ∙tg27Oo-3∙tg25Oo ∙tg27Oo) + + 3∙tg23Oo =9∙(δl-3∙tg2100 ∙tg25Oo ∙tg27Oo ×
х (ctg21 Oo + ctg2 50° + ctg2 7Oo)) ÷ 1 =
= 9∙(81-3∙tg23Oo∙33)+1 = 433 (рівність
ctg210° +ctg25Oo +ctg2 70° =33 рекомендується довести самостійно).
170


VIII. Формули тригонометрії.,.
10) 	Скористаємося формулою, яка легко доводиться
cosec2ce = ctgce - ctg2ce .
Маємо
cosec2ce + cosec4ce +...+cosec2"ce =
= ctgce - ctg2ce+ctg2ce - ctg4ce+... +
+ ctg2"'l а - ctg2" а -
zws>oιt cos2"ce ex —aj
sinα sin2"а since sin2"а
sin(2,'а -а\
Відповідь: — .
since sin2"се
171


101 порада абітурієнту
IX. 	ТРИГОНОМЕТРИЧНІ РІВНЯННЯ
У 59
Найпростіші тригонометричні piβ∏JLHHjL
Найпростіші
це рівняння вигляду
sin х = т, ∣w∣ ≤ 1;
cosx = т, |/и| ≤ 1;
tgx = т;
ctgx = т.
Хоч вони і мають найпростіший вигляд, але ми хотіли б запобігти появі помилок. Отже, почнемо.
sinx = т
Рекомендуємо звернути увагу на запис загального розв’язку:
х = (- l)n arcsinw + nπ, я ∈ Z
172


IX. Тригонометричні рівняння
По-перше, ∣w∣ повинен бути не більше за одиницю. По-друге,
≤ arcsm т ≤ —, a arcsιn(- т = - arcsιn т.
2 2 v 7
І, нарешті, типова помилка багатьох школярів:
не можна писати різні букви
в показнику (-l)n і в множнику п .
cosx = т
Це рівняння також підступне! |/л| також повинен бути не більше за одиницю. Тут часто пропускають знак" ÷ " у формулі
х = ±arccosw + 2Aπ, к ∈ X
Необхідно враховувати, що arccos(-w) = π-arccos т
Розв’яжемо декілька найпростіших тригонометричних рівнянь:
* До речі.
arctg(- т) = -arctg т; arcctg(- m) = π - arcctg т.
173


101 порада абітурієнту
П
sin 2x
х =
π π nπ — + — 12 8
heZ.
2 ’
2) cosx = ; х = ±arccos -~ + nπ,nEZ',
½ к 2√ 2тг
х - ±-+2nπ , п ∈ ∕L>.
3) ctg3x = -1; 3x = π -arcctgl + kπi k,EZ', πkπ
4 by,A∈Z.
1 (3π π
x = -- + kπ ,kEZ',x = ~ +
Наведемо таблицю «нулів». Наполегливо рекомендуємо розв’язувати найпростіші рівняння з нулем у правій частині не за загальною формулою, а користуючись наведеною таблицею.
174


IX. Тригонометричні рівняння
sinx = 0
х = kπ, к ∈ Z
cosx = 0
π ^7∕
x = ~ + nπ, yiEl/L
tgx = 0
x = lπ, 1 ∈ Z
ctgx = 0
х = — + tπ t ∈ Z 2
ну 60
Основні унетоди розв’язання тригоно- jueτnpu4HU7t рівнянь
Якими б різноманітними не були тригонометричні рівняння, врешті-решт існує два основні методи їх розв’язання:
• метод розкладання на множники;
• метод введення нової змінної.
175


101 порада абітурієнту
Задача 1. Розв’язати рівняння • 4 х .
sm2x = cos sin
2
. 4 ×
:п —
2
Розв’язання.
Маємо:
X . тХ
2 X . 2 x
9
2sinxcosx- cos'-+sin'— ∙ cos'—sin — =0,
2 2
або 2sinxcosx-cosx = 0, звідки
2
Тоді
cosx = 0
2 sin х -1 = 0
х = — + nπ.n ∈ X 2
6
Відповідь: і —
2
6
Задача 2. Розв’язати рівняння
3sinx + 4cosx = 5.
Розв’язання.
Виразимо тригонометричні функції через тангенс половинного аргументу.
176


IX. Тригонометричні рівняння
Покладемо tg— = t. Маємо:
2/ І-/2 1
3∙-—Γ + 4-i—Г = 5’ звідки/ = -,
1 + Г 1 + Г з
або tg— = —, х = 2arctg~ + 2nπ, neZ.
Відповідь: '
2arctg j + 2nπ ∣ п, ∈
Розглянемо тригонометричні рівняння, які можна впізнати за зовнішнім виглядом, а отже, застосувати «домашню заготівку».
61
Однорідні триіоноjuem- ричні piβHjMHjL
Коли в рівнянні містяться лише синуси та косинуси, радимо подивитися, чи не однорідне воно відносно цих функцій.
12-4-636
177


101 порада абітурієнту
Наприклад, рівняння 5sin х = 4cos х однорідне, а рівняння 5sin х = 4cos х + С неоднорідне. Рівняння 3sin2x + 4cos2x + 5sin xcos х = 0 однорідне (показник однорідності дорівнює 2), рівняння 3sin2x - V5 cos2x - sin х cos х = З також однорідне, тому що
З = 3(sin 2x + cos2 х).
Отже, при розв’язанні однорідного рівняння a sin х + b cosx = 0 (a ≠ 0, b ≠ 0) потрібно поділити обидві частини рівняння на cosx. Одержимо αtgx+Z> = 0.
Зауважимо, що при a ≠ 0 однорідному рівнянню не задовольняють ті значення х, при яких cosx = 0.
Тому ділення на cosх (або на coswx, якщо показник однорідності дорівнює п ) обох частин однорідного рівняння у випадку a ≠ 0 не приводить до втрати коренів.
178


IX. Тригонометричні рівняння
Задача 1. Розв’язати рівняння 7sinx-8cosx = 0.
Розв’язання.
Поділимо обидві частини рівняння почленно
на cosx. Одержимо
8 8 _
tgx = y; х = arctgy + πw, п ∈ /L .
г g
Відповідь: < arctg — + π п ∣ п ∈ Z .
Задача 2. Розв’язати рівняння
5sin2 х + л/з sinxcosx + 6cos2 х = 5.
Розв’язання.
Маємо
5 	sin 2 х + л/з sin х cosx + 6 cos2 х = = 5(sin2 x + cos2 х),
звідки
л/з sin х cosx + cos2 х = 0;
cosx = 0
л/з sinx + cosx = о’
12*
179


101 порада абітурієнту
cosx = 0
х = ~ + πk. k ∈ X
t і ;
tgx = -V3
2
π ч/
x=-~ + nπ, пе£ 6
<— + πk∖ ∖-nπ∖k,nE.'Z, •.
[2 6 ∫
Відповідь:
ry 62
TiβκjLHHjL
Ми продовжуємо вивчення рівнянь, які можна впізнати за зовнішнім
типу виглядом
αsinαx±6cosαx = с (на жаль, їх не так вже і багато).
Зустрічаючись з рівнянням типу
αsinαx±δcosαx = с
варто подумати, який із запропонованих способів розв’язання доцільно обрати.
180


IX. Тригонометричні рівняння
Перший спосіб. Будемо вважати, що с ≠ 0, a1 +b2 ≠0. Поділивши обидві частини рівняння на y∣a2 +b2 , одержуємо: a . b
. - sin а х + . r cos а х =
.∕x,2 і l2 «/„2 , д2
∙√α +Ь ya +Ь
С
ь
Оскільки
а
. l2
то
2
існує такий кут φ i що
а (*)-=== = cos φ
1 т2
b
rf - sin φ .
_ . . . С
Тоді sin а х cos φ + cos а х sin φ = . , або
√α2 + b2
С
= . Якщо
І іЛ
х = — - φ + (-1)" arcsin а
с
+ nπ ,
п ∈
де φ визначається з формули (*).
181


101 порада абітурієнту
Використання цього способу раціональне, у випадку, коли φ «гарне»,
(тобто легко знаходиться з формули (*)).
Другий спосіб. У випадку, коли φ — «не гарне», ми рекомендуємо застосовувати формули λ a 1 з а
2tg- l-tg'--
sin а = — :cosa = —
1 	а і . о а
l + tg"- l + tg"-
(доведення див. у ПОРАДІ 55). У результаті ах одержимо квадратне рівняння, відносно tg-^- • Ще одна порада: не загубіть розв’язок рівняння (2λ + l)π
— перевірте, чи не буде X = — , к є X.
Третій спосіб. Використавши формули . ах ах
smαx = 2sm cos ;
2 2
9 	ах . у ах cosa х = cos" sin" ;
2 2
r з ах . з axy с-с cos^ Fsιn"
І 	2
2 ) ’
182


IX. Тригонометричні рівняння
ми зведемо дане рівняння до однорідного, яке розглядалося в попередній ПОРАДІ.
Задача 1. Розв’язати рівняння
З 	sin х + д/з cosx = 3.
Розв’язання.
Маємо:
а
COS(P =24з=~^^ЇП(Р =
1 π
= τ,φ =~Σ
/ \П π π Г7/
х = (-1) — + nπ ,he7j.
_, ∙ ∕ . ∖ Z7 7Г 7Г І гту
Відповідь: -Ц-1 і - + nπ не /L ►.
' 3 6 і
Задача 2. Розв’язати рівняння
3sin5x -2cos5x = 3.
Розв’язання.
Маємо:
6⅛y l + tg2½
-) 5х rτ 2 5х
183


101 порада абітурієнту
2 5x , 5x „ л звідки tg 6tg 1-5 = 0, тоді
2 2
а звідси
5х
tgτ = ι
5х tgy = 5
π 2nπ r7,
х = — 4 , п є X
10 5
2 2ιτιτz і—™
х = —arctg5+ , т ∈ /L,
. π 2nπ 2 _ 2mπ ∣ n,,
Відповідь: ■ —+——, — arctg5+—— ∣ n,m ∈ /L -.
ΦiβHJLHHJL типу α(sinx±cosx)± ±Z>sinxcosx = с
Визначивши цей тип рівняння (іноді він «ховається»), радимо зробити  заміну sinx±cosx = t.
Оскільки
∣sinx±cosx∣ = y∣2
sin
≤ √2 ,то
184


IX. Тригонометричні рівняння
Далі, sinxcosx = ±—-— і ми приходимо до квадратного рівняння.
Ще одна порада: можлива поява сторонніх коренів, тому необхідно зробити перевірку.
Задача 1. Розв’язати рівняння sin2x + 12(sinx + cosx)-12 = 0.
Розв’язання.
Заміна sinх + cosx = t. Одержимо рівняння t1 + 12∕-13 = 0.
Звідси t = 1 (Z = -13 — не підходить). Далі, . ( π∖ 1 sin х + — -
2
7С
Відповідь: — + 2nπ; 2mπ |«, ти ∈ Z >.
. 2
Задача 2. Розв’язати рівняння
sinx + sin2 х + cos3 х = 0.
Розв’язання.
Маємо sinx(l + sinx) + cosx(l - sin2 х) = 0;
185


101 порада абітурієнту
(1 + sinx)∙(sinx + cosx-sinxcosx) = 0.
Звідси
sinx = -1
sin X + cosx - sin X cosx = 0
Друге рівняння сукупності розв’яжемо методом, що розглядається.
Відповідь:
- — + 2kπ∖
2
+ nπ І kin ∈ ► .
4 	1
іу 64
Cucmejuu триюно-
рівнянь
Порада дуже проста: не лякайтеся! Вони розв’язуються за допомогою звичайних прийомів розв’язання систем рівнянь і формул тригонометрії.
186


IX. Тригонометричні рівняння
Задача 1. Розв’язати систему рівнянь
5π х-у = — z 3 .
sinx = 2sin>>
Розв’язання.
. „ 5π
Маємо х = — + у. Підставимо це значення З
х у друге рівняння, одержимо
— • 7Г 7Г • , л
або -sι∏ycos>' + cosysιny-2sιny = 0, звідки √3cosy+ 3sinj> = 0,
z- √3 π ,
або tgy = ——, y = -- + kπ, З 6
5τr it . Зтг . . r-w
= + kπ=—+kπ, kE∕L
3 6 2
Відповідь: ’ (х;у)
±kπ∙,-- + kπ Λ∈Zt.
6 J
187


101 порада абітурієнту
Задача 2. Розв’язати систему рівнянь sinx + cosy = 1,5 sin2 х + cos2 у = 1,25 Розв’язання.
Зробимо заміну sin х = и; cosx = v. Тоді
w +v = 1,5
1 _ , звідки
u2 + v2 =1,25
w = 1
1 ,
V = —
2
sinx = 1
або
, отже, -
1 ,або - cosy = —
sinx = —
cosy = 1
Відповідь:
π -~+2kπ ;±~ + 2wr ;
и = —
2 v = l
π
Зауваження. Звертаємо увагу читача на відмінності у записі відповідей двох попередніх систем рівнянь:
• у першій системі х та у були «зв’язані» першим рівнянням системи, тому для запису відповіді використовується тільки одна буквар;
188


IX. Тригонометричні рівняння
• у другій же системі І X, і у стоять під знаком тригонометричної функції, яка «вбиває» період, тому букви к і п не пов’язані між собою.
iJTарауитр у триіоно/нетрички.^ piβκjLHκjc^
Звичайно, ми не могли обминути рівняння з параметром. Порада наша ппоста:
максимум уваги і більше практики!
Введення параметра у тригонометричне рівняння гарний привід, щоб повторити основні властивості не тільки тригонометричних функций, але й алгебраїчних нерівностей.
Задача 1. Розв’язати рівняння
cosx -sinx = а .
Розв’язання.
Дане рівняння еквівалентне рівнянню
cos
а
189


101 порада абітурієнту
Тоді при
≤ 1, тобто при а ∈
π а
х =-—±arccos-^ + 2Λπ, ⅛∈Z.
4 √2
При a ∈ {-∞,-y∣2)lj(V2∖∞)—рівняння не має розв’язків.
Задача 2. Розв’язати рівняння
tgx + tg2x = ∕wtg3x .
Розв’язання.
Дане рівняння еквівалентне рівнянню tg3x(l - tgx ∙ tg2x - т) = 0.
Тоді
kπ . <—» 2tg ∙x .
х = — , к ∈ /L або tg х — = 1 - т.
З l-tg*^x
Розглянемо другий варіант. Нехай tgx = у.
Маємо
2у2 = - y2 )(1 - т) 'iy2 (w - 3) = т - 1.
Останнє рівняння буде мати розв’язок, якщо
——j≥0, тобто при т є (-°°;і]и(3;<»). Тоді
190


IX. Тригонометричні рівняння
Відповідь:
∕w-l , i т-1
, х = ± arctgJ + nπ, п ∈ Z. т - З V т - З
при/иє(1;3] x = ∙y,A∈Zj
при т ∈ (-00∏]U(3
і °°)
х = —, к ∈ /L:
З
т-1 r77
+ nπ, не /L. 7И-3
191


101 порада абітурієнту
X. 	ТРИГОНОМЕТРИЧНІ НЕРІВНОСТІ
На відміну від рівнянь «найпростіші» нерівності не такі й вже прості!
Найпростіші тригоноуаетричні нерівності
Хоча за зовнішнім виглядом
вони дуже схожі sin х = —
Ми рекомендуємо методику розв’язання нерівностей з використанням тригонометрично¬
го круга.
В
Отже, sinx<-. Раді- 2
ус О А (див. мал.) розділи¬
мо навпіл (тобто прове-
1 ч
демо пряму у = —).
192


X, Тригонометричні нерівності
Від точки С униз йдуть значення sin х, менші
—. На тригонометричному крузі точці С 2 відповідають два кути, синуси яких О
1 π . 5π ^
дорівнюють — :— і —. Отже, між точками Е і
2 6 6
D знаходиться шукана дуга EBD, для точок якої 1 smx<-.
2
Можна було б написати 5π π
— < х < —, 6 6
але це явний абсурд!
Не зневіряйтеся! Користуйтеся таким правилом:
«якщо важко додайте 2 ».
Тобто замість — ми напишемо —+ 2π = 6 6
13π .
= і скористаємося тим, що період синуса
6
— 2π. Отже, остаточно,
5τr 1 1 3π . _ гу/
∖∙2kπ<x< н2£тг, ⅛∈Z∙
6 6
13-4-636
193


101 порада абітурієнту
Задача 1. Розв’язати нерівність tgx ≥ 1 .
відають значення
Радимо скористатися так званою «віссю тангенсів» — дотичною MN, проведеною в точці S. Точці D, такій що __ _ i . тг
DS = 1, відповідає кут —.
4 Точкам прямої MN, розташованим над точкою D, відпо- х, при яких tg х ≥ 1 . Додавши періоде функції y = tgx, одержимо шука-
π π .
ний розв’язок: — + kπ ≤x<~ + kπi
Задача 2. Розв’язати нерівність cosx <
Точка А має координати
точки Е і D від-
Розв’язання.
3π . 7π повідають кутам — і —.
4 4
194


X. Тригонометричні нерівності
Дуга DBE— шукана. Звідси 3π, 7π
— + 2kπ < х < — + 2kπ, ке /L.
4 4
У 67
Тозвязання триіоно- уаетрични^ нерівностей
Як і у випадку рівнянь, розв’язання тригонометричних нерівностей зводиться до розв’язання найпростіших.
Радимо застосовувати знання з розв’язання алгебраїчних нерівностей і користуватися властивостями тригонометричних функцій.
Задача 1. Розв’язати нерівність sinx > cos2 х .
Розв’язання.
Дана нерівність рівносильна наступній: sin2 x + sinx- 1 > 0,
із*
195


101 порада абітурієнту
л 1 ^*^ 1
Але —-— > 1, тому
1 + ->/5 sin х + > 0.
2
Отже, розв’язками даної нерівності будуть
розв’язки нерівності
√5 -1 sin х > .
2
√5-l
Відповідь: arcsin—-— + 2kπ <х<
√5-l <π -arcsin —-— + 2kπ, ⅛ ∈ Z.
Задача 2. Розв’язати нерівність
2 cos2x + sin 2x > tg х .
Розв’язання.
Перепишемо дану нерівність у вигляді
2⅛ + 2^--tgr>0,
l + tg"jc l + tg^x або tg3x + 2tg2x - tgr - 2 < 0,
або (tgr - 1) ∙ (tgr + 1) ∙ (tgx + 2) < 0 .
196


X. Тригонометричні нерівності
Звідси
A∈Z
tgx< 1
tgx > -1, тоді
tgx < -2
π
х > -~ + nπ
4
π
x<- + nπ
4
68
(Dθβe∂eHHJL триюно- juempu4HW^ нерівностей
Радимо повторити доведення алгебраїчних нерівностей і.,, знову і знову користуватися властивостями тригонометричних функцій, sin х + tox
Задача 1. Довести, що > 0 при всіх
cosx + ctgx
допустимих значеннях х.
Доведення.
Перетворимо чисельник і знаменник даної нерівності. Маємо:
197


101 порада абітурієнту
sinx∙ 1+ . 7 /, \
V cosxj _ sin" x∙(l+ cosx)
cosx∙ 1+
V sin х)
Задача 2. Довести, що cos(sinx) > sin(cosx).
Доведення.
cos(sinx) - sin(cosx) = co:
- cosx
„ . 1 π г- . π
= 2∙sm ∣-√2sm х
21 2
×sin
2І 2
∏- π
2 cos х
\ 4
√y^ І І
2< —, а оскільки ∣ sin a ∣ ≤ 1;
∣cosα∣≤l, то
π
2
_ π г- J π]
0 < √2 соя х < π, звідки
2 ∖ 4J
нерівність, яку треба було довести.
і випливає
198


X, Тригонометричні нерівності
7Tapajιιemρ у триюко- унетрични^ нерівностям
Тригонометричні нерівності з параметром одна з найважчих тем тригонометрії, Ми радимо розпочати її вивчення з найпростіших нерівностей, наприклад sin х < а, потім розглянути нерівності з оберненими тригонометричними функціями і тільки після цього розв’язувати задачі, в яких застосовуються властивості нелінійних алгебраїчних функцій.
Задача 1. Розв’язати нерівність sinx < а.
Розв’язання.
Якщо а > І, то х — довільне число.
Якщо -1 < a ≤ 1, то
π -arcsinα + 2Aτr <x <arcsinα + 2π (Л +1), k
Якщо a ≤ -1, то нерівність не має розв’язків.
199


101 порада абітурієнту
Задача 2. Розв’язати нерівність arcsinx < а .
Розв’язання.
_ 71 , ,
Якщо α>y,τo -1 ≤ х ≤ 1.
n τt π
Якщо <a≤ — , то -1 ≤ х < sιnα.
2 2
„ π ,
Якщо a ≤ , то розв язків нема.
Задача 3. Розв’язати нерівність ∣sinx∣ + ∣cosx∣ > а.
Розв’язання.
Оскільки при ВСІХ ДІЙСНИХ X
I sin x∣ ≥ sin2 X ,∣ cosx∣ ≥ cos2 X ,
ТО I sin X∣ +1 cosx∣ ≥ sin2 х + cos2 X = 1.
Отже, при а < 1 нерівність справедлива при ВСІХ ДІЙСНИХ X.
При а = 1 розв’язками нерівності будуть всі lπ / r7∕ числа, крім чисел вигляду х = —, I ∈ /L .
При a ≥ 2 нерівність не має розв’язків.
Розглянемо випадок, коли 1 < а < 2 . Маємо (після піднесення до квадрату):
200


X. Тригонометричні нерівності
I sin2x∣ > а2 -1, звідки
1 / у ∖ kπ
— arcsinlα -l) + -τ-<х<
2 v 7 2
7Г 1 . / 2 і ∖ . t~w
< arcsιn α -1 +—, ⅛∈∕^
2 2 \ і 2
Радимо читачеві не лякатися слова «аркус». Адже «аркус» це кут! А саме кутами та функціями від них займається тригонометрія.
⅝μJ70 Операції з оберненаjιιu триіоноуиепг- ричниуии
(fyn∕(iμjLjuu
Під час повторення означення обернених тригонометричних функцій, радимо звернути
увагу на те, що:
201


101 порада абітурієнту
При розв’язанні різних задач неодноразово застосовуються співвідношення:
arcsin(- х) = - arcsin х; arccos(- х) = π - arccosx; arctg(-x) = -arctgx; arctg(- х) = π - arctgx.
Радимо звернути увагу на доведення цих співвідношень (і багатьох інших з оберненими тригонометричними функціями).
Доведемо, наприклад, що
arccos(- х) = π - arccosx.
Позначимо ліву частину рівності через a ∣, праву — через a 2. Щоб довести рівність
a ∣= а 2, доведемо спочатку, що cosα 1= cos се 2 (І) • cos( arccos(- х)) = -х;
cos( π - arccos х) = - cos(arccos х) = -х.
Але рівність (1) є необхідною умовою, і не є достатньою (дійсно, наприклад, cos450 = cos3150, але 450 ≠ 315°). Тому доведемо, шосе l іα 2 належать одному інтервалу монотонності косинуса: 0 ≤ arccos(- х) ≤ π .
202


X. Тригонометричні нерівності
Далі,
0 ≤ arccosx ≤ π; 0 ≥ -arccosx > -π; π≥π - arccosx>0.
Отже, кути a 1 і a 2 належать інтервалу [О;тг]
— інтервалу монотонності косинуса.
Задача 1. Обчислити sin —arcct
Розв’язання.
Маємо
sin
Ґ1
ґ зї
= sin
/
∩f
— arcctg
l2
1 √
π -arcctg—
= sin
π
arcctg —
- cos
С 3^l arcctg —
2
2
2
\
I ∕
Л . а . ,ч
Оскільки гострий кут (доведіть!), то
а = cos—.
2
a ∕l + cosα cos— = J
2 V 2
о к ctgα
Застосуємо формулу cos а = —.
√1 + ctg2α
203


101 порада абітурієнту
г\ 4 3.
Одержимо: coset = = —, і, остаточно,
5
16
4_
2 V5 Js'
а cos— =
2
. 2
Відповідь: —=.
Задача 2. Знайти значення виразу arcsin(sin 3).
Розв’язання.
Користуючись формулами зведення, запишемо sin3 через синус деякого кутах, який . . π π задовольняє нерівність - — ≤ х ≤ —.
Маємо sin 3 = sin(π - 3), тому arcsin(sin3) = = arcsin(sin(π -3)). Причому число π -3 задовольняє цю нерівність, тому arcsin(sin 3) = arcsin(sin(π - 3)) = π - 3.
Відповідь: 7t-3.
204


XL Елементи аналізу
XI. 	ЕЛЕМЕНТИ АНАЛІЗУ
диференціюваккβ
Для розв’язання конкурсних задач з елементів математичного аналізу,
важливо вільно володіти таблицею похідних, знати правила диференціювання, вміти знаходити похідну складеної функції та.,, не губитися в нестандартних ситуаціях. Радимо таблицю похідних і правила диференціювання вивчити напам’ять.
Функція fix)
с (const)
X
^j~X
X
Хр, рє
sinx
COS X
Похідна fix)
0
1
1
2<[х
-Ги 1
pxp-'
COS X
-sinx
205


101 порада абітурієнту
Функція f(χ)
tgx
ctgx
ах
ех
∣θgfl*
In X
Похідна f'(χ)
1
cos2x
1 sιn^x
axina
ех
1 хіна
X
( (∕W))'= '(∕W)∙∕'W
206


XL Елементи аналізу
Задача 1. Знайти похідну: у = sin2(tg2x).
Розв’язання.
Маємо:
y' = (sin2(tg2x)) = 2sin(tg2x)∙(sin(tg2x))' =
= 2 sin(tg2x) ∙ cos(tg2x) ∙ (tg2x)' =
= 2 sin(tg2x) ∙ cos(tg2x) (2х)' =
cos2 2х
2 sin(2 ∙ tg2x)
cos2 2х
2 sin(2 ∙ tg2x)
Відповідь: l-∑
cos 2х
Задача 2. Знайти похідну: у = хх (х > 0).
Розв’язання.
Прологарифмуємо обидві частини співвідношення, даного в умові:
In у = In xx = xlnx.
Тоді, диференціюючи одержану тотожність, маємо:
207


101 порада абітурієнту
(in у)' = (х In х)';
—-у' = x' lnx + x(lnx)';
y, 1
— = lnx + x∙- = lnx + 1 ;
У х
y' = (lnx + 1)-у = (іпх + 1)• хх .
Відповідь: (1πx + 1)∙xλ.
Задача 3. Знайти суму:
l + 3x2 +5х4 + ... + (2л- l)x2"^2 (х ≠ ±1).
Розв’язання.
Помітимо, що
l + 3x2 +5х4 + ... + (2л-l)x2"~2 =
Крім того, х3 + х5 +...+ х2" 1 —сума п перших членів геометричної прогресії, перший член якої дорівнює х, а знаменник— х2 . Тоді:
(x + x3 +x5 +... + x2"^, )’ =
208


XL Елементи аналізу
]4-4-636
209


101 порада абітурієнту
72
критичні mo4f(u фун^ії
На жаль, часто доводиться чути таку фразу: «Знайдемо критичні точки функції, для цього прирівняємо похідну до нуля»!??
Радимо знати означення критичної точки функції і не розгубитися, якщо доведеться ним користуватися. Критичною точкою функції називається точка, яка належить внутрішній частині області визначення цієї функції, похідна в якій дорівнює нулю або не існує.
Задача 1. Знайти критичні точки функції: /(х) = х3 - Зх2 + 5.
Розв’язання.
Маємо: £>(/): xeR; ∕'(x) = 3x2 -6х ; E^f : х ∈ R ; f (х) = 0 , тоді х = 0 або х = 2 . Відповідь: х = 0 і х = 2 .
210


XI. Елементи аналізу
Задача 2. Знайти критичні точки функції: λ Зх - 2 х) = .
, 2х + З
Розв’язання.
Маємо:
6x + 9-6x + 4 13 ». .
= (2x + 3)2 = ; якщо f w = 0 ■тоді
х ∈ 0; f (х) не існує при х = - у, але
-∣≡D(∕) !!!
Відповідь: функція критичних точок не має.
Задача 3. Знайти критичні точки функції: ∕(x) = √4≡√ .
Розв’язання.
Маємо: £>(/): хє[-2;2]; f∖x') = -=½½=-.
√4-λ-2
f (х) = 0 , тоді х = 0 ; f (х) не існує при х = -2 і 14*
211


101 порада абітурієнту
при х = 2, але ці точки не належать внутрішній частині області визначення.
Відповідь: х = 0.
Задача 4. Знайти критичні точки функції:
f(x) = y∣x2 -1 .
Розв’язання.
Маємо: £>(/): х ∈ R.; f ’ (х) = —. _ •
З з// 2 1∖2 vvc ~ /
t 1
f (х) = 0 , тоді х = 0; f (х) не існує при х = -1 і при х = 1, і ці точки належать внутрішній частині області визначення.
Відповідь: х = -1; х = 0; х = 1.
Радимо пам’ятати, що якщо функція досягає экстремуму у критичній точці, де похідна не існує, то графік функції «гострий». (Приклад: у = | х |).
212


XI. Елементи аналізу
∏∩nα∏a 73 Використовуючи похідну У )ИД ' 1 * * 4-* для дослідження функцій, ґ Ви, мабуть, переконалися,
Монотонність „
у важливості
і e%cmpejuyjιιu неформального володіння
теорією.
Звертаємо Вашу увагу на те, що:
• якщо розривна функція є монотонною на кожному з інтервалів, де вона є неперервною, то вона не обов’язково буде монотонною на всій області визначення*;
• критична точка є «підозрілою» на екстремум, але не обов’язково є екстремальною (приклад: функція у = х3).
• максимум функції може бути менше за. її мінімум, оскільки ми, взагалі-то кажучи, досліджуємо функції на локальний екстремум. І взагалі, не варто ототожнювати мак1
Розгляньте функцію у = — : доведіть, що вона є X
спадною на кожному з інтервалів області визначення.
але не є монотонною на всій області визначення.
213


101 порада абітурієнту
симум з найбільшим, а мінімум — з найменшим значеннями функції.
Задача. Дослідити функцію
∕(x) = V(l-x)(x-2)2
на монотонність і екстремуми.
Розв’язання.
О(/): х ∈ R . / '(х) = -^~2)(4~ЗХ) ' ■ Зд/(1 -x)2(x-2)4
. 4
f (х) = 0, х = —— критична точка.
/' (х) не існує при х = 1 і х = 2.
— —точка min, 2 — точка max. З
214


XL Елементи аналізу
lW 74
ТҐо^ідна і дотична
Нехай задано функцію f(x).
Нехай у дотична до цієї
функції, проведена через точку (x0,∕(x0)).
Тоді рівняння дотичної до функції/ (х) в точці хо має вигляд
У =f(xo) +f '(xo)(x - Хо).
Якщо дане рівняння переписати у вигляді: У =f ∖xo)x + (∕Uo) -∕ ,(*o) *о)
і позначити
f(×o) ~f \хо) xo = b; f r(x0) = k , то
у = кх + Ь.
Радимо пам’ятати, що
f ,(x0) = к = tg а ,
де а — кут між дотичною і додатнім напрямком осі ОХ.
215


101 порада абітурієнту
Нехай j∕1) = Λ1x + Z>∣, j∕2) = Λ2r + ⅞ — рівняння деяких прямих. Тоді
Задача. Скласти рівняння дотичних до кривої у = x2 -4х + 3,
що проходять через точку Л/(2;-5).
Розв’язання.
Маємо
f(x) = Xі -4x + 3 *; f (x) = 2x-4.
Нехай х0 —точка дотику. Тоді рівняння дотичної, яка проходить через цю точку має вигляд:
T = (⅞2 -4x0 +3) + (2x0 -4)(x-x0).
За умовою задачі
x = 2,y = -5.
* Для зручності використання рівняння дотичної, радимо завжди «перейменовувати» дану функцію у на/(х).
216


XL Елементи аналізу
Отже,
- 5 = (x02 -4x0 + з) + (2x0 - 4)(2 - х0 х0 = 0 або х0 = 4.
Тоді при х0 = 0 :
y = (02 -4-0 + 3)+ (2∙0-4)(x-0), у =-4х + 3;
при х0 = 4 :
У = (42 -4∙4+3)+(2∙4-4)(x-4), y = 4x-13.
Відповідь: у = -4х + 3; у = 4х -13.
217


101 порада абітурієнту
XII. ПЛАНІМЕТРІЯ
ПОЗНАЧЕННЯ, ЯКІ ЗУСТРІЧАЮТЬСЯ У КНИЗІ:
• а, Ь, с — сторони трикутника АВС.
• Z.A, Z.B,Z.C — кути ВАС, ABC, АСВ.
• ha,hh,hc— висоти, опущені на сторони ВС, АСіАВ відповідно.
• ma,mh,mc— медіани трикутника ABC.
• la,lh,lc— бісектриси кутів ВАС, ABC, АСВ відповідно.
• О — центр кола, описаного навколо трикутника ABC, R — його радіус.
• І (інцентр) — центр кола, вписаного у трикутник ABC, г— його радіус.
• Н (ортоцентр)—точка перетину висот.
• М (центроїд, центр ваги) — точка перетину медіан.
• Λ∕1,ΛY2,Λ√3— середини сторін ВС, АС і АВ відповідно.
• n = α + + c — півпериметр трикутника ABC.
2
• S — площа трикутника АВС.
218


XIL Планіметрія
fDecjuwb а^тивнит^
Оскільки кожен екзамен включає розв’язання задач, то і в геометрії ми приділимо увагу
τmopejιι цьому питанню,
пушмі/иетрії
Сконцентрувавшись на цьому, ми умовно виділимо десять найбільш активних (тобто таких, що часто застосовуються при розв’язанні задач) теорем планіметрії
Такий собі рейтинг теорем, а точніше, можливість повторити теорію.
1) Теорема Піфагора.
2) Теорема синусів.
3) Теорема косинусів.
4) Метричні співвідношення у прямокут¬
ному трикутнику.
5) 	Теорема Фалеса.
219


101 порада абітурієнту
6) Теорема про властивості середньої лінії трикутника і трапеції.
7) Теорема про властивість бісектриси внутрішнього кута трикутника.
8) Властивість чотирикутника, вписаного у коло. Властивість чотирикутника, описаного навколо кола.
9) Теорема про добуток відрізків хорд.
10) Теорема про дотичну і хорду.
⅛a76
Основні форjuyjιu пjιaπijuempil
Ми рекомендуємо для розв’язання великої кількості геометричних задач знати і вміти застосовувати такі формули та співвідношення:
1 ( 1 1 А
• s = ^aha S = ~bhh, S = ~chc ;
2 V 2 2 √
• <S, = -αZ>sinC S = — δcsin A , S = — αcsin В
2 \ 2 2
220


XII. Планіметрія
• S,4-κyτ = — flf∣<⅞ s∙n y4 (площа чотирикутника дорівнює півдобутку діагоналей, помноженому на синус кута між ними);
а
• =2R ;
sin А
синусів);
λ abc
• Я = ;
4S
S
• г = —;
Р
а b с ,
= = (теорема sin A sin В sin С
,o
а + Ь-с
2
5 = p(p - a)(p - b)(p - с) (формула Герона);
• пг2
4
• a2 =b2 +c2 -2bccosA (теорема косинусів);
, 2bc А
• la = cos—;
a b + c 2
22!


101 порада абітурієнту
• d2 + d¾ = 2∖a2 +b2j (сума квадратів діагоналей паралелограма дорівнює подвоєній сумі квадратів двох його суміжних сторін);
1111
• —+— + — = -.
⅛ hb hc г
Доведемо останню формулу.
25
Оскільки ha = —, то
а
1 1 1 _ a + b + с _2р _ \
~⅛+~⅛+~⅛^ 2S ^2S~7'
c4y∂oβi mo4f(u mputyniHUfqi
До чудових точок трикутника відносяться точки
О, І, н, м.
З різних причин теореми про них у шкільних
підручниках з математики
розглядаються (і губляться!)
серед задач.


XII. Планіметрія
Радимо надати їм належне, як найважливішим теоремам планіметрії.
Отже,
Теорема 1.
г Центр кола, описаного навколо трикут- г> ника, співпадає з точкою перетину пер- д пендикулярів, проведених до сторін трикутника через їх середини.
Теорема 2.
? Центр вписаного у трикутник кола спів- £> падає з точкою перетину бісектрис цього /1, трикутника (ще раз нагадаємо, що він називається інцентром).
? Теорема 3.
Три медіани трикутника перетинаються в А одній точці і діляться точкою перетину у відношенні 2:1, рахуючи від вершини.
Теорема 4.
Три висоти трикутника перетинаються в одній точці.
223


101 порада абітурієнту
Доведемо теорему 3.
Нехай дві медіани перетинаються у точці М, точки F і Е — середини відрізків AM і CM, а чотирикутник M∖M-iFE — паралелограм. Тоді медіани АМ\ і CM3 точкою М діляться в одному і тому ж відношенні (1:2). Отже, перетинаючись, медіани діляться в одному і тому ж відношенні, тому точка поділу для трьох медіан — спільна.
Доведемо теорему 4.
Через вершини трикутника ABC проведемо прямі, паралельні сторонам цього трикутника. Одержимо трикутник A∖B∖C↑. Оскільки AC∖BC і ABCB∖ — паралелограми, то AC↑=ABγ=BC. Аналогічно,
BA↑=BC∖ і A↑C=CB∖. Отже, точка Н є центром кола, описаного навколо трикутника A↑B∖C∖i а він — єдиний.
224


XIL Планіметрія
78
Сьогодні їх взагалі не називають теоремами.
Задачі- А нам важливо
meopejuu
підкреслити їхню вагомість.
Отже,
Задача-теорема 1.
Кут з вершиною всередині круга вимірюється півсумою дуг, розташованих між прямими, що містять його сторони.
Доведення.
Доведемо, що
zχ = z^β = ^.
2
Позначимо
ΛCAS = φ ΛSCA = φ .
Тоді
1 1 n
£Х = φ^φ2 = -a+-β.
Задача-теорема 2.
Кут з вершиною зовні круга дорівнює модулю піврізниці дуг, розташованих між прямими, що містять його сторони.
(Доводиться аналогічно).
15-4-636
225


101 порада абітурієнту
Задача-теорема 3.
Кут між дотичною і хордою, проведеною через точку дотику, дорівнює половині дуги, розміщеної між його сторонами.
Задача-теорема 4.
У трикутнику ABC
1) ZBOC = 2ЛА ;
2) ЛВНС = 180° -/.А',
3) ZB∕C = 90° + —.
Доведемо формулу 3):
ZBZC= 180°-
Задача-теорема 5.
Нехай K↑, K2∙, Кз — точки дотику вписаного у трикутник ABC кола зі сторонами BC,AC, АВ , відповідно. Тоді
AK3 = р-a; BKi = p-b; CK2 = р-с.
226


XII. Планіметрія
Доведення.
b + c-a
Позначимо
AK3 = х, ВК\ = у, CK2 = z.
Тоді
x = b-z, х = с-у \ 2x = b + с - (у + z);
а
= р-а.
Дві інші рівності доводяться аналогічно.
Задача-теорема 6.
У рівнобедреній трапеції ABCD(ВС|| AD∖ ВС < AD) BKJ-AD і KeAD. Тоді відрі¬
зок KD дорівнює середній лінії трапеції.
Доведення.
З точки С опустимо перпендикуляр СЕ (Е ∈ AD).
KD=KE+ED =
„„ AD-ВС BC+AD
15*
227


101 порада абітурієнту
Задача-теорема 7.
Площі трикутників, які мають спільний кут, відносяться як добутки сторін, що утворюють цей кут. (Довести самостійно).
Що таке легка задача? Ну, дуже легка! Такі
Спочатку задачі ми розглядати не jιeif(i задачі будемо. А ось задачу, в якій потрібно застосувати лише одну-дві геометричні теореми, без несподіваних додаткових побудов, ми і будемо вважати легкою.
Радимо розв’язати більшість задач групи А з 10-глави збірника під редакцією Ска- наві. Тут труднощів бути не може!
Задача 1. У прямокутному трикутнику точка дотику вписаного кола ділить гіпотенузу на відрізки довжиною 5 і 12 см. Знайти катети трикутника.
228


XII. Планіметрія
Розв’язання.
А
В 5 Ki С
Нехай коло, вписане у прямокутний трикутник ABC, дотикається його сторін у точках Kl ,K2 ,K2t, г — радіус цього кола. Оскільки дотичні, проведені до кола з однієї точки рівні, то СК} = CK2=r,
AK2 = AK3 = 12см, BKy = BK3 = 5см. Застосовуючи теорему Піфагора, маємо
звідки г = 3 см і ВС = 8 см, АС =15 см.
Відповідь: 8 і 15 см.
Задача 2. Точка на гіпотенузі, рівновіддалена від обох катетів, ділить гіпотенузу на відрізки довжиною ЗО і 40 см. Знайти катети трикутника.
Розв’язання.
С
Нехай L — дана точка на гіпотенузі А В прямокутного трикутника АСВ (ЛАСВ = 90°).
229


101 порада абітурієнту
З точки L опустимо перпендикуляри LE і LF на катети АС і ВС. Оскільки, за умовою, LE = LFy то ΔCEL = ΔCFL і ZΛCL = Z5CL,
отже CL—бісектриса кута ВСА.
Позначимо ВС = х, тоді AC = λ∕702 -х2 і за властивістю бісектриси
ВС BL c х з
= , або —. = —, звідки х = 42 .
АС AL FF^F 4
Отже, #С = 42см, АС = 56 см.
Відповідь: 42 і 56 см.
80
Янатоуиіуг
Як анатомія повинна знати все про будову людини, так абітурієнт повинен
piβHθcmopθHK,b ого трищтни^а
знати все про рівносторонній
трикутник.
Отже, якщо дано сторону а рівносторон- нього трикутника, то:
230


XII. Планіметрія
Ці формули бажано знати напам’ять, вони стануть у нагоді вам і в стереометрії, володіння ними зекономить найцінніше на іспиті — час.
Задача 1. Площа рівностороннього трикутника, вписаного у коло, дорівнює Q1. Довести, що 20^3 радіус кола дорівнює —-—.
Доведення.
Нехай сторона даного рівностороннього трикутника дорівнює*. Тоді площа цього трикутни-
231


101 порада абітурієнту
ка дорівнює —-—. За умовою ——
∣4Q2 ~ . n хл/з
ЗВІДКИ X = І . Оскільки R = , то
V л/з З
√3 4Q2 4√3
R = — l-½=- = 20—■
з V √3 з
Задача 2. У ромб, який ділиться своєю діагоналлю на два рівносторонніх трикутники, вписано коло радіуса 2. Знайти сторону ромба.
Розв’язання.
ш
В
А
Оскільки діаметр кола співпадає з висотою ромба, то задача зводиться до знаходження сторони трикутника за його висотою. Вихо- , , Дл/з •
дячи з формули h = , і
2
позначивши сторону ромба через х, одержимо λ . 8 8√3
4 = ——, звідси х = — = —ї—.
2 √3 З
Відповідь: —
З
232


ХП. Планіметрія
81
«Очевидна.» подібність
Якщо в умові задачі можна знайти паралельні прямі, то це перша «вказівка» на те, що ключем до розв’язання може бути подібність трикутників (назвемо цей випадок «очевидною» подібністю).
Звертаємо увагу на рівність вписаних та інших кутів вони також виводять на подібність трикутників.
Задача 1. Два кола радіусів R = 3 і г = 1 дотикаються зовні. Знайти відстань від точки дотику кіл до їхньої спільної зовнішньої дотичної.
Розв’язання.
Нехай А і В — точки дотику кіл і дотичної, О\ і О2 — центри кіл, 5 — точка дотику кіл, SLLAB. Тоді LK = r ∖
233


101 порада абітурієнту
Δ O2 KS ~ Δ O2 EOx. Звідси
KS O2S KS_ EOl O2S
EOx ~ O2Ol ’ ~ OxO2 ’
(R-rVr 1 1 З
KS = - = -; LS = LK +KS =∖+- = -.
R + r 2 22
- 3
Відповідь: —.
Задача 2. Довести теорему: якщо до кола провести з однієї точки дотичну і січну, то добуток січної на її зовнішню частину дорівнює квадрату дотичної.
Доведення.
Нехай до кола проведено дотичну AD і січну DC. Оскільки
ЛАСВ = ZBAD i то
Δ ADB~ΔCDA.
AD BD ■>
Звідси = , або AD2 = BD∙DC.
DC AD
234


XII. Планіметрія
82
«Л’римована» подібність
Як читач здогадався, «прихована» подібність це подібність трикутників, яку важко побачити.
Радимо звернути увагу на застосування другої ознаки подібності: якщо дві сторони одного трикутника пропорціональні двом сторонам іншого трикутника і кути, утворені цими сторонами рівні, то трикутники подібні.
Крім того, практика розв’язання дозволяє побачити подібність при неочевидній рівності кутів.
Задача 1. Відрізки АВ і CD перетинаються в точці Е. Відомо, що АЕ ♦ ЕВ = DE ∙ EC . Довести, що точки Л, В, С, D належать колу.
Доведення.
АЕ ED Оскільки АЕ • ЕВ = DE ■ EC, то = .
ЕС ЕВ
235


101 порада абітурієнту
Враховуючи, що
AAED = ABEC, можна стверджувати, що Δ AED ~ Δ ВЕС .
Отже, Z.DAE = Z.BCE, а тому, точки AiB,CiD належать од¬
ному колу.
Задача 2. Два кола перетинаються, AD — їхня спільна хорда, А В і АС — хорди, що дотикають- . ττ AB2 BD
ся кожного з кіл. Довести, що — = .
AC2 DC
Доведення.
Оскільки
ZCAD = ΛABD, a /.BAD - AACD, то
ΔABD~ΔADC.
^ AD AB BD AB π Отже, = , = . Перемножив-
DC AC AD АС
ши ці дві рівності, одержимо потрібне.
236


XII. Планіметрія
Що nunςe точкой fW і «триβucHuiζj>
Радимо звернути увагу на точки перетину бісектрис кутів BAC,ABC,ACB з описаним колом.
їх ми позначимо VFι, W2, VF3,
відповідно. Ці точки мають цікаві властивості, які активно
використовуються у задачах.
Наприклад:
OlfKl ± ВС (О— центр описаного кола); ∩ • теорема «трилисника» 0z∣∕ = ∕4z∣ В = J4z∣ С.
Доведемо теорему «трилисника»:
Wr∣
Зрозуміло, що jylB = iylc (рівні дуги стягуються рівними хордами). Доведемо, що 0√ = 0r1 Я. Маємо:
Z∕^ = Z∕BC+ZCB^ =
=т+т:
237


101 порада абітурієнту
. ЛА Z.B
ABIWχ = + як зовнішній кут трикут-
ника ВІА. Отже, трикутник Wz1ВІ — рівнобедре- ний, тобто WλI = Ж] В, що і треба було довести.
Задача 1. Сторони трикутника ABC складають арифметичну прогресію (b < а < с) *. Довести, що Al = IWx.
Mx
wl
Доведення.
Нехай вписане коло дотикається сторони А В у точці К3. Маємо
р- а = =
2
а + 2а -2а а = = — = АК .
2 2 3
Оскільки ZMxCWx = ΛIAK3, то ΔCΛ∕∣JF1 = = ΔAK3I і CWi = А/. Але ∕Ψi =CWrl, отже, АІ = /Ж .
Такі трикутники називаються різницевими.
238


XII. Планіметрія
Задача 2 (формула Ейлера). Довести, що OI2 = R2-2Rr.
Доведення.
А
W1
N
В
Проведемо діаметр MN через точку І. Маємо AI∙IW↑ = MbIN = = (R + Ol)-(R-Ol) = = r2-oi2.
Оскільки
ZWyEB = ZIAB
(WrlE — діаметр), то
ΔW∖BE ~ΔIK3A.
Звідси
EWx _ BWλ
Al ~lκζ'
і тоді, враховуючи теорему «трилисника», маємо
EWγ>lK3 = AIIWλ∖ 2Rr = AI∙lW∖.
Таким чином,
R2 -Ol2 =2Rr.
239


101 порада абітурієнту
W 84
Метод допоміжного елемента популярний як завдяки своїй необхідності, Метод ∂onojιdy(Hθio ejιejιιewma. (Doιwjιriy(Huii ejιeju,eκm — відрізок
так і ефективності. Суть його полягає в тім, що при розв’язанні задачі вводиться елемент (його ми називаємо допоміжним), якого в умові немає.
З його допомогою складається рівняння (чи інше співвідношення), де невідомим буде шуканий елемент, або елемент, необхідний для його знаходження.
Під час розв’язання введений елемент «чудовим чином» скорочується, виконав- іии свою зв’язуючу функцію,
240


XII. Планіметрія
Ми розпочнемо з уведення допоміжного відрізка.
Радимо вводити його, вибравши подібні фігури.
Задача 1. Основи трапеції а і b (а> Ь). Пряма, що проходить через точку перетину діагоналей паралельно основам, перетинає бічні сторони
трапеції в точках М і N. Знайти довжину
відрізка MN.
Введемо як допоміжні елементи відрізки hx,h1'h — висоти трикутників МВО, AMO, ВСА. відповідно. Позначимо: МО = х.
Δ MBO~ΔAMO,
тоді — = — (1); Δ AMO~ΔABC, звідки a h
х h^> , ч х х /її + ¼
- = ~γ (2). Додамо (1) і (2): - + - = ——. b h а b п
16-4-636
241


101 порада абітурієнту
. , , , х х ab
Але hx + И-, = п, тому — + — = 1, х = .
а b а + Ь
Відрізок ON знаходиться аналогічно: MO = ON .
n. . 2αZ>
Відповідь: MN = .
а + Ь
Задача 2. Радіуси двох кіл, що не перетинаються, дорівнюють R і г. їхні спільні внутрішні дотичні взаємно перпендикулярні. Знайти площу трикутника, утвореного цими дотичними і спільною зовнішньою дотичною до цих кіл.
Розв’язання.
Позначимо (9і і О2
— центри кіл, і точки дотику — D, К, Е, F, Ex,F↑-, нехай
DK = ∕, DA = х, ВК = у,
S — площа трикутника ABC.
Оскільки чотирикутники ECEλO2 і FCFxOx — квадрати, і FC = F∣C = R,EC = CEx = г, то
AD = АЕ = х, ВК = BF} = у, DB - BEx, АК = AF, 242


XII. Планіметрія
звідки 1-х = R + r + x, ∕-y=R + r + y, отже, x = y,AB=R + r. За теоремою Піфагора,
(R + r)2 = (R + x)2 + (r + х)2, Rr = R х + гх + х2 . (1) Маємо
S = —(Я + х)(г + x) = —(Rr + Rx + γx + x2} . (2) 2 г
Підставимо (1) в (2), одержимо
S = i(Λr+flr) = Яг.
Відповідь: Rr.
Метод допоміжного ejιejueκma. rDonoуиі^ний ejiejueum — njιoιuμ
Введення площі як допоміжного елемента аналогічне введенню лінійного елемента. Порівнюючи площі фігур, можна одержати рівняння
16*
243


101 порада абітурієнту
відносно невідомих задачі або необхідні співвідношення у вигляді формул. Радимо знаходити або порівнювати ті площі, сума (різниця) яких дає площу заданої фігури або співвідношення площ тих фігур, в яких лінійні елементи шукані або є компонентами співвідношення у вигляді формули.
Задача 1. Довести, що у прямокутному трикутнику ЛВС (ZC = 90°) виконується співвідношення a-b = c-h, де h — висота трикутника.
Доведення.
Позначимо 5—площа трикутника ЛВС. Тоді
S = -ch.
2
З іншого боку,
S = -ab, 2
отже, — ch = — ab, або ch = ab.
244


XII. Планіметрія
Задача 2. Довести, що сума відстаней від довільної точки, взятої всередині правильного многокутника, до всіх прямих, що містять його сторони, є величина стала.
Доведення.
Нехай AxA2... Ап —правильний многокутник, точка X — довільна точка, взята всередині цього п-кутника. Позначимо сторону многокутника через а, а відстані від точки X до сторін многокутника або до їхніх продовжень— через dx, d2 ,∙..,dn.
З’єднавши точку Хз вершинами Al ,A2 ,...,A,j одержимо п трикутників з однаковими основами. Позначимо їхні площі через 51,...,Sn. Тоді 2*S,∣ = dxa∖ 2S2 = d2a;...; 2Sl1 = dna. Додавши рівності, одержимо 2S = a(dx +d2+...+dn), звідки
25 d∖+d2+...+ dl1 =— — величина стала.
245


101 порада абітурієнту
⅜j∣∏3 θθ Застосування
Метод ∂ ОПОJlliτζHOlO ejiejuewna. (D(moju⅛ζHuu ejiejitCHm — tςtjm
і кута як допоміжного елемента пов’язане
з тригонометрією. Теореми синусів, косинусів, розв’язання трикутників дозволяють звести задачу до доведення нескладної тригонометричної тотожності або до розв’язання рівнянь чи нерівностей.
Задача 1. Довести, що у трикутнику ABC AB BD AC~ DC'
де D — точка перетину бісектриси кута ВАС зі стороною ВС.
Доведення.
Введемо позначення:
ZDAB = а ; ZADB = β .
246


XII. Планіметрія
А
AC sin(18Oo -jS)
DC sin а
За теоремою синусів: з трикутника ADB одержимо
AB _ sin β
BD sin а ’
з трикутника CAD —
_ AC sιnθ або = ——
DC sin а
Отже,
АС АВ
DC ~ BD
Задача 2. Довести, що якщо діагоналі вписаного у коло чотирикутника взаємно перпендикулярні, то сума квадратів протилежних сторін чотирикутника дорівнює квадрату діаметра цього кола.
Доведення.
Введемо позначення у чотирикутнику ABCD ∖
ZADB = a ; ZCAD = β. Тоді a + β = 90°. З трикутників ABD і CAD маємо:
ΛB = 2∕Csinα ; CD = 2Rsinβ =2Rcosa .
247


101 порада абітурієнту
Отже,
AB2 + CD2 = 4Д2 (sin2 a + cos2 а ) = 4 Я2, що і треба було довести.
V 87
Метод допо_/иі?!(ноіо
Читач уже здогадався, що у стереометрії також «працює» метод допоміжного
cjιejuemna. елемента. Але ми
tDonoрадимо звернути увагу еуігуиент — на більш загальний
периjuemρ або підхід аналогію,
об'е/и
Аналогію між планіметрією (геометрією на площині) і стереометрією (геометрією в просторі).
І 	ми не відмовимо собі (і вам) у задоволенні процитувати блискучу думку Штефана Банаха:
248


XII. Планіметрія
«Математик це той, хто вміє знаходити аналогії мЬіс твердженнями; кращий математик той, хто встановлює аналогії доведень; більш сильний математик той, хто помічає аналогії теорій; але можна уявити собі і такого, хто між аналогіями бачить аналогії».
Задача 1. У прямокутному трикутнику ABC (zC = 9Oo) площею S через вершину С проведено відрізок CD (точка D належить стороні АВ), так, що кола, вписані у трикутники CAD,CBD, рівні. Довести, що CD = Vs .
Доведення.
Позначимо CD = х; очевидно, що
s = sACD+sDCB =Plrl + P2rl =(p∣ + Pl∖l, де pl і р2—півпериметри трикутників ACD і DCB , r∣ — радіус рівних кіл, вписаних у ці трикутники. Отже,
5 S
η = —т— = ~~ ■ P∖+p2 р + х
249


101 порада абітурієнту
Позначимо J1, J2 — ін- центри трикутників ACD і DCB . З подібності трикутників АІВ і √1∕√2 одержимо, що = . Не-
r-η Jl√2
хай F і N —точки дотику кіл до сторони АВ. Маємо
JlJ2 = FN = FD+ DN. Але
FD = p2-a ', DN = p↑-b. Таким чином,
J1J2 = p∖ - b + р2 - а = р + х- Ь — а.
Отже, маємо:
Р _ с .
S S р+х-Ь-а
Р Р + х
х2 = p(b + a-p) = р(р-с).
Але r = p-ci отже,
х2 = pr = S , звідки х - 4s .
250


XII. Планіметрія
Задача 2. Довести, що бісекторна площина двогранного кута тетраедра ділить протилежне ребро пропорціонально площам граней, які утворюють цей кут.
Доведення.
Нехай ADE — бісекторна площина двогранного кута з ребром AD. Розглянемо тетраедри EABD і EACD, вони мають рівні висоти, оскільки точка Е рівновіддале- на від площин ABD і ACD. Таким чином,
vACDE sACD
Спільну грань ADE тетраедрів EABD і EACD приймемо за їхню основу, тоді
yABDE = eb /2) v ACDE ЕС
Порівнюючи вирази (1) і (2), одержимо
ee = sABD
ЕС sACD
251


101 порада абітурієнту
гу 88 i)θβe∂eHHji (f>opjuyjι njunu,
Доведення різних геометричних формул один з популярних типів задач. Радимо широко застосовувати апарат алгебри, тригонометричних формул, попередньо використавши співвідношення типу a = 2R sinZ/4.
Задача 1. Довести формулу:
‰ 5 = -J4a2c2-(a2+c2-l>2)2 .
& 4V \ /
Доведення.
З 	формули Герона випливає, що
16S2 = (a + b + c)∖b + c- a)∙(a + c-b)∙(b+ а-с). Маємо:
16S2 = ((α + c)2 - b2) ∙ (b2 - (с - а)2) = = (α2 +2αc, + c2 -b2)∙(b2 -c2 +2ac-a2) = = 4a2c2-(a2+c2-b2)2.
* Цей наслідок з формули Герона іноді буває доцільно застосувати, якщо сторони трикутника ірраціональні.
252


XII. Планіметрія
Задача 2. Довести, що Л
S=R∙ph,
де рн — півпериметр трикутника, вершини якого співпадають з основами висот трикутника ABC*
Доведення.
Маємо:
Рн = U∏tH2+HiH3 + H2Hi) =
1 7
= — B(sin 2ZΛ + sin 2Z.B + sin 2ZC) =
1
= — ♦ R ∙ 4 ∙ sin ZΛ ∙ sin ZB ∙ sin ZC =
= 2 ∙ R ∙ sin ZΛ ∙ sin ZB ∙ sin ZC.
А враховуючи, що
S = 2' R2 ∙ sin Z-A - sin ZB ∙ sin ZC (довести самостійно!), одержимо формулу, яку й треба було довести.
‘Цей трикутник називається ортоцентричним.
253


101 порада абітурієнту
3acmocyβθHκjι φopjuyjι п/іощ
Формули площі трикутника (многокутника) пов’язані між собою, і цей зв’язок часто використовується при розв’язанні задач.
Задача 1. Довести, що S = -^Jabchahhhc .
2
Доведення.
Маємо, S = — ahπ ; S' = — bhh ; S = — ch... 2 2 2
Отже, S3 = ±abchah∕,hc , або S = abchahhhc .
Задача 2. Довести, що у трикутнику ЛВС
І X Ч "
∖abc)
Доведення.
Маємо:
, 2S 2S 2S + b + c = — + — + —
¼∙
¼∕ ¼ fy
254


ХП. Планіметрія
1 1 1 h(. + h∣i ÷ hc
І і і» ∙' С
а Ь с 2S
Отже,
= 25∙(Λσ+¼+Λc)∙y-∙
J_ 1 _L Λ+⅛+∕½
що і треба було довести.
поширена задач. Радимо
застосовувати різні формули площ, розбиття фігур,
90 "ς≡
Зна%рд?Кеннл
площ фігур
рівновеликість, порівняння площ фігур, подібність
(площі подібних трикутників відносяться як квадрати відповідних лінійних елементів).
Задача 1. Знайти площу паралелограма за двома діагоналями і d2 та гострим кутом а.
255


101 порада абітурієнту
Тоді маємо:
αf2 = x2 + y2 + 2xy cos а
Позначимо в паралелограмі ABCD'.
AC = d∖; BD = d2 ;
/.BAD = а ;
AB = х; AD = у.
d2 = х2 +y2-2xy cos а,
√12 -√2 =4x^cosα.
о ■ rf∣2-rf2 г.
Звідси, ху . Отже,
4 	cos а
d; - d,2 d- d}
S 	4RΓ∏ - ХУ sin ос = — — sin а = - tgα .
∙' 4 cos а 4
о. . di
Відповідь: tgα.
4
Задача 2. Довести, що якщо в опуклому чотирикутнику ABCD
y∣sABCD =τ∣sBOC +y∣sAOD ’
де О — точка перетину діагоналей, то ABCD — трапеція.
256


ХП. Планіметрія
Доведення.
Позначимо площі трикутників BOC,AODi АО В, COD через
S1 ,S2 ,S3 ,S4, відповідно.
Таким чином, нам дано, що
S, = S1 +S2 +2√S1S2 . (1)
(S— площа чотирикутника ABCD ). Крім того, очевидно, що
S = 51+S2+S3+S4. (2) Трикутники АВО і AOD мають спільну висоту, S9 DO a . S4 DO ^ тому —- = . Аналогічно, — = . Отже,
S3 OB s∣ ов — = —2-, тобто 51 ∙ S2 = S3∙S4. Звідси, врахо- S3 S,1
вуючи рівності (1) і (2), одержуємо
S3 +S4 = 2√S3S4 , або (√⅜ -√¾)2 =0.
Отже, S3 = S4 , а тому, Sa∩d =sACDi τa' ким чином, чотирикутник ABCD —трапеція.
17-4-636
257


91
Метод ∂onojιιi^HU2C точок
101 порада абітурієнту
Існує думка, що в геометрії додаткові побудови робляться інтуїтивно.
Проте існують «домашні наробки»,
з якими радимо ознайомитися.
Одна з них вміння користуватися точками, про які в умові нічого не говориться (тому ми називаємо їх допоміжними).
Розглянемо одну з них центр кола. (До речі, зауважимо, що формули _ λ abc „ _ л = pr , S = ; S = крн доводяться з
4R використанням саме цієї допоміжної точки).
Задача 1. Одна з точок перетину двох кіл — точка К. Пряма дотикається цих кіл в точках М і N. Радіуси кіл — Rλ і R1. Знайти радіус кола, описаного навколо трикутника KMN.
258


XIL Планіметрія
Розв’язання.
Введемо позначення: Oλ і О2 — центри кіл. що перетинаються; (9 — центр кола, описаного навколо трикутника MNK.
Доведемо, що трикутники МОК і NO2K подібні.
Нехай Z,KNO2 = a, Z.KMO- β. Але ж
a = Жр-AMNK = 90°--ЛМОК = 2
= 90° - -(1800 - 2β} = β .
2v 7
Отже, (X=βi а тому трикутники МОК і NO2K подібні. Тоді {Rx— радіус кола з центром у точці О)
Rx _ КМ
R2~ KN ‘
З подібності трикутників KON і X791М випливає, що
17*
259


101 порада абітурієнту
Rx KN
Rλ~ KM'
Перемноживши ці рівності, одержимо:
Rx = R↑ ' R2 ; Rx = y∣R] ' R2 ’ Відповідь: ^Rx R2 .
тинаються в крузі, є круга.
Задача 2. Довести, що сума квадратів відрізків двох взаємно перпендикулярних хорд, що пере- величина стала для цього ведення.
З центра О опустимо перпендикуляри OF і ОН на хорди А В і DC. Е — точка перетину хорд АВ і DC. Нехай EF = x, ЕН = у . Тоді
АЕ2 + BE2 +СЕ2 +DE2 =
= (AF-x)2 + (AF + x)2 +(c∏-y)2 +(CH + y)2 = = 2AF2 +2СН2 +2x2 +2y2 =
= 2(AF2 +y2) + 2(CH2 +x2) = 2R2 +2R2 = 4R2 .
260


XII. Планіметрія
tMenw∂ ∂onojuiτ∣(κoιo ∣(ojιa
Це найпопулярніший метод посеред тих, які використовують додаткові побудови. Радимо проводити коло:
щоб вписати в нього розглядуваний
чотирикутник (коли це можливо); у випадку рівності кутів, які після побудови стануть вписаними;
для застосування формули a = 2Rs∖nΛA .
Задача 1. Визначити кути трикутника, в якого бісектриса, медіана і висота, проведені з однієї вершини, ділять кут на чотири рівні частини. Розв’язання.
Нехай у трикутнику ABC ABAC = а , СН — висота, CL — бісектриса, CM — медіана. Опишемо навколо трикутника ABC коло, продовжимо медіану CM до перетину з колом у точці D.
261


101 порада абітурієнту
Тоді ZCDB = ZCAB = ZCAH = ai ZACH = = 90° - а.Оскільки
ZCBD = 180° - (ZCDB + ZBCD) = 90°, то трикутник CBD — прямокутний. Отже, CD — діаметр. Оскільки AM = МВ , то АВ— також діаметр (у протилежному випадку CDZAB}. Тоді 90° = ZACB = 4а, звідки a = 22o3θ'. Отже, ЛВАС = 22°3θ', ΛACB = 90° , ЛАВС = 67o3θ'.
Відповідь: 22o3θ', 90°, 67o3θ'.
Задача 2. АН — висота гострокутного трикутника ABC. Точки М і N— проекції точки Н на 5 сторони АВ і АС. Довести, що MN = —.
Доведення.
Опишемо коло навколо чотирикутника ANHM. Тоді MN = AHs∖nZA =
__ 2S ВС =S
~ ВС 2R~ R
262


XIII. Стереометрія
XIII. СТЕРЕОМЕТРІЯ
першої необхідності
Ми починали розмову про планіметрію з перерахування найактивніших теорем, що застосовуються в задачах
За аналогією, в стереометрії ми виділяємо таку саму групу теорем. Радимо порівняти їх формулювання з поданими у підручниках, зрозуміти відмінності й переваги.
Отже,
Теорема 1. (Ознака паралельності прямої і площини).
Якщо пряма, яка не належить площині, паралельна деякій прямій, що лежить у цій площині, то вона паралельна й самій площині.
263


101 порада абітурієнту
Теорема 2.
Якщо площина проходить через пряму, паралельну іншій площині, та перетинається з цією площиною, то пряма їх перетину паралельна даній прямій.
Теорема 3. (Ознака паралельності двох площин).
Якщо дві прямі однієї площини, які перетинаються, паралельні двом прямим іншої площини, то ці площини паралельні.
Теорема 4.
Якщо дві паралельні площини перетинаються третьою, то прямі перетину паралельні.
Означення 1.
Пряму, що перетинає площину, називають перпендикулярною цій площині, якщо вона перпендикулярна будь-якій прямій, що лежить у цій площині.
Теорема 5. (Ознака перпендикулярності прямої і площини).
Якщо пряма перпендикулярна двом непара- лельним прямим на площині, то вона перпендикулярна цій площині.
264


ХШ. Стереометрія
Означення 2.
Відрізок, що сполучає основи перпендикуляра і похилої, проведених з однієї точки до площини, називається проекцією похилої на цю площину.
Теорема 6.
Якщо пряма, проведена на площині, перпендикулярна проекції похилої, то вона перпендикулярна похилій.
Має місце обернена теорема:
Якщо пряма на площині перпендикулярна похилій, то вона перпендикулярна й проекції похилої (теорема про три перпендикуляри).
Теорема 7. (Ознака перпендикулярності двох площин).
Якщо площина проходить через пряму, перпендикулярну іншій площині, то ці площини перпендикулярні.
Теорема 8.
Пряма, проведена в одній з двох перпендикулярних площин перпендикулярно до прямої їх перетину, перпендикулярна до іншої площини.
265


101 порада абітурієнту
Теорема 9.
Якщо дві площини перпендикулярні третій, то лінія перетину цих двох площин також перпендикулярна третій площині.
Означення 3.
Кутом між прямою і площиною називають кут між прямою та її проекцією на цю площину.
Означення 4.
Кутом між площинами, що перетинаються, називається кут між прямими, проведеними в цих площинах перпендикулярно лінії їх перетину.
Теорема 10.
Кожний плоский кут тригранного кута менше за суму двох інших плоских кутів.
Теорема 11.
В опуклому многогранному куті сума плоских кутів менша 360°.
Теорема 12.
Кут між площиною і похилою є найменшим з усіх кутів, які похила утворює з прямими, проведеними в площині через основу похилої.
266


XIII. Стереометрія
У 94
Φopjuyjιa mprboχj
Корсику сів»
Радимо запам’ятати і навчитися застосовувати формулу, що пов’язує косинуси трьох кутів: між прямою, похилою та проекцією цієї похилої на деяку площину : cos = cos cos Звертаємо увагу, що кут між прямою і
АВ-ОА
Нехай SA — похила, SO — перпендикуляр до площини π, SBLBA. Тоді за теоремою про три перпендикуляри ОВ1АВ.
ОА AB o
cosy = = = cosα ∙ cosp .
AS∙OA AS OA
267


101 порада абітурієнту
Задача 1. Плоский кут при вершині правильної чотирикутної піраміди дорівнює а . Знайти кут нахилу бічного ребра до площини основи.
Розв’язання.
Нехай у заданій піраміді SABCD
ZDSC = a.
Тоді
Маємо
ZSCD = 90°- — і 2
cos Z.SCD =
= cos /.SCO ∙ cos Z.OCD,
= cosx∙cosZ450.
. а д/2
sin — = cosx , звідки
2 2
гт . а ( /т . оЛ
cos х = √2 sin —, х = arccos √2 sin —
2 ∖ 2)
Відповідь: arccos
268


XIII. Стереометрія
Задача 2. Діагоналі двох суміжних бічних граней, розташовані на мимобіжних прямих, прямокутного паралелепіпеда нахилені до площини його основи під кутами а і β. Знайти кут між цими діагоналями.
Розв’язання.
Кут між мимобіжними прямими А} D і В\А — це кут х між прямою АВ} і прямою В}С, яка паралельна AiD.
Оскільки CB-LBBi і AB-LBBi, то пряма СВ перпендикулярна до площини АА} В} В і відрізок BBx є проекцією похилої CBi. Застосуємо теорему «трьох косинусів»:
cosx = cosЛВВ}С cosХАВ} В .
Оскільки Z,BBλ С = 90° - а ; ΔABx В = 90° - β, то cosx = cos(900 -α)cos(900 - β^ = sinα sin β.
х = arccos(sin a sin β).
Відповідь: arccos(sin a sin β).
269


101 порада абітурієнту
lW 95
Перед тим, як вирушати в нелегку подорож до стереометрії,
Jeojumpijι непогано провести на цбі тренаж зі,
здавалося б, такої простої фігури, як куб. Його конструкція дозволяє повторити основні теореми стереометрії, щоб потім успішно застосовувати їх у задачах і, що не менш важливо, правильно їх формулювати.
Отже, нехай дано куб ABCDA↑BχC∖Db
270


XIIL Стереометрія
Задача 1. Довести, що ребро AλBx паралельне площині ABCD і площині DZ)1C1C.
Доведення.
Оскільки A1B∣^AB, то ребро ∕1∣B1 паралельне площині ABCD. Оскільки ΛlB1∣∣C∣Z)1 , то ребро AlBl паралельне площині DDlC1C.
Задача 2. Довести, що площини ABCD і DDxCλC паралельні.
Доведення.
Дійсно, Al Bl II АВ і B1C1II ВС, отже, твердження задачі доведено.
Задача 3. Довести, що прямі AlBl і AD мимобіжні.
Доведення.
Припустимо, що прямі Λ1B∣ і AD перетинаються. Тоді можна побудувати площину A}B}DA. За теоремою 4, AD∖∣AiB1, що не вірно. Отже, Al Bl і AD мимобіжні прямі.
271


101 порада абітурієнту
Задача 4. Довести, що ребро AA↑ перпендикулярне ребрам ВС, B1C1 , BD iBxDx , AC , AxCx.
Задача 5. Довести, що ребро AD перпендикулярне відрізку ABx. *
Задача 6. Довести, що диагональ ACx перпендикулярна перерізу Al DB.
Задача 7. Довести, що діагональ ACx перетинає площину BDAl у точці перетину медіан трикутника BDAx.
Задача 8. У кубі проведено два діагональних перерізи AxBD і BxDxC. Довести, що ці перерізи, перетинаючись з діагоналлю ACx, ділять її на три рівні частини.
272


XIII. Стереометрія
npoe.fQnyerrt'bCJi точщі S, JLfQUjO...
%Ly∂u
Розв’язання деяких стереометричних задач залежить від того, які висновки ви зробите, проаналізувавши проекцію однієї з точок, даних в умові задачі
Вам допоможе знання найбільш типових ситуацій.
О Нехай у тригранному куті ABCS
ZSAB = ZSAC . Доведемо, що якщо S∣ — проекція точки S на площину САВ, то відрізок ASj належить бісектрисі
В
кута САВ.
Дійсно, проведемо
SF1AB і SE1AC.
За теоремою про три перпендикуляри
SxFLAB і S∣E±ΛC.
Отже,
ΔS1ΛF = ΔS1ΛE і
ΔSxAF = ΛSxAE.
18-4-636
273


101 порада абітурієнту
θ S вершина піраміди з рівними ребрами.
У цьому випадку проекція точки 5 на основу піраміди співпадає з центром кола, описаного навколо основи піраміди.
Дійсно, прямокутні трикутники SS1∕1∣, SS∣A2, SSlA3i..., SSlAn рівні за катетом і гіпотенузою, отже, ∣S і А і = ιS∣ A2 ~
= S∣X3 = ...= S∣Λw, а тому S1 — центр кола, описаного навколо основи піраміди.
© Ребра піраміди утворюють з площиною основи рівні кути.
Вершина піраміди 5 проектується в центр кола, описаного навколо основи піраміди.
О Грані піраміди утворюють з площиною основи рівні кути.
Вершина піраміди S проектується в центр кола, вписаного в основу піраміди.
274


XIII. Стереометрія
Г Можливий випадок, коли вершина 5 проектується в центр зовні вписаного кола*.
У 97 fKymu в θ
стереометрії ©
Радимо звернути увагу на такі серії задач:
кут між прямою і площиною; кут між мимобіжними прямими;
кут між площинами.
Тут ми знову зустрінемося з формулою трьох косинусів, з паралельним переносом при знаходженні кутів між мимобіжними прямими, з ознакою перпендикулярності прямої і площини та теоремою про три перпендикуляри, коли мова піде про лінійний кут двогранного кута.
Задача 1. У тригранному куті О ABC дано:
ZAOC = 60°; ZBOC = 45°; Z4O5 = 45°.
Знайти кут між АО і площиною ВОС.
* Коло, яке дотикається однієї зі сторін трикутника і продовжень двох інших сторін називається зовні вписаним.
18*
275


101 порада абітурієнту
З 	точки Е, що належить ребру OAi опустимо перпендикуляр EF на площину ВОС. Позначимо AEOF = х ,∕-FOC = у.
Тоді Z.FOB = 45° — у . Маємо:
cos 60° = cosycosx
cos450 = cos(450 -y)cosx s. ' ,
Звідси, sin у = cosy, у = 45°. Відповідь: 45°.
Задача 2. Площина квадрата утворює кута з площиною, що проходить через одну з його сторін. Який кут утворює з тією ж площиною
діагональ квадрата?
Розв’язання.
Нехай ABCD — даний квадрат. З точки С опустим перпендикуляр СЕ на дану площину π.
276


XIII. Стереометрія
Оскільки AD A-DC, то за теоремою про три перпендикуляри ADA.DE, а отже, Z.CDE — лінійний кут двогранного кута з ребром AD. Нехай Z.CDE - a, Z.CAE = х.
СЕ = AC sin х, тоді
СЕ α sin α since
98
Muβlθ6iT!(Hi npjLJlli
Відповідь: arcsin
ю вважається, про такі прямі
Традиційно що задачі щ
найважчі. їх, в основному, два типи: задачі на знаходження кутів між мимобіжними прямими та на знаходження відстаней між ними.
Наша порада:
щоб знайти кут між мимобіжними прямими, потрібно за допомогою паралельного переносу розмістити ці
277


101 порада абітурієнту
прямі в одній площині й побудувати «площинний» кут;
щоб знайти відстань між мимобіжними прямими, потрібно знайти деякий відрізок, перпендикулярний цій площині.
Задача 1. У циліндрі твірна дорівнює діаметру основи. Точка А кола верхньої основи сполучена з точкою А і кола нижньої основи, О і О\ — центри основ, кут між відрізками ОА і CM∣ дорівнює 60°. Знайти кут між прямими (901 і AA↑.
Розв’язання.
Через точку Оі у площині нижньої основи проведемо пряму O↑B, паралельну ОА (точка В належить колу нижньої основи). Тоді кут між прямими ОО\ і АА\ дорівнює куту Л] АВ прямокутного трикутника AlAB.
Кут між мимобіжними прямими ОА і О[А\ дорівнює куту між прямими О]В і (91/41, тобто
278


XIIL Стереометрія
Z,BO↑ Л] = 60° . Отже, трикутник O∣ BAl
А В 1 рівносторонній, тоді tgZ∕4∣ А В = —.
Відповідь: arctg—.
2
Задача 2. У прямокутному паралелепіпеді ABCDAxBxCxDx довжина ребра AD дорівнює а, довжина ребра AA↑ дорівнює Ь. Знайти відстань між прямими, яким належать діагональ BD і сторона А В.
Розв’язання.
Проведемо діагональ AxD грані AAxDxD. Доведемо, що відстань між прямими BxD і А В дорівнює відрізку АК, де К належить діагоналі AxD і
AKLAxD.
Доведемо, що AKLAB і АК1. Bx D. Дійсно,
BAl,ADx ,BA1AA1. Отже, відрізок ВА перпен279


101 порада абітурієнту
дикулярний до грані АА} DλD, а тому і відрізку АК. Далі, маємо: AKJ-A1D(3a побудовою) і AKJ.CD, отже АК перпендикулярний площині А}BCD, тобто АКΔ-B↑D . Маємо: AKAiD=AA∣ AD.
√*, αb
α~ + b~ , то АК - . г.
√α2 +ft2
. αb Відповідь: —. .
√77F
Різні пірсуиіди
На уроках у школі, навіть у математичних класах, Ви, здебільшого, зустрічалися з трикутною та чотирикутною пірамідами. Звертаємо Вашу увагу на п-кутні піраміди (п = 5, 6, 8,12,...).
Задача 1. Відношення повної поверхні правильної n-кутної піраміди до площі основи дорівнює і. Знайти кут між бічним ребром і площиною основи.
280


XIII. Стереометрія
Розв’язання.
В п-кутній піраміді позначимо одну з граней SAj А2, О — центр основи, ΛSA2O = а : А}А2=а. Запишемо теорему синусів для трикутника ОА}А2:
а _ OA2 . π π ,
sin— cos—
п 2п
2 sin — 2п
_ . c, . OA2 а
Тоді SA2 = — = .
cosα n ∙ π Л 2 sin — cosα 2/7
Апофема
піраміди (Л):
і • 2 2
α1l-sιn —cos а
N 2/7
„ •
2 sin — cosα
2/7
Бічна поверхня піраміди (5):
281


101 порада абітурієнту
na2
S = -ha =
2
і ♦ 2 2
1 	- sin —cos а 2п
4 	sin — cos а 2п
Площа основи (S'):
2 	. 7l> 7 n
na sm— na cos—
n _ 2n
4 sin —
2n
И „2 . Я
S = — OAy sin — = 2 п o . 2
8 sin —
2n
За умовою = t, або
s'
1 . о 7Γ 2 π
I-sin"—cos α+cos—cosα
2n 2n t
π cos—cosα 2n
Звідси
l-sιn —cos" a =cosα cos— 2n 2n
2 ∙ 2 2 2
cos a sin — + cos a cos —
2n 2n
282


XIII. Стереометрія
tg^α =sι∏" —+ cos —(r-l)^-l = 2п 2п = co√^p-2∕)j
2n' ’
Відповідь: arctg cos—√Z"-2∕ .
∖ 2n J
Задача 2. У деякій неправильній піраміді усі внутрішні двогранні кути при основі дорівнюють а. Площа основи дорівнює S, а периметр основи дорівнює 2р. Знайти об’єм і повну поверхню цієї піраміди.
Розв’язання.
М
Справедливі формули:
V = ∖s∏ ,S = pr,
З
де V — об’єм піраміди, р— півпериметр основи, г — радіус вписаного в основу кола (довести самостійно, що його можна
283


101 порада абітурієнту
вписати!), Н = МО — висота піраміди. Нехай точка Е—середина сторони основи АВ. Тоді
г = —, Н = r tgα .
Р
Отже,
„ і о s і s2
V =^s-tga=-—tgα.
Зр Зр
Далі, використаємо дуже важливу й корисну теорему: якщо деяку плоску фігуру площею S ортогонально спроектувати на площину, яка утворює з нею кут а , то площу S' її проекції можна знайти за формулою
S'=S cos а .
Тоді
ПОВ ~ 1^OCH + ⅞
. 1 S2
Відповідь: tgα
З р
c 2Scos2-
■, $ 2
> н =
cosα cosа
2S cos2 —
2
cos а
284


XIII. Стереометрія
У100
УЇЇіла
Як правило, в школі стереометрія закінчується вивченням тіл
обертанню обертання.
Ми радимо вам «не розслаблятися». Самі по собі циліндр, сфера, конус, зрізаний конус не викликають особливих труднощів, але в комбінаціях з іншими тілами досить громіздкі й складні.
Ми розглянемо задачі середньої складності.
Задача 1. У зрізаний конус вписано кулю. Об’єм цієї кулі складає половину об’єму конуса. Знайти кут нахилу твірної конуса до площини основи. Розв’язання.
Побудуємо осьовий переріз конуса. Нехай точка О — центр вписаного в трапецію ABCD кола. Радіус цього кола позначимо через r1, а радіуси основ конуса—через R і г.
285


101 порада абітурієнту
З 	умови задачі маємо, що —πh(R1 + r1 + Rr) = ~πr∖, Де h — висота конуса. Оскільки h = 2rλ, то
Далі R = r1ctg
В результаті одержимо рівняння:
2 /_А ') Z-A Z.A Z.A .
ctg — + tg"- + ctg-tg—— = 4,
2 2 2 2
звідки
2 ЛА 3±√5
tg 2 " 2
. ЛА о Оскільки <45 , то
2
2ZA 3-√5 . yλ o
tg —- = —-—, і тоді tgZ/4 = 2 .
Відповідь: arctg 2.
286


ХШ. Стереометрія
Задача 2. Навколо сфери описана правильна трикутна призма, а навколо неї описана сфера. Знайти відношення площ поверхонь цих сфер.
Розв’язання.
Площі сферичних поверхонь відносяться, як квадрати їх радіусів:
S1ιS2 =R{i⅛, де S∣ — площа поверхні сфери, вписаної в призму, S2 — описаної, R∖ і R2 — їхні радіуси.
Нехай а — сторона основи призми. Тоді
Звідси,
а2 5а2
12 : 12
Отже,
S1ιS2 =1:5.
Відповідь: 1:5.
287


101 порада абітурієнту
Jftς oφoρjujιwβamu яіенаційну роботу
Розбірливо
Не сердіть перевіряючого
Нехай Ваша ручка пише добре
2 	Майте «у запасі» одну, дві, три ... ручки !
Не заіржавіють ...
288


Сто перша порада
З 	Малюнки можна робити чорнилом, але правильно - • ! И ЧІТКО •
4 	Краще розв’язати задачу правильно, хоча й нераціонально, ніж неправильно, але раціонально.
А ще краще — правильно й раціонально!
5 	При застосуванні формул, ■+■
не передбачених програмою, вимагається їхнє доведення. 11
19-4-636
289


101 порада абітурієнту
6 	Не вживайте слова:
«Легко бачити»,
«Очевидно, що ... » — f
краще доведіть •
7 	При посиланні на теорему вимагається її формулювання.
8 	Вмійте використовувати абзаци, формули винесіть !
на окремий рядок;
290


Сто перша порада
9
Після розв’язання задачі пишіть слово «Відповідь» і результат розв’язання.
10
Намагайтеся не перекреслювати написане, тим паче, не витирати гумкою.
⅛aτχae∕ιu) ycniχy!
19*
291


СТРУКТУРА книги
Передмова З
І. Числа 5
П. Алгебраїчні перетворення 16
III. Рівняння 53
IV. Нерівності 76
V. Системи рівнянь 93
VI. Прогресії 104
VIL Логарифми.
Логарифмічні рівняння та нерівності 109
292


VIII. Формули тригонометрії.
Тригонометричні тотожності та перетворення 132
IX. Тригонометричні рівняння 172
X. Тригонометричні нерівності 192
XI. Елементи аналізу 205
XII. Планіметрія 218
ХШ. Стереометрія 263
Сто перша порада 288
293


3I∖ΛIOT
JTeρe∂juoβa З
4ucjιa
ПОРАДА 1 5
ПОРАДА 2. «Не потрап у дроби» 6
ПОРАДА 3. Нескінченний періодичний дріб 7
ПОРАДА 4. Задачі про числа 9
ПОРАДА 5. Задачі на подільність 11
ПОРАДА 6. Абсолютна величина числа 13
Яліебраїчні перствореннл
ПОРАДА 7. Про типи алгебраїчних виразів 16
ПОРАДА 8. Формули скороченого множення 18
ПОРАДА 9. Про пропорції 20
294


ПОРАДА 10. Спрощення раціональних виразів 23
ПОРАДА 11. Умовні тотожності 25
ПОРАДА 12. Корінь и-ого степеня 28
ПОРАДА 13. Знищення ірраціональності в знаменнику (чисельнику) ЗО
ПОРАДА 14. Модуль і корені 34
ПОРАДА 15. Спрощення ірраціональних виразів 37
ПОРАДА 16. Формула «складного радикала» 40
ПОРАДА 17. Тотожні перетворення з кубічними коренями 42
ПОРАДА 18. Від’ємний і дробовий показник 44
ПОРАДА 19. Розкладання на множники 48
ПОРАДА 20. Подільність многочленів.
Теорема Везу 50
TiβκjLKHjL
ПОРАДА 21. Лінійні рівняння. Параметр....53
ПОРАДА 22. Що таке метод інтервалів в
розв’язанні задач з модулями.. 55
295


ПОРАДА 23. Квадратне рівняння.
Формула αx2+Z>x + c = α(x-xl )(x-x2) 58
ПОРАДА 24. Теорема Вієта 61
ПОРАДА 25. Параметр у квадратному рівнянні 66
ПОРАДА 26. Ірраціональні рівняння 68
ПОРАДА 27. ОДЗ ірраціональних рівнянь...70
ПОРАДА 28. Про методи розв’язання ірраціональних рівнянь 72
Нерівності
ПОРАДА 29. Лінійні нерівності.
Модуль. Параметр 76
ПОРАДА ЗО. Квадратні нерівності 79
ПОРАДА 31. Системи нерівностей 82
ПОРАДА 32. Ірраціональні нерівності 84
ПОРАДА 33. Доведення нерівностей 87
ПОРАДА 34. Нерівність Коші 89
Систедш рівнянь
ПОРАДА 35. Системи рівнянь першого степеня. Параметр 93
ПОРАДА 36. Нелінійні системи рівнянь 95
296


ПОРАДА 37. Системи ірраціональних рівнянь 98
ПОРАДА 38. Системи рівнянь з трьома невідомими 100
tJIρoιρecu
ПОРАДА 39. Арифметична та геометрична прогресії 104
floιapuφjιιu. fioιapuφjιti4∏i
рівняння та нерівності
ПОРАДА 40. Логарифми 109
ПОРАДА 41. Показникові рівняння 115
ПОРАДА 42. Логарифмічні рівняння 117
ПОРАДА 43. Показникові та логарифмічні рівняння з «родзинкою» 120
ПОРАДА 44. Параметр у показникових та логарифмічних рівняннях 125
ПОРАДА 45. Показникові та логарифмічні нерівності 128
297


Φoρjuyjιu тригонометрії. Тригонометричні тотожності та перетворенню
ПОРАДА 46. Основна тригонометрична
тотожність 132
ПОРАДА 47. Формули зведення 135
ПОРАДА 48. Формули додавання 138
ПОРАДА 49. Про формулу суми тангенсів двох кутів 139
ПОРАДА 50. Формули подвійного аргументу 141
ПОРАДА 51. Формули половинного аргументу 145
ПОРАДА 52. Формули зниження степеня 148
ПОРАДА 53. «Перетворити на добуток!» 150
ПОРАДА 54. Формули потрійного кута 154
ПОРАДА 55. Порада, якій ціни нема! 156
ПОРАДА 56. Знаходження тригонометричних сум 158
298


ПОРАДА 57. Тригонометричні функції кутів трикутника 160
ПОРАДА 58. Колекція тригонометричних задач з «родзинкою» 163
УІЇриіоноуііетричні piβujLKHji
ПОРАДА 59. Найпростіші тригонометричні рівняння 172
ПОРАДА 60. Основні методи розв’язання тригонометричних рівнянь.... 175
ПОРАДА 61. Однорідні тригонометричні рівняння 177
ПОРАДА 62. Рівняння типу a sin а х±bcosax - с 180
ПОРАДА 63. Рівняння типу α(sin х ± cosx) ± b sin х cosx = с 184
ПОРАДА 64. Системи тригонометричних рівнянь 186
ПОРАДА 65. Параметр у тригонометричних рівняннях 189
299


ТЙригоноуиетричні нерівності
ПОРАДА 66. Найпростіші тригонометричні нерівності 192
ПОРАДА 67. Розв’язання тригонометричних нерівностей 195
ПОРАДА 68. Доведення тригонометричних нерівностей 197
ПОРАДА 69. Параметр у тригонометричних нерівностях 199
ПОРАДА 70. Операції з оберненими тригоно¬
метричними функціями 201
cEjιejweHmu ана/іізу
ПОРАДА 71. Техніка диференціювання 205
ПОРАДА 72. Критичні точки функції 210
ПОРАДА 73. Монотонність і екстремуми 213
ПОРАДА 74. Похідна і дотична 215
cJTлані/иетрія
ПОРАДА 75. Десять активних теорем планіметрії 219
300


ПОРАДА 76. Основні формули планіметрії 220
ПОРАДА 77. Чудові точки трикутника 222
ПОРАДА 78. Задачі-теореми 225
ПОРАДА 79. Спочатку—легкі задачі .......228
ПОРАДА 80. Анатомія рівностороннього трикутника 230
ПОРАДА 81. «Очевидна» подібність 233
ПОРАДА 82. «Прихована» подібність 235
ПОРАДА 83. Що таке точка W і «трилисник» 237
ПОРАДА 84. Метод допоміжного елемента. Допоміжний елемент— відрізок 240
ПОРАДА 85. Метод допоміжного елемента. Допоміжний елемент— площа 243
ПОРАДА 86. Метод допоміжного елемента. Допоміжний елемент— кут 246
ПОРАДА 87. Метод допоміжного елемента. Допоміжний елемент— периметр або об’єм 248
ПОРАДА 88. Доведення формул площ 252
301


ПОРАДА 89. Застосування формул площ 254
ПОРАДА 90. Знаходження площ фігур 255
ПОРАДА 91. Метод допоміжних точок 258
ПОРАДА 92. Метод допоміжного кола 261
Стереоβtempiя
ПОРАДА 93. Теореми першої необхідності 263
ПОРАДА 94. Формула «трьох косинусів» 267
ПОРАДА 95. Геометрія на кубі 270
ПОРАДА 96. Куди проектується точка S, якщо 273
ПОРАДА 97. Кути в стереометрії 275
ПОРАДА 98. Мимобіжні прямі 277
ПОРАДА 99. Різні піраміди 280
ПОРАДА 100. Тіла обертання 285
Сто перша порада 288
302


Кушнір Ісаак, Фінкельштейн Леонід
К 96 Математика в задачах і прикладах: 101 порада абітурієнту. — Видання третє. — К.: Факт, 2004. — 304 с.: іл.
ISBN 966-7274-91-8
У книзі розглядається систематичний курс шкільної математики в оригінальній формі порад вступникам у вищі навчальні заклади. Кожна з цих порад є рекомендацією до певного класу задач, що пропонуються на конкурсному іспиті. Наводяться приклади з детальними розв’язаннями.
ББК 22.1я729
КУШНІР Ісаак ФІНКЕЛЬШТЕЙН Леонід
МАТЕМАТИКА В ЗАДАЧАХ І ПРИКЛАДАХ 101 ПОРАДА АБІТУРІЄНТУ Видання третє
Київ, «Факт», 2004, 304 с.
Редактор Олена Шарговська
Науковий редактор Наталія Попова Технічний редактор Дмитро Фінкельштейн Художнє оформлення Інокентій Вировий Коректор Олена Дейнеко


ТОВ «Видавництво ,,Факт“» Реєстраційне свідоцтво ДК№1284 від 19.03.2003 04080, Україна, Київ-80, а/с 76 Тел./факс: (044) 417 1366, 416 8754 E-mail: office@fact.kiev.ua Відділ збуту: (044) 463 6887 E-mail: sbyt@fact.kiev.ua www.fact.kiev.ua
Надруковано з готових форм на AT «Віпол», м. Київ, вул. Волинська, 60. Наклад 3 000 прим.
Зам. № 4-636
Здано до виробництва 02.03.2004. Підписано до друку 22.03.2004. Формат 60x84/32. Друк офсетний. Папір офсетний № 1. Гарнітура «Тайме». Ум. друк. арк. 8,87. Обл.-вид. арк. 12,2.


СУЧАСНІ КНИЖКИ СУЧАСНОГО ВИДАВНИЦТВА
ISBN 966-7274-91-8