І.А. Кушнір
ТРИКУТНИК
І ТЕТРАЕДР У ЗАДАЧАХ


І .А. Кушнір
ТРИКУТНИК І ТЕТРАЕДР У ЗАДАЧАХ
Книжка для вчителя
КИЇВ „РАДЯНСЬКА ШКОЛА" 1991


ББК 22.151
К96
Кушнір І. А. Трикутник і тетраедр у задачах: Для ст. шк. віку.— К-: Рад. шк., 1991.— 208 с.— Мова укр.
У книжці понад 400 цікавих (включаючи й класичні) теорем і задач, пов’язаних з визначними точками і лініями в трикутнику і тетраедрі, властивості яких лежать в основі властивостей усіх інших складніших геометричних фігур. Кожний параграф є циклом погоджених між собою задач, розміщених у міру зростання складності. До всіх задач наводяться розв’язання.
Для вчителів загальноосвітних шкіл, студентів фізико-мате- матичних факультетів педвузів, учнів старших класів.
Кушнир И. А. Треугольник и тетраэдр в задачах: Для ст. шк. возраста.— К.: Рад. шк., 1991.— 208 с.— На укр. яз.
В книге помещено более 400 интересных (в том числе и классических) теорем и задач, связанных с замечательными точками и линиями в треугольнике и тетраэдре, свойства которых лежат в основе свойств всех других более сложных геометрических фигур. Каждый параграф представляет собой цикл четко согласованных между собой задач, расположенных в порядке возрастания трудности. Ко всем задачам даны решения.
Для учителей общеобразовательных школ, студентов физико- математических факультетов педвузов, учащихся старших классов.
Рецензенти: Е. Г. Готман, кандидат фізико-математич- них наук (Арзамаський педінститут); В. В. Плахотник, кандидат фізико-математичних наук (Київський університет).
Редактор Л. Л. Розумова
„ 4306020000—230 „17 Q1
К М210(04)—91 61' УІ
ISBN 5-330-02081-6
© І А. Кушнір. 1991


ПЕРЕДМОВА
Рівень математичної культури багато в чому визначається умінням розв’язувати задачі. Мета цієї книжки — допомогти учням, які цікавляться геометричними задачами підвищеної складності. Пошук їх розв’язків розвиває ініціативу, логічне мислення, кмітливість і геометричну уяву.
Задачам про трикутник і тетраедр, як найпростішим геометричним фігурам на площині і в просторі, приділяється багато уваги в цій книжці. Вони розміщені за певними темами залежно від розглядуваних властивостей трикутника і тетраедра. Звертається увага на зв’язок між прийомами розв’язування різних задач. Адже знайдений прийом нерідко перетворюється в більш- менш загальний метод, якщо виявиться застосовним до деякого класу задач. А вміння знаходити загальні прийоми і методи, прагнення поповнити їх арсенал і розкрити можливості застосування також є істотною рисою математичної культури.
Перший розділ книжки присвячений трикутнику і визначним точкам і лініям, пов’язаним з ним.
Після вивчення властивостей трикутника читач перейде до другого розділу — «Тетраедр». У стереометрії тетраедр має таке саме значення, що й трикутник у планіметрії. Тут ми часто будемо користуватись аналогією — умінням виявити подібність між властивостями трикутника і трикутної піраміди. Використання аналогії сприяє оновленню знань, об’єднує, здавалося б, розрізнені факти.
Третій розділ присвячений векторам — необхідному апарату для вивчення геометрії.
Позначення, які використовуються при розв’язуванні задач, наведені у кінці книжки.
Ми не можемо гарантувати, що для розв’язання кожної задачі знайдено найкращий шлях. Будемо щиро раді, якщо читачеві поталанить і він знайде його.
З


ТРИКУТНИК
паралелограми АВСВ\ і АСВС\.
1. 	ВИСОТИ ТРИКУТНИКА.
ОРТОЦЕНТР
Задача 1. Якщо через вершини трикутника ABC провести прямі, паралельні його сторонам, то утворений трикутник А\В\С\ (мал. 1.1) буде гомотетичний трикутнику ABC з центром гомотетії в точці М перетину медіан трикутника ABC і коефіцієнтом k = — 2. Довести це.
Доведення. Розгляне
Оскільки ВС = АВ\ і ВС = АС\, то АВ\ = АС\, а звідси випливає: точка А ділить відрізок В\С\ пополам. Аналогічно точки В і С ділять пополам відповідно відрізки АіСі і ЛіВі. Тому МАї = — 2ЛМ, МВ\ = — 2 ЛІД МС\ == — 2МС і трикутник А і В\Сі буде гомотетичний трикутнику ABC з центром гомотетії в точці М перетину медіан трикутника А$С.
Задача 2. Прямі, що містять висоти трикутника, перетинаються в одній точці. Довести.
Доведення. Прямі, яким належать висоти трикутника ABC, перпендикулярні до сторін трикутника Лі^іСі в їх серединах (мал. 1.1). Отже, вони мають спільну точку — центр кола, описаного навколо трикутника ЛіДСі. Ця точка, спільна для висот трикутника ABC, називається ортоцентром. Позначимо її Н.
4


Пряма Ейлера
Задача 3. Довести, що у будь-якому трикутнику АВС центр О описаного кола, точка М перетину медіан і ортоцентр Н належать одній прямій (пряма Ейлера), причому 2ОМ = МН.
Доведення. Оскільки точка Н є центром кола, описаного навколо трикутника А іВі Сі (мал. 1.1), то точки О і Я відповідно гомотетичні при гомотетії з центром М і коефіцієнтом k = — 2, а отже, твердження доведено.
Задача 4. Довести, що в трикутнику ABC
20М\ = АН. (1.1)
Доведення. Оскільки точка Мі —середина відрізка ВС, а точка А—середина відрізка В\С\ (мал. 1.1), то для розглядуваної гомотетії вони відповідно гомотетичні. Гомотетичні також точки О і Н, тобто відрізки ОМ\ і НА гомотетичні з коефіцієнтом гомотетії k = — 2, що доводить твердження задачі.
Задача 5. Довести, що в трикутнику ABC:
AH2 = 4R2 — а2. (1.2)
Доведення. Справді, оскільки Н — центр кола, описаного навколо трикутника А\В\С\ і HC\ = 2R, то формула (1.2) випливає з розгляду трикутника НАС\ (мал. 1.1).
Наслідок: AH — 2R | cos А |. (1.3)
Точки Ейлера
Точками Ейлера називають точки Е\, Еч> Ез, які поділяють відрізки АН, ВН, СН пополам.
Задача 6. Довести, що відрізки М\Е\, М2Е2, М3Е3 мають спільну середину.
Доведення. Враховуючи співвідношення (1.1), стверджуємо, що чотирикутник ОМ\НЕ\ — паралелограм (мал. 1.2). Аналогічно чотирикутники ОМ2НЕ2 і ОМ^НЕз—також паралелограми. Всі вони мають спільну діагональ ОН, середина якої є спільною серединою розглядуваних відрізків.
5


Задача 7. Довести, що М\Е\ = М%Е2 = МзЕз= R-
Доведення. Справді, оскільки за співвідношенням (1.1)
ОМі = у АН = АЕі, то чотирикутник АОМ\Е\— паралелограм (мал. 1.2). Отже, М\Е\ = ОА = R. Аналогічно доводиться, що ЛЇ2В2 = R і М3Ез = R-
Задача 8. Довести, що для гострокутного трикутника
а-АН + b-BH + c-CH = 4S.
Як зміниться ця формула для тупокутного трикутника?
Доведення. Розглянемо трикутник В\НС\ (мал. 1.1). Його площа дорівнює а-АН\ площі трикутників А\НС\ і В\НА\ дорівнюють відповідно Ь'ВН і с-СН. Враховуючи, що площа трикутника АіВіСі дорівнює 4S, матимемо
а-АН + Ь-ВН + с-СН = 4S.
Для тупокутного трикутника: Ь-ВН-\~С'СН — a-AH=4S (тут і далі вважається, що тупий кут ВАС).
Зазначимо, що задачу можна розв’язати за допомогою формули (1.1).
Задача 9. Довести, що ортоцентр ділить висоти трикутника на частини, добуток яких є постійним для даного трикутника.
Доведення. Доведемо для гострокутного трикутника.
Оскільки Z_H\HB=Z_ACB (мал. 1.1), то НН\ = ВН cos С.
Враховуючи формулу (1.3), маємо:
НН] = 2R cos В cos С і АН-НН\ = 4R2 cos A cos В cos С, що доводить твердження задачі. Для негострокутного трикутника доведення аналогічне. Рекомендується знайти інші способи розв’язування цієї задачі.
Задача 10. Довести, що має місце формула
ОН2 = 9/?2 — (а2 + Ь2 + с2). (1.4)
Доведення. З трикутника ОАН (мал. 1.2) за теоремою косинусів:
ОН2 = О А2 + АН2 — 20 А • AH cos Z_ ОАН.
Розв’яжемо задачу спочатку для випадку, коли А <90°. Враховуючи співвідношення (1.2) і (1.3), а також те, що
Z_OAH = АСАН- АСАО = 90° - С-(90° - В) = В - С, маємо: ОН2 = R2 + 4/?2 — а2 — 2R-2R cos A cos (В — С) = = 5/?2 - а2 - 2R2 (cos (А + В - С) + cos (А - В + С)) =
= 5R2 — a2 —2R2(— cos 2С — cos 2В) = 5/?2 — а2 —
— 2/?2 (2 sin2 С — 1 +2 sin2 В - 1) = 9В — (а2 + б2 + с2).
Якщо А >>90°, то cosAcO, АН = — 2R cos А і cos Z. ОАН = = cos (180° —(В — С)) = — cos (В — С). Отже, знову дістанемо формулу (1.4).
6


Задача 11. У середині гострокутного трикутника ABC дано таку точку Н, що Z_HAC = = АНВС, Z-.HBA = Z.HCA, АНСВ= АНАВ.
Довести, що точка Н — ортоцентр трикутника ABC.
Доведення. Позначимо три пари даних кутів а, р, у (мал. 1.3). Очевидно, що 2(а + + 0 + y)=18O°, a + 0 + V = = 90°. Але АААіВ= ААСАі + -f- /С.СААі = сс -f" Р Д- у = 90°.
Отже, відрізок ААі — висота, аналогічно ВВ] і СС\ — висоти, а отже, Н — ортоцентр.
Задача 12. Довести, що радіус описаного навколо трикутника кола дорівнює радіусу кола, що проходить через дві вершини і ортоцентр цього трикутника.
Доведення. Якщо трикутник ABC гострокутний, то А.ВНС =\80°—Д, а радіус кола, описаного навколо трикут- ника ВНС, дорівнює R. Справді, 2sin(1f6C. _ Л) = -щ- = R-
Для випадку, коли Д>90°, Z.BHC дорівнює (180° — — Д), а радіус кола, описаного навколо трикутника ВИС, дорівнює R.
Задача 13. Точки, які симетричні ортоцентру відносно сторін трикутника, лежать на колі, описаному навколо цього трикутника. Довести.
Доведення. Продовжимо, наприклад, висоту АН\ (мал. 1.4) до перетину з колом в точці N\. Доведемо, що НН\ = = H\N\.
7


Справді, = /-АСВ = Z-BHN\. Тоді трикутник
BHN\ — рівнобедрений, а отже, НН\ = H{N].
Задача 14. Три кола однакового радіуса R перетинаються в спільній точці S і в точках М, /V, Р, причому точка S знаходиться всередині трикутника MNP. Довести, що точки М, N і Р лежать на колі того самого радіуса R.
Доведення. Сполучимо між собою точки М, /V, Р, S (мал. 1.5). Оскільки кола рівні, то дуги, що сполучають точки їх перетину; рівні, а отже, рівні і пари кутів (вони позначені на малюнку). Із задачі 11 випливає, що точка S — ортоцентр трикутника MNP, а із задачі 12 випливає, що коло, описане навколо трикутника MNP, має такий самий радіус, як будь-яке з трьох даних кіл, тобто R.
Задача 15. Якщо пряма Ейлера трикутника ABC (див. задачу 3) паралельна стороні АВ, то tgA-tgB = 3. Довести.
Доведення. Позначимо проекції ортоцентра Н і центра описаного кола О на сторону АВ відповідно Н\ і Л4ь За умовою НН\ = ОМ\ і OM\ = RcosC (формули 1.1 і 1.3). Але НН\ = = 2/? cos A cos В (див. задачу 9), отже, cos С = 2cos A cosB, або — cos (А + В) = 2cos A cos В, тобто sin A sin В — cos A cos В = = 2cosAcosS, звідси tgA-tgB = 3. (Зазначимо, що трикутник ABC — гострокутний, оскільки точки О і Н лежать з одного боку від відрізка АР).
2. 	ОРТОЦЕНТРИЧНИЙ
трикутник
Трикутник Н\Н2Нз, вершинами якого є основи висот даного трикутника ABC, називається орто- центричним (мал. 2.1).
Розглянемо трикутник N\N2N3, утворений відрізками, що сполучають точки перетину продовження висот гострокутного трикутника ABC з описаним навколо нього колом (мал. 2.2). Нехай Н — ортоцентр трикутника ABC. Тоді, = НН2 = H2N2, ННз = NiN2N3 гомотетичні, причому Н- гомотетії k — 2.
згідно з задачею 13 (с. 7), H3N3 і трикутники Н\Н2Нз і - центр гомотетії і коефіцієнт
Задача 1. Якщо радіус кола, описаного навколо трикутника ABC, дорівнює R, то радіус кола, описаного навколо ортоцент-
ричного трикутника, дорівнює R. Довести.
8


Доведення. Це випливає з гомотетичності / трикутників Н\Н2Н3 і NXN2N3.
Задача 2. Висоти гострокутного трикутника ABC є бісектрисами кутів ортоцентричного трикутника. Довести.
Доведення. Справді, ZW2AM = Z_N2BA, Z_AN]Nz = Z_ACN3 (мал.
2.2). Але Z_N2BA = /LACN3. Отже, Z_N2N\A = Z_AN}N3.
Задача 3. Довести, що величини кутів ортоцентричного трикутника дорівнюють
А//2/7|//з= 180° -2А, ЛН\Н2Н3 = 180°-2В,
Z.H}H3H2 = 180°-2С.
Мал. 2.2
Доведення. Справді, наприклад (мал. 2.2):
Z_H2H\H3 = 2 Z_AN\N2 =
= 2(90°-А) = 180° —2А.
Задача 4. Довести, що довжини сторін ортоцентричного трикутника дорівнюють:
Н2Н3= ВС cos А,
НіН3 = AC cos В,
Н\Н2 = ABcos С.
Доведення. Очевидно, що (мал. 2.2)
Н2Н3 = 4 W2W3 =
= 7? sin (180° — 24) = = ВС cos А.
Задача 5. Довести, що кути між сторонами орто¬
центричного трикутника і гострокутного трикутника ABC дорівнюють: Z_AH2H3 = В, Z_H3H\B = A, Z_AH3H2 = С (мал. 2.2).
Доведення. Справді, наприклад, відрізки АС і N2N3 перетинаються в точці Т.
Тоді ААН2Н3= Z_ATN3 = ^(^AN3 + оЛ72С) = 90°-Л+ 4-90° — С= 180° — (180° — В) = В.
9


Задача 6. Довести, що півпериметр рн ортоцентричного три- . ' S кутника дорівнює .
Доведення.
рн = у(Л^^2 + N2N3 + N\N$ = у R (зіп2Д + sin 2В + sin 2С) =
= у R (2sin (4 + В) cos (4 - В) + sin (2(я - (4 + В)))) =
= у R (2sin (4 + В) cos (4 — В) — 2 sin (4 + В) cos (4 + В)) =
= ^R (2sin (4 + В) • (cos(4 - В) - cos (4 + В))) =
- у R (2sin (я — С) • (— 2sin4 ■ sin (— В)) =
= у R • 4sin 4 • sin В • sin С = 2R sin 4 sin В sin С.
Оскільки
S = 2R2 sin 4 sin В sin С, to
= 4 • (2-4
Задача 7. Якщо з вершини ортоцентричного трикутника провести перпендикуляри до сторін трикутника ABC, то відрізок, який сполучає основи перпендикулярів, дорівнює півпериметру рн ортоцентричного трикутника. Довести.
Доведення. Нехай відрізок //|F| перпендикулярний до відрізка АС, відрізок H\Fz перпендикулярний до відрізка АВ (мал. 2.3). Навколо чотирикутника H\F\AF2 можна описати коло, діаметр якого дорівнює відрізку АН\. Тоді:
FxF2 = 4Bisin4 = 4- ' (2-2)
К
Порівнюючи вирази (2.1) та (2.2), бачимо, що F\F2 = pH. Задача 8. Якщо через довільну точку сторони трикутника
ABC провести перпендикуляри
до двох інших сторін, то довжина відрізка, що сполучає основи перпендикулярів, буде не меншою за півпериметр рн ортоцентричного трикутника. Довести.
Доведення. Візьмемо, наприклад, на стороні ВС точку F (мал. 2.3) і проведемо перпендикуляри FQ\ і FQ2 до сторін АС і АВ. Тоді QiQ2 = = AF • sin A, sin А — постійна величина, а довжина відрізка
Мал. 2.3
10


AF буде найменшою, якщо відрізок AF перпендикулярний до відрізка ВС. Отже,
Q1 F\F%,
або QiQ2>Ph. (2.3)
Задача 9. Довести, що з усіх трикутників, вписаних у даний гострокутний трикутник, орто- центричний має найменший периметр.
Доведення. Нехай довільний трикутник MFN вписаний в гострокутний трикутник АВС (мал. 2.4). Побудуємо точки, симетричні точці F відносно АС і АВ. Матимемо відповідно точки L та Е. Довжина ламаної LMNE дорівнює периметру 2р трикутника MFN. Q1Q2— середня лінія трикутника LFE, тому Q\Q^ = ЕЕ. Але довжина LE не більша від довжини ламаної LMNE. Отже, довжина відрізка Q1Q2 не більша від півпери- метра р трикутника MFN, тобто
QiQ2<p.
(2.4)
Порівнюючи вирази (2.3) і (2.4), дістаємо
QiQ2<P, або рн^р.
Знак рівності буде тоді і тільки тоді, коли трикутник MFN буде ортоцентричним. Справді, у цьому випадку (мал. 2.4) Z_FNB=C (задача 5, с. 9), AMNF = 180° — 2С (задача З, с. 9), отже Z.MNE — 180° — 2С + 2С= 180°, тобто MNE — пряма лінія. Аналогічно доводимо, що Z-LMN = 180°, а це означає, що ламана LMNE збігається з відрізком LE.
Задача 10. Довести, що відрізок ОА перпендикулярний до відрізка Н2Н3 (мал. 2.2).
Доведення. Справді, дуга AN2 дорівнює дузі АМз (мал. 2.2), а отже, радіус О А буде перпендикулярним до хорди Л^Мз, тобто й до відрізка Н2Н3.
Задача 11.
У трикутниках ABC і //1//2//3 відповідно р і рн—півпери- метри, R — радіус описаного навколо трикутника ABC кола, г — радіус вписаного в трикутник ABC кола. Довести, що
Р ~~ R • Доведення.
S = R-pH, S = г-р.
Отже, R • рн = г • р, або — = .
р к


Задача 12. (І^рло дев’яти точок). Довести, що середини Мі, Мг, Мз сторін трикутника ABC, основи висот Н\, Н2, Нз, а також точки Е], Е2, Ез— середини відрізків АН, ВН, СН—належать одному колу, яке називають колом дев'яти точок.
Доведення. Розглянемо гомотетію з центром в ортоцентрі Н трикутника ABC і коефіцієнтом k = у (мал. 2.2). Нехай со — коло, описане навколо трикутника Н\Н2Нз, wi — коло, описане навколо трикутника ABC. Е і О — центри цих кіл. При цій гомотетії коло сої переходить у коло (0, точки А, В і С — в точки £і, Е2, Ез. Оскільки точки А, В і С належать колу сої, то точки £і, £2 і Ез належать колу (о. Враховуючи коефіцієнт гомотетії, робимо висновок, що центр кола co (точка £) належить відрізку ОН, причому ОЕ = ЕН і радіус кола co дорівнює половині
Я
радіуса кола сої, тобто у.
Оскільки Мі£ = £]£ = у (див. задачу 7, с. 6), то колу co належить і середина Мі сторони ВС, а отже, й середини сторін АВ і АС.
Задача 13. Довести, що точка, яка симетрична ортоцентру трикутника ABC відносно середини його сторони, належить описаному навколо цього трикутника колу.
Доведення. При гомотетії з центром у точці Н і коефіцієнтом k = 2 коло дев’яти точок перейде в коло, описане навколо трикутника ABC, а точка Мі, наприклад, в точку, симетричну точці Н. Оскільки точка Мі належить колу дев’яти точок, то твердження задачі доведено.
3. 	МЕДІАНИ ТРИКУТНИКА. ЦЕНТРОЇД
Розглянемо задачі про медіани трикутника та їх точку перетину, яка називається центроїдом. У трикутнику ABC будемо позначати її буквою М.
Задача 1. У трикутнику ABC
tn2a= 2(<>2+4c.1-q2-. (3.1)
Довести.
Доведення. У трикутнику АВС (мал. 3.1) продовжимо медіану АМ\ і відкладемо на ній відрізок M\D = AM\. Тоді чотирикутник ABDC — паралелограм, а отже, 2(Д£2 + ЛС2) = = AD2 + ВС2, або 4/и2 + а2 = 2(/>2 + с2). Звідси дістанемо фор-
12


Мал. 3.1
Мал. 3.2
мулу (3.1). За допомогою векторів ця формула доведена на сторінці 174.
Задача 2. (Теорема Лейбніца). Довести, що алгебраїчні суми квадратів відстаней будь-якої точки X площини від вершини трикутника ABC і від його центроїда М пов’язані співвідношенням:
ХА2 + ХВ2 + ХС2 = AM2 + ВМ2 + CM2 + ЗХМ2. (3.2)
Доведення. Позначимо через Y проекцію точки X на медіану (мал. 3.2). Нехай для визначеності Z.XMA ^.90°.
З трикутників ХАМ і ХММ\\
ХА2 = ХМ2 + AM2 — 2АМ • МУ,
ХМ2 = ХМ2 + ММ2 + 2ММ| ■ MY.
Помножимо другу рівність на 2 і додамо до першої, враховуючи, що 2ММі = AM. Дістанемо:
ХА2 + 2ХМ2 = ЗХМ2 + AM2 + 2ММ2.
Але ХМ\ — медіана трикутника ВХС, а ММ\ — медіана трикутника ВМС. За формулою (3.1).
ХМ2 = 2(ХВ2 + ХС2)-ВС2
ММ2 = 2(М£2 + МС2)-£С2
1 4
Отже, ХА2 + ХВ2 + ХС2 - у ВС2 =
= ЗХМ2 + MA2 + MB2 + МС2 - у ВС2, тобто
ХА2 + ХВ2 + ХС2 = ЗХМ2 + MA2 + MB2 + МС2.
із


Задача 3. Знайти кути трикутника ABC, якщо мл2 + мя2ч-мс2 = з/?2.
Розв’язання. Нехай точка X (формула 3.2) збігається з точкою О — центром кола, описаного навколо трикутника ABC. Тоді ОА2 + ОВ2 + ОС2 = МА2 + МВ2 + МС2 + ^ОМ2 або, враховуючи умову задачі, дістанемо: ОМ = 0. А це можливо тоді і тільки тоді, коли трикутник ABC — рівносторонній, тобто А = = в= С=60°.
Задача 4. Довести, що в трикутнику ABC
т2а 4- ті + т2 = у (а2 + Ь2 + с2').
Доведення. За формулою (3.1):
2 1 2 І 2 а2 б2 с2 а2
та + ть + тс — Н—
Ь2 - с2 і а2 Ь2 с2 3 , 2 і л 2 і 2\  - + — + — + - = -у- (а2 + Ь2 + с2).
Задача 5. У трикутнику ABC деякі точки М\ і Mq належать відповідно сторонам ВС і АС. Відрізки AM і і ВМ2 перетинаються в точці М, причому кожен з цих відрізків ділиться у відношенні 2:1, починаючи від вершини. Довести, що відрізки АМі і ВМ2 — медіани трикутника.
Доведення. Трикутник АВМ і М1М2М — подібні (мал. 3.3):
AM __ ВМ _ о ммі — ММ2 ~
Тому МіМ2 = АВ і відрізок М1М2 паралельний відрізку АВ.
З подібності трикутників М2М1С та ABC випливає, що точки Мі й М2 — середини сторін ВС і АС. Отже, АМ\ та ВМ2 — медіани.
Задача 6. Висота і медіана трикутника, які виходять з однієї вершини і розміщені всередині його, утворюють із сторонами трикутника, які виходять з тієї самої вершини, рівні кути. Довести, що цей трикутник прямокутний або рівнобед- рений.
Доведення. Опишемо навколо трикутника ABC коло і продовжимо медіану АМ\ до перетину з колом в точці D (мал. 3.4). Оскільки Z_ACH\ = Z.ADB, то два кути трикутника АН\С дорівнюють двом кутам трикутника ADB, а отже, Z.ABD = = Z_AH\C = 90°. Таким чином, AD — діаметр і ділить хорду ВС в точці М\ пополам. А це можливо тоді й тільки тоді, коли діаметр перпендикулярний до хорди або хорда належить діаметру. Це означає, що трикутник ABC рівнобедрений чи прямокутний.
14


Мал. 3.3 Мал. 3.4
_ _ _ „ ab -4- be -4- ас ,
Задача 7. Довести, що R = 6(/ + , де /, т, п — від¬
стані від центроїда відповідно до сторін трикутника ВС, АС, АВ.
Доведення. Оскільки трикутники АВМ, ВМС, АМС — рівновеликі, то
аі Ьт сп S
Т=~=~ = ~3 ’
Поділимо ці рівності на у abc. Маємо:
І  т п 2S або / + /п + п 2S
Ьс ас ab ЗаЬс ’ ab + ас -J- Ьс ЗаЬс ’
~ abc але *=— •
Отже,
Р ab + ас + Ьс
6 (/ -Т tn 4” я)
Задача 8. У середині трикутника ABC дано деяку точку М — таку, що площі трикутників АМС, ВМС, АМВ рівні між собою. Довести, що М — центроїд трикутника.
Доведення. Нехай площа трикутника ABC дорівнює S. Тоді площі рівновеликих трикутників АВМ, ВМС, АМС дорів- 5
нюють у кожна. Розглянемо трикутники ABC і ВМС (мал. 3.3).
АН\ і МТ\ — висоти цих трикутників. Тоді
МТ} 1 . Л4Л4, 1 AM
~ан7~~ 1 Т4мГ"“Т’ зв,дки “млГ~2-
Аналогічно 2, М\ і Мъ — точки перетину продовжень 15


AM і BM із сторонами ВС і АС. Отже, (див. задачу 5, с. 14). AM і і ВМ2 — медіани; тобто М — центроїд.
Задача 9. Якщо в трикутнику ABC квадрати сторін утворюють арифметичну прогресію, то квадрати відповідних медіан також утворюють арифметичну прогресію. Довести.
Доведення. Нехай у трикутнику ABC АС — середня за величиною сторона. Тоді, за умовою задачі, 262 = а2 + с . Обчислюючи квадрат довжини медіани та, маємо:
2  2(/г + с2) — а2 2Ь2 + 2с'2 — а2 Зс2
т°- 4 4 =— •
Аналогічно ml = ^-b2, т2 = ^-а2. Тоді
2т2ь = у 2Ь2 = у (с2 + а2) = т2а + пї2с.
Задача 10. Знайти залежність між сторонами трикутника, якщо дві його медіани взаємно перпендикулярні.
Розв’язання. Нехай медіана ВМ2 перпендикулярна до медіани СМз- Тоді
4 / 2 і 2\ 2 4 2(а" + с~} — Ь~ 2{а2 Ь2} — с~ 2
--{ті + тії = або — • j = а2,
або Ь2 + с2 = 5а2.
Задача 11. У трикутнику ABC точки М\, М2, С, М належать одному й тому самому колу. Довести, що 2с2 = а2 + Ь2.
Доведення. Нехай N — середина середньої лінії Л4|Л42 (мал. 3.5). Оскільки CN = ^-mc, NM = -^mc. то, враховуючи, кт лх тс с2 пі'2 А 2 2(а2 + Ь2) — с2
що M\N • M2N = — — маємо — = —. Але ml=—-—L-rJ .
2 о 4 3 4
Отже, 2с2 = а2 + Ь2.
Задача 12. Якщо пряма Ей- лера перпендикулярна до медіани, то квадрати сторін і квадрати медіан складають арифметичні прогресії. Довести.
Доведення. Нехай О — центр описаного навколо трикутника ABC кола, R — його радіус. Нехай пряма Ейлера перпендикулярна до медіани АМ]. З прямокутного трикутника ОАМ (мал. 3.6) ОА2 = = ОМ2 + AM2. Враховуючи, що ОА = У?, і формулу (1.4), дістанемо:
іь


ОМ = ОН - 4л/9/?2 - (°2 + + с2) •' о о у
Тоді
г>2 __ D2 а2 + b2 + С2 . 2 (Z?2 + с2) - а2
К — К 9 + 9
Звідси
2а2 = Ь2 + с2.
За задачею 9, 2т2 = т2 + т2.
Задача 13. У коло вписаний трикутник ABC. Медіана СМз перетинає коло вдруге в точці D. Довести, що АС2 + ВС2 = = 2СМ3 ■ CD.
Доведення. Оскільки CD = СМз + M3D (мал. 3.7), то 2СМз • CD = 2тс (пгс + M3D) = 2т2 + 2пгс ■ M3D.
Але
2Мз£> • тс = 2АМ3 • М3В = ±-с2.
Отже,
2СМ3-CD = 2m? + у с2 = б2 + а2 - у с2 + у с2 = ft2 + а2.
Задача 14. Якщо на медіані СМз існує така точка N, що М42 + Л/В2 = 2Л/С2, то відрізок ON перпендикулярний до відрізка СМз- Довести.
Доведення. Із трикутника ANB (мал. 3.7) дістанемо: NMl= 20^ + ^2)--^2. .
Враховуючи умову, маємо:
NM23 = NC2 - .
2 0-172
17


З 	прямокутного трикутника ОМзВ:
-^-= М3В2 = R2 - ОМІ.
Отже, ЛШз = AfC2 4- ОМ2 — R2- Позначимо Z.0NM3 = Ф- Тоді
/?2 = CN2 + NO2 + 2CN ■ ЛЮ-созф. (1)
і
ОМІ = NO2 + NM2 - 2NO • NM3 • cos ф =
= NO2 + NC2 + ОМІ — R2 — 2NO • NM3 • cos ф.
Звідси
/?2 = NO2 + NC2 - 2NO • NM3 • cos ф. (2)
Порівнюючи (1) і (2), дістанемо:
NO(CN+ NM3) cos ф = 0.
Отже, ф=90°.
Задача 15. Нехай при продовженні медіан АМ\, ВМ2, СМз до перетину з колом, описаним навколо трикутника ABC, дістанемо точки М', М", М'".
п AM . ВМ . CM о
Довести, ЩО + .7777/ + w = 3.
ММ 1 ММ 1 мм
Доведення. Виразимо відношення через сторони трикутника (мал. 3.6). Маємо:
АМ = 4~та, ММ' = 4-та + МіМ'.
О о
Враховуючи, що Л4|ЛГ • АМі = СМі • М\В, маємо:
М\М' = -^—. 4та
Отже, ММ' = -^-та + -г~ та
AM
2та 8т,а — а2 + 2Ь2 + 2с2
ММ' о/ 1 _ і а2 \ 4/Па + За2 а2 + + с2
Л~^та + 4mfl )
Аналогічно
ВМ _ — б2 + 2а2 + 2с2 ММ" а2 + Ь2 + с2 ’
СМ — с2 + 2а2 + 2Ь2
ММ'" а2 + Ь2 + с2
Отже,
AM 1 ВМ ' CM _ „ ММ' ММ" ' ММ"' 6'
18


Задача 16. Обчислити кути трикутника ABC, якщо трикутник АММї — рівносторонній (мал. 3.8).
Роз в’ язання. Оскільки дм2= М2М = у, то
ВЛ12 = у6, AMt = -^b.
Тому
Звідси
9Ь2 = 2а2 + 2с2 — Ь2, 9Ь2 = 8Ь2 + 8с2 - 4а2, або 562 = а2 + с2, Ь2 = 8с2 — 4а2.
Тоді
1а2 = 13с2, 762 = 4бЛ 4а2 = 1362.
Ь2 + с2 - а2
cos А =
2Ьс
2с
±С2 + ^-
2 • с
Аналогічно
D а2 + с2 — Ь2
COS В = 5
2ас
8 _ Ь2 + а2 - с‘
COS С = 5-7
/пі 2аЬ
5
2д/ЇЗ
Задача 17. У трикутнику ABC проведені медіани і в трикутники АМ2М, СМ2М, СМ\М, ВМзМ, ВМ\М, АМзМ вписані кола. Довести, що коли три з них рівні між собою, то всі шість рівні.
Доведення. Розглянемо, наприклад, рівні кола радіуса г, вписані в трикутники ВМ$М, ВМ\М і СМ\М (мал. 3.9). Позначимо їхні центри Оі, О2, Оз, точки дотику кіл з центрами Оі і О2 до сторін АВ і ВС, відповідно Со, Ао.
Оскільки трикутники ВМ\М і СМ\М рівновеликі, то
+ у СВ) =
= г(С7И+ МіМ + у СВ),
звідси ВМ = CM і, отже, СМз =
= ВМ2.
Звідси трикутник ABC — рівнобедрений, тобто АВ = АС. Із рівновеликості трикутників ВМ\М і ВМзМ маємо:
Гр2 = Грз (р2 І Рз — ПІВПЄРИ-
метри цих трикутників),
або
г(ВМ + АоМі) =
= r(BM + С0М3).
19


Звідси ЛоМ| = СоЛїз- Тоді трикутник О2А0М[ дорівнює трикутнику 0\СоМз і Z-BM3M = Але Z_BM\M = 90°. Отже,
медіана СМз є висотою, тобто ВС = АС. Таким чином, трикутник ABC — рівносторонній, тобто всі шість кіл рівні між собою.
Інші випадки взаємного розміщення даних рівних кіл вимагають додаткового розгляду.
Задача 18. Довести, -що у трикутнику ABC
ctg Z~CM3B = y(ctg A — ctg В). (3.2)
Доведення. Позначимо ЛСЛ43В = ф. Нехай В>Л (мал. 3.10). Тоді М3Н3 = СН3 ctg <р, АН3 = СН3 ctgA ВН3 = = С//з ctg В.
Оскільки АМ3 = М3В, то АН3 — ВН3 = (ЛЛ43 + М3Н3) — (Л43В — - М3Н3) = 2М3Н3.
СН3 ctg А — СН3 ctg В = 2СН3 ctg <р, або
ctg <Р = у (ct6 А ~ ctg
або
ctg Z.СМ3В = у (ctg А — ctg В).
Задача 19. Довести, що в трикутнику ABC
З п2 І А- і <>2 ctgZ.BAMi + ctgZCBM2 + ctgZACM3 = ^- • .
Доведення. Можна показати (за допомогою теореми косинусів), що а2 = b2 + с2 — 4Sctg Z.BAC.
Тоді ВМ2 = с2 + AM2 — 4S| ctg Z_BAM\ (Si— площа трикутника AMB).
CM2 = a2 + BM2 - 4S2 ctg Z CBM2;
AM2 = b2 + CM2 - 4S3 ctg AACM3,
(S2— площа трикутника ВМС, S3 — площа трикутника АМС). Додаючи ці рівності і враховуючи, що площа кожного три-
1 с
кутника дорівнює nrS, маємо:
О
4 	• 4-3 (ctg Z_BAM\ + ctg АСВМ2 + ctg ААСМ3) = а2 + Ь2 + с2. О
Отже,
З я2 4- h2 -4- с2 ctgZBЛЛ4l+ctgACBЛl2 + ctgZДCЛ1з = 4~> "s ' •
Задача 20. У трикутнику ABC 3tgA + ctgB = 0. Довести, що тс = R.
Доведення. Перетворимо рівність, задану в умові, так:
З 	sin А . cos В Q
cos А ' sin В ’
20


3 sin A sin В + cos В cos А = О,
2 sin A • sin В + cos (Д — B) = 0, cos (Л — B) — cos (Д + B) + cos (Д — B) = 0. Отже,
2 cos (A — B) — cos (A -f- B) = 0. (1)
Далі маємо:
СЛ4з = -^- + 4 T= sin2y4 + 4 sin2# — 2 sin2C) =
d2
= y(2 — 2 cos 2Д + 2 — 2 cos 2B — 1 + cos(24 + 2B)) =
D2
= — 2 (cos 2A + cos 2B) + 2 cos2(4 + 5)) =
= 4~(2 — 2 cos (4 + B) (2 cos (4 — B) — cos (4 + B))).
Скористаємося співвідношенням (1). Дістанемо, що СМ3= R. Задача 21. Коло дотикається до двох сторін трикутника і двох його медіан. Довести, що цей трикутник рівнобедрений.
Доведення. У трикутнику ABC медіани АМі і ВМ2 перетинаються в точці М (мал. 3.11). Оскільки чотирикутник ММ\СМ2 описаний навколо кола, то ma t b гпь ! а ~ + — ' Т ’
або
та + у Ь = Шь + у а. (1)
Розглянемо трикутники АМ\С і ВМ2С. Вони рівновеликі, і коло, вписане в кожний із них, одне й те саме. Отже, рівні між собою й периметри цих трикутників. (
’ 4“ “2" 4“ А~. ~2~ 4“
21


або
, b .а
та-\-^= ть + у •
(2)
Віднімаючи рівності (1) і (2), дістаємо: а = Ь.
Задача 22. У площині трикутника знайти точку, сума квадратів відстаней якої від вершин трикутника має найменше значення.
Р оз в’ язання. Доведемо, що шукана точка — центроїд М трикутника ABC. Згідно з теоремою Лейбніца (див. задачу 2, с. 13) маємо:
ХА2 + ХВ2 + ХС2 = AM2 + ВМ2 + CM2 + ЗАМ2 =
= ^Ат2а + ml + ml) + ЗХМ2 = ±-(а2 + Ь2 + с2) + ЗХМ2.
У о
Вираз ХА2 + ХВ2 + ХС2 буде найменшим, якщо ХМ2 = 0, тобто якщо точки X і М збігаються. Це найменше значення дорівнює у (а2 + Ь2 + с2).
4. 	БІСЕКТРИСИ ТРИКУТНИКА. ІНЦЕНТР
Задача 1. Довести формули:
'“=H7C0ST (4Л)
12 = Ьс-ЬуС\ (4.2) (6і = CLi, Сі — BL\, Li — точка перетину бісектриси кута ВАС зі стороною ВС).
а — ь _|_ с (,‘*••>7
Доведення. Доведемо формулу (4.1).
Нехай Si і S2 — площі трикутників ABLi і ACLt (мал. 4.1). Тоді:
S 	= -^-bc sin A, Si = у-с • ZaSin-y , Sa = -j-bla sin -у .
Але S = S, 4- Sa, звідси
у be sin A = у cla sin у + у Ыа sin -у .
be sin A = la sin -y-(6 + c),
22


звідки
Доведемо формулу (4-2).
Перший спосіб. За теоремою косинусів (мал. 4.1)
6 	I = b2 + la — 2bla COS
c2 = c2 + la — 2cla COS ,
ЗВІДКИ
b2 + l2a — b2\ c2 + la — C?
2b ~~ 2c ’ або
ll(b — c) = be (b ~ c) — (cb2 — c2b).
Враховуючи властивість бісектриси внутрішнього кута трикутника, маємо у = або Ьс\ = Ь\С. Звідки cb2 — c2b = c\b\b — С\Ь\С = — с).
Отже, I2 (b — с) = be (b — с) — СіЬ] (Ь — с).
Нехай b У= с, тоді І2 = Ьс — Ь\С\. При b = с формула очевидна.
Другий спосіб. Опишемо навколо трикутника ABC коло і продовжимо бісектрису ALi до перетину з цим колом у точці W (мал. 4.2). З подібності трикутників AWB і ACL} (2_CAL[ = = Z_WAB, ААСВ= AAWB) маємо:
AW __ AB AC ~ АЦ *
Позначимо L\W = t. Тоді — j-- = , або I2 + la • t = be.
О la
Враховуючи, що la* і = b\C], дістанемо ll=bc — b\C\.
23


Доведемо формулу (4.3). Враховуючи, що ВЬ\ =
CL\ = с і застосовуючи формулу (4.2), маємо: звідки
,2 Ьс (а + Ь + с) (2р — 2а)
Іа~ (Г+7)5 ’
або (
. 2-д/ Ьср (р — а) '
la~ Ь + с
Задача 2. Довести, що в трикутнику ABC
ZB/C = 90°+4- (4-4)
Доведення. Справді,
ЛВІС= 180°-у(В + С)= 180°-4(180°-4) = 90°+ 4-
Задача 3. Довести, що якщо в трикутнику ABC Іа = Іь, то а = Ь.
Доведення. Враховуючи формулу (4.1), маємо:
A R
2 cos -у 2 cos J, ± = ± - ± ‘ b ' с а ' с
Припустимо, що а>Ь, або А > В. Тоді 1 1 . 1 - 1 1 , 1
— <ґ — і — -І- — — -4- —
a b b ' с а ' с '
Отже, cos -у > cos , або А < В, що суперечить припущенню. Аналогічно доводиться, що а не може бути меншим
за Ь. Залишається єдине: а=Ь.
Задача 4. У трикутнику ABC кут А дорівнює 60°. Довести, що точки В, С, Н, І належать одному колу.
Доведення. 1. Кути В і С—гострі. Оскільки Z_BIC = А
= 90° +“2“, a Z-BHC = 180° — А, то у даному випадку ЛВ/С = 90° + 30°= 120°, АВНС= 180°-60°= 120°, а це означає, що точки В, С, /, Н належать одному колу, оскільки відрізок ВС з точок І і Н видно під кутом 120°.
2. Один із кутів В і С — тупий, наприклад, В. Тоді Z.BIC + + /СВНС= 120° 4-60°= 180°. Тобто навколо чотирикутника СІВН можна описати коло, що доводить твердження задачі.
Задача 5. У трикутнику ABC В = 50°, С = 70°. Знайти кути трикутника АІН.
24


Мал. 4.3
Мал. 4.4
Розв’язання. Нескладно показати, що кут між відрізками АН і АІ дорівнює у |В — С |. Для трикутника 1НА (мал. 4.3) Z_IAH= 10°. Оскільки кут А = 60°, то точки С, Н, І, В належать одному колу (задача 4). Крім того, Z_AIH=Z_AIC — — АНІС. Але ZA/C = 90° +-^-= 90° + 25° = 115°, АНІС = = АНВС = <Ж° — С = 20°, тобто ААІН = 115° — 20° = 95° і, нарешті, А АНІ = 180° — 105° = 75°.
Задача 6. Один із кутів трикутника ABC дорівнює 60° (мал. 4.4). Довести, що ОІ=ІН.
Доведення. Нехай, наприклад, А = 60°. Тоді АН=Я (формула 1.3) і трикутник ОАІ дорівнює трикутнику НАІ (доведіть самостійно, що Z.OAI = Z-HAI). Отже, ОІ = ІН.
Задача 7. Довести, що кут <р між медіаною АМ\ і бісектрисою ЛЛ1 трикутника ABC обчислюється за формулою
> , 2 А А I# б"І
tg <Р = tg2 -у tg 2 .
Доведення. Припустимо, що В> С. У трикутнику АМіВ (мал. 4.4) Z_M\AB = — + ер. Згідно з теоремою синусів
МіВ AM,
■ / А . \ sin В s п \“2"
д
У трикутнику АМіС /_М\АС = -^ ф.
За теоремою синусів
М,С __ АМі (А \ sin С s,nkT-
25


Поділивши другу рівність на першу, маємо:
sin (4 + ф) = sin В
sin (4—ф) sin с
звідки
sin tg (pcos-^-= k (sin -у — cos 4-tg ф),
Далі
+ ~ і A k — 1 j A sin В — sin С
Xg Ф — 2 ’ k + 1 “ Xg Т ’ sTn В + sin С ~~
Л х л „„4 5inia=s
6 2 ' ,;„Д±С„,Я-С-,г 2 ' С„Л • тВ-С ~ £ £ £ Z,
= t^4-.tg^L.
Отже, , 1 2 А , ]В — С|
tg Ф = tg і”’ tg —2~ .
Задача 8. Довести, що в трикутнику АВС
АІ ь + с
Щ ~ ~ •
Доведення. Позначимо BL\ = х. Тоді CL\ = a — x та
x с ac
— -Г- , ЗВІДКИ X = -г-. .
a — x b b + c
' . Al AB Al c K
Оскільки -г;-- — st— > то -ГГ- = — , або 1 L\ dL\ I L\ X
Al b A- c
IL\ a
Задача 9. Бісектриси трикутника ABC діляться інцентром в одному й тому самому відношенні, починаючи від вершини. Довести, що трикутник ABC— рівносторонній.
Доведення. За умовою цієї задачі і, враховуючи результат задачі 8, маємо:
~І- ~Н /ґ с2 її. 2 і
= —-г— , або Іг + Ьс = а2 + а Ь 11
Далі
а с а А~ b »2і 2і
—7— = , або bz + ab = с2
Ьс 1 1
26


Віднімаючи рівняння, які дістали, маємо:
b (с — а) + {с — а) (а + с) = 0, звідки с = а.
Аналогічно доводиться, що а = Ь. Отже, трикутник ABC — рівносторонній.
Точки (і= 1; 2; 3)
Позначимо точки перетину продовження бісектрис Za, lb, ІС внутрішніх кутів трикутника з описаним колом W\, №2, №з (мал. 4.5).
Зазначимо, що діаметр цьоМал. 4.5
го кола, якому належить ,одна
з точок Wi (і = 1; 2; 3), належить осі симетрії відповідної сторони трикутника.
Задача 10.
Довести, що
Wil= W\B = WiC.
(4.5)
Доведення.
AICWt = ±-C +/LBCWi = ±-(С + А} (мал. 4.5). ♦
Але AWtIC = Z11CA + ZCA/ = y(C +A), отже, AICWi = AWtIC, тоді CWi = IWi. Але CW} = WtB, а тому Wil = WiB = WtC.
Задача 11. Довести, що у будь-якому нерівнобедреному трикутнику бісектриса лежить між медіаною і висотою, проведеними з тієї самої вершини.
Доведення. Розглянемо медіану АМі, бісектрису ALi і висоту АН\ (мал. 4.5). Оскільки точка W\ є серединою дуги BW\C, то проекцією точки І^і на сторону ВС є точка Л4|. Таким чином, якщо проектувати відрізок AW\ на відрізок ВС, то точки М\ і Н\ є проекціями його кінців, а це означає, що точка L\ лежить між точками М\ і Н\.
Задача 12. Бісектриса AL\ трикутника ABC перпендикулярна відрізку ОН\. Довести, що чотирикутник OAH\W\ — ромб.
Доведення. Оскільки відрізки OW\ і АН і паралельні (мал. 4.5), то AOW'A = AW1AH1, а оскільки OW} = ОА, то ЛОАГі = ЛОНМ, тобто AOAWi = Z_W\AH\, а отже, ОА = = АНі = OWi = W^Hi (відрізки ОА, ОВН WiH} на малюнку не показані).
27


Задача 13. Визначити кути трикутника, у якого медіана, бісектриса і висота, проведені з однієї вершини, поділяють кут при цій вершині на чотири рівні частини.
Розв’язання. Опишемо навколо трикутника ABC коло. Продовжимо бісектрису кута ВАС до перетину з колом в точці №| (мал. 4.5). Тоді AW\AH\ = Z_M\W\A. Враховуючи умову, маємо:
Z_M\AW\ = ZMiUM, а отже, AM, = M,W,.
Звідси випливає, що перпендикуляру до відрізка AW, у його середині належить і точка Мі, і точка О. Отже, ABAC = 90°.
Таким чином, ААСВ = AACH, = 22°30', ААВС = ААВН, = = 67°30'.
Задача 14. 1) Довести, що в трикутнику ABC бісектриса кута ВАС є бісектрисою кута ОАН\ 2) Знайти кут ВАС, якщо бісектриса AL (L належить відрізку ОН) кута ВАС перпендикулярна до відрізка ОН', 3) довести, що в цьому випадку довжина відрізка AL бісектриси дорівнює
4-дМ2 + b2 + c2- 5R2.
Розв’язання. 1) Оскільки відрізок OW, паралельний відрізку АН і OW, = ОА, то (мал. 4.5) AOW,A = AOAW, = = AW,АН.
2) Оскільки AL — бісектриса кута ОАН, то ОА = АН або згідно з формулою (1.3), враховуючи, що А < 90°, R = 2R cos А. Звідси cos А = y , А = 60°.
3) Оскільки в трикутнику ОАН відрізок AL ділить відрізок ОН навпіл, то з трикутника OAL, враховуючи формулу (1.4), маємо:
AL2 = ОА2 — OL2 = R2 — (9/?2 - (а2 + Ь2 + с2)) =
_ а2 + Ь2 + с2 - 5R2
4
Задача 15. Довести, що центром кола, описаного навколо трикутника В/С, є точка W,.
Розв’язання. Це випливає із співвідношення (4.5).
, Задача 16. Довести, що коли у трикутнику ABC інцентр / належить прямій Ейлера, то цей трикутник рівнобедрений.
Доведення. Оскільки відрізок ОМ і паралельний відрізку АН (мал. 4.6), то трикутник OIW, подібний трикутнику НІ А. Отже,
01 _ OWx
ІН ~ АН ’
к . 01 ОМз
Аналогічно -ггг = ~^тг
Іп Сп
Отже, АН — СН, а з цього випливає, що ВС = АВ.
28


Мал. 4.7
Задача 17. Бісектриса кута ВАС гострокутного трикут- ника АВС перпендикулярна до прямої Ейлера. Довести, що S = ^la{b + c).
Доведення. Оскільки Z_OW\A = Z_ W\AH = Z_OA W\ і Л// = 2/?созД (за формулою 1.3), то /? = 2/? cos Д A = 60°.
Враховуючи формули (4.1) і S = be sin А, дістанемо la (ft + с) = 4S, або S = у Іа (Ь + С).
Трикутник WiW2W3.
Задача 18. Довести, що інцентр / трикутника ABC є ортоцентром трикутника Wi (мал. 4.7).
Доведення. Позначимо точки перетину відрізків AW\, BW2, CW3 зі сторонами трикутника W\W2W3 як Qi, Q2, Q3. Доведемо, що Z_IQ3W\ = 90°. Справді, CW\ = W\I і Z_CW\W2 = = zLW2W\A. Отже, у рівнобедреному трикутнику CW\I відрізок —бісектриса, а отже, медіана і висота.
Аналогічно доводиться, що відрізки UPjQj і W2Q2 також висоти, тобто точка / — ортоцентр трикутника W\W2W3.
Задача 19. Довести, що кути трикутника Wi W2 W3 дорівнюють (мал. 4.7):
Д W2 W, W3 = 90° - 4; Z №, U72№3 = 90° - -f- і
AWtW'3W'2 = 90°
Доведення. Справді, AW2W[W3=AW2WlA + + Z-AWtW3 = Z. W2BA + AACW3 = 4 + 4 = 90° - 4 • Ана’ логічно знаходимо значення інших кутів.
29


Задача 20. Довести, що трикутник №і1Г2№з— гострокутний.
Вказівка. Це випливає із задачі 19.
Задача 21. Довести, що:
1) трикутник Q1Q2Q3 є ортоцентричним трикутником трикутника Wi №2^з (див. задачу 18);
2) трикутник ABC гомотетичний трикутнику Q1Q2Q3 при гомотетії з центром у точці / і коефіцієнтом k = 2;
3) пряма 01 є прямою Ейлера трикутника Wi №2№з.
Доведення.
1) Оскільки точка І є ортоцентром трикутника W\ їГ2І^з, то твердження задачі доведено.
2) Оскільки точки Qi, Q2, Q3 ділять відрізки Д/, В/, СІ навпіл, то твердження доведено.
3) Оскільки точка / — ортоцентр трикутника и^і1^2їГз і він вписаний в коло з центром О, то пряма 01 — пряма Ейлера цього трикутника.
Задача 22. Довести, що:
1) 	площа Sw трикутника W\ І^г^з дорівнює
sw = R • ± ;
2) якщо S — площа трикутника ABC, то
,$ 2г S„ ~ R '
3) S<SM.
Доведення. 1)3а формулою (2.1) Sw = R • ра,
Де Ра — півпериметр трикутника Q1Q2Q3 (див. задачу 18), який є ортоцентричним трикутником трикутника І^іІГгІГз. Але ра = = у р, а отже, S» = 7? у .
2) Враховуючи, що S == гр та Sw = R , маємо:
З гр 2г Sw R-Z- r
3) Нерівність 3) зводиться до нерівності R 2г (див. с. 32, співвідношення (5.4)).
Задача 23. Довести, що середини відрізків UZjU^2, W2І^з, Wi №3, IWi, IW2, IWz, I A, IB, ІС належать одному й тому самому колу.
Доведення. Із властивостей трикутника UZ| U^2U^3 робимо висновок, що всі дев’ять середин відрізків належать колу дев’яти точок трикутника U^|U^2U^3.
ЗО


5. 	ВПИСАНЕ
Й ОПИСАНЕ КОЛА
Задача 1. У трикутнику ABC АКз = АК2 = р — а, ВКх = ВКз = р-Ь, СК} = = СК2 = р — с.
Довести.
Доведення. Позначимо АКз = х, ВК\ = у, СК\ = = z. Тоді (мал. 5.1)
х = с — у, х = b — z, 2х = b + с — (у + z) = = Ь + с — а = 2р — 2а, х = р — а.
Аналогічно доводиться, що у = р — b, z = р — с.
Задача 2. Довести, що мають місце формули
r = (p-a)tg4-; (5.1)
г = 4/? sin sin sin -у. (5.2)
Доведення. Формулу (5.1) дістаємо, скориставшись задачею 1, розглянувши ДА/Аг- Доведемо формулу (5.2).
S 2R2 sin A sin В sin С 2R2 sin A sin В sin С
Г р R (sin А + sin В + sin С) лп А В С
и V 1 1 7 4R COS -<y COS -у COS -ту
лп . А . В . С = 4R sin — sin sin .
Задача 3. (Формула Ейлера), У трикутнику ABC ОІ2 = R2 — 2Rr.
(5.3)
Довести.
Доведення. Перший спосіб. Нехай W\ — середина дуги ВС (мал. 5.2). Проведемо перпендикуляр ID (точка D належить діаметру W\E кола, описаного навколо трикутника ABC) до W\E.
Із трикутника W\OI маємо: оі2 = owl + /г? -
— 2ОГ| • WjD.
Але Г1П=г+МіГі. Тому О/2=/?2 + /Г? —2/?(r-h + Мі W2,) = R2 - 2Rr +11Г? -
Мал. 5.1
31


Мал. 5.2
Доведемо, що CW'\ = 2R • MiW\. Справді, з прямокутного трикутника W\CE випливає, що CW2 = 2R • M\W\. Враховуючи, що CW\ = IW\ (співвідношення (4.5)), формула Ейлера доведена.
Другий спосіб.
Із трикутника 01В за теоремою косинусів (мал. 5.3)
О І2 = ОВ2 + В І2 — 2ОВ • BI cos ЛОВЕ
Але OB = R, ВІ = —, А.ОВІ = І 4- - (90° - А) |.
В 2
51пт-
О/2 =
.2 2/?r sin (A 4"
~ =
Sinv
ABC
4R sin sin sin -y
. 2 В s,n Т
z 5'п (А + -у-)
= R - 2/?г( 2
= R2 - 2Rr 2
sin 27? sin^
А — С А — С , А + С cos —2 eos —g h cos —у—
sin
cosl+C
= R2 - 2Rr = R2 - 2Rr.
sin 2"
Отже, О/2 = R2 — 2Rr.
Наслідок: R 2r. (5.4)
Задача 4. Довести, що в трикутнику ABC
abc mnl
P r 1
де m, nt I—відповідно відрізки ЛД ВД CI.
32


Доведення. З одного боку,
АІ = ’ ВІ = -Ч- ’ СІ = :
sin -J- sin sin
Al • BI- Cl = -4-'4\ r - — - 4/?r2.
4/? sin sin ”2~ sin -j- r
З іншого боку, abc 4/? • S • r
Отже, твердження задачі доведено.
Задача 5. Довести, що в гострокутному трикутнику ABC
OMj + ОМ2 + ОМз = R + г.
Доведення. Враховуючи формули (1.1) і (1.3), маємо:
ОМ] + ОМ2 + ОМз = R cos А + R cos В + R cos С =
= R (1 + 4 sin 4“sin nrsin =
= R + 4R sin -4-sin -^-sin -£-= R + r. £ £ z
Як зміниться формула для тупокутного трикутника?
Задача 6. Довести, що в трикутнику ABC:
1) S = -д/р(р — а) (р — Ь) (р — с),
2) sin — sin — sm — С у.
Доведення. 1) Доведіть самостійно, що
ctg-p+ ctg— +ctg— = ctgctg — ctg — .
До цього співвідношення застосуємо формулу (5.1). Тоді маємо:
р — а + р — Ь + р — с __ (р — а)(р — Ь)(р — с)  7 = Р ’
або
(Зр — 2р) г2 = (р — а) (р — Ь)(р — с).
Помноживши обидві частини рівності на р, дістанемо:
р2г2 = р (р — а) (р —' Ь) (р —• с).
Враховуючи, що S = гр, маємо:
S2 = р (р — а) (р — Ь) (р — с).
Звідси:
S = д/р(р — а) (р — Ь) (р — с),
З 0-172
33


2) Запишемо нерівність R 2г за допомогою формули (5.2), Дістанемо
R 8 R sin -^-sin -y-sin або
. А . В . С . 1 sin —sin -g—sin -g-.
Задача 7. У прямокутному трикутнику ABC (С = 90°) А/(з = т, ВКз = п. Знайти площу трикутника ABC.
Роз в’ язання. Згідно з задачею 1 (с. 31) АКз = р — а, ВКз = р- ь.
Тоді
S2 = р(р — а) (р — Ь)(р — с) = р-т-п-г, S2 = Smn, звідси S = тп.
Задача 8. Довести, що відрізок А/G (так само, як і відрізки ВКъ і СКз) розбиває трикутник на такі два трикутники, що вписані в них кола дотикаються одне одного.
Доведення. Припустимо, що кола, вписані в трикутники АК\В та Д/(іС, не дотикаються (мал. 5.4). Позначимо точки дотику кожного з кіл зі сторонами цих трикутників Ті, Г2, Тз, Г4, Т5, Тб. Відрізки Т\В = у, Т2А = и, Т3Т4 = /, Т5С = /, Т4К\ = х. Тоді t + х + І + х + у + у + и + І + и + t = 2р, або І + и = = р — (х + у + /). Але х t = Р — с, а у + и = с. Таким чином, І и = р — (р — с У) = с — У = и- Отже, І = 0, і точки Тз і Т4 збігаються.
Задача 9. У прямокутному трикутнику ABC (С = 90°) через вершину С проведено відрізок CD (точка D належить стороні АВ) так, що кола, вписані у трикутники CAD і CBD, рівні між собою. Довести, що CD = ^/s.
Доведення. Позначимо CD = х (мал. 5.5). Очевидно, що
5 = Вдсп + SdCB = Р\Г 1 + р2Г 1 = (рі + р2) гІ,
де р\ і р2 — півпериметри трикутників ACD і DCB\ г\ — радіус рівних кіл, вписаних у ці трикутники.
Отже,
S S
г\ = і = —і— •
Р\ + р2 р + х
Позначимо /і, /2 — інцентри трикутників ADC і CBD. Із подібності трикутників АІВ і І\ІІ2 дістанемо:
г __ с г — Г\ І}І2
Нехай F і N — точки дотику кіл до сторони АВ. Але І\І2 = FN = = FD + DN, де FD = р2 — a, DN = р\ — Ь (згідно з задачею 1, с. 31).
34


Мал. 5.4
Таким чином,
ЛЛ = pi — b р2 — а = р + х — Ь — а.
Отже,
S Р S = р + х- fe-a , *2 = Р (* + а - р) = р (р - с). Р Р + X
За формулою (5.1), г = р — с. Отже,
х2 = pr = S; звідси х = -yfs.
Задача 10. щу і периметр Довести.
Пряма, що проходить через інцентр, поділяє пло- трикутника в одному й тому самому відношенні.
35


Доведення. Нехай пряма, що проходить через інцентр /, перетинає сторони АВ і ВС в точках D і F відповідно (мал. 5.6). Тоді
q с і с і с 4rAD-r + -1-СГ«г
°ОЛСГ °Л0/ І °Л/С I °IFC Z Z Z
$BFD $DIB "Ь $BIF
AD + AC + CF BD + BF
Задача 11. З вершини С прямого кута прямокутного трикутника ABC проведена висота CD. Нехай CD = h\ r, r\, г 2— радіуси кіл, вписаних у трикутники'ABC, CBD, ACD-, R, R\, R2 — радіуси кіл, описаних навколо цих трикутників.
Довести, що:
1) Г1 + ГІ = г2\
2) /?? + /?!= Я2;
4) 	І\І2 = 2г2 (/і, І2 — інцентри трикутників BCD і ACD). Доведення. 1) Трикутники ABC, CBD, ACD — подібні.
Тоді
Г\ Si d S2
~~ ~~~ ’
(Si і S2 — площі трикутників BCD і ACD).
Таким чином,
.2
S, + S2 J
S — ’
Отже,
.2
2) Аналогічно можна показати, що /?2 + Rl = R2- (Можна показати, що /? +/1 =/2, де /і, /2, І—відповідні лінійні елементи трикутників, що розглядаються.)
3) Перший спосіб.
Г| Г2 Г а b с
або
Звідси
^-=h.
с
Другий спосіб. Позначимо BD = с\, AD = С2. З формули (5.1) випливає, що коли АС = 90°, то а + b — с Г = 2 ■
За цією формулою
2
h.
36


a zLI\DB = Z_hDA = 45°, to
4) Оскільки Z_I\Dh = 90°, в трикутнику I\Dh
ml = 2r? + 2ri = 2 (r? + r2) = 2r2 (див. задачу 11.1)).
Задача 12. Трикутник ABC вписаний у коло радіуса R.
Довести, що:
1) fC2 = ab — 4Rr;
2) ID2 = 4/?2 — ab, де D — точка, діаметрально протилежна точці С.
Доведення. 1) 3 трикутника СІК\ (мал. 5.7)
С/2 =
. 2 С ' inz
* о . 2 С . п . а2 -І- Ь2 — с2 2 (р — а)(р —*Ь)
Але 2 sin — = 1 - cos С - 1 = Ть
Звідси знаходимо, що
= ab (р — с)
Р
Оскільки
abc = 4/?S = 4/?pr,
то
СІ2 = ab — 4Rr.
2) За формулою Ейлера, ОІ2 = R2 — 2Rr. Оскільки 01 — медіана /\C1D, то
0/2 = ±(С/2 + О/2)--^ .
Звідси
-2Rr = ^ (ab - 4Rr) +±-ID*- R2.
37


Отже,
ID2 = 4/?2 - ab.
Задача 13. У трикутнику ABC проведені медіани АМ\, ВМ2, СМз. Довести, що коли радіуси кіл, вписаних в трикутники ВСМ2, САМз, АВМі, рівні між собою, то трикутник ABC — рівносторонній.
Доведення. Оскільки у трикутників ABMj, ВСМ2, САМз рівні площі і радіуси вписаних кіл, то рівні й їх периметри, тобто с + a + ~2'+^fe— + тс- Припустимо,
що трикутник ABC не рівносторонній, наприклад, а b с (інші випадки розглядаються аналогічно). Із рівності
■ а - . b .
с + "у + та — а + Т + ҐПь випливає, що
а^Ь С + (ть — та) = 0. (1)
Оскільки, за нашим припущенням, с — найменша сторона, то
Доведемо, що ть — та 0. За допомогою формули (3.1) перетворимо цю нерівність так:
2а2 + 2с2 - Ь2 > 2Ь2 + 2с2 - а2, За2 > 362, а > Z>, що справджується за припущенням а b > с. Отже, сі -f- b . ( \
2 І” (тЬ Ша) 0.
Знак рівності у співвідношенні (1) має місце тільки тоді, коли а = b = с.
Задача 14. Центроїд прямокутного трикутника лежить на колі, вписаному в цей трикутник. Знайти гострі кути цього трикутника.
Розв’язання. У трикутнику ABC (С = 90°), а — менший катет, b — більший катет (мал. 5.8). За умовою r2 = ІМ2, а також
C/-rV2. =
За теоремою косинусів
IM2 = СІ2 + CM2 — 2СІ ■ CM ■ cos гС/СМ,
А/СМ = ~ — А. 4
Отже,
r2= 2r2 + 4-2rV2 -fcos(^--A),
38


або
9 + (—У —
- \ г/ (П
— 6^2 -£-cos(-^-—д) = 0.
Враховуючи, що г = —~с t маемо:
с __ 2
r sin А + cos А — 1 ■
Оскільки -у] 2 cos — д) = = sin А + cos Л, то, позначивши х = sin А + cos Л, рівняння
(1), запишемо так:
Звідси Зх2 + 6х — 13 = 0.
Таким чином,
2
4 4
: = —= 1; cos Л + sin Л = —- 1;
-/з /л -\ 4
COSI Л ) = ——
\ 4 / -^6
А = —— arccos ( —
'4. \ 7б
Отже, В = 4- arccos (—
4 V Тб
1
/*2
Задача 15. Довести, що трикутники і /САгКз гомо-
D
тетичні з коефіцієнтом гомотетії k = — (мал. 5.9).
39


Доведення. Справді, якщо провести в точках UZ,, UZ2, №3 дотичні до кола, описаного навколо трикутника ABC, то дістанемо трикутник А'В'С', гомотетичний трикутнику ABC, а образом трикутника КіКгКз буде трикутник Wi UZ2UZ3. Оскільки коло, описане навколо трикутника ABC, буде вписане в трикутник А'В'С', то коефіцієнт гомотетії k = .
Задача 16. Довести, що пряма, якій належать центр О кола, описаного навколо трикутника ABC, й інцентр /, є прямою Ейлера трикутника КіК2Кз-
Доведення. Справді, пряма 01 є прямою Ейлера трикутника 1^|1^2^3, гомотетичного трикутнику Кі-Кг^Сз» І ЦІЙ прямій належить точка / — образ точки О.
Задача 17. Довести, що площа трикутника КхКчКз (ЗЦ дорів- рг2 НЮЄ .
Доведення. Оскільки трикутник Кі/’СгКз гомотетичний трикутнику з коефіцієнтом гомотетії а 5^,^ =
Задача 18. Довести, що S = 2^/$^ • Sk . Доведення.
о с _ n Р pr2 S2
К -у ,
звідси S = 2 ~y[sw • Sk.
6. 	ЗОВНІВПИСАНІ КОЛА
Коло, дотичне до однієї з сторін трикутника і до продовження двох інших, називається зовнівписаним. Центр зовнівписаного кола, що дотикається, наприклад, до сторони ВС трикутника ABC (/а), знаходиться в точці перетину бісектрис зовнішніх кутів при вершинах В і С або в точці перетину однієї з цих бісектрис і бісектриси внутрішнього кута ВАС. Позначимо радіуси зовнівписаних кіл, які дотикаються до сторін ВС, АС, АВ, відповідно га, гь, гс.
Задача 1. Відстані від точок дотику зовнівписаного кола які належать продовженню двох сторін трикутника ABC до їх спільної вершини дорівнюють півпериметру р трикутника ABC. Довести.
Доведення. Нехай, наприклад, зовнівписане коло з цент40


ром 1а дотикається до продовжень сторін АВ і АС трикутника ABC в точках Т2 і Тз, а до сторони ВС — в точці Т\ (мал. 6.1).
Позначимо С7’і = х, TtB = = у. Маємо:
АТ2=с + у, АТз = ЬА-х, 2р = а-\-Ь + с = х + у + -\-b + c= b-\-x-\-c-\-y =
= АТ2 -І- АТз.
Але АТ2 = АТз, тому 2Л7’2 = = 2р, звідки АТ2 = АТз = р.
Задача 2. Довести формули:
га = —?— ; (6.1)
р — a v 7
д
ra = ptg-r; (6.2)
Га = (Р- b) Ctg 4 • (6.3)
Доведення. Оскільки АТ% = р і = то га =
^4
~ ptg —. Дістанемо формулу (6.2). Застосуємо формулу (5.1).
Маємо:
+ A r S
ґа = Р tg -п- = р = .
м р — а р — а
Формулу (6.1) доведено. Формулу (6.3) можна дістати, розглядаючи трикутник СІаТз.
Задача 3. У трикутнику ABC IWx=WxIa, де Г1—точка перетину бісектриси кута ВАС з описаним навколо трикутника ABC колом. Довести.
Доведення. Оскільки АІаСІ прямий і СГ1 = Wil (див. співвідношення (4.5)), то IaW\ = Wil (мал. 6.2).
Задача 4. (Формула Ейлера для зовнівписаного кола). Довести, що:
0/2 = fl2 + 2R • га.
41


Мал. 6.5
Доведення. Із трикутника OW\la (мал. 6.3), опустивши перпендикуляр IaD на продовження відрізка OW\, маємо:
0/2 = 01Г? + IaW2\ +
+ 2OW7, . DW\.
Враховуючи, що W\Ia = CW\, дістаємо:
CW2} = 2R • M]W\.
Отже, ОІ2 = R2 + ^R ' M}W\ + + 2R-W[D = R2 + 2R(MlW} + + ГіО).= R2 + 2R • MiD.
Оскільки M]D = га, то формула Ейлера для зовнівписаного кола доведена.
Трикутник ІаІЬІс
Задача 5. Довести, що трикутник ABC є ортоцентричним трикутником у трикутнику ІаІЬІо Доведення. Справді, це випливає з того, що бісектриси внутрішніх кутів трикутника перпендикулярні до бісектрис його зовнішніх кутів.
Задача 6. Довести, що
1) В трикутнику ІаІЬІс (МЗЛ.
6.4) кути дорівнюють 90°
90° — 90° -
2) радіус кола, описаного навколо трикутника ІаІь1с, дорівнює 2R\
3) трикутники U/] W2W3 І ІаІЬІс ГОМОТЄТИЧНІ, Й КОефІЦІЄНТ гомотетії дорівнює 2.
Доведення. 1) Z-IcIaIb = = 180°— ЛВІС= 180° —(90° + + = 90° — Інші кути
знаходимо аналогічно; 2) це випливає з того, що радіус кола, описаного навколо ортоцентричного трикутника, для ІаІьіс дорівнює R\ 3) доведення випливає з задачі 3.
42


Задача 7. Довести, що центроїд трикутника ІаІьіс належить прямій 01.
Доведення. Справді, точка О — центр кола дев’яти точок трикутника Іаіьіс, а отже, твердження доведено.
Задача 8. Довести, що точки, симетричні точкам /а, /*, Іс відносно точки О, належать колу з центром у точці / й радіусом 2R.
Доведення. Позначимо центр кола, описаного навколо, трикутника Іаіьіс, через Т (мал. 6.5) і скористаємося властивостями кола дев’яти точок (с. 12).
Точка О є центром кола дев’яти точок у трикутнику ІаІьІс. Отже, ТІа = FD = 2R (F і D — середини відрізків ЛЛ, //а). Побудуємо точку Д, симетричну Іа відносно О. Оскільки ТО = О/, то ТІаІІ'а — паралелограм і ТІа = ІГа = 2R.
Аналогічно TI'b = 2R, Tlfc=2R, а отже, твердження доведено.
Задача 9. Довести, що:
2) Га + Гь + Гс = 4R + г;
3) d2 + d2 + d2b + d2c= \2R2
(d = О/, da = Ola. db = Olb. dc = O/c).
Доведення.
П1 P . 1 p — a \ p — b 1 p — c
— =^— ■ 7T = ^—; — =—Г~(див- (6-4- Додаючи ці рівності, дістанемо:
1 I 1 I 1_ p — a-\-p — b-\-p — c 1
Га ' гГЬ ’ rc S г ■
9Х r _ -S / p{p-b)(p- с) р(р- Ь)(р — с) .
Га - ~ \ ~ S ’
г _ р(р — а)(р — с) . _ р (р — а) (р — 6) .
Гь — s 1 Гс — s ’
S (р — а) (р — 6) (р — с) р (р — с) с .
г = у = S ’ Га + Гь = S ’
г _ г _ с (р — а) (р — &) .
с Г S
г і _ і r г с Цр — Ь) (р — а) + р (р — с)) abc
Г а ~\~ Г ь Г с — Г = £ = —— = 4R.
3) d2 + d2a + d2b + di = R2 - 2Rr + R2 + 2Rra + R2 + 2Rr„+ + R2 + 2Rrc = 4/?2 + 2R (ra + rb + rc) - 2Rr = 4/?2 + 2R (4/? + + r) — 2Rr - - 12R2.
Задача 10. Довести формулу Герона:
S = — а) (р — Ь) (р — с).
Доведення.
Га = (р — С) Ctg г=(р — Ь) tg
43


Отже, rar = (р — Ь) (р — с), або ■ ^-= (р — Ь) (р — с). Звідси
S2 = p(p — а)(р — Ь) (р — с), або S = -y/p(p — а) (р — Ь)(р — с).
Задача 11. Знайти залежність між радіусами га, гь, гс прямокутного трикутника ABC (С = 90°).
Розв’язання. За формулами (6.2) і (6.3)
Га = р — ь, гь = р — а, гс = р.
Звідси а = Гс — rb, b = Гс — Га, с = Га + Гь.
Але с2 = а2 + б2, тому
(Га + ГЬ)2 = (Гс — Гь)2 + (Гс — Га)2, або
Га • ГЬ + ГЬ * Гс 4- Гс • Га = Г2.
Задача 12. Якщо у гострокутному трикутнику АВС АСАВ = = 60°, то точки В, С, Іа, І, Н належать одному колу. Справедлива й обернена теорема. Довести.
Доведення. Позначимо АСІаВ = х, АСІВ = а, АСНВ = = ₽.
Тоді х = 90° - -4-= 60°, а = 90° + -j-= 120°, р = 180° - — 60° = 120°, а це доводить твердження задачі. (У чотирикутниках ВІСІа і ВНСІа сума протилежних кутів дорівнює 180°.)
Задача 13. Довести, що
//2= 4/?(ґа-г).
А Доведення. Оскільки На = 2IW\, a IW\ = 2В sin то формулу, яка доводиться, можна записати так:
. 2 Л Га — Г
s,n4- = ^-- (’)
Доводимо формулу (1)
$ $
S a sin А S 1 sin А ra sin А
2 ар (р — а) р — а р 2 р 2 , А . А А . 2 А = tg —sin —COS sin2 -g-.
Задача 14. Дано трикутник ABC з сторонами а, b і с, в який вписане коло. До нього проведено дотичну, яка перетинає сторони трикутника АВ і АС відповідно у точках Di і Z>2. Знайти периметр і площу трикутника AD[D2, якщо D\D2 = tn.
Розв’язання. Розглянемо трикутник AD\D2 (мал. 6.6). Коло, вписане в трикутник ABC, буде зовнівписане в трикут-
44


нику ЛР|£>2. Позначимо точки дотику вписаного кола до сторін АС і АВ відповідно через /Сг і Кз- Тоді півпериметр трикутника Л£)|£>2 дорівнюватиме відрізку АК2 (або ДКз), тобто р — а (див. с. 44), а периметр цього трикутника дорівнюватиме 2 (р — а) (р — півпериметр трикутника ABC).
Знайдемо площу Sx трикутника AD\D2:
Sx= г (рх — т), ІЛал. 6.6
де рх— півпериметр трикутника AD\D2.
Ми показали, що рх = р — а. Тоді
5
Sx = г (р — а — т), де г = — .
Задача 15. У трикутник ABC вписане коло. Дотичні до цього кола, паралельні сторонам трикутника, відсікають від нього три маленькі трикутники. Дано радіуси кіл гі, г2, гз, вписаних у ці трикутники. Знайти радіус кола, вписаного в трикутник ABC.
Розв’язання. Нехай рі, р2,-рз— півпериметри маленьких трикутників; р — півпериметр трикутника ABC. Тоді
Р\ + Р2 + Рз = Р-
Оскільки трикутники подібні, то
р\ r I Р2 Го рз Гз
~' р ~~ ~ ~ ~ ~
Звідси
Р\ + р2 + Рз п+гг + Гз „ ^1^1,
= , або г = Г\ + г2 + Гз.
Задача 16. Точки дотику зовнівписаного кола до сторони ВС І прямих АВ і АС позначимо Ті, Т2, Тз. Довести, що пряма АТ\ поділяє периметр трикутника ABC пополам (мал. 6.1).
Доведення. Оскільки АС CT \ = b Р — 6 = р, то
пряма АТ\ поділяє периметр пополам.
Задача 17. У трикутнику ABC проведено пряму, що перетинає сторони АС і ВС в точках М і N так, що MN = AM + BN. Довести, що всі такі прямі дотикаються до одного й того самого кола.
Доведення. Розглянемо трикутник MNC (мал. 6.7.), Для якого деяке коло буде зовнівписаним і дотикається до продовжень сторін CM і CN у точках Р і Q.
45


Тоді
СР = CQ = pCMN = 4(CM + MN + CN) = ^(CM + AM + + BN + CN) = -^-(CA + Cfi)’ а це означає, що положення точок Р і Q — сталі.
Задача 18. Через точку D, що міститься всередині кута, провести пряму так, щоб трикутник, який відтинається від кута цією прямою, був:
1) заданого периметру 2р;
2) найменшого периметру.
Розв’язання. 1) На сторонах кута MAN (мал. 6.8) відкладено рівні за довжиною відрізки АТ\ = AT% = р. Побудуємо коло, яке дотикається до сторін кута в точках Т\ і Г2, і через точку D проведемо до нього дотичну. Трикутник ABC — шуканий. Згідно з задачею 1 (с. 40), його периметр дорівнює 2р.
2) Проведемо через точку D (мал. 6.9) коло, яке дотикається до сторін кута, і дотичну до цього кола. Ця дотична перетинає сторони кута в точках В і С. Доведемо, що трикутник ABC — шуканий. Для цього порівняємо його периметр і периметр іншого 46


трикутника, наприклад В\С\А. Проведемо дотичну В2С2, паралельну відрізку В\С\, який проходить через точку D. Тоді периметр трикутника АВ2С2 дорівнює периметру трикутника ABC, а периметр трикутника ЛВіСі більший за периметр трикутника ЛВ2С2.
Задача 19. У кут вписане коло, яке дотикається до сторін кута в точках Аі і Вь Провести до меншої дуги, обмеженої точками дотику, дотичну так, щоб трикутник, який відтинається, мав найбільшу площу. Довести, що довжина цієї дотичної буде найменшою.
Розв’язання.
Нехай бісектриса заданого кута В\ОА] перетинає меншу дугу кола в точці D (мал. 6.10). Проведемо дотичну до кола в цій точці. Вона перетинає сторони кута в точках F й Е. Дістанемо трикутник OFE. Якщо в кожній точці дуги провести дотичні, то дістанемо множину трикутників. Доведемо, що трикутник OFE матиме найбільшу площу. Проведемо дотичну в довільній, відмінній від точки D, точці меншої дуги. Дістанемо трикутник OF\E\. Радіус кола, вписаного в трикутник OFE, буде більший, ніж радіус кола, вписаного в трикутник OF\E\ (оскільки центр Оі першого з цих кіл знаходиться далі від вершини кута, ніж центр О2 другого кола). А оскільки півпериметри цих трикутників рівні між собою (ОАі чи ОВі), то більшою буде площа трикутника OFE.
У трикутнику OF\E\ позначимо: гх — радіус вписаного кола, р — півпериметр, а\ — відрізок дотичної ЛіЕі, Z_A\OB\ = а. Тоді за формулою (5.1): rx ctg у = р — а\.
Якщо величина гх — найбільша, то відрізок а і — найменший. Отже, EF — найменша з дотичних. Друге твердження задачі доведено.
7. 	ВПИСАНЕ ПІВКОЛО
Назвемо півколо, що міститься всередині трикутника, вписаним у трикутник, якщо воно дотичне до двох його сторін, а його діаметр належить третій стороні трикутника.
Нехай Оі — центр півкола, який належить стороні ВС, a F] і F2 — точки дотику півкола до двох інших сторін
трикутника АВС (мал. 7.1). Оскільки кути CF\O\ і В/^Оі— прямі, то кути АСВ і ABC — гострі, а це означає, що три півкола
можна вписати в гострокутний і прямокутний трикутники.
47


Мал. 7.1
Задача 1. Розглянемо трикутник F]H\F2, де H\ — основа висоти Д/Л (мал. 7.1). Довести, що бісектриса кута F\H\F? належить висоті АН\.
Доведення. Оскільки Z_O\F\A = ЛОіЛ2Д = 90°, то точки 01, Гі, А, Л2 належать колу з'діаметром ОіА. А оскільки Z_AH\O\ = 90°, то цьому самому колу належить і точка Н\. тобто трикутник F\H\F2 буде вписаним у нього. Відрізок О\А
належить осі симетрії відрізка F\F2, а точка А — колу, яке розглядається. Отже, відрізку АН\ належить бісектриса трикутника F\H\F2, проведена з точки Н\.
Наслідок 1. Z_F\H\C = Z_F2H\B (I)
Задача 2. Розглянемо трикутники зі спільною стороною F\F2 і з третьою вершиною, яка належить діаметру D\D2 півкола (мал. 7.2). Довести, що серед таких трикутників трикутник H{F\F2 матиме найменший периметр.
Доведення. Для доведення цієї властивості розглянемо лему: «Точка, симетрична одній із двох вершин F\ або F2 трикутника F\H\F2 відносно діаметра Z)|Z)2, міститься з двома іншими вершинами цього трикутника на одній прямій».
Візьмемо, наприклад, точку Fj, симетричну точці F\ відносно діаметра Z)|O2. За властивістю симетрії і наслідком (1), дістанемо
Z_F\H\C + Z_CH\F\ + AF}HiF2 = = Z_CH\F\ + Z_F2H\B + AFlH]F2 = 180°.
Аналогічно доводиться лема для точки F2, симетричної точці F2 відносно діаметра £>|О2. Зауважимо надалі, що відрізки FjF2 і F2F| перетинаються в точці Н\.
Тепер доведемо розглядувану властивість. Нехай Н\ — довільна точка діаметра Z)|Z)2 — така, що Н\ не збігається з точкою Н\. Позначимо периметри трикутників F\H\F2 і F\H\F2 відповідно через Р і Р'. Тоді
Р = F,F2 + F2F', Pf = FxF2 + F\H\ + H\F2.
Отже, P' > P.
Задача 3. Якщо провести дотичні до дуги FiF2 (мал. 7.3) в будь-якій з її точок (крім точок F\ і F2), то дістанемо трикутники, у яких одна вершина спільна (точка А), а дві інші— точки перетину дотичної до дуги F,F2 із сторонами АВ й АС. Довести, що всі ці трикутники мають однаковий периметр 2AF\ =
48


= 2ЛЛ2, а найбільшу площу матиме трикутник, у якого сторона точкою дотику поділяється навпіл.
Доведення. Справді, для будь-яких із цих трикутників, півколо буде частиною зовнівписаного кола (с. 40), а отже, першу частину твердження доведено.
Друге твердження тотожне задачі 18 с. 46. Доведемо його іншим способом.
Позначимо точку перетину дуги F\F2 з бісектрисою кута САВ через F (мал. 7.3). У точці F проведемо дотичну до дуги ЛіЛ'г, яка перетинає сторони АС і АВ відповідно у точках D й Е. Доведемо, що площа трикутника ADE більша, ніж, наприклад, площа трикутника AMN, де MN—відрізок дотичної до дуги FiF2, проведеної через довільну її точку L. Трикутники ADE і AMN, які розглядаються, мають спільну частину — чотирикутник АЕКМ (К — точка перетину відрізків DE і MN). Порівняємо площі трикутників MKD і EAW. Оскільки кути при вершині К рівні між собою, то порівняймо сторони КЕ і МК. NK і KD. Покажемо, що КЕ < МК і КК < KD.
Справді, КЕ= FE- FK= DF - FK= DF - KL = DF\ - KL< < MFx — KL = ML — KL = MK, тобто KE < MK.
Далі NK= NL + LK= NF2 + LK = NF2 + FK< EF2 + KF = = EF + FK= DK, тобто W < KD.
Отже,
Samm <2 $ADE-
Метричні співвідношення
Позначимо радіуси півкіл, вписаних у гострокутний трикутник ABC, через Ra, Rb, Rc (центри цих півкіл належать відповідно сторонам ВС, АС, АВ).
Мають місце формули:
п р р ( 1
~ 2р — а ’ ~ 2р - b ’ Кс~ 2р — с ’ > 4 0-172
49


де 5, р — відповідно площа і півпериметр трикутника АВС\ 1112
^ + ^ + ^7=4 • (2°)
де г — радіус кола; вписаного в трикутник АВС\
р /дох
а (cosec В + cosec С) cosec А ' ' '
де R — радіус кола, описаного навколо трикутника ABC.
Доведемо формулу (1°). Очевидно, що (мал. 7.1)
5 = 5,4О|с + S/iOiB = -~2 Ra • b ~2~ Ra • С = -у Ra (Ь + с), де b = АС, с = АВ.
Звідси
Аналогічно доводяться дві інші рівності. Записуючи їх у вигляді.
1 2р — а 1 2р — b 1 2р — с
"r7 ~ 2S ’ — 2S ’ -R7 ~ 2S
і додаючи почленно, дістанемо формулу (2°).
Доведемо формулу (3°). Очевидно, що ВС = ВО\ СОї, але
ВО\ = , ВС = 2R sin 4, CO, =
sin В sin С
Тоді
2/? sin A = Ra (cosec В + cosec C), або
n =
(cosec В + cosec C) cosec A
Задача 4. Довести, що в трикутнику ABC Ra ’ Rb ■ Rc _ Г lu • Іь' /. — ~4R~ •
Доведення.
Ra = la sin Rb = lb sin ,
= lc Sin
Ra • Rb • Rc = lalblc 5ІП ^“Sin -|“Sin .
Враховуючи формулу (5.2), дістанемо:
<50


RaRbRc = lalblc ‘ , ЗВІДКИ
Ra • Rb • Rc ___ r la - lb ' Ic ~ 4/? ’
Задача 5. Довести, що в трикутнику ABC. .
Доведення:
1 2р — а р а 1 1
“£7— 2S — ТГ 2S ~ r ha ’
Задача 6. Довести, що коли Ra = Rb = Rc, то трикутник ABC — рівносторонній.
Доведення. За умовою
2S 2S _ 2S
2р — а 2р — b 2р — с
Звідси а = b = с.
Задача 7. Довести, що площа трикутника ABC
S = ±-F}F2 . AW, (7.1)
(IFі—точка перетину бісектриси кута САВ з описаним колом, F\, F<2— точки дотику півкола до сторін АС і АВ).
Доведення. З подібності трикутників ЛІГіВ і ACL] (мал. 7.4)
AW\ AC ~
або АВ - АС = AW\ • АЦ. До- множимо обидві частини рівно¬
сті на у sin А:
■у АВ • АС • sin А =
= • al> sin а-
Але ALi • sin А = FiFo, а -у АВ • AC sin А = S. Отже.
S = ^F\F2 • ЛГ|.
АВ
51


Задача 8і. У трикутнику АВС точка W\ сполучена з точками F\ і F2. Відрізки W\F\ і W\F2 перетинають сторону ВС у точках D\ І £>2- ДоВЄСТИ, ЩО ScF.O, + SbD2F2 = 5о,и7,о2.
Доведення. Розглянемо чотирикутник AF\ W\F2 (мал. 7.4). Його площа дорівнює • AW], тобто дорівнює площі три¬
кутника ABC. Оскільки у трикутника ABC і чотирикутника AFi W\F2 спільна частина — п’ятикутник F\AF2D2D\, то твердження задачі доведено.
Задача 9. У трикутник ABC вписано три півкола з центрами Оі, 02, Оз, що дотикаються до його сторін у точках відповідно F\, F2, Qi, Q2, Ті, Т2. Довести, що
FkC • Q2A • TyB __
F2B ■ QiC • T2A ~~ L
Доведення. Із подібності трикутників O\F2B і АН\В,
OiFiC і АН\С
(мал. 7.5)
маємо:
F2B _
Ra .
Ra
НуВ ~
АН{ 1
/7іС —
АНу
Звідси
F.C _
НуС
F2B ~~
НуВ •
Аналогічно
Q2A _
Н2А
ТуВ _
НзВ
QiC
Н2С ’
Т2А
НЛА
Отже,
FyC-Q2A-TyB __ Н{С-Н2А‘НъВ __ ctg C-^ctg A-/ifctgB
F2B-Q\C-T2A ~ НхВ-Н2С-НзА ~~ ha ci%B-hh ctgC-/if ctg 4
Задача 10. Якщо в трикутнику ABC Z_BCA = 90°, то
2) q1. = -gr , d — відстань між/ центрами опи¬
саного кола і вписаного півкола.
Довести.
Доведення. 1) Перша формула випливає із співвідношення (1°), якщо врахувати, що площа S дорівнює добутку катетів а та Ь.
1 Авторська задача, яка була прийнята від СРСР на XVIII Міжнародній математичній олімпіаді. Куба, 1987 р.
52


2) Доведемо другу формулу. Нехай О — середина гіпотенузи АВ. Оз — центр вписаного півкола, F\ і F2— точки дотику півкола до сторін ВС і АС. точки М і W — проекції точок дотику на гіпотенузу АВ (мал. 7.6)'.
Оскільки
ЛМ/7іОз= af2o3n = лв й O3F \ = O3F2. то МО3 = NF2 й ОзМ2 + Оз№ = Rc.
Але O3S = О В -І- ООз R -f- d, О3А = ОА - ОО3 = R - d.
Із прямокутних трикутників BO3F\ і AO3F2 маємо:
ОзМ =
O3N =
O3F2 _ ОзВ оЛ = ОіА
R2
R + d ’
R2
R — d •
Таким чином,
Re 1 Re _ r>2 (/? + d? (/? - d)2 —
б 1 і 1 _ 1
300 (R + d)'2 (/? - d)2 ~R*
Задача 11. У рівнобедрений трикутник ABC (АВ = ДС) вписане півколо з центром Оі, який належить стороні ВС. Це півколо дотикається до бічних сторін трикутника в точках F\ і F2. Дотична до довільної точки дуги F\F2 перетинає сторони АВ і АС в точках N і М. Довести, що добуток МС • NB є сталою величиною для даного трикутника ABC.
Доведення. Нехай від¬
різок MN дотикається до дуги дал 77
F\F2 у точці К (мал. 7.7). У три¬
кутниках М0\С і NOiB позначимо кути, як показано на малюнку 7.7. Тоді Z.CM01 = 90° — у, а оскільки а + 0 + у = 90°, то Z_BO\N = а + 0 = 90° — у. Звідси Z_CM0\ = ^_BO\N. Крім того, Z-ACB = Z..ABC. Отже, ДМОїС сю дОіЛ^В.
З подібності трикутників випливає, що
МС • NB = СОї • OtB = 4-ВС2 = 4- .
4 4
53


8. 	РІЗНИЦЕВІ
трикутники
Трикутник, довжини сторін якого складають арифметичну прогресію, називається різницевим.
Вважатимемо, що b > >а>с. Тоді b — а=а — с, або 2а = b + С-
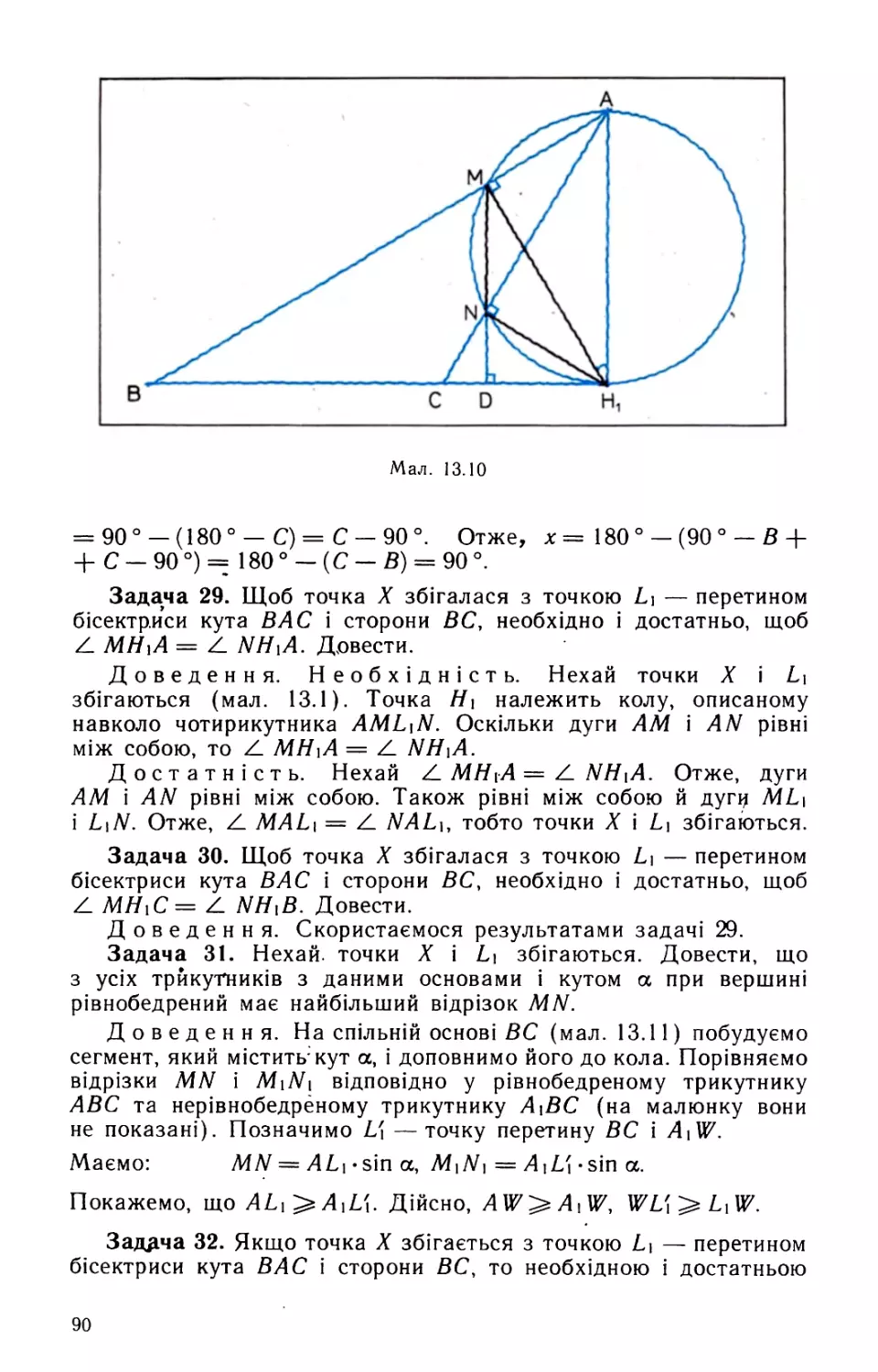
Задача 1. Щоб трикутник ABC був різницевим, необхідно й достатньо, щоб АІ =
= IWi, де / — інцентр, Ц7| — точка перетину бісектриси кута ВАС з кутника колом. Довести.
описаним навколо три-
Доведення. Необхідність, різницевого трикутника АВС (мал. 8.1).
Тоді
2
2
fl + Ь + с — 2а а + 2а — 2а
р — а = — — —
чу 1, с. 31).
Оскільки
Нехай р — півпериметр
= АКз (див. зада-
ЛМіСГі = ЛКзЛ/ і СМі = ДКз, то
ДСМіїГі = АЛКз/ і СГі = АІ.
Але CWx = IW{ ((4.5) с. 27). Отже, АІ = IWi.
Достатність. Нехай AI=IW\. Оскільки CW\ = IW\ = AI й Z.M1CU7, = АКзА/, то дСМіГі = АААз/. Отже, СМі = АКз. а / а я а а-\-Ь-[-с — 2а~ , .
Але CM і = -у , АКз = р — а, —= § ’ 2а = Ь + с,
тобто трикутник ABC — різницевий.
Задача 2. Щоб трикутник ABC був різницевим, необхідно і достатньо, щоб г =. Довести. О
5
Доведення. Необхідність. Оскільки г = — і р = -у , р 4
то
а • ha • 2 ha г ~ 2 -3 ■ а ~ Т •
Достатність доводиться аналогічно.
Задача 3. Щоб трикутник ABC був різницевим, необхідно і достатньо, щоб W\L\ = L\I. Довести.
Доведення. Необхідність. Трикутники CM\W\ і АКзІ рівні між собою (див. задачу 1). Звідси W\M\ = КзІ. З цього випливає, що рівні між собою і трикутники M\W\L\ й Кі/Ль Отже, ГіЛі = Li/.
Достатність доведіть самостійно.
54


Задача 4. Щоб трикутник ABC був різницевим, необхідно і достатньо, щоб:
1) відрізок 01 був перпендикулярний до відрізка АІ\
2) справджувалось рівняння АІ = -y]2Rr.
Довести.
Доведення. Необхідність. 1) Оскільки АІ = IWі, то відрізок 01 перпендикулярний до відрізка АІ.
2) Оскільки трикутник ОІА — прямокутний, і за формулою Ейлера О/2 = R2 — 2/?г, то АІ2 = R2 — R2 + ZRr, звідси АІ = = -^2Rr.
Достатність доводиться аналогічно.
Задача 5. Щоб трикутник ABC був різницевим, необхідно і достатньо, щоб Ьс = 6/?г. Довести.
Доведення. Необхідність. Рівність, яку треба довести, запишемо так:
abc = 6Rra.
_ ha гл abc
Враховуючи, що r = ~ * R = ’ ма€м0:
R • 4S = 6 • R , або 4S/? = 4S/?.
Достатність доводиться аналогічно.
Задача 6. Щоб трикутник був різницевим, необхідно і достатньо, щоб пряма, яка сполучає центроїд та інцентр, була паралельна середній за величиною*стороні трикутника. Довести.
Доведення. Необхідн цевий, то відстані від центроїда до сторони ВС дорівнюють 4-/г(
Достатність довести самостійно.
Задача 7. Щоб трикутник був різницевим, необхідно і достатньо, щоб сума відстаней від будь-якої з точок бісектриси кута, протилежного середній за величиною стороні трикутника, до сторін трикутника була сталою. Довести.
Доведення. Необхідність. Нехай d\, do, dz — відстані від довільної точки бісектриси Іа до сторін трикутника, ABC, відповідно ВС, АС, АВ. Тоді do = d?, = I.
с т ь. Якщо трикутник різнило сторони ВС і від інцентра = г. Отже, задачу доведено.
Мал. 8.1
55


Нехай S — площа трикутника. Маємо:
2S = d[a + d2b + d^c = dia + l(b + c).
Враховуючи, що b + c = 2a, маємо:
2S = d\ci 2/a = a (d\ -|- 2/), звідки
di + 2/ = -^ = /ie.
Достатність довести самостійно.
Задача 8. Щоб трикутник ABC був різницевим, необхідно і достатньо, щоб інцентр /, вершина, протилежна середній за величиною стороні трикутника, і середини двох інших сторін належали одному колу. Довести.
Доведення. Необхідність. Опишемо навколо трикутника АВС (мал. 8.2) коло і проведемо бісектрису кута ВАС до перетину з цим колом у ТОЧЦІ W\. Точки М і N— середини сторін АВ і АС. Оскільки АІ = IW\, то чотирикутники ABW\C і AMIN— гомотетичні і, отже, точки А, М, /, N належать колу.
Достатність довести самостійно.
Задача 9. Щоб трикутник був різницевим, необхідно і достатньо, щоб котангенси половин його кутів складали арифметичну прогресію. Довести.
Доведення. Необхідність. Оскільки ctg -^-= р ~ а ,
. В р — b . С р — с ctg -77-= , ctg -z-= .
& 2 Г ’ & 2 г
Числа Ь, а, с є членами арифметичної прогресії, тому числа р — Ь, р — а, р — с — також члени арифметичної прогресії, а отже, р — b р — а р — с ,
і числа —, —-—, ~^~г— також складають арифметичну прогресію.
Задача 10. Довести, що в різницевому трикутнику ABC Z_A < 60°.
Доведення. Відомо, що
А _ Г І (р- ь)(р- с)
g 2 - p-а р(р-а) •
Але
д/ (р —fe)(p —с) < -у(р — b +
+ Р — с) = у а’ Р = ~2а'
р — а = а.
Отже, tg
/-А 60° (рівність має місце
тільки при а = b = с).
Мал. 8.2 г
56


9. 	БІСЕКТРАЛЬНИЙ ТРИКУТНИК
Трикутник L1L2L3 назвемо бісектральним (мал. 9.1).
Задача 1. У трикутнику ABC
. 2 (sin А + sin В) п 1
tg ф =— і і о , (9.1)
& 14-2 cos С ' v '
де ф = ALiL3^2. Довести.
Доведення. Позначимо Z-AL3L2 = ос, Z_BL3L\ =
= р. Тоді ф = 180° — (а + р), tg ф = — tg (а + р).
Із трикутника AL2L3 (мал. 9.1) за теоремою синусів маємо:
Але
ALz sin а
ДВз sin (Д 4- а)
AL2 = —AL3=-^-7- . z а 4- с ’ л а 4- b
Отже,
ч а 4- b . sin а
а + с sin (Д 4- а)
Аналогічно з трикутника
L}BL3
а + b __ sin р
b 4- с sin (В 4- р)
Оскільки
а 4- С
CL 4“ Ь
2R (sin А + sin С)
2R (sin А 4- sin В)
Мал. 9.1
. а 4- с sin (Д 4- а)
а + b sin а
ТО
sin А 4“ sin С sin (Д + а)
sin А 4- sin В sin а
Знайдемо з цього співвідношення tg а,
sin A (sin А 4- sin В)
® а sin А 4- sin С — cos Д sin Д — cos Д sin В
Враховуючи, що sin С = sin (А 4" В), маємо:
. sin A (sin А + sin В)
g а sin Д (1 — cos Д) 4- sin A cos В + cos Д sin В — cos Д sin В ’
ЗВІДКИ
. sin Д 4- sin В
g а 1 4- c°s В — cos А ’
57


Аналогічно
, о sin А + sin В . , ( . tg а + tg Р
tgP= Г+cos—cos-B ■ tg<p=-tg(a+P)= t-\tgpli •
tg а + tg p = (, + cos B 2co^)0 + сТгл"— СОЇ5) ■ tga-tgp- 1 =  sinM-|-2sin/4 sinB H-sin2B—1+c°s2i4 — cos/4 cosB — cos4 cos£-|-cos2B (14- cos — cos 4) (1 + cos A — cos B)
1 — 2 cos (A + B)
(1 4- cos В — cos Л) (1 4~ c°s A — cos B)
Оскільки cos (A + B) =
= — COS C, TO tg ф =
2 (sin A + sin B) 1 + 2 cos C
Задача 2. Знайти площу бісектрального трикутника, якщо відомі сторони а. Ь, с трикутника ABC.
Розв’язання. Нехай Si, S2, S3 — площі трикутників CL\L2, AL2L3, BLzL\, S— площа трикутника ABC. SL — площа Д
S, =
s2 =
s3 =
CL\ - CL2 • sin С
. CL, =
ab
. cl2 =
ab
2
b 4- c ’
a + c
AL2 • AL3 • sin A
, al2 =
be
Д I .
be
2
a 4- c 1
a + b
BLz • BL\ • sin В
, BL3 =
ac
, BL, ==
ac
2
a + b ’
b + c
a2b2 sin C b2c2 sin A | a2c2 sin В
2(/? + c)(a + c) 2(a4" c)(a4- b) 2(a-|- b)(b + c)
/ ab {a 4- 6) 4- be (b 4" c) 4~ ac (a 4- c) \ (a 4- 4- c) (a 4- c) ,
Si + S2 + S3 —
Звідси маємо:
S/. = S — (Si + s2 + S3) =
/ (a + b) (b + c) (a + c) — ab (a + b) — be (b + c) — ac (a + c)>
“ \ (a + b)(b + c)(a + c) ,
Отже,
2S a • b • c
L ~ (a + b) (b + c) (a 4- c)
Мал. 9.2
Задача 3. Для будь-якої точки, яка належить стороні бісектрального трикутника, сума (або модуль різниці) відстаней до відповідних сторін дорівнює відстані до третьої сторони. Довести.
Доведення. Нехай точка X належить відрізку LiL2 (мал. 9.2). Нехай Р. R, L — проекції цієї точки на сторони 58


трикутника. Розглянемо гомотетію з центром L\ і коефіцієнтом k= L}X: L}L2.
Тоді трикутник ЛіВіСі буде гомотетичний трикутнику ЛВС, а образом бісектриси BL2 е бісектриса В\Х трикутника ЛіВіСі. Отже, відстані від точки X до сторін ЛіВі і В]С\ рівні між собою, тобто XQ = XP. Оскільки точка Лі належить бісектрисі ЛСі, то прямі А\В\ і А\С\ рівновіддалені відповідно від прямих АВ і АС. Тому QL = XR, а тоді XQ + LQ = ХР + XR, або XL = ХР + XR.
Якщо точка X належить продовженню відрізка L\L2, то розв’язання аналогічне, але замість суми відстаней доведеться розглянути модуль різниці відповідних відстаней.
Задача 4. Довести, що існування рівняння
sin (Л — В) — sin (Л — С) = sin 2С — sin 2В
для кутів трикутника ЛВС є необхідною і достатньою умовою того, щоб бісектральний трикутник був рівнобедреним (L|L3 = = B1L2).
Доведення. Необхідність. Отже, дано, що tg ері = = tg ф2, де ф| = Z-L1L3B2, Ф>2 = Z.L1L2B3.
За формулою (9.1) маємо
2 (sin А + sin В) 2 (sin А + sin С)
1 + 2 cos С 1 + 2 cos В ’
sin А + sin В sin А + sin С
1 -J- 2 cos С 1 -j- 2 cos В Звідси
2 cos В sin Л 4- sin В + sin 2В + sin А =
= sin А + 2 sin A cos С + sin С + sin 2С, або
sin (А — В) + sin 2S = sin (Л — С) + sin 2С; тобто
sin (Л — В) — sin (Л — С) = sin 2С — sin 2В.
Достатність доводиться аналогічно.
Задача 5. Довести, що площа бісектрального трикутника SL обчислюється за формулою
■ <9-3>
Доведення. Відомо (формула 4.3), що
z° = т4т— а) •
Аналогічно
/й = -^л/асР(Р - 1' = ТГТ(Р - с> ■
59


Перемножимо ці рівняння і застосуємо формулу (9.2). Дістанемо формулу, яку доводимо.
Задача 6. Довести, що площа бісектрального трикутника не більша за одну чверть площі трикутника ABC.
Доведення. Для додатних чисел а, Ь, с має місце співвідношення
(tz —|- 6) (tz -|- с) (Ь —|- с) 8abc.
5
Враховуючи формулу (9.2), маємо SL .
Задача 7. Серед прямокутних трикутників знайти такий, що має бісектральний трикутник із найбільшим кутом, протилежним прямому.
Розв’язання. '-Покажемо, що таку властивість має кут бісектрального трикутника у рівнобедреному прямокутному трикутнику ABC (С = 90°). За формулою (9.1) маємо:
tg ер = 2 (sin А + sin В) = 4 sin —— cos —— •
ГА ■ ± А л/2 А~В А~В 1 +
Оскільки tg ф = 4—^— cos 2 ’ але COS 2 ’ Т0 tg <Р ^2д/2. Причому tg ер =2^/2 при cos = то^то = = В = 45°:
Задача 8. Довести, що бісектральний трикутник буде прямокутним тоді й тільки тоді, коли один із кутів трикутника ABC дорівнюватиме 120°.
Доведення. Справді, це випливає безпосередньо з формули (9.1).
Задача 9. У рівнобедреному трикутнику ВС = АС. Знайти точку на стороні LjL2 бісектрального трикутника, добуток відстаней від якої до рівних сторін трикутника найбільший.
Розв’язання. Нехай X — довільна точка, яка належить відрізку L1L2, АТИі, XN\, ХКі,— відстані від цієї точки до сторін трикутника (мал. 9.3). Тоді ХМ\ + XNi = ХК\ (задача 3).
Оскільки відрізок L{L2 паралельний стороні АВ, то для змінних доданків ХМ\ і XN\ відрізок ХК\—сталий. Тому добуток відстаней від точки X до сторін ВС і АС набуває найбільшого значення, коли ХМ\ = XN\ = . Отже, таку властивість має
точка перетину Xq висоти СНз з відрізком L\L2.
Задача 10. Бісектриса кута А трикутника ABC перетинає сторону Ь2Ьз бісектрального трикутника Ь\Ь2Ьз у точці М (центроїді трикутника ABC). Знайти кути трикутника ABC.
Розв’язання. Позначимо відстань від точки М (мал. 9.4) до сторін АВ і АС через /і, а відстань до сторони ВС — через 12.
G0


Отже, /і • b = l\ • c, або b = c, тобто трикутник ABC — рівнобедреник Враховуючи задачу 3, маємо: 2/і = /2- Звідси b = 2а (оскільки 1\ • Ь = /2 • а).
Отже,
cos С = y ’ В = С = arccos , А = я — 2 arccos .
10. 	ПОБУДОВА ТРИКУТНИКА 1
Задача 1. Побудувати трикутник ABC за трьома висотами: /ifl, hb, hc.
Розв’язання. У трикутнику ABC а : b : с = -у-:
звідки
а b с hb ha ha • hb
he
Таким чином, сторони трикутника ABC пропорційні величинам hb, ha, hahhb • Тепер побудуємо трикутник MNP зі сторонами hb, ha, ha-~- . Він подібний трикутнику ABC. Отже, можна знайти кути Л, В, С, тобто побудувати трикутник ABC (а можна трикутник MNP перетворити за допомогою гомотетії у трикутник ABC).
1 У пропонованих задачах не ставиться мета розглянути всі етапи розв’язання задач на побудову.
61


Задача 2. Побудувати трикутник ABC за ha, hb, г.
Розв язання. Покажемо, що k k -7—= — .
ha 1 hb 1 he г Справді,
1.1.1 CL Ь С 2р 1
ИГ “Г "ST ' ~h7 = 2S = ~2S~ = ~ •
Знайдемо висоту hc і дістаємо задачу 1.
Задача 3. Побудувати гострокутний трикутник ABC, знаючи положення трьох точок Н\, Hz, Нз-
Розв’язання. Скористаємося властивостями ортоцентричного трикутника (с. 9). Будуємо трикутник НхН^Нз- У ньому проводимо бісектриси внутрішніх кутів і до кожної з них у відповідних точках Н\, Hz, Нз проводимо перпендикулярні прямі. Перетини цих прямих утворюють точки А, В, С, що є вершинами шуканого трикутника.
Задача 4. Побудувати гострокутний трикутник ABC за точками перетину продовжень висот з описаним навколо трикутника колом.
Розв’язання. Позначимо задані точки через 7V і, Мг, N3 (с. 8). Тоді, провівши бісектриси у трикутнику ЛЛМрМз до перетину з описаним навколо нього колом, дістанемо вершини трикутника ABC.
Задача 5. Побудувати трикутник ABC, знаючи положення точок Н<2 і Нз і прямої /, якій належить сторона ВС.
Розв’язання. Нехай точки Н2 і Нз розміщені з прямою / в одній півплощині (мал. 10.1). Оскільки точки В, С, Н2, Нз належать одному колу, то центр Е цього кола є перетином осі симетрії відрізка Н2Н3 і прямої /. Таким чином, будуємо коло радіусом ЕН2 з центром у точці Е, яке перетне пряму І в точках В і С, а перетин прямих ВНз і СН2 дасть точку А.
Задача 6. Побудувати трикутник ABC, знаючи положення вершини А, ортоцентра Н і центра О описаного кола.
Розв’язання. Перший спосіб. Скористаємося задачею 13 (с. 44). Побудуємо коло з центром у точці О,' радіус якого ОА. Оскільки НН[ = H\N\, то, провівши через точки А і Н пряму, яка перетинає коло в точці /Vi, поділимо відрізок HN\ пополам. Дістанемо точку Н\, а потім і точки В й С (мал. 10.2).
Другий спосіб. Скористаємося прямою Ейлера і знайдемо центроїд М(НМ = 2М0). Продовжуючи відрізок AM на одну другу його довжини (мал. 10.2), дістанемо точку М\, яка належить стороні ВС, а потім (опустивши перпендикуляр на відрізок Л/Vi) і точки В й С.
Задача 7. Побудувати трикутник ABC, знаючи положення вершини А, ортоцентра Н і середини М\ сторони ВС.
Розв’язання. Поділивши відрізок А М і у відношенні 2:1, починаючи від вершини, знайдемо положення точки М — цент-
62


роїда трикутника ЛВС, а продовжуючи відрізок НМ на половину його довжини, дістанемо точку О.
Задача 8. Дана пряма і дві точки, які лежать з різних боків від неї. Побудувати гострокутний трикутник, для якого дані точки були б основами двох висот, а третя висота лежала б на заданій прямій.
Розв’язання. Позначимо дані точки Н2 і //з, а пряму — І (мал. 10.3). Побудуємо точку Н\у яка належить прямій /, як вершину ортоцентричного трикутника Н\НїНз. Оскільки пряма І є бісектрисою кута //2/ЛЯ3 (с. 9), то будуємо точку симетричну ії2 відносно прямої І. Сполучимо точки Н2 і Яз, проведемо через них пряму до перетину з /, дістанемо точку Н\. Тепер можна побудувати трикутник В|//2//з, а отже, і трикутник ABC.
Задача 9. Побудувати трикутник, знаючи положення центра О описаного кола, вершини Л, центроїда М.
Розв’язання. Проведемо коло радіуса ОА з центром у точці О. На продовженні відрізка AM (мал. 10.2) відкладемо відрізок ММ\ = уЛМ, проведемо пряму, перпендикулярну до відрізка ОМ\. Вона перетинає коло в точках В і С.
Задача 10. Дано пряму і дві точки з одного боку від неї. Побудувати трикутник ЛВС, щоб ці точки були центроїдом і центром описаного кола, а одна із сторін належала цій прямій.
63


Розв’язання. Оскільки центроїд М належить прямій Ейлера і ОМ = -^МН, то можна знайти ортоцентр Н (мал. 10.2). Із точки Н на задану пряму / проведемо перпендикуляр НН\ і на продовженні відкладемо відрізок HiN\ = НН\. Оскільки точка М належить колу, описаному навколо трикутника ABC (с. 7), то з точки О радіусом ON\ проведемо це коло, яке перетне пряму / в точках В і С. Щоб дістати точку А, продовжимо перпендикуляр НН\ до перетину з побудованим колом.
Задача 11. Побудувати трикутник ABC за ha, ть, тс.
Розв’язання. Аналізуючи задачу, помічаємо, що коли подвоїти медіани ть і тс (мал. 10.4), то дістанемо прямокутні трикутники ЕКВ і LCD, які можна побудувати за гіпотенузою і катетом (він дорівнює висоті ha). Дістанемо кути МВС і МСВ, а отже, і трикутник СМВ. Тепер уже можна дістати точки Л42 і Мз, тобто і трикутник ABC.
Задача 12. Побудувати трикутник за кутом А, медіанами ть і тс.
Розв’язання. Якщо подвоїти медіану СМз, то дістанемо паралелограм ALBC (мал. 10.4). Оскільки Z-M3BL = А, а MB = = -у ть, то точку В можна дістати, побудувавши на відрізку МзС = тс сегмент, який вміщує даний кут А, і з точки М про- 2
вести дугу радіуса MB = у ть.
Задача 13. Побудувати трикутник за кутом А, відрізками В/, СІ.
Розв’язання. У трикутнику BIC Z.BIC = 90° + (див. с. 24, (4.4)). Побудуємо трикутник ВІС за сторонами В/, ІС і кутом ВІС, а потім побудуємо трикутник АВС (мал. 10.5).
Задача 14. Побудувати трикутник ABC, якщо відоме положення вершин В і С, а також пряма 1\, якій належить бісектриса /а.
Розв’язання. Перший спосіб. Якщо побудувати точку Ві, симетричну точці В (мал. 10.6) відносно прямої 1\, то вона належатиме стороні АС (бісектриса Іа належить осі симетрії кута ВАС). Отже, щоб дістати точку А, потрібно продовжити відрізок В\С до перетину з прямою 1\.
Другий спосіб. В основу розв’язання покладемо властивість точки Wi (с. 27). Проведемо вісь симетрії відрізка ВС до перетину з прямою /і у точці U7j. Маючи точки В, С, Wi, проведемо коло, яке містить ці точки, а також точку А.
Задача 15. Дано три прямі, що перетинаються в одній точці, і точка А на одній із них. Побудувати трикутник ABC, щоб вершини В і С належали двом іншим прямим, а ці прямі були б бісектрисами внутрішніх кутів трикутника ABC.
Розв’язання. Перший спосіб. Позначимо дані прямі /і, /2 і /з, а точку їх перетину / — інцентр трикутника ABC 64


(мал. 10.6). Оскільки кут BIC заданий (позначимо його ер), то ер = 90° + -у (с. 24), звідки ^-= ер — 90°.
Отже, з точки А під кутами ер — 90° проведемо промені, які перетнуть прямі І2 і h у точках В і С.
Другий спосіб. Розв’язання аналогічне до розв’язання задачі 14: симетрія точки А відносно прямих /2 і /з дасть точки Аі і А2 (вони належатимуть прямій ВС).
Задача 16. Побудувати трикутник ABC, знаючи положення точок Wi, Г2, Гз.
Розв’язання. Будуємо трикутник VV'i 1Г2№з і, враховуючи задачу 19 (с. 29), проводимо в ньому висоти, продовження яких перетнуть коло, описане навколо трикутника U/iU^2U^3 у точках А, В і С.
Задача 17. Побудувати трикутник ABC, знаючи положення центра О описаного кола, точки W\ та центроїда М.
Розв’язання. Побудуємо коло радіуса OW\ і за властивістю прямої Ейлера знайдемо ортоцентр Н. Через точку Н проведемо пряму, паралельну прямій OW\. її перетин із колом дасть точки А і А^. Побудуємо вісь симетрії відрізка HN\, знайдемо точки В і С (мал. 10.2).
Задача 18. Дано пряму і дві точки з різних боків від неї. Побудувати трикутник ABC, щоб одна з точок була інцент- ром, інша — а сторона ВС належала даній прямій.
Розв’язання. Побудуємо відрізок IW\ (мал. 10.5) і радіусом /ІГі, вважаючи центром точку W\, опишемо дугу, яка перетинає дану пряму в точках В і С.
5 0-172
65


Описане, вписане і зовнівписане кола
Задача 19. Побудувати трикутник за /?, г, а.
Розв’язання. Будуємо коло радіуса /?, центр якого позначимо точкою О. У цьому колі проведемо хорду ВС, довжина якої а. З усіх трикутників із стороною а, необхідно знайти такий, у якого радіус вписаного кола дорівнює г.
Це можна зробити трьома способами.
Перший спосіб. Проведемо на відстані г від хорди ВС пряму /, паралельну ВС, і з точки О проведемо дугу радіусом 01 = ~\] R2 -т 2Rr (скористаємося формулою Ейлера, див. с. 31) до перетину з прямою /.
д
Другий спосіб. Оскільки Z-.BIC = 90° + (4.4, с. 24),
^4 то на хорді ВС будуємо сегмент, який містить кут 90° + — (кут А відомий, оскільки відомі відрізки Ria).
Перетин сегмента і прямої І, яка паралельна ВС на відстані г, дасть точку /.
Третій спосіб. Скористаємося співвідношенням (4.5), (с. 25): поділимо дугу ВС пополам, дістаємо точку Wi і радіусом BW\ = CW\ робимо засічку на прямій /. Діставши точку /, продовжимо побудову, аналогічно до задачі 18.
Задача 20. Побудувати трикутник ABC за R, г, р.
Розв’язання. Відомо (5.1, с. 31), що
Г = (р — a) tg або
г = (р — 2/? sin Д) tg4-=(p_— tg^ )tg4 . v і + tgs47 2
Звідси знаходимо tg Отже, задача зводиться до поперед- ньої.
Задача 21. Побудувати трикутник за точками О, 1, Іа.
Розв’язання. Поділимо відрізок//fl пополам (мал. 10.7). Дістанемо точку И7| (див. с. 41). Тепер будуємо коло з центром в точці О радіусом OW], Оскільки ВГі = СГі = IWi, дістаємо вершини В і С.
Задача 22. Побудувати трикутник ABC, знаючи положення центрів /а, Іь, Іс зовнівписаних кіл.
Розв’язання. Будуємо трикутник ІаІЬІс- ОСНОВИ ЙОГО 66


висот є вершинами трикутника АВС (с. 42). Зауважимо, що трикутник IJblc—гострокутний (с. 42).
Задача 23. Побудувати трикутник ABC за двома кутами А і В та периметром 2р.
Розв’язання. Існують різні способи розв’язання цієї задачі. Покажемо побудову за допомогою зовнівписаного кола. На сторонах кута ВАС відкладемо відрізки АТ\ = АТ<2 = р. У кут впишемо коло так, щоб воно дотикалося до його сторін в точках Т\ і Т2, а потім під кутом В до однієї з сторін кута проведемо дотичну (див. с. 46).
Задача 24. Побудувати трикутник ABC, якщо відомі пряма, якій належить сторона ВС, і точки І та /а.
Розв’язання. Сполучимо / та /а. Поділимо відрізок ІІа пополам. Дістанемо точку Wi (с. 41). Оскільки відрізок /І^і відомий та = WiB = W\C, то маємо точки В і С. Побудуємо коло з центром в точці /, дотичне до прямої І, і з точок В і С проведемо до нього дотичні. їх перетин дасть точку А.
11. 	ПОБУДОВИ
В ТРИКУТНИКУ1
Задача 1. На стороні ВС трикутника ABC (або її продовженні) знайти таку точку, щоб сума радіусів кіл, описаних навколо трикутників АСХ і АВХ, була мінімальною.
Розв’язання. Шукана точка X — основа висоти АН\. Доведемо це.
Нехай і /?2 — радіуси
кіл, описаних навколо трикутників АСХ і АВХ. Тоді
/?! +/?2 = уИС + ЛВ)
1
sin Z.CX4
Сума R\ + /?2 буде мінімальною, якщо Z.CXA = 90°, тобто, коли точка X збігається з точкою Н\.
Задача 2. Всередині трикутника ABC побудувати точку X, для якої АК = BE = CD, а К, Е, D — основи перпендикулярів, опущених із точки X на сторони АВ, ВС, СА відповідно.
Розв’язання. Розглянемо трикутник А'В'С', утворений перпендикулярами в точках А, В, С відповідно до сторін АВ,
1 У пропонованих задачах не ставиться мета розглянути всі етапи задач на побудову.
67


ВС, СА (мал. 11.1). Із точки X опустимо перпендикуляри на сторони трикутника А'В'С'. Враховуючи умову задачі і розглядаючи утворені прямокутники, робимо висновок, що ХК' = ХЕ' = = XD'. А це означає, що точка X рівновіддалена від сторін трикутника А'В'С', тобто вона є інцентром цього трикутника.
Задача 3. Усередині трикутника ABC побудувати точку X, яка належить прямим, що проходять через вершини трикутника і перетинають відповідні сторони у точках Аі, Ві, Сі так, щоб АХ . ВХ СХ . .
сума -Vi—г —г була мінімальною.
Л/і і Л D і Л С і
Розв’язання. Позначимо площі трикутників ХВС, ХСА, ХАВ через Si, S2, S3. Площі трикутників ХСАі—через qi і ХАїВ — через ^2. Тоді (мал. 11.2)
АХ
_ So
ЛЛ' _
A
ХАі
1 Q\
XAt ~
<72
Отже,
АХ _
S2
== A =
S2 + S3
So -|" S3
ХА}
^2
<7l + <?2
— s.
Аналогічно
ВХ
S3 -|- Si
CX
Si + S2
ХВ} ~~ S2 ’ ХС1 ~ S3
Далі
АХ ВХ СХ _
"ХАТ “г ХВі + ХСі ~
= (іг + <)+(І7 + 4;)+(^ + С)>6- оскільки сума двох обернених додатних величин не менша від двох. Знак «дорівнює» має місце при Si = S2 = S3, тобто точка X — центроїд трикутника ABC (див. задачу 8, с. 15).
Задача 4. Всередині гострокутного трикутника ABC знайти таку точку X, щоб сума ХА -|- ХВ + ХС була мінімальною.
Розв’язання. Всередині трикутника ABC візьмемо довільну точку Y (мал. 11.3). Повернемо навколо вершини А на 60° трикутник AYC. Дістанемо трикутник AY'C'. Розглянемо суму
68


YA + YB + УС. Оскільки трикутник AYY' — рівносторонній, то ДУ = У Г', крім того, YC = = У'С'. Отже, УД + YB + + YC = BY + YY' + Y'C'. Ця сума буде мінімальною, коли точки В, У, У', С' належатимуть одній прямій. Причому A.AYB = Х.ДУ'С' = ABYC = = 120°. Отже, шукана точка X така, що з неї сторони трикутника видно під рівними кутами. Щоб знайти цю точку, на кожній стороні будуємо сегмент, який містить кут, що дорівнює 120°. Перетин сегментів дасть точку X.
Задача 5. Знайти всередині трикутника точку, добуток відстаней від якої до сторін трикутника набував би найбільшого значення.
Розв’язання. Нехай X—шукана точка, d\, dz— відстані від цієї точки до сторін ВС, ДС, АВ. Подвоєну площу трикутника можна записати так:
2S = ad\ + bdz + cdz^ 3^/ ad\ • bd% • cdz.
Добуток d\ • o?2 • dz набуває найбільшого значення тоді, коли ad\ • bd% • cdz також досягає найбільшого значення. Це можливо при
ad] = bd<z = cdz = -3-
звідки
1 25 сі • /іц ha f hb f he
d' =-^=-^r=— ’ d2 = — ’ d^ = —
А це означає, що точка X збігається з центроїдом.
Задача 6. У трикутнику ABC знайти точку X, сума квадратів відстаней від якої до сторін трикутника буде найменшою.
Розв’я-зання. Введемо позначення попередньої задачі.
Має місце нерівність (Коші-Буняковського)
(d2 d2 гіз) (я2 + Ь2 -|- с2) (ad 1 -|- bdv -|- cdz}*, звідки
Оскільки права частина нерівності — величина стала, то ліва частина набуває найменшого значення, якщо виконується рівність
d\ d-i ds
а b с ’
69


Справді, d] + dl + dl =
У результаті нескладних перетворень маємо:
(adz- bd\)2 + (ad3-cdt)2+ (bd3 - cd2)2 = 0.
Отже,
adz — bdi = ad3 — cdi = bd3 — cd? = 0, або
d\ d.2 d'i a b c ’
тобто відстані від шуканої точки X до сторін трикутника ABC пропорційні їх довжині. Щоб побудувати цю точку, треба провести прямі, паралельні сторонам трикутника, на відстанях, які дорівнюють довжині відповідної сторони. Дістанемо трикутник АіВіСі, гомотетичний трикутнику ABC. Відрізки, які сполучають відповідні вершини, перетинаються в центрі гомотетії, що є шуканою точкою X.
Задача 7. Знайти всередині трикутника ABC точку, сума квадратів відстаней від якої до вершини трикутника найменша.
Розв’язання. Із формули Лейбніца (3.2) випливає, що шуканою точкою є точка М — центроїд трикутника ABC (див. с. 22, задача 22).
Задача 8. На сторонах АВ і ВС трикутника ABC, або на їх продовженнях побудувати відповідно точки М і N так, щоб AM = MN=NC.
Розв’язання. Відкладемо на стороні АВ (мал. 11.4) довільний відрізок AD. На стороні ВС — відрізок СЕ, який дорівнює відрізку AD. Через точку Е проведемо пряму, паралельну АС. Із точки D розхилом циркуля, що дорівнює AD, зробимо на цій прямій засічку. Дістанемо точку L. Чотирикутник ADLK(LK II EC) гомотетичний чотирикутнику AMNC. Точки М і N — шукані. Центр гомотетії — точка А. Тому через точки А і L проводимо пряму до перетину із стороною ВС в точці N і потім проводимо відрізок NM паралельно відрізку DL.
Задача 9. У трикутнику ABC на стороні ВС знайти таку точку X, щоб довжина перпендикуляра XL дорівнювала довжині перпендикуляра XD (точки L і D належать відповідно сторонам АВ і ЛС). (XL Л_АВ, DXX.BC).
70


Роз в’язання. Нехай X — шукана точка і XL = XD (мал. 11.5). Проведемо висоту АН\. Тоді ХС-tg С = XB-sin В. Отже,
ХС: ХВ = sin В : tg С = =НіС '. АВ.
Ad /7 і С
Тепер зрозуміла побудова. Продовжимо сторону АВ за вершину А і відкладемо на її продовженні відрізок АЕ, який дорівнює Н\С. Сполучимо точки Е і С. Через точку А проведемо пряму, паралельну відрізку EC. Дістанемо точку X.
Задача 10. Через точку D, яка належить стороні ВС трикутника ABC, провести пряму, яка поділяє площу трикутника пополам.
Розв’ язання. Нехай DE — шуканий відрізок (мал. 11.6). Тоді
DC*CE __ 1 sabc ~ ВС-АС — 2 ’
Якщо Мі — середина відрізка ВС, то
DC-СЕ __ 1
ЧМіС-АС ~ 2 •
Отже,
DC __ АС
AfjC “ СЕ '
Таким чином, щоб знайти точку £, проведемо відрізок М\Е, паралельний AD. Відрізок DE — шуканий.
Задача 11. Через вершину А негострокутного трикутника ABC провести відрізок AD (точка D належить ВС), довжина якого була б середньою пропорційною величиною між довжинами відрізків BD і DC.
71


Розв’язання. Навколо трикутника ABC опишемо коло з центром у точці О (мал. 11.7). На відрізку АО як на діаметрі опишемо коло, що перетинає хорду ВС в точках D і D\. Оскільки відрізок OD (OD\) перпендикулярний до хорди АЕ(АЕ\) (Е і Е\ — точки перетину продовжень відрізків AD і AD\ з описаним колом), то AD = DE (AD\ = D[E\). Звідки
BD-DC = AD-DE AD2=BD-DC.
Аналогічно AD2 = BD\-D\C.
Задача 12. Через вершину А трикутника ABC провести пряму так, щоб відношення периметрів і площ трикутників, які утворилися, було однаковим.
Розв’язання. Нехай Si і pi, S2 і р2— площі і півпери- метри шуканих трикутників, г\ і г2 — радіуси кіл, вписаних у ці трикутники.
За умовою Si : S2 = р\ : Але Si = р\Г\, S2 = р%г2. Отже, р\Г\ : р\г2 = р\ : Р2, або г\ = г2.
Отже, через точку А потрібно провести відрізок AN (точка N належить стороні ВС) так, щоб кола, вписані в трикутники ABN і ACN, були рівними. Нехай /і і /2— центри кіл, вписаних у трикутники ABN і ACN (мал. 11.8). Очевидно, що відрізок
1 	\12 паралельний стороні ВС, a Z. 1\АІ2 = А.
На довільному відрізку І\Г2 з кінцями на бісектрисах кутів ABC і АСВ і паралельному стороні ВС, будуємо сегмент, що містить кут —А. Продовжимо бісектрису кута ВАС до перетину з сегментом — дістанемо точку А'. Трикутник /ЇА72 гомотетич- 72


НИЙ трикутнику і\АІ2 з центром гомотетії — точкою І. Отже, можна дістати точки І\ і /2, побудувати кола рівних радіусів і провести до них дотичну AN.
Задача 13. Даний трикутник поділити на дві рівновеликі частини відрізком DE найменшої довжини (точки D і Е належать відповідно сторонам АС і АВ).
Розв’язання. Позначимо AD = x, АЕ = у (мал. 11.9). Оскільки
*У _ 1
Ьс ~ 2 ’
Ьс
т°у = і7-
За теоремою косинусів
DE2 = х2 + у2 — 2хг/ cos Л, або
г^г-2 9 і Ь2С2 о ЬС л о . Ь2С2 . -
DE* = Xі + 2х--п— cos А = х2 be -cos А.
1 4х 2х 1 4xz
За допомогою похідної знайдемо, що відрізок DE буде міні-
2 	Ь2С2 * мальним тоді, коли х =—г, або х = 4х
Таким чином, AD = АЕ = ~л/ cos4) є міні-
мальним.
Задача 14. Всередині трикутника ABC дано точки М і N. Провести ламану MXiXzXzN мінімальної довжини, де Х]£ЛВ, х2єас, х3евс.
Розв’язання. Побудуємо трикутник АВ'С, симетричний трикутнику ABC відносно відрізка АС (мал. 11.10). Тоді точці М відповідатиме точка М'. Побудуємо точку Л4і, симетричну точці М' відносно відрізка АВ\ і точку Afj, симетричну точці
Мал. 11.9
73


N відносно відрізка ВС. Зрозуміло що довжина відрізка AfiAfi залежить тільки від взаємного розміщення точок А, В, С, М, N. Довжина ламаної MXiXzXzN дорівнює МХ\ + ^1^2 + Х2Х3 + X3N. Враховуючи, що X|X2 = XfX2 (точка Х'і відповідатиме точці Хі при симетрії відносно ДС), ХіМ = Х1ЛҐ = Х'їМі, XsN = X3Ni, знаходимо, що довжина ламаної MX1X2X3N дорівнює ЛїіХІ + + XjX2 + Х2Х3 + X3/Vj ^Afi/V|. Очевидно, що довжина ламаної дорівнює M\N\ тоді, коли точки XI, Х$, Хз, лежать на прямій MiNi.
12. ВИВЧЕННЯ ВЛАСТИВОСТЕЙ ТРИКУТНИКА ЗА ДОПОМОГОЮ ПАРАЛЕЛЬНОГО ПРОЕКТУВАННЯ
Нехай у просторі дано дві площини уі і ?2 і деяка пряма /, не паралельна жод¬
ній із цих площин (мал.
12.1). Нехай точка А і нале¬
жить площині 7і. Якщо через неї проведемо пряму, паралельну прямій І до перетину з площиною 72 у точці Д2, то точка А2 називається проекцією точки А і на площину 72. Очевидно, що кожна точка площини 71 має свою проекцію на 72 і навпаки, кожна точка площини 72 є проекцією деякої точки площини 7і. Таким чином, ми маємо справу з деяким взаємно- однозначним відображенням площини 71 на площину 72. Це відоб¬
раження називається паралельним проектуванням площини 7і на площину 72 в напрямку І.
Нагадаємо основні властивості паралельного проектування.
1°. Будь-яка пряма лінія при паралельному проектуванні переходить в пряму лінію.
2°. При паралельному проектуванні паралельні прямі переходять в паралельні прямі.
3°. При паралельному проектуванні зберігається відношення відрізків, які лежать на одній прямій або на паралельних прямих.
4°. При паралельному проектуванні зберігається відношення площ будь-яких фігур.
5°. Основна теорема про паралельне проектування. Довільний трикутник можна за допомогою паралельного проектування перетворити в трикутник, подібний даному трикутнику MNP.
Доведення. Нехай трикутник ABC належить площині 7і (мал. 12.2). За площину 72 візьмемо довільну (що не збігається
74


з 	уі) площину, якій належить сторона ВС, і побудуємо в ній трикутник ВАїС, подібний даному трикутнику MPN.
Якщо тепер напрям проектування вибрати паралельним прямій ААі, то проекцією трикутника ABC на площину уг буде трикутник АіВС. Теорему доведено.
Задача 1. Довести, що медіани довільного трикутника перетинаються в одній точці і діляться у відношенні 2:1, рахуючи від вершини.
Розв’язання. Спроектуємо паралельно довільний трикутник ABC у рівносторонній трикутник ЛіВіСі (мал. 12. 3). Згідно з властивістю 3°, медіани трикутника АВС АМ\, ВМї, СМ3 перейдуть в медіани ДіЛН, ВіМз, С\М3 трикутника ДіВіСі, які перетинаються в одній точці (як висоти чи бісектриси рівносто- роннього трикутника). Отже, і медіани трикутника ABC перетинаються в одній точці.
Мал. 12.2
Мал. 12.3
75


Мал. 12.4
Доведемо, що AM : ЛШі = 2: 1. Справді, М'В\=М'А\ і А\М': М'М\ = В\М': М'М\ = 2 : 1 (з прямокутного трикутника В'М'М'А і
AM : ММ} = АіМ': М'М\ = 2: 1
(властивість 3° паралельного проектування.)
Задача 2. Через довільну точку 7<, яка лежить всередині деякого трикутника ABC, проведено прямі, паралельні сторонам цього трикутника. Відрізки, які відтинаються на цих прямих сторонами трикутника, позначені відповідно через Д|В2, В\С%, С|Д2. Довести, що
A\Bo - ВіС? ] С\А’> __ q
~~АВ~~ + ~АС~ г- ~ВС~ ~
Розв’язання. Спроектуємо даний трикутник ABC в рівно- сторонній трикутник MNP (мал. 12.4). Тоді точка перейде в К\ відрізки ЛіВ2, ВіС2 і С|Л2 — у відрізки *Л|В2, BfC2, С!Д2, паралельні сторонам трикутника MNP. При цьому трикутники зі спільною вершиною К' рівносторонні. Нехай С\К' = х, A\Cf2 = у, К'А'ї = z. MP = PN = MN = a.
Маємо:
/41^2 і В\С'2 і СІЛ2 2
а * а * а а
А\Вч . В\Со і С і А 2
а отже, -^ + ^ + ^ = 2.
Задача 3. У трикутник ABC вписаний трикутник АіВ|Сі так, що його вершини Аі, В\, С} розміщені відповідно на сторонах ВС, АС, АВ, причому
/41Z3 В\С С\А
~7^С~="~В^А=~С^В= k’
Знайти відношення площ трикутників А\B\C\ і ABC.
76


Мал. 12.5
Роз в’язання. Спроектуємо трикутник АВС у рівносторон- ній трикутник MNP (мал. 12.5) зі стороною, що дорівнює fe+ 1. (Таку довжину ми дістанемо, враховуючи, що, наприклад,
Тоді трикутник А\В\С\ перейде у трикутник M\N\P\, а його сторона (позначимо її через х) за теоремою косинусів дорівнюватиме
х = д/ Z?2 + 1 — 2/г cos 60 ° = д/ fe2 + 1 — & .
Тоді дістанемо відношення площ трикутників
^л,Д|С| Л'2 £2 — fe 4-І
(/? + 1)2 (& 4- І)2 •
Задача 4. Через кожну вершину трикутника проведено дві прямі, які ділять протилежну сторону на три рівні частини. Довести, що діагоналі, які сполучають протилежні вершини шестикутника, утвореного цими шістьма прямими, перетинаються в одній точці.
Доведення. Спроектуємо трикутник ABC у рівносто- ронній трикутник А'В'С' (мал. 12.6). У правильному трикутнику шестикутник також правильний, він має три осі симетрії — медіани трикутника ABC. Цим осям належать діагоналі шестикутника, що сполучають протилежні вершини. Отже, вони перетинаються в одній точці — центрі рівностороннього трикутника.
Мал. 12.6
77


Задача 5. З медіан трикутника ABC складено трикутник XYZ. Довести, що
$XYZ _ 3
$АВС 4
Доведення. Справді, якщо трикутник ABC спроектувати в рівносторонній ЛіВіСі, то медіани трикутника ABC перейдуть в медіани трикутника ЛіВ|С|. Оскільки відношення площ збережеться, а для правильного трикутника SX1X1Z| =
3 с
— ~ > ТО
$XYZ = 3
SABC 4
Задача 6. Дано трикутник ABC і точка Р всередині його. Довести, що з трьох трикутників АМ\Р, ВМ^Р, СМ$Р сума площ двох з них дорівнює площі третього трикутника.
Доведення. Спроектуємо трикутник ABC в рівносторонній трикутник А'В'С'. Оскільки медіани рівностороннього трикутника рівні, то залишається довести, що сума висот двох трикутників дорівнює висоті третього трикутника.
З точки Р' опустимо на медіани Л'Мь В'Мг, С'М'з перпендикуляри Р'К, P'N, P'L (мал. 12.7). Треба довести Р'L + Р'К= Р'N• Нехай О — центр рівностороннього трикутника Л'В'С'. Позначимо Р'О = т, А Р'ОС' = а.
Маємо:
= т • sin (60 ° — а);
P'L = т • sin а;
P'N = пг • sin (60 ° + а).
Отже, P'N = P'L + Р'К, звідки
SpBMi = $РАМ' “I” SpCM-v
Задача 7. У даний трикутник XYZ вписаний інший трикутник XiTiZi, вершини якого ділять сторони трикутника XYZ у відомих співвідношеннях. Довести, що площа трикутника X\Y\Z\ не залежить від того, яка з сторін трикутника XYZ і в якому відношенні ділиться.
Доведення. Спроектуємо трикутник XYZ (мал. 12.8) у рівносторонній трикутник ABC. Тоді точки Хі, У|, Z\ перейдуть у точки Ль Ві, Сі і мають місце співвідношення:
ЛСі t . СВ] , . ВА\ .
~AB~==kl} ~СА~=“2' ~TC~=k3‘
5д)В|С| = SaBC — SaB'Ci SbAiCi
78


Нехай сторона рівностороннього трикутника дорівнює а. Тоді
с а2л/з а2д/з Z1 , a2J3 Z1 ,
5д,5,Сі — 4 4— (1 — ^2) k\ X— • (1 — k\) k3 —
4^ ( 1 — &з) &2 = SABC( 1 4" ^1^2 + &1&з4“ ^2&3— k\ —
— k2 — kz) ,
тобто площа трикутника X\Y\Z\ не залежить від того, яка із сторін трикутника XYZ і в якому відношенні ділиться.
Задача 8. Усередині трикутника ABC вказати точку М, таку, що
Здвм = $всм = Засм
Розв’ язання. Спроектуємо трикутник ABC у рівносторон- ній. Тоді М є точкою перетину медіан, для якої справджується співвідношення
ЗдВМ = Звем = Здсм-
Задача 9. Нехай І — довільна пряма, яка проходить через точку перетину медіан М трикутника ABC і перетинає його сторони (або їх продовження) в точках /?, S і Т, причому точки S і Т лежать з одного боку від точки М. Довести, що
MR MS ' МТ '
Доведення. Нехай трикутник ABC рівносторонній (мал.
12.9) і Z. MSB = а, АВ = а.
Маємо:
MS =
а
2 ^/з sin а
79


MT = і = 2
2уз sin (180 ° — а— 120°) 2-д/З sin (60 ° — а) ’
MR = —J- ,
2д/3 cos (ЗО ° - а)
MR і MR _ sin <z sin (60 ° — a) sin a-|- sin (60° — a)
MS ' MT cos (30° — a) cos (30° — a) — cos (30° — a) =
Оскільки відрізки MT, MS, MR належать одній прямій, тобто при паралельному проектуванні відношення між ними зберігаються, то співвідношення, яке доводиться, справджується для довільного трикутника.
Задача 10. На кожній із сторін трикутника XYZ відкладено відрізок, що дорівнює одній третій відповідної сторони:
XZ{ = ±-XY, YXi = 4- YZ, ZYi = ±-ZX.
ООО
Довести, що площа трикутника, утвореного прямими ХХ\, УУі, ZZi, дорівнює одній сьомій площі трикутника XYZ.
Доведення. Спроектуємо заданий трикутник у рівносторонній трикутник ABC. Тоді точки Хі, Z\ спроектуються в точки Аі, В], С\ (мал. 12.10). Точки перетину відрізків АА\ і СС\, ВВ\ і ААі, ВВі і ССі позначимо М, W і Р відповідно. Доведемо, що площа трикутника MNP дорівнює одній сьомій площі трикутника ABC. Таким чином, буде доведено дану задачу.
Трикутники АСС\, СВВ\, ВАА\ — рівні. За теоремою косинусів знайдемо ССі, позначивши АС\=х, АС = Зх (з трикутника'
АСС\)СС\ = ~\[ 1 х. Оскільки
Л Сі 1
— ;—, то площа трикут-
С,С у/ 7
ника АСіМ дорівнює одній сьомій площі трикутника АССг.
5дс,лі = —Saco
Знайдемо відношення площ трикутників ABC і С\СА:
SACCt = АС' = 1
$лвс АВ З
Отже,
ЗдСіМ = — 5дсс, = -2у5лвс.
80


Таким чином, площу трикутника MNP (SY) (мал. 12.10) знаходимо з рівності:
== Sabc 4" ЗХлсіМ — .
і і о
Нехай SA8C = S. Тоді S^cc, = ~у S, = урЗ і SY = S -|- тгр^ —
-s = 4-s.
із. проекції точки,
ЩО РУХАЄТЬСЯ вздовж СТОРОНИ трикутника, НА ДВІ ІНШІ ЙОГО СТОРОНИ
У нетупокутному трикутнику ABC точка X належить стороні ВС. Позначимо точками М і N її проекції на сторони АС і АВ і розглянемо властивості відрізка MN.
Задача 1. Довести, що М
<^АХ.
Доведення. Опишемо навколо чотирикутника ANXM коло (мал. 13.1). Тоді MN = ЛХ-sin А. Оскільки sin А 1, то MN^.AX. Зверніть увагу на співвідношення
= Д/.sin А.
(13.1)
Задача 2. Для того, щоб відрізок MN = АХУ необхідно і достатньо, щоб Z_ ВАС =90°.
Доведення. Це випливає із співвідношення (13.1).
Задача 3. Довести, що відрізок MN буде найменшим тоді і тільки тоді, коли точка X, довільна точка сторони ВС трикутника ABC, збігається з точкою Я і — основою висоти, проведеної з вершини А.
Доведення. Необхідність. Нехай M\Ni — найменший з відрізків MN під час руху точки X вздовж сторони ВС. Тоді найменшим буде вираз АХ • sin А. Оскільки sin А — величина стала, 6 0-172
81


то вираз АХ-sin А буде найменшим тоді й тільки тоді, коли відрізок АХ буде найменшим, тобто коли точки X і Н\ збігаються.
Достатність. Нехай точка X збігається з точкою Н\. Розглянемо співвідношення (13.1). Тут величина sin А стала. Отже, величина відрізка MN залежить від відрізка АХ, який є найменшим саме у цьому випадку.
Задача 4. У прямокутному трикутнику ABC(Z_ А = 90 °), точка X — довільна точка, яка належить гіпотенузі ВС.
Довести, що коли сума ХМ2 + XN2 найменша, то необхідно і достатньо, щоб точка X збігалася з точкою Н\, основою висоти, проведеної з вершини А.
Доведення. Необхідність. Нехай сума ХМ2 + A~XN2 = MN2— найменша. У прямокутнику XMAN діагоналі АХ і AW рівні. Але відрізок АХ буде найменшим, якщо точки X і Н\ збігаються.
Достатність. Нехай точки X і Н\ збігаються. Оскільки ХМ2 + XN2 = MN2, то, враховуючи задачу 3, стверджуємо, що відрізок MN буде найменшим, а отже, сума XM2A~XN2 також буде найменшою.
Задача 5. Щоб відрізок MN перетинав відрізок АХ у його середині, необхідно і достатньо, щоб кут ВАС трикутника ABC дорівнював 90 °. Довести.
Доведення. Достатність. Нехай Z_ ВАС = 90 °. Навколо чотирикутника XMAN можна описати коло з діаметром АХ, а оскільки відрізок ЛЇМ також є діаметром цього кола, то він перетинає АХ в його середині.
Задача 6. Щоб відрізок АХ перетинав відрізок у його середині, необхідно і достатньо, щоб точка X збігалася з точкою перетину бісектриси кута ВАС і сторони ВС, або Z_ ВАС = 90°. Довести.
Доведення. Необхідність. Опишемо коло навколо чотирикутника XMAN. Діаметр АХ поділить хорду MN пополам, а, отже, він належить бісектрисі кута ВАС трикутника ABC, або MN — діаметр і Z_ ВАС = 90 °.
Задача 7. Щоб трикутник ABC був рівнобедреним (АВ = АС), необхідно і достатньо, щоб величина XM-\~XN дорівнювала висоті, опущеній на сторону АВ або АС. Довести.
Доведення. Необхідність. Нехай АВ = АС=Ь, ВС = а. Позначимо ВХ = т, СХ=п, Z_ABC=a. Тоді ХМ = = и-sin a, XN = /n-sin а. Звідси
ХМ + XN = n-sin а+ /n-sin а= (т + n)sin а= а-ріп а= hb.
Достатність. Нехай ХМ + XN = АВ = с, АС = Ь. Оскільки
Sabx + Sacx = Sabc, то b • ХМ + с • XN = b - hb.
За умовою
XM + XN = hb, або XM = hb - XN.
82


Отже,
b(hb — XN) + c-XN= b-hb, або b-XN=c-XN. Звідси b = с.
Задача 8. Щоб центр О кола, описаного навколо трикутника ЛВС, належав відрізку АХ, необхідно і достатньо, щоб відрізок MN був паралельний стороні ВС. Довести.
Необхідність. Нехай AD — діаметр кола, описаного навколо трикутника ЛВС, якому належить точка X (мал. 13.2). Опишемо коло навколо чотирикутника XMAN.
Z. DCA = Z ХМА = 90 °, Z DCB = Z. DAB, Z. XMN = Z_ XAN.
Отже, Z_ DCB = Z- XMN і Z. ВСЛ = Z. NMA, тобто відрізки MN і ВС паралельні.
Достатність. Доведемо, що коли відрізок МN паралельний відрізку ВС, то центр О кола, описаного навколо трикутника ЛВС, належить відрізку АХ. Продовжимо відрізок АХ до перетину з описаним колом в точці D і доведемо, що точка О належить цьому відрізку. Оскільки MN || ВС, то трикутники AMN і ЛСВ гомотетичні. В гомотетичних колах, описаних навколо цих трикутників, відрізки АХ і AD — діаметри. Отже, твердження задачі доведено.
Задача 9. Площа S трикутника ЛВС обчислюється за формулою
S = -^MN-AF, (13.2)
де AF — хорда кола, описаного навколо трикутника ЛВС, причому відрізки AF і MN перпендикулярні. Довести.
Доведення. Доведемо спочатку подібність трикутників САХ і FAB (мал. 13.3). Щоб довести рівність відповідних кутів, опишемо навколо чотирикутника ANXM коло. Z_ МАХ = Z. MNX, Мал. 13.3
6
83


як вписані кути, що спираються на одну дугу, а /_ FAB = Z_ MNX, як кути із взаємно перпендикулярними сторонами, Z_ACX = = Z. AFB. Отже, подібність трикутників доведено. Із подібності випливає, що AB-AC = AX-AF, або -^-ЛВ-ЛС-біп А = — АХХ X ЛЛ-зіп А.
За формулою (13.1) ЛХ-sin А = MN, Отже, S = -у MN-AF, що й треба було довести.
Задача 10. Щоб точка X збігалася з серединою відрізка ВС точкою Мі, необхідно і достатньо, щоб МХ-АС = NX-AB. Довести.
Доведення. Необхідність. Нехай точка X збігається з точкою Мі. Тоді трикутники АВМ\ і ACM і рівновеликі, а отже, MlM-AC = MlN-AB.
Достатність. Нехай ХМ-АС = XN-АВ. Тоді трикутники АВХ і АСХ рівновеликі, а оскільки у них висота, проведена з вершини Л, спільна, то ВХ = СХ. Таким чином, точка X збігається з точкою М|.
Задача 11. З усіх трикутників XMN найбільшу площу має трикутник M\MN, де Мі — середина сторони ВС.
Доведення. Позначимо Sx — площу трикутника XMN. Нехай ВХ = х, тоді СХ = а — х (а — довжина сторони ВС).
Звідси
$х = ~2~ ХМ ‘ XN • sin (180 0 — А) = х(а — х) • sin А • sin В ■ sin С.
Оскільки х + (а — х) = а, то найбільшого значення площа набуває при х = а — х, або х = -^~. Отже, це буде трикутник M\MN.
Позначимо знайдену площу Q і далі будемо застосовувати це позначення.
Задача 12. Довести, що коли точка X збігається із серединою відрізка ВС точкою Мі, то площа трикутника M\MN дорівнює:
Q = -L sin2 Л-S, (13.3).
де Л — величина кута ВАС, S — площа трикутника ABC.
Доведення. Позначимо hb і hc — висоти, проведені з вершин В і С, Ь — величина сторони АС. Тоді
Q = ~2~MiM-MiW-sin (180 ° — А) = hb-hc-sin А =
о
1 h ь • b ' ч а 1 . о л _
= -J—2 Sln ~ Slr*2 * •$.
Задача 13. Довести, що площа трикутника M\MN не більша за —S, де З — площа трикутника ABC.
84


Доведення. За формулою (13.3) 5-ИіЛ<№ ~ sin2i4-S.
Але sin4<l, тому SMimn -^-S.
Задача 14. Маємо множину трикутників площею S із спільною стороною ВС. У кожному з таких трикутників можна побудувати трикутник M]MN. Довести, що в прямокутному трикутнику трикутник M\MN має найбільшу площу з усіх трикутників цієї множини.
Це випливає з формули (13.3).
Задача 15. Довести, що з усіх трикутників з даною основою ВС і даним кутом при вершині у випадку, коли X збігається з М, рівнобедрений має найбільший відрізок MN.
Доведення. На відрізку ВС будуємо сегмент, який містить кут ВАС=А, і доповнюємо його до кола з центром О (мал. 13.4). Порівняємо відрізки MN і M'N' (на малюнку вони не показані) відповідно у рівнобедреному трикутнику ABC і різносторонньому А[ВС\ MN = AAfisin A, M'N' = AjAfisin А. Покажемо, що АМі^АїМ]. Справді, оскільки ОАі = ОА, ОАі + ОМ] = АМі і ОАі + ОМ] АіЛїі, то AMi^AjM], отже, MN^M'N'.
Задача 16. У трикутнику ABC точки Мі, М2, N] і N2 — проекції середин Хі і Х2 сторін АС і АВ на дві інші сторони. Щоб відрізок M\N] дорівнював відрізку МгМг, необхідно і достатньо, щоб трикутник ABC був або рівнобедреним (АС = АВ), або квадрати його сторін складали б арифметичну прогресію (ВС — середня за величиною сторона трикутника ABC). Довести.
Доведення. Необхідність. Нехай M\N\ = M2N2 (мал. 13.5), тоді за формулою (13.1) маємо:
85


або
ть sin С
тс sin В
Враховуючи формулу медіани, маємо:
2а2 + 2с2 — *2 _ с2 2а2 4- 262 — с2 — ‘б’’’
або
2а\Ь2 - с2) = Ь4- с4, (Ь2 - с2) (2а2 - (Ь2 + є2)) = 0, звідки Ь = с, або 2а2 = Ь2 + с2.
Задача 17. Щоб точка X збігалася з основою висоти АН\ трикутника ABC, точкою Н\, необхідно і достатньо, щоб
МН = 4-- (13.4)
К
Довести.
Доведення. Необ/іідність. Нехай точка X збігається з точкою Н\. Діаметр кола, описаного навколо чотирикутника ANXM (мал. 13.1), дорівнює АН\ = ha. Тоді
MN = /iasin А = ~= 4.
u Zz\ і\
Достатність.
MN
- у JY11V о 2S ,
sin А /?«5ІпД а а'
S
а це означає, що точка X збігається з точкою Н\.
Задача 18. Щоб точка X збігалася з точкою Н\, основою висоти, опущеної з вершини А трикутника ABC, необхідно і достатньо, щоб Z_ AMN= Z_ ABC. Довести.
Доведення. Необхідність. Нехай точка X збігається з точкою Н\. Опишемо навколо чотирикутника AMXN коло (мал. 13.6).
Кути AMN і AXN рівні, як вписані. Але X. AXN = Z. ABC (доведіть!). Отже, Х_ AMN = = X. ABC.
Достатність. Отже, дано, що Х_ AMN = В, X- NXB = 90 ° — В, а оскільки Л AXN = В, то X- АХВ = 90 °. Отже, точка X збігається з точкою Н\.
Задача 19. Щоб точка X збігалася з точкою Н\, необхідно 86


і достатньо, щоб точки В, С, Л4, W належали одному й тому самому колу. Довести.
Необхідність. Доведемо, що навколо чотирикутника MNBC можна описати коло, якщо точки X і Н\ збігаються.
Справді, Z. AMN = Z. ABC = В (задача 18). Отже, / CMN + Z- NBC = 180 ° — В + В = 180 °, а це означає, що твердження задачі доведено.
Достатність. Нехай точки В, С, М і N належать колу. Доведемо, що Z- АХВ = 90 °. Позначимо /_ XMN = ф (мал. 13.6). Тоді ЛХДВ=ф і 90 ° + ф + В = 180 °. Отже, Л АХВ = = 90°, тобто точки X і Н] збігаються.
Задача 20. Нехай О — центр кола, описаного навколо трикутника ABC. Довести, що необхідною і достатньою умовою для того, щоб точки X і Н\ збігалися, є перпендикулярність прямих ОА і MN.
Доведення. Необхідність. Нехай точки X і Н\ збігаються (мал. 13.7). Доведемо перпендикулярність прямих ОА і MN. Точку їх перетину позначимо D. Обчислимо кут MDA. У трикутнику MDA Z_ MDA = 180 ° — (Z_ AMD-\~ Z- MAD). Але Z_ AMD = В. Кут МАО знайдемо з рівнобедреного трикутника АОС: Z. МАО = 90° — В. Отже, Л MDA = 180 ° — (В + + 90° —В) = 90°, а це означає, що відрізки MN й АО — перпендикулярні.
Достатність. Нехай ЛЛ4ВА = 90°. Тоді Z_AMD = = 90 ° - Л MAD = 90 ° — (90 ° — В) = В.
Опишемо навколо чотирикутника ANXM коло. Оскільки Z. AXN = Z. AMN = B, то Z. AXN + Z NXB = В + 90 ° - В = = 90°, тобто точки X і Н\ збігаються.
Задача 21. Нехай точка X збігається з основою висоти АН\, точкою Ні. Довести, що відрізок MN ділить площу S трикутника ABC навпіл тоді і тільки тоді, коли центр О кола,
описаного навколо трикутника ABC, належить цьому відрізку.
Доведення. Необхідність. Нехай площа трикутника AMN дорівнює -уЗ. Тоді MN-AK = S (АК — висота трикутника AMN). Враховуючи формулу (13.4), маємо -^-Х XAK=S, звідки А/(=/?. Отже, точка О збігається з точкою /С . Достатність. Нехай точка О належить відрізку MN. Згідно з задачею 20, відрізки MN і ОА перпендикулярні,
Мал. 13.7
87


а отже, Samn = ±MN-OA = ± ^-.R = -Ls.
Задача 22. У гострокутний трикутник ABC вписані трикутники XMN. Довести, ЩО де рх—півпериметр будь-якого
з цих трикутників, a M\N[ —довжина відрізка MN у разі, якщо точки X і Н\ збігаються.
Доведення. Справді, якщо точки X і Н\ збігаються, то 5
M\N\ = Отже, довжина цього відрізка дорівнює півпериметру ортоцентричного трикутника (с. 10, формула (2.1)).
Задача 23. Нехай точки X і Н\ збігаються. Довести, що з усіх трикутників з даними основами і кутом а при вершині рівнобедрений має найбільший відрізок MN.
Доведення. На спільній основі ВС (мал. 13.8) побудуємо сегмент, який вміщує кут а, і доповнюємо його до кола. Порівняємо відрізки MN і M'N' у рівнобедреному трикутнику ABC і нерівнобедреному трикутнику А\ВС (на малюнку вони не показані). За формулою (13.1)
MiV = X//i-sin a, M'N' = A i//2-sin а.
Оскільки sin а—величина стала, а АН і Л1Я2, то MNZ^M'N'.
Задача 24. Якщо найменша довжина відрізка MN дорівнює найменшій довжині відрізка, який ділить площу 5 трикутника ABC пополам, то S = 2tg-y/?2, де R — радіус кола, описаного навколо трикутника ABC. Довести.
Доведення. Ми довели (с. 72), що відрізок найменшої довжини, який ділить площу трикутника ABC пополам, дорівнює л/bc(l — cos Л). Отже,
Мал. 13.8
MN2 = Ьс (1 — cos Л-) = = 26с sin2 та
■^=2bc sin2^-,
або
S2 sin2 Д-
— Q.4
R2 ~~ 4 sin А •
Остаточно маємо:
S = 2/?2 tgA-
Задача 25. Довести, що коли в прямокутному трикутнику 88


АВС (А ВАС = 90°) S = -у- (a=BC), то найменша довжина
відрізка MN дорівнює найменшій довжині відрізка, який ділить площу трикутника пополам.
Доведення. Це випливає із задачі 24.
Задача 26. Нехай точки Х_ і Н\ збігаються. Довести, що коли висота АН\ дорівнює /?д/ 2, де R — радіус кола, описаного навколо трикутника ABC, то необхідно і достатньо, щоб відрізок MN ділив площу трикутника ABC пополам.
Доведення. Достатність. Нехай SAMN = -y-S.
Оскільки &AMNco ЛАВС (див. задачу 18), то Sa^n- = = _L
о ґіа 2
де h] — відповідна висота трикутника AMN. Враховуючи задачу
R2 1 /—
21, маємо: h\ = О А = /?. Отже, -гт= -тг, звідки ha = /?л/ 2 .
Ііц 2 *
Задача 27. Нехай точки X і Н\ збігаються. Довести, що точки М, М\, N\, N належать одній і тій самій прямій (Мі і Afi — проекції точки Н на дві висоти трикутника ABC).
Доведення. Доведемо, що Z. MMiAZi = 180° (мал. 13.9). Опишемо коло навколо чотирикутників СММ\Н\ і H\M\HN\ (Н — ортоцентр трикутника ABC). Тоді Z_ ММіС = Z МН\С = =90° — С, Z. HiMiNi = Z_ H\HN\ = С. Отже, Z. MMjA/j = = Z MMjC+Z. CMrfi + A //iMi/V1 = 90°-C + 90° + C= 180°. Аналогічно доводиться, що Z_ M\N\N = 180°, а це означає, що точки М, Mi Afi, TV належать одній і тій самій прямій.
Задача 28. Щоб відрізок МА ВС для випадку, коли точки і достатньо, щоб різниця кутів С 90 °. Довести.
Доведення. Необхідність. Відомо, що Л NDH] = = 90° (мал. 13.10), де D — точка перетину прямої • MN і прямої ВС. Опишемо навколо чотирикутника AMNH\ коло. Маємо:
A NDH\ = Z. DNH\ + Л NH\D.
Але Л DNH\= Z_ NCD=\W°-
— С, a Z_ NH\D = Л DMHx = = В. Отже, 90 ° = 180 ° - С + + В, С — В = 90 °
Достатність. Доведемо, що Z. NDH\ = 90 °, якщо С —
— В=90°. Нехай Z_NDH\=x. Тоді х= 180°—(Z. M//1D + + ^DMH{). Але гСМЩ) = =90°-В, Z_DMH\ = Z_NAHy =
був перпендикулярний до прямої X і Н\ збігаються, необхідно
і В трикутника ABC дорівнювала
Мал. 13.9
89


= 90° — (180° — С) = С — 90°. Отже, х = 180 ° — (90 ° — В + 4- С — 90°)= 180° — (С — В) = 90°.
Задача 29. Щоб точка X збігалася з точкою L\ — перетином бісектриси кута ВАС і сторони ВС, необхідно і достатньо, щоб Z. МН\А = 2 NH\A. Довести.
Доведення. Необхідність. Нехай точки X і L\ збігаються (мал. 13.1). Точка Н\ належить колу, описаному навколо чотирикутника AML\N. Оскільки дуги AM і AN рівні між собою, то /- МН\А = /- NH\A.
Достатність. Нехай Z. МН\А = Z_ NH\A. Отже, дуги AM і AN рівні між собою. Також рівні між собою й дугц ML\ і L\N. Отже, Z_ MAL\ = Z_ NAL\, тобто точки X і L\ збігаються.
Задача ЗО. Щоб точка X збігалася з точкою L\ — перетином бісектриси кута ВАС і сторони ВС, необхідно і достатньо, щоб Z_ МН\С = Z NHiB. Довести.
Доведення. Скористаємося результатами задачі 29.
Задача 31. Нехай, точки X і L\ збігаються. Довести, що з усіх трикутників з даними основами і кутом а при вершині рівнобедрений має найбільший відрізок MN.
Доведення. На спільній основі ВС (мал. 13.11) побудуємо сегмент, який містите кут а, і доповнимо його до кола. Порівняємо відрізки MN і MiNi відповідно у рівнобедреному трикутнику ABC та нерівнобедреному трикутнику А\ВС (на малюнку вони не показані). Позначимо L\ — точку перетину ВС і A\W.
Маємо: ММ = ЛСі-5Іпа, M\N\ = A\L\-sin а.
Покажемо, щоД£і>ДіМ. Дійсно, AW^ А\W, WL\^LXW.
Задача 32. Якщо точка X збігається з точкою L\ — перетином бісектриси кута ВАС і сторони ВС, то необхідною і достатньою
90


умовою того, щоб точка І (інцентр) належала відрізку MN, є рівність
2p-sin2 — = а,
де р — півпериметр трикутника ABC.
Доведення. Необхідність. Оскільки точка / (мал. 13.12) належить відрізку Л4М, а також бісектрисі AL\, то вона є точкою перетину відрізків MN й AL\. Отже, Л4/ = -у MN. Маємо:
г == ЛІ/«cos -у ; (1)
Л4/ = A. MN = AL1 • sin А = -^--^-ccos sin А ■
Отже, MI =2S- 6 + с • cos-y. (2)
Підставимо вираз (2) у вираз (1). Маємо.
2S 2 А , S 2S 2 А
Г = -г~1 cos -S-. а°° = А _1_ 7 ‘cos “о"
b + с 2 ’ р Ь + с 2
b + с= 2p-cos2 ,
2р — а = 2р • cos2 -у,
2р (1 — cos2 -у) = а,
звідки 2р • sin -у = а.
91


Достатність. Знаходимо довжину перпендикуляра ІК, де К—проекція точки / на сторону АС (мал. 13.12) і доведемо, що ІК=г, якщо 2p-sin2-^=a (/ — точка перетину відрізків MN і AL).
А I A о A 2prcos24-
//<=M/-Cos4=4^.cos4=^|t.cos24=^^.
Але за умовою 2p-sin2-^-= а, або 2р(1—cos2-^-)= а, або 2р — а = 2р • cos2-^-.
2pr-cos2^
Підставляючи останню формулу у вираз //< =—2р — а—* маємо:
Задача 33. Довести, що коли точка X збігається з точкою Li, перетину бісектриси кута ВАС зі стороною ВС, то площа S обчислюється за формулою
S = 4 MN-А
де Wi — точка перетину бісектриси кута ВАС з описаним навколо трикутника ABC колом.
Доведення випливає з формули (7.1) або з (13.2).
Задача 34. У гострокутному трикутнику ABC точки Лїь УУ| І ЛІ2, Л^2—проекції точок перетину бісектрис кутів ABC і АСВ зі сторонами АС і АВ на дві інші сторони. Довести, що для того, щоб відрізок дорівнював відрізку M2N2,
необхідно і достатньо, щоб трикутник ABC був рівнобедреним (АВ = АС).
Доведення. Необхідність. Позначимо бісектриси кутів В І С через /1 І І2. Оскільки M\N\ = M2N2. то 1\Ь=І2С, де b і с — довжини сторін АС і АВ. Враховуючи формулу (4.1) для бісектриси, маємо:
2ас В . 2ab С
—: • COS — - Ь = —- • COS -х- • С
і + с 2 а + b 2
або
а + с
cos-^ 4sin А - -cos А
’ аб° 4sinAi^.cos 4 ~
С cos"S
В ' с05 2-
92


Дістаємо cos А- у-— = cos Л 2 * тобто В=С (за умовою трикутник ABC — гострокутний).
Задача 35, Трикутник ABC вписаний в коло. Діаметри BF\ і CF2 перетинають сторони АС і ВА в точках D\ і £>2. Кожна з цих точок проектується на дві інші сторони. Дістанемо точки Mi, Ni і М2, ^2. Щоб відрізок M\N\ дорівнював M2N2, необхідно і достатньо, щоб трикутник ABC був рівнобедреним або /_ А = 60 °. Довести.
Доведення. Необхідність.
Mj/Vi = BD\ -sin В\
де Ф= ZBD.C;
мал. 13.13).
Але ер = 90 ° + А — С. Отже,
.... йь-sin В
М і /V і = ( л /-\ ■
1 1 cos (Л — С)
Аналогічно,
.. .. /іс-sinC
М^2~ COSH-В) •
Таким чином,
hb • sin В • cos (А — В) =
= йс-sin C-cos(A — С),
звідки
hb sin C-cos (Л — С) hc sin В -cos (Л — В)
sin С с Враховуючи, що -^-g- = т маємо:
hb-Ь-cos (A — B) =
= hc-c-cos (A — C), cos (A — B) = cos (A — C), звідки В = C, або А = 60 °.
Мал. 13.13


ТЕТРАЕДР
14. 	КУТИ, РЕБРА
І 	ГРАНІ ТЕТРАЕДРА
Задача 1. Визначити залежність між кутами бічних граней тетраедра, прилеглими до сторін основи.
Р о з в’ я з а н н я. У тетраедрі DABC (мал. 14.1) позначимо довжини ребер DA, DB, DC через с, а, Ь.
Позначимо кути:
Z_ DAC = ссі, Z_ BAD = ос2, Z ABD= Рь Z CBD = p2, Z_ BCD = yi, Z_ ACD = y2.
За теоремою синусів маємо:
sin p2 _b_
sin ті a ’
sin a2 a sin y2 c sin Pi c ' sin ai b '
Перемножимо ці рівності. Дістанемо:
sin a2 sin T2 sin p2 I
sin ai sin Pi sin Yi
Задача 2. Довести, що відношення синусів плоских • кутів будь-якого із тригранних кутів тетраедра дорівнює оберненому відношенню синусів відповідних лінійних кутів двогранних кутів тетраедра.
Доведення. У тетраедрі DABC (мал. 14.2) DO — висота тетраедра. Кути DEO і DFO — лінійні кути двогранних кутів
94


Мал. 14.2
між відповідними боковими гранями і основою ABC. Позначимо / DFO через х і звернемо увагу на те, що коли точка О міститься
поза площиною кута ВАС, то результат не зміниться, оскіль- ки sin (180 ° — х) = sin х. Позначимо X. DCB = а, Z_ ACD = у, X- DEO = у. Має-  DO =
мо DO = DF sin х, = DE sin у, звідки
DF sin у
DE sin x
З трикутників DFC маємо:
* DF sin а
і DEC
DE sin у ’
отже,
sin a
sin у sin х
Задача 3. Гострі кути а, р, у є плоскими кутами тригранного кута. Знайти його двогранні кути.
Розв’ язання. Перетнемо тригранний кут із вершиною D площиною MNP, яка перпендикулярна до ребра DM (мал. 14.3). Позначимо Z_ PMN через ф. Виразивши відрізок PN з трикутників MPN і DPN, за теоремою косинусів маємо:
MP2 + MN2 — 2 • МР • MN cos ф = DP2 + DN2 — 2DP -DN cos а.
Нехай MD = 1. Тоді МР= tg р, MN = tg у.
95


DP = —Ц- , DN = , DP2 — MP2 = DN2 - MN2 = 1.
COS p cos у
Тому
n j n і 2 cos а л
2 	tg 0 • tg у • cos ф = з 2,
b r b 1 v cos [J-cos у
cos a — cos P-cos у ... .
COS ф = —з— -. (14.1)
T sin p-sin у v '
Аналогічно знаходимо косинуси інших двогранних кутів.
Задача 4. Довести, що в тетраедрі:
1) не може бути більше ніж чотири тупих або прямих плоских кутів;
2) хоча б при одній вершині тетраедра всі його плоскі кути гострі;
3) якщо всі двогранні кути тетраедра гострі, то й всі плоскі кути також гострі. Чи справедлива обернена залежність?
Розв’язання. 1) Оскільки в тетраедрі чотири грані, а у трикутнику може бути тільки один тупий або прямий кут, то твердження задачі доведено.
2) Нехай при всіх вершинах тетраедра один з плоских кутів буде прямим чи тупим. Оскільки сума двох плоских кутів тригранного кута більша від третього, то сума трьох плоских кутів, які розглядаються, буде більшою за 180°, а сума всіх плоских кутів тетраедра більша за 720°. Але це неможливо, оскільки їх сума дорівнює 720°.
3) Розглянемо двогранні кути <р>, ф2, фз тригранного кута, плоскі кути якого а, 0, у. За формулою (14.1)
СО5фі =
cos a — cos p cos у
(1)
sin p siny ’
СОЧ (Do •
cos p — cos a cosy
(2)
sin a sin у '
PGQ ГЛо —- -
cos у — cos a cos p
(3)
sin a sin p
Оскільки за умовою кути ері, ф2, фз — гострі, то кути а, 0, у не можуть бути одночасно тупими, оскільки ліві частини рівностей (1), (2), (3) —додатні, а праві, якщо кути тупі,— від’ємні.
Припустимо, що кути а і 0 — тупі, а у — гострий. Тоді, якщо 0, то
cos а — cos 0 cos у < cos а — cos 0 < 0
і, відповідно до рівності (1), COS фі < 0.
Якщо а<0, то з рівності (2) випливає, що созф2<0, а це неможливо, ОСКІЛЬКИ Ф1 І ф2 — гострі кути.
96


Якщо ж припустити, що серед кутів а, р, у тільки один кут тупий, наприклад а, а решта гострі, то, згідно з рівністю (1), cos(pi<0, що також неможливо. Отже, кути а, 0, у — гострі.
Обернене твердження неправильне. Справді, розглянемо тетраедр DABC, всі ребра якого дорівнюють одиниці, крім ребра АВ, яке дорівнює 1,3. Тоді всі плоскі кути будуть гострими, а двогранний кут при ребрі CD дорівнюватиме cos ер =
0,155 — 0,25 , п ‘ пло
= < 0, тобто ф >> 90 .
0,/□ т
Задача 5. Довести, що коли всі двогранні кути тетраедра рівні між собою, то тетраедр — правильний.
Доведення. Нехай фі і фг — двогранні кути тригранного кута, плоскі кути якого а, 0, у.
Покажемо, що
COS фі — COS ф2 =
(cos (а + 0) — cos 7) sin (а — 0) sin а sin 0 sin у
Справді, за формулою (14.1) маємо:
cos а — cos 0 cos 7 cos 0 — cos a cos 7
COS ф! — COS ф2 = ■ Q . L : L
v Y sin 0 sin 7 sin a sin 7
sin a cos а — cos 0 sin g cos 7 — sin 0 cos 0 -|- cos a cos 7 sin 0
sin a sin 0 sin 7 sin a cos а — sin 0 cos 0 — cos 7- sin (a — 0) sin a sin 0 sin 7
sin (a — 0) cos (a + 0) — cos 7 sin (a — 0) sin a sin 0 sin 7
sin (a — 0) (cos (a + 0) — cos 7)
sin a sin 0 sin 7
Оскільки a+0>y й а+0 + у<2л, то cos (a + 0) =/= cos y. Отже, якщо фі = ф2, то а=0. Таким чином, усі плоскі кути при вершині рівні між собою. Доведення аналогічне для кожної вершини, а отже, всі грані тетраедра — правильні трикутники.
Задача 6. У тетраедрі три бічні ребра рівні між собою і площі трьох бічних граней також рівні між собою. Довести, що в основі тетраедра лежить рівнобедрений трикутник.
Доведення. Позначимо аі, аг, аз — плоскі кути при вершині, з якої виходять рівні ребра тетраедра. Якщо площу кожної грані записати у вигляді півдобутків довжин ребер на синуси кутів між ними, то дістанемо рівність:
sin ai = sin a2 = sin аз.
Звідки ai = аг, або ai = аз, або аг = а3, а це означає, що дві
7 0-172
97


з 	бічних граней рівні між собою, а отже, рівні між собою дві сторони основи. Твердження доведено.
Задача 7. Плоский кут при вершині правильної трикутної піраміди DABC дорівнює а. Знайти:
1) кут нахилу ребер до площини основи;
2) кут між бічною гранню і площиною основи;
3) кут між бічними гранями;
4) кут між мимобіжними ребрами.
Розв’язання. 1) Нехай О — проекція вершини D на основу піраміди АВС (мал. 14.4). Позначимо сторону основи а, /_ DBO = y. Тоді з трикутника DBO\
DB = — =
cos z. DBO 3 cos ф ■
З трикутника DA\B (Лі — основа висоти DA\ грані DCB) маємо:
Отже,
звідки
DB = —
sin Z. A\DB
З cos ф
а
2sin і-
а
; cos ф п • а '
2 sin -ж-
2) Позначимо шуканий кут DAiO через £. Тоді з трикутника DAiB (мал. 14.4):
DA, = 4 ctg
З трикутника DOA\\ звідки
cos Р = з" ~ 1 0 = arccos(—tg -y) .
3) Знайдемо кут між гранями ADC і BDA. Це буде кут ВЕС (мал. 14.4) (СЕ A. AD, BE J_ AD). Позначимо його через у. З трикутника ЕА\С'.
ЕС =
а
2 sin
а з трикутника АЕС\ EC = a cos
98


Звідси маємо рівняння: cos = ! . Звідки
2 sin -3J-
si„i=——
к 2 cos -S-
тобто 2
7=2 arcsin ( !-—) .
' 2 cos -?£-
4) 	Проведемо висоту осно- Мал. 14.4
ви ААі і висоту піраміди DO
(мал. 14.4). Ребро СВ перпендикулярне до відрізків ААі і DO, а отже, і до площини ADA\. Таким чином, ребра* СВ і AD перпендикулярні.
Задача 8. Знайти залежність між двогранними кутами правильної трикутної піраміди.
Р оз в’ язання. Позначимо площу основи піраміди DABC через S (мал. 14.4), площу бічної грані Si, лінійні кути двогранних кутів /_ ВЕС =у, Z. DA\A = 0. Спроектуємо бічні грані на основу піраміди. Тоді S = 3Si-cos0. Спроектуємо тепер грані на одну з бічних граней. Тоді Si = 2Si cos 7 -f- S cos p. Із цих рівностей маємо:
= 3 cos р, 1 = 2 cos 7 + 777 cos 0’ звідки
2 cos 7 + 3 cos2p = 1.
Мимобіжні ребра тетраедра с І С\.
Задача 9. Довести, що = + + + -
— а2 —а2), де AG і N2 — середини ребер ВС і AD.
Доведення. Розглянемо у тетраедрі DABC (мал. 14.5) медіани трикутників DBC, ABC, AN'D.
Тоді за формулою (3.1) маємо:
DABC позначимо а і ai, b і Ь\,
99


Л7 Лт2 2(Л/У? + D/V?) — а? б2 + ді + с2 + Сі — а2 — а?
/V і /V 2 = — —’—
4
4
Задача 10. Довести, що кут ер між мимобіжними ребрами а й а\ тетраедра DABC обчислюється за формулою
■ <'«)
Доведення. Побудуємо у тетраедрі DABC кут <р (мал. 14.6). Для цього проведемо середні лінії трикутників ABC і ADC L\Li, L1L3 відповідно.
З трикутника L\L2L3 маємо:
ЛзН = (-^-)2 + (^-)2 - 2 2-COS ф,
але ^задача
L3Ll = -^(а2 + а? + б2 + Ьі — с2 — с?) -
Отже
І- &2 - 6? + с2 + с?| cos Ф 2^1
Задача fl. Довести, що в тетраедрі DABC:
1) якщо ребро а перпендикулярне до ребра щ, а ребро о перпендикулярне до ребра 6і, то ребро с перпендикулярне до реб2)Э якщо а2 + а?=62 + 6і = с2 + сь то ребра а й аь с й Ci, b й 6і попарно перпендикулярні;
3) якщо а = аі, b = Ь\, с = Сі, то
|с2 - 62І
COS ф = •
Розв’язання. Доведемо твердження 1. Враховуючи умову
і формулу (14.2), стверджуємо, що с2 + с2{ = Ь2 + ІЇ\ а2 + а2х = — Ь2 4” Ь2.
Нехай а— кут між ребрами с і Сі- Тоді
Мал. 14.6
І— а2 — а? + b2 + b2\ п cos а= 2^ °’
отже ребра с і С\ взаємно перпендикулярні.
Твердження 2 і 3 випливають із формули (14.2).
100


Задача 12. Довести, що об’єм тетраедра обчислюється за формулою
V = -5-aa\d sin ср (14.3),
де а й а\ — мимобіжні ребра; d — відстань між ними; ср—кут між цими ребрами.
Доведення. Нехай в тетраедрі SABC ВС = а, ЗЛ = аі. Доповнимо його до паралелепіпеда з гранями BMNC і DESA (мал. 14.7). Тоді кут між мимобіжними ребрами ЛЗ й ВС є кутом між ребрами паралелепіпеда ВС і 2VC, тобто Z. BCN = ер.
Відрізки ЛЗ і ВС лежать в різних площинах, тобто відстань d між ними є висотою паралелепіпеда з основою BMNC. Але об’єм тетраедра дорівнює одній шостій об’єма побудованого паралелепіпеда:
V = -5- dSBMNC = -5- daa} sin <р,
що й потрібно було довести.
Задача 13. Вздовж двох прямих, які схрещуються, переміщаються два відрізки. Довести, що об’єм тетраедра з вершинами у кінцях цих відрізків не залежить від розміщення останніх.
Доведення випливає з формули (14.3).
Задача 14. Довести, що коли відстані між мимобіжними ребрами тетраедра гіі, гіг, гіз, то об’єм тетраедра не менший ніж 4- гіігіггіз. О
Доведення. Доповнимо тетраедр DABC до паралелепіпеда APCEMBND (мал. 14.8). Позначимо Ил і V — відповідно об’єми паралелепіпеда і тетраедра. Тоді V = -у Vn- Позначимо відстань між ребрами АС й BD, АВ й CD, AD та ВС відповідно rij, гіг, гіз. Позначимо висоти паралелограма АРСЕ, опущені на сторони АР й PC, через h\ і /іг- (На малюнку показана висота ЕН\ = h\). Зрозуміло, що висоти паралелепіпеда дорівнюють гіі, гіг, гіз.
Мал. 14.8
101


Маємо:
q «І«2 у j h\il2
^АРСЕ — Sin /_ рае ’ Vn ~~ a' ' sin Z. PAE ’
h\h2
Проведемо висоту паралелепіпеда £Я=гіг. З прямокутного трикутника ЕН\Н h\^d2. Аналогічно Отже, йійг^яМз
і 5ІПУрл£>^3' ТомУ Vn > dtd2d3, did-Ж.
Задача 15. У правильній трикутній піраміді плоский кут при вершині дорівнює а, відстань між двома мимобіжними ребрами дорівнює І. Знайти об’єм піраміди.
Розв’язання. У піраміді DABC (мал. 14.4) проведемо переріз через висоту DO і висоту основи ААі. Дістанемо трикутник DAAi. У ньому висота буде відстанню між ребрами ВС і AD. Маємо Z_BDC=a, Z_DAO = y. Ми довели (задача 7), що
2 . а
COS ф = —г=- Sin .
л/3 2
З трикутника AA\E маємо:
sin <p 2
а. Тоді
3 -
АА,
Позначимо ВС через
І2
$АВС~ 4 ~
DO = AO•tgq>= , b T 3 cos cp
у = 1 , /2 2/ = 2/3
3 <3 sin 2 tp 3 cos <p 9 sin2cp cos ф
3 sin 2 cp 2/
Далі маємо:
sin2 ф = 1 — cos2 ф = 1 у- sin2 "5" = “з" (3 — 4 sin2 -g-) =
За
(з sin-у
З sin -?Г
3sin-|-
fl2 У~з
Остаточно дістаємо:
2/3-3 sin-S--^3 J 3a
— = — /3 cosec a 3
_ -3g—-
9 ~y3 • sin-^" • 2 sin
102


Задача 16. Знайти відстань між мимобіжними висотами DD\ й ААі граней правильного тетраедра DABC, ребро якого дорівнює а.
Розв’язання. У тетраедрі DABC проведемо висоти ААі й DD] граней ABC та ADC (мал. 14.9).
Розглянемо тетраедр DAiADi, об’єм якого Q. За формулою (14.3) маємо:
Q = -±-DDi -ААі •/ sin ф, де І — відстань між ребрами DD\ й ААі, а ф — кут між цими ребрами. В той самий час Q = -5-
О
Мал. 14.9
S' -DO, де S' — площа трикут¬
ника AA\D\, DO — висота тетраедра DABC. Але S'= -^-S =
= а 3 (S — площа грані), a DO = a~yj -|- .
Отже,
Q = ~[2 Sa
(1)
Проведемо відрізок D\E, паралельний АА]. Тоді Z-ED\D = ^>. З трикутника DEA\:
de* = ^
ип 16 .
З трикутника DEDi за теоремою косинусів маємо:
13а2 , , /ад/"з \2
- DE2 + £)£)? + £)і£2 4 ) 1
COStp- 2DD,-D,E g/j З 6 •
Z 2 *“4
лі 35
Тоді sin ф = —. Отже (за формулою (14.3)),
г) 1 ал/~^ . л/35 /лх
Q ~~ 6 2 2 1 6 *
Порівнюючи вирази (1) й (2), дістаємо:
103


15. 	ВИСОТИ ТЕТРАЕДРА. ОРТОЦЕНТРИЧНИЙ
ТЕТРАЕДР
Висоти тетраедра (або їх продовження), на відміну від висот трикутника, не обов’язково проходять через одну й ту саму точку.
Задача 1. Побудувати тетраедр, у якого дві висоти
не перетинаються.
Розв’язання. Розглянемо тетраедр DABC (мал. 15.1), у якого грань DAB перпендикулярна до грані ABC, ребро BD дорівнює ребру AD, а ребра ВС й АС не рівні між собою. Висота тетраедра DD\ належить грані ADB, а висота тетраедра СС] належить грані ABC. Оскільки трикутник DAB рівнобедрений (DA = DB), то точка D\ поділяє сторону АВ пополам, а точка С\ — ні, оскільки ЛС=#ВС. Отже, точки D\ і Сі не збігаються, тобто висоти DD\ і СС\ не мають спільних точок.
Задача 2. Побудувати тетраедр, у якого дві висоти перетинаються в одній точці, а дві інші — в другій.
Розв’язання. Розглянемо тетраедр DABC, у якого ребро DA перпендикулярне до грані АВС (мал. 15.2) і точка А спільна для висот DA і АНі. Висоти тетраедра ВН2 і СНз належать грані ABC і мають спільну точку Q, яка не збігається з точкою А.
Задача 3. Довести, що в тетраедрі, у якого протилежні ребра рівні між собою, але не перпендикулярні, чотири висоти не мають спільної точки.
Доведення. Припустимо, що висоти DH4 і СНз мають спільну точку Q (мал. 15.3). Проведемо в рівних гранях ABD і ABC висоти DD\ і СС\. Трикутники ABD і ABC розміщені так, що точки D{ і Сі не збігаються.
Прямі DH3 і СНі перетинаються у точці Е, що лежить на ребрі АВ. За теоремою про три перпендикуляри відрізки DE та СЕ перпендикулярні до ребра АВ, що неможливо.
Задача 4. Якщо одна вершина тетраедра проектується в ортоцентр протилежної грані, то решта вершин також проектуються в ортоцентри відповідних протилежних граней. Довести.
Доведення. Нехай у тетраедрі DABC вершина D проектується в ортоцентр Н4 грані АВС (мал. 15.4). Проведемо площину через ребро AD і висоту DH4. Дістанемо трикутник ADA\, причому відрізки ААі, DAi, AD перпендикулярні до ребра ВС. Проведемо висоту тетраедра АН\. Оскільки площини DBC і ADA і взаємно перпендикулярні, то висота АНі належить площині ADA\. Продовжимо відрізок СН\ до перетину з ребром BD у точці ЛЛ Покажемо, що точка Н\ — ортоцентр трикутника
104


Мал. 15.1
Мал. 15.2
DCB. Справді, оскільки ребра DB і АС взаємно перпендикулярні, то за теоремою про три перпендикуляри відрізок DB перпендикулярний до відрізка CW, а отже, точка Н\ —ортоцентр трикутника DBC.
Задача 5. Щоб одна з вершин тетраедра проектувалася в ортоцентр протилежної грані, необхідно і достатньо, щоб мимобіжні ребра були попарно перпендикулярні. Довести.
Доведення випливає із задачі 4.
Задача 6. Щоб дві висоти тетраедра перетиналися, необхідно і достатньо, щоб ребро, з кінців якого проведені ці висоти, було перпендикулярне до протилежного ребра тетраедра. Довести.
Доведення. Достатність. Доведення достатності випливає із задачі 4.
105


Необхідність. Застосуємо векторний метод. Нехай висоти, проведені з вершин D й С тетраедра DABC, перетинаються в точці Н. Тоді
АВ ^Cb = Xb(hD—~HC) = HD-AB - НС-АВ = 0,
тобто А В ± CD.
Задача 7. Щоб два мимобіжних ребра тетраедра були взаємно перпендикулярні, необхідно і достатньо, щоб основи висот, проведених з кінців одного з цих ребер на інше ребро, збігалися. Довести.
Доведення випливає із задачі 4.
Задача 8. Щоб чотири висоти тетраедра перетиналися в одній точці, необхідно і достатньо, щоб одна з вершин тетраедра проектувалася в ортоцентр протилежної грані. Довести.
Доведення. Необхідність. Доведення випливає із задачі 4.
Доведення. Достатність. Якщо одна з висот тетраедра проходить через ортоцентр основи, то мимобіжні ребра попарно перпендикулярні, і кожні дві висоти тетраедра перетинаються одна з одною (задача 6). Але чотири прямі, які не лежать в одній площині і попарно перетинаються одна з одною, мають одну спільну точку.
Тетраедр, у якого висоти перетинаються в одній точці, називається ортоцентричним, а ця точка — ортоцентром тетраедра.
Задача 9. Довести, що вершини правильної трикутної піраміди проектуються в ортоцентри протилежних граней.
Доведення випливає із задачі 4.
Задача 10. Один із плоских кутів при вершині тетраедра прямий, а висота, проведена з цієї вершини, проходить через ортоцентр основи. Знайти решту плоских кутів при цій вершині.
Розв’язання. Враховуючи задачу 4, а також те, що ортоцентр прямокутного трикутника збігається з вершиною, протилежною гіпотенузі, робимо висновок, що два інших кути також дорівнюють 90 °.
Задача 11. Висоти тетраедра DH^ і АН\ перетинаються в точці Н, а висоти С//3 і ВН2 — у точці Q. Довести, що відрізок HQ належить спільному перпендикуляру до ребер AD і ВС.
Доведення. Проведемо переріз через кожну із вказаних пар висот. Дістанемо трикутники ADK і BCL (мал. 15.5). Точка //4 лежить на відрізку АК і АК ± ВС (задача 6). Сполучимо точки К і L. Тоді KL-LAD.
Із задачі 7 випливає, що ВС ± AD. Отже, ВС-L AD й ВС-LAK. Отже, ВС — перпендикуляр до площини AKD, й тоді ВС ± KL. Таким чином, доведено, що KL — спільний перпендикуляр ребер AD і ВС.
106


Висоти тетраедра DH^ й АН\ є одночасно і висотами трикутника ADK. Тому точка Н належить висоті ЛХ. Так само з трикутника BCL доводять, що точка Q лежить на відрізку ^L.
Задача 12. У тетраедрі DABC ребро AD перпендикулярне до ребра ВС\ Z_ САВ = = Z- CDB\ площа перерізу, який проходить через ребро ВС і середину ребра DA, дорівнює S; довжина ребра DA дорівнює а. Знайти об’єм тетраедра DABC.
Розв’язання. Проведемо у гранях DBA й ADC з точок В та С висоти (мал. 15.6). Згідно із задачею 7, вони матимуть спільну точку Qi на ребрі DA. З точок А й D проведемо висоти в гранях ABC та CDB. За задачею 7 вони будуть мати на ребрі ВС спільну точку А і. В трикутниках ABC і CDB сторона ВС — спільна, протилежні кути рівні між собою і основи висот, проведених з вершин D і Л, збігаються (точка Лі). Отже, ці трикутники рівні між собою, тобто DB = = ВА, і висота BQ\ є медіаною трикутника DBA. Таким чином, ребро DA перпендикулярне перерізу BQiC, площа якого дорівнює S. Оскільки DQ\ = -у, то об’єм V тетраедра DABC дорівнює двом об’ємам тетраедра
DQ\BC, тобто У =
Задача 13. У тетраедрі DABC при вершині D три кути прямі. Вершина D проектується в точку Н на основу ABC. Довести, що S = ~ySi-S2, де S, Si, S2 — площі трикутників ADB, АСВ, АНВ відповідно.
Доведення. Протилежні ребра тетраедра DABC (мал. 15.7) взаємно перпендикулярні, отже, висоти граней ABC й DAB, проведені з вершин С і D, матимуть спільну точку Е на ребрі АВ (задача 7). Точка Н належатиме відрізку СЕ.
107


Позначимо Z. DEH = а. Тоді
5 = ^- cos а
(1)
Оскільки Z. CDE = 90 °,
_ DE_ _ 2S-AB _ З С05 а— СЕ 23,-ЛВ — 3, ’ ставимо це співвідношення (1). Маємо:
s = -ф., або S = VS1-S2.
то
Під-
висоти піраміди, проведеної з об’єм тетраедра.
Задача 14. У правильній трикутній піраміді DABC сторона основи ABC дорівнює а, відстань від вершини D до вершини Л, дорівнює Ь. Знайти
в
Розв’язання. Оскільки вершина А (мал. 15.4) проектується в ортоцентр В і трикутника DBC (задача 9), то за формулою (1.3) маємо:
DH\ = 2/?|cos (pl,
де <р= Z. CDB, R — радіус кола, описаного навколо трикутника CDB.
Позначимо А і середину сторони ВС. Оскільки sin<p = ^, cos <р = ^ , то tg <р = -2- •
Звідси
ф — ь ± -д/б2 4- а2
2 — а
(1)
Позначимо Z_DA\A = a, проекцію точки- D на основу ABC через Я4. Оскільки
то
— Ь ± у]а2 Ь2 од/ З
sin а =
108


DH< = 4 алАз tg a = ^V°2 + b/a* + b*
лЛб (— 6 ± д/а2 4- 62 )
об’єм піраміди, яка розглядається, дорівнює
у а3^/~2 .~у/ а2 — b2 ± b-\ja2 -f- b2
~ 24(— ±Vfl2 + b2)
Якщо ф<С-^-, то буде знак « + », якщо -^-<С<р<Сл;, то знак «—».
Задача 15. У ортоцентричному тетраедрі проведено три відрізки, кожний з яких перпендикулярний до двох протилежних ребер, а кінці відрізків належать цим ребрам. Довести, що:
1) ці відрізки перетинаються в ортоцентрі тетраедра;
2) ортоцентр тетраедра ділить ці відрізки, як і висоти тетраедра, на частини, добуток яких сталий;
3) кінці цих відрізків належать сфері.
Доведення. 1) Розглянемо переріз ADA\ (мал. 15.4), якому належать ребро AD і висота тетраедра DH^. Проведемо у трикутнику ADA\ висоту AiQi. Відрізок ЛіQі перпендикулярний до ребер AD й ВС, і йому належатиме ортоцентр тетраедра — точка Н, оскільки вона збігається з ортоцентром трикутника ADA\. Аналогічно доводиться належність цієї точки двом іншим відрізкам, перпендикулярним до відповідної пари мимобіжних ребер тетраедра.
2) Оскільки Z_ DQ\A\ = Z_ DH^Aі = 90 °, то точки D, Qi, //4, А1 належатимуть одному й тому ж колу. Отже,
Q1/7.//A, = DH-HHi.
Позначимо два інших відрізки, перпендикулярні до пар мимо- . біжних ребер Q2Bi і Q3C1 (на мал. 15.4 ці точки не позначені). Маємо:
Q3H-HCx = DH-HfU
Оскільки добуток DH-HHi для тетраедра DABC сталий, то твердження доведено.
3) Оскільки Q\H • НА\ = Q^H - НВ\, то точки Qb Q2i Лі, В\ належать одному й тому самому колу. Аналогічно точки Qi, Q3, А і, Сі також належать одному й тому самому колу. Отже, точки Qi, Q2, (?з, Аі, Ві, Сі належать сфері.
109


16. 	ПРЯМОКУТНИЙ ТЕТРАЕДР
Тетраедр, у якого кожний плоский кут при одній із вершин прямий, називається прямокутним. Ця вершина проектується в ортоцентр протилежної грані (с. 104).
Вважатимемо, що в тетраедрі DABC плоскі кути при вершині D — прямі.
Деякі властивості прямокутного тетраедра зручно доводити, якщо доповнити цей тетраедр до прямокутного паралелепіпеда. Спочатку розв’яжемо допоміж¬
ну задачу.
Задача 1. Нехай а, р, у — кути, утворені довільною прямою d з трьома взаємно перпендикулярними прямими. Довести, що
cos2 а + cos2 Р + c°s2 Т = 1 •
(16.1)
Доведення. Виберемо на трьох перпендикулярних прямих такі відрізки а, b і с, щоб діагональ паралелепіпеда з ребрами а, b і с збігалася з даною прямою d (мал. 16.1). Тоді
а = d cos a, b = d cos р, с = d cos у.
Враховуючи, що d2 = а2 + Ь2 + с2, маємо:
d2 cos2 а + d2 cos2 р + d2 cos2 у = d2,
звідки
cos2a + cos2 p + cos 2 у = 1.
Задача 2. Довести, що в прямокутному тетраедрі DABC вершина D, точка перетину медіан грані ABC і центр описаної навколо цього тетраедра кулі лежать на одній прямій.
Доведення. Доповнимо тетраедр DABC до паралелепіпеда (мал. 16.1). Зрозуміло, що цей паралелепіпед прямокутний. Центр кулі, описаної навколо паралелепіпеда, збігається з точкою перетину діагоналей паралелепіпеда, а також є центром кулі, описаної навколо даного тетраедра DABC. Покажемо, що діагоналі ED належить центроїд грані ABC. Нехай М\—середина відрізка АВ. Тоді СМ\ — медіана трикутника ABC. Оскільки точки ЛІ! й С належать перерізу A\ECD, то діагональ ED перетинає медіану СЛ4] у точці М. З подібності трикутників ЕСМ 110


та DM\M випливає, що
ММ1 _ РМу 1 МС EC ~ 2 ’
а це означає, що М — центроїд трикутника ABC.
Задача 3. У прямокутному тетраедрі DABC ребра DC, DB, DA дорівнюють а, Ь, с. Довести, що
/? = -Ьуа2 + &2 + с2, Мал. 16.1
де R — радіус описаної навколо тетраедра DABC кулі.
Доведення. Оскільки діаметр кулі збігається з діагоналлю ED допоміжного паралелепіпеда (задача 2), то
/?=4^=4-Va2+^+c2.
Задача 4. У прямокутному тетраедрі DABC бічні ребра дорівнюють а, Ь, с. Довести, що
V = 4- а-Ь-с о
(V — об’єм тетраедра).
Доведення. Доведення очевидне, оскільки об’єм прямо- кутного тетраедра складає -g- об єму прямокутного паралелепіпеда з ребрами а, b і с.
Задача 5. У прямокутному тетраедрі DABC бічні ребра дорівнюють а, Ь, с. Висота DH = h. Довести, що
Доведення. Позначимо кути між висотою DH і ребрами DA, DB, DC через а, 0, у відповідно. Тоді (мал. 16.2)
DH h о h
cos a = -pr-p = — ; cos p = -r- ;
DA a ’ r b ’
За співвідношенням (16.1)
ill


звідки
Задача 6. У прямокутному тетраедрі DABC грані DAB, DBC, DAC утворюють з основою ABC кути а, 0, у. Довести, що cos2 а + cos2 0 4- cos2? = 1.
Доведення. Оскільки точка D проектується в ортоцентр Н трикутника ABC, то лінійні кути двогранних кутів при основі утворюватимуться висотами відповідних граней, наприклад, Z. DEC = а (мал. 16.2). Оскільки Z_ EDC =90°, то Z_HDC = = Z. DEC = а. Отже, два інших аналогічних лінійних кути дорівнюють y(Z. HDB) й 0(zC HD А) і за формулою (16.1)
cos2 а + cos2 0 + cos2 у = 1.
Задача 7 (Теорема Піфагора для прямокутного тетраедра). У прямокутному тетрадрі DABC сума квадратів площ граней, що містять прямий кут, дорівнює квадрату площі четвертої грані.
Доведення. Нехай грань DAB утворює з основою тетраедра кут а. Площа грані дорівнює Si, а площа основи — S. Дві інші грані утворюють з основою кути 0 і у, і їх площі дорівнюють S2 і S3. Тоді, оскільки ребро CD перпендикулярне до грані ADB, то
S1
— = cos а.
Аналогічно
5г о S3
-y=COS0, — =cosy,
звідки (задача 6)
S! 4- S2 + S3 cos2 а cos2 р _|_ cos2 у = ] , або
s? + si + si = s2.
Задача 8. Сторони основи ABC прямокутного тетраедра DABC дорівнюють а, Ь, с. Знайти висоту тетраедра DH.
Розв’язання. Позначимо AD = x, BD = у, CD = z. Об’єм піраміди V можна обчислити двома способами.
У = “у $авс'Ь
(h — висота тетраедра DH) й
112


V = -^-x-y-z (задача 4).
x-y-z
~ / 1
Отже, h = -5- -с .
2 о ABC
За теоремою Піфагора з прямокутних трикутників ADB, BDC, ADC дістанемо:
х2 + у2 = с2, y* + z2=a2, х2 + г2 = Ь2,
ЗВІДКИ
2 Ь2 + с2 — а2
X
2
2 а2 + с2 — Ь2
У 2
2 а2 + Ь2 — с2 z = !
2
Враховуючи формулу Герона, маємо:
h _ / (fl2 + б2 - с2) (fl2 + с2 - Ь2) (Ь2 + с2 - а2)
\ 2(а + b 4- с) (а + b — с) (Ь + с — а) (а + с — Ь)
Задача 9. Довести, що основа прямокутного тетраедра DABC, трикутник ABC,— гострокутний.
Доведення. Нехай сторони трикутника ABC дорівнюють а, Ь, с. Дослідимо підкореневий вираз у формулі для висоти h (див. попередню задачу). Якщо трикутник ABC — тупокутний й а < с, b <с, то а2 + Ь2 < с2, тобто вираз (а2 + Ь2 — с2) — від’ємний, а решта виразів у дужках — додатні. Якщо трикутник ABC прямокутний, то вираз, що міститься в одній із дужок, перетворюється на нуль. Отже, трикутник ABC — гострокутний.
Задача 10. У прямокутному тетраедрі DABC, S — площа основи, а, Ь, с — довжини ребер DA, DB, DC відповідно. Довести, що
Si S2 S3 s
а b ’ c h ’
де h — висота DH тетраедра DABC\ Si, S2, S3 — площі трикутників відповідно DBC, DAC, DAB.
Доведення. Нехай V — об’єм тетраедра. Тоді
ЗУ = aSi, 3V= bS2, 3V= cS3, 4V = hS.
Має місце рівність
(задача 5)
8 0-172
ИЗ


Помножимо обидві частини рівності на 3V. Маємо:
hS aSi . bS2 Пгг=^г + ~Ь^
cS3
"Г
звідки
S\ . S2 1 s3 S
а ’ b ' с h '
Задача 11. Довести, що відрізок, який сполучає середини двох мимобіжних ребер прямокутного тетраедра, дорівнює радіусу описаної навколо тетраедра кулі.
Розв’язання. Задачу можна розв’язувати так само, як задачу 3. Покажемо другий спосіб розв’язання цієї задачі.
Нехай Е\ і £2 — середини ребер ВС й AD тетраедра DABC (мал. 16.3). Застосуємо формулу медіани до відрізка £і£2 у трикутнику В£2С, враховуючи, що В£2 і С£2 — медіани трикутників ABD та ACD. Отже,
4£2£? = 2(В£і + С£і) - ВС2,
2ВЕІ = BD2 + АВ2--^- AD2,
2СЕІ= CD2 + АС2 - AD2,
4Е}Е22 = BD2 + АВ2 + CD2 + АС2 - AD2 - ВС2.
Позначимо DA = a, DB = b, DC = с Піфагора. Маємо:
застосуємо теорему
£і£г = -ул/ <? + Ь2 + с2 .
Отже, E\Ei = R, де R— радіус описаної навколо тетраедра кулі (задача 3). Аналогічно обчислюються й інші відрізки, що сполучають середини протилежних ребер.
Задача 12. Довести, що в прямокутному тетраедрі DABC радіус вписаної кулі г обчислюється за формулою
Р
де 5б — площа бічної поверхні, р — сума довжин ребер, які утворюють прямі кути при вершині £), S — площа основи ABC.
114


Доведення. Відомо, що (див. с. 131» (20. 1)).
_ 3V
Г ~ S6 + S ’
де У — об’єм тетраедра.
Позначимо довжини ребер, які утворюють прямий кут при вершині, а, Ь, с; площі прямокутних граней — Si, S2, S3.
Враховуючи, що V = -^~ а- b-с, маємо:
а - Ь - с (!• b • с {S\ S2 S3 — S)
Г — 2(S, + S2 + Зз + S) = 2 [(S, + S2 + S3)2 - S2]
_ а-6-с (З, + S2 + S3 — S)
— 2[S? + S2 + S2 + 2(S,S2 + S2S3 + S1S3) — S2] •
Оскільки
2St = be, 2Sz = ас, 2S3 = ab
s2 = s? + si + si,
маємо:
_ S|+ S2 + S3-S _ S6-S r a + b + c p
Задача 13. Серед усіх прямокутних тетраедрів з висотою h знайти тетраедр найменшого об’єму.
Розв’язання. Позначимо ребра, які утворюють прямі кути при вершині тетраедра, a, Ь й с. Тоді
а1 + б2 + ? > 3 V
1 aW
л 1 і 1 , 1 — 1
Але a2 + b2 + c2 h2 , тому
або
Тобто найменший об’єм дорівнює —Л3. Це буде в прямокутному тетраедрі з рівними бічними ребрами.
Задача 14. У прямокутному тетраедрі DABC R і г — радіуси відповідно описаної і вписаної куль. Знайти найменше значення відношення R: г.
8*
115


Розв’язання. Покажемо, що
Л’Ь'С / J \
Г ab Ьс + ас + -Ja2b2 + Ь2с2 + Л2 *
де а, Ь, с — довжини ребер, що утворюють прямий кут.
Справді, позначимо Si, S2, S3 — площі бічних граней, S — площу основи. Тоді
S = -^S? + S2 + S3 = ~Y~y/a2b2 + b2c2 + a2c2 .
Враховуючи, що г = ~$~ (20.1), дістанемо формулу (1).
Отже,
R (ab ас Ьс а2Ь2 4- Ь2с2 + а2? ) а2 4~ б2 4~ с2 >
r 2аЬс
(Зд/g2&V 4~ а4Ь4с4) 3 д/а2Ь2с2 З -^3 4~ З
J 2 а-b-с 2
Рівність справджується при а = b = с.
17. 	РІВНОГРАННИЙ ТЕТРАЕДР
Рівногранний тетраедр — це тетраедр, у якого всі грані — рівні трикутники.
Задача 1. Довести, що у рівногранного тетраедра мимобіжні ребра попарно рівні.
Доведення. Нехай у тетраедрі DABC ребро ВС не дорівнює ребру AD. Оскільки всі грані — рівні між собою трикутники, то з порівняння, наприклад, трикутників ADB й BDC випливає, що ВС=АВ, або BC=BD. Але тоді всі грані — не тільки рівнобедрені трикутники, але й рівносто- ронні, що суперечить припущенню. Отже, припущення неправильне, і AD = ВС.
Задача 2. Довести, що грані рівногранного тетраедра — гострокутні трикутники.
Доведення. Позначимо кути грані тетраедра а, 0, у. Тоді плоскі кути тригранних кутів тетраедра при кожній із вершин також дорівнюють а, р, у. За властивістю плоских кутів тригранного кута маємо: а + р + у = 180°, а < Р + у, звідки Р + у >90 ° 116


і а <90°. Аналогічно доводиться, що 0 і у — також гострі кути.
Задача 3. Довести, що у рівногранному тетраедрі сума косинусів усіх двогранних кутів дорівнює 2.
Доведення. Позначимо ои, 0і, уі— кути між бічними гранями ADC, BCD, ADB і основою ABC відповідно. Площа кожної грані — 3. Спроектуємо кожну з бічних граней на основу. Розглянемо випадок, коли всі двогранні кути — гострі. Тоді
3 = 3 cos осі + 3 cos 0і + 3 cos у і, звідки
cos аі + cos 0і + cos у і = 1.
Позначимо аг, 0г, уг — двогранні кути між бічними гранями, що мають спільні ребра DB, DA, DC відповідно. Оскільки в рівногранному тетраедрі тригранні кути рівні, то, враховуючи формулу (14.1), маємо: аі = аг, 0і = 0г, її = Уг- Отже,
cos аг + cos 0г + cos уг = 1.
Таким чином, сума косинусів всіх двогранних кутів дорівнює 2. Випадок, коли один із двогранних кутів — негострий, розгляньте самостійно.
Задача 4. У рівногранному тетраедрі мимобіжні ребра дорівнюють а, Ь, с. Знайти відстань між ними.
Розв’язання. Нехай DABC — даний тетраедр (мал. 17.1). AD = BC = a, АС = = BD=b, AB=CD=c. Через мимобіжні прямі DC й АВ, АС і BD, AD й ВС проведемо паралельні площини. При взаємному перетині вони утворюють паралелепіпед. Оскільки діагоналі граней рівні між собою, то ці грані — прямокутники, а паралелепіпед — прямокутний. Відстанню, наприклад, між ребрами тетраедра DC і АВ є ребро паралелепіпеда DE (або /(С). Отже, задача зводиться до знаходження ребер паралелепіпеда х, у, z, якщо діагоналі граней дорівнюють а, Ь, с:
х2 + у2=а2, х2 + z2 = Ь2, y> + z2=c2,
117


Розв’язавши цю систему відносно х, £/, z, маємо:
X = 2(а2 + б2 — С2) ,
у = -yV 2(а2 + с2 — б2) , z = 4*л/ 2(&2 + с2 —а2) .
Задача 5. У рівногранному тетраедрі мимобіжні ребра попарно дорівнюють а, Ь, с. Знайти його об’єм.
Розв’язання. Знаючи виміри прямокутного паралелепіпеда, знайдемо його об’єм Уі (задача 4). Об’єм тетраедра V
дорівнює -д- Уь Отже,
V = 2(с2 4-а2 - &2) (а2 Н-ft2 - с2) (б2 4-е2 - а2) .
Задача 6. Довести, що відрізки, які сполучають середини рівних протилежних ребер тетраедра, перпендикулярні до цих ребер, перпендикулярні один до одного і перетинаються в одній точці.
Доведення. Доведення випливає з розгляду відрізків, що сполучають центри симетрії граней прямокутного паралелепіпеда (мал. 17.1).
Задача 7. Довести, що в тетраедрі з рівними мимобіжними ребрами, центри описаної і вписаної куль збігаються з точкою перетину відрізків, які сполучають середини протилежних ребер цього тетраедра1. Знайти радіус /? описаної навколо тетраедра кулі, якщо довжини мимобіжних ребер дорівнюють а, Ь, с.
Доведення. Такою точкою є центр симетрії прямокутного паралелепіпеда, а
Задача 8. Позначимо плоскі кути рівногранного тетраедра а, р, у, а мимобіжні ребра попарно а, Ь і с. Довести, що об’єм
ї/ аЬс І о
V = —g—^/cos а-cos p-cos у .
Доведення. Оскільки плоскі кути тригранного кута розглядуваного тетраедра дорівнюють а, р, у, а ці кути в свою чергу дорівнюють кутам Л, В, С трикутника ABC (однієї з рівних граней тетраедра), то
1 Справджується й обернене твердження (с. 139).
118


а2 + с2 — b2 = 2 ас - cos p, a2 -|- b2 — c2 = 2 ab • cos y, b2 + c2 — a2 = 2 be • cos a.
Підставляючи ці значення в формулу задачі 5, дістанемо шукану формулу.
Задача 9. Довести, що об’єм рівногранного тетраедра дорівнює
V = у ^1/2/3, О
де /|, /2, ts — відрізки, які сполучають середини протилежних ребер тетраедра.
Доведення. Це випливає з того, що об’єм тетраедра 1
дорівнює -у об єму описаного паралелепіпеда.
Задача 10. Довести, що
ЇЇ + tl + tl = 4/?2,
де /і, /2, /з — відрізки, які сполучають середини протилежних ребер рівногранного тетраедра, R — радіус описаної сфери.
Доведення. Нехай a, 6, с — виміри прямокутного паралелепіпеда (задача 4). Тоді t\ = a, tz=b, t$= с. А оскільки діаметр описаної кулі — діагональ цього паралелепіпеда, то твердження задачі доведено.
Задача 11. Довести, що радіус кулі, вписаної в рівногранний 1 тетраедр, дорівнює — висоти цього тетраедра.
Доведення. Позначимо V — об’єм рівногранного тетраедра, S — площу його грані, h — висоту, г — радіус вписаної З у
в тетраедр кулі. На с. 131 ми покажемо, що г = -^у. Отже,
V = 4-S/і = 4 Зг, г = 4- о 3 4
Задача 12. Сума відстаней від довільної точки X, яка міститься всередині рівногранного тетраедра, до його граней дорівнює висоті цього тетраедра. Довести.
Доведення. Оскільки всі грані в тетраедрі рівні між собою (їх площі позначимо S), то
у Sxi -|—й- Sx2 Я—г S%3 -|—Sx4 = у Sh ООО О о
(xj, Х2, х3, х4 — відстані від точки X до граней), звідки
Х\ + Х2 + Хз + Х4 = й.
119


Задача 13. Довести, що проекція Q вершини рівногранного тетраедра на протилежну грань належить прямій Ейлера цієї грані, причому OQ = OH (О — центр кола, описаного навколо грані, Н — ортоцентр грані).
Доведення. Спочатку розглянемо лему: ортоцентр Q трикутника ДіВіСі (мал. 17.2), середні лінії якого збігаються зі сторонами трикутника ABC, належить прямій Ейлера трикутника ABC, причому OQ= ОН.
Справді, нехай М — центроїд трикутника ABC. Оскільки трикутники ABC і ДіВіСі — гомотетичні з центром гомотетії М і коефіцієнтом k = — 2, то точці Н відповідатиме точка Q, яка належить прямій НМ. Ця пряма — пряма Ейлера. Оскільки 2ОМ = НМ (с. 5), то НО = OQ.
Перейдемо до доведення задачі. У рівногранному тетраедрі DABC проведемо висоту DE бічної грані, сполучимо точки Е і Q та зробимо розгортку (мал. 17.3). В розгортці це відрізок А\Е перпендикулярний до сторони ВС, тоді відрізок АіН\ перпендикулярний до відрізка В\С\, звідки А]Н\ — висота трикутника ЛіВіСі. Аналогічно доводиться, що точка Q належить й іншій висоті цього трикутника. За лемою ортоцентр трикутника AiBiCj належить прямій Ейлера трикутника ABC й HO=OQ. Задачу доведено.
Пропонуємо наступну задачу розв’язати самостійно.
Задача 14. У рівногранному тетраедрі а, Ь, с — довжини мимобіжних ребер, — повна поверхня. Довести, що
я4 й4 с4 5^ Sn
120


18. 	МЕДІАНИ ТЕТРАЕДРА. ЦЕНТРОЇД
Відрізок, що сполучає вершину тетраедра з центро- їдом протилежної грані, називається медіаною тетраедра.
У цьому розділі користуватимемося такими позначеннями: тА, тв, тс, mD— медіани тетраедра, проведені з вершин відповідно А, В, С, D\ МА, Мв, Мс, MD~ центроїди відповідних гра¬
ней.
Описаний паралелепіпед
Через мимобіжні ребра тетраедра DABC проведемо паралельні площини. Дістанемо паралелепіпед AA\BB\CC\DD\, описаний навколо тетраедра DABC (мал. 18.1).
Лема. Діагональ описаного паралелепіпеда перетинає одну з граней у її центроїді. Довести.
Доведення. Доведемо, наприклад, що діагональ АС\ перетинає грань BCD у центроїді МА. Проведемо діагональний переріз ААіСіС. Йому належать відрізки АСі й C/V2 (W2— середина відрізка BD). Відрізок CW2 є медіаною у трикутнику BCD. Ця медіана перетинає діагональ паралелепіпеда АС\ у точці Q. З подібності трикутників N2QC\ та CQA випливає, що CQ : QN2 = АС : W2Ci = 2:1. Отже, точка Q — центроїд трикутника CBD, тобто Q==Ma.
Задача 1. Довести, що медіана тетраедра DABC належить діагоналі описаного навколо нього паралелепіпеда і дорівнює 2 . .. .
— цієї діагоналі.
Доведення випливає з леми.
Задача 2. Довести, що медіани тетраедра перетинаються в одній точці.
Доведення. Цією точкою є точка перетину діагоналей описаного паралелепіпеда. Вона називається центроїдом тетраедра. Позначимо її через G.
Задача 3. Довести, що центроїд тетраедра ділить кожний із відрізків, які сполучають середини мимобіжних ребер, пополам.
Доведення. Справді, якщо N2 і N\ — середини ребер BD і АС (мал. 18.1), то відрізку Af2?Vi належить точка перетину діагоналей описаного паралелепіпеда, тобто точка G.
Задача 4. Довести, що центроїд G ділить кожну медіану у відношенні 3:1, рахуючи від вершини.
121


Мал. 18.1
. Мал 18.2
Доведення. Трикутники N^GQ і CC\Q {Q = M^ подібні (мал. 18.1):
QN2 _ GQ _ 1
CQi Ci Q 2 ’
звідки ”” = і але C\G = AG, і тоді
C і О о
= 4 й 4G = 3GQ,
звідки випливає, що
GQ _ _ 1
AG ~ 3 •
Задача 5. Довести, що відстань від центроїда тетраедра до грані дорівнює гідній четвертій відповідної висоти тетраедра.
Доведення. Це випливає з подібності трикутників, наприклад, GMdK і DMdH\, де К і Н\ — основи перпендикулярів, проведених з точок G і D (мал. 18.2) на площину ABC.
Задача 6. Довести, що центроїд тетраедра DABC є спільною вершиною чотирьох тетраедрів, об’єми яких рівні між собою. Основами цих тетраедрів є грані тетраедра DABC.
Доведення випливає із задачі 5.
Задача 7. Довести, що у тетраедрі DABC точка, що є спільною з вершиною чотирьох рівновеликих тетраедрів, основи яких — бічні грані тетраедра DABC,— центроїд цього тетраедра.
Доведення випливає із задач 5 і 6.
Задача 8. Визначити вид тетраедра, чотири медіани якого рівні між собою.
Розв’язання. Якщо медіани тетраедра рівні між собою, то рівні й діагоналі описаного паралелепіпеда. Отже, він прямокутний, а тетраедр рівногранний.
122


Задача 9. Довести, що в рівногранному тетраедрі збігаються центроїд і центр описаної сфери.
Р оз в’ язання. Справді, це точка перетину діагоналей описаного паралелепіпеда.
Задача 10. Довести, що в рівногранному тетраедрі
тА = тв= tnc=^ tnD = -у/ 2(а2 + б2 + с2) ,
де а, Ь, с — протилежні ребра.
Розв’язання. Якщо тетраедр рівногранний, то діагоналі описаного паралелепіпеда рівні між собою. Отже,
тА = тв = тс = mD = -у R = -у У 2(а2 + б2 + с2) ,
де R — радіус описаної кулі (див. с. 118).
Задача 11. Довести, що в ортоцентричному тетраедрі центроїд G, ортоцентр Я, центр описаної сфери О належить одній прямій (прямій Ейлера), причому HG= GO.
Доведення. Розглянемо описаний паралелепіпед (мал. 18.3). Покажемо, що сторони трикутників HBD і OD\B\ попарно паралельні. Відрізок ОВ\ перпендикулярний до грані тетраедра ABC, оскільки ОС=ОВ=ОА, В\А = В\С=ВВ\ (грані описаного паралелепіпеда у випадку ортоцентричного тетраедра — ромби), і відрізок DH перпендикулярний до грані ABC. Отже, відрізки ОВ\ і DH паралельні. Аналогічно доводиться, що паралельні відрізки OD\ та ВН, а відрізки BD й B\D\ рівні і паралельні один одному. Отже, трикутники BHD та D\OB\— рівні між собою. Оскільки B0D\H — паралелограм, то він симетрично розміщений відносно центра симетрії, точки G, тобто HG= GO.
Задача 12. Дано тетраедр DABC. Довести, що коли пряма, якій належить точка G і центр описаної навколо даного тетраедра сфери — точка О, перетинає його мимобіжні ребра DA і ВС, то DB = АС та DC= АВ.
Доведення. Нехай пряма GO перетинає ребра DA та ВС відповідно в точках X і У (мал. 18.4). Оскільки точка G збігається з серединою відрізка, який сполучає середини К\ і К2 ребер DA і ВС, то відрізки XY і /СіХг перетинаються в точці G. А це означає, що ребра DA і ВС лежать в одній площині. Оскільки це не так, то точки X і Кі, У і /<2 збігаються. Оскільки ОА = ОВ — ОС = = OD, то трикутники AOD та ВОС — рівнобедрені і спільна
123


їх медіана /СКг перпендикулярна до ребер DA і ВС.
В описаному паралелепіпеді (мал. 18.5) відрізок /С1Д2 перпендикулярний до граней A\AD\D і В\ВСС\. Отже, грані паралелепіпеда — прямокутники, VDB = AC, DC=AB.
Задача 13. Довести, що якщо пряма, якій належать центроїд і центр вписаної сфери перетинає ребра DA і ВС. то DB = AC, DC = AB.
Доведення аналогічне задачі 12.
Задача 14. Якщо в тетраедрі DABC
1) точки G і Н збігаються, то тетраедр правильний (Н — ортоцентр тетраедра);
2) точки G й О або точки G та І збігаються (/ — центр вписаної в тетраедр сфери), то тетраедр — рівногранний.
Доведення. 1) Оскільки висота тетраедра проходить через центроїд грані, то ортоцентр грані збігається з цент- роїдом, і грань є правильним трикутником.
2) Якщо точки G й О збігаються, то прямокутні трикутники GK\A і GK2C рівні
(мал. 18.4). Отже, А/G = С/G. Аналогічно, /СіР = /СгВ, тобто AD = BC.
Так само доводиться рівність інших пар протилежних ребер. Якщо збігаються точки G і І. то за задачею 5
h\ hi h3 ju_
~~~~~ 4 ~ 4 ’
де r — радіус вписаної в тетраедр кулі, hi, h,2. Лз, tu— висоти тетраедра. Отже, висоти тетраедра рівні, тобто рівні й грані.
Позначимо площину, якій належить центроїд тетраедра і його бічне ребро, g.
Задача 15. Довести, що площина g ділить тетраедр на два рівновеликі тетраедри.
Доведення. Справді, у тетраедрів DBB\A і DBB\C висота спільна, а основи рівновеликі (мал. 18.6).
124


Задача 16. Знайти кут між площинами g правильного тетраедра. Відповідь. 120°.
Задача 17. Медіана тетраедра DMd збігається з його висотою, а і р — кути, під якими видно цю висоту з вершин перерізу g (ці вершини належать площині ABC). Довести, що відношення тангенсів кутів Р і а величина стала і дорівнює 2.
Доведення. Позначимо ( мал. 18.6) /- DAMd = а, Z. DAiMd= р.
Тоді
Мал. 18.6
, D№q , о DMd
tga DMq-MdAl 1
"tgT— AMd-DMd
Отже, tg p : tg a= 2.
Задача 18. У тетраедрі DABC проведено переріз g. У якому відношенні ділиться медіана тетраедра і медіана перерізу їх спільною точкою?
Розв’ язання. Позначимо Q — точку перетину медіани DMd і медіани AF перерізу ADA\ (мал. 18.7). Проведемо через точку D пряму, паралельну АА\ і продовжимо AF до перетину s цією прямою в точці L. Позначимо AMD=2x, МпА] = х, DF = FA\.
З рівності трикутників AFA\ і LFD дістанемо DL = 3x.
З подібності трикутників ЛфЛ4р і LQD маємо:
DL _ DQ .
AMD QMD '
DQ _ Зх З
QMd 2х 2
Проведемо через точку F пряму, паралельну DMd. Дістанемо MDF\ = F\Ai =.
AQ AMd 2x .
~QF~~~ MDF\ =~= 4-
125


Задача 19. У тетраедрі DABC а і а\, b і 6і, с і с, —довжини протилежних ребер. Довести, що
то = 4-V 3(а? + 6? + с2) - (а2 + &2 + с2) . (18.1)
Доведення. Позначимо через А\ і В\ середини ребер ВС і АС (мал. 18.6) 3 трикутника CMDA\:
2 2 і ^2 л ГП2
mD= т\ + -д 2гпі — cos а, де
т\ = DA\, гп2= АА\, Z_DA\M = a.
З трикутника AAiD знайдемо cos а
cos а =
^,2 І ~.2 J Ш\ 4“ ПІ2 — О|
2/П1/П2
Отже,
w2 2 і ^2
ГП\ -J” g
2zni/n2(mi 4- — а?) 9m? 4- mj — 3m? — Зт2 4~ За?
3-2тіт2 9
6т? — 2/Пг + За?
= 9 ’
Враховуючи формулу медіани трикутника, маємо
2 2(с? + 6?) - а2 . 2 2(Ь2 + с2) - а2 .
ті= , /и2 = 1 ,
2 12с? + 126? - 6а2 - 462 - 4с2 + 2а2 + 12а?
mD = Г9 =
12(с? + 6? + а?) — 4(62 4- с2 + а2) а? 4- 6? 4- с? а2 4- Ь2 4- с2
4-9 ~ 3 9
mD = ^la' + ^+c'-a2 + ^+c2 = ±7 За? + + Зс? - (а2 + Ь2 + с2).
Задача 20. Довести, що в тетраедрі
^2 і _,2 і ^2 і _,2 П
/пл + тв 4- ^с + — “9“ У»
де Q — сума квадратів ребер тетраедра.
Доведення випливає з формули (18.1).
Задача 21. Довести, що коли в тетраедрі DABC тА = tnB, то АС2 + AD2 = ВС2 + BD2.
’ Доведення випливає з формули (18.1).
126


19. 	ТЕТРАЕДР
І ОПИСАНА СФЕРА
Задача 1. Довести, що навколо тетраедра можна описати сферу.
Доведення. Знайдемо точку, рівновіддалену від вершин тетраедра DABC (мал. 19.1). Геометричним місцем точок, рівновіддале- них від вершин А, В і С є пряма п, яка проходить через точку Оі — центр кола, описаного навколо трикутника ABC, і перпендикулярна до площини цього кола. Геометричним місцем точок, рівновіддалених від вершин О і А, є площина а (на малюнку вона не показана), яка проходить через середину відрізка AD і перпендикулярна до нього. Площина а перетинає пряму п у точці О. Ця точка рівновіддалена від усіх вершин тетраедра, тобто є центром описаної навколо нього сфери.
Задача 2. Довести, що шість площин, які проходять через середини ребер тетраедра DABC і перпендикулярні до них, перетинаються в одній точці — центрі сфери, описаної навколо тетраедра DABC.
Доведення випливає з попередньої задачі.
Задача 3. У правильній трикутній піраміді довжина бічного ребра дорівнює а, висота дорівнює h. Дослідити, при якій залежності між а і h центр описаної сфери міститься:
1) всередині піраміди;
2) на поверхні піраміди;
3) поза пірамідою.
Розв’язання. Нехай у тетраедрі DABC Оі — центр правильного трикутника АВС {мал. 19.2). Нехай радіус сфери, описаної навколо даної піраміди, дорівнює R. Продовжимо висоту D0\ до перетину зі сферою у точці D\. Трикутник DAD\ прямокутний і 0\А — його висота.
Тоді DA2 = D0\• DD] або
* 2h *
1) Якщо R<Zh, то центр описаної сфери лежить всередині піраміди і а< h.-\j 2 .
127


2) Якщо R=h, то центр сфери збігається з точкою О\ і а = hryj 2 .
3) Якщо R > А, то центр лежить поза пірамідою і a>hr\j 2.
Задача 4. У сферу вписаний правильний тетраедр. Довести, що точка, діаметрально протилежна одній з вершин тетраедра, рівновіддалена від площин його граней.
Доведення. D\—точка, діаметрально протилежна вершині D правильного тетраедра DABC (мал. 19.2), О — центр сфери, Оі — центр основи ABC, R — радіус сфери. Знайдемо
відстань від точки D\ до основи ABC. Позначимо довжину ребра тетраедра а. Сполучимо точки D\ і А. Оскільки Z_ DADi = = 90 °, то Z. AD\D = A DAO\ = а. З трикутника AO\D\ D\O\ —
= /40i-ctga. З трикутника DAO\ знаходимо, що cos а =
Отже, а= ■■ г— і D\O\ = 3 7^~~ 2- .
V 2 ° у 2 -у 6
Проведемо з точки D\ перпендикуляр до площини DBC. Він перетинає продовження апофеми DA\ у точці Е. Тоді
D\E = DD\ -sin р,
де р = А £)|£Мі.
З трикутника DAD\ маємо
DD\ =——
sin а
2
Знайдемо sin р з трикутника DO\A\\ sin р = —. Тоді D\E = аг\] 3 1 а
~~ лЛ2" ~~
Отже, D\O\ = D]E.
Аналогічно доводимо, що точка D\ рівновіддалена від інших граней тетраедра.
Задача 5. Довести, що в ортоцентричному тетраедрі точки, симетричш основам висот тетраедра відносно ребер, які належать одній й тій самій грані, лежать на описаній сфері.
Доведення. Оскільки кожна вершина ортоцентричного тетраедра проектується в ортоцентр протилежної грані (див. с. 104) і точки, симетричні ортоцентру відносно сторін, належать
128


описаному навколо трикутника колу, то всі вони належать сфері, описаній навколо даного тетраедра.
Задача 6. У тетраедрі DABC а, b, с — довжини сторін основи ABC. Точки Оі, О2, Оз, 04 — проекції центра описаної навколо тетраедра сфери на грані DAB, DBC, DAC і ABC. З цих точок одні й ті самі ребра тетраедра видно під рівними кутами. Знайти радіус сфери.
Розв’язання. Оскільки точка О рівновіддалена від вершин тетраедра DABC, робимо висновок, що центр О описаної сфери проектується в центр кола, описаного навколо відповідної грані (мал. 19.3). Отже, точки Оі, О2, Оз, 04— є центрами кіл, описаних навколо відповідних граней. Трикутники DO\B і DO2B рівні, оскільки вони рівнобедрені з спільною стороною DB і рівними кутами при вершинах 0\ і О2. Отже, D0\ = DO2. Трикутники D00\ і DOO2 рівні (вони прямокутні з спільною гіпотенузою DO і рівними катетами DO] і DO2). Отже, ОО2 = 00]. Аналогічно доводимо, що 00г= 003, ООі = 004. Отже, ООі = 002= 00з= 004, тобто центр описаної сфери збігається з центром вписаної сфери. Таким чином, тетраедр DABC рівногранний і радіус описаної сфери обчислюється за формулою (див. с. 118, задача 7)
1 / а2 + б2 + с2
2
Задача 7. У тетраедрі DABC О — центр описаної сфери, R — її радіус; Оо, /0 — центри кіл відповідно описаного навколо трикутника ABC і вписаного в нього, Ro і го — їх радіуси. Довести, що
О/g = R2- 2Roro.
Доведення. Проведемо з точки О перпендикуляр на грань АВС (мал. 19.4). Тоді Оо — його основа. З А ООоІо маємо:
ОІ2о=002о + ОоП.
Але з А АООо
002о = R2 - R2'
9 0-172
129


За формулою Ейлера (5.3) маємо:
OqIq = У?2 — 2/?оГо-
Отже,
OIq = /?2 /?о + /?о — 2/?оГо =
— R2 — 2/?оП).
Задача 8. У сферу вписано тетраедр DABC, мимобіжні ребра якого AD == ВС = a, BD = = AC=b, CD=tn, АВ = п. Обчислити радіус сфери.
Мал- 195 Розв’язання. Нехай у
тетраедрі DABC (мал. 19.5) N і М — середини мимобіжних ребер АВ і DC. Покажемо, що відрізок MN перпендикулярний до ребер АВ і DC. Справді, трикутники ADC і BCD рівні, оскільки мають спільну сторону DC і пари рівних між собою сторін. Медіана ВМ дорівнює медіані AM. Отже, трикутник АМВ — рівнобедрений і його медіана MN перпендикулярна до сторони АВ.
Аналогічно показуємо, що MN — перпендикуляр до ребра DC. А отже, центр О описаної сфери належить відрізку MN. Нехай R — радіус сфери. Маємо:
ОМ = -д/я2 —ON = , MN=OM± ON.
Можна показати (за допомогою формули 3.1), що
MN2 = (а2 + а2 + Ь2 + Ь2 — т2 — п2) = -^-(2а2 + 2Ь2 — т2 — /г2).
Отже,
(“\/ Я2 - ± -д/я2-^- ) - ^(2а2 + 2Ь2 — т2 — п2).
Звідси
2Л, _ -грі ± 2д/(/г!-4)(^-4) = *+£ -
або
R2.
Після піднесення до квадрата обох частин рівності маємо:
(о2 + &2)2 - т2п2 4(2(а2 + &2) - т2 - п2) ’
І (а2"^- &2)2 — mV ТУ їіа1 + &2) — т2 - п2 •
130


Задача 9. Нехай R і г — відповідно радіуси описаної і вписаної куль тетраедра. Довести, що R Зг.
Доведення. Розглянемо тетраедр, вершини якого збігаються з центроїдами граней заданого тетраедра DABC. Вони гомотетичні з коефіцієнтом гомотетії ( . Доведемо
це. Нехай Мл, Мв, MQ, MD— центроїди граней DBC, ACD, ABD, ABC відповідно. Точка А гомотетична точці МА відносно центроїда М тетраедра з коефіцієнтом (—3). Аналогічно точка D гомотетична точці MD відносно точки М з коефіцієнтом (—3). Оскільки zL DMA = = Z. MDMMA (мал. 19.6) і MMD : MD = MMA : AM, то трикутники DMA і MdMMa гомотетичні відносно точки M. Отже, відрізки MDMA і DA гомотетичні. Аналогічно доводимо гомотетію інших ребер тетраедрів MAMBMCMD і ABCD. Таким чином, радіус сфери, описаної навколо тетраедра MAMBMCMD, дорівнює -yR. Оскільки він не менший за радіус сфери, вписаної в тетраедр DABC, то твердження задачі доведено.
20. 	КУЛЯ, ДОТИЧНА
ДО ГРАНЕЙ ТЕТРАЕДРА. СФЕРА, ВПИСАНА В ТЕТРАЕДР
Задача 1. Довести, що радіус г кулі, вписаної в тетраедр, обчислюється за формулою де V — об’єм тетраедра,
Sn — повна поверхня тетраедра.
Доведення. Вважатимемо центр кулі, вписаної в тетраедр, вершиною чотирьох пірамід, у яких висоти радіуси цієї 9 *
131


кулі, а площини, на які ці висоти опущені,— грані тетраедра. Позначимо площі граней Si, S2, S3, S4, а об’єми відповідних пірамід Vi, Уг, Уз, У4. Тоді
V = Уі + У2 4" Уз 4“ У4 = “о"г(5і 4- S2 4- S3 4- S4) = -я-rSn, О О
звідки
Задача 2. Нехай Vi і У2, Si і S2 відповідно об’єми і поверхні тетраедра і вписаної в нього кулі. Довести, що
Vj _ Si v2 “ s2 •
Доведення. Нехай г—радіус кулі, вписаної в тетраедр. Оскільки Уі = -^-r-Si, a V’2 = 4-r-S2, то твердження задачі О О
доведено.
Задача 3. У тетраедрі DABC h\, Й2, йз, й$ — висоти тетраедра. П 1 1 1 1 І 1 і 1
Довести, що— =“^"+■^■+77+77’ де г — радіус вписаної кулі.
Доведення. Нехай У — об’єм тетраедра; Si, S2, S3, S4 — площі граней, до яких проведено висоти відповідно /її, /12, йз, й4. Тоді j__ s, 1 _ s2 1 _ s3 1 _ £4
~h?~ 3V ’ h2 ~ 3V ’ /гз — 3V ’
Отже,
1 - 1 - 1 I 1 Si + S2 + S3 + *$4 Srt 1
Задача 4. У тетраедрі DABC h\, /12, /із, й4 — висоти тетраедра. Довести, що /її 4- Й2 4- йз 4- й4 16 г, де г — радіус вписаної кулі.
Доведення. Має місце нерівність:
(л,+/і2+/із+/14) 7+4+4+7 16-
Отже, твердження задачі доведено.
Задача 5. У тетраедр вписана сфера. Довести, що величини кутів, під якими з точки дотику сфери з гранню видно ребра цієї грані, однакові для всіх чотирьох граней.
Доведення. Позначимо вершини тетраедра DABC цифрами 1, 2, 3, 4 (мал. 20.1), / — центр вписаної сфери, Кі, /О. Кз, /С4 — точки дотику її з гранями.
132


Нехай точка /G належить грані ADC, а точка Лл — грані ABC. Трикутник ІК2С дорівнює трикутнику ІКьС (за гіпотенузою ІС і рівними катетами ІК2 і ІКа). Звідси К2С = КіС. Аналогічно доводимо, що К2А = = КїА. Отже, ААК2С = = ZLAKtC. Так само доводимо, що А СК\В= Z. СКіВ, A AKsB = А АК<В, A CK2D = = A CK\D, zL DKzB= zL DK\B, zL DK3A = zL DK2A.
Позначимо кути ZL AK2C = = сріз, ZL CK4B = фз2, Z_ АК^В = ф12, Z- CK2D = ф34, DK$B = ф42, Z_ DK2A = ері4.
Але
фіЗ + Ф34- + ф32 + ф34 -|- ф!4 + фі 2 + фіЗ “І” ф32 -|-
Мал. 20.1.
ф14 = 360 °, ф42 = 360 °, ф42 = 360 °, ф 12 = 360 °.
Віднімемо від першої рівності другу. Маємо: фі З + фі 4 = ф32 + ф42.
Віднімемо від третьої рівності четверту. Маємо: фі 4 + ф42 = фі 3 + ф32.
Звідси
фі 3 + фі 4 — ф32 — ф42 = фі 4 + ф42 — фі 3 — ф32,
ЗВІДКИ фіз = ф42.
Аналогічно доводимо решту рівностей.
Задача 6. У тетраедрі DABC довжини сторін основи АВ = = ДС=5, ВС=6. Висота тетраедра проходить через середину сторони ВС і дорівнює 1. Знайти радіус кулі, вписаної в цей тетраедр.
Розв’язання. Нехай DABC — даний тетраедр (мал. 20.2). £>Мі—дана висота. Радіус г вписаної кулі знайдемо за формулою (20,1).
133


З трикутника АВМ\ маємо:
AM і = дМв2 - ВМ2 = -д/52 —З2 = 4.
Тоді
І/ = -^-3-£>Л4і, деЗ—площа трикутника ABC.
Знаходимо площу ДЛВС: 3=3-4=12. Тоді V = 4.
У трикутнику DAB проведемо висоту DK. Тоді відрізок КМ\ перпендикулярний до відрізка АВ.
З трикутника АМ\В\
ax jz АМ\-ВМ\ 4-3
М^= АВ =~=2Л
З трикутника DM\K'.
DK = УЛ4|/<2 + ОЛ4? = У 2,42 + 1 = 2,6.
Оскільки трикутники DAB і DAC рівновеликі, то, позначивши їх площу Si, маємо:
S! = ± А В • DK = 4- 5 ■2’6 = 4-
Позначимо Зз площу трикутника BCD. Маємо:
33 = 4’ВС‘ОЛ1| = -Г’6‘1 =3-
Отже, Зн = S + 23і + Зз = 12 + 13 + 3 = 28. Оскільки г =
ЗУ 3-4 З
— S„ ’ то г~ 28 ~' 7 ’
Задача 7. У тетраедр вписано кулю, дотичну до граней у точках перетину їх медіан. Довести, що тетраедр правильний.
Доведення. Нехай дано тетраедр DABC (мал. 20.3). Л4і, М2, Мз, М4 — точки перетину медіан граней DBC, DCA, ABC, ABD відповідно. К, L, Р — середини ребер ВС, АС і АВ відповідно.
DM\ = DM2 = DM4, КМ\ = КМз, LM2=LM3, РМ4=РМ3 як відрізки дотичних, проведених з однієї точки. Але
DM\ = 4-DK, DM2 = 4-DL, DMt = 4-OP, О О о
KM3 = -^-AK,
<о о
lm2 = -^-dl, LM3 = 4-BL, о о
PMi = -^-DP, PM3 = -^PC
134


(відрізки BL і PC на малюнку не показані). Тому DK= DL = = DP = АК= ВІ2= СР, тобто медіани грані ABC рівні між собою, а отже, трикутник ABC — рівносторонній. Аналогічно доводимо, що трикутники DAC, CDB і ADB — рівносторонні. Отже, тетраедр DABC — правильний.
Задача 8. У тетраедр вписана куля, дотична до граней в їх ортоцентрах. Довести, що тетраедр правильний.
Доведення. Нехай в тетраедрі DABC (мал. 20.4) I — центр вписаної кулі, Н\, і Я2 — ортоцентри трикутників ABC і DBC. Через точки /, Н\, Н2 проведемо площину, яка перетинає ребро ВС в точці Р. Оскільки сфера дотична до граней тетраедра в ортоцентрах, то відрізки 1Н} і ІН2 перпендикулярні до цих гоаней, а отже, ребро ВС перпендикулярне до побудованої площини. Відрізки Н\Р і ВС взаємно перпендикулярні, а оскільки Н\ — ортоцентр трикутника ABC, то АР — висота цього трикутника. Аналогічно доводимо, що DP — висота трикутника BDC і площина перерізу збігається з трикутником DAP. Отже, ребра AD і ВС взаємно перпендикулярні. Так само доводимо перпендикулярність ребер DC і АВ, DB і АС. Таким чином, тетраедр DABC—ортоцентричний, a DH\ і АН2— його висоти.
За умовою ІН\ = ІН2. Отже, точка І рівновіддалена від сторін кута DPA і / — ортоцентр A DPA, тобто трикутник ADP — рівнобедрений (AP=DP} і AI=DI. Аналогічно доводимо, що BI = DI і CI = DI. Таким чином, точка / рівновіддалена від вершин тетраедра DABC'. збігаються центри вписаної і описаної сфер, отже, тетраедр DABC — правильний.
Задача 9. У трикутну піраміду вписано кулю, яка дотикається до чотирьох граней даної піраміди в інцентрах. Довести, що ця трикутна піраміда правильна.
135


Доведення. Нехай DABC — дана піраміда (мал. 20.5), /—центр вписаної кулі, /і, /2, /з — інцентри трикутників DCB, ADC і ABC відповідно. Через точки /і, /2 та І проведемо площину, яка перетинає ребро DC в точці F. Оскільки ІІ\ та ІІ2 перпендикулярні до DC, то пряма DC перпендикулярна до площини //1/2. Отже, відрізки I2F і I\F перпендикулярні до DC (див. задачу 8), тобто I\F і I2F — радіуси кіл, вписаних у трикутники CDB і ADC відповідно.
Оскільки трикутники І2ІС і І\ІС рівні (за гіпотенузою і катетом), то СІ2=СІ\. Отже, трикутники I2FC і I\FC також рівні. Таким чином, Z I}CF= Z_ I2CF і Z_ ACD= Z_ DCB. Аналогічно доводимо, що Z_ ADC= Z. CDB. Далі маємо:
Z DAC= Z CAB; Z CBD= Z CBA, Z DCA = Z ACB,
Z CAD+ Z ADC= 180° — Z ACD= zL CDB + Z CBD (оскільки Z DCB = Z ACD).
Зважаючи на те, що Z CDB= Z CDA, Z CBD = Z CBA і Z CAD = Z CAB, дістаємо: Z CAB = Z CBA. Отже, трикутник ABC — рівнобедрений.
Аналогічно доводимо, що Z_CAD=Z_CDA і /LCDB = = Z_ CBD, тобто трикутники ADC і CDB також рівнобедрені. Звідси випливає, що Л ABD — рівносторонній. Аналогічно доводимо те, що решта граней — рівносторонні трикутники.
Задача 10. У правильній трикутній піраміді R і г відповідно радіуси описаної і вписаної куль. Довести, що де а—кут між бічною гранню і основою піраміди.
Доведення. Нехай в правильній трикутній піраміді DABC О — центр описаної кулі, а І— центр вписаної кулі (мал. 20.6). Тоді OD = R, IH = r (Н— центр грані ABC). Проведемо ОЕ перпендикулярно до ребра DB. Побудуємо лінійний кут ALD двогранного кута при ребрі ВС. Позначимо Z_ALD = a. Сполучимо точки Н і В. З подібності трикутників DOE і DBH маємо:
DO _ DB
DE — DH ‘
Враховуючи, що DE = -^-DB, маємо:
ZDO-DH= DB2
або
2DO-DH=DH2 + HB2 (1)
Оскільки IL — бісектриса кута DLA, то
DH = HL tg сс= ІН-ctg ^-tg а = r ctg^-tg a. (2)
136


Оскільки
BH=2LH, то
Btf=2/tfctgf=2rctgf.
(3)
Підставляючи (2) і (3) в (1), маємо:
R ■ 2rctgf tga= r2ctg2f tg2a+4r2ctg2f.
Перетворимо цей вираз:
r_
tg2f
- tg«f
/? + г __ 1
r tg2-£_ tg<“. ’
S 2 Ls 2
r _ i~2a ±_.4a
R + tg 2“^ T
137


Можна показати, що існує (і до того ж єдина) куля, дотична до однієї з граней тетраедра і продовжень трьох інших граней (мал. 20.7). Така куля називається зовнівписаною.
Задача 11. Довести, що
= ЗУ
4~ S3 + S4 — Si
де га — радіус зовнівписаної кулі, дотичної до грані ABC тетраедра DABC; V—об’єм тетраедра; Si, S2, S3, S4 — площі відповідно граней ABC, ADC, ADB, DBC.
Доведення. Нехай Іа — центр зовнівписаної кулі радіуса га. Уі, У2, Уз, У4— об’єми тетраедрів /аАВС, IaADC, IaADB, IaDBC. Маємо:
V= УгЧ" УзЧ” У4— У1 = 4“Га52-|-4“Га5з4”"Тга‘54 ^aSi
О О О О'
звідки
ЗУ
S2 + S3 + S4 — S1
Задача 12. Довести, що
Га ГЬ Гс Га Г
де г — радіус вписаної в тетраедр DABC кулі; га, гь, rc, rd — радіуси зовнівписаних куль.
Доведення. Позначимо через Sn повну поверхню тетраедра DABC. Маємо:
1 і 1 і 1 і 1 З (S1 4- S2 + S3 + S4) — (Si 4- S2 + S3 + S4)
_ 2Sn __ 2
~ ЗУ ~ г '
Задача 13. У тетраедрі DABC ha, hb, hc, hd—висоти, ra, rb, rc. rd — радіуси зовнівписаних куль. Довести, що
Доведення. Нехай Si, S2, S3, S4 — площі граней, на які опущені висоти ha, hb, hc, hd. Тоді
4Ґ—4- — 4- — -k—= 4Ґ— 4- — 4- — 4- —=
X h2 h2 h2 ' h2J X 9У2 9У2 9У2 9У2/
4 (S? + Si + S32 + S?)
де У — об’єм тетраедра DABC.
Маємо:
^ = S4 + S3 + S2-Si = S„-2Slt
г а
138


ЗВІДКИ
Аналогічно
Г а
_ Sn-2S,
ЗУ
Sn — 2S2
гь
ЗУ
Sn - 2S3
Гс
3V
_ S„ — 2S<
rd
3 V
Отже,
7+
' а
r2 ' 2 1 _2
Гь Гс rd
(Sn - 2S,)2 + (Sn - 2S2)2 + (Sn - 2S3)2 + (Sn- 2S4)2 _ 9 V2
4S2 — 4Srt(Si + S2 + S3 + S4) 4~ 4(S2 + S2 + S3 + S2)
9V2 ~
4S2 - 4S2 + 4 (S? + Sj + Sj + Si)
9У2
4 (S2 -|~ S2 -|~ S2 -j~ S2)
9У2
Порівнюючи вирази (1) і (2), дістанемо твердження задачі.
Задача 14. Довжина двох мимобіжних ребер тетраедра дорівнює а, двох інших мимобіжних ребер — Ь, решти двох — с. Знайти відстань між центрами вписаної в тетраедр кулі і зовні- вписаної кулі.
Розв’язання. Навколо тетраедра DABC (мал. 20.8) опишемо паралелепіпед (див. с. 117). Він прямокутний. Центр вписаної кулі збігається з точкою перетину діагоналей паралелепіпеда, а центр зовнівписаної кулі збігається, наприклад, з вершиною L. Це неважко довести,
якщо врахувати, що тетраедр В'LCD (B'L = BL) дорівнює тетраедру BLCD. Отже, точки А, Z), В', С лежать в одній площині. Отже, точка L рівновіддалена від площин ADC і DCB. Аналогічно доводиться, що точка L рівновіддалена від площин DCB і ACB, DCB і ADB. Шукана відстань дорівнює половині діагоналі паралелепіпеда, тобто (с. 118)
1 / a2 + *2 + c2
2V 2 ’
139


21. 	КУЛЯ, ДОТИЧНА ДО РЕБЕР ТЕТРАЕДРА
Задача 1. Якщо куля дотикається до всіх ребер тетраедра, то суми довжин протилежних ребер тетраедра рівні між собою.
Доведення. Нехай куля дотична до ребер тетраедра DABC (мал. 21.1) уточках /<,, /<2, Яз, /<5, Ке. Оскільки дотичні, проведені з однієї точки до даної кулі, рівні між собою, то
D/<4, Л= Л/Сз == Л/Cs, В/(2=ВКз = В/(б, СКх = СК2=СКь.
Розглянемо суми 5і = Л£> + ВС і S<2=DC-\~AB. Оскільки 4D + BC=4tf4 + £tf4 + B/<2 + C7<2, a DC + AB= DK\ +КіС + + Л/Сз + ВКь, то, враховуючи (1), маємо, що Si = S2. Аналогічно доводиться рівність сум інших пар ребер тетраедра.
Задача 2. Довести, що коли в тетраедрі суми довжин протилежних ребер рівні між собою, то всі ребра дотичні до кулі.
Доведення. Нехай у тетраедрі DABC
AB+CD = AC + BD=AD + BC. (2)
Впишемо кола в грані ABC і DBC. Позначимо їх точки дотику до сторін трикутників ABC і DBC відповідно /Сі, Кз, L\, L2, 140


Ьз (мал. 21.2) Тоді (с. 31)
СК\=р — АВ
(р — півпериметр трикутника ABC), або
уг-,-г ВС-\-АС— АВ
СКі = 2
Аналогічно
л , ВС -|- CD — BD
сц = 5 .
За умовою (2) маємо AC — АВ= CD — BD. Тому C/G = CLi.
Таким чином, кола, вписані в грані ABC і DBC, дотичні до ребра ВС в одній і тій самій точці Т. Проведемо перпендикуляри з центрів вписаних в грані кіл. Усі вони перетинаються в точці О (доведіть), яка рівновіддалена від ребер тетраедра. Оскільки ці перпендикуляри є геометричним місцем точок рівно- віддалених від сторін трикутника, то О — центр кулі, дотичної до всіх ребер тетраедра.
Задача 3. Куля дотикається до всіх ребер трикутної піраміди. Центр кулі міститься всередині піраміди на її висоті. Довести, що піраміда правильна.
Доведення. Нехай DABC — дана піраміда. О — центр кулі (мал. 21.3). Куля дотична до ребер АС, ВС, АВ, DB, AD, CD відповідно в точках Р, М, N, К, L, F. Тоді
OL=OK= ON= ОМ=ОР = OF.
(1)
Трикутники LOD і KOD рівні між собою, тому Z_ADO = /LBDO. Аналогічно Z_CDO= Z-BDO і Z_ADO= Z.CDO. Оскільки DO] — висота піраміди, то з рівності кутів ADO, BDO\ і CDO\ випливає, що трикутники ADO], BDO], CDO] і О]А=О]В=О]С, тобто точка Оі — центр кола, описаного навколо трикутника ABC.
Оскільки куля дотична до сторін трикутника ABC в точках М, N і Р, то вони є точками дотику кола з центром Оі, вписаного в трикутник ABC (враховуючи (1)). Отже, точка Оі — центр вписаного і описаного кіл трикутника ABC. Таким чином, трикутник ABC — рівносторонній і вершина D проектується в його центр Оі, тобто піраміда DABC — правильна.
Задача 4. У трикутну піраміду вміщена куля, яка дотична
рівні. Отже, AD= DC= DB
Мал. 21.3
141


до всіх сторін основи у їх серединах, а середини бічних ребер піраміди лежать на поверхні кулі. Довести, що піраміда правильна.
Доведення. Нехай DABC — дана піраміда. Лі, В\, Сі, Мі, Мг, Мз — середини ребер AD, BD, CD, ВС, АС, АВ відповідно, О — центр даної кулі (мал. 21.4). Тоді відрізки ОМ\, ОМ2 та ОМз рівні між собою і перпендикулярні відповідно до ВС, АС та АВ. Трикутники ОМ2С і ОМ\С рівні (за катетом і спільною гіпотенузою) . Аналогічно рівні й трикутники ОМ\В і ОМзВ, МзОА і М2ОА. Отже, МгС= МіС = = М\В= МзВ = МзА = М2А. Звідси АС= ВС=АВ, тобто трикутник ABC — рівносторонній. Проведемо з точки О перпендикуляр ОМ на площину ABC. Тоді М — центр кола, вписаного в трикутник ABC, тобто М — центр трикутника ABC. Трикутник А іВіСі — правильний, причому площина А\В\Сі паралельна площині ABC. Площина АіВ]Сі перетинає кулю по колу, описаному навколо трикутника АіВіСі. Нехай Оі — центр цього кола. Тоді пряма ООі перпендикулярна до площини ЛіВіСь Пряма 0\М перпендикулярна до площин ABC і ЛіВіСі і точка О належить прямій 0\М. Трикутники ABC і ЛіВіСі гомотетичні з центром гомотетії D. Таким чином, образом точки Оі при цій гомотетії є точка М. Отже, точки Оі, D і М лежать на одній прямій. Оскільки пряма 0\М перпендикулярна до площини ABC і МА = МВ = МС, то DA = = DB= DC. Отже, дана піраміда правильна.
Задача 5. Центр кулі, дотичної до всіх ребер правильного тетраедра, віддалений від граней на відстані а, від вершини на відстань Ь. Знайти ребро тетраедра.
Р оз в’ язання. Центр кулі, дотичної до трьох ребер правильного тетраедра, що виходять з однієї вершини, належить висоті тетраедра, проведеній з тієї самої вершини. Оскільки правильний тетраедр — ортоцентричний, то всі висоти перетинаються в одній точці і ця точка збігається з центрами вписаної й описаної куль. Отже, висота тетраедра дорівнює а-\~Ь.
Позначимо ребро тетраедра х. Тоді х2 —у=(а + &)2 , звідки
х=Лдїїрі(а+(,).Лд:
142


Мал. 21.6
Задача 6. Сторона основи правильної трикутної піраміди дорівнює а, бічне ребро дорівнює І. Знайти радіус кулі, дотичної до всіх ребер піраміди.
Р оз в’ язання. Нехай DO — висота піраміди, Q — центр заданої кулі (мал. 21.5), точки Е і F — точки дотику кулі до ребер АВ і DB відповідно. Позначимо радіус кулі r. BE = BF, як дві дотичні до кулі, проведені з точки В, QE=QF=r, ВЕ=-^. Трикутники DQF і DBO подібні:
QF-.DF = BO.DO,
_ _ DF_ ■ BO (Z~t) а (2/-а)
Г~ ~ DO
Задача 7. У правильну зрізану трикутну піраміду з боковим ребром І вміщені куля, що дотикається до всіх ребер піраміди і куля, що дотикається до всіх її граней. Знайти сторони основ піраміди.
Розв’язання. Куля, вписана в дану зрізану піраміду, дотикається до її основ ABC і ЛіВіСі в центрах О і Оі (мал. 21. 6), а також апофеми DD\ у точці Е. Позначимо ЛВ = х, Л іВі = у.
Тоді
ddW-(V)’-
Оскільки DE=DO, D\E= DiO\, то
DO! = 004-010, =
2-^3
ЗВІДКИ
2 1
/2 _ = ±(Х _|_ уу
143


Оскільки куля дотикається до всіх ребер даної піраміди, то грань ВВіС]С перетинає її так, що в перерізі дістанемо коло, вписане в трапецію ВВ\С\С.
Отже, ВС + В\С* і = ВВ\~|~ x-J-f/=2/.
Розв’язуємо систему рівнянь:
. /2-(^-)2= І(* + у)2.
. х + у = 21.
Враховуючи, що х>у
22. 	ТРИКУТНИК
І ТЕТРАЕДР.
АНАЛОГІЧНІ ЗАДАЧІ
Задача 1. Довести, що коли з точки X, взятої всередині трикутника ABC, провести перпендикуляри da, db, dc на сторони ВС, АС, АВ відповідно, то
1) а-da+b•df>4-c-dc=2S;
2) -Г-+-Г-+-Г-=1-
7 ha 1 hb 1 hc
Задача 1". Довести, що коли з точки X, взятої всередині тетраедра DABC, опустити перпендикуляри da, db, dc, dd на грані, площі яких відповідно дорівнюють Si, S%, S3, S4, то:
1) S] • da И- S2 • db Я- S3 • dc -J- S4 • dd — ЗУ, де У — об єм тетраедра DABC\
2) Ь Де Ло, hb, hc, hd — відповідні перпен-
7 ha ' hb с hd
дикулярам висоти.
Доведення 1". Розв’яжемо другу частину задачі 1".
Нехай точка X міститься всередині тетраедра DABC. Позначимо об’єми тетраедрів DABC, ХАВС, XDBC, XADC, XADB відповідно V, Уі, V2, Уз, У4 (мал. 22.1).
Маємо:
_1_
V71 3 Здвс • dd dd
V j-SABC-hd
144


Мал. 22.1 Мал. 22.2
1 1 У2 3 SfiftC • da da Уз З $А[)С ’ db db
~v = Т = й7 ’ ,“7=Т = ~ь ■ З $DBC ‘ З SADC • hb
J_
У4 З SABD -dc dc V=T = Л?’
ЗВІДКИ 3 • hc
У' + Уї+Уз+Уа —da . db . de dd У ha^~ hb' hc “f" hd ’
або da і db і dc * dd .
I? ’ k
Задача 2. Довести, що бісектриса трикутника ділить протилежну сторону пропорційно прилеглим сторонам.
Задача 2". Довести, що бісекторна площина двогранного кута тетраедра ділить протилежне ребро пропорційно площам граней, що утворюють кут.
Доведення 2". Нехай ADE — бісекторна площина двогранного кута при ребрі AD тетраедра DABC (мал. 22.2).
Розглянемо тетраедри EABD і EACD, у яких основи — відповідно грані ABD і ACD. Ці тетраедри мають рівні між собою висоти, оскільки точка Е рівновіддалена від площин ABD і ACD. Таким чином,
VABDE $ABD ,
17 * \ /
VACDE ^ACD
Візьмемо за спільну основу розглядуваних тетраедрів грань ADE. Зрозуміло, що їх висоти відносяться як довжини ЕВ до EC.
10 0-172
145


Звідси маємо:
Vabde ВВ /2)
vacde ВС
Згідно (1) і (2)
В В SABD
ВС sACD
Задача 3. Довести, що коли в трикутниках ABC і AjBiСі рівні кути А і Лі, то
Вдвс АС-ВА
ВаіВіСі ’ В\Аі ‘
Задача 3". Довести, що об’єми двох тетраедрів зі спільним тригранним кутом відносяться як добутки ребер, які утворюють цей кут.
Доведення З". У тетраедрах DABC (мал. 22.3) і DA\B\C\ візьмемо за основи грані DAB і DA\B\ відповідно. Проведемо у цих тетраедрах висоти СН і С\Н\. Об’єми тетраедрів позначимо V і Vi, площі основ — S і Si, висоти, опущені на основи,— /і, /її, ребра, які утворюють спільний тригранний кут — а, Ь, с і аь 6|, С\ відповідно. .
Т ОДІ А і - Si hi • а\ • bi
V~~ h • S ~ h • a • b
З подібності трикутників DH\C\ і DHC маємо:
hi ci
h c ’ отже,
Vi ai bi ci
c •
Задача 4. Довести, що площа S трикутника ABC обчислюється за формулою
S = y absinC.
Задача 4". Довести, що об’єм V тетраедра DABC обчислюється за формулою де Si, S2 — площі двох довільних граней; а — довжина їх спільного ребра; ер — кут між цими гранями.
Доведення 4". Позначимо Si і S2 площі граней ABC і DBC тетраедра DABC (мал. 22.4). ВС —їх спільне ребро. D\ і Е — проекції точки tD на грань ABC і ребро ВС відповідно. Позначимо
146


Z_DED\ = q, BC = a. V=jSi-DDt, але
DD\ = DE sin <p= ^y-sincp, звідки
1Z 1 o 25г • sin cp 2S1 • S2
V= -3 s > Г-^= ~~зГ~ sin *₽•
Задача 5. Якщо через кожну вершину трикутника ABC провести прямі, паралельні його сторонам, то дістанемо трикутник А\B\C\. Довести, що їх площі відносяться, як 1:4.
Задача 5". Через кожне ребро тетраедра проведена площина, паралельна протилежному ребру. Довести, що об’єм тетраедра відноситься до об’єму утвореного паралелепіпеда, як 1 : 3.
Доведення 5". Нехай A\BC\D — даний тетраедр (мал. 22.5) Зрозуміло, що об’єм кожного з тетраедрів ABDA\, BDCC\, А\ІІ\С\В і A\D\C\D дорівнює одній шостій об’єму побудованого паралелепіпеда.
Позначимо об’єм паралелепіпеда і тетраедра A\BC\D — VT. Тоді
V V
п _ п о
~\Г л
т |/ —У
" 6 Л
Задача 6. Довести, що медіана трикутника ділить його площу пополам.
Задача 6". Довести, що площина, яка проведена чер/ез ребро тетраедра і середину протилежного ребра, ділить його на два тетраедри з рівними об’ємами.
10*
147


Доведення 6". Справді, в утворених тетраедрах основи рівновеликі і висота спільна.
Задача 7. Знайти всередині трикутника ABC таку точку X. щоб площі трикутників ХВС, ХАС. ХАВ були рівні між собою.
Розв’язання. Цю задачу розглядали в розділі «Медіани трикутника. Центроїд». Розв’яжемо її іншим способом. Позначимо точки перетину прямих АХ. ВХ. СХ зі сторонами трикутника Х\. %2, Х$. Трикутники АХВ і АХС (мал. 22.6) мають рівні площі і спільну сторону АХ. Опустимо на пряму АХ висоти ВНі і СТЛ- Чотирикутник ВН\СН<2 — паралелограм, оскільки ВН\ = СН2 і BHxWCHz. У паралелограмі ВН\СН<2 ВХ\ = СХ\. Отже, АХі — медіана трикутника ABC. Аналогічно доводимо, що ВХ2 і СХз — теж медіани, тобто X — центроїд трикутника ABC.
Задача 7". Знайти всередині тетраедра DABC таку точку X. щоб об’єми тетраедрів ХАВС. XDBC. XBDA. XACD були рівні між собою.
Задача розв’язана на с. 122 (задача 7).
Задача 8. У трикутник вписане коло радіуса г. Паралельно сторонам трикутника до кола проведені дотичні і в утворені малі трикутники вписані кола радіусів гі, Гг, г3. Довести, що г=г\Н-гг + гз.
Доведення. Цю задачу розв’язували за допомогою зовнівписаного кола (с. 45). Розв’яжемо її інакше: малі трикутники подібні трикутнику АВС (мал. 22.7). Отже,
або
Г\ ha —2г
Г ha
Аналогічно
Отже,
Ґ2=Г
1
Гз=Г
г, + г2 + г3 = Зг-г2(а+/ + с) = г.
Мал. 22.7
148


Задача 8". У тетраедр DABC вписана куля радіуса г. Площини, які дотикаються до цієї кулі і паралельні граням тетраедра, відтинають від тетраедра DABC чотири тетраедри. Нехай Г1, Г2, Гз, ^4 — радіуси куль, вписеяих у ці тетраедри. Довести, що Г\ 4-Г2 + гз + г4 = 2г.
Доведення 8". Проведем площину, що дотикається до кулі, вписаної в тетраедр, і паралельну грані АВС (мал. 22.8). У перетині дістанемо трикутник ДіВіСі. Радіус кулі,
вписаної в тетраедр DA\B\C\, позначимо г\. Тетраедри DA]B\C\ і DABC подібні, тому
г\ h —2г г h 1
де h — висота тетраедра ABCD, опущена з вершини D. Звідси
але Vі зі/ ) ’ = г( 1 — )
V ЗУ / ’ ==rfl_2£1S1\
V зу / ■
де V—об’єм тетраедра DABC, Si — площа грані ABC. Нехай S — повна поверхня тетраедра, 5’г — площа грані BCD\ S3, S4 — площі граней ACD, ABD.
Отже,
Г1
Аналогічно знаходимо
Г2
Гз
Отже, г і г і г і г г(л 2r(Si + S2 + S3 + S4) \
г І + г 2 + г з + г 4 = Г 4 зр \ =
= <4- А-)=2г.
Задача 9. Через деяку точку, взяту всередині трикутника ABC, проведено три прямі, відповідно паралельні сторонам три-
149


кутника. Ці прямі поділяють трикутник на шість частин, три з яких — трикутники з площами Si, S2, S3. Площа трикутника ABC дорівнює S. Довести, що
■д/S = д/Si Я- л/S2 + л/S3.
Доведення. Нехай X — точка перетину прямих, паралельних сторонам трикутника (мал. 22.9). Оскільки трикутники ЛВС, LXD, NEX, XKF подібні, то
-y/s} XD -y/S2 ХЕ ~/s3 FK
^S~~ ВС ' -yJ~S вс' BC '
Додамо ці рівності:
д/s, | I XD + XE + FK = J
-у/S -yjS -yjS BC
ЗВІДСИ
ys = ysl+ys2 + VS3.
Задача 9". Через точку О, яка міститься всередині тетраедра DABC, проведено площини, відповідно паралельні граням тетраедра. При цьому утворилися чотири тетраедри, у кожному з яких однією вершиною є точка О, а інші вершини лежать на відповідній грані тетраедра DABC. Позначимо об’єм тетраедра DABC—V, а об’єми утворених тетраедрів У|, V2, Уз, У4. Довести, що
V? = V Рі + V ^2 + л/^з + V .
Доведення 9". Площини, які проходять через точку О (мал. 22.10), утворюють перерізи, паралельні площинам СЛВ, DAB, CDB і CAD. Маємо чотири тетраедри ОА4В4С4, CM3B3S3, OB2C2S2, OA\C\S\. Усі вони подібні тетраедру DABC. Отже, де t\, h\ — відповідні висоти тетраедрів ОЛіСіВі, DABC, опущені на основи 5іЛіСі і DAC.
Аналогічно
<2 150


де /2, h>2 — відповідні висоти тетраедрів OB2C2S2, DABC, опущені на основи B2C2S2 і CDB. Далі
У~Йз _ /з
^/Й ^3 ’
де /3, ^3 — висоти тетраедрів OA3B3S3 і DABC, опущені на основи ЛзВзЗз і ABD. Нарешті,
t<
де /4, /і4 — висоти тетраедрів ОЛ4В4С4 і DABC, опущені на основи Л4В4С4 і ABC.
Маємо:
"V Vl + V Vi +V V3 + ’У V4 t\ І /2 f /3 ] Ц
^/й ='/ії + _£г +77 + '/ії =
(див. задачу 1"). Отже,
V V, + + V V3 + V?4 = V V .
Задача 10. У трикутник ABC вписане коло, дотичне до сторін трикутника в точках К\, /G, Кз- Довести, що бісектриси внутрішніх кутів трикутника ABC перпендикулярні до сторін трикутника
Задача 10". Довести, що точки, в яких вписана в тетраедр сфера дотикається до трьох його граней, належать площині, перпендикулярній до бісектриси тригранного кута, утвореного цими гранями.
Доведення 10". Нехай / — центр сфери, вписаної в тетраедр DABC (мал. 22.11); Т\, Т2, Тз, 7\— точки дотику
151


Рфери і граней. Доведемо, що площина ТгТзТ^ перпендикулярна io прямої DI. Відрізки DT%, DT3, DT4 рівні між собою, як дотичні до сфери, проведені з точки D. Тому рівні і прямокутні трикутники DIT2, DIT3, DI7\. Перпендикуляри, проведені з точок Т2, Гз, Г4 до бісектриси DI тетраедра, перетинають її в одній точці Q. Тоді промінь DI перпендикулярний до QT2, QT3, QT4. Отже, точка Q належить площині Т2Т3Т4.
З цього випливає, що відрізок DI перпендикулярний до цієї площини.
Задача 11. У трикутнику ABC ha, hb, hc — висоти, da, db, dc — відстані від точки X, яка належить трикутнику ABC, до відповідних сторін. Довести, що
h3an + h3bn + h3n З3л+1 • dna•dnb‘ dnc,
де n —, будь-яке натуральне число.
Доведення. Позначимо S— площу трикутника ABC’, S\, S2, S3 — площі трикутників ХВС, ХАС, ХАВ з висотами відповідно da, db, dc-
Тоді
- 5”((1?)’"+ (47)”+ (4гЛ = (Si+Л+s-)’'((f)’"+
+(4Л"+’з
= З3л+1 . dna . dnb • dnc.
Задача 11". У тетраедрі h\, h,2, h3, й4 — висоти; d\, d2, d3, d4 — відстані від точки X, яка міститься всередині тетраедра, до відповідних граней.
Довести, що для натуральних п
h]n + № + h3n + h\n 44л+ 1 • d? • dfi • • d4
Доведення 11". Позначимо площі граней Si. S2, S3, S4. Враховуючи, що
diSi -|“ d2&2 “F d3S3 + d4s4 = З V,
де V — об’єм тетраедра DABC, маємо:
hr + h42n + h43n + hr = (-^-+ * +17 +==) X \ st” St” st” st”/
X (diSi 4- d2S2 + d3S3 + ^54)4я > a L-та • 44л X
X ^(di-d2-d3-d4-Si-S2-S3-S4)4n = 44n+‘ • ctf • di • dS ■ dl
152


Задача 12. Довести, що у трикутнику АВС довжина бісектриси la обчислюється 33 формуЛОЮ
, 2Ьс А а~ b'+c cos-2'-
Задача 12". У тетраедрі DABC грані ABC і ABD мають площі S] і S2 і утворюють між собою кут а. Довести, що площа перерізу, який ділить кут а пополам, обчислюється за формулою
2Si • S2COS -у
S
5і + 52
Доведення 12". Враховуючи формулу (22.1), обчислимо об’єми даного тетраедра і тетраедрів, утворених перерізом, який ділить кут а пополам. Маємо:
2 5-5,sinT 2
3 а 'З
ЗВІДКИ S
5-52sinf 2 а =Т
2S|S2cosy
5і 52
Si • S2 • sin а
а
Задача 13. Коло, вписане в трикутник ABC, дотичне до його сторін у точках /G, ^2, Кз- Довести, що центр цього ;ола міститься всередині трикутника КхКчКз.
Доведення. Зазначимо, що основа висоти, опущеної з вершини прямого кута на гіпотенузу прямокутного трикутника, належить гіпотенузі, а не її продовженню. Тому точки А і І міс-, тяться з різних боків відрізка КгКз. Аналогічно доводиться, що точки В і /, С і І містяться з різних боків відрізка відповідно КхКз та К\Кч. що доводить твердження задачі.
Задача 13". Довести, що центр вписаної в тетраедр сфери, міститься всередині тетраедра, утвореного точками дотику.
Доведення 13". Позначимо точки дотику вписаної сфери до граней тетраедра К\, Л2, Кз, Ка, і — центр вписаної сфери. Ми показали (див. задачу 10), що площина, якій належать три з цих точок, перпендикулярна до бісектриси тригранного кута, утвореного відповідними гранями. Причому ця площина перетинає бісектрису в точці, яка належить відповідному відрізку, що сполучає вершину з центром вписаної кулі /. В тетраедрі DABC, за аналогією з попередньою задачею, точки D та І містяться з різних боків відрізка Для доведення можна розглянути прямокутні трикутники DK\I і ZW- Отже, вершини тетраедра DABC і центр кулі / містяться з різних боків граней тетраедра /<іЛ^зК4- Твердження задачі доведено.
Задача 14. Довести, що коли центр кола, описаного навколо трикутника ABC, збігається з інцентром, то цей трикутник рівно- сторонній.
Задача 14". Довести, що коли центри вписаної й описаної сфер тетраедра збігаються, то всі грані — рівні трикутники.
153


Доведення 14". Якщо сферу, описану навколо тетраедра DABC (мал. 22.12), перетинати площинами граней, то кола, описані навколо кожної з них, будуть рівними між собою, оскільки вони рівновіддалені від центра сфери. У рівних колах рівні хорди стягують рівні дуги. Тому, наприклад, Z_BDC = = /LB АС. Позначимо пари рівних кутів
Л BDC= /LBAC= аі ААВС= /LADC=a2 ZLACB= AADB=a3.
Аналогічно
Z_ABD=/LACD=fL /LBCD = ABAD=fr> /LCBD = Z_CAD = $3.
Далі маємо:
cti oc2 И- o&3 == 180°, Pi 4~ P2 4" аз = 180°, ai + Рз+ P2= 180°, P1 + CX2 -|- Рз = 180°.
Від першої рівності віднімемо другу, від третьої — четверту. Дістанемо:
аі + а2=Рі + р2, аі—а2=Рі — Р2, звідки аі = Ри 002= р2; аз=Рз.
Отже, грані рівні.
Задача 15. Довести, що сума квадратів відстаней від будь- якої точки кола до вершин вписаного в нього правильного трикутника є величина стала, незалежна від положення точки кола.
Доведення. Нехай X — довільна точка кола, в яке вписано рівносторонній трикутник АВС (мал. 22.13).
Позначимо АХ=Гі, ВХ=г2, СХ=г3. Але п = г2-\-г3 (доведіть!).
Позначимо ВС=а. З трикутника ХВС маємо:
a2=d + d — 2г2гзСО5 120°, або
г2 + гз + ''2 • гз = а2-
Далі
Г2 Г2 4“ Гз= (г2 4" гз)2 4” ^2 4“ ^3 = 2 (г2 Гз + Г2 • Гз) = 2d2
Задача 15". У сферу вписаний правильний тетраедр DABC. Довести, що для кожної точки М сфери
MA2 + MB2 + МС2 + MD2 = 8/?2, де R — радіус сфери.
154


Мал. 22.12
Мал. 22.13
Доведення 15". Позначимо О — центр сфери. Тоді
МА = ОА -ОМ,
МВ=ОВ — ОМ,
МС=ОС-ОМ,
MD= OD - ОМ.
Оскільки |ОЛ4|=|ОД |=Я, то
{МА |2+|7ЙВ|2 + |7ЙС|2+|Л4О|2= 4|ОЛ |2 + 4|ОЛ1|2-
— 2ОМ(ОА +ОВ +ОС +OD) = 8R2, або МА2 + МВ2 + М С2 + MD2= 8R2,
оскільки О А + О В + ОС A~OD = 0 (доведіть!). Рівність до- ведено.
Задача 16. У коло вписано трикутник АВС. Медіана СМз перетинає коло вдруге в точці D. Довести, що
АС2 + ВС2 = 2СМз*СО.
Задача 16". У сферу вписано тетраедр О АВС. Пряма, проведена через точку О і точку перетину медіан М трикутника АВС, перетинає сферу вдруге в точці D. Довести, що ОЛ2 + ОВ5 + ОС2=ЗОМ- OD.
Доведення 16". Нехай S — центр описаної сфери радіуса R. Позначимо через гі, Г2, гз, Н радіуси-вектори точок Л, В, С і О. Тоді _ _ _
35Л4 = Гі-р Г2 Я-Гз ,
О А = г\ — г4,
ОВ =Г2 — Г4,
ОС = г3 — г4.
155


Звідси
оа2+ов2+ос2=(71__-22+(72_74)2j_(j3__-)2== •
= б/?2-L2r4(ГI + Г2 + Гз) = б/?2 - бГ4 • SM.
Але SM= г4-|-ОМ, тому остання рівність набирає вигляду: ОА2 + О В2 + ОС2 = б/?2 - 6r4(r4 + ОМ) = - 6г4 • ОМ=
= 3 • ОМ -2tfcos Z-SOD.
Оскільки OD = 2R • cosZ.SOD, то ОА2 +ОВ2+ОС2 = = 3 • ОМ • OD.
Задача 17. На стороні АВ трикутника ABC взято точку F. Через неї проведено прямі FA\ і FB\, паралельні відповідно сторонам АС і АВ (Аі належить ВС, Ві належить АС). Довести, що ці прямі відтинають на сторонах ВС і АС трикутника відрізки СА\ = а\ і СВ\ = Ь\ такі, що
Qi . 61 і а “Г" b И
Доведення. Оскільки A\FB\C — паралелограм (мал. 22. 14), то FB\ = A\C=a\, FA\ = ВіС= b\. Тоді
а\ B\F AF b\ A\F FB
~a~~BC~~AB ’ ~b~~~AC~=-AB ' ЗВІДКИ
fli . 6i AF-\~FB .
~ + ~AB ~~ k
Задача 17". Через точку F на основі ABC тетраедра DABC проведено прямі, паралельні бічним ребрам, які перетинають грані DBC, DAC, DAB у ^очках -і, В< С|. Довести, що
v+t+t=1’ де ҐЛ| = С|’ ол = а-
FBi = 6i, DB=b, FC\ = c\, DC=c.
Доведення 17". Розглянемо тетраедри ADBC і FDBC (мал. 22.15). Позначимо відповідно їх об’єми V і VT Ці об’єми відносяться як висоти, опущені на спільну грань DBC. Оскільки відрізки DA і FA\ паралельні, то відношення висот цих пірамід дорівнює відношенню DA . FA\. Отже,
V1 FA\
V ~ DA ’
Позначимо об’єми пірамід з основами DBA і DAC і вершиною F через V2 і Уз. Тоді
V2_ FB\ 1/3 __ FCx
V ~ DB ’ V — DC •
Додаючи почленно ці рівності, маємо:
156


Ml , FB1 , FC1
DA ' DB DC — 1 ’ або
а ’ b “Г с ‘
Задача 18. Всередині рівно- стороннього трикутника ABC міститься точка X. Через центр трикутника М і точку X проведено пряму, яка перетинає сторони трикутника (або їх продовження) у точках Аі, Ві, С\. Довести, що
с,х _ Q о.
А\Х , В\Х
АхМ + В'М СіМ
Доведення. Позначимо проекції точок X і М на сторони ВС, АС і АВ через Xj, Х2, Х3 і Л4і, Лї2, Мз (мал. 22.16). З подібності трикутників А1ХХ1 і АіММі маємо:
АіХ ХХі
AtM
MMi ‘
Аналогічно
ВіХ _ хх2
ВіМ ■“ ММ2 ’
СіХ _ ХХз СіМ ~~ ММз ■
Позначимо площі трикутників ХВС, ХАС, ХАВ відповідно Si, S2, S3; сторону рівностороннього трикутника ABC — а. Тоді
XX, =-^, хх2 = -^, ХХз = -^ а а а
157


MMi = MM2=MM3 = ?^, ТО
А,Х В,Х С,Х _ XXt XX, ХХ3 _ ІТлГ 'Тмт+'сГлГ-’лТ/йТ-’- мль-*"~ммГ~
= 2(Si+S2 + S3)-6 = 120^3 = 3
а2 З а2 д/3 • 4
Задача 18". Точка І — центр кулі, вписаної в правильний тетраедр DABC. Точка X міститься всередині тетраедра. Пряма XI перетинає площини граней в точках А|, Ci, D\, Довести, що
Д,Х , В'Х , С\Х , DiX л АхІ + В,/ + Сі/ D,/ ~4
Доведення 18". Позначимо проекції точок X і І на грані тетраедра Хі, Х2, Лз, Х4 і /і, /2, /з, Л (мал. 22.17). З подібності трикутників Z/4Di і XXiD\ маємо:
D\X XX, Dd ~~ II, •
Аналогічно
AtX _ XX, ВіХ ХХ2 СіХ _ ХХз Ad ~~ //, ’ Bd — ІІ2 1 Cd ~ //з ’
Нехай г — радіус вписаної в тетраедр кулі; 16, V2, V3, 16— об’єми тетраедрів XDBC, XACD, XABD, ХАВС, V — об’єм даного тетраедра, S — площа кожної з граней. Тоді
YY ЗИ, YY ЗУ2 yY ЗУз1 yY 316
ЛЛ|——£—, ЛЛ2 — ——, ЛЛз — ——, лл4 — ——
Маємо: AiX BtX С,Х DiX _ Ad ' Bd + Cd г Dd ~
XX, + XX2 + ХХз + XX4 r
_ 3(1/, 4- У2 + Уз+ V,) 3V r-S r-S ’
але
Q 5n0B1I. 3V
s=~l“’ r=^—• °повн.
Отже, розглядувана сума дорівнює
4-3V 4r
158


23. 	ПЕРЕРІЗИ ТЕТРАЕДРА
Задача 1. У тетраедрі DABC на різних гранях задано точки М, Af, L. Побудувати переріз тетраедра площиною, яка проходить через ці точки.
Розв’язання. Через точки D, М, N проведемо допоміжну площину. Вона перетинає ребра АВ і ВС відповідно в точках М] і (мал. 23.1). У цій площині
проведемо дві прямі, які перетинаються в точці /(. Одна з них проходить через точки М, /V, а друга — через точки Mi, N\. Пряма ЛХ перетинає ребра ВС і АВ відповідно в точках X і Y. Проводячи через точки X і /V, Y і М прямі, дістанемо точки Z і U на ребрах DC і DA відповідно. Переріз XYUZ — шуканий.
Задача 2. Довести, що коли тетраедр перетнути площиною,
яка не паралельна жодній зі сторін основи, то три точки перетину продовжень відповідних сторін трикутників основи і перерізу належать одній і тій самій прямій.
Доведення. Нехай площина а перетинає ребра тетраедра DABC у точках Аі, Ві, Сі (мал. 23.2), а площину р, якій належить основа ABC, по прямій XY. Оскільки відрізки АВ і АіД не паралельні один одному і належать площині бічної грані тетраедра, то при продовженні вони перетинаються у деякій точці М. Ця точка належить площині а і площині р, тобто
159


вона належить лінії їх перетину X/. ’^алогічно доведемо, що прямі АС і ЛіСі, ВС і В\С\ перети 4аюто?я відповідно в точках L і К, які належать прямій XY. Таким чином, усі точки перетину продовжень відповідних сторін трикутників ABC і на¬
лежать одній і тій самій прямій XY.
Задача 3. Побудувати переріз тетраедра DABC площиною, проведеною через довільну точку ребра АВ і паралельною мимобіжним медіанам ВМ\ і СМ2 граней DBC і DAC.
Розв’язання. Проведемо у трикутнику DAC медіану ДМі (мал. 23.3). У трикутнику АМ\В проведемо М3М4ЦВМ1. Через точку М4, яка належить грані ADC, проведемо пряму, паралельну медіані СМ2. Пряма перетинає ребра АС і AD у точках X і Y відповідно. Переріз M3XY — шуканий.
Задача 4. Довести, що тетраедр можна перетнути площиною так, що в перетині дістанемо ромб.
Розв’язання. У гранях ABD і DAC через деяку точку М на ребрі AD проведемо прямі, паралельні мимобіжним ребрам АВ і DC. Через ці прямі проведемо площину перерізу і дістанемо паралелограм. Тепер знайдемо положення точки М, щоб паралелограм MNPQ перетворився у ромб (мал. 23.4). Позначимо АВ=с, DC=d, MN=x. З подібності трикутників AMQ і ADC маємо:
х AM
~d~~~~~AD~ ’
З подібності трикутників MDN і АЬВ\
х _ MD с — AD ’
160


або
X _ AD —AM с ~ AD
ЗВІДКИ
Таким чином,
MD^—^AD.
c-\-d
Отже, на ребрі AD завжди знайдеться така точка Л4, що переріз буде ромбом.
Задача 5. Правильний тетраедр перетнули площинами, паралельними двом ребрам, які не перетинаються. Довести, що периметри всіх утворених перерізів рівні між собою і дорівнюють 2а, де а — довжина ребра тетраедра.
Доведення. Побудуємо переріз MNPQ (мал. 23.4), паралельний ребрам АВ і CD. Цей переріз — паралелограм. Позначимо довжину відрізка PC через х. Тоді NP = BP = a — x. Оскільки NB = a — х, то DN = x і MN = DN = х. Отже, периметр паралелограма QMNP дорівнює 2(х-|-а— х)=2а.
Задача 6. У тетраедрі проведено перерізи, паралельні двом його ребрам, які не перетинаються. Знайти переріз з найбільшою площею.
Розв’язання. Позначимо площу перерізу, паралельного мимобіжним ребрам АВ і DC (паралелограма QMNP) (мал. 23.4), через S.
S= QP • QM • sin /LMQP.
Кут MQP дорівнює куту між мимобіжними ребрами АВ і DC. Отже, це величина стала для всіх розглядуваних паралельних перерізів і площа перерізу залежить тільки від добутку QP • QM. Позначимо QC=x. Тоді
QP х QM АС — х
~АВ~АС ’ ~DC~ АС~~ ’
Звідси
QP.QM= АВа£?С х(АС-х\
Сума % + (ДС —х) — стала. Отже, добуток х(АС — х) набуває найбільшого значення при х = уДС.
Таким чином, переріз з найбільшою площею утворюється при перетині тетраедра площиною, яка проходить через середини ребер AC, AD, ВС, BD.
Задача 7. Дано правильну трикутну піраміду, сторона основи якої дорівнює а, бічне ребро дорівнює 2а. Через середину
11 0 172
161


бічного ребра,перпендикулярно до нього, проведено площину. Знайти площу утвореного перерізу.
Розв’язання. Нехай MNP — переріз, проведений через середину М ребра AD і перпендикулярний до нього (мал. 23.5). Оскільки відрізок MD перпендикулярний до відрізка NP і відрізок ВС перпендикулярний до ребра AD, то відрізки NP і ВС — паралельні. Отже, DN=DP і MN = MP. Позначимо середини відрізків АВ і NP відповідно Е і /С Позначимо також /LED В = а. Тоді
1 л/15
sina=—, cosa=-V- , 4 _4
M№=atg2a=-24jl-
Знайдемо /VP і NN. Маємо:
NP _ DN а _ 8
ВС ~~ DB ’ UN— cos 2a “ 7 а'
Отже, NP=-~a, NK=-^NP=^-a.
Далі знайдемо MN'.
МК= =УД а.
"І”1
Отже, площа перерізу MNP дорівнює ~%МК • NP= 4Q а .
Задача 8. Правильний тетраедр з ребром а перетинають безліч площин так, що в перерізі утворюється трикутник, а сума бічних ребер кожного з утворених тетраедрів дорівнює а. Знайти тетраедр найбільшого об’єму серед утворених.
Розв’язання. Позначимо об’єм правильного тетраедра V, одного з утворених—Vx і бічні його ребра — Яі, ао, аз- Тоді (див. задачу 3", с. 146)
Vx aiasa3
~у~=—’ ЗВІДКИ
у у 01^2^3
а3
Але а\ ++ яз = а. Отже, добуток набуває найбільшого значення при ai = a2=a3 = y. Таким чином, шуканий тетраедр — той, у якого ребра дорівнюють .
162


Задача 9. Об’єм правильної трикутної піраміди DABC дорівнює V. В цій піраміді проведена площина, яка паралельна медіані основи BN, перетинає бічне ребро DB у точці Ві, бічне ребро DA — у точці Ді, причому
DA} = ±DA, DBi = ~DB.
о
Знайти об’єм тієї частини піраміди, яка міститься нижче від цієї площини.
Розв’язання. У площині DBN через точку В] проведемо відрізок B\N\, паралельний медіані BN (мал. 23.6) Через точки Bi, Afj і А] проведемо площину, яка перетинає ребро DC у точці Сі. Знайдемо відношення об’ємів тетраедрів DABC і DA]BiC\. Для цього потрібно знайти відношення DC\ : DC. Оскільки
_ DB, _ 1
DN ~ DB ~ 3 ’
то задача зводиться до планіметричної: у рівнобедреному трикутнику DAC медіана DN поділена у відношенні DN\ : DN = 1 : З, сторона DA — у відношенні DA і : DA = 1 : 2. Через точки ЛЛ і А і проведено пряму, яка перетинає сторону DC у точці Сі. Знайти відношення DCi .DC. Для розв’язання цієї задачі в рівнобедреному трикутнику DAC (мал. 23.7) проведемо середню лінію Л|Л2. Через точку D проведемо пряму /, паралельну відрізку А]А2, і продовжимо відрізок ЛіС| до перетину з І у точці Е. Тоді з подібності трикутників А\А2С\ і EDC\, позначивши DC\=x, DC = y, маємо:
DC, _ 2х _ ED _ ЕР С,А2 у—2х ЛіЛ2 2ЛА2/41
Враховуючи подібність трикутників EDN] і A\N2N\. маємо:
ED _ 1 DN, 2ЛМі — Т' ЩІГ2~~ '
163


Отже,
,, Or . . X 1
А__=1, ЗВІДКИ -=Г-
Отже, 4^"=Т- Тоді V='2^4(lZ1—об єм тетРаедРа ОДіВіСі) .
Звідси Vi=^--
Шуканий об’єм Vx дорівнює
у — у V_=%Ly
Vx~ V 24 24
Задача 10. У тетраедрі DABC через ребро DA проведено переріз, перпендикулярний до ребра ВС. Площа цього перерізу S, довжина ребра ВС дорівнює а. Знайти об’єм тетраедра.
Розв’язання. Позначимо об’єм тетраедра V, довжину ребра AD — Ь' відстань між мимобіжними ребрами AD і BC~dy кут <р між цими ребрами дорівнює 90°. Отже,
V=~abd sin ср, але sin<p= 1, d=~~.
Звідси І/ 1 а 25 Sa v=^ab—=-3~-
Задача 11. Через кожне ребро ортоцентричного тетраедра DABC проведено переріз, перпендикулярний до протилежного ребра. Довести, що:
1) всі перерізи мають спільну точку;
2) три перерізи, перпендикулярні трьом ребрам однієї грані, мають спільну пряму;
3) коли ці три перерізи рівновеликі, то тетраедр — правильна піраміда;
4) коли чотири з цих перерізів рівновеликі, то тетраедр правильний.
Справджуються й обернені теореми.
Доведення. 1) Оскільки кожному перерізу належить висота тетраедра, то спільною точкою є ортоцентр тетраедра;
2) 	цією прямою є висота тетраедра; 3) позначимо висоти, які належать розглядуваним граням h\, /і2, h$\ Н — спільна пряма цих перерізів, або висота тетраедра. Тоді Н • h\ = Hh,2 = НІіз. Отже, грань ABC (до неї проведена висота Н тетраедра DABC) — правильний трикутник; 4) міркування аналогічні до попередньої задачі.
164


24. 	ТЕОРЕМА ЧЕВИ
Задача 1. Теорема Чеви. Нехай Лі, В]у Сі —три точки, які лежать відповідно на сторонах ВС, СА, АВ трикутника ABC чи на їх продовженнях. Для того, щоб прямі АА\, ВВ], СС\ перетинались в одній точці або були між собою попарно паралельні, необхідно і достатньо, щоб
^6*1 В А і СВ] < /94 1 \ С|В ‘ Л,С ’ В}А ’ 1 1
Доведення. Необхідність. Нехай відрізки ААі, ВВ\, СС\ перетинаються в точці К (мал. 24.1).
Проведемо пряму / через точку А паралельно стороні ВС і продовжимо відрізки ВВ\ і СС\ до перетину з / у точках М і N. Позначимо /4Сі = Хі, С\В = х^ ВА\ = у\, А\С — у^ CB\ — z\, B\A = z<2, МА = а\, AN = ao.
Трикутник МВ\А подібний трикутнику ВВ\С. Тому
Q|Zi J
(Уі + Уг)22
Трикутник NC\A подібний трикутнику СС\В\
Л'і
У\ +У2 ~ Л'2
Звідси
02*2
<У\ +і/2)Х|
Поділимо вираз (1) на вираз (2), враховуючи, що (3 подібності трикутників BtfAi і МКА‘, СКАї і NKA). Дістанемо
Д1 • ^1(^/1 +і/2) • Х| __ J
(yt + yzjaz- х2- z2 ~ ’
або^--£!.= і.
У2 ■ А'2 • Z2
Випадок, коли точки В\ і С\ лежать на продовженні відрізків СА і ВА, розглядається аналогічно.
1.
(2)
Мал. 24.1
165


Достатність. На сторонах трикутника АВС (мал. 24.1) дано точки Л і, В\, С\ так, що
АС\ • ВА і • СВі _ . . .
ВС\ • СА} • АВ\ ~~ 1 ‘ ' 1
Проведемо відрізки ААі і ССі. Вони перетнуться в точці /С Нехай ВВ\ не проходить через цю точку. Проведемо, через неї пряму ВВ2 (Вг належить ЛС). За умовою (24.1) маємо:
АСі ’ ВАі • СВ2 _ .
ВСі • СЛі -ЛВ2 ~ 1'
З (1) і (2) дістанемо:
СВі _ СВ2
АВ\ АВ2
Отже, В\ і В? збігаються, що й потрібно було довести.
Задача 2. Довести, що в трикутнику ABC в одній точці перетинаються:
1) медіани трикутника;
2) бісектриси внутрішніх кутів трикутника;
3) висоти трикутника;
4) прямі, які сполучають вершини трикутника з точками дотику вписаного в нього кола;
5) прямі, які виходять з вершини трикутника і ділять протилежні сторони пропорційно одним і тим самим тригонометричним функціям прилеглих кутів;
6) прямі, які сполучають вершини трикутника з точками дотику відповідних зовнівписаних кіл.
Доведення. 1) Нехай Л4і, М2, Мз— середини сторін ВС, СЛ, АВ трикутника ЛВС. Тоді
Л/Из • М\В • СМ2 .
МзВ-СМі-М2Л = k
2) Нехай Lj, С2, Сз — точки перетину бісектрис із сторонами ВС, ЛС, АВ.
Тоді
AL3 • BL\ * CL2 abc .
BL3 • CL[ • AL2 abc
3) Нехай //і, //о, Яз— основи висот ha, hb. hc. Тоді
АНз • BH\ • СН2 _ hcdgA • ha • ctgB • /^ctgC .
НзВ • H\C • H2A = AcctgB • /ifl • ctgC • /uctg Л = *
4) Нехай /G, /С2, Кз— точки дотику вписаного кола зі сторонами трикутника ЛВС. Тоді, оскільки Л^з = Л^2, ВК\ = = ВКз. СКї= СК\, маємо:
166


АКз-KiB-Cfa _ !
КзВ • СК\ -КъА 1 •
5) Нехай ці прямі перетинають сторони трикутника ВС, АС, АВ відповідно в точках F\, F2, F3. А, В, С—кути трикутника. Тоді
AF2 _ ф(Л) . CFi _ ф(С) . BF3 _ ф(В)
F2C ~ ф(С) ’ F\B ~ ф(В) ; F3A ~ ф(Л) *
AF2 • CF, • BF3 _ ф(Л) • ф(С) • ф(В) _
F2C-F}B-F3A <р(С) • ч(В) - <р(А) k
6) Нехай зовнівписані кола дотичні до сторін ВС, АС, АВ трикутника ABC відповідно у точках Т\, Т2, Тз; а, Ь, с — довжини сторін трикутника, р — його півпериметр. Тоді (див. с. 40)
АТ2 = р — с, Т2С=р — а, СТ\ = р — Ь, Т\В = р — с,
ТзВ = р — а, ТзА = р — Ь. Звідси
АТ2-Т3В-СТ} __ (р — а)(р — Ь)(р — с)___ СТ2-АТ3-ВТі (р —а)(р —Ь)(р —с) ~~~ К
Отже, умова (24.1) виконується.
Задача 2. У трикутнику ABC прямі АА\, ВВ\, СС\ перетинаються в одній точці. F\, F2, F3 — середини прямих ААі, ВВі, ССі відповідно. Довести, що прямі AliFi, M2F2, M3F3 перетинаються в одній точці.
Доведення. Маємо:
ВАі СВ\ АС\ . р-.
—гт; в—і 7г-б“=1. Помножимо чисельник і знаменник кож-
А і G о і А С і d
ного дробу на у. Маємо:
“2“ В А і • -%СВ\ • А Сі
уЛ.С-уВіЛ -уСіВ
або
M3F\ M[F2 M2F3 .
що й доводить твердження задачі.
Задача 3. Знайти залежність між сторонами а, Ь, с трикутника ABC, якщо медіана АМ\, висота ВН2 і бісектриса СЬз перетинаються в одній точці.
Розв’язання. Очевидно, що АЬз: ЬзВ = ^~, М\В= М\С, а2А-Ь2—с2
CH2:H2A = ctgAACB:cigACAB= 7^^ ’
167


Підставляючи отримані формули в умову (24.1), маємо:
Ь(а2 + Ь2 — с2)
а(Ь2 + с2 — а2)
або
a3 + b3 = a(b2 + c2)-b(a2-c2}.
Задача 4. На медіані СМз трикутника ABC дана точка Р. Через неї проведені прямі АР і ВР, що перетинають сторони ВС і СА відповідно в точках А\ і В\. Довести, що коли AAt = = ВВі, то трикутник ABC — рівнобедрений.
Доведення. Оскільки точка Р — спільна для прямих ЛЛі, ВВ] і СМз, то, застосовуючи теорему Чеви, дістанемо:
СВ{ • ВА\ о СВ\ _ АіС
В\А-А\С ~~ а°° ~~В~іА~~ ВАх ’
тобто відрізок Д|В] паралельний відрізку АВ. Оскільки АіА = = ВВ\Ч то Z-^iBA = Z-В\АВ, тобто трикутник ABC — рівнобедрений.
Задача 5. Півколо дотикається до сторін АС і АВ трикутника ABC у точках F\ і Л2, а його діаметр належить стороні ВС. Довести, що відрізки BF\ і CF% перетинаються з висотою АНі трикутника ABC в одній точці.
Доведення. Позначимо радіус півкола — Ra.
Нам треба довести, що
AF2-BH' • CFi _
FzB-H'C-F'A L
У даному випадку
4/У| • ctgB • Ra • ctgC .
Ra-ctgB-AH' -ctgC= L
Отже; твердження задачі доведено.
Задача 6. На висоті АН\ трикутника ABC виберемо довільну точку X. Нехай К — точка перетину прямих АС і ВХ, Т — точка перетину прямих АВ і СХ. Довести, що
Z_TH\A = Z_KH\A.
Доведення. Позначимо (мал. 24.2) К\ і Ті—точки перетину прямих Н]К і Н\Т з прямою /, яка проведена через вершину А паралельно стороні ВС. Доведемо, що А/Сі=АГ|. За теоремою Чеви АК • СН\ • ВТ = КС • ВН\ -ТА. З подібності трикутників АКК\ і СКН\ випливає, що
ЛКі
СНх-АК СК
Аналогічно
АТ\
ВН} -AT
~ ВТ
168


Якщо АТ\ = АК\, то СН\Уі ХАК-ВТ=ВНі-АТ-СК, але це випливає з теореми Чеви. Отже, АК\=АТ\. Звідси
/7^, = //^! і ЛТНуА = ЛКНіА.
У тетраедрі також існує теорема, яка нагадує теорему Чеви.
Задача 7. Для того, щоб дві прямі, проведені через вершини А і D тетраедра перетинались, необхідно і достатньо, щоб виконувалося співвідношення
$ АР\С $APtB
SPA,C
SpA^B
(24.2),
де А] і Di—точки перетину, цих прямих з відповідними гранями.
Доведення. Необхідність. Нехай прямі АА, і DDt перетинаються в точці О. Через ці прямі проведемо площину ADF (мал. 24.3).
Зрозуміло, що
$FD\C CF
SFDtB
Отже,
SCAF~SFPlC SADiC CF
SBAF~SFD}B SAD}B
Аналогічно доводиться, що $DA\C CF SdA'B=~bF'
тобто виконується рівність (24.2)
Достатність. Припустимо, що прямі ААі і DD] не мають спільної точки. Нехай пряма DAi перетинає сторону ВС у точці Fg, а А£)| у точці F\. Зрозуміло, що
$ар}с CF\ SpAtC CF2 $АРіВ BF\ 1 SDA[B BF2
scaf CF
~S^—BF-
169


Отже,
CF\ _ CF2
BFi ~~ BF2 ’
BFi BF2 '
BC _ BC
BF\ ~~ BF2 ‘ або тобто
Звідси BF] = BF2
і точки F\ і F2 збігаються. Отже, прямі ААі і DD] перетинаються.
Можна показати, що умовою перетину прямих ААі, ВВ\, ССі, DDi в одній точці є виконання для кожних двох з них умови (24.2).
Задача 8. Довести, що медіани тетраедра перетинаються в одній точці.
Доведення. Оскільки точки D\ і А] центроїди граней ABC і DBC і площі трикутників AD\C, AD\B і DA\C, DA\B рівні (див. с. 15), то твердження задачі доведено.
Задача 9. На гранях ABC, DBC, DCA, DAB тетраедра DABC задано відповідно точки D\, Аь В\, С\. Вони сполучаються з усіма вершинами граней, яким належать. Площі кожного з утворених трикутників у сумі з площею грані, яка має спільну сторону з цим трикутником, рівні. Довести, що прямі ААі, ВВ\, СС\, DD\ мають спільну точку.
Розв’язання. Доведемо, що прямі ААі і DDi перетинаються. За умовою (мал. 24.3)
51 + 5,40,6 = S2 + Здя.в = Si + 50,4,6=52 + 50,4,0 = у.
де 5і, S2 — площі граней DAC і DAB; S — повна поверхня тетраедра.
Звідси
5д0Іб=50л1с=у —5і,
5д0|Д= 50д,в = у —S2.
Підстановка останніх рівностей у рівняння (24.2) перетворює його в тотожність, що доводить твердження задачі.
Задача 10. У гранях тетраедра DABC (див. задачу 9) задані точки D\, А\, В\, Сі, що сполучаються з усіма вершинами граней, яким належать. Відношення площ кожного з утворених трикутників до площі грані, яка має спільну сторону з трикутником, рівні. Довести, що прямі DD\, АА\, ВВ\, СС\ мають спільну точку.
Доведення. Позначимо 5і і S2 — площі граней відповідно ADC і ADB. Маешу.
$AD'C $ADxB . §A\DB $AJ)C
Si ’ ~ S2" 1 s2” — Si ’
звідки виконується умова (24.2).
170


Задача 11. Довести, що в тетраедрі DABC прямі DC АІі, ВІ2, СІз, де /, /і, Л, /з — інцентри відповідних граней перетинаються в одній точці, якщо добутки довжин протилежних ребер рівні між собою.
Доведення. Доведемо, що DI і ЛІ \ перетинаються. Нехай г і Г\ — радіуси кіл, вписаних в трикутники ABC і DBC.
Маємо:
^Здіс—г • Ь\ 2SA/B=r-c\ 2SDhC= r\b\; 2SDilB= г\С\
(b і 6і, с і Сі —довжини ребер відповідно АС і CD, АВ і BD). Підставляючи ці вирази в (24.2) і враховуючи умову Ьс\ = Ь\С, дістанемо твердження, яке доводиться.
Задача 12. Довести, що чотири висоти тетраедра перетинаються в одній точці, якщо добутки косинусів двогранних кутів при мимобіжних ребрах рівні..
Доведення. Нехай Н — проекція точки D на грань ABC, а Ні — проекція вершини А на грань DBC. За теоремою про площу проекції плоскої фігури маємо
$АНС = SadC • COS<pi,
де ері —лінійний кут двогранного кута з ребром АС.
Далі запишемо:
$АНВ = SaDB • COS<P2,
де ерг — лінійний кут двогранного кута з ребром АВ’,
Sadc • COS(?3,
де срз— лінійний кут двогранного кута з ребром CD\
Sdh}b= $ADB • COS(p4,
де ф4 — лінійний кут двогранного кута з ребром DB.
Підставляючи ці співвідношення у формулу (24.2) і врахувавши умову, дістанемо твердження задачі.


ЗАСТОСУВАННЯ ВЕКТОРІВ У ЗАДАЧАХ
25. 	ВЕКТОРИ В ЗАДАЧАХ ПРО ТРИКУТНИК
І ТЕТРАЕДР
Про деякі векторні співвідношення
І. Довести, що для довільної точки X простору і для деякого дійсного числа k рівність
XC=kXA+(\-k)XB (25.1) є необхідною умовою належ¬
ності точок А, В і С (Д^В)
одній прямій, причому ВС = kBA .
Співвідношення (25.1) можна записати так: точка С нале¬
жить прямій АВ тоді і тільки тоді, коли
ХС =аХА +ЬХВ a -j— b = 1
(а, b — дійсні числа, X — довільна точка простору).
Доведемо формулу (25.1).
Достатність. Нехай виконується рівність (25.1). Тоді
ХС -ХВ = k(XA —XBY
172


Звідси BC=kBA, отже вектори ВС і ВА колінеарні, а точки А, В, С належать одній прямій.
Необхідність. Оскільки точки А, В, С належать одній прямій, то вектори ВС і ВА колінеарні, або ВС = kBA . Звідси ХС -ХВ = k(XA -XBY або ХС =kXA +(1 -k)XB .
II. Довести, що коли точка С ділить відрізок АВ у відношенні АС : ВС= т : п {т, п — дійсні числа, X — довільна точка простору), то
ХС=-Х4 Н ~ХВ. (25.2)
ги4-и 1 т-\-п
Для доведення цієї формули у співвідношенні (25.1) візьмемо
т-\-п
Якщо точка С — середина відрізка. А В, то
ХС=у(ХЛ+ХВ). (25.2')
ПІ. Для довільної точки простору X і для деяких дійсних чисел k і / рівність
~XD=kXA +ЇХВ +(\-k-l)XC (25.3)
є необхідною і достатньою умовою належності точок Л, В, С, D одній площині. Співвідношення (25.3) можна записати інакше:
У5=а,ХЛ + а2ХВ + а3ХС ,
аі+а2 + аз=1 }
(аі, а2, а3 — дійсні числа, X — довільна точка простору).
Доведення необхідності. _ _
Позначимо ХА — а , ХВ =Ь , ХС =с , XD = d
Оскільки точки Л, В, С і D належать одній площині, то вектори d — с , а — с , Ь — с також належать одній площині, тобто d — с= k(a — с) + 1(Ь— с), або d= ka-\~ lb —kl^c-
Таким чином,
XD = kXA + lXB + ^-k-l}XC.
Достатність доведіть самостійно.
IV. Довести, що для довільної точки простору X і точки М перетину медіан трикутника ABC (центроїда трикутника ЛВС) виконується співвідношення
ЇШ = ±(ХА + ХВ + ХС\ (25.4)
173


Доведення. Позначимо М\ — середину сторони ВС. Врахо- _— J —•
вуючи, що ММ] = уЛМ, маємо:
ХМ,— XM = j-(XM,-XA), звідки
ХМ^ХА+^ХМі.
Але Жі = у(ХВЧ-ХС) отже,
ХМ = -Ь ХА + у • у (ХВ + ХС) = у (ХА + ХВ + ХС).
Задача 1. Довести, що медіани трикутника перетинаються в одній точці і діляться у відношенні 2:1, починаючи від вершини.
Доведення. Позначимо Мі, М2, Мз — середини сторін ВС, АС, АВ трикутника ABC, X — довільна точка площини. Тоді XMi = y(XB + ХС). Нехай Хі—довільна точка, яка ділить медіану AM і у відношенні АХі :Х]Мі = 2: 1. Тоді за співвідношенням (25.2):
xxt -1ХА+ у ХМі = у ХЛ + у (у<Х5 + ХС)) =
= у(ХА + Ж+ХС).
Аналогічно: якщо Х2 і Хз — точки, які ділять медіани ВМ2 і СМ3 у відношенні ВХ2: Х2М2 = СХ3:Х3М3=2: 1, то ХХ2=ХХ3 = = у(ХЛ+ ХВ + ХС), тобто точки Хі, Х2, Х3 збігаються.
Задача 2. У трикутнику АВС а, Ь, с — довжини сторін, та — медіана ЛМ|. Довести, що
2_ 2 (б2 + с?) — а2 гПа— 4 ■
Доведення. Нехай ВС=а, АС=Ь, АВ = с, АМ\ = та Тоді mfl = y(F+7), або m2 = ^(b2+ + 2Ьс). Але
- - 62+с2_а2
Ь • с = 2 •
Отже,
2 2(62 + с2)-а2
ГПа— 4
Задача 3. Довести, що три висоти трикутника перетинаються в одній точці.
Доведення. Нехай АН\ і ВН2 — висоти трикутника ABC (мал. 25.1). Позначимо точку перетину цих висот Н і через неї проведемо пряму СН до перетину з АВ в точці К- Позначимо також НА = а, НВ = Ь, НС=с. Тоді СВ=Ь — с, АС=с — а, ВА = а — Ь. _ _
Мають_ місце рівності Ь(с — а) = 0, а(Ь — с) = 0. Звідки с(а — &) = 0.
174


Отже, £
IM-^V2 + 2«sC=^V2'2«>s!f=^+7-
Задача 5. Довести теорему Лейбніца (див. с. 13) Доведення.
ХА = ХМ + МА.
ХВ = ХМ + МВ.
ХС=ХМ + МС.
Піднесемо обидві частини кожної рівності до квадрата, дода- мо їх та застосуємо співвідношення МА +Л4В + Л4С=0; ^41/в2+/с2=зхм2+мд2+мв2+мс2+2хм(мд+W+ + МС) = МД2 + МВ2 + МС2 + ЗХМ2
Задача 6. У площині трикутника ABC візьмемо довільну точку Р. Л4|, ЛІ2, Мз — середини сторін трикутника ВС. АС. АВ відповідно. Точки Лі, В\. С\—симетричні точці Р відносно точок М\. М2. Мз. Довести, що відрізки АА]. ВВ\. СС\ перетинаються в одній точці і діляться в ній пополам.
Доведення. Нехай X — довільна точка простору.
ХА = Т\. ХВ = Т2. ХС = 7з. Нехай точки Оі, О2. Оз належать відповідно відрізкам АА\. ВВ\. СС\. Тоді
XOi = XiZ4i+(l — ХОХДі. (1)
Оскільки РМ\ — М\А\ (мал. 25.2), то за формулою (25.2х) ХМ\ = -у (ХР + ХА і), звідки ХЛ| = 2ХМ| — ХР= Г2 + гз — ХР.
175


Мал. 25.2
Тепер вираз (1) можна записати так:
XO1 = Xi(f2 + ^ —ХР) + -|- ( 1 — Х1)Г1=(1 — Хі)г 1 + Х|Г2 +
Х| Гз —
Аналогічно
ХО2 = Х2Гі + ( 1 — Х2)г2 -|- + Л-2Г з — Х2ХР, ХОз = Хзгі -|- Хзг2 + + (1 — Хз)гз — ХзХР.
Якщо покласти Хі = Х2 =
= А,з=у, то Х0і = Х02 = Х0з, тобто відрізки АА], ВВі, СС\ перетинаються в одній точці і діляться в ній пополам.
Задача 7. Точка D належить стороні ВС трикутника ABC. Довести, що AD • ВС^.АВ • DC-\~АС • BD.
Доведення. За формулою (25.1)
а/ГВ + (1 — a)AC=AD.
Оскільки а=4£, то 1—а=^.
£>С £>С
| AD | =|а• АВ+ (1 -аЖ|<а|АВ|+(1 -а)|АС|=
= ^\АВ\+^\АС\.
Отже, AD • BC^DC -AB + BD • АС.
Задача 8. Довести, якщо центр гомотетії двох гомотетичних трикутників є центроїдом одного з них, то він е центроїдом і другого трикутника.
Доведення. Нехай G — центр гомотетії трикутників ABC і AjBiCi, k — коефіцієнт гомотетії, М— центроїд трикутника ABC (G = M\ Mi — центроїд трикутника AiBjCi, X — довільна точка простору. Тоді
XBi = GSi+XG = kMB + XM~,
XAi = kMA + XMy XCi = kMC + XM.
За формулою (25.4)
ХМі = У (ХА1 + ~ХВ і + XCt) = хм + у (МЛ+ MB + МС)=
= XM = XG, тобто XM, = XM = XG.
Отже, точки М і Мі збігаються.
Задача 9. У тетраедрі DABC ребро АС перпендикулярне до ребра BD, а ребро АВ перпендикулярне до ребра CD. Довести, що AD J_ ВС.
176


Доведення. Для довільних точок А, В, С, D має місце векторна рівність: АВ • CD + АС • DB + AD • ВС= 0.
Доведемо її:
ЛВ(С4+ЛО)+ЛС(ОЛ+Ав)+ДО(ВЛ+ЛС) = ЛВ-СЛ+ЛВХ
X АВ + ДС • DA+AC • АВ + AD - BA + AD • ЛС=0.
Враховуючи умову задачі, маємо:
AB-CD = 0 і AC-DB = 0.
Отже, рівність запишемо так: AD - BC=Q, тобто ребро AD перпендикулярне до ребра ВС.
Задача 10. Якщо в тетраедрі DABC суми квадратів довжин протилежних ребер рівні, то ці ребра взаємно перпендикулярні. Довести.
Доведення. Для чотирьох довільних точок А, В, С, D має місце векторна рівність:
\AB\2 + \CD\2-\AD\2-\BC\2 = 2AC-DB (довести!)
За умовою AB2 + CD2 = AD2 + BC2y а отже, ЛС-£>В = 0, тобто відрізки АС і DB — перпендикулярні.
Задача 11. Пари протилежних ребер тетраедра мають довжини а і аі, Ь і 6|, с і С\. Довести, що для кута <р між ребрами, довжини яких а і а\, справджується формула:
І б2+ 61 — с1 — С\ І COSG) = - •—т - .
Y 2ааі
Доведення. Позначимо DA = a, DB = b, DC = c, СВ = а\, ДВ = с~і, АС=Ь\. _
Доводжувана рівність рівносильна рівності: 12а • а\ |= | Ь2 — с2 + -|-62 — Н|. Оскільки СВ= b — с, АС=с — а, АВ = Ь — а, то \2а(Б—7:) | = |7>2 — c2 + (F— а)2 — (6 —^а)21, або |2а6 — 2ас |=|Ъ2 — —~с2 + ~с2 — 2ас + а2 — Ь2 + 2аЬ — а21.
Отже, 12аЬ— 2ас|=|2о5— 2ас|.
Задача 12. Довести, що коли плоскі кути при вершині тетраедра прямі, то центроїд основи, центр описаної кулі і вершина тетраедра належать одній прямій.
Доведення. Нехай у тетраедрі DABC М — центроїд основи, О — центр описаної кулі, DA = a, DB = b, DC=c, DO — n,DM=m (мал. 25.3).
Доведемо, що вектори т і п однаково напрямлені. За формулою DM = y(а + & + с), тобто вектор т і o’+'S’+c однаково напрямлені. Оскільки DO2 = АО2, то п2 = (7Г—~а)2=п2-\-а2 — 2па.
12 0-172
177


Мал. 25.3
Але п = аа + 06-|-Хс, тому и2 == и2 + a2 — 2a(aa + 06 + М-
Враховуючи, що ab = ac=0, маємо: a2 —2aa2 = 0, a=y.
Аналогічно доводиться, що 0=у=у. Таким чином, п=уХ Х(а + 6 + с) і вектори піт — однаково напрямлені, тобто точки D, О і М належать одній прямій.
26. 	РОЗВ’ЯЗУВАННЯ ЗАДАЧ ПРО ТРИКУТНИК ЗА ДОПОМОГОЮ РОЗКЛАДАННЯ ВЕКТОРІВ
Відомо, що коли дана пара х; у неколінеарних векторів, то для будь-якого вектора in, компланарного з ~х і 'у, існує єдина пара чисел а і 0, що задовольняє рівність m = (xx+0^ (1)
Отже, завжди можна підібрати числа
ють умову (1). _____ _
Тому, якщо_вектор т = а-\-Ь_, причому вектори а і Ь колінеарні векторам х і у, то a=ax, 6 = 0г/.
Звідси,
а і 0, які задовольняв
a Q b
ос=-—, p = ~zi"
* у
Задача 1. У трикутнику ABC точка X належить стороні ВС, причому ВХ : ХС— т : п. Довести, що
д7=-4—ASH ^—АС. (26.1)
пг-\-п ’ т-\-п ' 7
Р оз в’ язання. Через точку X проведемо прямі, пара-
0 Зауважимо, що якщо два вектори а і b (Ь =#0)_ колінеарні, то замість рівності a = kb іноді зручно писати a:b~k. Символ а : b застосовується тільки для колінеарних векторів а і 7Г при Г#=0. 178


лельні сторонам АВ і АС трикутника АВС (мал. 26.1). Дістанемо паралелограм ADXE. Маємо:
AX = AD + AE і АХ=аАВ + $АС,
звідки
AD Q АЕ а=—, р = ^=
АВ г АС
г\ • лгГ rV AD ЕХ СХ п
Оскільки AD = EX, то а=-^==^=-=-=^=
АВ АВ СВ tn -|- п
Аналогічно 6 =—:—. Отже, г т-\-п ’
АХ——^— АВ-\ ^—АС.
т-\-п 1 т-\-п
Співвідношення (26.1) називається формулою поділу відрізка у даному відношенні. За допомогою цієї формули можна проводити різноманітні розкладання векторів.
Задача 2. Довести, що в трикутнику медіани перетинаються в одній точці і діляться у відношенні 2:1, рахуючи від вершини.
Доведення. У трикутнику АВС (мал. 26.2):
2ММ\ = МВ-\-~МС. (1)
Розкладемо тепер вектор AM за векторами MB і МС:
АМ=аМВ + ^МС.
Далі зробимо паралельний перенос векторів MB і МС на вектор МА. Дістанемо паралелограм ADME. AM = AD -f-AE.
Отже,
AD АМъ . • о і
cz= -т== = 1, аналогічно 6=1.
МВ МзВ г
Таким чином, АМ = МВ-\-МС.
Порівнюючи (1) і (2), бачимо, що AM = 2ЛШ1, а це доводить твердження задачі.
Задача 3. Довести, що в трикутнику ABC:
1°. Три висоти перетинаються в одній точці.
2°. Якщо Н — точка перетину висот і А, В, С — величини кутів трикутника ABC, то tg А X X НА + tgB • HB + tgC - НС = 0.
12*
179


3°. Якщо Н\ — основа висоти, проведеної з вершини Л, то (tgB + = tgB • НВ + tgC • НС.
ло НА cos4
НН\ cos В cos С
Доведення. Доведемо спочатку задачу 2°. Спільну точку висот ВНъ і СНз позначимо Н (мал. 26.3). Розкладемо вектор НА за векторами НВ і НС:
НА = аНВ + $НС.
Зробимо паралельний перенос векторів НВ і НС на вектор НА. Дістанемо паралелограм AEHD і
ВЛ = аЯВ + ₽ВС=-(ЛВ + ЛЁ).
Отже,
_ - tgB
~ НВ ~ Н^В~ tg/l
Аналогічно р=—
Маємо
НА = -^г-НВ —^-НС, (1)
tg/4 tg/l ’ v 7
або_ tgAj НА = - tgB • НВ - tgC • НС- HAtgA + HBtgB + + //CtgC=0, що й потрібно було довести в задачі 2°.
Розв’яжемо тепер задачу 3°. Враховуючи, що Н\В:Н\С = = tgC: tgB, маємо (за формулою (26.1) задача 1):
™'=-їгЙ^г™+-етї<-^ або
(tgB + tgC)HH\ = tgB • НВ + tgC ■ НС. (2)
Порівнюючи (1) і (2), бачимо, що вектори Н\Н і НА колінеарні, а це означає, що висота АН\ проходить через точку Н. Отже, розв’язана і задача 1°.
180


Переходимо до задачі 4°.
Із колінеарності векторів АН і НН\ випливає, що
АН tgB + tgC cos А
НН\ tg A cos В • cos С
Задача 4. У трикутнику ABC Н\, Н2, Нз— основи висот. Довести, що
а2 АН і + Ь2ВН2 + с2СНз = (ї
Доведення. Зробимо паралельний перенос векторів Н2В і НзС відповідно на вектори Н2А і НзА. Дістанемо паралелограм AEH\D (мал. 26.4).
Тоді
АНх = аВН2 + $СНз,
А7Г} = - (H\D + ТГЁ) = DH 1 + ~ЁНі , тобто
__ ~РН\ _ АІГ £777 _ АР
а~~ BH2~~BH2 снз~с7Г3'
Позначимо AH\ = hi, BH2=h2, СНз=Из.
Очевидно, що
Л7МЕ = ЛС, ADAH} = ЛВ.
Розглянемо трикутник ЕН\А. Він подібний трикутнику ABC. Тоді
АЕ hi - h\b h\b
-7-=—; АЕ = ; а= —
b a a a - h.2
Знаючи, що
/її Ь
-1—=—, маємо /12 а ’
с2
Аналогічно р= — .
Отже, АН і = - -4 ВН2 -^СНз. а а2
Звідси маємо:
а2ЛЯ! + Ь2ВН2 + с2СН3=0?
Задача 5. Якщо І — центр вписаного в трикутник ABC кола, а, Ьу с — довжини сторін ВС, АС, АВ, р — півпериметр, то с7=-^-СЛ+^-^В. Довести.
181


Доведення. Зробимо паралельний перенос векторів АС і ВС на вектори АІ та ВІ. Дістанемо паралелограм CDIE (мал. 26.5). Маємо £7=аСТ+ + 0СВ, CI—CD + СЕ-
Отже. —-
CD а= -=■,
СА
н СВ
Мал 26 5 Позначимо CD = CE=x.
Тоді
Позначимо L\ точку перетину бісектриси кута САВ зі стороною ВС. AD = b — x. Тоді
, ^ ab L\C АС b
LiL~ Т+с’ ~7d~~Xd’ а0° (&4-с)х•
Звідси
х а
~~1р‘
Отже,
Наслідок. Якщо О — центр описаного кола, то о7= -X (адА + b ОВ + сОС).
Справді,
™+ОЇ-%сд+-^ОА + -^СО+^ОВ.
=^ол+^ов+І^
Задача 6. Нехай X — довільна точка всередині трикутника ABC, Si, S2, S3 — площі трикутників відповідно ХСВ, ХАС, ХАВ. Довести, що має місце рівність
SiX7+S2XB + S3XC=0. (26.2)
Д оведення. Розкладемо вектор ХА за векторами ХВ і ХС. Проведемо вектори АЕ і AD, що однаково напрямлені з векторами ХС і ХВ (мал. 26.6). Дістанемо паралелограм ADXE.
Тоді
XA = XE-\-XD, ХА = —аХВ — $ХС.
182


Отже,
Позначимо точку перетину прямих АВ і СХ через /С Тоді
_«__М=_Ь (доведіть!). хв KB S,
тобто а = ~.
Аналогічно р = ^. Отже, 5іХ
X ХА== - S2XB - S3XC7
Мал. 26.6
Задача 7. Довести що в трикутнику ABC:
1) OAsin2A + OBsin2B4~ OCsin2C = 0 (О — центр описаного
кола); __
2) al А 4- ЫВ + сі С = 0 (I — центр вписаного кола);
3) tgA • /М + tgB • ЯВ + tgC • ЯС=0 (В — ортоцентр гостро- кутного трикутника ABC)',
4) ЛЬ4 + Л1В-|-МС=0 (Л4 — центроїд).
Розв’язання. 1) У формулі (26.2) візьмемо Х = О.
Маємо: _
Si ♦ ОА +$2 • OB4-S3 • ОС = 0. Тоді
Si = y/?25Іп2Л, S2=yB2sin2B, S3=yB2sin2C.
Отже,
OAsin2A 4- OBsin2B 4- OCsin2C=0.
2) 	У формулі (26.2) візьмемо Х = І.
Тоді — _
SxIA + S2IB + S3IC = Q, с аг с Ьг с сг д,==^’ = 5з = Т-
Отже, аІА-\-ЬІВ-\-сІС = ії.
3) 	У формулі (26.2) візьмемо Х = Н. Тоді
S1ІНА + S2HB 4- ВзЯС = 0?
Маємо співвідношення:
32 _ АНз _ tgB . З3 __ tgC
Si “ НзВ tg4 ; Зі — tg4 ’
Отже,
tgA • НА 4- tgB • HB + tgC • НС= 0.
183


4) 	У формулі (26.2) візьмемо Х = М. Оскільки в цьому випадку S1 = tS2 = S3, то МА + + МВ + МС = 0.
Задача 8. Точки А і, В\, С\ — ортогональні проекції центроїда М трикутника ABC на сторони ВС, СА, АВ. Довести, що
а2-МІ1 + 62-Ж + + с2.Л4Сі = 0.
Доведення. Запишемо формулу (26.2) для випадку Х = М для трикутника А\В\С\ (мал. 26.7).
Маємо
Si • МА і + S2 • МВі + S3 • MCj = 0.
Нехай МА\ = т, МВ\ = 1, МС\ = п.
Тоді
51 n/sin А 1-а
52 mnsinB tn-b
Але -£ = у, оскільки площі трикутників АМС, СМВ, ВМА рівні і відповідні висоти обернено пропорційні сторонам, на які вони опущені.
Отже,
31__а2
S2 т b Т7" *
а • 5з с2
Аналогічно доводимо, що—=— , а це означає, що доведено Si а
твердження задачі.
Задача 9. У трикутнику ABC І — центр вписаного в трикутник кола, /Сі, /G, Кз — точки дотику його до сторін. Довести, що а-ЇКі + Ь-ПГі + с-ЇКз^
Доведення. Запишемо формулу (26.2) при Х = І для трикутника /СКгКз
S] 	-ЇК\ +s2.7a2+s3-7^3=o^
Але
S] 	= yr2sinA (г—радіус вписаного кола). Враховуючи, що
sinA=-^- (/? — радіус описаного кола), маємо:
184


Звідси аГКі + ь7Кг + сІКа = 0.
Задача 10. З довільної точки X, яка міститься всередині рівностороннього трикутника ABC, опущені перпендикуляри на сторони ВС, АС, АВ трикутника. Довжини перпендикулярів — а, Ь, с відповідно. Довести, що
аХЛ + 6ХВ + сХС = 0^
Доведення.' Позначимо т — довжину сторони рівностороннього трикутника ABC. Враховуючи, що в трикутниках ХВС, ХАС і ХАВ сторони ВС, АС, АВ рівні, формулу (26.2) записуємо так:
^-ХА + ^-ХВ+^ХС = 0,
а-ХА + Ь-ХВ + с-ХС=0.
27. 	ЗАСТОСУВАННЯ
ФОРМУЛИ ГАМІЛЬТОНА
Формула Гамільтона має вигляд:
ОН= ОА + ОВ + ОС (27.1) Доведемо її.
Маємо: ОН = ОА -j-AH.
За формулою £1.1) АН=
= 2ОМ. Але 2ОМ = ОВ + ОС, звідки випливає -формула
(27.1).
Задача 1. Дано трикутник ABC. Якщо І — центр вписаного кола, a Wi, U/2, W3 —
точки перетину бісектрис його внутрішніх кутів з описаним колом (з центром О), то
57= dW} + OW2 + OWi (27.2)
Доведення. Справді, точка І — ортоцентр трикутника UZir2UZ3 (с. 29). Отже, має місце формула (27.2).
Задача 2. Довести, що в трикутнику ABC центроїд М, ортоцентр Н, центр описаного кола — точка О належать одній прямій (прямій Ейлера), причому ОМ : МН =1:2.
Доведення. Відомо, що якщо X — довільна точка простору, то
ЗХМ = ХА+ХВ + ХС.
Якщо X збігається з точкою О, то ЗОМ = ОА + ОВ + ОС.
185


Звідси, враховуючи рівність а це доводить твердження задачі.
Задача 3. Точки О і /—центри описаного навколо трикутника ABC і вписаного в нього кіл, R і г — їхні радіуси. Довести, що
О/2 = /?2 —2/?г.
Доведення. Піднесемо обидві частини рівності (27.2) до скалярного квадрату.
Враховуючи, що r=4/?sinf sinf sin^-
(див. с. 31 (5.2)), дістанемо:
ОІ2=(OW, + OW2 + OW3)2=3R2 - 2/?2(совЛ 4- cosB + cosC) = З/?2 - 2R2 (1 + 4siny sin у sin -J) = 3R2 — 2R (r + R) = R2 — 2Rr.
Що й треба було довести.
Задача 4. Дано трикутник ABC. Знайти множину точок простору X таких, що XA2-j-XB2=2XC2.
Р оз в’ я з а н н я. Нехай О — центр кола, описаного навколо трикутника АВС (мал. 27.1). Рівність, дану в умові, запишемо так:
(ОД - ОХ)2 + (ОВ - ОХ)2 = 2 (ОС - ОХ)2, або
-4ОХ • ОС4-2ОХ. ОД+ 2ОХ - ОВ = ОД2 + ОВ2-2ОС2
Звідси
або
ОХ(ОА + ОВ-2ОС) = 0, ох (од + о в+ос—зос)=її
Враховуючи (27.1) і те, що ЗОМ=ОН (задача 2), дістанемо
здх(ол^оо_=о.
Отже, ОХ-СЛЇ = 0, або ОХ±СЛЇі, де Мі— середина сторони АВ. Отже, шукана множина є площина, яка перпендикулярна до 186


медіани трикутника, проведеної з вершини С, і проходить через центр описаного навколо трикутника кола.
Задача 5. У коло з центром О вписано трикутник ABC. На колі взято точки L і К такі, що сума квадратів відстаней від точки L до вершин трикутника ABC має найменше значення, а від точки К до вершин трикутника — найбільше. Довести, що ортоцентр Н і точки О, А, К належать одній прямій.
Доведення. Нехай X — довільна точка кола, описаного навколо трикутника ABC, R— радіус кола (мал. 27.2).
Нехай S{x) = XA2 + XB2 + XC2.
Тоді S(x)=(XO+O4)2 + (XO+OB)2 + (XO + OC)2 = 3XO^ + + ОА2 + ОВ2 + ОС2 + 2ХО(ОА + ОВ + ОС).
Враховуючи рівність (27.1), маємо:
S(x) = б/?2 + 2X0 • ОН = б/?2 + 2X0 • Otfcosq? (<р = 180° - А НОХ).
Очевидно, що S(x) буде мінімальна, тобто L = X, коли <р= 180°, і максимальна, тобто Х = коли ф = 0. А це можливо лише тоді, коли точки L, К, О, Н належать одній прямій. Що й треба було довести.
Задача 6. Довести, що пряма, якій належить центр описаного навколо трикутника кола і центр вписаного в нього кола, є прямою Ейлера трикутника АіКгКз, вершинами якого є точки дотику сторін до вписаного в трикутник кола.
Доведення. Трикутник гомотетичний трикут¬
нику /СіКгЛз- Позначимо k —коефіцієнт гомотетії, Hk— ортоцентр трикутника /САгЛз- Оскільки І—центр кола, описаного навколо цього трикутника, то за формулою (27.2) маємо:
ої= о¥і + о¥2+ow3=/г(7д7+ік2=/^)=ад.
Застосовуючи до виразу в дужках формулу (27.1), дістанемо 01 = kIHk, тобто точки О, /, Hk належать одній прямій.
Задача 7. Довести, що сума квадратів відстаней від довільної точки кола, описаного навколо правильного трикутника, до його вершин не залежить від положення точки на колі.
Доведення. Нехай X — довільна точка кола з центром О, А, В, С — вершини правильного трикутника, вписаного в це коло (мал. 27.2); R— радіус кола. Враховуючи розв’язання задачі 5, можна записати, що
S(x) = 6/?2 + 2XO- ОН, де Н — ортоцентр трикутника ABC.
Оскільки у рівносторонньому трикутнику ОН=0, то S(x) = 6/?2. Звідси й випливає доводжуване твердження
Задача 8. У трикутнику ABC а, b, с — довжини сторін, причому Ь>а>с. У цей трикутник вписано коло з центром / і навколо трикутника описано коло з центром О. Довести, що:
187


1) якщо пряма 01 перпендикулярна до бісектриси кута ВАС, то сторони трикутника ABC складають арифметичну прогресію;
2) якщо пряма ОМ перпендикулярна до медіани, проведеної через вершину А, то квадрати сторін трикутника складають арифметичну прогресію.
Доведення. 1) Бісектриса кута ВАС перетинає описане коло у точці Wi (мал. 27.3). Отже, використовуючи умову, можна записати, що AI = IW\ і 20I=0Wi + 0A.
Враховуючи формулу (27.2) маємо:
2(O¥2 + OW^)= OA-OW\.
Оскільки I OW\ |=| OW21= I OW31= R (/?— радіус описаного кола), то
8R2 — 8/?2созЛ = 2R2 (1 - соз(Л + 2С)), або
2siny=sin (А + с) .
Звідки
2sin4 = sinB + sinC, або 2а=ЬА~с.
2) 	Продовжимо медіану до перетину з описаним колом у точці М. Оскільки ортоцентр Н належить прямій ОМ (задача 2), то
ОН • AM = 0, ЗОМ = ОН, АМ=ОМ — ОА.
Отже, за формулою (27.1)
ЗАМ = ОС+ ОВ — ЇОА-
Враховуючи умову, дістанемо
(ОА + ОВ + ОС) (2ОА - ОВ - ОС) = 0.
Оскільки І О А |= І ОВ |= І ОС |= R,
то
2ОВ • ОС— О А • ОВ — О А - ОС=0, або 2соз2Л = cos2B4-cos2C. Звідки
2(1 -2зіп2Л)= 1 -2sin2B+ 1 -2sin2C, або
2зіп2Л = sin2B + sin2C.
Отже, 2а2 = Ь2 4-е2.
188


28. 	ПРО ОДНУ ВЕКТОРНУ ФОРМУЛУ
ДЛЯ ТРИКУТНИКА
Нехай X — довільна точка простору. У трикутнику ABC візьмемо на сторонах СА і СВ відповідно точки В\ і >41, які ділять сторони у відношеннях:
СВ і : В і А = р, СА і : А і В = q.
Позначимо У точку перетину АА] і ВВ]. Тоді має місце формула:
(28.1)
рХАqXBХС
XY =
? + <?+ 1
Доведення. Розглянемо вектори CQ і CD, які однаково напрямлені відповідно з векторами YA і YB, такі, що CY—CQA- + CD (мал. 28.1). З подібності трикутників AYB] і CQB], BA\Y і СА]Р маємо: CY=pYA+qYB. Оскільки CY=CX^XY, то pYA + qYB=CX + XY, але YA=YX + XA, YB=YX + XB.
Тому р(уГ+^4) + р(У% + ХВ)=С% + ХгГ або
ХУ(р + р + \) = рХА qXB ХС. Отже, формулу (28.1) доведено.
Покажемо застосування формули (28.1)
Задача 1. Довести, що в трикутнику ABC: 1) медіани АА], ВВ], СС] перетинаються в одній точці; 2) якщо X — довільна точка простору, а М — точка перетину медіан, то
ХМ = у(ХЛ+ХВ + %С); (1)
3) AL4 + MB + MC="K (2)
Доведення. 1) Припустимо, що медіани АА] і ВВ] перетинаються в точці Дії, а медіани АА] і СС] — в точці ЛІ2. Для даного випадку знайдемо значення р і q:
р= СВ\ : В]А= 1, q =: СА j : А і В = 1.
Підставимо ці значення в формулу (28.1) і, враховуючи, що АС] : С]В= 1, дістаМал. 28.1
немо:
189


VTT ХА + ХВ 4- ХС . V77 ХА + ХВ 4- ХС
ХМ\ = 5 1 ХМ2 = т ■, —•
□ о
Отже, ХМі = ХМ2, тобто точки М\ і М2 збігаються.
2) Нехай у формулі (28.1) У=М. Оскільки відрізки МА\, МВ\, МС\ — медіани, то p=q = 1. Тоді
ХЛГ= 4- (ХА + ХВ + ХС). о
3) Покладемо в формулі (28.1) Х = М =
Тоді ХМ = 0 і ЛЬ4 + МВ + МС=0.
Задача 2. Довести, що в трикутнику ABC:
1) висоти перетинаються в одній точці Я;
2) НА tg А + НВtg В+ HCtgC=Q.
Доведення. 1) Припустимо, що висоти АА\ і ВВ\ перетинаються в точці Н\, а висоти ААі і СС] — в точці Н2- 3 трикутників АВВі і СВВ\ маємо:
j л ВВ\ , ВВ\
’^С=в/Г
З трикутників ВАА\ і СААі запишемо, що tgB=4^-,tgC=^.
Тепер можемо ввести позначення:
р=СВі : B]A — tgA:tgC, q=CAi:AtB = tgB : tg С.
Нехай X — довільна точка простору. Тоді за формулою
(28.1)
777 XAtgA 4-*BtgB4-A'CtgC 1 tgA 4-tgB4-tgC
Розглянемо висоти, які перетинаються В ТОЧЦІ //2» і введемо нові позначення:
р=ВСі : СіД= tgi4: tgB, q=BA \ :>4iC==tgC: tgB.
Тепер, вважаючи в формулі (28.1) У = Я2, запишемо
у77 _ XAtgA + XBtgB + XCtgC Л/Ї2~ tg4 4- tgв 4- tg С
Отже, ХН} = ХН2, тобто НУ=Н2=Н і
у77 XAtgA 4-tgB 4-XCtgC ~ . tg А + tg В + tgC
2) Нехай Х = Н. Тоді ХН==ІЇ, і формула (3) матиме вигляд
НА tg А + НВtg В + tfCtg С= 0.
Задача 3. Довести, що в тетраедрі DABC:
І) відрізки, які сполучають вершини піраміди з точками (3)
190


перетину медіан протилежних граней, перетинаються в одній точці М;
2) якщо X — довільна точка простору, то
ХЛ4 = ±(ХЛ + XB + XC + XD); (4)
3) кожний з відрізків, які сполучають вершини тетраедра з точками перетину медіан протилежних граней, ділиться точкою М у відношенні 3: 1, починаючи від вершини;
4) справджується рівність: МА + MB + МС + MD = 0.
Доведення. 1) Позначимо точки перетину медіан граней тетраедра DABC через М\, М2, Лї3, Лї4 (мал. 28.2) і припустимо, що відрізки, які сполучають вершини піраміди з точками Мі, М2, Мз, М4, не перетинаються в одній точці.
Нехай відрізок DMi і відрізок АМ2 перетинаються в точці Q. Вводимо позначення: пряма АМ\ і відрізок ВС перетинаються в точці Лі; пряма ВМ] і відрізок АС перетинаються в точці В\. За властивістю медіан АА\ і DA\ запишемо, що
АіМі :М\А = 1 :2=р; ДіЛ12:М2/) = 1 :2=р.
Тепер за формулою (28.1) для довільної точки X простору маємо:
і —
XQ = п—Г “ -Г (ХА + XD + 2ХА ,) =
1 +— -4- — '2'2
= -і- (хл +хв+хс+хБ).
Позначимо тепер точку перетину відрізків ВМз і DMi точкою L. Тоді
і
XL = — -=- = 4- (ХЛ + ХВ + ХС + Х£>).
1 +— + — 4 1 2 ' 2
Це означає, що XQ = XL = XMy тобто Q = L = M. Аналогічно доводимо, що відрізок CM, перетинає відрізок ВМз в точці Л4, відрізок DM\ і відрізок СМ4 перетинаються в точці Л4, тобто відрізки DAfi, ВМз, СМ4, АМ2 перетинаються в точці М.
2) Тепер очевидно, що
ХМ = У (ХА + хв + ХС + XD).
3) 	Нехай у формулі (4) X збігається з Л4|. Тоді
М^М = у (+ ЛЇЇВ + М?С +
191


+ МID) = (M ,A + M1В + MIC) + M! D = M, D.
(див. формулу (2).) Отже, £>Л4 = ЗЛ4Л4і.
4) 	Нехай Х = М. Тоді MA =
Задача 4. У тетраедрі DABC плоскі кути при вершині D прямі. Довести, що відрізок, який сполучає вершину D з точкою перетину висот основи ABC, є висотою пираміди.
Доведення. Нехай в тетраедрі DABC (мал. 28.3) точка Н — ортоцентр трикутника АВС\ а, Ь, с — довжини його сторін. Нехай у формулі (3) X збігається з D. Тоді
п77 5Ttg4 + 5BtgB + 5ctgc ип— tg^+tgB + tgC
Враховуючи задачу 8, с. 113, маємо:
гч л 2 б2 + с2 — а2 . -
DA =— = be cos А,
DB2= ° ~ 2 = accos в» (5)
DC2= _ a b cos С,
DH-ВС= DH(DC — DB) = tg4+tg‘B+tgC (OC2tg C — DB2tgB).
Згідно з рівністю (5) запишемо:
DC2tgC—DB2tgB =
= ab cos С tg С — accos В tg В = = ab sin С — ас sin В =
= 23лвс— ^Sabc— 0.
Звідси DH-BC = 0, тобто відрізок DH перпендикулярний до відрізка ВС.
Аналогічно доводимо, що DH • АС=0, тобто відрізок DH перпендикулярний до відрізка АС. Отже, пряма DH перпендикулярна до площини трикутника ABC.
192


29. 	ПРО ОДНУ ВЕКТОРНУ ФОРМУЛУ
ДЛЯ ТЕТРАЕДРА
Розглянемо формулу, аналогічну формулі (28.1). Розглянемо тетраедр ХАВС (мал. 29.1). Позначимо в трикутнику ABC на сторонах СА і СВ точки В] і Аі такі, що СВ\ : В\А = р, СА і : А іВ = (/. Точку перетину відрізків ААі і ВВі позначимо У. Тоді
—Si.X4+S2-XB+S3-XC
Аї ~~ S, + S2 + S3
(29.1)
де Зі—площа трикутника СУВ; S% — площа трикутника ДУС; Зз — площа трикутника AYB.
Доведемо формулу (29.1).
З точок В і С проведемо відрізки CM і BN, які- перпендикулярні до прямої АА\. З подібності трикутників A\NB і А\МС випливає, що
q=CA\. А\В=СМ \ BN.
Трикутники AYB і AYC мають спільну сторону ДУ, а тому їх площі відносяться як відповідні висоти, тобто
Аналогічно
S2 __ CM _
S3~ BN ~
Підставляючи значення р і q у формулу (28.1), маємо формулу
(29.1). За допомогою формули (29.1) розв’яжемо задачі.
Задача 1. У тетраедрі DABC точка / — центр вписаної кулі. Точка /о — перетин прямої DI з площиною ABC. Довести, що
— _ -52 + 7с.5з
77о — s1+s2 + S3
де Si, S2, Зз — площі граней BDC, DAC, DBA відповідно.
Доведення. За формулою (29.1)
//о • SAbc = ІА • Зс/0вН-/В • Зд/оС + /С • Зд/0д. (1)
З точки /о опустимо перпендикуляри /0К і /0Кі на грані BCD і ABD тетраедра (мал. 29.2). Неважко показати, що ці перпендикуляри рівні. Справді, прямокутні трикутники DIL і DIL\,
13 0-172
193


де L і L\ — точки дотику- вписаної кулі до граней DBC і DAB, рівні. Отже, /LKDIq. Звідси
AD/oKi, тобто =
Позначимо довжину кожного перпендикуляра, проведеного з точки /о до грані, через /, а висоту тетраедра DABC на грань ABC через h. Тоді
Vdiqba = “у S^ab • h = -у Sdab • Л
Уя/оВС="у •S/ofiC • ■у SDBC ’
SaBC • h=-^-(SDAB-\-SACD-[-SDCB) • I.
З цих формул дістаємо:
^ІоАС— Sdac • у І
$І0ВА = $DAB * у і
S/0BC = $DBC • у і
З ABC— (5ддв + •5дср + '5рсв)у •
Підставляючи ці співвідношення в (1) маємо:
+ (29.2)
О| -1- 02 -h 03
Задача 2. Довести, що в тетраедрі DABC справджується рівність — _
IA •S1 + /B-S2 + /C,-S3 + /D -S4 = 0, 194


де I— центр вписаної кулі; Si, S2, S3, S4 — площі граней відповідно DBC, DAC, DAB і ABC.
Доведення. Нехай г — радіус вписаної в тетраедр DABC кулі, h — висота тетраедра, проведена до основи ABC (мал. 29.3). Тоді
DI о h / * \
”77^””“’ O'
де /о — точка перетину DI з площиною ABC.
Оскільки г = -у- (с. 131 (20.1)), де 5 = 5і+52 + 5з + $4, a 3V= h • S4, то
Dio _ DI + II0__ DI , .
//о //о “Г //о ’ }
Порівняємо вирази (1) і (2). ково напрямлені, то
77О=Б7-
Оскільки вектори IIq і DI одна-
$4
і + S2 + S3
Оскільки
уу _ ІА •S^/B-Sz + ZC-Sa /0— S.+S2 + S3
Та •s1+7b-s2+7c-s3+7z)-S4=o.
то
Задача 3. У тетраедрі DABC розкласти вектор DM за векторами DA, DB і DC (М — точка перетину медіан трикутника ABC).
Розв’язання. Позначимо Si, S2, S3 — площі трикутників АМС, ВМС, АМВ. Оскільки Si = S2 = S3=yS, то згідно з формулою (29.1)
DM • S = DA • у S + DB • ± S 4- DC • у S,
ЗВІДКИ
DM = 4- (DA + DB + DC). О
Задача 4. Розкласти вектор DI за векторами DA, DB i DC (I — центр кола, вписаного в трикутник ABC).
Розв’язання. Позначимо Sa, Sb, Sc — площі трикутників ІВС, І АС, ІАВ. Нехай г — радіус кола, вписаного в трикутник ABC, р — півпериметр ДДВС.
Оскільки Sa=yra; Sb = -^rb', Sc = ±-rc,
195
13*


то за формулою (29.1) DI= DA +-^- DC.
Задача 5. Розкласти вектор DO за векторами DA, DB, DC (О — центр описаного кола навколо трикутника ABC).
Розв’ язання. Оскільки О — центр описаного навколо трикутника ABC кола, R — його- радіус, то площі трикутників ДОС, ВОС, АОВ дорівнюють відповідно
ytf2sin2B, у/?2зіп2Л, у Я2 sin 2С,
а площа трикутника ABC дорівнює 2/?2sin A sin В sin С.
Тоді за формулою (29.1)
DO • 2R2 sin A sin В sin С= DA • у /?2sin 2Д + DB • у R2 sin 2В Д-
+ 5c-y/?2sin 2С.
Звідки
уГТ cos А гГл \ c°s В cos гчТ'
2 sin В sin С 2 sin Л sin С ' 2sinBsin4 '
Задача 6. Основа тетраедра DABC — рівносторонній трикутник ABC, X — довільна точка всередині цього трикутника, S— його площа, а х\, хг, х3— відстані від точки X до сторін відповідно ВС, СА, АВ трикутника. Довести, що
1)
ргт; x\DA x2DB + x3DC
UA — : : ',
2) V3S2 • DX = XiDA+x2DB + x3DC.
Доведення. 1) Нехай а — довжина сторони трикутника ABC. Тоді
= у Х\а,
SАХС = ~2~ Х2а> $АХВ = “2"
S = у а (%і +%2 + х3).
Таким чином,
XiDAХгОВ X3DC
Хі + х2 + Хз
2) Оскільки хі + Х2 + хз = h (h — висота трикутника ABC) 4 1
і h = ~\3S2 , то задачу доведено.
196


Різницевий тетраедр
Назвемо різницевим тетраедром першого роду такий тетраедр, у якого площа однієї з граней складає середнє арифметичне площ решти трьох граней, а різницевим тетраедром другого роду такий тетраедр, у якого площі чотирьох граней складають арифметичну прогресію.
Задача 7. Довести, що в різницевому тетраедрі першого роду пряма, яка проходить через центр вписаної кулі і центроїд тетраедра, паралельна одній з граней.
Лема. Доведемо, що в довільному тетраедрі DABC
^7 _ (3S,-(S2+S3+S4))D4+(3S2-(S1+^3+S4))DB+(3S3-(S1+S2+S4))DC 4(S,+S2 + S3 + 54)
де І — центр вписаної кулі, М— центроїд тетраедра, Si, S2, S3, S4 — відповідно площі граней DBC, DAC, DAB і ABC.
Доведення. Скористаємося формулою
їа .s1+/b-s2+7c-s3+7d-S4=’o.
Виразимо вектори М, IB і ІС через DA, DB, DC і /£>: м=75+5л, 7в=/о+5в, Tc=Td + dc.
Тоді після підстановки маємо:
y-j j Si • DA -|- S2 • DB -j~ S3 • DC
Si -j-S2H-S34-S4
Оскільки
DMt = -^(DA+DB + DC), DM = ^-DM{
(Л1і — центр тяжіння трикутника ABC, то DM = ^(DA-\-DB-\~ -\-DC). Далі маємо:
МІ=Ш-DM =
(3S,-(S2+S3+S4))OA + (3S2-(Si+S3 + S<))DB+(3S3-(Si+S2+S4))DC 4(S 1 + S2 + S3 + S4)
Переходимо до розв’язування задачі. Якщо, наприклад,
о S2 S3 -|- S4
то MI, DB і DC компланарні.
Отже, відрізок МІ паралельний грані DBC.
Задача 8. Довести, що в різницевому тетраедрі другого роду вектори IM, BA, DC компланарні, якщо
Sdbc^Sdac^Sdba
197


вектори IM, DA, ВС компланарні, якщо
Sda с < DBC <C S A Bc <C S D BA;
вектори IM, AC, BD компланарні, якщо
5двс<5DBA <^SdbC<^SDAC.
Доведення. Позначимо SDflC, SDac> Sdba, Sabc відповідно
S3, S4, S2. Нехай, Si<S3<S4<S2, тоді, Si+S2 = S3 + S4.
Звідси
3S1 — (S2-|-S3-|-S^)= — (3S2 — (Si -|-S3Ч-S4)), тобто вектори IM, DA — DB= BA і DC компланарні.


Додаток
Тільки одна задача
Розглянемо задачу з книги П. С. Моденова «Задачі з геометрії» (М.: Наука, 1979).
Задача. Нехай ABC — довільний трикутник. Розглянемо 12 векторів, початковими точками яких є центри вписаного і зовнівписаного кіл, а кінцями — точки дотику кіл до сторін трикутника Довести, що сума цих векторів дорівнює вектору ОН, де О — центр кола, описаного навколо трикутника ABC, Н— ортоцентр ABC.
Помилка в умові полягає в тому, що сума векторів дорівнює 40//, а не ОН, як стверджує задачник. Розв’яжемо цю задачу. Позначимо шукану суму S12, /<ь К2, Кз — точки дотику вписаного в трикутник ABC кола до сторін ВС, АС, АВ. Враховуючи гомо- тетичність вписаного і зовнівписаного кіл з коефіцієнтом гомотетії, що дорівнює відношенню їх радіусів, суму S]2 можна записати так:
с ІК\ ' Га 1 К.2 * Га /Кз ‘ Га /Аг * Гb . /К\ ' Гb .
5|2= ——Ч ~Г ~Г Ч — +
+ ІК3- г± ІК^- ГС + ІК,,- ГС + /&■ + — [ + —2 _|_ — з =
=7к,(і-^+у-+у-)+ 7к2(і-^+^+^-)+7/<3(і-
Г Г (*)
Лема 1. Довести, що в трикутнику ABC мають місце такі співвідношення: '
ABC
Га = 4/?S І П у COS у COS у,
ГЬ = 4/?SІП у COS у COS у , Tc=4/?siny cos у COS у-
Доведемо першу з цих формул (дві інші доводяться аналогічно) .
1 Автор мав на увазі точки дотику відповідних кіл не тільки до сторін, а й до їх продовжень.
199


S a • b sin C 4R2 sin A sin В sin C
Га== p — a= b + c — a 2/?(sin В + sin S + sin Л)
27? sin Л sin В sin C 27? sin Л sin В sin C _ 2sin cos _ 2 sin A cos ~ 2 cos у ( cos — cos
47? sin 4 cos 4sin 4 c°s 4sin 4cos 4  2 2 2 2 2 2
А . Д . C cos ~ sin sin —
2 2 2
= 47? sin у COS у COS у .
Лема 2. Довести, що у трикутнику ABC /Кі^у^- = ОВ + ОС, 7к2 -2/?c°s - = ОА+ОС,
2₽c°sC =OA + OB.
Доведення. Доведемо першу формулу методом розкладання вектора за двома неколінеарними векторами. Розкладемо вектор ІК\ за векторами ОВ\_ОС. Зробимо паралельний перенос векторів ОВ і ОС на вектор 01, а векторів CO і ВО відповідно на вектори СКі і ВКі.
Дістанемо ромб IDK\E (мал. 1). Маємо //G = aOB + pOC. З іншого боку,
ік^гБ+їе.
Звідси
№ п а~"бВ'
/Е
ОС'
Оскільки |//G|=r, ID = IE, то
а 2R cos А
Мал. 1
200


Таким чином,
IKi = 0D г . (ОВ + дс), ЇК} ■ — cosA = OB + OC. 2R cos А v ' г
За допомогою лем 1 і 2 запишемо вираз (>fc), враховуючи, що
r= 4R sin у sin у sin у .
Маємо:
О 7Т 4/? cos А . ГГ 4R cos В . 777 4R cos С
о 12 = 1 їх і Н і Л 2 Н і і\ з =
= 2(ОВ + ОД + ОС + ОС + ОА + ОВ) = 4(ОА + ОВ + ОС).
Враховуючи формулу Гамільтона, дістаємо:
S}2 = 4(OA + OB + OC) = AOH.


ОСНОВНІ ПОЗНАЧЕННЯ
а, Ь, с — сторони трикутника ABC;
А, В, С — кути трикутника ABC: ВАС, ABC, АСВ;
ha, hb, hc — висоти трикутника ABC, опущені відповідно на сторони ВС, АС, АВ;
Н\, Н2, Нз — основи висот ha, hb, hc трикутника ABC;
та, ть, тс — медіани, проведені до сторін ВС, АС, АВ;
Mi, М2, Л43 — середини сторін ВС, АС, АВ;
1а, 1ь, 1с — бісектриси кутів трикутника АВС: ВАС, АВС, АСВ; L\, Ьг, Ьз — основи бісектрис Іа, Іь, lc;
О, R — центр і радіус описаного навколо трикутника ABC кола;
/ — центр вписаного в трикутник ABC кола (інцентр); К\, К2, Кз— точки дотику вписаного в трикутник ABC кола до сторін ВС, АС, АВ;
г— радіус вписаного в трикутник ABC кола;
2р — периметр трикутника ABC;
S — площа трикутника ABC;
Іа, Іь, Іс — центри зовнівписаних кіл, які дотикаються до сторін ВС, АС, АВ;
га, гь, гс — радіуси зовнівписаних кіл з центрами Іа, Іь, Іс-


СПИСОК ВИКОРИСТАНОЇ
ТА РЕКОМЕНДОВАНОЇ ЛІТЕРАТУРИ
1. Бевз Г. П. Геометрія тетраедра,— К.: Рад. шк., 1974.— 106 с.
2. Г о т м а н Э. Г., С к о п е ц 3. А. Задача одна — решения разные.— К.: Рад. шк., 1988.— 17І с.
3. Г о т м а н Э. Г., С к о п е ц 3. А. Решение геометрических задач аналитическим методом.— М.: Просвещение, 1979.— 128 с.
4. Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике.— М.: Наука, 1986.— 512 с.
5. Понарин Я. П., Скопец 3. А. Перемещения и подобия плоскости.— К.: Рад. шк., 1981.— 176 с.
6. Прасолов В. В. Задачи по планиметрии. Ч.І.— М.: Наука, 1986.—272 с.
7. Прасолов В. В. Задачи по планиметрии. Ч. II.—М.: Наука, 1986.— 303 с.
8. Ш а р ы г и н И. Ф. Задачи по геометрии (планиметрия).— М.: Наука, 1986.— 224 с.
9. Шарыгин И. Ф. Задачи по геометрии (стереометрия).— М.: Наука, 1984.— 160 с.


ЗМІСТ
Передмова - , з
Трикутник
1. Висоти трикутника. Ортоцентр 4
2. Ортоцентричний трикутник 8
3. Медіани трикутника. Центроїд 12
4. Бісектриси трикутника. Інцентр 22
5. Вписане й описане кола 31
6. Зовнівписані кола 40
7. Вписане півколо 47
8. Різницеві трикутники 54
9. Бісектральний трикутник 57
10. Побудова трикутника 61
11. Побудови в трикутнику . 67
12. Вивчення властивостей трикутника за допомогою
паралельного проектування 74
13. Проекції точки, що рухається вздовж сторони трикутника,
на дві інші його сторони 81
Тетраедр
14. Кути, ребра і грані тетраедра 94
15. Висоти тетраедра. Ортоцентричний тетраедр 104
16. Прямокутний тетраедр 110
17. Рівногранний тетраедр 116
18. Медіани тетраедра. Центроїд 121
19. Тетраедр і описана сфера 127
20. Куля, дотична до граней тетраедра. Сфера, вписана
в тетраедр 131
21. Куля, дотична до ребер тетраедра 140
22. Трикутник і тетраедр. Аналогічні задачі 144
23. Перерізи тетраедра 159
24. Теорема Чеви 165
Застосування векторів у задачах
25. Вектори в задачах про трикутник і тетраедр 172
26. Розв’язування задач про трикутник за допомогою
розкладання векторів 178
27. Застосування формули Гамільтона 185
28. Про одну векторну формулу для трикутника 189
29. Про одну векторну формулу для тетраедра 193
Додаток
Тільки одна задача 199
Основні позначення 202
Список використаної та рекомендованої літератури 203


Учебное издание
Исаак Аркадьевич Куиінир
ТРЕУГОЛЬНИК И ТЕТРАЭДР В ЗАДАЧАХ
Книга для учителя
На украинском языке
Киев, «Радянська школа»
Завідуючий редакцією математики і фізики М. Ю. Зубченко.
Художній редактор В. Б. Волков
Художник, С. М. Кобрін
Технічний редактор И. М.- Горбунова.
Коректори Л. В. Ш уланська, Л. О. Волинська
И Б № 7353
Здано до набору 20 03 90 Підписано до друку 14 03 91 Формат 60Х 9О‘/ю Папір офсетн № 2 Гарнітура літературна Друк офсетн Умови друк арк 13 Умови фарбо-відб 26,37 Обл-вид арк 1 1,27.Тираж 24 000 пр Вид № 30326 Замовлення № 0-172 Ціна 2 крб 70 коп
Видавництво «Радянська школа» 254053, Київ, 1О Коцюбинського, 5
Харківська книжкова фабрика «Комуніст» 310012, Харків, вул Енгельса. II


Кушнір I. А.
К96 Трикутник і тетраедр у задачах: Книжка для вчителя.— К.: Рад. шк., 1991.— 204 с.
ISBN 5-330-02081-6.
У книжці понад 400 цікавих (включаючи й класичні) теорем і задач, пов’язаних з визначними точками і лініями в трикутнику і тетраедрі, властивості яких лежать в основі властивостей усіх інших складніших геометричних фігур. Кожний параграф є циклом погоджених між собою задач, розміщених у міру зростання складності. До всіх задач наводяться розв’язання-.
Для вчителів загальноосвітніх шкіл, студентів фізико- математичних факультетів педвузів, учнів старших класів.
„ 4306020000—230 qi7 Q1
14 М210(04)—91 дІ/ У1
ББК 22.151


2 крб. 70 к.
w шнояя