Бібліотека журналу «Математика в школах України» Заснована 2003 року
Випуск 9 (81)
І. 	А. Кушнір
ГЕОМЕТРІЯ ТРАПЕЦІЇ
В ЗАДАЧАХ
Харків Видавнича група «Основа» 2009


УДК 512
ББК 22.14
К96
Кушнір I. А.
К96 Геометрія трапеції в задачах. — X. : Вид. група «Основа», 2009. — 80 с. — (Б-ка журп. «Математика в школах України»; Вип. 9 (81)).
ISBN 978-611-00-0367-4.
Пропонована книга — перша книга в шкільній геометрії, що цілком присвячується трапеції. Властивості трапеції розглядаються у вигляді задач. Тут є задачі для початківців, але є й задачі підвищеної складності. Усі вони докладно розв’язані, багато які з них зустрічалися на конкурсних іспитах, на математичних олімпіадах різного рівня.
Для вчителів математики та учнів загальноосвітніх шкіл, ліцеїв, гімназій.
УДК 512
ББК 22.14
Навчальне видання КУШНІР Ісаак Аркадійович ГЕОМЕТРІЯ ТРАПЕЦІЇ В ЗАДАЧАХ Навчально-методичний посібник Головний редактор І. С. Маркова Редактор Г. О. Новак Коректор О. М. Журенко Комп’ютерна верстка О. В. Лебедева Підп. до друку 10.09.2009. Формат 60×90∕16. Папір офсет. Гарнітура шкільна. Друк офсет. Ум. друк. арк. 5,0. Зам. № 9-09/14-04. ТОВ «Видавнича група “Основа”».
Свідоцтво суб’єкта видавничої справи КВ № 1390-263Р від 26.06.2006. Україна, 61001 Харків, вул. Плеханівська, 66. Тел. (057) 731-96-33 Віддруковано з готових плівок ПП «Тріада+» Свідоцтво суб’єкта видавничої справи ДК № 1870 від 16.07.2007. Харків, вул. Киргизька, 19. Тел.: (057) 757-98-16, 757-98-15.
ISBN 978-611-00-0367-4
© Кушнір І. А., 2009
© ТОВ «Видавнича група “Основа”», 2009


ЗМІСТ
Передмова 4
Розділ 1. Властивості довільної трапеції 5
Розділ 2. Друга середня лінія трапеції 10
Розділ 3. Кути 14
Розділ 4. Теорема про середню лінію трапеції. Альтернативні способи доведення 19
Розділ 5. Середня лінія рівнобедреної трапеції. Альтернативні способи доведення 24
Розділ 6. Теорема про площу трапеції. Альтернативні способи доведення 26
Розділ 7. Паралелограм Варіньона і площа трапеції 31
Розділ 8. Чудовий трикутник трапеції 34
Розділ 9. Трапеція — привід для аналогій 37
Розділ 10. Трапеція з перпендикулярними діагоналями як привід для аналогій 41
Розділ 11. Пошук подібних трапецій 44
Розділ 12. Трапеція. Описане коло 49
Розділ 13. Вписане коло 54
Розділ 14. Кола і трапеція 58
Розділ 15. Прямокутна трапеція 62
Розділ 16. Площа трапеції 66
Розділ 17. Обернені задачі про трапецію 71
Розділ 18. Задачі на побудову 77


ПЕРЕДМОВА
Трапеція — одна з найпопулярніших і досліджуваних фігур шкільної геометрії. З нею учні знайомляться в молодшій школі, далі вивчають у 7-му, поглиблюють у 8-му й 9-му класах і продовжують вивчення в стереометрії.
Пропонована книга — перша книга в шкільній геометрії, що цілком присвячується трапеції. Властивості трапеції розглядаються у вигляді задач. Тут є задачі для початківців, але є й задачі підвищеної складності. Усі вони докладно розв’язані, багато які з них зустрічалися на конкурсних іспитах, на математичних олімпіадах різного рівня.
Вивчення трапеції — це можливість глибше вивчити подібність трикутників, геометричні перетворення, рівновеликість фігур і задачі на побудову. Зв’язок трапеції з колом аналогічний темі в геометрії трикутника, тому задачі за цією темою добиралися особливо ретельно. Читача не залишать байдужим три розділи на доведення більш, ніж десятьма способами (!). Йому надається можливість знайти нові способи, чим, як упевнений автор, він обов’язково скористається. Хочеться вірити, що книга не залишить байдужими не тільки учнів шкіл, ліцеїв, але й викладачів вищих навчальних закладів, студентів.
Бажаємо успіху!


Розділ 1. ВЛАСТИВОСТІ ДОВІЛЬНОЇ ТРАПЕЦІЇ
Задача 1. Довести, що в будь-якій трапеції середини основ, точка перетину діагоналей і точка перетину прямих, що містять бічні сторони, лежать на одній прямій.
Доведення
АО
Гомотетія з центром О і коефіцієнтом -^∙, як і гомотетія з центром S (рис. 1)(S — точка перетину прямих AD і ВС) і коефіцієнтом AD
, відображує відрізок АВ у CD, а середину М відрізка АВ у сере- SD
дину N відрізка CD. Отже, точки О, М, N і точки S, М, N колінеарні, це означає, що точки S, М, N, О лежать на одній прямій.
Задача 2. Довести, що сума квадратів діагоналей трапеції дорівнює сумі квадратів бічних сторін і подвоєного добутку основ.
Доведення
У трапеції ABCD (рис. 2) проведемо висоти BE і CF.
Маємо:
AC2-AF2 =CD2-FD2, BD2-ED2 = АВ2-АЕ2.
Додавши ці рівності, дістанемо:
AC2 +BD2 =AB2 +CD2 + AF2-FD2 +ED2-АЕ2 =
= АВ2 +CD2 + AD(AF-FD + ED-AE) =
Рис. 2
Рис. 1


6
/. Кушнір. Геометрія трапеції в задачах
= ΛB2 +CD2 +AD∙2EF = AB2 +CD2 +2ADBC.
Задача 3. (3-тя Всесоюзна олімпіада, 1969, Київ). На основі AD трапеції ABCD позначена точка Е така, що периметри трикутників ABE9 ВСЕ і CDE — рівні. Довести, що BC = -AD.
2
Доведення
На прямій ВС виберемо точку C1 таку, що ABC1E — паралелограм (рис. 3). Тоді периметри трикутників ABE, BEC1 і ВЕС рівні. Звідси випливає, що точки С і C1 збігаються. Тому BC = AE. Аналогічно доводиться, що ВС = ED. Отже, ВС - —AD.
Задача 4. Довести, що відрізок, паралельний основам трапеції і такий, що є їх середнім геометричним, ділить своїми кінцями бічні  ⅛
сторони трапеції у відношенні J—, де a і b — довжини основ трапеції.
Доведення
Нехай BC = a9 AD = b (рис. 4). Проведемо FC∣∣AB. Тоді
EN = Jab -a (ME = a)9 FD = b-a.
Маємо:
Ь-H Х+У ,s,'T АГ ТА Ч
—= = (CN = x9 ND = t∕);
y∣ab-a х
^Jb + Ja . у
7=^~ = 1 + “’
√α х
4b 1 у х
звідси — +1 = — +1, або — =
√α х у


Розділ 1. Властивості довільної трапеції
7
Задача 5. На основі АВ трапеції ABCD позначено довільну точку К і через неї проведені прямі паралельно діагоналям. Ці прямі перетинають сторони AD і ВС відповідно в точках М і N. Пряма MN перетинає діагоналі АС і BD в точках Р і Q. Довести, що MP = QN.
Доведення
Позначимо AB = α, CD = b (рис. 5).
^ . MP ME DO CD PN a λ MN a+b
Оскільки = = = , то = —, або =
PN EK OB AB MP b MP b
Задача 6. Точка M, що належить бічній стороні ВС трапеції ABCD, з’єднана з вершинами А і D. З вершини В проведена пряма, паралельна DM, а з вершини С — пряма, паралельна AM. Довести, що останні дві прямі перетинаються в точці, що належить стороні AD.
Доведення
Продовжимо сторони AD і ВС до перетину в точці О (рис. 6). Нехай пряма, проведена з точки С паралельно МА, перетинає сторону AD у точці N, а пряма, проведена з точки В паралельно MD, перетинає сторону AD у точці N1. 3 подібності трикутників AM О, NCO, АВО і DCO, N1BO і DMO маємо:
ОС OA=OD OB ОМ
ОА ~ ОМ' OB ~~ OC' ON1 ~ OD ’
Перемножуючи почленно ліві й праві частини цих пропорцій, дістанемо:


8
/. Кушнір. Геометрія трапеції в задачах
ON OA OB ОС OD OM * ON 1
OAOBON1 OMOCOD 0N1
тобто ON = ON1, отже, точки N і ΛΓ1 збігаються.
Задача 7 (Олімпіада механіко-математичного факультету КДУ ім. Т. Шевченка, 2009, заочний тур). У трапеції ABCD розглядаються три умови:
1) 	AC±BD∙, 2) AB = jAD BC∙, 3) ABJ.AD.
Довести, що з будь-яких двох умов випливає третя.
Доведення
1) Нехай виконуються перша і друга умови, тобто ACLBD і AB = y∣AD∙BC. Доведемо, що AB±AD (рис. 7).
Рис. 7
Проведемо В7С||СА. Тоді АКВС — паралелограм iAK-BC1 а отже,
AB2 = AXAD.
Опишемо навколо трикутника KBD коло γ і продовжимо ВА до перетину з γ у точці L (рис. 8).
Тоді BA AL = KA AD, BA2=AK AD.


Розділ 1. Властивості довільної трапеції
9
Тоді AL = АВ. Діаметр KD ділить хорду BL навпіл, тому KD.LBL, звідси BA1.AD, що й потрібно було довести.
2) 	Нехай виконуються умови (1) і (3), тобто BA±AD і BD1.AC, Доведемо, що AB = ^JBC AD. Проведемо BjE∣∣AC. Тоді трикутник EBD — прямокутний і з прямокутного трикутника EBD (рис. 9):
BA = ∙>JEAAD = jab.
Рис. 9
Рис. 10
3) 	Нехай виконуються умови (2) і (3), тобто
AB = -JADBC і AB1AD.
Доведемо, що AC±BD.
Доведення
Проведемо B1C∣∣AC (рис. 10). Тоді АК = ВС. У трикутнику KBD висота BA = y∣AK∙AD, звідси трикутник KBD — прямокутний і BD1.AC, що й необхідно довести.
Задача. У чотирикутник вписано трапецію, паралельні сторони якої паралельні його діагоналям. Довести, що непаралельні сторони трапеції перетинаються на другій діагоналі чотирикутника.
Вказівка. У чотирикутнику ABCD непаралельні сторони MN і LK трапеції MNKL ділять навпіл діагональ DB зовнішньо в одному й тому самому відношенні. Для доведення застосувати теорему Менелая до трикутника ABD і січноїMN, трикутника BCD і січної LK.


Розділ 2. ДРУГА СЕРЕДНЯ ЛІНІЯ ТРАПЕЦІЇ
Другою -середньою лінією трапеції назвемо відрізок, який сполучає середини основ трапеції.
Позначимо T1, T2, T3, Т\ середини бічних сторін АВ і CD, основ ВС і AD відповідно трапеції ABCD (рис. 1).
Відрізок T,1T2 — перша середня лінія трапеції, відрізок T3T4 — друга.
Задача 1. Довести, що чотирикутник TlT3T2T∖ — паралелограм.
Справді, його сторони — середні лінії трикутників, що утворені двома сторонами трапеції й діагоналями.
Паралелограм T1T3T2T4 називають паралелограмом Варіньона (1654-1722, Франція).
Задача 2. Середні лінії трапеції в точці перетину діляться навпіл. Довести.
Справді, середні лінії — діагоналі паралелограма Варіньона.
Задача 3. Якщо діагоналі трапеції взаємно перпендикулярні, то τ1τ2=τ3τ4.
Справді, це випливає з паралелограма Варіньона.
Задача 4. Середні лінії трапеції рівні. Довести, що точки T1, Т2, T3, Т4 належать одному колу.
Доведення
Оскільки T1T12 = 7,3T4, то паралелограм 7,1T3T2T4 — прямокутник. Твердження задачі доведено.
Задача 5. Точки T1, T2, T3, T,4 належать одному колу. Довести, що діагоналі трапеції взаємно перпендикулярні. Доведення випливає з попередньої задачі.


Розділ 2. Друга середня лінія трапеції
11
Задача 6. У чотирикутник T1T3T2Ti вписано коло. Довести, що трапеція ABCD — рівнобічна.
Доведення
Справді, оскільки в цьому випадку T1T3 = T3T2, то паралелограм T1T3T2T4 — ромб. Отже, AC = BD і AB = DC.
Площа
Задача 7. Довести, що друга середня лінія ділить площу трапеції навпіл.
Доведення
Справді, площі трапецій ABT31∖ і T3CDT4 рівні між собою.
Задача 8. Деяка пряма, перетинаючи основи трапеції, поділила її площу навпіл. Довести, що якщо вона ділить основи трапеції в одному відношенні, то вона збігається з другою середньої лінією.
Доведення
Нехай деяка пряма KN (рис. 2) ділить верхню і нижню основу в одному й тому самому відношенні: ВК = тпх, КС = nx, AN = my, ND = ny.
Оскільки за умовою Sabkn = Scdnk , то τn(x+r∕) = n(x+ι∕), або m = n.
Рис. 2
Рис. З
Задача 9. Довести, що площа трапеції дорівнює добутку другої середньої лінії, діагоналі трапеції і синуса кута між ними.
Доведення
З’єднаємо точки А і T3, С і Т4 (рис. 3). Тоді
^at3ct4 = 2 AC'rΓ3]∖ ’sinφ,
де φ — кут між відрізками АС і T3T4. Але


12
/. Кушнір. Геометрія трапеції в задачах
S>AT3CT4 ~ 2 &ABCD •
Отже, твердження задачі доведено.
Задача 10. Довести, що площа трапеції дорівнює добутку другої середньої лінії і суми перпендикулярів, проведених на цю середню лінію (або на її продовження) з двох вершин, які є кінцями однієї з діагоналей.
Доведення
Позначимо перпендикуляри AA1 і CC1, що проведені з точок А іС на відрізок T3T4 як ħ1 і ħ2 відповідно (рис. 4). Тоді твердження задачі.
Задача 11. Площа трапеції дорівнює S. Знайти площу паралелограма Варіньона.
Відповідь. — S.
2
Задача 12. Довести, що площа трапеції ABCD обчислюється за формулою
Sλbcd =4sτ1τiτ3 =⅛∣p(p-t2)(p-d1 yj>-<⅛),
де р — півпериметр трикутника T1T4T3, t2 — друга середня лінія, d, =-AC, d. =-BD.
1 2 2 2
Доведення
Розглянемо трикутник T1T3T4 (рис. 5). Його площа дорівнює половині площі паралелограма Варіньона й обчислюється за формулою Герона, оскільки
Т.71 =-AC, Т.Т. =-BD.
1 3 2 2


Розділ 2. Друга середня лінія трапеції 13
ОС _ Q
4joT1T3T2T4 *jABCD'
твердження задачі доведено.
Задача 13. Довести, що площа трапеції обчислюється за формулою S = 2713714 √, де І — відстань від точки T1 (або Т2) до другої середньої лінії.
Доведення, Нехай T1K = І (рис, 6),
Рис. 6
Тоді S = 4Sτ τ τ =4-T.KT.T. = 2T3T. І.
Задача 14. Довести, що площа трапеції дорівнює добутку однієї з непаралельних сторін і перпендикуляра, проведеного з середини другої сторони на першу.
Доведення, Доведення цієї задачі випливає з доведення попередньої задачі.
Справді, нехай у трапеції ABCD (рис, 7) T1F — перпендикуляр, проведений з точки 711 на сторону CD, Побудуємо трапецію ABC1D1 так, щоб відрізок CD був її другою середньою лінією. Введемо позначення Sabc d = Sl. Тоді за попередньою задачею маємо:
S1 =2SLβr∏ = 2CDT,F, або S = CD>T.F, що й потрібно було довести.


Розділ 3. КУТИ
Задача 1. У трапеції ABCD сума кутів при основі AD дорівнює 90°, KN — відрізок, що сполучає середини основ, TG — відрізок, що сполучає середини діагоналей. Довести, що KN = TG.
Е
Рис. 1
Доведення
Доповнимо трапецію ABCD до трикутника AED (рис. 1). Ураховуючи умову, дістанемо кут AED, що дорівнює 90°.
Чотирикутник TKGN — паралелограм
(GW∣∣AB, GN = -AB, XT∣∣AB, KT = -AB).
2 2
Але ZTKG = Z.AED = 90°, звідси TKGN — прямокутник і KN = TG.
Задача 2. У трапеції ABCD діагоналі АС і BD дорівнюють основі АВ. Точка М — середина CD, Z.MBC = Z.CAB. Знайти кути трапеції.
Розв’язання
Оскільки AC = BD (рис. 2), то трапеція ABCD — рівнобедрена. Застосуємо метод допоміжної точки й допоміжного кола.
Нехай точка К — середина відрізка AD. Тоді
KM∖∖ACi ZAKM + ZKAC = 180°.
Позначимо ZCAB = ZMBC = а. Отже,
ZKAC = Z А - а і ZMBA = ZB-a,
звідси ZAKM + Z.MBA = 180° і навколо чотирикутника АКМВ можна описати коло. Оскільки BD = ВА, то


Розділ 3. Кути
15
ZAKB = 90° і ZAMB = 90°, причому висота ME = EB. CN = ME = -^AB = -^AC. Отже, sinα = ^ (за умовою AC = AB), a = 30°. Тоді
ZBAB = ZCBA = 750, ZADC = ZBCD = 105°.
„ „ „ . . . . „ 15√3
Задача 3. У трапеції середня лінія дорівнює 7, висота , а кут
7
між діагоналями напроти основ дорівнює 120°. Знайти діагоналі трапеції.
Рис. З
Розв'язання
За умовою задачі в трапеції ABCD
AB+CD = 14, ZAOB = у, DH1.AB і DH = (рис. 3).
Через вершину С проведемо пряму, паралельну діагоналі BD, до перетину з продовженням сторони АВ у точці М. Дістанемо паралелограм DCMB9
DC = ВМ і AM = AB+CD = 14, ZACM = ZAOB = —.
З
Позначимо AC = х, CM = BD = у. З трикутника ACM за теоремою косинусів: 142 = x2 + if +ху.


16
І. Кушнір. Γеометрія трапеції в задачах
Площа трикутника ACM дорівнює
1 AM DH = —АС СМ sin—,
2 2 3
звідки 30л/3 = — хі/л/З. Розв’язуючи систему рівнянь 2
142 = x2 +yz + xyi iχy√3=30√3,
І2
дістанемо: х = 10, у = 6 або х = 6, у = 10.
Задача 4 (турнір Архімеда,
Московська математична регата)
Рівносторонні трикутники ABC1DPE розміщені на площині так, що вершина В належить відрізку DE, а вершина Р — відрізку АС. Визначити вид чотирикутника, вершинами якого є точки А, С, D і Р.
Розв'язання
Проведемо відрізок ВР (рис. 4). Доведемо, що AD і СЕ паралельні. Оскільки ZBAP= ZBDP = 60o, то чотирикутник ADBP — вписаний. Оскільки Z.BEP = Z.BCP, то, аналогічно, чотирикутник ВЕСР — вписаний.
Звідси ZADB + ZAPB = 180° і ZBEC + ZBPC = 180°.
Оскільки Z.APB і Z.BPC — суміжні, то
Z ADB + ZBEC = 3600 - ( А АР В + ZBPC) = 180°, звідси AD∣∣CjK, отже, ADEC — трапеція.
Якщо AC∣∣DE, то ADEC — паралелограм.


Розділ 3. Куги
17
Задача 5 (Соросівська олімпіада)
У чотирикутнику ABCD ZCAB = 30o, ΛDBC = 30o, ΛBCA = 20°, ZS2)C = 70°.
Довести, що чотирикутник ABCD — трапеція.
Доведення
Нехай О — точка перетину діагоналей (рис. 5). Обчислимо:
ОАОВ
OCOD
XT siπ20o
У трикутнику ОВС =
ОС sin30o
Маємо:
ΛABD = ЛВОС-ЛВАС = 180° -30° -20° -30° = 100°;
ЛАОВ = 180o - ЛВАО-ЛАВО = 50°;
ΛOCD = 180o - ΛCDB - ΛDOC = 60°.
ОЛ = slnlθθ∙ (д АОВ) AB _ sin201 (д AB sin50o 4 , ВС sin30o v Л
ВС cd'
.∞ML(ABCD), sin30o v ,
CD
DO
,^L(kCOD-} sin60o
або
ОА _ОА AB ВС CD _
OD~ АВ ВС CD OD
_ sinl00o ∙sin20° ∙sin70° 4sinl00o ∙sin20° ∙sin70o
sin2 30o ∙sin60° sin600


18
/. Кушнір. Геометрія трапеції в задачах
_ 4sin800 ∙sin20o ∙cos20o _ 2sin80o ∙sin40o β sin60o sin600
ОАОВ __ 2sin80o ∙sin40o sin20o _
OC∙OD sin60o sin30o
_4sin80o ∙sin40o ∙sin20o _ sin60o
sin60o sin600
^ . ОА ОВ 1 ОА OD . a ,^n ad^
Оскільки = 1, то = і ΔAOD - ΔBOC, звідси
OCOD ОС ОВ
BC∣∣AD.
Задача 6 («Квант»). У трапеції ABCD діагональ АС дорівнює бічній стороні ВС, точка Н — середина основи АВ. Нехай І — пряма, що проходить через Н, а Р і Q — точки перетину прямої І з прямими AD і BD відповідно. Довести, що
ZACP = Z.QCB або Z.ACP+Z.QCB = 180°.
Вказівка. Можна довести, обчисливши відношення відрізків, що СР і CQ перетинають сторону АВ на рівних відстанях від кінців.
А можна вийти у простір: провести нову площину р через АВ і розглянути проекцію нашої площини на р із центра О, що віддалена від р на ту саму відстань, що й CD.


Розділ 4. ТЕОРЕМА
ПРО СЕРЕДНЮ ЛІНІЮ ТРАПЕЦІЇ.
АЛЬТЕРНАТИВНІ СПОСОБИ ДОВЕДЕННЯ
Теорема. Середня лінія трапеції паралельна основам і дорівнює їх півсумі. Довести.
Доведення
Перший спосіб
Доведення першим способом (1) загальновідоме за шкільними підручниками з геометрії, хоча тут замість розглядання MN як середньої лінії трикутника АВК можна застосувати теорему, обернену до теореми Фалеса (рис. 1): якщо MA = MB, &.DN = CN і BC∣∣ AD, то
MN∣∣BC∣∣AD і MN = —АК.
2
Другий спосіб
Нехай MN — середня лінія трапеції ABCD (рис. 2). Позначимо: ВС = α, AD = Ь. Проведемо CE∣∣ AB, F — точка перетину СЕ і MN.
Оскільки CF = FE, то FN — середня лінія трикутника ECD
і FN∖∖ED, отже, MN∣∣AD. Доведемо, що MN = Справді,
2
ED = b-a, FN = ^-, a MN = MF + FN = a+^^ = ^-.
2 2 2
Третій спосіб
Через точки А і D проведемо перпендикуляри до прямої ВС (рис. 3). Дістанемо прямокутник AAvD1D. Позначимо:


20
/. Кушнір. Геометрія трапеції в задачах
A1B = m, CDl =п.
Очевидно, що m + n = b - а.
Нехай точки Е і F — середини відрізків AA1 і DD1. Тоді
MN∖∖AD і AD = EM + MN+NF = —+-+MN = —+MN, . 2 2 2
Четвертий спосіб
Доповнимо трапецію ABCD до паралелограма ABKD (рис. 4). Тоді NE — середня лінія трикутника DCK і ΛΓE∣∣CK,. Оскільки KC = b-a, то NE = ^^ і MN+- = b, звідки MN = 2 2 2
П'ятий спосіб
Проведемо висоти BB1 і CC1 (рис. 5).
Середні лінії МЕ і FN трикутників ABB1 і DCC1 паралельні AD. Позначимо їх т і п.
Оскільки т = — AB., п = — C.D, то 21 2 і
b-а ∙ njτxτ b-а а+Ь
т + п = і MN =a+m-∖-n =а-\ = .
2 2 2
Рис. 5
Шостий спосіб
Проведемо діагональ АС (рис. 6). Нехай точка Е — середина АС.
Тоді ME∣∣BC, EN∖∖AD, отже, ΛW∣∣BC∣∣AD.


Розділ 4. Теорема про середню лінію трапеції. Альтернативні способи доведення 21
ME = -BC, EN = -AD.
2 2
BC+AD
2
MN = ME + EN =
Сьомий спосіб
Проведемо ||В£> (рис. 7). У паралелограмі BDKC перетин прямої MN і діагоналі CD утворює центр симетрії — точку N.
ZΔABD-.
ML = -AD, LN = -LE = —ВС і LE∖∖BC.
2 2 2
MN = ML + LN =
AD+BC 2
Восьмий спосіб
Нехай точка О — середина AD (рис. 8), точки Е і К — середини відрізків ВО і СО:
ME = -AO, EK = -BC, KN = -OD і ME∣∣AO, EK∖∖BC, KN∖∖OD.
2 2 2
MN = ІАО+-ВС+-ОВ = - AD+-BC+-AD = ВС+—.
2 2 2 4 2 4 2
В С
Рис. 8
Дев'ятий спосіб
З 	точок В, С, М, N опустимо перпендикуляри на основу AD (рис. 9). Перпендикуляр МК буде середньою лінією трикутника


22
/. Кушнір. Геометрія трапеції в задачах
ABL (BL-LAD). Аналогічно, NF — середня лінія трикутника CED.
Позначимо АК = KL = zn, FD = FE = п. Маємо (ВС = a; AD = д):
b—a m+m+a+n+n = b∙, 2m+2n = b-a, m+n = .
2
MN = AD-(AK+FD) = b-(m+n) = b-- = -.
2 2
Десятий спосіб
Нехай точка Т — середина відрізка ВС (рис. 10). Відрізок MN перетинає відрізки AT і DT у точках Е і К відповідно.
ME = -, KN = -, EK = -.
4 4 2
Маємо:
a a b 2a+2b a+b
ЛГУ = -+-+- = = .
4 4 2 4 2
Одинадцятий спосіб
Нехай точка Т — середина відрізка ВС (рис. 11). Проведемо TE∖∖ АВ і 7T∣∣DC, L і К — точки перетину цих відрізків із прямою MN.
Маємо:
MN = ML+LK + KN =
n о\ а b-а а+Ь
= -+- b-2∙- +- = α+ = .
2 2\ 2) 2 2 2
Рис. 11


Розділ 4. Теорема про середню лінію трапеції. Альтернативні способи доведення 23
Дванадцятий спосіб За правилом многокутника
MN = MB+BC+CN і MN = MA+AD+DN.
Додавши ці рівності, дістанемо:
2MN^∖MB+MA ] + ∖BC+AΣ)∖ + ∖CN+DN
Але точки М і N — середини сторін АВ і CD, тому
МВ+МА = б і CN+DN = б.
Отже, 2MN = AD+BC, звідки
MN = -∖ AD+BC∣∙ 2k J
Оскільки вектори AD і ВС співнапрямлені, то вектори MN і AD також співнапрямлені, а довжина вектора ^AD÷Bcj дорівнює AD + BC. Звідси випливає, що
ЯуГАТІІ а г\ • П/ГАТ AD + BC MjV∣∣ AD і MN = .
(Атанасян Л. С. и др. Геометрия 7-9.— М.: Просвещение, 1990)


Розділ 5. СЕРЕДНЯ ЛІНІЯ РІВНОБЕДРЕНОЇ ТРАПЕЦІЇ. АЛЬТЕРНАТИВНІ СПОСОБИ ДОВЕДЕННЯ
У рівнобедреній трапеції ABCD (рис. 1) з вершини В проведено перпендикуляр ВК(Ке AD). Довести, що відрізок KD дорівнює середній лінії трапеції.
в
с
Рис. 1
Доведення
Перший спосіб
Проведемо СЕ (Е ∈ AD) паралельно ВК (рис. 2).
Нехай ВС = КЕ = zn, АК = ED = п.
Оскільки середня лінія MN дорівнює ^(BC + AD), то
MN = — (jn + m + n+n) = —∙2(τn + n) = KD. 2 2
Другий спосіб
Сполучимо точки М і К (рис. 3). У прямокутному трикутнику
АВК медіана


Розділ 5. Середня лінія рівнобедреної трапеції. Альтернативні способи доведення 25
MK = ~AB = ND.
2
Отже, чотирикутник MNDK — паралелограм, звідси
KD = MN.
Рис. З
Рис. 4
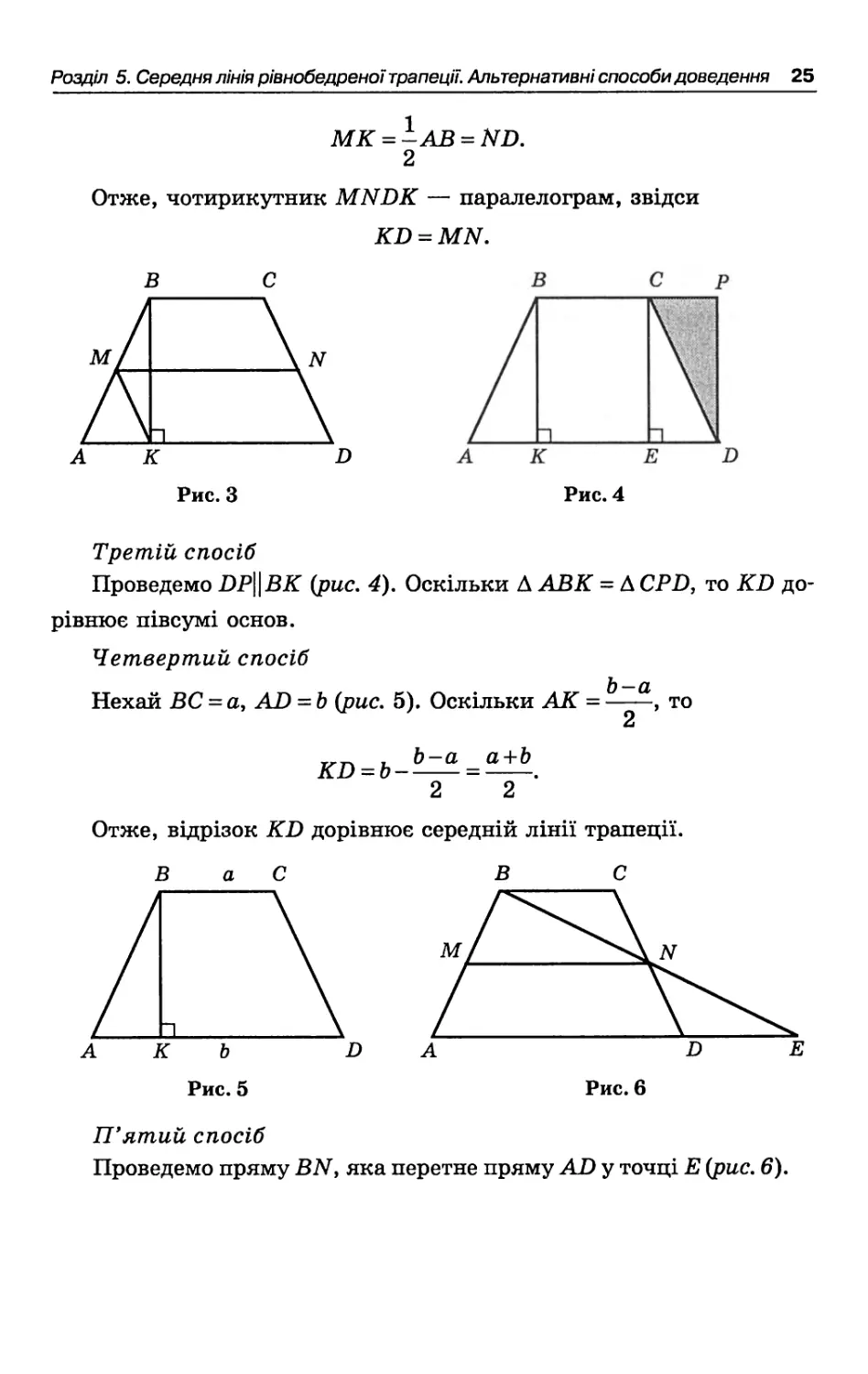
Третій спосіб
Проведемо DP∖∖ВК (рис, 4), Оскільки Δ АВК = Δ CPD, то KD дорівнює півсумі основ.
Четвертий спосіб
Нехай ВС = a, AD = b (рис. 5). Оскільки АК = ~~~> то
KD^b-b-^ = ^-.
2 2
Отже, відрізок KD дорівнює середній лінії трапеції.
П'ятий спосіб
Проведемо пряму BNi яка перетне пряму AD у точці Е (рис. 6).


Розділ 6. ТЕОРЕМА ПРО ПЛОЩУ ТРАПЕЦІЇ.
АЛЬТЕРНАТИВНІ СПОСОБИ ДОВЕДЕННЯ
Теорема. Площа трапеції В дорівнює добутку півсуми її основ на висоту.
Доведення
Перший спосіб
Нехай ABCD — трапеція, ВН — Ті висота.
Нехай точка Р (рис. 1) — середина сторони CD. Побудуємо трапецію CA1 BxD, симетричну заданій відносно точки Р. Чотирикутник ABAlB1 — паралелограм. (A1B1|| АВ і A1B∣∣AB1)
saba1b1 = abi ВН,
тоді
S = ∣⅛b1 =∣(BC + AD)BH.
Будемо далі позначати ВС = a, AD = b, ВН = h, площу трапеції — S, діагоналі — d1 id2.
Отже, S = ^(α+∂)Λ.
Другий спосіб
Проведемо CJS∣∣ АВ.
Тоді Sced = -h(b-a) (рис. 2), a Sabce = ah, отже, 2
S 	=—h(b-a)+ah = Λ∣ — +а | = — (а+І
2 v 7 І2 2 J 2v


Розділ 6. Теорема про площу трапеції. Альтернативні способи доведення
27
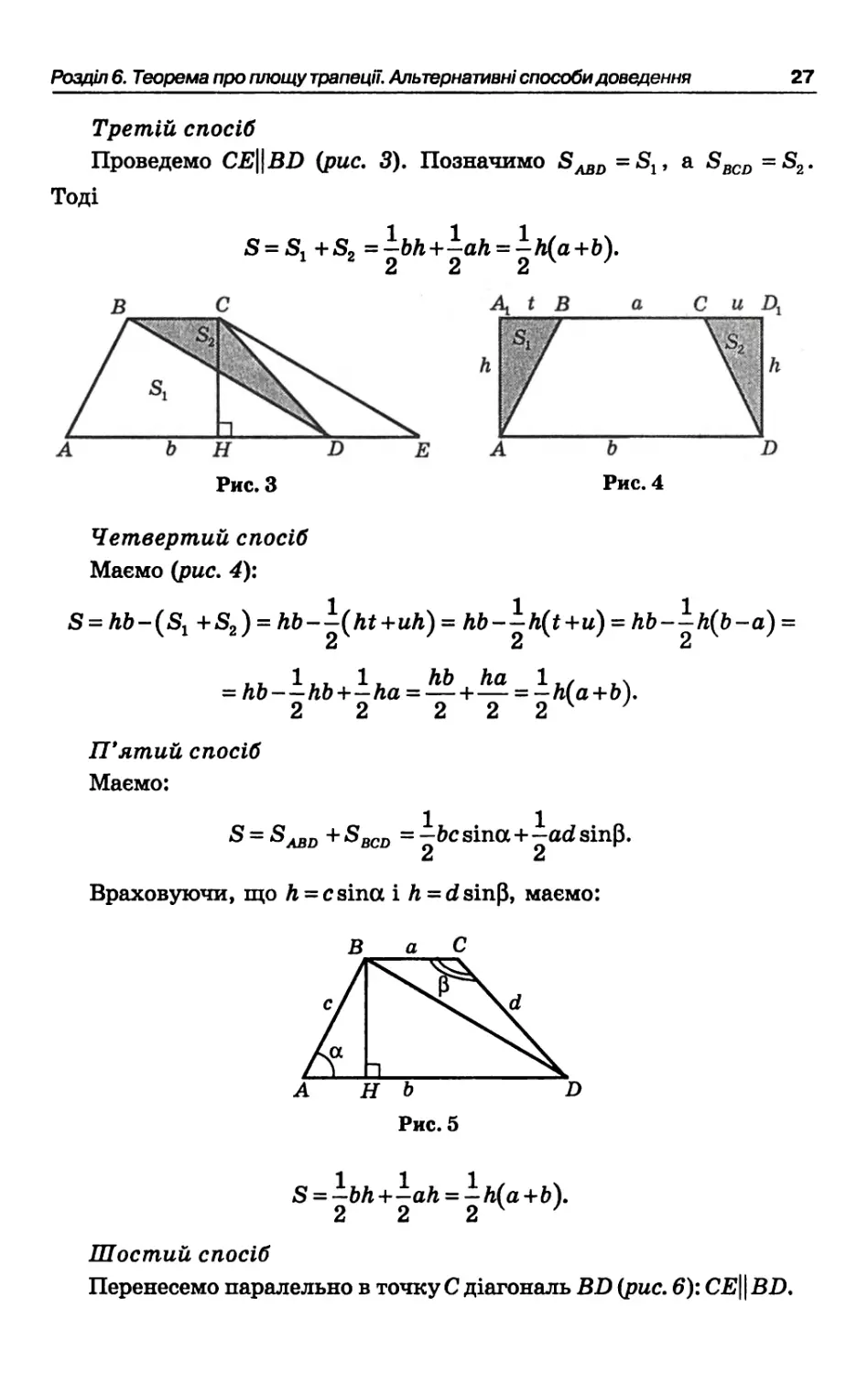
Третій спосіб
Проведемо CE∣∣BZ> (рис. 3). Позначимо Sabd =S1, a Sbcd =S2.
Тоді
S = S1 +S2 = -bh+-ah = -h(a+b).
2 2 2
Четвертий спосіб
Маємо (рис. 4):
S = hb-(S1 +S2) = hb--(ht+uh) = hb--h(t+u) = hb--h(b-a) =
2 2 2
= hb--hb+-ha = —+— = -⅛(α+ft).
2 2 2 2 2 v ’
П’ятий спосіб Маємо:
s~sabd
÷ ® BCD ~
llfc . 1^.0
—be sma+—ad sιnp.
2 2
Враховуючи, що Λ = csina і A = dsinβ, маємо:
S = -bh+-ah = -h(a+b).
2 2 2 v ,
Шостий спосіб
Перенесемо паралельно в точку С діагональ BD (рис. 6): CE∣ ∣ BD.


28
/. Кушнір. Геометрія трапеції в задачах
Оскільки Sase = Sabcd , то
S = ⅛H∙AE = iΛ(α+ft), 2 2
Перенесемо в точку С діагональ BD: CE∣∣BD (рис, 7).
&ABCD ” θ6Λ ’^2 sinCC - Sace .
Але Sace = -h(a+b) = S.
2
Восьмий спосіб
& 	~ ВНЕС ÷ 8 ABH + &CED
= ha+-ht+-hu= ha+-h(t+u) = -h(a+b) (рис. 8).
2 2 2 2
Дев’ятий спосіб
Позначимо висоту трикутника ВЕС як h1 (рис. 9).


Розділ 6. Теорема про площу трапеціїАльтернативні способи доведення
29
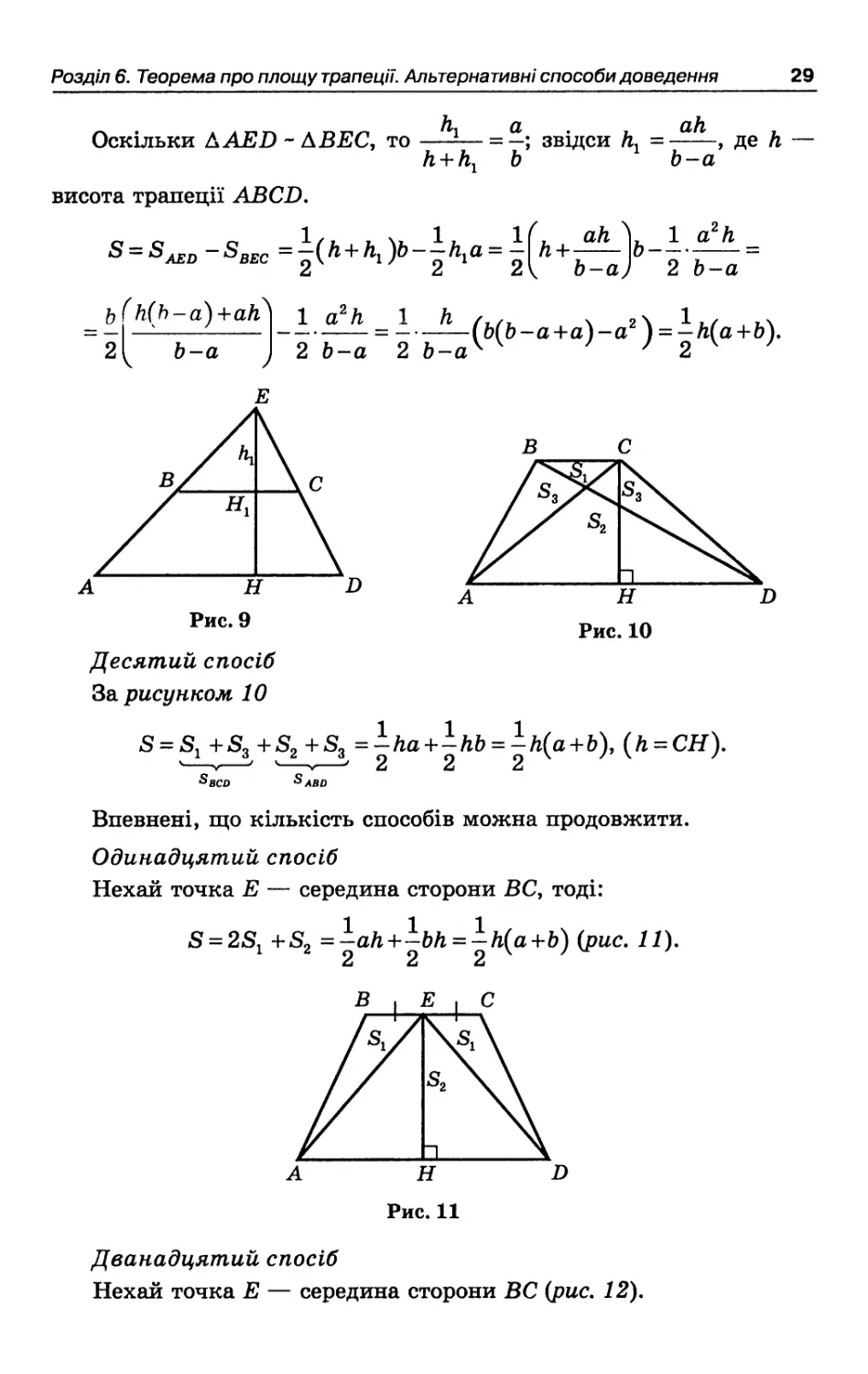
Оскільки AAED - АВЕС, то —-— = —; звідси h1 =——, де h — h + hl b b-a
висота трапеції ABCD.
cι ~ ci 1∕l і ∖> h 1|\ ah Y 1 a2h
S = Saed-Sbec = -(h+ħl)b--hla = -∖h+-∖b--- =
2 2 2 ∖ и a J 2 и d
b(h(ħ-a)+ah} ι a2ħ 1 h f,,, 4 2∖ 1. ∕ t4
= - — = (b(b-a+a)-a )--h(a+b).
2 b-a , 2 b-a 2 ft-αv v ’ , 2 v ,
Десятий спосіб
За рисунком 10
S = S1 +S3+S2+S3 =∣Λa+∣Λb = ∣Λ(o+ft), (Л = СЯ).
^BCD $ABD
Впевнені, що кількість способів можна продовжити.
Одинадцятий спосіб
Нехай точка Е — середина сторони ВС, тоді:
S = 2Sl +S2 =-ah+-bh = -h(a+b') (рис. 11).
2 2 2
D г п
А Н D
Рис. 11
Дванадцятий спосіб
Нехай точка Е — середина сторони ВС (рис. 12).


зо
/. Кушнір, Геометрія трапеції в задачах
Проведемо EK∖∖ АВ і EL∖∖CD. Площа паралелограма АВЕК — S1, площа трикутника EKL — S2.
S = 2S1+S2 =2—Л+—Λ(ft-α) = —(α+i>).
2 2 2
ВЕС
А К Н L В
Рис. 12
Тринадцятий спосіб
Довести, що площа трапеції обчислюється за формулою
&ABCD = 27^7*4 'l9
де T3T4 — друга середня лінія, І — відстань від точки T1 або Т2 до другої середньої лінії (точки T1, Т2 — середини сторін АВ і CD відповідно).
Доведення
Нехай T1K -І (рис, 13), Тоді
&ABCD = 4sT1TjT4 = ^4 = 2^ 'l∙
а
Чотирнадцятий спосіб — за читачами!


Розділ 7. ПАРАЛЕЛОГРАМ ВАРІНЬОНА І ПЛОЩА ТРАПЕЦІЇ
Теорема. Довести, що площа трапеції дорівнює подвоєній площі паралелограма Варіньона.
Доведення
Перший спосіб
Нехай Sb — площа паралелограма Варіньона T1T3T2T4 (точки Ti — середини сторін трапеції) (рис. 1).
Sb=2Sttt = 2--— = -h~ = -Sabcd в τ3τ,τ4 2 2 2 2 2 2
(а і b — основи ВС і AD, h — висота трапеції).
Другий спосіб
Нехай d1, d2 — діагоналі трапеції ABCD (рис. 2)j ZT3T1T4 =а,0 — точка перетину діагоналей трапеції. Маємо:
Sβ = 2Sτττ
-T1T3 TlT4 ∙sinα =
Рис. 2


32
/. Кушнір. Геометрія трапеції в задачах
d. d<i 1 1
——- sin Z.AOD = -d,d, sinα - — S
2 2 4 1 2 2
ABCD *
Третій спосіб SB =⅛'τ3τ,4 τiτ2 sin<P (Puc∙ 3)>
де φ = ZT2OT4. Оскільки ZTiT2H =φ (T1H±AD), то
Sb =-.-.T1H = -Sabcd. b 2 2 2
Четвертий спосіб
Маємо (рис. 1):
&в ~^^T2T3T1 ^z^^ABTlT2 ~(Sτ3BTl +SaT3T2 )) =
rt(l(a b∖ (1 h a 1 h 1, lfa + zΛ 1
lk2<2 2) І2 2 2 2 2 2)) 2 2∣k 2 ) 2 '
П'ятий спосіб
Sb — 2S7,27,37,4 = 2(Sat3t4d ^^^at3t2 ) =
.2flfΞ+6+6'∣.*-2∙li,∙*'∣.
1,2I 2 ) 2 2 2)
_2 (^fa+6 + 2b bYj-ЛҐa+ZΛ~ lg
\ЇЇІ 4 2))2∖~2~)2
Шостий спосіб
&в = ^^τ3τlτ4 = ^C^t3bt1t4 -2Sγ3bt1) •
Далі — аналогічно п’ятому способу.


Розділ 7, Паралелограм Варіньона і площа трапеції
33
Сьомий спосіб
Відомо, що Sabcd = 2T1T2 і, де l = T2K — висота трикутника T3TlT2 (рис. 4).
Sλrc∏=2∙2-T.T,1 = 22Sttt =2Sr,
J∖lSLrL) 2 ,* 1 ,* 2 * З t>,
що й потрібно було довести.
Восьмий спосіб
Якщо побудувати трикутник TγEK, рівновеликий трапеції
ABCD (рис. 5), то очевидно, що Sτιτ4τ2τ3
а отже, Sb
~ 2 ^TlEK '
2


Розділ 8. ЧУДОВИЙ ТРИКУТНИК ТРАПЕЦІЇ
У трапеції ABCD (рис. 1) проведемо прямі T1Т3 і 711Т4 (точки T1, Т2, T3, Т4 — середини сторін), вони перетнуть пряму AD у точках Е і F.
Рис. 1
Розглянемо трикутник T1EF. Оскільки ΔT1BT3 = ΔEAT3, то 771T3 = T3E9 тобто точка Т3 — середина відрізка TlE. Аналогічно, точка Т4 — середина відрізка T1F.
Розглянемо властивості трикутника T1EF шляхом розв’язування задач.
Задача 1. Довести, що середня лінія трапеції дорівнює півсумі основ.
Доведення
Дійсно, T3T4 =-EF = -(a + b).
2 2
Задача 2. Довести, що Sτ ef = Sabcd .
Доведення
Дійсно,
EA=DF = -a, AD = b, T.H = h 2 1
(а, b — основи трапеції, h — висота трапеції).
r, 11(a а Л , (a+b∖ „
Sτ ff —h∖ — ÷—ьд — h∖ — B4nrn.
1 2 \2 2 ) І 2 J
Задача 3. Довести, що площа паралелограма Варіньона дорівнює половині площі трапеції.


Розділ 8. Чудовий трикутник трапеції 35
Доведення
Дійсно, оскільки точки T2, T3, Т4 — середини сторін трикутника T1EF, то твердження доведено.
Задача 4. Довести теорему: сума квадратів діагоналей трапеції дорівнює сумі квадратів її бічних сторін, доданих до подвійного добутку основ.
Доведення
Нехай α, b,c,d — основи й бічні сторони трапеції ABCD, dl і d2 — п діагоналі. Необхідно довести:
d12+d2 =c2+d2+2ab. (*)
Позначимо ZT1EA = α, ZT1FD = β (рис. 1). За теоремою косинусів із Δ T3 АЕ:
або
c2 =df +a2 -2ad1 ∙cosa.
(1)
Аналогічно,
d2 = d2 +a2 -2ad2 ∙cosβ.
(2)
Додамо (1) і (2):
d12 +d2 =
c2 +d2 -2a2 +2a(d1 ∙cosa+d2 ∙cosβ).
(3)
Порівняючи вирази (3) і (*), залишається довести, що 2αb = 2α(d1 cosα+d2 cosβ)-2a2
або
b = d1 ∙cosa÷d2 ∙cosβ-a.
Проведемо висоту T1H. Маємо: d1 ∙cosa = EHi d2 ∙cosβ = FH. Отже, d1 ∙cosa+d2 cosfi-a = EF-a = b, що й потрібно було довести.
Задача 5 (МДУ, мехмат, 1973)
У трапеції діагоналі дорівнюють 3 і 5, а відрізок, що з’єднує середини основ, дорівнює 2. Знайти площу трапеції.
Розв'язання
У трикутнику T1EF потрібно знайти площу за сторонами 3 і 5 та медіаною T1T2, що дорівнює 2.


36
/. Кушнір. Геометрія трапеції в задачах
Рис. 2
Очевидно, що площа єгипетського трикутника (рис. 2) дорівнює 6.
Задача. Побудувати трапецію за двома основами і двома діагоналями.
Вказівка: побудуйте ΔT1EF.
Задам, в. У трапеції середні, лінія дорівнює 7. висота
а кут між діагоналями проти основ дорівнює 120°. Знайти діагоналі трапеції.
Розв'язання
З ΔT1EF
d12 +d2-2d.d2 ∙cosl20o =EF2 або d2 +d2 +d.d2 =142.
Площа ΔET1Fι
1 , , √3 14∙15√3 χ . . βn
-dyd9 = або dy d9 = 60.
2 1 2 2 2∙7 12
Отримаємо систему рівнянь:
'd12 +d2 +d1d2 = 196,
d1d2 =60,
звідки d1 = 10, d9 =6 або dy =6, d9 = 10.


Розділ 9. ТРАПЕЦІЯ - ПРИВІД ДЛЯ АНАЛОГІЙ
Математик — це той, хто вміє знаходити аналоги між твердженнями; кращий математик — той, хто встановлює аналоги доведень; більш сильний математик той, хто помічає аналоги теорій; але можна уявити собі й такого, хто між аналогіями бачить аналоги.
Стефан Банах
Думка розглянути трапецію як «вироджений» трикутник може виникнути у зв’язку з формулою середньої лінії (рис. 1):
MN = ^-. (1)
2
Рис. 1
Очевидно, що при α = 0 трапеція «вироджується» у трикутник і формула (1) стає формулою середньої лінії трикутника ABC:
MN = -
2
(точки М iN — середини сторін трикутника, b — відповідна сторона).
Задача 1. У рівнобедреній трапеції ABCD (BC<AD} точка К — проекція точки В на основу AD. Довести, що KD — відрізок, що дорівнює середній лінії трапеції.
Доведення загальновідоме.
Задача 1°. У рівнобедреному трикутнику ABC (AB = AC} відрізок HxB дорівнює середній лінії трикутника (точка Hγ — основа висоти, проведеної з вершини А).
Доведення очевидне.
Задача 2. Довести, що в трапеції ABCD чотирикутник 711713T2T4 — паралелограм (T1, T2, T3, Т4 — середини сторін трапеції).


38
/. Кушнір. Геометрія трапеції в задачах
Справді, це паралелограм Варіньона.
Задача 2°. У трикутнику ABC чотирикутник AM2M1M3 — паралелограм (рис. 2).
Аналогія очевидна.
Задача 3. У трапеції ABCD середні лінії T1T2 і T3T4 у точці перетину діляться навпіл (випливає із задачі 2).
Задача 3\ У трикутнику ABC середня лінія M2M3 і медіана AMl діляться точкою перетину навпіл.
Аналогія очевидна.
Задача 4. Якщо середні лінії трапеції рівні, то діагоналі трапеції перетинаються під прямим кутом.
Задача 4°. Якщо середня лінія трикутника дорівнює відповідній медіані, то трикутник прямокутний.
Задача 5. У трапеції ABCD друга середня лінія, відрізки AN і DM перетинаються в одній точці (рис. 3).
Доведення
Справді, друга середня лінія проходить через точку перетину діагоналей трапеції. Отже, вона належить відрізку T3T4.
Задача 5е. Три медіани трикутника перетинаються в одній точці. Довести.


Розділ 9. Трапеція — привід для аналогій
39
Доведення
Справді, відрізки трапеції AN і DM аналогічні медіанам CM3 і BM2, а друга середня лінія — медіані AMl (рис. 4).
Задача 6. Довести, що якщо в трапеції ABCD AN = DM (рис. 3), то трапеція рівнобедрена.
Доведення
Справді, оскільки MN — середня лінія трапеції, то чотирикутник AM ND — рівнобедрена трапеція, а отже, рівнобедреною є і трапеція ABCD.
Задача 6°. Довести, що якщо в трикутнику ABC медіана ть дорівнює медіані тс, то трикутник рівнобедрений.
Доведення очевидне.
Задача 7. Довести, що якщо в трапеції ABCD відрізок BN = CM (рис. 3), то трапеція рівнобедрена.
Задача 7°. Якщо в трикутнику ABC відрізок ВМ1 = BM3, то a = с.
Доведення очевидне.
Задача 8. Якщо в трапеції ABCD відрізок CM =DM (рис. 3), то трапеція прямокутна ( ZD = 90°).
Задача 8°. Якщо в трикутнику ABC τnc = —с, то ZC = 90°.
Задача 9. У трапеції ABCD Scmd
-ls
~ 2 abcd
. Довести.
Задача 9е. Довести, що медіана ділить трикутник на дві рівновеликі частини.
Трапеція і формула медіани трикутника
У трапеції ABCD розглянемо паралелограм Варіньона 711713T2T,4 (рис. 5). Нехай d1 і d2 — діагоналі трапеції. За властивістю паралелограма


40
/. Кушнір. Геометрія трапеції в задачах
(d і
+ v =t3γ42+t1t22 (Γ)∙ у /2 J І
У разі «виродження» в трикутник діагоналі стануть сторонами b і с, відрізки T3T4 і TlT2 — медіаною ma і середньою лінією, що дорівнює —. Тоді формула (1°) набуде вигляду:
ι12 і Z.2 л2 . 2 b +с a
звідки = .
fl 2 4


Розділ 10. ТРАПЕЦІЯ
З ПЕРПЕНДИКУЛЯРНИМИ ДІАГОНАЛЯМИ
ЯК ПРИВІД ДЛЯ АНАЛОГІЙ
Задачі про рівнобедрену трапецію з перпендикулярними діагоналями дуже багато років. У задачнику М. Рибкіна вона друкувалася мільйонними накладами (§ 13, № 82) і впродовж десятиліть її розв’язував увесь Радянський Союз. Розглянемо задачу.
У рівнобедреній трапеції ABCD з перпендикулярними діагоналями висота дорівнює середній лінії. Довести.
Доведення можна провести багатьма способами.
Наведемо один з них.
Доведення
Нехай Е — точка перетину діагоналей, ВН — висота (рис. 1).
Оскільки в рівнобедреній трапеції відрізок HD дорівнює середній лінії (довести!), то у випадку перпендикулярності діагоналей (ZBDH = 45°) ВН = HD (з Δ BHD).
Рис. 1
Київський учитель математики В. Химерик розглянув нерівно- бедрену трапецію з перпендикулярними діагоналями й отримав цікавий результат.
Нехай ВН і СК — висоти трапеції (рис. 2) і ZAED = 90°.
Позначимо проекції діагоналей: DH = т, АК = п. Тоді площа трапеції S дорівнює:
o zn + n /
S = √77171
2


42
/. Кушнір. Геометрія трапеції в задачах
тобто площа трапеції з перпендикулярними діагоналям дорівнює добутку середнього арифметичного проекцій діагоналей трапеції на їх середнє геометричне.
Введення відрізків ш і ті — проекцій діагоналей, «наштовхує» на аналогію з прямокутним трикутником. Формула h = yjmn для цього трикутника доводилася звичайно за допомогою двох прямокутних трикутників АСН і ВСН (рис. 3).
У нашому випадку аналогія, оскільки Z.HBD = Z.KAC (кути з взаємно перпендикулярними сторонами), то Δ АС К ~ Δ BDH, звідси
СК АК HD~ ВН
або h2 = ττιτι (h = CK = ВН). Залишається показати, що тп + тг =a + b, де α = AD, b = ВС.
Позначимо AH = х, KD = у.
Маємо: AD = АН + НК + KD =x+b+y або a = x + b + у.
Оскільки x+b = mΛy=n-b, а отже, й a = τn + n,-b, а.Ь = Ь, то
, , , . a+b тп + п
a+b = 7∏+7i-b+b = τn+τι і = ,
2 2
o 771+71 і
ЗВІДСИ S = — у]77171.


Розділ 10. Трапеція з перпендикулярними діагоналями як привід для аналогій 43
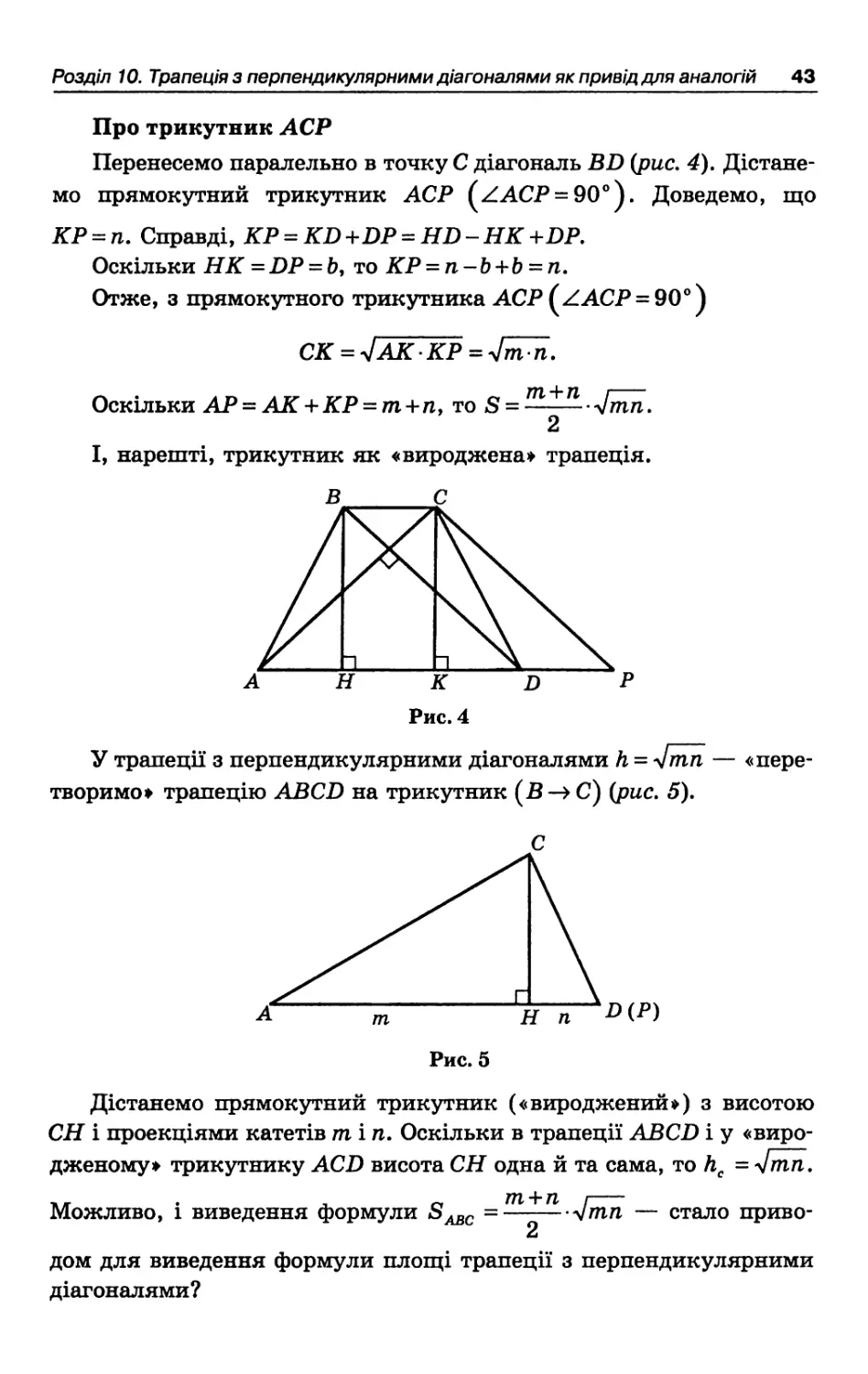
Про трикутник АСР
Перенесемо паралельно в точку С діагональ BD (рис. 4). Дістанемо прямокутний трикутник АСР (ZACP = 90°). Доведемо, що КР = п. Справді, КР = KD +DP = HD - НК +DP.
Оскільки НК = DP = b, то KP = n-b+b = n.
Отже, з прямокутного трикутника АСР (ZACP = 90°)
СК = -JAKKP = 4m÷n.
Оскільки AP = AK+KP = m+n, то S= m+n-Jm∏.
2
І, нарешті, трикутник як «вироджена» трапеція.
У трапеції з перпендикулярними діагоналями h = y∣τnn — «перетворимо» трапецію ABCD на трикутник (B->C) (рис. 5).
Дістанемо прямокутний трикутник («вироджений») з висотою СН і проекціями катетів min. Оскільки в трапеції ABCD і у «виродженому» трикутнику ACD висота СН одна й та сама, то hc = ^mn. τur • . о ТП + П і
Можливо, і виведення формули Sabc - ^jmn — стало приво-
2
дом для виведення формули площі трапеції з перпендикулярними діагоналями?


Розділ 11. ПОШУК ПОДІБНИХ ТРАПЕЦІЙ
1. Трапеції зі спільними основами
Нехай у трапеції ABCD проведено пряму EF паралельно основам.
Теорема. Якщо трапеції зі спільними основами подібні, то їх спільна основа є середнім геометричним двох інших основ (рис. 1).
Рис. 1
Справді, нехай EF∣∣BC∣∣AD і EF = х. Тоді = або — = —, EF AD х b звідси х = y[ab.
Теорема (обернена). Якщо EF = 4ab, то трапеції подібні.
Справді, з умови випливає пропорційність основ. Як буде показано, цього досить.
2. 	Основи трапецій не збігаються
Теорема. Дві або більше трапецій, вершини яких належать сторонам кута, будуть подібними, якщо відношення довжин основ рівні (коефіцієнт подібності).
Рис. 2


Розділ 11. Пошук подібних трапецій
45
Доведення
ВС В.С. Нехай у трапеціях ABCD і A1B1C1D1 (рис. 2) = ———.
AF) -A,γD∙γ
Доведемо, що ці трапеції подібні. Дістанемо:
СЕ _ CEED _ CE(AD-BC) _ ~AB~~ED~AE ED-BC
_ СЕ ґ АР _ C1E1 (A1D1 _
ED∖BC J E1D1{B1C1 J
_ C1E1 A1D1 -B1Cl _ C1E1 E1Dl _ ClEl
E1D1 B1C1 E12)1 A1E1
Тому трикутники АЕС і A1ElC1 подібні, а отже, паралелограми АВСЕ і A1B1C1E1 — подібні, отже, подібні й трапеції.
Задача 1. Прямою, що паралельна основам трапеції, поділити трапецію на дві подібних.
Розв'язання
Позначимо FE — шуканий відрізок. Нехай BC = a, AD = Ь. Тоді за першою теоремою EF = Jab.
Коефіцієнт подібності: k = a:Jab = Ja∖Jb (теорема 2).
Щоб знайти точку F, необхідно поділити відрізок АВ у відношенні Ja*.Jb.
Задача 2. У трапеції ABCD, основи якої дорівнюють aid, проведено середню лінію T1T2, паралельний їй відрізок MN через точку перетину діагоналей і паралельний основам відрізок EF = Jab (рис. 3).
Довести, що трапеції T1EF7,2 і EMNF — подібні.
Доведення
Доведемо, що EF = λ∣MN∙T1T2. Справді, (рис. 3)


46
/. Кушнір. Геометрія трапеції в задачах
v Vα+6 2
що доводить твердження задачі.
Теорема (!). У трапеції проведено пряму паралельно основам. Якщо в трапеції, що утворилися, можна вписати кола, то трапеції подібні. Довести (рис. 4).
Доведення
Нехай EF — відрізок прямої, паралельної основам трапеції ABCD. Продовжимо бічні сторони трапеції ABCD до перетину в точці S. Трикутники SAB, SEF, SDC — подібні. Позначимо радіуси кіл, вписаних у трапеції ABFE і FEDC як г і R. Для трикутників SAB і SEF вони є зовнівписаними. Позначимо: AB = α, DC = b, EF = х. З подібності трикутників SAB і SEF:
З подібності трикутників SEF і SDC (для трикутників SEF іSDC r iR — радіуси вписаних кіл):
Поділивши почленно рівності (1) і (2)
χ2 = а&. x = yfa⅛. EF = Jab,
хх Rr
доведемо твердження задачі.
Задача 4. Дві прямі, паралельні основам трапеції ABCD, ділять її на три трапеції, у кожну з яких вписано коло. Знайти радіус кола, вписаного в середню трапецію, якщо радіуси двох інших кіл R і г.


Розділ 11. Пошук подібних трапецій
47
Розв'язання
Оскільки всі три трапеції подібні, то їх відповідні лінійні елементи пропорційні. Позначимо EK - t1, LM = t2, радіус другого кола — х, ВС = а (рис. 5). Маємо (з подібності верхньої і середньої трапецій):
Рис. 5
З подібності середньої і нижньої трапецій:
r⅛∙ ,2)
Поділимо (1) на (2):
r-R at2 r∙R at2
= —— або = -√-.
XX t1 ∙t1 xz t{
Але tf =t2 а.
Γ,R ^^2 1 /п
Отже, —— = —— = 1, х = y∣Rr.
х t2 а
Діагональна трапеція
Відрізок EF, проведений паралельно основам трапеції так, що дві нові трапеції подібні, має ще одну властивість: чотирикутник AECF — трапеція! Доведемо це (рис. 6).
Оскільки = і ЛЕВС = Z.AEF, то трикутники ЕВС і AEF
EF ЕА
подібні. Отже, Z.ECB = Z.AFE = Z.CEF і звідси CE∣∣ AF.
І навпаки... (ознака подібності).


48
/. Кушнір. Геометрія трапеції в задачах
Рис. 6
Якщо CE∣∣AF, то трапеції EBCF і AEFD — подібні (EF = 4ao).
Справді, трикутник ЕВС подібний трикутнику AEF і трикутник CEF подібний трикутнику FAD — а це означає, що трапеції подібні.
Задача 3 (!). У трапеції ABCD проведено пряму EF, паралельно основам, причому EC∣∣ AF. Знайти відношення площі трапеції ABCD до площі трапеції AECF, якщо ВС = α, AD = Ь (рис. 7).
Оскільки трапеції AEFD і EBCF подібні, то EF = jab (рис. 7).
Позначимо площу AECF як S1. Маємо: S1 = — EF ∙ AC-sinφ (φ — кут
2
між діагоналями).
Але AC∙ sinφ -СН — висота трапеції ABCD. Отже,
1 1 OQ
S. = -EFCH = -Jab-^=-,
1 2 2 а+Ь
S а+Ь звідси — = —- ■ s. -Jab


Розділ 12. ТРАПЕЦІЯ. ОПИСАНЕ КОЛО
Задача 1. AD і ВС — основи трапеції ABCD. Точка Р — точка перетину її діагоналей Довести, що кола, описані навколо трикутників АВР і CDP, перетинаються в центрі описаного кола трапеції ABCD.
Доведення
Нехай О — центр кола (рис. 1). Кут CDB — вписаний, кут ВОС — відповідний йому центральний. У силу симетрії РО — бісектриса кута ВОС. Тому Z.BOP = ZCOP. Звідси випливає, що точки Р, С, D, О лежать на колі, описаному навколо трикутника CDP. Аналогічно — навколо трикутника АВР.
Задача 2. Основи трапеції а і Ь, бічна сторона І. Знайти радіус кола, описаного навколо цієї трапеції.
Рис. 2


50
/. Кушнір. Геометрія трапеції в задачах
Розв'язання
Трапеція, вписана в коло, рівнобедрена, радіус цього кола — це радіус кола, описаного навколо трикутника ACD (або ABC) (рис. 2).
Знайдемо його за відомою формулою R = . У нашому випадку
4S
AD = a, CD = І. Знайдемо АС і Sacd . Маємо:
AH = ^-, CH1.AD.
2
І 	7 , \2
CH = -Jl2-HD2 = z2- ≤L± .
V І 2 J
І / \2 / \2
AC = Jah2 +CH2 = Jl2 -1 ≤-∣ = √∕2 +ab.
\ < 2 J V 2 J
S = -ADCH = -aJl2-f—1 .
2 2 V V 2 √
al∙y∣l2 +ab . I l2 +ab
1 2 fα-bY ]4l2-(a-b)
2 V І 2 )
Задача 3. Трапецію ABCD вписано в коло. Продовження висоти СК трапеції перетинає описане коло в точці F. Знайти радіус кола й діагональ трапеції, якщо діагоналі трапеції перпендикулярні,
3.DF = тп, PT = n (Р — точка перетину діагоналей, PTLAD).
Розв'язання
Трапеція ABCD — рівнобедрена, а за умовою
Z.PAD = Z.PDA = 45° (рис. 3).
Рис. З


Розділ 12. Трапеція. Описане коло
51
ZACF = ZADF = 450, PT = AT = n.
3ΔKDF-.KD = ^=" √2 42
Тоді
AK = 2AT-KD = 2n-‰ AC = AK42 =∣2n--⅛∣√2 =2-j2n-m.
√2 І 42)
Оскільки ZBCF = 90°, то BF — діаметр описаного кола навколо трапеції ABCD. З Δ BDF:
BF2 =BD2 +DF2 = (2λ∕2ti-τn) +τn2 =8п2 -4л/2тпя+ 2τn2,
звідки BF = y∣8n2 -4∖[2m,n+2ιn2 і BO = -y∣8n2 -⅛j2τnn +2τn2.
2
Задача 4. У коло вписано дві трапеції з відповідно паралельними сторонами. Довести, що діагональ однієї з них дорівнює діагоналі Другої.
Доведення
Нехай ZABC = а (рис. 4). Тоді AC = 2Rsina (R — радіус кола).
Але ZA1B1C1 також дорівнює а і A1C1 = 2Rsina, тобто AC = A1C1.
Задача 5. Основи трапеції дорівнюють 4 і 16. Знайти радіуси кіл, вписаного в трапецію і описаного навколо неї, якщо відомо, що ці кола існують.
Розв’язання
Висота трапеції дорівнює діаметру вписаного кола. Оскільки
AB+CD = BC + AD,


52
І. Кушнір. Γеометрія трапеції в задачах
то AB = 10. Але AH = ^-- = 6 і ВН = √100-36 = 8, отже, г = 4.
2
Радіус кола, описаного навколо трапеції, знайдемо за теоремою синусів із Δ ABD:
д_ BP 2√415√41
2∙sinZBAD 8 4
5
Задача 6. У вписаній трапеції ABCD центр кола — середина основи AD. Довести, що ∣ZB - ZACB∣ = 90°.
Доведення
Нехай ZABC = α, Z.ACB = β (рис. 6).
Проведемо діагональ BD: Z.CAD = Z.DBC = β, a Z.ABD = 90°.
Отже,
90o = ZABC-ZΠBC = α-β = 90o.
Рис. 6
Рис. 7


Розділ 12. Трапеція. Описане коло
53
Задача 7. Знайти середню лінію трапеції, вписаної в коло, якщо висота трапеції h, а бічну сторону видно з центра кола під кутом 120°.
Розв'язання
Нехай точкаО — центр кола (рис. 7), тоді ZCOD = 120o, a ZCAD = = 60°. З ДАСИ:
AHr = CJT∙ctg60o = Л—.
З
Оскільки АН дорівнює середній лінії заданої трапеції, то діста- A√3 ємо відповідь: .
З
Задача 8. Основи трапеції, вписаної в коло й описаної, дорівнюють а і b (а > &). Знайти відстані між центрами цих кіл.
Рис. 8
Розв'язання Позначимо h — висоту трапеції (рис. 8): h = 2г (г — радіус вписа¬
ного кола, R — описаного).
о • . rτ J<*b
Зрозуміло, що h = ∙>Jab9 г - .
2
Нехай ОЕ = х, де точка Е — середина основи ВС, тоді із Δ AOTi маємо:
2 і_2 Л2 »2 , a jl2
τ⅜2 Л / , \2 А тл τ⅜2 2 —Р 4" 4/1
R = h(Λ- х) ; ДВОЕ: R = х ч—, звідки х ~.
4 v ’ 4 8Л
Нехай ОІ = d, d = ОЕ- ІЕ. a2 -b2 +4й2 Tab ,  = α. 8й 2


54
/. Кушнір. Геометрія трапеції в задачах
Враховуючи, що ħ = Vαb, маємо:
, a2 -b2 +4ab 4ab a2 -b2 a = — = —f=γ^∙
⅛Jab 2 bjab
Задача 9. У рівнобедреній трапеції ABCD Р — точка перетину діагоналей. Довести, що центр кола, описаного навколо трапеції, лежить на колі, описаному навколо трикутника АВР.
Доведення
Нехай точка О — центр кола, описаного навколо трапеції ABCD.
Позначимо ZBDA = а. Тоді ZАОВ = 2а.
≡'t'2" 2«
2
(кут з вершиною всередині круга), отже, твердження задачі доведено.


Розділ 13. ВПИСАНЕ КОЛО
Задача 1. У трапецію вписано коло радіуса г. Знайти площу трапеції, якщо кути при більшій основі дорівнюють а і β.
Розв’язання
Проведемо висоти ВН і СТ (рис. 1). Кожна з висот дорівнює діаметру вписаного кола.
З 	Δ ABH: = =
since sinα 9r 3ADCT: CD = ——. sinβ
Оскільки трапеція описана, то AB+CD = BC + AD. о • е» BC + AD . AB+CD . t
Звідси Sabcd = h h(h — висота трапеції, що
2 2
дорівнює 2г).
Отже,
S = (AB+CD')∙r = 2r2 —+-J— . ⅛4sina sinβ J
Задача 2. В описаній рівнобедреній трапеції ABCD (BC<AD) проведено висоту BE і відрізок MN (точки М і N — точки дотику кола до бічних сторін). Довести, що BE = y∣AB-MN.
Доведення
Нехай точка О — центр кола, вписаного в рівнобедрену трапецію ABCD (рис. 2). Проведемо висоту BE і OKLMN. Оскільки Z.ABE = ЛОМ К (кути зі взаємно перпендикулярними сторонами), то ААВЕ - АОМК:


56
/. Кушнір. Геометрія трапеції в задачах
Рис. 2
АВ _ BE 0M~ MK'
Оскільки ОМ = —BE і МК = -MN, то = звідки 2 2 BE MN
BE2 = AB∙MN.
Задача 3. У рівнобедрену трапецію вписано коло. Довести, що точки М і 7V дотику кола з бічними сторонами й точка перетину діагоналей лежать на одній прямій.
Рис. З
Доведення
Нехай Р — точка перетину діагоналей рівнобедреної трапеції ABCD. Нехай точка О — центр вписаного кола (рис. 3). Проведемо висоту ВН. Оскільки Z.ABH = Z.OMN (кути зі взаємно перпендикулярними сторонами), то ΔABH ~ ΔOMP. Нехай ВС = α, AD = Ь. Тоді
b-a о ГТ / \ МР ОМ
АН = , ВН = 2^jab (довести). = .
2 ВН АВ
Нехай BH = h — діаметр кола, тоді ОМ = ^ħ = ^Vab. Отже,
Л/ГП ВНОМ . a+b jitd hh ab
МР = . Оскільки АВ = , то МР = = .
AB 2 a+b a+b
Але ΛfP∣∣AD і МР = , що доводить твердження задачі.
а + &


Розділ 13. Вписане коло
57
Задача 4. В описаній трапеції
f12 +t2 +⅛ +t2i = c2 +d2
(ti — відстані від центра кола до вершин), AB = с, DC = d. Довести.
Доведення
Нехай точка О — центр кола (рис. 4), тобто точка перетину бісектрис кутів трапеції, звідси Z.AOB = ZCOD = 90°.
З Δ АОВ:
ОА2 +OB2 =с2.
З Δ СОВ:
OC2 +OD2 =d2.
Отже, OA2 +OB2 +OC2 +OB2 =c2 +d2.
Рис. 4 Рис. 5
Задача 5. Основи трапеції дорівнюють а і Ь, кути при більшій основі а дорівнюють а і β. Довести, що необхідною і достатньою умовою для того, щоб у цю трапецію можна було вписати коло, є рівність:
ь * α + β rtg2⅛
Доведення
Необхідність. Нехай г — радіус вписаного кола, К — точка дотику кола до сторони AD (рис. 5). Очевидно, що
x α x β а x а xβ
a = 7'ctg,- + rctg— або - = ctg—+ctg,-.
2 2 г 2 2
Л ∙ & , а , β
Аналогічно, - = tg,-+ tg,-.
г 2 2
Отже, — = te2+tgLt⅛⅛∣,


58
/. Кушнір. Геометрія трапеції в задачах
Достатність. Нехай деяке коло дотикається до бічних сторін трапеції, основи AD, але не дотикається до основи ВС (рис. 6).
Проведемо дотичну B1C1, паралельну основі AD. В описаній трапеції AB1C1D
⅛ = tg^.tg∣ (b1 =B1c1).
U1 & и
Але tg— ∙ tg— = —, звідси ∂1 = b. Отже, B1C1 = ВС і достатня умова
2 2 а
теореми доведена.
Задача 6. Навколо кола описано трапецію, бічні сторона якої у разі продовження перетинаються під кутом а. Основи трапеції дорівнюють а і b (а > Ь). Знайти радіус кола.
Доведення
Проведемо DF∖∖ВС (рис. 7).
Оскільки трапецію описано навколо кола, то
AD +DF — AD + ВС = а+Ь.
Проведемо висоту DH (DH = 2г, де г — радіус кола). Застосуємо формулу AF2 = (AD+DF)2 -4Sctg- (S — площа Δ ADF). Оскільки 2
AF=a-b1 то S = (a-b)r9 отже,
(α-∂)2 =(α+∂)2 -4(α-∂)r∙ctg-,
2
ab . а звідси г = tg—.
a-b 2


Розділ 14. КОЛА І ТРАПЕЦІЯ
Задача 1. У трапеції ABCD з основами АВ і CD діагоналі перетинаються в точці О. Довести, що кола, описані навколо трикутників АОВ і COD, дотикаються.
Доведення
Трикутники COD і ВОС гомотетичні відносно точки О (рис. І). Кола, описані навколо цих трикутників, гомотетичні відносно їх спільної точки (точки О). Тому точка О належить лінії центрів — O1O2, а отже, кола дотикаються в точці О.
Задача 2. Відомо, що в трапецію можна вписати коло. Довести, що кола, побудовані на її бічних сторонах як на діаметрах, дотикаються одне до одного.
Доведення
НехайRl iR2 — радіуси побудованих кіл (рис. 2), точки O1 iθ2 — їх центри. Доведемо, що O1O2 =R1 +R2.
Дійсно, O1O2 — середня лінія трапеції ABCD:


60
І. Кушнір. Γеометрія трапеції в задачах
O1O2 = -(AΣ>+BC) = -(AB+CD')=Rl +R2.
2 2
Задача 3. Три сторони трапеції рівні. Коло, діаметром якої є основи трапеції, ділить бічну сторону навпіл. Знайти величину кутів трапеції.
Розв'язання
Нехай AB = ВС = CD. Позначимо кут CBD: Z.CBD = х (рис. 3).
З трикутника BCD: Z.BDC = я, крім того, Z.BDA = я, Z.ADF = — я. 2
З прямокутного трикутника AFD:
2x+- = 90°, x = 36°. 2
Отже, кути трапеції 72° і 108°.
Помітимо, що рівність AB = AD = ВС — неможлива.
Задача 4. У трапеції ABCD основи AB<DC. Коло, описане на¬
вколо трикутника ABC, дотикається до сторони AD. Довести, що
AC = ^ABCD.
Доведення
Оскільки ZDAC = ZABC (рис. 4) і Z.BAC = Z.ACD, то трикутники ABC і CAD подібні.


Розділ 14. Кола і трапеція
61
— = — або AC = ∙JABCD. AC CD
Задача 5. Продовження бічних сторін AD і ВС рівнобедреної трапеції ABCD перетинаються в точці L. Довести, що кола, описані навколо трикутників ACL і BDL, перетинаються в центрі кола, описаного навколо заданої трапеції.
Доведення
Трикутник ABL — рівнобедрений. Його висота LM належить його осі симетрії (рис. 5). Через точки A,C,L і B,D,L проведемо кола. Вони симетричні відносно осі LM. При цій симетрії дуги КС і KD — симетричні як і дуги АК і КВ. Крім того, дута АК дорівнює дузі КС. Звідси випливає рівність чотирьох дуг. Тому рівні й хорди, що стягують ці дути, так що точка К є центром кола, описаного навколо трапеції ABCD.
Задача 6. Коло з центром у точці перетину діагоналей трапеції ABCD дотикається до меншої основи CD і бічних сторін. Знайти радіус кола, якщо основи трапеції дорівнюють 6 і 26.


62
/. Кушнір. Геометрія трапеції в задачах
Доведення
Оскільки точка О — центр кола, то відрізок СО належить бісектрисі кута BCD, звідси Z.OCD = Z.OCB = Z.CAB, отже, ВС = АВ = AD.
Проведемо висоту CD, СВ = АВ = 26, отже,
CD = √BC2 -BDi = √262-102 = 24.
З подібності трикутників COD і АОВ:
Е0 =—, ЕО = 4,5.
24-ЕО 26
Задача 7. Діагоналі трапеції ABCD перетинаються в точці К. На бічних сторонах трапеції як на діаметрах побудовані кола. Точка К лежить поза цими колами. Довести, що довжини дотичних, проведених до цих кіл з точки К, рівні.
Доведення
Нехай бічні сторони трапеції АВ і CD. Позначимо через М і N точки перетину прямих АС і BD відповідно до кіл (рис. 7). За теоремою про дотичну й січну добутки КМ -КА і KN KD є рівними. Отже, нам необхідно довести, що KM∙KA=KN∙KD. Оскільки кут АМВ спирається на діаметр, дістаємо, що ZAMB = 90°. Отже, Z,BMC = 90°. Аналогічно, ΛBNC = 90°, тому точки В, М, N і С лежать на колі з діаметром ВС, звідси ACMN = Z.CBN = Z.BDA (оскільки BC∣∣AD). Але тоді Z.AMN + Z.NDA = 180°, тому точки А, М, N, D лежать на одному колі і за теоремою про добуток всієї січної на її зовнішню частину KM ∙ KA = KN ∙ KD, що й потрібно було довести.


Розділ 15. ПРЯМОКУТНА ТРАПЕЦІЯ
Задача 1. Довести, що в описаній прямокутній трапеції висота є середнім гармонічним основ, а площа дорівнює їх добутку.
Доведення
Нехай в описаній трапеції ABCD (рис. 1) ВС = α, AD = b, CD = f, CH = h. Маємо:
t + Λ = α+b або ((α+∂)-Λ)2 = h2 +(∂-α)2,
, 2ab rr 2аЬ а+Ь .
a h = , отже, S = = ab.
а+Ь а+Ь 2
Задача 2. У прямокутній трапеції ABCD tlsl стороні, не перпендикулярній основі, як на діаметрі описано коло, що дотикається до протилежної сторони трапеції в точці М.
Довести, що AM2 =BC AD.
Рис. 2


64
Доведення нерівностей. Числові послідовності... Книга З
Доведення
Нехай у трапеції ABCD точка О — середина сторони CD, Е — точка перетину кола зі стороною AD (рис. 2).
ZCED = 9Q°, ЛАМО = 90” і BC = АЕ, BM = -AB.
2
Зрозуміло, що AM2 = АЕ AD. Але АЕ = ВС, отже, AM2 = BCAD, що й потрібно довести.
Задача 3. У прямокутну трапецію ABCD (AB∣∣CZ), AB<DC) на меншій бічній стороні АВ як на діаметрі описане півколо, що дотикається до сторони ВС. Довести, що AD2 = AB DC.
Доведення
Позначимо AB = ти, DC = n,ι радіус півкола (рис. 3), Е — точка дотику. Оскільки AB = BE і EC = DC, то
(zn + n)2 = 4r2 +(zn-n)2, звідси r2 = mn або AD2 = AB DC.
Рис. З Рис. 4
Задача 4. У прямокутній трапеції ABCD Е — точка перетину діагоналей; кут А — прямий, точка F — основа перпендикуляра, проведеного з точки Е на сторону АВ. Довести, що FE — бісектриса кута CFD.
Доведення
Подовжимо відрізок FE до перетину із CD у точці К (рис. 4). Тоді СК _FB _ FC KD~ AF~ FD,
що доводить твердження задачі.


Розділ 15. Прямокутна трапеція
65
Задача 5. У прямокутній трапеції ABCD з основою АВ і прямим кутом В до середини М сторони AD проведено перпендикуляр, що перетинає пряму ВС у точці N. Довести, що ZAND = ZCMB.
Рис. 5
Доведення
Оскільки DM = AM, то трикутники ADN і ВСМ — рівнобедрені. Оскільки ZBCD = ZDMB = 90°, то навколо чотирикутника NCDM можна описати коло, отже, ZADN = ZBCM, а отже,
Z AND = ZCMB.


Розділ 16. ПЛОЩА ТРАПЕЦІЇ
Задача 1. Бічні сторони трапеції дорівнюють 15 см і 20 см. Знайти периметр і площу цієї трапеції, якщо відомо, що одна з діагоналей є її висотою, а сума тупих кутів трапеції дорівнює 270°.
Розв'язання
Оскільки за умовою в трапеції ABCD (рис. 1) Z.B + ZD = 270°, а сума внутрішніх кутів 360°, то Z.A + ZC = 90°. Подовжимо за точку D відрізок AD (пряма AN). Тоді Z.CDN = ZC, а
ZBZ>C + Z.CDN = ZBDC + ZC = 900.
Отже, ZA + ZC= ZBDC + ZC, звідси ZA = ZBDC. Отже,
Δ ABD - ΔDCB∙. - = — = BD = 3t; BC = At. ВС 20 4
Далі
AD 15 3 λτ^ 3BD atλ 9t BD 20 4 4 4
З трикутника ABD
Q 1≠2 9f2 +2JL_ = 225, t = 4.
16
Отже, BD = 12 см, ВС = 16 см, AD = 9 см.
Звідси Р = 60 м, S = 150 см2.
Задача 2. У трапеції ABCD відомі основи AD = а, ВС = b і площа S трикутника ВОС (О — точка перетину діагоналей). Знайти площі трикутників ВОА і AOD.


Розділ 16. Площа трапеції
67
Рис. 2
Розв'язання
Позначимо шукані площі (рис. 2):
8 BO А = &DOC = ® AOD = ^*∙
Трикутники ВОС і AOD подібні:
Та2’ b2 ’
Далі Q+T = -h a (h — висота трапеції). 2
Q+S = -hb,
2
rp a2S отже, оскільки Т = ——, то b2
QfT = a o = ^(b∑^l = s- Q+S I) b(b-a) Ь
Рівновеликість — одна з наипопулярніших тем у геометрії. Чудово, що вона (тема) пов’язана з властивістю трапеції: площі трикутників АВО і COD рівні.
Рис. З
&АВС ~~ &DBC * & ABC & ВОС ~ ^DBC ^ВОС » отже, Sab0 =Socd.


68
/. Кушнір. Геометрія трапеції в задачах
Введемо новий термін: «рівноподільна»: пряма, що ділить площу фігури навпіл.
Розглянемо задачі із застосуванням властивості трапеції.
Задача 3. Три медіани трикутника ділять трикутник на шість рівновеликих (рис. 4),
Доведення
Оскільки Scmm = Smm b , то пара трикутників, що прилягають до однієї сторони, рівновеликі. Оскільки M2M3∖∖BC, то CM2M3B — трапеція і SCMiM =SMM}B.
Ріновеликість інших трикутників доводиться аналогічно.
Задача 4. Якщо в трикутнику ABC КР — рівноподільна і LN —
Доведення
Дійсно, розглянемо чотирикутник NPLK (рис. 5). Нехай NL і КР перетинаються в точці О. Оскільки КР і NL — рівноподільні, то 8 АКР = &ANL •


Розділ 16. Площа трапеції
69
Оскільки в трикутників ANL і АКРчотирикутник ANOP спільний, то Sonk = Sopl , а це означає, що KNPL — трапеція і KL∖∖NP, що й потрібно було довести.
Задача 5. У прямокутну трапецію вписано коло із центром О (BC∣∣ AD, BC<AD), Довести, що пряма OD — рівноподільна (ділить площу трапеції навпіл).
Доведення
Позначимо: F — точка перетину OD з АВ (рис, 6)∙f М, К, N, Е — точки дотику кола й сторін трапеції, Sκ — площа квадрата EON А, S1 — площа трикутника OND, Оскільки ΔEFO = АСОК (Z.ODN = ZFOE = ΛCOK∖ то Sefo = S2.
Маємо:
&AFD =⅜ +⅛ +⅜∙ (1)
Далі
^FBCD ~ К — 2SL 4" S, — Sn + Sκ + & . (2)
Порівнявши (1) і (2), доведемо потрібне.
Задача 6. Через точку О перетину діагоналей АС і BD трапеції ABCD проведено пряму, що паралельна основам і перетинає бічні сторони трапеції в точках М і N, Довести, що MO = ON,
Рис. 7


70
/. Кушнір. Геометрія трапеції в задачах
Доведення
Позначимо: MO = x9 NO = у, висоти трикутників АМО і BNO — відповідно ħ1 і h2 (рис. 7).
Тоді
&АВО = &COD ÷⅛)∙
Але S1 = S2.
Тому
∣x(Λ1 + h2) = →(Λ1 + Л2), х = у,
що й потрібно було довести.
Задача 7. Через точку на стороні трикутника провести пряму так, щоб вона поділила площу трикутника навпіл.
Рис. 8
Розв'язання
Нехай на стороні АС точка К — задана (рис. 8).
Необхідно на стороні ВС знайти таку точку X, щоб площі фігур КХС і КХВА були рівними між собою. Проведемо медіану AΛf1. Сполучимо точки M1 і К. Через точку А проведемо пряму, паралельну KM 1, яка перетинатиме сторону ВС у шуканій точці X.
Доведемо, що пряма КХ — шукана. Дійсно, чотирикутник AXM1К — трапеція. Отже, Sako =Sm ох. Але
Q — Q - 1 Q oAΛf1C - kjAMlB “2 abc'


Розділ 17. ОБЕРНЕНІ ЗАДАЧІ ПРО ТРАПЕЦІЮ
Задача 1. Якщо в чотирикутнику ABCD трикутники ABC і DBC рівновеликі, то цей чотирикутник — трапеція. Довести.
Доведення
Дійсно, оскільки площі трикутників рівні і в них спільна основа, то BC∣∣ AD.
Задача 2. Довести, що якщо в опуклому чотирикутнику ABCD (рис. 1)
y]^ABCD = >]&ВОС + λJ^AOD ’
то чотирикутник — трапеція.
Доведення
Позначимо площі (рис. 2).
Рис. 2
Маємо: Js = + (доведіть!) або S = S1 +S2 +2λ∕S1S2 . З ін¬
шого боку,
S = S1 ÷ S9 ÷ ∣SL ÷ Sλ . 1 і а 4


72
/. Кушнір. Геометрія трапеції в задачах
Звідси
⅜ + S4 “ 2λ∕S1S2.
(1)
Трикутники АБО і AOD мають спільну сторону, тому
52 DO
53 ~ OB'
m Sd DO S∙> Sλ „ „ „ „
Також — = , отже, — = —, S. ∙ S9 = S4 ∙ S4.
S1 OB s3 s1 1 2 3 4
Ураховуючи рівність (1), дістанемо:
S3 + *S∖
= 0.
Отже, S3 = S4, а це означає, що чотирикутник — трапеція.
Задача 3. Довести, що якщо середня лінія чотирикутника, яка відповідає одній парі протилежних сторін, дорівнює півсумі двох інших його сторін, то цей чотирикутник — трапеція (або — паралелограм).
Рис. З
(1)
Доведення
Припустимо, що чотирикутник ABCD — трапеція (рис. 3). Проведемо в ньому діагональ BD і середню лінію MN. Нехай точка Е — середина цієї діагоналі. За умовою
njrxτ AB + CD
MN = .
2
З трикутника ABD: ME = — АВ. З трикутника BDC:
2
EN = -DC.
2
З трикутника MEN:
HJTXT l∖jrrt ПАТ AB+CD - AB + CD
MN < ME + EN = або MN <
(2)
2
2


Розділ 17. Обернені задачі про трапецію
73
Порівнюючи вирази (1) і (2), доходимо протиріччя. Отже, чотирикутник ABCD — трапеція (або паралелограм).
Задача 4. Довести, що якщо пряма, яка проходить через середини двох протилежних сторін опуклого чотирикутника, проходить через точку перетину його діагоналей, то чотирикутник — трапеція (або паралелограм).
Доведення
Припустимо, що сторона DC не паралельна стороні АВ (рис. 4).
Нехай точки М і N — середини сторін АВ і CD відповідно, S — точка перетину діагоналей. За умовою точки М, N і S належать одній прямій. ПроведемоDCl || АВ (C1 є АС). Пряма MN перетне відрізок DCl у його середині, точці Р (оскільки
PD PS PC1 , АЛ/Г nnyr
= = L і AM = BMi MB SM AM
то DP = PC).
Отже, NP — середня лінія трикутника Z>CC1, тобто WP∣∣CC1, що неможливо (оскільки S ∈ NP, S ∈ CC1).
Задача 5. Якщо в чотирикутнику відрізок, кінці якого збігаються із серединами діагоналей, дорівнює піврізниці протилежних сторін, то цей чотирикутник — трапеція. Довести.
Рис. 5


74
/. Кушнір. Геомєтрія трапеції в задачах
Доведення
Позначимо в чотирикутнику ABCD (рис. 5) AB = α, CD = b; середини діагоналей АС і BD як E1 і Е2 відповідно.
За умовою
e1e2=^-,t1e1=^,t1e2=^
Сі и и
(точка T,1 — середина сторони ВС).
γ1e1-t1e2=^,
4U
отже, точка Е2 належить відрізку T∖E2. Отже, точки T1, E1, Е2 належать одній прямій. Але T1B21|DC, T1El || AB, DC∖∖ АВ, звідси, чотирикутник ABCD — трапеція.
Задача 6. Довести, що якщо в трапеції ABCD, де AD і ВС — основи (AD> ВС) AB + BD = AC+CD, то трапеція рівнобедрена.
Рис. 6
Доведення
Оскільки AB + BD - AC+CD, то периметр трикутника ABD (2р) дорівнює периметру трикутника ACD (2p1) (сторона AD у них спільна). Але трикутники ACD і ABD рівновеликі, а оскільки периметри в них рівні, то рівні радіуси вписаних кіл (точки I1 і І2 — їх центри) (рис. 6).
Позначимо Kl і К2 — точки дотику цих кіл до бічних сторін трапеції. Оскільки CK1 = p1- AD, a BK1 = p2- AD і p1 = р2, то CKγ = BK1, а отже, ZI1CK'1 = Z,I2BK1 або Z.ACD = Z.ABD, звідки очевидно, що трапеція рівнобедрена.
Задача 7. Якщо в трапеції ABCD периметр трикутника АВО дорівнює периметру трикутника COD (О — точка перетину діагоналей), то трапеція рівнобедрена. Довести. Доведення аналогічне попередній задачі, оскільки трикутники АВО і COD рівновеликі.


Розділ 17. Обернені задачі про трапецію
75
Задача 8 (!). Відрізок, що з’єднує середини сторін АВ і CD чотирикутника ABCD, ділиться діагоналями на три рівні частини. Довести, що ABCD — трапеція.
Рис. 7
Доведення
Лема. У трикутнику ABC медіана AM ділиться точкою Q навпіл. Пряма BQ перетинає сторону АС у точціD. Довести, що AD:DC = 1:2, a BQ: QD = 3.
Довести самостійно.
Розглянемо трикутник АВЕ (рис. 7). У ньому ЕМ — медіана, яка прямою AQ ділиться навпіл.
Тоді за лемою BO = 2t, ОЕ = t, ED = 3t.
Аналогічно, з трикутника COD: CO = 2p, QO = р, AO = Зр.
ВО СО 1
Звідси = = —, отже, трикутники ВОС і DO А гомотетичні
OD ОА 2
iBC∣∣AD.
Задача 9. У чотирикутнику ABCD T1T2 — середня лінія (рис. 8).
TlE = T2K.
Довести, що ABCD — трапеція.
Доведення
Нехай точки Р і L — середини діагоналей чотирикутника (рис. 8).
Трикутники Т\РЕ і T2LK рівні. ZT1EP= ZT2KL, тобто


76
/. Кушнір. Геометрія трапеції в задачах
ZAET2 = ZBKTl.
Розглянемо прямі АС і BD і січну T1T2.
Оскільки ZAET2 = ZBKTl, то AC∣∣BZ>, що неможливо, отже, Р ≡ К, К ≡ L, а це означає, що T1E і T2K - середні лінії трикутників ABC і BDC, тобто чотирикутник ABCD — трапеція.
Задача 10. Довести, що якщо тільки одна із середніх ліній чотирикутника ділить його площу навпіл, то чотирикутник — трапеція.
Доведення
Нехай точки М і N — середини основ чотирикутника. Оскільки площі трикутників BNM і CMN рівні, то рівні й площі трикутників ABN і CND. Оскільки AN = ND, то висоти цих трикутників рівні, а отже, BC∣∣AD.
Задачі для самостійного доведення
Задача. Нехай точка М1 — середина основи AD трапеції ABCD. Довести, що якщо AB + ВМ1 = CD +CM1, то трапеція рівнобедрена.
Задача. Нехай точки E1 і Е2 — середини сторін АВ і CD трапеції ABCD. Якщо периметри трикутників AExD і AE2E рівні, то трапеція ABCD — рівнобедрена. Довести.


Розділ 18. ЗАДАЧІ НА ПОБУДОВУ
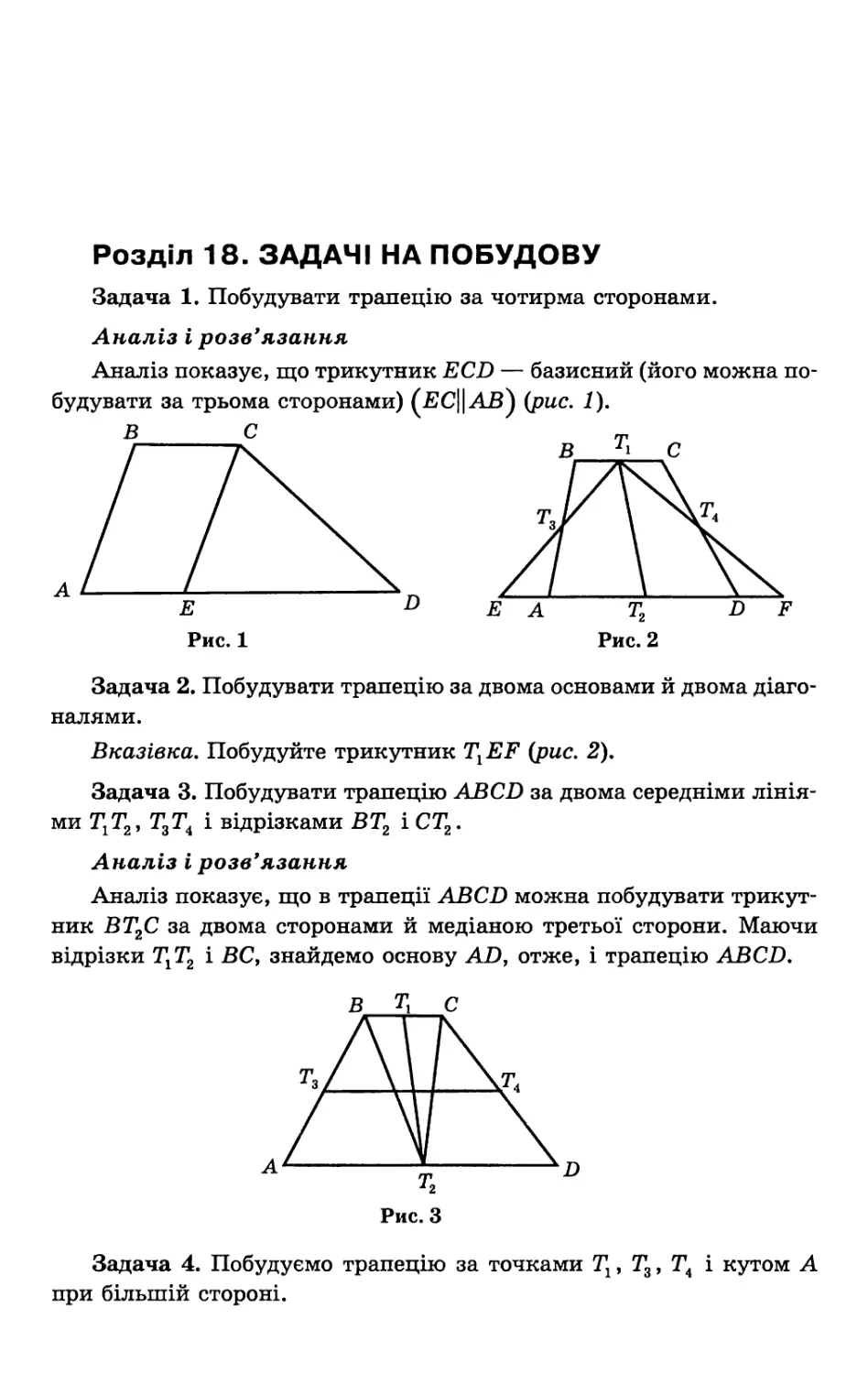
Задача 1. Побудувати трапецію за чотирма сторонами.
Аналіз і розв'язання
Аналіз показує, що трикутник ECD — базисний (його можна побудувати за трьома сторонами) (EC∣∣ АВ) (рис. 1).
Рис. 1 Рис. 2
Задача 2. Побудувати трапецію за двома основами й двома діагоналями.
Вказівка. Побудуйте трикутник TlEF (рис. 2).
Задача 3. Побудувати трапецію ABCD за двома середніми лініями T1T2, T3T4 і відрізками BT2 і CT2.
Аналіз і розв'язання
Аналіз показує, що в трапеції ABCD можна побудувати трикутник BT2C за двома сторонами й медіаною третьої сторони. Маючи відрізки T1T2 і ВС, знайдемо основу AD, отже, і трапецію ABCD.
Рис. З
Задача 4. Побудуємо трапецію за точками T1, T3, Т4 і кутом А при більшій стороні.


І. Кушнір. Γеометрія трапеції в задачах
78
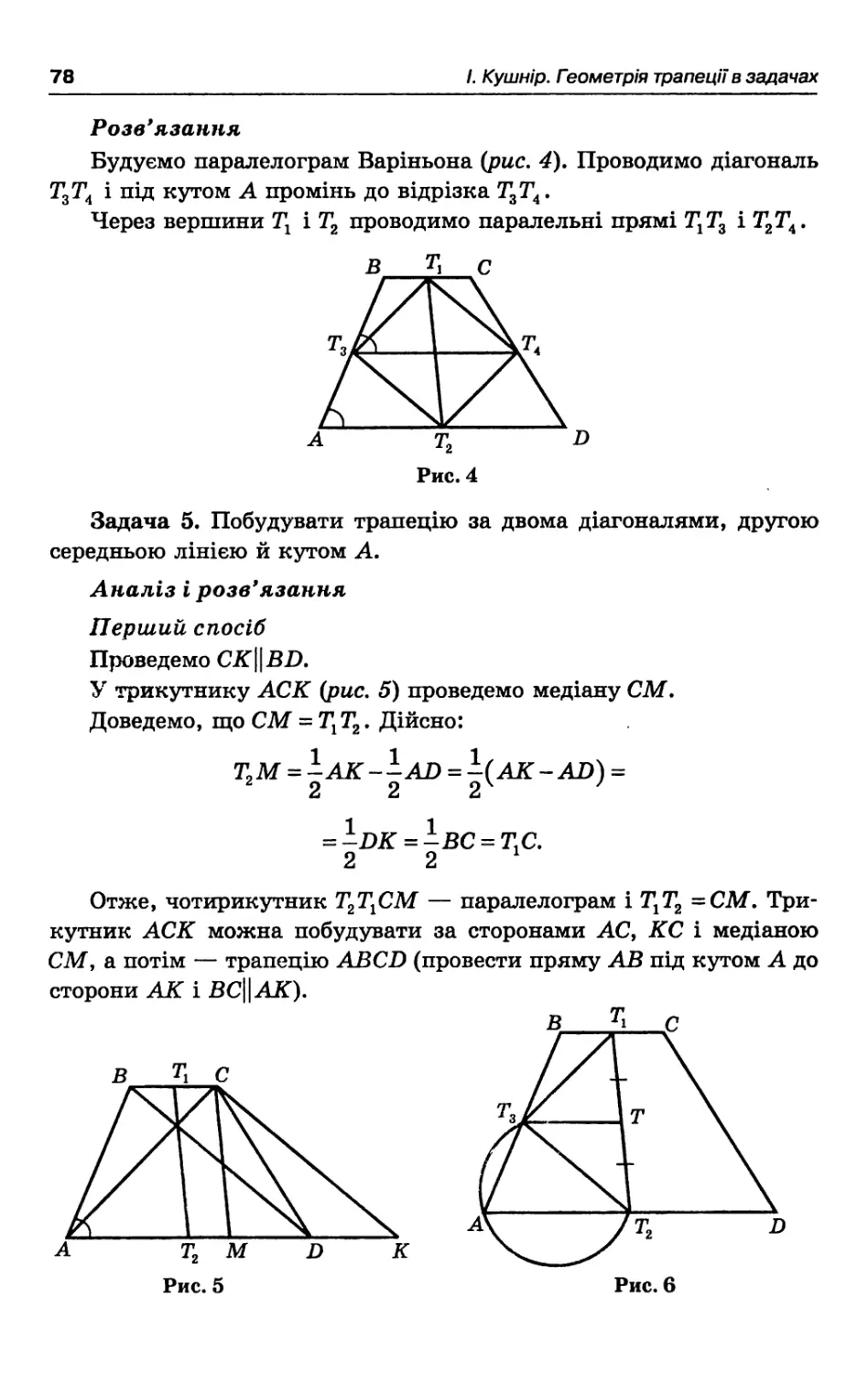
Розв'язання
Будуємо паралелограм Варіньона (рис. 4). Проводимо діагональ T3T4 і під кутом А промінь до відрізка T3T,4.
Через вершини 7,1 і Т2 проводимо паралельні прямі T1T3 і T2T4.
Рис. 4
Задача 5. Побудувати трапецію за двома діагоналями, другою середньою лінією й кутом А.
Аналіз і розв'язання
Перший спосіб
Проведемо СК11BD.
У трикутнику АСК (рис. 5) проведемо медіану CM.
Доведемо, що CM = T1T2. Дійсно:
T2M = -AK--AD = -(AK-AD) = 2 2 2
= -DK = -BC = T.C.
2 2 1
Отже, чотирикутник T2TlCM — паралелограм і T1T2 =СМ. Трикутник АСК можна побудувати за сторонами АС, КС і медіаною CM, а потім — трапецію ABCD (провести пряму АВ під кутом А до сторони АК і BC∣∣ АК*).


Розділ 18. Задачі на побудову
79
Другий спосіб
Побудуємо трикутник T1T2T3 (рис. 6). У ньому проведемо медіану T3T і через точки T1 і Т2 паралельні відрізку T3T прямі. На відрізку T2T3 будуємо сегмент, що містить кут А. Дістанемо вершину А.
Третій спосіб — скористатися трикутником TxEF.
Задача 6. Побудувати трапецію за двома основами, кутом між діагоналями і висотою.
Аналіз і розв'язання
Проведемо CjE∣∣ BD (рис. 7). Трикутник АСЕ можна побудувати за допомогою сегмента, що містить кут між діагоналями.
В С А (А')В
А Н D Е D М С'С
Рис. 7 Рис. 8
Задача 7. Побудувати трапецію ABCD (AB∣∣CZ)) за прямими ВС і AD, серединою діагоналі АС і точкою М на прямій CD.
Розв'язання
Позначимо точку О — середину відрізка АС (рис. 1). Пряма A'C,, симетрична ВС відносно точки О, в перетині з прямої AD визначить точку Р, відповідну вершині А шуканої трапеції. Після цього, провівши пряму АО, знайдемо вершину С і пряму МС, що дає вершину D і, нарешті, AB∣∣C7λ
Задача 8 (авторська). Дано трикутник ABC і довільну пряму І, що перетинає сторону ВС у точці X. Знайти на І таку точку У, щоб трикутник ABC був рівновеликим чотирикутнику ACXY.
Розв'язання
Проведемо відрізок АХ (рис. 9), а через точку В пряму, паралельну АХ, яка перетне пряму І у шуканій точці У. Справді, чотирикутник ABXY — трапеція, Sδfv = Sκ,nγ.
Задача 9. Менша основа трапеції DC = &; більша основа АВ = а. На продовженні меншої основи знайти точку X за умови, що пряма АХ поділила трапецію на дві рівновеликі частини.


80
І. Кушнір. Γеометрія трапеції в задачах
Розв'язання
Нехай СХ = t (рис. 3), висоти трикутників АВЕ і СХЕ відповідно
Λ1 і h2.
За умовою
-ahl = -(a+b}(hx + h2) або -^*- = = 1 + —.
2 2 a+b hl h2
х h.
Але з подібних трикутників АВЕ і ХСЕ маємо: — = —. Звідси
α h2
2а л х х а-Ь а-Ь
= 1+—, — = , х = а . а+& а а а+Ь а+Ь


Книжкові додатки не є дайджестом статей.
Актуальна тематика, інноваційні методики, високий індекс практичності. Сучасні книги для вчителя від найбільшого виробника методичної літератури в Україні.
Бібліотека журналу «Математика в школах України
У вартість передплати на місяць входить: З випуски журналу + книжковий додаток!
ISBN 978-611-00-0367-4
Оформити передплату на журнал «Математика в школах України» з книжковим додатком можна з кожного наступного місяця у будь-якому відділенні зв'язку України.
01651
передплачуйте
ЗАВЧАСНО!
з
ПЕРЕДПЛАТНИЙ
ІНДЕКС
9 "786110 003674