⅛ БІБЛІОТЕКА ЖУРНАЛУ
«МАТЕМАТИКА В ШКОЛАХ УКРАЇНИ»
Випуск 11 (131)
L А. КУШНІР
зззззш/ ЗЩМ/
Харків Видавнича група «Основа» 2013


УДК 514
ББК 22.151
К96
Кушнір І. Д.
К96 Позиційні задачі на побудову. — X. : Вид. група «Основа», 2013. — 62, [2] с. (Б-ка жури. «Математика в школах України»; Вип. 11 (131)).
ISBN 978-617-00-1945-5.
Книгу відомого автора, заслуженого вчителя України І. А. Кушніра присвячено позиційним задачам на побудову. Актуальність видання полягає в тому, що вперше тут зроблено спробу розглянути Позиційні задачі, чимало з яких підвищеної складності, та об’єднати їх в одну книгу.
Учителям математики, учням 8-11 класів загальноосвітніх закладів. Книга також стане у пригоді учням, які беруть участь у математичних олімпіадах.
УДК 514
ББК 22.151
ISBN 978-617-00-1945-5
© Кушнір І. А., 2013
© ТОВ «Видавнича група “Основа”», 2013


ЗМІСТ
Передмова 4
Розділ 1. Три позиційні точки 5
Розділ 2. Позиційні прямі 20
Розділ 3. Позиційні задачі з кутом 34
Розділ 4. Позиційні задачі. Багатоспосібність 38
Розділ 5. Пам’яті Л. М. Лоповка 55
Розділ 6. Позиційні задачі на українській математичній олімпіаді 59


ПЕРЕДМОВА
Задачам на побудову за допомогою циркуля і лінійки стільки років, скільки самій геометрії, тобто понад двадцять століть. На мою думку, емоційно вони такі заразливі, що не залишають байдужими тих, хто хоч трохи знайомий з геометрією.
1866 року в Копенгагені вийшла книга Юлія Петерсона «Методи і теорія для розв’язування геометричних задач на побудову».
У передмові автор писав: «Дехто вважає розв’язування геометричних задач на побудову певною мірою загадками, впоратися з якими вдається тільки одинакам, особливо обдарованим від природи. Через такі погляди геометричні задачі на побудову увійшли лише частково до системи шкільної освіти, тоді як саме в школі їх постійне місце, бо жодні інші задачі не сприяють так розвитку в учнів спостережливості, правильності мислення, водночас залишаючись особливо привабливими, як геометричні задачі на побудову»*.
Позиційні задачі відрізняються умовою від загальноприйнятих задач на побудову. Умова таких задач може містити лише точки або точки і відрізки; кути, точки, прямі (а не відрізки). Наприклад, пряма, якій належить відрізок ВС, позначається ax, ha — пряма, якій належить висота ha, тощо.
Такі задачі збагачують традиційну колекцію задач, їх значно менше, ніж у наявних задачниках, а окремо виданими можна назвати книгу В. А. Вишенського і В. І. Сущанського «Дано тільки точки» (Київ, Головне видавництво об’єднання «Вища школа», 1989). Ми зробили спробу розглянути задачі, які значно відрізняються від наведених у згаданій книзі, у чому читач зможе переконатися сам.
Здійснено боязку спробу об’єднати в одному виданні позиційні підсильні задачі, чимало з яких підвищеної складності. Усі задачі наведені з розв’язанням. Книга чекає продовження. У дорогу!
Автор
Цитируется по книге Петерсон Ю. «Методы и теоремы для решения геометрических задач на построение». К., Радянська школа, 1940.


РОЗДІЛ 1.ТРИ ПОЗИЦІЙНІ точки
ЗАДАЧА 1
А, І, О (І —інцентр, О —центр описаного кола).
Розв'язання
Аналіз показує, що, маючи точки Oil, можна побудувати відрізок 01 і застосувати теорему Леонарда Ейлера: ,
OI2=R2-2Rr. (1)
Маючи точки О і А (рис. 1.1), дістанемо радіус ОА, отже, з формули (1), відрізок г. І задача зводиться до задачі: R, г, А.
Рис. 1.1


6
Позиційні задачі на побудову
ЗАДАЧА 2
M1, О, Н.
Розв'язання
Скористаємося прямою Ейлера — побудуємо точку М (рис. 1.2): ОМ :МН = 1:2.
Маючи точку М і точку Н, побудуємо вершину А, отже, можна провести коло, пряму АН, на яку опустити перпендикуляр M1H1 і продовжити пряму M1Hγ до перетину з колом у точках В і С.


Розділ 1. Три позиційні точки
7
ЗАДАЧА З
Побудувати гострокутний трикутник за проекціями його вершин на протилежні сторони.
Розв'язання
Задачу можна сформулювати в інший спосіб: H1, H2, Н3 (основи висот) (рис. 1.3).
В
Рис. 1.3
Трикутник H1H2H3 — ортоцентричний, у ньому ортоцентр трикутника ABC буде інцентром. Задача ідентична до задачі Wl, W2, W3.


ЗАДАЧА4
M1, Д, I.
Розв'язання
Через точки M1, L1 (рис. 1.4) проводимо пряму M1L1. Чёрез точку M1 проведемо перпендикуляр, який перетне пряму ILl у точці Wi. Трикутник WlM1Ll —базисний.
Рис. 1.4
Застосуємо теорему трилисника: IWl = W1C = W1B. Коло з центром W1 і радіусом IW1 перетне пряму M1L1 уточках В і С.


Розділ 1. Три позиційні точки
ЗАДАЧА 5
W1, W2, W3 (W. — точки перетину бісектрис внутрішніх кутів трикутника ABC з описаним колом).
Розв'язання
Оскільки інцентр І трикутника ABC буде ортоцентром трикутника W1W2W3, то для того щоб дістати вершини А, В і С, потрібно провести висоти трикутника W1W2W3 (Puc∙ 1∙5)∙
Рис. 1.5


10
Позиційні задачі на побудову
ЗАДАЧА6
Λf1, Kl, M2 (M1, М2 —середини сторін BC9 AC; K1 —точка дотику вписаного кола до сторони ВС).
Розв'язання
Нехай а, Ь, с —довжини сторін трикутника ABC (рис. 1.6).
Оскільки K.C^z~~~~—то М.К. =———. Але M.M9 =—, отже, 1 2 1 1 2 1 2 2
можна знайти сторону Ь. Таким чином, через точки M1 і K1 (рис. 1.6) проводимо пряму. Оскільки M1C = ^, то можна побудувати трикутник M1M2C, отже, і трикутник ABC.
Рис. 1.6


Розділ 1. Три позиційні точки
11
ЗАДАЧА 7
А, Н, Ll.
Розв'язання
Побудувавши пряму АН (рис. 1.7), з точки L1 опустимо на неї перпендикуляр LlH1.
Пряма ВС, проведена через точки Ll і Hl, буде віссю симетрії точок Nli Н, причому точка N1 належатиме колу, описаному навколо трикутника ABC. Трикутник ALlH1 — базисний, з якого дістанемо кут L1AH1, а отже, і рівний йому кут OALl. Стороні АО цього кута належатиме діаметр кола, описаного навколо трикутника ABC. Відновивши із середини відрізка ANl точки F перпендикуляр, матимемо точку О.
Рис. 1.7


Позиційні задачі на побудову
ЗАДАЧА 8
H1,H2,H3
« Ml,M2,M3
E1,E2,E3
Hi — основи висот; М. — основи медіан; Ei — точки Ейлера, середини відрізків АЛ, ВН, СН.
Вказівка
Застосувати коло Ейлера.


Розділ 1. Три позиційні точки
13
ЗАДАЧА 9
A, H3, L2.
Розв'язання
Маючи точку Н3 — основу висоти з вершини С, L2 — основу бісектриси з вершини В, а також вершину А, можна побудувати прямі bx і сх — сторони кута А (рис. 1.8).
Рис. 1.8
Якщо відновити перпендикуляр у точці Н3, то він перетне пряму bx У точці С.
Оскільки
AL2:CL2=AB:BC,
то точка В належить геометричному місцю точок (ГМТ), відношення відстаней яких до двох точок задане. Це ГМТ називають колом Аполлонія, яке будуємо для точок А і С, і з точки А проводимо пряму AH3, яка перетне це коло в точці В.


14
Позиційні задачі на побудову
ЗАДАЧА 10
Д, Д А-
Розв'язання
Побудуємо трикутник LlIL2, дістанемо кут
Отже, дістанемо кут АСВ, що дорівнює куту С (рис. 1.9).
Позначимо середину дуги L1L2 (що не містить вершину С) літерою D. Через точки D і І проводимо пряму, яка перетне коло в точці С. Перетин прямих CL1 і L2I дасть точку В, CL2 і L1I — точку А.


Розділ 1. Три позиційні точки
15
ЗАДАЧА 11
О, Λf1, Н3.
Розв'язання
Будуємо пряму ВС, перпендикулярну до відрізка OM1 (рис. 1.10).
У прямокутному трикутнику CH3B є медіана MvH2, а отже, і відрізок ВС. Будуємо коло радіуса OB = OC і, провівши пряму BHv дістанемо вершину А.


16
Позиційні задачі на побудову
ЗАДАЧА 12
Побудувати прямокутний трикутник ABC (ZC = 90°) за точками M3, L3, Н3.
Розв'язання
Опустимо перпендикуляр L3K з точки L3 (рис. 1.11) на медіану CM3.
Відомо, що ZL3CK = ZL3CH3, а отже, трикутники CKL3 і CH3L3 рівні (за гіпотенузою і гострим кутом). Тоді L3K = L3H3. Звідси побудова: проводимо пряму M3H3, яка збігається з гіпотенузою ВС. З точки Н3 відновимо перпендикуляр (рис. 1.12).
Будуємо коло γ з центром у точці L3 радіусом L3H3.
З точки М3 проводимо дотичну до γ, дістанемо точку К, а отже, і точку С.


Розділ 1. Три позиційні точки 17
ЗАДАЧА 13
(Олімпіада/. Ф.Шаригіна). I, H1, Іа.
Іа —центр зовнівписаного кола, дотичного до сторони ВС.
Розв'язання
Для тих, хто знає теорему Мансіона
JW1=W'1∕fl,
умову задачі можна записати як I, Wl, Hl, і тоді застосувати «новинку»
QH1=rz
тут W1 — точка перетину бісектриси кута ВАС з описаним колом, Q —точка перетину прямої WlK1 і висоти AH1, Kl —точка дотику вписаного кола до сторони ВС (рис. 1.13).


18
Позиційні задачі на побудову
Оскільки IQH1Kl — прямокутник
(LK1=QH1=r, IKl∖∖QHl),
то W1K1 перетинає IH1 у точці V — середині відрізка IH1.
Перейдемо до побудови. Будуємо точку V — середину відрізка IH1. Коло γ, побудоване на відрізку IHl як на діаметрі, містить точку K1, Тому перетин прямої W1V з цим колом дасть точку Kl.
Проведемо пряму через точки K1 і Hv Цій прямій належать точки В і С, які тепер нескладно дістати, застосувавши «теорему трилисника». Із цих точок до кола з центром І і радіусом IKl проведемо дотичні, які перетнуться у точці А.


Розділ 1. Три позиційні точки
19
ЗАДАЧА 14
Побудувати трикутник за вершиною А і точками N2 і N3 перетину висот hb і hc з описаним навколо трикутника ABC колом.
Розв'язання
Ортоцентричний трикутник HlH2H3 гомотетичний трикутнику N1N2N3 (рис. 1.14), оскільки HH1 =H1N1.
Отже, точка А — середина дуги N2N3.


РОЗДІЛ 2. ПОЗИЦІЙНІ ПРЯМІ
задача і αx, H2, Н3.
Розв'язання
Аналіз показує, що чотирикутник CH2H3B вписаний у коло з діаметром ВС. Через середину відрізка H2H3 проведемо перпендикуляр, який перетне пряму ах у точці Q (рис, 2,1).
Радіусом QH2 = QH3 проводимо коло, яке перетне пряму ах уточках В і С.
Рис. 2.1


Розділ 2. Позиційні прямі
21
ЗАДАЧА 2
ax, M3, Н.
Розв'язання
Напряму ВС з точки Н опускаємо перпендикуляр, дістанемо точку H1 (рис. 2.2).
Оскільки AB = 2HlM,3, то дістанемо точки А і В. Через точку Н проведемо перпендикуляр HH3 до прямої АВ і, продовжуючи його до перетину з ах, дістанемо точку С.


22
Позиційні задачі на побудову
ЗАДАЧА З
Я,, H,, h .
Розв'язання
Розглянемо ортоцентричний трикутник H1H2H2 (рис. 2.3).
Оскільки пряма ha — бісектриса кута H2H1H3, то середина дуги H2H3 кола, описаного навколо ортоцентричного трикутника (точка E1), також належить прямій ha .
Провівши перпендикуляр через середину відрізка H2H3, дістанемо точку E1, і навколо трикутника H2E1H2 побудуємо коло, яке перетне пряму ha у точці H1.


Розділ 2. Позиційні прямі
23
ЗАДАЧА4
Побудувати прямокутний трикутник ABC (ZC = 90°) за M1, М2 і сх.
Розв'язання
Через точки Ml і М2 проведемо пряму і на відрізку MlM2, як на діаметрі, побудуємо коло γ (рис. 2.4).
Рис. 2.4
На прямій сх позначимо довільну точку X, сполучимо її з M1 і на прямій XM1 відкладемо відрізок X'M1, що дорівнює XM1. Через точку X' проведемо пряму t, паралельну прямій сх, яка перетне коло γ в точках С і C1. Трикутники СВА і ClBA шукані.


24
Позиційні задачі на побудову
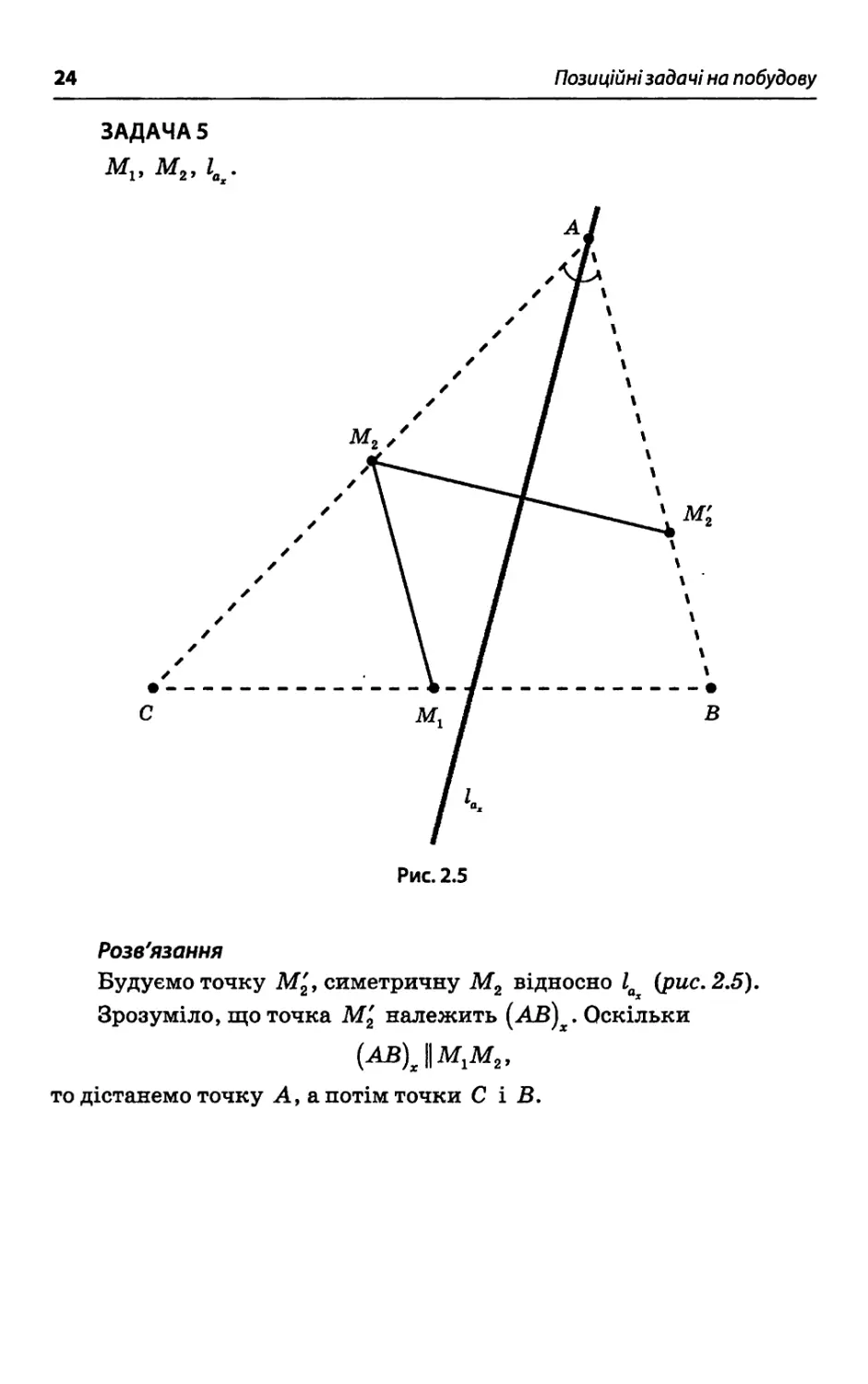
ЗАДАЧА5
to •
Розв'язання
Будуємо точку M2', симетричну М2 відносно la (рис. 2.5).
Зрозуміло, що точка M'2 належить (АВ) . Оскільки
(ab)x∖∖m1m2,
то дістанемо точку А, а потім точки С і В.


Розділ 2. Позиційні прямі
25
ЗАДАЧАб aχ9 О, М.
Розв'язання
Застосування прямої Ейлера дозволяє знайти точку Н (рис. 2.6). Потім можна дістати точки Ml і Hl. Провівши MM1 і HHγ, матимемо точку А.
Рис. 2.6
Маючи центр О, радіус ОА, дістанемо вершини В і С.


26
Позиційні задачі на побудову
ЗАДАЧА 7 (!)
Λflχ,M1,1.
Розв'язання
Застосуємо теорему про пряму MlI9 що відтинає на висоті AH1 відрізок AF = r (рис. 2.7).
З точки M1 на пряму ha опускаємо перпендикуляр, будуємо IKl. Зрозуміло, що
IK1=r.
Проводимо пряму M1I, дістаємо точки F і А. Будуємо коло (/; г).
З точки А проводимо дотичні, дістаємо точки В і С.


Розділ 2. Позиційні прямі 27
ЗАДАЧА 8
Побудувати трикутник за точками перетину продовжень ha, la, πιa з описаним навколо трикутника ABC колом.
Розв'язання
Нехай точки перетину— N1, Wl, Мо (рис. 2.8).
Оскільки коло задане, то його діаметр DW1 паралельний прямій AN1. Дістали точку А. Перетин діаметра WlD з хордою M0A дає середину Λf1 відрізка ВС, а отже, точки В і С.
Рис. 2.8


28
Позиційні задачі на побудову
ЗАДАЧА9
ax, М, Li.
Розв'язання
Якщо з центроїда М опустити перпендикуляр MDi на пряму ах, то можна знайти довжину висоти AHl (рис. 2.9):
ha=2MD1.
Напряму ах опустимо перпендикуляр L2F1. Доведемо, що
Рис. 2.9
L2F1=x.
Дійсно, позначимо
Маємо
х _CL2 ⅛ ^ АС
або


Розділ 2. Позиційні прямі
29
звідки
х AC-CL2 h ~ АС с
CL2 + АС — CL2
АС ~
hahc ha+flc'
Оскільки х і ha задані, то дістали довжину відрізка hc. Отже, маємо й довжину відрізка MD2 (MD2 ± bx). Тепер можна побудувати два кола γ1(L2,L2F1), γ2(M,MD2) і провести до них спільну дотичну сх, яка перетне ах у точці В.


зо
Позиційні задачі на побудову
ЗАДАЧА 10
αx, M2, Н3.
Розв'язання
З точки М2 опускаємо перпендикуляр на пряму ах (рис. 2.10).
Рис. 2.10
На відстані
2M2P = ha z а
проводимо пряму І, паралельну ах. Оскільки трикутник AHzC.
прямокутний, то
M2Hz=AM2=CM2,
і точка А — перетин кола радіуса M2Hz з центром М2 з прямою І.


Розділ 2. Позиційні прямі
31
ЗАДАЧА 11
ax, Н, W1.
Розв'язання
Розв’язання задачі базується на властивостях симетричних точок: ортоцентра відносно ах (точка N) і, знову ж таки, ортоцентра відносно M1 (рис. 2.11).
Рис. 2.11
Оскільки точки W1,N,D належать описаному колу, то можна знайти точки В, С, А.


32
Позиційні задачі на побудову
ЗАДАЧА 12 αx, M2, Н.
Розв'язання
Будуємо точку N, симетричну точці Н відносно ах (рис. 2.12).
З точки М2 опустимо перпендикуляр M2P на пряму a,x. Оскільки
МР = l,
2
Перетином серединних перпендикулярів до хорд AN і АВ дістанемо центр О, отже, і трикутник ABC.


Розділ 2. Позиційні прямі
33
ЗАДАЧА 13
aχ9 M2, Е2. Е2 —точка Ейлера, середина відрізка ВН.
Розв'язання
Маючи діаметр кола Ейлера M2E2, знайдемо центр Е' цього кола. Спроектуємо точку М2 на пряму αx, дістанемо точку Р
(рис. 2.13) і
, , _ h M2P = -±.
2 2
Рис. 2.13
Можна знайти вершину А, дістати точки В і С.


РОЗДІЛ 3. ПОЗИЦІЙНІ ЗАДАЧІ З КУТОМ
задача і
На площині розташований деякий гострий кут А і довільна пряма. Побудувати трикутник так, щоб заданий кут був кутом трикутника, а задана пряма — прямою Ейлера.
Аналіз
Нехай пряма Ейлера перетинає пряму AW1 у точці L (рис. 3.1).
W1
Рис. 3.1


Розділ 3. Позиційні задачі з кутом
35
Позначимо відрізок AL як І. Оскільки ΔALH ~ΔWlLO, то AHr AL OW1 ~W1L 2BcosA I  - , ЗВІДКИ R W1L I
Враховуючи, що AH = 2RcosA, то
W.L = ,
2cosA
отже, W1L можна побудувати.
Побудова. Проведемо бісектрису кута А, яка перетне пряму Ей- лера у точці L. Дістанемо відрізок AL = І. Побудуємо відрізок LW1, отже, і хорду AW1. Оскільки прямій Ейлера належить центр О, то, відновивши перпендикуляр t до середини хорди AW1, дістанемо точку О, а отже, і трикутник ABC.


36
Позиційні задачі на побудову
ЗАДАЧА 2
ZA, (M1l)χ.
Розв'язання
Скористаємося відомим фактом: пряма M1I відтинає від висоти AH1 відрізок AF, що дорівнює г (рис. 3.2).
Провівши бісектрису кута ВАС, знайдемо інцентр І, а отже, і радіус г вписаного в трикутник ABC кола.
Точка F належить прямій MlI і колу з центром у точці А радіуса г. Маючи напрям висоти AHl, інцентр І і радіус г, побудуємо дотичну до вписаного в трикутник кола, перпендикулярну до AH1, і продовжимо її до перетину зі сторонами кута А.


Розділ 3. Позиційні задачі з кутом
37
ЗАДАЧА З
ZA, I, (Ol)χ.
Розв'язання
Оскільки пряма ОІ є прямою Ейлера трикутника K1K2K3, а інцентр І — центр кола, описаного навколо трикутника KlK2K3, то розглядувана задача звелася до такої: побудувати трикутник за прямою Ейлера, центром О описаного кола і стороною (побудова трикутника K1K2K3 «автоматично» дає побудову трикутника ABC) (рис. 3.3).
Отже, нехай задана сторона ВС. Величина AH = 2OM1 — відома. Відкладемо на прямій OM1 відрізок AH = 2OMl. Побудуємо пряму Z1, що проходить через точку A1 паралельно прямій І. Оскільки радіус R відомий (ОВ = ОС = R), то знайдемо вершину А (A = llr∖OA).


РОЗДІЛ 4. ПОЗИЦІЙНІ ЗАДАЧІ. БАГАТОСПОСІБНІСТЬ
ЗАДАЧА 1
Дано кут А трикутника ABC, точки L2, L3 (основи бісектрис кутів В і С).
Розв'язання
1-й спосіб
Проведемо аналіз задачі. З точки L2 (рис. 4.1) проведемо перпендикуляри L2F1 і L2F2.
Рис. 4.1


Розділ 4. Позиційні задачі. Багатоспосібність
39
Оскільки L2F1 = L2F2, то на стороні АС поданого кута А побудуємо коло з центром у точці L2 і радіусом L2F2. Аналогічно — друге коло с центром у точці L3. Потім до цих кіл проводимо спільну дотичну, яка перетне сторони кута в точках В і С.
2-й спосіб
У трикутнику ABC
ZBIC = 90o + -.
2
Отже, на відрізку L2L3 будуємо сегмент, що містить кут
90° + —
2
(рис. 4.2).
Потім проводимо бісектрису кута L2AL3, дістанемо точку І. Через точки L2 і і проводимо пряму, маємо точку В. Аналогічно — точку С.


40
Позиційні задачі на побудову
ЗАДАЧА 2 (ЖУРНАЛ «КВАНТ»)
Прямі AH1 і BH2, точка О.
Розв'язання
1-й спосіб
Пряма OMl (рис, 4.3) паралельна висоті AHl, а тому вона може бути побудована.
Якщо пряму BH2 відобразити симетрично відносно OM1,toπ,h пряма пройде через точку С. Аналогічно, пряма, симетрична AH1 відносно OM2, пройде також через точку С. Через точку С проводимо перпендикуляр до AHl до перетину з прямою BH2 у точці В. Аналогічно будуємо точку А.
2-й спосіб
Аналіз показує, що кут між прямими ha і hb дорівнює Z.C (рис. 4.4).
Нехай точка Н — ортоцентр трикутника ABC. Тоді


Розділ 4. Позиційні задачі. Багатоспосібність
41
ЛАТІВ = 180o-ЛС, ΛAOB = 2ΛC,
ЛАОВ = 2(180o - ЛАН В) — відомий. z
За повороту з центром О на кут АОВ точка А перейде в точку В (поворот прямої AH1). Тому повернемо пряму ha на кут
2(180° -ЛАНС)
навколо точки О і в перетину з прямою hb дістанемо точку В. Аналогічно дістанемо точку А. З точки В опустимо перпендикуляр BH2 — перетин перпендикулярів у точці С дозволяє побудувати трикутник ABC.


42
Позиційні задачі на побудову
ЗАДАЧА 3 (!)
А, I, M1.
Розв'язання
1-й спосіб
Застосуємо теорему про відрізок АР (рис. 4.5), що дорівнює г (радіус вписаного кола), який відтинається на висоті AH1 прямою MJ.
Рис. 4.5
Аналіз показує, що якщо через точку А провести пряму, паралельну M1P, і на ній відкласти відрізок AN, що дорівнює M1I, то ΔAAP = ΔM1∕7f1
(AN = M1I, AP = IK1=r, ZNAP = ZMlPHi= ZM1IK1), отже, ZNPA = 90°.
Перейдемо до побудови. Побудуємо точку M1. Проведемо пряму M1I і пряму І через точку А паралельно M1I. На прямій І відкладемо відрізок


Розділ 4. Позиційні задачі. Багатоспосібність
43
AN = M1I
і побудуємо на ньому як на діаметрі коло, яке перетне пряму M1I у точці Р. Маючи відрізок AP = г, побудуємо коло, вписане в трикутник ABC, і дістанемо прямі АВ і АС. Потім будуємо пряму ha і з точки M1 опустимо на неї перпендикуляр, який перетне сторони кута А в точках В і С.
2-й спосіб
Точку Λf1, середину ВС, можна побудувати (рис. 4.6).
Нехай точка D діаметрально протилежна точці Kl, точці дотику вписаного кола. Нехай пряма AD перетинає ВС у точці T1, B1C1 — дотична до вписаного кола, що проходить через точку D.
Оскільки трикутники ABlC1 і ABC гомотетичні, точки D і Tλ відповідно гомотетичні, отже, T1 — точка дотику сторони ВС і зо- внівписаного кола трикутника ABC. Тоді
CTl=p-b = BK1
(р — півпериметр трикутника ABC).


44 Позиційні задачі на побудову
Отже,
MlTl = M1C1 - CT1 = M1B - BK1 = K1M1.
Отже,
T1Ml = K1M1.
Але DI = IK (радіуси), IM1 — середня лінія трикутника TvDKλ і IMl∖∖DTl.
Проведемо M1W∣∣∕A'1. Очевидно, що ΛΠ∣∣T1.K1, WM1∣∣LK1, а отже,
AINMγ =^IK1Tl =90°,
тобто точку N можна дістати як перетин прямої A771 і кола з діаметром IMλ.


Розділ 4. Позиційні задачі. Багатоспосібність
45
ЗАДАЧА4
Відновити паралелограм ABCD за променями AB, AD і точкою О — центром кола, описаного навколо трикутника BCD.
Розв'язання
1-й спосіб — Поворот
Аналіз. ZBOD = 2ZBCD = 2ZA — відомий (рис. 4.7).
За повороту навколо точки О на кут 2ZA проти руху годинникової стрілки точка В переходить у точку D.
Точки В у нас немає, але ми можемо повернути пряму АВ.
Побудова (рис. 4.8).
Рис. 4.8


46
Позиційні задачі на побудову
1. Повернемо AM навколо точки О проти руху годинникової стрілки на кут 2ZA. Дістанемо пряму А'М', яка перетне пряму AN у точці D (див. аналіз).
2. Точку В дістанемо аналогічно.
3. Побудова точки С є очевидною.
2-й спосіб — Симетрія
Аналіз
Проведемо OM1 —серединний перпендикуляр до ВС, OM1-LAD', OM2 — серединний перпендикуляр до CD, OM2 А_АВ (рис. 4.9).
За симетрії відносно OM1 пряма АВ перейде в пряму, що проходить через точку С. За симетрії відносно OM2 пряма AD перейде в пряму, що проходить через точку С.
Побудова (рис. 4.9)
1. Нехай A1P — пряма, симетрична прямій АР відносно OM2.
3. Аналогічно будуємо пряму SA2, симетричну АВ відносно OMl.
4. SA2r∖AxP = C.
5. Проводимо через точку С паралелі до поданих променів, дістанемо сторони паралелограма, яких бракує.


Розділ 4. Позиційні задачі. Багатоспосібність
47
ЗАДАЧА5
в, с, (κ2κ3)x.
Аналіз базується на теоремі, яку назвемо теоремою А.
Теорема А. Нехай бісектриса кута В перетинає відрізок K2K3 у точці Т.Тоді ZBTC дорівнює 90°.
Доведення
Доведемо, що навколо чотирикутника CTK2I можна описати коло (рис. 4.10).
Дійсно,
ЛСІТ = 180° - ЛСІВ = 180° -1 90° + — | = 90° -—.
І 2 ) 2
ΛCK2T = ΛAK2K3 = 180° ~za = 9о° _ ≤Δ = хсіТ.
2 2 3 2 2
Отже, навколо чотирикутника CTK2I можна описати коло і ZCTI = 90°.
Перейдемо до побудови (рис. 4.11).
На відрізку ВС як на діаметрі побудуємо коло. Дістанемо точки Т і N. Кут СТВ дорівнює 90° і за теоремою пряма ВТ — бісектриса трикутника ABC. Аналогічно CN — бісектриса кута С. Подальше є очевидним.


48
Позиційні задачі на побудову
А тепер про багато способів. Доведемо теорему А другим способом.
Нехай бісектриса кута В перетинає K2K3 у точці Т (рис. 4.12).
С
Kl
Рис. 4.12
В


Розділ 4. Позиційні задачі. Багатоспосібність
49
Тоді трикутник BTK1 дорівнює трикутнику BTK3
(ZTBKl = ZTBK3,
ВТ — спільна, BK1 = BK3). Тому
ZKlTB = ZK3TB,
отже, ТІ —бісектриса кута KγTK3.
Нехай бісектриса кута С перетинає продовження K2K3 у точці V, VI — бісектриса кута TVKγ, отже, І — інцентр трикутника TVKγ, тому IKγ — бісектриса кута TKγV, але IKγIKiC, тому KγC — бісектриса зовнішнього кута трикутника TVKγ.
Оскільки VC — бісектриса кута V трикутника TVKγ, KγC — зовнішня бісектриса трикутника TVKγ, то ТС — також зовнішня бісектриса трикутника TVKγ, отже, ТС .LTI (як внутрішня і зовнішня бісектриса), отже,
ZCTB = 90°.
2-й спосіб
Оскільки прямі ВС і K2K3 можна побудувати, отже, кут BDK3 заданий (рис. 4.13),
Маємо
ZZ) = 180o-(Z,KiBD + ABK3D} =
. ( /А А /В — /С
= 180o- 180o-ZB + 90o =
І 2 ) 2
Маємо в трикутнику ABC сторону а, різницю кутів ZB-ZC. Для побудови залишається знайти лінійний елемент. Покажемо, що ним буде різниця сторін b-с. Позначимо відрізок BD як t, р — півпериметр трикутника ABC.


50
Позиційні задачі на побудову
AK2 = AK3 = р-а, CK2 = p-c, BK3 = p-b, ВС = а.
За теоремою Менелая: ck2ak3bd 1 K2A∙K3B DC~ ’ або
(p-c)(jp-a)⅜ (p-α)(p-fr)(α + t) ЗВІДСИ
р-с _a + t р-b t або
д + Ь — с a, + t a+c-b t Нехай Ь-с = х.Тоді
α + x _ a + t а-х і ’
a, + %t
Оскільки відрізки BD-t і BC = α відомі, то
α2 b-c = .
a + 2f
Залишається побудувати трикутник ABC за a, ZB - Z.C, Ь-с.
Розв'язання
Аналіз показує, що якщо на стороні АС відкласти відрізок
CD = b-c9
то
Будуємо трикутник CDB (рис. 4.14) за а,


Розділ 4. Позиційні задачі. Багатоспосібність
51
Рис. 4.14
/ТУ __ /(У CD=b-c і ZDBC=- .
2
Потім продовжимо пряму CD, яка перетне серединний перпендикуляр І відрізка BD у вершині А шуканого трикутника ABC.
3-й спосіб
Аналіз показує, що трикутники CMK2 і BNK3 подібні (CM±K2K3, BN LK2K3) (рис. 4.15).
Рис. 4.15


52
Позиційні задачі на побудову
(1)
(2)
(3)
Дійсно, AK2 = AK3, отже, ZAK2K3 = ZAK3K2
і тоді AMK2C = ANK3B, а отже, ΔCMTf2 ~ ΔBNK3. Тоді
CKi CM
BK3 ~ BN'
Але
CK2=CKl, BK3=BKl.
Враховуючи (1) і (2), маємо
CK1 CM BKl “ BN ’
а отже, відоме відношення, у якому точка K1 ділить відрізок ВС.
Перейдемо до побудови. Опустимо з поданих точок В і С перпендикуляри BN і CM на подану пряму K2K3. Маємо
BK1=BC-CK1.
Враховуючи співвідношення (3):
BKi=BC-- BK1, 1 BN 1
ЗВІДКИ
_ BCBN Ї5Л, —
.1 BN + CM
— відрізок BK1 можна побудувати. З точки В радіусом BKl робимо засічку на прямій K2K3 — матимемо точку X3, аналогічно точку К2. Перетин прямих BK3 і CK2 дає точку А.


Розділ 4. Позиційні задачі. Багатоспосібність 53
ЗАДАЧА 6 (ЖУРНАЛ «КВАНТ»)
LiLl, laι,K,∙
Розв'язання
1-й спосіб
Оскільки
ZLlIL2 = 90°+^-,
то на відрізку L2Li будуємо сегмент, що містить цей кут, і доповнюємо його до кола (рис. 4.16).
Позначимо W середину дуги L2L1. Маючи точки І і W, знаходимо точку С.
2-й спосіб
Побудуємо точки, симетричні точкам L1 і L2 відносно прямих laχ, lbχ (рис. 4.17).


54
Позиційні задачі на побудову
Рис. 4.17
Ці точки (L' і L') належать стороні АВ. Подальше є очевидним.


РОЗДІЛ 5. ПАМ'ЯТІ Л. М. ЛОПОВКА
Розглянемо позиційні задачі, автором яких був Лев Михайлович Лоповок, видатний український педагог — математик, автор популярних книг, автор великої кількості цікавих задач.
ЗАДАЧА 1(ОСНОВНА ЗАДАЧА)
Дано кут і точку D всередині кута. Побудуйте відрізок з кінцями на сторонах цього кута, середина якого збігається з точкою D.
Розв'язання
Нехай кут ВАС заданий (рис. 5.1).
Рис. 5.1
Проведемо пряму AD і відкладемо відрізок DE, що дорівнює AD. Побудуємо паралелограм АВЕС з діагоналлю АЕ, діагональ ВС паралелограма — шуканий відрізок.


56
Позиційні задачі на побудову
ЗАДАЧА 2
Побудувати трикутник за точками M1 і P1, Р2 — серединами сторін ВС і висот BH2 і CH3.
Розв'язання
Будуємо прямі BH2 і CH3 (рис. 5.2).
Дістанемо кут ВНС і точку Ml усередині кута ВНС (Н —ортоцентр). За основною задачею будуємо точки В і С, а маючи точки Н2 і H3 (BP1 =PlH2, CP2 -P2H3)1 будуємо трикутник ABC.


Розділ 5. Пам'ятіл. М. Лоповка
57
ЗАДАЧА 3(H)
Побудувати трикутник ABC за точкою дотику вписаного кола зі стороною АВ і точками перетину цього кола з медіаною, проведеною з вершини А.
Розв'язання
Нехай вписане у трикутник ABC коло дотикається до сторони АВ у точці К і перетинає медіану AM в точках Т і N (рис. 5.3).
Маючи три точки К, Т, N можна побудувати вписане у трикутник ABC коло.
Проведемо дотичну до кола в точці К1 дістанемо пряму АВ. Перетин прямих АВ і NT дає точку А. Провівши з точки А дотичну до кола, відмінну від АВ, дістанемо пряму АС.
Рис. 5.3
Відкладемо на промені TD відрізок, що дорівнює AT. Побудуємо паралелограм AEDF (Е eAB, F ∈ АС). Оскільки Т — точка перетину діагоналей паралелограма, ЕТ = TF і AT — медіана трикутника AEF, провівши дотичну до кола, паралельну EF, дістанемо в перетину з прямими АВ і АС точки В і С.


58
Позиційні задачі на побудову
ЗАДАЧА4
Побудувати паралелограм ABCD за серединами його висот BB1, BB2 і DD1.
Розв'язання
Позначимо К, L, М середини відрізків BBl, AB, DDl (рис. 5.4).
Рис. 5.4
Оскільки трикутники ABB1 і DCD1 рівні, то
LK = MH.
Серединний перпендикуляр до відрізка BB2 ділить КМ навпіл. Побудувавши КМ, проводимо BB1 ± KM, DD1 ± КМ. Тепер можна знайти точку Т — середину КМ — і побудувати BB2 ± ОТ. Це визначає вершину В. Далі можна знайти BB2, побудувати ВА і CD, паралельні ОТ.


РОЗДІЛ б. ПОЗИЦІЙНІ ЗАДАЧІ
НА УКРАЇНСЬКІЙ МАТЕМАТИЧНІЙ
ОЛІМПІАДІ
1986 року в місті Рівне відбулася XXVI Українська математична олімпіада. У сьомому і восьмому класі було запропоновано дві позиційні задачі.
Крім олімпіадного характеру, ці задачі цікаві глибоким зв’язком: у першій задачі задані дві точки і позиційні медіана і бісектриса; у другій задачі — одна (!) точка і позиційні медіана і бісектриса. Щоправда, дещо інші. Цікаво!
ЗАДАЧА 1
Побудувати трикутник, якщо відомі дві його вершини А і В і прямі, на яких лежать медіана та і бісектриса la.
Рис. 6.1


60 Позиційні задачі на побудову
Розв'язання
Побудуємо точку B1, симетрично точці В, відносно прямої la. Вершина трикутника ABC (рис. 6.1) лежатиме на прямій AB1.
Аналіз показує, що якщо побудувати паралелограм АВВС, то вершина С трикутника ABC належатиме його діагоналі ВС. Проведемо через точку В пряму, паралельну (ΛBl)χ — вона перетне пряму (mβ)χ у точці D.


Розділ 6. Позиційні задачі на українській математичній олімпіаді
61
ЗАДАЧА 2
Побудувати трикутник ABC, якщо відомі вершина А і дві прямі, на яких лежать бісектриса кута С і медіана, проведена з вершини В.
Розв'язання
1-й спосіб
Побудуємо точку A1, симетричну точці А відносно прямої mb . Через точку A1 проведемо паралельно mb пряму t (рис. 6.2).
Тоді вершина С буде точкою перетину прямих t і lc .
2-й спосіб
Через точку А паралельно lc проведемо пряму t1 (рис. 6.3).
Позначимо D — точку перетину прямих t1 і mb . Через цю точку паралельно AQ проведемо пряму t2. Точка перетину прямих t2 і lc буде шуканою вершиною С. J∖jlsl знаходження вершини В відобразимо промінь СА відносно прямої lc . Точкою перетину побудованого променя з прямою mb буде вершина В.


62
Позиційні задачі на побудову
Задачі та їх розв’язання взято з книги «Українські математичні олімпіади» (Київ, «Вища школа», 1993).


Навчальне видання Бібліотека журналу «Математика в школах України» Випуск 11 (131)
КУШНІР Ісаак Аркадійович
ПОЗИЦІЙНІ ЗАДАЧІ НА ПОБУДОВУ
Навчально-методичний посібник
Головний редактор І. С. Маркова Редактор Г. О. Новак Коректор О. М. Журенко Комп’ютерне верстання О. В. Лебедева
Підп. до друку 05.11.2013. Формат 60x90/16. Папір газет. Гарнітура Шкільна. Друк офсет. Ум. друк. арк. 8,0. Зам. № 13-11/18-04.
ТОВ «Видавнича група “Основа”». Свідоцтво суб’єкта видавничої справи КВ № 11392-265Р від 25.07.2007. Україна, 61001 Харків, вул. Плеханівська, 66.
Тел. (057) 731-96-32. E-mail: math@osnova.com.ua
Віддруковано з готових плівок ПП «Тріада Принт» Свідоцтво суб’єкта видавничої справи ДК № 1870 від 16.07.2007. Харків, вул. Киргизька, 19. Тел.: (057) 757-98-16, 757-98-15.


«МАТЕМАТИКА В ШКОЛАХ УКРАІ
Книжкові додатки не є дайджестом статей.
Актуальна тематика, інноваційні методики, високий індекс практичності. Сучасні книги для вчителя від найбільшого виробника методичної літератури в Україні.
иАВшко^УНМІНИ”
«МАТ*"*
∣∣ιι∣
ПЕРЕДПЛАТНИМ
ПЕРЕДПЛАЧУЙТЕ ЗАВЧАСНО!
У вартість передплати на місяць входить: З випуски журналу + книжковий додаток!
Як оформити редакційну передплату зі знижкою, дізнайтеся за тел.: (057) 731-96-36
4
01651
Скачати
ІНДЕКС
Також придбайте посібник в електронному вигляді на сайті:
w⅛⅛⅛⅜l⅛higa.in.u¾
Оформити передплату на журнал «Математика в школах України» з книжковим додатком можна з кожного наступного місяця у будь-якому відділенні зв’язку України.