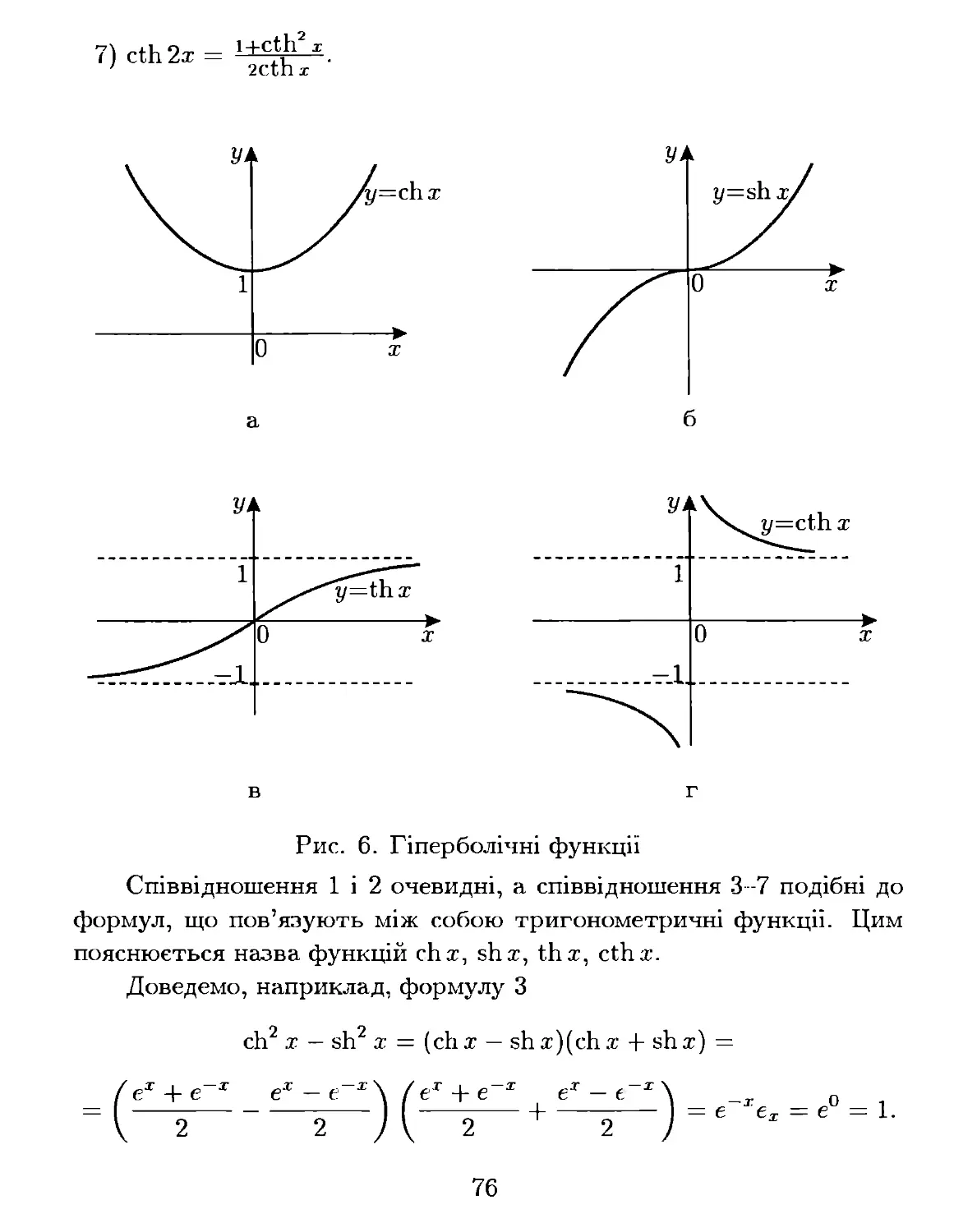
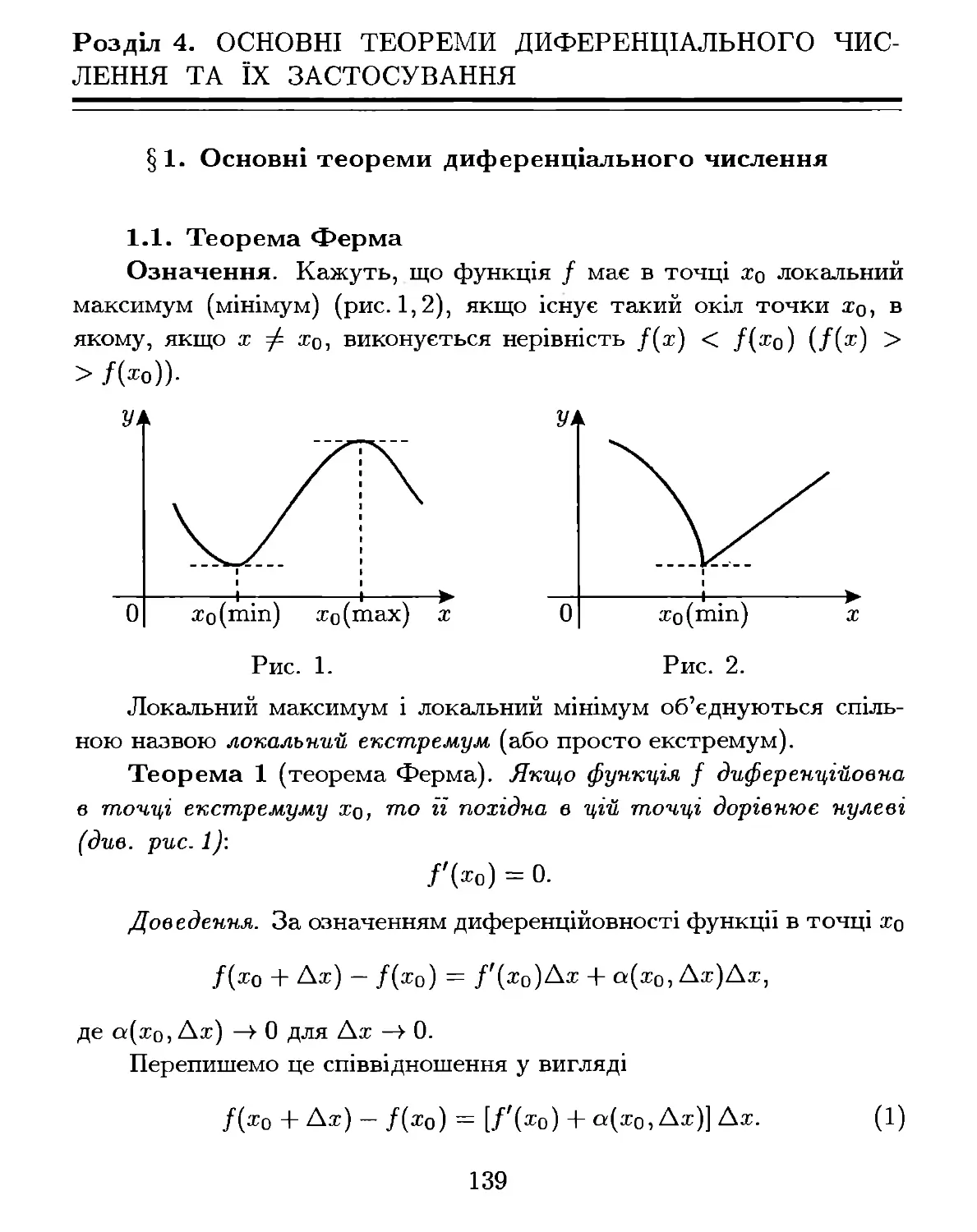
Текст
МІНІСТЕРСТВО ОСВІТИ і НАУКИ УКРАЇНИ
НAl{ІОНАЛЬНИЙ УНІВЕРСИТЕТ "ЛЬВІВСЬКА ПОЛІТЕХНІКА"
u
МАТЕМАТИЧНИИ
АНАЛІЗ
Частина І
Рекомендовано Науково-,м,етодичною радою
Національного університету "Львівська політехніка"
як навчальний посібник для студентів вищих uавча.аьнux закладів
Львів
Видавництво Національного університету "Львівська політехніка .....
2ОО3
ББК 22.161 я73
М 34
УДК 517(075.8)
Pekome'H-дова'Н-о Нацкоео-методичною радою
Націо'Н-мь'Н-OlО y'H-іверситету "Львівська політехніка" як 'H-авЧWLь'Н-ий посіб'Н-ик
для студентів вищих 'H-авЧWLь'Н-их за'/CJlадів (пpomoкол Мб від 12.09.2003 р.)
Рецензенти:
Сторож О.Г., доктор фіз.-мат. наук, професор Львівського національного універ
ситету ім. t.Франка;
Каленюк П.І., доктор фіз.-мат. наук, професор Національного університету
"Львівська політехніка";
СЛОНЬО8СЬКИЙ Р.Б., доктор фіз.-мат. наук, професор Національного універ
ситету "Львівська політехніка";
lСироїд 1.-п.п.l, канд. фіз.-мат. наук, старший науковий співробітник ІППММ
ім. я.с. Підстригача НАН України
Рудавський Ю.К. та ін.
М 34 Математичний аналіз: Навчальний посібник. - Ч. І. - /ю.к Ру-
давський, п.п. Костробій, Л.Л. Лібацький, А.З. Мохонько, т.я. Олексів,
Ів.в. ЮсілевичJ В.М. Бушмакін, О.А. Микитюк, М.М. Чип, В.М. Зеленяк,
сл. Томецька. - Львів: Видавництво Національного університету
"Львівська політехніка", 2003. - 404 с.
ISBN 966-553-340-1
Пропонований посібник з математичного аналізу написаний колективом
авторів, які упродовж тривалого часу читали цю дисципліну студентам різних
спеціальностей Львівської політехніки.
Вправи і задачі для закріплення теоретичного матеріалу на практичних
заняттях можна знайти у виданому Львівською політехнікою збірнику задач.
Посібник призначений для студентів інженерно-технічних спеціаль
ностей вищих навчальних закладів.
ББК 22.161 я73
© Рудавський ю.к., Костробій П.П.,
Лібацький Л.Л., Мохонько А.З.,
Олексів т.я., Кісілевич В.В.,
Бушмакін В.М., Микитюк О.А.,
Чип М.М., Зеленяк В.М.,
Томецька С.І., 2003
ISBN 966-553-340-1
© Національний університет
"Львівська політехніка", 2003
Передмова
Пропонований читачеві посібник з математичного аналізу напи-
. .
сано колективом авторів, ЯКІ УПРОДОВЖ тривалого часу читали цю
дисципліну студентам різних спеціальностеи Львівськоі політехніки.
Кількість годин, що виділялась на курс так званої вищої математи
ки, частиною якої є математичний аналіз, коливалась від 100 до 510
годин. Залежно від цього формувався відповідний обсяг відомос-
u • • • •
теи з ЦІЄІ ДИСЦИПЛІНи, а також РІВень доклаДНОСТІ під час доведення
теорем, формулювання означень тощо. Звичайно, це певною мірою
відобразилось і на цьому посібнику. Проте автори намагались по
дати основні положення математичного аналізу так, щоб, з одного
боку, забезпечити доступність засвоєння, а з іншого - не допустити
зниження наукового РІВНЯ викладення.
Зазначимо, що вправи і задачі для закріплення теоретичних по
ложень на практичних заняттях можна знайти у виданому Львів
ською політехнікою збірнику задач [11].
Автори
з
ПОЗНАЧЕННЯ
Множини
.4 = {а, Ь, с} - -- множина А складається з елементів а. Ь, с.
Е - на.;Іежить до ... , наприклад, а Е А --- елемент а на.тlежить
множині А.
f}. - не належить до .
с - включення в .
sup А -- точна верхня межа множини А.
inf А - точна нижня межа множини А.
u - об'єднання (додавання), AuB - об'єднання (сума) множин
А і В.
n -- перетин (множення), А n В -- перетин (добуток) множин
А іВ.
(j) - порожня множина.
N - множина натуральних чисел.
Z -- множина цілих чисел.
Q --- множина раціональних чисел.
R --- множина дійсних чисел.
R --- розширена множина дійсних чисел (з включенням -оо
+00).
С --- множина комплексних чисел.
(R) --- дійсна пряма.
[a;b]-- закритий проміжок (відрізок, сегмент), включає кінці а
і Ь.
(а; Ь) --- відкритий проміжок (інтервал), виключає кінці а і Ь.
[а; Ь), (а; Ь] --- напівзакритий (напіввідкритий) проміжки.
(R2), (R3), (Rn) --- двовимірний, тривимірний, n-вимірний дійсні
простори.
і = 1, п--- і набуває значень 1. 2, .... п,
n! ---- факторіал (добуток послідовних цілих чисел ВІД 1 ДО 11.
п!=1·2·3· .. _·n).
4
с: = ( n ) = I(n� )1 -- кількість комбінацій зп елементів по т.
111 m. n m.
lаl --- МОДУ.,lЬ числа.
{х Ilхl < є} ---- множина тих значень х, модуль яких менший за
є.
U(С)-- окіл точки С (відкритий проміжок, який містить точку
С).
U(С,є) -- епсилон-окіл точки С (U(С,є) = {х Ilх - хоl < є}), де
хо - - координата точки с.
'І( -оо, М), U( +00, А1) - околи нескінченно віддалених точок
(U(±оо, М) = {х !lхl > М}).
U � ( С), U + ( с) -- відповідно лівосторонній і правосторонній око-
ли точки с. -
X�Y} . і . X-'J
-- фУНКЦІЯ відображає множину у множину L •
i:X�Y
D(J) = Х --- область визначення функції і.
Е(Л = У --- область значень функції і.
і І ХІ -- звуження функції і на підмножину ХІ (ХІ еХ).
і-І --- функція, обернена до функції і.
[х] -- ціла частина числа х (найбільше ціле число, яке не переви
щує х).
{ х} = і: - [х]---- дробова частина числа х.
{І, якщо х > о,
SIgn х = О, якщо х = О,
-1, якщо х < о.
Логічні символи
:::::} -- випливає, слідує (імплікація, логічне слідування).
<=? -- еквівалентність.
V -- квантор заг-адьності (для всіх ... , Д.,lЯ кожного ... ).
з --- квантор існування (існує ... , знайдеться ... ).
А "і" .
V -- "або".
Розділ 1. ЧИСЛОВІ множини. ФУНКЦІЇ. ПОСЛІДОВНОСТІ
§1. Множини. Логічні символи
1.1. Поняття множини. Поняття множини - це одне з ос
новних, початкових понять математики, яке не визначається через
•• • • • v ,
ІНШІ ПРОСТІШІ поняття 1 яке приинято роз яснювати на прикладах.
Говорячи про множину, звичайно розуміють набір об'єктів (іх нази
вають елементами множини), що об'єднуються за деякими спільними
ознаками.
Так, припускаючи, що елементами множини можуть бути до
вільні об'єкти, можна говорити, наприклад, про множину студентів
групи, множину книг бібліотеки, множину планет Сонячної системи
тощо.
Множини позначатимемо великими літерами латинського алфа
ВІТУ, а елементи множин - малими.
Якщо елемент з: належить множині А, то записують х Е А. Якщо
х не належить А, то пишуть х fj. А. Запис А = {а, Ь, с, d} означає, що
множина А складається з елементів а, Ь, с, d.
Якщо кожен елемент множини А є одночасно елементом множи
ни В, то записують А С В або В :J А і говорять, що А є підмно
жиною множини В (а також що А належить В або В містить А).
Запис А = В означає, що множини А і В складаються з одних і тих
самих елементів, тобто що А С В і ВеА. Множина, яка не містить
жодного елемента, називається порожньою 1 позначається символом
А = ф. Якщо А -- довільна множина, то вважають, що CD С А.
Ми розглядатимемо переважно числові множини, тобто множи
ни, елементами яких є числа. Для числових множин будемо дотри
муватися позначень:
R --- множина дійсних чисел,
Q -- множина раціональних чисел,
Z = {О, ±1, ±2, ... } __ о множина Ш.ІИХ чисел,
G
N = {І, 2, 3, ... } -- множина натуральних чисел.
Очевидно, що NeZ с Q с н.
Елементи числових 1І1НОЖИН зображатимемо точками на число
вій ОСІ 1 ототожнюватимемо з цими точками. Отже, множина R
ототожнюється з усією числовою віссю, а множини N, Z, Q - з її
. .
гпдмножинами, що складаються з точок, координатами яких є ВІДПО-
відно натурвльні, цілі та раціональні числа. Нижче розглядатимемо
. . - .
деякі ІНШІ підмножини точок числової ОСІ, ЯКІ називатимемо також
точковими множинами.
1.2. Дії над множинами. Для множин вводять дії, що мають
алгебраїчні властивості, подібні до властивостей додавання, відні-
.. Оо.. ...... ..
мання І множення чисел, хоча за своєю суттю І ЗМІСТОМ ВІДМІННІ ВІД
цих арифметичних дій.
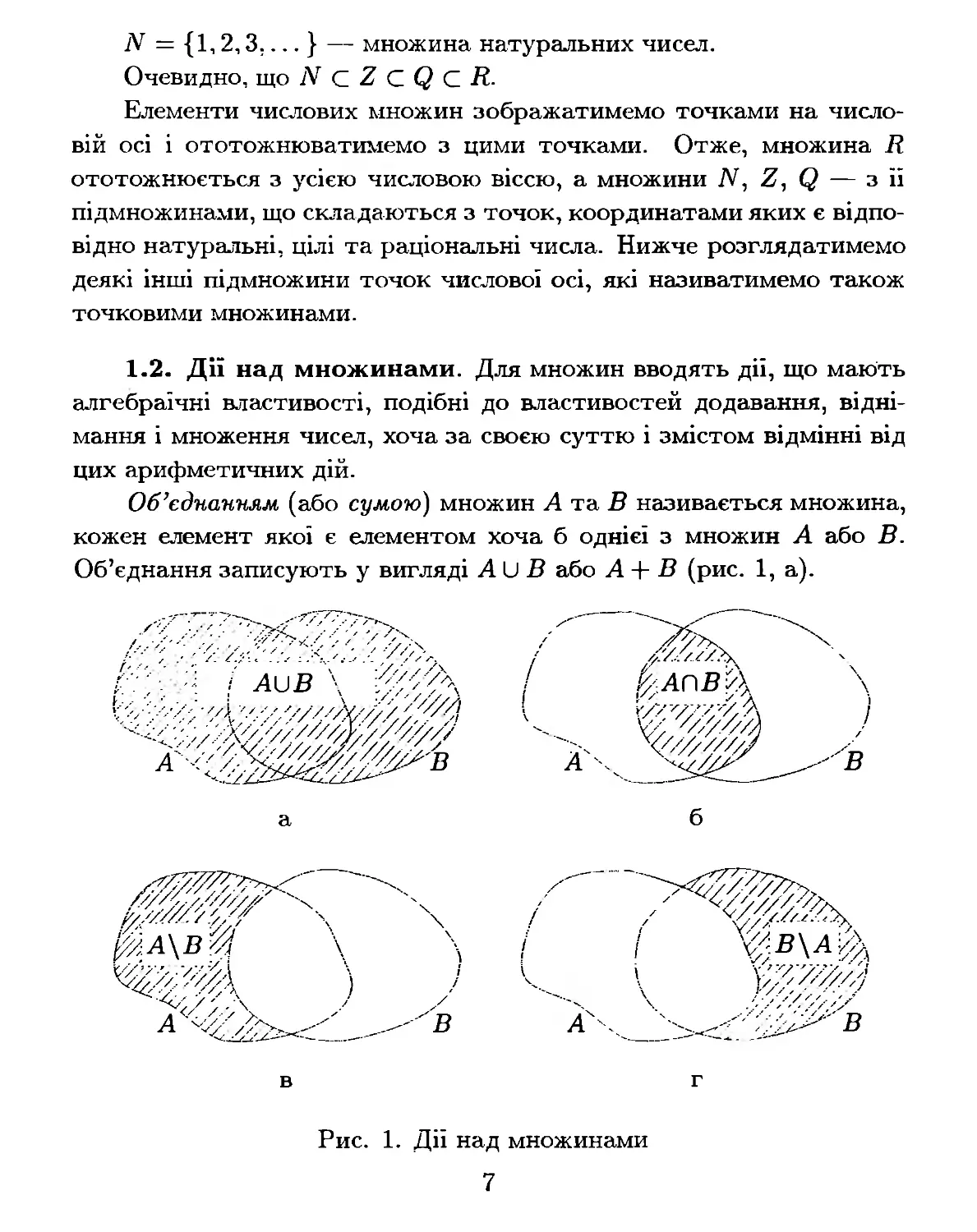
Об'єд'Н,а'Н:н,.я,м (або сумою) множин А та В називається множина,
кожен елемент якої є елементом хоча б однієї з множин А або В.
Об'єднання записують у вигляді А u В або А + В (рис. 1, а).
а
в
б
г
Рис. 1. Дії над множинами
7
Перерігом (або добуm:к"о.м) множин А та В називається множина,
яка складається з елементів, що є спільними дЛЯ �ІНОЖИН А та В.
Переріа записують у вигляді АПВ, або А·В (рис.1,б). Якщо Апв =
= (]), то кажуть, що множини не перетинаються.
Різницею множин А і В називається множина, ЩО складається з
тих елементів множини A� які не є елементами множини В. Різницю
записують у вигляді А\В або А - В (рис. 1, в).
Приклад 1. Для множини А = {-11, -8, -6,4,5, 10} і В
= {-8, -4, -2,4, 12} знайти А U В, А n В, А\В, (А\В) U (В\А).
РОЗб 'язання.
AuB = {-11,-8,-6,-4,-2,4,5,10,12},
АпВ = {-8;4}, А\В = {-11,-6,5,10},
(А\В) U (В\А) = {-11, -6, -4, -2,5,10, 12}.
Для дій над множинами справджуються такі співвідношення:
1) AuB = BUA;
2) (А U В) U С = А U (В U С);
3) (А n В) n С = А n (В n С);
4) (А U В) n С = (А n С) U (В n С);
5) Au А = А;
6) An А = А;
7)(A\B)UB=AUB;
8) А U (В n С) = (А U В) n (А U С).
Зауважимо, що лише перші чотири властивості аналогічні до від
повідних властивостей дій над числами, а решта відрізняються від
них.
Довести рівності 1--8 можна, скориставшись визначенням рівнос
ті множин. Доведемо, наприклад, рівність 8.
Нехай х Е AU(B n С). За визначенням суми л Е А або х Е ВпС.
Але тоді :r Е А U В і х Е Au С і, отже. :г. Е (А U В) n (А U С). Тому
А U (В n С) с (А U В) n (.4 U С).
8
Некай, навпаки, х Е (А u В)П(А u. С). Тодіг Е AuB і х Е AuC.
Звідси випливає, шо або х Е А, або х Е впС, а тому от Е Au (В n С).
Отже, (А u В) n (А u С) с А u (В n С).
Оскільки виконання співвідношень DeE і Е с D рівнозначне
D = Е, то рівність 8 доведена.
I.З. Деякі поняття і символи математичної логіки.
а) Необхідні і достатні умови. У формулюванні кожної тео
реми можна виділити дві частини. Першу частину становлять умови
теореми (їх позначимо А), у яких задаються математичні поняття
та співвідношення між ними, а другу --- висновки теореми (їх позна
чимо В), які потрібно отримати з цих умов.
Тоді формулювання теореми символічно записують у вигляді
А=::;. В
(1)
і говорять, що з умов А випливають умови В, а також коротко: "з
А випливає В", або "якщо А, то В". Знак =::;. називається логічним
знаком і.мnлі'К:шц,іі (наслідку).
Наприклад, у теоремі "діагоналі ромба взаємно перпендикуляр
ні" умова А -- задано ромб, умова В -- діагоналі взаємно перпенди
кулярні,
Якщо деяка теорема записана у вигляді (1), то умова В нази
вається необхідною для А (у тому розумінні, що коли не виконується
умова В, то неможливою є також А), а умова А називається доста т
ньою для В (у тому розумінні, що наслідком А завжди є умова В).
Якщо умова В є необхідною дЛЯ А, то не завжди вона є достат
ньою дЛЯ А, тобто не завжди справджується теорема
В=::;.А.
(2)
Так, для сформульованоі вище теореми, якщо діагоналі чотири
кутника взаємно перпендикулярні, то чотирикутник необов'язково є
ромбом.
9
Теорема (2) називається оберненою до теореми (1). Якщо обидві
теореми (1) і (2) справджуються, то Їх об'єднують записом
.4 {::;> В.
(3)
Умови А. і В називаються екеівалентнимь (або ріВНОСИ.1ЬНИМИ),
а знак {::;> --- еквівалентністю (рівносильністю]. Запис (3) читають
так:
1) умова А еквівалентна (або рівносильна) умові Ві
2) умова В необхідна і достатня для виконання Аі
3) для того, щоб виконувалася А, необхідно і достатньо, щоб вико
нувалася Ві
4) А виконується тоді і тільки тоді, якщо виконується В.
У наведених формулюваннях А та В можна поміняти місцями.
Часто замість слова "умова" вживають слово "ознака" і тоді
говорять "необхідна ознака", "достатня ознака", "необхідна й дос
татня ознака". В останньому випадку 4 кажуть також "критерій",
наприклад: умова В є критерієм для виконання умови А.
б) Квантори. Для чіткого і стислого формулювання мате-
. .
матичних понять 1 тверджень користуються спеціальними знаками
(символами) V і З, що називаються кванторамн (від лат. quantum
скільки).
Знак V називається 'К:ва'Н,торо,м, загальності, його застосовують
замість слів "Д.'ІЯ кожного", "для будь-якого", "кожний", "всякий",
"будь-який" .
Знак З називається квантором існивання його вживають за
мість слів "існує", "знайдеться", "хоча б один", "хоча б для одного" ,
"деякий", "для деякого" .
Застосування кванторів дає змогу спростити записи матема
тичних тверджень. Ось який вигляд звичайно можуть мати записи
твердження про те, що рівняння х + In у = 3 для кожного фіксованого
додатного числа у > О має розв'язок стосовно невідомої х:
Vy > О Зх Е R [х + Ін у = 3], або
Vy > О З.г Е R :::::} х + ln у = 3, або
10
Уу > О :::Іх Е R: х + Іп у = 3.
Кожний з цих записів читають так: для кожного додатного чис
ла у > О існує дійсне число х Е R таке, що виконується рівність
з: + Іп у = 3 (тобто рівняння х + Іп у = 3 має розв'язок стосовно х).
Інколи для зручності читання квантори розділяють дужками:
(Уу > О) (:::Іх Е R) [х + Іп у = 3].
Якщо з тексту зроауміло, якій множині належать змінні х і у (зокре
ма, х Е R у нашому твердженні), то можна також писати:
Уу > О :::Іх [х + Іп у = 3].
Для запису тверджень використовуються ще й інші логічні зна
ки. Так, знаком Л позначають сполучник "і", а знаком V - сполуч
ник "або".
Наприклад, запишемо твердження
Ух Е R: ху > О {:} (х > О Л У > О) V (х < О Л У < О),
яке означає, що ЩІЯ всіх дійсних значень х і у співвідношення ху > О
виконується ТОДІ і тільки тоді, коли з: > О і у > О або х < О і у < О.
Іншими словами: нерівність ху > О, записана для дії1СНИХ х і у, ек
вівалентна, ТОМУ що обидва співмножники х і у або додатні, або
від'ємні, тобто є числами однакових знаків.
1.4. Метод математичної індукції. Припустимо, що потріб
но довести НИЗКУ однотипних тверджень А (n) для всіх натуральних
п, Інколи це вдається зробити за методом математичної індукції.
Згідно з цим методом доведення ведуть в такіи послідовності:
1. Перевіряють, чи твердження справджується ДЛЯ n = 1, тобто
доводять твердження А (1). Ця частина називається базою і'Н,дУ1'і:'Ціі.
2. З припущення про те, що твердження справджується ДЛЯ
n = k, доводять його для n = k + 1, тобто що A(k) =} A(k + 1). ПЯ
. .-. .
частина, що називається кроком індукцп. заКІНЧУЄ доведення тверд-
ження А ( п) для всіх 11 Е lУ.
11
Якщо деяке твердження А (п) потрібно довести не для всіх
n ЕіУ, а лише Д.'ІЯ п � m, де т --- задане натуральне число, то
база іНДУКІІії полягає у перевірці того. шо справджується тверджен
ня А (т), а крок індукції залишається таКИ:�І самим, як і в загальному
випадку 2.
Приклад 1. Довести, що
2 2 2 п(п + 1)(2п + 1)
1 +2 +···+п = 6 .
(4)
Доведен/пл. 10. Якшо п = 1, то формула справджується:
2 1(1 + 1)(2 + 1)
1 = = 1.
6
20. Припустимо, шо 12 + 22 + ... + k2 = k(k+l�(2k+l). Доведемо,
що (4) правильна для п = k + 1, тобто що
Справді, маємо
k(k + 1)(2k + 1) + 6(k + 1)2
6
(k + 1)(k + 2)(2k + З)
6
Отже, формула правильна для довільного п.
Приклад 2. Довести нерівність Бернуллі
(1 + х) n � 1 + пх, якщо х > -1, n ЕіУ.
(5)
Дов еден/пл.
1 о. Якщо n = 1, то 1 + х = 1 + х.
12
20. ПРИПУСТИМО, що {І + X)k � 1 + k.r. ДовеДБЮ, що нерівність
задовольняється для п = k + 1, тобто що (1 + J;)k+1 � 1 + (А: + l)х.
Справді, ПОМНОЖИМО обидві частини нерівності (1 + x)k 2:: 1 + kx
на (1 + х) 2:: О:
(1 + .r)k(1 + :с) 2:: (1 + kx)(1 + х):
(1 + x)k+1 2:: 1 + (k + l)х + kx2 2:: 1 + (k + l)х.
Отже, нерівність ВИКОНУЄТЬСЯ для всіх n ЕіУ.
1.5. Формула бінома Ньютона. У записах різних формул
інколи ВИКОРИСТОВУЮТЬСЯ добутки n послідовних натуральних чисел
1 . 2 ..... n; іх скорочено позначають n! (читають "п. факторіал").
За означенням приймається, що О! = 1, І! = 1. Тоді 2! = 1 ·2 = 2,
З! = 1·2· З = 6 і Т.д.
Запишемо добре відомі формули для степенів бінома (а + Ь):
(а + ь)2 = а2 + 2аЬ + Ь2,
(а + Ь)3 = аЗ + За2Ь + ЗаЬ2 + Ь3.
у багатьох задачах доводиться користуватися формулами для
(а + Ь)О, якщо 0:- - дійсне число. Якщо о: = n ---- натуральне число,
маємо одну з найважливіших математичних формул, що називається
формулою бінома Ньютона:
n! n-І Ь n! n-2ы.
(а + ь)n = с" + а + а + ... +
1!(n - І)! 2!(n - 2)!
, , ,
n. n-тьт n. 2ьn-2 1l. ьn-1 ь"
+ '( _ ),а + ... +( _<J)'<Jї(l +( _ 'Іа +.
т. п т. n � .�. n 1).1.
(6)
Доведемо цю формулу методом математичної індукції.
10. Якщо n = 1, то (6) правильна, бо (а+Ь)l = а+Ь. Пропонуємо
читачеві переконатися, що (6) також справджується, якщо n = 2 і
n = З.
ІЗ
20. Припустимо, шо (6) правильна для n = k, тобто
)k k k! k-l k! k-2 2
(а + Ь = а + І! (k _ І)! а Ь + 2! (k _ 2)! а Ь + ... +
k! k-m m k! 2 ь -г k! k-l k
+ m!(k_m)!a Ь + ... + (k_2)!2!a Ь + (k __ l)!I!ob +Ь.
(7)
Доведемо цю ФОРМУ.:"ІУ, . якщо n = k + 1. Для цього по:множимо
обидві частини рівності (7) на (о + Ь):
)k+I _ ( k k! k-l k! . k-2 2
(о+Ь -(а+Ь) о + '(k- ),а Ь+ '(k- ),а Ь + ... +
. 1. 1 . 2. 2 .
k! k-m m k! 2 k-2 k! bk-1 bk)
+ m!(k_m)!a Ь + ... + (k-2)!2!0 Ь + (k-l)!I!a + .
Далі виконаємо множення на (о + Ь) у правій частині цієї рівнос
ті. Виділимо доданки, що містять добутки ak+1-ibi, і = О, k + 1, і
знайдемо коефіцієнти біля однакових добутків:
біля ok+l - 1
,
. kb k! (k+l)!
БІЛЯ а --- 1 + 1!(k _ І)! l!k!'
. k-l 2 k! k! (k + І)!
БІЛЯ а Ь --- '( _ )' + '(k _ )' = '( _ )" ... '
2. k 2. 1. 1. 2. k 1.
біля ak+1-mbm -
k! k! (k + І)! (8)
m!(k - т)! + (т - 1)!(k - m + І)! = m!(k + 1 - т)!'··· ,
біля a"lbk-I k! k! (k + І)!
_ .. - (k - 1)!1! + (k - 2)! = (k - 1)!2!'
біля abk-- k! 1 (k + І)!
(k - 1)!1! + = l!k! '
біля bk+1 ---- 1.
14
Враховуючи знаидені коефіцієнти, переконуємося, що (7)
справджується, якщо замінити k на �. + 1:
( b)k+l _ k+l (k + 1)1 kb (k + І)! k-1b2 ...
а + - а + 'k' а + ?'(k' _ )' а + +
1. . �. 1 .
(k + І)! k+l-mbm (k + І)! 2bk-1 (k + І)! bk bk+1
+ m!(k + 1 - т)!а + ... + (k _ 1)!2!а + k!l! а + .
Отже, (6) доведено.
Коефіцієнти біля одночленів аn-тьт, т = О, n, у (6) називають
ся біноміальними і позначаються с:;- або (;:.) (читається "кількіст�
комбінацій з n по т"), с:;- = т!(:�т)!' За визначенням приймають,
що c� = с;: = 1. Очевидно також, що с:;- = с;:-т. Формула (8),
якщо в ній k замінити на n, означає, що с:;- + с:;--І = С:;-+l' Фор
мулу бінома Ньютона за допомогою введених позначень записують
у ВИГЛЯДІ
(а + Ь)n = ап + C�an-lЬ + C�an-2ь2 + ... + С:;'аn-тьт + ... +
+ C�a2ьn-2 + C�aьn-l + ь",
(9)
або за допомогою знака суми L -
n
(а + Ь)n = L С:аn-тьт.
т=О
(10)
1.6. Модуль дійсного числа. Модулем (абсолютною вели
чиною) дійсного числа а називається таке невід'ємне ЧИС.10 lаl, яке
визначається умовами;
якщо а � О,
якщо а < О.
Очевидно, що 101 = о {::} а = О.
15
Точку, що має координату а на числовій осі , також позначимо
о. Геометрично �al означає відстань від точки а до початку відліку
(точки о). Неважко переконатися також, щО ІЬ- al дорівнює відстані
між точками Ь та а.
Як вправи ПРОПОНУО10 читачам довести такі властивості моду-
1) lal = 1- al; -Ial ::; ±а ::; lal; 1021 = lal2 = а2;
2) lal ::; Ibl {:} -Ibl < а ::; Ibl {:} або ь::; -101, або Ь � lal;
З) lal ::; Ibl {:} а2 ::; Ь2;
4) la . bl = lal· Ibl;
lаl lal
5) Ь = тьт' якщо Ibl і= о.
у математичному анаяізі часто застосовуються такі ЧОТИрИ не-
. ... ..
РІВНОСТІ, ЯКІ запишемо У ВИГЛЯДІ
Ilal - Ibll ::; la ± bl < lal + Ibl·
(11)
Доведемо одну з них (інші можна довести подібно), наприклад,
Ilal- Ibll ::; la - bl·
(12)
Користуючись властивостями З та 1, зведемо нерівність (12) до
• • u
низки еквівалентних нерівностєи:
Оскі.:'ІЬКИ остання нерівність справджується, то й (12) також ви
конується.
ВІІХОДЯЧИ З нерівності
(ІЗ)
16
· .-
І застосовуючи метод математичної індукцц , можна довести, що
(14)
1.7. Проміжки, розширена числова пряма, околи точок.
Нехай задано дійсні ЧИС.:1:а а і Ь, а < Ь. Множину точок Х, що задо
вольняють нерівності а ::; х ::; Ь, позначають [а; Ь] і називають відріз
пом або сегментам; точки а і Ь -- кінцями сегмента, Відрізку [а; Ь]
у множині дійсних чисел R відповідають усі числа, що знаходяться
між числами а і Ь, включаючи Їх.
Надалі запис {х І } означатиме множину точок х, для яких
виконується умова, записана після вертикальної риски. Зокрема, ви
значення ВІДРІзка можемо записати так: [а;Ь] = {х І а ::; х ::; Ь}.
Множина точок (а; Ь) = {х І а < х < Ь} називається інтервалом; а і
Ь - кінці інтервалу. Інтервалу (а; Ь) у множині R відповідають усі
числа, що знаходяться між числами а і Ь, за винятком останніх.
Множини точок [а; Ь) = {х І а ::; х < Ь} і (а; Ь] = {х І а < х < Ь}
називаються півінтереаламн (або півсегментамлі чи nіввідріз-х:а.мu);
а і Ь - кінці півінтервалу. Півінтервалу в множині R відповідають
усі числа, що знаходяться між числами а і Ь, включаючи лише одне
з них.
Відрізки, інтервали і півінтервали об'єднують назвою проміжки:
Якщо а і Ь - кінці проміжку, то число Ь - а називається довжиною
ПРОМІЖКУ.
Множина точок всієї числової осі позначається ( -оо; +00), тобто
R = (-оо; +00). Знакам -оо і +00 ("мінус нескінченність" і "плюс
нескінченність" ) не відповідають ніякі числа і для них на числовій осі
не існує відповідних точок. Самі ці знаки називаються нев лостиоими
(або нескінченними) числами; або нев пастлівимлі точками:
Множина дійсних чисел R, доповнена невластивими точками
-оо і +00, називається розширеною множиною дійсних чисел і поз
начається як R. На відміну від нескінченних чисел -оо і +00, дійсні
числа х Е R називають також скінченними числами.
17
За визначенням приимають, що -оо < +00 1, якщо Х Е Н; то
-оо < х < +00.
Вище МІ-І визначили проміжки, кінці ЯКИХ є скінченними числа-
-. .
ми; ІХ називають СКІнченними, вони мають СКІнченну довжину.
Можна визначити також проміжки, хоча б один 3 кінців яких є
невластивою точкою. Такі проміжки називаються нескінченними і
вважають, що Їх довжина є нескінченною. Нескінченними МОЖ)'ТЬ
бути інтервали: (-оо; +00) = {х І - оо < х < +оо} (уся числова
вісь R), (а;+оо) = {хІх> а, аЕ R}, (-оо;Ь) = {хІх < Ь, Ь Е R};
та півінтервали (або півсегменти]: [а; +00) = {х І х � а, а Е R},
(-оо; Ь] = {х І х ::; Ь, Ь Е R}. Сегменти вважають завжди скінченни
ми.
Важливим поняттям є поняття околу точки, яке ми введемо для
усіх елементів с Е R; окіл точки с позначатимемо U(с).
Якщо с - дійсне число, тобто с Е R, то околом U(с) точклі с на
зивається довільний інтервал (скінченний або нескінченний), який
містить цю точку (рис. 2, а). Зокрема, окіл (с-є; с-і-є), О<є<+оо
(рис.2,б), який має середину (центр) в точці с і довжину 2є, по
значають також U(с; є) і називають симетричним є-окопом точки с;
число є називають радіусом симетричного околу. Очевидно, що
U (с; є) = {х І с - Е < Х < с + є} = {х ІІ х - сІ < є}.
U(с)
и(с, є)
U_(с)
U+(с)
(
•
)
(
•
•
(
•
•
)
с
с-є
с
с+є
с
с
а
б
в
г
Рис.
2. Околи скінченних точок
Неважко переконатися, що в кожному околі точки с Е R містить
ся деякий симетричний її окіл і, навпаки, у кожному симетричному
околі точки с міститься деякий інший її окіл.
Якщо С = - оо, то окіл U ( - оо) о це довільний інтервал вигляду
(-оо; iV1), lviER, якии позначають також U( -оо; lV1). Якщо с = +00,
18
то окіл U(+оо) - це довільний інтервал вигляду (М;+оо), MER,
якии позначають також U( +00; М). Околи невластивих точок зоб
ражено на рис. 3.
U( -оо )=U( -оо; М)
М
U(oo;M)=(-оо; -M)U
U(+оо)=U(+оо;М) U(M;+oo), М>О
. . (
М -М О М
а
б в
Рис. 3. Околи невластивих точок
Інколи множину R доповнюють не двома невластивими точками
-оо і +00, а однією нескінченно віддаленою точкою оо (нескінчен
ність без знака), яку не пов'язують з дійсними числами відношен
нями порядку. Околом U(оо) точки оо називають об'єднання двох
нескінченних інтервалів (-оо; а) U (Ь;+оо), де -оо < а < Ь < +00.
Симетричний окіл U(оо; М), О < М < +00, точки оо визначають як
(див. рис. 3, в)
U(оо;М) = (-оо; -М) U (М; +00) = {х Ilхl > М}.
Лівостороннім околом U _ (с) (відповідно правостороннім око
лом U + ( с)) точки с Е R називається довільний півсегмент , що міс
тить точку с як його правий (лівий) кінець (див. рис. 2, в, г). Ліво
сторонній та правосторонній околи точки об'єднують однією назвою
"односторонній окіл точки" .
Для невластивої точки с = -оо ЇЇ окіл (-оо; М), М Е R, роз
глядають одночасно як правосторонній U+( -оо; М) = U( -оо; М) =
= (-оо;М). Для невластивої точки с = +00 її окіл (М;+оо), MER,
розглядають одночасно як лівосторонній U_(+оо; М) = U( +00; М) =
= (М; +00). Для невластивої точки с = оо поняття одностороннього
околу не вводять.
Приклади.
1. Нерівність Іх + 1,51 < 0,2 визначає симетричний ОКІл
U( -1,5; 0,2) з центром в точці с = -1,5 радіусом 0,2, тобто інтервал
(-1,7; -1,3). Цей інтервал є також околом будь-якої його точки.
19
2. Нерівність з: + 1,5 < -0,2 рівносильна нерівності з: < -1,7,
яка визначає нескінченний інтервал (-оо; -1,7). Цей інтервал можна
розглядати також як лівосторонній окіл U_( -1,7) точки с = -1,7,
або як окіл U( -оо; -1,7) точки -оо, або як окіл будь-якої його точки.
з. Нерівність І + 1,5 > 0,2 рівносильна нерівності І > -1,3,
яка визначає нескінченний інтервал (-1,3; +00). Цей інтервал можна
розглядати також як правосторонній окіл U+( -1,3) точки с = -1,3,
або як окіл U( +00; -1,3) точки +00, або як окіл будь-якої його точки.
4. Нерівність Іх + 1,51> 0,2 визначає окіл U(оо) точки оо, який є
об'єднанням двох інтервалів U(оо) = (-оо; -1,7) U (-1,3; +00) (вони
були розглянуті в прикладах 2 і 3).
1.8. Межі числових множин.
Означення 1. Числова множина А називається обмеженою
зверху, якщо j MER V І Е А[х ::; М].
Геометрично це означає, що множина А на числовій осі розміще
на ліворуч від точки М, яка називається верхньою межею множини
А, тобто Ас (-оо; М].
Аналогічно визначається обмеженість множини знизу, а саме,
множина А називається обмеженою знизи, якщо j mER V ІЕ А[І 2:
2: т]. Геометрично це означає, що множина А на числовій осі розмі
щена праворуч від точки т, яка називається нижньою межею А,
тобто Ас [т; +00).
Множина А називається обмеженою, якщо вона обмежена знизу
і зверху, тобто, якщо j т е Н j MER V х Е А[т ::; х ::; М], або, що
те саме, якщо Ас [т;М].
Очевидно, що множина А буде обмеженою, якщо j МІ > О
V І Е А [ІхІ::; МІ], оскільки остання нерівність еквівалентна двом
нерівностям - МІ < Х < МІ.
Якщо множина не обмежена зверху (знизу), то за її верхню
(нижню) межу беруть нескінченне число +00 (відповідно -оо) і тоді
для довільного х Е R виконуються нерівності -ас < І < +00.
Приклад. Які з поданих множин обмежені знизу, які обмежені
20
зверху, які обмежені: N - наТУР&11ЬНИХ чисел, Z -- цілих чисел, R-
дійсних чисел, АІ = {�I n EN}, А2 = {�I рЕ Z, q Е N, ІрІ < q},
Аз = { n : 1 Іп EN}, А4 = { n � 1 Іп EN}, А5 = {n-:21 Іп EN},
{(_1)nn21 }
А6 = n EN?
n+1
Відповідь. Обмежені знизу, але необмежені зверху: N (нижня
межа О), А4 (нижня межа О).
Обмежена зверху, але необмежена знизу - А5 (верхня межа О).
Обмежені: АІ (межі О і 1), А2 (межі -1 і 1), Аз (межі О і 1).
Необмежені зверху і знизу: Z, R, А6.
Якщо М - верхня межа множини А, то довільне число М' > М
також є верхньою межею множини А. Отже, існує нескінченна мно
жина верхніх меж для обмеженої зверху множини. Подібно існує
нескінченна множина нижніх меж для обмеженої знизу множини.
Означення 2. Найменшою з усіх верхніх меж обмеженої зверху
множини А є число, яке називається точною верхньою межею, або
верхньою гранню цієї множини і позначається sup А (від лат. supre
mum, що означає "найвище"). Найбільшою з усіх нижніх меж обме
женої знизу множини А є число, яке називається точною нижньою
межею, або нижньою гранню цієї множини і позначається inf А (від
лат. infimum, що означає "найнижче").
Число (3 = sup А має такі дві характеристичні властивості:
1 О. ДЛЯ всіх х Е А виконується нерівність х � (3.
20. Для довільного числа є > О існує хоча б один елемент х' Е А
такий, що х' > (3 - є.
За допомогою логічних символів ці властивості можна записати
так:
10. Vx Е А[х � (3]; 20 VE > О Зх' Е А[х' > rз - є]. (15)
Перша властивість випливає з того, що (3 - це верхня межа
множини А, а друга - з того, що (3 ---- це найменша верхня межа
21
(якщо властивість 20 не виконувалася б. то деяке число f3 - со < (J
було б верхньою межею: що менша за {З).
Цими двома властивостями точна верхня межа множини харак
теризується ПОВНІстю.
Аналогічно точна нижня межа 0= inf А характеризується подіб
ними двома властивостями. Запишемо їх, застосовуючи логічні сим
воли:
10. Vx Е А[х � оІ; 20. Vc > ОЗх" Е А[х" < 0+ сІ. (16)
Теорема (про існування верхньої й нижньої граней множини).
Якшо 'Чuслова множина обмежена зверху, то існцє ЇЇ с'К',і'Н,'Че'Н,'Н,а точ
на верхня межа. Яклио 'Чuслова множина обмежена з'Н,uзу, то існцє
zz скінченна точна нижня межа.
З доведенням теореми можна ознайомитися в [1, т.l, с.69].
Зауважимо, що самі числа supA та inf А можуть належати або не
належати множині А. Якщо supA Е А, то елемент supA називають
нсйбільшмм. або максимапьним елементом множини А і позначають
тахА (від лат. maximum, що означає "найбільше"}. Якщо inf А Е А,
то елемент inf А називають найменисим або ,м,і'Н,і,м,аль'Н,u,м, елементом
множини А і позначають тіпА (від лат. minimum, що означає "най
менше").
Якщо множина А необмежена зверху (знизу), то за визначенням
вважають, що sup А = +00 (inf А = -оо).
Для множин з попереднього прикладу маємо:
inf Z = inf R = inf А5 = inf А6 = -оо,
supN = supZ = supR = вцр А, = впр А, = +00,
inf N = minN = 1, inf АІ = О Є/:. АІ, supAI = піах А, = 1,
inf А2 = -1 Є/:. А2, supA2 = 1 Є/:. А2, inf Аз = гпіп А, = t:
вцр А, = 1 Є/:. Аз, inf А4 = гпіп А, = t, вцр А, = гпах А, = -to
Розглянемо тепер числові множини ХІ, ... , Хn. Визначимо дві
множини
22
A�C{XI· ... ·xnIXiEXi. і=l,n}.
Можна довести (див., наприклад, [1, п. 3.5]), що
supS = supXI + ... + supXn, inf S = inf ХІ + ... + inf Хn (17)
і. якщо елементи, з яких складаються множини ХІ, ... , Хn, невідєм
НІ. то
supA = зцр Х, ..... supXn, inf А = inf ХІ ..... inf Хn. (17')
Якщо числові множини Р, Q такі, що Р с Q, то
inf Р � infQ, supP � supQ.
(18)
§ 2. Функції. Послідовності
2.1. Поняття функції. Одним з основних понять математи
чного аналізу є поняття функції. На ідеї вивчення функціональних
залежностей між величинами грунтувалися математичні досліджен
ня (у ХУІІ столітті) творців диференціального числення англійського
вченого І. Ньютона та німецького вченогго Г.В. Лейбніца. У іхніх
працях вперше вживається термін "функція", хоча сучасне понят
тя функціі було сформульовано лише в 20--30-х роках ХІХ століття
у роботах російського математика М.І. Лобачевського і німецького
математика п. Діріхле.
Означення 1. Нехай задано дві множини дійсних чисел Х і У.
Якщо кожному числу х Е Х за певним правилом (законом) постав
лено у відповідність одне дійсне число у Е У, то говорять, що на
множині Х визначено числову функцію і записують у = Лх), х Е Х.
Кажуть також, що функція J відображає множину Х у множину У
і записують І: Х -+ У або Х � У.
Множина Х називається областю визначення (існування) функ
ціі, х '.- аргументом, або незалежною змінною, І(х) -- значенням
функції в точці Х. Множину тих значень у Е У, які набуває функція
Лх), якщо х Е Х, називають областю значень функції. Область
23
ензначення позначають також п(І) або п(у), а область значень -
de!
Е(!) або Е(у). Якщо А с Х, то множина ЛА) = {ЛХ) : х Е А}
називається образом множини А при відображенні І.
Якщо не виникає непорозумінь, то можна користуватися також
записом функції, не вказуючи область її визначення, наприклад,
у = Лх).
Якщо розглядають декілька різних функцій, то записують Їх за
допомогою різних літер у = Лх), z = g(x), ... або літер з індексами
УІ = 11 (х), У2 = І2(Х), ....
Означення 2. Нехай на множині Х задана функція І, а на
підмножині Х} с Х - функція ІІ така, що ІІ (х) = Л х) для всіх
х Е ХІ С Х. Тоді функція Л називається зецженням фУЮ'і':ції І на
підмножину ХІ, вона позначається І І ХІ, а функція І - продоежен
ням фУЮ'і':ції Л на множину Х.
2.2. Способи аадання функції. 3 означення у попередньому
параграфі випливає, що для аадання функції необхідні дві умови:
1) вказати множину Х, область визначення функції;
2) задати правило І, за яким для кожного елемента х Е Х можна
знайти відповідний йому елемент у Е У.
Щодо цих умов, то множина Х може бути довільною підмно
жиною множини дійсних чисел, а правило І може формулюватися
у довільному вигляді, Залежно від способу аадання відповідності
між елементами множин Х та У розглядають різні способи задання
функцій.
Аналітичний спосіб. У математичному аналізі функції най
частіше задаються математичними формулами. Такий спосіб аадан
ня функцій називається аналітичним. Формула вказує, які дії потріб
но виконати над аргументом х, щоб отримати відповідне значення
у.
Наприклад, аналітичними виразами задані функції
2
УІ = 2х - 1,
2х + 3
У2 = Х + 1 '
уз = Vl - х2, У4 = vfsin х-І.
24
Якщо, задаючи функцю, не вказали області її визначення, та
кою областю вважають множину всіх значень аргументу, для яких
аналітичний вираз має зміст. Так, областями визначення наведених
функцій є такі множини:
п(У4) = {х І х = 27rk + %' k Е Z} .
Багато прикладів функцій, заданих аналітичними виразами,
можна взяти з геометрії та фізики. Наприклад, S(r) = 7rr2 - площа
круга радіуса т, V(x) = х3 - об'єм куба, ребро якого дорівнює х,
S(t) = vt - шлях, пройдений тілом за час t під час рівномірного руху
зі швидкістю v, а( F) =: - прискорення, з яким рухається тіло ма
сою m під дією сили F (другий закон Ньютона), Q(t)=cm(t - іо) -
кількість теплоти, що потрібна для нагрівання від температури іо до
t тіла масою т, питома теплоємність якого дорівнює с.
Областями визначення наведених функцій як математичних
формул є множина R, але вона звужується до множини додатних
дійсних чисел, а для останньої функції - до множини [іо; +00), як
що врахувати геометричний чи фізичний зміст величин, які визна
чаються цими формулами.
Область визначення функцій може звузитися ще більше, якщо Їх
застосувати до розв'язування конкретних задач. Так, область визна
чення функції Q(t) є відрізком [іо; 100], якщо розглядається задача
про нагрівання води.
Інколи функція може задаватися на різних проміжках різними
формулами. Наприклад, двома формулами задається функція
{ х2 - 1, якщо х < -2,
у-
З + х, якщо х > -2.
Трьома формулами задається функція сигнум х, У = signx (від
25
лат. SIgnum, що означає "знак"):
1,
якщо
х> О,
у = S1gnx =
{ О,
якщо
х = О,
-1,
якщо
х < о.
Словесний (описовий) спосіб. Іноді закон відповідності між
елементами двох множин формулюється за допомогою слів.
Прикладом такої функції є функція Діріхле п(х), яка визначена
на множині дійсних чисел і кожному раціональному числу ставить у
відповідність число 1, а ірраціональному - О:
{ 1, якщо х -- раціональне число,
п(х) =
О, якщо х - ірраціональне число.
Функція - ціла частина числа х, позначають ЇЇ [х], ставить у
відповідність кожному дійсному числу х найбільше ціле число, що не
перевищує х, тобто [х] = k, якщо х Е [k; k + 1) де k Е Z. Наприклад,
[2,7] = 2, [-2,7] = -з.
Різницю х - [х] позначають {х} і називають функцією - дробо
воючастиноючислах. Зокрема, {2,7} = 0,7, {-2,7} = -2,7-[-2,7] =
= -2,7 - (-з) = О,з.
З визначення функцій [х] і {х} випливає, що Е([х]) = Z, Е( {х}) =
= [О; 1).
Графічний спосіб. Нехай у = f( х) - деяка функція і хОу -
декартова система координат на площині. Графі-к;о.м фу'Н,-к;-ціі у = f( х)
називається множина точок площини з координатами (х; І(х)),
х Е п(л.
Припустимо тепер, що деяка множина Е на площині має з кож
ною прямою, перпендикулярною до осі Ох, не більше від однієї спіль
ної точки і нехай проекція Е на вісь Ох --- це деяка множина п. Тоді
саму множину Е можна розглядати як графік функції у = f(х), яка
задана на множині D і в кожній-точці хЕп набуває значення f(х),
26
. . - ""
яке ДОРІВНЮЄ ординаті єдиноі точки перетину прямоі, перпендику-
.1ЯРНОЇ до осі абсцис з множиною Е. Такий спосіб задання функції
називається графічним. Графічним способом можна задати функ
цію лише наближено, оскільки довжини відрізків вдається виміряти
лише з певною ТОЧНІСТЮ.
х
Не кожну множину на площині можна
вважати графіком деякої функції. Так, лінія
L, зображена на рис. 4, не може бути графі
ком жодної функції у = Лх), оскільки деякі
прямі, перпендикулярні до осі Ох, перетина
ють L більше ніж в одній точці.
Графічний спосіб задання функцій особ
ливо поширений в експериментальних дос
лгдженнях. У метеорології користуються
о
Рис.4
. . .
кривими, що описують ЗМІНу температури ПОВІТРЯ залежно ВІД часу,
тиску повітря на різних висотах тощо. Хоча графік зображає функ
цію наближено, бо бу дується за скінченною кількістю точок, проте
часто допомагає створити загальне уявлення про хід функції та 11
влаСТИВОСТІ.
На рис. 5 зображено графіки функцій sign х, [х], {х}.
S1gnx
у
{х}
L�
1 2 з:
1
а
В
РИС.5.
Інші способи задання функцій використовуватимуться РІДко.
Серед них згадаємо лише табличний, уявлення про нього можуть да-
27
вати таблиці функцій (тригонометричних, десяткових і натуральних
логарифмів тощо).
2.3. Складена функція. Припустимо, що задано дві функції
Х � U і U .г; У, де Х, U, У - підмножини множини дійсних
чисел. Тоді кожному числу х Е Х поставлено у відповідність єдине
число и = ЛХ) Е U і можна розглядати число У = у(и) = уи(х)) Е У.
Отже, для кожного х Е Х визначена функція и = І(х), а потім через
неї - функція У = у(и), що відображає множину Х в множину У.
ЦЯ функція називається складеною, або суперпозицією фУ'Н,'/'ї,цій j і
у, і позначається У = уи(х)). Для складених функцій застосовують
також позначення У = 9 о f( х), іноді пишуть Х .Е, U .г; У.
Існують складені функції, що записуються за допомогою трьох
і більше функцій, наприклад, У = g(f(h(x))).
Приклад 1. Записати складені функції за допомогою декількох
функцій: а) У = уІ1- х2; б) Z = (хз + 1)2.
Розв 'язання. а) Якщо УІ = х2, У2 = 1 - УІ, уз = #2, то У
= Уз (У2 (УІ(Х))).
б) Якщо ZI = хз, Z2 = ZI + 1, Zз = zi, то z = ZЗ (Z2 (ZI(X))).
Приклад 2. Записати складені функції у=у (І(х)) і z=j (у(и)),
якщо ЛХ) = х2 + 4, у(и) = .JГ=U.
Розв 'язання. Знаходимо: Е(f) = [4; +00), п(у) = (-оо; 1]. Ос
кільки Е(f) if. п(у), то складена функція уи(х)) не існує.
Далі оскільки Е(у) = [О; +00) с R = п(f), то z = Лу(и)) =
2
= (vг=u) + 4 = 5 - и, и Е (-оо; 1].
2.4. Числові послідовності.
Означення. Функція j називається послідовністю, якщо облас
тю її визначення є множина натуральних чисел У = і(n), n Е N.
Традиційно для послідовностей використовують дещо інші по
значення і термінологію. Так, значення функції І(n) позначають Уп
(можна застосовувати також будь-які інші букви латинського алфа
віту) і називають n-м (або загальним) членом (або елементом) по-
28
елідовності (якщо n = 1, отримуємо перший член УІ, якщо n = 2 -
другий У2 і т.д.). Тоді послідовність Уn = Лn), n Е N можемо запи
сати у ВИГЛЯДІ
УІ , У2, ... ,Уn,···
(19)
Важливо, яке МІсце займає кожен елемент у цьому запису. Зміна
елементів місцями дає іншу послідовність. Для послідовності (19)
застосовують також записи {Уn} або Уn, n Е N.
Числову послідовність як частковий випадок функції можна за
давати тими самими способами, що й функцію дійсного аргументу
(аналітичним, словесним тощо). Послідовність можна також визна
чити, якщо задати перший її елемент або декілька перших елементів
і правило утворення n-го елемента за допомогою попередніх. Та
кий спосіб задання називається рекурентним (від лат. гесцггепв, що
означає "зворотний").
Прикладами послідовностей, що задаються рекурентним спосо
бом, є арифметична та геометрична прогресії. Справді, арифметич
на прогресія - це послідовність {ап}, кожен член якої, починаючи
. .
з другого, ДОРІВНЮЄ попередньому, до якого додається одне І те са-
ме стале число d. Тому арифметична прогресія задається умовами
аІ = а, аn+І = а., + d. Геометрична прогресія - це послідовність
{Ьn}, перший член якої Ь1 f= о, а кожен член, починаючи з друго-
. .
ГО, ДОРІВНЮЄ попередньому, помноженому на одне І те саме число
q f= о. Тому геометрична прогресія задається умовами ЬІ = Ь f= о,
Ьn+І = bnq.
Послідовність {Уn} можна зобразити графічно точками (n; Уn) у
декартовій системі координат. Однак зручніше зображати її точка
ми на числовій осі, що мають координати Уn, хоча так важче відтво-
. . . .
рити ВІдносне розташування елементгв ПОСЛІДОВНОСТІ.
Приклад 1. Записати перші 4 члени послідовності
( _1)71
Уn = n Е N.
n2 + І '
29
Розв 'язання.
1 1 1
У2 = 5"' УЗ = - 1 о' У4 = 17·
Приклад 2. Послідовність {ап} задана умовами аl = о, а2 = 1,
аn+2 = аn+l . ап - 1. �найти члени аз, а4, а5, аб.
Розв 'язання. аз = 0·1 - 1 = -1, а4 = -2, а5 = 1, аб = -з.
Приклад 3. Записати формулу загального члена послідовності,
заданоі умовами аІ = 1, ап = 2аn-l + 1, n = 2, з, ....
Розв 'язання. Очевидно, що для перших чотирьох членів послі
довності маємо аl = 1 = 21 - 1, а2 = З = 22 - 1, аз = 7 . 2З - 1,
а4 = 15 = 24 - 1. Тепер природно припустити, що ап = 2n - 1,
n Е N. ЦЮ формулу легко довести (зробіть це самостійно) методом
математичної шдукцп,
Введемо ще одне важливе поняття - поняття nідnослідов'Н,осmі.
Розглянемо послідовність {Уn} і деяку послідовність, складену з різ
них натуральних чисел Пl < П2 < ... < nk < ... , kEN, розташова
них за іх зростанням. Виберемо з послідовності {Уn} лише елементи
. . .
з номерами Пl, П2, ... , nk, ... І складемо з них нову ПОСЛІДОВНІСТЬ
ZI = УnІ' Z2 = Уn2' ... , Zk = Ynk' ... , kEN. (20)
Цю послідовність називають підпослідовністю послідовності {Уn} і
позначають {Ynk}. З побудови випливає, що під множина (20) елемен
тів послідовності (19) є підпослідовністю цієї послідовності, якщо для
будь-яких двох елементів YТIk' Ynk' нерівність k < k' справджується
тоді і тільки тоді, коли nk < nk', ь е н, k' Е N.
3ауваже'lt'Н,,я,. Якщо послідовність трактувати як функцію нату-
. . .
рального аргументу, то ПІДПОСЛІДОВНІСТЬ можна визначити також як
звуження послідовності на деяку необмежену підмножину множини
натуральних чисел.
Приклад 4. Серед послідовностєй
1, 2, з, 4, 5, ... , П, ...
(21)
зо
З, 4, 5, ... , n, ...
(22)
(2З)
(24)
2, З, 4, 5, ... , n, ...
З, 2, 4, 5, ... , n, ...
. . .
вказати ПІДПОСЛІДОВНОСТІ.
Розе'язання. Послідовність (24) є підпослідовністю (21), (22),
(2З); послідовність (22) є підпослідовністю (21); послідовності (21) і
(2З) не є підпослідовностями ніяких інших з цих послідовностей.
2.5. Загальні властивості функції.
а) Монотонні функції.
Означення 1. Функція у = ЛХ) називається зростаючою (1іе
сnад1іОЮ) на множині D, якщо для довільних двох точок ХІ < Х2 З
множини D виконується нерівність f( х І) < f( Х2) (f (Х 1) ::; f( Х2 )).
Ордината Лх) графіка зростаючої (неспадноі) функції збіль
шується (не зменшується), якщо абсциса Х збільшується (рис. 6, а, б).
у
у
у
о
о
х
х
х
х
а
б
в
г
Рис. 6. Монотонні функції
Означення 2. Функція у = ЛХ) називається спадною (1іезрос
таючоюї на множині D, якщо для довільних двох точок ХІ < Х2 З
множини D виконується нерівність Лх}) > ЛХ2) (Лх]) � ЛХ2)).
Ордината ЛХ) графіка спадної (незростаючої) функції зменшу
ється (не збільшується), якщо абсциса Х збільшується (рис. 6, в, г).
Зростаючі, неспадні, спадні та незростаючі функції об'єднують
ся однією назвою "монотонні" функції, причому зростаючі і спадні
ЗІ
називають строго монотонними, а незростаючі 1 неспадні ---- нестро
го монотонними.
Приклади.
1. Функція у = ох + Ь, де о і Ь - сталі, зростає на множині R,
якщо о > О і спадна, якщо 0<0.
Якщо о = О, то у = Ь - стала функція, а тому вона є і незрос
таючою, 1 неспадною.
2. Функція у = хЗ зростає на множині R.
3. Функція ЛХ) = � спадає на (-оо; О) і (О; +00), але не є спад
ною на множині R\{O}, бо, наприклад, Л-I) = -1 < ЛI) = 1.
4. Функція у = х2 не є монотонною, якщо її розглядати для усіх
дійсних значень х. Проте ця функція зростає на (О; +00) і спадна на
(-оо; О).
5. Неспадними є функції у = sgnx і у = [х] (рис.5,а, б).
6. Функція у = {х} не є монотонною на R, але на кожному про
міжку [k; k + 1), k Е Z, вона зростаюча (рис.5,в).
7. Функція Діріхле D(x) (див. п.2.2) не є монотонною на жод-
. - .
ному ПРОМІЖКУ числової ОСІ.
б) Парні та непарні функціі
Означення 3. Функція у = ЛХ), область визначення якої D(f)
є симетричною ВІДНОСНО початку координат, називається nар'Н,ою
(відповідно непарною'[, якщо для кожного х Е D(f) виконується рів
ність Л-Х) = ЛХ) (відповідно Л-Х) = -ЛХ)).
Приклади парних функцій -- х2; х2n, n Е Z; Іхl; cosx. Непарни
ми є функції sign х; х2n+1, n Е Z; sin х, tg хІ ctg х.
3 означення випливає, що графік парноі функції симетричний
відносно осі ординат Оу, а графік непарноі функції симетричний
відносно початку координат (точки 0(0; О)). Тому, щоб побудувати
графік парної чи непарної функціі, досить побудувати його для до
датних значень х 2:: О, а для х < О частину побудованого графіка
для парноі функції дзеркально відобразити відносно осі ординат, а
для непарної функції -- відобразити симетрично відносно початку
координат (тобто виконати подвійне дзеркальне відображення щодо
32
обох координатних осей).
х
У
а
б
Рис. 7. Парні і непарні функції
Зокрема, графік парної функції у = Іхl (рис. 7, а) можна отри
мати як об'єднання бісектрис двох координатних кутів: першого
(графік У = Іхl = х, якщо х � О) і другого (графік У = Іхl = -х,
якщо х < О).
Графік непарноі функції У = xlxl (рис. 7,б) можна одержати як
об'єднання правої гілки параболи У = х2 (графік У = xlxl = х2, якщо
Х � О) і лівої гілки параболи У = _х2 (графік У = xlxl = _х2, якщо
Х < О).
в) Періодичні функції.
Означення 4. Функція У = Лх), визначена на деякій множині
D, називається періодичною, якщо існує таке число Т f=. о, що для
усіх xED числа х - Т і х + Т також належать D і виконується
рівність ЛХ ± Т) = лх).
Число Т називається періодом фу'Н,'К'Ціі; кажуть також, що функ
ція лх) Т-періодична.
Кожна періодична функція має нескінченну множину періодів.
Пропонуємо читачам самостійно довести, що періодом T-періодичноЇ
функції є кожне з чисел ±nТ, де n - будь-яке натуральне число.
33
Якщо серед УСІХ періодів періодичної функції існує найменший
додатний період, то він називається основним періодом ФУ1f,'/\,чіі.
Приклади.
1. Функція у = const періодична, її періодом є будь-яке дійсне
число; основного періоду функція не має.
2. Функція Діріхле (п.2.2) періодична, її періодом є будь-яке
раціональне число; основного періоду функція не має.
з. Функція у = {х} (дробова частина числа х) періодична, її
періодом є довільне ціле число; основний період функції - 1.
4. Тригонометричні функції sin х, cos з: періодичні, основний пе
ріод -- 27r.
5. Тригонометричні функції tg х, ctg з: періодичні, основний пе
рІОД -- 7r.
Щоб одержати графік Т-періодичної функції, досить побудувати
його на довільному відрізку, що має довжину Т, після чого, змінюючи
побу дов ану частину графіка вздовж осі абсцис ліворуч і праворуч на
відстань Т, 2Т, 3Т тощо, отримаємо графік функції на всій області
визначення.
Встановлюючи періодичність функцій, часто користуються та
кими твердженнями.
Якщо у = f( х) - періодична функція з основним періодом Т, то
основний період функції у = f( ах + Ь) є I�I.
Якщо дві періодичні функції мають однаковий період Т (він мо
же бути дЛЯ них основним), то алгебраїчна сума, добуток і частка
цих функцій є періодичними, мають період Т, але дЛЯ НИХ вІН може
виявитися неосновним.
Наприклад, основним періодом функцій cos2 х, sin2 х, сов" х,
sin4 з: є л , але функція у = cos2 x+sin2 х = 1 не має основного періоду,
а основним періодом функції у = сов" Х + віп 4 з: є Т = і.
Сума, добуток і частка двох періодичних функцій, що мають
різні періоди ТІ і Т2, Є функціями періодичними, якщо �� -- ра
ціональне число, але й можуть виявитися неперІОДИЧНИМИ, якщо
f; _ .. ірраціональне число.
34
г) Обмежені та необмежені функції.
Означення 5. Функція у = лх) називається обмеженою на
множині D, якщо існує таке число М > О, що для всіх xED вико
нується нерівність IЛх)1 � М,
3 означення випливає, що графік обмеженої функції знаходить
ся в горизонтальній смузі {(х; у) І х Е R, - М � у -:; М}, симетричній
відносно осі абсцис.
Очевидно, що функція є обмеженою також і тоді, коли можна
вказати хоча б одну горизонтальну смугу {(х; у) І х Е R, m < у < М},
-оо < m < М < +00, що містить графік функції. Тому означення
5 еквівалентне такому: функція у = f( х) називається обмеженою на
множині D, якщо існують такі два дійсні числа m іМ, що для всіх
«є о виконуються нерівності m < f (х) � М.
Функція називається необмеженою на множині D, якщо вона мо
же набувати як завгодно великі значення тобто, якщо для бу дь- якого
числа М > О знайдеться таке хо Е D, що If(хо)1 > М. Графік необ
меженої функції виходить за межі будь-якої горизонтальної смуги.
Приклади.
1. Функція у = х2 обмежена на довільному скінченному проміж
ку [а; Ь]. Справді, якщо х Е [а; Ь], то, позначивши як М більше з двох
чисел а2, Ь2, маємо нерівність О � х2 � М. На всій числовій осі ця
функція є необмеженою, бо для довільного М > 1 і х � 1У! вико
нується нерівність х2 � 1'vf2 > М. Пропонуємо читачам довести, що
функція х2 необмежена на довільному нескінченному проміжку.
2. Функція у = � необмежена на проміжку (О; +00), бо вона на-
х
буває як завгодно великі значення в околі точки о. Ця сама функція
вже є обмеженою на проміжку [а; +00), а > О, бо О < � -:; �, якщо
х> а.
2.6. Обернена функція. Розглянемо функцію у = ЛХ), об
ласть визначення якої є Х = D(f), а область значень --- У = Е(!) =
= {Лх) І х Е Х}. Тоді кожному значенню х Е Х відповідає єдине
35
значення у Е У, що дорівнює ЛХ), тобто у = ЛХ).
Задамо тепер у і спробуємо розв'язати рівняння ЛХ) = у ВІД
носно Х У множині Х. Очевидно, що це рівняння має хоча б один
розв' язок, якщо у Е У (а всіх таких розв'язків може бути декілька
або й нескінченна кількість).
Якщо рівняння ЛХ) = у має лише один розв'язок з: Е Х, цей
розв'язок, очевидно, є функцією змінної у, яка кожному значенню
у Е У ставить у відповідність таке значення з: ЕХ, що у = f( х). Цю
функцію, областю визначення якої є множина У, а областю значень
- множина Х, позначають з: = і-І (у) і називають оберненою до
(прямої) фу'Н,'Х:'Ціі у = ЛХ).
Якщо х = і-І(у), У Е У, є функція, обернена до у = і(х), з: Е Х,
то очевидно, що у = f( х) є оберненою до функції з: = і-І (у). Тому
функції у = f( х) і з: = і-І (у) Є в заемно оберненими.
З вищесказаного випливає, що обернена функція існує тоді і
лише тоді, коли для кожного у Е У рівняння f( х) = у має один
розв'язок у множині Х. А розв'язок такого рівняння єдиний тоді і
лише тоді, коли будь-яким двом різним значенням хІ 1 Х2 З множини
Х відповідають різні значення функції:
(25)
Отже, ця умова (вона називається умовою однолистості ), вико
нання якої вимагається для будь-якої пари різних значень хІ і Х2
аргументу з множини Х, є необхідною і достатньою для існування
функції і-І (у), оберненої до ЛХ). Серед функцій, для яких вико
нується умова (25), тобто існують обернені, найбільший практичний
інтерес становлять строго монотонні функції.
З визначення оберненої функції випливають такі наслідки.
1. Області визначення і значень прямої та оберненої функцій і
і і-І пов'язані умовами D(f) = Еи-l), D(f-I) = Е(Л.
2. Для довільних Х Е D(f) і у Е D(f-I) виконуються рівності
і-І и(х)) = х, і и-І(у)) = У і правильним є твердження: ЛХ) =
= у {:} і-І (у) = х.
36
3. Якщо функція у = лх) є зростаючою (спадною), то обернена
функція х = І-l(у) Є також зростаючою (спадною).
4. Якщо для непарноі функції існує обернена функція, то ця
обернена функція є також непарною.
Розглянемо тепер функцію І, що не є однолистою на множині
Х; тоді оберненої до функціі j не існує. Але якщо вибрати таку
підмножину ХІ множини Х, на якій звуження /І = j І ХІ функції j
є однолистим, то можна побудувати функцію, обернену до звужен
ня /І. Оскільки для неоднолистих функцій існують різні однолисті
звуження, то обернені до цих звужень функції також будуть різними.
Приклади.
1. Розглянемо функцію
у = 2х + 3.
(26)
Тут Х = R = У і функція зростає. Розв'язуючи рівняння (26)
відносно х, знаходимо обернену функцію х = Ну - 3).
2. Дослідимо функцію у = х2 на множині R. Оскільки х2 -
неоднолиста функція (бо (_х)2 = х2), то оберненої до неі функції
не існує. Звузимо область визначення R, розглянувши іншу функцію
у = х2, Х Е [О; +00)_ Обернену до неї функцію знайдемо як невід'єм
ний розв'язок рівняння у = х2: х = Vfj. Функція у = х2, Х Е (-оо; О),
дає змогу побудувати ще одну обернену функцію х = -Vfj.
Зауважимо, що, вибираючи інші області однолистості функції
х2, можемо будувати інші обернені до неї функції. Так, наприклад,
оберненою до функції у = х2, х Е [-1; О) U [1; +00), є функція
{ Jy, у? 1,
х = _Jy, О < у < 1.
Нижче (п.2.7) наведемо інші приклади обернених функцій.
Розглянемо графік оберненої функції. З визначення взаємно
обернених функцій у = Лх), х Е Х і х = І-l(у), У Е У, випливає,
37
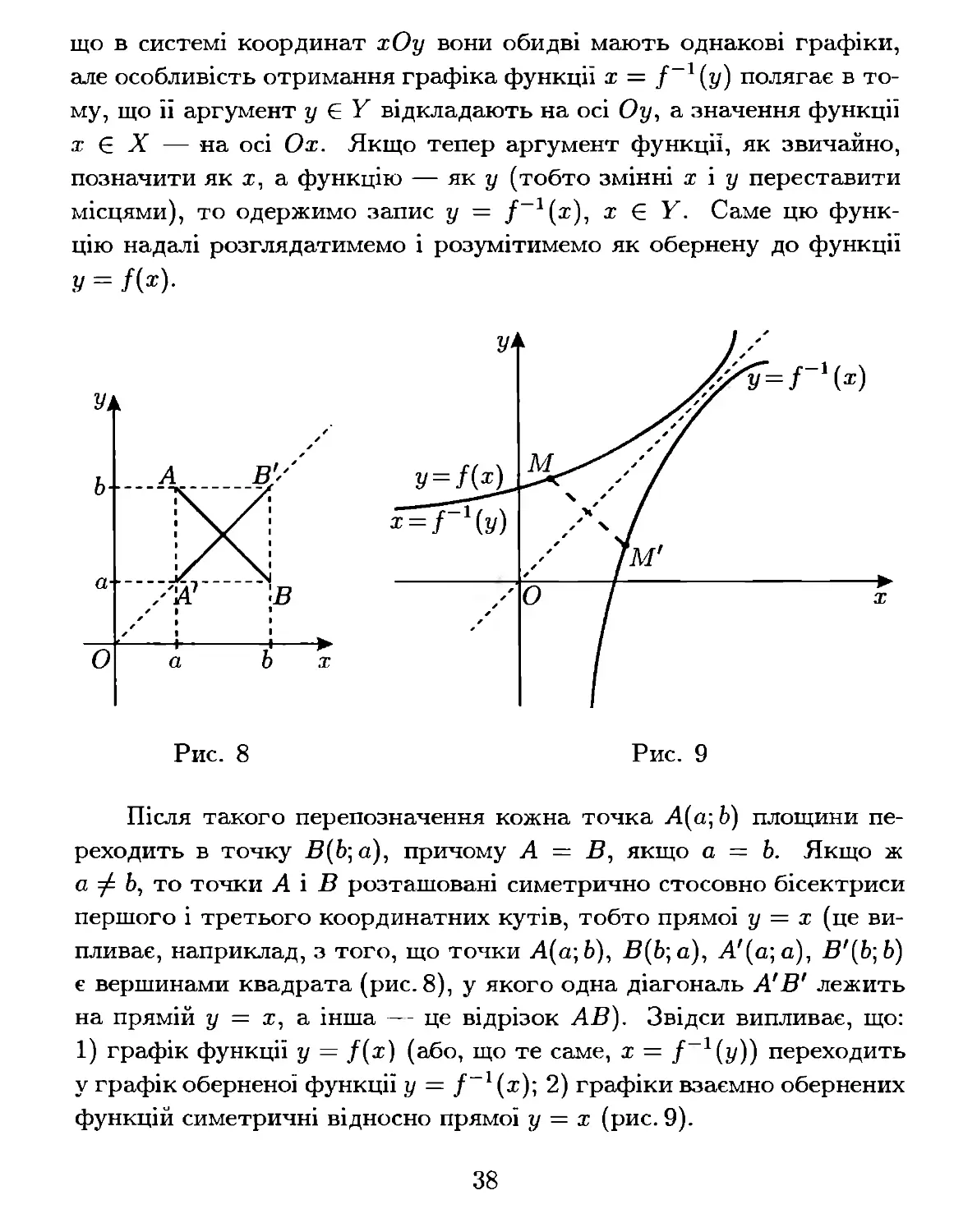
що в системі координат хОу вони обидві мають однакові графіки,
але особливість отримання графіка функції х = і-І (у) полягає в то
му, що її аргумент у Е У відкладають на осі Оу, а значення функції
х Е Х - на осі Ох. Якщо тепер аргумент функціі, як звичайно,
позначити як х, а функцію - як у (тобто змінні х і у переставити
місцями), то одержимо запис у = і-l(х), Х Е У. Саме цю функ
цію надалі розглядатимемо і розумітимемо як обернену до функції
у = лх).
у
у
,
,
,
Ь
,
,
,
,
,
,
О
х
,
,
,
,
,
,
,
О
а
Ь
х
Рис.8
Рис.9
Після такого перепозначення кожна точка А( а; Ь) площини пе
реходить в точку В(Ь; а), причому А = В, якщо а = Ь. Якщо ж
а =J Ь, то точки А і В розташовані симетрично стосовно бісектриси
першого і третього координатних кутів, тобто прямої у = х (це ви
пливає, наприклад, з того, що точки А(а; Ь), В(Ь; а), А'(а; а), В'(Ь; Ь)
є вершинами квадрата (рис. 8), у якого одна діагональ А' В' лежить
на прямій у = х, а інша-- це відрізок АВ). Звідси випливає, що:
1) графік функції у = ЛХ) (або, що те саме, х = і-І (у)) переходить
у графік оберненої функції у = і-l(х); 2) графіки взаємно обернених
функцій симетричні відносно прямої у = х (рис.9).
38
Отже, щоб побудувати графік оберненої функції, якщо відо
мо графік прямої, потрібно дзеркально відобразити графік прямої
функції відносно бісектриси першого і третього координатних ку
ТІв.
2.7. Основні елементарні функції.
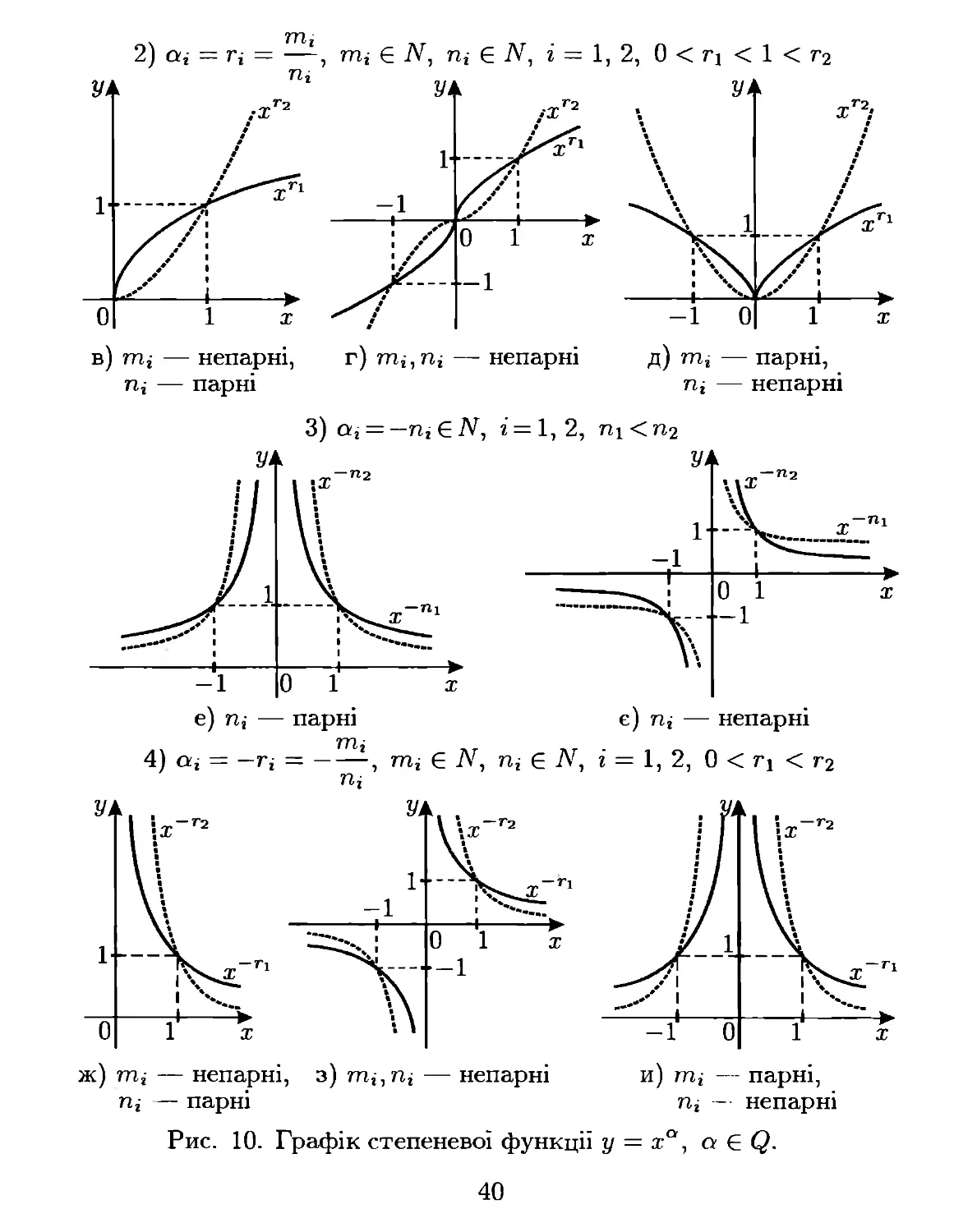
Степенева функція. Степеневою називається функція у = хО,
Q Е R. Розглянемо її для різних значень показника а.
Припустимо спочатку, що о: - раціональне число і о: > О; ТОДІ
у(О) = о.
1) о = n, n EN, у = хn, D(y) = R.
Якщо n парне, то Е(у) = [О; +00), функція парна, зростає на
[0;+00) і спадає на (-00;0] (рис.10,а)).
Якщо n непарне, то Е(у) = R, функція непарна, зростає
(рис.10,б)).
2) о = т, де mEN, n Е N і m - нескоротний дріб, у = x�.
n n
Якщо n парне, то D(y) = Е(у) = [О; +00), функція зростає
(рис. 10, в).
у
у
б) nі ---- непарні
39
у
1
о
В)
1 х
г)
ті - непарН1,
nі - парН1
непарні
1, 2, О < ТІ < 1 < Т2
У
-1 О 1
д) ті - парН1,
nі - непарН1
х
-1
о
х
1
у
х
1
\�-n2
'.
.... -nl
--- Х
: ._------------_.
-1
о 1
-1
є) nі - непарні
ті Е N, іі, Е N, z 1, 2, О < ТІ < Т2
у
у
1
-1
о 1
-1
х
х
ж) ті непарні, з) ті, nі - непарні
nі - парН1
Рис. 10. Графік степеневої функції у
40
х
и) ті парні,
nі непарні
xa,OEQ.
Якщо тіп непарні, то D(y) = Е(у) = R, функція непарна,
зростає (рис. 10, г).
Якщо m парне, n непарне, то D(y) = R, Е(у) = [О; +00), функція
парна, спадає на (-оо; О] і зростає на [О; +00) (рис.10, д).
Нехай тепер а - раціональне число і а < о. На рис.10, е-и зоб
ражено графіки функції у = ха, якщо 3) а = -n, n Е N, і 4) а = - ';:,
де mEN, n Е N і ';: - нескоротний дріб. Пропонуємо читачам за
цими графіками проаналізувати властивості функції аналогічно, як
це було зроблено для випадків 1 і 2.
Якщо а - ірраціональне число, то коли а > О, D(y) = Е(у)
= [О; +00) і функція у = ха зростає, а якщо а < О, D(y) = Е(у)
= (О; +00) і функція спадає.
Графіки функції у = ха, а Е R в околі точки х = 1 для РІЗНИХ
значень показника а зображені на рис. 11; всі графіки проходять
через точку (1;1).
2 х
у
2
І , .
1 -----------: "г:
у=х/З
Рис. 11. Графіки функції у = ха, а Е R, в околі точки х = 1.
Показникова функція у = а", а> О, а # 1 (рис. 12). D(y) = R,
Е(у) = (О; +00). Функція зростає, якщо а> 1 і спадає, якщо О < а < 1.
Графіки функції для різних значень а проходять через точку (0;1),
41
тобто аО = 1.
Рис. 12. Показникова функція
О < Ь2 < Ь1 < 1 < аl < а2
Рис. ІЗ. Логарифмічна функція
Логарифмічна функція у = loga І, а > О, а і= 1 (рис. ІЗ).
Функцію можна розглядати як обернену до показниковоі у = а":
Тому D(loga І) = (О; +00), Е(у) = R. Функція зростає, якщо а > 1
і спадає, якщо О < а < 1. Графіки функції для різних значень а
проходять через точку (1;0), тобто loga 1 = О.
Тригонометричні функції" у = sin І (рис. 14), у = cos І
(рис. 15). Для обох функцій п(у) = R, Е(у) = [-1; 1], обидві функції
періодичні з основним періодом Т = 2п. Функція У = sin І непарна,
а у = сов л - парна.
z=s:::::J7-�::::::: :
-21r :-=-:���"
Рис. 14. Графік у = sin І
Рис. 15. Графік у = cos І
* в математичному аналізі аргументи тригонометричних функцій
розглядаються в радіанній МІрІ.
42
Функція у = sin х монотонна на проміжках [k7r - f; k7r + І]'
k Е Z, а саме: проміжками зростання є відрізки [2nп - І; 2nп + І]'
nEZ, а проміжками спадання - [(2n + l)п - І; (2n + l)п + f],
n Е Z. Графік функціі перетинає вісь Ох у точках х = k7r, k Е Z.
Функція у = cos х монотонна на кожному проміжку (k7r; k7r + п],
k Е Z, а саме: проміжками зростання є відрізки (2nп-п; 2nп], nEZ,
а проміжками спадання - (2nп; 2nп + п], n Е Z. Графік функції
перетинає вісь Ох у точках х = k7r + І, k Е Z.
Тригонометричні функції y=tgx (рис. 16), y=ctgx (рис.17).
D(tgx) = (k7r-f;k7r+f), k Е Z, E(tgx) = R; D(ctgx) = (k7r;k7r+f),
k Е Z, Е( ctg х) = R. Обидві функції періодичні з основним періодом
т = п, обидві функції непарні.
Функція у = tg х зростає на кожному проміжку (k7r - f; k7r + І) ,
k Е Z. Графік функції перетинає вісь Ох у точках х = Іеп , k Е Z.
Функція необмежена в околах точок х = k7r + І, k Е Z.
Функція у = ctg х спадає на кожному проміжку (k7r; Ьг + п),
k Е Z. Графік функції перетинає вісь Ох в точках х = k7r + f, k Е Z.
Функція необмежена в околах точок х = Ісп , k Е Z.
у
у
:п х
І
І
Рис. 16. Графік функції y=tgx
Рис. 17. Графік функції у = ctg х
Обернені тригонометричні функції. Очевидно, що триго
нометричні функціі неоднолисті хоча б через те, що періодичні, а
43
тому ЗГІДно з п. 2.6 обернені до них функції не існують. Зате
існують однолисті звуження тригонометричних функцій і саме обер
нені функції до деяких з тих звужень називаються оберненими три
гонометричними функціями.
Детальніше опишемо побудову функції у = arcsinx. З-поміж різ
них можливих однолистих звужень функції у = sin х виділимо лише
монотонні звуження у = sinx, х Е [7rk - �;7rk + �], k Е Z, а серед
них, прийнявши k О, - одне, що монотонно зростає у = sin х,
х Е [-�; �], Е(у) = [-1; 1]. Функція, обернена до цього звужен
ня, називається арксинусом, у = arcsinx, х Е [-1; 1], E(arcsinx) =
= [-�; �]. Ця функція монотонно зростає, є непарною і аrсsіn 0= о.
Графік у = агсвіп х показано на рис. 18. Його, як графік оберненої
функції, можна отримати, відобразивши графік функції у = sin х,
х Е [ - �; �], симетрично відносно бісектриси першого і третього
координатних кутів.
Аналогічно визначають інші обернені тригонометричні функції.
Опишемо Їх коротко.
Функція у = arccosx, х Е [-1; 1] (рис. 19), _. це функція, оберне
на до звуження у = cosx, х Е [о; п]. Тоді E(arccosx) = [О; п], функція
спадає, агссов О = �.
у
у
х
Рис. 18. Графік у = агсвіп х
Рис. 19. Графік у = агссов х
Функція у = arctg х, х Е R (рис.20), -- це функція, обернена до
звуження у = tgx, х Е (-�; �). Тоді E(arctgx) = (-�; �), функція
непарна, зростає, arctg О = о.
44
Функція у = arcctgx, х Е R (рис. 21), - це функція, обернена
до звуження у = ctgx, х Е (О;п). Тоді E(arcctgx) = (О;п), функція
спадає, arcctg О = І.
у
Рис. 20. Графік у = arctg х
-3 -2 -1
о 1 2 3 х
Рис. 21. Графік у = arcctg х
Означення. Основними елементарними функціями називають
ся функції, розглянуті в цьому параграфі: у = С, С - стала, степе
нева - у = ха, Q Е R, показникова - у = аХ, а > О, логарифмічна -
у = loga х, а > О, а #- 1, тригонометричні - у = sinx, у = cosx,
у = tg х, у = ctg х, і обернені тригонометричні - у = агсвш х,
у = агссов х, у = arctg х, у = arcctg х.
45
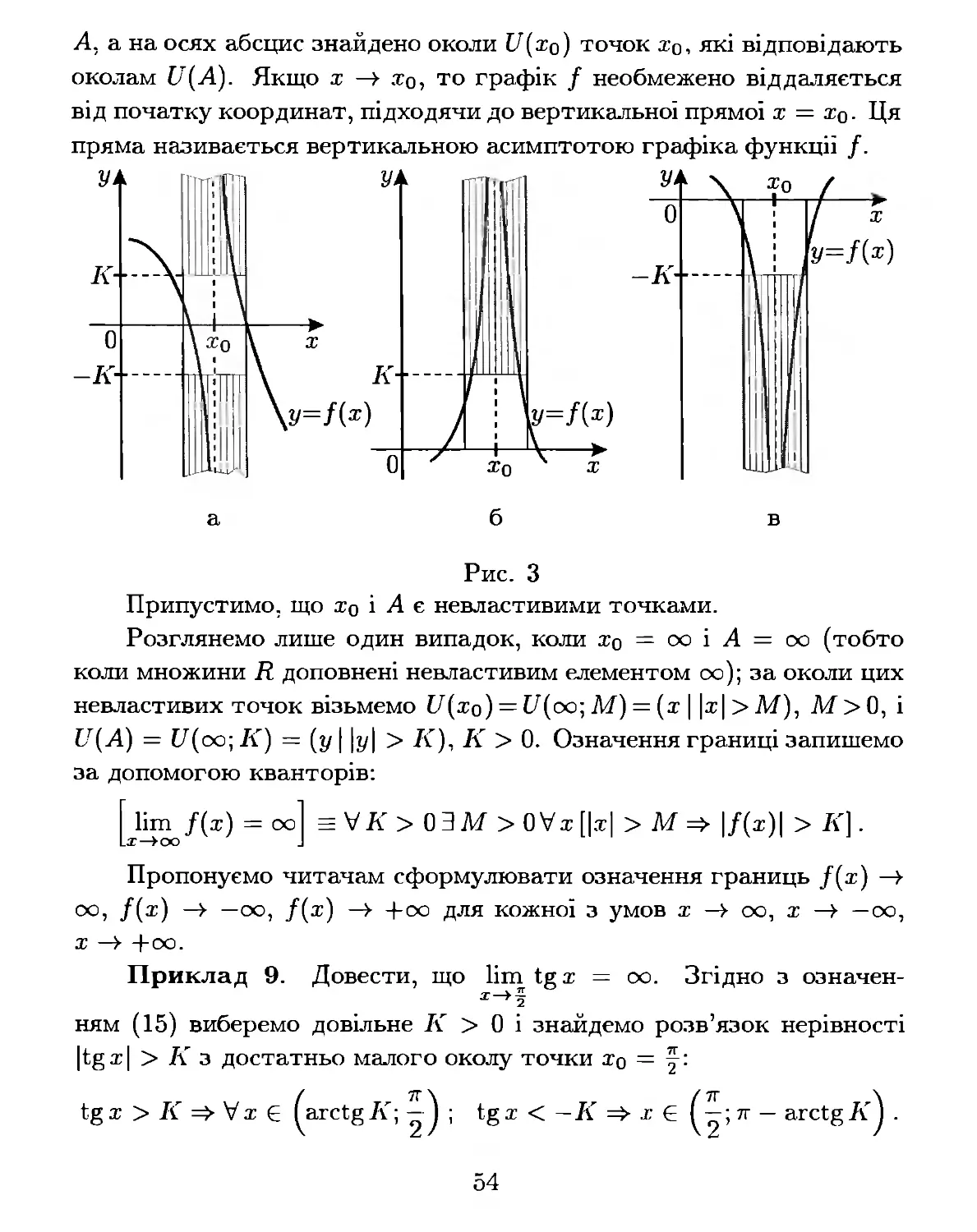
Розділ 2. ГР АНИЦЯ. НЕПЕРЕРВНІСТЬ ФУНКЦІЇ
§ 1. Границя функції
1.1. Означення границі функції.
а) Загальний випадок. Одним з основних понять в матема
тиці є поняття границі. Воно характеризує величину, яка, змінюю
чись, стає все ближчою і ближчою до деякої сталої; цю сталу звичай
но називають границею, Якщо змінною величиною є деяка функція
у = j (х), то для розв'язування практичних задач важливо окремо ви
ділити той випадок, коли значенням х, які наближаються до деякого
значення Хо, відповідають значення і(х), які наближаються до дея
кої сталої А. ДЛЯ описання подібної ситуації застосовують поняття
границі функції в точці.
Нехай у = f( х ) - функція, визначена в деякому околі точки
хо Е R, крім, можливо, самої точки хо і А Е R.
Означення 1. Число А Е R називається границею функції f( х )
в точці хо Е R, якщо для будь-якого околу И(А) числа А існує такий
окіл U (хо) точки Хо, що для всіх х Е U (хо) \ { хо} виконується умова
ЛХ) Е И(А).
Той факт, що А є границею функції f( х) в точці Хо, записують
так:
Ііш ЛХ) = А або ЛХ) -t А.
Х-+Хо Х-+Хо
Кажуть також, що А є границею функції ЛХ), якто х прямує
до хо. За допомогою кванторів означення границі в точш можна
подати так:
[Ііш f( х) = А] ===
Х-+Хо
(1)
='v'U(A)3U(;ro)'v'x[x Е и(хо)\{хо}::::} ЛХ) Е И(А)]
46
або, що те саме --
[Ііш Лх) = А] = 'v' И(А):3 и(Ха) [J (и(Ха)\{Ха}) с И(А)].
x-tхQ
Надалі частіше користуватимемося записом (1) означення границі.
Шодо самої точки Ха, то f( Ха) може дорівнювати довільному зна
ченню з R або навіть не існувати зовсім.
Приклад І. Довести, що Іігп С = С для кожного Ха Е R і
x-tхQ
с е н.
Розв 'язання. В означенні (1) приймемо f( Х) = С, Х Е R, А = С
і задамо довільний окіл И(С) точки С. Тоді для всіх Х Е R маємо
f( Х) = С Е U ( С). Тобто за окіл U (Ха) можна взяти всю множину Н.
Отже, Іігп С = С.
x-tХQ
Приклад 2. Довести, що Іігп Х = Ха для кожного Ха Е Н.
x-tХQ
Розв 'язання. В означенні (1) приймемо f( Х) = Х, Х Е R, А =
= Ха і задамо довільний окіл U (А) = U (Ха) точки А. Тоді для усіх
Х Е и(Ха) маємо Лх) = Х Е И(А). Тому Іітп Лх) = Іігп Х = Ха.
x-tХQ x-tХQ
Для аналізу означення 1 виділимо два випадки: 1) обидва числа
Ха і А скінченні, тобто Ха Е R і А Е R; 2) хоча б одне з чисел Ха або
А нескінченне (невластиве).
б) Скінченний випадок: Ха Е R, А Е Н.
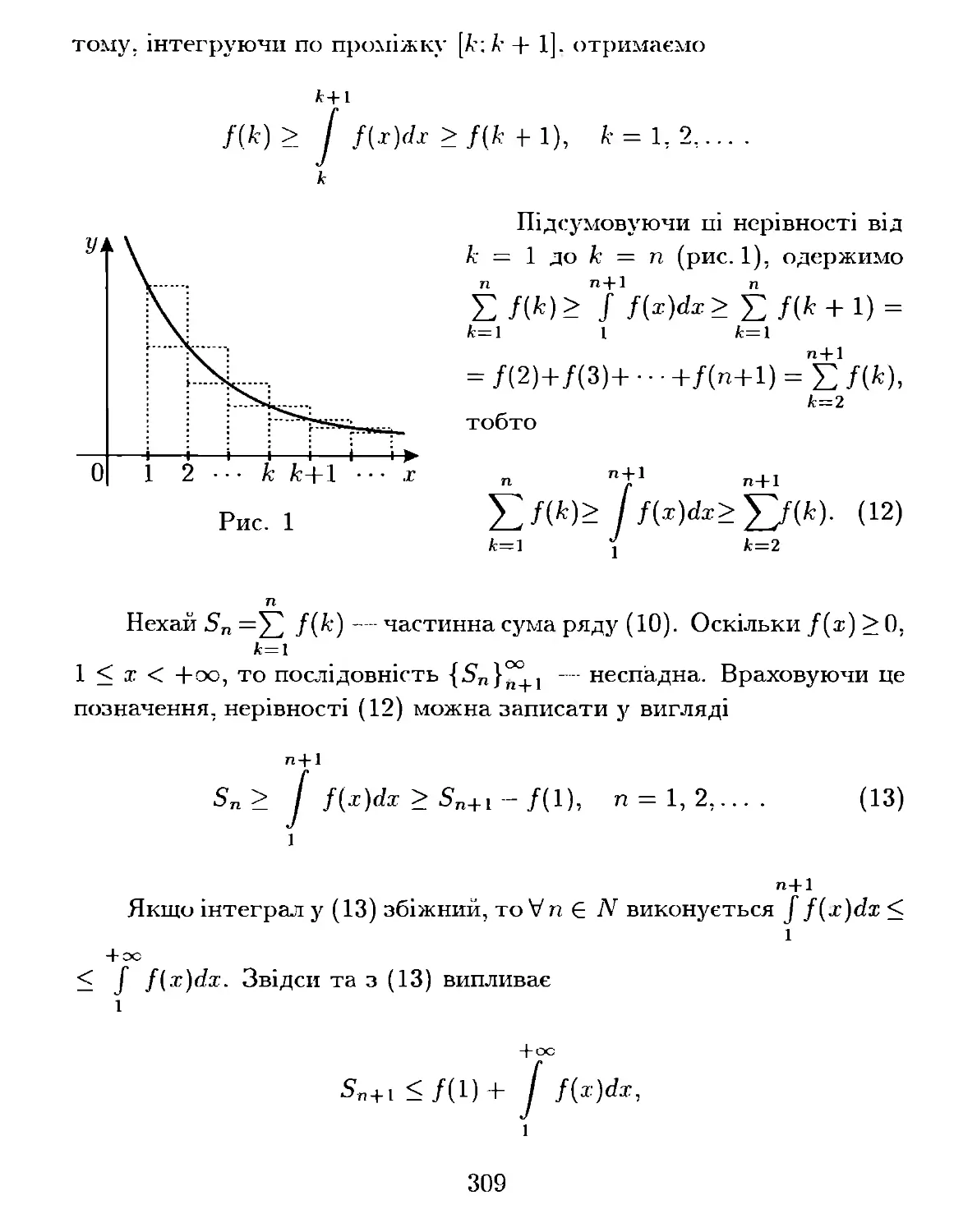
На рис. 1 наведено графік функції і, для якої Іігп Лх) = А.
x-tХQ
Справді, на осі ординат зображено довільний окіл И(А) точки А, а
на осі а6сцис за околом И(А) побудовано такий окіл и(ха) точки Ха,
що j (и (Ха) \ { Ха}) С U (А). Якщо значення Х мало відрізняються від
Ха, то значення функції Лх) мало відрізнятимуться від А. 3 рис. І
зрозуміло, що звуження околу U (А) не призводить до розширення
околу и(Ха).
Повернемося до означення І. Окіл И(А) часто замінюють симет
ричним околом U (А; є), а окіл U (Ха) .-- симетричним околом U (Ха; о).
Оскільки тоді ці околи залежать лише від чисел є та О, а умови
47
х Е И(хо;Ь)\{хо} і лх) Е и(А;є) еквівалентні відповідно нерівно
стям О < Іх - хоl < ь і IЛх) - АІ < є, то означення 1 еквівалентне
означенню 2.
О
Означення 2. Число А Е R
у = J( х ) називається границею функціі j
у
[--- ---- � ----_.
И(А) А _
�
- ->7 '!
...., , !
в точці хо Е R, якщо для довіль
ного є > О існує Ь > О, що для
.. .
ВСІХ Х, які задовольняють неРІВ-
ності О < Іх - хоl < ь, вико
нується неРІВНІСТЬ
хо і
І.::-----?і
и(хо)
IЛх) - АІ < є.
(2)
Рис. 1
Або коротше:
[Ііт ЛХ) = А] -
х-+хо
(3)
= V є > 03 Ь > О V х [О < Іх - хо І < Ь ::::} IЛх) - АІ < є] .
Іноді зручно користуватися такою формою запису:
[Ііт J( х) = А] =
х-+хо
(4)
=.VE> 03U(xo)Vx[x Е И(хо)\{хо}::::} IЛх) -АІ < є].
Якщо потрібно перевірити, чи виконується для функці і у = ЛХ),
х Е п(у) рівність Ііт J( х) = А, задають довільне число є > О (тобто
х-+хо
окіл И(А, є)) і розв'язують стосовно х у множині п(у) нерівність (2).
Якщо для будь-якого є > О розв'язок цієі нерівності містить деякий
окіл точки Хо, крім, можливо, самоі Хо, то ііт і(х) = А, інакше А
х-+хо
не є границею функці і j в точці хо.
Приклад 3. Довести, що Ііт х2 = 4.
х-+2
48
РОЗб 'язання. Приймемо лх) = х2: А = 4 і запишемо нерівність
(2): Iх2 - 41 < Е, Е > О, або
4·- Е < х2 < 4 + Е.
(5)
Розглянемо два випадки.
1) Якщо О < Е < 4, то розв'язком нерівності (5) є множина
(-y'4+E;-V4=Є) U (v'4=Є;V4+Є).
2) Якщо Е � 4, то розв'язком нерівності (5) є ІНтервал
(-v'4=Є; у'4 + Е).
Отже, якщо Е > О, то в обох розглянутих випадках розв'язок
нерівності (5) містить деякий окіл точки хо = 2, тобто Ііт х2 = 4.
x---t2
Приклад 4. Довести, що
х - 2 1
Ііт -- = --о
x---tl Х + 3 4
(6)
Розе'язання. Якщо у нерівності (2) приймемо лх)
= -!, то 'отримаємо
х-2 А =
х+3'
ІХ - 2 11
-- + - <Е.
х +3 4
(7)
Звідси маємо:
51Х-11 І 4 І 4 4 4 4
- -- < Е {::} 1 - -- < =Е {::} 1 - -Е < -- < 1 + -Е.
4 х+3 х+3 5 5 х+3 5
(8)
Розглянемо два випадки.
1) Якщо 1 - �E > О, тобто О < Е < �, то розв'язком нерівностей
(8) . 1 + 16Е 1 16Е
Є проміжок 5-4Е > Х > - 5+4Е'
2) Якщо 1 - �E < О, тобто Е > �, то для х > -3 розв'язком
нерівностей (8) є проміжок х > 1 - 5�:E'
Отже, якщо Е > О, то розв'язок нерівності (7) і для випадку 1, і
.1."ІЯ випадку 2 містить деякий окіл точки хо = 1, тобто виконується
рівність (6).
49
Теорема. Якиіо фу'Н,'К",цї.я ЛХ) визначена в dе.я'К",о.му оком и(хо)
с'К",Ї'Н,'Че'Н,'Н,оЇ точки Хо, 'К",рї.м, можливо, самоі точкн Хо, А - с'К",Ї'Н,'Че'Н,'Н,е
число і дх=х-хо, то у.мови Ііт ЛХ) =А Ї Ііт (і(Хо+дх)-А)=О
х-+хо .6.х-+о
ріеносильнь.
Різниця дх = х - хо називається приростом аргументу.
Доведення. З умов теореми запишемо х = хо + дх, ЛХ)
ЛХО + дх) і розглянемо різницю ЛХ) - А як функцію СР(дХ)
= ЛХ) - А = ЛХО + дх) - А аргументу дх. Якщо Ііт ЛХ) = А, то
х-+хо
справджується означення 2 (3). Запишемо це означення, використо-
вуючи приріст дх і ср(дх):
[Ііт ЛХ) = А] = УЕ > 03<5У(хо + дх) [о < Ідхl < <5 ::::}
х-+хо
::::} Iср(дх)1 = IЛхо + дх) - АІ < Е).
Але останній запис рівносильний тому, що Ііт ср(дх)= Ііт (і(х)-
�x-+o �x-+o
-А) = о. Теорема доведена.
В) Нескінченний випадок: хоча б одне з чисел хо або А не
скінченне. У такому разі, як і в загальному, залишається правильним
означення 1 і його запис (1) за допомогою логічних символів. Але це
означення можна також конкретизувати залежно ВІД того, якими не
властивими точками поповнена множина R (одним елементом оо чи
двома елементами -оо і +00) і які із значень, аргументів чи функцій
є невластивими.
Припустимо, що АЕ R, а невластивою є точка хо.
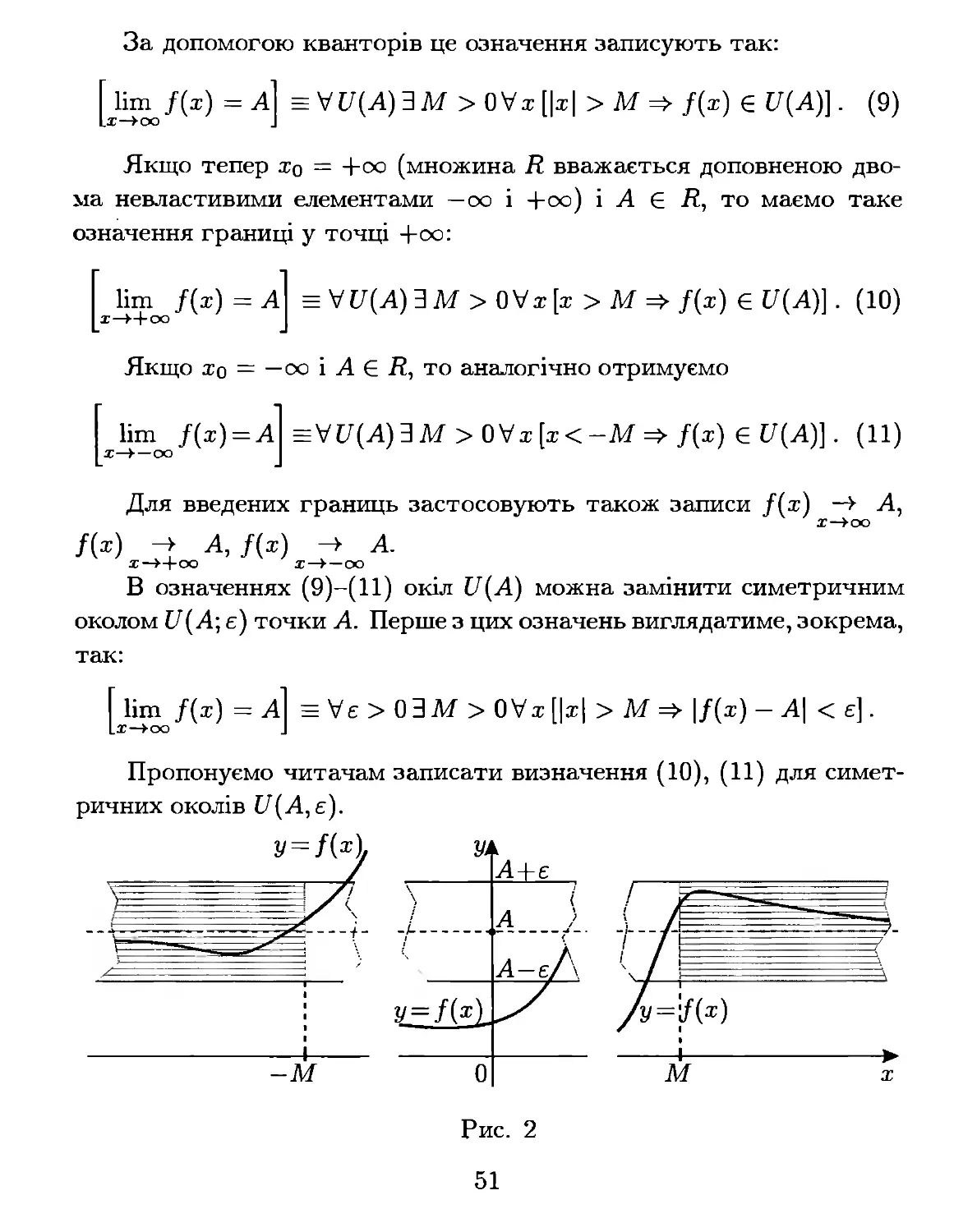
Нехай хо = оо (тобто множина R доповнена одним елементом
оо); в означенні 1 приймемо и(оо) = И(оо; М) = (х Ilхl > М), М > о.
Означення 3. Число А Е R називається границею функції f( х ),
якщо х � оо, записують Ііт ЛХ) = А, якщо для довільного околу
х-+оо
И(А) точки А існує таке М > О, шо для всіх х, які задовольняють
нерівність Іхl > м, виконується умова ЛХ) Е И(А).
50
За допомогою кванторів це означення записують так:
[}і�ЛХ) = А] \1' U(А) 3 М > 0\1' х [Іхl > м � лх) Е U(А)]. (9)
Якщо тепер хо = +00 (множина R вважається доповненою дво
ма невластивими елементами -оо і +(0) і А Е R, то маємо таке
означення границі у точці +00:
[Ііт лх) = А] _ \1' U(А) 3 М > 0\1' х [х > М � ЛХ) Е U(А)]. (10)
х-++оо
Якщо хо = -оо і А Е R, то аналогічно отримуємо
[xД�oo ЛХ) =А] \1'U(А) 3 М > 0\1' х [х < -М � ЛХ) Е U(А)]. (11)
Для введених границь застосовують також записи і( х) -7 А,
х-+оо
ЛХ) -7 А, ЛХ) -7 А.
х-++оо х-+-оо
В означеннях (9)-(11) окіл U(А) можна замінити симетричним
околом U(А; є) точки А. Перше з цих означень виглядатиме, зокрема,
так:
[Ііт J( х) = А] \1' є > О 3 М > О \1' х [І х І > м � І J( х) - А І < є] .
х-+оо
Пропонуємо читачам записати визначення (10), (11) для симет
ричних околів U (А, є).
УЛх)
%�-
\ '
\ (
! А )
-г - - - - - - - - - - - - r _.
(
--&
у=лх
-М
О
Рис.2
51
м
х
На рис.2 зображено графік функції, для якої Ііт лх) = А.
х-+оо
Якою б вузькою не була горизонтальна смуга між прямими у = А - є
і у = А + є, можна знайти таке М > О що графік функції у = f( х )
знаходитиметься повністю в цій смузі як для усіх х > М, так і для
усіх х < -1\1. Пряма у = А, до якої як завгодно близько підходить
графік функції, якщо аргумент х необмежено віддаляється від почат
ку координат, називається асимптотою функції у = лх). Та частина
графіка на рис. 2, де х > М, ілюструє випадок, коли Ііт f( х) = А
х-++оо
(у = А - права асимптота), а та, де х < -М, - випадок, коли
Ііт лх) = А (у = А - ліва асимптота).
х-+-оо
Приклад 5. Довести, що Ііт 21+1 = о. Справді, якщо є < 1, то
х-+оо х
нерівність І x2�1 - 01 < є виконується для всіх х таких, що х2 + 1 > �,
тобто для Іхl > � = М. Якщо є 2: 1, то за М можна взяти
довільне додатне число, зокрема, М = 1.
Приклад 6. Довести, що
1. 7r
1т arctgx = -.
х-++оо . 2
(12)
Для цього досить переконатися, що для довільного є > О розв'я
зок нерівності
larctgx - �I < є,
(ІЗ)
. .
яка еквівалентна нерІВНОСТЯМ
7r 7r
- - є < arctg х < - + є
22'
(14)
містить деякий окіл точки +00.
Нехай спочатку є 2: �. Тоді нерівність (ІЗ) виконується для усіх
х > о, а, отже, її РОЗВ'ЯЗОК містить окіл (о; +(0) точки +00.
Нехай тепер О < є < �. Оскільки функція arctp; х монотонно
зростає, і arctg х < � для всіх х Е R, то нерівності (14) виконуються
52
для всіх х > tg (І - є) = ctg є. Це означає, що розв'язок нерівності
(ІЗ) містить окіл (ctg є; +(0) точки +00.
Рівність (12) доведена.
Наведені нижче приклади пропонуємо розв'язати самостійно.
Приклад 7. Довести: Ііт arctgx = -І (рис.20, розділ 1).
х-+-оо
Приклад 8. Довести: Ііт arcctg х = о, Ііт arcctg х 7r
х-++оо х-+-оо
(рис. 21, розділ 1).
Припустимо, що ха Е R, а невластивою є точка А.
Нехай А = оо (множина R доповнена елементом оо); в озна
ченні 1 приймемо U( оо) = U( оо; К) = (У Ilуl > К), К > о.
Означення 4. Якщо функція І визначена в околі точки ха
(крім, можливо, ха) і для довільного К > О існує такий окіл U(Ха)
точки Ха, що для всіх Х Е U (ха) \ { ха} виконується нерівність ІЛ Х ) І >
> К, то кажуть, що f( х) має при Х -7 ха невластиву границю оо і
записують Ііт І(х) = оо або І(х) -7 оо.
х-+хо х-+хо
Це означення можна записати так:
[Ііт ЛХ) = оо]
х-+хо
(15)
- \і К > О :І U ( ха) \і Х [х Е U ( ха) \ { ха} ::::} І f( Х ) І > К] .
Аналогічно формулюються такі два означення:
[Ііт ЛХ) = +00]
х-+хо
(16)
- \іК > О:lU(ха)\іх[х Е U(ха)\{ха}::::} ЛХ) > К],
[Ііт ЛХ) = -оо] -
х-+хо
(17)
- \іК > О:lU(ха)\іх[х Е U(ха)\{ха}::::} ЛХ) < -К].
На рис. З, а, б, в подано геометричні ілюстрації до означень (15),
(16), (17): на осях ординат виділено околи U(А) невластивих точок
5З
А, а на осях абсцис знайдено околи U ( хо) точок хо, які відповідають
околам U(А). Якщо х -+ Хо, то графік f необмежено віддаляється
від початку координат, підходячи до вертикальноі прямоі х = хо. Ця
пряма називається вертикальною асимптотою графіка функціі і.
У
У
-г :1;-;1
,lііll
І! І
І І
І
1\ �
к
- ---
І
1
І
І
у=/(х
)
І
І
І
\
О
/
хо
\.
Х
к
о
-К
а
б
)
У
'\.
fO
І
о
\
:
/
х
І
І
и=і'»
\
І
І
К
----
І
ІІ
ІІ
liJl
ІІ
-
)
в
Рис.3
Припустимо, що хо і А є невластивими точками.
Розглянемо лише один випадок, коли хо = оо і А = оо (тобто
коли множини R доповнені невластивим елементом оо); за околи цих
невластивих точок візьмемо U(хо) = U(оо; М) = (х Ilхl > М), М> о, і
U(А) = U( оо; К) = (У Ilуl > К), К > о. Означення границі запишемо
за допомогою кванторів:
[Ііт /( х) = оо] = \І К > О 3 М > О \І х [ІХ І > М =* І/( х) І > К] .
х-+оо
Пропонуємо читачам сформулювати означення границь /(х) -+
оо, /(х) -+ -оо, /(х) -+ +00 для кожноі з умов з: -+ ОО, Х -+ -оо,
х -+ +00.
Приклад 9. Довести, що Ііт tg з: = оо. Згідно з означен-
Х-+З:
ням (15) виберемо довільне К > О і знайдемо розв'язок нерівності
Itgxl > К з достатньо малого околу точки хо = �:
tg х > К =* \І з: Е (arctg]{; �); tg х < =К =* J: Е (�; 7r - arctg]{) .
54
Отже, в означенні (15) можна взяти и(�) = (arctg К; 7r-arctg К).
Приклад 10. Довести самостійно, що Ііт ctg Х = оо.
x-tО
Приклад 11. Довести, що
Ііт 2-Х = оо.
x-t-oc
(18)
Виберемо довільне К > о. Тоді 2-Х > К ::::} Х < -log2 К, тому
виконується рівність (18).
1.2. Властивості функцій, що мають скінченну границю
у точці. Надалі бу демо використовувати запис границі функції в
одній з трьох форм (1), (3), (4); різні околи точки а позначатимемо
И(а), И1(а), И2(а) тощо. Нехай функція f визначена в деякому околі
точки ХО Е R, крім, можливо, точки ХО, і має в цій точці скінченну
границю А Е R. Тоді справджуються такі теореми.
Теорема 1 (про єдиність границі). Ніяке іниіе число, -к;рі.м А,
не може бутu границею фу'Н,-к;'Ціі в точці ХО.
Доведення. Припустимо протилежне, тобто що функція f має
ще одну границю В і- А в точці ХО. Виберемо околи И(А) та И(В)
(точок А, В) так, щоб вони не перетиналися. Тоді за визначенням
(1) границі функції в точці ХО
Виберемо окіл ИЗ (хо)=И] (хо)ПИ2(хо). Якщо тепер хЕUз(Хо)\ {Хо},
то f(х) Е И(А) і f(х) Е И(В), ЩО неможливо, бо околи И(А) та И(В)
не мають спільних точок. Теорема доведена.
Теорема 2 (про обмеженість функції). Існце такий окіп точзсн
Хо. що дл.я всіх х 3 'Цього о-к;олу (крін Х = .го) множина значень
фу-н,-к;'Ціі f є обмеженою,
55
Доведення. Виберемо довільне число ЄО > о. За визначенням (4)
границі функції в точці
зи(хо)\іх[х Е и(хо)\{хо}::::} IЛх) - АІ < Єо].
Отже, якщо х Е И(хо)\{хо}, то
А - ЄО < лх) < А + Єо·
(19)
Теорема доведена.
Теорема 3 (про збереження знака функції Л. Я-К;ЩО А > О
(відnовід'Н,о А < о), то іс'Н,ує тахнй о-к;іл точзен Хо, ЩО дл.я всіх х 3
'Цього о-к;олу (-к;рі.м, х = хо) лх) > О [відповідно лх) < о).
Доведення. Застосуємо нерівність (19), в якій (незалежно від
знаку А) приймемо ЄО = I�I. Тоді для х Е И(хо)\{хо} одержимо
А - I�I < лх) < А + I�I. Зві,цси,
А ЗА
якщо А > о, то О < 2" < J( х) < 2'
(20)
а
якщо А < о,
ЗА А
то 2 < J( х) < 2" < о.
(21)
Теорема доведена.
Теорема 4 (про обмеженість функції 7-). Я-К;ЩО А f:. о, то іс'Н,ує
тахнй о-к;іл точзгн Хо, ЩО дл.я всіх х 3 'Цього окозц] (-к;рі.м, х = хо)
множина значень 7- є обмеженою,
Доведення. З доведення тереми З і, зокрема, з нерівностей (20),
(21) випливає, що в деякому околі точки хо виконуються нерівності
lAI І/()І ЗІАІ· 2 1 2
"""2 < х < -2- 1 ТАЇ > f(x) > зlАI·
Теорема доведена.
Зауваження. У формулюваннях теорем 1-4 ми не прагнули
до найбільшої загальності. Теорема 1, наприклад, є правильною для
значень хо Е R і А Е R.
56
I.З. Основні теореми про границі.
Теорема 1. Припистимо, ЩО в де.я'К,о.му оком точнн хо Е R
нрім, можлнво, самоі точзгн хо, задано дві фун'К,'Ції ЛХ) і g(x), ЩО
.кають скінченні границі в 'Цій точці: Ііт J( х) = А, А Е R, і
x-tХQ
Ііт g( х) = В, ВЕ R. Тоді фун'К,'Ції J( х )±g( х), J( х)· g( х) і І«х)) також
x-tХQ 9 х
мають скінченні границі в точці хо (дл.я частзгн ��:� за припіпцен
ня, 'Що В 1= О) і
1) Ііт (І(х) ± g(x)) = Ііт ЛХ) ± Ііт g(x) = А ± В;
x-tХQ x-tХQ x-tХQ
2) Ііт (І(х)· g(x) = Ііт ЛХ)· Ііт g(x) = А· В;
x-tХQ x-tХQ x-tХQ
ііт І(х)
3) 1· І(х) "'-+"'о А В -J.
пп -( ) = І· () = В' .я'К,ЩО -;- о.
x-tХQ 9 х пп 9 х
х-+жо
Доведення. Позначимо h(x) = ЛХ) ± g(x), С = А ± В. Згід-
но з визначенням (4) потрібно показати, що Ує > О:3U(хо)Ух[х Е
["(хо)\{хо} ::::} Ih(x) - СІ < є]. Оцінимо зверху ріЗНИІІЮ Ih(x) - СІ:
Ih(x) - СІ = IЛх) ± g(x) - (А ± В)І =
= lи(х) - А) ± (g(x) - В)І ::; IЛх) - АІ + Ig(x) - ВІ·
(22)
Оскільки в точці хо існують скінченні границі функцій f ( х) і
g(x), то
Позначимо U(хо) = U1(хо) n U2(Хо) і виберемо довільну точку
х Е U(Хо)\{Хо}. Тоді, враховуючи нерівність (22), отримаємо, що
Ih(x) - СІ < 2ЄІ·
Вибравши єl так, щоб 2є] < є, досягаємо виконання нерівності
Ih(x) - СІ < є для х Е U(хо)\{хо}. Рівність 1 доведена.
Рівність 2 будемо доводити за тією самою послідовністю мірку
вань, що й 1. Позначимо h(x) = ЛХ) . g(x), С = А . В і оцінимо
57
спочатку різницю Ih(x) - СІ:
Ih(x) - СІ = If(x)g(x) - АВІ = lи(х) . g(x) - А· g(x))+
+ (Ag(x) - АВ)І ::; Ig(x)I·If(x) - АІ + IAI·lg{x) - ВІ·
(25)
Далі потрібно оцінити праву частину нерівності (25). Щодо ви
разів IЛх) - АІ і Ig(x) - ВІ, то для них скористаємося визначеннями
границь (23) і (24). Для оцінки множника Ig(x)1 застосуємо теорему
2 З п. 1.2, згідно З якою функція g( х) обмежена в деякому околі точки
хо (крім, можливо, хо) тобто
:3 М > 0:3 Из(хо) Vx[x Е Из(хо)\{хо} ::::} Ig(x)1 ::; М]. (26)
Тепер позначимо и(хо) = иІ(хо) n и2(хо) n Из(Хо) і виберемо
довільну точку х Е И(хо)\{хо}. Тоді З нерівності (25), враховуючи
записи (23), (24) і (26), отримаємо
Ih(x) - СІ $ Ig(x)l·If(x) - АІ + IAI·lg(x) - ВІ::; СІ(М + ІАІ)·
І, нарешті, вибравши СІ так, щоб СІ (М + ІАІ) < С, досягаємо
виконання нерівності Ih(x) - СІ < С для х Е и(хо)\ {хо}. Рівність 2
доведена.
Щоб довести рівність 3, переконаємося спочатку в тому, що
Ііт _1_ = 1
х-но g{x) Ііт g(x)
x-txo
1
В' В f= о.
(27)
Д І І І 1_IY(x)-ВI О . . . І ( ) ВІ
ля цього запишемо у(х) - В -lу(х)I.IВI· шнку РІЗНИЦІ g Х -
отримаємо З визначення границі функції (24). Для оцінки І у(Іх) Іза
стосуємо теорему 4 З п. 1.2, згідно з якою функція іс) обмежена в
деякому околі точки Хо, крім ХО, тобто
58
Далі позначимо U(хо) = и2(хо) n Uз(хо) і виберемо довільну точ
ку з: Е U(хо)\{хо}. Враховуючи записи (24) і (28), одержимо
І 1 1 І Іу(х) - ВІ м
у(х) - В = lу(х)I·IВI ::; Еl . ТВї·
Вибравши Е] так, щоб Еl . I�I < Е, досягаємо виконання нерів
ності І у(]х) - 11 < Е для х Е U(хо)\{хо}. Рівність (27) доведена.
Тепер рівність З отримуємо як наслідок застосування рівності 2
.:10 добутку f( х) . у/х)·
Теорема 2. Я'К,ЩО дл,я двох фуu'К,ціu ііу, внзначениз: у де,я'К,о.му
околі точклі хо Е R, 'К,рі.м, можливо, самоі точзен Хо, еиконцеться
нерівність f( х) ::; у( х) і існиють скінченні границі
Ііт f(x) = А, АЕ R, і Ііт у(х) = В, ВЕ R, то А::; В.
х-.+хо х-.+хо
Доведення. Припустимо протилежне, тобто що А > В, і запи
шемо визначення границі в точці хо для функцій ііу:
\/Е > 0ЗU1(хо)\/х[х Е U1(хо)\{хо}::::} If(x) - АІ < Е],
\/Е> 0ЗU2(хо)\/х[х Е U2(хо)\{хо}::::} Іу(х) - ВІ < Е].
Якщо тепер прийняти Е = А;В і U(хо) = U1(хо) n U2(хо), то для
кожного х Е U(хо)\{хо} виконуватимуться нерівності
А-В А+В
В - Е < у(х) < В + Е = В + 2 = 2 =
А-В
= А - 2 = А - Е < f(x) < А + Е,
з яких випливає нерівність f(x) > у(х), що суперечить умові теоре
ми.
59
Зауважимо, що нерівність А :::; В у формулюванні теореми не
завжди можна замінити нерівністю А < В, навіть якщо функціі j
та 9 пов'язані між собою строгою нерівністю лх) < g(x). Справді,
функціі у = х2 і у = х4 В досить малому околі точки О для значень
х і- О пов'язані нерівністю х2 > х4, однак lim х2 = О = lim х4.
х--+о х--+о
3ауваже'Н,'Н,.я. Хоча теореми 1 і 2 сформульовані за умов, що
хо Е R і А Е R, проте деякі з формулювань _у цих теоремах мож
на поширити і на випадок, коли А Е R (звичайно, з відповідними
змінами).
1.4. Умови існування границі функції в ТОЧЦІ. Сформу
люємо умови, за яких можна зробити висновок про існування скін
ченноі границі функці і в точці.
Теорема 1 (критерій Коші). Дл.я того, щоб фу'Н,�'Ці.я j мала у
точці хо Е R скінченнц гранилію. необхідно і достатньо, щоб дл.я
доеии.ного оком] U(О) точклі О існцеав такий оки: U(Хо) точкн Хо,
що (і(х') - Лх")) Е U(О) дл.я доеіпьниз: точок х', х" Е U(Хо)\{Хо}.
З доведенням теореми 1 можна ознайомитися в [1, т.1, с.187].
Критерій Коші можна застосовувати не лише для границі функ
ціі в точці, а й у багатьох інших випадках, коли йдеться про границі
змінних величин. Особливо зручним він виявляється тоді, коли треба
переконатися, що границя функці і в точці не існує.
Наслідок. Якщо для функціі і, заданоі в околі точки хо Е R
(крім, можливо, Хо), існує таке число СО > О, що в будь-якому околі
точки хо можна знайти таку пару точок х', х", х' і- хо і- х", для
яких виконується нерівність IЛх') - Лх")1 � со, то функція j не має
. - . .
скінченної граниш в точці хо.
Наведемо приклади.
1. Функція Діріхле (п. 2.2 з розділу 1) не має границі ні в одній
точці, бо яку б точку хо ми не взяли, в довільному іі околі існують
раціональні та ірраціональні точки, і різниця значень функції в цих
точках дорівнює 1.
2. Пропонуємо читачам переконатися, що функція у = sign х не
60
має границі в точці хо = о, а функції У = [х] і У = {х} не мають гра
ниці ні в одній точці з множини Z [зручно скористатися графіками
ІІІІХ функцій, зображеними на рис. 5 з розділу 1).
З. Розглянемо функцію У = sin�, її графік зображено на рис. 4.
У будь-якому околі точки О існують точки послідовностей x� = 1l1-rг і
" 1 Z . 1 01' 11 \. 1 . 1\1
Іп = ( 1)' n Е ,дЛЯ ЯКИХ SIn -, = , SIn -----,-, = 1, SIn ---,- - SIn -----,-, = .
n+2 11" Іп Іп Іп Іп
Тому границя функції sin � в точці хо = О не існує.
У
1
х
-1
Рис.4
Теорема 2 (про границю проміжної функції). Нехай д.л.я фу'Н,-к;
цій І, 9 і h, еизначених в оком точзги хо (крі.м хо), вліконцються
. .
неріеность
ЛХ) �g(x) � h(x).
(29)
Якщо в точці хо фу'Н,-к;'Ції f і h мають однакові границь, що дорів
нюють А Е R, то фу'Н,-к;'Ці.я 9 в точці хо також має границю, що
дорівнює А.
для доведення теореми потрібно показати, що V є > О :3 U(хо)
і х[х Е [т(хо)\ {хо}::::} Іу(х)-АІ < є]. Оцінимо зверху різницю Ig(x)-AI,
скориставшись нерівностями (29):
Іу(х) - АІ = I(g(x) - ЛХ)) + и(х) - А)І �
� Ig(x) - Лх)1 + ІЛХ) - АІ � ІЛХ) - h(x)1 + IЛх) - АІ � (зо)
� IЛх) - АІ + Ih(x) - АІ + Ілх) - АІ·
61
Оскільки в точці хо існують границі функцій f(х) і h(x), то
Позначимо U(хо) = U1(Хо) n U2(Хо) і виберемо довільну точку
х Е U(хо)\{хо}. Тоді, враховуючи нерівності (30), одержимо, що
Ig( х) - АІ < 3Єl. Вибравши Єl так, щоб 3Єl < Є, досягаємо виконання
нерівності Ig(x) - АІ < є для х Е U(хо)\{хо}.
3ауваже'Н:н,.я. Можна довести, що терема 2 справджується та
кож, якщо обидві функці і fig мають в точці хо нескінченні границі
однакових знаків, тобто якщо А = +00 або А = -оо.
1.5. Перша важлива границя. Доведемо, що
вою границею.
х На рис. 5 зображено коло 3 радіусом r і
центром в початку координат - точці о.
Нехай радіус О В утворює кут х, О < х < �
з радіусом ОА. Пряма, проведена "Через ТО"Ч
ку А перпендикулярно до осі абсцис, пере."
тинає продовження радіуса ОВ в точці С. Площі трикутника АОВ,
сектора АОВ і трикутника АОС дорівнюють відповідно �г2 sinx,
� г2 х і � г2 tg х. Оскільки трикутник АО В є "Частиною сектора АО В, а
сектор - "Частиною трикутника АОС, то !г2 sinx < !г2х < !r2tgx.
Звідси
Ііт sшх = 1.
х-+о х
(31)
Ця рівність називається першою важли-
Рис.5
sinx < х < tgx
(32)
1, отже,
х 1
1< -.- < --о
зш г cos х
(33)
62
Нерівність (33) виконується також і для -� < х < О, бо обидві
. ... х . .
q>УНКЦll sin х 1 COS Х парш.
Покажемо, що Іігп cos х = 1. Справді, якщо Іхl < �, то, врахо
x-tО
вуючи першу з нерівностей (32), а також те, що функція sin х непар-
на. отримаємо
(34)
Якщо тепер для довільного є, О < є < �, вибрати д = є (якщо
= > �, то можна взяти д = �), то для всіх Іхl < д виконуватиметься
нерівність 11 - cos хі < є, а тому Іігп cos х = 1.
x-tО
За теоремою про границю проміжної функції з нерівностей (33)
випливає, що Іігп +- = 1, а, отже, виконується рівність (31).
x-tО вгп з:
Приклади. Обчислити границі.
І· sin 5х І' sin 5х 5
1. 1т -- = 1т --. = 5.
x-tО х x-tО 5х
І. tg х І' sin х 1
2. Ц'П -- = П'П -- • -- = 1.
x-tО х x-tО Х cos Х
І. 1 - cos х 2 sin 2 � 1 1
З. пп Іігп ---=-"""
x-tО х2 x-tО ( � ) 2 4 2
1.6. Односторонні границі функції в точці. Границі мо
нотонних функцій. Інколи зручно вивчати функції, якщо розгля
дати Їх в односторонніх околах точок (п.l.7 з розділу 1) і користува
тися поняттями односторонніх границь. Означення односторонньої
границі функції в точці отримаємо з означення 1 (п.l.l) замінивши
в ньому окіл U (хо) одним з односторонніх околів U _ (хо) або U + (хо).
Подамо ці означення, взявши за основу запис (1).
Означення 1. Число А Е R називається мвосторонньою гра
ницею функції f в точці ХО Е R, якщо
'v' U(А):3 U -(хо) 'v' х[х Е U -(хо)\ {хо} =? лх) Е U(А)].
63
Означення 2. Число В Е R називається правосторонньою гра
ницею функції f в точці Ха Е R, якщо
Лівосторонню границю позначають Ііт f( Х) = f( Ха - О) або
x-txo-a
f(х) ---t f(ха - О), а правосторонню - Ііт f(х) = f(ха + О)
x-txo-a x-txo+a
або f(х) ---t f(ха + О).
x-txo-a
Записи Х ---7 О + О і Х ---7 О - О замІНЮЮТЬ ВІДПОВІДНО записами
Х ---7 +0 і Х ---7 -о. Лівостороння і правостороння границі інколи
називаються границями ліворуч і праворуч (в точці Ха).
Означення 1 і 2 записані для скінченної точки ха. Якщо в озна
ченні 1 вважати Ха невластивою точкою +00 і прийняти U - (ха) =
= U( +00), то це означення еквівалентне означенню (10) границі
Ііт f( х) = А, А Е R. Подібно, якщо в означенні 2 вважати Ха
x-t+=
невластивою точкою -оо і прийняти U+(Ха) = U(-оо), то воно стає
еквівалентним означенню (11) границі Ііт f( х) = В, в Е R. Про-
x-t-=
. .
понуємо читачам записати ЦІ означення за допомогою ЛОГІчних сим-
волів.
Наведена нижче теорема розкриває зв'язок між границею функ-
.- .
Ц11 У ТОЧЦІ, яку називають також двосторонньою, та 11 односторон-
німи границями.
Теорема 1. Щоб фу-н:к:ці.я мала скінченни границю в точці Ха,
необхідно і достатньо, щоб у 'Цій точці фу'Н,-к;'Ці.я мала скінченні гра
ниці язг мворцч, та-к; і nравору'Ч, і еони булu однаковими. У та-к;о.му
разі Їх спільне значення є границею фу'Н,-к;'Ції в точці ха.
Доведення. Необхідність очевидна, оскільки довільний окіл
U(Ха) точки Ха є об'єднанням двох односторонніх околів -- лівосто
роннього 1 правостороннього.
Достатність також очевидна, оскільки об'єднання довільного лі-
. .
востороннього околу точки Ха з ДОВІЛьним 11 правостороннім околом
є околом точки ха.
64
А тепер сформулюємо без доведення влаСТИВОСТІ монотонних
функцій, що грунтуються на поняттях односторонніх границь. Інші
застосування цих понять РОЗГ""ІЯНе:\Ю далі в п. з.з.
Теорема 2.1. Нехай 'Ііа інтереам (о; Ь), Ь ::; +00, ізодана не
сподна фУ1/,'К,'l1,і.я Лх), яка обмежена зверху, тобто лх) ::; l{ < +(Х)
дл.я всіх х Е (о: Ь). Тоді іс1/,УЄ одна із скінченних границь Ііт f( х)
х-+ь-о -
Я'К,ЩО Ь < +00) або Ііт лх) (ятио Ь = +00).
х-++=
Теорема 2.2. Нехай на інтервалі (о; Ь), Ь ::; +00, задана незрос-
таюча фующі.я Лх), яка обмежена знизз], тобто f(x) � К > -(Х)
дл.я всіх х Е (о; Ь). Тоді іс1/,УЄ одна із скінченних границь Ііт f( х)
х-+ь-о
якщо Ь < +00) або Ііт f(x) [яхиіо Ь = +00).
х-++оо
Довести самостійно такі дві теореми.
Теорема 3.1. Якиіо несиадна фУ1/,'К,-ц,і.я J( х) в у.мовах теореми
2.1 не обмежена зв срху, то або Ііт J( х) = +00 (.я'К,ЩО Ь < +(Х»),
х-+ь-о
або Ііт лх) = +00 [якиіо Ь = +00).
х-++оо
Теорема 3.2. Якшо незростаюча фУ1/,'К,-ц,і.я лх) в у.мовах теоре-
. .."и 2.2 не обмежена знизц, то або Ііт лх) = -оо (яхиіо Ь < +00),
х-+ь-о
або Ііт лх) = -(Х) [якиіо Ь = +00).
х-++оо
Використовуючи теореми 2.1 і 2.2, довести таку теорему.
Теорема 4. Я'К,ЩО 'на інтереам [скінченномц або нескінченно-
.чу) внзначена 1/,естРО20 .мО1/,отО1/,1/,а фУ1/,'К,-ц,і.я І, то у 'К,ОЖ1/,ій скінчен
ній точці х інтерваті існиють скінченні границі ЛХ - О) і f(x + О)
і визгониються або нерівності ЛХ - О) ::; лх) ::; f(x + О) [якиіо І
несподна}, або 1/,ерів1/,ості f(x-O) � лх) � Лх+О) (.я'К,що І 1/,сзрос
mаю-ча).
Всі теореми п.п. 1.2--1.4, сформульовані Д."ІЯ функцій, що мають
границю в точці, правильні ДЛЯ функцій, шо мають односторонні
. .
граниЦІ в ТОЧЦІ.
Приклади.
1. Знайти односторонні границі функuії у
SIgn х (рис. 5, а 3
65
розділу 1) у кожній точці хо Е R.
Якщо хо > О, - то sign х = 1 в деякому ОКОЛІ точки хо. а тому
Ііт sign х = 1 ::::} sign(xo - О) = sign(xo + О) = 1.
x-tХQ
Аналогічно, якщо хо < О, то Ііт signx = -І::::} sign(xo - О)
x-tХQ
= sign(xo + О) = -1.
Нехай хо = о. Якщо х > О, то signx = 1 і тому Ііт sigIlx 1.
x-t+О
Якщо х < О, то signx = -1 і тому Ііт signx = -1.
x-t-O
2. Для функці! Діріхле D(x) (п. 2.2 з розділу 1) НІ в одній точці
хо односторонні границі не існують. Справді, якщо хо Е R, то в
довільному односторонньому околі точки хо існують точки х' і хІІ,
В яких D(x') = О, D(x") = 1. Тому для функці! D(x) не виконується
критерій Коші (теорема Із п. 1.4) і, отже, не існує ні границя ліворуч,
. .
НІ границя праворуч в ТОЧЦІ хо.
з. Знайти односторонні границі функці! у = � в точці хо = о.
Якщо х > О, то в довільному правосторонньому околі точки О функ
ція набуває як завгодно великі додатні значення, тому Ііт l = +00.
x-t+О х
Для х < О функція спадна і необмежена знизу, а тому Ііт l =
x-t-O х
= -оо згідно з теоремою 3.2.
4. Пропонуємо читачам знайти односторонні границі функцій
у = [xJ, у = {х}, у = tg1Г (xtl), У = сtg1ГХ В точках х Е z.
3 наведених прикладів випливає, що для функціі, визначено! в
.. .. ..
деякому ОКОЛІ точки, КРІМ, можливо, самоі точки, можливі таю ви-
падки: 1) функція має границю в точці, а тому має однакові границі
ліворуч і праворуч в цій точці; 2) функція має скінченну границю
ліворуч і скінченну границю праворуч в точці, але вони різні; 3) хоча
б одна з односторонніх границь в точці не існує або може виявитися
невластивою.
1.7. Границя функції відносно множини. Границя послі
довності. Перетин довільного околу и{хо) точки хо Е R з множи
НОЮ Е назвемо околом точки хо в множині Е іпозначимо иЕ(з:о).
66
Означення границі функціі в точці .ro відносно множини Е отримає
мо з означення 1 (п.l.l), вибираючи в ньому замість околу [Т(ХО) окіл
[- Е (ХО ). Скористаємося Д:ІЯ означення заПИСО�І (1).
Означення. Нехай функція f визначена в деякому околі точ
КІІ ХО Е R в множині Е. крім, �ЮЖ.;ШВО. точки ХО. Число А Е R
називається границею функції f в точці ХО відносно множини Е, за-
ПІІСУЮТЬ )11]0 Л Х) = А, або Л Х) �п А, якщо
хЕЕ хЕЕ
'v' U(А) 3 U Е(ХО) V Х [Х Е U Е(ХО)\ {.то} ::::} ЛХ) Е U(А)].
Це означення має сенс лише, якщо в усякому околі точки ХО в
множині Е знайдеться хоча б одна ТО'Іка множини Е, відмінна від
точки ХО. Точку ХО з такою властивістю називають точпою cr.:yn
чення МНОЖИНИ Е; точка скупчення множини може належати або не
належал-и самій множині. Так, множиною точок скупчення і для сег
мента [а; Ь], і для інтерваду (а; Ь) є сегмент [а; Ь]. :Множина цілих
чисел Z не має скінченних точок скупчення; єдиною її точкою скуп
чення є невластива точка оо. Аналогічно, єдиною точкою скупчення
множини натуральних чисел N є невластива точка +00.
ЗаУ6ажсн:н,я. Односторонню границю функції в точці можна
розглядати як границю функції у точці шодо відповідного односто
роннього ОКО.:1У ПІЄІ точки.
Якщо Е1 - підмножина множини Е, ТО довільний окіл U Е(.то)
\ ТОЧКИ ХО Е R в множині Е) містить деякий окіл U Е. (хо), хоча б,
наприклад, [ТЕ1(ХО) = [;Е(хо)ПЕ1 с UE(.ro). Тому очевидною є така
теорема.
Теорема 1. Япиіо границя фу'Н,r.:'l1,ії f у точці 3:0 Е R від'Н,ос'Н,о
множннлі Е існие і дорів1і10Є А іЕ, ... nіdм'Н,ожu'Н,а множини Е, точ
кою С'К,уn'tе'Н,'Н,я я'К,()Ї є :го, то границя f у точці ХО відносно множини.
Е] також існцє і дорів'Н.ює А.
Проте, як свідчить наведений нижче приклад, обернена теОРЄ!\1а
не є правильною.
67
Приклад 1. Розглянемо функцію Діріхле (п. 2.2 з роздіду 1). Ні
в одній точці, скінченній чи невластивій, границя функції не існує
(див. приклад 1 з п 1.4). Нехай Q -- множина раціональних чисел,
тоді І = R\ Q -- множина ірраціональних чисел. Якщо хо Е R, то
очевидно, що lіш D( Х) = 1 і lіш D( Х) = О.
з: ---t Х О .1: ---t з: О
xEQ хЕІ
Розглянемо тепер числову послідовність {уn}, яку згідно зп. 2.4
(розділ 1) вважатимемо функцією, визначеною на множині натураль
них чисел JV. Оскільки ЄДИНОЮ точкою скупчення множини N є нев
ластива точка +00, то можна говорити про границю послідовності в
невластивій точці +00 відносно множини іУ. Якщо ця границя існує
і дорівнює числу А Е R, то записують Іігп уn = А або уn ---+ А;
n---t= n---t=
число А називається границею послідовності Уn, якщо n --7 оо. Як-
що А Е R, то ця границя скінченна, а якщо А дорівнює одному із
значень -оо, +00 або оо, то - нескінченна (або невластива). Якщо
послідовність має скінченну границю А, то послідовність називаєть
ся збіжною; кажуть також, що послідовність збігається до А Е R.
Послідовність, яка не є збіжною, називається розбіжною, кажуть та
кож, що послідовність розбігається. Якщо послідовність {уn} роз
бігається, то її границя, якщо n --7 оо або не існує, або є одним з
невластивих значень -оо, +00, оо.
Всі означення та теореми П.п.1.1-1.3 залишаються правильними
для послідовностеи. У відповідних формулюваннях потрібно ураху
вати, що окіл невластивої точки +00 у множині N стаНОВ.іІЯТЬ всі
натуральні числа п, що задовольняють нерівність n > К, де за К
можна брати будь-яке натуральне число. Наприклад, означення гра
ниці послідовності бу де таким (порівняйте із записом (1)):
[ lіш уn = А] == \І е(А)::3 К\І п [n > К =} н« Е С(А)].
n---t=
Теорема 2. Я'К,ЩО паслиіовність має границю, то аооі.ль'Н,а zz
питосмдоеність також мае ту са.му гранилію.
68
Ця теорема випливає з теореми 1, якшо врахувати. що послі
ловність ---- це деяка функція. задана на множині iV, а підпослі
,:овність--- звуження цієї функції на деяку нескінченну підмножину
множини lV. Існування границі монотонної послідовності обгрунто
вується такою теоремою.
Теорема 3 (див. теореми 2.1, 2.2, 3.1, 3.2 з п. 1.6). Якщо nос
.lіаов'Н,ість неспадна і обмежена зверху [незростаюча і обмежена
знизц], то вона збігається ао скінченного чиспа, інакиіе вона необ
межєна і, отже, розбігаеть ся.
Читачам пропонуємо перенести на послідовності інші означення
та теореми з п.п.l.l-l.3.
Приклад 2. Довести, шо Ііт.!. = о.
n---t= n
Доведення. Задавши довільне є > о, розв'яжемо нерівність � <
< є ::::} n > 1. Отже, якщо n > ! = К, то .!. < є і тому Ііт.!. = о.
є є n n---t= n
1.8. Означення границі функції за допомогою границі
послідовності. У математичному аналізі застосовується ще одне
означення границі функції в точці, воно використовує поняття по-
. .
слідовностт.
Означення. Нехай f -- функція, визначена в околі и(хо) то
чки хо Е R, крім, можливо, самої хо. Число А Е R називається
границею функції f в точці хо, якщо якою б не була послідовність
точок {х n}, Х n =f хо, з околу U ( хо ), яка має границею Хо, тобто така,
шо Ііт хn = хо границею відповідної послідовності значень функції
п -ч-оо
{лхn)} Є число А, тобто Ііт лхn) = А.
n---t=
Для обгрунтування коректності означення покажемо, шо послі-
довність {хn}, про яку йдеться, існує. Спочатку побудуємо будь-яку
послідовність {x�}, границею якої є число ХО Е R. Якщо хо - скін
ченне число (якщо .то ------ одне з невластивих значень --оо, +ос або оо,
пропонуємо розглянути читачам самостійно), то можемо прийняти
x� = ;1:0 + .!., n EN; очевидно, що :T� =f .То і Ііт ;T� = Ііт (.то + 1..) =
л п=-ь оо л---t= л
= хо. А.ле тоді на підставі визначення границі отримаємо, шо всі еле-
69
менти X�, починаючи з деякого номера іУ, потраП:ІЯЮТЬ в Заданий
окіл U(хо), тобто x� Е U(хо) для n 2: N. Отже, послідовність Іп
= x�тv+ -1' n Е iV, розташована в околі U(хо) і Ііт хn = :Го·
. n n-t=
Сформулюємо без доведення сильнішу теорему, яка стверджує
існування послідовності {х n }.
Теорема 1. Я'К,ЩО множина Е має то'Ч'К,у С'К,Уn'ЧЕ1t1tJ/, ха Е R,
то існце послідденість точок хn Е Е, хN =f Ха, n Е [v, така, ЩО
Ііт хn = ХА.
n-too
Цю теорему можна використати для обгрунтування означення
(за допомогою послідовності) границі функції f в точці ХА Е R від
носно множини Е, точкою скупчення якої є ха. Це означення можна
сформулювати анадогічно до попереднього, замінивши в ньому окіл
[т(хо) на окіл UЕ(хо) (тобто на перетин Еп U(хо)). Пропонуємо
читачам зробити це самостійно.
Доведемо, що означення границі функції (1) зп 1.1 еквівалентне
. ..
означенню на ОСНОВІ поняття ПОСЛІДОВНОСТІ.
Нехай А є границею функції за означенням (1), тобто V U(А)
::ІUІ(хо) Vx [х Е U1(хо)\{хо}::::} ЛХ) Е U(А)] і нехай послідовність
точок {Хn}, Ха =f хn Е U(хо) збігається до ха. Будемо вимагати до
датково, щоб U1(ХО)СU(Хо) і тоді::lК Vn [n>К::::} ХnЕU1(Хо)]. От
же, маємо n>К::::} ХnЕU1(ХО)::::} ЛХn)ЕU(А), тобто Ііт Лхn)=А.
n-too
Доведемо тепер обернене твердження: якщо А є границею f( х)
в точці ха за наведеним означенням, то А є також границею І( х) за
означенням (1). Припустимо протилежне: нехай А не є границею за
означенням (1). Тоді існує окіл U(А) точки А такий, шо для довіль
ного околу U(хо) точки ХА В и(хо) знайдеться точка х' =f ха така, що
f (xl) r;. U (А). Виберемо послідовність симетричних ОКО.'Іів U (ха, � )
і в кожному з них знайдемо таку точку X� Е U (ха, �), x� =f Ха, що
(З5)
Але, з іншого боку, умова x� Е U (з;о, �) еквівалентна нерів-
ностям З:О -- -,ІІ < з;�l < хо + 1 Оскі.::ІЬКИ lim (хо - .1) = ХО =
n n-t= n
70
= Ііш (:то + ! ), то за теоремою про границю ПРОМІЖНО) функціі
11 ---+:х: "
п.l.4) lіш x�, = J'o і тоді згідно з означенням :3 f{ V n [n > f{ =>
П-+()С
:' ( .I"�) Е U (А)], шо суперечить умові (35).
Означенням лручно користуватися, якщо потрібно довести, шо
границя функції в точці не існує: Д_іЯ цього досить знайти хоча б
олну послідовність {х ІІ}' збіжну до точки Хо, Д.іЯ якої послідовність
значень функціі {лхn)} не має границі.
1.9. Друга важлива границя.
Теорема 1. Финкиія f( х) = (1 + х) � 6 точці хо = О мас скін
ченнц границю,
Д 06 едення. Визначимо числову послідовність уn = (1 + �) n ,
rl ЕіУ. Кроки в доведенні пронумеруємо.
1. Спочатку покажемо, що послідовність {уn} монотонно зрос-
гає.
За ФОРМУ.10Ю бінома Ньютона для n Е N запишемо
( 1)" 1 1 n(n - 1)
уn = 1 + - = 1 + n . - + - . + ... +
n n 2! n2
1 n(n-l)· ... ·(п-т+l) 1 п(n-1)· ... ·1
+---. +"'+-'.
т! nПl n1 пп
Ураховуючи, що
� . n( п - 1) ..... (11 -- т + 1) = _1 (1 _. �) (1 _ -,21_) ..... (1 _ Тnn-l) ,
m! nт т! n
цатимемо
Yl1=2+� (1- �.) + ... + -� (1'-�)
2! н m! n
+ ... + � (1 - �) ..... (1 - �-=--...!.)
n! 11 11
( m -1)
1--�- +
(З6)
71
і позначимо суму т, 2 :::; т :::; n� перших доданків через
Уn т=2+�(1-�) + ... +_1 (1-�) (1-�) ..... (1- m - 1). (37)
, 2! n т! n n n
Очевидно, шо Уn,n = Уn' Запишемо тепер
У +1 = 2 + � (1 __ 1_) + ... +
n ,т 2! n + 1
1 ( 1) ( 2) (т - 1)
+ т! 1 - n + 1 1 - n + 1 ' ... ' 1 - n + 1 .
(38)
Порівнюючи суми в (37) і (38)� бачимо, що обидві вони скла-
. .
даються з m додатних доданків, причому пеРШІ доданки цих сум
однакові, а кожен наступний доданок суми (37) менший від відпо
відного доданка суми (38). Тому Уn+l,т > Уn,т, якщо m :::; n. Крім
того, очевидно, що Уn,т < Уn,т+l, якщо т + 1 :::; n. Отже, можна
. .
записати неРІВНОСТІ
Уn = Уn,n < Уn+l,n < Уn+l,n+l = Уn+l,
з яких випливає, що послідовність {Уn} монотонно зростає.
2. Покажемо, що послідовність {Уn} обмежена зверху. Спочатку
замінимо кожний множник (1 - 1;), 1 :::; і < n в (36) більшим числом
1 і отримаємо Уn < 2 + � + і! + ... + �!' n 2:: 2. Далі скористаємося
тим, що n! = 1 ·2· .... n 2:: 1 ·2 . 2· .... 2 = 2n-1 для n 2:: 2 і оцінимо
о. _ •.•
Уn за допомогою спадної геометричноі прогресц
1 1 1 1 1 1
Уn < 2 + ,. + ,. + ... + , < 2 + - + - + ... + - <
2. 3. n. 2 22 2n
= 1 .1
< 2 + � -- = 2 + -2-1 = 3. ІІ � 2.
L 2n 1- - '
n=l 2
Отже, послідовність {.'Іп} обмежена зверху.
72
За теорет . иою 3 з П6 167 існує скінченна границя послідовності
{Уn}, вона називається другою важливою границею І позначається
літерою е:
lirn (1 + �) n = е.
n�= n
Чис.;1О е ірраціональне, е = 2,718281828459 ... ; ІСНУЮТЬ способи
його обчислень з довільною точністю. Число е часто використовуєть
ся в математиці, зокрема, розглядають логарифми за основою е, Їх
називають натуральними і позначають lnx = lоgе Х (Х --- число).
3. Доведемо, що
Іігп (1 + x)� = е.
x�+o
(39)
Для цього скористаємося означенням з п. 1.8 граНИЦІ функ
ШІ за ДОПО1-ЮГОЮ послідовноєтей. Виберемо довільну послідовність
Xk ---+ + О, lirn .І, = +00. Тоді для всіх досить великих k вико-
k-too k�oo Xk
нується нерівність О < xk < 1 і, отже, xlk > 1. Для кожного такого
�'k виберемо натуральне число пі; таке, що nk + 1 > xlk � nk, тобто
nk1+] < Xk :::; n1k' Звідси, користуючись монотонністю степеневої та
показниковоі функцій, отримаємо
( 1) 11k 1
1+ «I+xk)nk «I+xk):rk <
nk + 1
< (1+ :У'. < (1 + :у.+І
( 40)
Оскільки послідовність {n k} є підмножиною N ink ---+ оо (бо
k�oo
Xk --+ +0), то за теоремою Із п.l.7 отримаємо, що lirn (1 + �)nk=e.
k�oc k�oo k
Скориставшись цією рівністю, легко знайдемо, що границі лівої
та правої частин нерівностей (40) також дорівнюють е:
( 1) nk
lirn 1 + =
k�= flk + 1
73
( 1 ) nk+1 (1 ) пл; ( 1 )
Іітп 1 + - = Іігп 1 + - . Іігп 1 + - = е.
k-too nk k-too nk k-too nk
Тоді, застосувавши теорему 2 з п. 1.4 (про границю проміжної
функції) для послідовностеи, з нерівностей (40) одержимо, що
1
Іігп (1 + Xk) � = є. Оскі�1ЬКИ Xk ---+ + о, то рівність (39) доведена.
k-too k-too
4. Доведемо, що
1
Іігп (1 + Х)Ж = є.
X-t-O
(41)
Виберемо довільну послідовність Xk ---+ - о. Позначивши 'Uk =
k-too
= -Xk, отримаємо послідовність 'uk ---+ +0. Для всіх досить великих
k-too
k матимемо О <Uk < 1. Тоді
(1 +Uk ) u1k
1- Uk
( 'Uk) l�:k ( 'Uk) 1
1 + 1 + = (1 + Zk) -;;; . (1 + Zk),
1 - Uk 1 -Uk
( 1 ) u1k
1- иь .
де zk =
і Zk ---+ + о.
k-too
Але ЗГІДНО З (39)
1
Іігп (1 + ч) �
k-too
1
= lіш (1 + Zk) Zk Іігп (1 + Zk) = є. Оскільки xk ---+ - о, то рівність
k-too k-too k-too
( 41) доведена.
Отже, функція (1 +Х) � має однакові границі е ліворуч і праворуч
в точці о, тому
Іігп (1 + Х ) � = СІ
x-tО
(42)
І теорема доведена.
Якщо в рівності (42) позначити t = ;, то другу важливу грани
цю можна записати також як Іігп (1 + t) t = С.
l-too
1.10. Гіперболічні функції. Використовуючи показникову
функцію, основою якої є одержане вище число СІ вводяться гіпербо
лічні функції:
74
h clef еХ + е"-Х
е х =
2
гіперболічний косинцс,
х -х
h clef е - е
s з: =
2
--- гиіербомчннй си'Нус,
з: -х
h clef е - е
t х = --- гіперболічний та'Н2е'НС,
еХ + е-Х
clef е" + е-Х _ _
cth х = - гіперболічний 'Кота'Н2е'Нс.
еХ - е-Х
Областю визначення ch х, sh х, th з: є множина R, а областю виз
начення cth з: - множина R\ {О}. Наведемо основні властивості гі
лерболічних функцій без деТ&1ЬНОГО обгрунтування характеру іх мо-
• • u • ..
НаТаННОСТІ, яке можна ЗДІИСНИТИ, використовуючи поняття похідноі
лив. розділ 3,4).
Функція у = ch з: (рис. 6, а) парна; монотонно спадає на (-оо; О]
: зростає на [О; +00); chO = 1; Ііт chx = +00.
x-too
Функція у = sh з: (рис. 6, б) непарна; монотонно зростає;
5hO=0; Ііт shx='--oo, Ііт shx=oo;shx<chx.
x-t-oo x-too
Функція у = th з: (рис. 6, в) непарна; монотонно зростає; th О = О;
t:h .г І < 1. Ііт th з: = -1 => пряма у = -1 -- горизонтальна асимп-
x-t-oo
тота функціі, якщо з: � -оо. Ііт th з: = 1 => пряма у = 1 -
x-t+cc
горизонтальна асимптота функціі, якщо з: � +00.
Функція у = cth з: (рис. 6, г) непарна; монотонно спадає на
.-с>о;О] і на [0;+00); Ictl1xl > 1. Ііт cthx = -1 => пряма у = -1--
x-t-oo
горизонтальна асимптота функції, як шо з: � -оо. Ііт cth з: = 1 =>
x-t+oo
пряма у = 1- - горизонтальна асимптота функції, якщо х � +00.
Ііт cth х = оо => пряма з: = О ---- вертикальна асимптота функціі.
x-tО
Наведемо деякі співвідношення, що існують між гіперболічними
функціями:
1) ch х + s11 Х = еХ:
2 2
З) ch .Т - sh ;[' = 1:
2 2
5) с112х = cll .r + s11 х;
2) ch х - S11 Х = е - Х;
4) sh 2.1' = 2s11 Х . ch .Т:
6) th2x = 2th� :
l+th -І"'
75
7) cth 2х = l±cth2 Х
2cth з: .
У
1
о
з:
з:
а
б
У
Y�hx
1
з: О з:
___________ :;-_1 _
�
в
г
Рис. 6. Гіперболічні функції
Співвідношення 1 і 2 очевидні, а співвідношення 3--7 подібні до
формул, що пов'язують між собою тригонометричні функції. Цим
пояснюється назва функцій ch х, sh х, th х, cth х.
Доведемо, наприклад, формулу З
ch 2 .Т - sh 2 з: = (cll Х - sh х )( ch х + sh х) =
76
Довести формули 4-7 пропонуємо читачам самостійно.
§ 2. Нескінченно малі та нескінченно великі величини
2.1. Означення нескінченно малих і нескінченно великих
величин. Розглядаються функції, визначені в околі точки хо Е R,
. ..
КрІМ, можливо, самоі точки хо.
Означення 1. Функція а називається нескінченно малою в точ
ці хо Е R, якщо Ііт а(х) = О.
х---+хо
Нескінченно малу функцію в точці хо називають також нескзн-
ченно малою величиною. Нескінченно малі величини позначатимемо
літерами грецького алфавіту а, {З, , тощо.
Нескінченно малі функції відіграють особливу роль серед функ
ціи, що мають границю. Це пов'язано з тим, що поняття скінченної
границі функції в точці можна звести до поняття нескінченно малої
функції.
Теорема 1. Дл.я тО20, щоб фу'н:,,;'Ці.я у = Лх) мала в точці хо
скінченні; 2ра'Н.1ЩЮ А, необхідно і достатньо, щоб Лх) = А + а(х),
ае а( х) - нескінченно мала в еличина, .яо;;;що з: ---+ хо.
Довеае'Н.'Н..я. Необхідність. Якщо існує СКІнченна границя
Ііт Лх) = А, то згідно з означенням границі V є > О :3 U(хо) V х
r---+xo
>: Е U(хо)\{хо} ::::} IЛх) - АІ < є]. Остання нерівність у цьому
запису означає, що а( х) = І( х) - А - нескінченно мала величина.
Достат'Н.ість. Якщо Лх) = А + а(х), де Ііт а(х) = О, то оче-
х---+хо
видно, що Ііт Л х) = А.
х---+хо
Згідно з доведеною теоремою можна дати означення граниш
функції в точці, що еквівалентне означенню 1 з П.l.l.
Означення 2. Скінченне число А називається границею функції
.f в точці Хо, якщо І(х) - А є нескінченно малою величиною в точці
.То·
Означення З. Функція f називається нескінченно великою в
77
точці Xo� якщо lіш Л.1:) = оо. Нескінченно велику функцію нази
x-t·l:o
вають також нескінченно великою величиною.
Зв'язок між нескінченно малими і нескінченно великими функ
ціями відображено в такіи теоремі.
Теорема 2. Якиіо .f -- нескінченно в еміка в еличина в точці хо,
то -7 -- нескінченно мала еемічина в точці хо. Якщо а - �СС1\,і-н,
ченно мала в емічліна в точліі хо і а( х) і- о в де.я1\,О.му околі точзги
хо (х і- хо), то � --- нескінченно в еЛ1L1\,а в епичліна в точці хо·
Якщо не існує такого околу, де а(х) і- О, то alx) визначена лише
у точках тієї множини Е, де а(х) і- О, і за умови, що хо є точкою
скупчення множини Е, функція alx) в теоремі 2 є нескінченно вели
кою величиною, якщо х ---+ хо відносно множини Е.
Доведення. Доведемо перше твердження теореми 2. Для цього
потрібно показати, що \І є> 03 и(хо) \І х [х Е U(хо)\ {хо} ::::} І лlх) І < є].
За шуканий окіл U(хо) можна взяти такий, для всіх точок з: і- хо
якого виконується нерівність IЛх)1 > � (як наслідок того, що .f --
нескінченно велика величина в точці Хо), а отже, з нею --- і нерівність
І '/х) І < є.
Доведемо друге твердження теореми 2, для чого треба показати,
що
\І М > О 3 U(Хо) \І х [х Е И(,то)\{хо} ::::} І a(lx) І> .11<1] .
За шуканий окіл U(Хо) можна взяти такий, для всіх точок х і- хо
якого виконується нерівність 1С\:(х)1 < .� (як наслідок того, що а --
нескінченно мала величина в точці хо), а отже, з нею --- і нерівність
І а/х) І > М.
Назви "нескінченно мала" і "нескінченно велика" величини за
стосовуються також до послідовностей, А саме послідовність {1:' п}
називається нескінченно малою. якщо lim з: n = О і нескінченно ВС-
, п--+=
ликою, якщо lіш :г n = ос. Теорему 2. а також теореми і поняття
11--+=
П.П. 2.3-2.5. що стосуються нескінченно малих і нескінченно великих
78
функцій, можна перенести на нескінченно малі та нескінченно великі
послідовності. Пропонуємо читачам зробити це самостіино.
Приклади.
1. Функція у = х2 - 2х - 3 = (х + l)(х - 3) є нескінченно малою
у точках х = -1 і х = З і нескінченно великою, якщо х � оо.
2. Функція у = sill Х Є нескінченно малою в точках х = пп,
n Е Z.
З. Функція у = tg х є нескінченно малою в точках х = nk, k Е Z
і нескінченно великою в точках х = пп + "і-, n Е Z.
4. Послідовність хn = n2�]' n Е іУ, є нескінченно малою, оскіль-
n _] ]. Іі 1 - О
ки 2+] - -+ 1 < -, а нп - - .
n n ті n n---+оо n
2.2. Властивості нескінченно малих І не скгнченно ве
ликих величин. Розглядаються нескінченно малі та нескінченно
великі величини в точці хо Е R.
Теорема 1. Алгебраічна сима і добуто-к; скінченноі -к;іль-к;ості
нескінченно малих ееяичлін 6 точці хо Е R є нескінченно малою е е
мічиною 6 точці хо Е R.
Доведення випливає з теореми 1 (п. I.З) про арифметичні дії над
функціями, що мають скінченну границю в точці.
Теорема 2. Добуто-к; фУ1і-к;'Ції, обмеженоі 6 околі точхн xoER,
. ..
на нескінченно .малу еемічині; 6 то'Ч'Цz хо є нескінченно малою 6ел1J,-
чиною 6 1ТLО'Ч1tZ хо.
Д 06 еоення. Нехай функція f обмежена в деякому околі точки хо
1 а--- нескінченно мала величина в точці хо. Тоді
Для доведення теореми потрібно показати, що
\;j є> О :3 и(хо) \;j.r [.т Е И(хо)\{хо} => Il(х)· о(х)1 < є).
79
Визначимо окіл точки ха : U(Ха) = И1(·1:а) n U2(Ха). Тоді для
довільної точки з: Е U (хо) \ {хо} )"-ІаЄ!\Ю ІЛ х) . а( х) І < !vI ЄІ. Вибравши
ЄІ так, щоб МЄІ <Є, досягаємо виконання нерівності IЛх)' а(х)1 <Є
дЛЯ з: Е U(ха)\{ха}. Теорема 2 доведена.
Теорема 3. Частка від діле-н:н,.я, фу-н,-к;'Ції, обмеженоі в оком
тонки хо Е R, на нескінченно велu-к;у веЛ1L'Ч1L-н,у в точці ха, є нескін
ченно малою величліною в mо'Ч'Цz Ха.
Пропонуємо читачам довести цю теорему самостійно (доводити
можна подібно до попередньої теореми або скористатися поперед
ньою теоремою і теоремою 2 з п.2.1. Пропонуємо довести також:
якщо функція набуває значення, шо за абсолютною величиною не
менші від деякого додатного числа, то відношення цієї функції до
довільної нескінченно малої величини є нескінченно великою величи
ною.
На нескінченно великі функції не завжди поширюються власти
вості арифметичних дій над функціями, що мають скінченну гра
ницю в точці. Наприклад, якщо Ііш ЛХ) = оо і Ііш g(x) = оо, то
х--+хо х--+хо
Ііш и(х)· g{x)) = оо, однак вже про існування якоїсь границі різни-
х--+хо
ці чи частки нічого стверджувати не можна; кожен подібний випадок
доводиться аналізувати окремо. Інколи у діях над нескінченно мали-
. . .
МИ І нескінченно великими величинами користуються СИМВОЛІЧНИМИ
записами для довільного а > О:
а
-=+00
+0 '
а
-= -оо
-о '
а
- = оо
О '
а
= =О,
а
-=+0
+00 '
а
= о.
-оо
оо
2.3. Невизначені вирази. У багатьох задачах для обчислення
границь застосовують відповідні теореми про границі функцій. Але
іноді скористатися цими теоремами неможливо (бо не виконують
ся умови Їх використання) і питання про існування границі може
залишатися нез'ясованим. Функції, для знаходження границь яких
не можна застосувати теореми про граНИЦІ, ІНКОЛИ називають не
визначеними виразами. або невизначеностями. Дослідження умов
80
існування та обчислення границь невизначених виразів називається
розкриттям невизначєностеи.
Розглянемо основні невизначені вирази. Якщо о' і {J -- нескін-
ченно малі величини: в точці ХО Е R, ТО для обчислення границі
1. о(х)
Ц'П --
І-Но {з(х)
( 43)
неможливо скористатися теоремою про границю частки. Відношен
ня ;�:� називається невизначеним виразом (g) або невизначеністю
(§) в точці Хо. Сама границя (43) може бути скінченним числом, не
скінченністю або не існувати зовсім. Відношення si: І, якщо Х -7 О,
є невизначеністю (§), яка розкрита в п.l.5: lim sin І = 1 (перша
. I�O І
важлива границя).
Невизначеність (:) означає, що ми маємо ВІдношення двох
функцій, які обидві є нескінченно великими в точці ХО. Невизна
ченість (О· оо) означає, що маємо добуток двох функцій, одна з яких
нескінченно мала, а інша нескінченно велика в точці Хо. Аналогічно
можна з'ясувати зміст невизначеностей (оо - оо), (ооо), (оо), (1=).
Зокрема, функція (1 + x)�, якщо Х -7 О, є невизначеністю (1 =); вона
розкрита в П.l.9: lim(1 + x)� = е (друга важлива границя).
I�O
Поняття "невизначені вирази" застосовується не тільки до функ-
uій, а й до послідовностеЙ. Наприклад, відношення Іп, n EN, на
Уn
зивається невизначеністю (§), якщо {х n} і {Уn} -- нескінченно малі
послідовності. Аналогічно можна розглядати інші невизначені вира-
• u
зи для послідовностеи.
Ми застосуємо нескінченно малі величини до розкриття неви
значеностей. Інші методи розкриття невизначеностей бу дуть роз
тлянуті в розділі 4 § 2.
2.4. Порівняння нескінченно малих величин. Нехай о' і
.3 _.- ДВІ нескінченно малі функції в точці ХО Е R (що може бути
скінченною або невластивою точкою). Розглянемо частку ��:� і, при-
81
пускаючи, що знаменник (3( х) не перетворюється на О в деякому околі
. .
точки ХО, КрІМ, можливо, Хо, дамо такі означення.
Означення 1. Якщо Ііт о{3«х» = О, то а називається нескін-
x-txn х
ченно малою вищого порядку, ніж {3 в точці Хо, кажуть також, що
(3 --- нескінченно мала нижчого порядку, ніж а. Це записують так:
а(х) = о({3(х)), Х � ХО (читають: "а(х) є о мале від (3(Х) в точці
хо").
Означення 2. Якщо Ііт О{3«Х» = с - скінченне число, с і= О, то а
x-tХQ х
і {3 називаються нескінченно малими однакового порядку в точці хо.
Означення З. Якщо Ііт (30«Х» = 1, то а і (3 називають еквіва-
x-tХQ х
лентними і записують а(х) '" (3(х) або (3(х) '" а(х), х � ХО.
Очевидно, що еквівалентні нескінченно малі є нескінченно мали
ми однакового порядку.
Приклад 1. Порівняти попарно нескінченно малі функції в точ
ці хо = О: а(х) = х, (3(Х) = х2, ,(х) '= VГ+X - 1, д(Х) = sшх,
є(х) = 1- сов г.
Розв 'язання. Знаходимо
Ііт а(х) = Ііт х = Ііт х( VГ+X + 1) = 2
x-tО ,(х) x-tО VГ+X - 1 x-tО з: '
(3(х) х2 х2
ііт -- = Ііт = Ііт = 2,
x-tО є( х) .c-tО 1 - cos х x-tО 2 sin2 �
1· ,(х) l' VГ+X - 1 l' Х 1
1т -- = 1т = 1т да.JIl
x-tО д( х) x-tО sin х x-tО ( VГ+X + 1) віп г 2
ііт а(х) = Ііт ,(х) = Ііт д(Х) = Ііт а(х) = Ііт ,(х) = Ііт д(Х) =00.
x-tО #( х) x-tО #( х) x-tО ,в( Х) x-tО є( Х) x-tО є( х) x-tО є( х) .
. а(х)
11т �( ) = 1.
x-tО о Х
Отже, якщо х --7 О, то нескінченно М<і.іІИМИ однакового порядку
є функції х, sin х, VГ+X -- 1, а також функціі х2 і 1 - СОБ х; крім
того, х2 = о(х), х2 = o(vг+;:- - 1), х2 = o(sinx), 1 - сов л = о(х),
1 - СОБ Х = о( VГ+X - 1), .Г '" sіп:г.
Нескінченно великі величини f і .Q в точці ХО можна порівнюва-
82
ТИ між собою так СЮ,Ю, як 1 нескінченно малі, Якщо lim І(х) = О,
:l:--txo у(.Т)
ТО І(.т.) називають нескінченно ве.::Ш:КОЮ НИЖЧОГО порядку. ніж g(x)
в точці хо, кажуть також. шо 9(Х) _. нескінченно велика вищо
го порядку, ніж лх) (записують лх) = o(g(x)), Х -7 .го); якшо
lim Іс<;» = с -- скінченне число с -# О, то f( х) і 9( х) нескінченно
r--tro .9
. ... '. l' Лх) - 1
великі функціі однакового порядку в ТОЧЦІ ХО, якщо пп -(О ) - ,
з: --txo 9 .с
ТО .f(:r) і g( х) називаються еквівалентними (записують f( х) rv g( х),
.1' � хо).
Приклад 2. Порівняти попарно між собою нескінченно великі
функціі, як шо х -7 оо: х, х2, vг+x" - 1.
РОЗб 'язання. Знаходимо
.І: . 1
lim - = 11т - = О;
--tOG х2 х --too Х
. х
11т
x--tOG Jl + х-І
. x(vг+x" + 1) -
= Ііш = lim (JI+ х +- 1) = оо;
x--t= (JI"+Т -- 1)( vг+x" + 1) x--too
аналогічно
2
lim --�--- = lіш х( Л +х + 1) = ОО.
:l:--t= уІІ + .1: - 1 .1'--t=
Отже, Х = 0(х2), vг+x" - 1 = o(:r), ).1+:;; -- 1 =::: 0(х2), якщо
l' � оо.
Надалі говоритимемо лише про нескінченно малі величини, хоча
більшість результатів пього та наступного параграфів можна сфор-
6.. .
мулювати з втдповідними змінами також для нескінченно великих
величин.
Означення 4. ЯКШО ДЛ! нескінченно малих функцій (\'(х) і ,3(х)
не існує границя lіш (�«'I:)). то о(х) і .и(х) називаються непорівнюва-
,l'--tcro' ,1
НП?>ІИ між собою в точці .1'0'
83
Приклад 3. Показати, що нескінченно малі величини а(х) = х,
�(x) = х (1 + sin �), 1](Х) = х (2 + sіп�) попарно непорівнювані між
собою в точці ха = о.
Розв 'язання. Розглянемо відношення:
а(х)
�(x)
1
�(x) . 1
-( -) = 1 + SIn -,
а х х
а(х)
1](Х)
1
1 + sin 1.'
х
2 + sin.!.'
х
1](Х) . 1
-( -) = 2 + sш -,
а х х
�(x)
1](Х)
1 + sin 1.
х
1](Х) 2 + sin �
� ( х) - 1 + sin � .
2 + sin 1.'
х
Оскільки згідно з прикладом 3 з п. 1.4 границя функції sin � в
точці хо = О не існує, то не існує також границя жодного із шести
записаних відношень в точці хо = о. Тому нескінченно малі а(х),
�(x) і 1](Х) попарно непорівнювані між собою.
Далі зауважимо, що відношення ;�:� і ��:j необмежені в довіль
ному околі точки о, бо знаменник дробів �(x) = 1 + sin � перетво
рюється в О.в точках хn = !і!І.:2Пn' n Е Z, дЛЯ яких точка хо = О є
2
точкою скупчення. Решта відношень обмежені:
1�(x)I<2
а(х) - ,
І а(х.) І
1](Х) < 1,
11](Х) І
-- <3
а(х) - ,
І � ( х) І 11 + sin � І І 1 І 2
1](Х) = 2+sin� = 1- 2+sіп� :::; з·
Означення 5. Якщо для нескінченно малих функцій а( х) і (3( х)
існує така стала с > о, що І ;�:� І < с в деякому околі точки хо (крім
х = Хо), то нескінченно мала а(х) називається обмеженою в околі
точки хо порівняно з нескінченно малою (3(х). Це записують так:
а(х) = О({3(х)), х ---+ хо (читають: "а(х) є О велике від (3(х) в точці
хо").
Для нескінченно малих а(х), �(x), 1](Х) з прикладу 3 можна запи
сати: �(x) = О(а(х)), а{х) = О(1](Х)), 1](Х) = О(а(х)), �(x) = О(1](Х)).
84
Зробимо декілька зауважень.
1. Означення 5 формулюється для двох нескінченно малих функ
цій незалежно від того, порівнювані вони чи ні між собою. До того ж ,
якщо а(х) = о(!3(х)), х --7 Хо, то тим більше а(х) = О(р(х)), х --7 хо.
Тому кожна з нескінченно малих функцій {3(х) і є(х) з прикладу 1 є
функцією О велике від усіх інших нескінченно малих цього прикладу.
2. Рівності, що містять символи о та О, не є рівностями у зви
чайному розумінні цього слова. Всі вони читаються зліва направо:
так, рівності а(х) = о(р(х)) і ,(х) = о(р(х)) означають лише, що а(х)
і ,(х) є нескінченно малими вищого порядку, ніж р(х), але звідси зо
всім не випливає, що а(х) = ,(х). Наприклад, х2 = о(х) і хЗ = о(х),
х --7 О, однак х2 -# хЗ.
З. Символи О та о можна застосовувати до довільних функ
цій (водночас і нескінченно великих) і до послідовностей, якщо у
відповідних означеннях замінити назву "нескінченно мала функція"
назвою "функція" або "послідовність". Записи а(х)=О(I), ,6(х)=о(l)
означають, що а( х) - обмежена функція, а,6( х )-- нескінченно мала.
2.5. Еквівалентні нескінченно малі функції.
Теорема 1. Нехай а і f3 - нескінченно малі фуu'К,'Ціі в mо'Ч.'Цz
хо Е R. У мови
1) а(х) г'v (З(х), х --7 Хо,
2) а(х) - р(х) = о(а(х)), х --7 хо,
3) а(х) - В(.с) = о({3(х)), х --7 хо,
еквівалентні одна одній.
Доведення. Доведемо теорему 1 у таюи послідовності: 1) �
2) � 3) � 1).
1) � 2). Оскі.'ІЬКИ Ііт �(I» = Ііт 3(І) = 1 (за умовою 1)), то
x-tХQ' Х .c--txo о з:
1· о(х) - ,3(х) l' (1 fЗ) О
llll = ІІIl - - = .
.c-t.co а(х) x-txo а
85
2) � 3). Оскільки lim o(./:)(:�(.!:) = О (за умовою 2)), то
.l.-t.1:0 О.І
1. 0'(Х)-3(.с) й-З o-{J
ІПl = lіш = Ііш О - = О.
т-Но П(:t·) t-tТQ (3 - о) + О' .г-trQ д-.Е:. + 1
о
3) � 1). Оскільки Ііт a(�'.:(�(x) = О (за умовою 3)), то
r-t.сQ .1 .г
о(х) (О' - (3 )
Ііт -- = Ііт -- + 1 = 1.
x-tХQ ,6{ х) x-tХQ (3
Читачам пропонуємо самостійно довести такі дві теореми.
Теорема 2. Якщо О'(Х), (З(х), ,(х) -- нескінченно .малі фУЮ't:'Ціі
в точці ха і О'(Х) "-' (3(х), (3(х) "-' ,(х), х --t Ха, то О'(Х) "-' ,(х),
Х ---t ха.
Теорема З. Нехай О'(Х) і (3(х) -- нескінченно мам фУ'Н.'r.;'Ціі в
точці з:«. Якшо Ііт �«x» =с-!-О, тоО'(х) "-'с{3(х), Х---+Хо, тобто
x-tХQ І-' а:
О'(Х) = сfJ(х) + О({3(Х)) і, отже, (3(Х) = �O'(X) + О(О'(Х)), Х ---+ ха·
Теорема 4. Нехай О'(Х), (3(Х), О'I(Х), (3І(Х) ... _- нескінченно мам
фУ'Н.'r.;'Ціі в точці ха і О'(Х) ;..., О'І(Х), (3(х) "-' (3І(Х), Х ---+ ха. Якиіо
існцє границя Іітп �I«X», то також існце границя Іігп �«x» z сnрав-
x-txo 1-'1 з: x-txo І-' Х
dжуєтьс.я рівність
Ііт о(х) = Ііт О'l(Х).
x-tХQ (3(х) x-tХQ (31(Х)
(44)
Доведення. У деякому околі точки ха виконується тотожність
а(х) _ о(х) ОІ(Т) {JI(X) 3' 4
{J(x) - 01 (х) • {JI(X) . {J(x)' ВІДСИ, ураховуючи умови теореми ,зна-
ходимо
. оСт) . а . 0'1 . ЗІ . 01(Х)
Inn --- = Іігп -. Іігп -. Ііш - = 11111 -, --.
J·-+.1:0 Ц(х) .Г-+·1"о 0'1 :/:-tJ:() 3] ..'-t.со:З r---t·t:o ііІ (х)
Оскільки ліва і права час.ТИШІ рівності (44) рівноправні, то або
обидві границі в цій рівності існують і тоді вони однакові, або обидві
86
вони не ІСНУЮТЬ. Тому, аастосовуючи теорему 4 ДО розкриття НСВПЗ
наченостеи (§), можна одну або обидві задані нескінченно малі ВС-
. . ...
.1ИЧИНИ ламінити СКВІва_1еНТНІІ�ІИ НІ нескінченно малими, не знаючи
навіть: чи існує границя Їх відношення . Для розкриття невизначено
стеи іншого виг.1ЛДУ. наПРИК1ад. (О· ас) і (�), можна скористатися
не ті"1ЬКИ еквіВп_1СНТНП),Ш нескінченно малими функціями, а и ЄК
вівалентними функціями а60 сквівалентними нескінченно великими
функціями. Пропонуємо читачам аналог-ічно до теореми 4 довести
са�ЮСТІИНО таку теорему.
Теорема 5. Нехай О'(Х) і О'І(Х) .- нескінченно мам, а ЛХ) і
ІІ(:Г) -� нескінченно еемікі фуu'К":ціі в точці Ха і О'(Х) '" О'І(Х), ЛХ) '"
ІІ(Х), Х ----+ ХА. Якшо існцє границя Іігп (О'І(Х) . ІІ(Х)), то також
x--tХQ
існие границя Іігп (О'(Х)' ЛХ)) і вонн однакові.
x--tХQ
Застосувавши теореми 4 і 5 можна, спростити обчислення гра-
ниць.
у табл. 1 подано перелік деяких еквівалентних нескінченно ма-
.1ИХ В точці ХА = О.
Таблиця 1
6.
In( 1 + .Т) '" .Г
-----
1.
Sin х ""' Х
--
--
:r
2.
tg Х '" Х
7.
Ioga (1 + Х) '" --.-
Ін а
Т- .
8.
є" - 1 '" х
.. -
'. a1"<:S1I1:r '" .Т
4.
alTtg х '" .1:
9. а" - 1 '" х . Іп а
7г
(1 + .TY�
u.
"2 - arccos х '" :r
10.
- 1 '" О.Т
--
Перша єквівалентнієть в табл. 1- це інша форма запису першої
важливоі границі. Еквіва .. тентність tg;r rv :с також випливає з першоі
.. .
важливої граниш:
. t g .г ( SIll Xl)
Ііш --- = Ііш --. ---
.г--tО:1" .г--tО J' cos ,1'
1
(бо Ііш cos ,1'
. г-+О
1 (ДІІВ. п. 1.5)) .
8ї
Можливості обгрунтування інших еквівалентностєи розглянемо
в П.3.5.
Приклади. Обчислити границі.
І' sinx ( sinx rv х )
1. x� In( 1 + tg х) In{ 1 + tg х) rv tg х
еБіп Х' _ 1 ( esill Х' - 1 rv sin х )
2. Ііт з� 1
Х-+О .vI + х-І уІ + х-І rv зх
І· tgx-sinx І' sinx(l-cosx)
З. пп = ІШ --=-----'-
x-+о.гЗ Х-+О хЗ . cos х
2х. х2 1
= (sin х rv х) = Іігп 4
Х-+О хЗ 2
Означення. ЯКЩО О'(Х) і {3(х) -- нескінченно малі функції в
точці хо і }��o (;�»k = с і- о, то О'(Х) називається нескінченно малою
порядку k щодо {3(х) в точці Хо, а c({3(x))k називається головною
частиною нескінченно малої О' ( х ), х --7 х О •
3 означення і теореми 3 випливає, ЩО
І. х
= 1т -- = 1.
х-+о tg х
вш т
ііт -- = З.
х-+о tx
sin х . 2 sin 2 f
Іігп ----,----...:::-
х-+о хЗ• cos х
тобто а(х) rv С (({3(x))k), Х --7 хо.
Аналогічне означення можна сформулювати для нескінченно ве
ликих функцій в точці хо.
Приклади.
4. Функції, що записані в табл. 1 праворуч від знаків еквіва-
лентності, є головними частинами функцій, що записані ліворуч від
цих знаків. Всі ліві частини співвідношень є нескінченно малими
першого порядку щодо х, ЯКЩО х --7 О.
5. Головною частиною многочлена
як нескінченно великої функціі, якщо х --7 оо, є функція а.,):", Отже,
многочлен Р n( х) є нескінченно великим порядку ТІ відносно л , ,]; --7 оо.
88
Можна записати також: Рn(Х) = аnхn + о(хn) або рn(х) rv аnх'!,
х -+ ОО.
Відповідно до означення за ГО"10ВНУ частину для нескінченно ма
лої функції можна взяти довільну еквівалентну їй нескінченно малу.
Задаючи конкретний вигляд головної частини, можна значно звузи
ти множину функцій, серед яких шукають головну частину і навіть
домогтися того, що вони визначатимуться однозначно. Цей пошук
ведуть звичайно серед простих (в деякому сенсі) нескінченно малих
функцій, що мають добре вивчені властивості (наприклад, степеневої
чи тригонометричної). Зокрема, задача про виділення для довільної
нескінченно малої а(х), х -+ Ха, головної частини у вигляді степе
невої функції А( х - xo)k зводиться до знаходження двох чисел А та
k > О.
Приклади.
6. Виділити головну степеневу частину функції а(х) = lп(І+
+2х2 - Зх3), Х -+ О.
Позначимо t = 2х2 - Зх3. Враховуючи, шо t -+ О, якщо х -+ О,
і, застосовуючи еквівалентність lп(І + t) rv t, t -+ О, одержимо
111(1 + 2х2 - Зх3) rv 2х2 - Зх3 = х2(2 - Зх) rv 2х2, Х -+ О.
7. Виділити головну степеневу частину функції (3(x)=V2 - х-І,
.г -+ 1.
Введемо змінну t = х-І; t -+ О, якщо х -+ 1. Тоді (3(х) =
= ,в( 1 + t) =.J[=t-I. Використовуючи еквівалентність .J[=t -1 rv - tt,
t -+ О, дістанемо
;3(х) = J2 - х-І =.Jl=t.- 1 rv -�t = -�(x - 1), х -+ 1.
§ з. Неперервність функції
З.1. Неперервність функції в точці. Поняття границі функ
ціі Лх) в точці ха вимагає, шоб функція БУ.;'Іа визначеною в околі точ
ки хо Е R крім, можливо, самої точки Ха, а значення І(хо), навіть
89
якщо воно існує, не враховується. Якщо ж говорять про неперерв
ність функціі в точці .1:0. то припускають, шо хо --- скінченна точка і
враховуть як поведінку функції біля точки Хо, так і значення функціі
в саМІИ точш.
Означення 1. Функція лх) називається неперервною в точці
хо Е R. якщо вона визначена в деякому околі точки хо і
Іігп лх) = лхо), лхо) Е R.
х-+хо
(45)
Ця умова означає, що границю неперервної функціі в точш хо
можна знайти, обчисливши значсння функції в точці Хо. Неперер
вність функції в точці відображає ту надзвичайно важливу влас
тивість функціі, що невеликі відхилення значень аргументу від хо
можуть спричинити лише невеликі відхилення значень функціі від
лхо).
Означення неперервності функції в точці можна формулювати
також, як і означення границі функції в точці, за допомогою околів,
(є, Ь)-запису чи посяідовностеи. Для цього потрібно звмінити в різ
них означеннях границі функції, які наведені в п. 1.1 і п. 1.8, ЧІІС.ло А
числом лхо). Пропонуємо читачам зробити це самостійно.
Для функцій, неперервних в точці, справджуються всі теореми
п.п.1.2, 1.3 про властивості функцій, що мають границю в точці.
Сформулюємо лише теорему про арифметичні дії над неперервними
функціями.
Теорема. Я'і'\,ЩО ФУU'і'\,'Ціі І(;г) і у(х) неперерені в точці хо, то
в 'Цій точці неперервними є також ФУU'і'\,'Ціі лх) ± у(х), лх)· у(:г) Z
��:�, остання за у.мови, ЩО у(хо) і- О.
Теорема насправді стверджує, шо виконуються рівності
1) Ііш и(х) ±у(х)) = л:го) ±У(:То):
x-t.l'О
2) Іігп (Л.1·)· у(.г)) = л·L·о)· У(.1·О):
x-txo
. Л:1.') лхо)
3) Іігп --(-) = -(-) , якщо у(то) і- О.
x-txo 9 Х У :1.'0
90
Ці рівності випливають з теореми 1 (п. 1.3), як ШО врахувати, шо
Ііт Лт) = лхо) і Іігп 9(;r) = .ч(хо).
-tХU .["-txo
Подамо ще одне означення функції, неперервної в точш. Для
цього нагадаємо, що відповідно до теоре1,Ш з п. 1.1 умова існування
скінченної границі Ііт f (х) = А ріВНОСЮІьна умові Ііт (f (.Т ) - А) = О,
x-txo D-х-tО
де 6.х = х _. хо -- - приріст аргумєнту. Якщо тепер у цих границях
прийняти А = f (хо ), то перша з них переходить в означення непе
рервності (45), а друга -- в ріВНОСИ.11ЬНУ цьому означенню умову
Ііт и(х) - лхо)) = О,
D-х-tО
(46)
яку можна записати як
Ііт 6.у = О,
D-х-tО
(47)
якщо позначити 6.у = ЛХ) - Лхо) = ЛХО + 6.х) - f(хо). Величи
на 6.у називається приростом функції f в точці Хо, який відповідає
приросту аргументу 6.х (або коротко -- приростом функції). Умову
(47) можна взяти за означення функції, неперервної в точці. Вона
означає, що нескінченно малому приросту аргументу 6.х відповідає
нескінченно малий приріст функції 6.у. Рівністю (47) зручно корис
туватися для доведення неперервності функції в точці.
Означення 2. Функція f(х), визначена на множині Е, нази
вається неперервною в точці хо Е Е відносно множини Е, якщо хо є
точкою скупчення для Е і \j є > О :3 <5 > О \j х [х Е U Е (ХО) ::::} І J( х)
-f(хо)1 < є], записують Іігп f(х) = ЛХО) або ііт f(х) = f(хо),
r-txo x-txo
хЕЕ
• u
якщо ВІдомо, про яку множину идеться.
Означення З. Функція називається неперервною на множині
Е, якщо вона неперервна у кожній точці множини Е.
Приклади.
1. Стала функція у = с неперервна на множині R (довести
самостіино] .
2. Показати, що степенева функція у = х": П Е .У, неперервна
на множині R.
91
Спочатку розглянемо функцію у = х. Для довільного ха Е R
маємо 6.у = 6.х і тому Ііт 6.у = о. Отже, за умовою (47) функція
D-x---ta
у = х неперервна на множині R. З теореми 1 випливає, що функція
у = хn, як добуток n неперервних функцій у = х, є неперервною на
R.
3. Показати, що многочлен Рn(Х) = аа + аІХ + а2Х + ... + аnхn,
n EN, ап =J. О, є неперервною функцією на множині R.
Кожна з (n + 1) функцій аіхі, і = О, n, неперервна на множині R
(за прикладом 2). Тому з теореми 1 випливає, що функція Рn(Х) є
неперервною на R.
4. Показати, що функція у = sinx неперервна на множині R.
Розглядаючи в п.1.5 першу важливу границю, ми скористалися
нерівністю І віп г] < іхІ, з якої випливає неперервність функції sinx
в точці ха = О (бо l6.уl = І sinx - зіп О] = І зіп г] < Іхl = l6.хl). Для
довільної іншої точки ха Е R запишемо
І І І І І· х - ха І І х + Ха І
6.у = sin х - sill Ха = 2 SIll 2 . cos 2 ::;
І· х - Ха І І І І І
::; 2 SIll 2 ::; х - Ха = 6.х.
Звідси випливає, що функція у = sin Х неперервна на множині R.
5. Функція у = cos Х неперервна на множині R (довести самос
тійно).
6. Функція tg Х неперервна, якщо Х =J. кп + �, n Е Z .
. Справді, якщо ха =J. п п +�, nEZ, то cosxa =J. О і функція tgx =
SIn Х· Ф . u
= cos х неперервна в точш ха 11К частка двох неперервних УНКЦІИ.
7. Функція у = ctgx неперервна на множині R\ ( U {n7Г}) (до
nEZ
вести самостійно).
3.2. Границя 1 неперервність складеної функції. Як
вище, через U (х) позначатимемо окіл точки .г Е R.
92
Теорема 1 (про заміну змінної для границі функції). Нехай дл.я
фу'Н,-к;'Цій у = лх) і z = g(y), заданиа: відnовід'Н,о на де.я-к;uх множинах
и(хо)\{хо}, хо Е R, і и(уо)\{уо}, уо Е R існцють скінченні або
нескінченні границі уо = Ііт J( х) і Ііт g(y). Тоді існцс склаоена
x---txo y---tyo
фу'Н,-к;'Ці.я 9 и(х)), визначена 6 де.я-к;о.му околі точхн Хо, але без точхн
хо, z границя
ііт 9 и(х)) = Ііт g(y).
x---txo y---tyo
(48)
З доведенням теореми 1 можна ознайомитися в [1, с.189-190].
Наступна теорема стосується неперервних функцій.
Теорема 2 (про неперервність складеної функції). Нехай зада
на фу'Н,-к;'Ці.я z = g(y) еизначена в околі U (уо) точхн уо Е R, а фу'Н,-к;'Ці.я
у = лх) визначена в оком и(хо) точкн хо Е R, уо = лхо), і об
ласть значень фу'Н,-к;'Ціі 1 е підмножиною о-к;олу и(уо). Якиіо фу'Н,-к;'Ці.я
у = J( х) неперервна в точці Хо, а фу'Н,-к;'Ці.я z = g(y) неперервна в
точці Уо, то складена фу'Н,-к;'Ці.я z = g(f(x)) неперервна в точці хо і
тоді сnравджуютьс.я такі рівності
Ііт 9 и(х)) = 9 (1 ( Ііт х)) = 9 (ЛХО)) =
x---txo x---txo
=g (Ііт ЛХ)) = g(yo) = Ііт g(yo).
x---txo y---tyo
(49)
Коротко цю теорему формулюють так: неперервна функція від
неперервної функції неперервна. Рівності (49), як і рівність (45),
показують, що операцію граничного переходу Ііт можна міняти міс
llЯМИ з операціями знаходження значень неперервних функцій.
Зауважимо, що формулювання теореми 2 відрізняється від фор
�Іулювання теореми 1 вимогами неперервності функцій J( х) (у точці
хо) і g(y) (у точці уо), Ці вимоги, по суті, зводяться до накладан
ня в теоремі 1 таких двох додаткових обмежень: 1) щоб значення
1'0, уо і обидві границі Ііт Лх), Ііт g(y) були скінченними; 2) щоб
x---txo y---tyo
Ііт ЛХ) = лхо) і Ііт g(y) = g(yo). Тому теорему 2 можна отри-
x---txo y---tyo
93
мати як наСЛІДОК з теореми 1 для неперервних функцій. Проте ми
подамо доведення теореми 2. не використовуючи теорему 1.
Д 06 едення теореми 2. За умовами теореми f (U (хо )) Е і: (уо), а
тому існує складена функція z =.9 (ЛХ)), визначена в ОКО.1і (т(хо).
Функція g(y) неперервна в точці уо і тому
V U(g(yo)) :3 [і(уо) Vy [у Е и(уо) =} g(y) с [і (g(yo))].
Функція у = f( х ), уо = f( хо ), неперервна в точці хо і тому для
вибраного околу [т(уо) :зи(хо) Vx [х Е и(хо) =} ЛХ) с и(уо)]. Отже,
якщо х Е и(хо), то g(f(x)) С U(g(yo)). Оскільки окіл U(g(yo))
довільний, то це означає, що lim 9 (ЛХ)) = g(yo) = 9 (ЛХО)) і, отже,
x-tХQ
виконується низка рівностей (49).
Теорему 2 можна поширити на суперпозиції скінченної кількості
функцій. Якщо не зупинятися на ТОЧНО�іУ формулюванні відповідної
тереми, то суть такого поширення ПО.·ІЯгає в тому, що супєрпозишя
скінченної кількості неперервних функцій є неперервною функцією.
Сформулюємо ще один практично важливий наслідок з тео
реми 1.
Наслідок. Якщо в теоремі 1 вважати функцію g(y) неперерв
ною в точці уо (а тому визначеною в околі и(уо)), то рівність (48)
можна записати як
lim o9(f(;r:)) = lіш g(y) =g(yo) =09 (liШ Л:1:)). (50)
x-txo y-t УО .Т -txn
Приклад. Показати, що функція у = cos2(2x3 +- .г] неперервна
на множині R.
Розв 'язання. Задану функцію можна записати ЯК суперпозицію
трьох функцій: у = v2, т = соз И, 11 = 2х3 + .С. ОскіЛЬКІІ кожна
з функцій неперервна на множині R, то функція у = cos2 (2.1:3 + .с)
неперервна на В.
Інші приклади застосування теореми 1 до обчислення границь
РОЗГ.1ЯН('МО в П. 3.5.
3.3. Неперервність оберненої функції. У п.2.6 з роз дьлу
1 було показано, що обернена до монотонноі функція завжди існує.
Сформулюємо без доведення ще дві теореми, в яких говориться про
існування оберненої неперервної функції.
Теорема 1. Нехай фу'Н:к;'Ці.я Лх) зростаюча і неперервна на сєа
менті [а; Ь] і А = Ла), В = ЛЬ). Тоді образом [а; Ь] є сегмент. [А; В]
і обернена фующі.я і:' (у) зростаюча і 'Н,еnереро'Н,а на сегменті [А: В]
(рис. 7, а).
В цій теоремі слово "зростаюча" можна замінити словом "спад
на" , але тоді образом [а; Ь] буде [В; А] (рис.7,б).
Теорема 2. Нехай фующі.я Лх) зростаюча і неперервна на
проміжки ( а; Ь), а Е R, Ь Е R, і нехай існиють односторонні гра
ниці А = Ііт і(х) і В = Ііт Лх), А Е R, В Е R. Тоді образом
x-tа+О x-tb-O
( а; Ь) є проміжок (А; В).
У цій теоремі слово "зростаюча" можна замінити словом "спад
на" , але тоді образом (а; Ь) буде (В; А).
у
о
а
ь х
о
а
ь х
а
б
Рис.7
Приклад 1. Показати, що функція у = агсsшх неперервна на
сегменті [-1; 1].
РО,30 'язання. Справді, оскільки функція sill х зростаюча і непе
рєрвна на сегменті [- і: і], sill (- і) = -1, sin (і) = 1, то обернена
функція. за теоремою 1. зростаюча і неперервна на [-·1; 1]; образом
відрізка [--1: 1] є відрізок [- і; і] .
95
Аналогічно можна довести неперервність функцій агссов х,
arctg х, arcctg х у точках, в яких вони визначені .
.
3.4. Неперервність основних елементарних функцій. У
п. 2.7 з розділу 1 розглянуто основні елементарні функції.
Теорема. Кожна 3 осноених еяементарниз: фу'Н,'к::ці'й неперервна
в тих точках, де вона еизначена.
Доведення теореми не подаємо, але зробимо декілька зауважень.
Неперервність функцій у = С, де С - стала, у = х n, n EN, і триго
нометричних функцій обгрунтована в прикладах у п.3.1. Питання
про неперервність обернених тригонометричних функцій розглянуто
в п. 3.3. Доведення неперервності степеневої функції у = хО, о: Е R,
і показниковоі у = аХ, а > О, а =f:. 1, виходить за межі цього курсу.
3 цими доведеннями можна ознайомитися в [1, § 7]. Логарифмічна
функція у = loga х, О < а =f:. 1 є неперервною як обернена до показни
ковоі.
3.5. Обгрунтування співвідношень еквівалентності. Об
грунтуємо співвідношення еквівалентності 3-10 з табл. 1 в п. 2.5.
Покажемо, що arcsinx '" х, х ---7 О, тобто що Ііт arcsinx = 1.
x-tО х
Розглянемо функцію у = arcsinx, х Е [-1; 1]. Оберненою до неї є
функція х = siny, у Е [-І; І]. Якщо у відношенні arc�nx прий
мемо аrсsіn х = у і х = sin у, то отримаємо функцію ....,lL-. Пере-
. Sin у
конаємося, що до функцій у = f( х) = аrсsіn х і z = g(y) = si� у
можна застосувати теорему 1 з п. 1.1. Справді, перша з цих функ
цій f( х) існує на множині (-1; 1), яка містить точку хо = О і УО =
= Ііт f( х) = Ііт аrсsіn х = О; друга функція g(y) існує на множині
x-txo x-tО
(- І; І) \ {уо = О} і Ііт .л.: = 1. Тоді згідно з теоремою 1 з п. 1.1
y-tуо=О SIn у
границю складеної функції g(f(x)) = sin(�rs:�i�x) - arc�nx В ТОЧЦІ
хо = О можна обчислити за (48), тобто
1· arcSIn х 1· у
пп = lПl -.--
x-tО Х y-tО Sill у
1.
96
Отже, доведено, що arcsin х rv х, Х ---+ О.
Аналогічно можна довести, що arctg х rv х, Х ---+ О.
Покажемо, що loga (1 +- х) rv І: а' .r --t О і, зокрема, якщо - а = е,
то ln(1 + х) rv х. Справді, Ііт loga(l+x) = Ііт loga ((1 + x)�)
x--tО х x--tО
= loga (Ііт (1 + х ) �) = loga е = -І 1 (тут для другої рівності вико-
x--tО па
ристано наслідок з теореми 1 в п. 1.1, а для третьої - другу важливу
границю).
Обгрунтуємо, що ах - 1 rv х In а, х ---+ О. Розглянемо функцію
у = ах - 1. Оскільки вона монотонна і неперервна на R, то існує
обернена функція х = Іп���у), яка --- монотонна і неперервна для
у > -1. Якщо у відношенні аХ;1 приймемо ах -1 = у і х = Іп���у), то
отримаємо функцію I:('���). Далі застосовуємо теорему 1 з п.l.l до
-1ВОХ функцій: у = Лх) = а" -1 і g(y) = I:('���). Першу з тих функцій
розглядаємо в околі точки ХО = О і тоді УО = Ііт (ах - 1) = О, а
x--tхо=О
-1РУГУ - в околі точки УО = О без точки О і тоді
1. У -Іп о
пп
y--tуо=О ln( 1 + у)
Ina
1. Iп(1+У) =(ln(l+y)rvy)=lna.
1т ---''----'--''-'-
y--tО у
Оскільки 9 (f(х))
ходимо
(aX-1)lпа
Iп(1+аХ-1)
аХ--=-!.. то за теоремою 1 з п. 1.1 зна-
І '
аХ - 1. . у In а
Ііт g(f(x)) = Ііт = 11т g(y) = 11т 1 ( ) =lna.
x--txo x--tО Х н+ис y--to n 1 + у
Отже, аХ - 1 rv xlna, х ---+ О, а якщо а = е, то е" - 1 '"" х.
Щодо не розглянутих ще співвідношень еквівалентностей 5 і 10
з табл. 1 в п.2.5, то Їх можна обгрунтувати аналогічно, до поперед
ніх (зокрема, еквівалентності 3 і 9) за допомогою відповідних замін
змінних. 1ІІи обмежимося лише двома вказівками, запропонувавши
деталі обгрунтувань як вправи для читачів.
97
Вказівка 1. Для обгрунтування еквівалентності � - а1"С"С"08.Т r..J
"-' х, Х ---7 О. можна виконати заміну у = � - arccosx. яка зведе
• 1':. - arccos:z'
ВІдношення 2 до вигляду -.-У-.
х • �"Y
Вказівка 2. Д.;1Я обгрунтування еквівалентності (1 + х)О - 1 r..J
r..J ах, х ---7 О, можна виконати заміну у = Іпі І + х), яка зведе відно-
O+x)O-l еа!і-l
шення ох до вигляду о(е!і-l)'
З.6. Точки розриву функції та ІХ класифікація.
Означення 1. Нехай функція І визначена в деякому околі скін
ченної точки Хо, крім, можливо, самої ЦІЄІ точки. Точка хо нази
вається точкою розриву функції І, якщо функція не визначена в
точці хо або якщо вона визначена в цій точці, але не є в ній не
перервною; саму функцію називають розривною в точці Хо, кажуть
також, що функція І має розрив у точці хо.
Означення 2. Якщо хо - точка розриву функції І і існують
односторонні скінченні границі (див. п. 1.6) ЛХО - О) = Іігп ЛХ) і
x---txo-O
ЛХО + О) = Іігп ЛХ), то хо називається точкою розриву першого
x---txo+o
роду.
Означення З. Якщо хо --- точка розриву першого роду функції
І, то різниця ЛХО + О) - ЛХО - О) називається стрибком функціі в
точці хо. Якщо стрибок дорівнює О, тобто існує границя Іігп Лх) =
x---txo
= ЛХО - О) = ЛХО + О), то хо називається точкою усувного розриву.
Розрив функції названо усувним тому, що можна побудувати
таку іншу функцію F, яка бу де неперервною в точці хо і відрізняти
меться від І значенням лише в точці хо; функцію F будують так:
{ ЛХ), якщо х =І- Хо,
F(x) = lіш ЛХ), якщо х = хо.
x---txo
Означення 4. Якщо для функції точка розриву не є точкою
розриву першого роду, то вона називається точкою розриву друго
го роду.
98
у точці розриву хо другого роду хоча б одна 3 односторонніх
границь ЛХО - О) або ЛХО -+- О) не існує або може виявитися невлас
тивою.
Означення 5. Функція j називається неперервною ліворуч в
точці Хо, якщо ЛХО - О) = лхо) і неперервною праворуч в точці Хо,
якщо ЛХО -+- О) = лхо).
Функція j є неперервною в точці хо тоді і тільки тоді, коли
вона є неперервною ліворуч і праворуч в точці Хо, тобто і(хо - О) =
= лхо) = ЛХО -+- О).
Приклади.
1. Функція signx неперервна, якщо х -І- о. Точка хо = О -
єдина її точка розриву першого роду, величина стрибка sign (+0) -
sign (-О) = 2.
2. Функція Isignxl має розрив першого роду в точці хо = О
(рис. 8 а)), але цей розрив усувний: бо існує неперервна функція
F( х) = 1, що відрізняється від функціі Isign х І значенням лише в
точці хо = О (рис. 8 б).
У y=lsignxl
У
у=1
1
1
х
О
О
б
х
а
Рис.8
3. Для функції Діріхле (п. 2.2 з розділу 1) кожна точка хо Е R є
. . . . .
точкою розриву другого РОДУ, ОСКІльки не ІСНУЄ НІ граниш ЛІВоруч
D(xo - О), ні границі праворуч D(xo -+- О) (приклад 2 з п. 1.6).
4. Функція � має розрив другого роду в точці хо = О, бо обидві
. .. �, .
односторонні граниш у ши ТОЧЦІ Є невластивими.
5. Із графічного зображення функцій [х] і {:г} на рис.5,б, в
з розділу 1 легко зробити висновок, що в кожній точці множини Z
обидві функції мають розриви першого роду, обидві вони неперервні
99
праворуч, але стрибок функції [х] дорівнює 1, а стрибок функції {х}
дорівнює (-1).
6. Розглянемо функцію sin � (рис.4). Аналогічно, до прикладу 3
зп. 1.4 було показано, що не існує границі Ііт sin;, можна показати
x-tО
також, що не існує односторонніх границь Ііт sin.1 і Ііт sin.1.
x-t-O х x-t+О х
Тому ХО = О --- точка розриву другого роду для функції sin �.
7. Знайти точки розриву функції у = � і вказати Їх тип.
21+х -4
Розв 'язання. Функція не визначена в точках, в яких 1 + х = О =}
1
Х = -1 і 21+х -- 4 = О =} х = - t. Тому ХІ = -1 і Х2 = - t - точки
розриву цієї функції. В усіх інших точках функція неперервна, бо
записується як суперпозиція, різниця і частка неперервних функцій.
Знайдемо односторонні границі функції в точці ХІ = -1. Нехай
1 1
Х ---+ -1 - О =} 1 + х ---+ -о =} -- ---+ -оо =} 2 l+х ---+ О =}
l+х
1 1
=}у= 1 ---+--.
21+х - 4 4
Приймемо
1 1
Х ---+ -1 + О =} 1 + Х ---+ +0 =} -- ---+ +00 =} 21+х ---+ +00 =>
l+х
1
=} у = 1 ---+ о.
21+х - 4
Отже, ХІ = -1 -- точка розриву першого роду, стрибок функції
дорівнює �.
Знайдемо односторонні границі в точці Х2 = - t. Нехай
1 1 1 1
Х ---+ - - - о =} ;!" + - ---+ -о =} Х + 1 =} - - о =} -- ---+ 2 + О =}
2 2 2 l+х
1 1
=} 2 т+х ---+ 4 + О =} У = ----,1:----
21+х - 4
---+ +00;
100
приимемо
1 1 1 1
х ---+ - - + о ::::} х + - ---+ + о ::::} х + 1 ::::} - + о ::::} -- ---* 2 - О ::::}
2 2 2 l+х
1 1
::::} 2 1 +"' ---+ 4 - О ::::} У = --'-1 -- ---+ - CXJ •
21+"' - 4
Отже, Х2 = -! -- точка розриву другого роду. Графік функції
поблизу точок розриву схематично зображено на рис. 9.
у
о х
І
� __ �_�_�_�_� __ �_�_�_�_�L::::�-::::
Рис.9
у
о а
х
Рис. 10
3.7. Функції, неперервні на сегменті. Сформулюємо без
доведення декілька властивостей неперервних функцій, заданих на
сегменті (тобто неперервних в кожній точці сегмента). Ці властивос-
ті застосовуються в теоретичних дослідженнях і розв'язаннях прак
тичних задач; з Їх доведенням можна ознайомитися в [1, § 6].
Теорема 1 (про обмеженість неперервної функції). Я'К,ЩО ФУ'Н,'К,
ція f неперервна на сегменті [а; Ь], то вона обмежена на ньомц,
тобто існцють такі два числа m і АІ, m � М, щО дл.я всіх х Е [а; Ь]
еиконцються нерівності m < лх) � АІ.
Геометричний зміст теореми полягає втому, що для графіка
неперервної на сегменті [а; Ь] функції f завжди існують дві горизон
тальні прямі у = m і у = ІУ!, У смузі між якими знаходиться її графік
101
(рис.10). Очевидно, що будь-яка горизонтальна смуга тІ <Іі» )<5,1\11
де тІ <5, т., МІ � 1\1 також міститиме цей графік.
Вимоги умови теореми, -- шоб функція була визначеною на сег
менті і неперервною на ньому, є істотними. Так, функція ЛХ) = � є
неперервною на півсегменті (О; 1], але не є обмеженою поблизу точки
о. Якщо цю функцію довизначити, прийнявши ЛО) = О, то вона буде
скінченною в кожній точці сегмента [О; 1], але не буде неперервною і
обмеженою на ньому.
Повернемося до теореми 1. Згідно з нею множина значень Е(f)
неперервної функції f на сегменті [а; Ь] обмежена. А тому за те
оремою 1 з п.1.8, розділ 1 існують скінченні точні межі множини
Е(f) -- нижня то = inf Е(f) і верхня МО = вцр Е(f)*. Тоді сму
га то <5, у <5, Мо буде найвужчою серед усіх горизонтальних смуг,
що містять графік функції І. З логічних міркувань можна припус
тити, що горизонтальні краї цієї смуги у = то і у = Мо повинні
дотикатися в деяких точках до графіка функції f (рис. 11). Це озна
чає, що на сегменті [а; Ь] повинні існувати такі точки ХІ і Х2, У яких
ЛХІ) = МО = supE(f) і ЛХ2) = то = infE(f), тобто у множині
Е(f) існують найбільший Мо і найменший то елементи.
у Число то називають найменшим
МО або мінімальним значенням функції f
Б Х
на сегментт
= гпіп ЛХ),
а<х<Ь
[а; Ь], записують то =
а Мо -- найбільшим
або максимальним значенням функції
f на сегменті [а; Ь], записують Мо =
= тах ЛХ).
а<х<Ь
Рис. 11
Точки ХІ і Х2, У яких ЛХІ) = Мо і
І(Х2) = то, називаються точками від
найменшого значень функції f на сегменті
повідно найбільшого
[а; Ь].
вцр ЛХ).
а<х<Ь
* Числа іпf Е(f) та БНР Е(f) ще позначають inf Л Х)
а<х<Ь
102
Наші евристичні міркування ПІ)О існування найменшого і наи
більшого значень функці] на сегменті підтверджуються такою тео
ремою.
Теорема 2 (ВеЙєрштрасса). Я'К,ЩО фУ'Н,'К,1І,і.я неперервна на сег
менті, то на ньомц існцють тонни: в якиз: вона 'Н,абуває своі най
менше і найбіпьии: значення (тобто нижню і верхню грані}.
Як і в теоремі 1, вимоги теореми 2, щоб функція була визначена
на сегменті і неперервна на ньому, також істотні. Так, функція у = х
неперервна на півсегменті (О; 1] і обмежена на ньому, але її точна
нижня межа то = О не досягається, бо немає такого х, для якого
функція дорівнює о.
Якщо функція розривна на сегменті, то вона не обов'язково до
сягає МІНІМУМУ. Такою, наприклад, є функ
ЦІЯ
1 х
{І, якщо - 1 < х < О,
Лх) = - -
х, якщо О < х :::; 1,
-1
Рис. 12 графік якої зображено на рис. 12.
Теорема 3 (Больцано-Коші). Я'К,ЩО фУ'Н,'К,1І,і.я f неперервна на
сегменті [а; Ь], а чисзиі Ла) і ЛЬ) не дорівнюють О і мають різні зна
ки, то на інтервалі (а; Ь) іс'Н,ує хоча б одна точка с, в якій Ле) = о.
у
А
х
у
Ла)
в
с
О а
ЛЬ)
Рис. 13
Рис. 14
На рис. 13 зображено графік неперервної Нп сегменті [а; Ь] функ
ціі і, що набуває значення Л а) > О, ЛЬ) < о. Цей графік уявляємо
103
собі у вигляді лінц , що можна провести, не відриваючи олівця від
паперу. Оскільки графік повинен знаходитися у вертикальніи смузі
а :::; х :::; Ь і з'єднувати точки (о; Ла)) і (Ь; ЛЬ)), що лежать у різ
них півплощинах щодо осі абсцис, то геометрично очевидно, що він
повинен перетинати хоча б один рІО інтєрвал (а; Ь). Це і стверджує
теорема З. ДЛЯ графіка функціі. зображеного на рис. ІЗ, на інтервалі
(а; Ь) існує нескінченна кількість точок є, в яких лс) = о.
Теорема 4 (Больцано-Коші). Якиіо фу'lt'К','l1,і.я f неперерена 'Ita
сегменті [а; Ь], 'Числа Ла) = А і ЛЬ) = В різні і С - оовільне 'Число,
що знагоонться між А і В, то 'Ita інтереам (а; Ь) існце хоча б одна
тонка с, в якій f( с) = с.
Теорема 4 стверджує, що неперервна на сегменті функція на
буває всі проміжні значення між іі значеннями на кінцях сегмента.
Тому цю теорему називають ще теоремою про проміжне значення
неперервноі функції.
На рис. 14 подано ілюстрацію до теореми 4. Міркуючи подібно,
як і для рис. ІЗ, переконуємося, що будь-яка горизонтальна пряма
у = С, А < С < В, хоча б в одній точці повинна перетинати графік
функціі лх) (на рис. 14 є три такі точки).
3 теореми 4 можна отримати такий наслідок.
Наслідок. Нехай функція f неперервна на сегменті [а; Ь] і
то = min f( х), Мо = тах f( х). Тоді множиною значень функції f
а<х<Ь а<х<Ь
Є сегмент [то; Мо]; зокрема, якщо то = j\;fo, то лх) = то = 1у10 ---
стала функція на сегменті [а; Ь].
З.8. Рівномірно неперервні функції. Припустимо, що функ
ЦІя f задана на такій множині, кожна точка якої є її точкою скуп
чення. Прикладами таких множин на прямій є проміжки, об'єднання
. .. . .
проміжків. множина рашональних чисел, множина іррацюнальних
чисел.
Означення. Функція у = Лх), визначена на множині Е с R,
називається рівномірно неперервною на Е, якщо для довільного
є > О існує таке J > о, шо для довільних двох точок х і х' множини
104
Е, які задовольняють умову
Іх - х'l < 6,
(51)
виконується також нер1ВНІСТЬ
IЛх) - Лх')1 < є.
(52)
Пропонуємо читачам записати це означення, користуючись ло
ГІЧНИМИ символами.
Зробимо декілька зауважень.
1. Якщо функція є рівномірно неперервною на множині Е, то
вона є також неперервною в кожній точці ха множини Е. Справді,
якщо в означенні прийняти х' = Ха, то воно перетворюється на озна
чення 2 з п. З.l функціі, неперервноі в точці Ха щодо множини Е.
2. Основна відмінність означення неперервноі функціі в точці
Ха Е Е щодо множини Е від означення рівномірно неперервноі функ
ціі на множині Е полягає в тому, що число 6 > О в першому означенні
залежить від є і від точки Ха і для іншої точки ХІ Е Е, в якій функція
неперервна, може бути іншим, в той час як друге означення вима
гає, щоб число 6 > О можна було вибрати однаковим для всіх точок
множини Е.
з. З неперервності функції на множині Е не випливає їі рівномір
на неперервність на множині Е (див. далі приклад 1).
4. Якщо функція рівномі рно неперервна на множині Е, то вона
також рівномірно неперервна на будь-якій підмножині ЕІ еЕ.
Наведений нижче приклад підтверджує зауваження, зроблене в
п.З.
Приклад 1. Показати, що функція ЛХ) = �, яка неперервна на
проміжку (О; 1], не є на ньому рівномірно неперервною.
Розв 'язання. Означення рівномірної неперервності вимагає, щоб
нерівності (51) і (52) справджувалися для довільного наперед зада
ного числа є > О, деякого вибраного числа 6 > О і будь-якої пари
точок х, х', що задовольняють нерівність (51).
105
Розглянемо точки хn = �, x� = n�]' n Е іУ, для яких IЛхn)-
-Лх�)1 = Іп - n + 11 = 1 і Іхn - x�1 = I� - n�ll = n(n1+l)· Звідси
отримуємо, що ні для одноі пари точок Хn, x� нерівність (52) не
виконується, хоча, якщо задати довільне 6 > О, то нерівність (51)
справджується для всіх Хn, x� з достатньо великими номерами п,
Це означає, що функція � не є рівномірно неперервною на проміжку
(О; 1].
Приклад 2. Показати, що функція лх) = � рівномірно непе
рервна на проміжку (а; 1], якщо О < а < 1.
Розв 'язання. Виберемо х і х' на (а; 1]. Оскільки х � а і х' � а,
то IЛх) - Лх')1 = І � - ;, І = Ix�:,xl � �2Ix' - хІ· Тому виконання
нерівності (52) можна досягти, якщо вимагати, щоб Іх' - хІ < єа2,
тобто вибрати 6 = єа2• Отже, функція � рівномірно неперервна на
сегменті (а; 1].
Теорема (Кантора). Якиіо фУ'Н,'К",1І,і.я f неперервна на сегменті
[а; Ь], то вона рівномірно неперервна на 1І,ьо.му сегменті.
З доведенням теореми можна ознайомитися в [1, т.l, с.446].
Приклад 1 підтверджує істотність вимог тереми, щоб функція
була неперервною на сегменті. Твердження прикладу 2 можна також
отримати як наслідок з теореми Кантора.
106
Розділ 3. ПОХІДНІ І ДИФЕРЕНЦІАЛИ
§ 1. ПОНЯТТЯ похідної
До поняття похідної впритул підходили такі вчені, як Галілей,
Барроу , Кеплер, Ферма і інші. Але остаточно і грунтовно воно бу
ло введене основоположниками математичного аналізу Ньютоном і
ЛеЙбніцем. Наведемо ймовірні (осучаснені) схеми ІХ МІркувань, наз
вавши скорочено ЦІ схеми задачами.
1.1. Задача Ньютона. Ньютон розглядав задачу про миттєву
швидкість нерівномірного прямолінійного руху, яку можна сформу
лювати так: вздовж деякої прямоі за законом s = s(t) (t -- час)
рухається точка. Знайти швидкість іі руху у момент часу t.
Розв 'язання: s(t) --- це шлях, який пройшла точка за час і. Якщо
б рух був рівномірним, то швидкість була б однаковою в будь-який
момент часу t і дорівнювала б
s( і)
t
(1)
Але якщо рух нерівномірний, то (1) дає лише значення середньої
швидкості руху (тобто швидкості такого рівномірного руху, за яко
го точка за час t проходить шлях s(t)). Щоб знайти точне значення
швидкості в момент і: Ньютон міркував так. Нехай час руху збіль
шився на 6.і. Пройдений точкою шлях збільшився відповідно на 6.s.
Середня швидкість руху на проміжку часу 6.t бу де
6.s
6.і
(2)
Швидкість 11еер буде тим ближчою до миттєвої швидкості в мо
мент часу і, чим меншим буде проміжок часу 6.t. Точне значення
... ...
мит-гєвоі ШВИДКОСТІ одержимо як границю середньої ШВИДКОСТІ за
107
умови, що 6.t ---+ о. Отже, миттєва швидкість v(t) буде дорівнювати
. . 6.s
v(t) = 11т Vеер = 11т л .
�t-+O �t-+O ut
(3)
Шлях 6.s називають приростом шляху, отриманим за ПРИРІСТ
часу 6.t. 3 простих міркувань (які уна-
s( t) 6.s
OC A-_=v= �B
очнює рис. 1), випливає, що
s(t+6.t)
6.s = s(t + 6.t) - s(t),
(4)
Рис. 1
і тому (3) можна продовжити
v(t) = Ііт 6.s = Ііт s(t + 6.t) - s(t) .
�t-+O 6.t �t-+O 6.t '
(5)
Границю в (3), чи (5) називають похідною від шляху за часом і
позначають або �;, за Лейбніцем або s' (t) за Лагранжем. Отже,
v(t) = Ііт 6.s = Ііт s(t + 6.t) - s(t) = ds = S'(t). (6)
�t-+O 6.t �t-+O 6.t dt
Тобто миттєва швидкість дорівнює похідній шляху за часом.
1.2. Задача ЛеЙбніца. Лейбніц (як і Ферма) прийшов до
� - . .
поняття похідноі, розглядаючи задачі на екстремум 1, зокрема, у
певний спосіб пов'язану з цим геометричну задачу про дотичну до
графіка функції. Сформулюємо цю задачу, використовуючи для уна
очнення рис.2.
На рис. 2 зображено криву, що є графіком заданої функції
У = f (х). Потрібно знайти рівняння дотичної до графіка цієї функції
у точці Мо(хо; Уо) (Уо = лхо)).
Розв 'язання. Позначивши через Х, У --- координати біжучої
оо •••
точки дотичноі, запишемо 11 РІВняння як РІВняння прямоі, що прохо-
дить через задану точку 1\10
у - УО = k(X - хо),
(7)
108
де k ----- кутовий коефіцієнт дотичної.
Якщо знайти кутовий коефіцієнт k і підставити його в рівняння
(7), то задача буде розв'язана.
у
хо
xo+�x х
Yo+�Y
уо
Рис.2.
Візьмемо на графіку точку М з координатами (хо + �x; уо + �y)
і проведемо січну МоМ. Ця січна утворює з віссю Ох кут 0*, а тому
кутовий коефіцієнт січної k* буде
k* = tgo*.
3 прямокутного трикутника MoLM знаходимо
* �y
tgo = �x.
Якщо точка М, рухаючись по кривій, наближається до точки
Мо (очевидно, що тоді �x --+ о) січна Mo1V!, повертаючись навколо
точки МО, буде прямувати до збігання з дотичною (0* --+ о), а, отже
k=tgo= Ііт k*= Ііт tgo*= Ііт �y =і'(хо). (8)
М--+Мо М--+Мо �x--+o �x
Тобто кутовий коефіцієнт дотичної до графіка функції у = f( х) в
точці Мо (хо; уо) дорівнює значенню похідної цієі функції в точці Мо·
log
Підставляючи значення k з (8) в (7), одержимо рівняння дотичної
у - лхо) = І'(хо)(Х - хо).
(9)
Якщо пригадати зв'язок між кутовими коефіцієнтами двох взає-
. .
мно перпендикулярних прямих, то можна записати РІВНЯННЯ нормалі
до кривої в точці Мо
1
У - лхо) = - І'(хо) (Х - хо).
(10)
I.З. Означення ПОХІДНOl. Розглянемо тепер формальне оз
начення похідної, яке не зв'язане з певними фізичними чи іншими
задачами. Отже, нехай маємо функцію у = Лх), х Е (а; Ь). Нада
мо аргументові деякого приросту І::::.х, тобто від точки х перейдемо
до точки х + І::::.х. Функція отримає певний приріст І::::. у , а значення
функції в точці х + І::::.х (нарощене значення ) буде таким
у + І::::.у = ЛХ + І::::.х).
Приріст функції дорівнює різниці між її значеннями в точках
х + І::::.х і з:
І::::.у = f( х + І::::.х) - у = f( х + І::::.х) - f( х).
Запишемо відношення приросту функції до приросту її аргумен-
ту
І::::. у ЛХ + І::::.х) -- лх)
І::::.х І::::.х
Якщо границя цього відношення за умови �T-t О існує, то вона
називається похідною функції в точці з: і тоді пишуть
, _ dy _ І'( ) _ df _ l' d.y _ l' f(;r + �<l:) -- f(:r)
у - - - х - -- - lIIl - - ІІIl - _
dx d;r .6.х-+о І::::.х .6.х-+о 1::::.,1:
(11 )
110
Тут штрихом праворуч вверху біля функції чи символом ddx перед
функцією позначено операцію диференціювання, тобто операцію зна
ходження границі відношення приросту функції до приросту ЇЇ аргу
менту, коли останніи прямує до нуля.
Символ d�T (чи штрих) називають оператором дuфере-н:ціЮ6а-н:н.я.
Кажуть, шо для знаходження похідної функції треба подіяти на неї
оператором диференціювання.
Функція називається диферєнційовною в точці х, якщо в цій точ
ІІі існує її похідна. Якщо похідна функції існує в усіх точках дея
кого ПРОМІЖКУ, то функція називається дuфере-н:ціU06'НОЮ на цьому
ПРОМІЖКУ.
1.4. Неперервність диференційовноі функції.
Теорема. Фцнкція, дuфере'Н'ЦіU06'На 6 точці, є й неперервною У
'Ніи.
д 06 едення. Нехай функція У = І( х) диференційовна в точці хо.
Це означає, що існує границя
1· ДУ - Іі І(хо + дх) - І(х) - І'( )
П'П - - П'П - хо.
6x�OДX 6x�0 дх
На основі теореми 1 п. 2.1 розділу 2 можемо записати
ДУ ,
Дх = j (То) + О(ДХ),
де Ііт О(ДХ) = О.
6.T�0
Домножимо обидві частини рівності на Дх
ДУ = j'(хо)д.r + Дхо(Дх).
Звідси випливає, ЩО
Ііш ДУ = Ііт [І(хо -+- Дх)- І(хо)] =
6I�0 6x�O
111
= і'(хо) ііт дх + Ііт дхо(дх) = О.
�х--tО �х--tО
Тобто нескінченно малому приросту аргументу відповідає не
скінченно малий приріст функції, що й підтверджує її неперервність.
у -уо= І'(хо-О)(Х-хо)
У-уо= '(xo+O)(X-хо)
Рис.3
Зауважимо, що аналогічно до
лівосторонніх (правосторонніх ) гра-
. .,
ниць ІСНУЮТЬ поняття ЛІВОСТОРОННІх
Г(х-О) чи правосторонніх Г(х+О)
похідних. Очевидно, що лівосторон
ню (правосторонню ) похідну ми
.. .
одержимо, якщо в СП1ВВІдношенНІ
(11) будемо вважати дх<О (дх>О).
Потреба в таких похідних ви-
. .
никає П1д час знаходження кута МІЖ
дугами графіка функціі в ТОЧЦІ иого зламу. Цей кут приймають
. ... .
таким, що ДОРІВнює кутові МІЖ ЛІВосторонньою 1 право сторонньою
дотичними (див. кут о на рис. 3)
Перш ніж переходити до практичного знаходження похідних, на
гадаємо ще раз, що:
1) Похідна - це границя відношення приросту функціі до приросту
11 аргументу, коли ПРИРІСТ аргументу прямує до нуля.
2) З фізичного погляду похідна- -- це швидкість (швидкість зміни
функції).
3) З геометричного погляду похідна ---- це кутовий коефіцієнт до
тичної до графіка функції.
1.5. Знаходження похідних на основі означення. Знайде-
мо похідні функцій: а) у = с; б) У = х; в) у = х2; У т "; n Е N;
д) у = sinx; е) у = о'Т; Х Е R.
Похідні знаходимо за ЄДИНОЮ схемою, а саме:
1) За нарощеним значенням аргументу з: + дх визначаємо нароще
не значення функції у + ду = Л:Г + д.І').
2) Обчислюємо приріст функціі ду= Лх+дх)-у= ЛХ+дх)- Лх).
112
3) Складаємо відношення приросту функції до приросту 11 аргу
ь..у
менту Ь..х'
4) Знаходимо похідну у' = Ііт �Y.
b..x-tО <.>.Х
а) у = с.
1) у + t::.y = с; 2) t::.y = с - у
4) у' = (с)' = Ііт О = О.
b..x-tО
Отже, якщо у = с, то у' = О.
б) У = х.
1) у + t::.y = х + t::.x; 2) t::.y
Ііт ь.. у = Ііт 1 = 1.
b..x-tО ь..х b..x-tО
Отже, якщо у = х, то у' = 1.
в) у = х2•
1) у + t::.y = (х + t::.x)2 = х2 + 2х . t::.x + (t::.x)2; 2) t::.y = х2+
+2х· t::.x + (t::.x)2 - У = х2 + 2х· t::.x + (t::.x)2 - х2 = 2х· t::.x + (t::.x?;
3) ь..у = 2х·Ь..х+(Ь..х)2 = 2х + t::.x; 4) у' = Ііт (2х + t::.x) = Ііт 2х+
ь..х ь..х b..x-tО b..x-tО
+ Ііт t::.x = 2х.
b..x-tО
Отже, якщо у = х2, то у' = (х2)' = 2х.
г)у=хП,nЕN.
1) y+t::.y = (x+t::.x)n = xn+nxn-l·t::.x+ n(�.;l) ·(t::.x)2+ .. ·+(t::.x)n;
2) t::.y = (х + t::.x)n - хп = nхп-l . t::.x + n(�.;l) хп-2 . (t::.x)2 + ... +
+(t::.x)n; 3) �� = nхп-l + n(�.;l) хп-2 . t::.x + ... + (t::.x)n-\ 4) у' =
= Ііт (nХП-1 + n(�.;I)xn-2. t::.x + ... + (t::.x)n-l) = nхп-І.
b..x-tО
Отже, якщо у = хп, то у' = (хп)' = nхп-І.
д) у = sinx;
1) у + t::.y = sin(x + t::.x); 2) ду = sin(x + дх) - sinx = 2sin �x х
х cos (х+ Ь..х): 3) ь..у = 2. sin t:>;x cos (х + Ь...т). 4) у' = Ііт ь..у =
2' ь..х ь..х 2 І b..x-tО ь..х
sin .t:>.x (Ь.. )
= Ііт � Ііт cos з: + --f = 1 . cos х = cos х (враховано непе-
ь"х-tО ""2 b..x-tО
рервність функціі косинус).
Розв 'язання.
с-с
О; 3)
О
ь..х
О'
,
дх; 3)
1; 4) у'
113
Отже, якщо у = sinx, то у' = (sinx)' = cosx.
) _ Х
е у - о .
1) у + ду = оХ+..6.х = а" . о..6.Х; 2) ду = оХ+..6.х - а" = оХ(о..6.Х - 1);
З) ..6.у = oxa.a.X-I. 4) у' = Ііт ..6.у = оХ Ііт а.а.Х_l = оХlпо •
..6.х ..6.х ' ..6.x---tО ..6.х ..6.x---tО..6.х
Отже, якщо у = а", то у' = (оХ)' = а" Іпо.
Зокрема, для о = е, у' = (еХ)' = е" -Іп е = е",
1.6. Правила диференціювання. Похідні багатьох функцій
можна знайти, використовуючи відповідні правила диференціюван
ня. Розглянемо ці правила, припускаючи, що всі функції, що розгля
даються тут, є диференційовними.
а) Дифере'l-/:ціюва-н:н,.я суми.
Нехай у = u(х) + vex). Тоді
у' = (u(х) + v(x))' = u'(х) + v'(x).
(12)
Доеедепня. 1) у+ду = u(x+tlx)+v(x+tlx). 2) ду = U(Х+дх)+
+v(x + дх) - (u(х) + v(x)) = u(х + дх) - u(х) + v(x + дх) - v(x) =
= tlu+tlv· З) ..6.у = ..6.u + ..6.v. 4) у' = Ііт ..6.u + Ііт ..6.v = u'(x)+v'(x).
, ..6.х ..6.х ..6.х' ..6.x---tО..6.х ..6.x---tО..6.х
Використовуючи сполучний закон додавання, теорему неважко
узагальнити на суму будь-якої скінченної кількості доданків, що ко
ротко можна сформулювати так: похідна суми дорівнює сумі похід-
. .
них ВІд доданків.
б) Дифере'Н,'/�іюва'Н,'Н,.R добуm-к;у.
Нехай у = u(х) . vex). Тоді
у' = (u(x)·v(x))' = u'(x)·v(x) + u(x)·v'(x).
(ІЗ)
Доведення. 1). y+.6.y=u(x+tlx)·v(x+tlX)j .6.y=u(x+tlx)·v(x+
+tlx)-u(x)-v(x). Нічого не зміниться, якщо в правій частині рівності
додати і відняти u(x)·v(x + дх). Тоді 2) ду = u(х + .6.x)·v(x + дх)
-u(x)·v(x + .6.х) + u(x).v(x + дх) - u(x)v(x) = (u(х + tlx)-u(x))·v(x+
+дх) + u(x)·(v(x+tlx)-v(x)) = .6.u·v(x+tlx)+u(x)·tlv. З) �� =
114
:;::: �u .v(x+.6x)+u(x). �v. 4) Іігп �u. Ііт v(x+.6x)+u(x) Ііт �v =
Х Х �X-40 Х �X-40 �X-40 Х
= u'(х) . v(x) + u(х) . V'(x) (тут враховано неперервність диференці-
йовної функції).
Тобто похідна добутку дорівнює добуткові похідної першого
співмножника на другий плюс добуток першого співмножника на по
хідну другого. Неважко узагальнити це правило на добуток трьох і
більше співмножників.
Наслідок. Якщо приймемо u(х) = С, тобто у = С· v(x), то,
. -. .
враховуючи, що ПОХІдна сталої ДОРІВнює нулеві, одержимо
уІ = (С . v)' = С . v'
тобто стале число можна виносити за символ (оператор) похідної.
Приклад. Знайти похідну функції у = 3еХ sinx.
Розв 'язання.
уІ = (3еХ sinx)' = 3(еХ sinx)' = 3 ((еХ)' sinx + eX(sinx)') =
= 3( еХ sin х + еХ cos х) = 3еХ (sin х + cos х).
Властивості похідної від суми функцій і від добутку сталот на
функцію часто об'єднують в одну властивість, яку називають влас
тивістю ліній�ості оператора диференціювання. Коротко цю влас
тивість можна сформулювати так: похідна від лінійної комбінації
функцій дорівнює лінійній комбінації похідних від функцій, що вхо
дять до лінійної комбінації. Тобто, якщо
у = СlУІ + С2У2 + ... + сьи«,
де СІ, С2,··· ,Ck - сталі, а УІ, У2,··· ,Yk --- диференційовні функції,
то
(14)
в) Дuфере'Н:ціювшн:н,.я дробу.
Нехай у = �; v і- о. Тоді
уІ =
(�)' =
u'v - uv'
v2
(15)
115
Доведення. 1) у + 6.у = :�:��:j. Використовуючи означення
приросту функції, можемо записати и( х+6.х) = и( х )+6.и; v( х+6.х) =
= v(x) + 6.v. Враховуючи ці співвідношення, матимемо
v
V· (и + 6.и) - и . (v + 6.v)
v· (v + 6.v)
6.и . v - и . 6.v
v·(v+6.v) .
6.у = и + 6.и
2) v + 6.v
и
Ділимо обидві частини на 6.х
3) 6.у
6.х
fluV _ И flv
flx flx
v·(v+6.v)·
Переходимо до границі
1· flu 1· flv
'flu flv V пп --л--- - и пп --л---, ,
, (и) . flx V - И flx flx---+O �x flx---+O �x И V - иv,_
4) у = - = 11т - ---------
v flx---+ОV·(v+6.v) v Ііт (v+6.v) v2
flx---+O
тут 1imflx---+o 6.v = О внаслідок неперервності функціі v(x).
Отже, похідною частки є частка, знаменник якоі дорівнює квад-
. . - ..
рат ОВІ знаменника вихгдноі частки, а чисельник є РІзницею МІЖ до-
бутком похідної чисельника на знаменник і добутком чисельника на
ПОХІДНУ знаменника.
Використаємо правило диференціювання дробу для знаходження
похідних тригонометричних функцій tg х і ctg х.
Розв 'язання.
вш г
y=tgx=--;
cosx
, ( )' (Sin х)'
у = tgx = --
cosx
( sin х)' cos х - sin х ( cos Х)'
сов? Х
cos2 Х - sin х( - sin х)
сов? Х
cos2 Х + sin2 х
сов? х
1
сов? х·
cosx
у = ctgx = -.--;
вш з:
(со. SX)' =
у' = (ctg х)' =
зш г
116
( cos х)' sin х - cos .r ( sin х)'
. 2
SIn х
- sin2 х - cos2 Х
. 2
SlIl Х
( -- sin х) sill:r - cos х cos х
sin2 х
sin2 х + cos2 Х
. 2
SIn з:
1
. 2
SIn з:
1.7. Диференціювання складної функції. Нехай у є функ
цією змінної х не безпосередньо, а за участю проміжної диференці
йовної функції u = и(х), тобто У є складною (складеною) функцією
відх: у=/(и(х)).
Будемо також вважати, що ли) є диференційовною функцією
від и. Надамо змінній з: деякий приріст .6х. Функція и(х) набуде
деякий приріст .6и, причому внаслідок неперервності [диференш
йовності) .6и ---+ О, якщо .6х ---+ О. Функція у набуде приріст fly,
причому flу ---+ О, якщо .6и ---+ О.
3а умовою функція у = J( и) є диференційовною, тобто існує
1· flу І ІІ
ІІП Л = уu = и'
�u-tО L).U
3 означення границі для flu і- о маємо
flу І
flu = Уи + (1,
де а ---+ О, якщо flu ---+ О.
Домножимо обидві частини останньої рівності на .6 u
.6у = y� . flu + (1 . flu.
Ця рівність правильна і для flu = О при довільному а, але ОСКІльки
а ---+ О, якщо flu ---+ О, то природно прийняти а = О для flu = О.
Після ділення обох частин на flx і переходу до границі, якщо
fl.r ---+ О, одержимо
1. .6у І І
пп -- = УХ = Уl1
�х-tО flr
.611 .6и І І
ііт + ііш о· lirп -- = уu . Их'
�l1-tО flJ: �l1-tО �х-tО flx
117
Тобто, якщо У = Ли); u = и(х), то
, і' , , ,
Ух = u· их = Уu . их·
(16)
Отже, похідна складної функції за кінцевим аргументом дорів
нює добуткові похідної цієї функції за проміжним аргументом на
.. .
ПОХІДНУ ПРОМІЖНОГО аргументу за КІнцевим аргументом.
Неважко узагальнити це правило і на випадок, коли проміжних
аргументів є декілька. Наприклад, якщо у виконаних вище мірку
ваннях вважати, що u є диференціиовною функцією проміжного ар
гументу v = v( х), який є диференційовною функцією х, то, очевидно,
що у співвідношенні (16) похідну и�, треба замінити на добуток и� ·v�
І ТОДІ
, і' , , , , ,
Ух = и " Uv . Vx = уu . Uv . vx·
(17)
тобто ланцюжок з добутку похідних у правій частині подовжився б
на одну ланку.
Приклад. Знайти y�, якщо У = In(sin5x).
Розв 'язання. Тут маємо У = Іп и, u = sin v, v = 5х, і тому
1
y� = (In(sin5x))� = (lпи)�· (sinv)�· v� = -. cosv· (5x)� =
u
1 cos 5х
= --. cos5x· 5 = 5-- = 5ctg5x.
sin5x sin5x
Звичайно, під час практичного знаходження похідних позначен
ня для проміжних аргументів не записують, а запам'ятовують. Для
розглянутого прикладу скорочені міркування мають такий вигляд
щоб знайти похідну від lп( sin 5х ), треба похідну від логарифма по-
... ..
множити на ПОХІДНУ ВІД синуса 1 помножити на ПОХІДНУ ВІД аргументу
синуса.
1.8. Похідна оберненої функції.
Теорема. Н ехай фУ'Н,'І'і:ці.я У = f( х) є строго монотонною z не
перервною на nро.м.іж'/'і,У [а; Ь], внасмдок 'Чого дл.я неі існце строго
118
монотонна і неперервна на проміжки [А; В] (А = Ла), В = ЛЬ))
обернена фу'Н,'К,'Ці.я g(y) (n.3.3 з розділу 1). Я'К,ЩО фу'Н,'К,'Ці.я у = лх)
мае в точці хо Е ( а; Ь) від.мі'Н,'Н,у від 'Н,ул.я nохід'Н,у f' (хо), то обернена
у
фу'Н,'К,'Ці.я g(y) має у відповідній точці уо = лхо) Е (А; В) nохід'Н,у,
д· 1
яха орівнюе І;(хо).
Дoвeдe'Н,'Н,.R� Надамо уо деякий приріст ду, тоді функція х =
= g(y) отримає відповідний приріст дх, причому якщо ду =J. о, то і
дх =J. о. Можемо записати
дх
ду
1
t::.y.
t::.x
(18)
Якщо тепер ду -+ о, то внаслідок неперервності функції х = g(y)
приріст дх -+ О і, отже,
ду І
дх -+ f (хо) =J. о.
Тому, з огляду на рівність (18), існує границя лівої частини і до
того ж вона дорівнює g'(yO).
т
Якщо позначити g' (уо) = x� а
f'(xo) = у'(Хо) = y�, то матимемо
І 1
х =-
у y�
(19)
або
Рис.4
І
ух= -.
х'
у
1
(20)
Формули (19) і (20) проілюстровані на рис.4, на якому зобра
жена дотична Т до графіка функції у = f( х) (х = g(y)) у точці
119
М(хо; уо) і кути о і {З, які вона утворює відповідно з осями Ох і Оу.
З геометричного змісту похідної y� = tgo; x� = tg,G, а оскільки
о + {З = �, то tg{З = t�Q' тобто маємо (19).
Якщо взяти у = loga х, то обернена функція бу де х = аУ, тоді
І І 1
х = (аУ) = аУlпа = хlпа = х· --о
У loga е
Тобто, якщо у = loga х, то уІ = хІ, = � loga е.
у
Знайдемо похідні для деяких обернених тригонометричних
функцій.
1) у = arcsinx; -1 < х < 1, а тому -� < у < �. Оберненою до
цієї функції є х = sin у, для якої похідна x� = cos у > о на вказаному
вище проміжку. Тоді x� = соsу = vI - sin2 у = vI -_х2
І • І 1 1 1
у = (агсsшх) = - = -- = ---;==�
з: з: x� cos у vI _ х2
2) Оскільки arcsinx + arccos х = �, звідки
1г •
arccos х = - - агсюп х,
2 .
то, отже,
І 1
( arccos х) = - .
Vl- х2
3) у = arctg х; -оо < х < оо. Обернена функція х = tg у, x�
lIt 2 1 2 'т' .
= -2- = + g у = + х . л.оді
cos У
І 111
У = (aretgx) = - = ---о
х. з: І 1+ 2
ХУ Х
4) Враховуючи, що arcctgx = � - arctgx, матимемо
(arcctg х)' = - 1 2
l+х
120
1.9. Логарифмічне диференціювання. Якщо функція, по
хідну якої треба знайти, є степенево-показниковою, або дробом, чи
сельник і знаменник якого мають вигляд добутку кількох множників,
які є диференційовними функціями, то доцільно спочатку пролога
рифмувати цю функцію, а вже після цього диференціювати одержа
ний вираз. Потрібно пам'ятати, що у є деякою функцією змінної х, а
тому похідну Іп у знаходимо як похідну від складної функції, тобто
(1 )' (1 )' , 1 , у:
пу з: = пу у. ух = -. ух = -.
у у
Такий метод і називають логарuф.мі'Ч'Н,u.м дuфере'Н,'Ціюва'Н,'Н,.я.м, причо
му похідну (Іп y)� від логарифма функції іноді називають логарuф
мічною похідною функції. Застосуємо його для обгрунтування фор
мули диференціювання степеневої функції з довільним дійсним по
казником.
Нехай у = х"; де n -- довільне дійсне число, Прологарифмуємо
обидві частини рівності і потім продиференціюємо одержані вирази
1, 1 , у х" n-l
Іпу = nlпх ::::} -у = n- ::::} у = n- = n- = nх
у х х х
Знайдемо формулу для диференціювання степенево-показнико
вої функції у = u ", де u і 17-- деякі функції змінної х.
Логарифмуємо задану функцію і диференціюємо отримані вира
зи за х
v 1" 1 ,
у = u ::::} Іп у = v Іп u ::::} -у = 17 Іп u + v-u ::::}
у u
::::}Y'=y(v'Inu+v�) =uv (v'Inu+v�)'
= (uv Іп u)v' + l.JUv-ІU'.
Отже,
(V)' (V 1 )' v-I'
U = 11 n и V + 17и U .
121
Як бачимо, похідна степеневопоказниковоі функції складаєть
ся з двох доданків: перший з них є похідною показниковоі функції
(одержаною за припущення, що основа ЇЇ - стале число), а другий
доданок є похідною степеневої функції (отримаємо за припущення,
що показник степеня v - стале число).
1.10. Диференціювання неявно І параметрично заданих
функцій.
а) Нехай дві змінні х і у зв'язані між собою рівнянням
Р(х,у) = О.
(21)
Якщо для кожного х з певного проміжку існує одне або декілька
значень у, які разом з х задовольняють рівняння (21), то кажуть, що
це рівняння визначає відповідно однозначну чи багатозначну функ
цію у = у(х). Функцію, задану рівнянням (21), називають неявною.
Якщо в рівняння (21) підставити явний вираз функції у = у(х), то
воно перетвориться в ТОТОЖНІсть
Р(х,у(х)) _ О.
На питання про існування неявної функції, її однозначність і не
перервність буде дана відповідь під час вивчення функцій багатьох
змінних. А тепер ми обмежимось практичними рекомендаціями для
знаходження похідної неявно заданої функції.
Нехай, наприклад, неявна функція у задана рівнянням
Вважаючи, що в це РІВняння підставлено явний вираз функції
у = у( х ), отримаємо тотожність
122
Очевидно, що дві тотожно рівні функції мають однакові похідні.
Тому, диференціюючи тотожність за х з урахуванням того, що у є
функцією х, одержимо
2х 2у ,
а2 + Ь2' у = О.
Звідси
ь2х
,
у =-
а2у'
Розглянемо ще один приклад неявного аадання функції і знаи
демо 11 ПОХІДНУ
Вважаючи, що замість у підставлено явний вираз ЦІЄІ функції
у = у(х), отримуємо тотожність
Диференціюємо обидві частини тотожності за х
2222,1, 'о
ху + х уу + -у - у - ху = =?
У
'( 2 1) 2' у2(1 - 2ху)
=? У 2х у + - - х = у - 2ху =? У = 2 2 •
У 1 + 2х у - ху
б) Говорять, що змінна у як функція аргументу х задана nара
метрично, якщо обидві змінні х і у задані як функції деякої третьої
змінної t: х = <p(t), У = ф(t). Змінну t називають параметром. У
теоретичній механіці за параметр t переважно приймають час і. тоді
задання х і у як функцій часу називають параметричним рівнянням
траєкторії рухомої точки М(х; у). Будемо вважати, що функції <p(t)
і ф(t) в області зміни параметра t є диференційовними, Зокрема, бу
демо вважати, що функція х = <p(t) в околі точки, що розглядається
123
t = to має обернену функцію t = <р-l(х), що Й дає змогу розглядати
У як складну функцію х: у(х) = Ф(t) = 'ф (<р-l(х)).
Теорема. Похідна параметрично заоаноі фу'Н,-к;'Ціі еизначаеться
за формулою
І ф'(t)
Ух= <p'(t)'
І .
(22)
д 06 едення. За правилом диференціювання складноі функціі
(див. п. 1.7) маємо
І І І ./.'() І
Ух = Yt . tx = <j.J t . tx·
Але, враховуючи зв'язок між похідними взаємно обернених функцій
(п. 1.8) t� = ..!" одержуємо
х!
І '() 1 фІ (t)
Ух = Ф t . x� = <p'(t)'
Часто використовують скорочений запис
І
І Yt
Ух =>:
xt
Приклад . Знайти похідну функціі У, заданої параметрично
{Х = a(t - sint),
у = a(l - cos t),
- оо < t < оо.
РОЗ6 'язання. Оскільки x� = а( 1 - cos t), y� = а sin і, то
І а sin t t
Ух = .- = ctg -.
а(l - cost) 2
Зауважимо, що крива, яка є графіком заданої функції, нази
вається циклощою.
124
1.11. Таблиця похідних основних елементарних функцій.
1.
І
=0
у=с
У
2.
у = х"
І n-І
у = пз:
y=�
І
1
2а.
у
-
х2
26.
y=VX
І
1
у
-
2VX
З.
у = а"
І
= а" Іпа
у
За.
у = е"
І
= е"
у
1
4.
у = loga х
уІ = -loga е
х
у = lпх
І
1
4а.
у
-
-
х
5.
І
У = вш г
у
= cosx
6.
І
У = cosx
У
= - SlnX
І
1
7.
у = tgx
у
-
--
сов? Х
І
1
8.
у = ctgx
У
-
- sin2 х
І
1
9.
у = агсвш г
у
-
уіІ - х2
І
1
10.
у = arccosx
у
-
-
у1- х2
І
1
11.
у = arctgx
у
-
1 + х2
12.
у = arcctgx
І 1
у = -1 + х2
ІЗ.
у = shx
І
= chx
у
14.
у = chx
І
= shx
у
15.
у = thx
І 1
у =ьг
с х
16.
у = cthx
І 1
у = --2-
sh х
125
§ 2. Диференціал
2.1. Означення диференціала. Якщо функція у
диференційовною в точці х, то
лх) є
ііт 6.у = Ііт ЛХ + 6.х) - ЛХ) = г(х) .
.6.х--+О 6.х .6.х--+О 6.х
На основі відповідної теореми про границю, опускаючи символ
граничного переходу, матимемо
6.у = ЛХ + 6.х) - ЛХ) = г(х) + а,
6.х 6.х
(23)
де а - нескінченно мала величина ( Ііт а = О) .
.6.х--+О
Домножуючи всі члени рівностей (23) на 6.х, одержуємо
6.у = ЛХ + 6.х) - ЛХ) = г(х)· 6.х + а· 6.х. (24)
Тобто приріст функції поданий у вигляді суми двох доданків, причо
му перший доданок Г(х)6.х лінійний щодо приросту аргументу 6.х,
а другий - а . 6.х є нескінченно малою величиною вищого порядку
порівняно з 6.х.
Означення. Головна частина приросту функції, лінійна від
носно приросту її аргументу, називається диференціалом функції і
позначається dy = df(x}. Як бачимо з (24)
(25)
тобто диференціал функції дорівнює добуткові її похідної на приріст
аргументу. Тоді
dx = (x)�6.x = 1· 6.х = 6.х.
(26)
Співвідношення (26) показує, що диференціал незалежної змінної
дорівнює її приросту. У зв'язку з цим співвідношення (25) можна
записати так
dy = y�dx = j'(x)dx.
(27)
126
Отже, дифере'Н,'Ціал фу'Н,-к;'Ціі дорівнюе добут-к;ові похіднді фу'Н,-к;'Ціі
на дифере'Н,'Ціал іі аргу.ме'Н,ту.
Формулу (27) ми одержали, вважаючи, що х є незалежною змін
ною. Однак виявляється, що вона правильна і тоді, коли х є залеж
ною змінною, тобто проміжним аргументом. Доведемо це.
Нехай х = x(t) і у = ЛХ) = f (х(і)) - складена функція від і.
Тоді
dy = І; . dt = I� " x� . dt.
Але x� . dt = dx і тому dy = I� . x�dt = I� . dx.
Доведене твердження становить так звану властивість інварі
антності (незмінності) форми першого диференціала, а саме: nер
'Ший дифере'Н,'Ціал завжди дорівнює добут-к;ові похіднді фу'Н,-к;'Ції на ди
фере'Н,'Ціал її аргу.ме'Н,ту, незалежно від того, 'Чи 'Цей аргименпі Є за
лежною, 'Чи незалежною змінною,
3 (27) можна одержати
(28)
так що вираз ��, який ми раніше трактували як символ, введений
Лейбніцем для позначення похідної, можна розглядати як дріб, а саме
відношення диференціала функції до диференціала аргументу. Так,
наприклад, для параметрично заданої функції
{Х = acost,
у = asin і,
dx = -asint· dt,
dy = а cos t . dt,
/ dy а costdt
ух = dx = -а sin tdt = -ctg і.
Не зупиняючись на деталях, зауважимо, що подання приросту
функції у вигляді суми двох доданків, перший з яких є лінійним від
носно приросту аргументу, а другий - нескінченно малою вищого
порядку, є достатньою умовою диференційовності функції. До того
127
ж множник біля приросту аргументу в лінійному доданку є похідною
функції.
2.2. Основні правила диференціювання. Оскільки знаход
ження похідної і диференціала тісно пов'язані, то знаходження ди
ференціала також називають диференціюванням функції. Основні
правила можна записати так:
1) d(cu) = с- du;
З) d(u . v) = udv + vdu;
2) d( u ± v) = du ± dv;
4) d (;) = vdu � udv .
(29)
Таблицю диференціалів основних елементарних функцій, як і на
ведені вище правила, одержуємо домноженням обох частин відповід
них формул для похідних на диференціал аргументу.
2.3. Застосування диференціала у наближених обчис
леннях. Рівність (24) з урахуванням (25) можна записати так
6.у = dy + а . 6.х.
• u
кидаЮТЬІприимають
у наближених обчисленнях другий доданок у правій частині від-
6.у � dy = f'(x)dx.
у
Лхо+6.х)
о
хо
х+6.х х
Рис.5
(ЗО)
3 геометричного погляду (див.
рис. 5) це означає, що приріст ор
динати графіка функції при пе
реході від точки МО до точки М
(N М) приймається таким, що до
рівнює приростові N Кординати
дотичної до графіка.
Іншими словами, частина
МоМ графіка функції, прилегла
до точки дотику Мо, заміняється
відповідною частиною МОК до-
128
тичноі. Згідно з рис. 5
dy = NK =!J.x· tga =!J.x· і'(хо) = j'(xo)!J.x,
!J.y = NM = у - уо = лхо + !J.x) - лхо).
Тоді рівність (30) набуде такий вигляд
лхо + !J.x) - лхо) � Г(хо) . !J.x,
ЗВІДКИ
лхо + !J.x) � лхо) + і'(хо) . !J.x.
(31 )
Розглянемо приклади застосування (31).
Приклад 1. Обчислити наближено lп(1,23).
Розв 'язання.
у = лх) = lпх,
, , 1
у =і(х)=-.
х
Приймемо хо = 1, тоді !J.x = 0,23
Лхо)=lп1=0,
Г(хо) = � = 1.
хо
Тоді lп(1,23) � 0+ 1·0,23 = 0,23. З таблиць знаходимо lп(1,23) = 0,21.
Приклад 2. Обчислити наближено .J4,I8.
Розв 'язання.
у = лх) = Vx; г(х) = 2�·
Якщо' прийняти хо = 4, то !J.x = 0,18, лхо) = v4 = 2, г(хо) =
І 1
- 2уГхО - 4·
За (31)
1
J4,i8 � 2 + 4 ·0,18 = 2 + 0,045 = 2,045,
129
що дорівнює табличному значенню.
Якщо позначити ха +D.x = х, то D.x = х-ха і (31) перепишеться
так
ЛХ) � ЛХа) + Г(ха)(х - ха).
(32)
у правій частині (32) маємо лінійну функцію змінної х, яка для
х близьких до ха дає наближені значення неперервної та диферен
ційовноі функції f( х ). Тому заміну функції f( х) правою частиною
(32) (нагадаємо, одержаної з рівності (30)) називають пінеаризсиісю
функції f( х ).
Крім обчислення наближеного значення функції, диференціал
використовується також для оцінки похибок, які виникають у наб
лижених обчисленнях, Наприклад, нехай нам відомо, що найбільша
похибка під час визначення х Е сх (сх 2:: lD.xl).
Треба знайти найбільшу похибку величини у, яку спричиняє по
хибка сх якщо у визначається через х за відомим законом у. _J(x).
Вважаючи похибки малими, можемо визначити залежність між
ними за співвідношенням (30)
D.y = Г(х) . D.x.
Перейдемо в цьому співвідношенні до абсолютних величин
ID.YI = 1j'(x)I·ID.xl·
(33)
Найбільше значення абсолютної похибки ID.YI позначимо як Су.
Значення цієї похибки одержимо, якщо в рівнянні (33) замінимо lD.xl
на е-. Тоді
Су = IГ(х)l' сх·
(34)
Для отримання найбільшої відносної похибки Оу потрібно обидві
частини рівності (34) розділити на lуl = IЛх)l. Тоді
Су І f'(x) І
Оу = ЇУТ = ЛХ) . СХ·
(35)
130
Зауважимо, що під знаком модуля у правіи частині (35) СТОІТЬ
похідна натурального логарифма функції лх).
Приклад. Знайти найбільшу відносну похибку під час обчис
лення площі квадрата, якщо під час вимірювання його сторони до
пускається похибка, яка не перевишує є х-
Розв 'язання. Площа квадрата у = х2, де х --- сторона квадрата,
In у = 2ln х диференціюємо � = 2� ::::} І � І = 21�1·
Підставляємо у (35)
де дх - найбільша відносна похибка під час вимірювання сторони
квадрата. Отже, відносна похибка під час визначення площі квадра
та дорівнює подвоєніи відносній похибці, яка виникає під час ВИМІ
рювання иого сторони.
§ 3. Похідні та диференціали вищих порядків
3.1. Похідні вищих порядків. Нехай перша похідна у' = г(х)
функції f існує для всіх точок деякого проміжку. Тоді вона є функ-
• • • • U"
ЦІЄЮ точок цього ПРОМІЖКУ І за ТІЄЮ самою схемою, що и для першоі
•.. u • -
ПОХІДНОІ, можна приити до поняття ПОХІДНОІ другого порядку:
у"(х) = и'(х))' = d2y = d2 f = lim г(х + �x) - г(х)
dx2 dx2 дх--+о �x
зрозуміло, що тут точки х і х + �x належать проміжкові існуван
ня першої похідної. Можна сказати, що похідна другого порядку є
. . . ..
першою ПОХІДНОЮ ВІД ПОХІДНОІ першого порядку:
у" = d2y = (у')' = � (dY)
dx2 dx dx
131
Цей процес можна продовжити і прийти до поняття похідної n
го порядку, яка є першою похідною від похідної (n - 1)-го порядку:
Останнє співвідношення називають рекурентним (зворотним),
бо воно повертає нас до попередньої похідної, тобто, знаходячи по
хідну n-го порядку, ми диференціюємо похідну (n - 1)-го порядку.
Взагалі, якщо, наприклад, нам потрібно знайти похідну четвертого
порядку, то ми діємо в такій послідовності: 1) спочатку знаходимо
похідну першого порядку; 2) диференціюємо вираз, який одержали
після першого кроку і отримуємо похідну другого порядку; 3) дифе
ренціюємо вираз, одержаний після другого кроку і отримуємо похід
ну третього порядку; 4) нарешті диференціюємо вираз, одержаний
після третього кроку, і отримуємо похідну четвертого порядку. Іно
ді, як буде показано нижче, можна вивести..формулу для похідної
будь-якого порядку, і тоді відразу переходять до останнього кроку,
пропускаючи ПРОМІЖН1.
Безпосередній фізичний зміст має лише друга похідна від шляху
за часом, яка визначає прискорення руху. Справді, швидкість руху
є першою похідною шляху за часом v(t) = �;. А прискорення - це
швидкість зміни швидкості руху, тобто а = �� = �:�.
Друга похідна довільної функції безпосереднього геометрично
го ЗМІСТУ не має. Вона присутня разом з першою у формулі для
кривини графіка функції. Загалом можна сказати, що похідна вищо
го порядку (довільного) - це швидкість зміни похідної на одиницю
нижчого порядку.
Приклад. Знайти похідну четвертого порядку від функції у =
= х2е-2х.
РОЗб '-ЯЗШН:Н"я.
1) у' = (х2е-2Х)' = 2хе-2х + х2( _2)е-2х = 2(х _ х2)е-2х;
2) уІІ = (2(х - х2)е-2х)' = 2(1 - 2х)е-2х + 2(х - х2)( _2)е-2х
= 2(1 - х - х2)е-2х;
132
3) у"'= (2(I-х _х2)е-2Х) '= 2( -1-2х )е-2х +2(I-х-х2)( _2)е-2х =
= 2( -3х - х2 )е-2х;
4) у(4)=(2( -3х-х2)е-2Х)' = 2( -3-2х )е-2х +2( -3х-х2)( _2)е-2х=
= 2( -3 - 5х - х2)е-2х = -2(3 + 5х + х2)е-2х.
3.2. Похідні вищих порядків параметрично заданої
функції. Для параметрично заданої функції вище (22) одержано
. Права частина у цьому співвідношенні загалом є функцією змін
ної t. Тому, якщо ми будемо диференціювати обидві частини за х,
то праву частину треба диференціювати як складену функцію
�(yl) = d2y = У"2 = � (y�) = � (y�) dt =
dx х dx2 х dx x� dt x� dx
х'
t
УІІ хІ - уІ хІІ
t2 t t t2
(x�P
(37)
--
За аналогією можна одержати похідні третього і вищих поряд-
кІВ.
Приклад. Знайти третю похідну параметрично заданої функції
х = а cos t, у = bsint.
РОЗб 'язання. Послідовно знаходимо:
dy
І
bcost
Ь
Yt
dx
х'
-asin t
= --ctgt;
t
а
:t (- �ctgt)
ь
ь
ь
а sin2 t
= --sіп-Зt·
dx
-asin t
а2 sіпЗ t
2 '
ті
а
.!L (_ J!... sin -з t)
dt а2
dx
ті
з� Sill-4 t cos t
а
-asin t
3bcos t
аЗsіп5t·
133
3.3. Загальні формули для похідних довільного порядку
деяких функцій. Розглянемо декілька прикладів на знаходження
похідних k-ro порядку. Довести наведені формули можна методом
математичноі гндукцп.
Приклад 1. у = т".
РОЗб 'язання. Виконуючи послідовне диференціювання, матиме-
мо:
іп (n),,, ( 1)( 2) n-З
у = х =nn- n- х ;
... ,
y(k) = (xn)(k) = n(n - 1)(n - 2) ... (n - (k - 1)) xn-k. (38)
Приклад 2. У = а":
РОЗб 'язання. Послідовно одержуємо:
у'" = ((aXlna)2)' = аХ(lпа)З;
y(k) = (ax)(k) = aX(lna)k.
... ,
(39)
Приклад 3. У = вш г.
РОЗб 'язання.
, [ві )' . ( 7r)
У = SIn х = cos х = SIn х +"2 ;
у" = (sin (х + �))' = cos (х + �) = sin ( х + � + �) = sin (х + 2;) ;
т (. ( 27r)) , (27r) (27r 7r) (37r)
У = ,SIll Х+2 =cos Х+2 =sin Х+2+"2 =sin Х+2 ; ... ;
y(k) = (sin x)(k) = sin (х + k;) .
(40)
Приклад 4. у = cos х.
134
РОЗб 'язання. За аналогією з попереднім прикладом
y(k) = (СОБ Х )(k) = СОБ (Х + �7r) .
(41)
3.4. Формула ЛеЙбніца. Нехай функція у є добутком двох
функцій u і v, які мають похідні до k-ro порядку включно. Знайдемо
вираз для похідної k-ro порядку функції у = uv.
Виконуючи послідовне диференціювання, матимемо:
" ,,,,, 2" " ,,, т ·3'" 3 ,,, т
у =и v+uv; у =и v+ u v +uv ; у =и v+ u v + u v +uv ; ...
Якщо саму функцію вважати похідною нульового порядку u =
и(О), v = v(O), то праві частини одержаних виразів нагадують
розклади відповідних степенів бінома, в якому степені доданків є
ПОХІДНИМИ певного порядку.
Для похідної k-ro порядку будемо мати так звану формулу Лейб
нща:
k
y(k) = (uv)(k) = L C�u(k-i)v(i) = u(k)v + ku(k-l)v'+
ї=о
(42)
k(k-l) (k-2) " k(k-l) ... (k- j + 1) (k-j) (і) (k)
+ u v + ... + __ . u v + .. ·+uv .
1·2 1·2 ... )
Доведення, яке також можна здійснити методом математичної
. .-
індукцц, опускаємо.
Приклад. Для функції у = хз sinx знайти похідну 7-го порядку.
РОЗб 'язання. Тут k = 7, u = хЗ, v = sin х.
и' = зх2; и" = 6х; и'" = 6; и(4) = и(5) = ... = о.
Це означає, що у (42), записаній для k = 7, відмінними від нуля
будуть лише чотири останні доданки. Нагадаємо, що коефіцієнти
бінома, рівновіддалені від кінців, є однаковими. Отже,
(7) з· (7) . ( 47r) . ( 57r )
У = (х БШ х) = 35 . 6 . БШ Х + 2 + 21 . 6х . БШ Х + 2 +
135
2 . ( б7Г) 3. ( 77Г ) .
+ 7 . 3 . х SIll Х + 2 + х SIll Х + 2 = 210 . SIll х + 12бх COS х-
-21х2 sin х - х3 cos х.
3.5. Диференціали вищих порндкш. За умови існування
похідних вищого порядку заданої функції можна прийти до понят
тя її диференціалів вищого порядку. Так, диференціалом другого
порядку або другим диференціалом функції у = f( х) називають ди
ференціал від її першого диференціала, що записують так:
За аналогією диференціалом k-ro порядку чи k-M диференціалом на
зивають диференціал від (k - 1)-го диференціала
(43)
Нагадаємо, що диференціал першого порядку для функції у = f( х )
записується так:
dy = df(x) = y'dx = f'(x)dx,
тобто завжди дорівнює добуткові похідної функції на диференціал
11 аргументу, незалежно від того, чи цей аргумент є незалежною
змінною, чи він є функцією іншої змінної (властивість інваріантності
форми). Як побачимо далі, властивість інваріантності не справджу
ється для диференціалів вищих порядків.
Розглянемо спочатку випадок, коли аргумент функції є неза
лежною змінною. Тоді dx є довільним числом, яке не залежить від х,
тобто диференціюючи за х, треба вважати dx сталим. Тому будемо
мати
dy = y'dx, d2y = d(y'dx) = (y'dx)'dx = y"(dx?
136
Для спрощення запису дужки в правій частині опускають і пи
шуть так:
(44)
вважаючи, що dx2 = (dx?
Продовжуючи, отримаємо:
(45)
З цього співвідношення маємо такий запис для похідної k-ro порядку
(46)
Треба пам'ятати, що це співвідношення справедливе лише за умо
ви, що х - незалежна ЗМІнна.
Нехай тепер х є функцією деякої незалежної змінної і, х = х(і).
Тоді dx = x� . dt, тобто dx є функцією змінної t і, диференціюючи,
11 вже не можна вважати сталою величиною (а, отже, d(dx) =f. О).
Внаслідок цього маємо
Як бачимо, вже у диференціалі другого порядку з'явився додат
ковий член, який показує, що для диференціалів другого, а, отже, і
вищих порядків властивість інваріантності форми загалом не справ
джується.
Зауважимо, що коли проміжний аргумент є лінійною функцією
КІнцевого аргументу
х = аі + Ь
( 45) справедлива, бо тоді dx = а, d2 х = d( dx) = О і у (47) другий
доданок відсутній, а множник d2x біля першого доданка буде сталим
числом dx2 = а2.
Приклад. Нехай у = х2, причому Х = і2, де t - незалежна
ЗМІНна. Знайдемо вирази для другого диференціала за (44) і (47).
137
Розв 'язання.
УІ = 2х.
х ,
" 2
Ух2 = ;
dx = 2tdt;
за (44)
за (47) маємо
Відмінність результатів зумовлена тим, що (44) справедлива ли-
. . .
ше ТОДІ, коли х Є незалежною ЗМІННОЮ, а у розглянутому прикладі х
залежить від змінної t.
138
Розділ 4. ОСНОВНІ ТЕОРЕМИ ДИФЕРЕНЦІАЛЬНОГО ЧИС
ЛЕННЯ ТА Іх ЗАСТОСУВАННЯ
§ 1. Основні теореми диференціального числення
1.1. Теорема Ферма
Означення. Кажуть, що функція f має в точці хо локальний
максимум (мінімум) (рис. І, 2), якщо існує такий окіл точки Хо, в
якому, якщо х f. Хо, виконується нерівність Лх) < лхо) (І(х) >
> лхо)).
у
xo(min) хо(mах) х
о
Рис. 1.
у
х
xo(min)
Рис.2.
о
Локальний максимум і локальний мінімум об'єднуються спіль
ною назвою покапьниі; екстремцм (або просто екстремум).
Теорема 1 (теорема Ферма). Я-К;ЩО фу'Н,-к;'Ці.я f дuфере'Н,'Ційов'Н,а
в то'Ч'Цz е-к;стре.м,у.м,у Хо, то її nохід'Н,а в 'Цій точці дорів'Н,ює 'Н,улеві
(див. рис.1):
г(хо) = о.
Доведення. За означенням диференційовності функції в точці хо
лхо + �x) - лхо) = Г(Xo)�X + а(хо, �x)�x,
де а(хо, �x) --+ О для �x --+ о.
Перепишемо це співвідношення у вигляді
лхо + �x) - лхо) = [г(хо) + a(xo,�x)] �x.
139
(1)
Оскільки хо - точка екстремуму, то ЛІва частина (1) або не
від'ємна, або недодатна одночасно для всіх достатньо малих !:lx.
Якщо б виконувалось г(хо) f. о, то для !:lх, достатньо близь
ких до нуля, величина г(хо) + a(xo,!:lx) мала б знак Г(хо), а тому
права частина рівності (1) змінювала б знак зі зміною знака !:lx. Це
. .
ПРОТИРІЧЧЯ заКІНЧУЄ доведення теореми.
Зауваження до теореми Ферма.
1. Теорема Ферма дає необхідну умову екстремуму диференці
йовної функції.
2. Геометрично теорема є цілком очевидною, оскільки вона
стверджує, що в точці екстремуму диференційовної функції дотична
до її графіка є паралельною до осі Ох (див. рис. І).
З. Фізично теорема означає, що при "плавному" русі вздовж
вертикальної прямої у момент початку зворотного руху (екстремум!)
. . .
ШВИДКІсть ДОРІВнює нулеві.
Із доведеної теореми, а також теореми Вейєрштрасса про існу
вання для неперервної на замкненому проміжку [а; Ь] функції j гло
бального мінімуму m = minf(x) та глобального максимуму М =
[а;Ь]
= mахі(х), випливає така теорема.
[а;Ь]
1.2. Теорема Ролля.
Теорема 2 (теорема Ролля). Нехай фу'Н,-к;'Ці.я, j задовопьняе у.м,о-
ви:
1) j неперервна на за.м,-к;'Н,е'Н,о.м,у nро.м,іж-к;у [а; Ь];
2) j дифере'Н,'Ційов'Н,а у від-к;рито.м,у проміжки ( а; Ь);
3) Ла) = ЛЬ).
Тоді існце точка с Е (а;Ь) така, що г(с) = О.
Доведення. Оскільки функція j неперервна на замкненому про
міжку [а; Ь], то знайдуться точки хт, хм Е [а; Ь], в яких вона набуває
відповідно найменше та найбільше із своїх значень на цьому проміж
ку. Якщо Лхт) = лхм), то функція є сталою на [а; Ь], а тому
Г(Х) == О і твердження теореми виконано. Якщо ж Лхт) < лхм),
140
то, оскільки і(а) = і(Ь), одна з точок хт, х м повинна міститися в
проміжку (а; Ь). ЦЮ точку і позначимо через с. За теоремою Ферма
f'(c) = о.
Фізична інтерпретація теореми Ролля. Нехай х - час, а
ЛХ) - координата точки, що рухається вздовж прямої, у момент
часу х. У початковий момент х = а точка має координату і(а),
далі рухається з певною швидкістю f' (х) і в момент часу х = Ь зно
ву опиняється в точці з координатою Ла) и(ь) = Ла». Перш ніж
почати зворотний рух в точку і(а), вона повинна зупинитись у де
який момент часу, тобто у деякий момент х = с Е (а; Ь) швидкість
f'(c) = о.
Геометрична інтерпретація теореми Ролля. Існує точка
с Е ( а; Ь) така, що дотична до графіка функції j в ТОЧЦІ (с; J( с)
паралельна до осі Ох.
Приклад 1. Довести, що рівняння 5Х + 12Х = lЗХ має єдиний
корінь х = 2.
Розв 'язання. Перетворимо це рівняння до вигляду (15з) Х + (��) Х =
= 1 і розглянемо допоміжну функцію ЛХ) = C5Jx + C�)X - 1, ди
фєренційовну для усіх х Е R. Вихідне рівняння рівносильне рівнянню
ЛХ) = о. Очевидно, що Л2) = о. Припустимо протилежне: нехай це
рівняння має ще один корінь хо і=- 2, тобто лхо) = о. За теоремою
Ролля на проміжку з кінцями в точках хо і 2 ((хо; 2) або (2; хо) існує
точка с, така, що f'(c) = о, проте f'(x) = С5з)Х In 15з + (��)X In �� < О
(In 15з < о, In �� < о) для всіх х Е R. Це протиріччя доводить, що
корінь х = 2 - єдиний.
I.З. Формула скінченних приростзн (теорема Лагран
жа).
Теорема З (теорема Лагранжа). Нехай фУ'Н,"к''Il;і.я j зсдовольняе
у,м,ови:
1) j неперервна на зомзененомі: nро,м,іж"к'У [а; Ь);
2) j дифере'Н,'Il;ійов'Н,а у від"к'рито,м,у nро,м,іж"к'У ( а; Ь).
141
Тоді іс'Н,ує точка с Е (а; Ь) така, що
ЛЬ) - Ла) = Г(с)(Ь - а).
(2)
Ця формула називається формулою Лагранжа, або формулою
скінченних nриростів, оскільки тут прирости функції та аргументу
можуть бути скінченними. Розглянуті раніше твердження пов'язува
ли лише локальний (нескінченно малий) приріст функції з похибкою
або диференціалом у фіксованій точці.
Теорему 3 називають ще теоремою про середнє значення (серед
німи у такому разі є як значення f' (с) швидкості зміни функції, так
і точка с, що лежить між а та Ь).
Доведення. Для доведення теореми розглянемо допоміжну функ-
ЦІЮ
F(X)defJ(X) _ ЛЬ) - Ла) (х - а),
Ь-а
яка, очевидно, є неперервною на замкненому ПРОМІЖКУ [а; Ь], ди
ференційовною у відкритому проміжку (а; Ь) і на його кінцях набирає
однакові значення: Р(а) = Р(Ь) = Ла).
Застосовуючи до Р(х) теорему Ролля, знайдемо точку с Е (а; Ь),
в якій Р'(с) = f'(c) - I(bi=�(b) = О, що приводить до (2).
Фізична інтерпретація теореми Лагранжа. Нехай х -
час, і(х) - координата точки, що рухається вздовж прямої, у мо
мент часу х. Запишемо формулу Лагранжа у вигляді
ЛЬ� = �(a) = г(с).
Величина у лівій частині рівності є, очевидно, середньою швид
кістю руху точки вздовж прямої за період часу від а до Ь. Формула
Лагранжа показує, що існує такий момент часу х = с, для якого мит-
•• • и· •
тєва ШВИДКІсть ДОРІВнює середніи ШВИДКОСТІ на часовому ПРОМІЖКУ
[а; Ь].
142
Геометрична інтерпретація теореми Лагранжа. Число
!(Ьі=:(а) є кутовим коефіцієнтом січноі, що проходить через кінці
графіка функції f - точки (а; J( а)), (Ь; J( Ь)), j' (с) -- кутовий коефі
цієнт дотичноі до графіка в точці (е; Ле)). Формула Лагранжа (2)
показує, що дотична до графіка в деякій точці (е; Ле)) паралельна
до січноі, що проходить через кінці графіка (або збігається з нею).
Розглянемо приклад, в якому на основі теореми Лагранжа дово
диться інтуітивно передбачуване твердження.
Приклад 2. Нехай функції f та q визначені та диференційовні
для х � Хо, причому лхо) = q(xa), г(х) > q'(x) для х > хо. Довести,
що ЛХ) > q(x) для х > ха.
РОЗб '.ЯЗа'Н:Н,.Я. Розглянемо функцію <.р = f - q на ДОВІльному
проміжку [хо; х] (х > хо). За формулою Лагранжа
<.р(Х) - <.р(Хо) = <.р'(е)(х - хо),
(3)
де е Е (хо; х).
Оскільки <.р(ха) = лхо) - q(xa) = О, <.р'(е) = г(е) - q'(e) > О,
х-ха > О, то із рівності (3) випливає, що <.р(Х) > О, тобто J(x)-q(x) >
> О для х > хо. Отже, ЛХ) > q(x) для х > ха.
Пропонуємо, використавши приклад 2, встановити самостіино
• • u
справеДЛИВІСТЬ нерівностеи
а) еХ > 1 + х, х > О;
б) ln(l + х) > l�x' Х > О.
Приклад З. Довести, що для всіх и, v Е R виконується нерів
ність І sin u - sin vi :::; lи - vi·
РОЗб 'язання. Функція sin х диференційовна для всіх х Е Н. За
формулою Лагранжа sin u - sin v = cos е( u - v), де е -- деяка точка,
яка лежить між u і v. Із нерівності І cos с] :::; 1 випливає потрібна
нерІВНІСТЬ.
Зауважимо, що для v = О з. доведеної нерівності маємо І sin u І :::;
:::; іиІ, u Е R.
143
1.4. Умови монотонності чи незмінності функції на від
критому ПРОМІЖКУ.
Теорема 4 (про монотонність та незмінність функції). Нехай
фУ'n1\,'Ці.я f дuфере,n'Ційов,nа в (а; Ь), тоді:
а) .я1\,що г(х) � О (J'(x) > О) дл.я усіх х Е (а;Ь), то f не спадає
(зростає) на (а; Ь);
б) .я1\,що г(х) :::; О (J'(x) < О) дл.я усіх х Е (а;Ь), то f не зростає
(спадає) 'па (а; Ь);
в) .я1\,що г(х) = О дл.я усіх х Е (а; Ь), то f стала 'па (а; Ь).
Доведення. Справедливість цих тверджень випливає із формули
Лагранжа ЛХ2) - f(XI) = Г(Х)(Х2 -ХІ), що справджується для будь
якої пари точок ХІ, Х2 із проміжку (а; Ь) дЛЯ деякого Х, що міститься
МІЖ ХІ та Х2.
Приклад 4. РозглянемофункціюJ(х) = -kx5+x+4. Знайдемо
похідну: г(х) = 1 - х4. Маємо: г(х) < О, якщо Х < -1, Х > 1;
г(х) > О, якщо -1 < Х < 1. Отже, f спадає на (оо; -1) U (1; оо) і
зростає на (-1; 1).
3ауваже,n,n.я. Із останнього твердження теореми 4 можна зро
бити такий (важливий для інтегрального числення) висновок: .я1\,що
noxia,ni Р{, p� двох фУ'n1\,'Цій РІ, Р2 збігаються 'па де.я1\,О.му проміж-
1\,у, тобто Р{(х) _ РНХ), то 'па 'Цьо.му проміжкц] різниця РІ - Р2 Є
сталою фУ'n1\,'Цією.
1.5. Узагальнена формула скінченних приростів (теоре
ма Коші).
Теорема 5 (теорема Коші). Нехай фУ'n1\,'Ціі f і q заоовольняють
у.мови:
1) f і q неперервні 'па замхненомц проміжт] [а; Ь];
2) f і q дuфере,n'Ційов,nі у від1\,рито.му nро.між1\,У (а; Ь);
3) q' (х) =І=- О дл.я будь-.я1\,Ог.о Х Е (а; Ь).
Тоді існце тО'Ч1\,а с Е ( а; Ь) така, що
ЛЬ) - Ла)
q(b) - q(a)
г(с)
q'( с) .
(4)
144
Формула (4) називається формулою Коті.
Доведення. Відзначимо, що q(b) - q(a) f= о, оскільки у іншому
разі (теорема Ролля) існувала б точка dE (а; Ь) така, що q' (d) = о, що
суперечить умові теореми. Утворимо допоміжну функцію
def ЛЬ) - Ла)
F(x) = лх) - Ла) - q(b) _ q(a) (q(x) - q(a)).
(5)
На основі умов теореми переконуємось, що для цієї функції ви
конуються всі умови теореми Ролля, а тому існує точка с Е (а; Ь),
в якій F'( с) = о. Підставивши в похідну від функції (5) замість х
точку с, приходимо до (4).
3ауваже'Н,'Н,.я.
1. Теорему Коші часто називають узагальненою теоремою про се
реднє значення. Теорема Лагранжа є її частковим випадком,
оскільки (2) випливає із рівняння (4) для q(x)derx.
2. Фізичний зміст теореми Коші. Якщо х інтерпретувати як час,
а значення пари функцій Лх), q(x) - як координати частинки,
що рухається в площині, то (і'(х); q'(x)) - вектор її швидкості
у момент часу х, а (І(Ь) - Ла); q(b) - q(a)) -- вектор переміщен
ня частинки за проміжок часу [а; Ь]. Теорема Коші стверджує,
що у деякий момент часу с Е (а; Ь) ці вектори є колінеарними
(координати векторів пропорційні).
Приклад 5. Перевірити, що функції ЛХ) = sinx і q(x) = cosx
задовольняють умову теореми Коші на проміжку [�; �] та знайти
точку с, що фігурує у формулі Коші (4).
Розв 'язання. Функції J( х) = sin х і q( х) = cos х неперервні на
замкненому проміжку [�; �]. Їх похідні f' ( х) = cos х і q' ( х) = - sin х
існують в усіх точках х Е (і; �), причому похідна q' (х) = - sin х f= о.
• 7r • 7г
3 К .. (ТГ ТГ) SIn - +вгп - cos С
а теоремою ОШ1 існує точка с Е -6; -3 така, що � � ві n с '
cos з-СОS"6
звідки ctg с = 1 і с = і.
145
§ 2. Правило Лопіталя
Теорема, наведена нижче, часто буває корисною для розкриття
u
невизначеностеи.
Теорема. Нехай внконані у.мови:
1) фУ7і'l'(;'Ції f і q визначені та дuфере7і'Ційов7іі в де,я'l'(;О.му окопі точ
'l'(;и а, за вннятхом, можпиео, самоі точкн а (Іаl :::; оо);
2) Ііт лх) = Ііт q(x) = О, або Ііт лх) = Іігп q(x) = оо;
х-+а х-+а х-+а х-+а
3) q( х) і=- О та q' (х) і=- О у вказаномц оком, за винятком, можміво,
самої точзсн а;
4) іС7іУЄ границя Ііт і:«х)) [можливо, нескінченна}.
х-+а q х
Тоді іС7іУЄ Ііт і(Х), nрu'Чо.му Ііт і(х) = Ііт і:(х) .
х-+а q(x) х-+а q(x) х-+а q (х)
3ауваже7і7і,я.
1. Наведена теорема відома під назвою праеила Лопітаея, яке ко
ротко, але не зовсім точно формулюють так: границя відношен
ня фУ'Н.'І'(;'ЦіЙ дорівнюе гранииі виіноиьення Їх похідниа: за у.мови,
що остання ьснце.
2. Якщо всі умови цієї теореми виконуються в правому (лівому)
півоколі точки а, то теорема є правильною щодо правої (лівої)
границі функції І. в точці а.
q
3. Правило Лопіталя дає змогу безпосередньо розкривати невизна-
ченості типу § або типу :.
4. Необхідно відзначити, що умова 4 є лише достатньою для існува
ння границі дробу (приклад 2).
Дов едення. Доведення теореми наведемо лише якщо Ііт f( х) =
х-+а
Ііт q(x) = О, причому вважатимемо, що а --- скінченне число (якщо
х-+а
а = оо, заміна х = t робить а скінченним: а = О).
Отже, нехай виконується умова Ііт f( х) = Ііт q( х) = о. Довиз-
х-+а х-+а
начимо функції f і q в точці х = а, приймаючи f( а) = q( а) = О, тоді ці
нові функції будуть неперервними в точці х = а. Отже, на проміжку
[х; а) ([а; х)), якщо х < а (якщо х > а), функції f і q є неперервними, а
146
на (х; а) ((а; х)) - диференціиовними, тому за теоремою Коші існує
точка сх Е (х; а) (сх Е (а; х)) така, що
Ла) - ЛХ) (ЛХ) - Ла)) = f'(x) або ЛХ)
q(a) - q(x) q(x) - q(a) q'(x) q(x)
Коли х ---t а, то і сх ---t а, а тому на підставі умови 4 теореми
випливає існування Ііт і(х) = Ііт і;(сх) = Ііт і;(х).
x---ta q( х) сх ---ta q (сь) x---ta q (х)
у можливості застосування правила Лопіталя завжди перекону
ємось після того, як знайдемо границю відношення похідних. Необ
хідно пам'ятати про перевірку виконання умов 2. Про важливість
цих умов свідчить такий приклад.
Приклад 1. Нехай ЛХ) = cos х, q(x) = sinx, тоді f'(x) = - sinx,
q'(x) = cos х і якщо х ---t +0 маємо �;�:� = -tg х ---t о, У той час
як ��:� = ctg х ---t +00. Правило Лопіталя "не спрацювало" внаслі
док невиконання умов 2: Ііт q( х) = Ііт sin х = о, а Ііт f( х) =
x---t+О x---t+О x---t+О
= Ііт cos х = 1 і=- о.
x---t+О
Приклад 2. Обчислити границю Ііт x+s�n х .
x---t= x-sIn х
РОЗб 'язання. Маємо невизначеність типу ::' застосовуємо пра
вило Лопіталя Ііт x+s!n х = Ііт 1 +cos х але бачимо що знаменник
x---t= x-sIn х x---t= I-cos х' ,
1 - cos х = О в точках xk = 2kn ---t оо (k ---t оо, k Е Z), а отже, ро
бимо висновок про те, що правило Лопіталя тут використовувати не
можна (не виконується пункт 3 правила Лопіталя).
+ . () І+зіпх 1+0
Робимо інакше· Ііт х s�n х = = = Ііт - -- - 1
. x---t= x-sIn х = x---t= 1- Sl� х - 1-0 - .
Приклад 3. Обчислити границю Ііт cos �x .
х---+ � cos х
РОЗб 'язання. Маємо невизначеність типу §, застосовуємо пра
вило Лопіталя
cos 7х
Ііт
x---t� cos 5х
Ііт 7 sin 7 х = 7· ( -1) = _ � .
x---t � 5 sin 5х 5 . 1 5
Іноді для розкриття невизначеності правило Лопіталя доводить-
. .
ся використовувати КІлька разів.
147
Приклад 4. Обчислити границю Ііт Iп2зх.
Х-++= х
РОЗб 'язання.
Ііт ln2 х = (ОО)
Х-++= х3 оо
. 2 In х (ОО) . 2 1
11т -. - = - = 11т -. - = о.
Х-++= 3 х3 оо Х-+= 9 х3
Невизначеності типів О· оо і оо - оо за допомогою простих алгеб
раічних перетворень зводяться спочатку до типу § або :' до яких
потім застосовують правило Лопіталя.
Приклад 5. Обчислити границю 11т з:> ln х.
Х-++О
РОЗб 'язання. Маємо невизначеність типу О . оо. Зводячи іі до
типу: (11Х) і використовуючи правило Лопіталя, отримаємо
lim xlnx=(O· 00)= Ііт l�x = (ОО) = Ііт �1 =- lim х=О.
Х-++О Х-++О;; оо Х-++О - х2 Х-++О
Рекомендуємо звернути увагу на те, що зведення заданої невиз
наченості типу О· оо до типу § ( f ) із подальшим застосуванням
Іп с
правила Лопіталя не дає бажаного результату: знову прийдемо до
невизначеності типу О· оо. Отже, вибирати зведення невизначеності
типу О . оо до типу : або типу § потрібно осмислено.
Приклад 6. Обчислити границю Ііт (! - Ж�l).
Х-+О х е
РОЗб 'язання. Маємо невизначеність типу оо - оо. Зводячи їі до
типу § і двічі застосовуючи правило Лопіталя, матимемо
lim (� - 1 ) = (оо _ оо) = Ііт _eX_-_1_-_х_
Х-+О х еХ - 1 Х-+О х(ех - 1)
(�)
= Ііт еХ - 1 _ (О) _ lim еХ
Х-+О еХ + хе" - 1 - О - Х-+О 2еХ + хе"
1
2
Невизначеності типів 00, 1 =, 000, які трапляються під час обчис
лення границь функцій вигляду (І( х)) q(x), за допомогою тотожності
(f(x))q(x) == eQ(x) Іп І(х) зводяться до невизначеності типу О . оо.
148
Приклад 7. Обчислити границю Ііт ( tg Х )COS Х.
x-+�-o
РОЗб 'язання. Маємо невизначеність типу 000. Подамо (tg Х )COS Х=
= eCos х Іп tg х і розглянемо Ііт (cos Х -Іп tg Х). Маємо невизначеність
X-+�-O
типу О· оо; зводячи її до типу :: із застосуванням правила Лопіталя,
отримаємо
1· ( 1 ) 1· In tg Х
пп cos Х· n tg Х = пп 1
X-+�-O X-+�-O
cos х
(:)
Ііт
X-+�-O
1 1
�.�
sin х
cos2 х
1. cos Х _
I� -.-2- - О,
Х-+2"-О SIn Х
звідки Ііт (tg Х )COS х = еО = 1.
X-+�-O
§ 3. Формула Тейлора
3.1. Многочлен Тейлора. Вивчаючи диференціальне числен
ня, можна прийти до правильного висновку про те, що чим більше
похідних (включаючи похідну нульового порядку) збігаються у двох
функцій в деякій точці, тим краще ці функції наближають одна одну
в ОКОЛІ ЦІЄІ точки.
Нехай задана функція і, яка має в точці ХО всі похідні до по
рядку п включно. Бажаючи наближати цю функцію алгебраїчним
многочленом (найпростіша функція в математичному аналізі), при
родно розглянути такии многочлен
(6)
похідні ЯКОГ() ДО порядку n включно в точці хо збігаються з ПОХІД
ними відповідного порядку функції і:
(7)
149
Многочлен (6) називається многочленом Тейлора n-го порядку
функції t з центром в точці хо·
3ауваже,n,nя. Одразу необхідно підкреслити: термін "порядок"
многочлена Тейлора заданої функції не тотожний терміну "степінь"
многочлена Тейлора: степінь може бути меншим за порядок, ос
кільки в (6) може бути І(n)(хо) = о. Так, наприклад, для функції
Л х) = sin х многочлен Тейлора 4- го порядку з центром в точці хо = О
є т (х О) = sinO + cosO· х + -sіПОх2 + -соsохз + sinOx4 = Х _ хЗ -
4 , 2! З! 4! З!
многочлен З-го степеня.
3.2. Формула Тейлора ІЗ залишковим членом у формі
Лагранжа.
Теорема 1. Якшо фУ'n1\,'Ція t має в 01\,олі тО'Ч1\,и хо неперервнц
noxia,ny І(n+l), то для будЬ-Я1\,О20 х 3 'ЦЬО20 01\,ОЛУ знайдеться тО'Ч1\,а
Сх,n, ЩО лежить між х і хо і така, що справедлива рівність
(8)
де
І(n+l)(с )
R () Х,n ( )n+l
n х, хо = ( )' х - хо .
n+ 1 .
(9)
Зауважимо, що точка Сх,n може бути записана в такому вигляді
Сх,n = хо + 8х,n(Х - хо),
де 8х,n --- певне число, що задовольняє умову О < 8х,n < 1.
Формула (8) має назву формули Тейлора n-го порядку для функ
ції t з центром в точці хо; Rn(x, хо) називається залишковим членом
(у формі Лагранжа) формули Тейлора, індекси х, n біля літери с по
казують, що точка с залежить від вибору х та n. Функція Rn(x, хо)
дає відхилення (похибку) многочлена Тейлора від функції І.
у частковому випадку хо = О формулу Тейлора ще називають
формулою Маклорена.
150
Знайдемо вираз Rn(x, ха) через похідну І(n+l)(х). Будемо врахо
вувати (внаслідок (7) і (8)), що Rn(xa, ха) = R�(xa, ха) = R�n)(xa, ха) =
= о. Приймемо <p(x)�C(x - ха)n+l, для цієі функції теж виконується
<р(ха) = <р'(Ха) = ... = <Р(n)(ха) = о. Застосовуючи теорему Коші до
пари функцій Rn(x,xa), <р(х) на проміжку [ха;х] (без обмеження в
загальності вважаємо, що х > ха), матимемо
Rn(x, ха) - Rn(xa, ха)
<р(х) - <р(ха)
R�(XI, ха) - R�(xa, ха)
<р'(ХІ) - <р'(Ха)
R�(X2,Xa)
<Р"(Х2)
R�(XI' Ха)
<р'(ХІ)
R�n)(xn, Ха)
<р(n)(хn)
(10)
R�n)(xn, Ха) - R�n)(xa, Ха)
<Р(n)(Хn) - <р(n)(Ха)
де ХІ Е (ха,х) і Xk+l Е (Xa,Xk), k = 1,n.
Враховуючи те, що <р(n+l)(х) - (n+ І)!, R�n+l)(x,xa) = І(n+l)(х)
та позначаючи Сх,n defxn+l, із (10) отримаємо (9).
Отже, (8) можна записати у вигляді
n jk( ) І(n+l)()
І( ) = � Ха (_ )k + Сх,n (_ )n+l
Х L...t k' Х Ха ( )' Х Ха .
. n + 1 .
k=a
(11)
Формула (11) називається формулою Тейлора із залишковим чле
ном у формі Лагранжа. Вона є узагальненням формули Лагранжа,
в яку переходить: якщо n = о.
3.3. Залишковий член у формі Пеано і Коші. Обмежимось
лише формулюванням такої теореми.
Теорема 2 (локальна формула Тейлора). Нехай фуu'К,ці.я, j має в
точці Ха всі потдн» Г(ха),··· , І(n)(ха) до nор.я,д'К,у n включно, тоді
відзшічасться зображення
n j(k)(xa)
ЛХ) = L k! (Х - xa)k + о[(х - хо)n] при Х -+ Ха· (12)
k=a
151
Співвідношення (12) називається локальною формулою Тейлора
n-го порядку з центром у точці Хо, оскільки вказаний в ньому вигляд
залишкового члена (так звана форма Пеано)
дає змогу робити висновки лише про асимптотичний зв' язок много
члена Тейлора і функції і, якщо х -+ хо. Отже, формула (12) зручна
для обчислення границь та описання асимптотики функції і, якщо
х -+ Хо, але вона не може використовуватися для наближеного обчис
лення значень функції доти, доки немає фактичної оцінки величини
Rn(x, хо) = о [(х - хо)n].
Формула Тейлора (12) із залишковим членом у формі Пеано, оче
видно, є узагальненням означення диференційовності функції в точ
ці, в яке вона переходить, якщо n = 1.
Зауважимо, що (11) практично завжди змістовніша, оскільки, з
одного боку, вона дає змогу оцінювати абсолютну величину залиш
кового члена, а з другого, наприклад, у разі обмеженості І(n+l)(х) в
околі хо з неї випливає (12).
Відомі й інші форми залишкового члена формули Тейлора, на
приклад, форма Коші:
R (х х ) = (х - хо)n+l(1 - ех,n)n І(n+l) (х + е (х - х ))
n , О І о Х,n о,
n.
де О < ех n < 1.
,
З.4. Формули Тейлора для деяких елементарних функ
цій. Найвживанішими розвинениями за формулою Маклорена є:
n k е х
І. еХ = L �! + Rn(x, О), де Rn(x, О) = (n��)! . хn+1;
k=O
• n k-l x2k-1
ІІ. SШ:Г = L (-1) (2k-l)! + R2n(x,0),
k=l
Де R (х О) - (_l)n cOS(8x,2nX) • х2n+1.
2n ,- (2n+l)! '
152
п k X2k
ПІ. COSX = L (-1) (2k)! + R2n+1(X, О),
k=O
R (. О) - (_l)n+l cos(8x.2n+1x). 2n+2.
де 2n+l х, - (2n+2)! Х,
п k
ІУ. lп(l + х) = L (_l)k-l xk + Rn(x, О),
k=l
R ( О) (_l)п n+l.
де n х, = (n+l)(1+8x•nx)n+l . х ,
n
У. (1 + х)а = 1 + L a(a-l)·k�a-k+l)xk + Rn(x,O),
k=l
R ( О) - a(a-l) ..... (а-n)(1+8х•nХ)"-n-l. n+l
де n х, - (n+l)! х.
Як приклад доведемо формулу І. ДЛЯ функції J( х) е" маємо
Лі) = f'(x) = І"(х) = ... = І(n+l)(х) = ех, тому
ЛО) = 1'(0) = І"(О) = ... = І(n+l)(О) = еО = 1,
отже, многочлен Тейлора n-го порядку (6) з центром у точці ХО = О
n (k) n
набуває вигляд Тn(Х,О) = L f k!(O)xk = L :!xk, причому залишко-
k=O k=O
вий член (9) у формі Лагранжа матиме такий вигляд
І(n+l)(с ) Сх п
R (х О) = Х,n хn+І = е· хn+1
n, (n+1)! (n+1)!
де Сх,n = 8х,nХ, (О < 8х,n < 1).
Аналогічно доводяться формули П·-ІV.
Розвинення багатьох інших функцій (наприклад, ch х, sh х,
arcsinx, arctgx) можна одержати самостійно або скористатись до-
. -
В1ДНИКОМ З ВИЩО1 математики.
Розглянемо тепер деякі приклади використання формули Тей
лора.
Приклад 1. Розвинути функцію ЛХ) = tgx за формулою Мак
лорена до члена із хЗ включно.
Розв 'язання. Маємо:
ЛХ) = tgx,
1'(х) = cos-2 х,
І"(х) = 2соs-З х· sinx,
і/l/(х) = 6cos-4 х· sin2 х + 2cos-2 х,
ЛО) = О,
1'(0) = 1,
=? І"(О) = О,
І/l/(О) = 2.
153
За формулою Маклорена із залишковим членом у формі Пеано
отримуємо
хз
tgx = х + 3 + о(хЗ).
Із обчислення похідних для f( х) = tg х легко зауважити, що
І(4)(0) = О, отже Тз(х,О) == Т4(х,0), а тому записану вище формулу
можна уточнити так:
Приклад 2. Розвинути функцію f(x) = lncosx за формулою
Маклорєна до члена із х4 включно.
Розв 'язання. Тут немає потреби обчислювати похідні функції
до четвертого порядку включно, а можна скористатися основними
розвиненнями ІІІ та IV.
Користуючись розвиненням ІІІ, отримаємо
( х2 х4 )
lncosx = Іп 1 - 2 + 24 + о(х4) = lп(l + t),
_ х2 х4 (4)
де t - -"""2 + 24 + О Х •
Тепер застосуємо розвинення IV:
t2 х2 х4
lncosx = Iп(l + t) = t - - + о(е) = -- + - + о(х4)-
2 2 24
Приклад З. Знайти значення перших з чотирьох ПОХІДНИХ
функції f(x) = lncos х в точці х = О.
154
РОЗб 'язання. Не будемо знаходити функціональні вирази цих
похідних, а скористаємось єдиністю многочлена Маклорена функціі
та результатом попереднього прикладу.
Якщо Лх) = СО + С1Х + ... + СNХN + о(хn), якщо Х -+ О, то_ Ck =
= J<k�!{o), а тому f{k) (О) = k!Ck.
Із прикладу 2 маємо:
Incosx = О+О·х+ (-t) х2 +0·х3 + (-112) х4 +о(х4), якщо Х ----+ О,
звідки знаходимо: (Іп cos )(0) = О, (Іп COS)' (О) = О, (Іп COS)" (О) =
= 2! (-�) = -1, (Incos)"'(O) = З!·О = О, (1ncos)(4)(0) = 4! (-112) = -2.
Приклад 4. Оцінити абсолютну похибку наближеноі формули
. 1 3 1 5
SlllX � Х - -Х + -Х при - 1 ::; Х ::; 1.
З! 5!
РОЗб 'язання. Многочлен 5-го степеня у правій частині наближе
ноі формули є многочленом Маклорена б-го порядку функціі Лх) =
= вш г:
. 1 3 1 5 6
SlllX = Х - ІХ + ІХ + О· Х + R6(x,0),
з. 5.
де залишковий член у формі Лагранжа матиме вигляд
R ( ) _ sin(7)(cx,6) 7
6 Х,О - 7! Х .
Оскільки sin(k) Х = sin (Х + k21!") і Iхl ::; 1, то
IR (Х 0)1 = Isin (Сх,6 + І;) І· IхІ7 < � < 10-3
6 , 7! 7!·
3аУбаже'Н,'Н,л. Для цього прикладу можна було відразу викорис
тати готову формулу для залишкового члена (див. формулу Макло
рена ІІ для Лх) = sinx, якщо n = з):
- cos(8x 6Х) 7
R6(x, О) = 7!' г : Х ,
155
де ех,вХ = Сх,в, а -соs(ех,вх) = -соsсх,в = sіп(сх,в + 727r).
О 1· tp; х+2 sin х-Зх
Приклад 5. бчислити границю 1Ш 4 •
х40 Х
Розв 'язання. Використовуючи результат прикладу 1 та розви-
нення ІІ, запишемо
Ііш tg х + 2 sin х - Зх = (Q)
Х40 х4 О
§ 4. Дослідження поведінки функцій
та побудова графіків
4.1. Асимптоти графіка функції.
Означення 1. Якщо точка М (Х, Л х )) графіка функції і, нес-
... . .
кінченно віддаляючись ВІД початку координат у неСКІнченНІСТЬ, як
завгодно близько наближається до деякої прямоі, то ця пряма нази
вається асимптотою графіка цієї функції.
Асимптоти графіка функції поділяються на в ертнкальні та nо-
хилz.
Означення 2. Пряма х = а називається еертикапьною асимп
тотою графіка функції і, якщо хоча б одна із односторонніх границь
Ііш ЛХ) або Іігп Лх) дорівнює -оо або +00. На рис. З, а,б пряма
Х4а-О Х4а+О
Х = 1 є вертикальною асимптотою зображених графіків функцій. Як
бачимо, вертикальні асимптоти необхідно шукати в точзгаз: розриву
функції.
Означення 3. Пряма у = kx + Ь називається лівою (правою)
nохилою асимптотою графіка функції І, якщо f( х) можна подати у
вигляді лх) = kx + Ь + о(х), де о(х) --t О для Х --t -оо (х --t +00).
3ауваженнл. Якщо k = О, то похила асимптота називається
горизонтальною. На рис. З, в, г, Д пряма у = х є відповідно лівою,
156
правою, одночасно лівою і правою похилими асимптотами графіків
функцій.
у
у
у=х,
,
,
а
б
в
х
,
,
,
,
,
,
,
,
,,'у=х
,
,
,
,
,
г
д
Рис.3
Теорема 1. Щоб графі'К, фун'К,v,іі f мав nохuлу асимптоти, не
обхідно і достатньо, щоб одночасно існувалu скінченні грани/ці
k - Ііт лх) Ь = Ііт [ЛХ) - kx] .
- х-+±оо х' х-+±оо
Тут знак "+" береться в обох формулах для правої асимптоти, а
знак "-" для лівої (-оо --- для лівої, +00 -- для правої). Тоді пряма
у = kx + Ь буде похилою асимптотою.
Доведення. Необхідність. Нехай функція f має, наприклад, пра
ву похилу асимптоту у = kx+b. Тоді f(x) = kx+b+o(x), де о(х) -+ О,
якщо х ---t +00.
157
Звідси
Ііт лх) = Ііт [k + � + а(х)] = k,
x-t+oo х x-t+oo х х
Ііт [ЛХ) - kx] = Ііт [Ь + а(х)] = ь.
x-t+oo x-t+oo
Достатність, Нехай вказані в теоремі границі існують для
х -+ +00, тоді рівність Ь = Ііт [ЛХ) - kx] еквівалентна співвід-
x-t+oo
ношенню ЛХ) - kx - Ь = а(х), де а(х) -+ О для х -+ +00, тобто
виконується ЛХ) = kx + Ь + а(х), а це означає, що пряма у = kx + Ь
-- права похила асимптота графіка функції І.
Приклад 1. Знайти асимптоти графіка функції ЛХ) = х2;:1.
Розв'язання. І) D(f) = (-00;0) u (0;00) =? х = О - точка роз
риву функції.
1)
Ііт ЛХ) = _1 = -оо, }
x-t-O -о
1 =? х = О --- вертикальна асимптота.
Ііт ЛХ) = - = +00,
x-t+О +0
2)
(ІІ) 1)
k = Ііт J( х) = Ііт х2 + 1 = 1 }
x-t±oo х x-t±oo х2' 1
=?у= -
ь= Ііт [J(x)-kx]= Ііт �=o,
x-t±oo x-t±oo х
2)
похила асимптота (і ліва, і права).
Приклад 2. Знайти асимптоти графіка функції ЛХ) = х + е1х•
Розв 'язання. І) D(f) = ( -оо; оо) ---- точок розриву немає, а отже,
158
вертикальних асимптот немає.
ІІ) 1) k = Ііт f( х) = Ііт (1 + _1 )
x-t±oo х x-t±oo хеХ
{ (лівої похилої)
оо, х ---+ -оо ::::} аси�птоти
= не ІСНУЄ,
1, х ---+ +00;
2) Ь = ііт [ЛХ) - kx] = Ііт � = о.
x-t+oo x-t+oo еХ
Отже, графік заданої функції має лише праву похилу асимптоту
у =х.
Приклад 3. Знайти асимптоти графіка функції лх) = хе",
Розв 'язання. І) D(f) = (-оо; оо), отже, вертикальних асимптот
немає.
{о, х ---+ -оо,
ІІ) 1) k= Ііт f( х) = Ііт ех= (правої похилої)
x-t±oo х x-t±oo +00, ----'. + ----'-
Х ---т оо -7 аси�птоти ;
не ІСНУЄ,
2) ь= ііт [ЛХ) - kx] = Ііт хе" = о.
x-t-oo x-t-oo
Отже, пряма у = О (вісь Ох) Є лівою горизонтальною асимпто
тою графіка цієї функції.
4.2. Монотонність функції.
Твердження 1. Між характером монотонності дuфереu'Ційов
ноі на від'К,рито.му nро.між'К,у (а; Ь) фуu'К,'Ціі f та знаком іі похіднді
і' на 'Цьо.му nро.між'К,у існие такий взає.мозв '.яЗО'К,:
г(х) > о
::::}
f зростає
::::}
г(х) � о,
г(х) � О
::::}
f не спадає
::::}
г(х) � о,
г(х) == О
::::}
f = const
::::}
г(х) == о,
г(х) < О
::::}
f не зростає
::::}
г(х) < о,
г(х) < О
::::}
f спадає
::::}
г(х) < о.
159
Доведення. Лівий стовпчик тверджень був доведений раніше як
наслідок із теореми Лагранжа. Правий стовпчик тверджень одер
жується безпосередньо із означення похідної. Доведемо, наприклад,
що якщо диференційовна на (а; Ь) функція f зростає, то і' ( х) � о на
(а; Ь).
Дійсно, 1'(х) = Ііт !(Х+ь';)-!(Х). Якщо 8.х > О, то лх + 8.х)-
Ь.Х--+О Х
- лх) > О, а якщо 8.х < О, то лх + 8.х) - лх) < О, тому дріб під
знаком границі є додатним, а отже, ЙОГО границя - невід'ємна.
Те, що із зростання диференційовноі функції випливає лише не
від'ємність її похідної (а не додатність), видно на простому прикладі
функції J( х) = хз. Ця функція зростає на всій числовій осі, а її
похідна не є скрізь додатною: 1'(0) = о.
Нагадаємо, що в записі А => В, А - умова, достатня для В, а
В - умова необхідна, для того щоб було А. Значить, із наведеного
вище твердження можна зробити такі висновки:
а) функція є сталою на інтервалі тоді і лише тоді, коли її по
хідна тотожно дорівнює нулеві на цьому інтервалі;
б) для того, щоб диференційовна на інтервалі функція спада
ла (зростала) на ньому, достатньо, щоб її похідна була від'є.м,ною
(додатною) в кожній точці інтервалу;
в) для того, щоб диференціиовна на інтервалі функція не спадала
(не зростала) на ньому, необхідно, щоб її похідна була недооотна
[невід'емна} на цьому інтервалі.
Приклад. Знайти проміжки монотонності функції лх) = хз_
-Зх + 2.
Розв 'язання. 1'(х) = зх2 - З = З(х2 - 1) і, оскільки 1'(х) < о
для Іхl < 1 і 1'(х) > о для Іхl > 1, то на проміжку (-00;-1) функція
зростає, на проміжку (-1; 1) спадає, а на проміжку (1; +00) знову
зростає.
4.3. Локальний екстремум функції. Означення локального
екстремуму було дано на початку § 4. Відразу зауважимо, що йдеть
ся про локальний внутрішній екстремум функції, тобто точка хо,
160
в ЯКІи досягається екстремум, є ВНУТРІШНЬОЮ точкою області за
дання функціі (:1:'0 входить В цю об.-ШСТЬ разом з деяким своім око
лом). Надалі під локальним екстремумом розуміємо саме такий
слово "внутрішній" домовимось опускати.
Враховуючи теорему Ферма (§ 1), можна сформулювати таку
теорему.
Теорема 2 (необхідна умова екстремуму]. Щоб точка Ха була
точкою е-к:сrnре.му.му фун-к:'Ції І, ензначеноі в цій точці і в її околі,
необхідне визгонання однієї з двох у.мов: або Г(Хо) = О, або Г(Хо) не
ьснце.
Прості приклади показують, що ці необхідні умови не є досrnаrn
німи.
Наприклад, для функції Il(X) = ХЗ (рис.4,а) маємо Л(О) = О,
але в точці ХА = О екстремуму немає.
у
н=І, (х)
Х
Х
а
б
Рис. '-1
Д .- f () {2;1:, Х < О, ( 4) . .
ля функціі 2 З' = '" > О рис.ч , б ІЗ зламом в НУ.1І, оче-
Х, ;[. _ .
видно, Л(О) не існує (немає дотичної), але в точці :то = О екстремуму
немає.
Для пояснення теореми 2 доцільно ввести таке означення.
Означення 1. Множиною крипьнчниз: точок І-го роду функціі
І(х) називається множина внутрішніх точок області її визначення,
для яких похідна f' дорівнює нулеві або не існує.
Точки. в яких f' = О, іноді називають столионсрнимлі точками
функції.
lGl
Отже, критична точка І-го роду функціі f є лише підозрюва
ною на локальний екстремум. Щоб остаточно вирішити питання,
потрібно ще мати критерії розпізнання: чи буде вона дійсно точкою
екстремуму, а якшо бу де, то якого - ),!аКСИМУМУ чи мінімуму.
Використовуючи встановлений в п. 4.2 зв'язок між знаком похід
ної та характером монотонності функціі, приходимо до таких дос
татніх умов наявності або відсутності локального екстремуму в точ
ЦІ.
Теорема 3 (достатня умова екстремуму в термінах першої по
хідної). Н ехай фУ1і-к:'Ці.я f визначена і непсрсрона в де.я-к:о.му околі
критичноі точзгн Ха, еключаючаі са.му то'Ч,-к:у, а похідна l' іС1іУЄ в
околі 'Цієї точхи; за еннятком, можлиео, самої точзгн Ха. Тоді:
1) .я-к:що 1'(х) > о [яназ« "+") nри Х < Ха і 1'(х) < о [знск "-"),
.я-к:що Х > О, то фУ1і-к:'Ці.я f в точці Ха досягае .ма-к:си.му.му;
2) .я-к:що 1'(х) < о [знск "-") nри Х < Ха і 1'(х) > о [янск "+"),
.я-к:що Х > О, то фУ1і-к:'Ці.я f в точці Ха досягае .мі1іі.му.му;
3) .я-к:що 1'(х) не змінюе знак, то е-к:стре.му.му немае.
Коротко можна сказати, що якщо в разі переходу через критич-
. .
ну точку ПОХІдна змінює знак, то екстремцм є, а якщо 11 знак не
змлнюеться, то екстремцмц немае.
Доведе1і1і.я. 1) Нехай Х -- довільна точка із лівого півоколу точ
ки Ха, тоді на [Х; Ха] f неперервна за умовою зростає внаСЛІДОК
додатності 1', тому очевидно, шо Лх) < ЛХа).
Нехай тепер Х --- довільна точка із правого півоколу точки Хо,
тоді на [Ха; Х] f неперервна і спадає внаслідок від'ємності 1', тому
1'(Ха) > ЛХ).
О тже, для будь-якого Х =І=- Ха із вказаного в теоремі околу точ
ки Ха виконується нерівність ЛХа) > ЛХ), щО й означає наявність
локального максимуму в точш ха.
Пункт 2 теореми доводиться аналогічно.
3) Оскільки l' не змінює знак під час переходу через точку Ха,
то функція f або зростає в лівому та правому півоколах точки, або
відповідно спадає, а із неперервності f в точці Ха робимо висновок,
162
що І зростає або спадає У ВСЬО;\іУ околі, ТОМУ екстремуму немає.
Відзначимо відразу, що ці У!\ЮВІІ є достатніми, але не є необхід
ними для наявності у функції екстремуму. Наведемо приклад.
{? 2 + 2,· І
Н u І() _Х х SIn - ,
ехаи х = І
О,
Оскільки х2 ::; f( х) � 3х2 (графік функції міститься між двома
параболами), то ясно, що функція має в точці ха = О локальний мі
німум, який дорівнює нулеві. Проте її похідна г(х) = 4х + 2х sin�
- cos! ні в якому півоколі точки Ха = О не зберігає знак. Дійсно,
х ,
для малих х знак похідної визначається доданком - COS �, який, якщо
з: --+ О (::::} � --+ оо), коливається нескінченну кількість разів між (-1)
та 1. Отже, маємо в Ха = О локальний мінімум, а знак похідної з 11_"
на "+" під час переходу через Ха = О не змінюється.
Теорема 4 (достатня умова екстре
муму в термінах вищих похідних). Не
хай фУ1і-к:v,ія І, еизначснс в околі ста
чіО1іаР1іОЇ точклі Ха, мас в Ха nохід1іі до
nоряд-к:у n в-К:ЛЮ'Ч1іО (n � 1).
Якиіо г(ха) = ... = І(n-l)(ха)
= О, l(n)(Ха)=І=О, то nри непарномц n у
у
О
Рис.5
Х =1= О: ( �)
Х = О рис. і) .
,
Х
Ха е-к:стре.му.му немає, а nри парномц n
е-к:стре.му.м є, причомц че локапьний .мі1іі.му.м, я-к:що І(n) (Ха) > О
ло-к:аЛЬ1іUU .ма-к:си.му.м, я-к:що І(n)(ха) < о.
Доведення. Використовуючи локальну формулу Тейлора n-го
порядку з центром в точці Ха ЛХ) = ЛХа)+ I(n:�Xo) +a(X)(x-Ха)n, де
о(х) --+ О, якщо Х --+ Ха, будеш міркувати так, як під час доведення
теореми Ферма (§ 1).
Перепишемо попередню формулу у вигляді
163
.' It") (с )
ОСКІЛЬКИ Рn)(:т.а) f. О, а 0(.1:) -+ о. якшо Х -+ Ха· то СУ!>'/Іа ---;г+
+о(х) !>'/ІаЄ знак І(n)(ха). коли змінна х достатньо близька до Ха.
Якщо ТІ неттарне. то при переході через Ха дужка (.7: - :Га) n змінює
знак і тоді зміниться знак ВСІЄІ правої, а, отже: і лівоі частини ос
танньої рівності. Отже. при п непариому в Ха екстремум відсутній.
Якщо ТІ парнє, то (х -- Ха)n > о, якщо Х # Ха, а тому в малому
околі точки Ха знак різниці f (х) - f (Ха) збігається із знаком і( n) (ха).
Оскільки похідна l' може змінювати знак лише в критичних точ
ках функції і, то, досліджуючи f на екстремум, паралельно визна
чаємо 11 Інтервали МОНОТОННОСТІ.
Практичний алгоритм застосування похідноі для знаходження
.. . .
інтервалів МОНОТОННОСТІ та екстремумів виглядає так:
1. Знаходять похідну 1'.
2. Знаходять множину критичних точок І-го роду функції і
з. Відкладають критичні точки на області визначення D(f)
отримують інтервали знакос талості похідної 1'.
4. Беруть на кожному із цих інтервалів довільну пробну точку і
визначають знак ПОХІДНОІ на ньому.
5. Аналізуючи кожну критичну точку функції f щодо зміни зна
ка похідної 1', встановлюють відсутність чи наявність екстремумів
та Їхній характер.
6. ОБЧИС-1ЮЮТЬ значення функції в екстремальних точках (тоб
то одержують числові значення екстремумів).
Приклад 1. Дослідити на екстремум функцію ЛХ) = (х2 -4х+
+з)2, знайти інтервали монотонності.
Розв 'язання. Знаходимо похідну 1'(х) =, 2(х2 - 4х + З)(2х - 4).
Маємо 1'(;г) = о {::} .Т] = 1, Х2 = 2, Хз = з; точок, в яких би l' не
існувала, немає. Отже, .r І, Х2 і .Lз .-- критичні точки.
Результати дослідження функції на екстремум подаємо у вигляді
такої таблиці
164
min
шах
min
Аналіз таблиці дає такі висновки:
1) Хтіп,l = 1, Утіп,l = ЛI) = О; 2) Хтіп,2 = 3, Утіп,2 = Л3) = О;
3) Хта.х = 2, Ута.х = Л2) = 1.
На множині (-оо; I)U(2; 3) J спадає, на (1; 2)U(3; +(0) J зростає.
Приклад 2. Знайти екстремуми та інтервали МОНОТОННОСТІ
функції ЛХ) = \!х2 - 1.
Розв 'язання. Знаходимо похідну j' (х) = ;>./ 2х . Звідси вип-
3 V (х2_1)2
ливає:
г(х) = О {:} х = О; І'(х) не існує {:} х = ±1 Е D(J),
отже, ХІ = -1, Х2 = О, Хз = 1 ---- критичні точки.
Наводимо таблицю знаків j' та поведінки І.
Х
(--оо; --1)
--1
(-1; О)
О
(О; 1)
1
(1;00)
г(х)
-
не ІСНУЄ
-
О
+
не ІСНУЄ
+
ЛХ)
-,
О
-,
1
/'
О
/'
пцп
Аналіз таблиці приводить до висновків:
1) функція J має єдиний екстремум: Хтіп = О, Утіп = ЛО) = -1;
2) на інтервалі (-оо; О) функція J монотонно спадає, а на інтер
валі (О; +(0) --- монотонно зростає.
Приклад 3. Дослідити на екстремум функцію ЛХ) = х3-3х2-4.
Розв 'язання. Критичними точками функції J є точки ХІ = О,
Х2 = 2, в яких похідна г(х) = 3.т2 - б.r дорівнює нулеві, Оскільки
165
І"(х) = 6х - 6, то 1"(0) = -6 < О, а 1"(2) = 6 > О, отже, згідно із
другою достатньою умовою екстремуму [теорема 4), функція І має
максимум в точці х = О і мінімум В точці х = 2.
Екстремальні значення цієї функції такі: Утах = /(0) = -4,
Утіп = /(2) = -8.
4.4. Напрямки опуклості графіка функції та точки пе
регину.
Означення 1. 1) Кажуть, що графік функції І є отргпим вго
ру (оnу-к:лu.м вннз] в точці Ха, якщо існує окіл точки Ха такий, що
для усіх його точок відповідні точки доmU'Ч1іОЇ до графіка функції
в точці Ма(ха; /(Ха)) лежать вuще [нижче} від графі-к:а (рис. 6, а,б),
за винятком самої точки дотику. Часто опуклість вгору називають
просто оnу-к:лісmю графіка, а опуклість вниз - увіг1іуmісmю.
2) Графік функції І опуклий вгору (опуклий вниз) на проміжки
(а; Ь), якщо він опуклий вгору (опуклий вниз) в �ОЖ1іі'Й точці цього
ПРОМІЖКУ.
3) Точка Ма(ха; ЛХа)) графіка функції І називається точкою
nереги1іУ цього графіка, якщо У цій точці графік має доmU'Ч1іУ та
існує такий окіл Ха, У межах якого графік функції І ліворуч та пра
воруч від Ма має різні напрямки опуклості (змінює опуклість на увіг
нутість або навпаки) (рис. 6, в).
У
О
О
О
Ха
Х
Ха
Х
Ха
з:
а
б
в
Рис.6
Геометрично цє означає, що під час переходу Х через абсцису Ха
166
точки перегину 1"110 точка і\I(:г: f( Х)) графіка переходить з одного
боку дотичної на другий її бік.
Можна довести, що властивість опуклості вниз графіка функ
ції f на проміжку (а; Ь) екеіоалентна такій аналітичній властивості
функції І: дЛЯ довільних точок ХІ, Х2 Е (а; Ь) (ХІ =1= Х2) і довільних
чисел 01 > О, 02 > О таких, що 01 + 02 = 1, виконується нерівність
Рис.7
(13)
Геометрично нерівність (13) озна
чає (див. рис. 7), що точки будь-якої
дуги АВ графіка функції f (Х) лежать
під хордою АВ, що її стягує. Дійс
но, у лівій частині нерівності (13) є
значення функції f в точці Х = 0IХІ+
+02Х2 Е (ХІ; Х2), а праворуч стоїть
значення у цій точці лінійної функ
цц , графік якої (пряма) проходить через точки А(ХІ; ЛХІ)) і
В(Х2; ЛХ2 )).
Якщо графік функції f є опуклим вгору на проміжку (а; Ь), то
виконується протилежна нерІВНІСТЬ
(14)
яка геометрично означає, що точки будь-якої дуги графіка функції
лежать над хордою, що стягує цю дугу.
Твердження 2. Щоб графік дuфере'Н,'/�ійов-н,ої на nро.м,іж.,,;у (а; Ь)
фу-н,.,,;'Ції f бу-в оnу.,,;лu.м, вниз (вгору) на ( а; Ь) необхідно і достатньо,
щоб її похідна f' зростала (спадала) на (а; Ь).
Доведення. Доведемо це твердження для опуклості вниз (увіг
нутості) графіка функції, для опуклості вгору всі викладки бу дуть
аналоГІЧНИМИ.
Необхідність, Нехай графік функції f є опуклим вниз (увіг
нутим) на проміжку (а; Ь), а тому виконується нерІВНІСТЬ (13), яку
167
елементарними перетвореннями, з урахуванням умов 0'1 + 0'2 1 і
Х = О'ІХІ + 0'2Х2, можна звести до вигляду
Х - ХІ
(15)
якщо ХІ < Х < Х2 та довільних ХІ, Х2 Е (а;Ь).
Нерівність (15) є іншою формою запису означення опуклості вниз
графіка функції на проміжку (а; Ь). Геометрично нерівність (15) оз
начає (див. рис.7), що кутовий коефіцієнт хорди AD, що з'єднує
точки А(ХІ; ЛХІ)) і D(x; Лх)), є меншим за кутовий коефіцієнт хор
ди BD, яка з'єднує точки D(x;J(x)) і В(Х2;ЛХ2)).
Спрямовуючи В нерівності (15) Х послідовно до ХІ та Х2, одер
жуємо
(16)
що означає неспадання похідної f' на проміжку (а; Ь). Покажемо,
що насправді відзначається строге зростання похідної [". Дійсно,
використовуючи в нерівності (15) теорему Лагранжа, а також вра
ховуючи нерівність (16), приходимо до такої оцінки
якщо ХІ < С] < Х < С2 < Х2, тобто маємо зростання похідної f' на
проміжку (а; Ь).
Достатність, Для а < ХІ < Х < Х2 < Ь за теоремою Лагранжа
ЛХ2) - Лх) = І'(С2)'
Х2 - Х
де ХІ < СІ < Х < С2 < Х2, і якщо похідна f' зростає на проміжку (а; Ь):
f' (СІ) < f' (С2 ), то виконується нерівність (15) увігнутості вниз.
168
Доведене породжує таке твердження.
Твердження з. Я-К:ЩО 1\10 (хо; J( хо)) - точха перегини графі-к:а
неперервно дuфере1іv,і'Йов1іоі фУ1і-к:v,іі І в оком тонкн Хо, то потдно.
f' має в точці хо локапьний екстремцм.
Внаслідок твердження 2 доведення твердження 3 цілком анало
гічне доведенню теореми 3 (пункт 30) із заміною І на f'.
Як наслідок із твердження 2 та твердження 1 (пункт 20) отриму
ємо достатню умову опуклості графіка функції І на проміжку (а; Ь)
в термінах другої похідної І".
Теорема 5 (достатня умова опуклості графіка функції на про
міжку). Я-К:ЩО друга похідна І" іС1іУЄ на проміжкц ( а; Ь) і не змінюе
знак на ньомц, то:
1) Л-К:ЩО І"(х) > о [знок "+"), графі-к: фУ1і-к:v,іі І OnY-К:ЛU'Й вниз
(увіг1іутu'Й) на nро.між-к:у (а; Ь);
2) Л-К:ЩО І"(х) < о [знозс "-") графі-к: фУ1і-к:v,іі І опикпнй вгору
(OnY-К:ЛU'Й) на проміжт; (а; Ь).
Це твердження, яке називають "правилом дощу" , символічно оз
начає, що якщо графік опуклий вниз, то дощ, що падає, начебто
наповнює його (знак "+"), а якщо графік опуклий вгору, то краплі
дощу начебто стікають з нього (знак "-").
у тому, що вказані умови є ллиие достатніми; можна перекона
тись, розглянувши функцію f( х) = х4: графік цієї функції є опуклим
вниз (опуклий) на всій числовій осі, а 1"(0) = О, тобто на всій осі не
виконується строга нерівність І" (х) > о.
Необхідну ознаку абсциси точки перегину графіка функції отри
маємо, порівнюючи твердження 3 та теорему 2 (пункт 30).
Теорема 6 (необхідна умова існування точки перегину). Щоб
точка 1\10 (хо; f( хо)) була точкою nереги1іУ неперервно дuфере1і
иійовноі в околі точклі хо ФУ1і-к:v,іі І, необхідне виконання одніеі із
двох у.мов: або І"(хо) = о або І"(хо) не іС1іУЄ.
Те, що ці умови не є достатніми, показують приклади функцій
11 (х) = х1, f () { х2, Х < О,
2 Х = !х2 Х > О
2' ,
169
ОСКІЛЬКИ /{'(О) = О, Л'(О) - не існує, проте Ха
точки перегину графіків обох функцій.
Теорема 6 приводить до такого означення.
Означення 2. Множиною кріпплічних точок Пгго роду функції
І називається множина внутрішніх точок її області визначення, в
яких друга похідна І" дорівнює нулеві або не існує.
Критичні точки 11- го роду необов' язково є точками перегину
графіка функції І, остаточно це питання вирішується за допомогою
такої теореми, яка є наслідком твердження 1 (п. 4.2) і твердження 2.
Теорема 7 (достатня умова існування точки перегину). Неиій
фую<;;'Ці.я І еизначена і 1іеnерерв1іа в де.я-к:о.му околі тонкн Ха, вклю
чаючлі са.му точпи, а друга похідна І" іС1іУЄ в оком 'Цієї точзеи, за
винятком, можлиео, самоі точзгн Ха. Тоді, .я-к:що в ліво.му півокопі
тонкн Ха друга похідна І" має всюди. один знак, а в правоми nіво
-к:олі - есюдн протилежний знак, то точка l'vla(xa; f(xa)) -- точка
перегинн графіка фУ1і-к:'Ції І.
Доведення. Те, що друга похідна І" в лівому та правому піво
колах точки Ха має різні знаки, є достатнім за твердженням 1 (§ 4),
щоб перша похідна f' в цих півоколах була строго монотонною, але
мала різний характер монотонності. Тоді, внаслідок твердження 2,
в точці М, а (ха; J( ха)) зміниться напрямок опуклості графіка, тобто
точка l'vla(xa; ЛХа)) буде точкою перегину.
Алгоритм застосування другої похідної для пошуку інтервалів
опуклості вгору та вниз (опуклості або увігнутості), а також точок
О не є абсцисою
• • и. •
перегину ЦІлком аналоГІЧНИИ алгоритму ВІДшукання екстрємумів та
інтервалів монотонності (див. пункт 30), тільки замість першої по
хідноі розглядається друга.
Приклад 1. Знайти інтервали опуклості вгору та вниз і точки
перегину графіка функції ЛХ) = (х2 - 4х + з)2.
Розв 'язання. Знаходимо другу похідну 1"( х) = 12 (х2 - 4х + ІзІ).
Маємо: І"(х) = О {::} ХІ = 2 - )з, Х2 = 2 + )з; точок, в яких би І"
не існувала, немає. Отже, критичні точки-- Х І і Х2. Результати
дослідження на опуклість та точки перегину зображаємо у вигляді
170
таблиці
х
(-ОО· 2 __ 1 )
2 __ 1
(2 __ 1 ·2+-1 )
2+_1
_(2+-1 . 001
' vГз
vГз
vГз' vГз
vГз
vГз'
і" (х)
-
О
+
О
-
ЛХ)
г>;
4
\....J
4
г\
9
9
перегин
перегин
З таблиці робимо такі висновки:
1) на інтервалах. (-оо; 2 - )з) u (2 + )з; оо) графік функціі
опуклий вгору, а на інтервалі (2 - )з; 2 + )з) - опуклий вниз;
2) хІ = 2 - )з, Х2 = 2 + Jз -- абсциси точок перегину графіка
функціі, іх ординати: УІ = (хі -4Х1 +3)2 = �,Y2 = (x� -4Х2 +3? = �.
Отже, МІ (2 - )з; �), М2 (2 + )з;�) - точки перегину.
Приклад 2. Знайти інтервали опуклості вгору та вниз і точки
перегину графіка функціі f( х) = � х2 - 1
2
РОЗб 'язання. Знаходимо другу похідну і" (х) = - � х +35 , має
(х2-1)3
мо:
і" # О; і"(х) не існує {::} х = ±1 Е D(f),
отже, ХІ = -1 і Х2 = 1 -- критичні точки. Тоді маємо таку таблицю
х
(-оо; -1)
-1
(-1;1)
1
(1;00)
і"(х)
-
О
+
О
-
лх)
г\
О
\....J
О
г\
перегин
перегин
Із таблиці випливає:
1) на інтервалах ( - оо; -1) U ( 1; оо) графік функції опуклий вгору,
а на інтервалі (-1; 1)--- опуклии вниз;
171
2) ХІ = -1, Х2 = 1 - абсциси точок перегину графіка функції,
знаходимо відповідні ординати: УІ = \І хі - 1 = о, У2 = \І x� - 1- = о.
Отже; МІ(-l;О), М2(1;0) - точки перегину.
4.5. Загальна схема дослідження функцій шд час побу
дови графіків. Для наочного описання функції досить часто вико
ристовують її графічне зображення. Як правило, таке зображення
буває корисним для вивчення якісних питань поведінки досліджу
ваної функції. Для точних розрахунків графіки використовуються
рідше. У зв'язку з цим практично важливим виявляється не стіль
ки ретельне відтворення функції у вигляді графіка, скільки побудова
ескіза графіка функції, який правильно відображає основні елементи
в повеД1НКИ.
Вивчати властивості функції під час побудови ескіза її графіка
ДОЦ1Льно за такою схемою.
1. Знаходять область визначення і точки розриву; обчислюють
значення функції (або відповідних границь) в граничних точках об
ласті визначення. Водночас вирішується питання стосовно існування
вертикальних асимптот.
2. Встановлюють парність або непарність, періодичність функ-
цп.
Призначення цього пункту - зменшити обсяг дослідження.
Дійсно, якщо функція парна чи непарна, то замість всієї області виз
начення достатньо розглянути лише ту в частину, яка належить до
датній півосі абсцис. На цій частині області визначення потрібне
повне дослідження функції та побудова ескіза графіка, а потім, ко
ристуючись симетрією, необхідно побудувати його на всій області
визначення.
Якщо функція періодична, то достатньо дослідити функцію на
будь-якому відрізку, довжина якого дорівнює періоду функції, а по
тім, побудувавши ескіз графіка на цьому відрізку, продовжити його
у періодичний спосіб на всю область визначення.
3. Визначають 'Нулі функції та ІНтервали в знакосталостл, а
172
також точку перетину графіка з віссю ордннат:
4. Знаходять похилі асимптоти, якщо функція визначена на
півпрямій або на всій числовій прямін.
5. Досліджують функцію на екстремцм; визначають гнтєрвали
11 монотонності.
6. Знаходять точки перегини та інтервали опиклості вгору
(опуклості) або вниз (увігнутості) графіка функції.
7. Використовуючи результати досліджень, отриманих в пунк
тах 1--6 будуємо графік функціі.
Приклад 1. Дослідити функцію та побудувати ескіз її графіка
хЗ
/(х) = 2(х + 1)2
РОЗб 'язання. 1. Область визначення - уся числова вісь, за ви
нятком точки х = -1, в якій функція має розрив. Граничні значення
функції:
.rЗ
Ііт -------- = ОО'
Х-4-00 2(х + 1)2 '
З
1. х
П'П -----,-,- = - оо;
Х-4-1-0 2(х + 1)2
хз
Ііт ---- = -ОО'
х-+-1+0 2(х + 1)2 ,
хЗ
Ііт ----- = +00.
Х-4+= 2( х + 1)2
Дослідження поведінки функції в околі точки розриву свідчить,
що існує вертикальна асимптота х = -1.
2. Функція загального вигляду � неперіодична.
3. Функція має один нуль в точці х = О, функція додатна для
х > О і від'ємна Д�1Я .Х: < О. Точка перетину з віссю ординат у = О.
4. Визначимо параметри похилоі асимптоти:
х
:ГЗ
liш 2
Т-+±= 2.т(х + 1)
1
2'
k = Ііш
Т-+±=
/(х)
ь = Ііт (/(:1:) -- k.r)
Х-4±=
ІіЗ
Рівняння похилої асимптоти (лівої і правої): У = �X - 1.
5 З . І/() х2(х+з)
. находимо похІДНУ х = 2(х+І)З.
f' = О {::} ХІ = -З, Х2 = О; f' не існує {::} Хз = -1 1:. D(f),
отже, ХІ = -З і Х2 = О ---- критичні точки.
Тоді таблиця зміни знаків f' та поведінки І бу де такою:
Х
(-оо; -З)
-З
(-З;-1)
(-1;0)
О
(0;00)
Г(Х)
+
О
-
О
+
+
Лх)
/'
-З�
-,
/'
немає
/'
8
екстр.
шах
із таблиці випливає, що:
а) Хтах = -З, Утах = f( -З) = -Зі;
б) на інтервалах (-оо; -З) U (-1; О) U (О; +00) функція зростає,
на інтервалі (-З; -1) -- спадає.
6 В . ІІІ Зх
. изначаємо другу ПОХІДНУ = (х+І)4.
ІІІ = О {::} ХІ = О; ІІІ не існує {::} Х2 = -1 1:. D(f),
а, отже, критична точка лише одна .'ТІ = о.
Зображаємо таблицю зміни знаків І" та вигляду графіка функ
ціі І:
Х
( --00;--1)
(-1;0)
О
(0;00)
--
І" (Х)
-
-
О
+
ЛХ)
г>;
г>;
О
\....J
перегин
Аналіз таблиці показує:
а) Х = 0-- абсциса точки перегину, ордината У = ЛО) = О;
174
б) на інтервалах (- оо; -1) U ( -1; О) графік функціі опуклий вго
РУ, на інтервалі (О; +00) -- опуклий вниз.
7. На основі одержаних даних рисуємо ескіз графіка.
у
У=2(х+1)2 ,,-'1
,,-"У=2х-1
-з
І
.. '
, І
І
, ..
, І
,.,' І
х
з
-з-
8
Рис.8
175
Розділ 5. КОМПЛЕКСНІ числх. многочлени. РАЦІО
НА . .1ЬНІ ДРОБИ
§ 1. Комплексні числа
1.1. Комплексне число як впорядкована пара дгисних
чисел. Відомо, що дійсних чисел недостатньо, щоб розв'язати будь
яке квадратне рівняння з дііІсНІІМІІ коефіцієнтами. Так, рівняння
х2 = -1 не має коренів серед дійсних чисел R. Тому виникає потреба
побудувати більш ширшу множину чисел С, таку, що R с С і в
якій алгебраїчні рівняння, зокрема, рівняння х2 = -1, вже мають
розв'язки.
Дійсні чиста можна зображати точками числовоі осі Ох. Розгля
немо на площині прямокутну систему координат хОу. Якщо дійсне
число х зобразити точкою осі Ох системи координат хОу, ТО ЧИС.:1У
Х буде відповідати на площині хОу точка з координатою (х; О), .1' Е R
(рис. І).
у
у
А(х; у)
О
:с
х
(.1";0)
Рис. 1.
Рис.2.
Компяексним числом z назнвасться впорядкована пара (х; у)
(}Ї-ЙС'Н,1LХ чисел х, у:
z =: (.су); Х.у Е R.
Число .І: називається дійс'Н,ою частліною, у УЯ(І'Н,ОЮ частиною
комплексного ЧИС.1а г і позначаються: .г = Не z. у = 1111 Z. :\ІНОЖlIна
усіх комплексних ЧИ<:('.-Т позначається СИ:--ІВО.10�1 С.
17G
Комплексне число Z = (х; У) зручно зображати на площині хОу
у вигляді точки А(х; у) з координатами х: у. І навпаки, кожній точ
ці А(х; у) площини відповідає комплексне число z = (Хі у). Число
Z = (Хі у) можна також ототожнювати з радіус-вектором ОА, по
чаток якого знаходиться в точці 0(0; О), а кінець -- в точці А(Хі у)
(рис.2). Площина хОу, точки якої є зображеннями комплексних
чисел, називається комплексною плоииіною с. у площині С вісь Ох
називається дійс'Н,ою, а вісь Оу - у.яв'Н,ою віссю.
Комплексні числа ZI = (ХІ і УІ) і Z2 = (Х2 і У2) називають рівними,
якщо ХІ = Х2, УІ = У2:
Су.ма і різниця комплексних чисел zl = (ХІ і УІ) 1 Z2
визначаються за формулами
ZI + Z2 = (ХІ і УІ) + (Х2і Y2)�f(X1 + Х2і УІ + У2),
Zl - Z2 = (ХІі УІ) - (X2iY2)def(XI - Х2іУ1 - У2),
(1)
тобто діі вихониються за правшиімлі додава'Н,'Н,.я [віднімання} е ех
торьв: відповідні координати додаються (віднімаються).
Рис.3
Якщо Zl і z2 розглядати як раДІУС
вектори, то сума Zl + Z2 визначається за
nравuло.м паралепограма (три1\",ут'Н,и1\",а):
ЧИс''10 Zl + Z2 зображується радіус-векто
ром, який збігається з діагоналлю пара
лелограма, сторонами якого є вектори zl
і Z2. Різниця zI - Z2 зображується век
тором, початок якого -- точка Z2, а КІ
нець ---- точка ZI (рис.3).
Добиток компяексниз: чисел Zl = (ХІіУІ) і Z2 = (Х2іУ2) визна
чається формулою:
177
Дл.я дій додавання і множення комплексниа: чисел. вихониють
ся законн 'К',о.мутатив'Н,ості, асоціативності і дuсmрuбуmuв'Н,осmі:
.я'К',що 2j = (Xj; Yj), j = 1, 2, З, то
10.21+22=22+21, 20. (21+22)+2з=21+(22+23),
зо. 21 . 22 = 22' 21, 40. (2122)23 = 21(2223),
50. (21 + 22)23 = 21ZЗ + 222з.
Доведемо властивість ЗО.
Інші властивості доведіть самостійно.
у множині комплексние чисел:
а) існце число (О; О) Е С [нейтральний елемент} таке, що дл.я
довіЛЬ'Н,О20 2 = (Х; у) Е С
2 + (О; О) = 2, 2' (О; О) = (О; О);
б) існце число (1; О) Е С [одиничний елемент] пиіке, що дл.я
довіЛЬ'Н,О20 2 = (Х; у) Е С
2·(1;0)=2.
Доведення випливає з означення множення, наприклад,
2' (1; О) = (Х; у)(l; О) = (х· 1- у. О; Х· О + у ·1) = (х; у) = 2.
Дл.я 'К',ОЖ'Н,О20 2 = (х;у) Е С існие комплексне нисло (-z)
= ( -х; -у) [протияежний елемент] таке, що
2 + (-2) = (0;0).
Дяя довіпьниз: 21 = (Хl;Уl), 22 = (Х2;У2) анкониються еласти
востл
178
Дов едення.
z + (-z) = (х;у) + (-х;-у) = (х + (-Х);У + (-у)) = (0;0);
Аналогічно перевіряється третя рівність.
Частхою �о.мnле-к:с'Н,uх чисел zl =(Хl; УІ) і Z2=(X2; У2), (Z2#(0; О))
'Н,азuваєтьс,я комплексне число z = (х; У) [позначаеться символом
z = �) таке, 'lцо
Z2·
Z2 . Z = ZI.
(3)
Частку можна знайти за формулою
(4)
Дійсно, запишемо рівність (3) у вигляді (Х2; У2)(Х; у)
Враховуючи правило множення комплексних чисел, отримаємо (Х2Х
-У2У; У2Х + Х2У) = (ХІ; УІ), тоді умова рівності комплексних чисел
{ Х2Х - У2У = ХІ,
визначається системою Розв'яжемо її за правилом
У2Х + Х2У = УІ·
Крамера: � = X� -+ уі, �x = ХІХ2 + УІУ2, �y = Х2УІ - ХІУ2; Х = �,
- [).у
у - """"Е"' отже,
Нижче (див. (8)) ми покажемо, як практично виконується ділен
ня комплексних чисел.
Дл,я довіль'Н,uх дійс'Н,их члісел а і Ь маемо
а) (а; О) + (Ь; О) = (а + Ь; О); б) (а; О)(Ь; О) = (аЬ; О);
) (а;О) _ (а.О) b..J..O (Д .. и )
В (Ь;О) - Ь' , ,я-к:що І· овести самостіино .
179
Встановимо взаємооднозначну відповідність (х; О) t-+ х між під
множиною комплексних чисел {(х; О) : х Е R} і множиною дійс
них чисел R. З а, б і в випливає, що ця відповідність "зберігає
операціі": якщо а, Ь Е R, то (а; О) + (Ь; О) = (а + Ь; О) t-+ а + Ь,
(а; О)(Ь; О) = (аЬ; О) t-+ аЬ, �:��� = (�; о) t-+ �, Ь =1= о.
Це твердження показує, що комплексні числа вигляду (а; О)
мають ті самі арифметичні властивості, що і дійсні числа а. То.му.ми
можемо ототожнювати. комплексне число (а; О) 3 діЙс'Н,и.м числом
а; 'Це ототожнення перетворює множини R усіх дійс'Н,их чисеп у
nід.м'Н,ожu'Н,у системи. компаексниа: чисел С, R с с. Отже, будемо
писати (а; О) = а, Va Е R.
Зокрема, запишемо (0;0) = О, (1;0) = 1, (-1;0) = -1.
1.2. Алгебраїчна форма комплексного числа. Через і поз
начимо комплексне число (0;1), яке називається у.яв'Н,ою одиницею
і яке зображено на рис. 4.
Знайдемо добуток і . і = і2, користуючись правилом (2):
і2 = (О; 1)(0; 1) = (О· О - 1 . 1; 0·1 + 1 . О) = (-1; О) = -1,
отже,
(5)
Рис.4
Отже, комплексне число і - корінь рівняння х2 = -1.
Аналогічно можна показати, що другим коренем цьо
го рівняння є число -і = (О; -1).
Дл.я буdь-.я-К:О20 z = (х; у) Е С спраеедлиеа рів-
юсть
z=(x;y)=x+iy.
Нехай у Е R. Знайдемо добуток і . у:
іу = (О; 1)(у; О) = (О· у-І· О; О· О + 1 . у) = (О; у).
180
Тоді
Z = (х;у) = (х;О) + (О;у) = (х;О) + (О; l)(у;О) = Х + іу.
Запис Z = х+іу називається алгебраінною фор.м,ою комплексного
числа Z = (х; у).
Нехай Zl = ХІ + іУІ, Z2 = Х2 + іУ2. Враховуючи, шо і2 = -1,
перемножимо числа Zl і z2 як двочлени за правилами алгебри:
ZlZ2 = (ХІ +іУІ)(Х2 +іУ2) = ХІХ2 +іХ2УІ +іХІУ2 +і2УІУ2 =
= ХІХ2 - УІУ2 + і(ХІУ2 + УІХ2) = (ХІХ2 - УІУ2;ХІУ2 + УІХ2).
Бачимо, що ми отримали той самий результат, що і в (2).
Як випливає з (1), (2), (4), додавання, віднімання, множення та
ділення комплексних чисел, записаних в алгебраічній формі zl = ХІ +
+іУІ, Z2 = Х2 + іУ2, виконують так:
Zl + Z2 = (ХІ + іУІ) + (Х2 +іУ2) = (ХІ + Х2) + і(УІ + У2);
Zl - Z2 = (ХІ + іУІ) - (Х2 + іУ2) = (ХІ - Х2) + і(УІ - У2);
ZIZ2 = (ХІ + іУІ)(Х2 + іУ2) = (ХІХ2 - УІУ2) + і(ХІУ2 + УІХ2);
ZI Х} + іУІ ХІХ2 + УІУ2 . Х2УІ - ХІУ2
-= . = 2 2 +z 2 2
Z2 Х2 + ZY2 Х2 + У2 Х2 + У2
Комтеексні числа Х + іу та Х - іу назиеаються спряженими
[езаємно]. Якщо Z = Х + іу, то число, спряжене з Z, позначається
через і: і = Х - і У. Знайдемо добуток Z • і:
(6)
( ')( ') 2 2· . 2 2
zi = Х + zy Х - zy = Х + У + zxY - zxY = Х + У .
(7)
Для частки чисел Zl і Z2 виконується рівність � = �, \;f аЕС,
Z2 Z2a
а "# О (доведіть самостійно). Формулу (6) для частки можна одержа-
ти, якщо чисельник і знаменник дробу � домножити на комплексне
Z2
число, спряжене до знаменника, і використати (7): .
ССI + іУІ)(Х2 - іУ2)
x� + Уі
ХІХ2 + УІУ2 + іХ2УІ - ХІУ2 (8)
x� + Уі x� + Уі
181
Приклади.
1. (1 - 7і) + (2 + 5і) = (1 + 2) + (-7 + 5)і = 3 - 2і.
2. (7 + і) - (3 - 9і) = (7 - 3) + (1 - (-9))і = 4 + 10і.
з. (3 - і) (1 + 2і) = (3 . 1 - ( -1) . 2) + (3 . 2 + ( -1) . 1) і = 5 + 5і.
4 23+.і = (23+і)(3-.і) = 23·3-1·(-I)+(l·3+23·(-I))і = 7 - 2і.
. 3+І (3+І)(3-І) 3-3+1-1
І.З. Комплексне число як вектор. Тригонометрична
форма комплексного числа. Візьмемо комплексне число z = х+
+і у = (х; у), і будемо розглядати його на комплексній площині як
вектор ОА, початок якого знаходиться в точці 0(0; О), а кінець - в
точці А(х; у). Довжина 10АІ = r вектора ОА називається .модуле.м
[абсопютною величиною] компяексного числа z і позначається Izl,
у
у А(х; у)
х х
Рис.5
Izl=r=Jx2+y2, z=x+iy=(x;y). (9)
Нехай tp -- кут між додатним напрямком
осі Ох і напрямком вектора ОА, щО зображає
число z, z =І о. Кут tp називається аргцмен
том комплексного числа z. Аргумент tp може
набувати як додатні, так і від'ємні значення,
. .
причому додатні кути ВІдраховуються проти
руху годинникової стрілки. Оскільки під час
оберту на кут 21Г навколо точки О вектор О А повертається в по
чаткове положення, то ми будемо визначати аргумент z з точністю
до кратних 21Г. Наприклад, якщо аргумент z дорівнює �, то як ар
гумент z можна взяти і f + 21Г і взагалі � + 2nk (k ---- ціле число).
Аргу.ме'Н,т комплепсного члісла z мас нескінченно багато значень,
.я,-к;і відріз'Н,.я,ютьс.я, однн від одного на дода'Н,-к;и вuгл.я,ду 2nk, k -- 'Ціле
число (k Е Z). Аргумент не визначений лише для числа О; це число
цілком визначається, однак, рівністю 101 = о. Множину всіх значень
аргументу комплексного числа z позначають символом Arg z. Якщо
'-Ро -- - яке- небу дь значення аргументу числа z, (tpo Е Arg z), то
Arg z = '-Ро + 27Гk, k = О, ±1, ±2, ...
(10)
182
Серед значень аргументу комплексного числа z і- О ІСнує од
не значення 'Р, яке задовольняє нерівності -7ї < 'Р � 7ї. Воно на
зивається головним значенням ар2у.ме'Н,тnу І позначається символом
argz. Отже,
-7ї < argz � 7ї, Argz = argz + 2Jrk, k Е Z.
Нехай о Е Arg z, Izl = т, z = х + іу. Тоді (див. рис.5) х = r cos 'Р,
у = г віп о: тому z = х+іу = rcos'P+i(rsill'P) = r(cos'P+isin'P), або
z = r ( cos 'Р + і sill 'Р ).
(11)
Права частина цієї формули називається трнгонометричною
фор.мою комплексного числа z. Очевидно, що комплексні числа дорів-
. . .
нюють одне одному ТОДІ І ТІЛЬКИ ТОДІ, КОЛИ ДОРІВнюють одне одному
Їх модулі і аргументи: .
(12)
Останню рівність ми розуміємо як рівність двох множин.
Відзначимо співвідношення: якщо z = :с + іу, то
Izl = Jx2 + у2, t,g(argz) = ?;
arg z = arctg 11.., х > О;
х
arg z = 7г + arctg ?, х < О, у 2: О;
argz = -7Г + arctg 1L, х < О, у < О;
х
arg z = �, х = О, у > О;
arg z = - �, х = О, у < О.
Приклади.
1. Подати в тригонометричній формі число z = -2 + 2vГзі.
РОЗб '.я,за'Н,'Н,.я,. Маємо х = Re z = -2, у = 1т z = 2vГз, Izl
J( -2)2 + (2vГз)2 = 4. ЯКЩО'Р -- одне із значень Arg z, 'Р Е Arg z,
то t,g'P = ? = - vГз, Ю'сtg � = -- f. Оскільки точка z = - 2 + 2JЗі
розміщена в другій чверті, то 3 попереднього випливає, шо al"g z =
= 7г + arct,g;: = 7ї - f = 2;. Тому Z = 4 (cos �171" + і зіп 2171").
183
2. Подати в тригонометричній формі додатне дійсне число а.
Розв 'язання. Число а має двочленний вигляд а + і . о. Звідси
модуль а дорівнює r = Va2 + 02 = а. Числу а відповідає вектор, що
лежить на дійсній ОСІ І утворює З цією віссю кут, що дорівнює нулеві.
Отже, arg а = о, і ми одержуємо: а = а( cos О + і sin о).
3. Подати в тригонометричній формі від'ємне дійсне число а.
Розв 'язання. Число а має двочленний вигляд а + і . о. Звідси
модуль а дорівнює r = va2 + 02 = lаl = -а. Числу а відповідає
вектор, що лежить на дійсній осі, але, на відміну від попереднього,
утворює з цією віссю кут, що дорівнює 1r. Отже, arg а = 1r, і ми
отримуємо: а = -а(СОБ1Г + isinn).
Як випливає з (11), щоб подати комплексне число Z =І о у триго
нометричній формі, необхідно знайти абсолютну величину Izl і яке
небудь значення tp аргументу числа z, tp Е Argz. У розглянутих
прикладах ми обмежились головним значенням аргументу.
Знайдемо формули множення комплексних чисел у тригономет
ричній формі. Якщо zI = ТІ (cos 'РІ +і sin 'РІ), Z2 = T2(COS 'Р2 +і sin 'Р2),
то
ZI . Z2 = T}r2(costpI + і sintpI)(coS'Р2 + isintp2) =
= Т}Т2 [(COStpI COStp2 - sintp} sintp2) + i(sintp} COStp2 + COStpI sintp2)] =
= Т}Т2 (COS(tpI + 'Р2) + isin(tpI + 'Р2)).
Отже,
(ІЗ)
Ми одержали запис добутку zI Z2 У тригонометричній формі, і
тому
тобто .модуль добут'К:у компяексниз: чисел дорівнюе добуткові .моду
лів співмножнихіе, а аргцмент. добут'К:у дорів'Н,ює су.мі аргцментів
. .
ствмножнизав,
Другу рівність в (14), як і всі рівності, що містять Arg, необхідно
розуміти як рівність відповідних множин, причому кожний елемент
184
• • u • •• •
множини в ЛІВІИ чаСТИНІ РІВНОСТІ є сумою деяких елементів ВІДПОВІДНО
з множин Arg zl Arg Z2. Методом математичної індукції можна
довести, що
Arg(ZIZ2 ... zn) = Argzl + Argz2 + ... + Argzn.
Звідси, якщо zl = z2 = ... = zn = Z для zn, п = 1, 2, ... отримаємо
Iznl = Izln, Argzn = nArgz + 27rk, k = О, ±1, ±2,... . (15)
Якщо z = r( cos If' + і sin <р), то <р Е Arg z, n<р Е Arg zn, отже
(16)
зокрема, якщо Izl = r = 1, то z = cos <р + і sin <р, і
(cos <р + і sin <р)n = cos n<р + і sin пір,
(17)
Формула (17) називається ФОРМУЛОЮ Муавра.
Зауважимо, що
Arg г" ::j:. nArg z.
Дійсно, якщо <р - яке-небудь значення аргументу числа z, то
множину всіх аргументів числа г" становлять числа вигляду n<р+
+ 2п k, k Е Z, а множина значень nArg z являє собою сукупність усіх
чисел вигляду n( <р + 2пт) = n<р + 2пnт, m Е Z, тобто ДО числа
пір додаються не всі можливі кратні числа 2п, як для Arg zn, а лише
кратні числа 27Тn.
Знайдемо частку � комплексних чисел у тригонометричній фор
Z2
мі. За означенням частки справджується рівність zl = � . Z2; звідси
Z2
таз рівностей (14) в�пливає: IZ11 = І �� 1·lz21, Argzl = Arg �� +Argz2,
або
ZI
Arg - = Arg ZI - Arg Z2,
Z2
(18)
185
тобто під 1ИС діле'Н:н,.я комплексних чисел Їх .модулі діл.яmьс.я, а ар-
2у.ме'Н,ти від'Н,і.маюmьс.я. Тому якщо ZI = ТІ (COS!PI + і sin УІ), Z2 =
= T2(COS!p2 + isin!p2), то
(19)
Для модуля суми справедливі нерівності:
(20)
Модуль комплексного числа Z = х + іу дорівнює довжині від
повідного йому вектора (х; у). Якщо розглядати числа ZI, z2 Е С
як радіус-вектори (рис. 6), то сума ZI + Z2 визначається за правилом
трикутника (паралелограма ).
х
Рис.6.
Рис.7.
Величина І ZI - z21 дорівнює відстані між точками, які зобра
жують комплексні числа ZI і Z2 (рис. 6,7). Довжина кожної сторони
трикутника не перевищує суми довжин двох інших його сторін, а
абсолютна величина різниці довжин двох сторін не перевищує дов
жини третьої сторони. Тому для довільних комплексних чисел ZI і
Z2 справедливі нерівності (20).
Оскільки zI - z2 = zl + (--Z2) і 1- z21 = IZ21, то з (20) випливають
. .
також нерівності
(21)
186
Враховуючи (14), (18), (20), (21), бачимо, що модуль комплексного
. .
числа має такі влаСТИВОСТІ:
Izl�O, і Izl=O{::} z = О; Ilz11-lz211:::;lzj±z21:::;lz11+lz21, \lzj,z2EC;
\z1'z21 = \z11·\z21, \lz1, Z2 Е С; I;�I = ::::' \lz1,z2 ЕС, Z2 -І- О. (22)
Розглянемо взаємно спряжені комплексні ЧИС-і"Іа z = х + іу та
і = х - іу. Числом, спряженим з і, буде, очевидно, z. Якщо а -
дійсне число, то а = а + і . О і тому сі = а. Дійсні числа. і тільки.
еони, спряжені самі собі. Геометрично числа z і і зображаються
векторами, симетричними відносно осі Ох (рис.8).
у
Рис.8
3 означення спряжених чисел випли-
. - .
ває, що МОДУЛІ ІХ ДОРІВнюють один одному,
а значення аргументу протилежні:
1 О. ІіІ = Izl, Arg z = -Arg z. (23)
Для спряжених чисел виконуються також
х
. .
РІВНОСТІ
20. (-)
z = z;
(24)
---
Z1 . Z2 = Z1 . Z2;
Якщо z = х + іу, то z = :с - іу, і тому (і) = х - іу = х + іу = z;
знайдемо добуток z - z = (:с + іу)(х - іу) = х2 + іху - іху - і2у2 =
= х2 +у2 = Iz12, отже, властивості 20,30 доведені. Властивості 50 і 60
випливають :3 того, щО МОДУЛІ 1 аргументи виразів у ЛІВИХ та в правих
частинах відповідних рівностей збігаються. Дійсно, використовуючи
(22) та властивість 1 О, одержимо
Zl
= --Arg- =
z2
187
= -(АrgzІ-Аrgz2) = -АrgzІ -(-Argz2) = ArgzI -Argz2 = Arg �I .
Z2
Це і означає, що виконується властивість 60. Властивість 4 о доведіть
• U
саМОСТІИНО.
ЯКЩО число О, О Е С, У певний спосіб виражено 'Через комп
лексні числа {ЗІ, {З2, ... , {Зk за допомогою додава'Н,'Н,.я" множення від
німання і діле'Н,'Н,.я" то, замінююнн в 'Цьо.му виразі всі числа {ЗВ Їх спря
женими, ми. одержимо число, спряжене з о. Зокрема, .я,-К;ЩО число
О діuс'Н,е, то воно не змінюеть ся із заміною всіх компяексниз: чисел
{ЗВ Їх спряженими.
Якщо k = 2, ця властивість випливає з (24). Для k ;:::: 3 тверд
ження доводиться індукцією за k.
1.4. Добування кореня з комплексного числа. Показни
кова форма комплексного числа.
Коренем n-20 стспеня (n - нстцрааьне] з комплексного числа Z
назиеається будь-.я,ке комплексне число Ш, яке заооеопьняе рівняння
(25)
позначають иого символом \jZ. Якщо Z = г( cos <р + і sin <р), а W =
= р( cos Ф + і sin Ф), то враховуючи (16), рівність (25) можна записати
так: pn(cos nф+і sin nф) = r(cos <р+і sin <р); звідси та з умови рівності
комплексних чисел (див.(12)) отримаємо р" = г; nф = <р + 27rk,
k = О, ±1, ±2, ... , або р = vгт > О, (\IF -- арифметичний корінь),
.1. = <е+21Тk отже
'f/ n' ,
n • (<P+27rk . <P+27rk)
.VfZ=\lГ(соs<р+іsш<р)=ifТ cos n +гвіп n ,kEZ. (26)
Можна переконатись, що надаючи k значення k = О, n - 1, одер
жимо n різних значень кореня, а саме, якщо через �'k позначити зна
чення аргументу Фk = <е+�lТk і прийняти Wk = \IF(cos Фk + і sin Фk),
(г =F О), то отримаємо різні комплексні числа Шо, ШІ, ... , Шn-l. На
188
комплексній площині С числа Wo, WI, ••. , wn-I розміщені у верши
нах правильного n-кутника, вписаного в коло радіуса р = � з
центром у початку координат. Це випливає з того, що значення
аргументу 'Фk числа wk відрізняється від значення аргументу 'Фk-І
числа Wk-I для усіх k = 1, п - 1 на одне і те саме число 2;:. Як
що до значення аргументу 'Фn-l числа Wn-I додати 2;:, то З точні
стю до повного оберту одержимо значення 'Фо аргументу числа WO:
'Фn-І + 2п = 'Р+2п(n-І) + 2п = !f. + 21Г = 'Фо + 21Г. Тому для інших
n n n n
значень k (k Е Z, k OF О,n -1) аргументи будуть відрізнятись від
отриманих на число, кратне 21Г, і, отже, одержимо значення кореня,
які збігаються з розглянутими. Отже, корінь Ф має, якщо z OF О
• • • u
РІВНО n РІЗНИХ значень Wo, WI, •.. , Wn-I, ЯКІ можна знаити, якщо у
(26) послідовно прийняти k = О, п - 1.
Приклад 1. Знайти корені рівняння w2 = -1.
Розв 'язання.
1-11 = 1; Arg(-I) = n+2nk, k Е Z; -1 = cosn+isinn;
1г + 2nk 1г + 2nk
wO,I = (V-l)О,І = cos 2 + isin 2 ' k = 0,1;
(г-1) 1Г .• 1г .
ШО = V -1 о = cos "2 + Z SIn "2 = Z,
З1Г .• З7r .
WI = (V-1)I = cos 2 + е вш 2 = -z,
(k = О);
(k = 1).
Нехай е = 2,71828 ... _.- число Ейлера, tp _. довільне дійсне число.
Символом еі...., позначимо комплексне число cos tp + і sin 'р:
.. def і....,
cos tp + ь SIll tp = е .
(27)
Ця формула називається формулою Ейлера. Використовуючи
11, кожне комплексне число z = r( cos tp + і sin 'р) можна записати у
показнихоеій формі
(28)
189
Розглянемо дії над комплексними числами у показникові й формі . .
Я-К;ЩО ZI = ТІ еі'РІ, Z2 = т2еі'Р2, Z = теі'Р, то: (
k = О,N -1.
Доведення.
= ТІ Т2( COS!PI + і sin!pI)( COS!p2 + і sin !Р2) = (див. (ІЗ)) =
= ТlТ2 (COS(!Pl + !Р2) + isin(!PI + t;Q2)) = (див. (27)) = ТІТ2еі('РІ+'Р2);
ZI = т1еі'РІ = ТІ(COS!PI + �s�n!PI) = (див. (19)) =
Z2 Т2 e�'P2 Т2 ( COS!p2 + Z SIn !Р2)
Zn = (теі'Р( = (r(cos!p + isin!p))n = (див. (16)) =
\/z = � = y/r(cos!p + isin!p) = (див. (26)) =
nс( !p+2nk .. !P+2nk) -с: i(.,,+27rk) k
УІ COS + Z SIn = \іте n , = О, п - 1.
n n
Приклад 2. Знайти корені рівняння ш3 = -1 - іVЗ.
Розв 'язання. Позначимо Z = -1 - і VЗ. Тоді х = Re Z = -1,
у = Imz = -VЗj Izl = JI+З = 2. Якщо ю одне із значень Argz,
!р Е Arg z, то tg!p = ? = jЗ; оскільки точка z = -1 - і VЗ розміщена
190
в третіи чверті, то з попереднього випливає, що <р
Тому z = -1- іvГз = 2 (cos 4з71" + isin 4з71") = 2ei�";
4з71" Е Argz.
\І . гп з ( 471" .. 471")
Wo 1 2 = -1 - і V 3 = 2 cos - + Z SIll -
, , З З
з!n ( 4з71" + 271"k .. 4з71" + 271"k) VI2 і(4"+б"k)
= V L cos + Z SIll = 2е 9 k = О 1 2·
З З " , ,
З!n і4"
Wo = V Le""9,
З!n іІО"
WI = VLe-g-,
3Гn іlб1Г
W2 = VLe-g-.
1.5. Представлення змінного струму у комплексній фор
мі. Правила дій з комплексними числами в алгебраїчній та показ
никовій формах використовуються для розрахунків електричних кіл.
у 189З році інженер Чарльз Протеус Штейнмец розробив метод роз-
.. -
рахунку КІл ЗМІНного синусоідного струму.
Нехай сила струму змінюється за законом
І = І.м sin(wt + <р),
(29)
де І.м = const > О - амплітуда струму, w -- циклічна частота, <р -
початкова фаза. За формулою Ейлера струм І можна розглядати як
уявну частину комплексного числа
(ЗО)
Дійсно, І І.м (co�( іоі + <р) + і sin( соі + <р)), тому, �раховуючи
(29), уявна частина lтІ = І.м sin(wt + <р) = І. Величину І називають
комплексним стрцмом. Їі можна записати у вигляді j = IMei(wt+<.p) =
= І.меі<.р. eil..li = jMeil..lt, де і; = І.меі<.р. Величина ім називається комп
пексною а.м,nліmудою струму. Отже,
І· І· il..li
=.мЕ ,
(ЗІ)
191
Приклад 1. У ланцюгу проходить змінний струм, значення
якого (в амперах) І = 25sin (50і + і). Яка комплексна амплітуда
струму? Який комплексний струм?
РОЗб 'язання. З умови випливає, що амплітуда струму І.м. = 25А,
циклічна частота w = 50с-l, а початкова фаза <р = і радіан. Отже,
(див. (31)), комплексна амплітуда струму і; = 25eif, комплексний
. .. ·(50t+")
струм І = I.Mel5ot = 25е1 "4 •
Експериментально встановлено, що коли в колі є дві гілки, з'єд
нані паралельно, в яких проходять синусоїдні струми 1', І" з однако
вими частотами w, то якщо об'єднати ці гілки в одне коло, по ньому
бу де проходити струм
І = ІІ + І".
За умовою
ІІ = і; sin(wt + <рІ) = 1т (I�ei(c..Jt+'f"») ,
І" = 1.: sin(wt + <р") = 1т (I.:ei(c..Jt+'f''')),
(32)
де w -- частота, І:М, I� .- амплітуди, <рІ, <р" --- фази. Струми І' і І"
мають комплексні амплітуди (31)
І· І = ІІ i'f" І·" = І" i'f'''
.М .м. е , .м. .М е .
(33)
Тоді
І = ІІ + І" = (див. (32)) = Im(I�ei(c..Jt+'f"») + Im(I.:ei(c..Jt+'f''')) =
= Im(1.�ei'f" eic..Jt + I.:ei'f''' eic..Jt) = 1т ((I.�ei'f" + I�ei'f''')eic..Jt) (34)
= (див. (33)) = 1т ((i� + i�)eic..Jt),
тобто струм І -- періодична функція часу t з частотою w. З (31),
(34) випливає, що комплексна амплітуда ім струму І дорівнює
192
Отже, додаючи синусоїдні струми ОДНІЄІ 1 ТІЄІ самоі частоти, Їх
комплексні амплітуди теж додають (хоча Їх авичайні амплітуди не
додаються) .
Приклад 2. Додати два струми однакової циклічної частоти
w = 50с-1, ЯКЩО відомо, ЩО вони мають такі комплексні амплітуди:
і: = 10 + 15і, Ї�� = 20 - 45і.
Розв 'язання. Знвйдємо комплексну амплітуду сумарного стру-
му: і; = i.�+ї�� = (10+15і)+{20-45і) = ЗО-ЗОі = зоJ2еі{-�О. То
му сумарний комплексний струм j дорівнює (див.(З1)): j = Ї.меі":і =
= ЗОV2еі{ -�) . ei50t = ЗОV2еі(50t-�), І = 1т j = ЗОJ2 sin (50і - �).
Комплексні числа використовуються також для обчислення пов
ного опору кола, електрорушійної сили (Ере), виведення закону Ома
для кола ЗМІНного струму.
§ 2. Деякі відомості з алгебри многочленів
2.1. Розклад многочлена на множники. Многочленом сте
пеня n (п -. ціле, невід'ємне) називається функція
Р ( ) n п-І
n Z = cnZ + Cn-IZ + ... + CIZ + Со,
Z Е С,
(З5)
де СП, Сп-І, ... , СІ, Со (Сп і- О, якщо n > 0)--- сталі дійсні або комп
лексні числа, які називаються 'l),оефі1l,іє-н,mа.м,u многочлена. Многоч
лени нульового степеня мають вигляд Po(z) == с, Z Е С, С --- стале
ЧИС.10.
Комплексне ЧИС-10 Zo таке, що Pn{Zo) = О, називається коренем
многочлена Pn{z). 3 алгебри відомо, що число Zo Є коренем многоч
лена Pn{z) (n � 1) тоді і тільнн тоді, копи. справедлиеа рівність
многочяен стспеня n - 1 [наслідок з теорема Бе-
зу). Комплексне ЧИС"10 Zo називається k-'І),ратn-н,u.м, коренем многоч
лена Pn{Z), якщо справедливе подання
(З6)
19З
де Ql-.k(Z) многочлен степєня 1/- Іг; причому (-2n -k(ZО) #- О. Якшо
В (36) k = 1, то Zo -- простий корінь,
()С'Н,О6'Н,а теорема алгебри стверджує. шо будь-який многочлен
степеня n 2: 1 має п коренів, якщо кожнии корінь рахувати стільки
• u •
раЗІВ, яка иого кра тнтсть.
Якщо ZI, ...• Zm .. _. всі можливі різні корені многочдена Pn{Z),
то З попередньої теореми випливає, що {ЮГ0 можна розкласти на
множники
Припустимо, шо всі коефіцієнти многочлена (35) Сп, Сп-1, .•• ,
со- дійсні числа. Тоді, Jl1l:'ЩО .м,'Н,О20'Чле'Н, (35) має корінь Zo = a-tbi Е СІ
то і спряжене 'Ч11СЛО 20 = а - Ьі є коренем 'ЦЬО20 ,м,'Н,О20'Чле'Н,а_
Для діисного числа а виконується а = а. За умовою
тому
о = Pn(ZO) = Pn{ZO), сп = Сп, Сп-l = Сп-І,· .. , со = со· (39)
Оскільки ZI + Z2 = z\ + Z2, ZI . Z2 = Z]. Z2, то З (38), (39) випливає
+- (_. І" + () '1--1 + + Р (-) о
со = Сп' Zo Сп-І' ·2"0 • . . СО =: ІІ Zo = ,
тобто іо _.- корінь многочлена Pn(z).
Можна довести таке твердження: Jl1l:ЩО комплексне 'Число Zo є
коренем кратності k многонлена Рn (z) з ()i-ііСЮl.м,1L 1І:оефічіє'Н,rnа.м,и.
то ь спряжене 1Lо.м,у чиспо іо також є .,.,:оре'Н,е.м, кратності k ЧЬО20
,м,'Н,О20'Чле'Н,а.
lD4
з цієі теореми випливає. ЩО в розкладі (37) многочлена Р,,(::)
комплексні корені входять попарно спряженими. Відзначимо. що а0-
буmо'l), (z - zo) . (.: - іо) є многоч-леном 3 Оі'ііс'н.и.м.1/. коефініентоми.
Діисно, нехай Zo = а + Ьі, а. ЬЕ R. Тоді іо = а _О Ьі, і, отже
(z - zo)(z - іо) = (z - а - Ьі)(.: - а + Ьі) = (див. формулу (7). § 1) =
= (z - а)2 + ь2 = z2 - 2az + а2 + ь2 = z2 + pz + q,
де р = -2а, q = а2 + Ь2; р, q Е R.
Дал:і ми бу демо розглядати многочлени в дійсній області. Тш.:ІУ
замість букви z, яка використо�ува:Іась вище Д.1Я позначення аргу
менту многочлена, бу демо за традицією вживати букву х.
Як випливає з вищесказаного, будь-,я'l),1/.U .м.'Н.О20'Ч,ле'Н. стспеня n
(п � 1) 3 діис'Н.1/.,м.1/. 'l),оефі1l,іє'Н.mа,м.1/. розплодасть ся, причомп) єди'Н.1; . .м.
способом, на множники.
де усі 'l),оефі1l,іє'Н.m1/. сп, аІ" . О , ат; РІ,' .. , Ps, ql" .. ,q.� 0- діис'Н.і 'Ч,1/.сла;
аl, ...• ат -- всі діис'Н.і корені .м.'Н.О20'Ч,ле'Н.а P,,(.r), /1 кожномлі комп
лексномц кореню Zo і ии.м.у спряженомлі іо відповідає ()іUс'Н.1/.Й ,м.'Н.ОЖ
ннк .1:2 + pl' + q = (х _о zo)(;1' - 20); сп Е R; аl,"" ат Е R; РІ,···; Р»
ql, ... , qs Е R: kl + ... + k/o + 2(11 + ... + ls) = п; Р; -- 4q] < О, (mР1LОILле'Н.
J.2 + PjX + qj .м.аt: 'l),u.м.nлс.,..с'Н.і .,..ире'Н.і), j = 1, .'І.
2.2. Розклад раціонального дробу на суму елементар
них. Нехаіі Рn(х), С}т(.Г) оо- �ІНогочлени з ді{IСНlНПI коефіцієнта�ш,
Рn(х) Ф. О. Будf'!\Ю вважати, щu ці МНОГUЧЛf'НИ НІ' мають СШ.1ЬНIІХ
кореНІВ. ВіДНОШ('ННfI двох !\Іногоч.1енів
Ьщ:с1l1 + ьт_1хт-І + ... -+ ьо
С" :1' /1 + СП _ 1 Х 11 - І-+-. . . + СО
(41)
О � Р' О'б (}rn(.Т)
Ш\3Ішається рачіо'Н.алt>'Н.оll.,мо ()роио.м.. аЦlOна.1ЬНIПl ДРl) Р" (.lo) нази-
вається nраО1/.ЛЬ'Н.1L.м., якшо ('тешнь !\ІНОГО'!.1('на (1т (./") !\:ІСНШИИ, ніж
1!)5
степінь многочлена Рn(Х) (тп < п), і неправильним якщо m � n.
Якщо раціональний дріб ��:\��; неправильний, то з нього можна ви
ділити 1l,ілу частини (�1НОГОЧ.1ен), тобто цей дріб можна аобразити у
вигляді суми многочлена і правильного раціонального дробу
де Rm-n(x), S(x) - деякі многочлени, J..<c2) правильний ра
ціональний дріб. Це досягається діленням чисельника на знаменник
за правилом ділення многочленів. Наприклад, справедлива рівність
x4-2хЗ+х-l = х2 -2х+2+ -3х+3. У цьому можна переконатись, якщо
х2-2 х2-2
виконати ДІлення з остачею
х 4 _ 2х' - Ох' + х-І І х' - 2
х4 - 2х2 х2 - 2х + 2
- 2х3 + 2х2 + Х - 1
- 2х3 + 4х
2х2 - Зх - 1
2х2 - 4
-Зх+З
Еле,м,е-н,тар-н,u,м,u [простимлі] називаються такі дроби
А
Вх+С
40. ...,..-
(х2 + рх + q)k '
,
х-а
де А, В, С, а,р, q Е R; k � 2, kEN; р2 - 4q < О (тобто тричлен
х2 + рх + q має комплексні корені). Розглянемо теорему.
Теорема. Праеильннй dріб �:'(<:i: де Qm(x), Рn(х) многочяенн
з діі1с-н,и,м,и �оефі1l,іє'Н.rnа.м,u, можна затісатлі у вU2л.яді су.м,и елемен
тарниз: дробів, Яхиіо Рn(Х) = сn(х - аl )k1 ••••• (х -- ar)kr(x2 + РІХ+
196
:-- Сп' Qm(X)
Рn(х)
(42)
. -
де всі 'К",оефі'Ціє-н,ти Аі,а, Bj,j3, Сз,fЗ --- дійс-н,і числа, л'К",і можна знайти.
за допамогою .м,етоду невизначених 'К",оефі'Ціє-н,тів.
З цієї теореми випливає, що длJ/, роз'К",ладу раціонального дробу
��(<:l потрібно: а) виділити 'Цілу частини дробу, J/,'К",'Що дріб ��(<:1
--- неправильний (т � n); б) знаменніік дробу Рn(;І:) зобразитн у
вигяяоі добут'К",у (40), длJ/, 'Чого досить знайти. всі корені рівняння
Рn(х) = О.
Приклад. Розкласти на елементарні дроби вираз
2х4 + 2х3 - 2х2 + Х - 2
х2(х - 2)(х2 -+- 1)
Розв 'язання. Цей дріб правильний. Відповідно до (42) множнику
знаменника х2 відповідають два дроби �, �; множнику (х - 2) -
один дріб хс:...2; множник (х2 -+- 1) .має комплексні кореніл тому йому
відповідає дріб �;�f; А, В, С, п, Е -- невідомі дійсні числа. Тоді
2х4 + 2х3 - 2х2 -+- Х - 2 А В С Пх -+- Е
---------- = - -+- - -+- -- -+- ---
x2(x-2)(x2-t-l) :Е х2 :Е-2 х2+1'
Для спрощення запису тут, на відміну від (42), опушено індекси,
тобто введено позначення А = А1.1, В = А1,2' С = А2,І, D = ВІ,І,
Е = СІ,І. Звівши праву частину до спільного знаменника, одержимо
197
два рівні дроби з однаковими анаменниками , це означає, що чисель
ники в них теж ДОРІВнюють один ОДНО).,ІУ:
2х4 + 2хЗ - 2.т.2 + Х - 2 = А.т.(х - 2)(х2 + 1)+
+В(х - 2)(х2 + 1) + Сх2(х2 + 1) + (пх + Е)х2(х - 2).
(43)
Далі можна діяти двома способами: 1) надавати аргументу х
конкретні значення; 2) прирівнювати коефіцієнти при однакових сте
пенях х ліворуч і праворуч у (43). Часто обидва способи комбінують,
це ми і зробимо нижче.
Рівні многочлени набувають однакові значення для усіх значень
х. Приймемо в (43) послідовно х = О і х = 2 (.1: = О і х = 2 - дійсні
корені знаменника Рп(х)). Отримаємо
х = О 1-2 = - 2В => В = 1
з: = 2 40 = 20С => С = 2. '
Тотожність (43) тепер можна переписати у вигляді
-(х - 2)(х2 + 1) - 2х2(х2 + 1) + 2х4 + 2хЗ - 2х2 + Х - 2 =
= Ах(х - 2)(х2 + 1) + (пх + Е)х2(х - 2),
або після спрощень у лівій частині
(х - 2)х2 = Ах(х - 2)(х2 + 1) + (пх + Е)х2(х - 2).
Скоротимо обидві частини цієї рівності на х(х - 2), (вважаючи з: і- о
і хі- 2), одержимо х = А(х2+1)+(пх+Е)х. Розмістивши многочлен
в правій частині за спадними степенями х, матимемо х = (А+п)х2 +
Ех + А, або О· х2 + 1 . з: + О = (А + п)х2 + Ех + А. Два МНОГОЧ.;1ени
дорівнюють один одному, якщо однакові коефіцієнти при однакових
степенях х. Тому
х2 О = А + п,
х! 1 = Е,
хО 0= А.
Звідки А = О, D = О, Е = 1, В = 1, С = 2. Остаточно
2х4 + 2хЗ - 2х2 + Х -- 2 1 2 1
х2(х - 2)(.1:2 + 1) = х2 + ;;-=-2 + .1'2 + 1 (44)
198
Розділ 6. НЕВИ3НА ЧЕНИЙ ІН ТЕ ГР АЛ
§ 1. Первісна. Невизначений інтеграл
у цьому розділі розглядатимемо функції, визначені не тільки на
відкритому проміжку (о.; Ь) = {х : а < х < Ь}, але і на замкнено
му [а; Ь] = {х : а ::; з: ::; Ь}, а також у націввідкритих проміжках
(а;Ь] = {х : а < х ::; Ь} і [а;Ь) = {х : а ::; з: < Ь}. Будь-яку із
вказаних множин будемо називати пр оміжком іпозначати СИМВО.'Іом
(а; Ь). Можливо також, шо проміжок (а; Ь) має нескінченну довжину.
Нехай да'liО фУ'li1l:'Цію Лх), ензначени 'Ііа nро.міЖ1l:У (а; Ь). ФУ'li1l:'Ці.я
р : (а; Ь) -+ R назиеається первісною фУ'li1l:'Ціі f 'Ііа проміжки (а; Ь),
.я1l:ЩО Р дuфере'li'ЦіЙО6'1іа 'Ііа (а;Ь),і енконцеться тотожність
рІ (х) = J( х ), V з: Е (а; Ь) .
Приклад 1. Функція Р(х) = cosx, -оо < з: < +00, є первісною
для функціі лх) = -sinx, -оо < х < +00 на проміжку (-оо; +00),
оскільки РІ ( х) = (cos х)' = - sin з: = J( х ), _. оо < з: < + оо.
у розділі 7 ми доведемо, що всі неперервні 'Ііа (а; Ь) фУ'li1l:'Ціі
. . .
мають 'Ііа 'Цьо.м,у проміжкі) первьсні.
Функція, яка має в точці з: похідну, неперервна в цій точці. Тому
з означення первісної випливає, що первісна Р функції f неперервна
на проміжку (а; Ь).
Якщо Р --- первісна функції f на (а; Ь), то функція Р(х) + С,
з: Е (а; Ь), С Е R --- довільна константа, також є первісною функції f
на проміжку (а; Ь). Дійсно, (р(.т.) + С)' = Р'(х) + СІ = F'(x) = Лх),
з: Е (а; Ь). Отже, .я1l:ЩО фУ'li1l:'Ці.я мае 'Ііа проміжки од'liУ переісни, то
вона має на 'Цьо.му nро.міЖ1l:У беялін первісних.
Нехай Ф(.І:), F(.I:), .г Е (а;Ь) _._- довільні первісні функції f на
проміжку (а:Ь). Розглянемо функцію .р()') = Ф(.т) - Р(х), х Е (а;Ь).
3 означення первісної випливає, ЩО похідна
ср'(х) = Ф'(:r) - Pl(x) = лх) -- Лх) == О, V.r· Е (а; Ь). (1)
199
Візьмемо Хо, х Е (о: Ь). ДЛЯ функції ср(х) на проміжку [ха: х] (на
[х: ха]: якщо з: < хо) виконуються умови теореми Лагранжа. Тому
існує таке <; Е (хо;х) С (о.:Ь), ШО у(Х) - СР(ХО) = <р'(<;)(х - ха). Ос
кільки <; Е (о.: Ь), то враховуючи (1), ср'(<;) = о. Отже, ср(х) - <р(хо) =
= о. Оскі_"ІЬКИ Х Е (о.; Ь), х --- довільне, то з попереднього випливає
<р(х) = <p(-!�=:= С = canst, Vx Е (о.;Ь). А_"Іе <р(х) = Ф(х) - Р(х), тому
Ф(х)-Ft�) = С, Ф(х) = Р(х)+С, Vx Е (о.;Ь), С = const. Отже, будь
.я:к;і дві первісні Ф iF ФУ'Н,1І:1l,іі f на проміжт] (о.; Ь) виірізняються між
собою на константи.
Ми довели, що якщо F - довільна первісна фУ'Н,1І:1l,іі f на проміж-
1І:У (о.; Ь), то множина всіх первісних дл.я фУ'Н,1І:1l,іі f на проміжт] (о.; Ь)
подається У внгляді {Р(х) + С, з: Е (о.;Ь), С Е R}.
Множина всіх первісниз: фУ'Н,1І:1l,іі f на nро.м,іЖ1l:У (о.; Ь) назиеа
ється нее изначеним інтегралом ФУ'Н,1І:1l,іі f на nро.м,іЖ1l:У (о.; Ь) і позна
чається символом J f(x)dx. Символ J назиеаеться з на 1І:О.м, інтегра
ла, а ЛХ) - nіді'Н,теграль'Н,ою фУ'Н,1І:1l,ією, ЛХ )dx-- підінтегральний
вираз, х - з.м,z'Н,'Н,а інтегриеання.
Отже, якщо F ----- довільна первісна функції f на проміжку (о.; Ь),
то записують
J f(x)dx = Р(х) + С, х Е (о.;Ь), С Е R,
(2)
хоча правильніше було б писати
J f(x)dx = {Р(х) + С, х Е (а.; Ь), С Е Н}.
Приклад 2. J sinxdx = - cosx + С, х Е R, бо функція Р(х) =
= - cos х є однією з первісних для функції f (х) = sin х на проміжку
-оо < х < +00. Дійсно, (-cosx)' = sinx, х Е R.
Приклад 3. J ";;:x2dx = vl -- хі + С, -1 < х < 1, бо функція
F(:r) = vl - х2 є однією з первісних для функції ЛХ) = - ";1�I2 на
проміжку -1 < х < 1.
200
Якщо Р(х) --- яка-небудь первісна функції лх) на (а; Ь), то ди
ференціал dF(x) = F'(x)dx = f(x)dx, і згідно З (2) під знаком інтег
рала стоїть диференціал функції F. За означенням будемо вважати
1 f(x)dx = 1 F'(x)dx = 1 dF(x).
§ 2. Властивості невизначеного інтеграла
1 о. Псаіона від інтеграла дорівнює підінтегрольчій ФУ'Н'/'І,'Ції
d� (1 f(X)dX) = ЛХ), V х Е (а; Ь).
Ця властивість випливає з означення первісної та невизначеного
інтеграла функції І.
20. Нехай фУ'Н'/'І,'Ці.я ЛХ) дифере'Н'Ційов'На 'На (а;Ь), тоді
1 f'(x)dx = ЛХ) + С, х Е (а; Ь)
або, що те саме,
1 df(x) = ЛХ) + С, х Е (а;Ь).
Ця властивість випливає з того, що функція f( х) є пеРВІСНОЮ
для похідної f' (х) цієї функції на (а; Ь) .
ЗО. Інтеграл від су.ми фУ'Н'/'І,'Цій дорівнює су.мі інтегралів від до-
1и(х) + g(x))dx = 1 ЛХ)��! g(x)dx.
(З)
у правій частині (З) -- сума двох множин первісних. Її треба
•• u
РОЗУМІТИ як множину ВСІХ можливих сум, У яких першии доданок
u _ U
взятии З першоі множини, а другии доданок--- З ДРУГОІ множини.
201
Оскільки дві первісні для однієї і тієї самої функції 1ЮЖУТЬ від
РІЗНЯТИСЬ лише на константу, то достатньо довести. шо якшо
р(х) -- первісна для Лх), С(х) -- первісна для g(x) на проміжку
(а; Ь), то р(х) + С(х) -- первісна для Лх) + .Q(x) на (а; Ь). Дійсно,
(р(х) + С(х))' = р'(х) + С'(х) = Лх) + .Q(x).
40. Стамій множник можна ои'Нести за знак інтеграла
J Af(x)dx = А J f(x)dx, А = const і о.
(4)
Нехай р- первісна функції f на проміжку (а; Ь), тобто F'(x) =
= f(x), х Е (а; Ь). Тоді функція А· F є первісною для функції А· f бо
(А· р(х))' = А· р'(х) = А· ЛХ), х Е (а; Ь). Тому інтеграл J Af(x)dx
складається з усіх можливих функцій вигляду А· р( х ) + С, а інтєград
А J f( х )dx - з усіх можливих функцій вигляду А( р( х)+ С) = А- р( х) +
+А·С. Оскільки С - довільна константа А і о, то обидві сукупності
функцій збігаються.
50. 3 означення невизначеного інтеграла випливає, що кожна
формула вигляду Р'(х) = ЛХ), х Е (а; Ь) може бути записана в інтег
ральній формі J f(x)dx = F(x) + С, х Е (а; Ь). Це даЄ:1МОГУ записати
таблицю інтегралів, використовуючи одержану раніше таблицю по
хідних елементарних функцій.
J хn+І•
1
xndx = -- + С,
n і-І
n+1
Jdx
2
- = lпlхl +С
х
J sіпхdх = - cosx + С
---:-
З
4
J гов алі« = sinx + С
- ----------------------
202
203
Для перевірки формул таблиці достатньо переконатись, що по
хідні виразів у правих частинах цих формул збігаються з відповід
ними підінтегральними функціями (перевірити самостійно).
Треба зауважити, що здебільшого інтеграли від елементарних
функцій не є сукупностями елементарних функцій. Наприклад, хоча
інтеграли J е-х2 dx, J cos x2dx, J sin x2dx, х Е R; J I�Xx' х > О, х і=- 1;
J si� х dx, х і=- о, як інтеграли від неперервних функцій, існують, але
вони утворюють нові класи функцій, відмінні від елементарних. Пер
шим довів існування таких інтегралів П.Л.Чебишов в середині ХІХ
го СТОЛІТТЯ.
§ з. Основні методи інтегрування
З.l. Інтегрування підстановкою (заміна змінної).
Теорема. Нехай да'Но фу'Н'К",'Ціі f(t), tE(a;{3) іі = <р(Х), ХЕ(а;Ь),
такі, що іс'Нує складна фу'Н'К",'Ці.я л<р(х)), х Е (а; Ь). Нехай фу'Н'К",'Ці.я
<р(х) дuфере'Н'Ційов'На 'На (а;Ь). Якшо фу'Н'К",'Ці.я f(t) має 'На (а,.В) nер
віс'Ну F(t) і, отже,
J f(t)dt = F(t) + С, t Е (а;,3) , (5)
то фу'Н'К",'Ці.я Л<р(Х))<р'(х) мас 'На (а;Ь) первісни F(<p(x)) Z
J f(<p(x))<p'(x)dx = F(<p(x)) + С = J j(t)dtlt=<p(:c)' х Е (а;Ь). (6)
204
За умовою функція F(t) - одна 3 первісних для f(t) на проміжку
( а; Ь), тому Р' (t) = f( t), t Е (а; {З). Підставивши в останній рівності
t = <р(Х), х Е (а, Ь), одержимо
F' ( <р ( х )) = f( -е ( х ) ) , х Е (а, Ь) .
(7)
Знайдемо похідну складної функції ddxF(<p(x)) = Р'(<р(Х))<р'(х) =
(див. (7)) = Л<р(Х))<р'(х), х Е (а; Ь). Це означає, що функція
Р(<р(Х)) є однією з первісних функції Л<р(Х))<р'(х) на проміжку (а; Ь).
Звідси згідно з означенням інтеграла випливає, що
J f(<p(x))<p'(x)dx = Р(<р(х)) + С, х Е (а;Ь). (8)
Підставивши в (5) t = <р(х), х Е (а; Ь), отримаємо
J f(t)dtlt=.,o(x) = Р(<р(Х)) + С, х Е (а; Ь) .
(9)
З (8) та (9) випливає (6).
Запишемо (6) у вигляді
J f(<p(x))<p'(x)dx = J f(t)dtlt=.,o(x), х Е (а; Ь). (10)
Метод інтегрування, що грунтується на застосуванні (10), нази
вається методом інтегрцеання підстаноекою, а саме підстановкою
t = <р(х). Ця назва пояснюється так: якщо урахувати, що диферен
ціал dt = d(<p(x)) = <p'(x)dx, то можна записати J f(<p(x))<p'(x)dx =
= J f(<p(x))d(<p(x)) = (підставл. <р(х) = t) = J f(t)dtlt=.,o(x), тобто,
обчислюємо інтеграл J f(t)dt, а потім повертаємось до змінної х,
прийнявши t = <р(х).
Іноді (10) зручно використовувати у зворотній послідовності -
справа наліво. А саме припустимо, що функція t = <р( х) має обернену
.r = <р-l(і); У (10) поміняємо місцями сторони рівності, одержимо
205
J f(t)dtl,=:p(I) = І f('P(x))..p'(x)dx: перейдемо в обох частинах Ц1ЄІ
формули ДО змінної t за допомогою заміни х = <p-l(t), враховуючи,
шо 'Р ( у-І ( t )) = t, отримаємо
(11)
-- . фор.мула інтегрцвання заміною змінноі. Те саме детальніше мож
на записати так
J ( t = <р(х) ) J '
f(t)dt = dt = 'P'(x)dx = Л<р(х))ср (x)dxlx=",,-l(t)·
Приклад 1. Знаити J cos(5x + 3)dx.
Розв 'язання. Зробимо підстановку t = 5х + 3, тоді
J ( t - 3 dt)
cos(5x + 3)dx = t = 5х + 3 * х = � * dx ="5 =
J dt 1 J 1
= cos t"5 = [; cos tdt = 5 sin t + С = (повертаємось
1
до змінної х, прийнявши t = 5х + 3) = � sіп(5х + 3) + С.
о
П 2 З u r xdx
риклад . наити. х2+5'
РОЗ(і 'язання. Виконаємо підстановку t = :f2 + 5, тоді
J xdx ( 2 dt)
-2--5 = t = х + 5 * dt = 2xdx * хіі« = _....:.
х + 2
J (ft 1 J <It 1 1
= - = - - = -lIlltl + С = -lп(:с2 + 5) + С
2t 2 t 2 2 .
Приклад З. Знайти J .rvrr=�lrl:T.
206
РОЗО '.ЯЗа'Н:Н.Я. Зробимо підстановку t = Vf.Т"=l, звідси .І = е, + 1
і dx = 2tdt, тому
Приклад 4. Знайти J e!�l'
Розв 'язання. Замінимо змінну х = Іп t, звідки t = е"; dx = �I,
тому
J dx - J dt - J (t + 1) - t dt - J �� -- J � -
еХ + 1 - (і + 1)і - (і + 1)t - t t + 1 -
= Іп t - J � = (t + 1 = у ::::} t = У - 1 ::::} dt = dy) = Іп t - J dy =
і+1 У
= Іп t - Іп у + С = Іп t - Іп( t + 1) + С = х -- Іп (eL' + 1) + с.
П 5 З U J ,P'(x)dx
риклад . наити .,о(х)'
Розв 'язання. Підстановка t = <р( х), тоді
J <p'(x)dx , J dt
-'--------'--� = (і = <р(х) ::::} dt = <р (x)dx) = -- =
<р(х) t
= Іп Itl + с = Іп 1'Р(х)1 + с.
Маючи деякі навики виконання підстановак, можна самої змін
ної t і не записувати. Наприклад, в інтегралі J sin2 х cos xdx =
= J sіп2 xd(sin т ) подумки розглядають sin х як нову змінну і одраау
переходять до результату:
J J . з
2 2 SIll Х
sin .Т cos Х(].І = sin хd(sіпх) = -3- + с.
207
Аналогічно J х sin х2 dx = � J sin х2 d( з,2) = - � СОБ .r2 + С.
3.2. Тригонометричні підстановки. Якщо інтеграл містить
радикал J а2 - х2, ТО зручно користуватись підстансвкою х = а Біп і,
а > О, -� < і < �; тоді VQ2 - х2 = Va2 - а2 Біп2 і= Ja2(I - sin2 і) =
= а cos і.
Якщо інтеграл містить радикал V х2 - а2, то використовують
підстановку х = _а_ тоді - / х2 _ а2 = / -.L _ а2 = а l-cos2 t
cos t ,У V cos2 t cos2 t
_ а sin t
- cos і '
В інтегралі, що МІСТИТЬ вираз V х2 + а2, застосовують підста-
новку х = а sin ь , тоді - /х2 + а2 = а2 sin2 t + а2 = а sin2 t+cos2 t
cos t ,У cos2 t <"082 t
а
cos ь:
Приклад.
J x2dx = (х = віп г, t = arcsinx) = J sin2tcostdt =
vI - х2 dx = costdt - VI - Біп2 t
J Біп2 tcostdt J 2 J 1 - СОБ2і t 1 J
= = віп tdt = dt = - - - СОБ 2tdt =
СОБі 2 2 2
t 1 J і віп 2і t віп і cos t
= 2 - 4: cos2td(2t) = 2 - -4- + С = 2 -- --2- + с =
= ! _ sin і) 1 - Біп 2 і + С = arcsin х
222
xvI - х2
--2---+С'
3.3. Метод інтегрування частинами.
Теорема. Я'/'І,ЩО фу'нхціі 1t(X) і {J(З') дuфере'Н:ці-Uовnі па nро.між-к;у
(а; Ь) і па 'Цьо.му проміжки ісnус інтеграл J v(x)u'(x)dx, то існцє і
інтеграл J u(x)v'(x)dx, nршчо.му
(12)
або
j ші» = lJ.V - j lJdu ..
Доведення. Знвйдемо похідну від добутку и(.т)·u(х), одержимо
(и(т}·u(х))' = u'(x)·'l..'(x)+U(X)·11'(X). Тоді и(х)· u'(.r) = (и(.1')· І·(.т.))'
--I1.'(x)·v(x). Проінтегруємо ліву і праву частини цієї рівності. Врахо
вуючи, шо І Г(х)сіх = Лх)+С, отримаємо (12). Доданок С у (12) !\1И
не пишемо тому, шо інтеграли в лівій і в правій частинах (12) визна
чені з точністю до константи. Якщо урахувати, що d'lJ(x) = 'lJ'(x)clJ.�,
dll(J.�) = и'(х)(lт, то 3 (12) випливає (ІЗ).
Приклади. Обчислити інтеграли: 1. І хе" ііз:
РОЗб '.ЯЗа'Н:Н,.Я. Приймемо и = г , dv = еІсіх, тоді duo = dx, v =
= J eXdx = еХ, (константу С беремо такою, що дорівнює нулеві, ос
кільки для обчислення інтеграла достатньо знати одну з первісних).
За (ІЗ) J xeTdx = хе" - е" + С.
2. J х2 cos xdx.
РОЗб 'язання. ПРИЙ�1емо И. = х2, dv cos xdx. Тоді duo = 2xdx,
v = J cos xdx = sin х. За (ІЗ)
(ІЗ)
j х2 cos xdx = х2 sin х - j 2х sin xdx.
(14)
До інтег-рала в правій частині ше раз застосуемо формулу інтег
рування частинами:
і. ( и = 2х * ([и = 2dx, )
2х SIll xdx =. .
dv = SIn xdx * v = J SIll ;l·сіІ = - СОБ Х
= -2xcosx - j('-СОSХ)2dІ = --2.rсоsJ: +- 2БіПІ + С.
Звідси та з (14) випливає
j .1'2 СОБ хчіх = J:2 зіц г + 2.1: СОБ J: - 2 Бів .1' + С.
20!)
J ( - VI 2 2 d - -xdx )
J 2 2d и - а - х * и - �,
3. а - х х = va--x- =
dv = dx * v = х
J -x2dx J (а2 - х2) - а2
= xJ а2 _. х2 - = xJ а2 - х2 - dx =
J а2 - х2 J а2 - х2
= xJa2 - х2 - J Ja2 - x2dx + а2 J dx =
Ja2 - х2
= Х J а2 - х2 - J J а2 - х2 dx + а2 аrсsіn � + СІ.
Порівнюючи початок і кінець цього виразу, бачимо, що одержали
рівняння відносно невідомого інтеграла J Ja2 - x2dx. Розв'язуючи
це РІВняння, знаходимо
J Ja2 - x2dx = �Ja2 - х2 + � arcsin � + С,
С = СІ.
2
(15)
4. Повторюючи попередні міркування, можна показати, що
J Jx2 + Adx = %Jx2 + А + � Іп Іх + Jx2 + АІ + с. (16)
(переві рити самостійно).
§ 4. Інтеграли, що містять квадратний тричлен
4.1. Інтеграли вигляду
J dx
ах2 + Ьх + с
J dx
та
Jax2 + Ьх + с
(17)
зводять до табличних інтегралів, виділяючи повний квадрат з квад
ра тного тричлена:
(Ье)
ах2 + Ьх + с = а х2 + �x + �
210
[2]
С Ь Ь2 С
-] = а (х + -) - -"2 + - .
а 2а 4а а
---lІриклад.
J dx J dx
J2x2 - 5х + 7 - -)2 [(х2 _ 2. �x + 25) _ 25 + 7..]
4 16 16 2
( 5)2 ЗІ
х - - + - + с.
4 16
4.2. Інтеграли вигляду
J тх + n d
ах2 + Ьх + с х
J тх+n d
та х.
Jax2+bx+c
(18)
Обчислюючи Їх, знаходять похідну (ах2 + Ьх + с)' = 2ах + Ь і у
чисельниках цих інтегралів виділяють вираз 2ах + Ь, що дає змогу
звести обчислення інтегралів (18) до інтегралів (17).
Приклад. Обчислити J x23�4-::�5 dx.
РОЗб 'язання. Похідна (х2 - 4х + 5)' = 2х - 4 і диференціал d( х2_
-4х + 5) = (2х - 4)dx; чисельник Зх - 2 можна записати у вигляді
Зх -- 2 = Н2х - 4) + 4, тому
J Зх - 2 d З J (2х -- 4)dx J dx
х-- ----+4 -
х2 - 4х + 5 - 2 х2 - 4х + 5 х2 -- 4х + 5 -
З J ах З 2
= -Іп Iх2 - 4х + 51 + 4 2 2 2 = -21п l:z� - 4х + 51+
2 х -- . x+4tl
J dx З 2
+4 ( )2 = -Ін Іх - 4х + 51 +- 4ю"Сtg(х - 2) + с.
х-2 +1 2
211
43 І J dx .
.. нтеграл вигляду (mх+п)Vа:r.:'ЧЬх+с за .:\ОПО:\ЮГОЮ під-
становни �+ = t зводиться до інтеграла попереднього типу.
1nХ n ...
Приклад. Обчисшти J (I-I��·
РОЗб 'язання. Підінтегральна функція визначена якщо х -І- 1,
:г2-1>О,тобто,на�шожині{х: -CXJ<х<--1}U{х: 1<x<+CXJ}.
Обчислимо інтеграл на проміжку -СХ) < з: < -1.
J dx (1 1 <іі)
(х _ 1)vx2 _ 1 = t = х -1 =?І = t + 1 =? d:r = - і2
Самостійно обчисліть цей інтеграл на проміжку 1 < х < +CXJ.
4.4. Інтеграл вигляду J Vax2 + Ьх + оіх виділяючи з ах2+
-t-bx + с повний квадрат, зводять до одного з інтегралів
J уІх2 + Adx = �yIx2 + А + .� Іп Іх + уІІ2 + АІ + с
(див. (15), (16)).
Приклад.
212
= f J-2((x + 1)2 - 2)dx = J2 f -/2- (х + 1)2а(х + 1) =
а: (х + 1 . х + 1 )
= v г -2-у!2 - (х + 1)2 + arcsin УІ2 + С .
§ 5. Інтегрування раціональних дробів
5.1. Інтегрування елементарних раціональних дробів.
Як встановлено раніше (розділ 5, п.2.2, (42)): кожен раціональний
дріб можна записати у вигляді суми многочлена і елементарних ра
ціональних дробів. Тому інтегрування раціональних дробів зводить
ся до інтегрування многочлена і елементарних раціональних дробів
А А Вх + С
х - а' (х - a)k' х2 + рх + ч'
Вх+С
( 2 )k' k = 2, 3, ... ,
х + рх + q
2
де А, В, С, а,р, q - дійсні числа, причому Р4 - q < О. Покажемо, що
невизначені інтеграли від таких дробів виражаються через елемен
тарні функціі.
1. f�dX=(X - а=і =? dх=dt)=Аjdt-=Аlп1tl+С=Аlп1х-аl+С.
х-а t
іА fdt гНІ (х - а)-НІ
2. ( )k dx = А і: = А k + С = А k + С, k > 1.
х-а t - +1 - +1
З. Розглянемо J (x2�;��q)k dx, k = 1, 2, .... Якщо k = 1, отримає
мо J хJЗ::Х�qdх ---- інтеграл, що містить квадратний тричлен, метод
інтегрування якого розглянули вище. Якщо k = 2,3, ... , застосо
вують метод пониження степеня, причому попередньо у квадратно
му тричлені х2 + рх + q рекомендується виділити повний квадрат
2 2 2 2
х2 + рх + q = х2 + 2 . ІХ + � - � + q = (х +�) - Р4 + q і зробити
підстановку х + � = і.
Приклад. Знайти І = J (I2�.ix�6)2a.г.
213
РОЗб 'язання. Оскільки х2 - 4х + 6 = (х - 2)2 + 2, то прийнявши
І-- 2 = і, одержимо:
J di 1 і і
(і2 + 2)2 = 4J2arctg J2 + 4(і2 +-2) + С.
Підставимо інтеграли (20), (21) в (19), отримаємо
1 2 _} З і Зі Зі - 2
1 = --(і + 2) + -arct,g м + (2 ) + С = - ( 2 ) +
2 4J2 v2 4 і + 2 4 і + 2
(21)
З і Зх - 8 З :1: -- 2
4J2arctg J2 + С = 4(х2 _ 4х + 6) + 4J2arctg J2 + с.
J' dt
Позначимо Іп = (і2+а2)п, п = 1,2, З,.... Використовуючи
спосіб, застосований для обчислення інтеграла (21), можна довести
рекцрентні; формулу
1 t 2п - 1
Іn+І = 2па2 . (i2+-�� + 2па2 . Іп, n = 1, 2, З,... . (22)
214
Інтеграл ІІ легко обчислюється (ДИВ. таб.'ІИЦЮ інтегралів}, (22)
дає змогу обчислити 12 (цей інтегра.л 1111 онайшли в (21)): знаючи 12,
за тією самою формулою можна знайти Із: продовжуючи цеи процес,
можна знайти будь-який інтег-рал Іп, n = 1, 2, ....
5.2. Загальний випадок інтегрування раціональних ,цро
бів. Нагадаємо, що раціОН3.:1ЬНИМ дробом називається функція ��:�,
де Р(х), Q(x) - многочлени з діисними коефіцієнтами, причому
Р(х) 1= о. 3 попередніх результатів випливає спосіб обчислення інте
грала Bi� раціонального дробу: якщо дріб ��:� .непра�ил�ниЙ, то спо
ча тку ДІЛенням чисельника на знаменник ВИДІЛЯЄТЬСЯ ЦІла частина,
тобто цей дріб ��: � подається у вигляді суми многочлена R( х) і пра-
вильного раціонального дробу ��:�. Якщо S(x) 1= о, то правильний
дріб розкладає�ься на суму елементарних дробів. Оскільки інтег
рал від суми функцій дорівнює сумі інтегралів й інтег-рали від еле
ментарних раціональних дробів виражаються в скінченному вигляді
через елементарні функції, то можна зробити висновок: нееизнсче
ний інтеграл від будь-.я:r.;ої раціональнді фу'Н,'/'щії ��:� на будь-.я:r.;о.м.у
проміжки, de знаменних Р( х) 'Н,С перетеорюється в 'Н,уль, існцє і ви
ражається у скінченномц вигляді.
5 3 2
П 3 "U J х +з.1" -4х +х"--2 І
риклад. наити х5-2х4+х3-2х2 (;1:.
РОЗ6 'язання. Оскільки підінтегральнии дріб неправильний, ДІ-
. .
ленням чисельника на знаменник ВИДІЛЯЄМО шлу частину:
Многочлен, який знаходиться у знаменнику, розкладемо на !\ІНОЖНИ
ки із дійсними коефіцієнтами:
54 З г 2З 'l <
Х - 2х + х --- 2:г =х (;г - 2.1' + Х --- 2) =
215
Вже відомо (див. розділ 5. п2.2, (44)), що
2х4 + 2х3 - 2х2 + Х - 2 1 2 1
--------- = - + -- + .
х2(х-2)(х2+1) х2 :1'-2 х2+1
Звідси та з (23) випливає
J х5 + 3хЗ - 4х2 + Х - 2 J d J dx J 2dx J dx
----,-----:-------::--dx = х + - + -- +
х5 - 2х4 + хЗ - 2х2 х2 Х - 2 х2 + 1
1
= х - - + 21n Іх - 21 + arctg х + С.
х
§ 6. Інтегрування ірраціональних функцій
Функція вигляду
(24)
де ak1 , ... ,kn, bj1 , ... .і« Е R, називається раціональною фую·щією від
ИІ, ... , ·иn. Якщо В (24) змінні ИІ, ... , Ип, своєю чергою, є функ
ціями змінної х : иі = <Рі(Х), і = l,n, то функція F(<PI(X), ... ,<Рn(Х))
називається рсціональною фую·щією від фУ'Н,'Ущій <р 1 (х), ... , <рn (х).
Розглянемо деякі класи ірраціональних функцій, інтеграли від
яких виражаються через елементарні функції.
Г-�.l. Інтеграл вигляду
J
І
J F ( (ах +.!!..) '::11 (ах.±.!!..) � (ах +.!!..) :;) d .
х, ех + d ' ех + d , ... , ех + d х,
"
'
'-----
216
де ті, п, --піді додатні числа (і = l,р); F(x, И], ... ,Ир) - раціональ
на функція від аргументів х, Иl, ... , Ир, зводиться до інтеграла від
раціональної функції змінної t за допомогою підстановки
ах + Ь ('
___ -{і)
ех + d - ,
(25)
де s -- спільний знаменник дробів 7:і ' і = 1, р.
Приклад.
J 1 р;і+ х ( 1 + х 2 1 - 2tdt )
� -- dx = -- = t =? х = -2--' =? dx = ( 2 )2
Х Х Х t -1 t -1
J 2 2 -2tdt J 2 2 3 2 J( 1 + х) 3
= (t - 1) t = -2 t dt = - -t + С = С - - -- .
(t2 - 1)2 З З х
6.2. Інтеграл вигляду
(26)
Вираз хт(а + ьхn)р, а,Ь і= о називається дифере'Н:ціаль'Н,и,м, біно
мом. Нехай а, Ь -- дійсні, ат, n, р -- раціональні числа. Як встано
вив п.л. Чебишов, інтеграл (26) еирожасться 'Через скінченни ком
бінацію епементарниз: фу'Н,к'Цій лите у таких випадках:
1) .якщо р -- 'Ціле 'Число;
2) .якщо т:І -- 'Ціле 'Число. Тоді використовиють nідста'Н,овку
II + Ьх" = і", де s -- знаменник дробу р;
3) .якщо т:І + р -- 'Ціле число, то застосовують підстановни
ах-n + Ь = tB, де s -- знаменнизг дробу р.
Приклад. Знайти J �.
]+х
Розв 'язання.
217
Тут m = О, n = 4, р = -�, s = 4. Маємо т:'l +р = �-� = о -- третій
випадок інтегровності. Приймемо х-4 + 1 = і4, t = \!х-4 + 1
= � х = (t4 - 1)-і- dx = -t3(t4 - l)-%dt отже 1 _ -.!... -
х ' , , VI + х4 іх
J t2dt О
Тому І = - і4 -1 . скільки
t2
----
t4 - 1
1 1 1
--- - --- - ----
4( t + 1) 4( t - 1) 2( t2 + 1) ,
то
І = � J� - � J� - � J -� = �ln[t+ 1[- �arctgt+ С
4 t + 1 4 t - 1 2 t2 + 1 4 t - 1 2 '
де t = {l'х-4 + 1.
6.З. Інтеграли вигляду J R(x, vax2 + Ьх + c)dx, а #- О, R(u,v)
--- раціонапьна фую'щі.я., розв'язуються за допомогою однієї з підста
новок Ейлера.
Першу nідсmа'Н,Об'К',У Ейлера застосовують, якщо а > О. Приима-
ють
J ах? + Ьх + с = ±хуГа + t.
Тоді ах2 + Ьх + с = (±xJa + t)2. Члени, ЩО містять х2, знишу-
2
ються; знаходимо х = b�27.Ja, отже. і dx раціонально виражається
через t. Підставляючи ці вирази в інтеграл, одержимо інтеграл від
раціональноі функції.
Приклад 1. Знайти 1= J ,,/: .
х+ х +х+l
РОЗб 'язання. Квадратний тричлен х2 + х + 1 має комплексні
корені, а = 1 > О, тому застосовуємо першу підстановку Ейлера
Vx2 + х + 1 = t -'т. Піднесемо до квадрата обидві частини цієі
рівності, отримаємо х2 + х + 1 = {І. - 2tx + :Е2 або .r + 1 = t2 - 2іх,
отже
е-l {І'+і+l
х -- --- =} аз· = 2----,--dt.
. - 1 + 2t( 1 + 2t) 2
218
Отже
І = 2 J і2 + t + 1 dt = J (А + _� + D ) dt
і(I+2і)2 t 1+2і (1+2і)2 .
Обчислюємо невизначені коефіцієнти: А = 2, В = -з, D = -з. Ос
таточно
І= (2In Ііl- � In 11 + 2іl + (з ) + с) .
2 2 1 + 2і t=х+vхЧх+І
Другу підстанотец Ейлера застосовують, якщо с > о. у цьому
• u / 2 Ь /: 3 . b-2tvc
разі приимаємо v ах + х + с = V с + хі. вІДСИ х = і2-а .
Третю підстанотец Ейлера використовцють, коли тричлен
ах2 + Ьх + с має дійсні корені. Нехай ХІ, Х2 - ці корені. Тоді прийме
мо vax2 + Ьх + с = і(х - хІ). Піднесемо обидві частини цієі рівності
до квадрата і скоротимо одержану рівність на Х-ХІ, отримаємо а(х
-Х2) = і2(х - ХІ), звідки знаходимо Х = Xl:�=�X2, vax2 + Ьх + с
a(X-Х2) t dx = 2a(X-Х2) dt
і2-а' (і2-а)2·
Приклад 2. Обчислити інтеграл І = J .J dx 2·
1+ 1-2х-х
Розв 'язання. Квадратний тричлен 1 - 2х - х2 має дійсні, різні
корені ХІ = -1- ../2, Х2 = -1 +../2. Тому зробимо третю підстановку
Ейлера t = V:;I2:h2• Піднесемо до квадрата обидві частини рівності
Vl -- 2х - х2 = і(х+ 1 + J2), отримаємо -Х -1 + J2 = і2(х + 1 + J2).
Отже, Х = -I+�;-�?+V2), ,)1- 2х - х2 = �f;:, dx = (-;24/:);dt. Тому
І = -4J2J (2 )( �dt vi і Одержали інтеграл від раціонального
t +1 t +2 2і+1
дробу, який обчислюється методом невизначених коефіцієнтів.
§ 7. Інтегрування раціональних виразів
від тригонометричних функцій
7.1. Інтеграли вигляду
І= J зіп'" Х сов" хіі»,
(27)
219
1. Якщо m = 2k + 1 --- непарнє додатне число, n -- шле: то
І і· 2k+l n d J ( . 2)k n . d
= SIn х COS х х = SIn х COS х SIn х х =
. .. .
-- ІНтеграл, що розглядається, привели до ВІдомого типу інтегралів
від раціональної функції. Аналогічно розглядаються інтеграли (27),
коли n - непарне ЧИС--1ІО, n > О.
Приклад 1.
J sin2 х cos3 xdx = J sin2 х cos2 х COS xdx =
J . 3 . 5
. 2 . 2 . SIn х SIn х
= SIll Х (1 - SIll х) d( SIll х) = -- - -- + С.
з 5
2. Якщо m = 2k 2: О, п = 28 2: О, то в інтегрвлі (27) понижують
показники степенів за допомогою формул
. 2 1 - cos 2х 2 1 + cos 2х
SIn х = 2 ,COS х = 2
. sin2x
вш т сов ,г = -2-'
(28)
Приклад 2.
J . 4 і' 2 2 J (1 - cos 2х ) 2
SIll xdx = (SIll х) dx = 2 dx =
= � J (1- 2cos2x + cos2 2х) dx = � - � J cos2xd(2x)+
. 1 J 1 + cos4x d х sin2x х sin4x
Т4 2 х ="4 - -4- +"8 + 32 + с.
7.2. Інтеграли вигляду
J R (sin2 х, COs2 х) dx,
(29)
220
ае R( и: и) -- раиіонапьна фующі.я, приводять ао інтеграмв від ра-
11,іо'Н.аЛЬ1іОЇ фующії за допомогою замінлі
t = tg х, х = arctg і,
dt
ах = --2'
1+{'
(ЗО)
ТОДІ
. 2 sin2 х tg2x
Sin х = 2 - 2
sin х + cos2 Х tg х + 1
cos2 Х 1
cos2 Х = --;0------=-
sin2 х + сов? Х - tg2x + 1
1
і2 + і
Приклад І,
J dx J 1 dx J 2 tgЗ Х
-- = --, -- = (tg x+l)d(tgx) = -+tgх+С.
cos4 х cos2 Х сов? Х З
Приклад 2.
J dx (і = tg х, dx = 1 �tt2 , )
2 =, 2 t2 2 1 =
sin х сов? х Sin х = t2+1' cos х = і2+1
_ J і2 + 1 (2 )2 dt _ J (і2 + 1)2d _
- __ о t +1 .--- і-
і2 і2 + 1 і2
J ( 2 1) tgЗх
= t + 2 + і2 dt = -З- + 2tgx - ctgx + С.
7.З. Універсальна тригонометрична підставовка. Розгля
даємо ІНтеграл
І= J R(sinx,cosx)dx,
де R( u, и) --- раціональна функція. Виконаємо підстановку
(ЗІ)
х
t = to' -
п 2'
х 2dt
2' = arctg і, dx = "1 + {l. '
(З2)
221
ТОДІ маємо
2 . І Х
. SIll"2 COS"2
вш т = 2
sin � + cos2 �
2 2
2і
1 + і2'
cos2 � - sin 2 � 1 - tg2 �
cos Х = 2 2 _ 2
sin2 � + cos2 � tg2 �2 + 1
2 . 2
1 - і2
1 + і2·
Інтеграл (31) після підстановки (32) набуває вигляд
J J (2і 1 - і2) 2dt
R{sinx,cosx)dx = R --2' --2 --2
l+і l+і l+і
(33)
._- інтеграл від раціональної функції. Доведемо, наприклад, формули
7, 8 таблиці інтегралів:
J s�:x = (tg� = і, sinx = 1 �\2' dx = 1 �ii2) =
J dx J dx
cos х = sin (х + �)
J 1 + і2 2dt J dt І х І
= --.--= -=lпltl+С=lпtg- +С.
2і 1 + і2 t 2
J d(x +!!:) І (Х 7Г)1
= 2 = In tg - + - + С
sin (х + �) 2 4 .
Приклад.
J dx
1 + sin х + cos т· =
= J �-- = In 11 + tl + С = In 11 + tg =-1 + С.
l+t 2
7.4. Інтеграли вигляду
(34)
222
де т - 'Ціле додатuе число, обчислюються, відповідно, за допомо
гою фор,м,ул
2 1
tg х = -- -1,
cos2 х
2 1
ct,g з: = -.-2- - 1.
SIn х
(З5)
Приклад 1.
і tgЗ xdx = і tg х . tg2 xdx = і tg х (co�2 х-І) dx =
і і tg2x і sin х tg2x
= tgxd(tgx) - tgxdx = -- - --dx = -- + In І сов г] + с.
2 cos х 2
Приклад 2.
і і 2 (1 ) tgЗх і
tg4xdx = tg х cos2 х-І dx = -з- - tg2xdx =
tgЗх і (1 ) tgЗх
=--- ---1 dx=---tgх+х+С.
З cos2 х З
7.5. Інтеграли вигляду
і sinmxcosnxdx, і sinmxsinnxdx, і cosmxcosnxdx (З6)
розв '.язуюmьс.я за допо,м,огою фор,м,ул
1
sin тх cosnx = 2 [sill(m + n)х + sin(m - n)х] j
sinmxsinnx = � [cos(m -- n)х - cos(m + n)х] j
1
cosmx cos пз: = 2 [cos(m - n)х + cos(m + n)х].
Приклад.
і sіпЗхсоs5хdх = � і [Біп8х + sin(-2x)] dx =
1 і 1 і cos2x cos8x
=16 sin8xd(8x)--4 sin2xd(2x)= 4 - 16 +С.
22З
Розділ 7 . ВИЗНАЧЕНИЙ IHTErPA.Jl
§ 1. Означення та існування інтеграла
Рімана (визначеного інтеграла)
1.1. Задача про площу криволінійної трапеції. Криволіній
ною трапецією називається фігура, обмежена віссю абсцис, ПРЯ�ПІМИ
х = а і х = Ь (а < Ь) і графіком функції у = ЛХ), а � х � Ь (рис. І).
у
х=а
х=Ь
о
а 6 Х]
Хn-І �n Ь Х
Рис. 1.
Розділимо відрізок [а; Ь] довільно на n частин точками ХІ < Х2 <
< ... < Хn-І іпозначимо хо = а, ХN = Ь. Тоді а = ХО < Х1 < ... <
< Хі-І < Хі < ... < Хn-] < Хn = Ь. Через ці точки проведемо
прямі, перпендикулярні до осі абсцис (див. рис. І). Цими прямими
ця трапеція ділиться на п смужок (елементарних трапецій). Дов
жину кожного з проміжків розбиття позначимо 6.Хі = Хі - Хі-І,
де і = 1, п, На кожному з проміжків візьмемо довільну точку (і
(Хі-І � (і � Хі, і = 1, n) і знайдемо ординату Л�і) відповідної то
чки кривої у = ЛІ). На проміжках розбиття як на основах побу
дуємо прямокутники з висотами Л�і). Одержимо ступінчасту фігу
ру, складену з усіх побудованих прямокутників. Складемо добуток
Л�l)' 6.Хі· Якщо Л.Т) � О, а � Х < Ь, то добуток Л�і)' �Xi дорівнює
площі прямокутника з основою 6.х і і висотою f( � і). Тоді площа Sn
224
ступінчастої фігури, ск.:таДСНОЇ з УСІХ ІШХ ПРЮЮКУТНІІків. ДОРШНЮЄ
5n = Л(І)6.ХІ + ... + л(z)с.Хі + ... + Л�n)сн" або
n
5n називають інтегральною гумою функціі ]". Чим дрібніше розбит
тя, тобто ЧИ�1 менше шах 6.J:i, і = Г,l, ТП�І мєншє площа побудованої
ступінчастої фігури відрізнятиметься від площі криволініиноі т'рапє
ції. Площею криволінійноі трапеціі називається границя СУ�ПІ 5" за
умови, що шах 6.Хі --+ О:
п
1.2. Задача про обчислення шляху. Знайти шлях, прои-
u • • • u • •
дении ТІЛОМ, що рухається прямозпніино, ла ПРО�ПЖОК часу ВІД а
до Ь (а < Ь), якщо в кожний момент часу і швидкість руху т'іла
V = Лі). Роаділимо відрізок [(1; Ь] довільно на n частин точками
а = іо < іІ < ... < іі-l < іі < ... < іп = Ь. Через 6.іі позначимо дов
жину проміжку подрібнення [і і _} ; t І]: 6.t і = і 1 - t і -1, і = 1, 11. На кож
ному з проміжків [іі--І: іі] виберемо довільнии момент часу [довільну
точку) �i, іі-І :S; (і :S; і.. Якшо ПРИПУСТИТИ. шо швидкість руху на
�ожному з проміжків [іі-.І: ti] стала і дорівнює значенню швидкості
у вибраний момент часу �i (І' = Л�і)), ТО Ш.:ІНХ. проидений за гіромі
жок часу [іі-l;і;], дорівнює Л(і)' !:lti [добуткові швидкості Л(і) на
час 6.іі, і = I�n). Ш.ІЯХ. пройдений тілом за проміжок часу Ь - а. на
ближено дорівнює СУ:\Іі 5п = Л�І )�il -+- ... + Л�і )6.і; + ... + Л�lI )�in
або
n
з; = L і«. )6.і;.
і=1
Чим дрібніше подрібнєння. ТИМ значення гуми 5п nуд{' б.1ижче дО
ІСТИННОГО значення Ш.1ЯХУ. ПРОІ1Дt'НОГО тілом за відрі;)()І( часу [о: Ь].
225
3а означенням шлях, пройдении тілом, шо рухається прямолініино,
за проміжок часу від а до Ь, якщо швидкість руху v = f( і) дорІВНЮЄ
границі суми Sn, коли шах Q.ti ---7 О:
n
5 = lіш L Л�і)�іі.
шах �ti--+O .
1=1
Розв'язання багатьох інших задач приводить ДО анаЛОГІЧНИХ
. .
границь, які називаються визначеними Інтегралами.
1.3. Верхні та нижні суми Дар бу. Інтеграл Рімана. Не
хай f( Х ), Х Е [а; Ь] --- обмежена дійсна функція,
m � Лх) � АІ, а < Х < Ь.
Розбиттям П відрізка [а; Ь] назиеається скінченна множина
точок {ХО,Хl"" ,Хn}, такие, що а = ХО � ХІ � Х2 � .. , � Хn-l �
� Хn = Ь. Позначимо �Xi = Хі - Хі-І, �Xl --- довжина відрізка
[Хі-І; Хі], і = 1, n. Кожному розбиттю П відрізка [а; Ь] ВІДПОВІДають
числа (див. розділ 1, п1.S) (і = 1,n)
де М, .-- точна верхня, а ті -- точна нижня межі значень функці і
Лх) на відрізку [Хі-І; Хі],
Позначимо
n n
U(П, Л = L м.с»; L(П, Л = L тi�:1:i;
;=1 і=1
(2)
цп, Л < U(П, Л. (3)
Число U(П, і) називають верхньою інтегральною симою, число
L(П, Л нижньою інтегральною сцмою [симою Дарбу).
22G
З'ясуємо геометричний зміст інтсгральних сум (2). Розглянемо
криволінійну трапецію, тобто фігуру, обмежену відрізком [а: Ь] осі
Ох, графіком невіл'ємноі неперервної функції у = Лх) � О, :r Е [а; Ь]
і прямими х = а, .Т = Ь (рис.2). Неперервна функція f на замкне
ному відрізку [Хі-І; Хі] досягає свого наибільшого 1Ні і наЙ:\1СНШО
го ті значень (розділ.Е, п.3.7), тому ті = іпі' Лх) = f(�:),
Xi-l�Х�Хі
�: Е [Хі-І; xJ Добуток Пlі�Хі дорівнює площі прямокутника, осно
вою якого є відрізок [Хі-І; Хі] і висота якого дорівнює ті = Л��) --
найменшому значенню функції f на відрізку [Хі-І; Хі]. Тому ниж
ня інтегральна сума L(П, f) (2) дорівнює площі ступінчастої фігури,
складеної з n прямокутників (рис.2), яка повністю знаходиться в
• • u • u .-
криволгніиніи. трапецц ,
Ха ХІ··· Хі-l
ХпХ
у
, "
.1 '
а
а
Ха ХІ
. Хі-l
ХnХ
Рис.2.
Рис.3.
Число 1\;1; = вцр Лх) = шах Лх) = Л�:'), �:' Е [Хі-І, xJ
X;-l �X�Xi Xi-l �X�Xi
Добуток i\1i�Xi дорівнює площі прямокутника, основою якого є від-
різок [Хі-І; Хі] і висота якого дорівнює М, = Л�:')-- найбільшому
значенню функції f на відрізку [Хі-І; Хі]. Тому верхня інтеграль
на сума U(П, f) (2) дорівнює площі ступінчастої фігури, складеної з
n прямокутників (рис.З}, яка повністю містить у собі криволінійну
трапецію.
Нижче ми доведемо таку властивість неперервної функції f( Х ),
Х Е [а; Ь]: якщо шах �Xi --+ О, і = 1, n, то інтегральні суми L(П, Л,
227
U(П. Л. які ДОРІВнюють плошам відповідних ступінчастих фігур,
прямують до ОДНІЄІ 1 тзєі самоі границі. Саме цю границю
11
11
5 = Ііш L Л�:).6.·Ті = lіш L Л�:')ДХі
maxD.x;---tО. maxD.x;---tО.
1=1 1=1
. .. .-
І назвемо площею криволініиноі трапецц.
11
Оскільки Ь - а = L �Xi, пі s:; ті ::; іНі::; АІ, то т(Ь - а) =
і=1
n n n
m L ДХі = L тДх; < L тіДХ; = L(П, Л: аналогічно можна
і=1 і=] і=1
показати, шо U(П, f) ::; Аl(Ь - а). Звідси та з (3) випливає, що для
бу дь-якого розбиття ІІ
т(Ь - а) ::; L(П, Л < U(П, Л ::; іН(Ь - а).
(4)
Нехай {П}_·- множина всіх можливих розбиттів відрізка [а; Ь];
розглянемо числа
(5)
які називають, відповідно, в ерх'Ні.м і нижнім інтегралами функції f
на відрізку [а; Ь]. фУ'Н'І\;'Ці.я f назнеаеться інтегровною за Ріманом 'На
відріз'l\;У [а; Ь], .я'l\;що J fdx = J fdx, а спільне значення верхнього та
нижнього інтегралів Рімана інтегровноі функції f позначають сим-
Ь Ь
волом J f(x)dx. ЧИС.іІо J f(x)dx називають визначеним ьнтегралом
а а
[інтегрслом Рімана} фУ'Н'І\;'Ції f 'На відріз'l\;У [а; Ь].
Верхній і нижній інтеграли Рімана обмеженої на ВІДРІЗКУ [а; Ь]
функції завжди існують. Питання про рівність цих інтегралів ви
магає додаткових досліджень, оскільки не кожна обмежена функція
інтегровна за Ріманом.
228
ь
Виізначимо. що І f(.r)liз: залежить оіа і. а, ь і НС залежнть від
а.
ь ь
:1:, то,м,у І ЛI1)аи, .г J(t)lit означають одне і те саме.
а. СІ
Приклад 1. ПокаЖБЮ, ШО функція Л.т) = є = canst, х Е [а: Ь]
інтегровна на [а; Ь], ЩШЧО�ІУ
ь
J ссіІ = с(Ь - а), с = const.
а.
(6)
РОЗб 'язання. Діисно, при будь-якому розбитті П справедливі рів
ності ті = АІі = є, де ті, М, визначені вище. Отже, L(П, f) =
n n n
= L: тідХі = L: едІі = с L: дТІ = с(Ь - а) для будь-якого розбит-
і=1 і=1 ;=1
тя п. Тому І ісі:!· = sup L(П, f) = е(Ь - а). Аналогічно, U(П, f) =
- {П}
n n n
=--:: L: j\;[itlXi = L: сдХі = с L: дХі = с(Ь - а) Д.'ІЯ будь-якого ро-
і=1 ;=1 ;=1
збиття п. Тому f іах = inf U(П, f) = с(Ь - а). Звідси випливає
. {П}
Ь
І fdx = І fdx = с(Ь - а) = І сах.
а.
Приклад 2. Функція Діріхле ЛХ), значення якої в раціональних
. ... . .
точках дорІВНЮЄ ОДИНИЦІ, а в іррашональних -- -- ну .. леві, не інтегровна
за Ріманом на [а; Ь].
РОЗВ 'язання. Візьмемо довільне розбиття П відрізка [а; Ь]. У
КОЖНШ.1у З відрізків [Хі--І; ;Гі] Є хоча б одна раціональна точка �i, �i Е
[:Тl-І; Хі], Л�і) = 1 та існують ірраціональні точки 'Іі, 'Іі Е [.1:;-1; Хі],
ЛlІі) = о. Отож, ті = inf ЛТ) = о: JJ; = Бар лх) = 1.
Т,-1 $_l"$ї, .l:і-1 �.l-$Li
n n
Тому L(П, f) = L: mі�Зї = L: о . �.I·i "= О Д.1Я будь-якого розбиття
і=1 і=1
п. Звідси :-'ІаЄМО ІііІ:1: sнрL(П, Л = о. Аналог-ічно U(П, f) =
{ІІ}
229
n n
L: мідхі = L: 1 . дхі
і=l і=І
n
L: дхі = Ь - а для будь-якого розбиття
і=l
п. Тому J Idx = inf U(П, f) = ь - а. Звідси випливає J fdx =f. J [іі«,
{П} -
ь
Було введено поняття інтеграла Рімана J f( х )dx функції І на
а
відрізку [а; Ь], а < ь. Дд.я фу'н:к:ціі І, інтегровноі 'На відріз'К:у [а; Ь],
приймемо, за означенням,
а Ь
J f(x)dx = - J f(x)dx,
ь а
а дд.я будь-.я'К:оі фу'Н'К:ціі І, визнсченоі в точці а приймемо, за озна
ч е 'Н ням,
а
J f(x)dx = о.
а
1.4. Властивості сум Дарбу. Умови інтегровності обме
женої функції. Розбиття П* називається nодріб'Не'Н'Н.я.м розбиття П,
якщо П с П* (тобто якщо кожна точка розбиття П є також точкою
розбиття П*). Нехай задано два розбиття П, і П2; будемо вважати,
що П* є Їх спільним подрібненням, якщо П* = Пl U П2.
Теорема 1. Я'К:ЩО П* - подрібнення розбиття П, то
L(П, f) ::; L(П*, Л,
(7)
U(П*, f) ::; U(П, Л·
(8)
Тобто nри подрібненні розбиття нижні су.ми Дарбу .можуть
пииіе зростати, а верхні - лилие змениіцеатлісь,
Доведення. Щоб довести нерівність (7), припустимо спочатку,
що П* містить рівно на одну точку більше ніж п. Позначимо цю
230
точку через х" і припустимо, ЩО Хі-l < х* < Хі, де Хі-l І Хі -- ДВІ
послідовні точки розбиття п. Нехай
V} = inf J(x), Хі-І::; Х ::; т"; V2 = inf J(x), х*::; Х ::; Хі·
Зрозуміло, ЩО VI � ті і �}2 � ті, де, як і раніше, ті = inf J(x),
Хі-І::; Х ::; Хі. Тому
Якщо П* містить на k точок більше ніж П, повторимо попе
реднє міркування k разів і отримаємо (7). Доведення нерівності (8)
аналогтчне.
Теорема 2. J fdx < J fdx.
Доведення. Нехай ПІ і П2 -- два розбиття, П* - Їх спільне
подрібнення. За попередньою теоремою
цп., л < L(П*, Л < U(П*, Л < U(П2, Л·
Тому для будь-яких двох розбиттів ПІ і П2
(9)
Вважаючи П2 фіксованим і обчислюючи верхню грань за всіма
ПІ, 3 (9) одержимо sup цп., Л = J fdx ::; U(П2, Л· Отже,
П! Е{П} -
J fdx < U(П2, Л·
(10)
231
Обчислимо нижню грань по всіх П2 в (10):
ііс1х � iIlf ["(Пl, Л =jfc1:r.
І12Е{П)
З означень верхнього і нижнього інтегралів для бу дь- якого ро
збиття П отримуємо нерівності L(П. Л < Ifdx� J fdx < [�(П� Л·
Звідси та з теореми 2 вип.::шває
L(П, Л:::; j fdx < j fdx < U(П� Л·
(11)
Теорема 3. Щоб фу'Н,-кv,ія Лх), х Е [а;Ь], обмежена на віdріз-ку
[а; Ь], буда інтегровною на [а; Ь], необхідно і достат'Н,ьо, щоб \;j є > О
існцеало та-ке розбиття П відріз-ка [а; Ь], що
о:::; U(П,Л - L(П,Л < є.
(12)
Необхідність, Нехай f інтегровна на [а; Ь] задане ДОВІльне
Ь
є > о. Тоді J fdx = J fdx = J f(x)dx і через властивості точних меж
а
числових множин [розділ 1, п.l.8, (15)� (16)) існують такі розбиття
ПІ і П2 відрізка [а; Ь], ЩО
ь
U(Пl,Л- jJ(X)dT<�,
ь
j J(x)dx - L(П2, Л < �.
(13)
а
а
Нехай П = Пl U П2. Згідно з теоремою 1 виконуються нерівності
[Г(ІІ, Л :::; L(П1, Л, U(П2, Л < L(П, Л· Тmлу, враховуючи (13),
ь ь
U(П,j) < j J(x)dJ: +�; j J(.r.)d:J: < L(П.Л +�. (14)
а
а
232
Звідси випливає U(П,J) < L(П,Л + є отже виконується (12).
Достатність, Нехай V Є > О, існує таке розбиття П відрізка
[а, Ь], шо О � U(П, Л - L(П, Л < є. ТО,.:Іі, враховуючи (11), О <
� J І dx - J І dx < є. Оскільки є > О можна взяти як завгодно малим,
то це означає шо J ІсІх = fIdx.
§ 2. Інтеграл Рімана як границя інтегральних сум
2.1. Поняття інтегральної суми. Зв'язок з інтегралом
Рімана. Нехай П = {а = Хо,ХІ, ... ,хп = Ь} - довільне розбиття
відрізка [а; Ь]. Позначимо d(П) = тах �Xi -- діаметр розбизптя п.
і=І,п
На кожному відрізку [Хі-І; Хі] візьмемо довільну точку �i і розгляне-
мо значення Л�і). Тоді
Розглянемо добуток Л�і)�Хі і утворимо так звану інтеграпьнц
n
суму l:= Л�і)�Хі. Оскільки �Xi 2: О, то з (15) випливає тi�Xi <
і=1
n n n
< Л�і)�Хі < м.с»; Тому l:= rni�.гi � l:= Л�і)�Хі < l:= м.с»,
і=1 і=1 і=1
. . .
для ІНтегральних сум виконуються нерІВНОСТІ
n
L(П, Л < L Л�і)�Хі < U(П, Л·
і=І
(16)
n
Число А називається гРU1іu'Цею інтегральноі суми l:= f( �i )�X і,
і=1
n
lіш � Л�і)�З·і == А, А Е Н,
ma.x/::"J°-tоL
• і=!
( 17)
233
якщо для будь-якого є > О існує 8 > О, таке, ЩО для будь-якого
розбиття П відрізка [а; Ь], дЛЯ якого d(П) = тах /::).Х1 < 8, виконується
неРІВНІСТЬ
n
(18)
L Л�і)/::).Хі - А < Є,
і=l
для будь-яких точок �i з відрізків [Хі-І; Хі], і 1, n. Границя ін
тегральноі суми не залежить як від способу розбиття відрізка [а; Ь]
на відрізки [Хі-І; Хі], і = 1, n, так і від вибору точок �i з відрізків
[Хі-І; Хі].
Введене поняття границі інтегральних сум є новим поняттям,
.. Оо.... ..
яке не вкладається НІ в поняття граниш ПОСЛІДОВНОСТІ, НІ В понят-
тя границі функціі. На границю інтегральноі суми поширюються
теорема про єдиність границі функціі В точці, про границю суми,
теореми про перехід ДО границі В нерівностях. Довести іх пропонує
мо читачеві.
n
Теорема. а) ,я-к:що існце Ііт l: Л�і)/::).Хі = А, то f інтег-
тах 6.Xi-tО і=l
ровна на [а; Ь] і
б) ,я-к:що f інтегровна на [а; Ь], то вихониється спіееідноиіення
( 19).
n
Доведення. Якщо Ііт "Л�і)/::).Хі = А, то Vc > 038> О:
шах 6.Xi-tО L
і=l
v П d(П) < 8 ::::}
(20)
для будь-яких точок �i З відрізків [Хі-І; Хі], і = 1, n. Зафіксуємо
таке розбиття П і візьмемо нижню і верхню межі множини чисел
234
{�Л�і)�Хі}' яка отримується при усіх припустимих вибираннях
точки �i у відрізку [Хі-І; Хі], і = 1, n. Одержимо (див. розділ 1, п.l.8,
n n n ( �
(17)) infi�J(�i)�Xi і�Хі_lі2[�х�Л�і)�Хі)=і� Хі_lі2[�ХіЛ�і)) �Xi =
n n
= l:mi�xi = L(П, Л. Аналогічно можна довести, що suPl: Л�і)�Хі =
і=І і=І
= U(П, Л. Тому, враховуючи (20) та означення верхньої і нижньої
. .
меж, приходимо до неРІВНОСТІ
є є
А - З < L(П,!) < U(П,!) < А + з·
(21)
Отже, V є > О :3 П: О ::; U(П, Л - L(П, Л < є, і за теоремою 3 п.l.4,
функція f інтегровна на [а; Ь]. Це означає, що" f fdx = f dx =
ь
= J J(x)dx. Звідси та з (11), (21) випдиває Аь-Ч < L(П,Л::; ffdx =
а
Ь _ Ь
= f J( Х )dx = f f dx < U (П,!) < А +J, або А - � < f J( Х )dx < А + �.
а а
Ь
Оскільки є > О як завгодно мале, то f J(x)dx = А. Властивість (а)
а
доведена.
Нехай функція f інтегровна на [а, Ь]. Візьмемо довільне є > о.
Існує розбиття П* відрізка [а, Ь]: а = хо < ХІ < ... < хn = Ь таке, що
ь
U(П*,Л < J J(x)dx +�.
(22)
а
Функція f обмежена на [а; Ь] (чому?). Нехай IЛх)1 < м, Х Е [а; Ь].
Число дІ означимо за правилом
дІ = mіП{-Є-'�ХІ'�Х2' ... ,�Xn}!
4nМ
(23)
де n ----- кількість відрізків розбиття П*, �Xi = Хі - Хі-І, і = 1, n.
235
Візьмемо довільне розбит-тя П відрізка [о,; Ь]: о, = tO < t1 < ... <
< ts = Ь, таке. ШО шах �tl' < й]. 6.і]' = t]' - t]'_I. J' = 1. з, Жоден
, 1< '<s' "
_1_,
відрізок [t j_l; t j] розбиття П не може містити більше від однієї точ-
ки розбиття П*. бо d(П) = шах 6.і]' < 151. Отже, будь-який відрізок
, 1< '<s •
-]-
[і j -1; t j ] розбиття П або належить деякому відрізку [х і -І ; :r і] розбит-
тя П*, або містить тільки одну точку розбиття П*. Через.1 позначи
мо множину номерів тих відрізків [і j-I; t j] розбиття П, які містять по
одній точці розбиття П*, (таких відрізків менше ніж п; бо розбиття
П* складається з n + 1 точки). Нехай J,/; = sup ЛХ). Розгля-
tj-l $,x$.tj
немо верхню суму U(П, Л. Оцінимо внесок в цю суму тих відрізків
розбиття П, які містять точки розбиття П*:
� * (n - l)єll.1 є
� 11.1j �tj < (n - 1) шах �tjjl1 < < -.
4А1n 4
jEl
(24)
Позначимо и, = {j : [tj_l;tj] С [ХО;ХІ]} ---- множина номерів
тих відрізків [tj_l;tj] розбит-тя П*, які належать відрізку [ХО;ХІ];
.12 = {j : [tj-l;tj] С [ХІ;Х2]},"" .1п = {j : [tj--l;tj] С [,Тп-I;Хп]}'
Тоді l: 6.tj::=; �Xl,"" l: �tj::=; �xn і Vj Е.11 відрізок [tj_l;tj] С
jEll jE.]n
С [ХО;ХІ] =} Іу!; = Б11р ЛХ)::=; .АІІ БНР Лх), отож
Іі_1 �I"5:Ii Хо$,Х$,ХI
(25)
),/1*
J
Б11р Лх) < іНn
t j -- І '5:1'"5:' з
зцр ЛХ), тешу
Хn-і $,х$,Хn
(26)
jE.J"
jEl"
2�Ю
3 (24), (25). (26) випливає U(П, Л = 2: АЧ t::.tj + 2: 1\11; t::.tj + ... +
JEJ jEll
+ 2: 1\1; t::.tj � � + 1\11 t::.x\ + ... + �wn�xn = � + U(П*, Л. Тому:
jEJn
враховуючи (22),
ь
U(П,Л < � + U(П*,Л < J j(x)dx +�: \in л d(П) < «5"1· (27)
а
Таким самим способом можна показати, що існує число «5"2 > О,
таке, що для всіх розбиттів П, дЛЯ яких d(П) < «5"2, виконується
ь
L(П, Л > J j(x)dx - �.
(28)
а
Вибираючи «5" = mіп(«5"I,<<5"2), ми бачимо, що нерівності (27), (28)
виконуються для кожного розбиття П, дЛЯ якого d(П) < «5". Оскільки
(див. (16))
n
L(П, Л < L j(�i)t::.Xi < U(П, Л,
і=1
то з (27), (28) випливає
ь n Ь
J лх )dx - � < ?= j(�i)t::.Xi < J Лх )dx + �.
а 1=1 а
n Ь
3 цих нерівностей видно, що 2: j(�i)t::.Xi - J f(x)dx < є для всіх П,
і=1 а
для яких d(П) < «5", тобто виконується (19).
2.2. Інтегровність неперервних, монотонних та куско
во-неперервних функцій. Доведемо інтегровність двох важливих
класів функцій.
237
Теорема 1. Якщо фу'Н,'К'U,і.я f неперерено на [а; Ь], то вона ін
тегровна на [а, Ь].
Доведе'Н,'Н,.я. Нехай задано число є > о. Згідно із теоремою Кан
тора (розділ. 2; п.3.8) з неперервності функції f на замкненому
відрізку [а; Ь] випливає, що функція f рівномірно неперервна на [а; Ь],
тобто V є > О :І 8 > о:
є
IЛх)-Лі)1 < Ь-а'
(29)
якщо Іі - хІ < 8. Виберемо розбиття П так, щоб d(П) < 8. Не
перервна функція f на замкненому відрізку [Хі-І; Хі] досягає сво
го найбільшого і найменшого значення (розділ 2, п.3.7), тому ті =
= inf ЛХ) = шіп Лх), М, = sup Лх) = тах ЛХ).
Xi-I:$X�Xi Xi_l�X�Xi Xi_l�X�Xi Xi_l�X�Xi
Тоді з нерівності (29) випливає, що
є
Мі - ті < Ь--' і = 1, n.
-а
n n n
Тоді, U(П,1) - L(П, 1) = l: Mit::.Xi - l: mit::.Xi = l: (Мі - mi)t::.Xi <
і=1
і=l
і=1
n
< Ь':'а l: t::.Xi = є. Отже, за теоремою 3 п. 1.4 функція f інтегровна
і=l
на [а; Ь].
Теорема 2. Якиіо фу'Н,'К'U,і.я f монотонна на [а; Ь], то вона і'Н,
тегровна на [а; Ь].
Доведення. Нехай задано є > о. Для довільного п виберемо роз
биття так, щоб t::.Xi = b�a, і = 1, n (тобто точки розбиття ділять
відрізок [а; Ь] на п відрізків однакової довжини). Припустимо, що
функція монотонно зростає (у іншому разі доведення аналогічне).
Тоді
отже,
11
n
n
і=1
і=1
і=]
238
Ь-а
+ j(хз) - ЛХ2) + ... + лхn) - лхn-l)) = -и(Ь) - Ла)) < Є,
п
якщо п достатньо велике. За теоремою 3 п. 1.4, функція f інтегровна
на [а:Ь].
Теорема 3. Якшо фу'Н,-к:v,і.я f обмежена і �ус-к:ово-'Н,еперерв'Н,а на
[а; Ь], тобто мас скінченнц -к:ідь-к:ість точок розрuву і всі вонн роз
ривн І-го роду, то вона інтегровна на [а;Ь]. (Довести самостійно).
§ 3. Властивості визначеного інтеграла
3.1. Адитивність відносно інтервалів інтегровності. Не
хай а < с < Ь. Через п� позначимо розбиття відрізка [а; Ь], яке
містить точку с, тобто а = Хо < ХІ < ... < Xk = С < Xk+l < ... <
< Хn = Ь. Цьому розбиттю відповідає розбиття П� відрізка [а; с]:
а = Хо < Х} < ... < xk = С
(3О)
і розбиття п� відрізка [с; Ь]:
С = xk < Xk+l < ... < Хn = Ь.
(31)
Для верхніх і нижніх інтегральних сум функції Лх), Х Е [а; Ь],
що відповідають розбиттям п�, П�, п�, виконуються співвідношення
u(п�, f) = U(П�, f) + u(п�, Л, L(П�, f) = L(П�, f) + L(П�, Л, (32)
U(П�, f) - L(П�, f) < u(п�, f) - L(П�, Л,
U(П�,f) - L(П�,f)::; U(П�,f) -- L(П�,f).
(33)
(34)
Дійсно, нехай ті і і\1і-- нижня і верхня грані функціі f на відріз-
n k
ку [Xi-l;:Гі] (див. (1)). Тоді U(П�,f) L м.ь», L j,[i6.xi+
1=1
і=1
239
і=l
і=l
і=l
k
-ml)�Хі 2=: Е (Мі - тi)�Xi = U(П�, f) - L(П�, Л· Аналогічно ДОВО-
і=l
ДЯТЬСЯ інші співвідношення (32) і (34).
Теорема 1. Нехай а < с < Ь. Фу'Н:к::u,і.я ЛХ), Х Е [а; Ь] інтегровна
на [а; Ь] тоді і тільзги тоді, ко аи вона інтегровна на еідрізкоа: [а; с]
і [с; Ь].
Доведення. 1. Якщо функція f інтегровна на [а; Ь], то Vc > о
існує таке розбиття П відрізка [а; Ь], що для верхніх і нижніх інтег
ральних сум виконується нерівність (див. (12))
U(П,f) - L(П,f) < є.
(35)
До точок розбиття П приєднаємо точку с. Одержимо подріб
нення розбиття П відрізка [а; Ь], яке позначимо П�. За теоремою 1
п. 1.4 з нерівності (35) випливає
u(п�,Л - L(П�,f) < с,
тому, враховуючи (33), U(П�,f)--L(П�,Л � U(П�,Л-L(П�,Л < є.
Отже, Vc > о існує розбиття П� відрізка [а, с], для якого U(П� ,J)
-L(П�,f) < є. Згідно з теоремою 3 П.1.4 функція f інтегровна на
[а; с].
2. Нехай функція f інтегровна на відрізках [а; с] і [с; Ь]. Тоді
згідно з теоремою 3 Vc > о існують розбиття П� і п� ВІДПОВІДНО
відрізків [а; с] і [с; Ь], дЛЯ яких
U(П�,f) - L(П�,f) <�, U(П�,f) - L(П�,J) < �. (36)
Через п� позначимо розбиття відрізка [а; Ь], яке виходить, якшо
до точок розбиття П� відрізка [а; r] додати точки розбит-тя п� відріз
ка [с; Ь]. дЛЯ верхніх і НИЖНІх інтегральних сум, що відповілають
240
розБИТТЮ1 п�, П�, п�, виконуються рівності (З2). Тому, враховуючи
(З6). U(П�,f)-L(П�,f) = U(П�.f)+U(П�,f)-L(П�,f)-- L(П�,J) <
< і + � = є, тобто \;fc > О існує розбиття п� відрізка [а: Ь], Д.іІЯ якого
виконується нерівність u(п�, f) - L(П�, f) < Є, а це означає (див.
теор. з), що функція f інтегровна на [а: Ь].
Теорема 2. Нехай а < с < Ь. Якиіо фу1t'К,1�і.я f інтегровна на
6ідріз'К,ах [а; с] і [с; Ь], то 601ta інтегроена на відріз'К,у [а; Ь), причомл)
(див. рис.4)
Ь с Ь
J f(x)dx = J f(x)dx + J f(x)dx.
а
(З7)
а
с
Доведення. Інтегровність функції f на [а; Ь] випливає з теореми
1 п. з.і. Доведемо (З7). Позначимо
Ь с Ь
І = J f(x)dx, ІІ = J ЛХ )dx, 12 = J f(x)dx. (З8)
а
у
а
с
а
с
/'f=f(x) -:
[�:
: с : ь :
� J f( .г )ах � J f( .г )dx �
І І І
І І ,
І а І с
, І
Нехай пЬ П'; пЬ --- розбит-
а' а' е
тя, відповідно, відрізків [а; Ь], [а; с],
[с; Ь]. Для кожного З цих розбиттів
побудуємо інтегральні суми функ
ції f на відрізках [а; Ь], [а; с], [с; Ь];
ІІІ суми скорочено позначимо через
"Ь "'с ",Ь' . О'
иа, �a' �e' ВІДПОВІДНО. СКІ.;1ЬКИ
Ь х функція f інтегровна на цих відріз
ках, то \;fc > О 36 > О, таке, що ос
кільки діаметри розбиттів d(П�),
а(п�), а(п�) < 6, то виконуються нерівності (див. (18), (19))
о
Рис.4
І ы С е г І ы є
І _. � < - І І( - � І < - 12 -- � <-
а з' а з' с З
(чому можна взяти одне і те саме f, для трьох різних інтетралів/].
Розбиття п� беремо таким, щоб d(П�) < 6, і щоб одна з точок ІІЬОГО
(З9)
241
розбиття збігалася з точкою е, тобто а = хо < хІ < ... < Xk =
= е < Xk+I < ... < Хn = Ь. Цьому розбиттю відповідає розбиття П�
відрізка [а; е] і розбиття п� відрізка [е; Ь]. Оскільки діаметр d(П�) <
< О, то і d(П�) < О, d(П�) < О. Тому виконуються нерівності (39).
Розділимо інтегральну суму E�, яка відповідає розбиттю п� відрізка
[а; Ь] на дві суми: суму E�, що відповідає відрізку [а; е] і суму E�, яка
відповідає відрізку [е; Ь]. Тоді E� = E� + E�, або E� - E� - E� =
= О. Отже, ІІ} + 12 - ІІ = ІІ] + 12 - І + E� - E� - E�I = (групуємо)
= IE�-I+II-E�+I2-E�1 :::; IE�-II+III-E�I+II2-E�1 < �+�+� = є,
тобто ІІІ + 12 - ІІ < Є. Оскільки число є довільне, то з останньої
нерівності випливає І = І І + 12.
3.2. Властивість лінійності інтеграла Рімана.
Теорема 1. Яхиіо фу'нхці.я Лх) інтегровна на [а; Ь] і е - стала,
то на 'Цьо.м.у відріз'К:у інтегровна фу'Н.'К:'Ці.я еЛх), nрu'Чо.м.у
ь ь
J ef(x)dx = е J f(x)dx, е = const.
(40)
а
а
Доведення. Коли е = о, то рівність (40) очевидна. Нехай е і= о.
Якщо функція f інтегровна на [а; Ь], то 'v є > О існує число о > о, таке,
що для будь-якого розбиття П, діаметр якого d(П) < О, виконується
неРІВНІСТЬ
n Ь
� Л�і)ДХі - J f(x)dx < 1:1·
а
(41)
Для розбиття П відрізка [а; Ь] інтегральна сума функції е f( з: )
n
має вигляд L: еЛ�і)ДХі, Враховуючи (41)
і=І
n Ь n Ь
L еЛ�і)ДХі - е J f(x)dx = ІсІ L Л�і)ДХі - J f(x)dx < є,
і=І а і=І а
242
n Ь
тобто L: СЛ�і)дХі - сІ J(x)dx < є при всіх розбиттях П, діаметр
і=l а
n
яких d(П) = гпах Аг, < Ь. Це означає, що З Ііт L СЛ�і)дХі =
тах �Xi-+O і=l .
Ь
= сІ f( З:). 3а теоремою п. 2.1 функція с J( х) інтегровна на [а; Ь] і
а
виконується рівність (40).
Теорема 2. Якшо ЛХ), g(x) - інтегровні фУ'li-к;'Ції 'Ііа відріз-к;у
[а; Ь], то 'Ііа 1�bO.мy відріз'К,у інтегроена ФУ'Іі'К,'Ці,я J( х) + g( х), nрu'Чо.му
ь ь ь
іи(х) + g(x))dx = j J(x)dx + j g(x)dx.
а
(42)
а
а
ь ь
Доведення. Позначимо 1/ = І J(x)dx, 19 = І g(x)dx. Оскільки
а а
функції і, 9 інтегровні на [а; Ь], то \;f є > О існує число Ь > О, таке,
що для будь-якого розбиття П відрізка [а; Ь], діаметр якого d(П) < Ь,
. .
виконуються неРІВНОСТІ
n Ь
L Л�і)дХі - j f(x)dx
і=l а
є
< -.
2'
є
< -. (43)
2
Для розбиття П відрізка [а, Ь] інтегральна сума функції ЛХ)+
n
+g(x) має вигляд L: (Л�і) + g(�i))LlXi, �i Е [Xi-l; Хі], і = 1, n. Врахо-
і=l
вуючи (43)
n
І)Л�і )+g(�i) )дз:і -1/-19
і=l
n
n
і=l
і=l
243
тобто \;f є > О, існує ЧИСІО Ь > О, таке, що для будь-якого розбиття
П, діаметр якого d(П) < Ь, виконується нерівність
n
�)Л�і) + У((і))дХі -- І! - 19 < є,
і=l
n Ь Ь
Це означає, що 3 Ііт L (Л�і) + Y(�i))ДXi = J ЛХ) + J у(х). За
max�xi---t°i=l а а
теоремою п. 2.1 функція f( х) + у( х) інтегровна на [а; Ь] і виконується
рівність (42).
3.3. Інтегрування нерівностей.
Теорема 1. Я-К;'ЩО фУ'li-К;1�і.я f( х) інтегровна 'Ііа [а; Ь], nР11:ЧО,м,у
ЛХ) � о, .r Е [а;Ь], то
ь
J f(x)dx � о. (44)
а
д Об едення. За умовою функція f( х) інтегровна на [а; Ь]. Тому
ь
J f(x)dx = J fdx = J fdx.
(45)
а
Візьмемо довільне розбиття П відрізка [а; Ь]. Якщо ЛХ) � о,
х Е [а, Ь], то М, = suр ЛХ) � о. З урахуванням цього верхня
Хі-І �X�Xi
n
інтегральна сума становить U(П, f) = L м.а«, � о. Тому J fdx =
і=l
= іпf U(П,f) � о. Звідси та з (45) випливає нерівність (44).
{п}
Теорема 2. Я'К,'ЩО ЛХ), у(х) -- інтегровні ФУЮ\,1�ії 'Ііа біdрізх:у
[а; Ь], і f(з.:) :::; у(х), з: Е [а; Ь], то
ь ь
J f(x)d.r ::; J g(х)dз.:.
( 46)
а
а
244
Доведення. Функція g(X) - ЛХ) -- інтегровна на [а; Ь] (див. те
ореми 1,2 п.3.2). причому g(x) - ЛХ) � о. Використовуючи влас-
Ь Ь
тивості (40), (42), (44), от�имаємо О � J(.q(x) - f(x))dx = J.q(x)dx-
а
а
ь
- J f(x)dx. 3 останньої нерівності випливає (46).
а
Якщо ЛХ), g(x) > о, х Е [а; Ь], то вказана властивість легко
ілюструється геометрично (рис. 5).
Оскільки ЛХ) � g(x), х Е [а; Ь], то площа криволінійної трапеціі
аА} ВІ Ь не більша від площі криволіній
ної трапеції аА2В2Ь.
Нагадаємо властивості точної ниж
ньої і точної верхньої граней (див.
розділ 1, п.l.8, (18)). Якщо множина
Р с Q с [т; М], то
у
а
о
х
inf Р � infQ, supP � supQ.
(47)
Рис.5
Теорема 3. Я'К:ЩО фУ'Н,'/'ї,'Ці.я f( х) інтегровна на відріз'К:у [а; Ь],
m � ЛХ) � !vI, х Е [а; Ь], і фу'Н,'К:'Ці.я cp(t), t Е [т; !vI] неперервна на
[т; М], то сцпсрпозиція фу'Н,'К:'Цій h(x) = ср(лх)), х Е [а; Ь] інтегровна
на [а; Ь].
Доееоення. Візьмемо Е > о. Функція ср рівномірно неперервна
на [т; М] [чому"}. Отже, існує {) > о, таке, що {) < Е і
І ср ( s) - ср (Т ) І < Е, V s, т, Is - r І � {) 1\ s, r Е [т, М]. ( 48)
3а умовою функція f інтегровна на [а; Ь], тому існує розбиття
П відрізка [а; Ь]: а = хо < хІ < ... < хn = Ь, таке, що для верхніх і
НИЖНІх інтегральних сум виконується неРІВНІСТЬ
U(П, f) - L(П, f) < {)2.
(49)
Нехай ті і М, мають той самий зміст, що і в (1). Оскільки ті �
-::; ЛХ) � Мі, х Е [Хі.-l; хі], то множина Е = {ЛХ) : Хі-І � х � хі} с
245
Звідси, враховуючи (41), т; = inf{;p(f(.1')) : ХІ-l ::; Х ::;,Хі} �
� inf{:p(t) : t Е [ті; АІі]} = :Р(.'», де s -. деяке ЧИС.10, з Е [ті; 1\;/і] (тут
ми ще врахували, що неперервна функція t.p на замкненому проміжку
[ті; АІі] досягає найменшого і набільшого значення (див. розділ 1,
п.3.7)). Аналогічно, А1і* = sup{t.p(f(x)) : Хі-І::; Х ::; Хі} ::; sup{t.p(t) :
t Е [ті; А1і]} = 'Р(т), r Е [ті; lVIJ Отже, y(s) ::; ті ::; Мі* S 'Р(т),
А1і* - т; ::; 'Р(т) - t.p(s), S,T Е [ті,Л;/і], Is - тl < Мі - ті,
s = s(i), т = т(і), і = 1,n.
(50)
Розділимо цілі числа 1, 2, ... ,n на дві множини: і Е А, якщо
М, - ті < О; і Е В, коли М, - ті � О. Якщо і Е А, то Мі - ті < О
і в (50) Is -- тІ < М; - ті < О, а тому з (48) випливає Мі* - т; S
::; 'Р(т) - 'Р(,с;) < є. Отже
(51)
Якщо і Е В, 1\1;* - т; ::; 11ІЦ 1-+ lт;1 ::; 2 sup :р(і) = К. Тому
m$t$M
АГ -- т * < К і Е В.
z z - ,
(52)
З означення множини В та 3 (49) випливає О L дх і = L О дх і S
іЕВ іЕВ
1l
< L (М, - Пlі)дХі ::; L (М, - ті)дХі = U(П, f) - L(П, f) < 02.
іЕВ і=1
Порівнюючи початок і кінець цієі нерівності, маємо L дХі < О. То
іЕВ
му, враховуючи (51), (52), інтегральні суми функції '�(x) можна оці-
нити у такий спосіб U(П,fz)·- L(П,h) = L (1'\11,* - m;)дХі -+ L (1\;1;*--
іЕА іЕlЗ
246
--тnДХі :::; є L: дхі + К L ilXi < Е(Ь'- а) + КЬ < Е(Ь - а + [{). Ви-
іЕА іЕП
ще ми скористались тим, шо й < г, Оскільки число г довільне. то з
попередньої нерівності випливає (див. теорема 3 п. 1.4), шо функція
h,(x) = <ри(х)) інтегровна на [а,Ь].
Теорема 4. Якииз фУ'Н,J;;'I�ії !(х), g(J:) інтегроені на [о.:Ь], то на
'Цьо.му віоріз"/'і,У і'Н,тС2РО(3'Н,а фУ'Н,J;;'Ці.я ЛХ) . g(.r).
ДО6сдс'Н,1і-Я. Приймемо :р(і) = і2. Тоді У(Л:Г)) = Р(х) і з по
передньої теореми випливає, що і2 -- інтегровна на [а; Ь], якшо f
_о. інтегровна. Тепер твердження теореми є наслідком- тотожності
4fg = (f + g)2 -- (f - g)2.
Теорема 5. Яклио фу'Н,кu,і.я !(х) і'Н,тС2РО6'Н,а на [а; Ь], то на 'ЦЬО
.му відріз-к;у і'Н,тС2РО6'Н,а фу'Н,ю�і.я І!( х) І, причомі)
ь ь
J f(x)dx :::; J 1f(:r}ldx.
(53)
а
а
Доведення. Розглянемо неперервну функцію :p(t) = Itl. За умо
вою функція t = ЛХ) інтегровна на [а; Ь], тому (теорема 3 цього пунк
ту) суперпозиція <р(Лх)) = IЛх)1 теж інтєгровна на [а; Ь]. За теоре
мою 2 цього самого пункту, з нерівностєи -1!(·г)l:::; Лх) :::; IЛх)1
ь ь ь
випливає - J lf(x)ldx :::; J !(x)dx :::; J l!(х)lах. тобто виконується
а
нерівність (53).
Теорема 6. ЯJ;;ЩО
l!(х)1 ::; АІ на [а; Ь], то
а
а
фУ'Н,J;;1�і.я f( х) z'Н,тС2рО(J'Н,а на [а; Ь] z .яJ;;ЩО
ь
J f(x)dx :::; lvJ(b - а).
(54)
а
ь
ДО6еdс'н,'Н,.я. Пише:\ІИ показали. шо J Jld;r' "= ""І(Ь - а), J.f =
(1
= COllst. Нерівність ІЛ l') І :::; JI еквіва.l('нтна такіЇІ -.\1:::;!( х) :::; J,[.
247
Якщо проінтегрувати всі частини цієї нерівності на відрізку [а; Ь], то
ь
враховуючи теорему 2, одержимо -М(Ь - а) :::; J f(x)dx :::; 1\1(Ь - а),
а
тобто виконується (54).
З.4. Середнє значення функції.
Теорема 1. Якиіо фУ'li-к;'Ці.я ЛХ) неперервна 'Ііа [а; Ь], то існие
точка с, а < е < Ь така, що
ь
J f(x)dx = Ле)(Ь - о).
(55)
а
Доведення: Неперервна на відрізку [а; Ь] функція ЛХ) досягає
на цьому відрізку найменше і найбільше значення (теорема Вейєр
штрасса), тобто існують точки ХІ, Х2 Е [а; Ь] такі, що
ь ь
Звідси, враховуючи теорему 2 п.3.3, маємо J mdx < J f(x)dx <
а а
ь
< J Mdx або
а
ь
rn(Ь - а) < J f(x)dx < М(Ь - а),
(56)
а
ь
тому m < b�a J f(x)dx sM.
а
Оскільки rn = ЛХІ), М = ЛХ2), то за теоремою про проміжне
ь
значення (теорема Больцано-Коші), для числа А = b�a J f(x)dx,
а
тn S А S М, існує точка С, е Е [хІ; Х2] С [а; Ь] і така, що А = Ле),
ь
тобто b�a J f(x)dx = Ле). Рівність (55) доведено.
а
248
ь
Значення функції Ле) = Ь�a J f(x)dx називають середнім зна-
а
ченням фУЮіщіі лх) на проміжку [а; Ь].
Формула (55) для невід'ємної на [а; Ь] функції f має простий гео
метричний зміст: площа криволінійної трапеції з основою [а; Ь], обме
женої графіком функції і, дорівнює площі прямокутника з основою
[а; Ь] довжини Ь - а і висотою довжини і(е) (рис.6).
У
М
: у=Лх)",,� :
Ле)
, '.'
, . , \: о', � , "
"", �����" ."
m
--f •• �
t � ,,:\.,-;,:-, ";-�" � .�
" .. " ". '. "
о
а
е
х
О
а'
Б
х
Рис.
6.
Рис.7.
Формула (56) геометрично означає, що площа криволінійної тра
пеції з основою [а; Ь], обмеженої графіком функції і, міститься між
. . . .
площами прямокутників з ТІЄЮ самою основою І висотами, що дорів-
нюють відповідно найменшому m і найбільшому М значенням функ
ції Лх), х Е [а; Ь] (рис.7).
§ 4. Визначений інтеграл із змінною верхньою
межею інтегрування. Існування первісної.
Формула Ньютона-Лейбніца
4.1. Неперервність і диференційовність визначеного ін
теграла із змінною верхньою межею. Нехай функція f( х) інте
гровна на [а; Ь]. Тоді за теоремою 8 вона інтегровна і на будь-якому
відрізку [а; х], де а � з: � Ь, тобто для будь-якого х Е [а; Ь] існує
249
ІНтеграл
х
J f(u)du�fF(x), х Е [а;Ь].
а
Ця функція називається інтегралом із змінною верхньою межею ін
тегрування.
Теорема. (а) Якиіо фУ'li-к;'Ці.я f інтегровна 'Ііа [а; Ь], то фУ'Іі-к;'Ці.я
х
Р(х) = J f(u)du рівномірно неперервна 'Ііа [а;Ь].
а
(6) Якшо фУ'Іі-К;1�і.я f неперервна в точці х, х Е [а; Ь], то фУ'Іі-К;1�і.я
F дифере'li'Ці'Й,оВ'liа 6 точці х і
Доведення. Функція лх) інтегровна на [а; Ь), тому вона обме
жена на цьому відрізку. Нехай IЛи)1 � ій, КО.,1И U Е [а; Ь). Якщо
а � s < t ::; Ь, то (теорема 2 п.3.1)
t s
Р(і) - F(s) = J f(u)du - J Ли)сІu =
а
а
(57)
s t s t
= J f(u)du + J f(u)du - J Лu)(lи = J Ли)сІи.
а s а s
Тому, враховуючи теорему 6 п. 3.3,
t
IР(і) -- F(s)1 = J f(u)du � 1vI(t - . .,).
s
Звідси випливає, що \;f Е > О нерівність IР(і) - F(s)1 < Е вико
нується \;f .5, t Е [а; Ь), Д.1Я яких It - sl < i�' Це означає, що фУНКІІія F
рівномірно неперf'рвна на [а; Ь).
250
Нехаи тепер функція f неперервна в точці х. Тоді \j є > О існує
таке 6 > О, що Д.-ІЯ всіх И Е [а; Ь], дЛЯ яких lu - .тl < 6, виконується
нерІВНІСТЬ
Іf(и) - Лх)1 < є.
(58)
Візьмемо х - 6 < s � х � t < х + 6, а ::; s < t � Ь. Рівність (57)
t
можна подати у вигляді F(t�=�(s) = t�s J f(u)dи. Точка х фіксова-
s
t
на, отож, ЛХ) теж фіксоване і тому (теорема 1 п.3.2) J f(х)dи =
s
t t
= ЛХ) J dи = Лх)(і - s), або ЛХ) = t�s J f(х)dи. Враховуючи ці
s s
співвідношення, а також теореми 2 п.3.2, 2 і 5 п.3.3 і нерівність
(58), отримаємо І F(t�=�(s) - Лх)1 = І t�s [ f(и)dи - t�s [ f(Х)dиl
= І t�s [f(Х)dиl = І t�s [(f(и) - f(Х))dиl < t�s [Іf(и) - f(х)ldи <
t
< t�s J єdи = t�s(t - s) = є. Отже,
s
І F(t) - F(s) І
t-s -ЛХ) <є, x-6<s�х�t<.т+6, a�s<t�b.
(59)
Якщо, наприклад, в нерівності (59) прийняти s = х, то одер
жимо І F(t�=�(x) - Лх)1 < є, з: < t < х + 6. Це означає, що існує
ііт F(t)=F(x) = ЛХ). Аналог-ічно доводиться, що ііт F(s)=F(x) =
t--+х+О t з: s--+x--o в з:
= ЛХ). Оскільки лівостороння і правостороння границі існують і
дорівнюють одна одній, то існує похідна Р'(х) = Ііт F(t)-F(x)
t--+x t-x
= ЛХ).
4.2. Існування первісної для неперервної функції. Тепер
, . . ..
ми можемо розв язати задачу про Існування первісної Д:ІЯ неперерв-
ноі функції.
251
Теорема 1. ЯК;ЩО фу'н:к;'Ці.я лх) неперерено на відріз,;;;у [а; Ь], то
х
на -н,ьо.му вона має переісщ) Р( х) = J f( и )du.
й
Доведення. Якщо функція лх) неперервна на відрізку [а; Ь], то
за теоремою 1 п. 2.2 вона інтегровна на [а; Ь]. 3 теореми попереднього
х
пункту випливає, що \;/х Е [а;Ь] існує похідна :х J f(u)du = лх). То-
й
х
му функція Р(;г) = J f( и )du є первісною для функції f( х) на відрізку
й
[а; Ь].
Операція інтегрування із змінною верхньою межею, яка засто
сована до неперервної функції, є операцією, оберненою до диферен
шювання:
F'(x) = (J і(u)аu) � = Лх), а S; х S; Ь,
- формула диференціювання визначеного інтеграла за верхньою ме
жею.
Теорема 2. Будь-.я,;;;а первісна фу-н,,;;;'Ціі Лх), неперервноі на
відріз';;;]/ [а; Ь], мае вИ2л.яд
х
J f(u)du + С, х Е [а; Ь],
й
С --- довільна константа.
х
Доведення: Ми показали, що функція Р(х) = J f(u)du, х Е [а; Ь]
а
є первісною функції Лх), х Е [а; Ь], а будь-яка інша її первісна може
відрізнятись від Р(х) лише на константу (див. розділ 6, § 1).
Отже: зв'язок між невизначеним і визначеним інтегралами ви
значається формулою
з:
J f(x)dx = J f(u)du + С, х Е [а;Ь], С = const.
й
252
4.3. Формула Ньютона-ЛеЙбніца.
Теорема 1. Н ехай фу'н:к;'Ці.я J( х) неперервна на відріз'к;У [а; Ь].
Я'к;1ЦО фУ'Н.'к;'Ці.я Ф( х)- .я'к;а-'Н.е6удь ЇЇ первісна на 'ЦЬОМУ відріЗЩІ, то
ь
J J(x)dx = Ф(Ь) - Ф(а). (60)
а
з:
Доведення. Візьмемо Р(х) = J J(u)du. Згідно із теоремою 1
а
п. 4.2 функція F є первісною для функції f на відрізку [а; Ь]. Отже, F
і Ф -- дві первісні однієї і тієї самої функції f на відрізку [а; Ь], тому
(див. розділ 6, § 1) Р(х) = Ф(х) + С, х Е [а; Ь], де С ---- певна конс-
з:
танта. Оскільки F(x) = J J(u)du, попереднє співвідношення можна
а
записати у ВИГЛЯДІ
з:
J J(u)du = Ф(х) + С, х Е [а; Ь].
(61 )
а
а
Якщо у (61) взяти х = а, одержимо J J(u)du = О = Ф(а) + С,
а
з:
або С = -Ф(а). Тому (61) можна записати у вигляді J J(u)du =
а
= Ф(х) - Ф(а). Якщо х = Ь, з цієї рівності випливає (60).
Для зручності користування цю формулу записують у вигляді
ь
J f(x)dx = Ф(х)l� = Ф(Ь) с... Ф(а).
а
3
J 4 І513 з5 (-_1)5 -1
Наприклад, х dx = - = -;:- .-- --- = 48�.
5 -·1 ,) 5 о
-1
253
Справедлива загальніша теорема.
Теорема 2. Я7'ОЩО ФУ'Н,7'Оці.я f інтегроена на [а; Ь] і має на ?.(,ьо
.му проміжт, первісно Ф (Ф'(х) = ЛХ), х Е [а: Ь]), то спроеедлиеа
фор.мула Ньютона-Лейбніца (60).
Доведення. Для цього розбиття П відрізка [а; Ь] виберемо точки
(і так, що Хі-І:::; (і :::; хі і Ф(Хі) - Ф(Хі-l) = (хі - Xi-I)Ф'((і) =
= (Хі - Хі-l )Л(і), і = 1, п, Це можливо за теоремою Лагранжа (див.
розділ 4, п. 1.3). Тоді, враховуючи, що Хо = а, Хn = Ь, маємо
n
n
і=l
і=l
ь
За теоремою п. 2.1 остання інтегральна сума прямує до J f(x)dx,
а
коли діаметр розбиття d(П) � о.
§ 5. Формули заміни змінної та інтегрування
частинами для визначеного Інтеграла
5.1. Інтегрування заміною змінної.
Теорема. Нехай фу'Н,,;;;чі.я ЛХ) неперервна на відріз7'ОУ [а; Ь], а
фу'Н,,;;;чі.я Х = <p(t) неперервна і мае непереренц nохід'Н,у на відріз,;;;у
[о,,в], nрuчо.му а = <р(о) :::; <p(t) :::; <р({3) = Ь дл.я t Е [о,{3]. Тоді
Ь (J
J f(x)dx = J f(<p(t))<p'(t)dt,
(62)
а
о
фор.мула заміни. зміннді дл.я визначеного інтеграпа.
Доведення. Неперервна на відрізку [а; Ь] функція ЛХ) має на
цьому відрізку первісну Ф(х) (теорема 1 п.4.2). Тому за формулою
Ньютона-Леибніца маємо
Ь
J f(x)dx = Ф(Ь) - Ф(а).
(63)
а
254
З того, що Ф(х) є первісною для функції ЛХ) на відрізку [а; Ь], випли
ває Ф'(х) = ЛХ), х Е [а; Ь]. Підставивши в останній рівності г = 'f'(t),
t Е [о; ,6], одержимо
ф'(х)lх=<р(t) = Ф'('f'(t)) = f('f'(t)), t Е [о; ,6]. (64)
Знайдемо похідну складної функції :tФ('f'(t)) = Ф'('f'(t))'f"(t) =
= (див.(64)) = f('f'(t))'f"(t). Це означає, що функція Ф('f'(t)) є однією
з первісних функції f('f'(t))'f"(t) на відрізку [о;,в]. За формулою
Ньютона-Леибніца
(3
J f('f'(t))'f"(t)dt = Ф('f'(,в)) - Ф('f'(о)) =
(65)
о
= ('f'(fЗ) = Ь, 'Р(о) = а) = Ф(Ь) - Ф(а).
Формула (62) є наслідком рівностей (63) і (65).
Нехай функція g(x) диференційовна на [а; Ь]. Якщо існує інтег
ь
рал J f( х )g' (х )dx, то приймемо, за означенням,
а
ь ь
J f(x)g'(x)dx = J f(x)dg(x).
а а
За допомогою цього означення (62) набирає вигляд
ь (3
J f(x)dx = J f('f'(t))d'f'(t).
а
о
ь
Отже, замінюючи змінну X='f'(t) в означеному інтегралі J f( х )dx,
а
необхідно всюди формально замінити х на �(t) і відповідно поміня-
ти межі інтегрування. (62) можна використовувати як зліва направо,
255
так і справа наліво. Однак на відміну від невизначеного інтеграла,
де в кінці обчислень потрібно повернутись до початкової змінної ін
тегрування, тут цього робити не потрібно, бо, як ми довели, числа,
які стоять в лівій і в правій частинах (62), однакові.
е 2
Приклад 1. Обчислити J ІПІ І dx.
1
Розв 'язання. Застосуємо (62) справа наліво (тут роль змінно;
t виконує х). Приймаємо t = Inx; тоді dt = d:; якщо х = 1, то
t = In 1 = О; якщо х = е, то t = In е = 1. Отже,
1е In 2 х 11 2 tЗІ1 1 з з 1
-dx = t dt = - = -(1 - О ) = -.
х 3 о 3 3
1 О
Можна, однак, діяти інакше: обчислити спочатку невизначений
інтеграл J Іп; І dx, а потім розглянути різницю його значень, .якшо
х = 1 і якщо х = е.
Для обчислення J Іп; І dx замінимо змінну за формулою t = In х.
Тоді dt = d: і J Іп; І dx = J t2dt = t; = Іп; І (беремо константу
е І 2 І з Іе IпЗ е IпЗ І
С = О). Тому J ..!!....Edx = ..!!....Е 1
І З 1 -з- - -з- з·
1
1
Приклад 2. Обчислити І = J "'\;І2 d.T .
..J2/2
Розв 'язання. Приймемо г = sin і. Тоді dx = cos tdt, t = arcsin х,
(} = arcsin V; = � і f3 = arcsin 1 = �. Отже,
тr/2 тr/2 тr/2
1 J 1 .- sin2 t 1 cos2 t 1 1 - sin2 t dt =
І = . 2 cos іаі = -.-2-dt = sl·n2 t
SIn t SIn t
тr/4 тr/4 тг /4
Iтr/2 7г 7г 7г
=(-ctgt--t) =---+1+-=1--.
тr /4 2 4 4
256
5.2. Інтегрування частинами.
Теорема. Я","ЩО ФУ1/,,,,"'Ції н(.с) і v(.r) неперерені разом із своімн
похідними и'(х), l"(X) 1/,0. оіuріз","у [o;bj, то
ь ь
j udv = lтl� - j іліи ,
(66)
а
а
фор,м,ула інтегрцеання частинами.
Доведення. Функція Ut' є первісною для функції (щ))' на [а; Ь].
Тому за формулою Ньютона-Лейбніца маємо
ь
j ( Иt' )' dx = l/"V І : .
(67)
а
Оскільки (НІ))' = l1'V + ии' = НІІ' + ии', то
Ь Ь Ь Ь
j(UI')'llJ' = j(Иl/ + VH')clx = j ші» + j іліи, (68)
а
а
а
а
Всі наведені інтеграли існують, бо підінтегральні функції непе-
ь Ь
рервні. Порівнявши (67), (68), одержимо рівність J Hclv + J ініи
а а
= u v І �, звідки і ВИП.1Иває (66).
1L
а
Приклад 1. Обчислити 1= ЛТ + 3) sin o.xdx.
о
Розв 'язання. Приймемо и = :с + 3, ар = sinaxdx, тоді du = dx,
v = J siIlon];r = ._!:о:ах (беремо константу С= О). Застосуємо фор-
1L
мулу інтегрування чаСТІІНЮШ: І = - X�3 cos от Ig + �. J cos o.xdx
о
= - !.�.� СОБ ш:I(� + si��,!: I(� = (;2 + �.
257
е
Приклад 2. Обчислити І = J In xd:r:.
1
Розв 'язання. Використовуючи (66), знаходимо
іе (и = In х ::::} du = dX) Іе іе
І = In xdx = х = ;т; In х - dx =
dv = dx ::::} t' = Х 1
І І
= е In е - Пп 1 - х І � = е - О - е + 1 = 1.
§ 6. Деякі застосування визначеного інтеграла
6.1. Загальні принципи. Розглянемо основні принципи за
стосування визначеного інтеграла, що лежать в основі розв'язування
задач механіки, фізики та інших галузей знань.
Нехай нас цікавить деяка величина Q, яка визначається як гра
ниця інтегральної суми. Ця величина зв'язана з деяким відрізком
[а; Ь] осі Ох і функцією ЛХ), визначеною і неперервною на [а; Ь]. Крім
цього, величина Q характеризується властивостями адитивності та
ЛІНlИНОСТl в малому.
1 О. Адитивність. Якщо поділити відрізок [а; Ь] точками поділу
а = Хо, ХІ, Х2,· .. , Хn-І, ХN = Ь на малі відрізки [Хі-І; хі] з довжиною
.6.Хі = Хі - Хі-І, (і = 1, n), то кожному з цих малих відрізків відпо
відає певне значення величини Q: .6.QI, .6.Q2, ... , .6.Qn. Величина Q
називається адитивною, якщо для довільного розбиття відрізка [а; Ь]
на .6.Хі справедлива рівність
n
(69)
20. Лінійність в малому. Нехай!'vІ довільно вибрана точ-
ка відрізка [а; Ь] і ЛІї Е [Хі-І; xJ Припустимо, шо величина .6.Qi,
відповідна .6.Хі, приблизно пропорцінна до довжини .6.Хі
258
Відношення ��: мало бу де ВІДРІЗНЯТИСЯ ВІД числа k: оскільки
ІСНУЄ Ііт �Qi = k за умови. шо �Xi довільно стягvється V точку
.6.х;-ю Хі' и и и
Мі. Кожній точці Мі відповідає певне значення коефіцієнта k, тобто
k = ЛМі), звідки
(70)
Покажемо, що коли шукана величина Q має властивості адитив
ності та лінійності в малому на [а; Ь], то її знаходження зводиться до
обчислення визначеного інтеграла.
Дійсно, розділяючи відрізок [а; Ь] на n Мд.;1ИХ відрізків довжиною
�Xi, внаслідок властивості 1 о маємо рівність (69); у межах кожного
малого відрізка �Xi величина �Qi задовольняє наближену рівність
(70)
Отже, для знаходження Q отримаємо наближений вираз
n
Q � L ЛМі)' �Xi.
і=l
(71)
Права частина в (71) є інтегральною сумою для функції ЛМ) на
[а; Ь]. Точність наближеної рівності (71) зростає із зменшенням роз
мірів �Xi.
Перейшовши до границі, одержимо
n Ь
Q = l��ЛМі)' �Xi = J f(M)dx,
z=l а
(72)
де л = тaX{�Xi}.
Вираз f(A1)dx називається едементом шуканої величини Q і поз
начається dQ.
6.2. Площа плоскої фігури. Нехай функція ЛХ) 2: О визначе
на і неперервна на відрізку [о; Ь]. Тоді площа криволінійної трапеції,
259
обмеженої зверху графіком функціі у = Лх). знизу --- відрізком [а; Ь]
осі Ох, з боків -- відрізками прямих з: = а, .С' = Ь виражається фор
мулою (див. геометричний: зміст визначеного інтеграла)
ь
S = J Лх)сі:l:.
(7З)
а
Зауваження 1. ЯКЩО лх) < О, то формула для обчислення
ПЛОЩІ має вигляд
Зауваження 2. ЯКЩО функція f( х) визначена І неперервна на
ь
[а; Ь] і змінює знак у скінченній кількості точок відрізка, то J f(x)dx
а
числово дорівнює алгебраічній сумі ПЛОЩ криволінійних трапецій,
утворених частинами графіка кривої у = Лх), відрізками осі Ох
і відрізками прямих: паралельних до осі Оу.
Приклад І, Обчислити площу фігури,
обмеженоі параболою у = х2 - Зх + 2, відріз
ком [О; З] осі Ох і відрізками прямих х = О,
х = З.
Розв 'язання. Шукана площа зображена
на рис.8. На відрізках [О; 1] і [2; З] функція
невід'ємна, а на відрізку [1; 2] вона недодат
ня. Отже, внаслідок зауваження 2 маємо
О
Рис.8
ь
S = - J f(x)dx.
(74)
а
3 :r
1 2 З
S = J (х2 - ЗJ' + 2)(1:1' - J (:1'2 -- З.1' + 2)сі.с' +- J (.е}. _. Зх + 2)dx.
() \ 2
Обчис.1ИВШИ інтеграли. отримаємо S = Ів\ кв. ОД.
260
у загальномц оиnад1\,У, Д.1Я обчислення площі плоскої фігури, об
меженої зверху графіком кривої У = У2(Х), знизу--- графіком кривої
У = УІ (х), використовують формулу
ь
5 = і[У2(Х) - Уl(х)]llх,
'---
абсциси точок перетину графіків функцій УІ (х), У2 (х), а
самі функції УІ (х), У2(Х) визначені і непе
рервні на [а; Ь].
Дійсно, площу шуканої фігури (заштри
хована на рис. 9) можна розглядати як різни
цю площі КРИВО.!1ініїІНОЇ трапеції, обмеженої
зверху графіком У = У2 (х), і площі криво
лінійної трапеції, обмеженої зверху графіком
У = УІ(Х)'
де а, Ь
У У=У2(Х)
-
І
І
: У=Уl (х) :
І І
а
ь
о
Рис.9
(75)
а
х
Приклад 2. Обчислити площу фігури, обмеженої параболою
У у=х2+1 У = х2 + 1 і прямою У = -2х + 1.
5
-2 -1
Рис. 10
Розв 'язання. Розв'язавши систему
{У = х2 + 1, u
знаидемо абсциси точок пе-
У = -2х + 1,
ретину цих графіків х = --2, х = О (рис. 10).
Площа фігури (див. формулу (75)) дорів
нює
х
о
5 = j [(-2х + 1) - (х2 + l)lllx = �KB.oд.
-2
Якщо рівняння границі плоскої області
задано в параметричній формі
{ .С = 'р(і),
t Е [о; д]
у = ф(t),
261
де функції <р(і), ф(t) визначені та неперервні на [а;,3], а ср(і) ди
ференційовна на [о:; ,В], то аналогом (73) є
{3
s = f Ф(t) . ср'(і)lIі. (76)
()
2 2
Приклад 3. Обчислити площу еліпса �2 + � = 1.
Розв 'язання. Можна знаити частину площі еліпса, яка лежить у
першій чверті у = %J а2 - х2, О s; х S; а і результат помножити на 4.
Отже,
іа ь V І х = а cos t І
s = 4 - а2 - х21Iх = . =
а dx = -аsш tdt
о
о �
4Ь f 2 2 f 1 - cos 2і
= - -;; а sill tdt = 4аЬ 2 аі = п аіз,
� о
Проте можна використати параметричне рівняння еліпса
{Х = acost,
у = bsin і,
t Е [О; 271-].
Тоді, застосувавши формулу (76), отримаємо
о � �
s = -4 f Ь sin t . а sin іlIі = 4аЬ f sin2 іlIі = 4аЬ f 1 - �os 2і аі = '!rab.
� о о
Зауважимо, що, використовуючи (76), потрібно пам'ятати, що
межі інтегрування (див. (73)) повязані між собою
а=<р(о), ь=:р(в).
262
Приклад 4. Визначити П.10ту під першою аркою циклоїди
{Х = a(t - віп г},
У = а(1- cost),
t Е [О: 27Г) (рис. 11).
Розв 'язання. Для обчислення використаємо (76). Оскільки
tp'(t)lIt = а(1 - cos t)lIt, то
2� 2п
S= j a2(1-соst)21It=а2 j(1-2соst+соs2t)lIt=
о о
2�
2 j ( 1 + cos 2і ) 2
= а 1 - 2cost + ----2-- аі = 37Га .
о
у
О
7Га
27Га х
Рис. 11.
О
р
Рис. 12.
Виведемо формулу для обчислення плоті плоскоі фігури у по
лярних координатах. Нехай маємо криволініянии сектор, обмежений
променями () = 0:, () = fJ і неперервною лінією р = р( ()) (рис. 12.). От
же, функція р(()) визначена і неперервна на відрізку [0:;,В). Розділимо
відрізок [о:;,в) довільно на n малих відрізків точками поділу
Отримаємо n малих криволінійних секторів площею /}.Si кожен, при
чому площа криволініиног-о сектора
263
Розглянемо і-ЇІ криволінійнии сектор ОАІ--І Аі. Вибравши довільно
точку лініі р = р(О) з полярним кутом у, Е [0'-1; Оі], замінимо площу
цього сектора наближено площею кругового сектора радіусом р( <.р і):
д5і � � . р2(<.рі) - ДОі, де ДОі = О, - Оі-І'
Таку заміну виконаємо для кожного з малих криволінійних сек
торів. Очевидно, що
1 n
5 � "2 L р2( <.рі) . ДОі.
і=]
(77)
Вираз праворуч - це інтегральна сума для неперервноі функ
ціі � р2 (О), а шукана величина 5 задовольняє умови 1 о, 20 пункту
1. Спрямувавши діаметр л поді .. 'ІУ відрізка [о:;,в] до нуля, отримаємо
формулу для обчислення площі в полярних координапиіх
(3
1 n 1 J
5 = Ііт - " р2(<.рі) . ДОі = - р2(О)llО.
��o2� 2
і=] Q
(78)
Приклад 5. Обчислити площу фігури, обмеженоі кардклдою
р = а(1 + cos О), О Е [О; 2ІТ] (рис. ІЗ).
у
в
2а
А
р
:М2
О
а
Xl
Х2
Хі--І
Хі
Ь
Х
Рис.
ІЗ.
Рис.
14.
Розв 'язання. Врахувавши симетрію фігури відноєно полярноі
осі і використовуючи формулу (78): маємо
п п
1 J 2 '2 2 J 2' З 2
5=2'"2 а (l-tсоsО) llО=а (1+2cosO+cos O)dO= "2ІТа.
О О
264
6.3. Довжина дуги кривої. Нехаи на плошині хОу крива
'-'
задана рівнянням у = лх). 3наІІДСМО довжину дуги АВ, яка від-
сікається від кривої відрізками вертикальних прямих х = а і х = Ь
(рис. 14).
'-'
Розділимо дугу АВ точками МІ, JVI2, ... , lVIi, .•• , А1n-1 на n
довільних частин. 3' єднавши сусідні точки, отримаємо ламану лінію,
'-'
вписану в дугу АВ, що складається з ланок l'vloiYlI, lVI1 А12, •.• ,
lVIi-ІМі, ... , Мп-І-Мп, (_МО = А, Мп = В). Позначивши довжину
кожної з ланок через 6.Li = IMi-1Міl, (і = 1, n), виразимо периметр
ЦІЄІ ламаної
n
(79)
Очевидно, що із зменшенням довжини кожноі ланки 6.Li сама
'-'
ламана лінія за формою наближаєтьсио дуги АВ.
Означення. Довжиною L дуги АВ називається границя, до якої
о. ••• •
прямує периметр вписаноі в цю дугу ламаноі, коли КІЛЬКІсть 11 ланок
необмежено зростає, а довжина найбільшої з ланок ПрЯМУЄ до нуля
n
L = Ііт L сл.;
тах LCI.Li-+О
і=І
(80)
Припускаємо, що границя (80) ІСНУЄ і не залежить ВІд вибору
вписаних ламаних. Криві, для яких границя (80) існує, називають
спрямлюваними.
Нехай функція лх) неперервна і диференційовна на [а; Ь]. Пока
жемо, що довжина дуги обчислюється за формулою
ь
L = J Jl + (J'(x))2dx.
(81)
а
265
де Уі - Уі-] = ЛХі) - ЛХі-1 ).
Застосувавши формулу Лагранжа Д.1Я [:[.і-1; хі], отримаємо
де Хі-] < � < Хі. Отже,
де вважається, що Хі- Хі-І;:::: О.
Позначивши дХі = Хі - Хі-І, одержимо вираз для периметра
ламаної
n
n
і; = L сл; = L VI + и/(�i))2ДXi'
і=1 і=1
(82)
Оскільки довжина дуги кривоі задовольняє умови 1 о, 20 п. 6.1,
то перейшовши до границі, коли шах дLі -+ О, отримаємо вираз (81):
n Ь
L= Іігп Ln= Іігп L Jl+(f/(�іW·ДХі=JJl+(f/(х))2llХ.
тах сл., -+0 тах сл; -+0
і=] а
Приклад 1. Обчислити довжину дуги ланцюговоі лініі У = chx
на відрізку [О; 1].
Розв 'язання. Оскі.1ЬКИ у/ = sllx, 1 + (у/)2 = 1 + S}12X = ch2x, то,
застосувавши фОР�ІУЛУ (81), одержимо
1
L = J chxllx = shxl� = sIll � 1,17.
о
Нехай крива L задана у парамстричній формі
{ .Г = .р(і), t Е [о; ,3],
.lJ = ':':(і),
266
де функції "р (і), 11' (і) неперервні і диференціиовні на [(}; ,3], причому
<р'(і) =F о.
dy 1,'.' (і) , .
Враховуючи, шо d� = �'(O' (іх = 'Р (t)dt, І ВИКОРИСТОВУЮЧИ (81),
отримаємо формулу д .. 1Я обчислення довжини дуги П.10СКОЇ кривої
{:J
L = J V(<p'(t))2 + (1/J'(t))2dt
(83)
о
(причому а = <р(а), Ь = <р({3)).
а
Приклад 2. ОБЧИС.1ИТИ довжину дуги
астроіди
х = acus3 t, у = аsіп3 і. t Е [о; 271-].
у
-а
Розв 'язання. Оскільки крива задана
у параметричній формі, то, знайшовши по
ХІДНІ
-а
Рис. 15
dy . 2
·-3а cos2 t sin t'dt = 3а SIll t cos t
використовуючи формулу (83), та враховуючи симетрію кривої
(рис. 15), маємо
� п
2 2
L = 4· J V9a2 сов" t siIl2 t + 9а2 sin'" t СОБ2 tdt = 12а J СОБ t sin tdt = 6а.
а а
якшо крива L просторова і сnр.я.м.л:юваuа, ТО, застосовуючи ана
логічні міркування, як і під час виведення (81), отримаємо вираз для
- .. -
довжини дуги просторової кривоі, заданоі nара.меmрu·чuо
{ з: = у(і),
У = lЬ(і),
z = x(t).
t Е (о; .О)
267
а
L = j V(<p'(t))2 + (ф'(t))2 + Сх'(і))21Iі.
(84)
о
Приклад 3. Обчислити довжину першого витка гвинтової ліні]
х = а cos і, У = а sin і, z = ат і.
Розв 'язання. Оскільки йдеться про перший виток, то t Е [О; 271-].
Застосовуючи формулу (84) та попередньо знайшовши похідні
lIх .
- = -аSlпt
аі '
dy
- = acost
lit '
liz
dt = ат,
маємо
2п 2п
L = j Va2 sіп2 t + а2 cos2 t + a2m2dt = а] VI + т21Iі = 27raVI + т2.
о о
Нехай плоска крива задана в полярних координатах р = р(О),
О Е [о:; ,В]. Цю криву можна вважати заданою параметрично, прий
нявши за параметр о. Враховуючи формули переходу
х = р( О) cos О, у = р( О) sin О
і використовуючи формулу (83), отримаємо вираз довжини дуги в
полярних коордннатоа:
іЗ
L = j V(p')2 + р21IО,
(85)
Q
, _ dp
де р - dO.
Приклад 4. Обчислити довжину дуги кардіоїди
p=a(I+cosO), OE[0;27r].
268
Розв 'язання. Оскільки рІ = -а sin О, то за (85) маємо
п п
L = 2 J Ja2 sin2 О + а2(1 + cosO)2dO = 4а J cos �llO = 8а.
о о
6.4. Обчислення об'єму тіла за відомим поперечним пе
рерізом. Нехай відомі площі перерізів тіла Т площинами, перпенди
кулярними до осі Ох. Такі перерізи називаємо поперечними (рис. 16).
Площа поперечного перерізу 5
визначається абсцисою Х: 5 = 5(х).
Розділимо відрізок [а; Ь] довільно на
n частин точками
, Х
Через точки поділу проведемо
Рис. 16 площини, перпендикулярні до осі Ох.
Об'єм елементарного шару на відрізку [Хі-І; Хі] (і = 1, n) позначимо
через 6.{)і. Отже, об'єм V тіла Т дорівнює
Замінимо елементарний шар прямим циліндром висотою 6.х і
Хі - Хі-І, а за основу циліндра приймемо площу поперечного пе
рерізу тіла, відповідно до абсциси �i, де Хі-І ::; �i ::; Хі·
Отже, 6.0; � 5(�i) . 6.Хі і
n
V � L 5(�i) . 6..1:;.
і=1
(86)
Вираз праворуч у (86) є інтегральною сумою Д.1Я функції 5(.1:).
Перейшовши до границі, коли /\ --t О, одержимо ФоРхІУЛУ для обчиє-
269
лення об'єму тіла Т
ь
V = Іігп t S(�i)· �Xi = J S(x)llx.
>'-+0
і=l а
(87)
2 2 2
Приклад. Обчислити об'єм еліпсоїда :2 + � + �2 = 1.
Розв 'язання. Перетинаючи еліпсоїд площиною х = h (-а < h < а),
в перерізі отримаємо е.ПІПс
Площа еліпса дорівнює (див. приклад З п.6.2)
S(h) = 7ГЬс (1- ::).
ІДа
Застосувавши формулу (87), одержимо вираз для об'єму еліпсо-
Зокрема, якщо а = Ь = с = R, то маємо кулю, об'єм якої, як
. V 4 R3
ВІДОМО, = з7Г .
у
Рис. 17
6.5. Об'єм тіла обертання. Не
хай криволінійна трапеція, обмежена
графіком функції у = ЛХ), х Е [а; Ь],
обертається навколо осі Ох (рис. 17).
Очевидно, що об'єм тіла обертан
ня можна знайти за допомогою мі р
кувань, наведених в п. 6.4. Дійсно, в
перерізі маємо круг 3 раДІУСОМ у
= ЛХ), отже, S(x) = п . и(х))2
270
ь
v=7Г j(f(x))2dX.
(88)
а
Зауваження. ЯКЩО криволінійна трапеція лежить над ВІСсю
Оу, х = ср(у), у Е [с; d], то об'єм тіла обертання навколо осі Оу
знаходимо за формулою
d
Vy = 7г j(cp(y))2dY.
с
(89)
Приклад. Знайти об'єм тіла, утвореного обертанням параБОЛІІ
у2 = х навколо осі Ох, х Е [О; h].
Розв 'язання. Використовуючи формулу (88), маємо
jh 7Гh2
V= xdx= т.
о
6.6. Площа поверхні обертання. Нехай поверхня утворена
'-' �
обертанням дуги АВ кривоі у = Лх), х Е [а; Ь] навколо осі Ох. Фун-
кція Лх) неперервна і диференційовна на [а; bJ.2,f(x) ? о. Розглянемо
довільну точку М(х; у), яка лежить на дузі АВ.
"""
Довжина дуги АМ є функцією від х
х
l(х) = J J1 + (f'(x))2dx.
(90)
а
причому функцією зростаючою, О :::; 1 :::; L, де L --- довжина дуги
'-"
АВ.
Отже, існує обернена неперервна функція з; = :г(l), але і у =
= лх) = у(х(l)) -- неперервна функція.
271
О . і( ) { .1: = х(і).
тже, функція з: може бути задана паРЮ,ІСТРИ'ІНО (і)'
- ." У = У .
--
Розділимо дугу АВ точками А = -\10' ",ІІ, .11.12,"" ;1-Іn-1, М; = В
на n частинних дуг. Поверхня обертання складається з частинних
поверхонь, кожна з яких наближено може бути замінсна бічною по
верхнею зрізаного конуса 56,к, = 27Г Пт, де т --,- твірна конуса (дов
жина хорди Ali-I�Hi (рис. 18)).
Оскільки m � діі, R = Уі = Y(€i).
Хі-l < �i < ХІ, ТО д5і � 27Г' Y(�i)c.ii,
а площа всієі поверхні обертання S;J'
у
х
наближено дорівнює
n
Рис. 18
з; � L 27Г . Y(�i) . діі.
і=l
Переишовши до границі, коли тах діі -t О, одержимо
n L
з, = lim L 27Г . Y(�i)дii = 27Г J y(l)(ll.
тах �li-НJ .
1=1 О
(91)
Із (90) маємо, що dl = Jl + (f'(x))2dx. Очевидно, що відріз
ку [О; L] відповідає відрізок [а: bj, а у(l) = Лх). Отже. отримаємо
шукану фОРМУ�'Іу
ь
з. = 27Г f f(x)J!+Tl'(x))2dJ".
(92)
а
Приклад 1. Знайти площу поверхні обертання синусоїди У
= sinx навколо осі 0.1:, .r Е [О; її].
Розв 'язання. За (92) маємо
п
511 О = 27Т J sinxJl + cos2 J"(JJ' = І �OS .1',= t It І =
. . - SIn .1'( J' = (
о
272
І
= 27Г J Jl -+- t2dt = 27.( J2 -+- ln(l -+- V2)).
-І
Якщо зру-чно використовувати параметричне задання кривоі
{Х = ;p(t),
У = Ф(t),
t Е [а; ,8], (див. п.6.3),
площа поверхні обертання обчислюється за формулою
Г�-- іЗ
і в.: = 27. J 1jj(t) . V('P'(t))2 -+- (1j,'(t))2dt.
'<; -- а
(93)
Приклад 2. Знайти площу поверхні обертання півкола у =
= .JIi2�;;2 навколо осі Ох.
. {х = R cos t,
Розв 'язання. Параметричне подання півкола R . t t Е
у= SIll,
[О; 7Г]. Звідки
х' = - R sill і;
н' = R cost
tJ ,
J(X')2 -+- (y')2dt = Rdt.
п
Sпд = 27. JR. sіпt . Rdt = 27ГR2( - cos t)l; = 47ГR2.
О
6.7. Знаходження статичних моменттв л центра маси
криво г, СтаТИЧНИ:\1 моментом К матєріальноі точки масою ІН від
носно деякої осі називається добуток маси m точки на іі відстань 6
до ОСІ
273
у
с.::»:»
К = тд,
Визначимо статичний момент
Кх відносно осі Ох мас, розподіде
них вздовж деякої плоскоі кривої АВ
(рис. 19).
Припустимо, що крива однорідна,
тобто її лінійна густина т (маса, що
припадає на одиницю довжини) -
'-'"
стала. Виділимо е-лемент діі дуги АВ, маса цього елемента дорівнює
дті = Т· tlk
Виберемо точку �i Е [Хі-І; хі], тоді відстань елемента діі до
осі Ох буде Y(�i), а статичний момент цього елемента ДКі = т .
діі· у. Підсумовуючи ці елементарні статичні моменти і здійснивши
граничний перехід (див. попередній пункт), отримаємо
А
о
а
х
Рис. 19
L
КХ = J Tydl,
о
або
ь
к; = т J f(x)Jl + (f'(x))2dx.
(94)
а
Аналогічно виражається і момент відносно осі Оу
ь
Ку = т J xJl + (f'{x))2dx.
(95)
а
Статичні моменти кривої дають змогу визначити положення 11
центра мас с{хс; Ус). Центр мас-- це така точка, ЩО якби в ній
.0 ••
зосередити всю масу m кривоі, то момент ЦІЄІ маси ВІдносно ОСІ до-
рівнював би моменту кривої щодо цієї осі
274
ЗВІДКИ
Ку к,
хс = -, Ус =
m m
(96)
де Кх, Ку визначаються за (94), (95), а маса m кривої дорівнює
L Ь
m = І J dl = І J Jl + (f'(x))2dx.
о а
(97)
Із формули т· ус = ИХ отримаємо цікавий геометричний наслі
док. Дійсно, маємо
L L
І . J dl . ус = І J ydl.
о о
Поділивши на І і помноживши обидві частини рівності на 27., одер
жимо
L L
27.Ус . J dl = 27Г J ydl.
о о
(98)
Права частина рівності (98) це площа Sx поверхні, утвореної
обертанням кривої АВ, у лівій частині вираз 27ГУс означає довжину
кола, описаного центром мас кривої під час її обертання навколо осі
L
Ох, а J dl .--- довжина цієї кривої.
о
Рівність (98) виражає зміст теореми Гульдина. n.lюща nоверх-
ні, ymBope,noї під 'Час обертання криеоі наекспо осі, Л'/'І,а ЇЇ не nере
тіінає, доріенюе довжu,nі дуги ціеі крнвоі, помноженій 'па довжu,nу
'/'І, о ла, описаного центром мас С �iєi кривоі.
Ця теорема дає змогу встановити ординату ус центра мас кри
вої, якщо відомі її довжина і площа описаної нею поверхні обертання.
Приклад. Знайти координати центра мас однорідного (І =
= const) півкола у = �R2 - х2.
275
РОЗб 'язання. Внаслідок симетрії хс = О. Обчислимо [{.с, ви
користавши параметричне представлення півкола (див. приклад 2
п.6.6):
71"
к, = �I J R2 sin tdt = 2R2/.
о
Маса півкола дорівнює m = 'YrrR. Отже, за (96) маємо
Ус =
'У7Г R 7г
Цей самий результат отримаємо за теоремою Гульдина. Дійсно,
площа поверхні обертання 5п.о. = 4rrR2 (див. приклад ІЗ), а довжина
дуги півкола 7г R.
Отже, із (98) маємо
4rrR2
УС = 27Г' rrR
2R
7г
§ 7 .Невласні інтеграли
7.1. Поняття невласного інтеграла. Побудова інтеграла
Рімана (див. § 1 2) здійснювалась на замкненому (а отже, скін-чен
ному) проміжку за припущення, що функція є обмеженою. Якщо
ж функція необмежена або проміжок інтегрування нескін-ченний, то
необхідні певні узагальнення поняття інтеграла. Ці узагальнення
назвали невласними інтегралами, на відміну від інтеграла Рімана,
який називають власним. Узагальнення поняття інтєграла для нес-
. .. .
кінченного ПРОМІЖКУ Інтегрування називають невласним Інтегралом
першого роду, а для необмеженої функції -- невласним інтегралом
другого роду.
Перейдемо до РО3Г.1ЯДУ цих інтєгралів.
276
7.2. Невласні інтеграли першого роду. Узага�1ЬНИТИ ПОНЯТ-
. . . . .
тя ІНтеграла можна на таю три випадки ПрОМІЖЮВ Інтегрування:
1) напівнескінченний проміжок а :::; .т < ас;
2) напівнескінчєннии проміжок - оо < х :::; Ь;
3) нескінченний проміжок (вся вісь O;r) -оо < х < оо.
Детально розглянемо перший: випадок. Нехай функція f(;r) ви
значена на напівнескінченному проміжку а :::; х < оо і Д.'ІЯ довільного
ТJ, але такого, що а < ТІ < оо, існує інтєграл Рімана
1J
I(ТJ) = J f(x)dx.
а
Означення. Якщо існує скінченна границя
1J
Ііт jf(x)dx,
1J---++oo
а
. .
то цю границю називають невласним інтегралом першого роду ВІД
функції f (на проміжку [а, +(0)) і позначають так
+::ю
J лх)сіх.
а
Отже, за означенням,
+= 1J
j f(x)dx = Ііт J лх)с1х.
1J---++=
(99)
а
а
+=
У такому разі кажуть, шо невласний інтеграл J Лх)(lх існце, або є
а
збіжним.
2ї7
Звернемо увагу читача, що далі ми, як і автори всіх без винятку
підру-чників, будемо використовувати і символ (99), і назву "невлас
ний інтеграл" також якщо скінченноі границі в (99) не існує, під
креслюю-чи, що тоді невдасний інтеграл не існує (є розбіжним).
Аналогі-чно визна-чається невласний інтеграл на проміжку -оо <
< х � Ь:
ь ь
J f(x)dx = Ііт j f(x)dx.
t-+-oo
-оо t
(100)
Якщо функція f визна-чена на інтервалі -оо < х < оо, і при
деякому довільному виборі то-чки с є (-оо; +(0) існують невласні ін-
с +00
теграли J f(x)dx (в сенсі (100)) J f(x)dx (в сенсі (99)), то, за
-оо
озна-ченням,
с
+00 с 7) с +00
jf(x)dx�f Ііт ff(x)dx+ Ііт ff(x)dx =jf(X)dx+jf(X)dx. (101)
t-+-oo І' 7}-++ОС І'
-оо t с -оо с
Зауваже'Н,'Н,.я 1. Якщо для підінтегральної функції існує первісна
F(x), то співвідношення (99), (100) і (101) можна записати так
+00
j f(х)dз.: = Ііт F(1]) - F(a);
7}-++0О
(99')
а
ь
J f(x)dx = F(b) - tE�� F(t);
( 100')
-оо
+00
j f(x)dx = Ііт F(1]) - Ііт F(t).
7}-++0О t-+--oo
(101')
-оо
278
+=
П Р U • J хЬ
риклад 1. озглянемо невласнии інтеграл І +х2 •
-оо
Розе'язання. Оскі.1ЬКИ існує первісна F(x) = tln(1 + х2). то
згідно із співвідношенням (101') маємо
+ех>
J
;rdx
---
1+ х2
-ех>
Перша границя у правій частині (друга також) дорівнює нескін
-ченності. Отже, невласний інтеграл розбіжний.
3ауваже1і1і-Я 2. Якщо збіжним є інтеграл по напівнескінченному
проміжку а ::; х < +00, то збіжним бу де і інтеграл по напівнескін
ченному проміжку а] ::; х < +00, де а < аl < ТJ < оо. Це є наслідком
о-чевидного співвідношення (див. п. З.l розділу 7)
1J а 1 1/
J f(x)dx = J f(x)dx + J f(x)dx,
(102)
а
а
у якому перший інтеграл правої частини є деякою сталою, незалеж
ною ВІД 'fl.
Тому, якщо існує границя інтеграла, що стоїть в лівій частині
рівності (102), за умови '/ --+ +00, то повинна існувати за цієї самої
умови і границя другого інтеграла у правій частині (102).
Розглянемо ще кілька прикладів на дослідження збіжності нев-
. .
ласних інтеграшв першого роду.
+=
Приклад 2. J �:' а > о.
а
Розв 'язання. Первісна підінтегральної функції F( х) = Іп ,є. Тоді,
згідно з (99')
Ііт Іп л -Іпа = +00,
І}--++ОО
а
279
отже, інтеграл розбіжний.
+00
Приклад 3. J :�, а =І- 1, а > о.
а
Розв 'язання. У такому разі первісна F( х )
шення (99') запишеться так
стиввідно-
+00
J dx
хо
1]1-0 а1-0
Ііт -----
1}--++ОО 1 - а 1 - а
а
Залежно від значень а будемо мати:
о > 1, тоді 1 - а < о;
+00
J dx а1-а
- = -- - інтеграл збіжний.
хо а-І
а
а < 1, тоді 1 - а > о;
+00
J dx . . v
- = +00 -lнтеграл розбіжний.
ХО
а
Результати прикладів 2 і 3 можна об'єднати
якщо а > 1, то
+00
J dx . v • • а1-о
- збіжний 1 дорівнює --;
з:" 1- а
а
(103)
якщо а � 1 то
+00
J dx . "
- розбіжнии,
хО
а
Розглянутий інтеграл часто використовується як еталон під час
застосування ознаки порівняння для дослідження збіжності невлас-
. .
них інтєгралів першого роду.
+00
П 4 J dx
риклад. 1 +х2 .
-()С
280
Розв 'язиння. Первісна для підінтегральної функції Р( х )=arctg х.
Використаємо співвідношення (1 О 1')
+00
J _d_X_2 = Ііт arctg 11 - Ііт arctg t = � -
1 + х 1)-++00 t-+-oo 2
(- ;) = 7Г.
-=
Отже, інтеграл збіжний і дорівнює 7Г.
Варто підкреслити, що значення інтеграла в цьому прикладі до
рівнює площі фігури, обмеженої зверху графіком функції у = І)х2,
а знизу віссю Ох (див. рис.20).
-3
-1
1
3 х
Рис. 20
7.3. Критерії збіжності невласного ІНтеграла першого
роду.
1 О. Критерій Коті. Для збіжності невласного інтеграла (99)
необхідно й достатньо, щоб для довільного як завгодно малого Е > О
можна було вказати таке М > а, що для довільних ТІ' > м і ТІ" > м
бу де справджуватися нерівність
1)"
J f(x)dx < Е.
1)'
Неважко встановити, що ця нерівність виражає критерій Коші ієну-
1)
вання границі на нескінченності для функції 1(-'7) = J f(x)dx (див.
а
п. 1.4 з розділу 2).
281
Дійсно, оскільки
"
п
J J(x)dx = l(т/,) - 1(т/),
т}'
то це означає, що існує такий окіл И( +00, �vI) нескінченно віддаленої
точки, що як тільки тІ' і тІ" потрапляють в цей окіл, різниця значень
функції l(т/') - 1(т/) потрапляє в є-окіл НУ.'Ія.
20. Ознака порівняння. Нехай на проміжку а � з: < +00 вико
нується нерівність
IЛх)1 s; <р(х), <р(х) � О.
(104)
ех>
Якщо інтеграл J <p(x)dx збіжний, то збіжним буде і інтеграл
а
ех> ех>
J IЛх)1 dx, а отже, і інтеграл J J(x)dx, причому цеї! останній інтег-
а а
рм називають у такому разі абсолютно збіжним.
ех>
Доведення. Припустимо, що інтеграл J <p(x)dx збіжний. Згідно
а
з критерієм Коші для 'v Е > О, 3М > а, шо для довільних Т7' і т/'
більших М справедлива нерівність
т}"
J <p(x)dx < Е.
Т}'
(105)
Враховуючи (104), (105) і правило інтегрування нерівностеи (див.
п. З.4 цього розділу), одержуємо
1]" ,," '1"
J J(x)dx <.! lJ(x)ld-f < .f :p(.r)dx < е.
1/'
ТІ'
л'
282
А це ІІ означає, що невласні інтеграли від функції лх) і від її модуля
є збіжними.
Зацеаження 1. Якщо нерівність (104) несправедлива, то може
трапитись, що невласний інтеграл від модуля функції розбіжний, але
DC
інтеграл від самоі функціі збіжний. Тоді інтеграл J л х )dx нази-
а
вають умовно збіжним.
3ауваже"н'"н',я 2. Якщо лх) > О, то IЛх)1 = Лх) і нерівність (104)
запишеться так
Лх) � <р(х).
(104')
Сформулюємо словами ознаку ПОРІВняння для цього випадку:
якщо для двох додатних на проміжку інтегрування функцій ви ко
оо
нується нерівність (104'), то збіжність невласного інтеграла J <р( х )dx
а
ос
забезпечує збіжність невласного інтеграла J л х )dx. Очевидно, що
а
оо
розбіжність невласного інтеграла J л х )dx зумовлює розбіжність не-
а
оо
власного інтеграла J <р( х )dx.
а
Ознаку порівняння для додатних функцій можна сформулювати
за допомогою границі Їх відношення, а саме: якщо д.;1Я двох додатних
на проміжку інтегрування функцій Лх) і у(х) справедливе співвід
ношення
Іігп Лх) = А
х-.++ос<р(х) ,
о < А < оо,
(105')
+=
то збіжність одного з інтегралів J Л з: )d.r,
+=
J у(:х; )dx забезпечує
а а
збіжність другого, а розбіжність одного з них зумовлює розбіжність
другого.
Доведення. 3 означення границі для довільного додатного Є < А
знаидеться таке М (11 < 1\1 < + оо ), що Д.ІЯ АІ < з: < + оо бу де
283
виконуватись нерІВНІСТЬ
IЛХ)-АI<є.
ср(х)
Опускаючи символ модуля і домножуючи всі члени нерівностей
на у(Х) > О, одержимо
(А - є)ср(х) < ЛХ) < (А + є)ср(х), М < х < оо.
(106)
+ОС>
Нехай інтеграл J cp(x)dx є збіжним. На основі зауваження 2
а
+ОС>
до п. 7.2 збіжним буде також інтеграл J cp(x)dx, а, отже, і інтеграл
м
+ОС>
J (А+є)ср(х)dх. Тоді з нерівності (106) випливає збіжність інтегра
м
+ОС> +ОС>
ла J f(x)dx, а, отже, і збіжність інтеграла J f(x)dx, оскільки він
м а
М
відрізняється від попереднього на сталу J f( х )dx.
а
+ОС>
Пропонуємо читачам довести розбіжність інтеграла J ср(х )dx
а
+ОС>
за умови розбіжності інтеграла J f(x)dx.
а
+ОС>
Приклад 1. Дослідити на збіжність інтеграл J х2(:�еж).
1
Р' О . 1 11< u
озв язання. СКІЛЬКИ х2(І+е"') < х2, _ х < оо, а нев.:'Іа.СНИИ
+ОС>
інтеграл J �� є збіжним (див. (103)), то збіжним є і досліджуваний
1
невлаСНИИІнтеграл.
Приклад 2. Дослідити на збіжність невласний інтеграл
+ОС>
f 3х + 2 _·х 1
---е (Т.
х
284
Розе 'язоння. Приймемо е-х = <р(х), 3х:2є-х = лх) 1 скористає
мось ознакою (105')
Іігп лх) = Іігп Зх + 2 = Іігп (з + �) = з.
x---t+= <р( х) x---t+oc х x---t+ou х
Але інтеграл
+00 оо
J <p(x)dx = J e-xdx = Іітп (-е-'7) + є-І
1)---t+=
І І
-І
=е
+=
збіжний. Тому збіжним є і нев.;ІаСНИЙ інтеграл J 3X:2e-xdx.
І
7.4. Невласні інтеграли другого роду. Узагальнення ін
теграла Рімана, якщо підінтегральна функція є необмеженою, нази
вають невласним інтегралом другого роду. Розрізняють три основні
випадки, коли:
1) f( х), а � х < Ь, необмежена в околі точки Ь;
2) ЛХ), а < х � Ь, необмежена в околі точки а;
з) ЛХ), х Е [а; Ь], х -# с, а < с < Ь, необмежена в околі точки с.
Вказані точки іноді називають особливими точками інтеграла.
Нехай функція f( х) є необмеженою в околі точки Ь, але інтег-
ровна за Ріманом на будь-якому проміжку [а; Ь - 1]], де 1] > О, тобто
існує функція
Ь-1)
1(1]) = J f(x)dx.
а
Якщо існує скінченна границя функції 1( rz) за умови ТІ ---+ О, то її
називають невласним інтегралом другого роду і позначають таким
самим символом, як і звичайнии інтеграл Рімана
Ь Ь-ц
J f(.r)d.r = Іігп J f(.l:)d.r.
ТI---t+o
(107)
а
а
285
Якщо скінченноі границі у правій частині (107) не існує, то нев
ласнии інтеграл називають розбіжним.
Аналогічно розглядається випадок, коли функція f( х) необме-
. -.
жена в ОКОЛІ нижньої межі а
ь ь
j f(x)dx = ііт j f(x)dx.
1)---t+О
а а+1)
(108)
Якщо функція ЛХ) необмежена в околі точки еЕ (а; Ь), ненласнии
інтеграл подається як сума невласних інтегралів типу (107) і (108)
ь с Ь
Іл х )dx = Іл х )dx + Іл х )dx = ііт
р р р 1)І-НО
С-1)} Ь
jf(x)dx+ ;��O jf(X)d�. (109)
)1 "
{
. і
а
а
с
а
у такому разі інтеграл вважається збіжним, якщо в (109) існують
обидві скінченні границі (у яких Тl1 і Тl2 прямують ДО нуля незалеж
но). Якщо ж хоча б одна з границь не існує, то інтеграл вважається
розбіжним.
3ауваже'Н,'Н,.я 1. Якщо для підінтегральноі функціі існує первісна
Р(х), то співвідношення (107), (108) і (109) запишуться ВІДПОВІДНО
так:
ь
j f(x)dx = ііт Р(Ь - "7) - Р(а);
]---t+О .
(107')
а
ь
j f(x)dx = Р(Ь) - ііт Р(а + "7);
1)---t+О
(108')
а
ь
j f(x)dx = Іітп Р(е - Тl1) - Ііт Р(с + 112) + Р(Ь) - Р(а). (109')
1)1 �+О 1)2---t+О
а
286
ь
Приклад 1. Дослідити на збіжність інтеграл J г.. с Е (а; Ь).
а
Розв 'язання. На кожному з проміжків [а; с - 171] і [с + '72; Ь] існує
первісна Р(х) = In Іх - с], а тому згідно із співвідношенням (109')
ь
J � = Ііт In І - 1]1 І - Ііш In 11]21 + In ІЬ - сІ - In І а - с] =
х - с 1}1 --++0 1}2--++0
а
І Ь- сІ
= Ііш In 1]1 - Ііт In 1]2 + In -- -
'11 --++0 1}2--++0 а - с
Перша границя (як і друга) у правій частині дорівнює -оо. Тому
невласний інтеграл розбіжний.
ь
Приклад 2. J b�x·
а
Розв 'язання. На проміжку [а; Ь - 1]] ІСНУЄ первісна Р( х )
= -In ІЬ - хІ. Тому за (107')
ь
J dx
-- = - Ііш In 1] + In(b - а) = +00,
Ь - х 1}--++О
а
інтеграл розбіжний.
ь
Приклад 3. J (b�:)O' Q -І 1.
а
Розв 'язання. Первісна підінтегральної функції Р(х) = _ (b���-O .
Тому за (107')
ь
J dx 1 (Ь - а) І - о
-,----- = --- Ііш '171-0 + ---'--------'---
(Ь -- х) о 1 - Q 1} --+0 1 - Q
а
Звідки маємо два випадки:
287
ь
1) (О" < 1 1 г'- > О J dx (Ь __ а)l-а інтеграл збіжнии ..
.< ,- L< , (ь-х)а = 1-0' .
а
ь
2) 1 1 О J dx . бі u
Q > , - Q < , (ь-х)а = +00, ІНтеграл роз ІЖНИИ.
а
Об'єднуючи приклади 2 і З, можемо записати:
ь 1 а
) J dx - (Ь-а) -. бі х,
1 о < 1, (Ь-х)<> - 1-0' .лнтеграл з ІЖНИИ,
а
Ь
2) о � 1, J (b�:)<> = +00, інтеграл розбіжний.
а
Ь
Приклад 4. J ;� .
о
Пропонуємо читачам переконатись, що для цього інтеграла від-
значаються таю результати:
Ь
1) 1 J dx ь1-<>. • u
Q < , х<> = 1-0" Інтеграл зБІЖНИИ;
о
Ь
2) Q � 1, J ;� = +00, інтеграл розбіжний.
о
7.5. Критерії збіжності невласного ІНтеграла другого
роду.
1 О. Критерій Коші.
Сформулюємо критерій Коші збіжності нсвласного інтеграла
другого роду, якщо підінтегральна функція необмежена в околі верх-
- .
ньоі межг.
Д.1Я збіжності інтеграла (107) необхідно й Достатньо, щоб для
будь-якого як завгодно малого Е > О можна було вказати таке (6) О),
що для довільних 17' і т/', які задовольняють умову О < 11" < 17' < 6
справедлива нерІВНІСТЬ
Ь-·т/'
J л·х; )ll.r < Е.
Ь--ч'
288
Як і у Па 7а3, можна переконатись, що ця нерівність означає іс
нування границі введеної више функціі І(у) за умови ТІ ----+ О.
Можна перефразувати умову Коші за допомогою околів, а са
ме: для збіжності неВ.'ІаСНОГО інтеграла другого роду необхідно й
достатньо. щоб ДЛЯ дові.1ЬНОГО як завгодно малого є > О можна було
вказати такий д-півокі.1 (д > О) особливої точки, що як тільки точки
Ь - ТІ' і Ь - Т/' потраплять в цей окіл, відповідне значення інтеграла
Ь--т/,'
J f(x)dx потрапить в є-окіл нуля.
Ь-1}'
20. Ознаки. порівняння.
Для невласного інтеграла другого роду характерні ознаки по-
. . . . ..
РІВняння, анадогтчні до ознак ПОРІВняння для невласного Інтеграла
першого роду, розглянуті в п.7.3. Треба лише пам'ятати, що у всіх
формулюваннях і доведеннях функція f( х) розглядається на напів
відкритих проміжках, а саме: на проміжку [а: Ь), якщо особливою
точкою є верхня межа інтеграла, на проміжку (а; Ь], якщо особли
вою є нижня межа і на проміжках [а; с) і (с; Ь], якщо особливою
є внутрішня точка інтервалу інтегрування. Часто як еталони для
порівняння використовуються інтеграли (або подібні), розглянуті у
прикладах 1, 3 і 4 п. 7.4.
7.6. Інтегрування частинами і заміною змінної в невлас
них Інтегралах.
1 о. Запишемо формулу інтегрування частинами для визначеного
ІНтеграла
Ь
J іиіи = uvl�
а
Ь
.f udu.
(110)
а
Якшо функції II ( х) і 1: (:r) �іаЮТЬ неперервні похідні на відповід
них напіввідкритих проміжках (які нє міст-ять особливих чи нескін
ченно віддалених точок) і існує границя добутку u(.r) . v(x) у від
повідній особливіи чи нескінченно віддаленіи точці, то із збіжності
289
одного з інтегралів, що входять в (110), випливає збіжність другого
інтеграла і справедлива рівність (11 о).
ос
Приклад 1. Дослідити на збіжність J si� Х dx, а> о.
а
Розв 'язання. Для довільного скінченного ТІ > (1, інтегруючи час-
тинами, одержимо
1]
J si:X dx =
а
( u = 1 =} du = - \ dx )
dv = si� xdx =} v = Х_ cos х
1] 1]
_ cos х \1] _ J cos х dx = _ cos ТІ + cos а _ J cos х dx.
х а х2 ТІ а х2
а
а
Якщо тепер перейти до границі, коли ТІ ---+ +00, то матимемо
� 1]
J sin х d 1· cos rJ cos а 1· J cos х d
-- х =- ІІП --+--- lIll -- х =
х 1]-++� ТІ а 1]-++00 х2
оо
cos а _ J cos х dx
а х2'
а
а
а
але
а
оо оо
< J 1 cos х І dx < J dx = � < оо.
- х2 - х2 а
оо
J cosx dx
х2
а
а
оо
Отже, інтеграл J Si� Х dx збіжний.
а
Аналогічно можна переконатись, що збіжним є також ІНтеграл
оо
J co;xdx. Однак обидва ці інтеграли є умовно збіжними, оскіль
а
ки розбіжними є інтеграли від абсолютних величин підінтегральних
функцій. Дійсно, внаслідок того, що І sill Х І � si1l2 Х, згідно з під
пунктом 20 п.7.3
оо ІХ оо .ас оо
J І si��dx � J sіп2 Х dx = J !----=- �ОБ 2·�d:r: = � J сІх - � J СОБ 2.т dx.
З· х �.E 2х 2 х
а
а
а
а
а
2DO
оо
О . U • J аІХ • ,. •• • •
СКІЛЬКИ першии інтеграл у правіи частині нерІВНОСТІ розбіж-
а
ех>
U ( U бі ) ,... u • • J І sin хі 1
нии другии є 3 пжним , то розоіжнии І ІНтеграл =г:" х.
а
20. Якшо функція f( х) неперервна на відповідному напіввідкри-
• t.." •• ••
тому проміжку, ЯКИИ Є множиною значень деякоі строго моно гонноі
і неперервно диферєнціиовноі функції .г = q(t) t Е [а: ,3], причому
ь
а = q(a), Ь = q(;3), то із збіжності одного з інтегралів J f(x)dx
а
(з
J f [q(t)] q'(t)dt ВИП.ІІиває збіжність другого інтеграла і справедлива
о
РІВНІсть
ь f3
J ЛХ )dx = J f [q(t)] q'(t)dt.
(111)
а
о
Зауважимо, що тут одна з граНИІІЬ (чи й обидві) у кожному з на
ведених інтегралів може бути нескінченною (для інтегралів першого
роду) ЧИ особливою точкою (для інтегралів другого роду). Про-
• •• • • u •
те ІНОДІ ПІС-ЛЯ заміни змшноі Інтегрування невласнии інтеград стає
власним ЧИ навпаки.
2
Приклад 2. J ---.4.!._
з: іп г '
1
РОЗб 'язання.
2
J x�=x =
І
(IПХ = t::::} х = et ::::} dx = Fldt)
х = 1; t = О
х = 2; t = ln2
О
Іп 2
J �t =
О
Іп 2
= Іігп J dt = lim (Int)lln2 = lпlп2 - lim lпт} = +00,
1/·"""*+0 t 1]-t+0· '/ 1/-t+0
І]
інтеграл розбіжний.
291
1
П 3 J dx
риклад . х+ф'
о
РОЗб 'язання.
і1 dx (і = VГX:::::} х = ";'. dx = 2іаі) іl 2tdt іl dt
--= - х - о· t - О - -- - 2 --
х + JX - = 1: t = 1 - і2 + t - t + 1 .
о х-, - о о
Одержали звичайний інтеграл
1
J � = Іп( t + 1) І � = Іп 2 - Іп 1 = Іп 2.
t + 1
о
Приклад 4.
+=
J
dx
xVl+x2 •
РОЗб 'язання.
+= (х = tgt:::::} t d arctgx) % dt
J dx dx = ---+t j Cos2 t
xJ1 + х2 = Х = 1; СО/=; 7г =.!С tgtJ1 + tg2t
х = +00; t = 2" 4
".
"2
=js�t=
".
"4
Невласний інтеграл зведи до власного інтеграла.
Варто звернути увагу на умову строгої монотонності функції
х = q( і) У кожному з наведених прикладів, оскільки вона забезпечує
. . .
законність ВСІХ спрощень гпдштет-раяьних виразів.
7.7. Головне значення невласних інтегралів. Далі, вив
чаючи інтеграл Фур'є, використовують дещо інший підхід до визна
чення невласного інтеграла, ніж в (101) (чи (109)).
Якщо там існування невласного інтеграла залежало від двох гра
ниць, в кожній з яких прямування на -оо і +00 {підході до точки с
292
ліворуч і праворуч) відбувалось незалежно, то тут пропонується в
а _ .....
означенні невласного Інтеграла застосовувати однаковни закон пря-
мування на -оо і +00 (симетричний підхід до точки с).
Означення 1. Нехай функція ЛХ) визначена для -оо < х < оо
інтегровна на будь-якому скінченному проміжку [-'7; ТІ], О <'7 < оо.
Якщо існує скінченна границя
ТJ
Ііт j ЛХ )d:r,
ТJ-++=
-ТJ
то вона називається головним значенням невласного Інтеграла пер
+=
шого роду J f( х )dx за Коші і позначається символом
-=
= ТJ
V.p. j f(x)dx = Ііт j Лх)ах.
1]-+=
(112)
-=
-ТJ
Якщо для підінтегральної функції існує первісна Р( х), то сгцв
відношення (112) запишеться так
оо
v.p.jf(x)dx= lim (F(1])·-F(-1])).
ТJ---t=
( 112')
-=
3 останнього співвідношення видно: якщо Р( х) є парною функ-
. .
цією, то головне значення невласного Інтеграла на нескінченному
. . .
ПРОМІЖКУ дорівнює нулеві.
оо
П 1 J хзі х
риклад . І+х2•
-=
РОЗб 'язання. Як було встановлена в п. 7.2, згідно з означенням
(101) цей невласний інтеграл розбіжний. Але головне значення існує
і, враховуючи парність первісної Р(х) = t Iп(1 + х2), дорівнює нулеві
оо
V.p. j
xd;r (1 '2 1 2 )
-1-+-x�2 = ТJД�= "2lп( 1 + 1] ) -- 21n(1 +'1) = о.
= оо
293
Подібно визначається і головне значення невласного Інтеграла
другого роду для функції, необмеженої в околі точки с, яка є внут-
. . .
РІШНЬОЮ точкою ПРОМІЖКУ Інтегрування.
Означення 2. Нехай функція лх) визначена для х Е [а; Ь], крім
точки с, а < с < Ь і інтегровна на проміжках [а; с -1]] і [С+1]; Ь], 1] > О.
ь
Тоді головне значення інтеграла J л х )dx визначається формулою
а
V.p. j лх)ах = �.!i'l'= l тлх)ах + j і(х)ах] .
а r _ а c+q
(113)
Якщо існує первісна F(x), то (113) набуде такий вигляд
ь
V.p. J f(x)dx = Р(Ь) - Р(а) + Ііт [Р(с -1]) - Р(с + 1])].
q---t+О
(113')
а
ь
Приклад 2. J xd�c' С Е (а; Ь).
а
РОЗб 'язання. 3а означенням (109) цей інтеграл розбіжний (див.
приклад 1 п.7.4). Однак головне значення існує 1, З урахуванням
первісної Р(х) = Іп Іх - с] і (113'), дорівнюватиме
ь
J dx І Ь - сІ
V.p. -- = llllb - cl-Illla - сІ + Ііт [Іп ] - 1]1- 11l1]) = III -- .
х-с q---t� а-с
а
294
Розділ 8. РЯДИ
§ 1. Числові ряди
1.1. Поняття числового ряду та його залишку. Нехай
задано ПОСЛІДОВНІСТЬ
дійсних чисел, яку позначимо {an}�. Утворимо на основі неї послі
ДОВНІсть
ДІИСНИХ чисел, яку позначимо {Sn}�. Члени послідовності {Sn}�
бу дуємо в такий спосіб
So = ао,
SI = ао + 0,1,
S2 = 0,0,+ 0,1 + 0,2,
Крапки після останнього рядка означають, шо послідовне додавання
може тривати як завгодно довго.
Означення 1. Вираз вигляду
ао + а І + 0,2 + ... + ап + ...
(1)
називається чзіслоеим рядом, член ап послідовності {an}� називаєть
ся загальним 'Ч,.лЕ1іО.м р.я,ду, член Sn послідовності {SIJ}� --- частин-
1іОЮ су.мою р.я,ду.
295
Означення 2. ЯКЩО існує скінченна границя
Ііт Б; = 5
п=-ь ос
(2)
то ряд (1) називається збіжним, а число 5 називається су.мою р.я,ду,
ос
і записують 5 = L ал,
п=О
Якщо границя (2) не існує а60 дорівнює оо, то ряд (1) називають
розбіжним.
оо
Приклад. Розглянемо ряд l+q+q2+ ... +qn+ ... = L qn, члени
п=О
ап = qn, п = О, 1, 2, .. , якого утворюють геометричну протресію.
ЯКЩО q =f- 1, то маємо
1 _ qn+l
Sn= ----
l-q
ЯКЩО Iql < 1, тобто ·-1 < q < 1, то
Ііт qn+l
п-+сх!
О, прогресія є
. .
нескінченно спад ною І
1
5 = Ііт Sn =--
п-+сх! 1 - q'
тобто ряд збіжний і отримане число 5 для кожного розглядуваного q
бу де його сумою. ЯКЩО q = 1, то одержуємо ряд 1 + 1 + 1 + ... + 1 + ... ,
для якого Sn = n + 1 і 5 = +00 -- ряд розбіжний. ЯКЩО q > 1,
то послідовність {Sn}� монотонно зростає і необмежена зверху, ЇЇ
границею є +00, ряд розбіжний. ЯКЩО q = -1, то отримуємо ряд
1 + ( -1) + 1 + ( -1) + ... , для якого частинні суми з парним номером
дорівнюють 1, частинні суми з непарним номером дорівнюють О __ О
границі послідовності частинних сум не існує, бо дві піппослідовності
мають різні границі; ряд розбіжний. ЯКЩО q < -1, то послідовність
частинних сум з пар ним номером прямує до +00, послідовність час
тинних сум з непарним номером прямує до -оо _.- ряд розбіжний. У
такому разі послідовність {І з; І} � монотонно зростає. і необмежена
зверху.
296
3ауваЖЕ'Н,'Н,.я,0 Між множиною числових рядів і множиною число-
о о о
вих послщовностєи ІХ частинних сум ІСНУЄ взаємно однозначна від-
=
повідність. Справді, якщо задано деякий числовий ряд L: ап, то
п=о
існує і єдина ПОСЛІДОВНІСТЬ {5n}� його частинних сум, члени якої
одержуються за правилом
Навпаки, якщо задано деяку числову ПОСЛІДОВНІСТЬ {5n}�, то
оо
існує і єдиний числовий ряд L: ап, для якого задана послідовність є
п=о
послідовністю його частинних СУ:-'1, тобто члени якого отримуються
за правилом
ао = So, ап = 5п - 5п-І, n = 1,2, о о о
Означення 30 Ряд вигляду
оо
ап+l + ап+2 + о о 0+ an+k + о о о = L ау
у=п+l
(3)
називається залu'Ш-r,;о.м, ряду ао + а} + а2 + о о о + ап + ап+l + о о о о
Зв'язок між рядом та його залишком досліджується на основі
співвідношень між Їхніми частинними сумами. Нехай Sn - частинна
сума з номером n самого ряду, тобто
rnk ---- частинна сума з номером k залишку з номером n цього ряду,
тобто
7°nk = ап+І + ап+2 -+- о о 0+ an+ko
Зауважуємо, що 5n+k = ао + а] + о о о + ап + ап+l + о о 0+ an+k
= 5п + Tnko Тому
297
Якщо залишок (3) є збіжним рядом, то існує граНИІІЯ
оо
гn = lim rnk
k�oc
(4)
и=n+l
Збіжність чи розбіжність ряду залежить ВІд збіжності чи роз
біжності його залишку.
1) Ряі) збіжний тоді і тіль1\,U тоді, коті збіжний 6удь-J/,1\,UЙ
його запииіок. Справді, якщо ряд збіжний, то із співвідношення
Tnk = Sn+k - Sn та існування скінченної границі у правій частині,
якщо k ---+ оо, випливає існування скінченної границі у лівій частині
при будь-якому n = 1'2' .... Якщо збіжний один із залишків ряду,
то з цього самого співвідношення при фіксованому п та існування
скінченної границі у лівій частині, якщо k ---+ оо, випливає існування
• - • • v •
скінченноі граНИЦІ у правіи частині.
2) Ряд розбіжний тоді і тількл: тоді, копи розбіжний 6удЬ-Л1\,иu
його запишок .. Справді, нехай ряд розбіжний. Якщо деякий його за
лишок був би збіжним, то за попередньою властивістю був би збіж
ним весь ряд. Суперечність. Нехай тепер розбіжний один із залиш
ків. Якщо весь ряд був би збіжним, то за попередньою властивістю
був би збіжним будь-який його залишок. Суперечність.
3ауваЖЕ'Іі'liJ/,. Відкидання від збіжного (розбіжного) ряду скін
ченної кі.лькості його членів чи додавання до збіжного (розбіжного)
ряду скінченної кількості деяких членів не впливає на його збіжність
(розбіжність).
Встановимо деякі властивості залишку.
1) Су,м,а залuш1\,У дорівнюе різнииі між сцмою рлду та його час
тлінною су,м,ою. З рівності 1'nk = Sn+k'- Sn, якто k ---+ оо, і п. фіксо
ване, враховуючи lim Sn+k = 5, отримуємо гn = 5 - Sn.
k�=
Звідси випливає, що
298
2) Су,м,а залuш'К',у збіжного р.я,ду язг завгодно бмизько наб ллі
жається до uул.я" .я,'К',що необмежено з6ільшуєmьс.я, U020 'Ііо,м,ер. З
рівності тп == S - Sn, враховуючи lim Sn == S, одержуємо
n�::ю
Ііт Т'п = о.
n�oc
3ауважеuu.я,. Оскільки гn = 5 - 5n і ї:« -+ о, якщо n -+ оо, то на
основі оцінки суми залишку можна оцінювати похибку при обчислен
ні суми ряду за допомогою його частинної суми. Якщо є - граничне
значення похибки, тобто IS - 5nl ::; Є, то ІтпІ::; Є, звідки знаходять
значення n, для якого різниця між сумою ряду та його частинною су
мою бу де меншою від заданої похибки. Число є називають точністю
обчислення суми ряду.
1.2. Критерій збіжності. Необхідна ознака збіжності.
Відповідність між множиною числових рядів та множиною числових
послідовностей дає змогу переформулювати ДЛЯ ряду критерій збіж-
.. .
НОСТІ ПОСЛІДОВНОСТІ.
оо
Розглянемо рЯД L ап ПОСЛІДОВНІСТЬ {5n}� його частинних
n=о
сум. Застосуємо ДО неї критерій Коші збіжності числової послідов-
ності, зауваживши, що для будь-якого натурального m буде
оо
Критерій збіжності. Для того, щоб ряд L а.; був збіжним,
n=о
необхідно і достатньо, щоб для кожного є > О існував такий номер
По, що для кожного n > по і будь-якого натурального m була б іс
тинною нерІВНІСТЬ
Нерівність стверджує, що сума будь-якої кількості членів ряду,
. .
ЯКІ роз гашоваш за достатньо далеким 11 членом, як завгодно мала.
299
Сформульовану ознаку називають критерьем Коші збіжності
числового ряду.
оо
Якщо ряд L ап збіжний, то на основі необхідної ознаки кри-
n=О
терію збіжності, прийнявши m = 1, одержуємо lan+ll < є, якщо
n > по, тобто аn+l ---+ о, якщо n ---+ оо, значить а.; ---+ О при n ---+ оо,
бо ап і аn+ 1 пробі гають одну і ту саму послідовність. Іншими слова
ми, справедлива
оо
Теорема (необхідна ознака збіжності). Яхщо ряд L ап
n=о
збіжний, то Ііт ап = о.
n-too
Обернене твердження не може бути істинним, ОСКІльки неРІВ-
ність в критерії збіжності є істинною для всіх m = 1, 2, ... , а не
тільки для m = 1.
Необхідну ознаку збіжності можна встановити іншим способом.
оо
Якщо ряд L ап збіжний, S -- його сума, Sn - частинна сума з
n=о
номером n, то Ііт Sn+l ііт Sn = S. Тому, оскільки аn+l =
n-too n-too
= Sn+l - Sn, маємо
Ііт аn+l = Ііт (Sn+l - Sn) = Ііт Sn+l - Іітп Sn = 5 - S = о,
n-too n-too n-too n-too
тобто ііт а.; = о.
n-t=
3 необхідної ознаки збіжності випливає достатня ознака роз-
оо
біжності: якщо Ііт а.; і= О, то ряд L а.; розбіжний. Справді, якби
n-too
n=о
ряд був збіжний, то було б Ііт ап = о. Суперечність.
n-too
Необхідна ознака збіжності не є достатньою: існують ряди, для
яких послідовність Їхніх членів є збіжною до нуля, а самі ряди роз
біжні.
Приклад. Розглянемо ряд
1 1 1 1 оо 1
1 + - + - + - + ... + - + ... = L -.
2 З 4 n n
n=1 .
зоо
Необхідна ознака збіжності, очевидно, виконується: Іігп .!. = О,
n-t= n
але, як ми покажемо нижче, ряд розбігається. Для доведення вико-
ристаємо таку нерІВНІСТЬ
і > In(i + 1), і > О.
Дійсно, позначивши Лі) = i-In(i+1), матимемо г(і) = i�I > О,
якщо і > О. Отже, Лі) зростає на [О; оо); оскільки ЛО) = О, то
Лі) > О або і > In(i + 1)� якщо і > О. Якщо і = �, одержуємо
� > In (� + 1). Тепер на основі цієї нерівності оцінюємо
1 1 1 1
Sn = 1 + - + - + ... + -- + - >
2 З п-1 n
з 4 n п+1
> In 2 + In - + In - + ... + In -- + In -- =
2 З п-1 n
= In 2 + In З - In 2 + In 4 - In З + ... + In n - In( n - 1) + In( n + 1) - In n =
= In(n + 1) -+ +00, n -+ +D?'
отже, і більша величина Sn -+ ОО, якщо n -+ +00. Це означає, що ряд
розбіжний.
оо
Ряд L � називається гармонічним рядом. Отже, гармонічний
n=І
ряд розбіжний.
Розглянемо ряд
(5)
де а --- деяке діисне число.
Якщо а < 1, то по < п, бо n > 1, тому пІа > �; частинні суми
оо
ряду L пІа бу дуть більші від частинних сум з тим самим номером
n=І
301
оо
РЯДУ L � Оскі.,"ІЬКИ останні необмежені, то и пеРШІ необмежені.
n=1
=
Отже, якщо о' < 1, то ряд L n10 розбіжний.
n=1
Нехай о' > 1 і {Sn} � --- послідовність частинних сум ряду, шо
розглядаються. Оскільки Sn - Sn-l = n1", > О, якщо n = 2, 3, ... :
тобто Sn > Sn-l, то ПОСЛІДОВНІСТЬ {Sn} ех>, виявляється монотонно
зростаючою. Тому
Sn < S2n+l = 1 + (210 + з10) + (410 + 510) + ... + ((2�)0 + (2n � 1)0) <
2 2 2 2 2 2
<1+-+-+···+--=1+-+ + ... +---
20 40 (2n)0 20 20' . 20 20 . п"
= 1 + _1_ (1 + � + � + ... +�) = 1 +�.
20-1 20 зО' ПО 20-1
Отже, Sn < 1 + 2��1 або (1 - 2<>�-1) Sn < 1. Оскільки о' > 1,
0-1 . 1 20-1
ТО 2 > 1 І 1 - 2<>-1 > О. Тому Sn < 20 І-І' Отже, МОНОТОННО
зростаюча послідовність {Sn}� обмежена зверху. На основі теореми
про ГІ?аницю монотонної та обмеженої послідовності випливає, що
ех>
послідовність {Sn}� є збіжною, тобто ряд L n1о Є збіжним.
n=І
ех)
Ряд L n1о при фіксованому дійсному значенні о' називається
n=1
узага.лЬ'Н,Е'Н,U.м гармонічним р.ядо.м (ряд Діріхле}. Він збіжний, якщо
о' > 1, і розбіжний, ЯКШО о' :::; 1 (якщо о' = 1, перетворюється в рар
монічний ряд).
I.З. Ряди з додатними членами. Достатні ознаки збіж-
ех>
ності. Розглянемо ряд L аrl в ЯКОМУ ап > О для всіх n = О, 1'2: ....
n=О
ЯКШО деякі члени ряду виявляться такими, що дорівнюють нуле-
. - . . . .
ВІ, то ІХ можна пропустити, ВІДМІННІ ВІД нуля члени перенумерува-
ти і одержати новий ряд, всі члени якого будуть додатними. Не
хай {Sn}� - - послідовність чаСТИННІІХ <'У),,1 цього ряду. Оскільки
302
Sn - Sn-I = ап > О для всіх n = 1, 2, ... , то послідовність {Sn}: ви
являється :монотонно зростаючою. На основі теореми про границю
монотонної та. обмеженоі послідовності отримуємо твердження.
оо
Лема. Нехай в р.яді L ап осі членн dодат'Н,і, {Sn}: - посм-
п=о
довність його чостинних су.м. Я1\,ЩО послідодність {Sn}: є обме-
женою зоерху, то р.яд збіжний. Я1\,ЩО поемдовність {Sn}: є необ
меженою зо ерху, то р.яд розбіжний.
Ознаки збіжності чи розбіжності рядів з додатними членами
встановлюють, враховуючи твердження цієї леми.
Перша ознака порівняння.
оо оо
Теорема 1. Нехай L ап і L Ьп --- р.ядu з додат'Н,и.ми членамн.
n=о п=о
дл,.я яти. іониють такс додатне число с та таке нотирольне число
По, що дл,.я всіх n > по буде
(6)
ех) оо оо
Я1\,ЩО р.яд L Ьп збіжний, то р.яд L ап збіжний. Я1\,ЩО р.яд L ап
п=о
п=о
п=о
оо
розбіжний, то р.яд L ь; розбіжний.
п=о
Доведення. Ми знаємо, що відкидання від ряду скінченної кіль-
кості його членів не впливає на його збіжність (розбіжність), тому
можна вважати, що нерівність (6) виконується 'r/n, n = О, 1'2' ....
оо
Нехай {рт} :--- послідовність частинних сум ряду L ап, {Чт}: ---
п=о
оо
ПОСЛІДОВНІСТЬ частинних сум ряду L ь.: Тоді
п=о
m
m
Рт = L аn ::; С L Ь« = СЧт·
п=о п=о
ех)
За умовою ряд L ь; збіжний, тому послідовність {чт}: також
n=о
збіжна, а тому обмежена зверху. Оскільки Рт ::; cqm, а послідов-
303
НІсть {qm} � обмежена зверху, то послідовність {Рт} � також обме-
оо
жена зверху. На основі леми встановлюємо, що ряд L ап збіжний.
п=о
ос оо
Нехай ряд L ап розбіжний. Якби ряд L Ьп був збіжним, то,
п=о п=о
оо
за доведеним, РЯД L ап був би також збіжним. Але він розбіжний.
п=о
оо
Суперечність. Тому РЯД L Ьп розбіжний.
п=о
Приклад 1. Дослідимо збіжність рядів
1
а) L 2n -1;
п=1
Розв 'язоння. а) 2П]-1 > 2�
оо
� . �,РЯД L � розбіжний � ряд
п=1
оо
,,1 б' u
г: 2п-l роз іжнии;
п=1
б) n�2п < 21п
оо оо
(�)n, ряд L (�)n збіжний � РЯД L n�2п
п=1 п=о
збіжний.
Друга ознака порівняння.
оо оо
Теорема 2. Нехай L а.; і L Ьп -- рядн З додат'Н.и.м.и членоми;
п=о п=о
д.л.я яких існцє скінченна та додат'Н.а гранилія
1· ап h h О
пп -ь =, >.
п--+= n
(7)
Якщо збіжний один З 'It1LX рядіе, то збіжний іниіий. Якшо розбіжний
один З 'Цих р.ядів, то розбіжний іниіий.
Доееоення. 3 означення границі випливає, що ДЛЯ кожного Е: > О
існує такий номер ПО, що для всіх n > по буде
304
Звідси одержуємо ІІ -- Є < � 11 < ІІ + Е:. тобто (/L - Є )Ьn < а n < (ІІ + Є )011'
"
.]аді застосовуємо ТРОРСМУ 1.
Приклад 2. Дослідимо збіжність рядів
XJ 1
б) '" .
г: п + 211
n=о
ас
Розв 'язанн . я. а) ап = 2n1_l' Ь« = �,ряд Е Ьn як відоь .. го. розбіж-
11=0
оо
ний, h = Ііт 2 n_1 = � > О, отже, ряд Е ап розбіжнии;
n-+ас n n=о
б) - 1 Ь
ап - n+2n' n
оо
= 21"., ряд Е Ьn як ві домо, збіжний, Jl =
n=о
Ііт +2"211 = Ііт (1 - +n211) = 1 ._- Іігп +n211 = 1 > О, отже, ряд
n-+оо n n-+оо n n-+= n .
оо
Е ап збіжний.
n=о
Ознака Даламбера.
оо
Теорема 3. Нехай Е ап _ ... р.яд з додатними. членами. Я1\,'ЩО
n=о
існце таке члісло q Е (О; 1) та існцс таке натцрпльне члісло По, 'Що
дл.я всіх n > по буде
то р.яд збіжний. Я1\,'ЩО дл.я всіх n > по буде
то р.яд розбіжний.
Доведення. Перенумеруємо члени ряду, починаючи з номера По,
тобто 'Іден з номером ПО позначимо ао. Ч.1ЄН з HO!vIepoM ПО + 1 позна
чимо аl, і так далі, член з номером ПО + 11 Д.1Я кожного натурального
n позначимо ап, Зауважимо, що
аn-l (1n
::; ОО . q . q ..... q = ао(/.
ОО 01
З05
ас
Ряд L qn. ЯКЩО q Е (О: 1). виражає нескінченно спадну геометричну
n=О
ос
протресію. Оскільки (Іп ::; Ооцn• а ряд L qn збіжний; то на основі
n=О
ас
першої ознаки порівняння ряд L (/n буде збіжним.
п=о
Нехаи � > 1. Тоді
а.,
аl а2 ап-І ап
ап = ао . - . - ..... -- . _._- � аа . 1 . 1 ..... 1 = ао,
аа аl аn-2 аn-]
1, отже, ап � аа > О, \;j n = О, 1, 2, ... ,тому Ііт ап =f. о - не вико-
n--+оо
нується необхідна ознака збіжності, а, отже, ряд розбіжний.
Наведемо спрощений варіант теореми З, який також називають
ознакою Даламбера.
ас
Теорема З * . Нехай L оп - р.яд 3 додатними. членамн. дл,.я
n=О
якого існие гранилія
Іігп аn+ І = d.
n-�= ап
(8)
Я1\,ЩО d < 1, то р.яд збіжний; .я1\,ЩО іЇ.'> 1, то р.яд розбіжний; .я1\,ЩО
d = 1, то р.яд може бути збіжним члі розбіжним.
Приклад З. Застосуємо ознаку Двламбера до рядів
оо � n!. � 1 � 1
а) L 2�' б) г: з-: в) г: п2' г) L-;;'
n=О n=О n=l n=1
Розв '.яза"-'''-'.я.) 11 - n+1 J
- єь єь а ап 271' Оп+1 - 271+1, (
! Ііт n+І = ! . 1 = ! < 1. ряд збіжний;
2 11--+00 n 2 2 '
б) n! (n+I)! 1 __ Іі (n+I)! 271
ап = 271 , аn+І 271+1, (- lIН 271+1 "
n --tao n.
1· n+І
лп 271+1
п-ч ос
271
n
= � Ііш (п+l) = ос,
n--+оо
ряд розбіжний;
:.І () 2
в) ап = п12' ОП + І - � �] )2: а = }�l� (п � 1)2 = }�]� 11 � ]
1. а.'Іе ряд збіжний, бо він f' РЯДО�І ВИГ.1ЯДУ (5) при о' = 2:
З06
Г) а -' а -' J = 11·111 n
n - -;;-. n+І - n+'- fJ---tх. 1/+1
він Є рядом вигляду (5) при о = 1.
Ознака Коші.
1, але ряд розбіжний, бо
ос
Теорема 4. Нехай L аІ! - - [І.яd з додаm:н:и . мн чяенами, Я1\,ЩО
n=о
існцє тане число q Е (О: 1) та lС'Н..УЄ таке 'Н.атураль1/.С "Число По, що
dл.я всіх n > по будс
"Га-- < ч.
y� n - -
то р.яd збіжний. ЯК/ЩО dл.я есіз: ТІ > ГІо буdе
то р.яd розбіжний,
оо
Доееоення. Оскільки ап :::; ч", а ряд L ч", виражаючи, якщо
n=о
q Е (О; 1), нескінченно спадну геометричну прогресію, є збіжний, то
оо
на основі першоі ознаки порівняння ряд L ап буде збіжним.
n=о
Нехай � � 1. Тоді ап � 1, ТІ > по і не виконується необхідна
ос
ознака збіжності. Ряд L ап --- розбіжний.
n=о
Спрощений варіант теореми 4 формулюється так.
оо
Теорема 4 *. Нехаі1 L о-п
- р.яd з додат'Н..и.ми ч.аенами, dл.я
п=о
Ііт уа;; = d.
n---too
(9)
Я1\,ЩО d < 1, то р.яа збіжний; .я1\,ЩО d > 1, то рзи) розбіжний; .я1\,ЩО
d = 1, то р.яd може бути збіжний чи розбіжний.
Приклад 4. 3астосує).ю ознаку Коші до рядів
"хі ( 1) п2
б) L 1 + ;�
11=0
:х: 1
в) L ;;2;
11=-'
ас 1
г) L-;;.
11=1
307
Розв 'язання.
а)
rl = Ііт (1 + -ч - л
Л-+Х; Л
= Ііт [(1 + l)Л] -] = (,-] = 1 < 1, ряд збіжний;
n-+= л �
2
б) ап = (1 + 1 ( .г = lіш (1 + 1 ( = є > 1, ряд розбіжний:
n n-+ос л
) 1 І Іі 1 Іі - �
в ап = 2, (= пп -пГ2 = пп 11 n,
n n-+сх: V n� 11-+00
2 2
Іп d = III Ііт 11 - 71 = Ііт Іп n - 71 = О, d = 1,
n-+= n·--+оо
але, як відомо, ряд в) збіжний;
) 1 d l' 1 Іі _1.
Г ап = -, = 1т nг.:: = нп Пп,
n n-+оо vn л-+=
І І
lnd = Іп Ііт 11-71 = Ііт Iпп-71 = О, d = 1,
n-+= n-+=
але, як відомо, ряд г) розбіжний.
Інтегральна ознака.
Теорема 5. Якщо фУ'Н,1\,'Ці.я f(x), Т Е [1; +00) незростаюна z
f( х) 2: о, х 2: 1, то ряд
оо
(10)
n=l
збіжний тоді і тільки. тоді, комі збіжний інтеграл
+00
J f(x)dJ:.
(11)
Доведення. За умовою функція ЛХ), х Е [1; +(0) монотонна.
ті
Тому (розділ 7, § 2) існує інтеграл Рімана J f(X)d.T, \;/ТJ Е [1; +00) і
1
можна РОЗГ.1Я,:ЩТИ новласнии інтеграл (11). Д.1Я незростаючоі функ-
ції ЛХ), 1 :::; х < +сс виконується
f(k) 2: ЛТ) 2: ЛІ.: + І), k::;.r::; k + 1. k = 1. 2, ...
308
тому, інтегруючи по проміжку [k: k + 1]. отримаємо
k+l
I(k) � J Л·г)rIх � f(k + 1), К' = І, 2, ....
k
у
О 1 2 ... k k+l .... Т
Рис. 1
Підсумовуючи ІІі нерівності від
k = 1 до k = n (рис. І), одержимо
n п+І n
L, f(k) � J f(x)dx � L, f(k + 1) =
k=I k=I
п+І
= /(2)+ Л3)+ " . + Лn+l) = L, f(k),
k=2
тобто
n n+І п-і-І
L f(k)� J f(x)dx� V(k). (12)
k=1 1 k=2
n
Нехай Sn =L, I(k) -.-- частинна сума ряду (10). Оскільки І(х) � О,
k=I
1 ::; х < +00, то послідовність {Sn} �+ І ---- неспадна. Враховуючи це
позначення, нерівності (12) можна записати у вигляді
п+І
з; � J лх)ах � Sn+l ._- /(1), n = 1, 2,... . (13)
1
n+l
Якщо інтеграл у (13) збіжний, то \;j n Е N виконується J Л.Г )dx ::;
1
+=
< J J(x)dx. Звідси та 3 (13) випливає
+ос
Sn+1 < ЛІ) + J I(;r:)dx,
309
тобто послідовність частинних сум ряду (1 о) неспадна і обмежена
зверху, а, отже, ряд (10) збіжний.
Якщо ряд (1 О) збіжний і його сума дорівнює 5, то 5 n ::; 5, \;j n =
= 1, 2, ... і з нерівності (13) випливає
n+l
J f(x)dx::; 5, \;j n = 1, 2, ....
Тоді
ті n
J f(x)dx < J f(x)dx ::; 5, 1:::; ТІ :::; п, n Е н.
ті
Отже, сукупність всіх інтегралів J Л х )dx < 5, ТІ � 1 обмежена звер
І
Лх)
ху, тому інтеграл (11) збіжний.
Геометрична ілюстрація. Графік
функції Лх) має ВИГЛЯД (рис. 2). Розгляне
мо криволінійну трапецію, обмежену звер
ху графіком функції f( х ), знизу віссю абс
цис, ЛІВоруч прямою Х = По, а праворуч
оо
необмежену. Збіжність інтеграла Jf(x)dx
по
означає, що площа криволінійної трапеції є скінченною; його розбіж-
о
по
Рис.2
х
. .
НІСТЬ означає, що 11 площа є нескінченно великою.
оо
Приклад 5. Дослідимо абіжність ряду L ';0' де а - фіксоване
п=І
діисне число.
Розв 'язання. Нехай а < о. Приймемо а = -{3, де {3 > о. Тоді
-1" = пР -+ +00, якщо п -+ оо, тобто Іігп -1" І- о. На основі необхід-
п n--too n
ної ознаки збіжності ряд розбіжний.
Нехай а � о. Застосуємо інтегра .. і'ІЬНУ ознаку. П риимемо f (х) =
= хІа і перевіримо сформульовані в теоремі 5 властивості цієї ФУНК
ції, яка визначена на проміжку [1; +00).
310
Додатиість: � > о.
х
Монотонність: якщо
1 < :1:1 < Х2, то О < л. < л. < 1, -k = =
Х2 ХІ Х2
хІо, отже, функція /(х) монотонно спадає. Функ
І
проміжку [1; +ос] заДОВО�1ЬНЯЄ умови теореми 5.
( xIJ а < (:1) а
ція /(х)
Да.пі,
Jood Jbd І-аІЬ
Х Х Х
- = lim - = lіш --
ха b--t+oo ха Ь--t+:ю 1 - о 1
1 1
1 (. 1)
-- Іігп .
1 - о b--t+oo Ьа-1 - 1
Якщо 0-1 < о, тобто о < 1, то lim Ь}-l
b--t+oo
lim Ь1-а - +00·
b--t+oo - ,
інтеграл і ряд розбіжні.
Якщо о - 1 > о, тобто о > 1, то lim ьо \ -1 = о; інтеграл і ряд
b--t+oo
збіжні.
оо Ь Ь
Якщо 0-1 = о, тобто 0= 1, то J d: = lim J d: = lim Inxl1 =
1 b·�+oo 1 b--t+oo
Ііш ln Ь = +00, інтеграл і ряд розбіжні.
b--t+oo
Якщо о = О, то наш ряд має вигляд 1 + 1 + 1 + ... -- розбіжний
ряд.
оо
Ряд L: nІо збіжний, якщо о > 1 і розбіжний, якщо о ::; 1.
n=1
1.4. 3накочергувальні ряди. Розглянемо ряди, члени ЯКИХ
є дійсними числами, причому послідовні члени ряду набувають зна-
. .
чення РІЗНИХ знаків,
Означення. Ряд вигляду
ас
І)-I)nаn = ао - аІ + а2 - аз + ... + (-I)llаn + ... , (14)
n=о
в якому ап > О або ап < О для УСІХ 11 = о, 1, 2, ... , називається
знакочерецеальним р.ядо.м. Будемо вважати, що аТІ > о. Якщо ап < о,
311
=
то можна прииняти а" = -Ь". де Ь" > О. Ряд L (-l)"+JЬ,, 6yд(�
11.=0
також знакочерг-уввльним рядом,
Для знакочергувальног-о ряду існує практично зручна достатня
ознака збіжності.
оо
Теорема (ознака Лєибніца). Нехай L (-·l)"а" -- знскочерги-
n=о
еальний р.яа. Якиіо
Ііт ап = О,
n--}оо
то р.яа збіжний.
Доведення. Нехай {S2n+l}� - послідовність частинних сум з
непарним номером. Запишемо її члени у вигляді
Оскільки ао � аl � а2 � аз � ... � аь« � а2n+l � ... , то значен
ня різниці в кожній дужці є невід'ємним, тобто члени послідовності
{S2n+l}� Є невід'ємними. Додавання нових членів ряду або збіль
шить значення частинної суми з непарним номером, або за.ПИШИТЬ
без зміни. Тому послідовність {S2n+l}� Є монотонно неспадною.
тобто
Запишемо тепер члени послідовності {S2n+l}� У вигляді
Оскільки значення різниці в кожній дужці є невід'ємним, а2n+1 > О.
то відкидання всіх ВІ,.]; Є!\!ІНІІКІВ )' правіи чаСТІІНЇ може ті.!1ЬКІІ збіль-
шити ЇЇ. Тому
312
тобто послідовність {52п+ І} � Є об).ІСЖСНОЮ.
З теореми про границю монотонноі та обмсжєноі послідовності
випливає, що послідовність {52n+I}� збіжна до скінченної т раниш ,
яку ми позначимо 5, тобто
Ііт 52п+1 = 5.
п--+=
Нехай тепер {52n}� - послідовність частинних сум з парним
номером, тобто
Зауважимо, що 52п = 52п+1 + а2п+l' Було доведено, що 52п+1 ---+ 5,
якщо n ---+ оо. З умови теореми випливає, що а2п+І ---+ О, якщо n ---+ оо,
бо підпослідовність {a2n+l}� збіжної послідовност-і {an}� є збіжною
до тієї самої границі. Тому
Ііт 52п = Ііт (52П+1 + а2п+l) = Ііт 52п+І + Ііт а2п+l = 5.
п--+оо п--+оо П--+СХ) n--tcx,
Позначимо 5k частинну суму з номером k. Оскільки для кожно
го фіксованого k значення Sk збігається з одним із значень 52п чи
52п+1, які, якщо n ---+ оо, як завгодно мало відрізняються від числа 5,
то якщо k ---+ оо значення 5 k також бу дуть як завгодно мало відріз
нятися від числа 5. Тому послідовність {5k}� виявляється збіжною,
причому
Іігп 5k = 5.
k--+CXJ
оо
Отже, ряд L ( -1) n ап збіжний.
п=О
Достатня ознака збіжності, встановлена в теоремі, називається
ознакою Лейбніца; ряд, члени якого задовольняють умови теореми,
називається рядом. Лейбніиа.
Наслідок. Абсолютна величина аалишку ряду Леибніца не пе
ревищує абсолютної величини: першого члена ІІЬОГО за.НІШКУ.
313
Справді, з нерівності 52n+ І ::; ао, якщо n ---+ ех" одержуємо
тобто сума ряду Леибніца не перевищує значення першого його чле
на. Умови теореми заДОВО.1:ЬНЯЄ також залишок
( 1)1/.+] + ( 1-)1l+2
Тп = - аn+І - аn+2 + ...
ряду, тобто за.1ИШОК є також рядом Леибніца. Тому дЛЯ ВСІХ n
=0,1,2, ... ,буде
оо (_l)n-l . u
-п риклад . Дослідимо збіжність ряду L -11-- та ОЦІНимо 1Ю-
n=l
го залишок. Маємо
оо (_l)n-І 1 ІІп 1 оо (_l)n
L n = 1 - 2 + з - 4 + ... + ( -1) -n -+-1 + ... = L -'-n -+'---1
n=І n=О
О . 1 1 Іі Іі 1
СКІЛЬКИ ап = -+1' аn+І = +2' то ап > аn+І; нп ап = ІПІ -+1 =
n n n .-+00 n-+оо n
= О; ряд збіжний; Ітnl ::; n�2' Для суми 5 ряду маємо 5::; 1.
1.5. Абсолютно збіжні ряди та умовно збіжні ряди. Роз-
оо
глянемо ряд L ап, члени якого є дійсними числами. Якщо ряд, що
п=О
!>О3г .... тядається, збіжний, Т() ряд З аБС()&І1ЮТНИХ величин иого членів
може бути збіжним чи розбіжним.
оо оо
Теорема 1. Якщо р.яd L lаnl збіжний, то р.яd L ап збіжний.
п=О п=о
оо
Доведення. Нехай ряд L lаnl збіжний. Тоді на основі необ-
n=О
хідноі ознаки критерію збіжності маємо: для кожного є > О існує
такии номер По, що Д.1Я кожного n > по і кожного натурального
m = 1, 2, 3 .... , буде
314
Тому, застосовуючи нерівність Д.'ІЯ абсолютної ве.1ИЧИНИ суми СКІн-
... .. ..
чеННОІ КІЛЬКОСТІ доданків, одержимо
На основі достатньої ознаки критерію збіжності встановлюємо, ЩО
оо
ряд L ап збіжний.
n=о
оо
Означення. Ряд L ап називається абсолютмо збіжним; якщо
n=о
оо оо оо
Є збіжним ряд L lаnl· Збіжний ряд L ап, для якого ряд L lаnl
n=о n=о n=О
розбіжний, називається у.мО6UО збіжним.
оо (_1)71-1 оо (_1)71-.1
Приклад. Ряди L n2 та L n збіжні за ознакою
n=1 n=1
оо ( )л-J оо
Лейбніца, Ряд L -�2 абсолютно збіжний, бо ряд L �2 збіжний;
n=l n=I
оо ( 71-! оо
ряд L -1� умовно збіжний, бо ряд L � розбіжний.
n=l n=]
оо
Ряд L Іап І Є рядом з додатними членами, ЯКЩО не враховувати
n=о
Ч .. лени, що дорівнюють нулеві. Тому кожну достатню ознаку ЙОГО
збіжності можна вважати достатньою ознакою абсолютної збіжності
оо
ряду L аtl·
n=о
оо
Ознака Даламбера. Нехай L ап
ряд з дійсними членами,
n=о
для яких ІСНУЄ границя
lim І аn+l І = d.
n-too ап
(15)
Якщо сі < 1, то ряд аБСО.1ЮТНО збіжний; якщо сі > 1, то ряд
розбіжний; якщо d = 1, то ряд може бути абсолютно збіжним <1.60
У!\,ЮВНО збіжним чи розбіжним.
315
ас
Ознака Коші. Нсхаи L un --- ряд :з діисними 'Іденами, для
п=о
яких ІСНУЄ границя
lіш VТaJ = d.
п-ч ос
(16)
Якщо d < 1, то ряд аБСО.1ЮТНО збіжнии; якщо d > 1, то ряд
розбіжний: якщо d = 1, то ряд може бути абсолютно збіжний або
умовно збіжний чи розбіжний.
Смисл понять абсо.1ЮТНОЇ збіжності та умовної збіжності вира
жається у такому твердженні.
ос оо
Теорема 2. Нехай L ап - р.яд 3 діисн;и.м;и членами, L Pk
п=О k=O
оо
р.яд з усіх його нееід'енниз: чяеніе, L q/ -- р.яд з сбсомотних величлін
/=0
усіх його еід'емниа: членів,
()Q ()Q оо
Якщо ряі) L ап абсолютно збіжний, то рядн L Pk та L q/
п=О k=O /=0
збіжні.
оо оо оо
Якщо р.яд L ап у,м,ооио збіжний, то ряди. L Pk та L q/ роз-
п=О k=O /=0
біжні.
()Q
Доведення. Цікавим є тільки випадок, коли ряд L ап містить
п=О
нескінченну кількість додатних і нескінченну кількість від'ємних
членів, інакше твердження теореми очевидне. Введемо позначення
(Ч = Ро + РІ + ... + рь ; {З/ = qO + ql + ... + qt·
у частинній сумі SlI виділимо в одну групу всі додатні та ті, шо
дорівнюють нулеві, члени, в іншу групу виділимо всі від'ємні члени.
Члени ряду з першої групи позначимо РО, РІ,", , Pk: члени ряду з
другої групи позначимо -чо, -ql,"', -qt. Тоді, оскільки п. = k + І,
одержимо
316
Звідси способом ПОЧ."І('ННОГО додавання та віднімання знаходимо
і« -- 5n
,зІ = -----
2
Якщо п � Х, то k � оо та l � ос.
ех;
Нехай ряд L о; абсолютно збіжнии. Тоді ІСнують скінченні
n=о
границі Ііт 5n та lіш tn.
тг-ч-оо n--}=
В отриманих співвідношеннях між частинними СУ),Іа),ПІ граниш
послідовностеп в правпх частинах, якщо п � оо, існують і скінченні.
Тому гранилі послідовноєтєй в лівих частинах, як шо k � оо та
оо ех;
l � оо, існують і скінченні. Отже, ряди L РІ.- та L q, збіжні.
k=O k=O
оо
Нехай ряд L ап умовно збіжнии. Тоді існує скінченна границя
n=О
Ііт 5n, З означення випливає, що послідовність {tn}� неспа.дна,
n- .... оо
Тому існує Ііт tn скінченна або нескінченна. Скінченною ця грани
n-t=
оо
ця бути не може, бо це б означало, що ряд L ап абсолютно збіжний.
п=о
Отже, Іігп tn = +00. Тому, Ііт O'k = +х, Ііт дІ = +00, Отже,
n--}= k--}ex; I-·t�)c
ех; ех;
ряди L Pk та L q, розбіжні.
1=0 1=0
ос
3аува:жс'Н,'Н,я. Нехай ряд L ап абсо."ІЮТНО збіж нии. Позначимо
n=О
Ііш 5n = 5, Іігп til = t, Іігп O'k = 0', lіrп 31 = 3. Тоді із співвідно-
n--t= П--}СХ; k--}cx; 1- .... =
шень 5n = ak -- {ЗІ та tn = O'k + (ЗІ в границі, якщо n --+ Х), отримуємо
5 = о' - (3, t = о' + ,З.
Вплив перестановки членів умовно збіжного ряду на його збіж-
. .
ність виражається у тако:ну твердженНl.
Теорема Рімана. Для будЬ-Я'КО20 'Н,аnереа :заcJа'Н,О20 rJіЙС'Н,О20
=
чuсла 5 .м,ОЖ'Н,(l nерестnаоuuш 'lлеЮJ. у.м,овно збіж'Н,о�() ряду L an
n=о
та'К, що oтnp·и.м,(L"Н,п-U після nepecтna'Н,oo'",;и чл(�'Н,і(J ряд буде збіж;юиJ.
ЗІ7
ао S. Членн у.лu)(j1{,О збіжного р.я.dу можна перестаеитлі так, що
опціиманий після нерестаноекн члснів ряі] бу()е розбіжним (j то.м.у
розу.м.іuuі, ЩО його су.М.О'/О буcJе ±х,
1.6. Властивості збіжних рядів. Частинна гума ряду є су
�ЮЮ скінченної кількості иого членів. Серед усіх властивостєи СУМИ
. ... .. .
єкінчєнноі кількості доданків пригадаємо ДВІ ---- С-ПО.1:УЧН.У та перес-
тавну. На іхніи основі побудовано ефективні способи О()ЧПСІСННЯ цієї
СУ�ПІ. Розглянемо обидві властивості Д.1:Я суми нескінченної кількості
доданків, тобто Д:ІЯ рЯДУ.
Сполучна властивість.
ос оо
Теорема 1. Нехай L ап -- рзи) з UіЙСU1L.м.'lL членами; L Сn---
n=о n=о
р.я.U, заг альннй член СП я-к:ого є су.м.ою тліз: членів заданого ряду, як:
об'єcJuа-н,і в групу з номером n при задаuій послідоаності Їх розта-
оо
ніцеання (див. нижче}. Якшо ряд L ап збіжний і його су.м.ою є
n=О
оо
члісло S, то ряд L сп збіжний і його су.м.ОЮ є тлікож число S.
n=о
ос
ДовеUеuuя. РЯД L ап має ВИГ.1:ЯД
n=о
оо
Lan = ао +- (1] +- ... +- апо + anotl +- аnо+2 +- ... +
n=о
ос
ряд L сп �ШЄ ВИГЛЯД
n=о
ос
L сп = (оо +- а] +- ... +- аnо) +- ((1/10+] +- аl/.о+2 +- ... +- а/l))+-
11=0
С'у:ну '1.1{'НlB У першпх дуж ках позю\'пп-ю Со. CY�IY Ч.1:('НlВ У других
. .
.Jужках позюl'ПВІО СІ. CY�IY ч.:ІРНlВ У трет]х дужках познаЧIl),Ю С·!
так дал.
318
Нехай {S1/}�
Х·
послідовність частинних сум РЯДУ LOll ,
11=0
оо
{bk}� --- послідовність частинних сум ряду L Ck. Оскі.1ЬЮ'І Д.1Я
k=O
скінченної кількості доданків сполучна властивість є істинною, тоб-
то дужки під час додавання можна опускати. то до = Со = Snn. дІ =
= СО+СІ = Sn\, 152 = СО+С1 +С2 = Sn2"'" 15k = СО+СІ +"'+Ck = Snk
при k = О, 1, 2, .... Отже. всі члени послідовності {дAc}� збігаються
з окремими членами послідовності {S1\}:, тобто містяться серед її
членів. Це означає, шо послідовність {bk}� є підпослідовністю пос
лідовності {S п} � .
оо
Нехай ряд L ап збіжнии і його сумою є число S, тобто послі
п=О
довність {Sn}� є збіжною до S. Тоді будь-яка ЇЇ пі дпослідовність
{Snk}� при k = О, 1,2, ... , зокрема {bk}� є збіжною, ПРИЧО).1у до S.
оо
Тому ряд L ск виявляється збіжним і ЙОГО сумою є також ЧИСЛО S.
k=O
На основі цієї теореми можна стверджувати, що в збіжному ряді
U • U • •
иого 'Ідени можна групувати як завгодно при ааданіи ПОСЛІДОВНОСТІ
ЇХ розташування, ПРИЧО).ІУ кожного разу одержується збіжний ряд і
Їюго сума збігається з сумою цього ряду.
Якщо ряд розбіжнии, то після групування його членів різними
способами отримувані ряди можуть бути збіжними ЧИ розбіжними;
у разі збіжності Їхні суми можуть бути різними.
Приклад. Розглянемо ряд
оо
1-1+1-1+1-1+···.
п=О
Він розбіжний, бо ПОСЛІДОВНІСТЬ ІЮГО членів не є збіжною до нуля.
Якщо {ЮГ0 члени згрупувати двома способами, то одержимо
L (.-1 )11 # (1 -- 1) + (1 -- 1) + (1 - 1) + ... = о.
319
L(-I)ll:f- 1-- (1-· 1) --- (1-1) -_. -. = 1_
11=0
Якто в КОЖНО�ІУ З ци:х рядів відкрити дужки, то отримаємо ряд,
то розглядається.
ЦС{І прпкла.д і.1ЮСТРУЄ також такс: якто агруповании ряд збіж
ний, то ряд, одержиний після відкриття дужок, може вияВІППСЯ роз
біжним,
Переставна властивість.
оо
Теорема 2_ Нехай L ап- ряі) :з аіЙс'Н:и.м:и чменами;
п=О
р.яа, отриманий з хьоао довільною перестановкою його
оо
L СП
п=О
чяеніе .
оо
Якиіо рзи) L а.; абсомотно збіжний і його сцмою є число 5, то рзи)
п=О
оо
L сп абсолютно збіжний і його снмою є також число 5_
п=О
оо
Доведеuuя. Нехай спочатку L оп --- збіжний ряд з додатни-
п=О
ми членами, 5 - його сума. Через {6n}� позначимо послідовність
оо
частинних сум ряду L сп· Послідовність {6п};; є монотонно зрос
п=О
таючою, оскільки 611+ 1 - 6п = СП > О. Члени послідовності {6n}�
оо
Є сумами деяких переставлених членів ряду Lan, тому б« < 5.
п=О
Отже, послідовність {6п};; є монотонно зростаючою і обмеженою
зверху. На основі теореми про границю монотонноі та обмеженої
послідовності стверджуємо, що послідовність {6п};;О є збіжною. Це
оо
означає, що ряд L сп збіжний. Його суму, тобто граНИІІЮ послі-
11=0
довності {Ьп};;О, позначимо Ь_ 3 нерівності ЬtI < 5, якто n � оо,
оо
випливає, що 6 ::; 5. Отже, якщо L Сп
11=0
. ряд з пєрєставленими '1.'1('-
ос
нами ряду La", то fJ s; 5 прп бу дь- ЯІ<ііІ перестановці його членів.
11=0
320
оо
Але І: а1l можна розглядати як ряд з переставленими членами ря
п=О
оо
ду І: Сп, які досить переставити у зворотній послідовності. Тому
п=О
5 < Ь. З нерівності 5 ::; 8 < 5 випливає, що 8 = s. Отже, якщо в
збіжному ряді з додатними членами переставити Їх будь-яким спо
собом, то одержании ряд виявиться збіжним, причому до тієї самої
суми.
оо
Нехай тепер І: ап
п=О
абсолютно збіжний ряд з діисними чле-
оо
нами. Тоді І: Іспl -- РЯД, одержании ПІсля переставляння членів
п=О
оо оо
збіжного ряду І: lапl· За доведеним вище ряд І: Іспl - збіжний.
п=О п=О
оо
На основі теореми 7 стверджуємо, що ряд І: сп збіжний. Отже, ряд
п=О
оо
І: СП виявляється абсолютно збіжним.
п=О
оо оо
Знайдемо суму ряду І: сп· Виділимо в РЯДІ І: а« ряд з не-
п=О п=О
від'ємних членів, суму якого позначимо а і ряд з абсолютних вели-
чин від' ємних членів, суму якого позначимо {З. Обидва виділені ряди
збіжні на основі теореми 8, причому 5 = а - {З. Перестановка членів
оо
ряду І: а.; спричинить перестановку членів у виділених рядах. Але
п=О
обидва вони є збіжними рядами з додатними членами. Тому Їхні су-
ми не ЗМІНяться і число 5 виявиться сумою ряду з переставленими
членами.
На основі цієї теореми можна стверджувати, що в абсолютно
збіжному ряді його члени можна переставляти як завгодно, причо
му кожного разу одержується збіжний ряд його сума збігається з
сумою иього ряду.
В умовно збіжному РЯДІ, як стверджує теорема Рімана, можна
так переставити його члени, шо отриманий ряд бу де мати іншу суму
321
або виявиться розбіжним,
1.7. Дії над числовими рядами. Д."ІЯ суми скінченної кількос-
. .. .
ТІ доданків є ІСТИННІІ).,ПІ Б.1аСТИВОСТІ поч .. лєнного множення на число,
почленного додавання чи ВІДНІмання: а також перемноження суми
на суму. Розглянемо ці властивості для суми нескінченної кількості
доданків.
оо
Теорема 1. Я-Г;;ЩО р.яд L: ап збіжннй і його су.ма дорів1і'ЮЄ 5,
n=о
оо
то р.яд L: сап, де С -- фіксоеане число, також збіжний і його су.ма
n=о
дорівнює С • 5.
Доведення. Позначимо {5n}: послідовність частинних сум ряду
оо оо
L: ап, {Ьn}: послідовність частинних сум ряду L: Сп, сп = С· ап·
n=о n=о
Маємо
Ьn = со + СІ + С2 + ... + Сп = С . ао + С • 01 + С • а2 + ... + С . ап =
= с(ао + аl + а2 + ... + ап) = С· 5n,
Послідовність {5n}: є збіжною до числа 5. Тоді з вищенаведеного
одержуємо
Іігп Ьn = Іігп с5n = с Іігп 5n =--= с5.
n�CX) n�oo n�cx)
Дію множення збіжного ряду на число записують у вигляді
оо оо
CLan = L сип,
n=о n=о
(17)
який означає, що постійнии множник можна внести шд знак суми
або винести з-під її знака.
оо
Теорема 2. Якиіо р.яд L: ап збіжний і су.мо'Ю його є члісло
n=о
оо оо
а, р.яd L: Ь; збіжний і сцмою його є число Ь, то р.яd L: (ип ± ьn)
n=о
збіжний і симою його є число а ± ь.
n=О
322
оо
Доведення. Послідовність ЧаСТИННИХ сум ряду L а; позначимо
п=о
оо
{Sn}�, послідовність частинних сум ряду L ЬП позначимо {(ln}�,
n=о
ех;
посшдовність частинних сум ряду L (ап ± Ьп) позначимо {in}�.
п=о
Маємо
Послідовність {Sn}� є збіжною до числа а, послідовність {(ln}�
є збіжною до ЧИСо:1а Ь. Тому з рівності іп = Sn ± а« випливає
Ііт і« = Ііт (Sn ± (Іп) = Ііт Sn ± Ііт (Іп = а ± ь.
n�= n�= n�= n�=
оо
Отже, ряд L (ап ± Ьn) збіжний і його сума дорівнює а ± ь.
n=о
Дію додавання та вгднімання двох збіжних рядів записують у
ВИГЛЯДІ
(18)
п=о
n=о
п=о
оо ос
3ауоаже'Н,'Н,.я. Якщо ряд L ап розбіжний, ряд L ь; розбіжний,
n=о
п=О
оо
то ряд L (ап - Ьn) може бути збіжний.
п=о
Приклад. Приймемо ап = Ьп. Тоді
І)ап - Ьп) = L о = о + о + о + ... + о + ... = О,
n=о
11=0
оо
тобто ряд L (ап - Ьп) ВИЯВИВСЯ збіЖНИ!'.І і сума ЙОГО дорівнює нулеві.
п=О
Множення рндгв.
оо
Означення 1. Добутком двох ЧИС,10ВИХ рядів L: ап
n=О
n=О
оо
називається такий числовий ряд L: сп, члени якого утворені до бут
n=О
ками кожного члена першого ряду на кожнии член другого.
Члени добутку утворені елементами нескінченної матриці
аоЬо
аоыl
аОЬ2
аоЬ,
аlЬО
аl ыl
аl Ь2
аІЬ'
а2ЬО
а2ыl
а2Ь2
а2Ь,
akbO
akbl
akb2
akb,
причому кожен елемент береться тільки один раз. Послідовність роз-
ташування елементів може бути довільна: ВЗДОВЖ сторін квадратів,
тобто
Со = аоЬо,
СІ = аоыl + аlЬО + а1Ь1,
С2 = ао Ь2 + а2 ЬО + а І Ь2 + а2 ыl + а2 Ь2 ,
(19)
чи вздовж діагоналей, тобто
Со = аоЬо,
СІ = аоыl + (11 ЬО,
С2 = аОЬ2 + а] Ь1 + а2ЬО,
(20)
оо
Означення 2. Ряд L: Сп, члени якого розміщені вздовж діа
n=О
гоналей, тобто загальний член має вигляд
324
оо оо
називається добут'/;:о.м за Коші рядів L 011 L ЬП• Сума номерів
n=о п=о
множників у КОЖНО).,ІУ доданку (див. фОР)"ІУ�1У для Сп) дорівнює но-
меРОВІ зага.1ЬНОГО члена.
оо
Теорема З. Нехай L а.;
п=о
оо
L Ьп --- рядн з ді'йС1іи.ми членами,
п=о
оо оо
L сп - ЇХ1іі'й добуто-г;;. Якшо рзи) L ап абсолютно збіжний і су-
n=о п=о
оо
мою 'його е число а, р.яд L ЬП абсолюпіно збіжний і сцмою 'його е
п=о
оо
число Ь, то р.яд L сп абсопютно збіжний і сцмою 'його е члісло аЬ.
п=о
3 доведенням можна ознайомитись в [1, т.2, с.38].
§ 2. Функціональні ряди
2.1. Поняття функціонального ряду та його області
збіжності. Нехай {! n (х)} :'=0 --- послідовність функцій, визначених
на множині D1. Розглянемо ряд
оо
L іn(х). х Е п.,
п=о
членами якого є елементи шєі послідовності. Ряд (21) називається
фУЮї.ціО1іаЛЬ1іU.м рядом. Для кожного фіксованого .:r, xED І він стає
числовим рядом, який може виявитися збіЖНІНІ чи розбіжним.
Означення 1. Множина тих значень :Г. при яких функціональ
ний ряд (21) збіжний, називається областю збіжності цього ряду.
Область збіжності ряду (21) позначатимемо через D. Коли х
змінюється на множині D. то. взагалі кажучи. змінюється і сума
ряду (21). Тобто в області збіжності цього ряду його сума є деякою
функцією від Х. ТО!\ІУ суму функціонального ряду (21) позначимо
через 5(х):
(21)
5(.1") = L іll(Х)' г е о.
п=О
(22)
It
Через Sn(x) позначимо частинну СУ1ІУ РЯДУ (21): Sn(.T) ='LJk(;r):
k=O
тоді S(x) = Ііт Sn{:r), .l� Е D.
11.-+=
Означення 2. Ряд. одержаний з ряду (21) відкиданням перших
n + 1 членів, тобто ряд
In+І(Х) + In+2{Х) + ... + In+k(X) + ...
(23)
називається зали иі �ом р.яду (21).
Властивості З3.;1ИШКУ функціонального ряду в його області збіж
ності збігаються з відповідними властивостями залишку числового
ряду. Позначивши
гn(х) = L Ik(X), xED,
k=n+I
(24)
отримаємо Ііт гn{х) = О, S(x) = Sn(X) + гn(х).
n-+оо
2.2. Ознаки збіжності та властивості. Ознаки збіжності
функціонального ряду в області збіжності є аналогічними до відпо
відних ознак збіжності для числового ряду.
оо
Необхідна ознака збіжності. Якщо ряд L: Іn(х) збіжний в
11.=0
деякій області, то в цій області
ііт In(Х)=О.
n-+=
Достатні ознаки збіжності функціональних рядів є також ана
ЛОГІчними до ВІДПОВІДНИХ достатніх ознак збіжності Д.1Я ЧИС-,10ВИХ
рядів.
оо ас
Означення. Ряд L: Іn(х) такии, що ряд L: I/n(.с)1 теж збіж-
n=О
n=О
оо
ний, називається абсолютно збіжним: збіжний ряд L: І" (3:) такии.
,,=0
ос
що ряд L: I/n(х)1 розбіжний, називається цмовно збіжни . .м ..
n=О
326
.Іля знаходження області аБСО.1ЮТНОЇ збіжності функціонального
ряду можна ластосувати такі ознаки .
. х;
Ознака Даламбера. Нехай L: іn (х) -- функціональний ряд,
п=о
для якого ІСНУЄ границя
Ііт І іп+І (х) І = d(x).
n--too іп(:с)
Тоді на множині {х : d( х) < І} ряд абсолютно збіжнии, на множині
{х : d(x) > І} ряд розбіжний, намножині {х : d(x) = І} ряд може
бути абсолютно збіжний або умовно збіжний чи розбіжний,
оо
Ознака Коші. Нехай L: f п (х) ---- функціональний ряд, для яко-
n=о
го ІСНУЄ границя
Іігп уІIІn(х)1 = d(x).
n--t<XJ
Тоді на множині {х : d( х) < І} ряд абсолютно збіжний на мно
жині {х : d( х) > І} ряд розбіжний, на множині {х : d( х) = І} ряд
може бути абсолютно збіжнии або умовно збіжний чи розбіжний.
Зв'язок між абсолютною збіжністю та збіжністю функціональ
ного ряду Є аналогічним до відповідного зв'язку для числового ряду.
оо оо
Теорема. Якиіо ряі) L: IІп(х)1 збіжний, то рзи) L: іn(х) збіж-
п=о п=о
ний.
Властивості збіжних функціональних рядів та арифметичні дії
над ними виконують� в кожній точці Їхніх областей збіжності і Є
аналог-ічними до відповідних властивостей збіжних числових рядів
та арифметичних дій над ними.
=
2.3. Рівномірна збіжність. Нехай L: Іn(.г) - функціональ-
п=О
ний ряд, {5" (.г)} � - - послідовність його частинних сум, 5 (х )-- СУМа
оо
ряду, D - ... область збіжності. Збіжність ряду L: іll(.I:) В області D
,,=0
327
до його суми S(x) означає, шо в кожній точці х області D послідов
ність {Sn(.I:)}� Є збіжною ДО функції S(x):
оо
lim Sn(x) = S(x) = L Іn(х);
n-+оо
n=о
іншими словами, для кожного xED і для кожного Е > О існує таке
натуральне число По, ПО = ПО ( Х, Е), ЩО для всіх натуральних n > по
бу де істин�ерівність
ISn(x) _оо S(x)1 < Е.
3а допомогою логічних символів це означення можна записати так:
(\Іх Е D)(\lE > 0)(3nо Е іУ)(\ln � по) : ISn(x) - S(x)1 < Е. (25)
Означення. Якщо ціле число По, вказане в (25), можна вибрати
незалежно від х, тобто воно є функцією лише від Е; іншими словами,
якщо для будь-якого Е > О існує такий номер По, що коли п � По, то
для всіх xED виконується
ISn(x) - S(x)1 S Е,
оо
то ряд L: Іn(х) називається рівномірно збіжним в області D до
n=о
функції 5 (х), а послідовність {S n (х) } � .. - називається рів номірно
збіжною в області D до функції S(x).
Це можна записати стисло:
(\Іє> 0)(3По Е іУ)(\lх Е D)(\lп � по): ISn(x) - S(x)1 < є, (26)
оо
Якщо ж такого числа ПО не існує, то ряд L: .f n (;(:) залишається
n=О
збіжним, a.;�e нерівномірно, а послідовність {Sn(x)}: оо .... збіжною, але
. .
нерівномірно.
328
Приклад. Геометрична прогрссія 1 + :І.: + х2 + ... + хn + ... =
оо n 71+1
L: xk, яка має частинну суму Sn (х) = L: xk = І ��x ,збігається
k=O k=O
абсолютно V з: Е (-1; 1) і має суму S(x) = І � .тхжільки Іігп Sn(x) =
х n---+сх)
І· I_xn+l І
пп І-х = І-х' -1 < з: < 1. Однак цей ряд збігається на
n---+сх)
-1 < з: < 1 нерівномірно. Дійсно, залишок ряду гn(х) = хn+l+
+2 n+l
+хn + ... утворює геометричну прогресію, тому гn(х) = �-x'
Інтервал (-1; 1) містить точки як завгодно близько до 1. Оскільки
1· () Іі xn+1 u
пп Гn Х = пп -1- = ОО, то яким би великим не було n, знаидуться
х---+l х---+І х
точки х, Х Е (-1; 1) для яких г n (х) більше від бу дь- якого як завгодно
великого числа. Отже, не можна підібрати таке По, щоб для n > по
нерівність Ігn (х) І < Е виконувалась у всіх точках інтервалу ( -1; 1), а
це і означає, що збіжність ряду в інтервалі (-1; 1) не є рівномірною.
оо
Критерій рівномірної збіжності. Для того, щоб ряд L: Іn(х)
n=О
був рівномірно збіжним в області С, необхідно і достатньо, щоб для
кожного Е > О існував такий номер По, що для кожного n > по і
будь-якого натурального m нерівність
IІn+l(Х) + Іn+2(Х) + ... + Іn+т(х)1 < Е
(27)
була істинною одразу для всіх з: Е С.
Сформульовану ознаку називають критерієм Коші рівномірної
збіжності функціонального ряду. �
оо
Наслідок. Якщо ряд L: Іn(х) рівномірно збіжний в області
n=О
оо
С, а функція лх) обмежена в ній, то ряд L: Лх)Іn(х) рівномірно
n=О
збіжний в області С.
Справді, оскільки існує таке число с > О, що для всіх з: Е G
буде ІЛ х) І ::; с, то застосовуючи властивість абсолютної ведичини
добутку двох функцій, а також необхідну ознаку критерію рівномір
ної збіжності, (див. (27)), одержуємо (V є > О) (3 по Е іУ) (V х Е С)
329
(\І n � по) (\І тЕіУ):
IЛх)ln+I(Х) + Лх)ln+2(Х) + ... + Лх)/n+т(х)1 =
= IЛх) (Іn+l(Х) + In+2(Х) + + In+т(х))1 =
= IЛх)I'l/n+І(Х) + In+2(Х) + + In+т(х)1 < СЕ,
звідки на основі достатньої ознаки критерію рівномірної збіжності
оо
випливає, що ряд L Лх)ln(х) рівномірно збіжний в області С.
n=О
оо оо
Теорема. Нехсй L Іn(х) -- фу-н,'К:ціо'НДль'н:uu р.яд, L ап -- чис-
n=О n=О
лоеий р.яд з додат-н,·и.ми членпми: Якиіо 'Іп (х) І s ап дл.я 'К:ож-н,020
оо оо
n = О, 1,2, ... і всіх х Е С, а р.яд L ап -- збіжний, то р.яд L Іn(х)
n� n�
абсопютно і рівномірно збіжний в області С.
оо
Дов едення. На основі ознаки порівняння маємо, що ряд L 'Іп (х) І
n=О
оо
збіжний в деякій області С, тому ряд LIn (х) абсолютно збіжний у
n=О
цій самій області.
Для доведення рівномірної збіжності застосуємо критеріи РІВ
номірної збіжності функціонального ряду та критерій збіжності чи
�.лового ряду. На основі нерівності для абсолютної величини суми
�ІНченнOl КІЛЬКОСТІ доданків та неРІВНОСТІ в УМОВІ теореми маємо
s I/n+І(х)1 + I/n+2(х)1 + ... + I/n+т(х)1 s аn+l + аn+2 + ... + аn+т
оо
для будь-якого rn = 1, 2, З, ... і всіх з: Е С. Оскільки ряд L ап
n=О
збіжний, то на основі необхідної ознаки критерію збіжності ЧИС:ЮВО-
го ряду \І є > О 3по Е і\', таке, що виконується (1n+1 + аn+2 + ... +
+аn+т < є. Враховуючи сказане вище, маТИМБЮ 1/"+1 (х)+ In+2(Х)+
330
+ ... + іn+т(х)1 < є для будь-якого т = 1� 2. 3� ... і всіх .r Е с. Це й
ас
означає, що ряд L .f n (х) рівномірно збіжнии в області с.
п=о
Доведена ознака називається ознакою Вейсристрасса.
оо
Збіжнии ЧІІСЛОВІШ ряд L ап з додатними членами функ
п=о
ос
ціональний ряд L.f n ( Х ), Д.1Я членів котрих виконується умова
п=о
lіп(х)1 < ап, часто називають відповідно мажоруючим і мажоро-
ваним. Тоді ознака Вейєрштрасса може бути сформульована так:
мажорований функціональнии ряд є рівномірно збіжним.
Однак рівномірно збіжний ряд може бути і немажорованим.
2.4. Неперервність суми ряду. Сума скінченної кількості
функцій, неперервних на деякому проміжку, є неперервною на цьо
му самому проміжку функцією. Розглянемо аналогічну властивість
для суми нескінченної кількості функцій, тобто для утвореного ними
функціонального ряду.
Теорема. Я?\,ЩО фу'Н?\''Ціі іn(х) дл.я кожного т = О, 1,2, ... є
оо
неперереними. 'На де.я?\,о.му nро.між?\'у [а; Ь], а р.яд L Іп(х) рівномірно
n=о
збіжний 'На ньоми, то су.ма р.яду буде 'Неnереро'Ною 'На 'Цьо.му самомц
nро.між?\'у фу'Н?\''Цією.
оо
Доведення: Нехай S(x) -- сума ряду L іп(х), Sn(x)
иого
n=о
частинна сума, r n (х )-- за.:1ИШОК ряду. У кожній точці ПРОМІЖКУ
[a� Ь], зокрема в точці хо, маємо
S(x) = Sn(x) + 1'п(х),
S(xo) = Sn(XO) + 1'11(ХО).
(28)
Віднімаючи нижню рівність від верхньої та застосовуючи нерів
ність для абсо.1ЮТНОЇ величини суми трьох доданків, одержимо
331
Функція Sn(X) при кожному фіксованому n = О, 1,2: ... має виг
ляд Sn(x) = Іо(х) +- ІІ (х) +- ... +- Іп(х), тобто є сумою скінченної кіль
кості функцій, неперервних на проміжку [а; Ь]. Тому вона неперервна
в кожній точці проміжку [а; Ь], зокрема в точці ха. Це означає, що
для кожного є > О існує таке й > О, шо для всіх х Е [а; Ь], дЛЯ яких
Іх - ха І < й, буде істинною нерівність
r
/ {- (І/ -
І ( ,
./" >'.';
оо
Ряд LIn (х) рівномірно збіжний на проміжку [а; Ь]. Це означає,
п=о
що для кожного є > О існує такий номер По, що для всіх n > по і
всіх х Е [а; Ь], зокрема, для х = ха будуть істинними нерівності (див.
(28), (26))
На основі одержаних нерівностей можна стверджувати, що для
кожного є > О існує таке й > О, що Д�1Я всіх х Е [а; Ь], Д.:1Я яких
Іх -- хаІ < й буде
IS(x) - S(xo)1 < 3є.
Це означає, що функція S(x) є неперервною в кожній точці ха
проміжку [а-; Ь], а: значить, і на всьому проміжку.
2.5. Границя суми ряду. Границя суми скінченної кількості
функцій при необмеженому наближенні значень аргументу до гра-
ничного значення дорівнює сумі границь кожної з них. Розгляне-
мо аналогічну властивість для суми нескінченної кількості функцій,
тобто для утвореного ними функціонального ряду.
оо
Теорема. Н ех ай р.яd LIn Ст), .Т є л», рівномірно збіжний
п=о
'На множині І); 'Нехай Ха ._--- гранична точка множини п. Я1\,що:3
332
Ііт Іn(х) = [n, [n Е Н, n = О, 1, 2, ... , то існує скінченна границя
x-txo
ос оо
Ііт L іn(х) = L Ііт Іn(х).
x-txo x-txo
n=о n=о
(29)
Доведення. На основі необхідної ознаки критерію рівномірної
оо
збіжності ряду L f n (х) для кожного є > О існує такий номер по, ЩО
n=о
для кожного n > по і будь-якого натурального m нерівність
є істинною одразу для всіх х Е [а; Ь]. Переходячи в цій нерівності до
границі, якщо з: � Ха, та враховуючи умову теореми, одержимо
На основі достатньої ознаки критерію збіжності числового ряду мож-
оо
на стверджувати, що ряд L [n збіжний.
n=о
оо
Для ряду L Іn(х) позначимо: S(x) -- його сума, Sn(X) - час-
n=о
тинна сума з номером 11, Тп(Х) ----- залишок з номером n. Для ряду
оо
L [n позначимо: а --- його сума, ап ---- частинна сума з номером n,
П=О
рП---- залишок з номером n. Тоді маємо
S(x) = Sn{x) + Тn(Х), а = о.; + рn·
Віднімаючи від лівої рівності праву та застосовуючи нерівність для
абсолютної величини суми трьох доданків, отримаємо
333
оо
Ряд L Іn{.1:) рівномірно збіжний на проміжку [а; Ь]. Це означає:
n=о
дЛЯ кожного Є > О ІСнує такии номер П1, шо для всіх n 2:: n 1 і усіх
:І: Е [а; Ь] буде
оо
Ряд L іп збіжнии. Це означає: для кожного є > О існує такии
n=о
номер П2, що Д�1:Я всіх n 2:: П2 буде
IРnl < Є.
Візьмемо ДОВІльне n > таХ(Пl' П2) і зафіксуємо його. функція
Sn(x) при фіксованому n є сумою скінченної кількості доданків, бо
n
Sn(x) = L І,,{х). Переходячи до границі, якщо х � Хо, та викорис-
,,=0
товуючи позначення, матимемо
n
n
n
Звідси, з урахуванням означення границі функції, випливає, що для
кожного є > О існує таке й > О, що для всіх х Е [а; Ь], дЛЯ яких
Іх - хоl < 8, буде
На ОСНОВІ одержаних нерівностей можна стверджувати: ДЛЯ
кожного є > О існує таке 8 > О, що дЛЯ ВСІХ Х Е [а; Ь], дЛЯ яких
Іх - хаІ < 8, буде
IS(x) - 0"1 < Зє.
Це означає, шо границею функції S(x), якщо з: � Хо, є число 0".
2.6. Диференціювання ряду. Похідна суми скінченної кіль
кості диференціиовних функцій дорівнює сумі похідних кожної з них.
РОЗГЛЯНБЮ аналогічну властивість для суми нескінченної кількості
функцій: тобто для утвореного ними функціонального ряду.
ЗЗ4
Теорема. Нехай фУ1і?\"ціі іn(х) nри ?\,ОЖ1іО.му n = О; 1,2;.,. d'/L-
оо
фере1і'Ційов1іі на проміжкл; [а; Ь]. Якиіо ряі) L fп (х) збіжний при-
п=о
ос
наймні в од1іій точці ха проміжкл; [а; Ь], а ряі) L I� (х) рівномірно
n=о
оо
збіжний на nро.між'К:у [а; Ь], то р.яд L Іn(х) рівномірно збіжний на
n=о
nро.між?\'у [а; Ь], його су.ма S(x) є дuфере1і'Ційов1іОЮ на проміжкл; [а; Ь]
фУ1і?\''Цією, причомц
(30)
Доведення: На основі необхідної ознаки критерію рівномірної
оо
збіжності ряду L I� (х) для кожного Є > О існує такий номер По, ЩО
n=о
для кожного п > по і будь-якого натурального l нерівність
n+т і
L I�(x) < є
v=n+l
n+т
є ІСТИННОЮ одразу дЛЯ ВСІХ з: Е [а; Ь]. Функція ЛХ) = L fv(x)
v=n+I
для кожних фіксованих тіп є сумою скінченної кількості доданків,
n+т
тому f'(x) = L I�(x). Враховуючи попередню нерівність, маємо
v=n+l
1f'(x)1 < є в проміжку [а; Ь]. ДЛЯ кожного з: -І- хо застосуємо до
функції ЛХ) на проміжку [ха; х] (на Іх; ха), якщо х < ха) теорему
про скінченні прирости. Одержимо J Il=�oxo) = Г(с), де с --- деяке
число, ха < с < х. Але
335
Тому для кожного є > О існує НО?УІер по, ЩО для кожного ТІ > по
будь-якого натурального т буде
n+m (
" І", х) - 1",(1:0) = 1/'(с)1 < є
� х-хо
",=n+l
на проміжку [а; Ь] при х # хо" На основі достатньої умови критерію
оо
рівномірної збіжності можна стверджувати, ЩО ряд L In(X:=��(Xo) є
n=о
рівномірно збіжним на [а; Ь], ЯКЩО х#хо. Множимо його на обмежену
оо
на проміжку [а;Ь] функцію л-є.єь. Одержаний ряд L иn(х) - Іn(:со)]
n=о
залишається рівномірно збіжним на [а; Ь], ЯКЩО з: # хо. 3а умовою
оо оо
ряд LIn (хо) збіжний. Тому збіжною є сума рядів L [J n (х) - Іп (хо)]
n=о
n=о
оо DC
і L Іn(хо), тобто ряд L Іn(х) виявляється рівномірно збіжним на
n=о n=о
проміжку [а; Ь].
оо оо
Приймемо L Іn(х) = S(x). Враховуючи, що L Іn(хо) = S(1:0)
n=о n=о
оо оо
одержимо L Іn(х)- Іn(хо) = S(x)-S(xa). Оскільки ряд L Іn(х)- Іn(Ха)
n=о Х-Хп Х-Хо n=о Х-Ха
рівномірно збіжний на [а; Ь], ЯКЩО .г # Хо, то виконуючи дію гранич
ного переходу під знаком ряду, ЯКШО :Г --+ хо, (див. теорема п.2.5),
та враховуючи диференційовність функціи Іn(х) в проміжку [а; Ь],
отримаємо
1· S(x) - S(xo) 1· f-- Іn(х) - Іn(хо)
пп = пп �
Х-+ХО Х - хо Х-+ХО Х - хо
n=О
DC
Ряд L I�(xo) збіжний в кожніи точш :то Е [а: Ь]. Тому граниля
n=О
Іігп �(.c)-S(IO) . . 3
ДОРІВНЮЄ деякому числу. а саме сумі нього ряду. а
ЗЗG
означенням похідної значє':ІНЯ Ц1ЄІ границі ДОР1ВНЮЄ 5'( :го ). Функ
ція 5(х) ВИЯВ:ІЯЄТЬСЯ дифсрєнціиовною у кожній фіксованій точці
оо
хо Е [а:Ь], причому 5'(хо) = L I�(;l'o).
n=О
оо
Рівність 5'(х) = L І:,(х) записують у вигляді (30). ЦЮ ДІЮ
n=о
називають дифере1щіюва'Н:н.я.м р.яду. І30на означає, шо похідна суми
ряду дорівнює сумі ряду похідних кожного иого доданка.
2.7. І нтегруванн.я ря ду. Інтеграл суми скінченної кількості
інтегровних функціи дорівнює сумі інтегралів кожної з них. Розгля
немо аналогічну властивість для СУ),1:И нескінченної кількості функ
цій, тобто для утвореного ними функціонального ряду.
Теорема. ЯКЩО фу'Н:к:ціі іn(х), Q � Х � Ь, інтегровні 'На [а; Ь]
оо
при кожноми n = О, 1, 2, ... і .я'К',ЩО 5(х) = L іn(х), а � х � Ь,
n=о
причомц р.яО збігається рівномірно 'На [а; Ь], то 5( х) інтегроена 'На
[а; ЬІ і р.яd можна почленно інтегрцеати:
ь ь ь
J S(x)dx = J (�fп(I)) ах = �! іn(х)ах. (ЗІ)
а а а
Доведення. Нехай задано є > О. Виберемо 1/ > О так, щоб ТJ <
3(Ь-=-а)' Оскільки ряд збігається рівномірно, то :3 по > О:
-17 � 5(.1') - 5n(х) � 17, 'ч п > По. Vx Е [а;Ь]. (32)
n
Зафіксуємо п . н ::::: ПО. Функція 5n(з:) = L fll(X) інтегровна на
11=0
[а; Ь] (як сума інтєгровних функцій). Тому (теорема 3, розділ 7) існує
розбиття П відрізка [а; Ь]: а = ХО < .Т] < ... < j'n < ХІ = Ь, такс. що
Д.,1Я верхньої і нижньої інтегральних сум функції 5 n ( .r) ВИКОНУЄТЬС Я:
(33)
337
t І
де U(П, 5n) = L ініс,.І:і, L(П, 5n) = L mi�;ri, �.1:, = Хі -- Х,--І,
,=1 і=l
і = 1,і; М, = sup5n(x) .. 1"і-1 ::; Х::; .Сі: т.; = inf 5n(х) .. 1',-I::;Х::; Ті·
Розглянемо також верхню і нижню інтегральні суми функuії 5(.1}
t
U(П,5) = L Al1�Xi, L(П,5) = L iiii�Xi,
і=1
і=1
1\1і = sup 5(х), Хі-І::; Х ::; Хі; іііі = inf 5(х), Хі-І::; Х ::; Хі·
3 (32) ВИШІИває, що 5n(х) - Т} ::; 5(х) ::; 5n(х) +- Т}, а ::; х ::; Ь, тому
t � t t t
Тоді U(П, 5) = L м.с», < L (Мі +- Т})!:Ні = L м.с», +- Т) L ь.Хі =
і=1 і=1
U(П, 5n) +- Т}(Ь - а) ::; U(П, 5n) +- �, тобто
і=l
і=l
U(П,5) < U(П, 5n) + �.
(34)
Аналогічно можна показати, що для нижніх інтегральних сум
�
L(П,5) 2: L(П, 5n) - �.
(35)
3 (33)(35) випливає
U(П,5) -- L(П,5) = [U(П,5) - U(П,5n)] +- [L'(П,5n) __ о L(П.5n)]+-
� =- ё
+-[L(П, 5n) - L(П, 5)] < � +- � +- 3" = Є.
338
Отже, \;f г > О існує розбиття П відрізка [а; Ь] таке, ЩО С(П,5)
-L(П,S) < Є, і за теоремою З (розділ 7) функція 5(1:) інтсгровна на
[а; Ь]. Враховуючи (ЗО), ЯКЩО n � N, !\ІаЄ\ІО
ь ь ь
j 5(J·)d.T -- j 5n(.г)d.г = і(5(.Т) - 5n(x))dx <
а
а
а
(З6)
ь
< j 15(х) - 5(х)1 dx < ТJ(Ь - а) < є.
а
оо
Оскільки є> О довільне, 5(х) = L іn(х),
n=о
ь ь ь
J Sn(x)dx � J (�цx)) ах � �J цх)ах,
а а а
то з (З6) та з означення суми ряду випливає (ЗІ).
§ 3. Степеневі ряди
3 функціональних рядів важливими є степеневі р.яди вигляду
оо
ао+аl(:с-хо)+а2(х--хо)2+ .. ·+аn(х-хо)n+ ... = L аn(х-хо)n. (З7)
n=О
Числа ап називаються коефіцієнтами ряду. Якщо в (З7) хо = О, то
одержимо ряд
(З8)
11=0
Дослідження збіжності ряду (З7) еквівалентне дослідженню
збіжності ряду (З8). Тш.,1У далі будемо розглядати ряди (З8).
ЗЗ9
З.l. Теорема Абеля. Радіус збіжності.
Теорема 1 (Теорема Абеля). ЯКЩО ]JJlO (38) збіжний (j oeJl7\.iii.
точці х ; #- О, то ві-н, абсолютна збіжний д.ая 6yOb-Jl7\.020 х, ОЛJl яко-
20 Іхl < Iх*l. Я"І\�ЩО ряд (38) розбіжний в деяній. то'Ч'Цz х", то Bzn
розбіжний д.ая всіх х, для якиз: Iтl > І:г* І·
Доведення. Нехай ряд (38) збіжний в точш т , #- ха. Тоді за
необхідною ознакою збіжності ряду Ііт lanx� І = О. Отже, існує
п+ь оо
таке ЧИС.10 1\1 > О, що lanx� І < 11-1, \;f п = О, 1, 2, .... Якщо Іхl < Іх* І,
то
де q = І ХХ. І < 1, тобто всі члени ряду (38) за абсолютною величи
ною менші від членів збіжної геометричної прогресії. За ознакою
порівняння ряд (38) збіжний абсолютно.
Нехай ряд (38) розбіжний в точці т" #- о. Припустимо, що він
збіжний в деякій точці х такій, що Іхl > Іх* І. Тоді, за доведеним
вище, він повинен бути збіжним в точці з:", Одержали суперечність.
Оскільки {х : Іхl < Iх*l} = {х : -lх*1 < з: < Iх*I}, то з першого
твердження теореми Абеля випливає, що ряд (38) абсолютно збіжний
в околі точки з: = О радіуса Iх*l. З другого твердження теореми
випливає, що РЯД (38) розбіжний зовні околу точки з: = О радіуса
Iх*l·
Степеневий ряд (38) завжди збіжний, якщо х = О, ОСКІльки у
таКО!\1)' разі усі члени ряду, крім ао, дорівнюють нулеві. Існують
ряди (38), які не мають інших точок збіжності, крім з: = О. Таким є
оо
ряд L п!хп. Використовуючи ознаку Да.n:амбсра, легко перевірити,
п=а
що він розбіжний \;f:r #- О. Ряди: які збіжні тільки в одній точці :Г = О,
. .-
нецікаві, 1 далі ми ІХ не РОЗГ.'ІядаЄ�10.
Теорема 2. длJl кожного степеневого РЩ)У (,'/8) існне П, П?:.О
або R = +х таке, що \;f .г , ОЛJl язгиз: 1.t'1 < R. рщ} (.'і8) збіжннй
абсолютно, а ЩJ'U всіх :Г, ()ЛJl нкиз: І.І:І > В. рщ) (:/8) роз6іжюиl..
340
На будь-якому проміжку [-1'; 1']. де l' фіксоване і l' < Н, ряд (38)
рівномірно збіжний.
Збіжність ряду (38) в точках з: = ±R досліджується додатко
во для кожного ряду (38). Число R називається радіусо.м, збіжності
степеневого ряду, а інтервал (-R; R) називається інтереалом збіж
ності.
Доведення. Позначимо через А множину чисел А = {х : з: � О,
з: належить області збіжності ряду (38)}. Оскільки в точці з: = О ряд
(38) збіжний, то О Е А f. (J). Позначимо R = sup А -- верхню грань
множини А (див. розділ 1, п.1.8). Покажемо, що R -- радіус збіжнос
ті ряду (38). Нехай число з: таке, що Іхl < R. Згідно з означенням
верхньоі грані існує таке х* Е А, що Іхl < т , :::; R. З означення
множини А випливає, що в точці х* (х* Е А) ряд (38) збіжний. Тому,
враховуючи перше твердження теореми Абеля, для вказаного з: ряд
(38) збіжнии абсолютно.
Якщо Іхl > R, то виберемо число з:" таке, щоб R < з:" < Іхl.
Оскільки R --- верхня грань тих чисел, в яких ряд (38) збіжний, а
з:" > R, то в точці х* ряд (38) розбіжний. Тому з другого твердження
теореми Абеля випливає, що в точці з: (Іхl > х*) ряд (38) розбіжнии.
Отже, дійсно, R є радіусом збіжності ряду (38).
Якщо тепер 0< т < R, то, як було доведено, ряд (38), якщо х = r
оо
абсолютно збіжний, тобто числовий ряд L: Іап Ітп збіжний. Для
n=О
будь-якого з: Е [-1'; 1'] виконується
тому за ознакою Веиєрштрасса (теорема 14) ряд (38) рівномірно
збіжнии на [-1'; т].
3ауважеuu.я. Повторюючи попередні міркування, можна по
казати, що для загального степеневого ряду (37) існує інтервал
(хо - R; хо + R) (іитерв ал збіжuосmі) з центром в точці з: = хо,
всередині якого ряд (37) збіжнии абсолютно, а зовні (якщо І;г -
хо І > > R)· . ряд розбіжний. На бу дь-якому проміжку [.го - г; хо + 1'],
341
де r фіксоване і О < r < В, ряд (37) рівномірно збіжний. Радіус
збіжності R може іноді дорівнювати також О і оо. У кінцевих точ
ках інтервалу збіжності з: = хо ± R МОЖ.ПІВа як збіжність, так і
розбіжність степеневого ряду.
у простих випадках радіус збіжності можна знайти за допомо
гою ознак Двламбера або Коші, застосовуючи іх до ряду, членами
якого є абсолютні величини членів ряду (37):
Наприклад, якщо існує границя
(39)
то за ознакою Даламбера, ряд (37) абсолютно збіжний, якщо q < 1
і розбіжний, нкщо q > 1. Тому з (39) випливає, шо для Іх - хо І <
< hн.!, ряд (37) збіжний. а для Іх - хо І > -_llа--І . цей ряд
Іі n 1 ' ,. �'
пп lапl пп [с І
п-+оо n-t-oc n
розбіжний. Отже, радіус збіжності
R=
1 = Ііш lаnl
Ііт � n-+= lаn+ll
n-+сю lапl
(40)
Аналогічне міркування і застосування ознаки Коші дає формулу
1
R= .
Ііш �'
n-+=
( 41)
справедливу. якщо існує фігуруюча в ній границя.
Користуватись (40). (41) треба дуже обережно, оскільки грани
ці, шо стоять в правих частинах цих формул, часто не існують. На
приклад, якщо нескінченна множина коефіпіентів а 11 перетворюється
в нуль (це, зокрема, справджується, як шо ряд містить ті.1ЬКИ члени
;) парними або тільки з непаРНІНШ стєпснями (х - xo))� то застосо
вувати вказані ФОР�ІУЛИ не можна. У зв'язку л ЦИ�1 рекомендується
для визначення інтервалів збіжності використовувати ознаки Далам
бера і Коші безпосередньо, як пе зроблено нижче, не звертаючись до
лагальних формул Д.1Я радіуса збіжності.
?о n 5n
Приклад. Дослідити на збіжність ряд L �nX_l.
n=1
РОЗб 'язання. Застосуємо ознаку Даламбера, Розглянемо ряд
2nlхl5n•
2n-l '
n=1
ип =
2n+1IхI5(n+l)
2n+ 1
2n+1IхI5(n+l)
2n+ 1
иn+] . 5 2n - 1 5. 2n - 1 5
Іігп -- = Ііш 21хl . = 21хl . 11Ш = 21хl = q.
n--+ех> ИП n--+ех> 2n + 1 n--+ех> 2n + 1
Ряд збіЖНИІІ, якщо q 21хl5 < 1, тобто Іхl < И. Ряд розбіжний,
коли q > 1, тобто Іхl > И. Розглянемо збіжність ряду на кінцях ін-
бі . ( 1 1) П· 1 О
тер валу з lЖНОСТl -- и; и· гдставимо в ряд х = и· держимо
ех>
ряд L 2n1_1· Цей ряд розбіжний (його можна порівняти з гармоніч-
n=1
ас ех>
ним рядом L �). Якщо х = - И' отримаємо ряд L ����, який є
n=1 n=]
умовно збіжним (за ознакою Леибніца). Отже, заданий ряд збіжний,
якщо - И :::; х < и·
au
3.2. Множення степеневих рядів. Нехай ряд L аn(х - хо)n
n=о
збіжнии на проміжку (1·0 - Н«: ;1:0 + R]), дf' R1 > О, і сумою його Є
оо
функція S(x), а ряд L ьn(х-.го)n збіжнии на проміжку (xo-R2: хо+
n=О
343
оо
R2), де R2 > О, і сумою його є функція а( х). Тоді ряд L сп (х -- хо) n ,
n=о
де СП = аоЬn + a1bn-1 + a2bn-2 + ... + аnЬо, збіжний на проміжку
(хо -R; хо +R). де R = шіll(R], R2), і сумою його є функція S(x)a(x).
Міркуємо так само, як при обгрунтуванні дії множення числових
оо
рядів, встановленої в теОРБІЇ ІЗ. Ряд L (аоЬn + a1bn-] + a2bn-2+
n=о
+ ... +аnЬо)(х - хо)n збіжний на спільному проміжку збіжності рядів
ех> оо
L аn(х - хо)n та L ьn(х - хо)n.
n=О n=О
Дію множення двох степеневих рядів записують у вигляді
n=о
n=о
(42)
ех>
І)аоЬn + a1bn-1 + a2bn-2 + ... + аnЬо)(х - хо)n.
n=О
Множення двох степеневих рядів виконується аналогічно до мно
ження двох а-лгебраїчних многочленів однакових степенів.
3.3. Диференціювання степеневих рядів. Нехай ряд
ех>
L аn(х - хо)n збіжний на проміжку (хо - R; хо + R), де R > О,
n=о
і сумою його є функція S(x). Тоді функція S(x) має на ПРОМІЖКУ
(хо - R; хо + R) похідну і виконується рівність
ех>
Позначимо R] радіус збіжності ряду L nаn(х - хо)n-l 1 пока-
n=]
жемо, що R. = R. На основі ознаки Коші маємо
R,=
Іігп �
n-+=
1
1
1
----==-R
Іігп � - ,
n-+=
Ііш \іп
п-ч-сс
344
ас
бо Ііш vn = 1. Отже, ряд L пап (.т - хо)п-] збіжний на проміжку
п--+=
п=1
(ха - R; ха + R), і будучи степеневим рядом, він рівномірно збіжнии
на кожному замкненому проміжку з проміжку збіжності (теорема
ех>
19). Тому на основі теореми 17 ряд L ап(х - :1:о)П можна почленно
п=о
диференціювати і сумою одержаного ряду буде функція 5'(.т). Отже,
( 43) правильна.
З.4. Інтегрування степеневого ряду. Нехай степеневии ряд
ех>
5(х) = L ап(х - хо)п збіжнии на проміжку (ха - R; ха + R), де
п=о
х
R > О, тоді для будь-якого х Е (ха - R; ха +R) існує інтеграл J 5(t)dt,
ХО
причому
(44)
Кожний степеневий ряд
оо
5(х) = L ап(х - хо)п,
п=о
(45)
збіжний на проміжку (ха - R; ха + R), рівномірно збіжний на відрізку
[ха - т; ха + Т], О < r < R (див. теорему 19), тому твердження про
можливість почденного інтегрування степеневого ряду безпосеред
ньо випливає з теореми 18.
§ 4 Деякі застосування степеневих рядів
4.1. Різні форми залишкового члена у формулах Тейлора
І Маклорена. У § 3 розділу 4 було показано, що Д.1Я функції f( х),
345
яка має всі похідні до (п + 1)-го порядку ВК.ІЮЧНО, В деякому околі
точки ;Т = .То справедлива формула Тейлора:
f'(.ro) /"(3:0) 2
ЛХ) = лхо)+ , (х - хо) + 'J'- (х - хо) + ... +
1. �.
/(71)(3:0) n
+ , (х - хо) + Rn(x, хо),
П.
(46)
де Rn(x, хо) залишковий член, який може бути ааписаним. наприклад:
а) у формі Лагранжа
( )n+1
_ х - ХО (n+1) _, ]
Rn(x, хо) - ( ),' / [хо + 0x,n(X -- хо) ,
п + 1 .
(47)
де О < 0х,n < 1;
б) у формі Коші
,. _ (х - xo)n+1(1 - 0х,п)П (п+1) _ ])
Rn(x,xo)- n! ./ [хо+0х,п(.Т-Хо), (48
де О < 0х,п < 1;
в) у формі Пеано
(49)
Запишемо також формулу Маклорена для довільної функції f( х)
(як частковий випадок формули Тейлора для хо = О) із залишковим
членом у різних формах
1'(0) /"(0) 2 /(П)(О)
ЛХ) = ЛО) + і!х + �x + ... + ----;,- + Rn(x, О), (50)
де залишковий член має вигляд (для спрощення запису пишемо
Rn(x,O) = Rn(.r), 0І,л = 0):
а) у формі Лагранжа
хл+1
Rn(.r) = /Л+1)(0х), (О < е < 1);
(11+1)! .
(51)
346
б) У формі Коші
в) у формі Пеано
(53)
4.2. Оцінка залишкового члена ДЛЯ довільної фукціі Оці
нимо ДЛЯ довільноі функціі f( х) аалишковий член формули Макдоре
на, взятий у формі Лагранжа.
Припустимо, ЩО функція І(х), яка розглядається, має такі влас
тивості: існує таке дійсне число М: ЩО для всіх номерів п і Д.:'ІЯ всіх
значень аргументу х із деякого околу точки х = О справедлива нерів-
НІСТЬ
(54)
із нерівності (54) випливає, що і
а тому із (51) маємо
І ІП+І І Iп+І
IRn(x)1 = _:..- ·IІ(П+l)(0х)1 � м . -.!_' -,-о
(n+1)! (n+l)!
Отже, ми одержали таку універсальну опінку залишкового члена
для функції, сукупність всіх похідних котроі обмежена в околі точки
х = О:
(55)
Доведемо тепер, ЩО для довільного фіксованого х
(56)
347
Д . . {} .. х,,+І
.'ІЯ ІІЬОГО покажемо, шо ПОСЛІДОВНІСТЬ СП ,для якоі СП = (n+l)!'
має для довільного фіксованого х границю, що дорівнює нулеві. Ос
кільки для достатньо великого n дріб �:II < 1, то, починаючи з
деякого номера по, маємо нерівність IСп+ІI < Іспl, тому що
Звідси випливає, що починаючи з номера По, послідовність {Ісnl}
буде монотонно спадною і обмеженою знизу (наприклад, нулем). То
ді за відомою теоремою (теорема 2 розділ 2 п.1.6) послідовність
{lenl} є збіжною. Нехай с - границя цієї послідовності, вона є також
границею і для послідовності {leп+ ІІ}, оскільки остання пробігає ті
самі значення, що і {Іспl}. Переходячи у співвідношенні
до границі, якщо n -+ оо, і враховуючи те, що �:12 -+ о, отримуємо
с = с- О = о. Отже; рівність (56) доведена.
Тоді, на основі рівності (56), вибираючи достатньо великий но
мер n, ми можемо зробити праву частину (55) як завгодно малою.
Отже, якщо виконується нерівність (54), то
Ііт Rn(x) = о.
n--+СХ>
4.3. Оцінка залишкового члена у формулі Маклорєна
для деяких елементарних функцій.
а) лх) = е": Оскільки ДЮ! будь-якого n і(П)(х) = еХ, і тому
і(n)(О) = 1, то формула Маклорєна (54) набирає такий вигляд
х х2 хП
еХ = 1 + - + - + ... + - + R (х)
1! 2! n! n,
(57)
348
де залишковий член у фОР�Іі Лагранжа дорівнює
.т"+1
( ) ех
Rn х = ( )' . е
п+1.
(О < е < 1).
На довільному відрізку [-1': 1'] (1' > О), внаслідок того, шо \te.l-\ <
< е", одержимо таку оцінку для залишкового члена:
(58)
Із оцінки (58) і рівності (56) очевидно, що для всіх Х Е R виконується
Ііт Rn(x) = О.
n�cx>
б) ЛХ) = sіпх. Оскільки І<П)(х) = sin (х -+- �n), то
п = 2k (парне),
п = 2k + 1 (непарне),
(k = 0,1,2, ... )
і тоді формула Маклорєна має вигляд
. хЗ х5 х7 k x2k+1
SlIlX = Х - - + - - -;::;-, + ... + (-1) + R2k+2(X). (59)
3! 5� І. (2k + І)!
а за�'ІИШК()ВИі'І член в формі Лагранжа дорівнює
;г2k+З ( 7г )
Ва+2(х) = (2k + 3)� . sin ех + "2(2k + 3) ,
(О < е < 1).
Очевидно, ШО на довільному відрізку [-1'; 1'] (1' > О) ДЛЯ за.'ІИШКО
вого члена справедлива така ОІІІнка:
(60)
а з (60) і (56) ВИП.1Иває, ШО R а+2 (;с) -* О за умови �. -� оо Д.1Я всіх
.1" Е н.
349
в) л х) = COS з:. Оскі.1ЬКИ І( n) (:с) = COS (х + іп), то
n = 2k + 1 (нспарне),
(k = О, 1, 2, ... )
n = 2k (парне).
і тоді формула Маклорсна :VIae таЮІІІ вигляд
:с2 х4 х6 k x2k
cosx=I--+---+···+(-I) ·--+Н2k+l(Х) (61)
2! 4� 6! (2k)! '
а залишковий член у формі Лагранжа дорівнює
X2k+2 ( 7r )
R2k+l(X) = (2k + 2)� . COS 0х + "2(2k + 2) ,
(О < 0 < 1).
На довільному відрізку [-г; г] (г > О) одержимо для залишкового
. (60) R () r2k+2 А . . .
члена ОЦІНку типу :2k+1 з: :s; (2k+2)!. налогтчно, як 1 для SIll Х
із цієї оцінки і (56) маємо Іігп R2k+l(X) = О для всіх з: Е R.
1(�=
г) ЛХ) = lп(1 + х). Оскільки для п :::: 1
( (П - 1)'
J n)(х) = (_l)n-l (1 + x)�, то ЛО) = О,
І( n) (О) = ( -1) n -1 . (п - І)!,
і формула Маклорєна запишеться так
х2 хЗ x� тп
111(1 + х) = х - - + -- -- - + ... + (_I)П-1 . - + Rn(:z:). (62)
2 З 4 n
Залишковий Ч.1ЄН на цей раз запишемо і оцінимо як У формі Лаг
ранжа, так і у формі Коші:
( _1)nхП+1
Rn(.r.) = ._-- (у формі Лагранжа); (63)
(п + 1)(1 + 0х)n+1
1)( ( nll+1 (1-0)"
L" .1:) = -1) :1.. ( 0)· +1
1+-;сll
(у формі Коші).
(64)
350
Для значень Х, які належать відрізку О < .1' < 1, зручніше вико
ристати залишковий член в формі Лагранжа, Перейшовши у (63) до
абсолютних величин, отримаємо
(65)
Із оцінки (65) очевидно, ЩО Rn (х) -t О за умови n -t ос для всіх
О < х < 1.
Для від'ємних значень х із відрізка -Т � Х < О, де О < r < 1,
використаємо залишковии член в формі Коші. ПереПИШе:\ІО (64) у
ВИГЛЯДІ
Rn(x) = (_I)n ( 1-: )n
1 + -х
1 + ех'
(66)
Врахувавши, ЩО ДЛЯ значень х які розглядаються, виконується
нерівність (1- е)(1 + ех) < 1, з (66) одержимо
тn+1
IRn(x)1 < -. (67)
l-т
Оскільки О < r < 1, то оцінка (67) дає змогу стверджувати, ЩО
ііт Rn(x) = О.
n-tCXJ
4.4. Достатні умови розвинення функції в ряд Тейлора.
ЯКЩО функція f( х) має похідні всіх порядків (безмежно диференці
иовна] в околі точки х = Ха, то в формулі Тейлора (66) число n можна
брати як завгодно великим. Припустимо, шо в околі, який розгля
дається, залишковий член Rn(x,xo) прямує ДО нуля, ЯКЩО n -t оо,
тобто Ііш Rn(x,xo) = О. Тоді, перейшовши у (66) до границі, як-
n-tCXJ
ЩО n -t оо, отримаємо праворуч безмежний степеневий ряд, який
називається рядом Тейлора функціі f( .г ):
f'(xo) І"(хо) 2
лх) = f(хо)+ , (х - ;го) + -,),-(,г - ха) + ... +
1. �.
І( n) (ха)
+ r (х - :го)n + ....
n.
(68)
351
Остання рівність справедлива лише тоді. КО.НІ Rn(x, ха) --+ о Д.1Я
11 --+ ОС. У такому разі написаний праворуч в (68) ряд збігається і
його СУ).1а дорівнює цій функції Л.т). Доведемо цє.
Нсха:lI f(.T) = Тn(.Т.'ТО) + Л,,(З',:То), де
г(·то) І"(хо) 2 І(n)(хо) n
Т,,(.г,.го)=Л:го)+ , (х-хо)+ ?' (.т-хо) + ... + , (.г-.то),
1. �. n.
Оскільки за умовою Ііт Rn(x,xo) = О, то f(x) = Ііт тn(:г, ха).
n�= n��
Але Тn(Х, :1:0) Є n-на частинна сума ряду (68), і її границя дорівнює
сумі безмежного ряду, ЯЮІіі стоїть в правіи частині рівності (68).
Отже, рівність (68) справедлива.
Із попереднього випливає, шо ряд Теилора збігається до функції
ЛХ) ті.1ЬЮІ тоді, коли Ііт Rn(x,xo) = О. Якщо ж Ііт Rn(x,xo} t= О,
n�� n��
то цеи ряд не збігається до функції f( х ), хоч може бути збіжним до
іншої функції.
Якщо в ряді Тейлора (68) ПРИІШЯТИ хо = О, то одержимо частко
вий випадок ряду, який називається рядом Маклорєна функції f(.T):
Отже, якщо Д:1Я деякої функції формально написати ряд Тей
лора, то Д:ІЯ того, щоб цей ряд збігався до цієї функції, необхід
но довести, ШО залишковий член формули Теилора прямує до нуля,
або іншим способом впевнитись, що написаний ряд збігається до цієї
функції.
4.5. Розвинення деяких функцій в ряд Маклорена.
а] В п. 3 було одержано формулу Маклорєна для функції Л.с) =
= ( г (69) і доведено. шо Ііш Rn{x) = О для всіх х Е R. Тоді на основі
" -�'X-
сказаного В п. 4 отримаємо розвинення функції еХ в ряд Маклорсна:
.г .1·2 .с·:1 .t:"
("'=1+ -- +._-+--+ ... +-+ ...
1 � 2' 3� n �
(,О)
332
Якщо в розкладі (70) замінити х на (-х), то одержимо:
х х2 хз
е-І = 1 - - + - - - + ...
1! 2! 3!
б) На основі П.п. 3,4 отримаємо розвинення функцій sin х і cos х
в ряд
• ХЗ х5 хї k x2k+1
SlIl Х = Х - 3т + 5т - 7т + ... + ( -1 ) (2k + 1)! + . . . (71)
для всіх х Е R.
х2 х4 х6 x2k
cos Х = 1 - - + - - - + ... + ( _1)k -- + . . . (72)
2! 4! 6! (2k)!
для всіх х Е R, k = О, 1'2' ....
в) У п. 4.3 було одержано формулу Маклорена для функції J( х) =
= 1п(1 + х) (62) і доведено, -ЩО, ЯКЩО -1 < х .::; 1, виконується умова
Ііт Rn (х) = О. Тоді на підставі п. 4 функція lп( 1 + х) розвивається
n--+СХ)
В ряд Маклорена:
х2 ХЗ х4 ХN
1п(1 + х) = х - 2 + 3 - 4 + ... + (_l)n-;- +... (73)
для всіх х Е (-1; 1].
ЯКЩО у (73) замінити х на (-х), то отримаємо:
х2 хз
1п(1 - х) = -х - - - - - ...
2 3
(74)
для всіх х з інтервалу [-1; 1).
г) Розвинемо в ряд Маклорєна функцію J( х) = (1 + х) т, де m -
ДОВІльне число.
Тут оцінка за.1ИШКОВОГО члена доволі складна, тому розвинення
цієї функції ми одержимо по-іншому.
353
Враховуючи, ЩО функція лх) = (1 + х)7n задовольняє РІВняння
(1 + х) . І' ( х) = т Л х)
(75)
і умову ЛО) = 1, знайдемо такии степеневий ряд, сума якого sex)
задовольняє рівняння (75) і умову 5(0) = 1:
(76)
Підставивши (76) в (75), одержимо:
Прирівнявши коефіцієнти при однакових степенях х в лівій
• U •
правіи частинах останньої рІВНОСТІ, знаходимо:
т(т -1)
1·2
аз =
т(т - l)(т - 2)
1·2·3
т(т-l)· ... ·(т-n+l)
... , ап =
1 ·2· .... 11
Це біноміальні коефіцієнти. Підставляючи ІХ у (76)� отри-
маємо:
т(т - 1)
S(x)=I+mx+ 1.2 ·х2+ ... +
т(т -- 1) ..... [т - (n- 1)] n
+ Х + ....
1·2· ... · n
(77)
Якщо т ----- ціле додатне число, то, очевидно, починаючи з члена,
який містить хт+1, всі коефіцієнти дорівнюють нулю і ряд перетво
рюється в многочлен, Якщо m ---- дробове або ціле віл'ємне число, то
маємо безмежний ряд.
354
Визначимо радіус збіжності ряду (77), використавши ознаку
збіжності Двламбера. Маємо
т(т - 1) ..... [т - (n - 1)]
"Иn+l =
1· 2· ... · n
т(т - 1) ..... [т - (n - 2)] n-І
"Ип = . Х •
1 ·2· .... (n - 1) ,
1· IИn+11 1· lт-(n-l)111 ІІ
П'П --- = П'П . х = х.
n-+СХ) ИП n-+сх) n
Тоді згідно з ознакою Двламбера ряд (77) збігається, якщо Iхl<l.
Отже, в інтервалі (-1; 1) ряд (77) збігається до функції 5 ( х),
яка задовольняє диференціальне рівняння (75) і умову 5(0) = 1. Але
оскільки рівняння (75) і умову 5(0) = 1 задовольняє єдина функція,
то, отже, сума ряду (77) тотожно дорівнює функції (1 + х)т.
Отже, в результаті одержуємо розвинення в ряд Маклорена
m,(т-l) т(т-l)(т-2),
(l+х)т=l+тх+ х2+ ·хз+ ... +
- 2! 3!
т(т - 1) (т - n + 1) n
+ , ·х + ....
n.
(78)
Отримане розвинення функції в ряд справедливе:
якщо rn � О, коли -1 < х < 1;
якщо -1 < т < О, коли -1 < х � 1;
якщо rn � -1, коли -1 < х < 1.
4.6. Застосування розвинення бінома для розвинення в
ряд інших функцій. Розвинемо в ряд Маклорєна функцію лх) =
= arctgx. Із (78), якщо m = --·1, одержимо:
1 2 З '1
(1 + х)-l = -- = 1 -- х + з: -- х + х
1 +;Г
3.5.5
Підставивши в останню рівність замість з: вираз і2 отримаємо:
1 2 4 6
--=l-і +і -і + ... (-l<і<l).
1 + t2
Тоді на основі тсоре:ми про інтегрування степеневих рядів, при
пускаючи, що проміжок інтегрування (О; х) належить області збіж
ності (-1; 1) підінтегрального ряду (тобто Іхl < 1), одержимо шука
НИІІ розклад, якщо Іхl < 1:
Х
J dt х3 XS х7 k x2k+I
arctgx= --=х--+---+···+(-l) + .... (79)
1 + і2 3 5 7 2k + 1
о
Легко показати за ознакою Лейбніца, що ряд в правій частині
(79) збігається і якщо х = ±1. Тоді, прийнявши х = 1 в (79), отри
маємо формулу для обчислення 7Г:
7г 111
arctg 1 = - = 1 - - + - - - + ...
435 7
4.7. Наближене обчислення значень функцій. Для набли
женого обчислення значень функції f(x) зберігають перші п членів
11 розвинення в степеневий ряд, а інші члени не враховують. Для
оцінки похибки знайденого наближеного значення необхідно оцінити
суму відкинутих членів ряду, тобто залишковий член Rn (х). Якщо
u v и. • •
цеи ряд знакосталии, то ряд, складении ІЗ відкинутих членів, мож-
на порівняти із безмежно спадною геометричною прогресією. Якщо
ряд знакозмінний, члени якого задовольняють ознаку Лейбніца, то
використовується оцінка IRn(x)1 < Іиn.tll, де иn+І-- перший із від
кинутих членів ряду.
Приклад 1. Обчис.'ІИТИ ifE з точністю до 0,001.
Розв 'язання. Застосувавши розвинення (78) функції f( х) = еХ у
ряд, одержимо:
1 1 1 1
1 + І! . 3 + 2! ·32 + З! . 33 + 4! . З-І + ...
356
Визначимо число n так, шоб похибка наближеноі рівності
� � 1 + _1_ + _1_ + ... +- _1_
1�·3 2! ·32 п! ·3"
не перевищувала 0,001. Для цього скористаємось оцінкою похибки
за (58), тобто оцінкою залишкового члена. Прийнявши в (58) r = !'
одержимо:
0(+1 1 е 3 1
Rn < (n+ І)! . ез < (n + І)! . 3п+1 < (n+ І)! . 3" ·3= (n+ І)! . з-: (80)
Підбираючи, визначимо, при якому значенні n буде виконува
тись нерівність Rn < 0,001. Взявши, наприклад, n = 3 отримаємо із
(80) Rз < 4!�ЗЗ' тобто н; < 6�8· Нехай n = 4; тоді R4 < 5!�З4' тобто
Rn < 9 �20 < 1 �oo· Отже, приймаємо n = 4. Тоді маємо
= 1 + 0,3333 + 0,0555 + 0,0070 + 0,0005 = 1,3963.
Отже, f(ё � 1,396. Кожний доданок ми обчислювали з точністю
до 0,0001 (брали чотири знаки після коми) для того, щоб під час
додавання не одержати похибку, яка перевищує 0,001.
Приклад 2. Обчислити � з точністю до 0,0001.
Розв 'язання. Скористаємось розвиненням функції лх) = (l+х)т
у ряд за (78), прийнявши х = 0,2, m = і. Маємо
5 � = (1 + О 2) � = 1 + � . О 2 + -k . (і - 1) . О 22 +
V .L,L. , 5' 2! '
!·(J.-1)(!-2) !(!-1)(!-2)(!·-3)
+ 5;) 5 . О 23 + 5 5 5 5 . О 24 + . . . =
3! ' 4! '
= 1 + 0,04 - 0,0032 + 0,00038 - 0,00005 + ....
357
'Члени ряду, починаючи з другого, утворюють знакочергуваль
ний, монотонно спаДНИІІ ряд. Зг-ідно в наслідком теореми 6 (п. 1.4.
розділ 7) п'ятий і наступні 'Ідени ряду відкидаємо, оскільки П'ЯТІІЙ
член меншин, ніж 0�0001. Отже,
w ::::; 1 + 0,04 - 0,0032 + 0,00038 = 1,0371.
Приклад З. Обчислити Іlll,08 з точністю до 0,0001.
Розе'язання. Скористаємось розвиненням Іп(1 +х) у ряд за (73),
прийнявши х = 0,08. Маємо знакочергувальнии, монотонно спадний
ряд
0,082 0,083 0,084
Іп 1 08 = Іll( 1 + О 08) = О 08 - -- + -- - -- + ... =
, "2 3 4
= 0,08 - 0,0032 + 0,00051 - 0,00004 + ....
Четвертий і наступні члени одержаного ряду відкидаємо, оскіль
ки 0,00004 < 0,0001. Отже,
Іlll,08 ::::; 0,08 - 0,0032 + 0,00051 = 0,0767.
За допомогою рядів (73), (74) можна обчислювати логарифми
чисел, які знаходяться між нулем і двійкою. Виведемо формулу для
обчислення натуральних логарифмів будь-яких цілих додатних чи
сел.
Оскільки при почленному відніманні двох збіжних рядів одер
жується збіжний ряд, то, віднімаючи почленно рівність (74) ІЗ рІВ
ності (73), отримаємо:
1 + х ( х3 х5 х7 )
Іп] 1 + х) - Іп( 1 - х) = Іп -- = 2 :,; + - + -;:-. + -- + . - . .
І-х 3 о 7
П � l+х і+l 'Т" І Д б t О
риимемо І-х = -І-' годі Х = 2t+l' ц; ІЯ удь-якого > маємо
О < х < 1. Отже
Іп 1 +::. = Ін t -+- 1 = 2 (_1_ + _.� + __ �_--:- + ... ) _
1-.t· t 2t+l 3(2і+l)3 5(2t+l)" .
358
ЗВІДки
( 1 1 1 )
Ill(t + 1) = Іп t + 2 -- + ----- + --- + ... .
2t + 1 3(2t + 1)3 5(2t + 1)5
(81)
Оцінимо суму залишку Rп ряду в правій частині (81).
R (1 1
n = 2 (2n + 1)(2t + 1)2П+l + (2n + 3)(2t + 1)2П+3 +
+ (2n + 5)(:t + l)2п+5 + ... ) .
Замінимо кожнии із множників 2n + 3, 2n + 5, 2n + 7, . .. меншим
числом 2n + 1. Тоді
2 (1 1 1 )
Rn < 2n + 1· (2t + 1)2П+l + (2t + I)2П+3 + (2t + l)2п+5 + ... .
Ряд, що знаходиться в квадратних дужках останньої нерів
ності, -- це безмежно спадна геометрична прогресія, сума якої до
РІВнює
(2t + �)2n+l : (1 - (2t � 1)2 ) = (2t +'-I-)2-П---\ 1_. 4-·-t-· -(t-+-l-)·
Отже,
R < 1
n 2(2n + l)t(t + 1)(2t + I)2П-l
(82)
Приклад 4. Обчислити Іll2 з точністю до 0,0001.
Розв 'язання. Приймемо у (81) і нерівності (82) t = 1, тоді
(1 1 1 )
Іп 2 = Іп 1 + 2 - + -- + -- + ...
3 3·33 5·35 '
1
л; < ) .
4(211 + 1 ·32п-1
359
Підбираючи, визначимо, при ПКО).ІУ значенні ТІ буде виконува
тись нерівність ЛN < 0.0001. Якщо п = з. то Rз < 4)35 = 6 �O.1:
якщо ПРИІІмаою n = 4� то Д.1Я обчислення lп2 наближено одержимо
(1 1 1 1)
lп2 ::; 2 - + -- + -� - + --_ =
з з . зз о . З5 7 . З'
= 0,66667 + 0,02469 + 0,00165 + 0,00012 = 0.69З14.
4.8. Обчислення визначених інтегралів. Визначені інтегра
ли, які не вдається обчислити за формулою Ньютона-Лейбніца, або
навіть тоді, коли первісна виражається через елементарні функції але
має громіздкий вигляд, іноді можна досить ефективно обчислити за
допомогою степеневих рядів. Така ситуація може відзначатись, ко-
. . . ..
ли верхня 1 нижня межт визначеного ІНтеграла належать інтервалові
збіжності (іноді навіть є межею інтєрвалу] степеневого ряду, в який
розвивається підінтегральна функція. Розглянемо
1
"2
Приклад. Обчислити J l-��БХ dx з точністю до 0,0001.
о
Розв 'язання. Замінивши cos х його розвиненням в степеневий
ряд, одержимо:
1 1
"2 "2 х2 х4 6
J 1 - COS х J 1 - 1 + , - тт + � -- ...
-----:,----dx = 2. 4. 6·-----dx =
х2 х2
О О
(�x-�+�-···)I�
?' 4'·З 61.�
�. • . u О
1 1 1 1 1 1
-- - + ----- -- ... = - - ---- -t- ----.- - .. -
2!·2 4!·З·23 6!·5·2.'> 4 576 115200
360
Третій і наступнии ч.1ЄНІІ ряду відкидаємо. оскільки 1 152 ооо <
< 10 Ьоо' Отже,
1
2
J 1- cosx
х2 dx � 0,25 - 0,0017 = 0,2483.
о
4.9. Інтегрування диференціальних рівнянь за допомо
гою рядів. Іноді, коли інтегрування диференціального рівняння в
елементарних функціях неможливе, шукають розв'язок рівняння у
ВИГЛЯДІ ряду
у(х) = L Сn(Х - хо(.
n=О
(83)
Невизначені коефіцієнти Сп (n = О, 1, 2, ... ) знаходять, підстав
ляючи ряд (83) в диференціальне рівняння і прирівнюючи коефіцієн
ти при однакових стєпенях різниці (х - хо) в обох частинах одер
жаної рівності. Якщо вдається знайти всі коефіцієнти ряду (83), то
отриманий ряд визначає розв'язок рівняння у всій області збіжності
ряду.
Нехай, наприклад, потрібно проінтегрувати рівняння у" - х2у =
= О. Будемо шукати його розв'язок у вигляді ряду
Далі, підставивши у і у" в диференціальне рівняння, одержимо:
2 2 n_
---х . (Со + СІ . Х + С2х + ... + СNХ + ... ) = О.
Згрупуємо члени з однаковими єтепенями х:
оо
2·1· С2 + 3·2· Сзх2 + L ((n + 4)(1l + 3)Сn+-1 -- СІІ) хn+2 = О.
11=0
3G1
Прирівнявши до нуля всі коефіцієнти останнього ряду, знаходи-
мо
Останнє співвідношення дає З:\ІОгу виразити послідовно всі ко
ефіцієнти ряду через СО і СІ, які є довільними і ВІДІграють родь
довільних сталих інтегрування. Тоді
СО СІ
C4k = ---------:----. , C4k+1 = ._------)'
3 . 4 . 7 . 8 ..... (4k - 1) 4k 4 . 5 . 8 . 9 ..... 4k (4k + 1
C4k+2 = C4k+3 = О, (k = 1, 2, ... ).
Отже
X4k ос x4k+I
у(х) = СО . L 3.4.7.8 ..... ( 4Л; _ 1)4k + СІ . L 4.5.8.9 .... ·4k(4k + 1)·
k=I k=l
оо
На основі ознаки збіжності Двдамбера одержані ряди збігають
ся на всій чиєловій ОСІ 1 визначають два дініино незалежні часткові
розв'язки цього диференціального рівняння.
Якщо для рівняння уІ = ЛХ, у) потрібно розв'язати задачу Коші
з початковою умовою у(Хо) = Уо, розв'язок слід шукати у вигляді
ряду Тейлора:
оо у<n)(хо)
у(х)=І: , ·(х-хо)n,
n.
n=о
(84)
де У(Хо) = Уо, у'(хо) = ЛХО, уо), а наступні похідні У<n)(хо) знахо
дяться послідовним ДИференціюванням рівняння уІ = J( х, у) і під
становкою в результат диференціювання замість х, у, н', ... значень
хо, уо, уь і усіх наступних похідних. Сума скінченної кількості членів
ряду (84) буде наближеним розв'язком рівняння. Аналогічно за до
помогою ряду Тейлора можна проінтегрувати і рівняння вищих по
рядків.
362
Знайдемо перші чотири (відмінні ВІД НУ�"ІЯ) члени розвинення
розв'язку диференціального рівняння у' = 2 сов х - чР з початко
вою умовою у(О) = 1 . Для цього знаидємо у'(О) = 2 cos О = 2. Далі,
диференціюючи рівняння, послідовно ОТРlI:мао.ю:
" ? 2?' <; ,» 4'? (( ')2 ІІ)
У = -� SIll Х - У - �xyy, у = -� cos Х - уу - � у + у . у .
Прийнявши Х = О і використовуючи значення у(О) = 1, у'(О) = 2,
знаходимо:
у" (О) = - 2 sin О - 1 - 2 . О . 1 . 2 = -1,
у"'(О) = -2соsО - 4·1· 2 - 2· (1- 1) = -10.
Підставивши вст-ановлені значення похідних в ряд (84), і враху
вавши, шо ХО = О, одержимо наближений розв'язок рівняння
1 2 5 3
у(х) = 1 + 2х - -Х - -х .
2 3
363
Розділ 9. РЯДИ ФУР'Є. ІНТЕГРАЛ І ПЕРЕТВОРЕННЯ ФУР'Є
§ 1. Тригонометричні ряди. Ряди Фур'є
Використання рядів Фур'є тісно пов'язане з такими роздшами
фізики, як теорія коливань і теорія поширення тепла. Менш жорсткі
умови, ніж при розвиненні функції в степеневий ряд та інші переваги
сприяли перетворенню рядів Фур'є в зручний засіб для розв'язування
багатьох задач матєматичноі фізики. Разом з тим, проблеми, шо
виникли під час вивчення рядів Фур'є, спричинили перегляд і пе
ребу дову всієї теорії функцій дійсної змінноі, над якою працювали
такі вчені, як Ріман, Кантор, Лебег. Тому ряди Фур'є є важливим
. .
РОЗДІЛом математичного аналізу.
1.1. Тригонометричні ряди.
Означення. Тригонометричним рядом називається ряд, якии
має такии вигляд
ао + а 1 cos Х + ЬІ sin х + а2 cos 2х + Ь2 sin 2х + ... +
2
ех) (1)
+ап cosnx + Ьп sinnx + ... = � + 2,)ал cosnx + Ьл sinnx),
� п=l
де ао, аl"", ап,··· , ы •.. ,, Ьп, ... - -- сталі, які називаються коефі
цієнтами ряду. Якщо кількість доданків в (1) є скінченною, то та
кий вираз називають тригонометричним многочленом. Зауважимо,
що тригонометричнии ряд можна записати інакше, якщо об'єднати
члени з однаковими аргументами синуса І косинуса прийняти до
датково
А 1::21+ Ь2 t ап
тут n = V (J л т л' [!, ср л = Ь;:.
Тоді
ап cos nх +ЬП sin ТІ х = Ап (cos п х -зіп 'Р n +віп 77;]: -єов :.рл) = Ап sin( н.т+:.р n),
364
Ап - амплітуда, а 'Рn -- початкова фаза п-Ї гармоніки.
Ряд (1) запишеться так
оо
ао �
- + � Ап sin(nx + 'Рn),
2
n=l
тобто тригонометричний ряд представлено сумою нескінченної кіль-
. .
кості простих гармонік.
1.2. Тригонометричні ряди Фур'є. Нехай маємо функцію
і, задану та інтегровну на проміжку [-1Г; 1Г]. Спробуємо подати її
у вигляді суми збіжного тригонометричного ряду (1), тобто знайти
коефіцієнти ао, ап, Ьщ n EN, цього ряду такі, щоб виконувалася
рІВЮСТЬ
оо
ао � .
f(x) = - + �(an cosnx + ЬN sшпх).
2 ..
n=о
(2)
Тут відразу виникає декілька запитань. По-перше, які умови
повинна задовольняти функція і, щоб було можливе розвинення (2)?
По-друге, як знайти коефіцієнти цього розвинення? По-третє, який
характер збіжності тригонометричного ряду у (2)?
Відповіді на перше і третє запитання сформулюємо далі в теоре
мах 1 і 2. Тепер отримаємо відповідь на друге з поставлених питань,
припускаючи, шо функцію j можна розкласти в збіжний тригоно
метричний ряд (2), який можна почленно інтегрувати на проміжку
[-1Г; 1Г]. Інтегруючи обидві частини рівності (2) в межах від -1Г до
+1Г, З урахуванням того, що
тг
J - cosnx IП
sin nxdx = = о для ДОВІЛьного n
n -п
(3)
-п
(для n = О внаслідок того, що sill пх = sill О = О),
тг
J +- sill пх 171"
СОБ nxdx = = о для ДОВІЛьного ТІ ::І О,
n -п
(4)
-п
365
одержимо
71"
1 f(x)dx = ао о п ,
-і'і'"
;ЗВІДКИ
71"
ао = � 1 f( х ) сіх о
(5)
-11"
Для знаходження коефіцієнтів аь ; де kEN домножимо обидві
частини рівності (2) на coskx і проінтегруємо в межах від -7Г до 7Го
Враховуючи (3), (4) і співвідношення
1
cos kx sin пх = - [sin(k + п)х + siIl(n - k)x],
2
1
coskxcosnx = - [cos(k + п)х + cos(n 0- k)x],
2
sin kx sin пх = � [cos(k - п)х .- cos(k + n)х] ,
можна встановити, що
11"
1 cos kx sin nxdx = О ДЛЯ довільних kin,
-71"
111" {О дЛЯ k f. п,
cos kx СОБ nхl1х = .,.,.',
ІІ для k = n f. О,
-11"
для k f. п,
для k = ТІ. -І Оо
366
Отже, коефіцієнти розвинення функціі л.г) у тригоно:метрпч
ний ряд зв'язані з нею співвідношеннями
тг
ап = � J Л:г) cos nхсіх,
(6)
("-
11'
1 J .
ьn =;. f(:г)sшn:гdх.
(7)
-11'
Зауважимо, що з (6) для n = О одержуємо (5).
Означення 1. Якщо функція f абсолютно інтегровна на сег
менті [-1Т'; 1Т'], то тригонометричний ряд (1), коефіцієнти якого ви
значаються за (5), (6), (7), називається (тригонометричним) рядом
Фур' є для функції І. Застосовують запис
оо
ао � .
лх) rv - + �(an cos пз: + ЬN SШ nх),
2
n=о
який означає, шо функції f ставиться у відповідність її ряд Фур'є
(про збіжність ряду тут не йдеться).
Якщо ряд Фур'є функції f збіжний в точці з: Е R, то його суму
позначимо через S(x). Очевидно, що S(x) -- періодична функція з
періодом 21Т' (як сума ряду (1), складеного з 2їr-періодичних функцій).
Тоді рівність (2) можна записати як рівність двох функцій, але лише
на сегменті [-1Т'; 1Т']
лх) = S(x), х Е [-1Т'; 71"].
(8)
є приклади функцій і, для яких ЦЯ РІВНІсть не виконується. Щоб
забезпечити виконання рівності (8), функція f повинна задовольняти
. .
дєякі додаТКОВІ умови,
Говорять, що функція f заДОВО.1ЬНЯЄ умови Діріхле на сегменті
[-71"; 71"], якщо вона на цьому сегмєнт; має не більше ніж СКІнченну
З67
. . .
КІЛЬКІсть точок розриву першого роду, І якщо, ДО того, сегмент
[-їr; 1Г] можна розділити на скінченну кількість таких проміжків. на
кожному з яких І є монотонною функцією.
Теорема 1. Якиіо фу'нхu,іл лх) заоана на сегменті [-1Г; 1Г] і
задовопьняе у.м.ови Діріхле на ньомц, то рлд Фур 'є цієї фу'Н,'/\,ції збі
гаєmьсл в кожній точці сегмента [-1Г; 1Г] і його су.м.а
1) S(x) = Лх), л'/\,що х Е (-1Г; 1Г) і є тонкою неперервності ФУ'Н,'/\,
ції і,
2) S(x) = лх-о)� Лх+О), л'/\,що х Е (-1Г; 1Г) і є точкою розриву ФУ'Н,'/\,
ції і:
3) S(x) = /(-11+0)2+/(71"-0), л'/\,що х = �1Г або х = 1Г.
Означення 2. Функція І, задана на сегменті [а; Ь], називаєть
ся кусково диференційовною на [а; Ь], якщо вона неперервна на [а; Ь]
і диференційовна в кожній точці сегмента, за винятком скінченної
. .
КІЛЬКОСТІ точок.
Теорема 2. Яклцо І -- '/\,ус'/\,ово дифере'Н,ційов'Н,а фу'Н,'/\,ціл на сєа
менті [-1Г; 1Г], то рлд Фур 'є цієї фу'Н,'/\,ції збігаеться у кожній точці
сегмента і його су.м.а
{ ЛХ - О) + ЛХ + О)
S(x) = 2 ' якщо х Е (-1Г; 1Г),
Л-1Г + О) + Л1Г - О)
----'- с...-_----=----_---С.., якщо Х = -1Г або
2
х = 1Г.
3 доведенням теореми 1 можна ознаиомитися в [4, с.443 ], а
теореми 2 --- в [1, с. 25].
I.З. Тригонометричні ряди Фур'є для парних і непарних
функцій.
а) Нехай функція Лх), х Е [-1Г;1Г] Є парною (f(-х) = лх)) і
задовольняє умови теореми 2. Тоді добуток f( х) . sin х є непарною
функцією і згідно з (7) одержимо Ьn = О (оскільки інтеграл від не
парноі функції в симетричних межах дорівнює нулеві).
368
Дешо інакше запишуться фОР�іУ:ІИ (5) і (6), наприклад,
;;
ап = � 1 л:с) cos паах =
ті
-п
(9)
� (! ЛХ) со, nxdx + jлх) соо nXdx) = � jлх) cosnxdx,
-п о О
. ..
тут використано нсзалежність визначеного інтеграла ВІД позначення
змінної інтегрування і зроблено заміну х = -і У першому інтегралі
в дужках.
Отже, у разі парності функції J( х) матимемо
оо
ао ,
лх) = -- + Lan cosnx,
2
n=1
(10)
де коефіцієнти обчислюються за (9).
б) Нехай тепер функція J( х ), х Е [-7r; 7r] непарна І задовольняє
умови теореми 2. Тоді добуток лх) СОБ nх є непарною функцією і
тому ао = О; а.; = О ДЛЯ всіх n Е iV, а ДЛЯ коефіцієнтів Ьn справедлива
формула
тг
21
ьn = _. f( х) Бів 11 :Td.r.
7r
О
Розклад функції в ряд Фур'є матиме вигляд
( 11)
оо
f( х) = L ЬN sill пх,
n=l
(12)
де коефіцієнти Ьn оБЧИС.1ЮЮТЬСЯ за ( 11).
Приклад 1. Побудувати ряд Фур'є і графік СУШІ ряду Фур'є
для функції
369
з:
{х, якщо - 7г ::::; Х < О,
І(х) = '
о, якщо о::::; х ::::; 7Г.
7г
Рис. 1
Графік функціі j зображено на рис. 1.
Розв 'язання. Оскільки функція ні парна, ні
непарна, то коефіцієнти її ряду Фур'є шукаємо
за (5), (6), (7)
71" (О 71" )
an=�] j(x)cosnxdx=� J xcosnxdx+ Jo.cosnxdx =
-71" 71" О
(О)
U = х => du = dx 1 х. О 1 .
= . = - - SIn nх - - SIn nxdx =
І dv = cos nxdx * v = * sm nх І 1г n 1-. n L
_ 1 cos пз: 10 _ 1 ( ( )п)
-- - - 1- -1
7г n2 n27Г '
-71"
71" О
Ьп = � J f(x)sinnxdx = � J xsinnxdx =
(О)
U = х => du = dx 1 х о 1
=. 1 = - - - COS nх + - COS nxdx =
І dv = sш піиі» * v = -;; е"" lІХ І 1г 11 1-. 11!.
1 (7Г n 1. о) (_1)П
=- --(-1) +-sшnхl._ =---.
7г ТІ 112 71" п
370
Запишемо СУ),.ІУ ряду Фур' є для функці] j ( .С )
7г оо (1-(-l)П (--1)".)
S(x) = -- + "" сов лл + -'--Sll1nХ .
4 L 7Гn2 п
п=1
( 13)
Оскільки Лх) кускова диференціиовна на сєгмєнті [-7Г; 7Г], то за
теоремою 2 ряд Фур' є збігається в кожній точці інтервалу (-7Г; 7Г)
до і(х), а на кінцях х = -7Г і Х = п --- до значення /<-1І+0)2+f(1І'-0)
f(--;г)+f(1І') __ � ( <J)
2 - 2 рис. - .
І І І
І І І
-- ..... -- --------.-- -------- -е- -
х
Рис.2.
Зауважимо, що члени ряду (13) є функціі неперервні і навіть ди
ференціиовні бу дь- яку кількість разів у кожній точці х Е R, проте
сума ряду S(x) не є неперервною функцією; ії точками розриву (пер
шого роду) є точки Xk = (2k + 1)7Г, k Е Z (рис.2). Звідси випливає;
що ряд Фур'є (ІЗ) не збігається рівномірно до своєї суми S(x) (бо
інакше сума S(x) була б неперервною).
Отже, на інтервалі (-7Г; 7Г) матимемо
J( х) = - � + � (�=- ( � 1 ):. cos nх + (-1) n sill nх) . (14)
4 L 7Гn2 17,
,,=1
Точка х = О є точкою неперервності функці], а тому, приймаючи
у рівності (14) х = О, одержимо
371
ЗВІДКИ
r ( )11 _ {О для п = 2k,
тут враховано, що 1 - -1 - ') _ _ <Jk + 1.
� дляп-_- ,
Побудованим ряд Фур'є дав змогу анайти суму такого числового
ряду
1 1 1 �2
1 + - + - + ... + ---- + ... = -.
32 52 (2k + 1)2 8
3ауваже-н:н,.я 1. Якто ряд Фур'є для функції ЛХ), х Е [-�; �],
збігається, то мого сума S(x) є періодичною функцією. Тому саму
функцію ЛХ) інколи продовжують до 2�-періодичної функції і(х) на
усій числовій осі. Практично, тоб отримати і(х), для кожної точки
х Е (-�;�), приймають і(х + 2k�) = ЛХ), k Е Z, а в кожній точці
х k = (2k + 1)� приймають j (ч) = а, де а -- довільне дійсне число,
однакове дЛЯ ВСІХ х k .
3ауваже-Н:/і.я 2. Якщо функція f періодична з періодом 2�, ін
тегровна на сегменті [-�;�] (а тому вона, очевидно, інтегровна на
довільному скінченному проміжку (а; {З)), то за проміжок інтегру
вання у (5), (6), (7) можна взяти довільний проміжок довжиною 2�.
Обгрунтуемо це зауваження. Для довільних а Е R і Ь Е R можна
записати
а+211" а+2;т а Ь+2;т а+2;т а
j f(x)dx = j f(X)dx-j f(x)dx = j f(x)dx+ j f(x)dx- j f(x)dx.
а ь Ь ь Ь+211" Ь
Якщо в передостанньому з написаних інтег-ралів виконати замшу
х -. 2� = t, dx = dt, то отримаємо
a+2;r Ь+2;т (j а Ь+2;т
j f(x)d.r = j f(x)dx + j f(.r)dx - j Лх)сІх = j ЛХ)(/:С:.
а
ь
ь
ь
ь
372
Звідси випливає, що за проміжок інтегрування у (5), (6), (7)
можна взяти довільний проміжок з ДОВЖИНОЮ 27Г, зокрема [О; 27Г]
(частковий випадок одержаної вище рівності при а = -7Г, Ь = О), і
тоді користуватися такими формулами
2r.
au = � J f(x)dx,
о
2r.
а.; = � J ЛХ) cos п хііх ;
7г
о
n := О, 1, 2, ... ,
2r.
1 J .
Ьn=; f(х)sшnхdх,
о
n = 1,2, З, ....
Приклад 2. Побудувати ряд Фур'є для функції ЛХ) = х,
х Е [-7Г; 7Г] (рис. З, а).
РОЗб 'язання. Згідно із зауваженням 1 функцію ЛХ)=Х, хЕ( -71";71")
можна продовжити періодично на інтервали ((2k - 1)71"; (2k + 1)71"),
k Е Z, а в точках xk = (2k + 1)71", приймаємо j(ч) = О (рис.З,б).
у
у
х
х
--71"
а
б
РІІС. З
Оскільки функція І непарна. то всі коефіцієнти (І" = О. а коефі
цієнти ЬN оБЧИ:С.;ІЮЮТЬСЯ за (11)
З/З
11"
2 J .
ьn =;: Х SIn nxdx =
о
2 (7Г n 1. 111") 2 n+І
= - --(-1) + -sшnх = -(-1) .
п n n2 о n
Шуканий ряд Фур'є має такий вигляд:
ех> (_l)n+l
S(x) = 2 L sin nх.
n
n=1
(15)
За теоремою 2 S(x) = х, якщо х Е (-7Г; 7Г) і S( -7Г) = S(7Г) = о.
Оскільки функція S(x) є розривною, то збіжність ряду (15) до своєї
суми не є рівномірною. Сума ряду Фур'є S(x) і продовжена функція
f(x) мають однакові графіки (рис. 3, б).
На рис.4 зображено графік функції лх) = Х, (-7Г � Х � 7Г) і
графіки функцій, одержаних з правої частини (15) зі збереженням у
. .
СУМІ одного, двох чи трьох перших доданків.
у
п ----------------.f(x)=x
2
11"
2
-2
-7Г
Рис.4.
374
Розглянемо тепер побудову ряду Фур'є для функції І, заданої на
сегменті [О; 71"]. Спочатку продовжують функцію І до функції It на
сегменті [-71"; 71"] і далі ряд Фур'є будують для продовженоі функції
іІ· Оскільки можна побудувати різні продовження It на проміжок
(-71"; О), то і відповідні ряди Фур'є для цих продовжень будуть різ
ними, але всі такі ряди збігатимуться до однієї і тієї самої функції
S(x) на інтервалі (О; 71").
Серед багатьох типів продовжень виділимо лише найуживаніші.
1. Функцію І продовжують до парної функції ІІ на сегменті
[-71"; 71"]:
{ Лх), якщо х Е [О; 71"],
It(х) =
Л-х), якщо х Е [-71";0],
(рис. 5, а).
у ряд Фур'є такої функції входитимуть члени, які містять лише
косинуси (див. (10)).
у
,
.
I�
I�
І'
І �
І �
І '.
І '.
І •
І .. , ...... ,.
І
а
у
71" Х
у
в
2. Функцію І продовжують до непарноі функції 11 на сегменті
[-71";71"]:
б
Рис.5.
Лх),
якщо
х Е (О; 71"],
ІІ (х) =
{ О,
якщо
х = О,
(рис. 5, б).
- f( -х),
якщо
х Е [-71"; О),
375
у ряд Фур'є такої функціі входитимуть члени, які містять дише
синуси (див. (11)).
3. Функцію І "зсувають" на -'7Г вздовж осі Ох і отримують
продовження ІІ (х):
якщо х Е [О: 7Г],
якщо х Е [-7Г; О),
(рис.Б;в].
Тоді ряд Фур'є для функціі ІІ (х) можна бу дувати на основі (5),
(6), (7). Однак пропонуємо читачам після ознайомлення зп. 1.4 пере
конатися в тому, ЩО зручніше скористатися (23), (24) для функцій,
що мають період 2і, якщо прийняти в цих формулах l = f.
3ауваже'Н:н,,я З. Коефіцієнти ряду Фур'є для функuіі ІІ повністю
визначаються поведінкою функціі ІІ на інтервалах (-7Г; О) і (О; 7Г) і
не залежать від ії значень (які повинні бути скінченними) на кінцях
інтервалів, у точках х = О, х = -7Г, Х = 7Г. 3 цієі причини функцію
ІІ у точках х = О, х = -7Г, Х = 7г можна визначити по-іншому, ніж
це зроблено вище, або, як часто роблять на практиці, й не визначати
ЗОВСІМ.
Приклад З. Побудувати ряди Фур'є для функціі лх) х,
х Е [О; 7Г], продовживши її:
а) до парноі функції ІІ спочатку на сегмент [-7Г; 7Г], а далі --- на
всю ВІСЬ;
б) до непарноі функції 12 спочатку на інтервал ( -7Г; 7Г), а далі -- на
всю ВІСЬ.
Розв 'язання. а) Приимємо
{ .1". .г Е [О; Ті], } _
ІІ (.т) = = І·гl, .г Е [-Ті; 7Г].
---.1:, .г Е [--7Г; О)
376
На рис. 6 зображено графік продовження функції ІІ на всю ВІсь.
Рис.6.
Оскільки функція є парною, то ЬN О. а решту коефіцієнтів
обчислюємо за (9)
2І71" ') 2171"
ао = -; xdx = ;- . Х2 о = 7Г,
О
71" ( 7r)
ап = �Ix cos nxdx = � :. sin nxl� - �fSіП nxdx = � (�cos nxl�) =
7г п л п п 7Гn
о о
2 n. {О, якщо n = 2k, k Е Z,
= - (( -1) - 1) = 4
7Гn2 - "rr(2k + 1)2' якщо п = 2л� + 1,
Запишемо шуканий ряд
k Е Z.
ті 4 � 1
S(x) = - - - L (k )2 cos(2k + l)7ГХ.
2 7г 2 +1
k=O
(16)
За теоремою 2 S(x) = іхІ, х Е [-7Г; 7Г], тобто ряд (16) збігається
до функції І х І в кожній точці х, х Е [-- Ті: 7Г].
далі, оскільки
1 __ 1 __ . cos(2k + l)rrJ"1 < --�"--"-
І (2k + 1)2 - (2k + 1)2'
З77
тобто члени ряду (16) не більші від членів збіжного числового ряду
:XJ •
L (2k�1)2' то за теоремою Вейєрштрасса ряд (16) збігається рів
k=O
номірно на всій числовій осі до S(x) (рис.6).
б) Ця задача зводиться до прикладу 2. Справді, непарна фун
кція 12(Х) = Х, Х Е (-7r; 7r) є продовженням функції ЛХ), х Е (О; 7r)
на інтервал х Е (-7r; л ). Рядом Фур'є для функції 11. є ряд (15),
побудований у прикладі 2, його сума S (х) зображена на рис. 3, б.
1.4. Ряд Фур'є для функції з періодом Т = 21. Нехай
функція ЛХ) задовольняє умови теореми 2 на проміжку [-І; І]. Після
заміни х = � проміжку -І < х < І відповідає проміжок -7r < t < 7r, а
функції ЛХ) -- суперпозиція І (*). Приймемо F(t)c!!.fl (�) і розви
немо F(t) в ряд Фур'є на проміжку [-7r; 7r]
(и) ао �
F(t) = І 7r ="2 + �(ancosnt+bnsinnt), t Е (-7r;7r),
(17)
де
тг
ап = .!. J І (и) cosntdt, n = О, 1,2, ... ,
7r 7r
-тг
(18)
тг
ьn = .!. J І (и) sinntdt n = О, 1,2, ....
7r 7r
(19)
-.
Якщо тепер у (17), (18), (19) виконати заміну' (_ тХ, dt = 1��J
то одержимо розклад функції ЛХ) у ряд Фур'є на проміжку (-І; І)
оо
ао � ( n7r . n7r )
Лх) = "2 + L «« cos л= + ЬN sш-1-х , Х Е (-І; І),
n=l
(20)
де
І
1 J пз:
ап = І Лх) cos -l-xdx,
-І
п = 0,1,2, ...
(21)
378
/
1 J rlТi
ЬП = 1 f(x)sin -І xdx
-І
n = 0,1,2, ....
(22)
Якщо функція f( х) періодична з періодом 21 і інтегровна на
[-І; І], то на основі зауваження 2 у (21), (22) проміжок інтегруван
ня можна замінити на довільний проміжок з довжиною 21. 30КРб1а,
можна записати
2/
1 J пз:
ап = 1 лх) cos -I-xdx,
о
n = 0,1,2, ...
(23)
21
1 J . пл:
ЬП = 1 f( х) sin -I-xdx
о
n = 0,1,2, ....
(24)
Приклад. Побудувати ряд Фур'є для функції лх) = х на
проміжку [О; 7Г].
РОЗб 'язання. Оскільки функція f( х) визначена на відрізку [О; 7Г]
довжиною 7Г, то приймаємо Т = 21 = 7г і І = �. Коефіцієнти ряду
Фур'є обчислюємо за (23), (24).
11"
ао = � J xdx = 7Г,
О
1 111"
= --2 СОБ2nх о = О,
27Гn
ЬП = � І xsin2nxdx = - 2�n (х. cos2nxl� -І COS2nXdX)
1
n
379
Записуємо ряд Фур: є
5(:r) = � _. f-. sin 2nх .
2 г: n
n=l
(25)
За теоремою 2 5(х) = х, якщо тЕ (O;7r) і 5(+0) = S(7r - О) =�.
Оскі.1ЬКИ функція 5 (х) розривна, то ряд (25) не збігається рівномі рно
до своєї суми. Графік суми 5 (х) зображено на рис. 7.
у
х
Рис.7.
у прикладах 1·4 отримано розвинення в ряди Фур'є деяких
функцій. Результати розвинень свідчать про те, шо різні тригоно
метричні ряди не обов' язково мають різні суми. Так, всі три ряди
(15), (16) і (25) мають однакову суму 5(х) = х на інтервалі (О; 7r), а
ряди (14) і (15) -- однакову суму 5\(;1") = х на інтервалі (-7r;О).
1.5. Комплексна форма тригонометричного ряду Фу
р'є. Нехай на сегменті [о; т задані дві дійсні інтегровні функціі а(х)
і Ь(х). Розглянемо комплексну функцію дійсного аргументу а(х)+
+іЬ(х), а S х � Ь. За означенням приймемо
;3 в в
./[а(.і') + іЬ(х)]llт = ./ а(х)f1х + і ./ b(x)d.r.
о
о
п рипуг тимо. ШО функція f( х) ладовольняє умови теОРБІИ 2 на
проміжку (-/: /). Тоді ЇЇ можна розвинути в ряд Фур'є (20).
380
Введемо позначення wn
лера, запишемо
"Г І, скориставшись формулами Ей-
{ еІ":пХ + e-1(.о)nХ
COSWnx = 2 ..
eZ:..JnX _ e-І(.о)nХ • e1:..JnX _ e-1·(.о)nХ
SIllwnX = ------- = -Z-------
2і 2
(26)
Підставляючи вирази (26) в (20) і прийнявши ЬО = О, одержимо
(27)
Позначимо сп = an-;іЬn Враховуючи (21), (22) можна записати
сп =
І
1 J .
-lL.V7tХ
21 Лх) о е dxo
-І
(28)
Тоді аn1іЬn = сп clеrс_nо Тобто коефіцієнти другої суми в (27) отри
муються з (28) простою заміною п на -по Далі, оскільки w-n = -Wn,
то e-і:..Jnх = ei:..J-nх і тоді другу суму в (27) можемо записати так:
оо оь оо
Lan + l n -і:..) Х L і(.о)_ Х
-----е n = сеп
2 -n' о
n=1 n=1
-1
Останній ряд домовимося позначати L сnеі(.о)пІ і тоді (27) перспи-
n=-СХ)
шємо у ВИГЛЯДІ
ас
лх) = L cnei:..Jn.l·o
(29)
_·ОС
381
Співвідношення (29), в якому сП визначаються (28), називається
комплексною формою тригонометричного ряду Фур'є.
1.6. Узагальнений ряд Фур'є. Нехай задана система комп
лекснозначних функцій ді:і'ІСНОГО аргументу
'Р І (х), <р2 (х), ... , х Е [а; Ь]:
(30)
інтегровних на сегменті [а; Ь].
Означення 1. Система функцій (30) називається ортогональ
ною на сегменті [а; Ь], якщо для будь-яких двох функцій цієї СИСТБШ
виконується умова ортогональності
Ь
J <pn(x)<Pm(x)dx = О, п ст. = 1,2, ... , п =1= т,
а
а якщо до того ж для кожної функції <рn(х) виконується умова нор
малЬНОСТІ
ь ь
J <pn(x):pn(x)dx = J l'Pn(x)12dx = 1,
а
а
то система (30) називається ортонормальною (або ортонормованою)
на сегменті [а; Ь].
Означеннями ортогональноі та ортонормальноі систем функцій
можна користуватися і якщо (30)--- система дійсних функцій, ін
тегровних на [а; Ь]. ДЛЯ цього, враховучи, що кожне дійсне число є
комплексно спряженим самому собі, потрібно в умовах ортогональ
ності та нормальності замінити <рт (х) і <рn (х) на <рт (х) і <рn (х).
у п. 1.2 ми розглядали систему тригонометричних дійсних функ
цій f!](x) = 1, <Р2(Х) = сов г , <Рз(Х) = sinx, <Р4(Х) = cos2x, <Р5(Х) =
= віп Зт , ... , з: Е [-їr; їr]. Було показано, що ця система є ортогональ
ною, ОСКІЛЬКИ
ь
J <pn(x};pm(.r)dx = О, як шо n =1= т; плп > 1,2, ... ,
а
382
але не є ор гонормальною, оскільки
ь { '1 }
-.n=l.
J <p;(x)dx = 21' _ ')' -І- 1.
а , n - _,З, ...
ЇГ
Пропонуємо читачам переконатися, що ортонормальну систему
на [-1Г; 1Г] становлять функції
( .) _ <Рl(Х) __ 1_ (. _ <Р2(Х) _ cosx
<РІ Х - ..j2i -..j2i' <р2 Х) - YI7r - yI7r'
'Рз(Х) = <Pj;) = s�, 'Р4(Х) = <Pj;) = c�x, (31)
( ) _ <Р5 (х) _ sin 2х
<р5 х - YI7r - --YI7r , ....
Означення 2. Якщо функція f абсолютно інтегровна на [а; Ь] і
система функцій (30) ортонормальна на [а; Ь], то числа
ь
сп = J f(t)<pn(t)dt, n = 1,2, ...
а
(З2)
r,
називаються коефіцієнтами Фур'є функції f щодо системи (30), а
ряд
оо
(33)
рядом Фур'є для функції f відносно цієї системи.
Легко переконатися (пропонуємо пе для вправи читачам). що
тригонометричний ряд Фур'є для функції f (див. п.l.2) є рядом
Фур'є відносно ортонормальноі системи функцій (ЗІ). Якими бу
дуть коефіцієнти Фур'є щодо системи функцій (ЗІ)? Чи можна іх
обчислювати за (5), (6), (7)?
383
1.7. Властивість мінімальності частинних сум ряду Фу
р'є. Розглянемо функцію Л;l'), абсолютно інтегровну на сегменті
[а; b]� "і ті-ну частинну суму ряду Фур'є (33) (за ортонормальною сис
Те:\ЮЮ (30))
n
Sn(:Г) = L Ck'r'k(X),
n=]
(34)
а також деяку суму
n
аn(х) = L л«: 'Pk(X),
k=]
(35)
коефіцієнти якої "ik є довільними комплексними числами.
Теорема. Дл.я фу'н:к:u,ій Sn(x) і аn(х), .я'К,і еизнсчаються (34) z
(35), справедливе спіевідноиіення
ь ь
J IЛх) - Sn(x)12 dx < J IЛх) - аn(х)12 dx
(36)
а
а
nри1ЮМУ PUI1f.zcmb досягоеться лите за умови
'УІ; = СІ; (k = 1,2, ... ,п).
(37)
Де означає, шо з усіх функцій ап(І), які визначаються співвідно
шенням (35), наикрашс середньоквадратичне наближення до функuії
Л:r) дає та функція ап (.r) 1 коефіцієнти якої є коефіцієнтами Фур'є
функuії .f(.r).
Доеедення.
Ь Ь ТІ n Ь n
J f . (jnl/.r = J f . L ik;.?U/X = L 1І; J f . ..p�дy =-.: L ;;YkC/.-. (38)
а а k=] k= 1 а k= 1
384
Аналогічно
(39)
Зважаючи на ортонормованість системи {\fJn}, останню рівність
можна записати так
(40)
Враховуючи (38), (39) і (40), а також те, що lu-vl2 = (u-v)( й-й) =
= lиl2 - иі) - vii + It'12, будемо мати
ь ь ь ь ь
іl/ - o-nl2dx= jlЛ2dх - j fandx - j І· o-ndx + jlo-nl2dx =
а а а а а
Ь n n n
= j Iл2 dx - L Ck;Yk - L Ck . Ik + L ,k'ik =
а k=l k=l k=l
(41)
Очевидно, що останній вираз набуде найменше значення за умо
ви ,k = Ck, що рівнозначно заміні в (41) о- n на S п- Теорема доведена.
Приймаючи в (41) ,k = Ck і враховуючи, що права частина (41)
є невід'ємною, одержимо
� 2 іЬ 2
г: lekl::; ІЛ dx.
k=l а
(42)
385
Останнє співвідношення називається нерівністю Бесселя. Прав
да, частіше нерівністю Бессе.пя називають нерівність, яка отримуєть
ся з (42), якщо n ---7 ОО, тобто для випадку, КО.ІИ функція f( х) пред
ставлена розвиненням у ряд Фур'є
f(x) = L CnIPn(X).
п=l
Відзначимо, що для тригонометричного ряду Фур'є (29) нерів
ність Бесселя переходить у рівність Парсеваля
(43)
І і
І
/
§ 2. Інтеграл Фур'є. Перетворення Фур'є
2.1. Інтеграл Фур'є. Припустимо, що функція f(x) може бути
розвинена в ряд Фур'є на будь-якому проміжку (-1; І) і є абсолютно
інтегровною на всій числовій осі, тобто
оо
J lf(t)1 dt = м < оо.
(44)
-оо
Введемо позначення шп = n,7r і змінну інтегрування у (21), (22)
позначимо літерою t. Тоді (20), (21), (22) запишуться так
(45)
,
ап = t J f(t) соsшпtаt,
-,
(46)
386
І
ь; = � j Лі) sіпшntdt.
-І
( 47)
Якщо коефіцієнти у співвідношенні (45) замінити Їх виразами з
(46) і (47), то одержимо
lі' 1 =і'
лх) = 21 Лt)dt + 1 L f(t)[соsшntсоsшnх+
-І n=I_1
І оо І
+sіпшnt· sіпшnх]dt= �I jf(t)dt+t L jf(t)Соsшn(t - x)dt.
-І n=I_1
(48)
:Можна переконатись, що перший доданок у правій частині (48)
прямує до НУЛЯ, якщо І ---7 оо. Дійсно
І І оо
�I jЛt)dt 5:. �I іlЛі)1 dt 5:. �I j lf(t)ldt < 1� ---7 О, якщо І ---7 оо. (49)
-І -І --оо
Суму у співвідношенні (48) запишемо в дещо іншому ВИГЛЯДІ,
ввівши позначення дшn = "'-'n+l - WN = Т (n = О, 1, 2, ... )
оо І оо І
t L j Лt) соsшn(t - x)dt = � L дWn j Лі) соsшn(t - x)dt. (50)
n=I_1 n=1 -І
Інтеграл в останньому виразі є абсолютно збіжним на всій чис-
• U· •
ЛОВІИ ОСІ, ОСКІЛЬКИ
IЛt) соsшn(t- х)1 5:. lf(t)1
і справедливе співвідношення (44).
387
Д . 1 n;r
ля як завгодно великого, 8..:1е СКІнченного значення Ш11 = "Г
.. . .
ЗМІНюється ВІД дуже малого Д.:ІЯ СКІнченних n до нескінченно велико-
го для п --+ оо. Тому суму у співвідношенні (50) можна розглядати
як інтегральну суму деякої функції від змінної шn (детальне обгрун
тування цього твердження опускаємо). Границя ж цієї суми, якщо
дшn --+ О, Є невласним Інтегралом за змінною Шn' Враховуючи все
сказане, можемо записати (індекс n при змінній шn опустимо)
оо оо
ЛХ) = � J dw J f(t)· cosw(t - x)dt.
о -оо
(51)
Інтеграл у правій частині останньої рівності називається інтег
ралом Фур'є. Його існування і справедливість рівності (51) в точках
неперервності функці! j (х) обгрунтовує така теорема.
Теорема. Як,ЩО фу'Н,-к;v,їл Лх), х Е (-00;00), абсомотно інтег
ров'Н,а на (-оо; оо), то в кожній точці х Е (-оо; оо), в л-к;іu існцють
односторонні границі Лх+О), Лх-О) і односторонні nохід'Н,і Г(х+О),
г(х - О), викониеться рівність
+00 +00
� J dw J ЛХ) cos ш(х - t)dt = ЛХ + О) ; ЛХ - О) . (52)
о -оо
у точках неперервності права частина дорів'Н,юс ЛХ), бо в низ:
ЛХ - О) = ЛХ + О) = ЛХ).
3 доведенням теореми можна ознайомитись в [1, т. З, с.75].-
2.2. Інтеграли Фур'є для парних і непарних функцій.
Косинус- і синус-перетворення Фур'є. Якщо використати фор
мулу для косинуса РІЗНИЦІ, то співвідношення (51) можна записати
так
оо оо оо оо
і(;т)= �JcoswXdW J f(t)coswtdt+�Jsinwxdw J .f(t)sinwtdt. (53)
о -(Х) О-ас
388
Якщо f( і) парна функція. то .f( і) cos iJJt також буде парною. а
J( і) sill ші -- непарною функцією і тому
оо ех;
J f(t)coswt = 2 J J(i)cosiJJtdi:
-оо о
оо
J f(i)sinwidi = О.
Інтеграл Фур'є, записаний у вигляді (51), набуде такий вигляд
ех; оо
ЛХ) = � J соswхdш J Лі) cos widi =
о о
оо оо
= [!; J COSWXdW[!; J лі) cos widi.
о о
(54)
Внутрішній інтеграл у співвідношенні (54) називають косинус
перетворенням Фур'є функції f( і) і позначають так
оо
Fc(w) = [!; J f(i)cOSL<Jtdi.
о
(55)
Співвідношення (54) набуде такий вигляд
оо
лх) = [!; J рс(ш) . coswxdw;
о
(56)
його називають оберненим косинус-перетворенням (або оберненням
косинус- перетворення) Фур'є.
Якщо вважа ти Е; ((;J) відомою функцією. то співвідношення (55)
являє собою інтегральне рівняння для функції Лх), а (56) дає роз-
. .
в язок ПЬОГО РІВняння.
389
для непарноі функції f(t) інтеграл Фур'є запишеться так
ас оо
лх) = � J sinwxdw J f(t)sinwtdt =
о о
ас оо
= Л J Sin",х.ьдЛ J f(t)sin"'tdt>\
о \._-- -о ----
(57)
Запишемо також синус-перетворення Фур'є
оо
Fs(W) = Л J J(t)sinwtdt
о
(58)
і обернене синус-перетворення Фур'є
оо
ЛХ) = Л J Fs(W) sinwxdw.
о
(59)
Приклад. Подати у вигляді інтеграла Фур'є функцію
ЛХ)={�
для
для
Іхl � 1,
Іхl > 1.
Розв 'язання. Оскільки функція f( х) парна, то скористаємось
(54)
оо 1 оо
2 J J 2 J sillw
J(:r) = - coswxdw coswtdt = - coswx· --dw.
7r 7r w
О о о
Зауважимо, що згідно з властивостями інтеграла Фур'є
оо {І д.'ІЯ
2 J sinw І
- cosu..:x--dw = 2" для
ЇГ UJ
О О Д.ІЯ
І.тl < 1,
Iтl = 1,
Iтl > 1.
390
2.3. Комплексна форма інтеграла Фур'є. Пряме і обер
нене перетворення Фур'є. Внутрішніи інтеграл у співвідношенні
( 51) є па рН<)ю функцією відносно частоти w. ТО!\ІУ. розширюючи
. . ... .
проміжок інтегрування у зовнішньому інтегралі на симетричну ліву
частину, можна записати
оо оо
л х) = 217Г .І elw .І л і) cos U)( t - х )сІі.
(60)
-= -оо
для непарноі відносно w функції справедлива рівність
оо оо
0= 2� .І dw .І Лt) sinw(t - х)сІі.
-ос -оо
(61)
Домножуючи обидві частини останньої рівності на уявну одини
цю і, після почленного віднімання від (60) матимемо
оо ас
лх) = 2� .І dw .І Лt) (cosw(t - х) - і sinw(t - х)) сіі =
--оо -оо
(62)
1 lое 1= ";() 1 [оо _ 1 ІОС -
= -- dw Лt)· е-І і-х сіі = -- е'''-'І dш-- Лі)є-1,,-,ісІі_
27Г. • �.�.
--�; -ос
--:::>С
--=
Співвідношення (62) являє собою комплексну форму ІНтеграла
Фур'є.
Внутрішній інтег-рал в (62) називають прямим перетворенням
Фур' є функції Л х) і позначають
оо
F(U)) = �I f(t)t --і.,;аі.
V г п .
-::х;
(63)
зю
Формула (62), записана тепер у таКО:\ІУ ВИГ.:'Іяді
оо
лх) = _1_[ F(ш). еі!.JХdш,
..j2i. .
= оо
(64)
називається оберненим перетворенням (оригіналом) Фур 7 Є.
392
СПИСОК .ЛТЕР АТУРИ
І. Кудрявцев л.Д., Куре матсматического анализа. В З-х томах.
--- ),1.: Вьтєшая школа, 1988 1989.
2. Фихтєнгольц Г.�I .. Курс диффсренциального и интег-ральног-о
исчисления, ІЗ З-Х томах. -- �I.: Наука. нпо.
з .. .Іяшко 1.1., Є",ІЄ.1ЬЯНОВ В.Ф., Боярчук О.К., �ЛаТбіаТИЧНИЙ ана
ліз. В 2-·х частинах. - - К.: Виша шкода, 1992.
4. Смирнов В.И., Курс вьгсшеи математики. Т.2. -- Мл ГИТТЛ,
1956.
о. Пак В.ІЗ., Носенко ю.л. Вища математика, ---- К.: Либідь, 1996.
6. Дввьщов tЛ.о. Курс математичного аналізу. В З-Х ТО",ШХ. --- К.:
Вища школа, 1990.
7. Дорог-овцев А.Я. Математичний аналіз. У 2-х частинах. - К.:
Либідь, 199З.
8. Рудин и. ОСНОВЬІ математического анализа г--є- М.: Мир, 1991.
9. Пискунов Н.С. Диффсренциальное и интєградьное исчисления.
В 2-х томах. -- М.: Наука, 1978.
10. Бугров Я.С., Никольскии С.М. Дифференциальное и интеграль
ное исчисление.---- М.: Наука, 1980.
11. Збірник задач з маТбіаТИЧНОГО аналізу. Ч.1 / За ред. проф.
Ю.К. Рудавського. - Львів: Видавництво Національного універ
ситету "Львівська політєхника", 200l.
З9З
Предметний покажчик
Абе.'ІЯ теоре",-,Іа 340
Абсолютна величина (С1.ЮДУ.'Іь)
дійсного числа 15
Алгебраїчна форма комплексно
го числа 181
Аналітичнии спосіб задання
функції 24-
Аргумент комплексного чис
ла 182
Аргумент функції 23
Арксинус, арккосинус 44
Асиптота графіка функці] 156
Бернуллі нерівність 12
Біном Ньютона 13
Больцано-Коші теорема 104
Вейєрштрасса теорема 103
Верхній інтеграл 228
Верхня інтегральна сума 226
Верхня межа 20
Визначений інтег-рал 226
Вищого порядку нескінченно ма
ла 82
- - -- - велика 83
Вищого порядку похідні 1:31
дифєренціали 136
Геомє-тричнии зміст похі дноі 109
- - диференціала 128
Гіперболічні функції 75
Головне значення аргументв 183
--- -- HeB.laCHoro інтеграла 293
Границя послідовності 69
--- друга важлива 71
-- одностороння 63
-- перша важлива 62
- функціі 46
-- функці] відносно множини 67
Даламбера ознака 305
Дарбу сума 226
Диференціал ПЕ'РШОГО поряд
ку 126
Диференціальнии біном 217
Диференціиовна функція 111
- вищих порядків 136
Діаметр розбиття 233
Дійсна вісь 177
Дійсна частина комплексного
числа 176
Діріхле функція 26
Еквівалентні величини 82, 97
Елементарні дроби 196
Задача Лейбніца 108
Ньютона 107
Залежна змінна 23
Залишковий 'І.1СИ у формі Лаг
ранжа 150
Коші 152
394
Пе(-LНО 152
Замкнении проміжок 17
Інваріантність форми дцферен
ціала 127
Інтеграл визначений, верхніи,
нижній 228
-- невизначений 200
-- невласнии І-го роду 277
-- нєвяасний ІІ-го роду 285
--- - Рімана 228
--- Фур'є 388
Інтег-ральнв сума верхня, ниж
ня 226
Інтегровна функція 228
Квантори 10
Класифікація точок розриву 98
Комплексна площина 177
Комплексне число 176
Корінь з комплексного числа 188
Корінь многочлена 193
Косинус тригонометричний 12
--- гіперболічний 75
Коші критерій 299
- - ознака 307
теорема 144
Логарифмічна похідна 121
.Тогарифмічна функція 42
Макгимум функціі 138
Межа �ІНОЖИНИ 20
Мєтод математичноі індукціі 11
Мінімум функціі 139
Многочлен 193
Множина значень функціі 23
Модуль дійсного числа 15
--- комплексного ЧИС.1а 182
Монотон:іш функція 31
Найбільше значення 102
Найменше значення 102
Невизначеність 80
Невласний інтеграл І-го роду 277
-- - ІІ-го роду 285
Необхідна умова 9
Неперервність функціі в точці 90
--- -- на проміжку 101
- -- оберненої 95
--- ---- рівномірна 104
-- --- складеної 93
Неправильний дріб 196
Нескінченно велика величина 78
---- мала величина 77
Обернена функція 36
Обернені тригонометричні фун
кції 44
Область визначення функції 23
-- значень функції 23
Односторонняграниця63
-- похідна 112
О дносторонній окіл 19
Окіл точки 18
Основні єлемєнтарні функціі 39
393
Оцінка похибки 130
Первісна 199
Перетворення Фур' є 391
Період функції 33
Підпоєлідовність 30
Підстановка Еилера 218
Подрібнення розбиття 230
Показникова форма комплекєно
го числа 189
функція 41
Порядок диференціала 136
. ..
нескінченно ведИКОІ вєличи-
ни 83
--- - ма.10Ї величини 82
- похідної 133
Послідовність 28
Правило Лопіталя 146
паралелограма, трикутни
ка 186
Правильний дріб 195
Приріст аргумента 91
функції 91
Проміжок 17
Простий корінь 194
Радіус збіжності степеневого ря
ДV 341
Раціональнии дріб 195
Розбитт-я відрізка 224
Розкриття невизначеностеи 146
Розширена ЧИС.1Ова пряма 1 ї
Ряд збіжнии , розбіжнии 29G
абсо.1ЮТНО 315
рівномірно 328
- умовно 315
Фурє 3G7
Сєрслнє значення функuії 248
Синус тригонометричний 42
-- гіпєрболічнии 75
Спільне по дрібнення 230
Спряжені числа 181
Стапіонарна точка 161
Степенева функція 39
Степєневопоказникова
функ-
ція 121
Сума Днрбу 226
-- інтегральна 233
-.- ряду 296
Супєрпозиція функцій 28
Тангенс тригонометричний 43
- -- гіперболічний 75
Теорема Ро.1ЛЯ 140
--- Ферма 139
Точка розриву 98
Точна верхня межа 21
---- нижня межа 21
Тригонометрична форма комп
лєкгного числа 183
Тригонометричні функuії 42
Універсальна тригоноз .. ІеТІНІчна
пілстановка 221
).'СУВН<і точка розриву 98
39G
Уявна вісь 177
---- одиниця 180
---- частина 176
Формула Ейлера 189
--- Лагранжа скінченного при
росту 141
-- Лейбніца 135
-- Маклорена 150
--- Муавра 185
- - Ньютона 253
---- Тейлора 149
Функція 23
---- Діріхле 26
.-- задана парах .. IЄТРИЧНО 133
.- - -. неявно 122
.--- обмежена, необмежена 35
---- парна, непарна 32
---- періодична 33
397
3�ПСТ
Перє-л мова 1
110:311:\ чі: ІІ НЯ ·1
Роз ліл 1. числові :\ІНО}КІІШІ. ФУНКЦІЇ. ПОСЛІДОВНОСТІ
§1 . .\Іножини. Логічні СИМНО.1И r;
1.1. ПОНЯТТЯ МнОЖИни 6
1.2. Дії над множ ипам и ..............•............................... ї
I.З. деякі ПОНЯТТЯ і г и м воли математичної логіки , 9
1.4 . Ме-год м ат ем а-ги ч иоі індукціі 11
1.5. Формула бінома Ньютона ІЗ
1.6. Мо луль дійсного числа 1.5
1.7. Проміжки, розширена числова пряма, околи точок 17
1.8. Межі числових множ и н 20
§ 2. Функції. Послідовності 2З
2.1. Поняття функціі 2З
2.2. Способи з а д ан ня функції 24
2.З. Складена функція ....................................•......... 28
2.4. Числові послідовності ....•...•................................. 28
2.5. Загальні властивості функції ЗІ
2.6. Обернена функція ..................•........................... З5
2.7. Основні елементарні функції З9
Розділ 2. ГРАНИUЯ. НЕПЕРЕРВНІСТЬ ФУНКШЇ
§ 1. Границя функції , 46
1.1. Означення границі функції 46
. 1.2. Властивості функцій, що мають скінченну границю у точці 55
1.З. Основні теореми про границі 57
1.4. Умови існування границі функції в точці 60
1.5. Перша важ.ти ва границя .................................•...... 62
І ) 1.6. Односторонні границі функції в точці. Границі монотонних функцій 6З
1.7. Границя функції ві лносно множини. Границя послідовності 66
1.8. Означення гран и ці функції за допомогою границі пос.яідовност-і .......• 69
] .9. Лру га важлива границя .... о • О ••••••••••••• о •• о •• о О •••••• о ••••• 071
] .10. Гіперболічні функції о • О ••• о •• о ••••••• о • О ••••• о ••••••••••••••••• 74
§ 2. Нескінченно малі та нескінченно великі величини 77
2.1. Означення неск іи че и но м ал и х і нескінченно ве.1ИКИХ величин 77
2.2. В.lас'Гивості нескінченно м ал их і нескінченно великих ве.1ИЧИН 79
2.З. Нев из н ачені вирази ..................................•......... 80
2..1. Порівняння нескінченно малих ве.1ИЧИН 81
2.5. Еквівалентні нескіН''''1І11О малі функції 85
§ З. Неперервність функціі 89
398
1.1. Нсперервиіс-гь фун к піі В точні f.<J
:J.2. Границя і нг-перервиість ск ла леноі фуик піі !'Jl
3.3. Неперєрвиість об ерпе ноі фун к піі fl5
З.4. Неперервність осн овн и х еле мсптар н и х фу п к пі и 96
3.5. Обг рунту нан н я співвідношень еквівалеитност і Вб
З.6. Точки РОЗРНВУ фу нк піі та іх к.аасифікв пія fl8
З.7. Функ піі, неисрервні ІІа се г меп т і 101
З.8. Рівномірпо неперервні фун к піі 104
Розділ З. ПОХlдlІІ І :llIФЕРЕН ШАЛИ
§ 1. Поняття похілпоі 107
1.1. Зв.дача Ньюг о н а ІОї
1.2. Зв дач а Лсибніц а 108
I.З. Означення похі лноі 11 О
1.4. Неперервність диферєн шиовноі функціі 111
1.5. Знаходження похідних на основі оз п ачеин я 112
1.6. Правила диференціювання 114
1.7. Диференціювання ск.я а лноі фу н к піі 117
1 8. Похідна обе риспоі функніі 118
1.9. Логарифмічне ДІІференціювання 121
1.10. Диферениіюван нн неявно і иарам ет ри чно заданих функцій 122
1.11. Таб.1ИЦЯ похідних основних елементарних функцій 125
§ 2. Дифереиціал : 126
2.1. Озиачеиия дифе рен піал а ..........••................ , 126
2.2. Осиовні правила лиференшюванн ня 128
2.З. Заст-осувапия диферен піал а у п абл и ж ен и х об ч ис.лен н я х 128
§ 1. Похідні і дифе рен иіал и виших порядків ІЗІ
З.1. Похідні виших порядків ІЗІ
З.2. Похідні вищих порядків п араме-гри ч ио заданоі функніі 1ЗЗ
З.З. Зага.lьні формули для похідних довільного порядку деяких функцій 1З4
ЗА. Форму.га Леибніц а ІЗ5
З.5. Ди ферен шали вищих порядкін lЗ6
Роа аіл ч , ОСНОВНІ ТЕОРЕМИ ДИФЕРЕНІlIАЛЬНОJ"О ЧИСЛЕННЯ
ТА ЇХ ЗАСТОСУВАННЯ
§ І. Основні теореми л иферснпі ал ьног-о числення.................... 139
1.1. Теорема Ферма 1З9
1.2. Теорема РО.1ЛЯ 140
І.З. Формул а ск ін ч ен н и х п ри рост ів (теорема Лагранж а) 1·11
1.-1. Умови ион о-т-оииост-і '1И не-змін нос-гі функції на відкритому проміжку 1·1-1
1.·5. Уз агал ьие-н а фо рм у.та ск ін чєн н и х п ри рост ів (ч'ео рем а Коші). О. О О О. О. 01·1·1
� 1.. Пр а вило .·lопіта.1Н О • О • О О О •••• О ••••• О О О •••••• О О О О •••• О О О О • О О О • О • О • 1·1(;
§ 3. Формул а Те и.то ра О •••••• О • О О • О ••• О О ••• О ••••• О • О ••••• О • О • О •• О О •• О 1·1!!
3.1. \11101·0'I.lell Теи лора О' О ••• О ••••••••••••••••••••••••• О О ••• 11�}
399
3.2. Формула Теииора і.з аал ишковим членом у фОР�1і Лаг ран жа 150
3.3. Зааишковий член у формі Пеано і Коші 151
3.4. Формули Теилора Д.1Я лея ки х е.яемен гарн и х функuій •.........•..... 152
§ 4. Дослі дженн я поведінки функцій та побудова графіків .•............... 156
4.1. Асимптоти графіка функпіі ...............•..................... 156
4.2. Монотонність фуи к піі ..........•................•....•........ 159
4.3. Локвльни я екстремум фу н кпіі 160
4.4. Напрямки опуклості графіка функuіі та точки перегину 166
4.5. Загальна схема дослідження функпіи під час побудови графіків 172
Розділ 5. КОМПЛЕКСНІ ЧИСЛА. МНОГОЧЛЕНИ. РАЦІОНАЛЬНІ ДРОБИ
§ І. Комплексні числа 176
1.1. Комплексне число як впорядкована пара дійсних чисел ....•......... 176
1.2. Алгебраічна форма комплексного числа 180
1.3. Комплексне число як вектор. Тригонометрична форма комплексного
числа .............................................•........• 182
1.4. Добування кореня з комплексного числа. Показникова форма
комплексного числа ...................•••.................•... 188
1.5. Представлення змінного струму у комплексній формі 191
§ 2. Деякі відомості з алгебри многочленів 193
2.1. Розклад многочлена на множники .........................•....• 193
2.2. Розклад раціонального дробу на суму елементарних 195
Розділ 6. НЕВИЗНАЧЕНИЙ ІНТЕГРАЛ
§ І. Первісна. Невизначений інтеграл .........................•........ 199
§ 2. Властивості н евиз наченог о інтеграла ..•...............•............ 201
§ 3. Основні методи інтегрування .....................•.............•. 204
3.1. Інтегрування пі.аствновкою (заміна змінноі) ...................•... 204
3.2. Тригонометричні пі.аствновки ..........................•........ 208
3.3. Метод інтегрування частинами .....................•............ 208
§ 4. Інтеграли, шо містять квадратнии тричлен ............•............. 210
І dx І d.r
4.1. Інтеграли вигл яду ах2+Ьх+с та vlax2+bx+c 210
І тх+п d І тх+п d
4.2. Інтеграли вигляду 2+Ь + Х та ./ 2 Ь х 211
,.\ ах х с уах + х+с
4.4. Інтеграл вигляду І уІах2 + Ьх + cdx 212
§ 5. Інтегрування рац іон ал ьни х дробів ...............................•. 213
5.1. Інтегрування еле мен т-арн и х раціональних дробів ..•................ 213
5.2. Заг а.аьи и и випадок інтегрування рапіон ал ьних дробів 215
(-6:- Інте�р�вання і�раUіональних функпіи ...........•.................. 216
і; 6.1. Інт ет рал ви г.тя ду
jF (х. (uх+ь) :: (ax+ь)�
'(·.I·+d 'c:r+d
7nР)
ах+Ь ПР
, C'X+d) dx 216
400
6.2. Інтеграл вигляду J хln(а + ЬхП)Рах· 217
б.З. Іп-гег рали ви гл ялу J R( х. V;;;:X + Ьх + с )сІ.с 218
§7. Інтегрування рапіональиих вирааів від �РНГОIIО)lе'JРИЧНИХ функuій 219
7.1. Ін-гег рая и ВИГ.1Я..1У І = J зіп'" х сов" ха;[" ................•...... 219
7.2. Інтеграли вигляду J R (sin2 х, cos2 х) ах 220
7.З. Універсальна ТРИГОIIO�lетрична підс-г аповк а .....••................ 221
7.4. Інтеграли ВИГ_1ЯДУ J tgmxdx та J ctgmxcl.r 222
7.5. Інтеграли вигляду J sin тх cos п.хііх, І sin тх sin п ззіх,
J cos тх cos пхііх 22З
Розділ 7. ВИЗНА ЧЕНИЙ ІНТЕГРАЛ
§ 1. Означення та існування інтеграла Рімана (визначеного інтеграла) 224
1:1. Задача про площу криволінійної т-рапеціі 224
1.2. Задача про обч исле ння шляху ..........................•...•.... 225
I.З. Верхні та нижні суми Дарбу. Інтеграл Рімана ..........•.•..•••.•. 22б
1.4. Властивості сум Дарбу. Умови інтегровності обмеженоі функuіі 2ЗО
§ 2. Інтеграл Рімана як г рани цн інтегральних сум 2ЗЗ
2.1. Поняття інтегральної суми. Зв'язок з інтегралом Рімана 2ЗЗ
2.2. Інтегровність неперервних, монотонних та кусково-неперервних
функuій ' .......•.•....••...•...................... 2З7
§ З. Властивості визначеного інтеграла 2З9
З.l. Адитивність відносно інтервалів інтегровності ............•.••..... 2З9
З.2. Властивість лінійності інтеграла Рімана ...................••..... 242
З.З. Інтегрування нерівностей ......•....•.......•......•..•.•..•... 244
З.4. Середнє значення функuіі ..........•.....•......•.•••......•... 248
§ 4. Визначений і н-гег рал із змінною верхньою межею інтегрування.
Існування первісної. Формула Ньютона-Лейбніuа 249
4.1. Неперервність і дифереиційовність визначеного інтеграла із
змінною верхньою межею 249
4.2. Існування первісної для неnерервноі фун кціі ......•.•..•........... 251
4.З. Формула Нью-гонв-Ле йбніцв 25З
§ 5. Формули заміни змінної та інтегрування частина.ми для визначеного
інтеграла ..••..........•.•........................•.•......•... 254
5.1. Інтегрування заміною змінної ........•.........•...••..•..•..... 254
5.2. Інтегрування частинами .........•..•..•..............•........ 257
§ б. Деякі застосування визначеного інтеграла 258
б.l. Загальні прин ц и пи ..... , ..................................•.•. 258
б.2. Площа плоєкоі фігури ..............................•........... 259·
б.З. Довжина дуги кривої .........••............................... 2б5
б.4. Обчислення об'єму л іл а з а відомим гюперечни м переріасм 2б9
б.5. Об'єм тіла обертання 270
401
6.6. Площа поверхні обертання .........•..•......................... 271
6.7. Зн акодж еи пя ст ат-и чн их момент-ів і центра маси к ривоі 27З
§ 7. Нев.а асн і ін-гег рал и ............................................•. 276
7.1. Поняття иев.я асиого інтеграла ......•............................ 276
7.2. Невласні іиге г рали нершого роду 277
7.3. Критеріі збіжності ие власного інтеграла першого роду 281
7.4. Нев.я асиі іи гег рали другого роду ........••.............•........ 285
7.5. Критєріі збіжності невдаСІІОГО інтеграла другого роду 288
7.6. Інтегрування частинами і заміною з мін ноі в невласних інтегралах .••• 289
7.7. Головне з н ачєннн невл аспи х інтегралів 292
Розділ 8. РЯДИ
§ 1. Числові ряди .•.......•....•.............. , ..•.................. 295
1.1. Поняття числового ряду та його залишку .......................•. 295
1.2. Критерій збіжності. Необхідна ознака збіжності .........•......... 299
1.3. Ряди з додатними членами , Достатні ознаки збіжності ....•......... 302
1.4. Знакочергувальні ряди .....•.•................................. 311
1.5. Абсолютно збіжні ряди та умовно збіжні ряди 314
1.6. Властивості збіжних рядів .....•................................ 318
1.7. Діі над числовими рядами ...•••................................ 322
§ 2. Функціональиі ряди ..............•...........•••...•..•••..•...• 325
2.1. Поняття функціонального ряду та його області збіжності ...••....•.• 325
2.2. Ознаки збіжності та властивості ...............................• 326
2.3. Рівномірна збіжність •.............................••....•..... 327
2.4. Неперервність суми ряду ...••..•...........•..•....••.......•.• 331
2.5. Границя суми ряду ......•............•........................ 332
2.6. Диференціювання ряду 334
2.7. Інтегрування ряду ...............................•••.......... 337
§ 3. Степеневі ряди ....••••.......................•.............•••• 339
3.1. Теорема Абеля. Радіус збіжності ............•................•.. 340
3.2. Множення степеневих рядів 343
3.3. Диференціювання степеневих рядів 344
3.4. Інтегрування степеневого ряду ......•.•....•.................... 345
§ 4 Деякі застосування степеневих рядів .......................•....•... 345
4.1. Різні форми залишкового члена в формулах Тейлора і Маклорен а 345
4.2. Оцінка залишкового члена для довіл ьноі фу кпіі 347
4.3. Оцінка залишкового члена у формулі Маклорена для деяких
елементарних функцій ......•...............................•.. 348
4.4. Достатні умови розвинення функціі в ряд Тейлора .........•........ 351
4.5. Розвинення деяких функuій в ряд Маклорен а ...•.......••........• 352
4.6. Застосування розвинення бінома для роз ви ие нн я в ряд інших функцій •• 355
4.7. Наближене обчислення значень функцій 356
4.8. Об численнн визначених інтегралів " ...................••.. 360
402
4.9. Інтегрування диференціальних рівнянь за допомогою рядів 361
Розділ 9. РЯДИ ФУР'Є. ІНТЕГРАЛ І ПЕРЕТВОРЕННЯ ФУР'Є
§ 1. Тригонометричні ряди. Ряди Фур'є 36-1
1.1. Тригонометричні ряди 364
1.2. Тригонометричні рндн Фур'є 365
1.3. Тригонометричні ряди Фур'є для парних і неnарних функцій 368
1.4. Ряд Фур'є для функціі з періодом Т = 2/ 378
1.5. Комплексна форма тригонометричного ряду Фур'є 380
1.6. Уаагальиении ряд Фур'є 382
1.7. Властивість мінімальності частинних сум ряду Фур'є 384
§ 2. Інтеграл Фур'є. Перетворення Фур'є 386
2.1. Інтеграл Фур'є 386
2.2. Інтеграли Фур'є для парних і неnарних функцій. Косинус- і синус-
перетворення Фур'є 388
2.3. Комплексна форма інтеграла Фур'є. Пряме і обернене перетворення
Фур'є 391
СПИСОК ЛІТЕРАТУРИ 393
Предметиий покажчик .- 394
ЗМІСТ 398
403
НАВЧАЛЬНЕ ВИДАННЯ
Рудавський Юрій Кирилович, Костробій Петро Петрович,
Лібацький Леонід Львович, Мохонько Анатолій Захарович,
Олексів Ігор Ярославович, IКісілевич Володимир Васильович�
Бушмаків Віктор Миколайович, Микитюк Олег Андріанович,
Чип Максим Миколайович, Зеленяк Володимир Михайлович,
Томецька Світлана Іванівна
МАТЕМАТИЧНИЙ
АНАліз
Частина І
Редолетор Оксана Чернигевич
Технічний редакто Лілія Саламін
Комп'ютерне складання Воло ими а Кісілевича
Художни'К-дизайнер Уляна Келеман
Здано у видавництво 20.08.2003. Підписано до друку 18.12.2003.
Формат 70х90/16. Папір офсетний. Друк офсетний.
Умовн. друк. арк. 29,5. Обл.-вид. арк. 15,7.
Наклад 2000 прим. Зам. 30573.
Видавництво Національного університету "Львівська політехніка"
Реєстраційне свідоцтво серії ДК ом 751 від 27.12.2001
Поліграфічний центр
Видавництва Національного університету "Львівська політехніка"
вул. Ф. Колесси, 2, 79000, Львів
у = !(С;,
• •
І
. .-
МА"ЕМА"�ВЧВВВ
АВААІ3 (с;ї) ь:
- .� .�() І-
І
, t