■•• V- ^/ »*-'» Ju^»*- /-#■■-».
іШ'іТіЖМ!
УЦІ
.A

ББК 22.161
3-415
УДК 517
Рекомендовано Науково-методичною радою Національного
університету "Львівська політехніка" як навчальний посібник
для студентів інженерно-технічних спеціальностей
(протокол № 7/2007 від 25.06.2007р.)
Рецензенти:
Каленюк П.І., доктор фізико-математичних наук, професор,
Національний університет "Львівська політехніка";
Копич І.М., кандидат фізико-математичних наук, професор,
Львівська комерційна академія;
Мохонько А.З., доктор фізико-математичних наук, професор,
Національний університет "Львівська політехніка";
Сторож О.Г., доктор фізико-математичних наук, професор,
Львівський національний університет імені Івана Франка
Укладачі:
Ю.К. Рудавський |, М.А. Сухорольський, Д.М. Білонога, І.О. Бобик,
О.Я. Бродяк, О.В. Веселовська, М.І. Вовк, Х.Т. Дрогомирецька, І.М. Зашкільт
няк, І.Ф. Клюйник, В.О. Коломієць, В.А. Лазько, Є.М. Луцев, І.В. Мандзинець,
О.А. Микитюк 1, О.М. Рибицька, СІ. Томецька, М.М. Чип.
Збірник задач з математичного аналізу. - 2-ге вид., виправ, і
3-415 доп. - Львів: Видавництво Національного університету "Львівська
політехніка", 2008. - Ч. І. - 352 с
ISBN 978-966-553-702-1
Збірник укладено відповідно до типових навчальних програм для
вищих технічних навчальних закладів. Перша частина містить задачі з
диференціального числення, інтегрального числення, числових та
функціональних рядів. У збірнику наведено довідковий теоретичний матеріал
з кожного розділу, а також численні приклади розв'язування задач.
Порівняно з першим виданням у цьому виданні значно збільшено
кількість завдань у кожному з розділів.
ББК 22.161
© Національний університет
ISBN 978-966-553-702 1 "Львівська політехніка", 2008

ЗМІСТ
Розділ І. Вступ до математичного аналізу 5
§ 1. Основні поняття 6
§ 2. Елементи поведінки функції 20
§ 3. Границя числової послідовності та границя функції 29
§ 4. Нескінченно малі і нескінченно великі величини 48
§ 5. Неперервність і точки розриву функції 54
Розділ II. Диференціальне числення функцій однієї змінної 64
§ 1. Похідна функції 66
§ 2. Теореми про середнє для диференційовних функцій 98
§ 3. Правило Лопіталя. Формула Тейлора 103
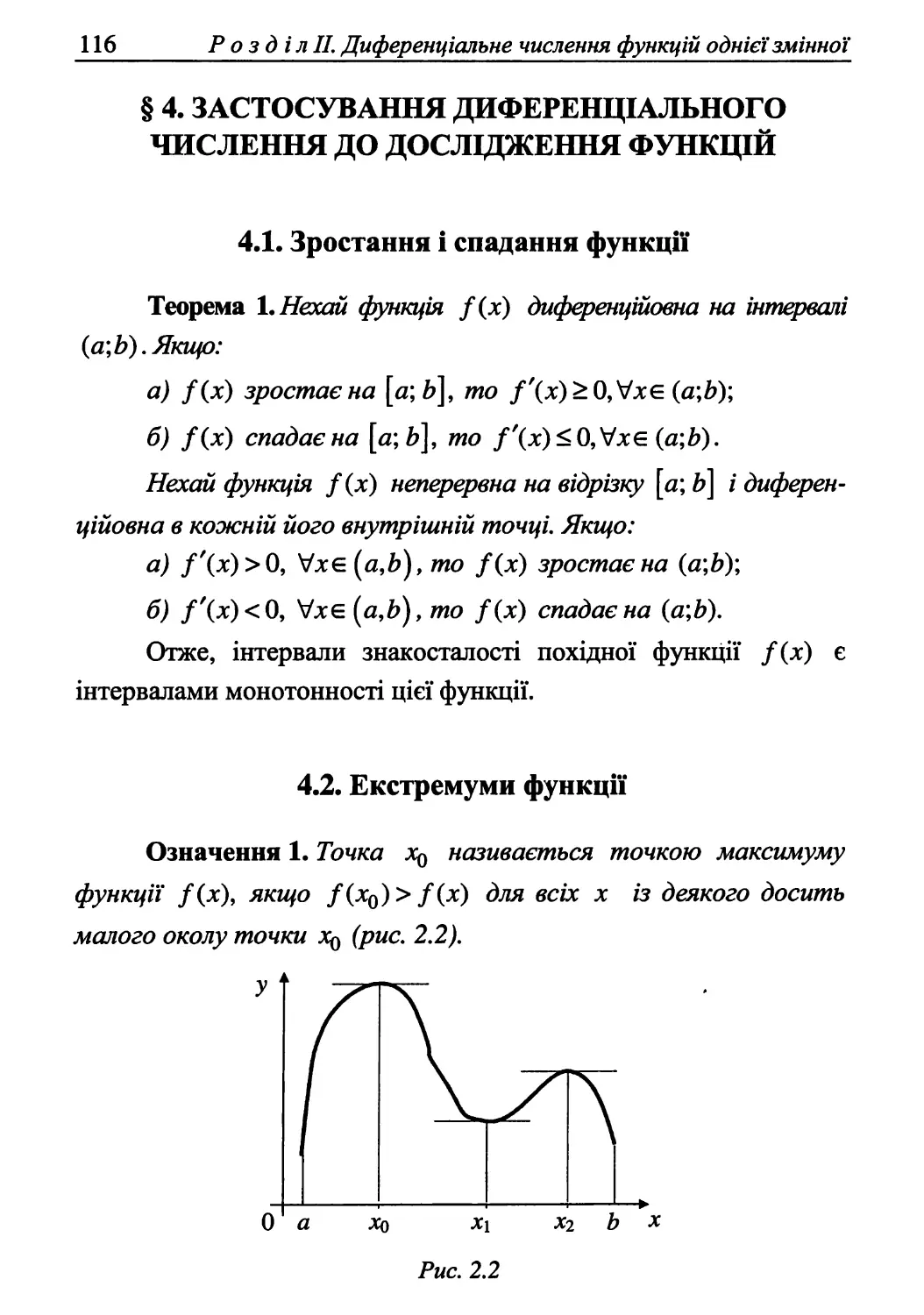
§ 4. Застосування диференціального числення
до дослідження функцій 116
Розділ III. Невизначений інтеграл 149
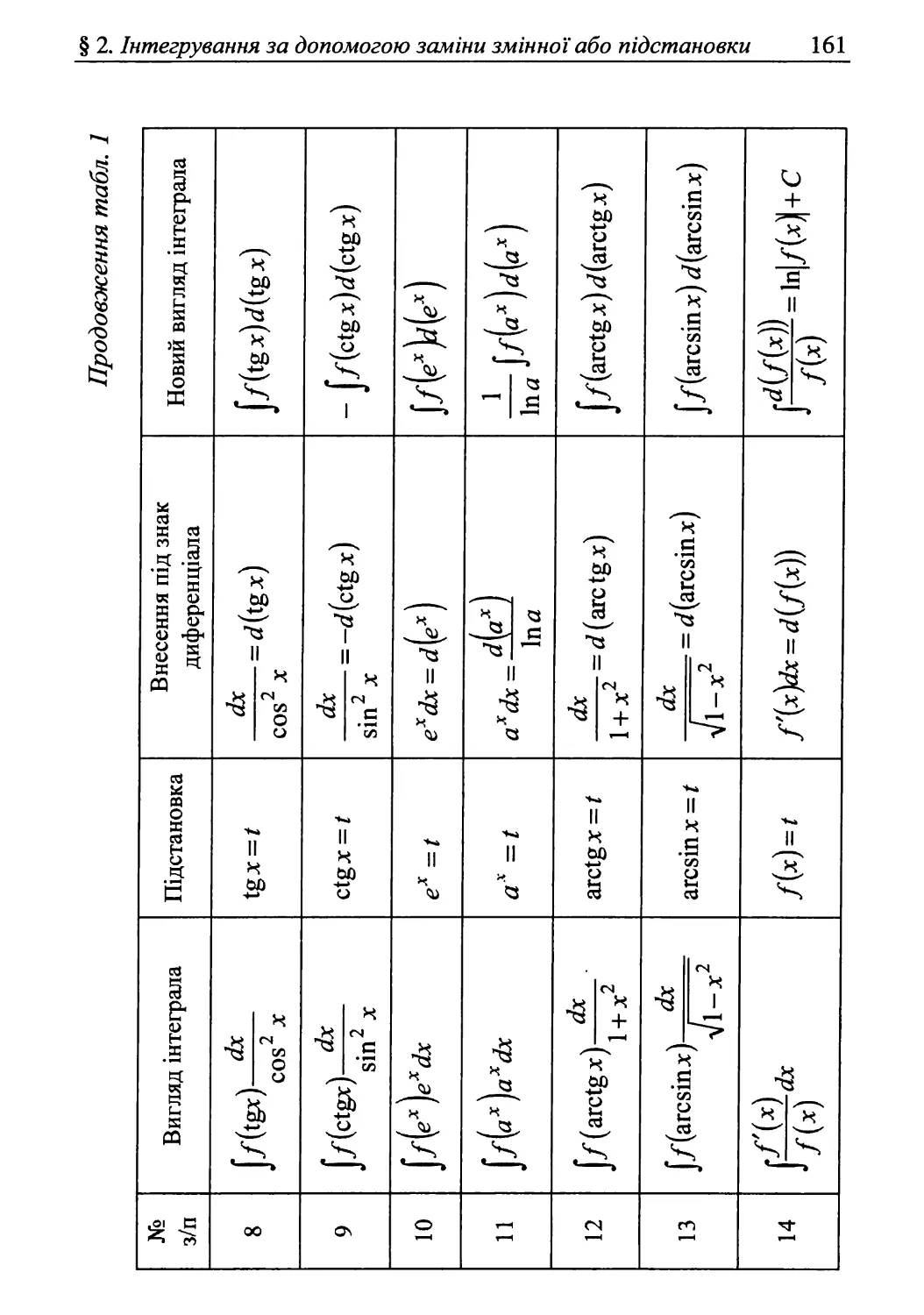
§ 1. Безпосереднє інтегрування 150
§ 2. Інтегрування за допомогою заміни змінної
або підстановки 158
§ 3. Інтегрування виразів, що містять квадратний тричлен 167
§ 4. Інтегрування частинами 175
§ 5. Інтегрування дробово-раціональних функцій 187

§ 6. Інтегрування ірраціональних функцій 202
§ 7. Інтегрування раціональних виразів
від тригонометричних функцій 222
§ 8. Інтегрування гіперболічних функцій 236
Розділ IV. Визначений інтеграл 243
§ 1. Обчислення визначених інтегралів 244
§ 2. Невластиві інтеграли 259
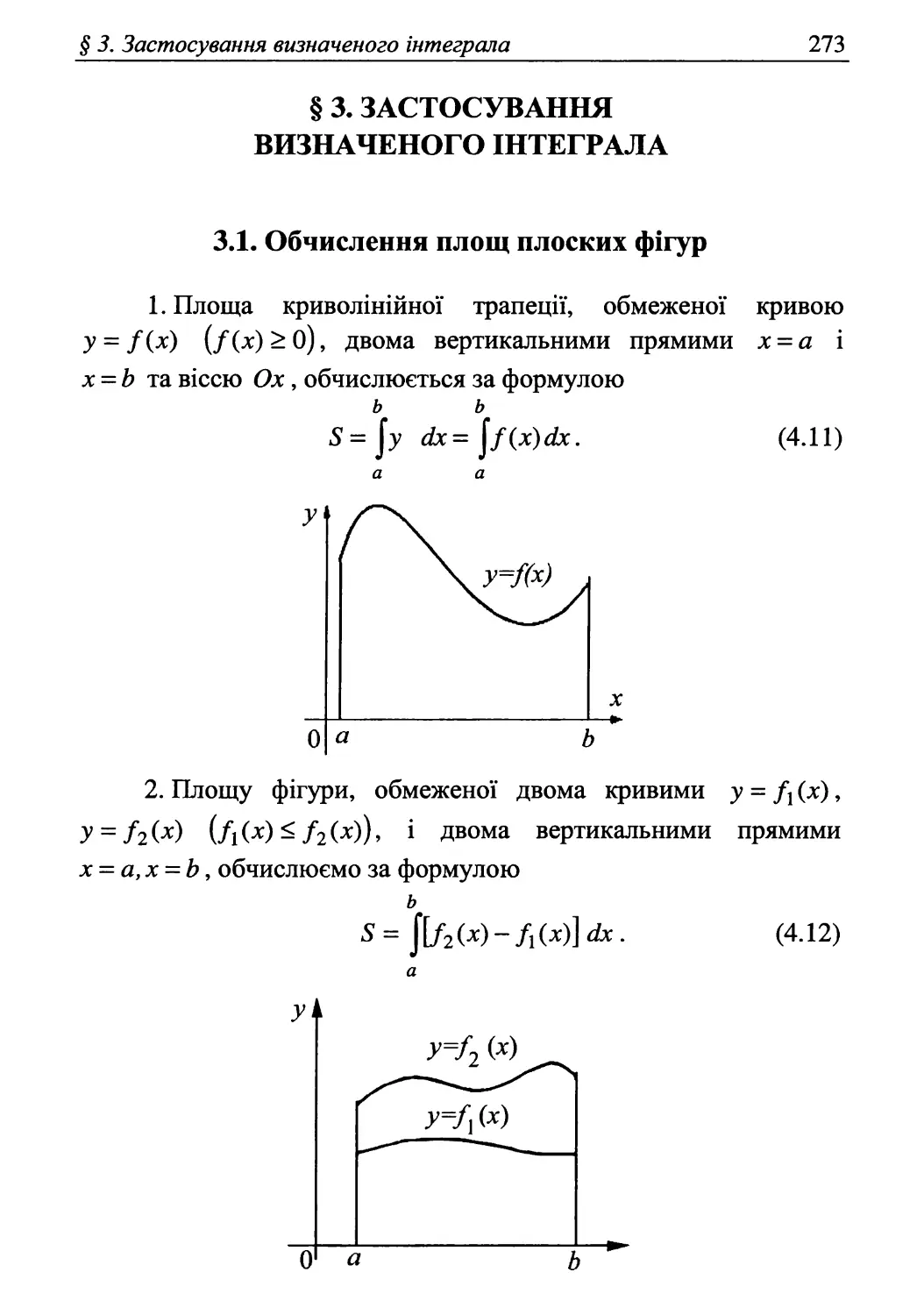
§ 3. Застосування визначеного інтеграла 273
Розділ V. Ряди 293
§ 1. Числові ряди 294
§ 2. Функціональні ряди 315
Список літератури 351

Розділ І
ВСТУП
ДО МАТЕМАТИЧНОГО АНАЛІЗУ

6
Розділі. Вступ до математичного аналізу
§ 1. ОСНОВНІ поняття
1.1. Функція
Означення 1. Якщо кожному числу хє X с R за правилом
f ставиться у відповідність певне число yeY qR , то кажуть,
що у є функцією від х, і записують y = f(x). Величину х
називають незалежною змінною або аргументом. Множину X
називають областю визначення функції і позначають D(f),
(D(f) = X). Множину E(f)={yeR\y = f(x),xeD(f)}
називають множиною значень функції.
Якщо функцію задають тільки формулою у = f{x), не
вказуючи області визначення X , то вважають, що область визначення цієї
функції збігається з множиною тих значень змінної х, для яких вираз
f(x) має зміст. У такому разі область визначення функції називають
областю допустимих значень або природною областю визначення.
Означення 2. Графіком функції f називається множина
точок
Gf={ (x;y)eR2\xeD(f\y = f(x)}.
З означення функції випливає, що плоска крива є графіком
деякої функції, якщо будь-яка пряма, паралельна до осі ординат,
перетинається з цією кривою не більше, ніж в одній точці.
1.2. Числова послідовність
Означення 3. Функція, визначена на множині натуральних
чисел N, називається числовою послідовністю і позначається
символом {хп}.
Значення такої функції позначають хп і називають членами
послідовності, а число п називають номером члена хп.

§ 1. Основні поняття
7
Послідовність можна задати формулою загального члена
хп= f(n) ,пє N, що виражає хп через номер п.
Для задания послідовності використовують і так звані
рекурентні формули, тобто формули, що виражають п-й член
через члени з меншими номерами.
Прикладами послідовностей можуть бути арифметична та
геометрична прогресії. їх можна подавати формулою загального
члена ап =ах +(n-l)d {ах - перший член, d - різниця
арифметичної прогресії), bn -bxqn~x (bx - перший член, q- знаменник
геометричної прогресії), а також рекурентними формулами
відповідно ап = ап_х +d, bn= bn_xq.
1.3. Способи аналітичного задания функції
Основними способами задания функції є табличний,
графічний та аналітичний. Аналітичний спосіб задания функції -
це задания її за допомогою однієї або декількох формул. Якщо
залежність між х і у задана у вигляді y = f(x), то кажуть, що
функція / задана явно. Наприклад,
(sin*,*є (-°°;0)
о г \ •
Якщо змінні х і у зв'язані між собою рівнянням вигляду
F(jc, у) = 0 (не розв'язаним відносно у), то кажуть, що функція
У-fM задана неявно. Наприклад,
tg(x-y) + xy = 0.
Параметричний спосіб полягає в тому, що х і у задаються
як функції допоміжної змінної - параметра t
\x = cp(t) ,
te[a;j3]. (1.1)

8 Розділі. Вступ до математичного аналізу
Наприклад, функцію, графіком якої є верхнє півколо
радіуса г з центром у точці <9(0;0), можна задати такими способами:
/~2 2
у = уг -х - явне задания;
9' 9 9
х +у —г = 0, у>0 - неявне задания;
(x = rcost г -,
, t є [0; 7iJ - параметричне задания.
у = rsint
1.4. Обернена та складна функції
Нехай дано функцію у = f{x), і виконується умова
(V*!,*2 є D(f),xx * x2)=>{f(xx) Ф f{x2)\
Тоді кожному значеїшю у можна поставити у відповідність єдине
значення хе D(f) таке, що f(x) = y. Так визначену обернену
відповідність називають оберненою функцією і позначають
х = f~l(y). Звичним є позначення аргументу літерою х, а значення
функції - літерою у. Перейшовши до цих позначень, одержимо
у = f~l(x) - обернена функція до функції y = f(x). Очевидно, що
Ж/"1) = £(/),а Ж/"1) = £>(/)
Функція, що має обернену, називається оборотною.
Графік оберненої функції f~l симетричний графікові
функції / відносно бісектриси першого і третього координатних кутів.
Нехай функції y = f(z) і z = g(x) визначені відповідно на
множинах £>(/) і D(g). Якщо E(g) с D{f), то на множині D(g)
можна визначити функцію h(x), яка кожному хе D(g) ставить у
відповідність y = h(x) = f[g(x)\. Функція h(x) називається
складною функцією або суперпозицією (накладанням) функцій fig.
Розв'язування типових прикладів. Задачі на знаходження
області визначення функції часто зводяться до розв'язання
нерівностей. Розглянемо приклади розв'язання типових нерівностей.

§ 1. Основні поняття
9
Приклад 1. Розв'язати нерівність - Зх < 2х + 5 < 1 - 6х.
Подвійна нерівність - Зх < 2х + 5 < 1 - 6х еквівалентна
системі нерівностей
J-3jc<2jc + 5 U>-1
{2х + 5<\-6х^\х<-У2
Отже, ця подвійна нерівність виконується для
Приклад 2. Розв'язати нерівність х - х - 2 < 0.
Графіком функції у = ах +Ьх + с є парабола, яка перетинає
вісь Ох у точках, що є коренями відповідного квадратного рівняння.
Вітай параболи спрямовані вверх (вниз), якщо коефіцієнт а
додатний (від'ємний). Коренями рівняння х2 -х-2 = 0 є х{ =-1;
х2 = 2, коефіцієнт а = 1 >0. Отже, значення виразу х -х-2
від'ємне для всіх х, що лежать між коренями хх і х2, тобто
Приклад 3. Розв'язати нерівність \2х - 5| < 1.
Нерівність \2х - 5| < 1 рівносильна подвійній нерівності
-1<2jc-5<1, 4<2jc<6, 2<*<З.Отже, *є(2;3).
Приклад 4. Розв'язати нерівність \2х -1| < |3л: +1|.
Оскільки обидві частини нерівності \2х -1| < \3х +1| є
невід'ємними, і областю допустимих значень лівої і правої
9 9
частин є вся числова вісь, то нерівність (2х -1) < (З* +1)
рівносильна вихідній. Розв'язуючи цю нерівність, одержимо
*є(-оо;-2]и[0;+оо).

10
Розділі. Вступ до математичного аналізу
Приклад 5. Розв'язати нерівність
х + 3
х-2
>0.
Областю допустимих значень виразу
х + З
х-2
є вся числова
вісь, крім точки, у якій знаменник дорівнює нулю, тобто точки
х = 2. Для всіх х з ОДЗ нерівність
jc + 3
х-2
> 0 рівносильна
нерівності (х + ЗХ* - 2) > 0. Отже, хє{- оо;-з] (J (2;+оо).
Приклад 6. Зобразити на числовій осі множину
{xeR\ |jc-1|<2}.
Ця множина - сукупність точок числової осі, відстань яких
від точки х = 1 менша за 2, тобто інтервал (-1;3).
у у уу уу у уу,/,/,/1 ►
-1
1
Розглянемо деякі типові приклади на дослідження
властивостей функції, а також на знаходження області визначення та
множини значень функції.
Приклад 7. Нехай /(*) = . Перевірити, що
1-х
П
а) f\-\ = -x'f(x)>
б) /І
1-х
1
*•/(*)
1
Знайдемо значення функції для аргументу —. Маємо
х
/і^
XJ !_
1 х-1
х * ft \
= -х- = -*•/(*).
1-х
Аналогічно
Ґ 1
/
1-х
1—
1-х
1-JC-1
1
1-х
1-х
*•/(*)

§ 1. Основні поняття
11
Приклад 8. Знайти значення а і b у виразі функції
f(x) = ах2 + Ьх + 5 , за яких справедлива тотожність
Д*)-/(* + 1)н8* + 3.
Оскільки
f(x + l) = a(x + l)2 +b(x + l) + 5 = ax2 +2ax + a + bx + b + 5 = ,
-ах2 л-(2а + b)x + (а + b + 5),
то
f(x) - f(x +1) = ax2 + bx + 5 - ax2 - (2a + b)x - (a + b + 5) =
= -2ax -(a + b).
Тотожність - 2ax - (a + b) = Sx + З перетворимо до вигляду
(S + 2a)x + (3 + a + b) = 0.
Многочлен тотожньо дорівнює нулю, якщо всі його коефі-
цієнти-нулі,тобто {з^+їіо^і^Г4-
Приклад 9. Знайти області визначення таких функцій:
а) у = у/х + 2; б) у = ^/д:-3; в) у = lg^ »
4-jc
г) у = — ; д) у = л[^ + 1е(5х-х2-6)-1/ї::х.
х2 -9
а) Корінь парного (у цьому прикладі - другого) степеня
існує лише для невід'ємних значень підкореневого виразу.
Тоді d(Vjc + 2)={jce/?|jc + 2>0}=[-2;+oo).
б) Корінь непарного степеня (у тому числі третього) існує
для будь-якого значення підкореневого виразу.
Тому d(^JC-3)={jcE/?}=(-oo;+oo).
в) Функція logfl и існує для всіх и > 0. У цьому прикладі
и = . Отже,
4-х
J, х + ЪЛ Г Іх+3 J / „ ч
D lg- = хеЯ- >0 =(-3;4).
І 4-х) { \4-х J

12
Розділі. Вступ до математичного аналізу
г) Функція у = — існує для будь-яких значень хе R,
х2 -9
крім тих, для яких Xі - 9 = О, тобто х = ±3. Тому область визна-
чення D\ -
i_l = (-oo;-3)U(-3^)U(3;-H»)-
д) Ця функція є сумою функцій f1(x) = ylx-l,
/2(jc) = lg(5;t-Jc2-6), /3(х) = Щ-х.
Область визначення функції, що є сумою інших функцій,
дорівнює перетину областей визначення останніх, тобто
D(f) = D(fl)riD(f2)nD(f3).
D(fO = {xe R\x-l>0}=[l;+oo)-
D(f2) = {xeR\5x-x2-6>o} = (2;3); D(/3) = (-~;+~).
Отже, D(/) = [l;+oo) П(2;3)П(-~;+~) =(2;3).
Приклад 10. Знайти множину значень функцій
а) у--Xі +6jc-4; б) y = l + 2cosjc;
в) у - л/jc + l ; г) у = V* +1.
а) Використаємо метод доповнення до повного квадрата:
у = -х2+6х-4 = -(х2-6х)-4 = -(х2-2-Зх + 32) + 32-4 =
= -(jc-3)2+5 = 5-(jc-3)2.
Оскільки (х - З)2 > 0 для будь-яких х, тому 5 - (х - З)2 < 5.
Отже, у < 5 , тобто ^(-jc2 + 6х - 4) = (- °о;5].
б) Оскільки -1<cosjc<1, то -2<2cosjc<2, і
-1<2со8л; + 1<З.Отже, £(1+ 2 cos х) = [-1;3].
в) Очевидно, що D(<yjx +1) = {х є R\x +1 > о} = [- 1;-н»). Для
довільного jc з ОДЗ справедлива нерівність vjc + 1 >0. Отже,

§ 1. Основні поняття
13
. Для всіх х з ОДЗ виконується
нерівність л/х>0, отже V* +1 > 1. Тоді, Е{>[х +1) = [і;+°°).
Приклад 11. Записати складну функцію у = h(x), якщо
у = lgw , и = yv , V = COSJC .
Маємо y = lgu = lgy/v=lgyJcosx .
Приклад 12, Суперпозицією яких функцій є функція
y = lgtg|?
Очевидно, ЩО V = — х, и = tgv, у = lgw .
Приклад 13. Записати в явному вигляді функції у, задані
рівняннями, та знайти їх області визначення.
а) 10х + 10^ -10 = 0; б) х + \у\-ху = 0.
а) Знайдемо у з такого рівняння:
10^ +10^ -10 = 0<=> Ю3' =10-10х =>lgl0^ =lg(10-10x)=>
=> у = lg(10(l - lO^"1)) => у = igio + lg(l - ю^-1) =>
^^l+igd-io*-1).
Оскільки логарифмічна функція визначена лише для
додатних аргументів, то
D(l + lg(l-10x"1)) = {^e/?|l-10x"1>0} = (-oo;i).
\у = х, у>0
, , \х + у-2у = 0, у>0
б) х + \у\-2у = 0<*\ <=><{
и ' Ь-у-2у = 0, у<0
У=-х, У<0
Знак функції тут збігається зі знаком аргументу. Тому
fjc, х>0

14
Розділі. Вступ до математичного аналізу
Приклад 14. Чи є оборотними функції
а)/(л:) = л:2, £>(/) = (-~;+оо);
б) f(X) = 2x + 3, D(/) = (-oo;+oo);
B)/0t) = 5\D(/) = (-oo;+oo)?
Якщо так, то знайти обернені.
а) Задана функція не є оборотною, оскільки вона двом
різним значенням х{ = -а, х2 = а із області визначення ставить у
відповідність одне число f(a) = f(-a) = а2, тобто не
виконується умова існування оберненої функції .
б) Для функції f(x) = 2х + З з умови хх Ф х2 випливає, що
2хх + З Ф 2х2 + 3 . Отже, функція оборотна. Розв'яжемо рівняння
у = 2х + 3 відносно jc, х = — (у-3). Отже, функція у = —(jc-3) -
обернена до вихідної. Область визначення цієї функції
D
-(х-3)
= Е(2х + 3) = (-оо;+оо).
в) Рівність 5*1 = 5*2 виконується лише тоді, коли хх-х2,
тобто виконується умова оборотності функції. Знайдемо
функцію, обернену до функції у = 5х. Прологарифмувавши ліву і
праву частини, одержимо log5 у = х. Перейшовши до звичних
позначень, одержимо обернену функцію у = log5 х. Область її
визначення D(log5 х) = Е(5Х) = (0;+°о).
Задачі для самостійного розв'язування
У задачах 1.1-1,9 розв'язати нерівності:
1.1, 2jc - 3 > 0. 1.2. jc-6<2jc-5<jc-3.
1.3. 18jc-3;c2>0. 1.4. х2 -5jc + 24<0.

§ 1. Основні поняття
15
1.5. |2* + 1|<1
Зх + 1
1.6. bc-l|<bc + l|. 1.7. ^^>3.
1111 JC + 1
1.8
jc-3
<3.
1.9. —і—+ —^—<1.
2-дг 2 + jc
У задачах 1.10-1.15 зобразити на числовій осі множину,
задану вказаними нерівностями:
1.10. |*| < 2 . 1.11. |х| > 3. 1.12. |* - 3| < 1. 1.13. |jc - 2| > 3.
1.14. 1<|;с-і|<3. 1.15. 0<|;с + 2|<4.
1.16. Які з множин, записаних у лівому і правому стовпцях,
збігаються?
а) множина чисел, відстань яких а\ | є /?| be - її > Ія + ill*
від числа 3 менша за 2;
б) множина чисел, відстань яких б) \х є Щ \х -1| < \х + l|j;
від числа -1 більша, ніж 3; ч Г „і і .і Л1
в) \хе R\\x-3 <2f;
в) множина чисел, відстань яких 1 і' ' J
від числа -2 менша, ніж 4 і г) [хе r\ \х-і\ >з};
більша, ніж 1; г j
г) множина чисел, відстань яких д) Iх є ^| г + Ч < г ~ а\< г + ЧJ
від точки -1 менша, ніж відстань е) {ХЕ д| |х + 1| < j^}.
від точки 1;
д) множина чисел, відстань яких є) \хє Щ \х +1| > З/;
від точки 0 більша за їх відстань ч Г „і, . , Л.\
. * ж) \хе R\\х\>\х-2\\\
від точки 2; ' L Iм ' IJ'
є) множина чисел, відстань яких з) \х є r\ і < Ijc + 2І < 4/;
від точки 1 більша, ніж відстань г і і і 1
від а до точки-1. и)1*бД|*<|*|<* + 1).
1.17. Нехай f(x) =
х-1
х + 1
Перевірити, що
а)/
б)/
і
/(*)
1.18. Дано fix) = -. Довести, що fid) - fib) = f
х
b-a

16
Розділі. Вступ до математичного аналізу
1.19. Дано F(z) = аг. Довести, що F(-z) ■ F(z) -1 = 0.
1.20. Дано <р(х) = lg*. Довести, що
<р(х) + ц>(х +1) = q>(x(x +1)).
У задачах 1.21-1.26 знайти області визначення функцій:
2х ч х2-1
1.21. а) у = уІх2+4; 6)у = - * - ; в) у= .
{х-2\х + 1) х2+1
1.22. a) y = V*2-4; б)у = -^-; в) y = -=L-
* + 3 V9-
х1
1.23. а) у = ; 6)y = lg—^; в) y = J-^-.
д/jc — |jc| 2-jc V2-x
2х-3
х-5
1.24. a) y = -yJx + 6-y/4-x; б) у = ліх2 -7х + 12 +
в) y = lg(8x-x2).
1.25. а) у = 4х1 +9х; б) у = V3-* + IgO + 5);
в) у = л/8л:-л:2-12+ Ї-—.
25-ж2
З
1.26. a) y = j2-lgx; б) у = -
l + lg(6-*)
в) y = lg(l-8jc) + ln(3* + 2).
У задачах 1.27-1.29 встановити, чи збігаються області
визначення таких функцій:
1.27. /(*) = -=— І8(х) = ^(х + 5)(х-2).
х2-3л: + 10
1.28. /(х) = л[х-ліх-5 і g(x) = -yjx(x-5).
1.29. /(*) = -Г-І \ і g(x) = ■ *
у[х{х-10)(х-0,ї) lg2JC-l

§ 1. Основні поняття
17
У задачах 1.30,1.31 знайти множину значень функцій:
1.30.а) у = 2 —|дс|; б) у = х2 -8* + 13.
З 1
1.31.6) у = —; б) ;y = 3-4sin;c; в) у = ——.
х х1
У задачах 1.32-1.38 записати складну функцію, якщо задані
проміжні функції:
1.32. у = и , w = sin;c. 1.36. ;y = arctgw, w=Vv, v = igx
1.33. y = u\ u = 4x-l. 1.37. У = {о"'^о°' U = x2 "L
1 1 9
1.34. у = —, и = tgjc. 1.38. у = , w = v , v = sinw,
w4 и-I
w = 2x + 3.
1.35. y = 2M, w = -cosv, v = 5* + l.
У задачах 1.39-1.48 вказати функції, суперпозицією яких є
такі складні функції:
1.39. у = (6х-6)7.
1.40. у = lgcos;c.
1.41. y = V?-4.
1.42. у = sin л/'х- 6 .
141 v-
cos (л:+ 71/4)
1.44. ;y = (2;c-5)10.
1.45. y = 2cosx.
1.46. у = lgctg—.
л:
1.47. y = cos(3~x2).
14Я v-
ig(*3)
У задачах 1.49-1.53 записати в явному вигляді функції,
задані рівняннями, та знайти їх області визначення:
1.49. ху = 15. 1.50. Зх+У = 10. 1.51. х2 + у2 = 4.
1.52. lgx + lgy = 4. 1.53. х(9-у2) = 1.

18
Розділі. Вступ до математичного аналізу
У задачах 1.54-1.59 встановити, чи є оборотними задані
функції. Якщо так, то знайти обернені:
1.54. у = х2 -1, х& (0;+°о). 1.55. у = —!—. 1.56. у = lg(x +1);
х-4
(х, х<0
1.57. у = 1-2~х. 1.58. у = \ . . 1.59. у = 5х.
1.60. Показати, що функції збігаються з оберненими:
2* + 3 _ч 3* + 5
а) у = ; б) у = .
5ж-2 2д;-3
Відповіді
1.1. (%;+~). 1.2. (-1;2]. 1.3. [0;б]. 1.4.0. 1.5. (-1;0).
1.6. (0;+оо). 1.7. (- 2;-і). 1.8. (- ~; ^). 1.9. (- ~;-2) U (2;+-).
1.10. (-2;2). 1.11. (-°о;-3]и[3;+~). 1.12. [2;4].
1.13. (-оо;-і)и(5;+о°).1.14. [-2;0]U[2;4].1.15. (-6;-2)U(-2;2).
1.16. а) і в); б) і є); в) і з); г) і є); д) і ж); є) і а). 1.17. а) так; б) так.
1.21. а) (-~;+оо); б) (-oo;-i)U(-1;2)U(2;-H;b) (~то;+Ч
1.22. а) (- ~;-2] (J [2;-Юо); б) (- °=;-3) U (- 3;+«.); в) (- 3;3).
1.23. а) 0;б)(-2;2);в) [0;2).
1.24. а) [- 6;4]; б) (- оо;з] U [4;5) U (5;-Юо); в) (0;8).
1.25. a) (-oo;-9]U[0;+oo);6) (-5;3];в) [2;5)и(5;б].
1.26.а) (0;100];б) (-oo;5,9)U(5,9;6);b) f-|;jl.
V З 8J
1.27. ні. 1.28. ні. 1.29. так. 1.30. а) (-°о;2];б) [-3;-Юо).
1.31. a) (-~;0)U(0;+oo); б) [-1;7]; в) (-~;0). 1.32. у = sin 2 х;
1.33. у = (4х-1)3. 1.34. у = l/tg4*. 1.35. у = 2-cos(5x+l\

§ 1. Основні поняття
19
1.36. у = arctgV^. 1.37. у = \2/ 2'хе [ $ ..
[О, JCG(-oo;-1)U(1;+oo)
1.38. у = , * . 1.49. у = —, хе (- оо;0) (J (0;+~).
sinz(2jc + 3)-l л:
1.50. у = х, хе (-°°;+°о).
Ig3
1.51. Уі = -УІЛ-х2 , у2 = -УІ4-х2 , хе[-2;2].
10000 /л ч
1.52. у = , д:є(0;+оо).
л:
1.54. у = л/лг + 1, жє [-1;+°°).
1.55. у = - + 4, * є (- °о;о) U (0;+°°).
1.56. у = 10*-1, Д:є(-оо;+оо).
1.57. >- = log2- , д:є(-оо;і).
1-х
\х, х < 0
1.58. У = І /- > *є(-°о;+оо).
[Vx, jc > О
1.59. у = log5х, хе(0;-н»).

20
Розділі. Вступ до математичного аналізу
§ 2. ЕЛЕМЕНТИ ПОВЕДІНКИ ФУНКЦІЇ
2.1. Монотонність та знакосталість
Означення 1. Нулем функції f називається таке значення
аргументу хє D(f), при якому f(x) = 0. Інтервали, на яких знак
функції не змінюється, називаються інтервалами знакосталості функції
Нулі функції ділять область визначення функції на
інтервали знакосталості.
Означення 2. Функція f називається обмеженою на
множині X, якщо існують сталі т і М такі, що т< f(x)<M,
\/хєХ.
Якщо для будь-яких двох чисел т і М , т<М , умова
т< f(x)<M не виконується хоча б для одного х Є X , то
функція / називається необмеженою на множині X.
Означення 3. Функція f називається зростаючою на
множині X, якщо більшому значенню аргументу хє X відповідає більше
значення функції f(x), тобто f - зростаюча функція, якщо для
довільних х{,х2є Xз того, що х{<х2, випливає f(xl)<f(x2)^
Аналогічно, f - спадна функція, якщо для довільних хх,х2є X з
того, що хх <х2, випливає f(x{)>f(x2).
Зростаючі та спадні функції називаються монотонними.
Якщо з того, що хх<х2, випливає, що f(x{)<f(x2) для
довільних хх,х2є X, то функція / називається неспадною на X .
Якщо ж з того, що х{ < х2 випливає, що f(x{)> f(x2) для
довільних хх,х2 є X, то функція / називається незростаючою на X.

§ 2. Елементи поведінки функції
21
2.2. Парність, непарність, періодичність
Означення 4. Функція /, визначена на симетричній відносно
початку координат множині X, називається парною, якщо
/(*) = /(-*)> VjcgX. Якщо ж /(-*) = -/(*), VjcgX, mo
функція f називається непарною.
Графік парної функції симетричний відносно осі Оу, а графік
непарної функції симетричний відносно початку координат.
Означення 5. Функція f називається періодичною, якщо існує
таке дійсне число Т Ф 0, що для всіх хе D(f) точки х±Т також:
належать множині D(f) і виконується рівність f(x + T) = f(x).
Очевидно, що для довільних хе D(f) справджується також
умова f(x-T) = f(x). Найменше із чисел Т > 0, для якого
виконуються вказані умови, називається основним періодом функції.
Розв'язування типових прикладів
Приклад 1. Знайти нулі та інтервали знакосталості функції
г, ч jc2-5jc + 6
f(x) = —.
х-4
Область визначення цієї функції
D\
Гх2-5х + 6Л
х-4
= (-oo;4)U(4;+~).
f(x) = 0=><х х => хх=2, jc2 = 3 — нулі функції. Отже,
[хФ4
точки х = 2 і х = 3 ділять D(f) на інтервали знакосталості
(-оо; 2), (2; 3), (3; 4), (4; +<*>). Обчисливши значення функції в
довільній точці інтервалу знакосталості, визначимо знак функції на
З
цьому інтервалі. Наприклад, в точці х = Оє (-©о; 2) /(0) = — < 0.
Отже, на інтервалі (-©о;2) ця функція від'ємна. Аналогічно

22
Розділі. Вступ до математичного аналізу
отримаємо, що f(x)<0 на проміжку (3;4), і f(x)>0 на
проміжках (2; 3) і (4;+оо).
Приклад 2. Визначити, чи задані функції парні (непарні):
а) f(x) = (ax+a~x)/2.
Замінивши у виразі для f(x) аргумент х на -х,
отримаємо /(-*) = (а~х +ах)/2 = (ax + a~x)/2 = f(x).
Отже, функція / (х) - парна.
б) f(x) = (ax-a-x)/2.
f(-x) = (a~x-ax)/2 = -(ax-a~x)/2 = -f(x) - функція
f(x) -непарна.
3*-1 3~*-1 3~*-1
в) /(*)= —і. /(-*) = - - = -- -.
х -хх
Очевидно, f(-x)*f(x) і /(-*)*-/(*). Отже, функція
f(x) ні парна, ні непарна.
Приклад 3. Нехай задано функцію f{x)-ex, х> 0. До-
визначити функцію f(x) в області л;<0 так, щоб одержана
функція на множині (- <»;+оо) була
а) парною функцією; б) непарною функцією.
Графік парної функції є симетричним відносно осі Оу.
Симетричним до графіка функції у = ех, х> 0, є графік функції у = е~х,
\е~х х<0'
х < 0. Отже, довизначена функція має вигляд f(x) = < ' '
[ех, х>0.
Аналогічно одержимо для пункту б) довизначену до
\-е~х, *<0;
непарної функцію f(x) = 1 ех, х>0;
0, х = 0.

§ 2. Елементи поведінки функції
23
Приклад 4. Знайти період функції f(x) = 5 , хє R.
Оскільки f(x) = 5 для довільного хє R, то для довільного
TeR виконується рівність f(x±T) = f(x), тобто виконується
умова періодичності. Проте найменшого числа Т > 0, для якого
виконується умова періодичності, не існує, а тому періодична
функція f(x) = 5 не має основного періоду.
Приклад 5. Перевірити, чи число Т = 1 є періодом функції
f(x) = {х}, де символом {х} позначимо дробову частину числа х.
Нагадаємо, що символом [х] позначають цілу частину
числа х (наприклад, [2,3] = 2, {2,3} = 0,3). Очевидно, що
f(x + l) = {x + l}=x + l-[x + l] = x + l-{[x] + l) = x-[x] = f(x).
Крім того, якщо 0 < а < 1, то маємо
ч г Л г -, J*+*-[4 [*+fl] = H _
f(x + a) = \x + a\ = x + a-\x + a\ = < /r . ч _ _ _ _-
1 J L J |jc + a-([jc] + l), [;c + a]>[jc]
[/(д:) + а, [л + а] = [д:]
[f(x) + a-l [x + a]>[x]
Отже, T = 1 - найменше число, для якого виконується умова
періодичності. Зауважимо, що функція у = [х] не є періодичною.
Приклад 6. Знайти період функції f(x) = sin foe.
Область визначення цієї функції D(f) = R. Тому, якщо
х є D(f), то і х ± Т є D(f). Нехай Т - період функції f(x). Тоді,
за означенням періодичної функції, справджується рівність
f(x + T) = f(x), тобто sin k(x + Т) = sin kx. Для знаходження Т
перепишемо цю рівність у вигляді sin£(jc + r)-sinfo; = 0. Звідси
„ / ТЛ . кТ Л
2cos£ Jt + — sin— = 0 дня всіх значень х, що можливо лише при
І 2J 2
£Т ЛТ 2гп7Г
sin— = 0. Отже, —— = ттг, meZ=>Tm= , me Z . Наймен-
2 2 ifc

24
Розділі. Вступ до математичного аналізу
_ 2тл „ 2л г^_ ,
шим додатним із чисел Тт = є число Т = —. Отже, функція
к к
2л
f (х) = sin кх має період Т = —.
к
Приклад 7. Знайти період функції f(x) = a cos(a х + /3).
ОСКІЛЬКИ D(f) = (- °о;+оо) і
/О) = acos(a x + /3) = acos [(а х + /3) + 2л ] =
( 2л\
= acos [а(х + 2л/а ) + /3] = f \х +— ,
v &)
то періодом функції f(x) = a cos(a x + j3) є Т = 2л/а.
Зауваження. Порівнюючи методи розв'язування прикладів
6 і 7, бачимо, що другий із них ефективніший. Дійсно,
скориставшись цим методом для розв'язання прикладу 6, одержимо
ґ
f (х) = sin кх = sin(kx + 2л) = sin к
2л] J 2л
х + — =/ JC + -
к J{ к
2л
Отже, Т = —. При цьому використовується та обставина, що
к
функція y = sinx має період 2л. Метод розв'язування,
використаний у прикладі 6, не застосовує періодичності функції у = sin х, і
через те є загальнішим.
Задачі для самостійного розв'язування
У задачах 1.61-1.70 знайти нулі та інтервали знакосталості
заданих функцій:
1.61. у = 2-х. 1.66. у =
jc2 — 5jc + 6
1.62. у = 2 + х-х2. 1.67. у = - Р—ч -.
(4 - х)х
jc —1 ^ ^0 2jc2 + 4jc + 2
1.63. у = —0 . 1.68. у =
л: — 5jc + 6 х + 1

§ 2. Елементи поведінки функції
25
1.64. у = х3-4х.
2х
1.65. y = lg- .
1 + д:
У задачах 1.71-
1.71. f(x) = x4-2x2
1 7Л f(r\- Х
2*-1
1.73. f(x) = sin х - со
1-х2
1.74. /(д) = _±-.
1 + д:2
1.75. /(jc) = jc2-jc.
-1.80
SX.
х2-4
1.69. )/ = -—І.
л- + 2
1.70. у = 21п|л|.
дослідити на парність вказані функції:
1.76. f(x) = sin л:-cos*.
1.77.f(x) = xlg^.
1 + X
1.78. f(x) = y/x2-3x-4.
1.79. /0) = ;c3+3sinjc.
e~*-l
1.80. f(x) = —r .
ex+l
В задачах 1.81-1.84 встановити, чи функція h є парною
(непарною):
1.81. h(x) = f(x)g (х), f -парна, g -непарна;
1.82. h(x) = f(x)-g(x), f , g - парні функції;
1.83. h(x) = f(x) + g(x), / , g - непарні функції;
1.84. /i(jc) = f(x)g(x), /, g - непарні функції.
1.85. Чи існують визначені на R функції, що є одночасно:
а) парними і зростаючими на всій області визначення;
б) непарними і спадними; в) непарними і додатними на всій
області визначення?
У задачах 1.86-1.103 з'ясувати, які з наведених функцій є
періодичними, та визначити їх основний період:
1.86. y = 10cos3jt. 1.87. y = 2tg[3jt-—1. 1.88. y = l + sin2jc.
1.89. у = cos(jc2). 1.90. у = tgV*. 1.91. у = sin
х + —
\
З

26
Розділі. Вступ до математичного аналізу
*-§,.
1.92. y = l + ctg|
1.94. y = V^-
1.96. у = х2 +1,
Ґ1, х - раціональне,
1.98. у = \
[О, х- ірраціональне.
1.100. ;у = AcosAx + BsinAx;
1.101. у = sin jc + 0,5 sin 2jc + 0,3 sin Зх
1.102. y = cos(l-;c2).
' Л^
1.93. y = 3-5cos
1.95. у = sin x + sin(V2;c)
2jc + —
з;
1.97. y = 2tg- + 4tg-.
2 3
1.99. y = sin2jc.
1.103. y = tg^-3tg^.
1.104. Знайти /(/(/(*))), якщо /(*) =
1
1-JC
1.105. Знайти /(л:), якщо /(л; + 1) = л; -Зл; + 2.
У задачах 1.106-1.109 довести, що задані функції є
монотонно зростаючими на вказаних проміжках:
1.106. f(x) = x, л;є[0;+оо). 1.108. /(jc) = tgjc, хє
л л
'2'2,
1.107. /(>:) = sin*, хе
л л
1.109. /(x) = 2^: + sinjc, jce(-oo;+oo).
У задачах 1.110-1.112 довести, що задані функції є
монотонно спадними на вказаних проміжках:
1.110. f(x) = x2; хє(-оо;0]. 1.111. /U) = ctgjc; хе (0;/г).
1.112. /(jc) = cos;t; хє[0;/г] .
1.113. Нехай (р(х), f(x), у/(х) - монотонно зростаючі функції.
Довести, що, якщо р(х) <f(x)< уг(х), то
q>((p(x))<f(f(x))<y/(ii/(x)).

§ 2. Елементи поведінки функції
27
1.114. Визначити обернену функцію y = f 1(х), якщо
їх, -оо<л:<1
х2, 1<jc<4.
\2Х, 4<л:<оо
У =
1.115. Довести, що всяку функцію f(x), визначену в
симетричному інтервалі (-/; І), можна подати у вигляді суми парної і
непарної функції.
Відповіді
1.61. 2; у > 0 при хе (- оо;2); у < 0 при хє (2;+оо).
1.62.-1; 2; у>0 при *є(-1;2); у<0 при хє (-oo;-i)(j(2;+«>).
1.63. 1; у>0 при jcg(1;2)U(3;+oo); у<0 при хє (-оо;і)(J(2;3).
1.64. -2; 0; 2; у > 0 при хе (- 2;0)U (2;+«>);
у<0 при jce(-oo;-2)U(0;2).
1.65.1; у > 0 при хє (-oo;-i)(j(l;+oo); у < 0 при хє (0;і).
1.66.2; 3; у > 0 при хе (l;2)U (3;+«>); у < 0 при хє (- oo;l)|J (2;3).
1.67. -3; у > 0 при хє (-oo;-3)U (0;4);
у<0 при л:є(-3;0)и(4;+оо).
1.68. 0; у>0 при л:є(-1;+оо); у<0 при хє(-°о;-і).
1.69.2; у>0 при хє(2;+оо); у<0 прихє (-оо;-2)U(-2;2).
1.70.-1;1; ;у>0 при хє (-oo;-i)|j(l;+oo); у<0 при хє (-l;0)U(0;l).
1.71. Парна. 1.72. Ні парна, ні непарна. 1.73. Ні парна, ні непарна.
1.74. Парна. 1.75. Ні парна, ні непарна. 1.76. Непарна. 1.77. Парна.
1.78. Ні парна, ні непарна. 1.79. Непарна. 1.80. Ні парна, ні непарна.
1.81. Парна. 1.82. Парна. 1.83. Непарна. 1.84. Парна.
1.85. а) ні; б) так, наприклад у = -х ; в) ні.

28
Розділі. Вступ до математичного аналізу
2я л
1.86. Т = — . 1.87. Т = -.
3 3
1.89. Неперіодична. 1.90. Неперіодична.
1.92. Т = -. 1.93. Т = л. 1.94. Т = л.
3
1.88. Т = л.
1.91. Т = 2л.
1.95. Неперіодична.
1.96. Неперіодична. 1.97. Т = 6тт.
1.98. Періодична з довільним раціональним періодом, проте
основного періоду немає.
2л
1.99. Т = л . 1.100. Т = —. 1.101. Г = 2/г. 1.102. Неперіодична.
л
1.103. Т = 6л. 1.104.x.
ЇХ ХЄ(-°°;і);
1.114. y = \jx~ хє[і;1б];
log2x хе (16;-н»)
1.105. я2-5*+ 6.

§ 3. Границя послідовності та границя функції
29
§ 3. ГРАНИЦЯ ЧИСЛОВОЇ ПОСЛІДОВНОСТІ
ТА ГРАНИЦЯ ФУНКЦІЇ
Означення 1. Число а називається границею числової
послідовності {хп), якщо для довільного, як завгодно малого додатного
числа Є можна вказати таке натуральне число N = N(e), що
для кожного натурального числа п> N виконується нерівність
\хп -а\<є.
Той факт, що число а є границею послідовності {хп]
записується як lim хп=а або хп —> а при п —> °о. Послідовність
{хп), яка має границю, називається збіжною, у протилежному
випадку -розбіжною.
Означення 2. Послідовність {хп} називається нескінченно
великою, якщо для довільного числа К > 0, яким би великим воно
не було, можна вказати таке натуральне число N = N(K), що
для довільного п>N справедлива нерівність \хп\ > К.
Те, що послідовність {хп) є нескінченно великою,
прийнято записувати так: limjc„=°o, або jtn—>оо при я—><». Якщо
limjcn = ©о, і при цьому існує таке натуральне N , що для
довільні —>оо
ного п > N виконується нерівність хп > 0 (хп < 0), то пишуть
відповідно lim хп = +°о (lim хп = -оо). у всіх цих випадках
твердять, що послідовність має нескінченну границю.
Означення 3 (Коші). Число А називається границею
функції f(x) в точці а (або при х —> а), якщо для кожного числа
є > 0, яким би малим воно не було, існує таке число S (£)>0, що
для всіх х, які задовольняють умову 0<|х-я|<£, виконується
нерівність |/(де) - А\ < Є.

зо
Розділі. Вступ до математичного аналізу
Якщо число А є границею функції f(x) в точці а, то
пишуть lim f(x) = а , або f(x) -> а при х -> а .
Зауважимо, що в означенні Коші ніяких умов на спосіб
прямування х до а не накладається. Якщо ж х —> а так, що х > а,
то така границя називається правосторонньою границею функції
f(x) в точці а , і позначається lim /(jc) . Аналогічно lim f(x) =
*-»а+0 *-»а-0
= lim/(л;) - лівостороння границя функції /(jc) у точці а. Якщо
а = 0, то правосторонню і лівосторонню границю функції /(jc) у
точці а позначають відповідно lim f(x) і lim /(jc).
*->+0 *->-0
Означення 4. Число А називається границею функції
f(x) при *—>°о, я/аг/о для кожного, як завгодно малого, числа
є > 0 існує таке число К >0, що для всіх X у ЯКІ задовольняють
умову |л:| > К, виконується нерівність |/(jc) - А\ < є.
При цьому записують lim /(jc) = А. Якщо ж jc —> ©о так, що
jc>0 (jc< 0), то кажуть, що число А є границею функції f(x) при
лг—>+оо (х—^-оо) і записують lim /(jc) = A ( lim /(jc) = A).
Означення 5. Границя функції f(x) в точці а дорівнює
нескінченності: lim f(x) = <», якщо для кожного числа К > 0,
х—>а
яким би великим воно не було, існує таке число S>0, що для
всіх х, що задовольняють умову \x-a\<S, виконується
нерівність |/(jc)| > К.
Якщо lim /(jc) = оо і до того ж f(x) > 0 (f(x) < О) в деяко-
х—>а
му околі точки а , то пишуть lim f(x) = +<» (lim f(x) = -©о).
x—>a x-^>a

§ 3. Границя послідовності та границя функції
31
Аналогічно, lim f(x) = «>, якщо для кожного числа К > 0
X—»оо
існує таке число 5 > 0, що для всіх х, що задовольняють умову
|jc| > S, виконується нерівність |/(х)| > К .
Для функцій, що мають границю, справедливі такі
твердження (властивості):
1. Якщо границя функції у = f(x) при х —> а існує, то вона
єдина.
2. Якщо функція f(x) тотожньо дорівнює сталій С, то
lim f(x) = С.
х—>а
3. Якщо точка х = а разом з деяким околом належить області
визначення елементарної функції f(x), то існує границя функції
/О) при х —> а і вона дорівнює f(a), тобто lim f(x) = f(a).
х->а
4. Якщо lim/О) = А і lim g(x) = В (а - скінченне або
х—>а х-*а
дорівнює +°о чи -°°), А, 5- скінченні числа, то
а) lim(/(jc) ± g(x)) = lim /(*) ± Urn g(x) = А ± Я;
х->а х->а х->а
б) lim (f(x) ■ g(x)) = lim f(x) ■ lim g(x) = AB;
x->a x—>a x->a
в) lim(C • f(x)) = С • lim /(jc) = С • A, де С - const;
f(V> Um/<» л
г) lim^-^ = ^ = -,якщо 5*0;
x-^a g(x) limg(x) В
д) lim[/(jc)]
g(x) _
и lim g(x)
Urn /(jc) И" = AB , якщо A > 0 ;
є) якщо /(х)ФЬ при д: * а та існує lim h(y), то
lim h(f(x)) = lim Л(у).
jc—»a y—>&
5. Якщо lim /(jc) = +°o і lim g(x) = +©o, то
jc—>a jc—>a
a) lim(/00 + $(x)) = +oo; 6) lim (/(*)• *(*)) = +«>.
jc—>a jc—>a

32
Розділі. Вступ до математичного аналізу
6. Якщо lim f(x) = ©о і lim g(x) = А (А - скінченне число,
відмінне від нуля), ТО
a) Um(/(jc)-*(jc)) = oo; б) lim(/(jc)±y(jc)) = oo.
7. Якщо lim /0) = °°, то lim = 0.
*—>а *—>а f(x)
8. Якщо 1іт/(;с) = 0, і /(х)Ф0 в деякому околі точки
х = а , то lim = оо .
Зауважимо, що аналогічні властивості можна
сформулювати для границі числової послідовності.
3.1. Невизначені вирази
х->а g(x)
fix)
Кажуть, що lim {а - скінченне, або дорівнює +«>
чи - ©о) є невизначеністю типу \ — \9 якщо lim f(x) = lim g(x) = О,
[OJ x^>a x^>a
і записують lim- = \ — >. Аналогічно
*->°g(x) [OJ
fix) fool
а) lim = < — k якщо lim f(x) = lim g(x) = oo;
x^>a g(x) [ooj x^a x^a
б) lim(/(x)-^(x)) = {oo-oo}, якщо lim f(x)= lim g(;c) = +o°;
*—>a jc—>a jc—>я
в) lim[/(x)-g(*)] = {0-oo}, якщо lim/O) = 0, limgO) = oo;
г) 1іт[/(д:)]8М = JO0], якщо lim/(jc) = limg(x) = 0;
д) lim[/(^)]gW = loo0] , якщо lim /(*) = «,, lim g(x) = 0;
е) lim[/(x)]gW = ІГ], якщо lim f(x) = 1, lim $(*) = °°.
*—>a *—>a

§ 3. Границя послідовності та границя функції
33
3.2. Важливі границі
При обчисленні границь часто використовують такі
формули:
sin*
lim
*->0 х
= 1 - перша важлива границя;
1ІШІ1 + -
*->°Ч х)
= lim(l +у)у = є - друга важлива границя, а
у->0
також наслідки з другої формули:
г lQg*(1 + *) , г (1 + *Ґ-1
lim — - = logfle, lim-^ '- =
jc-»0 X *-»0 X
.. ax-\
lim
;c^0 X
= lna, /ИФО, я>0,а*1.
Розв'язування типових прикладів
Приклад 1. Користуючись означенням, довести, що число 2
. Ґ2л + і1 ^ Л. 2n + l ^
є границею послідовності <j }, тобто lim = 2.
п ) л—>°о п
Потрібно довести, що для кожного додатного числа є існує
таке натуральне число N, що для довільного натурального
|2л + 1
п > N справедлива нерівність
<є.
Оскільки
2л+ 1
-2
= —, то нерівність
п
2п + 1
-2
п
< є рівнозначна нерів-
носп — < є, звідки п > —. Якщо взяти деяке натуральне число N,
п є
що більше за число —, наприклад, число
є
+ 1 (U-ці
ціла частина
числа), то для кожного натурального п, яке більше за число N,

34
Розділі. Вступ до математичного аналізу
виконується нерівність
2л+ 1
-2
— < — = є. Отже,
+ 1 -
для довільного числа є>0 можна визначити таке число N
|2п + 1
такий, що при всіх п > N справедлива нерівність
2п + \
'—2
<є.
Значить, lim
■ = 2.
и—>°° П
Приклад 2. Довести, що lim
х2-16
*->4jc2-4jc
означення Коші границі функції в точці.
= 2, використовуючи
Розглянемо функцію f(x) =
;с2-16
х2 -4*
у деякому околі точки
х = 4, наприклад, на інтервалі (2; 5). Візьмемо довільне додатне
число є , і перетворимо вираз \f(x) - А\ при д: ^ 4,
jc2 -16
х2 -4х
х + 4
нерівність
\х-4\
Xі -16
jc2 -4*
-2
Враховуючи умову хє(2;5), отримаємо
|х-4|
<J L, з якої видно, що для 8 = 2є і
2
всіх х є (2; 5), 0 < \х - 4| < 5, виконується нерівність
х2-\в
х1-Ах
-2
< — = є. За означенням Коші, число А = 2 є грани-
jc2-16
цею функції /О) = — у точці X = 4 .
jc -4х
Приклад 3. Обчислити границю lim
2х3 + 3х2 -5х
*->°° 5х3 -їх2 +4

§ 3. Границя послідовності та границя функції
35
Оскільки lim(2jc +3jc -5jc) = °o і lim(5x -їх +4) = оо,то
маємо невизначеність типу \ — >. Для знаходження границі дробу
ігри х —> ©о 9 чисельник і знаменник якого є многочленом ВІДНОСНО X,
доцільно поділити чисельник і знаменник цього дробу на хк, де к -
степінь многочлена в знаменнику. Поділивши чисельник і знаменник
cz з 2jc3+3jc2-5jc х х2 _
дробу на х , отримаємо —г = —~-. Зауважимо,
5jc3-7jc2+4 5-- + А
1 1 1
що lim — = 0, lim — = 0 і lim — = 0. Тому
х—>оо х *—>°о х х—>°° х
' 3 5 ^ Л Г 7 4
lim 2 + — = 2, a lim 5 — + -~- =5. Отже, існують границі
чисельника і знаменника дробу, і границя знаменника відмінна від
нуля. Тому можна перейти до границі в чисельнику і знаменнику.
,.„35
її г -ч lim 2 + —
їх5 +3xz -5х _ ) оо| _ ^-»оо х х2 _ 2
*^~ 5jc3-7jc2+4 1°°J lim5-Z + A 5*
jc->oo х х3
rr г л/*5+2-^2х2+1
Приклад 4. Обчислити границю lim . —. .
x^°°fcx4+2-<Jx3+l
Поділимо чисельник і знаменник дробу на \х3 = х2.
Отримаємо
lim . , = lim -—г- =

36
Розділі. Вступ до математичного аналізу
J1 2 І 2 1
= lim
*2 *2 О
х->- ІЗ 2 ,1-1
*2 Л2
= 0.
Приклад 5. Обчислити границю lim
Оскільки lim ух -1 = +°° і lim ух +1 = -Н», тс
маємо невизначеність типу {©о-©о}. Вираз \ух -І-ух +1
домножимо і розділимо на спряжений до нього вираз
lim
= lim
х—»«>
im (VJc^T - V?+l ] = {°° - с»}=
= Um/^-(^=Um.
-2
,(^/7Л + ^/77ї) ~~(л£М + 777І)
= lim
2
•444
> 2
Приклад 6. Обчислити границю lim —
*^3^2-8x + 15

§ 3. Границя послідовності та границя функції
Ъ1
При я—»3 чисельник і знаменник прямують до нуля.
Отже, ця границя є невизначеністю типу < — k Оскільки х —> 3,
то нулі в чисельнику і знаменнику отримаємо за рахунок виразу
(дс-З)—»0. Для розкриття цієї невизначеності потрібно в
чисельнику і в знаменнику виділити множник (х - З). Розклавши
чисельник і знаменник на множники, одержимо
х2-5х + в (х-Ъ\х-2) х-2 _ / 0\
—z = т г/ \= • Тут скорочення на ід: — 3) є
законним, оскільки х —> 3, але х Ф 3 , так що х - З Ф 0.
Отже, на основі властивості З
jc2-5jc + 6 ГОІ ,. jc-2 3-2 1
lim — = < — > = lim
х-*Ъх2 -Ъх + 15 10J jc->3j-5 3-5 2
2jc-3
Приклад 7. Обчислити границю lim— .
*->ijc -3jc + 2
Оскільки lim be2 - Ъх + 21= І2 - 3 • 1 + 2 = 0, lim (2jc - 3) =
jc->1x ' JC—>l
2.1-3 = -1^0,то lim „2*~3 =oo.
*-^jc2-3jc + 2
Приклад 8. Обчислити границю lim •
*^°V*2+16-4
Маємо невизначеність типу к — >. Оскільки х—>0, то в
чисельнику і в знаменнику треба виділити множник х. Для цього
домножимо чисельник і знаменник дробу на спряжені до них
вирази. Матимемо

38
Розділі. Вступ до математичного аналізу
*2(л/7^ + 4) 77^ + 4 л/іб + 4 ,
—- = km = = ^
Приклад 9. Обчислити границю lim
lim
= lim-
*->0
Jt->0 X [0>
(i-jc)-g+jc)
-2
= lim
jc-»0
= lim
*->о /3
(л/ь1*) +^ї^^ї+7 + (^ї+І)'
sin&x
Приклад 10. lim , де к є R.
х->0 х
Маємо невизначеність типу < — L Введемо змінну у = кх.
Оскільки х —> 0, то і у —> 0. Використовуючи першу важливу
,. sinfar Го] Л. sin у , ,. sin у 7
границю, знаходимо lim = < — f = lim — = к lim — = к .
jc-»o jc [0J у-»о у_ у->о у
к
Приклад 11. Обчислити границю lim -
2
П
— -Х

§ 3. Границя послідовності та границя функції
39
Маємо невизначеність типу < — v. Безпосередньо застосувати
. ,. sin* ,
формулу lim = 1 тут неможливо, оскільки змшна х не прямує
*->0 х
до нуля. Введемо нову змінну z так, щоб z —> 0. Оскільки х —> —,
го приймемо z = х. Тоді
lim
1 + япЗх_ГОІ_15„ U J,. 1-
-де
= ^ = lim
2 10 z^o
= lim-
cos3z
2sin'
гГЗг
= lim-
г->0
• = 2
sin
'зг^2
V
lim
z->0 z
\ J
= 2-
Ґ3\1
\^J
9
2
_ _ ^ i- arcsin3x
Приклад 12. Обчислити границю lim .
jc->0 x
Нехай arcsin3x=y. Тоді x = — sin у і у—>0 при x—>0.
Отже,
-. arcsin3x Г 01
lim = < — > = lim T
jc-»0 x 101 y-»o 1
-2—= 3 lim-2-
sin у ' ^ lim
sin у
у-Ю у
= 3.
Приклад 13. Обчислити границю lim
х + 1
\2jc-1
х-*х>[ Х + 3
Маємо невизначеність типу |і°°}, бо lim
І J г—*ос
^JC + O
= 1, a
lim (2jc -1) = о». Отже, потрібно використати другу важливу

40
Розділі. Вступ до математичного аналізу
границю. Для цього виділимо у виразі
х + 1
х + 3
одиницю, тобто
запишемо цей вираз у вигляді 1 + а (х). Це можна зробити,
наприклад, якщо поділити чисельник на знаменник або додати до
цього виразу і відняти від нього одиницю. Будемо мати
jc + 1 Л (х + 1 Л л х+\-х-3 -2 ^ .
= 1+ 1 =1 + = 1 + .Тоді
х + 3 \х + 3 J х + 3 х + 3
lim ГіІіГ"1 = {і°°} = lim fl + —Г"' =
= lim
X—»оо
jc+3
1 +
-2
jc + 3
-2(2jc-1)
jc+3
Оскільки
jc+3
-2
JC-»~l X+3
lim 1 +
jc + 3
-2=У>
= lim 1 + — = e,
,. -2(2jc-1) .. -4x + 2 r 4+x
lim — = lim = lim - =
JC->oo X + 3 *->oo X + 3 *->°° л , 3_
= -4,
то
lim
л:+3
1 +
-2
x + 3
-2(2jc-1)
jc+3
v
jc+3
lim' \
JC->°o^ x + 3
h» -2(2*-1}
г—*oo JC+3
= £
2
Приклад 14. Обчислити границю lim(cos6x)ctg x •
jc-»0
Um(cos6jc)ctg2x ={Г] = lim(l + cos6;c-l)ctg2* = Um(l-2sin23;c)ctg2* =
г—>П L J r—tf) r-*0
JC-Ю

$ J. Границя послідовності та границя функції
41
= lim
2 2
j \-2sin 3*-ctg х
(l-2sin23jc)
2sin23*
= lim
*-»0
2 2
Л \ lim (-2sin 3*-ctg x)
1 U->0
(l-2sin23jc)
2sin23x
= e
■18
Приклад 15. Обчислити границю lim jc(ln(jc +1) - In x).
X—»+«>
За наслідком з другої важливої границі lim = 1.
*->0 х
Тому
lim jc(ln(jc + l)-lnjc)= lim jcln
JC + 1
*-»+°°
*-»+«> X
= lim jcln| 1 + — | =
1 1
\-=y9 * = —і
y->+0
.ШпіїйІЙ.,.
;y-»+0 у
Задачі для самостійного розв'язування
У задачах 1.129-1.138, користуючись означенням границі
послідовності, довести:
п 1
1.129. lim-^ = l, beR.
1.130. lim
1.131. lim
Зп З
л->~2п-1 2
л->~ 2п + 3 2
1.132. 1іт^- = -1.
и-»» 2 + п

42
Розділі. Вступ до математичного аналізу
Л 2п2+1 2
1.133. lim z— =—.
и->°° Ъп З
* *^ і- у4п2 +а2 -
1.135. lim- = 2, а є/?.
1.134. lim
n2-31n + 4 1
nsin-
1.137. lim
nn
n-»~ n2+5
= 0.
«^~2n2 + 17n-57 2'
2"+3
1.136. lim^^ = 0.
n->~3" + 2
1.138. lim 2n + 1 =0.
>(n + l)2n
У задачах 1.139-1.144 за означенням Коші границі функції
в точці довести справедливість вказаних границь:
1.139. lim(5x-3) = 7.
*-»2
1.141. lim(x2 + 2;c-3) = -4.
х1 -9
1.140. lim-—- = -6.
*->-з х+3
1.142. 1іт(л:3 + 2) = 3.
1.143. lim
1
1.144. lim
'х^Лх2+4 5' *-+2(1-jc):
У задачах 1.145-1.235 знайти вказані границі
- = 4.
1.145. lim
х3-2х
х-+°оХ4+5х2-ї
1.146. Urn
п2 + 2
п-4~и +П + 1
1.147. lim
хг -1
*-»~2лг+1
1.148. lim
/1—>оо
1.149. lim
(2и + 1)3-(2п-1)3
»-*» (и + 2)2+(и-2)2
і 1 1 1
1 + - + - + ... + —
2 4 2"
l + 2 + З + ... + и
1Л50. lim (" + 2)! .
n-»»(n + 3)!-(n + l)!
/
1.151. lim
И—*» - 1 1
. 1.152. lim
1 + - + - + ... + —
3 9 З"
П—>оо
1 1 1
+ + ...+
1-2 2-3 n(n + l)
ш 1іт<1±*Хі+2,)...(і+1ад
X—>оо
*10+1

$ 3. Границя послідовності та границя функції
43
,.,54. lim C*-'A3'-f, 1Л55. 1іт W + a.'-!
1.156. Ііт
лІ4п2+1 + п)
1.157. Ііт
V9n3-3n2+2 + \/n4+l
"->" \/l6n6 + 3n5 + In - Цп1 + Ъпъ
, 1ce .. уІх2 + 2-Ухг+1 Л 1еа .. Vx2+4+Vl6x4+l
1.158. hm , . 1.159. Ііт
*-*- VT^I ' ' '*-*- V77
2
,Л60. lim 2ЁЗр[. 1.161. Ііт ^+g + ^,
х->+оо 1 + Vjc " *->+°° V2jc + 1
,Л62. lim V* + V^ . 1.163. limV4*2Wg77
*->+~ V*+l *->°° л]х2+4
1.164. ИтГл/л:2-2;с-1-л/*2-7л: + з\
1.165. lim L/(n + 2)(п +1) - V« (n -1)1
1.166. 1ітГл/4д:4+13л:2-7-2л:21.
>ooV
1.167. lim [jc-Vjc2 + jc + 2 ].
—^*->±°Л У
1.168. limlljx3 +3x2 -ijx3 -3x2).
1.169. lim f^/(jc +1)2 - V(^ ~ !)21 •
1.170. lim (^n3+n2+1984 -n\
/1->ooV у

44
Розділі. Вступ до математичного аналізу
1.171.
1.172.
1.174.
1.176.
1.178.
1.180.
1.182.
1.184.
1.186.
1,188.
1.190.
1.192.
1.194.
1.196.
lim
X—»оо
lim
у х1 + \х2 + 4 х1 -ліх2
jc2+4jc-5
*->і х1-\
Л. (1 + jc)3-(1 + 3jc)2
*->о jcz+jT
lt„ r 2jc2-11jc-21
1.173. lim—r .
— *->7 jc2-9jc + 14
1.175. lim
jc-3jc + 2
lim
V*
3+l JC + 1
1__^
1.177. lim
*->2
*->1jc-4jc + 3
1
lim
*->il
lim
[ jc2-4jc + 6 jc-4
1 +
jc2-5jc + 4 3jc2-9jc + 6
jc4-jc3 + jc2-3jc + 2
1.179. lim
2jc-jc2 jc2-3jc + 2,
8jc3-1
>I6jc2-5jc + 1
2
*->i jc3 — jc2 — JC + 1
л. V5-JC-2
lim і —.
*->W2-jc-1
-. jc - V3jc - 2
lim r .
x-*2 jc2-4
.. V7 + 2jc-jc2 -Vl + Jc + jc2
lim
1.181. lim
V^I-2
*-»5 JC - 5
1 їді r V6-JC-1
1.183. lim ,
^->53-V4 + jc
1.185. lim
*->0
2vjc2 + jc + 1-2-jc
*->2
lim
*->i^/jc-1
2л: -jc
*2-i
.. W+x + x + 7
lim , .
*-»-8 3/l5 + 2;c + l
1.187. lim
*->0
1.189. lim
ДГ-»-
1.191. lim
ЙЇ7-1
V^-x3
і x+i
V9 + 2x-5
*-*8 3/x-2
,. Ці + хг -h + x2
lim
*-»i jc -1
lim-^.
*-»o sin 3jc
sinjc
lim .
*->o sin 6jc - sin 7jc
1.193. lim
sinfcc
x->0Sin/7U
1.195. Iimjcctg5jc.
*->0
1.197. lim
cos 3jc3 -1
*->° sin6 2jc

§ 3. Границя послідовності та границя функції
45
1.198.
1.200.
1.202.
*->о siir2jc
lim .
*-»2sin;rjc
1 + cos3jc
lim
Х_Д tgz6x
з
1.204. lim
я
-2;ctgjc
1.206.
2
. x + 5 nx
lim sin tg .
*->-5 3 10
1.208.
1.209.
1.211.
1.213.
Vl + 2sin3jc-Vl-4sin5jc
sin6jc
lim
1# vcos4x-vcos5jc
lim
*->o 1-cos3jc
arctg3jc
lim
*->o arcsin 2jc
-. tg2jc-3 arcsin 4jc
lim — .
*-»o sin5jc-6arctg7x
1.199.
1.201.
1.203.
1.205.
lim
sin 77t X
*-»i sin 2n x
cosjc-cosv3
lim j= .
*->л/з sin v 3 - sin X
v-Д V2cOSJC-l
1.207. lim
lim (l-sinjc)tg2jc.
ctgx-1
7t
*^cos2jc'
. %/shTx-\/sinx
1.210. lim —
л
jc->—
2
COS JC
1.212.
lim
*-»з
arctg(jc-3)
^3
„ ^ „ ,. л/і + arcsin jc - 111 + arctg2x
1.214. lim *
*->o д/і + arctg3jc - Vl- arcsin Ax
1.215. lim
l + — , t,me #.
1.216.
lim
*-*»v jc + 3
jc+2
1.217.
rj
jc2
lim
1.219. lim
*z +4
*2-4.
l + x
1.218. lim
x2-2x + \
*-4 x -Ax + 2
*->°\\-x
1.220. lim(Vl + x - xfx.
*-»0

46
Розділі. Вступ до математичного аналізу
\х _J_
1.221. lim І^Іі] . 1.222. lim (cos jc) x\
nx
xfgT
1
1.223. Urn 2-- . 1.224. lim(l + tg2V^)2*.
x->3\ Ъ) *->0
1.225. Um(sinjc)tg2^ •
1.227. lim(l + ctgx)tg3*.
л /%/%л і- lncos3jc
1.229. lim .
*->olncos5jc
ax __ bx
1.231. lim- —.
1.226.
1.228.
1.230.
1.232.
і
]im(l + 3x4yin2
x->0
Iimln(a + X)"
11111
*-»0 X
-. shx
lim .
*->0 X
limiH^).
X
-Ina
jc->0 X Jt-»0 x2
r\X о r\X cX
1.233. lim-—-. 1.234. lim-
*->3sin#"jt *-»o sin л: - sin 2x
1.235. lim(ln(e + jt))ctg*.
ВІДПОВІДІ
1.145.0. 1.146.1. 1.147. °o. 1.148.-. 1.149.12. 1.150.0.
2
1.151.-. 1.152.1. 1.153.10! 1.154. 215 З31. 1.155.1. 1.156.9.
З
з
1.157. —. 1.158.0, якщо х —» +°°; 2, якщо х —» -°°.
2
V2
1.159. З, якщо л: —» +°°; -3, якщо *—>-«>. 1.160.1. 1.161. —.
1.162.1. 1.163. VJ.1.164.-. 1.165.2. 1.166.—.
2 4 •

§.і. Границя послідовності та границя функції
47
1.167.—,якщо х —» +оо;-°°,якщо х —>-«>. 1.168.2. 1.169.0.
2
1.170 — . 1.171. -. 1.172.3. 1.173.—. 1.174. ос. 1.175. ос.
3 2 5
1.176.1. 1.177.-І. 1.178.1.1.179.6. 1.180.2. 1.181. і.
2 4
1.182. —. 1.183.3. 1.184.—. 1.185.-. 1.186.—. 1.187.-.
2 16 4 4 З
1.188.6. 1.189. --. 1.190.2.1.191—. 1.192.--. 1.193. —.
З 5 4т
1.194.-. 1.195. -. 1.196.-1. 1.197.——. 1.198.—.
3 5 128 16
1.199. - -. 1.200. -. 1.201. tgV3 . 1.202. -. 1.203.4.
2 п & 8
1.204.2. 1.205.-. 1.206.-—. 1207.0. 1.208.—. 1.209.-.
2 Зл- 6 3
1.210.—. 1.211.-. 1.212.1. 1.213.—. 1.214.- — .
24 2 37 21
1.215. еы. 1.216. е-\ 1.217. е\ 1.218. є2. 1.219. е\
_)_
1.220. є 2 . 1.221. +°о, якщо х —>+«>; 0, якщо л:—»-оо.
І _і І _І І
1.222. є2. 1.223. е~* . 1.224. є2. 1.225. є"2 . 1.226.1. 1.227. є3.
1. а-Ь. 1.232.—.
2
1.228. -.
а
1.233.^.
п
9
1.229. —.
25
1.234. In-.
2
1.230.1. 1
і
1.235. ее.

48
Розділі. Вступ до математичного аналізу
§ 4. НЕСКІНЧЕННО МАЛІ
І НЕСКІНЧЕННО ВЕЛИКІ ВЕЛИЧИНИ
Означення 1. Функція а(х) називається нескінченно малою
при jc —» а, якщо lim СХ(х) = 0.
х-*а
Означення 2. Функція f(x) називається нескінченно великою
при х—їа,якщо lim f(x) = «>.
Означення 3. Нехай а(х) і 0(х)- нескінченно малі при
сс(х)
х—>а, тобто ]іта(х) = 0 і lim/?(jc) = 0. Нехай lim = А.
*—»д х->а *—»д /3(х)
Якщо
а) А - скінченне число і АФО, то а(х) і J3(x)
називаються нескінченно малими однакового порядку малості при х —> а.
У цьому разі пишуть а(х) = О(0(х)) при х—>а (читається: а(х)
є О велике від /3(х) при х, що прямує до а).
б) А = 1, то а(х) і 0(х) називаються еквівалентними
нескінченно малими при х —> а. Еквівалентність нескінченно
малих а(х) і j8(x) позначають символом ~ і пишуть а(х) ~ 0(х) при
х —> а (читається а(х) еквівалентна до /?(*) при х —> а);
в) А = 0, то а(х) називається нескінченно малою вищого
порядку малості, ніж: J3(x) (а величина ^(х) - нескінченно малою
нижчого порядкуу ніж сс(х)); записується a(x) = o(j3(x)) при х—>а
(читається: а(х) є о мале від J3(x) при х, що прямує до а).
Означення 4. Якщо а(х) = 0((j3(x))k), k>0, при х —> а, то
сс(х) називається нескінченно малою к -го порядку малості відносно
нескінченної малої J3(x).
Обчислення границь функцій здебільшого спрощується, якщо
використати еквівалентність функцій, а також таку теорему:

# */. Нескінченно малі і нескінченно великі величини
49
Теорема 1.Якщо f(x)~fx(x) і g(x)-gl(x) при jc—>я, і
jm//o існує hm , /wo hmjL-L-i- = limjii .
Зауважимо, зокрема, що при х —> 0 нескінченно малі х, sin jc,
Igx, arcsin*, arctg*, ln(l + jc), ex -1 попарно еквівалентні.
Розв'язування типових прикладів
Приклад 1. Встановити, чи правильним є співвідношення
4-jc
= 0(2 - 4х) при jc —> 4.
4 + jc
4 — х І г~Л 4 —jc
Оскільки lim = 0 і lim 12 -Vjc)=0, то функції і
*->4 4 + JC *->4v 4 + JC
є нескінченно малими при х —> 4. Обчислимо границю їх
підношення при х —> 4.
Hm "-' ,. = щ<**ЯЮ-р. lim 0±Л) =і.
*->4(4 + jc)(2-Vjc) *->4 (4 + jc)(2-Vjc) *->4 (4 + jc) 2
Отже, за означенням 3 функції і (2-VJc) є одного
4 + jc х '
порядку малості при х —> 4, тобто це твердження правильне.
Приклад 2. Визначити порядок відносно х функції
/ ( jc) = V4 - jc4 + jc2 - 2, нескінченно малої при jc —> 0.
Згідно з означенням 4, потрібно знайти таке число k, що
/(jc) = OIjc* ) при х —> 0, тобто, lim—— = A, де A - скінченне
число, відмінне від нуля. Обчислимо границю
hm т = hm - . /x '- =

50
Розділі. Вступ до математичного аналізу
4-jc4-(jc2-2)2 Л. -2х4+4х2
= lim—, , г= Ііт-
*-»0
/(V4^7-U2-2)) **°**[^4^-х>+2
= lim
-2jc2 + 4
= lim x
*-»0
2-А:
При 2 - £ > 0, і відповідно £<2, маємо А = limjc2"* = 0, і
*-»о
тому f(x) = o(xk) при х—»0.Якщо 2-к <0, тобто £>2,то
Л = оо. Отже, величина х і задана функція не є величинами
одного порядку малості. При к = 2 маємо А = lim х° = 1. Отже,
*->о
л/4-jc4 + jc2 - 2 = 0(jc2) при jc -> 0, або л/4 - х4 + х2 - 2 ~ х2 при
*->0.
Приклад 3. Визначити порядок відносно х функції
/(jc) = sin (y/l + x -1J, нескінченно малої при х —> 0.
sin(Vl + JC — lj
Знайдемо значення к, при якому lim —-—T = А Ф 0.
*-»0
Отримаємо
sin(vl + jc-l)
= lim ^ L = її
A = lim-
*->0
= lim
sin(vm-i) уп^__і
Vf+jc-1 хк
sin(vm-i) vr+^-i
= hm ) • lim - .
*->o Vi + jc-i x->o xk
Обчислимо границю в першому співмножнику. Для цього
використаємо заміну змінної
sin
(>/і+*-і)
lim .
yJl + X~l=y
x —> 0 => у -» 01
г Sln;y і
= hm = 1.
у->0 у

§ 4. Нескінченно малі і нескінченно великі величини
51
Обчислимо границю в другому співмножнику
hm = km- ,—г -
*-*о xk *-*о xk\^l + x + l)
= lim
*-*() Yk
(л/ї+JC+l)
= ium^.
2*->o
J-*
Очевидно, що limjc має скінченне, відмінне від нуля
значення лише при к = 1, тоді хх~к = 1, Л = —. Отже,
sin(л/ITjc — і) = O(jc) при Jt—>0.
Приклад 4. Обчислити границю lim — —
*->0 Х + х + X
Оскільки limSm Х = 1, то sin3*~3* при х—>0. Замінив-
^° 3jc
ній sin З* еквівалентним значенням Зх, отримаємо
sin З* ,. Зх ,. З
lim — г = lim — = lim — = 3.
*->o x + xz + x x->o X + X + x *->0jt4jc + 1
Задачі для самостійного розв'язування
У задачах 1.236-1.244 встановити, чи правильними є
нказані твердження:
1.236. 2х-х2 =0(х) при *->0.
( ъ\
1.237. JcsinvJc=0
х
\ J
при х -» 0.
1.238. -^tl = of- I при *->«>.
х +1

52
Розділі. Вступ до математичного аналізу
1.239. sec* - tg х ~ п - 2* при х —> —.
1.240. l-x-1-lfx при *-»1.
1.241. * ~l-cos— при *—»0.
2
1.242. ^+I)=0(^) при *->0.
1 + V* V '
1.243. jc3-3jc + 2 = o(jc-1) при jc—»1.
1.244. l-cos3* = o(sin2*) при x—>0.
У задачах 1.245-1.257 визначити порядок відносно х
функцій, нескінченно малих при х —> 0:
1.245. /(*) = 2*-3*3+*5.
1.246. /(*) = ^1 + V*-1.
1.247. /(*) = yll + x2-Jl-x2.
1.248. /(де) = 3/1-2* - 3/1-3*.
1.249. /(*) = 3sin2*2-5*5.
1.250. /(я) = 1-х4-cos*2.
1.251. /(*) = 2sin*-tg2*.
1.252. /(*) = еЛ-1.
1.253. /(*) = є -cosх.
1.254. /(*) = sin(V*2+9 -з\
1.255. / (*) = arcsin(Vl + *5 - Л
1.256. /(*) = Vl + *2tg—.
1.257. /(*) = ln(l + V*sin*).

§ 4. Нескінченно малі і нескінченно великі величини
53
1.258. lim
*->2
У задачах 1.258-1.263 знайти вказані границі:
2
1.259. lim
1.260. lim
arctg(2-jt)
х2-4
ln(cosjc)
1.262. lim
*-»o tgjr
sin2 3jc
*->oln(l-2;c)
sin3jc
*->o
1.261. lim
1-Vl + JC3
sin2jc
*->oln(l + 3jt)
1.263. lim
yjl + x2
+ jc3-1
*->o ln(cos4jc)
Відповіді
1.236. Правильне.
1.238. Правильне.
1.240. Неправильне.
1.242. Правильне.
1.244. Правильне.
1.246.1/3.
1.248.1.
1.250.4.
1.252.1.
2
1.254.2.
1.256. 1.
1.258.0.
1.260.-І.
2
1.262.0.
1.237. Правильне.
1.239. Неправильне.
1.241. Неправильне.
1.243. Правильне.
1.245.1.
1.247. 2.
1.249.4.
1.251. 3.
1.253. 2.
1.255. 5.
1.257.1.
1.259. -2.
1.261.-.
3
1.263. —L.
16

54
Розділі. Вступ до математичного аналізу
§ 5. НЕПЕРЕРВНІСТЬ
І ТОЧКИ РОЗРИВУ ФУНКЦІЇ
Означення 1. Функцію f(x), визначену в околі точки х0,
називають неперервною в точці х0, якщо lim f(x) = f(x0).
Різницю x - x0 називають приростом аргументу в точці jc0 і
позначають через Ах, а різницю f(x) -f(x0) називають приростом
функції в точці х0, що відповідає цьому приросту аргументу Ах, і
позначають через Ау, тобто Ах = х - х0, Ay = f(x0 + Ах) - /(jcq).
Означення 2
ij Функцію f(x), визначену в околі точки х$, називають
неперервною в точці х$, якщо lim Ay = 0.
Дх->0
2J Функцію f(x), визначену на півінтервалі (a;jc0J,
називають неперервною зліва в точці х0, якщо lim f(x) = /(jc0) .
дг->Л()-0
З) Функцію f(x), визначену на півінтервалі [xQ\b),
називають неперервною справа в точці Xq, якщо lim /(*) = /(л^).
X-+XQ+0
Справедливе твердження: для того, щоб функція f(x),
визначена в околі точки х0, була неперервною в цій точці,
необхідно і достатньо, щоб lim f(x) = lim f(x) = f(x0).
x-*xq-0 x-*xq+0
Означення 3. Нехай функція f(x), визначена в околі точки
Xq , крім, можливо, самої точки х$. Точку х$ називають точкою
розриву функції f(x) у таких випадках:
1) функція f(x) не визначена в цій точці;
2) функція f(x) визначена в точці х0, але
а) не існує lim f(x) або lim /(л:) = ±оо;
X-+XQ X-+XQ
б) існує lim f(x), але lim f(x) Ф f(x0).
X—>Xq X-+XQ

і' 5. Неперервність і точки розриву функції
55
5.1. Класифікація точок розриву
а) Якщо існує lim f(x), але функція f(x) не визначена в точці
*->*ь
х{) (рис. 1.1), або в точці х0 функція визначена, однак
\\т /(х)Ф /(xq) (рис. 1.2), то х0 називають точкою усувного
/юзриву. Якщо функцію f(x) довизначити в точці х0, або змінити її
шачення в цій точці так, щоб f(x0) = lim f(x), то ця функція буде
неперервною в точці х0.
Рис. 1.1
і
Л*о)
0
^
т
Xq
У=Лх)
Рис. 1.2

56
Розділі. Вступ до математичного аналізу
б) Якщо в точці розриву х0 існують скінченні границі
однак,
lim f(x) = f(x0+0\
X-+XQ+0
lim f(x) = f(x0-0),
X->Xq~0
f(xQ+0)*f(xQ-0), то Xq називають точкою розриву першого
роду, а різницю A/(jc0) = f(x0 + 0) - f(x0 - 0) - стрибком функції
f(x) в точці х0 (рис. 1.3).
Рис. 1.3
в) Якщо в точці розриву jcq , принаймні одна з границь
lim f(x) або lim f(x) не існує чи дорівнює нескінченності,
X-+XQ+0 x-*xq-0
то jcq називають точкою розриву другого роду (рис. 1.4, 1.5).
Якщо х0 - точка розриву функції, то цю функцію
називають рОЗривНОЮ В ТОЧЦІ Xq .
Використовують терміни: неперервна функція, розривна
функція. Неперервною функцією називається функція,
неперервна в кожній точці області визначення (якщо функція
визначена в кінцевій точці проміжку, то мається на увазі
неперервність відповідно зліва або справа). Розривною
функцією називається функція, що має принаймні одну точку
розриву.

;У 5. Неперервність і точки розриву функції
51
У
Рис. 1.4
Рис. 1.5
Справедливі такі твердження:
1) всі основні елементарні функції (показникова,
логарифмічна, степенева, тригонометричні, обернені тригонометричні) є
неперервними в областях їх визначення;

58
Розділі. Вступ до математичного аналізу
2) якщо функції f(x) і g(x) неперервні в точці jcq , то в
деякому околі цієї точки визначеними є функції cf(x) (с - стала),
f(x)±g(x), f(x)-g(x), які також неперервні в точці х$. Якщо,
крім того, g(x0)*0, то в деякому околі точки Xq визначена
функція , і вона неперервна в точці х$ .
3) якщо функція у = g(x) неперервна в точці х0, а функція
f(y) неперервна в точці у0 = g(x0), то в деякому околі точки х0
визначена складна функція (композиція) f(g(x)), і вона
неперервна В ТОЧЦІ Xq .
З цих тверджень випливає, що будь-яка елементарна
функція неперервна в області її визначення.
Розв'язування типових прикладів
Приклад 1. Користуючись означенням неперервності
функції, довести, що функція /(jc) = sin3* неперервна в кожній точці
області її визначення.
Область визначення цієї функції D(f) = R. Доведемо
неперервність sin Зх в довільній точці Xq g R на основі означення 2.
Знайдемо приріст Ау і покажемо, що lim Ay = 0.
Ajc->0
Ay = f(x0 + Ax) - f(x0) = sin3(jc0 + Ax) - sin3*0 =
„ . ЗА* 3(2jc0+Ax)
= 2 sin cos-^-^ ,
2 2
r A г о • ЗДх 3(2*0+ Ax)
km Ay= lim 2 sin cos =
Ax->0 Ax-*0 2 2
■ (зд^|
0 r Sm[ 2 J A 3(2*0+ Ax)
= 2 lim --Ax-cos = 0,
Ax->0 Ac 2

§ 5. Неперервність і точки розриву функції
59
• (ЗАх)
г r Sml 2 J з г а п л • 3(2*0+Дх)
Гю hm— - = -£-» lim Ддс = 0, а функція cos
Дх->0 Ах 2 Ах->0 2
обмежена.
Приклад 2. Користуючись означенням неперервності
функції, довести, що функціяf(x) = \ogax (а>0,аФІ) неперервна в
кожній точці області її визначення.
Ця функція визначена в інтервалі (0;+°о). Покажемо, що
lim Ду = 0 для довільного х0 є (0;+°о). Знайдемо приріст Ду :
Л*->0
Ay = f(x0+Ax)-f(x0) = logfl (х0 + Ах) - logfl х0 = logfl 1+
Дх
х0
\
_ r logfl(l + *) ,
Враховуючи, що lim —— = loga є, отримуємо
х-+0 X
lim Ay = lim log^
Ajc->0 Ajc->0 "
1+^
l0Sa
= lim
1+
V XQJ
Ax
{ x0) a*-*o *x x0
Ax
l°ea
= lim
1+—
V XQJ
Ac->0 A* Ax->0 JC0
Ax
lim — = loga e • 0 = 0.
Отже, за означенням 2 функція loga х неперервна в кожній
точці інтервалу (0;+°о).
Приклад 3. Дослідити на неперервність функцію
/(*) = -
tg х-
п
, знайти точки розриву, встановити їх рід.
jc--

60
Розділі. Вступ до математичного аналізу
Оскільки ця функція є елементарною функцією, то вона
неперервна в кожній точці своєї області визначення
D(f) = R\\—;-— + яп, n = 0,±l,±2,...l. Дослідимо /(*) на
неперервність у точках х = — і х = + япу п = 0,±1,±2,...
4 4
п
а) Ця функція визначена в околі точки х = — (за винятком
4
п
самої точки), тому х = — є точкою розриву функції. Знаходимо
4
односторонні границі
tg
lim
п
х
4
4 * 4
п
х — -а
4
яг->+0
*_>£_о ж_^ *-»-о or
4 * 4
Оскільки односторонні границі існують і дорівнють одна одній,
то х = точка усувного розриву. Якщо прийняти / — = 1, то
функція ДХ) =
/
tg
п
х
1Т ' ^ А Я
х-— 4 буде неперервною В ТОЧЦІ X = —.
І,
п
4
я-
б) Точки х = + яуі також є точками розриву функції.
7t
Нехай п = 0, тобто х = —.
4

§ 5. Неперервність і точки розриву функції
61
tg \х
lim
л
4 х 4
п
х + — = а
4
дг->+0
tglar-|
= lim —- - = -н>о,
ar->-K) #
^зг
2
tg
lim
х
V
п
х + — = а
4
дг->-0
= lim -
ог->-0
tg дг-
Л"
^зг-
Л"
4 4
Отже, jc = — є точкою розриву другого роду. Аналогіч-
4
71
ними міркуваннями можна показати, що всі точки х = — + пп,
4
п - ±1,±2,... є точками розриву другого роду.
Приклад 4. Дослідити на неперервність функцію
f{x) = j—, знайти точки розриву і встановити їх рід.
\ + ехЛ
Область визначення цієї функції £>(/*) = /?\{l}. Оскільки
f(x)e елементарною функцією, то вона неперервна при всіх
xeR, крім jc = 1, яка є точкою розриву функції. Знаходимо
односторонні границі в точці х = 1:
lim
*->1+0
1
lim
*->і-о
\ + ехЛ
1
J_
\ + ехЛ
х-1 = а ,|
дг->+0
= lim -
1
Г = 0>
х-\ = а ,
дг-*-0
= lim
ог->-0
1 + еа
1
1 + еа
=1.
Отже, односторонні границі існують, але не дорівнюють
одна одній, тому д: = 1 є точкою розриву першого роду;
А/(1) = 0 -1 = -1 - стрибок функції в точці х = 1.

62
Розділі. Вступ до математичного аналізу
Приклад 5. Дослідити на неперервність функцію, знайти
точки розриву і встановити їх рід.
/(*) =
cosjc, jc<0,
jc + 1? 0<jc<2,
1
, х>2
jc-2
Ця функція не є елементарною. Кожна з елементарних функцій
cosjc, jc + 1, неперервна у внутрішніх точках області свого
jc-2
задания, тобто на інтервалах відповідно (-°°;0), (0;2), (2;-н»). Тому
f(x) може мати розрив лише у тих точках, де змінюється її
аналітичний вираз, тобто при jc = 0 і jc = 2. Дослідимо f(x) на
неперервність у цих точках. Для цього обчислимо односторонні
границі і значення функції f(x) у точках х = 0 і х = 2.
lim f(x) = lim cos x = 1, lim f(x) = lim (jc +1) = 1,
*->-o jc->-0 *->+o x-*+0
/(0) = cosO = l.
Оскільки lim f(x)= lim /(х) = /(0) = 1, то f(x) неперервна
jc->-0 jc->40
В ТОЧЦІ X = 0.
lim f(x)= lim (jc + 1) = 3, lim f(x)= lim = +«>.
jc->2-0 jc->2-0 д:->2+0 jc->2+0jc~2
Отже, в точці x = 2 функція f(x) має розрив другого роду.
Задачі для самостійного розв'язування
У задачах 1.264-1.269, користуючись означенням
неперервності функції, довести, що функція неперервна в кожній точці
області її визначення:
1.264. f(x) = хъ + 2х. 1.265. /(*) = ах. 1.266. f(x) = —.
х

<S 5. Неперервність і точки розриву функції
63
1.270./(*) =
|jc2 + 2, jc<0,
br-1, х>0.
1.267. у = cos2jc . 1.268. у = sin3 х.
1.269. у = cos(ojc + fe), а,Ьє R,a*0.
У задачах 1.270-1.277 дослідити на неперервність функцію,
'шайти точки розриву, встановити їх рід:
1-jc3, jc<0,
(jc-1)3, 0<jc<2,
4-jc, jc>2.
2*, jc<0,
1, 0<jc<1,
jc-1, x>l.
jc2 -1, jc<0,
flg(2-jc), jc<2,
1.274. /« = очз .о L275- /(*H
l(*-2) , x>2
1.272. f(x) = \
, л:<0,
x
5x-x , x>0.
1.271. f(x) = \
1.273. /(*) =
1.276. /(*) =
cos , JC<1,
2 ' ' 1.277. /(jc) =
[|jc-1|, |jc|>1.
. X
sin—,
2
3
Я
' 1
*2
і
2
ЛГ + 1,
-1
»
+ JC
»
0 < x < я,
X>7T.
jc*0,
jc = 0.
У задачах 1.278-1.284 знайти точки розриву функцій,
встановити їх рід, довизначити функції до неперервності в точках
усувного розриву:
cos
пх
1.278. у = -
х + х-6
1.279. у =іт% 1.280.у= }22
х1 -1
* ^о-і sin3jc
1.281. у = .
sin2jc
1.282. у = 31'х . 1.283. у=-
jc -jc
arctgjc

64
Розділі. Вступ до математичного аналізу
ВІДПОВІДІ
1.270. л: = 0 - точка розриву першого роду.
1.271. х = 0 і х = 2 - точки розриву першого роду.
1.272. jc = 0 - точка розриву другого роду.
1.273. jc = 1 - точка розриву першого роду.
1.274. х = 2 - точка розриву другого роду.
1.275. х = 0 і х = л - точки розриву першого роду.
1.276. х--\ - точка розриву першого роду.
1.277. jc = 0 - точка розриву першого роду.
1.278. jc = -3 і jc = 2 - точки розриву другого роду.
1.279. х = 1 - точка усувного розриву.
1.280. jc = 1 - точка усувного розриву,
х = 0 - точка розриву другого роду.
1.281. х - як, keZ - точки усувного розриву,
7Г(2к-1) ,_
jc = , к є Z - точки розриву другого роду.
1.282. jc = ±1 - точки розриву другого роду.
1.283. х = 0 - точка розриву першого роду.

Розділ II
ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ
ФУНКЦІЙ ОДНІЄЇ ЗМІННОЇ

66 Роз д і л II. Диференціальне числения функцій однієї змінної
§ 1. ПОХІДНА ФУНКЦІЇ
1.1. Означення похідної
Нехай функція у = /(х) визначена в деякому інтервалі.
Надамо аргументові х приросту Ах довільного знака в межах
інтервалу, тоді відповідний приріст функції дорівнює
Ду = /(* + Дх)-/(х).
Означення 1. Похідною функції у = f(x) за аргументом х
називається границя (якщо вона існує) відношення приросту функції
Ау до приросту аргументу Ах, коли останній прямує до нуля.
Похідна функції у = /(х) в точці х позначається одним із
символів: у'х, Щ-, -j-, у'(х), /'(*). Отже,
ах ах
у (х) = lim — = hm — у J ч у. (2.1)
Ах->0 Дх Ах->0 Дх
Знаходження похідної називають диференціюванням.
Функція, що має похідну, називається диференційовною.
1.2. Таблиця похідних
Якщо х - незалежна змінна, то мають місце формули:
1) (хаУ = ах?-1; 2) (ах)' = ах1па;
3)(ехГ = ех; 4)(loge*)' = -^-;
хта
5) (In x)f =—; 6) (sin x)f = cos х;
х
7) (cosx)' = -sinx; 8) (tg х)' =
2 :
cos X
9) (ctgx)' = —\-; 10) (arcsin x)f = *
sin X
^7*

♦ / Похідна функції
61
11) (arccos х)' = —==; 12) (arctg х)' =
Vl-JC2' 1 + х
2 '
І \) (arctg jc)' = l—; 14) (sh jc)' = ch x;
1 + лГ
И) (ch jc)' = sh jc; 16) (th *)' = —L_; 17) (cth *)' = - !
ch2 л: sh2 x
1.3. Основні правила диференціювання
Нехай w(jc), v(jc) - диференційовні функції, а С = соияґ. Тоді:
1. С' = 0; 2. (Cw)' = CV;
3. (і/ ± v)' = и' ± v'; 4. (от)' = w'v + v'i/;
. (иЛ u'v-v'u
6. Правило диференціювання складної функції: якщо
функції у-fiu) і и = <р(х) диференційовні, то і складна функція
у -f[(p(x)] диференційовна, причому у'х = /J -и^..
Геометричний зміст похідної полягає в тому, що вона
дорівнює кутовому коефіцієнту дотичної до графіка функції
*'-/(*) в точці з координатами (x0,f(x0)), тобто /'(jc0) = tgar,
де а - кут, між дотичною до точки графіка функції з
координатами (x0;f(x0)) та додатним напрямком осі Ох.
РІВНЯННЯ ДОТИЧНОЇ ДО КрИВОЇ У = /(х) В Т. M0(xQ;f(x0))
має вигляд
>>-/(*о) = /'(*оХ*-*о). (2.2)
Рівняння нормалі до кривої y = f(x) в т. М0 (х0; f(x0))
має вигляд
У-/(х0) = -—^-(х-х0). (2.3)

68 Роз д і л II. Диференціальне числення функцій однієї змінної
Кутом між кривими y = f(x) і у = fii*) в точці їх
перетину М0 (х0, у0) називається кут між дотичними до цих кривих у
точці М0. Цей кут (позначимо його в) можна знайти з формули
в=яы-яы (24)
1 + /і'(*оХ/2'(*о)
Значення похідної f'(x0) характеризує швидкість зміни
функції у = f(x) в точці х0. Зокрема, якщо функція S = S(t) опи~
сує прямолінійний рух точки (S - шлях, / - час), то швидкість руху
V точки в момент часу t0 дорівнює S'(t0). Отже, V(t) = S'(t).
1.4. Логарифмічне диференціювання
Логарифмічною похідною функції y = f(x) називається
похідна від натурального логарифма цієї функції, тобто
* '- у /«
звідки
У = у.(\пу)'х. (2.5)
Отже, для знаходження похідної цієї функції спочатку
знаходимо похідну від її натурального логарифма. Цей метод
знаходження похідної називається логарифмічним
диференціюванням. Застосування попереднього логарифмування функції
інколи значно спрощує знаходження її похідної.
Приклад. Знайти похідну показниково-степеневої функції
У = (и(х)У(х).
Знайдемо логарифмічну похідну функції за формулою
^- = (]п(и(х)У(х)) =(v(jc).lnw(jc))' =vf(Jc)lnw(jc) + v(jc).-^^,
у \ ч 7 / v и(х)

§ І. Похідна функції
69
і ому У = | v'lnw + v— \у, отже
(u(x)vM) =uvv']nu + vuv-lu'. (2.6)
1.5. Похідна оберненої функції
Якщо похідна функції y = f(x) не дорівнює нулю, тобто
/v*0, то обернена функція x = f~x{y) є диференційовною,
причому
*>у=\. (2.7)
Ух
1.6. Похідна неявної функції
Якщо диференційовна функція y = f(x) задана рівнянням
/''(*> у) = 0, то її похідну ух можна знайти так: продиференціювавпш
по х обидві частини рівняння F(x9y) = 09 отримаємо рівняння
першого степеня відносно ух (треба пам'ятати, що х - незалежна
імінна, а у є функцією від х). З цього рівняння знаходимо ух.
1.7. Похідна функції, заданої параметрично
Якщо диференційовна функція y = f(x) задана
параметрично, тобто \ ' де <p{t\y/{t) - диференційовні функції, то
для її похідної справедлива формула
%Ж W0). (2.8)
ах q>t

70 Розділ II. Диференціальне числення функцій однієї змінної
1.8. Похідні вищих порядків
Нехай функція y = f(x) в інтервалі (а; Ь) має похідну
У = /'(*)• Припустимо, що похідну /'(*) можна
диференціювати в точці х є (а; Ь).
Означення 2. Похідною другого порядку або другою
похідною функції у = f(x) називається похідна від Ті похідної
Друга похідна позначається одним із символів:
/./'(*)> 4т'-тт- 0тже'
dx1 dx1
У КУ),У dx'y dxidx
Зауважимо, що друга похідна S" від шляху S = S(t) є
прискоренням.
Означення 3. Похідною п -го порядку, або п -ю похідною
функції у = f(x), називають похідну від її похідної (п -1) -го порядку.
Для позначення п-ї похідної функції y = f(x)
ВИКОЛИ1П f
ристовують такі символи: у^п\ f^n\x), ——, ——. Отже,
14Ж \ЛЛ/
У») =(/"-1)) або
d"f = d(d"-lf)dy("-l)
dx" dx[dx"~l) dx
Легко перевірити, що справедливі такі формули:
(ха)(п)=а(а-і)(а-2)...(а-п + і)ха-п;
(ах)(П)=ах]п"а, (а>0>
(sinx) =sin х + п~ ; (cosx) =cos х + п— .

I /, Похідна функції
71
При обчисленні похідних л-го порядку використовують
і и к і правила:
І, (си)(п) = си("\ де с = const;
І (//±v)(wWw)±v(w);
чМ "
», (w. v)(w) = £ Cnku(kV"~k) - (формула Лейбніца),
Ыо
дсм(о)=м> v(0)=v>c/=^! ;(0!=1)>
Якщо функція y-f{x) задана параметрично, тобто
\ , то похідні ух, у ж, у ххх,— послідовно можна знайти за
\у = ф(і)
(формулами
, \Ух) t лт _/\." \ _ \Ухх) t
кжрема, /„^У"**"*» 'У*.
(x't)
Розв'язування типових прикладів
Приклад 1. Враховуючи означення похідної, знайти
похідні таких функцій:
а) у = 2л:3 - Зх2 +5; б) у = х + ctg х.
а)Знайдемо приріст Ду функції у = 2х -Зх +5, що
відповідає приростові аргументу Ах,
A^ = /(^ + Ax)-/(jc) = 2(jc + Ax)3-3(jc + Ax)2+5-2jc3+3jc2-5 =
= 6х2Дх + бхДх2 + 2Ах3 - бхАх - ЗДх2.
Отже, згідно з означенням похідної
у' = lim — = lim (бх2 + бхДх + 2Дх2 - 6х - ЗДх)= 6х2 - 6л:.
Дх->0 Ах Дх->(Г 7

72 Роз д і л II. Диференціальне числення функцій однієї змінної
б) Як і в попередньому прикладі, знаходимо
ДУ = /(* + А*) ~ /(*) = х + Ах + ctg(jc + Дх) - х - ctg х =
а . / а ч a sin(-Ax)
= Дх + ctg(jc + Ах) - ctg jc = Ах + .
sin х • sin(jc + Ах)
Тому,
/=lim^=lim
Дх->0 Дх Лх->0І
1--
1 sinAx
л
sin х • sin(x + Дх) Дх
= 1-
sin2 X
Приклад 2. Використовуючи основні правила
диференціювання і табличні похідні, знайти /'(*) і /'(*о):
а)/(х) = 2х4-Зх2+8х-2, х0=1;
6)/(х) = (л/^ + л/з)(2^і), х0=4;
в) /(*) = х2 arccosx, х0 = 0;
х2
г) /(*) = -—, *о=е.
lnx
а) Оскільки похідна суми дорівнює сумі похідних, то
/'(*) = (2х4 - Зх2 + 8х - 2)' = (2х4 )' - (Зх2)' + (8*)' - (2)'.
Враховуючи, що сталий множник можна виносити за знак
похідної, і похідна від сталої дорівнює нулю, знаходимо
/'(х) = 2(х4 )' - 3(х2 )' + 8(х)', звідки, застосовуючи формулу
(ха )' = аха_1, отримаємо /'(*) = 8х3 - 6х + 8.
Тому /'(1) = 8.13 -6-1 + 8 = 10.
б) Функція f(x) = є добутком двох
співмножників и = л/х + л/3 і v = 2х -1. Тому
/'(*) = u'v + v'u = W1 + л/3 ) (lx -1) + (л/х + л/3 )(2* -1)' =
= 1*^(2*-і)+(^х+^зУ
2 2vx

>v /, Похідна функції
73
Отже, Л4) = ^^ + (л/4+л/з)241п2 = —+ 1б(2 + л/з)іп2.
в) За правилом диференціювання добутку знаходимо
х1
f\x) = (jc2)'arccosjc + jc2(arccosjc)' = 2jcarccos;c -
VbV
Тому/'(х0) = /'(0) = 0.
г) Для знаходження похідної цієї функції використаємо
привило диференціювання частки
( х1 \ = (jc2) lnjc-x2(lnx)' = s(21ns-l)
У&х) ~ (in*)2 ~ In2*
/'(*) =
,,, е(21пе-і)
()гже, / (є) = -і— '- = є.
In є
Приклад 3. Знайти похідні функцій: а) у = vjc; б) у = —.
*"
і
а) Оскільки у = у/х = х", то
У = — JCW = — X п =■
() гже,
(«£)'= _* (2.9)
б) Перепишемо функцію у вигляді у = х~м. Тоді У = Іх~м) =
^х"""1 = -//*-(//+1) =~^г, тобто
1 ' ** (2.10)
x"J х"+1
Безпосереднє використання формул (2.9) і (2.10) при
диференціюванні функцій полегшує спрощення отриманих виразів.

74 Розд і л II. Диференціальне числення функцій однієї змінної
Приклад 4. Знайти похідні таких функцій:
а) у = ІЗх4 + — -tfx + 2 ; б) .y = sin2jc;
г) j; = lntg-;
в) j; = cos -;
2х2
д) .y = arcsin г;
1 + х
ч sinjc - 1 + sinjc ч _v . _v _r
є) 7 = г— + lg ; ж) у = е -sine -cose .
ё) у = ех arctg є* - In д/1 + ?2*;
cos2jc
COSJC
а) Нехай u(x) = 3x4 + — - v* + 2, тоді <y = w5 і за прави-
x
лом диференціювання складної функції знаходимо
у'(х) = (и5) и-и'х=5и4(зх4 +\-fc + 2) =
= 5[3jc4+-4~^ +
2)4\3И+І?]-№І+еі
„4.2 5
= 5 \3хч+-=г- iJx + 2
12л:3-4- 1
х4 5547
б) Позначимо и(х) = sin jc, тоді у-и і, використуючи
правило диференціювання складної функції, знаходимо
у'х =\и2)и Vx=2w(sinjc)' = 2sinjccosjc = sin2jc.
х 3
в) Аналогічно и{х) = cos—, у = и . Тоді
^і =г)" 'wx =3w2 cos— = 3cos2 — -sin—
3 2 X . JC
=—cos —sin—.
5 5 5

§ 1. Похідна функції
75
f
1 1
1
1 1
tg— cos — v J
B2 2
1
. x їх 2 x x sinx
tg— cos — 2sm —-cos—
2 2 2 2
• = cosec X.
д) у' = (arcsim/) • u'x = .
Vl-M2
l + x4
r-2-
2x(l + x4)-x2-4x3 Ax
1-
2xl
l + x4
d + *4)2
1 + д;4
e) y'= Yzxc\%ex) -[Wl+e2* j =[ex) arctge^+e^arctge*) -
I
. * -fVl + g2*! = e*arcfge*+ex Ц-(ехї-
л/Г+Т*7 V J i + e2*v '
•(l + e2*) = e* arctg e* +
,2x
l + e
2x
Vl + e2* 2л/і + е2*
:— e2* • (2дг) = e* arctge* + ; 1 тЛ = ex arctge*
2(l + e2jc) V ' l + e2* 2І1+12*)
є)У =
f sinjc ^ (. І + зіплЛ _ (sinjc) cos2 x - sin jc(cos2 jc)
Vcos2JcJ v cos* ) cos4jc
COSJC
\ 4 2
1 + sin JC і cos x + 2sm JCCOS JC
cos4jc
(l + sinjc)lnlO ^ COSJC
cos2jc + sinjc(l + sinjc)_(l + sin2^)tol0 + cos2x
COSJC
(l + sinjc)lnlO
COS JC
cos3jc-lnlO

76 Роз д і л II Диференціальне числення функцій однієї змінної
ж) Запишемо цю функцію у вигляді у = є х —sin2e *. Тоді
/ = (*-*)' --(sin2e-*)' =e~x(-xj --cos2e"*(2e-*)' = -*"* -
—cos2e~* -2e~*(-jc) = -е~х +е~хсо$2е~х =-2e~xsm2e~x.
2 v }
Приклад 5. Написати рівняння дотичної і нормалі до кри-
і 2
вої у = є в точках перетину її з прямою у = 1.
Для знаходження точок перетину прямої у = 1 і кривої
і 2
у = є розв'яжемо систему рівнянь
Отже, ця крива перетинається з прямою у = \ в точках
А(1; 1) і 5(-1; 1). Знайдемо кутові коефіцієнти дотичних до графі-
1 2 1 2
ка кривої в точках А і В. Оскільки у = є (~2х) = -2хе , то
кутовий коефіцієнт дотичної до кривої в точці А дорівнює
У(1) = -2, а в точці В він дорівнює у\-\) = 2. Тому дотичною до
кривої в точці А є пряма у-1 = -2(х-ї) або у = -2х + 3, а в
точці В дотичною є пряма <у-1 = 2(х + 1) або у = 2х + 3.
Нормаллю в точці А є пряма у-1 = — (х-1) або у-— (х + 1)9 а в
точці В - є пряма у = —(* " 0 •
<5
Приклад 6. Під яким кутом перетинаються лінії у = х і
х2
'=-т?
Координати точки перетину даних ліній є розв'язком
.3
системи рівнянь
у = х
1 ■
X

§ 1. Похідна функції
11
Розв'язавши цю систему, бачимо, що криві перетинаються
в точці (1;1). Оскільки похідні функцій f\(x) = x3 і /г(х) = —г-
х2
і 2
відповідно дорівнюють //(jc) = 3jc і f{(x) = -, то /і'(1) = 3 і
X
t f'(D — Ґ(1)
А (1) = —2 і за формулою tgfl= 2 —^^- знаходимо tg# = l.
і+//(і)/2Чі)
Отже, криві перетинаються під кутом в = 45°.
Приклад 7. Тіло рухається прямолінійно, причому
залежність шляху S, пройденого тілом, від часу t (тобто закон руху)
виражається рівнянням S = t2 + It + 3, де S подано в метрах, t - в
секундах. Знайти швидкість руху точки наприкінці п'ятої секунди.
Швидкість V руху точки - це похідна від шляху S за
часом /. Отже,
V(t) = S't=2i + 2.
Тому Г(5) = 2-5 + 2 = 12 м/с.
Приклад 8. Знайти похідні функцій:
.)>-, ^ ;б)д,42+і)^.
а) Безпосереднє диференціювання вказаної функції
спричиняє громіздкі обчислення. Для знаходження похідної функції
>>= , =—, застосуємо логарифмічне диференцію-
Щх + 2)2-у1(х + 3)ъ
наиня. Прологарифмувавши цю функцію, отримаємо
12 3
]ny = -]n(x-l)—ln(jc + 2)—ln(jc + 3),
jL J jL
ІНІДКИ
I t t
(ln^=filn(^-l)l -f|ln(x + 2)l -f|ln(* + 3)l ,

78 Розділ II. Диференціальне числення функцій однієї змінної
або
J__ , = і._1 2#_1 З 1
у 2 х-1 3 х+2 2х+3'
З останньої рівності знаходимо
1 2 3 ^
7 =Я
2(х-ї) 3(д: + 2) 2(x + 3)J
Замінивши j його виразом, отримаємо
УлГ^І f 1 2 3 "\
У ~ $x72jJ(x~^l2(x-V 3(х + 2) 2(* + 3)|
б) Для знаходження похідної функції у = \х2 +1 j
ристаємо формулу (2.6). Прийнявши и(х) = х2 +1, v(jt) = v* , за
цією формулою знайдемо
^(*2 +if] = (*2 + if (V?)' 1п(*2 +1) + V*"(*2 + if'' (х2 +1)' =
вико-
=Ы'
іТї
1п(лг2+1) _ 2хл/хЛ\
2yfx
Xі +1)
Приклад 9. Знайти у'х, якщо х = уг + Ъу.
За формулою (2.7) диференціювання оберненої функції
знаходимо
y>=±-=-±-=—L-\
х'у Зу2+3 3(/+1)
Приклад 10. Знайти похідну у'х, якщо
arctg^-lnJjc2+/ =0.
Функція j/(jc) задана неявно. Диференціюємо по х обидві
частини рівняння. Отримаємо

§ І. Похідна функції
79
1 у'х-уЛ 1 1 /^ - л л
1 + 2L * V*W 2Vx2+/
х2
ІІІІДКИ
ух-у х + уу xJ^x + y
і і і і у
х2+у2 х1 л-у1 х-у
Приклад 11. Скласти рівняння дотичної і нормалі до кривої
л2 4- 2ху2 + ЪуА - 6 = 0 в точці М(1;-1).
Це рівняння визначає функцію ^(jc) неявно. Диференцію-
гмо рівняння ПО X
2
2х + 2у2+4хуу'х+12у3.у'х=0 => у'х=-* + У 3-
2ху + 6у5
іиайдемо значення похідної ух в точці М(1;-1)
v1 1 + Н)2 =1
ІМ(1;-1' 2.Ь(-1) + 6.(-1)3 4*
Отже, дотичною до цієї кривої в точці Af(l;-1) є пряма
у + 1 =—(лг-і) або jc-4j/-5 = 0, нормаллю в цій точці пряма
у +1 = -40 -1) або 4jc + у - 3 = 0.
Приклад 12. Визначити кути, під якими перетинаються
9 9 9
лінії х + у =2 і у =х.
{9 9
*2 ^ ~ , знаходимо точки перети-
у =х
му кривих Mj(l;l) і М2(1;-1). З рівняння першої кривої маємо
X
2х + 2у • У = 0, тобто у' = —, а з рівняння другої кривої знахо-
У
димо 2уу'-\ тобто У = —. Тому кутові коефіцієнти дотичних
2j>

80 Розд і л II. Диференціальне числения функцій однієї змінної
до цих krhbhx в точці Afj(l;l) (тобто значення похідних в точці
AfjCljl)) дорівнюють, відповідно, kx = -1 - для першої кривої і
к2 = для другої кривої. В точці Мі для кута між кривими маємо
2
Аналогічно знаходимо кут #2 = arctg(-3) між кривими в точці
Л/2(1;-1).
{2
JC == COS Ґ
y = sinf
Оскільки jcJ =-2 cos f sin/, y\ = cos/, то за формулою (2.8)
диференціювання параметрично заданої функції матимемо
, yt cos*
1
x't -2cos/sin/ 2sin/
Приклад 14. Знайти похідну х'у, якщо
х = -
t-\
^=V^7T.
Оскільки для вказаної функції
t-\ |'_
* =
:4t^:
t+l
t2 + \
(t2+l)ylt2+l'
v Jt 2V/2+l V/2+l
TO X' = — =
/+1
*; ?(/2+i)

/І І. Похідна функції
81
Приклад 15. Знайти похідну третього порядку функції
у = Щ-х).
Послідовним диференціюванням знаходимо
/ = (іп(1-*))'=--!-;
1-х
/-^-f-r-l'-rV-
І і-х) а-х)2
у
,fff
=(/')'=
(1-хУ
{ 1 V 2
(1-х)2) (1-х)3'
Приклад 16. Знайти у^ \ якщо у = х є .
Функція є добутком функцій и і v, де « = jc3, v = e2x.
Застосовуючи формулу Лейбніца, знайдемо
(А*р - f^A^f"' -С?.И<">(«,*Г +
fc=0
4cj,(x>)n(/-f +с2 (*f yf >+WVVT+
Оскільки И0)=Л H'W, (,3У2,=6,, (*f>=6,
(jc3| =0 при к>4, то
(Л2')<">)=СЇ>ох3(е2')<">> + С11І,Зї2(е2'')(')+С1206х(Є2')<,,+
к и1
За формулою С„ = : знайдемо
к\(п-к)\
і 10! о 10! <і 10!
Cfo= —= 10, С^ —= 45, Cfi, = — = 120,
1!9! 2!8! 3!7!

82 Ро з д і л II. Диференціальне числення функцій однієї змінної
( 2x\k) ~k їх
і, врахувавши, що \е ) =2 є , матимемо
(х3е2х)(Щ = хг-210е2х +30*2 -29е2х + 45-6*-28 -е2х +
+120 • 6 • 27 • е2х = 27е2х (Sx3 + 120jc2 + 540* + 720).
Приклад 17. Знайти похідну другого порядку —^г функ-
!x = arcsinf
і .
~T=t{~2t)
Знайдемо першу похідну — = -—- = ^ "" = Ч.
dx xt 1
(-о;
Vw2
=-V^7.
Приклад 18. Знайти другу похідну у11 неявно заданої
функції у = х + arctg у .
Продиференціювавши по х ліву і праву частини рівності,
матимемо 7=1 + - • у , звідки
1 + /
/ = 1 + Л" (2Л1)
Продиференціюємо останню рівність по jc. Отримаємо
2
у" =—-у', і підставивши замість похідної у' її значення з
У
виразу (2.11), остаточно знайдемо
У уъ
1 + —
2(1 + /)

«У І. Похідна функції
83
Задачі для самостійного розв'язування
Знайти похідні функцій:
11 2 4
2.1. v = 3jc3 -2jc5 + jc 3. 2.2. у = -ху[х jc5Vjc.
' 7 11
* *> х 2 «з/— _ . 5v*+* + l
2.3. .у = 7 + 3v*. 2-4- >> = ——г= •
З х2 V*
2.5.^ = ^+4^-^/3. 2.6.7 6 3
jc2+1
З/Т хЧЇ
2.7. у=~ ' ^arctgx. 2.8. >> = Зл;31пл;-л;3.
JC
/ 0 ч (l + jc2)arctgjc-jc
2.9. y = lx2 -2)sinx + 2xcosx. 2.10. у = ± '- .
^ _ sinx + cosx _„ /~/„і ~\
2.11. у = . 2.12. у = х^х(3\пх-2).
sinx-cosx
- ,. arcsin д: _ . . - х є
2.13. .у = . 2.14. 7 = lntg .
2.15. у = sin4 —. 2.16. у = cos2 —.
'2 З
2 1 + jc
2.17. j^ = tg2jc ч— tg2 2лг. 2.18. y = arctg .
3 1 — jc
2.19. y = exyl-e2x -arcsine*. 2.20. >> = lncos-—.
x
2.21. <y = jcsin lnjc . 2.22. у = д/д: + v* + V*.
+ **> і V* +4+X __. sin2*/ x i\2
2.23. y = ln-1== . 2.24. y = asm x(x tgx-1) .
V*2-4-jc
2.25. у = - tg2 V* + In cos 4x. 2.26. у = lntg— - —
2 2 sin л:

84 Ро з діл II. Диференціальне числення функцій однієї змінної
2.27. ^ = 2*rato3"+(l-arccos3i)2. ТПу дг"міпх ■ Іл'/Г^
VTT
2.29. j =
2.31. у ■■
З, jc^+1 1
—є *(3sin3jc-cos3jc). 2.30. v = —In—=— +—arctgjc.
10 v 7 4 x2-l 2 б
log2(log3(log4(log5;c))).
lnfVl + ^-lVlnfVi
l + e*+l .
2.32. у
2.33. j = -y/x2-4 - 21nf jc + 7*2-4І
2.34. у
2.35. ^ = In
In arcsin jc +—In2 jc + arcsin In jc.
2
1 + Vsin JC - і—.—
+ 2arctgvsinjc.
1-Vsi
sin л:
2.36. у
2.38. у
2.40. у
2.42. j
2.43. ^
2.44. у
2.45. j =
2.46. у-
2.47. у-
1 . W3"
= -rarctg =-
V3 1-х2
2.37. у = In cos arctg
є —є
= *.
1-JC
1 + jc2
sin2 JC cos2 JC
2.39. у = + .
1 + CtgJC 1 + tgJC
1 + jc arctg ;c
= JCI
, 2.41. y = ln|jc + V*2-l)—, X .
(arcsin jc)2 - 2x + 2v 1 - x2
arcsin jc.
= 2 ln(2jc - 3>/l-4jc2) - 6 arcsin 2x.
. JC-2 fZ " J
2arcsin—r^-y2 + 4x-x .
S
: 3jc3 arcsin jc + (jc2 + 2)Vl - x2.
■ \n(ex cos* + e~x sinx).

§ /. Похідна функції
85
х
2.48. у = In tg— ctg x ln(l + sin x) - x.
2.49. y = X + lnVl + x2 + arctgx.
3xJ
2.50. >> = -(3-х)л/і-2х-х2 +2 arcsin^J-.
2 V2
2.51. Скласти рівняння дотичної та нормалі до кривої:
а) у = уіх3 в точці л((і;і);
б) у = х3 - 2jc2 +1 в точці А(2;І);
в) у = \jx-\ 4 в точці ^4(1;0);
г) у = arcsin в точці перетину з віссю Ох;
д) у = arccos3x в точці перетину з віссю Оу\
є) >> = tg 2 х в початку координат.
є) х3 + у1 + 2х - 6 = 0 в точці з ординатою у = 3;
ж) х5 + >>5 - 2ху = 0 в точці А(1; 1);
з) ;;4 = 4х4 + бху в точці А(1; 2);
и)х = 2е', у = е~* при / = 0;
і) х = sin /, у = cos 2/ при / = —;
6
ї) х = 21n ctg/ +1, >> = tg/ + ctg/ при / = —;
4
З/ З/2
й)х = -, у = при/= 2;
1 + Г 1 + Г
ч fx = /(/cos/-2sin/), /г
к) ^ при / = —.
[>> = /(/sin/ + 2cos/), 4
% *~ ^ .. x - 6 ...
2.52. В яких точках кривої у-—^ дотичні до неї пара-
х -2х-8
ІІСЛЬНІ до осі Ох?

86 Роз д і л II. Диференціальне числення функцій однієї змінної
2.53. Знайти точки, в яких дотичні до кривої у = Зх4 + 4х3 -
-12л:2 +20 паралельні до осі абсцис.
* «j п .. 1 з 3 2 4 ...
2.54. В яких точках кривої у = -х—лг+ — u дотична пара-
Э £ D
лельна до прямої у = -2х + 7?
1 2
2.55. Скласти рівняння дотичної до параболи у = —х -Зх-б,
перпендикулярної до прямої х + 5у -10 = 0.
2.56. Під яким кутом крива у = ln(jc +1) перетинає вісь абсцис?
JC — 1
2.57. Під яким кутом крива у = — перетинає вісь абсцис?
Xі +1
2.58. Під яким кутом перетинаються криві:
а) у = (х-2)2 і у = 6х-х2 -4; б) 2у = х2 і 2y = S-x2;
в) у = х-х3 і у = 5х; г) y = ^sinx і <y = V2cosjc?
2.59. Залежність пройденого шляху від часу при русі тіла по
прямій має вигляд S = — t4 - 4t3 + I6t2 (t - в секундах, S - в метрах).
4
Знайти швидкість тіла: а) в кінці першої секунди; б) в кінці
четвертої секунди.
2.60. Залежність шляху від часу при прямолінійному русі точки
задана формулою S = — t5 +— sin— (t -в секундах; S - в мет-
5 я- 8
pax). Визначити швидкість руху в кінці другої секунди.
2.61. В який момент часу швидкість тіла, що рухається
прямолінійно за законом S = t3 -Ш2 +64f (S - в метрах, t - в
секундах) дорівнює нулю?
2.62. Тіло масою 3 кг рухається прямолінійно за законом
S = l + t + t (S - в сантиметрах, t - в секундах). Знайти
кінетичну енергію тіла через 5 с після початку руху (вказівка:
1 2
Wk = — mV , де V - швидкість тіла).

§ L Похідна функції
87
2.63. Кут а повороту шківа залежно від часу t виражається
формулою a = t2 +3t-5 (t - в секундах, а - в радіанах). Знайти
кутову швидкість шківа при t = 5 с.
2.64. По параболі у = х(8 - х) рухається точка так, що її абсциса
змінюється залежно від часу t за законом х = ґл/7 (/ - в секундах,
х - в метрах). Яка швидкість зміни ординати в точці М(1;7)?
2.65. Залежність шляху від часу задана рівнянням S = t ln(t +1)
(/ - в секундах, S - в метрах). Знайти швидкість руху в кінці
другої секунди.
2.66. Колесо обертається так, що кут повороту пропорційний
квадратові часу.
Перший оберт був зроблений колесом за 8 с Знайти кутову
швидкість со через 32 с після початку руху.
2.67. Кут в, на який повертається колесо через t с, дорівнює
0-at -bt + c, де а,Ь,с - додатні сталі. Знайти кутову
швидкість со руху колеса. В який момент часу кутова швидкість
дорівнюватиме нулю?
2.68. Кількість електрики, що протікає через провідник,
починаючи з моменту часу t = 0, задається формулою Q = It1 + 3t +1
(кулонів). Знайти силу струму в кінці п'ятої секунди.
2.69. Точка рухається по архімедовій спіралі р = а<р(а = 10 см) так,
що кутова швидкість обертання її полярного радіуса стала і
дорівнює 6° за секунду. Визначити швидкість видовження
полярного радіуса р в момент, коли р = 25 см.
2.70. Куля, випущена з швидкістю 250 м/с під кутом 30° до
обрію, пройшла за t с у горизонтальному напрямі віддаль
д: = 125л/3ґ, а у вертикальному - y = \25t-499t2 (опором повітря
нехтуємо). Знайти швидкість кулі наприкінці п'ятої секунди.

88 Роз діл II. Диференціальне числення функцій однієї змінної
2.71. Використовуючи логарифмічне диференціювання, знайти
похідні функцій:
а) у = -
(2х + З)3
уі(х-2)1(х + 4)9'
в) y = (x + lf(2x + lf(3x + \);
1/х + ї(х-2)2
д) у=-^^;
є) у = V* sin Wl - є* ;
jce*arctgjc
б)7 = .
0 + 2)(3jc-1)3
г) у = (х - 5)(3х + 2)4зУ5д:-1
#^2(jc + 1)3
є) у = - ■
ж) Д>
_ /l-arcsinx
Vl + arcsinA:'
з) j =
In5*
и) 7 =
2.72. Знайти похідні функцій:
а) у = хх ;
г) y = (arctgx)*;
є) 7 = (arcsinx:)slt
6)y = xsiax;
д) у = Ух)';
(arccosx)3
в) j> = (cos;c)s
є) y = (sinx)cl
ж) у= 1 +
2.73. Знайти похідні 7*> якщо:
б) х = у + 1пу;
^ 1 5
а) х = у+-у ;
1
в) х = 2у + е2у;
є) jc=arcsin2:)'.
2.74. Знайти похідні у'х неявно заданих функцій:
г) x = y--cosy; д) х = 3у + у ;
а) х3 + х2у + у2 = 0; б) е^дг + д'; в) \пу + — = 5; г) >'-2sin>' = x;
д) arctg(*+ >>) = *; є) tgj = A^; є) * - д> = tg j;
ж) xsiny + ysinx = 0; з) exsiny-eycosjc = 0; и) xy = arctg—.
У

$ І. Похідна функції
89
I) sin(xy) + cos(xy) = tg(x + y); ї) 3* + 3' = 3x+y;
II) cos(xy) = x; к) x - у = arcsin x - arcsin y.
2.75. Знайти похідні y'x функцій, заданих параметрично:
fjc = 2f-l,
b-*3;
Ь=#; V=e2'; ;b='2+2'3;
ч І л: = е~' cost, p.\ \x = cos f, ч /jc = f(l - sin t),
;UU = e-'sin/; ;U = sin3/; } \y = tcost;
Л* = 1п(1-И>), з)
[y = t-arctgt;
x = arccos
y- arcsin-
^V1' и)
x=(/+i)-i2,
4tV
2.76. Знайти похідну другого порядку уп функцій:
її) у - ех ; б) у = sin2 д:; в) у = ln(x + л/4 + х2);
г) y = ln%Jl + x2; fl)j; = (l + jc2)arctgjc; є) у = е2х sin5х;
г) у = у 1-х2 arcsinх; ж) .у = yja2 -х2.
2.77. Знайти вказані похідні:
a)(x2sin2xf5); б) (xe^f2). в) (А"*)00;
і)(дґ1пж) ; д)(хех) ; є) ~7^ •
2.78. Знайти похідну у^ функцій, заданих параметрично:
а)
(x = \nt,
\y=t3;
б)
|x = ln(l + /2),
[y=t2;
в)
jc = arctgf,
|v = ln(l + /2);
ч lx = tfCOS f,
|y = tfsin3f;
ч f jc = ґ — sin ґ,
д' 1^ = l-cosf;
ч Jjx^e'cosf,
|y = e'sinf.

90 Розділ II. Диференціальне числення функцій однієї змінної
2.79. Знайти у^ функцій, заданих неявно:
а) у = sin(> + у); б) ху = ех+у; в) х - у = tgy;
г) у = х + Іпу; д) х3 + у3 -Загу = 0; є) tg>> = ху.
2.80. Знайти загальний вираз для похідної у^п\ якщо:
х + З 1 — jc
д) y = sin2x ; є) j; = xln:x:; є) у = —2—-;
х -І
ж) у = sin4 x + cos4x.
Відповіді
2.1./ = А_ 2 __^_ 2.2./ = Аз/^-2х4^.
2.3. / = х2 + Аг + -^. 2.4. у' = -ЦІ. 2.5. / = є* + 4-
я:3 Цх2 2xjx уїх
2.6. / = -==—==. 2.7. v' = -r-(x:-2arctgjc). 2.8. у' = 9дг21іис.
2.9. у' = х2 cosjc. 2.10. / = jtarctg де. 2.11. / = 2/(sin2*-l).
9 r- x-Jl-
2.12. / = -VJclnx 2.13. / = —-—
x1 arcsinx
x4l-x2
олл , 3e2sin3*cos3x __ , - . з* x
2.14. / = —? r-. 2.15. у = 2siir -cos-.
1 2sin3jc I 2 2
sin — e
2
12 2 ( 4 л
2.16. / = --sin-jc. 2.17. / = г l + -tg2x
3 3 cos22jc^ 3

§ І. Похідна функції
91
2.18. У = (і + дг2)_1. 2.19. / = - 2Є
Jl^T*"
1 x-l
2.20. у' = —-tg . 2.21. у' = sin In х- cos In x.
x2 x
U2 y= l + 2jx- + 4jxjx7^ 223 y, = 2(x2 + 4~
8v W* + Vjc д/jc + V* + vx
2.24. У = ^sin2x(jctgjc-l)(sin2;c(jctgjc-l)ln^ + 2tgjc+ -^-Д
cos xj
2.25. / = —rtg4x. 2.26. / = —-.
2v* sin jc
2.27. У = (2-2arccos3jt+ 2arcsin3* In2)-
^
9x'
2.28. / = - , 2.29. y' = e *cos3;c.
(і-х2)л/Г^7'
2.30. / = -(x2-6x-l)(x4-l)_1.
2.31. y = [xln2]n31n41n5(log5x)log4(log5x)-log3(log4(log5jf))] ;
2.32. y' = . * . 2.33. у' = ліх2 -4.
, ,. , In* 1 1 -,_ , 2
2.34. / = + +—■===• 2*35. y' = -
x ліі-х2 arcsin* Wl-ln2* cosWsinx
1 + jc e-JC — e*
2.36. у' = , .. 2.37. / = —.
l + x +x e x +ex
2.38. У = 2 Зх x Д-4^. 2.39. y = -cos2x.
2(1-*)(1 + jc2)V1 + x2
2.40. у = «SSi-. 2.41./ = ^^
Vo+*2)3' ' ' Vc*2-1)3

92 Ро з д і л II. Диференціальне числення функцій однієї змінної
2.42.
2.44.
2.46.
2.48.
2 50
2.51.
У
У
У'
У'
у'
а)
= (arcsinjc)2.
_V*2+i
X
= 9jc2arcsinjc.
ln(l + sinjc)
sin2jc
x2
yjl-2x-x2
3x-2y-l = 0,
2.43. У = 4°
2x-3\l\-4x2
2.45. У =
V2 + 4jc-
x
2.47. y'=(C0SX-sinx)(eX + e X)
e^cosx + e ^sinx
JC5+1
2.49. У = -^
2x + 3y-5 = 0;
6) 4x-y-l = 0, x + 4y-6 = 0;
b)x-1 = 0, y = 0; r) x-2y-l = 0, 2x+y-2 = 0;
д) 6х + 2у-л = 0, 2x-6j> + 3;r = 0; e) y = 2x, у-—x;
є) 5;c + 6.>>-13 = 0,6jt-5>> + 21 = 0;
ж) x + y-2 = 0, х-у = 0;
з) 14x-13>> + 12 = 0, 13л: + 14у- 41 = 0;
и) x + 2y-4 = 0, 2x-y-3 = 0;
і) 4x + 2y-3 = 0, 2x-4y + l = 0;
ї)у = 2, x = l;
й) 4x + 3j>-12 = 0,3;c-4.>> + 6 = 0;
ч v 2 л v 2 я-
к) x + y = , y-x = .
' 16 * 16
2.52.M^2;£)i М2(щ^
2.53. Af,(0;20), M2(l;15), Л/3(-2;-12)

^ /. Похідна функції
93
2.54. MAI;-) і М2(2;-2). 2.55. 5jc->>-38 = 0.
2.56. Крива перетинає вісь абсцис під кутом —.
4
2.57. Крива перетинає вісь абсцис під кутом arctg—.
2.58.a)tg^=-|; tg02=|; 6)tg^=-|; tg02=|;
•0 tg^=j;
2
2.59. a) V = 21 м/с; б) Г = 0. 2.60. V =
(
16 + — м/с.
8
2.62. Wk =0,01815 kt-mVc2
2.61. /, =- c; r,=8c.
1 3 2
2.63. ю = 13 c1. 2.64. Г = 9 м/с. 2.65. К = (-+1пЗІ м/с.
2.66. й> = 2*^,
с
2.67. co = (2at-b)-—; швидкість
с
дорівнюватиме нулю при t = — с. 2.68.23 ампери.
2а
2.70. Приблизно 229,4 м/с.
п
2.69. — см/с.
3
1.71. а) У = , t2"3'3
V(*-2)'(x+4)'l2*+3 2(*"2) 2(i+4)J'
Г,) ■■■ Kh* + 2)Qx-l)f( 1,9 П
" 5V і7 U+2 Зх-1 *J'
,,/=(,-5)(з,+:Гй^т(^+^+^

94 Роз д і л II. Диференціальне числення функцій однієї змінної
3(х-5)4Щх + 1)2
е)У = -
57л:2-302s2+361 (х + 1)2$/х~^2ш
20(*-2)(x-3) ' ^З)2" '
г) у =—\xsmxyjl-e —+ctgx-
2(l-e*)J
ж)/ =
Vl - х2 ((arcsinx)2 ) -1V1 + arcsinx'
1-arcsin л:
л , e* arctg* [,
3) y'=——2-\l + x +
In X {
ч , (l-x2)e3*-1cosjt
(l + x2) arctg* lnx
3-2x-3x2
(arccosx)
1-^
— tgx +
Vi-"2
x arccosjcy
2.72. a) y = x* +1(21njc + l); 6) / = jtsin* cosjtlnx +
smjc
в) j> = (cosjt)
(
cosjclncosjc-
• 2 Л
sin X !
COSJC
л: ;
г) j/ = (arctgx)x In arctgx + -
^ (l + x2)arctgxy
Д)У = (^)
e) j> = (sin x)
У* lnx + 3
6
f з
' COS JC
smjc
-sin2jcln(sinjc)
є) j> = ( arcsin д; J
cosjc In (arcsin jc) +
sinjc
ІГ-
x arcsin я: у

$ І. Похідна функції
95
ж)/ = х(і + -1 •[ 21n[l-f-—J
2.73.0) ух=(\ + улУ;
п)у'х=0,5(і + е2уУ;
>Х) ух={Ъ + 2у)-\
х + 3
б)У,=
у + у
і .
*• /1»
*)Ух
tO Ух
*')У'х
і\ Vі
*> Ух
х1 +2у
= У .
х-у'
= (х + у)2;
cos2 у
1 + COS J>
e-^ sinjt + e* sinj;
ey COSJt-Є* cosj>
г) УІ =11 + —sin^ | ;
e) Ух = •
' 2У ln2
б)у'х=(ЄУ-іУ;
1
r)/x =
1-2 cos у
ycos у .
1 - jccos у
. , vcosjf + siny
ж)Ух=— -,
jfcosy + sinx
и)У,=А
, _ ycos2(x + jv) (cos(xy)-sin(xy))-l
jfcos2(x + j) (cos(xv)-sin(xv))-!
л=-
3^-1
0^;=з^-—-
1-3*
_ , l + ysin(xy)
и)л=—., ' ;
к)^; =
f ^7 (i-^7)
2.75.a)y;=|/2;
б)у;=тіг;

96 Роз д і л II. Диференціальне числення функцій однієї змінної
в)д/=-2е3';
ч , sinf-cosf
д) Ух=-г- -;
sin ґ +cos*
ч f cost-tsint
z) Ух =
1-sinf-fcosf'
, ґ-1, якщо t<0
3) У*=\ 1 ,^л
[ 1, якщо t > 0,
2.76.а)/ = 2(1 + 2*2)е*2;
г) у;
є) у;
ж)^і
и)У,
б)/.
= /;
= -tg/;
1
-It
/+Г
= 2cos2x;
в) / = --*_; г) / = |(і-Л2)(і + х2)-2;
д) / = 2 arctgx+
1 + х2)'
e)/ = e2*(20cos5;c-21sin5jc); є) .»_ 1 L , arcsins
х1-\
4T7J
ч . «2
2.77. a) 214(l05cos2x-30xsin2jf-2x2cos2A:);
6)5ne5*(5;t + 12);
в) 2"-le-2x(2(-l)"x2 +2П(-1)"-1х + ^^-(-1)п-2
ч (-1)"6(и-4)!
г) я_3—- при «>4 ;
ч , ч (-1)""1-1.3...(2и-3)/ „ ,ч
д) (х + п)ех ; є) ^ ^ '-(х-2п + 1).
2"х~
2.78. а) ^=9>3; б)^=1 + ґ2;
в) /xx = 2(l-3t2)-(l + t2)-4; г) ^ =(3acos4^sin0-1;

§ 1. Похідна функції
97
д) у'„ =-(l-cosO 2; є) у"хх=2е '(cos/- sin/)"
2.79. а)/ = «5СЩЦ.
(l-cos(x + y)y
б)/=
,y(jc2+>y2-2jc-2>y + 2)
х2(і-7)3 ;
„з
, 2sm£COS_2. ,_ j
*> У - ( , \з ' -* у ~ /і чЗ
(l + cos2j>/ 0 -У)
д)/ = -2в3ху(у2-азс)"3;
с)/ =
2 j> cos3 ^(cos j; - x cos3 j> - j> sin y)
(1-jccos2>>)3
2.80.a)>>(w)=(-l)w+1-
n\
Ч/1+1
6)/">=-
2и!
чЛ+1 '
(х + 3)и+1 ' ' (1-дс)и
b)/w)=(-3)V3*; т) у{п) =(іх+(-\)п2~х} In"2.
Д) У
W=2"-1sinf2^ + ^^l
с)/0 =(_!)» £l-J>J при »>2;
с)/"> = (-!)"-
1 1
-+■

98 РозділІІ. Диференціальне числення функцій однієї змінної
§ 2. ТЕОРЕМИ ПРО СЕРЕДНЄ
ДЛЯ ДИФЕРЕНЦІЙОВНИХ ФУНКЦІЙ
Теорема Ролля. Якщо функція f(x) неперервна на
відрізку [a; b], диференційовна в інтервалі (а, Ь) і f{a) = f(b), то
існує принаймні одна точка £є (а, Ь) така, що /'(£) = 0.
Якщо, зокрема f(a) = f(b) = 0, то теорема Ролля означає,
що між двома коренями рівняння f(x) = 0 міститься принаймні
один корінь рівняння f'(x) = 0.
Теорема Лагранжа (про скінченний приріст). Якщо
функція f(x) неперервна на відрізку [a; b] і диференційовна в
інтервалі (а, Ь), то існує принаймні одна точка £є(а, Ь)
така, що fib) - f(a) = /'(£) (b - а) (формула Лагранжа).
Ці теореми мають такий геометричний зміст: на дузі АВ
неперервної кривої у = f(x), яка має в кожній внутрішній точці
визначену дотичну (не паралельну осі Оу), знайдеться принаймні
одна внутрішня точка, в якій дотична паралельна хорді АВ
(в теоремі Ролля хорда АВ і дотична паралельні осі Ох).
Теорема Коші. Якщо функції f(x) і <р(х) неперервні на
відрізку [a; b], диференційовні в інтервалі (а, Ь) і <р'(х) Ф 0 в
інтервалі (а, Ь), то існує принаймні одна точка £є (а, Ь) така, що
f(b)-f(a)=m (формулаКоші).
<р(Ь)-<р(а) <р'(£)
Приклад 1. Чи виконується теорема Ролля для функції
f(x) = ySx — х2 на відрізку [0; 8] ? Знайти відповідне значення £.
Задана функція f(x) неперервна для всіх значень хє R і
має похідну
ЗЩЯх-х2)2

§ 2. Теорема про середнє для диференційовних функцій
99
для х Ф О, х Ф 8, тобто диференційовна в інтервалі (0; 8). Крім
того, /(0) = /(8) = 0. Отже, теорема Ролля на відрізку [0; 8]
виконується. Дійсно, f\x) = 0 для х = £ = 4.
Приклад 2. Задана функція f{x) = щх-S)2 . Нехай
я = 0, fe = 16. Тоді /(0) = /(16) = 4. Але похідна
f'(x) = 2/(3yjx-&j не перетворюється в нуль ні в одній точці
інтервала (0; 16). Чи протирічить це теоремі Ролля?
Не протирічить, оскільки в точці х = 8 інтервала (0; 16)
похідна не існує, і умови теореми Ролля порушені.
Приклад 3. Показати, що похідна многочлена
f(x) = хъ - х2 - х +1 має дійсний корінь в інтервалі (-1; 1).
Знайдемо корені цього многочлена: х -х -jc + 1 = 0, або
jc2(jc—1)—(jc—1)=0, (jt-l)2(;t+l) = 0, тобто jc1=x2=1, Лз=-1.
Оскільки /(-1) = /(1) = 0, то за теоремою Ролля рівняння
f'(x) має корінь в інтервалі (-1; 1). Знайдемо корені похідної:
f'(x) = 3x2-2х-1 = 0. Вони дорівнюють хг =—, лг2 = 1- Отже,
між коренями -1 і 1 функції міститься корінь похідної в точці
1
х = —.
з
Приклад 4. На дузі АВ кривої у = 2х - х2 знайти точку
М , в якій дотична паралельна хорді АВ, якщо А(ї91) і 5(3; - 3).
Функція у = 2х - х2 неперервна і диференційовна при всіх
значеннях х. За теоремою Лагранжа між двома значеннями
а = 1 і b = 3 існує значення х = £, що задовольняє рівність
УФ) - У(а) = ф- а)у\4), де у\х) = 2-2*.
Підставивши а=1;Ь = 3, одержимо
у(3)-у(1) = (3-і)/(£);

100 Р о з д і л II. Диференціальне числення функцій однієї змінної
(2.3-32)-(2-1-12) = (3-1).(2-2£); -4 = 4(1-£).
Звідси £ = 2, у(2) = 0. Отже, точка М має координати (2; 0).
Приклад 5. На дузі АВ кривої, заданої параметрично рівняй-
ням х = t , у = f , знайти точку М , в якій дотична паралельна
хорді АВ . Точкам А і 5 відповідають значення t = 1 і f = 3.
гг д> • • ,п . У(3)-у(1)
Кутовий коефіцієнт хорди АВ дорівнює , а
х(3)-*(1)
кутовий коефіцієнт дотичної в точці М (при t = £) дорівнює
4^, де*; =2;, >>;=з;2.
Для визначення £ за формулою Коші отримуємо рівняння
y(3)-yq) = y;(fl або 27-1 = з^
х(3)-*(1) *;(£)' 9-1 2<f'
^ 13 3 г ^ .13
або — = —с . Отже с = —.
4 2* Ь 6
Знайдене значення £ задовольняє нерівності 1 < £ < 3.
Підставивши значення t = £ в параметричне рівння кривої,
169 2197 _
одержимо х=—, у = . Отже, шукана точка М
Ґ169. 2197^
36' 216 У
Задачі для самостійного розв'язування
2.86. Перевірити справедливість теореми Ролля для функції f(x)
на відрізку [a; b], якщо:
а) f(x) = x3+4x2-7x-l0, а = -1, Ь = 2;
б) f(x) = ]nsinx, а = —, Ь = -Г*
о о
в)/(х) = 48Іп*, а = 0, Ь = я;

§ 2. Теорема про середнє для диференційовних функцій 101
г) /U) = V*2-3jc + 2, a = 1, b = 2;
д) /(jc) = \/jc2-5jc + 6, a = 2, & = 3;
c) /(jc) = jc3-6jc2+11jc-6, я = 1, & = 3;
(:)/(*) = 2*H a = 0, & = 1;
ж) /W = tgjc, я = 0, & = я\
2-jc2
2.87. Функція у = J— приймає однакові значення на кінцях
х
підрізка [-1; і]. Переконатися в тому, що похідна від цієї
функції ніде в інтервалі (-1; 1) в нуль не перетворюється. Пояснити,
чому не виконується твердження теореми Ролля.
2.88. Функція у = \х\ приймає однакові значення на кінцях
відрізка [- 3; 3]. Переконатися в тому, що похідна від цієї
функції ніде в інтервалі (-3; 3) в нуль не перетворюється. Пояснити,
чому не виконується твердження теореми Ролля.
2.89. Чи застосовна теорема Ролля до функції f(x) = 1 — на
відрізку [-1; і]?
2.90. Показати, що функція f(x) = х-х3 на відрізках [—1; О] і
[0; і] задовольняє умови теореми Ролля. Знайти відповідне
значення £ .
2.91. Нехай f(x) = jc(jc - 1)(jc - 2)(jc - 3). Довести , що всі три
корені рівняння f\x) = 0 дійсні.
2.92. Показати, що між коренями функції f(x) = х2 -7л;+ 12
міститься корінь її похідної.
2.93. Рівняння ех = Jt + І, очевидно, має корінь х = 0. Показати,
що це рівняння не може мати іншого дійсного кореня.
2.94. Перевірити виконання умов теореми Лагранжа для функції
f(x) = х-х3 на відрізку [- 2; і] і знайти відповідне значення £.
2.95. Перевірити виконання умов теореми Лагранжа для функції
f(x) = Ух4 на відрізку [-1; і] і знайти відповідне значення £ .

102 РозділІІ. Диференціальне числення функцій однієї змінної
2.96. Записавши формулу Лагранжа для функції f(x) = v3 х3 + Зх
на відрізку [0; lj, знайти на інтервалі (0; 1) відповідне значення £.
2.97. Записати формулу Лагранжа для функції у = sin Зх на
відрізку [х^, х2].
2.98. Записати формулу Лагранжа для функції у = х(1 - Іпх) на
відрізку [а; Ь\.
2.99. Перевірити справедливість теореми Лагранжа для функції
у = \х на відрізку [О; 4].
2.100. Перевірити справедливість теореми Лагранжа для функції
у = In х на відрізку [і; є].
2.101. Застосовуючи формулу Лагранжа до функції
f(x) = х3 -Зх2 +х + \ на відрізку [і; 3], визначити відповідне
значення %.
2.102. Записати формулу Лагранжа для функції f(x) = 2х на
відрізку [О; і] і знайти відповідне значення £.
2.103 Для дуги параболи у = х2, що міститься між точками А(1; 1)
і 5(3; 9), знайти точку М , дотична в якій паралельна хорді АВ.
2.104. Перевірити справедливість теореми Коші для функцій
f(x) і ф{х) на відрізку [а; й],якщо
а) /(*) = х3, <р(х) = х2 +1, а = 1, b = 2;
б) /(jc) = sinjc, 0?(jt) = JC + COSJC, tf = 0, & = —.
2.105. Записати формулу Коші для функцій /(jc) та ^(jc) на
проміжку [a; b] та знайти відповідне значення %, якщо
a) f(x) = 2x3+5x + l, 0?(jt) = jt2+4, я = 0, & = 2;
6)/(jc) = jc4, <р(х) = х2, я = 1, & = 3;
Л" Л"
в) /C*) = sinjt, <p(x) = cosx9 а =—, b = — .
6 З

§ 3. Правило Лопіталя. Формула Тейлора
103
§ 3. ПРАВИЛО ЛОШТАЛЯ.
ФОРМУЛА ТЕЙЛОРА
3.1. Правило Лопіталя
Теорема 1 (правило Лопіталя). Нехай функції fix) і <p(x)
визначені та диференційовні в окопі точки а, за винятком, можливо,
fix)
самої точки а, причому <р'(х)ї0, а відношення при х—>а є
<р(х)
невизначеністю типу \ — > або \ — >. Якщо існує lim^-г—, то
. r /(*) t. f(x) t. f(x)
існує і lim- , причому lim- ^m-^—.
x->a (p{x) x-*a ф(х) x-*a ф (x)
f'(x)
Зауваження 1. Якщо вираз • при х —> а є невизна-
(р(х)
ченістю типу < — > або < — к а функції f'(x) і (p'(x) задоволь-
,. fix) -. fix) t. fix)
няють умови теореми 1, то lim = lim —f— = lim -^—,
x-*a q>{x) x->a q> (x) x->a q> (x)
r fix)
зауважимо, що існує lim -^—.
x->a (p (x)
Зауваження 2. Теорема Лопіталя правильна і у випадку а = <*>.
Зауваження 3. Невизначеності типу {()•<»} і {оо-оо}
/°1 * Ы
зводяться до невизначеностеи типу < — > або < — > за допомогою
простих алгебраїчних перетворень. Дійсно, якщо lim/(x) = 0, а
х->а
lim #>(jt) = ©о, то записавши добуток fix) • <р(х), який при л: —> а
х->а
є невизначеністю типу {()•«>}, у вигляді дробу — або
(<РІх)Т1

104 Р о зд і л II. Диференціальне числення функцій однієї змінної
<р(х) ... (0
—, приходимо до невизначеності, відповідно, типу «{ —
(/«Г1 r J Ю
або \ — >. Якщо lim f(x) = lim <р(х) = -н», то записавши різницю
[ooj х->а х->а
f(x)-<p(x), яка при х —>а є невизначеністю типу {оо-оо}, у
вигляді
(f(x))~1 ((Р(х))-1 (Я*))"1-(Я*))"1
/01
приходимо до невизначеності типу < — > .
Зауваження 4. Розкриття невизначеностей типів |і°° 1, JO01 і
І*»0} для виразу (/(*)) зводиться до розкриття
невизначеностей типу {О-оо}. Для цього потрібно прологарифмувати
(при/(л:)>0) вираз (/(*))^(дг). Якщо ]im(<p(x)lnf(x)) = k, то
х—>а
Um[/(x)fМ =ек, оскільки [f(x)fx) =^«1п/«
х->а
3.2. Формула Тейлора
Теорема 2. Якщо функція f(x) має похідні до (п + 1)-го по-
рядку включно в деякому окопі точки х = а, то справедлива формула
(п + 1)! V ; V '
яка називається формулою Тейлора п -го порядку.

§ 3. Правило Лопіталя. Формула Тейлора
105
У випадку а = 0 ця формула називається формулою Мак-
лорена і має вигляд
1! 2! и!
(л + 1)! V ;
Розв'язування типових прикладів
Приклад 1. Обчислити Km
*4-81
Функції /(jc) = jc4-81, <р(х) = х-3 задовольняють умови
теореми 1:
а) lim/(jc) = lim^(jc) = 0;
х->3 jc—>3
б) похідні /'(jc) = 4л:3 і <р'(х) = 1 існують в околі точки х = З,
причому (р\х) Ф 0;
Ґ(х) 4х3
в) існує границя lim —— = lim = 108.
jc->3 <р (х) jc—>з 1
fix)
Отже, відношення при jc —> 3 є невизначеністю типу
#>(*)
\ — L і за правилом Лопіталя lim = 108.
lOj «з jc-3
Законність застосування правила Лопіталя в подальших
прикладах перевіряється аналогічно.
_ л _- ,. Insin2;c
Приклад 2. Обчислити lim .
*->о lnsinjc
Маємо невизначеність типу <— k За правилом Лопіталя
знаходимо

106 РозділІІ. Диференціальне числення функцій однієї змінної
1# Insin2jc Л. (In sin 2х)' ,. 2cos2jc sinjc Л
lim = lim — = lim = 1.
*->o In sin л: *->o (lnsinjc) *->o cosjc sin2jc
ex-e~x -2x
Приклад 3. Обчислити lim .
*->o ;c-sin;c
Застосувавши правило Лопіталя тричі, знайдемо
.. ех-ё~х-2х Г0] v (ех-е~х-2хУ v ex+e~x-2
lim =< — ^ = lim ^= hm ■
*->0 л:-sin л: [OJ *->0 (jc-sinjc) *->o l-cosx
— =um -
OJ *->o (1-cosjc)
. ^ZzlLJI].щи ifl£l=Um£±£:=2=2.
lim = ^ — f = lim- 7L-=lim = —
*->o sinjc [OJ *->o (sinjc) *-»o cos л: 1
Приклад 4. Обчислити lim be• sin— І.
Оскільки lim;c = °o, a lim sin—= 0, то цей вираз є невизна-
х—*» х—>оо д;
ченістю типу {<»• О}. Зведемо цю невизначеність до
невизначеності І — > і застосуємо правило Лопіталя:
• fl (sin-
Umf^sin-l = {oo.0}= Шп^£. = (-1= lim^—^- =
*->~^ XJ x~*°° _ [OJ *~>co fl
a-\ —г- cos—
= lim ^ x X=a.
2

§ 3. Правило Лопіталя. Формула Тейлора
107
Приклад 5. Обчислити lim ctgjc— .
Для х—>0 функція ctg х є невизначеністю типу
х
{оо - оо}. Враховуючи, що
1 cosjc 1 jccosjc-sinjc
ctgx— = — = : ,
х sinjc х xsmx
причому lim(jccosx-sinx) = 0, lim(jcsinjc) = 0, приходимо до
невизначеності типу < — L і за правилом Лопіталя отримаємо
( І\ „ jc cosjc-sin jc Г0
l ctgx— =
lim ctgjc— =lim
x^o\ x) *->o jcsinjc [0
.. cosjc-л: sin л:-cosjc Ґ0І t. -sin л:-л: cos л: 0 .
= hm = < — f=hm = — = 0
x->o jccosjc + sinjc [OJ *->o2cosjc-jcsinjc 2
j_
Приклад 6. Обчислити lim
x->0{ X
tt л sin* 1 1 r^
Для jc —> 0 маємо > 1, — —>«>. Отже, маємо невизна-
х xl
J_
ченість типу {l°°). Прологарифмуємо вираз Г . Отрима-
j_
. (ътх\хг 1 , sin*
ємо In =—т •
\ x ) x2 x
Знайдемо границю
і - sinjc
x-¥i У X ) x-^Q^x2 X ) l J x->0 x2 [OJ
COS X 1
= lim (hlsinx~lnxy - цт sin* ~ x _ 1 Ит *cos*-sin;c _ fOJ =
*-><> (x2)' *->o 2x 2*->o л:2 sin* [О]

108 Р о з д і л II. Диференціальне числення функцій однієї змінної
1-. (jccosjc-sinjc/ 1 t. -jcsinjc
= — lim- г - = — lim-
2*->o (jc2sinjc/ 2*->0 2jtsinjt + jt2cosjt
11. -sinjc f0] 1,. -cosjc 1-1 1
= — lim = < — > = — hm -
2*->o2sinx + jtcos;c І0І 2*->o3cosjt-;csinjt 2 3 6
Тому hm Iх = lime v
x->o\ X ) x->o
fsinx^ 2 1 . sin*
= lim ex x
x—>o
_,,*->oU2 x ) -p в __L
1
Приклад 7. Обчислити lim (ctg x)lnx.
Маємо невизначеність типу { 00°j. Логарифмуємо вираз
і
(ctg*)ln*
J- і
ln(ctgjc)111* = lnctgjc.
lnjc
Оскільки
1
Umln(ctg^ = Um^^ = i-j= Цт ^g^sin2x =
X
TO
=-Hmf— A-| = -l,
*->(\cosx sinjc
I _L lnctg*
Um(ctg*)In7 = limeta(ctg*)InJC = lime ta* =
*-»0 *-»0 *->0

§ 3. Правило Лопіталя. Формула Тейлора
109
Приклад 8, Обчислити lim;csin*.
х—>о
Маемо невизначеність типу і0°]. Оскільки
Umln(jcsin^) = lim(sinA:.lnjc) = {0-oo} =
TO
= lim
*->0
lnjc
sinjc
*->0 v
-ft-
lim
*->0
lim-
*->0
Х§ІП*
x->0
1
л:
cos л:
sin2jc
= lim-
lim( sin x-\n л:)
sinjc
X
= e°
(-
= 1
sinjc
COS*
= 1-0 = 0,
Приклад 9. Написати формулу Тейлора третього порядку
для функції f(x) = s[x9 якщо a = 1.
Формула Тейлора третього порядку для функції /(*) має
вигляд
m = f(a)+^(x-a)+fM(x-af+£^(x-af +
+ /"r<a;f-)W. *(«!)•
Знайдемо значення функції /(а) і її похідних
/'(а), /'(в), /», fIV {а + в{х-а)). Маємо
/(*) = >£=» /'(*) = -V =*• /#(х) = - j •
1 1
2V^ 4 77
/"(*)=-A^ =*/"(*) = • 15
8jc2vjc 16jc3vjc
Тому, при я = 1,
/(і) = і,//(і)=^,Г(і) = ~,Г(і)=|,

ПО РозділІІ. Диференціальне числення функцій однієї змінної
гпг, ~ч 15
Ґу(і + Є(х-1)) = -
Іб^І + віХ-І))1
Отже,
Г , 1/ іч 1(*-1) 3(*-1)3
Jx = l + -(x-l)—- —+ -- —
2 4 2! 8 3!
"Т?^(1+^-1))_К' *є(0;1)-
Приклад 10. Написати формулу Маклорена п-го порядку
для функції f(x) = ех.
Диференціюючи послідовно функцію f(x) = ex9 знайдемо
/(*) = ех^ ДО) = 1, /'(*) = ех=> /'(0) = 1,
/*(*) = ех => Ґ(0) = 1, fM(x) = ех=> f w(0) = 1,
/(w+1) (jc) = ex => /(n+1) (вх) = евх.
Підставивши отримані значення в формулу Маклорена,
отримаємо
Є* =1 +х + £_ + ... + £- + -І ** ^ /Q j4
2! п! (л + 1)! V ;
Приклад 11. Знайти наближене значення числа є,
використавши формулу Маклорена п'ятого порядку для функції ех.
Формула Маклорена п'ятого порядку для функції ех має
вигляд
2! З! 4! 5! 6! v '
Приймемо в цій формулі, х = 1. Отримаємо
11111
2! З! 4! 5! 6!
е = 1 + 1 + —+ - + — + —+ —ее, 0є(О; 1),
2! З! 4! 5! 6! v ;

§ 3. Правило Лопіталя. Формула Тейлора
111
Отже,
е«1 + 1 + ~ + - + —+ — = 2,72,
2 6 24 120
при цьому знайдемо похибку є = —ев, ве (0; і).
6!
Враховуючи, що в є (0; і), е<% для похибки є знайдемо
таку оцінку
є = —<-<- = —<0,01.
6! 6! 6! 240
Задачі для самостійного розв'язування
2.106. Записати формулу Тейлора п -го порядку для таких функцій:
а) /(х) = —,якщо я = -1; б) f(x) = Jx, якщо а = 4;
х
з 1
в) f(x) = x Injc, якщо а = 1; г) f(x) = —j=, якщо я = 1, и = 3;
Д) /(*) = lnjc, якщо я = 1, п = 3 ; є) /О) = л/jc, якщо а = 1, п = 5.
2.107. Записати формулу Маклорена n-го порядку для таких
функцій:
a) /(jc) = хех\ б) /(jc) = Vm, п = 2;
в) f(x) = %Jl + x9 и = 2; г) /(jc) = sinjc;
Д) /С*) = tg x, n = 2; e) /(jc) = arcsinjc, и = 3.
2.108. Використовуючи наближену формулу
х 1 *2
Є «1 + JC +—,
2
_j_
знайти є 4 і оцінити похибку.
2.109. Використовуючи наближену формулулу
2 3 4
ln(l + jc)«jc + ,
V } 2 3 4
обчислити In 1,5.

112 Р о з д і л II. Диференціальне числення функцій однієї змінної
2.110. Обчислити з точністю до 0,001 значення таких функцій:
a) sinl0; б) cos41°; в) 3/Ї2Ї; г) ^29~; д) Ч~е\ є) VU9.
Обчислити границі:
-+ЛЛ ,. lncosjc „--„,. Є* -1 ~лл~> ,. 1 — JC
2.111. lim . 2.112 hm . 2.113. lim-
*->0 X *->0 sinJC х-*\Л . 7tX
1-sin
2
2.114. lim*3-2*2-* + 2 2.115.1im^A 2.116. lim ^.
*->l x -ІХ + 6 x^° InjC *->«> jc
*ллт і- tg* ^**o і- e* *+m i- JCCOS^-SinJC
2.117. hrn-2—. 2.118. lim —. 2.119. lim г .
x^*tg5x *->+~л;3 *-><> x5
2
x3
x_ -*o S111JC-JC +
2.120. lim-— —. 2.121. lim &-.
Jt->0 1-COSJC *->0 x
2.122. lim 2.. 2.123. Hm^f".
JC^l CtgflK *->0 x
ln(l + jc) - x + —
2.124. lim - —. 2.125. lim - .
*->o jc3 *->o jr-sinjc
<*<%** і- Jc2-l + lnjc ..._ t. <?3*-3jc-1
2.126. lim . 2.127. lim-
*->i ex-e *->o sin25jc
r3 ^
e — 1 —jc ^ ._ ,. lnjc
2.128. lim- ^——. 2.129. lim-
*->° sin 2 jc *->o 1 + 2 In sin jc
2.130. Пт^-Д 2.131. liml
*->l Ctg 7DC x->V
Ґ
1 1
JC -1 In JC y
' о ..«tof ' >].
2.132. lim -y-ctg^jc. 2.133. xxxxx, 9 -
*->(\a;z у *-><\sinzjc jcz
2.134. lim — . 2.135. lim(l - cos jc)ctg jc.
*->i^lnjc hue у *->0

§ і. Правило Лопіталя. Формула Тейлора
113
2.136. lim(l-jc)tg—. 2.137. HmJjtV*).
2.138. lim(^-2jc)tgjc.
*->+«>
2.139. lim
X—>oo|
( I ^
Є*"1
2.140. lim
*->o|
( \\
2 r2
2.141. linut1+ln*. 2.142. Um(^-2jc)c
*->o
У
ях
2.143. Um(l-Jt) 2 . 2.144. lim(sinjt)*. 2.145. Um(ctgjt) .
tg*
л
2.146. liml-I . 2.147. lim(jt + 2*k 2.148. lim (tg*)2* *.
2
.і. і
2.149. lim xx. 2.150. lim(tg x)2cosx. 2.151. lim (** + *)*.
2.152. lim{l + xfnx. 2.153. lim(cos2jt)* .
*->0
*->0
1 3
2.154. Um(3-2jc)lgT. 2.155. lim*1"*. 2.156. 1іт(і + Л.
2.157. Urn
tg~T
tg-
l
. 2.158. limjtln(* 4). 2.159. lim l + -y I •
1
nx
2.160. lim(2-jt)g2 .

114 Р о з діл II. Диференціальне числення функцій однієї змінної
ВІДПОВІДІ
2.106. a) f{x) = -1 - (jc +1) - (jc +1)2 -... - (jc + Vf +
+ (-!)»* (x + l) _„, 0є(О;1);
Л+1
/i+2
[-l + 0(jC + l)J
4 64 512 n!(n-l)!24""2
. (-№)!(,-4Г' r>ff£(0.>]);
22п+1п!(п + 1)!А/[4 + ^(д;-4)]
2n+l
ч */ n / i4 5 / i\2 ll/ t\3 (-І)"6(д:-І)п
.) /w-cx-Ot-^-l) +-(*-i) +...+-^L^_L_+
(-.r'6(,-i)- ._
m-2
(n - 2)(n - І)и(и +1) [І + в(х -l) J
D /w=i-i(*-,)+±l(*-i)*-.L3|(,-i)> +
+ 1^7 (,-.)' (ад);
24 »■ J[U<Kx-»t
д. ^.(,-^-^aztf - <->4 ,вв№.
2 3 4[l + 0(;t-l)]4
w/ ч . jc-1 2(jc-l)2 ІО(дг-І)3 80(jc-1)4 880(;t-l)5
є) /(д:) = 1+ ^ —+— — + —
З 9-2! 27-3! 81-4! 243-5!
. 12320CX-IJ» _
729-6!fl + 0(x-l)]%
г2 г3 г" гп+1 „
2.107. а) *+—+—+...+—— + —А 0є(О;1);
1 2! (п-1)! п!

§ 3. Правило Лотталя. Формула Тейлора
115
9 Ч
б) l + Z-?L + ?L(l + ex)-%t 0Є(О;1);
2 о lo
B)l + -- — + — (1 + вх)-%, в€(0-ЛУ,
3 9 81 V '
х3 х5 х1 хп . пп хп+1 . (л я{
г) л: + I-...+—sin h sin 0л: +
3! 5! 7! л! 2 (и + 1)!
ве (0;1);
я + іЛ
2 Г
д) Л+—-
л3 l + 2sin30;t
3 cos4 вх
, ве (0,1);
*3 jc4 90х + 6(0;с)3 . ..„
с) х+— + — ^-=4-, 0є(О;1).
3! 4! (1_в2х2/2
2.108. 0,78, £ < 0,01. 2.109.0,4.
2.110. а) 0,841; б) 0,754; в) 4,946; г) 3,072; д) 1,395; е) 2,002.
2.111.0. 2.112.1. 2.113. оо. 2.114.0,5. 2.115. -ее.
2.116. 0. 2.117. 5. 2.118. оо. 2.119. --. 2.120. 0.
3
2.121.—. 2.122.-2. 2.123.--. 2.124.-. 2.125.--.
120 3 3 3
2.126. -. 2.127. 0,18. 2.128. —. 2.129. 0,5. 2.130.0.
е 128
2.131.-0,5. 2.132. -. 2.133.І. 2134.-1. 2.135.0.
3 3
2.136. —. 2.137.0. 2.138.2. 2.139.1. 2.140. о».
п
2.141. е2. 2.142.1. 2.143.1. 2.144.1. 2.145.1.
2.146.1. 2.147.2. 2.148.1. 2.149.1. 2.150.1.
2.151. е2. 2.152.1. 2.153. <Г6. 2.154. ея. 2.155. е~\
2.156.1. 2.157. ё~\ 2.158. е. 2.159.1. 2.160. еп'.

116 РозділІІ, Диференціальне числення функцій однієї змінної
§ 4. ЗАСТОСУВАННЯ ДИФЕРЕНЦІАЛЬНОГО
ЧИСЛЕННЯ ДО ДОСЛІДЖЕННЯ ФУНКЦІЙ
4.1. Зростання і спадання функції
Теорема 1. Нехай функція f(x) диференційовна на інтервалі
(а\Ь).Якщо:
а) f(x) зростає на [a;b], то f\x)>0,\/xG(a\b)\
б) f(x) спадає на [a;b], то f'(x)<0,Vxe(a;b).
Нехай функція f(x) неперервна на відрізку \а\ b] і
диференційовна в кожній його внутрішній точці. Якщо:
а) /'(*)>0, Ухє(а,Ь), то f(x) зростає на (а;Ь);
б) /'(*)< 0, Vjc€ (a,b), то f(x) спадає на (а;Ь).
Отже, інтервали знакосталості похідної функції f(x) є
інтервалами монотонності цієї функції.
4.2. Екстремуми функції
Означення 1. Точка Xq називається точкою максимуму
функції /(*), якщо f(x0)>f(x) для всіх х із деякого досить
малого околу точки х$ (рис. 2.2).
У
0 а
Рис. 2.2

§ 4. Застосування диференціального числення до дослідження функцій 117
Точка хх називається точкою мінімуму функції /(*),
якщо f(xx)<f(x) для всіх х із деякого досить малого околу
точки хх (рис. 2.2).
Точки максимуму і мінімуму називаються точками
екстремуму (екстремальними точками), а значення функції в цих
точках - екстремумами.
Теорема 2 (необхідна умова існування екстремуму). Якщо
точка jq є екстремальною точкою диференційовної функції
/(*), то f'(x1) = 0, або f'(xx) не існує.
Ця теорема має очевидну геометричну інтерпретацію: якщо
в точці екстремуму функція f(x) має похідну, то дотична до
кривої y = f(x) в цій точці паралельна до осі Ох (рис. 2.2).
Висновок. Якщо функція f(x) є диференційовною, то
вона може мати екстремум тільки в тих точках, в яких її
похідна /'(*) = 0.
і
-1
1
Т
(
'У
2.
0
1у=х3
1 JC
Рис. 2.3
Обернене твердження неправильне. Наприклад, функція
у = х3 є диференційовною і в точці х = 0 її похідна /(0) = 0.
Однак точка х = 0 не є точкою екстремуму (рис. 2.3).

118 Р озділІІ. Диференціальне числення функцій однієї змінної
У -
0
і
Х\
Х2
Рис. 2.4
х3
X
Зауваження. Точки, в яких похідна функції f'(x) не існує,
можуть бути точками екстремуму, а можуть і не бути (рис. 2.4). У
точках хІ9х2,х3 похідна не існує. Однак, х{- точка максимуму,
х2 - точка мінімуму, а х$ - не є точкою екстремуму.
Означення 2. Точки, в яких похідна обертається в нуль або
не існує, називаються критичними точками.
Теорема 3 (достатні умови існування екстремуму
функції). Нехай функція f(x) неперервна в деякому інтервалі,
що містить критичну точку х{, / диференційовна в усіх точках
цього інтервалу (крім, можливо, самої точки хх). Якщо:
/'(*)> 0 при jc<jc1
f'(x)<0 при х>х{
(рис. 2.5, а);
f'(x)<0 при jc<jc1
/'(jt)>0 при x>xlj
(рис. 2.5, б).
На підставі сформульованої теореми можна дослідити на
екстремум функцію y = f(x) за такою схемою:
1. Знайти область визначення функції D(/);
2. Знайти критичні точки функції. Дня цього шукаємо похідну
f'(x) і, розв'язавши рівняння f'(x) = 0, знаходимо точки, в яких
а)
б)
то хх - точка максимуму функції f(x)
то хх - точка мінімуму функції f(x)

§ 4. Застосування диференціального числення до дослідження функцій 119
похідна обертається в нуль. Крім того, дослідивши область
визначення похідної /)(/'), знаходимо точки, в яких похідна не існує.
Рис. 2.5
3. Знайти точки екстремуму функції. Для цього визначають
знак похідної ліворуч і праворуч від кожної критичної точки.
Якщо при переході через критичну точку зліва направо знак
похідної змінюється з мінуса на плюс, то в цій точці функція має
мінімум (min), якщо знак змінюється з плюса на мінус, то
функція в цій точці має максимум (max). Якщо при переході
через критичну точку похідна знака не змінює, то ця критична
точка не є точкою екстремуму.
4. Знайти екстремум функції, обчисливши її значення в
екстремальних точках.
Результат досліджень корисно записувати в таблицю.
Інтервали
монотонності.
Критичні точки
Знак і значення
похідної
Поведінка
функції, екстремуми
(<h\ аі)
+
Функція
зростає
71
х = а2
0
max
f(a2)
(я2; аъ)
-
Функція
спадає
^1
х = а3
0
min
/(«з)
(я3; <*4)
+
Функція І
зростає
7\ |

120 Р о з д і л II. Диференціальне числення функцій однієї змінної
Дослідити диференційовну функцію на екстремум можна
також і за допомогою другої її похідної, якщо вона існує.
Теорема 4. Нехай в околі точки хх функція f(xx) є двічі
диференційовноЮу причому f'(xx) = 0. Якщо:
а) f"(xx)>0> то в точці хх функція f(x) має мінімум;
б) /'(*і)<0> то в точці jq функція f(x) має максимум.
Відомо, що неперервна на відрізку [a, b] функція f(x)
досягає на цьому відрізку свого найменшого min/(jc) і НаЙбІЛЬ-
шого max / (jc) значень. Ці значення функція набуває або в точках
екстремуму функції, що належать відрізку [a;b], або на кінцях
цього відрізка. Отже, для знаходження min/(jc) і max/(jc)
[a,b] [aj>]
потрібно:
1. Знайти критичні точки функції y-f{x\ які належать
(а; Ь);
2. Обчислити значення функції /(jc) в критичних точках і
на кінцях відрізка;
3. З отриманих значень функції знайти найменше і
найбільше.
Розв'язування типових прикладів
Приклад 1. Знайти інтервали зростання і спадання функцій
х2
а) у = 4х2+х\ б) у = г-.
9-х2
а) Областю визначення функції у = 4х2 +х є множина
D = (-<»; +<»). Знаходимо похідну / = 8jc + 1. Щоб знайти
інтервали зростання функції, розв'язуємо нерівність />0, тобто

§ 4. Застосування диференціального числення до дослідження функцій \2\
8* +1 >0. Одержимо х>—. Отже, функція y = 4jc2+jc зростає в
о
інтервалі —; оо І Розв'язавши нерівність /<0, тобто 8jc + 1<0,
знаходимо, що ця функція спадає в інтервалі -оо; —
х2
б) Функція у = - визначена на множині
9-х2
D = (-«>; -3)и(-3; 3)u u(3; оо). Знаходимо похідну
,_ 2jc(9-х2)- х2(-2х) _ 18л:
У " (9-Jt2)2 "(9-jc2)2'
Знаменник дробу f 9-х2) >0,\/хє D. Тому /> 0 при всіх
jc>0, xeD. Отже, ця функція зростає при *є(0; 3)и(3; «>).
Для тих значень xeD, які задовольняють нерівність д:<0,
маємо у <0. Отже, інтервалами спадання функції є
(-оо;-3)и(-3;0).
Приклад 2. Дослідити на екстремум функцію
1*1 5
У Ъ 2
Будемо дотримуватись наведеної вище схеми дослідження
функції на екстремум.
1. Область визначення. Очевидно, що областю визначення
ЦІЄЇ фуНКЦІЇ Є ДІЙСНа ВІСЬ D = (-оо; +оо) .
2. Критичні точки. Знаходимо похідну функції
у=х2 -4jc + 3.
а) Розв'яжемо рівняння / = 0,
х2 -4jc + 3 = 0=>jc1 =1, лг2 = 3.
Отже, критичними точками є : хх = 1, х2 = 3.

122 Р о з д і л II. Диференціальне числення функцій однієї змінної
б) Знаходимо точки розриву похідної. У нашому випадку
похідна у визначена на всій осі, тобто точок розриву немає.
Тому інших критичних точок, крім хх = 1, х2 = 3, немає.
3. Точки екстремуму. Критичні точки хх =1 І JC2 =3 ділять
область визначення функції £> = (-оо; +оо) на інтервали
монотонності (-оо; l)u(l; 3)и(3; «>). На кожному з цих інтервалів знак
похідної не змінюється. Отже, щоб визначити знак похідної на
інтервалі монотонності, досить визначити його в довільній точці
цього інтервалу:
-вточці л; = 0є(-оо; і) похідна /(0) = 02 -4-0 + 3 = 3>0;
-вточці д: = 2є(і; 3) похідна /(2) = 22 -4-2 + 3 = -1<0;
-вточці д: = 4є(3;+«>) похідна /(4) = 42 -4-у + 3 = 3>0.
Значить, на інтервалах (-оо; і) і (3; оо) похідна />0
(має знак "+"), а на інтервалі (і; 3) похідна /<0 (має
знак "-").
Отже, під час переходу через точку д: = 1 зліва направо
похідна змінює знак з плюса на мінус, і тому точка хх = 1 є
точкою максимуму цієї функції. У разі переходу зліва направо
через точку jc2 = 3 похідна змінює знак з мінуса на плюс. Тому
х2 = 3 є точкою мінімуму функції.
4. Екстремуми. Знайдемо значення функції в точках хх = 1 і
Ушах=)'(1) = ^12-2-12+3-1 + | = 3,
Уті„=ЯЗ)=|-33-2.32+3-3 + | = |.

§ 4. Застосування диференціального числення до дослідження функцій 123
Для наочності запишемо результати пунктів 1-4 в таблицю:
Інтервали
монотонності.
Критичні точки
Знак і значення
похідної
Поведінка
функції, екстремуми
(—,і)
+
я
*1=1
0
max
/d) = 3
Н з)
-
^
jc2 =3
0
min
(з; ~)
+
^
З таблиці видно, що (-°°; 1), (3; °°) є інтервалами
зростання, а інтервал (-1; 3) - інтервалом спадання функції.
Зауваження. Продиференціювавши функцію у ,
отримаємо у" = 2jc-4. Очевидно, що у" визначена на всій числовій
осі, зокрема в критичних точках хх=1 і лг2 = 3. Тому для
дослідженя критичних точок можна використати другу похідну.
Дійсно, оскільки у"(1) = 2-1-4<0, а /(3) = 2-3-4>0, то хг=1
є точкою максимуму, a jc2 = 3 - точкою мінімуму.
Приклад 3. Дослідити на екстремум функцію
у = (х-7)у/х + 1.
1. ОблаСТЬ ВИЗНачеННЯ фуНКЦІЇ D = (-оо; +оо) .
2. Критичні точки.
у' = 1[7+ї + (х-7) ■ 1 =- *~1 .
а) / = 0=>*2=1.
б) в точці хх = -1 похідна функції у' не існує. Отже, точки
хх = -1 і Х2 = 1 є критичними.
3. Точки екстремуму. Розглянемо інтервали (-©о; 1),
(-1; 1),(1; оо). Оскільки /(-2)<0, /(0)<0, /(2)>0, то jc1=-1
не є точкою екстремуму, а д>2 = 1 є точкою мінімуму.

124 Р о з діл II. Диференціальне числення функцій однієї змінної
4. Екстремуми. Обчислимо у^ = у(1) = (1 - 7)Ш +1 = -6\І2.
Заповнимо таблицю:
Інтервали
монотонності.
Критичні точки
Знак і значення
похідної
Поведінка
функції, екстремуми
(-;і)
-
^1
хх =-1
у не
існує
немає
Н і)
-
^1
*2 =1
0
min
у(1) = -6^/2
(і;~)
+
71
Зауважимо, що для дослідження критичної точки хх = -1
застосувати другу похідну не можна, оскільки в цій точці вона
не існує.
Приклад 4. Дослідити на екстремум функцію y = xyjl-x2.
1. Область визначення фунції D = {хє R:\x\<l} = [-1; і].
2. Знайдемо похідну у' = л/і - х +.
-2х \-2х1
2^11-х2 л/і-д:2 '
а) розв'яжемо рівняння у' = 0, або 1-2л:2=0, тобто
1_ 1
Xl~ J2,X2~J2-
б) значення функції у не існують, якщо 1 - х = 0, тобто
Х$ = ~1» х^ = 1.
Оіже, точки хх =—т=, х2 =-т=, Лз =-1,^4 =1 є критичними.
3. Точки Хз = -1, дг4 = 1 є граничними точками області
визначення функції. Тому вони не можуть бути точками
екстремуму (точками екстремуму можуть бути лише внутрішні точки

§ 4. Застосування диференціального числення до дослідження функцій 125
області _*. Дослід™» криги™, TO™, b—felx, -j-
за допомогою другої похідної. Маємо
У =
х(2х2-У)
\И
Оскільки у"\ —j= > 0, а у*\ —j= < 0, то в точці хх = —j=
функція має мінімум, а в точці дг2 = —т= - максимум.
v2
4. Знайдемо екстремуми функції
Утах У| ^J
1 ^
Ш 2 2'
Приклад 5. Знайти найбільше та найменше значення
функції у = х4 - 2jc2 + 5 на відрізку [-2; 2].
Знайдемо критичні точки цієї функції. Оскільки у' = 4х3 - 4дг,
то критичними точками є розв'язки рівняння 4х -4х = 0, тобто
хх = -1, дг2 =0, jc3 = 1. Точки jc1? jc2, Д3 лежать в середині
відрізка [-2,2]. Знайдемо значення функції в критичних точках і на кінцях
відрізка [-2; 2]. Маємо
у(-2) = 13, у(-1) = 4, у(0) = 5, у(1) = 4, у(2) = 13.
З отриманих значень виберемо найменше і найбільше
min (х4 - 2х2 + 5) = 4, max (х4 - 2х2 + 5) = 13.
[-2;2]\ / [-2;2] \ '

126 Р о з д і л II. Диференціальне числення функцій однієї змінної
Приклад 6. Сітка для огородження має довжину / (метрів).
Які розміри повинна мати прямокутна ділянка, що прилягає до
будинку, огороджена сіткою, щоб площа її була найбільшою?
Оскільки ділянка прилягає до будинку, огороджувати її
потрібно лише з трьох сторін. Довжину сторони ділянки, що
знаходиться навпроти будинку, позначимо через х. Тоді, довжина
сторін прямокутної ділянки, що примикають до будинку, дорівнює
х(1 - х)
(1-х)/2, а площа ділянки 5=-* . Очевидно, 0<jt</.
2
Отже, потрібно знайти найбільше значення функції
(Іх-х2)
5 = на відрізку [0; /]. Як і в попередньому прикладі,
знаходимо критичні точки функції 5,5' = => / — 2jc = 0 => jcx = —.
їх-х1
Обчислимо значення функції 5 = в критичній точці
*!=—є[0;/] і на кінцях відрізка [0;/], 5
5(0) = 0, 5(/) = 0
Отже, 5тах=5||
т /
2
Л і2
= —. Довжина сторони, що знаходиться
о
навпроти будинку х = —, а довжина прилеглої до , будинку
/
сторони дорівнює —.
4
Приклад 7. Знайти розміри (висоту і радіус основи) циліндра,
який при даній повній поверхні 5 мав би найбільший об'єм.
Нехай радіус основи циліндра дорівнює х, а висота у. Тоді
5 = 2ях2 + 2яху, звідки

§ 4. Застосування диференціального числення до дослідження функцій 127
y = (s~2nx2)l2nx = — і--2пх\
S <*
Тому об'єм циліндра V = — х - ют, лс>0.
5 з
Дослідимо на максимум функцію V = — х-пх , лс>0. Зна-
ходимо похідну V'= Злх2. Розв'язавши рівняння V' = 0 або
— ЗЛ"д:2 = 0, знаходимо критичне значення х = х \—. Друга
2 убл-
похідна У" = -6ях. У критичній точці V" = -6nA—<0. Отже,
об'єм V циліндра, повна поверхня якого дорівнює 5, набуває
максимального значення, якщо радіус його основи x = J—.
убл-
Підставивши це значення радіуса в формулу для висоти циліндра,
знайдемо y = 2J—.
V6#
Задачі для самостійного розв'язування
2.161. Знайти інтервали монотонності функцій
a) у = -х3-2х2+Зх + 2; б) у = -х4-2х2 +1; в) y = ;cV*;
З 4
г) y = arctgx-lnA; ; д) у = -; є) y = (x-3)<Jx;
х-2
є) у=£-3£; ж) у = 2ех2~4х; з) у =—;
З jc
и) у = (л:2-і) ; і) У = -г~\ ї) у = ху]і-х
\ І In г

128 Р о зділІІ. Диференціальне числення функцій однієї змінної
2.162. Знайти екстремуми функцій:
4 j
а) у = 2х2-—; б) у = х5 +5jc4 +5jc3 -2; в) у = *2—-;
4 jc2
г) y = jc^/T^ ; д) y = (jc-5)2^/(jc + l)2; є) у = * -1п(* + 1);
є) y = jcV"*; ж) у = л;е* ; з) y = jcln2jc;
и) у=у(**+*~*); О y = ^/(*2-D2; D у = і](х-і)6.
й) у = 1-^(*-2)4; к) у = (2* + 1$0с-2)2;
л) y = (2jt-l)^/(jc-3)2; м) j = ^ + 2V3^jc;
н) у =—jc v6jc-7; о) у = (л; -2jc)ln*—д: +4дг;
п) у = 2х + Зу[х*; р) y = arctgx—ln(jc2+l).
2.163. Знайти найменше і найбільше значення функції y = f(x)
на відрізку [я; Ь], якщо:
а) у = 3х-х\ [-2;3]; б) у = *4 -2jc2 +3, [-3;2];
в) y = jc-31njc, [2; 4]; г) y = Vl69-x2, [-12; 5];
д)у = *2--, [-2;-0,5]; є) у = *-1п(* + 1), [-0,5; і];
є) у = * + 2^, [0;4]; ж) У = ^р [0;4];
1-JC
з) у = ^ї+ї-З/І^ї, [0; 1]; и) у = arctg- , [0;l].
1 + JC
2.164. Число 60 розкласти на два доданки так, щоб сума подвоєного
одного доданка та квадрата другого була найменшою.
2.165. Число 8 розкласти на два доданки, сума кубів яких
найменша.
2.166.3 квадратного бляшаного листа, сторона якого дорівнює а ,
треба зробити відкриту зверху скриньку з найбільшою місткістю,

§ 4. Застосування диференціального числення до дослідження функцій Y19
вирізаючи рівні квадрати по кутах і відкидаючи їх, а потім
згинаючи бляху так, щоб утворити боки скриньки. Яка повинна
бути сторона вирізуваного квадрата?
2.167. Відомо, що міцність балки з прямокутним поперечним
перерізом пропорційна ширині та квадратові висоти цього перерізу.
Вирізати з круглої колоди, діаметр якої d, балку з прямокутним
перерізом так, щоб вона в горизонтальному стані чинила
найбільший опір згинові (найбільший опір згинові буде тоді, коли
міцність матиме максимум).
2.168. Тиск води по твірній на конічну посудину при витіканні
визначають за формулою р = ax(h - х), де h - висота посудини, х -
відстань до рівня води, а - стала. На якій глибині тиск найбільший?
2.169. Треба повісити над центром круглого майданчика з
радіусом а електричний ліхтар. На якій висоті h ліхтаря доріжка,
що оточує (проходить по краю) майданчик найкраще буде
освітлена? (освітленість прямо пропорційна косинусу кута падіння та
обернено пропорційна квадратові відстань від джерела світла).
2.170. Треба виготовити бляшану посудину циліндричної форми
місткістю 3 л, відкриту зверху. Які повинні бути розміри посудини,
щоб на її виготовлення витратили найменшу кількість матеріалу?
2.171.3 усіх прямокутників, що мають дану площу 5, знайти
той, периметр якого найбільший.
2.172. У конус з висотою Н і радіусом основи г вписано
циліндр. Знайти той, що має найбільший об'єм.
2.173. Прямокутний трикутник, обертаючись навколо одного з
його катетів, утворює прямий конус. Знайти об'єм найбільшого з
них, якщо гіпотенуза трикутника дорівнює 3 см.
2.174. Переріз тунелю має форму прямокутника з насадженим
півкругом. Периметр перерізу дорівнює а метрів. За яких
розмірів сторін прямокутника площа перерізу буде найбільшою?
2.175. На пароплаві витрати на паливо пропорційні кубові його
швидкості; при швидкості в 10 км/год витрати на паливо
становлять 25 грн. на годину, інші витрати (не залежні від
швидкості) становлять 400 грн. За якої швидкості пароплава загальна

130 РозділІІ. Диференціальне числення функцій однієї змінної
сума витрат на кілометр шляху буде найменшою та яка буде при
тому загальна сума витрат на годину?
2.176. Довести нерівності:
a) 2vjc>3— при х>\;
х
в) jc>ln(l + jc) при лг>0;
ч 2(jc-1) ,
д) — -<\пх при jc>0;
Jt + 1
jc3
є) х <sinjc при лг>0;
б) ех > 1 + х при х Ф 0;
г) ln(l + ;c2)<2jcarctgjc;
є) — <1п(1 + дс) при jc>0;
1 + JC
ж) jc + — <tgjc при 0<л:<—;
з) х <1п(1 + дг) при лг>0;
и) 1 <cosjc при хФО;
і) х <arctgjc при 0<jc< 1; ї) х + — <arcsinjc при 0<л;<1.
З 6
Відповіді
2.161. a) (-°°;l)u(3;<*>)- зростає; (1;3) - спадає;
б) (-2;0) u (2;оо) - зростає;(-оо;-2) и (0;2) - спадає;
в) (-<>о;0)и(0;3)-зростає;(З;**)-спадає; г) (0;°°)-спадає;
д) (-оо;2)и(2;оо)-спадає; є) (і;°°)-зростає;(0;1)-спадає;
є) (-°°;-l)u(і;оо}-зростає;(-1;1)-спадає;
ж) (2; ©о) - зростає; (-°°; 2) - спадає;
з) (1; °°) - зростає; (-«>; -0) u (0; 1) - спадає;
и) (-1;©о) - зростає; (-°°; -1) - спадає;
і) (^°°) ~ зростає; (0;1) u (1;е) - спадає;
ї)
V2 V2^
Г
- зростає;
-1:"Т
л/2І ҐЛ
U
л
т;1
- спадає.

§ 4. Застосування диференціального числення до дослідження функцій 131
2.162. а) Упйп = у(0) = 0; у^ = у(2) = у(-2) = 4;
б) Утах = У(-3) = 25;Утіп = у(-1) = -3; в) Утіп = у(-1) = у(1) = 2;
г) ^„^х = у — = —^0,25; при х = 1 екстремуму немає;
\4J 4
Д) ушх=у(0,5) = 20,251/2Л5;уЫп=у(-1) = 0;уЫп=у(5) = 0;
є) Ушп = УФ) = 0; є) у^ = у(0) = 0; Утах = у(2) = 4<Г2;
ж) Утіп = У(-1) = -є"1; з) ущз, = у(е-2) = 4е~2; у^ = у (1) = 0;
и) Угйп = У(0) = і; і) Ушп = y(-D = yd) = 0; у,™ = у(0) = 1;
0 Утіп = УШ = 0. й) утах = у(2) = 1 ;
к) Ушах = У(2) = 0, jw = у(1) = 3 ;
л) Утіп = У(3) =0, Уіоах = у(2) = 3 ; м) Утах = у(2) = 4 ;
2
н) Утіп = У(!) = -J. Утах = У(°) = ° J
е(4-е)
О) Утіп = У(«) = . Утах = У0) = 2,5 ;
п)Утіп=У(0) = 0. Утах=У(-1) = 1 ;
Р)Утах=У(1)=|-|іп2 .
2.163. а) тіпу = у(3) = 18; max у = у(-2) = у(1) = 2;
[-2;3] [-23]
б) тіп у = у(-1) = 2; max у = у(-3) = 66;
[-3;2] [-3;2]
в) тіпу = у(3) = 3-1п27; таху = у(2) = 2-1п8;
[2-А] [2А]
г) гтіп у = у(-12) = 5; max у = у(0) = 13;
[-12;5] f-12;5]
д) тіп у = у(-1) = 3; max у = у(-2) = 5;
[-2;-0,5] [-2;-0,5]
є) гтіп у = у(0) = 0; max у = у(1) = 1-1п2;
[-0,5;1] [-0,5:1]
є) тіпу = у(0) = 0; таху = у(4) = 8;
[0;4] [0;4]

132 Р о з д і л II. Диференціальне числення функцій однієї змінної
ж) min у = у(0) = -1; max у = у (4) = 0,6;
[0;4] [0;4]
з) min у = у(ї) = ІІ2; max у = у(0) = 2;
л
и) miny = y(l) = 0; maxy = y(0) = —.
[0;i] J [0;i] У yK ' 4
2.164.1 і 59. 2.165.4 і 4. 2.166. -.
6
V3'
2.167. Ширина поперечного перерізу x = —j=; висота у = dj—.
2.168. Глибина x = —. 2.169. A = -т=. 2.170. Радіус основи посуди-
2 v2
ни дорівнює висоті А = з/—. 2.171. Квадрат із стороною а = VS.
4 2
2.172. Об'єм циліндра дорівнює —nr Н. 2.173. Об'єм конуса
дорівнює 2уіЗя. 2.174. Радіус півкруга дорівнює висоті
прямоті
кутника h- . 2.175. v = 20 км /год; загальна сума витрат на
яч-4
годину 600 грн.
4.3. Опуклість та увігнутість кривої
Нехай функція y = f(x) диференційовна в кожній точці
інтервалу (а; Ь).
Означення 3. Крива y = f(x) називається опуклою на
інтервалі (а; Ь), якщо всі її точки (х; /(*)), хе (а; Ь) лежать
нижнє довільної дотичної проведеної до кривої в будь-якій точці
цього інтервалу (рис. 2.6, а). Крива y = f(x) називається увігнутою
на інтервалі (я; Ь),якщо всі їїточки (jc; /(*)), хе (a; b), лежать

§ 4. Застосування диференціального числення до дослідження функцій 133
вище довільної дотичної проведеної до кривої в будь-якій точці цього
інтервалу (рис. 2.6, б).
Рис. 2.6
Теорема 5 (достатні умови опуклості чи увігнутості).
Якщо в усіх точках інтервалу (я; Ь) друга похідна /'(*)< 0, то
на цьому інтервалі крива y = f(x) опукла. Якщо в усіх точках
інтервалу (а\ Ь) друга похідна f"(x) > 0, то на цьому інтервалі
крива y = f(x) увігнута.
Означення 4. Точка кривої, яка відокремлює її опуклу
частину від увігнутої, називається точкою перегину.
Теорема 6 (достатні умови, за яких точка кривої є
точкою перегину). Якщо в точці х§ друга похідна f"(x^) = 0 або
не існує і при переході через цю точку f"(x) змінює знак, то
точка кривої (xQ\f(x0)) є точкою перегину.
Дослідити графік функції y-f(x) на опуклість та
увігнутість і знайти точки перегину можна за схемою:
- знайти другу похідну f"(x)\

134 Р о зд і л II. Диференціальне числення функцій однієї змінної
- розв'язати рівняння /'(*) = 0, а також знайти ті точки, в
яких f"(x) не існує;
- дослідити зміну знака похідної f"(x) при переході через
ті точки, в яких /'(jc) = 0 або f"(x) не існує. Якщо при переході
через таку точку f"(x) змінює знак, то ця точка кривої є точкою
перегину, а якщо f"(x) знака не змінює, точка не є точкою
перегину. У точках, де f"(x) > 0, крива увігнута, а в точках, де
f"(x) < 0, крива опукла.
4.4. Асимптоти
Під час побудови графіка функції, область визначення або
множина значень якої є необмеженими, доцільно
використовувати асимптоти графіків.
Означення 5. Пряма І називається асимптотою кривої
У = І (х) у якщо відстань d змінної точки M(jc;/(jc)) кривої від
цієї прямої при необмеженому віддаленні точки М від початку
координат прямує до нуля (рис. 2.7).
У +
о
х
Рис. 2.7

§ 4. Застосування диференціального числення до дослідження функцій 135
Розрізняють вертикальні та похилі (зокрема горизонтальні)
асимптоти.
Якщо хоч би одна з границь lim /(jc) або lim /(jc)
х—>а+0 х->а-0
дорівнює -И» або -оо, то пряма х = а є вертикальною
асимптотою кривої у = /(jc).
Наприклад, графік функції у = має вертикальну асимп-
jc-3
2 2
тоту х = 3 (рис. 2.8), оскільки lim = -н», Цт
*-»з+о jc — З
*->3-ojc-3
Pwc. 2.5
Графік функції може мати довільну кількість вертикальних
асимптот. Наприклад, графік функції у = tgjc має їх нескінченну
кількість:х = ±—, х = ±—, ....
2 2
Теорема 7. Пряма y = kx + b є правою похилою
асимптотою кривої y = f(x) тоді і тільки тоді, коли існують
fix)
скінченні границі k = Urn Щ±9 6= Urn [f(x)-kx] .
Jt-»+°o
JC->+w

136 Р озділІІ. Диференціальне числення функцій однієї змінної
Якщо k= lim , b= lim [/(jc)-fcc] , то пряма
X->-°° X X—»-oo
у = he + b є лівою похилою асимптотою.
Похилих асимптот може бути не більше двох (ліва і права).
4.5. Загальна схема дослідження функцій
Досліджують функції за допомогою похідних і будують їх
графіки за такою схемою:
1. Знаходять область визначення функції. При тому
встановлюють точки розриву та інтервали неперервності функції, а
також вертикальні асимптоти.
2. Досліджують функцію на парність чи непарність, на
періодичність, знаходять точки перетину графіка з осями
координат, а також інтервали знакосталості функції.
3. Знаходять точки екстремумів функції, інтервали
монотонності та екстремальні значення.
4. Знаходять інтервали опуклості і увігнутості графіка,
точки перегину.
5. Знаходять похилі асимптоти графіка функції.
6. Будують графік функції.
Розв'язування типових прикладів
Приклад 1. Знайти точки перегину та дослідити на опук-
2
лість і увігнутість графік функції у = є
Областю визначення цієї функції є вся дійсна вісь
Dy=(-<x>;°o).
Знаходимо першу та другу похідні
у' = -2хе-**9 / = -2е"*2(і-2;с2).

§ 4, Застосування диференціального числення до дослідження функцій 137
Розв'яжемо рівняння У = 0,
1
-2е~х (i-2jc2) = 0=>1-2jc2=0=>*u=±-^.
Зауважимо, що друга похідна у" існує на всій дійсній осі.
Визначимо знак функції у" на кожному з інтервалів
W [~І2 \/2 J' (V2 ;С
. Для цього в кожному із цих
інтервалів візьмемо точку і визначимо знак у в цій точці.
Заповнимо таблицю
X
/(*)
У(х)
h-т)
+
u
і
0
Перегин
1
У"Т
V& я)
-
п
1
0
Перегин
1
У"Т
щ
+
U
У першому рядку таблиці вказані інтервали з граничними
точками, в яких у" = 0 або у" не існує (якщо такі є).
У другому рядку записано знак похідної у" на кожному із
вказаних інтервалів, а також її значення у відповідних точках.
У третьому рядку зображено схематично вигляд графіка
функції на відповідному інтервалі (графік опуклий -п, графік
увігнутий -и), вказано, чи є в "підозрілих" точках перегин, та
обчислено значення функції в цих точках. З таблиці видно, що
точки —
1 1
V2'VJJ І Л'Je~
1
є точками перегину графіка.
Приклад 2. Дослідити на опуклість і увігнутість графік
функції у = v х2 .

138 Р о зд і л II. Диференціальне числення функцій однієї змінної
Область визначення функції - дійсна вісь D = (-«>; -н»).
2 2
Знайдемо похідні / і /, / = —=, / = -=.
Ъ<1х 9х<Іх
Друга похідна не існує в точці х = 0. Складемо відповідну
таблицю
X
/(*)
Уіх)
(-оо; 0)
-
п
jc = 0
Не існує
Перегину немає
(0; +оо)
-
п
Отже, точок перегину немає. Крива опукла на інтервалах
(-оо; 0) и (0; +оо).
Приклад 3. Знайти асимптоти кривої у =
х2 +2х-Ъ
Область визначення функції - D = (-©о; 0) и (0; +°°).
Дослідимо задану функцію в точці дг = 0. Оскільки
jc2+2jc-3 ,. jc2+2*-3
km = +оо, lim = -°0, то пряма * = 0 є
jc—>о-о х *->о+о х
вертикальною асимптотою.
Знайдемо похилі асимптоти
k= lim ±-^-= hm - = 1,
Jt-»-H» X Х-ї+оо
b= lim [f(x)-kx] = lim
^*2 + 2jc-3
X->+°o
-hx
= lim = 2.
*->+« x
Отже, пряма y = x + 2 є правою асимптотою графіка цієї
функції. Аналогічно знаходимо
*2+2jc-3
к= lim
= 1, fe= lim
^jc2+2jc-3
-їх
= 2.

§ 4. Застосування диференціального числення до дослідження функцій 139
Тому пряма у = jc + 2 є також і лівою асимптотою графіка
цієї функції, (рис. 2.9).
у
'/
' /'
>'-2
і\У
2.
/ /
о/і
/У
X
Рис. 2.9
Приклад 4. Знайти асимптоти кривої у =
W-1
Функція визначена на множині
D = {jcetf||*|-l*o] =(-<*>; -1)и(-1; l)u(l; -к»).
Шукаємо вертикальні асимптоти. При х > 0
У = -
2 2
X X
lim - = +оо, lim
jc-1 *-»i+0jc-1 jc->i-0jc-1
Отже, пряма х = 1 є вертикальною асимптотою. Знайдемо
праву похилу асимптоту графіка функції
2 Ґ 2 \
k= lim = 1, b= lim
*-*-Н» x(x -1) JC-^+oo
f 2
JC
~1
-1-jc
= 1.
Отже, пряма y = x + l є правою похилою асимптотою
графіка цієї функції.
х2
При х < 0 ця крива має рівняння у = . Тому
JC + 1
lim = -и»,
lim
*-»-і-о jc +1 *-»-i+o jc +1
і пряма jc = -1 є вертикальною асимптотою.

140 Р о зділІІ. Диференціальне числення функцій однієї змінної
Знайдемо k і b для лівої похилої асимптоти графіка
Л ґ 2 \
k= lim
-JC
=-1, Ъ- lim
*->-«> х{х + 1) *-»-«
д: + 1
+ 1-JC
= 1.
Отже, ліва асимптота має рівняння у = -х +1.
Графік функції у = г-:— зображено на рис. 2.10.
Ы-1
у = -х + 1
y = jc + l
Рис. 2.10
Приклад 5. Дослідити функцію у = 3х-х3 і побудувати її
графік.
Дослідження функції здійснюватимемо за наведеною вище
схемою.
1. Область визначення функції D - (-<»; оо). Точок розриву
немає.
2. Дослідимо функцію /(jc) = 3jc-;c3 на парність. Маємо
/(-jc) = -3jc-(-jc)3 =-3jc + jc3 = -(3jc-jc3) = -/(*).

§ 4. Застосування диференціального числення до дослідження функцій 141
Отже, функція є непарною, а її графік є симетричним
відносно початку координат.
Очевидно, що функція /(jc) = 3jc-jc3 не задовольняє умову
f(x + T) = /Ос), Т > 0. Отже, ця функція не є періодичною.
Знайдемо точки перетину графіка функції з осями
координат. Маємо
)> = 0=>3jc-jc3=0, jc(3-jc2) = 0=>jc2=0, jq=->/3, лг3=л/з.
х = 0=>у = 0.
Отже, графік цієї функції перетинає вісь Ох в точках
хх = -у/З, Xj = 0, *з = V3, а тому інтервалами знакосталості
функції є інтервали: (-оо; ->/з), (->/з^ О), (О; >/з), (73; +<*>).
Вісь <9у графік функції перетинає лише в початку
координат.
3. Знаходимо першу похідну: / = 3 -Зх2. Очевидно, що у'
існує на всій числовій осі, а тому критичними точками будуть
лише ті точки, в яких у = 0:
3-3jc2=0=>3(1-jc2) = 0=>jc1=-1,jc2=1.
Отже, функція має такі інтервали монотонності:
(-o;-l), (-l;l),(l;+oo)-
Заповнимо таблицю
Інтервали
монотонності.
Критичні точки
Знак і значення у
Поведінка функції.
Екстремуми
(-оо; -1)
-
^
jcx =-1
0
min
у = -2
(-і; і)
+
71
*2=1
0
max
у = 2
(і; Н
-
^

142 Р оз д ілІІ. Диференціальне числення функцій однієї змінної
4. Дослідимо графік функції на опуклість і увігнутість та
знайдемо точки перегину. Для цього знайдемо другу похідну.
у" = -6х9 у" = 0 при jc = 0. ^
Складемо таблицю
X
/(*)
У(*)
(-оо;0)
+
U
jc = 0
0
Перегин у = 0
(0;+~)
-
п
5. Оскільки ця функція неперервна на всій осі, то
вертикальних асимптот немає.
Знайдемо праву похилу асимптоту
*= lim £&= lim £fLJL= Цщ (з-*2) = -~.
Отже, правої похилої асимптоти графік не має. Оскільки
графік функції симетричний відносно початку координат, то і
лівої похилої асимптоти він не має.
Рис. 2.11
6. Будуємо графік функції (рис. 2.11).

§ 4. Застосування диференціального числення до дослідження функцій 143
Приклад 6. Дослідити функцію у = ех і побудувати її графік.
1. Область визначення - D = (-«>; 0) и (0; +°°); точка
розриву функції х = 0.
2. Функція ні парна, ні непарна. Вона не періодична і не
j_
перетинає осі Ох, оскільки ех * 0. Точка х = 0 не належить
області визначення функції. Тому графік функції не перетинає
j_
вісь Оу. При довільному хФО маємо ех >0. Отже, функція
приймає тільки додатні значення.
j_
ех
3. Знайдемо критичні точки функції, у -—-. Оскільки в
х
області визначення у *0 критичних точок немає. Хоч / = оо
при jc = 0, однак ця точка не є критичною, оскільки вона не
належить області визначення. Похідна /<0, для \/хе D Тому
фукція спадає на інтервалах (-«>; 0), (0; <»).
( \\
-pX,
ел
4. Знайдемо другу похідну, у' =
х
Розв'язавши рівняння У = 0, маємо
—Ц ^ = 0=>1 + 2jc = 0=>jc =—.
jc4 2
Заповнимо таблицю
_ех(і + 2х)
jc
/(*)
Я*)
Ь-3
-
п
1
2
0
Перегин
(-Н
+
U
(0; «о)
+
U

144 РозділІІ. Диференціальне числення функцій однієї змінної
5. Знайдемо асимптоти графіка функції
lim ех = 0, lim ех = -н»,
х->0-0 х->0+0
k= lim — = 0, b= lim [f(x)-kx] = ]imex =1.
0
Pwc. 2.12
Отже, пряма jc = 0 є вертикальною асимптотою, а пряма
у = 1 є одночасно лівою і правою горизонтальною асимптотою.
6. Будуємо графік функції (рис. 2.12).
Задачі для самостійного розв'язування
2.177. Дослідити на опуклість та увігнутість і знайти точки
перегину таких кривих:
a) у = х3-6х2 + 2х + 10; б) у = х4 -6х2 +2; в) у = 2-%х-3;
X X
т) у = — ; д) у = хех; є) y = arctg*-A;; є) у = — ;
лГ+1 JT+12
із
ж) у = (1 + х2)ех; з) )/ = (jc-4)5+4jc + 4; и) у = (х-ї)1 .

§ 4. Застосування диференціального числення до дослідження функцій 145
2.178. Знайти асимптоти графіків функцій:
їх 1 х3
а)у = -; б)у = х + -; в) у = -; г) у = х2е~х;
х + 2 х 3-х
Д) У
х2-2х + Ъ ч In2* „ ч зП 7Т
= ; є) у = Зх; є) у = ух -6х ;
х + 2
ж) )> = ;carctg;<:; з) у = ух2-1; и) у =
х2+1
1 г і
і) ;y = 2jc + arctg—; ї) ;y = jce*; й) y = xln\е + — | .
2.179. Дослідити функції і побудувати їх графіки:
а) у=-х3-4х\ б) у = (*-1)2(х + 2); в) У = ^^;
З jcz+1
1 х3 4
г)у = ^—; д)у = -—; є) >; = * +—;
jc-1 jc -4 jc
є) У = *—т; ж) ;у = л:е 2 ; з) у = х3е~3х\
х
и) y = jc-ln(jc + l); і) у = у]1-х3; ї) y = yfx + ^4-x;
Й) у = хе~х\ к) у = (2 + х2)е'х1; л) у = уі6х2-х3.
Відповіді
2.177. а) (-°°;2) -інтервал опуклості, (2;°°)- інтервал увігнутості,
(2; -2) - точка перегину;
б) (-оо; 1), (1; ©о) - інтервали увігнутості, (-1;1) - інтервал
опуклості, (-1;-3) і (1;-3)- точки перегину;
в) (-°°;3) - інтервал опуклості, (3; «>) - інтервал увігнутості,
(3; 2) - точка перегину;

146 Р озділІІ. Диференціальне числення функцій однієї змінної
г) (-оо; -у/з)9 (0; л/з) - інтервали опуклості, (-v3;0j, (v3;°°] - ін-
( «lb] ( >ІЬ\
тервапиувігнутості, -V3; , (0;0), V3;— -точкиперегину;
V 4 ) V 4 )
Д) (-°°;-2) - інтервал опуклості, (-2;°°) - інтервал увігнутості,
-2; —j" " точка перегину;
є) (-«>;0) - інтервал опуклості, (0;«>) - інтервал увігнутості,
(0;0) - точка перегину;
є) (-°°;-6),(0;6) - інтервали опуклості, (-6;0),(6,<^) - інтервали
увігнутості, (-6;-4,5), (0;0), (6; 4,5) - точки перегину;
ж) (-°°;-3), (-1;°°) - інтервали опуклості, (-3;-1) - інтервал
увігнутості, (-3;10е~3), (-ї92е~~1) - точки перегину;
з) (-°°;4) - інтервал опуклості, (4;«>) - інтервал увігнутості,
(4; 20) - точка перегину;
и) (-°°;1) - інтервал опуклості, (1;°°) - інтервал увігнутості, (1;0) -
точка перегину.
2.178. а) х = -2 - вертикальна асимптота, у = 2 - горизонтальна
асимптоти;
б) jc = 0 - вертикальна асимптота, у = х - ліва і права похилі
асимптоти;
в) jc = -v3 і jc = v3 - вертикальні асимптоти, у = -х - ліва і
права похилі асимптоти;
г) у = 0 - горизонтальна асимптота;
д) х = -2 - вертикальна асимптота, у = х - 4 - ліва і права похилі
асимптоти;
є) х = 0 - вертикальна асимптота, )> = -3jc - права похила асимптота;
є) у = х - 6 - ліва і права похилі асимптоти;
ж) у = — jc-1 - права похила асимптота, у-—х-\ - ліва
похила асимптота;
з) у = -х - ліва похила асимптота, у = х- права похила асимптота;

§ 4. Застосування диференціального числення до дослідження функцій 147
и) jc = -1 і jc = 1 - вертикальні асимптоти, у = -х - ліва похила
асимптота, у = х - права похила асимптота.
і) у = 2jc+ права похила асимптота, у = 2jc ліва похила
асимптота;
ї) y = jc + l - похила асимптота, jc = 0 - права вертикальна
асимптота;
1 1 . .
и) х = права вертикальна асимптота, у = х + ліва і права
похила асимптота.
2.179. а) Функція визначена на (-00;00). Точка максимуму -
-2;— ;(-°о;0) - інтервал опуклості; (0;°°) - інтервал
увігнутості ; (0;0) - точка перегину;
б) функція визначена на (—«э;00). (—1;4) - точка максимуму;
(1;0) - точка мінімуму; (0;2) - точка перегину; (-°°;0) -
інтервал опуклості; (0;©°) - інтервал увігнутості;
в) функція визначена на (-00;00). (1;0,5) - точка максимуму;
(—1;—0,5) - точка мінімуму; jc = -v3,jc = 0,jc = v3 - точки
перегину; f—оо;—д/31 і f 0;v3J - інтервали опуклості; і (v3;°°) -
інтервали увігнутості; у = 0 - асимптота;
г) функція визначена на (-°°;-1),(-1;1),(1;°°). (0;-1) - точка
максимуму; (-©о;—і) і (1;°°) - інтервали увігнутості; (—1; 1) -
інтервал опуклості; jc = 1, jc = -1, у = 0 - асимптоти;
д) функція визначена на (-~;-2),(-2;2),(2;«>). (-2>/3;-3>/з) -
точка максимуму; - точка мінімуму; (0;0) - точка
перегину; (-°°;0) - інтервал опуклості; (0;°°) - інтервал
увігнутості; х = 2, х = -2, у = х - асимптоти;

148 РозділІІ. Диференціальне числення функцій однієї змінної
є) функція визначена на (-°°;0),(0;«>). (2;3) - точка мінімуму;
точок перегину немає; у = х, х = 0 - асимптоти;
є) функція визначена на (-оо;0),(0;оо). (-°°;0),(0;°о). (-2;-2,5)-
точка максимуму; точок перегину немає; х = 0 і у = х - асимптоти;
ж) функція визначена на (-о0;*»). (-1;-е~°'5) точка мінімуму;
її,є '5J - точки максимуму; jc = 0,jc = -v3,jc = v3 - точки
перегину; у = 0 - асимптота;
з) функція визначена на (-^°;°°). (1;г~3) - точка максимуму;
п Л 7з . л&
jc = 0,jc = 1 і jc = 1 + точки перегину; у = 0 -асимптота;
и) функція визначена на (-1;°°). (0;0) - точка мінімуму; крива
увігнута скрізь; х = -1 - асимптота;
і) функція визначена на (-«>; ©о ). Екстремумів немає; (-°°;0) і
(1;°°) - інтервали увігнутості; (0;1) - інтервал опуклості; (0;1) і
(1;0) - точки перегину; у = -х - асимптота;
ї) функція визначена на [0; 4], (2; 2V21 - точка максимуму;
й) функція визначена на (-00;00) , (і^1) - точка максимуму;
(2; 2е~2] - точка перегину; у = 0 - асимптота;
к) функція визначена на (-00;00). (0;2) - точка максимуму;
(-1; Зе"1) і (1; Зе'1) - точки перегину;
л) функція визначена на (-<»; -и»); (0; 0) - точка мінімуму;
(4; 2л/4] - точка максимуму; (6; 0) - точка перегину; (-<»; 0) і
(0; 6) - інтервали опуклості; (6; -н») - інтервал увігнутості;
у = -х + 2 -асимптота.

Розділ III
НЕВИЗНАЧЕНИЙ ІНТЕГРАЛ

150
Розділ III. Невизначений інтеграл
§ 1. БЕЗПОСЕРЕДНЄ ІНТЕГРУВАННЯ
1.1. Основні поняття
Означення 1. Функція F(x) називається первісною функції
f(x) на інтервалі (а;Ь), якщо F'(x) = f(x), або dF(x) = f(x)dx
для всіх хе (а;Ь).
При цьому функції f(x) на інтервалі (а;Ь) існує безліч
первісних. Всі вони відрізняються одна від одної лише сталим доданком,
тобто
0(jc) = F(jc) + C, де ФО), F(x) -первісні, С = const.
Означення 2. Сукупність усіх первісних функції f(x)
називається її невизначеним інтегралом і позначається \f(x)dx.
Записують \f(x)dx = F(x) + C, де J - знак інтеграла,
f(x) - підінтегральна функція, f(x)dx - підінтегральний вираз,
х - змінна інтегрування. Знаходження невизначеного інтеграла
функції f(x) називається інтегруванням функції. Інтегрування є
дією, оберненою до диференціювання. Якщо функція f(x)
неперервна на інтервалі (а;Ь), то вона інтегровна на цьому
відрізку.
1.2. Основні властивості невизначеного інтеграла
1. ({/(*№))' = /(*).
2. d[ jf(x)dx) = f(x)dx.
3. jdF(x) = F(x) + C.

§ 1. Безпосереднє інтегрування
151
4. \kf{x)dx = к \f{x)dx, де к = const.
5. \[Мх)±/2(х)]с1х= jf^dxl jf2(x)dx.
6. Якщо \f{x)dx = F(x) + С , то:
а) \f(ax + b)dx =—F(ax + b) + C, зокрема,
J a
якщо b=0, то \f(ax)dx = — F(ax) + C,
J a
якщоа=1,то \f(x + b)dx = F(x + b) + C.
б) jf{<p(x))(p'(x)dx = F(<p(x)) + C.
1.3. Таблиця основних інтегралів
1. Г^ = ^_ + С) (a*-l). 8. f_^- = Iarctg- + C.
J a + 1 jjc z+a a a
rdx 1 _ 0 r dk _
la. — =— + C. 8a. - = arctgjc + C.
Jxz x j1 + jT
f4 = -I + C. 8a. f-A
•<& Л г- „ „ с dx 1
16. f« =2^ + С. 9. f^L* In
JV^ V-д2 2я
jc-a
х + а
+ C.
^,ii^ *Л Г dx . x
2. J— = ln|jc| + C. 10. J-
/~~2 J
dx
= arcsin — + C.
3. \axdx-^— + C. 10a. f . =arcsinjc + C.
J In a JVJT7
(a>0, афі).
3*.[exdx = ex+C. 11. f , *** =lnljc + Vjc2±fl2
J J /2.2
yjx ±a '
4. Jsinjc^: = -cosjc + C. 12. Jsh*dk = ch.x + C.
+ C.

152
Розділ III. Невизначений інтеграл
5. jcosjftic = sinjc + C.
dx _
4:
cos2jc
—T- = -ctgx + C.
sin JC
13. fchjc^c = shjc + C
14. f-*
'ch2jc
15. J-
sh2jc
= thjt+C.
= -cthjc + C.
1.4. Безпосереднє інтегрування
Безпосереднє інтегрування - це інтегрування з
використанням властивостей 1-6 невизначеного інтеграла, тотожних
перетворень підінтегральної функції та таблиці основних інтегралів (1.3).
dx
Приклад 1. Знайти інтеграл [ ,—
W9-
25jcz
Використовуючи властивість 4 і табличний інтеграл 10,
одержимо
dx
'4.
9-25*'
-f
dx
КїИ
=u
dx
з^2
1 • 5x _
■ =—arcsin— + C.
5 3
-jc
Приклад 2. Знайти інтеграл
Перетворимо підінтегральний вираз
7 і
Тоді на основі властивості 5 та табличного інтеграла 1, ма-
5 J_
г2
ємо
( 1
іїл/* + і) Jxdx= Л х6 +2х6 +х
5 Л
г2
У
*£с =—*6 +—j;6 +-х2+С.
13 11 з

§ 1. Безпосереднє інтегрування
153
Приклад 3. Знайти інтеграл [— j.
JJT+jc4
Додаючи та віднімаючи в чисельнику підінтегральної функ-
ції х , отримаємо (згідно з властивістю 5 та табличними
інтегралами 1а і 8а)
г dx _fl + *2-*2,_f l + x2 __ г x2
J777= J7(IT7y J7(I^) Щї7)'
-йЬс =
r^ic f dk 1 _
= T" 5" = arctg* + C.
Jjr j1 + jT x
Приклад 4. Знайти інтеграл f
Перетворимо підінтегральну функцію
dx.
2*_1+3*+1_2_1-2*+3-3*_l 2* з3""-1
6х ~ 6х ~2вх+ \х~ 2
fiY
- +3-
riY
<2j '
Згідно з властивостями 4, 5 та табличним інтегралом 3,
одержимо
flY flY
J 6* 2JUJ JUJ 21ni lni
3 2
3-* л 2-д:
=--—^-^+c.
21n3 ln2
„ , „ ■„ . rl + 2sin2x ,
Приклад 5. Знайти інтеграл f dx.
J 1 + cos2jc
Використовуючи формули 1 + cos 2x = 2 cos x,
sin2jc = l-cos2x властивості 4, 5 та табличний інтеграл 6,
знайдемо
rl + 2sinzjc , fl + 2sin2^:J 1 г
-dx = — -
? J,
J 1 + cos2jc j
2cos2 jc
(ic rsin2jc ,
+ -r-dx-
2 J cos2 jc J cos2 x

154
Розділ III. Невизначений інтеграл
1 г dx rl-cos x , 3 r dx
і r ax cl - cos x , з r ax r, 5 „
= -I — + I - dx=- I г <£c = -tg;c-Jc + C.
2 J cos x J cos jc 2 J cos jc J 2
Задачі для самостійного розв'язування
"■ м
У задачах 3.1-3.45 знайти невизначені інтеграли:
, JC" JCVJC
3.3. Nxyjxyfxdx.
+ —t= + 2 \dx.
3.5. J-
dx
УІЗх2-2
3.7. sinjc-
VT
Ax1
3.9. IU2+^
etc.
3.11. J5x~lexdx.
3.13. J(3*-2)(3"*+2)dr.
Д25. f+4x + 2dx.
3.17. J-
2л:
з-2*-2-зЛ
dx.
e2x-A
U9. p_J:
dx.
Ul-2x + x2
4vi^
<&.
3.2. | yyl^—r + . —
dy.
dx
ЯА. f- , .
J16;c2-9
d!x
Ш\
VT
5*z
<&. 3.8. jV?(5%/?-lW.
3.10. p =-^-<fe.
3.12. |(ел-е_д:)2^д;.
3.14. f(3ctg.x:-l)(3tg;<: + l)d!x.
зле. f2-^17
^
dx.
3.18. J-
лЛ+1 _ cX-\
10*
e3*+l
<&.
(ІХ.
3.20. P-^i
V4-JC4

§ 1. Безпосереднє інтегрування
155
3.23. j^J^dx.
х2+4
•x4dx
V+1
3.27. l^^-dx.
}х2-1
3.29. Й±^ .
J л:2(1 + д;2)
3.31. [sin xdx.
3.33. Jsin3^-sin5^dbc.
3.35. [cos л; sin Зх (it.
3.37. f(tg2 лг + tg4 x)dx.
3.39. f-*_.
J1-C0SJC
3.41. j- л
' sm2 jccos2 JC
3.43. Г-^
Jsin jc + cos2jc
3.45. f- C0S2X
cos2jc-sin2;t
dk.
rvl + jc2 + vl - x2
3.24. у , ^ dx.
УІЇ^?
3 + jc
3.26. Лс.
J3-jc
3.28. f»ff£
J jc2+1
<£t.
І1ТЛ
».30. fi- L_<fo.
jjc(1 + jc2
c(l + ;t2)'
3.32. Jcos2jc^c.
3.34. Jcos2jccos3jc^c .
3.36. \ctg2xdx.
3.38. J(2tgjc + 3ctgjc)2rfjc.
3.40. Г—
•>1 +
1-COSJC
dx.
.42. fll
•4 +
3.44. f
COSJC
1 + cos2 X
cos2jc
dx.
cos x + 3cosjt-2
cos2jc
d*.
1 8
3.1. j= + 2x + C.
x V*
3.3. — xtf7 + C.
15
Відповіді
5 y + 2
3.4. —In
24
Ах-Ъ
4х + Ъ
+ C.

156
Розділ III. Невизначений інтеграл
3.5. -т=1п
х + Лх
+ С. 3.6. —т= arcsin х + С.
n/5
З ЗО ^ 2 *
3.7.—arcsin дг- cos х + С. 3.8.—д:6 —х2+С.
2 19 5
3.9. — + -х2^ + З^/л7 + С
5 4
3.10.
3.11.
2т+-
X 2
1 "
2т + -
2
іК
1
т+п+—
X 2
m + n + —
2
•+С.
2л+-
X 2
+—г
2п + -
2
3.12
+ с.
(е2х-е-2х)-2х + С.
51п5 + 1 2^ /
3.13. (3*+3"*)-Зл- + С. 3.14. 8x + 31n|sin2;t| + C.
х2
3.15. — + 2* + In Ы + С 3.16. 2 arcsin л- - х + С
4 ' '
3.17. Зя-2'(1,5)*+С.
In 1,5
3.19. ех-2х + С.
3.18.
1п5І5
v і (\ у
51п2
+ С.
3.20. -e2*-e*+x + C.
2
3.21.--^/(і-^+С.
3.22. In
: + V2 + :
+ arcsin —рг + С.
72
* + V.*2+4
3.23. In
3.24. arcsin л: + In
- 3arctg- + C.
* +
Vl+~
+ С. 3.25. л: + arctg х + С.
3.26. -лг-61п|3-д:| + С.
3.27. х+ 2 In
*-l
д: + 1
+ С.
3.28. л- + 1п(л:2+1) + С.
3.29. arctg л- — + С.
Л"

§ /. Безпосереднє інтегрування
157
3.30. \n\x\ + 2axctgx + C.
3.32.± + ^+С.
2 4
3.34. —sin5x +—sinx + C.
10 2
3.36. -*-ctg.x + C.
л: 1
3.31. sin 2* +С.
2 4
3.33. — sin 2* sin 8* + С.
4 16
3.35. —cos4x—cos 2* +С.
8 4
1 і
3.37. -tg^x + C.
3 6
3.38. 4tg*-9ctg.x-.*: + C.
3.39. C-ctg-.
2
3.40. 2Щ--Х + С.
*2
3.41. tgx-ctgx + C.
3.42. -(tgJc + Jc) + C.
3
3.44. jc +—In
2
1 + sin X
1 - sin X
3.43. tgjc + C.
-2tgJc + C. 3.45. C-ctgjc- tgx

158
Розділ III. Невизначений інтеграл
§ 2. ІНТЕГРУВАННЯ ЗА ДОПОМОГОЮ
ЗАМІНИ ЗМІННОЇ АБО ПІДСТАНОВКИ
В основі інтегрування за допомогою заміни змінної лежить
перехід від змінної х до змінної t за допомогою співвідношення
x = <p(t), dx = cp'(t)dt9 тобто
jf(x)dx=jf(<p(t))<p'(t)dt. (3.1)
Функцію х = cp{t) треба так вибрати, щоб невизначений
інтеграл в правій частині (3.1) можна було звести до табличного.
В остаточному результаті треба повернутись до змінної
х згідно із формулою t = (p~l(x), де (р~1{х) - функція,
обернена до <p(t).
Приклад 1. Знайти інтеграл [ -—.
Jjc(9 + ln2jc)
Зробимо заміну х = є*, t = In х. Тоді dx = exdt,
г dx с e*dt r dt 1 t _
z—= ;r-= r- = -arctg- + C.
j49 + ln2jc) V(9 + f2) J9 + t2 З 3
Залишається лише повернутись до змінної jc, підставляючи In х
замість t
с dx 1 lnjc _
—=-arctg + C .
Jjc(9 + ln2jc) З 3
Формулу (3.1) можна використати і в зворотному порядку.
Нехай треба знайти інтеграл вигляду \f{(p{x))(pXx)dx. Внесемо в
цьому інтегралі множник (р\х) під знак диференціала,
(p\x)dx = dcp(x), та зробимо підстановку t = <р(х),
\f{(p{x))(p\x)dx = \f((p(x))d((p(x)) = \f{t)dt. (3.2)

§ 2. Інтегрування за допомогою заміни змінної або підстановки 159
Такий спосіб перетворення підінтегрального виразу
називають внесенням під знак диференціала.
Приклад 1 можна розв'язати також способом внесення під
знак диференціала,
Jjc(9 + ln2jc) j9 + ln2jc* j9 + ln2jc J9 + t2
1 t „ 1 hue „
= -arctg- + С = -arctg + С.
3 53 3 5 3
Тут, очевидно, In X = t.
При достатніх навичках саму підстановку можна не
виписувати, а відразу переходити до результату
—7 ^г= ^—rf (In jc) =-arctg + C.
J*(9 + ln2;c) J9 + ln2* V ; З 3
Корисну інформацію, що спрощує відшукання вдалої
підстановки, можна знайти в табл. 1.
Приклад 2. Знайти інтеграл \43х+1 dx.
Вносячи вираз Ъх+l під знак диференціала, знайдемо
і л3*+7
f43*+7dx=- №х+1 d(3x+i)=-—+с.
J З J у ' 31n4
Приклад 3. Знайти інтеграл |3sin хsinlxdx.
Показник sin х функції 3sin х замінимо новою змінною t. Тоді
,2V г оіп2,
J3sin xsin2xdx = J3sin *2sinjccosjc<£t =
r = sin JC
df = 2sinjccosjc<£c|
. 2
o/ osin JC
= Гз'л=—+c=-—+c.
J ІпЗ ІпЗ

160
Розділ III. Невизначений інтеграл
К
cq
«
к
BQ
PC
Внесення під знак
диференціала
s
g
є
е-
S
X
m
^» СО
4з
43
II
1
II
Н
с-)
-
СП
СП
-|т
СП
-н|т
II
Н
•**
II
СП
X
•3
-Л-
(N
N У
43
1
43
1
II
и
-1 н
Ґ "N
со
s
43
II
II
4f
"Г
ж
II
•81 x
и
H
4lH\
«o
"*4
.s
.s
'go
43
II
СЛ
О
О
II
X
.3
■3
ХЛ
°
•3
40
о
о
О
р.
1
о
43
1
II
•S
и
*
О
.3
'ел
о
О
к

§ 2. Інтегрування за допомогою заміни змінної або підстановки 161
03
5
0>
н
.5
ч
«
2
я
cq
Я
CQ
s*
оЗ
Я 03
со к
ч .2
•в 5
Внесення
дифереї
оЗ
*
CQ
03
ЕС
й
03
.5
к
PQ
,©! и
1?
£р
*
""к4
1
■3
5
3
1
<N
ел
о
о
II
х
•8
<N
ел
о
+-*" 1
.*>->
00
К
о
^
-4-*
^
1
тг
с
1
•8
J,
3
1
X
.S
'ел
II
X
О
•8
.s
*ел
о 1
.^
ON
"—^
1 ^
^
II
•3
>->
Ъ)
II
^
^
•8
^ ^
.^
о
"a
4^
1 s
чз
1
I
Q
***
II
Q
^ q^
,^
-
^
ЭД
+^
1
^
S3
^
I
43
II
l<N
•3
X
+
"***
II
•8
>
с
•4-
X
+
>
H I
Oj і
^
<N
^
•S
'ел
p
^
4S
*
.£
'ел
о
J,
X
"ел
2
^52-
4s
II
1 ^
%
1
^*
-^
II
к
.S
СЛ
p
1-І
03
*e7
<N
X
1
Г
H
>
o3
4^
m
^
+
^
^
•fi
"к4
^3
1
Гк4
£=^
J2,
^3
II
^
4
II
^
^
*
ЧЦ
^
ТҐ

162
Розділ III. Невизначений інтеграл
Приклад 4. Знайти інтеграл Г-
dx
Знаменник дробу замінимо новою змінною t\
\
dx
ліЗ + і
і = уІЗ + ех; 3 + ex=t2; ex=t2-3\
ltdt
t dt
-^т^к-.-ч
exdx = 2tdf, dx =
dt
t2-3
(t2-3)t V-f^f 2^
*-V3
t +
S
+c=
= —In
3
7з + е*-л/3
л/з + ^+л/з
/г (уіЗ + єх -л/з)
3 + е*-3
3 e* 3 \ /3
r \/2x — 3dx
Приклад 5. Знайти інтеграл —== .
J^/2;c-3+ 1
Підінтегральний вираз є раціональною функцією від змінної
уі2х-3. Тому приймемо 2д:-3 = ґ6, звідки dx- 3t5dt ;
%2x-3=t2 ; >/2д:-3=ґ3.Отже,
ry/2x-3dx c3tsdt j,6 4 2 ^ч, ^ С dt
\тг——= b = 3f(r6-r4+r-1)^ + 3 [ - =
f7 f5 f3
= 3 3—+ 3 3f + 3arctgf + C.
7 5 3 5
Повертаючись до змінної jc, одержимо
7 5
rj2x-3dx 3(2*-З)6 3(2*-З)6 „ ^ „„ „Jj
L „ = ' + (2*-3)2 -3(2*-3)6 +
j^/2jc-3 + 1 7 5

§ 2. Інтегрування за допомогою заміни змінної або підстановки 163
+3arctg(2jc-3)6 +С\
2.x і
Приклад 6. Знайти інтеграл [ .
Jex +1
Застосуємо заміну змінної,
„2*
V+1
t = ex; x = lnt
dt
dx = —
t
- f {2dt [tdt - f(i±£lzi-
~ h(\+t)~ n+t~' i+t
= jdt-j^ll!l=t-ln\l + t\ + C =ex-\n(l + ex) + C.
Задачі для самостійного розв'язування
У задачах 3.46-3.90 знайти вказані інтеграли:
(х + l)dx
3.46. [л/З + xdx.
e(x-l)dx
3.48. р, і—
Чіх-х2
3.50. J2x(x2+l)4dx.
3.52. jx-5~x2dx.
3.54. j2^+1x4rfr.
3.56. J
exdx
уії-е
2*
3.58. JTctge*)^.
3.47. f-^liSi
Jx2 + 2x+:
z+4x+3,
xdx
3.49. Jejr+J,x"(jc + 2)<k
$.51. f-^L
V+l
і
3.53. I—^-dx.
3.55. J-
exdx
ee2xdx
3'57' f-f—5Г •
32 + e2x
3.59. d*+±*dx.

164
Розділ III. Невизначений інтеграл
3.60. J-
dx
л/9-In2
2x
S.62. \x\lx
+ ldx.
3.64. f Tdx.
J16 + *4
1
3.66. j(3-4sinjc)3 cosxdx.
3.68. —— dx.
Jshr x
3.70. jctgjcdk.
3.72. J- Л
2 • 2
X sin I -
3.74. f
3.76. f-*
3ctg2*-l
cos2 л:
<£t.
jclnjc
3.78. рЕЁ£& .
J X
3.8О. |±^-&.
jjc + cos*
3.82. fcos2 sin— cos—dx.
J I 2) 2
3.84. p
rarccos x
dx .
3.61. j(l-;c) xdx.
3.63. p-^
x2-e^+l
3.65. J
л: dx
Я77Ї
dx.
3.67. J cos8 xsinxdx .
„ ^л с cosxdx
3.69. .
J2sin;c + 3
3.71. \x• cos(;c2 + l)dx.
dx
J.73. f-
J7i
Vtg5*-sin2jc
<£t
3.75. J I^-T-.
J 25cos ;c + 9sinz;c
3.77. J- Л
3.79. J-
Wl-ln2*
sin(lgx)
<£t.
3.81. f;tfg(;c2-5W
3.83. J-
dx
VI - x2 arcsin л:
arctg л:
3.85. №&.

§ 2. Інтегрування за допомогою заміни змінної або підстановки 165
5.86. \——
J х2+1
dx
(x2+l)Jaictgx + l
3.88. f_*
J Х + у/х
3.90. f—^Ц-Л.
J(3-*)?
3.87. J-
3.89. J-
4х^г
e3xdx
rdx.
3.46. -^(3 + xf +C.
3.48. -^2x-x2 +C.
3.50. i(*2+l)5+C.
5
Відповіді
3.47. -1п(л:2+2;с + з) + С.
3.49. {Lex2+4x+3+C.
h
3.51.-ln(x2+l) + C.
3.52.
3.54.
3.56.
1 r2
— -5~x +C
21n5
0x5+l
+ C.
51n2
arcsine* + С
3.58. In
sine
+ C.
. In 2*
3.60. arcsm—!—*- + C.
3
3.62. -Mx2+lf +C.
7tx
3.53.--— + C.
2ІПЯ-
3.55.
■ + C.
l-ex
3.57.-ln(2 + e2jc) + C.
3.59. 2y[^+^- + C.
2
10100
3.63. -e^l+C.
3

166
Розд і л III. Невизначений інтеграл
1 хА
3.64. -arctg—+C.
8 & 4
З і
3.66. (3-4sinx)3 +C.
16V '
3.68. — + C.
sin*
3.70. ln|sinx| + C.
3.72. ctg
fi'l+c.
3.74. -3ctg;c-tg;c + C.
3.76. ln|lnjc| + C.
3.78. -yl(l + ]nx)3 +C.
3.80. ln|x+ cos;c| + C.
3.82. sin—+ - sin 2sin- | + C.
2 2^2,
1 -
3.84. —arccos jc + C.
3
3.86. 2yJaictgx + l + C.
3.88. 21n(V*+l) + C.
3.65. -In
3
■^
дґ+Vx +1
+ C.
3.67. -cos9x + C.
9
3.69. -ln(2sin;c + 3) + C.
3.71. -sin(x2+l) + C.
2
7 -
3.73. ctg7 x + C.
12 6
3.75. —arctg ^ + С
15 6 5
3.77. arcsin(lnx) + C
3.79. -In 10 cos(lgx) + C.
(д;2-5) l + C.
3.83. ln|arcsinx| + C.
3.81. --In
2
cos
1 9
3.85. -arctg^x + C.
3.87. e^3+C.

§ 3. Інтегрування виразів, що містять квадратний тричлен 167
§ 3. ІНТЕГРУВАННЯ ВИРАЗІВ,
ЩО МІСТЯТЬ КВАДРАТНИЙ ТРИЧЛЕН
3.1. Інтеграли вигляду
_ Г dx __ f dx
1 " J 2 ' У2 - J / - = •
Jax + fo + c 4ax2+bx + c
Такі інтеграли зводяться до табличних інтегралів 8-11 за
допомогою виділення повного квадрата з квадратного тричлена
(ґ и \* . ul \
2 , І 2 Ь С ,
ЬГ с bz
х + — +
2а J а 4а2
Застосовуючи це при обчисленні інтегралів Іх та /2,
матимемо:
dx
Jax +bx + c a J>
ЪЛ2 с Ъ2
х+— + —-
2а J а 4а2
с Ъ2 л с Ъ2 у2 с Ъ2
>0 позначимо т = ''
« 4а2
l2
При ->0 позначимо - = k , при 7<^ відпо-
я 4а2 а 4а2 а 4а1
відно = -к2 . Причому знак плюс або мінус береться залеж-
а 4сГ
но від того, чи вираз буде додатним чи від'ємним, тобто чи
а 4сГ
будуть корені квадратного тричлена ах + Ъх + с дійсними чи
ROMAIC
лексними. Зробивши заміну х + — = t\ dx = dt, одержимо
2а
1 г dt - Т 1 г dt . . с b2
I\ =— К т або /і =— \-z залежно від знака різниці -.
а^2+к2 ah2-k2 а 4а2
Далі необхідно скористатись табличними інтегралами 8 або 9.

168
Розділ III. Невизначений інтеграл
Виконуючи подібні дії при обчисленні інтеграла /2 , матимемо
dx r dx
w
yjax +bx + (
■=\-
(
b)2 с b2^
x + — I + —
\-Jr=ia6ozn\-
2a
dt
J
Ja \lt2+k2 Ja~4t2-k2
1 r dt
a 4a
при a > 0,
]4i^?
при a<0.
Отже, цей інтеграл зводиться до табличних інтегралів 10
або 11.
dx
2
Приклад 1. Знайти інтеграл Г-
jl5-9xL-6x
У знаменнику дробу виділимо повний квадрат:
15-9jc2-6jc = -(9jc2 +6jc-15) = -((3jc)2+2-3* + 1-1б) =
= -(3;с + 1)2+16=16-(3* + 1)2.
Отже,
dx
-\
dx
1 r d(3x + l)
15-9x2-6x J16-(3x + lf 3J42-(3x + l)
-ІУ
1 *,
= In
3 8
(3* + l) + 4
(3* + l)-4
+ C=—In
24
3* + 5
Здг-3
+ C.
dx
I-
г ax
Приклад 2. Знайти інтеграл -====.
V3 + 2jc-jc2
Виділимо повний квадрат у знаменнику дробу
3 + 2х-х2=-((х2-2х + ї)-4)) = 4-(х-ї)
Тоді
dx с dx с d(x-l)
-і
УІЗ + 2х-х2 3уІ4-(х-1)2 1^22-(х-1)
■f
• х-1 _
= arcsin + С.

§ 3. Інтегрування виразів, що містять квадратний тричлен 169
3.2. Інтеграли вигляду
г Ах + В , _ г Ах + В
І3 = J—J— <&, /4 = |-т== •<& •
Jax +bx + c \Jax2+bx + c
зводяться до попередніх інтегралів ІХ,І2 виділенням у
чисельнику дробу похідної від квадратного тричлена, що міститься в
знаменнику. Дійсно
Ах + В
(2ах + Ь)— +
2а
В
ах +Ьх + с
_АЬ)
~-^1ах =
J ах + bx + с J
_ A rd(ax2 +bx + c) ( Ab\ r dx
2a* ax2+bx + c V 2a)*ax2+bx + c
= —In
2a
ax +bx + c\
2a
LN A (D Ab\
(2ax + b)—+ В
= j a*+b ..- j OL-L-bd*.
4
ax* +bx + c
A rd(ax +bx + c)
V
dx =
ax +bx + c
On і
Ab
-£J-
2a \lax2+bx + c v 2aJ Jax2+bx + c
dx
= —yjax2 +bx + c+\ B-
a {
АЬЛ
2a J
h-
Приклад 3. Знайти інтеграл J-
(x + 2)dx
]х2-4х + \Ъ
Розкладемо чисельник дробу на суму двох доданків так,
щоб один з них містив похідну від знаменника. Враховуючи, що
d(x2 - 4х +13) = (2х - 4)dx , матимемо
. -(2*-4) + 4
l-Y^—^lh
jjc2 -4^ + 13 J x2 -4;c + 13
dx =

170
Розділ III. Невизначений інтеграл
1 г(2*-4) dx
■'J
+ 4
2V-4X + 13 J;c2-4;c + 13
J-
etc
1 rd(x2-4x + l3)
d(x-2)
_ і rfl(x -4X + 13) r акх-і)
~2J x2-4x + 13 *(x-2)2+32~
2
* -4* + 13i
4 jc-2 ^
+ -arctg + C.
3 3
Приклад 4. Знайти інтеграл J-
Зх-5
75
r<£t .
\2xL -12^ + 15
Запишемо чисельник дробу у вигляді суми двох доданків,
один з яких містить похідну від підкореневого виразу, і
розкладемо заданий інтеграл на суму двох інтегралів
і-
Зх-5
rdx= Г-
-(4*-12) + 4
уі2х2-12х + 5 уі2х2~^12х + 15 4 W2x2-12x + 15
dx = —\-
А J
4л;-12
rdx +
+4
dx
З rd{2x2-\2х + \5) 4 r d{x-3)
-if-
f
l2^_6,+Mj 4J^-12, + 15 ^'f^~-
= -\І2х2-12х + 5 + 2л/2 In
2
JC-3 + Jx2 -6д; +—
+ C
3.91. J-
Задачі для самостійного розв'язування
dx
Знайти вказані інтервали:
6dx
х +4х-5
3.92. J-
3.93. [-у-*
3.95. J
*2+3;c-10
д: -х + 2
dx
7з
д: -7* + 10
3.94. Г« .
Jx2+V3 *+і
3.96. Г—
J4x2+4x + 5

§ 3. Інтегрування виразів, що містять квадратний тричлен
171
3.97. f
dx
Ъх1-2х + 2
3.99. f—
Jl +
3.101. J-
Adx
2x -3xl
dx
4x2 + x
dx
3.103. f- ,
-]x2+x + l
3.105. J- Л
3.107. J-
3.109. J-
УІ4х-3-х2
dx
^8 + 6x-9x2
V4-6jc-3jc2
4x-5
3.111. f , dx.
3.113. J
3.115. J-
3.117. f-
1 A
(3x-2)dx
5jc2-3jc + 2
<3jc-l)dbc
x2-x + l'
2-3*
'4jc -b-xL
3.119. f * *? <&■
V-jc2 + 2
3.121. J- **
3.123. J-
V*2-6x + l
(л: + 3)gfcc
V4x2+4;c + 3
3.98.
3.100.
3.102.
3.104.
3.106.
3.108.
3.110.
3.112.
3.114.
3.116.
3.118.
3.120.
3.122.
3.124.
dx
Ax -x1 -5
Axdx
x4-2x2-l
dx
l2xz-x + 2
dx
fcx-x2
dx
УІ2-6х-9х2
dx
\2-Ъх-Ах2
dx
\\-2x -x1
xdx
xz-lx + U
(6x-l)dx
Ъх-lx + ll
(lx + \)dx
6xz+x-\
x dx
*2-6л: + 10'
x5dx
x6-x3-2
(x-3)dx
УІХ2 + 6x
2x-\
\І5-4х-х2
dx.

172
Розділ III. Невизначений інтеграл
6х + \
3.125. J- .
УІХ-Х
3.127. J- 2Х~8
dx.
3.129. j
yjl-x-x2
exdx
dx.
e2x+&ex+\5
xdx
3.126. J-,
W5jc2-2jc + 1
3.128. \- (x + 3)dx
W3 + 4jc-
4л"
cosxtic
3.130. J C0S^
ВІДПОВІДІ
3.91. In
x-1
3.93. -In
7
3.95. -In
3
x + 5
x-2
x + 5
x-5\
+ C.
+ C.
x-2
+ C.
3.97. -;= arctg -^=- + C.
у/5 V5
3.99. In
3x + l
*-l
+ C.
3.101. In
і п—
2
+ C.
1
3.102. -^ln
V2
1 2 1 t
*— + Ax —x + l
4 V 2
_-. 2 2jc-1 ^
3.92. -,=arctg—?=- + С
V7 л/7
3.94. 2arctg(2* + V3) + C.
3.96. -arctg^±1 + С
4 б 2
3.98. arctg(2-;c) + C.
3.100. -^ln
n/2
-л/2-l
*2+л/2-1
+ C.
+ C.
3.103. In
Х + - + ЫХ2 +x + l
2
+ C.
x-4
3.104. arcsin + C.
4
3.105. arcsin(jc-2) + C.

§ 3. Інтегрування виразів, що містять квадратний тричлен 173
3.106.
3.108.
3.110.
3.111.
3.112.
3.113.
3.114.
3.115.
3.116.
3.117.
3.118.
3.119.
3.120.
3.121.
3.122.
1 . Зх + 1 _
—arcsin —т=- + С.
з 7з
1 . 8* + 3 „
—arcsin —т=^ + С
2 V41
• х + 1 „
arcsin—^- + С.
-Я
, .,л_ 1 . Ъх-\ _
3.107. -arcsin + С.
З З
„<лл >/з . л/3(х + 1) ^
3.109. —arcsin V '+ С.
З V7
21п
jc2-2jc + 5
1 х-1 _
-arctg + С.
2 & 2
2х-1
я * я
1 9 7
-1п(;Г -7д: +13) + -^=- arctg
2
Го
+ с.
з, .. 2 о ^ и 10*-з ^
—1п(5д:2-Зд: + 2) т= arctg
5л/зї л/зї
1пІЗл:2-7л:+1і| + С.
З, , 2 1Ч І 2л: —І _
-ln(*z-* + l) + -^=arctg—т^- + С.
2 V3 V3
-Іп|3л-І| + -Іп|2л + І| + С.
-In (хг - Ах + 5) + 4arctg(;c - 2) + С.
х + 3ln (х1 - 6х + ІО) + 8arctg(;c - 3) + С.
I, / 4 2 „\ I 2x2-l _
-In[x* -xl + 2+—;=arctg—j=— + C.
4 \ ' 2л/7 V7
Iln
9
p-2)2(^+l)
+ C
V*2-6x + l + 3lnLc-3 + V*2-6;t + l
+ C.
4x?+6x-6ln be + 3 + V*2 + 6x
+ C.

174
Розділ III. Невизначений інтеграл
3.124. -2sJ5 + 4x-x2 +3
• х-2 _
arcsin + С
3.125. -бл/х-х2 + 4arcsin(2x-l) + C.
3.126.
5^5
In
1 2 2 1
5 V 5 5
+ -V5*2-2x + l + C.
3.127. —2л/і — л: — jc2 -9arcsin * + С.
V5
3.128. —л/3 + 4д;-4л:2 + -arcsin—— + С.
4 4 2
3.129. -In
2
е*+3
є*+5
+ C.
3.130. arcsin(sinх-2) +С.

§ 4. Інтегрування частинами
175
§ 4. ІНТЕГРУВАННЯ ЧАСТИНАМИ
Якщо и(х) і v(x) - диференційовні функції, то
справедлива формула інтегрування частинами
\udv = uv- \vdu . (3.3)
Застосовуючи формулу (3.3), обчислення інтегралу iudv
зводимо до обчислення інтегралу \vdu, і якщо останній інтеграл
простіший від заданого або табличний, то формула використана
доцільно.
Інтегрування частинами найчастіше використовують тоді,
коли підінтегральний вираз містить:
а) добутки вигляду Рп (х)екх, Рп (х)акх, Рп (х) sin кх,
Рп (х) cos кх, де Рп (х) - многочлен степеня п;
б) добутки многочленів Рп(х) та логарифмічних функцій:
\gx, \пх, loga*;
в) добутки многочленів Рп (х) та обернених
тригонометричних функцій arcsin х, arccos*, arctgx, arcctg*.
Щоб застосувати формулу інтегрування частинами, треба
підінтегральний вираз розбити на два множники, один з яких
позначити через и, інший - dv. При тому: 1) dx необхідно
включити до<іу; 2) вираз для dv повинен бути таким, щоб
інтегруванням можна було легко знайти функцію v (v= \dv);
константу С додавати не потрібно, оскільки для використання
формули (3.3) достатньо мати одну довільну первісну. Табл. 2
допомагає встановити, який із співмножників в підінтеграль-
ному виразі доцільно позначити через и, а який через dv.

176
Розділ III. Невизначений інтеграл
Таблиця 2
1 №
з/п
1
2
3
Вид інтеграла
Jw<
\pnw
1
Г kx "ї
sin be
cos be J
arcsinfoc
arccos/bc
arctgfct
■N
ftffcc
^ lnw kx J
j|si\(!nlU
J [cos(ln X) J
J [cos raj
U/я -л: <£c
Множник и
u = Pn(x)
u=<
arcsinfcc
arccoso
arctg/bc
L lnw /bcJ
_fsin(ln ;c)~l
~ \cos(ln x)J
Доі
и =
вільний ви
множника
= у]a2 -х
бір
7
Множник dv
dv=<
sin kx
w cos fo
►cbc
dv = Рп (х) dx
dv -dx
Довільний вибір
множника
<
iv = *&c
Приклад 1. Знайти інтеграл Jjcsin 2х dx.
Згідно з першим пунктом таблиці, за и доцільно вибрати
многочлен Рп (х) = х. Тоді
І и = х;
\dv = sin2x dx; v = --
h;sin2.x<ic =
du-dx
cos 2л:
= —cos2;c + — \Q,b$2xdx =—;ccos2;c + —sin2;c + C.
7 7 і 7 Л

§ 4. Інтегрування частинами
111
Приклад 2. Знайти інтеграл $(х2-2х + з) \nxdx.
Згідно з другим пунктом таблиці, за и вибираємо In х:
\(x2-2x + 3\\nxdx =
и = In х\
dx
du =—;
x
9 X О
dv = (x -2x + 3)dx; v = jc + 3x
(J
— -x2+3x
l(x3 о '
In*- I x +3x
J
—dx-
x
(хз Л
x2+3x In*-
Ч3 J
--X + 3
xz+3x \]nx + 3x + C.
3 9 2
dx =
J
V
Приклад 3. Знайти інтеграл Jjc arctg 3* dk.
Згідно з табл. 2, за и вибираємо arctg Зх
3 dx
\х arctg 3xdx =
и = arctg3.r, du =
l + 9;c2
dv = xdx\ v = —
2
2 И 1
лґ+- —
x „ 3 с xL J xL , If 9 >
= —arctg3*— Trdx-—arctg 3x— -—;
2 ё 2h + 9x2 2 B 6 J i + x
9 9
dx =
x о 1 1 Г
=—arctg3*—x+— —
2 6 6 54 Yl
dx xl 0 1 1 „ ^
=—arctg 3x—x+—arctg3;c + C.
■ 0 2 B 6 18 6
Часто формулу інтегрування частинами необхідно
застосовувати послідовно декілька разів.

178
Роз д і л III. Невизначений інтеграл
\(2х2-Ъ)
exdx =
= i^2x2-3)jex-4Jxexdx =
Приклад 4. Знайти інтеграл j(2x2 - 3) exdx.
Відповідно до п. 1 табл. 2 маемо
и = 2*2-3; du = 4xdx\
dv = exdx\ v = ex
= (їх2 - з)ех - а[хєх - jexdx)= (їх2 -3)ех-
- 4хех +4ех +С = ex(lx2 -4х + і)+С.
Приклад 5. Знайти інтеграл f (arcsin xfdx.
Цей приклад вимагає двократного застосування методу
інтегрування частинами:
и = (arcsin х)2\ du = 2arcsin х-
и-х\ du = dx\
\dv = exdx; v = e
[(arcsin x) dx =
= jc(arcsin x)2 - jarcsinx
"Vb^
dv = dx\ v = x
2xdx
VbV
и = arcsin x; du =
dv =
dx
S^x1
= ^(arcsin x)
(
■2v 1 - x2 arcsin x +
J2VT7.
dx
VTv
= ^(arcsin x)2 +2vl- x2 arcsin jc- 2* + С.
Інколи повторне застосування формули інтегрування
частинами приводить до алгебраїчного рівняння відносно шуканого
інтеграла (див. табл. 2, п. 3).

§ 4. Інтегрування частинами
179
Приклад 6. Знайти інтеграл fsin х e3xdx.
Два рази інтегруємо частинами, причому під час другого
інтегрування функцію и необхідно вибрати так, як її було
вибрано при першому інтегруванні:
fsin;c£3*<#c =
и = е3х, du=3e3xdx,\
dv = sinx dx, v = -cos*
= -e3x cos x + 3 Jcos xe3xdx =
Яг I
и = e"", du-Ъе dx\
dv = cos xdx, v = sin x
=- e3x cos x + 3 (e3* sin л: - 3 Jsin ;ce3*<£c)=
= є3*(З sin jc - cos jc) - 9 [sin *е3*б£с.
Отже, ми отримали рівняння відносно шуканого інтеграла:
fsin xe3xdx = е3х (Зsin х - cosх) - 9 fsin *е3хб£с.
Звідси 10 fsin;ce3*d[x; = e3*(3sinjt-cos.x). Отже,
fsin xe3xdx = — е3х (З sin х - cos ;с) + С.
J 10 V '
Приклад 7. Знайти інтеграл fsin(ln;*;)d[x;.
fsin(ln;c)d[x: =
\u = sin(ln x); dw = cos(ln *) —|
rfv = dx; v = x
= ;c-sin(ln;c)- f;tcos(ln;c) = jc-sin(ln*)- jcos(ln.x;) dx =
dx,
и = cos(ln x); du = - sin(ln л:) 1
x
dv-dx\ v = x
\dx
- x • sin(ln x) - *cos(ln x) -
- Jx • sin (in x)— = x sin(ln x)-x cos(ln *) - Jsin(ln x)dx.

180
Розділ III. Невизначений інтеграл
Позначимо інтеграл \sm(\nx)dx через /. Тоді отримаємо
рівняння / = *sin(ln;c) - ^cos(ln^) - /, звідки
/ = — ;c[sin(ln х) - cos(ln х)] + С.
Приклад 8. Знайти інтеграл |-
xdx
sin2 х
И
xdx
sin2 x
u = x\ du = dx\
dx
dv = ——; v = -ctg*
sin x '
= -;cctgJt + jctg*d[x: = -;cctg;*; +
rf(sin^)
+ — dx = -xoXgx+ —: = -*ctg;c + ln sin* +C.
J sin r J sin r
sin*
Приклад 9. Знайти інтеграл IV4 - x2 dx.
Маємо
=j^
л: dbc =
и = \1А-х ; aw = —.
v = *
4-;c2-4
dv = <ic;
= jcv4-jc2 - [ . dx=x\l4-x2 - \—. dx =
J Л.T J Га 72
V4-jr
V4-x
",2
= W4-jc2 - fV4-jc2<£c + 4arcsin— = xyj4-x2 -7 + 4arcsin—.
J 2 2
Отже, 2/ = xy4-х2 + 4arcsin—.
2
Звідси
/= U4-x2dx = -x^4-x2 + 2arcsin— + C.
J 2 2

§ 4. Інтегрування частинами
181
Інколи інтегрування частинами дає змогу отримати
співвідношення між невизначеним інтегралом, що містить степінь
деякої функції, і аналогічним інтегралом, але з меншим
показником степеня тієї самої функції. Подібні співвідношення
називаються рекурентними формулами.
Приклад 10. Вивести рекурентну формулу для інтеграла
г dx . -
In = І—о Ъ— 1 обчислити за її допомогою інтеграл
(х2 +а2)п
і)
Маємо
9 9 9
_ Г d* _ * К* +а )-х , _ 1 r dx
п ~~ J/v2 , Л2уі ~~Т J ,2 ,„2чл "Т J/ 2 ,Л2чл-1 "
*(л;+я) а " {х + а ) а (х +а )
и = х; dv =
(х2+а2)"
\du = dx; v = -[(x2+a2) "d(x2+a2) = = ?—г
1 , x 1 r dx
= -r/„_i +
a2 nl a2(2n-2)(jc2+a2)"-1 a2(2n-2) J(jc2+a2)"-1
b^J:
а2(2и-2)(л:2+а2)
• + /-
'l 1 ^
„— TJn-l
az 2az(n-l)
2w-3
2/o„ i\ /J x л2чіі-1 ' 2— — n_1
<Г(2л-2)(дГ+<ГГ""1 az(2n-2)
Отже, шукана рекурентна формула має вигляд
1 х 2п-3
п~(2п-2)а2 (х2+а2)"~1 а2{2п-2) "

182
Розділ III. Невизначений інтеграл
Застосовуючи її для п = 2 і а = 1, матимемо
с dx х І с dx х І ^ „
h = \—3 Т = 5 + ^Г "9 = 5 + -arctgx + C;
J(jc2+1)2 2(jc2+1) 2V+1 2(jc2+1) 2
Для л = З і а = 1 отримаємо
г Л _ д: 3 _
3"J(77l?"4(x2+l)2+4 2"
х Зх 3 _
= 5 т +—ъ + ~arctgx + C.
4(jc2+1)2 8(jc2+1) 8
Задачі для самостійного розв'язування
У задачах 3.131-3.175 знайти вказані інтеграли:
3.131. j(3x2 -Sx)e2xdx.
3.133. Г—dx.
3.135. be sin* cos **£*:.
3.137. [sin yfxdx .
3.139. \xtg2xdx.
3.141. jln(l-x)dx.
3.143. jx"ln;c<£c.
3.145. j]a(x2+l)dx .
3.147. \b^dx.
J X
3.149. jjx]n2xdx.
3.132.
3.134.
3.136.
3.138.
3.140.
3.142.
3.144.
3.146.
3.148.
3.150.
jx2e~2xdx.
je^dx.
\x sinxdx.
brcos2 xdx.
cxcosx ,
l—t—dx.
J sin X
\x2ln(l + x)dx.
jlnf x + V1 + x2 )dx.
jjcarcsinxdk.

§ 4. Інтегрування частинами
183
3.151. j(arcsinjc)2dic.
3.153. [^Udx.
3.155. jarctgjcrfx.
3.157. jarctg д/jc dx.
3.159. \*^**dx.
3.161. \exsmxdx.
3.163. je2*sin2jcd!x;.
3.165. jsin(ln;t)dk.
3.167. jcos2(lnjc)d!x;.
3.169. jja2-x2dx.
arcsmjc
U7i. Г-зА
J(;c2+a
2ч2
rfx.
3.152. [""її
3.154. J
d[*.
л:
arcsinjc
dx.
3.156. jxarctgxdk.
3.158. Р^£Й£&.
J x2+l
3.160. [(arctgx) xdk.
3.162. \e3xcos2xdx.
3.164. JV** sin feed!*.
3.166. jcoslnjcdx.
3.168. f-^L.
3.170. [4a + x?dx.
3.172. J^<£c.
У задачах 3.173-3.175 знайти рекурентні формули для
інтегралів
3.173. /„ = jxk ln"xdx (neN).
3.174. In = jsinnxdx.
(Зауваження. Подати sin" x = (sin;c)n-2(l-cos2;t], і прийняти
л-2
dv = (sin *) cos x dx.

184
Розділ III. Невизначений інтеграл
ВІДПОВІДІ
Лх
3.131.
3.132.
—(бх2-22х + и)+С.
'л:2+;с + -| + С.
2
3~х
(*1пЗ + і)+С.
3.133.
3.134.
3.135.
3.136. - х3 cos х + Зх2 sin х + бх cos х - 6 sin х + С.
In2 З
2e^(jx~-l)+C.
1 • ^ 1 ^ ^
—sin 2х —xcos 2х + С
8 4
3.137.
3.138.
3.139.
3.140.
3.141.
3.142.
3.143.
3.144.
3.145.
3.146.
З l2-yJx^\cosyfx + 2^x~smsfx
х2 1 • „ 1 „ ^
— +—jcsin 2х +—cos 2л + С.
4 4 8
х2
xtgx + ln|cos;c| + C.
+ C.
• + ln
.«I+c-
sin* V. 2)
-x-(l-;c) ln(l-;c) + C.
-(хъ+\)\п{1 + х)- — + — -- +С.
3V ' 9 6 З
ІПДС--
+ С.
п + іу n + 1,
С—^lg(xVel
2xl
*ln(x2+l) -2jc + 2arctgjc + C.
—(ln3jc + 31n2jc+61njc + 6) + C.

§ 4. Інтегрування частинами
185
3.147. [ln(lnjc)-l]lnx + C.
3.148. x\nix + 4l + *2)-Vl + x2 +C.
3.149. -хї f In2 x - -In x + -1 + C.
ЗІ 3 9
3.150. -,
4L
(2;c2-l)arcsin x + xjl-x2 \ + C.
3.151. jc(arcsinjc)2 +2arcsin;c у 1-х2 -2x + C.
3.152. 2Vl + *arcsin x + 4yll-x + C.
3.153. 2jx~ arcsin
3.154. =+lh(l-,2) + C.
3.155. jcarctgjc—ln(l + jc2)+C.
x 1 + x2
3.156. — + arctg x + С
2 2
3.157. jc arctg 4x-4x + arctg V* + С
3.158. jc arctg jc—ln(l + jc2)—arctg2 x + C.
3.159. Vl + Jc2 arctg jc-In (jc + Vl + Jc2 ] + C.
jc2 +1 9 1 9
3.160. (arctgjc)-jc arctgjc + -ln(l + jr) + C.
3.161. — e*(sinjc-cos;t) + C.
2
e3x
3.162. (3cos2jc + 2sin2jc) + C.
13
e2x
3.163. (2-sin2jc-cos2jc)+ С
8

186
Розділ III Невизначений інтеграл
ълил £"(ЯSinfot-fcCOSfot) _
J.164. hC.
a2+b2
3.165. —(sin(lnjc) -cos(lnx)) + C.
3.166. — (coslnjc + sinlnjc) + C.
2V '
і ллп x *cos(21njc) + 2jcsin(21njt)
3.167. —I HC.
2 10
3.168. Wl + x2-- J(1 + jc2)3+C.
3
3.169. —л/я -jc +—arcsm— + C.
2 2 a
3.170. — \la + x2 +-\n\x + \la + x2
2 2 I
3.171. -Lflarctg-+ —ІЦ-1 + С.
3.172. 2(л/ї-і)^ + С.
3.173. / =— jc*+1ln"jc ——/„ч.
n k + l k + l n l
~+mA T sin^jtcosjt n-1 .
3.174. /„ = + In_v
+ C.
n n
X
3.175. /„ =±— 5—r + — /„
2a2(n-l)(jc2+a2)n_1 a2(2n-2)

§ 5. Інтегрування дробово-раціональних функцій
187
§ 5. ІНТЕГРУВАННЯ
ДРОБОВО-РАЦІОНАЛЬНИХ ФУНКЦІЙ
5.1. Основні теоретичні відомості
Означення І. Дробово-раціональною функцією, або
раціональним дробом, називається функція вигляду
QmW
де Рп(х), Qm(x) -многочлени з дійсними коефіцієнтами степенів
п та т відповідно.
Раціональний дріб називається правильним, якщо степінь
п многочлена Рп (х) менший від степеня т многочлена Qm (jc).
У протилежному випадку дріб називається неправильним.
•є Рп(*)
Якщо дріб — неправильний, то в ньому можна виділи-
QmW
ти цілу частину, тобто подати його у вигляді
|f^ = M_W + ^-, (3.5)
де Мп_т(х) і Ri(x) - многочлени степенів п-т>0 та / відпо-
відно, причому / < т, тобто, дріб — правильний.
QmW
Тому інтегрування неправильного раціонального дробу
зводиться до інтегрування многочлена та правильного
раціонального дробу.
Для виділення цілої частини у дробі його чисельник ділять
на знаменник.
Зауважимо, що при діленні многочлена на многочлен їх
треба записати за спаданням степенів змінної. За відсутності
доданка певного степеня потрібно вважати числовий множник,
який він містить, нулем.

188
Розділ III. Невизначений інтеграл
Приклад 1. Виділити цілу частину дробу
5jc4+10jc3+3jc2-21jc + 4
х1 + 2х -1
Використовуємо ділення "кутом"
5jc4+10jc3+3*2-21jc + 4
5jc4+10jc3-5jc2
;Г+2jc-1
5jc2+8
8jc -21л:+ 4
8л:2 + 16л:-8
-37jc + 12
Обмежимося поясненням перших кроків: ділимо старший
член діленого (5 л:4) на старший член дільника (jc2) і отримуємо
5л: . Множимо дільник на 5л: і результат підписуємо під діленим.
Віднімаємо цей результат від діленого і ділимо старший член
різниці на старший член дільника і т. д. Процес закінчується, коли
залишок має степінь, менший від степеня дільника, або ж дорівнює 0.
Многочлен 5л: + 8 - частка, а - 37л: +12 - залишок.
Отже,
5л;4+10л;3+Зл;2-21л; + 4
л:2+2л:-1
■ = 5л;' + 8 +
12-37л:
л:2+2л:-1
5.2. Інтегрування простих дробів
Розглянемо дроби
А „ А
х-а
II.
(x-df
III.
Mx + N
2 '
х + px + q
IV.
Mx + N
(x2 +px + q)P
Тут дг = 2,3,..., /7 = 2,3,..., Л, M, N9 а, р і q -дійсні
числа, причому тричлен х2 + рх + q не має дійсних коренів, тобто
його дискримінант від'ємний р - Aq < 0,

§ 5. Інтегрування дробово-раціональних функцій
189
Наведені вище дроби називаються простими дробами
/, //, ///, IV типів.
Розглянемо інтеграли від простих дробів усіх чотирьох типів
і. \^-dx=A[^z^L=A]n\x-a\+c.
}х-а J х-а
II. f—-—dx = A[{x-aYad(x-a) = — Г + С.
Для обчислення інтегралів від дробів Ш та IV типів
запишемо квадратний тричлен так:
х + px + q =
х + ^-\ +
2 ( п2\
р2 Л р2
і, враховуючи, що q - J— > 0, введемо сталу а = \lq—£—
4 V 4
r(Mx + N)dx _
J х + px + q
P P
t = x +—; x = t- —
2 2
dt-dx
Mt + \ N-
Mp
J r+ar
_M r ltdt ( МрЛ r dt
О J Л . „2 + о J .2 , 2 ~~
2 ' (2+<!2 I 2 Іа'ґгЛ 2
;)+' 2
2N-Mp t _ M, . 2
+ -arctg— + C = —ln(;c +p* + g) +
2a a 2
/
2N-Mp
+ — =arctg
2f^
Л
x + -
+ C.

190
Розділ III. Невизначений інтеграл
\xHpX + qf J (,2 + я2)' 2'(l2+a2)"
. МрЛ r dt
+ N-
Останній інтеграл обчислено вище (див. приклад 9).
5.3. Інтегрування
правильних раціональних дробів
Нехай дріб (3.4) - правильний, і його знаменник
Qm (х) = Ьтхт + bm_1xm~l +... + bxx + Ь0 має дійсні корені
ах,...,аг кратностей sx,...,sr та пари комплексно-спряжених
коренів /?!,/?!,...,/?£,/?£, кратностей відповідно tl9..Jk
(sx +... + st + 2tx +... + 2tk = m), отже,
Qm(x) = bm(x-aiyi...{x-ar)5r[x2 + pxx + qxf ...(x2 + pkx + qkf Л3.6)
де Xі + pvx + qv =(x-J3v)(x-/?v), v = l,...,fc.
Тоді розклад дробу — на суму простих дробів має вигляд:
QmW
РпМ А(1) <} А(г) <г)
" = 1- + ... + 1- + ... + —2 + ... + L +
Qm(x) х-ах (х-цУ1 х-аг (х-агУг
вРх + С® Bf*>x + C$> В^х + С^
+— — + ... + + ... + — —...+
x2+plx + q1 (x2 + plx + ql) h x2 + pkx + qk

§ 5. Інтегрування дробово-раціональних функцій
191
+-Г Чг- (з-7)
(xz + pkx + qkyk
Числа Af, Bf, Cf у цьому розкладі визначаються методом
невизначених коефіцієнтів: прирівнюємо коефіцієнти при
однакових степенях х у многочлена Рп(х) і многочлена, який
отримується у чисельнику правої частини (3.7) після зведення її
до спільного знаменника. Можна також визначати ці коефіцієнти,
надаючи змінній х конкретних числових значень (насамперед
значень дійсних коренів знаменника Qm(x)). Інколи доцільно
комбінувати обидва ці методи.
Отже, завдяки рівності (3.7), інтегрування правильного
раціонального дробу зводиться до інтегрування простих дробів
вказаних чотирьох типів.
2х2 -1
Приклад 2. Знайти інтеграл J— dx.
х -5х +6х
2х2-\
Дріб — правильний. Оскільки корені знамен-
х -5х +6х
ника прості і дійсні,
х -5х +6х = х(х -5х + 6) = х(х-2)(х-3),
то розклад цього дробу на прості дроби має вигляд
2jc2-1 ABC
. = — + + -
х3-5х2+6х х х-2 х-3'
Зводячи дроби в правій частині останньої рівності до
спільного знаменника і прирівнюючи чисельники, отриманих
дробів, матимемо
2х2 -1 = А(х - 2)(х - 3) + Вх(х - 3) + Сх(х - 2).
Визначимо коефіцієнти ДДС, надаючи змінним значень
л; = 0, х-2, х = 3:
* = 0: -1 = Л-(-2)-(-3); -1 = 6Д; А = --;
6

192
Розділ III. Невизначений інтеграл
х = 2: 2-22-1 = £-2(-1); 7 = -25; В = --\
х = 3: 2-32-1 = С-3-1; 17 = ЗС; С =—.
З
Отже,
їх1 -\
117 1 17 1
• +
-5л:2+6* 6 х 2 х-2 З х-3
тому
2л;2-1
1 tdx 1 td(x-2) 17 rd(x-3)
6 J г 9 J
!л;3-5л;26л; 6 J x 2J jc-2 3J jc-3
= -—ln|jc| -—ln|jc - 2| +—ln|jc-3| + C = ln
6 2 3 '
17
(*-3)3
I z
jc6 -(jc-2)2
+ C.
rjc3 - 2jc2 + 4
Приклад 3. Знайти інтеграл —- —dx.
J x3(x-2)2
Знаменник дробу має кратні корені: корінь jc = 0 кратності
З, та корінь х = 2 кратності 2. Тому розклад підінтегральної
функції на прості дроби має вигляд:
jc3-2jc2+4 А А2 А3 Д В2
= —- + —— + —— + —— + —.
jc3(jc-2)2 х х2 х3 х-2 (х-2)2
Зведемо дроби в правій частині рівності до спільного
знаменника і прирівняємо чисельники її правої та лівої частин:
jc3-2jc2+4
jc3(jc-2)2
_ Ахх2(х-2)2 + А2х(х-2)2 +А$(х-2)2 + Вххъ{х-2) + В2хъ
х3(х-2)2
д:3-2д:2+4 = д(д:4-4д:3+4д:2) + Л2(д:3-4д:2+4д:) +

§ 5. Інтегрування дробово-раціональних функцій
193
+ А3 (jc2 - 4х + 4)+ Вг (jc4 - 2jc3 )+ В2хъ ,
jc3 -2jc2 + 4 = jc4^ +51) + jc3(-4A1 +A2 -2Bx + B2) +
+ jc2(4A1-4A2+A3)+jc(4A2-4A3) + 4A3.
Прирівнюючи коефіцієнти при однакових степенях JC,
одержуємо систему рівнянь:
ґд + я^о,
-4 Д + А2 - 2ВХ + В2 = 1,
І4А1-4А2 + А3 =-2,
4А2-4А3=0,
[4Л3=4.
Звідси знаходимо А3= 1; А2= 1; Aj=—; Вх = ; В2=—.
Отже,
гд:3-2д:2+4, /ill 1
J jc3(jc-2)2 J 4jc x1 x3 4(jc-2)
1
4(*-2) 2(jc-2)2
<іх =
і)
4J x Jx2 Jx3 4 J jc-2 2 j(jc-2)2
dx rdx 1 fd(jc-2) J_rd(>-2)
1 r<£c rax гал і г
1, 11 1
= -1пЫ + -
1
x -2xL 4
.-Ilnb-2|-i-i- + C =
=Il„|
4
jc-2
1
1
* 2л:2 2U-2)
2д:-2
+ C.
Приклад 4. Знайти інтеграл j-
*£х
(jc + і) (л:2+4)
Оскільки знаменник дробу має дійсний корінь jq = -1 і два
комплексно-спряжених корені х2 = 2/, д:3 = -2/, то розклад на
прості дроби матиме вигляд
1
А Вх + С
■ + •
(> + 1)(л-2+4) * + 1 л-2+4

194
Розділ III. Невизначений інтеграл
Звівши праву частину до спільного знаменника і
прирівнявши чисельники дробів, матимемо
і = а(х2 +4} + (Вх + С)(х + і),
1 = (А + В)х2 + (В + С)х + (4А+С).
Прирівнюючи коефіцієнти при однакових степенях X,
отримаємо
и + в=о,
\в + с=о,
[4А + С = 1.
Звідси А =—,В = — ,С =—.
5 5 5
Отже,
1
1 х-1
(х + 1) (х2+4) 5(* + і) 5 л:2+4
Тоді,
r dx 1 rd(x + l) 1 f л—1 , 1, , ,, 1г
г- г = - — -— \-z dtc = -InЬс+1— -
J(* + l) (*2 + 4) 5J jc + l 5^2+4 5 ' ' 5 J.
5V+4 5 ' ' 2-5J х2+4 5 2
xdx
х2+4
х
arctg- =
= -ln|x + l| ln(;c2+4)+ — arctg- + C =
5 і ' 10 V Mo 2
J_
10
(. (л- + 1)2 хЛ
ln-4-^- + arctg-
x +4 2y
+ C.
x +x-l
Приклад 5. Знайти інтеграл f -dx.
.Оскільки знаменник дробу має кратні комплексні корені, то
x3+x-l Ах + В Cx + D
■ +
(х2+2)
2 х2 + 2
(х2+2)2'

§ 5. Інтегрування дробово-раціональних функцій
195
Зведемо праву частину рівності до спільного знаменника і
прирівняємо чисельники отриманих дробів
х3 + jc-1 = (Ах + В)(х2 + 2) + Сх + Д
х3 + х-1 = Ах3 + Вх2 + (2А + С)х + 2В + D.
Прирівнявши коефіцієнти при однакових степенях х, матимемо
U=i,
15 = 0,
12Л + С = 1,
\2B + D = -1,
звідки С = -1; D = -1. Отже,
Xі +х-1
x + l
(J+г)
2 х2 + 2
(Х2+2Ї
ВІДПОВІДНО,
f
X +JC-1
xdx
-h
_ с хах г ха
= l Мх2 + 2) t d(x2+2) ^
= 2J x2+2 ~^^ + 2)2~\x2+2)2~
= lUx2+2)^-^—\-^-,.
2 \ ) 2,42 y+2)2
Для обчислення інтеграла f використаємо реку-
рентну формулу (приклад 9, § 4), згідно з якою
1 х 1 с dx 1 л: , 1 . х
In = ^ + l-s = —^ + —1= arctg-= + C.
2 2-2 (x2+2) 2.2^2+2 4x2+2 4^2 Л
Остаточно одержимо
Гі!±^1Л = І1п(/+2) +
\х2+2)2 2 1 '
2-х
1 х _
arctg-T= + C.
4{х2+2) 4л/2 6V2

196
Розділ III. Невизначений інтеграл
5.4. Загальний випадок
Дробово-раціональна функція в загальному випадку
інтегрується так:
1. Виділяємо цілу частину, тобто дробово-раціональну
функцію записуємо у вигляді (3.5). Ціла частина інтегрується
безпосередньо.
2. Знаменник Qm (х) дробово-раціональної функції
розкладаємо на лінійні та квадратичні множники, тобто записуємо його
у вигляді (3.6).
3. Частину підінтегральної функції, що є правильним
раціональним дробом, розкладаємо на прості дроби (див.
співвідношення (3.7)) інтегруємо кожний з доданків.
Приклад 6. Знайти інтеграл: f—- dx.
j(x 2-1)(jc + 2)
Оскільки степінь полінома в чисельнику більший від
степеня полінома в знаменнику, то підінтегральна функція -
неправильний дріб. Виділимо цілу частину цього дробу:
/+4jc3+4
х6 + 2х5-х4-2х3
х3 +2х2-х-2
jc3-2jc2+5jc-6
-2х5 +х4 +6х3 +4
-2х5-4хА+2х3+4х2
_5jc4+4jc3-4jc2+4
5jc4+10jc3-5jc2-10jc
Отже,
(X
(х2-
3+2)2
-!)(* +2)
-6х3
-6х3
= х3-
+ jc2+10jc + 4
-12jc2+6;c + 12
13jc2+4jc-8
о 2 * ; ІЗ*2
-2х +5jc-6 + ——
(х2-
+ 4х-
-!)(* +
-8
2)

§ 5. Інтегрування дробово-раціональних функцій
197
._ 13jc2+4jc-8
Розкладемо дріб -. г на прості дроби
(*2-і) (х + 2)
13jc2+4jc-8
ABC
- + + -
(х2-1)(х + 2) де —1 х + 1 х + 2
Зведемо праву частину рівності до спільного знаменника і
прирівняємо чисельники отриманих дробів
ІЗ*2 + 4х - 8 = А(х + 1)(х + 2) + В(х - ї)(х + 2) + С(х -1) (х +1).
Надаючи змінній х значення 0 і значень, які дорівнюють
кореням знаменника, матимемо
х = 0: -8 = 2Л-25-С;
х = -1: 1 = -2В, В = --\
2
* = 1:
С= 8+2Л-2Я=8+3+1= 12.
9 = 6Л, А = -;
2
Отже,
13*2+4;t-8 3 1 1 1 ,„ 1
- + 12-
(х2-ї)(х + 2) 2 х-1 2 х + 1 х + 2
(x3+2fdx
З rd(x-l)
M£_+fL«_e \x'dx-2\x2dx + 5\xdx-6\dx + ^\^^
Ux2-V)(x + 2) J J J J 2 J jc-1
1 rd(x + l)
d(x + 2) x4 2 з 5 2
- — -+12 — - = Xі +-хг -6x + -ln\x-l\
2J x + 1 J x + 2 4 3 2 2 ' '
1, і ,, ,., | -| _ 3*4-8;c3+30;c2-72;c
—1п|дг + 1| + 121п|дс+2|+С = +
2
(jc-1)3(jc + 2)24
(* + D
+ C.

198
Розділ III. Невизначений інтеграл
Задачі для самостійного розв'язування
У задачах 3.176-3.187 знайти інтеграли (знаменник має
різні дійсні корені):
3.176. Г *£ . 3.177. f-*U
J(jc + 1)(2jc + 1) Jjc(jc-I)
xdx - .,__ r (2x-l)dx
3.178. [ ,** . 3.179. f-^
3.180. \/+23 dx. 3.181. f 2*2+41x-91 dx.
ix3-x2-6x j(jc-1)(jc + 3)(jc-4)
3.182. f 45x t2 dx. 3.183. f . * dx.
Jx3-5x2+4x Jx4-3x2 + 2
~.+ot r;c5+;c4-8J „ <oe. r lx2-22x + 21
3.184. Г—r dx. 3.185. [ dx.
} Xі-4x j(jc + 5)(2jc2-5jc + 3)
3.186. f (* +2) dx. 3.187. [— % dx.
J(x2-V)(x + 2) J(x2-x)(x2-5x + 6)
У задачах 3.188-3.195 знайти вказані інтеграли (знаменник
має лише дійсні корені; деякі корені кратні):
З.Ш. f £—5.. 3.189. {-^dx.
}(х + ї)(х-ї)2 J0-2)3
,,м г х2-Ъх + 2 , „ <Л„ /х+2^ dx
3.190. ; <&. 3.191. —.
Jx(x2+2x+l) \x-l) х
3.192. \—^—. 3.193. J f ~8x+\dx.
V(jt-l)2 j(jc2-3a:-10)2
_10. f/+3^3-l, r*4-6x3+12*2+6
3.194. т—dx. 3.195. — dx.
J (jc + 1)2 J jc3-6jc2+12x-8

§ 5. Інтегрування дробово-раціональних функцій
199
У задачах 3.196-3.203 знайти інтеграли (знаменник має
різні комплексні корені):
3.196. J-
3.198. {
3.200. J
dx
dx
x4+x2
jc3+3jc2-3;c + 1
(jc + 1)2(jc2+1)
3.197. f-^.
V+l
3.199. j2x2:3x+1dx
dx.
3.201. J
jc3+1
x3-6
x4+6x2+S
dx.
3.202. \-^—dx.
3.203. Г dx.
}x(x2+l)
У задачах 3.204-3.210 знайти вказані інтеграли (знаменник
має кратні комплексні корені):
3.204. J-
3.206. J
Зл + 5
0c2 + 2* + 2)2
dx
dx.
3.205. {•
dx
(l + *)(;c2+Jt + l)2
3.207. J-
(1 + *2)2'
2x
(l + x )(1 + jc2)2
dx.
3.208. J
(x4-D2
x dx
dx.
3.209. \-^—dx.
3(x2 + 2x + 2y
3.210. Г-4-2Ї-.
jjc15-1
Відповіді
Lc + 1
3.176. In ' +C
3.177. In
V2* + l
3.178. -In ((* -2)2 V2jc + l) + C. 3.179. In
*-l
+ C.
(Х-2У
x-1
+ C.
3.180. --1пЫ + — ln|jc + 2| + —ln|jc-3| + C.
2 ' ' 10 ' ' 5 ' '

200
Розділ III. Невизначений інтеграл
3.181. In
(х-1)Л(х-4)5
(Х + 3?
+ С. 3.182. 5* +In
І 161
jc2(jc-4)6
3.183. In,
їх2-2 „ _„. х3 х2
х2-1
+ С. 3.184.— + —+4х+1п
З 2
(*-1)3
х2(х-2)5
(Х+2У
+ С.
+ С.
3.185. In
(x + 5)4j(2x-3)3
(х-іУ
+ С.
3.186. + 6* + ln|
4 З
V(x-l)3U+2)12
л/л+ї
+ С,
3.187. In
3.189. -
0t-l)3(;c-3)
(х-2Ух
7
+ С. 3.188. - l +-ln
2(jc-1) 4
2
JC + 1
2(x-2)2 Л-2
+ C.
3.190. In
д: + 1
*-l
6
д; + 1
+ C.
+c.
3.191. 4 In be - 3 In be -1 + C.
11 ' ' x-l
3.192. K- — + 31n
2x x x-l
x-l
3.193.
8
27 30 ,
-+ In
+ C.
x-5
49(*-5) 49(x + 2) 343
x + 2
+ C.
11 3 і і
3.194. -л:3+-л;2-3л:+ + 51nbc + l+C
3 2
3.195.^- П
x + l
■ + C.
2 (x-2)2 x-2
3.196. — lnlx - 2| -—In (x2 + 2x + 4] - —^arctg^i- + С
12 ' ' 24 V I AS S

§ 5. Інтегрування дробово-раціональних функцій
201
3.197.
3.198.
3.200.
3.201.
3.202.
3.204.
3.205.
3.206.
3.207.
3.208.
3.209.
r u+1)2 , і
-In
н—^= arctg-
2*-1
+ С.
6 х2-х+1 у/З S
arctg* + С. 3.199. 21n|jc+1| —^arctg^^- + С.
х V3 л/3
З 1
+-InO2 +1) - 2arctgx + С.
x+1 2
, jc2+4 3 x Ъу[2 хЛ „
ln-7» - + - arctg-—— arctg—- + C.
уіх2+2 2 22 2
In
4 4
*4-l| + C.
3.203. лг + іп
і
x2+l
+ C.
2x-l
2(д;2+2д; + 2)
x arctg*
2(1+ x2)
+ arctg(x+l) + C.
+ C.
, і ,i * + 2 5 2jc + 1 1, . 2 n Л
H* + 1| + 7To ~+:Птагс,£—Tz—-1п(дґ+ * + l) + C.
3(x2 + x + l) Зл/З V3 2
x-l 1
--ln|* + l| + -ln(jt2+l) + C.
2(*z+l) 2
l(2x6-3x2 3, .
—з +—In
x4-l 2
x2-l
+ C
*2+l|
5x3+15;c2+18;c + 8
-arctg(*+l)- , ,
8 8(x2+2;c+2)2
3.210. —
1, (x5-І)2 n/з 2х5 +1
-In— ; arctg j^-
2 *10+;c5+l 3 & S
+ C.
+c.

202
Розділ III. Невизначений інтеграл
§ 6. ІНТЕГРУВАННЯ
ІРРАЦІОНАЛЬНИХ ФУНКЦІЙ
Будемо позначати через R(u, v, w, ...) вираз в якому
використовуються лише арифметичні дії над величинами и, v, w, ...
6.1. Інтеграл вигляду
R
х,
ах + Ь
cx + d
щ
ах + Ь
cx + d
т2
п2
\dx,
де ті,Пі,т2,п2,... - цілі числа, a, b,c,d - сталі, причому
ad-ЬсФО, зводиться до інтеграла від раціональної функції
ax + b _ k
аргумента t підстановкою
дробів —,—*-,....
CJt+rf
= / , де А:- спільний знаменник
dx
Приклад 1. Знайти інтеграл f-=—-т=.
УІХ - V JC
Тут fl = d = l, 6 = с = 0, — = —, —*- = -.
nj 2 п2 З
Оскільки А: = 6 - спільний знаменник дробів — і —, то раціо-
2 3
налізацію підінтегрального виразу можна здійснити підстановкою
х = t6, звідки Г = vjc, dx = 6t5dt. Отже,
г й rr t5dt r r t5dt , rf3df , rf3 -1 + 1 .
,6filzl,(+6f.JL=6f('-'X'^»i)A+6fj(£zl) =
J*-l h-\ J r-l J f-1

§ 6. Інтегрування ірраціональних функцій
203
= 6\{t2+t + \)dt+6\n\t-\\ = 6
( Ъ 2 Л
— + — + t
З 2
+6ink-i+c=
= 2t3 +3t2 +6t + 6ln\t-l\ + C = 2-Jx + 3^x + 6^x + 6]nWx-l\ + C,
Приклад 2. Знайти інтеграл j-
<£t
(л/л + 2-^+2) tyjt + 2*
Приймемо x + 2 = t6, звідки dx = 6t5dt, t = л/дг + 2. Тоді
г dx r 6t5dt r t5dt _ r t2
\4хТ2-Их~щ Ух~ї2~Кр-(2) t~ K\t-\)~ ta
Л =
гГ-1 + 1
rf(r-l)
= б/і-^^Л = б|(ї + 1)Л + б|^^ = 6 - + ґ + Ц
^f2
—+ f + ln|f-l|
+ C =
Гз,
= 6
tyc + 2
+ tyjc + 2 + lntyjt + 2-l +C.
1-л:
r\\i — xj
Приклад 3. Знайти інтеграл / = J— , dx
x +
1-х
Після підстановки
1-JC
= t одержимо
X 2 t , ltdt
= t ; x = г-; dx =
1-х
1 + Ґ
(l + t2)2'
Тому
It
1 =
(1 + f2)2 A
J г2 J(l+f2) (f3 + r2 + o
1+^

204
Розділ III. Невизначений інтеграл
= 2/ /;
J(l + f2)(r+f-
-Л.
'(і+ *)(*+* +1)
Розкладемо підінтегральну функцію на прості дроби
ґ3 At + B Ct + D
+ ■
(1+г2)('2+г + і) г2 + 1 г2+г + Г
г3 = (At + B)(t2 +t + l) + (Ct + D)(t2 +1),
t3=(A + C)P + (A + B + D)t2 + (A + B + C)t + (B + D).
Прирівнявши коефіцієнти при однакових степенях змінної
t, одержуємо систему
1 = А + С,
0 = A + B + D,
0 = А + В + С,
0 = B + D,
звідки А = 0, B = -l, С = \, D = l.
Отже,
(2t + l) + l
І = -2 f-r + 2 Щ dt = -2arctg t + Г
1
Л2
-<Й =
d(r+t + l)
ravt+t + i) r
= -2arctg ґ+ -^ i+ -
J Г+t + l \
t + -
d\t + £
+ -
У _
if 3
2 4
/
= -2arctg t + ki
r+t + 1
^arctg
1
f + -
2
. 2
+ C =
= -2arctg
1-JC
+ ln
1-х
+ 1
^arctg
Vi-*
+1
V3
+ c.

§ 6. Інтегрування ірраціональних функцій
205
6.2. Інтеграли вигляду ІК їх, у/ах2 +bx + c \dx (аФО)
зводяться до інтеграла від раціональної функції за допомогою
однієї з підстановок Ейлера.
Першу підстановку Ейлера застосовуємо при а>0.
Приймаємо
jax2+bx + c=±x\[a±t (3.8)
(знаки можна брати в довільній комбінації). Тоді
ах2 + Ьх + с = \± xyfa ± tj.
Члени, що містять х , взаємно знищуються, отже, змінна х
. , ч . t2-c
(а, значить, і ах) раціонально виражається через t: х = т=.
b ± 2На
Підставивши цей вираз у (3.8), знайдемо раціональний
вираз і для радикала у/ах +Ьх + с.
dx
Приклад 4. Знайти інтеграл J-
' х + ліх2 +Х + 1
Тут а = 1 > 0, тому застосовуємо першу пістановку Ейлера
V*2 +x + l=-x + t. Звідси х2 +x + l = x2 -2xt + t2, х = ;
1 + 2*
2t2 + 2t + 2
dx- г— dt. Підставивши одержані вирази в інтеграл,
(1 + 20
отримаємо
//г л?/2 4- Ъ А- 2
-dt.
с ах _ rzt +
■20
Розклад підінтегральної функції на прості дроби шукаємо у
вигляді
2t2+2t + 2 А ВС
t(l + 2t)2 (1 + 20 l + 2t l

206
Розділ III. Невизначений інтеграл
Для визначення невідомих А, В, С отримуємо систему
2 = 2В + 4С, 2 = А + В + 4С, 2 = С,
звідки А = -З, В = -З, С = 2.
Отже,
f—^ , = -3 Г—*--З Г-^- + 2 f^ =
3 1, t4
• + -ln =- + C,
2(1 + 20 2 |i + 2,|J
де t = x + y]x +ЛГ + 1.
Другу підстановку Ейлера застосовують при с>0. У
цьому разі приймемо \ах +Ьх + с =±4с± xt (комбінація знаків
b±2tyfc
довільна). Звідси х =
Г -а
dx
Приклад 5. Знайти інтеграл J ,—.
V1 - л:2 -1
Оскільки с = 1 > 0, застосовуємо другу підстановку Ейлера
Vl-Jc2 = tx-l.
Піднесемо обидві частини рівності до квадрата, одержимо
1-jc2 =t2x2 -2tx + l, * = -
f2+l
J 2(l + f2)-4f2 2(l-f2).
Тому d^c = — ^—Л = -1ТуА
(1 + Г2)2 (l + r)2
Виразимо Vl — jc2 -1 через f
jl-x2 -l = tx-2 = t~—2 = 2
2f . .r2-r2-l
r2+l t2+l t2+\

§ 6. Інтегрування ірраціональних функцій
207
J7T^-i J0+<2)2-— ' +1 ^ ' +1')
Г2+1
^ Vi-*2+i ^ Vi-*2+i „
= f-2arctg f + C = 2arctg + С.
Третю підстановку Ейлера застосовуємо, коли тричлен
ах2 + Ьх + с має дійсні корені, зокрема, при а < 0.
Нехай jcl5 jc2- корені тричлена ах2 +Ьх + с . Тоді приймемо
звідки знаходимо раціональний вираз для х:
с маємо
lajx-x^ =^
\ a:-a:2
Д^2^ — #Д^
Г-Я
Для радикала \Іах2 +Ьх + і
\Іах +bx + c =Ja(x-xl)(x-x2) = / —-(jc-j^) = г і jc — jc2 І.
у Jt-Jt2
Приклад 6. Знайти інтеграл J , =.
(х-і)уі-х2+Зх-2
Тричлен - x2 + Зх - 2 має дійсні корені хг = 1, х2 = 2, тому
-jc2 + 3jc - 2 = -(jc - 2)(jc -1).
Підкореневий вираз - х2 + Зх - 2 додатний при 1 < х < 2.
Можна покласти
-с-1) =L
х-2
Звідси
2ґ2+1 . ltdt
х = -^ , dx =
t2+l' (f2 + l)2

208
Розділ III. Невизначений інтеграл
Завдяки нерівності \<х<2 величина х-2 від'ємна. Тоді
підставляючи в праву частину вираз х через t, знаходимо
^-(jc-2)(jc-l)=J^^|jc-2| = r|jc-2| = -r(jc-2)f
J-(x-2)(x-l)=^—.
t2+l
Отже,
f ^ _ f ^ _ о f ^ - ^ -
\х-1)лі-х2+Зх-2 ~ Чх-1)уІ-(х-2)(х-1) ~ J7""7"
V-(^-i) Vi-*
Зауваження 1. Інтеграли вигляду \R[x, *Jax + b, sjcx + djdx
9
підстановкою t =ax + b зводяться до інтегралів, розглянутих вище.
Справді
х = -
t2-b , It , і - \с о cb
а а у а а
, dx = —dt, yjcx + d =J-t2- — + d =VAr2+5,
. с n cb ,
де A = —, 5 = + d, тому
\r[x, y/ax + b, y/cx + djdx = (Vf t, 4At1 + В j dt.
Зауваження 2. Обчислення інтегралів з використанням
підстановок Ейлера може призвести до громіздких виразів, тому
їх треба застосовувати лише тоді, коли розглядуваний інтеграл не
вдається обчислити іншим способом.

§ 6. Інтегрування ірраціональних функцій
209
6.3. Тригонометричні підстановки
Виділенням повного квадрата в квадратному тричлені
2 . • Ъ
ах +Ьх + с і подальшою заміною и = х + — інтеграл
2а
\R[x, yjax2 +bx + c\dx (аФО) зводиться до інтеграла одного з
таких трьох типів:
1
|/?(м,л// -и \du\
2. ЩиАі1 +u2\du;
3. J/?LVm2-/2W
Ці інтеграли тригонометричною чи гіперболічною
підстановкою відповідно
1. M=/sinr,a6o u=lcost, або u=ltht;
2. w=/tgr, a6ow=/ctgr, a6ow=/shr;
3. и= , або u= , або u=lcht
cost sint
зводяться до інтегралів вигляду fi?(sinr, cost)dt чи
\R(sht, cht)dt.
Приклад. 7. Знайти інтеграл J ***•
Приймемо x = 4sin<p. Тоді dx = 4cos <р d<p. Отже,
гл/іб-jc2 , r4cos#?-4cos^<i^ 1 r ctgV ,
^ jc4 ^ 44sin4^ 16 J sin2 #?

210
Розділ III. Невизначений інтеграл
Приклад 8. Знайти інтеграл J-
dx
(jc2-2jc + 5)2
Перетворимо ісвадратний тричлен: х - 2х + 5 = (х -1) +4.
Приймемо х -1 = 2ig(p, тоді dx -
cos2 ер
dq>\
jc2-2x + 5 = (jt-l)2+4 = 4(l + tgV)= 4
cos2 cp
J
dx
-f
2d(p
(**-*,+ 5)5 cos>Jv 4
= —|cos^J^ = —sin^7+C =
1 4cp +c = j д x-1 +c
4VtgV + l 4V*2-2jc + 5
r^—
Приклад 9. Знайти інтеграл [ —die.
Нехай jc = , тоді dx = T—d<p ,
cos#> cos #>
2 і 1 - l-COS2fi? Sin2 Ф 2
cos2#?
cos2 <p cos2 #>
Знаходимо
rh?-
г—dx= -^- r_ri= \tg<psm<pd<p= -d<p =
cos (p—2
COS 0>
rl-cos2#? г d#? r , , /V n
= -d<p= —-— cospdp = ln tg —+ —
J cos#? Jcos#? J v2 4
-sin^ + C =
= ln
Ix + ylx2-]
47^\
+ C.

§ 6. Інтегрування ірраціональних функцій
211
■•[
Приклад 10. Знайти інтеграл f .
yja2 -х2
Маємо інтеграл першого типу
adt\
ca3th3t adt _ 3 fth3r _
л: die
£Г-
\x = a thf; die =
ch2t
thr = -
ch/
з rsh2f-shf _, і , ,, ,i зги2-1 . з cdu
= a —dt = \cht = u; shtdt = du\ = a —-—du = a —т~
J ch4t ' ' J u4 V
з г^м з 1 a 1 _ a a^, a a ,-,
V и 3 M3 Зм3 и 3ch3f ch/
Оскільки = VI - th2f , то
cht
/ = £lV(l-th203-a3V^h^ + C = ^- Jl-f-1
З 3 V[ l^aj
die
Приклад 11. Знайти інтеграл J ,
Після заміни jc - 1 = t одержимо інтеграл третього типу
dx
j-
уіх2-2х
\t = chu, dt = shudu
w = archr
|f = jc-l, dx = dt\
x = t + l
- f dt
= f—-du=u + C = archt + C =
Jshu
= fo(t + ylt2 -l\ + C = ]n(x-l + \lx2 -2x\ + C.

212
Розділ III. Невизначений інтеграл
Приклад 12. Знайти інтеграл
= JV(*2-D3
dx =
2
x = cht, dx = shtdt\
t = arch x
ft(x2-lfdx.
= \sh3t • sh tdt = \sh4 tdt =
= j| ch2£—1 j dt = Lj(ch^2t-2ch2t + l)dt = -jch22tdt-
— \ch2tdt + -t = - dt—sh2f + -f = - \cYi4tdt +
2* 4 4J 2 4 4 8J
1 1 i_~ 1 1 ,.„ 1 uo 3 „
+ -f sh2f +—f =—sh4r sh2f + -t + С
8 4 4 32 4 8
Виразимо гіперболічний синус через гіперболічний косинус
sh4f = 2sh2f ch2f = 4sh t ch t (sh2f + ch2f) = 4shfchf (2ch2f -1) =
= WchV-1 • chf(2ch2f -1);
sh 2t = 2sh tcht = 2vch2f -1 • chr.
Тому
/=J_.4Vch2r-l.chK2ch2r-l)---2Vch2r-bchr + -r + C =
32 4 8
= ^Vch2r-bch/i(2ch2r-l)-l| + -^ + C = -
2
= -Vch2r-l-chr-
8
2 A) 8
= -Vch2;-l-(2ch3*-5chO +lf + C =
= ^Vjc2 -1 -(2*3 -5д:)+-1пд; + л/л:2 -і
+ C.

§ 6. Інтегрування ірраціональних функцій
213
6.4. Інтеграл від диференціального бінома
Диференціальним біномом називається вираз
xm(a + bxn)pdx,
де а,Ь - сталі, відмінні від нуля, а т,п, р - раціональні числа.
Інтеграл
jxm(a + bxn)pdx
виражається через елементарні функції лише в таких трьох
випадках:
а) р - ціле число. Тоді потрібно зробити заміну х = ts, де
s - найменше спільне кратне знаменників дробів m in;
б) - ціле число. Тоді треба зробити заміну
п
а + bxn = ts, де s - знаменник дробу р;
ч /и + 1 . _ . - -
в) + р - ціле число. Тоді треба зробити заміну
п
ах~п +b = ts, де s - знаменник дробу р.
dx
Приклад 13. Знайти інтеграл Г
2'
хҐ - '
Маємо р = -2 - ціле число, тому це перший з наведених
вище випадків інтегрування диференціального бінома. За умовою
т = -1, п = —, тобто s-Ъ. Приймаємо х = t , тоді dx = 3t dt і
с dx _ с 3t dt _ г Л
*(l+^)2"Jf3(1+02" Jfd+02'
Розклавши підінтегральну функцію на прості дроби
1 = —+ —+ С ,; А(1 + 02+Я»(1 + 0 + С/ = 1;
/(1 + 0 f 1 + f (1 + 0

214
Розділ III. Невизначений інтеграл
t = 0:A = l; t = -l:C = -l; t2:A + B = 0, B = -A = -l,
отримаємо
Г ^—^ = 3 jf I—і L_U = 31nH-31n|l+f|+— +
х(і+Щ2 V l+t a+o2J ' ' i+r
c=
= 31n
1 + </д;
+ -
1 + Vx
r + C.
Приклад 14. Знайти інтеграл f dx.
1 x
Оскільки m = -l; n =—; p =—; = -r = 0, то маємо ви-
2 3л 1
падок б) інтегрування диференціального бінома. Підстановка
1 + *fx = t3 дає х = О3 -1)2, dx = 2(t3 -1) • 3t2dt. Тому
, r^/l + VJc j rf-6f2t3-l), ,/t 1 V - ^r rfr
/= [- —<£c = [ , ' 4, ;rf( = 6 1 + 1 №=6f + 6 -—.
* u3-ir v ' _1' ' *
1
Розкладемо підінтегральну функцію —— на прості дроби:
г-1
1
A Bt + C
■ + ■
f*-l f-lV+f + 1
Знаходимо невідомі коефіцієнти А, В, С
A(t2+t + l)} + (Bt + C)(t-l) = l,
А + В = 0,
А + С-В = 0,
А-С = \,
звідки А = —, В = —, С = —.
3 3 3

§ 6. Інтегрування ірраціональних функцій
215
Отже,
/ = 6r + 2 2 A = 6f + 21nf-l- -Ц— dt =
h-l 42+t+\ ' ' J t2+t + \
d(t2+t + l)
dU+-
1 ' J t2+t+i Y і
f+2j +4
= 6f + 21nf-l -In
r+f + 1
-3-^arctg
' 1^
t + -
2
V3
2 ;
+ C = 6^/l + V* +
+ln
(^W^-i)2
ш+7І)2+^/ГЙ/ї
+i
- 2V3arctg * * +1
Приклад 15. Знайти інтеграл dx.
гт, 2 m + 1 . . ^
Тут m = -6, л = 3, р =—, + р = -1- ціле число. Тому
З п
маємо третій випадок інтегрування диференціального бінома.
Приймемо
jc"3 + 2 = t3, x~4dx = -t2dt.
Оскільки 1 + 2x3 = x3 lx~3 + 2J, то
2 2
JV6 (l + 2x3 fdx= J*-4 (х-3 +2fdx= j? (-t2dt) = --t5 +C =
= --X-$(l + 2x3p+C.

216
Розділ ПІ. Невизначений інтеграл
6.5. Інтеграли вигляду J . п ==dx,
\lax2 +bx + c
де а Ф О, Рп (х) - многочлен степеня п > 1.
Ці інтеграли завжди можна звести до інтегралів від
раціональних дробів за допомогою однієї із підстановок Ейлера. Проте
тут значно швидше до цілі приводить наступний метод.
Запишемо:
\ W <Ь =Pw_lW>/ax2+fa + c+f f£ !f (3.9)
V ах2 +bx + c у] ах2 +bx + c
де Рп-\(х) - многочлен степеня «-Із невідомими
коефіцієнтами, І - невідома стала. Для знаходження коефіцієнтів
многочлена Рп-\(х) і сталої / диференціюємо ліву та праву частини
рівності (3.9), множимо її на л]ах + Ьх + с , а потім прирівнюємо
коефіцієнти при однакових степенях х в лівій і правій частинах
одержаного виразу.
Приклад 16. Знайти інтеграл / = | , —dx.
J уіх2-2х
Приймемо
І = (Ах2+Вх + С)\Іх2-2х+і\ , *** .
Чх2-2х
Продиференціювавши (3.10), одержимо
3x3-Sx2+4x
(3.10)
4І~-
2х
= (2Ах + В)у]х2-2х + (Ах2+Вх + С) * + .
2уІх2-2 у]х2-2х
Помножимо обидві частини отриманої рівності на yjx -2х . Тоді
3jc3 - 8jc2 + 4jc = (2Ах + В)(х2 - 2х) + (Ах2 +Вх + С)(х -1) + /,

§ 6. Інтегрування ірраціональних функцій
217
звідки, розкривши дужки, отримаємо
Зх3 - Sx2 + Ах = 3Ах3 + (25 - 5А)х2 + (С - ЗВ)х -С + 1.
Прирівнявши коефіцієнти при однакових степенях х, матимемо
А = 1, 5 = -|, С = ~ / = —.
2 2 2
Отже,
' 2 З О
jc —д; —
2 2
д; Nx -2х-
2 2
— f , ' = х1—х—W*2-2jt—In Lc -1 + л/л2 - 2jc
2J^)M I 2 2j 2 I
+ C.
Задачі для самостійного розв'язування
3.211. І -==dx.
h + Jx
,213. f-£*L ;
J *(* + !)
Л:
3.:
3.215. f ,
3.217. J *
JyJx + \/x
. „., ryfxdx
3.221. -—t=.
3.223. J-
dx
fax + l)2 -yl2x + l
3.212. f1 ^X^dx.
3.214. J-
3.216. J
3.218. J
x-l4x
(x + l)<£t
xy/x-2
x + 3
х2л/2х + 3
dx
*x^Tx
dx
dx.
3.220. f- .
3.222. \X + fX+ff dx.
3'224' і-2j;+&;+&'

218
Розділ III. Невизначений інтеграл
3.225.
3.227.
3.229.
3.231.
3.233.
3.235.
3.237.
3.239.
3.241.
3.243.
3.245.
3.247.
3.249.
4х>-Тх
dx.
Yjc-1
1-х dx
l + x(l + x)2'
dx
>V7^
dx
/(5-х2)3
ll + xz
dx.
dx
(x2+4)yj4x2+l
\jl-4x-x dx.
\l2x-x2dx.
yjxdx
і
x3+l
dx
Нй7'
dx
V7^
e2xdx
(ex+l)4
3.226. \xj dx.
J Vjc + 1
x-\
3.228. f -\l±±dx.
>(1-х)а + х)2 Vl-x
3.230. jjx2-9dx.
3.232. jV^
x dx.
3.234. y1 * dx.
3.236. J- Л
3.238. J-
xyjl + x2
dx
d
(jc + 1)Vjc +ДС + 1
3.240. J- dx;
3.242. J-
dx
Wi-*3
5*
3.244. f . <fr.
JVT^7
3.246. J- Л
x4l + x2
3.248. jyf^+x^dx.
. ._л rsh vI-jc ,
3.250. —т=—*-*£c.

§ 6. Інтегрування ірраціональних функцій
219
ВІДПОВІДІ
3.211. х-2у[х + 2ln(y[x +і)+С. 3.212. -2(>/Jc + ln|>/Jc-2|) + C.
х-2
3.213. 2arctgVJc + С. 3.214. 2а/*-2 + ЛarctgJ + С
3.215. 2arctgV* + l + C.
3.217. -\/? - Зл^ + 3lnk/x + її + С.
2 І І
3.218. 2lfx +31n|V3c - її + С.
3.219. 2^-4^ + 41п(і + ^) + С.
3.220. -2($[5^f -41n(l + ij5-x)+ С
3.216.-^±3+С
3.221. -f5-3f2 + In -—^
6
—і
5
2f-l
a+ir
+2л/з arctg —p- + C, t = yfx.
s
3.222. -у[х*+бУх- 6arctg^c + С
2
+ C.
3.223. - V2x + 1 + 3^2*+1 + 3 lnR/2* + l -1
2 I I
3.224. -V^--V^-V^--V^-3'^- —ln|'^-l|
4 4 5
3
+ —In
40
2^/Jc + 212/x +1 + —arctg b1^* +1
I 20 I I
+ C.
3.225.— V7--'^F + C.
27 13
3.226. — 0-2) +-lnLc +
2 2 I
VT^T
+ c.
3.227. -In
1, z^ + z + 1 2
+ -t= arctg
2z + l 2z
3 (Z-1)2 V3 6 ч/з z3-l
+ C, де z = 3.
ЛГ + 1
*-l*

220
Розділ III. Невизначений інтеграл
3.228.
VTT
■+с.
3.229. --
8
(1-хУ
1 + х
+ С.
3.230. V*2-9--lnL + V*2-9
2
+ С. 3.231.— - + С.
9х
3.232. 2arcsin- + *^4 * + С.
2 2
3.233.
„„„, Vi-*2
3.234. arcsin х + С.
3.235. -
Vo+7)
+ С.
З*3
■+с.
3.236. In
3.237.
i+V*2+i
+с.
4>/Ї5
In
ху/Ї5+2лІ4х2+1
к^іЇ5-2уі4х2+1
+ С.
3.238. In
3.239. -
2
V*2+*+1+.
+с.
V*2 +JC + 1 + X + 2
/ лг + 2
(л: + 2)л/і-4л:-л:2 + 5 arcsin —=-
V5 .
+ С.
3.240. V*2 +2д;+1пл: + 1 + л/л2 + 2*
3.241.
І[(*-1)>/2^Г
л; + arcsin(x -1)
+ С.
+ С.
3.242. -In
З
л/Г^5"-:
+ с.
Vl-л;3 +]
3.243. |Г^-Ц</7 + і)] + С.
3.244. —lnljc2 + Vl + x4| + С.
2 І І

§ 6. Інтегрування ірраціональних функцій
221
-,-,,* і, (z-i)2 л/з 2z+i ^ з/;—
3.245. — 1п4г—— + —arctg-^ + C, де z = Vl + -
Ю z2 + z + l 5
S
3.246.
(2х2-і)л/
1 + лґ
3*J
■ + C,
3.247. -2j(* ^+l) +C.
3.248. 2]n\x + Jx2 +4 + -уіх2 +4 + C.
I I 2
3.249. l^+l)7-|^+l)3+C.
3.250. -2chVl-* + C

222
Розділ III. Невизначений інтеграл
§ 7. ІНТЕГРУВАННЯ РАЦІОНАЛЬНИХ ВИРАЗІВ
ВІД ТРИГОНОМЕТРИЧНИХ ФУНКЦІЙ
7.1. Інтеграли виду \R(smx,cosx)dx,
де R - раціональна функція своїх аргументів, зводяться до
інтегралів від раціональної функції нового аргументу t за допомогою
універсальної тригонометричної підстановки
х . , 2dt
ig—-t, тоді х = zarctgf; ах = -.
2 1 + Г
При цьому використовують відомі тригонометричні формули
X
2 _:
sinjc =
2*f _ 2,
1+tg
2* l + t
2 '
COSJC = -
2 X
Приклад 1. Знайти інтеграл J-
1 + tg2* 1 + '
6 2
2 '
'8-4sinjc + 7cosjc
Застосовуючи універсальну тригонометричну підстановку
х . 2f
tg—= f, матимемо sin;c = -,
2 l + t2
1-Ґ J 2dt
cosa: = -, ax-
l + t'
2 '
Ь
Отже
dx
8-4sinjc + 7cosjc
-!■
1
2dt
2t 1-t2 l + t2
8-4^ + 7^-Л-
-J:
l + t
2dt
t-8t + 15
= lnk-5-lnk-3+C = ln
1 + Ґ l + t
3)-(f-5
(t~3)(t-5)
t-5
_ г 2dt _ r(t-3)-(t-5) _ e dt с dt
~ 4t-3)(t-5) ~J (t-3)(t-5) '" h-5 h-3~
t-3
+ C=ln
,§-*
«f-3
+c.

§ 7. Інтегрування тригонометричних функцій
223
На практиці універсальна тригонометрична підстановка іноді
зумовлює дуже громіздкі обчислення. У частинних випадках
застосовують простіші підстановки:
а) якщо функція /?(sinjc, cosjc) непарна відносно sinjc, тобто
^(-sinjc,cosjc) = -^(sinjc,cosjc), то підстановка t = cosx
приводить до інтеграла від раціональної функції;
б) якщо функція /?(sin jc, cos jc) непарна відносно cosx,
тобто /?(sin jc,- cos jc) = -i?(sin jc, cos jc) , то підстановка t = sin jc дає
інтеграл від раціональної функції;
в) якщо функція i?(sin jc, cos jc) парна відносно sin jc та
cosjc, тобто /?(-sinjc,-cosjc) = /?(sinjc,cosjc), то підстановкою
t = tg jc отримують інтеграл від раціональної функції.
Приклад 2. Знайти інтеграл J-
sinjc
-dx.
sin JC + 6COS JC
Підінтегральна функція непарна відносно синуса, тому
використаємо підстановку cosjc = f, звідки -sinxdx-dt
Отже,
r sinjc r sinjc
Л„ , *~~ЛХ J1 + c_„2
'sin JC + 6COS
5 cos jc
=--— arctg
t
+C = —j=arctgU5t\ + C = —T=rarctg(V5 cosjc) + C.
Приклад 3. Знайти інтеграл jcos jc^sin jc dx.
Підінтегральна функція непарна відносно косинуса, тому
зробимо підстановку t = sin jc . Отже, dt = cosxdx і
jcos jeVsin jc dx = jcos4 Wsin jc cos xdx =
= f(l - sin2 jc)2 • Vsin jc cos xdx = \(l-t2)2yftdt= \(l-2t2 +tA)t2dt =

224
Розділ III. Невизначений інтеграл
( 1
-і
9Л
t2 -It1 +t2
J
~ З Л 7 л 11
2 - 4 - 2 —
dt = -t2 --t2 +—t2 +C =
3 7 11
2/. ч2 4/. J 2/. чіі .
= --(sinJCJ2 (S1IUCJ2 +— (sin jc; 2 +C.
Приклад 4. Знайти інтеграл / = Г
2sinjc + 3cosjc
dx.
Sin JC +COS JC
Оскільки
n/ . v 2(-sinjc)-3cosA: 2sinjc + 3cosjc n/ . ч
/?(-sinjc,-cosjc) = — = = /c(sinjc,cosx),
-sinjC-COSJC SHIJC + COSJC
приймемо t = tg jc. Тоді
1 ?
df = jdx = (tg jc + l)dx
COS
rcosjc(2tgJc + 3) _ r
J cosjc(tgjc + l) ■*(* +
2f + 3
-dt.
(* + l) (Г+1)
Для обчислення отриманого інтеграла розкладемо під-
інтегральну функцію на прості дроби:
2t + 3
A Bt + C
■ + -
(* + i)(r+i) f + i r+i
звідки A(f2 +1) + (Л + C)(f +1) = It + 3. .
Для визначення коефіцієнта А приймемо в останній
тотожності г = -1, тоді 2А = 1, А = —.
2
Щоб знайти сталі В і С , прирівняємо коефіцієнти при t і
Г° у цій самій тотожності
t2: А + В = 0У В = --\ t°:A + C = 3; С = -.
Тоді шуканий інтеграл набуде вигляду

§ 7. Інтегрування тригонометричних функцій
225
=-In If + її--In
2 ' ' 4
';2+1|
2
5 ^1, (t + iy 5
+ -arctgf + C = -ln\ + -arctg; + C.
2 4 ,2+l 2
Повертаючись до змінної х, отримаємо
\2
/=-ln^g^+ j +-arctg(tgJc) + C = -ln((tgA: + l)2cos2A:) + -A:+C =
4 tg2x + l 2 4 VV* /2
= — lnlsin JC + cos jc| + — X + C.
2 ' '2
7.2. Інтеграли виду Jsinm jccosw jc^c.
Можливі три випадки:
а) якщо принаймні одне з чисел т або п - непарне
додатне ціле число, то, відокремлюючи від непарного степеня
співмножник у парному степені і виражаючи його за допомогою
формули sin jc + cos jc = 1 через іншу функцію (sin х через COS X
або навпаки), приходимо до табличного інтеграла.
б) якщо /піп- парні невід'ємні числа, то степені
понижуються за допомогою переходу до подвійного аргументу:
? 1 + cos2jc . 2 1-cos2jc . 1 . Л
cos jc = , sin jc = , sinjccosjc = —sin2;c;
2 2 2
в) якщо m + n = -2k, k є TV, тобто m + n - ціле парне
від'ємне число, то доцільно використати підстановки tgx = t або ctg jc = t.
„ _ ^ w fsin jcdbc
Приклад 5. Знайти інтеграл ,
J л/cosjc
Маємо
rsin3jcdbc r sin2* . , rl-cos2jc ., ч rd(cosjc)
J 4/ Jl7—Sm^^ = "J 4/ rf(COSJK) = -l 4/ +
J VCOSJC J>/COSJC J yJCOSX J VCOSJC
fCOS2JC Jr ч 4 4/ Г~" 4 J jT~ ^
+ , <i(cosjc) =—vcos JC+—vcos X + C.
WCOSJC 3 11

226
Розділ III. Невизначений інтеграл
Приклад 6. Знайти інтеграл [sin2 х cos4 xdx.
Оскільки sin xt cos х мають парні додатні степені, •
С . 2 4 , rl-cos2jcfl + cos2jc>\ ,
sin jccos xdx= dx =
J J 2 L 2 J
= — j(l + cos 2x - cos2 2x - cos3 2x) dx =
1 1 . _ 1 rl + cos4jc , If 2 m »• • ~ ч *
= — jc +—sin2;c— dx cos 2jcrf(sin2jc) = — +
8 16 8J 2 16J 16
1 . - 1 sin Ax If,- . 2^ ч i/ • л» \ *
+—sm2jc (1-sin 2jc)d(sin2jc) =— +
16 16 4 16J v J 16
1 . о 1 . A 1 . о 1 sin32jc „
+—sin2jc sui4jc sin2;c + + C=
16 64 16 16 3
x sin4x sin32jc _
= + + C.
16 64 48
2
Приклад 7. Знайти інтеграл j—— dx .
J cos JC
\^Adx = ftg2* г —= ftg2x(l + tg2*y(tg*) =
JCOS JC J COS X COS JC J
= Jtg2*. rf(tg*) + Jtg4ja/(tg*) =
= f(r2+r4Wr = ^ + ^ + C = ^ + -^ + C.
JV /35 35
У загальному випадку такі інтеграли обчислюють за допомогою
рекурентних формул, які отримують інтегруванням частинами.
Приклад 8. Вивести рекурентну формулу для обчислення
г dx с dx
інтеграла ——— і за її допомогою знайти інтеграл —-—.
J sin2*+1 jc J sin3 JC

§ 7. Інтегрування тригонометричних функцій
227
Рекурентну формулу виводимо, використовуючи в
чисельнику тригонометричну тотожність sin2 х + cos2 X = 1.
_ r dx _ rsin jc + cos x _ с dx r cos x _
*2*+l - J 2*+l " J e:„2*+l **" J~2kT~+ L„2*+l **~
sin
sin2*+1jc
г cos л: ,
= /2fc-l + J . 2*+l ^ =
sin x " sin
w = cosjc; du=-sinxdx
COSJC
aV = aX\ V = —
• 2Jfc+l '
siir*+1 JC
1
2fcsin2*jc
— IlV-\ —
COSJC
smjc
d* - hk-\
2Jfcsmz*jc J2ifcsin *jc
^ т ft 1), cos*
Тому /2jfc+1 = I"— /2*-l -——"2^—-
^ 2fc; 2fcsmz*jc
COSJC
.--Ц
2£sin2*jc 2fc
2*-l'
Зокрема, при k = 1 отримаємо
* CI
Л:
cos л:
sm3jc 2sin2jc
1Л r dx
1 f ax _
2 J J sin jc
COSJC
2sin2jc
. 2 * 2 *
sin —+ COS — л
+-f—2 1Л = __£«* +1
2J 2Sin±cos* 2sil>2* 2
2 2
і s
( X X ^
sivi—dx cos—dx
f ^—+ f ^—
2cos— 2 sin —
v 2 2
JC JC
л dcos— л dsin —
cos л: 1 r 2+1 f 2 =
2sin2x 2 J x 2* . x
zsm x * CQS_ * sm_
2 2
COSJC lt
In
2sin2jc 2
JC
cos—l
2
2
. x
sin—|
2
_ cos* 1 ,
2 sin2 л; 2
tg:
+ C.

228
Розділ III. Невизначений інтеграл
7.3. Інтеграли виду [sin" xdx.
Запишемо sin" jc = sin" ^-sinjc і використаємо формулу
інтегрування частинами. Тоді
Іп = fsin"jcdlx: = jsin^jc-sinjcd^
_ \ и = sin""1 jc; du = (n-1) sin""2 jccos xdx\ _
| dv = sinxdx\ v =-cosjc |
= -cosjc sin""1 x + (n -1) fsin""2 jccos2 xdx= - cos jcsin""1 x +
+ (n -1) fsin""2 jc(1 - sin2 jc) dx = - cos x sin""1 X 4
+ (n-1) j(sin"~2 jc- sin" jc)dbc -cos jc sin""1 JC + in - l)/n_2 - (л - l)/n.
Звідси отримуємо рекурентну формулу
/„=— (w-1) Іп_2 -cosjc sin""1 JC , л=3,4, ...
Зауваження. Для степенів тригонометричних функцій
відомі формули
1 т_1 1
мп^-х = -2^гХ(-1)т"':С2тсо8[2(ш-^] + -^С2г
Jt=0
та
sin
2m+l
1 w
* = Т5г£<"1>^*с^іві,1[<2т-2* + 1)я]-
2 *=0
Для високих степенів синусів доцільно використовувати
такі рівності:
\sm2mxdx = -гЦ- У іг\)т~кС\т sin [2(m - к)х\ +
9
Z Jt=0
\w-l m-1
2(m-k)
+ІС^^+С=Ч^-^Н)^—-sin[2(m-*)*WC,*+C,
2 2 £q лг-А: 2

§ 7. Інтегрування тригонометричних функцій
229
-cos[(2m-2ifc + l)jc] +
і т
+С = -^ У(-1)*С|т+1 cos[(2m-2£ + l)jcl + С.
22w Й (2m-2ifc + l) L J
Приклад 9. Знайти інтеграл jsin4 xdx.
Знаходимо
/ = jsin7 jcA=— 6 jsin5 ju£c-cosjc-sin6jc =— jsin5 xdx—
cos jc-sin JC =
—14 jsin3 xdx - cos x • sin4 x J
= — sin jcdx
1 • 6
COS Jt'sin jc =
7
35
cos jc • sin4 x—cos x • sin6 X =
24
35
-12 jsin xdx - cos x • sin2 jc]
6 . 4 1 -6
COS jc-sin JC—COS jc-sin JC =
35 7
16 8 . 2 6 . 4 1 . 6 „
= COSJC COS JC-sin JC COSJC-Sin JC—COSJC-Sin JC + C,
35 35 35 7
7.4. Інтеграли виду jcos" xdx.
Для такого інтеграла теж існує рекурентна формула,
аналогічна до наведеної в п. 7.3:
Іп = jcosn xdx = — sinjc cos""1 jc + (n-1) In_2 , «=3,4,...
Ґрунтуючись на формулах для степенів тригонометричних
функцій
1 т_1 1
Z k=Q Z
та
1 т
cos2m+1 х = ^rZ Clm+i cos[(2m - 2* +1)*],
2 *=0

230
Розділ III. Невизначений інтеграл
знаходимо
1 1 1
fcos2m xdx = — £ Ск2т -sin[2(m-k)x] +—C?mx+ С,
J 2 £Ґ0 (m-k) 2
. і m
* 1
2Lmt^s 2m+1(.2m-2k + l)
sin[(2m-2k + l)x] + C.
Приклад 10. Знайти інтеграл [cos7 xdx.
Маємо
jCos10xdx = ^f^C1k0-^-sm[2(5-k)x] + ^C^x + C =
2 £=o ^ k' 2
>io
Cfo •—sinIOjc + Cio •—sin8jc + Q20 • -sin6jc +
1
+Ci3n •—sin 4jc + Ci4n sin 2jc
-10
10 г
+ ^шСюх + С-^Го
—sinl0jc +—sin8jc +
5 2
+ 15sin6jc + 60sin4jc + 210sin2jc
63
+ jc + C.
256
7.5. Інтегрування добутків синусів
та косинусів різних аргументів
У цьому випадку застосовують тригонометричні формули
cos a cos (3 =—[cos(ar -j3) + cos(a + /?)],
sinasm/3 = —[cos(a-j3)-cos(a + j3)],
sin a cos J3 =—[sin(or -j3) + sin(a + /?)].
Приклад 11. Знайти інтеграл Jcosjc cos2jc cos3jcdbc.
Перетворимо добуток тригонометричних функцій у суму і
проінтегруємо. Отримаємо

§ 7. Інтегрування тригонометричних функцій
231
jcos л; cos 2xcos3xdx = — j(cos х + cos3jc)cos 3xdx =
= — jcosxcos3jcйЬс + — jcos2 3xdx = — J(cos2x + cos4jc) dx +
+— J(l + cos 6x)dx=— Jcos 2x^ + —Jcos4x&+ —(*£*+— Jcos 6xdx-
1 • „ 1 • , 1 1 -^ ^
= -sm 2jc +—sm 4jc +—jc +—sin ox + C.
8 16 4 24
7.6. Інтеграли виду \tgmxdx, \ctgmxdx,
де m = 2,3,...
Для обчислення таких інтегралів використовуємо
тригонометричні формули
2 1 , 2 1
tg х = — 1; ctg * = —2
cos х
Тоді
sin х
1-1.
[tgmxdx= ftgW-2JC —^ llfe = -2-i- \tgm-2xdx
J J Icos2jc У m-1 J
Аналогічно
VCOS x J
-1
\ctgmxdx = ctgw_1jc- [ctgm~2xdx.
J m-1 J
Приклад 12. Знайти інтеграл jtg6jtd!x.
/= [tg6xdx = ftg4jc r 1 d!x = -tg5jt- ftg4;cd!x =
J J Uos2jc у 5 J
_ tg5* tg3* pin2* = tg5* tg3* r
5 3 Jcos2* 5 3 J
rl-cos2 x
dx =
'cos x
^5„ 4_3.
COS JC
tg3JC tgJjc
= -2 2— + tgJC-Jt + C.
5 3

232
Розділ III. Невизначений інтеграл
Задачі для самостійного розв'язування
3.251. jsin3;cd!x. 3.252. jsin2 jccos3 xdx.
3.253. fsin3-cos5 — dx. 3.254. |cos52;csin2;cd!x.
J 3 2 - J
3.255. t^Ldx . 3.256. i^dx.
J cos* Jsiirjc
. • з
3.257. \\lsin2xcos3xdx. 3.258. f ,Sm * dx.
V cos4 ;c
^ ~m Г sin* , „ _,Л f cosjc
3.259. -dfr. 3.260. —г dx.
(l-cosx) sin x-6sinx + 5
sin3 л: , ^ л,л f sin3 л:
3.261. [ Sm * dbc- 3.262. f—
Jcosx-3 Jl +
sin 2л:
cos2 л:
d!x.
3.263. [ T—dx. 3.264. [sin2;c-cos2;cd!x.
Jl + sin2x J
3.265. jsin4;cd!x. 3.266. jcos 3xdx.
3.267. fsin2jccos4jrc&. 3.268. f .
J Jsinx
* ~^ rcosjc + sinx , „ __л r d!x
3.269. dfr. 3.270. — .
J sin 2л: J sin x cos л:
3.271. /-з^гз-. 3.272. f.4^ 4 ■
Jcos jcsin jc Jsin JCCOS JC
3.273. f-4-. 3.274. Г *
Jcos x sin л:
г Г X X
3.275. sin;csin3;tt£t. 3.276. sin—sin—dx.
J J 3 2
3.277. jsin—cos—dx. 3.278. jsin л; sin 2;c sin 3jtd!x.

§ 7. Інтегрування тригонометричних функцій
233
3.279. Jcos;ccos3jtcos5;cd!x.
3.281. |-
dx
З sin2 л;+ 5 cos2 л;
dx
3.283. f—
3.285. jtg ;cd!x.
3.287. f *
J4 + tgx +
3.289. f-^i
tgx + 4ctgx
sinxdx
sm л:-cos л:
3.291. f
J(l + cos;c)
3.293. f—^—
2'
dx
4-5sinx
3.295. Г—^
J4-5si
3.297. f- Л
3.299. |
sin 2л: -2 sin л;
1-sinjc
<it.
3.280.
3.282.
3.284.
3.286.
3.288.
3.290.
3.292.
3.294.
3.296.
3.298.
3.300.
cos л:
cos 2л:
cos4 x + sin4 x
dx.
dx
sin2 x + 3sin л:cosx - cos2 x
1 + tgx
1-tgx
dx
dx.
igx
dx
1 + sin x
cosxdx
1 + cosjc
dx
(sin x + cos ;c)
dx
2 "
5-3cos;c
5-4sinx + 3cosx
cos2jc
1 + sin л: cos л:
-dx.
1 + cos x
1 + cos 2x
dx.
Відповіді
1 о
3.251. -cos x-cosx + C.
3
3.253. -cos8---cos6- + C.
4 2 3 2
„ „- sin3 л: sin5 л: _
3.252. + С.
3.254. -—cos6 2л: + С.
12

234
Р о зд і л III. Невизначений інтеграл
3.255.
3.256.
3.257.
3.258.
3.260.
3.262.
3.264.
3.266.
3.267.
3.269.
3.271.
3.272.
3.274.
3.276.
3.278.
1 2 II
— cos дс-ln cosjq + C
sin2 де
— 21n|sin;t| + C.
2sin x
5 11
3 - ~
—cos3;c + 3cos 3x + C.
5
3.259. —
1
2(1 -cos jc)
- + C.
1, 5-sin* _ „ _,. cos2л: . 01 ,. ч _
-In + C. 3.261. +3cos;c + 81n(3-cos;c) + C.
4 1 - sin x 2
■ + C.
cosjc- 2arctg(cos;c) + С. 3.263. ln(l + sin jc) + С
x sin Ax
8~~~32~
5 1 . , 1 • m 1 • з* -
—;c +—sinojc + — sin 12* + sin ojc + C.
16 12 64 144
^/%^^ 3jc sin2x sin4x _
3.265. + + C.
8 4 32
jc sin4jc sin32jc _
+ + C.
16 64 48
1, (l-cosx)(l + sinx) _
-In- - + C.
4 (cos;c + l)(l-sin;c)
-(tg2x-ctg2x) + 21n|tgx|+C.
(tg2x-l)(tg4jc + 10tg2x + l)
3.268. In
*,
«*
+ c.
3.270. lnltgjcl V + c-
2tg2x
1
3tg3x
+ С 3.273. tg * + - tg3 x + C.
2 1 11
-ctgx—ctg3x—ctg5x + C. 3.275. — sin2x—sin 4* +С
6 3 5 4 8
о • X 3 . 5 _
3sm sm—x + C.
6 5 6
3.277. —cos cos x + C.
2 3 2
—совбде cos4x cos2x + C.
24 16 8

§ 7. Інтегрування тригонометричних функцій
235
3.279.
3.280.
—sm9jc +—sin;c +—sin/jc +—sin3;c+ С.
36 4 28 12
1 , V2+sin2x „ .„^ 1
ЛпЛ= + C. 3.281. -т= arctg
2л/2 V2-sin2x
7Ї5
V3tg.
V5
+c.
Vis
In
2tg х+3-л/ЇЗ
2tg *+3 + \/ІЗ
3.282.
3.284. -ln|cosx-sinx| + C.
3.286.
3.287.
3.288.
3.290
+ C. 3.283. -[x + ln|sin;t + cos;t|] + C.
1 4
3.285. -tg* x-tgx + x + С
-ln(;y + l)--ln(;y2->> + l)+—-arctg^^ + C, де у
2 4 2 V3
4 3 2 3
25 25 |6^ ' 5(tgjc + 2) 25 ' '
-parctg(72~tgx)+C.
= ^c.
x-tg- + C.
x 1
3.289. lnlsinx + cosjcl + C.
2 2 ' '
3.291.-tg-+ +-tg3- + C.
2 62 6 6 2
3.292. С —
1
1 + tgx
3.293. -Un
л/5
л/5 + tg-
V5-,gf
+ c.
3.294.
3.296.
1
-arctg
2tg| |+ C.
3.295. -In
3
Ч5-2
2„§-l
+c.
2-lf
-+c.
3.297. С--In
4
л:
,g5
+ -
8 sin
2X
3.298. ln(2 + sin2x) + C.
3.300.
3.299. ln(l + sin;c) + C.
1
-(tgjt + *) + C.

236
Розділ III. Невизначений інтеграл
§ 8. ІНТЕГРУВАННЯ
ГІПЕРБОЛІЧНИХ ФУНКЦІЙ
8.1. Заміна гіперболічних функцій показниковими
Інтеграли, що містять гіперболічні функції, можна
обчислити, замінивши гіперболічні функції на показникові
є —є , є +е
sh* = , chx = -
2
є —є , є +е
thx = , cthx =
є +е є —є
„ . _ г є dx
Приклад 1. Знайти інтеграл .
J chjc + shjc
Замінюючи гіперболічні функції на показникові, маємо
r exdx r exdx cexdx r, „
= = —= = \dx = x + C.
Jchx + shx Jex+ex ex-ex J ex J
+
2 2
Приклад 2. Знайти інтеграл Jth4;cd!x.
є — є є — 1
Оскільки th х = — = — , то після заміни th х = z
ех +е х є + 1
матимемо є = ; д: = —In ;
1-z 2 1-z
2 1 + г (1-z)2 (l+z)(l-z)
Тому

§ 8. Інтегрування гіперболічних функцій
237
с dz z3 1.
Jl-z2 3 2
1-z
1 + z
+ C =—th3x- thx +
3
2
1-th x
l + thx
1 і 1
+ C= —thJx-thx + -ln
3 2
1-
1 +
g*-g-*
g*+g-y
~x ~~x
e —e
ex + e~x
+ c =
= —\h3x-\hx—Ые2х + C = —th3x-thx-x + C.
8.2. Інтегрування із застосуванням
гіперболічної тригонометрії
Інтегрувати гіперболічні функції можна аналогічно до
тригонометричних, використовуючи такі формули:
sh х
ch х
= th х\
due
sh x
= cth x,
ch2x-sh2x = l,
О 1 9 1
2shxchx = sh2x, chzjc = -(ch2x + l) , shzx = -(ch2x-l),
1 - th2x = ——, 1 - cth2x = ——.
ch jc sh л:
Приклад 3. Знайти інтеграл jth2;cd!x.
Оскільки th2;c =
sh2jc ch2x-l
ch2;c ch2;c
■, TO
\th2xdx= ifl 5r-Uc= frfr- f-
J Jl ch2jj J J.
ch2x
= jc- thjc + C.
Приклад 4. Знайти інтеграл fsh2;cch3;cd!x.
fsh2xch3jc^c = Jsh2jcch2;cch.xY£t = |sh2xfl + sh2xjj(shx) =

238
Розділ III. Невизначений інтеграл
= fsh2* d(shx)+ \sh4x d(shx) = + + C.
Приклад 5. Знайти інтеграл Г .
с dx 1 г dx 1 rchx dx 1 rd(thx) 1 h ,
= - = - — = - \—K- ^ = -ln thx +C.
!sh2x 2Jshxchjc 2Jshxch2x 2 J thx 2 ' '
Приклад 6. Знайти інтеграл jsh 2д:йЬс .
\sh32xdx = Uh22x• sh2xdx = - f(ch22x-l)rf(ch2x) =
1 ch32jc 1 ^ л 1 l3/1 1 ^
= ch2x +С = -dr 2;c—ch2x + C.
2 3 2 6 2
Приклад 7. Знайти інтеграл Jsh2* ch2xdx.
\sh2xch2xdx= j —-2shjcchx d!x = — jsh22jtd!x =
= f(ch4jc-l)tffct = -
-jc
V 4 j
+ C = —sh4x—x + C.
32 8
Приклад 8. Знайти інтеграл J .
Помножимо чисельник та знаменник підінтегрального
дробу на ch х +1. Одержимо
r dx rchx + 1 , fch* + l , r t _2 ,/, \
7 = = — dx- —dx- sh xJ(shjc) +
Jchx-1 Jch2;c-1 J sh2* J V
J:
d!x _ 1
sh2x shx
-cthx+C.

§ 8. Інтегрування гіперболічних функцій
239
Задачі для самостійного розв'язування
У задачах 3.301-3.320 знайти інтеграли від гіперболічних
функцій:
3.301. І^ЕЕл*. 3.302. f Shxchx. dx.
L {E^Z*.*. 3.302. f-Eif
J Vl^c Jsh2;c +
3.311.
2.
ch x
sh4xdx.
3.303. jsh3xdx. 3.304. f:
3.305. f A . 3.306. fcth^dbc.
Jsh;tch x J
3.307. f *** . 3.308. fsh2*dbc.
Jsh j + ch2* J
3.309. Jsh3xdbc. 3.310. fcth5jcdr.
dx „. rxdx
f-^-. 3.312. Г
'shx "" Jch2x
3.313. j;c2shjcd!x. 3.314. \(ch2ax + sh2ax)dx.
3.315. f^thjc^. 3.316. f
dx
shx-1
3.317. f *** „ . 3.318. fJchx + ldx.
JshVch2;c J
3.319. fsh2;cch;c<£c. 3.320. f -.
J J(l + ch;c)2
Знайти інтеграли, використовуючи різні методи
інтегрування:
3.321. j(x + l)jx2+2xdx. 3.322. jex2+4x+3(x + 2)dx.
3.323. i^^fdx. 3.324. tf^.
J 1 + x2 J cos6*
3.325. J^/tg^sec4*^. 3.326. \x2^4-x2dx.

240
Розділ III. Невизначений інтеграл
„ „_ г/ г-— \2 j <, ^о f 12л:2 + 21л:+ 14 ,
3.327. Vsinjc + cosjc йЬс. 3.328. , =-flfr.
Д ' JV3x2+3x + 4
3.329. Jjc2arctg;c<£c. 3.330. J-
sin2;cd!x
З
х dx
>х*-4
3.331. fi£±!ML. 3.332. |*°»£а.
JJC(1 + JC£*) Jcos2x
3.333. [sin yjxdx. 3.334. Jsin8;cd!x.
rx + sinx , „ „„^ r d!x
/ - 4 *
'sin X
3.335. f* + Sm*<fr. 3.336. f-
Jl + cos;c Js
3.337. |xln(l + x3)^. 3.338. j^*"1)^
In2 л:
tffo л /ЩЛЛ r dx
3.339. Г — . 3.340. f—
Jl + sin^ + cosA: Jl +
3.341. [хе*2 (x2+l)dx. 3.342. f—
J 3(l +
cos2 л:
xexdx
d + x)2
3.343. J—j —. 3.344. \sin4xdx.
Jcos x + sin x J
.345. J-^j. 3.346. \eTxdx.
3.347. P^-dx. 3.348. f*^fc
3.349. f tsxdx? . 3.350. Г££!ІН^.
Відповіді
3.301. -ijl^x + С. 3.302. — Inсп2л: + С.
4
3.303. -ch3x-chx + C. 3.304. 2;с + ^ + ^І£ + С.
З 8 4 32

§ 8. Інтегрування гіперболічних функцій
241
3.305. In
th-
2
1
chx
3.307. arctg(thjc) + С.
■ + С.
3.306. ln|sh*|-^-^ + C.
3.308. - (sh л: ch x - x)+C.
3.309. sh* + -sh3* + С 3.310. lnlshjcl cth2*—cth4jc + C.
3 ' ' 2 4
3.311. In
«si
+c.
3.312. л th л - In cth jd + C.
■> 1
3.313. jrchx-2jcshjc + 2chjc + С 3.314. — sh2ax + C.
3.3X5. 1^ 1 + Vjh^ / /^) + c.
2 1-Jthxl v '
2a
3.316. cthx + C.
shjc
3.318. 2V2sh- + C.
2
3.320.-th---th3- + C.
2 2 6 2
3.322. -ex2+4x+3 + C.
2
3.324. -tg5;t + C.
5 6
3.317. -2cth2x + C.
3.319. ^-£ + c.
32 8
3.321. -yj(x2 + 2x)3 +C.
3.323. С +
(arctg*)
n + 1
n+l
(n*-l).
3.325. — 7tg^(5 tg2 * + 9) + С.
3.326. -(jc2 -2)4A-x2 + 2arcsin- + C.
4 2
3.327. — + —sin 2x +—Vsin3 x + cosx + C.
2 4 3
3.328. 2(jc+2)V3^+3jc+4+C.
3.329. —arctg*--*2 +-ln(*2 +1) + C.
3 6 6

242
Розділ III. Невизначений інтеграл
3.330. —In
16
jc4-2
jc4+2
+ С.
3.331. In
хе
+ С.
3.332. 2*-tgjc+C
35 1 7 1
3.334. — х—sin 2х н sin 4jc +—sin"1 2jc +
ll+jce*1
3.333. 2{sin\fx-\lxoos4x)+C.
1
1024
- sin 8x + С
1 ч
3.336. —ctg jc - ctg x + С
28 4 128 24
3.335. xtg-+C.
3.337. -jc2 ln(l + jc3)--*2 + -ln(jc2 -jc + l)--ln(jc + l) +
2 4 4 2
>/3 2*-l ,_
+тапяв^г+с-
3.339. In
1
3.341. -jcV +C.
l + tg-|
.2.^
+ c.
3.338.— +С
In л;
3.340.-^arctg-^ + C.
V2 %/2
3.342.
. + C
3.343. arctg(tg2 jc) + C.
1 + JC
3.345. -In
4 |l-jc
3.347. 2VJc + l(ln|jc + l|-2) + C.
3.348. — arcsin jc \l-x2 +1
2 2
3.349. jc—^arctg1 + 2*g* + C.
7з 7з
1 +JC
3.344. 2lsin-v/x-v^cosv^j + C.
+ -arctgjc + С 3.346. 3e^ /#? - 2#c" + 2) + C.
3.350. In
-VI^c2
arcsin jc
+ C.

Розділ IV
ВИЗНАЧЕНИЙ ІНТЕГРАЛ

244
Р о з д і л IV. Визначений інтеграл
§ 1. ОБЧИСЛЕННЯ ВИЗНАЧЕНИХ ІНТЕГРАЛІВ
1.1. Метод інтегральних сум
Нехай функція f(x) визначена на відрізку [a,b]. Розіб'ємо
його на п елементарних відрізків точками хк, £ = 0,..., п:
а = х0<хх< х2...< хп_х < хп = b.
Виберемо на кожному відрізку [**_і,**] довільно точки ^, і
знайдемо їх довжини
А*к =хк~~ Хк-\ •
Позначимо через X довжину найбільшого серед відрізків
[**_!»**]: Л = тахАхк, к = 1, ... ,п.
Означення 1. Інтегральною сумою для функції f(x) на
відрізку [a,b] називається сума вигляду
± /(& К = /(й К + /(& )Ах2 +...+f(€n К •
Означення 2. Визначеним інтегралом від функції f(x) на
відрізку [a,b] називається границя інтегральної суми при п—»«>
за умови, що така границя існує і не залежить від способу
розбиття відрізка [a,b] на частини і вибору точки £k
ь
f/(*)<fe=lim £/(&)Д**.' (4.1)
Числа а і й називаються відповідно нижньою і верхньою
межами інтегрування.
Теорема. Якщо функція f(x) неперервна на [a,b], то границя
інтегральної суми існує і не залежить ні від способу розбиття відрізка
[a,b] на елементарні відрізки, ні від вибору точок €k.

§ 1. Обчислення визначених інтегралів
245
Геометричний зміст. Якщо f(x) > 0 на [a,b], то визначений
ь
інтеграл \f(x)dx числово дорівнює площі відповідної криволінійної
а
трапеції, тобто фігури, обмеженої лініями y = f(x), у = 0,
х = а, х = Ь.
1.2. Формула Ньютона-Лейбніца
Зв'язок між визначеним інтегралом і первісною підінтеграль-
ної функції встановлює формула Ньютона-Лейбніца:
ьг \ь
= F(b)-F(a), (4.2)
де F(x) - будь-яка первісна функції f(x), F'(x) = f(x).
In З
Приклад 1. Обчислити визначений інтеграл J є xdx.
1п2
Оскільки функція F(jc) = — е3х є первісною функції є х, то
за формулою Ньютона-Лейбніца знайдемо
p^ = F(ln3)-F(ln2) = i,31n3-i,31n2=i(,In27-eIn8)=^.
In 2
S dx
Приклад 2. Обчислити f .
1 X
Первісною підінтегральної функції є F{x) = — arctg—, тому
1^--^м-^^4-ї^
3 j
ЗІ 6"~l~6"J Г 9"

246
Р о з д і л IV. Визначений інтеграл
1.3. Основні властивості визначеного інтеграла
1. Визначений інтеграл змінює знак при заміні місцями
його меж
b а
jf{x)dx = -jf(x)dx.
a b
2. Визначений інтеграл дорівнює нулю, якщо верхня і
нижня межі інтегрування однакові
і*
jf(x)dx = 0.
3. Для довільних чисел а,Ь,сз множини визначення функції
f(x) справедлива така рівність (адитивність визначеного
інтеграла) :
b с b
\f(x)dx= \f(x)dx+ \f(x)dx.
а а с
4. Визначений інтеграл суми (різниці) двох функцій
дорівнює сумі (різниці) відповідних визначених інтегралів
b b b
j[Mx)±f2(x)]dx= JMx)dx± jf2(x)dx.
a a a
5. Сталий множник можна виносити за знак визначеного
інтеграла
ь ь
jC-f(x)dx = CJf(x)dx (С = const).
а а
Властивості 4 і 5 називають властивостями лінійності
визначеного інтеграла.
6. Оцінка визначеного інтеграла. Якщо справедлива оцінка
m<f(x)<M на відрізку [a,b], то
ь
m(b-a)< \f(x)dx<M(b-a).

§ 1. Обчислення визначених інтегралів
247
7. Теорема про середнє. Якщо функція f(x) неперервна на
ь
[a,b], то існує число се (а,Ь) таке, що \f(x)dx = f(c)(b - а).
Значення функції f(x) при х = с називається її середнім
1 ь
значенням на відрізку [a,b], /(c) = \f(x)dx.
h — п J
2
x2J
dx.
Приклад 3. Обчислити / = | . + —j=
За властивостями лінійності 4 і 5 визначеного інтеграла маємо
9 9
dx Л с dx
'-'JtttW
о Vl-x2 о л/з-л2
= 3 arcsin jc
1 л ■ Х
+ 4arcsin—т=г
о V3
2
= 3
. л/3
arcsin arcsin 0
2
+ 4
arcsin
2-V3
\
- arcsin 0
/
^71 A 71 ЪП
= 3- —+ 4- —=—.
3 6 3
Приклад 4. Обчислити / = \Л—
cos2jc
dx.
1 + cos2jc
Оскільки X ' ww*"v = д/cos2 д: = Icosx\ =
я*
cosjc при 0<x<—,
-cosjc w/?M — <д:<Л",
то за властивістю адитивності визначеного інтеграла маємо
п
\к
2 71
І- Jcosja£c + J(-cosjc)^=sin^
п
~2
+ (-sinjc)
п
= (1-0)-(0-1) = 2.

248
Р о з д і л IV. Визначений інтеграл
Приклад 5. Оцінити інтеграл /
я\ х J
dx.
Похідна підінтегральної функції
w/ \ ґsinjc^ cosjc-jc-sinjc cosx(jc-tgx)
/{х)=Ьг) ' 7 =—7—
в жодній точці відрізка
п п
4'Т
не дорівнює нулю і приймає лише
від'ємні значення, отже, функція /(х)на цьому відрізку моно-
.(п\ 2уі2
4
тонно спадає. Тому М = /
Vі
п
є її найбільшим, а
m = f
яЛ Тз-з
- найменшим значенням. За властивістю 6
Ь
справедливою є оцінка m(b-а)< \f(x)dx<M(b-a). Довжина
, я и и
відрізка інтегрування дорівнює о-а- = — .
Тому для цього інтеграла маємо
3^ *<7<^.*, або 0,2іЛ^<0,24.
12 п 12 їх
2п
4
Приклад 6. Знайти середнє значення функції /(*) =
на відрізку [0;і].
За властивістю 7 визначеного інтеграла
ь
\f{x)dx = f(c)(b-a\
4а-х2

§ 1. Обчислення визначених інтегралів
249
тому
її
f(c) = \—j=dx =
. X
= arcsin—
2
_ п
о~~б'
Отже, середнє значення функції f(x) = —j= на відрізку
л/4-r2
-х
[0;і] дорівнює —.
6
1А Заміна змінної у визначеному інтегралі
Теорема. Якщо функція f(x) неперервна на відрізку [а;Ь],
а функція q>(t) і її похідна q>\t) - неперервні на відрізку [a;j3],
причому а = (р(сс), b = cp(j3), то справедливою є формула
ь Р
\f(x)dx=\f[<p{t)]<pXt)dt. (4.3)
а а
V2
Приклад 7. Обчислити / = f sA - х2 dx.
-їг
Виконаємо заміну змінної jt = 2shu, dx = d{2sint) =
= 2 cos tdt. Знайдемо нові межі інтегрування. Для цього вирази-
. х
мо змінну t через х: маємо f = arcsin—.
Для нижньої межі х = -у/2 одержимо t- , і відповідно
4
при х = V2 маємо t = —.
4
Отже,
л_ п_
1 . 4
/= JV4-4sin2r2cosr^ = 4 \\cost\costdt =
_П_ _7t_
~4 4

250
Р о з д і л IV. Визначений інтеграл
л_
4
л_
~4
= 4 jcos2tdt = 2 j(l + cos2t)dt = 2u +
л_
~4
л
~4
sin2f
= 2 + я.
^arct ъх
Приклад 8. Обчислити / = [ ^Ц-<йс.
о 1 + х
Зробимо заміну arctg x = t, dt = d(arctg jc) =
dx
l + x2

Визначимо нові межі інтегрування. При jc = 0 маємо t = 0, при
х = v3 одержуємо t = — . Отже
i=jPdt={-
з = —
О 4
(«А ^
^--0
V81 у
324
1.5. Інтегрування частинами
Теорема. Якщо функції и(х) та v(x) неперервні і диферен-
ційовні на відрізку \a\h\, то справедлива формула інтегрування
частинами
г \Ь с
\udv = uv\ -\vdu.
а І а
1
Приклад 9. Обчислити / = Jjcln(l + x2)dx.
(4.4)
Позначимо 1п(1 + х ) = и , лгйЬс = rfv . Тоді dw =
2xdx
l + x2
На проміжку [0;l] функції u(x),v(x) неперервні разом зі своїми
похідними. Використовуючи формулу інтегрування частинами,
одержимо

§ 1. Обчислення визначених інтегралів
251
І = uv
- \vdu =
о і
yln(l + *2)
1 ^
*z 2*<іх In 2 с х
1 г* z*<ix _ inz г л:
о J 2 1 + jc2 " 2 Jl +
■*& =
о
In 2 r[ jc
2 "Д^і+х2;
V In 2
кзЬс =
2
^jc2 ln(l + ;c2)^
_ln2_j_ ln2 2_j_
Г 2 2 2 2'
і
Приклад 10. Обчислити / = J (х - ї)е xdx.
Позначимо х-1 = и, є xdx = dv, тоді du=dx, -є x=v.
Отже,
І = (1-х)е~
1 Г-*
+ є *dfr = -l-e
о ^
= -е
Приклад 11. Обчислити / = \xsin(\nx)dx.
Приймемо и = sin(ln х), dv = xdx. Тоді du = dx, v = —
л; 2
/ = —sin(lnjc)
2
2 12ґ
— bccos(ln^)tic •
1 2 j1
Ще раз застосуємо інтегрування частинами, приймаючи
w = cos(ln jc), dv = лг^Ьс. Звідси du = dx, v = —. Одержимо
x 2
I = —sin(ln^)
2
2_l
і 2
—cosfliuc)
2
f 2 2 A
X X
—sin(ln x) cos(ln x)
V2 4 J
+ — Ijcsinflnjc)
2 l2f
— \xsm(}n x)dx.
і 4J

252
Р о з д і л IV. Визначений інтеграл
Маємо лінійне алгебраїчне рівняння відносно шуканого
інтеграла
1 1
pcsin(lnjc)d[x; + — \xsm()nx)dx = 2 sin In 2 - cos In 2 + —.
4f
Звідси I x sin(ln x)dx = —
2sin In 2 - cos In 2 + —
4
1.6. Інтеграли від парних та непарних функцій
Якщо функція f(x) є непарною на симетричному відносно
а
початку координат відрізку [-а; а], то \f(x)dx = 0.
-а
Якщо функція/(лс) на відрізку [-а; а] парна, то
а а
jf(x)dx = 2Jf(x)dx.
-а 0
Приклад 12. Обчислити інтеграл
Ч 2хп +Ъх6 -\0х5 -1хг -\2хг + х + 1 _,
т. dx.
-к х+2
Підінтегральну функцію подамо як суму непарної та парної
функцій і використаємо властивості інтегралів від цих функцій.
Матимемо
(^Л
'-Jt
^3;cV-4) + l
2Х1 - ІО*5 - 1хъ + х Зх6 -\2х2 +1
х2 + 2
х2+2
dx =
oJ х2+2 oJ h2+2
Ґ^.Ахг 2 a^jOK_1бГіп =V2>-64)
,5 V2 V2j о 5 2n/2 20

§ 1. Обчислення визначених інтегралів
253
Задачі для самостійного розв'язування
Обчислити визначені інтеграли, користуючись формулою
Ньютона-Лейбніца:
2 4 З
4.1. j(x2+4x)dx. 4.2. J2xdx.
8 4, Г
4.4. \(4Ъс + Щс1х. 4.5. j^4^-dx.
4.3. \e3x+4dx.
-2
0
4.6. У2 -3xdx.
A- Л + Іпх .
4.7. dx.
-3
4.8. J-
dx
-l
і
oV25 + 3*
4.9. J-
d!x
0
x + Ax + 5
4.10. J
V+3
4.13. J-
x-2
3dx
dx.
4.11. J
2dx
x2+A
1 e*
1.12. H
«1 +
,2*
tie.
4?~-
Ax
4.14. J
д: dx
n
б"
oV?
+ 4
4.15. J
dx
ncos 2x
f 3
4.16. I sin xdx.
к
3
. 17 4r sin 2л: Ac
|.1 + cos2jc
sin(ln^)
4.18. j(l + tg2x)dx.
^ н.л ґ 4 t ^ лл rsinun;*;) ,
4.19. )ctg*xdx. 4.20. J—* '-dx.
Обчислити інтеграли, застосовуючи властивість адитивності:
4.21. jf(x)dr, f(x) =
-о
2
4.22. J/(*)&; /(*) =
"і
\x2 при 0<jc<1,
[vjc при \<x<2.
cos* при <*<0,
Л 2x л ^л-
1 при 0<л;<—.
л- 2

254
Р о з д і л IV. Визначений інтеграл
4.23. jf(x)dx, /(*) =
_1
X
хе
є
1
х(1 + \п2х)
,*є[і;е].
і Гл, о<л<?,
4.24. \f{x)dx, f(x) = \ i-x
о
t , t<x<\.
I 1-f
e- {x2+4x + 4
4.25. [
4.27. p-dx .
■fifo.
Vs
4.29. J л: arctg | x \ dx.
3
Оцінити інтеграл:
4.31. jx2exdx.
4.33. J
2x2+5
■dx.
оДГ+2
і
4.35. jyl4 + x2dx.
4.37. J^/jcCjc-1 ;2^fcc.
4.39.
№її
sin xdx.
4.26. J|l-jc|<fe.
о
e
4.28. Jjlnjc|d*.
I
e
Юл:
4.30. J Vl-cos2*d[x;.
4.32. J-
dx
8 + x*
4.34. J
xdx
-2
1
4.36. J
4jc2-3jc + 4
tic
олІ2 + х-х2
In
1.38. f ■
і 10 +
dx
3cos*
4.40. Jjc^/tg^dk.

§ 1. Обчислення визначених інтегралів
255
Знайти середнє значення функції заданих на відрізках:
4.41. /(jc) = jc2, *є[0;і]. 4.42. /(jc) = 2 + 3cosjc, хє[-я,я].
4.43. f(x) = sin2 х, хе [0;я]. 4.44. f(x) = cos2 х, хе [0;я].
4.45. /(;c) = tg jc, хе
*7
4.46. /(;c) = sin jc, хе
*f
4.47. /(*) = -JL-f *є[2;3]. 4.48. /(*) = _J , *є[-1;0].
лГ+1
jc2+2jc + 2
4.49. /(jc)= , 1 *є[0;і].4.50. /(х) = лІ4-х2 , *є[0;2].
V2 + JC + JC2
Обчислити інтеграли, використовуючи заміну змінної
4.51. f;c<r*2<£c. 4.52. f-^_
4.53. J-
3-sin3 X
COS*
■dx.
dx
4.54. Ш±5£л. 4.55. f-^=,
1 /r^~~ 29
4.57. U—-dtc. 4.58. J-
(x-2)3dx
7Г
2(л-2)3+3
dx. 4.61. F -d!x:
4.56. p£*
fl + VJc
4*f *
4.60. J^^b. 4.61. J«-±
:(jc-1)VjcT6
#5 2.
4.62. J
*6-6;с3 + 13'
2
In 2
lnV
VT^i
4.63. j y}ex-\ dx. 4.64. J^^ -dx. 4.65. JV4-
* d!x.
ex+3
2 / 9 1 ,
4.66. N2x-x2dx. 4.67. |W81-;c2<&. 4.68. f—=L_^
о oJ -id + ^2)2
4.69. ) ** .
•5-3cos*
1.70. f—
Лс
2 cos*

256
Р о з д і л IV. Визначений інтеграл
Обчислити, застосовуючи інтегрування частинами:
л_ я
1 2 2
4.71. jxe~xdx. 4.72. \xcos2xdx. 4.73. fjc2sinArcbc.
ооо
1 1 %
4.74. jx3e2xdx. 4.75. Lshxdx. 4.76. \ex
0 о 0
1 e-2 e
4.77. farcsinjcdx. 4.78. J ln(;c + 2)dx. 4.79. JVlnjcdi.
о о і
4.80. j]n3xdx. 4.81. J[ —] dx. 4.82. J-
IV * J і x5
к к
4 3 т 1
4.83. Jjctg2;crfx. 4.84. J-^y^. 4.85. |Лх.
0 *sin x о
4
4.86. jylx2+ldx. 4.87. jfjc Wl + x2 W
о о
з і і
arcsin;t;<ix
4.88. [xaictgxdx. 4.89. JVarccosjcdk. 4.90. f—.
0 -1 Q УІ1 + Х
Обчислити інтеграли, використовуючи парність чи непар-
ність підінтегральних функцій:
АМ 2гх3+х + 2^ АМ Зг2jc7 + 3jc5 -3jc4 -h jc3 -6jc2 j
4.91. — dx. 4.92. dx.
і Jc2+4 4 jc2+2
In in
4.93. J x2 cos x dx . 4.94. f (x - я) sin 2x dx.
-In 0
К
Юп 2 9
4.95. J лее* ~7cos2;c<ix:. 4.96. J jc8cosjcsin32jctic.
-ion s.
9

§ 1. Обчислення визначених інтегралів
257
1 л
4.97. j\x\dx. 4.98. je^smxclx.
-і -п
к
2 71
4.99. J|jc|cos;c<ix;. 4.100. f sh*sh2jtsh3jc<ix;.
Відповіді
4.1. 51-. 4.2. Л. 4.3.^1. ul. 45.2.
3 In 2 3e2 3 4
4.6. 10^~4^ . 4.7. -. 4.8. - -. 4.9. arctg 3 - arctg 2.
9 2 3 6 6
4.10. 5,5 + 7 In 2. 4.11. -. 4.12. arctg(e) -—.
4 4
A1* 11 4 + 2л/3 ... 1, 1 + V5 .„ л/З-1
4.13. 31n 1=^. 4.14. —In . 4.15. .
3 + V5 3 2 2
4.16.-. 4.17.0. 4.18.1- — . 4.19.^ + -.
3 3 27 6
4.20. 1 - cos 1. 4.21. illzl. 4.22. ^±*. 4.23. - +1.
3 4 4
4.24. -. 4.25. e +1. 4.26. 1. 4.27. 5. 4.28. 2[ 1 - -
4.29. — - —. 4.30. 20V2 . 4.31. 0 </ <e. 4.32. -</<-.
9 3 9 7
4.33. 3<7<5. 4.34.-—</<i. 4.35. 2</<V5.
13
4.36. -<I<-\=. 4.37. 0</<2З/2. 4.38.—</< — .
3 V2 13 7
4.39. -</<-,/-. 4.40. 0 < / < —. 4.41. і. 4.42. 2.
2 2V2 16 3

258
Роз д і л IV. Визначений інтеграл
4.43.-. 4.44.- 4.45.^—^. 4.46. — . 4.47.-In2.
2 2л Ъж 2
п 7 71 еА -1 3
4.48.-. 4.49. In —i=. 4.50.—. 4.51.^—^. 4.52. In-.
4 1 + 2V2 2 2е4 2
4.53. 1п2--. 4.54.-(2^2-і). 4.55. 2-21п2. 4.56. 1 + 1п—.
8 4V > 4
4.57.--1. 4.58. Зл/Зл. 4.59. 4=ln16 + 5^7 . 4.60.1--.
2 V7 9 4
4.61. л/3-—-1. 4.62.—. 4.63.2--. 4.64. 4-л.
12 12 2
, ,_ л л/3 . ,, л- . ,_ 6561л . ,„ 1 л . ,_ arctg 2
4.65. — + — .4.66. —. 4.67. . 4.68. - + —. 4.69. —.
3 2 2 16 2 4 2
4.70. Дг. 4.71. 1 --. 4.72. - -. 4.73. л - 2. 4.74, * + 3
л/5 е 2 8
1 ел +1 л 1 + 2е3
4.75. —. 4.76. ——. 4.77. - -1. 4.78. 2 - In 4. 4.79. ——.
2е 2 2 9
4.80. 6-2е. 4.81. е--. 4.82. — -—. 4.83. --lnV2-—.
е 256 64 4 32
/3 л-(9-4ч/з) /2 , =
4.84. In. - + —і '-. 4.85. 2. 4.86. — + In VI + V2 .
\2 36 2
4.87. -(l + л/2 + In (l + л/2)). 4.88. 5arctg3 - -. 4.89. -.
4.90. лV2 - 4. 4.91. -. 4.92. - 54. 4.93. 8л. 4.94. -л.
2
4.95.0. 4.96.0. 4.97.1. 4.98.0. 4.99. л-2. 4.100.0.

§ 2. Невластиві інтеграли
259
§ 2. НЕВЛАСТИВІ ІНТЕГРАЛИ
Означення 1. Невластивими інтегралами називаються
1) інтеграли з нескінченними межами інтегрування
(невластиві інтеграли першого роду);
2) інтеграли від необмежених функцій (невластиві
інтеграли другого роду).
2.1. Невластиві інтеграли першого роду
Нехай функція f(x) визначена і неперервна при всіх
значених хе [а;-!-00). Розглянемо інтеграл
ь
F(b)=jf(x)dx.
а
Цей інтеграл має сенс для будь-якого Ь>а і є неперервною
функцією від змінної верхньої межі Ъ.
ь
Означення 2. Границя lim \f(x)dx називається невлас-
а
тивим інтегралом першого роду в межах від а до +«э і
позначається через Г / (x)dx,
а
-и» Ъ
\f(x)dx= lim \f(x)dx. (4.5)
a a
b
Якщо при £—>+oo функція F(b)= \f(x)dx має скінченну
a
CO
границю, то невластивий інтеграл першого роду \f(x)dx існує і
називається збіжним.

260
Р о з д і л IV. Визначений інтеграл
Якщо ж при Ь—>+°о функція F(b) не має скінченної
границі або не існує, то невластивий інтеграл першого роду
називається розбіжним.
Аналогічно визначаються невластиві інтеграли в межах від
-°о до Ь,
ь ь
[f(x)dx = lim \f(x)dx, (4.6)
J /7—^-00 J
а також невластиві інтеграли в межах від — °° до + °°:
-И» b
\f(x)dx= lim \f{x)dx.
J П—Ь—oo J
a->-
(4.7)
Іноді проміжок інтегрування доцільно розбити на дві
частини, тоді
+оо с -И»
jf(x)dx = ff(x)dx+ \f(x)dx =
—oo —oo с
С Ь
= lim \f(x)dx + lim \f(x)dx.
n—b—oo J Л—k-J-oo J
a—>-oo * b—>+°° *
а с
де с - довільно вибрана точка числової осі, найчастіше
вибирають с = 0.
Приклад 1. Обчислити Г
dx
х1 +х-2
За означенням
dx
с dx Л. с dx с dx
— =hm — =hm - —
zxz+x-2 *->~*лг +x-2 b^ooJf іу,
2
9
4
= lim —In
x-l
x + 2
= lim -| In
2 fc-»+oo 3
&-1
fc + 2
-In
2-1
2 + 2
= Umifln^i-lnll = ^ln2
*->+~ЗІ Ь + 2 A) 3
- невластивий інтеграл збігається.

§ 2. Невластиві інтеграли
261
dx
-х
Приклад 2. Дослідити на збіжність інтеграл [
J 1 + .
—оо
За означенням,
■«з, 07+оо, 0, Ь j
г ах с ах г ах t. с ах v с ах
7 = 7+ 7= hm 7+ hm 7 =
<» -оо о a 0
= lim arctg jc| + lim arctgxl = lim (arctg 0-arctg a) +
+ lim (arctgft-arctg 0) = — + — = яг.
Невластивий інтеграл збігається.
оо
Приклад 3. Дослідити на збіжність інтеграл Icos xdx.
о
Маємо lim [cosAofcc = lim sinjd = lim (sin£-sinO) = limsinfe.
b-H°oJ Ь-Ноо 'O b-*°o b-^oo
0
Ця границя не існує, тому невластивий інтеграл є розбіжним.
хе
о
Г -х2
Приклад 4. Дослідити на збіжність інтеграл І хе dx.
їхе dx- lim їхе х dx = lim
о о
-Іе-'!
b=limfl-V!U.
о ь^+х>{2 2 ) 2
dx
7*
Невластивий інтеграл збігається
Приклад 5. Дослідити на збіжність інтеграл Г—
J v"
\ x~p+l
І lim —
f—= lim \x~pdx =
J YP Л-V+oo J
limine I
ПрИ/7 = 1.

262
Р о з д і л IV. Визначений інтеграл
]Розглянемо випадок рф\\
0-
ь~р+х
-р+1
а~р+1 а~р+1
-р + 1 -р + \у
при р>1
-р + 1 р-1
п-Р+і
оо при р<\.
-р + 1
При р = 1 одержимо
[—= lim lnjq = lim [1п£-1пя] = <
Отже, інтеграл j— є збіжним при р > 1, і розбіжним при
/><і.
Твердження. Якщо невластивий інтеграл І-
Ф{х)а\к

містить обмежену на проміжку [а; <*>) функцію Ф(х), то в*н
збігається при р>1 і розбігається при р<\.
Приклад 6. Дослідити на збіжність інтеграл
°°г 2 + sin х
г- , dx.
fy/x(x2-X + l)
Перетворимо підінтегральний вираз
2 + sin;c _ 2 + sin;c _Ф(х)
yfx(x2-x + l) U і і
Х2\ 1 + ~z
X X
Функція Ф(л:) = — обмежена при хє [1;°°).
1 —+ ~2
х xL

§ 2. Невластиві інтеграли
263
Чисельник цієї функції не менший, ніж 1 і не більший, ніж З,
знаменник дорівнює одиниці при х = 1 та х —> °°, і має
З
найменше значення при х = 2, що дорівнює —. Отже,
4
1 < Ф(л:) < 4 при хе [1;оо).
°г 2 +sin* , . . , . °°сФ(х)с1х
Інтеграл -т=—^ ах відповідає формі .
(yfc(x2-X + l) і ХР
Оскільки в цьому випадку маємо р = —>1, то згідно зі
зробленим вище зауваженням цей інтеграл збігається.
dx
Приклад 7. Обчислити J
xz +4х + 9
Згідно з формулою (4.7):
°°е dx є dx ,. r dx
— = km - + lim 5 =
J x2+4x + 9 «->— J(x + 2)2 + 5 b^+~)(x + 2Y + 5
1 x + 2
= lim -^arctg—j=-
0 v 1 x+2
+ lim -^arctg
Приклад 8. Обчислити Г—ydx.
o">/5"
За означенням f—^-dfr= lim Г—т-d!*
fc_»oo J XJ
Скористаємося формулою (4.4) для інтегрування визначеного
інтеграла частинами. Приймаючи и = 1пл;, dv = x dx, одержимо
dx 1
du=—, v = -
x 2x
Обчислимо
b
2 "
>*л \b r, і Г і T i>

264
Р о з діл IV. Визначений інтеграл
\пх
2xl
Тоді
і 4xz
b_ \nb 1_ І_
і 2b2 2b2 4
ГІПЛ
■dx= lim
J_ 1 ]n&
4 Ab2 2b2
1 1 ,. Infe
4 2г>->~ fe2
1 1 .. \b) 1 ,. 1 1
= hm-^^- = — lim—- = —.
4 2fc->~ 2b 4 ь-*~2Ь2 4
Приклад 9. Дослідити на збіжність інтеграл je~pxdx, де
а, р - будь-які дійсні числа.
При р * 0 за означенням
оо b
\e-pxdx= lim \e~pxdx= lim
= lim
1
1 Ї
*-P*
= lim
la b—>«>
е-рв_е-рь
ype>" pepbJ
aPa
pe
pa
при p>0,
-оо ПрИ p<0.
Тому інтеграл є збіжним при р > 0 та розбіжним при р < 0.
Нарешті, при р = 0 маємо
оо оо О
\e~pxdx= \dx- lim \dx= lim (b-a) = +°°,
a
тобто і в цьому випадку інтеграл є розбіжним.
оо 2
Отже, інтеграл збігається при р> 0: \e-pxdx=
РеР"
розбігається при р < 0.
Приклад 10. Дослідити на збіжність інтеграл (■
dx
При х>1 справедлива нерівність
1
(х\і + ех)
1
х3(1 + ех) х3

§ 2. Невластиві інтеграли
265
Обчислимо
ь
6->оо
[— = lim їх 3dx = lim
1 Л
oo
Отже, |
2
= lim
lL-2 1
—fe z+-
2 2
2
dlx _. .1
- збігається, і його значення менше, ніж —.
(х3(1 + ех) 2
°°х2+\
Приклад 11. Дослідити на збіжність інтеграл [ .— dx
1 УІХ5
Очевидно, що
х2+1 х1 1
= —7= ДЛЯ ВСІХ X > 1.
J7 J7 ^
Інтеграл \—j= = lim J—= = lim 2у[х\ = ©о _ розбіжний. Отже,
вихідний інтеграл також розбіжний.
Приклад 12. Дослідити на збіжність інтеграл f——dx .
Підінтегральна функція є знакозмінною. Оскільки Icos д:| < 1,
то
cos*
< —. Обчислюємо допоміжний інтеграл:
rdx
[— = lim \х dx- lim
jt &->°°
2
= lim
2 2
2
Отже, інтеграл jj——\dx збігається, а інтеграл J——dx
\\ x | x л:
збігається абсолютно.
У деяких випадках необхідно лише встановити, чи є
збіжним заданий інтеграл і оцінити його значення. Для цього
користуються ознаками порівняння.

266
Р о з д і л IV. Визначений інтеграл
1.Якщо для всіх х>а виконується нерівність 0<f(x)<(р{х),
а інтеграл \ <р(х) dx збігається, то збігається також; інтеграл
а
+оо оо оо
J / (х) dx, при цьому \f (х) dx < \<р(х) dx.
а а а
2.Якщо для всіх х>а виконується нерівність 0<ф(х) <f(x),
і інтеграл \cp{x)dx є розбіжним, то розбіжним є також: інтеграл
а
+оо
J f(x)dx.
а
оо
З.Якщо інтеграл \\f(x)dx\ збігається, то збігається і
а
+оо
інтеграл \ f(x)dx. У цьому разі останній інтеграл називається
а
абсолютно збіжним.
2.2. Невластиві інтеграли другого роду
Нехай функція f(x) визначена і інтегровна на відрізку
[а; b-є] (є > 0), а при х = b необмежена.
ь-є
Означення 3. Границя вигляду lim \ f{x)dx називається
а
невластивим інтегралом другого роду від необмеженої функції при
b
x = b функції і позначається через \f(x)dx,
а
b b-є
f/(jc)£fe= Um f f(x)dx. (4.8)
a a

§ 2. Невластиві інтеграли
267
b-є
Якщо при є—»0 функція ^(є)= } f(x)dx має скінченну
а
b
границю, то невластивий інтеграл \f(x)dx існує і називається
а
збіжним.
Якщо ж при є —> 0 функція F(e) має нескінченну
границю, або ж ця границя не існує, то вказаний інтеграл не існує і
називається розбіжним.
Нехай тепер функція f(x) визначена і інтегровна на
відрізку [я + є\b\ (є > 0), але необмежена у точці х = а.
ь
Інтеграл \f(x)dx є невластивим інтегралом другого роду.
а
За означенням,
ъ ъ
\f{x)dx= lim \f(x)dx. (4.9)
Якщо функція f(x) необмежена в точці х = с, яка лежить
всередині відрізка [a,b], і неперервна у всіх інших точках цього
відрізка, то за означенням
Ь с
jf(x)dx= \f{x)dx+ jf(x)dx =
а а с
с-Є\ Ь
= lim f f(x)dx+ lim f f(x)dx. (4.10)
С+Є2
1
Приклад 13. Дослідити на збіжність інтеграл [—.
0
При х = 0 підінтегральна функція — необмежена, тому за
х
означенням

268
Р о з д і л IV. Визначений інтеграл
rdx ,. cdx
\—= lim [—= lim lnjcl = lim [lnl-ln£] = +°o,
J X є->0+ • X є->o+ Є є->0+
тобто невластивий інтеграл розбіжний.
dx
Приклад 14.0бчислити [ . .
Підінтегральна функція має нескінченний розрив в точці
х = 1, яка лежить всередині відрізка інтегрування [-1; 2]. Тому,
за означенням,
r dx г1 dx r dx
і lim . + lim .
-i#*-l)2 *-** і з/(х-1)2 -2^^2з/^Г^
= Urn зЭДс-1 + Urn 3#c-l
= 3 Um+(3/^"-^2) + 3 lim (#-^) = з(#2 + і).
Інтеграл збігається.
Для визначення збіжності невластивих інтегралів від
розривних функцій і оцінки їх значень застосовують наступні ознаки
порівняння.
1. Нехай функції f(x) і (р(х) необмежені в точці х = с, і
задовольняють нерівність 0 < ф{х) < f(x) при а<х<су тоді:
с
а) якщо збігається інтеграл [f(x)dx> то збігається і
а
с
інтеграл j(p(x)dx>'
а
с
б) якщо інтеграл [q){x)dx розбігається, то розбігається і
інтеграл \f{x)dx.
а

§ 2. Невластиві інтеграли
269
2. Якщо f(x) - знакозмінна функція на відрізку [а,с] інеоб-
с
межена тільки в точці х = с, і невластивий інтеграл j]/(jt)|dbt
а
с
збігається, то збігається також інтеграл \f(x)dx.
dx
Приклад 15. Дослідити збіжність інтеграла [—j= .
Підінтегральна функція необмежено зростає при jc —> 0.
Оскільки при х > 0 маємо л/х +5х > уіх , то --== — < —т=.
л/х+5х л}х
Обчислимо невластивий інтеграл
\—j== lim \—j== lim 2yfx\ = lim 2\у[І-4є~\ = 2.
Інтеграл |—j= збігається. Згідно з першою ознакою
r dx
порівняння, збігається також інтеграл —т= .
Nx+5xz
dx
г ах
Приклад 16. Дослідити збіжність інтеграла . .
* / 2 2
oVtf -х
Підінтегральна функція f(x) = —= при х = а необме-
ліа2 -. "
■х2
жена, тому
dx " с dx
\ , = lim f , = lim -
Ma2-x2 *-*+ І УІа2-х2 <-*+L
. x
arcsin—
a
. а-є n
- lim arcsin = —.
є^о+ a 2
Отже, заданий інтеграл є збіжним і дорівнює —

270
Р о з д і л IV. Визначений інтеграл
Приклад 17. Дослідити на збіжність невластивий інтеграл
'-і
dx
о
*2-4jc + 3
У точці х = 1 знаменник підінтегральної функції дорівнює
нулю, тому функція має розрив другого роду. Згідно з (4.10), маємо
1,2 , 1,2
/ =
0
1-Єі , 2
_ С dx с dx _ r dx r dx
~' \х2-4х + Ъ \{x2 -4jc + 3)(jc-1)~ \(x-2)2 -1 \{x-2)2-\
с dx с dx
= lim + lim =
e^o+ 0J (x-2)2-l e2^o+1+J (x-2)2-l
= lim —In
El-*o+ 2
x-3
x-l
l+e2
l+ lim -In
0 e2^o+ 2
x-3
x-l
l + e»
= lim —
Є!^0+ 2
f
In
Ej+2
^
+ ln3
r l
+ km -
є2->о+ 2
f
lnl-ll-ln
є9-2
4
= oo — oo
Одержана невизначеність не може бути усунена, оскільки єх
та Є2 незалежні. Це означає, що скінченна границя відсутня, тобто
інтеграл розбіжний.
Задачі для самостійного розв'язування
Обчислити невластиві інтеграли (або встановити їх
розбіжність).
1. Інтеграли з нескінченними межами
4.101. pj. 4.102. [е~ах(Іх(а>0). 4.103. {—„ Т(а*0).
J"4 X iaz+xz
і*
. п
~ ~sm— о ,
4.104. \x%\VLxdx. 4.105. J—^dx. 4.106. J^ j {a*
0).

§ 2. Невластиві інтеграли
271
4.107. f-^r. 4.108. f ****, (д*0).
iV* аа +х
r dx r dx
4.109. f 5 г- (a*0). 4.110. \—. T(a*0).
£x(a +x ) 2вл °
4.111. j — . 4.112. —.
Jmx2 + 2x + 2 ^(1 + л 2)2
4.113. f(;c2-l)cos;td!x;. 4.114. f , .
0J _і*2-4х + 7
4.115. J .*** . 4.116. f«rexsin&c<fe (a>0).
і W*2 -1 о
dx
4.117. jV^cos&ctfr (a>0). 4.118. J-
0 ~°(л;2+л; + 1]
4.119. ~pk 4.120. 7^Й* Л.
nl + л „Jl + *2
2. Інтеграли від необмежених функцій
4.121. f *!*L. 4.122. \-jL-. 4.123. j^.
ол/4^7 0w*a-*) V
, 4.125. J-7==
/і-л2 oVl-;
1 j„ б , з
4.124. J . . 4.125. J . . 4.126. jlnxdtx.
QSl-X2 Ол/і-Л2 0
4.127. Г« . 4.128. [ . M . 4.129. USL
2 2 2
4.130. -. 4.131. ——. 4.132. H—
QJ(*-1)2 J2X2-l {yf^l

272
Р о з д і л IV. Визначений інтеграл
1_ і
°гех V ес dx
4.133. І—jdx. 4.134. Jjtlnjtdk. 4.135. J —.
—\Х о о ХІТІ X
4.136. f—$=. 4.137. \Zfldx. 4.138. Г—.
/Win* 4V7 i*ln*
*<& . .. .л V xAdx
4.139. f , . 4.140. f
J /772 7/o J
2\/0c2-4)3 oVl-x5
Відповіді
4.101. -. 4.102. -. 4.103. —. 4.104. oo. 4.105. -.
3 a 2a ft
4.106. —. 4.107. oo. 4.108. oo. 4.109. Щг. 4.110. —.
2a 2a2 2a
4.111. я. 4.112.-. 4.113. oo. 4.114.^-. 4.115.-.
2 3 2
4.116.^-^. 4.117. ^A-^. 4.118.^. 4.119. ІП
a2+b2' ' ' a2+b2' ' ' 9 ' ' ' Зл/з '
4.120. —. 4.121. —. 4.122. п. 4.123. ~. 4.124.1. 4.125. -.
8 15 2
4.126.-1. 4.127.-. 4.128.6^/2. 4.129. -3/Ї25. 4.130. oo.
2 3
4.131. °o. 4.132.-. 4.133. e-1. 4.134.--. 4.135.1.
3 4
10 2
4.136.2. 4.137.—. 4.138. oo. 4.139. oo. 4.140.-.
7 5

§ 3. Застосування визначеного інтеграла
273
§ 3. ЗАСТОСУВАННЯ
ВИЗНАЧЕНОГО ІНТЕГРАЛА
3.1. Обчислення площ плоских фігур
1. Площа криволінійної трапеції, обмеженої кривою
У = /00 (/(*) ^ О)> двома вертикальними прямими jc = а і
л: = b та віссю Ojc , обчислюється за формулою
S= Jy <fc= J/(jc)dbc.
(4.11)
2. Площу фігури, обмеженої двома кривими у = fx (х),
у = f2 (х) (/j (х) < /2 (х)), і двома вертикальними прямими
х = а, х = b, обчислюємо за формулою
ь
S=\[f2(x)-Mx)]dx. (4.12)

274
Р о з д і л IV. Визначений інтеграл
З.Якщо функція у = f{x) знакозмінна на відрізку [а,Ь],
то площа криволінійної трапеції, обмеженої графіком цієї
функції, віссю абсцис та прямими х = а та х = b обчислюється
за формулою
ь
S = j\f(x)\dx.
а
4. Якщо крива, що обмежує криволінійну трапецію зверху,
задана параметричними рівняннями
то площа трапеції, обмеженої цією кривою, віссю абсцис та
прямими х = х(а), х = x(j3) дорівнює
Р
S = jy(t)x(t)dt.
а
Тут а та Р - значення, між якими змінюється параметр t,
коли точка зліва направо пробігає всю криву, що обмежує
криволінійну трапецію зверху.
Площу фігури, обмеженої замкненою параметрично
заданою кривою, яку точка пробігає проти годинникової
стрілки при зміні параметра t від а до J3, можна обчислити
за формулою
S = - j(xy'-yx')dt.
а
5. Площу криволінійного сектора, який обмежений кривою, що
задана в полярних координатах рівнянням р = р(в), і двома
полярними радіусами в = а, в = /3 (a<j3), обчислюємо за формулою
\Р
S = -\p2(6)de.
а

§ 3. Застосування визначеного інтеграла
275
Приклад 1. Обчислити площу фігури, обмеженої
параболою у = З*2 - 6х і віссю Ох на відрізку [0,4].
У
20
10
\
0
/
/
у
>s ""г 4
/
X
Парабола у = Зх -6х = 3(х -1) - 3 перетинає вісь Ох в
точках хх = 0; х2 = 2. За властивістю адитивності визначеного
інтеграла
ь
S=j\f(x)\dx=S =
j(3x2-6x)dx\
+ J(3jc2 -6x)dx = 24 (кв. од.).
Приклад 2. Знайти площу фігури, обмеженої параболою
2 а • 8
х =4у і кривою у =
х2+4
Знайдемо спочатку абсциси точок перетину кривих
х2
У =
8
х2+4

276
Р о з д і л IV. Визначений інтеграл
З рівності правих частин маємо х4 + 4л:2 - 32 = 0. Дійсними
коренями рівняння є хх = -2, х2 = 2.
З рисунка видно, що на проміжку [-2; 2] (наприклад, в
точці х = 0) виконується нерівність
8 >Ґ
х2+4 4
8 х2
Тому у формулі (4.12) приймемо f2{x) =—z , fx{x) = —. Отже
лг+4 4
S=j{f2(x)-fl(x))dx= П
8
„2 Л
х2+4 4
dx =
2/
-ч
л\
х1 +2г
dx =
х ~х
8arctg—2—
52 12
о
8 4
= 8arctgl — = 2я— (кв. од.).
6 3
Приклад 3. Знайти площу петлі кривої
Ця крива задана параметрично, тому скористаємось формулою
S=\){xy'-yx')dt.
При ti = 0 точка кривої має координати л: = 0, у = 0.

§ 3. Застосування визначеного інтеграла
277
При t = 6 крива повертається у ту саму точку, утворюючи
петлю. Тому
S =1(1(6-0
2І3
Ґ 2
1 t
-(6-0
^ <г
J
—(6-0
8
If/
-іДс-о
f
2oJ3
-(6-0 —
4V 8
2Л ( Л
Т(6-,)
-(6-0
6-г г
<# =
dt =
1 V(6-0 J 1 (W 2 ^ 3 44 _, 27 ,
= - — —dt= — (36Г-12Г +r)dt = — (кв. од.)
21 24 48 J 5
Приклад 4. Обчислити площу петлі листа Декарта
х3 + у3 -3аху = 0.
Перейдемо до полярних координат
І y = psin<p.
Знайдемо
зз з-з о 2 • гл/- 3acos#?sin0
р cos <р + р sin ф-Ъар cos^sm#? = 0 або /7 = —-—-—^1
sin3 #> + cos3 ^

278
Р о з д і л IV. Визначений інтеграл
Ця крива симетрична відносно прямої у = х. Площа,
обмежена петлею, дорівнює подвоєній площі області ОАМ . Відпо-
1 > 2
відний інтеграл у полярних координатах S = — \р d(p. Тому
7t_
>ОАМ
4
у
9а
За cos #> sin <р
sin3#> + cos3^
її tgg>
2 0\cos^(tgV + l).
2 4Y
^="f \
Sin ^7
cos <p(tg <р + 1)
d<p =
2Ї
9а
2 7
, \)а с
tg <pd<p
2 0Jcos>(tg> + ir
Проведемо заміну змінної tg<p = t, тоді —j— = dt.
cos #J
Визначимо нові межі інтегрування <р = 0 => г = 0;
<р = — => t = l.
4
9а2 V t2dt За2 \d(t3+1) За2 1
*ОАМ
r t at __ за ra {t +ij _
„V+D2 " 2 J(f3+1)2 "
2 0V+D2 2 0J(r3+l)2 2 (r3+l)
За2 За2 3a2
і, відповідно 5 = 2S0AM =
3al
3.2. Обчислення довжини дуги плоскої кривої
1. Якщо крива y-f(x) на відрізку [a,b] є гладкою (тобто
вона і її похідна у' = f'(x) неперервні), то довжина відповідної
дуги цієї кривої обчислюється за формулою

§ 3. Застосування визначеного інтеграла
279
L = \ij\ + y'2dx = ^l + [f'(x)]2dx. (4.13)
а а
2. Якщо крива задана параметричними рівняннями
\x = x(t),
[y = y(t),
a<t<(5, де функції x(t),y(t) - неперервно диферен-
цшовні, то довжина дуги цієї кривої задається інтегралом
А
■=№+у?
dt.
(4.14)
3. Якщо гладка крива задана в полярних координатах
рівнянням р = f((p)9 де а < (р < Р, то довжина дуги дорівнює
fi
L=^p2+p'2d<p. (4.15)
Приклад 5. Обчислити довжину дуги кривої у = In х, що
лежить між точками з абсцисами x = yJ3 і х = v 8 .
Щоб застосовувати формулу (4.13) знаходимо похідну
у = —. Тоді шукана довжина
х
Ь V8 І
,= yi+y'2dx= JJl +
(і V
J*l 2+1
dk = Г dx= \
і х і
jo/* +1
dx.
X + 1 = t, ТОДІ JC + 1 = t ,
jt<£c = fcfr, x2 = t2 -1. Знайдемо нові межі інтегрування:
х = у/з => t = 2; jc = V8 => Г = 3.
Тоді
З .2
L= \- = l + -r \dt=\ t + -ln
\t2-\ A t2-l) I 2 f + 1
і 1, 3
= l + -ln-.
2 2

280
Р о з д і л IV. Визначений інтеграл
Приклад 6. Обчислити довжину гіпоциклоїди
t 2t
х = 27? cos— + /?cos—,
3 * 0<1<2я.
у = 27? sin— Rsin—,
З З
Ця крива задана параметрично, тому для обчислення її
довжини застосуємо формулу (4.14).
Спочатку знайдемо похідні
2n. f 2n, 2г . 2 „ t 2 „ It
х =—/?sin /?sin—, у =— Rcos Rcos—,
3 33 3 3 33 3
/ 5 7 4 t
івираз уііху+іу1)= -tfsin-.
Тоді
'2
L= jVu')2+(y')2^= fl/?sin-^ = --/?cos-|
J J 4 7 4 7
2Л-
З
Приклад 7. Знайти довжину кардіоїди р = 2а (і - cos (р).
Крива задана полярним рівнянням, тому для обчислення її
довжини необхідно застосовувати формулу (4.15).
Знаходимо похідну р' = 2а sin <р і обчислюємо вираз
*\р2 + р'2 =yJ4a2(l-cos<p)2 + 4a2sin2<p =
= 2ay]l + cos2 <p- 2cos^ + sin2 q> = 2a<sj2(l-cos<p) =
= 2aJ4sin2—=
V 2
4a sin-
Коли точка кардіоїди пробігає всю криву, полярний кут
змінюється від 0 до 2я, тому
Р 2л- і
L= Up2 + p'2d<p= J4asm—d(p = -4a-2cos—\
In
= 16a.

§ 3. Застосування визначеного інтеграла
281
3.3. Обчислення об'ємів тіл
1. Обчислення об'ємів тіл за відомими площами поперечних
перерізів. Якщо площу перерізу тіла площиною, перпендикулярною
до осі Ох, можна виразити у вигляді функції S = S( х ), а < х < Ь, то
об'єм частини тіла, що міститься між перпендикулярними до осі
Ох площинами х = а, х = Ь, обчислюємо за формулою
ь
V= js(x)dx. (4.16)
а
2. Обчислення об'єму тіла обертання. Якщо криволінійна
трапеція, обмежена кривою y = f(x) і прямими х = 0, x = afх = Ь,
обертається навколо осі Ох, то об'єм тіла обертання, що
утворюється, обчислюється за формулою
ь ь
Vx=7rjy2dx = 7rj[f(x)fdx. (4.17)
а а
Якщо обертання криволінійної трапеції здійснюється навколо
осі Оу , тоді об'єм тіла обертання, що утворюється, обчислюється
за формулою
ь
Vy=27rjxf(x)dx. (4.18)
а
Якщо ж фігура, обмежена кривими у = /і(*)» У = їг(х)
0</i(jc)</2(jc)) і прямими х = а, х = Ь, обертається навколо осі
Ох, то об'єм тіла обертання обчислюємо за формулою
ь
Vx=*l([f2(x)]2 -[/i(*)]2)<fc. (4.19)
а
Приклад 8. Знайти об'єм тіла, обмеженого однопорожнин-
2 2
X У 2
ним гіперболоїдом — + z = 1 і площинами z = -1, z = 2.
4 9

282
Р о з д і л IV. Визначений інтеграл
Перетин гіперболоїда площиною z = const є еліпсом
2 2
— + — = l + z2 з півосями a = 2\ll + z2', Ь = Зл/l + z2. Площа
4 9
еліпса 5 = ;гя£ = бяч 1 + z2). Тому об'єм гіперболоїда
Z2 2
V= ]s(z)dz = 6n j(l + z2)dz = 367T.
Приклад 9. Криволінійна трапеція, обмежена гіперболою
ху = 4, прямими л: = 1, л: = 2 і віссю Ох, обертається навколо осі
Ох. Знайти об'єм тіла обертання.
Об'єм цього тіла обчислюємо за формулою (4.17):
ь
Vx=7t\[f(x)]2dx.
а
4
Маємо /(*) = — , межі інтегрування 1 < х < 2. Отже,
х
ух
= #• — ах = яЧ
j\xj ^ х)
2
= 8л-.
і
3.4. Обчислення площі поверхні тіла обертання
Якщо дуга гладкої кривої y = f(x) (a<x<b) обертається
навколо осі Ох, то площу поверхні обертання обчислюють за
формулою
Sx = 27i\\y\4l+y2dx. (4.20)
Якщо крива задана параметричними рівняннями
x = x(t), y = y(t) {a<t</3),
то р
Sx = In j\y\ylx2 + y'2dt. (4.21)

§ 3. Застосування визначеного інтеграла
283
Приклад 10. Знайти площу бічної поверхні тіла, утвореного
обертанням однієї арки циклоїди х = R(t -sint), у = R(l-cost),
0 < t < In, навколо осі Ox.
Оскільки крива задана параметрично, площу поверхні тіла
знайдемо за формулою (4.21),
Sx=2n\\y\4x'2 + y'2dt.
Обчислимо вираз
х'2 + у'2 =(R(l-cost)f +(Rsmtf = R2 -4sinz-.
-2І
2
Тоді
Sx=ZnR2 Jsin3l^ = -16^/?2 jsm2-d cos- =
In ґ \
= -\6nR2 J 1-cos2-
cos—
v 2y
= -\6nRz
t 1 зО
cos cos —
2 3 2
In
0
9 4 64 9
= 16ягЛ2-- = — ягЛ2 (кв. од.).
3 3
3.5. Механічні застосування визначеного інтеграла
Означення 1. Статичним моментом матеріальної точки
А відносно осі І називається величина
Мх =m-d,
де т -маса точки A, d - віддаль від точки А до осі І.
Для плоскої кривої y-f(x) статичні моменти Мх і Му
відносно координатних осей Ох і Оу обчислюємо за формулами
ь ь
Mx = jf(xyJl + [fXx)]2dx, My = \x4\ + [f\x)fdx. (4.22)

284
Р о з діл IV. Визначений інтеграл
Для плоскої фігури, обмеженої кривою у = у(х), віссю Ох
і двома вертикальними прямими х = а та х = b, статичні
моменти обчислюємо за формулами
. ь ь
Мх =- \y\y\dr, Му = \x\y\dx. (4.23)
а а
Означення 2. Моментом інерції матеріальної точки маси
т відносно осі І, віддаленої від цієї осі на відстань d,
називається величина Ii=m-d .
Момент інерції плоскої фігури, обмеженої кривими Уі = ^(jc)
і У2 ~ Уі(х) {уі(х) - Уі(х))> та прямими jc = а і х = b, відносно
осі Cty визначається формулою
ь
Iy = jx2(y2-yi)dx. (4.24)
а
Координати центра маси плоскої кривої обчислюються за
формулами
-МУ.
Ус=-
де L = U/1 + [/ '(*)] Л - довжина кривої.
а
Центр маси плоскої фігури має координати
(4.25)
*„=^*
^; ?с=% (4-26)
і
а
0
1 У
^^щ^ВЯІ
«К
а
л:
де 5 - площа фігури.
Приклад 11. Обчислити
статичні моменти відносно кожної
сторони прямокутного рівнобедренного
трикутника з катетом а .
Розмістимо катети трикутника
вздовж координатних осей.

§ 3. Застосування визначеного інтеграла
285
Тоді рівняння його гіпотенузи у = а - х.
За формулами (4.23) знаходимо
М,
1*ґ 2
= —\{а-х) dx = -
1(а-хУ
а а3
М,
u
= \х(а - x)dx =
Ґ 2 З'
ах х*
3 3 3
а* а* а
Для знаходження статичного моменту відносно гіпотенузи
розмістимо трикутник так, щоб вісь Оу була віссю його симетрії,
а початок координат лежав на середині гіпотенузи.
V2
Рівняння сторони АВ: у = я х.
Тоді
М =2-— Г я х Лс = -
2 оЧ 2 J
лз
г V2
я х
і 2 У
2 = я\/2
о 12
Приклад 12. Знайти координати центра маси півкола
д: +у = я2, розташованого над віссю Ох.

286
Р о з д і л IV. Визначений інтеграл
Для спрощення обчислень знайдемо спочатку диференціал
довжини дуги кривої.
З рівняння кола маємо у = v а2 - х2 . Отже,
ds = Jl + [f'(x)f dx = Jl + -/-i;dx= adx
V я -х у/а -х
За формулами (4.25) обчислюємо координати центра маси
кривої
МЛ
и
г а
-а ча -.
rdx
-а\Іс
2-х1
г a dx
J / 2 2
-а\Іа -х
. х
tf-arcsin— і
а
= 0;
а і
77^7
dx
2az 2а
. х
я-arcsin— і
а
а-я л
Задачі для самостійного розв'язування
ці фігур, обмежених вказаними лініями:
2. 4.142. у = 2-х2; х + у = 0.
Обчислити ПЛОЩІ '
> = 3.
4.141. у = х2; х+у = 2.
4.143. 2х = у2; 2у = х2. 4.144. у = *2 +1; х + у ■■
4.145. у = х +1; у = cos*; у = 0.
4.146. у = х3-6х2+Пх-6;у = 0.
4.147. лу = 4;х+у-5 = 0. 4.148. у = 4-х2;х-5у + 2 = 0.
4.149. y = ;t2-5jc + 4;;y = 0;;c = 0;;t = 4.
4.150. y2=x + l;y2=9-x
4.151. y=|lgx|; у = 0; * = 0Д; * = 10. 4.152. у = 2х; у = 2; х = 0.

§ 3. Застосування визначеного інтеграла
287
4.153.^ + ^- = !.
^2 U1
а о
4.155. \ Х'Ъ~,г- .
Jjc = 2cosr-cos2r,
" \y = 2sint-sin2t.
4.154. \ 0<t<27t.
[y = 3sinr,
4.156.\X = a(t-Sm> ,e[0;2*];, = 0.
[y = a(l-cost),
4.158.
x = acost,
a sin2/
2 + siiU
з '
* = 2cos —,
4 0<Г<2л-.
x = 2f-f2,
4.160.
Iy = 2f2-r3.
4.162. уО = 3<г?; 0<е»<2я\
4.164. p = a(l + cos<p).
4.159. <
U = 2sin3-
l 4
4.161. /0 = a sin 2<p.
4.163. /? = 2 + cosft» .
4.165. p2 =2a2coslcp; -—<<p< —.
4 4
4.166. *3 + у3 -Ъху = 0; x > 0; у < x.
4.167./? = ; ф = — , 67 = —. 4.168./7 = .
l-cosc> 4 2 l + 0.5cosfi»
Обчислити довжини дуг кривих.
).y = 24x;Q<x<\. 4.170. у = ех; 0<х<1.
і -.3 _ „2 . Л ^ „ ^ о 4 172 9ау2 = Х(Х _ Зау
4.169. у = 2-Jx ;
4.171. у3 = х2; 0 < х < 8.
4.173. дг2 + у2=Л2.
2 2 2
4.175. х^ +у3 =а3.
4.174. у = -
7 2
де- jaj
\еа +е а
0<*<а.
ж
4.176. y = lncosjc; 0<jc<— .
= -y2--lnj, 1<у<е. 4.178. j; = ln^—sl<*<2.
А 2 ' «*_i
4.177. * = -у'
47 2

288
Р о з д і л IV. Визначений інтеграл
4.179.
|jc = i?cosr,
І у = Rsint.
4.180.
fx = <я(2 cos t - cos It),
І у = a(2siiu-sin20.
f.x = tf(cosr + fsinO,
4.181 J 0<ґ<2лг.
І у = a(sinf-fcosf)t
4.182.
\ = y[bt2,
y = t-t\
■l<t<l.
4.183.
з *
JC = /?COS —,
4
T, . 3 t
y = Rsm-.
4
4.185. p = <p2\ Q<(p<~.
4.187. /? = я(1 + cos cp).
4.184. p = a<p; 0<<р<2я.
4.186. /? = *2*; 0<#?<-.
4.188. /? = tfsin3^; 0<^<3лг.
Знайти об'єми тіл обертання навколо заданих осей
4.189. y = sinx; хє[0;я]; Ох. 4.190. y = sinx; хє[0;;г]; Оу.
4.191. у = 2х-х2; у = 0; Ох. 4.192. у = 2х-х2; у = 0; Оу.
4.193. у = ех; х = 0; у = 0; Ох. 4.194. )> = £*; х = 0; у = 0; Оу.
4.195. у2 =jc3; у = 0; jc = 1; Ох.4.196. у2 =х3; у = 0; jc = 1; Оу.
4.197. у2=8х; х = 2; Оу. 4.198. х=у2; х = 1; у = 0; Оу.
4.199. y = jc2; 8jc = j2; Оу.
4.200. лу = -2; jc = 1; x = 2; y = 0; Ox.
2 < 2
4.201. x2+(y-b)2=a2 (b>d);Ox. 4.202. —+ ^ = 1; Ox.
4 16
Обчислити об'єми тіл за відомими площами поперечних
перерізів:
2 2
4.203. z = —+ iL;z = i
4 2
2 2
4.204. (z - 2)2 = — + -2-; z = 0.
3 2
2 2
4.205.— + -^ Z2=1;Z = -1;Z = 1.
4 9

§ 3. Застосування визначеного інтеграла
289
Обчислити площі поверхонь обертання навколо заданих осей:
4.206. 9у2 = х(х - З)2; Ох. 4.207. х2 + (у - 2)2 = 1; Ох.
X3 9
4.208. у = —; |х|<1; Ох. 4.209. х = у2;х = 0\х = 1'Ох.
4.210. у = tgx; х = 0; jc = —; Ox. 4.211. у = е'х;х = 0; х = «>; Ох.
4
2 2
4.212. у = sin jc; х = 0; х = п\Ох. 4.213. ^- + -^ = 1 (а>Ь); Ох.
а2 Ь2
2 2
4.214.^ + ^ = 1 (fl>fc); Оу.
4.215. Обчислити статичний момент прямокутника з основою а і
висотою в відносно його основи.
4.216. Знайти статичні моменти відносно осей Ох, Оу
трикутника, обмеженого прямими
bx + ay = ab; х = 0; у = 0.
4.217. Обчислити статичний момент верхньої половини еліпса
2 2
X у
— + — = 1 відносно осі Ох.
25 9
4.218. Знайти момент інерції відносно осі Оу фігури, обмеженої
параболою у2=4х та прямою х = 1.
4.219. Знайти момент інерції прямокутника зі сторонами а і Ь
відносно сторони в.
4.220. Знайти координати центра маси дуги першої арки циклоїди
x = a(t-sint),
y = a(l-cost),
0<t<27t.
4.221. Визначити координати центра маси сегмента параболи
у2 = 2х, що відтинається прямою х = 2.

290
РозділІУ. Визначений інтеграл
ВІДПОВІДІ
4.141.4.5. 4.142.4.5. 4.143.-. 4.144.4.5.
З
4.145. 0,5. 4.146. 0.5. 4.147. 7,5-41п4. 4.148. 9—.
ЗО
4.149. —. 4.150. ^^-. 4.151. 9,9 - 8,llge.
6 3 &
4.152.2——. 4.153. лаЬ. 4.154. 6л. 4.155. 8
1п2 15
\6_
Я'
4.156. Зла2. 4.157. 6л. 4.158. ла11 ^ - 9 І.
л2
4.159. —. 4.160. — . 4.161. ^—. 4.162. 12л"
Зя" 8 W з
8 15 8
4.163.—. 4.164.^-. 4.165. а2. 4.166.-.
4 2 2
4.167. 3 + 4^2 . 4.168.-, f ■. 4.169. V2+ln(l +л/2).
6 Vd"0'25)3
4.170. л/l + e2 - л/2 + lnfVl + e2-l] + 1п(л/2 +1)-1.
4.171. —(іОл/ЇО-
4.П4.^-І)-
4.177. -(1 + є1).
4
4.180. 16а.
■')■
4.172. 2а7з .
4.175. ва.
е4-1
4.178. Іп-^-ї-.
є -є
4.181. 2ая2.
4.173. 2л-/?.
1л
4.176. lntg—
8
4.179. 2лЯ.
4.182.4.

§ 3. Застосування визначеного інтеграла
291
4.183. 6R.
4.184. -(2я7і + 4я2 + 1п(2я + Vl + 4л2 )1.
з
(л"2+1б)2-64 JI/ г
4.185. ^ і . 4.186. — [є* -1 . 4.187. 8а .
Злй
4.188.
4.191.
4.194.
4.197.
4.200.
4.203.
4.206.
4.209.
2
16л-
15 *
2л-.
128л-
5
2я.
Лл/2.
Зл-.
fH-
-■)
4.189.
4.192.
4.195.
4.198.
4.201.
4.204.
2 х
^1
2 "
8л-
3 '
Л"
7'
4л-
~5~'
2яа2Ь
8лч/б
4.190. 2я2.
4.193. -.
2
4.196. і^.
7
4.199.
4.202.
24л-
5
128л-
4.205. 16л-.
4.207. 8я2. 4.208. -я(іу[2 -1).
4.210. я\
'Я-Я+Ы^*2"
л/5+1
4.211. яШ + \п(^2 + \)\. 4.212. 2л-(72 + 1п(72 + і)).
4.213. 2яЬ + arcsinf
Ґ 4а^Л
є =
V
(
л*,л ^ 2 лЬ2 л 1 + є ( \Іа2-Ь2
4.214. 2па1 + In І є = -
є 1-є
а
\

292
Р о з д і л IV. Визначений інтеграл
4.215.
аЪ1
2
4.217. ЗО.
4
4.220. хс =ла\ ус=—а.
9 9
4.216. Мх = ; Му =
6 6
4.218.
8
4.219.
агЬ
7 З
4.221. хс= 1.2; ус=0.

Розділ V
РЯДИ

294
Р озділУ. Ряди
§ 1. ЧИСЛОВІ РЯДИ
1.1. Основні теоретичні положення
Означення 1. Нехай задана нескінченна послідовність
Чисел (21,(225^3'*"'(2n'---
Вираз вигляду
оо
al+a2+... + an+... = Yjan (5.1)
п=1
називається числовим рядом, де а, аІ9а2,..ап,... - дійсні числа;
ап - п-й член ряду.
Ряд заданий, якщо вказано його загальний (n-й) член.
Наприклад, якщо n-й член ряду ап = , то, надаючи
(2п - ї)(2п +1)
порядковому номерові п конкретні значення 1,2,..., п,... одержимо
його члени
1 1 _ 1 _ 1
(24-1X2.1 + 1) ЬЗ ' 3-5 л (2*-1)(2* + 1)
Тоді ряд має вигляд
111 1
- + + + ... + -
ЬЗ 3-5 5-7 (2л-1)(2л + 1)
Практично задають декілька перших членів ряду, за
якими можна встановити формулу для ап. Наприклад, якщо
маємо ряд н -н г + "-> то легко бачити, що
1-2 3-23 5-25
1
(2п-ї)22пш~1

§ 1. Числові ряди
295
Утворимо послідовність чисел Sx, S2,..., Sn,... за схемою
*^2 == ^1 ^2'
(5.2)
Число 5Л називають и-ю частковою сумою ряду (5.1).
Означення 2 Числовий ряд називається збіжним, якщо
послідовність його п -х часткових сум має скінченну границю. Тоді
число S = Ііііі Sn називається сумою ряду. Якщо границя не існує
або дорівнює нескінченності, то ряд називається розбіжним.
Приклад 1. Дослідити на збіжність ряд 1 + 2 + 3 +... + п +...
Знаходимо послідовність часткових сум ряду
Sl=l9 S2 =1 + 2 = 3, 53 =1 + 2 + 3 = 6,...,
л ~ -і (1 + и)и
S =1 + 2 + 3 + ... + п = - —,...
2
Маємо Urn Sn = lim = °°, отже, цей ряд - розбіжний.
П—>°° П—>оо 2
Приклад 2. Знайти суму ряду + + +...
Загальний член ряду такий а„ = або після
" (2п-1)(2и + 1)
розкладу на прості дроби
if 1 1
" 2\2п-\ 2п + 1
тобто

296
Р о з д ілУ. Ряди
Знайдемо часткову суму і її границю
,.4/і-іі+ігі_іиш '
213 5
2И 7
1
.+ ' '
1
2\2п-\ 2п + 1,
1
і L 1 1 1 1 1
= -1 — + + + ...-
2{ 3 3 5 5 7 2n + l 2n-\j
-Уі-_!_
2І 2и + 1
Urn S„ = — lim 1 —
2 П—>оо'
2и + 1
1
Отже, ряд збігається, і його сума дорівнює —.
Приклад 3. Знайти суму ряду ]|Г-
1
п=і п +5/1 + 6
Знайдемо я-ну часткову суму ряду. Для цього зручно
розкласти загальний член ряду на прості дроби.
1 111
а„ =
п л2+5п + 6 (л + 2)(л + 3) п + 2 п + З'
Тоді
п Із 4І U 5І І6 1) U + 2 п + З
1
1
З п + З
1
Звідси знайдемо S = lim 5W = lim
И_>оо Л->ооІ З П + З) З
Приклад 4. Дослідити на збіжність ряд
я + а# +aq2+aq3 +... + aqn +..., (tf*0). (5.3)
Цей ряд утворений з елементів геометричної прогресії
я,ш7 ,од ,...,## ,... Його я-на часткова сума дорівнює сумі
.w+i
перших п членів геометричної прогресії Sn =
a-aq
1-Я
При \q\<l члени ряду (53) утворюють безмежно спадну
геометричну прогресію, і тому існує границя

§ 1. Числові ряди
297
Iim5ll = lim^^l = -5L. (5.4)
п—>оо п—>оо 1 — q 1 — ^
У цьому випадку ряд є збіжним. Якщо ж |д|-1» то
відповідно границя є безмежність і ряд розбігається.
При q = -1 ряд (5.3) набуде вигляду а-а + а-а + ... Тоді
(0, якщо п - парне число,
я, якщо п - непарне число.
Отже послідовність {Sn} при п-^оо не має границі, і
відповідно, не є збіжною.
Наведемо основні теореми про збіжність числових рядів.
Теорема 1. На збіжність числового ряду не впливає
відкидання скінченної кількості його членів.
Теорема 2. Якщо числовий ряд а1+а2+... + ап+... збігається,
і його сума дорівнює S, то для довільного числа С збігатиметься
також:ряд Сах + Са2 +... + Сап +...,/ сума його дорівнює CS.
Теорема 3. Якщо ряди а1+а2+а3+... + ап+... та
Ьх + b2+b3 + ... + Ьп +... збігаються, і суми їх відповідно
дорівнюють А і В, то збіжними є також ряди
(a1+b[) + (a2+b2) + (a3+b3) + ... + (an+bn) + ...,
(al-bl) + (a2-b2) + (a3-b3) + ... + (an-bn) + ..„
і суми їх відповідно дорівнюють А + В, А-В.
Теорема 4 (необхідна умова збіжності ряду). Якщо число-
оо
вий ряд ^ап збігається, то його п-ий член прямує до нуля при
П->°о;
1ітап=0. (5.5)
П—>оо

298
РозділУ.Ряди
Зауважимо, що виконання умови (5.5) не є достатнім для
висновку про збіжність числового ряду, а саме: ряд, у якого
загальний член прямує до нуля, може бути як збіжним, так і розбіжним.
Наприклад, гармонічний ряд
> - = 1 + - + - + ... + - + ...
拾п 2 3 п
розбігається, хоча його загальний член прямує до нуля.
Якщо ж lim ап Ф 0, то ряд розбігається. Як наслідок теореми 4
одержимо достатню умову розбіжності.
Приклад 5. Дослідити на збіжність ряд — + - + — + — + ...,
який утворений з членів безмежно спадної геометричної прогресії
2 f 2 1
a,aq ,aq ,...,aq ,...\a =—,q = —
Його сума дорівнює
a-aqn+l а 2 4
lim Sn = lim — = - = ™7 \ =— •
n->oo n<r-°° l-q l-q J 1) 3
I ~2
Приклад 6. Дослідити на збіжність ряд — + — + — +...
11 12 13
Загальний член ряду тут має вигляд ап = —, п = 11, 12, ...
п
Цей ряд отримують з гармонічного ряду відкиданням перших
його десяти членів. Відомо, що гармонічний ряд - розбіжний.
Оскільки відкидання скінченного числа членів ряду не впливає
на його збіжність, то заданий ряд теж є розбіжним (теорема 1).
Приклад 7. Дослідити на збіжність ряд
12 8 4 п
- + - + - + — + ... + -
2 5 3 11 Зп-1
Перевіримо необхідну умову збіжності цього ряду.

§ 1. Числові ряди
299
Знаходимо lim ап = lim = lim — = — Ф 0 .
П—>оо П—>оо 3/1 — 1 П—>оо 1 З
Необхідна умова збіжності не виконується, отже, цей ряд -
розбіжний.
1.2. Достатні ознаки збіжності рядів
з додатними членами
Теорема 5 (ознака порівняння). Нехай задані два ряди з
додатними членами
а1+а2+а3+ ...ап +... = ^ап , (5.6)
оо
/ нехай кожен член ряду (5.6) не більший від відповідного члена
ряду (5.7), тобто
ап<Ьп , (я = 1,2,3,...). (5.8)
Тоді: а) якщо збігається ряд (5.7), то збіжним є і ряд (5.6);
б) якщо ряд (5.6) -розбіжний, то і ряд (5.7) є розбіжним.
Ця ознака зберігає силу і тоді, коли нерівність (5.8)
виконується, починаючи з деякого члена ряду з порядковим номером
п = п0 < оо. Це пов'язано з тим, що відкидання скінченного числа
елементів ряду не впливає на його збіжність (теорема 1).
Для порівняння найчастіше використовується узагальнений
гармонічний ряд
> = + + + ... (5.9)
^(an + b)p (a + ЪУ (2a + b)p &а + Ь)р
(a,b - довільні числа), який збігається для р>\ і
розбігається для р < 1, а також наведений вище ряд (5.3)
а + aq + aq2 + aq3 +... + aqn +..., який є збіжним при \q\ < 1.

300
РозділУ.Ряди
Встановити, чи виконується нерівність типу (5.8) для
конкретних рядів не завжди достатньо просто, тому на практиці ознаку
порівняння часто використовують в такій граничній формі:
якщо існує скінченна границя
lim^- = A, (А*о,А*±оо) (5.10)
то ряди (5.6) і (5.7) або обидва - збіжні, або обидва -розбіжні.
^ 1
Приклад 8. Дослідити на збіжність ряд 2^ •
Порівняємо цей ряд з рядом ^—, який утворюється за
п=і2П
формулою (5.3), при а = 1, q = — .
Позначимо ап = , Ьп = —. Застосовуючи умову
п 4-2" -3 п 2п
а 2п 11
(5.10), отримаємо lim —— =lim = lim — = —. Гра-
л->оо Ъп л->оо 4. 2п — 3 я-»00 а 3 4
оо ■*
ап ^, 1
ниця відношення —— скінченна і не дорівнює нулю, а ряд 2^—
Ьп п=і 2П
збігається, тому збіжним є і вихідний ряд.
oof 1 ^
Приклад 9. Дослідити на збіжність ряд ^
л=1
еп-1
V J
оо j
Порівняємо цей ряд з гармонічним рядом У]—, який, як
п=1П
відомо, розбігається. Використовуючи правило Лопіталя, обчис-

§ 1. Числові ряди
ЗОЇ
1 І
рП 12 —
лимо lim = lim —- = lim еп = 1 • Границя відношення
П—>оо 1 W_»оо 1 п—»°°
оо
загальних членів цих рядів скінченна, отже, ряд Vі
розбігається, як і гармонічний ряд.
Приклад 10. Дослідити на збіжність ряд ^
е"-1
"«2+1
Порівняємо цей ряд з розбіжним гармонічним рядом Л — .
Позначимо tfw = — , Ьп = —, і обчислимо
п2+1 я
п-^оЪп "->°°n +1
Отже, заданий ряд розбігається, як і гармонічний ряд.
Теорема 6 (ознака Даламбера). Нехай для числового ряду
(5.1) з додатними членами існує границя
lim^- = Z. (5.11)
п->оо ап
Тоді: якщо І < 1 -ряд збігається;
якщо 1> 1 - ряд розбігається;
якщо 1 = 1- ознака відповіді не дає.
оо еП
Приклад 11. Дослідити на збіжність ряд V—.
£іп !
5п
Використовуючи ознаку Даламбера, маємо а =—,
п !
5п+1
ап+і=1 777 і відповідно,
(п + 1)!

302
Р о з д ілУ. Ряди
Z= hm-^±L= 1ші7 г = lim = 0<1;
Значення І менше від одиниці, отже, ряд збігається.
Теорема 7 (радикальна ознака Коші). Нехай для ряду
(5.1) з додатними членами існує границя
limff/fl7 = Z. (5.12)
Тоді: якщо І < 1 -ряд збігається;
якщо 1> 1 - ряд розбігається;
якщо 1 = 1- ознака відповіді не дає.
Ґ і Vі
1 + -
оо j
Приклад 12. Дослідити на збіжність ряд ^—
Використовуючи радикальну ознаку Коші, знайдемо.
і, відповідно,
І = lim Щап = - lim
, 1+- =-<1.
І п) З
Отже, ряд збігається.
Теорема 8 (інтегральна ознака Коші). Нехай члени ряду
(5.1) додатні.
Нехай існує така монотонно спадаюча при хе [1; ©о) функція
fix), що
f(l) = al9f(2) = a29...9f(n) = an...
Тоді справедливі такі твердження:
оо
1) якщо невластивий інтеграл jf(x)dx збігається, то збі-
і
гається і ряд (5.1);
2) якщо цей інтеграл розбігається, то і ряд (5.1)
розбігається.

§ 1. Числові ряди
303
00 1
Приклад 13. Дослідити на збіжність ряд У) .
„=1(n + l)ln(n + l)
Використаємо інтегральну ознаку Коші. Зауважимо,
що члени цього ряду ап = , п = 1, 2, 3, ..., можна
(n + l)ln(n + l)
одержати за допомогою функції /(*) = при
(л; + 1)1п(л: + 1)
* = 1,2,...,п,...
Обчислимо інтеграл
оо
f/(jc)dbc = [ = f-1-^ " = In 1п(л: +1) = оо.
\J /(* + 1)1п(* + 1) J ln(jc + l) 'х
Оскільки інтеграл є розбіжним, розбігається і заданий ряд.
1.3. Знакозмінні ряди
Означення 3. Якщо серед членів ряду (5.1) є як додатні,
так і від'ємні числа, то ряд називається знакозмінним.
Дослідження знакозмінного ряду на збіжність найпростіше
здійснювати переходом до ряду, складеного з абсолютних
значень його членів.
Теорема 9. Якщо для знакозмінного ряду
ах +а2+а3 +...ап +... (5.13)
ряд, складений з абсолютних значень його членів
збігається, то збіжним є заданий знакозмінний ряд.
Приклад 14. Дослідити на збіжність ряд
ґ~\ ґ*~\ ґ*~\ '(2п-1)яЛ
cos
яЛ (ЪяЛ (5яЛ (
— cos — cos — COS
4J. UJ. UJ. A_l
32 33 3„

304
Р озділУ. Ряди
Для довільного п можна записати
Г(2п-1)яЛ
cos
І 4 )
<±
Зп Зп
Отже, члени ряду, складеного з абсолютних величин
вихідного ряду, не перевищують відповідних членів ряду
11 1 ^. .
— + -т- +... + — +..., звідки слідує збіжність заданого ряду.
З З2 З"
Означення 4. Знакозмінний ряд (5.13) називається
абсолютно збіжним, якщо збігається ряд (5.14), утворений з
абсолютних величин його членів.
Означення 5. Якщо знакозмінний ряд (5.13) збігається, а
ряд, утворений з абсолютних величин його членів, розбігається,
то цей знакозмінний ряд називається умовно збіжним.
Означення 6. Якщо знаки членів знакозмінного ряду
чергуються, тобто ряд має вигляд
ах -а2+а3-а4 +... + (-1)п+1ап +..., (ап >0), (5.15)
то ряд називається знакопочерговим (знакопочережним).
Теорема 10 (ознака Лейбніца).
Якщо для членів знакопочергового ряду (5.15) виконуються
умови:
1) ах >а2>а3 >...>ап >..., 2) Km ап =0,
п—>°°
то ряд (5.15) збігається, його сума додатна і не більша від
першого члена. Залишок цього ряду за абсолютною величиною не
перевищує першого відкинутого члена.
Приклад 15. Дослідити на збіжність ряд V (-1)п+1 —.
Й п
Заданий ряд - знакопочерговий. Дослідимо його збіжність
за допомогою ознаки Лейбніца. Маємо І) ап= —, ап>ап+1;
п
2) lim ап = 0. Умови ознаки Лейбніца виконуються, отже, даний

§ 1. Числові ряди
305
ряд збігається. При цьому ряд У*—, утворений з абсолютних
величин членів заданого ряду, розбіжний. Отже, заданий ряд є
умовно збіжним (означення 5).
ОО -І
Приклад 16. Дослідити на збіжність ряд ^](-1)Л .
Дослідимо цей ряд на збіжність, використовуючи теорему 9.
Утворимо ряд з абсолютних величин заданого ряду ^ , і
застосуємо для дослідження його збіжності ознаку Даламбера:
/ = 1іш^=1іш'*ЦІ).-?1Лит'2(2±1) = {!іи
и->°° ап п-+°° 2 In и 2w->°° Inn [ooj
1
= - hm -^ll = _ iim = - < 1.
2 w—>«> 1 2 И—>°° п + 1 2
и
Отже, ряд з абсолютних величин збігається. Тому заданий
ряд збігається абсолютно.
Завдання для самостійного розв'язування
Записати вираз для загального члена ряду:
є* і 2 3 4 __ 1 2 3 4
5.1. 1 + - + - + - +... 5.2. - + - + — + — +...
2 4 8 3 7 15 31
sin(;z72)_sin0z74) sin(;z76) sin(;z78)
V2 V4 7б y/s
ГА л ЬЗ 2-4 3-5 __ Л 1 1 1
5.4.0+ + + + ... 5.5. 1—Т + -Г—г + -
1-2 1-2-3 1-2- 3-4 22 З3 44

306
Р озділУ. Ряди
5.6. 1-1 + 1-1 + ...
го 10 100 1000 10000
5.8. + + ...
7 9 11 13
еп 1 2 3 4
5.9. + —+ -
11 101 1001 10001
Записати кілька перших членів рядів:
„ 1 4 9 16
5.7. - + — + — + — + .
2 3 4 5
^Л 2 4 8 16
5.10. - + - + - + — + ..
1 2 6 24
5.11. X
2п2+1
п=іл/2"+1
5.12. £
п=1
п + 2
2л-1
Л2
оо •
5.13, У ^
=1 Л
и=1
5.14. X
2 + (-1)"
л=1
ПІ
5.15. J]
£(3п-1)(3п + 1)
5.16. Y,
(-D
л-1
#
п=1
5.17. / cos «я-- sin—.
^ 2"
л=1
-і« ^ (-!)"• n _1Q ^ (*(я-1)
>.18. > . 5.19. > sin'
^(n + l)ln(n + l) ^
п=1
5.20.
5.21.
5.22.
5.23.
5.24.
л=1 z
Знайти суми рядів:
1 1
+ + .
1-4 2-5
1 1
1-3 + 3-5 +"
1 1
+ + .
1-4 4-7
1 1
1
1-2-3 2-3
і
п-(
. +
(2и
. +
(Зи
і
1 ...
4
1
:«+з)
і
-1)-(2и-
...
— + ...
И)
1
-2)-(Зп + 1)+"
f
и-(и +
1
•
2)

§ 1. Числові ряди
307
5.25. Y.—^
оо 1
5.26. Х^—
~^іґ +7п + 12
5.27. £
л=1
а-1
а
п-\
cos
, а>1. 5.28. £(-l)
п-1
'яЛ
v-v
л=1
з"
5.29. ft!
п=1 Z
In
5.30. X
л=1 6
л+1 •
5.31. ^(Vn + 2-2Vn + l+V«).
З 1
w=l
5.32. X
w=lL
5.33. J]
Vn + 3-Vn y/n + 2-yJn + l
yjn + l- yfn
2-(n2+3n + 3)
' ~п(л + 1)(п + 2)(п + 3)'
w=l УН +П
Скориставшись ознаками порівняння, дослідити вказані
ряди на збіжність:
оо о/І оо ґ\П , -і
5.35. У-?—. 5.36. У±-ti.
5.37. £ 2 — *» + !
л=1
5.39. £
Зи + 4
2л-1
5.38. І4^Т
„=і Зп - 2п
5.40. — + — + ... + -
3-4 4-5 (л + 2)-(л + 3)
гЛ< . 4 + 2 9 + 2 п2+2
5.41. 1 + + + ... + ^ + .
• + ...
8 + 2 27 + 2 и3+2
п
Т
7t 71 ТС
5.42. sin— + sin— + ... +sin— + ...
2 4

308
РозділУ.Ряди
5.43. — + — + ...+
In 2 In 3 ln(n + l)
5.44. tg- + tg- + ... + tg—+ ..
3 6 Зи
■ + ...
5.45. £
1
„=i п -Зи + 13
5.46. £
. я
5.47. £
«2+3
^("2+9)-3"'
5.48. У sin—.
5.50. У—-
5.49. X
п=2
И + ІПИ
5.51. ]Г In
п=1л/«(и + 2)(и + 4)
п4+3и2
оо і оо
5.52. £-(>/й+ї->/л^ї). 5.53. £
и=1И л=1
„=1 п*+3
nlv2 + sinvnj
£ 2N^
Дослідити вказані ряди на збіжність, використавши ознаку
Даламбера:
оо І __ "І 1^ оо /__2 ■ /^ оо і
5.54. У Я-11-.
2"
5.57. У——=.
5.60. - + — + ...+
3 З2
5.55. У^ЧР-
ІІ^ гл+1
оо Ол
5.58. £—.
п=1 И
+ ... 5.61. —
2!
5.56. У — .
п=1 ^
5.59. У 4--
2 w
+ — + ...+
3! (л + 1)!
5.62.1 + ^ + ...+ (!і±1^ + .
З З
з"
2 4-2
2"-п!
5.63. - + —— + ... + —77Г + ...
1 2
10
„. 3 3-5 3-5-...(2л + 1)
564. - + + ... + - + ...
п
оо о"
10
1 1-4
1-4-...(Зл-2)
5.65. Yr
5.66. у (2nz«!. 5.67. У п ■ tgНЧ • 5.68. У-і .

§ 1. Числові ряди
309
5.69. £
10
Зп
5.72. £
п=\ ПІ
оо ~П
5.70. £
(2п)п
5.71. £*-
п=і И!
5.73. У ^^. 5.74. У ^
3-5...(2л-1)
_ (2и + 1)1
^ї(2«)! й я! " ""*' Йї 3-(п!) '
5.75.У3'5-(2П + 1). 5.76. Уї±
ЙЗ-8...(5л-2) £ 3>-1)!
5.77. £
W
sm
Г-5-
«=і 2"
5.78. У
/1=1 1
\Ьл.
5.79.
^ . (2п
У nsin —
^ ІЗ"
п=\
Дослідити ряди на збіжність, використавши радикальну
ознаку Коші:
.ОЛ 1 1 1
5.80. ^ + ^— + ... + 7 г + ...
In 2 In'З
Іп"(л + 1)
оо 1
5.81. У—
п + 1
„=lV2n-l,
**• Я^І • **• яш ■ **■ І
и=1
И + 3
/і=1
5.85. У f -±-
оо
5.88. £
Ч
5.86.
2п + 1
S^J-^Sl^i
Г2л-1
[Sn + l
2n + l}
5n-l)
,2/г
2/г-І
3n-2f"3" ._ ^ . її2 —. ^,Гп + 2л("+1)2
л=Г
7и + 5
5.89. X 1 + _ • 5-90- Z
5.91. £
П=\
[а
V я,
5.92. У П " ,. 5.93. У 2" —
5.94. ^З"1
и=1
П + 1
«=lf 1
п + -
п
п
и
. 5.95. У—.
п=ї J
5.96. ^
(n + lf
ли+1
и=1

310
РозділУ.Ряди
°° ґ 1 \п\п~Ч °° і
5.97. У — . 5.98. У -
ifU + U ЙЬ-(л
оо я
5.99.Х 7 V
п
Дослідити на збіжність ряди, використовуючи інтегральну
ознаку Коші:
оо -• оо ґ> оо
5.100. У—. 5.101. У —=—. 5.102. У-^—.
5.103. У-^т- 5.104. У -J—. 5.105. У^— .
5.Ю6 У^ . 5.107. У^-. 5.108. УІ2ІЙ-.
£^4n2+4n-8 tf«3+l п=2"3-1
5.109. У —?-=. 5.110. У^Ц. 5.111. У-^—.
^ 1 + Vn ^ї(1 + п)2 £?л2+3
5.Ц2. У " 5.113. У—П—. 5.114. У <£«Щ?.
tri + n4 Й 16 + п4 ~ 1 + п2
5.115. У п2п . 5.116. У —. 5.117. У і .
£ ^ еп Й(л-1)1п(и-1)
5.И8.І;—^—. 5.П9.І; *
^ n(In4 n +1) ^ (п +1) ln(n +1) ln(ln(n +1))
Дослідити на збіжність ряди:
5.120. —=г + —= + ...+ == + ...
2V2 3V3 (n + l)Vn + l
5.121. + + ... + + ...
101 201 ЮОи + 1
ода" » „|
5.122. - + - + ... + — +... 5.123. У—.
2 8 п2п ї£пп

§ 1. Числові ряди
311
5.124. £Л-
п=і 2"
5.126. £
1
00 и"
5.125. У —-
£» + 1)
оо .
5.127. ^arctg"-
и=1
5.128. Xі"
w=i
5.130. У sin—-.
^ In1
w=i
5.129. У | nzl
5.131. Уіп(і + -
п
л(п-1)
Дослідити на збіжність знакозмінні ряди:
ч/1+l
1
5.132.1-і+ ... + (-1)"+1—!— + ... 5.133. У (-1)"
З 2n-l ±f (Зп + 2)2
/1=1
5.134. I-I.i- + ... + (-l)"+1I.J- + .
2 2 22 п 2"
5.135. Y(-irlh4-7--(3n-2).
^ 7-9-Ц....-(2л + 5)
5.136. ^(-ІГ1^-.
п=і 2
5.138. у(-»П-\2п + 3)
ЇҐі п (я+ 2)
5.137. £(-1)'
п=1
/1+1
Зп
5.139. £
(-D
4п + 3
л-1
Й>/л ^(я + З)"
5.140. £(-1)
„Vn2 +2/1 + 1 -Vn2-2n + l
л=1
5.141. £
n=l
5.143. £-
(-1)" я
7n-l
(-D
/i+i
n_1n + cos
V\/nJ
5.142. У(-1)й
^ l-3-5-...-(2n-
5.144. E ^ . 2 ■
w=1 nv« + sm n
1)

312
РозділУ.Ряди
5.145.
5.147.
5.149.
5.151.
5.1. а,
5.4. а,
5.7. а,
5.9. а,
5.11. -
оо
І
/1=1
cos и
и!
Ес-іг'іп
ґнЛІ.
л=1 V п" J
Е(-іґ—•
оо
І
/1=1
'(-І)"-1 і"
•
5 146 Y Sin"
^плУп + 1
5.148. £(-1)" *
w=2 nlnn^lnlnn;
5.150. £(-l)»_L_.
^2 Л - In Л
Відповіді
-— 52
1 2""1
(п-1)(п + 1)
,=-^. 5.8.
1 и + 1
= (_!)»_?_. 5.10
' V ' 10" +1
3 9 19 33
у/З л/5 л/9 л/І7 "
5.13. 1 + -
2
2 3
+ —+ —
9 32
2
+ —
б:
4
— + ..
>5
sin
f—1
12л J
" 2"+l-l л/2^
йл=(-і)"_1~; 5Ав,=(-і)и.
„ ( IV* 10"
2n + 5
2"
•an= — .
S^ n 16 . 36
5.12. 9 + —+ 1 + — + ...
9 49
5.14. 1 + - + - + -
2 6 J
1
- + ..
3
eilr 1 2 3 4
5.15. - + — + — + + ...
8 35 80 143
„.,_ , V2 . n . n
5.17. -1 + sin— + sm—+...
2 8 16
5.16. 1—t= + -f=—;= + •••
V2 3V3 V4

§ 1. Числові ряди
313
5.18. —+ —-
2 In 2 ЗІпЗ
3 4
41п4 51п5
5.19. 0 + — + 1 + — + 0-... 5.20. 1 + -
2 2 2
5.21. —. 5.22.
18
23
5.25. —. 5.26.
45
5.29. —. 5.30.
12
5.33.1. 5.34.
5.37. Розбіжний.
5.40. Збіжний.
5.43. Розбіжний.
5.46. Збіжний.
5.49. Збіжний.
5.52. Збіжний.
5.55. Збіжний.
5.58. Розбіжний.
5.61. Збіжний.
5.64. Збіжний.
5.67. Збіжний.
5.70. Розбіжний.
5.73. Розбіжний.
5.76. Збіжний.
5.79. Збіжний.
5.82. Збіжний.
5.85. Збіжний.
5.88. Розбіжний.
5.91. Збіжний.
1 е^ 1
-. 5.23.-.
2 3
—. 5.27. а.
4
-. 5.31. 1-V2.
2
4
—. 5.35. Збіжний.
3
5.38. Розбіжний.
5.41. Розбіжний.
5.44. Розбіжний.
5.47. Збіжний.
5.50. Розбіжний.
5.53. Збіжний.
5.56. Збіжний.
5.59. Збіжний.
5.62. Збіжний.
5.65. Збіжний.
5.68. Розбіжний.
5.71. Розбіжний.
5.74. Розбіжний.
5.77. Збіжний.
5.80. Збіжний.
5.83. Збіжний.
5.86. Збіжний.
5.89. Розбіжний.
5.92. Розбіжний.
1 1
+ — + - + ...
4 8
5.24. -.
4
5.28. -.
7
5.32. 1-л/з.
5.36. Збіжний.
5.39. Розбіжний.
5.42. Збіжний.
5.45. Збіжний.
5.48. Розбіжний.
5.51. Збіжний.
5.54. Збіжний.
5.57. Збіжний.
5.60. Збіжний.
5.63. Розбіжний.
5.66. Розбіжний.
5.69. Збіжний.
5.72. Збіжний.
5.75. Збіжний.
5.78. Збіжний.
5.81. Збіжний.
5.84. Збіжний.
5.87. Збіжний.
5.90. Розбіжний.
5.93. Збіжний.

314
РозділУ. Ряди
5.94. Збіжний.
5.97. Збіжний.
5.100. Розбіжний.
5.103. Розбіжний.
5.106. Збіжний.
5.109. Розбіжний.
5.112. Збіжний.
5.115. Розбіжний.
5.118. Збіжний.
5.121. Розбіжний.
5.124. Збіжний.
5.127. Збіжний.
5.130. Збіжний
5.132. Умовно збіжний.
5.134. Абсолютно збіжний.
5.136. Абсолютно збіжний.
5.138. Умовно збіжний .
5.140. Умовно збіжний.
5.142. Абсолютно збіжний.
5.144. Абсолютно збіжний.
5.146. Абсолютно збіжний.
5.148. Абсолютно збіжний.
5.150. Умовно збіжний.
5.95. Збіжний.
5.98. Збіжний.
5.101. Розбіжний.
5.104. Збіжний.
5.107. Збіжний.
5.110. Збіжний.
5.113.36ІЖНИЙ.
5.116. Збіжний.
5.119. Розбіжний.
5.122. Розбіжний.
5.125. Розбіжний.
5.128. Збіжний.
5.96. Збіжний.
5.99. Збіжний.
5.102. Розбіжний.
5.105. Збіжний.
5.108. Розбіжний.
5.111. Збіжний.
5.114. Збіжний.
5.117. Розбіжний.
5.120. Збіжний.
5.123. Збіжний.
5.126. Збіжний.
5.129. Збіжний.
5.131. Розбіжний.
5.133. Абсолютно збіжний.
5.135. Розбіжний.
5.137. Розбіжний.
5.139. Умовно збіжний.
5.141. Розбіжний.
5.143 Умовно збіжний.
5.145. Абсолютно збіжний.
5.147. Абсолютно збіжний.
5.149. Умовно збіжний.
5.151. Розбіжний.

§ 2. Функціональні ряди
315
§ 2. ФУНКЦІОНАЛЬНІ РЯДИ
2.1. Загальні поняття
Означення 1. Ряд
U1(x) + U2(x) + ... + Un(x) + ... = XUn(x) (5.16)
членами якого є функції Un{x), п = 1,2,...,©о, визначені в одній і
тій же області, називається функціональним рядом.
При заданому значенні змінної х = х0 одержимо числовий ряд
оо
2Х(*о). (5.17)
Означення 2. Множина X значень змінної х, для яких
функціональний ряд (5.16) збігається, називається областю збіжності
цього ряду.
Кожному значенню хе X ряду відповідає певне значення
п
величини S(x)= limV U(x) (якщо границя існує), яка
називаєгься сумою функціонального ряду. Запишемо суму ряду у вигляді
S(x) = Sn(x) + Rn(x),
де Sn(x) = Ul(x) + U2(x) + ... + Un(x) - п - часткова сума,
Rn(х) = Un+l(х) + Un+2(х) +... - залишок функціонального ряду
після п -то члена.
Означення 3. Функціональний ряд (5.16) називається
рівномірно збіжним в області X, якщо для як завгодно малого числа,
Є>0 можна вказати такий порядковий номер члена ряду и0, що
при п>п0 виконується нерівність \Rn(x)\ < є для всіх хе X.
Ознака Вейєрштраса (достатня ознака рівномірної
збіжності функціонального ряду).

316
Р о зд ілУ. Ряди
Нехай ^ап, (ап > 0) - збіжний числовий ряд. Якщо при
всіх ХЕ: X для членів функціонального ряду (5.16) виконується
нерівність \Un(x)\ <ап, то такий функціональний ряд рівномірно
збігається в області X .
Приклад 1. Довести рівномірну збіжність ряду
sin2 2л; sin3 Зх . / ч
Sin X + + + ... На ПрОМІЖКу (- oo;ooj .
Загальний член цього функціонального ряду
задовольняє нерівність
sinw пх
п2
<—, для всіх хе(-°°,оо), а
п2
00 1 11 1
числовий ряд У-т- = 1 + —Т + Т + — + —т + — -збіжний.
п=іп 15 п
Отже, за ознакою Вейєрштраса цей ряд рівномірно
збігається при хе (-00,00).
Для рівномірно збіжних функціональних рядів справедливі
наступні теореми.
Теорема 1.Якщо для всіх хє {а,Ь) члени функціонального
ряду (5.16) - неперервні функції) а сам ряд рівномірно збігається в
цій області, і сума його дорівнює S(x), то збігається і ряд
ь ь
\г(х)(Іх+ \u2(x)dx + ... + Un(x)dx + ...9
а
Ь
і сума його дорівнює \S(x)dx (сума рівномірно збіжного ряду -
а
неперервна функція; рівномірно збіжний ряд можна почленно
інтегрувати).
Теорема 2. Нехай члени ряду (5.16) визначені в області Х9
і мають в цій області неперервні похідні U[(x), U'2(x)9...,U'n(x),...

§ 2. Функціональні ряди
317
Якщо в цій області ряд (5.16) збігається, а ряд ^ІҐп(х) -
збігається рівномірно, то сума S(x) ряду (5.16) має похідну,
оо
причому S\x)= ^U'n(x).
w=i
2.2. Степеневі ряди
Означення 4. Степеневим рядом називається
функціональний ряд
оо
а0+аї(х-Хь)+а2(х-х0)2+..ЛаЛ{х-^ (5.18)
и=0
де х0 - стала величина, а0, ах, а2,.... - коефіцієнти ряду.
У частковому випадку х0 = 0 степеневий ряд має вигляд
оо
а0+ ахх + а2х2 +... + апхп + ...= ^апхп. (5.19)
/г=0
Очевидно, що заміною х-х0 = z ряд (5.18) можна звести до
виду (5.19).
Теорема 3 (Абеля). Якщо степеневий ряд (5.19) збігається
для деякого значення х = х0 ї 0, то він абсолютно збіжний при
всіх х, для яких — \х01 < х < \х01, Якщо ж ряд (5.19) розбігається
при х = х0, то він розбігається для всіх \х\ > \х0\.
З теореми Абеля слідує, що існує значення |*| = R, яке
відділяє область збіжності степеневого ряду від області його
розбіжності. Число R називається радіусом збіжності ряду (5.19), а
інтервал (-R,R) - інтервалом збіжності.
Знаходження радіуса збіжності степеневого ряду
грунтується на застосуванні ознаки Даламбера або ознаки Коші за
формулами

318
Р о з д ілУ. Ряди
R= lim
П—¥°°\
1П + 1
(5.20)
R = 1-г=. (5.21)
lim tf\a„\
Збіжність ряду в граничних точках х = +R підлягає
окремому аналізу.
Теорема 4. В інтервалі збіжності (-R,R) степеневого
ряду (5.19) його сума
S(x) = а0 + ах х + а2х2 +... + апхп +...
є неперервною функцією. Степеневий ряд (5.19) в межах
інтервалу (~R,R) є рівномірно збіжним, тому його можна почленно
інтегрувати та диференціювати довільне число разів. При цьому
радіус збіжності ряду, отриманого почленним диференціюван-
оо оо X X
ням ^(апхп)'= S'(x), чи інтегруванням ^ \antndt= \S(t)dt9
w=l n=la а
(а, х) с (-R, R), дорівнює радіусові збіжності вихідного ряду.
Приклад 2. Знайти інтервал збіжності та суму ряду
1-2-х + 2-3-х2 +3-4х3 +... + п(п + 1)хп +...
Знайдемо радіус збіжності цього ряду за формулою (5.20):
R= lim
и—>°°
гп+1
-lim W(W + 1) =1.
п->оо (п + \){п + 2)
Ряд є збіжним, причому рівномірно, для 1*1 < 1.
При х = 1 маємо числовий ряд
1-2 + 2-3 + 3-4 + ... + /і(и + 1) + ...,
при х = -1 одержуємо 1 • 2 - 2 • 3 + 3 • 4 +... + n(n + l)(-l)(w+1) +...
Кожен з цих числових рядів розбігається, оскільки для
першого з них не виконується необхідна умова збіжності, для другого -

§ 2. Функціональні ряди
319
умови ознаки Лейбніца. Отже, граничні точки інтервалу (-1,1) не
належать до області збіжності заданого степеневого ряду.
Знайдемо тепер суму S(x) даного ряду
S(x) = l-2-x + 2-3-x2 +3-4jc3 + ... + п(п + 1)хп + ...
Для цього проінтегруємо обидві частини останнього виразу
в межах від 0 до z, z Є (— 1, і).
Z
Одержуємо z2 + 2z3 + 3z4 +... + nzn+l +... = js(t)dt.
о
Поділимо обидві частини цього співвідношення на z , і
проінтегруємо його в межах (/?, х) с (-1,1), 0 < /3 < 1. Отримуємо
2 З
х + х +х +
х jS(t)dt
... + *"+...= J° 2 dz + C
/з z
2 3 Р
Тут С = Р + (3 +/3 +...= - стала, що виникає при
підстановці нижньої межі інтегрування в ліву частину виразу.
Використовуючи вираз для суми членів нескінченої
геометричної прогресії, маємо
х
X
4.
\S{t)dt
£-Ь^+с-
Знайдемо похідну по х від двох частин цього виразу,
пам'ятаючи, що визначений інтеграл є функцією верхньої межі інтегрування
х
1 X t
,=-—--—, звідки -= \S(t)dt.
(1-х)2 х2 (1-х)2 0J
Ще раз продиференціюємо останню рівність, отримаємо
а-*)3

320
Р озділУ. Ряди
У результаті для суми заданого степеневого ряду маємо
їх
S(x) = l-2-x + 2-3-x2+3-4-x3 + ... + п(п + ї)хп + ...=
(1-х)3
Приклад 3. Знайти суму степеневого ряду
v3 v5 г7 г2п+1
X X X ( л\п X
X + + ... + (-1) + ...
3 5 7 v ; 2л + 1
Радіус збіжності ряду дорівнює одиниці (перевірити !): R = 1.
Для обчислення суми ряду
г3 v5 v7 г2"+1
5(jc) = jc- —+ — - — + ... + (-1)Я- + ...,
3 5 7 V } 2п + \
враховуючи його рівномірну збіжність в інтервалі (-1,1),
знайдемо спочатку похідну від обох частин останнього виразу
S'(jc) = 1-jc2+jc4-jc6+...
У правій частині при кожному |х| < 1 маємо нескінчено
спадну геометричну прогресію із знаменником q = -х , для якої
1-х2 +хА-х6 +... = - 1
1 + х2 '
Отже, S'(x) =
1 + JC2
Проінтегруємо одержаний вираз в межах від 0 до х, pj < 1.
XX X
js\t)dt = jd(S(t)) = S(x) - 5(0) = j-^y =arctg;c.
о о о1+'
Враховуючи, що 5(0) = 0, отримуємо
*3 *5 К" , іч» Я2"*
S(x) = x- — + — - — + ... + (-1)"- - + ... = arctgjc.
3 5 7 2п + 1

§ 2. Функціональні ряди
321
2.3. Розклад функцій у степеневі ряди
Нехай функція f(x) на проміжку [а, /?] є (п +1) разів
неперервно диференційована. Тоді для довільних х і х0 з цього
проміжку справедлива формула
f(x) = f(x0) + ^^-(x-x0) + ^^-(x-x0) + ...+
+ І__Ш(Х_1Ь)"+^, (5.23)
яка називається формулою Тейлора для функції f(x); /?„ -
залишковий член формули Тейлора
Rn =l — (x - x0 )n+l, (5.24)
n (л + 1)! °
£ -точка в інтервалі (jc0;jc) : £ = x0 +в- (л: — jc0), 0 < в < 1.
Означення 5. Рядом Тейлора для функції f(x)
називається степеневий ряд
1! 2! пі
У частковому випадку х0 = 0 (розклад в околі точки
jc0 = 0) одержуємо ряд
т+тх+ішх+...+і^<?±х.+..., (5.26)
1! 2! л!
який називається рядом Маклорена.
Залишковий член в формулі Тейлора (5.24) для функції
f(x) не обов'язково є залишком ряду Тейлора (5.25) цієї
функції. Тому із збіжності ряду Тейлора ще не випливає його
збіжність саме до функції f(x).
Нижче наведено розклади деяких елементарних функцій в
степеневий ряд (ряд Маклорена)

322
Р о з ділУ. Ряди
2 З
XXX
є =1 + —+ — + — + ...+— + ...,
1! 2! З!
л
х3 х5 х1 , 1ЧІІ х2п+1
sin X = х + +... + (-1)"
З! 5! 7! (2л+ 1)!
, х2 х4 х6 , пя х2»
C0SJC = 1 + + ... + (-1)" + ...,
2! 4! 6! (2л)!
chjc =
є +е
л Xі х4 х2п
2! 4! (2л)!
u ех-е-х х3 х3 х2п+1
sh х = = х + — + — +... +
чт л т m(m-l) 2
(l + jc)m=l + — х+ v ' ~1
1! 2!
т(т - 1)...(т - л +1) п
З! 5! (2л+ 1)!
лґ*+...+
• + ...
-°о<х<°о;
-оо<д;<оо;
-oo<jc<«> ;
-оо<д:<оо;
-oo<jc<oo;
Л
*"+...
-1<х<1, m>0;
—1 < jc < 1, -Km<0;
—1< jc<1, m<-l.
-Л+1
2 3
ln(l-Jt) = Jt- — + — + ...+ (-1)" —+ ...,
2 3 л + 1
—1< jc<1;
arcsiiuc = x + — •
1 x3 1-3 jc5 1-3-5 jc7
2 3 2-4 5 2-4-6 7
- + ...+
1-3-5-...-(2л-1) x
,2/г+1
2-4-6-...-2л 2л + 1
+ ...,
-1 < jc < 1;
.2/2+1
jc3 x5 x1 x-
arctgx=*- — + - — + ... + Г-1Г- + — -1<*<1.
3 5 7 2л + 1
Приклад 4. Розкласти за степенями х-х0 функцію
f(x) = lnx; х0 =1 у степеневий ряд і знайти інтервал його
збіжності.
Обчислюємо
Д*0) = 1п1 = 0, /'(*) = -,
х
/"(*„) = і;

§ 2. Функціональні ряди
323
/'(*) =-Л-. /*(*ь) = -1;
л:
rw=-
,3 '
Г(;с0) = 2;
Зауважимо, що
/"іх) = =Ц; /*(х0) = -2.3.
\П+1,
/«ад.НОїіВ!.
:(")/
\П+1/
Враховуючи це, одержимо In х = X ("" 1/ + "^
Знайдемо область збіжності цього ряду за допомогою
ознаки Даламбера
/= lim
П—>оо
с/,
Л+1
£/„
= lim
П—>оо
л(*-1>
/г+1
= Ьс-1<1.
|(n + l)(jc-l)"|
Отже, ряд збігається при -1<jc-1<1, або 0 < х < 2.
Точка л; = 0 не входить в область визначення функції
у = In х. При л: = 2 отримуємо збіжний знакопочерговий ряд.
Отже ряд збігається при 0 < х < 2.
/(*) =
Приклад 5. Розкласти за степенями х - х0 функцію
1
-, jc0 = —1, у степеневий ряд і знайти інтервал його
3 + 2jc
збіжності.
Використовуємо для знаходження розкладу вказаної
функції в ряд за степенями х - х0 = х +1 вираз для суми членів
нескінченно спадної геометричної прогресії. Для цього запишемо
функцію f(x) =
1
3 + 2*
/(*) =
у вигляді:
1
3 + 2[(jc + 1)-1] 1 + 2U + 1)

324
Р о з д inV. Ряди
= 1-2(jc + 1) + 4(jc + 1)2-8(jc + 1)3+... (я0=1; q = -2(x + l)).
Ряд збіжний при |g| = 2|jc +1| < 1, або — < jc +1 < —, тобто
З 1
<*< — .
2 2
2.4. Множення рядів
Нехай задано ряди
оо оо
Yuan Та Yuhn-
лг=1 /г=1
Добутком рядів називається ряд, що складається з усіх
можливих попарних добутків акЬт (к = 1,...,°°;т = 1,...,°°, к<т).
Теорема 5. Добуток двох абсолютно збіжних рядів
оо оо
^ап = А, ^Ьп = В є абсолютно збіжним рядом, сума якого до-
/г=1 /г=1
рівнює АВ: ^] ^] я^т = АВ, незалежно від порядку, за яким
k=lm=l
розташовані добутки akbm при сумуванні.
Означення 6. Добутком за Коші називається ряд 2^сп >
членами якого є
с} = арх у с2 = арг + а2Ь1,
с3 = аръ+а2Ъ2+аъЪх ,..., сп = £ акК >•••
k+m=n+l

§ 2. Функціональні ряди
325
2.5. Застосування рядів
1. Обчислення значень функції
Розклад функції в степеневий ряд можна використовувати
для обчислення з будь-якою точністю її значення в точці з
проміжку збіжності цього ряду.
Приклад 6. Обчислити -Je з точністю 10 .
Запишемо розклад функції ех в степеневий ряд при х = — .
Одержимо
\ ^ 1 1 1 1 1
е2=У = 1 + - + —— + —— + ...
£02п-п\ 2 22-2 23-6
Оцінимо залишковий член гп цього ряду. Оскільки члени ряду
додатні, то для оцінки можна використати мажоруючий ряд. Маємо
= у J_ = 1
1
-,п+2
■ + ... + ■
1
■ + ...=
~+іГк\ 2"+1(« + 1)! 2"+z(n + 2)! 2"+m(n + m)!
Тп\
1
1
■ + ...+-
1
2(п+1) 22(и+1)(п+2) 2m(n+l)(n+2)-...-(n + m)
1
2пп !
1 1
1 1
- + -
2(л + 1) [2(п + 1)]2
1 1
+ ... + -
1
[2(/г + 1)Г
1
2пп\ 2(п + 1) х 1 2"-и! 2(л + 1)-1 2"и!(2п + 1)
2(п + 1)
CO j
Мажоруючим рядом тут є ряд V -, що являє
£о[2(л + 1)]*
собою суму членів нескінченно спадної геометричної прогресії зі
1
знаменником
2(и + 1)

326
Р о з д ілУ. Ряди
Отже, гп < . Знайдемо найменше натуральне
2пп\(2п + ї)
число я, при якому гп <10~4. Зауваживши, що гх < —, г2 <—,
6 40
Гі < , Гл < , Гс < < 10"4, знаходимо п = 5 . Тоді
3 336 4 3456 5 42240
1 5 1 11 1 1 1
4~е=е2 = У = 1 + - + — +
ЇҐ02п-п\ 2 22-2! 23-3! 24-4! 25-5!
і 1 1 1 1 1 2491 л ^лоп
= 1 + - + - + — + + = 1 + «1.6487.
2 8 48 384 3480 3480
Отже, Ve« 1.6487.
Приклад 7. Обчислити cosl з точністю 10~4.
Запишемо розклад функції cos* в степеневий ряд,
поклавши х = 1. Одержимо
~(-l)" 111 (-1)"
cosl= У-—— = 1 + + ... + -^—+ ...
£>(2п)\ 2! 4! 6! (2л)!
Оскільки цей ряд - знакопочерговий, то для оцінки його
залишкового члена гп застосуємо нерівність \гп\< ап+1, де ак- абсолютні
величини відповідних членів ряду. Отже, \гп\< . Знаходимо
найменше натуральне число п, при якому |г„|<10 . Зауваживши,
що|гі|<—, |г9|< , |rJ< < 10-4,знаходимо п = 3.Тоді
111 24 |21 720 '3| 40320
, V^(-l)" ,111,11 1 389 пелм
cosl= > -—— = 1 + = 1 — + = = 0.5403.
£о(2л)! 2! 4! 6! 2 24 720 720

§ 2. Функціональні ряди
327
2. Інтегрування функцій
Використовуючи розклад підінтеграпьної функції в
степеневий ряд, та застосовуючи теорему про інтегрування рівномірно
збіжних рядів, заданий інтеграл можна виразити у вигляді
степеневого ряду. Одержаний вираз можна використати для
обчислення з довільною точністю значення цього інтеграла в будь-якій
точці з проміжку збіжності одержаного ряду.
хл *-t
гі — Є
Приклад 8. Розкласти dt в ряд за степенями х.
о '
Розкладемо функцію е~%, а потім і підінтегральну функцію,
в ряд за степенями t; одержаний ряд інтегруємо почленно.
Маємо
,(-і)*/*^
0 1 оЧ к=0 К' J оЧ *=1
л 1 ( °° ґ л\к+1 Л Л хл( °° ґ 1\П+2+П+і\ х оо лі
о^Й *! J М h (п + 1)! J Й (п + 1)!
0 V л=0
/г .п+1
..«+1
= yiil2_fr»<u = yiii2_.i_J =У(-і)"—^ .
„t-0(n + l)!0J £(« + 1)1 И0 «=о (я + ІЖп + 1)
Степеневий ряд функції е~1 збіжний на проміжку (-00,00).
Одержаний після інтегрування ряд збіжний на цьому ж проміжку.
Отже,
J г Й (л + 1)!(л + 1)
Приклад 9. Обчислити Л з точністю
10"
Запишемо значення вказаного інтеграла у вигляді суми
числового ряду. Для цього підінтегральну функцію розкладаємо в
степеневий ряд і почленно його інтегруємо. Одержуємо

328
Р о з д inV. Ряди
03 і и , 1\ азі °° *я+1 0.3
,J f iff* n + 1 J±-v л + 1
0 л=0 " т x о «=0
, л 0.3
(-1} b,, *(-!)- f*1
:y^_ |W,= yi±L21
„То» + 1 о „=o" + l" +
°'3=E(-ir^,
0 n=0
(П + 1Г
22 З2 42 (и+ 1)2
Для оцінки залишкового члена гп одержаного знакопочерго-
вого ряду застосуємо нерівність |г„| < ап+1, де <я„ - абсолютні зна-
(0 3)"+2
чення відповідних членів ряду. Отже, \гп І < —'■ —. Знайдемо най-
(и + 2)1
менше натуральне число п, при якому |г„|<10-4. Зауваживши, що
(0.3)3 3 | | (0.3)4 81 | | (0.3)5 243
11 З2 103 ' ' 42 16-104 " 52 25-105
243 1 ш-4
= г<Ю »знаходимо п = 3.
250 Ю4
Отже,
°?1п(ґ + П з (о.зГ1 ло (0.3)2 , (0.3)3 (0.3)4
0J ' Й (я + 1)2 22
ІІ^ 40 100 16000 J
З2 42
A !_A + J___^_LilZ^0.2800.
101 40 100 16000J 16000
3. Знаходження сум рядів
Застосовуючи відомі розклади функцій в степеневі ряди, а
також дії над степеневими рядами, суму числового ряду можна
виразити через значення заданої функції в точці з проміжку
збіжності ряду, а також знаходити суми інших степеневих рядів.

§ 2. Функціональні ряди
329
°° 1
Приклад 10. Обчислити суму ряду V .
Застосовуючи розклад функції 1п(;с + 1) в степеневий ряд,
маємо
/2=0
/2=0
1 °° 1 ( \\ 1
Приймаючи х = —, одержимо ^ = -1п 1— = -1п—= 1п2 ,
2 и=і л 2 \ 2) 2
л=1'
Зауважимо, що при підстановці інших значень ;сє (-1, і]
. ~ 1
знаходимо суми інших рядів. Так, приймаючи х = —, одержуємо
/2=1 П Z J
оо
Приклад 11. Обчислити суму ряду V (-1)" -
£ (2и +1)!
Зауваживши, що
1 1
(2л)! (2л+ 1)! (2л)!
1 <х- ■
2л
2л + і; (2л+ 1)!
та застосовуючи розклади функцій cos* та sin* в степеневі
ряди, маємо
2У(-1)П——х2п+1 = У (-1)"
Й (2и + 1)! Й
1
1
(2л)! (2л+ 1)!
х2п+1 =
°° х2п °° х2п+1
= *У (-1)" У (-1)" = *COS X - Sin X , -оо < х < о» .
^ (2л)! ±-v (2л + 1)!
% (2л)! £ (2л + 1)!
Поклавши дг = 1, одержуємо
У(-і)п——=
±Г (2л+ 1)!
cos 1-sin 1
n=0 (2n + l)! 2
Цей результат можна також отримати, прийнявши х = -1.
Зауважимо, що при підстановці інших значень хє (-00,00) знахо-

330
Р о з д ілУ. Ряди
димо суми інших числових рядів. Так, приймаючи х = ±л,
одержуємо ]£](-1)Л
71=0
(2л+ 1)!
-71 =
оо Z
Приклад 12. Знайти суму ряду ^—хп .
/г=1
2
Цей ряд рівномірно збіжний на проміжку хє(-°°,°°).
Позначимо його суму через f(x). Прийнявши п -1 = £, маємо
/г=1
.2
оо Z. оо
(*+1)V
J0(* + l)!
/(дт) = у(Я-1)2^
Обчислимо інтеграл від обох частин одержаного виразу в
межах від 0 до х, позначивши змінну інтегрування через t:
fit)
І t і £і(* + 1)!
<* + 1>>Л.
Враховуючи, що означений інтеграл є функцією верхньої
межі інтегрування, знайдемо похідні за змінною х від обох
частин цього виразу. У лівій частині маємо
d_
dx
Л
/(0
vo
dt
fix)
J
У правій частіші попередньо виконаємо почленне інтегрування
ряду. Ця дія обгрунтована, оскільки ряд - рівномірно збіжний.
Враховуючи вигляд степеневого ряду для функції ех, одержуємо
■(*+1)У.а-у(*+1)2*-
Тоді
Отже,
(*+1)
л
fV^liL^ \ = ±(х.е*) = е* + х.е*
і SU* + 1)! dx\ І
= ех +х-ех.

§ 2. Функціональні ряди
331
Знаходимо вираз для суми заданого ряду
оо 2
Yr-:*? = х(\ + х)е\хє(-~>~).
*=і"'
Зауважимо, що при кожному значенні хе (-<» ,оо) на
основі одержаного виразу знаходимо суму відповідного
числового ряду. Так, при ;с = -1 та при х = 1 відповідно маємо
2 оо 2
I(-irV0;£V2*-
2.6. Ряди Фур'є
Нехай f(x) - періодична функція з періодом 2я, яка на
проміжку (-п,7і) неперервна або має скінченне число точок
розриву першого роду, і абсолютно інтегровна на цьому проміжку.
Означення 7. Рядом Фур ує функції f(x) називається ряд
— + а{ cos х + \\ sin х + а2 cos 2х + Ь2 sin2jc +...
(5.27)
+ап cos пх + bn sin пх + ... = — + ^ (ап cos пх + Ьп sin пх),
2 л=1
коефіцієнти а0, ап, Ьп якого обчислюють за такими
формулами
1 л
ао=— \f(x)dx9
7Г J
~п (5.28)
1 1
ап=— \ f(x)cosnxdx, bn=— \ f(x)sinnxdx, п = 1, 2, З,...
Л" J Л" J
-я" -л-
Сума 5(л:) ряду Фур'є, побудованого для функції f(x),
S (х) = ^ (aw cos nx + bn sin ш:),
л=1

332
Розд ілУ. Ряди
дорівнює значенню функції f(x) в точках її неперервності, в
точці розриву х = с дорівнює півсумі границь функції справа і
зліва точки розриву:
5(с) = |(Дс-0) + Дс + 0)).
У випадку парної функції f(x) коефіцієнти Ьп (п = 1,...,°°)
дорівнюють нулю, і ряд Фур'є має вигляд
ап _. ао ^
-^- + а{ cos х + а2 cos 2х +... + ап cos пх +... = -^ + 2J°Ln cos пх.
2 2 71=1
Коефіцієнти а0,...9 ап,.. (л = 1,...,оо) при цьому можна
обчислювати за формулами
2*г 2п
Z г Z с
а0 = — \f(x)dx, ап =— \f(x)cosnxdx.
У випадку непарної функції ряд Фур'є має вигляд
\\ sin х + b2 sin 2х +... + bn sin ш: +... = ^bn sin пх.
71=1
Для коефіцієнтів ряду в цьому випадку маємо
Iя
= 0, ап=0, п = 1,...,°°, bn=— \f(x)sinnxdx, л = 1,...,
*о
Приклад 13. Розкласти в ряд Фур'є функцію
ГО, -я-<л;<0,
[1, 0 < х < п.
Обчислимо коефіцієнти а0,ап,Ьп:
\лт \пг 1 п
а0=— \f(x)dx = — \l-dx = — х І =1,
п J пJ я о
-л о
І * і* і п
ап=— \ f(x)cosnxdx = — \cosnxdx = —sinnx І =0,
п J пJ Л"Л о

§ 2. Функціональні ряди
333
1 п \л
Ъп-— Г f(x) sin nxdx = — jsin nxdx =
= cos ял;
nn
о n n
-(1-cos яті).
Для парних значень п маємо cos7Tn = l. Отже, ряд містить
лише доданки, що відповідають непарним п: n = 2k + l, к = 0,1,...
Значить, Ь2к = 0, Ь2к+1 =
тг(2к + 1)
, * = 0,1,2,.
n /y ч 1 2f,sin[(2* + l)*]
Одержимо /(*) = — + — 2^-
2 п
к=0
2к + 1
Для періодичної функції f(x) з довільним періодом 21,
яка є неперервною і абсолютно інтегровною на проміжку (-/, /),
або має на цьому проміжку скінченне число точок розриву
першого роду, ряд Фур'є має вигляд
ап ^( ппх , . і
Чг + 2, \ancos-— + bnsm-
п=1
ппх
(5.29)
де
.і 1 /
а° =7 lf(x>>dx> an=J jf(x)cos——dx,
-і -і 1
1 г ., ч . ппх , л _ .
fc„ =- J/U)sin—— rtx, л = 1,2,3,...,
-/
причому ряд Фурє для парної функції містить лише доданки
—+ 2^tf„cos , а для непарної - доданки 2^fyisin •
Коефіцієнти ряду Фур'є для парної функції дорівнюють

334
РозділУ.Ряди
2Zr_, 2і
ao=- \f(x)dx9 an=- \f(x)cos——dx, bn = 0, n = l,...,oo, івідпо-
1 l n l
о 0
відно для непарної bn = — f/(jt)sin d[x, я0 = 0, n = l,...,°o.
2.7. Інтеграл Фур'є
Нехай f(x) - неперервна (або кусково неперервна) і
абсолютно інтегровна функція, задана у всіх точках хє (-оо,оо)
дійсної осі. Розкладом фікції f(x) в інтеграл Фур'є називається
зображення її у вигляді
оо оо
f(x) = -jda)jf(t)cosaKt-x)dt (5.30)
*о
що дійсний у всіх точках хє (-00,00), за винятком точок розриву.
У точках розриву х = с виконується рівність
/(с + 0) + /(с-0)_1
оо оо
= — \dco [ f (с) cos a)(t-x)dt.
7Г * *
*o
Права частина виразу (5.30) називається інтегралом Фур'є
функції /(*).
Для інтеграла Фур'є використовують також форму
оо
/(*)= j(а(со) cos сох + b(co) sin cox)dco, (5.31)
де
оо оо
а(со) = — і f(t)cos(ax)dt, b(co) = — {fit) sin cotdt.
n J n J
—oo —oo
Величини a{aS) та Ь(ю) називаються перетвореннями
Фур'є функції f(x) .

§ 2. Функціональні ряди
335
У випадку парної функції маємо Ь{со) = 0, отже
оо
/(*) = \a(Q))cos((Dx)d(D,
о
1 °° 2 °°
а(со) = — [ f(t)cos(ax)dt = — [f(t)cos(cot)dt,
п J пі
-оо О
у випадку непарної функції відповідно а(со) = 0,
оо
f(x)= \b(co) sin coxd(Q,
0
оо оо
If 2 г
b(co) = — \f(t)sm(a)t)dt=— \f(t)sm(cot)dt.
n J n {
-оо О
Задачі для самостійного розв'язування
Знайти область рівномірної збіжності рядів:
5.152. У±Vj. 5.153. У^. 5.154. У^^
п=\х +п „=1 п л=1 п !
5.155. V-1-У . 5.156. У4г. 5.157. У—.
n=1w(* + 2) „=1и „=1е
" (-1)"
^і я*
5.158. Yrr' 5.159. 2-
n=\vn п=і
х"
5.160. Довести рівномірну збіжність ряду Y— У будь-якому
п>0ПІ
скінченному інтервалі.
2* + 1 ч"
5.161. Довести, що ряд ^J є рівномірно збіжним на
проміжку (-1,1).

336
РозділУ.Ряди
Використовуючи почленне диференціювання або почленне
інтегрування, знайти суму вказаних рядів в інтервалі (-1, 1).
Обгрунтувати методику обчислень:
1.162. х + — + — + ... + — + ...
2 3 п
в,« х х1 х3 х4 хп
5.163. - + — + — +— + ...+ + .
2 8 24 64
х3 х5 jc2"-1
5.164. х + — + — + ...+
З 5 2п-1
п-2п
+ ...
2л-1
г3 г5 г-
5.165. *- — + — -...+(-І)"4- + ...
3 5 2л-1
ГУ3!5 J"-1
5.166. ^-^+^+...+(4)^ ^——+... 5.167. У/їх" .
2 24 160 (2л-1).22*-1 ~
оо оо
5.168. £(-1)я(2/і + 1)*2я . 5.169. £/і(/і + 1)*я"\ (**0).
л=0 л=1
г^л ї * ЬЗ 2 ЬЗ-5 з 1-3-5-7 4
5.170. 1 + - + х1 + jr + jc4 +...
2 2-4 2-4.6 2-4-6-8
5.171. х - 4х2 + 9х3 -... + (-І)"'1/г V"1 +...
Дослідити вказані ряди на збіжність, встановити їх
поведінку на границях інтервалу збіжності:
оо п
5.172. £—.
71=1
5.173. У—. 5.174. У—
£«5" -ДлОі + І)
5.175. ^
(*-2)и
5.177. J 1-1
л=0
Л"
5.176. У *<**? .
ОО
5.178. ^U3+l)n.
п=0
ОО ч ОО ч
5Л79- Z 2 . 2 • 5Л80- Z *
=n/i + sin X
п=0
п=0
n + cosx

§2. Функціональні ряди
337
5.181. £(2* + 1)и.
л=0
5.183. Д- + 1
2/1+1
5.182. £(л:2-1)\
л=0
оо
5.184. ^
л=0
' *2^
1- —
V 2J
2л+1
5.185. £-
If 2х
n=lnU + x^J
5.186. J£-
/
п=1'
5.187. J]
л=1
д:-1
5.190. £(лх)" .
л=1
Д + х + д:2.
5.188. У (-1) —. 5.189. У—.
5.191. У(;С + 2)П. 5.192. УУ*)"
n=l Z" + 1 л=1
Л-1
5.193. У-^—-(х-2)п
5.194. 2-^2дс-1)и.
л=і5
5.195. У—
ІЇ4-7
1-3-5-..-(2и-1)
10-...-(Зп + 1)
(* + 1)в.
5Л96. f«*«
л=1
П!
5J97.|;^^U-l)2w.
/г=1
П!
оо п оо я
5.198. У — . 5.199. У —.
Й(* + 2)я Й«я
5.200. Радіус збіжності ряду ^апхп дорівнює 2. Знайти радіус
збіжності ряду ^Г я„*2,г •
л->0
5.201. Радіус збіжності ряду ^ап(х-а)п дорівнює R. Чому
дорівнює радіус збіжності ряду ^ ап (х - а)п+к, де і - ціле
додатне число ?
л>0

338
Роз д inV. Ряди
Розкласти в ряд за степенями х функцію f(x), вказати
область збіжності одержаного ряду:
5.202. f(x) = —. 5.203. /Ос) = —^.
1 + х 1 + х2
5.204. /(jc) = 2х. 5.205. /(*) = =¥-.
х
5.206. f(x) = е2х. 5.207. /(*) = jccosjc .
5.208. /(jc) = є"*2. 5.209. / (jc) = * V.
5.210. Використовуючи розклад у ряд за степенями jc функцій
sin* та cosд:, обчислити:
-. shuc-jccosx _ ,. sinx-xcosx
a) lim ; б) lim .
jc-»0 X *->0 х
5.211. Використовуючи вираз для суми членів збіжної
геометричної прогресії, знайти розклад за степенями х вказаних функцій.
а)/(*) = -*--; б)/(дс)= Х
1 + х 1+х
в)/(д:) = —!—; г)/(*) = ■ 1
2 '
х(1 + х)' "' " Ч "' І-*3'
X2 1
Д)/(*) = - , (а>0); є) /(jc)=- ,(а*0);
1-ах 1 + ах
х2+\ . _ , _ 1
є)/(*) = , (*>0); ж)/(*) = -.
я + * ;c2(2 + x)
5.212. Розкласти в ряд за степенями х вказані функції:
а) /(*) = *chx + shjc; б)/(.*) = sh2x; в)/(д:) = ;
т) f(x) = ^-^; д) f(x) = ex(l + x); є) f(x) = esinx;
х
є) /(*) = е™*х; ж) f(x) = е2х ; з) /(де) = 1п(10 + х);
0 /U) = xln(l + Jc).

§ 2. Функціональні ряди
339
Для заданих значень х0 розкласти вказані функції в ряд за
степенями х-х0:
5.213. /(*) = 2х, jc0=-2.
5.215. f(x) = yfl + x , jc0 = 0.
7t
5.214. f(x) = sin x, x0 = —.
5.216. f(x) = —\ x0=2.
x
5.217. /(jc) = 4s *o=l.
jcz
5.218. /(jc) = л:2 + 2jc + 2; x0 = -1.
5.219. /(x = ^±^±^±16 _2
jc + 2 °
5.220. /(jc) = jc • (jc2 + 2jc +1), jc0 = -1.
5.221. /(jc) = jc3-jc2+1, jc0=1. 5.222. f(x) = exsinjc, Jfy=0.
5.223. /(jc) = In jc, jc0 = 1. 5.224. /(jc) = Vj?, Jc0 = 1.
5.225. / (jc) = chx, jc0 = 0.
5.226. /(jc) = cos
n
jc + —
71
, x0 = 0. 5.227. / (x) = tgx, x0= —
5.228. Використовуючи вираз для суми членів нескінченно
спадної геометричної прогресії, розкласти за степенями х-х0
вказані функції:
а) /(*) = —;-, *о=-2;
в) /00 =
х + 3
х2+1
х-1
) *0 "" ~1 '
б)/(*) =
г)/00 =
1
jc(jc + 1)
jc2 + jc + 1
х + 1
, Xq — 1;
, jcq = 1;
x2+* + l #
д)/оо = ;—. ■^о=-1;
1
є) /(*) = -. *o=-L
jc-1 " ' ' х
Розкласти в ряд Фур'є вказані функції:
-1, -7T<jc<0,
5.229. /(*) =
1, 0<jc<^.
5.230. /(jc) = х9 -п<х<п.

340
Розділ V. Ряди
5.231. f{x) =
5333. /(*) = ■
j-x, -л<х<0,
{ х, 0<х<л.
[і, -1<хй0,
\х, 0<jc<1.
5.232. f(x) =
Г0, -л<х<0,
5.235. fix) = x, хєіО; 4).
ґ-1, —К jc < 0,
х, 0<х<л.
5234. fix) = \x\,xei-l; 1).
0, -2<дс<0,
5.237. fix) = -
1, 0<jc<1.
5.236. f(x) =
5.238. f(x) =
2, 0<*<2.
-X, -Л<Х<0,
2x, 0<х<л.
5.239. /(*) = ^-A 0<д;<2я-.
5.240. /(д;) = <?*-1, 0<;t<2/r.
Розкласти в ряд Фур'є задані функції у вказаних інтервалах,
продовживши їх, як парні:
5.241. /0с) = —, х&ф,л). 5.242. fix) = x-sinx, хеф,л).
4 2
5.243. /(де) = х + 2л, хе (-3/г,-2л).
5.244. fix) =
1, 0<jc<— ,
1, U<x<-, г о<л:<05
2 5.245. /(*)=' и<ж-и'Э'
-, — <дс<я. 1
L2 2
[-*, -1<jc<0,
[ х, 0<х<1.
Розкласти в ряд Фур'є задані функції у вказаних інтервалах,
продовживши їх, як непарні:
5.246. /(*) = •
5.247. / (де) = cos 2х, хеф,л). 5.248. fix) = \
х, 0<дг<—,
2
л-х, —<Х<Л.
2

§ 2. Функціональні ряди
341
5.249. f(x) = 1, хе (0; 2). 5.250. /(*) = ех9 хе(0; л)
5.251. /О) = х-4л-, хе (4я, 5яг). 5.252. f(x) = \
х, 0<л;<1,
1, 1<*<2,
3-х, 2<*<3.
Зобразити інтегралом Фур'є задані функції:
5.253. f(x) = \
5.254. /(*) =
-JC-2, -2<д:<-1,
л:, —і < jc < і,
-jc + 2, 1<д:<2,
[О, |jc| > 2.
1, -1<х<0,
—, х = -1,х = 0,х = 1,
2
л:, 0<л;<1,
0, |jc| >1.
5.255. f(x) = e~
5.256. /(*) =
fsinjc, |jcJ <Я\
[ 0, |jc| > п.
5.257. f(x) = \
cosx, jc<—,
1 ' 2
о,И>|.
5.258. f(x) = e~x .
5.259. /(*) =
fl, И<1,
0.5, jc = 1,
0, |jc| > 1.
(Вказівка: використати значення інтеграла І af = —).

342
Р о з д ілУ. Ряди
5.260. Зобразити задану функцію інтегралом Фур'є,
продовживши її на інтервал (0,-°о), як непарну:
а)/(*) =
[sinjc, 0<Х<7Г,
І 0, Х>7Г.
б) f(x) =
2-3jc, 0<л:<-,
З
2
0, х>—.
З
5.261. Зобразити задану функцію інтегралом Фур'є,
продовживши її на інтервал (0,-°°), як парну:
Ґ1, 0<*<1,
/(*) = «
0, jc>1.
5.265. In 2.
Обчислити з точністю 10 :
5.262. є'1. 5.263. sinl2°. 5.264. Vl5.
Розкласти в ряд за степенями х.
5.266. j^lLldt. 5.267. jcos(f2)A. 5.268. J—А.
о
Обчислити з точністю 10
0.5
о
-4,
5.269. jV' dt,
о
Обчислити з точністю 10 :
5.271. V_* .
Знайти суму ряду.
5.273. У—.
5.270. dt
і t
100
5.272. J
ln(l + jc)
dx.
10
5.274. У-Ь
(-і)"
5.275. ]Г(-1)"
и + 1
„=o (2n + l) !
^Ї3"(2п) !
и + 1
n=0
5.276. £(-1)я
Л

§ 2. Функціональні ряди
343
5.277. £nV_1.
п=\
5.279. £(-1)"
Jin
ЇҐі п(2п-\)
5.278. £
и=0
2п + 1х2п
П !
5.280. у JL—xn,
5.152. д;є(-оо,оо).
5.154. д:є(-«>,оо).
5.156. лє[-1;і].
5.158. хе (0; 1).
1
Э.Ю<£. *MJC)=lIl7-
|1
5.164. 5(д:) = -1п
2
-*г
1 + *
5.166. S(;t) = arctg-.
5.168. S(x)= l~* .
(1 + JC2)2
5.170. S(jc) = -=L-.
Відповіді
5.153. ДС Є (-оо.оо).
5.155. д;є(-оо; -3)и[-1; »),
5.157. *є [0; оо).
5.159. хе (0; °о).
1-3
2
5.163. ад=-іп
5.165. S(;t) = arctg х.
5.167. 5(jc) =
5.169. ад =
5.171. ад =
(i-*r
_2
(І-*)3'
дс(1 - дс)
vi-дс
5.172. -1<jc<1.
5.174. -1<д;<1.
5.176. -2,5 < л: < 0,5.
5.177. Збіжний при 0<д;<4.
5.178. -^2<л;<0 .
5.179. Збіжний при - оо < х < °°
5.180. Розбіжний.
(1 + х)
5.173. -5<*<5.
5.175. 1<*<3.
з •

344
РозділУ.Ряди
5.181. Збіжний при -1 < х < О .
5.182. Збіжний при -Л<х< О, 0 < * < V2 .
5.183. Збіжний, -4 < х < О.
5.184. Збіжний при -2 < х < 2 .
5.185. Абсолютно збіжний при всіх значеннях х, крім х = 1 та
jc = -1, при яких він умовно збіжний.
5.186. Абсолютно збіжний при х Ф — 1, при jc = —1 — умовно збіжний.
5.187. Збіжний при — < х < °°.
5.188. Збіжний при -1 < х < 1.
5.189. Збіжний при - °° < х < °°.
5.190. Збіжний лише при х = 0.
5.191. Збіжний при -3 < х < 1.
5.192. Збіжний при -1< х < 1.
5.193. Збіжний при 1< х < 3.
5.194. Збіжний лише при х=0,5.
5.195. Збіжний при -2,5 < х < 0,5.
5.196. Збіжний при — < х < —.
є є
5.197. Збіжний при 1—7=-<jc<1 + -t=-.
5.198. Розбіжний.
5.199. Збіжний при —1 < jc < 1
5.200. R = лІ2.
5.201. Радіус збіжності дорівнює R.
5.202. f(x) = l-x + x2-x3+... Ряд збіжний при |jc| < 1.
оо
5.203. /(*) = £ (-1)" х2п . Ряд збіжний при |jc| < 1.
00 хп
5.204. /(jc) = У* (In 2)п —. Ряд збіжний на всій дійсній осі.
и=0 П'

§ 2. Функціональні ряди
345
оо / і\/г-1
5.205. f(x) = У х2п~2 . Ряд збіжний на всій дійсній осі.
Й(2п-1)!
00 2пхп
5.206. /(х) = УУ . Ряд збіжний на всій дійсній осі.
°° (—і)пх2п+1
5.207. f(x) = V . Ряд збіжний на всій дійсній осі.
ЇҐо (2л)!
5.208. f(x) = V . Ряд збіжний на всій дійсній осі.
5.209. /(*) = £■
*"+1
й(»-1)«
5.210. а) 0; б)-.
6
5.211. а) /(де) = £ (-1)";с"+1, |*| < 1;
б) /0t) = f>2n+1, |*|<1; в) /W = |](-ir^-1, Н<1;
г) /(л) = f>3\ \х\ < 1; д) /(*) = £ Л'"2 , Н < -;
л=0 n=0 а
e)/(;t) = £(-l)"aV\ И<7^т;
е)/(*) = Е(-1)"^^, N<a;
ж)/(*) = £<-1)"£1, Н<2.
л=0
2"
5.212. a) /<*) = Z^T^"+1; б) f{x) = 2
oo гу2п~\ 2П
„=o (2л)! Д (2л)!

346
Р озділУ. Ряди
w/ ч 1 1 ^ (-1)лл:2"+1
2 2±- (2п + 1)
і °° гя-1
г)/(*)=--+2£г;
* п=0 и!
Д)/(*) = £
~ хп(х + 1) . х2 Зх4 8х5 Зх{
л=0
; e)/(*) = l + * + + + ...;
п! 2! 4! 5! 6!
Xі х3 їх4
є) /00 = 1+*+ + +...
2 3! 4!
ж
й (»-W
п=1
иЮ"
i)/w=Z(-1>
и-1 *
/1+1
л=1
5.2І3. /w.If;<!s2a£±2; и
<оо.
Ги=0
^
5.214. /W = ^_2(-1)L
2 n=0
я-
l+il 4
т2-. Н<~.
и!
де
- ціла частина дробу —.
5.215. /(*) = ! + --
х х2 \-Зхг 1-3-5-д:5
2 2!-22 3!-2J 4!-24
• + ...
5.216. /(*) = £(-!)«llJtf!.. 5.217. -U £(-!)>+ 1)*".
/і=0
п=0
5.218. /(;с) = 1 + (;с + 1)2.
5.220. f(x) = -(х +1)2 + (х +1)3.
5.219. /U) = 2(;t + 2) + (jt + 2)2
5.221. /(;t) = l + (;t-l) + 2(jt-l)2+(;c-l)3.
5.222. т = £уІГ*т^£ 5.223./(*) = £ (-і)""1 ^-Х
и=0
/г=1

§ 2. Функціональні ряди
347
5.224. /(*)=!+-
ю+1к±-^!±££Э0£2.+.
2 2!
•уП-1
п\
V
00 „2л
5.225./(*) = £^-. 5.226. /(д) = 2£_£(-1)»
п=02и- 2 /і=0
V2^. „„(Vя *2п+1
2п! (2п + 1)!
5.227. /0с) = 1 + 2| *-—] + 2[ х-—
\2
+ ...
5.228. а) /(*) = (*+2)-(*+2)2 + (* + 2)3-(;с + 2)4 + ...;
6)/(,)=i-3(£zi)+2(fzi)!-^-i)3 +
2 4 8 16
в)/(;с) = _1+£±1_(£±1)1+(£±і)1_...;
2 4 8
w, ч 3 3(*-1) (х-1)2 (*-1)3 (*-1)4
Г) /(д;) = _ + -і і + і і і І- + .І І- + ... ;
2 4 8 16 32
w, ч 1 дс + 1 3(дг+1)2 3(*+1)3 3(дс + 1)4
2 4 8
оо
е)/(*)=-2>+іг.
16
32
л=0
4 -£, sin f (2и +ГЫ
5.229. /(*) = -£-
я-^5 2и + 1
5.230. /0с) = 2£(-1Г-
„_х sinnx
/1=1
n
5.231./(,)^-lyCOs[(2" + f].
2 л-^ (2и + 1)2
5.232. f(x) = *_lf™(Vn + l)x) + y(-irlsmrvc
4 я:^ (2n + l)2 ~ n

348
Розд ілУ. Ряди
5.233.
З 2 y,cos[(2w-l)/rx]
/(Л) = 4"^Й (2п-1)2
ґ(2л-1)*>Л
sin
^ 1 .
h> SI
5.234.
1 4 ^,cos[(&i + l)g*]
* ~2 я:2^ (2и + 1)2
- «-,- /.^ ч „ 4 ^і 1 . (ппх\
5.235./(де) = 2 2j_sin
5.236.
5.237.
5.238.
*;^л 12;
/(*) = 1 + -X- -si-|V
n=l'
,. , 4 ysin^w + lj/rj;)
я- Іо 2n + l
Зя- _ 6 ^ cos((2n - 1)лг)
5.239. /(*) = £
4 л-^ (2и-1)2 ^
sin(nx)
з£(-і>
„_! sin(m;)
и=1
п
5.240. /(х) = ^(і + £со^)-^іп(дх)^
і2 „=1 1 + П у
я-
2 ^,cos[(2/i + l);tl
л^ (2п + 1)2
5.241.
5.242. /W = l-^± + 22(-D
cos де
„_1 cos/а
5.243./(*) = -- + -£
2 „^ ' n2-\
л 4^cos[(2n-l);t]
5.244./(д:) = ^ + -Х
2 *~ (2n-l)2
3 l^cos[(2n-l);t]
4 л-^ї (2n-l)2

§ 2. Функціональні ряди
349
5.245. f(x) = 4-У ( 1)И , sin((2n -\)жх)
5.246. /(,) = -1 + 4ЁС08[(2П"Г]-
2 л-2^ (2п-1)2
5.247. /(;с) = 1у^ + 1)^ + 1^.
»Й (2п + 1)2-4
5.248. /«ЛуН)»*^ВД.
*Й (2п + 1)2
sin
Г(2я + 1)л
5.249./(*)=*f;~~"l 2 ^
5.250. f(x) = -
п
1 + е* . 2{\-еп) . „ Ъ(\ + ея) . „
■sin х + —^ sin 2х + —-z sin Ъх +.
22+1
32+1
5.251. /W = 2^(-l)"-
to 2" + 1
„ 1 . ((2п + \)х
sin1
/
5.252. f{x) =
eS
л
ях . 5ях . І7ІХ
sin— sin sin
3_ 3_ + . 3_
I2 52 72
5.253. - Г
7Г J
4 г (1-cos or) sin or .
1 —г smax-da.
пЬ a"
1 °°г[
5.254. - Л
7Г J
2arsinar + cosar-l sin «- — лг .
- cos ах + -—sin ах
я-qL ос1 а1
da.
_„_ 2°°rcosarjc ,
5.255. — Tda.
я il + az
_„, 2°°rsma7r . ,
5.256. — -smax-da.
nlx-a1

350
РозділУ.Ряди
5.257.
5.259.
5.260.
5.261.
5.263.
5.265.
( ал\
со COS со
— [ ^ . 'cosax-da. 5.258. —j= \e
nl 1-а2 у/я 0J
2 °rsin a
— cosax-da.
4 cosax-da.
4
1Г J
>2ar-3sin
'2^
V •* J
sinax-da
a
о
2°°rsinar
— cosax-da,
*o a
0.2094.
0.6931.
5.267. £(-l)"
..4/I+1
5.269.
5.271.
5.273.
5.275.
5.277.
5.279.
5.280.
„=0 (2n)\ (4n + l)
0.927.
0.927.
e2-l.
cos l + sin l
l + x
(l-JC)
3 '
-l<JC<l.
2xarctg x - ln(l + x2).
><л:<оо
x(x + 2)^ ^
4
5.262. 0.3679.
5.264. 3.8730.
5.266. _Lf>l)"
Jln+2
(n + l)
2n+l
,2 •
5.268. У (-1)" -
~ (2n + l)(2n + l)!
5.270.0.9461.
5.272. 8.040.
5.274. cos .
5.276.0.
.2 ,.xz
5.278. Q. + 2x2)e

СПИСОК ЛІТЕРАТУРИ
І.БерманГ.Н. Сборник задач по курсу математического
анализа. -М.: Наука, 1975.
2. Бугров А.С., Никольский СМ. Дифференциальное и
интегральное исчисление. - М.: Наука, 1980. - Ч. 1.
3. Вірченко Н.О., Ляшко І.І., Швецов К.І. Графіки функцій
(довідник). - К.: Наук, думка, 1977.
4. Данко П.Е., Попов А.Г. Высшая математика в
упражнениях и задачах. Ч. 1, 2. - М.: Высш. пік., 1974.
5. Двайт Г.Б. Таблицы интегралов и другие математические
формулы. -М.: Наука, 1977.
6. Запорожец Г.И. Руководство к решению задач по
математическому анализу. - М.: Высш. шк., 1966. - 460 с.
7. Ильин В.А., Позняк Э.Г. Основы математического
анализа. -М.: Наука, 1980. -Ч. 1.
8. Кузнецов Л.А. Сборник задач по высшей математике
(типовые расчеты). - М.: Высш. шк., 1983. -174 с.
9. Ляшко И.И., Боярчук А.К., Гай Я.Г., Головач Г.П.
Математический анализ в примерах и задачах. - К.: Вища шк,. 1975. -
Ч. 1: Введение в анализ, производная, интеграл. - 677 с.
10. Ляшко И.И., Боярчук А.К., Гай Я.Г., Головач Г.П.
Математический анализ в примерах и задачах. - К.: Вища шк., 1977. -
Ч. 2: Ряды, функции нескольких пременных, кратные и
криволинейные интегралы. - 671 с.
11. Марон И.А. Дифференциальное и интегральное
исчисление в примерах и задачах. - М.: Наука, 1973. - 400 с.
12. Пискунов Н.С. Дифференциальное и интегральное
исчисление для втузов. - М.: Наука, 1978. - Т. 1.
13. Сборник задач по математике для втузов. Линейная
алгебра и основы математического анализа / Под ред. А.В. Ефимова,
Г.П. Демидовича. -М.: Наука, 1981.
14. Шмелёв П.А. Теория рядов в задачах и упражнениях. -
М.: Высш. шк., 1983. - 176 с.

НАВЧАЛЬНЕ ВИДАННЯ
Укладачі
уРудавський Юрій Кирилович |, Сухорольський Михайло Антоновичу
Білонога Дарія Михайлівна, Бобик Ігор Омелянович,
Бродяк Оксана Ярославівна, Веселовська Ольга Володимирівна,
Вовк Мирослава Іванівна, Дрогомирецька Христина Теофілівна,
Зашкільняк Іванна Михайлівна, Клюйниківан Федорович,
Коломієць Віктор Олександрович, Лазько Віктор Анатолійович,
Луцев Євген Михайлович, Мандзинець Іван Васильович,
Щикитюк Олег Андрійович \, Рибицька Ольга Мар'янівна,
Томецька Світлана Іванівна, Чип Максим Миколайович
ЗБІРНИК ЗАДАЧ
З МАТЕМАТИЧНОГО
АНАЛІЗУ
Частина І
Редактор Галина Клим
Коректор Ольга Дорошенко
Комп'ютерне верстання Галини Сукмановської
Технічний редактор Лілія Саламін
Художник-дизайнер Уляна Келеман
Здано у видавництво 2.01.2008. Підписано до друку 29.05.2008.
Формат 60x90/16. Папір офсетний. Друк офсетний.
Умови, друк. 22,0 арк. Обл.-вид. арк. 13,70.
Наклад 2000 прим. Зам. 80002.
Видавництво Національного університету "Львівська політехніка"
Реєстраційне свідоцтво серіїДК№ 751 від 27.12.2001 р.
Поліграфічний центр
Видавництва Національного університету "Львівська політехніка"
вул. Ф. Колесси, 2, Львів, 79000

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ "ЛЬВІВСЬКА ПОЛІТЕХНІКА"
ЗБІРНИК ЗАДАЧ
З МАТЕМАТИЧНОГО
АНАЛІЗУ
Частина І
Рекомендовано Науково-методичною радою
Національного університету "Львівська політехніка"
як навчальний посібник для студентів
інженерно-технічних спеціальностей
2-ге видання, виправлене і доповнене
Львів
Видавництво Національного університету "Львівська політехніка'
2008