C. T. ЗАВАЛО, С. С. ЛЕВІЩЕНКО,
В. В. ПИЛАЄВ, І. О. РОКИЦЬКИЙ
ПРАКТИКУМ
АЛГЕБРА
І ТЕОРІЯ
ЧИСЕЛ
Частина 2
Допущено Міністерством освіти УРСР
як навчальний посібник для студентів
фізико-математичних факультетів
педагогічних інститутів
Київський педагогічний
Іінстяту т їм. 0. ЛІ. Горьк#г#|
БІБЛІОТЕКА
КИЇВ
ГОЛОВНЕ ВИДАВНИЦТВО
ВИДАВНИЧОГО ОБ'ЄДНАННЯ
сВИЩА ШКОЛА»
1986

22.14я73
А45
УДК 512 + 511 (076.5)
Алгебра и теория чисел: Практикум. Часть
2/Завало С. Т., Левищенко С. С, Пьілаев В. В., Рокиц*
кий И. А. — К.: Вища шк. Головное изд-во, 1986.—
264 с. — Яз. укр.
Практикум составлен в соответствии с действующей
программой курса «Алгебра и теория чисел» для физи-
ко-математических факультетов педагогических инсти-
тутов.
Каждьій параграф пособия имеет следующую
структуру: сначала помещен список рекомендованной литера-
турьі с ссьілкой на соответствующие параграфи и стра-
ницьі, затем даньї основньїе теоретические сведения и
приведеньї подробньїе решения нескольких типичньїх
задач. В конце параграфа имеютея задачи для само-
стоятельного решения. К зтим задачам даньї ответьі,
указания, а иногда и полньїе решения.
Приложение содержит таблицу квадратов
натуральних чисел от 1 до 99, таблицу простьіх чисел от 2 до
4057 и их наименьшие первообразнне корни, таблицу
первообразньїх корней и индексов по простому модулю
от 2 до 97.
Предназначен для студентов физико-математических
факультетов педагогических институтов.
Табл. 66. Ил. 2. Библиогр.: 44 назв.
Рецензенти: доценти В. Г. Тарнопольський, М. М. Му»
рач (Чернігівський педагогічний інститут), доцент
/. /. Мельник (Херсонський педагогічний інститут)
Редакція літератури з математики і фізики
Зав. редакцією Є. Л. Корженевич
1702030000—201 © Видавниче об'єднання
М211(04)-86 125~~86 «Вища школа», 1986

Розділ /. ТЕОРІЯ ПОДІЛЬНОСТІ
В КІЛЬЦІ ЦІЛИХ ЧИСЕЛ
§ 1. Відношення подільності, його найпростіші властивості.
Теорема про ділення з остачею
Література
1] - § 5, с. 70-72;
2] — § 5, с. 66—69;
3] —гл. 4, § 4, с. 141 —146;
4] —гл. II, § 2, 4, с. 83-84, с. 104—105;
8] — гл. 1, § 8, с. 59—60;
0] —гл. І, § 1, с. 7—9;
II}—гл. 1, § 2, с. 18—20;
12]- гл. І, § 1, с. 23—25;
14] — § 1, с. 17-19.
ТЕОРЕТИЧНІ ВІДОМОСТІ
Якщо для цілих чисел а і b в кільці цілих чисел Z існує таке ціле число q,
цо a=bq, то кажуть, що «а ділиться на Ь» або «6 ділить а» і пишуть відпо-
идно а\ b, b\a. Число а при цьому називають кратним числа b, a b —
дільником числа а. Якщо в кільці Z не існує числа q такого, що й = bq, го кажуть,
цо «а не ділиться на 6», або «6 не ділить а» і пишуть відповідно а не : b, b не | а.
Нехай a, b, c, d, m, n — довільні цілі числа. Тоді:
1°. ага;
2°. 0': а;
3°. а\±\;
4°. Якщо а : 0, то а = 0;
5°. Якщо a: b і b:cf то а\с;
6°. Якщо а\с, то 'ab\c;
7°. Якщо а-.с і 6: с, 'то (а ± b) \ с\
8°. Якщо а-.с, (а ± Ь)\с, то b: c;
9°. Якщо а:с, 6 не : с, то (а ± Ь) не : с;
10°. Якщо а: ft, то ас \ be;
11°. Якщо ас: be і с Ф 0, то а; Ь;
12°. Якщо с:а, d : b, то cd\ab;
13°. Якщо а:с, £:с, то (та ± nb)\c\
14°. Якщо а:Ь і b : а, то а= ±6;
15°. Якщо а: b і | 6 | > | а |, то а = 0.
Для будь-яких цілих чисел а і Ь, де 6 ^ 0, існує єдина пара цілих чисел
q і г така, що a = bq-\-r, 0 < r < | b | (узагальнення теореми про ділення з
остачею). Число q називають неповною часткою, а т — остачею від ділення а на Ь.
Ціле число а тоді і тільки тоді кратне цілому числу b Ф 0, коли остача
від ділення а на b дорівнює нулю.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. При діленні цілого числа а на 17 неповна частка дорівнює 13. Знайти
найбільше значення а.
Розв'язання. Маємо а = 17 • 13 + г, де 0 < т < 17. Отже, найбільше
значення для а дорівнює 17 • 13+16= 237.
2. При діленні числа а —50 на число b остача r = 6. Знайти b і неповну частку q.
Розв'язання. Маємо 50 — bq-\-6, де 6 < Ь. Тоді ^ = 44 = 44 • 1 =
= 1 -44 = 22.2 = 2-22= 11 -4 =4 11. Оскільки b > 6, то b є одним з
чисел 44, 22 або 11. Тоді q відповідно дорівнює 1, 2 або 4.
З

3. Знайти неповну частку q і остачу г від ділення цілого числа а на ціле число bt
якщо: а) а = 37, b = 8; б) а =-- 8, ft = 37; в) а = 37, ft = —8; г) а = —37,
fc = 8; д) а = 8, ft = —37; є) а ™ —8, ft = —37; є) а = — 8, ft =» 37; ж) а = —37,
ft = — 8.
Р о з в'я з а н н я. Щоб знайти неповну частку q і остачу т при діленні цілого
числа а на ціле число ft, треба знайти найбільше ціле число k, яке кратне ft
і не перевищує а. Тоді неповну частку q дістають як частку від ділення k
иа ft, а остачу г—як різницю між а та k. а) & = 32 = 8 • 4. Отже» б/ = 4,
г = 5; б) А = 0 = 37 • 0, (7 = 0, /- = 8; в) Л = 32 = (—8) • (—4), q = —4 г ---=5;
г) /г = —40 = 8 . (—5), (7 = —5» ' « 3; д) k --=■ 0 = (—37) .-0, (7 — 0, г = 8;
є) * = —37 =і (—37) • 1, q = І, т = 29; є) k ■-= — 37 = 37 • (—1), ¢ = -1,/- = 29;
ж) k = —40 = (—8) .5, (7 = 5, /■ = 3.
Зауваження. Згідно з теорією, існує єдина пара чисел q і г для довільних
цілих чисел а і ft, ft =^ 0, така, що а — ft^ + г, 0<r<|ft|. Тому аналогічну
задачу можна розв'язувати у загальному випадку для довільних а і ft, ft ф 0.
Наприклад, а) а > 0, ft > 0, а > ft; тут діленням а на ft знаходимо (7 і г>
б) а > 0, ft > 0, а < ft; тут ¢ = 0, г = а; в) а > 0, ft < 0, а > | ft |; діленням а
на | ft | знаходимо q1 і г, тоді (7 = —Я і* г) я < 0> ft > 0, | а | > ft; діленням
| а | на ft знаходимо а1 і г, тоді q = —(^ + 1); д) а > 0, ft < 0, а < | ft |; тут
<7 = 0, г = а; є) а < 0, ft < 0, | а \ < | ft |; тут q = 1, r = | ft | — | а |; є) а < 0,
ft > 0, | а | < ft; тут (7 = —1, r = ft + а; ж) а < 0, ft < 0, | а | > | ft |; діленням
| а | на | ft | знаходимо qt і г, тоді (7 = <7i + 1-
4. Довести, що п(п-\- 1)(2/1+ 1) : б при довільному натуральному п.
Р о з в'я з а н н я. / спосіб (ьа методом математичної індукції).
При я = 1 маємо л(л+1) (2п+1) = 6 : 6. Припустимо, що при /і = &
/г (6 + 1) (2& +1) : 6, і доведемо, що твердження справедливе й при п = k + lt
тобто (£ + 1) • (k + 2) (2k + 3) : 6. Оскільки
(k+\)(k + 2)(2k + 3) = k(k+l)(2k+\) + 6(k+l)*,
то твердження очевидне, бо перший доданок ділиться на 6 за припущенням,
а другий має своїм множником 6, тобто теж ділиться на 6. Тоді твердження
я(/і + 1)(2/і+ 1) : 6 справедливе для довільного натурального числа п.
II спосіб (за методом повної індукції). Оскільки л(/г+1) є добуток двох
послідовних натуральних чисел, то п (п+ 1) : 2 і тому п(п+ 1)(2я + 1) : 2.
Оскільки 6 = 2 • 3, а числа 2 і 3 не мають спільних дільників, то для того
щоб п(п+ 1)(2/і+ 1) : 6, треба показати, що п(п+ 1) (2/і + 1) : 3. Згідно
з теоремою про ділення з остачею, можливі такі випадки: а) /і =» 3k; б) п =
==:3/5+1; в) /і = 3& + 2, де Л —деяке ціле невід'ємне число. У випадку
а) на 3 ділиться число я = 3&, у випадку б)—число 2/і+ 1 = 6Л + 3, а у
випадку в) —число /і+1=3£ + 3. Цим доведено, що п (л+ 1) (2п+ 1)
завжди ділиться на 3. Твердження доведено.
III слоа'6" (штучний). Оскільки
п(п + 1) (2/1+ 1) = /і(п+ 1) [(я- 1) + (n+ 2)] =
= (л- 1)п(/г +1) + /і(/і+ 1)(/г + 2),
то доводжуване твердження випливає з того, що кожен доданок утвореної
суми є добуток трьох послідовних чисел, а отже, він ділиться на 6.
Зауваження
1. При розв'язуванні аналогічних задач не можна віддати перевагу жодному
з розглянутих способів. Так, для задачі 4 найраціональнішим є третій спосіб.
Твердження, аналогічні розглянутим, завжди можна довести першим способом,
хоч процес використання кроку індукції (кроку припущення) не завжди простий
(при цьому часто використовується й узагальнена форма математичної індукції).
Зрозуміло, що тільки вдале комбінування наведених та інших способів може
зробити процес доведення ефективним і економним.
2. Доведення другим і третім способами свідчить про те, що твердження
п (п + 1 (2/і + 1) : 6 справедливе для будь-якого цілого числа п.
4

Задачі
1.1. Знайти неповну частку і остачу при діленні цілого числа
а на ціле число 6, якщо: а) а= 131, 6 = 31; б) а = 31, fe = 131; в) а =
= -131, 6 = 31; г) а = -31, 6=131; д)а = 131, 6 = -31; є) а = 31,
& = —131; є) а = —31, 6 = —131; ж) а = —131, 6=-31.
vM.2. При діленні цілого числа а на ціле число 6 дістають
неповну частку q і остачу г. Знайти 6 і qy якщо: а) а=100, г = 6; б) а =
= 148, г = 37; в) а = 298, г= 10; г) а = 497, г= 16; д) а = 28, г = 2;
є) а=14, г=14.
v 1.3. При діленні цілого числа а на ціле число 6 утворюється
неповна частка q і остача г. Знайти 6 і г, якщо: а) а = 371, q=l4>
б) а =826, ? = 83; в) а = 441, ? = 25; г) а = 57, q = 0\ д) а=13 127,
47= 121; є) а=100, ^= 100.
1.4. Знайти загальний вид усіх тих цілих чисел, які: а)
діляться на 2; б) діляться на 3; в) діляться на 8; г) при діленні на 7
дають остачу 3; д) при діленні на —4 дають остачу 1; є) не
діляться на 2; є) не діляться на —3; ж) не діляться на 2 і на 3.
1.5. Довести, що: а) з трьох послідових цілих чисел одне і
тільки одне ділиться на 3; б) з двох послідовних парних цілих
чисел одне і тільки одне ділиться на 4; в) з п'яти послідовних цілих
чисел одне і тільки одне ділиться на 5; г) з п послідовних цілих
чисел одне і тільки одне ділиться на п.
1.6. Довести, що: а) добуток двох послідовних цілих чисел
ділиться на 2; б) добуток трьох послідовних цілих чисел ділиться
на 6; в) добуток чотирьох послідовних цілих чисел ділиться на 24;
г) добуток п послідовних цілих чисел ділиться на /г!.
1.7. Нехай w, n, р, q — цілі числа і (mn + pq) \{m — /?).Довести,
що (mq + np) • (т — р).
1.8. Довести, що:
а) квадрат непарного цілого числа при діленні на 8 дає
остачу 1;
б) сума квадратів двох послідовних цілих чисел при діленні на
4 дає остачу 1;
в) числа виду 3£ + 2, k^Z не можуть бути квадратами цілих
чисел;
г) сума квадратів двох непарних цілих чисел не може бути
квадратом цілого числа;
д) (я3— 1) • 7, або (л3 + 1) : 7, якщо п не і 7, ngZ;
є) сума квадратів п'яти послідовних цілих чисел не може бути
квадратом цілого числа;
є) якщо остача від ділення деякого цілого числа на 9 є одне
з чисел 2, 3, 5, 6, 8, то це число не може бути квадратом цілого
числа;
ж) якщо чисельник дробу є різниця квадратів двох непарних
цілих чисел, а знаменник — сума квадратів цих чисел, то такий
дріб можна завжди скоротити на 2, але не на 4.
1.9. Довести, що:
а) (8 • 2323 —71 • 3232) і 10;
б) (II10 —1) : 100;
5

в) (22225555 + 55552222) : 7.
1.10« Довести, що для довільних цілих чисел т і т
а) (л3 — л) • 6;
б) (л5 — п) • ЗО;
В) (л (Л2 + 5)) : 6;
г) (л7 — л) і 42;
д) тп (т4 — л4) : ЗО;
є) (я* — 5л3 + 4л) • 120;
є) (я4 + 6л3 + Ил2 + 6л) •: 24;
ж) (л3 + И/і) • 6;
з) (л2 + Зл + 5) не :• 121.
1.11. Довести, що для довільного натурального числа п:
а) (2і* — 6) і 10;
б) (42« — З2" — 7) : 84;
в) (62*-' + 1): 7;
г) (л+1)(л + 2)...(л + л) :2";
д) (З2" + 5) не і 8.
1.12. Довести, що для довільного цілого невід'ємного числа пі
а) (5*n_ j) . 24; є) (10Л + 18л— 1) s 27;
б) (Ю3* — 1) : 27; є) (32"+3 + 40/1 — 27) s 64;
в) (15" — 1) ; 7; ж) (4* +6л — 1)і9;
Г) (36« _ 26") ; 35; з) (ЇСИ-1 — 9л — 10) •: 81;
д) (11«+2 + 12^+1) і 133; к) (9*+і_8л —9) •: 16.
1.13. Довести, що (22лі—6) • 10 для будь-якого натурального
числа л > 2.
1.14. Довести, що числа 48, 4488, 444888, ... можна подати у
вигляді добутку двох послідовних парних натуральних чисел.
1.15. Довести, що сума 2л+1 послідовних натуральних чисел
ділиться на 2п + 1.
1.16. Довести, що в піфагоровому трикутнику (прямокутному
трикутнику, довжини сторін якого натуральні числа):
а) довжина, принаймні, одного катета ділиться на 3;
б) довжина, принаймні, однієї із сторін ділиться на 5.
1.17. Довести, що коли довжини сторін і діагоналей
прямокутника є натуральні числа, то його площа ділиться на 12.
1.18. Довести, що корені квадратного рівняння ax2 + bx+c = 0
з цілими непарними коефіцієнтами а, Ь, с не можуть бути
раціональними.
1.19. Довести, що сума кубів трьох послідовних цілих чисел
ділиться на 9.
§ 2. Означення і властивості простих та складених чисел.
Решето Ератосфена. Канонічна форма натурального числа.
Розподіл простих чисел серед чисел
натурального ряду
Література
[1]-§ 7, с. 89-92; § 8, с. 95-99;
[2] — § 7, с. 86—91; § 8, с. 93—98;
[3] —гл. П, § 1, с. 365—372;
[4] —гл. II, § 7, с. 124-134;

[81- гл. 1, § 8, с. 57—58;
[101—гл. І» § 4, 5, с. 13—16;
[11] —гл. 2, § 1, 2, с. 28—38;
[12] — гл. І, § 4, с. 31-35.
ТЕОРЕТИЧНІ ВІДОМОСТІ
Натуральне число а, яке більше від 1 і дільниками якого є тільки 1 і а,
називають простим. Натуральне число а, яке більше від J і в якого є дільники,
відмінні від 1 і а, називають складеним. Число 1 має тільки один ' натуральний
дільник — одиницю, тому воно не належить ні до простих, ні до складених
чисел.
Найменший натуральний дільник складеного числа я, відмінний від 1, є число
просте і не перевищує У а.
Теорема Е в к л і д а- Множина простих чисел нескінченна.
Основна теорема арифметики. Кожне відмінне від 1 натуральне
число можна записати у вигляді добутку простих чисел і притому єдиними
способом, якщо не брати до уваги порядок розміщення множників. ^
Для складання таблиці простих чисел, які не перевищують даного
натурального числа с, існує загальний спосіб, який називається решетом Ератосфена. Він
полягає у послідовному викреслюванні з ряду 1, 2, ..., а числа 1, потім всіх
чисел, кратних числу 2 (крім 2), потім — кратних числу 3 (крім 3) і т. д. Отже,
слід викреслити всі числа, кратні простим числам: рх = 2, р2 = 3, р3 = 5
pk < Yа (удосконалення решета Ератосфена).
Усі невикреслені числа і складають таблицю простих чисел, які не переви-
щуть числа а.
Якщо в розкладі натурального числа а > 1 на прості множники об'єднати
однакові множники, то дістанемо так зване канонічне зображення числа
а = р{ р2 ... рт ,
Ае Pit Р/ — різні прості числа, і, / = 1, 2, . . ., m, і Ф /; fy —натуральні числа.
Зрозуміло, що довільний дільник d числа а має такий вид: d = p^pfc •. •
і
Рт> 0 < /^ < fy, і — It 2, . . ., т (це узагальнена канонічна форма числа d).
Через тс (х) позначають число простих чисел, які не перевищують
натурального числа х.
Відомо, що 1ітмс(х):-— =1 (асимптотичний закон розподілу простих
чисел).
Відомо також, що
0,92129 • -jjjj <*(*)< 1,10555 . -^~
(нерівності Чебишова).
Теорема Діріхле. У кожній арифметичній прогресії, перший член
і різниця якої є взаємно прості числа, тобто не мають ніяких спільних діль*
ників, крім 1, міститься нескінченна множина простих чисел.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Просте чи складене число 323?
Розв'язання. Відомо, що натуральне число пч п > 1, є простим тоді
і тільки тоді, коли воно не ділиться на жодне з простих чисел, які не
перевищують Уп. Знаходимо з надвишком 1^323^18 і виписуємо всі прості
числа, які не перевищують числа 18:
2, 3, 5, 7, 11, 13, 17.
7

Перевіряємо, чи ділиться число 323 на виписані числа. За ознаками
подільності це число не ділиться на 2, 3, 5. Подільність на решту чисел перевіряємо
безпосередньо.
В результаті дістаємо, що 323 не ділиться на 7, 11, 13, а ділиться на 17.
Відповідь. Число 323 є складеним.
Зауваження. Якщо існує точне значення У~п, тобто Уп = k, k £ N, то
п є складеним числом, бо п : к.
Процес безпосередньої перевірки подільності числа п на виписані прості
числа р{=2, р2 = 3, ..-., pki Pk <Vn припиняється тільки у двох випадках:
а) коли знайдеться таке число рІУ на яке ділиться п; б) коли перевірено
подільність числа п на всі числа р^ і = 1, 2, . . ., k.
2. Знайти всі значення простого числа р, якщо 4р2 + 1 і 6р2*-\-\ прості числа.
Р о з в'я з а н н я. Усі натуральні числа містяться серед чисел виду: 5л, Ьп ± 1,
5/г ± 2, де п £ Z. Числа виду 5я є простими тільки пр и п = 1; тоді р — 5, 4р2 +
+ 1 = 101, 6р2+ 1 = 151. Оскільки числа 101 і 151 прості, то значення р = 5
задовольняє умову.
Покажемо тепер, що інших значень р немає. Справді, якщо р =Ьп ± 1, то
4р2 + 1 =5 (20аі2 ±8/і+1) є складене число; якщо р = Ьп ± 2, то 6р2 + 1 =^
= 5 (30/г2 ± 24л+ 1) теж складене число.
8. Знайти канонічний розклад числа 4725.
Розв'язання. Оскільки 4725 = 3-1575, а 1575 = 3-525, 525 = 3-175,
175 = 5 • 35, 35 = 5 • 7, то 4725 = 3 . З . З . 5 • 5 . 7 = 3^ . 52 . 7.
Скорочено цей процес записують так:
4725
1575
525
175
35
7
1
3
3
3
5
5
7
Зауваження
1. Якщо треба знайти канонічний розклад числа виду k • 10s, то слід знайти
канонічний розклад числа k і здобутий результат домножити на число 2s • 5s.
2. Зрозуміло, що не завжди процес розкладу на прості множники є простим.
Для непарних чисел існує спеціальний спосіб розкладу на прості множники.
Розглянемо його у наступному прикладі.
4. Довести, що коли непарне натуральне число k, k > 1, можна подяти у вигляді
різниці квадратів двох цілих невід'ємних чисел єдиним способом, то воно
просте. У противному разі k складене.
Доведення. Нехай k — деяке непарне натуральне число і fc = 2s+l,
де s — деяке натуральне число. Припустимо, що k розкладається на множники
k = mn. He порушуючи загальності, можна вважати, що т > п. Тоді існують
такі невід'ємні цілі числа х і у, що має місце система
{
х + у = т,
х— у = п,
в якої
m + n т —
Отже, якщо k складене, то
Якщо k просте, то його можна єдиним способом подати у вигляді добутку
k = (2s + 1) • 1. Тоді т = 2s + 1 = £ і я = 1.

Таким чином, якщо зображення
-т-м'
(воно завжди існує, бо k непарне) є єдине, то k — просте.
Якщо, крім того,
(=w-(=*-")■
де п Ф 1, то k — складене. Зазначимо, що коли k є квадрат числа т, то х — т,
у = 0.
Зауваження
1. З доведення цього твердження випливає спосіб розкладання непарних
чисел k, k> 1, на множники (х+ у)(х — у). Справді, з рівності k = x2—y2
дістаємо k -J- у2 = х2. Отже, щоб знайти х і у, досить для числа k підібрати
k — 1
квадрат такого цілого невід'ємного числа у, щоб у < —п— * сУма ^ + У бУла
повним квадратом, тобто £-f-j/2 = я2. Знайшовши таким способом х і у, маємо
* = (* + у) (X — у) = /ял.
2. Застосовуючи цей спосіб до розв'язування задач, доцільно користуватися
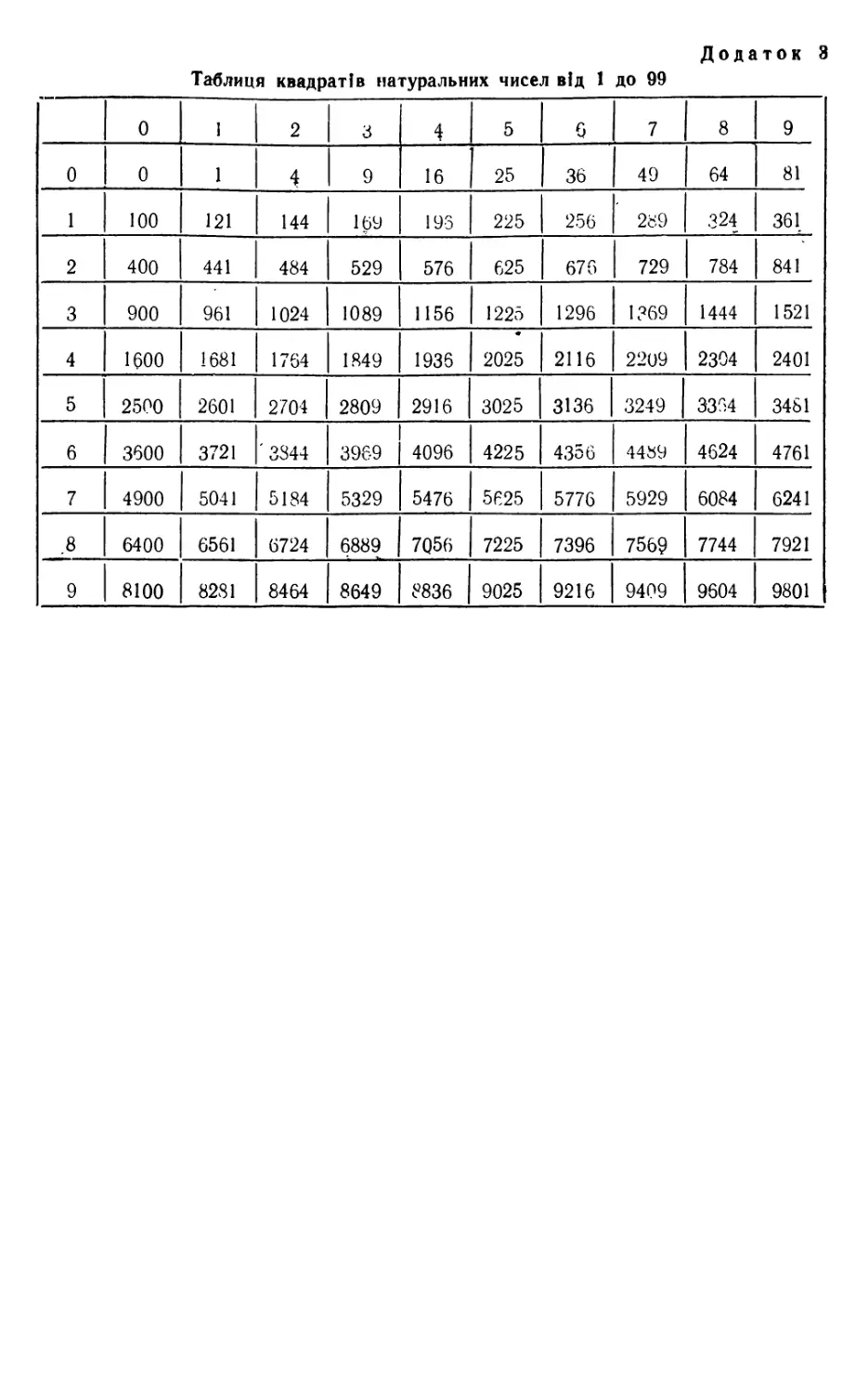
таблицями квадратів натуральних чисел.
3. Для знаходження числа у іноді доводиться випробовувати кілька
найближчих квадратів до числа k.
5. Знайти канонічний розклад чисел 4725 і 1769.
Розв'язання. Найближчий квадрат до числа 4725 є число 4761.
Знаходимо різницю 4761 — 4725 = 36 = ба. Отже, 4725 + 36 = 4761, або 4725 + 6а »
= 692. Тоді 4725 = 692 — б2 = (69+ 6) • (69-6) = 75-63 = 3-5.5 -3-3-7 =
= З3 • 52 • 7. Остаточно маємо 4725 = З3 • 52 • 7. Результат, зрозуміло,
збігається з результатом прикладу 3.
За таблицею квадратів знаходимо найближчий квадрат до числа 1769. Це
число 1849. Потім знаходимо різницю 1849—1769 = 80. Оскільки числово
не є квадратом, то беремо наступний квадрат — число 1936. Тоді 1936— 1769 =
= 167. Число 167 знову не є квадратом. Випробуємо наступний квадрат —
число 2025 = 452. Оскільки 2025 — 1769 = 256 = 162, то у = 4. Отже, 1769 +
+ 16а = 45а. Тоді 1769 = 452 - 162 = (45 + 16) (45 — 16) = 61 . 29 = 29 • 6І.
Остаточно маємо 1769 = 29-61.
Задачі
2.1. Чи є числа 127, 919, 1033, 1643, 1657, 2647, 2773, 3163, 3621,
3623, 3631, 3763, 3767, 3769, 7429 простими?
2.2. Знайти всі прості числа, які містяться між числами:
а) 1 і 100; д) 1250 і 1300;
б) 100 і 150; є) 2300 і 2350;
в) 150 і 200; є) 2550 і 2600;
г) 550 і 600; ж) 4300 і 4350.
2.3. Знайти канонічний розклад числа п9 якщо;
а) п= 160; є) п= 1800;
б) м = 494; * є) я = 3551;
в) п = 1001; ж) п = 82798848;
г) п = 1009; з) п = 81057226635000.
д) аі= 1769;
2.4. Довести, що дане число а є складеним, якщої
а) а = 230— 1;
б) а = п4 + 4, п Ф ± 1 (теорема С о ф і ї Ж є р м є н);
в) а = п4 + п2 + 1, п > 1;

Г) а = л8 + 4, пф ±1;
д) а = п8 + я4 + 1, п > 1.
2.5. Знайти канонічний розклад числа а, якщо!
а) а = 26 + З6; д) а = 2і* + З18;
б) а = 54 + 53- 6; є) а = 2352 + 9722;
в) а = 56 + 53 —2; є) а = З10 + 3* + 1.
г) а = 78 + 74—6;
2.6. Знайти таке просте число р, щоб простими були також
числа:
а) р + 5; д) р + 4 і р + 14;
б) 2/?2 + 1; е)р + 2ір+4;
в) р2 + 8; є) 8/?2 + 1 і 8р2 + 2р + 1;
г) р + 10 і /> + 14; ж) 2/7 + 1 і Ар + 1.
2.7. Довести, що три числа /7, /7 + #*» /7 + аі не можуть бути
одночасно простими, якщо р > 3 і натуральні числа т і я дають
при діленні на 3 відповідно остачі 1 і 2.
2.8. Довести, що з усіх цілих чисел виду 2/7+1, де /7 — просте
число, тільки одне є точним кубом.
2.9. Довести, що одночасно простими не можуть бути такі
числа:
а) /7 + 5 і /7 + 10;
б) /7, /7 + 2, /7 + 5;
в) 2п — 1 і 2" + 1, де п > 2.
2.10. Нехай /7—просте число і р > 5. Довести, що /72 при
діленні на ЗО дає остачу 1 або 19.
2.11. Нехай pk є fc-те просте число (р\ = 2, /72 = 3, /73 = 5, р4 = 7 і
т. д.). Довести, що:
а) pk<22k~\ причому рівність виконується тільки при k = 1;
б) pk > 26, де ft > 5;
В) /7*+1 </7]/72 . . .pb fe > 1,
Г) /7і/72 . . . /7Л > П, ДЄ /7* < П І /2 > 2.
2.12. Довести, що коли пронумерувати всі прості числа,
починаючи з 5, тобто р\ = 5, /72 = 7, /?з = 11 і т.ДГ, то рп>3п.
2.13. Нехай /14,1 = 2^—1, п£ N. Показати, що коли Мп є
просте число, то простим є також число п.
Примітка. Прості числа виду Мп = 2п—1 називаються числами Мерсенна.
(Мер сени Марен (1588—1648)—французький математик, фізик і філософ.)
Нині відомо 27 чисел Мерсенна, причому 27-е число дістали при п = 44497.
Скінченною чи нескінченною є множина чисел Мерсенна, невідомо.
2.14. Нехай Fn = 2n + 1, n£N. Довести, що коли Fn просте
число, то n = 2k, де k — деяке ціле невід'ємне число.
Примітка. Прості числа виду Fk—2 +1 називаються числами Ферма.
(Ферма П'єр (1601—1665)—французький математик і юрист.) Досі не знайдено
жодного простого числа виду 22 + 1 ПРИ k > Ь (при k — 0, 1, 2, 3, 4 числа Fk
є простими), а також невідомо, скінченною чи нескінченною є множина чисел
Ферма.
2.15. Довести, що (р2 — q2) • 24, якщо р і q — прості числа,
більші від 3.
10

2.16. Знайти всі прості числа, які є одночасно сумами і
різницями простих чисел.
2.17. Нехай р — просте число і р > 5. Довести, що (р2— 1) ; 24.
2.18. Довести, що для будь-якого n£N знайдеться таке #£Nt
що пх + 1 є складене.
2.19. Знайти натуральне число я, якщої
а) п = 2а, п + 1 = 3^, де а, р —деякі натуральні числа;
б) п = За, п+1 = 2Р, де а, р — деякі натуральні числа.
2.20. Довести, що між натуральними числами п і пі, де п > 2,
міститься, принаймні, одне просте число.
2.21. Знайти п послідовних складених натуральних чисел, якщої
а) /г = 10; б) п =12; в) /і = 100; г) п = 1000; д) /г = £.
2.22. Довести нескінченність множини простих чисел видуі
а) р = 3* + 2, k Є N; г) р = 4£ + 3, fe £ N;
б) р = 36 + 1, fcgN; д) p = 6ft + l, ft£N;
в) p = 4fe + l,>e~N; є) р= 6£+5, fc£N.
§ 3. Найбільший спільний дільник і найменше спільне кратне
та способи знаходження їх. Взаємно прості числа
Література
[1] —$ 5, с. 72—79;
[2] — § 5, с. 69—76;
[3] —гл. 11, § 2—3, с. 372—379;
[4] —гл. II, § 5, с. 109—119;
[8] —гл. 1, § 8, с. 59;
[Ю] —гл. І, § 2, 3, с. 9—13;
[11] —гл. З, с. 38—48;
[12] —гл. І, § 2, 3, с. 25—31;
[14] — ^ 2, 3/5, 6, с. 19—22, с. 24—28.
ТЕОРЕТИЧНІ ВІДОМОСТІ
Якщо кожне з цілих чисел av а2, ..., ап ділиться на ціле число d, то число d
називають спільним дільником чисел av а2, . . ., ап* Найбільший із спільних
дільників чисел Яр а2, .. ., ап називається найбільшим спільним дільником (НСД)
цих чисел і позначається символом (t/p а2, . . ,, ап).
Якщо найбільший спільний дільник чисел а^ а2, .. ., ап дорівнює 1, то ці
числа називають взаємно простими. Якщо кожне з чисел а{, а2, . . ., ап взаємно
просте з кожним з решти з них, то числа av а2, .. ., ап називають попарно
взаємно простими. Зрозуміло, що попарно взаємно прості числа завжди і взаємно
прості (але не завжди навпаки). Для двох чисел поняття «попарно взаємно прості»
збігається з поняттям «взаємно прості».
Нехай av a2, . . ., an_v an — будь-які цілі числа, серед яких хоч одне
відмінне від 0. Нехай (Яр а2) = d2, (d2, а3) = dv . . ., {dn_2, an_x) = d„_p (dn_v
an) = dn. Тоді (ар a2, ..., an) = ((ap a2)} д3), .. .). Ha основі цього факту
можна дати інше означення найбільшого спільного дільника.
Найбільшим спільним дільником чисел а[у а2і .. ., ап називають невід'ємний
спільний дільник цих чисел, який ділиться на будь-який їхній спільний дільник.
Якщо а : Ь, то (а, Ь) = | Ь |.
11

Якщо а = bq + r, де a, b, q, r— цілі числа, то (a, b) = (b} г).
Якщо а, Ь, т — цілі числа, то (am, Z?m) = (a, 6) • | m |.
Якщо a, 6—цілі числа, а k—який-небудь їхній спільний дільник, то
(а Ь\ (а, Ь) ,.-.-4
І у, -т-І = . , ■ (при цьому хоч одне з чисел с чи о відмінне від нуля).
(а Ь\
Якщо (a, b) = d, то ^-j, -j J = 1.
Якщо dj a, <i 1 6 і (-j, -j) = 1, то \d\ = (a, b).
Для знаходження найбільшого спільного дільника двох чисел користуються
способом послідовного ділення, який називають алгоритмом Евкліда. Розглянемо
цей спосіб. Якщо а і b натуральні числа, то за теоремою про ділення з остачею
послідовно дістаємо:
a = bq{ +rv де 0 < г{ < Ь,
b = r{q2 + r2t де 0 < r2 < rv
'і = г2% + г3» Ае ° < гз < г2>
Гп-2 = rn-\Qn + Тп> Де °<rn< rn-V
'„_i=W/i+i» Де гЛ+і=0-
Остання відмінна від нуля остача тп і є найбільшим спільним дільником чисел а і Ь.
Згідно з алгоритмом Евкліда, якщо (a, b) = d, то існують такі цілі числа х
і у, що "d = ах + by, і навпаки (лінійне зображення найбільшого спільного
дільника).
Для взаємно простих чисел справедливі такі властивості:
1°. Цілі числа а і b взаємно прості тоді і тільки тоді, коли існують цілі
числа и та v такі, що аи + bv = 1;
2°. Якщо (а, Ь) =---. 1, то (ас, b) = (с, b)\
3°. Якщо (а, Ь) = (а, с) == 1, то (a, be) = 1;
4°. Якщо а£ : с, причому (6, с) = 1, то а : с;
5°. Якщо а | Н о ; с, причому (Ь, с) ■— 1* то а : 6с;
6°. Якщо (а, 6) = 1, то (а^ £m) = і для будь-яких цілих невід'ємних чисел
л і т;
7°. Якщо для деяких двох натуральних чисел я і m (an, bm)= 1, то (а, Ь) = \\
8°. Якщо рр р2 — різні прості числа, то (рр p2l) = 1 для будь-яких цілих
невід'ємних /г і т.
Нехай ap a2, .. ., а>п — відмінні від нуля цілі числа. Ціле число k, яке
ділиться на всі ці числа а{> а2, ...» ап, називають спільним кратним цих чисел.
Найменше з додатних спільних кратних чисел а{, а2, .. ., ап називають
найменшим спільним кратним (НСК) цих чисел і позначають символом \av а2, . . ., an].
ab
Відомо, що [a, b] = /fl и\ » де a, b — довільні цілі числа, з яких хоча б
одне відмінне від нуля. Ця формула лежить в основі nepiiiortr-способу
знаходження найменшого спільного кратного двох чисел. Зокрема, найменше спільне
кратне взаємно простих чисел дорівнює їхньому добутку.
Нехай [ap a2\=m2, [m2, a3]=m3, ..., [mn_2, аЛ-1]=тЛ_р [mn__v
an] = mn. Тоді [Др a2, . . ., an] = mn. Це дає змогу звести питання знаходження
НСК кількох чисел до питання знаходження НСК двох чисел: [ap а2, ..., ап] =
= [. ..[[ap а2], a3], . . .J.
Наведемо інше означення найменшого спільного кратного.
Найменшим спільним кратним цілих чисел ар а2, . . ., ап називають
невід'ємне спільне кратне цих чисел, на яке ділиться будь-яке їхнє спільне кратне-
Другий спосіб знаходження НСД і НСК цілих чисел ар а2, ..., ап грун-
12

туеться на канонічному зображенні цих чисел. Нехай числа а ї b мають так!
канонічні розклади:
Позначимо символами рр р2» • • •» Рп УСІ P*3Hi прості множники, кожен з яких
входить до розкладу хоч одного з чисел а і Ь. Якщо при цьому простий
множник р{ не міститься в розкладі якого-небудь з чисел а і Ь, то вважатимемо, що
він входить до цього розкладу в нульовому степені. За цієї умови канонічні
розклади а \ Ь можна записати так: a = pl lp2 .. . pn , b = р{ р2 . . . рп (ие
узагальнені канонічні форми запису чисел а і [b)t де кожен з показників k( і т0
і = \, 2, .. ., л, є ціле невід'ємне число. Тоді іклраведливі такі рівності:
(а, Ь) = р{ Ір22 . .. рпп, де d{ = min {ki% m,), і = 1, 2 n.
\a, b] = PiV22 .. . рлп, де /t = max (fy, m,), і = 1, 2, ..., n.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
Знайти найбільший спільний дільник і найменше спільне кратне чисел 1917
і 1985.
Розв'язання. 1 спосіб. Скористаємося алгоритмом Евкліда для
знаходження найбільшого спільного дільника.
1) Ділимо 19£б на 1917, дістаємо частку 1 і першу остачу 68;
2) ділимо 1917 на 68, дістаємо частку 28 і другу остачу 13;
3) ділимо 68 на 13, дістаємо частку 5 і третю остачу 3;
4) ділимо 13 на 3, дістаємо частку 4 і четверту остачу 1;
5) ділимо 3 на 1, дістаємо частку 3 і п'яту остачу 0.
Остання відмінна від нуля остача 1. Отже, (1985, 1917) = 1,
Наведені обчислення записують тах:
г_1985
1917
_19Ї7
1363
"^557
544
681 13
^35 1515
fi
,68
|"23^
13
1
У
з
Отже, числа 1985 і 1917 взаємно прості. Найменше спільне кратне цих чисел
дорівнює їхньому добутку, тобто [1985, 1917] = 1985 • 1917-=3805245.
II спосіб. Знайдемо канонічні розклади чисел 1917 і 1985:
1917 = 33 • 71, 1985 = 5 -397.
Запишемо ці числа в узагальнених канонічних формах:
1917 = З3-5° .71' • 397°, 1985 = 3° -5і . 71° • 3974
Тоді (1917, 1985) = 3° • 5° . 71° . 397° = 1, а
[1917, 1985] = 3^-51. 7і] . 397і = 3805245.
13

Зауваження. Цей спосіб доцільно застосовувати в тих задачах, де треба
знайти НСД і НСК в канонічнім формі.
2. Знайти найбільший спільний дільник d чисел 1917 і 1985, а також цілі числа
х і у, за допомогою яких число d лінійно виражається через числа 1917
і 1985, тобто d = 1917*+ 1985//.
Р о з в'я з а н н я. Скористаємося попереднім прикладом. Маємо:
1985=1-1917 + 68,
1917 = 28 • 68+13,
68 = 5. 13 + 3,
13 = 4 -3+1,
3 = 3-1+0.
Починаючи з передостанньої рівності, знаходимо остачі:
d= 1 = 13 —4 • З, (1)
З = 63 — 5 • 13, (2)
13= 1917 — 28 -68, (3)
68= 1985—1 • 1917. (4)
Замінюватимемо послідовно остачі в цих рівностях, поки не залишаться числа
1917 і 1985. Остачу 3 у виразі (1) замінюємо виразом (2) і зводимо подібні
члени (13 і 68):
1 = із - 4 • З = 13 — 4 • (68 — 5 . 13) = 21 - 13 — 4 . 68.
У цій рівності замість множника 13 підставляємо вираз (3) і" знову зводимо
подібні члени (68 і 1917): ,
1 =21 13— 4 . 68 = 21 (1917 — 28 -68)-4. 68 = -592 • 68 + 21 . 1917.
У знайденому виразі замість множника 68 підставляємо вираз (4) і знову
зводимо подібні члени (1917 і 1985):
1 :=а _592 -68 + 21 • 1917 = -592 (1985 - 1 . 1917) + 21 • 1917 =
= 613 • 1917-592 • 1985.
Отже, 1 =613 . 1917 — 592 . 1985, звідси « = 613, (/ = —592.
Зауваження
1. Може трапитись, що у виразах для остач (особливо на проміжних етапах,
в процесі знаходження лінійного виразу для НСД) деякі неповні частки
збігаються з якоюсь остачею. Тоді слід пильно стежити, щоб замість таких частот
не було підставлено вираз для остачі.
2. Часто лінійне зображення НСД чисел а .і 6 є громіздким і тому, щоб не
робити повну перевірку, можна обмежитися тим, що ліва і права частини
рівності ах-\- by = d повинні мати однакові останні цифри. Так, у розглянутому
прикладі права частина виразу і = 613 • 1917 — 592 . 1985 закінчується цифрою 1,
а ліва частина є 1.
3. Довести, що (а, 6) = (5а+ 36, 13а+ 86) для довільних цілих чисел а і 6.
Розв'язання. Введемо позначення (a, b) = dlt (5а + 36, 13а + 86) = d2.
Доведемо, що d1 = d2> Оскільки dx і d2 — натуральні числа, то досить
показати, що dx | 0*2 і d21 di-
З означення d± маємо: dx \ а і а\ | 6. Тоді а\|5а + 36 і dt\ 13a+ 86. Згідно
з означенням числа d2, dx \ d2.
Покажемо, що d2| d^. Виразимо числа 5а + 36 і 13а+ 86 через d2. Дістанемо
5a + 36 = d2*, 13a + 86 = d2#, де х і у — деякі цілі числа. Домноживши
першу рівність на 8, а другу на 3 і віднявши від першої рівності другу,
знайдемо a = d2 (8х — Зу). Аналогічно дістаємо 6 = d2 (5у — 13х). Отже, d21 a
і d2|6. З означення числа а\ випливає, що d2|dlt що й треба4 було довести.
Зауваження. З доведення цього твердження випливає, що (а, 6) = {raxa + т2Ь,
л1а-\-п2Ь)9 якщо | тхп2 — т2п1 | = 1, де mv т2, nv n2—цілі числа.
4. Знайти натуральні числа т і я, якщо їхня сума дорівнює 168, а
найбільший спільний дільник 24.
14

Розв'язання. Використаємо факт: якщо (а, Ь) = d \ a = da^ Ь = dbi% то
(av Ьг) = \.
У цьому разі (т, п) = 24. Тоді т = 24mlf n = 24nv де (m^, nj = 1. Оскільки
т + п= 168, то 24т1 + Шіх = 168, тобто т1 + лх « 7. Оскільки натуральні
числа тх і п^ взаємно прості, то розглядаючи всі можливі випадки, дістаємо,
що т1 і пг набувають таких значень: 1 і 6, 2 і 5, 3 і 4, і навпаки. Отже,
числа т і п дорівнюють 24 і 144, 48 і 120, 72 і 96, і навпаки.
Задачі
3.1. Знайти найбільший спільний дільник чисел:
а) 0 і 0; є) 1173 і 323;
б) 0 і —7; є) 2585 і 7975;
в) —231 і 546; ж) 2091 і 1681;
г) 1001 і 6253; з) 3763 і 3337;
д) 1066 і 1970; к) 6791400 і 178500;
л) / та Я, де / — ваш поштовий індекс, а Н — ваш рік
народження;
м) Т та Я, де Т — номер телефону деканату, а Н — рік
заснування факультету;
н) двох послідовних цілих чисел п і /і+1.
3.2. Знайти найбільший спільний дільник таких чисел:
а) 819, 702 і 689; є) 31605, 13524, 12915 і 11067;
б) 3059, 2737 і 943; є) 42598, 2324 і 498;
в) 2737, 9163 і 9639; ж) 1023, 1518 і 14883;
г) 299, 391 і 667; з) 3655, 2516, 731 і 663;
д) 588, 2058 і 2849; к) 91476, 3960 і 3360;
л) років народження всіх членів вашої сім'ї;
м) трьох послідовних цілих чисел п, л+1 і я+2.
3.3. Знайти найменше спільне кратне чисел:
а) 0 і 0; . є) 252 і 468;
б) 0 і 1; є) 279 і 372;
в) 360 і 504; ж) 178 і -381;
г) 187 і 533; з) двох послідовних цілих
д) -2520 і 6600; чисел п і /і+1.
3.4. Знайти найменше спільне кратне чисел:
а) 126, 420 і 525; г) я, /7+1 і /г+2, де /z<=Z;
б) 91, 252 і 462; д) 1058, 1403 і 3266;
в) 84, 147 і 245; є) 356, 1068 і 1424.
3.5. Знайти лінійне зображення найбільшого спільного дільника
чисел*
а) 21 і 51; є) 1786 і 705;
б) -26 і 174; є) 822 і 1734;
в) 899 і 493; ж) 4373 і -826;
г) 1445 і 629; з) -3791 і 3281.
д) 903 і 731;
3.6. Довести, що для довільних натуральних чисел а і Ь:
а) (a, b)=*(a+b, a+2b);
б) (a, b) = (2a+3b, За+46);
в) (а, Ь) = (7а + 5Ь, 4а+3й);
г) (а, &) = (За+5&, 8а+№);
15

д) (а, Ь) = (4а+36, 5а + 4Ь);
є) (а, b) = {ma-\-nb, ka + lb), де m, n, k, /Z — натуральні числа,
причому |mZ — /г£|=1.
3.7. Знайти натуральні числа а і ft, якщо:
(а, Ь) = 4,
а)
б)
в)
г)
д)
є)
є)
(а + Ь =
І (а,
Ь) =
І (а, Ь) =
tab
\[а,
(ab
\(а,
ІаЬ
І (а,
1 (а.
І (а,
= 20,
61 =
150,
ЗО;
144,
24;
і
10;
= 8400,
Ь) =
20;
= 720,
Ь) = 4;
11
— 7-,
Ь) =
5.
~~ 9'
Ь) =
:45;
28;
ж).
" [a, b] = 24;
з)
к)
л)
(a, &) = 4,
[а, 6] = 12;
(а, *>) = 24,
[а, b] = 2496;
а + b = 667,
[а, 6] = 120 (а, Ь)\
м) (а, 6) т (а, ¢)
І [а, 6] = 975;
. [аЬ= 168,
н) І
\(а,6)=14.
3.8. Довести, що для довільних натуральних чисел а, Ь, с\
а) (a, b) = (—a, b) = (a, а± b) = (a ± b, b);
б) (ab, be, са) ! (а, Ь, с)2;
в) (a, b) = (a + b, [a, b]), якщо (а, Ь) Ф 0;
г) (а, Ь, С) =/£±^-, і±£, *±£\, якщо а, Ь, с- непарні
V * * . і числа;
ж) \а Ь с\= аЬс(а' Ь' с) ■
А) Щ, О, С\-(а,ь)(а,с)(Ь,сї
є) (a, b) (a, с) (Ь, c) [а, b] [а, с] [b, с] = а W;
є) abc = [а, Ь, с] • (ab, ас, be);
ж) (а, [&, с]) = [(а, &), (а, с)];
з) [а, (6, с)] = ([а, 6], (а, с]);
к) [аа\, bb\, ab\, a\b) — ddi, якщо d = (а, 6), а\ = (fli, &i)5
л) ([a, b], (a, b)) = (a, b);
м) ([а, ft], ab) = fa, fe].
3.9. Довести, що для довільних натуральних чисел a, b, ct
а) (а, а + 1) = (а + 1, 2а + 1) = (а, 2а + 1) = 1;
б) (а, 2а + 1) = (а, 2а— 1) = 1;
в)(2а + 1, -^^-) -1;
г) (І4а + 3, 21а+ 4)= 1;
д) (6—а, 6)= 1, якщо (а, 6) = 1;
є) (а + 6, ab) = 1, якщо (a, b) = 1;
16

є) (а, а + Ь) = (а + 6, 2а + Ь) = (а, 2д + b) = 1, якщо (я, b) = І;
ж) (ас, Ь) = (с, Ь), зокрема, с • (ас, Ь), якщо (а, 6) = 1;
з) (а + Ь, а — Ь) = 1 або 2, якщо (а, 6) = 1;
к) (2а—1, 2* —1)=1, якщо (а, 6)=1;
л) (Па+ 26, 18а +56)=1 або 19, якщо (а, 6)=1;
н) (я3 + 2а, а4 + 3а2 + 1)= 1.
ЗЛО, Знайти найбільший спільний дільник чисел:
а) ап—1 \ ат—1, якщо а — ціле, а т і п — натуральні числа;
б) а2 + 1 і 2а + 3, якщо а — ціле число;
в) 26 — 1 і 215 —1.
3.11. Довести, що з п'яти послідовних цілих чисел завжди
можна вибрати одне, взаємно просте з усіма іншими.
3.12. Довести, що:
а) 2903я — 803" — 464"+261* : 1897, якщо « — натуральне число;
б) п (п + 1) (п + 2) [ 504, якщо п + 1 є кубом деякого
натурального числа;
в) а4п+!—а | ЗО, якщо а —ціле, a n — невід'ємне ціле число;
г) а3 — Ь3 } 2п тоді і тільки тоді, коли а — Ь \ 2п, де а, Ь — цілі
непарні числа, п — натуральне число;
д) (я+1, а2*+1) = І, якщо а—парне натуральне число, a k —
довільне натуральне число.
§ 4. Числові функції. Число і сума натуральних дільників.
Ціла і дробова частини дійсного числа. Функція Ейлера
Література
[1] —§ 7, с. 93—95, § 16, с. 169—174;
[2]—§ 7, с. 92—93, § 16, с. 173—178;
[3] — гл. 11, § 1, с. 368—369, гл. 12, § 3, с. 406—408;
[4] —гл. II, § 8, с. 134—146;
[10] —гл. II, с. 25—32;
[11] — гл. 10, с. 92—95; гл. 33, с. 315—322;
[12] —гл. II, § 4, с. 52—56; гл. VIII, с. 229—246;
ги] —§ 11—14, с. 49—63.
ТЕОРЕТИЧНІ ВІДОМОСТІ
Функцію f (х) називають числовою, якщо вона визначена при всіх
натуральних значеннях аргументу х.
Через х (п) позначають числову функцію, значення якої для будь-якого
натурального числа п дорівнює числу всіх його натуральних дільників.
Через а (п) позначають числову функцію, значення якої для будь-якого
натурального числа п дорівнює сумі всіх його натуральних дільників.
Через ер (п) позначають числову функцію, значення якої для будь-якого
натурального числа п дорівнює кількості натуральних (цілих невід'ємних) чисел»
взаємно простих з п, які не перевищують (відповідно менших) п. Функцію ер (л>
називають функцією Ейлера.
Через [х] (читається «антьє від х») позначають числову функцію, значення
якої для будь-якого дійсного числа х дорівнює найбільшому цілому числу, яке
не перевищує х. Функцію [х] називають цілою частиною від х.
17

Через {*} позначають числову функцію, значення якої для будь-якого
дійсного числа х дорівнює різниці х—[х]. Функція {х} /називається дробовою
частиною від х.
Числова функція f (п) накривається мультиплікативною, якщо для кожного п
функція f (п) ф 0 і для будь-яких взаємно простих натуральних чисел п і т
виконується рівність / (т • п) = / (т) • f(n).
Мультиплікативні функції мають такі властивості:
1°. /(1) = 1;
2°. Добуток мультиплікативних функцій є мультиплікативна функція;
3°. Якщо числа nv п2, . . ., nk попарно взаємно прості, то / (п{ • п2 . . . nk) =
Числові функції х (я), а (п)у <р (п) мультиплікативні. Якщо п = Р\Р2~ ••• Рт —
канонічний розклад натурального числа я, то
х («) — (*, +"1) (*а + 1) - - • (*т+ 1),
р;.-и_і р»гит.1 ру._х
°с) = -77=т *=г—• Рт-\ •
*«-('-;9('-і)-(-£)-
Зрозуміло, що т (1) == а (1) = ер (1) =і 1, згідно з означенням цих функцій.
Сума значень функції Ейлера для всіх дільників df числа п дорівнює п:
S ? (**/) = л (формула Гаусса).
[МІ Г*1
Якщо х — дійсне додатне число, а я— натуральне число, то [—] = [—-І.
Показник о простого числа р, яке входить до канонічного розкладу
натурального числа лі, обчислюється за формулою
де ps < п< р*+1.
п
[р\
+
' п '
IP J
+ ..
•+И1
І р і
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Знайти суму дільників, число дільників і дільники числа 680.
Розв'язання. Знаходимо канонічний розклад числа 680:
680 = 2*. 5*. 17. Тоді
Т (660) = (3+ 1)(1 + 1)(1 + 1) = 16,
23+х 1 б1*1 — 1 171*1 —1 .
. (680) - ї—fL • іт_т1. ІІ__!_ ,б20.
Дільники числа 680 дістанемо, коли розкриємо дужки-у виразі
(1 + 2 + 4 + 8).(1+5)-(1 + 17).
Матимемо:
1, 2, 4, 8, б, Ю, 20, 40, 17, 34, 68, 136, 85, 170, 340, 680.
2, Знайти натуральне число де, якщо воно має тільки два різних простих
дільники і х (х) й= 6, о (*) = 28.
Розв'язання. Оскільки число х мав тільки два різних простих дільники
(нехай це числа р і q)> то канонічний розклад числа х має вид: х =* pyqz, де
у і г — деякі натуральні числа. Тоді
_ рН-і _ і д*+і _ і
Ч*) = (0+1)(*+1). 3«= . .
р—\ q — \
18

Оскільки т (х) = 6, то (у + 1) (г + 1) = 6. Внаслідок того що числа у і г на-
туральні, 0=1, 2 = 2 або навпаки. Тоді х = р^а і а (х) = (р + 1) (¢2 J|_ ^ _i_ п
Оскільки а (х) = 28, то (р + 1) to2 + qf + 1) « 28.
Через те що р і q — різні прості числа, слід розглянути такі можливі
випадки: /7+1=4, q2 + q + 1 = 7 або навпаки. Якщо /? + 1 =- 4, q2+q+1 =7,
то р = 3, a q = 2. Тоді х = 3і . 2а = 12. Якщо р + 1 •-= 7, ¢2 + </ + 1 = 4, то
р = —-б, що суперечить вибору числа р. Отже, єдиним числом, яке
задовольняє умову задачі, є число х = 12.
3. Знайти натуральне число я, якщо ер (п) =•• 600 і п = 3а . 5?, де а, р —
натуральні числа.
P о з в' язання. Оскільки
то
600 = За5р • у • 4"
Звідси
3253 = 3*5?.
Ця рівність можлива тільки при а = 2 і р = 3. Тоді п = З2 • 53 = 1125.
4. Знайти кількість нулів, якими закінчується число 295!
Розв'язання. Щоб розв'язати цю задачу, треба знайти канонічний
розклад заданого числа. Справді, якщо п\ = paq$. . . гт, то кількість нулів,
якими закінчується число, збігатиметься з числом т, де т — менше з чисел k
і s, a k і s — показники чисел 2 і 5 відповідно в канонічному розкладі числа п\.
Оскільки до канонічного розкладу числа п\ просте число 5 входить з меншим
показником, ніж просте число 2, то для розв'язання задачі досить знайти
показник s, з я-ким просте число 5 входить до добутку пі. Як відомо, s
знаходять за формулою
Оскільки
*.]-[
/.'+
-Ж + ІЯ + ДОн-
If]
то для нашого прикладу маємо
»-[?г1 + [т1 + Іт]-59+11+2=72-
Отже, число 295! закінчується 72-ма нулями.
Задачі
4.1. Знайти число і суму всіх натуральних дільників таких
чисел: а) 60; б) 100; в) 360;т) 375; д) 720; є) 957; є) 988; ж) 990;
з) 1000; к) 1200; л) 1542; м) 3500.
4.2. Знайти всі натуральні дільники чисел: а) 24; б) 50; в) 100;
г) 360; д) 375.
4.3. Знайти натуральне число /г, якщо:
а) п ділиться тільки на два простих числа і т(аі)=6, а
а(п)=42;
б) т (/г) = 1, 2, 3, 4, 5 або 6 відповідно;
•в) п має тільки два простих дільники, т(/і) = 12, о{п) =1240;
г) п має тільки два простих дільники, т(п) = 12, о (я) =465;
д) п ! 12 і т (я) = 14;
є) п — найменше натуральне число, для якого т(/0 = 14;
19

є) п — найменше натуральне число, для якого т'(л) = 18;
ж) п — найменше натуральне число, для якого т(/г) == 100;
з) добуток усіх його натуральних дільників дорівнює 5832;
к) п = 2*3*5*, т(|п)=т (л) — ЗО, т /1 п\ = х (л) — 35,
т(і-п) = т(л)-42;
л) п—-найменше натуральне число виду 2хр\р^ ДЄ рі і рч—
різні непарні прості числа і о (п) = Зп (задача Ферма);
м) добуток усіх його натуральних дільників дорівнює 330-540;
н) я = 2* • 3" • 5*, х (5п) = т (/і) + 8, х(7п) = х(л) + 12, х(8/г) =
«т (л) + 18.
4.4. Довести, що:
а) існує нескінченна множина натуральних чисел т, для яких
о(т) = 2т—1;
б) множина всіх натуральних чисел, більших від одиниці,
кожне з яких дорівнює добутку всіх своїх натуральних дільників,
збігається з множиною всіх простих чисел;
в) х(п) непарне тоді і тільки тоді, коли п — квадрат
натурального числа;
*(*)
г) добуток усіх дільників числа п дорівнює п 2;
д) .(nt.. х (тп)) == 1, де /і, т — натуральні числа;
€) х (т) х (п) > х (тл)7"якщо (т, п) > 1;
є) а (т) а^д),> д (/ял), якщ^ (т, п) > 1;
^1 + d2 + • • • + dk
ж)п = —х j р, де du d2y ..., dk — усі дільники
^ + ^ + --+¾
числа п.
4.5. Нехай /і — натуральне число. Знайти т(/і3), якщо:
а) т(/г2) = 15 і п має тільки два простих дільники;
б) т(/г2)=81 і /г має тільки два простих дільники;
в) т(п2) = 105 і п має тільки три простих дільники.
4.6. Натуральне число п називається досконалим1, якщо
с(/г)=2/г. Довести, що:
а) 6, 28, 496, 8128 — досконалі числа;
б) парне число п є досконалим тоді і тільки тоді, коли п =»
= 2k~{ • (2k— 1), де k > 2, а /? = 2k — 1 — просте число2 (теорема
Евкліда — Ейлера);
в) довільне натуральне число з одним простим дільником не
€ досконалим;
г) непарне натуральне число з двома простими дільниками не
є досконалим.
4.7. Два натуральних числа т і п називаються дружніми3,
1 Нині відомо 27 досконалих чисел. Усі вони — парні числа. Ще невідомо,
чи існують непарні досконалі числа і чи скінченна множина досконалих чисел.
2 Так зване просте число Мерсенна (див. § 2). Зрозуміло, що кожне просте
число Мерсенна дає нам деяке досконале число.
3 Найбільшої пари дружніх чисел ще не знайдено.
20

якщо а(т) =т + п. Довести, що дружніми є такі пари чисел:
а) 220 і 284; б) 1184 і 1210; в) 2620 і 2924.
4.8. Побудувати графіки функцій у=г(х) і у = а(х), де
1<jc<20.
4.9. Знайти функцію Ейлера для чисел: а) 17; б) 31; в) 100;
г) 200; д) 375; є) 625; є) 720; ж) 1000; з) 1200.
4.10. Знайти кількість натуральних чисел, які менші від числа
п і мають з ним найбільший спільний дільник d, якщо:
а) n = 300, d = 20;
б) /і =1476, d = 41; д) лг= 1072, d = 8;
в) /г=1665, d = 37; є) я = 2500, d = 50;
r) /г = 975, d=13; є) л = 2476, d=619.
4.11. Довести, що:
а) ер (п) — парне число при п > 3;
б) ер (4/г) = 2? (2/г), /i£N;
в) ср(4/г + 2) = ср(2/г+1), n^N;
r) S = у/і? (п), де S — сума натуральних чисел, які взаємно
прості з числом п і менші від п\
д) ер (5/і) Ф ер (7/і) для всіх п £ N;
є) якщо рівняння ср(л:) = а має корінь х = т, де m не : 2, то
воно має також корінь х = 2m;
є) ср(тл) =. 7(т) - Ф(л) - ¢^¾. m, "£N;
ж) ер (тл) = ер ((т, /г))ер([т/п]), т, /i£N;
з) ер (тгі) > ер (т) <р (/г), якщо (т, /г) > 1.
4.12. Розв'язати рівняння:
а) ?(*) =8; Є) <р(х) = Ь
6)?(*)=12; х
в) 9(x) = 14; »)?W-T'
г) ер (я) = р — 1, р — просте число; 3) ? М = т-*;
д) ер (х) = 2*. k Є N; к) ер (*) = |-х;
є) <р(*) = -|; л) ер (2х) = ер (Зх);
м) ер (6*) = 72.
4.13. Знайти натуральне число п, якщо:
а) п = 3*57% ft, /, s£ N і ер (п) = 3600;
б) n = pq, де /7 і ^ — різні прості числа такі, що р— д = 2 і
<р(п)= 120;
в) n = p2q2, де р і ^ —Різні прості числа і ер(/г) = 11424;
г) /і = /?V ... sm, де р, 9,...,s — різні прості числа, k, /,...,
m — натуральні числа, більші від 1 і ер (я) = 462000;
Д) п = 7*, k б N і ср(л) ==« 294;
є) /i = 5*741, k9 /Є N і ер (л) = 42 000;
є) n = pkql, де /?, ^ — різні прості числа, ky / ^ N і ер (n) = 120;
ж) п = pky де /7 — просте число, k є N, ер (я) = бр*-2.
4.14. Побудувати графік функції t/ = ep(#), де 1 < * < 20.
21

4.15. Знайти:
а) [є];
б) 1-е];
в) [1-/2];
г) [Igl28|;
л) [Ц^];
є) [/2бо];
4.16. Знайтиі
а) {*};
б) {-*};
B){l+sin|};
г) {2,1+cos |};
є) [/580+1];
*>[4 + «»ж]:
з) [2-lg2512];
к) [1 — In 501;
«ш
Д) {1.5 —tg^};
є) {1,3 + cos I};
є) {-2,6};
ж) {-?}.
4.17. Розв'язати рівняння*
а) [2,3x] = 3;
б) [3,2*] — 3 = 2;
в) [ах] = m,
де а Ф 0 і х — дійсне число;
г) [12,4*] =86;
Д) [*2І = 2;
4.18. Довести, що:
а) [х + у] > [х] + [у], *, y£R, узагальнити цей результат для
більшої кількості доданків;
= [2г|, де г Є R і 0 < г < 1;
є) [З*2 — *] = *+!;
є) М =т*;
ж) [*2| = *;
з) [12,4*| =87;
X
К
т— 1
т>2.
б) И + Іг + І
в)
г)
Д)
/7— 1 . /7 — 3
—^— аоо —-—, де р —просте непарне число;
о —г
т
, де г — остача від ділення цілого числа а на
натуральне число т\
е) l2l<x<!2L + ifngN;
=
X
п
4-
і
п
або
X
п
+
п
4 + 4+1;
ж) пг =t—2—» якщо т — непарне натуральне число;
22

JL
+
+
■^ якщо (m, 4) = lj
(fe— l)ml __ (/г— l)(m- 1)
якщо (m,
* +
[лл:] для будь-якого дійс-
з) [я*] > п [*], л Є N, л: g R;
»>[т] + [т] + [т]-8("
*>[-?№]+•••
Л)= 1, т> 2 і А; > 2;
м) M + jx + lj + ..
ного л: і п > 2;
н) [х] — 2 [-2-1==0 або 1, x£R.
4.19. Знайти показник степеня простого числа р, яке міститься
в добутку /г!, якщо:
а) р = 3, л = 100; в) р = 13, л = 10 000;
б) р = 11, /і = 1000; Г) /7 = 7, n = 81 561.
4.20. Знайти канонічний розклад чисел: а) 111; б) 181; в) 401;
ч тс і ч ^1
г) 75!; д) -їоТТої-
4.21. Скількома нулями закінчується число я!, якщо: а) п =*
= 50; б)п= 123; в) п = 1985.
4.22. Побудувати графіки функцій:
а) У =
б)у =
в) «/ =
г) «/ =
М;
2М;
[2дс];
т4
Д) У = -у №.
є) У = 2 f-j *1;
є) г/ =
і [2л;];
ж) г/ = [*] + х;
3ЇУ = Щ''
^У = Щ'
Ч 1*]
н) У = {*}.
4.23. Довести, що:
а) 288! : (16!)18;
б) 288! : (18!)16;
В) Ь10000 : /,
, г) п\ • (а! М ... £!), якщо а + b + ... + k < я;
д) (k + 1) (Л + 2).. . (k + п) і /і!, k9 n Є N;
є) (/і!)! : (п!)^-1)';
є) (* + d)(k + 2d),
ж) [л-
+ 1
+
п + 2
.(k + nd) і п\у якщо (d, n!)
Гл + 2* і
і;
+ ...+
2*+і
+
я.
4.24. Скільки є натуральних чисел, які:
а) кратні 786 і містяться між 106 і 107;
б) менші від числа 1000 і не діляться ні на 5, ні на 7;
в) не більші від 100 і взаємно прості з 36;
23

rj не більші від 2311 ї не діляться на жодне з чисел 5, 7, 13, 17;
д) не більші від 12 317 і взаємно прості з 1575;
є) не більші від 1000 і не взаємно прості з 363?
4.25. Турист перебував у дорозі ціле число днів і проїжджав
кожен день стільки кілометрів, скільки днів він подорожував.
Якби він проїжджав щодня по 20 км і зупинявся на один день
через кожні 40 км, то час його подорожування збільшився б на
37 днів. Скільки днів подорожував турист?
§ 5. Ланцюгові дроби. Підхідні дроби ланцюгового дробу
Література
П
[3]
и:
[10
ці
[12
— § 9, с. 99—111;
— § 9, с. 98—111;
— гл. 11, § 3, с. 379-385;
-гл. IV, § 14, 15, с. 260-278;
— гл. І, § б, с. 18—22;
— гл. 5, § 1, 2, с. 58—66;
— гл. III, § 3, с. 69-79;
[14] — § 7—9, с. 31—41.
ТЕОРЕТИЧНІ ВІДОМОСТІ
Нехай а —довільне дійсне число. Позначимо через qx найбільше ціле число,
яке не перевищує а. При дробовому а маємо о = ^0+ -£-, де а±> 1. Аналогічно
при дробових Op ..., cts_j маємо
1
ai = ?i + ""Z' a»sl»
«s-i=<7s-i +—' as> *'
і тому дістаємо розклад в елементарний ланцюговий, або елементарний
неперервний, дріб:
« = <7о + Ц . (]>
*1 +
<72 + «
1
* «-і + Т
Якщо а—ірраціональне, то а{1 а2, . . ., а& — ірраціональні (якщо as
—раціональне, то згідно з розкладом (1) число а теж раціональне), і через це
зазначений процес можна нескінченно продовжити, і в результаті дістанемо
нескінченний ланцюговий дріб.
а
Якщо a — раціональне, то існує такий раціональний нескоротний дріб у,
а
що а ==-г-, Ь > 0. Тоді зазначений процес скінченний і його можна здійснити
за допомогою алгоритму Евкліда. Справді, для чисел а і Ь маємо:
24

a = tyo + rv
b = 'i<7i + '2
r/i-2 = ^-l^-
'«_! = ^¾.
-£- = <7n +
Я\ +
»
\+rn,
<72 + «-
b
b
ri
rn-2
ra-\
rn-\
_1
і
1
.
•
T^
= ?o +
= <7i +
= ^-1
= <7Л>
1
</*-! +
1
T
1
Si!
r2
+ і
5=T
'«
■*
"7
Яп
(2)
Числа <7o, ft, ..., які містяться в розкладі числа о ь ланцюговий дріб,
навивають неповними частками або елементами цього ланцюгового дробу.
Скорочено довільний ланцюговий дріб записують так:
а = [Яо'> Qv Як •••> Яп* •••]•
Число q0 є цілою частиною числа а, а [0; q^ q2, . ..]—дробовою частиною
числа а. Правильні дроби —, —, ... називаються відповідно першою, другою
Яі Я*
і т. д. ланкою ланцюгового дробу.
Будь-яке раціональне число а можні подати у вигляді деякого скінченного
ланцюгового дробу:
а = [Яо'> Я\> ?2> • ••* Яп]-
Якщо qn > 1 при п > 0, то такий розклад єдиний.
Будь-яке ірраціональне число можна подати у вигляді деякого нескінченного
ланцюгового дробу, причому цей розклад єдиний.
Нескінченний ланцюговий дріб називається чистим періодичним, якщо його
неповні частки перюдично повторюються в тій самій послідовності, починаючи
в <7о» тобто, якщо дріб має вигляд
[Яоі <7і> Я2> •••» ЯП' Яо> Я\* <72» ••■•• ЯП' •••]
або
[(Яо\ Я\* Яч> ..•» Яп)]-
Ланцюговий дріб називається мішаним періодичним, якщо період
ланцюгового дробу розпочинається не з qQt тобто якщо дріб має вигляд [qQ\ <7р • • •> Ят*
я-, pv .. ., рп, Р0. . . ., рп, . . .], або [<70; Я\> • • •» Ят* (Ро> • • •» Рп)]-
Будь-який нескінченний періодичний ланцюговий дріб (чистий чи мішаний)
є дійсним коренем квадратного рівняння в цілими коефіцієнтами, тобто є так
званою квадратичною ірраціональністю.
Будь-який ірраціональний корінь довільного квадратного рівняння в цілими
коефіцієнтами розкладається в нескінченний періодичний ланцюговий дріб (чистий
чи мішаний).
25

Дроби
*1+^
<7<г
91 +
(3)
+■
1к
називаються підхідними дробами. При цьому -тг- називається підхідним дробом
k-то порядку. Якщо k—парне (непарне), то дріб -тг- називається підхідним дро-
бом парного (непарного) порядку. Зрозуміло, що для скінченного ланцюгового
дробу порядку п виконується рівність
Рп
"57'
звідси -г = a, a а — раціональне число, для якого будувався ланцюговий дріб.
Правило утворення підхідних дробів (скінченних і нескінченних):
^.=^.-1 + ^,-2. Qs = ?sQs-l + Qs-2> «>!• (4)
Звідси Р0= q0, Q0 = 1. Щоб формула (4) виконувалася 1 при s= 1,
покладають P_j = 1, Q_j = 0. Усі обчислення зручно виконувати за. такою схемою
(табл. 1).
k
Як
?к
Qk
—і
т-
1
0
0
Яо
Яо
1
1
Яі
Рі = ЯіРо + Р-і
Qi = <7iQo + Q-i
2
Я2
Р% = ЯіРі + Ро
Q2 = я&і + Qo
. . .
Таблиця 1
п
Яп
Рп = ЯпРп-\+
+Рп-2
+ <?п-2 1
Щоб обчислити Ps, s =s 1, 2, . . ., пУ треба число <73> яке стоїть над Ps,
помножити на число Ps_v яке передує Ps з цього самого ряду, і до добутку
додати число Я$_2» яке стоїть в тому самому рядку і передує Ps_i. Аналогічно
обчислюють і Qs.
Справедливі такі властивості підхідних дробів для скінченного ланцюгового
дробу:
і°. P,Q_i-P.-iQ, = (-1)-1. *>U
2°. Кожен підхідний дріб нескоротний;
26

3°- PsQ*-2 - Ps-zQs = (-l)s <7S, s > 2;
4°. Підхідні дроби парного порядку даного ланцюгового дробу утворюють
вростаючу послідовність, а підхідні дроби непарного порядку — спадну
послідовність;
5°. Кожен підхідний дріб парного порядку даного ланцюгового дробу
менший за будь-який підхідний дріб непарного порядку цього ланцюгового дробу.
Якщо дійсне число а розкладено в ланцюговий дріб (скінченний чи
нескінченний)
а = [?o; Qv 9і> • • •]
І тг— є значенням fc-го підхідного дробу, то
і %
і і
QkQk+i КЩ
/ м
І оцінка похибки наближення числа а підхідним дробом уг-1
Рк
Якщо а— дійсне число, -Q——&-й підхідний дріб розкладу а у ланцюговий
X
дріб, — — довільний раціональний дріб із знаменником у, меншим від Qk, то
Pk І І X
виконується нерівність
—"ЗГ ГІ—7
(теорема про найкраще
наближення).
Ланцюгові дроби знаходять широке застосування. Сформулюємо теорему, за
якою знаходять загальний розв'язок у цілих числах лінійного рівняння з двома
невідомими, коефіцієнти і вільний член якого є цілі числа (так звані невизна-
чені рівняння).
Загальний розв'язок у цілих числах рівняння ах-{- by = с, де a, b, c—цілі
числа, a (a, b) = 1, можна подати у вигляді
х = (-І)*-1 cQn_{ + bt, y = (-1)" сРп_{ - at,
де t — довільне ціле число, а Рп__{ і Qn_i — чисельник і знаменник передостан-
а
нього підхідного дробу розкладу числа -г у ланцюговий дріб. Оскільки тут t —
довільне ціле число, то можна користуватися формулами х = (—1)л—1 cQn__i — bt,
y-i-lfcP^+at.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
602 .
1. Розкласти в ланцюговий дріб число — ogy 1 знайти всі підхідні дроби.
а
Розв'язання. Якщо -т—додатний дріб, то застосовуємо алгоритм Ев-
а о, а*
кліда. Якщо "т- < 0, то спочатку подаємо його у вигляді -г = —k + -т-, де
аі -* ^
k—натуральне число, а -г-—правильний дріб. Отже, маємо
°і
602_ К32
~ 367 - ""2 + 367*
27

Далі, за алгоритмом ЕвклІда дістаємо
132
103
103
"" 87
29
3
29 1 16
~~іб|Т
""13 1 1
13
12
3
Т
367
"2Є4
103
1
132
2
з|і
0
Отже, — ^«[-г2;-2, 1,3, 1,1, 4,3], зокрема, q0 = — 2, qx = 2, q2 = 1, ?3=3,
Qi = 1» <7e = 1, <7e = 4, ^77 == 3. Для обчислення підхідних дробів складаємо
таблицю (табл. 2).
k
Як
?к
Qk
—і
—
і
0
0
—2
—2
1
1
2
—3
2
2
1
—5
3
3
3
-18
11
4
1
—23
14
Т
.5
1
-41
25
а бл и ця 2
6
4
—187
114
7
3
—602
3G7
Звідси
Р4 23
"57 __ 14;
Зауваження
рі 3.
Q, ~ ~ 2 •
Р5 41
Q, ~ ~ 25 :
Ра 5 Р3 18
Qt ~~ з; q3 -- ір
Р, 187 Р, 602
Qt ~ — 114 : Q, - — 367
п и
1. Оскільки -g—=-Т-, то нижні дві клітинки останнього стовпчика в таблиці
для обчислення підхідних дробів є своєрідною перевіркою правильності
виконання всіх обчислень.
а
2. Якщо звичайний дріб -т- розкласти в ланцюговий, то останній підхідний
р
дріб 75— буде нескоротний, ланцюговий дріб дає змогу водночас скорочувати
•* а
дріб -j.
28

3. Обчисливши всі підхідні дроби за даним ланцюговим дробом [gQ; qv q2, ...,
а
qn], можна дістати нескоротний дріб -у, що відповідає йому.
2. Ірраціональне число розкласти в ланцюговий дріб і обчислити з точністіо
до 0,0001 значення jA~R.
Розв'язання. Щоб розкласти дійсне число а в ланцюговий дріб, вико-
ристовують алгоритм Ейлера — алгоритм виділення цілої частини.
1
<* = <7о + —» Де <7о = М * «і > 1;
аі = <7і +т"» де Яі = K1 * a2 > і;
«2
<*2 = ?2 + Г' ДЄ ?2 = К1 І «З > 1 J
Про послідовність q0, <7і» ^2» • • •» кажуть, що її побудовано з числа а за
допомогою алгоритму виділення цілої частини. Всі члени цієї послідовності —
цілі числа, причому ql > 1 для і = 1, 2, ....
Процес побудови цієї послідовності закінчується тоді, коли деяке ап буде
цілим числом (тобто тоді, коли ап , j = 1).
а
Якщо а— раціональне число, тобто а = -г , де а £ Z, 6 £ N, то,
застосовуючи алгоритм Евкліда до а і до чисел а і fc, дістанемо ту саму послідовність.
Тоді матимемо скінченну послідовність <70, qv q2, • . •» qn і розклад числа а «=
а а
= -у в скінченний ланцюговий дріб: а = -у = [^0; </р . . ., дл].
Якщо а—ірраціональне число, то, очевидно, послідовність q0, qv q2, .. „
нескінченна (тоді всі at > 1, і = 1, 2, ...).
Використовуючи алгоритм виділення цілої частини для числа )^14, маємо:
і УТГ + з , , і
1 5 УІ4 + 2 п 1
—г~
1 2 /Й + 2 1
-Т! = 1 + Т-.
/14+2 9 УТі — 2' 5
5
1 5 — 1
= )/14 + 3 = 6 + -,
а4 = Т7т?
/14 + 2 _, /14-3 r ^ ^ «•
5
1 1
4= }Па + 3 — 6 = УІ4 - З
ОСКІЛЬКИ а5 --= Oj, TO
/Ї4 = [3; (1,2, 1,6)]-
29

За наближене значення /і 4 можна взяти один з підхідних дробів
побудованого ланцюгового дробу. Для обчислення підхідних дробів складемо таблицю
(табл. 3).
k
Як
Pk
Qk
—і
—
і
0
0
3
3
1
1
1
4
1
2
2
11
3
3
1
15
4
4
6
101
27
5
1
116
31
т
6
2
333
89
а бл и ця 3
7
1
449
120
• • •
. . . 1
• • •
. . .
Як відомо, похибка наближення числа а підхідним дробом тг" не перевищує
1
або —J.
_1_
QkQk+i
Оскільки в даному разі
1
Q6Q7 ~- 89
-J2Q < 0,0001, то за наближене значення
Р6 333
/14 з точністю до 0,0001 можна взяти підхідний дріб тг-, тобто *зо"~ 3,7416.
Зауваження. Будь-який наступний за tj" підхідний дріб буде точнішим ра-
ціональним наближенням до /і 4. Проте краще вибирати за наближення той
з підхідних дробів, в якого знаменник найменший.
3. Знайти квадратичну ірраціональність а, якщо а = [4; 3,(2,1)].
Розв'язання. Перетворимо спочатку нескінченний чистий періодичний
ланцюговий дріб, який дістаємо із заданого ланцюгового дробу після того, як
відкинемо цифри, що стоять до періоду:
^ = [(2,1)] = 2 +
Маємо
і +
У = 2 +
!
1 +
-)•
'+7
звідки
^-20-2 = 0, ^ = 1+/3,.^ = 1-/3. ^
Оскільки у— додатна квадратична ірраціональність, то у = \ 4-/3.
Тепер перетворимо в квадратичну ірраціональність заданий нескінченний
мішаний періодичний ланцюговий дріб:
[4; 3, (2, 1)] = [4; 3, у) = 4 f
3 +
1 + /З
30

14-/3 17+13/3 49 — УЗ
= 4 + 4 + 3/3~~ 4 + 3/3 ~~ Н
Отже,
49—Кз
[4; 3, (2, 1)]= ^—.
4. Розв'язати в цілих числах рівняння —117* + 343# = 119.
Розв'язання. Запишемо це рівняння так:
117 (—х) + 343у = 119. (1)
Визначимо невідомі — х та у. Загальний розв'язок у цілих числах рівняння
сіх-\-Ьу=*с, де а, Ь% с — цілі числа й (я, b) = І, подамо у вигляді
(2)
#=(-1)^-1-^
де / — довільне ціле число, а Рп_\ і Q„_i — чисельник і знаменник
передом
останнього підхідного дробу розкладу -у у ланцюговий дріб.
У цьому разі а =117, 6 = 343, (117, 343)=1.
117
Розкладемо дріб щ в ланцюговий: а = [0; 2, 1, 13, 1, 1, J, 2].
Отже, п = 7. Обчислимо Рп_х = Рб і Qn_x = Q6. Маємо Р6 = 44, Q6 = 129.
Тоді одним з окремих розв'язків є
-*о = (— 1)в • 119- 129= 15 351, у0 =(—І)7 .119- 44 = -5236.
Згідно з формулами (2), загальний розв'язок запишемо як
—а; = 15 351 +- 343/, у = —5236 — 117/,
або
д: = — 15351 — 343/, у = - 5236 — 117/.
Маємо порівняно великі за абсолютною величиною окремі значення для х9
і у0, проте із загального розв'язку можна дістати інші окремі значення для
х і уу які будуть найменші за абсолютною величиною. Нехай / = —45. Тоді
хх = 84, t/i = 29 і загальний розв'язок рівняння (1) є
х = 84 + 3436, # = 29+1176 (тут замінено — / на k).
Зауваження.
1. У розглянутому прикладі значення х і у можна було визначити відразу»
Справді, розкладаючи — grg B ланцюговий дріб, дістаємо
-ks = [^1; *' *' *'13' *' *'Іі 2]-
Тоді я«8, а = -117, 6 = 343, с= 119, /^ = /^ = -44, Qn_x = Q7 = \29~
Згідно з формулами (2). х0 = (—1)М19 • 129 = -15351, </0 = (-1)8.119-(-44) =
=:-44 • 119 = -5236.
Отже, х = — 15 351 + 343/, у = 5236 + 117/.
При / = 45 маємо той самий результат, що й раніше:
* = 84+ 343/, 0 = 29+117/.
2. Часто при розв'язуванні аналогічних задач треба обчислити тільки під-
р
хІдний дріб п"~ . Проте доцільно заповнювати всю таблицю для підхідних
^л—1
Рп
дробів, оскільки, обчисливши дріб q-, можна перевірити розь*язання.
31

є)
ж)
з)
к)
я)
521.
143*
83.
217*
99.
170*
0,375;
-0,4
(51).
Задачі
5.1. Розкласти в ланцюгові дроби і обчислити їхні підхідні
дроби для раціональних чиселі
ч 23
*)ї8'
*\ 36-
б> І9'
в) 2,55;
г) -1,425;
602
Д) -36Г
є) -5Й;
5.2. За допомогою розкладу в ланцюгові дроби скоротити дробиі
1180. v \24Л. 1872
*) 7825» А; 6059» 3' ""1560'
А\ ШІ- Р\ ^І- ч 3523
°' 991Г Є' 2147' К) 1300;
R\ І5І3. *\ 32671. ч 309 672
В) 3427' ^ 10 027' Л' 464 508'
1857, 70 757 ,
Г' 9153' Ж) 491 209'
5.3. Знайти звичайні нескоротні дроби, що відповідають
ланцюговим дробам:
а) [2; 1,3,4,2]; є) [-3; 1,2, 1, 1,5];
б) [2; 1, 19, 1,3]; ж) [-5; 2, 1, 1,3,2];
в) [2; 1, 1,3, 1,2]; з) [1; 3, 2, 4, 3, 1, 1,1,5];
г) [1; 1, 2, 3, 4]; к) [а; а, а, а, а];
д) [0;4, 1,2,5,6]; л) [a; b, a, b, а],
є) [-2; 1,3, 1, 1,5];
Рп-\
5.4. Нехай -~ передостанній підхідний дріб у розкладі
раціонального числа -г в ланцюговий дріб. Довести, що (а, Ь) =?
= (—l)nQn-ia + (-ІГ-1Рп-іЬ.
5.5. Користуючись результатом задачі 5.4, розв'язати задачу 5.3.
Б.6. Розкласти звичайний дріб у в ланцюговий, замінити його
Р
підхідним дробом тг» знайти похибку заміни, замінити наближену
рівність із зазначенням похибки, якщо:
\ а 29 , , *s а 648 , л
а> Т = 37' * = 4; 6>Т = 385' fe==4;
571
ч а 0/1 и с
Ь ~~ 359'
32

5.7. За допомогою підхідних дробів знайти наближення до дробу
1Щ. з точністю до: а) 0,001; б) 0,0001.
5066
5.8. Розв'язати рівняння!
7Q 1Q
а) [*; 2, 3, 4] = g; б) [2; 1, 2, х] = у.
5.9. Знайти ланцюговий дріб 1^0", <7ь ..., дп], якщо qn m З,
Рп-і 14
5Л0. Нехай для деякого скінченного ланцюгового дробу [qQ>
Pq 3 Р\ 10 ^33 0 х
¢,, ..., <?„] маємо $p~f' «Г~Т' ^їо' Знайти ?*
5.11. Треба побудувати зубчасту передачу за допомогою двох
валів з кількістю зубців, що дорівнює відношенню 587:113. Чи
можна замінити це відношення відношенням з меншими
чисельниками і знаменниками, але похибкою, яка не перевищує 0,001?
Як зміниться відповідь, коли: а) початкове відношення 355:118,
а похибка 0,002; б) початкове відношення 12 532:3921, а похибка
0,00005?
5.12. Розв'язати в цілих числах рівняння:
а) 38* + 117у = 209; є) 37* + 23*/ = 15;
б) 119л: — 68г/ — 34; т є) 53*+17*/= 25;
в) 41*+ 114*/ = 5; ж) 64* — 39*/= 15;
г) 49* + 9у - 400; ' з) 3827* + 3293*/= 1869 j
д) 12*+ 31*/ = 170; к) 571* + 359у - —10.
5.13. Розв'язати в натуральних числах рівняння:
а) 8*+ 13*/ = 15;
б) 23* — 42*/= 72;
в) 15* + 28у = 185.
5.14. Розкласти число 100 на суму таких двох натуральних
чисел,_щоб одне з них ділилось на 7, а друге — на 11.
5.15. Для настилання підлоги завширшки 3 м є дошки
завширшки 11 і 13 см. Скільки треба взяти дощок різної ширини, якщо
довжина кімнати 1 довжина дощок однакові, а дошки кладуть
вздовж кімнати?
5.16. Для перевезення зерна є мішки по 60 і 80 кг. Скільки
треба таких мішків для перевезення 440 кг зерна?
5.17. Скільки білетів вартістю ЗО і 50 коп. можна купити на
14 крб. 90 коп?
5Л8. Купили ЗО птахів за ЗО монет однієї вартості; причому
за кожних трьох горобців заплатили 1 монету, за кожні дві
2 5-271
33

горлиці також 1 монету і за кожного голуба — по 2 монети.
Скільки купили птахів кожного виду?
5.19. 26 студентів посадили разом 88 дерев, причому кожен
студент І, II і III курсу повинен був посадити відповідно 6,
4 і 2 дерева. Скільки було студентів І, II і III курсу?
5.20. Розкласти в ланцюгову дроби такі квадратичні
ірраціональності: _а) /2;_б) /3;_в) /б; £)_ /б; Д)_ /7; е)_/8; є) /10;
ж) /11; з) /12; к) /13; л) /28; м) /ЗО; н) /59.
5.21. Розкласти в ланцюгові дроби такі квадратичні ірраціо»
нальності:
2
2-f-VT
а) 1 + /2;
6)l+VT
в)
г)
Д)
З
3+)/5",
2
2 + VT
ж) 1 —/31;
з + Гю,
к)
л)
м)
н)
б—YJ,
2 •
3-/7".
■V5.
76 + /285
94 '
€) 5 —/15;
5.22. Знайти квадратичні ірраціональності, якщо відомі їхні
розклади у нескінченні періодичні ланцюгові дроби:
а) [(1,2)]; ж) [0; (1,3)];
б) [1; (3)]; з) [0; (2, 1)];
в) [2; (5)]; к) [0; (1,4)];
г) [0; (4)]; л) [2; (1,2)];
Д) [0; (7)]; м) [1; (3,2)];
є) [(2,3)]; н) [1; (3, 1)].
є) [3; (4, 11)];
5.23. Знайти квадратичні ірраціональності, якщо відомі їхні
розклади у нескінченні періодичні ланцюгові дроби:
а) [0; (1,3,2)]; ж) [2; (3,2,1,2)];
б) [1; (2,3, 12)]; з) [4; 3, (2, 1,3, 1)];
в) [1; (1,2, 11)]; к) [3; 2; 1, (3, 1)];
г) [2; (3, 1,4)]; л) [1; 1,2, 1, 1, (4)];
д) [1; (1,2,3)]; м) [(1,2,4,6)];
є) [2; (3, 1,2)]; н) [1; (1, 1, 1, 1, 2,5)].
є) [3; (1, 1,6];
5.24. Знайти квадратні рівняння з цілими коефіцієнтами, корені
яких розкладаються в такі нескінченні періодичні ланцюгові дроби:
а) [10; (10, 20)]; д) [(2, 4, 1, 3)];
б) [9; (1,1,2,4,2, 1,1, 18)]; є) [2; 1,2,(1, 1,3)];
в) [2; (1,1,3)]; є) [1; 2,(3,4)].
г) [1; (1,2,2,1)];
34

6.25. Знайти квадратичну ірраціональність х, якщої
а) х=[д; (2д)\, q£fi;
б) * = [<r. [q\ {q, 2q)\, <?£N.
5.26. Розкласти в ланцюговий дрібі
а) УУТЇ, q£N; в) У(д + І)2 =2, <7 Є N;
б) Vq* + 2q, q£ N; г) У> + 2?, <?€ N.
5.27. Замінити числа підхідними дробами третього порядку І
оцінити похибку:
а, Ц; б) 3, .4159; =, =1^2; г) l=f*.
5.28. За допомогою ланцюгових дробів обчислити з точністю до
0,0001 обидва корені квадратних рівнянь з цілими коефіцієнтами!
а) 2х2 — 15* + 26 = 0; г) ** — 5х + 2 = 0;
б) х2 + 9х + 6 = 0; д) 4а? + 20л; + 23 = 0.
в) 2х2 — Зх — 6 = 0;
5.29. Знайти підхідні дроби ^ у розкладі /2, якщо 0<k < 3.
5.30. Знайти другий підхідний дріб у розкладі кореня
рівняння 2* = 5.
5.31. Розкласти в нескінченний ланцюговий дріб і обчислити
з точністю до 0,0001:
а) КЗО; б) К59; в) *±£Ц г) l±fL,
5.32. Довести, що:
Р2 2а 4- 1 /•
б) тг = —3— при розкладі ірраціональності у а? +а + 1 в
ланцюговий дріб;
в) дріб
а* + За' + 1
, а б N є нескоротним;
а3 + 2а
г) (Рп, Pn_i) = (Q/., Q.-0-1;
д) Pn_i = Qn для дробу [?о; <7і, ?2, ..., ?*], в якому go=qnf
e)
^H'-^H^-'H'-^)
є) [2; 2, 2 2] =
ж)
3;
n-
Qn>2
Pk
2 , якщо п «
< Т7Г a6°
2Q*
>2;
Pk-x
- »
" 2<#_l
для заданого дійсного додатного числа а і натурального числа k,
k>\\
35

л)
к) — є підхідним дробом розкладу дійсного додатного числа а
у ланцюговий дріб, якщо р, q£N, (p, q) = 1 і а=И=—, а —— <
Ч \ Ч \
-£!><;.№.+<,-.)•Д0ВІВШИ' шо к' ferfe лежать
по один бік від а;
м) підхідний дріб /г-го порядку збільшиться (зменшиться), якщо
неповну частку qn збільшити на кілька одиниць, де п — парне
(непарне) натуральне число.
5.33. Довести, що:
а) додатний корінь тричлена Ьх2— аЬх— а, де а, Ь — натуральні
числа, розкладається в нескінченний чистий періодичний ланцюговий
дріб, довжина періоду якого дорівнює 2;
б) квадратне рівняння з цілими коефіцієнтами має другий
корінь -г-г—г—, якщо перший його корінь є число [(а, Ь)];
в) квадратне рівняння з цілими коефіцієнтами має корінь а —
— [(с9 &)], якщо перший його корінь є х= [(a, fc, c)]\
г) числа а = [а; Ь9-с] і р = [с; Ьу а] пропорційні числам х =
= [(а, 6, с)] і у = [(с, 6, а)]; __
д) ірраціональність виду )Лп, mgN розкладається в
ланцюговий дріб, період якого починається з другої неповної частки.
5.34. Знайти ірраціональність а, якщо:
а) Q"ft = T' a*+i = V2;
ГИ Р* - 37 1+/Т
б) О; - ІЗ' "*+1 = _2 •
5.35. Знайти загальний вигляд квадратичних ірраціональностей,
які розкладаються в ланцюговий дріб з однаковими неповними
частками.
§ 6. Системні числа, операції над ними;
переведення з однієї системи в іншу
Література
[1]- § 6, с. 79-88;
[2] — § 6, с. 76—86;
[3]—гл. II, § 4, с. 385—389;
[4]—гл. II, § 3, с. 88—104.
ТЕОРЕТИЧНІ ВІДОМОСТІ
Той чи інший спосіб найменування та записування чисел називають
нумерацією (від лат. numeres — лічба) або системою числення.
Розрізняють усну й письмову нумерації. Усна нумерація—це спосіб
називання чисел за допомогою слів. Письмовою нумерацією Називають спосіб
записування чисел за допомогою знаків (символів), які називаються цифрами.
Розрізняють позиційні і непозиційні системи числення.
36

Під позиційною системою числення розуміють систему, в якій значення кож*
ної цифри визначається не тільки цифрою, а й позицією, яку вона займав
в запису числа.
Під непозиційною системою числення розуміють систему, в якій кожна
цифра завжди позначає те саме число незалежно від її місця (позиції) в ва~
пису числа. Прикладом непозиційної системи числення є римська система, яка
дійшла до нас із Стародавнього Риму. В ній для запису чисел використовують
сім цифр: цифра І означає одиницю, цифра V — п'ять, цифра X —десять, L —
п'ятдесят, С — сто, D — п'ятсот, М — тисячу. За допомогою цих цифр можна записати
будь-яке число, використовуючи принцип додавання і віднімання. Якщо менша
цифра стоїть справа від більшої, то Бона додається до неї (причому вона може
повторюватися не більш як 3 рази), якщо зліва — то віднімається (повторення
меншої цифри не дозволяється). Наприклад, 19£5 —MCMLXXXV.
Хоч символу для зображення нуля у римській систем' числення немає,
проте можна записувати числа, які містять нуль. Наприклад, 1809 — MDCCCIX.
Записи чисел у римській нумерації громіздкі, до того ж множення і ділення
на письмі виконувати неможливо, їх доводиться виконувати усно. Тому римська
система числення в математичній практиці не застосовується.
З'ясуємо суть позиційного принципу запису чисел. Нехай g—деяке фіксоване
число, більше від 1. Назвемо це число основою системи числення.
Кожне натуральне число т можна записати і притому єдиним способом
у вигляді
м = ап8П + ап-\£~Х + • • • + аі2 + я<>, П)
де а0 2 = 0,1..., п — цілі невід'ємні числа, менші від g, причому ап =£ 0.
Вираз (1) називають записом числа т у системі числення з основою g.
Символи, якими позначають числа ап, an__lt . . . , av a0, називають цифрами
числа т у системі числення з основою g (або «g-кова» система числення).
Вираз (1) скорочено записують так:
^ = (^^-1---^1¾)^ (2)
У системі числення з основою g використовуються g цифр: 0, 1, 2, ..., g — 1.
При цьому основа числення g записується як 10.
Запис додатного дробового числа у будь-якій системі числення є зображення
цього числа у вигляді суми степенів основи з цілими невід'ємними
коефіцієнтами, меншими від основи, але не лише додатних і нульового, а й від'ємних
цілих степенів. Для запису дробового числа, крім цифр, використовують ще один
знак — кому. Дробове число 1 - 83 + 2 - 82 + 5 • 8і + 4 • 8° + 7 - 8_1 + 6 - 8~2 +
+ 3 • 8—3 + 2 • 8~4, наприклад, записують так: 1254, 76328.
Для кожного додатного дробового числа так само, як і для кожного
натурального числа, в g-ковій системі числення існує тільки один запис.
Застосовуючи знак мінус, можна записувати в g-ковій системі числення
й від'ємні числа.
Загальновживаною тепер є позиційна система числення з основою g = 10.
її називають десятковою позиційною системою.
Виконуючи арифметичні операції над числами, записаними в g-ковій системі
числення, користуються правилами додавання, віднімання і множення «стовпцем»
і ділення — «кутом». При цьому використовуються g-кові таблиці додавання
і множення однозначних чисел.
Нехай натуральне число т задано в g-ковій системі числення. Щоб
записати це число в s-козій системі числення, треба спочатку записати число s
в g-ковій системі, а потім виконати (в g-ковій системі числення!) кілька ділень
числа mg на число sg і послідовно утворюваних часток доти, поки дістанемо
частку, яка дорівнюз нулю. Здобуті остачі треба спочатку виразити цифрами
і-козої сиггеми числення, записати їх у зворотному порядку. Записані таким
чином остачі (це вже цифри в s-козій системі числення) і є s-ковим записом
числа mg.
Перехід від g-кової системи числення до 10-кової виконують ще й так. Число
ag записують у вигляді
ag = anSn + an-iSn~l + • • • + a IS1 + *og°.
37

Потім замість чисел ап, an_v • . ., av a0 \ g підставляють їхні десяткові записи
і роблять відповідні обчислення. Десятковий запис результату є шуканим числом.
Оскільки десяткова система числення найзручніша для виконання тих або
інших дій, то, щоб перейти від g-кової системи числення до s-кової, спочатку
переходять від g-кової системи числення до Ю-кової, а потім від 10-кової
до s-кової.
Якщо g = sky k£N, то перехід від однієї системи числення до іншо! значно
спрощується.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Обчислити:
а) 2023324+222224; б) 2201114 — 323234; в) 232303014: П34.
Розв'язання. У четвірко вій системі числення цифрами є: 0, 1, 2, 3.
Складемо для них таблиці додавання і множення (табл. 4 і 5).
Таблиця 4 Таблиця 5
1 +
0
1
2
3
0
0
1
2
3
1
1
2
3
10
2
2
3
10
11
3
3
10
11
12
Тепер виконуємо дії:
а)
,202 3324
~т~ 222224
231 2204
б)
220 1114
" 32 3234
121 1224
, 23230301,
в' ~232
303
"232
113,
200 2034
1101
"1011
Зо4 (остача)
2. Перевести з однієї системи в іншу:
X
0
1
2
3
0
0
0
0
0
1
0
1
2
3
2
0
2
10
12
3
0
3
12
21
Перевірка:
231 2204
"~ 22 2224
202 3324
Перевірка:
+
121 1224
32 323,
220 11U
Перевірка:
X
2002034
ИЗі
1201221
+ 200203
200203
23 230 2114
23 230 2114+ 304 =232330І4.
а) 138
в) Ю0324
іо-
*4Ї
б) 1340і0
г) 20324 н
' ХІ5>
Розв'язання. Перехід від десяткової системи числення до s-кової системи
відбувається за допомогою послідовного ділення числа т, заданого в десят-
38

ковій системі, на число s, записане теж у десятковій системі. Маємо т ••
■=s<7i + г;- Тепер неповну частку qi ділимо на л. Дістаємо Яі = sq2 + r2.
Процес ділення продовжуємо доти, поки знайдемо неповну частку qk < 5.
При цьому запишемо число т у s-ковін системі: {Q)fkrk—\ • • • r2ri)s*
Цей процес можна записати у вигляді такої схеми:
__ т \_s__
sq3 I ft
sq2
\ \Г2\ "р=
\гА
«• •
Як-Ч.
~*Як-\
гк-\
І 5
1 Як-1
Чк
1 s
\~Як
■ U
*
-\як\
Стрілкою показано напрям від вищих до нижчих розрядів числа, записанога
в системі з основою s, цифри числа т у цій системі взято в рамки,
a) 1381Q-**4
Оскільки 4 < 10, то всі остачі є цифрам»
в новій системі числення.
1с
"15
«10
* L
18
16
2
*ю
*ь«
32
7
<и
±
~ и
Отже, 13810 = 20224.
б) 134010-*і5
-2ю
12І
Чо
_І34010
120
У 15-ковій системі числення число 14 є
цифрою і позначається (14) або 4.
Отже, 134010 = 5(14) 515-
Щоб перевести число с g-ковоі системи числення в s-кову, діють аналогічна,
причому всі обчислення виконуються в g-ковій системі числення.
в) 100324-*3. .
Число 3 в четвірковій системі числення записують так само. Тоді
100324
3
10
3
13
12
12
~12
1 о 1
t
34
1122,,
~~ 3
22
21
12
~12
\о]
34
1324| 34
. І2 1 224 1 З.
-і2 1HL ГІГ
'2 1=7 3
7= 1 ~=
34
_1і l_3j
J 01 — / 0 | -1L10
ИІ
1 1 і
1
Отже, 100324 = ЮЮ003.
39

Перевірка. Число 4 у тріиковій системі числення записують як 113.
Використовуючи таблиці додавання і множення одноцифрових чисел у тріиковій
системі числення (табл. б, 7), матимемо
Таблиця 6
Таблиця 7
+
0
1
2
0
0
1
2
1
1
2
10
2
0
10
11
X
0
1
2
0
0
0
0
1
0
1
2
2
0
2
11
1010008
" 22
20
""11
20
""11
20
Zli
0
и»
2111,
11
101
"" 22
21
"11
Mil
Hs
121s
—11
11
11
ПГГ
1 о 1
11,
11я
11
1 о 1
1 Us
П7
s
111
I
Отже, ІОЮООз = 100 (103) 24 = 100324, оскільки 108 = 34.
r) 20324 -* x10.
І спосіб. Число 10 в четвірковій системі числення записують так:
4lft
_Ю10
8__
Ш
t
0
0
І2|
Тоді
20324
132
112
""ПО
Й
t
224
32 4
~22
По]
224
U
~0
ЇЙ
1
Ю10 = 224.
224
0
Отже, 20324 = 1 (104) 2,-0 = 14210.
II спосіб. 20324 = 2 • 4*+ 0 • 42 + 3 • 4і + 2 • 4° = 2 • 64 + 0 + 12 + 2 = 142І0.
Як бачимо, результати однакові.
3. Перевести з однієї системи в іншу:
а) 11І0ІИ0001112->*5; б) 367340І8 -> х2.
Розв'язання. Застосуємо досить простий спосіб переведення з двійкової
системи числення в вісімкову і навпаки (аналогічний спосіб використовують,
коли g-юза і s-кова системи числення пов'язані співвідношенням s = g ).
40

Складемо таблицю виразі ь> цифр вісімковоТ системи числення в двійковій системі
%
»8
2а
За
V
58
%
V
= 0002,
=0012,
= ою2,
= ои2,
= Ю02,
= Ю12,
= по2,
= 1112.
Щоб перевести число з вісімкової системи числення в двійкову, треба кожну
цифру цього числа замінити двійковою тріадою за формулами (1). В свою чергу,
щоб перевести число з двійкової системи числення в вісімкову, треба розбити
це число справа наліво на грані, кожна з яких містить по три цифри (якщо
треба, то останню грань доповнюють до тріади нулями). Потім кожну з
двійкових тріад замінюють вісімковою цифрою за формулами (1).
а) 11101110001112 -^ jc8.
(001) (1Ю) (111) (000) (111)2 = 167078.
б) 36734018 = 0111101110111000000012 = 111101110111000000012-
Задачі
6.1. Записати в десятковій системі числення такі числа
римської нумерації: a) LXIV; б) CLIX; в) DXCVI; r) MCCV;
д) MCDXXIX; e) MDCCCLXXIV.
6.2. Записати в римській нумерації числа: а) 26; б) 112;
в) 1980.
6.3. Записати в десятковій системі числення: а) мільярд,
б) більйон, в) трильйон.
6.4. Обчислити:
а) 1101а -Н 1011а;
б) 1011а - 1101а;
в) 1000110а —11011а;"
г) 10001 la J 1012;
д) 36047 • 4237;
є) 7(10)112. 5(11)73,а;
є) 230547 + 43267;
ж) (10) (11) 792і. + 9534(10),2 + 70(10)0«;
з) 26153? і 3267;
к) 8(10)05(11)^19(10),2-,
л) 1018і32в.
6.5. Обчислити!
а) 11011,101а + 101,011а;
б) 11,001а-1,01а;
в) 111,0І2-101,1012;
г) 0,258-0,438;
д) 2,5.-3,4«.
41

6.6. Обчислитиі
а) 7306» + 25645« — 6774, — 261568;
б) (4256 • 54« — 5316 • 436) і 2456;
в) 2067І8! 1318— 1408;
г) 2321351 325 + 1135 • 35 — 12425;
д) 23201ЦІ 104. + 1234,-322Б— 10221315;
є) (5638 + 217«) • 158 + (23658 — 6368) і 17„ — 15122«;
є) 12011 Із і 102з + 2013- 123— 112203;
ж) 63257 — 456т — 15033571 237 — 5517;
з) 32157 • 247— 114617(257 + 15327— 115044 7;
к) (41238 — 42218) • 118 + (12228 + 7738) і 38;
д) (33334 + 22224) • 12« — (2310204 + 33333334) і 234;
м) і(215» + 532і). 168 —(ПОЗІ, —5278):328]і 147758;
н) [(351 в • 146 — 115361 31в — 150в) і 205,311 256.
6.7. Записати в десятковій системі числення такі числаї
а) 1001112; є) 46027;
б) 11001101а; ж) (10)6(11)і2;
в) 3458; з) 260147;
г) 5071,; к) 421256;
д) 13008; л) 5304156.
є) 333117;
6.8. Записати в десятковій системі числення такі числаї
а) 0,111s; г) 437,3218;
б) 0,110а; Д) 0,0278.
в) 11001, 11112;
6.9. Перевести з однієї системи в іншуі
а) 333117 -> хіа; д) 21066754и -*■ х2;
б) 21000122122з -+*9; є) 206315т -+ х5;
в) 46725109 -*хз; є) 320145-*х8.
г) 11110111011100001а т*х8;
6.10. Перевести з десяткової системи числення в інші системи:
а) 2042-*2, уз, z5; г) 231632 -*хт;
б) 2786 ^х2, уз, гь\ Д) 23163-**,;
в) 729-*дг7; є) 17527 -+*8.
6.11. Знайти х, якщої
а) 201, = 418; є) 541, = 20146;
б) 203, = 5310; є) 364ж = 30014;
в) 106, = 1537; ж) 401, = 2657;
г) 236, = 12405; з) 100, = 347.
д) 324, = 100223;
6.12. Визначити основу системи числення, в якій виконуються
такі рівностії
а) 12+13 = 30; в) 35 + 40 = 115;
б) 15 + 16 = 33; г) 236— 145 = 61;
42

6.13. Довести, що:
а) число 144 є квадратом натурального числа в будь-якій g-ковій
системі числення, g*>4;
б) число 1331 є кубом натурального числа в будь-якій ^-ковій
системі числення, g > 3;
в) в g-ковій системі числення числа 2(g—1) і (g—І)2
записуються тими самими цифрами, але в зворотному порядку;
г) число А = {апап-\.. .ДіЯо)і2 ділиться на 8 (на 9), якщо на 8
(на 9) ділиться число, утворене йсго останніми двома цифрами
(0іяо)і2;
д) число А = {апап—\... 0іяо)й ділиться на g— 1, якщо ап +
+ ап-\ + ... +0і +#о ділиться на g— 1;
є) натуральне число, десятковий запис якого є Зп одиниць,
ділиться на З".
6.14. Записати в двійковій системі числення.'
а) числа Ферма Fk= 22*+1, fcgN;
б) парні досконалі числа D = 2Р~1 (2Р — 1), де р — просте число.
6.15. Знайти частку від ділення числа (62ху427)ю на 99ю, а таксж
невідомі цифри х і у> якщо ділення виконується без остачі.
6.16. Знайти невідсмі цифри, якщо множення виконується в
десятковій системі числення:
а)
*2*3
**
***87
2*004*
б)
шість
х шість
******
******
******
*****шість
6.17. Знайти таке найменше натуральне число т, яке в
десятковій системі числення закінчується цифрою 6, причому, якщо цю
цифру записати на початку числа, то воно збільшиться в 4 рази.
6.18. Число (42л;4#)ю ділиться на 72ю. Знайти цифри х і у.
6.19. У десятковій системі числення знайти тризначне число х
таке, що добуток його цифр дорівнює а і х = а2.
6.20. Довести, що сума цифр квадрата будь-якого натурального
числа не може дорівнювати числу 1985ю.
6.21. Нехай 2 х (xyz)w = (xyz)g. Знайти (xyz)w і g.
6.22. Знайти в десятковій системі числення таке двозначне число»
яке у двійковій, четвірковій і еісімковій системах числення
зображується однаковими цифрами, але різними для різних систем.
43

Розділ II. КІЛЬЦЯ
§ 7. Кільце, підкільце. Найпростіші властивості подільності
в комутативному кільці. Дільники нуля та одиниці.
Асоційовані елементи. Область цілісності, поле
Література
\\] - § 12, с. 132—136;
[2]—§ 12, с. 133—141;
(3] —гл. З, § 4, с. 104—107;
14] —гл. VII, § 3, с. 350-358;
[8]—гл. 4, § 4, с. 172—176;
(24] — § 9, с. 30-32.
ТЕОРЕТИЧНІ ВІДОМОСТІ
Кільцем називається непорожня множина К> в якій визначено дві бінарні
алгебраїчні операції — додавання і множення, причому ва додаванням К є абелева
група — адитивна група кільця К, а операція множення — асоціативна і пов'я*
вана дистрибутивними законами (лівим і правим) в операцією додавання.
Якщо операція множення в кільці К комутативна, то кільце називається
комутативним.
Кільце, яке містить тільки один нульовий елемент, називається нульовим.
Ненульове кільце, в якому є нейтральний елемент відносно множення,
називається кільцем з одиницею.
Комутативне кільце з одиницею, в якому для кожного його ненульового
елемента існує обернений елемент, називається полем.
Елементи а і Ь кільця К називаються дільниками нуля, якщо а Ф 0, Ь Ф0
і ab = 0. При цьому а називають лівим, а Ь — правим дільником нуля.
Ненульове комутативне кільце з одиницею без дільників нуля називається
сбластю цілісності.
Підмножина Кх кільця К називається підкільцем кільця К, якщо К{ є
кільце відносно операцій додавання і множення, визначених у кільці К. Якщо К± e
підкільцем кільця /С, то записують К{ < /С.
Для того щоб непорожня підмножина К{ кільця К була його підкільцем, не*
обхідно і достатньо, щоб сума а-\-Ь, різниця а—Ь і добуток аЬ будь-яких
елементів а і Ь підмножини Кх належали до Кх (критерій підкільця).
Елемент Ь кільця К називається лівим (правим) дільником елемента а £ К,
якщо існує елемент с Є К такий, що а = be (відповідно a-—cb)\ при цьому а
називається правим (лівим) кратним елемента Ь. Якщо К — комутативне кільце, то
елементи b і а називають просто «дільник» і «кратне» і записують а і b (а ділиться
на Ь) або Ь\а (Ь є дільником а). У противному разі записують відповідно а не і b
і b не | а.
Кільце називається числовим, якщо воно є підмножиною множини всіх
комплексних чисел С.
Нехай К—деяке підкільце кільця раціональних чисел Q. Множину всіх
чисел виду a-\-bYpy де a, b £ К і р—деяке натуральне число, що не є точним
квадратом, позначатимемо символом К [}/Гр]1 а множину всіх чисел виду a-\-bYpi—
символом КіУріЬ Зокрема, Z[i] є множина всіх чисел виду а-\-Ьі% де я, b £ Z
і Q [і] — множина всіх чисел виду a+W, де a,b £ Q. Зауважимо, що кільце Z\i]
називають кільцем цілих гауссових чисел.
Елемент а, для якого в кільці К з одиницею існує обернений елемент а-1,
називають оборотним або дільником одиниці. Множина К* всіх дільників одиниці
кільця К з одиницею є мультиплікативною групою. К* називають ще групою
44

дільників одиничного елемента або групою одиниць кільця К. Елементи а і b
області цілісності К називаються асоційованими, якщо а = be, де є — дільник
одиниці. При цьому для асоційованих елементів а і b вживають таке
позначення: а ~ Ь.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Довести, що множина Z [Уз] усіх чисел виду а + б/з, де а І b — цілі
числа, є кільцем відносно звичайних операцій додавання і множення.
Розв'язання. Застосуємо прийом, який дає змогу скоротити процес
доведення. Якщо треба довести, що деяка непорожня множина К{ є кільцем, то
її поміщають (якщо це можливо) в якесь відоме кільце /Є. Тоді треба лише
довести, що Кх є підкільце кільця Ку звідки випливатиме, що К{—кільце.
Оскільки Ziyi}] e підмножиною, наприклад, кільця всіх дійсних чисел R,
то доведемо, що Z [/з]— підкільце кільця R. Застосуємо критерій підкільця.
Насамперед, покажемо, що Z [/з] =£ 0. Це справді так, бо, наприклад, 0 =
= 0 + 0 • /з € Z [Уз]. Нехай тепер t = а + ьУз, s = с + аУз, де a,b,c,d Є Z,
*,s£Z[]/3]. Покажемо, що * + s€Zj/3], / — s £ Z [/з] і / • s g Z ["Кз].
Справді, t ± s^ia + ьУз) ±(с + (іУз) = (а ±с) + (Ь ±(і)Уз^г[Узі
оскільки п ± с £ Zt b ± d 6 Z. Аналогічно для добутку дістаємо t • s = (а+б/з)
(с + аУз) = (ас + 3bd) + (ad + be) /з € Z [Уз], оскільки для цілих чисел
а, Ь, с, d, 3 маємо ас, 3bd, ad, be £ Z.
Отже, Z [/з] — підкільце кільця дійсних чисел R, а тому Z[/3]— кільце.
Зауваження. У цій задачі замість кільця дійсних чисел R можна було б взяти,
наприклад, кільце комплексних чисел С і, взагалі, таке довільне кільце К, що
К > Z [У^З], тобто кільце К не обов'язково повинно бути мінімальним з усіх
тих кілець, які містять підмножину Z[/3].
2. Довести, що в кільці Z\i] цілих гауссових чисел
(23 + 20:(2 + 3/).
Розв'язання. За правилом ділення двох комплексних чисел, записаних
в алгебраїчній формі, маємо
23 + 2/ (23+20(2 — 30 52 — 65/
2 + 3* - (2 + 30(2 — 30 - 13 ~4~5*'
Отже, 23 + 2/ = (2 + 30(4-50, де 4 — 5i£Z[i], а тому (23 + 20 42 + 30-
г з з \ з
3. Довести, що в кільці S = [а + Ь\Г2 + сУї, a,b,c g Z] число — 19 + 101^2 +
з _ / з _ з \
+ 20/4 ділиться на число VI — 31^2 + 5|^4J.
з з _
Розв'язання. Покажемо, що в кільці S існує таке число х + уУ2 + г/4,
що
з 3_/r 3 _ 3 W 3 г \
-19+10/2 + 20/4=11-3/2 + 5/Ш* + ^ + г/4,).
Розкриваючи дужки в правій частині останньої рівності, дістаємо
з з
¢+10^-62) + (-3^ + 4/+102)/2 + (5^-3^ + 2)/4 =
з _ з
= —19+10/2 + 20/4.
Ця рівність можлива тільки тоді, коли х, у, г задовольняють систему рівнянь
х+ 10*/ — 6г = — 19,
— З* + #+10г=10,
.5^ — 3^ + 2 = 20.
45

Розв'язавши цю систему* знаходимо дг=3, у =— 1. г = 2. Оскільки 3 —
з _ з
— /2+21^4 6 5, то
(— 19 + 101/2 + 20/4) Л\ — ЗУ2 + 51/¾).
4. У кільці Z [і) цілих гауссових чисел знайти всі дільники одиниці.
Розв* язання. Оскільки одиничним елементом у кільці Z [і] цілих
гауссових чисел є число 1 +0 • t = 1, то треба знайти всі такі числа х + уі та
г + ti% де х, у,г, і £ 2, що виконується рівність
(* + j0(* + /O = i.
Така рівність можлива, коли | (х+уі) (z-\-ti) | == |1|, тобто коли |*+#і'| |г+#| = 1.
Звідси (х2 + #2) (z2 + і2) = 1. Оскільки х, у, г, t — цілі числа, то остання
рівність можлива при умові х2 + у2 = z2 + t2 = 1. Рівність х2 + у2 = 1 можлива,
в свою чергу, в таких випадках: 1) *=1, #=--0; 2) х =— 1, # = 0; 3) х ■= 0,
# = 1; 4) я = 0, г/ = — 1. Це означає, що *+ #/ (відповідно z+ *0 може мати
лише чотири значення: 1,--1, і, —і. При цьому г-\-іі набуває відповідно
значень: 1, — 1, —/, /. Отже, в кільці Z[i] цілих гауссових чисел є чотири
дільники одиниці: 1,-1, і, — *. Ці елементи і утворюють групу одиниць
кільця Z \і]у тобто
Z\i]*= {1, —1, и — і].
З адач і
7.1. Які з заданих числових множин утворюють кільце відносно
операцій додавання і множину? У кільцях з одиницею знайти всі
дільники одиниці. Визначити пари таких кілець, в яких перше є
підкільцем другого.
<а) Z;
б) ті (множина цілих чисел, кратних m, m(=Z); окремо
розглянути випадки т = 0 і т = 1;
в) Z[—V"2] (множина чисел виду a + b{—1/2), де я, b£Z);
v0 mZ[)/2] (множина чисел виду а + Ь 1/2, де а, Ь £тї)\
д) Z[i] (множина всіх чисел виду а + bi, де a, b£Z);
є) mZ[i] (множина всіх чисел виду а + Ьі, де а, b^mZ)\
Щ Z[]f2i] (множина всіх чисел виду а + b (і 1/2), я, ft £Z);
ж) mZ\V%i] (множина всіх чисел виду а + b (і 1/2), a, b£mZ);
з _ з _
з) Z[]/2] (множина всіх чисел виду а + Ь/2, а, &^Z);
па Z\Yp\ (множина всіх чисел видуа + 6і/р, де a, b£Z,p£ti
і /? не є точним квадратом);
л) Q[|/^2] (множина всіх чисел виду a + b 1/2, де a, fc^Q);
з _ з _
м) Q[l/2] (множина всіх чисел виду a + b "j/2, де a, bgQ);
„,{=
2
a, b — цілі числа однакової парності |
7.2. Довести, що в довільному кільці К\
а) нуль — є елемент єдиний;
б) для будь-якого а£К протилежний елемент — а єдиний;
в) рівняння Ь+х=*а для будь-яких a, b£K має єдиний
розв'язок х = а + (—&);
46

г) якщо а + Ь = а + с, то Ь = с;
д) а-0 = 0-а = 0 для всіх а£К\
є) а (—fc) = (—а) Ь = —аб;
є) а (Ь — c) = ab — ас\
ж) (Ь — с)а = Ьа — са\
з) якщо ах = ауу а Ф 0 і а не є дільником нуля, то х = у;
к) а(—Ь) = (—Ь) а, якщо ab = ba\
л) а-яЬ = /ifc-а, tt^Z, якщо аб = 6а.
7.3. Довести, що:
а) перетин довільного числа підкілець деякого кільця є його
підкільцем;
б) множина К* всіх дільників одиниці кільця К з одиницею
утворює мультиплікативну групу (так звану групу одиниць
кільця К);
в) у кільці, яке містить п елементів, для кожного елемента а
з кільця виконується рівність па = 0;
г) кільце з чотирьох елементів 0, 1, а, & і з правилами дій a2 *=s
= ft, b2 = a, ab = ba= 1, 1 + 1=0, 1 + a = 6 утворює поле;
д) підмножина /Сі = {те\т£1) кільця К з одиницею є утворює
підкільце;
є) непорожня скінченна підмножина К\ кільця К є підкільцем
тоді і тільки тоді, коли (а + Ь)£К\ і ab^Kx для будь-яких
елементів а, Ь^Ки
є) поле не містить дільників нуля;
ж) дільник одиниці кільця з одиницею не може бути дільником
нуля;
з) підкільцем у кільці раціональних чисел Q є множина т-цілих
чисел, тобто всіх таких раціональних чисел, в яких знаменник
взаємно простий з т> m£N;
к) QlVT?] — поле, де pgN не є квадратом натурального числа;
ji)_Z[VJ\ =_Z [Ks~], Z[]Tsi] =_Z[VhH Q~[V~s) = Q [V7X]9
Q[Vsi] = Q[Vs\i]> якщо Ys = t Ys\ і s\ не є квадратом
натурального числа, s, t, S\£N.
7.4. Які із заданих множин матриць утворюють кільце відносно
операцій додавання і множення? Які з кілець комутативні? Які
містять одиницю? Знайти дільники нуля і одиниці. Знайти пари
таких кілець, в яких перше є підкільцем другого.
а) М(п, N) — множина квадратних матриць и-го порядку, еле-
менти яких є натуральні числа;
б) М(п, Z); ж){(* а j L Ь € 3ZJ;
[fa 2,
в) М(/і, Q); з) (^ а
la 2b
\b a
г) М (л, R); к) {^ ~а
А) М (л, С); л) |l ~a
a, &€Q|;
а, 6 Є ZJ;
a, &£2zj;
47

є) М(п, 2Z);
fa 2b
\b a
*>{СГ)Ь"4 *{(» *)
m)
h)
a
—b
a, b€QJ;
a, ft£R
fa —b
\b
(a
\b a)
7.5.- Які із заданих множин матриць утворюють кільце відносно
операцій додавання і множення? Які з кілець комутативні? Які
містять одиницю? У кільцях з одиницею знайти дільники нуля і
одиниці. Знайти пари таких кілець, в яких перше є підкільцем
другого.
nha -3hb\t
\а, b — цілі числа однакової парностіп
а)
б)
в)
г)
Д)
є)
а 0
хка)
a, &€ZJ;
-ЗЬ
а
a, b£Q\;
a, b£z\\
а, & eQ{;
а, ЬШ;
к)
'а
(а
Ф
'а
.0
(а
о
\о
І)
°\
ь)
ь\
«)|
ь
а
0
а,
а,
а,
с%
Ь
а
а9 Ь$1 ;
а, Ь, с£1
7.6. Нехай К — комутативна група відносно додавання. Чи буде
К кільцем, якщо операцію множення введено так»
а) a . b = 0, a, b£K\
б) а - b = a + b, a, b £К\
в) а • b =a — b, a, b £К\
г) а • b = а, а, & £ K\
д) а . Ь =в &, а, Ь g/C?
7.7, Які із заданих множин пар цілих чисел (я, b),a, b £Z
утворюють кільце, якщо операції додавання і множення пар введено'
так (дві пари рівні, якщо рівні їхні однойменні компоненти)!
+ (с9 d) = (асу bd)y
.(Су d) = (a+Cy b + d);
+ (Су d)^(a+Cy b + d)y
-(Су d) = (a + b + c + dy 0);
+ (Су d)=(a+Cy b + d)y
. (Су d) = (0, 0);
+ (Су d) =(a+Cy b + d)y
• (Су d) = (acy bd)\
+ (Су d) = (a + by c + d)y
• (Су d) = (aby cd)\
+ (Су d) = (a + Су b + d)y
• (Су d) = (ac + bdy ad + be);
a) (a,
(a,
6) (a,
(a,
в) (a,
(a,
r) (a,
(a,
Д) (a,
(a,
e) (a,
(a,
b)
b)
b)
b)
b)
b)
b)
b)
b)
b)
b)
b)
48

є) (я, Ь) + (с, d) = (a + cy & + d),
(a, 6)- (c, d) = (ас + 3bd, ad + be);
ж) (я, b) + (c> d) *ш(а + с, b + d),
(я, b) • (су d) = (ac — 3bd9 ad + be)?
Визначити комутативні кільця. Знайти дільники нуля та одиниці.
7.8. Довести, що:
а) скінченна область цілісності є полем;
б) усі елементи виду ab є дільниками нуля в кільці /С, якщо
а — дільник нуля, a b—довільний елемент з К\
в) 4:(1+//3), 4 не : (2 + 2//3) в кільці Z[/3t];
Г) (_8 + 3/5): (1 +2/5) в кільці Z[/B];
Д) (_з + 390: (3 — 5і), 34Ї: (5 + 3/), 25 ? (4 + ЗО, 5 \ (1 + 20,
(8 + 60 не : (7 + 50 в кільці Z\i]\
є) (-7 + 18/3): (4-/3), (5 + 2/3):(4-/3), 13-:(4-/3),
13:(5-2/3) в кільці Z[/3];
є) множина всіх дільників одиниці в кільці Z[/3] складається
з елементів виду ± (2 + /З)", де п£І\
ж) кільце К комутативне, якщо я2 = я для кожного а£К. Чи
справджується це твердження при умові я3 = я?
з) ат *= а для будь-якего елемента а поля Р, яке містить т
елементів.
7.9. Довести, що в області цілісності К:
а) а\ау а^К\
б) а-Су ЯКЩО Я: 6 І &іС, Я, Ь, С([/(;
в) яЬ-с, якщо а і Су я, b, cgK;
г) (a ±b)\Су якщо а • с і й • су я, 6, с£К\
д) (я ± Ь) не; Су якщо я-с і ft не і Су я, Ь, с £ /Є;
є) Оія, flg/C;
є) а-1, а(іК\
ж) я-fee, якщо я- b і б — дільник одиниці, я, Ь, є £/Є;
з) а\Ь і & -а тоді і тільки тоді, коли я = &е, де є — дільник
одиниці, я, by e£Ky афО.
7.10. Які з кілець задач 7.1, 7.4, 7.5, 7.6, 7.7 є областями
цілісності? полями?
7.11. У множині D виразів а + Ьеу де я, 6 ^ R, введемо операції
додавання і множення!
(a + be) + (с + de) = (a + c) + (b + d)ef
(a + be) (с + de) = (ас + bd) + (ad + fee) e.
Довести, що D — комутативне кільце з одиницею і знайти всі
дільники нуля (множина D називається множиною подвійних чисел).
7.12. Нехай у множині Q виразів а + 6г, де я, b g R, введено
операції додавання і множення»
(я + be) + (с + de) = (я + c) + (b + d) є,
(я + Ьв) (с + de) = ac + (ad + fee) є.
Довести, що 2 — комутативне кільце з одиницею і знайти всі
дільники нуля (множина 2 називається множиною дуальних чисел).
49

7.13. У множині К виразів a + bi + cj + dk, де р = p = k2 =¾
= —1,// = fe, ji = —k, ik = —jy ki = j\ jk = i, kj = —iya,b,c,
d£R, введено операції додавання і множення,-
(а і + Ьхі + с\] + dxk) + (а2 + Ь2і + с2\ + d2k) =
= (fli + а2) + (bx + b2) і + (ex + c2) j + (di + d2) k\
(ax + b\i + cxj + dxk) (a2 + b2i + c2j + d2k) = axa2 — bxb2 — c\C2 —
— d{d2 + (a{b2 + bxa2 + d{c2 — Cid2)i + (axc2 + c{a2 —
— b{d2 + d{b2)j + (axd2 + d{a2 + bxc2 — cxb2)k.
Довести, що К — некомутативне кільце з одиницею без дільників
нуля (таку множину називають множиною кватерніонів).
7.14. Довести, що задані множини утворюють область цілісності
(відносно операцій додавання і множення)!
а) множина всіх раціональних чисел виду-у, де m, fegZ, £>0;
б) множина всіх дійсних чисел виду ах2х* + а22х* + . .. + ап2Кп,
де я£ІМ, fli, а2, . .., ап£1> л:ь х2і ..., хп — раціональні числа
виду —, де mt k — цілі невід'ємні числа.
7.15. Нехай М—деяка множина, а 90? — множина всіх підмно-
жин множини М. Довести, що 9Я є кільцем з одиницею, всі
елементи адитивної групи якого мають порядок 2, якщо операції
додавання і множення введено так:
А +В = (А U В)\(А П В), А-В = А (] В9 Л, В£Ж
*'■ 7.16. Довести, що в області цілісності /0
а) відношення асоційованості на множині К є бінарним
відношенням еквівалентності;
б) елементна і b тоді і тільки тоді асоційовані, коли а\Ь \b\a\
в) ax'tbx, якщо а асоційовано з fli, а 6 з &і і alb)
г) елементи 5 + 2 J/3 і 4—j/З асоційовані, якщо /C = Z[Vr3];
д) елементи 25— 17 У2 і 7— V2 асоційовані, якщо К = Z\V2\\
-є) елементи 3 — 71/5 і 113 + 511/5 асоційовані, якщо К =
-Z[l/61;
, є) елементи 7 — 2і і 2 — Ті асоційовані, якщо K = Z\i].
§ 8. Ідеали кільця та операції над ними. Конгруенції і класи
лишків за ідеалом. Фактор-кільце
Література
[1] —§ 13, с 141-147;
12] —§ 13, с. 143-150;
[3] —гл. 13, § 1, с. 430-434;
[8J —гл. 4, § 4, с. 176—183.
50

ТЕОРЕТИЧНІ ВІДОМОСТІ
Непорожня підмножина І кільця К називається лівим (правим) ідеалом
цього кільця, якщо виконуються такі умови:
1) а ± Ь £ /, де а, Ь £ /;
2) ka £ І (ak£l), де а £ /, £ Є Я.
Підмножина / кільця К, яка одночасно є лівим і правим ідеалом,
називається двостороннім ідеалом або ідеалом кільця К.
У комутативному кільці кожен лівий і правий ідеали є двостороннім.
Кожен лівий і правий, а отже, двосторонній ідеал, є підкільцем кільця К.
Одиничним ідеалом кільця К називається кільце К.
Нульовим ідеалом кільця К називається нульове підкільце.
Нехай К — деяке комутативне кільце і а — будь-який його елемент. Множина
елементів виду ха-\-па% де х—будь-який елемент кільця К, а п — будь-яке ціле
число, є ідеал кільця К. Цей ідеал називають головним ідеалом, породженим
елементом а, і позначають <а>. Якщо в кільці К є одиниця, то <а> =Ка =
= {ka, де k^K).
Аналогічно визначають поняття ідеалу, породженого кількома елементами
s s
av а2, .. ., as, комутативного кільця К: <ах, а2, . . ., as> = V х£ас + J] /гуа-,
& /=і
де *, £ A:, tij £ Z.
Множину всіх елементів виду а + Ь, де а £ А, Ь £ В, А> В — ідеали кільця К,
називають сумою Ідеалів Л, В і позначають Л + В.
Множину всіх елементів виду axbx + a2b2 + . . . + anbn, де av a2> ..., ап^А%
bv b2t . . ., bn£By Л, В — ідеали кільця /С, називають добутком ідеалів Л, В і
позначають АВ. Перетин, сума \ добуток ідеалів кільця К є також ідеал
кільця К.
Елементи а і b кільця К називають конгруентними за ідеалом / (за
модулем /), якщо а—b£ І. Це рівносильно тому, що елементи а і b належать тому
самому суміжному класу адитивної групи К за її підгрупою /.
Висловлення «а конгруентно b за ідеалом /» записують так: а = b (mod /).
Якщо /= <£>, то пишуть a = b (mod k).
Відношення конгруентності елементів нз множині деякого кільця К за його
ідеалом / є бінарним відношенням еквівалентності. Класи еквівалентності
називають ще класами лишків кільця К за ідеалом / або суміжними класами групи
К за підгрупою /.
Властивості конгруенцій за ідеалом / в кільці К:
1°. Обидві частини конгруенції можна помножити на будь-яке ціле число;
2°. До обох частин конгруенції можна додати будь-який елемент з кільця К:
3°. Обидві частини конгруенції можна помножити на будь-який елемент
з кільця К;
4°. Конгруенції можна почленно додавати, віднімати і множити;
5° Клас а+/ лишків кільця К за ідеалом / з представником а позначають
так: а = а-\- /, як позначали раніше суміжний клас а + / групи К за її підгрупою
/ з представником а.
Множину всіх класів лишків кільця К за мого ідеалом / позначають К/І = К.
У цій множині алгебраїчними є операції додавання і множення класів лишків:
а + Т> — a + b, a -~b — ab.
Відносно цих операцій множина К утворює кільце, яке називають фактор-кільцем
кільця К за ідеалом /. Фактор-кільце К/І називають ще кільцем класів лишків.
Якщо К = Z, а / — ідеал кільця Z, то / — головний ідеал, породжений деяким
числом m, m £ Z. Фактор-кільце ZlI = Z/<m> позначають Zm.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
І. Нехай Кг — підкільце кільця /(, Т—ідеал кільця К- Довести, що Кх П J —
ідеал кільця Kv
Розв'язання. Введемо позначення D = Кг П І- Покажемо спочатку, що
ідеал /, як і будь-який ідеал, містить нуль-елемент кільця /Є. Справді,
51

оскільки /=£0, то в / Існує хоч один елемент си Тоді, зґідно з першим
пунктом означення ідеалу, елемента — а, тобто 0, теж належить ідеалу /. Оскіль*
ки 0 £ Kv 0 Є /, то 0 € D і тому D + 0.
Якщо a, b £ D, то a, b £ Кі і a, b $ І. Згідно з означенням ідеалу і
критерієм підкільця, а ± b £ /, a ± b £ Кі, а тому а ± b £ D.
Нехай а Є D, b £ /С§1. Покажемо, що ab і £а належать D. Справді, оскільки
D ^ Кіу то a, b £ Кі і за критерієм підкільця Кх маємо, що
ab, ba£ Kv (1)
Оскільки D ^ /, а / — ідеал кільця /Є, то для будь-якого елемента а £ D ^ /
і будь-якого елемента b £ /С2 *= А" маємо, що
а&, £а £ /. (2)
З включень (1) і (2) випливає, що ab, ba £ Кі [] І = D.
Отже, D = Кі [} І — ідеал кільця Kf,
[а Ь\
2. Довести, що в кільці М (2, Z) матриць другого порядку з цілими
\с dj
/° т\
елементами лівий ідеал утворює підмножина Т матриць виду , де пг,
\0 п]
п £ Z.
/0 0\
Розв'язання. Оскільки І € 7\ то Т ф 0. Якщо Л, £ £ 7\ то
й /0 т\ п /0 k\ L , „ ^ , ■ /0 т±А>\
оскільки m ± k, п ± І £ Z. Нехай тепер
X(EM(2, Z) і X-/* Ь\
№ a, b, c, d £ Z і А £Т. Знайдемо добуток
Х.А = (а Ь)(° m) = f° ат+Ьп\
\с dj\0 nj \0 cm + dn)
Оскільки am-j-bn, cm + dn^Z і в матриці X • А на місцях з номерами 11
і 21 стоять нулі, то X • Л £ Т. Отже, Г — лівий ідеал кільця М (2, Z).
Зауваження. Зрозуміло, що Т не є правим ідеалом цього кільця, оскільки
(mc md\
І і тому не завжди А . X £ 7і. Отже, Г не є двостороннім
ідеалом.
3. Побудувати фактор-кільце Z/<6> = Ze кільця цілих чисел Z за головним
ідеалом / = <6>, породженим числом 6. Скласти таблиці додавання і множення
для елементів фактор-кільця. Знайти всі дільники нуля цього фактор-кільця і
обернені елементи.
Розв'язання. Як відомо, фактор-кільце /С/7 довільного кільця К за його
ідеалом / є сукупність суміжних класів б =*=/, х = х-\-1, # = #+/,..., для
яких введено операції додавання і множення:
* + У*=х + у, х*у = ху. (і)
У цьому разі
tf = Z={0, ±1, ±2, ...},
/=<6> = {0, ±6, ±12, ...}.
Тоді
б = 0+<6> = {0, ±6, ±12, ±18, ...},
Т і^/г Я' 7' 13' 19'"-\
52

4-4+<6>=( _2> _8?_14>
5 = 5+<6>={
5, 11, 17, 23, .
-1, -7, -13, .
Побудовані класи лишків 0, 1,2, 3, 4, 5 вичерпують всі класи лишків за
модулем 6. Розглянемо, наприклад, клас лишків 341. Оскільки 341=336 + 5,
а 336 € <6>, __то 341 = 341+ <6> =(5 + 336) + <6> =5 + (336+ <6>) =
= 5+ <6> =5 (використано властивість класів лишків за ідеалом: якщо а £ /,
то а-\-1 = І). Користуючись формулами (1), складемо таблиці додавання і
множення класів лишків —таблиці Келі (табл. 8, 9).
+
0
І
2
3
І
5
б
0
ї
2
3
4
5
Т
І
2
3
4
5
0
2
2
3
4
5
б
Г
Таблиця 8
3
3
4
5
б
Т
2
4
4
5
б
І
2
3
5
5
б
І
2
3
4
X
б
Т
2
3
4
5
0
б
б
б
б
б
б
1
б
т
2
я
4
5
2
б
2
4
б
2
4
Таб
3
б
3
б
3
б
3
л и ця 9
4
б
4
2
б
4
2
5
б
5
4
3
2
І
Для прикладу знайдемо:
4 + 5 = 4 + 5 = 9 = 9 — 6 = 3,
4.5 = 4-5 = 20 = 20 — 6-3 = 20— 18 = 2,
g . 5 = 26 = 25 — 6 . 4 = 25-24 = ї.
За таблицею множення, дільниками нуля є 2, 3, 4, оскільки 2 ф б, З ф б, 4 =£ б",
але 2-3 = 3»2=^4.3 = 0. З цієї самої таблиці маємо І-1 = 1, 5—1 = 5J
оскільки Т • Т = 1, 5 • 5 = 1.
Задачі
8.1. Чи є ідеалами (лівим, правим, двостороннім):
а) перетин, сума і добуток двох ідеалів Іи /2 в довільному
кільці К\
53

б) МНОЖИНа / ВСІХ елементів ВИДУ Г\й\ +/*202 + . . . +Гпап> ДЄ
0і, 02, . . ., ап— деякі елементи підмножини А комутативного
кільця /Є, а ги /*2, . .., гп—деякі елементи з К\
в) множина Ка всіх елементів виду ха, де х — будь-який
елемент кільця К, а — довільний фіксований елемент цього кільця;
г) множина аК всіх елементів виду ах, де х — будь-який елемент
кільця Ку а а — довільний фіксований елемент цього кільця;
' д) множина КаК всіх елементів виду
ххау\ + х2ау2 + .. . + хпауП9
де я —будь-яке натуральне число, Хі і ус — будь-які елементи
кільця К, а — довільний фіксований елемент цього кільця;
є) множина 2Z в кільці Z;
є) множина ті в кільці Z;
* ж) множина 2Z[|/3] в кільці Z[]/3];
з) множина 3Z\i] в кільці Z[i]\
. к) множина пК = [nx \ x £ K) в /Є, де х — довільний елемент
кільця К> п — фіксоване ціле число;
л) множина таких функцій g(x)y що g-(l/3) = 0 в кільці
неперервних функцій на відрізку [—1; 1]?
8.2. Чи є ідеалами такі підмножини:
\(т п\\
п в кільці М (2, Z), якщо т, п£І\
а) множина
б) множина
в) множина
г) множина
д) множина
є) множина
і є) множина
ж) множина
з) множина
'0 0
)| в кільці М{2, Z), якщо т, п£І\
| в кільці М (2, Z), якщо т, n£Z;
а £1} в кільці
flfZ в кільці М (2, Z);
0, &(jz[ в кільці М(2У Z);
rf, e^Z
0, 6 £Z
в кільці
'а
0
,0
&
0
0
су
Ь
а,
a, b,c£Z ;
a, b, c£Z
в кільці М (З, Z);
0^Z
в кільці М (З, Z)?
8.3. Довести, що:
а) непорожня підмножина / кільця К є його правим ідеалом
тоді і тільки тоді, коли / — підкільце кільця К, причому І-К<1}
54

б) непорожня підмножина / кільця К є його правим ідеалом
тоді і тільки тоді, коли / — така підгрупа адитивної групи кільця /С,
що І * Ksl\
в) в кільці цілих чисел Z кожен його ідеал головний;
г) відношення конгруентності за ідеалом для елементів кільця
К є бінарним відношенням еквівалентності;
д) а Є (а + /) для будь-якого елемента а кільця К і його ідеалу /;
є) І-\-х = І тоді і тільки тоді, коли х£І, де / — ідеал кільця
/С, а х —елемент з К\
є) / +x= I + d, I+y = I+d9 якщо d£(I + x) (] (I + у), де
/ — ідеал, а х, у, d — представники класів лишків;
ж)І + х[}І + у=0, якщо І + хф І + уу де / — ідеал кільця
/С, а х, у — представники класів лишків;
з) підмножина {х\хт = 0, х£К, т£1) є ідеал кільця /С;
к) аК = К, якщо а—дільник одиниці комутативного кільця К
з одиницею, і навпаки, якщо а такий елемент комутативного кільця
/С, що аК = К, то К — кільце з одиницею і а — дільник одиниці.
8.4. Довести, що в комутативному кільці К з одиницею:
-' а) а£<а>, а$К\
б) <0> = {0}, <1> = /(;
в) Ь — с£<а>, якщо by c£<a>\
г) rb£<a>, якщо b£<a>, де г£К\
д) а\Ь тоді і тільки тоді, коли <a>f£<fc>, де a, b£K\
є) асоційовані елементи кільця К породжують той самий
головний ідеал;
є) головний ідеал, породжений дільником є одиниці 1 кільця /С,
збігається з /(, тобто <е> *= <1> =К;
ж) головні ідеали, породжені елементами а і 6, збігаються тоді
І тільки тоді, коли а і b — асоційовані елементи і /С — область
цілісності;
з) у К всі ідеали головні, якщо К — поле, причому в К лише
два ідеали* нульовий і одиничний;
к) мінімальний ідеал 1(A) кільця /С, який містить підмножину
А цього кільця, збігається з ідеалом <Л>, породженим підмно-
жиною Л.
8.5. У кільці цілих чисел Z виконати такі дії над його ідеаламиї
а) <2> + <3>; є) <4> + <10>;
б) <2> П <3>; ж) <4> П <Ю>;
в) <2> • <3>; з) <4> . <10>;
г) <3> + <6>; - к) <5> + <7>;
д) <3> П <6>; * л) <5> П <7>;
є) <3> - <6>; м) <5> • <7>.
8.6. Довести, що в довільному кільці К для будь-якого ідеалу /і
а) <0>+/ = /; д) *П / = Л
б) <0> П / = <0>; є) /С •/£./,
в) <0> ./ = <0>;
г) К + І = /С;
причому /(./ = /, якщо К — кільце з одиницею.
65

8.7. Довести, що:
а) <2-V3>=Z\V3];
б) <2 + V$>=Z[V5k
в) <3 + ]/7>=d<13 + 5]/7> в Z[V7];
г) <8-3]/7>=Z[/7];
Д) <i> = Z[i];
є) <2i>=-2ZW;
є) <—3> = 3Z[/];
ж) <3 + 4/> = <4 - 3/> в Z [/].
8.8. У кільці цілих чисел Z знайти ідеали:
а) <2, 5>; д) <2, 4, 6>;
б) <4, 6>; є) <2, 3, 5>;
в) <6, 15>; є) <4, 6, 8>.
г) <-1, 3>;
8.9. Нехай / — ідеал кільця К і a = b(modI), a, b£K.
Довести, що:
а) а + с= b + c(modI), c£K\
б) a + c^b+ d(modI), якщо c==d(mod/), с, d£/(;
В) —а**—Ь(т6йІ);
г) ma = mb (mod /), m£Z;
д) ас = be (mod/), c^K;
є) ас== bd(mod/), якщо c = d(mod/), с, dg/C;
є) a*=sfc"(mod/), n£N.
8.10. Довести, що в кільці цілих чисел Z при т > 1 а == 6 (modm)
тоді і тільки тоді, коли (а—Ь) • т. Що означає a==b(mod0)?
8.11. Побудувати фактор-кільця Zi, Z3, Z4, Z5. Скласти для їхніх
елементів таблиці доДабання і множення. Знайти всі дільники нуля
і обернені елементи.
8.12. Які з фактор-кілець Z2, Z3, Z4, Z6 є полями?
8.13. Довести, що:
а) Zm — поле, якщо т — просте число;
б) Zm — кільце з дільниками нуля, якщо т — складене число;
в) кільце /(, яке містить принаймні два елементи, є полем тоді
і тільки тоді, коли в К немає ідеалів, крім <0> і К.
8.14. Знайти всі дільники нуля у фактор-кільці Zm, якщо:
а) т = 8; б) т = 9; в) т = 10; г) т= 12;
д) т = 14; є) т = 15; є) m = 16.
8.15. Знайти обернені елементи для елементів фактор-кільця Zm,
ЯКЩО!
а) т = 7; б) m = 8; в) т = 9;
г)т—10; д)т=11; е)т=12;
є) т = 13; ж) т = 14; з) т = 15; к) т = 16.
8.16. У кільці цілих гауссових чисел Z[i] побудувати фактор-
кільце Z[i]/<m>. Скласти для елементів фактор-кільця таблиці
додавання і множення, знайти всі дільники нуля і обернені
елементи, якщо:
a) т = 2; б) т = 3; в) т = 2і\
г) m = —3/; д) m = і".
56

8.17. У фактор-кільці Z[i]/<m> кільця цілих гауссових чисел
Z [і] за ідеалом <т>, породженим елементом т, знайти кількість
елементів, усі дільники нуля і елементи а~\ якщої
а) т = 4, ~а = ~і\ 1і\ 1 +2і;
б) т = 5, а = 2; 4і; 3 +_2^_
в) т = 6і, а = 2 + 5і; 4 + *.
8.18. Побудувати фактор-кільце Z[1^3)/21 [У3] кільця Z[V3]
за його ідеалом 2Z[|/3]. Скласти для елементів фактор-кільця
таблиці додавання і множення, знайти всі дільники нуля і обернені
елементи.
8.19. Довести, що фактор-кільце К/І кільця К з одиницею за
будь-яким його ідеалом / містить також одиничний елемент.
§ 9. Гомоморфізми та ізоморфізми кілець.
Теорема про гомоморфізми кілець
Література
[!]_§ із, с. 147—150;
[2] —§ 13, с. 150-153;
[3] —гл. 13, § 1, с. 434-437;
[4] —гл. VII, $ 4, с. 360-362;
[8] —гл. 4, § 4, с. 178—183.
ТЕОРЕТИЧНІ ВІДОМОСТІ
Однозначним (взаємно однозначним) відображенням множини А на множину
В називається таке відображення ер, при якому:
1) кожен елемент а з множини А відображується на єдиний елемент Ь з
множини В; при цьому кажуть, що Ь — образ елемента а, а а — прообраз елемента
Ь, і пишуть ер (a) =¾ Ь\
2) кожен елемент Ь з множини В € образом хоч одного (єдиного) елемента
а з А.
Існують ще однозначні і взаємно однозначні відображення з множини в
множину, з множини на множину, множини в множину.
Ми користуватимемося в основному відображенням всієї першої множини на всю
другу множину.
Однозначне (взаємно однозначне) відображення ер кільця К на кільце /Cf
називається гомоморфним (ізоморфним) відображенням, якщо виконуються такі
дві умови:
1) образ суми довільних двох елементів а і Ь з кільця дорівнює сумі їхніх
образів: ер (а + Ь) — ер (а) + ер (Ь);
2) образ добутку довільних двох елементів а і b з кільця К дорівнює добутку
їхніх образів: ер (а • Ь) = ер (а) • ер (Ь).
Якщо «р — гомоморфізм кільця К на кільце Kv то ер є епіморфізм кільця К.
У цьому разі кажуть, що Кх є гомоморфним образом кільця /С, і пишуть
К « /Сі або ер: К « /^.
Якщо /С ізоморфно відображується на /Сі, то пишуть
К s /Сі або ер: /С з /С*.
Будь-яке ізоморфне відображення є одночасно і гомоморфним відображенням,
але не завжди навпаки.
Властивості гомоморфних (ізоморфних) відображень кільця К на кільце Кх такі:
1Q. Образом нульового елемента першого кільця є нульовий елемент другого
кільця: ер(0) = 0±;
67

2°. Образом ер (—а) елемента — я, протилежного даному елементу а, є
елемент —- ер (д), протилежний образу ер (а), тобто <р (—а) = — ер (а);
3°. Якщо в кільці К є одиничний елемент є, то його образ ер (є) € одиничний
елемент кільця Кг\ якщо в кільці К для елемента а існує обернений елемент а~{,
то ер fa""1) є оберненим елементом до елемента ер (а) в кільці Кл.
Нехай ? є гомоморфне відображення , кільця К на кільце /Є*. Множину D всіх
елементів кільця /С, які гомоморфізмом ер відображуються в Ох кільця /Cj,
називають ядром гомоморфізму ер і позначають так: D = Кег ер. Отже, Кег ер ={d j\d £ К>
Ядро D = Kerep будь-якого гомоморфізму ¥ кільця К на кільце /С^ є
ідеалом кільця К.
Теорема про гомоморфізми кілець. Фактор-кільце К І Кег ер кільця К ва ядром
Кег ер гомоморфізму К ^ Kt ізоморфне кільцю Kv тобто КІ Кег-f = /Сі.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Встановити гомоморфне відображення довільного кільця К на фактор-кільце
^ = /(// кільця К за будь-яким його ідеалом /.
Розв'язання. Задамо відображення ер множини К на множину Ж так:
ер (а) = а, тобто ер (а) = а+ /, де а £ #. Інакше кажучи, кожному елементу а
з кільця К поставимо у відповідність клас лишків а з кільця К з
представником а. Тоді ер є однозначним відображенням всього кільця К на все кільце
'R. Справді, якщо 5"£ /С, то 6 = 6 + /, де Ь £ К і тому ер (6) = Ь, Покажемо,
що ер (a + fc) =* «р (а) + ер (6) і ер (а • 6) = ер (а) • ер (6) для довільних елементів а,
6 Є /Є. Знаходимо:
ер (a -f 6) ==а+ 6, і ер (а) + ер (6) = а + 6.
Оскільки а + 6 = а +_£, _то ер (a -f b) ■— ер (а) + ер_(£). Далі маємо: ер (a b) =
= а~£ і ер (а) . ер (Ь) = а • 6. Оскільки а - b = а • Ьу то ер (а . 6) = ер (а) . ер (6).
Отже, ер є гомоморфним відображенням кільця К на кільце /0 Його називають
природним гомоморфізмом кільця К на фактор-кільце /(//.
Зауваження. Якщо / ф {0}, то ер не є ізоморфізмом.
2. Встановити гомоморфне відображення ер кільця цілих чисел Z на кільце Г
і побудувати фактор-кільце Z / Кег ер кільця Z за ядром Кег ер гомоморфізму <р»
якщоГ={0, є], а операції додавання і множення в Т задано табл. 10, 11.
Таблиця 10 Таблиця 11
+
0
є
0
0
є
є 1
є 1
в 1
X
0
є
0
0
0
є
0
б 1
Розв'язання. Згідно з таблицями, елемент 0 — нульовий, а є — одиничний
елемент кільця Т. Задамо відображення ер кільця Z на кільце Т так:
Ф^)=Л8, якщо z паРне;
Y v ' \е, якщо г непарне, де z £ Z.
Зрозуміло, що ер — однозначне відображення всієї множини Z на всю
множину Т. Покажемо, що ер (г + /) == ер (г) -)- ер (^) і ер (г • t) = ер (г) . ер (/) для
довільних Z, / £ Z.
З точністю до позначень можливі три випадки: 1) г і і — парні; 2) z і t —
непарні; 3) z— парне, t — непарне. Розглянемо кожен з них.
1) Якщо z і t парні, то ер (z) = cp (t) = 0. Тоді ер (z) + ер (/) = ер (г) • ер (/) = 0.
Оскільки г+/, z-/ —парні, то ер (г + /) = ер (г • Q = 0. Отже, ер (г + 0 =
= ?(*) + *(') і *<*-0 = *(*)-?(0г
58

2) якщо г і / непарні, то ер (?) = ер (t) = є, <р (г).+ <р (/) = є + є = 6 і <р (г) • <р(0 =
= є . є = є. Оскільки г~М— парне, а г«/ непарне, то <р (z +/) — 0,
щ (2 • /) = Є. ТОДІ ЗНОВУ ер (2 + 0 = <р (г) + ер (/) І ер (2 • 0 = cp (z) . cp (/);
3) якщо 2 парне, а / непарне, то cp (z) -■= 0, cp (*) = є. Тоді ер (г) + ер (/) =
= 0 + є = є, ер (г) . ер (/) = 8 • є = 0. Оскільки z + t непарне, a z • / парне, то
ер (2 + 0 = Є, ер (2 . О = 0 і ТОМУ ер (2 + 0 = ер (2) + ер (*) і ер (2 • /) = ер (z) . ер ¢).
Отже, ер є гомоморфне відображення кільця /С на кільце 7і. Із задання
відображення ер випливає, що Кег ер = 2Z. Тоді Z/Кег <р =Z/2Z = {0, ~1}, де
0 = 2Z= {0, ±2, ±4,...},
Очевидно, що Z / 2Z s Г. Це досягається за допомогою нового відображення
Ф : ф (0) = 6, ф(1)=в.
Зауваження. На практиці не завжди вдається відразу вдало підібрати
відображення ер. Його треба задавати таким чином, щоб задовольнялися вже перші
загальновідомі ознаки. Так, у розглянутому прикладі не можна покласти ер (г) = є
при парному г, бо тоді б нульовий елемент першого кільця перейшов би в
одиничний елемент другого кільця, що суперечить теорії і т. д.
Задачі
9.1. Довести, що:
а) відображення y(a + bi) =a+bi і ty{a+bi) =а — Ьі
вичерпують усі ізоморфні відображення поля комплексних чисел С на
себе; _
б) відображеннями <?(а + Ь\Ґ2) =а +b |/"2~ і ф (a + b j/T) =
= а — b \Ґ2 вичерпуються всі ізоморфізми поля Q[\r2] на себе,
при яких у(х) = х і ф(л;) = л; для довільного x£Q\
в) гомоморфізм двох кілець є їхнім ізоморфізмом тоді і тільки
тоді, коли ядро цього гомоморфізму збігається з нульовим
елементом першого кільця;
г) гомоморфний образ області цілісності є кільцем, але не
завжди є областю цілісності;
д) кільця Z\Vl\ і Z[KllJ не ізоморфні між собою.
9.2. Довести, що при гомоморфізмі ф двох кілець К і К\і
а) ср(0) =0,;
б) ф(—а) = — ф(а);
в) ф(а-&)=ф(а)-ф(6);
г) ф(в)=еі (якщо в К існує одиниця е)\
д) ер (а-1) = [ер (а)]-1 (якщо в К для а існує обернений елемент а-1);
є) ядро гомоморфізму Кег ф є ідеалом кільця К.
9.3. Які можливі гомоморфізми поля Р на поле Рі?
9.4. Довести, що ненульове комутативне кільце К з одиницею є
полем тоді і тільки тоді, коли довільний гомоморфізм кільця К на
ненульове кільце є ізоморфізмом.
9.5. Довести, що ізоморфними між собою є такі кільця:
а) Z[V2] і
б) 2Z [КЗ] і
а
2b a
а ЗЬ
b a
a, b£Z
a, b£2Z
59

а, Ь — цілі числа однакової парності | 1
а, Ь — цілі числа однакової
парності
я, b£Q .
(а —36
9.6. Нехай ер — відображення кільця К
(а Ь
a, b£l\ на
кільце Z цілих чисел, причому <р
Ь а
а Ь\
Ь а)
= а — Ь. Довести, що <р —
гомоморфізм, і знайти його ядро.
9.7. Нехай ер — від^ажейня кільця цілих чисел Z на кільце
класів лишків Zz = {б, 1, 2}, причому
( б, якщо z ділиться на 3;
vp (з:) = | Т, якщо z при діленні на 3 дає остачу 1;
І 2, якщо z при діленні на 3 дає остачу 2.
Довести, щр ? є гомоморфізм, і знайти його ядро.
9.8. Нехай ер — відображення кільця діагональних матриць
К= U J\ a> b£Q\ на кільце раціональних чисел Q, причому
ер М ))==61 Для будь-яких я, bgQ. Довести, що ер — гомоморфізм,
і знайти його ядро.
9.9. Нехай ф — відображення кільця К всіх неперервних
функцій на відрізку [—1; 2] на кільце дійсних чисел R, причому
ф(^)=[(1) для будь-якої функції f^K. Довести, що ф —
гомоморфізм, і знайти його ядро.
9.10. Нехай М і М\ — множини з бінарними операціями
додавання і множення. Довести, що Мі є кільце, якщо М є кільце,
і існує гомоморфне відображення множини М на М\.
60

a, ft, c, d£R
9.11. Довести, що:
а) будь-який ідеал / кільця К є ядром гомоморфізму при
відображенні кільця К на фактор-кільце К/І\
б) підмножина / кільця К є ядром гомоморфізму цього кільця
на деяке кільце К\ тоді і тільки тоді, коли / є ідеалом кільця К\
в) будь-яке кільце, гомоморфне кільцю /(, ізоморфне деякому
фактор-кільцю цього кільця.
9.12. Знайти (з точністю до ізоморфізму) всі скінченні кільця
з чотирьох елементів, які містять Oil.
9.13. Знайти (з точністю до ізоморфізму) всі скінченні кільця,
які містять pq елементів, де р і q — різні прості числа.
9.14. Довести, що довільне кільце, яке містить просте число
р елементів, або ізоморфне полю класів лишків Zp, або ізоморфне
адитивній групі лишків з нульовим множенням.
9.15. Довести, що кільце матриць
( a + bi c + di\
\—с + di a — bij
ізоморфне кільцю кватерніонів a+bl+cj+dk над полем дійсних
чисел (див. задачу 7.13).
9.16. Довести, що:
а) Z4/2Z4 ^ Z2;
б) Z6/2Z6 ^ Z2;
в) Z6/3Z6^Z3;
г) Z8/4Z8<sZ4;
д) ZmlnZms&Zn, якщо я, /л£ N і т \ п\
є) [QV7]^Q[VTt].
§ 10. Характеристика кільця з одиницею. Поле часток
області цілісності. Прості та складені елементи
області цілісності. Арифметика кільця головних
ідеалів та евклідового кільця
Література
[1]—§ 12, с. 136-141, § 13, с. 150—153, § 14, с. 153—155;
[2] —§ 12, с. 137—143, § 13, с. 153 — 156, § 14, с. 156-188;
[3J —гл. 13, § 2, с. 439—445, § 3, с. 445—448.
ТЕОРЕТИЧНІ ВІДОМОСТІ
Характеристикою кільця К з одиницею є називають число 0, якщо пе =* 0
тільки при п = 0; характеристикою кільця К називають натуральне число р,
якщо ре = 0 і немає такого натурального числа т < /?, що те = 0.
Характеристика будь-якого числового кільця дорівнює нулю. Кожне
натуральне число п є характеристикою деякого кільця з одиницею, наприклад, п
є характеристикою кільця класів лишків Zn.
Якщо ^С — кільце характеристики п, то для будь-якого елемента а £ К маємо
па = 0.
Характеристикою області цілісності (характеристикою будь-якого поля)
є або нуль, або просте число.
Якщо К — область цілісності характеристики 0, то па Ф 0 для будь-якого
ненульового злемента а £ К і будь-якого ЦіЛоГб числа п £ Z, п ф 0.
61

Для кожної області цілісності К існує поле 7\ що містить як иідкільце
область цілісності К. При цьому кожен елемент поля Т дорівнює частці
деяких двох елементів області цілісності К. Поле Т називають полем часток або
полем відношень області цілісності К. Будь-які два поля часток Т і Тх тієї
самої області цілісності К ізоморфні між собою: Т = Т{.
Поле часток кільця цілих чисел Z є полем раціональних чисел Q.
Запис а ~ Ь означає, що елементи а І Ь кільця К з одиницею асоційовані.
Елемент а області цілісності К називають простим або нерозкладним, не-
звідним, якщо:
1) а ф 0;
2) а не є дільником одиниці;
3) а, крім дільників одиниці і асоційованих ним, ніяких інших дільників
не має.
Елемент а області цілісності К називається складеним або розкладним,
звідним, якщо а, крім дільників одиниці та асоційованих з ним, має ще хоча б один
дільник.
Будь-який елемент Ь області цілісності К, асоційований з простим
елементом а, також простий.
Елемент с області цілісності К називають спільним дільником елементів
ov а2, . . ., ап, якщо кожен з цих елементів ділиться на с. Найбільшим
спільним дільником елементів ар а2, • • •» ап називають такий спільний дільник цих
елементів, який ділиться на будь-який інший їхній спільний дільник.
Найбільший спільний дільник елементів а{, а2, ..., ап позначається
символом (ар а2, . . ., ап) і визначається з точністю до множника, що є дільником
одиниці.
Елементи а і b області цілісності К називають взаємно простими, якщо
вони не мають спільних дільників, відмінних від дільників одиниці, тобто якщо
(а, Ь)=\.
Якщо а—будь-який, a p —простий елемент області цілісності /С, то (а,
р) = 1 або р.
Ідеал /j комутативного з одиницею кільця К ділиться на ідеал /2 цього ж
кільця, якщо /tcz /p.
Відношення подільності ідеалів транзитивне і рефлексивне.
Ідеал / комутативного^ з о диницеюе кільця К називається найбільшим
спільним дільником ідеалів /j і /2 цього кільця, якщо:
а) / є дільником 1Х і /2;
б) / ділиться на будь-який спільний дільник 1Х і /2.
Будь-які два ідеали /|.і /2 комутативного кільця з одиницею К мають
найбільший спільний дільник, яким є ідеал, породжений множиною /j (J /2, тобто
найменший ідеал, який містить ідеали І{ і /2.
Найбільший спільний дільник головних ідеалів <а> і <Ь> комутативного
кільця з одиницею К складається з елементів виду ra-\-sU де г, s £ К.
Найменшим спільним кратним ідеалів /j і /2 комутативного кільця з
одиницею К називають такий ід^ал / цього кільця, що / • /t і / • /2 і будь-який
ідеал, кратний І{ і /2, ділиться на /-.
Найменшим спільним кратним ідеалів /j і /2 є їх перетин /j f) /2.
Об'єднання зростаючого ряду lx rz /2 с , •. c In cz .. . ідеалів кільця К
є ідеалом цього кільця.
Область цілісності, в якій кожен ідеал головний, називається кільцем
головних ідеалів.
У кільці головних ідеалів К виконуються такі властивості:
1°. Будь-який набір елементів а{, а2, . . ., ап кільця К має найбільший
спільний дільник d, причому d = /г1а1 + k2a2 + . .. + knan, де kv k2, . .., kn £ K;
2°. Будь-які два найбільші спільні дільники елементів av а2, .. ., ап кільця
К асоційовані в К\
62

3°. d = (av a2, ..., ап) тоді і тільки тоді, коли <яг д2, . . ., ал> =
= <d>, av а2, . . ., any d £ К\
і a b \
4°. Якщо d = (а, Ь) і d =£ 0, то І-j, -j J = 1, де a, b% d £ К\
5°. Елементи а і 6 кільця К взаємно прості тоді і тільки тоді, коли в
кільці /С є такі елементи т і s, що та-\- sb = 1;
6°. Якщо а, Ь, с£ К і (a, &) = (а, с) = 1, то (а, &, с) = 1;
7°. Якщо а, Ь, с £ К, ab \ сі (а, с) = 1, то b ] с;
8°. Якщо а, Ь, с £ К% а \ Ь, а \ с і (Ь, с) = 1, то a • to;
9°. Якщо р—-простий елемент кільця /С, то фактор-кільце КІ<р> є поле;
10°. Якщо добуток кількох елементів кільця К ділиться на простий
елемент р £ К, то, принаймні, один із множників ділиться на р;
11°. У кільці К не існує нескінченної строго зростаючої послідовності
ідеалів;
12°. У кільці К кожен відмінний від нуля елемент, що не є дільником
одиниці, розкладається в добуток простих множників;
13°. Якщо а = р{р2 ... рг і a = q{q2 . . . qs e два розклади елемента а
кільця К в добутки простих множників, то r — s, і при відповідній нумерації
множників справджуються рівності qt = p{e{, і == 1, 2, ..., г, де ^ — деякий дільник
одиниці кільця К.
Елемент с називають спільним кратним елементів а{, а2, . . ., ап кільця
головних ідеалів К, якщо с ділиться в К на кожен з цих елементів.
Найменшим спільним кратним елементів а{1 av ..., an кільця головних
ідеалів К називають таке їхнє спільне кратне, на яке ділиться будь-яке спільне
кратне цих елементів. Найменше спільне кратне елементів а{а2, ..., ап
позначають [ар а2, • • •» °п].
Будь-які два найменших спільних кратних елементів а{1 а2, ..., ап кільця
головних ідеалів К асоційовані в К.
Якщо К — кільце головних ідеалів, то т=[ар а2, . .., ап] тоді і тільки
тоді, коли <а1>П<а2>п ••• П <<*„>=</я >, av а2, ..., an £ К,
md К.
Для будь-якого набору av а2, . . ., ап елементів кільця головних ідеалів К
існує найменше спільне кратне.
Якщо К — кільце головних ідеалів, то [act be] ~ c [a, b] для будь-яких
елементів а, b, c £ К>
Якщо а, Ь — ненульові елементи кільця головних ідеалів /Є, то
ab
Область цілісності К називають евклідовим кільцем, якщо існує
відображення ер множини відмінних від 0 елементів цієї області цілісності в множину
цілих невід'ємних чисел №, тобто Я"\{0}-»-№, яке задовольняє таку умову:
для будь-яких елементів a, b £ К, b =£0 в К існують такі елементи q і г, що
a = bq + r, причому г « 0 або у (г) < у (Ь).
Число ер (а) називають ще нормою елемента а.
Кожне евклідове кільце є кільцем головних ідеалів.
Кільце К називають факторіальним, якщо воно є областю цілісності і будь-
який елемент кільця, відмінний від нуля і дільників одиниці, однозначно (з
точністю до дільників одиниці і порядку множників) розкладається на добуток
простих множників.
Кільця головних ідеалів і евклідові кільця факторіальні.
Нехай а = ир\'р\г. . . /?^m, b = vp{lp22 . . . ртт, де pv pv .. ., pm — попарно
різні прості елементи факторіального кільця /Є, и, v — дільники одиниці цього
кільця. Тоді [a, b] = p]lp]2 . . . p^m, де
ТГ, = max {а., р,}, (а, Ь) = р{хр2 . . . ртт,
де 5t. = тіп [alt ^.}, 1 = 1,2,.. ., т.
63

ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Довести, що характеристикою області цілісності в або нуль, або просте
число.
Розв'язання. Нехай К — область цілісності, а є — одиниця кільця К.
Якщо те ф 0 для жодного натурального числа т\ то характеристика кільця
К дорівнює нулю.
Нехай тепер те «=-- 0 і т найменше натуральне число, що має цю властивість,
тобто т — характеристика кільця /Є. Тоді т Ф 1, оскільки є Ф 0. Якщо т
просте число, то твердження задачі доведено.
Нехай т складене число. Тоді існують натуральні числам і і такі, що 1 < s,
t < т і m — st. Внаслідок комутативноеті кільця К маємо
0 = me = (5/) e = (se) (te).
Крім того, оскільки т — характеристика кільця К і s < m, t < m, то se Ф 0,
te ф С і тому (se) • (te) = me Ф 0, бо /Є, як область цілісності, є кільцем без
дільників нуля. Отже, прийшли до суперечності.
2. У кільці цілих гуассових чисел Z [і] знайти найбільшим спільний дільник
чисел 6 — Пі та 18 + і.
Розв'язання. Алгоритм Евкліда для знаходження найбільшого спільного
дільника деох цілих гауссових чисел такий самий, як і відповідний алгоритм
для цілих чисел, тільки замість порівняння абсолютних величин виконується
порівняння норм. Нагадаємо, що нормою цілого гауссового числа г, г=а +
+ Ьі, а, Ь £ Z називається число а + Ь , яке позначають Nrz. Очевидно, що
Nrz = | г |2 = z • г, де | z | — модуль, а г — спряжене до а. Остання, відмінна
від нуля, остача в алгоритмі Евкліда і є найбільшим спільним дільником
заданих чисел.
Застосуємо алгоритм Евкліда до чисел 6— Пі та 18 + (.
Оскільки Nr(6—17(') = Nr(18 + (') = 325, т° 6—17/ ділимо з остачею на
18 + і. Використовуємо правило ділення комплексних чисел в алгебраїчній
формі:
6 — Пі (6 — 17t)(18 — 0 91—312*
18 +і = (18 + 0(18 — 0 = 325 *
Зрозуміло, що Nr(91—312Q > Nr (325), оскільки 912 +3122 > 3252.
Виділимо тоді цілу частину так, щоб у дробу, який залишається, норма
чисельника була строго менша норми знаменника. Дістанемо
91 — 312t 91+ 13/-325/ -325(
325 = ~Ш = 325 +
91 + 13( _ 91 + 13*
+ 325 = -' + ЩГ~"•
Тут Nr(9l + 130 < Nr(325), бо 9І2 + ІЗ2 < 3252. Тоді
6 — 17* 91+ 13і
18 + / = ~~* + 325 '
Звідси
6_17ї = (18 + 0(-0 + (5 + 0, «
причому
Nr (б + і) < Nr (18 + 0 і 5 + і — перша остача.
Оскільки Nr (18 + ().> Nr (5 + і), то
18 + t 91-13( 7 — і
5 + ( ~" 26 = 2 *
Внаслідок того що Nr (7 — (') > Nr (2), можна виділити цілу частину:
7-і 6 + 1 — і 1-і
—2~ = § = 3 + -2-.
64

Тут Nr (1—0 < Nr (2), бо І2 + І2 < 22. Тоді
18 + і п 1-і
Звідси
18 + і = (5 + 0 • З + (3 — 2t), (2)
Іг (5 + і) і 3 — 2і є
5 + і ділимо на З
5+/ 13+ J3t
причому Nr (3 — 2/) < Nr (5 + 0 і 3 — 2і є друга остача. Оскільки Nr (5 + 0 >
> Nr (3 — 20, то число 5 + і ділимо на 3 — 2/ з остачею:
• 2/ - 13
= 1 + /.
Отже, 5 + і = (3 — 20 (1 + 0 + 0> і т°му третя остача дорівнює нулю.
Згідно з алгоритмом Евкліда, найбільший спільний дільник чисел 6— 17/ та
18 + і дорівнює останній відмінній від нуля остачі в алгоритмі послідовного
ділення з остачею, тобто
(6— 17/, 18 + 0 ~ 3 — 2/
(тут поставлено знак асоційованості, бо найбільшим спільним дільником
чисел 6 — 17/ та 18 + / є також числа (3 — 20 (—1) = — 3 + 2/, (3 — 20 / = 2 +
+ 3/, (3 — 20 (—0 = —2 — 3/, тобто всі числа, асоційовані з числом 3 — %
в Z [/]).
Зауваження
1. Якщо задано два цілих гауссових числа гх і г2 і Nr^j)> Nr(z2), то
ділення з остачею можна виконувати не за правилом ділення комплексних чисел
в алгебраїчній формі, а за тим самим прийомом, який застосовували до виді-
а+ Ьі
лення цілої частини з дробу виду —-—, де a, b, c £ Z. Наприклад, для чисел
18 + / і 5 + і маємо
18 + / 15 + 3/ + 3 — 2/ _ 3—2/
5 + / = 5 + ї =3+ 5 + /
і тому 18 + і = (5 + /) • 3 + (3 — 2/). Тут процес ділення з остачею коротший.
Проте, оскільки це не завжди можливо, то краще для всіх г2 6 Z і Nr (г{) >
> Nr (z2) ділення виконувати так, як у прикладі 2.
2. На закінчення розв'язання треба зробити перевірку. Слід, наприклад,
перевірити, чи діляться задані числа на знайдений найбільший спільний дільник.
Маємо
6 — 17/ = (3 — 2/) (4 — 3/), 18 + / = (3 — 2/) (4 + З/).
Ще можна було б перевірити, чи будуть числа 4 — 3/ та 4 + 3/ взаємно простими.
3. Як своєрідну перевірку можна використати також лінійне зображення
найбільшого спільного дільника через задані числа. Так, з рівності (2) дістаємо
З — 2/ = (18 + /) — (5 + 0 • 3. (3)
З рівності (1) знаходимо
5 + і = (6 — 17/) — (18 + і) (—0.
Підставляємо це значення в рівність (3): -
3-2/ = (18 + /) — [(6 — 17/) — (18 + /) (—/)] . З =
= (6 - 17/) (-3) + (18 + /)(1- Зі).
Виконавши в правій частині останньої рівності необхідні перетворення,
впевнюємося, що лінійне зображення знайдено правильно.
4. Аналогічно знаходиться найбільший спільний дільник чисел у кільці
Z [Vр] або Z [Vpi]t де р не є точним квадратом. При цьому
Nr (а+ Ь V~pi) = a2 + b2p, Nr (а + Ь V~p) = \ а2 — Ь2р \, a, b £ Z.
З 5-27І 65

3. Простим чи складеним є ціле гауссове число 3 + 2f?
Розв'язання. Зрозуміло, що 3 + 2і ф 0 і 3 + 2/ не є дільником одиниці
в кільці Z [і] (в Z [і] дільниками одиниці є числа 1,-1, і, — і).
Використаємо норму цілого гауссового числа і покажемо, що 3 + 2« є простим числом.
Оскільки Nr (3 + 2і) = 13, то, припустивши, що 3 + Ті є складене число,
дістаємо
З + її = (a + bi) (c + di), (I)
де a + bi, c + di не є дільниками одиниці і не є асоційованими з числом
3 + 2t, a, bt c, d £ Z. З рівності (1) маємо
13 = (a2 -fftW + d2). (2)
Для цілих чисел я, fc, c, d ця рівність можлива тільки тоді, коли a2 + b2 =
= 13, с2 + d2 = 1 або а2 + б2 = 1, с2 + d2 = 13. При цьому дістаємо, що
c-\-di або відповідно a + W є дільниками одиниці, що суперечить
припущенню. Отже, 3 + 2/ не може бути складеним числом. Оскільки 3 + 2* ф 0
і 3 + 2/ не є дільником одиниці, то 3 + 2і є просте число в кільці Z [і].
4. Довести, що число 4 в кільці Z [У Зі] неоднозначно розкладається в добуток
простих множників.
Розв'язання. Знайдемо спочатку дільники одиниці в Z [Узі]. Нехай
а-\-ьУЗі, c-\-dY& — дільники одиниці, а, Ь, су d £ Z. Тоді
(а + &/з0(* + <*}/з0 = 1.
Знайдемо норму обох частин цієї рівності:
(a2 + 362)(^-,- 3d2) = 1. (1)
(Нагадаємо, що норму числа а+ьУзі знаходять за формулою
Nr(a + bV3i)=(a2+.3b2).
Рівність (1) виконується, якщо
a2+3b2 = c2 + 3d2=\. (2)
Рівність (2), в свою чергу, виконується при а = ± 1, b = 0, с = ± 1, d = 0«
Отже, в кільці Z [УЗі] лише два дільники одиниці: 1, —1.
Доведемо, що для числа 4 в кільці Z [УЗі] є два різних розклади в добуток
простих множників: 4 = 2 .2 = (1+ V3i) (l — У Зі). Для цього покажемо*
що 2, 1 + У Зі, 1 — V3i є прості числа в Z [У Зі], а пари_ чисел 2, 1 + У Зі та
2, 1 — У Зі не є асоційованими. Оскільки в кільці Z [Узі] асоційовані числа
відрізняються _тільки знаком, то покажемо, що 2, 1 + і/"3/, 1—У Зі є прості
числа в Z[j/*3/]. Якщо 2 = (а + ьУ^і) (с + dYZi), то знайшовши норми рід
обох частин, дістанемо 4 = (a2 + 362) (с2 + 3d2). Число 4 розкладається в
добуток натуральних чисел двома способами: 4 = 2-2=1-4. Якщо а2 + ЗЬ2=
= 2, то Ь2 < 1, тобто Ь = 0. Тоді а2 = 2, що неможливо для цілого числа
а. Отже, а2 + 362 = 1 або a2 + 362 = 4. Якщо а2 + ЗЬ2 = 1, то а + 61/¾ —
дільник одиниці. Якщо а2 + 362 = 4, то с2 + 3d2 = 1 і с + d У Зі — діл_ьник
одиниці. Отже, 2 є просте число в кільці Z [УЗі]. Оскільки Nr (l ±Узі) =
= 4, то аналогічно доводять, що числа 1 ± У Зі є простими. Отже, число 4
в кільці Z [УЗі] розкладається на прості множники двома різними способами.
Зауваження
1. Зрозуміло, що цей метод доведення можна перенести на будь-яке кільце
Z[ypi], де р не є точним квадратом, а р + 1 —складене натуральне число. Тоді
в Z [Урі] число р + 1 разкладатиметься на прості множники двома різними
способами.
66

2. Аналогічно можна довести неоднозначність розкладу на добуток простих
множників чисел виду р— їв кільцях Z \Vp\* де р не є квадратом
натурального числа, ар— 1 є складене натуральне число.
Задачі
10.1. Довести, що:
а) характеристикою будь-якого поля є нуль або просте число;
б) найменше підполе будь-якого поля характеристики нуль
ізоморфне полю раціональних чисел;
в) характеристика фактор-кільця Z/mZ кільця цілих чисел за
ідеалом ті дорівнює числу т\
г) па = 0 для будь-якого елемента а кільця К
характеристики п\
д) характеристика будь-якого числового кільця дорівнює нулю,
10.2. Довести, що в будь-якому полі Р для його елементів а
6, Су d, де 6 =£ 0, d ф 0і
а) у = у тоді і тільки тоді, коли ad ~ be;
0) b + d ~~ bd ;
v а с ad — Ьсл
v _а_ c_ act
Т) b # d ~~bdT
.ас ad . r\
е)(у)"1=Т при a =^= 0.
10.3. Нехай К— область цілісності, Р — множина всіх дробів
j- елементів a, b£K, b Ф0. На множині Р існує бінарне
відношення у R ~ тоді і тільки тоді, коли ad = be, d Ф 0. Довести, щоі
а) R— бінарне відношення еквівалентності;
б) ((а, 6)) = ((с, d)), ((0, Ь)) =, ((0, d)),
((ad, 6d)) = ((a, 6)), ((6, 6)) = ((d, d)), де ((а:, у)) —клас
еквівалентності /?, який визначається парою (х, у), # ф 0;
в) якщо ((а, Ь)) + ((с, d)) = ((ad + 6с, 6d)), ((a, b)). ((c, d)) =;
= ((ac, 6d)), то з рівностей ((a, 6)) = ((a', 6')) і ((c, d)) = ((<?', d'))
випливають рівності ((a, 6)) + ((c, d)) = ((a', 67)) + ((<;', d)) і ((a,
W) • ((^ d)) = ((a', 6')) • ((*', d'));
г) множина 5 класів еквівалентності R з введеними в п. в)
операціями додавання і множення є полем (його називають полем
часток області цілісності К);
д) множина К' = {((а, е))\а£К] є підкільцем кільця S, де
є — одиниця кільця К, причому /(' ізоморфне К.
З* 67

10.4. Довести, що:
а) будь-яке підполе Si поля S, яке містить ненульове підкільце
К, містить також всі дроби у, де а(=/(, Ь^К, ЬфО. Точніше
кажучи, всі елементи х з S такі, що х = у;
б) підмножина Р поля S, яка складається з елементів виду
х =-Г-, де а, Ь^К, ЬФО, є мінімальним підполем, що містить К,
якщо К" — ненульове підкільце поля S;
в) якщо К — підкільце поля S, то найменше підполе в S, яке
містить /С, складається з дробів у, а£К, Ь^К, ЬфО. Дроби ^
і -j рівні тоді і тільки тоді, коли ad = be;
г) будь-яка область цілісності К є підкільцем деякого поля 5;
д) поле часток кільця цілих чисел Z є полем раціональних
чисел Q;
є) поле часток кільця цілих гауссових чисел Zli] є полем раціо:
нальних комплексних чисел Q[i];
є) множина Р = |~6, п£і\ є мінімальним підполем поля /?,
якщо є — одиниця поля R\
ж) існує єдиний ізоморфізм поля Р на поле Р', який
продовжує ізоморфізм ф, якщо Р і Р/ — поля часток відповідно областей
цілісності К і К! і ф— ізоморфізм К на К'.
з) поле часток 5 довільного поля Р з точністю до ізоморфізму
є цим самим полем Р;
10.5. Нехай К — область цілісності. Довести, що:
а) ae<d>, 6e<d>, якщо <a, b> = <d>\
б) d|(a, fc), якщо <a, 6> = <d>;
в) існують такі х,у£К, що ах + by = d, якщо <a, fe> = <d>;
r) d • c, якщо a • c, b і c і <a, b> = <d>\
д) d~(a, b)9 якщо <a, ft> = <d> (знак «~» означає асоці-
йованість);
є) ненульовий елемент а кільця К, який не є дільником
одиниці і не розкладається на прості множники, має хоч один власний
дільник, який теж не розкладається на прості множники;
є) якщо виконується п. є), то існує така нескінченна
послідовність елементів кільця К\а> аи а<і,.. .,ап,. ..., в якій кожен
наступний елемент є власним дільником попереднього; при цьому
<а> а <а\> a <a2>cz ... c=<a^>c ..., тобто в К існує
нескінченна послідовність ідеалів, в якій кожен наступний ідеал
строго містить попередній;
ж) (а, Ь)~пі, якщо (a, b) — d і п — дільник одиниці;
з) c~d, якщо (a, b)~d, (a, b)~c\
к) К — факторіальне кільце, якщо в К кожен ненульовий
елемент, який не є дільником одиниці, розкладається в добуток
простих множників і для будь-якого простого елемента р£К
виконується умова: якщо ab і р, то а •: р або b • p.
68

10.6. Нехай К — кільце головних ідеалів. Довести, що:
а) кожні два елементи а, ft, ЬФО, мають (а, ft);
б) (а, р)~\ або р, якщо р — простий елемент;
в) якщо а\а2*..ап : р> то хоча б один з елементів щ ділиться
на р, коли р — простий елемент;
г) якщо <аі>с:<а2>с:<аз>с= ... <zz<an>cz ..., то при де-
оо
якому аЛ U <Щ> =<ап>\
і=і
д) в К не існує жодної послідовності ідеалів, в якій кожен
наступний ідеал строго містить попередній;
є) в К кожен ненульовий елемент, який не є дільником одиниці,
розкладається в добуток простих множників;
є) d — (я, ft) тоді і тільки тоді, коли <d> = <a> + <&>,
а ф 0, Ь ф 0;
ж) k~[a, ft] тоді і тільки тоді, коли <k> = <a> []<b>>
аФО, ЬФ0\
з) К — факторіальне кільце.
10.7. Нехай /( —евклідове кільце. Довести, щоз
а) якщо а~ ft, то Nr(a) = Nr(ft);
б) якщо а • ft і Nr(a) = Nr(ft), то а~Ь\
в) Nr(a) = Nr(l) тоді і тільки тоді, коли 1—а;
г) якщо а Ф 0 і а не —» 1, то Nr (a) > Nr (1);
д) Nr (ft) < Nr (а), якщо b — власний дільник а;
є) у будь-якому ненульовому ідеалі / кільця К існує такий не-
нульовий елемент г, що Nr(r)<Nr(c) для будь-якого ненульового
елемента с£І\ при цьому / = <т>;
є) /( — кільце головних ідеалів;
ж) К — факторіальне кільце.
10.8. Нехай К—факторіальне кільце. Довести, що:
а) а • d тоді і тільки тоді, коли d ~ ррр**... />S якщо а~
~рп\хрп2 ... Ps\ 0 < ki< пи і = 1, 2,..., s;
б) [а, Ь]~рІ7# .../£» Де 7<=max{af, (3,}; (a, b)~p\lpbj ...р*£
де 8/=тіп{аь р,}, ї==1, 2, .. ., s, якщо ~a~p\xp\\. . /?*% 6~
— Рі1/?^8 • - • Р^% рі> Рі—попарно різні прості елементи, /, /«1,
2,..., s, іФ}\
в) (а, &і&2. ..&s)~ 1» якщо (a, &i)~...~(a, k)~l;
г) с • аі^2.. .as, якщо с \ щ і (a/, aj) ~ 1, /, /' = 1, 2,..., s, t ^ /;
д) с і а, якщо (a, ft) — 1 і be - a;
є) (а, р) ~1 або р, якщо /7 — простий елемент;
є) якщо aiCL2...as • р, то хоча б один з елементів я/ ділиться
на р, коли р — простий елемент;
ж) (ka, kb)~kd, якщо k Ф 0 і (a, b)~d\
з) (-j, -j)^1, якщо (a> fe)~d;
к) якщо (a, t)^d, діє і ft і с, то f—, —);
Q \ C CI
л) [a, b\~abt якщо (a, ft) ^ 1 і a, ft — ненульові елементи;
69

nh
м) k\a, b]~\ka> kb], -j~[a, b], якщо a, b, k — ненульові
елементи;
н) існують такі елементи х, у£К, що а~хп, Ь~уп, якщо
(я, Ь)~ 1; ab = сп\
о) [а, (6, с)]~([а, ft], [а, с\).
10.9. Нехай Z [і]|— кільце цілих гауссових чисел. Довести, що!
а) для кожного a£Q[i] існує таке z£Z[i], що \а — z|2< -^-;
б) для будь-яких г, t£Z[i] існує таке u£Z\i]y що |г — /и|2<
<Ut2;
в) Z[f]—евклідове кільце з нормою Nr(г) = Іг|2, z£Z[i].
10.10. Нехай К= | 2 Іа> ^Z, а, ^ однакової парності!.
Довести, що:
а) для кожного a£Q[/] існує таке z£K, що |а— z|2<-j;
б) для будь-яких z, t^K існує таке и^/С, що |г — ^|2<|/|2;
в) К — евклідове кільце з нормою Nr(z) = |z|2, z£K.
1-0.11. Довести, що наступні кільця є кільцями головних ідеалів:
а) кільце всіх раціональних чисел ^- з непарним натуральним
знаменником п і цілим чисельником т\
б) довільне поле Р\
в) кільце Z [y^lJWj.
10.12. Довести, що дані кільця € евклідовими:
а) кільце Z[V2] з нормою Ют (a + b V~2) = \a2 — 262|, а,
b£Z.
б) кільце Z [КЗ] з нормою Nr [а + 6J/3] =|а2 — 36 2|, а, b£Z.
10.13. Довести, що в довільному кільці /(•
оо
а) / = (J h Є ІДеаЛ КІЛЬЦЯ К, ЯКЩО /iS/jC.^c/^g,,, Є
ft=l
послідовність зростаючих ідеалів кільця К\
б) a = be тоді і тільки тоді, коли в кільці К <а> <= <Ь>\
в) a — b тоді і тільки тоді, коли <а> = <&>, /С — кільце
з одиницею;
г) а не ~Ь тоді і тільки тоді, коли <а> ф <&>, a K —
кільце з одиницею.
10.14. Знайти породжуючі елементи даних ідеалів кільця цілих
чисел Z:
а) <4, 6, 8> + <10, 15, 20>;
б) <4, 6, 8>П<Ю, 15, 20>;
в) <3, 6, 9> + <15, ЗО, 45>;
г) <3, 6, 9> П <15, ЗО, 45>;
Д) <*п, п, s> + <k, t, />, k% m, ft, s, t, f£l\
e) <m, ft, s> П <&> U f>> k, m, ft, s, /, /£Z.
10.15. Знайти найбільший спільний дільник і найменше спільне
кратне таких цілих гауссових чисел:
70

а) 4 + З/ та 3 + г,
б) 6 + / та 5 + //;
в) 8+12/та 10 + 4/;
г) 5 — 5/ та У — /;
д) 11—3/ та 3 + 7/;
є) 5 + 6/ та 6 + 5/;
є) 7 + 3/ та 5 + 2/.
10.16. Знайти найбільший спільний дільник даних елементів
кільця Z[Y2]:
а) 7 + /2 і — 5-5]/2;
б) 5 + 2/2 і 6 — V2.
10.17. Знайти лінійне зображення найбільшого спільного
дільника d=ax+by, де числа a, b задано в задачах 10.15 і 10.16.
10.18. Довести, що:
а) ціле гауссове число є простим, якщо його норма є простим
натуральним числом;
б) будь-яке просте ціле гауссове число є дільником одного і
тільки одного простого натурального числа;
в) норма простого цілого гауссового числа є або простим
натуральним числом, або квадратом простого натурального числа;
г) просте натуральне число тоді і тільки тоді є нормою цілого
гауссового числа, коли воно дорівнює сумі квадратів двох
натуральних чисел;
д) усі прості натуральні числа виду р = 4/г + 3, л = 0, 1, 2, ...
є простими цілими гауссовими числами.
10.19. Нехай К — множина дійсних чисел виду а\ • 2Л« + а2-2*'+
+ ... +сіп • 2?пу де п—довільна натуральне число, а\9 а<і> ...,ап —
т
будь-які цілі числа, х\9 Х2, .. ., хп — будь-які числа виду 2ky де
m, k — цілі невід'ємні числа, k=fc0. Довести, що К є область
цілісності, в якій порушується існування розкладу на прості
множники (як приклад взяти число 2).
10.20. Довести, що наступні кільця є прикладом кілець з
порушенням однозначності розкладу на прості множники: a) Z[]/3/];
б) Z[VEi]; в) Z[V\7i); r) Z[/T9/].
10.21. Довести, що в кільці Z[/3/] простими є такі елементні
а) 2; б) —2; в) 1 + /3/; г) 1 — )/3/.
10.22. Довести, що в кільці Z [/] простими є такі елементи:
а) 3; б) —3; в) 7; г) -7; д) 2 + /; є) 2 — /; є) 3 + 2/; ж) 3 — 2/;
з) 4 + 5/; к) 4 — 5/.
10.23. Довести, що прості натуральні числа 2, 5, 11, 13 не є
простими цілими гауссовими числами.
10.24. Знайти канонічний розклад цілих гауссових чиселз
а) 5; б) 5 — 5/; в) 3 + /; г) —90 + 180/;
Д) —182—126/; є) 7+8/; є) 41.
71

Розділ III. ТЕОРІЯ КОНГРУЕНЦІИ З
АРИФМЕТИЧНИМИ ЗАСТОСУВАННЯМИ
§ 11. Конгруенції в кільці цілих чисел
та їхні найпростіші властивості
Література
[1]—§ 15, с. 162-167;
12] —§ 15, с. 166—169;
[3] —гл. 12, § 1, с. 397—399;
110]-гл. III, § 1—3, с. 41-44;
J11] — гл. 7, с. 72—77;
[12] —гл. II, § 1, с. 36—43;
(14] —§ 15, с. 66—71.
ТЕОРЕТИЧНІ ВІДОМОСТІ
Серед багатьох означень конгруентності двох цілих чисел а і Ь за модулем
m розглянемо три.
Означення /. Цілі числа а і b називають конгруентними за модулем т,
де т — ціле число, якщо їхня річниця а — b ділиться на т. Позначення:
а = b (mod m).
Якщо а і b не конгруентні за модулем т, то пишуть
а ф b (mod m).
Означення 2. Цілі числа а і b називають конгруентними за модулем т, де
m £ Z, якщо вони при діленні на т дають однакові остачі.
Означення 3, Цілі числа а і b називають конгруентними за модулем т, де
m £ Z, якщо існує таке ціле число qt що a = b-\- mq.
Означення 1, 2, 3 рівносильні.
Основні властивості конгруенцій
1°. Відношення конгруентності за даним модулем є бінарне відношення
еквівалентності на множині цілих чисел. Класи еквівалентності називають класами
лишків за даним модулем;
2°. Конгруенції о а одним модулем можна иочленно додавати, віднімати
і множити;
3°. До обох частин конгруенції можна додати будь-яке ціле число (це дає
змогу переносити будь-який доданок з однієї сторони в другу з протилежним
знаком);
4°. До будь-якої частини конгруенції можна додати довільне ціле число,
кратне модулю;
5°. Обидві частини конгруенції можна помножити на те саме ціле число;
6°. Обидві частини конгруенції можно поділити на їхній спільний дільник,
якщо він взаємно простий з модулем;
7°. Якщо у виразі
f(avai в*)в^йі^-в?
усі коефіцієнти А і числа ар а2, ..., ak замінити на конгруентні їм за модулем
т коефіцієнти В і числа bv b2, ..., bk відповідно, то вираз
«(»„*, bk) = ^BbnX2---blk
Суде конгруентний заданому за модулем т:
( (av а2, ..., ak) = g (bv Ь2, ..., bk) (mod m)
72

8°. Обидві частини конгруенції І модуль можна множити на те саме ціле-
число.
9°. Обидві частини конгруенції і модуль можна скорочувати на їхній
спільний дільник.
10°. Якщо конгруенція має місце за кількома модулями, то вона має місце
і за модулем, який дорівнює спільному найменшому кратному цих модулів.
11°. Якщо конгруенція має місце за модулем т9 то вона має місце за
модулем а\ де d — довільний дільник числа т.
12°. Якщо одна частина конгруенції і модуль діляться на деяке число, то
й друга частина конгруенції ділиться на те саме число.
13°. Якщо а = Ь (mod m), то (а, т) = (6, т).
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Чи конгруентні числа 78, 210 і 346 з числом 27 за модулем 11?
Розв'язання. Віднімемо від даних чисел число 27. Дістанемо 51, 183
і 319. З них тільки 319 ділиться на 11, а тому тільки 346 конгруентне 27 за
модулем 11, тобто 346 ss 27 (mod 11).
2. Довести, що коли 100а + 106 + с = 0 (mod 21), то а — 26 + 4с ш 0 (mod 21),
а, 6, сЄ2.
Розв'язання. Нехай 100а + 106 + с в 0 (mod 21). Помноживши обидві
частини цієї конгруенції на 4, матимемо
400а + 406 + 4c a 0 (mod 21). (1)
При цьому мають місце конгруенції:
400а = a (mod 21), бо 400а— а = 399а • 21, (2)
406 = —26 (mod 21), бо 406 — (—26) = 426 і 21, (3>
4с = 4с (mod 21), бо 4с — 4с = 0: 21. (4>
Додавши почленно ці конгруенції, дістанемо
400а + 406 + 4с == а — 26 + 4c (mod 21). (5>
Беручи до уваги конгруенцію (1), матимемо
а—26 +4с = 0 (mod 21).
3. Знайти остачу від ділення 15325 — 1 на 9.
Розв'язання. Зрозуміло, що нераціонально знаходити число 15325 — 1;.
а потім остачу від ділення цього числа на 9. Слід скористатися властивостям»
конгруенцій за модулем 9. Нам треба знайти таке ціле невід'ємне число jc,
що х= 15325— 1 (mod9) і х < 9. Оскільки 1530:9, то 15325 = (1532 —
— 1530)5 (mod 9), тобто 1532^ = 25 (mod 9). Проте 25 = 32 в 5 (mod 9). Отже,
15325 = 5 (mod 9). Віднімемо почленно від цієї конгруенції конгруенцію Із
= 1 (mod 9). Матимемо 15325 —1 = 4 (mod 9). Оскільки 0<4<9, то х = 4-
Отже, ?исло 1532 — 1 нри діленні на 9 дає остачу 4.
4. Довести, що числя виду З2 + 2, я £ N є складеними.
Розв'язання. Оскільки 4 = — 1 (mod 5), то 24л+1 = 2 . 42п в 2 (mod Б\
Тоді число 24"+1 має вид bk + 2, де k Є N, а тому з24"+1 + 2 = 35М~2 + 2.
Оскільки 243 = 1 (mod 11), а З5 = 323, то 35fe+2 +2 = 9- 243* + 2а
= 0(mod 11). Отже,324"+1 +2:11. Беручи до уваги нерівність 324"+I+2 > 11,.
маємо, що 3 + 2 t складене число.
73

Задачі
11.1. Серед чисел а\у a<L,...,an знайти всі пари різних чисел,
конгруентних за модулем т, якщо:
а) ах = 216, а2 = 134, а3 = 214, аА = 303, аь = 21, т = 5;
б) аі = 135, а2=106, аз =181, а4 = 225, а5 = 167, а6 = 452,
т = 15;
в) ах = 217, а2 = 42, а3 = 182, а4 = 241, т = 12.
11.2. Які з чисел а, fc, c конгруентні числу d за модулем т,
якщо:
а) а = 137, 6 = 343, с = 633, d = 13, m = 31;
б) а = 217, 6 = 201, с= 186," d = 11, т= 19;
в) а = 2.34,"6 = 634, с = 104, d = 9, m = 25.
11.3. Довести, що:
а) означення 1—3 еквівалентні між собою;
б) властивості 1 —13 справедливі;
в) якщо у многочлені з цілими коефіцієнтами / (х) = апхп +
-\-ап-\хп~х + .. • +#i* + #o, який задано на множині цілих чисел Z,
усі коефіцієнти аі замінити на коефіцієнти ЬІУ конгруентні at за
модулем т, то дістанемо многочлен g (x) = bnxn + bn-xxn~l + ... +
+ Ьхх + boy конгруентний многочлену / (х), тобто f (x) = g (x) (mod m);
г) якщо / (х) = апхп + ап-\хп-1 + . . . + ахх + ао — многочлен від
одного аргументу х з цілими коефіцієнтами і х = x' (rnodm), то
f(x) = /(л;') (rnodm);
д) п2—1=0 (mod8), якщо п — непарне число;
є) а = г (rnodm), де г — остача від ділення а на т.
є) a = b (mod m ), якщо ax = bx (rnodm);
ж) якщо ас = bd(rnodm), a=.fc(modm) і (a, m)=*l, то с=.
^rf(modm).
11.4. Записати у вигляді конгруенцій такі умови:
а) —38 і —3 дають при діленні на 7 однакові остачі;
б) при діленні на 8 число 53 дає остачу 5;
в) а + 2 ділиться на 5;
г) а2 — Ь2 ділиться на а — Ь (аФЬ)\
д) знайти остачу г від ділення —73 на 8;
є) 20 є остача від ділення числа 389 на 41;
є) числа 219 і 129 дають неоднакові остачі при діленні на 7#
11.5. Охарактеризувати конгруенціями числа п, якщо:
а) п — парне число;
б) п — непарне число;
в) п має вид 4k -f 1, k£Z;
г) п має вид 5ft + З, k Q Z;
д) п має вид Ik — 2, k£Z;
є) п має вид —3 + 8ft, ft£Z.
11.6. Довести, що:
а) 121 = 13145 (mod2);
б) 121347 = 92817 (mod 10);
в) 31 = —9 (mod 10);
г) (m—1)2=1 (rnodm);
74

д) 2m + 1 = (m + I)2 (modm);
е) 2630 — 1 =0 (mod5- 7-11- 31);
€) 26^ + 1=0 (mod 3-7-31);
ж) 2626 =1414 (mod 10);
з) 1772 = 1 (mod 10);
к) 2и-зі = 2 (mod 11 -31);
л) 314 = —1 (mod 29);
м) 11 • 13- 18- 19-2322 = 6 (mod 7).
11.7. Довести, що:
а) 51812 ф 1964 (mod 25);
б) 7103 ф 3 (mod 27);
в) 41965 #25 (mod 10);
r) 30- 17 #81 • 19 (mod 6);
д) її207 ф& (mod 27);
є) б89ф7 (mod 16);
є) ІЗ25 фЬ (mod 30);
ж) 710I#3 (mod35);
з) 8107 ф 7 (mod 14);
к) 2615 — 1 ф 0 (mod 5 • 7);
л) 7I00#3 (mod 125);
м) (2п + \)(2т + 1)ф2к (mod6), n, tn, k£Z.
11.8. Нехай p— просте число. Довести, щоі
а) (a + b)p = aP + bP (modp), a, b£Z;
б) C£_i = (-l)*(modp);
в) С*_2 = (-1)М* + 1) (modp);
г) a" = &p(modp'I+1), якщо as=b (modp");
д) 12*+' + 22*+< + 32*+> + ... + (р — 1)2*+і = 0 (modp), де р> 2;
є) рр+2 + (р + 2)" = 0 (mod 2р + 2), якщо р > 2;
€) ч„сЛа -£^1, _£^і, ...,-1, 0, 1, .... р-=±, ^zl
попарно неконгруентні між собою за модулем р, р > 2.
11.9. Знайти остачу від діленняі
а) 15231 на 14;
б) 15231+2 на 16;
в) 15325—1 на 9;
г) 121231 + 14*324 на 13;
д) 208208 на 23;
є) 2^3-7 на 25;
. є) З79821 + 5 на 17;
ж) 102732 + 10 на 22;
з) IS28'* —3 на 14;
к) 2100 + 5200 на 29;
л) 13^-23-16^ + 2217 на 15;
м) 292929 — 343434 +29 • 41 - б231 — 24 • 17120 на 31;
н) а на 73, якщо а100 = 2 (mod 73) і ат = 69 (mod 73). Як.
зміниться відповідь, якщо а ділити на 79 і а25 = 3 (mod 79), а26=з
ss 29 (mod79), (а, 79) = 1?
75

11.10.. Довести, що:
, а) а — 6 — с • 2, якщо а + 6 — с і 2;
б) 18а + 56 ■ 19, якщо Па + 26 ■ 19;
в) 2а+ 76 і 17, якщо а — 56 • 17;
г) 4а + 236 • 16, якщо 12а —76 • 16;
д) 10а + 76 • 19, якщо а —56 • 19;
є) На —6 +2с = 21, якщо 16а— 116 + с ■ 21;
є) а — 76 • 31, якщо 6а—116 • 31;
ж)а + 6 + 8с-21, якщо 50а + 86+с-21;
з) 5а + b • 17, якщо 15а + 36 :• 17;
к) а —46 +41с • 199, якщо 50а — 6 + 60с • 388.
11.11. Довести, що при будь-якому натуральному ш
а) 23" = — 1 (mod 3"+');
б) 10" +17 = 0 (mod 3);
в) 34л+3 = 17 (mod 10);
г) 242"+і • 21"+2 = 3"+2 • 172"+' (mod 19);
д) 483"+' + 16^+1 + 1=0 (mod 13);
є) 2з4л+1 + 3 — складене число;
є) (т— l)m" = —1 (mod mn+l), де т > 1 —непарне число;
ж) 3"+4 = _і (mod 10), якщо 3" = —1 (mod 10);
з) 25n=l (mod 31);
к) 3 • 10" + 24 = 0 (mod 54).
11.12. Довести, що задані рівняння не мають розв'язків у
натуральних числах:
а) 2х + 1у = 19г; в) 24* + 36" = 61*;
б) 2х + 5» = 19г; г) 20* + 50* = 71*.
11.13. Довести, що при будь-яких цілих а, 6 і невід'ємному п:
а) (Па+5)^+1 +(116 + 6)^+1 ==0 (mod 11);
б) (13а + 3)3"+2 + (136 —4)3"+2 + 1 =0 (mod 13);
в) 9^+1 + 33"+' + 1=0 (mod 13).
11.14. Знайти такі натуральні k, І, т, щоб при будь-якому
цілому а справджувалися такі конгруенції:
а) а3* + а3'+і + а3т+2 = 0 (mod а2 + а 4- 1);
б) а3*—а3'+'+а3т+2 = 0 (mod а2 —а + 1);
в) а3* + а31+1 + а3т+2 = 0 (mod а4 + а2 + 1).
11.15. Знайти останню цифру чисел:
а) 234;
б) 999;
в) (,.. (((77)7] ] ) —піднесення до степеня повторюється 1000 раз;
г) 7(7",(7 —піднесення до степеня повторюється 1000 раз,
11.16. Знайти останні дві цифри чисел:
76

(a) 2999;
б) З"9;
в) 2341;
г) 289289;
д) 203203203;
є) 141<14;
є) 999;
ж) 79".
11.17. Нехай Fn = 22" + 1 — число Ферма, де п = 0, 1, 2,....
Довести, що:
а) F5 : 641і;
б) число Fn закінчується цифрою 7 при всіх п, крім я = 0
І AZ = 1.
§ 12. Класи лишків, повна
і зведена системи лишків за даним модулем
Література
[1] —§ 15, с. 166—168, § 16, с. 168—170;
[2]—§ 15, с. 169—171, § 16, с. 171—173;
[3] —гл. 12, § 2, 3, с. 399—404;
[Ю] — гл. III, § 4, 5, с. 45—46;
[11]—гл. 8, 9, с. 77—92;
112] — гл. II, § 2, 3, с. 43—51;
ІI3J — § 16—18, с. 66—78.
ТЕОРЕТИЧНІ ВІДОМОСТІ
Відношення конгруентності за даним модулем т є бінарним відношенням
еквівалентності на множині цілих чисел Z. Класи еквівалентностей називають
класами лишків за даним модулем. Лишком (або представником) класу за модулем
т називають будь-яке число цього класу. Кільце цілих чисел Z розкладається
на т класів лишків. До класу лишків, який містить число а, належать усі
цілі числа х виду х«а + ті, де t £ Z. Цей клас позначатимемо символом
/Є(гп\ причому, якщо йдеться тільки про класи лишків за тим самим модулем т,
то можна писати /Cfl. Число а називають представником класу лишків К^К
Представником класу лишків /CJm) може бути будь-який елемент цього
класу, тобто К{ат) =* К{ьт\ якщо Ь £ К(атК Якщо К{ат)глК{^ Ф 0, то /^т>= Д^).
Якщо d > Ь то К? = /С<Г - 'CfU - *i#L - ..- - К%-і)пг'>
Kf) + *<«>. *й>ь> 4т)*(Г = * <?>.
Множина всіх класів лишків за модулем т відносно додавання класів
утворює комутативну групу, П називають групою класів лишків.
Множина класів лишків кільця цілих чисел за даним модулем т утворює
комутативне кільце з одиницею, його позначають Z^.
Якщо т — складене число, то в Zm є дільники нуля, причому, якщо т «
™ т^тг, то зокрема,
<><> = *Г\ Де <> + *(т) і <> + *,"">•
Якщо т — просте число, то Zm—скінченне'поле.
Повною системою лишків за модулем т називають будь-яку систему лишків,
утворену з т чисел, взятих по одному з кожного класу лишків. " "
Існують такі основні повні системи лишків:
1 Це було доведено щеЛ. Ейлером (1707—1783).
77

а) повна система найменших невід'ємних лишків;
б) повна система найменших за абсолютною величиною лишків;
в) повна система найменших натуральних лишків.
Якщо (а, т) = 1, то клас К^ називають взаємно простим з модулем т.
Зведеною системою лишків за модулем т називають будь-яку систему лишків,
утворену з <р (т) чисел, взятих по одному з кожного класу, взаємно простого
з модулем т.
Якщо (а, т) =• 1, Ь — довільне ціле число, а дг пробігає повну систему
лишків за модулем т, то й вираз ах-\- b також пробігає деяку повну систему
лишків за модулем т (не обов'язково ту саму).
Якщо (я, т) = 1, ах пробігає зведену систему лишків за модулем т, то
лінійна форма ах також пробігає деяку зведену систему лишків за модулем т
(не обов'язково ту саму).
Множина класів лишків за модулем т, взаємно простих з т, утворює
відносно множення класів комутативну групу, її називають мультиплікативною
групою класів лишків, взаємно простих з модулем.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Чи утворює повну систему лишків за модулем 8 система чисел
S= {—7, 2, 16, 20, 27, 39, 46, -3}?
Ро з в'я з а н н я. Щоб визначити, чи є деяка система чисел повною системою
лишків за деяким модулем т, треба: 1) впевнитися, що цих чисел є /я, 2)
показати, що всі вони між собою попарно неконгруентні за модулем т. При
цьому доцільно замінити кожне з даних чисел конгруентним йому
найменшим невід'ємним числом (це неважко зробити, знайшовши остачу від ділення
заданого числа на модуль).
У розглядуваному прикладі маємо: 1) чисел у системі є 8; 2) — 7 s l(mod 8),
2^2 (mod 8), 16=0 (mod 8), 20 s 4 (mod 8), 27 в 3 (mod 8), 39 з 7 (mod 8),
46 s 6 (mod 8), - 3 s 5 (mod 8). Дістали нову систему 1, 2, 0, 4, 3, 7, 6, 5,
яка є повною системою лишків за модулем 8.
Зауваження. 1. Якщо модуль т є невелике число, можна знайти всі
попарні різниці заданих чисел і довести їхню подільність на т. Якщо жодна
з різниць не ділиться на т, то задана сукупність чисел є повною системою
лишків за модулем /я, у противному разі — не є нею.
2. Замінивши кожне число системи S його остачею від ділення на 8,
визначимо, до якого класу К^ належить кожне число із системи S, а саме —
-7f6 *}8\ 2 є /С<8>, 16 є Kg», 20 Є К(*К 27 Є Kf\ 39 є К{78)* 46 € #68\ ~3 Є*£8>-
Оскільки всі числа з 5 належать до різних класів за модулем 8 і всі
класи мають представників у цій системі, то S — повна система лишків за
модулем 8.
2. Показати, що коли х пробігає зведену систему лишків за модулем 10., то й
х3 пробігає зведену систему лишків за модулем 10.
Розв'язання, Відомо, що числа зведеної системи лишків взаємно прості
з модулем. Взаємно простими з 10 є лише такі цілі числа, які закінчуються
цифрами 1, 3, 7, 9. Четвірки І таких чисел попарно неконгруентні між собою
за модулем 10, а оскільки <р (10) = ер (2 - 5)=2 -БИ— -у)(1 *~1П e 4f T0 5"~
зведена система лишків за модулем 10. Нехай х пробігає довільну зведену систему
лишків S за модулем 10. Якщо числа системи S, що закінчуються цифрами 1,
З, 7, 9, піднести до куба, то дістанемо систему S' чисел, які закінчуються
цифрами 1, 7, 3, 9. Цю систему й пробігає де8. Система S' утворює також зведену
систему лишків за модулем 10, оскільки: а) чисел у системі є 4 = ер (10), б) усі
числа системи S' попарно неконгруентні між собою за модулем 10; в) усі числа
системи S' взаємно прості з числом 1Q.
3. У множині класів лишків за модулем 15 знайти:
а) усі дільники нуля;
б) усі дільники одиниці;
78

і в) клас, протилежний класу К715);
\ г) клас, обернений до класу К[\5\
Розв'язання, а) Оскільки дільником нуля є кожен клас /(£15\ для якого
знайдеться такий клас К{х15), що К{а15) К(хі5) = К(015), де К(а15) Ф /С(015> Ф tf<15),
тобто такий клас К}15)* Що ах і 15, де 1 < а, х < 14, то фактично дільниками
нуля є всі ті класи К^ь\ в яких представник а не взаємно простий з 15.
Отже, дільниками нуля є такі класи: /с£15Г, ЩІЬК К$5)> К{915К К{$, К[\5\
б) Аналогічні міркування для дільників одиниці показують, що дільниками
одиниці є всі ті класи /(д15\ в яких представник а взаємно простий з 15.
Справді, якщо (a, 15) = 1, то знайдуться такі цілі числа и і v, що
т+ 15»:=1. Тоді Kau+l5v = Kv ^оте Kau+lbv = Kau + Kl5v, a Kl5v =
= Яо. Каи = ^а * **• 0тже' Ка'Ки = #г Звідси, зокрема, (Kfl)-i = /Cw, тобто
ми вивели формулу для знаходження класу, оберненого до класу /Є якщо
(a, 15) = 1.
Випишемо дільники одиниці: К\хь\ К{2]5\ К[15\ К^^К^К К\\5\ K\f, К[\5)
в) Знайдемо такий клас К[15\ що К7ІЬ)+К[15) = /Cj)15). Оскільки 7^15> + /С<15> =
= М+!с» т0 шукатимемо таке ціле число х, що 7+*: 15. Найменшим таким
є 8. Отже, х = 8 і тому — K(7l5) = /C(f
15).
8
числом
г) Знайдемо такий клас К(и15), що К[\5) • К{и15) = К[15). Оскільки (11, 15) = 1,
то, згідно з пунктом б), цей клас можна знайти, знайшовши спочатку за
допомогою алгоритму Евкліда число и. До чисел 11 і 15 застосуємо алгоритм
Евкліда. Маємо:
15 = 11 . 1+4,
11=4- 2+3,
4= 3-1 + 1.
Звідси
4 = 15-11 • 1,
3=11—4 ■ 2,
1 =4 — 3 • 1.
Тоді
1=4 — 3-1=4- (11— 4-2). 1 = 11 .(-1) + 4 -3 =
= 11 .(-1) + (15-11 • 1) .3 = 11 .(-4)+15-3.
Отже, м = -4, а /(</5) = /Сі!?.
Оскільки К^-^К^К то (к[\5))~~ = К[\5), тобто клас К[\5) є оберненим
до себе.
Зауваження
1. У подальшому, знайшовши дільники нуля (дільники одиниці),
говоритимемо, що. відмінні від дільників нуля і самого нуля елементи є дільниками
одиниці (відмінні від дільників одиниці і від нуля елементи є дільниками нуля).
2. У пунктах а) і б), не обмежуючись тільки переліком дільників нуля та
одиниці, можна виписати відповідні конкретні пари. У розглянутому прикладі
такими парами відповідно є:
415) і *Г'' *Р і 4І5) і т. д..
415> і *»». *У5> і <5) і т. д.
3. Клас /СуШ\ обернений до класу /СдШ\ можна іноді швидко знаходити усно>
підбираючи таке число и, щоб добуток а • и при діленні на т давав остачу 1.
79

Так для класу К\\Б) класи К[ІБ) t К$5), К[15), Я7(15), К{815) не підійшли б,
оскільки числа 1 • 11 = 11, 2 . 11 = 22, 4 • 11 =44, 7- 11 = 77, 8. 11 =88 при
діленні на 15 дають остачу, відмінну від 1. При цьому, звичайно, дільники нуля
Кз15)* ^515)» ^б15) ^915)' ^іо5> не випробовуються, бо вони вже дільниками
одиниці не можуть бути. Оскільки 11-11^=121 і 121 = 15-8+1» то
4. Для знаходження класу (К{ат)) \ оберненого до класу К{атК існує ще один
спосіб. Нехай (а, т) = 1, у противному разі клас К^ взагалі не має
оберненого класу. Нехай Рп__х — чисельник передостаннього підхідного дробу
Рп—\ т т Рп т
7ї для числа ~7> 7 = 7Г- Оскільки - — нескоротний дріб, то т = РПу
a=Qn. За однією з властивостей підхідних дробів маємо
Рп Vi (-1)^1
я-1
(-1)"
а -* Qn_x " Qn_{ • Qn '
Отже,
Звідси
Тоді
а{—\)пРп-іЕз l(modm).
Згідно з цією конгруенцією, клас /С^л—і Р є оберненим до класу /С(ат).
Отже,
Для розглянутого прикладу маємо (табл. 12), де т = 15, а = 11, п = З,
Рл_і = Р2 = 4.Тоді
(/(05))-1 = дс<Д ..4 = ^ = /Сі1,5»-
Таблиця 12
1 і
Яі
?і
Qt
—і
—
і
0
0
1
1
1
1
2
3
2
2
1
4
3
3
3
15
11
Задачі
12.1. Замінити найменшим невід'ємним і найменшим за
абсолютною величиною лишками такі числа:
а) 70 за модулем 32;
б) 327 за модулем ЗО;
в) 184 за модулем 16;
г) 333 за модулем 67;
д) 586 за модулем 13;
є) 799 за модулем 99;
80

є) 14 за модулем 15; л) 1000 за модулем— 17;
ж) 5353 за модулем 781; м) 501 за модулем 503;
з) —337 за модулем 56; н) —700 за модулем — 51.
к) 337 за модулем — 56;
12.2 Знайти повну систему найменших невід'ємних лишків
за модулем: а) 1; б) 2; в) 3; г) 4; д) 5; є) 6; є) 7; ж) 8;
з) 9; к) 10; л) 12; м) 15; н) 20.
12.3. Знайти повну систему найменших за абсолютною
величиною лишків за модулем: а) 1; б) 2; в) 3; г) 4; д) 5;
є) 6; є) 7; ж) 8; з) 9; к) 10; л) 12; м) 15; н) 20.
12.4. Знайти повну систему найменших натуральних лишків
за модулем: а) 1; б) 2; в) 3; г) 4; д) 5; є) 6; є) 7; ж) 8;
з) 9; к) 10; л) 12; м) 15; н) 20.
12.5. Знайти повну систему найбільших недодатних лишків
за модулем: а) 1; б) 2; в) 3; г) 4; д) 5; є) 6; є) 7; ж) 8;
з) 9; к) 10; л) 12; м) 15; н) 20.
12.6. Знайти повну систему найбільших від'ємних лишків
за модулем: а) 1; б) 2; в) 3; г) 4; д) 5; є) 6; є) 7; ж) 8;
з) 9; к) 10; л) 12; м) 15; н) 20.
12.7. Знайти хоч одну довільну повну систему лишків,
відмінну від знайдених у задачах 12.2—12.6, за модулем: а) 1;
б) 2; в) 3; г) 4; д) 5; є) 6; є) 7; ж) 8; з) 9; к) 10; л) 12;
м) 15; н) 20.
12.8. Знайти відповідні зведені системи лишків для задач
12.2—12.7.
12.9. Чи утворюють повну систему лишків за модулем т
такі числа:
а) 25, —20, 16, 54, —21, 26, 37, —17, якщо ш = 8;
б) 25, —9, —6, 420, —18, ЗО, 6, якщо т = 7;
в) —46, —45, 37, 32, —48, —40, якщо т = 6;
г) 43, 25, —23, 28, —50, —40, 31, якщо т = 7;
д) —261, —130, 170, 313, 973, 1000, 55, 1668, якщо т = 8;
є) 605, —189, 242, —311, 143, 40, —51, 194, якщо т = 8;
є) 809, 402, 1616, 220, 227, 439, 446, якщо т = 8;
ж) 921, 92, —18, 28, —109, 40, —22, —2, 15, якщо т = 9;
з) 134, 128,-19, 37, 28, —23, —32, 5, 41, —35, —33,
якщо т = 11;
к) 39, 66, 30, 19, —11, 55, 31, 46, 25, 47, 50, 35, 101,
якщо т=13?
12.10. Чи утворюють зведену систему лишків за модулем
т такі числа:
а) 19, —1, 25, —19, якщо т = 8;
б) 19, 95, 29, 49, —20, —64, 27, якщо т = 9;
в) 13, —13, 29, —29, якщо т=10;
г) 19, 35, 25, —19, якщо т=12;
д) —11, —55, —29, 35, якщо т=12;
є) —181, 231, 413, —349, якщо т=12?
8і

12.11. Довести, що:
а) коли х пробігає повну систему лишків за модулем 11, то
й 3# + 2 теж пробігає повну систему лишків за модулем 11;
б) коли х пробігає повну систему лишків за модулем 10,
то й х5 пробігає повну систему лишків за модулем 10;
в) система чисел 2, 4, ..., 2т становить повну систему лиш-
ків за модулем т, якщо т непарне;
г) члени арифметичної прогресії а, а + rf, ..., a + d(n—1)
утворюють повну систему лишків за модулем /г, якщо (d, л) = 1;
д) коли (a, 6) = 1, х пробігає повну систему лишків за
модулем 6, у пробігає повну систему лишків за модулем a, a c —
будь-яке число, то ax+by + с пробігає повну систему лишків
за модулем ab\
с) коли т = а\а2.. .aSy де всі щ попарно взаємно прості, тс =
= —, і = 1, 2, . . ., s, с — довільне ціле число, хі пробігають від-
і
ПОВІДНО ПОВНІ СИСТемИ ЛИШКІВ За МОДулеМ ГЛі, ТО Ш\Х\ +ГП2Х2 +
+ . . , + т&Хь + с пробігає повну систему лишків за модулем т\
є) система чисел 0, 2і, 22,. . ., 210 утворює повну систему
лишків за модулем 11;
ж) вираз За: + Ту пробігає повну систему лишків за модулем 21,
якщо а:—0, 1, 2, 3, 4, 5, 6, а у = 0, 1, 2;
з) повну систему лишків за модулем т\гп2 ... ms пробігає вираз
х\ + т\Х2 + гп\Ш2Хі + ... + гп\гп2... ms-ixs, якщо ти т>2, ..., ms —
натуральні, попарно взаємно прості числа, а хи *2,...» xs
пробігають повні системи лишків за модулем ти т2і...ут відповідно.
12.12. Довести, що:
а) коли х пробігає зведену систему лишків за модулем 7,
то й Юх пробігає зведену систему лишків за модулем 7;
б) коли х пробігає зведену систему лишків за модулем 9,
то 7х5 теж пробігає зведену систему лишків за модулем 9;
в) числа 6т—1, і 6т+1 при кожному цілому т утворюють
зведену систему лишків за модулем 6;
г) система чисел +1, ±2,..., + P~Z , Р~Г є зведеною
системою лишків за непарним простим модулем /?;
д) система чисел 8і, З2, З3, З4, З5, З6 утворює зведену систему
лишків за модулем 7;
є) система чисел 5і, 52, 53, 54, 55, 56 утворює зведену систему
лишків за модулем 7;
є) коли числа ахи ах2,.. ., ах9(т) утворюють зведену систему
лишків за модулем т, то відповідні числа Хи Хі> .. .,x9(m) також
утворюють зведену систему лишків за модулем /я;
ж) якщо (а, т) = 1, ЬзО (modm) і х пробігає зведену систему
лишків за модулем т, то ах + b також пробігає зведену систему
лишків за модулем т\
з) якщо (я, т) = d і х пробігає зведену систему лишків за
модулем ^-» то й —а: також пробігає зведену систему лишків за
модулем ~;
32

к) К$-\ = К\"\ де р— просте число, а не ділиться на р.
12.13. Об'єднанням яких класів лишків є класи лишків;
а) К(\\ Кг\ Kf за модулем 48;
б) К\13\ *Г\ К(5п\ К(713) за модулем 52;
в) К(2Щ, КЇ°\ *Г. Кіщ за модулем ЗО.
1§.14. Знайти класи лишків, обернені до таких класіві
а) ^3);б)М4,;в)К(з5);г) Кр;
д) М8); є) КГ; є) КГ; ж) *<»»>;
з) *»'>; к) /fffi»; л) М%»; м) К^з98); и) tfjjf».
§ 13. Теореми Ейлера і Ферма
Література
[1]-§ 16, с. 174-175;
[2] —§ 16, с. 178-179;
[31 —гл. 12, § 3, с. 408—409;
[10] —гл. З, § 6;
[11] —гл. 2, с. 96—106;
[12] —гл. II, § 5, с. 57—60;
[14] —§ 19, с. 79—80.
ТЕОРЕТИЧНІ ВІДОМОСТІ
Теорема Ейлера. Якщо m > 1 і (a, m) = 1, то
а^т) ш 1 (mod m).
Теорема Ферма (мала теорема Ферма). Якщо число р просте і (а, р) =
= 1, то аР~~х ss 1 (modp).
Наслідок. Якщо р — просте число, а — будь-яке ціле число, то аР = a (mod p).
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Знайти остачу від ділення: а) 223*123 на 52; б) 264102° на 138.
Р о з в* я з а н н я. а) Якщо треба знайти остачу від ділення as на т, де
(s, т) *= 1 is > <р(т)» то s можна подати у вигляді (за теоремою про ділення
остачею): s = 9 (m) q + г, де 0 < г < 9 (m). Оскільки a9(m) == 1 (mod т), то
fls = a9(m)Q+r = (^(m))^#er ш аг (mod m)>
де flf може бути значно меншим, ніж as.
У цьому разі маємо
52 = 2».13, Т(52) = 2з. ІЗ (і-^.j (і--^)=24,
223 = 52 . 4 + 15, 2123 = 24-88+11.
Тоді
2232123 = (52-4 + 15)24'88+п ^ 15й = 159 . 152 = (153)3 . 225 .
ш (3375)3 • 17 з (—5)3 . 17 >р (-125) . 17 а (-21) • 17 = -357 ss 7 (mod 52).
Отже, 223а123 при діленні ні 52 дає остачу 7.
б) Якщо (а, т) Ф 1 і (as, m) = d > І, то знаходимо спочатку таке найменше k,
що Qk Id. Тоді ak = atdt m — mxdy де вже (a, /nt) = 1- Позначимо через х
остачу від ділення as на т. Тоді
. as—A # ak __ as—k щ Q^d £mo(j щ^ dy
83

Звідси х = xxdi де
xt s= a5 Rat (mod mj.
ns—k
Тепер Хі знайдемо як добуток сстач від ділення as K і а^ на т^. Оскільки
(а, т^} =1, то остачу від ділення as~~k на т^ можна знайти за теоремою
Ейлера.
Маємо (264, 138) = 6. Якщо х = 2641020 (mod 138), то x = 6xv Оскільки 264 =
== 126 (mod 138), то 2641020 ш 1261020 (mod 138). Найменшим k таким, що
126*: 6, є 1. Тоді % = 126: 6=21, тг = 138 : 6 — 23 і хх = 21 . 126 (mod 23).
Оскільки ер (23) = 22 і 1019 =- 22 . 46 + 7, то
Хі-21. 111019-21.1122-4б+7 = 21.(П22)46. 117^
а= 2М17 = (—2) • 11 . 11е = —22-11е з 11в = (121)3 =
s б3 = 36 . 6 be (—10) . 6 = —60 ш 9 (mod 23).
Тоді х = 9 • 6 = 54. Отже, 2641020 при діленні на 138 дає остачу 54.
2. Знайти останні дві цифри числа 243402.
Розв'язання. Досить знайти остачу від ділення 243402 на 100. Маємо
243402 ш 4340а (mod 100).
Оскільки (43, 100)= 1, а
ср(100) = 22-52 (l-i-Wl-i-)=40,
то 4340 = 1 (mod 100). Оскільки 402 = 40 . 10 + 2, то
43402 = 4340.10+2 ^ 432 в ,849 s 4g (mod ,00)e
Отже, останніми двома цифрами числа 243402 є 4 і 9.
Зауваження. Щоб знайти k останніх цифр числа а, досить знайти остачу від
ділення цього числа на 10^.
3. Довести, що ІЗ176— 1 і 89.
Розв'язання. Оскільки ІЗ176— 1 = (1388)2— 1 = (ІЗ88 — 1) (ІЗ88 + 1), а
89 — просте число, то досить показати, що на 89 ділиться хоч один з
множників ІЗ88—1 чи 1388+ 1. Згідно з малою теоремою Ферма,
ІЗ88« 1 (mod 89),
. звідки ІЗ83 — 1 • 89. Отже, ІЗ176 — 1 \ 89.
Задачі
13.1. Чи справджується теорема Ейлера для таких чисел;
а) а = 2, т = 9; є) а = 4, т = 9;
є) а = 5, m = 24;
ж) а = 2, т = 33;
(з) а = 3, т = 24? ^^9-
б) а = 2, m = 15;
в) а = 3, /72 = 4;
г.) а = 3, /72 = 9;
д) а = 3, /72 = 16;
13.2. Чи справджується мала теорема Ферма для таких чиселі
а) а - 2, /7 = 3:
б) а = 2, /? = 5
в) я = 3, /? = 2
г) а = 10, /? = 5
д) а = 5, /7 = 2
є) а = 5, р = З
є) а = 5, /7 = 7
ж) а = 4, /7 = 3:
з) а = 4, /7 = 5
к) а= 14, /7 = 7?
84

13.3. Користуючись теоремою Ейлера, знайти остачу від ділення!
а) ?67 на 12;
б) 109345 на 14;
в) 197
157
на
є) 293275
є) 439291
ж) 527і44
з) 353160
к) 48584
на
на
на
на
на
48:
60:
65
75
129.
35;
г) 356273 на 39;
д) 383і76 на 45;
13.4. Користуючись малою теоремою Ферма, знайти остачу від
ділення:
а) 93253 на 7;
б) 500810000 на 5, 7, 11, 13;
в) 4250 на 17;
г) 20441 на
д) 460150 на
на
на
на
на
від ділення:
5;
г) 2059 на 17;
13.5. Знайти остачу від ділення:
а) 4583 на 24
б) б76 на 26
в) 96і 13 на 92
13.6. Знайти остачу
а) 7100 + 8100
б) іоіо°4-40100
В) З100 + 4100
г) 55° + 2570
д) 2580 + 4080
13.7. Знайти дві останні
а) З100; д) 17900;
б) З219; є) 19882;
в) 1124І>; є) 9031294;
г) ІЗ219; ж) 5731931;
13.8. Розв'язати ті з задач
д) 259833
є) 230347
є) 7150
ж) 512402
на 17;
на 37;
на 67;
на 101.
111;
425.
7;
7;
9;
на 11;
є) 1560 + 2030 на 13;
є) 570 + 750 на 12;
ж) 35оо + 75°о на 101;
з) (12 37156 + 145)28 на 111;
к) 3 • 575 + 4 - 7100 на 132.
цифри числа:
з) 2100;
к) 2153;
л) 10254.
сувати теореми Ейлера і Ферма.
13.9. Довести, що:
а) 21131 = 2(mod 11 -31);
б) 219<73-'> = 1 (mod 19 • 73);
в) 517-І9 = 23 (mod 17- 19);
Г) 2Ю931092=1 (mod 10932);
д) 273-37-1 == 1 (mod 73 • 37).
13.10. Довести, що:
а) а7 —а • 42;
б) а11—а •: 66;
11.9 і 11 16, до яких можна засто-
27;
100;
125;
■а2 ■ 100;
в) а21-
г) а42-
д) ат-
є) а12 — Ь12 ; 65, якщо (а, 65) =
є) а>г—а ■ 2730;
ж) а560—1 і 561, (аі 561)= 1;
з) а5Є1—а 5 11;
(Ь, 65) = 1;
85

к) а10 — а6 — а* + 1 і 35, (а, 35)= І.
13.11. Нехай р — просте число. Довести, щоі
а) ар = bp (modp2), якщо ар = Ьр(mod/?);
б) а1+2+-+<р~1) + 1 • р або а1+2+-+<р~1) —1 •/?, якщо р>2,
(а, /7)= 1;
в) а1+2+-+(^-1> + 1 : р і аЧ-2+...+<Р-і>_ 1 : Pf якщо р = 2;
(я, 2)=1;
Г) іА(р-і) + 2^-1) + . . . + (/7-1)^-1) = — 1 (mod/7);
Д) яр= ± 1 (mod/72), якщо ар == ± 1 (modp);
є) р^1 + Яр~х = 1 (mod/;?), якщо ? — просте число і р ф q\
є) 8/72 + 1 є простим числом, якщо р = 3;
ж) /7 = 3, якщо 5р2 + 1 = 0 (mod/?2);
з) 4/7 + 1 є складеним числом, якщо р > 3, а 2/? + 1 — простим
числом;
к) дар + paq = a(p + q) (mod pq), якщо ? — просте число, (а,
Р) = (*. <7) = 1-
13.12. Знайти остачу від ділення;
а) а100 на 125, a£Z;
б) 2^(т)_1 на число /я, якщо воно непарне і т> 1;
в) 4^^-1 на число т, якщо воно непарне і т> 1.
13.13. Довести, щоі
а) а\ +al + ... + fl£ = 0(mod 30), якщо а\ + #2 +...+an =
= 0 (modЗО), fli, ^2,..., ^^Z;
б) a100"*1 = a (mod 1000), якщо n£ N, (а, 10) = 1;
в) п2 = 1 (mod 24), якщо (я, 6) = 1;
г) a6tn+ a6n = 0(mod7) тоді і тільки тоді, коли а • 7, m, n^N;
д) (а — 1)а (а + 2) = 0 (mod 504), якщо а є кубом деякого цілого
числа.
§ 14. Конгруенції першого степеня
з одним невідомим та застосування їх
Література
[1] —§ 17, с. 175—180;
[2] —§ 17, с. 179-183;
[3] —гл. 12, § 4, с. 409—411;
[10] —гл. IV, § 2, 3, с. 54—58;
[12] —гл. III, § 2, 4, 5, с. 64—68, 79—87;
[14] —§ 21, 22, с. 85—94.
ТЕОРЕТИЧНІ ВІДОМОСТІ
Конгруенцією з одним невідомим за модулем m називають конгруенцію виду
/ (х) = anxn + an^-x + ... + ^ + ^-0 (mod m), (1)
ліва частина якої містить многочлен з цілими коефіцієнтами. Якщо ап неіт,
то п називається степенем конгруенції.
Розв'язком конгруенції (1) називають клас лишків за модулем т, кожне
число якого задовольняє цю конгруенцію.
Якщо а— число, яке задовольняє конгруенцію (1), то записують х зз a (mod m),
або х = /c£m), де о < а < т.

Конгруенції з одним невідомим називають рівносильними, якщо множини
їхніх розв'язків збігаються.
Операції, як-і ке порушують мнсжину розв'язків конгруенцій (у подальшому
називатимемо їхніми елементарними перетвореннями):
а) додавання до обох частин конгруенції будь-якого многочлена з цілими
коефіцієнтами;
б) додавання до однієї частини конгруенції многочлена з коефіцієнтами,
кратними модулю;
в) множення (ділення) обох частин конгруенції на число, яке взаємно просте
8 модулем (яке є їхнім спільним дільником);
г) множення обох частин конгруенції та їхнього модуля на натуральне
число.
Конгруенція
ах^Ь (mod m), (2)
де а не:т, називається конгруенцією 1-го степеня з одним невідомим.
Якщо (а, т) = 1, то конгруенція (2) має єдиний розв'язок.
Якщо (а, т) = d, d > I і b\dy то конгруенція (2) має d розв'язків.
Якщо (a, m) = d, d > 1 і Ь не : d, то конгруенція (2) ке має розв'язків.
Найбільш поширеними способами розв'язування конгруенції 1-го степеня
є такі:
I. Спосіб спроб. Підстановка в конгруенцію (2) чисел повної системи
лишків за модулем т (доцільно брати повну систему найменших за абсолютною
еєличиною лишків). Цей спссіб використовується при невеликих модулях.
II. Штучний спосіб. Зведення даної конгруенції за допомогою елементарних
перетворень до рівносильної їй конгруенції з коефіцієнтом при х, який
дорівнює 1.
III. Спосіб Ейлера: Розв'язок знаходять за формулою
х ss ba^m)-1 (mod /я), (3)
де ер (т) — функція Ейлера.
IV. Застосування ланцюгових дробів. Розв'язок знаходять за формулою
х**(-\)пРп__хЬ(т<Ат), (4)
. . т
де Рп_і — чисельник передостаннього підхідного дробу у розкладі -*- в
ланцюговий дріб.
V. Застосування класів лишків. Розв'язок знаходять за формулою
* = кГ(*Г)_1. (5)
де (К(™^)~~{ — клас лишків, обернений до класу лишків К(™К
Зауваження
1. Формули (3)-(5) справедливі тільки при (а, т) — 1. Тому
розв'язування конгруенції (2) будь-яким способом треба починати з відшукання (а, т).
2. Число х0 (клас лишків К^) вважається розв'язком конгруенції (2),
якщо х0 задовольняє (2) і 0 < х0 < т.
За допомогою конгр>енцій першого степеня з одним невідомим можна
розв'язувати невизначені рівняння першого степеня з двома невідомими (див. § 5).
Якщо х0 — розв'язок конгруенції (2), то \х0, -\ є розв'язком невизна-
ченого рівняння першого степеня з двома невідомими
ах + ту = Ь. (6)
Якщо {х0У у0} —деякий розв'язок рівняння (6), то множину розв'язків
цього рівняння знаходять за формулами
т а
*=-*o + -jU У = Уо — -jU (7)
де / — довільне ціле число, a d = (а. т).
87

Якщо числа /Яр m2, ..., mk попарно взаємно прості, то система з одним
невідомим
х = сг (mod m^y
х = с2 (mod m2), (8)
має єдиний розв'язок
x = ck (mod тЛ)
х = x0 (mod М), (9)
де
М = т^з . . . mk, х0 = М1у1с] + М2у2с2 + ... + М$#к,
причому числа Мі і у. визначають з таких умов:
М
М. = — , МіУі = 1 (mod т()9 і = 1, 2, . . ., k.
У загальному випадку, коли числа mp m2, . . ., тЛ можуть не бути попарно
взаємно простими, систему (8) розв'язують ще так: з першої конгруенції системи
(8) знаходять
x = c, + m1t1, де іл £ Z. (10)
Це значення х підставляють у другу конгруенцію системи (8) і розв'язують її
відносно tv Значення /, підставляють у рівність ПО) і здобуте значення х
підставляють у третю конгруенцію системи (8) і т. д. Зрозуміло, що на якомусь
кроці можна дістати конгруенцію, яка не має розв'язків. Тоді вся система
несумісна.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Користуючись способом спроб, розв'язати конгруенцію
2х = 5 (mod 9).
Розв'язання. Спочатку знаходимо (2, 9) = 1. Отже, задана конгруенція
має єдиний розв'язок. Випробуємо лишки з повної системи абсолютно найменших
лишків за модулем 9, тобто числа 0, ±1, ±2, ±3, ±4. Маємо:
2 • 0 = 0^5 (mod 9),
2 • 1 = 2^5 (mod 9),
2(— 1) = — 2 =£5 (mod 9),
2 . 2 = 4 ФЬ (mod 9),
2 (—2) = -4 = 5 (mod 9).
Отже, число— 4 задовольняє конгруенцію. Запишемо загальний розв'язок, який
відповідає цьому окремому розв'язку. Оскільки — 4£/CJ?\ то
* = 5(mod9), або х = Kf].
Процес випробування можна вже припинити, оскільки довели, що
конгруенція маз єдиний розв'язок.
2 Користуючись штучним способом, розв'язати конгруенцію
27* = 47 (mod 38).
Розв'язання. Знаходимо (27, 38) = 1. Отже, задана конгруенція має
єдиний розв'язок. Додамо до правої частини конгруенції число — 38, яке
кратне модулю. Дістаємо
27* = 9 (mod 38).
Поділимо обидві частини цієї конгруенції на 9:
Зх = 1 (mod 38).
88

Додамо до правої частини модуль:
За = 39 (mod 38).
Поділимо обидві частини останньої конгруенції на 3:
х а 13 (mod 38).
Це і є розь*язок заданої конгруенції.
Зауваження. Відомо, що коли (а, т) = 1, то для будь-якого цілого числа Ь
[снують такі цілі числа s і ty що 0 < s < а і Ь -f-sm = at. Отже, розв'язком
конгруенції о* а 6 (mod/л), де (а, т) = 1 є * = /(modm), і тому будь-яку
конгруенцію першого степеня з одним невідомим можна розв'язати штучним
способом. Справді, якщо конгруенція має розв'язки, то досить розглянути випадок,
коли (a, m)s=l. Тоді конгруенцію ах а Ь (mod m) послідовно замінюють
еквівалентними їй конгруенціями:
a* a b ± m (mod m), ax = b ± 2m (mod m), ...,
поки не дістануть конгруенцію, в якій ліву і праву частини можна скоротити
на а.
3. Користуючись способом Ейлера, розв'язати конгруенцію
27* а 24 (mod 102).
Розв'язання. Знаходимо (27, 102) = 3. Задана конгруенція має три
розв'язки, оскільки 24 ;. 3. Поділимо обидві частини і модуль заданої
конгруенції на 3:
9* а 8 (mod 34).
Оскільки тут а = 9, т = 34, b = 8, то за формулою (3) маємо
х a ba^m)-{ (mod m),
або
х а 8 • 9*34*-1 (mod 34).
Тепер знайдемо <р(34). Оскільки 34 = 2-17, то
,(34)=2.17.(14)(1-1.) = 16.
Тоді *а 8-915(mod34). Число 8-9^ замінимо найменшим невід'ємним лишком
за модулем 34. Дістаємо
* = 8-916 = 8. З30 = 8 -З14 з=8. (2187)2 = 8. 11* а 16 (mod 34).
Отже, *а 16 (mod 34) є розв'язок конгруенції 9х а 8 (mod 34). Тоді
конгруенція 27* = 24 (mod 102) має розв'язки:
*а 16 (mod 102),
х а 50 (mod 102),
х = 84 (mod 102),
або коротше
*а 16; 50; 84 (mod 102).
Зауваження. Недоліком способу Ейлера є те, що при великому ер (т)
знаходження найменшого невід'ємного лишку того класу чисел за модулем т, до якого
належить число ba^m)"lt стає громіздким.
4. Використовуючи ланцюгові дроби, розв'язати конгруенцію
220* а 28 (mod 348).
Розв'язання. Знаходимо (220,348) = 4. Оскільки 28:4, то задана
конгруенція має чотири розв'язки. Поділимо обидві частини і модуль заданої
конгруенції на 4:
55* а 7 (mod 87).
Розв'яжемо цю конгруенцію за допомогою ланцюгових дробів. Розкладемо
87
eg у ланцюговий дріб і обчислимо його підхідні дроби. Дістанемо таблицю
елементів qc і чисельників Р( (табл. 13).
89

Таблиця 13
і
Яі
1 р<_
—1
1
0
1
1
1
1
2
2
1
3
3
2
8 і
4
1
11
5
1
19
6
4
87 1
Отже, п = 6, РЛ_! = 19. Оскільки Ь = 7, m = 87, то за формулою (4)
х = (— \)пРп_хЬ (mod т).
Отже,
* к (—І)6 19 . 7 s 133 з 46 (mod 87)
є розв'язком конгруенції 55* =z 7 (mod 87). Тоді задана конгруенція має
розв'язки
х ш 46; 133; 220; 307 (mod 348).
Зауваження. Перш ніж застосувати цей спосіб, слід спочатку (якщо це
необхідно), використовуючи властивості конгруенцій, зробити коефіцієнт при
невідомому невід'ємним і меншим за модуль.
5. Застосовуючи класи лишків, розв'язати конгруенцію
37* = 25 (mod 107).
Розв'язання. Знаходимо (37, 107)=1. Отже, задана конгруенція має
єдиний розв'язок. Запишемо конгруенцію у вигляді
Знайдемо (/Сз7°7>)~1 ~"клас лишків за модулем 107, обернений до класу К$7)щ
Для цього застосуємо до чисел 107 і 37 алгоритм ділення з остачею. Матимемо
107 = 37 • 2 + 33,
37 = 33 • 1 + 4,
33 = 4-8+1.
Розглядаючи цей процес знизу вверх, виразимо 1 через числа 107 і 33:
1 = 33 — 4 • 8 = 33 — (37 — 33 • 1) • 8 = 33 • 9 + 37 (—8) =
= (107 — 37 - 2) . 9 + 37 (—8) =107-9 + 37 (—26).
Отже, 1 = 107 . 9 + 37 (—26). Це означає, що (К{3\07))~1 = К(Щ\ тобто
Тоді за формулою (5) маємо
х = кГ (Є*)-1. аб° * = *Г> • <7) = <275> = <07)-
Отже, х = К$7) є розв'язком заданої конгруенції, тобто х зз 99 (mod 107).
Зауваження. Процес розв'язування конгруенції першого степеня з одним
невідомим будь-яким способом слід закінчувати перевіркою.
6. Розь*лзати в цілих числах невианачене рівняння 27* + 38у = 47.
Розв'язання. Оскільки число у повинно бути цілим, то різниця 27* — 47
має ділитися на 38. Дістаємо
27* = 47 (mod 38).
Розв'яжемо цю конгруенцію. Знаходимо (27, 38)= 1. Отже, конгруенція має
єдиний розв'язок. Застосуємо штучний спосіб. Додамо до правої частини число
—38, яке кратне модулю:
27* s 9 (mod 38).
Поділимо обидві частини^цієї конгруенції на 9:
З* = 1 (mod 38).
Додамо до правої частини модуль:
З* s 39 (mod 38).
90

Поділимо обидві частини на 3:
х я 13 (mod 38).
Отже, х = 13 (mod 38) є розв'язком конгруенції 27* s 47 (mod 38). Тоді
" — 27-13)
{l3, 11^^1=(,3.-8}
є окремим розв'язком заданого рівняння,
няння дістаємо за формулами (7):
Загальний розв'язок заданого рів»
де х0 = 13, у0 = —8, т = 38, а = 27, d = 1. Отже,
{*' = 13 + 38/, уГ = — 8 — 27/} —
загальний розв'язок заданого невизначеного рівняння, де і — довільне ціле
число.
Розв'язати систему конгруенцій
Зд: = 11 (mod 17),
15* н= 35 (mod 13),
121* s 33 (mod 30).
Розв'язання. Розв'язуючи кожну конгруенцію, замінимо задану систему
еквівалентною їй системою конгруенцій:
(хш 15 (mod 17),
|хз 11 (mod 13),
Us 3 (mod 10).
Оскільки модулі конгруенцій попарно взаємно прості, то можна використати
формулу (9). Знаходимо:
М = 17. 13. 10 = 2210,
2210
^ = -^ = 130,
2210
13
= 170,
22\у3= l(mod 10).
Уз= І-
М2 =
2210
^3 = -10- = 221.
Розв'яжемо такі конгруенції:
130^ s= 1 (mod 17), \70у2 = 1 (mod 13),
^і= 14, г/2= 1,
Згідно з формулою (9), дістанемо
* = *0= 130-14-15+ 170.1-11 + 211.1.3 = 29 833= 1103 (mod 2210).
Зауваження. 1. Якщо деяка з конгруенцій системи має кілька розв'язків, то
їх слід об'єднати і записати як один розв'язок за меншим модулем, бо в
противному разі треба буде розв'язувати стільки систем, скільки розв'язків має
конгруенція.
2. Розв'язки системи конгруенцій можуть мати різні форми запису,
розв'язки третьої конгруенції з прикладу 7 ми записали б у вигляді
23 (mod ЗО), то довелося б розв'язувати такі три системи конгруенцій:
Так, якщо
*s3, 13,
|* s 15 (mod 17),
Us 11 (mod 13),
Іде з 3 (mod ЗО);
Дістали б три розв'язки:
х = 5523 (mod 6630),
Зазначимо, що мнощина чисел,
[*== 15 (mod 17),
*= 11 (mod 13),
U= 13 (mod 30);
x = 15 (mod 17),
x = 11 (mod 13),
x S3 23 (mod 30).
x S3 3313 (mod 6630), * s 1103 (mod 6630).
які визначаються цими розв'язками, збігається з
множиною чисел, що визначаються одним розв'язком, здобутим раніше,
jcs= 1103 (mod 2210).
91

8. Розв'язати систему конгруенцій
(2х = 19 (mod 15),
І3х = 41 (mod 20),
[6* =37 (mod 35).
Розв'язання. Розв'язуючи кожну конгруенцію, замінимо задану систему
еквівалентною їй системою конгруенцій:
іх= 2 (mod 15),
*= 7 (mod 20),
U= 12 (mod 35).
З першої конгруенції маємо * = 2+l5f, де / £ Z. Щоб визначити t,
підставимо значення х у другу конгруенцію:
2+15/= 7 (mod 20).
Звідси / = 3 (mod 4), або / = 3 + 4s, де s є Z. Тоді
х = 2 + 15/ = 2 + 15 (3 + 4s) = 47 + 60s,
причому х задовольняє вже перші дві конгруенції системи. Серед чисел х вибе*
ремотакі, які б задовольняли й третю конгруенцію. Для цього знайдемо s
з умови
47 + 60s = 12 (mod 35).
Звідси s = 0 (mod 7), тобто s — lky де k £ Z. Маємо х = 47 + 60s = 47 +
+ 60-7^ = 47 + 420/г. Отже, х = 47 (mod 420) — розв'язок заданої системи.
N Задачі
14.1. За способом спроб розв'язати такі конгруенціїї
а) 2х = 1 (mod 3); д) 4х == 6 (mod 10);
б) 8* = 3 (mod 4); є) 12л: = 1 (mod 7);
в) бх = 7 (mod 5); є) 5л: = 7 (mod 11);
г) За: = 22 (mod 7); ж) 8* =16 (mod 12).
14.2. За штучним способом розв'язати такі конгруенціїї
а) їх = 8 (mod 13); д) 16* = 50 (mod 23);
б) 6л: = 11 (mod 14); є) 25л: = 1 (mod 37);
в) 8л: = 10 (mod 14); є) 17л: = 23 (mod 41);
г) 11л: = —32 (mod 27); ж) 32л: = 43 (mod 51).
14.3. За способом Ейлера розв'язати такі конгруенціїї
а) 5* = 7 (mod 13); д) 27л: = 11 (mod 34);
б) 2ux = 3(mod 12); є) 24л: = 1 (mod 15);
в) 5* = 26 (mod 12); є) 15л: = 23 (mod 22);
г) 8л: =17 (mod 19); ж) 12л: = 51 (mod 39).
14.4. Застосовуючи ланцюгові дроби, розв'язати такі
конгруенції:
а) 15л: = 37 (mod 98); є) 192л: = 9 (mod 327);
б) 32л: =182 (mod 119); ж) 365л: = 50 (mod 395);
в) 105л: = 72 (mod 147); з) —639л: = 177 (mod 924);
г) 97* = 53(mod 169); к) 1296л: = 1105(mod 2413);
д) —50л: = 67 (mod 177); л) 1215* = 560 (mod 2755);
є) 69.x: = 393(mod 201); м) 1919л: = 1717 (mod 4009).
92

14.5. Застосовуючи класи лишків, розв'язати такі конгруенції:
а) 21* = 17 (mod 23); д) 28* = 33 (mod 35);
б) 5* = 7 (mod 24); є) 12* = 24 (mod ЗО);
в) 17*= 19 (mod 24); є) 9*= 18 (mod 41);
г) 13* == —1 (mod ЗО); ж) 11* = 31 (mod 50).
14.6. Розв'язати штучним способом конгруенції задач 14.3 і 14.5.
1.4.7. Розв'язати такі конгруенції:
а) (a + b)x = a2 +b2(mod ab), (а, Ь) = 1;
б) (a2 + b2)x = a — b(mod ab), (а, Ь) = 1;
в) (a + b)2 x = a2 —b2 (mod ab), (а, Ь) = 1;
г) (a — b)x = a2 + b2 (mod ab), (a, ft) - 1;
д) 2* = 1 + p (mod р), де р — просте непарне число;
є) (т— 1)*= 1 (mod/n);
є) (т + І)2* = a (mod m);
ж) а*= 1 (mod р), де р — просте число і (а, />) = 1.
14.8. Скласти конгруенцію першого степеня з одним невідомим
за модулем 15 так, щоб вона мала:
а) єдиний розв'язок;
б) 3 або 5 розв'язків;
в) 2, 4, 6, 14 розв'язків.
14.9. Розв'язати в цілих числах невизначенГрівнянняі
а)2* + Зг/ = 4; ж) 17* — 16г/ = 31;
б) 4* — Зу = 2; з) 91* — 28у = 35;
в) 3* + 4(/ = 13f к) 17* — 39у = 26;
г) 5* + 4у = 3; л) 50* — 42у = 34;
д) 3* + By = 5; м) 47* — 105(/ = 4;
є) 17*+130=1; н) 47*— 1 Ну = 89.
є) 23*+15у= 19;
14.10. Розв'язати системи конгруенцію
З* = 5 (mod 7), (*==&і (mod 13),
а) 12* з= 1 (mod 5); Д) \x = b2(mod 17);
^ ( 3* = 1 (mod 20), І 3* + 4у == 29 (mod 143),
б) 0„_Q/ 1 1«. Є)
.2* = 3 (mod 15); ' І2* — 9у = 59 (mod 143);
} 3* = 1 (mod 5), | * + 2у = 0 (mod 5),
В) 15* = 4 (mod 7); є) \ 3* + 2(/ == 2 (mod 5);
2 (mod 5);
(mod 6),
* = b (mod 25); m; 12* + 2y = 5 (mod 6).
f 14* = 12(mod 18), ( 5* — #==3(mod 6),
93

14.11. Розв'язати системи конгруенційі
а)
б)
в)
г)
Д) *s
є)
Хі
х\
XI
X =
Хі
X ■
XI
Хі
Хі
л: =
х е
х =
X =
X:
XI
х\
х\
х\
s3(mod 8),
е 11 (mod 20),
е 1 (mod 15);
-=2(mod 3),
= 3(mod 4),
= 4 (mod 5);
11 (mod 2),
:3 (mod 5),
E6(mod 9);
= 2 (mod 7),
= 5 (mod 9),
: 11 (mod 15);
;4 (mod 7),
;9(mod 13),
; 1 (mod 17);
:5 (mod 12),
2 (mod 8),
2 (mod 11);
* = 2(mod 15),
е) \ x = 7(mod 20),
,x= 12(mod 35);
# = 4 (mod 5),
ж) | x= 1 (mod 12);
x = 7 (mod 14);
'* = 5(mod 8),
з) I л: == 4 (mod 11),
4* = 6(mod 17);
л: = b\ (mod 25),
к) \ x = 62(mod 27),
x = bi (mod 59);
x= 1 (mod 3),
л:== 4 (mod 5),
л) { # = 2(mod 7),
x = 9 (mod 11),
Ar=3(mod 13).
14.12. Розв'язати системи конгруенцію
3x= l(mod 10),
а) | 4л: = 3(mod 5),
2л: = 7 (mod 9);
2л: =3 (mod 5),
б) J Зл: = 5 (mod 7),
3x = 3(mod 9);
4л: = l(mod 9),
B) ) 5x = 3(mod 7),
4л: = 5 (mod 12);
7x = 3(mod 11),
Г) I 3x = 2(mod 5),
15л: = 5 (mod 35);
Д)
e)
e)
Зл: == 7 (mod 10),
2л: = 5 (mod 15),
7л: = 5 (mod 12);
5л: = 3 (mod 9),
4* = 7 (mod 13),
8л: = 4 (mod 14),
x he 2 (mod 17);
2л: = 7 (mod 13),
5л: = 8 (mod 17),
14^ = 35 (mod 19),
3x = 7(mod 31).
14.13. Знайти точки з цілими координатами, які лежать на
прямих 4х—7f/ = 9, 2x + 9f/=15 і 5л:— 1 Зг/ =12 на одному
перпендикулярі до осі абсцис.
94

14.14. При яких значеннях а мають розв'язки такі системні
| х == a (mod 6),
х= l(mod 10),
1 х = 2 (mod 21),
І x = 3(mod 11);
(2* = a (mod 4),
ІЗ* = 4 (mod 10);
[ х = 5 (mod 18),
в) J * = 8(mod 21),
[ х == a (mod 35);
( *==3(mod 11),
г)
* = 11 (mod 20),
х = 1 (mod 15),
. * = a(mod 8)?
14.15. Знайти хоча б одне значення m, при якому несумісною
є система
х == 3(mod 6),
х = 7 (mod m).
14.16. Скільки точок з цілими координатами лежать на прямій
8х— ІЗу + б = 0 між прямими х = —100 і х = 150?
14.17. Довести, що всередині прямокутника, обмеженого
прямими х = —2, * = 5 і у = — 1, # = 2, на прямій З* — Ту = 1 не має
жодної точки з цілими координатами.
14.18. Скільки точок з цілими координатами лежать на заданих
прямих між точками з абсцисами а\ і а2\
а) 10л:— 11г/ = 15, ах = —ЗО, а2 = 50;
б) 31* — 47*/ = 23, а{ = 23, а2 = —50;
в) 101* — 39у = 89, аі=0, а2 = 100;
г) 8л:— 13(/ + 6 = 0, аі = —100, а2 = 150;
д) 7* + 29г/ = 584, а\ = —20, а2 = 160;
є) 90* —74у = 50, ах = —100, а2 = 200?
14.19. Нехай точки А і В мають цілі координати А (хи У\)>
В(х2, #2). Довести, що на відрізку АВ число внутрішніх точок з
цілими координатами дорівнює d—1, де
d = (у\ — У2, *і—*2).
14.20. Через скільки точок з цілими координатами проходять
сторони трикутника з вершинами:
а) Л(2, 3), 6(7, 8), С(13, 5);
б) Л(2, 1), В (20, 7), С(8, 15)?
14.21. Знайти відстань г між сусідніми точками з цілими
координатами, які лежать на прямій ах + by = c, (a, 6)=1.
14.22. При якій умові дріб -^- можна подати у вигляді суми
двох дробів із знаменниками а і b (a>bfc £ Z)?
14.23. Відгадати день народження, якщо сума добутків числа
місяця на 12 і номера місяця на 31 дорівнює 339. У чому суть
відгадування?
95

14.24. Для перевезення зерна є мішки по 60 і 80 кг. Скільки
таких мішків потрібно для перевезення 440 кг зерна?
14.25. На будівницгво газопроводу на трасу завдовжки 283 м
було доставлено труби, довжина яких 5 і 7 м. Скільки труб
доставили?
14.26. Скільки квитків по ЗО і 50 коп. можна купити на 14 крб.
90 коп.?
§ 15. Конгруенції вищих степенів з одним невідомим
Література
[1] —§ 18, с. 180—184;
[2]-§ 18, с. 183—187;
[3] —гл. 12, § 4, с. 411—413;
[5] —гл. VIII, § 4, с. 297—316;
[10] — гл. IV, § 4, 5, с. 58—63;
[11] —гл. 15, § 1, гл. 16, с. 126—131, с. 135—139;
[12] — гл. III, § 6, 7, с. 87—101;
[14] —§ 24, 25, с. 94—105.
ТЕОРЕТИЧНІ ВІДОМОСТІ
Якщо mp т2,...» tns — полярно взаємно прості числа, то конгруенція
/ (де) = а0хл + а,*"""1 + • • • + ап-\х + an s ° (mod mim2 • • • ms> (1)
еквівалентна системі конгруенцій
f (х) зз 0 (mod mx), \
fW^O (mod m2),
(2)
f (x) = 0 (mo і ms). )
Число розв'язків конгруенції (1) дорівнює kxk2 ... ks, де kv k2,..., ks
дорівнює відповідно числу розв'язків кожної з конгруенцій (2). Отже, треба
розв'язати конгруенцію виду
f (х) s 0 (mod pa), (3)
де р — просте число, а Є N.
Будь-який розв'язок
х =5 a (mod р) (4)
конгруенції
/ (х) = 0 (mod p) (5)
при умові, що f (а) не-/?, є одним з розв'язків конгруенції (3).
Якщо f (а):р, то розв'язок (4) або не дає жодного розв'язку для (3), або
дає кілька розв'язків.
Нехай х= a(modpk~~1) — розв'язок конгруенції / (х) =0 (mod pk~~x). Тоді
число х = a + pk~4, t£Z, є розв'язком конгруенції / (я) == 0 (modpfe) тоді
і тільки тоді, коли відповідне значення t задовольняє конгруенцію
Па)'= -4¾ (mod р). (6)
Якщо конгруенція (6) не має розв'язків, то в класі розв'язків х =
s= a(modpfe~'1) конгруенції / (х) = 0 (modpk~l) немає жодного розв'язку
конгруенції / (x) = 0{mcupk).
96

Якщо конгруенція (6) має розв'язки \ f (a) \ р, то будь-яке ціле число t
задовольняє конгруенцію (6), а тому / = 0, 1, . . ., р— 1 (mod/?) є розв'язками (6).
Тоді клас розв'язків х = a (modpk~~l) конгруенції / (x) ss 0 (modpk~~l) дає р
розв'язків конгруенції І(х) = 0 (mod pk), а саме: х = at a-\-pk~~{, a-{-2pk~lt
..., а + {р-1)рк~1(то<ірк).
Якщо конгруенція (6) має розв'язки і f (а) не ділиться на р, то це є
єдиний розв'язок / = /0(modp). Тоді з класу розв'язків х = a(modpk~l)
конгруенції f (х) г= 0(modp*—1) дістаємо єдиний розв'язок х = a-\-pk~~l t0 (modpk)
конгруенції f (x) 5= 0 (mod pk).
Конгруенцію (5) завжди можна замінити еквівалентною конгруенцією того
самого степеня із старшим коефіцієнтом, що дорівнює одиниці. Для цього слід
обидві частини конгруенції (5) домножити на число Ь} яке задовольняє
конгруенцію aQy = 1 (modp). Це'число визначається однозначно, оскільки (а0,р\= 1.
Конгруенцію (5) можна замінити еквівалентною їй конгруенцією степеня не
вище р — 1 за тим самим модулем (згідно з теоремою про пониження степеня
конгруенції). Для цього треба в конгруенції (5) замінити вираз / (х) на т (х),
де г (х) — остача від ділення fix) на хр — де. Ділення / (х) на хр — х можна
фактично й не виконувати, а просто замінювати кожне Xs у лівій частині (5) на
хг, де т — остача від ділення s на р—1 при умові, що остачу 0 замінюємо
числом р — 1.
Якщо а0 не ділиться на р, то конгруенція (5) степеня п < р має не більш
ніж п різних розв'язків.
Конгруенція (5) має більш як п розв'язків тоді і тільки тоді, коли всі
коефіцієнти в ліеій частині (п) діляться на р, тобто коли конгруенція тотожна.
Конгруенція (5) степеня п < р, в якій а0= 1, (ап>р) = 1, має п розв'язків
тоді і тільки тоді, коли всі коефіцієнти остачі від ділення хр — х на f (х)
діляться на р.
Теорема ВІльсона. Натуральне число п > 1 тоді і тільки тоді а про-
стим, коли (я— 1)! -f- 1 = 0(mod /і).
Якщо р — просте число, то конгруенція
хр-{ — 1 =0(modp)
має точно р^—1 розв'язок.
Якщо р — просте число і d — натуральний дільник числа р — 1, то
конгруенція
xd = 1 (mod p)
має точно d розв'язків.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Розв'язати конгруенцію / (*) s де17 + 2х11 + З*8 — $х7 + 2л: — 3 ss 0 (mod5)#
Розв'язання. Замінимо цю конгруенцію еквівалентною їй конгруенцією
степеня не вище 4 за тим самим модулем 5. Поділимо / (х) на хь — х. Дістанемо
/ (х) = (хь — х)(х12 + х* + 2х6 + *4 + З*3 — 2х2 + 1) + 3jc4 — 2х3 + 3* — 3.
Замінивши всі коефіцієнти остачі найменшими лишками за модулем 5,
дістанемо, що задана конгруенція еквівалентна конгруенції
т (х) = З*4 + З*3 + 3* + 2 = 0 (mod 5). (1)
Замінимо цю конгруенцію еквівалентною їй конгруенцією із старшим
коефіцієнтом, що дорівнює 1. Спочатку розв'яжемо конгруенцію
Зу = 1 (mod 5).
Додамо до правої частини модуль:
Зу = 6 (mod 5).
4 5-271
97

Поділимо обидві частини на 3:
у = 2 (mod 5).
Домножимо конгруенцію (1) на 2:
б*4 + б*3 + 6* + 4 = 0 (mod 5).
Замінимо останню конгруенцію еквівалентною їй:
хА + х3 + х — 1 s 0 (mod 5). (2)
Оскільки х Ф 0 (mod 5), то (я, 5) = 1, а тому х5~~{ = 1 (mod 5). Тоді
конгруенція (2) матиме вигляд
х3 + х = 0 (mod 5). (3)
Оскільки (х, 5) = 1, то обидві частини конгруенції (3) можна скоротити на х:
х2 + 1 = 0 (mod 5). (4)
Конгруенція (4) має такі очевидні розв'язки: х = 2 (mod 5) і х = 3 (mod 5).
Отже, конгруенція (1) має два розв'язки: х = 2; 3 (mod 5).
Зауваження. Замість того щоб ділити f (х) на хь — xt можна було б
замінити Xs на /у де г — остача від ділення s на 5 — 1=4, причому, якщо s
ділиться на 4, то покладемо т = 4. Тоді
х17 = * (mod 5),
2*11 =2x3(mod5),
Зх8 = 3jc4 (mod 5),
—4jc7 = x3(mod5).
Отже,
f (x) = 3x4 + 3x3 + 3x + 2 = 0 (mod 5).
2. Розв'язати конгруенцію
f(x) = x5 + I0x3 + x + 6 e= 0 (mod 108). (1)
Розв'язання. Оскільки 108 = 22 • З3, то задана конгруенція еквівалентна
системі
(/(*) = 0(mod4), (2)
|/ (х) = 0 (mod 27). w
Перша з цих конгруенцій після спрощення матиме вигляд
х5 + 2*3 + х + 2 = 0 (mod 4). (3)
Випробовуючи лишки 0, ±1,2 за модулем 4, впевнюємося, що конгруенція (3)
має єдиний розв'язок
х = 2 (mod 4). (4)
Щоб розв'язати другу конгруенцію системи (2), треба спочатку розв'язати
конгруенцію
/ (*) s 0 (mod 3), (5)
або після спрощення
*5 + х3 + х = 0 (mod 3). (6)
Оскільки
*5 = я1 (mod 3),
х6 = хх (mod3),
98

то конгруенція (6) еквівалентна конгруенції
Зх s 0 (mod 3),
тобто 0 = 0 (mod 3).
Отже, конгруенція (5) виконується при будь-якому значенні х. Це означає,
що вона має такі розв'язки:
х = 0; 1; 2(mod3).
Використовуючи ці класи чисел за модулем 3, розв'яжемо конгруенцію
хь + Юх3 + х + 6 = 0 (mod 9),
або еквівалентну їй конгруенцію
х5+а3 + * + 6 = 0 (mod 9). (7)
Нехай
g(x) = xb + x3 + x + 6.
Випробуємо тепер кожен клас за модулем 3.
У класі х = 0 (mod 3) беремо числа х = 3*, де t задовольняє співвідношення
g'(0) •/ = — ^P(mod3).
Оскільки g(x) = ЬхА + Зх2 + 1, g' (0) = 1 і g(0) = 6, то / а —2 (mod 3), тобто
/ = 1 (mod 3), або t = 3s + 1, s £ Z.
Дістаємо x = 3/ = 3 (3s + 1) = 9s + 3. Ці числа утворюють один клас
розв'язків конгруенції (7):
х = 3 (mod 9). (8)
У класі х == 1 (mod 3) беремо числа х = 1 + 3/, де / задовольняє
співвідношення
g (1) . t = -^->od 3).
Оскільки g' (1) = 9, g (1) = 9, то
9/ == —3 (mod 3).
Цю конгруенцію задовольняє будь-яке значення t, тобто t = 3s, / = 3s+l,
t = 3s + 2, де s £ Z. Тоді x = 1 + 9s, де = 4 + 9s, x = 7 + 9s. Отже, маємо
ще три розв'язки конгруенції (7);
х= 1; 4; 7 (mod 9). (9)
У класі jc == 2 (mod 3) беремо числі х = 2 + 3/, де * задовольняє
співвідношення
g'(2).* = ~^(mod3).
Оскільки g' (2) = 93, g (2) = 48, то
93/ = —16(mod3)
або 0 = 2(mod3).
Ця суперечність свідчить про те, що в класі чисел xs2 (mod 3) немає
розв'язків конгруенції (7).
За допомогою знайдених класів розв'язків / (х) = 0 (mod 9) дістасмо
розв'язки конгруенції
/ (х) = хь + ІОх3 + х + G = 0 (mod 27). (10)
Випробовуємо кожен з класів (8) і (9).
У класі х == 3 (mod 9) беремо числа х = 9/ + 3, де t задовольняє конгруенцію
/(3)
/'(3) ./^-^(mod3).
Оскільки /'(*) = 5*4 + ЗО*2 + 1, /' (3) = 676, / (3) = 522, то 676/ =з
ss —58 (mod 3), або / = 2 (mod 3), звідки / = 3s + 2, s £ Z.
4* 99

Тоді х = 9 (3s + 2) + 3 = 27s + 21, s£ Z.
Ці числа утворюють один клас розв'язків конгруенції (10)
х = 21 (mod 27). (11)
У класі х = 1 (mod 9) беремо числа * = 9/+ 1, де / задовольняє конгруенцію
/0)
/ (!)■* = --V (mod 3).
Оскільки /' (1) = 36, / (1) = 18, то 36/ = —2 (mod 3). Тут (36,3) = 3, а —2 не
ділиться на 3, тому остання конгруенція розв'язків не має. Це означає, що в
класі чисел х = 1 (mod 9) немає розв'язків конгруенції (10).
У класі х = 4 (mod 9) візьмемо числа х = 9/ + 4, де t задовольняє конгруенцію
/ (4)
/ (4)./ = -'-y(mod3).
Оскільки /' (4) = 1761, / (4) = 1674, то
1761/= —186 (mod 3).
Тут (1761,3) = 3, —186:3 і тому остання конгруенція має три розв'язки / =
==0; 1; 2(mod3). Отже, дістаємо ще три розв'язки конгруенції (10):
х = 4; 13; 22 (mod 27). (12)
У класі х = 7 (mod 9) знаходимо числа х = 9/ + 7, де / задовольняє конгруенцію
/(7)
/'(^•'---^(modS).
Оскільки /'(7) = 13 476, / (7) = 20 250, то
13 476/ = —2250 (mod 3).
Тут (13 476,3) = 3 і —2250:3 і тому остання конгруенція має три розв'язки
/ = 0, 1, 2(mod3).
Відповідно до цього, маємо останні три розв'язки конгруенції (Ю):
* = 7; 16; 25 (mod 27). (ІЗ)
Таким чином, щоб знайти розв'язки конгруенції (1), треба розв'язати сім
систем:
\)(х = 2 (mod 4), 4)(х = 2 (mod 4),
U = 4 (mod 27); U = 16 (mod 27);
2)(x = 2 (mod 4), 5)(x = 2 (mod 4),
U = 7 (mod 27); U = 21 (mod 27);
3) f x = 2 (mod 4), 6) і x = 2 (mod 4),
13 (mod 27); U = 22 (mod 27);
)j* = 2(mod4), 6)1 jc =
U= 13 (mod 27); U = :
7)fx = 2-(mod4),
U = 25 (mod 27).
Розв'язуючи ці системи, знаходимо:
1) х = 58 (mod 108); 2) х = 34 (mod 108); 3) х = 94 (mod 108); 4) х = 70 (mod 108);
5) х = 102 (mod 108); 6) x = 22 (mod 108); 7) x = 106 (mod 108).
Отже, конгруенція (1) має сім розв'язків: х = 22; 34; 58; 70; 94; 102;
106 (mod 108).
Задачі
15.1. Знайти конгруенції того самого степеня із старшим
коефіцієнтом 1, еквівалентні таким конгруенціям:
а) Зх3 — 5х2— 2 = 0(modll);
б) 27х3 + 14х2 — 10* + 13 = 0 (mod59);
100

в) 70х6 4 78х5 4 25х4 4 68л;3 + 52л:2 4 4х 4 3 = 0 (mod 101);
г) аох" 4 а\Хп~х + ... 4 ап-\х 4 ап = 0 (modm), (a0, m) = 1.
15.2. Звести задані конгруенції до еквівалентних їм конгруенцій,
степінь яких менше за модуль:
а) х8 + 2х7 + х5 — Xі — х + 3 = 0 (mod 5);
б) Зх14 + 4л:13 + Зх12 4 2хп 4 *9 4 2х8 + 4х7 4 *6 4 Зх4 + х3 +
+ 4x2 + 2x = 0(mod5);
в) х16 + 3х8 —5х7 —х4 + 6х —2 = 0(mod7);
г) 2х17 + 6х16 4 х14 4 5х12 + Зх11 + 2x10 + x9 + 5xs + 2x7 +
4 Зх5 + 4х4 + 6х3 + 4х2 + х + 4 = 0 (mod 7);
д) 6х18 + 18х15 + Зх4 - 8х3 + х2 + 3 5= 0 (mod 11).
15.3. Спростити задані конгруенції (понизити степені, зменшити
коефіцієнти за абсолютною величиною, зробити так, щоб старший
коефіцієнт дорівнював 1) і розв'язати способом підбору;
а) х5 + Xі + х2 + 4 = 0 (mod 3);
б) 6х4 + 17х2 —16 = 0 (mod 3);
в) 28х9 + 29х8 — 26х7 + 20х4 — 17х + 23 = 0 (mod 3);
г) хБ + 2х4 — 2х3 — 2х2 + 2х — 1 = 0 (mod 3);
д) хЧ- х4 — х2 — 5х + 1 з= 0 (mod 3);
є) х7 + 2х6 + х5 + 4х3 — 2х2 — 4х + 2 = 0 (mod 5);
є) х7 + Зх6 + х5 — х3 — Зх2 — 4х + 4 = 0 (mod 5);
ж) х7 + 5хБ — х3 — 9х + 3 = 0 (mod 5);
з) 34х10 — 29х7 + 43х4 — 19х + 37 = 0(mod5);
к) 6х10 — 12х + 1 = 0 (mod 5);
л) х7 — Зх6 + хБ — 15х4 — х3 + 4х2 — 4х + 2 = 0 (mod 5).
15.4. Спростити задані конгруенції і розв'язати їх способом
підбору:
а) 5х24 + 4х23 + 4х22 + 2х21 + х20 + 6х19 + 4х18 + Зх17 + 4х16 +
+ 6х15 + 5х14 + 2х13 + х12 + 2x" + -¾10 + Зх9 + 4х8 + 2х7 + 5х6 +
+ 6х5 + 5х4 + Зх3 + 4х2 + 4х + 2 = 0 (mod 7);
б) х13 —х11 +х9 — х7 + х5 + *3 + * + 1 =0(mod7);
в) 10х42 — 5х30 + 10х18 + 9х12 + 4 = 0 (mod 7);
г) 75х13 — 62х12 — 53хп — 24х6 + ІЗх — 27 = 0 (mod 7);
д) 6х13 — Зх12 — 2Х11 — 6х3 + Зх2 + 7х + 2 = 0 (mod П);
є) ІЗх23 —30х22 —2x13 + l=0(modll);
є) 120х91 + 14х15 + х11 — Зх5 + 9х2 —х 4- 6 = 0(mod 11);
ж) х1+ — х13 + 12х2 + 2х + 1 = 0 (mod 13);
з) ЗОЗх90 4 259х67 — 95х23 — 1=0 (mod 23).
15.5. Розкласти конгруенції на лінійні множники за заданим
модулем:
а) х34 4х2 — 3 = 0 (mod 5);
б) х3 —2x41 =0(mod5);
в) х4 — 20х3 4 90х2 — 135х 4 54 = 0 (mod 5);
г) Зх3 4 2х2 — 2х — 3 я- 0 (mod 5);
д) х4 — 12х3 4 46х2 — 53х — 12 = 0 (mod 7);
є) 5х3 4 4х2 — 8х — 1 = 0 (mod-7);
є) 6х3 4 5х2 — 2х — 9 з= 0 (mod 11);
ж) х3 4 Зх2 — 3 =. 0 (mod 17);
з) х3 4 11*2 4 8х 4 3 = 0 (mod 23);
к) х4 4 15х3 4 4х2 4 4х — 15 = 0 (mod 29);
101

л) х3 — 13х2 -Зх + 11 = 0 (mod 31).
15.6. Довести, що:
а) конгруенція х3 + ах + b s= 0(mod7) при (а, 7) = (b, 7) = 1 не
має трьох розв'язків;
б) (р— 2)1 = 1 (mod р), якщо р — просте число;
в) 2(р— 3)1 + 1 S 0 (mod/?), якщо р — просте число;
г) числа р і р + 2 є простими (тобто простими числами-близню-
ками) тоді і тільки тоді, коли 4 [(р — 1)! + 11 + p = 0(modp (p + 2))
(теорема Клемента);
д) [(2n)!]2 =—l(modp), якщо р — просте число і р = 4я + 1,
ngN;
є) [(2п + 1)І]2 = 1 (modp), якщо р — просте число і р =Ап + З,
i€N;
є) ар + (р—1)1 a = O(modp), якщо a — довільне ціле число І р —
просте число;
ж) натуральне число р > 2 є простим тоді і тільки тоді, коли
(р — 2)! — 1 s O(modp) (критерій Лейбніца).
15.7. Розв'язати такі конгруенції!
а) х2 — Зх + 2 = 0 (mod 6);
б) х* + 2х3 — х2 — х— 1 =0(mod6);
в) Зх3 — х2 + іх + 2 = 0 (mod 10);
г) 2хь + х3 + 2х = 0 (mod 10);
д) х6 — х5 — Xі + 4л: — 1 = 0 (mod 10);
є) х8 + 5л:6 — х5— Xі — 5х2 +8х — 3s0(modl5);
є) х6 + 3х5 — х2— х — 7 = 0(modl5);
ж) Зх3 + 6л:2 + х + 10 == 0 (mod 15);
з) л9 + л-7 —л3 + 4л-+ 1 =0(mod21);
к) Зл:2 + їх + 5 s 0 (mod 34);
л) Xі + х2 = 0 (mod 35);
м) 2х2 — 7л + 6 = 0 (mod 55).
15.8. Розв'язати такі конгруенції:
а) 6л3 + 27л2 + 17л + 20 = 0 (mod ЗО);
б) 4л3 — 5х2 + 7л: + 21 = 0 (mod 105).
15.9. Розв'язати такі конгруенції:
а) л6 + л5 — л2 + 2х + 2 = 0(ішмі25);
б) х6 — х5 — х2 + 4л: + 2 s 0 (mod 25);
в) х4 — 4х3 + 2х2 + х + 6 s 0 (mod 25);
г) 5х3 + Зх + 1 = 0 (mod 25);
д) Зх3 — 5х2 — 15 = 0 (mod 49);
є) Зх4 — 2х2 + Зх + 1 = 0 (mod 49);
є) 5х3 + 4х2 — бх + 5 s 0 (mod 49);
ж) х9 —2х7—x3 + 7x + 2 = 0(mod49);
з) x^ + 3x + 5 = 0(modl21).
15.10. Розв'язати такі конгруенції:
а) 4х3 — 8х — 13 = 0 (mod 27);
б) х5 + 2х4 + Зх3 + х2 + х + 1 н= 0 (mod 27);
в) x4 + 7x + 4 = 0(mod27);
г) 7х4 + 19х + 25 5= 0 (mod 27);
д) 9х2 + 29х + 62 = 0 (mod 64);
є) х3 — 2х2 — ЗОх + 41 = 0 (mod 125);
.102

є) х3 + 2x + 2 = 0 (mod 125);
ж) 6х3 — 7х— И =0 (mod 125);
з) Зх3 — їх — 69 = 0 (mod 125);
к) х4 + 4л;3 + 2л:2 + 2х + 12 = 0 (mod 625).
15.11. Розв'язати такі конгруенції:
а) Х5 __ 7л;4 + 11л:3 — 5х + 1 = 0 (mod 12);
б) х5 — х4 + 2х3 — х2 + 5х — 2 = 0(modl2);
в) х5 — 2х3 + 5х — 2 = 0 (mod 18);
г) х3 + 2х5 — х2 + x + 4 = 0(mod40);
д) xs — х6 + х3 + х + 3 == 0 (mod 45);
є) х4 + Зх3 + 2х + 6 = 0 (mod 45);
є) х4 + 4х3 + 2х2 + х + 12 = 0 (mod 45);
ж) х4 — Зх3 — 4х2 — 2х — 2 = 0 (mod 50);
з) х8 + 2х7 —х2 + Зх - 2 = 0(mod63);
к) х2 — Зх +23 = 0 (mod63);
л) х74-х5 —х3 + 3х —3 = 0(modl75);
м) 2х3 — 5х — 32 = 0 (mod 175);
н) 31х4 + 57х3 + 96х + 191=0 (mod 225).
15.12. Знайти необхідну і достатню умову того, що конгруенція
хп = a(mod/?), де р — просте число, (а, р) = 1, п < р, має тільки п
розв'язків.
15.13. Які з наступних конгруенцій мають п розв'язків, де п —
степінь конгруенції;
а) х3 =ее 1 (mod 7);
б) х4= 1 (mod 11);
в) х5 = 10 (mod 11)?
Знайти ці розв'язки.
15.14. Скільки розв'язків мають конгруенціїї
а) х6 = 1 (mod 7);
б) хр-1 == 1 (mod/?), де р — просте число;
в) x?<?0> = l(mod20);
г) **<"*>== l(modm);
р-Л
д) х 2 ==l(mod/?), де р — непарне просте число;
р-Л
є) х 2 =—l(modp), де р — непарне просте число?
15.15. Довести, що конгруенція хп == 1 (mod/?) має п розв'язків,
якщо р — просте число і /? = 1 (mod/і).
15.16. Конгруенцію 1 їх2 е= 65 (mod 103) задовольняє число хо = 31.
Знайти всі розв'язки цієї конгруенції.
15.17. Перевірити теорему Вільсона при: а) р = 5; б) р = 7\
в) р=11; г) р= 13.
15.18. Довести, що х5р+[ = x6(modp), де р — просте число.
15.19. Розв'язати систему конгруенцію
|х4+2х+ 1 =0(mod4);
(х3+ 3==0 (mod 10).
103

§ 16. Конгруенції другого степеня, квадратичні лишки
і квадратичні нелишки, символ Лежандра
Література
[1] —§ 18, с. 184—192;
[2] —§ 18, с. 187—196;
г10] — гл. V, § 1—4, с. 68—80;
11] —гл. 21, 22, с. 172-200;
12] —гл. III, § 10, с. 110—124;
114] — § 25—28, с. 105—136.
ТЕОРЕТИЧНІ ВІДОМОСТІ
Конгруенцію другого степеня виду
а\У2 + а2У + аг = 0 (тос* п)' аі ^ и lmod n) 0)
завжди можна звести до двочленної конгруенції виду
х2 = a (mod m), (2)
де а = а2 — 4(2^31 * — 2^(/ + a2» m = 4ая.
Для цього слід обидві частини і модуль конгруенції (1) домножити на 4а і
зробити відповідні перетворення.
Якщо конгруенція (2) має хоча б один розв'язок, то а називається
квадратичним лишком за модулем т, у противному разі а називається квадратичним не
лишком за модулем т. При цьому (а, т) = 1.
Розв'язування конгруенції виду (2) за складеним модулем зводиться до
розв'язування таких конгруенцій:
1) х2 == a (mod р), де р —непарне просте число; (3)
2) *2 = a(mod ра), де р — непарне просте число, а > 1; (4)
3) *2 = a(mod 2а), де <х> 1. (5)
Найбільш важливим є той випадок, коли модуль є непарним простим числом.
При цьому досить обмежитися випадком, коли (а, р) = 1, оскільки в противному
разі конгруенція (3) має єдиний розв'язок х as 0 (mod p).
Отже, надалі розглядатимемо таку конгруенцію:
х ^ a (mod р), (а, р) = 1, де р— просте непарне число. (6)
Якщо а—квадратичний лишок за модулем р, то конгруенція (6) має два
розв'язки.
Для будь-якого простого непарного числа р половина лишків зведеної
системи лишків є квадратичними лишками, а половина — квадратичними нелишками.
При простому непарному р число а є квадратичним лишком за модулем р тоді
р— і
і тільки тоді, коли а 2 = 1 (mod р), і квадратичним нелишком тоді і тільки
р— і
тоді, коли а 2 == — 1 (mod p) (критерій Ейлера).
Теорема Ейлера. Добуток двох квадратичних лишків або нелишків в
квадратичним лишком за модулем р; добуток квадратичного лишку на нелишок
є квадратичним нелишком.
Добуток ряду чисел а, Ь, .. ., с дає квадратичний лишок або нелишок
залежно від того, парне чи непарне число нелишків буде серед множників.
Для ефективного використання критерію Ейлера вводиться так званий символ
Лежандра І — І (читається: «символ Лежандра а відносно р», або коротше «а
відносно р», або «а до р»), а називається чисельником, ар — знаменником симво*
лу Лежандра.
104

Символ Лежандра І— 1 визначається для всіх цілих чисел а, які не діляться
на просте непарне число р, рівністю
1, якщо а є квадратичним лишком за модулем р,
якщо а є квадратичним нелишком за модулем р.
Критерій Ейлера тоді коротко записується так:
у—і / \
° 2 =\7"/(m°d P)'
(тН-Г
Основні властивості символу Лежандра:
1°. Якщо а^Ь (mod р), то (Л. \ = (A.Y
(І)-'-
2°.
р-1
> 2
6Ч^)-(т)Ш-(т>
Р'-І
8°. [-f_) = ,_n 8
9°. Якщо р і ^7 — різні непарні прості числа, то
р-1 7-1
.—.. 2 2
(закон взаємності квадратичних лишків).
(іНі)-<-.г
Узагальненням символу Лежандра є символ Якобі І — І (читається:
«символ
Якобі а відносно т»). Він визначається для будь-яких непарних натуральних
чисел т > 1 і чисел а, взаємно простих з т, рівністю
(±)-(f)(f )•••(*)•
де т = р- q . . . т є розкладом m на прості множники (серед них можуть бути і
рівні), тобто як добуток символГв Лежандра. Для символу Якобі зберігаються
властивості 1) — 9) символу Лежанлра, проте для символу Якобі йдеться не про
непарні прості числа рУ а про непарні натуральні числа m > 1, для властивості
9) — про взаємно прості непарні числа, відмінні від 1. Тому при визначенні
символу Лежандра зручно розглядати його як символ Якобі. ҐІри цьому часто немає
потреби виділяти з чисельника символу його непарні прості множники.
Конгруенція х2 = а (mod рп), де р —непарне просте число, п > 1, (а, р) = 1,
має два розв'язки, якщо І — 1 = 1, і не має їх зовсім, якщо (— 1 = — 1.
Для конгруенції х2 = о (mod 27), (a, 2)= 1, необхідними умовами існування
розв'язків є а =s 1 (mod 4) при а = 2; а= \ (mod 8) при о > 3.
105

Якщо ці умови виконуються, то існує один розв'язок гри а= 1; два розв'язки
при а — 2 і чотири розв'язки при а > 3.
Для конгруенції загального виду *2 = a(mod m), m = 2flp\xp\t ••• Pkk>
(а, т) = І, необхідними і достатніми умовами існування розв'язків є: а =1 (mod 4)
при а = 2; а = 1 (mod 8) при а > З
Ші)--(£К
Якщо жодну з цих умов не порушено, то число розв'язків дорівнюватиме:
2* _ при а = 0 і а = 1; 2k+] — при а = 2; 2*+2 — при а > 3.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Звести конгруенцію другого степеня 4х2 — \\х— 3 = 0 (mod 13) до двочленної.
Розв'язання. Для простого модуля старший коефіцієнт взаємно
простий з ним. Тоді процес зведення заданої конгруенції до двочленної можна
скоротити і навіть залишити модуль незмінним. Визначимо множник k так,
щоб 4/г = 1 (mod 13). Матимемо & = 10 (mod 13). Домножаючи обидві частини
заданої конгруенції на 10 за модулем 13, дістаємо
40х2 — 110* — ЗО = 0 (mod 13),
або
х2 — 6*-4 = 0 (mod 13). (1)
Виділимо в лівій частині цієї конгруенції повний квадрат
*2 — 2- Зх + 9 — 9 — 4 = 0 (mod 13),
або
(* _3)2— 13 = 0 (mod 13).
Остаточно
(х — З)2 = 0 (mod 13).
Зауваження
1. При розв'язуванні задач такого типу треба намагатися спростити процес
виділення повного квадрату, для цього є різні способи. Зокрема, у розглянутому
прикладі від заданої конгруенції можна було б перейти до такої конгруенції:
4х2- 24*-1Є = 0 (mod 13). (2)
Оскільки (4, 13) = 1, то на 4 можна скоротити обидві частини
конгруенції (2):
х2 — 6х-4==0 (mod 13).
Дістали конгруенцію (1).
2. Часто процес зведення конгруенції до двочленної завершується простим
розв'язанням її. Так,
* - 3 = 0 (mod 13), або х = 3 (mod 13).
2. Скільки розв'язків має конгруенція х2 г= 219 (mod 383)?
Розв'язання. Знайдемо символ Лежандра І -_і І. Оскільки 219 === 3 • 73,
а 383— просте число, то, згідно з властивістю 5,
219\ = /_£\ /73 \
383/ 1383/ 1383/'
106

Обчислимо окремо символи Лежандра -- і (^)- Оскільки 3 і 383— різні
прості непарні числа, то внаслідок закону взаємності 9) дістаємо
381—1 3—1
(А)_(»).м>-т--г__ф
За властивістю 1) маємо
бо 383 = 2 (mod 3).
За властивістю 8)
о
(4)-,-.,^--..
Отже, f—) = — (—1) = 1. Щоб спростити запис, а також полегшити процео
перевірки, доцільно при кожному переході під знаком рівності ставити номер
властивості, на основі якої відбувається цей перехід. Наприклад,
381—1 73—1
/.73\ /383\ г_п—2 ~ /383\ /18\
І383/ 9 \73/М \ 73/ і 173/
Остаточно
\3S3' V383/ \383/
Таким чином, задана конгруенція має два розв'язки.
Зауваження
1. Слід уважно застосовувати властивість 9), оскільки якщо хоч одне з чисел
р чи q є складеним, застосування цієї властивості може призвести до помилок в
обчисленні символу Лежандра.
2. Розглядаючи символ Лежандра як окремий випадок символу Якобі і ко«
ристуючись властивостями останнього, можна символ Лежандра обчислити швидше.
Наприклад,
383—1 219—1
/219 \ /383^ г_П~ ^ = -/¾ /164\
І383/ 9 \219/ \219/ і \219/
219—1 41-1
--(^--(Йт-ШШ-'-'^а)-
Ч*)Н^'>"Н4т)т-#)т-^»¥-'-
3. Зауважимо, що коли р — просте непарне число, то символ Лежандра І—1
є для конгруенції x* = a(mod р) символом Якобі І—І і навпаки. Тому для
107

конгруенцій за простим модулем можна не розрізняти символів Лежандра і Якобі,
що дає змогу при обчисленні символів Лежандра не розкладати чисельник на
прості множники. Треба тільки виділяти множники, що дорівнюють 2. Якщо
І— J = 1, то ця конгруенція має два розв'язки; якщо (—І = —1» конгруенція
розв'язків не має. Для конгруенції х2 s a (mod m), де т — непарне складене
число, символ Лежандра не існує, а символ Якобі існує. Проте, якщо символ
Якобі І — =1 і т — непарне складене число, то це ще не означає, що
конгруенція х2 = a (mod m) має розв'язки. Так, конгруенція х =2 (mod 15) розв'язків
/ 152-*
не має, а символ Якобі для неї І-—І = (—1) s = 1.
Задачі
16.1. Розв'язати конгруенції, звівши їх до двочленних.
а) За;2 — Ьх — 7 = 0 (mod 5); є) Зх2 + 2х = 1 (mod 7);
б) Зх2 — x = 0(mod5); є) 4х2 = 7х + 3 (mod 11);
в) 2х2 + 4х— 1 =0(mod5); ж) Ьх2 + їх + 1 == 0(mod 13);
г) 2х2-4х — 5 = 0(mod7); з) \х2 — 11х —3 = 0(mod 13).
д) 2х2 + Ьх — 1 =EE0(mod7);
16.2. Розв'язати задані конгруенції, звівши їх до двочленних!
а) 3%2 + 6x + 1 =0(mod 10); є) \2х2 — Єх— 7 = 0(mod 19);
б) 4*2+ 3^ + 3 = 0 (mod 15); є) 7х2 + 15л: — 11 =0(mod23);
в) Зх2 + 7х + 8 = 0 (mod 17); ж) х2 — 5х + 6 = 0 (mod 24);
г) 6х* + 3х+ 1 =0 (mod 17); з) \2х2 — 8х— 15 = 0 (mod 44).
д) Зх*+ ІЗх— 10 = 0 (mod 19);
16.3. Користуючись критерієм Ейлера, знайти всі квадратичні
лишки за модулями: а) 5; б) 7; в) 11; г) 13; д) 17; є) 23; є) 37;
ж) 53.
16.4. Розв'язати способом проб такі конгруенції!
а) х2 = 2 (mod 7);
б) x2 = 4(mod7);
в) х2 = 3 (mod 7).
16.5. Обчислити символи Лежандра»
а) (| б) (g); в) Щ г) (*); д) (£); є) (*);
16.6. Користуючись символом Якобі, обчислити символи Лежандраї
,/283^ ,, /251\ . /241 \ . / 323 \ пЧ f 346 \. . (3153\.
а> (ж);б) \тї' в> lw); г> \ж); д) \шЬ е) Ііж)'
. / 20 470 \ /-2108^ /3149 \
€' І 1847 /' Ж' І20Ш' 3) V 5987 і*
16.7. Знайти кількість розв'язків таких конгруенцій!
є) х2 = 429 (mod 563);
є) х2 = 579 (mod 821);
ж) x2 = 728 (mod 919);
а) x2 = 3(mod31)
б) x2 = 2(mod31)
в) х2 = 5 (mod 73)
г) x2 = 3(modl01); з) х2 =847 (mod 1087);
д) х2 = 226 (mod 563); к) х2 = 3766 (mod 5987).
108

16.8. Знайти х, якщо:
*> Ш - '• 6> (І) = '= "> (f) " '• г> (тг) = '• « (І) = '>
16.9. Довести, що:
а) конгруенція x2=za(modp) має розв'язки
х = а*+*, /? — а*+! (mod/?),
якщо /? — просте число виду 4& + З, a число а — квадратичний
лишок за модулем р\
б) конгруенція х2 =a(modp) має розв'язки
x^ak+l . 2<2*+*>'(mod/?),
де / = 0 при а2*+! == 1 (mod/?) і / = 1 при а2/г+1 = —1 (mod/?),
якщо /? — просте число виду 8k + 5 і а — квадратичний лишок за
модулем р\
в) рівняння 11# = 5л:2— 7 не виконується при жодних цілих
числах х і у\
г) при діленні добутку двох послідовних цілих чисел на число
13 остача ніколи не дорівнює 1;
£z± (1 (mod/?), якщо р — просте число виду 8k + 7,
д) 2 2 ==
7 [—1 (mod/?), якщо р — просте число виду 8k + З,
«)(т)(т)-{-..
якщо р — просте число виду \k + 1,
якщо р — просте число виду 4/г + 3;
З \ (1, якщо/? — просте число виду 12/¾ + 1 або 126 + 11,
' \Р J \—1, якщо/? — просте число виду 126 + 5 або 126 + 7;
ж) конгруенція х2 = a (mod 16), а = 1 (mod 8) має розв'язки:
х = хо, 16 — хо> хо + 8, 8 —*о (mod 16), де хо — один з розв'язків
заданої конгруенції; аналогічно за модулем 2а, а > 4,
х~х0у 2а — *о, хо+2*-1, 2а~1—хо (mod 2а).
16.10. Використовуючи результати задач 16,9, а), б), розв'язати
конгруенції:
а) л;2^ 2 (mod 311); в) х2 = 7 (mod 29);
б) х2 == 3 (mod 47); г) л:2 = З (mod 37).
16.11. Чи проходять через точки з цілими координатами такі
параболи:
а) 43у = х2 — 42; в) 83у = х2 — 34;
б) 73*/ = х2 — 37; г) 443*/ = х2 — 152?
16.12. Розв'язати в цілих числах рівняння:
а) 4л:2 — 5// — 6 = 0; г) х2 — 10* — 1 \у + 5 = 0;
б) 15л:2 — V — 9 = 0; д) х2 — 2\х— 13г/ + 110 = 0.
в) 5х2— Ну —7 = 0;
16.13. Довести, що:
а) розв'язки конгруенції л:2 + 1 ^0(mod/?), де р — просте число
виду 4т + 1, мають вид х = 1 • 2 . .. 2т; р — 1 • 2 ... 2m (mod /?);
б) конгруенція л:2 + 1 = 0(modp) має розв'язки тоді і тільки
тоді, коли р — просте число виду 4m + 1;
109

в) конгруенція х2 + 2 = O(modp) має розв'язки тоді і тільки
тоді, коли р — прссте число виду 8т + 1 або 8т + 3;
г) конгруенція х2 + 3 = 0(mod/?) має розв'язки тоді і тільки
тоді, коли р — просте число виду 6m + 1;
д) множина простих чисел виду Am + 1 нескінченна;
є) множина простих чисел виду 6т + 1 нескінченна;
є) канонічний розклад числа виду а2 + Ь2, де (a, 6)=1,
містить тільки прості числа виду 4т + 1;
ж) незалежно від простого непарного модуля р конгруенції
(х2 — 13) (х2 — 17) (х2 - 221) = 0 (mod/?),
(х2 — 3) (х2 — 5) (х2 — 7) (х2 — 11) (х2 — 1155) = 0 (mod/?)
мають завжди хоч один розв'язок;
з) конгруенція х2 ==—7(mod/?a), де /7— непарне просте число
виду 7/г+І, має розв'язки при будь-якому натуральному а;
к) конгруенція х2==—11 (mod 4р), де р — непарне просте число
виду П/і + 2, не має розв'язків;
л) для будь-якого натурального п число 1 + 2 + ... + п не
може закінчуватися цифрою 7.
16.14. Використовуючи результат задачі 16.9, ж), розв'язати
такі конгруенції!
а) х2 = 9 (mod 16); д) х2 = 57 (mod 64);
б) х2 = 17 (mod 32); є) х2 = 65 (mod 128);
в) х2 = 25 (mod 32); є) х2 = 73 (mod 128);
г) х2 == 41 (mod 64); ж) х2 = 145 (mod 256).
16.15. Розв'язати конгруенції!
а) х1 = 7 (mod 27); в) х2 = 91 (mod 243);
б) х2 ss 59 (mod 125); г) х2 — Зх + 2 = 0 (mod 400).
16.16. Довести, що:
1, якщо р — просте число і /?=1, 5, 7, 11 (mod 24),
якщо /7 — просте число і /7 == 13, 17, 19, 23 (mod 24);
б) (—j == (—1) 2 , якщо /7 — непарний простий дільник числа
ах2 -\-bif1, де а, Ь, х, у — цілі числа і (ах, by) = 1;
в) 10541 = 83 . 127, якщо 10541 = 3 . 592 + 2 . 72;
г) непарні прості дільники р чисел виду х2 + 2у2 при (х, у) =
= 1 мають вид р = 8п + 1, р = 8/г + 3;
д) непарні прості дільники р чисел виду 2л:2 — у і х2 — 2#2 при
(х, у) = 1 мають вид р = 8/г + 1, /? = 8/г + 7.
§ 17. Порядок числа і класу лишків за модулем.
Первісні корені, існування їх та кількість
за простим модулем
Література
[1]_§ 19, с. 193—201;
[2] — § 19, с. 196—204;
[3] —гл. 12, § 5, с. 413—416;
[10] — гл. VI, § 1—3, с. 86—90;
3)(тМ-і,
по

Ill] — гл. 17, 18, c. 139—152;
[12]-гл. IV, § 1, 2, c. 125-136;
114]—§ 29, ЗО, с. 137—144.
ТЕОРЕТИЧНІ ВІДОМОСТІ
Нехай а Є Z, т Є N і (а, т) — 1. Порядком числа а за модулем m називається
таке найменше натуральне число б, що а =1 (mod m). Число В позначають ще
як В = Рт(а) і називають показником, до якого належить число а за модулем т.
Оскільки за теоремою Ейлера а9(т) = 1 (modm), to число & завжди існує
і В < <f (m). Якщо В = ер (т), то число а називають первісним коренем за модулем т.
Якщо а =5 6 (mod /я), то Pm(a) = ^т(£)- Ця властивість дає змогу казати про
порядок класу лишків, а саме: клас лишків К^ має порядок 5 за модулем т.
якщо порядок його представника за цим самим модулем дорівнює В.
Якщо В = cp (т), то клас лишків називається класом первісних коренів за
модулем т.
Якщо В = Рт(а)> то числа 1 = а0, а1, а2,..., а6*"1 попарно неконгруентні
між собою за модулем т.
Якщо а—первісний корінь за модулем т, тобто Pm(a) = cp(m), то числа
1 = о», а1, а2, . . ., а^т) утворюють зведену систему лишків за модулем т.
Якщо Рт(а) = В, то ал ss az(mod т) тоді і тільки тоді, коли k == /(mod В).
Зокрема, ak = 1 (mod m) тоді і тільки тоді, коли k \ В.
Якщо Рт(а) = В і afe = 1 (mod т), то & : В.
Якщо Рт{а) = В, то ? (m): В.
Якщо (Pm(a), Pm{b)) = 1, то Pm (a . Ь) = Рт(а) • Рт(Ь).
Якщо Рт(дг) = аЬ, то Рт(^) = ft.
Якщо Рт(а), Рт(Ь), ..., Рт{с) — попарно озаємно
Рт(аЬ...с) = Рт(а)Рт(Ь)...Рт(с). Рт^) = Рт(а) тоді і
(s. ^ш («)) = 1.
ft PmW
Pm(a ) ~ (рт(в), ft) •
Якщо Рт(а) = ft, то класи лишків К{™\ К{£\ .... Klf
прості числа, то
тільки тоді, коли
є різними розв'яз-
ками конгруенції х = 1 (mod m).
Якщо т — просте число, то зазначені класи лишків вичерпують усі розв'язки
даної конгруенції.
За простим модулем р кожен дільник d числа р—1 є порядком для cp(d)
класів лишків. Зокрема, існує ер (р—1) класів первісних коренів (теорема Гаусса).
Якщо g—первісний корінь за простим модулем р, то інші первісні корені
містяться серед степенів g2, g3,..., gp~l і мають вигляд gk, де (k, р— 1) = 1
і k< р — 1.
Якщо р— 1 — q\xq**... q^s —канонічний розклад числа р— 1, то число g
тоді і тільки тоді є первісним коренем за простим модулем р, коли
р-1
gqi ф 1 (mod p)
для всіх і = 1, 2, ..., s.
Первісні корені існують тільки за модулями т — 2, 4, р* і 2р", де р—,
просте непарне число, а a > 1.
Нехай g—первісний корінь за простим модулем р. Тоді можна знайти таке
число tf що число ц, яке визначається з умови
пі

не ділиться на р. Відповідне число g+pt є первісним коренем за модулем ра
при будь-якому а > 1.
Неха-й о> 1 і g—первісний корінь за модулем ра- Непарне з чисел g
1 g-\~P є також первісним коренем за модулем 2ра-
Якщо с = ер (т) і qlt q2, . . ., ^- різні прості дільники числа с, то число gf
взаємно просте з т, тоді і тільки тоді є первісним коренем за модулем т\ коли
с
gqi ф\ (mod m)
для всіх і=1, 2,. .., к.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Знайти порядок Рт(а) числа а за модулем т, якщо:
а) а = 2, m = 15; б) а = 3, m = 15; в) а = 8, m = 15.
Розв* язання. Щоб знайти порядок Рт(а) числа а за модулем т, слід
забезпечити виконання таких вимог:
1) (а, т) = 1;
2) Рт(а) — дільник числа <р(т);
3) Ят(а) — найменше з тих натуральних чисел k, для яких виконується
конгруенція
ak = 1 (mod т)-
а) Маємо (2, 15) = 1. Знаходимо ер (15). Оскільки 15 = 3-5, то ер (15) =
_з.5(,-і)(,-І) = в.
Отже, Р15 (2) міститься серед чисел 1, 2, 4, 8. Записуємо послідовно:
21 = 2^1(mod 15),
22^4щф 1 (mod 15),
24= 16= 1 (mod 15).
Отже, Р15(2) = 4.
б) Оскільки (З, 15) = 3=£ 1, то для числа я = 3 за модулем 15 порядку не
існує.
в) Оскільки (8, 15) = 1 і 8 = 23, то Р15(8) існує, його визначають за формулою
Hu{Z)~(Pn (2), 3)-(4, З)"4'
Зауваження
1. Щоб знайти порядок Рт(а) числа а за модулем т, слід використовувати
обчислення, зроблені на попередньому етапі. Так, якщо вже знайдено ak =
= a0 (mod m), де k / cp (m), то щоб знайти а'де/>&і//ср (т), треба використати
те, що afe 2= q0 (mod m).
2. Процес знаходження порядку числа може водночас бути процесом
знаходження первісних коренів за даним модулем т. Для цього слід визначити, які
з чисел мають порядок tp (m).
2. Знайти всі первісні корені за модулем 7.
Розв'язання. Первісних коренів за простим модулем/? = 7 є ср(/? —1) =
= ер (6) = 2. Вони містяться серед чисел ЗСЛ7:
ЗСЛ7=- {1, 2, 3, 4, 5, 6).
Оскільки р— 1 = 6 у канонічному розкладі має вигляд р — 1 = 2-3, то дослід-
р—і р—і
жувати слід числа виду а 3 і а 2 , тобто числа а1 і а3, де а£ЗСЛ7.
Знайдемо перший первісний корінь. Перевіряємо число 2 (зрозуміло, що число
1 тільки за модулем 2 є первісним і тому в інших випадках перевірка не має
смислу).
22 е= —3 (mod 7), 23 s 1 (mod 7).
112

Оскільки 3 < б, то 2 не є первісним коренем за модулем 7.
Перевіряємо число 3:
З2 = 2 (mod 7), З3 = — 1 (mod 7).
Тоді 3е = 1 (mod 7). Отже, порядком числа 3 є 6, тобто 3 є первісним коренем
за модулем 7.
Другий первісний корінь міститься серед чисел виду 3*, де (&, р — 1) = (&, 6) = 1
і 1 < k < 6. Ці умови задовольняє тільки число k = 5. Отже, другим первісним
коренем є число З6. Оскільки З6 = 5 (mod 7), то первісними коренями за
модулем 7 є числа 3 і 5.
З адач і
17.1. Знайти порядок числа а за модулем /я, якщо:
а) а = 2, т = 5; ж) а = 7, т = 20;
б) а = 4, m = 5; з) а = 7, m = 22;
в) а = 5, /я = 8: к) а = 6, m = 39;
г) а =10, /я =13; л) а = 7, /я = 43;
д) а = 4, /я = 15; м) а = 5, m = 108;
є) а = 2, т=15; н) а = 2, /я =133.
є) а = 2, /я = 17;
17.2. Знайти порядки всіх класів лишків за модулем /я, якщо:
а) /я = 11; б) /я = 19; в) /я = 21.
17.3. Знайти порядки чисел a, ft, c, d за модулем т, якщо:
а) а = 7, 6 = 9, с = 12; m = 13;
б) а = 5, 6 = 8, с = 13; /я = 17;
в) а = 5. ft = 8, с = 10; d = 16; m = 33;
г) а = 10, 6 = 25, с = 50; /я = 39;
д) а = 5, ft = 15, с = 21, d = 35; т = 44.
17.4. Знайти порядок числа: а) 10 за модулем 13-31; б) т—1
за модулем /я.
17.5. Знайти всі первісні корені за такими модулями: а) 11;
б) 13; в) 15; г) 19; д) 49; є) 81.
17.6. Знайти число первісних коренів і найменший з них за
такими модулями: а) 10; б) 18; в) 19; г) 31; д) 37.
17.7. Знайти найменший первісний корінь за такими модулями:
а) 7; б) 17; в) 23; г) 41; д) 53; є) 50; є) 54; ж) 71; з) 242; к) 289;
л) 578; м) 625.
17.8. Знаючи, що 3 є первісним коренем за модулем 29, знайти
решту первісних коренів за цим модулем.
17.9. Знаючи, що 2 задовольняє конгруенцію а;8 = 1 (mod 17),
знайти всі розв'язки цієї конгруенції.
17.10. Знаючи, що Р29(4)= 14, знайти решту чисел, які мають
порядок 14 за модулем 29.
. 17.11. Знаючи, що 2 — первісний корінь за модулем 37, довести,
що 218 = 62(mod37).
17.12. Знаючи, що Р29(12) = 4, Р29(23) = 7, знайти Л>9(15).
17.13. Знайти всі натуральні значення х> які задовольняють
конгруенції:
а) 4х = 1 (mod 3); г) 2х = 1 (mod 25);
113

б) 5* = 1 (mod8); д) 6* = 1 (mod 49);
в) 5* = 1 (mod 9); є) 2х = 1 (mod 49).
17.14. Знаючи, що 2 є первісний корінь за модулем 131, знайти
всі розв'язки конгруенції х3 = 16(mod 131).
17.15. Знайти ті значення ft, при яких мають розв'язки
конгруенції: а) 4* == 6 (mod 9); б) 5*== ft (mod 9).
17.16. Нехай р — просте непарне число. Довести, що:
а) серед первісних коренів за модулем р не може бути
квадратів;
б) ( —) = 1, якщо а — первісний корінь за модулем р\
І a2n+l \
в) ( ) = 1» якщо а — первісний корінь за модулем р і п£ N;
г) Рр (аЬ) - Рр (а) . Рр (ft), якщо (Рр (а), Рр (ft)) == 1;
д) за модулем р існують первісні корені;
є) ак + 1 і /?, якщо Рр (a) = 2k\
є) добуток двох первісних коренів за модулем р не є первісним
коренем за цим модулем;
ж) якщо п>1, то існує (/?— 1)*?(р—1) різних первісних
коренів за модулем рпу не конгруентних за модулем р2\
з) якщо я>1, то існує тільки ер (<р (/?")) різних первісних
коренів за модулем рп\
к) якщо п>1, то існує <р (ер (/?")) різних первісних коренів за
модулем 2/Л
л) а • ft не є первісним коренем за модулем /?, якщо а і ft не
є ними за цим самим модулем;
м) якщо р — число виду 4й + 1 і g—первісний корінь за
модулем р\ то р — g—первісний корінь за модулем; р;
н) ak = —1 (mod/?), якщо Рр (а) = 2k і а не • р.
ПЛІ. Довести, що не існує первісних коренів за модулем т,
якщо:
а) т = 8;
б) т = 2а, а > 3;
в) т = 36;
г) m = 2ар, де а > 1 і р — непарне просте число;
д) т — непарне складене число, яке ділиться, принаймні, на два
різних простих множники.
17.18. Нехай р — просте непарне число. Довести, що
а) р має вигляд 1 + k • 2^+1, якщо р/22П + 1 і п > 1;
б) р має вигляд 1 + k • 2Л, якщо р/22П— 1 і /і > 1;
в) прості непарні дільники числа а*7— 1, де а£ N і а > 1 є
дільниками числа а — 1 або мають вигляд 2рх + 1;
г) прості непарні дільники числа aD + 1 є дільниками числа
а + 1 або мають вигляд 2рх + 1;
д) множина простих чисел виду 2рх + 1, х£ N, є нескінченною;
є) а є первісним коренем за модулем /Л а > 2, якщо а є
первісним коренем за модулем р2\

є) РрЬ(а) = P2Pk(a), якщо а — непарне число, а\р, fe^N;
зокрема, довільний непарний первісний корінь g за модулем pk є ним
і за модулем 2pk.
17.19. Довести, що:
а) первісний корінь за модулем т>2 завжди є квадратичним
нелишком за модулем т\
б) Рат~х (а) = /я, якщо а, т£ N і а > 1;
в) ср(ат— 1) = O(modm), якщо я, т£ N і а > 1;
г) Рт(а) = |Ppttl(а), Яра2(а), ..., Ppas(a)j, якщо (а, т) = 1 і т =
= Р?7>28 • • • PsS — канонічний розклад числа т\
д) Ppk (a) = rf, якщо ad = 1 (mod/?*), де d = Ppk-\{a)y p~ просте
число, ft Є N, ft > 1, і (a, pk) = 1;
є) PDfe(a) = р\ якщо а<* # 1 (mod/?*), де d = Ppk-\ (a), р — просте
число, ft g N, ft > 1, і (а, /?*) = І;
є) Р5929(16)= 1155;
ж) число а є первісним коренем за модулем т тоді і тільки
тоді, коли клас лишків КТ] є твірним елементом мультиплікатив-
ної групи кільця Zm.
§ 18. Індекси за простим модулем. Двочленні конгруенції
за простим модулем; таблиці індексів
і застосування їх
Література
[1] —§ 19, с. 201—204;
[2] —§ 19, с. 204—207;
[3] —і\л. 12, § 5, с. 416—420;
[10] —гл. VI, § 4, с. 90-92;
[11] — гл. 19, гл. 20, с. 163—172;
[12] —гл. IV, § 3, 4, с. 136—146;
[13] —§ 31, 32; с. 144—152.
ТЕОРЕТИЧНІ ВІДОМОСТІ
Нехай g — первісний корінь за простим модулем /?, a£Z і (а, р)=\. Ціле
невід'ємне число т називається індексом числа а за модулем р при основі g, якщо
gT = a(modp). (1)
Взагалі, довільне значення х, яке задовольняє конгруенцію
Ьх = d (mod m), (2)
називається індексом числа d за модулем m при основі Ь і позначається
х = indbd (mod m). (3)
При цьому m може бути й складеним числом, проте
(dtm) = (btm) = 1.
Означення індексу можна записати ще так:
Ь fc sd (mod m), (4)
115

Користуючись цим означенням, складають таблицю Індексів за даною
основою і модулем. Таблиці індексів за кожним простим модулем р (не дуже
великим) містять дві таблиці: одна — знаходження індексу за числом, а друга—
знаходження числа за Індексом (таблиця анти індексі в).
Основні властивості індексів
1°. Усі індекси числа а за простим модулем р утворюють клас чисел за
модулем р — 1. Точніше, якщо f і 7і — індекси числа аза модулем р (при будь-
якій тій самій основі), то
І as fi (modp — 1);
2°. Для того щоб a = £(modp), необхідно і достатньо, щоб indga =
== indgb (modp — 1);
Якщо значення чисел або індексів виходять за межі таблиць, то ці дві
властивості дають змогу переходити до найменших невід'ємних лишків: для
чисел — за модулем /?, для індексів—за модулем.р — 1.
3°. indgf sO(modp — 1);
4°. indgg==s 1 (mod p- 1);
5°. indg(a1a1 . . . as) = indgaj + indga2+ ... + indgas (modp— 1);
6°. ind^ в n inq^a (modp— 1);
7°. Якщо a і b, то indgi = indga— indg6 (mod p — 1).
Зазначимо, що перехід від конгруенції між числами до конгруенції їхніх
індексів називається індексацією, а зворотний перехід — потенціюванням.
Якщо задано двочленну конгруенцію я-го степеня за простим модулем
ахп з Ь (mod р), (а, р) = 1, п £ 14, (5)
то її розв'язок знаходять з конгруенції
п ind х = ind b— ind a (modp — 1). (6)
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Скласти таблиці індексів та антиіндексів за модулем 23.
Розв'язання. Знайдемо один з первісних коренів за модулем 23
(найчастіше це найменший з первісних коренів). Перевіряючи безпосередньо, дістанемо,
що число 5 є одним з первісних коренів за модулем 23, причому найменшим
з них. Справді,
ер (23) = 22 і 52 Ф 1 (mod 23), 5і х ф 1 (mod 23), а 522 = 1 (mod 23).
Отже, 523 (5) = 22, тому 5 є первісний корінь за модулем 23. Візьмемо його
за основу таблиці індексів і знайдемо найменші невід'ємні лишки степенів
:22
516 я 3 (mod 23),
517= 15 (mod 23),
518 = 6 (mod 23),
53 = Ю (mod 23), 511 = 22 (mod 23), 519 в 7 (mod 23),
54 = 4 (mod 23), 512 = 18 (mod 23), 520 == 12 (mod 23),
55 = 20 (mod 23). 513 = 21 (mod 23), 521 = 14 (mod 23).
56 = 8 (mod 23), 514 = 13 (mod 23),
57 =- 17 (mod 23), 515 s 19 (mod 23),
Отже, ind5l=0, ind55=l, ind52 = 2, ind5l0 = 3, ind54 = 0, ind520 = 5,.
Складаємо таблицю індексів за модулем 23 з основою 5 (табл. 14).
^а модулем 23:
5° а 1 (mod 23),
5і в 5 (mod 23),
52 = 2 (mod 23),
Б°. 5і. Б» 52
58 = 16 (mod 23),
59== 11 (mod 23),
510 = 9(mod23),
116

Таблиця 14
N
0
1
l_ 2
0
3
5
1
0
9
13
2
2
20
11
3
16
14
4
4
21
5
1
17
6
18
8
7
19
7
8
6
12
9 1
10
15
Тут номер рядка означає число десятків, а номер стовпця — число одиниць
заданого числа. $а перетині певного рядка і стовпця знаходиться відповідний
індекс. Так, індекс числа 18 знайдемо на перетині рядка з номером 1 і стовпця
з номером 8, тобто ind518 = 12.
Щоб побудувати таблиці антиіндексів, використаємо таблицю індексів. Маємо
(табл. 15):
Таблиця 15
/
0
1
1 2
0
1
9
12
1
5
22
14
2
2
18
3
10
21
4
4
13
5
20
19
6
8
3
7
17
15
8
16
6
9
11
7
Зауваження. Оскільки вибір основи для складання таблиць індексів за даним
модулем є довільним, то в різних підручниках і посібниках такі таблиці не
не завжди збігаються. Проте це не впливу на остаточний результат при
розв'язуванні задач за допомогою індексів. У таблицях індексів, які наведено
в кінці цього посібника, вказано основу £, а також канонічний розклад числа
р — 1 для даного простого модуля р.
2. Розв'язати конгруенцію
17*18 = 22 (mod 23). (1)
Розв'язання. Беремо індекси від обох частин конгруенції
ind 17 + 18 ind x ^ ind 22 (mod 22).
За табл. 14 маємо
ind 17 = 7, ind 22= 11
і тому
7+ 18 ind jc = 11 (mod 22),
або
18 ind x s 4 (mod 22). (2)
Дістали лінійну конгруенцію відносно ind х. Розв'яжемо її. Оскільки (18, 22)=
=« 2 і 4 і 2, то ця конгруенція має двя розв'язки. Знайдемо їх штучним
способом. Скоротимо спочатку обидві частини і модуль на 2:
9 ind де а 2 (mod 11).
Додамо до правої частини число —11:
9 ind х = —9 (mod 11).
Скоротимо обидві частини на 9:
indx = —1 (mod 11).
117

Звідси дістаємо два розв'язки конгруенції (2):
Шх= 10,21 (mod 22).
За табл. 15 знаходимо відповідні два значення невідомого х:
*s9f 14 (mod 23).
Зауваження
1. Зрозуміло, що розв'язування конгруенцій за допомогою індексів можливе
для довільного модуля, якщо тільки Є відповідні таблиці індексів.
2. При індексуванні конгруенції за модулем т відбувається перехід до
конгруенції за модулем ер (т), а при потенціюванні конгруенції за модулем
<р (пі) — перехід до конгруенції за модулем т.
Задачі
18.1. Скласти таблиці індексів за модулем р з основою g, якщої
а) р = З, g = 2; д) р = 7, g = б;
б) р = 5, g = 2; є) р=11, £ = 2;
в) /7 = 5, г=3; є) р= 13; g = 2-
г) Р = 7, £ = 3; ж) р = 29, ^ = 2.
18.2. Скласти таблицю індексів за складеним модулем т = 27
з основою g = 5.
18.3. Нехай g—первісний корінь за модулем т. Довести, що;
а) конгруенція b = c(modm) виконується тоді і тільки тоді,
коли indgb = indgC(modcp(m)) (тут (ft, m) = 1);
б) indma = ind2m^, якщо т = ра, р — просте непарне число, (a,
2р)=1.
18.4. Нехай g і / — два первісних корені за простим модулем
р. Довести, що:
а) indga = ind,a- indgt (mod(p — 1));
б) ind,a = indga • \nd(g(mod(p — 1));
в) indtg . \ndgt = 1 (mod (p — 1));
r) indga = ind,a (ind,g)^-^-1 (mod (p — 1))
(формула переходу від системи індексів з основою t до системи
індексів з основою g).
18.5. Розв'язати лінійні конгруенції;
а) 7* = 23 (mod 17); є) 125* == 7 (mod 79);
б) 5* = 13 (mod 27); є) 65* == 38 (mod 83);
в) 8* = —11 (mod 37); ж) 23* = 9 (mod 97);
г) 47* = 23(mod 73); з) 37* = 5 (mod 221).
д) 53*= 37 (mod 79);
18.6. Розв'язати конгруенції другого степеня:
а) *2= 15 (mod 17); ж) *2 = 40 (mod83);
б) х2== 10(mod 27); з) З*2 — 5* —2 = 0(mod 11);
в) *2 = 47 (mod 53); к) 2*2 - 7* + 28 = 0 (mod 43);
г) х1 = 58 (mod 61); л) З*2 — 8* + 44 = 0 (mod 47);
д) *2 = 59 (mod 67); м) *2 = 29 (mod 592);
є) *2 = —28 (mod 67); н) *2 = 61 (mod 732).
є) *2 = 54(mod71);
18.7. Довести, що:
а) конгруенція хп = a(modm), (a, m) = 1 має тоді і тільки тоді
розв'язки, коли \nda\d, де d = (я, <р(т)). Якщо конгруенція має
розв'язки, то їх всього d\
•18

б) конгруенція хп ==a(mod/?), де р— просте непарне число, має
розв'язки тоді і тільки тоді, коли
р-1
ad = 1 (modp), де d= (я, p— 1);
в) число а тоді і тільки тоді є квадратичним лишком за
модулем непарного простого числа р, коли за цим модулем inda —
число парне;
г) порядок Ь = Рт(а) визначається рівністю (inda, cp(m)) =
— с . Зокрема, належність числа а до первісних коренів за
модулем т визначається рівністю (inda, cp(m))= 1;
д) користуючись властивостями індексів, можна встановити
справедливість теореми Вільсона;
є) для простого числа р виду 2п + 1, де п > 3, число 3 є
первісним коренем;
є) індекс числа — 1 за простим непарним модулем р при будь-
р— і
якій сенові дорівнює ^—п—.
18.8. Скільки розв'язків мають такі конгруенції:
а) x15 = 6(mod37); є) х5 = 3(mod71)f
б) х16 = 10 (mod 37); ж) х21 = 5 (mod 71);
в) Зх3 == 2 (mod 37); з) х15 е= 46 (mod 97);
г) 7х7 = 11 (mod 41); к) х55 = 17 (mod 97);
д) 3xI2 = 31(mod41); л) х60 = 79(mod97)?
є) 5x30 = 37(mod41);
18.9. Розв'язати такі двочленні конгруенції:
а) х10 = 33 (mod 37); є) х27 = 39 (mod 43);
б) х3 = 34 (mod41); є) х35 = 17(mod67);
в) х8 = 31 (mod 41); ж) х30 = 14 (mod 67);
г) х12 = 37 (mod 41); з) х12 == 27 (mod83);
д) х5 = 37 (mod 43); к) х48 = 2 (mod 97).
18.10. Розв'язати такі двочленні конгруенції:
а) Зх3 = 4 (mod 7); є) 23х5 s 15 (mod 73);
б) 2х8 == 5 (mod 13); ж) 37х6 == 69 (mod 73);
в) 15х4= 17(mod23); з) 37х16 == 62(mod73);
г) 27x5 = 25(mod31); к) 44х21 = 53 (mod 73);
д) 13х3 = 24 (mod 37); л) 27х30 = 41 (mod79).
є) 3?x8 = 59(mod61);
18.11. Розв'язати конгруенції:
а) 5хп + 19 = 0 (mod 29); д) 7х13 + 23 = 0(mod47);
б) 25x7 + 7 = 0(mod31); є) х7 + 27 = 0(mod53);
в) 17x5 + 3 = 0(mod37); є) х11 + 36 = 0(mod71).
г) 8х9+ 17 s0(mod41);
18.12. Знайти найменше натуральне число х, яке задовольняє
такі конгруенції:
а) 8*==1 (mod 13); д) 24* = 1 (mod 31);
б) 27* = 1 (mod 17); є) 32* = 15 (mod 37);
в) 5* = 17(mod 31); є) 23* = 37 (mod4li;
г) 11*= 17 (mod 31); ж) 13* == 25 (mod 43);
119

з) 16*= 11 (mod53); л) 44* = 19(mod71);
к) 2х = 7 (mod 67); м) 18* = 53 (mod 79).
18.13. Розв'язати двочленні показникові конгруенції:
а) 3-8* = 7 (mod 23); г) 15 • 72* ~ 8 • З3* (mod 31);
б) 127*= 15 (mod 31); д) 255* = 47 (mod 61);
в) 213*=215(mod29); є) 6- 11* = 56 (mod 61).
18.14. Розв'язати конгруенції:
а) 13.75*+ 1 =.0 (mod 67);
б) 7-5^+1 =0(mod73);
в) 11 • 53* + 70 = 0(mod79);
г) 8.7^ + 4 = 0(mod83).
18.15. Знайти порядок числа а за модулем т, якщо:
а) а = 6, т = 7; д) а = 27, т = 47;
б) а = 6, т = 23; є) а = 13, т = 53;
в) а = 7, т = 29; є) а = 10, m = 1739.
г) а = 18, т= 41; ж) а = 32, m = 4331.
18.16. Знаючи, що за простим модулем р indg(a) =. b(mod(p —
— 1)), знайти за цим модулем ind/a, якщо:
а) Р = 47, g = 5, а = 34, Ь = 34, ^ = 10;
б) р = 73, # = 5, а = 54, Ь = 26, /=11;
в) р = 71, g = 7, a = 66, fc = 63, /= 13;
г) р = 71, g = 7, а = 56, 6= 19, /=11.
18.17. Чи є первісними коренями за модулем 59 такі числа!
а) 2; б) 3; в) 6; г) 8; д) 12; є) 13; є) 14; ж) 19?
18.18. Знаючи, що 2 є первісний корінь за модулями 101 і 163,
розв'язати конгруенції:
а) 3-5* = 4- З2**1 (mod 101);
б) 2< = 3-53*(modl63).
18.19. Користуючись критерієм Ейлера та застосовуючи
властивості індексів, з'ясувати, які з чисел 15, 16, 17, 18, 19, 20 є
квадратичними лишками за такими модулями: а) 23; б) 29; в) 41; г) 59;
Д) 79; є) 89.
18.20. Серед чисел зведеної системи лишків за модулем р
знайти ті, порядок яких дорівнює числу г, якщо:
а) /? = 43, г = 6; в) /? = 61, г= 10;
б) р = 43, г = 42; г) р =61, т = 60.
§ 19. Арифметичні застосування теорії конгруенцій
Література
[!]_§ 20, с. 205-210;
[2] —§ 20, с. 207—213;
[31 —гл. 12, § 6, с. 421—429;
[10] —гл. XXIII, с. 201-209;
[12] —гл. V, с. 147—160;
[14]—§ 33-36, с. 154—169.
ТЕОРЕТИЧНІ ВІДОМОСТІ
Теорія конгруенцій має ряд арифметичних застосувань. Основними з них є:
1) виведення ознак подільності;
2) обчислення остач при діленні;
120

3) перевірка результатів арифметичних дій;
4) визначення довжини періоду при перетворенні звичайного дробу в
десятковий.
Нехай в g-ковій системі числення число N має вигляд
М=а0 + а^+ ...+angn.
Позначимо через rk абсолютно найменші лишки числа gk за модулем т,
тобто g* = /"fe(mod m), k = 0, 1, ..., п і г0=Ч. Тоді N =s Rm(mod m), де Rm =
s <Vo + ^1^1 + • • • + VaiC1110^ m) (03нака подільності Паскаля).
З конгруенції N = #m(mod m) випливає, що при діленні на т числа N і Я
дають однакові остачі. Зокрема, число N ділиться на т тоді і тільки тоді, коли
на т ділиться Rm. Покладаючи g— 10, т = 2, 3, 4, 5. . . , дістаємо конкретні
ознаки подільності. З метою обчислення остач від ділення, крім ознаки Паскаля,
використовують також теореми Ейлера і Ферма, властивості індексів тощо.
Якщо
N = f(Nv Nv...t Nk)y (1)
де / — многочлен від цілих чисел N\t М2. .. , Nk з цілими коефіцієнтами, то
виконується конгруенція
N =f (N\ N'f ..., N'k) (mod m), (2)
де m—будь-яке натуральне число, Nt — остача від ділення Nt на т, i =
= 1, 2, . . ., k. Конгруенція (2) є умова, необхідна для рівності (1), але не
достатня. Інакше кажучи, якщо (2) не виконується, то не виконується й (1); якщо
(2) виконується, наприклад, для т = 9 або т *=* 11, то напевно помилки в
обчисленнях (1) не виявлено. Так, виконуючи перевірку для т = 9, помилку не
виявили, оскільки: 1) не було взято до уваги нуль у доданку або множнику;
2) в результаті цифри записані не в тому порядку; 3) неповні добутки
перебувають не на своїх місцях; 4) взагалі, помилка становить число, кратне 9.
Під час складних обчислень доцільно робити дві перевірки: одну за модулем 9,
а другу — за модулем 11.
а
Нескоротний дріб виду ——-^-, де с>1, сф2 і с =£ 5, у скінченний
десятковий дріб не перетворюється.
а
Якщо у— нескоротний дріб і (b, 10)-1, то цей дріб перетворюється
у чистий періодичний десятковий дріб. При цьому число цифр у періоді дорівнює
порядку рь(\0) числа 10 за модулем Ь.
а а
Якщо у — нескоротний дріб і Ь = 2а5р&і, де (bit 10) = 1, то цей дріб
перетворюється в мішаний періодичний десятковий дріб. При цьом/ число цифр
у періоді дорівнюг f» де f— більше з чисел ч і (3; число ци})р у періоді
дорівнює порядку рь (10) числа 10 за модулем bv
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Вивести ознаку подільності на 11.
Роз в'яза н ня. Нехай W =а0 + а,; • 10і + а2 • 102 + . . . + ап • 10n
—десятковий запис числа N. Оскільки m = 11, то 10* s= (—l)R(mod 11) і тому R^ =
= До — ах + а2 —•... , або Rn -= (а0 + а2 + а4 + ...)—• («і + аз + <*-ь + • • • )•
Враховуючи, що цифри a2fc 3 парними індексами в числі N стоять на непарних
місцях (починаючи справа наліво), то мзжна таким, чином сформулювати ознаку
подільності на 11:
Число N ділиться на П тоді і тільки тоді, коли різниця ніж сумою
цифр, які стоять на непарних місцях, і сумою цифр, що стоять на парних
місцях, ділиться на 11.
121

Зауваження. Беручи до уваги, що 102=l(mod 11), можна дістати іншу
ознаку подільності числа N на т ■-= 11. Маємо: N = Ь0 + ^102 + ... + 6/(10)2)1,
де Ь0 = аха0 — цифра одиниць першого розряду, Ь1 = а3а2 — цифра одиниць
другого розряду і т. д. Враховуючи, що (\02)k = 1 (mod 11), £=1, 2, . . . , /,
дістаємо: N 5s Rfi =z b0 + b1 + .. . + bl (mod 11). Інакше кажучи, число N ділиться
на 11 тоді і тільки тоді, коли на 11 ділиться сума двоцифрових чисел,
утворених відповідними гранями числа N при його розбитті справа наліво.
2. Знайти остачу від ділення N = ІЗ37 • 1241 на 35.
Р о з в'я з а н н я. Оскільки 35 = 5 • 7, то шукану остачу знаходять як
найменший невід'ємний розв'язок системи конгруенцій
х = /^(mod 5),
х = r2(mod І),
де гх і г2— відповідні остачі від ділення числа N на числа 5 і 7. Спочатку
знайдемо остачу від ділення N на 5:
/is ІЗ37 • 1241 = 337 -241 (mod 5).
Беручи індекси в обох частинах конгруенції, маємо
indri = 37 ind 3-J-41 ind 2 н= ind 3 -f- ind 2 = 3+1 = 0 (mod 4).
Звідси r ss 1 (mod 5).
Аналогічно знаходимо остачу від ділення N на 7:
т2 = 1L87 • 1241 = (-1)37 • (—2)41 = 241(mod 7);
ind r2 = 41 ind 2 з= 41 . 2 = 82 ss 4 (mod 6),
звідки r2 = 4 (mod 7).
Розв'язуємо систему конгруенцій
x ss 1 (mod 5),
x = 4 (mod 7).
З першої конгруенції знаходимо * = 5& + 1, k £ N.
Підставляємо це значення в другу конгруенцію bk + 1 = 4 (mod 7) і
розв'язуємо її відносно k:
bk ш 3 (mod 7),
bk= 10 (mod 7),
k = 2 (mod 7),
k = 7s + 2,s£ N.
Тоді x = bk + 1 = 5 (7s + 2) + 1 = 35s+ 11, тобто x = 11 (mod 35). Отже, шукана
остача дорівнює числу 11.
Зауваження. Зрозуміло, що цю остачу можна було знайти, скориставшись
лише теоремами Ейлера і Ферма, що значно скорочує обчислення. Справді,
? (35) = 24, (13, 35) = (12, 35)= 1, тому 13¾4 s= 1224 = 1 (mod 35). Тоді
ІЗ37 • 124і =з (13 • 12)37 • 12* з 16і3 • 2а . З4 s=i 280(-324) =
і= 280 з* 28 s= 2б • 23 S3 — 3 • 8 ss 11 (mod 35).
Отже, при діленні на 35 число ІЗ37 • 1241 дає остачу 11.
3. Перевірити правильність виконання арифметичних дій над цілими числами:
а) 1042 • 10182 + 42932— 18265= 10634311,
б) 4325-897 = 451425.
Розв'яз а н н я. Замінимо рівності а) і б) конгруенціями за модулем 9:
а) 7 • 12 + 20—22 = 19 (mod 9), або 1 я 1 (mod 9);
б) 14 • 24 з, 21 (mod 9). Застосуймо ще раз «правило дев'ятки»: 5*6 = 3 (mod 9),
або 3 з- 3 (mod 9).
Отже, перевірка числом 9 не виявила помилок в обох обчисленнях. Щоб бути
впевненим у правильності виконаних арифметичних дій, треба перевірити ці
результати за модулем 11:
а) (-3)(-4) + Ю + 6 з — 5 (mod 11), або 6 з 6 (mod 11);
б) 2 • 6 Ф7 (mod 11).
Отже, у прикладі б) дії виконано неправильно, тоді як у виконанні
арифметичних дій над цілими числами у прикладі а) помилки не виявлено.
122

Зауваження. На практиці розглянуті обчислення виконуються простіше:
для кожного числа обчислюється остача від ділення його на 9 (на 11); потім
здобуті остачі замінюються своїми остачами і т. д. Це стосується і всіх
проміжних обчислень.
4. Знайти число цифр до періоду і довжину періоду періодичного дробу, в який
13
перетворюється дріб 72Q •
Розв'язання. Знаменник цього дробу має канонічний розклад:
420 = 22 • 3 • 5 . 7. Оскільки f = max (a, p) = 2— більший з показників
степенів цифр 2 і 5, то періодичний десятковий дріб має дві цифри до періоду.
Щоб знайти порядок 5 = Р21 (10) числа 10 за модулем 21, використаємо один
загальний прийом. З конгруенції 105 = 1 (mod b) випливає, що 99...9 =
5 раз
== 0 (mod b). Отже, 5 можна знайти так: ділимо 9 на Ь, потім 99 на b і т. д.,
поки не дістанемо в остачі нуль. Число дев'яток при цьому, а отже, й число
цифр частки (якщо b > 9, то враховувати слід і нуль, який відповідає першій
дев'ятці) дорівнюватимуть шуканому порядку 5 -.= Рь (10) числа Юза модулем Ь.
У розглядуваному прикладі Ь = 2> • 7 = 21. Виконаємо ділення:
99 | 21
84 І 047619
159
""147
129
~Ц26_
39
"21
189
"189
0
У частці маємо 6 цифр, беручи до уваги також 0, який відповідає першій
13
дев'ятці. Отже, 5 = й2І(Ю) = 6, тобто період дробу -т^тс складається
з шести цифр.
Задачі
19.1. Вивести ознаки подільності на: а) 2; б) 3; в) 4; г) 5;
д) 7; є) 9; є) 10; ж) 11; з) 13; к) 25; л) 37; м) 50.
19.2. Довести, що:
а) число а= Юа\+ао ділиться на 7 тоді і тільки тоді, коли
(а\ — 2а0) • 7;
б) на 11 діляться ті і тільки ті цілі числа, в яких різниця між
числом, записаним всіма цифрами, крім останньої, і числом,
записаним цією останньою цифрою, ділиться на 11;
в) на 11 діляться ті і тільки ті цілі числа, в яких сума двох
чисел, одне з яких записане двома останніми цифрами, а друге —
рештою цифр, ділиться на 11.
19.3. Довести, що в g-ковій системі числення:
а) число а ділиться на /л, де m\g+ 1, тоді і тільки тоді, коли
різниця між сумами цифр числа а на парних і непарних місцях
ділиться на т;
б) число а ділиться на т, де m\g— 1, тоді- і тільки тоді, коли
сума цифр числа а ділиться на т\
123

в) число а ділиться на т, де m\gk, тоді і тільки тоді, коли
число, записане останніми k цифрами числа я, ділиться на /я.
19.4. Користуючись ознаками подільності, встановити, чи
ділиться число а на т, якщо:
а) а = 56704, т = 7; 11 або 13; є) а = 973126, т = 13;
б) а *= 24829, т = 7; є) а = 96736068, т = 11;
в) а = 454111, т = 7; ж) а = 20794, /я = 37;
г) а = 53746, т = 11; з) а = 2575163, /я = 37.
д) а = 63364, т = 7;
19.5. Користуючись ознаками подільності:
а) знайти канонічний розклад числа 244943325;
б) знайти канонічний розклад числа 282321246671737;
в) знайти х, у, z, якщо (13*'./45z)io:792;
г) знайти ху у, якщо (7*36^5; і о 11375;
д) знайти канонічний розклад числа 90799;
є) знайти канонічний розклад числа 3058487;
є) записати п'ятизначні числа, які діляться на 55 і середні цифри
яких становлять число 809;
ж) довести, що коли до будь-якого тризначного числа дописати
справа це саме число, то утворене число ділиться на 7, 11, 13.
19.6. Не виконуючи ділення, знайти остачу відділення а на /п,
якщо:
а) а = 3989713, т = 37; г) а = 125 • 465, т = 61;
б) а = 27 877 165, т = 37; д) а = 34 5217, т = 67.
в) а = 31 127567,т = 37;
19.7. Знайти остачу від ділення:
а) 763і7 на 29; є) 34124¾ на 89;
б) 342256 на 29; ж) 175411 на 629:
в) 5813792 на 37; з) 272і141 на 135;
г) 10і0 на 67; к) 35100 на 1242;
д) 244408 на 73; л) 206л+5 на 9, п 6 N.
є) 749193 на 79;
19.8. Знайти остачу від ділення:
а) 5329 • 4317 на 37;
ч,б) 378561 .427е21 на 41;
в) 3720-2312 на 61;
г) З19-37-1 на 19-37;
д) (5 622 + 179 — 346). 923 на 23;
є) (63157 + 25028) • 926 на 12;
Є) у161 — З60 на 100;
ж) (12 37156 + 34)28 на 111.
19.9. Довести, що
а) 14120 — 1:45; д) 4323 + 2343 і 66;
б) ІЗ176 — 1; 89; є) 222555 + 555222:7;
в) 372654500 + 72 • 107118; є) 220і 19' + 6922°119 + П9д9"° J102.
Г) 21093 —2-10932;
19.10. Нехай m, ngN. Довести, що:
а) /г7 + 6яі7;
б) 10л(9/г—1) + 1:9;
в) 3 • 5^+1 + 2^+1 і 17;
124

Г) 6^+54+2:31-,
д) 20m + 16m — З™ — 1 ; 323, якщо т = 2n;
є) тп(т60 — п60) ;56 786 730;
є) т96 — ft96:144, якщо (m, 12) = (л, 12)=1.
19.11. За правилом «дев'ятки» перевірити правильність
виконання арифметичних дій над цілими числами:
а) 375 819 + 726 345 + 807 611 = 1 909 775;
б) 732-421=308172;
в) 73416 • 8539 = 626899224;
г) 24667+18265 = 42932;
д) 5433153:4371 = 1243;
є) 375426-3846=1443888276;
є) /73818 = 2712+ 377.
19.12. Перевірити правильність виконання арифметичних дій
числами 9 і 11:
а) 387912—203756=185146;
б) 8740297—561245 = 8179052;
в) 5839131309:67377 = 85847.
19.13. Знайти довжину періоду при перетворенні у
десятковий дріб нескоротного звичайного дробу із знаменником: а) 17;
б) 19; в) 29; г) 37; д) 43; є) 59; є) 67; ж) 73; з) 89; к) 97.
19.14. Знайти довжину періоду при перетворенні у
десятковий дріб нескоротного звичайного дробу із 'знаменником: а) 21;
б) 33; в) 39; г) 49; д) 51; є) 77; є) 91; ж) 11-17; з) 13-17;
к) 17-23; л) 53-59; м) 53-73.
19.15. Знайти кількість цифр до періоду і довжину періоду
при перетворенні у десятковий дріб нескоротного звичайного
дробу із знаменником: а) 140; б) 220; в) 450; г) 528; д) 540;
є) 550; є) 665; ж) 816; з) 950; к) 1150; л) 2380; м) 26500.
19.16. Знайти знаменник дробу у, який перетворюється у
десятковий чистий періодичний дріб:
а) з двома цифрами в періоді;
б) з трьома цифрами в періоді.
19.17. Знайти:
а) -|і, знаючи, що ~ = 0, (052 631 578 947 368 421);
б) ig-, якщо ± = 0, (09) і -1 = 0, (076 923);
в) а, якщо jz = 0, (86 301 369) і -^ = 0, (01 369 863);
г) а, якщо -^- = 0, (ЗО 136 986) і ± = 0, (01 369 863).
19.18. Довести, що
ill
а) сума ——-г -\ 1——•, я>1, перетворюзться у мішаний
десятковий періодичний дріб;
б) коли р — просте число, р ф 2, р ф 5 і дріб — перетворюєть-
125

ся в чистий періодичний дріб з парним числом Ь цифр у періоді
— = 0, (a\a2.. .а ь аь_аь . ..Яб-іДб), то а^__ . = 9 — аІ9 і'■ = 1,
2, ..., -^-- (Перевірити для числа у];
в) звичайний дріб —, де р, q — прості числа, відмінні від 2
і 5, перетворюється в нескінченний періодичний дріб з довжиною
періоду [-^Л ^х^-]. де
d = (indlO, р — 1), 8 = (indl0, ¢-1)
(у першому випадку indlO беруть за модулем/?, у другому —
за модулем q)\
г) коли 10 є первісним коренем за модулем т, то леріоди
всіх нескоротних дробів із знаменником т утворюються в
результаті кругових перестановок тієї самої системи й = ф(т) цифр,
19.19. Перетворити у звичайні такі періодичні дроби: а) З,
(27); б) 0,35 (62); в) 11, 12 (31); г) 5, 1 (538),
Розділ IV, МНОГОЧЛЕНИ ВІД ОДНІЄЇ ЗМІННОЇ
§ 20. Кільце многочленів над областю цілісності •
Алгебраїчна і функціональна рівність многочленів
Література
11] — § 21, с. 211—227;
12] — § 21, с. 214—230;
J3] —гл. 14, § 1, с. 459—468;
17] —§ 7, с. 42-50;
]6] —§ 20, с. 130—133;
]8] — гл. 5, § 2, с. 207—211.
ТЕОРЕТИЧНІ ВІДОМОСТІ
Нехай К—довільна область цілісності з одиницею і R—ЇЇ підкільце з
одиницею.
Елемент х£К називається алгебраїчним над кільцем R, якщо в R існують
такі елементи а0, av а2, ..., ал, які не всі дорівнюють 0, що
апхп + ап__ххп~х + ... + ахх + а0 = 0.
Елемент, який не є алгебраїчним над R, називається трансцендентним над R
Мінімальне розширення кільця R, яке містить трансцендентний над R
елемент х, називається простим трансцендентним розширенням кільця R, або кільцем
многочленів від однієї змінної над R, і позначається через R[x]. Елементи цього
кільця називають многочленами від х над R і позначають символами / (x)} g (х)
і т. д. Нуль кільця R [х] називають нулевим многочленом або нуль-многочленом.
Будь-який ненульовий многочлен f(x) над кільцем R можна єдиним чином
подати у вигляді
/ (х) = апхп + ап_{хп-{ +9..+аїх + а09 (1)
Де aQ, а{, ..., ап £ R і ап Ф 0.
і 26

Вираз (1) називають канонічною формою ненульового многочлена f (х).
Канонічною формою нуль-многочлена вважатимемо 0.
Доданок akxk (k = 0, 1, 2 . . ., я) канонічної форми (1) ненульового многочлена
f (х) називається k-м членом (членом Л-го степеня), ak — k-м коефіцієнтом
(коефіцієнтом £-го члена), а0 називається також вільним членом многочлена f(x).
Член п-то (найбільшого) степеня називається старшим членом, його коефіцієнт
ап—старшим коефіцієнтом, а його степінь — степенем многочлена f (х) і
позначають deg /.
Нуль-многочлену не приписують ніякого степеня.
Два многочлени з кільця R[x] дорівнюють один одному тоді і тільки тоді»
коли вони мають однакові степені і попарно рівні відповідні коефіцієнти
(алгебраїчна рівність многочленів).
Кільце многочленів R [х\ є областю цілісності.
Степінь суми двох многочленів (з яких хоча б один є ненульовим) не
перевищує більшого з степенів цих многочленів. Степінь добутку двох многочленів
(відмінних від нуль-многочлена) дорівнює сумі степенів цих многочленів.
Якщо многочлен f (х) з кільця R [х] має канонічну форму (1) І a£R, то елемент
апаП + ап-\аП~Х + • • • + а\а + а0
кільця R називають значенням многочлена f (х) при х = а і позначають через f (а).
Кожен многочлен f (х) з кільця R [х] визначає відображення ср« : R -> R
таке, що (ff (а) = / (а).
Якщо область цілісності R має характеристику 0, то многочлени f(x)>g(x) £ R[x)
дорівнюють один одному тоді і тільки тоді, коли рівні функції cfy та cpg, які вони
визначають (функціональна рівність многочленів).
Алгебраїчне і функціональне тлумачення многочленів рівносильні над
областю цілісності характеристики 0.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Знайти всі цілі числа а і 6, при яких многочлен / (х) = х4 + ах3 + Ьх2 — 8* + 4
є квадратом деякого многочлена g(x) з кільця Z [х], та записати многочлен g (x).
Розв'язання. Многочлен / (х) має степінь 4. Тому степінь шуканого
многочлена g(x) (якщо він існує!) дорівнює 2. Нехай g(x) = mx2 -\-nx + pt тфО,
і многочлени / (х) та (g (х))2 дорівнюють один одному.
Запишемо многочлен (g(x)) У канонічній формі:
(g (х))2 = (тх2 + пх + р)2= т2хА + 2тпхг + (2тр + п2) х2 + 2пр + р2.
З умови рівності многочленів маємо систему рівнянь:
т = 1,
2m/i = а,
2тр + п2 = 6,
2пр = —8,
З першого рівняння системи знаходимо, що /я£{1, —1}, а з останнього
р£ {2, —2}. Це означає що дана система рівнянь рівносильна сукупності
чотирьох систем:
/и=1,
/> = 2,
я = —2,
а = -4,
ft = 8,
( m=l,
/7 = -2,
/1 = 2,
а = 4,
.6 = 0,
' т = —1,
/7 = 2,
п = — 2,
a = 4,
.6 = 0,
' т = —1,
Р = -2,
п =2,
a = -4,
,6 = 8.
Таким чином, якщо а = —4 і Ь = 8, то існують два многочлени %х (х) — — х -f-
+ 2jc — 2 і g2 (jc) = ^2 — 2х + 2, які задовольняють умову задачі. Якщо а = 4
127

1 b = 0, то gj (*) = x + 2x — 2 і g2 (де) = —х1 — 2л: + 2. Цим вичерпуються
всі можливі випадки шуканого зображення многочлена / (jc).
2. Перевірити, чи є кільцем множина К всіх многочленів з кільця Z [х\, в яких
вільний член ділиться на 5.
Розв'язання. Нехай
ї(х)=апхп + ...+а{х + 5а0,
g(*) = bmxm + ... + b{x + 5bQ і т> п.
Тоді
/W + gM = *m*m + --- + (^ + ^+- •- + («! + ^і)* + (5¾ + 5¾) =»
--=bmxm+... + (an + bn)xn + ... + (a, + b])x + 5(a0 + b0)y
f(x)-g(x) = (-bm)xm+... + (an-bn)xn + ... + (a{-bl)x + 5(a0-b0),
/(*)•* (x) = onbmxn+m + ... + (5a Д + Sa0b{) x + 5 . 5¾¾.
Це означає, що / (-де) + g (*), /(*)—g(*) і / (*) -g(*) також є елементами мно^
жини К. Отже, К є підкільцем кільця Z[x].
3. Многочлен / (х) з кільця Z5[x], степінь якого не вище за 4, має ту властивість,
що / (а) = 0 для всіх а £ Z5. Довести, що / (х) є нуль-многочленом.
Розв'язання. Нехай /(х) = ax4 + Ьхг + с*2 + dx + б. Тоді
/(0) = е = 0,
/(Т) = а + 6 + с + 3 + е = б,
/ (2) = 3 + 36 + 4с + 23 + є = б,
/ (3) = З + 26+ 4с + 33 + ~е = 0,
/ (4) = а + 46 + с + 45 + є = 0.
Звідси дістаємо систему рівнянь у полі Z5:
a + 6 + c + 3 = 0>
a + 6 + c + d = 0,
a + 36 + 4c + 23 = 0,
3 + 26 + 4с + зЗ = б,
a + 46 + c+43 = 0
або
26 + Зс + d = 0,
6 + Зс + 23 = б,
гь + зЗ = б.
Далі
( а + 6 + с + 3 = б,
6 — 3 = 0,
6 + Зс + 23 = б,
І 6 + 3 = 0
a = 6 = c = d = 0.
Таким чином, усі коефіцієнти многочлена f (х) дорівнюють нулю, тобто / (jc)
є нуль-многочленом.
4. Довести, що в многочлена
/ (*) = (_ sin2 a • *3 + COS2 a • X + *)1983
з дійсними коефіцієнтами суми коефіцієнтів членів парного і непарного
степенів однакові, і знайти їх.
Розв'язання. Якщо g(х) = апхп + . . . + а{х + а0 — деякий многочлен над
областю цілісності К з одиницею, то g (1) = ап + . .. +я, + а0 і g(— 1) =
= (—\)пап + ... — а{ + я0, тобто значення многочлена при х = 1 дорівнює
128

сумі всіх коефіцієнтів, а при х = —1 дорівнює різниці між сумами
коефіцієнтів парного і непарного степенів.
Позначимо суми коефіцієнтів членів парного і непарного степенів многочлена
/ (х) Через SQ І Sj ВІДПОВІДНО.
Тоді
^ + ,,-/(1)=-- (- sin2* + cos2* + І)1983 = (1 + cos 2a)1983 = 21983 . COS3966a,
s0 - S] = і (—1) = (sin2a + cos2a - 1)1983 = 0.
З другбї рівності маємо s0 = sv аз першої
Sq = Si = 21982.^3966^
Задачі
20.1. Знайти канонічну форму многочлена;
а) f{X) = (x+ K2)4 + U — V2Y-(x3 + 3x— l)(x2+7x + 2) у
кільці R \х\\
б) f(x) = (x— Т)3 у кільці Zz\x]\
в) / (х) = (4л:8 + 2л;2 — Зл; + ї) (х2 — 2х + 3) у кільці Z5 \x].
20.2. Встановити рівність чи відмінність між многочленами!
а) f{ (х) = 5-І0в.2*з _ \г\ — 2 J/3 *- + 2* - tg -J-,
/2W = (l-sin-j)x3 + (t-l)2x2 + 2-r,
/з (х) = yjc3 + (КЗ — і)*2 — 2/2jc — i\
f4 (x) = cos ^- хд + 2i3x2 + і7 + 2,
/6W = (| + tg2^)x3 + (tg~-l)jc2-4cos2|x-2° у кіль-
ці С[х]\
б) /і (*) = (4* + З)2, /2 (х) = — х2 + їх + 4 та /з (х) = 4х2 — х + З
у кільці Z5 [jcJ.
20.3. Довести, що в кільці Z5 [х] многочлени / (х) = (л: + З)5 і
g (х) = х5 + 3 дорівнюють один одному.
20.4. Довести, що для будь-якого простого числа р і цілого а,
1 < а < /? — 1, многочлени / (х) = (х + а)р і g (х) = хр + а рівні
в кільці Zp [х]л
20.5. При яких значеннях a, b \ c наступні многочлени з кільця
Z[x\ рівні між собою:
а) f(x)=ax2(x+ l) + b(x2 + l)(x — 6) + сх(х2 + 1) та g(x) =
= х2 -І- 5л: -і- 6*
б) /(x) = ajt(jt2 + 3)+ &*(*— 1)+C(jc+1) та g(x) = 2х3+ 5х2 +
+ 8х + 7?
20.6. Знайти всі значення а, при яких наступні многочлени є
квадратом деякого многочлгна g(x) з того самого кільця, і
записати g(x):
а) f(x) = tf -f 6%3 + 1 їх2 + ах -f 1 з кільця Z [х\\
6 5-271 129

б) f (x) = 4л:4 -\-ах2 — 1 з кільця Z5 [x];
в) /(х) = 9л:4 — 12х3 + 16л:2 — 8л: + а з кільця Z [х].
20.7. Знайти всі цілі а і 6, при яких многочлен
f(x) = x3+ax2+ I2x + b
є кубом деякого многочлена з кільця Z [х\.
20.8. Знайти всі цілі числа а і Ь, при яких многочлен f(x) =
= х* + ax3 -\- bx — 8л: + 1 є квадратом деякого многочлена g (x)
з кільця Z\x]y та записати многочлен g(x).
20.9. Чи може многочлен
f (х) = 8х* — Збах* + 66а2*4 — 63а3л:3 + ЗЗа'х2 — 9а5х + а6
з дійсними коефіцієнтами бути кубом многочлена g(x) з цілими
коефіцієнтами?
20.10. Яким умовам мають задовольняти цілі числа a, b і с> щоб
многочлен / (х) = 4л:4 — 4ал:3 + 4bx2 + 2а(с -\- 1) х + (с + І)2 був
квадратом деякого многочлена з цілими коефіцієнтами?
20.11. Знайти цілі числа a, b і с, для яких виконується рів-
х+5 а • Ь с
Н1СТЬ (х-\)(х — 2) (х — 3) ~~ *^7 + ^^2 + х~^Гз'
20.12. Чи існує в кільці R [х] квадратний тричлен, який є
квадратом деякого многочлена і такий, що зберігає цю властивість при
будь-якій перестановці своїх коефіцієнтів?
20.13. Кожен з двох многочленів f (х) і g(x) над областю
цілісності К є сумою квадратів двох многочленів з кільця К [х\.
Довести, що многочлен s(x) =f (x) • g (x) має цю властивість.
20.14. Записати у вигляді суми квадратів двох многочленів
з кільця Z[x] такі многочлени:
а)/(х) = (х2+1)(х2 + 9);
б) / (х) = (л;2 — 2х + 5) (л:2 + 16* + 73).
20.15. Чи є кільцем множина всіх многочленів з кільця Z[x\
а) в яких змінна х має тільки парний степінь;
б) в яких змінна х має тільки непарний степінь;
в) які не містять вільного члена;
г) коефіцієнти яких кратні даному натуральному числу k\
д) степінь яких нз перевищує числа 10;
є) степінь яких не менший числа 2?
20.16. Довести, що з функціональної точки гзору наступні
многочлени дорівнюють один одному:
а) f(x) = xs — 2x2 і g(x) = x2 — 2x з_кільця Zi[x]\
б) f(x) = 2x2 + x+l і g(x) = 2х3 + 2х2 + 2л: + 1 з кільцяZ3 [x];
в) f (х) = х10 + Ах2 і g(x) = 4л:5 + х з кільця Z5 [x].
20.17. За допомогою многочлена з кільця Z2 [л:] задати кожне
відображення поля Z<i в себе.
20.18. Довести, що для будь-якої області цілісності К в кільці
К[х] не існує двох многочленів першого степеня, які різні в
алгебраїчному і рівні у функціональному розумінні.
130

20.19. Довести, що для будь-якої скінченної області цілісності К
існує ненульовий многочлен f(x) в кільці К\х\ такий, що f(a) = 0
для всіх аеК
20.20. Довести, що кожне відображення скінченної області ці-
л існості К в себе можна задати деяким многочленом з К[х].
б_
20.21. Довести, що відображення f(x) = \fx множини дійсних
чисел R в себе не можна задати деяким многочленом з кільця R [х].
20.22. Знайти суму коефіцієнтів таких многочленів:
а) / (х) = (1 — 5а; + 4а:3) (За; + 5)3 в кільці Z [х]\
{) б) f (х) = (і + 2х — 4х2)19_83 - (1 —7х + 5*2)1982 в кільці Z [*];_
в) f(x) = 2 +_(х2 — 6х + 5) (х5 + Зх4 — 2х3 + а;2 — х) + (х2 — Зх +
+ 1)(а;3 + 5х + 2) у кільці Z7\x].
20.23. Многочлен g(x) над областю цілісності К з одиницею має
однакові суми коефіцієнтів членів парного і непарного степенів,
які дорівнюють s. Знайти суму коефіцієнтів членів парного степеня
многочлена f(x) = [g(x)]k, де k£ N.
20.24. Довести, що многочлен
f(x) = (1 — х + 2х2 — За;3 + ... + 50а:50) (і + х + 2х2 + . .. + 50а:50)
не містить членів з непарними степенями.
20.25. Довести, що кожен коефіцієнт при парному степені змін-
ної х члена многочлена f(x) = (1 -\-5х2 — x3)k не менший коефіцієнта
при такому самому степені х члена многочлена g(x) = (1 — 5л;2 — а3)*.
20.26. Знайти цілі числа а, при яких наступні многочлени
розкладаються в добуток двох многочленів gi(x) = х+ b і g2(x) = х + с
з цілими коефіцієнтами:
а) f(x) = (x-a)(x- 10)+1,
б) f(X)==(x + a)(x+ 1)-1.
20.27. Довести, що в кільці Z[x] немає многочлена f (х) такого,
щоб /(7)= 11 і /(11)= 13.
20.28. Довести, що многочлен f(x) = —- а; (а:— і) ... (х—(п— 1))з
кільця Q[x\, заданий для деякого фіксованого натурального числа п>
набуває цілих значень при будь-яких цілих значеннях змінної х*
20.29. Довести, що для кожного многочлена f(x) з кільця Z\x\
і будь-яких цілих чисел а і b число f(a+ V~b) + / (а — У"Ь) є цілим.
§ 21. Відношення подільності в кільці многочленів.
Ділення з остачею. Ідеали кільця многочленів
Література
{1] —і 22, с. 227—238;
[2J —§ 22, с. 231-241;
[3] —гл. 14, § 2, с. 469—470;
[5] —гл. VII, § 3, с. 262—265; гл. IX, § 1, 2, с. 316—322;
[6]-§ 20, 21, с. 133-137;
17] — * 8, с. 50—54.
[8] —гл. 5, § 2, с. 216—218.

ТЕОРЕТИЧНІ ВІДОМОСТІ
Нехай Р — деяке поле. Многочлен f (х) £ Р [х] ділиться на g (х) Є Р [х]
(записують / (х) і g(x)), якщо існує многочлен s(x) £ Р [х] такий, що f (x) — g (х) • s (х).
Відношення подільності многочленів над полем Р має такі властивості:
1°. V [/ (х): g(x) Ag (x) lh(x)=$f (х) і h (x)];
f(x),g(x)Mx)£Plx]
2°. V [f (x) lh(x)Ag (x) S h (x) =# (/ (*) ± g (x)): A (a:)];
f(x),g(x),h(x)£P[x]
3°. V [/W:AW4 V lf(x)g(x):h(x)]];
Hx)Mx)€Plx] g{x)£P[x]
4°. V V If (x) lc];
Hx)£Plx] c£p\{0}
5°. V V [f(x):g(x)^f(x):Cg(x)];
f{x),g(x)£P[x] c€p\{0}
6°. V [f(x):g(x)Ag(x)lf(x)^3 f(x) = Cg(x)].
?(x),g(x)£P[x] c£p
Говорять, що многочлен f (x) £ P [x] ділиться з остачею на многочлен g (x) Ф
Ф 0 з кільця Р [х], якщо в Р [х] існують такі многочлени s(x) і г(х), що:
1) f{x) = g(x).s(x) + r(x);
2) r (x) = 0 або deg r < deg g.
При цьому f(x) називають діленим, g(x) — дільником, s (х) — часткою, г (х) —
остачею.
Довільний многочлен f (х) з кільця Р [х] ділиться з остачею на будь-який
ненульовий многочлен g(x) з цього кільця, причому частка і остача визначаються
однозначно.
Кільце Р [х] многочленів над довільним полем Р є кільцем головних ідеалів.
Кільце Р [х] многочленів над полем Р є евклідовим.
Для знаходження частки і остачі від ділення многочлена
/ (де) - апхп + . . . + а{х + а0 на g (х) = Ьтхт + тшл + ьіх + Ь0
над полем Р (а при певних умовах і над областю цілісності К) застосовують
різні методи. Зокрема, метод ділення кутом, метод невизначених коефіцієнтів та
за допомогою табличних схем.
Розглянемо одну з можливих табличних схем, яка мав іноді переваги перед
рештою методів. Нехай п > т. Якщо
/ (*) =g(x)s (х) + г(х) і s (х) = сп_тхп-т+ . .. + с{х + с0
та т {х) = dm_lxm~l -(-...+ d{x + d0, то схема має вигляд (табл. 16).
У таблиці є п + 2 стовпці і п — m + 3 рядки. Через ait J < і < п — т,
позначено суму елементів (і + 2)-го стовпця, які стоять між першим та (і + 2)-м
рядками. Через 5;., 0 < / < /я— 1, позначено суму елементів відповідного
стовпця, які стоять між першим і останнім рядками. Таблиця заповнюється так:
ап .
1) знаходять -г- і записують його в останній рядок другого стовпця;
2) число сп_т множать на коефіцієнти дільника і послідовно записують
у другий рядок зліва направо (при цьому кілька останніх клітин можуть бути
порожніми);
3) обчислюють різницю #„_! — aj і записують її у клітинці на перетині
третього рядка і третього стовпця;
ап-\ — °і ., .
4) знаходять число сп_т_1 = т і записують його в третій клітинці
останнього рядка;
5) за аналогією з 2) заповнюють третій рядок (при цьому порожньою буде
клітинка з другого стовпця).
132

Таблиця 16
*»
А.-1
\bm-2
*
V
'ь0
an
an
an
cn—m
an-\
h a"
bm-x —
an-\ -ai
an-l-ai
cn—m—\
an-2
-i
t a«-i-°i
"-' ьт
an-2 — a2
an-2 — a2
bm
cn—m—2
...
<%
am~°«-m
am~Qn-m
*m
Co
am-\
bm-i><
aM—vn_m
am-l-5m-l
dm-\
...
...
^0
m
ao — 5o
4)
Цей процес продовжують доти, поки не буде обчислено вільний член £0
частки. Після цього знаходять коефіцієнти остачі як різниці між числом, що
стоїть у першому та останніх заповнених рядках відповідного стовпця.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Встановити подільність многочлена
/ (х) = х19 + xw + х13 + хп + х1 + х5 — б*3
на многочлен g (х) = х2—1 в кільці Z [х].
розв'язання. Запишемо многочлен f (х) у вигляді суми многочленів,
виділивши, якщо це можливо, в кожному з них множник-многочлен g(x):
f (x) = (х19 - хи) + (2х17 - 2х15) + (2л:15 - 2х13) + (з*13 - З*11) +
+ (4*11 - 4*9) + (4*9 - 4х7) + (5/ - 5/) + (6/ - б*3) = х17 (х2 - і) +
+ 2*15 (У - 1) + 2*13 U2 - 0 + З*11 (х2 - 1) + 4х9 Or -1) +
+ 4/ (х2 - І) + 5*5 (х2 - 1) + б*3 (х2 - і).
Оскільки кожен з многочленів-доданків ділиться на многочлен g (x) в кільці
Z[x]t то многочлен f (х) ділиться на g(x) в Z[x].
2. Знайти остачу від ділення многочлена
/(х) = (*-2)100 + (*-1)50+1
на многочлен g (х) = х2 — 3* + 2 в кільці R [х].
133

Розв'язання. До многочленів f (#), g (x) застосуймо в кільці R [х]
теорему про ділення з остачею. Тоді існують многочлени s (х) і г (х) такі, що
t [х) = g (x) • s (x) + т (х) і deg г (х) < 2.
Остання нерівність означає, що г (х) = ах + Ь. Тому
(* _ 2)100 + (х - І)50 + 1 = (jc2 — Зх + 2) s (*) + ах + Ь.
Враховуючи те, що g (\) = g (2) = 0, підставимо х = 1 і * = 2 у ?добуту
рівність. Маємо систему рівнянь:
f а+6 = 2, або (а=0,
І2а + * = 2
Отже, г (*) = 2.
3. Виконати ділення з остачею многочлена
/ (х) = Зх" + *4 -- 10x3 + 12х2 + 10* — 8 на многочлен g (х) = Зх2 + х — 1.
Розв'язання. Застосуємо описану вище табличну схему. В таблиці по»
винно бути 7 стовпців і 6 рядків. Маємо (табл. 17).
І*
■ 1
—1
.4
3
1
1
1
0
0
-10
—1
0
—9
—3
Та
12
0
о
15
5
б л и ця 17
Ю
3
5
2
—8
-5
—3
Отже, при діленні і (х) на ^ (л:) дістали частку s(x) = x'6 — 3*+ 5 і остачу
г(х) = 2х — 3.
Зауваження
1. Оскільки рядок, що містить тільки число 0, не впливає на обчислення,
то його можна не писати. При цьому в таблиці залишиться незаповиеним
передостанній рядок.
2. Для спрощення в таблиці відділяють лініями тільки перший і останні
рядки та перший і m останніх стовпців.
Задачі
21.1. Перевірити, чи ділиться:
а) f(x) = (3x2 — 2х — ї)(10х3+ 10* — 20) + 2*4 — 2 на g(x)=*
= 5х2—5 у кільцях Z[x] і Q[x]\
б) f(x) = х2+ х + ї на g(x) = х—1 у кільці Z3[*];
в) f(x) =*I00 + x98 + *96 + ... +х* +х2 +х — і uag(x) = x2 + 1
у кільці С \х\.
21.2. Довести, що многочлен f(x) = x3 + 2 не ділиться на жоден
многочлен першого степеня в кільці Z [х].
21.3. Довести, що многочлен f(x) = x3 + 2 ділиться на деякий
многочлен першого степеня в кільці Z?>\x\.
134

21.4. При яких значеннях а многочлен f(x) = 3xA — 2x2 — 5
ділиться на многочлен g(x) = x2 — а: а) в кільці Z[x\? б) в кільці
Q №
21.5. Довести, що при будь-якому натуральному п, кратному З
многочлен f(x) = xn — 1 ділиться на многочлен g (х) = х1 + х + 1
у кільці Z[x].
21.6. Знайти необхідні ; достатні умови подільності таких
многочленів:
а) / (х) = х6 + Ьх + с на g(х) = х2 + ах — 1 в кільці R [х\\
б) /(х) = х3 + Ьх + с на g(х) = х2 + 1 в кільці Z [х]\
в) f (х) = х4 + Ьх2 + с на g (х) = х1 + ах + 1 в кільці Z [х].
21.7. Довести, що многочлен f(x) = xn — an ділиться на
многочлен g{x) = x — а над областю цілісності К при будь-якому
натуральному п.
21.8. Перевірити справедливість твердження! «Довільний
многочлен f (x) з кільця Z [х] ділиться з остачею на будь-який
многочлен g(x) з цього кільця, відмінний від нуль-многочлена».
21.9. Довести, що коли в кільці К[х] над областю цілісності К
можна виконати ділення з остачею многочлена f(x) на g(x), то
частка і остача визначаються однозначно.
21.10. Довести, що в кільці К [х] над областю цілісності К з
одиницею можна виконати ділення з остачею довільного многочлена
f(x) на будь-який многочлен g(x), старший коефіцієнт якого
дорівнює одиниці.
21.11. Знайти остачу від ділення:
а) f(x) = xim0+xl0™+xm + xl0+x— 1 на g(x) = ix— 1 у
кільці (Z[i])\x\\
б) f(x) = x30 + х2*+х20+ х1-+х[0+х + 1 на g(x) = xb — l у
кільці Z\x\\
в) f(jc) = x19e2+*991+ 1 на g(x) = x2 — 1 у кільці Z[x]\
г) f(x) = xm2+x+l на g(x) = х2 — (1 +і)х+ів кільці С[х)\
Z) f(X)= xm + x"—2x9s —Зх3+ 2х + Ь nag(x) = x2 + х — 2
в кільці Z\x\.
21.12. Виконати ділення многочленів!
а) / (х) = \хь — 6л:3 + 2л;2 — 4 на g (х) = 2х2 — 5л: + 1 в кільці
QM;
q б) / (х) = (2і + 3) х6 — Мх + і — 2 на g (х) = х2 + і в кільці
с М; _ _ _v
в) f(x) = Ах6 + 2х2 — х + 1 на g(x) = 2х + З^в ^кільці Z5 \x]\
D г) / (x) = \0х7 — 36х" + 13л:5 + 38л:4 — 6л:3 + Зл:2 — 20л: — 13 на
g(x) = 2х2 — 4л: — 3_в кільці R [х]\
д) / (х) = (2л:3 + 3) (х — 2) —_*2 на g (*) = (л: + З)2 в кільці Z5 [*];
є) / (я) = Зл;7 + 6л:3 + Зл:' + 6 на g(x) = x2 + 6х +5 у кільці
Z7 [x]\
0 e)f(x) =-x6 + j-xb — x3+х2—1 на g(x) = х3—-g х+ 1 у
кільці Q[x\\
ж) / (л:) == ix« + (1 + *) * + (1 — 0 на g (л:) = л:3 + (1 + і) в кільці
С [х\.
135

21.13. Можна вважати, що многочлени f(x) = xP) + 3x* + x3 +
+ 4%2 — За:—1 і g(x) = x2+x+l належать кільцям Z[x] та Zb\x\
залежно від того, як інтерпретувати їхні коефіцієнти. Довести, що
в першому випадку f (х) не ділиться на g(x), а в другому—ділиться.
Чи можлива реалізація оберненого варіанта?
21.14. Довести, що многочлен / (х) = х6 + х3 +а не ділиться на
многочлен g(x) = х3 + х + а в кільці Q \х] при жодному значенні
числа а.
21.15. При яких значеннях а і Ь многочлен /(х) = х3 + 2х2 +
+ ах + b ділиться на многочлен g(x) = х2 + x + ab в кільці Q [х\?
21.10. При діленні многочлена f (х) на g(x) в кільці Z [я] дістали
остачу г(х) = Зх2 — \х + 1. Знайти остачу від ділення (/ (х))2 на
g(x), якщо degg = 5.
21.17. При діленні f(x) на g(x) в кільці Ц [х] дістали остачу З,
а при діленні (f(x))2 на (#(*)) —остачу 9. Яка буде остача,
якщо f(x) ділити на {g(x))2?
21.18. Остачі від ділення многочленів f\{x) і f^{x) на g (x) в
2
КІЛЬЦІ Q [X] ВІДПОВІДНО ДОрІВНЮЮТЬ Г\ (Х) = —2Х + -j І Ґ2 (X) = X2 +
+ Зх — 1. Знайти остачу від ділення многочлена f (х) = З/і (х) +
+ 2f2(x) на g(x).
21.19. При діленні f(x) на g(x) у кільці С [х] дістали частку
s(x) = іх + 3-7-2/ та остачу г(х) = (і—1)л:2 + 2. Знайти остачу від
ділення f(x) на s{x).
21.20. Знайти найменший ідеал / кільця Z[x]> який міститьі
а) многочлен / (х) = 3х — 5;
б) многочлени /і (х) = 2х — 1 і /2 {х) = Зх + 2;
в) многочлени /і (а:) = х2 — 1 і /г (х) *=* х2 — За; + 2.
21.21. Чи є ідеалом в кільці R [х] множина / всіх многочленів,
у яких вільний член є парним числом?
2Ь22. Множина / містить число 0 і всі многочлени / (х) з кільця
Z[x], які містять змінну х9 не нижче другого степеня. Довести, що
множина / € ідеалом кільця Z[x], Чи є цей ідеал головним?
21.23, Довести, що множина / всіх многочленів кільця Z[x]9
коефіцієнти яких діляться на число п, є головним ідеалом bZ[x].
21.24. Довести, що множина / всіх многочленів кільця Z[x],
вільний член яких дорівнює парному числу, є ідеалом в Z[x]. Чи
є цей ідеал головним?
§ 22. Ділення многочлена на двочлен х — а.
Розклад многочлена за степенями двочлена х — а
Література
[1] —§ 22, с. 231—235;
12] —§ 22, с. 234—239;
ІЗ]-—гл. 14, § 4, с. 481—482;
15] — гл. VII, § 3, с. 266—268;
16] —§ 22, с. І44—145;
17] —§ 12, с. 71—72;
[S] _ гл. 6, § 1, с. 243—244.
136

ТЕОРЕТИЧНІ ВІДОМОСТІ
У попередньому параграфі було наведено табличну схему для виконання
ділення з остачею многочлена / (х) на многочлен g (x) над полем Р. Ця схема
значно спрощується, якщо многочлен g (x) є двочленом виду g(x) = Ьтхт+ Ь0л
Справді, вона має вигляд (табл. 18). З другого по передостанній рядок цієї
таблиці в кожному стовпці міститься не більш як одне число, відмінне від
нуля. Наприклад, з другого по (т+ 1)-й стовпець — це ап, an_v . . ., an_m,lm
Таблиця 18
L
0
0
•
0
k
ап
ап
ап
Ь,п
ап-\
0
ап-\
ап-\
ьт
т
ап-2
1 °
0
ап-2
ап-2
ап-т+\
0
0
0
ап—т-\-\
ап-т+\
ьт 1
ап-т
ап ■
ит
0
0
0
п—т °т
т |
...
Яг»
т
а —о
т п—т
т ап—т\
т— І
0
ат-\ —
—Ьт-\
а()
а —а
т п—т\
&<> —ь—
а0 — Ь0
, ап . а"-1 . аг\—т-\-\
У наступних стовпцях: Ь0 -т—^ bQ —r , . . ., Ь0 —*~г*—- , тобто добутки вільного
mm m
члена &Q дільника g(x) на коефіцієнти частки сп_т> сп_т^_х, . . ., сп_2т_,1
і т. д. Це означає, що в таблиці можна обмежитися тільки трьома рядками
і заповнювати її в такій послідовності:
1) спочатку розіб'ємо коефіцієнти многочлена / (х) у групи по т членів
зліва направо (в останній групі може бути менше ніж т членів);
2) коефіцієнти Ьт і bQ записують у першому стовпці в першому і другому
рядках;
3) кожен ряд першої групи (ап, . . ., ап__т . і) ділять на старший член
дільника Ьт і заґіиоують у третій рядок під ним; у другому рядку з другої по
(т+ 1)-у клітину можна не вписувати чисел;
4) вільний член Ь0 послідовно множать на знайдені коефіцієнти частки і
вписують у другий рядок, починаючи з (т-|-2)-ї клітини;
5) знаходять наступні коефіцієнти частки, і процес продовжують доти, поки
не запевнять останню клітину таблиці в третьому рядку.
137

Якщо двочлен g(x) має вигляд g (х) = хт + &0, то при обчисленні
коефіцієнтів частки за наведеною табличною схемою не треба виконувати ділення чисел,
тоді ця схема нагадує схему Горнера. При цьому число 1 можна також не
писати в лівому верхньому кутку таблиці.
При діленні многочлена / (х) на двочлен g (х) = х—а описану схему можна
спростити. Так, якщо усно обчислювати різницю коефіцієнтів а{, 0 < і < п, і
добутків вільного члена — а на знайдений коефіцієнт частки Q—і, то в таблиці
стає - айвим другий рядок. Тоді розглядувана таблична схема відрізняється від
схеми Горнера тільки тим, що в першому стовпці міститься число—а замість а.
Нехай f (х) — деякий многочлен над полем Р. Для будь-якого елемента а
з поля Р остача при діленні многочлена f (х) на двочлен х — о дорівнює f (а)
Многочлен f (х) ділиться на двочлен х — а тоді і тільки тоді, коли остача
дорівнює нулю.
Подамо многочлен / (х) з кільця Р [х] у вигляді
f(x) = cn(x^a)n'\-cn_l(x^a)n-'l + ... + cl(x-a) + c0f
де с0, cv • • •> сп£Р називається розкладом многочлена за степенями х — а.
Коефіцієнти розкладу с0, сх сп можна знайти в результаті послідовного
ділення f (х) на х — а, потім здобутої першої частки на х—а і т. д.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Виконати ділення многочлена / (х) = 2х' + 4хг> — х4 — 6л:3 — х2 + Зх — 2 на
двочлен g (х) = 2х3 — 1 в кільці R [х].
Розв'язання. Виконуємо ділення за описаною вище табличною схемою
(табл. 19).
Та блиця 19
2
—1
2
1
0
0
4
2
—1
— 1
0
—6
0 1
—3
—1
—2
1
3
0
3
—2
3
—5 1
Отже, при діленні / (х) на двочлен g (х) дістали частку s (х) = х4 + 2х2 — З
і остачу т (х) = х1 + Зх — 5.
2. Розкласти многочлен
/ (х) = 2х7 + 4хь — хА — 6х3 — х2 + Зх — 2
за степенями двочлена g (х) = х2 + 1 в кільці Q[x].
Розв'язання. Щоб розв'язати задачу, треба знайти многочлени h3 (х),
h2(x), h{(x), h0(x) в кільці Q [х] такі, що виконується рівність
f (X) = fl3 (X) (*2 + 1)3 + /22 (X) (х2 + І)2 + hx (X) (х2 + 1) + hQ (X)
і deg/jt- < с^^длявсіхО < і < 3. Із записаної рівності бачимо, що h0 (x) є
остача відділення многочлена / (х) на х2 + 1, h{ (x) є остача від ділення здобутої
частки на х2 + 1, h2 (х) є остача від ділення нової частки на х2 + 1 і h3 (x) є
остача від ділення останньої частки на многочлен х2+1. Виконуємо послідовно
ділення за описаною схемою (табл. 20). Отже,
/ (х) = 2х {х2 + І)3 + (-2* - 1) (х2 + І)2 + (—8х + 1) (х2 + 1) + 11* — 2.
3. Знайти остачу від ділення многочлена
/ (х) = іх4 + (3-20 х3 + (2( — 4) х2 + (3 - ЗО х + Зі + 2
на двочлен g(х) = х + 1-і.
138

Таблиця 20
1
1
1
1
2
2
2
2
2
о
0 '
0
0
1 о
4 J
2
2
2
0
о
1 —2
-1
0
-1
' 0
—1
0
-І
—6
2
-8
0
* —8
— 1
—1
0
— 1
1
д
—8
11
__2
0
—2
hQ (х) = 11л: — 2; /z2 (х) = —2х — 1;
Розв'язання. Ділення виконуємо за спрощеною табличною схемою
(табл. 21).
Таблиця 21
1 1— і
і
і
3—2/
2-.ЗІ
2/ —4
—3+7/
3—Зі
—1 — 13/
3/+2
К>+5/
Щоб знайти коефіцієнти частки І остачі, доцільно (незалежно від того, яку
схему застосувати) виконати проміжні обчислення:
З—2/ —/(1-/) = 3-2/ — /— 1 =2—3/,
2і _ 4 — (1 — /) (2 — ЗО = 2/ — 4 — 2 + 3/ + 2/ + 3 = -3 + 7/,
3-3/-(1-/) (—3 + 70 = 3-3/ + 3- 7/ -3/-7 = -1- 13/,
Зі+ 2-(1-/)(-1 — 13/) = 3/ + 2+ 1 + 13/ — /+ 13= 16+ 15/.
Отже, остача дорівнює 16+ 1б/.
4. Довести, що многочлен
f {х) =.{х+ а+ б)1983 -*1983 -а1983 - б1983
ділиться на двочлени g{ (х)=х+ а і g2 (х) = х + Ь в кільці С [де].
Розв'язання. Знайдемо значення многочлена / (*) при * = — а і д: = —Ь
/(-а) = 61983+а1983-а1983-^1983=0,
/(_Ц = а1983 + 61983_а1983 _ ^1983 = ^
За теоремою Безу многочлен ділиться на двочлени gx {х) і g2 (x).
Задачі
22.1. Виконати ділення многочленів
a) f(x)=\Qx* — 23x3 + 26x2 — 9x — 2 на g(x) = 2x — 3 в кільці:
139

б) f(*) = (2 + 2/)*4 — 6х3 + (2 — 4l)x2 + (l + Ш)х + 2 — 5/ на
g(x) = (l — і)х + 3і в кільці С\х}\
в) / (х) = 2x* + 12,5х3 — Ах2 + 5,5* — 2,5 на g(x) = Ax2 + 1 в
кільці Q [л:];
г) /(*)= — 5х6 + 5х5 — 2л:3 + Зл:2 — 2л: + 5 на g(x) = 6x3 + 4 в
кільці Z7 [л:];
Д) ^(л;) = (2 + 0^ + 2^4 + (—2 + 60*3 — &с2 + (2 Ч- Зі")* +1 —
— 6/ на g(x) = ix2— 3 в кільці С[х].
22.2. Знайти частку і остачу від ділення!
а) f (х) = хА — 2л:3 + 4л:2 — 6л: + 8 на g (х) = х — 1 в кільці Z [х]\
б) / (*) = 4л:4 + л:3 на_#(л:) = х + 1 +і в кільці С \х]\
в) f (х) = 6х6 + х5 + 1 на g(x) = х + 3 в кільці Z7 [л:];
0/(^) = (1+/2)^+^^^ + 1 на g(x) = x-l+V2 в
кільці Q(K2) [х].
22.3. Знайти значення многочлена f{x) з кільця К[х] в точці
х = *о, якщо:
а) / (*) = л:4 — Зл'3 + 6л:2 — 10л: + 16, х0 = 4 і Я - Z;
б) / (л:) = л:5 + (1 + 20*4 —(1 +3t)x2 + 7, x0 = —2 — if К = C;
в) / (х) = х* + л:4 + Зх2_ + 1, хо =-- З, /С = Z5;
г) / (х) = х3 - (1 + |/~2) л:2 + (1 +V2), xo=l- V%
К= Q(V2).
22А. Знайти такі значення а і 6, при яких многочлен f(x) =
= хь — а2х2 + Ьх + 1 ділиться на двочлени g\ (х) = х — 1 і g2 (х) =
= х + 1 у кільці R [х].
22.5. Довести, що многочлен f(x) = xn — an для кожного п£ N
ділиться на двочлен £(л:) = л: — а над будь-якою областю цілісності
К з одиницею.
22.6. Довести, що многочлен f(x)£K[x] ділиться на g(x) =
= х — а для довільного a ¢/(, якщо:
а) f (х) = х1 — х і К = Z7;
б) f(x) = x10— х5 і /t = Z5;
в) /(*) = *р — х і К = ZP.
22.7. Остачі від ділення многочлена f(x) з кільця Z[x] на gi (л:)=
= х — 2 і g2 (я) = х — 1 відповідно дорівнюють 1 та 2. Знайти остачу
при діленні цього многочлена на g(x) = (x—1)(л: — 2).
22.8. Остачі відділення многочлена f(x) з кільця Z[x] на g\ (л:) =
= х — 1, g2 (х) = х — 2, g3 (х) = х + 1 відповідно дорівнюють 3, 15
та 0. Знайти остачу від ділення f{x) на g(x) = x3— 2х2 — л: + 2.
22.9. Многочлен f(x) з кільця С [х] ділиться на g\(x) = x+l;
при діленні на g2(x)=*x—1 цей многочлен дає остачу 2, а при
діленні на g3(x) = x — і остачу —і. Знайти остачу від ділення
многочлена f (х) на ^(л:) = (л:2 — 1) (х — *)•
22.10. Знайти остачу від ділення многочлена / (л:) = л:243 + xsl +
+ х27 + х9 + л:3 + х + 1 на двочлени:
a) g (х) = х + і\ б) g (х) = л:2 + 1.
140

22.11. Довести, що многочлен
f (jc) = (cos a — х sin a)n — cos па + x sin пт.
ділиться на g\(x) = х + і і g2(x) = x — i в кільці CM для всіх
л£ N і а £ R.
22.12. Довести, що многочлен f(x) = xn + an ділиться на
двочлен g(x) = х + а в Z2 [x].
22.13. Довести, що многочлен f(x) = (x + a)n — xn — an ділитьсяі
а) на g (х) = х над областю цілісності К з одиницею;
б) на g(x) = x + а над областю цілісності К з одиницею при
непарному п\
в) на §-(л:) = л: + а в кільці Z2 M-
22.14. Довести, що при непарному п многочлен
f(x) = (x + a + Ь)п —хп — ап — Ьп
ділиться на g\(x) = x + a і g2(x) = x + b в кільці R[x].
22.15. Довести, що при .непарному п многочлен
f(x) = (x — a)n + (a — b)n + (b—x)n
ділиться на g\ (х) = х — а і g2{x) = x— Ь в кільці R\x].
22.16. Довести, що многочлен f(x)> утворений з многочлена h (у)
заміною у = хпу n^N, при діленні на двочлен g(х) = хп—а над
областю цілісності К з одиницею дає остачу /(a).
22.17. Знайти остачу від ділення многочлена f (х) = х4 — 2л:2 + 6
на g (х) = х1 — 1 в Z \х].
22.18. Знайти остачу від ділення многочлена f{x) = хь + 2х3 + 2
на ^(л:) = л;3 + ї в кільці Zz[x].
22.19. Довести, що многочлен / (#) = хр — х +1 з кільця Zp \x]>
де р— просте число, не ділиться на двочлен g (х) = х—а при
жодному a£Zp.
* 22.20. Довести, що многочлен f (х) не ділиться на многочлен
g(x) в кільці К[х], якщо:
а) f(x) = x1984 + x+_l, g(x) = x2 — l і К = Z;
б) f(x) = x^ + 2x + 2t g(x)=x* + 4: і ЛГ = Z5;
в) 1(х)=хг — 6х2 + Пх — 69 g(x)--=x2 — 5x + 4: і К = 1.
22.21. Визначити а і b так, щоб многочлен f(x) = ахА + Ьх3 + І
ділився на g{x) = (x—І)2 в кільці Z[x]
* 22.22. Розкласти многочлен f(x) за степенями двочлена g(x) =
= х — а, якщо:
а) f (х) = х4 — 2х3 + Зх2 — 5х + 1, а = 1 в кільці QM;
б) / (х) = 2л:4 + Xі + х2 +|, а = Т в кільці Z3 [л:];
в) / (х) = хь — За3.*-- 4]&.$Ьіх — 1, а = —і в кільці С [х].
22.23. Розкласти*
а) / (л:) = х*— 4л:5 — 7л;1 +х3 + 2х2 —х — 1 за степенями двочлена
g{x) = x2—\ в кільці Z[x\\
б) / (л:) = х1 -f ї за степенями двочлена g(x) = х3 + 2 в кільці
Zb[x]\
в) f(x) = x)—2x + i за степенями двочлена g (х) = х3 + і в
кільці CM.
Ні

§ 23. Найбільший спільний дільник
і найменше спільне кратне многочленів
Література
[1] —§ 22, с. 238—243;
[2] — § 22, с. 242—247;
[3] —гл. 14, § 2, с. 470—471;
[5] —гл. IX, § 3, с 323—333;
[6] —§ 21, с. 137—143;
[7]-§8, с. 55-60;
[8] —гл. 5, § 3, с. 226—229.
ТЕОРЕТИЧНІ ВІДОМОСТІ
Нехай / (х) і g {х) — многочлени над полем Р. Якщо / (х) і g (x) діляться на
многочлен d(x) з кільця Р [х], то d (x) називають їхнім спільним дільником.
Спільний дільник многочленів / (х) і g(x), який ділиться на кожний їхній
спільний дільник, називають найбільшим спільним дільником многочленів / (х)у
g (x) і позначають символом (/, g).
Найбільший спільний дільник ааданих многочленів визначається однозначно
з точністю до сталого множника.
Для будь-яких двох многочленів /(х) і g{x) з кЦьця Р [х] (з яких хоча б
один відмінний від 0) існує найбільший спільний дільник, ян*й дорівнює
останній відмінній від нуля остачі в алгоритмі Евкліда.
Найбільший спільний дільник d (х) многочленів / (х) і g (х) з кільця Р [х]
завжди можна подати у вигляді
d(x) = f(x)u(x) + g(x)v(x),
де и (х) і v (х) — деякі многочлени з кільця Р [х]. Многочлени / (х), g(x) Є Р [х]
називаються взаємно простими, яцщо кожен їхній спільний дільник є
многочленом нульового степеня. При цьому пишуть (/, g) = 1.
Многочлени f (х) і g (х) з кільця Р [х] є взаємно простими тоді і тільки
тоді, коли існують многочлени и (х), v (х) £ Р [х] такі, що
f(x)u(x) + g(x)v(x)=\.
Взаємно прості многочлени мають такі властивості:
1°. V [(/, я)=іл(Л, /)=1=М/, *Л) = 1];
f(x),g{x),h(x)£P[x]
2°. V [/ (х) g(x)\h (X) Л (/, Л) = 1 # g (X) : h (*)];
f(x),f>(x).h(x)£P[x\
3°. V Ц(х)18(х)л f(x)lk(x),\(g, h) = \*$f(x)lg(x)h(x)].
f(x),g(x)Ji(x)£P[x\
Спільним кратним многочленів / (x), g (x) з кільця Р [х] називають
многочлен s (x) £ P [x] такий, що s (x) ділиться на / (#) і g(x). Найменшим спільним
кратним многочленів / (х) і g(x) навивавться таке ї^нє спільне кратне, на яке
ділиться кожне спільне кратне цих многочленів.
Найменше спільне кратне многочленів f (x) \ g (x) визначається однозначно
з точністю до сталого множника і позначається через [/, g].
Для довільних відмінних від нуля многочленів f (х) і g(x) з кільця Р [х]
найменше спільне кратне існує в Р [х] і визначається за формулою
[/'*]= (/.¾ '
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Знайти найбільший спільний дільник і найменше спільне кратне многочленів
f (х) = Зх3 — 6а:2 Н- 5а;— 10 і g (х) = 2х3 — 4х2 + 3* — 6 в кільці Q [х].
142

Розв'язання. Розглянемо многочлен s(x) = 2f (x) — 3g (х) = х — 2. З
властивостей подільності та означення найбільшого спільного дільника
многочленів маємо (/ (х), g (x)) = (s (x), g (х)). Оскільки g (2) = 0, то за теоремою Безу
g (x): s (х). Тому
.(/, g) = s(x) = * —2.
Для обчислення найменшого спільного кратного [/, g] цих многочленів
використаємо формулу
Оскільки g (х) = (2л:2 + 3) (х — 2), то
[/, g] = (3х^ ~ 6*2 + Бх - 10) (2*2 + 3) (* - 2> = (з* 3- 6л:2 +
+ 5л+10)(2а:2 + 3).
2. Для многочленів / (х) = а;4 + 4л:3 + 4а:2 + 6л: + 6 і #(л) = х3 — 1 з кільцяZ7 [x]
знайти їхній найбільший спільний дільник і многочлени и (х) і v (x) такі, що
f(x)u(x) + g(x)o(x) = (f, g).
Розв'язання. Застосуємо алгоритм Евкліда до многочленів f (x) і g (x)
(табл. 22—24). Звідси
Тому
(f» g) = r2(x) = x + 6,
r2 (x) = g(x) — r, (x) s2 (x) = g (x) — (/ (*) — g W Sj (a:)) s2 (x) =
= / (a:) (—s2 (a:)) + g (*) (1 + st (*) s2 (де)).
u (x) = —s2 (x) = —2x = 5a:,
v(x) = l + sx (x) s2 (x) = T + (x + 4) 2* = 2a:2 + x+ Г.
Таблиця 22
f W = g W «і (*) + 'i (*).
s, (a:) = * +1,
гі (де) = 4a:2 + 3:
-T
1
T
4
4
4
4
6
1 — Ї
1 o
6
—4
3
4
3
]
1
2
T
б
б І
аблиця 23
1 б
1 6
—Є
—Т
б
—Г 1
g(x) = ^(x)s2(x) + r2(x)y
s2 (х) = йх,
г2(х) = — 6*— 1 = * + б;
Таблиця 24
1
1 6
4
4
0 1
—3
1 з
1 б
4(x)=-r2(x)s9(x)%
s3 (x) = 4л — 3.
143

3. Нехай f (x), g(x) і h (x) — деякі многочлени з кільця Р [х] над полем Р. Знайти
всі многочлени и (х) і v (х) в кільці Р [х] такі, що
f(x)u(x) + g(x)v(x) = h(x), (1)
коли деякі многочлени «0 (х), v0 (х), над полем Р задовольняють цю рівність.
Розв'язан ня. Позначимо (/, g) = d (x), fx (x) = -jtgr і g{ (x) = jj^j. Тоді
кожна пара многочленів
(и (х) = и0 (х) + gx (х) s (х),
\v(x) = v0(x)-fl(x)s(x), ( }
де s (х) € Р [х], також задовольняє рівність (1). Покажемо, що кожен
розв'язок рівняння (1) у кільці Р [х] відносно и(х) і v (х) можна подати у вигляд}
(2). Справді, нехай и{ (х) і v2 (х) також є розв'язком рівняння (1), тобто
/ (д) и0 (х) + g (x) v0 {х) = h (x),
f(x)ul(x) + g(x)vl(x) = h(x).
Тоді
f(x)(u0(x)-ul(x)) + g(x)(v0(x)-vl(x))^Ot
f (х) («о (*) — Н (*)) = —5 (*) (»o W — »1(*))»
f, (X) (tt0 W — ttj (ДС)) = —ft (*) (t/0 (*) — »! (*)).
Оскільки (/j, gj) = 1, то за властивістю взаємно простих многочленів в кільці
Р [х] існує многочлен s (х) такий, що
f"о (*) — и\ (*) = —£і W * W»
\і>0 (X ) — 1>! (ДС) = /j (X) "s (Х).
Тому
\и1(х) = и0(х) + д1(х)ї(х),
\vx{x) = v0(x) — fl(x)s(x),
тобто будь-який розв'язок рівняння (1) можна подати у вигляді (2).
Таким чином, рівності (2) задають всі пари многочленів и (х) і v (x), які
задовольняють рівність (1).
4. Розв'язати рівняння
и (х) (х2 - 1) + v (х) (х2 + 2х + 1) = х3 + 1
відносно многочленів и(х) і v(x) у кільці Q[x].
Розв'язання. Задане рівняння в кільці Q [х] рівносильне рівнянням
u(x)(x-\)(x+\) + v(x)(x+\)*=(x+\)(x*-x+\)
і
и (х) (х — 1) + v (х) (х + 1) = х2 — х + 1.
Двочлени ft (х) = х — 1 і g2 (де) = де + 1 є взаємно простими і
— "§"£i(*) + "2"&W = К
Звідси
- у («»-*+l)ftW + -J-(x«--x+l)ftW==^-*+l,
тобто одним з розв'язків останнього, а, отже, і заданого рівняння відносно и (х)
і і; (де) є многочлени
144

Щ (*) = — "jf (*2 — * + 1),
v0(x) =-j(x2 — x+ 1).
Застосовуючи тепер формулу (2) з прикладу 3, маємо
и(х)=-^-(х*-х+ 1) + (*+1) s(x)9
V(x) = -2(x*-x+ \)-(x- \)s(x)i
де s(x)£Q [x].
Задачі
23.1. Нехай f(x) і g(x) є многочлени над полем Р, s(x) = f(x)-j-
+ g(x), Л (*) = / (x)—g(x). Довести, що (/, g) = (s, А).
23.2. Нехай f (х) і g(x) — многочлени над полем Р. Знайти
необхідну і достатню умови, при яких многочлени s(x) = anf(x) +
+ a\2g(x) і h (x) = a2\f (x) + a22g (х) з кільця Р [х] мають той самий
найбільший спільний дільник, що й многочлени f(x) і g{x).
23.3. Не застосовуючи алгоритм Евкліда, знайти найбільший
спільний дільник таких многочленів^ л
a) /(^) = ^ + 3^-2, /Х-*^/
g(x) = X3 + 3x2—X—3', (/ /
• б) f(x) = x4+x3 — 3x2 — 2x — 2, (a)
£(*) = _*з + Зх2 + 2х + 2; і ІJ
в) f(x) = x4+x3 — 3x2 — 2x— 1, f/\ )
g(x)~x3 + x2-3x-3; L y
г) /(*) = 2x3 + x2 + 4x + 2, UY)+ll
g(x) = 2x3+x2 + 6x + 3. \C^ y
23А. Довести, що многочлени / (х) = апхп + ... + а\х + ао, де
д0 ф 0 і g(x) = апхп + ... + аіх, є взаємно простими.
\] 23.5. Користуючись алгоритмом Евкліда, знайти найбільший
спільний дільник таких многочленів:
a) f(x) = x3+x2 — 4x — 6t
g (x) = х3 + х2 — Юх — 6 в кільці Q [х]\
•б) f(x) = За:4 — Зх3 + 4х2 — х + 1,
g(х) = 2х3 — х2 + х + 1 в кільці Q[х];
в) /(*) = х4 + х3 + х2 + х+1,
g до = 4л:3 + Зх2 +2х + 1 в кільці Q [х]\
г) /(х) = х3 + 3х2 + 2х + ї,
g (x) = х3 + Sx2 + х + 5 в кільці Z6 [х];
Д) )р(х) = х4 + 2а3 — 2х2 — 2/х+1,
g (х) = х3 + (і + 1)х2 + їх в кільці С [х].
V23.6. Знайти найменше спільне кратне таких многочленів:
а) / (х) = х4 — 4х3 + 4х2 — 5х — 2,
g (jc) = х2 — х + 2 в кільці Q [х]\
б) /(х) = 2х3 + 7х2 + 4х —З,
g (х) = х3 + х2 — Зл: + 1 в кільці Q [х];
145

в) f (х) = х3 + 6л;2 + 4х +1,
g (х) = х'3 + х1 + Зх — 4 в кільці Z7 \x];
г) f(x) = х3 — х2 + 3х — 3,
g(x) = х4 + 2х3 + 2х— 1 в кільці R\x\;
д) f(x) = х4 + 2іх3 — 2х2 — 2іх + 1,
g(x) = х6 + (і + 1) х1 4- іх в кільці С [х].
N/23.7. Визначити многочлени и(х) і и(я) так, щоб для
многочленів f{x) і g(x) виконувалась рівність f(x)u(x)+g(x)v(x) = (f, g),
якщо:
а) f(x) = x3 + 5x2 + 6x + 2, gix) = x2 + 6x + 5 в кільці Q[x]\
б) f(x) = x3 + 3_x2 + 2x+_l,
g(x) = х3 + 2х2 -\-х + 2 в кільці Z5 [x]\
*в) f (*) - 4л:4 — 2л:3 — 16х2 + 5х + 9,
^(л:) = 2л;3— х2 — 5л;+ 4 в кільці Q[x]\
г) f(x) = x* + l9
g(x) = x3 — 2іх — х в кільці С\х].
23.8. Нехай Р — деяке поле, f(x) і g(x) — многочлени з кільця
Р [х]. Довести, що1 найменший ідеал / в кільиі Р [х], що містить
многочлени f(x) і g(x)j збігається з головним ідеалом, породженим
многочленом (/, g).
23.9. Довести, що множина / всіх спільних кратних
многочленів f (х) і g(x) з кільця Р[х] многочленів над полем Р є ідеал.
Яким многочленом породжується цей ідеал?
23.10. У кільці Р[х] многочленів над полем Р знайти найм'ен-
ший ідеал /, який містить многочлени f[(x)y її{х), ..., fn(x).
23.11. Яким умовам повинні задовольняти многочлени f(x), g(x)
і hix) над полем Я, щоб рівняння/(л:) и(х) +g(x)v (x) = h(x) мало
розв'язок у кільці Р[х] відносно и(х) і v(x)?
23.12. Знайти множину всіх розв'язків рівняння
f (x) u(x)+g (x) v(x) = h (x)
в кільці К [х], якщо:
a) f(x) = x2-l,
g(x) = x2-2x+l,
h(x) = x3 — \
б) /(х) = х3-1,
g(x) = x2 + 3,
h (x) = х3 — 2х2+х
в) f(x) = x2 + (2 + i)x
g(x) = x2-4,
h (x) = Xі 4- 2ix
r) f(x) = (x2 + l)2,
g(x) = x + i,
h{x) = x2 + (\ +i)x
+ 2i,
і /\ .-
i K-
i K-
і K-
= Q;
= Z$\
= C;
= C.
23.13. Визначити найбільший спільний дільник многочленів:
а) /(л:) = л:44-*3 — Зх2 — 4л:— 1,
g (х) = х3 + х2 — х — 1,
h (х) = 2л*3 + 4л;2 + 2х в кільці Q [х\\
146

♦ 6) f(x) = x* + x4 + U
g(x) = x*+x2 + l,
h (x) = x3 + 1 в кільці Z2 [x]i
в) f (x) = x3 — x2 + x — 1,
g(x) = x3 — (2i + l)x2 + (2i- l)* + .l,
h (x) = x2 + (1 + i) x + і в кільці С [х].
23.14. З'ясувати, чи має розв'язок рівняння
/ (x) u(x) +g (x) v (x) + h (x) w(x) = s (x)
в кільці К [х], якщо:
а) / (х) =
8(х) =
h (х) =
5 (X) =
б)/(*) =
Я(х) =
h(x) =
s(x) =
■х4 + 2х3 — 2х— 1,
= х2—1,
= д;3 — х,
х3 — Зх2 + 1
:*4 + 2x2+ 1,
= л:3 — х2 -\- х — 1,
-.х2 + (і + 1)х + і,
х2 + (і— \)х — і
\к
\к
§ 24. Незвідні многочлени ящ полем.
Розклад многочленів на незвідні множники
Література
[1] — § 22, с. 243—247;
[2]—§ 22, с. 247—252;
[3] —гл. 14, § 2, с. 471—474;
[5] —гл. IX, § 3, с. 333—339;
[6] —§ 48, с. '290—295;
[7J — § 9, с. 60—64;
[8] — гл. 5, § 3, 4, с. 229—232.
ТЕОРЕТИЧНІ ВІДОМОСТІ
Нехай / (х) — деякий многочлен над по,лем Р. Многочлен f (х) називається
незвідним в Р \х] (або над полем Р), якщо він не є константою і не м^,€ в Р [х]
інших дільників, крім констант і многочленів виду cf(x), де е£ Р \ {0}.
Многочлен f (х) називається звідним в Р \х] (над полем Р), якщо deg/ > 1
і в кільці Р [х] існують такі многочлени g (х), s (х), що / (x) =g(x)s(x), degg>
> 1 і deg s > 1.
Незвідні над полем Р многочлени мають такі найпростіші властивості:
1°. Многочлен першого степеня над будь-яким полем Р є незвідним у
кільці Р[х];
2°. Якщо многочлен р (х) є незвідним над полем Р, то для кожного с£Р\
\{0} многочлен ер (х) також незвідний над Р;
3°. Якщо многочлен р (х) є незвідним над полем Р, то для Зудь-якого
многочлена / (х) з кільця Р [х] f(x):.p(x) або / (х) і р (х) є взаємно прості;
4°. Якщо незвідниД многочлен р (х) над полем Р ділиться на незвідний
многочлен q (х) з кільця Р [х], то ці многочлени відрізняються тільки сталим
множником.
Будь-який многочлен ненульового степеня над полем Р можна подати у
вигляді добутку незвідних многочленів pk(x)y 1 < k < /, над полем Р:
f(x) = pl(x)p2(x). ..Ptix).
Такий розклад є єдиним з точністю до сталих множників і порядку нумерації
многочленів pk (х).
147

Зображення многочлена f (х) з кільця Р [х] у вигляд! добутку
f(x) = [PlM]kllP2(*)fi'--\Pm(*)]km,
де р{ (х), р2 (х)у . . ., рт(х) — попарно взаємно прості і незвідні над полем Р
многочлени, називають канонічним розкладом многочлена / (х) над полем Р.
Канонічний розклад для будь-якого многочлена ненульового степеня f (х)
над полем Р завжди існує і єдиний з/точністю до сталих множників та порядку
нумерації множників.
Якщо многочлени f (х) і g (x) розкладено в добуток незвідних множників
над полем Р, то їхній найбільший спільний дільник (/, g) дорівнює добутку
всіх незвідних множників, які входять у розклад як f (х), так і g(x). Якщо
таких спільних незвідних множників немяє, то многочлени f (x) і g (x) є взаємно
простими.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
І. Чи є звідним у полі Q многочлен
f (х) = Xа + 2*3 — Зх2 — Ьх + 2?
Розв'язання. Нехай многочлен / (х) є звідним у полі Q, тобто його
можна розкласти в добуток не менше як двох многочленів ненульового степеня
з кільця Q [х]. Щоб розкласти многочлен / (х) на множники, застосуємо метод
невизначених коефіцієнтів. При цьому досить розглянути два випадки
можливого розкладу:
1) обидва множники мають степінь 2;
2) один множник має степінь 1, а другий 3.
Нехай
/ (х) = (ax2 + bx + c)(dx2 + тх + п). (1)
Тоді з рівності х4 + 2х3 — Зх2 — 5*+ 2 = adx4 + (am + bd) x3 + (an + bm +
+ cd) х2 + (bn + cm) x + en
маємо
(ad = 1,
\am + bd = 2,
| an + bm + cd = —3, (2)
bn + cm = —5,
[en = 2.
Розв'яжемо цю систему рівнянь у цілих числах. З першого знаходимо а= d =
= 1 або a = d= —1, з останнього с = 1, /2=2; с = 2, л= 1; с = —2, п = —1;
с = —1, л =—2. Розглянемо кожен з восьми можливих варіантів. Якщо
a = d—\ і с= 1, п = 2, то система набирає вигляду
/72+6 = 2,
bm = —6,
26 + т = —5.
Ця система несумісна.
У кожному з решти варіантів несумісними також є системи рівнянь:
/72 + 6 = 2, (/72 + 6 = 2, [/72 + 6 = 2, [т+6 = — 2,
bm = —6, І bm = 0, j 6т = 0, I bm = 0,
6 + 2т=—5, (—26 — т = -5, l—26 — m = —5, І26 + /Т2 = —5,
т + 6 = —2, [т+6 = —2, Гт + 6 = —2,
bm = 0, < 6т = —6, < 6т = —6,
6 + 2/72 = -5, 1-6-2/72 = -5, І—26 — т = — 5.
148

Це означає, що система рівнянь (2) несумісна ї многочлен f (х) не
розкладається в добуток двох многочленів другого степеня з цілими коефіцієнтами.
Припустимо, що розклад (1) виконується при дробових числах а, Ь, с, d> m, n.
Зведемо до найменшого спільного знаменника коефіцієнти многочленів g1 (х) =
= ах2 + Ьх + с і g2 (x) = dx2 + mx-\- n та винесемо за дужки ці знаменники
і найбільші спільні дільники чисельників обох многочленів. Дістанемо розклад
f (х) = "s {axx2 + bxx + сх)(dxx2 + тхх + пх),
де (г, s) = (av bv сх) = (dv тх ,пх) = 1. Оскільки коефіцієнти многочлена f (х)
€ цілими числами, то всі коефіцієнти многочлена
g (х) = (ахх2 + Ьхх + cx)(dxx2 + тхх + пх)
мають ділитися на число s, а тому й на кожен його простий дільник р»
Разом з тим, серед- кожної трійки чисел av bx, сх та dv mv nx знайдуться
числа, які не діляться на р. Тому серед коефіцієнтів axdv axmx-\-bxdv
ахпх + Ьхтх + cxdx, bxnx-\-cxmx і схпх многочлена g(x) знайдеться такий, що
не ділиться на р. Тому s = 1 і ми дістанемо розклад (1) з цілими
коефіцієнтами, що неможливо.
Нехай
f (х) = (ах + b)(cx3 + dx2 + mx+ п). (3)
Тоді з рівності хА + 2а:3 — Зх2 — Бх + 2 = асх4 + (ad + bc)x3 + (am + bd)x2 +
-f- (an+bm) x-\- bn маємо:
(ас = 1,
\ad + be = 2,
< am + bd = —3, (4)
an-\-bm=z —5,
I bn = 2.
Одним з розв'язків системи (4) є a = c = я = 1, 6 = 2, d = 0 і m = —3.
Отже, / (я) = (х + 2)(хг — Зх + 1), тобто многочлен f (х) звідний у полі Q.
2. Довести, що многочлен / (х) = 2а:2 + х +Т незвідний у полі Z3.
Розв'язання. Якщо многочлен f (х) є звідним у полі Z3, то його можна
подати у вигляді / (а:) = (ах + 1)(сх + 3), де асфО. Звідси /(аг) = 3(а: +
6 ^ - 1
-\--=г\(сх-\- d) і згідно з теоремою Безу многочлен f (х) має коренем х = —-=•.
а _ _ а
Проте /(0)=1, /(1) = Т і /(5) = 2, тобто многочлен f (х) не має коренів
в Z3. Отже, многочлен / (x) незвідний у полі 23.
3. Довести, що фактор-кільце Р [х]/<р (х)> кільця многочленів Р [х]
надішлем Р за ідеалом <р(х)>у породженим незвідним у полі Р многочленом
р (*), є полем.
Розв'язання. Відомо, що елементи кільця Р [х]/І мають вигляд
A=*f(x)+{g(x)pfr)\g(x)tP[x]},
де f (х) — представник класу А. З означення операції множення у фактор-
кільці і того, що Р [х] є областю цілісності, випливає її комутативність. Клас
Е = 1 + <р (х)> є одиницею в Р [х]/<р (х)>.
Візьмемо тепер довільний елемент В фактор-кільця Р [х]/<р (х)> такий, що
В Ф <р(х)>. Тоді у множині В існує многочлен h(x)t який не ділиться на
многочлен р (я), В = h (х) + <р (х) > і за властивістю незвідних многочленів
h(x) і р (х) є взаємно простими. Отже, в кільці Р [а:] існують многочлени
и (х) і v (х) такі, що
Л(*)и(*) + р(*)0(*) = 1.
Звідси h (х) и (х) = 1 — р (*) v (х). Тому оберненим елементом до В є 5—1 =
= «(*)+ <Р(*)>.
149

Таким чином, фактор-кільце Р [х]/<р (х)> є полем.
4. Знайти найбільший спільний дільник і найменше спільне кратне многочленів
/ (де) = (х - 2)(х - 3)2(х + О
і
g (х) == х3 — За;2 — 2х + 6 з кільця Q [х].
Розв' язання. Для многочлена / (х) відомий канонічний розклад у полі Q-
Щоб знайти найбільший спільний дільник і найменше спільне кратне даних
многочленів, дрцільно знайти канонічний розклад многочлена g(x) у полі Q.
Це можна зробити групуванням його членів і винесенням сильного множника:
g (х) = (х3 — Зх2) — (2х ~ 6) = х2 (х — 3) — 2 (х — 3) = (х —3)(х2 — 2).
Тепер за теоремою про знаходження найбільшого спільного дільника і
найменшого спільного кратного многочленів, розкладених на незвідні у полі Q
множники, маємо-:
(/, $)«* —3;
І/. *]-(*- 2)<*2 - 2)(х - 3)2(х + 1).
Задачі
24.1. Довести, що многочлен
а) f(x) = x3— 2 незвідний у полі Q;
б) f(x) = х2 + х + 1 незвідний у полі Q;
в) f(x) = x2 + x+l незвідний у полі Z5;
г) f (х) = хА + 1 незвідний у полі Q;
д) f(x) = Xа +ї ЗВІДНИЙ у ПОЛІ Z5;
є) f (х) = х6 + х3 + 1 незвідний у полі Q.
24.2. У кільці Zs[x\ знайти всі многочлени другого степеня, які
є незвідними у полі £з.
24.3. У кільці Z5[x] справджуються рівності:
х2 + х + 4 = (х + З)2 і х2 +х + 4 = (їх + 2)2.
Чи не суперечать воци теоремі про розклад многочлена на незвідні
множники у полі ^5?
24.4. Довести, що кожен многочлен другого сте-пеня над полем С
є звідним у полі С.
24.5. Многочлен f(x) = x2 + 2x + 2 можна розглядати в кільцях
Z5[x] і Zz\x\. Він є звідним у полі Zp і незвідним у полі Z3. Чиє
такий многочлен, що належить обом кільцям і є звідним у полі7з,
а незвідним у полі Z5?
24.6. Довести, що в кільці Zv \x\ при довільному простому р
існують незвідні у полі Zp многочлени як завгодно великого
степеня.
24.7. Довести, що множина н&звідних многочленів у будь-якому
полі Р є нескінченною.
24.8. Многочлен /(*) = 2х3 + Зх2 + Зх + 2 розкласти на незвідні
в полі Z5 множники, якщо відомо, що цей многочлен має два корені,
які є протилежними елементами в полі Z5.
160

24.9. Розкласти на незвідні множники в полі Q такі многочлени:
а) f (х) = 2хь — хА — 6л:3 + Зх2 + \х — 2;
б) / (х) = Зх5 + х4 — 15л;3 — 5л:2 + 12х + 4,
які мають по дві пари коренів, що відрізняються тільки знаком.
24.10. Розкласти на незвідні множники многочлен
f (х) = 2х5 — л;4 — 2л:3 + х2 — 4х + 2
в полях Q, R і С, якщо він має дві пари коренів у полі, які є
протилежними числами.
24.11. Довести, що многочлен третього степеня звідний у полі Q
тоді і тільки тоді, коли один з його коренів є раціональним числом.
24.12. Нехай многочлен f(x) належить кільцям Zp [x] і Z[x]
залежно від інтерпретації його коефіцієнтів. Довести, що кожен
незвідний у полі Zp многочлен не можна розкласти на множники
в кільці Z \х].
24.13. Довести незвідність у кільці Z[x] таких многочленів:
а) f(x) = jfi — x2 + l\
б) f(x) = x5 + x* + x3 + x2+ 1;
в) f(x) = x3 — x2+x + 1.
24.14. Довести, що многочлен / (х) = х2к + хк + 1 є незвідним
у полі Q при будь-якому k б N.
24.15. Чи є звідним многочлен / (х) = х4 + 4 в таких поляхі
a) Z5; б) Q; в) R; г) С?
24.16. Розкласти на незвідні в полі Р множники такі
многочлени:
а) / (х) = х4 — 2х3 — 27х2 — 44л: + 7, якщо Р = Q;
б) /(л:) = л:4 — 6л:3 + 11л:2 — 6л: + 1, якщо Р= R;
в) f (х) = 4л:4 + 4л:3 + 13х2 + 6х + 9, якщо Р = Q;
г) f(x) = x4 — 5x3 — 8x2+ 19л: —3, якщо Р = Q;
Д) f(x) = (x2 + x—l)2 + 3x(x2+x—l) + 2x2, якщо Р= R;
є) /(л:) = л:2(л:—3)2 + 4л:2— 12л: + 4, якщо Я= R;
є) fW = (^ + 2)(x + 3)(^ + 4)(x + 5) + l, якщо Р= R;
ж) /(л:) = (л; + а)(л: + 2а)(л; + 3а)(л; + 4а)+а2, якщо Р = Q,
з) / (х) = (jc + 1) (jc + 3) (^ + 9) (JC + 11) + 15, якщо P = Q;
і) / (х) = х4 — 10л:2 + 169, якщо Р = R;
к) f(x) = л:4 + х2 + Г, якщо Я = Z3;
л) f (х) == л:8 + *4 + 1, якщо /> = Q;
м) f (х) = х8 — 1, якщо Р = R;
н) / W = х9 — 1» якщо Р = Q;
о) /(jc) = х12— 1, якщо P--=Q;
п) f (х) = л;4 + 1, якщо Р = С;
р) f (х) = хь — ху якщо Р = Z5.
24.17. Знайти найбільший спільний дільник і найменше спільне
кратне таких многочленів:
а) f(x) = (x—l)2 (х2+1) (х2 — 5х + 6),
g(x) = х2 — х — 2 .з кільця Z\x\\
б) f(x) = (х2 — 2х + З)2 (х2 + 5х — б)2,
g (х) = (л:2 — 8л: + 12)2 (л:3 — 1) з кільця Q [х]\
в) /(л:) = л:4 + 2л:3—2л:—1,
151

g (x) = (x + 1) (x2 — x — 2) з кільця Q [x];
r) f(x) = (x + l)*(x*+l)(x*—l)9
g (x) = (X — І)2 (X + 1) З КІЛЬЦЯ C [X]\
д) f (x) = xb — x,
g (x) = (x2 + x + 1)2 (¾ + 4) з кільця Z5 [x];
е) /(*) = *9-l,
§-(л:) = л:12—1 з кільця Q[x].
24.18. Чи є полем кільце Q[x]/<x2— 1>?
24.19. У фгктор-кільці Q[#]/<x2+l> знайти елемент, оберне
ний до класу A = {x + (x2 + i)s(x)\s(x)£Q[x]}.
24.20. У фактор-кільці Q[x]/<—х+ї> знайти елемент,
обернений до класу Л, одним з представників якого є многочлен
/ (х) = х.
24.21. У фактор-кільці Q[x]/<x2— 4> знайти елемент,
обернений до класу Л, одним з представників якого є такий многочлен:
а) / (х) ==х2 — Ьх + 6; 6) / (х) = х2 — 1.
24.22. Довести, що фактор-кільце R [х]/<х2 + 1> ізоморфне
полю комплексних чисел С.
§ 25. Похідна многочлена. Кратні корені многочлена.
Виділення кратних множників многочлена
Література
[1] —§ 22, с. 235; § 23, с. 247—262;
12] —§ 23, с. 252-267;
[3] —гл. 14, § 4, с. 479-484;
15]— гл. IX, § 3, с. 340—343;
[6] —§ 22, с. 145—147, § 48, с. 295—298;
]7] — § 10, 11, с. 64^-70;
[8] —гл. 6, § 1, с. 243—257.
ТЕОРЕТИЧНІ ВІДОМОСТІ
Нехай t (х) = а пхп + а п__-{хп~х + ... -\-ахх + а0 — деякий многочлен над
полем Р.
Похідною многочлена / (х) називають многочлен
/'(*) - папхп-1 + (^-1) ап-\*П~2 + • • • + 2*а* + ах.
Вважають, що похідна многочлена нульового степеня і нуль-многочлека дорівнює
нулю (нуль-многочлену).
Виконуються такі рівності:
1°. V [f{x) + g(x)Y = f(x) + g'(x)\
)(х), g(x) Є Р[х]
2°- V [/ (х) g (*).]' = f'(x) g (х) + і (х) g(x);
/(*). g(x) Є P[x]
3°. V [cf(x)Y-=cf(x);
fix) Є P[x], c£P
4°. V {[f(x)]kY = k[f(x)]k-Y(x).
I(x) Є РМ, k£N
Якщо поле Р має,характеристику 0, то для кожного многочлена f (х) з
кільця Р [х] такого, що degf > 1, виконується рівність deg/' = deg/ — 1.
152

Наведемо два означення кореня многочлена.
Елемент а поля Р називають коренем многочлена / (х) з кільця Р \х], якщо
f*0 = 0.
Елемент а поля Р називають коренем многочлена f (х) з кільця Р [х], якщо
f (х) ділиться на g (х) = х —а.
Ці означення рівносильні над будь-яким полем Р.
Елемент п £ Р називається ^-кратним коренем (або коренем k-'i кратності)
многочлена f (х) з кільця Р [х], якщо f (х) ділиться на (х — ау і не ділиться на
(х — а)*"*"1. Корені кратності 1 називають простими, а корені, кратність яких
більша 1, — кра/гними.
Для того щоб елемент q, поля Р характеристики 0 був коренем кратності k
для многочлена / (*) з кільця Р [х}9 необхідно і достатньо, щоб
/ (a) = f'(a) = ... = fk~Ha) = 0 і fk(a) + 0, (1)
де через fm(x) позначено w-y похідну многочлена / (х). Нехай / (x) = [рх (x)]kx X
X [р2 (x)]k2 . .• [Р[ (x)]k[ — канонічний розклад многочлена f (х) над полем Я. Не-
звідний многочлен pt (х)у 1 < і < І, називають множником кратності kt многочлена
f(x), якщо -(х) ділиться на [рі (x)]ki> але не ділиться на [Pi(x)]ki+l.
Якщо незвіднин над полем Р характеристики 0 многочлен р (х) є множником
кратності k > 2 многочлена / (х)> то він є множником кратності k— 1 для
похідної і'(х). Якщо р (х)—множник першої кратності многочлена / (х), то він не
міститься в розкладі f (х) на незвідиі множники. Для того щоб многочлен не мав
кратних множників, необхідно і достатньо, щоб він був взаємно простим із своєю
похідною.
Позначимо через cpj (x) добуток всіх незвідних множників першої кратності
многочлена і (х), через <р2 0*0—добуток всіх незвідних множників другої
кратності і т. д. Тоді
/W = fiW[%W]2---[T«W]m.
або
/ = ?і*$РІ---С (і)
Якщо многочлен не має множників кратності k < m, то вважають, що yk = 1.
Подання многочлена у вигляді (1) називається відокремленням кратних множ»
ників. У будь-якого многочлена над полем Р характеристики 0 можна
відокремити кратні множники за допомогою скінченного числа раціональних дій над
деякими многочленами.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Знайти значення похідних / {х)> f (х), ■ (х) та tlV(x) для многочлена / (*) =
= іх4 + (\ — і)х3 — (2 + і)х2 + Зх — З — М з кільця С [х] при х = 2t та
розкласти многочлен за степенями двочлена х — 2і.
Розв'язання. І спосіб. Знайдемо похідні многочлена t (x):
і'(х) == Ux6 + 3 (1 — і) х2 — 2 (2 + 0 х + З,
Г(х) = \2іх2 + 6 (1 — і) х — 2 (2 + і),
/>) = 240 + 6(1-/),
fIVW = 24t.
Тоді
f'(2i) = 4і (203 + 3(1—0 (202 — 2 (2 + 0 21 + 3 = 27 + 4і,
f"(2i) = 12* (2f)2 + ti (1 — і) 2і — 2 (2 + 0 = 8 — 3«t,
153

f (20 = 24/ (20 + 6 (1 - 0 = —42 - 6/,
/IV(20 = 24i.
Щоб знайти розклад многочлена f (х) за степенями двочлена * — 2/,
застосуємо формулу Тейлора, яка справджується для многочленів над полем
характеристики 0:
/ (х) = / (20 + /7(20 (х -2і) + іШ(х- 202 + У?р (х - 203 +
^4!
Оскільки
' (20 = і (204 + (1 — 0 (203 — (2 + 0 (202 + 3 (20 — 3 — 4/ =- —3 + 14/,
то
/ (х) = і (х — 204 + (— 7 — 0 (х — 203 + (4 — 190 (х — 2if +
+ (27 + 40 (х — 20 — 3 + 14*.
II спосіб. Знайдемо розклад многочлена f (х) за степенями двочлена х — 2і
(див. § 22), застосувавши для знаходження його коефіцієнтів схему Горнера
(табл. 25).
Таблиця 25
/
2і
2і
21
2і
21
і
у
і
і
і.
і
1 — і
—1-і
—3—t
—5 — /
—7 — f
—2—/
—3/
2 — 9/
4— 19/
3
9
27 -h 4/
—3 — 4*
—3 + 14/
/(2/) =-3+14/; /'(20 = 27 + 4/;
-і-/'1 (20 = 4-19;; .^-,111 (И) = _7_/;
-ТГ-/,У(20=/.
Отже,
/ (дг) = і (х _ 2/)4 + (—7 - 0 (* — 203 + (4 ~ 19/) (х - 2/)2 +
+ (27 + 4/) (х — 20 — 3 + 14/,
/'(2/) = 27 + 4/, /"(20 = 8 — 38/, Г(2і) = —42 — 6/ та /1 v(2/) = 24/.
Знайти всі дійсні числа Ь, при яких многочлен / (а*) = хь — 5дг3 + Ь з кільця
R[x] має кратний корінь у полі R. Знайти цей корінь.
Розв'язання. Нехай а є кратним коренем заданого многочлена. Тоді (х)
ділиться на (х — а)2, тобто існує многочлен s(x)£R [х\ такий, що f (х) =
= {х —- а)2 - s (х). Знайдемо його похідну:
}'(х) =2(x-a)s(x) + s'(x) (x - а)2.

Звідси f'(a) = 0. Це означає, що число а ?адовольняє систему рівнянь
от — 5а3 + &=0,
.5а4— 15а2 =0.
Розв'язуючи друге рівняння, дістаємо
ctj =0, а2 = —і/З, а3 = УЗ.
Тому число Ь може набувати тільки одне із значень:
Ьг = 0, Ь9 = —б Уз або &з = 6 ^3.
Таким чином, при Ь == 0 кратним.коренем є число 0, при 6 = —6У^З —
число —Уз і при 6 = 6 Уз — число Уз.
3« Трикратним коренем многочлена f (х) з кільця Q [х] є число 2. Якою є
кратність цього кореня для многочлена
й (*) = ffy) (** + 3) + (^ + 3) Ґ(х)?
Розв'язання. Оскільки число 2 є трикратним коренем многочлена f(де),
то f (2) = f (2) = i"(U) = 0 і Г(2) =£ 0. Знайдемо g (2):
, (2) = /(2) (4 + 3) + (2 + 3) f (2) = 0.
Отже, число 2 є коренем многочлена g (х). Обчислимо похідну:
g(x) = Г(х) (х2 + 3) + 2xf (*) + З/» + (* + 3) /»,
,/(2) = !"(2) (4 + 3) + 4^(2) + 3/"(2) + 5Г(2) = 5Г(2) Ф 0.
Це означає, іцо число 2 є простим коренем многочлена g (*).
1. Відокремити кратні множники многочлена
,(л-) = л-4 — 2* А'3 — 2**— 1.
Розв'язання. Щоб відокремити кратні множники многочлена f(х), треба
подати його у вигляді
де ер/— добуток всіх незвідних множників і-'і кратності в канонічному роз"
кладі многочлена ?(х) над полем С при BGix і < і < т. Схему знаходження
многочленів у( для всіх 1 < і < /и подамо таблицею (табл. 26).
Таблиця 26
ат
f
d,
d2
-1
= <Рі92?3"
= (/.
= (d,
-("
n =
.«'І)
7T—2»
?2?3"
= <РЗ"
4-2)
ст-2
* ■ т
= ?т
fiL= I
}^ = Ч" =
ТіМз-Тт
?2 = "^Т5^^3 •" ^
?т =
лт—\
}?1 =
}<Р2 =
<7і
^2
9з
Знайдемо многочлени du d2, .. ., dm для многочлена f (а*). Застосуємо алгоритм
Евкліда:
/>) = 4л-3 —би2—2*.
155

Оскільки найбільший спільний дільник многочленів ми визначаємо з точністю
до сталого множника, то щоб уникнути дробових коефіцієнтів, помножимо
результати проміжних обчислень на відповідний множник. Ділення
виконуватимемо «кутом»:
уЛ 2i#3 2іх — 1 1
(множимо на 2) ^ _ ^ _ ^ _ ^ ™3 ^2 (Ділимо на 2)
2х4 — Зіх3 — іх
4х3
2а:3
- Єіх2 -
— Зі'*2 -
х+\
-2і
-і
-їх3-
2х3
2х3
— Зіх
— Ьх-
— Зіх
-2
-4і
— і
(множимо на 2і)
. . о;ч Зіх2 + 6* — Зі
(ділимо на ЗО — о '
х* — 2іх—\~
2х3 — Зіх2 — і
2х6 — \іх2 —2х
х2 — 2іх—\
2х + і
_іх2 + 2х — і
іх2 А-2х — і
0
Отже,
dx
d{
*2
= х2-
= 2х-
= X —
- 2іх -
-2і =
■ *,
- 1 =
= 2(х-
(х-
-1),
■if
d2 = l,
d3 = (d2, d2)=\.
Обчислимо многочлени: qv q2 і <?з:
"з
Тепер знайдемо множники <рр ср2 і <р3:
Ь=^~Х + І' f2=f" = 1' «Гз = ?з = *-'-
Таким чином, маємо
f(x) = (x + i)(x-if.
Задачі
25.1. Знайти похідну таких многочленів:
а) f(x) = 9(x2 + x — 1)3(х3 — 2) з кільця Q[x\\
б) f (х) = 21 (іх3 — Зх) ((1 + 0 х2 — і) з кільця С [х]\
в) / (*) = 4х10 + Зх2 (х + 3) з кільця Z5 [x\.
25.2. Знайти /''(2), якщо:
а) / (х) = 2х3 (х3 + 4) — (х + Т)2 є многочлен з кільця Z6 [x}\
б) f(x)= (5xs + 8)3(x — 3)2 є многочлен з кільця 1\г\х\.
156

25.3. Довести, що різниця deg/— cleg/' для многочлена f (х)
з кільця Zp[x]y де р — деяке просте число, може бути як завгодно
великою.
25.4. Довести, що многочлен f(x) з кільця Zp[x], степінь якого
дорівнює р—1, не може бути похідною жодного многочлена з цьога
кільця.
25.5. Довести, що похідна /7-го порядку від будь-якого
многочлена / (х) з кільця Zp [x] дорівнює 0.
25.6. Знайти многочлен шостого степеня f(x) з кільця Z^[x]^
якщо /'(*) = 2*+ ї і /(Г)= 1.
25.7. Знайти многочлен f (х) з кільця Q[x]> якщо /" (х) = 24л: +
+2, /(0) = 1 і /(1) = 5.
25.8. Многочлен f(x) з кільця Q[x] при діленні на многочлен
g(x) = (х2 + І)3 дає остачу г(х) = х2 — 1. Знайти остачу від
ділення /" (х) на многочлен h (х) = х2 + 1.
25.9. Довести, що многочлен п-то степеня f(x) над полем R
характеристики 0 ділиться на свою похідну /' (х) тоді і тільки тоді,
коли f(x) = a(x + b)n, де а, Ь £ Р, а Ф 0 і я £ N.
25.10. У кільці Z2[x] знайти всі многочлени f(x) такі, що
діляться на свою похідну і степінь яких не перевищує 3.
25.11. У кільці Zz[x\ знайти число всіх многочленів третього-
степеня, які діляться на свою похідну.
25.12. Розкласти многочлен f(x) за степенями двочлена g(x) =
= х — а і знайти /' (а), /" (а), f" {a), /IV (а), якщо:
а) / (х) = л:4 — 2л:3 + Зл:2 — 5л: + 1 належить Q[x] і а = 1;
б) / (х) = хБ — Зіх3 — 4л:2 + 5іх — 1 належить С [х] і а = —І;
в) f(x) = (х — 3)(х — 2)(х + 1)(х + 4) + 1 належить Q\x] \a =
=-1; _
г) / W = 4я5 + 10л:3 — х + 2 належить Zn [л:] і а = 3;
Д) / (*) = 2л:4 + л:3 + л:2 + 2 належить Z3 М і а = Г.
25.13. Многочлен четвертого степеня з кільця С[л:], старший
коефіцієнт якого дорівнює 2/, має число І—і трикратним коренем,
а при діленні на х -\-і дає остачу 2 — і. Знайти цей многочлен.
25.14. Довести, що число—3 є простим коренем многочлена
/ (х) = хп + 3я з кільця Q[x] при будь-якому непарному
натуральному п.
25.15. Знайти кратність кореня:
а) х = 3 многочлена / (л:) = л:4 — 6л:3 + Ю*2 — 6л: + 9 з кільця:
б) х = 2 многочлена / (я) = хь + 4л:4 — 7л:3 — 11л:2 + 4 з кільця=
Q М;
в) л: = 1 + t многочлена / (*) = л:4 — (3 + 4і) л:3 + (3 + 3/) л:2 +
+ (8 — 2і)х — 2 — 2f з кільця С[л:];_
г) л: = 3 многочлена / (х) = х6 + 2х з кільця Z5 [л:].
25.16. Відмінне від нуля дійсне число а є трикратним коренем:
многочлена f(x) з кільця R[x]. Знайти кратність кореня а для
многочлена
g(x) = (x-a)f(x).+ (x + a)f'(x).
157'

25.17. При яких дійсних значеннях а мають кратні" корені такі
многочлени:
а) / (х) = х3 + х2 + ах + 3;
б) f(x) = x3 — 4х2 — Зх+а;
в) f(x) = x* + 3x2 + 3ах — 4?
25.18. Многочлен f(x) = x3 + 5x2+8x + a має кратний корінь.
Знайти число а і розкласти многочлен на незвідні множники в
полі Q. /
25.19. При яких необхідних і достатніх умовах наступні
многочлени з кільця R [х] мають кратні корені:
а) f(x) = х3 +ах + Ь\
б) f{x) = x4+ax + b;
в) flx) = х5 + Q>x + Ь\
г) / (х) = хБ + ахг + 6?
25.20. Чи мають кратні множники такі многочлени з кільця
CM:
а) f(X) = x* + 4x2 + x — 6;
б) f(x) = x* + (3 — 2і)х2 — (1 +60^ — 3;
в) f (x) = x4 — 2хг — Зх2 + 4х + 4\
г) f(x) = x6 — 6л^ — 4х3 + 9х2 + 12л: + 4;
д) f(X) = хА + (1 — Зі)х3 — (3 + Зі) а:2 — (3 — 0x4- ї?
25.21. Відокремити кратні множники лтаких многочленів:
а) f (х) = х*-Зх2 + 4; (r-JLj^fr+V
б) f(x) = х4 + (4 —8і)*3 + (—18 —240 а:2 + (—44 + 8і) х+ (—7+
в) } (х) = хь + 4*4 + 7х3 + 8х2 + 5х + 2; И^ ^J />*-*/
г) / (*) = хь — іх* + 5х3 — іх2 +8х + 4г,
д) / (х) = х5 + 5%* + (6 — і) х6 — (4 + 60 х2 — (8 + 120 * — 8г,
є) f(x) = jfi + (—1+Зі)*5 + (6 — Зі)х* + (—6+ 10ї)*3 + (21 —
— 100 л:2 —(21 +9i)x + 9L
25.22. Довести, що кожний незвідний у полі Q многочлен не
може мати кратних множників у кільці' Р [х] для кожного
числового поля Р.
26. Інтерполяційні многочлени,
оле раціональних дробів
Література
[1] —§ 23, с. 250—251; § 24, с. 2^2—272;
[2] —§ 23, с. 253—256, § 24, с. 267—278;
[5] —гл. X, § 1—3, с. 357—373;
[6] —§ 24, с/ 158; § 50, с. 305—311;
£Sj — гл. 5, § 4, с. 233—242; гл. 6, § 1, с. 246—247.
ТЕОРЕТИЧНІ ВІДОМОСТІ
Нехай Р — деяке поле, av а2і . . ., ап, ап,1—різні елементи поля Р і b{f
Ь2, . • •> bn, bn,{—довільні елементи поля Р.
Існує один і тільки один многочлен / (х) в кільці Р [х], степінь якого не
перевищує п І який набуває в (п + і)-й точці at£P задані значення Ь{£Р, і =
= 1, 2 п+ 1.
.158
і

Шуканий многочлен ма? вигляд
У ь (*-"!)■-• (* -flf-l) (* - аі+\) - • ' (*~ */і+і)
м' Zj ' (^-^1)...(^-^-1)(^-^+1).-.(^-^+1)
Многочлен (1) називають інтерполяційним многочленом Лагранжа.
Іноді доцільно многочлен f (x) записувати у вигляді
f(x) = c0 + cl(x-al)+.. . + сп(х — аг)(х -а2). ..{х — ап)9 (2),
де коефіцієнти с0, cv ..., cn визначаються послідовним підставленням значень
x=^av х — а2, .. ., х=ап+1. Многочлен (2) називають інтерполяційним
многочленом Ньютона.
Для будь-якого поля Р існує єдине (з точністю до ізоморфізму) поле Р [*],.
яке містить кільце Р [х] многочленів над полем Р і кожен елемент якого можна
подати як частку
jjfcy де ї (де), g (х) £ Р [х] і 8(х)Ф 0. (3).
Зауважимо, що відповідно до загально! теорії елементом поля Р [х] є не кожна
окрема частка (3), а клас часток, як: дорівнюють одна одній.
Дві частки , v = 7j~T^) Д0РІВНЮЮТЬ °Дна одній, якщо /, (x) g2 (х) = /2 (х)Х
t W
X gx (*). Як правило, раціональний дріб подають тією часткою —т-т , для якої
</. g) = і.
Нехай раціональні дроби задано нескоротними частками і старший
коефіцієнт знаменника дорівнює І.
Раціональний дріб —ттг називається правильним, якщо степінь / (х) менше-
степеня g (x). У противному разі раціональний дріб називається неправильним.
Елементарний дробом над полем Р називається раціональний дріб виду
1, де g (х) — незвідний многочлен над полем Р, deg f < degg і k £ N.
lg(x)]
f{x)
Якщо „ /v _ /yv —-7-7 — правильний раціональний дріб над полем Р і
&\ W s2 v*/ • • • 6m vv
многочлени gx (x)t g2(x), . .., gm(x) — попарно взаємно прості, то в кільці Р [х]\
існують многочлени f{(x), . .., fm(x) такі, що
Пх) /і (*) /2W frnW
#1 (*) #2 (*)••• £m W " Si (X) + S2 № + * " * + Sm (*)
і кожен з дробів у правій частині є правильним.
f (x)
Правильний дріб над полем Р виду ^, де g(x) — незвідний над Р
многочлен і 6(=N, можна подати як суму елементарних дробів над цим полем.
t(x) t\ (х) /2 (де) fk(x)
[g(x)]k - Six) + [g{x)]2 + ••• + [g(x)]k •
Правильний дріб над полем Р можна подати як суму елементарних дробів*
над цим полем і до того єдиним способом.
f (х)
Неправильний дріб —-гт можна подати як суму многочлена і правильного
дробу.
.159-

ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
il„ Довести тотожність
а2
(х — а)(х — с) (х —Ь)(х — а)
Розв'язання. Розглянемо многочлен
(x-b){x-c) (x-q)(x-c) (х-Ь)(х-а)
tW-a (a_^b){a_c)-t-° (b-a)(b-C)^c (с—Ь)(с-аУ
Обчислимо його значення, якщо х £ {а, Ь, с):
f(a) = a\ f(b) = b*t f(c) = c\
Це означає, що / (х) є многочленом Лагранжа, степінь якого не вище 2.
Многочлен g (х) = х2 при х £ {а, Ь, с] набуває значень:
£(а) = "2, g(b) = b*, g(c) = A
Як відомо (див., наприклад, [2], § 23, теорема 3), над полем R існує тільки
один многочлен, степінь якого не більше 2 і який при трьох різних дійсних
числах a, b і с набуває значень а2, Ь2 і с2. Це означає, що многочлени f (х)
і g (x) дорівнюють один одному.
На координатній площині задано чотири точки Л (0; 1), В (— 1; 2), С(1; 4)
і D (2; 2). Знайти многочлен третього степеня, графік якого проходить через
ці точки.
Розв'язання. Складемо таблицю значень для шуканого многочлена / (х)
(табл. 27).
Таблиця 27
1 х
/(*)
0
1
—1
2
1 -
4
2
2 '
Щоб знайти коефіцієнти многочлена f (x), застосуємо інтерполяційну формулу
Ньютона:
f(x) = c0 + clX + c2x(x+\) + c3x(x+\)(x-^\). (1)
Підставивши значення х£ {0, —1, 1, 2), дістаємо:
ґ 1 = С0,
2 = с0 — Cf,
4 = c0 + (¾ + 2с2,
2 = ^ + 2^+ 6с2 + 6с3>
або
/^0 = 1,
4= —ь
с2 = 2,
3
£д = — 2 •
Отже,
/(*) = —1*(* +0(^-1) + 2*(*+1)- * + 1=-^-|г*+2л;2 + у х+1,
«3. Розкласти на елементарні дроби над полем Q дріб
/ (х) х2 + 4х + З
g(x)~ (д:2 _ 4л: -f- 4)(x + 3)2*
Розв'язання. Перевіримо, чи с даний дріб нескоротним. Для цього
знайдемо найбільший спільний дільник його чисельника і знаменника. Розкладемо
їх на незвідні множники в полі Q:
/ (х) - х* + Ах + 3 = (х + 1) (х + 3),
g (х) = (х2 — 4* + 4) (х + З)2 = (х — 2)2 (* + З)2.
Звідси (/, g) = x-f-3. Це означає, що перш ніж розкласти заданий дріб на
елементарні, треба замінити його нескоротним дробом, що дорівнює йому. Отже,
/(*) х+\
8(х)~ (х-2)*(х + 3)-

Шуканий розклад повинен мати такий вигляд (див., наприклад, [1], § 24»
с. 269, теорема 1):
х+\ А В С
(х — 2)*(х+3) ~ х — 2~т~ (*_ 2)2 "Ї'я + З'
де А у £, С — невизначені коефіцієнти. Отже, маємо
х + 1 = А (х - 2) (х + 3) + В (х + 3) + С (х - 2)\
Оскільки многочлени рівні між собою, то:
1) при х =■ 2, 5Б = З, В = -g-.
2
2) при х = —З, 25С = —2, С = - ■%.
2
3) Л + С = 0 і Л-25-
Остаточно дістаємо
/(*) *+1
g W■ (* — 2)2 (х + 3) -25(дс —2)Т" 5(* —2)а"~25(* + 3)'
4. Розкласти на елементарні дроби над полями Q і R дріб
fix) х + 3
g(x)~ (*8_2)(*+1)-
Розв'язання. Спочатку розв'яжемо задачу в полі Q. Многочлен g|(*)»
= *3 —2 у цьому полі незвідний. Тому заданий дріб є правильним і
нескоротним. Шуканий розклад матиме вигляд:
х + 3 Л__ Вх* + Cx + D
(Xs — 2) (де + 1) " х + 1 + х3 — 2 '
де Л, 5, С і D — невизначені коефіцієнти. Звідси
* + 3 = А (х3 — 2) + (Bx* + Cx + D)(x + 1).
Прирівнюючи коефіцієнти многочленів при однакових степенях невідомого в
лівій і правій частинах рівності, дістаємо систему рівнянь:
А + В=0,
В + С = 0,
C + D=l,
D — 2 А = 3.
2 2 2 5
Звідси Л = — -q-, £ = — , С = — -о-, D =* -^-, тобто шуканий розклад
заданого дробу на елементарні дроби над полем Q має вигляд:
х+3 2 2*2 — 2х + 5
(х3 — 2)(*+ 1) "- 3(х + 1) + 3(х3-2) •
Перший з доданків правої частини є елементарним дробом над полем R.
Розкладемо на елементарні дроби другий доданок:
2х2 — 2х + 5 2х2 — 2х + 5 ^1 Яі* + Сі
__2~~/ 3 W 3 з\— з"Г з__ з _»
U-/2jU2 + /2* + /4j * —/5 x2 + /2x + /4
2х2 - 2л + 5 = А, (х2 + /2а + /ї) + (Я^ + Cx) (* - /§),
Лі + ^-2,
з з_
Л,/2-^/2 + ^ = -2,
з_ з
U, /4-Ci/2 = 5.
6 5-2/1 161

Розв'язуючи цю систему, дістаємо:
2 2^- 5^
Cf = ~T+ T/2-T]A.
Отже, розклад дробу , 3 __ 2) (х + 1) на елементаРн1 ДР°би над полем R
має вигляд:
2 5 * 1 •*
Т + 72^2^Т^4
+ 5 +
*+3
(а:3 — 2) (х-j- 1) -— 3(х+ 1)
з , з
з
+
(т-і52^+т^)-т+т^^т^
з з_
Зауваження. Наведений приклад свідчить про те, що розклад дробу на
елементарні дроби залежить від поля, над яким розглядається дріб.
Задачі
26.1. Скільки існує многочленів f (х) першого та другого
степенів над полем R таких, що /(—1) = —1 і /(2) = 2?
26.2. Чи може графік многочлена третього степеня над полем R
мати з прямою у = kx більше трьох спільних точок?
26.3. Довести, що графік многочлена степеня п перетинає будь-
яку пряму не більш ніж в п точках.
26.4. Довести, що коли при будь-якому раціональному значенні
змінної х многочлен f(x) набуває раціональних значень, то всі
коефіцієнти многочлена є раціональними числами.
26.5. Довести тотожності:
а) а
(*-6)(*-*)
(а — Ь) (а — с)
+ ь
(х — а)(х — с)
(х-а)(х-Ь)
б)
(d — a)(d-
+
■b)(d- c)
(Ь-
+
а)(Ь-с)
(х—а)(х — Ь)(х — с) _^ (х — Ь){х — с) (х — d)
(a — b)(a— c) (a — d)
b)(x-d)
+
(с — а)(с— Ь)
+
= 1.
= х;
(b — a)(b—c)(b-d) ' (c — a)(c-b)(c — d)
26.6. Використовуючи формулу інтерполяційного многочлена
Лагранжа, побудувати многочлени найменшого степеня f(x)£Q[x]
за такими таблицями значень (табл. 28—ЗО).
Таблиця 28
Таблиця 29
а)
X
fix)
~3
22
1
2
2
7
б)
X
/М
0
2
1
1
3
1
4
2
26.7, Використовуючи інтерполяційну формулу Ньютона,
побудувати многочлени найменшого степеня f(x)£Q[x\ за такими
таблицями значень (табл. 31—33).
162

Таблиця ЗО
в)
X
f W
—2
—4
—1
—2
0
0
1
2
2
4
*
1 /(*)
— 1
4
Та
0
1
б л и ц я 31
1
2
2
7
б)
X
/W
0
і
і
2
Та(
2
3
5лиця 32
3
4
4
6
в)
Таблиця 33
X
/м
0
1
1
3
2
9
...
я
3*
26.8. Знайти многочлени найменшого степеня f(x)£Q[x] за
такими таблицями значень: (табл. 34—37).
а)
Таблиця 34
X
/(*)
—1
2
0
—1
1
2
б)
*
/(*)
1
4
Та
2
3
блиця 35
3
2
4
1
в)
Таблиця 36
1 х
1 /W
1
і
і
1
—1
—f
—* I
—1 1
, обчислити / (20 та / (0).
г)
X
/м
1
1
Та
4
2
блиця 37
9
3
16
4
, обчислити / (3) та / (2).
26.9. Відображення / поля Z5 в себе задається так: /(0) =/(2) =
= /(4) = 0 і f (1) = /(3) = 1. Задати це відображення за допомогою
многочлена з кільця Z5 [x] найменшого степеня.
26.10. Задати всі взаємно однозначні відображення поля Z3 в себе
за допомогою многочленів з кільця Za[x], степінь яких не
перевищує 2.
26.11. Довести, що для будь-якого простого числа р всі
відображення поля Zp в себе можна задати многочленами з кільця
Zp[x]y степінь яких не перевищує р—1.
6*
163

26.12. У полі R(x) знайти нескоротний дріб, який дорівнює
таким дробам:
< .^-4, + 3. з*2 - , — 2 .
а) ,2-5, + 61 б) ,6-1 '
,« + ,<+!. _х *2-,-1
В) х2 + х+\ ' Г) х3-х2-*-2'
/ (х)
26.13. Перевірити, чи є раціональний дріб -*-~г елементарним
S W
над полем Р, якщо:
а) І^^ і Р = *
б) Ш = *8-' і я = о-
J g W (,3 + 3)2 W>
. _/W _ 5,+ 6 . p _ R.
B,gW~ ,< + 2,2+l ' И~К
f(x) = i_
«W ,2 + ,+ l
D^-rrbri >> = *
e)IWe^±T ip = z
7 gW (* + 3)2
f (x)
26.14. Розкласти дріб -^ на елементарні дроби над полем R,
якщо:
/(,) ,^-5,+ 6 , . /(х) ,л-1
4W (2,-l)(,2-2,)' '«W U2 + ,+ l)2(,2+l)'
fix 1W x2 . /(x) ,4+ 2,3-18,2+54 .
;gW (, + 2)(, + 3) ' fc'eM ,5 + 6д.4 + 9лз >
^ Ш= *3+і жч И*) = ^2+ з, +2 .
' g(*) (,2 + 2,+ l)2' ' g(*) (,4 + 4)(J( + 2),
f(x) 2, /W_ ,2
*V w3 — 7^ л /„2 , ,\' <v
(,) (,_l)(x2+l)* '«(*) /_4-
д)Ш ^ •
A> h Iy\ (..1 , .. і n\2 '
«W (,2+ ,+ 2)'
якщо:
26.15. Розкласти дріб -^ на елементарні дроби над полем С,
' g(x)~ ix-l)ix + 2i) > °>g® (,^-2, + :
!, + 2) (, — 1 + 0'
Лч /(*).. 2* гч /(*)^ *2
°> g (,) ~ (,_ 1) (,2 +0* U g (,) ,4-4*
26.16. Розкласти дріб -£-|— на елементарні дроби над полем Q,
якщо:
,° + ,
164

26.17. Розкласти дріб -^ на елементарні дроби над полем Z5f
якщо:
a^W"x3+*f 'ГМ~*6-*' ^«"^-ї
26.18. Розкласти дріб -^j = -^— на елементарні дроби над
полем Zp, де /7 — довільне просте число.
Розділ V. МНОГОЧЛЕНИ ВІД КІЛЬКОХ ЗМІННИХ
§ 27. Кільце многочленів від п змінних
над областю цілісності. Розклад многочлена
на добуток незвідних множників
Література
[11 —§ 25, с. 272-288;
[2] —§ 25, с. 279—297;
[3] —гл. 14, § 1, с. 485-493;
15] —гл. XI, § 1, 2, с. 392—413;
[6]—§ 61, с. 312—320;
[7] —§ 21, с. 113—123;
[8] —гл. 5, § 2, с. 212—216.
ТЕОРЕТИЧНІ ВІДОМОСТІ
Кільцем многочленів R[xv xv ..., xn__v хп] від п змінних *р х2, • ♦ «J
*л_і> хп над областю цілісності R називається кільце многочленів від змінній
хп над кільцем R[xx, х2, . . ., хп_х].
Кільце многочленів R [xv х2у . . ., хп] над областю цілісності R є область
цілісності, причому кожен елемент f£R[xv х2, . . ., хп] можна подати як
скінченну суму:
/ = |vN*2'... *„*"'• (і)
де at£ R, fyy£ Z_j_, *'£.{!, 2, . . ., m} та /£ {1, 2, . . ., я}. Будь-який вираз виду
(1) є елементом кільця R[xv х2, . . ., хп].
Елементи кільця R [х{і х2, . . ., хп] називають многочленами від п змінних
над R і позначають f (xv x2, . . ., *л), g (xv x2l . . ., хп), .... Кожен доданок
а{х{1 х22і. . . хппі в сумі (1) називають членом многочлена / (хv х2, . . ., хл),
елемент <*[£ R — коефіцієнтом цього члена. Два члени, які відрізняються тільки
коефіцієнтами, називають подібними.
У подальшому вважатимемо, що в сумі (1) подібних членів немає. Така
форма запису многочлена називається канонічною і кожен многочлен з кільця
&[*і» х2, . . ., хп] можна записати в такій формі тільки єдиним способом.
Степенем члена ах{ {х22 . . . хпп многочлена називають суму fcj + #2 + • • • +
+ kn. Число kCj і =>. 1, 2, . . ., п; називають степенем даного члена відносно х.ф
165

Найбільший із степенів членів називають степенем многочлена, а член з най"
більшим степенем — старшим членом многочлена. Якщо всі члепи многочлена
мають степінь /, то кажуть, що це однорідний многочлен степеня /.
Нехай ах{1х22 . . . хпп і Ьх^х2 . . . х* — два члени многочлена / (xv х2, . ..,
хпу Вважають, що перший член вищий від другого, якщо k{ = /p k2 = /2, . . .,
k(_i = l(__i і kt > l{. Відношення «бути вищим» на множині членів многочлена
є лінійним строгим порядком, його називають лексикографічним.
Нехай члени многочлена / (*р *2, . . ., хп) упорядковані лексикографічно.
Тоді перший по порядку член називають вищим членом многочлена.
Вищий член добутку двох многочленів дорівнює добутку вищих членів цих
многочленів.
Означення подільності многочленів, його властивості, поняття звідного та
незвідного многочленів у кільці Р [х{> х2, . . ., хп] залишаються тими самими,
що й в кільці Р[х] (див. § 21, 24).
Будь-який многочлен / (*j, х2, . . ., хп} над полем Р ненульового степеня
можна подати у вигляді добутку многочленів, незвідних у полі Р і при тому
єдиним способом з точністю до сталих множників і порядку множників.
Кільце Р [xv х2у . . ., хп] не є кільцем головних ідеалів, а отже, воно не
може бути евклідовим кільцем.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Подати многочлен
f (х, у, z) = (х+2у) (*"_ 1) + (у —«)» — (*+ г) (у-2)
у вигляді суми однорідних многочленів, кожен з яких упорядкований
лексикографічно, і знайти його вищий член.
Розв'язання. Знайдемо канонічну форму заданого многочлена:
f(x,y, z) = xz* — x + 2yz* — 2y + y* — 2yz + z* — xy+2x —
— zy+2z = xz* + x + 2yz* —2y + y2 — 3yz + z* — xy + 2z.
Оскільки многочлен має члени першого, другого і третього степенів, то Кого
можна подати у вигляді суми трьох однорідних многочленів:
/ (*, у% z) = («» + 2у*) + & - 3yz + 2* - xy) + (х — 2у + 2г).
Упорядкуємо кожен з однорідних многочленів-доданків лексикографічно:
/ (*, у, 2) = (*z» + 2yz*) + (-ху + У2- № + *2) + (х - 2у + 2«).
Вищими членами кожного з доданків відповідно є xz\ —xy та х. Вищим серед
них, а, отже, і вищим членом многочлена f (х, у, z) є —ху.
2. Відображення множини Z3xZs в Z9' задано табл. 38.
(0,0)1 (0, 1)
1 0 1 2
Таблиця 38
(б, 2)1 (ї, 6)1 (Г, І) 1 (І, 2) 1 (2, 0)1 (2,1)
0 1 2 1 0 1 2 1 0 1 2
(2,2")
б
Знайти канонічну форму многочлена з кільця £.,[*, у], який задає це саме
відображення.
Розв'язання. Позначимо: х1 = Уі=0, х2 = у2 = 1, хя = у3 = 2. У кільці
Z3[*, у] розглянемо многочлен
, , , _ о (* — Хг) (X — Х3) (У — уг) (у — у3)
Т <*• У) -2(Хі- х2) (х, - х3) (у2 - Уі) (у2 - у3) +
■ ? (х — *і) (х — хг) (У — Уг) (У — Уз) ,
+ (*а — Хх) (Х2 — Хз) (Ух — У2) (Уі — Уз) "*"
166

fx — xt) (де — Хд) (у — Уі) (У — Уа) ,
"t" (де* — х,) (Д^, — *«) (//я— vt) (у2 — r/.ч) "*"
, -J І* — *і) (* — *г) (У ^ Уі) (У — #з)
"*" (*я — *і) (ДСа ~ *8) (^2 — Уі) (//2 — Уз) *
Оскільки
/ (*і. </і) = /" (*і> Уз) = / (*2> 0і) = / (*а, Уі) = / (*з, Уз) = О,
f {*v У*) = / (*2. Уі) = / (*2» 08) = / (*з> Уа) = 2»
то многочлен / (л, г/) є шуканим. Знайдемо його канонічну форму;
) ~(Х-~Х}(Х-\(У--У У + -7 М*-2)(У-Т)(у-2)
А I*. W - (_1} (.2) 1 (-1) ~*~ Т (-7) (-Т) (-2) +
4-2 ^^-^1¾ У +2 x^Jir>y(y-5>
"*" 1(-1)2-1 + 2-1 -Т (—Т)
= 2(х + 2)(х + 1)уії + Т) + 2х(х+ї)(у + 2)(у + \) + 2ху(х+\)(у + 2) +
+ 2ху {х + 2) (у + Т) = (2деу + 2де2у + # + у) + (2х*у* + 2уЧ + Xі' + де) +
+ (2*У + *2У + 2деу2 + ху) + (2*У + де*/2 + 2х*у + ху) =
= 2де V + 2х*у + х' + 2ху* + 2ху + де'+ у* + у.
3. Розкласти у полі Q на незвідні множники такий многочлен:
/(де, y) = (x+yy—* — tf.
Розв'язання. Розглянемо многочлен І (х, у) як многочлен від змінної у
над областю цілісності v І*]. Тоді / (де, 0) = / (х, — х) = 0. Це означає, що
/ {х, у) ділиться на многочлени у — 0 = у та у + х. Розглядаючи / (де, у) як
многочлен від змінної х над областю цілісності Q [у], маємо / (0, у) = / (—#,
і/) = 0, тобто заданий многочлен ділиться на х — 0 = де. Проте / (де, у) є одно»
рідним многочленом, тому його можна подати у вигляді
/ (де, у) = ху(у + де) (ах2 + bxy + су*)%
де я, b, c£Q — невизначені коефіцієнти. Запишемо многочлен /(де, у) у
канонічній формі:
/ (х, у) = 5 Xіу + lOrfy2 + 10*у + 5длД
Прирівнюючи тепер коефіцієнти при х*у і у4дс, знаходимо а = 5, с = 5, Якщо
де = у = 1, то а+6+с= 15, & = 5. Тому /(де, */) = 5^ (у + де) (де* + деу + у*).
Многочлен g (де, у) = де2 + ху + у2 є незвідним у полі U. Справді,
припустивши, що
*а + *У + Уг = ("Ч* + «7 У) (Щ* + "г*/)
для деяких щ9 m„ nj, rtf€Q, дістаємо систему рівнянь
mim2 =1, | 1_
п,п2 = 1, m* ~ та'
2
Щ П2
яка у множині Q розв'язків не має.
Отже, шуканий розклад в
/ (*» У) = ЬхУ ІУ + х) (де* +ху + у*).
167

Задачі
27.1. Знайти канонічну форму таких многочленів:
a) /(*, y) = (X-y)2(x2 + xy + y2)(x + 2y) + x2-U
б)/(*, y) = (x — y){y — z)(x — z)xyz.
27.2. Довести, що множина всіх однорідних многочленів кільця
Р[х\, Х2, ..., хп] многочленів над полем Р є підкільцем.
27.3. Скільки членів може мати канонічна форма однорідного
многочлена* а) другого степеня від двох змінних; б) другого
степеня від трьох змінних; в) третього степеня від двох змінних;
г) третього степеня від трьох змінних?
27.4. Довести, що однорідний многочлен степеня т, де т > 0,
від п змінних має в загальному вигляді *—!
27.5. Довести, що канонічна форма
від п змінних має в загальному вигляді
т\ (п— 1)!
многочлена
(т + п)\
членів.
m-го степеня
п\т\
членів.
27.6. Скільки існує однорідних многочленів другого степеня від
трьох змінних над полем: a) Zi\ б) Z3?
27.7. Довести, що над полем Zp існує р6 — 1 однорідних
многочленів другого степеня від трьох змінних.
(т+п—1)1
27.8. Довести, що над полем Zp існує p«K*-i)i— 1 однорідних
многочленів m-го степеня від п змінних.
27.9. Упорядкувати лексикографічно і знайти вищий член таких
многочленів:
а) / (*» У» *) = 2я3 (у + z) — Зу2х2 (х2 + z2) + 5xAyz2 з кільця Z [я,
У* *1;
б) f(x, у у г) = (2х + 3y)2z — х (у +j — 3xz) з_кільця Zb[x, //, z\\
в) f(x9 у, z, t) = (x + y)(z + у) + 2х(у + t + І) + (у + tf з
кільця Z3 [я, у у г, t].
27.10. Знайти два різних многочлени від двох змінних над
полем Z2, які визначають те саме відображення Z2XZ2 в Z2, задане
такими таблицями (табл. 39, 40).
а)
(0,0)
Т
Та
(о,Т)
б
б л и ц я 39
(ьо)
0
(ї.ї)
Т
б)
(о,о)
Т
Та
(о,Т)
0
б л и ц я 40
(Г.о)
г
(ї.ї)
б
27.11. Довести, що кожне відображення множини Znp у
множину Zp можна подати многочленом від п змінних над полем Zp.
27.12. Довести, що многочлен f (х\, #2, . .м хп) над областю
цілісності К ділиться на многочлен g\x\y #2, ..., xn) = xn — s(x\,
Х2, ..., Хп-\) з цього самого кільця тоді і тільки тоді, коли f(xi>
Х2> . . .yXn-\yS(X\y X2, ..., Хп-і)) Є НУЛЬОВИМ МНОГОЧЛЄНОМ.
27.13. Перевірити подільність многочлена f(x, у, г, t) = (xy —
— ztf -f (zx — ytf на многочлен g(x, у, zy t) = {у + z) (x — t) у
кільці Z[x, yf zy t\.
168

27.14. Довести, що многочлен f(x, у, z) = (л: 4- у + z)n — хп
— if — zn ділиться на многочлен g(x, у, г) = (х + у) (у + z) (x + г)
при будь-якому натуральному п.
27.15. Довести, що многочлен f(x, у) = х2 + у2— 1 незвідний
у полі Q.
27.16. Довести, що будь-який однорідний многочлен &-го
степеня від двох змінних f(x, у) над полем Р можна за допомогою
введення нової змінної подати у вигляді добутку двох многочленів,
кожен з яких має одну змінну.
27.17. Застосовуючи заміну x = ty, розкласти на незвідні у полі
Р множники многочлен /(#, у)у якщо:
а) / (х, у) = 9х4 — 12х3у — 2\х2у2 — 40ху3 — 16у4 і Р = Q;
• б) / (х, у) = 4х< + 4х3у + 13х2у2 + бху* + 9у4 і Р = Q;
•в) /(*, y) = x2 + xj + y2 і P = Z3;
г) /(*, у) = х* + 4у* і P = Z5;
Д) / (х, У) = (х2 - ху)2 + 2х2у2 - 2ху3 + у* і Р = Q.
27.18. Розкласти на незвідні у полі Q множники такі многочлени:
а) f(x, у, z) = (x + y + z)3~x3 — y3 — z3;
б) /(а, 6, с) = (Ь -с)(Ь + с)2 + (с — а)(с + а)2 + (а - Ь)(а + б)2;
в) f(ay b, c) = а(Ь — с)3 + Ь(с — а)3 + с(а — Ь)3\
Т) f(x9 у, z) = x(y2-z2) + y(z2-х2) + z(x2-у2);
Д) f(x, у, г) = (х + у + г)* — (у + г)* — (х + у)4-(z + х)4 + х4 +
+ У4 + г4\
є) /(а, Ь, c) = (a-b)(a + b)3 + (b-c)(b+c)3+(c-a)(c+a)*;
Є) / (Х> У у Z) = Х3у2 + y3Z2 + Z3X2 — Х2у3 — y2Z3 — Z2X3\
ж) /(а, b, c) = a4(b—c) + b4(c — a) + c4(a — b);
з) f(x, у, г) = (x + y + zf — x5 — y5 — z5\
к) f (х, у у z) = (y — zf + (z — a:)5 + (x — yf.
27.19. Довести, що многочлен f(x> у, г) = (х + у + z)2n+l—
— х2п+\—у2п+\—22л+1 ДІЛИТЬСЯ На МНОГОЧЛЄН g (x9 (/, Z) = (х + у +-
+ z)3 — я3 — */3— z3 при будь-якому /z, n£N.
27.20. Довести, що в кільці Р [х, у] многочленів від двох
змінних над полем Р не всі ідеали є головними.
27.21. Довести, що фактор-кільце Р [х, у]/<х — у> ізоморфне
кільцю Р [х].
§ 28. Симетричні многочлени
Література
[1] —§ 26, с. 288—295;
[2] — § 26, с. 298—305;
[31 —гл. 14, § 2, с. 493—500;
[5] —гл. XI, § 3, с. 413—423;
[6] —§ 52, с. 321—328;
[7]—§ 22, с. 123—130;
[8] —гл. 6, § 2, с. 257—263;
[44] —§1, 3, с. 8—19, 47—61; § 7, є. 115—137.

ТЕОРЕТИЧНІ ВІДОМОСТІ
'Многочлен / (хх, л2> . ., хг) з кільця Р \хх, х2, . . ., хп] називають
симетричним відносно змінних Jtj, х2, . . ., хп, якщо внаслідок довільної перестановки
змінних Хр *2, . . ., дсЛ утворюється многочлен, який дорівнює гаданому.
Симетричні многочлени мають такі властивості:
1°. Множина всіх симетричних многочленів від п змінних над полем Р
утворює область цілісності -> одиницею;
2°. Якщо симетричний многочлен t (Xj, х2, . . ., хп) містить деякий член
«Jfj лг2 . . . хп , то він містить і член, утворений з заданого, внаслідок будь-якої
перестановки показників /р /2, . . ., Іп;
3°. ?кщо ахх х2 .. . хпп є вищий член симетричного многочлена, то /t >
> '2 > - • • > /л.
Симетричні многочлени
а1=*1+*2+••.+*„,
а2 = *,*2 + Х{хг + .. . + хп_ххп%
називають елементарними симетричними многочленами.
Будь-який симетричний многочлен / (Яр *2, . . ., хп) від п змінних над
полем Р можна подати у вигляді многочлена від елементарних симетричних
многочленів 0|, а2, .. ., ап цих змінних, коефіцієнти якого належать тому самому
полю Р. Таке зображення є єдиним.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Виразити через елементарні симетричні многочлени такий многочлен:
t (*р *2> *з) = 3«? + 3*2 + 3*з + 5*1*1*3 + 2«? + 2*! + 24
Розв'язання. Заданий многочлен є сумою двох однорідних многочленів
М*1» *2> *з)=3*? + 3*2 + 3*3 + 5*!*2*3
І
М*і- *2> *з) = 2*і + 2д4 + 2^
відповідно третього і другого степенів. Розв'яжемо цю задачу для кожного
многочлена окремо.
Щоб виразити многочлен fx (*j, дс2, х9) через елементарні симетричні
многочлени, застосуємо загальну схему і метод невизначених коефіцієнтів. Складемо
таблицю [табл. 41].
При складанні всіх можливих систем показників вищого члена враховано, що:
1) сума показників у всіх змінних дорівнює степеню многочлена f1(xv x2, *з);
2) послідовність показників у змінних xv xv х9 незростаюча.
Тому
t\(*\> х2, х3) = За* + ао,а2 + 6а3,
де а, Ь — невизначені коефіцієнти. Обчислення коефіцієнтів а і Ь подаємо у ви*
гляді такої таблиці (табл. 42). Отже, а — —9, 6=14. Тоді
f\ (Х[> *2> *з) = 3а? — 9аі°2 + 14аз-
Застосуємо тепер формули скороченого множення. Як відомо,
(хх +х2 + х3)2 = х\-\-х\ + х\ + 2х{х2 + 2ххх3 + 2х2хг.
Звідси
*1 + *2 + *3 = (*1 + *2 + ^з)2 — 2 (*1*2 + *і*3 + *2*з)>
тому /2 (х{, x2t хг) = 2af — 4a2.
170

Таблиця 41
Система показників
вищого члена
*і
3
2
І
*«
0
1
1
х*
0
0
1
Вищий
член
зх\
ах\х2
^ 1*2*3
Відповідний добуток
елементарних симетричних
многочленів 1
•я^3—о„о— оо о з
ао?~1а2~°аЗ==аа102
і,„1—1 1—1 І h„
Таблиця 42
*1
1
1
*2
1
1
ч
0
—2
аі
2
0
а2
1
—3
а3
0
-2
M*b *2, ^) = ^1+^2 + ^3
6 = 24+2а
—28 = -26
Остаточно маємо
/ (*1> *2» *з) = /і ІХ\> Х2> хз) + /2 (х1> *2» *з) =
= 3^ — 9о,о2 + I4a3 + 2a* — 4о2.
2. Знайти симетричний многочлен від п змінних з найменшим числом членів
який містить член х\х\, і виразити його через елементарн'і симетричні
многочлени.
Розв'язання. Позначимо шуканий многочлен через о (Xj, х2, .. ♦, xnY
Згідно з означенням симетричного многочлена, многочлен о (д^, jc2, ..., хЛ
разом з членом *і*2*з • • • х°п містить усі члени, утворені із заданого
переставлянням змінних1. Це означає, що
о (*,, х2, . .., х„) = х\х\ + . .. + х\х\ +
Складемо таблицю (табл. 43).
Таблиця 43
[ Система показників вищого члена
Ч
2
2
1
*2
2
1
1
*3
0
1
1
и
0
0
1
...
...
...
* п
0
0
0
Вищий член
Х\х2
ох\х2хг
Ьх{х2х3х4
Відповідний добуток
елементарних многочленів
,2-2 2-0 2
J1 a2 =a2
'jal""lo2"~lc3 = aaia3
ba{ a2 a3 o4 = &«4
1 Многочлен о (jtj, jc2> . . ., xn) іноді позначають через о (х^х2) і називають
орбітою ххх2 і або моногенним многочленом, породженим членом х\х\.
171

Звідси
О (*,, ДГ2, . . ., Xn) =--4+ aa\°3 + **4-
Покладемо хх = *2 = х3=1, х4 = х5 — . . . = хп — 0. Тоді о1==3, <*2 ~ З,
о$ = 1, а4 = 0 і 9 + За = 3, тобто а = —2. Якщо дсх = дс2 = х3 = лс4 = 1 і хь =
= . .. = хп = 0, то <xt = 4, а2 = 6, о3 = 3, о4 = 1 і ЗО + 16а + Ь = 6. Тому
Ь = 2. Отже,
o(*lf ДГ2, ..., ^)==^- 2а,а3+2а4.
3. Виразити многочлен f (х, у) = х* + у" через елементарні симетричні
многочлени.
Розв'язання. Застосовуючи формули скороченого множення, дістаємо
/ (,, у) = (х2 + у2) (*4 - х2у2 + у') = ((х + у)2 - 2ху) X
X ((*2 + у2)2 - ЗЛ2) - («? - 2,2) ((,2 - 2,2)2 - За|) =
=■• («і - ^2? ~ 3*2 («І - 2«2) = «? - &f »2 + 9а2а2 _ 2*32.
Наведенші приклад свідчить про те, що не завжди загальна схема процесу
подання симетричного многочлена через елементарні є раціональною.
Задачі
28.1. Чи є симетричними такі многочлени:
а) / (хь х2, х3) = х\х2 + х2\Хз + х\хх + х\х6 + хх + х2 + хг\
б) / (хь х2, хз) = 2д:? + 2x1 + 2x1 + х\х2хз — 1;
В) f{Xu Х2, Хз, Х4) = {Х\Х2 + ХзХ4) (Х\ХА + Х2Х3) (*іХ3 + Х2Х4);
г) / (хи х2, Хз) = (х\ — х2) (х2 — Хз) (хз — х\)\
Д) / (Х\, Х2, . . ., Хп) = Х\Х2 . . . Хп-\ + Х\Х2 . . . Хп-2Хп + . . . +
-f- Х2Хз . . . Хпг
28.2. Доповнити задані многочлени найменшим числом нових
членів так, щоб вони стали симетричними:
а)/(хь х*) = 4 + 2x2;+ 1^+¼ ,5-7^2¾¾
б) /(*,, х2, jc3) = х\ + 2.^X2 + 2х2х3 + 5;* tf + 13 * + ** J
в) /(хь х2, хз) = (хі2+х5)2 + 2хіхз + хіх2хз. ^Хз +гу№
28.3. Знайти вищи^ члін'та$$% многочленів!
а) /(хі, х2) = Ьо\о2оз\
б) / (ХЬ Х2, Хз) = а? + 2а2а3 — За§.
28.4. Виразити через елементарні симетричні многочлени такі
многочлени:
а) / {х, у) = х3г/ + уЧ + 2х2 + 2у2;
б) / (х, у) = 2х*у — 5х*у + 2ху* - Ьху\
28.5. Нехай sn(x, у) = хп + уп, де п Є N. Довести, що для всіх
k > 2 виконується рекурентне співвідношення
Sk = aiSfc-l — c2Sfc_2.
28.6. При позначеннях задачі 28.5 перевірити справедливість
таких рівностей:
а) s2 = о\ — 2о<2\
б) S3 = о\ — Заіог;
172

^2 2
в) Si = <3\ — 4оіа2 -f 2а2;
Г) S5 = аі — 5а!02 + 5аіо2;
д) S6 = 0[ — 6а{о2 + 9оі02 — 2а2;
Є) S7 = а\ — 7аіа2 + 14аіа2 — 7оіа2.
28.7. Нехай sn (х, у, z) = хп + уп + zn, де /г б N. Довести, що для
всіх k > 3 виконується рекурентне співвідношення
Sk =OiS/j-i — 02Sk-2 + <33S*-3.
28.8. При позначеннях задачі 28.7 перевірити справедливість
таких рівностей:
а) s2 = оі — 2а2;
б) S3 = зі — Заіо2 -f- Зоз;
в) s4 = °і — 4аіс2 + 2о2 + 4at03;
Г) S5 = af — 5оіа2 + 5oja2 + 5аіаз — 5а2азв,
д) S6 = о\ — 6о\о2 + 9оіа2 — 2а2 + баїоз — 12аі<з2оз + Заз.
28.9. Виразити через елементарні симетричні многочлени такі
многочлени:
а) / (хи х2і хг) = х] + х\ + х\ — хх — х2 — Хз\
б) / (хи х2, хз) = лг^Хз + х2х\Хз + Х\Х2х\ + 2х\Х2х$\
в) / (х\, х2, хз) = х\х\ + x\x\ + x\xl + x\x\ + х\х\ + х2х\\
г) / (хи х2, хз) = (хі — х2)2 + (хі — хз)2 + (х2 — хз)2;
Д) f {хи х2у хз) = (х\ + х2 — 5лг3) (х2 + хз — 5х\) (хх + Хз — Ьх2)\
є) /Ч*і, *2, *з) = (*і — х2хз){х\ — х\Хз)(х\ — ххх2).
28.10. Виразити через елементарні симетричні многочлени чисель-
f (х ... х \
ник і знаменник раціонального дробу , р " ч та знайти його
g(*p . . ., Хп)
значення, якщої
а) і7^Г^7 ^ТТ^Г1 -і = 2, а2 = і,
g(x{, х2> *3) х2 х3 х\ х\х2 х\хз хчхг
о2 = 1, аз = 2;
/(*р x2) х\ + х\ . . .
в) -т г = —9 о- ! змінні *ь х2 набувають значень, що до-
S(X\> X2) Х\+Х2
рівнюють кореням рівняння х2 + х + 2 = 0.
28.11. Виразити через елементарні симетричні многочлени такі
орбіти многочленів!
а) х3]Хз в кільці Р[Х\, х2, хз]\
б) Х\Х2Хз В КІЛЬЦІ Р[Х\, Х2, Хз, Хі]\
в) х\ в кільці Р[хи х2у ..., хп].
28.12. Многочлен f(xx, x2t ..., xn), який змінює знак при
перестановці будь-яких двох змінних, називається антисиметричним.
Довести, що:
а) квадрат антисиметричного многочлена є симетричним
многочленом;
173

б) добуток симетричного і антисиметричного многочленів є ан-
тисиметричним многочленом;
в) будь-який антисиметричний многочлен від двох змінних
f(x\, x2) можна подати у вигляді f(xu х2) = (х{—x2)g(xu х2), де
g(xu х2) є симетричним многочленом;
г) будь-який антисиметричний многочлен від трьох змінних /(х\у
Х2> Хз) можна подати у вигляді f {х\> *2, *з) = (л:і—Хг) (х\ — лгз) X
X (х2 — x$)g (jci, X2, *з), Де g(x\, Х2у хз) є симетричним многочленом.
28.13. ДоВЄСТИ, ЩО КОЛИ СИМетриЧНИЙ МНОГОЧЛеН f(X\, Х2)
ДІЛИТЬСЯ на х\—Х2, то він ділиться також на (х\—х2)2.
28.14. Довести, що коли симетричний многочлен f(x\% х2, Хз)
ділиться на х\ — х2, то він ділиться на многочлен g(x\, х2> Хз) =
= (Х\ — Х2)2 (Х\ — Хз)2 (Х2 — Хз)2.
28.15. Довести, що будь-який многочлен від двох змінних є
сумою деяких симетричного і антисиметричного многочленів.
§ 29. Застосування симетричних многочленів
до розв'язування
деяких задач з елементарної алгебри
Література
[2] — § 26, с. 305—309;
[6] — § 53, с. 328—334;
[44] — § 2, 4, с. 19—46, 62—89.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
\. Розв'язати рівняння
з з
Розв'язання. Зробимо заміну:
з з
Тоді матимемо систему рівнянь
\и3 + vs = 1
16.
Позначивши и + v = df і uv = a2, дістаємо
иг + v3 = (и + v) {(и + v)2 - 3uv) = а? — 3^а2.
Система набуває вигляду
(°1 = '* або Г1 = ''
Повертаючись до змінних и і v, знаходимо
\uv = —5.
Розв'язками цієї системи є
\+V2\ t„ _1-/2Т
Ч-
v. =
"2 ■
2
1-/21 Т3 | п _ 1+/21
174

Враховуючи введену заміну, маємо сукупність рівнянь
2
її розв'язками є: х^ = ЗУ^, х2 = —sV^\.
2. Розв'язати систему рівнянь
(х + у + г = Ь,
lxy + xz + yz = 5,
U3 + ^ + z3= 125.
Розв'язання. Ліва частина кожного з рівнянь системи є симетричним
многочленом, а в перших двох рівняннях — навіть елементарним. Згідно з
прикладом 1, § 27,
З*3 + З/ + 3z3 + Ьхуг = За3 — 9а{а2 + 14а3.
Отже, х3 + у3 + z3 = а3 — Зало2 + Зо3. Тому маємо таку систему:
і = 5, або <xy + xz + yz = 5,
1с9 = 0 [хуг ^0.
Якщо
jc = 0, то \ -
Одним з розв'язків заданої системи рівнянь є: х = 0, у = 1, г = б. Усі інші
розв'язки дістаємо перестановкою чисел 0, 1, 5. Таким чином,
(х, у, г) 6 {(0, 1, б), (0, 5, 1), (1, 0, 5), (1, б, 0), (5, 0, 1), (5, І, 0)}.
3. Розкласти на множники найменшого степеня з раціональними коефіцієнтами
многочлен
f (jc, yt z) » 2*У + 2x*z* + 2(/¾2 — x4 — / — z4.
Розв'язання. Цей многочлен є симетричним. Виразимо його через елемен-
тарні симетричні многочлени (див. задачу 28, 8, в):
х4 + У4 + гА - с4 - 4о?а2 + 2а* + ЬхЧ.
Крім того,
*V + х2г2 + y2z2 = (ди/ + *z + yz)2 — 2*2#z — 2xy2z —
— 2jcf/z2 = 02 — 2ato3.
Тому
І (X, У, z) = 2af — 4ata3 — a4 + 4aja2 — 2a£ — 4ata3 =
^a1(4a1a2 — <y3 —8a3).
Це означає, що многочлен / (jc, у, г) ділиться на многочлен
£і (х, у,г) = х + у + 2.
Оскільки заданий многочлен містить змінні х, у і г тільки в парному степе*
ні, то він не зміниться при заміні х на —х, у на —у та г на —z. Це
означає, що / (х, у, z) ділиться також на многочлени:
ft(*. </> *) = —х + у + г,
8ш(*> У> *) = х — у + ж,
&(*, yt z)=x + y — z.
175

Враховуючи те, що многочлени gt (x, yt z), g2(x, у, z), g3(x, у, г) \ gi(x,y,z)
є попарно взаємно простими і deg / (х, у, г) = 4, маємо
/(х, у, Z) = k(x + y+z)(x + y — 2) (де- у + г)(у + г — х).
Покладаючи тепер х = у = г= 1, дістаємо 3k = 3 і k = \.
Отже, шуканий розклад є
/(х, у, г) = (х + у + г)(х + у — г) (х — у + г)(у + г— х).
4. Скласти квадратне рівняння з коренями х{ і х2, якщо x'j + х2 = 7 і Xj +
+ х2=1.
Розв'язання. Нехай шукане рівняння має вигляд х2 + ох + Ь = 0. Згідно
з теоремою ВІєта, його корені задовольняють умови х1 + х2 = —а і х^ = Ь.
Оскільки х\-\-х\ = <з\ — 3ata2, то
(^-За1а2 = 7, к = 1,
1а, = 1 К = -2.
Отже, Ь = —2, і шукане рівняння є
х2 —х —2 = 0.
б. Довести, що коли х, у, г— цілі числа і х + у + г ділиться на 6, то число
*3 + У3 + *3 також ділиться на 6.
Розв'язання. Розглянемо многочлен /(х, г/, z) = х3 + у3 + z3. Згідно з
прикладом 2, х3 + у3 + z3 = a3 — 33^ + 3a3. Число <jj = x + y + г ділиться
на 6 і тому є парним. Це означає, що хоча б одне з чисел х, у, г парне.
Тому as = xyz ділиться на 2, а Зая ділиться на 6. Отже, х3 + г/3 + z3
ділиться на 6.
Задачі
29.1. У множині дійсних чисел розв'язати такі системи рівнянь!
(*3 + t/3 = 35, U*-y)(x*-y*) = 3,
1 * + у = 5; \(х + у)(х* + у2) = 15;
'*5 + f/5 = 33, f X + t/+2=l,
б) ,
І * + У = 3; е) *2 + у2 + z2 = 9,
в) іх2+ху + у2 = 49, U3 + r/3+z3=l;
U4 +x2t/2 +f/4 = 931; , (x — */ + z = 6,
Г, jx3 + y* + xy(x + y)=l3, Q) U2 + t/2 + 22=14,
' W(x2+ */*) = 468; U3-t/3 + z3 = 36.
29.2. Розв'язати систему ірраціональних рівнянь:
Vx + Vj = 9,
з з
29.3. Розв'язати такі рівняння»
а) * + )Л7 —*2 + *Кі7 —х2 -« 9;
а)
б)
176

«M-?ff(*+$?)-">
з з
в) У\0 — х—УЗ — х= 1;
г) У!Г^х+ /89 + х = 5;
д) ]/ 78 + K24 + Vx — V 84 — КЗО — /л; = 0.
29.4. Розкласти на множники найменшого степеня з дійсними
коефіцієнтами такі многочлени:
а) f(х, у) = ІОх4 — 27х3у — 1 \0х2у2 — 27л;//3 + Юу4;
б) / (х, у) = 6х4 — 1 \х3у — 18х2у2 — 1 Іху3 + 6у4;
в) / (х, у) = 2х4 — х3і/ + Зх2у2 — хі/3 + 2г/4;
г) / (*, і/) = 18х4 — 21r3t/ — 94xV — 2\ху3 + 18t/4.
29.5. Подати у вигляді добутку такі многочлени;
а) f (х, у, г) = (х + у) (х + г) (у + г) + хуг;
б) /(*, у, z) = x3(y + z) + y3(x + z) + z3(x + y)+xyz(x + y + z);
в) f(x, у, z) = (x — y)* + (y — zY + (x — zY;
г) f(x, у, z) = (x2 + y2 + z2+xy + xz + yz)2-(x + y + z)2(x2 +
+ У2 + z2).
29.6. Скоротити дріб
/(де, ц, г) уг — х2 + хг — і/ + ху — г2
g (*. У, г) ~~ х (уг — х2) + у (хг — у2) + z (*(/ — г2)
29.7. Скласти квадратне рівняння з коренями х\ і де', якщо Х\,
Х2 є коренями квадратного рівняння х2 — Ах + 3 = 0.
29.8. Довести, що коли х\, Х2 є коренями квадратного рівняння
х2 — бх + 1=0, то сума х" -f & є цілим числом при будь-якому
натуральному я і при жодному з них не ділиться на 5.
29.9. Скласти кубічне рівняння, коренями якого є квадрати
коренів рівняння
х3 — 2х2 + х— 12 = 0.
29.10. Довести такі тотожності:
а) х* + у* + (х + у)* = 2(х2 + ху + у2)2;
б) (х + у)3 + Зху(1 -х-у)- І = (х + у- 1)(х2 + у2-ху +
+ х + у+1);
в) а(Ь + с)2+ Ь(с+а)2+с(а + Ь)2= (Ь + с)(а+ с)(а + Ь) + АаЬс;
г) xyz (x + y + z)3 — (yz + xz + ху)3 = (х2 — уг) (у2 — хг) (z2 — ху);
д) (ху + хг + уг)2 + (х2 - уг)2 + (у2 - xz)2 + (z2 - ху)2 = (х2 +
+ У2 + z2)2.
' 29.11. Довести, що коли х + у + 2 = 0, тої
а) x4 + (/4 + 24 = 2(;n/ + *2 + «/2)2;
б) 2 (х* + у* + г4) = (х2 +у2 + z2)2;
в) 2 (х5 + у5 + z5) а. Ьхуг (х2 + у2 + za).
177

29.12. Довести, що коли ху + xz + yz = 0, то (х + у)2 (х + z)2 X
X (у + z)2 + 2x*yh* = x*(y + z? + у4(х + zf + z* (х + у)2.
29.13. Довести, що коли ху + xz + yz = 1, то
1
+ ■
+ ■
4хуг
l_v2^1_22 (1 _ jc2) (1 — у») (1 — ^2) *
29.14. Довести, що коли х + у + z = 0 і ху + xz + yz = 0, то
виконується рівність
З (A/3 + x3z3 + yh3) = (х3 -\-у3 + z3)2.
§ ЗО. Результант двох многочленів. Виключення невідомих
з системи двох рівнянь з двома невідомими
Література
[1]~ § 27, с. 296—311;
[2] —§ 27, с. 310-325;
[3] —гл. 15, § 3, с. 500-504;
[б]— гл. XI, § 5, с. 432—438;
[6] — $ 54, с. 334—345;
[8]- гл. 6, § 2, о. 265—271.
ТЕОРЕТИЧНІ ВІДОМОСТІ
Нехай
t (х) = апхп + ап_ххп-х + .. . + axx + Oq»
gixy-Ь^ + Ь^іР-1 + .
, + b{x+b0
є многочленами над полем Pt anbm ^ 0 і а{, а2, .. ., ап — корені многочлена
Результантом многочленів f (x) і g(x) називається вираз
*</. *)- <8 («і) в («2) •••«(«„)•
Результант /? (/, g) є симетричним многочленом від ар а2» • • •» ал> Т0МУ
результант довільних двох многочленів над полем Р є елементом цього поля.
Нехай 7р І2> •• •» Km— корені многочлена g(x). Тоді:
1°. Я </.«)-«JX П («,-!/);
1</<т
2°. /?(e. /) = (-!)""*(/, g).
Для того щоб многочлени f (x) і g(*) мали спільний корінь, необхідно і
достатньо, щоб їхній результант дорівнював нулю.
Результант многочленів f (x) \ g (x) можна подати у формі Сільвестра:
RQ,g) =
п
о
ип-1
ап
' 6 '
6 '
ym-l
«0
0
m рядків
' я рядків
178

Дискримінантом D (f) многочлена f (x) називається вираз
n(n—\)
D (/) = (-1) 2 a-*R{f,n
де R (/, /') — результант многочлена / (x) і його похідної /' (х).
4 При цьому справджується рівність
D(/) = a*"-2 П («,-«,)■•
\<І<І<П
Многочлен / (х) має кратний корінь тоді і тільки тоді, коли його дискримінант
дорівнює нулю.
Нехай задано систему двох алгебраїчних рівнянь з двома невідомими, що
мають коефіцієнти з поля Р:
(fix, t/) = 0,
\g(x. ї/) = 0.
Схема виключення невідомих з цієї системи така:
1) упорядковуємо многочлени fix, у) і ц(х, у) за спадними степенями
однієї із змінних, наприклад, х;
2) складаємо результант R (/, g), розглядаючи змінну у як параметр;
3) знаходимо всі корені результанта pj, р2» • • •> Р/;
4) підставляємо в задану систему замість змінної у значення рр Р2» • • • Р/;
дістаємо сукупність / систем двох рівнянь з одним невідомим х\
5) розв'язуємо цю сукупність систем рівнянь і складаємо відповідні пари
розв'язків.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
Обчислити результант R (/, g) для многочленів
f(x) = x2 — 3*+ 6 і §М = ^ + хг-л'-1.
Розв'язання. 1 спосіб. Заданий многочлен / (х) має комплексні корені.
Многочлен g(x) = (x2— \)(х + 1) має коренями числа —1 і 1. Оскільки
R(f, g) = (-D3,2« fc, f) = R(g, /),
то
Ж/, £)=/(-0/(-0/(1)=10. 10-4 = 400.
II спосіб. Нехай аІ9 о2 — карені многочлена / (х). Тоді
*(Л £Г> — («і -Ь «і — «і — 0 («І Н- «| _ «2 — 1) « («!«2)3 +
+ (aia2)2 (ai + az) - aia2 (ai + 4) — (а\ + 4) +
+ (aia2)2 — aia2 (ai + a2J — (ai + 4) + aia2 + (ai + аг) + !'•
За теоремою Вієта, a^ == 6 і 0¾ + a2 = 3. Тоді
al + a2 = (al + аг)2 — 2ata2 = З і
a? + a3=(a1+a2){(a1 + a2)2-3a1a2)=-27.
Отже,
Я (/, g) = 216+ 108+ 18 + 27 + 36— 18 + 3 + 3 + 3+1 =400.
III спосіб. Обчислимо результант R (/, g) у формі Сільвестра:
*(/,£) =
, 1
0
0
1
о
—3
1
0
1
1
6
—3
1
—1
1
0
6
—3
-1
—1
0 І
0
6
0
-1 1
1
0
0
0
10
—3
1
0
4
1
6
—3
1
—7
1
0
6
—3
-1
—1
0
0
6
0
—1
179

=
1—360
6 7—90
4—7-1 0
1 1 —1 — 1
(—7 + 36 • 3 — 36 • 7
—З 6
7 —9
—7 —1
7-168-63-18) = 400.
Зауваження. Найбільш раціональний тут І спосіб. Проте, якщо важко знайти
корені заданих многочленів, то доцільно застосувати II або III спосіб.
2. Довести, що многочлен
f (х) = *4 — 2*3 + (а + 1) *2 — 2а* + а
має кратний корінь при будь-якому аєС.
Розв'язання. Достатньою умовою існування кратного кореня
многочлена
4J3
2
X 1
-1
є те, що дискримінант многочлена дорівнює нулю. Крім того, D(f) = (—1)
R (/, /'). Знайдемо похідну:
П*) = 4*3 — 6*2 + 2(а + 1)* —2а.
X
Тоді
R (/, П
') =
11
0
0
0
0
0
о
1
0
0
4
0
0
0
—2
1
0
2
4
0
0
= 24
«=2<
—
-2
(а+1)
1 —2
0 1
-6 2(а+1)
4 -6
0 4
0 0
(а+1)
—2
1
-2(о+1)
—6
4
0
1 —2
0 1
1 -(*+!)
2 -3
0 2
0 1
'а
1 —2
0 (1-а)
0 1
0 2
0 1
24
а
—а
—2а
(в+П
—2
—2а
2(а+1)
—6
4
—2а
(в + О
—2
6а
2 (а+1)
—6
4
(а+ 1)
—2
За
(я + 0
—3
0
(а+1)
(2а - 1)
(-а-1)
—3
0
За
1 (-а-І)
0 (2а—1) (-
0 (а + 1) -
а
—2а
(в+1)
0
—2а
0
а
—2а
0
0
2(а+1) —2а
—6
а
—2а
(я+ О
—4а
—2а
2(а+1)
—6
—2а
(а+1)
—2а
—а
(а + \)
(а-2)
-2а
0
За
(я + 1)
(а-2)
-За
За
-5а + І)
2 (а + 1)
2(а+1)
0
а
—2а
0
0
—2а
2 (а+1) -
а 0
—2а а
0 0
0 0
—а 0
(1-а) 0
а
—а
—2а
—а
(1 -а)
а 1
-2а
За
0+в) 1
0
0
а
0
0
0
-2а
0
0
а
0
0
0
-2а
=
180

Якщо а = 0, то R (/, f) = 0; якщо а Ф 0, то
0 __ а + 2 3 (а — 1)
Я(/,/')=2*.а
—2а +
1 — (а + 1) За —2а
0 2а—1 (—5а+1) За
0 а+1 -2(а+1) 1+а
І —а + 2 а — 2 —2а + 1 1
= —24а 2а — 1 —2а +1 За =0.
І а+1 —а — 1 1 + а |
Отже, при будь-яких а £ С, #(/,/') = 0 і £>(/) = 0. Тому многочлен f (x) має
кратний корінь.
3. Розв'язати систему рівнянь
Г*/2 + х2-*/-Зх=0,
[у^^вху —х2+Му+ 7х—\2=0.
Розв'язання. Застосуємо метод виключення невідомих. Для цього в лівих
частинах рівнянь впорядкуємо многочлени за спадними степенями змінної у
(можна взяти і змінну х):
(уг — у+х2—3х = 0,
[у* + (і і — бх) у — х2 + 7х — 12 *= 0.
Складемо результант для цих многочленів і знайдемо його корені:
R(x)
с) =
1 1
0
0
1 о
=
=
1
-3
1
1 -
0 1
1 11 -
0 1
—1
1
12 — 6а:
1
1
12 — 6*
1
2 (х — 2)
0
—X
12— 6а:
1 х2 — 3*
— 1
- 6* —а:2 + 7х —
11—6*
а:2 —3*
-1
—2а:2 + 10* — 12
11—6а:
0
—2а:2 + 4х
12— 6л:
1 0
—3 -х
1 12 — 6* -
х2 — Зх
—х
—х2 + х
= 2х (х
0
*2—3*
12 0
—*2 + 7х — 12
0
х2 —3*
0
—х2+7х — 12
х2 — Зх
0
-х2+7х — 12
а:2 —3*
0
_*2+7*_ 12
-2)
1
—3
1 12-
=
=
=
=
0
-6*
х —3
—1
: 2 (X — 2)
= 2х (х — 2) (х2 — х — 3 (х — 3) (12 — 6х) + х2 — Зх + 12 — 6х) =
= 2х (х — 2) (20х2 — ІООх + 120) = 40х (х — 2)2 (х — 3).
Отже, коренями результанта є 0, 2 ІЗ. Підставимо їх у задану систему
замість змінної х.
а) Якщо х = 0, то матимемо систему з одним невідомим:
(</2-</ = о,
\^2+ Цу_і2 = 0.
її розв'язком є у= 1. Це означає, що xt=0, ^• = 1 є розв'язком заданої
системи.
б) Якщо х = 2, то дістаємо
|ї/2-г/-2=0,
І//3 — і/ — 2 = 0.
181

Розв'язками цієї системи є: у =—І, у = 2. Тоді розв'язками заданої
системи є: х2 = 2, у2 = — 1 і х3 = 2, і/з = 2.
в) Якщо х = 3, то система набуває вигляду
(f-y = 0,
lj,« — 7у = 0.
її розв'язком є у = 0. Отже, х4 = 3, і/4 = 0 є розв'язком заданої системи.
Таким чином, задана система рівнянь має розв'язки:
(*, г/)Є«0, 1), (2, -1), (2, 2), (3, 0)}.
Задачі
30.1. Обчислити результант R(f, g) для таких пар многочленів:
а) /(х) = Єх2+х — 2, є) /(х) = х4 —2х2 + 3,
g(x) = 3x2-4x + 2; £(х) = х2-х + 1;
б) /(х) = х3 + 2х—1, ж) /(х) = 3х3 + х — 1,
g(x) = x2-2x — 3; #(x) = x2 —2x + 4;
в) /(х) = 2х3-{ х2 — 2х— 1, з) /(х) = х3 —2х + 2,
g (х) = Зх3 — 4х2 + 7; £ (х) = х2 + 2х + 2;
г) /(х) = х<-Зх2-4, к) /(х) = х3 +х2+х-1,
£(х) = 3х3 + х2 + 3х-1; g(x) = x3-x- 1;
д) /(х) = 2х2+х — 2, л) /(х) = х3 + 2х2+х-2,
£(х) = х4+5х2 + 4; g(x) = x2 —2х + 3;
є) /(х) = х2-2х + 2, м) /(х) = х3 + 2х2 + 4х+1,
£(х) = 2х2 + х —5; £(х) = Зх2+4х + 4.
30.2. Довести, що:
а) R if, gx ±g2) = R if, gx) ± R if, g2), коли deg/ = 1;
б) Rif, gx-g2) = R(f, gx)-Rif, g2);
B) R ifx • /2, £l -g2) = R (fx, gx) ■ R (/,, g2) • # (/2, gx) • R (/2, #)•
30.3. При якому значенні X мають спільний корінь такі
многочлени:
а) /(х) = 2х2 + Хх — 3, в) /(х) = х3 — Ьх2 + 4Хх — 4,
g(x) = Xx2+x — 2; £(х) = 3х2 — 5Хх + 8;
б) f(x) = х2 + X, г) / (х) = х3 + Хх* + 2,
# (х) = х3 — Зх2 + Хх — 3; g(x) = х3 + 2Хх — 1?
30.4. Обчислити дискримінант таких многочленів:
а) /(х) = х3 + 6х + 2;
б) / (х) = х3 — біх + 4 — 4і;
в) /(х) = х3 —9х2 + 21х—5;
r\ t <х\ _ хі х2 і J j
д) /(х) = х<-(1 + 2І)х3-(4-2()х2 + (1 + 6t)x + 3;
є) / (х) = х4 — х3 — Зх2 + х + 1;
є) /(х) = х5 + 2;
ж) / (х) — х" + а, де п € N і а £ С.
30.5. Знаючи, що дискримінант многочлена
/ (х) = аьх? + с4х4 + аз*3 + агх2 + а\Х + ао
182

дорівнює нулю, знайти дискримінант многочлена
cf (х) — аох5 -f а\хА + сцх6 + азх2 + сцх + а5.
Результат узагальнити.
30.6. Довести, що дискримінант многочлена / (х) = Xі + ах2 +
+ bx -f- c дорівнює дискримінанту многочлена
g (х) = 8х3 — 4ах2 — 8сх — (Ь2 — 4ас).
30.7. Довести, що:
а) D((x-a)-f(x)) = D(f(x)).lf(a)}2;
б) D(f-g) = D(f)-D(g)-[R(f, g))2.
30.8. При якому значенні X мають кратні корені такі
многочлени:
а)/ (х) = 4х3 — 1х + \;
б) f(x) = x3 — Зх2 + \2;
в) f(x) = x3 + (2-3i)x2 — he — 2?
30.9. Розв'язати такі системи рівняньї
а) (х2 + 2і/2 = 17,
(б*2 — ху— 12«/2 = 0;
б) (^-^-3 = 0,
Ь2+;п/ — і/ — 3 = 0;
в) (у2-5у + 4х-4 = 0,
\2у2 + у-х2 + \=0;
г) (л:2# — 2х2 — ху — 4 = 0,
\ л:2*/ — 2л;2 + 2х + у — 2 = 0;
д) 15л:2 — 5у2 — Зх + 9у = 0,
(5л:3 + 5«/3 — 15л:2 — ІЗху — у2 = 0;
є) ((«/ — 1)х2+л-у — 3 = 0,
((</-
1(</-
(</_1)л;2 —2л:+ (/-1=0.
Розділ VI. МНОГОЧЛЕНИ НАД ПОЛЕМ
КОМПЛЕКСНИХ ЧИСЕЛ
І НАД ПОЛЕМ ДІЙСНИХ ЧИСЕЛ
§ 31. Многочлени над полем комплексних чисел.
Алгебраїчна замкненість поля комплексних чисел
Література
її] —§ 28, 29, с. 311—319;
І2] — § 28, § 29, о. 325—334;
ІЗ] —гл. 16, § 1,с. 505—512;
І5]— гл. VII, § 2, с. 255—261; гл. VIII, § 3, с. 291—297; гл. IX, § 4, с. 343-347;
183

[6] —§ 23, 24, c. 147—158;
[7]_§ 13, c. 76—83;
[8] —гл. G, § 3, c. 272—281.
ТЕОРЕТИЧНІ ВІДОМОСТІ
Нехай f (x)— деякий многочлен над пслем P. Якщо deg / > 1, то існує
розширення К поля Р, в якому міститься деякий корінь многочлена / (х). З цього
твердження випливає, що для будь-якого многочлена /(*)£ Р [х] степеня degf > 1
існує таке розширення L поля Р, що f (х) можна подати в L [х] у вигляді добутку
лінійних множників.
Поле Р називають полем розкладу многочлена/ (*), якщо f (х) розкладається
в Р [х], на лінійні множники. Поле Р, якеє полем розкладу будь-якого
многочлена / (х) £ Р [х], називають алгебраїчно замкненим.
Нехай f (z) = anzn + .. . + fli? + aQ— многочлен ненульового степеня над
полем С комплексних чисел, а М — як завгодно велике додатне дійсне число.
2Л
Введемо позначення Л^ = 1 + ггт , де А — найбільший з модулів коефіцієнтів
\ап\
|лЛ_і|> • • • » \а\\» | ао |* Тоді Аля будь-якого г £ С, | / (г) | > М, як тільки
1#і» 1/ 2^ } • Многочлен /(z) має тільки ті корені, модуль яких
V \ап\)
А
менший за число N0 = 1 + -rj-т . Крім того, як тільки \z\>N0, то модуль
старшого члена многочлена / (х) більше за модуль суми решти членів цього
многочлена.
Кожен многочлен ненульового степеня з комплексними коефіцієнтами
f(z)^anzn + ... + a1z+a{i
має хоча б один комплексний корінь. Звідси випливає, що незвідними над полем
комплексних чисел є тільки многочлени першого степеня, а кожен многочлен
л-го степеня (п > 0) над полем комплексних чисел «диним способом (з точністю
до порядку множників) розкладається над цим полем на лінійні множники:
/ (*) = ая (*-*i)('-*i> ••• (*-*«)'
де 2і, zv ... , Zn — корені многочлена / (г). Отже, поле С є алгебраїчно
замкненим і для коренів многочлена / (z) у полі С є справедливими формули Вієта:
ап—\
Zi+z2+... + zn = -——t
| z I > max
а,
1п-2
ЧЧ + ¥г + • • • + *„_!*„ = —
«A---^-(-1) V
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Довести, що фактор-кільце Q[x]/ <х2—2> кільця Q [х] за головним ідеалом
<х2 — 2> є полем розкладу многочлена f(x)=x2 — 2 з кільця Q[x].
Розв'язання. Многочлен / (*) = х2— 2 не має раціональних коренів і тому
є незвідним над полем Q. Ідеал </> =« <х2 — 2> відіграє роль нуля
в фактор-кільці Q[x]/<x2—2>, а елементи останнього мають вигляд а =
= &(*)+</>> де g(x)£Q[x]. Оскільки в кільці Q [х] можна виконувати
ділення многочленів з остачею, то вважатимемо, що deg g < 2. Нехай а —
184

m ї
= &(*) + </> =5^ </>• Тоді многочлени /(x) і g(x) € взаємно простими. Тому
існують многочлени и (х), v (х) £ Q [х] такі, що / (х) u (x) + g(x)v (х) = 1.
Звідси g(x) v (х) = 1 — / (x) w (х), тому в кільці Q [х] І <х2— 2> виконується
рівність [g(x) + </>] [v (x) + </>] = 1 + </>• Це означає, що для еле.
мента а £ Q[x]/ <х2—2> існує обернений елемент а~[ = v (x) + </>.
Отже, Q[x]/ <х2 — 2> є полем, яке містить поле Q = \ — + </>
ізоморфне Q. Ототожнимо число —— £ Q з класом — + </> .
Нехай Ь = х + </> € Q [*]/ <х2 —2>.
Вважаючи, що — 2 = -2+ </>, маємо: f (b) = Ь2 + <—2> ^.- [х + </>]2+
+ 1-2+</>] = [х2 + </>] + [_ 2+</>] = х2-2+</> = </>.
Аналогічно / (—Ь) = / (—х + </>)= </>. Це означає, що многочлен / (х) =
= х2—2 має в полі Q [х] / <х2—2> два корені: д^ = £ і х2 = — Ь, Тоді
/ (х) = (х — b)(x + b) і поле Q [x] / <х2 — 2> є полем розкладу многочлена
/(*) = *»_ 2.
Розкласти на незвідні над полем С множники многочлен
f (х) = (2і — 3)х3 — 2 — Зі.
Розв'язання. Знайдемо корені многочлена / (х):
(21 — 3)х3 — 2 — Зі = 0, х3 = — і,
З З
З "q"tc + 2&тс -й-іс + 2&тс
«12, 3^=1^7 аб° *1. 2, 3=cos з + 'sin з ' ДЄ k==0t I>2'
Кз і- ^з і
і.
Тому *! = *, х2 = — — — -J і* Хя =■
0тже- /(^(2,-3)(,-0(,+^:+^)(,-11:+^).
3. Знайти зведений многочлен за його коренями х\, Хі х2 і х\, якщо числа хх і х2
є коренями рівняння
х2 + (і + 2)х — і = 0.
Розв'я за ння. Нехай / (х) = х3 + ах2 + Ьх + с — шуканий многочлен. За
формулами Вієта маємо
х\ + хгх2 + Xg = — а,
3 , 2 2 , 3
х\х2 ~Г •*! х2 ~Т" *1**2 ™
V3J3
[*1*2 ~ C*
Проте ах + х2 = — і— 2 і Х]Х2 = — і. Тому
а = — (дсх + х2)2 + ххх2 = - (- і: - 2)2 _ t = - 3 - 5t\
6 = xxx2 (х* + Xtx2 + х\) -= xxx2 [(*! + *2)2 — *і*2] =
= — f [(1 + 2)2+ і] = _5 — З/,
с = — (хл)3 = — /.
Отже,
Задачі
f (х) = х3 — (3 + 5t)x2 — (5 + Зі)х — t.
31.1. Довести, що Q[x]/<x2 — 3> є полем розкладу многочлена
f (x) = х2 — 3.
31.2, Довести, що поля Q\x]/<x2 — 3> і Q(V3) ізоморфні.
185

з
v 31.3. Чи є поле QiV^) полем розкладу многочлена f(x) = х3—2?
31.4. Знайти мінімальне поле розкладу многочлена f (х) = х2 — 5
з кільця QM.
31.5. Знайти мінімальне поле розкладу многочлена / (х) = х4—1
з кільця Q [х].
31.6. Довести, що поле R [х]/<х2 + 1> є алгебраїчно замкненим.
31.7. Чи є алгебраїчно замкненим поле Q [х]/<х2 + 1>?
31.8. Знайти додатне число т таке, що з нерівності \z\>m
випливають такі нерівності:
а) І z4 + 4z3 — 4z2 — 21 > 648;
б) jz4 —4z3 + 2z + 6|>8;
в) |4z4 + z3 — 2z2 + l + t|>512;
г) |/(z)|>|/(fl)|, якщо f(z) = 2z* — z*+z3 — (2 + i)z2 + iz-
-(3 + 2ї) та а = і.
31.9. Чи може число 3 — 41 бути коренем таких многочленів!
а) f(z) = 2/z5 + 3z4 — (1 +і)г* + (2 — Зі)г — 4і,
б) Дг) = г4 — 6z3 + 5z2 + tz — 3 + 4*?
v 31.10. Розкласти многочлен f (х) на незвідні над полем С
множники:
- а) /(*)-5х*+2*+10;
-б) f(x) = x2-(l+ і)х + і\
в) /(д:) = х4 —6л:3+ 11х2 —6л:+ 1;
< г) f(x) = x4 — 10х2+169;
Д) /(х)=х8-1;
•є) /(х) = *4+8х3 + 8х — 1.
31.11. Знайти многочлен найменшого степеня, в якого!
а) число і є подвійним коренем, а 1—і — простим;
б) число 2 є подвійним коренем, а 2t, 3 + /, 3 — і — простими
коренями;
в) число — 2і є потрійним коренем, а —3 — простим.
31.12. Знайти суму квадратів коренів многочлена
/(*) = *3 + 3x2 — 7л:+ 1.
31 .13. Знайти суму кубів коренів многочлена
f(x) = x3 + 2x2 + x — 3.
31.14. Довести, що коли комплексні числа ai,a2, ..., ап
задовольняють умови
ai + a2 + . . . + a„ = — ап-и
aioi2 + ...+ <Xn—\bn = a>n—2»
aia2.. .<хя =ч (—l^ao,
то ці числа є коренями многочлена
f (z) = zn + a^iz"-1 + ... + aiz + a0.
31.15. Знайти зведені многочлени, в яких:
а) корені дорівнюють у\ = х2Хз, у2 = х\Хз, у* = хм, а хи *2»
хз є коренями многочлена / (х) = х3 — 2х — 5;
186

б) корені дорівнюють у і = --І-, у2= -р—, уз = J!L, а хи х2,
X2XZ х\х3 х\х2
Хз є коренями многочлена / (х) =* — 2л:3 + х2 + 2х + 3.
31.16. Довести, що всі корені наступних многочленів є
дійсними числами:
а) f(X) = x3 + 3x — 1;
б) /(^) = a:3 + 7x2 + 25a;+1.
31.17. Корені многочлена f(x) утворюють арифметичну
прогресію. Знайти цей многочлен і його корені, якщо:
а) / (х) = х3 + 6х2 + 5х + г,
б) / (х) = *3 — 18л:2 + дх + 24.
-••■ 31.18. Один з коренів многочлена
f(>) = x3 — 7х2 + Их + г
вдвоє більший за другий. Знайти f (х) і його корені.
31.19. За формулами Віета знайти зведений многочлен f(x)
найменшого степеня, якщо його похідна має прості корені 2 та
1—і, двократні корені і, а 1 є коренем многочлена f(x).
31.20. Довести, що рівність ab = c є необхідною і достатньою
умовою того, щоб серед коренів рівняння
х3+ах2 + Ьх + с = 0, сФ0у
були два протилежні числа.
31.21. Розв'язати рівняння х3— 3\ҐЗх2 +7х—|/3 = 0, якщо
один з його коренів більше від другого на У2.
31.22. Розв'язати рівняння 8х3 + 4х2— 34*+15 = 0, якщо два
його корені Х\ і X2 задовольняють рівняння 2х\ — 4x2= 1.
*' 31.23. Корені рівняння х3 — 6х2 + px + q = 0 задовольняють
співвідношення Х[ :х2 :хз = 1: 2: 3. Знайти ці корені та
коефіцієнти р і q.
§ 32. Многочлени над полем дійсних чисел
11
[2
[З
[5
[6]
[7
і»:
Література
— § 29, с. 320—323;
— § 29, с. 334-337;
— гл. 16, § 2, с. 513—514;
— гл. IX, § 5, с. 347—350;
— § 24, с. 159—161;
— § 14, с. 84-86;
— гл. 6, § 4, с. 282—283.
ТЕОРЕТИЧНІ ВІДОМОСТІ
Нехай / (z) = anzn + an__lzn 1 + ... +a{z + a0 — многочлен з дійсними
коефіцієнтами. Якщо комплексне число г0 є коренем многочлена / (z), то
спряжене комплексне число zQ також є коренем цього многочлена. Крім того, якщо
комплексне число z0 є коренем 6-ї кратності многочлена / (z), то спряжене комп -
лексне число ~z0 також є коренем многочлена тієї самої кратності.
Кожен многочлен з дійсними коефіцієнтами, степінь якого більше 2, є
звідним над полем дійсних чисел.
187

Кожен многочлен f (г) з дійсними коефіцієнтами єдиним способом
розкладається над полем R у добуток лінійних множників і квадратних тричленів:
/ (2) = ап (г - г^ .. . (z - z,)*/ (z2 + pi+lz + в/+1)*'+і . .. (г2 +
+ Pm* + gm)krn.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Розв'язати рівняння
jc4 — х3 + х2 + 9д: — Ю = 0,
якщо один з його коренів дорівнює 1—2і.
Розв'язання. Задане рівняння має дійсні коефіцієнти. Тому число 1 + 2і
також є його коренем, а многочлен
/ (х) = х4 — х3 + х2 + 9* — Ю
ділиться на квадратний тричлен х2 — 2х + 5.
Виконаємо ділення «кутом»
х4—х* + х2 + 9х — \0\ х2 — 2х + Ь
— хА — 2хг + Ьх2>
■ *з __ 2х2 + Бх
х2 + х-
— 2х2+ 4*—10
— 2jc2 + 4х — 10
0
Щоб знайти інші корені заданого рівняння, розв'язуємо рівняння хг-\-х —
— 2 = 0. Маємо х = — 2, х = 1. Отжг,
хг = 1 — 2і, х2 = 1 + 2/, х3 = — 2, *4 = 1.
2. Знайти многочлен найменшого степеня з дійсними коефіцієнтами і старшим
коефіцієнтом, що дорівнює 5, якщо цей многочлен має потрійний корінь
1 — і і простий корінь 2.
Розв'язання. Оскільки шуканий многочлен / (х) має потрійний корінь
1 + /, то його розклад на незвідні множники над полем С має вигляд: / (х) =
= 5 (х — 1 + іу (х — 1 — О3 (х - 2).
Звідси
/ (х) =-- 5 {х2 — 2х + 2)3 (х — 2).
З адач і
32.1. Розв'язати такі рівняння:
а) х4 + х3 — х2 — Юх —12 = 0, якщо хх = — 1 + і |/3;
б) л:4 — х3 + х2 + 4х + 10 = 0, якщо хі = —1+і\
в) х4 — хг — 1 їх2 + 31* — 20 «= 0, якщо хі = 2 + і;
г) х4 — 10г3 + 36л:2 — 58л: + 35 = 0, якщо х{ = 2 — 1.
32.2. Число —3 -+- і є коренем рівняння з дійсними
коефіцієнтами х3 -\-х2 +ах + b = 0. Знайти числа а і b та два інших корені
рівняння.
32.3. Довести, що коли зведений многочлен з дійсними
коефіцієнтами має тільки уявні корені, то його можна подати у вигляді
суми квадратів двох многочленів з дійсними коефіцієнтами.
188

32.4. Довести, що многочлен
/ (х) = апхп + ...+а{х + ао
s дійсними коефіцієнтами має суто уявні корені тоді і тільки тоді,
коли многочлени
£і (У) = яо — а2у2 + аАу* —...
і
g2(y)=a{— asy2 + аьу* —...
мають спільний дійсний корінь.
32.5. Чи мають суто уявні корені такі многочлени з дійсними
коефіцієнтами:
а) /(х) = х* — 4х3 + Зх2 — 8х + 2;
б) f(x) = x* + 2x* + x2 + 11* + 3;
в) f(x) = xA+x* — 4х2 + 3х — 21;
г) / (х) = х5 + Зх3 — х2 + 4х + 4?
32.6. Многочлен f{x) = а:4 — 2х3 + 6х2— 18х + а має суто уявний
корінь. Знайти дійсне число а і всі корені цього многочлена.
32.7. Зведений многочлен четвертого степеня з дійсними
коефіцієнтами має всі уявні корені. Довести, що цей многочлен можна
подати у вигляді суми квадратів зведеного квадратного тричлена і
многочлена першого степеня з дійсними коефіцієнтами.
32.8. Довести, що многочлен
f(x) = хА + 2а:3 + 4х2 + Зх + З
не має дійсних коренів.
32.9. Довести, що при дійсних a, b і с рівняння
Xs + а2х6 + Ь2х4 + с2х2 « 0
не має дійсних коренів, відмінних від нуля.
32.10. Розкласти наступні многочлени на незвідні над полем R
множники:
а) f(x) = хА + 4х3 + 2х2 + 20* + 25;
б) f (х) = а:4 + 2х3 + 4а:2 + За: + 1;
в) f(x)=x* + x* + x2 + x+ 1;
г) / (х) = х* — 2а:3 + х2 + 3;
д) f(x) = х6 + х5 + х* + 2х3 + х2 + х + І.
32.11. Чи мають дійсні корені такі многочлени:
а) f(x) = 2x6 + x* + x2+ 1,
б) f(x) = 4x* + 2x* + 3x2+tf
32.12. Чи має многочлен /(а:) = 2а:3— За:2 + 4а:—1 корінь з
проміжку [4, 10]?
32.13. Довести, що многочлен
/ (х) = 6х5 — 4а:3 + 2а:2 + За: — і
при всіх х > 2 набуває тільки додатних значень.
189

§ 33. Рівняння третього і четвертого степенів
Література
[2] —§ ЗО, с. 337—348;
[3] —гл. 10, § 3, с. 515—521;
[5] —гл. VIII, § 2, с. 284-291;
[6] —§ 38, с. 233—240.
ТЕОРЕТИЧНІ ВІДОМОСТІ
Нехай х3 + а2х2 + а{х + а0 = 0 — рівняння третього степеня з
комплексам
ними коефіцієнтами. За допомогою підстановки х = у — — зведемо його до виду
о
х3 + px + q = 0. (1)
2 З
Число D = !L-|- -Е- називають дискримінантом рівняння (1). Корені цього
рівняння знаходять за формулою
з з
..-У-\+ут> + УЦ-у*^
яка називається формулою Кардано.
з з
Якщо и{= у —-о" + VD і Pj — І/ —~2 —V& е тими значеннями
кубічних коренів, при яких" ' х{ = u{ + v{ є коренем рівняння (1), то решту
коренів цього рівняння обчислюють так:
1 іУТ
х2 = - Т ("і + vi) + ~2~ (wi - vi)>
і іУТ
*з = - Т ("і + v\) - -2- ("і - vl)>
р
Числа Wj і Vi знаходять з умови и^{ = — -т.
Якщо коефіцієнти р і я рівняння (1) є дійсними числами, то:
а) при D > 0 рівняння має один дійсний і два комплексних спряжених
корені;
б) при D = 0 рівняння має три дійсних корені, два з яких дорівнюють
один одному;
в) при D < 0 рівняння має три дійсних різних корені.
Рівняння четвертого степеня
хА + а3х3 + а2х2 + ахх + а0 = 0 (2)
в результаті введення допоміжної змінної t запишемо у вигляді
[Л , аЗХ t \2 (4 \ 2 /^ \ І2
Значення змінної t беруть таке, щоб у правій частині рівності утворювався
квадрат деякого двочлена ах + Ь. Для цього розв'язують допоміжне кубічне
рівняння
І* - a2t2 + (а^а\ - 4а0) t - (а23а0 - 4a2aQ + а\) *= 0, (3)
яке називають кубічною резольвентою рівняння (2),
190

Якщо f0— один з коренів рівняння (3), то рівняння (2) рівносильне
сукупності рівнянь:
І * + -jp * + "з" = а* + &.
х2+-^х + - = -(ах + Ь).
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Розв'язати рівняння и3 — 3/* + 2 = 0.
Розв'яз а н н я. Зведемо це рівняння до виду (1). Для цього помножимо
обидві його частини на —і. Матимемо
х3 + Зх — 2і = 0.
з
Тут р = 3, ¢--21 iD = 0. Тоді Y-\ + VD-=VT. Нехай и1=в-і.
Оскільки MjUj = — 1, то vx = — t. Звідси х{ = — 2t, *2 = і, *3 = і.
2. При якому значенні дійсного числа а рівняння
У6 + З/ + 3 (і + Va ) у + 2а + 3 Уа+ 1 = 0
має три дійсних різних корені?
Розв' язання. Введемо заміну у = х — 1, Матимемо
(х - І)3 + 3 (де- І)2 + s(\+Va)(x^\) + 2а + 3/5"+ 1=0,
з _
х3 + 3 Yax + 2а = 0.
Дискримінант цього рівняння D =■ а2 + а. Розв'яжемо нерівність D < 0,
знаходимо а2 + а < 0 і — 1 < а < 0.
Отже, задане рівняня має 3 дійсних і різних корені тоді, коли «* 1 < а < 0.
3. Розв'язати рівняння де4 — 2хг + 6к2 — 2х + 5 = 0.
Розв'язання. Застосуємо метод Феррарі. Залишимо в лівій частині рів»
няння перші два доданки, а решту перенесемо в праву частину:
Y — 2*3= — 6х2 + 2х — 5.
У лівій частині виділимо повний квадрат, додавши до обох частин вираз х2.
Матимемо
(^-^2 = -5^ + 2^-5.
Доповнимо ліву частину цього рівняння до повного квадрата, ввівши нову
змінну t:
(# - xf + 2t(x2 - х) +t2 = 2t(x2 - x) - Ьх\[ + 2x +t2 - 5,
(x2 — * + t)2 = (2/ — 5) x2 + (2 — 20 * + £—6.
Виберемо t так, щоб у правій частині рівняння був теж повний квадрат.
При цьому дискримінант квадратного тричлгна відносно змінної х має
дорівнювати нулю:
(1 — О2 — (f2 — 5) (2/ — б) =х 0,
1— 2/ + /2 — 2/3 + 5/2+10/-25 = 0,
t* _ st2 -4/+12 = 0.
Знайдемо один з коренів останнього рівняння. У цьому разі можна не
застосовувати формулу Кардано. Тоді
/2(/ —3) — 4(/-3) = 0,
(/-3)(*2-4) = 0.
191

Одним з коренів останнього рівняння є t{ = 3. Отже, маємо
(*2__х+3)2 = *2_4* + 4,
(х2-* + 3)2-(*-2)2=0,
(*2__2*+5;(*2+ 1) = 0.
Останнє рівняння рівносильне сукупності рІЕнянь:
\х2 — 2х + 5 = 0,
х2 + 1 = 0.
Розв'язуючи її, знаходимо
*1і2 = ± і, *з,4 = 1 ± 2і.
Зауваження. Задане рівняння можна розв'язати за допомогою заміни * =
= # + "о\ Тоді здобуте рівняння не міститиме змінну у в третьому степені. Тому
в лівій частині рівняння залишають тільки г/4 і знову вводять змінну t.
Задачі
33.1. Обчислити дискримінант таких рівнянь:
а) х3 — 9х —4 = 0; г) х3 + х2 — х — ^ = 0;
б) х3 —4jc + 1 =0; д) х3 — би+ 4(1— /) = 0;
в) а:3 — їх = 0; є) хг — Зіх2 + 4 = 0.
33.2. Розв'язати такі рівняння:
а) х3 — Зл: + 2 = 0; ^д) л:3 — 6л:2 + 4х— 1 =0;
б) х3 + 3л: —2/ = 0; є) л:3 —2х2 + л: —3 = 0;
в) Xs — 24л: — 56 = 0; є) х3 + би + 4 + 4/ « 0;
з
г) 2л:3 —Зл:2 + 1 =0; ж) л:3 + ЗУбх + Ті = 0.
33.3. При яких дійсних значеннях а рівняння ах3— Зл: + 2а = 0
має один дійсний і два комплексних корені?
33.4. При яких дійсних значеннях а рівняння ах3 + (а — \)х +
+ а— 1 =0 має кратний корінь? Знайти його.
33.5. Довести, що корені рівняння л:3 + Зал:2 — За3 = 0 є
дійсними при будь-якому дійсному значенні числа а.
33.6. Які корені залежно від значення числа а має рівняння з
дійсними коефіцієнтами л:3 — Зл:2 — ах + 2а2 — За — 4 = 0?
33.7. Довести, що при а>0 і довільному дійсному b рівняння
х3 +ах + b = 0 має тільки один дійсний корінь.
33.8. Довести, що при довільному дійсному с рівняння л:3 —
— х2-\-х + с = 0 має тільки один дійсний корінь.
33.9. Довести, що будь-яке кубічне рівняння з дійсними
коефіцієнтами і від'ємним дискримінантом можна за допомогою заміни
х = ту + п звести до вигляду ау3 — ЗЬу2 — Зау + b = 0, де a, b —
дійсні числа.
33.10. Звести до вигляду ау3 — ЗЬу2 — Зау + b = 0, де a, b —
дійсні числа, такі рівняння:
а) л:3 + 6х2 + 6л: — 8 = 0;
б) л:3 — Зл:2--4л:+ 1 =0;
в) %3+4*2 +* —^ = 0.
192

33.11. Довести, що кубічне рівняння з дійсними коефіцієнтами
ш/3 — ЗЬу2 — Зау + Ь = 0 має корені ух = tg-|-, у2 = tgMp^, і/з =
= tgy Q п, де кут ер визначається з умови
о
Sin ер
Уа* + Ь*У
COS ер =
іп
с
0
D(c,d)
Cv
\^^*^
! £
Лл*
X
Рис. 1
Ка2 + 62'
33.12. Застосовуючи формули із задачі 33.11, розв'язати такі
рівняння;
а) у3-3//2~3//+1=0;
б) уз _ з 1^3^ _ Зі/ + |^3 = 0;
в) У3 + 3//2 — Зу— 1 =0;
г) у3 + 6*/2-3*/-2 = 0.
33.13. Знайти корені рівняння
axz + bx2 + ex + d = 0, якщо його
коефіцієнти задовольняють умову
ad = be.
33.14. Коефіцієнти членів
кубічного рівняння, розміщених у
порядку спадання степенів
невідомого, утворюють геометричну
прогресію. Довести, що корені цього
рівняння також утворюють геометричну прогресію із знаменником і.
33.15. Точки Л, В, C, D побудовано так, що ^АВС = ^.BCD =
= у (рис. 1). Координати точок Л і D є коефіцієнтами кубічного
рівняння з дійсними коефіцієнтами
ах3 + Ьх2 + ex + d = 0.
хБ — b
Довести, що число хо = —-—, де хв~ абсциса точки В, є дійсним
коренем цього кубічного рівняння.
33.16. За умовою попередньої задачі описати геометрично
області, в яких знаходяться точки А і D, якщо кубічне рівняння з
дійсними коефіцієнтами ax3 + bx2 + cx + d = 0, має: а) три дійсних
різних корені; б) два дійсних різних корені; в) тільки один дійс-.
ний корінь.
33.17. Розв'язати графічно такі рівняння!
а) 4%3 + 11*2 + 14.v + 6 = 0;
б) 4х3+6;к2 + 2л; — 3 = 0;
в) 2х3 + Ьх2 — х — 2 = 0;
г) 2а-3 + Ах2 — 5х + 3 = 0;
д) 2х3 + 5х2 — х—1=0.
33.18. Розв'язати такі рівняння четвертого степеня:
а) хА + Зх2 + 2*+ 3 = 0;
б) хА + х3 + 6х2 + 2х + 8 = 0;
7 5-271
193

в) х4 - 6х3 + 6л;2 + 27л; — 56 = 0;
г) 9л;4 + 6х3 — Зх2 + \х — 1 = 0;
д) 4л^ — 4*3 — 6х2 + 2х + 1 = 0.
33.19. Довести, що многочлен з дійсними коефіцієнтами
/ (х) = хА + а3х3 + а2х2 + а\Х + а0
можна подати у вигляді / (л;) = (х2 + px + q)2 + r2 тоді і тільки
тоді, коли
аз —4я2аз +8а\ = 0.
33.20. Застосовуючи твердження задачі 33.19, розв'язати такі
рівняння-
а) х4 + 4л;3 + Пх2 + 14л; +10 = 0;
б) л;4 — 2л;3 + х — 2 = 0.
33.21. Довести, що многочлен з дійсними коефіцієнтами
/ (х) = л;4 + азл;3 + а2х2 + а\Х + яо
можна подати у вигляді
f(x) = (x2+px + q)2 + (rx)2
тоді і тільки тоді, коли
2 2
cl\ = aoa3.
33.22. Застосовуючи твердження задачі 33.21, розв'язати такі
рівняння;
а) хА — 2 V2x3 + 5x2 — 4 /2* + 4 = 0;
б) л;4 + 6л;3 + 9*2 + 12* + 4 = 0.
§ 34. Відокремлення дійсних коренів многочлена
Література
[1] —§ ЗО, с. 323—336;
12] — § 31, с 348—363;
[3] —гл. 16, § 4, с. 521—525;
[6] —§ 39—41, с. 241—259;
[7] —§ 15, 16, с. 86—97;
[8]—гл. 6, § 4, с. 283—290.
ТЕОРЕТИЧНІ ВІДОМОСТІ
Нехай / (z) = апгп + ап_хгп~х + ... + a{z + aQ — многочлен з комплексними
коефіцієнтами, A = max {|я„_і|>... ♦ |^і|» |^о|} * ^о = 1 + ,—г* Тоді всі корені
\ап\
многочлена / (г) лежатимуть всередині круга з центром у початку координат
і радіусом jV0. Якщо многочлен f (г) маг дійсні корені, то вони знаходяться
в інтервалі ]—УУ0; N0[.
Одним з мгтодів знаходження верхньої межі додатних коренів многочлена
з дійсними коефіцієнтам:! є метод Ньютона. В основі цього методу лежить той
факт, що коли при х = М многочлзн / (х) маг додатне значення, а всі його
похідні—невід'ємні, то число М є верхньою межею додатних коренів многочлена.
194

Якщо W0, Nv N2 і W3 —верхні межі відповідно додатних коренів
многочленів з дійсними коефіцієнтами f (х), ynf[~)> t (—у) і упІ \~~Z)> то до"
датні корені многочлена / (х) знаходяться в проміжку 1-^-; jV01 » а від'ємні —
в проміжку І— iV2; ~ "Jv"! •
Нехай ср с2, .. ., ст — деяка впорядкована послідовність дійсних чисел.
Кількість пар сусідніх чисел цієї послідовності, які мають протилежні знаки,
називають кількістю змін знаків даної послідовності.
Правило Декарта: число додатних коренів многочлена в дійсними коефщієн.
тами f (х) = апхп + ап_]хп"1 + . . , + а{х + а0 дорівнює або на парне число
менше кількості змм знаків у послідовності його коефіцієнтів. Це правило за
допомогою заміни х = —у можна застосувати для оцінки кількості від'ємних
коренів многочлена / (х).
Задача відокремлення дійсних коренів многочлена / (х) полягає в
знаходженні тих інтервалів, у кожному з яких лежить тільки один корінь.
Відокремити корені многочлена / (х), який не має кратних коренів, можна методом
Штурма. При цьому для многочлена f (х) будують насамперед ряд Штурма:
f(x), /'(*), F\(*). F2{x),.. ., Fmamml{x), Fm.
Щоб знайти многочлени Ft(x)% \<i<m, застосовують алгоритм, аналогічний
алгоритму Евкліда:
f(x) = f'(x)<!>l(x)-Fl(x)t
f\x) = Fx(x)<k2(x) — F2ix).
Рт-\(х) = РтФт+х(х).
Відмінність цього алгоритму від алгоритму Евкліда поляга? тільки в тому, що
всі остачі rk(x) беруть з протилежними знаками, тобто Fk(x) = —^(*).
Після цього застосовують теорему Штурма:
Якщо а і b — довільні дійсні числа, які не є коренями многочлена / (де), то
число р дійсних коренів многочлена f (х) в інтервалі ]а\ Ь[ дорівнює р = s(a) — s (b),
де s(a) і s (b) — кількість вмін знаків у ряді Штурма відповідно при х = а і х = Ь.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Знайти кільце, в якому знаходяться всі корені рівняння
5*7 + Зх3+ 10л:2 —2 = 0.
Розв'язання. Маємо A = max {3, 10, 2} = 10 і laJ = 5. Тому W0 = 1 +
10
+ "5" = 3. Це означає, що всі корені х{, 1<к7, заданого рівняння
задовольняють нерівність |*(.| < 3.
Введемо заміну х = -. Маємо
у
-2у' + 10/ + З^4 + 5 = 0.
7» 195

Тут А = 10, \ап\ = 2 і М0 = 1 + ~2 = 6. Тому корені yit ]<i<7t
задовольняють нерівність \у,\ < 6. Виконуючи обернену заміну у =-, дістаємо г—. < 6,
1 1 х \хі 1
тобто |х,| > g.
Отже, всі корені заданого рівняння лежать всередині кільця з центром у
початку координат, радіусом зовнішнього кола 3, а внутрішнього g (рис. 2).
2. Знайти верхню межу від'ємних коренів многочлена
/ (х) = хь — 8*3 — б*2 + 6* — 3.
Розв'язання. Введемо заміну х = —-. Тоді
у
1
_1_ 8_ ^_ 6
Розглянемо многочлен
= 3^+6^ + 5/-8/+1,
який має ті самі корені, що й многочлен
Н)-
Щоб знайти верхню м«жу його додатних
коренів, застосуємо метод Ньютона. Знайдемо
всі похідні многочлена g (у):
Рис 2 g{y)== з/ + б*/4 + 5у3 - 8у2 + 1,
^0/)=15^ + 24/+15^-16*/,
gllQ/) = C0/ + 72r/2 + 3(h/-16,
gU](y)= 180^+144(/ + 30,
glV(*/) = 360^/+144,
gv(</) = 360.
Неважко перевірити, що число 1 є верхньою межею додатних коренів
многочлена g(y). Тоді число—1 є верхньою межею від'ємних коренів заданого
многочлена.
3. Відокремити дійсні корені многочлена
f(*) = *4 — 2j*2+4jc— і.
Розв'язання. Для цього многочлена А = 4, laJ = 1, jV0 = 5. Тому його
дійсні корені знаходяться в інтервалі ]—5; 5[.
Складемо ряд Штурма (многочлени ряду знаходитимемо з точністю до сталого
множника).
f (х) = 4х3 — 4* + 4 - 4 {X3 — х + 1);
2*2 + 4х — 1
" ХА — X2 + X
JC3 — X + 1
— *2+3* — 1
:> /^)=^-3^+^
196

x*-x + 1
x2 — 3x+ I
x + 3
3x2 — 2x + 1
"З*2 — 9x + 3
7x—2
:> Fa(*)«=-7* + 2;
^2 _ з* + 1
7*a — 21л: + 7
" 7x1 — 2x
-7*+ 2
-* + у
— 19л: + 7
38
—19*+y
ЇЇ
7
Таким чином, ряд Штурма утворюють многочлени:
*4 __ 2х2 + 4х — 1, л3 —х + 1, x2-3jc+ і, —7*+ 2, —1.
Складемо таблицю (табл. 44).
:> F8——1.
\ Знак
\
*• \
—5
5
0
f(xt)
+
+
І'(х.)
_
+
+
Fl(x,)
+
+
F,<*„>
+
+
т
F,
_
'
а б л и ц я 44
Кількість
змін знаків
3
1
2
Отже, заданий многочлен має два дійсних корені, один з яких від'ємний
і знаходиться в інтервалі ]—5; 0[, а другий — додатний і знаходиться в
інтервалі ]0; 5[.
Задачі
34.1. Знайти на комплексній площині кільце, в якому
знаходяться всі комплексні корені таких рівнянь:
а) хі982 _ 4л:24 + Ах3 — 7а;2 + 1 = 0;
б) х6 — х5 + *4 — х3 + х + 7 = 0;
в) х12 + хп— 5х5 + 6х2 — 6 = 0;
г) 2хь + Єх4 + х3 — х2 — 54* + 27 = 0.
34.2. Знайти методом Ньютона верхню межу додатних коренів
таких многочленів:
а) f(x)>=2x3 — За;2+ 5;
б) f(x\*=x* — 8x+l;
в)/(х) = (х-2)6 + (*-1)3;
г) / (х) = — 2х4 + 6х3 — 7х + 3.
34.3. Знайти методом Ньютона нижню межу додатних коренів
таких многочленів:
а) / (х) = 5х* — Зх3 + х2 + 1;
б) / (х) = 4х* — 12а:2 + 8х — 1;
в) / (х) = х5 + 6а;4
Па:3—Па:2+ 6*+ 1.
197

34.4. Знайти число змін знаків у коефіцієнтах таких
многочленів:
а) f(X) = bx7 — 2хь + 3хг> — х* + 6х3 + 2х2 — х+ 1;
б) /(*)= 12х4 —х3 —3*2 + 2а: + 4;
в) /(*) = 19х"> — 2х3 + х— 1;
г) /(*) = (*-І)100.
34.5. Оцінити за правилом Декарта число додатних і від'ємних
коренів таких многочленів.'
а) f(x) = x* — 2x? — 7x2 — 8x+U
б) f(x) = 2x3 — Зх2 +х— 1;
в) / (х) = х5 — 5а:3 — \0х2 + 2;
г) / (х) = хь + х5 — 12г* — 13г3 — 27а:2 — 14* — 14,
д)/(*) = х3-12*-4.
34.6. Знайти межі доданих та від'ємних коренів таких
многочленів:
а) / (х) = —За:4 + Ьх3 +9х2 — х+1;
б) f(x) = x* + 5x* — 7x + 2\
в) /5 (а:) = Зх1 — 12а:3 + 8а:2 + 2х + 4;
г) / (а:) = —2а:7 + За:5 — х3 + х — І;
Д) f(x) = x3 — \2x — 4.
34.7. Знайти число дійсних коренів многочленів-
а) f(x) = а:1 — 2а:3 — 6х2 + 4а: + 4 на проміжку [2; 4];
б) /(а:) = а:4 -+- За:3 — 4х—1 на проміжку [0; 2];
в) f (х) = хА — 2х3 — 4 на проміжку [—3; 5|;
г) f (х) = а:' + 5х2 — 10 на проміжку [Г; 3].
34.8. Відокремити дійсні корені таких многочленіві
а) ї(х) = 2х3 — 5х—1\
б) /(*) = _8а:3+ 16л: — 2;
в) f(x) = x3 + 6x— 2;
г) /(*) = х4 —4х3—12* + 9;
д) /(а:) = 2а:5 - 10а:3 + Ю*2 — 2;
є) f (х) = х4 — 4х + 1,
Є) / (х) = х4 — 2х3 + Зх2 — 2х + 2.
Розділ VII. МНОГОЧЛЕНИ НАД ПОЛЕМ
РАЦІОНАЛЬНИХ ЧИСЕЛ
І АЛГЕБРАЇЧНІ ЧИСЛА
§ 35. Цілі і раціональні корені многочлена з цілими
коефіцієнтами. Критерій незвідності Ейзенштейна
Література
[1] —§ 31, с. 337—343;
[2] — § 32, с. 363-369;
[3] —гл. 17, § 1, с. 526—528;
[51 —гл. IX, § 6, с. 350—355;
[6] —§ 56, 57, с. 350—358;
[7] —§ 17, 13, с. 97—104.
198

ТЕОРЕТИЧНІ ВІДОМОСТІ
Нехай/ (х) = апхп + ап_1хп"х + ... + а{х + а0 — многочлен з цілими
коефіцієнтами.
р
Якщо нескоротний дріб - є коренем многочлена / (х), то р є дільником
вільного члена а0, а 9— дільником старшого коефіцієнта ап цього многочлена.
Якщо ап= 1, то всі раціональні корені многочлена / (*) є цілими числами.
Оскільки многочлени / (х) і a^~~l f (х) мають однакові корені, то знаходження
раціональних коренів многочлена / (х) можна за допомогою заміни у -^fca /звести
до відшукання цілих коренів многочлена '
С1 / w - s (у) -=уп + ап-\уп~х + %-2апУп~2 + •. ■ +*і*Г2у + ^Г1-
Існують інші необхідні умови для того, щоб раціональне число було
коренем многочлена з цілими коефіцієнтами. Зокрема, щоб нескоротний дріб - був
раціональним коренем многочлена / (*), необхідно, щоб при довільному цілому k
число / (k) ділилося на р — qk, де p — qk=£Q. Така умова на практиці
найчастіше використовується для k = ± 1,при цьому числа і | мають бути
цілими.
Многочлен / (л;) з цілими коефіцієнтами є звідним у полі Q раціональних
чисел тоді і тільки тоді, коли існують многочлени /j(x) і f2(x) ненульового
степеня з цілими коефіцієнтами такі, що / (x) =fl(x)f2(x)1 тобто коли многочлен / (х)
є звідним у кільці Z.
Критерій Ейзенштейна незвідності многочлена з цілими коефіцієнтами:
Якщо коефіцієнти а0, av . . ., ап_х многочлена f (х) в кільця Z [х] діляться
на деяке просте число р, причому а0 не ділиться на р2, а старший коефіцієнт
ап не ділиться на р, то многочлен f (x) несвідний у полі раціональних чисел.
Отже, у кільці многочленів над полем раціональних чисел є многочлени
довільного степеня, які незвідні у полі Q.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Розв'язати рівняння
24*5 + 10*4 — х3 — 19jc2 — 5* + 6 = 0.
Розв'язання. Знайдемо спочатку раціональні корені цього рівняння (якщо
вони є). Раціональними коренями тут можуть бути такі числа:
±1; ±2; ±3; ±6; ±^ ±2; ±5; ±3: ±f ±| 4і ±8= ±8: ±Ї2; ±2? <'>
Знайдемо межі дійсних коренів заданого рівняння. Оскільки А = 19 і ап = 24,
19 19
то N0 = 1 + од = І94- Отже, всі дійсні корені знаходяться в інтервалі
]19 19[
—Іоі; Іод • Серед чисел ряду (1) у цей інтервал входять такі числа:
±1; ±2Ї ±2: ±3; ±3; ±4; ±4: ±6; ±8; ^81 ±12; ±24* ®
Для заданого рівняння маємо: /-(1) = 15 і /(—1) =—21. Поставимо умову,
15 . 21
щоб числа і — . були цілими. Тоді залишаться числа
І 3 2 II 3 2
±2; ~2; ~~3; ~4; 4; 6* (3)
199

Оскільки «кандидатів» на корені ще багато, то знаходимо \ (—2) = —660
—G60
і перевіряємо, для якого з чисел ряду (3) дріб , 9 в цілим числом. Цю
умову задовольняють тільки числа
І
2 З
±2; 2; 3; 4*
Застосуємо схему Горнера для перевірки того, яке з останніх чисел є
коренем заданого рівняння (табл. 45).
Таблиця 45
1 1
2
1
2
1 1
2
3
2
2
3
2
3
3
4
24
24
24
24
24
24
24
24 і
10
22
34
10
-14
6
-10
24
— 1
10
27
5
31
6
38
3
24
— 19
— 14
І
2
-4
-Ч
— 18
-24
0
—5
-12
-'4
'-4
771
4
0
6
0
У йхемі виділено коефіцієнти повних часток. Отже, задане рівняння мав
2 13
три раціональних корені: —g; о 1 1* РештУ коренів рівняння знайдемо,
прирівнюючи останню частку до нуля. Матимемо
24Г + 24* + 24 = 0,
х2 + х + 1 = 0.
,; -1 ± Узі
У цьому рівнянні комплексні корені —' -^ г °\ Тому задане рівняння мав
п'ять різних коренів:
2 ]_ 3 —1 —іУз —1 +іУз
~~3' 2' 4' 2 ' 2
2. Розкласти на незвідні у полі Q множники многочлен
/ (*) = х6—х5+2х3—2х2+6*—6.
Розв'язання. Згрупуємо в цьому многочлені по два члени, що стоять
поряд, і винесемо спільні множники за дужки. Тоді
/ (х) = хь(х - 1) + 2*2 (*- 1) + 6 (*- 1) = (х - 1)(*ь + 2*2 + 6).
200

Многочлен g (х) = хь + 2х2 + 6 в незвідним у полі Q за критерієм Ейзенштейна
(простим дільником є число 2). Отже, дістали шуканий розклад.
3. Довести, що многочлен
f (х) = х6 — 2х3 + Зх2 — 6*+ 7
є незвідним у полі Q.
Розв'язання. До заданого многочлена безпосередньо застосувати критерій
Ейзенштейна не можна. Зробимо заміну * = #+ 1. Маємо
/ (У+ 1) = g(y) = (0+ О6- 2 (у+1)3 + 3(у + 1)2- 6(^/+ 1) + 7 = /+6/+
+ 15^ + 20^+15/ + 6(/+1-2/-6^-6^/-2 + 3^ + 6^/ + 3-61/-6+
+ 7 = / + 6/+ 15/ + 18/ + 12/ + 3.
Усі коефіцієнти многочлена g (у), крім старшого, діляться на 3, а вільний
член не ділиться на 9. Не означає, що многочлен q (у) є незвідним у полі Q.
Отже, многочлен / (де) також є незвідним у полі Q.
4. Чи є звідним у полі Q многочлен
t {х) = х3 — б*2 + 12*-4?
Ро з в* я з а н н я. Подамо заданий многочлен у вигляді / (х) = (х — 2)3 + 4.
Зробимо заміну: у = * — 2. Тоді / (*/ + 2) = g (г/) = j/3 + 4. Оскільки кубічний
многочлен g (у) не має раціональних коренів, то він є незвідним у полі Q.
Отже, многочлен / (х) також незвідний у полі О.
Задачі
35.1. Розв'язати такі рівняння:
а) я4 —4г3— ІЗ*2 + 28л; + 12 = 0;
б) *з_2х2 —Зх + 10 = 0;
В) х4—х* — 22л:2 + 16* + 96 = 0;
г) 2х3 —5х2 + 6л: —2 = 0;
д) 12x3-x2 + 2jt-l =0;
є) Юх3 — Зл:2 — 2х + 1 =0;
є) 2x3 + 3x2 + 6jc —4 = 0;
ж) х4 + 4х3 — 2л2 — 12л: + 9 = 0;
з) л:3 — (а + Ь + c) х2 + (aft + ac + be) л: — а&с = 0;
к) х3 — (За — 1) х2 + (2а2 — За) х + 2а2 = 0;
л) х3 — 2х2 — (а2 — а— 1)л: + (а2 —а) = 0;
м) х3 — (2а + 1)х2 + (а2 + 2а —62)х + (Ь2 —а2) = 0.
35.2. Знайти раціональні корені таких рівнянь!
а) х*-х2-т^-т = 2;
Xі — ДГ
б) 2л:3 — Зх2 + 4л: — 5 = 0;
Л 16 5 .
В) —о о 5 5 ** 1 і
х3 + 3*2 — х + Ь *3 + 3х2 — х + 2
З
г) л:3 — (р2 — /? + 7)л: — 3(/?2 — р — 2) = 0, якщо р = /2;
д) (2л:2 + Зл:— І)2 —5х2(2х° + 3*— 1) + 5л:4 — х = 0.
35.3. Розкласти на незвідні у полі Q множники такі
многочлени:
а) / (х) = х" +х6 — 6х2 — їх — 7;
б) / (х) = хл — х* — 6х2 + 8х — 2;
в) / (х) = 6х4 - ІЗ*3 + 12х2 — 13* + 6;
г) / (х) = 9л4 — 15*я + 28л2 — 20х + 16;
д) f(x) = (x + 3y + (x + 5Y-\6;
є) /(*) = (*+ If— 9(х+ І)3+ 20.
201

35.4. Довести, що незвідними у полі Q є такі многочлениі
а) f(x) = x3 — Зх2 + 1;
б) f(x) = x* + 2;
в) / (х) = х5 + 5* + 9;
г) f(x) = х4 + х3 + х2 + х + 1;
д) f (x) = xs + х5 + х4 + х3 + х2 + х + 1;
є) / (х) = х^-1 + хр-2 + ... + х + 1, де /? — просте число.
35.5. Дослідити на звідність у полі Q такі многочлени:
а) f(x) = x4 + x3—\0x2 + x+U
б) f(x) = (5-х)4 + (2-х)4- 17;
в) /(х) =х3+х2—1;
г) / (х) = х4 + 2х + 3.
35.6. Довести, що коли многочлен /(х) можна розглядати як
елемент кілець Z [х] і Zm[x], залежно від інтерпретації його
коефіцієнтів, і f(x) є незвідним у кільці Zm[x], то він незвідний
також у кільці Z[x].
35.7. Довести незвідність у кільці Z[x] таких многочленів:
а) Дх) = х5+х2+1;
б) /(х) = х5 + х4+х2 + х+1;
в) / (х) = х6 + х4 + х2 + х + 1;
г) /(х) = 5х3 + х—1;
д) /(х) = 2х3 —Зх + 5.
§ 36. Алгебраїчні і трансцендентні числа.
Будова простого алгебраїчного розширення поля
Література
[1] —§ 32, 33, с. 344—360;
[2] — § 33, с. 370—374;
[3] — гл. 17, § 2, с. 528—531;
[4] —гл. VI, § 1, с. 316—320; § 5, с. 327—332;
[5] —гл. X, § 5, 6, с. 380—391;
[6] — § 58, с. 358—363;
[8] —гл. 9, § 1, с. 420—424.
ТЕОРЕТИЧНІ ВІДОМОСТІ
Нехай Р — деяке числове поле. Число а називають алгебраїчним відносно
поля Р, якщо воно є коренем деякого многочлена над полем Р. Число, яке не
є алгебраїчним відносно поля Р, називають трансцендентним відносно Р.
Зокрема, алгебраїчні і трансцендентні числа відносно поля раціональних чисел Q
називають відповідно просто алгебраїчними і трансцендентними.
Якщо а є алгебраїчним числом відносно поля Р, то в кільці Р [х] існує
єдиний незвідний зведений многочлен1 f (х)у який має а своїм коренем, а його
степінь п є найменшим серед степенів усіх многочленів з коренем а. При цьому
многочлен / (*) називають мінімальним многочленом числа а, а його степінь п —
степенем алгебраїчного числа а відносно поля Р.
Мінімальне розширення поля Р, яке містить число а£Р, називають простим
розширенням поля Р, утвореним приєднанням числа а, і позначають через Р (а).
Якщо а є алгебраїчним (трансцендентним) відносно поля Р, то Р (а) називають
простим алгебраїчним (трансцендентним) розширенням.
1 Многочлен називають зведеним, якщо його старший коефіцієнт дорівнює
одиниці.
202

Поле Р (а), утворене з поля Р приєднанням кореня а незвідного у полі Р
многочлена л-го степеня
/ (х) = хп + an_{xn~l + ... + а{х + а0,
складається з усіх чисел виду
Р = С0 + С{а + с2а2 + . . . +cn_{an-1,
де с0, cv . . ., сп_{ £ Р.
Нехай F — деяке підполе поля Р. Тоді Р можна розглядати як векторний
простір над полем F. При цьому розширення Р поля F називають скінченним,
якщо Р є скінченно-вимірним векторним простором над F. При цьому розмір
ність простору Р називають степенем розширення Р над полем F.
Просте алгебраїчне розширення Р (а) є скінченним розширенням поля Р
а степінь розширення Р (а) над полем Р дорівнює степеню числа а відносно Р
Розширення Р поля Ft утворене за допомогою кількох послідовно виконаних
простих алгебраїчних розширень, називають складеним алгебраїчним розширенням
Розширення Р поля F називають алгебраїчним, якщо всі його елементи є алгеб
раїчними відносно поля F.
Будь-яке скінченне розширення поля Р є його алгебраїчним та складеним
розширенням. Кожне складене алгебраїчне розширення поля Р є простим
розширенням цього поля.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Довести, що число а = і/ 3А є алгебраїчним, і знайти його міні-
мальний многочлен.
Розв'язання. Позбавимося радикалів у правій частині заданої рівності.
Для цього послідовно піднесемо обидві частини рівності до четвертого,
третього і другого степенів. Матимемо:
з
*-2--vT+7I'
(а4—2)3 = —1 -/З,
(а4 - 2)3 + 1 = -/З,
((а4_2)3+ 1)* = 3.
Остання рівність означає, що число а є коренем многочлена / (х) = ((*4— 2)3 +
-f- І)2 — 3 з раціональними коефіцієнтами, тобто а є алгебраїчним числом.
Знайдемо канонічну форму многочлена / (х):
f (х) = (хх2 - G*8 + 12*4 - 7)2 -3 - хи - 12*20 + 60*16 - 158*12 +
+ 228а:8 —168л:4 + 46.
Оскільки всі коефіцієнти многочлена / (дг), крім старшого, діляться на 2,
а вільний член 46 не ділиться на 4, то, за критерієм Ейзенштейна,
многочлен / (х) є незвідним у полі Q. Отже, f (х) є мінімальним многочленом
алгебраїчного числа а.
2. Знайти алгебраїчне число, приєднанням _якого до поля Q можна дістати
складене алгебраїчне розширення J2 (V^XV^h
Розв'язання. Число а = \^3 є алгебраїчним над полем Q (У 2) і його
мінімальний многочлен / (дг) = *2 — 3. Тому всі числа з поля Q(V2%V"s)
203

запишемо у _ вигляд! р = с0 + q/з, де с0» ^і £_Q (/¾. Оскільки всі числа
з поля Q(|^2) можна подати у вигляді а-\-Ь\% де a, b£Qt то
^ = (00 + ¾ /2) + (¾ + ^/2)/3 = а0+^о/2 + аУІ + ^/б, (1)
де а0, 60, %, 6f £ Q.
Якщо а0 = *і = ° і *о = <*і: = 1. то дістанемо 7 = /2 + /з £ Q (/2)(/5).
Тому Q (/2 + Уз) <^ Q (/2)(/5). Число ? є алгебраїчним і / (*) = х4 —
— 10jt2+1— його мінімальний многочлен. Це означає, ща Q (7) є простим
алгебраїчним розширенням і його елементи мають вигляд
4) + dfl + drf + drf, (2)
де d0, dp d2, d3£ Q.
Покажемо, що кожне число вигляду (1) можна подати у вигляді (2).
Маємо ч* = 5 + 2/б і /б = ^ (Т2 — 5). Застосовуючи тепер формулу (*+#)3 =
= х3 + //3 + Зл# (jc + */), знаходимо
7* =-- 2/2 + 3/3 + 3/6 (V2 + /3) = 2^ + /з~+ |т(т2 - 5).
Звідси /З = у7 — 2Г3 і ^2 = 2^-^. Тому
Р = *о + *о (5Т3 ~ Ь) + аі (-У + Т?) + 4 <ї* - 5) = (а° - 2Ьі) +
+ ("2"Яі ~2^)^ + 2^2+ (2^"" 2аі)^3-
Отже, ,3 £ Q (-у), тобто
0(/2)(/3)(=0(/2 + /3)
і
Q (/2)(/3) = Q (/2 +/3).
3. Знайти степінь розширення С (поля комплексних чисел) над полем R. '*
Розв'язання. Векторний простір С над полем R має розмірність 2.
Справді, числа 1 та і утворюють лінійно незалежну систему і кожне комплексне число
має вигляд а- 1 + 6/, де a, b£R. Тому розширення С над полем R має
степінь 2.
Задачі
36.1. Довести, що число а є алгебраїчним, і знайти його
мінімальний многочлен, якщо:
а) a = ]/~2 + j/3| д) a==j/5-K3;
б) а=1+]/з-і/5; Ї/ТҐ—75"
Vv
г)а + /2+1=0; е)а=1+ V /6+1;
ж) а = Г/3+ 1.
204

36.2. Знайти алгебраїчне число, приєднанням якого до поля Q
можна дістати складене алгебраїчне розширення:
а) Q(j/2)(/5);
б) Q (КЗ) (|/4);
в) (3(/5)(/7):
г) Q {Vp) (Vq), де р, q — прості числа;
д) Q(/2)(K3)(K6);
є) Q ()/2)(/3) (J/5).
36.3. Знайти базис векторного простору Р над полем Q, якщо:
('-) г) P = Q(j/2)(i);
VpZZtm ^=«<KW3HK5).
в) Р = ¢(/3)(/5):
36.4. Довести, що поле дійсних чисел R не'є скінченним розши"
ренням поля Q.
36.5 Довести, що розширення Р числового поля F, яке має
третій степінь, не має інших підполів, крім F і Р,
36.6. Довести, що розширення Р числового поля F, яке має
простий степінь, не має підполів, відмінних від F і Р.
36.7. Довести, що множина всіх алгебраїчних чисел є зчисленною.
36.8. Довести, що множина всіх трансцендентних чисел є
незчисленною.
36.9. Довести, що множина всіх алгебраїчних чисел є полем.
36.10. Алгебраїчне число називають цілихМ, якщо воно є коренем
зведеного многочлена з цілими коефіцієнтами. Чи утворюють цілі
алгебраїчні числа поле?
§ 37. Позбавлення від алгебраїчної ірраціональності
в знаменнику дробу
Література
[!]_§ 26, с. 294; § 32, с. 347—348;
[2] — § 26, с. 305—307; § 33, с. 374;
[3] —гл. 17, § 2, с. 532;
[7] —§ 23, с. 130—133.
ТЕОРЕТИЧНІ ВІДОМОСТІ
Основні методи розв'язування задач на позбавлення від ірраціональності
в знаменнику дробу грунтуються на таких фактах.
1. Якщо f (х)— многочлен від однієї змінної над полем Р з коренями
аг, а2, . . . , ап (які можуть не належати Р), то будь-який симетричний многочлен
g(xi> *2' • • •' Хп) наД полем Р при х± = аь х2 = «2» • • -'і *л — <*л набуває значення,
яке є елементом поля Р.
205

2. Поле Я (а), утворене з числового поля Р приєднанням кореня а, незвід-
ного у полі Р многочлена п-то степеня
-л—1
f (х) = хп + ап_ххГ-1 + ... + ахх + а0,
складається з усіх чисел виду
а = cQ + сла + С2а2 + . . . + С^а"""1,
де с0і Сі, . . . , сгг_1 — довільні числа з поля Р.
Крім цього, при розв'язуванні таких задач застосовуються формули
скороченого множення:
хп - у" = (х - у)(х«-і + хп~2у + ... + у—1),
,2*+1 + ^+1 = (х + y)(x2k _ X2k-Xy+ _ + y2k).
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Позбавитися від ірраціональності в знаменнику дробу
■, де о), — один
з коренів рівняння х3 — х— 1=0.
Розв'язання. Нехай со2 і о)3—решта коренів заданого рівняння. Тоді
1
(1 — а)2)(1 — со8)
1—0), (1 — 0),)(1 — 0)2)(1 — 0)3)
_ І — Ц2~ Щ3+ ^2^3
— 1^(0,-0)2-0)3+ 0)^2 + 0),0)3 + 0)20)3 — 0),0)20)3.
Згідно з теоремою Вієта,
^1+^2 + ^3= °> ^1^2 + ^1^3 + ^2^3 = —! І ^,0)20)3 = 1.
1 1 (0)о + 0)3) + 0)20)д
" __ ^ =-1+(^2 + ^3)- Vs» причому со2
Тому 13-^Г,=
л-з __ х __ і
і о)а є коренями рівняння —■ — = 0.
Знайдемо його ліву чаатину. Виконаємо ділення многочленів у лівій частині
за схемою Горнера (табл. 46).
Таблиця 46
1 <»і
1
1
0
0>1
—1
0)2—1
-1
0
Звідси х 2 + o)jjc + o)j — 1 = 0. Це означає, що ш2+ о)3 — — o)j і о)2о)3 =-- со2 — 1.
0тже> Г^^ = -1-а)і-((0і-1)=-а)!І-а)і-
2. Позбавитися від ірраціональності в знаменнику дробу
з __ з _
^49 — ^7+3
Розв'язання. Заданий дріб є значенням раціонального дробу ~-~r\ =
1 з_
= х2 х + 3 ГіРи х ■—у' 7, яке є коренем незвідного у полі 0 многочлена
h(x) = х2 — 7. Многочлени g(x) і h (x) взаємно прості. Знайдемо лінійне
зображення їхнього найбільшого спільного дільника (див. приклад 2, § 23).
206

Ділення многочленів виконаємо «кутом»:
*з __ 7 |х2 — х + З
—^_ха+3дг| ^4-1 >
г2 — Зл: — 7
~ *2_ , _|_3
або
і
— 2а:— 10
*з — 7 = (л-2 — х + 3)(* + 1) —2л: - 10,
h(x) = g(x)(x+ l)-(2*+ 10)
2х+10 = -М*)+ £«(*+!);
*2 — х + 3 1
*2+5x
— 6* + 3
_- 6* — ЗО
— 2л: — 10
1
~~~2Х + 6
33
33
або
Звідси
Xі - х + 3 = (— 2х — 10)f—2"* + з) +
g(*) - - (2х + 10)(- у* + з) + 33.
33 = g (х) + (2х + 10) (—2 * + 3) = g W + (- h (x) +
1
+
+ gW(^+i))(~-2^ + 3) = gw(1 + (x + l)(-Tx + 3)))
+ /i (х) (у*- з) = g(x) (- -1-ДІ + ^ + 4J + /і (*)(у*~ ЗІ
Оскільки /і І |/у І = 0, то
3_ 3 __
1 _ 1 -/49 + 5^7 + 8.
(З \ З З
VT) /49~/f + 3
66
8. Позбавитися від ірраціональності в знаменнику дробу 3 _ 5 __.
/5 +/З
Розв'язання. І спосіб. Застосуймо формулу скороченого множення:
х16 — уі* = (х + у){х™у — xl3y2 + x^f — хиу* + х10у* —
— А*6 + *У — *У + *У — *У° + * Vі — х3у12 + *V3 — *Уи)-
Тоді
1 і/3 — 5.. 3 —5 _ 5 _
з 5— = зЇ52 54/25 V3 - 54 /5 /9 + 54/27 -
/5"+/З V
З 5 3_ 3__ 3_-5_ 3 5
— 53/25 /81 + 533/5 — 533 /5 + 52 /25 . З /9 — 52 /б" • 3 /27+
5 3 3 — 5 _ 5 __ 3 5
+ 523 /81—5/25 -32 + 5/5 -З2/3-5. З2 /9 + /25 -З2/27-
207

З 5 \ | / Б _3 3 __5 __ 5 __
- VI • З »/81 + З3 J = -3152( 625 /3 /25 - 625 /5 /9 + 625 /27 -
- 125 |^25 /8Ї + 375 f$ - 375 /3" + 75 /25 /9 -
- 75 / 5 /27 + 75 VS\ - 45 /25 + 45 /5/З" - 45 /Г +
+ 9/25/27-9/Г/8Т +27).
II спосіб. Якщо в знаменнику дробу є кілька радикалів, то їх можна
поступово позбуватися одним із розглянутих вище способів (див. приклади 1 і 2)
з _ з _
Позбавимося від ірраціональності у~§. Число к = Y§ є коренем многочлена
h (х) = х3 — 5. Многочлени h (х) і £ (х) = x + j^3 є взашно простими і h (x) =
5 _ 5 5 _
= g(*)(*2— /3 ^ + /^)-/27-5 ТомУ
в(/5")(/Т5 - /3 /5" + /9") = 5 + /27
я ft 3 __ f.
1 /25—/3" /5 +/9*
3 - 5 — ~~ 5 _
/5 +/3 5 + у^27
5 __
Число і/ = /27 є коренем многочлена h, {у) = ць — 27, многочлени Ьл(у) та
gi(y) = у-{- Ь є взаємно простими і
(/6 — 27 = (.у — 5)(і/4— бу3 + 25(/2 — І25і/Н- 625) — 3152*
Звідси
(ь\ 3152
Si W21) = —5-3 ~ ~ ~ '
9/9—15 /81 +75/3 - 125 /27 + 625
Отже,
1 1 /3 __ 5 _^ _ 5 \/ 5 _ 5 _ 5
3~І ~ = ЗЇ52 1/25-/3 /5 + /9 Д 9 /9 - 15 /81 + 75/3 —
/5 +/3
-125/27 + 625)
Виконавши множення, ми побачимо, що результат однаковий.
4. По бавитися від ірраціональності в знаменнику дробу
1
/З + /5 + /7 '
Розв'язання. Введемо позначення: х = /з, у = /5, ? = Vl. Тод дріб
1 1
набуває- вигляду —ц—X~z =—» де аі — елементарний симетричний
многочлен від трьох змінних. Складемо вираз із степеневих сум $п(х, у, z) (див.
задач' 28.7 28.8) і парними індексами п так, щоб у ньому був множником
многочлен av Оскільки >2 = а? — 2з2 ' *4 ~ Q\ — ^1*2 + ^Q\ + 4аіаз > т°
<jj = а J — 4а|а2 + Щ,
s\ — 2s4 = aj (43^2 — а^ — 8о3).
208

Звідси
4а1а2_а13 — 8а3
Враховуючи те, що s2 = 15 і s4 — 83, маємо
Vs+ Уь + VT = k^ W* + ^ + ^)(^ + /21 + /з5) -
~ (/з" + /5"+ /f)3 - 8/Ї05).
Задачі
37.1. Позбавитися від ірраціональності в знаменнику дробуі
а) —, де и>2 + и>— 1 = 0;
б) -JL- де о)3 ~2(о —3 = 0;
в) НЧ> *е «>4-4а)-2 = 0;
1 + ш
г) -^-, де а)3 —8а) + 2 = 0;
7 а)3 + 5
д) -о , де а)4 —5 = 0.
Ш — (0
* 37.2. Позбавитися від ірраціональності в знаменнику дробу:
\ 7 . 2
а; ~ j г' з~^—~ »
1 — У2 + /2 /49 — Vl + З
3^ ч 1
Яч /2 . Д) — Г^—4 •
°' з і j /27 —2/9 + /3—1
/5 + 2^2
в) ~ ~;
1+/2 + 3/4
37.3. Позбавитися від ірраціональності в знаменнику дробу:
\ ' ч 1
3/ з 5 » В' 8 8 '
/6-/5 /3+ /2
1 ч 1
б) 5 _ В » Г) 9 9—'
/3-J/2 /5 + /З
37.4. Позбавитися від ірраціональності в знаменнику дробу:
і ч 1
а) \Га + VI 4- /с' 3 3 3 ;
б) 3 ї —і гч '
К a + у ь + ус
209

сих
37.5. Позбавитися від Ірраціональності в таких співвідношеннях!
з з
а) ]Га + Va2 + 6 = 0;
3 _ 3
б) pVa* + qV^ + r = 0;
_ 4 .
в) Va + Vb — Va* + b2 = 0.

ВІДПОВІДІ. ВКАЗІВКИ. РОЗВ'ЯЗАННЯ
Р озд іл І
§ і
1.1. a) q = 4, л = 7; б) q = 0, г = ЗІ; в) <? = — 5, т = 24; г) ^ = —1, r = 100
д) </ = —4, г = 7; є) <7 = 0, г = 31; є) <7= 1, '= 100; ж) ¢ = 5, r = 24.
1.2. a) ft = 47, ¢= 2; ft = 94, ¢= 1; б) .6 = 111, q = 1; в) ^ = 288, ^ = 1;'
ft2 = 144,' ^2 = 2; Л3 = 7І <?? = 4; ЬА = 28, ?4 = 11; ft5 = 11, <75= 28; г) ft = 481,
q = 1; ft = 37, 9 = 13; д) ft = 26, g = 1; ft = 13, q = 2; e) 3a ft можна взяти
довільне ціле число таке, що |ft| > 14, ¢ = 0.
1.3. a) ft = 25, г = 21; ft = 26, т = 7; б) таких ft і а не існує; в) ft = 17, т =
= 16; г) ft—довільне ціле число, причому | ft | > 57, г = 57; д) ft = 108, r = 59;
є) ft= I, /-,.-=0.
1.4 а) 2-А-, &£Z; б) 3/?, *fcZ; в) 8/?, k £ Z; г) 7£ + З, Л £ Z; д) 4/?+ 1, k £ Z;
є) 2/г + 1, * Є Z; є) 3k + r, г = 1,2, £ £ Z; ж) 6/г + г, л = 1,5 k £ Z.
mq -f- яр /я/z — РЯ
1.7. Розглянути різницю m_ — -m_ p і показати, що вона є цілим
числом.
1.9. б) Розкласти II10— 1 на множники: (11 — 1) (119 + 118 + . . . + 11 + 1);
в) 22225555 + 55552222 = (22225555 + 45555) + (55552222 - 42222) - (45555 - 42222).
Розглянути кожен вираз у круглих дужках, використавши той факт, що сума
однакових непарних степенів ділиться на суму основ, а різниця будь-яких
однакових цілих степенів ділиться на різницю основ.
§2
2.1. Прості числа: 127, 919, 1033, 1657, 2647, 3163, 3623, 3631, 3767, 3769.
2.2. а) 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67,
71, 73, 79, 83, 89, 97; б) 101, 103, Ю7, 109, 113, 127, 131, 137, 139, 149; в) 151,
157, 163, 167, 173, 179, 181, 191, 193, 197, 199; г) 557, 563, 569, 571, 577, 587,
593, 599; д) 1259, 1277, 1279, 1283, 1289, 1291,1297; є) 2309, 2311, 2333, 2339,
2341, 2347Гє) 2551, 2557, 2579, 2591, 2593; ж) 4327, 4337, 4339, 4349.
2.3. а) 25 . 5; б^в • З2 • 7; в) 7 . 11 . 13; г) 1009; д) 29 • 61; є) 23 . З2 • 52;
€) 53 • 67; ж) 28 • З5 • 113; з) 23 • З3 • 54 • 73 . 112 • 17 • 23 • 37.
2.5. а) 13 • 61; 6} 23 • 3 • 31; в) 22 • 31 • 127; г) Позначити число 74 через*
і розкласти число а на лінійні множники (х — 2) (* + $). Після спрощень дістаємо
а = 22 • 601 . 2399; д) 13-61 - 37 • 73 • 181; є) 293 • 3413; є) 13 • 4561.
2.6. а) р = 2; б) р = 3; в) р = 3; г) р = 3; д) р = 3; є) р = 3. Числа 3, 5
І 7 є єдиною трійкою простих чисел-близнят (прості числа р і р + 2 називають
простими числами-близнятами); є) р = 3. Якщо р = 3&+ 1 або р = 3k + 2, то
число 8р2 -f- 1 є складеним. Якщо р = 3k, то k = 1 і р = 3. Тоді 8р2 + 1 = 73
і 8р2 + 2/? + 1 =79; ж) р = 3.
2.8. р = 13. Розглянути рівняння 2р+ 1 = (2* + І)3.
2.9. а) Якщо р — парне, то р -f- 10 — складене, якщо р — непарне, то р -f- 5 —
складене; в) Якщо 2п = 3q + 1, то 2п — І =3^ —складене число, оскільки п > 2;
якщо 2п = 3q + 2, то 2п + 1 = Zq + 3 —складене число.
2.10. Усі натуральні числа містяться серед чисел виду 30& ± s, де k — ціле
число, a s = 0, 1, 2, . . ., 15. З них простими можуть бути числа виду р%~ ЗОЛ ± 1,
ЗОЛ ± 7, 30& ±11, 30& ± 13. Розглянути всі можливі випадки.
2.11. а), б) Використати метод математичної індукції;
в) РчР2 ... Pk_i = Psq (s > k, q> 1), звідки ps < p{p2 ... pk_l і ps< p{p2 ... pkm
Тоді pk+x < Plp2 ... pk;
211

г) Нехай pk—найбільше просте число, що не перевищує я > 2. Канонічний
розклад числа t = р{р2 . . . Р^—\ містить тільки прості числа, більші за п. Отже,
t > я, а тому рхр2 . . . pk> п.
2.13. Якщо я складене, то п = аЬ, а > 1, 6 > 1. Тоді 2Л — 1 = 2а6 — 1 =
= (2а)ь — 1 — складене.
2.14. Якщо я має хоч один непарний дільник d > 1,
то
" «w_1} "(,_2) "
2Л+1 = (2d +l)(2rf -2<* + ...,_2d + 1),
де обидва множники більші від 1, оскільки я > 3, d > 3. Тоді число 2Л + 1
було б складеним, що суперечить умові. Отже, я = 2 .
2.15. Використати рівність р2 — q2 = (р — \)(р + 1) — (q — \)(q + 1).
2.16. 5. Використати задачу 2.6, є).
2.18. Якщо /і = 1, то покласти х = 3; якщо я > 2, то покласти х = /і2.
2.19. а) я = 2, я = 8, б) я = 3.
2.20. Нехай /? — простий дільник я! — 1. Оскільки р < я! — 1,ти /? < я!. Крім
того, я! неір, звідки я < р. Отже, п < р < п\ (3 доведеного випливає, що
множина простих чисел нескінченна.)
2.21. („+ 1)1 + 2, (я+1)1 + 3, ..., (я + 1)1 + (я+1).
2.22. а) Припустимо, що множина простих чисел виду 3k + 2 скінченна-
Нехай це числа рх < р2 < . . . < ps. Розглянемо число t = Зрхр2 ... ps + 2-
Зрозуміло, що це число виду 3& + 2. Оскільки t > ps і / > 1, то t складене.
Отже, воно ділиться хоча б на одне просте число. На 3 воно не ділиться.
Зрозуміло також, що всі прості дільники числа і не є виду 3k + 1. Отже, число /
ділиться хоча б на один простий дільник виду ЗА» -+ 2. Оскільки всі такі прості
числа знаходяться серед чисел pv р2, . . . , ps, то t ділиться на одне з них.
Тоді з рівності / = ЗРіР2 ... ps + 2 випливає, що на це число поділиться
й число 2. Дістали суперечність.
§3
3.1. а)0; б) 7; в) 21; г) 13; д) 2; є) 17; є) 55; ж) 41; з) 71; к) 420; н) 1.
3.2. а) 13; б) 23; в) 119; г) 23; д) 7; є) 21; є)-2; ж) 33; з) 17; к) 12; м) 1.
3.3. а) 2; б) 0; в) 2520; г) 99671; д) 138600; є) 3276; є) 1116; ж) 67818;
з)я(я+1). ;.::
3.4. а) 88200; б) 36036; в) 2940; г) уя (я + 1 )(я + 2) при я парному і
я(я+1)(я + 2) при я непарному; д) 4582198; є) 4272.
3.5.3)3 = 5.21—2-51; б) 2 = 20 • (-26) + 3 • 174; в) 29 = -6-899 +
+ 11-49Ї; г) 17 = — 10 • 1445 + 23 -629; д) 43 = — 4 • 903 + 5 • 73І; є) 47 =
= 2 • 1786 — 5 • 705; є) 6 = — 135 - 822 + 64 -1734; ж) 1 = 17 - 4373 + 90 • (—826):
з) 17^ = 45 • (-3791) + 52-3281.
3.6. Див. приклад 3, § 3.
3.7. а) а = 30, 6 = 120; а = 60, 6 = 90 і навпаки; б) а = 24, Ь = 120 і
навпаки; в) а =» 2, Ь = 10 і навпаки; г) а = 20, Ь = 420; а = 60, Ь = 140 і навпаки;
д) а = 4, 6=180; а = 20, 6 = 36 і' навпаки; є) а = 495, 6 = 315 і навпаки;
є) а= 140, 6 = 252 і навпаки; ж) а = 4, 6 = 24; .а = 8, 6 = 12 і навпаки; з) а = 4,
6=12 і навпаки; к) а = 24, 6 = 2496;*а = 192,* 6 = 312 і навпаки; л) а =552,
6= 115; а = 435, 6 = 232 і навпаки; м) а = 75, 6= 195 і навпаки; н) не існує]
3.10. a) nd— 1, де cf = (m, я); б) 13, якщо (а —5): 13; 1, якщо (а — 5) не
МЗ. Скористатися рівністю 4 (а2+1) = (2а + 3)(2а — 3) + 13; в) 7.
3.12. а) Групуючи доданку, показати послідовно, що це число ділиться на
271 і на 7, і використати співвідношення (7, 271) = 1, 7 • 271 = 1897; б) покласти
п+ 1 = а3 і показати, що (а3— 1) а3 (а3*+ 1) ділиться на 7, 8 і 9;
в) Застосувати індукцію (за числом я, починаючи з я = 0);
д) Розглянути різницю (а2/г+ 1)— .(а+ 1).
212

§4
4.1. a) 12 і 168; 6) 9 і 217; в) 24 і 1170; г) 8 і 624; д) ЗО і 2418; є) 8 і 1440-
є) 12 і 1960; ж) 24 і 2808; з) 16 і 2340; к) 3Q і 3844; л) 8 і 3096; м) 24 і 8736.'
4.2. а) 1, 2, 4, 8, 3, 6, 12, 24; б) 1, 5, 25, 2, 10, 50; в) 1,5, 25, 2, 10, 50,
4, 20, 100; г) 1, 2, 4, 8, 3, 6, 12, 24, 9, 18, 36, 72, 5, 10, 20, 40, 15, ЗО, 60
120, 45, 90, 180, 360; д) 1, 5, 25, 125, 3, 15, 75, 375.
4.3. а) 20; б) 1, якщо т (п) = 1; р, якщо т (п) = 2; р2, якщо х (п) = 3; р3 або
ро, якщо т (п) = 4; р4, якщо т (п) = 5; р5 або р% якщо т (п) = 6, де скрізь р
і а— різні прості числа; в) 675; г) 200; д) 192; є) 192; є) 180; ж) 45 360; з) 18'
к) 2е З5 54; Л) 120; м) З3 5*; н) 1 400.
4.4. а) т = 2k, де k — довільне натуральне число.
4.5. а) 28; б) 160 або lf.9; в) 280.
4.9. а) 16; б) ЗО; в) 40; г) 80; д) 200; є) 500; є) 192; ж) 400; з) 320.
4.10. а) 8; б) 12; в) 24; г) 40; д) 66; є) 20; є) 2.
4.12. а) х= 16, 24, 20, ЗО, 15; б) х = 36, 28, 13, 26, 21, 42; в) розв'язків
немає; г) х = 2 при р = 2; х = р, х =■■ 2р при р > 2; д) х = 2*+1; 2k • 3; 2k~l • 5;
2fe~2 • 15 при k > 2; х= 15 при ^ == 3; є) х = 2*, ££ІЧ; є) х = 2* • 3', £, /£N;
ж) розв'язків немає; з) х = 5*, k £ N; к) х = 3*, £ 6 N л) * = 2к • s, де &, s£ N
і (s, 6) = 1; м) х ■--= 3.
4.13. а) 7875; б) 143; в) 14 161; г) 741 125; д) 343; є) 67 375; є) 143, 183, 225,
244, 248; ж) гри р Ф 3 розв'язків немає, при р =- Зза k можна взяти будь-яке
натуральне число, відмінне від 1.
4.15. а) 2; б) —3; в) — 1; г) 2; д) 4; є) 3; є) 5; ж) 4; з) -2; к) —3; л) 2.
4.16. Іа) 0,14; б) 0,86; в) 0,5; г) 0,6; д) 0,5; є) 0,15; є) 0,4; ж) -| .
4.17. а) [2,3*] = 3, тоді 2,3* — а = 3 або 2,3* = 3+ а, де 0 < а < 1. Отже,
З 4 л
З < 2, Зх < 4, тоді 2~3 < ^ < ~2~3 • 0стато.1,но маємо * £
ЗО 40
23: 23
;б)*є
50
32 ;
в) х
2І:
т-\- а
де 0 < а < 1; г) х = 7; д) , f [/2 ; /3 [; є) х = 1; є) х = 0; 1-і;
ж) *=.0;1; з) *£0; к) х£[ту; (т — \)(у + 1)[, де */—ціле число,

причому у < т — 1.
4.18. а) Нехай х=[х] + г і у --= [у] + s, де 0 < г < 1 і 0 < s < 1. Тоді
* + </ = [*] + [</]+ (' + *)• Якщо 0 <r + s < 1, то \х + у] = [х] + [у]. Якщо
1 < r + s < 2, то [* + у] > [*] + [у]. Отже, [х + у]> [х] + [*/]; в) якщо р = 46 + 1,
то
k='-
1
якщо р = 4& + 3, то
т. Тоді ^ = q + ^y де 0<^-< 1,
L4
=*-*
ЗВІДКИ і/ =
— 3
4
а 1
m J
; г) a = mq-\-rt де
і тому
\а_~\ а — г
m n l m m
з) використати твердження з п. а) цієї задачі; к) розглянути випадки m = 4k 4- І
і/п = 4НЗ.
13589.
216 , g8
31 • 37;
• 47 -53
4.19. а) 48; б) 98; в) 832;
4.20. a) 2s -З4-5 і. 7 • 11;
+ 7б • її3- ІЗ3 • 172- 192- 23 •
X 193 • 233 • 292 • ЗІ2 • 37а- 41
X 17 • 19.
4.21. а) 12; б) 28; в) 494,
4.24. а) | Ш -
б) 999
г)
б)
29-
43
53 .
J)
59
72.
271
. 61
11 .
. 335
• 67
13-
. 5і»
•71
17;
в)
•711-
• 73;
д)
238 .
П6 .
22
• З18
ІЗ5-
• 11
•5»х
174Х
• 13 X
в) 100
-т-
-т-
г108]
786J
999]
7
N00
L 3
+
+
11450
ті
7
j1001
L 6
=
= 686;
33;
213

г) 1378; д) 5634; є) 393.
4.25. ЗО.
§5
л Pk 1 4 5 9 23
5.1. а) [1; 3, 1, 1. 21.^ = 7- "З ' Т ' У' ІЗ;
*\ п і я 9, -* І 2 17 36.
6)115 ^ 2J' <?*=T' Т' 9- Г9:
г) [-2; 1, 1, 2, 1, 5], £= -т. - у. --j, _т -у. -^
^ JL A JL 23 ііі
в) [2; 1, 1, 4, 2], ^ = j , ,, 2 ' "9"' 20;
P_k 2 1 3 7 10 57
V
0 , , pk 2 3—5—18—23 jzii
д) —2; 2, 1, 3, 1, 1, 4, 3], ^ = — у. — -j. —> -ур» -уу > 25 '
— 187 602
~7Ї4~ ' 367 ;
wo ■ , , . ,п, ^* 3 4 7 п 51. 521.
е)[3;1, 1, 1,.4, Ю|, ^=---. -, т. т. w щ.
Рь 10 1 1 2 Ч
ж)[-1; 1, 1, 1, 1, 1, 1, 2,61,^=,-, у> —J'—з- -Т- —8'
_5_ ]3 _83_.
""13* ""34' 217 '
з) [-1; 2, 2, 1, 1, 6. 2], ^ -^, -І ~f "У' -й- ~8'
99_.
— 170 *
Pk 0 1 1 З
к)[0;2, 1, 2], р; = Т- Т'Т'Т:
Р_к 10 1 4 5 9
л) [-1; 1, 1,4, 1, 1, 1, Ю], Q-b = -T, - —5- — Т"- — ТТ- — 2Р
U _]49
""ЗР ~330-
20 131 7 97 17 359 883 73
5'2- а) ЗТ; б> 583; в> 23: г) ТІЗ: д) §3; е) ТЇЗ; є) 27ї; ж) Ї20І;
234 271 2_
з) 195; к) ~~ 100: л) З"
105 245 64 73 99 11 11 25
5.3. а) -з§; б) ж; в) ^: г) ^ д) Щ1 є) -1 ^; є) -2^; ж) -4 jy;
2633 . а* + 4с3 + 3д fl3^?2 f- 4a2fr + Зд
3) 1810; к) о'+За* : Л) л«62 + 3а&+1
5.4. Використати те, що
(а, 6) "' (а, 6)
* -Qn^a«n-l-^-lQn = (-lA
214

5.6. a) ^1^-^-(+0,01) = 0,78. Знак похибки «+», оскільки £< < JL.
3/9 Q4 Ь »
б) з^-J! (+0,0003) ^1,6830; в) 359^22(--0,0005)¾ 1,5909. Знак похибки
Рь а
«—», оскільки -Q- > -у.
85 5 Л 277
5.7. а) от з надвишком; о) щ з недостачею.
5.8. а) х = [щ| = 2; б) х = 2.
5.9. [1; 1, 1, 4, 3]. Розкласти -^- в ланцюговий дріб.
5.10. ?2 = 3.
* 587 • .
5.11. Замінити дріб тт^ підхідним дробом з похибкою, яка не перевищує
587
0,001. щ = [5; 5, 7, 3]. Підхідні дроби:
^о__5_ ^j__26 ^2 _ 187 ^з_587
Q0~ 1 ' Q, — 5' Q2- 36' Q3~ 1 ІЗ'
26 1 1
Якщо взяти дріб -g-, то похибка становитиме 5Т36 = Щ ~ ^»^^- Оскільки
26 ' 187
0,006 > 0,001, то дріб -g- не підходить. Беремо дріб-og-. Знаходимо похибку
36—ІТя^ 4068— °'00^ < ^00^ Отже, можна побудувати передачу за
допомогою валів з кількістю зубців 187 і 36, що технічно можливо, а) 22 і 7;
б) 163 і 51.
5.12. а) х = — 8360— 117/, #=-2717 + 38/, /gZ;
б) х = — 2 + 4/, у = — 4 + 7/, t £ Z;
в) * = —125 — 114/, # = 45 + 41/, / G Z;
г) л: = 1 — 9/, # = 39 + 49/, / Є Z;
Д)х = 9 + 31/, # = 2-12/, /£Z;
є) * = 75 + 23/, # = —120 — 37/, / £ Z;
є)* = 4+17/, # = —11—53/, /£Z;
ж) * = —15 — 39/, # = —25 — 64/, / £ Z;
з) * = —15 + 37/, #=18-43/, /<EZ;
к) х= 1270 + 359/, # = —2020 — 571/, / £ Z.
5.13. а) Розв'язків немає; б) л: = 4+42/, # = 23/, /£N; в) * = 3, # = 5.
5.14. 56 і 44.
5.15. 19 дощок 11 см завширшки і 7 дощок ІЗ см завширшки або 6 дощок
11 см завширшки і 18 дощок 13 см завширшки.
5.16. 2 мішки по 60 кг і 4 мішки по 80 кг.
5.17. З—5/ білетів по ЗО коп. і 28 + 3/ білетів по 50 коп., де —9 < / < 0.
5.18. Горобців — 9, горлиць—10, голубів—11.
5.19. (0, 18, 8); (1, 16, 9); (2, 14, 10), (3, 12, 11); (4, 10, 12); (5 , 8, ІЗ);
(6, 6, 14); (7, 4, 15); (8, 2, 16); (9, 0, 17).
5.20. а) [1; (2)]; б) [1; (1, 2)]; в) [2; (4)]; г) [2; (2, 4)]; д) [2; (1,1, 1, 4)];
є) [2; [1, 4)]; є) [3; (6)]; ж) [3; (3, 6)]; з) [3; (2, 6)]; к) [3; (1, 1, 1, 1, 6)];
л) [5; (3, 2, 3, 10)]; м) [5; (2, 10)]; н) [7; (1, 2, 7, 2, 1, 14)].
5.21. а) [(2)]; б) [(1, 2)]; в) [1; (2, 2, 2, 1, 12, 1)];^ г) [2; (1)]; д) [1; (1,
1, 4, 1)]; є) [2; (18, 2)]; є) [1; 7, (1, 6)]; ж) [-5; 2, (3, 5, 3, 1, 1, 10, 1, 1)];
з) [3; (3, 1, 1, 40, 1, 1, 3, 5)];- к) [2; 7, (2, 6)]; л) [0; 14, (8, 1, 2, 1, 8, 13)];
м) [1; І, 1, (2,_2, 1, 12, 1,_2)]; н) ]2; 1,_4, (5, 3)]. __
5.22. а) П+1; б) VI^ZI; в) Щіі; г) /5-2; д) Щ^І;
215

e) 1+VT76); є) /33-2,5; ж) ^212~3; з) Qfl; к) 2 (/2-і);
л)1+УЇ; м) ^1; „) К^+і.
5.23. a) Vj7=3. б) £^25-^69. в) 5 /ІЗ - 13 } /Ш -1
_ 4 ' _ 14 3_ 4
гі ^37-1. еї ^37 + 3, . 5/2. 2(/14 + 2). . 25-/бї.
Д) J Є) 4 ' ~2~' Б 4
„» 29+_/2Ї. 138-/5. . 18 + /506. . 4/95-18
' 10 ' ' 79 '28 13 '
5.24. а) Xі— 102 = 0; б)*2 — 92 == 0; в) Xі— х — 4 = 0; г) 10л:2—17л: —
-5=,0; д) 19л-2—_37£— 11 =0; є) 2-У2— 15* + 26 = 0; є) 16л:2 —32а: + 13 = 0.
5.25. а) *• = /а2 + 1; б) л: = V> + 2.
5.26 a) \q; (2q)]- б) \q\ (q, 2<,2)]; в) [q; (I, ¢-1. 1, 2<?)]; г) [cf>; fa2, 2<?3)].
5«7
5.27 a) fo3=(5; 1, 2. 3, 10]« 5,7 (+0,0002);
355
6) 3,14159 = [3; 7, 15, 1, 25, 1, 7, 41^^(+0,000004):
B) 1 (+0,07) = Z±±J_1; r) JL (+0,00005) = 2 ~~ ^
3 2 37 5
349 155
5.28. a) ^ ^ ^3 (—0,0001) « 4,7808, *2 «-gy (—0,0001) « 2,7192;
29 331
б) *i ~ — 55 (—0,0001) « —0,7250, x2 » — ^g- (—0,0001) « —8,2750;
в) *, % — -щ- (—0,0001) « —2,6375, *2 « Іщ (—0,0001) « 1,0332;
593 „ 57
r) *, « J3Q (-0,0001)¾ 4,5615, r, =^-J3Q (+0,0001)¾ 0,4384;
251 449
Д) *i* —]2g (+0,0001)¾ -2,008, *2« —щ (+0,0001) ^-3,2071.
,90 £>_-L _J_± ^_Jt ^-^
^' 0„- 1 • (?,- 3 ' Q2~ 4' Q3~23'
65
5.3). s.
241 530
5.31. a) f5; (2, 10)1«-^-- 6) [7; (1, 2, 7, 2, 1, 14)]¾ gg-;
271 !09
в) [2; (1, 4, 1, 1)1« gg-; r) [(1; 12, 1, 1, 1, 2, 1, Щ^щ.
5.32. а) Через x позначити дріб ,,< ., Тоді [(a, b)] = a + x і треба довести,
a л І
що * (a + *) = -j-. Оскільки х = j—, то в результаті перетворень маємо
b +
х2 + адг — -т- — 0, тобто х (а + х) = -т~;
a +*
_4 і Ол" | 1
в) Показати, що ^ = [а; о, а, а]. Якщо дріб [а; а, а, а] обчис-
я3 + 2я
лити, то дістанемо 3 , що свідчить про нескоротність останнього;
a4 + 3fl2+l
a3 + 2a
г) якщо (Р„, P/I_1) = d, то Р„ = ^Рл_! + Р„_2, звідки (Pn_v Pn_2) = d.
При я = 2 маємо д* = (Рр Р0)-= (0^+1. я0)= L Твердження (<?„, Qn_x) = 1
доводять аналогічно; д) використати результати ~адачі 5.32, г); є) застосувати
216

формули Pk = qkPk_x + Pk_2 і Qk = qkQk_x+ Qk__2 при k = n + 2 і k = n+ I;
є) використати індукцію за числом /і; ж) використати індукцію за числом п і
співвідношення Qn = qnQn_{ + Qn_2 > 2Qn__2;
л) Знак різниці
+
а~ Q„ + Qn+i =<?n+2Q„+i + Qn ~ Qn + Qn+i =
(-1^(^+2-1)
(<?n+2Qn+1+Q„)(Qn + Qn+1)
рп + Рп+і оь pn + Pn+i
залежить від парності п; п , п < а ПРИ п = 2«. а < тї—, /ч пои
V„ і- «п+і «п + Vn-и
, P. + P/.+1 • . Рп _ .
п = 2/г+ 1. Дріб 7ГТГ7І лежить між о і ;*-. Тоді
*л т ч:л+і ^п
P„ + ^
n+l
a~Qn r Q. + Q.+i ««
q„(Q„ + Q„+1)-
Зауваження. Встановлена нерівність дає нижню границю для
І, отже, доповнює відому нерівність
«—7Г <;
м) Твердження випливає з рівності
(qn + m)Qn_l+Qn_2 qnQn_{ + Qn_2 =
де Л > 0 — добуток знаменників підхідних дробів;
ab + YaW + 4a6
:(_1)«-2 . m . _
Л'
5.33. а)
26
[(а. Ь)];
б) маємо рівняння Ьх2 — abx — а = 0 (див. задачу 5.32, а)). Сума коренів
цього рівняння дорівнює а, звідки х2 = а— [(а, 6)] = — ^ .,;
в) оскільки х = [а; (6, с)] = a + [Tg^Tt то [(Ь, с)] = ^^г* Число Ш с)\ *
коренем рівняння сх2 — Ьсх — Ь = 0 (див. задачу 5.33, б)). Отже, другий корінь
можна знайти з умови —— =—., ,ч, звідки * = а— [(с, Ь)];
а аЬ + 1
г) -g- == . / у Числа х і у задовольняють умову
(Ьс + \)x* — (abc+a + c — b)x — (ab+ 1) = 0,
(ab + \)у* — (abc + a+ c — b) у — (bc+ 1) = 0,
х ab+ 1
звідки — =
У
be + 1» отже р = у ;
д) Якщо j/m = [?0; <7і> <72, • • + т0 00 + ^ = [2<70; <7р ?2, . . .\ > 1 і —1<
< q0—Vm < 0. Отже, <70 + ^^71 виражається чистим періодичним ланцюговим
дробом, тобто qQ + Vm = [(2qQ; qv q2, . .., qn)]. Тоді Vm = [q0\ (qv q* • • •> ?„)].
5.34. a) a:
£—1
10 /2 + P
[3; 3],
217

10/2 + 3 57-)^2
°"~ 3/2+ 1 ~ 17 ;
6) « = [2; 1, 5, 2, 1, (2, 1)] =23 '
a _i_ |/"fl2 і 4
6.35. Якщо д: = [a; a, a, . ..] = [a, x], то x = ~ •
§6
6.1. а) 64; б) 159; в) 596; г) 1205; д) 1429; є) 1874.
6.2. а) XXVI; б) СХІІ; в) MCMLXXX.
6.3. а) 109; б) 1012; в) 1015.
6.4. а) 110002; б) 10001 1112;в) 101 0112; г> 1112;д) 2255 0257; є) 3(10)94 91312;
є) ЗО 4І37; ж) 190 00012; з) 567 і остача 2027; к) (10) 9412 і 8712 в остачі; л) 2,48!
6.5. а) 1000012; б) 11, 111012: в) 100000, 110012; г) 0, 13378; д) 11, І48!
6.6. а) 18; б) 16; в) 18; г) 15; д) 15; є) 18; є) 13; ж) 17; з) 17; к) 18; л) 14|
м) h> н) !б.
6.7. а) 39; б) 205; в) 229; г) 2617; д) 704; є) 8387; є) 1668; ж) 1523; з) 6871;
к) 5669; л) 42 923.
6.8. а) 0,875; б) 0,75; в) 25,9365; г) 287,388671875; д) 0,044921875.
6.9. а) 4(10)2(!1)12; б) 230 5789; в) 11202 102 120 1003; г) 367 34І8;
д) 10001000 110 110 111 101 1002; є) 2 121 ЗІ 15; є) 41268.
6.10. а) 11 111 111 0102 = 221 01223 -= 31 1325 б) 1 010 111 000 0Ю2 =
= 10 211 0123 = 42 1215; в) 20617; г) 1653 2127; д) 55 1738; є) 42 1678.
6.11. а)°4; б) 5; в) 9; г) 9; д) 5; є) 9; є) 7; ж) 6; з) 5.
6.12. а) 5; б) 8; в) 6; г) 7; д) 7; є) 7; є) 7; ж) 9; з) 6; к) будь-яка основа
g> g > 2.
6.14. а) (Ю0...01)2; б) (11...1100.. . 00)2.
2^—1 Р Р—!
6.15. х = 2, і/ = 4.
6.16. а) 7243 -29-=210 047.
6.17. 153 846.
6.18. х{ = 0, У[ = 8; х2 = 8, у2 = 0.
6.19. 361.
6.21. (хуг){0 = \50, ^-= 15.
6.22. 6310 = 778 = 3334 = 111 1112#
Розділ II
§7
7.1. Усі множини, крім множин з) і м). Усі кільця з одиницями. Кільця
б), г), є), ж) містять одиницю при_ /п= ± 1, Дільники одиниці: а) 1, —1; б) 1,
-1 при т= ± 1; в) ±(3 + 2/2)", де п € Z; д) 1, -1, і, — і; є) 1, -1, ',
— / при т= ± 1; є) 1, —1; ж) 1, —1 при т = ± 1; к) 1, —1; л) усі ненульові
ч і 1 l *'^3 -Х *'^3
елементи; н) 1, —1, s » 9 '
7.4. Усі множини, крім а), є кільцями. Усі кільця, крім є), ж), л), містять
одиничний елемент. Дільники одиниці: б) такі матриці Л, що | А \ = ± 1;
ч /1 0\ /—1 0\ ч л
в), г), д) будь-яка невироджена матриця; є) І 1, І 1; з) будь-яка не-
/1 0\ / — 1 0\ ч л
нульова матриця; к) Iі h M^ будь-яка ненульова матриця;
218

н) будь-яка ненульова матриця. Дільники нуля мають б) — є), це вироджені
ненульові матриці. Комутативними є кільця є) — н).
7.5. Усі множини є кільцями. Всі кільця, крім б)—д), є комутативними і
/1 0\
містять одиницю. Дільники одиниці: а) І»
(
—1
0
°\
-&
Iі
U
3
""" 2
1
2
-І 2\ /1 3'
2 2 \ / ~~ 2 ~2
1 1 Г II 1
2 ~~ 2 / \ 2 "Т
є) будь-яка ненульова матриця; є) / \ і ( Q j; ж) ( Ь
П J)' ҐІ і)' (I -ЇЙ (І Йаб° Ґо _')'Д^~Довільне ціле
(1 Ь с\ /—1 Ь с\
0 1 Ь І, І 0—1 6 І. Дільники нуля: а) немає;
0 0 1/ \ 0 0 -1/
(а а\ І а — а\
б) — д) усі ненульові матриці; є) немає; є) матриці виду І } і
а а \—а а
(а 0\ /0 0\
де а=£0; ж) матриці виду І І і І І, де а, Ь ф 0; з) довільна матриця
/0 6\
виду І, ft^O; к) матриці виду
'0 ft c\
0 0 Ь 1, де б2 + с2 ^ 0.
\0 0 0/
7.6. Кільцем є тільки а).
7.7. Не утворюють кільце множини з пп. б), д). Усі кільця комутативні.
Дільники одиниці: а) усі елементи (одиницею в цьому кільці є пара
(0, 0){ в) немає одиниці; г) (1, 1), (1, —1), (—1, 1), (—1, —1) (одиницею тут є
(1, 1); є) — ж) (1, 0), (-1, 0); (одиниця тут (1, 0)).Дільники нуля: а) усі
пари, крім нульової (1, 1) і одиничної (0, 0); в) усі пари, крім нульової (0, 0);
г) fa 0), (0, Ь\ де а, ЬФО; є) (а, а), (а, —а), де а ф0; є), ж) дільників нуля
немає.
7.10. Областями цілісності є 7.1: а), б) при т= 1; в), г) при т = 1; д),
є) при т=1; є), ж) при т=1; к), л), н; 7.4: є), з), к), м), н); 7,5: а), є);
7.7: є), ж). Полями є 7.1: л); 7.4: з), м), н); 7.5: є).
7.11. Дільниками нуля є вирази виду а-\-ае, афО.
7.12. Дільниками нуля є вирази виду 6s, Ь Ф 0.
§8
8.1. а) Двосторонні ідеали; б) двосторонній ідеал; в) лівий ідеал; г)
правий ідеал; д) двосторонній ідеал; є) двосторонній ідеал; є) двосторонній ідеал;
ж) двосторонній ідеал; з) двосторонній ідеал; к) двосторонній ідеал; л)
двосторонній ідеал.
8.2. а) Правий ідеал; б) правий ідеал; в) лівий ідеал; г) двосторонній ідеал;
д) не є ідеалом при афО; є) не є ідеалом при а Ф 0 і Ь Ф 0; є) двосторонній
ідеал; ж) не є ідеалом при а ф 0; з) не є ідеалом при а Ф 0.
8.5. а) <1> =Z; б) <б>; в) <6>; г) <3>; д) <6>; є) <18>; є) <2>;
ж) <20>; з) <40>; к) < 1 > = Z; л) <35>; м) <35>.
8.8. а) <1> =1; б) <2>; в) <3>; г) <1> = Z; д) <2>; є) < 1 > = Z;
є) <2>.
219

8.10. Використати задачу 8.3, в); а = Ь (mod 0) тоді і тільки тоді, коли числа
а і Ь дорівнюють одне одному.
8.11. Для фактор-кільця Z2 = Z/<2> маємо табл. 47, 48. Дільників нуля
в Z2 немає; Г-1 = ї.
Таблиця 47
1 +
б
1 т
б
б
ї
т
т
б 1
Для Z3 —табл. 49, 60.
Таблиця 49
+
б
т
2
| 0
б
Г
2
т
Т
2
б
2
2
б
г
-1
Дільників нуля в Z3 немає; 1
Для Z4 — табл. 51, 52.
Таблиця 51
1 +
б
т
2
3
б
б
т
2
3
т
І
2
3
б
2
2
3
б
Т
сої
3
б
т
2
Дільник нуля 2; 1 1 = 1, 3 * =■• 3.
Для Z5 — табл. 53,54.
Таблиця 53
+
б
г
2
3
1 *
б
б
т
2
3
4
Т
т
2
3
4
б
2
2
3
4
б
Т
3
3
4
б
Т
2
4
4
б
Т
2
; з 1
Таблиця 48
X
б
1 І
X
б
Г
1 2
б
б
б
Та
б
б
б
б 1
1 т
1 б
1 9
б л и ц я 50
т
б
т
2
2
б
5
т 1
о-1
= 2.
Таблиця 52
X
б
7
5
з
б
б
б
б
б
Т
б
т
2
3
2
б
2
б
2
3
б
3
2
т
X
б
Г
2
3
1 4
б
б
б
б
б
б
т
б
Т
2
3
4
Таб
2
б
2
4
І
3
лиця 54
3
5
3
Т
4
2
4
б
4
3
2
т'
220

Дільників нуля в Z5 немає; 1 ] = 1, 2 ! = 3, 3 1 = 2, 4 ] = 4.
8.12. Z2, Z3 і Z5.
8.14. а) 2, 4, 6; б) 3, б; в) 2, £ 5\ 6\ 8; г) 2, 37 4, б" 8, 9, Ю; д) 2, ї, б,
7, 8, ЇО, Г2; є) 3, 5, 6, 9", 10, Ї2; є) 2, 4, 6, 8І ІО, Ї2, J4.
8.15. а) Т"1 =Т, 2~1 =4, З"1 = б, 4"1 =2, б"1 =3, б"1 = 6; б) Г"1 «
= Т, 3^=3, 5^=6, 7-1 = 7; в) J"1 = T, 2^=5, 4^=7, 5^=2,
Г"1 = 4, в"1 = 8; г) Т"1 ~ Т, З"1 = 7, 7"1 = З, ЇЇ-1 = 9~У д) І"1 = Т, 2"1 =
= 6, З-1--?, 4_1=3, 5^=9, 6^=2, 7_1=8, 8^=7, 9^=5, КГ"1 =
= Т0; є) J"1 =Т; 5^ = 5, 7^=7, ЇЇ"1 = ЇЇ; є) ї"1 = Г, 2"1 = 7, З"1-
=--9, 4~1=Ї0, ^=8, 1^= ТТ, У-1-^, ^=5, 9^=^3, TO"1 = 4,
ТІ-1 = 6, Т^-1 =Т2; ж) Т_1=Т, З'1 = 5, 5-^3, 9""1 =-ТТ, П"-1 = 9,
ЇЗ"1 = ІЗ; з) І-1 = Т, 2-1 =8; 4-1 = 4, 7""1 - ІЗ, 8"1 = £ ЇЇ-1 = ТТ,
ІЗ-1 = 7, "U-1 = Ті; к) І-1 = Г, З-1 - ТТ, %-{ = T5, 7"1 = 7, 9"1 = 9,
ЇЇ"1 = З, ІЗ-1 =-• 5, І5-1 =_Тб.
8.16. a) Z[i]/<2> = {0, Т, /, 1+0. де 0 = 0+<2> = {2£ + 2s/|fc, s£
£Z}, Г= 1 + <2> = {2*+l+2s/|£, s£Z}, Г = і+ <2> = {2k + (2s +
+ \)i\k, seZ>, Г+/ = 1 + / + <2> = {2fc+l + (2s + 1) /1 k, s£Z}.
Таблиці додавання і множення (табл. 55, 56).
Таблиця 55 Таблиця 56
X
0
Т
і
\Г+і
б
0
0
б
б
ї
б
Т
і
гйм
/
б
і
т
Г+ї
1 + ч
б 1
Ти
Г+7
б
+
б
т
1 і
1 Нр
б
б
г
І
П1";
т
т
б
т+ї
і
і
і
гп
б
т
1 + t
~і
і
т
б
Дільник нуля Т+7; Т_1=Т, І-1 =7. б) Z[/]/<3> ={0, Т, 2, /, 277 І+і',
Г+2^ 2+Т7 2+¾ Де
б"=:0 + <3> ={3k + 3st\k, s£Z},
Т = 1+ <3> ={3/г+ l+3s/|£, s£Z},
2 = 2+ <3> = (3£ + 2 + 3s/| £, s£ Z},
7=/ + <3> = {3£ + (3s + \)i\k, s£Z},
"2/ = 2/+ <3> = {3* + (3s+ 2)*'І £, s£ Z},
Т+7 = І+/+ <3> = {36 + l + (3s+ \)i\k, s£Z},
1+2/=1+2/+ <3> = {3k + l + (3s + 2)/|£, s£ Z},
2+1 = 2 + /+ <3> = {36 + 2 +(3s + 1)/1 6, s£Z},
2~+2/= 2 + 2/ + <3> = (ЗА;+ 2 +(3s+ 2)/1 k, s£ Z}.
Таблиці додавання і множення для елементів Z[/]/<3> (табл. 57, 58).
221

Таблиця 57
+
0
1
2
і
Ті
ї+1
Г+"Й
2~+1
\2~2i
б
0
Т
2
і
Ті
Г+1
Г+ПЙ
2 + і
2~+~Й
Т
Т
2
б
г+1
Г+~2І
2 + «
2"+^/
і
Ті
2
2
б
ї
2"+!
2~+"Й
/
Й
ТТі
Г+~Й
і
7
!+'
2+1
Й
б
1~+~Й
Т
2~+~Й
2
Й !
Я
1~+~Й
2"+~Й
б
і
т
ї+1
2
2 + /
ї+1-
ї+1
2+1
і
Г+~Й
т
Й+~Й
2
Й
б
Ґ+"й|
1 + 2і\
2~+"й|
Й
"і
Г+1
' 2
:"2+1
б
1
2+ М
2 +і
і
TTi
2~+~Й
2
Ті
б
Г+~й
г
2~+~2И
2~+"Й
2/
Г+2Л
2
2 + М
б
f 1
т
І"Г+1І
Таблиця 58
X
б
І
5
1 '
Ті
г~
1~+2І
2Т«
[2~+~Й
о
б
о
б
о 1
б
б
б
б
б
Т
б
Г
2
/
Ті
Т+1
ґ+"й
т+-і
2~+~Й
2
б
2
т
й
і
2~+~Й
2+1
Г+2І
ї+1
і
б
і
Ті
2
т
й+1
Т+1
І2"+~Й
Г+2І
Й
б
Й
і
І
2
Г+2І
2+ 2/
!ї+1
2+1
1 + /
б
ї+1
2~+~Й
2+1
1 +2/
2/
2
І
/
Г+~Й
б
ґ+"2<
2+1
Г+1
2~+~Й
2
і
Ті
т
2 + *
б
2+1
Г+~Й
2~+~Й
Г+1
1
й
І
2
Й+~Й
б
й+~й
Тр
1 +2 /
й+1
і
т
2
1 й
Дільників нуля нецае; Г""1 = 1, 2~* = 2, і~{ = 2t, 2Г"1 = і\ 1 + t"1 =
=1Й+1, ї+~#-1 = 2 + 2ї, 2+^ = 1 + і, 2 + 2Г~1 --= 1 + 2і\ в) <2/> =
= <2>; г) <—Зі> = <3>; д) </>=Z[/]i тому Z [<]/<*> = {Z [і]} =
= {б}.
222

8.17. a) 16 елементів; дільники нуля; 2, 2/, 1 +/, 2 + 2/, 3 + /, 3 + 3/;
М=% зі~{ =1 7+^--1 = "П+2Г;
б) 25 елементів; дільники нуля: lj-2/, 1 + 3/, 2 + /, 2 + 4/, 3 +/,
3 + 4/, 4 + 2/, 4 + 3/; 2"1 =3, 4Г"1 =_/, 3 +2/~|_= 1_+/^
в) 36 елементів; дільники нуля; 2, 3, 4, 2/, 3/, 4/, 1 + /, 1 + З/,
1 + 5/, 2+"2^ 2 + 4/, 3+Т 3 + 3/, 3 + 5/, 4 + 2/, 4 + 4/, 5~=К 5 + З/,
5 + 5/; 2 + 5/-1 =2+3/, 4 + Г"1 = 2 + /.
8.18. Z[/3]/2Z[/3j= {0, 1, /3, 1+/3}, де 0 = 0 + 2Z [/3 ] = {26 +
+ 2s/3U, s£Z}, T=l+2Z[/3]={2A!+l + 2s/3lfe, s^Z}, '7Т=/з +
+ 2Z [/3] = {26+ (25+1)/3^, s£Z}, 1+3=1+/3 +2Z [/3] ={26 +
+ l+(2s+l)/3*U, s£Z}.
Таблиці додавання і множення (табл. 59, 60).
Дільник нуля
1+/3; І"1*!, /3^=/3.
Таблиця 59
Таблиця 60
+
б
"і
VI
і+У"з
1
0
0
І
Ft
1+/3
Т
Т
б
1+/3
Ті
75
7?
ї+75
б
І
1+/ЗІ
1+71
75
г
б
X
б
т
7¾
і+75
б
б
б
б
б
т
б
т
71
1+/3
п
б
75
т
1+/3
\+vi
б
ї+75
Г+75
б
§ 9
9.3. Оскільки в довільному полі Р є тільки два ідеали {0} і Р, а ядро
Кегср гомоморфізму ер двох полів Р і Р{ повинно бути ідеалом в полі Р, то
при гомоморфному відображенні поля Р на поле Р{ ці поля ізоморфні.
Зауваження. Якщо розглядати відображення поля в поле, то можливий ще
очевидний гомоморфізм поля Р в поле Р{:
<|> (a) = 01 для будь-якого а £ Р.
9.4. Використати задачу 8.4, з).
9.6. Кегс
■не з
9.7. Кегср = 3Z.
а$ Z
*€Q
9.9. Кегср = {/€ /С|/( 1) = 0}.
9.12. 1) Кільце класів лишків Z4; 2) поле із задачі 7.3, г); 3) 0, І, а, а+ 1
при 1 + 1=0, а2 = а, а (а+ 1) = 0, (а + І)2 = а + 1; 4) 0, 1, я, а+1 при
1 + 1=0, а2 = 0, (а+1)2=1, а(а+1) = а. Усі кільця комутативні.
9.13. Кільце складається з елементів {та}\ т = 0, 1, . . ., pq—1. Елемент
а можна вибрати так, що виконуватиметься один з чотирьох випадків: а) а2 =
= а (кільце, ізоморфне кільцю класів лишків; 2) а2 = 0 (нульове множення);
3) а2 = ра; 4) а2 = qa.
223

§ ю
10.14. a) 1; б) 10; в) 3; г) 15; д) ((/я, я, s), (k, tt /=)); є) [(m, n, s)'
(*, '> /)!•
(4 + і) (3 + і)
10.15. а) (4 + 3/, 3 + 0- 1+2*, [4 + 3/, 3 +/] - 1 = 2/ ~ 7~~/;
б) (6 + і, 5 + 7/) - 6 + і, [6 + t, 5 + 7/] - 5 + 7/;
в) (8 + 12/, 10 + 40 - 2; [8 + 12/, 10 + 4/] - 16 + 76/;
г) (5 — 5і, 7 — 0 - 3 + і; [5 — 5і, 7-і] 5 + 15/;
Д) (і і _ зі, 3 + 70 ~ 1 + і, [ 11 — Зі, 3 + 7і] - 61 + 7/;
є) (5+ 6/, 6 + 50- 1; [5 + 6/, 6 + 5/] - 61;
є) (7 + Зі, 5 + 2і) - 1; [7 + % 5 + 2і] - 29 + 29і.
10.16. а) (7 4-/2, -5-5/2)-1; [7 + /2, -5-5/2)-45 +
+ 40/2; б) (5 + 2/2, 6-/2)-5 + 2/2; 15 + 2/2, 6-2/2]-
-26 + 7 /2.
10.17. Для задачі 10.15: a) d = 1 + 2/ = (4 + Зі) . 1 + (3 + /)(—1); б) d =*
= 6 + / = (6 + 0-1+(5 + 7/)^ в) d = 2 = (8+12/)(-1-3/) + (10+ 4/) X
X (—1 +40;
г) d = 3 + / = (7 - і) (-1) + (5 - 5/) (1 + 0;
Д) <*= 1 + / = (11-3/)(1-2/) + (3 + 7/)(1 + 0;
є) d = 1 = (5 + 6І) (-6) + (6 + 50 (6 + 0;
є) d= 1=(7 + 30(-2) + (5 + 2/)-3. _
Дл_я задачі 10.16: а)_ d = 1 = (7 + /2 ) (- 4 + 2_/2) + (— 5 — 5 /2 ) (9-
-7/2); б) ^ = 5+2/2 = (5+2/2) . 1+(6-/2) . 0.
10.18. а) Нехай г — ціле гауссове число і Nr (2) = р— просте число. Якщо
г = ху, де х, у £ Z [/], то р = Nr (2) = Nr (де) • Nr (у). Оскільки Nr (*) і
Nr (#) — натуральні числа і р — просте число, то або Nr (*) = 1, або Nr (у) = 1,
тобто одне з чисел л: або # є дільником одиниці в Z [/]. Це означає, що 2 б
просте ціле гауссове число.
11 111 і 2 і J
10.19. Показати, що 2 = 2^ = 2^2424 = 2224282=...
10.20. Знайти елементи, які неоднозначно розкладаються на прості
множники, довівши простоту множників та їхню неасоційованість: а) 4 = 2-2 =
= (І + /3/) (1 -/ЗІ); б) 6 = 2-3 = (1+ /57) (j_-/o7); в) 18 = 2 . З • 3 =
= (1 + /17/) (1 -/17/); г) 20 == 2 • 2 • 5 = (1 + /l9t) (і - /19/).
10.21. Використати норму Nr (а + Ь /з/) = a2 + 362.
10.22. Використати норму Nr (а + Ьі) = а2 + Ь2.
10.24. a) 5=(2 + /)(2- /); б) 5 — 5/ = (1 — і) (2 — і) (2 + /); в) 3 + /=.
= (1 + /)(2-/); г; -90+180/ = 32 (1+/)2 (2 +/)2 (2-0; д) —182-126/ =
= 7(1+/)3(2 + /)3; є) 7 + 8/ = 7 + 8/; є) 41=(4 + 5/)(4-5/).
Розділ III
§ П
11.1. а) 216 і 21, 134 і 214; б) 135 і 225, 106 і 181, 167 і 452; в) 217
і 241.
11.2. а) 137, 620; б) 201; в) 234, 634.
224

11.4. a) —38 з—3 (mod 7); б) 53= 5 (mod 8); в) а +2 s 0 (mod5); r) аа —
-і2 = 0 (mod (а — Ь)); д) — 73 є a (mod 8); 0 < г < 8; є) 20 ш 389 (mod 41);
a) 219 ф 129 (mod 7).
11.5. a) ns0(mod2); б) леї (mod 2); в) лезі (mod 4); г) лез 3 (mod 5);
д) п в — 2 (mod 7); є) л в — 3 (mod 8).
11.6. a) —д) Показати, що в заданій конгруенції різниця частин ділиться
на модуль; є), є) показати, що ліва частина заданої конгруенції ділиться на
кожен множник модуля; ж), з) показати, що обидві частини заданої конгруенції
закінчуються однаковими цифрами; к) оскільки 11 • 31 — 1 = 340 = 5 • 68 і 25 =з
є —1 (mod 11), то (2^ = 2340^11,31^ в 1 (mod 11). Оскільки 25 в 1 (mod 31),
то (г5)68^11'31""1- 1 (mod 31). Тоді 2ій31-1 в 1 (mod 11 .31). Звідси 211,31в
в 2 (mod 11 • 31); л) З н = (З3)432 = 274 . З2 а (-2)432 = 144 в -1 (mod 29).
11.7. а) —з), м) Показати, що обидві частини заданої конгруенції мають
з модулем різні найбільші спільні дільники.
11.8. а) Використати формулу розкладу бінома:
(а + Ь)р = аР + С\ар~хЬ + C2pap~2b2 + ... + Cpp~labp~l + Ьр.
У правій частині цієї формули всі члени, крім ар і вділяться на р.
б) Ср = j ,2ttj • Тоді р — Is— 1 (modp); р_ 2s —2
J mod р), . . ., р-*є~іг (mod р).
Іомножаючи почленно ці конгруенції, дістаємо:
(р - 1) (р-2). .. (р- k) ш (-1)*1 . 2.. .k (mod p).
Оскільки k\ і р взаємно прості і кожна частина конгруенції ділиться на k\. то
(р-1)(р-2)..,(р-*) n*/fmwlfrt
£j s(~1) (modp);
г) Оскільки а = Ь + p% t £ Z, то при піднесенні цієї рівності до степеня р
дістанемо ар = Ьр + рл+Ч q Є Z, тобто ар в бр (modp'1*1);
р — 1 р + 1 п і
д) 3 чисел 1, 2, 3,..., -g—, —g—, .,„/?-2, р — 1 складемо -=-^-
конгруенцій:
1 а — (р — 1) (mod p),
2в — (р — 2) (modp),
—2— а — —2— *т р'т
Тепер піднесемо кожну з цих конгруенцій до степеня 2k + 1 і результати до*
дамо; є) з конгруенції р з р + 2 в 1 (mod 2) дістаємо конгруенцію P*7"1"2 + (p +
+ 2)р в 0 (mod 2), з конгруенції раз— l(modp+l) і р+ 2 в 1 (modp+1)
маємо рр+2 + (р + 2)р в 0 (mod р + 1). Тоді рр+2 + (р + 2)" а 0 (mod 2p + 2);
Р — п
є) усі задані числа, крім нуля, мають вигляд ± —*—, л=1, 2, ,. #| р—2.
Конгруенції
р —л Р — пх Р — п2
± —%- s ° (mod rt» —2— * ~— s ° (mod rt
призводять до неправильних конгруенцій
л £з р (mod d), n{ в і л2 (modp).
8 6-271 225

11.9. a) 1; б) 1; в) 4; г) 0; д) 1; є) 1); в) 0; ж) 0; з) 1; к) 12; л) 3; м) 1}
н) 71. Остача дорівнюватиме 36.
11.10. б) Нехай \\a + 2b\9. Тоді 11д + 2Ь = 0 (mod 9). Домножимо цю
конгруенцію на 12. Матимемо 132я + 346 =з 0 (mod 19). Звідси 18а-f-56 =
= 0 (mod 19), тобто 18а + ЬЬ І 19.
11.12. Застосувати метод доведення «від супротивного», в) Нехай xQ, yQ
г0 — розв'язок рівняння 24^ + 36^ = 612. Тоді 24*° + 36-Vo = 61z°. Якщо числа
рівні, то вони конгруентні за будь-яким модулем. Отже, (—1)*0+1^°==
£= 12° (mod 5). Звідси (—1)*° = 0 (mod 5), що неможливо.
11.14. а) &, /, т — будь-які; б) k, /, m одночасно парні або непарні; в) kf
/+ 1, т одночасно парні або непарні.
11.15. а) 2; б) 9; в) 7; г) 3.
11.16. а) 88; б) 67; в) 24; г) 9; д) 27; є) 36; є) оскільки 9*°== 1 (mod 100),
то 910<7+r=9r(mod 100). Оскільки 99 s 9 (mod 10), то 9»9 = 99 = 89 (mod 100).
Шуканими цифрами є 8 і 9; ж) оскільки 74 = 2401 = 1 (mod 100), то і 710°¾
= 1 (mod 100), звідки 7»"s 7100^+89 г 789 (mod 100). Проте 788= 1 (mod 100),
тому 78е= 7 (mod 100). Отже, шуканими цифрами є 0 і 7.
11.17. а) 225 + 1 = 232 + 1, 232 = (28)4 = (2562)2 = 655362 ^ 1542 = 23716 ш
s — 1 (mod 641). Отже, 232 + 1 є 0 (mod 641). Справді, 232 + 1 = 4 294 967 297 =
= 641 • 6 700 417;
2 п
б) Це твердження рівносильне твердженню, що числа 2 , п — 2, 3, ...
закінчуються цифрою 6. Застосуємо метод математичної індукції. При k = 2 маємо
22"= 16 == 6 (mod 10). Припустимо, що 22 =6 (mod 10) і доведемо, що ^ =
= 6 (mod 10). Оскільки (22 ) =22'2 = 22 , то при піднесенні до квадрата
конгруенції 2^ = 6 (mod 10) дістанемо 22 = 36 s 6 (mod 10), що й треба було
довести.
§ 12
12.1. а) 6; б) 27 і —3; в) 8; г) 65 і —2; д) 1; є) 7; є) 14 і —1; ж) 667 і —114;
з) 55 і —1; к) 1; л) 14 і —3; м) 501 і —2; н) 37 і —14.
12.2. 0, 1, 2, . . ., т—1, якщо т — модуль.
гп і
12.3. 0, ±1, ±2,..., ±—2~, якщо т— непарне число; 0, ±1, ±2, ...р
(т А т л (т \ т
±1-2—1), 2 аб° °' ±Х% ±2'"" ±\~2~~-Ч* -¾. якщо /я—парне число.
12.4. 1, 2, . . ., m, якщо т — модуль.
12.5 0, —1, —2,..., — (т —1), якщо т — модуль.
12.6. —1, —2, . . ., —т, якщо т — модуль.
12.7. Наприклад: а) 3; б) 0, 5; в) 3, 4, 5; г) 0, 9, 10, —1; д) 0, 1, 2, 3, 100,
є) 36, 1, 2, 3, 4, 5; є) 7, 8, 9, 10, 11, 12, 13; ж) 0, ±1, ±2, ±3, 12; з) 0, —Ь
—2, —3, —4, —5, —6, —7, 1; к) 10, ±1, ±2, ±3, ±4, 5; л) 3, 2, 4, 5, 6, 7, 8,
9, 10, 11, 12, 13; м)-3, -4,-5, -6,-7, —8, -9, -10, -11, —12, —13, —14;
-15, —16, -17; н) 20, ±1, ±2, ±3, ±4, ±5, ±6, ±7, ±8, ±9, —10.
12.8. Використати відповіді до задач 12.2—12.7, виключивши у відповідних
повних системах числа, не взаємно прості з модулем.
12.9. а), б), г), д), ж), з), к) —так; в), є), є) — Ні.
12.10. а), в), г), д) — так; б), є) —ні.
12.13. а) *<»>' = К«? U *<478) U tf'f? U *(498) U *<£> U K(|f U К^ U *($;
*<!> = К™ и * (498> U * (4|> U К(42? U /СІ78) U К^ U К<№ U К<#; *<? = К(4Б8) U
и *(48> и к(478) и к($ и к(\1> и * !8> и * <4?> и k(4j>.
12.14. а) К<32>; б) К(з4>. в, /С(|>; -) к%; д) К^; є) /С<|>; є) /((130); ж) К1?1
в) /Г^>; к) не існує, оскільки (198, 501)-.3* 1; л) К%}; м) К(\\1$; К^-
226

§ із
13.1. г), з) Теорема Ейлера не справджується.
13.2. г), л) Мала теорема Ферма не справджується.
13.3. а) 7; б) 1; в) 22; г) 5; д) 32; є) 29; є) 19; ж) 1; з) 1; к) 1.
13.4. а) 2; б) 1, 4, 1, 4; в)13; г) 7; д) 14; є) 14; є) 65; ж) 49.
13.5. а) 21; б) 22; в) 64; г) 21; д) 375.
13.6. а) 2; б) 6; в) 1; г) 5; д) 2; є) 0; є) 2; ж) 2; з) 70; к) 7.
13.7. а) 01; б) 67; в) 31; г) 97; д) 01; є; 61; є) 61; ж) 97; з) 76; к) 92; л) 84.
_, 1 + т 1 + т
13.12. а) 0, якщо а\Ь і 1, якщо не ділиться на 5; б) —^—; в) —^—, якщо
Зт+ 1
т = 4k — 1 і —г— , якщо т = 4k + 1.
§ 14
14.1. a) xs=2(mod3); б) розв'язків немає; в) x3 2(mod5); г) х = 5 (mod 7);
д) х з 4, 9 (mod 10); є)^еЗ (mod 7У; є) х = 8 (mod 11); ж) х = 2, 5, 8, 11 (mod 12).
14.2. а) х ss 3 (mod 13); б) розв'язків немає; в) х = 3, 10 (mod 14); г) х з
= 2 (mod 27); д) *= 6 (mod 23); є) * = 3(mod37); є) х з 11 (mod 41); ж) х з
= 38 (mod 51).
14.3. a)jts4 (mod 13); б) х з 3 (mod 12); в) х з 10 (mod 12); г) х = 14 (mod 19);
д) х з 13 (mod 34); є) Розв'язків немає; є) х з 3 (mod 22); ж) х з Ґ, 14, 27 (mod 39).
14.4. а) * = 9 (mod 93); б) х ш 28 (mod 119); в) розв'язків немає; г) х з
з 11 (mod 169); д) х з 73 (mod 177); є) хз 29 (mod 201 £ є}"* з 29, 138, 247 (mod 327);
ж) хзІ7, 96, 175, 254, 333 (mod 395); з) х = 153, 461, 769 (mod 924); к) х з
^ 1630 (mod 2413); л) * з 200, 751, 1302, 1853, 2404 (mod 2755); м) розв'язків
немає.
14.6. a)jts3 (mod 23); б) х з 11 (mod 24); в) х з 11 (mod 24); г) * з 23 (mod ЗО);
д) розв'язків немає; є) х = 2, 7, 12, 17, 22, 27(mod30); є) X32(mod41);
ж) хз 21 (mod 50).
14.7. a) x = a+b (mod ab)\ б) * з (а — 6)(p(fl£>)~1 (mod аб); в) х = (а — &)(а +
+ £)<Р<а*)-і (mod ab). г) Xs(a —6)(moda6); д) х з -у^ (mod /?); є) х з m —
— 1 (mod m); є) x = a (mod m); ж) x з ap~~2 (mod /?).
14.8. a) Будь-яка конгруенція виду ax з b (mod 15), де (a, 15) = 1; 6) ajcs
ss b (mod 15), (a, 15) = 3, b\3 або (a, 15) = 5, 6 і 5; в) такої конгруенції скласти
не можна.
14.9. а) х = 2 + 3/, .і/ = —2/, * € Z; б) х = 2 + 3/, г/ = 2 + 4/, /g Z; в) х =
= 3 + 4/, #= 1 — З/, /*£Z; г) х = 3 + 4/,г/ = — 3— 5/, /£Z; д) х = 7 + 8/, */ =
= _2 — З/, /£Z; є) х = —3+13/, у = 4 — 17/, / £ Z; є) х = — 7+15/, r/= 12 —
— 23/, /£Z; ж) * = —1 + 16/, у = —8+17/, / £ Z; з) х = 1 + 4/, і/ = 2 + 13/,
t£Z; к) розв'язків немає; л) х = 20 + 2І/, у = 23 + 25/, /£Z; м) х = 47+105/,
у = 21+47/, /£Z; н) х = 94+111/, # = 39 + 47/, / £ Z.
14.10. а) х == 18 (mod 35); б) розв'язків немає; в) хз 12 (mod 35); г) х з
з 105 (mod 225); д) х з 170¾ + 52¾ (mod 221); є) х з 100 (mod 143), у =*
= 111 (mod 143); є) хз 1 (mod5); у з 2 (mod5); ж) розв'язків немає.
14.11. а) х з 91 (mod 120); б) х з 59 (mod 60); в) х з 33 (mod 90); г) х з
з 86 (mod 315); д) х з 256 (mod 1547); є) розв'язків немає; є) х з 47 (mod 420);
ж) х з 49 (mod 420); з) х з 125 (mod 1496); к) х з 11151¾ + 11800¾ +
+ 16875¾ (mod 39825); л) х з 8479 (mod 15015).
14.12. а) х з 17 (mod 90); б) х з 4 (mod 105); в) розв'язків немає; г) х з
=299 (mod 385); д) розв'язків немає; є) хз9573 (mod 13923); є) хз8505б (modl30169).
14.13. Абсциси точок такі; х з 291 (mod 819). Ординати знаходять за
допомогою рівнянь прямих.
14.14. а) а з 5 (mod 6); б) а з 0 (mod 4); в) а з 1 (mod 7); г) а з 1 (mod 6).
14.15. Необхідно і достатньо, щоб 7 — 3 = 4 ф 0 (mod (6, m)). Якщо,
наприклад, (6, т) = 3, то можна взяти т = 15.
14.16. 19.
14.18. а) 7; б) 2; в) 2; г) 19; д) 7; є) 8.
14.20. а), б) через 12 точок.
8*
227

14.21. r = Va* + b*.
14.22. c\(a, b).
14.23. 5 вересня. Задача зводиться до розв'язування невизначеного
рівняння 12*+ 31*/ = 8, 1<х<31 (або 1<у<12). Оскільки (12, 31)=1, то таке
рівняння з обмеженнями на х 1 у має єдиний розв'язок.
14.24. 2 і 4 або 6 і 1.
14.25. Можливі вісім варіантів: 2 J 39, 9 і 34, 16 і 29, 23 124, ЗО І 19,
37 і 14, 44 і 9, 51 1 4. Найкращим є перший, бо в ньому треба зробити
найменшу кількість стикувань труб.
14.26. Можливі 10 варіантів: 3 і 28, 8 і 25, ІЗ і 22, 18 і 19, 23 і 16, 28 і
13, 33 і Ю, 38 і 7, 43 і 4, 48 і 1.
§ 15
15.1. а) х3+ 2х2 +$ ж 0 (mod 11); б) х3 + 18х2 + 4*— 17 т 0 (mod 59); в) х6+
+ 4а:5 + 22х4 + 76х3 + 70л:2 + 52* + 39 в 0 (mod 101); г) хп + axxn~lh + ... +
+ anh в 0 (mod m), де h аадовольняє умову a0h в 1 (mod m).
15.2. a) 2x3 + 3 в 0 (mod 5); 6) 3x4 + 2x3 + 3x2 + 2x в 0 (mod 5); в) З*2 +
+ * — 2 в 0 (mod 7); r) 5x6 + x5 + 5*4 + За2 + 3* + 4 ш 0 (mod 7); д) б*8 + 7х5+
+ За-4 + З*3 + х2 + 3 в 0 (mod 11).
15.3. a) хв2(то(іЗ); б) розв'язків немає; в)о1, 2(mod3); г) х в
в 1 (mod 3); д)^| (mod 3); е)хз4 (mod 5); є) х в Я (mod 5); ж) * в 2 (mod 5);
з) розв'язків немає; к) х ж l(mod5); л)хв1, 2 (mod 5).
15.4. а) х в 2 (mod 7); б) * в 4 (mod 7); в) * в 1, 2, 3, 4, 5, 6 (mod 7); г) х а
в 4, 5 (mod 7); д) * в 4 (mod 11); є) розв'язків немає; є) * в 7, 9 (mod 11); ж) * в
в 12 (mod 13); з) * в 7, 13 (mod 23).
15.5. а) Випробовуючи лишки 0, ±1, ±2, знаходимо перший розв'язок х1 в
в 4 (mod 5). Запишемо тотожну конгруенцію
/(*)-(*-4)/^) (mod 5). (1)
Знаходимо /х(х) як частку від ділення / (х) на х —4 і визначаємо його корені
за модулем 5:
fr (х) = *а + 8* + 32 в х* + 3* + 2 в 0 (mod 5).
Ця конгруенція має розв'язок х2 в 3 (mod 5), отже
M*)-(*-3)M*)(mod5). (2)
Знаходимо /а (х) як частку від ділення /t (х) на х — 3 і його корені за
модулем 5:
/2 (х) = х + 11 в 0 (mod 5).
Розв'язуючи цю конгруенцію, дістаємо а* в 4 (mod 5), отже
f2(x) в* — 4 (mod 5). (3)
З конгруенцій (1) — (3) маємо
f (х) в (х — 3) (х — 4)а (mod 5).
Зауважимо, що розв'язок * в 4 (mod 5) e двократним.
Конгруенція (х — 3) (х — 4)а в 0 (mod 5) є еквівалентною заданій. Ліва
частина її і є розкладом на лінійні множники функції /(х) = х3 + 4ха— 3 за
модулем 5;
б) (х — 1) (аг — 2)as0(mod5);
в) (х — 1) (х — 2) (де — 3) (х — 4) з 0 (mod 5);
г) 3 (де — 1) (х - 2) (х — 3) в 0 (mod Б);
д) (х-1)(х-2)(х-3)(х-6)в0(пкгі7);
є) 5 (х — 1) (х — 3) (х — 5) в 0 (mod 7);
є) 6(х — 1)(х —2)(х —9)в0(пкгі 11);
Ж) (х — 2)(х — 3) (х — 9) в 0 (mod 17);
з) (х— 1)(х- 13) (х — 21) в 0 (mod 23);
к) (х — 2)2 (х — 11) (х — 28) в 0 (mod 29);
л) (х — 17) (х - 28) (х - ЗО) в 0 (mod ЗІ).
228

15.6. б) — є) Використати теорему Вільсона; є) треба гточленно перемножити
конгруенції а = ар (mod р) і (р — 1)1 = — 1 (mod p).
15.7. a) jts 1, 2, 4, 5 (mod 6); б) х = 1 (mod 6); в) x==2(mod 10); г) х в 0,
4, 6 (mod 10); д) х в 7 (mod 10); е)^9 (mod 15); є) х = 11 (mod 15); ж) х в 2, 5,
11 (mod 15); з) *s4(mod21); к) розв'язків немає; л) х в 0, 14, 20, 34(mod35);
м) х = 2, 7, 24, 29 (mod 55).
15.8. а) хв2, 5, 11, 17, 20, 26 (mod ЗО); б) лг = 3, 26, 28, 49, 63, 73, 84,
94 (mod 105).
15.9. а) хв 21 (mod 25); б) х в 16 (mod 25);
в) хв 2, 3(mod25); г) хв J3(mod 25);
д)ха 17 (mod 49); є) хв 18,33 (mod 49);
є) хв2, 9, 16, 23, ЗО, 33, 37, 44 (mod 49);
ж) х в 8 (mod 49); з) розв'язків немає.
15.10. a) хв 8 (mod 27); б) х в 19 (mod 27);
в) х в 22 (mod 27); г) х в 16 (mod 27);
д) хв 22,53(т&ї64); є) хв 61 (mod 125);
є) хв 113 (mod 125); ж) хв 84 (mod 125);
з) хе 19(mod 125); к) х в 43, 123, 168, 248, 293, 373,418,498, 543
623 (mod 625).
15.11. а) Розв'язків немає; б) х в 2(mod 12);
в) х в 4, 13 (mod 18); г) х в 12 (mod 40);
д) лг в 6, 33, 42 (mod 45); є) х в 42 (mod 45);
є) хвб, 24, 4? (mod 45); ж) х в 12, 24, 37, 49 s (mod 50);
в) хв 13 (mod 63); к) хв8, 44, 58 (mod 63);
л) х в 32, 82, 132 (mod 175); м) х в 36, 136 (mod 175);
н) х=22. 76, 122, 176 (mod 225).
р-\
15.12. Необхідно і достатньо, щоб ps 1 (mod п) і а п е] (mod/?).
15.13. a) xss 1, 2, 4(mod7); б) х в 2, 6, 7, 10 (mod 11); в) конгруенція
має лише два розв'язки х в 2, 9 (mod 11).
15.14. а) 6; б) р — 1; в)8;г)<р(т); д) ^=^; є) ^-=^-.
15.16. Оскільки 103 —просте число і 103= l(mod2), то дана конгруенція
має лише два розв'язки. Оскільки ж числа 31 і —31 задовольняють її і
31 ^—31 (mod 103), то маємо такі два розв'язки: хвЗІ, 72(mod 103).
15.19. х в З, 13 (mod 20).
§ 1«
16.1. а) х2 в 4 (mod 5), х в 2, 3 (mod 5);
б) (6х — І)2 в 1 (mod б), х з 0, 2 (mod 5);
в) (2х + 2)2в 1 (mod 5), хв 1, 2 (mod 5);
г) (2х — 2)2 в 0 (mod 7), х в 1 (mod 7);
д) (2х— І)2 в 3 (mod 7), розв'язків немає;
є) (Зх+ І)2 з 4 (mod 7), хвб, 6 (mod 7);
є) (х — 5)2в 1 (mod 11), хв4, Є (mod 11);
ж) (Юх + 7)2 в 4 (mod 13), х в 1, 8 (mod 13);
з) (х — З)2 в 0 (mod 13), х в з (mod 13).
16.2. а) (х+ І)2 в 4 (mod 10), хв 1,7 (mod 10);
б) (х+б)2 в 9 (mod 15), хвб, 12 (mod 16);
в) (6x + 7)2B4(modl7), хе 2, 7 (mod 17);
г) (х — 4)2 в 13 (mod 17), х в 12, 13 (mod 17);
д) (х — І)2 в 17 (mod 19), х в 7, 14 (mod 19);
є) (х - 5)2 в 5 (mod 19), х в U, 15 (mod 19);
є) (х + б)2 в 8 (mod 23), х в 4, 7 (mod 23);
ж) (2х — 5)2в— 39 (mod 96), хв 13, 16 (mod 24);
з) (6х + 2)а в 5 (mod 44), розв'язків немає.
16.3. а) а в 1, 4 (mod 5); б) а в І, 2, 4 (mod 7);
в) а= 1, 3, 4, 5, 9(mod 11); г) а в 1, 3, 4, 9, 10, 12 (mod 13);
д) ав 1, 2, 4, 8, 9, 13, 15, 16 (mod 17); є) а в 1, 2, 3, 4, 6, 8, 9, 12, 13,
16, 18 (mod 23); є) а в 1, 3, 4, 7, 9, 10, 11, 12, 16, 21, 25, 26, 27, 28, ЗО, 33,
34, 36 (mod 37);
229

JK)flsl, 4, 6, 7, 9, 10, 11, 13, 15, 16, 17, 24, 25, 28, 29, 36, 37, 38, 40,
42, 43, 44, 46, 47, 49, 52 (mod 53).
16,4. a) x =3 3, 4 (mod 7); 6) x ss 2, 5 (mod 7); в) розв'язків немає.
16.6. a) —1; 6У 1; в) 1; г) 1; д) —1; є) —1; є) —1; ж) —1; з) 1.
16.6. а) —1; б) 1; в) —1; г) —1; д) —1; є) 1; є) —1; ж) 1; з) 1.
16.7. а) 0; б) 2; В) Q; г) 0;'д) 0; є) 2; є) 0; ж) 0; з) 0; к) 0.
16.8. а) *= 1 (mod 31; б) *я 1, 4 (mod 5);
в) х= 1, 2, 4 (ntod 7); г) лг= 1, 3, 4, 5, 9 (mod 11);
д)^1, 2, 4, 8 (mod 15); є) х а 7, 11, 13, 14 (mod 15).
16.10. а) *чз"66, 245 (mod311); б)х& 12, 35 (mod 47);
в) * S3 6, 23 (mod 29); г) х щ 15, 22 (mod 37).
16.11. а) Ні; б) так; в) ні; г) так.
16.12. а) хз ±2 + 5?, у=*2\± 16g + 20<72, q$Z\ б) розв'язків немає;
в) розв'язків немає; ї) * = 8.+ ЩІ у = — 1 + Qq + 1 \q2 або x = 2+\\q, (/=»
= — 1 — 6q+ Uq\ q$Z; д) x = \0 + \3q або x = 11 — 13?, у = ІЗ?2— 1, q$Z.
16.14. a)jcs3, 5, 11, 13 (mod 16);
6) xsT, 9, 23, 25 (mod 32);
в)хаб, 11, 21, 27(jriod32);
г) *я ІЗ, 19, 45, 51 (mod 64);
д) *?* Jl, 21, 4І 53 (mod 64);
е) x ^31, 33, 95, 97 (mod 128);
є)* = 29, 35, 93, 99 (mod 128);
ж) * ==41, 87, 169, 215 (mod 256).
16.15. a) x= 13, 14 (mod 27); 6) x 5= 53, 72 (mod 125);
в) * = 116, 127 (mod 243); r) x^ 1, 2, 177, 226 (mod 400).
§ 17
17.1. a) 4; 6) 2; в) 2; r) 6; д) 2; e) 4; є) 8; ж) 4; з) 10; к) не існує; л) 6;
м) 18; н) 18.
17.2. а) клас Кі має порядок 1; клас /Сп0 — 2; класи К9* К4, Кь> Кь — Ь,
класи /Є2, #в» ^7» ^я—^; ^) клас %і мае порядок 1; клас /Є18 — 2; класи Кі,
/Сц — 3; /С8, /С12 —6; класи /С4, /Сб, /Ce, /C9, /Cle, /Ct7—9; класи 7(2, /С3, tfi0;
^із» ^Сі4» ^і5 ~ 18; в) клас /Сі має порядок 1; класи Ks> #13» АГ20 — 2; класи
^4» Km— 3; класи /Є2, К5У /С10» /Сц-, #із» ^Сі9 — 6.
17.3. а) 12, 3 і 2; б) 8,8 і 4; в) 10, 10, 2 і 5; г) 6, 2 і 12; д) 5, 10, 2 і 10.
17.4. а) 30; б) 2.
17.5. а) 2, 6, 7, 8; б) 2, 6, 7, 11; в) не існує; г) 2, 3, 10, 13, 14, 15; д) З,
5, 10, 12, 17, 19, 24, 26, 38, 40, 45, 47; є) 2, 5, 11, 14, 20, 23, 29, 32, 38, 41,
47, 50, 56, 59, 65, 68, 74, 77.
17.6. а) 2, 3; б) 2, 5; в) 6, 2; г) 8, 3; д) 12, 2.
17.7. а) 3; б) 3; в) 5; г) 6; д) 2; є) 27; є) 5; ж) 7; з) 7; к) 3; л) 3; м) 2.
17.8. 2, 8, 10, 11, 14, 15, 18, 19, 21, 26, 27.
17.9. *зз 1, 2, 4, 8, 9, 13, 15, 16 (mod 17).
17.10. 5, 6, 9, 13, 22. 17.12. 28.
17.13. а) # —довільне натуральне число; б) Р8 (5) = 2, тому х = 2л, л£ІМ;
в) х = 6/г, л Є N; г) х = 20л, л £ N;
д) х = 14л, л Є N; є) х = 21л, л Є N.
17.14. *і= 108 (mod 131).
17.15. а) Оскільки Р9 (4) = 3, то задана конгруенція має розв'язки тільки
при 6^=1, 4, 7 (mod 9); б) оскільки Р9 (5) = ер (9) = 6, то задана конгруенція
має розв'язки при умові, що (6, 9)= 1.
17.16. д) Використати результат задачі 17.16, г), н) дослідити конгруенцію
{a*- \)(ak+ l)aO(modp).
17.17. б) Довести за індукцією, що Р (а) < 2а-"2, де а —непарне
натуральне число, а > 3.
17.18. а) Нехай число 22П + 1 має простий дільник р. Тоді 22 + 1 ==
= 0(modp), тобто 22П=з —1 (mod/?). Звідси 22Л s=l(modp). Це означає, що
Рр (2) = 2П+1. Тоді р — 1 : 2*+1, тобто р =г 1 (mod 2n+1). Оскільки конгруенція
справджується при всіх п > 1, зокрема /7 в 1 (mod23), то р = St + Ь
230

За критерієм Ейлера про квадратичні лишки
р2-і
22 ш [ —J (mod р).
(M+Q'-l р-\
= 1. Отже, 2 2 =1 (modp). Звідси
Проте І у )-(-1) 8 --=(-1) *
£Zli : 2^+1 і тому р — 1 : 2Л+2 або р s 1 (mod 2"+2). Це означає, що р =
= \ + k- 2"+2;
в) якщо q— просте непарне число і ар г= 1 (mod q), то Ь = P q(a) — \ або р.
При & = 1 маємо а= 1 (mod q), а при В =р маємо q— 1 = 2/?*, *£ N;
г) якщо q — просте непарне число і аР + 1 = 0 (mod q), то а р = 1 (mod ¢).
Тому В = Р (а) є одним з чисел 1, 2, р або 2р. Випадки 5 *= 1 і В=р
неможливі. При В = 2 маємо: а2 == 1 (mod q), а+ 1 = 0 (mod q). При В = 2р маємо:
<7 — 1 = 2рху х£ N.
д) Використати результат задачі 17.18, а), поклавши а = 2, і провести
доведення методом від супротивного.
17.19. в) Очевидно, що Р т (a) = m і тому ер /ат — 1\ : т; є) використати
результати задач 17.19, г) — 17.19, є).
§ 18
18.1. а), б), г), є), є), ж)—див. таблиці індексів за відповідними модулями
в додатку; в) табл. 61, 62; д) табл. 63, 64.
18.2. Табл. 65, 66.
N
0
0
1
0
Таб
2
3
лиця 61
3
1
4
2
/
0
0
1
1
3
Таб
2
4
лиця
3
2
62
4
N
0
0
1
0
2
4
Тг
3
5
б л и ц я
4
2
5
1
63
6
3
І
0
0
1
1
5
2
4
Таблиця
3
6
4
2
5
3
64
6
N
0
1
2
0
12
5
1
0
17
—
2
11
10
3
16
13
4
4
7
—
5
1
2
6
8
9
Та
7
14
3
б л и ц я 65
8
15
9
6
18.5. а) х = 13 (mod 17); б) х = 8 (mod 27). Використати відповідь до задачі
18.2; в) х = 31 (mod 37);
г) х = ЗО (mod 73); д) х = 32 (тосі 79);
є) х = 74 (mod 79); є) х = 44 (mod 83);
ж) х s 51 (mod 97); з) х = ЗО (mod 221).
Оскільки 221 — 13« 17, то слід розглянути систему конгруенцій
137*= 5 (mod 13),
\37x = 5(mod 17).
231

Таблиця 66
/
! о
і
2
0
22
1
5
2
2
25
10
3
17
23
4
4
7
5
20
8
6
19
7
14
8
16
9
26
18.6. а) де = 7, 10 (mod 17); б) х = 8, 19 (mod 27). Використати відповідь до
задачі 18.2; в) х = 10, 43 (mod 53j;
г) * ss 27, 34 (mod 61); д) х === 27, 40 (mod 67){
є) х = 21, 46 (mod 67); є) х а 14, 57 (mod 71);
ж) *е= 17, 66 (mod 83); з) * а 2, 7 (mod 11);
к) х = 5, 20 (mod 43); л) * = З, 31 (mod 47);
м) х= 1634, 1847 (mod 592); н) х з 253, 4076 (mod 732).
18.8. а) 3; б) 4; в) 0; г) 1; д) 0; є) 10; є) 0; ж) 7; з) 3; к) 1; л) 0.
18.9. а) х = 4, 33 (mod 37); б) х ш 17 (mod 41);
в) розв'язків немає; г) х з= 2, 18, 23, 39 (mod 41);
д) *=7(mod43); e) розв'язків немає;
є) *= 17 (mod 67); ж) х з 8, 28, 31, 36, 39, 59 (mod 67);
з) де = ЗО, 53 (mod 83); к) розв'язків немає.
18.10. а) *з=3, 5, 6 (mod 7); б) х = 2, 3, 10, 11 (mod 13);
в) х = 10, 13 (mod 23); г) розв'язків немає;
д) *з= 11, 27, 36 (mod 37); є) х є 25, ЗО, 31, 36 (mod 61);
є) х= 17 (mod 73); ж) х ш 12, 23, 35, 38, 50, 61 (mod 73);
з) дс = 17, 63, 66(mod73); к) ^3, 24, 46 (mod 73);
л) де зз 6, 14, 20, 59, 65, 73 (mod 79).
18.11. а) х= 10 (mod 29); б) х == 29 (mod 31);
в) * = 24 (mod 37); г) х = 14 (mod 41);
д) х = 24 (mod 47); є) х ш 34 (mod 53);
є) х з=47 (mod 71).
18.12. а) 4; б) 16; в) не існує; г) 29; д) ЗО; є) 17; є) 2; ж) 16; з) не існує;
к) 23; л) 2; м) не існує.
18.13. а) Розв'язків немає; б) х =з 27 (mod ЗО);
в) х s 11 (mod 28); г) х з= 27 (mod ЗО);
д) х з= 2, 5, 8, ..., 56, 59 (mod 60); є) х =з 3, 7, 11, ..., 55, 59 (mod 60).
18.14. а) *з= 38 (mod 66); б) х = 3 (mod 72); в) хзаЗ, 16, 29, 42, 55,
68 (mod 78); г) х з= 5, 46 (mod 82).
18.15. а) 2; б) 11; в) 7; г) 5; д) 23; є) 13; є) 138. Оскільки 1739 = 37-47, то
Рі739 (10) = [Р37 (10), Р47 (10)] = [3, 46] = 138; ж) 84. Оскільки 4331 = 61-71, то
^433, (32) = [Р.х (32), Р71 (32)] = [12, 7] =84.
18.16. а) 26; б) 62; в) 7; г) 16.
18.17. а), в), г), є), є)—є; б),д), ж) — не є.
18.18. а) *з=*7, 57 (mod 100); б) розв#язків немає.
18.19. а) 15, 17; 19; 20; б) 15; 18; 19; в) 15; 17; 19; г) 18; д) жодне;
є) 15, 19.
18.20. а) 7; 37; б) 3; 5; 12; 18; 19; 20; 26; 28; 29; ЗО; 33; 34; в) 3; 27; 41;
52; г) 2; 6; 7; 10; 17; 18; 26; ЗО; ЗІ; 35; 43; 44; 51; 54; 55; 59.
§ 19
19.1. а) Ті і тільки ті цілі числа, в яких остання ци})ра парна; б), є) ті і
тільки ті цілі числа, в яких сума цифр ділиться на 3 (на 9); в), к), м) ті і тільки
ті цілі числа, в яких на 4 (на 25, на 50) ділиться двоцифрове число, утворене
їхніми останніми двома цифрами; г) ті і тільки ті цілі числа, які закінчуються
0 або 5; д), ж), з) ті і тільки ті цілі числа, в яких різниця між числом,
записаним останніми трьома цифрами, і числом, записаним рештою цифр заданого
числа (або навпаки), ділиться на 7 (на 11, на 13); є) ті і тільки ті цілі числа,
які закінчуються 0; л) ті і тільки ті цілі числа, в яких сума трицифрових
232

чисел, утворених відповідними гранями заданого числа при його розбитті справа
наліво, ділиться на 37.
19.4. а) Ні; б) так; в) так; г) так; д) так; є) ні; є) так; ж) так; з) так.
19.6. а) 33-52.112.2999; б) 7-13-17-19-37-73-101 • 137-257; в) х = 8, у = 0,
*«=6; г) *=* 1, */ = 2; д) 29-ЗМ01; є) 17а-19-557; є) 18095 і 68090.
19.6. а) 3; б) 33; в) 22; г) 63; д) 37 (використати задачу 19.3, б)).
19.7. а) 4; б) 24; в) 1; г) 23; д) 8; є) 8; є) 60; ж) 147; з) 48; к) 127; л) 5.
19.8. а) 19; б) ЗО; в) 20; г) 1; д) 12; є) 10; є) 6; ж) 70.
19.11. а), б), в), г), д), є) —помилки не виявлено; є) обчислення виконано
неправильно.
19.12. а) Помилки не виявлено, хоч насправді обчислення виконано
неправильно; б) помилки не виявлено; в) за модулем 9 помилки не виявлено, за
модулем 11—виявлено.
19.13. а) 16; б) 18; в) 28; г) 3; д) 21; є) 58; є) 33; ж) 8; з) 44; к) 96.
19.14. а) 6; б) 2; в) 6; г) 42; д) 16; є) 6; є) 6; ж) 16; з) 48; к) 176; л) 754;
м) 104. Конгруенція 10* s= 1 (mod 53-73) рівносильна системі
(10*= 1 (mod 53),
W= 1 (mod 73).
Розв'язуючи кожну з цих конгруенцій індексуванням, дістаємо
(х ш 0 (mod 13),
U = 0 (mod 8).
Звідси х ш 0 (mod 104). Отже, Рб3.73 (Ю) =.Ю4.
19.15. а) 2; 6; б) 2; 2; в) 2; 1; г) 4; 2; д) 2; 1; є) 2; 2; є) 1; 18; ж) 4; 16;
з) 2; 18; к) 2; 22; л) 4; 48; м) 3; 13.
19.16. а) Ь*= 11, 33 або 99; б) 6 = 27, 37, 111, 333 або 999.
19.17. а) 0, (736842105263157894); б) 0, (748251). Використати рівність
^ = 1+А;в)63;22.
1 1 1 3/г2 — 1
19.18. а) Показати, що ^—[ + ^Г ~*~ п 4- 1 = ~Т~2 ІУ * Р03ГЛЯНУТИ ви"
падки, коли п — парне, п — непарне; в) конгруенція 10* s 1 (modp<y) рівносильна
системі
10* = 1 (mod р), [х (ind 10) = 0 (mod р - 1),
або <
10* = 1 (mod q) [* (ind 10)^ = 0 (mod q — 1),
або
Звідси
/ p — 1\
: = 0 (mod —-j— j,
reOfmod^-y-A
г) Розглянемо будь-який період, який містить цифри zv z2, ..., Zfc і утворюе-
п
ться при перетворенні дробу — у десятковий, а також систему г0, r{t . . ^rk_{
усіх остач, що утворюються при нумерації їх по порядку, починаючи з п = г0.
Оскільки при діленні гг на т дістанемо в частці г2 і остачу г2 і т. д., то періоди
*і го Г\ rk-\ . .
дробів —, —, . . ., відрізнятимуться один від одного круговою
перестати т т
новкою цифр; період для другого дробу почнеться з z2, для третього — з z3 і
т. д. Якщо 10—первісний корінь за модулем т, то k = y(m) і числа гі вичер-
9 5-271 233

нують усю зведену систему лишків за модулем т. Тоді періоди всіх
нескоротних дробів із знаменником т знаходять як результат кругових перестановок
тієї само! системи k = y(m) цифр zv г2, ..., zk.
ю ю л ^ Лч 5521 ч 1Ї0119 ч 51487
19.19. а) п; О)9900: в) gggg ; r) gg()().
Розділ IV
§ 20
20.1. а) /(*) = — *5 —б*4 — 5х* + 4х2 + х+ 10;
б) /(д)=дв+-2;
в) /(а:) = 4*5 + 4х4 + 3*2 + 4а: + 3.
20.2. a) fl(x) = f3(x), f2(x) = fA(x)\
6)/iW=/2W.
20.4. Застосувати формулу бінома Ньютона і наслідок з теореми Ферма про
те, що ар =а (mod р).
20.5. а) а = —5, 6 = — 1, с=6;
б) а = 2, 6 = 5, с = 7.
20.6. а) а = 6, ^ (jc) = х2 + За: + 1, g2 (л:) = — х2 — З* — 1 ;
_ б) а== 3, g, (*) = 2* + 2, £2 (х) = З* + 3; а = 2, g{ (х) = 2* + З, g2 (x) =
= Зл: + 2;
в) а = 4, £і (а;) = За:2 — 2х + 2, g2 (х) = — З*2 + 2* — 2.
20.7. а =6, 6 = 2.
20.8. а = —8, 6=18, ^ (х) = х2 — 4х + 1, g2 (х) = — х2 + 4х — 1; а = 8,
6= 14, £^)=^+4^- 1, #2(а:) = — л:2 — Ах + 1.
20.9. Так, якщо а £ Z. Тоді g (*) = 2х2 — Зах + а2.
20.10. а2 = 46+4(с + 1).
20.11. а = 3, 6 = —7, с = 4.
20.12. Ні.
20.14. а) / (х) = (а:2 + З)2 + (2х)2;
б) / (х) = (а:2 + 6а: — ІЗ)2 + (2а: — 14)2.
20.15. а) Так; б) ні; в) так; г) так; д) ні; є) ні.
20.16. в) Застосувати наслідок з теореми Ферма та показати, що g (x) є нуль-
многочленом і f (x) = g(x) • h (х), де h (х) £ Z5 [x].
20.22. а) 0; б) —1; в) Т.
20.23. 2k~lsk.
20.24. Показати, що многочлен / (jc) не зміниться при замлні х на —х.
20.25. Розглянути многочлен h (х) = (1 + 5а:2 + я3)*, коефіцієнти якого при
парних степенях змінної х дорівнюють відповідним коефіцієнтам многочлена / (я).
20.26. а) а £ {8, 12}; б) а = 1.
§ 21
21. 1. а) У кільці Z [х] многочлен f (х) не ділиться на g(x), а в кільці
Q[x]—ділиться; б) ділиться; в) ні.
21.3. f(x) = (x + ~2)(x2 + x + ~\).
21
.4. а) а = -1; б) ає{-1, І-}.
21.5. Взяти до уваги, що х? — 1 = (х — 1) (х2 + х + 1).
21.6. а) 6 = — 1— а2, а = с;
б) 6=1, с = 0;
в) якщо а = 0, то Ь = с + 1 і с £ Z; якщо а £ Z\{0}, то b = 2 — а2 і с = 1.
21.8. Твердження хибне.
21.11. а) г= 1— і; б) г = 7; в) г (*)=* +2;
г) /■(*) = (2 + 0 * + 0-0; Д) г(х)=-7х+\\.
/о « 17 79^ 361 95
21.12. a) f(x) = g(x)[2x3 + 5*> + -s-x + -i-) + -rx--T;
234

б) f ( x) = g(x) (3 + 20* + (2-70* + (-2 + 0;
в) f(x) = g(x)(2x2 + 3x)+\-
г) s ^) = 5^-8^-2^ + 3^+6, л(л) = 4* + 5;
є) s {х) = Зх* + 3* + 2х* + х* + Ьх + 39 г(л) = 3л + 3;
1 , 1 2 1 71 / ч 449 2 71 7
€) s(x) = -g-x3 + Tx2 + -g4X—gj, '(*)= 5Ї2"* -*5T2"^+ 6?^
ж) s (л) = u, r (х) = 2х + 1 — і.
21.13. Ні.
21.15. а= 1, 6 = 0.
21.16. fj (^)=:(3^-4^+ І)2.
21.17. г = 3.
21.18. г(л) = 2х2.
21.19. г = —11 + 13*.
21.20. а) /«={(3* —5)/(*)|/(*)gZ[*]}; б) /=Z[*];
в) /={(*-1)/(*)|/(*)ЄЯМ}.
21.23. /={«/W|/WeZM}.
21.24. Ні.
§ 22
22.1. a) s (х) = 5л8 — 4л2 + їх + 6, r (a:) = 16;
б) s (х) = 2іх* + (3 — і)х — 2, г (х) = 2 + і;
в) s (л) = 0,5а;3 + Зх — 1, г(х) = 2,5х --1,5;
г) s (х) =-- 5л3 + 2л:2 + Т, /• (л) = 2л2 — 2х + Т;
Д) s (л) = {1 — 20 х3 + 2*2 — іл + 2/, г (х) = 2а: + 1.
22.2. a) s(*) = л3 — л2+3л — 3, г(де) —= 5;
б) s (*)'= 4л:3 _ (_3 + 40 а:2 + (—1 + 70 х + 8 - Гч\ г (л) = -14 + 2t]
в) $ (х) =%^Чл1+ 2л:3 + х2 + 4* + 5,__ r (x) = 2;
г/s (^) = (1+/2)^-^+^ + 1-/2, /■(*) = 4 — 2/2.
22.3. а) 136; б) —1 — 46/; в) 2; г) 9 — б/2.
22.4. а= 1, Ь = — 1.
22.7. г(л) = — х + 3.
22.8. /-(*) = 3,5**+ 1,5л: — 2.
22.9. г(л) = ((Т,5 + 0а:2 + л + 0,5 — і.
22.10. а) 1; б) 1.
22.17. 5.
22.18. 1.
22.19. Застосувати задачу 22.6, в) і теорему Безу.
22.21. а = 3, Ь = —4.
22.22. a) /(л) = (*—1)4 + 2(л — І)3 + 3 (х — І)2 — (л- 1) - 2;
б) / (х) = 2 (л - І)4 + (х- 1)2 + (л- Т);
в) / (*) = (* + О5 - 5/ (х + О4 - (Зі + Ю) (л + О3 + (-13 + 100 (х + О2 +
+ (22*+5) (*+/) + 11 —ї.
22.23. а) / (х) = (х2 — і)3 — 4 (л + 1) (х2 — і)2 — (7л + 9) (л2 — і) — 4* — 5;
б) / (л) = х (х3 + 2)2 + х (л3 + 2) + 4л;
в) / (х) = (л3 + і)2 — 2t (л3 + і) — 2л + / — І.
§ 23
23.2. апа22 — а\2а2\ =£ °-
23.3. a) (/, g) = х+ 1;. б) (/, g) = 1; в) (/, $) = 1; г) (/, g) = 2л + 1.
23.5. а) (/, g)=x-3; б) (/, *) =-*•-*+ 1; в) (/, g) - 1;
D (/, g)=x + 3; д)*(/, #)~х2 + (\+і)х + і.
23.6. а) [/, g]=x*- 4л5 + 4л2— 5л — 2;
б) [/, g] = (2л3 + 7х* + 4л - 3) (л - 1);
в) [/, g] = (*3 + 6л2 + 4л+і)(х3 + л2 + Зл-4):(л + 2);
г) [/, g] = (я* _ л2 + Зл - 3) (х4 + 2л3 + 2л- 1);
д) [/, g] = х5 + 2ІЛ4 — 2л3 — 2(л2 + л.
23.7. а) и(х) = 1, у(л)=—л+1;
9* 235

б) м (jc) = —дг — 1, v (x) = x + 2;
r) a (x) = — -g- (3x2 + 10/x — 17), о fxj = -ggr (l8x3 + 57/x2 — 158дг - 78/).
23.8. Використати те, що
/ = {/(*) и (x) + g(x)v(x) І fi (де), v(x) £ Р [х]}.
23.9. Ідеал / породжується многочленом [/, g].
23.10. Ідеал / породжується найбільшим спільним дільником многочленів
/iW, М*). •••• /BW-
23.11. Многочлен h(x) має ділитися на найбільший спільний дільник
многочленів / (х) і g(x).
23.12. а) и(х)=^(х2 + х + 1) + (*- 1) в (де), о (х) = ~у(х2 + х + 1) -
— (x+l)s(x), де f(x)6Q[x];
б) к (х) = ^^4^ + (*+2) s (х),о (х) = ^^-(х2 + їх) -U2 + х + ї) s (х),
де s (х) € £5 М;
в) рівняння розв'язків не має;
Г) U (X) = Х+ 1 + S (X), 0(Х) = — Х« + (* - ПХ3 + (і — 1) Х2+ ** + * + 1 -
— (х — i)*(x + i)s(x), де s(x)gC[x].
23.13. а) (/, g, /і) = х+1; б) (/, gt h) = ї; в) (/, g, Л) ex«+(/+l)x + *.
23.14. а) Рівняння розв'язків не має, оскільки многочлен s(x) не ділиться
на многочлен (/, gt h); б) рівняння має розв'язок, s(x) ділиться на многочлен
(/, * Л).
§ 24
24.2. /1(х) = х2 + ї, f2(x) = x2 + x + 2, f3W = *2 + 2^ + 2.
24.5. Так (наприклад, / (х) = х2 + 2).
24.8. /(х) = (2~х + 3")(* + Т)(х + 4).
24.9. а) /(х) = (х—1)(х + 1) (х* — 2) (2х — 1);
б) /(х) = (*-!)(хі-4)(Зх+1).
24.10. f (х) = (х2 + 1) (х2 — 2) (2х — 1) = (х* + 1) (х — /§) (х + /5) (2х —1)-
= (х-0(х + 0(х->^2)(х + /2)(2х-1).
24.15. а) /(*) = (х_+ї)(х + 2)(х + 3)(х + 4); б) незвідний;
в) / (х) = (х2 — /2х + 2) (х2 + /2х + 2); г) звідний.
24.16. а) / (х) = (х2 — 7х + 1) (х2 + 5х + 7);
й,„,_(,-з=/і)!(,-і+і2)!;
в) /(х) = (2*» + * + 3)«;
г) /(д) = (*»-6* + 1) (л:2 -|- де — 3);
в/(,,_(,-=!^)(,-=н^)(,_=з±іт?)а
х (.-=2^),
є) /(х).-=(*-1)«(х-2)»;
«)/(,)=(,-=і=Д)!(._=ці^)^
ж) / (х) = (х2 + 5ax + 5a2)2;
з) / (х) = (х2 + 12х + 26) (х2 + 12х + 12);
і)/(х) = (х2-18)(х2 + 8);
к)/(х) = (х + 1)2(х + 2)2;
л) незвідний;
236

м) f (x) = (ж- 1) (*+ 1) (** + !)(*• + 1);
н) / (де) = (д: — 1) (де« + ж+ 1) (Jt« + *■ + 1)ї
о) /М = (*-1)<*+ D(*2 + 1)(^ + ^ + 1):
„,/М-(,-^1^)(*-Л4^)(,+ 0+£й)х
р)/(х) = х(х-Т)(х-2)(х-3)(х-4).
24.17. a) (/, g)=x2_*_2, [/, g] = (x-l)2(*2+l)(*2--5*+6);
б) (/, g) = x-l, [/, g] = (x2-2x + 3)2(x + 6)2(x-l)2(x-2)2(x-6)2(x2-b
+ х+1);
в) (/, g) = (x+l)2, [/, *] = (*+1)8(*-1)(*-2);
г) (/, $) = (*-*)(*+1), [/, g] = (*+l)3(*a+D(*-D(*-0;
д) (/, g)=*x + 2, [/, g] = x(x + T)(x + 3)(x + 4)(x2 + x + f)2;
є) (/, я)=х-1, [/, *] = (**_ !)(*■ + *+1) (*• + *»+1).
24.18. Ні.
24.19. Л"1 = {_*+(*«+l)s(x)|s(x)e Q[x]}.
24.20. А"х = {1 + (—* + 1) s (х) | s (х) € Q [*]} = А
24.21. а) Оберненого елемента не існує;
б) A-1 = |^ + (** + 4) s (х) | s (х) є Q [х]J.
24.22. Ізоморфізмом є відображення
f ({gW + x*+ \)s(x)\s(x) £ R[x]}) = g(i).
§ 26
25.1. a) /' (x) = 27 (x2 + x — I)2 (2x + 1) (x3 — 2) + 27x2 (x2 + x — l)3;
б) /' (x) = 6/ (3/x2_- 1) ((/ + 1) x2 - 0 + 4x (—1 + 0 (/x3 - 3x);
в) /'(*)==x(x + 3) + 3x2.
25.2. a) 4; 6) 9.
25.6. f (x) = 2x6 + x3 + x2 + x + 2.
25.7. /(x) = 4x3 + x2 — x+ 1.
25.8. 2.
25.10. Усі, крім /і (x) = T, /2 (х) = х2, /з W - х2 + Г, /4 (х) = х3 + х2 + х.
25.11. 54.
25.12. a) /(*) = (*-1)4 + 2(х-1)3 + 3(х-1)2-(х-1)-2, f(l)=— 1.
/"(1) = 6, f (1)=12, /=IV (1) = 24;
б) /(д) = (* + /)*_ 5/(x+ /)4-(3/+ 10) (x + 08 + (10t — 13) (* + /)2 + (6 +
+ 220 (x + 0 + 11 - /, f (-/) = 22/ + 5, f (— 0 = 20/ - 26, f" (-/) = -60 —
— is/, /IV(-0 = —120/, /v (—/) = 120;
в) /(х) = (х+1)4-4(х+1)3-9(х+1)2 + 36(х+1)+1,Г(~1) = Зб, ГХ
X (-1) = -18, f" (-1) = -24, /IV (-1) = 24;
r) /,(x) = 4(x — 3)5 + 5(x — 3)* + 7(x — 3)3 + 4(x_-3)2 + 8(x-3) + 9, /'X
X ГЗ) = 8, f (3) = \ f (3) = 9, /1 v (3) = 10, /v -(3) = 7;
д) fjx) =2 (л:— 1)4 + (A;_ 1)2 + (x _ 1)f ,' (1) = 1f f ([) e 2, f(T) = 0, /'V(l)=
= 0.
25.13. / (jp) = 2/ (x4 + (5i — 2) x3 + (9/ —9) x2 + (14 — 4r) x + (6/ — 2)).
25.15. a) 2; 6) 1; в) 0; r) 5.
25.16. 1.
25.17. a) a = —5; 6) a £ j— ii, 18j; в) a = 0.
4, то /
(*+4)2 (*+t)
102
25.18. Якщо a = 4, то / (x) = (x + 2)2 (x + 1). Якщо a = -^-, то /(*)<
237

26.19. a) 4a3 + 2762 = 0; 6) 27a« = 25663;
в) 256a5 + 312564 = 0; r) 312562+ 108я5 = 0.
25.20. а) Не має; б) має; в) має; г) має; д) має.
25.21. а) / (х) = (х- 2)2 (х + 1); б) / (де) = (* + (1 — 2t))4;
в) /(*) = (*■ + *+ 1)»(*+ 2); г) /(*) = (*+ *)»(*-Я)»;
д) /(х) = (х + 2)3^2-л:-0; є) f (х) = (х — 1)* (х + М)*{х—\).
§ 26
26.1. Існує єдиний многочлен першого степеня f (х) «ху який задовольняє
умову задачі. Кожен многочлен / (х) = (4с — 1) х2 — (6 + Зс) х — 7с при с £ R\ і —і
також задовольняє умову задачі.
26.2. Ні.
26.4. Якщо deg/ = Пу то слід розглянути множину, що містить я+ 1 різних
раціональних чисел і застосувати інтерполяційну формулу Лагранжа.
26.6. а) /(*) = 2х«—*+1; б) /(*) = * ~^+6; в) 'W^2*-
26.7. aj/(X) = 2*2--* + 1;
б) /W = 24*(*— 1)(* —2)(*-3) + * + 1:
в) /(*?- і + 9у + 2^(ДС~ U + - - - + 2**('~ ° • ' * {Х~П+ °
2! ^ ^ п\
26.8. а) / (х) = 3jc2 — -1;
б) /(*) = -дг + 5;
в) / (х) = * (х2 - 1) (дг — 0 - (х - 1) (х- і) - *+ 1 - і, f (2і) = 8, /(0) = 0;
1 1 1
г) /(*)= І + Х (*~~ 1)el8 (*~~ ]) (*~4) +720(л:"~ 0(^-4)^-9),
/(3) =1120= !'72'5' № = ^732 ' ■ •)» * (2) = ^ = ]'39<4)' (^2 = 1>4142 • • •>
26.9. Цх)~=3(х + 3)*х(х+~\).
26.10. fx_(x) = x, f2(x) = 2x, /3(*) = 2*+1, ,4 (*) = * + !, /б (*) = 2"л; + 2,
/,(*) = *+2.
26.12. а) ^-у; б) ^ ±
(х* + х+\)(х*+\У .
в) (х2 — х-\- l)(jp* —л;2+ 1); г) заданий дріб нескоротний.
26.13. а) Так; б) ні; в) так; г) так; д) ні; є) ні.
26.14.3) (27^) + |;
б) заданий дріб неправильний;
1 З З
в) х+\ {x+\f+ (х+\/*
1 х— 1 1 лг —2
г)*-1-*2+і: д) *2 + JC + 2~(*2 + * + 2)2;
х+ 1 jc + 2 _^ _4__ 1 З
е) х*+{-х2 + х+\;е) хз- ^2 +^ + з + (^ + з)2;
* де —4
ж)
з)
8 (*2 + 2л: + 2) 8 (*2 - 2л: + 2) '
V2 __ ^2 ]
8 (л: - /2) 8 (л: + V2) ""*" 2 (*2 + 2)
1 1
26.15. а) з(х-0~~3(* + 20;
238

1 } + l , *-} -
б) 7=7"" 2(*-ї) + 2(x + i)'
1 1 , *
B) "4(jc—1+0""4(jc—1 -0 ^ 2 (jc — 1 + c)a '
/2 _ /2 /2 _ ^2
Г) 8 (x - /2) 8 (x + /2) + 8 (x - V2i) 8 (* + V*)'
1 *2 1 J
26.16. a) — 2F+ 2(x3-2); 6) 2(*2-2) + 2(*2 + 2);
1 *
2 2
26.17. a)T + JT2-r^+^
_L і і і і
6) 4x + 4(x + T) + 4(* + 2) + 4(a: + 3) + 4(x + 4) '*
2 1 4 3
B) F+2 + X + 3 + JC+4 + (^+ 4)2>
p-i
26
18. V—J
Al(p-l)(* + a)
a=0
Розділ V
§ 27
27.1. a) /(*, #) =** + *•? — 2*V — ^ + 2^ + ^- 1;
6) / (x, */, z) = x3f/2z + y*z2x + zx2# — xy2z9 — */z2*3 — z*2*/3.
27.3. а) Від одного до трьох членів; б) від одного до шести членів; в) від
одного до чотирьох членів; г) від одного до 10 членів.
27.6. а) 63; б) 728.
27.7. Однорідний многочлен другого степеня від трьох змінних у загальному
вигляді містить 6 членів. Кожен з шести коефіцієнтів цих членів може
набувати одне із значень 0, 1, 2..., р — 1, і всі можливі варіанти повністю
вичерпуються елементами множини ZJJ. Множина Zp містить р6 елементів. Якщо всі
коефіцієнти дорівнюють 0, то матимемо нуль-многочлен. Отже, число всіх
однорідних многочленів другого степеня від трьох змінних дорівнює рб— 1.
27.9. а) Вищий член — Зу2х*; б) вищий член 2л:2г; в) вищий член хг.
27.10. а) наприклад, к(х, у) = х +у+\ і f2(xt у)=х2 + у2 + 1;
б) /,(*. у) = х*+х + у+\ і ft(x, у) = х2 + у2 + х+Т.
27.16. Зробити заміну х = іу.
21М. а) / (х9 у) = (З*2 — 7ху — 4г/2) (З*2 + Зху + 4у2);
б) Пху у) = (2х2-ху + 3у2)2;
JU(x> У) = (*- УУ\ '
r) f(x, у) = (х-у)(х + у){х + 2у)(х + 3у);
Д) / (*, у) ■■= (х2 -ху + у2) (х2 - Зху + у2).
27.18. а)/(х, yt z) = 3(x + y)(x + z)(y + z); ,
б) /(а, Ь, с) = — (a — b) (b — с) (с — а);
B)JM-J>>cl^M9 — Ь)(Ь — с) (с - а);
г) / (х, у, г) = (х — у) (у — г)(г — xj;
Д) / (х> у, г) = \2xyz (х + у + г);
є) / (a, bt с) = 2(а — Ь) (Ь — с) (а — с) (а + Ь + с)\
- €) м*» у» г> =1* •—v)to —*) (* —*) (*// + /yz + ^)-
ІЇТТТС^ с) ^7#^ + а& + ас + to?);
з) /(*, у, г) = 5(х + У)(х+г)(у + г)(х2 + у2 + г2 + ху + хг + уг);
і) /(*, у, z) = 5(x-y)(y-z)(z-x)(x2 + y2 + z2-xy-xz-yz).
27.19. Використати розклад многочлена g (x, yt z) = (х + у + г)3 — *3 — і/3 —
г3 на незвідні множники (див. задачу 27.18, а)*
239

§28
28.1. a) Hi; б) так; в) так;г) ні; д) так.
28.2. а) Додати х\ і 2х{; б) додати х\у х\ і 2х1х3\ в) додати х\ 1 2*2*3.
28.3. а) Ьх\х\хг\ б) —2>х\х\х\.
28.4. а) / (*, у) = of а2 + 2а2 - 2о| - 4о2;
б)/(*> ^) = 20^2-63^1-50,02.
28.9. a) /(*,, x2, *3) = о3, — Зз,о2 + Зо3 —о,;
Ф / (*р *2, *3) = °1а3 ~ 4^а2а3 + 2а2а3 + 4а1°3 + 2аЗЇ
,2 28 З З 10
В) / (*,, Х2, Х3) = ofо2 + -J- ofo3 — 05 + -3- ^^2а3;
б) /(*,, *2, ^з) = 2о^—6о2. *
Д) / (*р *2> *з) = ~5а1 + Зба1а2 + 132а3?
Є) f(xv X2, ^3) = а^3-а2-
28.10. а) 0; б) ~ в) - -|.
28.11. а) o(Xj, х2, ^3) = 0^2--3-02-
б) о (*,, х2, х3, х4) = о2;
В) 0 (хр ДГ2, . . ., Хп) = 0^—30,02 + 3^3-
§ 29
29.1. а) (де, у) 6 {(2, 3), (3, 2)); б) (х, (/)6 {(1, 2), (2, 1)};
в) (х, у)¢{(5, 3), (3, 5), (-3, -5), (-5, -3)); г) (х, у)€ {(3, -2); (-2, 3)}{
Д) (ж, «/)€ {(1. 2), (2, 1)}; є) (х, у, -.)€{(!, 2, -2), (І, -2, 2), (2, І, -2),
(2, -2, 1), (-2, 2, 1), (-2, 1, 2)};
є) (х, У, *)€{(!. -2. 3), (1, -3, 2), (2, -1, 3), (2, -3, 1), (3, -1, 2), (З,
-2, 1)}.
29.2. а) (х, (/)6((1, 64). (64, 1)};
б) (ж. у)€ {(16, 81), (81, 16), (-16, -81), (-81, -16)}.
29.3. а) {1, 4}; б) {з, 4, 6 ±/29}; в) (2, 11};
г) {-8, -73}; д) х = 0.
29.4. а) / (х, у) = (2х + *)(*+ 2у) (ж - 5(/) (5х - у);
б) / (ж, (/) = (2** + Зху + 2(/2) (ж - Зу) (Зх - (/);
в) / (ж, у) = (X» - ху + </2) (2ж* + х(/ + 2</2);
г) / (ж, у) = (ж - Зу) (Зж - у) (2х + Зі/) (Зж + 2у).
29.5. а) / (х, у, г) = 0іа2 = (х + у + г) {ху + жг + г/г);
б) / (ж, у, г) = (ху + жг + уг) (х2 + У2 + га);
в) / (ж, {/, г) = 2 ((ж + у + г)2 - Зж</ - Зжг - 3//г)2;
г) / (ж, у, 2) = (х(/ + хг + yz)2.
296 UbJ!±JL = !
' ' g (ж, у, z) х + у + Ґ
29.7. х2—12х-)-27 = 0.
29.8. Застосувавши рекурентну формулу задачі 28.5 і метод математичної
Індукції, довести, що х" + уп є цілим числом. Далі, показати, що sn = —sn_3-f*
+ 5 (7s„_2 — s„_3) для всіх /г > 3. Подільність на 5 числа sn приведе до по*
дільності на 5 одного з чисел Sj, s2 або s3, що неможливо.
29.9. *3 —2/2— 47*—144 = 0.
§ ЗО
30.1. а) 162; б) —128; в) 0; г) —3564; д) 1768; є) 41; є) 10; ж) 651; з) 44;
К) —7; л) 136; м) 59.
30.3. а) X = 1; б) X = 2; г) X = 2; д) І = —1.
240

30.4. a) —108; б) 0; в) —27036; г) 144; д) 0; є) 725; є) 50000;
/г(я—і)
Ж) (__1) 2 лла/і-1ф
30.8. а) Х = 3; б) Х£{0, ±2}; в) Х = 2 + 4/.
30.9. а) (*, //) € {(3, 2), (-3, -2), ^2/2, --^), (-2/2, 1р.));
б) (*, і/) ^ {(/3, 0), (-/3, 0), (2, -1)}; _
в) (,, ^) €{(1. 0), (2, 1), (^I^IGIL, iL+flZL)};
г) (xt |/)=*(-l, 3);
Д) (*, у)£{(0, 0), (2, -1), (1, 2), (1, 68), (2, 52)};
є) (х, у) = (\, 2).
Розділ VI
§ 31
31.3. Ні.
31.4. Q(/5).
31.5. Q[*]/<*2+l>.
31.6. Можна, наприклад, встановити ізоморфізм між полем /?[*]/<**+!>
і полем комплексних чисел С.
31.7. Ні (наприклад, рівняння *а + 2 = 0 не має_коренів у цьому полі).
31.8. а) т = 9; б) т= 13; в) т = 4; г) т = 1+/13.
31.9. а) Ні; б) так.
31.10. аЖ,) = 5(* + і^)(, + Ш);
б) / (х) = (ж - 1) (дг -і);
г) f (х) = (jc — 3 + 2«) (х + 3 — 2«) (* — 3 — 2») (* + 3 + 2/);. ,
д) t(x) = (x-l)(x+\){x-i)(x + i)^x-^.-l^i\L
e)/W-(x-o^+o^+JL±pL)(g+^p),
31.11. а) / (х) = х3 — (1 + 0*2 + (1 + 20^ + 1-«;
б) / (х) = х* - (10 + 20 х* + (14 + 200 ** - (64 + 280 *2 + (40 + 1280 х - 80*;;
в) / (х) = ** + (3 + 60 я3 + (-12 + 180 *а — (36 + 80 * -24*.
31.12. 23.
31.13. 7.
31.15. а) ^ + 2^+25=0; б) f - 6^- -| */- у = 0.
31.16. Знайти суму квадратів коренів многочлена.
31.17. a) f(x) = x* + 6x* + bx — 6 і *! = — 2, х23 = — 2 ± /7;
б) / (х) = jc8 — 18лг2 + 68* + 24 і *і = 6, х23 = 6 ± 2/ЇО.
31.18. Якщог=8,то^ = 1,д:а = 2,д:з^=4;'якщол = 20,то^ =-2, jt2 = —1,
*з= 10; якщо г = 28 —12/2, то ^ = /2, x2= 2/2, *я = 7-3/2; якщол =
= 28+12/2, то*1==-2/2, *2 = -/2, *8 = 7+з/2.
5 10
31.19. / (х) = *6 — -^ (3 + 0 ** + — (1 + 50 х3 - 10 (1 + ЗО *2 - 40 (1 -0 *-
і 605 . 305
/2
12 І2
31.21, ^ = /3 - /2, *2 = /3, х3 = /3 + /2.
241

A L _ ±
31.22. xj = — о » %2 — о ' *я — 2*
31.23. xx = 1, *a = 2, *8 = 3, та p = 11 і q = —6.
32.1. a)*12 = — 1 ±*Уз, *
3,4 :
§ 32
і ±Уїз
• 6)*lt2 = -1 ±1, хзл=1±^ПІ
2 • -- -1.¾ -о.» 2
в) xx 2 = 2 ± i, *8 = — 4, *4 = 1; r) *lf2 = 2 ± /, *3 4 = 3 ± УЙ.
32.2. 'a = —20, b = —50, *3 = —3 — і, *„ = 5.
32.5. а) Так; б) ні; в) так; г) ні.
32.6. а •.= —243, jcj 2 = ± 9і, х8= —1, х4 = 3.
32.10. а) / (*) = (a:2'— 2* + 5) (* + !)(* + 5);
б) ї(х) = [х* + х-\
З + Уб
)(
*s+*4
З—У"5
>
в) / (х) = -^-(2^+(1+ 1^5) ж+ 2) (2*"+ (1 — Уб) *+ 2);
г) /(х)»(**_аг + 3)(*»+х+І);
Д) /(*) = (**+1)(*+ І)2(*»-*+!).
32.11. а) Ні; б) так.
32.12. Ні.
§ 33
229 і 175
33.1. а) 31; б) -щ; в) <^; г) — 29І6; д) 0; е) 4 + 1'
33.2. а) хг = —2, л:2 з = 1;
З —УЗ, —3 —Уз.
б) хі = і, х2 = —2 1» х* = 2 і;
з з
в) Xl = K28 + У272 + V28 - У272,
з з
З /28 + У 272 — )^28 - У272 г-
*2,з — "~2 ± 2 " ;
Г) *і= — 2' *2,3 **= ^
з
і/"9 , і/139, і/"9 і/139
Д)*і = [/ 2+ К Ї08+ К 2— К Ю8
+2« - й±і+!3х
ш
108
і- |/ 54+ 3 + К 54~ з
-2±^(і3/?
*2,3 =
___ З^і -
79 У77
54 + ~~Г~
|/~79 У/7
К 54" 3 ,
+і
є) *і.2, 3 = 2У-2-2і;
г- і+Уб. і-Уб Уз,
ж) *! - (1 + Уб)і, х2>3 - —^-< ± —2~ • — '•
зз.з. а€]-оо;0[ и її;+<*>[•
242

4 З
33.4. Якщо а=1, то х = 0. Якщо а = тгу, то х == — ^.
З
33.5. £ = -^.
33.6. Якщо а£]—оо;—l[eU ]—1;0[ U ]3;+°оІ, то рівняння має один
дійсний і два комплексних корені; якщо а£{ — 1, 0, 3}, то рівняння має три
дійсних корені, два з яких дорівнюють один одному; якщо а£]0;3[, то рівняння
має три різних дійсних корені.
33.9. Зробити заміну. Прирівнявши коефіцієнти при відповідних степенях
9а0 — а2а1
змінної в здобутому і шуканому рівняннях, матимемо п = , 2_ а ~~у т =
/Зп2 + 2а0п + Ді , . . з .
_ !—д= , a = mJ і & = л8 + я2ла+ ^/1 + ¾.
33.10. а) п = —3, т=1 і у3 — Зуа — З/у + 1 = 0;
1 5 _ 125 г- 27 125 ._ 9
б) Л = j, т = gf/"3» "72"^ 3 ^ + Т^ — "24"^ 3 ^ ~~ 4 = 0#
2
в) п = — 2, m = 1, ^- 2у*— Зу + g = 0.
33.12.3) ер = ^: ^^tgjg, #2 = -^ І/з = tgj5«; б) 9 = -g; у, = tg-jg, ya =
13 7 3 11 7 .1
= tg^7t, v«=tgfgre; в) <p = jw; і/і = 1, І/2 == ^ї^^» ^s=tgj2TC; г) <р =arcsin-7~;
ер ср+2тс ср + 4гс
01 = tgg, У 2 = tg 3 ' У'3 = tg 3 #
33.13. a) *і=~4 *2,з = ±l/-"7
З 1
33.17. а) * = — у б) х = 2,' в) ^=—2, *2 = 1; г) х = —3; д) дг^ —2, 6,
*2 ж —0,4, х3 = 2'
бд.ІЬ. а) дгЬ2 = , *3,4 = 1 .
^ і/о ~] ± /ї&
б) xU2 =V2f, хЗА = 2 ;
. +1 ±/29 5 ± Ї\Г1.
в) х12 — 2 ' *з,4 = ■ з
гі * - -1 ±'УП , -3 ± /5Т.
Г> *1,2 g » *3,4 = g •
«W - ^+/3 ± 1^12 + 2/3 ж 1-/3 ± K12-2/3
Д) ДГІ>2 ^ , *3,4 = 4
33.20. а) *1§2 =«1 ± 2t, *3,4 = -1 ± І; б) *U2 = 1 ±^У *я = -1, х, =2
33 22 а) х - /2-1 ±^5+2/2 _ f2 + і ± г/5 - 2/г.
де.и. а; *12 _ _, *3,4 = 2^ -
б)х --S±/17 „ _-1 ±/7>
°J *l.2 e § ' 3»4 2
243

§ 34
! 7 і
34.1. a) g < |*| < 8; 6) g < |*| < 8; в) 2 < |*| < 7; r) gg < |*| < 28.
3
34.2. a) o; 6) 2; в) 2; r) 4, розглянути многочлен ер (х) = —f (x).
34.3. a) 1; 6) 1; в) 2.
34.4. a) 6; 6) 2; в) 3; r) 100.
34.5- а) Додатних коренів два або жодного, від'ємних — два або жодного;
б) додатних коренів три або один, від'ємних — нем.ає; в) додатних коренів два
або жодного, від'ємних — п'ять або один; г) додатний корінь один, від'ємних —
п'ять, три або один; д) додатний корінь один; від'ємних — два або жодного.
34.6. а) ]-2; -1[, ]1; 3[; б) ]-|.— і[. |;1['* в> ]~5'> Ч[' J? б[*
г> ]-2; -?[• ]ї s[; д) ]-* -*[• ]ї: 4[*
34.8. а) х{£]—2; -1[, *2Є]—1; 0[, лг3 Є ] 1; 2[;
б)^€]-2; -1[, *2^]0; 1[, лг3 Є ] 1; 2[;
в) один дійсний корінь: *Є]0; 1[;
г) два дійсних корені: хх £ ]0; 1[, х2 Є ]5; 6f;
д) три дійсних корені: хх ^ ]—3; —2[, *2£]—1; 0[; х3 = 1;
є) два дійсних корені: х{£]0; 1[, *2£]1; 2[;
є) дійсних коренів многочлен не має.
Розділ VII
§ 35
35.1. а) хх = —3, х2 = 2, хЗА = 5±^17; б) Хі = —2, *2, 8 = 2 ± /; в) xt -
« -2, х2 = 3, дг3,4 = ±4; г) xl = j, х2і3= 1 ± і; д) хх = у *2,з - ""* % *л
1 2 ± і 1 ._
е)*і = — J» *2,з ="Т"; е) ^1 = 2^2.3=-1 і гЗ*;ж) *и2=Ь лг34 *= — 3;
з) хх = а, *2 = 6, *3 = с; к) *j = 2а, х2 «= а, х3 = — 1; л) д^ = 1, *2 = а, *3 =»
«= 1 — а; м) *j я* 1, х2 = 6 — а, *3 = £ + а.
35.2. a) *j=—Ь х2 = 2; б) рівняння раціональних коренів не має; в) х{=*
= —3, х2 = —1, лг3 = 1; г) х = —3; д) *lf 2 = 1.
35.3. a) f(x) = (x* + x+\)(x+\)(x-\); б) f (х) = (х- 1)(х3 - 6* + 2);
в) / (х) = (х2 + 1)(6*2 — 13jc + 6); г) / (*) = (З*2 - х + 4)(3*2 — 4а: + 4);
д) / (х) = 2 (х2 + 8х + 23)(х + 3)(* + 5); є) / (*) = (х3 + З*2 + Зх - 4)(х3 + Зх2 +
Н-Заг — 3).
35.4. а) Многочлен не має цілих коренів; б) застосувати критерій Ейзенштейна;
в) зробити заміну х = у + 1 і застосувати критерій Ейзенштейна; г) многочлен
не має цілих коренів і не розкладається у добуток двох квадратних тричленів з
з кільця Q[x]\ є) зробити заміну х = у-\-ї і застосувати критерій Ейзенштейна.
35.5. а) / (х) = (х2 + 4* + 1)(х2 — Зх -f- 1); б) незвідний; в) незвідний; г)
зробити заміну х = у— 1 і довести, що / (х) є незвідним.
244

35.7. а) Довести, що f (х) не ділиться на многочлени у1(х) = х, <р2 (х) =
«=*+1 і <р3(*) = х2 + х-\- 1 у кільці Z2[*] і застосувати задачу 35.6; г)
многочлен не має раціональних коренів.
§ 36
36.1. а) /(*) = х4 — 4дг2— 1; б) / (х) = *4 — 4дс3 + 8*- 1; в) /(*) = *4 —
—5 б/+ 4; г) /(х) = *3 + 3*2 + 3* + 3; д) / (*) = лг6 — 15л:4 + 6*3 + 75*2 +
+ 90* — 116; є) / (х) = х6 — 4*3 — 3; є) / (*) = а:6 — 6х5 + 12лг4 — 8х3 — 6; ж) /(*)=
==^^2^ + 4.
36.2. a) Q (У 2 + VI); б) Q (/З); в) Q (/5 + /7); г) Q (Vp + >^); д) Q (/2 +
+ /з); є) Q(V2 + V3 + Vb).
з з __
36.3. а) Ь /3, /9; б) 1, /3; вМ, /з, /б, /15; г) 1, /б, /7, /35;
д) 1, /2, /3, /5, УІО, /б\ УІ5, /ЗО.
§ 37
37.1. а) —1 —to; б) gw (со2 — w — 1); в) ^go> (а>2—1)(64о>з— 16а)2+ 4со—257);
г) -Щ° (64(°2 ~ 24а) ~~ 5°3); А) 20 (w" + "Х"1 + б).
4 4 4 _ j /З З \ 1/3
37.2. а) -/§-/¾ + 3/2 + 1; б) g 1/4-2/2 + 4J; в) 93І-2/4 +
з \ \ ( 3 г - \ \ ( 4 4 4 \
+ 17/2-5); г) ^^-1^ + 6/7 + 8^)-5^181/27+345/9 + 821/3+81).
З 3 __ 3 — 5 _5 5 5 /8
37.3. а) /36 +/30 +/25; б) /її +/54+ /36 + /24 + /І6; в) \/з +
+ /2)(/3 + /2)(/3 + /2)1 г) ^(/58-9/5^.3 + /6^.32--... + /38)
37 4 (У a + Vb + У'сКУії + УІс + /5Ь) — (а/а + б/5 + сУс) - 5/Ж.
* 2(а* + ас+6с) — (а?+Ь* + с*) '
/з _ з з _ 3 __ 3 _ 3 _\/ 8 3 ^
■л l/fl2 + /^2 + Ус*—УаЬ--Уас--УЬс)[(а+Ь+с)*+3 (д+Ь+с)У abc+яУ (abc)*)
} (a + b + cf — 27abc
37.5. a) q + q2 + *>3 — За& = 0; б) а2р3 + of + r* — 3qpqr = 0; в) q& = 0.

Дода ток 1
Таблиця простих чисел від 2 до 4057 та їхніх первісних коренів
1 р
2
з
5
7
11
13
17
19
23
29
31
37
41
43
47
53
59
61
67
71
73
79
83
89
97
101
ЮЗ
107
109
113
127
131
| 137
139
! 149
! 151
і 157
і 163
і 167
| 173
g
' 1
2
2
3
2
2
3
2
5
2
з
2
6
з
5
2
2
2
2
7
5
з
2
3
5
2
5
2
6
з
з
2
з
2
2
6
5
2
5
2
р
179
181
191
193
197
199
211
223
227
229
233
239
241
251
257
263
269
271
277
281
283
293
307
ЗП
зіз
317
ззі
337
347
349
353
359
367
373
379
383
389
397
401
409
g
2
2
19
5
2
3
2
3
2
6
з
7
7
6
3
5
2
6
5
3
3
2
5
17
10
2
з
10
2
2
3
7
6
2
2
5
2
5
з
21
р
419
421
431
433
439
443
449
457
461
463
467
479
487
491
499
503
509
521
523
541
547
557
563
569
571
577
587
593
599
601
607
613
617
619
631
641
643
647
653
659
и
2
2
7
5
15
2
3
13
2
3
2
13
з
2
7
5
2
з
2
2
2
2
2
з
з
5
2
3
7
7
з
2
з
2
2
з
Н
5
2
2І
р
661
673
677
683
691
701
709
719
727
733
739
743
751
757
761
769
773
787
797
| 809
811
821
823
827
829
839
853
857
859
863
877
881
833
887
907
911
919
929
937
941
1
я
2
5
2
5
3
2
2
П
5
6
*>
5
3
2
6
1.1
2
2
2
3
3
2
з
2
2
И
2
2
5
2
з
2
5
2
17
7
з
5
2
р
947
953
967
971
977
983
991
997
1009
1013
1019
1021
1031
1033
1039
1049
1051
1061
ІОСЗ
1069
1087
1091
1093
1097
ПОЗ
1109
1117
1123
1129
1151
1153
1163
1171
1181
1187
1193
1201
1213
1217
1223
g
2
з
5
6
3
5
1 6
7
П
3
2
10
14
5
3
з
7
2
з
6
з
2
5
з
5
2
2
2
її
17
5
5
2
7
2
и
2
з
5І
р
1229
1231
1237
1249
1259
1277
1279
1283
1289
1291
1297
1301
1303
1307
1319
1321
1327
1361
1367
1373
1331
1399
1409
1423
1427
1429
1433
1439
1447
1451 і
1453
1459
1471
1481
1483
1437
1489
1493
1499
1511
g
2
3
2
7
2
1 2
3
2
6
2
10 і
2
6
2
13
13
3
з
5
2
2
13
з
3
2
6
3
7
з
2
2
5
6
3
2
5
14
2
2
11
р
1523
1531
1543
1549
1553
1559
1567
1571
1579
1583
1597
1601
1607
1609
161,?
1619
1621
1627
1637
1657
1663 1
1667
1669
1693
1697
169Q
1709
1721
1723
1733
1741
1747
1753
1759
1777
1783
1787
1789
1801
1811
g
2
2
5
2
3
19
з
2
з
5
11
3
5
7
з
2
2
3
2
11
3
2
2
2
3
3
з
3
3
2
2
2
7
6
5
10
2
6
П
6

Продовження додатка 1
1
1 р
1823
1831
1847
1861
1867
1871
1873
1877
1879
1889
1901
1907
1913
1931
1933
1949
1951
1973
1979
1987
1993
1997
1999
2003
2011
2017
2027
2029
2039
2053
2063
2069
2081
2083
2087
2089
2099
2111
2113
2129
g
[
5
3
5
2
2
14
1°
2
6
з
2
2
з
2
5
2
з
2
2 1
2
5
2
3
5
з
5
2
2
7
2
5
2
з
2
5
7
2
7
б
3
р
2131
2137
1 2141
2143
2153
2161
2179
2203
2207
2213
2221
2237
2239
2243
2251
2267
2269
2273
2281
2287
2293
2297
2309
2311
2333
2339
2341
2347
2351
2357
2371
2377
2381
2383
23с 9
2393
2399
2411
2417
2423
g
2
10
2
з
з
23
7
5
5
2
2
2
з.
2
7
2
2
з
7
19
2
б
2
з
2
2
7
3
13
2
2
5
3
5
2
3
U
6
3
5
р
2437
2441
2447
2459
2467
2473
2477
2503
2521
2531
2639
2543
2649
2551
2557
2579
2591
2593
2609
2617
2621
2633
2647
2657
2659
2663
2671
2677
2683
2687
2Є89
2693
2699
2707
2711
2713
2719
2729
2731
2741
g
2
6
5
2
2
5
2
3
І7
2
2
5
2
6
2
2
7
7
3
5
2
з
з
3
2
5
7
2
2
5
19
2
2
2
7
5
з
з
3
2
р
2749
2753 !
2767
2777
2789
2791
2797
2801
2803
2819
2833
2837
2843
2851
2857
2861
28.79
2887
2897
2903
2909
2917
2927
2939
2953
2957
2963
2969
2971
2999
3001
ЗОН
3019
3023
3037
3041
3049
30G1
3067
'3079
g
6
з
3
з
2
6
2
з
2
2
5
2
2
2
11
2
7
5
з
5
2
5
5
2
із
2
2
3
Ю
І7
ц
2
2
5
2
з
11
6
2
6
р
3083
3089
3109
3119
3121
3137
3163
3167
3169
3181 1
3187
3191
3203
3209
3217
3221
3229
3251
3253
3257
3259
3271
3299
3301
3307
3313
3319
3323
3329
3331
3343
3347
3359
3361
3371
3373
3389
3391
3407
3413
g
2
з
6
7
7
з
3
5
7
7
2
П
2
3
5
10
6
6
2
3
3
3
2
6
2
10
6
2
3
з
5
2
11
22
2
5
3
3
5
і 2
р
3433
3449
3457
3461
3463
3467
3469
3491
3499
3511
3517
3527
3529
3533
3539
3541
3547
3557
3559
3571
3581
3583
3593
3607
3613
3617
3623
3631
3637
3643
3659
3671
3673
3677
3691
3697
3701
3709
3719
3727
g
5
3
7
2
3
2
2
2
2
7
2
5
17
2
2
7
2
2
•3
2-
21
3
з
5
2
3
5
15
2
2
2
13
5
2
2
5
2
2
7
3
р
3733
3739
3761
3767
3769
3779
3793
3797
3803
3821
3823
3833
3847
3851
3853
3863
3877
3881
3889
3907
39П
3917
3919'
3923
3929
3931
3943
3947
3967
3989
4001
4003
4007
4013
4019
4021
4027
4049
4051
4057
g
2
7
3
5
7
2
5
2
2
3
3
3
5
2
2
5
2
13
11
2
13
2
3
2
3
2
3
2
6
2
3
1 2
5
2
2
2
3
3
6
5
247

Додаток З
ТАБЛИЦІ ПЕРВІСНИХ КОРЕНІВ ТА ІНДЕКСІВ
Просте число З
Первісні корені: 2
\ч
о
0
1
0
2
1
3
4
5
б
7
а
8
9
/
1 о
0
1
1
2
2
3
4
5
6
7
8
9
Просте число 5
Первісні корені: 2, З
N
ІЛ
0
і
0
2
1
3
3
4
2
5
6
7
8
9
/
0
0
1
1
2
2
1 4
ЗІ
3
4
5
6
7
8| 9
11
Просте число 7
Первісні корені: 3, 5
\n
0
0
1
0
2
2
3
1
4
4
5
5
6
3
7
8
9
/
0
0
1
1
3
2
2
3
б
4
4
5
5
6
7
8
9
' 1 '
Просте число II
Первісні корені: 2,6,7,8
N
0
1 1
0
5
1
0
2
1
3
8
4
2
5
4
6
9
7
7
8
3
9
6
/
1 о
0
1
1
2
2
3
4 | 8
4
5
5
10
6
9
7
7
8
3
9
б|
Просте число ІЗ
Первісні корені: 2, 6, 7, 11
/
0
1
0
1
10_
1
2
_7_
2
4
3
8
4
3
5
6
6
12
7
11
8
9
9 1
51
—•'
N
0
1 1
0
10
1
0
7
2
1
6
3
4
4
2
5
9
6
5
7
11
8
3
9
8
1
Просте число 17
Первісні корені: 3, 5, 6, 7, 11, 12, 14.
/
о
1
0
1
8
1
3
7
2
9
4
3
10
12
4
13
2
5
5
6
6
15
7
11
8
16
9
14
\і
0
1 1
0
3
1
0
7
2
14
13
3
1
4
4
12
9
5
5
6
6
15
8
7
11
8
10
9
2
1 Скрізь за основу таблиці індексів береться найменший первісний корінь.
248

Просте число 19
Первісні корені: 2, 3, 10, 14, 15
/
о
1 1
0
1
17
1
2
15
2
4
11
3
8
3
4
16
6
б
13
12
б
7
5
| 7
14
10
8
9
9
18
N
о
1 1
0
17
1
0
12
2
1
15
3
13
5
4
2
7
5
16
і"
в
14
7
в
_10_
8
3
_9_
_9
8
Просте число 23
Первісні корен і: 5, 7, 10 11, 14, 15, 17, 19, 20, 21
/
0
1
2
0
1
9
12
1
5
22
14
2
2
18
' 3
10
21
4
4
13
5
20
19
Є
8
3
Т
17
15
8
16
6
9І
11
7
\n
о
1
2
0
3
5
1
0
9
13
2
2
20
11
3
16
14
4
4
21
5
1
17
6
18
8
7
19
7
8
6
12
9
10
15
Просте число 29
Первісні корені: 2, 3, 8, 10, 11, 14, 15, 18, 19, 21, 26, 27
\
/
о
1
2
0
1
9
123
1
2
18
17
2
4
7
5
3
8
14
10
4
16
28
20
5
3
27
11
6
6
25
22
7
12
21
15
8
24
13
9
19
26
1 N
о
1
2
0
23
24
1
0
25
17
2
1
7
26
3
5
18
20
4
2
13
8
б
22
27
16
6
6
4
19
7
12
21
15
8
3
11
14
9
10
9
Просте число 31
Первісні корен і: 3, 11, 12, ЇЗ, 17, 21, 22, 24
N
о
1
2
3
0
14
8
15
1
0
23
29
2
24
19
17
3
1
11
27
4
18
22
13
5
20
21
10
6
25
6
5
7
28
7
3
8
12
26
16
9
2 1
4
9
/
0
1
1 2
0
1
25
5
1
3
13
15
2
9
8
14
3
27
24
11
4
19
10
2
5
26
ЗО
6
6
16
28
18
7
17
22
23
8
20
4
7
9
29
12
21
Просте число 37
Первісні корені: 2, 5, 13, 15, 17, 18, 19, 20, 22, 24, 32, 35
N
о
1
2
3
0
24
25
14
1
0
ЗО
22
9
2
1
28
31
5
3
26
11
15
2d
4
2
33
29
/8
5
23
13
10
19
6
27
4
12
18
7
32
7
6
8
3
17
34
9
16
35
21
/
0
1
2
3
0
1
26
33
11
1
2
13
29
22
2
4
26
21
7
3
8
15
5
14
4
10
30
10
28
5
32
23
20
19
6
27
9
3
7
17
18
6
8
34
36
12
9
31
35
24
249

Просте число 41
Первісні корені: 6, 7, 11, 12, 13, 15, 17, 19, 22, 24, 26, 28, 29. ЗО, 34, 35
N
' 0
1
2
3
4
0
8
34
23
20
1
0
3
14
28
2
26
27
29
10
3
15
31
36
18
4
12
25
13
19
5
22
37
4
21
6
1
24
17
2
7
39
33
5
32
8
38
16
11
35
91
ЗО
91
7
6
/
о
1
2
3
0
1
32
40
9
1
6
28
35
13
2J
3fi
4
5
і 37
3
11
24
30
17
4
25
21
16
20
б
27
3
14
38
6
39
18
2
23
7
29
26
12
15
8
10
33
31
8
9
19
34
22
7І
Просте число 43
Первісні корені: 3, 5, 12, 18, 19, 20, 26, 28, 29, ЗО, 33, 34
N
0
1
2
3
4 1
0
10
37
11
22
1
0
ЗО
36
34
G
2
27
13
15
9
21
3.
1
32
16
31 і
4
12
20
40
23
5
25
26
8
18
6
28
24
17
14
7
35
38
3
7
8
39
29
5
4
9
2
19
41
33
/
о
1
2
1 з
1 4
0
1
10
14
11
24
1
3
зо
42
33
29 |
2
9
4
40
13
3
27
12
34
39
4
38
36
16
31
б
28
22
5
7
6
41
23
15
21
7
37
26
2
20
8
25
35
6
17
9
32
19
18
8
Просте число 47
Первісні корені: 5, 10, 11, 13, 15, 19, 20, 22, 23, 26, 29, ЗО, 31, 33,
35, 39, 40, 41, 43, 44, 45
N
0
1
2
3
1 4
0
19
37
39
9
1
0
7
6
3
15
2
18
10
25
44
24
3
20
11
5
27
13
4
36
4
28
34
43
5
1
21
2
33
41
6
38
26
29
ЗО
23 |
7
32
16
14
42
8
8
12
22
17
9І
40
45
35
31
/
0
1
2
3
1 4
0
1
12
3
36
9
1
5
13
15
39
45
2
25
18
28
7
37
3
31
43
46
35
44
4
14
27
42
34
32
5
23
41
22
29
19
6
21
17
16
4
7
11
38
33
20
8
8
2
24
6
9
40
10
26
ЗО
Просте число 53
Первісні кор єн і: 2, 3, 5, 8, 12, 14, 18, 19, 20, 21, 22, 26, 27, 31, 32,
33, 34, 35, 39, 41, 45, 48, 50, 51
/
о
І
2
з
4
5
0
1
17
24
37
46
40
1
2
34
48
21
39
27
2
4
15
43
42
25
3
8
ЗО
33
31
50
4
16
7
13
9
47
5
32
14
26
18
41
6
11
28
52
36
29
7
22
3
51
19
5
8
44
6
49
38
10
9
35
12
45
23
20
N
о
1
2
3
4
5
0
48
49
13
50
43
1
0
6
31
33
45
27
2
1
19
7
5
32
26
1 3
17
24
39
23
22
1 4
2
15
20
11
8
1 5
47
12
42
9
29
1 6
18
4
25
36
40
1 7
14
10
51
ЗО
44
8
3
36
16
38
21
9
34
37
46
41
28
250

Просте число 59
Первісні корені: 2, б, 8, 10, П, 13, 14, 18, 23, 24, ЗО, 31, 32, 33, 34,
37, 38, 39, 40, 42, 43, 44, 47, 50, 52, 54, 55, 56
У
о
1
2
3
4
5
0
1
21
28
57
17
3
1
2
42
50
55
34
6
2
4
21
53
51
9
12
3
8
50
47
43
18
24
4
16
41
35
27
3G
48
5
32
23
11
54
13
37
6
5
46
22
49
26
15
7
Ю
33
44
39
52
ЗО
8
20
7
29
19
45
9
40
14
58
38
31
N
0
1
2
3
4
5
0
7
8
57
9
13
1
0
25
10
49
14
32
2
1
52
2G
5
11
47
3
50
45
15
17
33
22
4
2
19
53
41
27
35
5
6
56
12
24
48
31
6
51
4
46
44
16
21
7
18
40
34
55
23
ЗО
8
3
43
20
39
54
29
9
42
38
28
37
36
Просте число 61
Первісні корені: 2, 6, 7, 10, 17, 18, 26, 30, 31, 35, 43, 44, 51, 54, 55, 59
/
0
1
2
3
4
5
0
1
48
47
60
13
14
1
2
35
33
59
26
28
2
4
9
5
57
52
56
3
8
18
10
53
43-
51
4
16
36
20
45
25
41
5
32
11
40
29
50
21
6
3
22
19
58
39
42
7
6
44
38
55.
17
23
8
12
27
15
49
34
46
9
24
54
ЗО
37
7
31
N
о
1
2
3
4
5
! 6
0
23
24
29
25
45
ЗО
1
0
15
55
59
54
53
2
1
8
16
5
56
42
3
6
40
57
21
43
33
1 4
2
50
9
48
17
19
5
22
28
44
11
34
37
6
7
4
41
14
58
52
7
49
47
18
39
20
32
8
3
13
51
27
Ю
36
9
12
26
35
46
38
31
Просте число 67
Первісні корені: 2, 7, 11, 12, 13, 18, 20, 28, 31, 32, 34, 41, 44, 46,
48, 50, 51, 57, 61, 63
N
0
1
2
3
4
5
6
0
16
17
55
18
31
56
1
0
59
62
47
53
37
7
2
1
41
60
5
63
21
48
3
39
19
28
32
9
57
35
4
2
24
42
65
61
52
6
5
15
54
ЗО
38
27
8
34
6
40
4
20
14
29
26
33
7
23
64
51
22
50
49
8
3
13
25
11
43
45
9
12
10
44
58
46
36
1 /
о
1
2
3
4
5
6
о
1
19
26
25
(у
47
22
1
2
38
52
50
12
1 27
44
2
4
9
137
33
24
54
21
3
8
18
7
66
48
41
42
4
16
36
14
65
29
15
17
5
32
5
28'
63
58
ЗО
34
6
64
Ю
56
59
49
60
7
61
20
45
51
31
53
8
55
40
23
35
62
39
9
43
13
46
3
57
11
251

СПИСОК ЛІТЕРАТУРИ
1. Зава ло С. Т. та ін. Алгебра і теорія чисел.—К.: Вища шк. Головне вид-во,
1976.— Ч. 2.—384 с.
2. З а в а ло С. Т. и др. Алгебра и теория чисел.—К.: Вища шк. Головное изі-
во, 1980.—Ч. 2.—402 с. '
3. Кулик о в Л. Я. Алгебра и теория чисел.— М.: Вьісш. шк., 1979.—559 с.
4. Ляпин Е. С., Е в се є в А. Е. Алгебра и теория чисел.—М.: Просвещение,
1974.— Ч. 1.— 383 с.
5. Л я п и н Е. С, Е в сеє в А. Е. Алгебра и теория чисел.—М.: Просвещение,
1978.—Ч. 2.-448 с. , ,
6. Курош А. Г. Курс вьісшей алгебрьі.—М.: Наука, 1971.—432 с.
7. Окунев Л. Я. Бьісшая алгебра.— М.: Просвещение, 1966.—336 с.
8. Кострикин А. И. Введение в алгебру.— М.: Наука, 1977.—496 с.
9. Проскуряков И. В. Числа и многочленьї.— М.: Просвещение, 1965.—>
284 с.
10. Виноградов И. М. Основи теории чисел.— М.: Наука, 1981.—176 с.
11. Бухштаб А. А. Теория чисел.— М.: Просвещение, 1966.— 384 с.
12. Михелович Ш. X. Теория чисел.— М.: Вьісш. шк., 1967.—336 с.
13. Гриба нов В. У., Т и т о в П. И. Сборник упражнений по теории чисел.—
М.: Просвещение, 1964.— 143 с.
14. Бородін О. І. Теорія чисел.— К.: Вища шк. Головне вид-во, 1970.—274 ct
15. Фаддеев Д. К., Соминский И. С. Сборник задач по вьісшей алгебре.—
М.: Наука, 1977.—288 с.
16. Кудреватов Г. А. Сборник задач по теории чисел.— М.: Просвещение,
1970.—128 с.
17. Оре О. Приглашение в теорию чисел.— М.: Наука, 1980.— 128 с.
18. Фаддеев Д. К. Лекции по алгебре.— М.: Наука, 1984.—416 с.
19. Алгебра и теория чисел/ Н. А. Казачек, Г. Н. Перлатов, Н. Я. Ви-
ленкин, А. И. Бородин — М.: Просвещение, 1974.— 200 с.
20. Яковкин М. В. Вьічислительньїе действия над многочленами.— М.: Учпед-
гиз, 1961.—80 с.
21. Давьідов А. К. Сборник задач по алгебре и злементарньїм функциям.—
М.: Учпедгиз, 1959.-150 с.
22. Ляпин С. Е. и др. Сборник задач по злементарной алгебре.— М.:
Просвещение, 1973.-351 с.
23. Окунев Л. Я. Сборник задач по вьісшей алгебре.—М.: Просвещение,
1964.—185 с.
24. Алгебра і теорія чисел: Практикум: В 2-х ч. / С. Т. Завало,
С. С. Левіщенко, В. В. Пилаєв, І. О. Рокицький —К.: Вища шк. Головне
вид-во, 1983.—Ч. 1.—232 с.
25. Пр о ску р я к о в И. В. Сборник задач по линейной алгебре.—М.: Наука,
1974.—384 с.
26. Боревич 3. И., Шафаревич И. Р. Теория чисел.— М.: Наука, 1972.—-
495 с.
27. Кал ужни н Л. А. Введение в общую алгебру.— М.: Наука, 1973.—448 с.
28. Ван-дер-Варден Б. Л. Алгебра.—М.: Мир, 1977.—623 с.
29. Постников М. М. Теория Галуа.— М.: Физматгиз, 1963.—220 с.
30. Постников М. М. Введение в теорию алгебраических чисел.— М.: Наука,
1982.—239 с.
31. Здвардс Г. Последияя теорема Ферма.—М.: Мир, 1980.—484 с.
32. Хинчин А. Я. Цепньїе дроби.—М.: Наука, 1978.— 112 с.
33. Кантор И. Л., С о л о д о в н ико в А. С. Гиперкомплексньїе числа.— М.:
Наука, 1973.—144 с.
34. Скорняков Л. А. Злементьі алгебрьі.—М.: Наука, 1980.—240 с.
35. Хассе Г. Лекции по теории чисел.— М.: Изд-во иностр. лит., 1953.—528 с.
255

36. Дзвенпорт Г. Вьісшая арифметика.—М.: Наука. 1965.—175 с.
37. Джекобсон Н. Теория колец.— М.: Изд-во иностр. лит., 1947.-288 с.
38. Ленг С. Алгебра.—М.: Мир, 1968.—564 с.
39. Садовничий В. А., Подколозин А. С. Задачи студенческих олимпиад
по математике.— М.: Наука, 1978.— 207 с.
40. Венгерские математические о л и м п и а д ьі.—М.: Мир, 1976.—
543 с.
41. З у б а левич Г. И. Сборник задач московских математических олимпиад.—
М.: Просвещение, 1967.— 232 с.
42. Ш к л я р с к и й Д. О. и др. Избранньїе задачи и теореми злементарной
математики: Арифметика и алгебра.—М.: Наука, 1976.—378 с.
43. Г л у х о в М. М., С о л о д о в н и к о в А. С. Задачник-практикум по курсу
вьісшей алгебри.— М.: Просвещение, 1965.— 207 с.
44. Б о лтя нски й В. Г., Виленкин Н. Я. Симметрия в алгебре.—М.:
Наука, 1967.—283 с.

ОСНОВНІ ПОЗНАЧЕННЯ
%{*) — число простих чисел, які не перевищують *, 7
(а, 6) — найбільший спільний дільник цілих чисел а і Ь, 11
[а, Ь] — найменше спільне кра'тне цілих чисел а і Ь, 12
т(я) — число всіх натуральних дільників п, 17
а (я) —сума всіх натуральних дільників м, 17
<р(/г) — функція Ейлера, 17
[х]— ціла частина дійсного числа х, 17
{х} —дробова частина дійсного числа х, 18
[<7о'> <7і» Я2> • • •» <7rt» • • .] —ланцюговий дріб, 25
[ІЯо'у Яі> Й2> • • •» Яп)\ ~~ чистий періодичний ланцюговий дріб, 25
[<70; Я\* • • •» <7т» (Ро> • • •» ^д)] —мішаний періодичний ланцюговий дріб, 25
mg — запис числа m в g-ковій системі числення, 37
знак асоційованості, 45
<ху —головний ідеал, породжений елементом х, 51
К/1 — фактор-кільце кільця К за ідеалом /, 5і
Zm — фактор -кільце Z/<m> кільця Z цілих чисел за головним ідеалом <т>, 51
а — клас лишків з представником а, 51
= — знак конгруентності, 51
^ —знак гомоморфізму, 57
= — знак ізоморфізму, 57
Кегср — ядро гомоморфізму «р, 58
Nr(Z) — норма елемента Z, 64
К*"£ — клас лишків з представником а за модулем т, 77
©-<
v ) -символ Лежандра, -104
Рт(а) = Ьт(а) — показник числа а за модулем т, 111
indga(modm) — індекс числа а за модулем т при основі gt 115
Р [х] — кільце многочленів від однієї змінної х над кільцем Р, 126
deg / — степінь многочлена /, 127
(/, g) —найбільший спільний дільник многочленів / і g, 142
U> g] —найменше спільне кратне многочленів / і g, 142
R [xv х2, • • •» хп\ —кільце многочленів від п змінних xv х2, .. ч хп над областю
цілісності R, 165
0^ о2, ..., <?п — елементарні симетричні многочлени, 170
#(/» g) — результант, многочленів / і g, 178
D(/) —дискримінант многочлена /(*), 179
Р (а) — просте розширення поля Р, 202

ПРЕДМЕТНИЙ ПОКАЖЧИК
Алгебраїчне число 202
— розширення 203
Алгебраїчний елемент 126
Алгебраїчно замкнене поле 184
Алгоритм Евкліда 12, 142, 195
— Ейлера 29
— послідовного ділення з остачею 12
Антисиметричний многочлен 173
Асимптотичний закон 7
Асоційовані елементи 45
Верхня межа 194
Виключення невідомих 179
Вищий член многочлена 166
Відображення кілець 57 .
Відокремлення дійсних коренів 194
— кратних множників 153
Взаємно однозначне відображення 57
— прості елементи 62
многочлени 142
числа 11
Властивості взаємно простих чисел 12
— гомоморфізму кілець 57
— ізоморфізму кілець 57
— індексів 116
— конгруенцій 51, 72
— мультиплікативних функцій 18
— незвідних многочленів 147
— підхідних дробів 26
— подільності З
— символу Лежандра 105
■~ симетричних многочленів 170
Головний ідеал 51, 136
Гомоморфне відображення 57
Гомоморфізм кілець 57
Група дільників одиниці 45
— класів лишків 77
— одиниць кільця 45
Двійкова тріада 41
Двосторонній ідеал 51
Десяткова система числення 37
Дискримінант многочлена 179
— рівняння 190
Ділене 132
Ділення кутом 156
— многочлена на двочлен 136
Дільник 3, 132
Дільники нуля 44
— одиниці 44
Добуток ідеалів 51
Довжина періоду 121
Досконале число 20
Дробова частина дійсного числа 18
Дружні числа 20
Евклідове кільце 63
Елементарний ланцюговий дріб 24
— дріб 159
Елементарні перетворення конгруенцій
87
— симетричні многочлени 170
Елементи ланцюгового дробу 25
Епіморфізм кілець 57
Задача Ферма 20
Закон взаємності квадратичних лишків
105
Запис числа 37
Застосування класів лишків 87
— ланцюгових дробів 87
— симетричних многочленів 174
Зведена система лишків 78
Звідний елемент 62
— многочлен 147
Знаходження НСД і НСК 12
Ідеал кільця 51
Індексація 116
Індекс числа 115
Інтерполяційний многочлен Лагранжа
159
Ньютона 159
Канонічна форма многочлена 127 165
■ числа 7
Канонічний розклад многочлена 148
числа 7
Квадратична ірраціональність 25
258

Квадратичний лишок 104
^. нелишок 104
Кількість змін знаків 195
Кільце 44
.— головних ідеалів 62
— з одиницею 44
^- кватерніонів 50
— класів лишків 51
— многочленів від п змінних 165
. однієї змінної 126
— цілих гауссових чисел 44
Класи лишків за даним модулем 72, 77
Клас первісних коренів 111
Коефіцієнти члена многочлена 165
Комутативне кільце 44
Конгруентні за модулем цілі числа 72
ідеалом елементи кільця 51
Конгруенції вищих степенів з одним
невідомим 96
— першого степеня з одним невідомим
87
Конгруенція з одним невідомим 86
/г-кратний корінь 153
Корінь многочлена 153
Кратне З
Кратний корінь 153
Кратні множники 153
Критерій Ейзенштейна 199
— Ейлера 104
— Лейбніца 102
— підкільця 44
Кубічна резольвента 190
Ланка ланцюгового дробу 25
Ланцюговий дріб 24
Лексикографічний порядок 166
Лишок класу 77
Лівий дільник елемента 44
■ нуля 44
— ідеал кільця 51
— кратний елемента 44
Лінійне аображення НСД 12
Метод ділення кутом 132
•— математичної індукції 4
— невизначених коефіцієнтів 132
■— Ньютона 194
•— повної індукції 4
— табличних схем 132
—- Феррарі 191
— Штурма 195
Мінімальний многочлен 202
Мішаний періодичний ланцюговий дріб
25
Многочлен від п змінних 165
однієї змінної 126
Множина дуальних чисел 49
— кватерніонів 50
—- подвійних чисел 49
Моногенний многочлен 171
Мультиплікативна група класів
лишків 78
— числова функція 18
Найбільший спільний дільник головних
ідеалів 62
елементів 62
ідеалів 52
— многочленів 142
чисел 11
Найменше спільне кратне елементів 63
< ідеалів 62
многочленів 142
чисел 12
Невизначені рівняння 27
Незвідний елемент 62
~ многочлен 147
Неперервні дроби 24
Неповна частка З
Неповні частки ланцюгового дробу 25
Непозиційна система числення 36
Нерівності Чебишова 7
Нерозкладний елемент 62
Нескінченний ланцюговий дріб 24
Норма елемента 63
НСД 11
НСК 12
Нульове кільце 44
Нульовий ідеал кільця 51
— многочлен 126
Нумерація 36
Область цілісності 44
Оборотний елемент 44
Образ елемента 57
Обчислення остач при діленні 120
Одиничний ідеал кільця 51
Однорідний многочлен 166
Ознака подільності Паскаля 121
Основа системи числення 37
Основна теорема арифметики 7
Остача 3, 132
259

Оцінка похибки наближення числа
підхідним дробом 27
Первісний корінь 111
Переведення з однієї системи
числення в іншу 36, 37
Перевірка результатів арифметичних
дій 121
Перший спосіб знаходження НСК 12
Письмова нумерація 36
Підкільце 44
Підхідні дроби 6-го порядку 26
ланцюгового дробу 26
непарного порядку 26
парного порядку 26
Піфагоровий трикутник 6
Повна система лишків 77
найменших абсолютно лишків 78
натуральних лишків 78
невід'ємних лишків 78
Подібні члени 165
Позбавлення від ірраціональності 205
Позиційна система числення 36
Показник числа 111
Поле 44
— відношень області цілісності 62
— раціональних дробів 158
— розкладу 184
— часток області цілісності 61, 62
Попарно взаємно прості числа 11
Порядок числа 111
•— класу 111
Потенціювання 116
Похідна многочлена 152
Правий дільник елемента 44
нуля 44
— ідеал кільця 51
— кратний елемента 44
Правило дев'ятки 122
— Декарта 195
— утворення підхідних дробів 26
Представник класу за модулем 77
лишків 77
Природний гомоморфізм кілець 58
Прообраз елемента 57
Просте алгебраїчне розширення 202
— трансцендентне розширення 126,
202
— число 7
Простий елемент 62
— корінь 153
Раціональний дріб 159 [
неправильний 159
правильний 159
Резольвента 190
Результант 178
Решето Ератосфена 6, 7
Римська система числення 37
Рівність многочленів алгебраїчна 127
функціональна 127
Рівносильні конгруенції 87
Розв'язок конгруенції 86
Розклад многочлена за степенями
двочлена 136
Розкладний елемент 62
Ряд Штурма 195
Символ Лежандра 104
— Якобі 105
Симетричний многочлен 170
Система конгруенцій 88
— числення 36
Системні числа 36
Скінченне розширення 203
Скінченний ланцюговий дріб 25'
Складне алгебраїчне розширення 203
.— число 7
Складений елемент 62
Спеціальний спосіб розкладу на прості
множники 8
Спільне кратне елементів 63
— — многочленів 142
чисел 12
Спільний дільник елементів 62
. многочленів 142
чисел 11
Спосіб Ейлера 87
— послідовного ділення 12
— спроб 87
Старший член многочлена 127, 166
— коефіцієнт многочлена 127
Степінь алгебраїчного числа 202
— конгруенції 86
— многочлена 127, 166
— розширення 203
~- члена многочлена 165
Сума значень функції Ейлера 18
— ідеалів 51
— натуральних дільників 17
Схема виключення невідомих 179
— Горнера 138, 154
260

Таблиця антиїндексів 116, 248
— індексів 116, 248
— квадратів 246
— Келі 53
— первісних коренів 248
— простих чисел 246
Теорема Безу 143
— Віета 176
— Вільсона 97
— Гаусса 111
— Діріхле 7
— Евкліда 7
— Евкліда ~ Ейлера 20
— Ейлера 83
— Клемента 102
— про гомоморфізми кілець 58
— — ділення з остачею 3, 132
найкраще наближення 27
— Софії Жермен 9
— Ферма 83
— Штурма 195
Трансцендентне розширення 202
— число 202
Трансцендентний елемент 126
Удосконалення решета Ератосфена 7
Узагальнена канонічна форма числа 7
— теорема про ділення з остачею З
Усна нумерація 36
Факторіальне кільце 63
Фактор-кільце 51
Форма сільвестра 178
Формула Гаусса 18
— Кардано 190
— переходу від однієї системи індексів
до іншої 118
— Тейлора 154
Формула Вієта 184
— скороченого множення 206
Функція Ейлера 17
Характеристика кільця з одиницею 61
Цифра 36
Ціла частина дійсного числа 17
Частка 132
Числа-близнята 211
— Мерсенна 10
— Ферма 10
Числова функція 117
Числове кільце 44
Число натуральних дільників 17
Чистий періодичний ланцюговий дріб
25
Член многочлена 165
Штучний спосіб 4, 87
Ядро гомоморфізму 58

ЗМІСТ
Розділ І. Теорія подільності в кільці цілих чисел
§ 1. Відношення подільності, його найпростіші властивості. Теорема про
ділення з остачею З
§ 2. Означення і властивості простих та складених чисел. Решето Ера-
тосфена. Канонічна форма натурального числа. Розподіл простих
чисел серед чисел натурального ряду- 6
§ 3. Йайбільший спільний дільник і найменше спільне кратне та способи
знаходження їх. Взаємно прості числа 11
§ 4. Числові функції. Число і сума натуральних дільників. Ціла і
дробова частини дійсного числа. Функція Ейлера 17
§ 5. Ланцюгові дроби. Підхідні дроби ланцюгового дробу 24
§ 6. Системні числа, операції над ними; переведення з однієї системи
в іншу 36
Розділ II. Кільця
§ 7. Кільце, підкільце. Найпростіші властивості подільності в
комутативному кільці. Дільники нуля та одиниці. Асоційовані елементи.
Область цілісності, поле 44
§ 8. Ідеали кільця та операції над ними. Конгруенції і класи лишків за
ідеалом. Фактор-кільце 50
§ 9. Гомоморфізми та ізоморфізми кілець. Теорема про гомоморфізми
кілець , 57
§ 10. Характеристика кільця з одиницею. Поле часток області цілісності.
Прості та складені елементи області цілісності. Арифметика кільця
головних ідеалів та езклідовог© кільця 61
Розділ III. Теорія квнгруенцій з арифметичними застосуваннями
§ 11. Конгруенції в кільці цілих чисел та їхні найпростіші властивості 72
§ 12. Класи лишків-, повна і зведена системи лишків за даним модулем . 77
§ 13. Теореми Ейлера і Ферма 83
| 14. Конгруенції першого степеня з одним невідомим та застосування їх 86
§ 15. Конгруенції вищих степенів з одним невідомим 96
§ 16. Конгруенції другого степеня, квадратичні лишки і квадратичні не-
лишки, символ Лежандра jq4
§ 17. Порядок числа і класу лишків за модулем. Первісні корені,
існування їх та кількість за простим модулем jjq
§ 18. Індекси за простим модулем. Двочленні конгруенції за простим
модулем; таблиці індексів і застосування їх 115
§ 19. Арифметичні застосування теорії конгруенцій 120
Розділ IV. Многочлени від однієї змінної
§ 20. Кільце многочленів над областю цілісності. Алгебраїчна і
функціональна рівність многочленів 126
§ 21. Відношення подільності в кільці многочленів. Ділення з остачею.
Ідеали кільця многочленів 131
§ 22. Ділення многочлена на двочлен х — а. Розклад многочлена за
степенями двочлена х — а 136
§ 23. Найбільший спільний дільник і найменше спільне кратне многочленів 142
§ 24. Незвідні многочлени над полем. Розклад многочленів на незвідні
множники 147
§ 25. Похідна многочлена. Кратні корені многочлена. Виділення кратних
множників многочлена 152
§ 26. Інтерполяційні многочлени. Поле раціональних дробів 15g
262

Розділ V. Многочлени від кількох змінних
§ 27. Кільце многочленів від /і змінних над областю цілісності. Розклад
многочлена на добуток незвідних множників 165
& 28. Симетричні многочлени 169
§ 29. Застосування симетричних многочленів до розв'язування деяких
задач з елементарної алгебри 174
§ ЗО. Результант двох многочленів. Виключення невідомих з системи двох
рівнянь з двома невідомими 178
Розділ VI. Многочлени над полем комплексних чисел і над полем
дійсних чисел
§31. Многочлени над полем комплексних чисел. Алгебраїчна замкненість
поля комплексних чисел , 183
§ 32. Многочлени над полем дійсних чисел . . . , , 187
§ 33. Рівняння третього і четвертого степенів . • , , , , 190
§ 34. Відокремлення дійсних коренів многочлена .»,.♦.,... 194
Розділ VII. Многочлени над полем раціональних чисел І
алгебраїчні числа
§ 35. Цілі і раціональні корені многочлена з цілими коефіцієнтами.
Критерій незвідності Ейзенштейна 198
§ 36. Алгебраїчні і трансцендентні числа. Будова простого алгебраїчного
розширення поля , 202
§ 37. Позбавлення від алгебраїчної ірраціональності в знаменнику дробу 205
Відповіді. Вказівки. Розв'язання 211
Додаток 1 ♦ . ♦ ♦ 246
Додаток 2 248
Додаток 3 254
Список літератури , 255
Основні позначення 257
Предметний покажчик , . . , » , 258

Сергей Трофимович Завало
Сергей Сергеевин Левищенко
Владимир Владимирович Пьілаев
Йван Александрович Рокицкий
АЛГЕБРА И ТЕОРИЯ ЧИСЕЛ
ПРАКТИКУМ
Часть 2
Допущено Министерством просвещения УССР
в качестве учебного пособия для студентов
физико-матвматических факультетов
педагогических институтов
(На украинском язьіке)
Киев,
Головное издательство
издательского обгединения «Вища школа»
Редактор Г. П. Трофімчук
Художній редактор С. В. Анненков
Технічний редактор І. І. Каткова
Коректор Н. В. В о л к о в а
Здано до набору 19.03.85. Підп. до друку 07.03.86. Формат
60Х90/1в. Папір друк. № 2. Літ. гарн. Вис. друк. Друк. арк.
16,6. Фарб.-відб. 16,14. Обл.-вид. арк. 20,18. Тираж 3460 пр.
Вид. № 7082. Зам. М 5-271. Ціна 85 к.
Головне видавництво видавничого об'єднання «Вища школа>,
252054, Київ-54, вул. Гоголівська, 7
Харківська книжкова фабрика «Комуніст», 310012,
Харків, вул. Енгельса, 11.