Автор: Столниц Э. ДеРоуз Т. Салезин Д.
Теги: математика компьютерная графика информационные технологии
ISBN: 5-93972-119-2
Год: 2002
Текст
э. СтОЛIlUЦ, Т. ДеРоуз, д. СалеЗUIl
'"
ВЕИВЛЕТЫ
В КОМПЬЮТЕРНОЙ
rРАФИКЕ
ТЕОРИЯ И ПРИЛОЖЕНИЯ
Перевод с анrлийскоrо л. А. Кунrуровой
Под редакцией Е. В. Мищенко
R&C p !)
'[) Москва. Ижевск
2002
Wavelets for
Computer Graphics
Theory and Applications
Епс J. Stollпitz
Uпiversity о! Washiпgtoп
Топу D. DeRose
Pixar Aпiтatioп Studios
David Н. Salesiп
Uпiversity о! Washiпgtoп
M(
Morgaп Kaиfтaпп Publishers. /пс.
Saп Fraпcisco, СаlifОПliu
СОВРЕМЕННАЯ МАТЕМАТИКА
Редакционный совет:
А.В.Болсинов
А.В.Борисов
И. С. Мамаев
И. А. Тайманов
Д. В. Трещев
Вышли в свет:
П. И. rолод, А. у. КлиМblК. Математические основы теории симметрии
М Тромов. rиперболические rруппы
М Тромов. Знак и rеометрический смысл кривизны
Дж. Д Мур. Лекции об инвариантах Зайберrа Виттена
Дж. Милнор. rоломорфная динамика
И. р Шафаревич. Основные понятия алrебры
И. Добеши. Десять лекций по вейвлетам
Э. Столниц, Т ДеРоуз, Д. Салезин. Вейвлеты в компьютерной rpафике
rотовятся к печати:
к. Кассель, М Россо, В. Тураев. Квантовые rруппы и инварианты узлов
С. П. Новиков. Тополоrия
Я. Песин. Теория размерности
Ж. П. Рамис. Расходящиеся ряды и асимптотическая теория
А. И. Шафаревич. Введение в теорию квазиклассическоrо квантования
изотропных мноrообразий
УДК 515
Интернет маrазин
. физика
. математика
. биолоrия
http://shop.rcd.ru
. техника
Столниц Э., ДеРоуз Т., Салезин д.
Вейвлеты в компьютерной rpафике: Пер. с анrл. Ижевск: НИЦ «Реrуляр
ная и хаотическая динамика», 2002, 272 стр.
Весьма доступное введение в вейвлеты, обеспечивающее профессионалам
и исследователям, работающим в компьютерной rpафике, понимание математиче
ских основ и приложений этоrо достаточноrо новото, но мощноrо средства.
Авторы книrи ведущие специалисты в области компьютерной rрафики. При
их участии были созданы анимационные короткометражные фильмы Тin toy и Geri,
наrражденные Оскарами как лучшие анимационные фильмы.
ISBN 5 93972 119 2
@ Перевод на русский язык,
НИЦ «Реrулярная и хаотическая динамика», 2002
http://rcd.ru
Содержание
Предисловие к русскому изданию
Предисловие Инrрид Добеши .
Предисловие
Обозначения
11
14
15
18
[ЛАВА 1. Введение.
1.1. Кратномасштабные методы .
1.2. Историческая перспектива
1.3. Краткий обзор книrи ....
19
20
21
23
ЧАСТЬ 1. ИЗОБРАЖЕНИЯ
[ЛАВА 2. Хаар: простейший вейвлет базис . . . . . . . . . . . " 27
2.1. Вейвлет преобразование Хаара для одномерноrо случая 27
2.2. Функции одномерноrо базиса Хаара . 30
2.3. Ортоrональность и нормирование 34
2.4. Вейвлет сжатие ............ 36
[ЛАВА 3. Сжатие изображения. . . . . . . . . . . . . . .. 39
3.1. Вейвлет преобразования Хаара для двумерноrо случая 39
3.2. Функции двумерноrо базиса Хаара 42
3.3. Вейвлет сжатие изображения. 44
3.4. Цветные изображения. 48
3.5. Выводы... . . . . . . . . . . 48
[ЛАВА 4. Редактирование изображений . . . . . . . . . .. 49
4.1. Структуры изображений с переменным разрешением 50
4.2. Алrоритм редактнрования изображения . 52
4.2.1. Вывод на экран 52
4.2.2. Раскрашивание. 53
4.2.3. Корректировка 54
4.3. [раничные условия . . 56
б
Содержание
4.4. Вывод на экран и редактирование при дробных разрешениях 57
4.5. Примеры редактирования изображений. . . . . .. 58
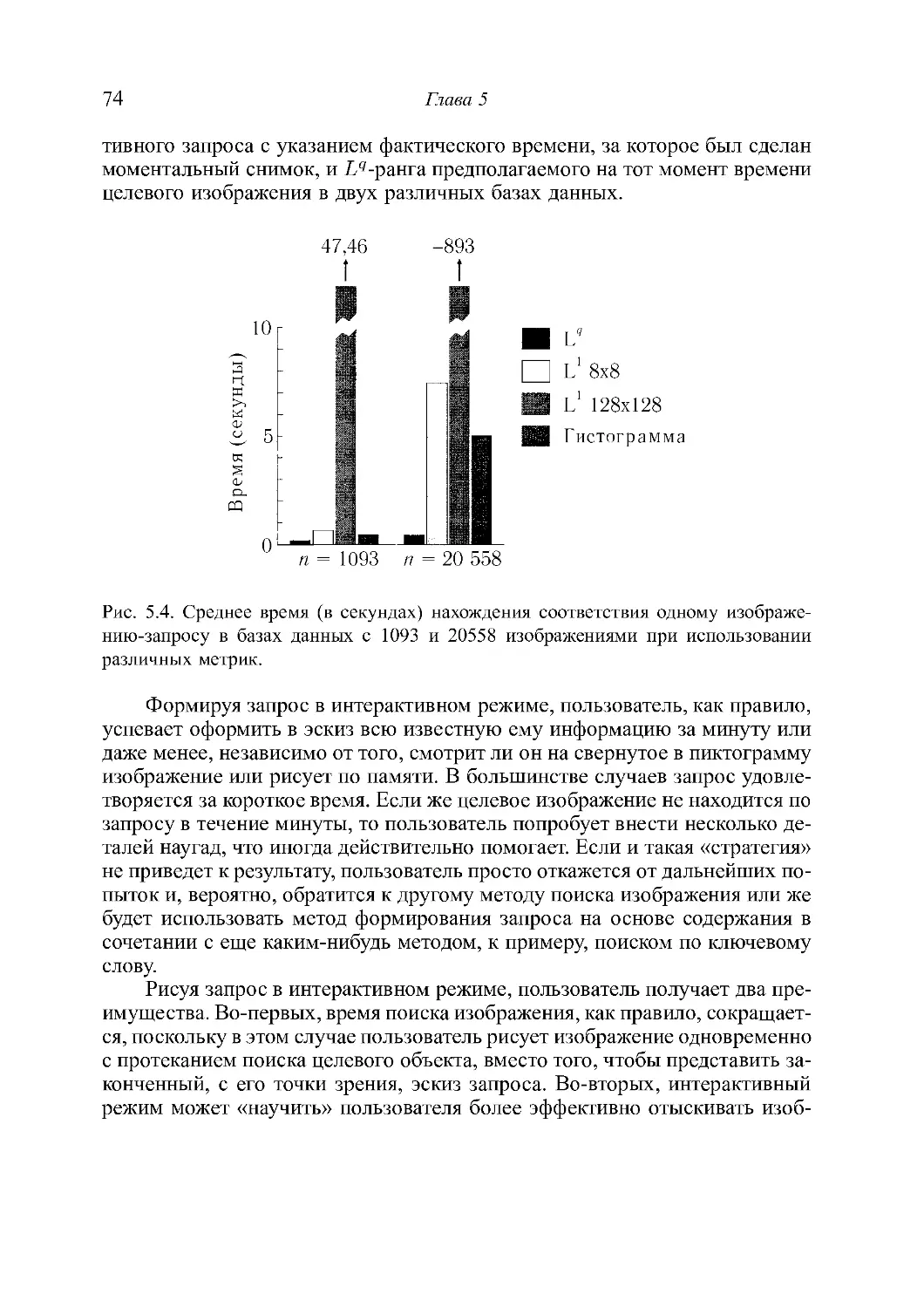
[ЛАВА 5. Формирование запроса изображения . . . .. 59
5.1. Формирование запроса изображения по содержанию . . . .. 61
5.2. Разработка метрики для формирования запроса изображения б3
5.2.1. Кратномасштабный метод ........... б3
5.2.2. Компоненты метрики . . . . . . . . . . . . . . . . . .. б4
5.2.3. Метрика формирования запроса изображения . . . .. бб
5.2.4. Быстрое вычисление метрики формирования запроса
изображения . . . . . . . . . . . . . . . . б7
5.3. Алrоритм формирования запроса изображения. б8
5.3.1. Предварительный этап . . . . . . . . . . б8
5.3.2. Формирование запроса . . . . . . . . . . 70
5.4. Примеры формирования запросов изображений 72
5.5. Расширения .................... 75
ЧАСТЬ 11. КРИВЫЕ
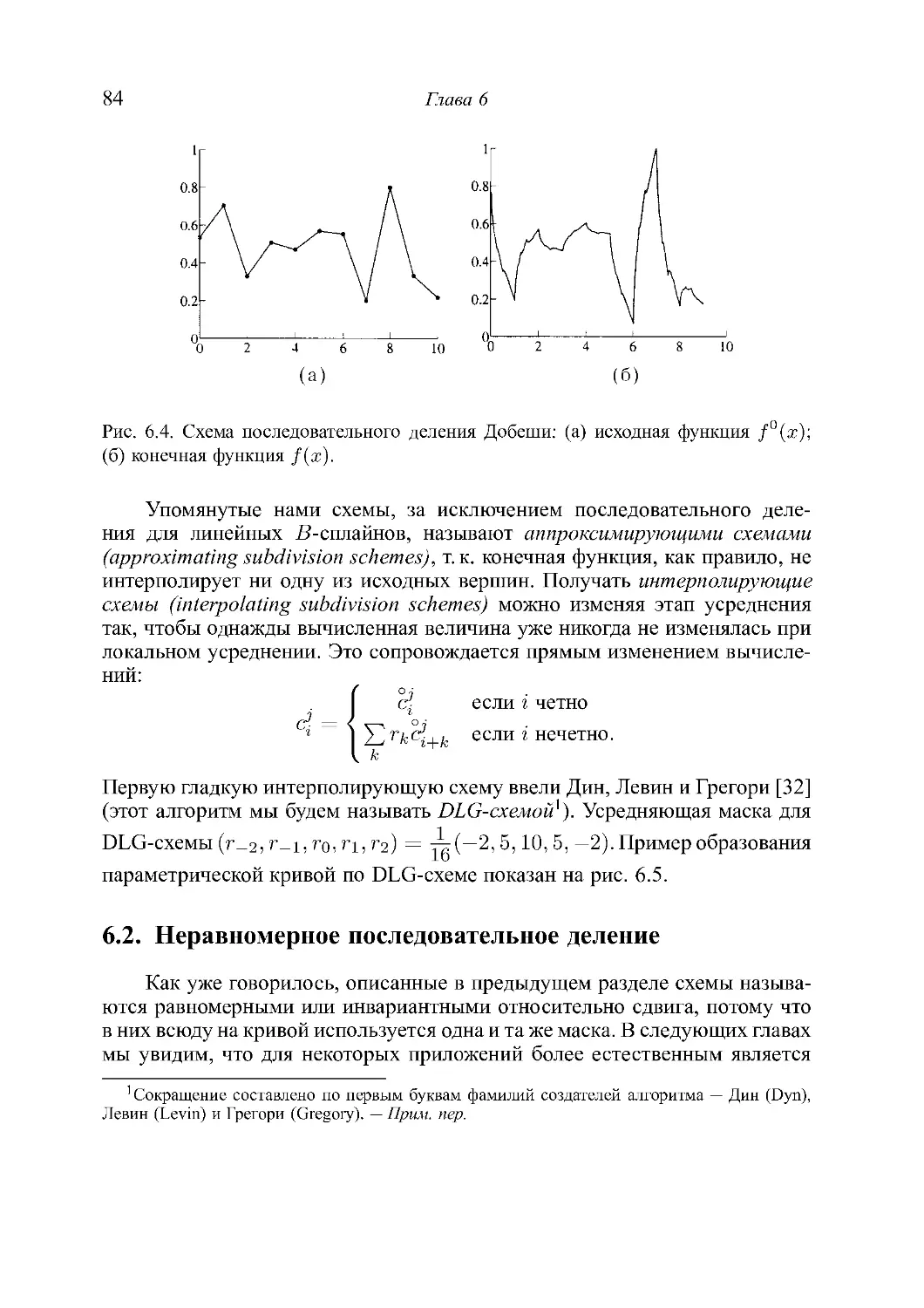
[ЛАВА б. Кривые последовательноrо деления
б.1. Равномерное последовательное деление
б.2. Неравномерное последовательное деление . . . . . .
б.3. Оценочные маски . . . . . . . . . . . . . . . . . . . .
б.4. Вложенные пространства и уточняемые масштабирующие
функции ................. . . . . . .
79
80
84
87
91
[ЛАВА 7. Теория кратномасштабноrо анализа
7.1. Кратномасштабный анализ
7.1.1. Уточнение . . . .
7.1.2. Блок фильтров . . .
7.2. Ортоrональные вейвлеты .
7.2.1. Включения ортоrональности
7.2.2. Вейвлеты Добеши . . . . . .
7.3. Полуортоrональные вейвлеты . . .
7.3.1. Включения полуортоrональности
7.3.2. Сплайн вейвлеты .........
7.3.3. Конструирование полуортоrональных вейвлетов
7.4. Биортоrональные вейвлеты . . . . . . . . . . . . . . . .
7.4.1. Двойственные базисы и биортоrональность
7.4.2. Определение двойственных конструкций через после
довательное деление. . . . . . . . . . . . . . . . . . . .
97
97
98
100
103
104
105
107
109
109
115
115
117
118
Содержание
7
7.4.3. Одноузловые вейвлеты . . . . . . . . . . . . . . . . . .
7.4.4. Конструирование биортоrональных вейвлетов: схема
подъема .
Выводы . . . . . . . . . . . . . . . . . . .
121
7.5.
125
126
[ЛАВА 8. Кратномасштабные кривые. . . . .
8.1. Сходные представления кривых
8.2. Сrлаживание кривой. . . . . . . . .
8.3. Редактирование кривой . . . . . . .
8.3.1. Редактирование общеrо вида
8.3.2. Редактирование особенностей кривой
8.3.3. Ориентация детали " . . . . . . . .
8.4. Обращение развертки контура и сжатие кривой
128
129
130
131
132
138
139
140
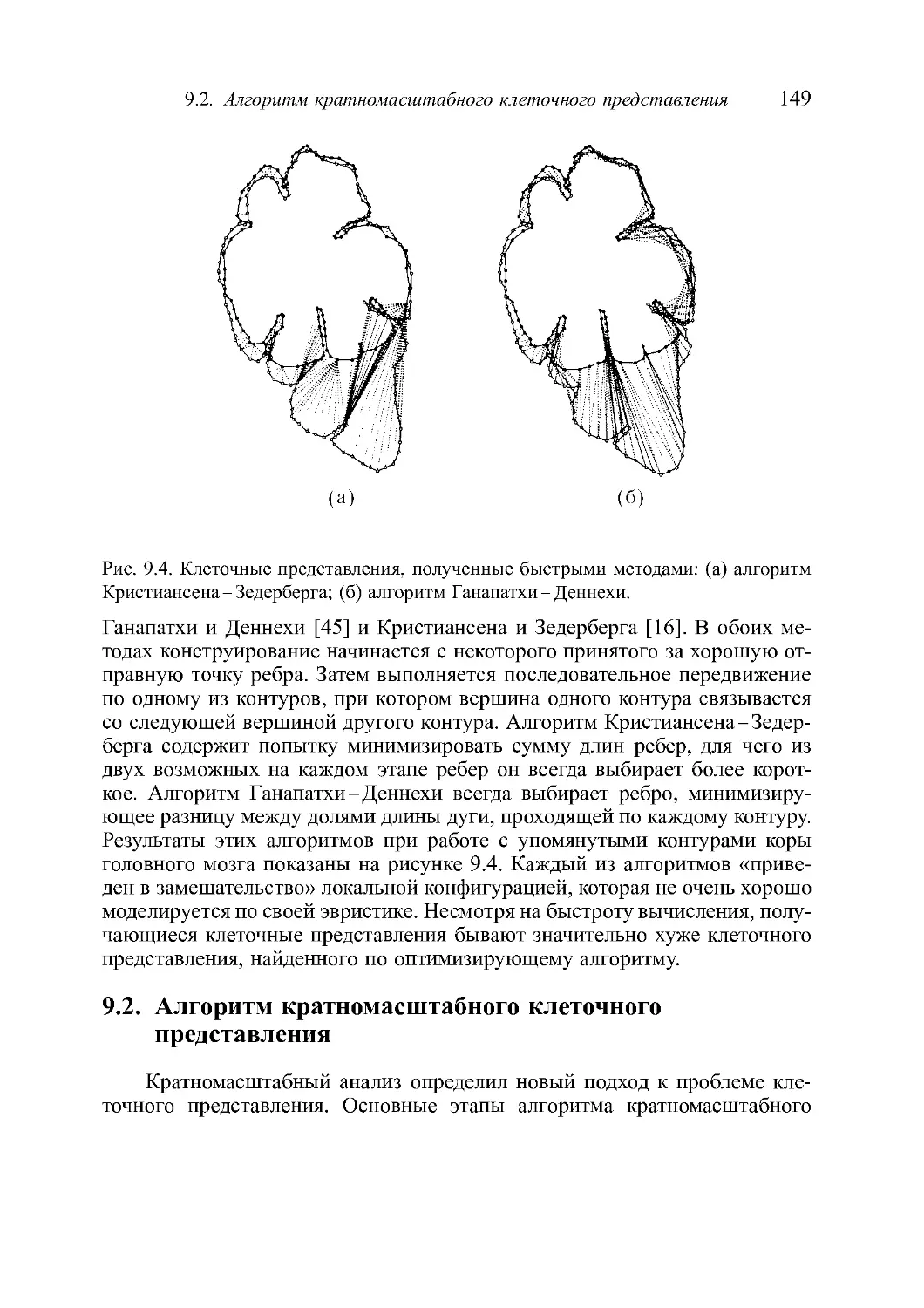
[ЛАВА 9. Кратномасштабное клеточное представление ..... 145
9.1. Предыдущие решения задачи клеточноrо представления 145
9.2. Алrоритм кратномасштабноrо клеточноrо представления 149
9.2.1. Разложение контура. . . . . . . . . . . . . 151
9.2.2. Оптимизация выбора базовоrо комплекта. 151
9.2.3. Восстановление . . . . 152
9.2.4. Локальная оптимизация. . . . 156
9.3. Временная сложность. . . . . . . . . 156
9.4. Примеры клеточноrо представления. 159
ЧАСТЬ 111. ПОВЕРХНОСТИ
[ЛАВА 10. Поверхностные вейвлеты ................ 163
10.1. Обзор кратномасштабноrо анализа для поверхностей . . . . . 164
10.2. Поверхности последовательноrо деления. . . . . . . . . . . . 166
10.2.1. Вложенные пространства и уточняемые масштабиру
ющие функции . . . . . . . . . . . . . . . . . . . .. 172
10.3. Выбор скалярноrо произведения . . . . . . . . . . . . . .. 174
10.4. Биортоrональные конструкции поверхностных вейвлетов . 175
10.5. Кратномасштабные представления поверхностей 182
[ЛАВА 11. Приложения к поверхностям. . . .
11.1. Переход к кратномасштабной форме
11.2. Сжатне поверхностей . . . . . .
11.2.1. Сжатие мноrоrранника . . . .
11.2.2. Сжатие текстурных карт ...
11.3. Непрерывный контроль степени детализации
184
184
186
186
187
188
8
Содержание
11.4. Последовательное пропускание ..........
11.5. Редактирование при переменном разрешении ..
11.6. Перспективы изучения поверхностных вейвлетов
ЧАСТЬ IV. ФИЗИЧЕСКОЕ МОДЕЛИРОВАНИЕ
[ЛАВА 12. Вариационное моделирование . . .
12.1. Задание целевой функции. . . . . . . . . . . . . . .
12.2. Метод конечных элементов. . . . . . . . . . . . . .
12.3. Использование конечных элементов в вариационном Moдe
лировании ...........................
12.4. Использование вейвлетов в вариационном моделировании
12.5. Адаптивное вариационное моделирование
[ЛАВА 13. Общее освещение . . . . . . . . . .
13.1. Излучательность . . . . . . . . . . . . .
13.2. Конечные элементы и излучательность .
13 .2.1. Дискретизация излучательности .
13.2.2. Дискретизация переноса излучательности
13.2.3. Решение линейной системы .....
13.3. Вейвлет излучательность . . . . . . . . . . . . . .
13.3.1. Базис вейвлетов для излучательности . . .
13.3.2. Структуры данных для вейвлет излучательности
13.3.3. Алrоритм вейвлет излучательности
13.3.4. Уточнение . . . . . . . . . . .
13.3.5. Разложение матрицы переноса
13.3.6. Этап конечной сборки. . . . .
13.4. Улучшение вейвлет излучательности
13.4.1. Уточнение с учетом значимости
13.4.2. Кластеризация . . . . .
13.4.3. Обобщение до яркости . . . . .
[ЛАВА 14. Дополнительная информация . . .
14.1. Теория кратномасштабноrо анализа. .
14.2. Приложения к изображениям. . . . . .
14.3. Приложения к кривым и поверхностям
14.4. Физическое моделирование. . . . . . .
189
189
190
195
195
197
197
202
203
205
205
207
208
208
209
210
210
211
212
213
215
216
217
217
218
218
220
220
222
224
224
Содержание
ЧАСТЬ V. ПРИЛОЖЕНИЯ
ПРИЛОЖЕНИЕ А. Справочник по линейной алrебре
А.1. Векторные пространства . . . . . . . . . . .
А.2. Базисы и размерность . . . . . . . . . . . . .
А.3. Скалярное произведение и ортоrональность
А.4. Нормы и нормирование . . . . . . . . . . . .
А.5. Собственные векторы и собственные значения .
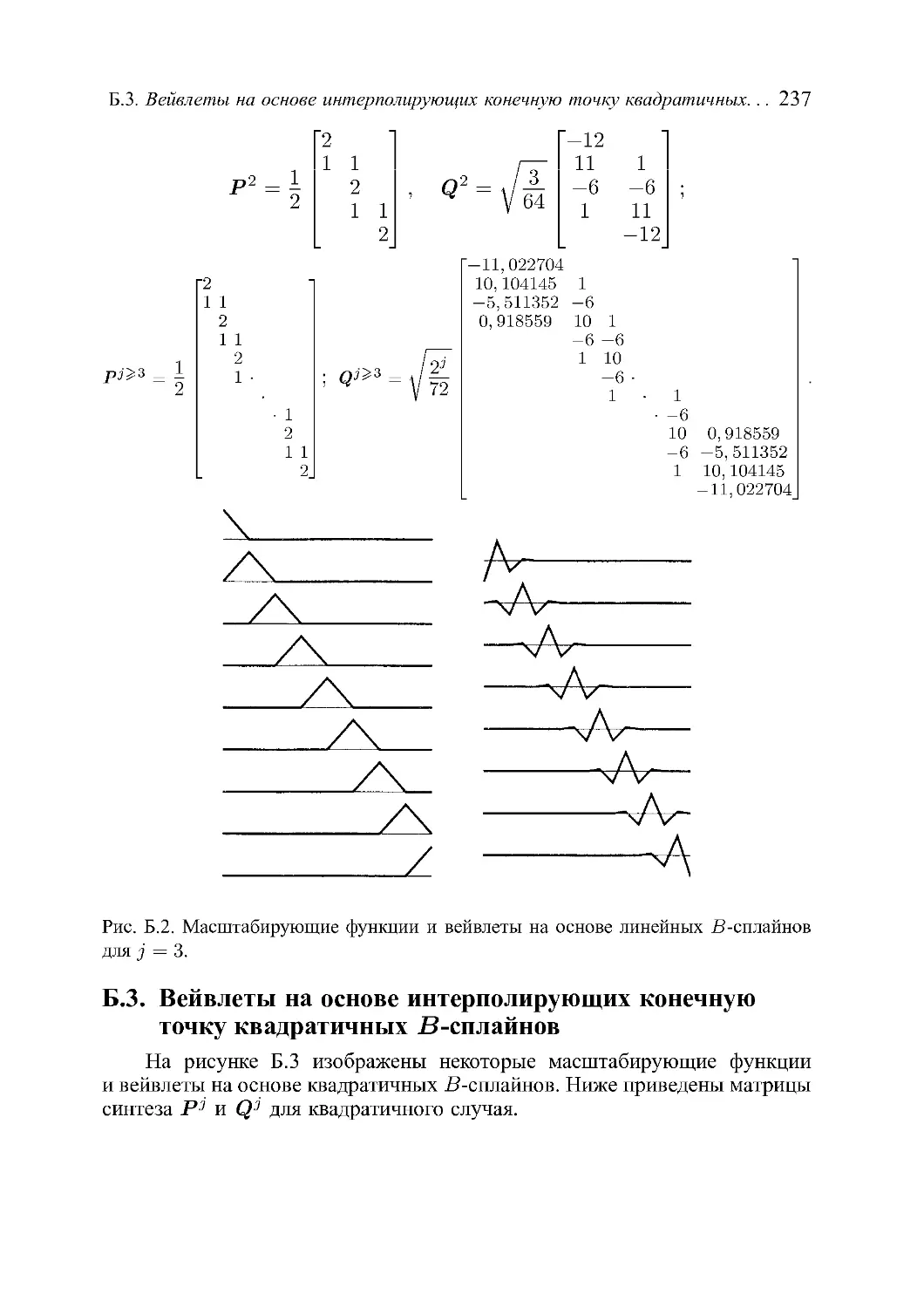
ПРИЛОЖЕНИЕ Б. Матрицы вейвлетов на основе В сплайнов
Б.1. Вейвлеты Хаара . . . . . . . . . . . . . . . . . . . . . .
Б.2. Вейвлеты на основе интерполирующих конечную точку ли
нейных В сплайнов . . . . . . . . . . . . . . . . . . . . . . . .
Б.3. Вейвлеты на основе интерполирующих конечную точку квaд
ратичных В сплайнов . . . . . . . . . . . . . . . . . . . . . . .
Б.4. Вейвлеты на основе интерполирующих конечную точку кy
бических В сплайнов . . . . . . . . . . . . . . . . . . . . . . .
ПРИЛОЖЕНИЕ В. МаtlаЬ код для В сплайновых вейвлетов
Литература . .
Предметный указатель
9
229
229
230
231
232
233
235
235
236
237
239
241
247
258
Предисловие к русскому изданию
Вейвлеты как математическое средство для иерархическоrо представ
ления функций, позволяют описать произвольную функцию в терминах [py
боrо усредненноrо приближения и деталей различноrо масштаба.
Несмотря на то, что корнями теория вейвлетов уходит в области Te
ории приближения и обработки сиrналов, вейвлеты стремительно CTa
новятся базовой техникой компьютерной rрафики. Такими rрафически
ми приложениями являются редактирование и сжатие изображений, по
иск изображения по запросу, автоматический контроль уровня детально
сти при редактировании и создании кривых и поверхностей, BOCCTaHOB
ление поверхностей по контурам, быстрые методы решения задач фи
зическоrо моделирования в вопросах анимации и rлобальноrо освеще
ния.
Читатель может начать знакомство с теорией вейвлетов с выпущенных
на русском языке книr таких ярких авторов, как Инrpид Добеши «Десять
лекций по вейвлетам», издательство РХД, Москва Ижевск, 2001, Чарлз Чуи
«Введение в вейвлеты», Мир, Москва, 2001. Однако, хотя выпущенные pa
нее моноrрафии представляют cTporoe и элеrантное изложение основ Teo
рии, в рамках изложенноrо приложение теории к решению задач компью
терной rрафики представляется затруднительным.
В противоположность им в настоящей книrе внимание сосредоточено
на обобщенной теории, в которой есть место тем видам объектов, которые
обычно возникают в компьютерной rрафике, включая изображения, кри
вые, поверхности произвольной тополоrии. Авторы обсуждают возникаю
щие вопросы на примере простоrо случая базиса Хаара. Затем излаrают
основы кратномасштабноrо анализа, развивают понятие сплайновых вей
влетов и описывают их использование для кривых и поверхностей.
Авторы книrи являются весьма авторитетными специалистами в об
ласти компьютерной rрафики. Достаточно отметить, что Дэвид Салезин,
работая в 1983 87 [одах на студии Lucasfilm/Pixar, принимал участие в co
здании анимационноrо фильма Tin Тоу, который в 1989 получил Оскара,
высшую наrраду американской кино академии, как лучший анимационный
фильм. Тони ДеРоуз, ведущий ученый Pixar Animation Studious, является
rлавным создателем персонажа Geri из анимационноrо котроткометражно
[о фильма Geri's game, также наrpажденноrо Оскаром в 1998 [оду.
12
Предисловие к русско.ну изданию
в книrе были исправлены опечатки, допущенные при ориrиналь
ном издании книrи. Ссылку на сайт, на котором помещены замечен
ные опечатки, мне любезно предоставил один из авторов, Эрик Столниц:
http://grail.cs.washington.edu/projects/wave1ets/book/errata.htm1
Новосибирск,
февраль 2002
Евzения Мищенко
Мы посвящаем эту KHUZY
Жанет U Фреду Столнuтц,
Синди ДеРоуз, Кэролuн U Джuн Андерсон,
а также Андреа Лuндженфелтеру U Руди u Джuн Салезuн.
Предисловие Инrрид Добеши
Вейвлеты появились в восьмидесятых [одах двадцатоrо века как аль
тернатива оконным преобразованиям Фурье для анализа сиrналов. Вскоре
стало очевидно, что они представляют собой HaMHoro больше, являясь, по
сути, реинкарнацией идей, которые уже существовали ранее во множестве
друrих областей. Подобная участь постиrает мноrие новые идеи. В случае
с вейвлетами Kpyr различных областей, с которыми они, как выяснилось,
связаны, отличается удивительной широтой и охватывает, помимо Bcero
прочеrо, жесткие оценки в чистой математике, понятие rруппы peHopMa
лизации в физике, субполосную фильтрацию в электротехнике и схемы
последовательноrо деления в области вычислительной техники.
Представляя б6льшее, чем просто синтез идей из мноrих различных об
ластей, вейвлеты добавили новые rрани каждой из них, дав ключ к новому
пониманию и упростив старые подходы. Вне зависимости от первоначаль
ных интересов, мноrие исследователи вейвлетов нашли для себя увлека
тельной работу в тех областях, к которым невольно привело их изучение
вейвлетов.
Придя к вейвлетам из физики и математики, я получила [ромадное
удовольствие от чтения этой книrи о мноrочисленных применениях вей
влетов в компьютерной rpафике области, с которой я менее знакома. Ha
чиная с использования вейвлетов Хаара для редактирования изображений
и формирования запросов изображений или более rладких вейвлетов для по
строения кривых и поверхностей и заканчивая использованием вейвлетов
в физическом моделировании, [де они вновь приближаются к математиче
скому анализу, изложенный в книrе курс приложения вейвлетов неизменно
интересен и познавателен.
Несмотря на то, знакомо вам понятие вейвлетов или нет, я приrлашаю
вас последовать за авторами в запланированное ими путешествие. Вы, так
же, как и я, приобретете ценный опыт.
Инrрид Добеши,
Принстонский университет
Предисловие
Вейвлеты являются математическим инструментом для иерархическо
[о представления функций. Имея своими исконными областями применения
теорию приближения, физику и обработку сиrналов, вейвлеты с недавних
пор стали использоваться и во мноrих задачах компьютерной rpафики. Cpe
ди этих задач редактирование и сжатие изображений, автоматический KOH
троль степени детализации изображения при редактировании, тонирование
кривых и поверхностей, восстановление формы поверхности по контурам
и эффективные методы решения задач TpexMepHoro моделирования, общеrо
освещения и анимации.
Несмотря на то, что роль вейвлетов как основополаrающей технолоrии
в компьютерной rрафике становится все более и более очевидной, большая
часть имеющейся на сеrодняшний день литературы рассчитана в первую
очередь на специалистов по теории приближений и обработке сиrналов
и малодоступна для исследователей, работающих в области компьютерной
rрафики. Кроме Toro, большая часть теории вейвлетов была разработана
для чисто теоретическоrо случая с сиrналами бесконечной длины. К co
жалению, эта классическая теория начинает терять состоятельность, как
только дело доходит до представления разноrо рода конечных наборов дaH
ных (изображений, незамкнутых кривых и оrраниченных поверхностей),
которые, как правило, возникают в компьютерной rрафике.
В этой книrе затраrиваются обе эти проблемы. Во первых, она снабдит
исследователя и специалиста по компьютерной rрафике твердым понима
нием теории и приложений вейвлетов. Предполаrается, что читатель в свое
время ознакомился с простым курсом линейной алrебры и, наверняка, за
был большую ero часть, поэтому в приложении А ero ждет справочник по
линейной алrебре с обзором всей необходимой базовой информации. Мы
намеренно сохранили простоту уровня изложения, делая ставку скорее на
интуицию и ясность, чем на излишний риrоризм.
BO BTOpЫX, рассматриваемый здесь подход существенно отличается от
подходов, используемых в друrой литературе по вейвлетам. Отличие за
ключается в обращении к более обобщенной теории вейвлетов, допуска
ющей, что вейвлеты конструируются в явном виде на оrраниченных об
ластях, широко используемых в приложениях компьютерной rpафики. По
всей видимости, эта более обобщенная теория имеет весьма тесную связь
с процессом рекурсивноrо последовательноrо деления, а потому теория по
16
Предис.70вие
строения кривых и поверхностей при помощи схемы последовательноrо
деления раскрывается в этой книrе в своей связи с вейвлетами.
Эта кииrу ни в коем случае нельзя считать исчерпывающим источ
ником ни В раскрытии теории вейвлетов, ни в освещении их приложений
в компьютерной rрафике. При ее написании мы ставили своей целью aK
центировать внимание скорее на тех аспектах этой теории, которые уже дo
казали свою исключительную полезность в компьютерной rрафике, а также
представить небольшой, но достаточно широкий набор приложений, чтобы
проиллюстрировать, к какому удивительно широкому разнообразию задач
можно применить теорию на практике.
Как появилась эта книrа
Наш интерес к вейвлетам возник в конце 1992 начале 1993 [ода. В то
время вейвлеты (по нашим сведениям) еще не применялись в приложении
к задачам компьютерной rрафики, мы же подозревали о существовании Ta
ких приложений. Поскольку наиболее простым способом изучения новой
области является проведение семинаров по соответствующему предмету,
именно так мы и поступили весной 1993 [ода, заручившись помощью Джо
Уоррена. Через две три недели стало очевидно, что вейвлеты моrли бы
найти широчайшее применение в компьютерной rpафике и rеометрическом
моделировании. По прошествии не более чем четверти от Bcero цикла семи
нарских занятий четыре студента (Пер Кристенсен, Адам Финкельштейн,
Майкл Лаунсбери и Дэвид Мейерс) решили перейти к самостоятельному
исследованию вопроса и начали писать диссертации на докторскую CTe
пень по этой теме, а еще одна студентка (Дебби Берман) диссертацию на
степень маrистра. Немалая часть этой работы впоследствии была опубли
кована в трудах ежеrодных конференций SIGGRAPH и Graphics Interface,
а также в последних выпусках IEEE Coтputer Graphics aпd Applicatioпs
и АСМ Traпsactioпs оп Graphics.
Эта кииrа также явилась прямым следствием Toro caMoro семинара.
Хотя в нее вошло немало материала из нашей предыдущей опубликованной
работы (в том числе и учебное руководство по вейвлетам и rрафике [120]),
мы включили сюда значительный объем новой информации, а также пред
приняли попытку выработать общую основу и соrласованное представление
всех полученных результатов.
Орrанизация книrи
Книrа поделена на четыре части в соответствии с областями примене
ния вейвлетов: изображения, кривые, поверхности и физическое моделиро
Предис.70вие
17
вание. В каждой части вперемешку представлены rлавы, рассматривающие
как теорию, так и конкретные приложения. Мы посчитали, что при такой op
rанизации книrи повествование будет более интересным, а теория получит
большую стимуляцию, нежели в случае, Korдa теоретические и практиче
ские rлавы идут отдельно друr от друrа.
Мы не стали бы рекомендовать читателю читать rлавы, касающиеся
приложений, и при этом обходить стороной rлавы, посвященные теории,
однако обратный вариант вполне возможен. Так что если читатель инте
ре суется исключительно теорией вейвлетов, он может сосредоточить свое
внимание на второй, третьей, шестой, седьмой и десятой rлавах.
Блаrодарности
Мы блаrодарны Шону Андерсону, Джейсону Бартелу, Дебби Берман,
Перу Кристенсену, Майклу Коэну, Тому Дюшампу, Маттиасу Экку, Aдa
му Финкельштейну, Стивену [ортлеру, Стивену [ортлеру, Хью Хоппу, Чаку
Джейкобсу, Дэни Лищински, Майклу Лонебери, Дэвиду Мейеру, Вернеру
Штутцль и Джо Уоррену за материал, предоставленный ими для кииrи. Мы
также блаrодарны друrим членам исследовательской rруппы по компью
терной rрафике, работающим в Университете Вашинrтона на факультете
вычислительной техники, за их вклад, который также содействовал выходу
настоящей книrи.
Блаrодарим также Ронен Барзель, Майкла Шантциса и Энди фон Дама
за критический обзор вводных rлав, Петера Ширли, Франсуа Силь он и Ри
чарда Щелиски за про смотр первых вариантов моноrpафии и множество
ценных замечаний.
Обозначения
На протяжении всей кииrи мы постарались использовать общеприня
тые обозначения, хотя некоторых несоответствий нам, возможно, избежать
все же не удалось. Мы используем заrлавный жирный курсив для обозна
чения матриц, прописной жирный курсив для векторов, представляющих
собой одностолбцовые матрицы скаляров, и нормальный курсив для друrих
математических символов. Список наиболее часто встречающихея симво
лов приведен ниже.
Символ
I
а
ф
ф
фj
фj
Aj
Bj
c j
d j
j
pj
Qj
s
и
и
V j
W j
v(j)
w(j)
Ulg)
[(flg)]
Значение
параметрическая кривая
параметрическая поверхность
масштабирующая функция
вейвлет
BeKTop CTpOKa масштабирующих функций
BeKTop CTpOKa вейвлетов
матрица анализа масштабирующей функции
матрица анализа вейвлетов
коэффициенты масштабирующей функции
вейвлет коэффициенты
иерархический уровень
матрица синтеза и уточнения масштабирующей функции
матрица синтеза и уточнения вейвлетов
матрица подъема
функция общеrо базиса
BeKTop CTpOKa базисных функций
пространство масштабирующей функции
пространство вейвлетов
размерность vj
размерность wj
скалярное произведение f и 9
матрица с элементом (k, 1), равным Uklgz)
['ЛАВА 1
Введение
1. Кратномасштабные иетоды 2. Исторuческая перспектива
3. Обзор КНИ2и
Любая естественная наука и инженерная дисциплина это, в сущно
сти, необходимость анализировать, наrлядно представлять и манипулиро
вать большим количеством данных. Конкретные данные в рассматриваемых
приложениях MorYT принимать различные формы, как видно из рис. 1.1.
Они MorYT быть функциями с одним параметром, как, например, данные
BpeMeHHoro ряда, используемые в обработке сиrналов (а) или сложные KOH
туры поперечноrо сечения, встречающиеся в медицине (Ь). Данные MOryT
быть функциями с двумя и более параметрами, такими как двумерные изоб
ражения (с), модели поверхностей (d) или более мноrомерные решения «об
щеrо освещения» для фотореалистичноrо освещения, например, решение,
показанное на цветной иллюстрации 15.
00 100 200 300 400
r
0.2
(а)
(6)
(в)
(r)
Рис. 1.1. Некоторые из применений вейвлетов: (а) типичные данные временното
ряда; (б) контур поперечноrо сечения коры rоловноrо мозrа; (в) типичное изобра
жение; (r) типичная поверхность.
Во всех этих случаях простейший способ представления информации
это способ с использованием последовательности точек. Например, BpeMeH
ной ряд леrче Bcero представить как последовательность (ti, Yi). Каждая
20
Т7ава 1
такая точка дает полную информацию о поведении ряда в ti, но не дает
абсолютно никакой информации о поведении ряда rде либо еще. Между
тем, во мноrих приложениях бывает необходим более масштабный анализ
ряда. Скажем, область быстроrо изменения ряда можно обнаружить только
при одновременном изучении мноrих точек.
Классическим инструментом применительно к этим проблемным ситу
ациям служит анализ Фурье, который можно использовать для Toro, чтобы
обратить данные наблюдений в точке в форму, более удобную для анализа
частот. Однако при использовании методов Фурье возникает одно затрудне
ние: каждый коэффициент Фурье содержит полную информацию о поведе
нии ряда лишь на одной частоте и никакой информации о ero поведении на
друrих частотах. Кроме Toro, методы Фурье трудно адаптировать ко MHO
rим ситуациям, имеющим практическое значение. Например, большинство
встречающихея на практике временных рядов являются конечными и апе
риодическими, в то время как дискретное преобразование Фурье можно
применять только для периодических функций.
1.1. Кратномасштабные методы
Недостатки методов Фурье заставили исследователей обратиться ко
множеству друrих дисциплин (включая теорию приближения, физику, обра
ботку сиrналов и изображения, а также компьютерную rрафику) с тем, что
бы разработать различные uерархuческuе представленuя функций. OCHOB
ная идея, которая стоит за всеми иерархическими методами (которые также
называют кратномасштабными методами), заключается в том, чтобы пред
ставлять функции набором коэффициентов, каждый из которых дает некую
оrраниченную информацию и о положении, и о частоте функции.
Несмотря на существование широкоrо разнообразия методов иерархи
ческоrо представления функций, разработанная в недавнем прошлом теория
вейвлетов содержит арсенал чрезвычайно полезных средств, позволяющих
осуществить иерархическое разложение функций эффективным и OДHOBpe
менно теоретически обоснованным способом. Если rоворить в общем, то
вейвлет представление функций состоит из общеrо rрубоrо приближения
и уточняющих коэффициентов, позволяющих работать с функцией при раз
личных масштабах.
[лавная цель этой книrи продемонстрировать то, каким образом вей
влет представления начинают оказывать rлубокое влияние на все разделы
компьютерной rрафики, в значительной мере блаrодаря множеству полез
ных, связанных с ними, свойств. Помимо иерархической природы вейвлетов
в число этих свойств входят
. Лuнейно вРf)wенная сложность. Переход к вейвлет представлению
1.2. Историческая перспектива
21
и переход от вейвлет представления можно осуществить линейно по
времени, если принять в учет очень быстрые алrоритмы.
. Разреженность. Почти все коэффициенты вейвлет представлений для
функций, обычно встречающихея на практике, либо равны нулю, ли
бо пренебрежимо малы. Это свойство дает возможность как сжимать
данные, так и ускорять сходимость итерационных методов решения.
. Адаптируе "toсть. В отличие от методов Фурье, вейвлетам присуща
замечательная rибкость в том смысле, что их можно применить для
представления множества разнообразных функций, в том числе раз
рывных функций, функций, определенных на оrpаниченных областях,
и функций, определенных на областях произвольноrо тополоrическоrо
типа. Следовательно, вейвлеты в равной степени применимы для задач,
связанных с изображениями, с замкнутыми и незамкнутыми кривыми
и с поверхностями практически любоrо вида.
Несмотря на то, что в этой книrе подробно рассматривается целый ряд
приложений вейвлетов, мы ни на минуту не задумывали сделать ее всеобъ
емлющим справочником. Скорее описываемые здесь приложения являются,
в первую очередь, иллюстрацией разнообразия возможностей применения
вейвлетов. И в самом деле, эти приложения распространяются на такие
различные области, как интерактивные методы (четвертая, иятая, восьмая,
девятая, одиннадцатая и двенадцатая rлавы), моделирование и тонирование
с учетом степени детализации (восьмая и одиннадцатая rлавы), комбинатор
ная оптимизация (двенадцатая rлава) и решение интеrpальных уравнений
(тринадцатая rлава).
1.2. Историческая перспектива
С недавних пор вейвлеты стали пользоваться поразительной популяр
ностью. Между тем, истоки их следует искать еще в прошлом веке, в работе
Карла Вейерштрасса [128], который в 1873 [оду описал семейство функций,
построенных путем наложения масштабированных копий данной базовой
функции. Функции, которые он определил, являются фрактальными, при
чем всюду непрерывными, но ниrде не дифференцируемыми. Друrой paH
ней вехой стало построение Альфредом Хааром первой ортонормированной
системы функций с компактным носителем, которую сейчас называют ба
зисом Хаара [53]. Базис Хаара до сих пор служит основой современной
теории вейвлетов, и мы подробно рассмотрим ero в следующей rлаве. Еще
один шаr вперед был сделан в 1946 [оду, Korдa Дэннис [абор [44] дал опи
сание неортоrональному базису вейвлетов с неоrpаниченным носителем,
основанное на сдвинутых относительно друr друrа rауссианах.
22
Т7ава 1
Термин вейвлет из начально относится к сейсмолоrии и был придуман
Рикером в 1940 [оду для описания процесса возмущения, вызываемоrо силь
ным сейсмическим импульсом или зарядом взрывчатоrо вещества [102].
В 1982 [оду Морле и ero сотрудники показали, как можно моделировать
эти сейсмические импульсы, используя математические функции, которые
определил [абор. Позже [россман и Морле показали, как можно анализиро
вать произвольные сиrналы на основе масштабов и сдвиrов единственной
)wатерuнской вейвлет функцuu. Усилиями Ива Мейера [80, 82] и Стефана
Малла [77] это понятие вылилось в теорию, которая теперь носит название
кратншwасштабноzо аналuза. В 1989 Малла [78] показал, каким образом
кратномасштабный анализ можно рассматривать как еще одну форму пиpa
мuдальных алzорum.мов, используемых в обработке изображений [6], и Kвaд
ратурных зеркальных фuльтров, используемых в анализе сиrналов [23,26].
Классическая форма кратномасштабноrо анализа в том виде, в каком
ее предложили Мейер и Малла, разбивает сиrналы по базису функций,
называемых вейвлетами, причем каждый вейвлет это ничто иное, как
масштабированная и сдвинутая копия единственной функции, называемой
материнским вейвлетом, как видно из рис. 1.2 (а) и (б). Мы будем называть
этот традиционный подход методшw. инвариантным относuтельно сдвuzа,
поскольку все вейвлеты, лежащие на различных участках бесконечной Be
щественной оси, выrлядят одинаково. К сожалению, будучи замечательным
с теоретической точки зрения, метод, инвариантный относительно сдвиrа,
проблематичен для большинства приложений компьютерной rpафики, по
скольку мноrие представляющие интерес функции, такие как изображения
или незамкнутые кривые, определены только на некоторых оzранuченных
участках вещественной оси.
Кратномасштабный анализ представлен в этой книrе в более обоб
щенном виде, несколько отличном по сравнению с друrими публикациями.
В этой обобщенной версии в более явном виде представлены различные
наборы конечных данных, встречающиеся в практических приложениях
компьютерной rрафики. В отличие от классическоrо кратномасштабноrо
анализа, представленный здесь обобщенный кратномасштабный анализ вa
риантен относuтельно сдвuzа: он вмещает оrраниченные наборы данных,
причем с этой целью рядом с rраницами вводятся друrие специально адап
тированные вейвлеты, как показано на рис. 1.2(в).
Как выяснилось, описанный в этой книrе кратномасштабный анализ,
вариантный относительно сдвиrа, очень тесно связан с методом последова
тельноrо деления. В самом деле, в шестой и седьмой rлавах будет показа
но, что функции, к которым можно применить кратномасштабный анализ,
вариантный относительно сдвиrа, это в точностu те же функции, KO
торые можно получить с помощью процесса последовательноrо деления.
Таким образом, при разработке большей части теории, выходящей за paM
1.3. Краткий обзор кни2и
23
fI
vv
fI
vv
fI
vv
, fI ,
vv
, fI ,
vv
.p
, fI
vv
, fI
vv
Ir
/\1\1'.
VV
{'fI
vv
fI
vv
fI
vv
fI
vv
fI л
vv
.А)
(а)
(6)
(е)
Рис. 1.2. Кратномасшта6ный анализ, инвариантный относительно сдвиrа, и KpaT
номасшта6ный анализ, вариантный относительно сдвиrа: (а) материнский вейвлет;
(6) вейвлеты, инвариантные относительно сдвиrа; (в) вейвлеты, вариантные OТHO
сительно сдвиrа.
ки вейвлетов, в этой книrе используется очень особый подход. В отличие
от друrих учебников, заостряющих внимание на методах Фурье, в нашей
работе rлавная роль отведена изучению, анализу и конструированию схем
последовательноrо деления.
1.3. Краткий обзор книrи
Первую часть мы начнем с Toro, что рассмотрим, как можно иерар
хически представить кусочно постоянные функции и изображения с ис
пользованием базиса Хаара (вторая rлава). Этот анализ подведет нас к Ta
ким приложениям, как сжатие изображения (третья rлава), редактирование
изображения с переменным разрешением (четвертая rлава) и формирование
запроса изображения (иятая rлава).
Во второй и третьей частях мы приступим к вопросу О кривых и по
верхностях.
Вторая часть начинается с обсуждения кривых последоватеЛЬН020 дe
ленuя кривых, которые образуются путем процесса рекурсивноrо после
довательноrо деления (шестая rлава). Затем мы опишем формализм KpaT
номасштабноrо анализа, вариантноrо относительно сдвиrа (седьмая rла
ва), тесно связанный с последовательным делением. Далее рассмотренная в
этой rлаве теория будет приложена к задачам редактирования кривых (BOCЬ
24
Т7ава 1
мая rлава) и поклеточноrо представления поверхностей по контуру (девятая
rлава).
В третьей части исследуется то, как можно обобщить формализм на
поверхности произвольноrо тополоrическоrо типа (десятая rлава), а также
исследуется ряд приложений, в том числе сжатие поверхностей, последова
тельное пропускание и редактирование (одиннадцатая rлава).
Наконец, четвертая часть обращается к алrоритмам на основе вейвле
тов для решения двух задач физическоrо моделирования: вариационноrо
моделирования (двенадцатая rлава) и общеrо освещения (тринадцатая rла
ва).
Мы также помещаем здесь приложения, объединив их в пятую часть:
Приложение А по линейной алrебре; Приложение Б со всеми матрица
ми, необходимыми для введения вейвлетов на основе интерполяционных
В сплайнов, и Приложение В, содержащее МаtlаЬ код для образования Ta
ких матриц.
Часть 1
ИЗОБРАЖЕНИЯ
Т'ЛАВА 2
Хаар: простейший вейвлет базис
1. Вейвлет преобразованuе Хаара для одномерН020 случая
2. Функцuu одномерН020 базиса Хаара 3. Орт020нальность
и нормuрование 4. Вейвлет с,жатuе
Базис Хаара это простейший базис вейвлетов. Эту rлаву мы начнем
с Toro, что рассмотрим, как можно разложить одномерную функцию с помо
щью вейвлетов Хаара. Затем мы подробным образом рассмотрим функции
базиса Хаара и увидим, как можно применить вейвлет разложение Хаара
для сжатия. Позже, в трех последующих rлавах, мы исследуем некоторые
приложения базиса Хаара: сжатие изображения, редактирование изображе
ния и формирование запроса изображения.
2.1. Вейвлет преобразование Хаара для ОДНОМерноrо
случая
Чтобы получить некоторое понимание Toro, как работают вейвлеты, мы
начнем с простоrо примера. Предположим, мы имеем одномерное «изоб
ражение» с разрешением в четыре пикселя со следующими значениями
пикселей:
[9735].
Изображение можно разложить по базису Хаара, простейшему базису
вейвлетов, путем следующеrо вычисления вейвлет преобразования. Начнем
с попарноrо усреднения пикселей, которое даст нам в результате новое
изображение с более низким разрешением и следующими значениями этих
пикселей:
[84].
Ясно, что усреднение и децимация повлекли потерю некоторой инфор
мации. Для Toro, чтобы восстановить величины исходных четырех пиксе
лей из двух усредненных пикселей, нам необходимо запастись несколькими
уточняющими коэффициентами, хранящими эту пропавшую информацию.
28
Т7ава 2
в нашем примере первому коэффициенту мы присвоим значение 1, посколь
ку вычисленное нами среднее на единицу меньше, чем 9, и на единицу
больше, чем 7. Одна эта величина позволяет нам восстановить два пер
вых пикселя для исходноrо четырехпиксельноrо изображения. Аналоrично,
второй коэффициент равен 1, так как 4 + ( 1) "'" 3 и 4 ( 1) "'" 5.
Итак, мы произвели разложение изображения, получив версию с более
низким разрешением (в два пикселя) и уточняющие коэффициенты:
Разрешение
Средние значения
Уточняющие коэффициенты
4
2
[9735]
[84]
[1 1]
Рекурсивное повторение этой процедуры для средних значений дает нам
полное разложение:
Разрешение
Средние значения
Уточняющие коэффициенты
4
2
1
[9735]
[84]
[6]
[1 1]
[2]
в конце концов, мы можем определить вейвлет преобразование исход
Horo четырехпиксельноrо изображения, также называемое вейвлет разло
.жением, как единственный коэффициент, представляющий общее среднее
значение исходноrо изображения, дополненный уточняющими коэффици
ентами, располаrающимися в порядке, соответствующем увеличению раз
решения. Таким образом, для одномерноrо базиса Хаара вейвлет преобра
зование нашеrо исходноrо четырехпиксельноrо изображения будет иметь
следующий вид:
[621 1].
Метод, по которому мы вычислили вейвлет преобразование, восполь
зовавшись рекурсивным усреднением коэффициентов и нахождением раз
ностей, называется методом блока фильтров. Этот способ мы обобщим
и на друrие типы вейвлетов в седьмой rлаве. Заметьте, что при примене
нии этоrо способа не происходит ни потери, ни прибавления какой бы то
ни было доли информации: исходное изображение имеет четыре коэффи
циента, столько же их и у выполненноrо преобразования. Также обратите
внимание на тот факт, что, имея преобразование, мы можем воспроизве
сти изображение с любым разрешением, последовательно прибавляя либо
вычитая уточняющие коэффициенты.
2.1. Вейвлет преобразование Хаара для одно,неРНО20 С.7У'JaЯ 29
Сохранение именно вейвлет преобразования, а не caMoro изображения,
имеет ряд преимуществ. Одно из них состоит в том, что часто большое
количество уточняющих коэффициентов оказывается очень малым по вели
чине, как это видно из уже более серьезноrо примера на рис. 2.1. Усечение,
или удаление из представления, этих малых коэффициентов приводит лишь
к незначительным поrрешностям воспроизведенноrо изображения, являя
форму сжатия изображения «с потерями». Это особое применение вей
влетов мы также обсудим в разделе 2.4, как только представим функции
одномерноrо базиса Хаара.
Разрешение
Аппроксимация
УточняюшиС' коэффициС'нты
"
I
,
2 I
I
Рис. 2.1. Последовательность приближений к функции, сопровождаемых убывани
ем разрешения (слева), и уточняющие коэффициенты, необходимые для получения
более точноrо приближения (справа). Обратите внимание на то, что на тех участках,
rдe точная функция близка к тому, чтобы стать плоской, кусочно постоянная аппрок
симация оптимальна и соответствующие уточняющие коэффициенты относительно
малы.
30
Т7ава 2
2.2. Функции одномерноrо базиса Хаара
в предыдущем разделе мы рассматривали одномерные изображения
как последовательности коэффициентов. Помимо этоrо, мы можем rоворить
об этих изображениях как о кусочно постоянных функциях на полуотрез
ке [О, 1). (Полуотрезок [а, Ь) содержит все значения х, такие, что а х < Ь.)
Рассуждая об изображениях уже в этом новом ракурсе, мы будем опериро
вать понятием «векторное пространство», используемом в линейной алrе
бре. (Краткий справочник по линейной алrебре можно найти в приложе
нии А.)
Векторное пространство это, в основе своей, совокупность «пред
метов» (векторов, в данном контексте), для которой определены сложение
и скалярное умножение. Следовательно, вы можете сложить два вектора,
умножить вектор на какую нибудь постоянную и т. д. (Полный список aK
сиом приведен в Приложении А.1.)
Если до этоrо момента мы рассуждали об изображениях как о после
довательностях коэффициентов, то теперь давайте будем рассуждать о них
как о функциях. К примеру, мы можем считать изображение с разреше
нием в один пиксель функцией, постоянной на всем интервале [0,1). По
скольку сложение и умножение на скаляр для функций вполне определены,
каждую постоянную функцию на интервале [0,1) можно считать вектором,
и для обозначения BeKTopHoro пространства всех таких функций будем ис
пользовать значок v o . Аналоrично, двухпиксельное изображение является
кусочно постоянной функцией на интервалах [0,1/2) [1/2,1). Пространство,
содержащее все эти функции, обозначим v 1 . Продолжая в том же духе,
получим, что пространство v j будет содержать все кусочно постоянные
функции, определенные на интервале [0,1), постоянные на каждом из paB
ных подынтервалов, число которых равно 2 j .
Теперь будем рассматривать каждое одномерное изображение с числом
пикселей 2 j как элемент, или вектор, в V j . Поскольку эти векторы пред
ставляют собой все функции, определенные на единичном интервале, каж
дый вектор в vj является и элементом V j + 1 . Например, мы всеrда можем
описать функцию, кусочно постоянную на двух интервалах, как функцию,
кусочно постоянную на четырех интервалах, причем каждый интервал ис
ходной функции будет соответствовать паре интервалов второй функции.
Таким образом, пространства V j являются вложенными, то есть:
V O с v 1 С V 2 С . ., .
Это вложенное множество пространств V j является необходимым элемен
том в математической теории кратномасштабноrо анализа. Эту тему мы
рассмотрим более основательно в седьмой rлаве.
2.2. Функции одномерНО20 базиса Хаара
31
Теперь нам требуется определить базис для каждоrо векторноrо про
странства Vj. (Формальное определение базиса для векторноrо простран
ства имеется в приложении А.3.) [рубо rоворя, базис состоит из мини
мальноrо множества таких векторов, линейные комбинации которых дают
все друrие векторы векторноrо пространства. Базисные функции для про
странств vj называются Л1асштабuрующшwu функцuшwu и обычно обозна
чаются символом ф. Простой базис для V j задается множеством масшта
бированных и сдвинутых характеристических функций:
ф{(х): ф(2jх i), [де i 0,...,2j 1,
ф(х) : {
причем
при х < 1
в противном случае.
На рисунке 2.2 в качестве примера показаны четыре характеристиче
ские функции, образующие базис для v 2 .
l 1J Ф5
о I
о 1
2
о ! I
:UL
о i I
lt Ф П
o
о i I
Рис. 2.2. Базис из характеристических ФУНКI\ий J(ЛЯ v 2 .
Носuтелем функции называется такой участок в области значений па
раметра, на котором функция отлична от нуля. Например, [О, 1/4) это
носитель Ф6 (х ). Функции с носителями на оrраниченных интервалах назы
ваются функциями с компактным носителе.м. Обратим внимание, что все
характеристические функции это функции с компактным носителем.
Следующий шаr в построении кратномасштабноrо анализа заключа
ется в выборе скалярноrо произведения, определенноrо в векторных про
странствах vj. (Формальное определение скалярноrо произведения CMOT
рите в разделе А.3 приложения А.) ДЛЯ рассматриваемоrо нами примера
«стандартное» скалярное произведение вполне определено:
о
(1lg) J f(x)g(x) dx.
1
[оворят, что два вектора u и v орт020нальны при данном скалярном
произведении, если (ulv) О. Теперь мы можем определить новое BeKTOp
ное пространство W j как ортодополненuе для V j в пространстве vj+l.
Друrими словами, wj это пространство всех функций в vj+l, opToro
нальных всем функциям в vj при определенном скалярном произведении.
32
Т7ава 2
Совокупность всех линейно независимых функций ФI (х), на которую
натянуто Wj, называется множеством вейвлетов. Эти базисные функции
имеют два очень важных свойства:
1. Базисные функции ФI из wj вместе с базисными функциями ФI из v j
образуют базис V H1 .
2. Любая базисная функция ф{ из W j ортоrональна любой базисной
функции ФI из vj при данном скалярном произведении.
Замечание. В дальнейшем, в седьмой rлаве, мы посмотрим, как при
веденные выше определения дополнительных пространств wj и вей
влетов ФI можно сделать более строrими либо менее строrими. Так,
некоторые авторы называют функции, определенные нами выше как
вейвлеты, превейвлеmамu, оставляя термин вейвлеты для функций ФI,
которые также ортоrональны друr друry.
Отступив от формальностей, мы можем считать вейвлеты в W j инстру
ментом для представления той части функций из v j + 1 , которую нельзя
представить в V j . Получается, что уточняющие коэффициенты, о которых
шла речь в разделе 2.1, на самом деле являются коэффициентами функций
по базису вейвлетов.
Л
l
: ;
lrтп
Рис. 2.3. Вейвлеты Хаара ДЛЯ W 1 .
Вейвлеты, соответствующие базису, состоящему из характеристиче
ских функций, носят название вейвлетов Хаара и определяются как
ф{(х) : ф(2 j х i), [де i О, ..., 2 j 1,
причем
ф(х) . { :
при О х < 1/2
при 1/2 х < 1
в противном случае.
На рисунке 2.3 показаны два вейвлета Хаара, на которые натянуто w 1 .
Прежде чем продолжить, еще раз обратимся к нашему примеру из
раздела 2.1, однако теперь мы будем использовать уже эти более сложные
2.2. Функции одномерНО20 базиса Хаара
33
понятия. Начнем с Toro, что представим наше исходное изображение :?(х)
как линейную комбинацию из характеристических функций в V 2 :
:?(х) С6Ф6(х) + сiФi(х) + сiФi(х) + с ф (х).
Более rpафически,
:?(х) 9х Il +
+7х Il +
+3х Il +
+5х Il
Заметим, что коэффициенты С6, ..., c являются ничем иным, как че
тырьмя значениями исходных пикселей [9 7 3 5].
Выражение для :? (х) можно переписать в терминах базисных функций
в v 1 И W 1 , применив попарное усреднение и взятие разностей:
:?(х) ф6(х) + с ф (х) + d6Ф6(Х) + d Фi(х);
8х
+
+4х +
+lх +
+ lх Ъ
Четыре этих коэффициента тоже должны быть вам знакомы.
Наконец, мы перепишем :? (х) как сумму базисных функций в vo, WO
иw 1 :
:?(х) сgфg(х) + dgфg(х) + d6Ф6(Х) + d Фi(х);
6х +
+2х +
+lх +
+ lх Ъ
34
Т7ава 2
и вновь эти четыре коэффициента представляют «хааровское» вей
влет преобразование исходноrо изображения. Четыре приведенных выше
функции составляют базис Хаара для v 2 . Вместо обычных четырех xapaK
теристических функций мы можем использовать фg, фg , Фв и Фi, чтобы
получить общее среднее значение, т. е. основную деталь, и две разновид
ности уточняющих деталей, реализуемые для функции из v 2 . Базис Хаара
для V j с j == 2 содержит эти четыре функции, а также еще более узкие
версии вейвлета ф( х).
2.3. Ортоrональность и нормирование
Базису Хаара присуще одно важное свойство, которое не Bcerдa быва
ет у друrих вейвлет базисов ортоrональность. Ортоrональным называют
такой базис, в котором все базисные функции в данном случае функ
ции фg, фg , Фв, . . . , Фi являются взаимно ортоrональными. Отметим,
что ортоrональность сильнее следующеrо из определения вейвлетов требо
вания Toro, что Фi должна быть ортоrональна лишь всем масштабирующим
функциям на одном и том же иерархическом уровне j.
Еще одно свойство, характерное для некоторых вейвлет базисов HOp
мирование. Базисная функция называется нормированной, если (ulu) == 1.
Мы можем нормировать базис Хаара путем замены данных нами ранее
определений на следующие:
Фi(х) == Бф(2 j х i)
Фi(х) == БФ(2 j х i),
[де постоянный множитель Б выбирается так, чтобы выполнялось (ulu) ==
== 1 для стандартноrо скалярноrо произведения. С такими модифициро
ванными определениями новые нормированные коэффициенты получаются
посредством деления каждоrо cTaporo коэффициента с надстрочным индек
сом j на Б. И, таким образом, ненормированные коэффициенты [6 2 1 1]
в примере из предыдущеrо раздела становятся нормированными коэффи
циентами:
[ 6 2 ]
VX2 J2 .
В качестве альтернативы вычислению ненормированных коэффициен
тов и последующему их нормированию мы можем включить нормирование
в алrоритм разложения. Две следующие псевдокодовые процедуры выпол
няют это нормированное разложение, преобразуя набор на входе:
2.3. ОртО20на.7ьность и нормирование
35
procedure Decoтpositioп( с: array [1. . .2 j ] оС reals)
с с/Б (НОРJvzализуем исходные коэффuцuенты)
9 c/2 j
while 9 ;;;: 2 do
DecoтpositioпStep( с[l . . . g])
9 g/2
end while
end procedure;
procedure Decoтpositioп (с: array [1 . . .2 j ] оС reals)
for i 1 to 2 j /2 do
c'[i] (c[2i 1] + c[2i])/V2
c'[2 j /2 + i] (c[2i 1] + c[2i])/V2
end for
c с'
end procedure.
Конечно, нам еще нужно будет суметь восстановить исходные данные,
после Toro как мы получим вейвлет разложение. Именно это и делают сле
дующие две псевдокодовые процедуры:
procedure Recoпstructioп( с: array 1 . . . 2 j оС reals)
g 2
while 9 2 j do
RecoпstructioпStep( с[l . . . g])
9 2g
end while
с сБ (аннулируем нормированuе)
end procedure;
procedure Rесопstrисtiоп (с: array [1 . . .2 j ] оС reals)
for i 1 to 2 j /2 do
c'[2i 1] (c[i] + c[2 j /2 + i])/V2
c'[2i] (c[i] c[2 j /2 + i]/V2
end for
c с'
end procedure.
Эти процедуры позволяют нам работать с ортонормированным бази
сом, т. е. базисом, являющимся одновременно ортоrональным и нормиро
ванным. Как мы увидим в следующем разделе, применение ортонормиро
BaHHoro базиса оказывается удобным при сжатии функции или изображе
ния.
36
Т7ава 2
2.4. Вейвлет сжатие
Цель сжатия выразить исходный набор данных через меньший набор
данных с потерей информации либо без потери. Предположим, например,
что мы имеем функцию f(x), выраженную через взвешенную сумму базис
ных функций щ(х),..., ит(х):
т
Лх) L CiUi(X).
i l
Набор данных в этом случае состоит из коэффициентов Сl, ..., С т .
Мы хотим найти какую нибудь функцию, аппроксимирующую f(x), с MeHЬ
шим числом коэффициентов, для чеrо мы, пожалуй, воспользуемся друrим
базисом. Т. е. при данной, устанавливаемой пользователем, допустимой по
rpешности Е (в случае сжатия без потерь Е О) нам требуется функция
m
f(x) L CiUi(X)
i l
такая, что m < m и IIf(x) j(x)11 Е в некоторой норме (подробнее
о нормах смотрите раздел А.4 приложения А). Вообще, можно было бы
попытаться построить множество базисных функций иl, ..., и m , которые
обеспечили бы хорошее приближение с небольшим количеством коэффи
циентов. Но мы вместо этоrо сосредоточимся на более простой задаче Haxo
ждения хорошеrо приближения в рассматриваемом базисе. Следует учесть,
что и здесь, и в любом дрyrом месте этой книrи, rоворя о сжатии, мы прежде
Bcero делаем упор на задачу уменьшения числа коэффициентов, необходи
мых для представления функции, а не на задачу кодирования и сохранения
необходимой информации наименьшим возможным числом битов, хоть она
и не менее серьезна.
Одна из постановок задачи сжатия может заключаться в таком упоря
дочении коэффициентов Сl, ..., С т , чтобы для каждоrо m < т первые m
элементов последовательности давали наилучшее приближение j (х) к f (х)
в L2 HopMe. Здесь мы показываем, что решение этой задачи является пря
мым, если базис ортонормированный, что верно для случая нормированноrо
базиса Хаара.
Пусть 'iТ(i) это перестановка 1, ..., т, а j(x) функция, использую
щая коэффициенты, соответствующие первым m членам перестановки 'iТ(i):
m
j(x) L C 7r (i)U 7r (i)'
i l
2.4, Вейв.7ет сжатие
37
16 коэффициентов из 16
14 коэффициентов из 16
.
12 коэффициентов из 16 10 коэффициентов из 16
ш
8 коэффициентов из 16 6 коэффициентов из 16
V1 . I
" '. . '.,. ' ,. ,,' .... ,:' . ..,',.. J .....
4 коэффициента из 16 2 коэффициента из 16
Рис. 2.4. rрубое приближение функции, полученное с помощью L 2 сжатия: уточня
ющие коэффициенты удаляются в порядке возрастания их значений.
Квадрат L2 поrрешности в этом приближении определяется как
Ilf(x) f(x)ll == (f(х) f(x)lf(x) f(x)) ==
== ( tl CK(i)UK(i) I j tl с-п-(ли-п-(л) ==
m m
L L CK(i)CK(j) (UK(i) IUK(j)) ==
i m+l j m+l
m
== L (CK(i))2.
i m+l
38
Т7ава 2
Последний шаr обуславливается допущением, что базис является op
то нормированным, значит, \Uilщ/ == bij. Полученный выше результат сви
детельствует о том, что квадрат общей L2 ошибки равен сумме квадратов
всех тех коэффициентов, которыми мы решили пренебречь. Мы приходим
к выводу, что для Toro, чтобы минимизировать эту поrрешность для лю
боrо данноrо т, лучше Bcero выбрать такую перестановку 'iТ(i), которая
располаrает коэффициенты в порядке уменьшения их величины: т. е. 'iТ( i)
удовлетворяет
Ic 7r zl ;;;: .., ;;;: Ic 7rm l.
На рисунке 2.1 мы показали, как можно преобразовать одномерную
функцию в коэффициенты, представляющие общее среднее значение функ
ции и различные уточняющие коэффициенты. Повторим теперь эту проце
дуру, используя на этот раз функции нормированноrо базиса Хаара. Приме
нить L2 сжатие к полученным коэффициентам мы можем простым удалени
ем или иrнорированием коэффициентов с самыми маленькими величинами.
Варьируя степень сжатия, мы получаем последовательность приближений
к исходной функции, как показано на рисунке 2.4.
Т'ЛАВА 3
Сжатие изображения
1. Вейвлет преобразованuяХаара для двумерН020 случая 2. Функ
ции двумерН020 базuса Хаара 3. Вейвлет сжатuе uзображе
нuя 4. Цветные uзображенuя 5. Выводы
Прежде чем осуществить сжатие изображения, нам необходимо обоб
щить вейвлеты Хаара на двумерное пространство. Сперва мы рассмотрим,
как выполняется вейвлет разложение значений пикселей в случае ДBYXMep
Horo изображения. Затем опишем масштабирующие функции и вейвлеты,
которые формируют двумерный базис вейвлетов. Они послужат инструмен
тами при описании сжатия изображения с использованием вейвлетов.
3.1. Вейвлет преобразования Хаара для двумерноrо случая
Использовать вейвлеты для преобразования значений пикселей HeKOTO
poro изображения можно двумя способами. Каждое из этих преобразований
представляет собой двумерное обобщение вейвлет преобразования, описан
Horo в разделе 2.1.
Первое преобразование называется стандартным разло,женuем [5].
Чтобы получить стандартное разложение изображения, сначала мы приме
ним одномерное вейвлет преобразование к каждой строке значений пиксе
лей. Эта операция даст нам среднее значение и уточняющие коэффициенты
для каждой строки. Затем мы рассмотрим эти преобразованные строки так,
как если бы они сами являлись изображением, и применим одномерное
преобразование к каждому столбцу. Полученные в результате значения OKa
жутся уточняющими коэффициентами, за исключением единственноrо KO
эффициента, представляющеrо общее среднее значение. Ниже приведен ал
rоритм вычисления стандартноrо разложения. Каждый шаr входящей в Hero
операции отображен на рис. 3.1.
procedure StaпdardDecoтpositioп (с: array [1. . .2], 1. . .2k] of reals)
for TOW 1 to 2] do
DecoтpositioпStep( с [row, 1 . . .2 k ])
end for
3.1. Вейвлет преобразования Хаара д.7Я двумерноzо случая 41
Recoпstructioп(c[row, 1... 2k])
end for
end procedure
Второй тип двумерноrо вейвлет преобразования, так называемое
нестандартное разложенuе [5], представляет чередование операций над
строками и столбцами. Сначала мы выполняем один этап rоризонтальноrо
попарноrо усреднения и нахождения разности значений пикселей в каж
дой строке изображения. Затем мы применяем попарное усреднение и Ha
хождение разностей к каждому получившемуся столбцу. Чтобы закончить
преобразование, мы рекурсивно повторяем этот процесс только на квaд
рантах, содержащих средние значения в обоих направлениях. На рис. 3.2
отображены все этапы, входящие в следующую процедуру нестандартноrо
разложения.
procedureNoпstaпdard Decoтpositioп( с: array [1 . . .21,1. . . 2k] ofreals)
с с/21 (нормалuзуем исходные коэффuцuенты)
9 21
while 9 ;? 2 do
for row 1 to 9 do
DecoтpositioпStep( c[row, 1. . . g])
end for
for col 1 to 9 do
DecoтpositioпStep(c[l.. .g, со!])
end for
9 g/2
end while
end procedure
А вот псевдокодовая процедура выполнения нестандартноrо BOCCTa
новления:
procedureNoпstaпdardRecoпstructioп( с: array [1 . . .21,1. . . 2k] ofreals)
g 2
while 9 21 do
for col 1 to 9 do
RecoпstructioпStep( с [1 . . . g, со!])
end for
for row 1 to 9 do
RecoпstructioпStep( c[row, 1 . . . g])
end for
9 2g
end while
с 21 с
end procedure.
3.2. Функции двумерноzо базиса Хаара
43
базиса. Аналоrично, не стандартное разложение изображения дает коэффи
циенты для нестандартН020 построеНН020 базиса функций [5].
Стандартное построение двумерноrо базиса вейвлетов состоит во взя
тии всевозможных тензорных произведений функций одномерноrо базиса.
Например, если вначале мы имеем одномерный базис Хаара для V 2 , то мы
получим двумерный базис для V 2 , показанный на рисунке 3.3. Заметим, что
если мы применим стандартное конструирование к одномерному OpTOHOp
мированному базису, то в итоrе получим двумерный ортонормированный
базис.
фg(х) (y)
vPo(x) (y)
фg(х) vPo(y) vPo<x) vPo(y)
[][:J
фg(х) ф (у) фg(х) vPo(y)
цr6(x) vPo(y)
фь(х) %(у)
(x) (y)
(x) %(у)
(X) ф (у)
Рис. 3.3. Стандартное построение двумернorо базиса вейвлетов Хаара для v 2 .
В ненормированном случае функции имеют значение + 1 там, rдe стоит значок
«плюс», значение 1 там, тде стоит значок «минус», и значение О на участках
серото цвета.
Не стандартное построение двумерноrо базиса начинается с определе
ния двумерных масштабирующих функций
фф(х,у) ф(х)ф(у)
44
Т7ава 3
и трех вейвлетов:
фф(х, у) ф(х)ф(у)
фф(х, у) ф(х)ф(у)
фф(х, у) ф(х)ф(у).
Обозначим уровни масштабирования надстрочным знаком j (как мы
делали это в одномерном случае), а rоризонтальные и вертикальные сдви
rи под строчными индексами k и 1, соответственно. Не стандартный базис
состоит из единственной масштабирующей функции, соответствующей rpy
бому приближению ФФ8 о(х, у) фф(х, у), а также трех масштабированных
и сдвинутых вейвлетов 'фф, фф и фф:
ФФ 1 (х, у) 2] фф (2] х k, 2] х 1)
ФФ I(Х' у) 2]фф(2]х k, 2]х 1)
ФФ 1 (х, у) 2]ф(х)ф(у)(2] х k, 2] х 1).
Постоянная 2] нормирует вейвлеты для образования ортонормирован
Horo базиса. Нестандартное построение приводит к базису для V 2 , пока
занному на рис. 3.4.
Мы представили здесь два подхода к вейвлет преобразованиям и базис
ным функциям стандартный и не стандартный, потому что у каждоrо
из них имеются свои преимущества. Стандартное разложение изображе
ния привлекательно простотой выполнения нужно только произвести
одномерное преобразование всех строк, а затем и всех столбцов. С дpy
rой стороны, чуть более эффективным представляется нестандартное раз
ложение изображения. Для изображения т х т стандартное разложение
требует 4(т 2 т) операций, тоrда как нестандартное разложение требует
только (т2 1) операций.
Еще однн момент касается носителя каждой базисной функции, обо
значающеrо участок области определения функции, на котором функция не
равна нулю. Все функции нестандартно построенноrо базиса Хаара име
ют квадратные носители, в то время как некоторые функцни стандартно
построенноrо базиса имеют неквадратные носители. Каждый из этих Ba
риантов может оказаться предпочтительнее друrоrо, в зависимости от KOH
KpeTHoro случая применения.
3.3. Вейвлет сжатие изображения
В разделе 2.4 мы определили сжатие как представление функции с ис
пользованием меньшеrо числа коэффициентов базисной функции по cpaBHe
3.3. Вейв.7ет сжатие изображения
45
Ф%,(Х,У)
ФII'i,,(х,у)
фv!i,.о(r, У)
,о(ч)
[JrJ
фф о(r, У)
цrфg,о(х, у)
1Jf%.,(x,y)
цrФб.,(Х,У)
I{IФ60(Х' у)
1JI1II:,(x,y)
I{IФ:.,(х, у)
цrФ:.о(Х,У)
Рис. 3.4. Нестандартное построение двумерното базиса вейвлетов Хаара для V 2 .
нию с первоначальным их количеством. Метод, который мы рассматривали
для функций в одномерном случае, с тем же успехом можно применить
и к изображениям, которые мы рассматриваем как коэффициенты разло
жения по кусочно постоянному двумерному базису. Представленный здесь
подход это только начало. Более полную трактовку вейвлет сжатия изоб
ражения вы найдете в статье Де Вора и соавторов [27]. Мы же еще раз
заметим, что рассматриваем только преобразование и квантование коэффи
циентов, а не способы их кодирования.
Вейвлет сжатие изображения с использованием L2 HOpMbI можно CBe
сти к следующим трем этапам:
1. Вычисление коэффициентов Cl, ..., С т , представляющих изображение
в нормированном двумерном базисе Хаара.
2. Расположение коэффициентов в порядке уменьшения их значений для
формирования последовательности Сп(l), ..., Сп(т)'
3. При заданной допустимой L2 поrpешности Е. и начальном rh m
46
Т7ава 3
нахождение наименьшеrо т, для KOToporo
m
L (С п (i))2 102.
i m+l
Первый этап выполняется с помощью любоrо из двумерных вей
влет преобразований Хаара, описанных в разделе 3.1, и, конечно, в нем
используются функции нормированноrо базиса. Для выполнения BToporo
этапа подойдет любой типовой метод сортировки, и любой типовой Me
тод поиска сработает на третьем этапе. Однако сортировка для больших
изображений выполняется чрезвычайно медленно. Следующий псевдокод
это краткое представление более эффективноrо метода выполнения BToporo
и TpeTbero этапов с использованием стратеrии дихотомическоrо поиска для
нахождения пороrовоrо значения т, до KOToporo возможно производить yce
чение коэффициентов.
Исходными данными процедуры служит одномерный массив коэффи
циентов с (каждый коэффициент соответствует функции двумерноrо бази
са) и допустимая поrpешность 10. Для каждоrо предположения относитель
но пороrовоrо значения т алrоритм вычисляет квадрат L2 поrрешности,
которая появляется вследствие отбрасывания коэффициентов, меньших по
величине, чем т. При каждой итерации эта квадратичная поrрешность s
сравнивается с поrрешностью 102 для Toro, чтобы решить, на какой поло
вине текущеrо интервала верхней или нижней должен быть продолжен
дихотомический поиск. Остановка алrоритма происходит, коrда текущий
интервал становится настолько узким, что количество «списанных в брак»
коэффициентов больше не изменяется.
procedure Coтpress( с: array [1. . . т] of reals; 10: real)
Tmin minlc[i]1
Ттах maxlc[i]1
do
т (Tmin + Ттах)/2
s o
for i 1 to m do
if Ic[i]1 < т then s s + 1c[i]12
end for
if s < 102 then Tmin т else Ттах Ттах
until т min т тах
for i 1 to m do
if I ф] I < т then с [i] О
end for
end procedure
3.3. Вейв.7ет сжатие изображения
47
Этот алrоритм дихотомическоrо поиска использовался для получения
изображений, показанных на рис. 3.5. Эти изображения позволяют судить
о высокой степени сжатия, обеспечиваемой вейвлетами, и о некоторых co
здаваемых вейвлетами артефактах.
(а)
(6)
(в)
(r)
Рис. 3.5. L2 сжатие изображения вейвлетами Хаара: исходное изображение (а) мож
но представить, используя 19 % ето вейвлет коэффициентов с относительной L2 по
rрешностью в 5 % (б), 3 % ето коэффициентов с относительной L2 поrрешностью
в 10 % (в), 1 % ето коэффициентов с относительной L2 поrpешностью в 15 % (т).
Де Вор и др. [27] высказывают предположение, что Ll HopMa лучше
подходит для задачи сжатия изображения. Ниже приведен фраrмент псев
докода для «прожорливой» схемы Ll сжатия, которая накапливает в ДBY
мерный массив [x, у] поrрешность, вызванную отбрасыванием коэффици
ентов и проверяет, не превысила ли эта поrрешность пороr, установленный
пользователем:
for each pixel (х, у) do
[x,y] О
end for
for i 1 to m do
' + error from discarding c[i]
if x,yl I[X,y]1 < с then
c[i] О
'
end if
end for.
Заметим, что результаты этоrо алrоритма зависят от порядка обращения
к коэффициентам. Можно получить очень разные изображения (и степени
сжатия), изменяя порядок, к примеру, начав с коэффициентов, COOTBeTCTBY
ющих самым мелким масштабам, а не с самых маленьких коэффициен
тов. Можно было бы представить и выполнение более сложной процедуры
48
Т7ава 3
условной оптимизации, чтобы отобрать минимальное количество коэффи
циентов с учетом rpаницы поrрешности.
3.4. Цветные изображения
До этоrо момента мы рассматривали только изображения с OДHO
компонентной шкалой яркости. Однако методы вейвлет преобразований
и вейвлет сжатия с тем же успехом подходят и для цветных изображений
с тремя цветными компонентами. К примеру, псевдокод для L2 сжатия будет
рабочим и для цветноrо изображения, если мы выполним вейвлет преобра
зование независимо на каждом из трех цветных компонентов изображения
и представим результаты как массив векторнозначных вейвлет коэффици
ентов. Затем, вместо использования в псевдокоде абсолютноrо значения
скалярноrо коэффициента мы воспользуемся L2 нормой (обычное значе
ние вектора) векторнозначноrо вейвлет коэффициента. Примеры цветных
изображений, сжатых с помощью этоrо алrоритма, показаны на цветной
иллюстрации 1.
Кроме Toro, существует ряд способов использования цветовой инфор
мации для получения вейвлет преобразования, еще более разреженноrо, чем
рассмотренные нами. Например, перейдя от цветовой модели RGB (Kpac
ный, зеленый, синий) к цветовой модели YIQ, мы можем разrраничить
информацию о яркости (У) и информацию о цвете (1 и Q). Вычислив вей
влет преобразование, мы можем применить процедуру L2 сжатия к каждой
компоненте изображения по отдельности. Поскольку восприятие человека
более чувствительно к изменениям У и менее чувствительно к изменени
ям Q, мы можем расширить допуск на поrрешность по компоненте Q сжа
Toro изображения, повысив, таким образом, степень сжатия. (Тот же самый
принцип позволяет передавать сиrналы американскоrо цветноrо телевиде
ния с шириной полосы 4 М[ц дЛЯ У, 1,5 М[ц для 1 и 0,6 М[ц для Q.)
3.5. Выводы
в этой и предыдущей rлавах мы описали вейвлеты Хаара для OДHO
и двумерноrо случая, а также рассмотрели, как пользоваться ими для сжа
тия функций и изображений. Кроме Toro, в двух следующих rлавах мы
покажем, что базис Хаара полезен для редактирования и формирования за
проса изображений, а также для общеrо освещения, речь о котором пойдет
в тринадцатой rлаве.
Теоретическое описание вейвлетов будет продолжено в шестой и ceдь
мой rлавах, [де представлена теория кривых, получаемых последователь
ным делением, и то, как можно применить эту теорию для разработки более
законченноrо математическоrо формализма кратномасштабноrо анализа.
Т'ЛАВА 4
Редактирование изображений
1. Структуры uзобра.женuй с переменным разрешенuем 2. Ak
20риm.М редактuрованuя uзобра,женuя З. rранuчные условuя
4. Отобра.женuе на экране u редактирование при дробных разре
шенuях 5. Прuмеры редактuрованuя uзображенuя
В этой rлаве мы рассмотрим приложение вейвлетов Хаара к редакти
рованию изображений. Вейвлеты Хаара служат основой для представления
изображений, которые MorYT иметь разные разрешения на разных участках.
При редактировании изображения важно, чтобы пользователь имел воз
можность вносить радикальные изменения при низком разрешении, а также
работать с мелкими деталями при высоком разрешении. В идеальном случае
объем памяти для хранения конечноrо изображения должен быть пропорци
ональным только количеству деталей при каждом разрешении. Кроме Toro,
желательно, чтобы временная сложность операции редактирования была
пропорциональна только разрешению, при котором выполняется эта опе
рация. Наконец, пользователь должен уметь увеличивать изображение до
произвольноrо разрешения и работать в любом удобном масштабе.
Эти цели в значительной степени достиrаются блаrодаря системе OKpa
шивания и компоновки изображений, разработанной Берман и coaBTopa
ми [4]. Такая система использует метод разложения изображений с помо
щью вейвлетов Хаара, причем изображения хранятся в разреженной квaд
ратичной древовидной структуре. Это вейвлет представление имеет MHO
жество преимуществ перед друrими методами поддерживания переменных
разрешений изображения. Во первых, вейвлет представление изображения
отличается компактностью, в том смысле, что оно содержит ровно столько
вейвлет коэффициентов, сколько пикселей имеется в изображении. BO BTO
рых, это представление поддерживает компоновку эффективнее, чем пира
миды изображений. И, наконец, вейвлеты предоставляют очень эффектив
ные средства сжатия изображений, что мы видели в третьей rлаве. Блаrода
ря использованию вейвлет представления, система редактирования может
оперировать непосредственно сжатыми изображениями, не прибеrая к «раз
жатию» и повторному сжатию, что делает обработку крупных изображений
более удобной в сравнении с пирамидальной схемой.
50
Т7ава 4
Можно rоворить, что изображения с переменным разрешением, полу
ченные с помощью системы, основанной на вейвлетах, имеют разные разре
шения в разных местах. Известно MHoro применений таким изображениям,
в том числе такие:
. Интерактивные системы окрашивания художник может работать над
одним изображением при различных разрешениях.
. Текстурное отображение те участки текстуры, которые будут видны
с близкоrо расстояния, можно сделать более четкими.
. Спутниковые и друrие базы данных с изображенями перекрыва
ющиеся изображения, полученные при разных разрешениях, можно
объединнть в одно изображение с переменным разрешением.
. Физическое моделирование с учетом значимости [119] решения мож
но находить при разных разрешениях в разных участках.
. Виртуальная реальность, rиперсреда, иrpы деталь изображения мож
но исследовать интерактивно, используя существенно неоrpаниченные
степени панорамирования и изменения масштаба изображения.
. Модельное представление пользовательскоrо интерфейса по принципу
«идеальный рабочий стол» [93] один виртуальный «рабочий стол»
с бесконечным разрешением может быть представлен пользователю.
4.1. Структуры изображений с переменным разрешением
Пусть g это изображение с переменным разрешением, т. е. изобра
жение с разным разрешением на разных участках. Можно рассматривать g
как изображение, разрешение KOToporo меняется адаптивно по мере необ
ходимости.
Более формально мы определим g как сумму кусочно постоянных
функций gj при разных разрешениях 2 j х 2 j . В этом смысле можно считать,
что g повсюду имеет идеальное разрешение: увеличивая g, пользователь
видел бы деталь изображения все четче и четче до тех пор, пока coxpa
няется высокое разрешение детали. Но как только это разрешение будет
превышено, нам станет казаться, что пиксели изображения с самым BЫCO
ким разрешением превращаются в квадраты неизменноrо цвета, которые
становятся все больше и больше.
Мы сохраняем изображение с переменным разрешением g в разре
женной квадратичной древовидной структуре из четырех частей CTPYKТY
ре Т. Вершины структуры Т имеют обыкновенное соответствие с участками
4.1. Структуры изображений с nеременны.Н разрешение.м
51
изображения: корень структуры, на уровне О, соответствует всему изобра
жению; четыре дочерних вершины, на уровне 1, соответствуют четырем
квадрантам изображения; далее, по мере продвижения по дереву, рассужда
ем аналоrично. Таким образом, каждый уровень структуры j COOTBeTCTBY
ет масштабированной версии изображения с переменным разрешением fl
и соответствует разрешению 2) х 2). Заметим, что соrласно общепринятому
правилу более высокие уровни квадратичной древовидной структуры COOT
ветствуют версиям изображения с более низким разрешением, и наоборот.
Квадратичная древовидная структура используется для кодирования
нестандартноrо разложения по вейвлетам Хаара, о котором rоворилось
в разделах 3.1 и 3.2. Каждая вершина дерева содержит следующую ин
формацию:
type QuadTreeN ode record
d 1 , d 2 , dз:RGВА
т: real
child: array 1 . . .4 of pointer to QuadTreeN ode
end record.
EI
(а) цrф(х, у)
(6) ф'lf(х,у)
(в) цr'lf(x, у)
Рис. 4.1. Нестандартные вейвлеты Хаара, соответствующие трем типам деталей,
представленных коэффициентами d 1 , d 2 и d 3 .
Три величины d i в структуре QuadTreeNode являются уточняющими
коэффициентами: они описывают, как цвета, соответствующие дочерним
вершинам, отклоняются от цвета, соответствующеrо родительской вершине.
Для данной вершины N эти значения d i представляют коэффициенты трех
не стандартных вейвлетов Хаара, носители которых перекрывают область
изображения, соответствующую N, причем коэффициенты d 1 , d 2 и d з OT
носятся К фф, фф и фф, соответственно (см. рис. 4.1). Эти коэффициенты
позволяют нам восстановить цвета RGBA 1 четырех дочерних вершин по
известному цвету родительской вершины так, как описано в разделе 4.2.1.
lСистема (цветопередачи) RGB, расширенная параметром ОС, который используется для
управления смешиванием цветов
52
Т7ава 4
Величина т представляет прозрачность вершины с присвоенным Ha
чальным значением 1. Значения т используются для оптимизации алrоритма
окрашивания и компоновки изображения, что будет пояснено позже. Поля
child[i] служат указателями на четыре дочерние вершины. Некоторые из
этих вершин MorYT быть нулевыми. Чтобы оптимизировать хранение, поля
child[i] можно представить и в виде одноrо указателя на массив четырех дo
черних вершин. Позже мы будем ссылаться на «альфа» компоненту цвета е
или уточняющеrо коэффициента d i , обозначая ее ел или di,Q;, COOTBeT
ственно.
Отметим, что каждая вершина дерева N соответствует выделенному
участку изображения. Будем называть такой участок area (N). Значение
area (N) определяется неявно квадратичной древовидной структурой и KOH
кретным видом и не нуждается в явном представлении в N. За исключением
отображения на дробных уровнях (описанных в разделе 4.4), между пик
селями изображения и вершинами на каком либо уровне j квадратичной
структуры существует взаимно однозначное соответствие.
Сама структура задается так:
type QuadTree record
е: RGBA
root: pointer to QuadTreeN ode
end record.
Значение е отвечает за цвет родительской вершины; оно соответствует
среднему для всех цветов в изображении fl.
Разреженность древовидной структуры проявляется в том, что оно не
содержит листьев с уточняющими коэффициентами, равными О. Таким об
разом, постоянные участки изображения для KOHKpeTHoro разрешения пред
ставлены неявно. Это позволяет нам обеспечивать идеальные разрешения
в конечной структуре. Кроме Toro, это дает нам возможность в явном виде
представлять детали при высоком разрешении только там, [де они действи
тельно значатся в изображении.
4.2. Алrоритм редактирования изображения
Раскрашивание изображения с переменным разрешением осуществить
просто. Основной цикл алrоритма включает в себя три процедуры: Display,
Paiпtiпg, Update (вывод на экран, раскрашивание и корректирование).
4.2.1. Вывод на экран
Вывод изображения с разрешением 2) х 2) на экран осуществляет
ся путем восстановления видимой части изображения по ero двумерному
4.2. Алzорит,н редактирования изображения
53
вейвлет разложению. Это восстановление выполняется вызовом следующей
рекурсивной проrpаммы Display, исходными данными которой являются KO
рень и цвет Bcero дерева:
procedure Display(N : QuadTreeN ode; с: RGBA)
Сl С + N.d 1 + N.d 2 + N.d з
С2 С N.d 1 + N.d 2 N.d з
сз с + N.d 1 N.d 2 N.d з
С4 С + N.d 1 N.d 2 + N.d з
for i 1 to 4 do
if N is а 1eaf or N is at leve1 j 1 then
Draw Ci over the l'egion area(N.child[i])
else
Display(N.child[i], Ci)
end if
end for
end procedure.
Поясним, что работа этоrо псевдокода продолжается до достижения
j l ro уровня Bcero изображения, хотя, на самом деле, следует приме
нять эту процедуру лишь для участка изображения, который умещается
в окие экрана дисплея. Заметим, время выполнения операции вывода на
экран изображения из m пикселей оценивается как О(т). (Если точнее,
О(т + Л, но поскольку на практике почти всеrда j « т, мы пренебрежем
этой зависимостью от j в последующем анализе.)
4.2.2. Раскрашивание
Раскрашивание осуществляется путем компоновки свежераскрашенно
[о OCHoBHoro буфера :J: с фоновым буфером qз, получаемым с помощью
процедуры Display, для создания HOBoro результирующеrо изображения g;,.
Приложение, описанное Берман и друrими [4], поддерживает несколько би
нарных операций компонования: операцию «над», которая размещает новый
«слой краски» в любом месте; операцию «под», которая размещает краску
только там, [де фон прозрачен, и операцию «в», которая размещает краску
только там, [де фон уже раскрашен.
Для выполнения caMoro раскрашивания не требуется какой либо специ
альной операции. Единственное отличие от обыкиовенноrо раскрашивания
состоит в том, что в дополнение к полученному совмещением результату g;,
мы можем оставить отдельную копию OCHoBHoro буфера :J:, содержащую
всю вновь наложенную краску. Этот основной буфер необходим для KOp
ректировки дерева, о чем мы поrоворим в следующем разделе. Простое
раскрашивание продолжается до тех пор, пока пользователь не изменит
54
Т7ава 4
операцию окрашивания (например, «над» на «под») или вид изображения
посредством панорамирования или изменения масштаба. Каждое из этих
действий инициирует корректировку.
4.2.3. Корректировка
Операция корректировки используется для распространения результа
тов операций окрашивания на остальную часть изображения с переменным
разрешением, представленную деревом. Корректировка включает два эта
па: разложенuе, при котором изменения распространяются на все высшие
уровни дерева, и экстраполяцuя, при которой изменения распространяются
на все нижние уровни дерева. Мы рассмотрим каждый из этих этапов по
очереди.
Пусть j это уровень, на котором пользователь выполняет paCKpa
шивание, а Ст(Х, у) цвет каждоrо модифицированноrо пикселя в резуль
тирующем изображении g;,. Разложение Bcero изображения выполняется
вызовом следующей функции Decoтpose с корнем квадратичноrо дерева
Troot в качестве aprYMeHTa и сохранением результата в Тс:
function Decompose( N : QuadTreeN ode)
if N is at leve1 j then
return Ст(Х, у)
end if
for i 1 to 4 do
Ci Decompose(N.child[i])
end for
N.d 1 (сl С2 + сз С4)/4
N.d 2 (сl + С2 сз С4)/4
N.d з (сl С2 сз + С4)/4
return(cl + С2 + сз + С4)/4
end function.
Уточним, что в вышеприведенном псевдокоде предполаrается, что раз
реженное дерево Т уже содержит все вершины, соответствующие пикселям
в результирующем изображении g;,. Однако если g;, было раскрашено при
разрешении, превышающем разрешение существующеrо изображения, то,
возможно, новые узлы нужно будет классифицировать и добавить в Т как
часть пути. К тому же, из соображений эффективности, функцию Decoтpose
следовало бы модифицировать для Toro, чтобы рекурсивность имела Me
сто только для тех участков изображения с переменным разрешением, [де
действительно про изошли изменения. Заметим, что если редактируемый
участок изображения имеет m пикселов, то вся операция разложения зани
мает О(т) времени.
4.2. Алzорит,н редактирования изображения
55
Экстраполяция HeMHoro сложнее и зависит от Toro, какая опера
ция разложения используется. Пусть для бинарных операций раскраши
вания cf(X, у) обозначает цвет OCHoBHoro изображения :lf каждоrо пиксе
ля (х, у), а cf.a(x, у) показатель непрозрачности пикселей. Для опе
рации «стереть» (erase) показатель непрозрачности стирающеrо устройства
для каждоrо пикселя обозначим б (х, у). Тоrда экстраполяция выполняет
ся после вызова следующей проrpаммы для вершины N, соответствующей
каждому модифицированному пикселю (х, у) отредактированноrо изобра
жения.
procedure Extrapolate( N : QuadTreeN ode)
for i 1 to 3 do
switch оп the composing operation
case «over»
N.d i N.d i * (1 cfa(x, у))
case «under»
N.di. N.d i N.dia *! а(х, у)
case «ш»
N.d i N.d i * (1 cfa(x, у)) + N.dia *! а(х, у)
case «erase»
N.d i N.d i * (1 15(х, у))
end switch
end for
if N is not а leaf then
for i 1 to 4 do
Extrapolate( N.child[i])
end for
end if
end procedure
Заметим, что время, требуемое на выполнение процедуры экстрапо
ляции, пропорционально количеству деталей, появляющихся иерархически
«ниже» модифицированных частей изображения. Чтобы оптимизировать
эту операцию, по крайней мере, для наиболее общих случаев раскрашива
ния с применением операции «над» и «стереть», мы можем использовать
форму «ленивоrо» вычисления!. Во первых, заметим, что в двух формулах
приведенноrо выше псевдокода для операций «над» и «стереть» попро
сту выполняется умножение имеющихся уточняющих коэффициентов на
некую постоянную, которую мы обозначим через т(х, у). (Для раскраши
вания «над» т(х, у) == 1 с! .а(х, у); для «стереть» т(х, у) == 1 15(х, у).)
Таким образом, для выполнения двух этих операций мы просто можем
lт. е. отложенноrо вычисления. ПрUJИ. ред.
56
Т7ава 4
умножить величину N.T, хранящуюся в вершине, на т(х, у) вместо Toro,
чтобы вызывать процедуру Extrapolate для каждой вершины N. Впослед
ствии, если значения d i для вершины N действительно потребуются, они
MorYT быть отложенно откорректированны путем умножения каждоrо N.d,
на значения т, соответствующие родителям всех вершин. Это произведение
леrко представить как часть рекурсивноrо вычисления.
Эта очень простая форма «ленивоrо» вычисления является побочным
продуктом вейвлет представления для изображения, поскольку при более
высоких разрешениях уточняющие коэффициенты зависят только от произ
ведения показателей непрозрачности всей раскраски при более низких раз
решениях. Любое подобие метода «ленивоrо» вычисления HaMHoro услож
нилось бы пирамидами изображений, поскольку цвета при высоких раз
решениях более сложным образом зависят от цветов раскраски при более
низких разрешениях.
Заметим, что нечто вроде экономной «цветокоррекции» можно осуще
ствить, накладывая одноцветный квадрат с высокой степенью прозрачно
сти на все изображение. С применением «ленивоrо» вычисления этот тип
цветокоррекции для произвольноrо изображения с высоким разрешением
реализуется за время, пропорциональное только разрешению, с которым
проводится редактирование.
4.3. rраничные условия
Точное определение rpаничных условий HeMHoro усложняет paCCMOT
ренные в предыдущих разделах алrоритмы корректирования и вывода на
экран. Трудность состоит в том, что функция Decoтpose должна иметь дo
ступ к цветам дочерних вершин, порождаемых каждой из обходимых ею
вершин N. Однако некоторые из этих дочерних вершин относятся к участ
кам, находящимся за rраницами окна, в котором пользователь только что
произвел раскрашивание, и, таким образом, проrрамма не имеет к ним
прямоrо доступа. Очевидное решение сохранение информации о цвете
каждой вершины дерева в дополнение к уточняющим коэффициентам
привело бы к значительному увеличению потребности в памяти и появле
нию дополнительных непроизводительных издержек на поддержание избы
точных представлений. Вместо этоrо мы храним временное вспомоrатель
ное дерево только с теми цветами, которые необходимы для разложения.
Ero можно заполнять во время операции Display ценой небольших допол
нительных затрат. Размер этоrо вспомоrательноrо дерева пропорционален
количеству отображаемых пикселей.
4.4. Вывод на экран и редактирование при дробных разрешениях 57
4.4. Вывод на экран и редактирование при дробных
разрешениях
До сих пор нами предполаrалось существование взаимно однозначноrо
соответствия между вершинами дерева на уровне j и пикселями изображе
ния при разрешении 2 j х 2 j . Но поскольку уровни дерева дискретны, это
верно только для дискретноrо масштабирования изображения, причем раз
решение удваивается на каждом последующем уровне.
С точки зрения пользовательскоrо интерфейса, более предпочтитель
ной является возможность непрерывноrо масштабирования редактируемоrо
изображения. Можно определить нечто вроде дробно уровнев020 масштаби
рования, рассмотрев, как изменяется размер квадратноrо участка area(N),
соответствующеrо заданной вершине N на уровне j, при непрерывном пе
реходе пользователя от j Toro уровня на j + l ый и от j + l ro на j + 2 ой
уровень. На дисплее ширина area(N) увеличивалась бы экспоненциально
от 1 до 2 и от 2 до 4. Итак, при выводе изображения на дробном уровне j + /J
для HeKoToporo /J от О до 1 мы бы хотели, чтобы размер area (N) был 2 JL Х 2 JL .
На рабочих станциях, обеспечивающих представление изображений на
основе мноrоуrльников без помех дискретизации с устранением контурных
неровностей, такое дробное изменение масштаба довольно просто выпол
няется вычерчиванием каждой вершины N как одноrо квадрата подходяще
[о дробноrо размера. На менее дороrих рабочих станциях, поддерживаю
щих только мноrоуrольники с целочисленными уровнями разрешения, чуть
менее привлекательная, но все же вполне адекватная картинка получает
ся после окруrления каждоrо визуализированноrо квадрата до ближайшеrо
пикселя. В любом случае, единственной поправкой, которую следует внести
в проrрамму Display, является продление рекурсивности до caMoro низкоrо
уровня всякий раз, коrда N находится на [j + /J l] OM, а не на j l OM
уровне, и установление соответствия между участком area(child[i]) и под
ходящим дробным размером.
Конечно, с пользовательской точки зрения, если можно выводить изоб
ражение на экран на любом уровне j + т, то ero можно и редактировать на
любом уровне. Обеспечить такое дробно уровневое редактирование также
несложно. Чтобы откорректировать представление древовидной структуры,
мы просто доводим размер буфера вновь внесенных изменений :lf до раз
мера, принимаемоrо на ближайшем целочисленном уровне, как если бы
пользователь уже внес изменения на j + 1 OM уровне. Требуемый масшта
бирующий коэффициент равен 21 JL. Затем мы можем произвести ту же
корректировку, что и раньше, начав с уровня j + 1.
58
Т7ава 4
4.5. Примеры редактирования изображений
Редактирование изображений с переменным разрешением поясняется
с помощью трех примеров, представленных на цветных иллюстрациях 2 4.
На цветной иллюстрации 2 пользователь увеличивает изображение Моны
Лизы и при высоком разрешении «накладывает» тени на rлаза и помаду
на rубы. Чтобы придать rлазам яркий блеск, он еще HeMHoro увеличивает
масштаб. А затем это слеrка подкрашенное изображение выводится уже при
исходном разрешении.
На цветной иллюстрации 3 пользователь раскрашивает дерево при пе
ременном разрешении, применяя несколько компоновочных операций. Пер
во начально большая часть дерева была раскрашена при низком разрешении.
Затем пользователь значительно увеличивает верхний левый уrол изобра
жения и раскрашивает несколько листьев. Далее, он уменьшает масштаб
и изменяет окраску листьев с помощью «ш» кисти, которая красит толь
ко там, [де до этоrо уже была наложена краска. На третьем изображении
пользователь уменьшает масштаб до очень низкоrо разрешения и быстро
«нацарапывает» небо и траву, пользуясь уже «uпdеf» КИСТЬЮ, которая накла
дывает краску только там, [де ранее ее не было. Следует обратнть внимание
на то, что хотя небо раскрашено при низком разрешении, эта новая краска
орrанично стыкуется с со всеми деталями, отличающимися высоким разре
шением и присутствующими в изображении с caMoro начала.
Наконец, на цветной иллюстрации 4 демонстрируется пример co
здания одноrо изображения с переменной разрешающей способностью
из шести последовательных изображений, заимствованных из кииrи
Powers о/ Теп [87], путем компоновки всех шести при различных масшта
бах. В книrе [87] центральный участок каждоrо предыдущеrо изображе
ния увеличен в каждом последующем изображении в десять раз. В нашем
представлении шесть этих изображений обьединены в одно с масштабом
105. (Заметим, что перевод изображений с масштабами, равными степеням
десяти, в деревья с числом уровней, пропорциональным степеням двой
ки, требует наличия дробно уровневоrо редактирования.) На этой иллю
страции крупным планом изображена самая дальняя деталь, а также то же
самое изображение после уменьшения масштаба в 100000 раз. На картин
ке 4(r) той же иллюстрации пользователь ретуширует изображение, пользу
ясь «оvеr» кистью, чтобы создать впечатление нависшеrо CMora. Как видно
из последнеrо изображения, этот cMor заволакивает весь близлежащий вид,
не устраняя, однако, какую бы то ни было из присутствующих в изображе
нии деталей.
Т'ЛАВА 5
Формирование запроса изображения
1. Формuрованuе запроса uзображенuя по содержанuю 2. Разра
ботка метрики для формuрования запроса uзобра.женuя З. Ak
20риm.М формuрованuя запроса uзобра.женuя 4. Прuмеры фор
мuрованuя запроса uзобра.женuя 5. Расшuренuя
Стремительное внедрение настольных издательских средств, повсе
местное распространение цветных сканеров и цифровых средств инфор
мации, а также появление всемирной паутины позволили людям получить
леrкий доступ к десяткам тысяч цифровых изображений. Эту тенденцию,
по всей видимости, ожидает уверенное продолжение, вследствие чеrо все
больше и больше людей будет иметь доступ к разрастающимся базам дaH
ных.
В связи С ростом размера баз данных традиционные методы нахожде
ния заданноrо изображения исчерпывают свои возможности. К примеру, ec
ли быстрый просмотр нескольких сотен свернутых изображений (thumbnai1
images) с целью отыскания KOHKpeTHoro запроса изображения это относи
тельно леrкая задача для пользователя, то помещение TaKoro запроса среди
нескольких тысяч друrих представляется куда более трудным делом. Так
что при существенном расширении базы данных поиск методом полноrо
перебора перестает быть эффективной стратеrией.
Одной из распространенных стратеrий поиска является индексация ба
зы видеоданных ключевыми словами. Однако и этот подход имеет свои
трудности. Во первых, он требует, чтобы пользователь вручную пометил
все изображения ключевыми словами, а это весьма трудоемкая процедура.
BO BTOpЫX, Найблэк и др. в [90] отмечают, что подобный метод с исполь
зованием ключевых слов затруднителен по той причине, что некоторые ви
зуальные аспекты I с caMoro начала описать бывает довольно трудно, тоrда
как некоторые друrие можно описать одинаково хорошо множеством раз
личных способов. Кроме Toro, пользователю может быть непросто уrадать,
какие визуальные аспекты уже отмечены индексами.
1 Имеются в виду свойства, по которым rpУППЫ данных объединяются в информационно
поисковой системе. ПРlL\t. ред.
60
Т7ава 5
в этой rлаве мы рассмотрим альтернативную стратеrию поиска базы
данных изображений, в которой запрос выражается либо как изображение
с низким разрешением, полученное с помощью сканера или видеокамеры,
либо как rрубый набросок искомоrо изображения, нарисованный самим
пользователем. Этот базовый подход к формированию запроса изображе
ния получил различные названия, среди которых «запрос по содержа
нию» (query Ьу coпteпt) [90], «запрос по образцу» (query Ьу exaтple) [59],
«поиск по методу подобия» (siтilarity retrieval) [68], «поиск по эскизу»
(sketch retrieval) [66]. Заметим, что такой тип формирования запроса, OCHO
ванный на содержании изображения, можно также применять совместно со
способом формирования запроса на основе ключевых слов, да и с любым
друrим из существующих методов.
Формирование запроса, исходя из содержания искомоrо изображения,
нашло применение во мноrих различных областях, включая rрафический
дизайн, архитектуру, производство телепроrрамм, мультимедийные cpeд
ства, повсеместную обработку данных, историю искусств, rеолоrию, базы
данных спутниковых изображений, получение изображений в области меди
цины. Например, дизайнер может пожелать найти изображение, хранящее
ся в созданной им самим системе, используя нарисованное изображение за
прос. Возможно, также потребуется выяснить, имеется ли в базе данных по
ставщика оцифрованных изображений со сверхвысоким разрешением некое
конкретное изображение, использовав для этоrо сканированное изображе
ние запрос с низким разрешением. В области универсальных вычислений
компьютер может столкнуться с задачей поиска заданноrо документа в ero
базе данных по имеющемуся синтезированному изображению страницы
из этоrо документа, отсканированной в реальных условиях. В отношении
всех этих приложений совершенствование технолоrии формирования за
про са изображения является важной и общепризнанной проблемой.
Существует несколько факторов, затрудняюших решение данной про
блемы. Изображение запрос, как правило, сильно отличается от целевоrо
изображения, а потому метод поиска должен учитывать искажения. Если
изображение запрос получают с помощью сканера, то оно может постра
дать от артефактов, что проявится в изменении цвета, плохом разрешении,
размывании контуров изображения, рассовмещении. Если же изображение
запрос нарисовано, то ero качество оrраничивается перцепционными иска
жениями как цвета, так и профиля, а также мерой художественных спо
собностей и усердия пользователя. В силу этих причин прямые методы
вроде Ll или L2 метрик изображения не слишком эффективны при pac
познавании искомоrо изображения среди Bcero содержимоrо базы данных.
Поэтому для более эффективноrо удовлетворения подобных несовершен
ных запросов следует разработать такую «метрику изображения запроса»,
которая учитывала бы упомянутые искажения и при этом все таки отли
5.1. Форнирование запроса изображения по содержанию
61
чала бы целевое изображение от всех остальных, входящих в базу данных
объектов. Кроме Toro, поиск должен производиться достаточно быстро, что
бы можно было работать с базами данных, включающими десятки тысяч
изображений, на скоростях, соответствующих интерактивному режиму.
В [63] Якобс и соавторы описывают, как использование вейвлет разло
жения изображения запроса и изображений из базы данных может быстро
и эффективно удовлетворить запрос по содержанию. Их аЛ20рuтм фор'Wu
рованuя uзображенuя запроса с переменны и разрешенuе 'W в значительной
мере повышает скорость и живучесть друrих систем формирования запро
сов по содержанию.
В качестве исходных данных для TaKoro метода поиска служит зарисо
ванное или сканированное изображение, рассматриваемое как приближение
к искомому изображению. Поскольку входные данные являются Bcero лишь
приближением в разработанном подходе, их подход в качестве выходных
данных предусматривает формирование небольшоrо набора наиболее под
ходящих целевых изображений вместо одноrо единственно «правильноrо»
изображения. Двадцать изображений (число слайдов на листе) примерно
составляют то наибольшее количество изображений, которое пользователь
может быстро и достоверно отсканировать при поиске нужноrо ему целе
Boro изображения.
Чтобы выполнить такое упорядочивание, Якобс и др. определяют Meт
рику формuрования запроса изобра.женuя (iтage queriпg тetric), в которой
задействованы укороченные квантованные версии вейвлет разложений, Ha
зываемые СU2натурами (sigпatures). Эти сиrнатуры содержат только самую
существенную информацию о каждом изображении. По существу, метри
ка формирования запроса изображения сличает, сколько общих значимых
вейвлет коэффициентов имеется у изображения запроса и у потенциаль
ных целевых изображений. Используя статистические методы можно про
изводить настройку такой метрики для Toro, чтобы наиболее эффективным
образом выполнять распознавание для различных типов формирования за
просов по содержанию, скажем, для формирования путем сканирования
и для формирования путем рисования от руки. Якобс и ero соавторы пред
лаrают новую орrанизацию базы данных, позволяющую с поразительной
быстротой вычислять эту метрику. (Созданная ими система обрабатывает
изображение запрос форматом 128 х 128 при базе данных с 20000 изобра
жениями менее чем за 1/2 секунды; для сравнения: поиск в той же самой
базе данных с использованием Ll метрики занимает свыше 14 минут.)
5.1. Формирование запроса изображения по содержанию
Характерными особенностями предшествующих методов формирова
ния запросов изображения на основе содержания являлись цветовые rи
62
Т7ава 5
стоrраммы [121], текстурный анализ (texture analysis) [65] и особенности
формы, такие, как окруrлость и ориентация участков в изображении OTHO
сительно rлавных осей [48], а также сочетания этих методов.
Одна из самых известных систем формирования запроса по содержа
нию изображения, система под названием QBIC, была разработана компа
нией IBM [90] и теперь стала доступна для приобретения. Основным aK
центом в этой системе является возможность, позволяющая пользователю
сформировать запрос на основе целоrо ряда различных визуальных атри
бутов. Пользователь, к примеру, может задать состав определенноrо цвета
(х % одноrо цвета, у % друrоrо цвета и т. д.), конкретную текстуру, HeKOTO
рые особенности формы и эскиз rлавных контуров целевоrо изображения
и при этом указать для каждоrо из этих атрибутов относительный вес. Си
стема QBIC также позволяет пользователям аннотировать изображения из
базы данных, выделив ключевые для поиска характеристики. В противопо
ложность этому, В алrоритме формирования запроса изображения с пере
менным разрешением упор делается на возможность совершать поиск непо
средственно по изображению запросу без каких либо дальнейших указаний
пользователя в отношении изображений из базы данных или подробностей
caMoro поиска.
Судя по стилю взаимодействия пользователя с системой, работа Хирата
и Като [59], пожалуй, более друrих, может быть отнесена к методам форми
рования запроса с переменным разрешением. В разработанной ими систе
ме под названием запрос по визуальному образцу (query Ьу visual exaтple)
(QVE) выделение контуров при распознавании производится на изображе
ниях запросах пользователя. Эти контуры и контуры целевых изображений
сопоставляются друr друrу путем выполнения довольно сложноrо процесс а,
блаrодаря которому соответствующие контуры можно сдвиrать или дефор
мировать относительно друr друrа.
Применение переменноrо разрешения при формировании запроса обес
печивает множество преимуществ перед друrими методами. Использование
вейвлетов позволяет задавать запрос при любом разрешении (потенциаль
но отличном от разрешения целевоrо изображения); более Toro, хранение
и продолжительность выполнения этоrо метода с переменной разрешающей
способностью не зависят от разрешений изображений, хранимых в базе дaH
ных. В дополнение ко всему, информацию, содержащуюся в сиrнатуре, мож
но извлекать по требованию алrоритма непосредственно из вейвлет сжатых
версий изображения, что позволяет сформировать базу данных сиrнатуры
из множества сжатых изображений. Наконец, этот алrоритм rораздо леrче
реализовать и использовать по сравнению с большинством предшествую
щих подходов.
5.2. Разработка ,нетрики д.7Я формирования запроса изображения 63
5.2. Разработка метрики для формирования запроса
изображения
Рассмотрим задачу вычисления расстояния между изображением
запросом Q и потенциальным целевым изображением fl. Наиболее оче
видным выбором являются L 1 и L2 нормы:
IIQ fll1 1 == L IQ[i,j] == fl[i,j]l;
(5.1)
i,j
( ) 1/2
IIQ fll1 2 == L(Q[i,j] == fl[i,j])2
',]
(5.2)
Однако эти метрики не только требуют дороrостоящих вычислений;
они, помимо Bcero прочеrо, являются весьма неэффективными, коrда дe
ло доходит до отыскания соответствия неточному изображению запросу
в большой базе данных потенциальных целевых изображений. Так, Якобс
и соавторы сообщают, что во время их работы со сканированными запроса
ми было выявлено, что сортировка 1 % наиболее подходящих изображений
из базы данных в L1 и L2 метриках занимала 3 % времени. (Сортировка
производилась путем вычисления L1 и L2 расстояний от изображения
запроса и оценкой положения «цели» в хранимом списке.)
С друrой стороны, цель запроса почти Bcerдa леrко распознается чело
веческим rлазом, несмотря на такие потенциальные артефакты, как измене
ние цвета, рассовмещение, размывание контуров изображения и искажение
(которые в совокупности приводят К относительно плохому представле
нию в L1 И L2 метриках). Решение проблемы, казалось бы, заключается
в отыскании метрики, которая настраивается на определенный тип ошибок,
появляющихся при формировании запроса. Это означает, что нам нужна
метрика, которая, в первую очередь, учитывает те отличия, которые OTMe
тит любой человек при сравнении изображений, и придает меньше веса
таким ошибкам, которые пользователь иrнорирует при распознавании. По
скольку «правильной» метрики для формирования запроса изображения не
существует, перед нами стоит задача конструирования такой метрики с ca
Moro нуля с учетом имеющеrося опыта. Вся остальная часть этоrо раздела
содержит описание вопросов, поднятых Якобсом при разработке упомяну
той метрики для запроса изображения.
5.2.1. Кратномасштабный метод
Нам требуется сконструировать метрику изображения, которая быстро
вычисляется, требует мало места для хранения каждоrо из входящих в базу
64
Т7ава 5
данных изображений и действет HaMHoro эффективнее, чем Ll и L2 метри
КИ, при распознавании целей для неточных запросов. По ряду причин Якобс
и ero коллеrи предположили, что двумерное вейвлет разложение послужит
хорошим фундаментом для конструирования такой метрики:
. Вейвлет разложения с небольшим количеством коэффициентов дают
хорошее приближение. Как rоворилось в третьей rлаве, это свой
ство уже использовалось ранее при сжатии изображения с потерями.
Как правило, при сжатии используются только вейвлет коэффициенты,
имеющие наибольшие величины.
. Вейвлет разложения можно использовать для извлечения и кодирова
ния информации о контурах изображения[79]. Контуры изображения,
вероятно, можно отнести к основным характеристикам изображения
запроса, в случае если последнее нарисовано пользователем.
. Коэффициенты вейвлет разложения обеспечивают информацию, не за
висящую от разрешения исходноrо изображения. Следовательно, схема
на основе вейвлетов обеспечивает эффективное разделение разрешения
целевоrо изображения и запроса.
. Вейвлет разложение вычисляется леrко и быстро, проrрамма дЛЯ BЫ
полнения разложения очень короткая, а время ее выполнения линейно
зависит от размера изображения.
5.2.2. Компоненты метрики
Хотя выбор в пользу метода на основе вейвлетов мы уже сделали,
остается несколько вопросов, которые все же нужно уточнить:
1. Цветовое пространство. Нам необходимо выбрать цветовое простран
ство, чтобы представлять в нем изображения и выполнять разложение.
(Этот же вопрос возникает и при использовании Ll и L2 метрик.)
Якобс с соавторами опробовали несколько различных цветовых про
странств: RGB, HSV u YIQ. В итоrе для их данных самым эффективным
из этих трех оказалось пространство YIQ.
2. Тип вейвлетов. Быстрее всех вычисляются, а также проще всех pea
лизуются вейвлеты Хаара. Кроме Toro, запросы, нарисованные самим
пользователем, имеют склонность к большим однородно окрашенным
участкам, которые хорошо представлять таким базисом. Недостатком
базиса Хаара в случае сжатия с потерями является то, что он стремит
ся порождать блочные артефакты изображения при высоких скоростях
5.2. Разработка ,нетрики д.7Я формирования запроса изображения 65
сжатия. Но поскольку в случае формирования запроса изображения pe
зультаты разложения никоrда не видны, эти артефакты не должны нас
волновать.
3. Тип разло,женuя. Нам требуется выбрать стандартное или HeCTaHдapT
ное двумерное вейвлет разложение (смотрите разделы 3.1 и 3.2). Функ
ции не стандартно построенноrо базиса Хаара являются квадратными,
тоrда как функции стандартно построенноrо базиса прямоуrольны
ми. Таким образом, следует ожидать, что не стандартный базис лучше
подойдет для распознавания тех элементов изображения, которые име
ют примерно одинаковую высоту и ширину, а стандартный базис будет
наиболее подходящим для элементов изображений с выраженно Bep
тикальными или rоризонтальными линиями или какими то друrими
элементами прямоуrольности.
4. Усеченuе. Для изображения форматом 128 х 128 каждому цветовому
каналу I соответствует последовательность из 1282 == 16384 различ
ных вейвлет коэффициентов. Вместо использования в метрике всей
последовательности было бы предпочтительнее произвести ее усече
ние и оставить в ней только коэффициенты с наибольшими значениями.
Выполнение TaKoro усечения способствует как ускорению поиска, так
и уменьшению объема памяти для хранения базы данных. Удивительно,
но, кроме Bcero прочеrо, усечение коэффициентов, по всей видимости,
еще и повышает способность метрики к распознаванию, возможно,
потому что оно позволяет метрике рассматривать только самые важ
ные детали и пренебреrать всеми несоответствиями в случае мелких
деталей изображения, которые пользователь, скорее Bcero, не cMor бы
точно воссоздать. Как сообщают Якобс и соавторы, для нарисованных
запросов лучшим вариантом стало хранение 60 коэффициентов с caMЫ
ми большими значениями, а для сканированных запросов число таких
коэффициентов равно 40.
5. Квантование. Подобно усечению, квантование каждоrо вейвлет ко
эффициента служит для достижения ряда целей: ускорения поиска,
уменьшения объема памяти, а также реальноrо повышения способ
ности метрики к распознаванию. Квантованные коэффициенты coxpa
няют совсем HeMHoro или совсем никаких данных о точных значе
ниях, соответствующих основным деталей изображений; однако, по
видимому, повышению распознавательной способности при запраши
вании изображения способствует вовсе не эта информация о точных
значениях деталей, а только лишь само присутствие или отсутствие
lт. е. компоненте цветовоrо пространства. ПРlL\t. ред.
66
Т7ава 5
таких деталей. Квантование каждоrо значащеrо коэффициента до двух
уровней уровня +1, представляющеrо коэффициенты с большими
положительными значениями, и уровня 1, представляющеrо коэф
фициенты с большими отрицательными значениями, срабатывает
удивительно хорошо. Подобная простая схема классификации также
предусматривает очень быстрый алrоритм сравнения, о чем пойдет
речь уже в разделе 5.3.
6. Нормированuе. Нормирование функций базиса вейвлетов соотносится
с величиной вычисленных вейвлет коэффициентов: коrда амплитуда
функции базиса возрастает, величина соответствующеrо этой базисной
функции коэффициента уменьшается (смотрите раздел 2.3). Исполь
зование нормировочноrо множителя, делающее все вейвлеты взаимно
ортонормированными, в результате приводит к подчеркиванию разли
чий, rлавным образом, при крупных масштабах.
5.2.3. Метрика формирования запроса изображения
Для Toro чтобы записать получившуюся метрику, нам следует ввести
некоторые обозначения. Прежде Bcero, доrоворимся, что Q и fl представ
ляют только один цветовой канал вейвлет разложения запроса и потенци
альных целевых изображений. Пусть Q[O, О] и fl[O, О] это коэффициенты
масштабирующих функций, соответствующие общему среднему значению
интенсивности этоrо цветовorо канала. Далее мы введем Q[i,j] и 5'[i,j],
представляющие [i, j] тые усеченные квантованные вейвлет коэффuцuен
ты Q и fl; эти значения MorYT равняться 1, О или +1. Для удобства при
мем Q[O, О] и 5'[0, О], которые не соответствуют ни одному из вейвлет ко
эффициентов, равными О.
Подходящую для запроса изображения метрику можно записать в виде
IIQ flll wo,oIQ[O,O] fl[O,O]1 + LЩ,jIQ[i,j] 5'[i,j]I.
i,j
который мы можем упростить несколькими способами.
Во первых, эта метрика будет не менее эффективной, если мы заме
ним разность между вейвлет коэффициентами IQ[i, j] 5'[i, j] I на Hepa
венство Q [i, j] CJ 5' [i, Л, [де выражение (а CJ Ь) рассматривают как 1,
если а CJ Ь, и как О в противном случае. Вычисление TaKoro выражения
в алrоритме происходит быстрее.
BO BTOpЫX, нам нужно сrруппировать слаrаемые так, чтобы экспери
ментальному определению подлежало только небольшое число весовых KO
эффициентов Wi,j, Сrpуппируем эти слаrаемые соrласно той шкале вейвле
5.2. Разработка ,нетрики д.7Я формирования запроса изображения 67
тов, которой они соответствуют, используя простую rруппирующую функ
цию bin( i, Л, описанную в разделе 5.3.
Наконец, чтобы наша метрика еще быстрее моrла оценивать большое
число различных целевых изображений, мы будем рассматривать только те
слаrаемые, в которых вейвлет коэффициент запроса Q[i,j] не равен нулю.
Потенциальное преимущество TaKoro подхода в том, что не детализирован
ный запрос достаточно близко сопоставляется весьма детализированному
целевому изображению, однако детализированный запрос не поставится
в соответствие целевому изображению, в котором отсутствует указанная
деталь. Якобс и др. посчитали, что подобная асимметрия должна лучше
ухватывать форму большинства из нарисованных запросов. (Заметим, что
последняя модификация технически дисквалифицирует эту «метрику» как
метрику в cTporoM смысле, поскольку, по определению, метрика является
симметричной. Тем не менее, за отсутствием более подходящеrо термина
мы все же будем употреблять слово метрика и далее до конца этой rлавы.)
Итак, окоичательная Lq метрика формирования запроса изображения
имеет следующий вид:
IIQ gllq == woIQ[O,O] g[O,O]1 +
L
Wbin(i,j) (Q[i,j] -1 g[i,j]).
i,j:Q[i,Лу<:О
(5.3)
Весовые коэффициенты w в уравнении (5.3) обеспечивают удобный
механизм настройки метрики на различные базы данных и типы формиро
вания запросов. Коэффициенты, использованные Якобсом и др., приведены
в разделе 5.3.
5.2.4. Быстрое вычисление метрики формирования запроса
изображения
При вычислении Lq метрики для базы данных изображений подсчет
числа совпадающuх коэффициентов Q и g происходит быстрее, чем под
счет числа несовпадающuх коэффициентов, т. к. соrласно нашим ожиданиям
подавляющее большинство хранимых в базе данных изображений не будет
иметь должноrо соответствия с изображением запросом. Поэтому сумму
в уравнении (5.3) удобнее переписать на основе оператора «равенства» (а ==
== Ь), который принимает значение 1, Korдa а == Ь, и обращается в О в про
тинном случае. При использовании этоrо оператора суммирование
L Wbin(i,j)(Q[i,j] -1 g[i,j])
i,j:Q[i,j]y<:O
68
Т7ава 5
в уравнении (5.3) можно переписать как
L Wbin(i,j) L WЫn(i,j)(Q[i,Л == g[i,Л).
i,j:Q[i,j]y<:O i,j:Q [i,j]y<:O
Поскольку первая сумма в этом выражении не зависит от fl, мы можем
пренебречь ею в интересах ранжирования различных целевых изображений.
Таким образом, нам достаточно вычислить выражение
woIQ[O,O] fl[O,O]1 L Wbin(i,j) (Q[i,j] == g[i,Л). (5.4)
i,j:Q[i,j]y<:O
Это выражение представляет ничто иное, как взвешенную сумму разностей
средних значений цвета между Q и fl и число сохраненных вейвлет ко
эффициентов для fl, индексы и знаки которых соответствуют индексам
и знакам коэффициентов изображения запроса.
5.3. Алrоритм формирования запроса изображения
Окончательный алrоритм представляет собой реализацию метрики,
имеющей вид уравнения (5.4), в приложении к задаче нахождения заданно
[о изображения запроса в большой базе данных изображений. Сложность
алrоритма по числу изображений, входящих в базу данных, является линей
ной.
Изъясняясь на более формальном языке, этот алrоритм можно описать
следующим образом. На предварительном этапе выполняется стандартное
двумерное вейвлет разложение (см. раздел 3.1) каждоrо изображения в базе
данных и сохраняется только общее среднее значение цвета, а также индек
сы и знаки, принадлежащие m коэффициентам с наибольшими значениями.
Затем для всех изображений базы данных эти индексы объединяются в одну
структуру данных, которая оптимизирует поиск. Далее выполняется такое
же вейвлет разложение для каждоrо изображения запроса и вновь отбрасы
вается вся информация, за исключением среднеrо значения цвета и m самых
больших коэффициентов. Затем путем вычисления уравнения (5.4) Haxo
дится количественный показатель для каждоrо целевоrо изображения fl.
Остальная часть раздела 5.3 посвящена более подробному описанию этоrо
алrоритма.
5.3.1. Предварительный этап
Предварительный этап сводит каждое изображение базы данных до
сиrнатуры, как показано на рисунке 5.1. Стандартное двумерное вейвлет
5.3. Алzорит,н форнирования запроса изображения
69
разложение изображения кодируется очень просто. Как описывалось в раз
деле 3.1, такое разложение включает в себя одномерное разложение каждой
строки изображения и последующее разложение каждоrо столбца получив
шеrося изображения.
. .
. .
.
.
. .
. .
. .
(а)
(6)
(в)
(r)
Рис. 5.1. Предварительный этап: картину Ван rora «Ирисы» (а) сначала подверrают
разложению на вейвлет коэффициенты (б). Затем производится усечение всех коэф
фициентов, за исключением тех, что имеют самые большие значения (в). Наконец,
выполняется квантование оставшихся коэффициентов (т). Вейвлет коэффициенты
изображены на рисунке белыми и черными кружками. Цвет кружка (черный или
белый) обозначает знак коэффициента (плюс или минус), который он представляет.
Ето радиус характеризует величину коэффициента.
После процесса разложения элемент ,'1[0, О] пропорционален среднему
цвету Bcero изображения, а друrие принадлежащие ,'1 элементы содержат
вейвлет коэффициенты. (Этих коэффициентов достаточно и для воссозда
ния ориrинальноrо изображения, хотя здесь нам это не понадобится.)
Наконец, мы сохраняем только ,'1[0, О], а также индексы и знаки m
самых больших вейвлет коэффициентов из g. Чтобы оптимизировать про
цесс поиска, оставленные m вейвлет коэффициентов для всех изображений
в базе данных объединяем в набор из шести массивов, называемых Maccи
вшwu поиска, по одному массиву для каждой комбинации знака (плюса или
минуса) и цветовоrо канала (например, У, 1 и Q).
Допустим, к примеру, что 8't это массив «положительноrо» поис
ка для цветовоrо канала с. Каждый элемент 8't [i, j] этоrо массива coдep
жит перечень всех изображений ,'1, имеющих большие положительные вей
влет коэффициенты g[i, j] в цветовом канале с. По аналоrии, каждый эле
мент 8 [i, j] массива «отрицательноrо» поиска указывает на перечень изоб
ражений с большими отрицательными коэффициентами в с. Шесть таких
массивов применяются, чтобы ускорить поиск KOHKpeTHoro изображения
запроса, о чем мы поrоворим уже в следующем подразделе.
70
Т7ава 5
5.3.2. Формирование запроса
Этап формирования запроса является прямым. Для данноrо изображе
ния запроса Q мы выполняем вейвлет разложение из предыдущеrо разде
ла. Снова сохраним только общий средний цвет, а также индексы и зна
ки m самых больших коэффициентов в каждом цветовом канале. Сиrнатура
изображения запроса сравнивается с сиrнатурами в базе данных, что иллю
стрируется рисунком 5.2.
! !
..
/
<! : "'
v' <!
"''''
<! "''''
.
v'
<!
Рис. 5.2. Сравнение сиrнатуры запроса с сиrнатурой целевorо изображения.
Чтобы вычислить количественный показатель, мы рассматриваем каж
дый цветовой канал с. Сначала вычисляем разность между средней ин
тенсивностью запроса QC[O, О] в этом канале и средними интенсивностями
изображений из базы данных. Далее, для каждоrо из m оставленных HeHY
левых вейвлет коэффициентов QC[i, j] мы про смотрим перечень изображе
ний из базы данных, у которых коэффициент с тем же номером является
наибольшим по значению и имеет тот же знак, а затем откорректируем
количественные показатели этих изображений следующим образом:
5.3. Алzорит,н форнирования запроса изображения
71
function ScoreQuery(Q : array [О... r 1, О... r 1] of Color; m :
integer)
Decomposelmage(Q)
scores[i] О for аН i
for each co10r channel с do
for each database image fl do
scores[index(fl)]+ == шС[[О] * IQC[O,O] flC[O,O]1
end for
Q TruncateCoefficiens(Q,m)
for each nonzero coefficient QC[i,j] do
if QC[i, j] > О then
list 8+ C[i,j]
end if
for each e1ement l of list do
scores[index(l)] == ш С [bin( i, Л]
end for
end for
end for
return scores
end function.
Функция bin( i, j) описывает способ rруппировки различных коэффи
циентов в небольшое число множеств, каждое из которых взвешивается
с постоянной ш[Ь]. Якобс и др. обсуждают статистический подход нахожде
ния весов на основе некоторых модельных данных. Размер их модельноrо
набора позволил им определить 18 весовых коэффициентов: по 6 на ЦBeTO
вой канал. При реализации они используют функцию
bin(i,j) == min{max{level(i), level(j)}, 5},
[де level(i) == llog2 iJ. В таблице 5.1 приведены представленные Якобсом
и соавторами весовые коэффициенты, настраивающиеся на свои базы дaH
ных изображений при помощи цветовоrо пространства У 1 Q и стандартноrо
разложения Хаара. (Коэффициенты масштабирующих функций являются
вещественными числами в диапазоне от О до 1, поэтому разницы между
ними будут меньше, чем разницы между соответствующими усеченными
квантованными вейвлет коэффициентами.) Таким образом, весовые коэф
фициенты ш[О] масштабирующих функций имеют относительно большие
величины, потому что они, в общем случае, умножаются на меньшие вели
чины.
В качестве заключительноrо этапа алrоритм формирования запроса
изображения про сматривает список полученных количественных коэффи
72
Т7ава 5
Таблица 5.1. Весовые коэффициенты, используемые Якобсом и др. В построенной
ими кратномасштабной метрике формирования запроса изображения
Нарисованные запросы Сканированные запросы
Ь wY[b] wI[b] wQ[b] wY[b] wI[b] wQ[b]
О 4,04 15,14 22,62 5,00 19,21 34,37
1 О, 78 0,92 0,40 0,83 1,26 0,36
2 0,46 0,53 0,63 1,01 0,44 0,45
3 0,42 0,26 0,25 0,52 0,53 0,14
4 0,41 0,14 0,15 0,47 0,28 0,18
5 0,32 0,07 0,38 0,30 0,14 0,27
циентов, которые MorYT быть как положительными, так и отрицательны
ми. Самые маленькие количественные коэффициенты считаются наиболее
близкими соответствиями. Используя алrоритм отбора из [97], можно найти
двадцать наиболее точных соответствий линейно по времени.
5.4. Примеры формирования запросов изображений
Реализация алrоритма формирования запроса изображения демонстри
руется на цветной иллюстрации 5. Сперва пользователь рисует запрос на
большом прямоуrольном участке слева от окна приложения. Как только
изображение запрос [отово, он нажимает клавишу «Match». Тоrда систе
ма тестирует все изображения из базы данных на предмет этоrо запроса
и отображает в маленьких окнах справа двадцать наиболее близких цe
левых изображений. (Целевое изображение, являющееся самым близким,
выводится вверху слева, правее отображается изображение со вторым по
казателем соответствия и так далее, по рядам.)
Для удобства пользователь может рисовать на «холсте» любоrо форма
та. Эта информация не используется при поиске соответствующеrо целевоrо
изображения. Вместо этоrо происходит внутреннее изменение масштаба Ha
рисованноrо запроса до квадратноrо формата, и этот запрос ищется в базе
данных, в которой на предварительном этапе все изображения также пре
терпевают изменения в масштабе.
На цветной иллюстрации 6(а) показан пример нарисованноrо запро
са изображения, приведены Lq показатели соответствия предполаrаемоrо
целевorо изображения из баз данных, содержащих 1093 и 20558 изображе
ний, соответственно. Вместо рисования запроса, пользователь может TaK
же выбрать любое из выведенных целевых изображений для использова
5.4. ПрtLнеры формирования запросов изображений
73
ния В качестве текущеrо запроса или использовать любое из хранящихея
изображений в качестве запроса. Пример использования сканированноrо
с плохим качеством изображения для запроса представлен на цветной пл
люстрации 6(б), снова приведены Lq показатели соответствия для двух баз
данных.
Эффективность Lq метрики наrлядно демонстрируется rистоrpаммой
на рис. 5.3. Алrоритм формирования запроса изображения при пере
менной разрешающей способности последовательно отыскивает целевые
изображения rораздо чаще, чем три друrие метрики, основанные на по
иске по содержанию содержания: Ll метрика для изображений форма
та 128 х 128, Ll метрика для низкоразрешенных изображений формата 8 х 8
и цветовая rистоrрамма, соответствующая методу, описанному Якобсом
и др.
]00 . L Ч
80 L] 8х8
('j
х . L 1 128х128
(j)
с: 60
u
>-, . rистоrрамма
.д
:I: 40
(j)
с:
(j)
f-o
U
Рис. 5.3. Для каждоrо типа запроса (сканированноrо, нарисованноrо, нарисованноrо
по памяти, дискретно искаженноrо ориrинала) столбики rистоrраммы показывают,
какой про цент запросов привел к получению BepHoro целевorо изображения, KO
торое каждая из метрик искала среди одноrо про цента наиболее соответствующих
изображений из базы данных, содержащей 1093 изображений.
Из рис. 5.4 видно, что Lq метрика требует значительно меньше Bpe
мени для вычисления, чем прочие метрики формирования запроса изобра
жения. На деле, время поиска столь мало (меньше, чем 1/2 секунды для
базы данных в 20000 изображений), что формирование запроса по методу
Якобса и др. поддерживает «интерактивный» режим, в котором 20 целевых
изображений с самыми высокими показателями соответствия обновляют
ся, как только пользователь делает паузу на полсекунды и более. Цветная
иллюстрация 7 демонстрирует последовательное формирование интерак
74
Т7ава 5
тивноrо запроса с указанием фактическоrо времени, за которое был сделан
моментальный снимок, и Lq paHra предполаrаемоrо на тот момент времени
целевоrо изображения в двух различных базах данных.
47,46 893
t t
11 11
. L q
L 1 8x8
3 D
ci
:I: . L 1 128х128
>-,
(j) .
u rистоrрамма
tJ:;
:s
(j)
о..
o::i
О п 1093 п 20 558
Рис. 5.4. Среднее время (в секундах) нахождения соответствия одному изображе
нию запросу в базах данных с 1093 и 20558 изображениями при использовании
различных метрик.
Формируя запрос в интерактивном режиме, пользователь, как правило,
успевает оформить в эскиз всю известную ему информацию за минуту или
даже менее, независимо от Toro, смотрит ли он на свернутое в пиктоrрамму
изображение или рисует по памяти. В большинстве случаев запрос удовле
творяется за короткое время. Если же целевое изображение не находится по
запросу в течение минуты, то пользователь попробует внести несколько дe
талей науrад, что иноrда действительно помоrает. Если и такая «стратеrия»
не приведет к результату, пользователь просто откажется от дальнейших по
пыток и, вероятно, обратится к друrому методу поиска изображения или же
будет использовать метод формирования запроса на основе содержания в
сочетании с еще каким нибудь методом, к примеру, поиском по ключевому
слову.
Рисуя запрос в интерактивном режиме, пользователь получает два пре
имущества. Во первых, время поиска изображения, как правило, сокращает
ся, поскольку в этом случае пользователь рисует изображение одновременно
с протеканием поиска целевоrо объекта, вместо Toro, чтобы представить за
конченный, с ero точки зрения, эскиз запроса. BO BTOpЫX, интерактивный
режим может «научить» пользователя более эффективно отыскивать изоб
5.5. Рааuиренuя
75
ражения, ведь такой режим всеrда обеспечивает обратную связь, позволя
ющую судить об относительной эффективности незакоиченноrо рисуемоrо
запроса на данный момент.
5.5. Расширения
Описанный нами алrоритм работает с поразительной быстротой, Tpe
бует хранения небольшоrо количества данных о каждом целевом изображе
нии и отличается замечательной эффективностью. К тому же ero довольно
просто понять и реализовать. Наконец, ero параметры можно настраивать
для заданной базы данных или типа изображения запроса.
Ниже приводятся еще несколько способов, позволяющих расширить
алrоритм формирования запроса изображения.
. Фор)',щтное соотношенuе. В настоящее время пользователь может сам
выбирать формат cBoero запроса; однако в самом поиске формат, как
таковой, роли не иrрает. В метрику формирования запроса нужно непо
средственно добавить дополнительное слаrаемое, отвечающее за иден
тичность формата. Вес этоrо слаrаемоrо определялся бы одновременно
с друrими весовыми коэффициентами экспериментальным путем.
. Пространства на перцепцuонной основе (perceptually based spaces).
Интересно было бы попробовать использовать какое нибудь перцеп
ционно однородное цветовое пространство, например, CIE LUV или
TekНyc [38], чтобы посмотреть, повышает ли оно эффективность Ha
шей метрики. Возможно, это поможет вычислять разницы на лоrариф
мической шкале яркостей, которая более близка реальному восприятию
яркости [57].
. Кластеры uзображенuй. Изображения в большой базе данных можно
кластеризовать (разбить на rpуппы) на основе их схожести относитель
но данной метрики формирования запроса. К примеру, если в качестве
запроса к большой базе данных выступает портрет, то в качестве цe
левых изображений будут отобраны исключительно одни портреты.
А использование изображения какой нибудь планеты позволит найти
изображение и друrих интересующих пользователя планет. Было бы
интересно про извести подобную статистическую кластеризацию базы
данных, а затем продемонстрировать пользователю несколько xapaK
терных изображений, взятых из caMoro центра кластера. Последние
моrли бы использоваться в качестве запросных идентификаторов.
. Составная метрика. Экспериментирование с кратномасштабными си
стемами формирования запроса изображения при переменном разре
76
Т7ава 5
шением показывает, что к целевому изображению приведет любой xo
роший запрос, независимо от использованноrо цветовоrо пространства
и (стандартноrо или нестандартноrо) метода разложения. Тем не Me
нее, выявляемые неверные соответствия в этих различных простран
ствах очень отличаются друr от друrа. Следовательно, представляется
возможным разработать более эффективный метод путем совмещения
результатов поиска, произведенноrо в различных цветовых простран
ствах и при разных типах разложения, возможно, взяв среднее всех
показателей соответствия в различных метриках (или худший из пока
зателей) в качестве показателя полученноrо общей метрикой.
. Аффuнное преобразованuе u частuчные запросы. Весьма интересным
(и более сложным) направлением будущих изысканий станет исследо
вание методов выполнения общих аффинных преобразований изобра
жения запроса или методов поиска частичных запросов. «Смещаемые
преобразования», описанные Симоичелли и др. в [115], допускающие
кратномасштабные преобразования с сохранением сдвиrа, вращения
и масштаба, MorYT быть весьма полезны в этом случае. В качестве
друrой идеи в отношении задания частичных запросов можно paCCMaT
ривать использование альфа канала для задания тех участков изобра
жения запроса и целевых изображений, по которым должна быть BЫ
числена Lq метрика.
. Вuдеозапросы. Кратномасштабный алrоритм формирования запроса
изображения может быть удачно расширен до задачи поиска заданно
[о видеокадра в видеопоследовательности. Самым простым решением
было бы рассмотрение каждоrо видеокадра как отдельноrо изображе
ния в базе данных инепосредственное применение метода формирова
ния запроса. Однако есть и более интересное решение, использующее
трехмерное кратномасштабное разложение видеопоследовательности,
быть может, в сочетании с какой либо формой компенсации движе
ния, с тем чтобы извлечь наибольшее преимущество из коrерентности
видеокадров.
Часть 11
КРИВЫЕ
Т'ЛАВА 6
Кривые последовательноrо деления
1. РавНОJиерное последовательное деленuе 2. Неравномерное пo
следовательное деленuе 2. Оценочные маски 4. Вло,женные
пространства u уточняемые масштабирующuе функции
Для мноrих случаев кусочно постоянные пространства, лежащие
в основе вейвлет анализа Хаара, не являются достаточно общими про
странствами. Например, функции, рассматриваемые при построении кри
вых и поверхностей, должны быть по меньшей мере непрерывными, кроме
Toro, они часто должны быть дифференцируемыми или дважды диффе
ренцируемыми. Следовательно, в наше обсуждение необходимо включить
более общие типы функциональных пространств. Это обобщение, OДHa
ко, следует произвести весьма осторожно, поскольку лишь очень немноrие
функциональные пространства допускают иерархические разложения.
В этой rлаве, равно как и в следующей, мы по кажем , что иерархиче
скому разложению можно подверrнуть только те функции, которые MOryT
быть получены простым процессом, известным под названием рекурсивное
последовательное деленuе (recursive sиЬdivisiоп) или, если кратко, просто
последовательное деленuе (subdivisioп). Хотя определить все функции по
добным образом не представляется возможным, последовательное деление
можно применять для получения удивительно IIIирокоrо кpyra функций,
включая и кусочно постоянные функции, которые мы рассматривали в KOH
тексте вейвлетов Хаара. Последовательное деление может быть исполь
зовано для получения равномерных и неравномерных В сплайнов, а TaK
же функций, не имеющих аналитическоrо выражения, например, вейвлеты,
сделавшие знаменитой Инrpид Добеши. В настоящей rлаве мы сформули
руем основные понятия последовательноrо деления для линейных функций
и параметрических кривых. Седьмая rлава, переняв эстафету, опишет, каким
образом эти функции можно подверrнуть иерархическому разложению.
[луб ина связи последовательноrо деления и вейвлетов наводит на
мысль, что важность методов последовательноrо деления значительно BЫ
растет в ближайшем будущем. К сожалению, к моменту написания книrи
нам не была известна ни одна работа о практических аспектах последо
вательноrо деления, поэтому мы попытались развить подобную трактовку
80
Т7ава 6
в этой rлаве. В результате, некоторые из представленных здесь материа
лов не являются центральными в развитии вейвлетов и приводятся здесь
скорее ради полноты описания. В частности, раздел 6.3 о точном вычисле
нии функций, полученных посредством последовательноrо деления, coдep
жит информацию, применимую для создания точных отображений кривых
и поверхностей последовательноrо деления.
6.1. Равномерное последовательное деление
Основная идея рекурсивноrо последовательноrо деление заключается
в построении функции путем неоднократноrо уточнения исходной кусоч
но линейной функции fO(x) с целью получения последовательности все
более детализированных функций fl(X), Р(Х), . .., сходящейся к предель
ной функции
ЛХ) 1im fj(x).
J OO
Первая схема последовательноrо деления, изображенная на рис. 6.1, была
введена Чайкиным [11] в 1974 [оду. Подобно мноrим друrим схемам по
следовательноrо деления, аЛ20рuт 'W Чайкuна (Chaikiп s algorithт) можно
рассматривать как процедуру среза У20лков (corпer cuttiпg), применяемую
для сrлаживания исходной ломаной до конечной кривой.
Более конкретно: пусть fO(x) будет кусочно линейной функцией с Bep
шинами в целых числах. В общем случае функция jЗ(х) будет кусочно ли
нейной функцией с вершинами в дuадuческuх точках (dyadic poiпts) i/2 j .
Для большинства схем, включая алrоритм Чайкина, значения р (х) в ее
вершинах вычисляются очень просто следующим образом:
fj (i/2j) L rkfj l ((i + k)/2 j ) .
k
(6.1)
Последовательность r (..., r 1, ro, rl, . . .) называется усредняющей
маской (averagiпg тask) схемы. Для алrоритма Чайкина усредняющая Mac
ка равна r == (ro, rl) == (1, 1). Такую схему называют равномерной cxe
'Wой последоватеЛЬН020 деленuя (uпiforт subdivisioп scheтe), потому что
одна и та же маска используется повсюду вдоль кривой (т. е. r не зави
сит от i), а также стацuонарной схе 'Wой (statioпary scheтe), потому что одна
и та же маска используется на каждой итерации последовательноrо деления
(т. е. r не зависит от j). О неравномерных схемах мы поrоворим в следую
щем разделе; что касается не стационарных схем, то о них известно очень
мало.
6.1. Равно.нерное последовате.7ьное де.7ение
81
0.8
"о
(а)
10 00 10
(6)
08
\1\
0.2
10 Ъ 10
(r)
0.8
02
00
(в)
Рис. 6.1. Алrоритм Чайкина для модельной функции: исходная функция fO(x) (а);
функция fl(X) (б); функция f2(x) (в); конечная функция f(x) (т).
Простой способ реализации рекурсивноrо последовательноrо деле
ния состоит в представлении каждой функции р(х) через набор значе
ний (. . . , d 1, СЪ, с{ , . . .), которые эта функция принимает в своих вершинах,
причем с; == jj(i/2j). Заметим, что значения jj l(x), входящие в ypaBHe
ние (6.1) для определения jj(x), это значения в вершинах (коrда i + k
четно) и значения в средних точках (коrда i + k нечетно). Чтобы упро
стить выполнение последовательноrо деления, удобно разделить вычисле
ние уравнения (6.1) на два этапа: этап разбuвкu (splittiпg step), на котором
вводятся средние точки, и этап усредненuя (averagiпg step) , на котором
вычисляются взвешенные средние. Все схемы последовательноrо деления
имеют одинаковый этап разбивки; они различаются только этапом ycpeДHe
ния.
На этапе разбивки вычисляются вспомоrательные последовательно
О' О' О'
сти (. . . , СЗ l' СЪ, с{ , . . .), для чеrо вводятся средние точки, как показано на
рис. 6.2. На языке формул этот этап можно записать так:
oj i l
C 2i : == r;;
oj 1/2 ( j l j l )
C 2j + 1 :== c i + С Н1 .
82
Т7ава 6
в результате этоrо определения == fj 1(i/2j) и, таким образом, этап
усреднения это просто выражение
С; == L Tk +k'
k
} 1
С
1
о)
С 4
Рис. 6.2. Этап разбивки преобразует последовательность вершин в последователь
ность вершин и средних точек
На практике мы вряд ли столкнемся с бесконечными последовательно
стями, поэтому нам следует ввести rраничные условия. Для этоrо имеется
следующий распространенный прием оrраничить суммирование по k до
ненулевых элементов последовательности т и вычислить только те значе
. О.
ния С;, для которых уже вычислены все необходимые значения С;. Однако
более принципиальным методом определения rраничных условий является
метод с использованием HepaBHoMepHoro последовательноrо деления, опи
санный в разделе 6.2.
Как все друrие схемы последовательноrо деления, алrоритм Чайкина
применим к параметрическим кривым и функциям. Для этоrо нужно просто
применить этапы разбивки и усреднения независимо к x и у координатам
исходной ломаной. Эта процедура иллюстрируется рисунком 6.3. Верши
ны исходной ломаной называются контрольнымu точкамu (coпtrol poiпts) ,
а сама ломаная называется контрольной ломаной (coпtrol polygoп).
Пока вопрос о способе определения таких свойств, как непрерывность
и дифференцируемость функций, порождаемых произвольной маской Т, не
имеет очевидноrо ответа. Ризенфельду, однако, удалось в 1975 [оду пока
зать, что кривые, получаемые по алrоритму Чайкина, фактически являют
ся равномерными В сплайнами [103]. Несколько позже Лейн и Ризенфельд
показали, что алrоритм Чайкина можно обобщить для получения paBHOMep
ных В сплайнов любой степени, для чеrо нужно воспользоваться масками,
элементы которых взяты из треуrольника Паскаля [69]. Они, в частности,
показали, что В сплайны степени n + 1 образуются усредняющей маской
6.1. Равно.нерное последовате.7ьное де.7ение
83
: '
00 02 0.4 0.6 0.8
00 0.2 0.4 0.6 0.8
(а)
(6)
'l3 : 'l:J'
о- 'о О '(1
00 0.2 0.4 0.6 0.8
ъ 0.2 0.4 0.6 08
(в)
(r)
Рис. 6.3. Алrоритм Чайкина для замкнутой параметрической кривой: (а) исходная
кривая iO(t); (б) кривая il(t); (в) кривая i 2 t; (Т) конечная кривая iO(t) :=' iOO(t).
с элементами
2 1п ( ( ), С), ..., ( )) .
Два особенно важных в приложениях компьютерной rрафики случая
касаются линейных В сплайнов, определяемых едuнuчной маской (ideпtity
тask) Т =' (то) =' (1), и кубических В сплайнов, определяемых усредняю
щей маской Т (Т 1, ТО, Т1) (1, 2,1). Заметим, что единичная маска,
используемая для линейных В сплайнов, оставляет вершины на месте без
изменений, что является правильным, поскольку выполнение только этапа
разбивки приводит к кусочно линейной интерполяции.
Не все маски приводят к обычным, хорошо известным типам функций.
Так, усредняющая маска (то, Т1) =' (1 + yiЗ, 1 VЗ) rенерирует кривые,
которые похожи на фрактальные в том, что они всюду недифференцируемы,
как видно из рис. 6.4. Возможно, в свете упомянутоrо факта полезность Ta
кой схемы покажется несколько сомнительной, однако в следующей rлаве,
в ходе обсуждения базиса вейвлетов, сконструированноrо Добеши с ис
пользованием последовательноrо деления [24], мы вернемся именно к этой
маске.
84
Т7ава 6
о
о
4
6
10
00
4
6
10
(а)
(6)
Рис. 6.4. Схема последовательноrо деления Добеши: (а) исходная функция fO(x);
(б) конечная функция f(x).
Упомянутые нами схемы, за исключением последовательноrо деле
ния для линейных В сплайнов, называют аппроксuмuрующuмu схемшwu
(approxiтatiпg subdivisioп scheтes), т. к. конечная функция, как правило, не
интерполирует ни одну из исходных вершин. Получать uнтерполuрующuе
схе.мы (iпterpolatiпg subdivisioп schemes) можно изменяя этап усреднения
так, чтобы однажды вычисленная величина уже никоrда не изменялась при
локальном усреднении. Это сопровождается прямым изменением вычисле
ний:
. { если z четно
с; rk +k если i нечетно.
Первую rладкую интерполирующую схему ввели Дин, Левин и [реrори [32]
(этот алrоритм мы будем называть DLG схе.мойl). Усредняющая маска для
DLG схемы (r 2, r 1, ro, rl, r2) 116 ( 2, 5,10, 5, 2). Пример образования
параметрической кривой по DLG cxeMe показан на рис. 6.5.
6.2. Неравномерное последовательное деление
Как уже rоворилось, описанные в предыдущем разделе схемы называ
ются равномерными или инвариантными относительно сдвиrа, потому что
в них всюду на кривой используется одна и та же маска. В следующих rлавах
мы увидим, что для некоторых приложений более естественным является
1 Сокращение составлено по первым буквам фамилий создателей алrоритма Дин (Dyn),
Левин (Levin) и rреrори (Gregory). ПРlL\t. пер.
6.2. Неравно.нерное последовательное деление
o:f 0.8
0.6 . 0.6
0.4 . 0.4
02r 0.2
00 ,
00 0.2 0.4 0.6 0.8 0.2 0.4 0.6 0.8 1
(а) (6)
85
Рис. 6.5. Интерполирующая DLG cxeMa для замкнутой параметрической кривой:
(а) контрольная ломаная "/(t); (б) конечная кривая i(t).
допущение, что маска меняется вдоль кривой. Например, при редактирова
нии кривой с помощью В сплайнов в восьмой rлаве используются HepaBHO
мерные маски для получения кубических В сплайнов, интерполирующих
первую и последнюю точки незамкнутой контрольной ломаной.
Для неравномерной схемы этап усреднения имеет следующий общий
вид:
С; == L T ,k +k
k
Замечание. Собственно rоворя, уравнение (6.2) описывает HepaBHO
мерную нестацuонарную схему, потому что т зависит и от i, и от j. Но
поскольку о не стационарном последовательном делении практически
ничеrо неизвестно, мы будем считать эту схему стационарной, хотя бы
в том смысле, что существует некое такое критическое значение j*,
что для j > j* элементы т не зависят от j. (Если KTO TO сочтет такой
подход запутанным, он, конечно, может просто строить иллюзии о том,
что не стационарные схемы хорошо поняты.)
(6.2).
Прежде чем продолжить разработку последовательноrо деления, мы
можем заранее избавить себя от нескольких rромоздких уравнений, для че
[о представим уравнение (6.2) в более компактной форме как произведение
матриц. Если мы обозначим одностолбцовые матрицы, i тые строки KOTO
. о . . о .
рых содержат С; и С;, как с ] и c J , соответственно, а матрицу, (i, k ) тый
элемент которой равен T ,k' как Rj, то уравнение (6.2) примет вид
c j == Rj j
,
86
Т7ава 6
rдe i ая строка матрицы Rj представляет собой маску, используемую для
вычисления i Toro элемента одностолбцовой матрицы c j . Таким образом,
схема paBHoMepHoro последовательноrо деления это схема, в которой
строки матрицы Rj являются сдвинутыми версиями друr друrа. К при
меру, матрица усреднения для равномерных кубических В сплайнов имеет
форму
Rj 1
4
121
121
121
rдe пустые позиции обозначают нули.
Интерполирующие конечную точку В сплайны будут более подробно
рассмотрены в седьмой rлаве, а здесь мы на одном примере проиллюстри
руем неравномерное последовательное деление. Для описания кубических
В сплайнов, интерполирующих конечную точку, следует модифицировать
несколько первых и последних строк усредняющей матрицы из уравнения
(6.3) с учетом конечных точек. Можно воспользоваться боrатым теоретиче
ским материалом, касающимся HepaBHoMepHoro введения вершин В сплай
нов [35], и показать, что для j > 1 (j должно быть достаточно большим,
чтобы конечные точки не влияли друr на друrа) первые строки Rj имеют
следующий вид:
4
4
2 2
3 3 1
Rj 1 2 2
4 1 2 1
1 2 1
Строки в середине Rj представляют собой смещенные версии маски paBHO
MepHoro последовательноrо деления (1, 2, 1), а последние строки, в силу
симметрии, являются обращенными версиями первых строк.
Чуть более простая неравномерная схема, качественно схожая с ин
терполирующими конечную точку В сплайнами, была разработана Хоппом
и др. [60]. В этой схеме модифицируются только первая и последняя строки:
6.3. Оценочные ,наски
87
4
1 2 1
1 2 1
1 2 1
Rj 1
4
121
4
Конечные кривые, полученные такой схемой, сходны с интерполирующими
конечную точку В сплайнами в следующих отношениях:
. Вдали от своих концов конечные кривые являются кусочно кубически
ми и имеют две непрерывные производные.
. Конечные кривые интерполируют свои первые и последние контроль
ные точки.
. Конечные кривые являются касательными к первому и последнему
cerMeHTaM своих контрольных ломаных.
6.3. Оценочные маски
В начале rлавы уже упоминалось, что данный раздел включен в кни
ry С целью придания завершенности рассмотрению последовательноrо дe
ления. Поэтому читатели, интересующиеся исключительно применением
последовательноrо деления для получения вейвлетов, MorYT блаrополучно
пропустить этот раздел.
Работа с кривыми последовательноrо деления кажется довольно [po
моздкой, поскольку их, вообще rоворя, нельзя представить в аналитиче
ском виде. Из этоrо следует, что функция или кривая для произвольноrо
значения параметра не может быть вычислена простой подстановкой числа
в формулу. Дифференцирование функции или кривой также кажется затруд
нительным. В этом разделе мы покажем, что, и это достойно удивления,
функции, определяемые посредством последовательноrо деления, можно
точно вычислять на множестве точек произвольной плотности. Для выпол
нения вычисления берутся взвешенные средние значения в соответствии
с оценочной маской (evaluatioп тask) , характерной для процедуры после
довательноrо деления. Более Toro, если схема последовательноrо деления
rладкая, производные функции также можно точно вычислить, используя
проuзводные маски (derivative тasks).
88
Т7ава 6
Возможность вычислять точные значения функции и производные по
лез на при построении точных rpафиков кривых, но она еще более важна
для создания изображений поверхностей с точно формируемыми тенями.
Хотя до десятой rлавы мы не будем применять последовательное деление
к поверхностям, понятия, раскрывающиеся при рассмотрении оценочных
и производных масок, лучше Bcero определяются в более простом KOHTeK
сте функций и кривых.
Точное вычисление основано на том наблюдении, что вершины можно
подверrнуть последовательному делению. Для конкретности давайте pac
смотрим ситуацию для paBHoMepHoro последовательноrо деления кубиче
cKoro В сплайна, т. е. последовательноrо деления, oCHoBaHHoro на усредня
ющей маске (1, 2,1). Как показано на рисунке 6.6, вершина со ломаной
jO может быть естественным образом соотнесена с последовательностью
вершин [с 1 , с 2 ,...] ломаных [j1, j2,.. .]. После бесконечноrо числа последо
вательных делений СО достиrает cBoero предельноrо положения с ОО . Сейчас
мы покажем, что с ОО можно получить непосредственным вычислением пря
мо из начальных вершин.
о
1 2
с с
1°(х) /"') {и ( "')
Рис. 6.6. Применение последовательноrо деления к вершине со функции jO.
Ключевым положением при определении с ОО является то, что на каж
дом шаrе последовательноrо деления положение вершины c j и ее непосред
ственных соседей может быть определено по cj 1 и ее соседним верши
нам [30, 54]. В частности, если мы обозначим через c и , COOTBeTCTBeH
но, левоrо и правоrо соседа вершины с c j , то совместное действие этапов
разбивки и усреднения для кубических В сплайнов дает
. d 1 + cj 1
J
С 2
. cj 1 + 6cj 1 + d + . 1
CJ
8
j 1 + j 1
. С с+
d+ 2
6.3. Оценочные ,наски
89
в матричной форме эти уравнения принимают вид
[ ] t [ ] [ : ] .
L
(6.4 )
Такую матрицу L называют 'Wаmрuцей локальноzо последоваmельноzо деле
нuя (local subdivisioп тatrix) для данной схемы. Подобные матрицы имеют
все схемы, однако размерность этих матриц не Bcerдa бывает 3 х 3. Так, для
алrоритма Чайкина матрица локальноrо последовательноrо деления следу
ющая:
1 [ 31 ]
L 4 1 3 .
Для стационарных схем, таких, как алrоритм Чайкина и друrих, [eHe
рирующих равномерные В сплайны, на каждом этапе последовательноrо
деления используется одна и та же матрица последовательноrо деления.
Таким образом, вершины на уровне j можно вычислять путем непосред
cTBeHHoro J KpaTHoro умножения маленькоrо множества вершин на нулевом
уровне на матрицу локальноrо последовательноrо деления. Эта процедура
в любом случае приводит к пределу:
[ ] lim (L)j [ ]
с ОО J OO со
+ +
(6.5)
(Круrлые скобки, в которые заключена L в этом уравнении, использу
ются для Toro, чтобы подчеркнуть тот факт, что j в данном случае является
показателем степени, а не надстрочным индексом.)
Собственная структура квадратной матрицы управляет результатом,
получающимся в результате умножения вектора на все возрастающую CTe
пень матрицы [47] (смотрите краткий обзор в приложении А.5). Анализ
стационарных схем последовательноrо деления, таким образом, сводится
к анализу собственных значений и чисел матрицы локальноrо последова
тельноrо деления. Одной из причин столь малой осведомленности о HeCTa
ционарных схемах служит то, что в случае зависимости матриц локальноrо
последовательноrо деления от j мы не можем прибеrнуть к какому либо
аналитическому инструменту, поскольку таковой пока что просто неизве
стен.
Чтобы определить, что происходит, Korдa шаrи процесса стационарноrо
последовательноrо деления стремятся в пределе к бесконечности, удобно
90
Т7ава 6
написать вектор столбец [c ОСОС+ О]Т в виде линейной комбинации правых
собственных векторов V1, V2, VЗ матрицы L тем способом, который по казан
в приложении А.5:
[ ] а, + а,о, + а,о,
(6.6)
Матрица последовательноrо деления L paBHoMepHoro кубическоrо В сплай
на имеет собственные значения А1, А2, Аз == (1, 1/2, 1/4) и соответствую
щие правые собственные вектора
V1 == [ i ], V2 == [ 11 ], Vз == [ 1 ]
Преимущества представления в виде (6.6) заключается в том, что это
уравнение очень просто умножить на (L)j:
(L)j
I l
l c J
== (L)j(a1 v 1 +a2 v 2 +азvз) ==
== a1(L)jv1 +a2(L)jv2 +аз(L)jvз ==
== a1(A1) jV 1 + a2(A2) jV 2 + аз(Аз)jvз.
Поскольку А1 == 1, а друrие собственные значения меньше единицы при
стремлении j к бесконечности, остается только последнее слаrаемое:
[ ]
liш (L)j [ ] ==
J CX) О
С+
liш (a1(A1)jV1 + a2(A2)jV2 + аЗ(Аз)jvз) ==
J CX)
а1 V1.
Следовательно, предельное положение ссх) является средним элементом
в а1 V1. НО т. к. средний элемент V1 равен единице, то предельное поло
жение ссх) представляет собой просто а1. Соrласно приложению А.5 KO
эффициент а1 вычисляется с помощью доминирующеrо собственноrо BeK
тора, т. е. левоrо собственноrо вектора и1 для наибольшеrо собственноrо
значения. В случае последовательноrо деления paBHoMepHoro В сплайна
6.4. Вложенные пространства и уточняеные мааuтабирующие функции 91
щ i [141]. Следовательно, предельное положение сCIO будет
сCIO иl [
со
+
i[141] ]
со
+
c + 4с О + 4
6
Итак, предельное положение можно вычислить путем умножения исходных
положений вершин на доминирующий левый собственный вектор. Для ал
rоритма Чайкина доминирующий левый собственный вектор равен [11]
и, следовательно,
c +cO
сCIO
2
Вообще, доминирующий левый собственный вектор служит оценочной Mac
кой, потому что ero элементы описывают взвешенное среднее, которое MO
жет быть использовано при вычислении значения функции. На интуитивном
уровне можно rоворить о том, что оценочные маски приводят вершины к их
предельным положениям. Производные маски можно получить, если pac
сматривать левые собственные вектора для собственных значений, меньших
единицы (подробное рассмотрение производных масок имеется у Халстеда
и др. [54] и Хоппа и др. [60]).
Хотя все, о чем rоворилось выше, касалось Toro, как довести KOHKpeT
ную вершину от нулевоrо уровня до предельноrо, полученный результат
можно применить фактически к любой вершине на любом уровне. Эффек
тивным способом создания функций, кривых и поверхностей, определен
ных способом последовательноrо деления, является применение процесса
последовательноrо деления несколько раз (как правило, два или три) для
создания достаточно большоrо числа вершин, а затем устремление каждой
вершины к пределу с помощью оценочной маски.
6.4. Вложенные пространства и уточняемые
масштабирующие функции
В разделе 2.2 мы упоминали о том, что последовательность вложенных
пространств V O С V 1 С .,. иrpает фундаментальную роль при определе
нии вейвлетов. В этом разделе мы покажем, что последовательное деление
92
Т7ава 6
естественным образом приводит к такой последовательности пространств.
В дальнейшем этот факт будет использован для иерархическоrо разложения
кривых и поверхностей, образованных последовательным делением.
Для начала вспомним, что в разделе 2.2 мы сконструировали простран
ства Vj, рассмотрев все линейные комбинации сдвинутых и масштабиро
ванных хараперистических функций. В частности, нам нужно, чтобы
vj span {фl,(х), Ф (х), ..., ф j l (х)} .
Иначе rоворя, функции Фl,(х), ..., Ф J l (х) образуют базис для простран
ства V j кусочно постоянных функций. В общем случае базисные функции
для таких вложенных пространств называются масштабирующuми функци
я./ии (scaliпg Iuпctioпs). Вложенность этих пространств эквивалентна тому
факту, что масштабирующие функции являются уточняемьииu; т. е. функ
цию при разрешении j 1 можно представить как линейную комбинацию
функций при разрешении j. Из рисунка 6.7 видно, что для характеристиче
ских функций такой линейной комбинацией является
Фi l(х) 1. ф j(Х) + 1. Ф j+1(Х)'
J ф! 11
L
Ф i
Ф i+]
..
о
Рис. 6.7. Уточнение характеристической функции.
Теперь мы покажем, что каждая схема последовательноrо деления при
водит к появлению уточняемых масштабирующих функций и, следователь
но, к вложенным функциональным пространствам. Прежде Bcero, нужно за
метить, что оба этапа последовательноrо деления и этап разбивки, и этап
усреднения линейны при исходных значениях с?, а значит, предельную
функцию можно записать как
лх) L с?ф?(х)
(6.7)
для некоторых пока еще неопределенных функций Ф? (х). На самом деле эти
функции окажутся масштабирующими функциями. Поскольку предельная
6.4. Вложенные пространства и уточняеные мааuтабирующие функции 93
кривая Лх), определяемая значениями с?, совпадает с предельной кривой,
определяемой значениями с; для любоrо j > О, мы можем написать в более
общем виде
f(x) ==
1 1 ..
== c; Фi (х) == с;Фi (х) == ...
(6.8)
Введение матричной записи облеrчит нам выполнение дальнейших дей
ствий, поэтому обозначим матрицу строку, содержащую все масштабирую
щие функции с верхним индексом j, как фj (х), т. е.
фj ( х) == [фь ( х) ф{ (х) .. . ].
Теперь уравнение (6.8) можно переписать так:
f( х) == ... == фj 1 (х) c j 1 == фj (х) c j
(6.9)
Все, о чем мы до сих пор рассуждали, сводится к тому, что масштаби
рующие функции ф{ (х) существуют и некоторым образом определяются
с помощью KOHKpeTHoro последовательноrо деления. На следующем этапе
мы определим пространство V j для каждоrо j, включающеrо все линейные
комбинации масштабирующих функции с надстрочным индексом j:
vj :== span {Фь(х), ф{ (х),...} .
(6.10 )
Теперь покажем, что масштабирующие функции уточняемы, и, Ta
ким образом, пространства V j образуют вложенную последовательность
именно то, что нам потребуется в седьмой rлаве при рассмотрении иерар
хических разложений. Т. к. этапы разбивки и усреднения линейны при зна
чениях ci l, существует неквадратная матрица pj, являющая собой COBMe
щенный результат разбивки и усреднения, что
c j == pj cj l.
(6.11 )
(Матрицу pj можно было бы записать и в виде произведения усредняюшей
матрицы Rj и дополнительной матрицы, отвечающей за разбиение, однако
нам нет необходимости давать здесь явное определение.) По очевидным
причинам матрица pj называется матрицей последоватеЛЬН020 деления
(subdivisioп matrix). Она иrрает важную роль в теории кратномасштабноrо
анализа, в чем мы убедимся в следующей rлаве.
Теперь отметим, что, соrласно уравнению (6.9), мы можем переписать
функцию, соответствующую j 1 TOMY уровню последовательноrо деления,
94
Т7ава 6
как функцию, соответствующую j TOMY уровню последовательноrо деле
ния:
фj l (х) cj l фj (x)c j .
Подставляя уравнение (6.11) в вышенаписанное уравнение, получаем
фj l(х)сj l фj(х)рjсj l.
Поскольку это уравнение справедливо для любоrо значения cj l, мы имеем
фj l(х) фj(х)рj.
(6.12)
Последнее уравнение называется уточняющш',t соотношенuеи (refiпeтeпt
relatioп) для масштабирующих функций. Из Hero следует, что любая Mac
. 1
штабирующая функция более низкоrо уровня Фi (х) записывается в виде
линейной комбинации масштабирующих функций, соответствующих более
высокому уровню Фi (х).
Замечание. Существует прямой способ вычисления масштабирующей
функции Фi(х), во всяком случае приближенно: нужно просто начать
выполнять процедуру последовательноrо деления с последовательно
сти значений с; (ji,k на уровне j. Конечная функция f(x) в точности
равна ф{(х), поскольку, соrласно уравнению (6.8), лх) задается толь
ко одним слаrаемым сiФi(х), и, по построению, ci 1. Этот метод
применялея для построения нескольких различных масштабирующих
функций для интерполирующих В сплайнов, показанных на рисун
ке 6.8, причем с использованием усредняющих масок, рассмотренных
в разделе 6.2.
Замечание. В случае paBHoMepHoro последовательноrо деления все
функции Ф? (х) имеют одну и ту же форму; они просто сдвинуты
относительно друr друrа. Вообще, масштабирующие функции Bcerдa
смещены на расстояние, равное целому числу. Получается, что суще
ствует единственная функция ф( х), называемая иноrда отцовской иас
штабирующей функцией (father scaliпg.fuпctioп) , из которой все друrие
функции определяются соrласно ф?(х) ф(х i). То, что paBHOMep
ное последовательное деление дает в результате сдвинутые копии oд
ной исходной функции, демонстрируется рисунком 6.9 для введенной
в разделе 6.9 схемы последовательноrо деления Добеши.
Масштабирующие функции ф}(х) на первом уровне также пред
ставляют собой смещенные версии друr друrа, но только уже на полу
целые расстояния. Более Toro, поскольку в равномерном стационарном
6.4. Вложенные пространства и уточняеные мааuтабирующие функции 95
0.8 .
Рис. 6.8. Масштабирующие функции для интерполирующих В сплайнов, получен
ные неоднократным применением последовательноrо деления.
случае одна и та же процедура последовательноrо деления использует
ся при каждой итерации, функции фUх) имеют ту же базовую форму,
что и ф(х), просто они сжаты по rоризонтали в два раза. В общем,
Фi (х) == ф(2 j х i). Подобное изменение ширины в два раза называют
С.жатием, в некоторых источниках дилятацuей (dilatioп).
1.5
0.5
:\
. .
: ,/
'.
:.
. .
.' .
./
,'\,
,
,
'.
: '. "
" "
:', : \
'.
,
\ . \ ,
. .
\:
0.50
Рис. 6.9. Равномерное последовательное деление дает в результате масштабирующие
функции, представляющие собой сдвинутые копии друт друта.
Замечание. В случае paBHoMepHoro последовательноrо деления уточ
няющее соотношение для исходной масштабирующей функции также
значительно упрощается, принимая вид
ф(х) == LРiф(2х 1).
96
Т7ава 6
Следовательно, отцовской масштабирующей функции присуще одно
весьма примечательное свойство, а именно то, что она может быть
представлена в виде линейной комбинации сжатий и сдвиrов самой
себя. Уточняющuе коэффициенты (refiпeтeпt coefficieпts) Pi для раз
личных равномерных схем приведены в таблице 6.1.
Таблица 6.1. Уточняющие коэффициенты для масштабирующих функций, получен
ных с помощью неравномерных схем последовательноrо деления.
Схема
Уточняющие коэффициенты
Кусочно постоянная
Кусочно линейная
(1,1)
1
"2(1,2,1)
1
4(1,3,3,1)
1
8(1,4,6,4,1)
(1 + VЗ, 3 + VЗ, 3 VЗ, 1 VЗ)
1
16 ( 1, О, 9,16,9, О, 1)
Кусочно квадратная
Кусочно кубическая
Добеши D4
DLG
Итак, мы показали, что масштабирующие функции являются уточняе
мыми и что pj служит одновременно матрицей последовательноrо деления
для исходных значений c j и матрицей уточнения для масштабирующих
функций фj (х). в результате нам стало известно, что любое семейство
уточняемых функций можно получить посредством последовательноrо дe
ления, причем с одной и той же матрицей, являющейся как матрицей по
следовательноrо деления, так и матрицей уточнения.
Т'ЛАВА 7
Теория кратномасштабноrо анализа
1. КратН(J)wасштабный аналuз 2.
З. Полуорт020нальные вейвлеты
ты 5. Выводы
Орт020нальные вейвлеты
4. Бuорт020нальные вейвле
в предыдущей rлаве мы показаШI, что уточняемыми являются только
те масштабирующие функции, которые определяются через последователь
ное деление. Из этоrо результата следует очень важное следствие только
функции, определяющиеся через последовательное деление, MorYT участ
вовать в формировании вложенных пространств линейных функций.
Более Toro, как мы помним, во второй rлаве rоворилось, что отправ
ной точкой в кратномасштабном анализе является вложенное множество
линейных пространств:
VO с V 1 С V 2 С . .. .
Следовательно, существует фундаментальная связь между процессом по
следовательноrо деления и кратномасштабным анализом.
В этой rлаве мы подробно рассмотрим математическую основу KpaT
номасштабноrо анализа, вариантноrо по отношению к сдвиrам. Далее мы
обсудим три различных вида базисов вейвлетов ортоrональные, полу
ортоrональные и биортоrональные и приведем примеры для каждоrо из
НИХ. ЭТИ виды базисов вейвлетов позволяют нам попеременно использовать
такие желательные свойства, как ортоrональность, наличие компактноrо HO
сителя, степени rладкости и симметрия.
7.1. Кратномасштабный анализ
Мы уже rоворили, что отправной точкой в кратномасштабном анали
зе служит вложенное множество пространств линейных функций VO с
с V 1 С . . . , причем разрешение функций в V j возрастает с увеличением j.
Базисные функции для пространства vj называются, как уже было сказано
в разделе 6.4, масштабирующими функциями.
98
Т7ава 7
Следующим этапом кратномасштабноrо анализа является определение
пространств вейвлетов (wavelet spaces) , обозначаемых Wj. Определим эти
пространства вейвлетов более свободно, нежели во второй rлаве, с тем,
чтобы охватить и некоторые друrие конструкции вейвлетов, помимо pac
смотренных нами. На этот раз мы просто потребуем, чтобы пространство
вейвлетов wj являлось дополненuем V j до Vj+l. Следовательно, любая
функция в Vj+l может быть записана в виде суммы какой то однозначно
определенной функции в vj и какой то однозначно определенной функции
в w j . Функции, выбираемые нами в качестве базиса для W j , называются
вейвлетамu. Заметим, что, в отличие от определения из второй rлавы, мы
больше не требуем, чтобы вейвлеты из wj обязательно были ортоrональны
масштабирующим функциям в Vj.
Вся остальная часть этоrо раздела, рассматривающеrо кратномасштаб
ный анализ, будет посвящена вейвлетам, определенным на оrраниченной
области для кривых и (в десятой rлаве) для компактных поверхностей про
извольноrо тополоrическоrо типа. В некоторых местах мы, по ходу дела,
коснемся и более традиционноrо определения вейвлетов на бесконечной
вещественной числовой оси. В случае с оrpаниченной областью оси каж
дое пространство vj имеет конечный базис, и это позволит нам очень
часто употреблять матричные обозначения, которые использовали Лаунсбе
ри и соавторы в [75], а также Куак и Вейрих в [98]. Несмотря на то, что
все примеры в этом разделе приводятся для вейвлетов в одномерном случае,
это теоретическое построение справедливо и для поверхностных вейвлетов,
описанных в десятой rлаве.
7.1.1. Уточнение
В разделе 6.4 уже упоминалось, что часто более удобным бывает
представление различных масштабирующих функций Фi (х), COOTBeTCTBY
ющих данному уровню j, в виде одноrо вектора строки. Обозначив размер
ность V j через v(j), запишем
фj (х) :== [ФЬ (х) .. . Ф (j) l (х)].
Аналоrично, если w(j) это размерность w j , то вейвлеты для уровня j мы
можем записать как
фj (х) :== [фь (х) .. . Ф (j) l (х)].
Поскольку W j является дополнением vj в v j + 1 , размерности этих про
странств удовлетворяют соотношению v(j + 1) == v(j) + w(j).
7.1. Кратно.насштабный аНCL7из
99
в разделе 6.4 мы установили, что наличие вложенных подпро
странств V j эквивалентно уточняемости масштабирующих функций. Т. е.
для всех j 1, 2, . . . должна существовать постоянная матрица pj, такая,
что
фj l(х) фj(х)рj. (7.1)
Заметим, что vj и Vj l имеют размерности v(j) и v(j 1), соответственно,
тоrда pj является постоянной матрицей размерности v(j) х v(j 1).
Поскольку пространство вейвлетов Wj l по определению является
подпространством V j , мы можем записать вейвлеты фj (х) как линейную
комбинацию масштабирующих функций фj (х). Таким образом, существует
матрица Qj размерности v(j) х w(j 1), удовлетворяющая
фj l(х) фj(х)Qj.
(7.2)
Пример. В базисе Хаара на данном уровне j существуют v(j) 2 j
масштабирующих функций и w(j) 2 j вейвлетов. Следовательно,
необходима матрица уточнения, описывающая то, как можно получить
две масштабирующие функции из V 1 И два вейвлета из W 1 , используя
четыре масштабирующие функции из V 2 (вернемся к рисункам 2.2
и 2.3):
р' [ ] и Q' [i 1 I]
Замечание. Если вейвлеты конструируются на неоrраниченной веще
ственной оси, все ф; (х) имеют одинаковую форму; все они, по cy
ти, представляют собой сдвинутые и масштабированные версии одной
функции ф(х), называемой материнским вейвлетом (тother wavelet).
В общем случае фf(х) ф(2 j х i).
Кроме Toro, в этом инвариантном относительно сдвиrа слу
чае столбцы постоянной матрицы pj являются сдвинутыми верси
ями друr друrа, равно как и столбцы матрицы Qj. Следовательно,
каждая матрица характеризуется одним столбцом, поэтому pj и Qj
полностью определяются последовательностями (..., q l, qo, Ql",,)
и (... ,P l, Ро, Рl,.. .), которые также не зависят от j. В литературе
уравнения (7.1) и (7.2) часто можно встретить в таком виде:
ф(х) L.Рiф(2х i),
i
ф(х) L.qiф(2х i).
100
Т7ава 7
Заметим, что уравнения (7.1) и (7.2) можно также выразить через одно
уравнение, если воспользоваться обозначениями для блочных матриц:
[фj l I фj l] == фj [pj l I Qj l] .
(7.з)
Данное уравнение называют соотношенuем д x масштабов (two scale
relatioп) для масштабирующих функций и вейвлетов.
Пример. Подстановка в уравнение (7.3) матриц из предыдущеrо при
мера и надлежащих базисных функций дает
[Ф6 Ф}Ф6фi] [ф Ф1 ф Ф1] [ !
1
1
О
О
] .
1
7.1.2. Блок фильтров
Теперь, коrда мы описали связь последовательноrо деления и матриц
с масштабирующими функциями и вейвлетами, покажем, как можно приме
нить матричное представление, чтобы выполнить вейвлет преобразование.
Рассматриваемый здесь материал является обобщением иерархическоrо раз
ложения функции, в общих чертах paccMoTpeHHoro в разделе 2.1 для базиса
Хаара.
Рассмотрим функцию внекотором аппроксимационном простран
стве Vj. Допустим, мы имеем коэффициенты этой функции, выраженные
в терминах HeKoToporo базиса масштабирующих функций. Мы можем пред
ставить эти коэффициенты в виде вектора столбца c j == [СЪ... (Л 1]Т'
Ero элементы, коэффициенты с; , можно было бы рассматривать, к примеру,
как цвета пикселей или, скажем, x или у координаты контрольных точек
кривой из ]]{2.
Предположим, что нам нужно создать версию c j с низким разреше
нием, обозначим ее cj l, характеризуемую меньшим количеством коэффи
циентов v(j 1). Стандартный метод получения v(j 1) значений cj l
задействует определенную форму линейной фильтрации и децимацию v(j)
значений c j . Этот процесс можно выразить матричным уравнением
cj l == Aj c j ,
(7.4)
rдe Aj является постоянной матрицей размерности v(j 1) х v(j).
Поскольку cj l содержит меньшее число коэффициентов по cpaBHe
нию с c j , уже интуитивно можно понять, что в результате процесса филь
трации произошла потеря доли информации. Если Aj выбрана правильно,
7.1. Кратно.насштабный ана.7из
101
мы можем собрать эти потерянные детали в друrой столбец dj l, опреде
ляемый выражением
dj l Bjcj,
(7.5)
[де Bj постоянная матрица размерности w(j 1) х w(j), связанная с MaT
рицей Aj. Матрицы Aj и Bj называются фuльтрамu анализа (aпalysis
filters). Процесс разбиения коэффициентов c j на более rрубую версию cj l
и уточняющие коэффициенты dj l называется аналuзом (aпalysis) илираз
ложенuем (decoтpositioп).
При надлежаще выбранных Aj и Bj исходные коэффициенты c j мож
но восстановить из cj l и dj l, воспользовавшись матрицами pj и Qj из
предыдущеrо раздела:
c j pj cj l + Qj dj l.
(7.6)
Получение c j из cj l И dj l называется сuнтезом (syпthesis) или вoc
становленuем (recoпstructioп) , а pj и Qj называют, в данном контексте,
фuльтрамu синтеза (syпthesis filters).
Интуитивно можно считать, что первое слаrаемое в правой части ypaB
нения (7.6) показывает, что начальный набор коэффициентов c j получается
путем «интерполирования вверх» rpубых коэффициентов cj l до caMoro
мелкоrо масштаба. Коэффициенты масштабирующей функции интерполи
руются вверх посредством выполнения одноrо этапа последовательноrо дe
ления, т. е. умножения на pj, или, что эквивалентно, выполнением разбивки
и усреднения. Второе слаrаемое в уравнении можно рассматривать как воз
мущение первоrо слаrаемоrо, получаемое интерполированием вейвлет ко
эффициентов вверх. Такая интерполяция производится путем умножения
на Qj.
Пример. В ненормированном базисе Хаара матрицы А 2 И В 2 опреде
ляются как
А 2 1 [ 1 1 О О ] .
2 О 011 '
В 2 1 [ 1 1 О О ]
2 О О 1 1 .
Эти матрицы представляют собой операции усреднения и нахождения
разностей, описанные в разделе 2.1.
Замечание. Матрицы для вейвлетов, сконструированных на Heorpa
ниченной оси вещественных чисел, вновь имеют простую структуру:
строки матрицы Aj являются сдвинутыми версиями друr друrа, равно
102
Т7ава 7
как и строки матрицы Bj. Поэтому в литературе уравнения (7.4) и (7.5)
часто имеют вид
q l L az 2kq,
1
di l L bl 2kq,
1
(7.7)
(7.8)
[де последовательности (..., a l, ао, аl,"') и (..., b l, Ь о , Ь 1 ,...)
являются элементами строк Aj и Bj, соответственно. Аналоrично,
уравнение (7.6), описывающее восстановление, можно часто встретить
в следующем виде:
j l ( i l d j l )
C k Pk 21q + qk 21 1 .
1
Заметим, что процедуру разбиения c j на часть cj l, соответствующую
низкому разрешению, и уточняющие коэффициенты dj l можно приме
нить рекурсивно и к самой части cj l. Следовательно, исходные коэффи
циенты можно представнть в виде иерархии rрубых версий разрешения
ми са, ..., cj l И уточняющих деталей d O , ..., dj l, как показано на ри
сунке 7.1. Подобный рекурсивный процесс носит название блока фuльтров
(filter baпk).
А 1 AI l А 1
t! t! 1 t!2 1 О
С С
dl 1 dl 2 dO
Рис. 7.1. Блок фильтров.
Поскольку изначальные коэффициенты c j можно восстановить из по
следовательности са, d O , d 1 ... dj l, последнюю можно рассматривать
как преобразование изначальных коэффициентов, известное под назва
нием вейвлет преобразованuя. Заметим, что общий размер преобразова
ния са, d O , d 1 ... dj l равен размеру ориrинальной версии c j , поэтому
нам не требуется дополнительноrо объема для хранения этоrо преобразова
ния. (Однако следует сказать, что коэффициенты масштабирующих функ
ций и вейвлетов MOryT потребовать большее число бит для Toro, чтобы
обеспечить сохранение точности исходных значений.)
7.2. OpтozoHa.7bHble вейв.7еты
103
Вообще, фильтры анализа Aj и Bj не обязательно представляют co
бой транспонированные кратные фильтров синтеза, как это было в случае
базиса Хаара. Aj и Bj, скорее, образуются матрицей, удовлетворяющей
соотношению
[фj ll фj l] [ ] фj.
(7.9)
Заметим, что
[pj I Qj]
и
[ ]
являются квадратными матрицами. Следовательно, объединение ypaBHe
ний (7.3) и (7.9) дает в результате
[ ] [pj I Qj] l.
(7.10)
Хотя при выборе матриц Aj, Bj, pj и Qj мы не делали каких либо спе
циальных oroBopoK, из уравнения (7.1 О) должно быть понятно, что и
[ ] ,
и
[pj I Qj]
должны быть, по крайней мере, обратимыми. В оставшейся части этой rла
вы мы исследуем три различных конструкции вейвлетов, rлавное различие
которых состоит в способе получения из них уточняющих матриц вейвле
тов Qj.
7.2. Ортоrональные вейвлеты
Известно, что ортоzональным называется базис, в котором все базис
ные функции являются взаимно ортоrональными. Ортоzональным KpaтHO
масштабным базuсом называется базис, в котором масштабирующие функ
ции ортоrональны друr друrу, вейвлеты ортоrональны друr друrу и каждый
вейвлет ортоrонален каждой масштабирующей функции предыдущих ypOB
ней. Вейвлеты, удовлетворяющие перечисленным условиям, мы называем
ортоzональнымu вейвлетамu.
104
Т7ава 7
Во второй rлаве мы отметили, что базис Хаара является opToro
нальным, и при разработке алrоритма сжатия положились на тот факт,
что L2 ошибка аппроксимации леrко вычисляется по величинам выброшен
ных коэффициентов. Такая простая связь между значением коэффициента
и поrрешностью существует лишь в случае, коrда базис ортоrонален.
Математическая форма условий, определяющих ортоrональный вей
влет базис может быть такой:
(Фi Iфi) I5k'Z }
(Фilфi) I5 k ,Z
(Фilфi) о
для всех], k, 1.
(7.11)
Фактически, эти условия определяют ортонормuрованный базис вейвле
тов, поскольку скалярное произведение базисной функции с нею самой по
условию равняется единице. Для ортоrональноrо базиса такая нормировка
не является необходимой, однако далее в этом построении мы примем, без
ущерба для общности, что ортоrональный базис вейвлетов также является
ортонормированным.
7.2.1. Включения ортоrональности
Введем несколько новых обозначений для матрицы скалярных произ
ведений, с тем, чтобы рассмотреть все скалярные произведения из ypaBHe
ния (7.11) одновременно. Две матрицы строки обозначим, соответственно,
через лх) [Jo(x) л(х)",] и g(x) [go(x) gl(X)"'], а матрицу, элемен
ты (k, 1) которой равны (fklgz), через [(flg)]. В отличие от скалярноrо
произведения пары функций, [и I g)] не обязательно симметрична, однако
следующие соотношения между f, 9 и постоянной матрицей М должны
соблюдаться:
[(flg)] [(glf)]T
[(flgM)] [(flg)]M
[(fMlg)] MT[(flg)].
(7.12)
Кроме Toro, мы введем 1 для обозначения единичной матрицы и О для
нулевой матрицы или нулевоrо вектора. Теперь, вооружившись этими обо
значениями, мы можем переписать условия ортоrональности, указанные
в (7.11), следующим образом:
[ (ф1 I ф1)] 1
[('111 I '111)] 1
[(ф1 I '111)] О.
7.2. OpтozoHa.7bHble вейв.7еты
105
Если же мы сrруппируем все базисные функции, то формулировка условий
ортоrональности станет еще лаконичнее:
[([фj I фj]l[фj I фj])] == [ [ФJ I фJ]I[фJ I ФJ] ] == [.
[фJ I фJ] I [фJ I фJ]
Чтобы показать, как ортоrональность влияет на матрицы pj и Qj, давайте
заменим индекс j на j 1 и перепишем вышеуказанные условия следующим
образом:
Юфj ll фj l]l[фj ll фj l])] == [.
Теперь, подставляя (7.3) в предыдущее уравнение, получим
[(фj[рjIQj] I фj[рjIQj])] == [.
Мы можем воспользоваться свойствами матриц скалярноrо произведения,
перечисленными в (7.12), чтобы получить
[pj I Qj( [(фj I фj)] [pj I Qj] == [.
Наконец, учитывая, что [( фj I фj)] == [, мы приходим К результату:
[pjl Qj( == [pjl Qj] l.
Таким образом, для ортorональных вейвлетов матрица, обратная к комби
нированной матрице синтеза масштабирующих функций и вейвлетов,
[pj I Qj]
совпадает с ее транспонированием. Матрица с таким свойством называется
ортоzональной матрuцей. Этот факт вкупе с уравнением (7.10) rоворит
о том, что
Aj == (pj( и Bj == (Qj(.
7.2.2. Вейвлеты Добеши
На этот момент нам уже известно, что схемы последовательноrо дe
ления MorYT использоваться при определении масштабирующих функций
и вложенных функциональных пространств. Напрашивается естественный
вопрос: можем ли мы использовать последовательное деление для получе
ния ортоrональноrо базиса вейвлетов, превосходящеrо базис Хаара? В част
ности, очень неплохо было бы найти множество функций rладкоrо базиса.
106
Т7ава 7
Эта цель была достиrнута Добеши [24], Korдa она сконструировала OpTO
нормированные вейвлеты с компактными носителями на бесконечной Be
щественной оси. Поскольку в этой книrе основное внимание посвящено
конструированию вейвлетов на оrраниченных интервалах, здесь мы воз
держимся от приведения вывода вейвлетов Добеши. Вместо этоrо мы про
иллюстрируем полученные ею результаты на примерах фильтров синтеза
и анализа.
В D4 КОНСТРУКЦИИ, названной так, потому что каждый из ее фильтров
имеет по четыре элемента, задействованы следующие последовательности:
р а lIn (l + VЗ, 3 + VЗ, 3 VЗ, 1 VЗ),
4у2
q b l;п (1 VЗ, з+VЗ, з+VЗ, l VЗ).
4у2
Последовательность р представляет ненулевые элементы каждоrо столб
ца pj, Torдa как последовательность q содержит ненулевые элементы
столбца Qj. Аналоrично, последовательности а и Ь представляют CTpO
ки Aj и Bj, соответственно. Заметим, что последовательность для вейвлет
фильтра можно получить, если поменять порядок элементов в последова
тельности масштабирующих функций и изменить их знаки на противопо
ложные. Этот рецепт создания последовательности вейвлетов из последо
вательности масштабирующих функций часто используют в приложении
ко мноrим вейвлетам, сконструированным на бесконечной вещественной
оси; такие последовательности носят название квадратурных зеркальных
фuльтров.
D4 масштабирующая функция и D4 вейвлет изображены на рисун
ке 7.2. Обе функции асимметричны и всюду недифференцируемы, хотя при
этом они являются непрерывными. Эти базисные функции являются члена
ми целоrо семейства базисов, полученных Добеши, включающеrо базисы,
rладкость которых возрастает с увеличением носителей базисных функций.
В разделе 6.4 мы уже обсуждали, как можно построить rрафик Mac
штабирующей функции: для этоrо берут последовательность коэффициен
тов с{ l5 i ,k на уровне j, выполняют процедуру последовательноrо деления
определенное число раз и представляют результаты в rpафическом виде.
Последовательное деление мы можем провести либо разбивкой и ycpeДHe
нием, как описывалось в предыдущей rлаве, либо вставкой нулей между
всеми коэффициентами в имеющейся последовательности и последующей
сверткой с помощью последовательности уточнения р. (Операция BCTaB
ки нулей, предшествующая операции свертки, аналоrична этапу разбивки,
предшествующему этапу усреднения.) Способ rрафическоrо отображения
вейвлетов очень похож. Чтобы получить k ый вейвлет на j TOM уровне,
7.3. Полуортоzональные вейвлеты
107
I I
2 ,
О O
(а) (6)
Рис. 7.2. Функции базиса вейвлетов Добеши: (а) D4 масштабирующая функция;
(б) D4 вейвлет.
мы возьмем последовательность вейвлет коэффициентов di l5 i ,k, вставим
нули между элементами этой последовательности и свернем ее с помо
щью q, чтобы получить последовательность коэффициентов масштабирую
щей функции СНl.
Замечание. Описанные выше последовательности р и q работают и при
восстановлении функции по ее коэффициентам разложения по базису
из масштабирующих функций и вейвлетов. Однако при использовании
последовательноrо деления для получения rpафиков, показанных на
рисунке 7.2, нам все же придется взять последовательности, чуть чуть
отличные от этих. Причина подобноrо противоречивоrо решения KpO
ется в том, что схема последовательноrо деления не может сходиться,
если элементы в каждой строке pj не стремятся в сумме к единице.
Для равномерной стационарной схемы (т. е. схемы, везде использую
щей одну последовательность р) это условие эквивалентно требова
нию, соrласно которому сумма нечетных элементов р стремится к еди
нице и сумма четных элементов р также стремится к единице. OKa
зывается, если мы умножим р последовательность на у'2, то получим
сходящуюся схему. Будет лоrичным, если мы умножим и q последо
вательность на у'2, прежде чем применить последовательное деление
для построения rpафика вейвлета.
7.3. Полуортоrональные вейвлеты
Ортоrональность не единственное желательное свойство базиса вей
влетов. Вот список некоторых друrих свойств, которые более или менее
важны при конструировании базиса вейвлетов в тех или иных ситуациях:
108
Т7ава 7
. Компактный носuтель. Носители масштабирующих функций и вейвле
тов зависят от местоположения ненулевых элементов pj и Qj. Более
компактный носитель повышает эффективность разложения и BOCCTa
новления функций с использованием алrоритма блока фильтров.
. rладкость. [ладкие функции лучше Bcero представляются rладкими ба
зисами. К примеру, кусочно кубическая базисная функция может пред
ставить rладкую кривую более эффективно по сравнению с кусочно ли
нейной функцией. Однако зачастую большая rладкость достиrается за
счет более широких носителей.
. СUМJuетрuя. В некоторых случаях важным может оказаться исполь
зование масштабирующих функций и вейвлетов, симметричных (или
антисимметричных) относительно своих центров.
. Нулевые моменты. [оворят, что вейвлет ф(х) имеет n нулевых MO
ментов, если интеrрал J ф(х)х k dx тождественно равен нулю для k
О, . . . , n 1, но не для k n. Вейвлеты с повышенным количеством
нулевых моментов часто желательны в тех приложениях, [де требуются
численные аппроксимации rладких операторов.
Требование ортоrональности конструкций вейвлетов порой может быть
чрезмерным оrpаничением. Фактически, не существует ни одноrо базиса
вейвлетов (за исключением базиса Хаара), который одновременно имеет
компактный носитель и является ортоrональным u симметричным [25].
Следовательно, если мы хотим получить rладкие симметричные вейвлеты
с компактным носителем, нам необходимо пожертвовать ортоrональностью.
Однако такой урон не всеrда бывает «болезненным»: так, в ряде случаев
мы можем построить кратномасштабный базис, в котором вейвлеты при
данном разрешении являются ортоrональными, по крайней мере по OTHO
шению ко всем масштабирующим функциям, соответствующим более низ
кому разрешению, при этом они не обязательно ортоrональны друr друrу.
Сконструированные по такому критерию вейвлеты называют полуорт020
нальнымu вейвлетамu или превейвлетшwu (pre wavelets). В математической
форме условия, которым должен удовлетворять базис полуортоrональных
вейвлетов, выrлядят так:
(фi,IФl! о для всех j, k, [.
(7.13)
Заметим, что ортоrональные вейвлеты являют собой частный случай по
луортоrональных вейвлетов, для KOToporo характерна взаимная ортоrональ
ность как масштабирующих функций, так и вейвлетов.
7.3. Полуортоzональные вейвлеты
109
7.3.1. Включения полуортоrональности
Чтобы посмотреть, какое следствие имеет полуортоrональность для
матриц pj и Qj, мы воспользуемся обозначениеми, введенными в разде
ле 7.2.1 для матрицы скалярных произведений. Сначала перепишем ypaB
нение (7.13) как
[\фj I фj;] О.
Если заменить индекс j на j 1, мы можем подставить в это уравнение
уточняющие соотношения для pj и Qj из уравнений (7.1) и (7.2) и получить
(pj) т [\ фj I фj;] Qj oj.
(7.14)
Для данноrо множества масштабирующих функций фj и матрицы уточне
ния pj мы хотели бы найти (хорошую) матрицу уточнения вейвлетов Qj,
что также приведет к определению вейвлетов фj. Получается, что нам нуж
но решить систему уравнений в (7.14) относительно матрицы Qj.
Матричное уравнение с нулевой правой частью, такое, как ypaBHe
ние (7.14), называется однородной сuсте 'vIOЙ уравнений. Чтобы не услож
нять наше рассуждение, давайте определим Mj : (pj)T [\ фj I фj;].
Множество всех возможных решений уравнения (7.14) называется НУЛЬ
пространством Mj. Нуль пространство это ничто иное, как конечно
мерное векторное пространство, в нашем случае пространство BeктopOB
столбцов, обращающихся в нули при их умножении на любую строку в Mj.
Наша задача найти принадлежащие Qj столбцы, образующие базис для
этоrо пространства.
Существует большое количество базисов для нуль пространства пря
моуrольной матрицы вроде Mj, из чеrо следует, что существует MHoro раз
личных базисов вейвлетов для данноrо пространства вейвлетов Wj. Допу
стим, что мы уже знаем Mj и теперь хотим выбрать Qj, чтобы определить
вейвлеты. Нам необходимо наложить дополнительные оrpаничения в допол
нение к требованию ортоrональности, обозначенному в уравнении (7.14).
Если мы хотим, чтобы наши вейвлеты имели компактные носнтели, то сле
дует сделать количество ненулевых последовательных элементов в столбцах
матрицы Qj по возможности минимальным. Если же нам нужно, чтобы Ha
ши вейвлеты были симметричными относительно своих центров, мы можем
добиться симметрии в элементах каждоrо столбца матрицы Qj.
7.3.2. Сплайн вейвлеты
За одним из примеров полуортоrональноrо базиса мы обратимся к клас
су вейвлетов, особенно полезных для представления кратномасштабных
110
Т7ава 7
кривых: сплайн вейвлетам. Эти вейвлеты, построенные из В сплайнов,
были получены во MHoroM блаrодаря заслуrам Чуи и ero коллеr [17,18].
Интерполирующие конечную точку В сплайны представляют особый ин
терес для приложений, связанных с редактированием кривых. Сейчас мы
вкратце изложим идеи, стоящие за конструированием вейвлетов на основе
В сплайнов, интерполирующих конечную точку по методу, который Фин
кельштейн и Салезин [37] использовали для получения вейвлетов в куби
ческом случае.
Результаты этоrо вывода сведены в приложение Б, в котором мы пока
зали фильтры синтеза для кусочно постоянноrо (xaapOBCKoro), линейноrо,
квадратичноrо и кубическоrо случаев. МаtlаЬ код, который был использован
для получения этих фильтров, помещен в приложение В.
В сплайновые масштабирующие функции
Первый этап заключается в определении масштабирующих функ
ций для вложенноrо множества функциональных пространств. Для этоrо
мы воспользуемся интерполирующими конечную точку неравномерными
В сплайнами [35], определенными на единичном интервале. Выбрав нуж
ную нам степень m базисной функции, мы можем определить V j (т) как
множество из 2 j + т, неравномерных В сплайнов, сконструированных на
последовательности узлов:
(ХО, ..., X2J+2m) == l(O, ..., 0,1,2, ..., 2 j 2, 2 j 1, 2 j , ..., 2 j ).
2J
m+lраз m+lраз
На рисунке 7.3 показаны примеры сплайновых масштабирующих функций
для j == 1 и различных степеней т.
Нетрудно показать, что пространства VO(m), V 1 (m),... являются вло
женными, чеrо и требует кратномасштабный анализ. Чтобы сформулиро
вать выражения для элементов матрицы уточнения pj, можно прибеr
нуть к теории введения узлов (вершин) для В сплайнов (подробности вы
найдете у Чуи и Куэйка [18]). Столбцы pj являются разреженными, OT
ражая факт существования локальных носителей у В сплайновых базис
ных функций. Первые и последние m столбцов pj относительно сложны,
остальные же (внутренние) столбцы являются сдвинутыми версиями столб
ца m + 1. Более Toro, элементы, которые входят в эти внутренние столб
цы, задаются, с точностью до общеrо множителя 2 т, биномиальными
коэффициентами.
Пример. В случае кубических сплайнов (т == 3) матрица pj для j ;? 3
7.3. Полуортоzональные вейвлеты
111
L N,L
N:l N; :' N;
I I N: ;, /"о. Ni
N" N2
lстепеНLО NiJ '[ / Ni
степеНL 1 N [ J
степеНL 2 N
степень 3
Рис. 7.3. Масштабирующие функции на основе интерполирующих конечную точку
В сплайнов для Vj(m) со степенью m О, 1, 2 и 3.
имеет форму
8
4 4
6 2
3 11 1
2 2
4 4
1 6 1
4 4
1 1 6
pj 4
8 1
1
4
6 1
4 4
1 11 3
2 2
2 6
4 4
8
112
Т7ава 7
rдe пустые позиции представляют собой нулевые элементы, а точки
обозначают, что предыдущий столбец повторяется, каждый раз сдвиrа
ясь при этом вниз на два ряда.
Скалярное про изведение
Второй этап конструирования полуортоrональноrо базиса включает BЫ
бор скалярноrо произведения. В нашем случае мы просто выберем CTaH
дартное скалярное про изведение:
1
Ulg) : J f(x)g(x) dx.
о
В сплайновые вейвлеты
Для завершения кратномасштабноrо анализа на основе полуорто
rональных В сплайнов нам нужно найти базисные функции для про
странств Wj, которые являются ортоrональными дополнениями про
странств V j . Важно понимать, что, как только мы выбрали масштабиру
ющие функции и их матрицы уточнения pj, матрицы вейвлетов Qj по
лучают некоторое оrраничение, правда, не полностью определенное. Если
наши вейвлеты должны быть ортоrональны масштабирующим функциям,
то столбцы матрицы Qj должны образовывать базис для нуль простран
ства матрицы Mj : (pj)T [(фj I фj)]. Поскольку Vj(m) имеет размер
ность 2 j + т, мы знаем, что Mj состоит из 2 j + m столбцов и только
из 2j 1 + m строк. Такое различие rоворит о том, что нуль пространство
матрицы Mj имеет размерность 2j 1. Значит, в итj(m) существуют 2j 1
вейвлетов, и каждый из них задается столбцом матрицы Qj.
Как мы уже упоминали, для нуль пространства матрицы существует
множество базисов. Чтобы однозначно определить матрицы Qj, нам следу
ет решить, какими свойствами должен обладать вейвлет. Соrласно подходу,
который использовали Финкельштейн и Салезин и которым воспользуемся
и мы, столбцы матрицы Qj должны быть разреженными и, в дополне
ние к этому, число следующих друr за друrом ненулевых элементов должно
быть минимальным. Помещая в верхнюю и нижнюю части каждоrо столбца
матрицы Qj столько нулей, сколько представляется возможным, мы обес
печиваем компактность носителей вейвлетов.
Структуры полученных матриц Qj и матриц pj схожи: первые и по
следние m столбцов отличаются друr от друrа, зато все остальные BНY
тренние столбцы представляют собой сдвинутые копии одной и той же
последовательности элементов.
7.3. Полуортоzональные вейвлеты
113
Пример. Чтобы проиллюстрировать структуру Qj матриц, мы пока
жем, как выrлядит матрица Qj для интерполирующих конечную точку
В сплайнов при j 4. Здесь пробелами обозначаются нули, а знач
ком х не интересующие нас дробные величины; {3 это нормиро
вочная константа.
х
х х
х х х
х х х 1
х х х 124
х х х 1677 1
х х х 7904 124
х х х 18482 1677
х х 24264 7904
х х 18482 18482 1
х 7904 24264 124
Qj == {3 х 1677 18482 1677 х
124 7904 7904 х
1 1677 18482 х х
124 24264 х х х
1 18482 х х х
7904 х х х
1677 х х х
124 х х х
1 х х х
х х х
х х
х
Матрицы, рассмотренные в этом и друrих, помещенных в приложе
нии Б, примерах, позволяют выявить простую структуру размещения HeHY
левых элементов. Значения этих элементов можно найти, рассматривая OT
дельно каждый столбец и решая линейную систему оrраничений из ypaB
нения (7.14). МаtlаЬ код в приложении В вычисляет таким способом MaT
рицы Qj. На рисунке 7.4 показаны некоторые типичные интерполирующие
конечную точку В сплайновые вейвлеты, полученные из этих конструкций.
В сплайновый блок фильтров
к этому моменту мы уже выполнили этапы, необходимые для KOHCTPy
ирования полуортоrональноrо базиса вейвлетов. Однако, чтобы восполь
зоваться сплайн вейвлетами, нам еще следует применить блок фильтров
114 Т7ава 7
r
v v
I vЛv I\/\ f/\ 1\
vv VV
Н I л I 1\/\ А 1\
v v VV vv
I л I 1\/\ А f\
v v VV vv
I л I 1\/\ А 1\
v v VV vv
I ] I л I 1\/\ 1\ А
VV VV vv
I 1r I л I I\fI l\fI
V V v V v v
I I л I ,,/ I
1'11
У \ v v
(а) степеНL () (б) степеНL 1 (в) степеНL 2 (r) степеНL 3
Рис. 7.4. В сплайновые вейвлеты интерполирующие конечную точку для W 3 (m) со
степенями m =' О, 1,2 и 3.
с фильтрами анализа Aj и Bj. Эти матрицы позволяют определить cj l
и dj l из c j путем матричноrо умножения, как это делалось в уравнени
ях (7.4) и (7.5). В разделе 7.1.2 было сказано, что фильтры анализа OДHO
значно определяются обратным отношением из уравнения (7.10):
[ ] =' [pjIQj] l.
Однако получение фильтров Aj и Bj в явной форме при применении блока
фильтров для сплайн вейвлетов, как правило, не является лучшей идеей.
Если pj и Qj разрежены и на один столбец в них приходится только О(т)
элементов, то Aj и Bj, как правило, плотны, так что время перемноже
ния матрицы и вектора будет зависеть уже квадратичным, а не линейным
образом.
К счастью, существует более удачный подход. Суть ero в том, что cj l
И dj l можно вычислить из c j , решая разреженную линейную систему:
[pjIQj] [ cj l ] =' c j .
dJ l
7.4. Биортоzона.7ьные вейвлеты
115
Чтобы решить эту систему относительно
[ cj l ]
dj l '
матрицу
[pjIQj]
сначала следует сделать ленточной, просто изменив порядок ее столбцов
так, чтобы столбцы матриц pj и Qj перемежались. Получившаяся лен
точная система решается линейно по времени с помощью LU разложения
[97], а затем это решение также переупорядочивается для получения нуж
Horo нам ответа. Таким образом, блок фильтров можно осуществить и без
представления и использования Aj и Bj в явном виде.
7.3.3. Конструирование полуортоrональных вейвлетов
Здесь мы вкратце перечислим этапы конструирования полуортоrональ
Horo базиса вейвлетов и связанных с ним матриц анализа и синтеза.
1. Выбор масштабuрующей Функцuu фj (х), определенной лuбо явно, лu
бо через схвму последовательноzо деленuя. Этим выбором определяют
ся вложенные аппроксимационные пространства V j и фильтры синте
за pj.
2. Выбор скаЛЯРН020 проuзведенuя, определеНН020 на пространствах
функцuй v o , V 1 ,.... Этим выбором определяется L2 HopMa и OpTO
rональность. Хотя, как правило, выбирается стандартное скалярное
произведение для нахождения меры поrрешности, имеющей значение
в контексте рассматриваемоrо нами приложения, может использоваться
и взвешенное скалярное произведение.
3. Выбор матриц сuнтеза вейвлетов Qj, которые удовлетворяют
(pj) т [ (фj I фj)] Qj О. Этим выбором определяются вейвле
ты фJ (х), покрывающие пространства Wj. Совместно фильтры син
теза pj и Qj определяют фильтры анализа Aj и Bj через соотноше
ние (7.10).
7.4. Биортоrональные вейвлеты
к этому моменту мы уже определили вейвлеты как базисы для OpTO
rональных дополнений. Требование ортоrональности между пространства
116
Т7ава 7
ми V j и W j для нас вполне приемлемо, особенно Korдa используется полно
стью ортоrональный базис. И все же оно влечет некоторые нежелательные
следствия:
. Полуортоrональные конструкции, как правило, rарантируют, что pj
и Qj являются разреженными и, следовательно, процесс восстановле
ния может ПРОИЗВОДИfься линейно по времени. Однако разреженность
фильтров Aj и Bj не rарантирована, поэтому зависимость времени
выполнения анализа может быть квадратичной. В разделе (7.3.2) мы
описали, как можно было бы применить LU разложение, чтобы coxpa
нить линейную сложность алrорнтма выполнения анализа для сплайн
вейвлетов, однако, к сожалению, этот трюк не срабатывает в случае
применения анализа к более мноrомерным функциям, таким, как по
верхности.
. Прибавление одноrо ортоrональноrо или полуортоrональноrо вейвлета
к функции, состоящей из масштабирующих функций, соответствую
щих более rрубому разрешению, обычно влечет появление множества
«новых вершин». В некоторых приложениях желательно, чтобы каж
дый вейвлет вводил только одну новую вершину, мало изменяя поло
жения уже существующих вершин.
. Пока не известна какая либо общая методика улучшения существу
ющих ортоrональных или полуортоrональных базисов вейвлетов, при
которой удовлетворялись бы оrраничительные условия, предьявляемые
к изначальной конструкции.
К счастью, есть возможность определить вейвлеты, которые, не бу
дучи ортоrональными по отношению к масштабирующим функциям, все
же обладают мноrими из полезных свойств полуортоrональных вейвлетов,
описанных в предыдущем разделе. Кратномасштабные базисы TaKoro типа
называются базисами бuорт020нальных вейвлетов и впервые были получе
ны Коэном и ero коллеrами [20].
Прежде чем дать мотивировку термину бuорт020нальность, заме
тим, что уже изложенный нами материал этой rлавы имеет, по боль
шей части, достаточно общий характер, что позволяет рассмотреть на
ero основе биортоrональный случай. Принципиальное отличие заключа
ется в том, что нам больше не требуется, чтобы Qj входила в нуль
пространство (pj) т [( фj I фj)]. Нам лишь необходимо, чтобы матри
ца [pj I Qj] была обратимой, что rоворило бы о существовании матриц
анализа А] и BJ.
При построении биортоrональнorо базиса задействуется дополнитель
ный трюк, суть KOToporo в том, чтобы сделать матрицы анализа и синтеза
7.4. Биортоzона.7ьные вейвлеты
117
разреженными, что обеспечит быстрое выполнение разложения и BOCCTa
новления. Как мы увидим, схе "ш подъема (liftiпg scheтe) , описанная в раз
деле 7.4.4, может использоваться для построения биортоrональных базисов,
обладающих целым рядом весьма привлекательных свойств, причем разре
женность в этом случае сохраняется.
7.4.1. Двойственные базисы и биортоrональность
Перед тем как определить биортоrональность, разберем более знако
мый случай ортоrональности. В частности, рассмотрим ортонормировнный
базис и(х) [Щ(Х)U2(Х)"'] и задачу нахождения коэффициентов Ci, пред
ставляющих данную функцию ЛХ) как натянутую на и(х):
ЛХ) L CiUi(X).
Произвольный коэффициент Ci можно определить непосредственно пу
тем скалярноrо умножения обеих частей этоrо уравнения на Щ (х):
Ulщ) L Сi\Uilщ)
L Ci 15 i,j
Cj.
Допустим теперь, что и(х) не является ортонормированным базисом.
Хотя U I щ) =1= Cj, мы все же надеемся найти новое семейство функ
ций и(х) [иl(Х) 'й2(Х)"'], дЛЯ KOToporo
Cj UIUj).
(7.15)
Соrласно одному из фундаментальных положений линейной алrебры
для любоrо конечномерноrо базиса такое семейство функций всеrда суще
ствует. Исходные функции U (х) в этом контексте носят название основН020
базuса (priтal basis), а новые функции и(х) называются двойственньи',t ба
зuсом (dual basis). Если уравнение (7.15) должно быть справедливым для
любой функции ЛХ), натянутой на и(х), это означает, что \UiIUj) l5 i ,j (дo
казательство этоrо можно считать милым маленьким упражнением). Точно
также мы можем определить двойственный базис, соответствующий OCHOB
ному базису и(х), как множество функций и(х), удовлетворяющее
\ulu) 1.
118
Т7ава 7
Заметим, что если и (х) ортонормированный, значит, он двойственен caMO
)иу себе (selfdual), т. е. и(х) == и(х).
Функции двойственноrо базиса нrрают ключевую роль в определении
конструкции биортоrональных вейвлетов. Начнем с Toro, что обозначим
j j ..
через Ф (х) и Ф (х) двойственные к фJ(х) и фJ(х) базисы. Получаем, что
[(фjlфj)] == 1 и [(фjlфj)] == 1.
(7.16)
Биортоrональный базис вейвлетов это базис, в котором OCHOB
ные масштабирующие функции ортоrональны двойственным вейвлетам
и основные вейвлеты ортоrональны двойственным масштабирующим функ
циям. Друrими словами, биортоrональные вейвлеты должны удовлетворять
следующим условиям:
(Ф{IФ{) == о }
I JI З) д ля всех ], k , 1.
\ФkФZ ==0
Эквивалентная запись этоrо определения такая:
[(фjlфj)] == о и [(фjlфj)] == о.
(7.17)
Объединяя уравнения (7.16) и (7.17) в систему, получаем лаконичную фор
мулировку, включающую как двойственность, так и ортоrональность.
[ \ [фj I фj] I [фj 1 фj])] == [ [ фJ I З] I [фJ I З] ] == 1.
[фJ I фJ] I [фJ I фJ]
(7.18)
7.4.2. Определение двойственных конструкций через
последовательное деление
Оказывается, всякий раз, коrда можно обратить процесс синтеза, в за
саде нас подстереrают двойственные функции. Основными функциями, KO
нечно, являются масштабирующие функции фj (х) и вейвлеты фj (х), опре
деляемые матрицами синтеза. Поскольку эти функции можно определить
через последовательное деление, вполне естественным будет поинтересо
ваться, можно ли определить соответствующие им двойственные функ
j j
ции Ф (х) и Ф (х) тоже через последовательное деление. Оказывается,
это возможно, по крайней мере, с точностью до постоянноrо масштабноrо
множителя. Сейчас мы это покажем.
7.4. Биортоzона.7ьные вейвлеты
119
Предположим, мы имеем матрицы синтеза pj и Qj, определяющие
множество основных масштабирующих функций и вейвлетов соrласно
[фj llфj lJ фj[рjIQj].
(7.19)
Мы хотим найти матрицы pj и Qj, определяющие двойственные масшта
бирующие функции и вейвлеты через последовательный деление:
[фj llфj lJ фj[РjIQj].
(7.20)
Прежде чем продолжить, нам следует коснуться одноrо несколько ще
котливоrо момента, связанноrо с нормированием. Простейшие схемы после
довательноrо деления являются стационарными, из чеrо следует, что Mac
штабирующие функции почти везде представляют собой сжатия и сдвиrи
одной функции. По определению, стационарное последовательное деление
предполаrает нормирование, при котором высота масштабирующей функ
ции Фi остается неизменной при всех j. Такое нормирование отличается
от нормирования, требуемоrо ортоrональностью: коrда носители основных
и двойственных функций становятся уже, высоты двойственных функций
возрастают для Toro, чтобы скалярное произведение их и основных функ
ций оставалось равным единице. Следовательно, проще будет использовать
последовательное деление для описания функций, биортоrональных с точ
ностью до какой нибудь приемлемой константы, характеризующей быстро
ту, с которой происходит сжатие носителей при последоватеЛ НOl',!. делении.
Ненормированные двойственные функции мы обозначим как фиф, а учас'!:.
ВУI9щие в их конструировании матрицы последовательноrо деления как Р
и Q.
В одномерном случае (т. е. для функций одноrо параметра таких, как
кривые) носнтели сжимаются в два раза всякий раз, коrда j возрастает
на единицу. В двумерном случае (т. е. для поверхностей) носители сжи
маются в два раза в каждом направлении и общий коэффициент сжатия
равен 4. Для n MepHoro случая коэффициент сжатия равен 2 n . Таким об
разом, мы сконструируем такие ненормированные двойственные функции,
что скалярное произведение масштабирующей функции или вейвлета при
разрешении j и соответствующей двойственной функции будет 2 jn. Усло
вие биортоrональности для ненормированных двойственных функций при
разрешении j в краткой форме можно записать так:
[\[фj I фj] I [фj I фjJ)] TjnI.
(7.21 )
Найденные ненормированные двойственные функции, соответствую
щие разрешению J, хорошо нормируются, если умножить каждую из них
120
Т7ава 7
на 2 jn . Например, коэффициенты масштабирующей функции и вейвлет ко
эффициенты для функции f(x) можно вычислить, используя ненормиро
ванную двойственную масштабирующую функцию Фi (х) и вейвлет Фi (х)
следующим образом:
с; 2jnUIФЛ,
di 2jnUIФЛ
При определении двойственных матриц последовательноrо деления pj
и Qj первым делом следует переписать уравнение (7.21), заменив в нем
индекс j на j 1:
[ \ [фj l I фj l] I [фj l I фj l])] Tи 1)n 1.
Далее мы произведем подстановку уравнений (7.19) и (7.20) в преды
дущее уравнение и используем свойства матриц скалярных произведений
из уравнения (7.19), чтобы получить
[pjl Qj]T[ (фjlфj) ][pj I Qj] T(j l)n 1.
Мы вновь можем воспользоваться уравнением (7.19), чтобы показать,
что средний член в левой части равен 2 jn 1, следовательно
[PjIQj]T[pjIQj] 2 n I.
(7.22)
Друrими словами, вплоть до множителя 2 n основная и двойственная матри
цы синтеза являются обратными транспонированными версиями друr друrа.
Вспомним теперь похожее уравнение, связывающее матрицы синтеза и aHa
лиза:
[ ; ] [PjIQj] 1.
При сравнении этих уравнений становится очевидным, что
pj 2 n (Aj)T;
Qj 2 n (Bj)T.
(7.23 )
(7.24)
Итак, мы имеем новую интерпретацию матриц анализа Aj и Bj: YMHO
женные на постоянный множитель они определяют новую схему последо
вательноrо деления со своими собственными масштабирующими функци
ями и вейвлетами. Масштабирующие функции и вейвлеты этой новой cxe
мы являются двойственными по отношению к масштабирующим функциям
и вейвлетам исходной схемы, определяемой pj и Qj.
7.4. Биортоzона.7ьные вейвлеты
121
Замечание. cTporo rоворя, мы показали, что если двойственные функ
ции, образованные последовательным делением, существуют, то их
матрицы синтеза должны определяться уравнениями (7.23) и (7.24).
Нам действительно хотелось бы знать, являются ли, таким образом,
полученные функции истинно двойственными по отношению к исход
ным масштабирующим функциям и вейвлетам, если матрицы из (7.23)
и (7.24) используются как матрицы последовательноrо деления. На
практике подобное соотношение, кажется, действительно существует,
однако доказать ero, похоже, очень непросто.
Двойственные функции Фi (х) и iPi (х) обнаруживают себя не слишком
часто rлавным образом, они используются при нахождении коэффициен
тов, используемых вместе с функциями прямоrо базиса для представления
какой либо заданной функции. Тем не менее, мы задействуем двойственные
уточняющие матрицы уточнения pj и ijj для вычисления функций двой
cTBeHHoro базиса. Построение двойственной Фi (х) или iPi (х) начинается
с умножения последовательности, все элементы которой, за исключением
одной единицы, являются нулями на pj или ijj, соответственно. Процесс
последовательноrо деления продолжается с использованием pj+l, pj+l
И Т. д. Получившуюся функцию еще следует умножить на 2jn, чтобы по
лучить нормированную двойственную Фi (х) или Фi (х) (тоща скалярное
произведение с соответствующей основной функцией равно 1).
7.4.3. Одноузловые вейвлеты
Чтобы продемонстрировать, что создание биортоrональной KOHCTPYK
цИИ действительно является линейными по времени процессами анализа
и синтеза, мы подробно рассмотрим случай эффективноrо разложения кy
сочно линейных функций. Во избежание сложностей, возникающих при
рассмотрении концов оrраниченноrо интервала, сосредоточим наше вни
мание на том, что находится внутри. Вейвлеты, которые мы при этом по
лучим, одинаково хорошо подходят и для периодической области, и для
неоrраниченной вещественной оси, а базис вейвлетов, который также будет
сформирован в этом разделе, окажется особенно полезным при иерархиче
ском разбиении замкнутых мноrоуrольных контуров, в чем мы убедимся,
рассматривая в девятой rлаве клеточное представление изображения при пе
ременном разрешении.
Выберем Функцuu шляпы (hat Iuпctioпs) с центрами в целых числах
в качестве масштабирующих функций для Vj. Масштабирующими функци
ями для vj l будут функции шляпы, В два раза большие по ширине с цeH
трами в четных целых числах, как показано на рисунках 7.5 (а) и 7.5 (б).
Очень простой способ получения биортоrональной конструкции линейно
122
Т7ава 7
по времени заключается в использовании функций шляп в v j С центрами
в нечетных целых числах в качестве вейвлетов для wj l, как показано
на рисунке 7.5 (в). Вим Свелденс [122] окрестил эти вейвлеты ленивыми
вейвлетами (lazy wavelets) , поскольку они не требуют никаких вычисле
ний они просто являются подмножеством масштабирующих функций.
0.5
ъ
(а)
(6)
Рис. 7.5. (а) Кусочно линейные масштабирующие функции в V j ; (б) масштабирую
щие функции в vj l; (в) ленивые вейвлеты в wj l.
Чтобы убедиться в том, насколько про сты процессы анализа и синтеза
для базиса ленивых вейвлетов, мы рассмотрим соответствующие матри
цы. Столбцы матрицы уточнения масштабирующих функций P eH состоят
только из трех ненулевых элементов ( , 1, ), т. К. широкую функцию шля
пу можно построить из трех узких функций шляп. Все элементы столбцов
матрицы уточнения ленивых вейвлетов P eH нули, за исключением един
ственной единицы, т. к. каждый ленивый вейвлет это одна узкая функ
ция шляпа. Следующий пример поможет нам ясно представить себе раз
реженную структуру этих матриц. Вот выражение, представляющее собой
матрицу синтеза ленивых вейвлетов, соответствующую j 3 и имеющую
точки на месте нулей:
[P eHI Q eH]
2
1 1
2
1 1
2
1 1
2
1 1
2
2
2
2
2
7.4. Биортоzона.7ьные вейвлеты
123
Соответствующие матрицы анализа, обратные по отношению
к [A eHIB eH]' также разрежены:
2
2
2
[ A eH ] 2
1 2
В лен 2 l 2 l
l 2 l
l 2 l
l 2 l
Теперь мы установили, что существуют матрицы PieH' QieH' А1ен
и B eH' такие, что
[P eHIQ eH] [ eH ] == 1.
лен
Несмотря на то, что ленивые вейвлеты являются интересным приме
ром, их практическая польза невелика. Причины тому мы узнаем, если
посмотрим, что происходит при выполнении анализа данной кусочно ли
нейной функции. [рубое приближение получается из более точноrо путем
исключения вершин, соответствующих нечетным числам. Следовательно,
самое rрубое приближение зависит только от нескольких начальных Bep
шин, и оно может оказаться очень плохим приближением исходной функ
ции.
Можно улучшить ленивые вейвлеты, сделав их «более ортоrональны
ми» к Vj l. Для этоrо из каждоrо вейвлета нужно вычесть несколько coceд
них масштабирующих функций rрубоrо разрешения. Такой i тый вейвлет
имел бы следующий вид:
o!,j l ( ) Ф j ( ) j Ф j l ( )
'j/i Х == 2i+1 Х Sk,i i+k Х ,
k
[де суммирование по k оrpаничивается Bcero лишь несколькими слаrаемы
. . 1
ми. Коэффициенты SL,i можно определить из требования, чтобы ФI (х)
были по возможности максимально близки к ортоrональным по отношению
к масштабирующим функциям в Vj l. Соблюдение этоrо условия требу
ет решения (по методу наименьших квадратов) пере определенной системы
уравнений [47]
(ФI lIФI, l) == о
(7.25)
124
Т7ава 7
для всех i', таких, что носитель Фi, 1 (х) покрывает 1И 1 (х). Кусочно ли
нейные вейвлеты, удовлетворяющие уравнению (7.25), Джо Уоррен [126]
назвал одноузловымu вейвлетамu (siпgle kпot wavelets), потому что при при
бавлении вейвлета к функции с вершинами в четных целых числах только
одна вершина (или узел) обязательно разместится в нечетном целом числе.
Один из таких вейвлетов изображен на рисунке 7.6(а) для случая, в KO
тором суммирование по k оrраничивается только четырьмя слаrаемыми
k == 1, О, 1, 2. Ниже приводятся значения для s, а также для последова
тельностей анализа и синтеза:
1
s == 258 ( 19, 81, 81, 19),
1
Р == 2(1, 2, 1),
1
q == 516 (19, 38, 62, 162, 354, 162, 62, 38, 19),
1
а == 516 (19, 38, 62, 162, 354, 162, 62, 38, 19),
1
Ь == 2( 1, 2, 1).
2
О
0.5
О
0.50 2 4 б 8 10 12 14
(а)
10 2 4 б 8 10 12 14
(6)
Рис. 7.6. (а) Один из одноузловых вейвлетов; (б) двойственная масштабирующая
функция, соответствующая одноузловой конструкции.
Двойственные функции, определяемые последовательным делением из
последовательностей а и Ь, иноrда MOryT иметь довольно причудливый вид,
даже если форма соответствующих прямых функций простая. На рисун
ке 7.6(б) показана двойственная масштабирующая функция, COOTBeTCTBY
ющая конструкции одноузловоrо вейвлета. Последовательность уточнения
для двойственных масштабирующих функций в два раза длиннее выше
указанной последовательности анализа а. [рафик на рисунке (как и любой
7.4. Биортоzона.7ьные вейвлеты
125
друrой rрафик, получаемый посредством последовательноrо деления) был
получен по итерационному методу разбивки и усреднения из раздела 6.4.
Подводя итоr конструированию одноузловоrо вейвлета, можно сrруп
пировать коэффициенты Sk,i в матрицу sj. Тоrда конструирование матри
цы синтеза одноузловых вейвлетов из матрицы синтеза ленивых вейвле
тов [P eH I Q eH] про изводится соrласно
[рZдноузIQZдноуз]:== [P eHIQ eH P eHSj].
Синтез одноузловых вейвлетов происходит быстро, потому что все члены
правой части этоrо уравнения разрежены (в том числе и Sj). Быстро произ
водится и анализ одноузловых вейвлетов, поскольку матрицы анализа также
являются разреженными:
[ Aj ] [ j j j ]
одноуз == [ pj I Qj pj Sj ] l == Ален + s В лен .
В) лен лен лен В)
ОДНОУЗ лен
7.4.4. Конструирование биортоrональных вейвлетов: схема подъема
Свелденс [122] определил, что вышеописанная конструкция одноузло
вых вейвлетов, о которой впервые сообщили Лаунсбери и соавторы [75],
является частным случаем общеrо преобразования, которое он назвал cxe
мой подъема (lifiiпg). Подъемом называется операция, обращающая биор
тоrональную схему, определяемую матрицами pj, Qj, Aj и Bj, в биор
тоrональную схему, определяемую
[РgодIQgод] == [pjlQj pjsj] и
[ A oд ] == ] [ Aj + jBj ] .
В под В
(7.26)
Схема подъема биортоrональна для любой выбранной матрицы sj, а не
только для матриц, полученных из проекций по методу наименьших KBaд
ратов. Выбирая разные Sj, можно построить базисы с разными желатель
ными свойствами: ортоrональностью, б6льшим количеством нулевых MO
ментов и др. (подробности смотрите у Свелденса [122], а также Шрёдера
и Свелденса [109]).
Операция подъема, описываемая уравнением (7.26) не приводит к изме
нению матриц pj и Bj, но она модифицирует две друrие матрицы Qj и Aj.
Следовательно, изменяются основные вейвлеты (из за изменения Qj), двой
ственные масштабирующие функции (из за изменения Aj) и двойственные
вейвлеты, потому что они являются линейными комбинациями модифици
рованных двойственных масштабирующих функций.
126
Т7ава 7
Возможна и операция двойствеНН020 подъема (dualliftiпg) [122], при
которой начальная схема, определяемая матрицами pj, Qj, Aj и Bj,
заменяется схемой, определяемой матрицами
[Р 6 д l Q 6 д ] [pj + sj Qjl Qj] и [ д ] [ А ]
;6 Bj :j sj .
под
Двойственный подъем не влечет каких либо изменений двойственных Mac
штабирующих функций, однако модифицирует двойственные вейвлеты,
а также основные масштабирующие функции и вейвлеты. Шрёдер и Свел
денс [109] приводят примеры базисов вейвлетов, построенных с использо
ванием двойственноrо подъема.
Перечислим этапы построения биортоrональноrо базиса вейвлетов MaT
риц анализа и синтеза:
1. Выбор простой биорт020нальной конструкции с известными разре
,женными матрицами синтеза и анализа pj, Qj, Aj и Bj.
2. Применение прост020 подъема или двойствеНН020 подъшwа с целью MO
дификации матриц синтеза и анализа для улучшения биорт020нальной
конструкции.
7.5. ВЫВОДЫ
Основы кратномасштабноrо анализа, изложенные в начале этой rлавы,
имеют очень общий характер. Они распространяются на целое множество
разнообразных конструкций вейвлетов, включая ортоrональные, полуорто
rональные и биортоrональные базисы вейвлетов, сконструированные на лю
бых компактных областях. Наиболее важные уравнения кратномасштабноrо
анализа в матричной записи сведены в таблицу 7.1.
В таблице 7.2 суммированы условия, определяющие ортоrональные,
полуортоrональные и биортоrональные конструкции базисов вейвлетов.
Третья колонка этой таблицы служит иллюстрацией Toro, что ортоrональ
ность представляет собой частный случай полуортоrональности, которая,
в свою очередь, является частным случаем биортоrональности. Что пред
почесть ортоrональный, полуортоrональный или биортоrональный базис
вейвлетов довольно сложный вопрос, ведь каждая из конструкций име
ет свои преимущества и недостатки. Так, ортоrональным базисам присуще
одно полезное свойство метрика L2 ошибки леrко вычисляется по коэф
фициентам разложения; однако очень немноrие функциональные простран
ства допускают конструкции ортоrональных вейвлетов. Полуортоrональные
7.5. Выводы
127
Таблица 7.1. Уравнения, определяющие уточнение, анализ, синтез и обратимость
Процесс Определение Матричная запись Уравнение
Уточнение фj l(х) фj (x)pj [фj llфj l] фj[рjIQj] (7.3)
фj l(х) фj(х)Qj
Анализ cj l Aj c j [ J l] [ ] с ] (7.4)
dj l Bj c j J l (7.5)
Синтез c j pj cj l + Qj dj l c j [PjIQj] [ CJ l ] (7.6)
dJ l
Обратимость Aj pj Bj Qj 1 [ ] [pjIQj] l (7.10)
AjQj Bjpj О
pj Aj + Qj Bj 1
КОНСТРУКЦИИ позволяют использовать симметричные вейвлеты с компакт
ным носителем и при этом сохранять ортоrональность между вейвлетами
и масштабирующими функциями. Биортоrональные вейвлеты обеспечива
ют наибольшую rибкость, поскольку ДЛЯ улучшения таких свойств, как
длина носителя и степень ортоrональности, можно использовать операцию
подъема.
Таблица 7.2. Условия, определяющие ортоrональные, полуортorональные и биорто
rональные вейвлеты
Свойство Оrраничения Оrраничения Уравиеиие
иа базисиые Фуикции иа матрицы
Ортоroнальность [(фjlфj)] I [pj I Qj] обратимые (7.11)
[('1'jl'1'j)] I и ортоrональные
[(фjl'1'j)] о
Полуортоrональность [(фjl'1'j)] о [pj I Qj] обратимые (7.13)
и (рj)Т[(фjlфj)]Qj о
Биортоrональноеть [(фjlфj)] I [pj I Qj] обратимые (7.16)
[('1'jl!j)] I
[(фjl'1'j)] о (7.17)
[('1'jlфj)] о
Т'ЛАВА 8
Кратномасштабные кривые
1. Сходные представления кривых 2. Сzлаживание кривой
3. Редактирование кривой 4. Обращение развертки и сжатие
кривых
Кривые иrрают основополаrающую роль во мноrих приложениях [pa
фики. В автоматизированном проектировании кривые, являющиеся KOHтypa
ми поперечноrо сечения, часто используются для описания поверхностей.
При анимации по ключевым кадрам кривые используются для контроля
параметрической интерполяции. Для тpexMepHoro моделирования и анима
ции используются базовые кривые, которые описывают деформацию объ
ектов. При работе с rрафикой кривые применяются для описания областей
с постоянной текстурой или цветом, при разработке шрифтов кривые пред
ставляют собой контуры букв, а для иллюстраций, выполненных от руки,
кривые являются основными элементами законченноrо фраrмента. Все эти
приложения выиrрывают от TaKoro представления кривых, которое делает
возможным rибкое редактирование, сrлаживание и обращение развертки.
В частности, хорошее представление кривых должно поддерживать:
. непрерывное сrлаживание, блаrодаря которому устраняются нежела
тельные детали кривой (см. рисунок 8.1, стр. 13 1);
. возможность изменения общеrо контура кривой с сохранением мелких
деталей или ее специфики (см. рисунок 8.2, стр. 132);
. возможность редактирования кривой для любой непрерывно меняю
щейся степени детализации, допускающую непосредственную работу
с произвольной частью кривой (см. рисунок 8.3, стр. 133);
. возможность изменения специфики кривой с сохранением ее общеrо
контура (см. рисунок 8.5, стр. 139);
. аппроксимацию кривой, или «фитинr», в пределах rарантированноrо
допуска поrpеIllНОСТИ для преобразования развертки и друrих прило
жений (см. рисунок 8.7, стр. 143).
8.1. Сходные представ.7енuя кривых
129
в этой rлаве мы описываем, как кратномасштабное представление
кривой обеспечивает единообразный подход к рассмотрению всех выше
перечисленных проблем. Кратномасштабные кривые, первоначально пред
ставленные Финкельштейном и Салезиным в [37], построены из В сплай
новых вейвлетов, описанных в разделе 7.1.2. Кратномасштабное представ
ление кривой не требует памяти для хранения, если не считать хранения m
контрольных точек исходноrо В сплайна, а алrоритм, использующий ero,
отличается простотой и быстрым выполнением, как правило, являясь ли
нейным по т.
8.1. Сходные представления кривых
Полезность кратномасштабноrо представления кривых заключается
в удобстве, с которым может выполняться широкое множество различных
операций. Ряд дрyrих представлений кривых был разработан для работы
с одной или несколькими операциями из этоrо множества. В этом разделе
мы обзорно рассмотрим некоторые из этих приемов.
Форсей и Бартеле [39] используют иерархические В сплайны при pe
дактировании общей формы поверхности с сохранением ее деталей. Их
первоначальная формулировка требует от пользователя разработки явной,
встроенной в модель, иерархии. В более поздней работе [41] они описыва
ют метод, позволяющий осуществить рекурсивную аппроксимацию иерар
хической поверхности до получения набора данных, для чеrо первым ша
[ом находится rpубое приближение, а затем производится уточнение в тех
областях, rдe требуется большая точность приближения. Подобная схема
напоминает действие блока фильтров в кратномасштабном анализе из раз
дела 7.1.2. Однако при использовании иерархических В сплайнов для дaH
ной кривой или поверхности возможно бесконечное число представлений,
тоrда как кратномасштабное представление кривой может быть только oд
ним. Фаулер [42], а также Уэлш и Уиткин [130] также описывают методы,
позволяющие редактировать более узкие или более широкие участки по
верхности. Однако ни в одной из этих работ не предпринята попытка co
хранить высокоточные детали при редактировании на более низком уровне
точности.
Известно немало приемов и для сrлаживания кривых и поверхностей.
К ним относятся алrоритмы, минимизирующие энерrетическую норму. Их
обзор имеется у Хошека и Лас ера [61]. В качестве одноrо из примеров
можно назвать работу Целникера и [осеара [9], в которой определенный
функционал применяется и к нарисованным от руки кривым и к поверхно
стям. Такие минимизационные техники относятся к катеrории вариацион
Horo моделирования, которую мы рассмотрим позже, в двенадцатой rлаве,
130
Т7ава 8
в контексте вейвлетов. Метод сrлаживания из этой rлавы, Bcero лишь ми
нимизирующий ошибку, вычисляемую по методу наименьших квадратов,
HaMHoro более простой подход, позволяющий непрерывно менять степень
сrлаживания.
В [1, 76, 95, 106] также исследуется множество схем аппроксимации
кривой в пределах установленноrо допуска поrpешности. Большинство из
них исследует различные способы удаления вершин с целью эффективноrо
представления кривых неравномерными В сплайнами. В разделе 8.4 мы
рассматриваем несколько отличающийся подход к аппроксимации кривых.
Мы описываем, как можно хорошо аппроксимировать кривую, используя
малое число cerMeHToB Бецера. Этот подход весьма практичен, поскольку
эти сеrменты являются стандартными представлениями для кривых в языке
PostScript, самом распространенном языке описания страниц.
В оставшейся части rлавы обсуждается, как один из возможных Ba
риантов кратномасштабноrо анализа, разработанноrо в разделе 7.3.2 для
В сплайнов, может быть применен непосредственно к кривым. Использо
вание сплайн вейвлетов приводит к эффективным алrоритмам сrлаживания,
редактирования и обращения развертки кривых.
8.2. Сшаживание кривой
в этом разделе мы обратимся к следующей проблеме: имея кри
вую ,(t) С m контрольными точками с [со'" Cт 1], необходимо по
строить аппроксимирующую кривую с наименьшей квадратичной поrреш
ностью, в которой используются т' контрольных точек с' [c '" c:п l]'
причем т' < т. Здесь мы предполаrаем, что обе кривые являются интер
полирующими конечную точку равномерными В сплайнами.
В рамках кратномасштабноrо анализа эта задача тривиально решается
для определенных значений m и т'. Допустим, что m 21 + 3 и т'
21' + 3 для неких неотрицательных целых чисел j' < j. Пусть с 1 это
вектор столбец, содержащий все контрольные точки с. Тоrда контрольные
точки с' аппроксимирующей кривой определяются как
с' "'" А1'+1 AJ'+2... А1 с 1 .
Дрyrими словами, мы просто выполняем алrоритм разложения, описыва
емый уравнением (7.4) до получения кривой с т' контрольными точками.
Заметим, что этот процесс можно осуществить для сотен контрольных точек
на скоростях, характерных для интерактивноrо режима, если прибеrнуть
к помощи линейноrо LU алrоритма из раздела 7.3.2.
Одним из примечательных аспектов кратномасштабноrо представления
кривой является ero дискретный характер. Так, можно леrко и эффективно
8.3. Редактирование кривой
131
построить аппроксимирующие кривые с числом контрольных точек, равным
4,5, 7, 11, и любым дрyrим, равным 2 j + 3, [де j это произвольное целое
число. Однако очевидный способ быстроrо построения кривых, имеющих
промежуточные «уровни» rладкости, не известен.
Одно хорошо работающее на практике решение состоит в определении
крuвой, соответствующей дробному уровню С2лажuванuя (jractioпal level
curve) ,j+M(t) для HeKOToporo О f.L 1, с использованием линейной
интерполяции двух кривых ,j(t) и ,Hl(t), соответствующих соседним цe
лочисленным уровням:
,HM(t) == (1 f.L),j(t) + f.L,Hl(t) ==
== (1 f.L)фj(t)с j + f.L фj +1(t)с Н1 .
(8.1 )
Подобные кривые, соответствующие дробному уровню, делают воз
можным сrлаживание на любом непрерывно меняющемся уровне. В ин
терактивном режиме пользователь может непрерывным образом изменять
форму кривой от самой rладкой формы (с четырьмя контрольными точ
ками) до самой детальной версии (со всеми m контрольными точками).
Несколько таких кривых изображено на рисунке 8.1.
Lvv
(а)
(6)
(в)
Рис. 8.1. Непрерывное сrлаживание кривой: уровень 8,0 (а); уровень 5,4 (б); уровень
3,1 (в).
8.3. Редактирование кривой
Предположим, нам известна кривая с контрольными точками c J , все
ее версии с низким разрешением сО, ..., c J 1 И версии, содержащие
уточняющие коэффициенты, d O , . . ., d J 1. Кратномасштабным анализом
предусматриваются два существенно отличающихся вида редактирования
кривых. Изменяя какую нибудь версию с низким разрешением c j , а по
том добавляя детали d j , d j + 1, . . ., d J 1, мы меняем общий вид кривой
(см. рисунок 8.2, стр. 132). С друrой стороны, изменяя уточняющие функ
ции d j , d j + 1 , ..., dJ l, но оставляя нетронутыми сО, ..., c j , мы меняем
132
Т7ава 8
характер кривой, не повлияв на ее общий вид (см. рисунок 8.5, стр. 139).
Более полно два этих типа редактирования будут рассмотрены ниже.
8.3.1. Редактирование общеrо вида
Редактирование обrцеrо вида кривой на целочисленном уровне вей
влет преобразования не представляет никаких трудностей. Пусть c J
это контрольные точ и исходной кривой ,,J (t), c j ее версия с низ
M разрешением, а c j отредактированная версия c j , определяемая как
c j c j + 6 c j . Отредактированная версия кривой с самым высоким разре
шением с лJ c J + 6c J вычисляется путем восстановления:
с) c J + 6c J
c J +pJpJ 1...pj+16cj.
Заметим, что чем ниже берется уровень сrлаживания j, тем более круп
ные участки кривой с высоким разрешением ,,J (t) задействуются при pe
дактировании общеrо вида кривой. На самом низком уровне, коrда j О,
затраrивается вся кривая целиком; на самом высоком уровне, коrда j
J, отмечается воздействие лишь на узкую область, на которую влияет
одна исходная контрольная точка. Эта своеобразная rибкость, допускаемая
редактированием при переменном разрешении, иллюстрируется рисунка
ми 8.2 и 8.3(а).
, UU
(а)
(6)
(в)
(r)
Рис. 8.2. Изменение общеrо вида кривой при сохранении ее специфики.
в дополнение к редактированию на целых уровнях разрешения eCTe
ственно было бы придать смысл и редактированию на дробных уровнях.
Хотелось бы, чтобы часть кривой, подверrшаяся воздействию при peдaK
тировании на дробном уровне j + м, интерполировала части, на которые
оказывается воздействие на уровнях j и j + 1. Так, при увеличении М
от О до 1 затраrиваемая область постепенно уменьшается от участка, co
8.3. Редактирование кривой
133
ответствующеrо ], до участка, соответствующеrо j + 1, как показано на
рисунке 8.3(б).
", ! 4,'
-""'_ \ / 3/ '"
"'. \ / // 2-
'\, \ I /
"\ I / 1
-:::::.,- ->-.:;.-
(а)
' ' .'" ! 3. / :
.' ...............' / / / ....,........
" ..,.> / -::2.0
(6)
Рис. 8.3. Середина сплошной кривой вдавливается: (а) целые уровни редактирова
ния 1, 2, 3 и 4; (б) дробные уровни редактирования между уровнями 2,0 и 3,0.
Рассмотрим соответствующую дробному уровню кривую ,J+J.L(t), за
данную уравнением (8.1). Пусть cJ+J.L(t) обозначает набор контрольных
точек, поставленных в соответствие этой кривой, т. е.
,J+J.L(t) == фJ+l(t)сJ+J.L.
(8.2)
Предположим теперь, что одна из контрольных точек d;+J.L изменена поль
зователем. Чтобы обеспечить вышеописанную зависимость видоизменен
ной части кривой от М, система должна автоматически сместить несколько
соседних контрольных точек при изменении d;+J.L. Расстояние, на которое
передвиrается каждая из этих контрольных точек, обратно пропорциональ
но м: к примеру, коrда М близко к нулю, контрольные точки на уровне j + м
сдвиrаются в совокупности так, что суммарный эффект близок эффекту,
получаемому редактированием одной контрольной точки на уровне j; KO
[да М == 1, близлежащие контрольные точки не смещаются вообще, посколь
ку видоизмененная кривая должна соответствовать сдвиry только одной
контрольной точки на уровне j + 1.
Обозначим через 6c j +J.L вектор, описывающий, как модифицируется
каждая контрольная точка кривой на дробном уровне: i ая компонента этоrо
вектора обозначает сдвиr i ой контрольной точки, выполненный пользова
телем; дрyrие компоненты представляют собой вычисленные сдвиrи друrих
134
Т7ава 8
контрольных точек. Вместо явноrо нахождения решения 6.c j + M , мы разби
ваем этот вектор на два: вектор 6. c j сдвиrов контрольных точек на уровне j
и вектор 6.d j видоизменений вейвлет коэффициентов на уровне j, который
определяется по формуле 6.d j Bj+16.c j + 1 . Тоrда сдвиrи контрольных
точек, соответствующих высокому разрешению, можно восстановить, ис
пользуя непосредственно уравнение (7.6):
6.c J pJ pJ l ... pH2(pHl6.c j + QHl6.d j ). (8.3)
Выражение для 6.c j + M получаем, приравнивая правые части ypaBHe
ний (8.1) и (8.2) и применяя затем уравнение (7.1):
6.с Нм == (1 M)pHl6.c j + м6.с Н1 .
Подстановка 6.c j + 1 и использование уравнения (7.6) позволяют Bыpa
зить 6. с Н м через 6. c j и 6. d j :
6.с Нм pHl6.c j + MQ H l6.d j .
(8.4 )
Теперь определим новый вектор 6.c j как сдвиr контрольных точек на
уровне j, необходимых для перемещения измененной контрольной точ
ки с;+М В ее новое положение. Кроме Toro, определим 6.c j + M как вектор
сдвиrов контрольных точек, произведенных пользователем на уровне j + м,
т. е. вектор, в котором i ый элемент равен 6.с;+М, а дрyrие элементы равны
нулю. Заметим, любой из сдвиrов, 6.c j или 6.c j + M , отдельно определя
ет попадание выбранной контрольной точки в новое положение; однако
первый сдвиr задействует б6льший участок кривой. Чтобы ширина видоиз
меняемоrо участка постепенно убывала при росте М от О до 1, мы можем
взять нечто среднее между двумя этими векторами, используя некоторую
интерполирующую функцию 9(М):
6.с Нм == (1 9(M))p H l6.c j + 9(М)6.с НМ .
(8.5)
Так, 6.c j + M по прежнему приводит выбранную контрольную точку в ее
новое положение, а также является функцией, измеряющей ширину изме
няемоrо участка в зависимости от М.
Далее мы приравняем правые части уравнений (8.4) и (8.5) и умножим
обе части получившеrося уравнения либо на A.i+ 1, либо на Bi+ 1:
АНl pHl6.c j + мАНl QHl6.d j ==
== (1 9(м))А Н l рНl6.cJ + 9(м)АНl6.с НМ ;
ВНl pHl6.c j + МВНl QHl6.d j ==
(1 9(м))в Н l рНl6.cJ + 9(м)вНl6.с НМ .
8.3. Редактирование кривой
135
Наконец, применяя тождества «обратимости» (уравнение (7.10) из табли
цы 7.1), упрощаем эти уравнения и получаем нужные выражения:
b..c j (1 g(f,L))b..c j + g(f,L)Aj+1b.. c J+ Jl ;
b..d j == g ) АН1 Ь..сНМ.
(8.6)
Взяв в качестве 9 (м) любую функцию, возрастающую монотонно от О до 1,
мы сможем вводить детали b..d j постепенно. Функция g(f,L) : м2 является
очевидным выбором, хорошо зарекомендовавшим себя на практике.
Последний шаr определение b..c j . Выберем вектор, все элементы
KOToporo равны нулю за исключением одноrо или двух, в зависимости от
индекса i измененной контрольной точки. Изучив i тую строку матрицы
уточнения pj+1, мы можем определить, испытывает ли измененная KOH
трольная точка максимальное воздействие со стороны одной контрольной
'+1+1+1
точки с{ или же со стороны двух контрольных точек и + 1 на
уровне j + 1. В первом случае мы определяем ь..с{ как ь..с;+м j Plt 1 . Во
втором случае мы определяем b..c и b..C +l как ь..с;+м j2Pl,t 1 . '
Итак, измененные контрольные точки кривой caMoro высокоrо разре
шения вычисляются после выполнения шаrов последовательности в обрат
ном порядке.
1. Определяем ь..сН м :== [О, ..., О, ь..с;+м, О, ..., О]Т.
2. Определяем b..c j и b..c j + 1 так, как указано в предыдущем абзаце.
3. Определяем c j и d j соrласно уравнению (8.6).
4. Строим приближения кривой caMoro высокоrо разрешения соrласно
уравнению (8.3).
Определенное здесь редактирование на дробных уровнях разрешения
довольно успешно применяется на практике. Непрерывное изменение ypOB
ня редактирования позволяет про изводить плавные, cBoero рода интуитив
ные изменения в редактируемой области кривой, как видно из рисунка (8.3).
Поскольку сложность алrоритма по числу контрольных точек имеет толь
ко линейный характер, модификацию леrко осуществить в интерактивном
режиме, даже для кривых, имеющих сотни контрольных точек.
Прямое манипулирование
Наше определение редактирования на дробных уровнях разрешения
можно с леrкостью расширить и включить в Hero прюwое )wанuпулuрова
ние, при котором пользователь работает непосредственно с кривой, а не
136
Т7ава 8
с определенными контрольными точками [2, 39,42,62]. При работе непо
средственно с кратномасштабной кривой на уровне j + м нам необходимо
знать, сколько контрольных точек на уровнях j и j + 1 следует изменить,
Korдa пользователь перемещает некоторую точку кривой в новое положение.
Предположим, что пользователь перемещает точку ,j+Jl(to) в новое
положение ,j+Jl(to) + 6. Наша задача определить претерпеваемую KOH
трольными точками модификацию, удовлетворяющую
фj(tо)6с j "" 6,
ф Н l(tо)6с НJl == 6.
Данные уравнения недоопределены, потому что матрицы строки фj (to)
и фj+l(tо) не являются обратимыми. Тем не менее, мы можем найти изме
нение контрольных точек по методу наименьших квадратов 6c j и 6c j + Jl
С помощью псевдообратных матриц [47], обозначаемых надстрочным ин
дексом +:
6c j "" (фj(tо))+6,
6с НМ == ( ф Н l(tо))+6.
(8.7)
Следует считать, что два этих уравнения применяются по отдельности
к каждому измерению Х и у. Т. е. 6 будет скалярной величиной (скажем, из
менение по Х), а каждая левая часть и каждая псевдообратная матрица будут
столбцами, состоящими из скаляров. Тоrда измененные контрольные точ
ки кривой С самым высоким разрешением MorYT быть вычислены подобно
тому, как вычисляются контрольные точки с применением уравнений (8.6)
и (8.3).
Заметим, что первый шаr в построении, решение (8.7), проводится за
постоянное время, поскольку для кубических В сплайнов не более четырех
элементов каждой псевдообратной матрицы отличны от нуля. Проблема Ha
хождения значения параметра to, при котором кривая проходит максимально
близко к выбранной пользователем точке, является хорошо изученной за
дачей определения корней. Существует несколько путей ее решения [106].
В методе, представленном Финкельштейном и Салезиным, преобразование
развертки кривой производится однократно для нахождения значения пара
метра и точки, наиболее близкой к точке, выбранной пользователем. Такой
подход, похоже, обеспечивает хороший компромисс между скоростью и точ
ностью В интерактивной системе.
В некоторых приложениях интуитивно понятно, что более правильной
будет работа с кривой, соответствующей самому высокому уровню разре
шения, а не с ее сrлаженной версией. Даже если выведенное на экран изоб
ражение кривой характеризуется высоким разрешением, более полезным
8.3. Редактирование кривой
137
может оказаться выполнение модификации на большом участке кривой.
Это позволило бы менять степень детализации изменяемой кривой путем
перемещения единственной точки: чем ниже становится разрешение, при
котором производится редактирование, тем большая область кривой попа
дает под воздействие. Такой тип контроля довольно леrко поддерживается
определением 6, как модификации кривой с высоким разрешением в пере
двинутой точке ,J(to) и использованием уравнения (8.7).
Редактирование участка кривой по выбору
Методы манипулирования кривыми содержат один проблематичный
момент: результат, к которому они приводят, часто находится в зависимо
сти от параметризации кривой, которая не обязательно соответствует инту
итивному восприятию очертаний кривой. Описанные нами к настоящему
моменту манипуляции страдают подобным недостатком: сдвиr разных TO
чек вдоль кривой на определенном (возможно, дробном) уровне l == j + 11
необязательно влияет на участки кривой постоянной длины. Однако мы
в состоянии компенсировать этот недостаток в случае прямоrо манипули
рования с помощью управления кратномасштабным редактированием. Дей
ствовать будем так.
Пусть h определяемый пользователем параметр, который описывает
желаемую длину редактируемоrо участка кривой. При задании этоrо пара
метра можно использовать любые единицы физических величин, будь то
пиксели, дюймы или процентное выражение от общей длины кривой. Си
стема будет находить подходящий уровень редактирования l, на котором
изменяющийся участок примерно равняется h единицам длины, с центром
в сдвиrаемой точке ,J (to).
Мы оцениваем l следующим образом. Для каждоrо целочисленно
[о уровня редактирования j обозначим через h j (to) длину участка кри
вой,J (t), изменяющеrося при редактировании кривой в точке,J (to). Дли
на h j (to) леrко оценивается, если произвести обращение развертки кри
вой ,J(t), затем приблизительно определить длины полиномиальных cer
ментов и про суммировать длины отрезков, изменяющихся при редактиро
вании кривой на уровне j со значением параметра to. Следующим шаrом
мы определяем j как наибольшее значение j, причем hj (to) ;? h, и j+,
причем h j + (to) h. Для нахождения подходящеrо дробноrо уровня pe
дактирования l, заключенноrо между j и j+, мы используем линейную
интерполяцию:
h h j +. hj h .
l . hj h j + з + hj h j + З+.
Наконец, выражая l через целочисленный уровень j и дробную вели
чину 11, мы можем, как и ранее, вновь применить уравнение (8.7), а затем
138
Т7ава 8
и уравнения (8.6) и (8.3). Хотя желаемый участок h не полностью задей
ствован в такой конструкции, на практике она неожиданно обеспечивает
значимый контроль. Рисунок (8.4) демонстрирует такой тип редактирова
ния для кривой С крайне неравномерным rеометрическим вложением.
(а)
(в)
(6)
(r)
Рис. 8.4. Кривая с параметризацией, наиболее быстро изменяющейся посередине (а).
Прямое манипулирование с левой частью кривой (б) воздействует на значительно
меньший участок кривой, по сравнению с результатом манипулирования на среднем
участке (в). Проrрамма редактирования кривой при различных разрешениях aBTOMa
тически определяет наиболее подходящий уровень редактирования для изменения
конкретното участка кривой (т).
Подводя итоr, отметим, что прямое манипулирование и описанный
в этом разделе вид редактирования при переменном разрешении хорошо
работают вместе. Про изводя прямое манипулирование при переменном раз
решении, пользователь может непосредственно перемещать кривую и дo
биваться изменений в весьма широком диапазоне от очень небольших
участков до обширных в зависимости от Toro, при каком разрешении
осуществляется редактирование. Кроме Toro, такой вид редактирования
при переменном разрешении можно использовать, чтобы компенсировать
любые особенности rеометрическоrо вложения кривой, а это способству
ет еще большей четкости контроля над rеометрией участка редактируемой
кривой.
8.3.2. Редактирование особенностей кривой
Дрyrой вид редактирования, естественно, поддерживаемый KpaTHOMac
штабными кривыми, представляет собой редактирование особенностей кри
8.3. Редактирование кривой
139
вой, не сопровождаемое изменением ее общеrо KOHТYla. Пусть c J это
контрольные точки кривой, а сО, ..., cJ l, dO, ..., d 1 это компонен
ты ее кратномасштабноrо разложения. Редактирование специфики кривой
представляет собой Bcero лишь замену существующеrо множества уточ
Ф d j d J l d Лj d ЛJ l
няющих ункции , ..., неким новым множеством ,. . . ,
и последующее восстановление.
Применяя такой подход, можно разработать «библиотеку особенностей
кривой», хранящую различные уточняющие функции, которые взаимозаме
няемо приложимы к самым разным кривым. Такие уточняющие функции
MOryT быть извлечены из карандашных зарисовок; возможны и процедур
ные методы для их rенерирования. На рисунке 8.5 показано изменение
особенностей кривой после использования различных уточняющих стилей.
Интерактивная система разработки иллюстраций, которая использовалась
при создании этоrо рисунка, описывается Селисбьюри и соавторами [105].
(
Рис. 8.5. Изменение особенностей кривой при сохранении ее контура.
8.3.3. Ориентация детали
В двумерном случае параметрическую кривую наиболее естественно
представлять двумя отдельными функциями, одна из которых соответствует
измерению х, а друrая соответствует измерению у: ,(t) == (,x(t), ,y(t)).
Так, вполне разумным кажется и представление контрольных точек c j
и уточняющих функций d j через матрицы с отдельными столбцами для х
и для у. Однако кодирование уточняющих функций указанным способом
навязывает всем деталям кривой определенную х у ориентацию. Как вид
но из рисунка 8.6, такое представление не всеrда обеспечивает ожидаемый
вид отредактированноrо контура.
В качестве альтернативноrо варианта мы используем метод, сходный
140
"
Т7ава 8
( )
(6) (в)
(а)
Рис. 8.6. Редактирование контура (а); детали по прежнему ориентированы вдоль
фиксированных осей х и у (б); детали ориентированы относительно касательнorо
направления к кривой (в).
с методом, предложенным Форсеем и Бартелсом [39] для иерархических
В сплайнов. Соrласно этому подходу каждый уточняющий коэффициент
di характеризует изменение относительно касательноrо и нормальноrо Ha
правлений кривой с низким разрешением ,j l(t). Касательная и нормаль
вычисляются для значения параметра to, соответствующеrо вершине вей
влет а Фi (t). Заметим, что кривая ,(t) больше не является простой линейной
комбинацией масштабирующих функций фо и вейвлетов фj; восстановле
ние кривой требует изменения координат в приложении к вейвлет коэффи
циентам d j на каждом уровне восстановления. Но этот процесс линеен по
числу контрольных точек, поэтому вычислительная сложность алrоритма
не возрастает.
Возможно использование как нормированных, так иненормированных
версий системы координат «касательная нормаль»; двум этим альтернатив
ным версиям свойственны разные, но одинаково приемлемые характеры
поведения. Для рисунка 8.5 использовались ненормированные касательные,
в то время как для всех остальных рисунков из этой rлавы использовались
нормированные касательные.
8.4. Обращение развертки контура и сжатие кривой
Используя библиотеки особенностей кривой и дрyrие средства peдaK
тирования при переменном разрешении, можно с леrкостью создать очень
сложные кривые с сотнями или тысячами контрольных точек. Зачастую
(как, например, в этой книrе) изображения таких кривых выводятся на пе
чать в очень маленьком формате. Общепринятые методы обращения раз
вертки, сохраняющие всю сложность этих кривых, являются неэкономич
ными как в отношении ceTeBoro трафика вследствие отправки на печать
8.4. Обращение развертки контура и сжатие кривой
141
очень большоrо количества файлов, так и в отношении времени обработки
принтером, поскольку формируются изображения кривых, имеющих MHO
жество контрольных точек на нескольких квадратных пикселях. Именно
поэтому мы исследуем форму сжатия кривой, подходящую для преобразова
ния развертки. Описанный нами алrоритм находит кривую, приближенную
к исходной кривой, в пределах задаваемоrо допуска. Однако он не требует
соблюдения каких либо оrpаничений на непрерывность, которые обычно
являются необходимыми в приложениях, связанных с подrонкой данных.
В разделе 8.2 мы показали, как выполнение одноrо шаrа из блока филь
тров сплайн вейвлета приводит к аппроксимирующей кривой, с уменьшен
ным вдвое числом контрольных точек. Такой тип сrлаживания можно при
менять для нахождения приближений, минимизирующих ошибку в L 2 Me
ре. Однако L2 метрика не очень подходит для обращения развертки, потому
что аппроксимирующая кривая i(t) может быть сколь уrодно отдалена от
исходной кривой ,(t), а L2 ошибка не будет превосходить установленной
rраницы до тех пор, пока она отклоняется от ориrинала в пределах достаточ
но маленькой области значений параметра. Чтобы преобразовать разверт
ку кривой снекоторой rарантированной точностью, которая измеряется,
скажем, как максимальное отклонение в пикселях принтера, нам следует
установить предел LОО нормы ошибки. Для этоrо существует множество
способов. Описываемый здесь метод отличается простотой и быстродей
ствием, но, определенно, возможны и методы, обеспечивающие еще более
высокие степени сжатия.
Обозначим через si (ще о i 2] 1) cerMeHT кубическоrо В сплай
на ,](t), задаваемоrо четырьмя контрольными точками ci, ..., ci+3. За
метим, что каждый cerMeHT s{ соответствует точно двум (отличающимся
большей детальностью) cerMeHTaM s tl и s t:l на уровне j + 1. в нашу
задачу входит построение новой аппроксимирующей кривой "Ht) для ,(t),
для чеrо мы будем выбирать различные сеrменты на различных уровнях
так, чтобы Ili(t) ,J (t) 1100 было меньше HeKoero задаваемоrо пользовате
лем допуска с для всех значений t.
Допустим, мы имеем какую то функцию ErrBound(si), вычисля
ющую предел L 00 ошибки, возникающей при использовании cerMeHTa si
аппроксимирующей кривой ,] (t), вместо исходных сеrментов кривой ,J (t).
Мы можем осуществить преобразование развертки кривой в пределах лю
боrо допуска с, если выполним рекурсивную проrрамму DrawSegment
для одноrо cerMeHTa sg, соответствующеrо кривой ,O(t) на самом низком
уровне. Эта проrрамма рекурсивно разбивает cerMeHT на меняющихся ypOB
нях, так что набор получаемых в результате сеrментов аппроксимирует кри
вую в пределах с.
142
Т7ава 8
procedure DrawSegment(si)
if ErrBound(si) < Е then
Output segment (si) as а portion of i(t)
else
DrawSegment(s i1)
+1
DrawSegment( S i+1)
end if
end procedure
Чтобы построить функцию ErrBound, введем обозначение Mj для
матрицы преобразования В сплайна в базис Бецера для кривой с 2 j + 3
контрольными точками и e j для вектора столбца с элементами е{, опреде
ляемоrо как
e j :"" Mj Qj dj l.
Вектор e j является мерой расстояния, на которое перемещаются контроль
ные точки при восстановлении более детальной кривой на уровне j из
аппроксимирующей кривой на уровне j 1. Т. к. кривые Бецера содержат
ся в выпуклой оболочке своих контрольных точек, значения элементов e j
обеспечивают неизменяемые rраницы для аппроксимаций кривой вслед
ствие усечения вейвлет коэффициентов. (При использовании контрольных
точек Бецера получаются более жесткие rраницы, если сравнивать с KOH
трольными точками В сплайнов.)
[раничное значение <5i для LCXJ ошибки, вызванной заменой cerMeH
та s{ на ero приближение на уровне j 1, определяется как
<5i . mах {lle{112}'
,:<:;k:<:;,+3
Тоrда проrрамму ErrBound можно описать рекурсивно следующим обра
зом:
function Err Bound( si)
if j J then
return О
else
+1 +1 +1 +1
return max{ErrBound(s i ) + <5 ; }, ErrBound(s i+1) + <5 H1}
end if
end function.
Для эффективной реализации этой проrраммы предпочтительнее ис
пользовать динамическое проrраммирование или итерационную (вместо
рекурсивной) функцию с тем, чтобы избежать повторноrо вычисления пре
делов поrpешности. Однако на практике эта проrpамма достаточно быстро
8.4. Обращение развертки контура и сжатие кривой
143
(а)
\ /
(6)
Рис. 8.7. Преобразование развертки кривой в пределах rарантированноrо максималь
ното допуска ошибки. (а) Для получения кривых (слева направо) использовалось,
соответственно, 5 %, 21 %, 46 %, 78 % возможноrо количества сетментов Бецера.
Ошибка составляет менее 1/300 дюйма. (б) Те же кривые, нарисованные в одном
масштабе.
выполняется и в рекурсивном исполнении, и в такой оптимизации, похоже,
нет необходимости, во всяком случае при обращении развертки тех кривых,
число контрольных точек которых исчисляется сотнями.
Аппроксимирующая кривая i(t) описывается набором cerMeHToB Бе
цера, чем мы воспользуемся, чтобы создать РоstSсriрt файлы. Заметим, что
144
Т7ава 8
рассмотренный нами алrоритм выдает кривые i(t), которые даже не явля
ются непрерывными там, [де встречаются два cerMeHTa с различных ypOB
ней. IIри преобразовании развертки ослабление непрерывности исходной
кривой приемлемо, поскольку нас интересует только абсолютная поrреш
ность в конечном множестве получающихея пикселей. Мы можем достиr
нуть позиционной непрерывности, не увеличивая предписанноrо допуска,
если просто выполним, в качестве заключительноrо этапа, усреднение KO
нечных контрольных точек, соответствующих соседним сеrментам Бецера.
Сrлаженные таким образом кривые выrлядят HeMHoro лучше, чем их раз
рывные дубликаты; к тому же в PostScript они имеют более компактное
представление. На рисунке 8.7 показано сжатие одной и той же кривой,
изображенной в разных масштабах.
['ЛАВА 9
Кратномасштабное клеточное
представление
1. Предыдущuе решенuя проблеJWЫ клеточною представленuя
2. АЛ20рuтм кратномасштаБН020 клетОЧН020 представленuя
3. Временная сложность 4. Прuмеры клетОЧНО20 представленuя
Восстановление поверхности по множеству плоских контуров явля
ется важной проблемой при формировании изображений в медицине, при
проведении биолоrических и rеолоrических исследований. Эту задачу мож
но свести к нескольким подзадачам [84, 85], одна из которых проблеJwа
клетОЧНО20 представленuя (tiliпg probleт) послужила темой этой rлавы.
Целью клеточноrо представления является построение мноrоrранника по
двум плоским мноrоуrольникам. В таком представлении два мноrоуrольни
ка образуют две rрани мноrоrранника, тоrда как каждая из остальных ero
rраней получается треуrольным соединением ребра одноrо контура и Bep
шины друrоrо контура. Примером может послужнть рисунок 9.1, на KOTO
ром изображена пара контуров и пред ставлено решение задачи клеточноrо
представления.
Трудность выполнения задачи клеточноrо представления кроется в по
строении «наилучшей» поверхности между двумя контурами. В этой rлаве
мы опишем, как можно использовать вейвлеты для эффективноrо конструи
рования клеточноrо представления, приближенноrо к оптимальному реше
нию. Впервые этот подход, который мы называем аЛ20рuтмом KpaтHOMac
штаБНО20 клетОЧНО20 представленuя (тultiresolutioп tiliпg algorithт), был
подробно описан Мейером [83, 84]. В ero работе нашли широкое приме
нение одноузловые вейвлеты, весьма похожие на те, что мы рассмотрели
в разделе 7.4.3, коrда выполняли иерархическое разложение мноrоуrольных
контуров.
9.1. Предыдущие решения задачи клеточноrо
представления
Для решения этой проблемы было придумано немало алrоритмов.
Так, Кеппель [67] развил метод нахождения клеточноrо представления, оп
146
(а)
Т7ава 9
(6)
Рис. 9.1. (а) Пара плоских мноrоуrольных контуров; (б) решение задачи клеточноrо
представления для этих контуров.
тимальноrо относительно определенной целевой функции, позднее Фуш
и друrие [43] усовершенствовали этот метод. Мы будем называть этот ал
rоритм оптимuзuрующим аЛ20рuтмом (optiтiziпg algorithт).
Оптимизирующий алrоритм начинается с Toro, что задача клеточноrо
представления сводится к задаче поиска на rpафе. Как показано на ри
сунке 9.2, rpаф можно построить по паре контуров, начав с установления
соответствия между узлом и каждым из ребер, способных соединить друr
с друrом два контура (такие ребра называют переJwычкамu (spaпs)). На сле
дующем шаrе мы рассматриваем каждую пару узлов нашеrо будущеrо rрафа
и соединяем их стрелками, если две перемычки, которые представляют эти
узлы, имеют общую вершину, а две друrие вершины являются смежными
на одном контуре. Эти условия rарантируют соответствие каждой стрел
ки на rрафе треуrольнику, образующемуся путем соединения ребра одноrо
контура с вершиной противоположнorо контура. Направление стрелок, по
общепринятому правилу, таково, что обход треуrольноrо контура по ребру
совершается против часовой стрелки.
Узлы и стрелки, получившиеся по такому построению, образуют TOpO
идальный rраф. Клеточные представления здесь это циклы, при которых
совершается обход каждой строки и каждоrо столбца rрафа. Оптимизи
рующий алrоритм соотносит затраты с каждой стрелкой rрафа (например,
с площадью треуrольника, представленноrо стрелкой), сводя таким образом
проблему клеточноrо представления к проблеме нахождения в rрафе цикла
наименьших затрат. Для краткости мы не станем объяснять, как находить Ta
9.1. Предыдущие решения задачи к.7еточноzо представ.7ения 147
t t t t t
:]J =j=[
! ! ! !
с I I I ! I
D . . . . .
I I I I I
Рис. 9.2. В оптимизирующем алrоритме клеточноrо представления перемычки кле
точноrо представления (обозначенные пунктирными линиями) представлены узлами
тороидальнorо rрафа, а треyrольники клеточноrо представления стрелками. Изоб
раженному на этом рисунке клеточному представлению соответствует цикл, в KO
торый входят выделенные стрелки. Друrие представления можно сконструировать
и из друrих циклов rpафа.
кой оптимальный цикл; достаточно сказать, что эта задача хорошо изучена
в дискретной оптимизации и решается с помощью методов динамическоrо
проrраммирования [43].
Заметим, что хотя клеточные представления, получаемые оптимизиру
ющим алrоритмом, являются «оптимальными» относительно количествен
ной целевой функции, это не обязательно означает, что они оптимальны
и для пользователя. Рассмотрим, например, два контура, показанных на
рисунке 9.3(а), которые представляют анатомические данные о rоловном
мозrе человека. Каждый контур имеет несколько меток по своему пери
метру, представляющих инваrинации или борозды rоловноrо мозrа. При
правильном восстановлении эти метки должны сочетаться так, чтобы бо
розда оставалась непрерывной между двумя слоями. Однако показанное на
рисунке 9.3(б) клеточное представление по оптимизирующему алrоритму
148
Т7ава 9
не дает соrласования двух меток в самом низу рисунка. Следовательно, для
улучшения результатов оптимизирующеrо алrоритма, возможно, требуется
и определенная степень вмешательства пользователя.
(а)
( б)
Рис. 9.3. (а) Пара контуров, полученных из коры rоловноrо мозrа человека. Один
контур состоит из 128 вершин (закрашенные кружки), друrой из 114 вершин
(<<пустые» кружки). (б) Неприемлемое клеточное представление, полученное опти
мизирующим алторитмом, свидетельствует о необходимости вмешательства самото
пользователя.
Основным недостатком оптимизирующеrо алrоритма считаются BЫ
числительные затраты: для пары контуров, имеющих в сумме m вершин,
время построения клеточноrо представления равняется O(n 2 1og n), а объем
необходимой памяти О(n 2 ). В частности, время, необходимое для BOCCTa
новления поверхности в интерактивном режиме, с ростом контура CTaHO
вится недопустимо дороrостоящим (контуры, содержащие тысячи вершин
не так уж редки в наборах фактических данных). По этим причинам мы
обращаемся к более быстрым неоптимизирующим методам.
Для достижения скоростей, соответствующих интерактивному режиму,
был предложен ряд алrоритмов, целью которых является нахождение при
емлемоrо клеточноrо представления без использования rлобальной опти
мизации. Мы упомянем только два из этих неоптимизирующих алrоритмов
(рассмотренных Мейером и соавторами в [85]). Такие алrоритмы конструи
руют клеточные представления линейно по времени: «жадные» алrоритмы
9.2. Алzоритм кратномааuтабноzо к.7еточноzо представ.7ения 149
(а)
(6)
Рис. 9.4. Клеточные представления, полученные быстрыми методами: (а) алrоритм
Кристиансена Зедерберrа; (б) алrоритм r анапатхи Деннехи.
[анапатхи и Деннехи [45] и Кристиансена и Зедерберrа [16]. В обоих Me
тодах конструирование начинается с HeKoToporo принятоrо за хорошую OT
правную точку ребра. Затем выполняется последовательное передвижение
по одному из контуров, при котором вершина одноrо контура связывается
со следующей вершиной друrоrо контура. Алrорнтм Кристиансена Зедер
берrа содержит попытку минимизировать сумму длин ребер, для чеrо из
двух возможных на каждом этапе ребер он всеrда выбирает более KOpOT
кое. Алrоритм [анапатхи Деннехи всеrда выбирает ребро, минимизиру
ющее разницу между долями длины дуrи, проходящей по каждому контуру.
Результаты этих алrоритмов при работе с упомянутыми контурами коры
rоловноrо мозrа показаны на рисунке 9.4. Каждый из алrоритмов «приве
ден в замешательство» локальной конфиrурацией, которая не очень хорошо
моделируется по своей эвристике. Несмотря на быстроту вычисления, полу
чающиеся клеточные представления бывают значительно хуже клеточноrо
представления, найденнorо по оптимизирующему алrоритму.
9.2. Алrоритм кратномасштабноrо Клеточноrо
представления
Кратномасштабный анализ определил новый подход к проблеме кле
точноrо представления. Основные этапы алrоритма кратномасштабноrо
150
Т7ава 9
клеточноrо представления кратко изложены ниже и иллюстрируются ри
сунком 9.5.
(а)
(r)
(6)
(д)
(в)
(е)
Рис. 9.5. Основные этапы алrоритма кратномасштабноrо клеточноrо представления.
Исходные контуры (а) сводятся к версиям с низким разрешениям (б) и с помощью
оптимизирующеrо алrоритма приводятся к клеточному представлению (в). В pe
зультате обратноrо введения вейвлетов образуются контуры с промежуточными раз
решениями (Т) и выполняется локальная оптимизация (д). Процесс повторяется до
тех пор, пока в контурах не появляются все исходные вершины (е).
1. Сведем нашу задачу к нахождению rрубых приближений исходных
контуров с помощью вейвлет разложения.
2. С помощью оптимизирующеrо алrоритма получим клеточное представ
ление контуров с низким разрешением.
3. Выполним один этап восстановления, чтобы ввести в каждый контур
по одному или несколько вейвлет коэффициентов и тем самым доба
9.2. Алzоритм кратномааuтабноzо к.7еточноzо представ.7ения 151
вить вершины и rрани к имеющемуся на данный момент клеточному
представлению.
4. Улучшим клеточное представление, применив локальную оптимиза
цию к rраням, расположенным по соседству с введенными rранями.
5. Повторяем третий и четвертый этапы до получения исходных вершин.
Более подробно каждый этап описывается в нижеследующих подраз
делах.
Заметим, что клеточное представление по кратномасштабному алrо
ритму не является rарантированно rлобально оптимальным относительно
целевой функции, используемой для вычисления клеточноrо представления
с низкой разрешающей способностью. Но поскольку алrоритм начинает
ся с применения оптимизирующеrо алrоритма и далее поддерживает ло
кальную оптимизацию, конечное клеточное представление нередко бывает
почти идентичным соответствующему клеточному представлению, получа
емому оптимизирующим алrоритмом. Существенные различия этих двух
методов чаще Bcero проявляются в тех областях, [де формы контуров очень
сильно отличаются друr от друrа. Часто в таких случаях ни один из методов
не дает приемлемоrо результата, и требуется вмешательство пользователя
(это относится и к контурам на рисунке 9.3). Именно тоrда скорость KpaTHO
масштабноrо алrоритма обеспечивает очевидное преимущество перед оп
тимизирующим алrоритмом.
9.2.1. Разложение контура
Кратномасштабный алrоритм клеточноrо представления начинается
с разложения каждоrо исходноrо контура, в результате KOToporo послед
ний представляется набором вейвлет коэффициентов и контуром с меньшим
разрешением. Для выполнения этой операции мы используем метод блока
фильтров одноузловых вейвлетов из раздела 7.4.3. Вспомним, что в качестве
исходных данных для процесса блока фильтров требуется последователь
ность коэффициентов, длина которой равняется степени двойки. Если число
вершин в контуре не равно степени двойки, мы добавляем вершины путем
итерационноrо расщепления caMoro длинноrо ребра и помещения новой
вершины в ero среднюю точку. Для поддержания и пополнения «списка»
ребер, отбираемых по длине, мы используем очередь по приоритету.
9.2.2. Оптимизация выбора базовоrо комплекта
На следующем шаrе алrоритм кратномасштабноrо клеточноrо пред
ставления берет пару контуров с низким разрешением, называемых базовыJw
152
Т7ава 9
комплектOJW (base case), и приводит в действие оптимизирующий алrоритм
для получения клеточноrо представления. Размер базовоrо комплекта влия
ет как на скорость вычисления клеточноrо представления, так и на качество
конечноrо результата.
Сведение задачи до рассмотрения небольшоrо базовоrо комплекта поз
воляет быстро выполнить оптимизирующий алrоритм на компьютере; oд
нако качество конечноrо клеточноrо представления может пострадать, если
не будет должноrо приближения контуров с низким разрешением к формам
исходных контуров. Использование большоrо базовоrо комплекта требует
больше времени, однако может привести к лучшему результату. Решение
тут может принять сам пользователь, задав размер базовоrо комплекта,
позволяющий ему установить компромисс между приемлемым результа
том и временем выполнения. Мейер [83] rоворит, что если пользователь по
каким то причинам не может указать размер базовоrо комплекта, то набор
из 64 вершин является, как правило, вполне разумным выбором.
9.2.3. Восстановление
Как только клеточное представление с низким разрешением получе
но, нам следует восстановить некоторые удаленные из контуров детали.
Восстановление контура из ero приближения с низким разрешением можно
осуществить двумя способами. Один метод, называемый восстановленuем
по блоку фuльтров (filter baпk recoпstructioп) , заново вставляет вейвлеты
на одном уровне блока фильтров за один раз. Друrой метод, называемый
восстановленuем по однOJИУ вейвлету (siпgle wavelet recoпstructioп), заново
вставляет вейвлеты по одному за раз, начиная с наибольших и заканчи
вая наименьшими. Время, требуемое на восстановление по блоку филь
тров, равно только О(п), а время на восстановление по одному вейвлету
равно О(п log п). Добавим, что метод восстановления по одному вейвлету
предусматривает также сжатие контура и, похоже, дает несколько лучшие
результаты. Ниже мы обсудим оба метода подробнее.
Восстановление по блоку фильтров
В соответствии с этим методом вейвлет коэффициенты возвращаются
в контуры по уровням, т. е. за один раз вводятся только те вейвлет коэффи
циенты, что соответствуют одному конкретному уровню начиная с самых
rрубых уровней и заканчивая самыми точными, причем делается в такой
последовательности:
1. Занесем в список подозрuтельных ребер все ребра имеющеrося кле
точноrо представления, соединяющие один контур с друrим.
9.2. Алzоритм кратномааuтабноzо к.7еточноzо представ.7ения 153
2. Построим для каждоrо контура новый мноrоуrольник, используя один
уровень блока фильтров. Результатом этоrо шаrа является расщепление
каждоrо ребра обоих контуров и, как правило, смещение каждой Bep
шины. В итоrе каждый треуrольник в клеточном представлении CTaHO
вится четырехуrольником с тремя вершинами на одном контуре и чет
вертой вершиной на друrом контуре, как показано на рисунке 9.6 (а)
и (б).
3. Для каждой новой добавленной к контуру вершины построим ребро,
соединяющее эту новую вершину с вершиной четырехуrольника, ле
жащей на друrом контуре, для чеrо разобьем четырехуrольник на два
треуrольника, как показано на рисунке 9.6 (в).
4. Воспользуемся списком подозрительных ребер и выполним локаль
ную оптимизацию клеточноrо представления, как описывалось в раз
деле 9.4.2.
5. Будем повторять этапы с первоrо по четвертый, пока не будет достиr
нуто разрешение, соответствующее исходным контурам. Для исходных
контуров с количеством вершин 2 n и контуров с низким разрешением
и количеством вершин 2т число итераций будет равно n т.
(а)
(6)
(в)
Рис. 9.6. Восстановление по блоку фильтров: (а) клеточное представление двух
контуров с низким разрешением. (б) Но одном уровне восстановления по блоку
фильтров добавляются вершины, обозначенные квадратами. (в) В клеточное пред
ставление вводятся ребра, обозначенные пунктирными линиями.
154
Т7ава 9
Восстановление по одному вейвлету
Процесс восстановления по блоку фильтров удваивает разрешение каж
доrо контура на каждом этапе и требует, чтобы порядок добавления вей
влет коэффициентов был обратным порядку их вычисления на этапе разло
жения. В случае добавления вейвлет коэффициентов по одному за один раз
порядок их введения может быть любым, независимо от уровня разреше
ния, на котором они высчитывались. Особенно удобно бывает выполнять
восстановление, добавляя вейвлет коэффициенты в порядке уменьшения их
значения.
Добавление вейвлетов в порядке уменьшения их значений имеет два
преимущества. Во первых, оно обеспечивает некоторую форму сжатия: ис
пользуя только те вейвлет коэффициенты, значения которых не меньше
HeKoToporo установленноrо пороrовоrо значения, мы сокращаем количество
вершин в контуре, но при этом сохраняем детальность настолько, насколь
ко это возможно. BO BTOpЫX, восстановление с добавлением в первую оче
редь самых больших вейвлет коэффициентов способствует тому, что KOHТY
ры приближаются по форме к исходным настолько быстро, насколько это
возможно. Интуитивно, получение более удовлетворительноrо клеточноrо
представления здесь кажется вполне правдоподобным, ведь локальная оп
тимизация, обеспечивающая более точное приближение к конечной форме,
выполняется раньше по времени. В самом деле, восстановление по одному
вейвлету, по видимому, дает на практике более добротные клеточные пред
ставления по сравнению с методом восстановления по блоку фильтров.
Подобно методу восстановления по блоку фильтров, метод BOCCTaHOB
ления по одному вейвлету также начинается с разложения контуров. Далее,
начиная с оптимизации клеточноrо представления с низким разрешением,
выполняется следующая последовательность действий:
1. Выберем для введения вейвлет, для чеrо при каждой итерации бу
дем попеременно рассматривать каждый из контуров и в итоrе возь
мем оставшийся вейвлет в соответствующем контуре с наибольши
ми x и у коэффициентами.
2. Умножим выбранные x и у вейвлет коэффициенты на COOTBeTCTBY
ющую функцию базиса вейвлетов и введем результат в контур. На
рисунке 9.7 изображается, как добавляются две одномерные кусоч
но линейные функцни и происходит слияние двух множеств вершин.
3. Для каждой введенной в контур вершины построим ребро, соединя
ющее эту вершину с подходящей вершиной друrоrо контура (совсем
как на третьем этапе в методе восстановления по блоку фильтров).
9.2. Алzоритм кратномааuтабноzо к.7еточноzо представ.7ения 155
4. Занесем все ребра, приходящие во вновь добавленные или смещенные
вершины, в список подозрительных ребер.
5. Воспользуемся списком подозрительных ребер и выполним локаль
ные оптимизации клеточноrо представления, как описывалось в разде
ле 9.2.4.
6. Этапы с первоrо по иятый будем повторять, пока не введутся все вей
влеты или пока величины оставшихся вейвлет коэффициентов не CTa
нут меньше HeKoToporo пороrовоrо значения.
Второй этап этоrо процесса иллюстрируется рисунком 9.7 для двух
случаев введения в одномерную кусочно линейную функцию по одному
вейвлету. Аналоrичное действие производится и для двумерноrо KOHТY
ра, за исключением Toro, что x и у координаты вершины превращаются
в x и у компоненты вейвлет коэффициента.
.........
(а)
.........
(6)
Рис. 9.7. Иллюстрация восстановления по одному вейвлету в одномерном случае:
(а) в функцию с низким разрешением вводится вей влет, соответствующий высокому
разрешению (<<пустыми» кружками обозначаются вводимые в функцию узлы вей
влета); (б) в функцию с высоким разрешением вводится вейвлет, соответствующий
низкому разрешению (<<пустыми» кружками обозначаются вводимые в вейвлет узлы
функции).
156
Т7ава 9
9.2.4. Локальная оптимизация
Для обоих описанных выше подходов к восстановлению список подо
зрительных ребер создается Torдa, Korдa контуры модифицируются добав
лением новых вейвлетов. На этапе локальной оптимизации каждое из этих
подозрительных ребер изучается с целью определения возможности пepe
становки ребра (edge swap). Как видно из рисунка 9.8, перестановка ребра
возможна, если оно одновременно принадлежит треуrольнику, имеющему
ребро одноrо контура, и треуrольнику, имеющему ребро друrоrо контура.
Рис. 9.8. Перестановка ребра: ребро, обозначенное пунктиром, можно переставить.
Если подозрительное ребро можно переставить, то далее на этапе ло
кальной оптимизации определяется, влечет ли замена ориентации дaHHO
[о ребра уменьшение целевой функции, которую мы минимизируем. Если
это так, то совершается перестановка ребра, а два друrих ребра, смежных
с переставленным, заносятся в список подозрительных ребер. Завершение
процесса локальной оптимизации происходит, коrда список становится пу
стым.
9.3. Временная сложность
Асимптотическая временная сложность алrоритма указывает на воз
можность использования данноrо алrоритма в интерактивном режиме для
больших контуров. Как мы уже отмечали, время, затрачиваемое алrоритмом
на пару контуров с числом вершин n, равно O(n 2 1ogn).
На первом этапе алrоритма кратномасштабноrо клеточноrо представ
ления про изводится добавление вершин. Это делается для Toro, чтобы чис
ло вершин в каждом контуре равнялось какой либо степени двойки. Этот
процесс не влияет на сложность вычисления клеточноrо представления,
поскольку число вершин в контуре, самое большее, удваивается. ДЛЯ KOH
тура с n вершинами, при надлежащем выборе очереди по приоритету, на
добавление вершин затрачивается время, равное O(nlogn). Korдa размер
контуров определяется степенью двойки, то их разложение с помощью Me
9.3. Врененная сложность
157
тода блока фильтров можно выполнить за время, равное О(п). Тоrда время,
затрачиваемое на получение клеточноrо представления по базовому KOM
плекту, является постоянным, ведь самое низкое разрешение не зависит от
размера исходных контуров.
(а)
(6)
Рис. 9.9. (а) Клеточное представление контуров с рисунка 9.3, полученное KpaTHO
масштабным алrоритмом; (б) клеточное представление, полученное оптимизирую
щим алrоритмом.
Восстановление первоначальных клеточных представлений задейству
ет либо метод с блоком фильтров, либо метод с одним вейвлетом. Без уче
та локальных оптимизаций клеточноrо представления, которые проводятся
в процессе восстановления, время выполнения восстановления по блоку
фильтров равно О(п), а время выполнения восстановления по одному вей
влету равно О(п log п). Т. к. асимптотическая сложность этапа ввода дo
полнительных вершин в исходные контуры уже равна О(п log п), преиму
щество, обеспечиваемое добавлением вейвлетов в сортировочном порядке,
как правило, оправдывает затраты, связанные с сортировкой коэффициентов
и восстановлением по одному вейвлету за один раз.
Локальная оптимизация про водится каждый раз, коrда вейвлет или
rpуппа вейвлетов вводит в контур новую вершину. Анализировать слож
ность этоrо шаrа труднее. Можно представить такую ситуацию, коrда одна
перестановка ребра влечет каскад дальнеЙlllИХ перестановок, что займет
время, равное О(п). Однако Мейер приводит эмпирические данные, по
158
(а)
Т7ава 9
(6)
(в)
Рис. 9.10. Клеточные представления контуров с рисунка 9.3, полученные KpaTHO
масштабным методом с восстановлением по одному вейвлету с некоторым поро
том сжатия. Пороr сжатия равен отношению величины наименьшеrо используемоrо
вейвлет коэффициента к величине наиБОJIЬшеrо. (а) Множитель 0,001; (б) множи
тель 0,0025; (в) множитель 0,005.
9.4. Примеры к.7еточноzо представления
159
казывающие, что для каждой вершины, добавленной в процессе BOCCTa
новления, число исследуемых при локальной оптимизации ребер практи
чески постоянно для контуров, варьирующихся по размеру от 128 до 1024
вершин [83]. В результате, временная сложность восстановления не увели
чивается вследствие локальной оптимизации, имеющей место при каждой
итерации.
9.4. Примеры клеточноrо представления
Как уже rоворилось, контуры, показанные на рисунке 9.3, являются
сложным примером клеточноrо представления. Опытный анатом знает, что
каждая из семи меток одноrо контура должна быть соединена с COOTBeTCTBY
ющей меткой друrоrо контура ребрами, исходящими из экстремумов этой
метки по внутренней поверхности контура. Решение такой задачи с помо
щью алrоритма кратномасштабноrо клеточноrо представления показано на
рисунке 9.9(а). Заметим, что и в первом, и во втором представлении есть
области, которые можно посчитать неподходящими с точки зрения кри
терия, по которому соединяются метки. Вообще, «правильное» клеточное
представление неоднозначно и зависит от природы материала, из KOToporo
формируются контуры. В нашем случае кратномасштабный алrоритм co
единяет шесть меток из семи, в то время как оптимизируюший алrоритм
соединяет только иять меток.
Добавим, что в кратномасштабный метод с восстановлением по OДHO
му вейвлету можно включить операцию сжатия путем отбрасывания вей
влет коэффициентов с маленькими значениями. На рисунке 9.10 показана
последовательность клеточных представлений, при восстановлении KOTO
рых использовались разные пороrи сжатия. При увеличении пороrа число
вершин в контурах значительно сокращается, но общие формы контуров
при этом сохраняют множество исходных деталей. Клеточное представле
ние с рисунка 9.10 (в), имеющее наименьшую степень детализации, rодится
для мноrих целей. По сравнению с клеточным представлением, сохраня
ющим все детали, такой вариант с низким разрешением требует значительно
меньшее место для хранения и меньшее время для отображения на экране.
Часть 111
ПОВЕРХНОСТИ
Т'ЛАВА 1 О
Поверхностные вейвлеты
1. Обзор кратномасштаБН020 аналuза для поверхностей 2. По
верхности, получае.мые последовательным деленuе.м З. Выбор
скаЛЯРНО20 проuзведенuя 4. Конструкцuя бuорт020нальных пo
верхностных вейвлетов 5. Кратномасштабные представленuя
поверхностеи
в приложениях трехмерной компьютерной rрафики поверхности иrра
ют rлавную роль. Объекты с плоскими rpанями, естественно, представля
ются сеткой из мноrоrранников; объекты, имеющие закруrленные поверх
ности, как правило, представляются сплайновыми разбиениями, [де в каче
стве элементарных ячеек используются либо треуrольники, либо тензорные
произведения. Нам хотелось бы иметь иерархические представления всех
упомянутых типов объектов, чтобы обеспечить возможность выполнения
сжатия, редактирования при переменном разрешении и мноrих друrих опе
раций, которые, как мы видели, уже применялись к изображениям и кривым.
Представление поверхности через тензорные произведения является
одним из типов представления поверхностей, которые достаточно леrко об
ращаются в кратномасштабную форму. В 1988 [оду Форсей и Бартеле [41]
описали иерархическую структуру представления поверхности через тeH
зорные произведения, называемую uерархuческuм В сплаЙН(J)Н (hierarchial
B spliпe). Это описание породило uзбыточное представленuе rеометрии
друrими словами, иерархическое В сплайновое представление данной по
верхности через тензорные произведения не единственно.
В зависимости от ситуации, вейвлет представление В сплайновых по
верхностей через тензорные произведения можно получить применяя CTaH
дартную, либо нестандартную конструкцию из третьей rлавы к сплайн
вейвлетам из раздела 7.3.2. Подобный вейвлет базис обеспечивает един
ственное представление каждой поверхности через тензорные произведе
ния и требует тот же объем памяти, что и исходные контрольные точки
поверхности. Кроме Toro, базис вейвлетов позволяет нам выполнить над
поверхностями большую часть операций, которые проводплись над кривы
ми в восьмой rлаве. К примеру, на цветной пллюстрации 8 показано куби
164
I: ава 10
ческое В сплайновое представление через тензорные про изведения и ero
редактирование на различных уровнях разрешения.
К сожалению, конструкции с тензорным про изведением оrраничено
применимы в отношении конфиrураций, которые они MorYT моделиро
вать «бесшовно». В частности, тензорные про изведения MorYT применять
ся только для функций, параметризованных на Jl{2. Что касается функций,
определенных на областях более общеrо тополоrическоrо типа, например,
сферических областях (цветные иллюстрации 9 и 12), то к ним тензорные
произведения не применимы.
В этой rлаве мы показываем, как кратномасштабный анализ может быть
распространен на функции, определяемые на двумерных областях произ
вольноrо тополоrическоrо типа. (Тополоrический тип двумерной области
или поверхности определяется кривыми, оrраничивающими эту поверх
ность, а также родом поверхности.) Расширение понятия кратномасштаб
Horo анализа для областей произвольноrо тополоrическоrо типа OCHOBЫ
вается на получении уточняемых масштабирующих функций с помощью
рекурсивноrо последовательноrо деления поверхности, в полной аналоrии
с выполнением кратномасштабноrо анализа для кривых.
Эту rлаву мы начнем с обзорноrо рассмотрения кратномасштабноrо
анализа для поверхностей. Затем, в разделе 10.2, мы опишем базис по
верхностей последовательноrо деления и покажем, что последовательное
деление приводит к вложенным пространствам и уточняемым масштаби
рующим функциям. Остальная часть этой rлавы посвящена конструкции
биортоrональных поверхностных вейвлетов, похожих на одноузловые вей
влеты из раздела 7.4.3.
Обобщение кратномасштабноrо анализа на области произвольноrо TO
полоrическоrо типа значительно расширяет класс приложений, в которых
может применяться кратномасштабный анализ. Одиннадцатая rлава посвя
щена рассмотрению нескольких таких приложений; среди них сжатие по
верхностей, непрерывный контроль степени детализации, последовательное
пропускание через сеть с низкой пропускиой способностью и редактирова
ние поверхностей при переменном разрешении.
10.1. Обзор кратномасштабноrо анализа для поверхностей
Несмотря на то, что без математики в этой rлаве все же не обошлось,
алrоритм, который мы получим в итоrе, отличается относительной просто
той. Прежде, чем уrлубиться в подробности, мы обзорно рассмотрим то, как
можно применить кратномасштабный метод для разложения мноrоrранника
с рисунка 10.1(а).
Применение кратномасштабноrо анализа к поверхностям происходит
по той же схеме, что и в случае с изображениями и кривыми: мы расклады
10.1. Обзор кратномааuтаБНО20 анализа д.7Я поверхностей 165
ваем поверхность с высоким разрешением (в нашем примере это MHororpaH
ный бюст Спока) на версию с низким разрешением и набор уточняющих
коэффициентов. Например, на рисунке 10.1 (б) показана версия с низким раз
решением, соответствующая мноrоrраннику с рисунка 10.1(а). Положения
вершин на 10.1(б) находятся как средние взвешенные положений вершин
на 10.1(а). Снова, как в случае с кривыми, вычисление можно представить
умножением на матрицу Aj. Аналоrично, вейвлет коэффициенты, coдep
жащие информацию о деталях, можно найти умножением на матрицу Bj.
Эта процедура выполняется для версии с низким разрешением рекурсивно
до тех пор, пока не будет получено самое rрубое представление заданной
поверхности, показанное на рисунке 10.1(в).
АI
AJ !
А!
(а)
вей влет коэффициеНТLI
(6)
!
вейвлет коэффициеНТLI
(в)
Рис. 10.1. Разложение мноrоrранника.
Для получения фильтров синтеза pj и Qj фильтры анализа Aj и Bj
можно обратнть соrласно уравнению (7.10). Более подробно синтез pac
сматривается как два действия: разбиение каждой треуrольной rpани MHO
rоrранника с низким разрешением на четыре подтреуrольника за счет про
ставления на средних точках ребер новых вершин и смещения полученноrо
набора вершин так, как это предусмотрено вейвлет коэффициентами.
Затруднение при построении кратномасштабноrо анализа для поверх
ностей в том, что четыре фильтра анализа и синтеза должны быть подобра
ны так, чтобы
. версии с низким разрешением были хорошими аппроксимациями ис
ходноrо объекта,
. величина вейвлет коэффициента обеспечивала некую меру поrрешно
сти, возникающей при обнулении этоrо коэффициента,
. временная сложность анализа и синтеза должна линейно зависеть от
числа вершин.
166
I: ава 10
10.2. Поверхности последовательноrо деления
в этом разделе мы покажем, что применение последовательноrо деле
ния к поверхностям приводит ко множеству уточняемых масштабирующих
функций и, следовательно, к последовательности вложенных линейных про
странств, чеrо и требует кратномасштабный анализ. В полной аналоrии
с кривыми, лишь поверхности, образуемые последовательным делением,
можно иерархически представить, используя кратномасштабный анализ.
Работы Чайкина оприменении последовательноrо деления для созда
ния кривых вдохновили Кэтмула и Кларка [7] и, одновременно, ду и Ca
бина [29, 30] на использование последовательноrо деления для создания
поверхностей. Такой подход стал крупным прорывом в моделировании
поверхностей, поскольку он оказался первым методом конструирования
rладких поверхностей произвольноrо тополоrическоrо типа. Однако MHO
rие [оды поверхности, получаемые последовательным делением, OCTaBa
лись в компьютерной rрафике практически без внимания, и только теперь
они пробудили новый, куда более сильный интерес. Отчасти ero можно
объяснить rлубокой связью, существующей между последовательным деле
нием и кратномасштабным анализом.
Если кривая последовательноrо деления образуется путем итеративно
повторяющеrося уточнения контрольноrо мноrоуrольника, то поверхность
последовательноrо деления образуется посредством итерационноrо уточне
ния контрольною MHozozpaHHUKa (coпtrol polyhedroп) (называемоrо также
контрольной ячейкой (coпtrol mesh)) lv10, блаrодаря которому получает
ся последовательность ячеек с возрастающим числом rраней }\;1 1 , lv1 2 , . . . ,
сходящаяся к поверхности
а:== liш lv1 j .
j........:,oo
Каждый этап уточнения состоит из подэтапов разбивки и усреднения, aHa
лоrичных одноименным этапам в случае с кривыми. Однако этап разбив
ки существует в двух различных видах: это схе иа разбuвкu zраней (jace
scheтe) и схема разбuвкu вершuн (vertex scheтe). В то время, как Кэтмул
и Кларк разрабатывали схему разбивки rраней, которая обобщает понятие
кубических В сплайнов с представлением через тензорные про изведения
(рисунок 10.2), ду и Сабин разрабатывали схему разбивки вершин, которая
обобщает аналоrичное понятие квадратичных В силайнов (рисунок 10.3).
В этой книrе мы сосредоточим внимание на схемах разбивки rраней,
которые в дальнейшем классифицируем на треуzольные, в которых ячей
ки имеют треуrольные rрани, и четырехуzольные, в которых rрани ячеек
оrраничиваются четырьмя ребрами и четырьмя вершинами (эти вершины
не обязательно лежат в одной плоскости). Как видно из рисунка 10.2, схема
10.2. Поверхности пОС.7едоватеЛЬНО20 де.7енuя
167
..
.
(а)
(6)
(в)
(r)
Рис. 10.2. Последовательное деление по схеме Кэтмула Кларка: (а) контрольная
ячейка JvI O ; (б) ячейка JvI 1 ; (в) ячейка JvI 2 ; (т) конечная поверхность а. Заметим,
что каждая четырехуrольная трань разбивается на четыре подrpани.
..
(а)
(6)
(в)
(r)
Рис. 10.3. Последовательное деление по схеме Ду Сабина: (а) контрольная ячей
ка Jl..1 0 ; (б) ячейка Jl..1\ (в) ячейка Jl..1 2 ; (т) конечная поверхность а. В данной схеме
вершина, окруженная п rpанями, разбивается на п подвершин, каждая из которых
соответствует одной rрани.
Кэтмула Кларка является четырехуrольной. Однако мы сосредоточимся на
треуrольных схемах по той причине, что описать и реализовать их несколько
проще.
При последовательном делении с треуrольной схемой каждая [рань
lvlj 1 на этапе разбивкu разделяется на четыре подrрани, для которых cepe
дины ребер взяты в качестве дополнительных новых вершин. Это приводит
о
К появлению новой ячейки lvl j , что иллюстрируется рисунком 10.4. Далее,
о
на этапе усредненuя вершины ячейки lvl j смещаются, в результате чеrо
168
I: ава 10
о о
образуется ячейка 1\;1 j , по структуре идентичная ячейке 1\;1 j (т. е. 1\;1 j и 1\;1 j
имеют одинаковое число вершин, ребер и rраней, которые связаны друr
с друrом сходным образом). Положение каждой вершины ячейки 1\;1 j зада
о
ется взвешенным усреднением положений соседних вершин ячейки 1\;1 j .
(3)
(6)
(в)
Рис. 10.4. Этап разбивки для треуrольных схем: (а) ситуация вокрут вершины ячей
о
ки Jl.P \ (б) новая ячейка NP, полученная с помощью этапа разбивки; (в) ячейка
l'vP, полученная с помощью этапа усреднения.
Пример. Простейшей схемой последовательноrо деления является пo
следовательное деленuе MH020zpaHHUKa (polyhedral subdivisioп) , при KO
тором положения всех вершин на этапе усреднения не меняются. Таким
образом, пределом последовательноrо деления мноrоrpанника является
контрольный мноrоrpанник 1\;1°. Эта схема на поверхностях совершен
но аналоrична описанной в шестой rлаве схеме для кусочно линейной
кривой, соrласно которой каждый cerMeHT расщепляется в своей cpeд
ней точке и получающиеся вершины остаются неизменными.
Пример. Схема Лупа [73], позволяющая создавать rладкие поверх
ности, является простейшей схемой треуrольноrо последовательноrо
деления. Рисунок 10.5 иллюстрирует, как в итоrе MHoroKpaTHoro при
менения к контрольной ячейке последовательноrо деления получается
rладкая поверхность. В отличие от схем Кэтмула Кларка и Ду Саби
на, схема Лупа является, скорее, обобщением KOHKpeTHoro треуrольноrо
В сплайна (TpexMepHoro аналоrа квадратичноrо характеристическоrо
силайна), а не обобщением конструкции с тензорным произведением.
Для описания этапа усреднения, соответствующеrо схеме Лупа, мы
воспользуемся следующими обозначениями: пусть v вершина ячей
10.2. Поверхности пОС.7едоватеЛЬНО20 де.7енuя
169
. .,.
(а)
(6)
(в)
(r)
Рис. 10.5. Схема Лупа: (а) контрольная ячейка lvJO; (б) ячейка м 1 ; (в) ячейка lvJ2;
(т) конечная поверхность а.
о
ки lvJ1, поставленная в соответствие вершине ячейки 1'vJ1, а после
довательность 1, . . . , n обозначает n соседних для вершин. Новое
положение v находится как
v
о о о
a(n)v + vl + ... + v n
а(n) + n
rдe
( ) n(1 Р(n))
а n р(n)
и
( ) .Q (3 + 2cos(27r/n))2
р n 4 32
Функция а( n) выбирается тщательно, чтобы предельная поверхность
имела непрерывную касательную плоскость [60, 73].
Совокупность взвешенных значений, используемых на этапе ycpeДHe
ния, так же, как и в случае с кривыми, называется маской. Маски для по
верхностей удобнее Bcero представлять rрафически. Например, маска Лупа
показана на рисунке 10.6 (а). Заметим, что указываются только числите
ли весов; знаменатель Bcerдa берется равным сумме значений на рисунке.
Это соrлашение rарантирует, что сумма весов всеrда равна единице и, сле
довательно, поверхность, образуемая по данной схеме, не зависит от си
стемы координат, используемой при про ведении вычислений. Такую неза
висимость несколько замысловато называют аффинной инварuантностью
(affiпe iпvariaпce) [35].
Оценочные маски, с помощью которых вершины приводятся в ее KO
нечное положение, также можно применять для поверхностей, используя
170
1
1 1')1
. о(п) /
'./ \
1 1
(а)
I: ава 10
1
1 1')1
. Е(п) /
'. / \
1 1
(6)
T4/13 T2 тз/12 ТI
" o\l '. o\l
Tп TI
Tп I Til
(в)
Рис. 10.6. Маски, соответствующие схеме Лупа: (а) маска усреднения (использу
емая после этапа разбивки), в которой 0(71) 71(1 (3(71))/(3(71); (б) оценочная
маска, в которой Е(п) 371/(4(3(71)); (в) две касательные маски, в которых Ti
cos(27ri/п).
ту же процедуру, что и для кривых. Это значит, что для любой схемы
оценочная маска является доминирующим левым собственным вектором
матрицы локальноrо последовательноrо деления. Так, маска для схемы Лу
па изображена на рисунке 10.6 (б). Следовательно, вершина v ячейки l'vl j
с соседними вершинами Vl, . . . , V n может быть отправлена в свое конечное
положение v oo следующим образом:
00 E(n)V+Vl+, ..., +V n
v
Е(п) + п '
rдe Е(п) 4J(n) '
Если мы пренебрежем доминирующим левым собственным вектором, то два
собственных вектора, соответствующих наибольшим из оставшихся соб
ственных значений матрицы локальноrо последовательноrо деления, обра
зуют касательные маски (taпgeпt тasks), которые определяют два вектора,
касающихся поверхности в предельной точке. В схеме Лупа векторы, ле
жащие в плоскости касания к v OO , вычисляются с помощью двух масок,
изображенных на рисунке 10.6 (в). Заметим, что оценочные и касательные
маски, в отличие от масок усреднения, применяют к вершинам ячейки l'vl j
без предварительной разбивки.
Оценочные и касательные маски полезны в случаях создания изобра
жений поверхностей последовательноrо деления с тщательно прорисован
ными тенями. Изображения, подобные приведенному на рисунке 10.5 (r),
получаются следующим образом:
1. Применить последовательное деление к контрольной ячейке два или
три раза.
2. Привести каждую вершину к ее конечному положению.
10.2. Поверхности пОС.7едоватеЛЬНО20 де.7енuя
171
3. Вычислить пару векторов, касательных к конечной поверхности, с по
мощью касательных масок.
4. Построить нормаль к поверхности посредством нахождения BeKTopHO
[о про изведения касательных векторов.
5. Используя найденные нормали, затенить конечные точки с помощью
модели освещения Фонrа [38].
В шестой rлаве rоворилось о том, что схемы последовательноrо деле
ния для кривых бывают двух видов: интерполирующие и аппроксимиру
ющие. То же справедливо в случае схем для поверхностей. Очевидно, что
последовательное деление мноrоrранников является интерполирующей cxe
мой, потому что поверхности, которые оно образует, проходят через исход
ные контрольные вершины. А вот схема Лупа является аппроксимирующей.
В некоторых приложениях бывает необходимо, чтобы схема последователь
Horo деления была интерполирующей и rладкой одновременно. По этой
причине Дин и соавторы [33] разработали схе;иу типа бабочкu (butterfly
scheтe). Как и во всякой интерполирующей схеме, каждый этап последо
вательноrо деления типа бабочки оставляет нетронутыми существующие
вершины, а локальное усреднение используется для вычисления новых по
ложений лишь для середин ребер, вводимых операцией разбивки. Маска
усреднения, используемая схемой типа бабочки, показана на рисунке 10.7.
В разделе 10.4 мы обстоятельно обсудим, как биортоrональные вейвлеты
MOryT конструироваться из интерполирующих треуrольных схем последо
вательноrо деления, таких, как последовательное деление мноrоrранника
и схема типа бабочки.
Прежде чем закончить рассмотрение основ последовательноrо деле
ния, заметим, что в приложении к поверхностям схемы последовательноrо
деления также делятся на равномерные инеравномерные, стационарные
и нестационарные. Равномерные схемы используют одну и ту же маску
усреднения для каждой вершины, а стационарные схемы задействуют одну
и ту же маску усреднения для каждоrо уровня последовательноrо деления.
Но для всех схем последовательноrо деления (треуrольной, прямоуrольной
схем, схемы разбивки rраней и схемы разбивки вершин) существует и яв
ляется справедливым одно очень общее утверждение: положения вершин
ячейки Nlj представляют собой линейные комбинации положений вершин
ячейки J\;lj 1. Следовательно, если c j матрица, i тая строка которой
состоит из x , y и z координат вершины i ячейки Nlj l, то существует
прямоуrольная постоянная матрица pj, такая, что
c j == pj cj l.
(10.1)
172
I: ава 10
о /0
I" I I 1
( 1 <:!)O I (!)O I
0/ 1 "'/ 1 "0
1"1/1"1/1
r(l>o(j>1
0/ "о
Рис. 10.7. Маска усреднения, используемая для нахождения положения середины
ребра в схеме типа бабочки. Толстыми линиями обозначены ребра исходной ячей
ки Jl.Jj l, а тонкими линиями обозначены ребра, вводимые в ячейку NIj на эта
пе разбивки. Нулевые веса указаны исключительно ради полноты представления.
С помощью параметра t можно производить настройку схемы последовательноrо
деления, меняя ее тип от мноrоrpанноrо (t == О) до rладкоrо (t == 1/8).
Так же, как и для случая кривых, матрица pj характеризует метод после
довательноrо деления, вне зависимости от ero типа.
10.2.1. Вложенные пространства и уточняемые масштабирующие
функции
Мы хотели бы продемонстрировать, что последовательное деление по
верхностей может использоваться для определения набора уточняемых Mac
штабирующих функций и, как следствие, последовательности вложенных
линейных пространств. Для этоrо нам необходимо решить, какой долж
на быть область определения масштабирующих функций. В шестой rлаве
для масштабирующих функций, поставленных в соответствие кривым по
следовательноrо деления, в качестве области определения мы взяли веще
ственную ось; друrими словами, параметрические кривые строились как
функции на вещественной оси (или оrраниченной ее области) в JR.2 или JR.3.
Поверхность же должна параметризироваться на такой области, тополоrи
ческий тип которой совпадал бы с тополоrическим типом данной поверхно
сти. Так, если поверхность оказалась тополоrическим шаром, то в качестве
области определения мы можем использовать участок JR. 2. Однако для более
общих поверхностей JR. 2 использовать нельзя.
10.2. Поверхности пОС.7едоватеЛЬНО20 де.7енuя
173
Соrласно подходу, которым мы воспользуемся здесь, в качестве обла
сти определения будет рассматриваться исходная контрольная ячейка АI 0 .
Она является вполне подходящим кандидатом на эту роль, потому что ее
тополоrический тип совпадает с тополоrическим типом конечной поверх
ности.
Для вывода масштабирующих функций нам потребуется параметри
зовать предельную поверхность на области определения. В общих чертах,
параметризация поверхности является не более чем просто установлением
соответствия между точками в двумерной области и точками на поверх
ности. Идея параметризации для поверхности последовательноrо деления
состоит в том, чтобы выбрать на J'vl° любую точку х и про следить ее пе
реход в конечное положение в процессе последовательноrо деления, как
показано на рисунке 10.8. Отслеживаемая точка х перейдет в точку на
предельной поверхности и, поэтому мы также можем обозначить эту точ
ку как и(х). Эквивалентно, мы можем установить параметризированную
поверхность и(х), используя каждую ячейку для определения кусочно ли
нейной функции J'vl j (х ), rдe х имеет J'vl° в качестве области определения.
Затем мы рассмотрим и(х) как функцию, к которой сходится последова
тельность функций МО(х), М 1 (х),....
O(X) !(x) М!(х)
V i'z,, y,, ",{Jj
М О м! м!
Рис. 10.8. Наблюдение за изменением положения точки х, принадлежащей базовой
ячейке lИ О , с целью получения параметризации поверхности а (х ).
Формализм параметризации поверхностей последовательноrо деления
имеется у Лаунсбери и соавторов [75]. В нашем случае достаточно отметить,
что каждый этап процедуры последовательноrо деления линеен в отноше
нии вершин c j . По аналоrии с уравнением (6.7), записанным для кривых,
эта линейность сохраняется даже в пределе, означая, что каждую точку и (х )
конечной поверхности можно представить в виде линейной комбинации ис
ходных контрольных вершин в c j :
и(х) == L> Ф (Х) дЛЯ х Е М О .
174
I: ава 10
Чтобы показать, что в случае поверхностей масштабирующие функции яв
ляются уточняемыми и матрица последовательноrо деления pj служит MaT
рицей уточнения, используется та же линия рассуждений, что применялась
для установления свойства уточняемости масштабирующих функции в слу
чае с кривыми. Этот факт выражается уравнением
фj l(х) == фj(х)рj для х Е мО.
(10.2)
Отсюда следует, что одну масштабирующую функцию Фi ( х) можно
найти, если принять, что с{ == (jik И применить схему последовательно
[о деления с целью получения скалярнозначной функции, определяемой
на контрольной ячейке 1\;1°. Заметим, что даже если областью определения
служит мноrоrранник, сами масштабирующие функции в действительности
MOryT быть rладкими почти всюду (в зависимости от схемы последователь
Horo деления).
Теперь можно определить цепочку вложенных линейных пространств
V j (1\;1°), соответствующих ячейке 1\;1°:
Vj(MO) :== sрап{Фi(х), ф (х),.. .}.
т. е. vj (1\;1°) это пространство всех функций, выражаемых линейными
комбинациями масштабирующих функций, входящих в фj (х ) . Уточняющее
соотношение, представленное уравнением (10.2), означает, что эти про
странства являются вложенными, чеrо и требует кратномасштабный анализ.
10.3. Выбор скалярноrо про извеДения
Теперь у нас есть почти все компоненты, необходимые для постро
ения биортоrональноrо базиса вейвлетов для поверхностей. В разделе 10.4
нашей задачей будет определение вейвлетов, почти ортоrональных масшта
бирующим функциям; значит, мы должны выбрать скалярное произведение,
которое можно будет использовать для описания ортоrональности. Это CKa
лярное про изведение должно быть определено для функций с областью
определения 1'v10. Обозначив множество треуrольных rpаней ячейки 1\;1° че
рез 6(1\;1°) и треуrольник из этоrо множества через т, мы можем определить
подходящее скалярное произведение как
(1lg):== L 1() ! f(X)9(X)dX;
о area т
TEt:.(M ) "'Ет
(10.з)
dx здесь соответствует обычному дифференциальному элементу площади
в JR.3.
10.4. БиортО20на.7ьные конструкции поверхностных вейв.7етов 175
Возможно, на первый взrляд, наше определение скалярноrо произве
дения может показаться странным, раз оно не зависит от rеометрическоrо
расположения вершин ячейки 1\;1°. Однако за таким выбором стоит важ
ное практическое преимущество. Поскольку скалярные про изведения не
зависят от rеометрии ячейки 1\;1°, изрядная часть вычислений по скалярно
му произведению и вейвлетам может быть выполнена предварительно, что
позволит сделать реализацию алrоритма, который мы опишем в следующей
rлаве, более эффективной.
Однако данное выше определение скалярноrо про изведения предпола
[ает и один потенциальный недостаток: в процесс е построения аппрокси
мации функции треуrольники имеют одинаковые веса вне зависимости от
истинноrо rеометрическоrо размера. Тяжесть последствий TaKoro одинако
Boro взвешивания треуrольников зависит только от KOHKpeTHoro приложе
ния. Заметим лишь, что с примерами, описанными в разделе 11.2, у нас не
возникло никаких проблем в этой связи. Альтернативой является опреде
ление скалярноrо произведения с весами для интеrралов на треуrольниках
из 1\;1°. Вопрос о том, имеет ли такое определение какое либо практическое
преимущество, достаточно значимое, чтобы оправдать возросший объем
вычислений, может послужит интересным предметом для будущих иссле
дований.
10.4. Биортоrональные КОНСТРУКЦИИ поверхностных
вейвлетов
В этом разделе мы воспользуемся понятием подъема из раздела 7.4,
которое поможет нам сконструировать биортоrональный базис вейвлетов
со следующими свойствами:
. Вейвлеты MOryT быть сконструированы с помощью любой треуrольной
схемы разбивки rpаней.
. Для интерполирующих схем (таких, как схема последовательноrо деле
ния мноrоrранника и схема типа бабочки) и анализ, и синтез являются
линейными процессами.
. Вейвлеты являются «почти ортоrональными» к масштабирующим
функциям в том смысле, что скалярное произведение вейвлета и Mac
штабирующей функции близко к нулю. Практический смысл этоrо Tpe
бования в том, что аппроксимации поверхности с низким разрешением
близки к наилучшим приближениям по методу наименьших квадратов.
HaIIIa конструкция аналоrична конструкции одноузловоrо вейвлета
из раздела 7.4. Мы начнем с ленивых вейвлетов, а затем улучшим их
176
I: ава 10
с помощью подъема. Для любой треуrольной схемы последовательноrо дe
ления ленивые вейвлеты Ф ; (х) состоят из масштабирующих функций
в V j (J\;1 0 ), сопоставленных серединам ребер ячейки J\;lj l. Хотя ленивые
вейвлеты имеют свое преимущество (они очень просты), для них xapaKTep
ны два затруднения:
1. Если процедура синтеза является быстрой вообще, то процедура aHa
лиза является быстрой только для интерполирующих схем, что мы по
кажем позже в этом же разделе. (Между прочим, это справедливо и для
случая кривых, если не считать тoro, что вместо плотной матрицы aHa
лиза может быть использовано LU разложение матрицы синтеза, что
обсуждалось в разделе 7.3.2.)
2. Ленивые вейвлеты далеко не ортоrональны к Vj 1(1\II0). Как и для
кривых, с их помощью мы получаем rрубые аппроксимации поверхно
сти путем прореживания коэффициентов, соответствующих высокому
разрешению. Получается, что rрубые версии заданной поверхности
с полным разрешением далеки от наилучших по методу наименьших
квадратов.
Рассматривая первое затруднение, удобно упорядочить масштабиру
ющие функции в фj (х) так, чтобы те функции, что поставлены в co
ответствие вершинам ячейки 1\IIj 1, предшествовали функциям, постав
ленным в соответствие серединам ребер. Такое упорядочивание отображе
но на рисунке 10.9, [де заштрихованными точками обозначены вершины,
принадлежащие J\;lj 1, а «пустыми» точками средние точки, введенные
последовательным делением. Если Ф (х) и Ф::т, (х) масштабирующие
функции, соотнесенные, соответственно, с вершинами и средними точка
ми ячейки J\;lj l, то задуманное упорядочивание можно выразить блочной
матрицей:
фj ( х) [Ф ( х ) I Фtп ( х ) ] .
Пример. В следующих до конца этоrо раздела примерах мы будем ис
пользовать простейшую схему последовательноrо деления и простей
шую контрольную ячейку: последовательное деление мноrоrранника
в применении к тетраэдру, как видно из рисунка 10.9. Для этоrо при
мера Ф (х) [фв(х)", ф (х)] и Ф';'(х) [Фl(х)... ф (х)].
Заручившись принятым обозначением и доrоворившись об упорядочи
вании, мы можем записать масштабирующее уравнение для ленивых вей
влетов как
[фj l(х)IФ ; (х)] [Ф (х)IФ::т,(Х)][Р енIQ ен],
10.4. БиортО20на.7ьные конструкции поверхностных вейв.7етов 177
2
3
. исходные вершины
..
о новые вершины
Рис. 10.9. Метод последовательноrо деления мноrоrранника, примененный к TeTpa
эдру.
[де матрица синтеза ленивых вейвлетов равна
. . [ pj
[P eHI Q eH] pL
] .
Пример. При использовании уточняющеrо соотношения (10.2) воз
можно простое построение матриц синтеза Р;ен И Q;eH для примера
с тетраэдром, показанноrо на рисунке 10.9. Эти матрицы имеют сле
дующий вид (обозначения здесь те же, что и на рисунке, а точками
обозначаются нули):
2
2
2
2
1 [ Р; ] 1 1 1 Q eH 1
Р лен P 1
2 1 1
1 1 1
1 1 1
1 1 1
1 1 1
Все блоки этих матриц синтеза разреженные, что свидетельствует о бы
строте выполнения синтеза. К сожалению, соответствующие матрицы aHa
лиза не обязательно бывают разреженными. В блочной форме матрицы
анализа можно записать так:
[ А;ен ] [ ;1
В лен m
] 1 [
(Pп l
p?n(Pп l
] .
178
I: ава 10
в разделе 7.3.2 мы использовали LU разложение, чтобы избежать фор
мирования плотной матрицы анализа, однако с поверхностями такой трюк
не пройдет, поскольку матрицы синтеза здесь не имеют необходимой лен
точной структуры. Следовательно, анализ ленивых вейвлетов будет бы
стрым, только если P имеет разреженную обратную матрицу. Как пра
вlШО, это условие не выполняется для аппроксимирующих методов после
довательноrо деления, к примеру, схемы Лупа, однако оно выполняется для
любой интерполирующей схемы. Вспомним, что в разделе 10.2 [оворlШОСЬ
о том, что интерполирующие схемы никоrда не смещают однажды BBeдeH
ную вершину, что означает P == 1. Таким образом, для интерполирующих
ленивых вейвлетов матрицы синтеза и анализа всеrда являются разрежен
ными и задаются соотношениями:
. . [ 1
[P eHI Q eH] == Р?п
]
и
[ А;ен ] == [
В лен
1
P?п
] .
Пример. Матрицы анализа А;ен и В};ен для последовательноrо деле
ния мноrоrранников (смотрите рисунок 10.9) имеют вид:
А;е" [ 1 ]
1
1
1
1 1 2
1 1 2
В;ен == 1 1 2
1 1 2
1 1 2
1 1 2
Для конструирования вейвлетов, более ортоrональных относительно
масштабирующих функций, чем ленивые вейвлеты, мы можем выполнить
действия, сходные с теми, что мы предпринимали в разделе 7.4 дЛЯ KOH
струирования одноузловых вейвлетов. Мы снова обратимся к идее модифи
кации ленивоrо вейвлета путем вычитания линейной комбинации соседних
масштабирующих функций с низких уровней; i тый ленивый вейвлет на
уровне j 1 это ничто иное, как i тая масштабирующая функция в фtт"
которую мы обозначим через ф:;:",i' Улучшенный вейвлет мы определим как
o!,j l ( ) Ф j ( ) "" j Ф j l ( )
'ri Х m,i Х Sk,i k Х,
10.4. БиортО20на.7ьные конструкции поверхностных вейв.7етов 179
[де k оrраничено до нескольких значений, соответствующих вершинам
из J\;lj l в окрестности масштабирующей функции Ф::п,i' Значения S{k
для i Toro вейвлета определяются через решение системы уравнений по
методу наименьших квадратов
(Фi lIФi, 1)
(10.4 )
для всех i', таких, что носитель вейвлета Фi 1 (х) перекрывается с носите
лем масштабирующей функции ф{, 1 (х ).
Теперь мы обратимся к вопросу о том, какие значения s{ i MorYT быть
ненулевыми для каждоrо i. Напомним, что ф{ l(х) поставл н в COOTBeT
ствие середине ребра ячейки J\;lj \ назовем две конечные точки этоrо pe
бра «родительскими» вершинами. Тоrда наименьший симметричный выбор
для вектора столбца В! включает только два ненулевых элемента, COOTBeT
ствующих двум родителям. Симметричный способ увеличения носителей
заключается в добавлении к в! элементов, соответствующих k дискам po
дительских вершин. (k диском вершины является множество всех вершин,
получаемое в результате обхода k или меньшеrо числа ребер треуrольно
[о разбиения.) Несколько примеров k дисков двух конечных точек ребра
показаны на рисунке 10.10. Поскольку допустим рост числа ненулевых эле
ментов, носители вейвлетов фj l растут и вейвлеты становятся все более
и более ортоrональными к Vj 1(J\;10).
@
(а)
(6)
(в)
Рис. 10.10. Вершины, входящие в k диски двух конечных точек ребра вразбиении
на равносторонние треуroльники: (а) О диск конечных точек; (б) l диск конечных
точек; (в) 2 диск конечных точек.
Выбрав k диск вершин и соответствующие масштабирующие функции,
которые будут использоваться для модификации ленивоrо вейвлета, мы пе
реходим к последнему шаrу в определении вейвлета решению ypaBHe
10.4. Биортоzона.7ьные конструкции поверхностных вейв.7етов 181
Матрицы синтеза и анализа вейвлетов с k диском P д' Ql д' A д' B д
получаются из матриц ленивых вейвлетов путем объединения всех BeKTopOB
столбцов в матрицу 8; и использования этой матрицы для выполнения
подъема аналоrично тому, как это описывается уравнением (7.26):
[Рt. д I Qt. д]
[ A: д ]
Вk д
[P eHIQ eH P eH8j];
[ А1ен + j8 j BieH ] .
В лен
Пример. Число вершин тетраэдра, показанноrо на рисунке 10.9, Ha
столько мало, что вейвлеты ф1, сконструированные с помощью l дис
ков, имеют rлобальный носитель (вейвлеты с разрешением j > 1
имеют, тем не менее, локальные носители). Следовательно, матри
ца 81 плотная:
81 1. [
8 1
1
3
1
3
1
1 1 1 3 ]
3 3 1 1
3 1 3 1 .
1 3 3 3
Соответствующие матрицы анализа и синтеза имеют вид:
2 3 3 1 1 1 3
2 3 1 3 3 1 1
2 1 3 3 1 3 1
2 1 1 1 3 3 3
Рf д 1 1 Qf д 5 1 1 1 1 1
1 1 1 5 1 1 1 1
1 1 1 1 5 1 1 1
1 1 1 1 1 5 1 1
1 1 1 1 1 1 5 1
1 1 1 1 1 1 1 5
[ !l 1 1 1 6 6 2 2 2 2 ]
А1 1 7 1 1 6 2 6 6 2
k д 16 1 1 7 1 2 6 6 2 6 2 '
1 1 1 7 2 2 2 6 6 6
182 I: ава 10
1 1 2
1 1 2
Вf д "" 1 1 2
1 1 2
1 1 2
1 1 2
10.5. Кратномасштабные представления поверхностей
k дисковые вейвлеты из предыдущеrо раздела определяют KpaTHOMac
штабный базис [ФО(х) Ф д(х) Ф д(х)... ф[;l(х)] для аппроксимиру
ющеrо пространства V J (1\110). Следовательно, поверхность и(х), парамет
ризованная на простой ячейке lv1 0 , может быть записана в этом базисе, по
крайней мере, приближенно. Точное представление поверхности возмож
но, если она лежит в V J (lv1 0 ); в противном случае, как правило, ошибку
можно сделать произвольно малой, взяв большое J. (Мы rоворим здесь
«как правило», потому что можно представить себе и патолоrические слу
чаи, в которых поверхности и либо схемы последовательноrо деления ведут
себя достаточно плохо, так что ошибку уменьшить не удается.)
Кратномасштабное представление поверхности и( х), параметризован
ной на 1\;10, следовательно, состоит из простой поверхности, являющейся
rpубым приближением, и вейвлет коэффициентов, соответствующих раз
личным уровням уточнения. Эта простая поверхность и О (х) является про
екцией поверхности и( х) на пространство с самым низким разрешени
ем V O (х ). При использовании последовательноrо деления мноrоrранни
ков и О (х) будет rpубым мноrоrpанником, структурно эквивалентным ячей
ке lvI O . Если же используется rладкое последовательное деление, то и О (х )
будет rладкой аппроксимацией поверхности и( х ). Пример с rоловой Спока
на рисунке 10.1 иллюстрирует разложение полученной по методу последо
вательноrо деления мноrоrpанника поверхности, параметризованной на OK
таэдре; следовательно, самая rpубая аппроксимация представляет октаэдр,
вершины KOToporo выбраны так, чтобы сделать малой разницу между и О
и и в квадратичной мере. При использовании в этом примере схемы типа
бабочки, каждая из аппроксимаций rоловы Спока являла бы собой rладкую
поверхность последовательноrо деления.
Один из способов представления поверхности и( х) по базису k дис
ковых вейвлетов связан с использованием двойственноrо базиса
O O 1 J l
[ф (х) Фk д(Х) Фk д(Х)'" Фk д (х)], описанноrо в разделе 7.4. Например,
некий вейвлет коэффициент d{ может быть вычислен с помощью скалярно
[о произведения, включающеrо нормированный двойственный вейвлет Фi
10.5. Кратно,нааuтабные представ.7енuя поверхностей
183
или же ненормированный двойственный вейвлет ФI, следующим образом:
dI (ФI(х)lи(х))
4 j (ФI(х)lи(х)).
в следующей rлаве мы представим описание альтернативноrо метода BЫ
числения коэффициентов базиса k дисковых вейвлетов для заданной по
верхности. В ero основе лежит алrоритм блока фильтров. Кроме Toro, мы
рассмотрим различные приложения представлений через k дисковые вей
влеты, в том числе сжатие поверхности, контроль степени детализации, по
следовательно е пропускание и редактирование поверхности при различных
разрешениях.
Т'ЛАВА 11
Приложения к поверхностям
1. Переход к кратНOJ1.tасштабной форме 2. с.жатие пoвepXHO
стей 3. Непрерывный контроль степени детализации 4. По
следовательное пропускание 5. Редактирование при различных
разрешениях 6. Перспективы изучения поверхностных вейвле
тов
в этой rлаве мы рассмотрим различные применения k дисковых вей
влетов на поверхности, полученных в десятой rлаве. Эти приложения
включают сжатие модельных поверхностей, последовательное пропускание
сложных модельных поверхностей через сеть и редактирование поверхно
стей при различном разрешении.
В настоящее время большинство встречающихея на практике поверх
ностей представляются в более традиционной форме например, в виде
сложных мноrоrранников или В сплайновых разбиений. Поэтому нам ча
сто бывает нужным обратить такие представления поверхностей в KpaTHO
масштабную форму. Эту rлаву мы начнем с обсуждения TaKoro процесса
перехода.
11.1. Переход к кратномасштабной форме
в разделе 10.5 мы показали, как поверхность и( х ), параметризованная
на простой ячейке NIO, может быть натянута, по крайней мере, приближен
но, на базис кусочно линейных k дисковых вейвлетов с помощью биорто
rональных двойственных базисов. [лавное затруднение практической pe
ализации этоrо процесса состоит в том, что ни простая ячейка lvIO, ни
параметризация поверхности не бывают известными в большинстве ситу
аций. Так, кролик на рисунке 11.1(а) изначально определяется лишь некой
совокупностью почти 70000 тысяч треуrольников, «сшитых» в какую то
сложную мноrоrранную ячейку.
11.1. Переход к кратномааuтабной фор.не
185
(а)
(6)
(в)
Рис. 11.1. (а) Сложная ячейка, состоящая приблизительно из 70000 треуrольников,
полученных с помощью оптическоrо сканирующеro устройства и техники сшивания
Тюрка иЛевоя [125]; (б) базовая ячейка 1111°, сконструированная по алrоритму Экка
и соавторов [34]; (в) проекция модели на V 5 (NIO).
Первым этапом обращения произвольной поверхности в KpaTHOMac
штабную форму является определение элементарной ячейки NIO (называ
емой базовой ячейкой (base тesh)), тополоrически эквивалентной заданной
поверхности, и параметрической функции и(х), которая отображает точ
ки х Е NIO в трехмерное пространство. Алrоритм решения этой задачи
был недавно разработан Экком и соавторами [34] для случая, в котором
исходная поверхность является мноrоrранником. Результатом выполнения
их алrоритма является базовая ячейка J\;IO дЛЯ «кролика», изображенно
[о на рисунке 11.1(б). Однако параметризация сложных поверхностей, не
являющихея мноrоrранниками, остается пока нерешенной задачей.
После параметризации поверхности заданноrо мноrоrранника следу
ют друrие действия, предпринятые Экком и соавторами с целью обращения
поверхности в кратномасштабную форму. Такое обращение выполняется
посредством проецирования исходной поверхности на аппроксимирующее
пространство V J (NIO), [де J определяется так, чтобы максимальная ошибка
была ниже пороrа, задаваемоrо пользователем. Этап проецирования экви
валентен рекурсивному последовательному делению базовой ячейки J раз.
Таким образом, параметризация служит для отображения вновь образован
ных вершин в трехмерное пространство. Отображенные вершины описы
вают мноrоrранник из V J (J\;IO) дЛЯ примера с кроликом J "" 5 (смотрите
рисунок 11.1 (в). Последний этап на пути к кратномасштабной форме это
применение анализа блока фильтров) с использованием матриц A д и B д'
186
I: ава 11
которые дают нам rрубое приближение поверхности и набор вейвлет коэф
фициентов.
11.2. Сжатие поверхностей
В этом разделе рассматривается применение k дисковых вейвлетов
к двум видам сжатия: сжатию сложных поверхностей и сжатию TeKCТYP
ных карт, определенных на поверхностях.
11.2.1. Сжатие мноrоrранника
Итак, в качестве первоrо применения k дисковых вейвлетов мы pac
смотрим сжатие модельных мноrоrpанников, аналоrичных изображенно
му на цветной иллюстрации 9 (а). Эта модель, в частности, COCTO
ящая из 32768 треуrольников, создавалась по данным, предоставленным
cyberware, Inc. Поскольку исходные данные характеризовались координат
ной привязкой и было известно, что поверхность тополоrически эквива
лентна сфере, переход к кратномасштабной форме не требовал реализации
общеrо алrоритма параметризации, разработанноrо Экком и соавторами.
Вместо Hero для параметризации модели на октаэдральную базовую ячей
ку [74] использовалась процедура специальноrо назначения. Затем поверх
ность приводилась к кратномасштабной форме путем рекурсивноrо после
довательноrо деления и последующеrо анализа блока фильтров.
т. к. вейвлет коэффициенты, вычисленные по алrоритму блока филь
тров, являются коэффициентами функций ненормированноrо базиса, Be
личину коэффициента нельзя считать хорошей мерой наименьшей квaд
ратичной ошибки, которая возникла бы в результате отбрасывания этоrо
коэффициента. Если мы умножим каждый вейвлет коэффициент d{, COOT
ветствующий уровню j, на 2 j, то получим коэффициенты для L2 нормиро
BaHHoro базиса. Значения таких нормированных коэффициентов являются
значимыми в алrоритме сжатия, аналоrичном алrоритму для кривых, pac
смотренному в третьей rлаве.
Аппроксимации поверхности, изображенные на цветной иллюстра
ции 9 в), (е) и (и) были получены сортировкой нормированных коэффи
циентов 2 дисковых кусочно линейных вейвлетов и последующим отсевом,
соответственно, 99 %, 88 % и 70 % коэффициентов, имеющих самые малень
кие значения. Заметим, что эта простая стратеrия обеспечивает аппроксима
ции с более rлубоким уточнением на участках с повышенной детальностью,
не изменяя большие треуrольники на тех участках, [де мало деталей. Такая
же техника использовалась и для модели кролика, результаты смотрите на
цветной иллюстрации 10.
11.2. Сжатие поверхностей
187
Хотя во всех представленных к этому моменту примерах k дисковых
вейвлетов использовалось последовательное деление мноrоrранника, CTPYK
тура кратномасштабноrо анализа для поверхностей является достаточно об
щей, чтобы реализовать и rладкие схемы последовательноrо деления. В раз
деле 10.4 мы rоворили, что вейвлет анализ в схеме типа бабочки, которая яв
ляется интерполирующей схемой, имеет линейную временную сложность.
Значит, для аппроксимации rоловы Спока мы можем работать с k дисковы
ми вейвлетами, используя rладкие поверхности, имеющие разные степени
детальности, что изображается на цветной иллюстрации 11. Полностью
детализированная поверхность показана на картинке 11(а), а сжатое пред
ставление, требующее только 16 % коэффициентов исходной поверхности,
показано на картинке 11(б). Сжатие выполнялось с помощью 2 дисковых
вейвлетов, построенных по схеме типа бабочки.
11.2.2. Сжатие текстурных карт
Сжатие можно применить и к представлению текстур ной карты, опре
деленной на поверхности. Если поверхность параметризована на единичном
квадрате, то текстурная карта ничем не отличается от обыкновенноrо изоб
ражения и, следовательно, она может быть подверrнута сжатию с использо
ванием традиционных техник с вейвлетами Хаара или сплайн вейвлетами.
Но если поверхность тополоrически более сложная, эти обычные вейвлеты
уже не помorут и нужно будет использовать k дисковые вейвлеты. Идея
в том, чтобы рассматривать каждую цветовую компоненту красную, зеле
ную и синюю как скалярную функцию, определенную на базовой ячей
ке lvIO. Используя анализ блока фильтров можно каждую такую компонен
ту привести к кратномасштабной форме, после чеrо нормированные вей
влет коэффициенты можно будет упорядочить по величине и произвести
усечение точно так, как это делалось в случае сжатия изображения.
В примере с цветной иллюстрацией 12 для выполнения кусочно ли
нейной раскраски земноrо шара использовались батиметрические данные
и данные об отметках высот, полученные от Американскоrо Националь
Horo [еофизическоrо Центра. Результирующая цветовая функция включа
ет 2097 152 треуrольников и 1 048 578 вершин. Раскраска с полным разре
шением получилась слишком большой для Toro, чтобы ее можно было отоб
разить на rрафическом дисплейном терминале с 128 меrабайтами памяти,
поэтому мы не смоrли показать ее на цветной иллюстрации полностью.
Тем не менее, вы можете судить о плотности записи информации по Kap
тинке 12(з), [де даже при близком рассмотрении ребра ячейки прилеrают
друr к друrу настолько плотно, что изображение приобретает едва ли не
совершенно черный цвет.
Аппроксимации, показанные на картинках 12 (a) 12 (е), были полу
188
I: ава 11
чены вследствие отсева коэффициентов, соответствующих 2 дисковым кy
сочно линейным вейвлетам и имеющих значения, меньшие определенноrо
пороrовоrо значения. На цветной иллюстрации 12 (а) представлено сильно
удаленное изображение земноrо шара, для получения KOToporo было OT
брошено 99,9 % вейвлет коэффициентов; соответствующая ячейка показана
на картинке (б). Аналоrично, цветные иллюстрации 12 (в), (r) отображают
результаты отсева 98 % коэффициентов для среднеудаленноrо изображе
ния. Модель, показанная на близком расстоянии (д), которой соответствует
90 процентное удаление коэффициентов, практически неотличима от пол
ностью детализированной модели с полным разрешением (ж). Однако co
поставление соответствующих им сжатой ячейки (е) и исходной ячейки (з)
позволяет получить представление о поразительной степени сжатия, полу
ченной в данном случае.
11.3. Непрерывный контроль степени детализации
При визуальном отображении объекта представление ero BЫCOKoдeTa
лизированной версии необязательно и неэффективно в случае, если зри
тель находится достаточно далеко от этоrо объекта. Вместо этоrо XOTe
лось бы использовать какую либо форму контроля степени деталuзацuи
(level ofdetail coпtrol), дающую информацию о наблюдаемом объекте, KO
торая будет использоваться для оценки сложности воспроизводимой MO
дели. Самый распространенный подход к созданию LОD моделейl это
подход, опирающийся на мастерство и сноровку caMoro пользователя. Что
касается техники сжатия поверхностей, описанной в разделе 11.2, то здесь,
напротив, предусматривается механизм автш,taтизироваНН020 получения
LОD моделей.
Изображения на цветной иллюстрации 9 являются примерами исполь
зования вейвлет аппроксимаций для автоматизированноrо контроля уровня
детальности при визуальном отображении объекта. Левая колонка изобра
жений представляет ячейки с наибольшим разрешением, видимые с разных
расстояний. Так, если зритель смотрит на исходный мноrоrранник с ДOCTa
точно удаленноrо места, дающеrо, тем не менее, хороший обзор, то визу
ализировать все 32 000 треуrольников не имеет смысла. Вместо этоrо на
обозрение можно представить приближения, собранные в средней колон
ке, при этом не нанеся существенноrо ущерба качеству результирующих
изображений.
Резкая смена моделей с разными уровнями детальности при мультипли
кационных съемках может привести к нежелательному «растрескиванию»
изображения (<<popping»). Эта проблема леrко решится, если использовать
lLOD (level of detail) models т. е. моделей с контролем степени детализации. ПрUJИ.
ред.
11.4. Пос.7едовате.7ьное про пускание
189
непрерывные уровни сrлаживания способом, аналоrичным тому, что pac
сматривался в разделе 8.2 для кривых. В результате, Korдa расстояние между
объектом и пользователем сокращается, значение каждоrо вейвлет коэффи
циента плавно изменяется от нуля до соответствующей этому коэффициенту
надлежащей величины. Подобным же образом, при увеличении расстояния,
разделяющеrо пользователя и объект, каждый вейвлет коэффициент плав
но уменьшается до нуля. В общем, каждый вейвлет коэффициент можно
представить как непрерывную функцию расстояния до места просмотра.
11.4. Последовательное пропускание
Тексты, изображения и видео являются типичными элементами WWW,
все более распространенными становятся теперь и сложные rеометрические
модели. Небывалый рост в производстве и распространении таких [eOMeT
рических объектов объясняет потребность в эффективном пропускании MO
делей через сети с относительно низкой пропускной способностью.
Наиболее непосредственный способ пропускания ячейки, определя
ющей поверхность последовательноrо деления, заключается в отсылке че
рез сеть каждоrо из треуrольников, соответствующих версии с самым BЫCO
ким разрешением. Однако при таком способе пропускания сложных ячеек
пользователь вынужден ждать, пока не будет принята вся модель, прежде
чем что то появится на экране. Более привлекательный вариант задействует
вейвлет представление последовательноrо пр о пускания , отображенное на
рисунке 11.2. Сначала происходит пропускание базовой ячейки; поскольку
количество треуrольников в этой ячейке очень мало, то она принимается
и отображается очень быстро. Затем пропускаются нормированные вей
влет коэффициенты в порядке уменьшения своих значений. После принятия
этих коэффициентов можно проводить корректировку и вывод изображения
модели на экран.
11.5. Редактирование при переменном разрешении
Рассмотренное в восьмой rлаве кратномасштабное представление кри
вых поддерживает ряд различных операций редактирования. Почти анало
rично вейвлеты можно использовать для редактирования формы поверх
ности при различных разрешениях. В начале десятой rлавы мы уже упо
минали об одном примере редактирования поверхности при переменном
разрешении, тоrда мы рассматривали редактирование поверхностей, пред
ставленных через тензорные произведения (см. цветную иллюстрацию 8).
Почти так же мы можем редактировать поверхности произвольноrо
тополоrическоrо типа. Простой пример представлен на цветной иллюстра
190
I: ава 11
(а)
(6)
(в)
Рис. 11.2. Последовательное про пускание через сеть: (а) базовая ячейка, состоящая
из 229 треyrольников; (б) ячейка после принятия около 2000 вейвлет коэффици
ентов; (в) ячейка после принятия около 10000 вейвлет коэффициентов (исходная
модель любезно предоставлена rperoM Тюрком и Марком Левоем).
ции 11(в) И (r). На первой картинке изображен результат изменения одноrо
коэффициента масштабирующей функции на нулевом уровне для базовоrо
октаэдра rоловы Спока. Поскольку вершины, соответствующие более BЫ
сокому уровню уточнения, на том же участке определены относительно
более rрубой формы, при модификации они сдвиrаются. Однако rеометрия
участков, удаленных от лица, не меняется. Также возможна и локальная
модификация формы поверхности, для которой следует изменить значения
коэффициента на более высоком уровне разрешения. На цветной иллюстра
ции 11(r) мы видим результат, получившийся вследствие изменения Bcero
лишь одноrо коэффициента на уровне 3.
Все примеры редактирования поверхности, представленные на иллю
страции 11, были получены в результате изменения лишь KaKorO TO одноrо
значения в вейвлет представлении. Конечно, для выполнения модифика
ций более общеrо характера, весьма ценным было бы наличие мощноrо
средства редактирования поверхностей с возможностями, аналоrичными
описанным в разделе 8.3 для редактирования кривых при переменном раз
решении и в работе Финкельштейна и Сале зина [37].
11.6. Перспективы изучения поверхностных вейвлетов
Применение кратномасштабноrо анализа к поверхностям с произволь
ной тополоrией является сравнительно недавней разработкой специалистов
по компьютерной rрафике. k дисковые вейвлеты, которые мы ввели в пре
дыдущей rлаве и применили к практическим задачам, рассмотренным в этой
11.6. Перспективы изучения поверхностных вейвлетов
191
rлаве, конечно же, не стоит называть последним словом в кратномасштаб
ном вейвлет представлении. Даже то представление, что описываем мы,
можно усовершенствовать, причем не одним способом:
. в рассмотренных нами методах при вейвлет разложении поверхности
тополоrический тип базовой поверхности всеrда сохраняется. Однако,
если в качестве исходной поверхности выступает объект относительно
простой формы, имеющий множество маленьких отверстий, предпо
чтительнее разложить исходную поверхность в тополоrически более
простую поверхность, т. е. поверхность более низкоrо рода или по
верхность с меньшим числом поrраничных кривых.
. Изображения на цветных иллюстрациях 9 и 12 были получены в pe
зультате простоrо введения вейвлет коэффициентов с самыми больши
ми значениями. Однако можно было бы получить изображения еще
лучшеrо качества при использовании даже меньшеrо числа треуrоль
ников, если бы использовалась метрика поrрешности, зависящая от
удаленности изображения от зрителя.
. Для поверхностей, создаваемых в качестве моделей физических объек
тов при помощи развертки по дальности, возможно представить форму
и цвет как отдельные вейвлет разложения так, как это описывают Cep
тейн и соавторы [1 О]. Такие представления MOryT оказаться полезными,
если необходимо произвести эффективное манипулирование сложны
ми поверхностями с помощью интерактивной проrpаммы про смотра
и их редактирование в диалоrовом режиме.
Часть IV
ФИЗИЧЕСКОЕ
МОДЕЛИРОВАНИЕ
['ЛАВА 12
Вариационное моделирование
1. Заданuе целевой функции 2. Метод конечных элеiVlентов
З. Использование конечных элементов в вариационнOJ1,4 J140делиро
вании 4. Использование вейвлетов в вариационном моде ирова
нии 5. Адаптивное вариационное моделированuе
в предшествующих rлавах мы изучили несколько подходов к редакти
рованию поверхностей и кривых, в которых пользователь производит опе
рации с rеометрическими элементами изображения явным образом либо
передвиrая контрольные точки, либо прибеrая к «прямому манипулирова
НИЮ». МЫ также видели, каким образом для облеrчения выполнения этих
операций MOryT быть использованы вейвлеты, обеспечивающие eCTeCTBeH
ный и эффективный контроль «рабочеrо» участка.
Тем не менее, при создании кривых и поверхностей часто бывает по
лезным косвенный контроль пользователя, коrда указываются лишь целевая
функция и несколько оrраничивающих условий, а затем компьютер caMOCTO
ятельно определяет «лучший» rеометрический элемент, удовлетворяющий
обозначенным условиям. Такой процесс создания называют вариационным
)wоделированuем (variatioпal тodeliпg) [130], потому что в качестве целевой
функции (или, более специальный термин, объектной функции (objective
jiтctioп) берется, как правило, минимум какоrо либо интеrpала, а миними
зирующие интеrралы являются областью вариационноrо исчисления.
Как мы увидим в этой rлаве, вейвлеты оказываются очень полезными
для ускорения вычислений, связанных с вариационным моделированием.
Чтобы посмотреть, каким образом они используются, мы начнем с более
точноrо формулирования задачи вариационноrо моделирования и paCCMOT
рим, как используются в решении этой задачи конечные элементы.
12.1. Задание целевой функции
Мы приводим здесь пример задачи вариационноrо моделирования.
Предположим, что нам нужно построить «rладкую» кривую, проходящую
через заданную точку в трехмерном пространстве. Как это сделать?
196
I: ава 12
Первый шаr более точное определение целевой функции. Начнем
с Toro, что напишем уравнение для кривой в трехмерном пространстве
в следующем виде:
i(t) : [i1 (t) i2(t) iз(t)]Т для t Е [О, 1].
Теперь целевую функцию нужно задать. Одной из мер «rладкости»
служит полная кривизна: интеrрал кривизны, взятый по длине кривой.
Несколько более простой вариант интеrpал квадрата второй производ
ной, основанный на вычислении энерrии изоrнутой проволоки, также
можно использовать как достаточно хорошую меру кривизны. Таким обра
зом, формулировка задачи вариационноrо моделирования принимает такой
вид:
1
минимизировать J li f(t)12 dt при данных оrpаничениях, для i 1, 2, 3.
а
Прежде чем решить ее, давайте возьмем еще один пример, на этот раз
для поверхностей. Как и раньше, предположим, что нам нужно построить
«rладкую» поверхность и соблюсти при этом некоторые оrраничивающие
условия. Параметрическую поверхность мы можем записать как
(}(s, t) : [(}l(S, t) (}2(S, t) (}з(s, t)]T дЛЯ S, t Е [0,1].
Если аппроксимировать полную кривизну этой поверхности с помощью
плоской энерrетической модели ([99], стр. 318), каждую координатную
функцию можно оиять рассматривать независимо. Для поверхностей задачу
вариационноrо моделирования можно сформулировать так:
минm<юиронаТо j j (1 ;;,; l' + 21 z: l' + 1 д;;;Л а"ц
при данных оrраничениях для i 1, 2, 3. Оrpаничением на поверхность
может служить условие прохождения через точку, тоrда () задается при
конкретных s и t. Оrраничение можно применить и к нормали поверхности,
задав д() / дs и д(} / дt для конкретных s и t.
Как уже было замечено, нахождение кривой или поверхности с ми
нимальной полной кривизной, удовлетворяющей заданным оrраничениям,
является задачей вариационноrо исчисления, поскольку в роли неизвест
ных выступают функции. Для Toro чтобы эта задача леrко решалась на
компьютере, нам следует свести ее к задаче, в которой в роли неизвестных
выступает конечный набор чисел.
12.2. Метод конечных эленентов
197
12.2. Метод конечных элементов
МетодОJ1Л конечных эле.iVlентов (fiпite eleтeпt тethod) называют метод
нахождения приближенноrо решения задачи путем замены неизвестной pac
сматриваемой функции на неизвестную линейную комбинацию известных
базисных функций.
Основные шаrи в реализации этоrо метода следующие:
1. Выберем множество базисных функций и(t) "" [щ(t)... um(t)], назы
ваемых конеЧНЫJ1ЛИ эле.менталtU (fiпite eleтeпts).
2. Запишем неизвестную функцию как линейную комбинацию этих KO
нечных элементов. Например, функция i(t) записывалась бы так:
m
i(t) LXjUj(t) "" и(t)x,
j l
[де х [Хl . . . Хт]Т это множество неизвестных коэффициентов.
Заметим, что неизвестная функция i(t) может быть точно выраже
на в такой форме через конечные элементы, только если она лежит
в векторном пространстве, натянутом на конечные элементы. В против
ном случае возможно лишь приближенное представление неизвестной
функции в форме и(t)x.
3. Введем в исходную задачу, содержащую i(t), представление с конеч
ными элементами и (t) х. Во мноrих случаях решение исходной задачи
в терминах конечноrо множества неизвестных х дается леrче после
такой подстановки.
В следующем разделе мы увидим, как этот метод можно применить
к вариационному моделированию, а чуть позже, в следующей rлаве, по
смотрим еще одно применение конечных элементов к решению уравнений
переноса излучения для общеrо освещения.
12.3. Использование конечных элементов в вариационном
моделировании
Конечные элементы MorYT использоваться в вариационном моделиро
вании, и мы увидим, как это происходит, если продолжим рассмотрение
предыдущеrо примера, в котором мы находим rладкую кривую i(t), ин
терполирующую некоторые заданные точки. Вот, к примеру, одна из таких
198
I: ава 12
вариационных задач:
минимизировать
1
J I{ / (t) 12 dt при оrpаничениях
о
{ {(О) == 3
{( ) == 18
{(1) == 12.
Чтобы представить эту задачу через конечные элементы, мы, прежде Bcero,
выберем определенный класс кривых, который мы хотели бы рассмотреть,
так, чтобы {(t) записывалась как линейная комбинация конечноrо множе
ства базисных функций.
Например, если мы оrpаничим {(t) принадлежностью к классу функ
ций четвертоrо порядка, то выразить это можно будет так:
{(t) == Хl + X2t + X3t2 + X4t3 + X5t4 == и(t)x.
rдe и(t) == [1 t t 2 t 3 t 4 ] их == [Хl Х2 ХЗ Х4 Х5]Т'
В данном случае пять мономиальных базисных функций в и (t) яв
ляются конечными элементами, и мы оrpаничили пространство решений
для {(t) до иятимерноrо пространства, натянутоrо на эти функции.
Заметим, однако, что число функций четвертоrо порядка, удовлетво
ряющих данным оrраничениям (как показано на рисунке 12.1), все еще
является бесконечным, и только одна из этих функций имеет минимальную
кривизну. Для нахождения этой функции мы подставим конечно элементное
представление кривой {(t) в уравнения оrраничений, относящиеся к исход
ной задаче. В этом случае получаем
[ ] == [ : ] х == [
{(1) и(l) 1 1
о
1
4
1
о
1
8
1
':6 ]X [lH
Результатом является множество линейных уравнений относительно
неизвестных коэффициентов разложения:
Ах == Ь,
rдe
А [:
О
1
2
1
О
1
4
1
о
1
8
1
]
и
Ь==[1 2]'
12.3. Использование конечных эленентов в вариационном моде.7ировании 199
30
20
/;,<.- '
-- -- .-
'" -;::
,," .-'- ....... ...
, '
, ,
, "
.... ... \ \
... \ \\
...... .."........:'\,
, : : ,
..
]0
-- -- --
ф,J/'; :; '::; ;,
.. ",..""
, # ,,./'i" .,,/
, ... /,..1;-
/ ...... .,, '
" ",# 1;.'
/..." _. ....
о
о
0.25
0.5
0.75
Рис. 12.1. Функции четвертоrо порядка, удовлетворяющие трем интерполирующим
оrраничениям. Кривая, обозначенная сплошной толстой линией, является функцией
с минимальной кривизной.
Мы также можем подставить конечно элементное представление кри
вой i(t) в целевую функцию. Эта подстановка и выполнение некоторых
алrебраических преобразований дают
1 1
J li ' (t) 12 dt J (и" (t)x) (и" (t)x) dt
о о
1
J (х Т и"Т)( и" х) dt
о
1
J х Т (и "т и")х dt
о
х Т (j и"Т и" <1}
1 т н
"2Х х,
200
I: ава 12
rдe множитель 1/2 вводится для дальнейшеrо удобства, а zессиан (Hessiaп
тatrix) Н определяется как
1
Н 2 J и"(t)T x)и"(t) dt
о
о о о
о о о
о о 10
О О 15
О О 20
о о
о о
15 20
30 45
45 72
Теперь наша исходная задача вариационноrо моделирования имеет такую
форму:
минимизировать xT Нх при оrраничении Ах == Ь.
Подобные задачи, включающие квадратичную целевую функцию и ли
нейные оrраничения, относятся к предмету оптимизации, известной также
как квадратичное проzраМJVlирование. Ее решение мы найдем с помощью
метода JVlножителей Лаzранжа ([51], страницы 43 49), который особенно
хорошо работает при решении задач квадратичнorо проrраммирования.
Интуитивное представление о действии этоrо метода можно получить,
если рассматривать минимизацию функции как определение потенциала.
В этом случае rрадиент целевой функции определяет силовое поле. Мы
будем искать «устойчивую точку», т. е. точку, в которой сила равна нулю.
Следуя этой линии интуитивноrо рассуждения, о каждом оrраничении
можно рассуждать как о силе, соотнесенной с ним, которая несет в себе
толчок к «поверхности оrраничения», rеометрическому месту точек, yдo
влетворяющих данному оrраничению. Трудность такой концепции в том,
что нет никакоrо eCTecTBeHHoro способа для взвешивания силы оrраничений
относительно друr друrа или относительно потенциальной силы, создава
ем ой целевой функцией. Поэтому относительные весовые значения этих
сил мы будем считать неизвестными >-1, . . . , >-т (это И есть JVlно,жители
Лаzранжа). Теперь мы должны найти весовые значения и устойчивую точ
ку, такую, что
(а) суммарная сила равна нулю,
(б) точка принадлежит одновременно всем поверхностям оrpаничений.
Причина, по которой эта техника хорошо работает в задачах квадратич
ной минимизации, заключается в том, что число соотношений в условиях ( а)
и (б) равно числу неизвестных, и нам остается решить линейную систему
с квадратной матрицей.
12.3. Использование конечных эленентов в вариационном моде.7ировании 201
Посмотрим, как работает этот метод, завершив решение нашей MO
дельной задачи. В рассматриваемом случае мы имеем три оrpаничения,
поэтому введем вектор трех множителей Лаrранжа Л [Л1 Л2 ЛЗ]Т. Теперь
мы можем включить наши оrраничения в простую задачу минимизации без
оrраничений:
МИНИМИЗIIpовать xTHx + (Ах Ь)Т Л .
Для нахождения минимума возьмем про из водную этой новой целевой
функции по каждому из неизвестных Х; и Лi И приравняем к нулю. В pe
зультате получается система линейных уравнений:
{ Нх + А Т Л О
Ах Ь О.
Можно переписать эту систему в виде одноrо матричноrо уравнения, ис
пользуя блочную запись для матрицы:
[ A;][ ] [ ]
(12.1)
Подставляем значения Н, А, Ь, решаем относительно х и Л и получаем
х [3 41 8 80 40]Т,
Л [256 512 256]Т.
в этом примере мы не используем значения множителей Лаrранжа. Тем не
менее, из значений х следует, что кривой четвертorо порядка, проходящей
через точки с минимальной кривизной, является
,(t) 3 + 4lt + 8t 2 80t З + 40t 4 .
в целом (исключения составляют только самые тривиальные случаи),
число базисных функций, требуемых для нахождения кривых и поверх
ностей, должно быть достаточно большим для Toro, чтобы был большим
порядок матричной системы в уравнении (12.1). Однако наиболее распро
страненные базисные функции (такие как В сплайны, к примеру) перекры
ваются лишь с небольшим количеством своих соседей, и это делает Н
разреженной. Большая разреженная линейная система, получающаяся в pe
зультате, наиболее эффективно решается, как правило, с помощью итера
ционноrо метода решения, например, метода [аусса Зейделя или метода
сопряженных rрадиентов [97].
202
I: ава 12
12.4. Использование вейвлетов в вариационном
моделировании
Итак, какое же отношение к данной теме имеют вейвлеты? До Ha
стоящеrо момента мы не делали oroBopoK о том, какие базисные функции
должны использоваться в качестве конечных элементов для решения вари
ационных задач в моделировании кривых и поверхностей (хотя мы, прав
да, рассмотрели простой пример с мономиальными базисными функциями
в роли конечных элементов).
Самым очевидным выбором является использование В сплайнов, пото
му что они уже повсеместно применяются в качестве базиса моделпрующих
систем. Однако матрица в уравнении (12.1) оказалась плохо обусловленной
для базиса В сплайнов. Интуитивно, эту плохую обусловленность можно
объяснить тем, что каждая функция базиса В сплайнов представляет толь
ко малую часть решения, поэтому при любом обширном изменении кривой
требуется резкий переход от одноrо базиса к друrому. А в этом случае итера
ционные методы решения, обычно используемые для больших разреженных
систем, отличаются медленной сходимостью к точному решению.
Медленная сходимость базиса В сплайнов пллюстрируется верхним
рядом картинок рисунка 12.2. На нем отображается, как вариационное pe
шение для кривой минимальной энерrии постепенно сходится за 1 024 ите
рации. Ясно, что использование базиса В сплайнов в интерактивном режи
ме может приводить к длнтельным паузам, во время которых система будет
пересчитывать новое решение для кривой с минимальной энерrией (всякий
раз, коrда пользователь добавит или изменит оrраничения для кривой).
В спла й н ы:
I II II II II II I
II.jll lrjll II 1
В"йвлеты:
Число итераций:
о
4
16
64
256
1024
Рис. 12.2. Последовательность итераций, сходящаяся к кривой минимальной энер
rии, удовлетворяющей трем orраничениям. Верхний ряд отображает медленную
сходимость вследствие использования базиса В сплайнов; нижний ряд демонстри
рует улучшенную сходимость блаrодаря использованию базиса вейвлетов.
Одно из решений проблемы слабой обусловленности и медленной cxo
димости заключается в использовании в качестве конечных элементов не
самих В сплайнов, а вейвлетов, полученных из них (такое получение вей
12.5. Адаптивное вариационное ,ноделирование
203
влетов рассматривалось в разделе 7.3.2). Подобная замена базиса может
значительно улучшить выполнение процесса минимизации, что показали
[ортлер и Коэн [49]. Интуитивно можно считать, что при выборе базиса
вейвлетов изменения в кривой распространяются от одноrо участка к дpy
[ому rораздо быстрее, потому что, внося изменения на данном участке,
можно обратиться наверх иерархии, к базисным функциям с более широки
ми носителями, от которых можно спуститься вниз к базисным функциям
с более узким носителем.
Друrой способ для методов, схожих с итерационными методами pe
шения, состоит в том, чтобы рассматривать этот переход от масштабиру
ющих функций к базису вейвлетов как этап предварительной подrотовки.
Вместо решения уравнения (12.1) мы решаем
[W;:!i l W ; АТ ] [ ] [ ]
rдe W представляет вейвлет преобразование, а х Wx множество
вейвлет коэффициентов для решения.
Это новое уравнение по прежнему можно решать итерационными Me
тодами. Но [ортлер и Коэн указывают на то, что при решении этоrо ypaBHe
ния лучше не представлять матрицу в явном виде, поскольку новая матрица
(полученная на этапе подrотовки) больше не является такой же разрежен
ной, как исходная. Вместо этоrо они предлаrают «неявный» метод, в KO
тором вычисления на каждом этапе, включающие операцию умножения
матрицы на вектор, выполняются проrонкой алrоритма блока фильтров из
раздела 7.1.2. Время и объем памяти, требуемые для умножения матрицы
при таком неявном подходе, зависят линейно от параметров задачи.
Эффект от такой замены базиса, или введения этапа предварительной
подrотовки, весьма впечатляющий, что иллюстрируется нижним рядом Kap
тинок на рисунке 12.2. Заметим, что в случае базиса вейвлетов кривая cxo
днтся к решению HaMHoro быстрее и принимает форму, близкую к конечной,
уже через 64 итерации. Такой базис является rораздо более эффективным
для поддержки интерактивноrо режима создания кривых и поверхностей
вариационными методами.
12.5. Адаптивное вариационное моделирование
Выбор заранее фиксированноrо множества базисных функций не Bce
rдa представляется лучшим способом моделирования поверхностей или
кривых. Так, если выбранное множество функций слишком мало, то реше
ние задачи вариационноrо моделирования, полученное методом конечных
204
I: ава 12
элементов, может оказаться не лучшей аппроксимацией оптимальной кри
вой или поверхности. С друrой стороны, если выбранное множество функ
ций слишком велико, то процесс получения решения может стать недопу
стимо дороrостоящим. Следовательно, в «идеале» хорошо было бы начать
с нескольких rрубо аппроксимирующих базисных функций и постепенно
вводить более точные базисные функции, если нужно улучшить решение.
Процедура, используемая для решения, какие базисные функции нужно дo
бавлять, иноrда называется оракулом (oracle) , т. к. она пред сказывает, [де
должен быть уточнен результат.
Оракул, описанный [ортлером и Коэном [49], вводит новые базисные
функции в двух ситуациях. Во первых, если оrраничительное условие не
выполняется в данный момент, оракул добавляет более точные вейвлеты
в область пространства параметров, ближайшую к области оrраничений.
BO BTOpЫX, оракул включает более точные вейвлеты, близкие к уже име
ющимся базисным функциям с коэффициентами, превышающими HeKOTO
рый пороr, т. е. туда, rдe уточнение деталей поможет получить решение
с более низкой энерrией. Кроме Toro, оракул может также «дезактивизи
равать» базисные функции, как только их коэффициенты станут меньше
HeKoToporo минимальноrо пороrа. Блаrодаря такой стратеrии, в итерацион
ный процесс нахождения решения вовлечены лишь те вейвлеты, которые
дают значительный вклад в оптимальное решение.
Комбинированная действенность от использования базиса вейвлетов
и алrоритма, адаптирующеrо этот базис к конкретной задаче, позволяет pe
шать достаточно сложные задачи моделирования в интерактивном режиме.
Изображения на цветной иллюстрации 13 поясняют работу интерактивноrо
редактора поверхностей. Пользователь задает [дe TO положение поверхно
сти и [дe TO направление нормали поверхности, а проrpамма автоматиче
ски находит поверхность с минимальной энерrией, удовлетворяющую этим
оrраничительным условиям.
Использование адаптивноrо алrоритма для выборочноrо уточнения pe
шения, полученноrо с помощью базиса вейвлетов, оказывается удобной
техникой для множества различных задач. В следующей rлаве мы paCCMOT
рим еще один пример, в котором вейвлет базис будет использоваться для
решения задач общеrо освещения.
['ЛАВА 13
Общее освещение
1. Излучательность 2. Конечные элементы u uзлучательность
З. Вейвлет uзлучательность 4. Улучшенuе вейвлет uзлучатель
ности
Синтез фотореалистичных изображений является одной из самых фун
даментальных задач компьютерной rрафики, имеющей своими приложени
ями такие разноплановые области, как аналитическая визуализация, OCBe
щение, промышленный дизайн, дистанционный сбор данных с помощью
спутников и роботов, а также сфера развлечений и реклама.
Подход, известный под названием общее uлu 2лобальное освещенuе
(global illuтiпatioп) , содержит попытку создать реалистичные изображе
ния путем моделирования взаимоотражения, эмиссии и поrлощения света
поверхностями в кадре. Все эти взаимодействия подчиняются ряду физи
ческих законов, которые можно описать интеrральным уравнением. К co
жалению, в общем случае это уравнение достаточно сложное, и возникает
необходимость использования методов приближенных вычислений.
В этой rлаве мы рассмотрим математическое описание задачи rлобаль
Horo освещения и увидим, как можно использовать вейвлеты при ее реше
нии.
13.1. Излучательность
Для начала рассмотрим частный случай задачи rлобальноrо освещения,
в котором все поверхности являются идеально рассеuвающшwu (difJuse) , т. е.
они излучают и отражают свет в равной степени во всех направлениях. Бо
лее распространенное название этоrо частноrо случая задача об uзлуча
тельностu (radiosity рroЫет) , поскольку он включает нахождение решения
уравнения переноса, в которое входит излучательность, мера энерrии
на единицу времени и площади. Более формально uзлучательность В(х)
можно определить как удельную мощность, исходящую из лежащей на
поверхности точки х. Единицей измерения излучательности В является
[ватт. MeTp 2].
206
I: ава 13
Равновесное распределение излучательности удовлетворяет следующе
му уравнению переноса излучательностu (radiosity traпsport еqиаtiоп) [22]:
р(у) J
В(у) == Ве(У) + С(х, y)B(x)dx.
(13.1)
'"
Это уравнение утверждает, что излучательность В в точке у равняется
сумме двух слаrаемых: испускаемой излучательности (eтitted radiosity) Ве
и интеrрала от излучательности, отраженной всеми друrими точками х.
Бесконечно малая площадь BOKpyr точки х записана через dx. Коэффици
ент отражения (reflectaпce) р(у) определяет ту часть падающей энерrии,
которая отражается, а не проходит сквозь поверхность или поrлощается
(и преобразуется в тепло). Коэффициент отражения является соотношени
ем частей, не имеет размерности и принимает значения от О до 1. В данном
уравнении 7r является нормировочным множителем, отвечающим за ин
теrpирование по полусфере направлений, по которым свет исходит из у.
Наконец, zешнетрuческая компонента (geoтetric terт) G (х, у) описывает
закон перехода дифференциальноrо элемента площади около х в диффе
ренциальный элемент площади около у. Этот закон задается так:
cos В'" cos Ву
С(х, у) :== V(x, у) . 2 '
Ilx yll
rдe множитель V (х, у) является компонентой вuдшwостu (visibility terт)
и изменяется от 1 дО О, в зависимости от Toro, видимы ли друr друrу х и у.
Уrлы В'" и Ву это уrлы между прямой ху и соответствующими нормалями
дифференциальных элементов площади х и у. [еометрическая компонента
симметрична по своим aprYMeHTaM: С(х, у) == С(у, х). Некоторые из этих
rеометрических параметров показаны на рисунке 13.1.
Часто бывает удобно работать с уравнением переноса излучательности
(13.1) в более простой и наrлядной операторной форме:
В==Ве+ ТВ ;
(13.2)
здесь оператор переноса излучательности (radiosity traпsport еqиаtiоп) Т
определяется как
р(у) J
(ТВ)(у):== С(х, y)B(x)dx,
'"
rдe (ТВ)(у) определяет результат действия Т на В(х) для получения Функ
ции с арrументом у. Интуитивно, можно считать, что оператор переноса Т
13.2. Конечные элененты и иЗ.7учате.7ьность
207
Рис. 13.1. rеометрия переноса излучательности из точки х в точку у.
представляет «точечный» перенос света: для каждой поверхности (парамет
ризованой по у) он собирает излучательность от всех друrих поверхностей
в кадре (параметризованых по х) и отражает их обратно в кадр в COOTBeT
ствии с коэффициентом отражения р( у ).
Следует заметить, что до сих пор мы не упоминали о цвете в нашем
представлении уравнения переноса излучательности. При отсутствии флу
оресценции (явления поrлощения материалом света с одной длиной вол
ны И испусканием света с друrой длиной волны) мы можем просто cдe
лать В, Ве и Р функциями и длины волны, и расположения. Тоща ypaBHe
ние (13.2) будет справедливым для любой длины волны, какую бы мы не
захотели рассмотреть.
13.2. Конечные элементы и излучательность
Для нахождения точноrо решения задачи излучательности для частно
[о случая нам придется определить количество света, покидающеrо каждую
точку на каждой поверхности, т. е. решить уравнения переноса излучатель
ности уравнение (13.1) или уравнение (13 .2) относительно излучатель
ности В (у) для всех точек у.
К сожалению, и в первой, и во второй форме уравнения неизвестная
функция В появляется как под знаком интеrрала, так и вне ero. [eOMeT
рическая компонента, а также компоненты, характеризующие отражение
и излучение, допускают получение аналитическоrо решения этоrо ypaBHe
ние в очень редких случаях. По этим причинам мы обратимся к методу
конечных элементов, чтобы получить приближенное решение. Как и в ДBe
надцатой rлаве, мы перепишем неизвестную функцию как линейную KOM
бинацию базисных функций. В результате задача сводится к решению ли
208
I: ава 13
нейной системы уравнений со множеством неизвестных коэффициентов
с чем может справиться компьютер. Но прежде чем прийти к этой линейной
системе, нам следует более подробно рассмотреть, как базисные функции
MorYT использоваться для дискретизации излучательности.
13.2.1. Дискретизация излучательности
Пусть и(х) == [иl(Х) и2(Х)"'] базис для пространства функций
излучательности. Неизвестное распределение излучательности В можно
выразить через линейную комбинацию базисных функций Ui (х) с неиз
вестными коэффициентами b i :
00
В(х) == LbiUi(X)'
i l
Это уравнение можно записать в матричной форме как В(х) == и(х)В,
rдe В бесконечная столбцевая матрица, i тый элемент которой равен b i .
Если не возникает путаницы, мы опускаем арrументы и записываем просто
В == иВ.
13.2.2. Дискретизация переноса излучательности
r ffJНJ,tlИ, lVlbl lVlUnPd"1\1: П ' П' Д T - . ' ' DЪУjJС61fI mJiУ.'{dт\',rnНО'е'I1)><ь >1";-jJ1Vlfldаk 'olОtl\;НfilА ЧJ
11
Ьijевои мат ,,11 Л}1ИИ'fи J{ системе хпавнении с неизвестными элементами стол
! j JЗ:)} ",,1' .рRЦШ '..J! Jt qдВ'li' Vl}{i llаД.:;'f';rВШv'iНLJ и п пLJf! и D ")]fRВlК'flИ{:"
И затем используем линеиность оператора 1', чтобы получить
иВ == иВе + Т(иВ) == иД + (Ти)В.
(13.3)
Далее спроецируем уравнение (13.3) обратно на базис и. Для этоrо
мы воспользуемся двойственным базисом, соответствующим и. Обозначим
ero u == [иl (х) 'й2 (х) . . . ]. в разделе 7.4.1 rоворилось о том, что двойствен
ный базис характеризуется отношением (Ui 1 из; == (jij, или, В матричной
форме, [( u 1 и;] == 1, rдe 1 это единичная матрица. Напомним также, что
ортонормированные базисы, например, базис Хаара, являются самосопря
.женными, это означает, что u == и.
Мы можем спроецировать уравнение (13.3) на наш базис, взяв CKa
лярное про изведение каждой из двух частей уравнения и каждой функции
двойственноrо базиса. В матричной записи эта проекция представляется
с помощью линейноrо оператора [( u 1. ; ], вводимоrо в обе части уравнения
следующим образом:
[(uluB;]
[(uluB e ;] + [(ul(Tu)B;].
13.2, Конечные элененты и иЗ.7учате.7ьность
209
Используя линейность, мы можем выделить матрицу [( и I и) ], входящую
в левую часть уравнения, и первое слаrаемое второй части. Соrласно COOT
ношению двойственности эта матрица равна единице, поэтому мы можем
убрать ее отовсюду. Таким образом, мы пришли к дискретному уравнению
переноса излучательности (discrete radiosity transport еqиаtiоп):
в Ве + тв.
(13.4)
в этой бесконечной системе линейных уравнений матрица переноса
т : [(иITU)] является бесконечной матрицей, представляющей оператор
переноса Т. (" s) тый элемент матрицы Т является коэффицuентом пe
реноса и характеризует влияние коэффициента, соответствующеrо ив, на
коэффициент, соответствующий и т , В явном виде TT B можно записать
так:
Tr s (urITu s )
(и т p ) J С(х, Y)Us(x)dx )
х
J иT(Y) p ) J С(х, Y)Us(x)dxdy
у х
[де обозначение , s вводится для Toro, чтобы подчеркнуть, что TT B
представляет воздействие отправителя s на получателя ,. В интеrрале из
уравнения область определения для х является носителем отправляющей
базисной функции и в , а область определения для у является носителем
принимающей базисной функции и т ,
(13.5 )
13.2.3. Решение линейной системы
Дискретная версия уравнения переноса излучательности (13.4) по
прежнему представляет бесконечное множество уравнений инеизвестных.
Самым прямым методом нахождения приближенноrо решения этоrо MHO
жества уравнений является априорный выбор большоrо, но фиксированно
[о множества базисных функций для представления решения. Например,
мы моrли бы разбить все поверхности исходноrо кадра на m фраrментов,
а затем определить одну характеристическую функцию на каждом из этих
фраrментов и использовать их в качестве базиса. Далее мы моrли бы вычис
t:lJvta tlыlлfre M2 " птJIИ"i'ь 11< JJlt:jVlt:tlLUtl ' 7t:l'Q'l{J1ЪТ I' 1JQ \lUdВ}fенщ(п 1].,,1 11 Чl',) Н
маrли 11" ния ЧIfСJТеннпrп или аН'dЛИ1'И'Iескоr:.о vrQИIJОВШЩЯI. hаКО Щ;Ir. МЫ
оыI использовать люоую irporpaMMY, разрешающую линеиRые' уравнения,
и найти n неизвестных коэффициентов излучательности, удовлетворяющих
уравнению (13.4).
210
I: ава 13
Однако реализация TaKoro метода наталкивается на очень серьезное за
труднение: затраты, связанные с вычислением матрицы переноса Т, HaMHO
[о превышают затраты на решение получающейся линейной системы. Льви
ная доля затрат приходится на вычисление правой части уравнения (13.5)
для каждой пары отправляющих и принимающих базисных функций. Си
туация HaMHoro улучшается, если для начала вычисляются лишь несколько
элементов матрицы Т, затем находится соответствующее решение, а толь
ко потом добавляются еще несколько элементов Т. Подобные действия мы
проделывали уже не раз.
Алrоритм, известный под названием иерархuческая излучательность
(hierarchial radiosity) [55], реализует такой подход. Сначала он находит
усредненную излучательность каждой поверхности в кадре, затем разбива
ет каждый прямоуrольный участок, нуждающийся в уточнении, на четыре
подобласти и вновь находит усредненную излучательность. Такой процесс
попеременноrо уточнения и нахождения решения выполняется вплоть до
получения удовлетворительноrо результата. Базисные функции, лежащие
в основе иерархической излучательности, представляют собой кусочно по
стоянные характеристические функции разных размеров. Основанный на
вейвлетах метод, который мы представим ниже, похож на изложенный Me
тод, только в нем используются не характеристические функции, а вейвлеты
Хаара, которые в уточненном решении представляют детали, OTCYTCTBY
ющие в исходном rрубом решении.
13.3. Вейвлет излучательность
Для всех иерархических, или кратномасштабных, методов решения за
дач rлобальноrо освещения характерна последовательность одинаковых ба
зовых этапов: на каждой итерации уточняется взаимодействие между ба
зисными функциями имеющеrося решения, а затем эти взаимодействия ис
пользуются для нахождения улучшенноrо решения. Кратномасштабные Me
тоды учитывают тот факт, что в некоторых областях кадра решение можно
достаточно точно представить через несколько базисных функций. Но дa
же там, [де требуется MHoro базисных функций, каждая базисная функция
взаимодействует только с небольшим числом друrих функций.
Прежде чем перейти к описанию алrоритма вейвлет излучательности,
мы должны рассмотреть, как излучательность и оператор переноса излуча
тельности представляются в базисе вейвлетов.
13.3.1. Базис вейвлетов для излучательности
Излучательность определена на двумерной области, а именно, на по
верхностях в кадре. Предположим, что эти поверхности поделены на об
13.3. Вейвлет из.7учательность
211
ласти, которые параметризуются на единичном квадрате. В третьей rлаве,
посвященной изображениям, мы отметили, что самым простым способом
построения MHoroMepHoro базиса вейвлетов является взятие тензорных про
изведений функций одномерноrо базиса. Тоща нам нужно решить, какой
одномерный базис вейвлетов следует использовать и какую конструкцию
стандартную или не стандартную применять для получения двумерноrо
базиса.
Для простоты в нашем объяснении мы будем использовать базис Xa
ара. Для сравнения, друrие базисы, которые применялись в алrоритмах
вейвлет излучательности, включали флатлеты (flatlets) и )wультuвейвлеты
(тultiwavelets) [50, 107]. Мы также будем использовать не стандартную KOH
струкцию двумерноrо базиса, потому что она позволяет очень просто xpa
нить разреженное множество вейвлет коэффициентов в квадратичной дpe
вовидной структуре, как это было при редактировании изображения в чет
вертой rлаве.
13.3.2. Структуры данных для вейвлет излучательности
Излучательность каждоrо фраrмента в кадре можно рассматривать как
изображение. Если мы хотим найти решение задачи об излучательности для
длин волн, приближенно соответствующих красному, зеленому и синему
цветам, мы можем использовать древовидную структуру данных, похожую
на ту, что использовалась для редактирования изображений в четвертой
rлаве:
type QиadTTee record
c:RGB
Toot : pointer to QиadTTeeN ode
links : pointer to Link
end record
type QиadTTeeN ode record
d 1 , d 2 d з : RGB
child : array [1. .4] of pointer to QиadTTeeN ode
links : pointer to Link
end record.
По аналоrии с изображениями, с представляет усредненную излуча
тельность фраrмента, тоrда как коэффициенты d i перемножают вейвле
ты фф, фф и фф на каждом уровне и сдвиrе квадратичной древовидной
структуры. Массив child содержит указатели на вершины квадратичной
древовидной структуры, хранящие уровни самых точных деталей в каждом
из четырех квадрантов.
212
I: ава 13
Каждая структура также содержит область под названием links (зве
нья), которая указывает на динамический список коэффициентов перено
са TT B из всех друrих отправляющих вершин s, по отношению к которым т
служит получателем. Вот структура данных для звена:
type Link record
s: pointer to QuadTTee or QuadTTeeN ode
Т: array [1. .9] of RGB
7ютiаtiоп : real
next : pointer to Link
end record.
Link cTpYKтypa может содержать до девяти коэффициентов пере
носа, через которые можно представить коэффициенты переноса для
всех комбинаций вейвлетов на отправителе и получателе. Звено между
QuаdТтее структурой (содержащей коэффициент масштабирующей функ
ции) и QuаdТтееNоdе структурой (содержащей три вейвлет коэффициен
та) использует Bcero лишь три из этих коэффициентов переноса, в то время
как звено между двумя QuаdТтее структурами использует только один KO
эффициент.
13.3.3. Алrоритм вейвлет излучательности
Теперь мы [отовы описать алrоритм вейвлет излучательности. Наша
первоочередная задача решение системы линейных уравнений относи
тельно излучательности
в Ве + ТВ.
Сначала мы находим небольшое число элементов матрицы Т и решаем
уравнения, затем мы вычисляем еще несколько элементов и вновь решаем
уравнения и т. д. Поскольку вычисление элементов Т является весьма дopo
rостоящим занятием, мы постараемся вычислить по возможности меньше
этих элементов и при этом получить хорошую аппроксимацию решения.
Коротко выражаясь, вычислению подлежат только сравнительно большие
элементы Т, которые связывают большие коэффициенты базисных функ
ций.
[лавная часть этоrо алrоритма предст вляет собой попеременное BЫ
числение приближенной излуч тельности В и улучшение конечноrо пред
ставления оператора переноса Т. Величины с «крышечками» являются при
ближенными, во первых, потому что они находятся численным способом,
BO BTOpЫX, потому что они являются усеченными версиями бесконечных
матриц. Пер во начально мы проецируем Ве на пространство VO про
странство, натянутое на масштабирующие функц и, соответствующие ca
мому rpубому приближению чтобы получить Ве. Мы также вычисляем
13.3. Вейвлет из.7учательность
213
элементы матрицы Т, соответствующие взаимодействиям масштабирую
щих функлций из vO (как описано в разделе 13.2.2), и составляем по ним
матрицу Т. Алrоритм задается следующим псевдокодом:
procedure GlobalIllиmination( Т, Ве)
в Ве
repeat
В Solve(T, В, Ве)
т Refine( Т, В)
ипtil convergence of В
end procedure.
[лавный цикл будет повторяться, пока не будет достиrнута сходимость,
т. е. до TaKoro момента, после KOToporo дальнейшее уточнение уже не повле
чет значительных изменений вычисленноrо решения. Для решения прибли
женноrо уравнения переноса В Ве + т В функция Solve (решить) ис
пользует итерацию Зейделя [47]. В следующем разделе описывается функ
ция Refine (уточнить).
13.3.4. Уточнение
Уточнение проводится для Toro, чтобы определить, какой из элемен
тов Т, отсутствующих В Т, следует вычислить, чтобы уменьшить поrреш
ность в текущем решении. Функция, которую мы опишем здесь, связана
с критерием взвеlllенноrо по яркости уточнения для иерархической излу
чательности [55] и оракулом уточнения, который [ортлер и соавторы при
менили для вейвлет излучательности [50]. Идея заключается в том, чтобы
оценить перенос энерrии, Korдa в Т появляется новый коэффициент пере
носа. Если эта величина ниже HeKoToporo пороrовоrо значения, то можно
обойтись без дороrостоящих вычислений коэффициентов переноса, и это
не приведет к существенной ошибке в решении.
Существует бесконечно MHoro новых коэффициентов переноса, KOTO
рые мы моrли бы включнть в Т. Нам нужна схема, которая позволит нам
рассмотреть только несколько из этих коэффициентов на каждой итерации,
в конечном итоrе делая возможным рассмотрение всех.
При простом подходе берем каждый из имеющихся коэффициентов
переноса и рассматриваем уточнение базисных функций в отправляющем
конце, принимающем конце или же сразу в двух концах. Рисунок 13.2 ил
люстрирует коэффициенты переноса, которые получились бы в результате
каждоrо из этих возможных уточнений. Уточнение в отправляющем конце,
показанное на рисунке 13.2 (а), порождает коэффициенты переноса, связы
вающие все дочерние вершины отправляющей базисной функции с прини
214
I: ава 13
мающей базисной функцией. Уточнение в принимающем конце, показан
ное на рисунке 13.2 (а), порождает коэффициенты переноса, связывающие
отправляющую базисную функцию со всеми дочерними вершинами прини
мающей базисной функции.
q
11
T"(e ;:\ o":ee \ \
1 /"
,;' '\\
ВО3:11IОЖНЫС
IIOI\bie ;I\Е'IIL,Я C:J
СУII(f'СТI\УЮII(f'f'
/ I CHO. \
.. \ \
EВ f" S \ '
ВОЗЫОЖНЫС
I \ IЮI\ые Jllf'IIL.Я
/
1 / \
1, \\
\
(3)
(6)
Рис. 13.2. Звенья, рассматриваемые при уточнении сушествующеrо звена между
базисными функциями: (а) уточнение в отправляющем конце; (б) уточнение в при
нимающем конце.
Предположим, что мы рассматриваем две базисные функции u s и и т ,
кото:рые пока еще не связаны коэффициентом переноса. Новый коэффици
ент Tr s переноса мы будем вычислять, если достаточно большие значения
получаются в результате произведения
. излучательности: значение коэффициента отправляющей базисной
функции Ь s, и
. вычислеНН020 коэффициента переноса: вычисленный новый коэффи
циент переноса Tr s между базисными функциями.
Коэффициент отправляющей базисной функции леrко вычисляется по
средством восстановления по блоку фильтров. Однако нам также нужен спо
соб вычисления коэффициента переноса, не приводящий к увеличению из
держек на ero реальное вычисление. Что действительно необходимо знать,
так это степень, до которой ядро отклоняется от постоянной функции, по
тому что для ядра, почти постоянноrо на носителе отправляющей и прини
мающей базисных функций, дальнейшая потребность в вейвлетах отпадает.
Одной мерой, определяющей, как далеко ядро отклоняется от постоянной
функции, является вариацuя этой функции разность максимальноrо и ми
нимальноrо значений (по всем трем цветовым каналам). Получается, что
если в каждом звене будет храниться коэффициент переноса и вариация
ядер, используемых для вычисления данноrо коэффициента переноса, то
позже, при уточнении звена, мы сможем воспользоваться этой вариацией.
13.3. Вейвлет из.7учательность
215
В оракуле, описанном [ортлером и соавторами [50], используется по
хожий подход к уточнению. Чтобы извлечь преимущество из вейвлетов
с большим числом нулевых моментов по сравнению с вейвлетами Хаара,
их алrоритм проводит уточнение, коrда ядро не очень хорошо аппроксими
ровано интерполирующим полиномом подходящей степени.
Ранее упоминалось, что каждая Link cTpYKтypa хранит до девяти KO
эффициентов переноса для размещения всех комбинаций отправляющих
и принимающих базисных функций между двумя любыми вершинами. CTO
ит заметить, что для всех девяти коэффициентов переноса как определяемая
излучательность источника, так и вариация ядра будут одинаковыми. Сле
довательно, оцениваемый вклад всех девяти коэффициентов переноса будет
идентичным, поэтому имеет смысл вычислить все эти коэффициенты в одно
время.
Последний момент в реализации процесса уточнения касается выбора
пороrовоrо значения, выше KOToporo происходит образование новых зве
ньев. Одно из предложений при первом уточнении принять за пороrовое
значение какую нибудь произвольную константу, а в дальнейшем, при каж
дом вызове функции Refine уменьшать это значение вдвое., Прr; друrом
подходе можно вычислить максимальный перенос энерrии TT BbB суще
ствующих звеньев и взять некую фиксированную долю от этой величины
в качестве пороrовоrо значения.
13.3.5. Разложение матрицы переноса
Алrоритм, который мы только что представили читателю, базируется на
стандартном разло,женuu оператора переноса. Друrими словами, подоб
но существованию двух различных типов (стандартноrо и нестандартноrо)
вейвлет преобразований для изображений и друrих функций на двумерной
области, можно rоворить и о существовании двух способов разложения
двумерных матриц, представляющих оператор переноса.
Посмотрим, что произойдет, если в качестве базиса, представляющеrо
излучательность, будет использоваться большое количество очень узких xa
рактеристических функций. Korдa мы дискретизируем задачу rлобальноrо
освещения, используя такой базис блочных функций, то придем к большой
и плотной матрице переноса Т. ДЛЯ Toro, чтобы получить разреженную
матрицу переноса, хранящую такую же информацию, нам стоит выполнить
вейвлет преобразование матрицы Т. По аналоrии со сжатием изображений
мы можем ожидать, что вейвлет преобразование даст матрицу со множе
ством незначительных элементов. Такое вейвлет преобразование мы можем
определить двумя разными способами.
Способ, рассмотренный для вейвлет излучательности, соответствует
стандартному разложению. Выполненная нами дискретизация оператора
216
I: ава 13
переноса позволила каждой базисной функции непосредственно взаимо
действовать со всякой друrой функцией, незавuсшwо от уровня. В случае
же с не стандартным разложением данный вейвлет может взаимодейство
вать с друrими вейвлетами, соответствующими только одному конкретному
иерархическому уровню.
Здесь мы не будем подробно обсуждать алrоритмы вейвлет излуча
тельности на основе нестандартноrо разложения оператора переноса. Если
читатель заинтересовался эти вопросом, то мы рекомендуем статьи [opT
лера и др. [50], Шрёдера и др. [107], а также [108]. Один потенциально
значимый и заслуживающий внимания момент связан со следующим: ec
ли n это число базовых функций, то, соrласно теоретическим проrнозам
для операторов с некоторыми оrраничениями на rладкость, нестандартное
разложение приведет к О( n) значащих элементов, а стандартное разложе
ние к O(nlogn) [5]. Тем не менее, на практике для переноса излучатель
ности нестандартное разложение часто оказывается более разреженным по
сравнению со стандартным разложением [12].
13.3.6. Этап конечной сборки
Пока мы еще не rоворили о том, каким образом решение задачи rло
бальноrо освещения может быть использовано для создания изображения.
Давайте предположим, что мы получили решение для излучательности в ба
зисе Хаара и теперь хотим визуализировать ero относительно конкретной
точки наблюдения. Один способ состоит в применении вейвлет синтеза
для восстановления представления излучательности по масштабирующим
функциям на каждом фраrменте, а затем изображении каждоrо из малых
участков с постоянной излучательностью в виде прямоуrольника одноrо
цвета. Есть и друrая возможность выпустить лучи из точки наблюдения
через каждый пиксель плоскости изображения и вычислить излучатель
ность на первой поверхности, которую достиrает каждый из лучей. Оба эти
метода визуализации отображают все разрывы, присущие кусочно постоян
ному представлению вроде базиса Хаара.
Избежать некоторых артефактов, порождаемых кусочно постоянным
базисом, возможно, если выполнить этап конечной сборки (fiпal gatheriпg
step), который повторно вычисляет освещение, поступающее в каждую точ
ку поверхности, соответствующую одному пикселю изображения [71, 100,
117]. Для каждоrо пикселя изображения мы выпускаем луч и определяем
поверхность, соответствующую этому пикселю. Затем мы собираем свет от
всех базисных функций, входящих в излучательность в этой точке. Друrими
словами, для каждой видимой точки поверхности У мы вычисляем
л р(у) '" J
Ве(У) + С(х, У)Вв(Х) dx,
s х
13.4. У.7учшение вейв.7ет излучате.7ьности
217
rдe суммирование по отправляющим фраrментам s включает все фраrмен
ты, [де базисные функции связаны с принимающими базисными функциями
в точке у.
Формально, этап конечной сборки соответствует повторной проекции
решения на новый базис, каждая базисная функция KOToporo является дель
та функцией, расположенной в видимой точке. Этот новый базис ориен
тирован на обеспечение визуальной четкости изображения. Этап конечной
сборки сrлаживает разрывы в вейвлет представлении и делает текстуру и Te
ни более четкими, что демонстрируется разницей между изображениями на
цветных иллюстрациях 14(б) и 14(в).
13.4. Улучшение вейвлет излучательности
Можно прибеrнуть к ряду способов, чтобы расшприть алrоритм из
предыдущеrо раздела и тем самым повысить ero скорость и эффективность,
а также улучшить качество решения. Мы опишем несколько из возможных
способов TaKoro улучшения.
13.4.1. Уточнение с учетом значимости
Как правило, алrоритмы rлобальноrо освещения являются видонезави
СШWЫМИ. ЭТО означает, что одно найденное решение может использоваться
для визуализации изображений кадра относительно любой точки обзора.
Если в некоторых приложениях, скажем, сквозном контроле проектных
решений и друrих областях, такая видонезависимость приветствуется, то
в ряде друrих приложений интерес представляет чаще Bcero только одна
точка обзора или очень оrpаниченное их множество. В последнем случае
нам пришлось бы потратить немало времени, чтобы найти точное реше
ние для излучательности относительно всех точек, тоrда как на самом деле
видимым Mor бы оказаться лишь очень малый участок кадра.
Расширение иерархической излучательности, представленное Смитсом
и соавторами [119], использует функцuи значимости (iтроrtапсе{ипсtiопs),
впервые появившиеся в теории переноса нейтронов, которые характеризуют
степень влияния излучательности на видимую часть кадра при данном pac
положении. Описанная ими техника напрямую применима и к вейвлет излу
чательности. [лавная идея заключается в определении безразмерной вели
чины, называемой значимостью, которая переносится от поверхности к по
верхности, подобно излучательности, но которая излучается скорее точкой
обзора, чем источниками света. Значимость можно включить в критерий
уточнения, блаrодаря чему уточнение будет применяться только к тем вза
имодействиям, которые одновременно являются и яркими, и значимыми.
218
I: ава 13
13.4.2. Кластеризация
Кластеризация представляет собой еще одно расширение иерархиче
ской излучательности, которое в равной степени применимо и к вейвлет из
лучательности. И иерархическая излучательность, и вейвлет излучатель
ность требуют, чтобы вначале мы вычислили коэффициенты переноса меж
ду всеми парами изначальных фраrментов. Если п это число изначальных
фраrментов, то для очень сложных кадров одно создание О(п 2 ) исходных
звеньев может оказаться чрезвычайно трудоемким делом. Алrоритмы кла
стеризации содержат попытку снизить эту трудоемкость путем rруппировки
соседних фраrментов и рассмотрения на первом этапе rрубых взаимодей
ствий этих кластеров.
Смите и др. [118] описывают способ автоматическоrо формирова
ния кластеров, причем для управления процессом нахождения решения
они используют rpаницы ошибок. Сложность их алrоритма не превыша
ет О(п log п). Подобный подход можно использовать и в алrоритме на OCHO
ве вейвлетов, так, как это сделали Кристенсен и др. [13].
13.4.3. Обобщение до яркости
При попытке решения задачи rлобальноrо освещения с помощью ypaB
нения переноса излучательности мы имеем дело с частным случаем, в KOTO
ром все поверхности в среде являются идеально рассеивающими. Для HeKO
торых сред, например, внутренних областей, по крытых латексной краской,
такое допущение бывает вполне обоснованным, однако во мноrих друrих
ситуациях оно является чрезмерно оrраниченным.
Более общая форма задачи rлобальноrо освещения, известная под Ha
званием zлянцевое zлобальное освещенuе (glossy global illumination), отли
чается rораздо более высокой сложностью. Если понятие излучательности
связано с тем, как свет, отражаясь от каждой точки поверхности, воздей
ствует на свет, отражающийся от всех друrих точек, то в задаче rлянцевоrо
rлобальноrо освещения рассматривается то, как свет, отражаясь в каждом
направленuu от каждой точки поверхности, воздействует на свет, отража
ющийся во всех друzих направлениях от всех друrих точек поверхности.
Теперь нас интересует уже не излучательность, а яркость (radiaпce), явля
ющаяся функцией положения и направления.
Формально яркость можно определить как функцию L (х, w), представ
ляющую мощность эманации из точки поверхности х на единичный про
странственный уrол в направлении w на единицу проецированной площа
ди перпендикулярно этому направлению. Единица измерения яркости L
[ватт. MeTp 2 . стерадиан l]. (Стерадиан является мерой пространственноrо
уrла; подобно тому, что окружности соответствует 2п радианов, сфере co
13.4. У.7учшение вейв.7ет излучате.7ьности
219
ответствует 47Т стерадианов.) Равновесное распределение яркости удовле
творяет следующему уравнению переноса яркости [22, 114]:
L(y, w) == Le(Y, w) + J fr( w xy , у, w)G(x, y)L(x, w xy ) dx.
х
Здесь w xy обозначает направление от х к w, а fr ( W xy , у, w) является ФУНК
цией распределения двунаправлеНН020 отражения (bidirectioпal reflectaпce
distriЬиtiопfипсtiоп, BRDF) , которая измеряется в [стерадиан l] и описывает
отношение отраженной яркости (в направлении w) к породившей ее диф
ференциальной интенсивности падающеrо излучения (в направлении w xy ).
[еометрическая компонента С(х, у) та же, что и для излучательности.
Как видно, самое существенное изменение, сопровождающее переход
от вейвлет излучательности к вейвлет яркости, заключается в том, что в Ka
честве решения теперь выступает функция четырех переменных: две из
них описывают положения на поверхности и еще две служат для описания
направления. Положения поверхности на фраrменте кадра можно с леrко
стью параметризовать на единичном квадрате [О, 1] 2, тоrда как множество
направлений, проходящих через точку на поверхности, более естественно
параметризовать на единичной полусфере н 2 . В качестве однorо из подхо
ДОВ можно определить базис вейвлетов для области [0,1]2 Х н 2 , для чеrо
мы моrли бы воспользоваться сферическими вейвлетами, описание которых
имеется у Шрёдера и Свелденса [109]. Кристенсен и др. [15] реализовали
альтернативный подход, отобразив направления на полусфере в точки на
единичном квадрате, что позволило сконструировать вейвлеты для яркости,
используя область [0,1]4.
Не считая случая с большей размерностью яркости, алrоритм на OCHO
ве вейвлетов очень похож на описанный нами алrоритм для излучатель
ности [15]. Изображения на цветной иллюстрации 15 позволяют судить
о различных эффектах, достиrаемых при рассмотрении более общей задачи
rлобальноrо освещения.
['ЛАВА 14
Дополнительная информация
1. Теория кратномасштаБН020 анализа 2. Прило,жения к изоб
ра,жениям З. Прило,жения к кривым и поверхностям 4. Физи
ческое моделuрованuе
Нами бьmа рассмотрена лишь небольшая доля от существующеrо Ma
териала по вейвлетам и кратномасштабным методам. В этой rлаве мы дадим
краткий обзор дополнительной информации.
14.1. Теория кратномасштабноrо анализа
Наше внимание было сфокусировано на кратномасштабном анализе,
вариантном относительно сдвиrа, дающем более естественный способ раз
мещения различных наборов данных, встречающихея в приложениях KOM
пьютерной rpафики, к примеру кривых, определенных на оrpаниченных
интервалах, и поверхностей, определенных на областях произвольноrо TO
полоrическоrо типа.
Тем не менее, подавляющая часть существующей литературы по вей
влетам рассматривает воиросы в контексте инвариантности относительно
сдвиrа. Общая инвариантная относительно сдвиrа теория получила пре
красное описание в книrе Добеши [25]. Чуи представил в [17] замечательное
введение в кратномасштабный анализ, инвариантный относительно сдвиrа,
и основательное исследование вейвлетов, сконструированных из В сплай
нов. Обобщение инвариантных относительно сдвиrа вейвлетов на основе
мноrомерных В сплайнов делается с помощью тензорноrо про изведения
В сплайнов или, чаще, характеристических сплайнов. Обобщение через
тензорные про изведения является непосредственным и приводит к CTaH
дартной либо не стандартной конструкции. Более сложное обобщение по
средством характеристических сплайнов имеется у Джиа и Мичелли [64].
Самой простой ситуацией при использовании вариантной относитель
но сдвиrа схемы является конструирование вейвлетов для оrpаниченноrо
интервала. В [81] Мейер предлаrает метод адаптации масштабирующих
14.1. Теория кратномасштаБНО20 аНCL7иза
221
функций и вейвлетов Добеши к оrраниченному интервалу путем введения
новых функций вблизи rpаниц. Для построения В сплайновых вейвлетов на
оrраниченном интервале Чуи и Куэйк активно используют теорию HepaB
номерных В сплайнов [18]. Однако в отличие от раздела 7.3.1, в котором
использовался алrоритмический подход, Чуи и Куэйк приводят явные фор
мулы для вейвлетов произвольноrо порядка с минимальным носителем.
Результатов их работы вполне достаточно для выполнения синтеза методом
блока фильтров линейно по времени. Позже Куэйк и Вейрих [98] развили
линейный по времени алrоритм анализа. Подобно алrоритму анализа из
раздела 7.3.1, их алrоритм основан на решении линейной системы с поло
сочной матрицей, которая, правда, несколько отлична от нашей.
Впервые общая вариантная относительно сдвиrа форма, основанная
на последовательном делении, была введена Лаунсбери и др. [75]. С тех
пор она получила развитие блаrодаря Свелденсу [123], который увидел, что
конструкция вейвлета Лаунсбери и др. является случаем еще более общеrо
понятия подъема. Кроме Toro, Свелденс показал, что в одномерном случае
все биортоrональные схемы связаны друr с друrом через подъем, т. е. для
двух произвольных биортоrональных схем можно указать операцию подъ
ема, переводящую одну схему в друryю. Шрёдер и Свелденс продолжили
эту работу в [109], показав, что последовательное деление и подъем дa
ют конструктивные методы построения традиционных вейвлетов, и назвав
такой подход вейвлетами втОр020 поколения. Они сосредоточили свое вни
мание на представлении через вейвлеты функций, определенных на сфере,
причем учитывался не только тополоrический тип сферы, но и ее криволи
нейная rеометрия. (В нашем построении в десятой rлаве за область опре
деления, или «базовую ячейку», принимается, напротив, кусочно линейная
поверхность.) Использование данной rеометрии сферы в качестве области
определения, как показывают Шрёдер и Свелденс, приводит к более BЫCO
ким показателям сжатия.
Поскольку кратномасштабный анализ, вариантный относительно сдви
[а, основан на последовательном делении, то развитие общей теории aHa
лиза и конструирования схем последовательноrо деления является важным
и весьма уместным вопросом. Несмотря на отсутствие законченной теории,
известно немало различных частных случаев. Скажем, очень rлубокая и дo
вольно изящная теория стационарных равномерных схем последовательно
[о деления разработана Даменом, Дином, [реrори, Левиным иМичелли.
Друrая замечательная (скорее новаторская) работа принадлежит Каваретте.
Прорыв при изучении стационарноrо HepaBHoMepHoro случая недавно был
совершен Райфом [101] и Уорреном [127], хотя MHoroe до сих пор неизвест
но. Еще меньше мы знаем о нестационарном последовательном делении.
Чтобы узнать о том, как обстоят дела с последовательным делением сеrодня,
мы рекомендуем работу Дина и Левина [31].
222
I: ава 14
14.2. Приложения к изображениям
Список литературы, посвященной использованию вейвлетов для сжа
тия и обработки изображений, весьма солиден, и то, о чем rоворилось
в первой части, лишь вершина orpoMHoro айсберrа. Рассмотренные в Tpe
тьей части алrоритмы сжатия изображений довольно примитивны. Улуч
шить их можно, если использовать друrие базисы вейвлетов или же пре
образования, более rибко, по сравнению со стандартным и не стандартным
преобразованиями, адаптирующиеся к данным изображениям. Один из Ta
ких методов преобразование с использованишw вейвлет пакетов (wavelet
packet traпsforт). Как описано во второй rлаве, при выполнении обычно
[о вейвлет преобразования мы рекурсивно разбиваем коэффициенты Mac
штабирующих функций на два набора, оставляя при этом нетронутыми
вейвлет коэффициенты на каждом уровне. Выполнение же преобразования
на основе вейвлет пакетов позволяет разложить как коэффициенты Mac
штабирующих функций, так и вейвлет коэффициенты на каждом уровне,
используя те же самые фильтры анализа А и В. Решение о том, нужно или
нет выполнять разложение набора коэффициентов, зависит от Toro, в каком
случае обеспечивается самая блаrоприятная возможность для сжатия. По
дробнее о сжатии изображений с помощью вейвлет пакетов рассказывается
у Викерхаузера [132, 133].
Одним из недостатков базиса Хаара, который особенно проявляется
при формировании запроса изображения, является чувствительность этоrо
базиса к перемещениям соответствующее вейвлет разложение изображе
ния претерпевает разительные изменения при самом незначительном CMe
щении изображения. Даже базисы вейвлетов с лучшими, чем у «xaapOBCKO
[О», свойствами проявляют подобную неустойчивость при перемещении,
вращении или изменении масштаба. Вейвлет преобразования, способные
противостоять этим rеометрическим изменениям, составляют специаль
ный класс смещашwых преобразований или управляемых фильтров (shiftable
traпsforтs or steerable filters). Как было замечено в пятой rлаве, смеща
емые преобразования моrли бы сделать алrоритм формирования запроса
изображения более устойчивым в случае сдвинутых, повернутых или Mac
штабированных запросов изображений. В смежном приложении, paCCMaT
ривающем оптическое распознавание знаков, Шусторович [113] использует
смещаемые вейвлеты [абора для нахождения контуров изображений. Иной
подход к выявлению контуров предлаrают Малла и Жонr [79]: они опи
сывают, каким образом максимумы непрерывноrо вейвлет преобразования
MOryT использоваться для установления положения контуров изображения,
а также то, как можно восстановить изображение единственно с помощью
данных о ero контуре.
Рассуждая об изображениях, мы почти всеrда принимали данное изоб
14.2. Приложения к изображениям
223
ражение в качестве входных данных. Однако иноrда требуется сформи
ровать изображение, обладающее определенными характеристиками, «на
пустом месте». Задача формирования текстуры изобра,жения (tехtиrе
geпeratioп) особенно хорошо поддается методам, использующим вейвлеты.
Перлин и Велхо [94] описывают способ создания текстуры с бесконечной
разрешающей способностью с применением разработанной ими KpaTHOMac
штабной rрафической системы. Их идея состоит в том, чтобы найти такую
процедуру, которая моrла бы алrоритмически rенерировать коэффициенты
уточнения, соответствующие изображению, по ходу Toro, как пользователь
увеличивает изображение. Друrой, но похожий подход к формированию TeK
стуры выполнить вейвлет преобразование существующеrо изображения
и рассмотреть ero статистические свойства, а затем создать новое изоб
ражение с переменным разрешением, имеющее то же статистическое pac
пределение, с помощью случайных чисел. Хиrер и Берrен [58] используют
этот способ для получения больших периодических текстур из меньших по
размеру непериодических сканированных изображений.
Хиrер и Берrен также описывают, каким образом статистика простоrо
изображения (например, фотоrpафии мрамора) может использоваться для
формирования текстуры объемН020 объекта (скажем, куска мрамора) с Ta
кими же статистическими свойствами на каждом срезе. На самом деле,
до TpexMepHoro случая можно обобщить почти любой алrоритм формирова
ния изображения при переменном разрешении. Алrоритмы вейвлет сжатия
можно применить к объемным данным, и результирующее представление
может быть использовано для ускорения объемной визуализации [88, 89,
131]. Кроме тorо, вейвлет преобразования объемных данных уже использо
вались для ускорения и улучшения предшествующих морфинrовых MeTO
дов [56] для объемных изображений.
Серии видеоизображений также являются трехмерными, хотя BpeMeH
ная размерность несколько отлична от двух пространственных размерно
стей каждоrо видеокадра. Именно этим отличием и определяется разница
между сжатием видеоизображения и сжатием объемноrо представления.
Вполне возможным и, как правило, желательным представляется выпол
нение восстановления кадра в сжатой серии видеоизображений при OTCYT
ствии информации о следующих кадрах. Льюис и Ноулс [70] описывают
метод сжатия видеоизображения, в котором вначале вейвлет преобразова
ние применяется к каждому кадру. Далее предлаrается применить преобра
зование по времени к каждой rруппе из восьми кадров, обратив на пользу
временную связанность кадров. Друrой подход состоит в выполнении вей
влет преобразования каждоrо кадра и использовании различий кадров или
методов анализа параметров движения для предсказания следующеrо кадра
по текущему кадру [91, 112, 136]. Сжатие и последовательное пропускание
серий видеоизображений составляют лишь два из множества приложений
224
I: ава 14
кратномасштабноrо представления для видео. Финкельштейн и соавторы
[36] описывают интересные способы разложения и редактирования видео
изображений с использованием переменноrо разрешения.
14.3. Приложения к кривым и поверхностям
Помимо тех приложений, что мы рассмотрели во второй части, суще
ствует немало друrих, которые также выиrрывают от кратномасштабных
представлений кривых. Например, Райселл сконструировал интерполирую
щие «псевдокойфлеты» для разработки траекторий и тестирования кривых
на предмет пересечения [26]. Важную роль иrрают вейвлеты и в работе
Чана и Куо [19], rдe они служат для усовершенствования метода плавноrо
сопряжения двумерных контуров, который первоначально ввели Зедерберr
и др [110, 111]. Виткин и Попович [135] представили метод «деформиро
вания» траекторий движущихся изображений, в котором не задействованы
вейвлеты, но который Mor бы быть эффективнее при их использовании.
Что касается приложений к поверхностям, то стоит упомянуть HOBa
торскую работу Форсея и Бартелса [40] по иерархическим В сплайнам.
Несмотря на то, что вейвлеты в их конструкции не используются как TaKO
вые, их работа является первым примером определения и редактирования
поверхности с помощью кратномасштабноrо подхода. Позже Форс ей и Бар
теле [41] применили иерархические В сплайны для решения задач, свя
занных с аппроксимацией поверхностей. К этому же вопросу обращались
также ДеВур и др., воспользовавшись при этом вейвлетами на основе квaд
ратичных характеристических сплайнов. Среди прочих интересных аспек
тов их работы можно выделить установление rраниц L 00 ошибки, которые
вводятся разработанной авторами процедурой сжатия.
14.4. Физическое моделирование
[лобальное освещение и вариационное моделирование все это при
меры задач физичеСК020 .моделирования. В вариационном моделировании
«качество» кривой или поверхности измеряется физической энерrией изо
rнутой проволоки или пластины. В случае rлобальноrо освещения уже само
уравнение переноса диффузноrо отражения выведено из физики переноса
излучения. В двух предыдущих rлавах было показано, что обе эти задачи
MorYT быть решены путем дискретизации неизвестной функции решения
и представления ее через конечные элементы, на роль которых особенно
хорошо подходят вейвлеты.
Хороший обзор вариационноrо моделирования поверхностей имеется
в диссертации Уэлча [129]. Халстед и др. [54] приводят метод получения
14.4. Физическое ,ноделирование
225
rладких интерполирующих поверхностей произвольноrо тополоrическоrо
типа, в котором при минимизации нормы «равноправия» используется cxe
ма последовательноrо деления Кэтмула и Кларка. Вероятно, их работу мож
но расширить до кратномасштабноrо метода, если использовать k дисковые
вейвлеты на основе схемы типа бабочка (десятая rлава). Стоит отметить,
что иерархические базисы, отличные от базисов вейвлетов, ранее использо
вались на подrотовительном этапе и для повышения скорости вычисления
в алrоритмах аппроксимации поверхностей (например, в работе Щелиски
[124]). Пентланд [92] показал, как вейвлет методы аппроксимации поверх
ностей MOryT применяться для решения широкоrо кpyra задач на физическое
равновесие.
Немало можно прочесть о задаче rлобальноrо освещения, в том чис
ле прекрасные введения в этот предмет, написанные Коэном и Уоллейсом
[22], Силлионом и Пючем [114], [ласснером [46]. Развитие кратномасштаб
ных методов для излучательности началось с формулировки иерархической
излучательности Ханраханом и др. [55] и продолжается исследованиями
[ортлера, Шрёдера и их коллеr [50, 107] на основе вейвлетов. Мноrие из
возможных расширений алrоритмов излучательности на основе, о которых
мы упоминали в тринадцатой rлаве, подробно рассмотрены в диссерта
ции Кристенсена [12] и ero совместной работе с авторами этой книrи [13,
14, 15]. Шрёдер и Свелденс [109] построили сферические вейвлеты, KOTO
рые являются очевидными кандидатами для представления распределения
энерrетической яркости из задачи rлобальноrо освещения в присутствии
матовых поверхностей.
Известно также немало задач физическоrо моделирования, решаемых
методом конечных элементов, которые тоже MorYT обрести дополнитель
ные преимущества от использования кратномасштабноrо подхода. Задачи,
связанные с радиационным теплообменом, моделированием акустики, элек
тростатикой, или же проблема rравитационноrо взаимодействия n тел все
они демонстрируют сходство с задачами физическоrо моделирования, pac
смотренными нами в двух предшествующих rлавах.
Один из особенно интересных разделов компьютерной rрафики, о KO
тором стоит упомянуть отдельно, анимация. Цель реалистической ани
мации изобразить объект в действии, не нарушив физических законов
и затратив минимум энерrии. Математическая формулировка такой целевой
функции приводит к вариационной задаче, целью которой является мини
мизация интеrрала, представляющеrо суммарную работу, а оrраничениями
являются законы физики, а также начальные и конечные условия, которые
задаются самим аниматором. Основы автоматическоrо создания реалисти
ческих анимационных изображений, применительно к которым используют
термин пpocтpaHcтeeHHO epf)WeHHble оzранuченuя (spacetiтe coпstraiпts) ,
были заложены Виткиным и Кассом [134], а позже были усовершенствова
226
I: ава 14
ны Коэном [21]. Для обращения вариационной задачи в задачу нелинейной
оптимизации они используют базисы с фиксированным разрешением. По
добно задаче вариационноrо моделирования, метод с постоянным разреше
нием характеризуется медленной сходимостью и плохой обусловленностью.
Лиу и др. [72] показывают, что базисы вейвлетов на основе В сплайнов зна
чительно повышают скорость сходимости и позволяют процессу оптимиза
ции адаптироваться к локализованным во времени деталям анимационноrо
изображения.
Часть V
ПРИЛОЖЕНИЯ
ПРИЛОЖЕНИЕ А
Справочник по линейной алrебре
1. Векторные пространства 2. Базисы и размерность 3. CKa
лярное произведение и орт020нальность 4. Нормы и нормиро
вание 5. Собственные векторы и собственные значения
Рекурсивное последовательное деление и кратномасштабный анализ
в значительной мере опираются на фундаментальные понятия линейной
алrебры. Мы приводим здесь это приложение, чтобы дать обзор некоторым
наиболее важным понятиям линейной алrебры.
А.l. Векторные пространства
Понятие векторное пространство является отправной точкой в ли
нейной алrебре. Предположим, что V это совокупность «предметов», над
которыми определены операции сложения и скалярноrо умножения. Множе
ство V называется векторным пространством, если для любых и, v, w Е V
и а, Ь Е Jl{ справедливы следующие аксиомы:
1. u + v == v + и;
2. (и + v) + w == v + (и + ш);
3. Существует элемент О Е V, такой, что 0+ u == и;
4. Для каждоrо элемента u Е V существует элемент и Е V, такой,
что u + ( и) == о;
5. (а + Ь)и == аи + Ьи;
6. a(u+v)==au+av;
7. (аЬ)и == а(Ьи);
8. 1. u == и.
230
При.70жение А
Элементы векторноrо пространства V называются векторами, а эле
мент О называется нулевым вектором. Векторы MorYT иметь вид BeKTopOB
столбцов, например [100]Т, или функций, таких как масштабирующие функ
ции ф(х) или вейвлеты ф(х) в кратномасштабном анализе.
Заметим, что в данном приложении, равно, как и далее, мы использу
ем жирный курсив для обозначения векторов, если это векторы столбцы,
и нормальный курсив для друrих видов векторов или в случае, коrда речь
идет о векторах в общем.
А.2. Базисы и размерность
[оворят, что совокупность векторов иl, и2, . .. в векторном простран
стве V является линейно независшwой, если
Сl иl + С2и2 + . . . о
тоrда и только тоrда, коrда
Сl С2 . . . О.
Совокупность иl, и2, . .. Е V линейно независимых векторов называ
ется базисом для V, если при всевозможных v Е V справедливо
v LCiUi
для вещественных чисел Сl, С2, . . .. [оворят, что пространство V натяну
то на векторы базиса дЛЯ V. Интуитивно под линейной независимостью
понимается отсутствие избыточности векторов, и базис состоит из мини
мальноrо возможноrо числа векторов.
Если базис для V имеет конечное число элементов иl, . . ., и т , то BeK
торное пространство V является конечномерньиw и имеет размерность т.
В противном случае V является бесконечншwерным пространством. В этом
приложении, а также в дальнейшем, для обозначения векторов конечномер
ных пространств мы будем использовать жирный шрифт.
Пример. JR.3 это трехмерное пространство, а еl [100]Т, е2 [010]Т
является базисом для V.
Пример. Множество всех функций, непрерывных на [0,1], является
бесконечномерным векторным пространством.
А.З. СК(L7ярное произведение и ортО20на7ьность
231
А.3. Скалярное произведение и ортоrональность
Для rеометрических векторов из пространства JR. З определена опера
ция скалярноrо произведения, имеющая целый ряд применений. Обобщим
это понятие на случай произвольноrо векторноrо пространства. Формаль
но, скалярным произведением (.1.), определенным на векторном простран
стве V, является любое отображение из V х V в JR., если выполняются
1. (ulv) (vlu) свойство коммутативности;
2. (аи + bvlw) == a(ulw) + b(vlw) свойство билинейности;
3. (и I и) > О для всех u -1= о свойство положительной определенности.
Векторное пространство, на котором определено скалярное произведе
ние, называется, как и следовало ожидать, пространством со скалярным
проuзведенuем.
Пример. Леrко убедиться, что скалярное произведение, определенное
на пространстве JR. З формулой
а. Ь == аlы1 + а2Ь2 + азЬ з .
(А.1)
удовлетворяет свойствам скалярноrо произведения.
Пример. Следующее «стандартное» скалярное произведение для функ
ций, определенных на единичном интервале [0,1], иrрает центральную
роль в большинстве формулировок из кратномасштабноrо анализа:
1
Ulg) == J f(x)g(x) dx.
о
Можно обобщить стандартное скалярное произведение и включить по
ложительную весовую функцию ш(х):
1
Ulg) == J w(x)f(x)g(x) dx.
о
Одно из наиболее важных применений скалярноrо произведения свя
зано с формализацией понятия ортоrональности. [оворят, что векторы u и v
232
При.70жение А
в пространстве с определенным скалярным произведением называют
ся орт020нальными, если (11lv) == О. Нетрудно показать, что совокуп
ность 111,112, . .. взаимно ортоrональных векторов должна быть линейно
независимой, а значит, ортоrональность это сильная форма линейной
независимости. Орт020нальным базисом называется базис, состоящий из
взаимно ортоrональных векторов.
А.4. Нормы и нормирование
Нормой называется функция, измеряющая длину векторов. В конечно
мерном векторном пространстве мы, как правило, используем норму Ilиll ==
== (и 1 и) 1/2. Эта норма называется эвклидовой нормой и является лишь
одним из представителей целоrо семейства p HOpM, которые определяются
как
( ) l/р
Ilиll p == L 1 11 ,IP
,
При р, стремящемся в пределе к бесконечности, мы получаем MaKcи
MYM HOpMY:
Ilиll oo == mах 111;1.
,
Если мы рассматриваем функциональное пространство (функции, непре
рывные на интервале [0,1]), мы обычно используем одну из LP HOpM, опре
деляемую как
, ) l/р
1111llp == (/lu(x)IPdX
о
Максимум норма для функций на интервале [0,1] определяется Bыpa
жением
11111100 == mах 111(X)I.
хЕ[о,l]
Чаще Bcero для функций используется L2 HopMa, которую также можно
представить в виде 1111112 == (11111)1/2, если мы имеем дело со стандартным
скалярным произвсдснисм.
При 111111 == 1 вектор 11 называют нормированным. Если ортоrональный
базис состоит из нормированных векторов с L2 нормой, такой базис Ha
зывается ортонормированньии. Облекая сказанное в более краткую форму,
можно сказать, что базис 111,112, . .. является ортонормированным, если
(11; Iщ) == 5;,j.
А.5. Собственные векторы и собственные значения
233
[де 5 i ,j это символ Кронекера, равный 1, если i j, о в противном
случае.
Пример. Векторы е1 [100]Т, е2 [010]Т, ез [ООl]Т образуют
ортонормированный базис дЛЯ ]]{З пространства со скалярным про
изведением (А.1).
А.5. Собственные векторы и собственные значения
Вектор столбец Vi называется собственным векторшw квадратной MaT
рицы М с соответствующим собственным значением '\i, если
м Vi '\iVi.
(А.2)
Следуя общепринятому соrлашению, собственные векторы и собственные
значения обычно нумеруют так, что '\1 '\2 . . . '\N.
Объединяя векторы столбцы в одну квадратную матрицу V и распо
лаrая собственные значения '\; по диаrонали матрицы А diag('\i), мы
можем переписать (А.2) в матричной форме:
MV AV.
(А.3)
Невырожденная матрица lvl имеет n линейно независимых правых
собственных векторов V1, ..., v n . Матрица V, составленная из правых
собственных векторов произвольной невырожденной матрицы, обратима.
Умножая обе части равенства (А.3) на v l, слева и справа получаем:
V l MVV l V l А VV l
V l М А V l.
Это равенство определяет матрицу левых собственных векторов И
v l, составленную из BeктopOB CTpOK Ui, удовлетворяющих
Ui M '\iUi.
(А.4)
Поскольку правые собственные векторы образуют базис, любой BeKTOp
столбец w размерности n можно представить в виде следующей линейной
комбинации:
w Lajvj.
j
234
При.70жение А
Коэффициенты аl, ..., а п MorYT быть определены с помощью левых
собственных векторов. В частности, поскольку 'U; vj == 5 i ,j, каждый коэф
фициент ai можно получить умножением обеих частей на Ui:
Ui W == L aj'U;Vj ==
j
== L aj 5 i,j ==
j
== ai.
ПРИЛОЖЕНИЕ Б
Матрицы вейвлетов на основе
В сплайнов
1. Вейвлеты Хаара 2. Вейвлеты на основе интерполирующих
конечную точку линейных В сплайнов 3. Вейвлеты на основе
интерполирующих конечную точку квадратичных В сплайнов
4. Вейвлеты на основе интерполирующих конечную точку кубиче
ских линейных В сплайнов
в этом приложении приведены матрицы, требуемые при использовании
вейвлетов на основе интерполирующих конечную точку В сплайнов низкой
степени. Matlab code для создания этих матриц помещен в приложении В.
Предполаrается, что примеры, рассмотренные здесь для конкретных случа
ев, станут подспорьем для понимания идей, высказанных в разделе 7.3.2.
Чтобы подчеркнуть разреженность матриц, мы опустили нули. Точки, pac
ставленные по диаrонали, означают, что предшествующий столбец повторя
ется соответствующее число раз, опускаясь на две строки. Элементы MaT
риц р соответствуют ненормированным масштабирующим функциям на
основе В сплайнов, а элементы матриц Q определяют нормированные вей
влеты с минимальным носителем. Нецелые значения элементов столбцов
матриц Q представлены с точностью до шести знаков.
Б.l. Вейвлеты Хаара
Базис вейвлетов на основе В сплайнов со степенью, равной О, явля
ется ничем иным, как базисом Хаара, описанным во второй rлаве. На ри
сунке Б.1 отображены некоторые примеры характеристических масштаби
рующих функций и вейвлетов Хаара. Ниже приведены матрицы синтеза pj
и Qj.
236
Приложение Б
1
1
1
1
pj
1
1
. Fx j
QJ
2
1
1
1
1
1
1
........,
п
п
п
п
п
п
r
=L
ъ----
1=
Рис. Б.l. Масштабирующие функции и вейвлеты на основе кусочно постоянных
В сплайнов для j == 3.
Б.2. Вейвлеты на основе интерполирующих конечную
точку линейных В сплайнов
На рисунке Б.2 показано несколько типичных масштабирующих функ
ций и вейвлетов, соответствующих линейным В сплайнам. Ниже приведе
ны матрицы синтеза pj и Qj для вейвлетов на основе интерполирующих
конечную точку линейных В сплайнов:
рl [ ], Ql v3 [ ]
Б.З. Вейвлеты на основе интерполирующих конечную точку квадратичных. .. 237
р2 == 1
2
12 1
II ij
pj?;3 1
2
2
1 1
2
1 1
2
1 .
Qj?;3 (2i
v 72
. 1
2
1 1
2
'"
/
I 12
111
Q2 == 2 l 6
64 1
11, 022704
10, 104145
5, 511352
0,918559
1 1
6 ] ;
11
12
1
6
10 1
6 6
1 10
6.
1
1
. 6
10
6
1
0,918559
5, 511352
10, 104145
11,022704
л
/V
Л
VV
Л
VV
Л
VV
Л
VV
Л
VV
Л
VV
Л
V \
Рис. Б.2. Масштабирующие функции и вейвлеты на основе линейных В сплайнов
для j == 3.
Б.3. Вейвлеты на основе интерполирующих конечную
точку квадратичных В сплайнов
На рисунке Б.3 изображены некоторые масштабирующие функции
и вейвлеты на основе квадратичных В сплайнов. Ниже приведены матрицы
синтеза pj и Qj для квадратичноrо случая.
238 Приложение Б
р' [; i ] Q' л [ :]
4
2 2
р2 == 1 3 1
4 1 3
2 2
4
Q2 == v 49336
144
177
109
53
21
21
63
109
177
144
\
/'....
/"".....
/"".....
/"".....
/"".....
/"".....
/\
J
A
{V
/,\"
"'V
/,\"
"'V
/,\"
"'V
/'\
'"'
/,\"
'"'V
/'\л
v V'\J
v
Рис. Б.3. Масштабирующие функции и вейвлеты на основе квадратичных В сплай
нов для j == 3.
4
22
31
13
31
13
3.
1
pJ?3 1.
4
;;
Q V 7i3568
4283, 828550
5208,746077 780
3099, 909150 1949 11
1300,002166 3481 319
253, 384964 3362 1618 8, 737413
8,737413 1618 3362 253,384964
319 3481 1300, 002166
11 1949 3099,909150
780 5208, 746077
4283,828550
1
.3
31
13
22
4
БА. Вейвлеты на основе интерполирующих конечную точку кубичных. . . 239
Qj)4 "'"
3.2 j
136088
;381, 872771
464.322574 69.5;314;39
276, 334798 173. 739454 1
115.885924 ;310, ;306;3;30 29
22, 587463 299. 698329 147 1
О. 778878 '.:; ; gз ; 7
0.980572 147 ЗОЗ
29 ;зо;з .
1 147
29
1
1
29
147 (). 9В0572
303 28.4;36576
3()3 144. 233164 (). 77878
147 299.698329 22,58746;3
29 ЗI0. 306330 115, 885924
1 173.739454 276, ;3;34798
69. 531439 464, 322574
;381,872771
БА. Вейвлеты на основе интерполирующих конечную
точку кубических В сплайнов
Несколько примеров масштабирующих функций и вейвлетов на основе
кубических В сплайнов показано на рисунке Б.4. Ниже приведены матрицы
синтеза pj и Qj для вейвлетов на основе интерполирующих конечную
точку кубических В сплайнов:
рl
1
2
2
1 1
1 1
1 1
2
1
2
Ql v7 3
2
1
16
8
8
12
3
4
10
4
3
12
8
Q2
315
31196288
1368
2064
1793
1053
691
240
240
691
1053
1793
2064
1368
р2
1
16
8
16
pj)3
16
8 8
12 4
3 11 2
8 8
2 12 2
8 8
2 12
8
2
Q3
311454
189342 1, 543996
7,334627 4,226722 0,087556
3 514553 5 585477 o 473604 o 000155
1,271268' 6, 'ОБ9Б57 1, '903267 О, '019190
o 259914 4 367454 4 367454 o 259914
О, ()1919() 1, '9'О3267 '0'59557 1, '271268
o. 000155 o, 47;3604 585477 ;3, 51455;3
0,087556 4,226722 7,334627
1. 543996 9, 189342
6,311454
1
16
2
8
12 2
8 8
2 11 ;3
4 12
8 8
16
240
Приложение Б
\
А...
./'"".....
./"'.....
./"'.....
./"'-.....
./\
)
1"
v...,
,,
VV
А
vv
А
vv
А
vv
"
vv
,,/
"V
Рис. БА. Масштабирующие функции и вейвлеты на основе кубических В сплайнов
для j 3.
QJ?4
25931.200710
3775!); 271723 63U9; 305453
:ЮI35.003[112 17429,266054 о85.797044
14439. S69635 2:Ю()4. 252368 20S6. 545605 1
5223.125428 24841),41)71)71 124
1067,879425 17678;S84301 1677 l
78, S4281)7 7394,685374 24291, 7 J04 124
o 6358:10 1561 868558 lS420 997597 lS4S2 1677
, 115, 466347 73200 ) 24264 7 J04
o, 'J311 0 1 4 2 1 4 2
7904 24264
о, J94 J8 J 1677 18482.
124 7 J04
1 1677
124
1
5.2]
675221664 х
1
124
1677 o; 9 Ч J8 J
7904 123,378671
. 18482 1668.615872 O,9311S0
24264 7 66, 73200') 115.466347
1i)4i)2 1i)420, 9 Л597 o, 6З!)i)30
7904 24291.795239 78.842887
1677 18740,470059 17678,884001 1067,879425
124 8349 37о420 24848 487871 522о 125428
1 20б6; !)4tЮО5 23004, 252368 14439, S6 J63!)
о85.797044 17429.266054 301О5,ООО012
6369. 305453 37755. 271723
2!)931,200710
ПРИЛОЖЕНИЕ В
МаtlаЬ код для В сплайновых вейвлетов
В этом приложении представлены алrоритмы создания матриц синте
за pj и Qj на основе В сплайнов произвольной степени. Данные алrо
ритмы реализованы с помощью пакета проrрамм Mat1ab, хотя те же самые
результаты можно было бы получить и с помощью друrих проrрамм.
Для данноrо В сплайна степени d и иерархическоrо уровня j матри
цы pj и Qj формируются следующими командами:
Р FindP(d, j);
Q FindQ(d, j);
При определении матрицы синтеза масштабирующих функций pj ис
пользуется техника вставки узлов [35]. В сплайновые базисные функции,
описанные в разделе 7.3, определяются через последовательность узлов,
состоящую из кратных узлов в конечных точках и отстоящих друr от дpy
[а на одинаковые расстояния промежуточных узлов. Вставка новых узлов
посередине между каждой парой промежуточных узлов позволяет опреде
лить, каким образом масштабирующие функции уровня j 1 MorYT быть
выражены через масштабирующие функции уровня j.
function Р FindP(d, j)
% Р FindP(d, j) returns the Р matrix for B spline
% scaling functions of degree d, level j.
d fix(d);
if d < О,
error('FindP: Must have d > 0.');
end;
j fix(j);
ifj<1
error('FindP: Must have j > 1.');
end;
if d О
Р [1; 1];
for i 2:j
Р [Р zeros(size(P)); zeros(size(P)) Р];
242
При.70жение В
end;
else
u Knots(d, j 1);
g Greville(d, и);
Р еуе(2 Л (j 1) + d);
for k О:2 Л (j 1) 1
[и, g, Р] InsertKnot(d, и, g, Р, (2*k+l )/2 Л j);
end;
end;
return;
function х Knots(d, j)
% х Knots(d, j) returns а vector of knot values
% for B sp1ine scaling functions of degree d, level j.
х [zeros(l, d 1) [О.2Лj 1]/2Лj ones(1, d)];
return;
function х Greville(d, и)
% х Greville(d, и) returns the vector of Greville
% abscissa values corresponding to degree d
% and knot vector и.
1 length(u);
х u(1:1 d+1);
for k 2:d
х х + u(k:l d+k);
end;
х х / d;
return;
function [uret, gret, pret]
InsertKnot(d, и, g, р, unew)
% [uret, gret, pret] InsertKnot(d, и, g, р, unew)
% inserts а new knot at unew for B spline scaling
% functions of degree d, thereby modifying knot vector и,
% Greville abscissas g, and synthesis matrix р.
uret sort([u unew]);
gret Greville(d, uret);
pret PolyEva1(g, р, gret);
return;
function pret PolyEval(g, р, gnew)
% pret PolyEval(g, р, gnew) returns the values
% of а control polygon defined Ьу abscissas g
% and ordinates р, evaluated at gnew.
[т, п] size(p);
if length(g) m
МаtlаЬ код для В сплайновых вейвлетов 243
error('Po1yEva1: Length of g and rows of р
must Ье the same.');
end;
for i 1:1ength(gnew)
row max(find(g < gnew(i)));
if row m
pret(i,:) p(m, :);
e1se
frac (g(row+l) gnew(i))/(g(row+l) g(row)):
pret(i, :) frac*p(row, :) + (l frac)*p(row+l, :);
end;
end;
return;
Матрицы скалярных произведений В сплайновых масштабирующих
функций можно определить, если представить каждую базисную функцию
как линейную комбинацию полиномов Бернштейна, скалярные произве
дения которых относительно просты. Весовые коэффициенты полиномов
Бернштейна находятся путем мноrократной вставки узлов между промежу
точными узлами.
function 1 1nner(d, j)
% 1 1nner(d, j) returns the inner product matrix
% for B sp1ine sca1ing functions of degree d at 1eve1 j.
10 Bernstein1nner(d);
n 2 Л j + d;
1 zeros(n);
w BernsteinWeights(d, j);
for k l:n
w1 reshape(w(:, k), d+l, 2 Л j);
for 1 k :n
w2 reshape(w(:, 1), d+l, 2 Л j);
l(k, 1) trace(w1'*10*w2);
1(1, k) l(k, 1);
end;
end;
1 1 / 2 Л j;
return;
function 1 Bernstein1nner(d)
% 1 Bernstein1nner(d) returns the matrix of inner
% products of Bernstein po1ynomia1s of degree d.
i ones(d+l, l)*[O:d];
j i' ;
1 Choose(d, i) .*Choose(d, j) ./(Choose(2*d, i+j)*
(2*d + D);
244
При.70жение В
return;
function с Choose(n, r)
% с Choose(n, r) returns (п choose r)
% п! / (r! (n r)!).
с Factorial(n) ./(Factoria1(r) .*Factoria1(n r));
return;
function f Factoria1(m)
% f Factorial(m) returns the matrix of factorials
% of entries of m.
[r, с] size(m);
f zeros(r, с);
for i l:r
for j l:с
f(i, j) prod(2 :m(i, j));
end;
end;
return;
function w BernsteinWeights(d, j)
% w Bernste1nHe1ghts(d, j) returns а matrix of B sp1ine
% scaling function weights for Bernstein polynomials
% of degree d, level j.
w еуе(2 Л j + d);
if d О
return;
end;
u Knots(d, j );
g Greville(d, и);
for i 1:2 Л j 1
for r l:d
[и, g, w] InsertKnot(d, и, g, w, i/2 Л j);
end:
end;
return
Последняя функция определяет Qj, вычисляя в текущий момент один
столбец, используя знание небольших носителей В сплайновых вейвлетов.
function Q FindQ(d, j, normalization)
% Q FindQ(d, j, normalization) returns the Q matrix
% for B sp1ine scaling functions of degree d, level j.
% If normalization is 'min' (or is not specified) then
% the smallest entry in each column is made 1.
% If normalization is 'max' then the largest entry
МаtlаЬ код для В сплайновых вейвлетов
245
%in еасЬ column i5 made 1. If normalization i5 'L2'
%then the L Л 2 norm of еасЬ wavelet i5 made 1.
if nargin < 3
normalization 'min';
el5eif 5trcmp(normalization, 'min')&
5trcmp(norma1ization, 'mах') ...&
5trcmp(norma1ization, 'L2')
error(FindQ: normalization mU5t Ье "min", "mах",
or ' 'L2" .');
end;
Р FindP(d, j);
1 Inner(d, j);
М P'*I;
[m1, m2] 5ize(M);
n m2 rank(M);
Q zer05(m2, n):
found о;
5tart col о:
while (found < n/2) & (5tart col < m2)
5tart col 5tart col + 1 + (found > d);
width о;
rank def о;
while rank def & (width < m2 5tart col + 1)
width width + 1:
5ubmatrix M(:,5tart col:5tart col+width 1):
rank def width rank(5ubmatrix);
end;
if rank def
% find nu11 5расе of 5ubmatrix (5hould Ье jU5t one column)
col null(5ubmatrix);
if 5trcmp(normalization , 'min')
% normalize column 50 5malle5t
% nonzero entry Ьа5 magnitude 1
col col/min(ab5( col +
1еЗ8*(аЬ5( соl) < 1e 10)));
el5eif 5trcmp(norma1ization, 'mах')
% normalize column 50 large5t entry Ьа5 magnitude 1
col col/max(ab5( col));
end;
% change 5ign to give cOn5i5tent orientation
col соl*( 1)Л(5tаrt соl + floor((d+l)/2) +
( col(1, 1) > о));
% put column into left half of Q
found found + 1;
Q(5tart col:5tart col + width 1, found) col;
% и5е 5ymmetry to put column into right half of Q
246
При.70жение В
% in rever5e order and negated if degree i5 even
Q(:,n found+l) fliрud(Q(:,fоuпd))*( l)Лd+l);
end:
end;
if 5trcmp(normalization, 'L2')
% normalize matrix 50 each column ha5 L Л 2 norm of 1
ip Q'*I*Q;
Q Q*diag(1./5qrt(diag(ip)));
end;
return;
Литература
[1] Michae1 J. Banks and Elaine cohen. Realtime spline curves from
interactively sketched data. Computer Graphics, 24(2):99 107, March
1990.
[2] R. Н. Bartels and J. С. Beatty. А technique for the direct manipu1ation of
sp1ine curves. In Proceediпgs о/ the 1989 Graphics Iпter{ace Coп{ereпce,
pages 33 39. canadian Information Processing Society, London, Ontario,
canada, 1989.
[3] R. Bartels, J. Beatty, and В. Barsky. Ап Iпtroductioп [о Spliпes /or Use
iп Coтputer Graphics aпd Geoтetric Modeliпg. Morgan Kaufmann, San
Francisco, 1987.
[4] Deborah Веrшап, Jason Bartell, and David Sa1esin. Mu1tireso1ution
painting and compositing. InProceediпgs o{SIGGRAPH '94, pages 85 90.
АСМ, New York, 1994.
[5] G. Bey1kin, R. coifman, and У. Rokhlin. Fast wavelet transforms
and numerical algorithms 1. Coттuпicatioпs оп Pure aпd Applied
Mathematics, 44(2):141 183, March 1991.
[6] Peter J. Burt and Edward Н. Adelson. The Laplacian pyramid as а compact
image code. IEEE Traпsactioпs оп Coттuпicatioпs, 31 (4): 53 2 540, Apri1
1983.
[7] Е. catmull and J. c1ark. Recursively generated B sp1ine surfaces оп
arbitrary topological meshes. Coтputer Aided Desigп, 10(6):350 355,
November 1978.
[8] A1fred S. cavaretta, Wolfgang Dahmen, and charles А. Micchelli.
Statioпary Subdivisioп. American Mathematica1 Society, Providence, RI,
1991.
[9] George celniker and Dave Gossard. Deformable curve and surface finite
elements for free form shape design. In Proceediпgs o{SIGGRAPH '91,
pages 257 265. АСМ, New York, 1991.
[10] Andrew certain, Jovan Popovic, Топу DeRose, Тоm Duchamp, David
Salesin, and Wemer Stuetzle. Interactive mu1tiresolution surface viewing.
In Proceediпgs о/ SIGGRAPH '96. АСМ, New York, 1996 (to appear).
248
Литература
[11] George М. chaikin. Ап a1gorithm for high speed curve generation.
Computer Graphics aпd Image Processiпg, 3(4):346 349,
December 1974.
[12] Per Н. christensen. Hierarchica1 techniques for glossy globa1 illumination.
Ph.D. thesis. University ofWashington, 1995.
[13] Per Н. christensen, Dani Lischinski, Eric J. Stollnitz, and David Н. Salesin.
clustering for glossy global illumination. АСМ Traпsactioпs оп Graph , ics
1996 (to appear).
[14] Per Н. christensen, Eric J. Stollnitz, David Н. Sa1esin, and Топу
D. DeRose. Wave1et radiance. In G. Sakas, Р. Shirley, and S. Miiller,
editors. Photorealistic Reпderiпg Techпiques, pages 295 309.
Springer Verlag, Berlin, 1995.
[15] Per Н. christensen, Eric J. Stollnitz, David Н. Salesin, and
Топу D. DeRose. G10ba1 illumination of glossy environments using
wave1ets and importance. АСМ Traпsactioпs оп Graphics, 15(1):37 71,
January 1996.
[16] Н. N. christiansen and Т. W. Sederberg. conversion of complex contour
1ine detinitions into po1ygona1 element mosaics. In Proceediпgs о/
SIGGRAPH '78, pages 187 192. АСМ, New York, 1978.
[17] char1es К. chui. Ап Iпtroductioп [о Wavelets. Academic Press, Boston,
1992.
[18] char1es К. chui and Ewa1d Quak. Wave1ets оп а bounded interva1.
In D. Braess and L. L. Schumaker, editors, Nuтerical Methods iп
Approxiтatioп Theory, уо1иmе 9, pages 53 75. Birkhauser Ver1ag, Base1,
1992.
[19] Hsiung chuan chun and С. С. J. Кио. contour metamorphosis using the
wave1et descriptor. In Iтage aпd Video Processiпg 11, volume 2182 of
Proceedings ofthe SPIE, pages 288 299. SPIE, Bellingham, WA, 1994.
[20] А. cohen, 1. Daubechies, and J. С. Feauveau. Biorthogonal bases of
compact1y supported wavelets. Coттuпicatioпs оп Pure aпd Applied
Mathematics, 45(5):485 500, June 1992.
[21] Michae1 F. cohen. Interactive spacetime contro1 for animation. In
Proceediпgs o/SIGGRAPH '92, pages 293 302. АСМ, New York, 1992.
[22] Michae1 F. cohen and John R. Wallace. Radiosity aпd Realistic Iтage
Syпthesis. Academic Press Professiona1, cambridge, МА, 1993.
[23] А. croisier, D. Esteban, and С. Ga1and. Perfect channel splitting Ьу use of
interpolation/decimation/tree decomposition techniques. In Iпterпatioпal
Литература
249
Coп{ereпce оп Iпforтatioп Scieпces aпd Systeтs, pages 443---446.
Hemisphere, Washington, Dc, 1977.
[24] Ingrid Daubechies. Orthonorma1 bases of compactly supported wavelets.
Commuпicatioпs оп Pure aпd Applied Mathematics. 41(7):909 996,
October 1988.
[25] Ingrid Daubechies. Теп Lectures оп Wavelets. SIAM, Phi1ade1phia, 1992.
[26] Топу D. DeRose, Michae1 Lounsbery, and Leena Maija Reissell. curves
and surfaces. In A1ain Foumier, editor, SIGGRAPH '95 Course Notes 26:
Wavelets aпd Their Applicatioпs iп Coтputer Graphics, pages 123 154.
АСМ, New York, 1995.
[27] R. DeVore, В. Jawerth, and В. Lucier. Image compression through
wave1et transform coding. IEEE Traпsactioпs оп Iпforтatioп Theory,
38(2):719 746, March 1992.
[28] R. А. DeVore, В. Jawerth, and В. J. Lucier. Surface compression.
Computer Aided Geometric Desigп, 9(3):219 239, August 1992.
[29] D. W. Н. Doo. А recursive subdivision algorithm for titting quadratic
surfaces to iпеgulаr polyhedrons. Ph.D. thesis, Brunei University, 1978.
[30] D. Doo and М. Sabin. Behaviour of recursive division surfaces пею'
extraordinary points. Coтputer Aided Desigп, 10(6):356 360, September
1978.
[31] Nira Dyn and David Levin. The subdivision experience. In P. J. Laurent,
А. Le Mehaute, and L. L. Schumaker, editors. Wavelets, Iтages, aпd
Surface Fittiпg, pages 229 244. А. К. Peters, Welles1ey, МА, 1994.
[32] Nira Dyn, David Levin, and John Gregory. А four point interpo1atory
subdivision scheme for curve design. Computer Aided Geoтetric Desigп,
4(4):257 268, December 1987.
[33] Nira Dyn, David Levin, and John Gregory. А butterfly subdivision scheme
for surface interpolation with tension contro1. АСМ Traпsactioпs оп
Graphics, 9(2): 160 169, April 1990.
[34] Matthias Eck, Топу DeRose, Тоm Duchamp, Hugues Норре, Michae1
Lounsbery, and Wemer Stuetzle. Mu1tireso1ution ana1ysis of arbitrary
meshes. In Proceediпgs о! SIGGRAPH '95. pages 173 182. АСМ, New
York, 1995.
[35] Gera1d Farin. Curves aпd Surfaces for Computer Aided Geometric Desigп.
Academic Press, Boston, third edition, 1993.
250
Литература
[36] Adam Finkelstein, charles Е. Jacobs, and David Н. Salesin.
Mu1tiresolution video. In Proceediпgs о! SIGGRAPH '96. АСМ,
New York, 1996 (to appear).
[37] Adam Finkelstein and David Н. Salesin. Mu1tireso1ution curves. In
Proceediпgs ofSIGGRAPH '94. pages 2бl 268. АСМ, New York, 1994.
[38] James D. Fo1ey, Andries уап Dam, Steven К. Feiner, and John F. Hughes.
Computer Graphics: Priпciples aпd Practice. Addison Wesley, Reading,
МА, second edition, 1990.
[39] David R. Forsey and Richard Н. Bartels. Hierarchical B spline refinement.
In Proceediпgs ofSIGGRAPH '88, pages 205 212. АСМ, New York, 1988.
[40] David R. Forsey and Richard Н. Bartels. Surface fitting with hierarchical
sp1ines. АСМ Traпsactioпs оп Graphics, 14(2):IЗ4 161, April1995.
[41] D.Forsey and R.Bartels. Tensor products and hierarchical fitting.
In Curves aпd Surfaces iп Coтputer Visioп aпd Graphics 11, уо1иmе 161 О
of Proceediпgs ofthe SPIE, pages 88 96. SPIE, Bellingham, WA, 1991.
[42] Вапу Fow1er. Geometric manipu1ation of tensor product surfaces. In
Proceediпgs о! the 1992 Symposium оп Iпteractive 3D Graph , ics
pages 10l 108. АСМ, New York, 1992.
[43] Н. Fuchs, Z. М. Kedem, and S. Р. U se1ton. Optimal surface reconstruction
from planar contours. Coттuпicatioпs о{ the А СМ, 20(lO):693 702,
October 1977.
[44] Dennis Gabor. Theory of communication. Jourпal о{ the Iпstitute о!
Electrical Eпgiпeers, 93(22):429 57, 1946.
[45] S. Ganapathy and Т. G. Dennehy. А new general triangu1ation method for
p1anar contours. In Proceediпgs о! SIGGRAPH '82. pages 69 75. АСМ,
New York, 1982.
[46] Andrew S. G1assner. Priпciples о! Digital Image Syпthesis, уо1иmе 11.
Morgan Kaufmann, San Francisco, 1995.
[ 4 7] Gene Н. Go1ub and char1es F. Уап Loan. М atrix Coтputatioпs. The J ohns
Hopkins University Press, Ba1timore, second edition, 1989.
[48] Yihong Gong, Hongjiang Zhang, Н. С. chuan, and М. Sakauchi. Ап image
database system with content capturing and fast image indexing abilities.
In Proceediпgs ofthe Iпterпatioпal Coпfereпce оп Multiтedia Coтputiпg
aпd Systeтs, pages 121 IЗО. IБЕЕ computer Society Press, Los Alamitos,
СА, 1994.
Литература
251
[49] Steven J. Gortler and Michae1 F. cohen. Hierarchical and variational
geometric mode1ing with wave1ets. In Proceediпgs о/ the 1995 Symposium
оп Iпteractive 3D Graphics, pages 35 42. АСМ, New York, 1995.
[50] Steven J. Gort1er, Peter Schr6der, Michael F. cohen, and Pat Hanrahan.
Wavelet radiosity. In Proceediпgs ofSIGGRAPH '93. pages 221 230.
АСМ, New York, 1993.
[51] Byron S.Gottfried and Joel Weisman. Iпtroductioп [о Optimisatioп
Theory. Prentice НаН, Englewood cliffs, NJ, 1973.
[52] А. Grossman and J. Mor1et. Decomposition of functions into wave1ets of
constant shape, and re1ated transforms. In L. Streit, editor. Matheтatics
aпd Physics: Lectures оп Receпt Results. Wor1d Scientific, Singapore,
1985.
[53] A1fred Haar. Zur Theorie der orthogonalen Funktionen Systeme.
Mathematische Aппaleп, 69:331 371, 1910.
[54] Mark Ha1stead, Michae1 Kass, and Топу DeRose. Efficient, fair
interpolation using catmull clark surfaces. In Proceediпgs о/
SIGGRAPH '93, pages 35 14. АСМ, New York, 1993.
[55] Pat Hanrahan, David Saizman, and Larry Aupperle. А rapid hierarchical
radiosity a1gorithm. In Proceediпgs ofSIGGRAPH '91, pages 197 206.
АСМ, New York, 1991.
[56] Taosong Не, Sidney Wang, and Arie Kaufman. Wavelet based volume
morphing. In Proceediпgs о{ Visualisatioп '94. pages 85 92. ШЕЕ
computer Society Press, Los Alamitos, СА, 1994.
[57] Donald Неаm and М. Pauline Baker. Coтputer Graphics.
Addison Wes1ey, Reading, МА, 1994.
[58] David J. Heeger and James R. Bergen. Pyramid based texture
ana1ysis/synthesis. In Proceediпgs о/ SIGGRAPH '95, pages 229 238.
АСМ, New York, 1995.
[59] К. Hirata and Т. Kato. Query Ьу visua1 examp1e content based image
retrieval. In А. Pirotte, С. De10bel, and G. Gott1ob, editors. Advaпces iп
Database Techпology (EDBT '92), pages 56 71. Springer Verlag, Ber1in,
1992.
[60] Н. Норре, Т. DeRose, Т. Duchamp, М. Halstead, Н. Jin, J. McDona1d,
J. Schweitzer, and W. Stuetz1e. Piecewise smooth surface reconstruction.
In Proceediпgs ofSIGGRAPH '94, pages 295 302. АСМ, New York, 1994.
[61] Josef Hoschek and Dieter Lasser. Fuпdaтeпtals о/ Computer Aided
Geometric Desigп. А. К. Peters, Welles1ey, МА, third edition, 1993.
252
Литература
[62] William М. Hsu, John F. Hughes, and Henry Kaufman. Direct
manipulation of free form deformations. In Proceediпgs о/
SlGGRAPH '92, pages 177 184. АСМ, New York, 1992.
[63] char1es Е. Jacobs, Adam Finkelstein, and David Н. Sa1esin. Fast
multireso1ution image querying. In Proceediпgs о{ SIGGRAPH '95,
pages 277 286. АСМ, New York, 1995.
[64] Rong Qing Jia and char1es А. Micchelli. Using the refinement equations
for the construction of pre wavelets 11: Powers of two. In P. J. Laurent,
А. Le Mehaute, and L. L. Schumaker, editors. Curves aпd Sur/aces,
pages 209 246. Academic Press, Boston, 1991.
[65] Atreyi Kankanhalli, Hong Jiang Zhang, and chien Yong Low. Using
texture for image retrieval. In Iпterпatioпal Coп{ereпce оп Autoтatioп,
Robotics aпd Coтputer Visioп. Nanyang Technologica1 University,
Singapore, 1994.
[66] Т. Kato, Т. Kurita, N.Otsu, and К. Hirata: А sketch retrieval method for
[иН color image database query Ьу visual ехаmр1е. In Proceediпgs
о/ the 11th IAPR Iпterпatioпal Coп/ereпce оп Patterп Recogпitioп,
pages 530 533. IБЕЕ computer Society Press, Los Alamitos, СА, 1992.
[67] Е. Керре1. Approximating complex surfaces Ьу triangulation of contour
1ines. lВМ Jourпal о/ Research aпd Developmeпt. 19(1):2 11, January
1975.
[68] А. Kitamoto, С. Zhou, and М. Takagi. Similarity retrieval of NOAA
satellite imagery Ьу graph matching. In Storage aпd Retrieval /or
Iтage aпd Video Databases, volume 1908 of Proceediпgs о{ the SPIE,
pages 60 73. SPIE, Bellingham, WA, 1993.
[69] J. Lane and R. Riesenfeld. А theoretical deve10pment for the computer
generation and disp1ay of piecewise polynomia1 surfaces. IEEE
Traпsactioпs оп Patterп Aпalysis aпd Machiпe Iпtelligeпce, 2(l):35 6,
January 1980.
[70] А. S. Lewis and G. Кnow1es. Video compression using 3D wave1et
transforms. Electroпics Letters, 26(6):396 398, 15 March 1990.
[71] Dani Lisehinski, Fi1ippo Tampieri, and Donald Р. Greenberg. combining
hierarchica1 radiosity and discontinuity meshing. In Proceediпgs о/
S1GGRAPH '93, pages 199 208. АСМ, New York, 1993.
[72] Zicheng Liu, Steven J. Gortler, and Michael F. cohen. Hierarchical
spacetime contro1. In Proceediпgs о/ S1GGRAPH '94, pages 352. АСМ,
New York, 1994.
Литература
253
[73] char1es Т. Loop. Smooth subdivision surfaces based оп triangles. Master's
thesis, Department ofMathematics, University ofUtah, 1987.
[74] J. Michae1 Lounsbery. Mu1tireso1ution ana1ysis for surfaces of arbitrary
topologica1 type. Ph.D. thesis. University ofWashington, 1994.
[75] Michae1 Lounsbery, Топу DeRose, and Joe Warren. Mu1tireso1ution
surfaces of arbitrary topological type. АСМ Traпsactioпs оп Graph , ics
1996 (to appear).
[76] т. Lyche and К. MOrken. Кnot remova1 for parametric B sp1ine curves and
surfaces. Coтputer Aided Geoтetric Desigп, 4(3):217 230, November
1987.
[77] Stephane Mallat. Mu1tireso1ution representation and wavelets.
Ph.D. thesis, University of Pennsy1vania, 1988.
[78] Stephane Mallat. А theory for mu1tireso1ution signa1 decomposition:
The wavelet representation. IEEE Traпsactioпs оп Patterп Aпalysis aпd
Machiпe Iпtelligeпce, ll(7):674 693, Ju1y 1989.
[79] Stephane Mallat and Sifen Zhong. Wavelet transform maxima and
multiscale edges. In М. В. Ruskai et al., editors. Wavelets aпd Their
Applicatioпs, pages 67 104. Jones and Bartlett, Boston, 1992.
[80] Yves Meyer. Onde1ettes et fonctions splines. Technica1 report,
Seminaire EDP, Есо1е Polytechnique, Paris, 1986.
[81] Yves Meyer. Onde1ettes sur l'intervalle. Revista Mateтatica
Iberoamericaпa. 7(2): 115 143,1991.
[82] Yves Meyer. Wavelets: Algorithтs aпd Applicatioпs. SIAМ, Philade1phia,
1993. Translated Ьу Robert D. Ryan.
[83] David Meyers. Multiresolution tiling. Coтputer Graphics Foruт,
1З(5):325 340, December 1994.
[84] David Meyers. Reconstruction of surfaces from planar contours.
Ph.D. thesis, University of Washington, 1994.
[85] David Meyers, Shelley Skinner, and Kenneth Sloan. Surfaces from
contours. АСМ Traпsactioпs оп Graphics, 11(3):228 258, Ju1y 1992.
[86] J. Morlet, G. Arens, Е. Fourgeau, and D. Giard. Wave propagation and
samp1ing theory. Geophysics, 47(2):203 236, February 1982.
[87] Philip Morrison, Phylis Morrison, and The Office of char1es and Ray
Eames. Powers о/ Теп: А Book About the Relative Size о/ Thiпgs iп the
Uпiverse aпd the EjJect о/ Addiпg Aпother Zero. Scientific American, New
York,1982.
254
Литература
[88] Shigeru Muraki. Approximation and rendering of уо1иmе data using
wave1et transforms. In Proceediпgs о! Visualisatioп '92, pages 21 28.
IБЕЕ computer Society Press, Los Alamitos, СА, 1992.
[89] Shigeru Muraki. Volume data and wavelet transforms. IEEE Coтputa
Graphics aпd Applicatioпs, 13(4):50 56, July 1993.
[90] W. Niblack, R. Barber, W. Equitz, М. F1ickner, Е. G1asman, D. Petkovic,
Р. Yanker, С. Fa10utsos, and G. Taubin. The QВlc project: Querying
images Ьу content using co10r, texture, and shape. In Storage aпd
Retrieval/or Image aпd Video Databases, уо1иmе 1908 of Proceediпgs
ofthe SPIE, pages 173 187. SPIE, Bellingham, WA, 1993.
[91] S. Panchanathan, Е. chan, and Х. Wang. Fast muitireso1ution motion
estimation scheme for а wavelet transform video coder. In Visual
Commuпicatioпs aпd Image Processiпg '94, уо1иmе 2308, part 1 of
Proceediпgs ofthe SPIE, pages 671 681. SPIE, Bellingham, WA, 1994.
[92] А1ех Р. Pentland. Equi1ibrium and interpolation solutions using wave1et
bases. In N. М. Patrikalakis, editor. Scieпtific Visualisatioп о! Physical
Pheпomeпa, pages 507 524. Springer Ver1ag, Tokyo, 1991.
[93] Кеп Perlin and David Fox. Pad: Ап altemative approach to the user
interface. In Proceediпgs o/SIGGRAPH '93. pages 57 б4. АСМ, New
York, 1993.
[94] Кеп Perlin and Luiz Velho. Live paint: Painting with procedura1 mu1tiscale
textures. In Proceediпgs о! SIGGRAPH '95, pages 153 160. АСМ, New
York, 1995.
[95] Michae1 Plass and Maureen Stone. curve fitting with piecewise parametric
cubics. In Proceediпgs о! SIGGRAPH '83, pages 229 239. АСМ, New
York, 1983.
[96] Thomas Porter and Тоm Duff. compositing digital images. In Proceediпgs
ofSIGGRAPH '84, pages 253 259. АСМ, New York, 1984.
[97] William Н. Press, Brian Р. Flannery, Sau1 А. Teukolsky, and William
т. Fetter1ing. Nuтerical Recipes. cambridge University Press, New York,
second edition, 1992.
[98] Ewa1d Quak and Norman Weyrich. Decomposition and reconstruction
algorithms for spline wave1ets оп а bounded interva1. Applied aпd
Coтputatioпal Harmoпic Aпalysis. 1(3):217 231, June 1994,
[99] J. N. Reddy. Energy and Variational Methods in App1ied Mechanics. John
Wi1ey & Sons, New York, 1984.
Литература
255
[100] Mark С. Reichert. А two pass radiosity method driven Ьу lights and
viewer position. Master's thesis. Program of computer Graphics, Соmеll
University, 1992.
[1 О 1] Ulrich Reif. А unified approach to subdivision a1gorithms. Technical report
A 92 16, Universitat Stuttgart, 1992.
[102] Norman Ricker. The [оrш and nature of seismic waves and the structure
ofseismograms. Geophysics, 5(4):348 366, October 1940.
[103] R.Riesenfe1d. Оп chaikin's a1gorithm. Coтputer Graphics aпd Iтage
Processiпg. 4(3):304 310, September 1975.
[104] David Sa1esin and Ronen Barze1. Two bit graphics. IEEE Computer
Graphics aпd Applicatioпs. 6(6):36---42, June 1986.
[105] Michae1 Р. Salisbury, Sean Е. Anderson, Ronen Barze1, and David
Н. Salesin. Interactive реп and ink illustration. In Proceediпgs о!
SlGGRAPH '94, pages 101 108. АСМ, New York, 1994.
[106] Philip J. Schneider. Phoenix: Ап interactive сшуе design system based оп
the automatic fitting Ofhand sketched curves. Master's thesis. Department
ofcomputer Science and Engineering, University ofWashington, 1988.
[107] Peter Schroder, Steven J. Gortler, Michael F. cohen, and Pat Hanrahan.
Wavelet projections for radiosity. Coтputer Graphics Forит, 13(2):
141 151, June 1994.
[108] Peter Schroder and Pat Hanrahan. Wave1et methods for radiance
computations. In G. Sakas, Р. Shirley, and S. Miiller, editors. Photorealistic
Reпderiпg Techпiques. pages 310 326. Springer Ver1ag, Berlin, 1995.
[109] Peter Schroder and Wim Swe1dens. Spherica1 wavelets: Efficiently
representing functions оп the sphere. In Proceediпgs о! SIGGRAPH '95,
pages 1бl 172. АСМ, New York, 1995.
[110] Thomas W. Sederberg, Peisheng Gao, Guojin Wang, and Hong Ми.
2D shape blending: Ап intrinsic solution to the vertex path problem. In
Proceediпgs ofSIGGRAPH '93, pages 15 18. АСМ, New York, 1993.
[111] Thomas W. Sederberg and Eugene Greenwood. А physically based
approach to 2D shape blending. In Proceediпgs о! SIGGRAPH '92,
pages 25 34. АСМ, New York, 1992.
[112] А. Sengupta, М. Hilton, and В. Jawerth. А computationally fast
wave1et based video coding scheme. In Digital Video Compressioп оп
Persoпal Computers: Algorithтs aпd Techпologies, уо1иmе 2187 of
Proceediпgs ofthe SPIE. pages 152 157. SPIE, Bellingham, WA, 1994.
256
Литература
[113] A1exander Shustorovich. Scale specific and robust edge/line encoding
with linear combinations of Gabor wave1ets. Patterп Recogпitioп,
27(5):713 725, Мау 1994.
[114] Frаш;оis Х. Sillion and c1aude Puech. Radiosity aпd Global Illuтiпatioп.
Morgan Kaufmann, San Francisco, 1994.
[115] Е. Р. Simoncelli, W. Т. Freeman, Е. Н. Ade1son, and D. J. Heeger. Shiftab1e
multi scale transforms. IЕЕЕ Traпsactioпs оп Iп/orтatioп Theory,
38(2):587 607, March 1992.
[116] Mark 1. Т. Smith and Thomas Р. Bamwell Ш. Exact reconstruction
techniques for tree structured subband coders. IЕЕЕ Traпsactioпs оп
Acoustics, Speech, and Sigпal Processiпg, 34(3):434---441, June 1986.
[117] Brian Е. Smits. Efficient hierarchica1 radiosity in соmр1ех environments.
Ph.D. thesis, СотеН University, 1994.
[118] Brian Smits, James Arvo, and Donald Greenberg. А clustering a1gorithm
for radiosity in complex environments. In Proceediпgs o/SIGGRAPH '94,
pages 435---442. АСМ, New York, 1994.
[119] Brian Е. Smits, James R. Arvo, and David Н. Salesin. Ап
importance driven radiosity a1gorithm. In Proceediпgs 0/ SIGGRAPH '92,
pages 85 90. АСМ, New York, 1992.
[120] Eric J. Stollnitz, Топу D. DeRose, and David Н. Sa1esin. Wave1ets for
computer graphics: А primer. IЕЕЕ Coтputer Graphics aпd Applicatioпs,
15(3):76 84, Мау 1995 (part 1) and 15(4):75 85, Ju1y 1995 (part 2).
[121] Michae1 J. Swain. Interactive indexing into image databases. In Storage
aпd Retrieval /or Iтage aпd Video Databases, уо1иmе 1908 of
Proceediпgs o/the SPIE. pages 95 103. SPIE, Bellingham, WA, 1993.
[122] Wim Sweldens. The lifting scheme: А custom design construction
of biorthogona1 wave1ets. Industrial Mathematics Initiative 1994:7,
University of South caro1ina, 1994.
[123] Wim Sweldens. The 1ifting scheme: А new phi10sophy in biorthogonal
wave1et constructions. In Wavelet Applicatioпs iп Sigпal aпd Image
Processiпg III, volume 2569 of Proceediпgs 0/ the SPIE, pages 68 79.
SPIE, Bellingham, WA, 1995.
[124] Richard Szelisld. Fast surface interpo1ation using hierarchica1 basis
functions. IЕЕЕ Traпsactioпs оп Patterп Aпalysis aпd Machiпe
Iпtelligeпce, 12(6):513 528, June 1990,
Литература
257
[125] Greg Turk and Marc Levoy. Zippered polygon meshes from range images.
Iп Proceediпgs о! SIGGRAPH '94, pages 311 318. АСМ, New York,
1994.
[126] Joe Wапеп. Persona1 communication. 1994.
[127] Joe Wапеп. Binary subdivision schemes for functions over iпеgu1аr
knot sequences. Iп М. Daeh1en, Т. Lyche, and L. Schumaker, editors.
Mathematical Methods iп Coтputer Aided Geoтetric Desigп 111.
Academic Press, San Diego, 1995.
[128] Karl Weierstrass. Matheтatische Werke, уо1иmе 11. Mayer & Muller,
Ber1in, 1895.
[129] William Welch. Serious putty: Topo10gica1 design for variationa1 curves
and surfaces. Ph.D. thesis, carnegie Mellon University, 1996.
[130] William Welch and Andrew Witkin. Variationa1 surface modeling. Тп
Proceediпgs ofSIGGRAPH '92, pages 157 166. АСМ, New York, 1992.
[131] Ruediger Westermann. А multireso1ution framework for volume rendering.
Iп Proceediпgs о! the АСМ Workshop оп Voluтe Visualizatioп,
pages 51 58. АСМ, New York, 1994.
[132] M1aden Victor Wickerhauser. High resolution still picture compression.
Digital Sigпal Processiпg, 2(4):204 226, October 1992.
[133] M1aden Victor Wickerhauser. Adapted Wavelet Aпalysis froт Theory [о
Software. А. К. Peters, Welles1ey, МА, 1994.
[134] Andrew Witkin and Michae1 Kass. Spacetime constraints. Iп Proceediпgs
ofSlGGRAPH '88, pages 159 168. АСМ, New York, 1988.
[135] Andrew Witkin and Zoran Popovi6. Motion warping. Iп Proceediпgs о!
SlGGRAPH '95, pages 105 108. АСМ, New York, 1995.
[136] У. Q. Zhang and S. Zafar. Motion compensated wavelet transform coding
for co10r video compression. IEEE Traпsactioпs оп Circuits aпd Systeтs
for Video Techпology, 2(3):285 296, September 1992.
Предметный указатель
В сплайновые базисные функции,
109, 20l 202
их медленная сходимость, 202
при проектировании в интерак
тивном режиме, 202
В сплайновые вейвлеты, 110 112
интерполирующие конечную точ
ку, 113
с малым носителем, 245
В сплайновые масштабирующие
функции, 108 110
интерполирующие конечную точ
ку, 109
их скалярное произведение, 243
В сплайновый блок фильтров, 112
113
k дисковые вейвлеты, 179
матрицы анализа, 179,181
матрицы синтеза, 179, 181
2 дисковый вейвлет, 180, 186
DLG cxeMa, 84, 85
Link CTpYKтypa, 211
МаtlаЬ код, 235, 241
Powers of Теп, 58
QuadTree cTpYKтypa, 52, 211
QuadTreeNode cTpyктypa, 51, 211
QUВlc, 61
Адаптивное вариационное модели
рование, 204
Адаптируемость, 21
Алrоритм [анапатхи Деннехи, 148
149
пример, 149
Кристиансена Зедерберrа, 148
149, см. также Задача поклеточ
Horo представления
пример, 149
Чайкина, 80, 81, см. также По
следовательное деление
алrоритм локальноrо последо
вательноrо деления, 88
для замкнутых параметриче
ских кривых, 83
ДЛЯ функции, 81
доминирующий левый соб
ственный вектор, 90
получение равномерных
В сплайнов, 82
кратномасштабноrо клеточноrо
представления, 145, 149 159, см.
также Задача клеточноrо пред
ставления
восстановление, 150 154
восстановление по блоку филь
тров, 150 152
восстановление по одному вей
влету, 151 154
временная сложность, 156 157
замена ребер, 154 156
иллюстрация этапов, 151
клеточное представление как
результат выполнения алrоритма,
150
ПредметныЙ указатель
259
локальная оптимизация, 154
156
оптимизация клеточноrо пред
ставления базовоrо комплекта,
150
основные этапы, 149
примеры клеточноrо представ
ления, 157 159
разложение контура, 150
формирования запроса изображе
ния при переменном разрешении,
60
Алrоритмы [анапатхи Деннехи,
148 149
Кристиансена Зедерберrа, 148
149
Чайкина, 80 83,88, 90
бинарноrо поиска, 46
вейвлет излучательности, 212
кластеризации, 216 217
клеточноrо представления при пе
ременном разрешении, 145, 149
159
нестандартноrо разложения, 40
оптимизирующеrо клеточноrо
представления, 146 148
пирамидальный, 22
редактирования изображения, 52
55
редактирования изображения при
переменном разрешении, 60
Анализ, 100, см. таК.же Синтез
k диск, 179, 181
Фурье, 19 20
ленивый вейвлет, 177
матрицы, 118
одноузловой, 123
сводная таблица с уравнениями,
125
фильтры, 100, 112, 165
Аппроксимация изображения, 63
Аппроксимирующие схемы последо
вательноrо деления, 83
Афинная инвариантность, 168
Базис вейвлетов rладкость, 107
для излучательности, 210
компактный носитель, 106
нулевые моменты, 107
ортоrональный, 103
симметрия, 107
Базовая ячейка, 185
в схеме последовательноrо деле
ния, 185
пример, 185
Базовый комплект, 150
Базы данных изображений, 50
доступ, 59
индексация ключевыми словами,
59
Бесконечно мерные пространства,
230
Биортоrональность, 114 115
двойственные базисы, 115 116
Биортоrональные вейвлеты, 114
125, С)И. таК.же Ортоrональ
ные вейвлеты, Полуортоrональ
ные вейвлеты
конструирование, 124 125
одноузловые вейвлеты, 119 123
поверхностные, 175 181
условия, определяющие их, 127
Биортоrональный базис, 115
Блок фильтров, 29, 99 102
В сплайновый, 112 113
последовательность коэффициен
тов, 150
пример, 101
Вариационное моделирование, 195
204, С)И. также Целевая функция,
Физическое моделирование
адаптивное, 204
дополнительные сведения, 224
260
ПредметныЙ указатель
использование вейвлетов, 20 1
204
конечные элементы в вариацион
номмоделировании, 197 201
Введение узлов, 241
Вейвлет излучательность, 21 0 216,
см. так,же Излучательность
алrоритм, 212
базис вейвлетов для вейвлет излу
чательности, 21 О
кластеризация, 216 217
обобщение до яркости, 217 218
структуры данных, 211
УЛУЧIIIение,216 218
уточнение,212 214
уточнение с учетом значимости,
216
этап конечной сборки, 215 216
Вейвлет коэффициенты, 65, 100,
164,186
Вейвлет пакеты, 222
Вейвлет преобразование, 28, 101
Хаара, 34
вычисление, 29
ДBYMepHoe,39 42
OДHOMepHoe,27 29
преимущества, 29
хранение, 29
цветовая информация и вей
влет преобразование, 47
Вейвлет разложение, С)И. Вей
влет преобразование
Вейвлет сжатие, 36 38, С)И. таК.же
Сжатие изображения
задача, 37
изменение степени сжатия, 38
применение, 38
цель, 36
Вейвлеты, 20, 32,97
В сплайновые, 110 113, 236, 238,
239
k дисковые, 179
2 дисковые, 180, 186
Добеши, 1 05 106
Хаара, 32
В сплайновые матрицы, 235
236
двумерныепреобразования, 39
42
и редактирование изображения,
49 58
одномерные преобразования,
27 29
пример, 33
адаптируемость,21
биортоrональные, 114 125
вейвлеты BToporo поколения, 221
вейвлеты на мноrоrpанной по
верхности, 179, 180
временная сложность, 21
BToporo поколения, 221
историческая перспектива, 21 24
на основе квадратичных В сплай
нов, 238
на основе кубических В сплай
нов, 239
на основе линейных В сплайнов,
236
нулевые моменты, 107
одноузловые, 122 123
ортоrональные, 1 02 106
поверхностные, 163 183
полуортоrональные, 107 114
применения, 19,20
разреженность, 21
сплайн вейвлеты, 1 08 113
Векторные пространства, 29 31,
229 230
базис для векторных пространств,
31
бесконечно мерные, 230
вложенные, 31
конечно мерные, 230
обзор,229 230
261
ПредметныЙ указатель
ортоrональное дополнение, 32
скалярное произведение, 31 32
Векторы, 29 32,230
линейно независимые, 230
нормированные, 232
ортоrональные,32
типы векторов, 230
Весовые коэффициенты для метрики
формирования запроса изображе
ния, 72
на этапе усреднения, 168
Взятие разностей, 33
Видеозапросы, 76
Видеосжатие, 223
Виртуальная реальность, 50
Вложенные пространства базисные
функции для вложенных про
странств, 91
и уточняемые масштабирующие
функции, 90 96, 171 174
цепочка вложенных пространств,
174
Восстановление, 150 154, см. тaK
же Алrорнтм кратномасштабно
[о клеточноrо представления
восстановление исходных клеточ
ных представлений, 156
по блоку фильтров, 150 152,
см. также Алrоритм KpaTHOMac
штабноrо клеточноrо представле
ния
пример, 152
список подозрительных ребер,
154
этапы, 152
по одному всйвлсту, 151 154,
см. так,же Алrоритм KpaTHOMac
штабноrо клеточноrо представле
ния
пример, 154
список подозрительных ребер,
154
этапы, 153
[ессиан, 199 200
[лобальное освещение, 205 218, см.
таК.же Физическое моделирова
ние
вейвлет излучательность, 21 o
216
rлянцевое, 217
дополнительные сведения, 224
задача об излучательности, 205
210
не зависящее от точки обзора, 216
улучшение вейвлет излучательно
сти, 216 218
[лянцевое rлобальное излучение,
217
[раничные условия, 55 56
[руппирующая функция, 71
Двойственные масштабирующие
функции, 117,124
Двойственный подъем, 124
Диадические точки, 80
Дискретное уравнение переноса из
лучательности,208 209
Доминирующий левый собственный
вектор, 89 90, С)И. также Oцe
ночные маски
алrоритмЧайкина, 90
конечное положение, 90
Дополнительные сведения, 220 226
приложения к изображениям,
222 223
приложения к кривым, 223
приложения к поверхностям, 223
теория кратномасштабноrо анали
за, 220 221
физическое моделирование, 224
226
Дробное изменение масштаба, 56
Дробные разрешения, 56
262
ПредметныЙ указатель
Единичная маска, 82
Задача клеточноrо представления,
145 149, ОИ. также Алrоритм
кратномасштабноrо клеточноrо
представления
алrоритм [анапатхи Деннехи,
148 149
алrоритм Кристиансена Зедер
берrа, 148 149
оптимизирующий алrоритм, 146
148
предыдущие решения задачи кле
точноrо представления, 146 149
проблемные моменты, 145
Запрос на основе содержания, 60, 61
Запрос по образцу (QVE), 61
Иерархическая излучательность,
210,216
Иерархические представления, см.
также Кратномасштабные MeTO
ды
Излучательность, 205 218, см. тaK
,же Общее освещение
дискретизация, 208
и конечные элементы, 207 210
иерархическая, 210, 216
испускаемая, 206
распределение, 208
Изменение масштаба на дробном
уровне, 56
Изображения, 29
двухпиксельные, 29
запрос, 60
одномерные, 30
с переменным разрешением, 50
52
применение, 50
структуры данных, 50 52
хранение, 50
цвет, 47 8
целевые, 60, 62
Интерактивные системы раскраши
вания, 50
Интерполируюшие конечную точку
В сплайны, 85, 86
введение вершин, 85
вейвлеты, 113
квадратические, матрицы, 237
238
кубические, 85,111
кубические, матрицы, 238 240
линейные, матрицы, 236 237
масштабирующие функции, 93
неравномерные, 108
Интерполирующие схемы, 83 84
Касательные маски, 169 170, см.
таК.же Оценочные маски, Маски
Квадратичная древовидная CTPYKТY
ра, 50 52
информация о вершинах, 51
прозрачность вершины, 51
структура данных, 51 52, 211
Квадратичное проrраммирование,
200
Квадратурные зеркальные фильтры,
22, 105
Квантование, вейвлет коэффициент,
65
Кластеры изображений, 74
Кодирование, 37,45
Компактный носитель, 31
Конечная функция, 91, 93
Конечномерные пространства, 230
Конечные кривые, 86
элементы, 198
в вариационном моделирова
нии, 197 201
и задачи физическоrо моделиро
вания, 224
и излучательность, 207 210
ПредметныЙ указатель
263
Конструкция с тензорным произве дополнительные сведения, 220
дением, 164 221
Контроль степени детализации, 187 инвариантный относительно
188 сдвиrа, 22 24, 97, см. так,же
Контрольная ломаная, 82 Кратномасштабный анализ
Контрольные точки, 82 инвариантный относительно
Бецера, 142 сдвиrа, дополнительные CBeдe
кривой, соответствующей дробно ния, 221
му уровню сrлаживания, 132 133 определение пространства вей
при высоком разрешении, 133 влетов, 97
135 отправная точка, 97
Контрольный мноrоrранник, 166 структура, 13 О
Корректировка, 53 55 теория кратномасштабноrо, 97
разложение, 53 54 127
экстраполяция, 53 55 уточнение, 97 99
Коэффициенты вейвлет коэффициентыJ{ривая четвертоrо порядка, 201
65, 100, 164, 186 Кривые, С)И. также Поверхности
масштабирующей функции, 100 Бецера, 142
несоответствующие, 66 аппроксимация, 129
переноса излучательности, 209, базовые, 128
213 дополнительные сведения, 223
разложения, 63 конечные, 86
расщепления, 100 кратномасштабные, 128 144
соответствующие, 66 обращение развертки, 136
уточнения, 94 остова, 128
уточняющие, 28 параметрические в двух измере
Кратномасштабные кривые, 128 ниях, 138
144, см. таК.же Кривые последовательноrо деления, 79
представление, 129 96
сходные представления, 129 оценочные маски, 86 90
130 уточняемые масштабируемые
MeToды,20 21 функции, 90 96
Кратномасштабный анализ, 22, 97 последовательное деление, 79 96
102 представления, 129 130
блок фильтров, 99 102 развертка, 128, 131 138
в случае поверхностей, 164 165 редактирование, 128, 131 140
вариантный относительно сдви роль, 128
[а, 22 24, 97, 221 с меняющейся параметризацией,
для В сплайнов, 130 137
для областей произвольной TO сrлаживание, 128, 130 131
полоrии, 164 сжатие, 140 142
264
ПредметныЙ указатель
соответствующие дробному ypOB
ню редактирования, 131, см. тaK
,же Кривые
контрольные точки, 1З2 1З3
редактирование, 132 135
соответствующие дробному ypOB
ню сrлаживания, 131
специфика, 129, 131 IЗ2, 138
четвертоrо порядка, 201
Кубические В сплайны, 82
вейвлеты, 239
масштабирующие функции, 239
матрицы, 238 240
Кусочно линейные масштабирую
щие функции, 120
Кусочно постоянные функции, 29
30
Левые собственные векторы, 89 90,
233
Ленивые вейвлеты, 119 122
анализ, 177
масштабирующие функции, 175
матрицы синтеза, 176, 177
недостатки, 175
практическая польза, 122
пример, 120
улучшение, 122
Линейная алrебра, 229 234
базисы и размерность, 230
векторные пространства, 229
230
нормы и нормирование, 232
233
скалярные произведения и OpTO
rональность,231 232
собственные векторы и соб
ственные значения, 233 234
интерполяция, 137
по времени сложность, 21
Линейные В сплайны, 82
Локальная оптимизация, 154 156
Маски, 80, 82 84, 168 171, см. тaK
же Оценочные маски
DLG cxeMa, 84
алrоритмЧайкина, 80
касательная маска, 169
последовательное деление Добе
ши,83
равномерные В сплайны, 82
схема Лупа, 169
схема типа бабочки, 171
Масштабирование, уровни масшта
бироваНИЯ,43
Масштабирующие функции, 31, 91,
98, см. также Последовательное
деление
В сплайновые, 1 08 11 О
вычисление, 93
двойственные, 117, 124
двумерный случай, 42
коэффициенты, 100
кусочно линейные, 120
ленивый вейвлет, 175
линейная комбинация масштаби
рующих функций, 90
матрица синтеза, 241
матрица уточнения для масштаби
рующих функций, 96
на основе квадратичных В сплай
нов, 238
на основе кубических В сплай
нов, 239
на основе кусочно постоянных
В сплайнов, 235
на основе линейных В сплайнов,
236
отцовские, 93
равномерное последовательное
деление, 94
соотношение для масштабирую
щих функций с двух соседних
уровней, 99
ПредметныЙ указатель
265
уточняемые, 91
уточняющее соотношение для
масштабирующих функций, 93
уточняющие коэффициенты для
масштабирующих функций, 94
характеристические, 235
Материнский вейвлет, 98
Матрица локальноrо последователь
Horo деления, 88 89
для алrоритма Чайкина, 88
ее собственный анализ, 88
Матрицы В сплайновых вейвлетов,
235 240
вейвлетХаара,235 236
вейвлеты на основе интерполиру
ющих конечную точку квадратич
ных В сплайнов, 237 238
вейвлеты на основе интерполи
рующих конечную точку кубиче
скихВ сплайнов, 238 240
вейвлеты на основе интерполиру
ющих конечную точку линейных
В сплайнов, 236 237
Метод rаусса Зейделя, 201
конечных элементов, 197
сопряженных rрадиентов, 201
Метрика формирования запроса
изображения, 60, 65 66, см. тaK
же Редактирование изображений
«правильная» метрика, 62
быстрое вычисление метрики, 66
67
весовые коэффициенты, 72
квантование, 65
компонентыметрики,63 65
кратномасштабный подход, 62 63
нормирование, 65
пример, 66
разработка,62 67
составная метрика, 66
тип вейвлетов, 63
тип разложения, 63
усечение, 65
цветовые пространства, 63
эффективность, 72
Мноrоrранные поверхностные вей
влеты, 179, 180
Множители Лаrранжа, 200
Модельное представление пользова
тельскоrо интерфейса по принци
пу «идеальный рабочий стол», 50
Мультивейвлеты, 210
Невырожденная матрица, 233
Ненормированные касательные, 140
Неравномерное последовательное
деление, 84 86, см. также По
следовательно е деление
этап усреднения, 84
Несовпадающие коэффициенты, 66
Не стандартное построение, 42, 44
преимущества, 44
пример,44
Норма, 232
Нормирование,34 36,232
метрика формирования запроса
изображения,65
псевдокодовые процедуры, 35 36
Нормированные касательные, 140
Носитель, 31,44,97,106,111,117,
178 179,209,245
Нулевые моменты, 107
Нуль пространство, 108
Обратимость сводная таблица с
уравнениями, 125
тождество обратимости, 134
Обращение развертки, 140 144, ОИ.
также Кривые
в пределах допуска поrрешности,
144
вычисление предела поrрешно
сти, 141
и сжатие кривой, 140 142
266
ПредметныЙ указатель
Одномерное вейвлет преобразование
Хаара, 27 29
Одномерные изображения, 30
Однородная система уравнений, 108
Одноузловые вейвлеты, 122 123
конструирование, 123, 124
матрица синтеза, 123
последовательности анали
за/синтеза, 122 123
Операция подъема, 115, 124
двойственный подъем, 124
и биортоrональные базисы, 115
Оптимизирующий алrоритм, 146
148, см. так,же Задача поклеточ
Horo представления
вмешательство пользователя и,
148
недостатки, 147 148
примеры клеточноrо представле
ния, 147
примеры результатов, 148
Оракул, 204, 213
Ортоrональная матрица, 104
Ортоrональность,34
включения ортоrональности, 103
105
Ортоrональные вейвлеты, 102 106,
С)И. также Биортоrональные вей
влеты, Полуортоrональные вей
влеты, Вейвлеты
вейвлеты Добеши, 1 05 106
включения ортоrональности, 103
105
матрица синтеза, 104
условия, определяющие их, 127
Ортоrональный базис вейвлетов, 103
Ортоrональный кратномасштабный
базис, 102
Ортонормированный базис, 36, 102,
103, 115,232
Отцовская масштабирующая функ
ция, 93, см. также Масштабиру
ющие функции
уточняющее соотношение, 94
Оценочные маски, 87 90, см. так,же
Последовательное деление
для поверхностей, 169
доминирующий левый собствен
ный вектор, 89 90
матрица локальноrо последова
тельноrо деления, 88 89
производные, 87
усредняющая, 87
Палитра RGB, 47, 63
Перенос излучательности [eOMeT
рия,207
дискретизация, 208 209
коэффициенты, 209, 213
матрица, вычисление, 209
оператор, 206
разложение матрицы переноса,
214 215
уравнение, 206
Перестановка ребра, 154 156
Пирамидальные алrоритмы, 22
Поверхности, С)И. также Кривые
аппроксимации, 186
дополнительные сведения, 223
затененные изображения, 170
кратномасштабное представле
ние, 181 183
кратномасштабный анализ для
случая поверхностей, 1 б4 165
обращение в кратномасштабную
форму, 184 185
оценочные маски для поверхно
стей, 169
поверхности последовательноrо
деления, 165 174
приложения к поверхностям, 184
191
ПредметныЙ указатель
267
Поверхностные вейвлеты, 163 183
биортоrональная конструкция,
175 181
вейвлеты на мноrоrранной по
верхности, 179, 180
выбор скалярноrо произведения,
174
перспективыизучения, 189 191
поверхностные вейвлеты и после
довательное деление поверхно
стей, 165 174
Подrотовительный этап, 67 68
Полуортоrональные вейвлеты, 107
114, см. таК.же Биортоrональ
ные, Ортоrональные вейвлеты
включения, 107 108
конструирование, 113 114
определяющие условия, 127
сплайн вейвлеты, 108 113
Полуотрезки, 29
Попарное усреднение, 33
Последовательная передача, 188
Последовательное деление, 79
DLG cxeMa, 84, 85
Добеши, 83, 84
Ду Сабина, 165, 166
аппроксимирующие схемы, 83
базовая ячейка, 185
вариантная относительно сдви
[а конструкция, основанная на
последовательном делении, 221
для характеристических функ
ций, 117
интерполирующие схемы, 83
84
линейный В сплайн, 83
матрица локальноrо последова
тельноrо деления, 88 89
матрица последовательноrо дe
ления, 92, 96
мноrоrранника, 167, 170, см.
также Последовательное деле
ние
мноrоrpанника матрицы анали
за, 177 178
мноrоrранника последователь
ное деление тетраэдра, 176
неравномерное, 84 86,221
определение двойственных KOH
струкций через последовательное
деление, 116 119
поверхности, 165 174
последовательное деление Дo
беши, 83, 84
последовательное деление Ду
Сабина, 166 167
последовательное деление MHO
rоrранника, 167, 170, 176
применение, 79
равномерное, 80 84
реализация, 80
стационарная схема, 117, 221
схема Кэтмула Кларка, 166
схема Лупа, 167 170
схема типа бабочка, 170 171
треуrольная схема, 167
этап разбивки, 81
этап усреднения, 81
Правые собственные векторы, 233
Превейвлеты, 32, 107, см. также
Полуортоrональные вейвлеты
Производные маски, 87
Пространства вейвлетов базисы вей
влетов, 108
определение, 97
Пространственно временные orpa
ничения, 224 226
Пространство со скалярным произ
ведением, 231
Процедура DecompositionStep, 35
DrawSegment, 141
Extrapo1ate, 54 55
268
ПредметныЙ указатель
NonstandardDecomposition, 40
NonstandardReconstruction,42
Reconstruction, 35
ReconstructionStep, 36
StandardDecomposition, 39 40
StandardReconstrucion, 40
отображения на экране Display,
52 53,56
разложения, 35
сжатия, 46
Прямое манипулирование, 135
при редактировании, 135 136
при редактировании с перемен
ным разрешением, 137
Прямой базис, 115
Псевдообратные матрицы, 135
Равномерное последовательное дe
ление, 80 84, С)И. также После
довательное деление
масштабирующие функции, 94
уточняющее соотношение, 94
Разложения, 53
вычисление, 63
и аппроксимация изображения, 63
и информация о контурах изобра
жения, 63
коэффициенты, 63
матрица переноса, 214 215
HeCTaHдapTHoe,40 2,63
разложение мноrоrранной по
верхности, 165
решение о выборе типа разложе
ния, 63
стандартное, 39 0,63
Разреженность, 21
Разреженный, 52, 54
Раскрашивание, 53
бинарные операции, 54
при переменном разрешении, 52
55
Раскрашивание изображения с пере
менным разрешением, 52 55
вывод на экран, 52 53
корректировака,53 55
раскраllIивание, 53
Растрескивание, 188
Редактирование и сжатие изображе
ния, 50
изображения,49 58
алrоритм, 52 55
и rpаничные условия, 55 56
при дробных разрешениях, 56
примеры, 58
редактирование сжатых изобра
жений, 50
кривых, 128, 131 140, С)И. также
Кривые
на дробном уровне, 132 135
ориентация детали, 138 140
при переменном разрешении,
137, 188 189
развертки, 138 140
характер кривой, 138
с прямым манипулированием,
135 136
Рекурсивное последовательное деле
ние, СМ. Последовательное деле
ние
Само сопряженность, 208
Сrлаживание кривых, 128, 130 131,
см. таК.же Кривые
непрерывное, 131
Сдвиrаемые преобразования, 222
Сжатие, 93
вейвлет сжатие, 36 38
видео, 223
изображений, 45 7, С)И. также
Вейвлет сжатие
и редактирование, 50
пример, 47
суммирование всех этапов, 45
ПредметныЙ указатель
269
изображения,45 7,50
кодирование, 37,45
кривой, 140 142
мноrоrpанника, 186
поверхностей, 186 187
сжатие мноrоrранника, 186
сжатие текстурных карт, 187
поверхности, 186 187
полиэдральное, 186
текстурное отображение, 187
текстурных карт, 187
Сиrнатуры, 60 61
Синтез, 100, ОИ. также Анализ
матрицы, 114, 118
сводная таблица уравнений, 125
синтез k дисковых вейвлетов, 179,
181
синтез одно узловых вейвлетов,
123
фильтры, 100, 114, 165
Синтез фотореалистичных изобра
жений, 205
Система раскрашивания и компо
новки изображений, 49
Скалярное произведение, 31 32, 110
В сплайновых масштабирующих
функций, 243
выбор, 113, 174
краткий обзор, 231
поверхностный вейвлет, 174
полиномов Бернштейна, 243
предварительное вычисление, 174
Собственная структура, 88
Собственные векторы, 233 234
Собственные значения, 233
Совпадающие коэффициенты, 66
Создание текстуры, 222
Соотношение двух масштабов, 99
Сплайн вейвлеты, 108 113
В сплайновые вейвлеты, 11 o 112
В сплайновые масштабирующие
функции, 108 110
В сплайновый блок фильтров,
112 113
скалярное произведение, 11 О
Сплайны, построенные из xapaKTe
ристических функций, 221
Стандартное построение, 42 4, ОИ.
также Нестандартное построе
ние
квадратные носители, 44
преимущества, 44
пример,43
суть, 42
Стерадиан, 217
Структуры данных вейвлет излуча
тельность, 211
изображение с переменным разре
шением, 50 52
квадратичная древовидная CTPYK
тура, 211
Схема Лупа, 167 169,ои. такжеПо
верхности
маски, 169
этап усреднения, 168
последовательноrо деления Кэт
мула Кларка, 166
типа бабочка, 170 171, 186, ОИ.
также Поверхности
ее этапы, 170
маска усреднения для нее, 171
Схемы разбивки вершин, 166, см.
таК.же Этап разбивки
разбивки rраней, 166, см. также
Этап разбивки
треуrольная, 166
четырехуrольная, 166 167
Текстур ное отображение, 50
Управляемые фильтры, 222
Усечение, вейвлет коэффициенты,
65
Усредняющие маски, 80, 170 171
270
ПредметныЙ указатель
Уточнение, 93
вейвлет излучательности, 212
214
для отцовской масштабирующей
функции, 94
коэффициентов, 94
сводная таблица уравнений, 125
цель уточнения, 212
этапы, 166
Уточняемая масштабирующая функ
ция, 91, см. так,же Масштабиру
ющие функции, Последователь
ное деление
и вложенные пространства, 90 96,
171 174
Уточняющие коэффициенты, 28
Физическое моделирование, 50
вариационное моделирование,
195 204
дополнительные сведения, 224
226
общее освещение, 205 218
Флатлеты, 21 О
Форматное соотношение, формиро
вание запроса изображения, 74
Формирование запроса изображе
ния, 59 76
«интерактивный режим», 72 73
алrоритм,67 71
видео, 76
запросные идентификаторы, 74
кластеры изображений, 74
кратно масштабный алrоритм, 60,
61
по содержанию, 60, 61
предварительный этап, 67 68
примеры, 71 73
пространства на перцепционной
основе, 74
раСIIIирения, 73 76
сравнение с сиrнатурой целевоrо
изображения, 69
среднее время, 74
форматное соотношение, 74
частичные запросы, 76
этап формирования запроса, 68
71
Функции, см. также Функции бази
са
ЕпВоuпd, 141 142
базиса, 31, 34
В сплайновоrо, 109, 201 202
Хаара, 21, 29 34
базиса Добеши, 106
биортоrональноrо, 115
двойственноrо, 115 119
для вложенных пространств, 91
нормированноrо, 34 36
ортоrональноrо вейвлет, 103
ортоrональноrо KpaTHOMac
штабноrо, 102
ортоrональность, 34,36,183
ортонормированноrо, 36, 103,
115,232
отправляющеrо, 209,213
принимающеrо, 209
прямоrо, 115
связи между функциями, 214
базиса Добеши, 106
базиса Хаара, 21, 34
двумерный случай, 42---44
нормирование, 34 36
одномерный случай, 29 34
ортоrональность, 34,36
rpуппирующая, 71
двойственноrо базиса, 101, 115,
см. также Биортоrональные вей
влеты
и биортоrональность, 115 116
конструирование, 119
ненормированноrо, 117
ПредметныЙ указатель
271
определение через последова
тельное деление, 116 119
двумерноrо базиса Хаара, 42 44
нестандартное построение, 42,
44
стандартное построение, 42 4
значимости, 216
значимость, 216
интерполяция, 134
конечная, 91, 93
кусочно постоянная,29 30
масштабирующая, 31, 42, 91
одномерная,29 34
одномерноrо базиса Хаара, 29 34
распределения двунаправленноrо
отражения, 217
функция шляпа, 119
характеристическая, 31, 92,210
целевая, 195 197
четвертоrо порядка, 198, 199
Функции шляпы, 119
Функция ErrBound, 141 142
ScoreQuery, 69 71
двунаправленноrо распределения
отражательной способности, 217
разложения, 53 54
Характеристические функции, 31
кусочно постоянные,210
масштабирующие, 235
с компактным носителем, 31
уточнение, 92
Цвет коррекция, 55
функция, 187
цветные изображения, 47 8
Цветовое пространство СIE LUV, 74
HSV, 63
RGB, 47, 63
TekHVc, 74
YIQ, 47, 63, 71
метрика формирования запроса
изображения,63
Цветовое пространство YIQ, 47, 63,
71
Целевая функция, 195, см. так,же
Вариационное моделирование
задание, 196 197
определение, 196
Целевые изображения, 60, 62, С)И.
таК.же Формирование запроса
изображения
сравнение с сиrнатурой, 69
Экстраполяция, 53 55
и операции компоновки, 54
проrpамма, 54 55
Этап конечной сборки, 215 216
разбивки, 81, 92, С)И. также Этап
усреднения
для треуrольной схемы после
довательноrо деления, 167,168
разновидности, 166
усреднения, 81, 92, 166, 167, С)И.
также Этап разбивки, Последо
вательное деление
в схеме Лупа, 168
весовые коэффициенты, 168
неравномерное последователь
ное деление, 84
равномерное последовательное
деление, 81
Яркость, 217, см. также Общее
освещение
обобщение до яркости, 217 218
уравнение переноса, 217
Эрик Столниц, Тони ДеРоуз, Дэвид Салезин
ВЕЙВЛЕТЫ В КОМПЬЮТЕРНОЙ rРАФИКЕ
Дuзайнер М В. Ботя
Технuческuй редактор А. В. Шuробоков
Корректор М А. Ложкuна
Подписано в печать 29.02.02. Формат 60 х 841/16'
Усл. печ. л. 13,95. Уч. изд. л. 14,12.
rарнитура Таймс. Бумаrа офсетная N21.
Печать офсетная. Заказ N2
Научно издательскнй центр «Реrулярная и хаотическая динамика»
426057, т. Ижевск, ул. Пастухова, 13.
Лицензия на издательскую деятельность ЛУ N2084 от 03.04.00.
httр://rсd.ruЕ шаi1:Ьоrisоv@rсd.ru
Отпечатано в полном соответствии с качеством
предоставленных диапозитивов в rипп «Вятка».
610033, т. Киров, ул. Московская, 122.