Автор: Рыбин В.В.
Теги: программирование математика тригонометрия учебное пособие издательство маи компьютеризация
Год: 2004
Текст
Мос^а • 2/WM
ПРИБЛИЖЕНИЕ
ФУНКЦИЙ.
КОМПЬЮТЕРНАЯ
ПРАКТИКА В СИСТЕМЕ
КОМПЬЮТЕРНОЙ
МАТЕМАТИКИ
МА I HCAI)
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ
(государственный технический университет)
В.В. РЫБИН
ПРИБЛИЖЕНИЕ ФУНКЦИЙ.
КОМПЬЮТЕРНАЯ ПРАКТИКА В СИСТЕМЕ
КОМПЬЮТЕРНОЙ МАТЕМАТИКИ MATHCAD
Учебное пособие
Утверждено
на заседании редсовета
13 октября 2003 г.
Москва
Издательство МАИ
2004
Рыбин В.В.
Приближение функций* Компьютерная практика в системе
компьютерной математики MATHCAD: Учебное пособие* — М.:
Изд-во МАИ, 2004* — 80 с.: ил.
В пособии кратко рассмотрена задача приближения одномерных функций и
разные схемы ее решения с использованием широкого круга базисных систем функ-
' ций, от традиционных систем функций — тригонометрических до современных —
базисных систем вейвлет-функций. Рассмотрены типовые примеры программирова-
ния и изучения задач приближения функций в системе Mathcad.
Пособие Предназначено для студентов специальности “Прикладная математи-
ка”, обучающихся по курсу “Компьютерная практика по математическим дисцип-
линам”, Оно также может быть полезным при проведении практических занятий в
дисплейном классе по курсу “Оптимизация и численные методы”, читаемого на тех-
нических и экономическом факультетах.
Рецензенты: каф. “Автоматизация биотехнических систем” МГУ прикладной
биотехнологии (зав. каф. В.И. Попов); В. Б. Чадов.
ISBN 5-7036*1434-7
® Московский авиационный институт
(государственный технический
университет), 2004
Тем. план 2004, поз, 32
Рыбин Владимир Васильевич
ПРИБЛИЖЕНИЕ ФУНКЦИЙ.
КОМПЬЮТЕРНАЯ ПРАКТИКА В СИСТЕМЕ
КОМПЬЮТЕРНОЙ МАТЕМАТИКИ MATHCAD
Редактор ГЛ. Моисеева
Компьютерная верстка Т.С. Евгеньева
Сдано в набор 17.03.04. Подписано в печать 17.06.04^
Бумага газетная. Формат 60 х 84 1/16.
Печать офсетная. Усл. печ. л. 4,65. Уч.-изд. л. 5,00.
Тираж 500. Зак. 2767/1709. С. 197.
Издательство МАИ
“МАИ”, Волоколамское шоссе, д. 4, Москва, А-80, ГСП-3 125993
Типография Издательства МАИ
“МАИ”, Волоколамское шоссе, Д. 4, Москва, А-80, ГСП-3 125993
ПРЕДИСЛОВИЕ
В настоящее время методы приближения функций широко
применяются в инженерной практике. Аппарат представления
функций и сигналов в виде обобщенных рядов Фурье нашел широ-
кое применение как в теории цифровой обработки сигналов и изо-
бражений, так и в теории управления. Так, например, конец про-
шлого века характеризуется появлением нового спектрального ме-
тода расчета нестационарных систем управления, специально при-
способленного для ЦВМ [9, 10, 16], Его истоки лежат в представ-
лении сигналов и временных характеристик системы управления
в виде ортогональных рядов. Коэффициенты этих временных
рядов, отделенные от самих рядов, рассматриваются как характе-
ристики сигналов и систем управления. Эти характеристики и со-
ставляют аппарат анализа систем управления. Теория обобщен-
ных рядов Фурье для представления функций все время развива-
лась под воздействием задач инженерной практики, В 60-х годах
прошлого века получил распространение метод приближения
функций сплайнами [6, 7], а в 90-х годах прошлого века возникла
и получила широкое распространение теория вейвлетов [11, 12],
Вейвлеты, особенно ортогональные вейвлеты с компактными но-
сителями, позволяют представлять и исследовать сигналы с ло-
кальными особенностями в виде обобщенных рядов Фурье — вейв-
лет-рядов.
Применение всех этих методов приближения функций невоз-
можно без использования вычислительной техники, и особенно
современных автоматизированных математических систем чис-
ленной и символьной математики [13—16], В последние годы по-
лучили широкое распространение такие программные системы
компьютерной математики, как Mathcad, Matlab, Mathematica,
Maple. Эти программные системы являются мировыми лидерами
среди компьютерных систем численной и символьной математики
для ПК. Они позволяют готовить отчетные документы, которые
объединяют исходные данные, описание алгоритмов решения
3
задач, программ и результатов решения в самой разнообразной
форме.
Данное пособие предназначено для проведения компьютерной
практики по приближению функций с использованием программ-
ной системы Mat head [13].
В первой главе рассматривается постановка задачи о прибли-
жении одномерных функций. Приводятся примеры базисных сис-
тем функций, ортогональных на конечном отрезке или на системе
точек этого отрезка. Более детально изучаются базисные сплайны
и ортогональные вейвлеты. Кроме того, изучаются задачи и схемы
интерполирования, точечного и интегрального квадратичного апп-
роксимирования функций.
Во второй главе рассматриваются примеры задач интерполя-
ции и аппроксимации с использованием различных базисных сис-
тем функций и различных численных схем решения искомых
задач. Каждый изучаемый пример является рабочим документом
программной системы Mathcad. Ввод и воспроизведение этого до-
кумента студентом на практике позволяют ему глубже понять ал-
горитм решаемой задачи и особенности его программной реализа-
ции, а также выполнить полученное задание на компьютерную
практику по приближению функций.
В приложении приводятся некоторые схемы решения задач
интерполяции и аппроксимации, а также задания на компьютер-
ную практику по приближению функций.
Глава 1. ПРИБЛИЖЕНИЕ ФУНКЦИЙ
1.1. Постановка задачи о приближении функций
Пусть дана базисная система функций ^90(х), ср^х), ...» ф^х),...} *
Функции вида
Qm(x) = с0 ФоО) + С1 <P1W + с2 Ф2<х> + + ст ’ <1Л)
где Cq , сх , ст — постоянные коэффициенты) называются обоб-
щенными многочленами или обобщенными полиномами.
Рассмотрим некоторую функцию f(x).
Задача о приближении ставится следующим образом: данную
функцию Дх) требуется приближенно заменить (аппроксимиро-
вать) обобщенным полиномом Qw(x) (1Л> так, чтобы отклонение,
в некотором смысле, функции f(x) от Q^r) на заданном множестве
М было наименьшим.
Этого можно достичь, вообще говоря, за счет надлежащего
подбора коэффициентов с- , i = 0, 1, 2, ...» т. При этом полином
Qm(x) называется аппроксимирующим. Что касается смысла тер-
мина “отклонение двух функций’*, то в зависимости от обстоя-
тельств его можно понимать по-разному.
Если множество М состоит из отдельных точек
х0 , хп , то приближение называется точечным; если же
М есть отрезок а < х < Ь, то приближение называется интегралы
ным.
В самом простом случае базисная система функций {Д(х)}
представляет собой последовательность целых неотрицательных
степеней переменной х:
5
фо(х) = 1 ; <р1(х) = х; ф2(х) = х2 ; ... фт(х) = хт ; ...
В этом случае функции (1.1) являются обычными алгебраичес-
кими полиномами:
= а0 + а1 х + а2 X2 + — + ат х™ ’ С1’2)
где а- — постоянные. Таким образом, приходим к задаче аппрок-
симирования функции /(х) полиномом Q,,/*) (1.2).
1.2. Примеры базисных систем функций
1,2,1. Ортонор мированные непрерывные системы
функций
Система функций {фД, в общем случае комплексных, опреде-
ленных на отрезке [0, fj, называется ортонормированной на этом
отрезке с весом р, если все функции этой системы удовлетворяют
условию
t
(p<PA’<p/)=f р(х)фй(х)ф/х)«/х=8Аи . (1.3)
' О
1,2,1.1. Полиномы Лежандра
Непрерывные ортонормированные полиномы Лежандра, опре-
деленные на отрезке [0, t], задаются формулой
I i у
Pi(t,x)=№j± ltiV i = 0,1,2,3.............. (1.4)
u = 0 '
где
iitP = (- 1Гис/+17с/-у.
Непрерывные полиномы Лежандра (1.4) ортонормировании
на отрезка [0, t] с весом p(t, х) = 1.
6
Для непрерывных полиномов Лежандра справедлива рекур-
рентная формула
Pi+1(«, =—г ж) х) -
I Т 1 t I > о
(1.5)
,i=l, 2, 3.....
'*• X J
которая позволяет найти все полиномы Лежандра по первым двум
р0<*’х) = ; Р1(*>х) = ру - il •
1.2.1.2. Полиномы Чебышева первого рода
Непрерывные ортонормированные полиномы Чебышева пер-
вого рода, определенные на отрезке [0, $], задаются формулой
х) =
(1-6)
где
Непрерывные полиномы Чебышева первого рода (1.6) ортонор-
мировании на отрезка [0, £] с весом
. 1
p<,’x> = W^r
Для непрерывных полиномов Чебышева первого рода справед-
лива рекуррентная формула
7
Tt + у/, x) = л/2л ту/, x) ту/, x) - Tt _ j(t, x) , i = 3, 4, ..
T2{t, x) = >/2л Tf(t, x) - VT T0(t, x) ,
(1.7)
которая позволяет найти все полиномы Чебышева первого рода по
первым двум
То(/, х) = ; Ту/, х) = № № - 1
и л 1 ТС I *
1.2.1.3. Полиномы Чебышева второго рода
Непрерывные ортонормированные полиномы Чебышева второ-
го рода, определенные на отрезке [0, £], задаются формулой ц
sin (г + 1) arccos — - 1
= 7 ' 7 - /2х^ у- ’ (1-8)
sin arccos — - 1
где
_ Л _ у л/тйГ(1 + и + 2)
Ч, и-^1) / ЯЛ
2Г и + -г- (i - и)! и!
1 I
Непрерывные полиномы Чебышева второго рода (1.8) ортонор-
мировании на отрезка [0, £] с весом
р(t, х) = ^x(t -^с) .
1.2.1.4. Тригонометрические функции
Непрерывные ортонормированные тригонометрические функ-
ции, определенные на отрезке [0, t], задаются формулами
8
, i = 0
C^t, x) = <
— cos
in
t
i= 1, 2
(1.9)
yt(l, x) = V-* sin Г* * ” x , i = 0, 1, 2,..
V 1 Г
(1.10)
Непрерывные тригонометрические функции ортонормирован-
ны на отрезке [0, с весом р(£, jc) = 1.
1.2.1.5. Комплексные экспоненциальные функции
Непрерывные ортонормированные комплексные экспоненциаль-
ные функции, определенные на отрезке [0, t], задаются формулой
__ . 2ук
Fl(t,x) = y~e~X,i = Q,±\,±2<... (1.11)
Непрерывные комплексные экспоненциальные функции
(1.11) ортонормировании на отрезка [0, £] с весом p(t, x)sl.
1.2.2. Ортонормированные дискретные
системы функций
Систему функций {(pj, в общем случае комплексных, опреде-
ленных на системе точек (I - 0, 1, L - 1) отрезка [0, £], назо-
вем ортонормированной на этом отрезке с весом р, если все функ-
ции этой системы удовлетворяют условию
L- 1
(РЧ>Л > <р/) = X РЮ <₽лЮ = 5h,i- С1-12)
7 / = 0
1.2.2.1. Полиномы Чебышева
Дискретные ортонормированные полиномы Чебышева, опре-
деленные на отрезке [0, 1], задаются формулой
9
; J(2i + 1)(L - 1)1“ Л . • П
и = О
i = 0, 1, L - 1 ; 1 = 0, 1, 1 ; L = 2, 3, 4,
где
= S(S - - v + 1) ; lk „ = (- 1)‘ - “ C,‘t „ c‘ - " .
Для точечного аппроксимирования удобно считать, что дис-
кретные полиномы Чебышева (1.13) заданы на системе точек
М = jx0 = 0 , хх , х2 > •••» х£ -1} отрезка [0, £] с постоянным шагом
h = xL + । - х(. . Они ортонормировании на этой системе точек с
весом p(L, Z) = 1.
Для дискретных полиномов Чебышева справедлива рекур-
рентная формула
*i + 1 ’ i+l -/-!)(£ +i+l)
x <
л/W* - 1) > ~ .J (£ + 0(ГП)~ * 1
N 3 PX(L. I) Pi(L, I) N (2. + 1){2. _ 1} Pi _ I) > .
i = 0,l, 2..L~ 1 ,
(1.14)
которая позволяет найти все полиномы Чебышева по первым двум
3(L - 1) f 21
(L + 1) L L - 1 “
1.2.2,2. Полиномы Кравчука
Дискретные ортонормированные полиномы Кравчука, опреде-
ленные на отрезке [О, £], задаются формулой
ЦЬ, Z) =
a „.o - 1’1"1 ’
(1.15)
10
i = О, 1, .... L - 1 ; 1 = 0,1. L - 1 ; L = 2, 3, 4..........................
где p > 0 ; q > 0 и p + q = 1 ,
a = s(s - - и + 1) .
Для точечного аппроксимирования удобно считать» что дис-
кретные полиномы Кравчука (1.15) заданы на системе точек
М ~ = 0 , » х2 > xl - i| отрезка [0, t] с постоянным шагом
h ~ xi + xi * Они ортонормированию на этой системе точек с
весом p(L» I) - ClL _ ! pl qL " 1 ~ \
Для дискретных полиномов Кравчука справедлива рекуррент- .
ная формула
х f(2p - l)i + ^pq(L- i) k^L, Z)i x
I * I
x kAL, I) - V---—Ц—- kt ,(L, I) ,
(1.16)
i = 1, 2,..„L - 1 ,
которая позволяет найти все полиномы Кравчука по первым двум
k0(L, /) = 1 ;
1.2.2,3. Тригонометрические функции
Дискретные ортонормированные тригонометрические функ-
ции, определенные на отрезке [О, Z], задаются формулами
л/у , i = 0 ;
Ci<X, 1) =
1 = 0, 1,.
2
Y cos
.„L-l ;
, i= 1, 2,...,L - 1;
L = 2, 3, 4....
(1.17)
11
(1Л8)
~ ,т ~ J 2 • ГО + 1) я ,, ,,
V/L, 1) = N-—.- sin \ (I + 1) ,
* Lt + 1 1 Lt + 1
t = О, 1» ..o L - 1 ; I = О, 1, L - 1 ; L = 2» 3, 4, ...
Для точечного аппроксимирования удобно считать» что дис-
кретные косинусоиды (1.17) заданы на системе точек
_ М - - h/2 , , х2 > **., xL _ отрезка [0< t] с постоянным
шагом , а дискретные синусоиды (1.18) заданы на системе точек
М - jx0 = h , , х2 , ...» xL _ отрезка [0, с постоянным шагом
h = xi+ j - xt . Дискретные косинусоиды и синусоиды ортонорм и -
рованны на указанных системах точек с весом p(L, 1) = 1.
1.2.2.4. Комплексные экспоненциальные функции
Дискретные ортонормированные комплексные функции, опре-
деленные на отрезке [0, £]» задаются формулами
F^L, l) = ^eL
L л _ , L .
i 2 , .... 1, О, 1...... 2 1 ; (1 ig)
I = 0, 1. L- 1 ; £ = 2,4,6,.,.
Для точечного аппроксимирования удобно считать/что дис-
кретные комплексные функции (1.19) заданы на системе точек
М = |х0 > Х1 » х2 ’ •••> XL-1| 0ТРезка [0* И с постоянным шагом
~ xi + 1~ xt * Они ортонормировании на этой системе точек с
весом р(1ч Z) = 1.
1.2.3. Базисные сплайны с конечными носителями
минимальной длины
।
1.2.3.1. Основные понятия
Введем понятие сплайна.
Функция £л(х)» заданная на отрезке [а, д] и имеющая п - v не-
прерывных производных» называется сплайном степени п дефекта
v (о — целое число, 0^и^п+1) с узлами на сетке
12
a = x0 < Xj < ... < xL _ j = b, если на каждом отрезке [хг, х/ + J
функция Sn(x) является многочленом степени п, т.е.
п
3„(х) = £ а*Гх-х/ , (1.20)
fc = 0 J
где х € [х^ , х* * , I - 0, 1, 2,..., L - 1.
Множество сплайнов, удовлетворяющих уравнению (1.20), об-
разует линейное пространство. В этом пространстве можно задать
различные базисные системы функций.
Рассмотрим базисные сплайны с конечными носителями ми-
нимальной длины (В-сплайны), которые образуют базис конечно-
мерного пространства размерности L + п - 1 сплайнов степени п
дефекта 1.
Если п = 0, то В-сплайн имеет вид
В0(х) =
1, х G [- 1/2, 1/2] ;
0, хе [- 1/2, 1/2] .
(1-21>
Любой В-сплайн порядка п можно найти, используя свертку
Вп(х) = Вп _ х(х) • В0(х) = J Вп _ г(у) В0(х - у) dy . (1.22)
Полученная в результате функция В^(х) есть полином степени
п на каждом единичном
г . (п + 1) . - (д + 1) I
отрезке [ j---%— , ] + 1---— J ’
/ = О, 1,...,
п, и равна 0 вне отрезка
(п + 1)
2
(ft + 1) ~|
2 J
. Заметим,
что для В-сплайнов справедлива рекуррентная формула
dBn(x)
dx
Используя свертку (1.22), находим В-сплайны порядка
р = 1,2,3. Они имеют вид
13
х + 1, хе [- 1, 0];
Bj(x) = < 1 — х, хе [0,1] ;
0, х«[-1, 1] ;
_3 _Г1
2 ’ 2J ’
* 1 Г .
2’2]’
(1.23)
(1-24)
О,
(2 + л)3
6,
хе [-2,- 1];
1 + 3(1 + х) + 3(1 + х)2 - 3(1 + х)3
1 + 3(1 - х) + 3(1 - х)2 - 3(1 - х)3
6,
(2 - х)3
6,
х е [О, 1];
х е [1, 2] ;
(1.25)
хе [-2, 2]
и являются наиболее приемлемыми в практических вычислениях.
В частном случае для построения базисной системы из
В-сплайнов на отрезке [0, t] преобразуем конечный носитель
В-сплайна порядка п, отрезок
(» + 1)
2
(п + 1) ~|
2 J
в отрезок
[Z А» (I + п• + 1) A], h = * . Получим
(В — 1)
14
а-2®)
I ** л
L2.3.2. Кусочно-постоянные базисные сплайны
Простейшие кусочно-постоянные финитные функции, опреде-
ленные на отрезке [0, задаются формулой
П/х) = V——
1, хе [lh, (I + 1)Л] ;
(1.27)
О, хе [/Л, (Z + 1)Л] .
1 = 0, 1.
Простейшие кусочно-постоянные финитные функции построе-
ны на сетке xt = hl, h =
t
L- 1
I = 0, L - 1, разбивают отрезок
[0, £] на L - 1 подобластей [lh, (i + 1)Л] , I - 0, 1,..., L - 2, и образует
ортонормированный базис линейной оболочки функций П^х), т.е.
t
j П/х) Л/х) dx -\j.
о
1.2.3,3. Кусочно-линейные базисные сплайны
Кусочно-линейные финитные функции (функции-крышки),
определенные на отрезке [0, t], задаются формулами
KQ(x) =
1 - Y X е [0, А] ;
0, х й [0, Л] ;
^+1(х) =
| - 1, хе [lh, (I + 1)й] ;
I + 2 - j , х е [(I + 1)Л, (Z + 2)Л] ;
0, xt [(lh, (I + 2)Л] ,
(1.28)
I = 0, 1,..., L - 3;
15
KL_1(x) =
%-L + 2,
h
xe[(L- 2)h, (L - l)ft] ;
x £ [(£ - 2)Л, (L - 1)Л] .
Кусочно-линейные финитные функции построены на сетке
= h = —Ц- , / = 0, 1
, L - 1, разбивают отрезок [0, #] на
L - 1 подобластей [/ Д (I + 1)Л], Z = 0, 1,,,,, L - 2, и образуют ор-
тонормированный базис линейной оболочки функций К^(х), при-
чем
i
J К£х) KjCx) dx =
О
= 0 при |i - j\ > 1 ;
# 0 при |i - j\ < 1 ,
т.е. только для соседних функций скалярное произведение отлич-
но от нуля (почти ортогональнрсть).
1.2 А. Ортогональные вейвлеты с компактными
носителями
1.2 АЛ. Основные понятия’
Введем понятие ортогонального вейвлета.
Квадратично интегрируемая функция xg называется ортого-
нальным вейвлетом, если семейство
ft(x) = 2 ;/z у(2' x - й) , j,keZ, (1.29)
является ортонормированным базисом квадратично интегрируе-
мых функций на R. Это означает, что
(Ч.*’ Vi,m)=5j,!5Atm> jtk,l,meZ, (ИЗО)
и любая квадратично интегрируемая функция f может быть пред-
ставлена сходящимся рядом
DO DO
= £ (1.31)
У = — <»&= — оо
16
Ряды, представляющие функции f в (1*31), называются вейв-
лет-рядами или обобщенными рядами Фурье, а вейвлет-коэффи-
циенты Су k определяются формулой
+ «
% k = I fW V* к(х) dx . (1.32)
Для ортогональных вейвлетов возможно точное восстановле-
ние функции, если использовать дополнительную аппроксимацию с
помощью масштабирующей функции ф(х). При. этом вейвлет-пред-
ставление функции (1.31) разбивается на две составляющие: грубую
(аппроксимирующую) и уточняющую (детализирующую)* Мас-
штабирующая функция ф, как и вейвлет у, порождает семейство
fe(x) = 2'?г Ф(2' х - k) , i.keZ, (1.33) \J
которое получено из одной масштабирующей функции ф (одного
Вейвлета ф) в результате двоичного сжатия в 2У раз и двухпарамет-
рического сдвига на /г/27.
Следовательно, можно считать, что задан ортонормированный
вейвлет-базис k , ф; , т*е. базис, отвечающий условиям
’ ДО. =$*,»,• у'
*>VAm)=0. j'keZ-, (1.34)
ДО,*’j<k,l,mEZ,
а поэтому любая квадратично интегрируемая функция на R пред-
ставляется рядом
+ « оо о®
K*)eZ Sj, k <Pj. + Z Z (1-35)
k = — » j = j k = — °°
и полностью характеризуется ее вейвлет-коэффициентами Sj
(аппроксимации) и k (детализации) разложения по этому бази-
су, которые можно вычислить по формулам
17
+ «
«/. ft = J fix) k(x) dx ; — PO (1.36)
+ « ft = J fM V* Й(Г) dX . (1.37)
Обращение функции можно проводить на любом J-м уровне
разрешения.
1.2.4.2, Функции Хаара
Исторически первым ортонормированным базисом вейвлетов
был базис Хаара, построенный задолго до того, как сформировал-
ся термин “вейвлет”. Масштабирующей функцией <р базиса Хаара
является функция (р(х) = 1, если 0 < х < 1, q>(x) = 0 в противном
случае (<рд k(x) - 1, если k/2J < х < (А + 1)/2; , *(х) = 0 в против-
ном случае), а вейвлетом является (базисной системой вейвле-
тов)
II, О £ х < ;
&
- 1, |<Х< 1 ;
&
0 в противном
случае
, 2А + 1 А + 1
- 1, —:—— <х< ;
2; + 1 Я
0 в противном
случае
(1.38)
Тогда базис вейвлетов Хаара с компактными носи-
телями образует ортонормированный базис квадратично-интегри-
руемых функций на Л.
1.2.4.3. Функции Добеши порядка М
Базис Добеши порядка М = 1 является базисом Хаара, т,е.
базис Хаара является частным случаем базиса Добеши. Масштаби-
рующая функция <р(х) и вейвлет Добеши \|/(х) не имеют явных ана-
литических формул, за исключением базиса Добеши—Хаара. Тем
18
№ не менее, если <р непрерывна, для заданного х можно вычислить
L <р(х) с любой точностью.
Е Построение вейвлета Добеши порядка М с компактным носи-
| телём сводится к построению масштабирующей функции Добеши
I порядка М.
I Уравнение, определяющее масштабирующую функцию, имеет вид
I 2М-1
[ <р(х) = £ hk <p(2r -k) , (1.39)
f fc = о
< а вейвлет Добеши строится по формуле
2М-1
i ф(х) = ^2 £ gk tp(2x -k) . (1.40)
j к = 0
t Можно показать (16], что для вейвлета Добеши (1.40) параметры
[ Я* = (-1)*Л2М-й~1? ft = 0-1..»2М-1, (1.41)
| т.е. выражаются через параметры hk однозначно. Сами параметры
hk (k = 0, 1,..., 2М - 1) находятся из решения следующей системы
уравнений:
гм - 1
Е hk hk-2т = So. т > т = °’ М - 1 ’
й = 0
2М - 1 2М - 1
Е kngk = 0; Е Afe = ^2 . (1.42)
k=0 k=0
Например, для вейвлетов Добеши порядка два, т.е* для М = 2
(т = 0,1), уравнения (1Л2) можно записать в виде системы
hl + hf + hj + Л| = 1 ;
ft-Q /ig "I" — 0
ЗЛ0 - + A2 = 0 ;
Ло + fti + Z«2 + Аз = 'fZ >
(1.43)
19
которая имеет два решения:
h 1 (1 + Vi) , А1 = ~ 1 4 >/2 (3 + Vs),
2 4 Vjf (3 - V3) , (1.44)
Йо = -Д= 0 4 -V2 (1 - V3) , (3 - V3),
й2 = —L= 2 4 V2 (3 + <3) , , 1 3 4 ^2 (1 + Vs).
Эти коэффициенты определяют простейший вейвлет Добеши
второго порядка. Коэффициенты для вейвлетов Добеши более вы-
сокого порядка могут быть получены аналогично [11]. Однако из-
за необходимости решать уравнения степени 2М, в общем случае
для них можно выписать лишь численные значения, хотя и с
любой заданной точностью. Область задания вейвлета равна
2М - 1. Вейвлеты Добеши более высокого порядка более гладкие.
По мере роста гладкости вейвлета увеличивается и размер его об-
ласти определения.
1.24.4. Вейвлет-базисы на отрезке
Рассмотренные ранее вейвлеты приводили к базисам квадра-
тично-интегрируемых функций на R. Исключение составляет
базис Хаара [9, 10, 16]. В приложениях обычно используют разло-
жение функции f(x) на конечном интервале. Если функция f(x) за-
дана на конечном интервале, то для ее анализа можно использо-
вать обычные базисы вейвлетов. Например, доопределим функцию
f(x)t полагая ее равной нулю вне [0,1]. Тогда при восстановлении
функции по формуле обращения (1.35) получим искуственные
“скачки” на краях отрезка, отраженные в значениях коэффициен-
тов вейвлетов. Таким образом, полезными были бы вейвлеты, при-
способленные для “жизни на интервале” [11]. Одним из способов
достижения этого является использование периодизированных
вейвлетов, которые удобно записывать в виде
20
cp0 0(х) = 1 при Л = О ;
^fc(x) =
^2Л =*£,*(*) ПРИ Л = 2П + А
I А I
п = О, 1, 2,...; k = О, 1, 2,..., 2” - 1 ,
где периодизированные базисы вейвлетов
<р£* = £ <Mx + z>; а = о,
/е Z
V- = Z Vj,*(x + Z); A = 0, 1, .... 2n - 1
Ze Z
(1.45)
(1.46)
(1-47)
Анализ функций, заданных на отрезке в базисе (1.45), эффек-
тивен при проведении вычислений, однако его использование оз-
начает анализ периодизированной функции /”(х), определенной
как /п(х) = /п(х - LXJ )) (где LXJ означает наибольшее целое, не пре-
восходящее х) с помощью обычных (непериодизированных) вейв-
летов. И хотя / уже периодична, на границах 0, 1 снова возникают
“скачки”. Избежать скачков на границах можно, заменив функцию
ftx), заданную на отрезке, инверсно-периодизированной функцией
А*) = 1 + (~1)W Ах - LxJ) +
I _ (_ nL*J
+-----(1 - Ах - L*J ) (1-48)
Существуют и другие способы задания вейвлет-базисов на от-
резке [11].
1.3« Интерполирование функций
Будем считать данную функцию /(х) и полином Q^(x) (1.2)
близкими (т.е. имеющими малое “отклонение”), если они совпадают
на заданной системе точек х0 , xt xL_ t (узлы интерполирова-
ния). Таким образом, мы приходим к следующей задаче интерпо-
лирования: для данной функции f(x) найти полином бщ(*)» воз-
21
можно низшёй степени т, принимающий в заданных точках х-
(i = О, 1, ..., L - 1 ; х- Ху при i - j) те же значения, что и функция
f(x), т.е. такой, что Q^x-) = f(xt) (t = 0, 1, ...» L - 1).
Полином называется интерполяционным.
Если L - 1 < пг9 то можно положить т - L - 1 и определить ко-
эффициенты из системы уравнений
а0 + Д1 х0 +... aL_i Хф X = f(xo);,
а0 + аг хг + ... аь_г xf " 1 = Дхр ;
а0 + xL _ х + ... aL _ i xf Z { = f(xL _ р .
Определитель этой системы А есть определитель Вандермонда:
д= П
О < р < q < Л /
и, следовательно, система (1.49) имеет единственное решение.
Полином Qm(x) ~ - i(*)» коэффициенты которого определя-
ются из системы (1.49), называется интерполяционным полино-
мом Лагранжа для функции /(х) и может быть записан в явном
виде:
L-1
К*) = Е f(xi) , (1.50)
1 = 0
где
(x-x0)...(x-xz_1)(x-xf ^...(х-х^,!)
Р*„(х) =-----ii—-----—--------—---------— . (1.51)
(Xi Xq)..,(Xj Xj _ jXXj Xj+2)...(Xi Xl _ i)
Это классический метод решения задачи алгебраического ин-
терполирования функций. Интерполяционный полином Лагранжа
явным образом выражается через фундаментальные многочлены
(1.51), такие, что каждый из них принимает значение, равное еди-
нице, в одном из узлов интерполяции и нулевые значения в ос-
тальных.
Задачу интерполяции можно решать с использованием других
базисных систем функций, которые были рассмотрены выше. Ос-
22
тановимся здесь только на применении сплайнов. Отметим, что
найдены такие фундаментальные сплайны порядка п дефекта 1
по которым построена интерполяционная формула Лагран-
жа для сплайнов
L- 1
Six) = Z Кх1> • <1.52)
/ = 0
Рассмотрим простейшую задачу приближения сплайнами. По-
строим сплайн 8г(х) = Sr(f; x)t совпадающий с f(x) в точках
r; = AZe[O, f] , 1 = 0, 1.L-l, h = ~~, (1.53)
— 1
Из определения сплайна (1.20) получается система 2L - 2
уравнений:
«1(А х<) = f(xi) , I = 0, 1..L - 1 ;
= + » / = 0>1.....Ь-1.
Эта система распадается на системы уравнений относительно
коэффициентов отдельных многочленов
si(f> xi) = а? = f(xi) ;
S^f; xl + 1) = a^ + a}(x( + 1-X{) = f(xt + J,
отсюда находим
где ft = f^Xj) .
Тогда из определения сплайна (1.20) будем иметь
51(Ах) = (1-т)^ + т// + 1, (1.54)
где т = (х - hty/h.
Это уравнение интерполяционного сплайна первой степени
дефекта 1.
23
Заметим, что эту формулу можно получить из формулы (1.52),
если в качестве фундаментальных сплайнов взять базисную систе-
му (1.28).
Усложним задачу приближения сплайнами. Построим теперь
сплайн S2(x) = S2(ft х), совпадающий с /(х) в точках (1.53) и имею-
щий первую непрерывную производную. Такой сплайн на отрезке
[xt > X/ + j] есть многочлен второй степени, который можно пред-
ставить в форме суммы линейного многочлена, принимающего на
концах отрезка значения и fl + ± , и многочлена второй степени,
обращающегося в нуль на концах отрезка. Легко проверить, что
такое представление имеет вид
S2№x) = (l^)f/ + VH1+p^(^l), (1.55)
Это уравнение интерполяционного сплайна второй степени
дефекта /, в котором неизвестные параметры выбираются так,
чтобы производная S2(/; х) в точке - hl, где соединяются отрез-
ки [х^ _ х , xj и [х, , Xj + была непрерывна. Это дает систему, со-
держащую L - 1 уравнение с L неизвестными. Один из параметров
pt остается произвольным и может быть выбран из дополнительно-
го условия или задан произвольно. Например, если известно зна-
чение производной от f(x) в точке х = 0, то параметр р$ может быть
найден из условия S2(/; 0) = f(0). Тогда для определения парамет-
ров находим систему уравнений
Ро ~ fl ~ ~ hfo ;
Л+1+Л“Л+1^2Л + Л-1> = 2,..., L - 2.
Наибольшее распространение при интерполяции функций по-
лучили сплайны третей степени S$(x) = S$(f; х).
Кубическим интерполяционным сплайном дефекта 2 (эрми-
товым кубическим сплайном) называют функцию S3(x), удовле-
творяющую следующим условиям:
1) на каждом из промежутков [х^ , xL + х]
S3(x) - af+ а*(х - хр -к af(x - х^)2 + af(x - хг)3 ;
24
2) S3(xz)-/z, 5^) = /;, I -0,1.....L-l. ;
Для вычисления 4L - 4 коэффициентов , k = 0, 1, 2, 3, при
каждом Z имеем систему уравнений
5з<хР = Л’ ЗД+, 1) ” fl + 1 ’ 5з(хР"Л’ 53^+1)”Л + 1’
Решив эту систему, получаем на Гх£ , xL + Л
S3(f; X) = ft (1 - т)2 (1 + 2т) + + д т2(3 - 2т) +
г' +Лт(1-т)р/1-т)-Г; + 1т]. (1.56)
Если производная в узлах сетки неизвестна, то ее можно апп-
роксимировать на основе разделенных разностей, положив
- _ 3/0“ 3/\ + f2 _fl+l~ fl-1
Т°~ 2h 'fl- 2h
1 = 0,1, .... L - 1 ;
6.-3 ~ 4fr, - 2 + 3^L - 1
'i-1- 2h
Заметим, что вторая производная эрмитова кубического
сплайна, вообще говоря, разрывна в узлах сетки. Однако можно
определить кубический сплайн, который является дважды непре-
i рывно дифференцируемой функцией.
Кубическим интерполяционным сплайном дефекта 1 называ-
J ют сплайн S3(x) , удовлетворяющий условиям
s^xi> = fi > l = Q> 1.L~ 1 •
Дополнительные условия
S'3(f; xz) = тг, Z - 0, 1, L - 1 ,
позволяют рассматривать сплайн S3(x) как эрмитов кубический
сплайн, т.е. представить его в виде
S3(A х) = ft (1 - т)2 (1 + 2т) + + (3 - 2т) +
+ hi (1 - т) Гтг (1 - т) - т1 + ! т
(1.57)
25
и выбрать величины так, чтобы была непрерывна и вторая произ-
водная S3(x) , т.е* выполнялось условие S3(/; х^ + 0) = S3(/; - 0) в
точках Хр I - 0, 1, ..., L - 1 .
Эти условия вместе с краевыми условиями (употребляются
различные виды краевых условий) достаточны для определения L
неизвестных из решения некоторой системы линейных алгебра-
ических уравнений.
В некоторых случаях более удобным является другое пред-
ставление кубического сплайна, в котором вместо величин ис-
пользуются = S3(x^) , Z-0,1, L - 1 . В этом случае интерпо-
ляционный кубический сплайн можно представить в виде
53(Ах) = ^(1-т) + /г + 1т +
>2
+ ^-T(l-T)[(2-T)zz + (l + T)z/ + 1]. (1.58)
Численные схемы вычисления интерполяционных кубических
сплайнов на равномерной сетке в разных постановках и для раз-
ных краевых условиях приведены в приложении 1.
Заметим, что если L - 1 > тп, т.е. число узлов интерполирова-
ния превосходит степень полинома больше, чем на единицу, то за-
дача интерполирования становится, вообще говоря, невозможной.
В этом случае обычно прибегают к точечному квадратичному апп-
роксимированию функции.
1.4. Точечное квадратичное аппроксимирование
функций
1.4.1. Метод алгебраических полиномов
При точечном квадратичном аппроксимировании за меру от-
клонения полинома
(?т(х) = а0 + ах ж + а2 г2 + ... + <хт х™ <1-59>
от данной функции у = /(х) на множестве точек х0 , хх _ i
принимают величину
26
К 1-1
' 8 = 2 [«Л)-/(*!>]2 . (1-60) "
Е z = оL
В называемую квадратичным отклонением.
К Для построения аппроксимирующего полинома требуется по-
t добрать коэффициенты а0 , , а2 ат так> чт°бьт величина S
с была наименьшей. Предположим, что В случае
•f т = L - 1 коэффициенты а- (у = 0, 1, L - 1) можно определить
из системы уравнений
: QL.1(xJ = /(x.) при i = 0, 1, L - 1 , (1.61)
причем S = 0, и приходим к разработанной выше проблеме интер-
полирования функций. При т £ L - 1 система (1.49), вообще гово-
I ря, несовместна. Поэтому сама постановка вопроса о точном ре-
шении теряет смысл. Решение нашей задачи аппроксимирова-
ния следует из минимизации функционала (1.60) и приводит к
? решению
у . А = [хт х]- 1 ХТ FT , (1.62)
f где
Г1 г т2 гт
, . 1 Хо Хо ... Хо
L х= 1 х’ **
— матрица-строка т + 1 основных функций ф0(х) = 1 , ф^х) ~ х,
Ф2(х) = х2,..., Фт(х) = х'71,..., значения которой, вычисленные в точ-
ках xt (I = 0, 1, L - 1), развернуты в вертикальный столбец;
Г F = [/(х0) , /(хх), pj — матрица-строка L значений задан-
ной функции на системе точек х0 , х^ , ...» xL _
L АТ = |~а0 , транспонированная матрица-столбец неиз-
f вестных коэффициентов полинома (1.59).
27
Можно доказать» что если среди точек х0 , хг , ...» xL_1 нет
совпадающих и т <L - 1, то определитель системы (1*62) отли-
чен от нуля.» и, следовательно, эта система имеет единственное
решение.
Е4Л. Метод ортогональных полиномов
/
Пусть
Ро(х) , р^х), ...» рт(х) , (1.63)
заданная система ортогональных квадратично суммируемых на
множестве точек jx0 , хх , ...» xL полиномов (функций). Так
как полиномы (1.63) линейно независимы» то произвольный поли-
ном Qm(x) степени можно представить в виде линейной комбина-
ции полиномов из системы (1.63), т.е.
= ъо р0(х) + ..., + Ът Рт(х) . (1.64)
Это представление называется разложением полинома Q^Cx)
по системе (1*63)-
Задача аппроксимации заданной функции у - f(x) на множест-
ве точек Xq , Xj х^_ 1 ортонормированным полиномом (функ-
цией) данной степени т(т<Ь-1)из условия минимума квадра-
тичного отклонения
L -1
У р(*х) ’ л*1)] =пнп
/ = 0
приводит к алгоритму вычисления коэффициентов (i = 0, 1, ...» т)
по формуле
L- 1
»< = Е • п-65)
1 — 0 »
28
Эта формула получается из (1,62) при условии ортонормиро-
ванности полиномов р/х), так как в этом случае ^Х7* Х^ = Е, а
X = P = P(L, т) =
' Р0(Д°) * Pq(L, 1) * о) Р1(Д 1) * р2(Л, 0) ... * Рт(Д0) ' РМ(Ь.1) *
* • •
* ж
Р0(Ь> L -: 1) P1(L, L - 1) p2(L,L-l) ... рж(ДЬ-1)!
* * * ♦
и элементы матрицы Хт имеют вид
pt(Lt 0 - p(L, 1) ;*(£, I) .
Отсюда искомый аппроксимационный полином имеет вид
т
= (166)
i = 0
Пример. Возьмем в качестве системы ортонормированных
функций полиномы Чебышева (1.14). Пологая I - (х - xQ)/h и учи-
тывая, что для полиномов Чебышева х0 = 0, h = t/Lf находим апп-
роксимационную формулу Чебышева
т
<?«(*) = £ V
»=о Л )
при т < L - 1.
(1.67)
1.5. Интегральное квадратичное аппроксимирование
функций на отрезке
Предположим, что данную непрерывную функцию f(x) нужно
аппроксимировать на Конечном отрезке [0, t] с помощью обобщен-
ных полиномов
Чп<*) = са Фо + С1 <Р1 + ”• + ст <Pm > С1-68)
29
где |фг(х)| — заданная система непрерывных функций и — посто-
янные коэффициенты.
Согласно способу наименьших квадратов коэффициенты q
(i — 0, 1, т) подбираются так, чтобы квадратичное отклоне-
ние полинома Qm(x) от функции Дх), равное
ь
Jw = j p(x)[Qm(X)-f(X>]2dx = min, (1.69)
а
имело наименьшее значение.
Как известно, минимум функции 1т
= 1т(с0...залают
коэффициенты, найденные из системы
МФо • Фо) + С1(Ф1 ’ Фо) + ••• + Ст(Фт • Фо) = Фо> >
<\)(Фо » Ф1) + С1<Ф1 г Ф1) + ... + cm«pm , ФР - (А фх);
t
со(Фо ’ Фт) + С1(Ф1 • Фт) + - + ст(Фт > Фт> = <А ФМ) ’
где
b
(рФг » фЛ = J Р(х) Ф*О) Ф/х) dx .
\ 7 а * •
Доказывается, что если <р0(х) Фт(х) линейно независимые
на отрезке [а, Ь], то система (1.70) имеет единственное решение,
которое соответствует наименьшему квадратичному отклонению.
При этом если система j<pjx)| есть система базисных сплайнов
(1.22), то матрица системы (1.70) есть матрица с диагональным
преобладанием и может быть решена методом прогонки. Более
того, если система {(^(х^ортонормированна, то коэффициенты
(^вычисляются особенно просто:
30
d
= J P(*) Я*) Ф*(х) dx • (1-71)
a
Коэффициенты cL , определяемые формулой (1.71), называют-
ся коэффициентами Фурье функции f(x) относительно заданной
ортонормированной системы с весом р(х).
Таким образом, справедлив вывод: обобщенный полином с ко-
эффициентами Фурье данной функции обладает наименьшим
квадратичным отклонением от этой функции по сравнению со
всеми другими обобщенными полиномами того же порядка т.
Замечание 1. Если система ортонормированных функций |<р^(х)| тако-
ва, что для любой непрерывной функции f(x) справедливо соотношение
Нт 1т = О, то эта система называется полной. В противном случае — не*
т —> «
полной.
Замечание 2. Формула (1.71) называется прямым преобразованием
Фурье, а формула (1.68) — обратным преобразованием Фурье.
Глава 2. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
НА ПРИБЛИЖЕНИЕ ФУНКЦИЙ В СРЕДЕ MATHCAD
В этой главе приведены примеры решения задач в среде Math-
cad на методы приближения функций, рассмотренные в первой
главе. Каждый рассмотренный пример является рабочим докумен-
том Mathcad и может быть полностью воспроизведен в системе
Mathcad.
Пусть на конечном отрезке заданы функции:
/1(х) =
вх+4
____о
2х7 + 5
/2(х) = cos
(2.1)
(2.2)
31
/3(х) = 1(х - 0,25) - 1(х - 0,77) ; (2.3)
/4(х) = 1(х - 1/4) - 2 • 1(х - 1/2) + 1(х - 3/4) ; (2.4)
/5(х) = 1(х - 0,105) - 1(х - 0,205) ; (2.5)
Г6(х) = 10/4(х) sin (8ях) + 20f5(x) ; (2.6)
Рассмотрим различные методы их приближения.
2.1. Интерполирование функций на отрезке
Пример 1. Требуется интерполировать функцию (2.1), задан-
ную на системе точек (на равномерной сетке или таблично) х{ = hl,
I = 0, 1, ..., L - 1, где хг е [0, t] и h = — кубическим интерпо-
XJ — 1
ляционным сплайном (П.1), который удовлетворяет краевым ус*
ловиям (П*3).
Решение задачи*
1. Зададим функцию (2*1) табличным способом.
Положим:
хп := 0 хк:=» t - начальное и конечное
1 значение функции (2.1)
1:=O..L-1 Н;=£-“ xi:=hl У1= Г(*1)
Находим:
? = ( 0 1 2 3) ут = ( 0.033 0.881 0.047 4.149 х 10"3 )
2. Интерполируем функцию (2.1) кубическим сплайном на
равномерной сетке*
32
г
2.1. Составим и решим систему алгебраических уравнений
(П.6), обеспечивающих выполнение непрерывности первой и вто-
рой производной кубического сплайна:
а) представим эту систему в матричном виде DV = С, где мат-
рицы D и С находятся с использованием программирования:
Щ):- Do o*~2 > for ie 1..L-2 n 1 1 D л xk- xn h< L- 1 CL ХП Co 2 I —f(ct) | ^da J for le 1..L-2 r 3 [f[h (1+ l)]-f[h(l-l)J]
1 2-h a xk Сц <- 2 • i-f(a) da C
Замечание. Сеточная (табличная) функция f(X[) и значение ее произ-
• водных в начальной и конечной точках отрезка [0* 0 формируются в про-
; грамме С(/, L, xnt xk) по передаваемой в нее аналитически заданной функ-
L: ' ции Дх);
б) решаем эту систему методом обращения матрицы D:
Mi-DfL)"1 C(f,L,xn,x$ < 2 0 0 0 ^ <2.4 A 0.5 2 0.5 0 0.02 D(L)» C(f ,L,xn,ri$ - M = 0 0.5 2 0.5 -1.315 0 0 □ 2 J -0 .017 ) ' 1.2 A -0.135 -0.622 < -8.2» x 10“3 J
i
Столбец М содержит L неизвестных /nz (I = 0, 1, L - 1), ко-
торые гарантируют непрерывность первой и второй производной
сплайна S3(/; х).
33
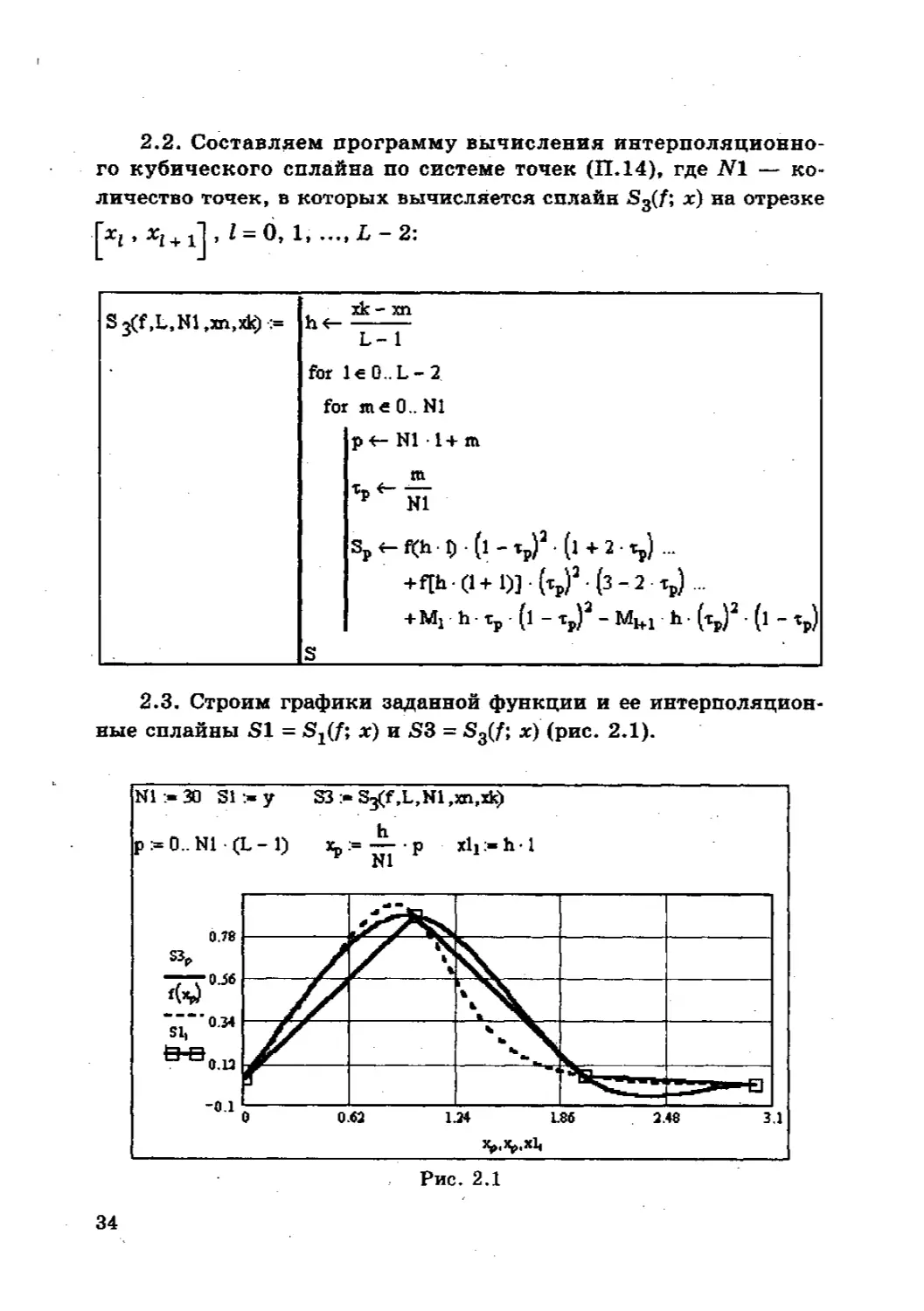
2.2. Составляем программу вычисления интерполяционно-
го кубического сплайна по системе точек (ПЛ4), где JV1 — ко-
личество точек, в которых вычисляется сплайн S3(/; х) на отрезке
ГХ1, , Z = 0, 1» ...» L - 2:
эск)-:=
xk - xn
--------
L- 1
for leO„L-2
for me 0.. N1
p -f- N1 1+ m
tn
p N1
Sp<-fl<h l) (l-»p)2 (1+2 tp) -
+f[h (l+l)]-(tp)J (3-2 tp) ...
+Mj h rp (1 - TP)S - MM h- (tp)2 . (1 - tp)
2.3. Строим графики заданной функции и ее интерполяцион-
ные сплайны SI = х) и S3 = S3(f; х) (рис. 2.1).
34
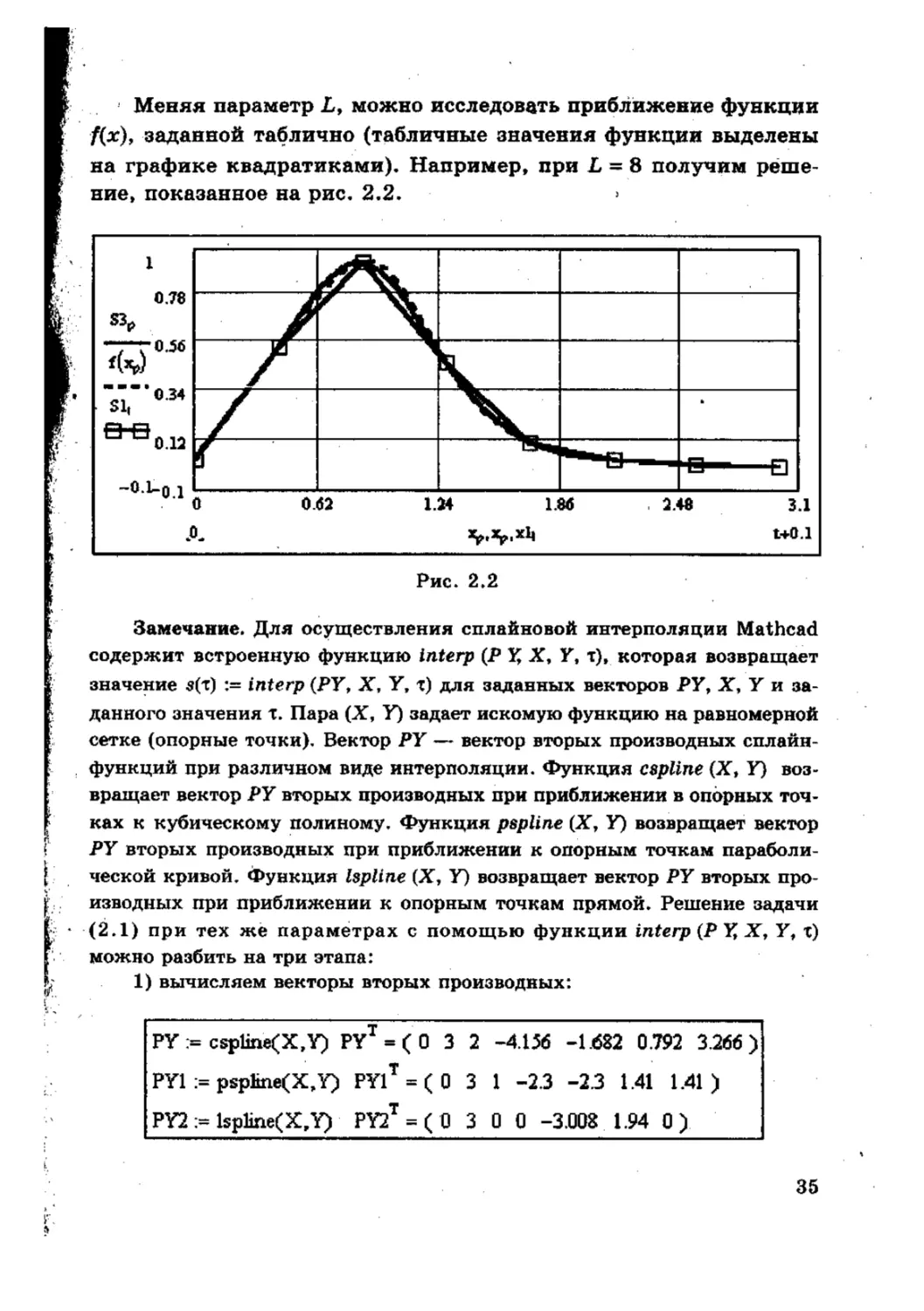
Меняя параметр L, можно исследовать приближение функции
f(x), заданной таблично (табличные значения функции выделены
на графике квадратиками). Например» при L = 8 получим реше-
ние, показанное на рис, 2.2,
Рис, 2.2
Замечание. Для осуществления сплайновой интерполяции Mathcad
содержит встроенную функцию interp (Р Y, X, У, т), которая возвращает
значение з(т) := interp (PY, X, У, т) для заданных векторов РУ, X, Y и за-
данного значения т. Пара (X, У) задает искомую функцию на равномерной
сетке (опорные точки). Вектор РУ — вектор вторых производных сплайн-
функций при различном виде интерполяции. Функция cspline (Xt У) воз-
вращает вектор РУ вторых производных при приближении в опорных точ-
ках к кубическому полиному. Функция pspline (Xf У) возвращает вектор
РУ вторых производных при приближении к опорным точкам параболи-
ческой кривой. Функция Ispline (X, У) возвращает вектор РУ вторых про-
изводных при приближении к опорным точкам прямой. Решение задачи
(2.1) при тех же параметрах с помощью функции interp (Р X У» т)
можно разбить на три этапа:
1) вычисляем векторы вторых производных:
PY := cspline(X.Y) PYT = ( 0 3 2 -4.156 -1.682 0.792 3.266)
PY1 := psplme(X,Y) PY1T = ( 0 3 1 -2.3 -2.3 1.41 1.41)
PY2 := lspline(X,Y) PY2T = ( 0 3 0 0 -3.008 1.94 0)
35
2) формируем сплайн-функции трех типов:
ЗМ(т) intMp(PY,X,Y,t) SMl('t)'inteip(PYl,X,Y,т)
SM2(t) := mteip(PY2,X,Y,t)
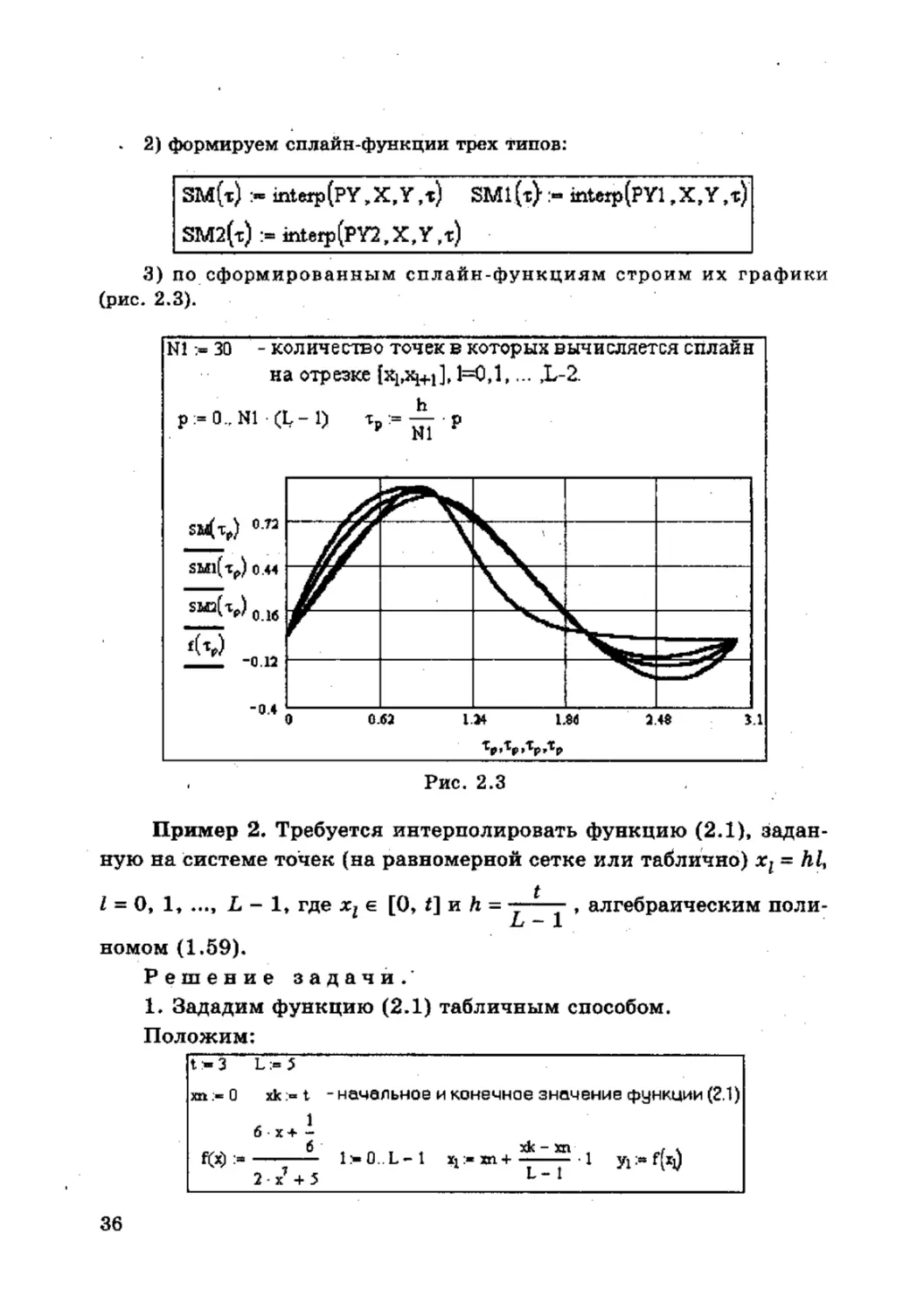
3) по сформированным сплайн-функциям строим их графики
(рис. 2.3).
Пример 2. Требуется интерполировать функцию (2.1), задан-
ную на системе точек (на равномерной сетке или таблично) xt - hl,
I = 0, 1.
L - lt где X} g [0> f] и h = —
Lj “ 1
алгебраическим поли-
номом (1.59).
Решение задачи/
1. Зададим функцию (2.1) табличным способом.
Положим:
t>3 L:=5
xn > 0 xk := t - начальное и конечное значение функции (2,1)
1
б х + -
l^O L-1 xtхп + 1
2 х7 + 3 L”t
36
Находим:
хТ = ( 0 0.75 1.5 2.25 3) у^Л оДЗЗ 0.886 0.234 0,023 4.149 хИГ*)
2. Интерполируем функцию (2.1) алгебраическим полиномом
на равномерной сетке но алгоритму (ПД9).
2.1. Составляем программу вычисления коэффициентов ин-
терполирующего полинома (П.16) по алгоритму (ПЛ 9):
A(f,L.xn,d$ := . . хк- хп hl < L- 1 for he0..L - 1 Fhi0<-f(hl-h) for he0..L- 1 for i e 1.. L - 1 Plhii,4- (hl • h/ B<-PCl-F В
2.2. По составленной программе находим коэффициенты а( ал-
гебраического полинома Q(x) и формируем его:
L-1
аA(f,L,xn,xk) аТ = ( 0 .033 3.737 -4.856 2.07 -0.289) Q(x) ®i х1
i =0
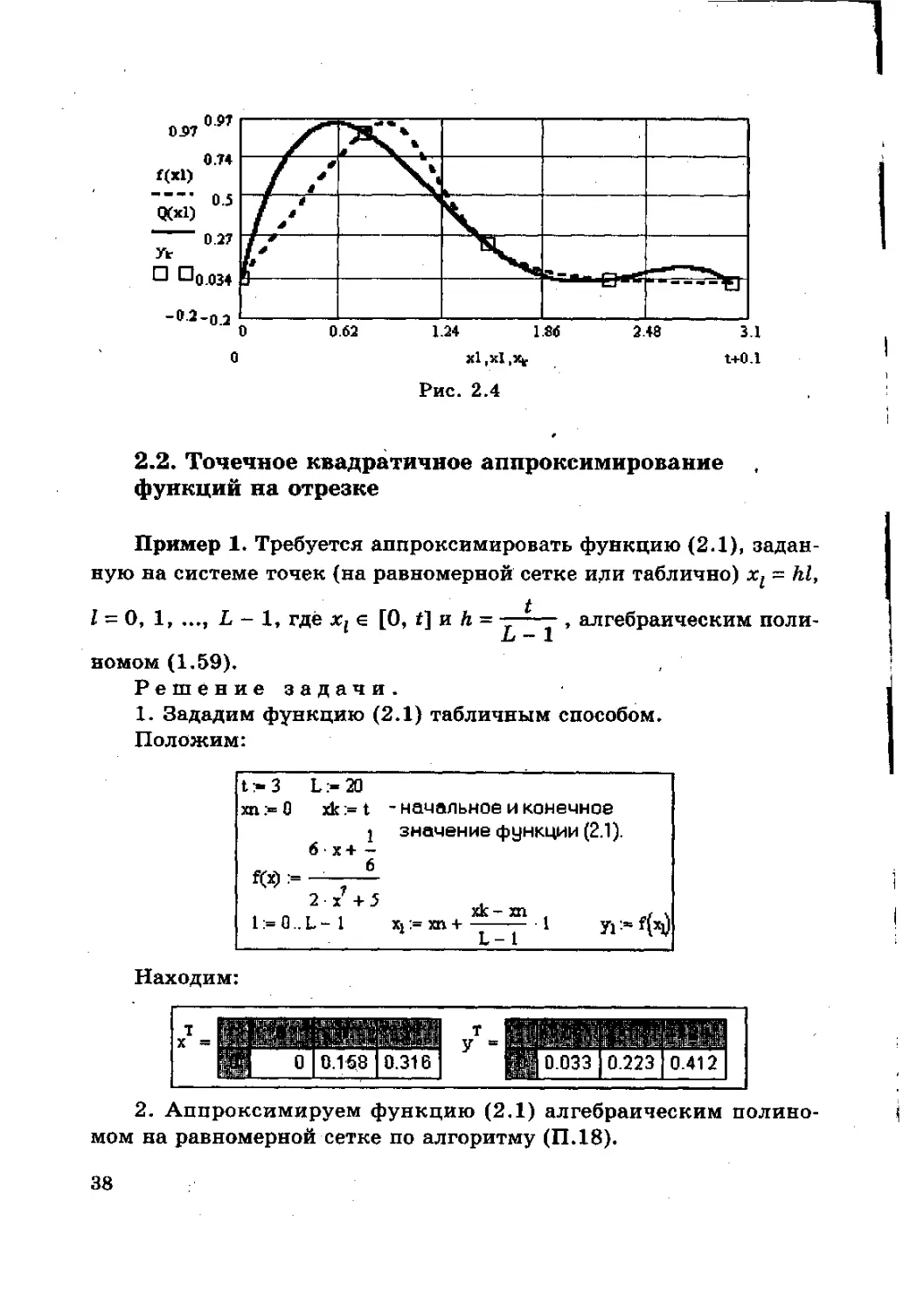
2.3. Строим графики заданной функции (2Л) и ее интерполя-
ционного полинома Q(x) (рис. 2,4). Сеточные (табличные) значе-
ния функции, по которой строится интерполяционный полином,
выделены на графике квадратиками.
37
Рис. 2.4
2.2. Точечное квадратичное аппроксимирование
функций на отрезке
Пример 1. Требуется аппроксимировать функцию (2.1), задан-
ную на системе точек (на равномерной сетке иди таблично) = hl,
1 = 0, 1, ..., L - 1, где х( е [0, f] и h = —-—
Lt — 1
алгебраическим поли-
номом (1,59).
Решение задачи.
1. Зададим функцию (2Л) табличным способом.
Положим:
t>3 L>20
xn := 0 хк := t
6-хЛ
ОД:=——
2 х7 + 5
1:=O..L- 1
- начальное и конечное
значение функции (2.1).
Находим;
yi>fM
xk- хп 4
Xi := хп +---- 1
1 L- 1
2. Аппроксимируем функцию (2Л) алгебраическим полино-
мом на равномерной сетке по алгоритму (ПЛ8).
38
2Л. Составляем программу вычисления коэффициентов апп-
роксимирующего полинома (ПЛ6) по алгоритму (ПЛ8):
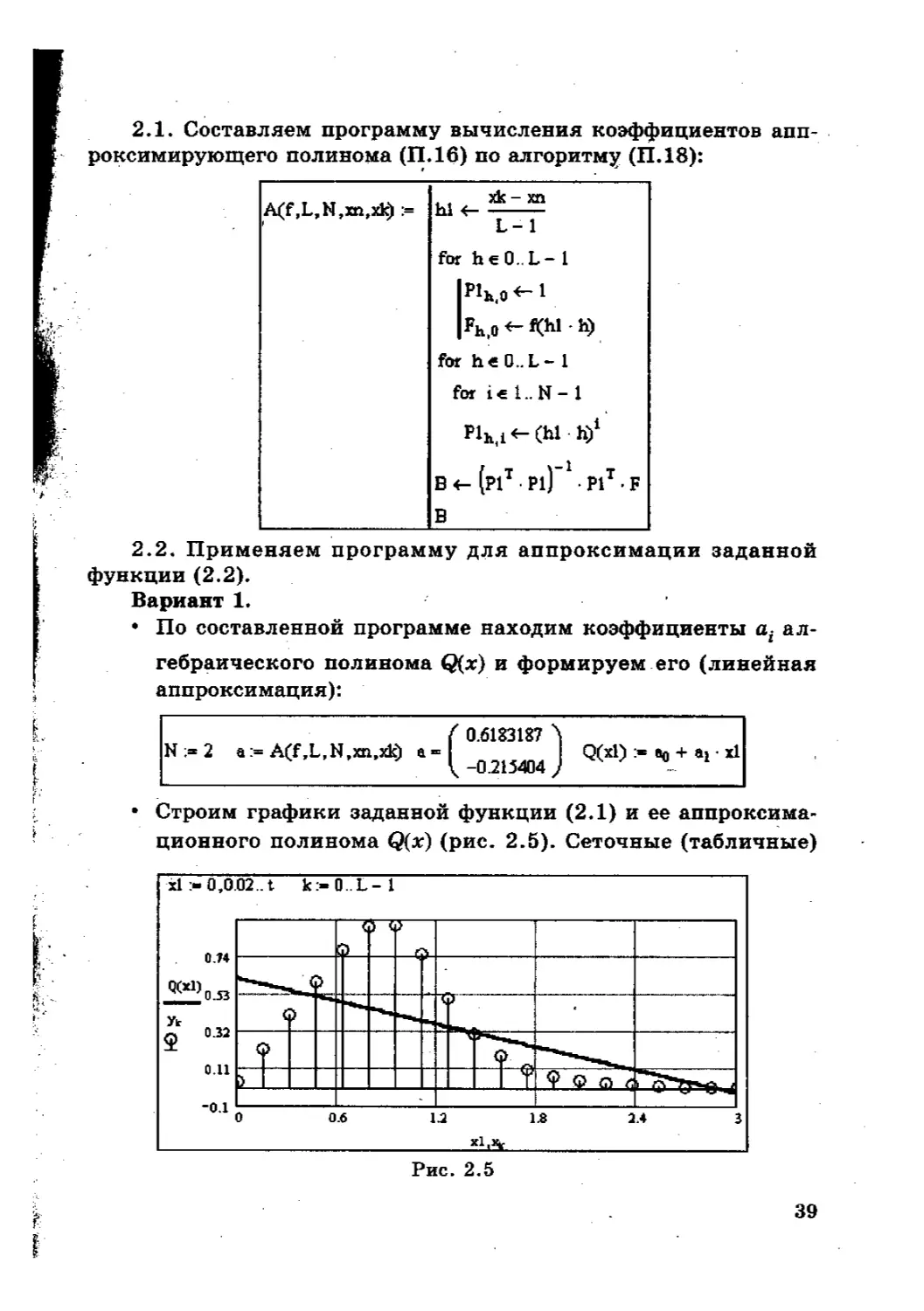
A(f,L,N,xn,xk) := 4 t xk - xn hl < L- 1 for heO. L- 1 |Hh|0 4- 1 h) for heO..L-l for i e 1.. N - 1 Plhll<-(hl h)1 В <- (plT Pl)-1 P1T . F В
2.2. Применяем программу для аппроксимации заданной
функции (2.2).
Вариант 1.
• По составленной программе находим коэффициенты ал-
гебраического полинома Q(x) и формируем его (линейная
аппроксимация):
( 0.6183187 А
N ;» 2 а:= A(f,L,N,xn,xfc) Q(xl) > (ц, + ar х1
V -0.215404 ) 4 '
• Строим графики заданной функции (2Л) и ее аппроксима-
ционного полинома Q(x) (рис. 2.5). Сеточные (табличные)
39
значения функции, по которой строится аппроксимацион-
ный полином, выделены на графике кружочками.
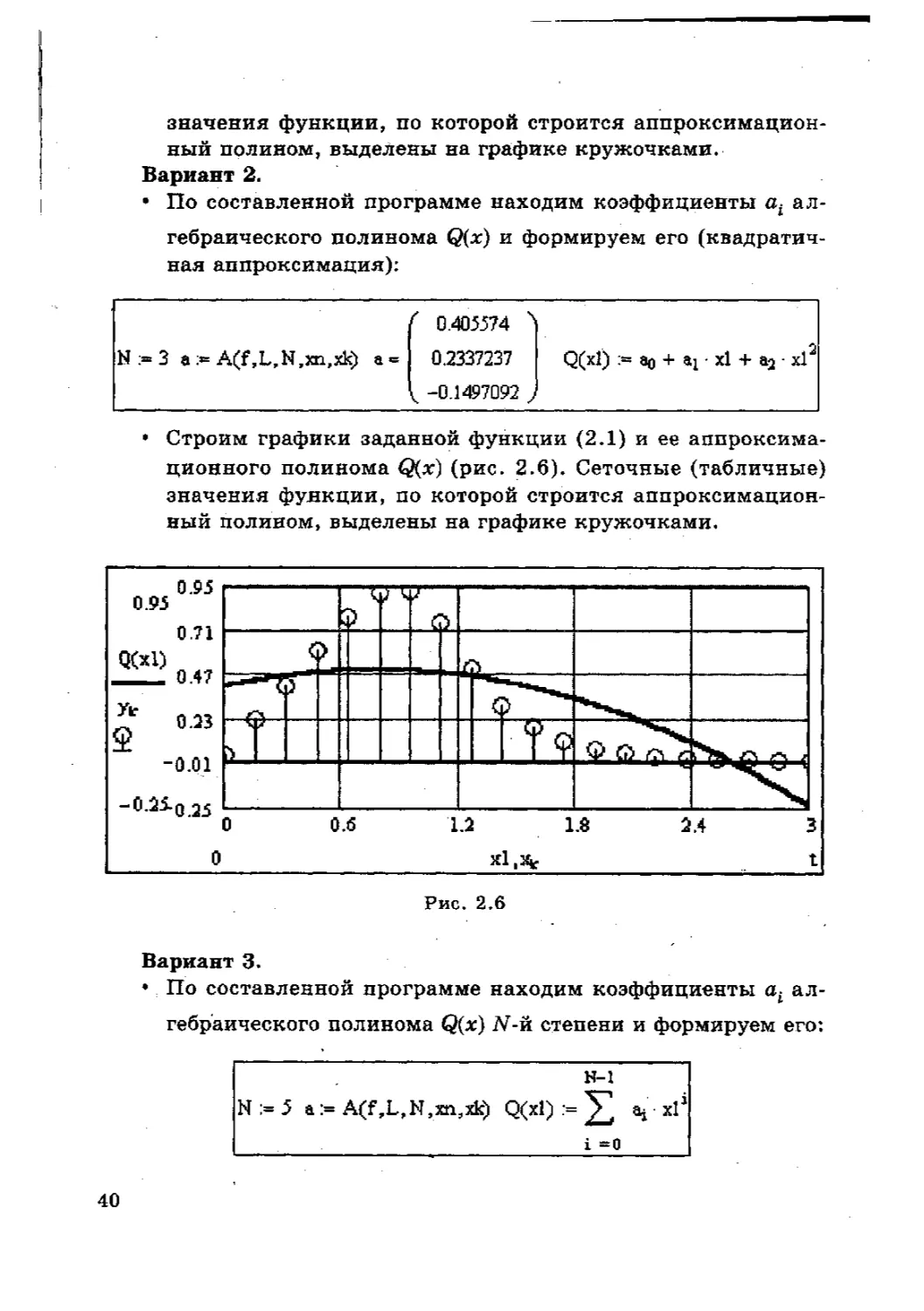
Вариант 2.
• По составленной программе находим коэффициенты ал-
гебраического полинома Q(x) и формируем его (квадратич-
ная аппроксимация):
( 0.405574 >
N := 3 а :•= A(f,L,N,xn,xk) а = 0.2337237
о
Q(xl) ао + • xl 4- xl
V -0.1497092 )
• Строим графики заданной функции (2.1) и ее аппроксима-
ционного полинома Q(x) (рис. 2.6). Сеточные (табличные)
значения функции, по которой строится аппроксимацион-
ный полином, выделены на графике кружочками.
Рис. 2.6
Вариант 3.
• По составленной программе находим коэффициенты ал-
гебраического полинома Q(x) Л’-й степени и формируем его:
N-1
N := 5 а:= Q(xl) := ^ а, х?
i =0
40
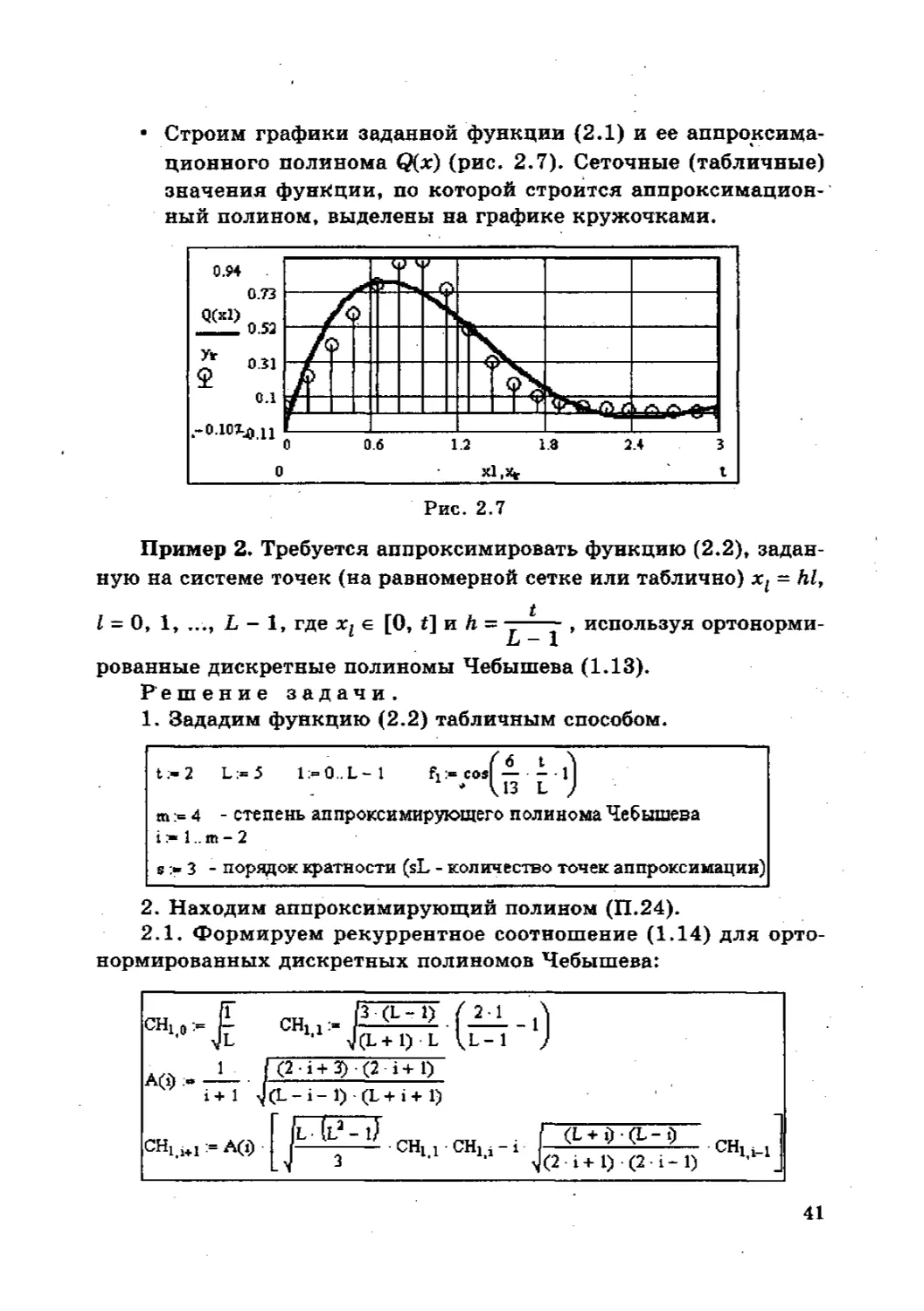
• Строим графики заданной функции (2.1) и ее аппроксима-
ционного полинома Q(x) (рис. 2.7). Сеточные (табличные)
значения функции, по которой строится аппроксимацион-
ный полином, выделены на графике кружочками.
Пример 2. Требуется аппроксимировать функцию (2*2), задан-
ную на системе точек (на равномерной сетке или таблично) х; - hl,
I - 0» 1, L - 1, где X} е [0, i]n й = —-—
L — 1
используя ортонорми-
рованные дискретные полиномы Чебышева (1.13).
Решение задачи.
1. Зададим функцию (2.2) табличным способом.
(6 t 1
t;-2 L:=5 ft > cos-1
* V3 L )
tn > 4 - степень аппроксимирующего полинома Чебышева
s > 3 - породой кратности (sL - количество точек аппроксимации)
2. Находим аппроксимирующий полином (П.24).
2.1. Формируем рекуррентное соотношение (1.14) для про-
нормированных дискретных полиномов Чебышева:
сн £ сн •- Р ( 21 11
ЬгЦ ft .₽ f— Uni j “ " * 1---1
’ JL J(L+1) L )
A „ 1 ПГЗТзПГТИГ
All J .«* / r
i+1 ^(L-i-1) (L+i+1)
CHlii+1:=A(i)
fb 1) "-СНц-СНц 1 ' vtll »_1
3 5 (2 i+1) (2 i-1) ’ _
41
2*2. Вычисляем коэффициенты разложения аппроксимирую-
щего полинома Чебышева (П.23) для функции /(х):
________________________________/____
а:» • СН - коэффициенты разложения
а" (2.0149768 -0.2066513 -0.0587214 1.4240153х 10“3 )
2.3. Формируем рекуррентное соотношение дискретных поли-
номов Чебышева для аппроксимационной формулы (П.24):
1:=0.. s L
i:= l 2
CHl'°;= J
/3(L-1) Г 2 1 1
^(L+ 1) L [(к-!) -s J
A(i) :=
[ (2 -1+ 3) (2 1 + 1)
<L-i- 1) (L + i+ 1)
CHlti+lAQ -
-СН1(1-СНм-1
1 (L+i)(L-i)
(2 • i+1) • (2 • 1-1)
2.4. Формируем аппроксимирующий полином по системе дис-
кретных ортонормированных полиномов Чебышева:
Q а СНТ
2.5. Строим графики заданной функции (2.2) и ее аппроксима-
ционного полинома Q(x) (рис. 2.8). Сеточные (табличные) значе-
t .
q > - • 1 - система точек на которой заданы
L исходные данные.
k:=O .s L
хь > —— к -система точек на которой вычисляется
s L аппроксимационное приближение.
Рис. 2.8
42
ния функции, по которой строится аппроксимационный полином,
выделены на графике кружочками.
Пример 3. Требуется аппроксимировать функцию (2.3), задан-
ную на системе точек (равномерной сетке или таблично), исполь-
зуя быстрое вейвлет-преобразование Добеши порядка два (П.40),
(ПЛ5).
Решение задачи.
1. Зададим табличную функцию по аналитически заданной,
функции (2.3) и построим ее график (рис.2.9).
Рис. 2.9
2. Сформируем программу вычисления аппроксимирующих
вейвлет-коэффициентов на J-м уровне разрешения, предполагая,
что функция продолжена периодически на всю числовую ось и
8J, k ~ :
Sd2phi(g,J) :» forke0..2J-l
Isiа, |sk si 3 :и for i e D.. 2 for k e 0.. 2J - 1 ST _ 51 . Зъ И оТ'оТ 1 Г1 1 ТПТо
51
3. Сформируем программу вычисления аппроксимирующих и
детализирующих вейвлет-коэффициентов уровней J - 1,J -
43
по аппроксимирующим коэффициентам J-ro уровня (см. приложе-
ние 2).
• Формируем матрицу коэффициентов фильтра Добеши по-
рядка два. 4 * *
h := т4'(1*'5) Т~ё (з^> A'11’1® Гл (1"#1 4 • ^2 4 ^2 4 • 4*^2 J
Формируем программу:
DS_d2(J,A,h) := for v eD..3- (sJ- 1) <- Av for pe U for veOJ-2J"p-3 3 m =0 3 dJ-p,V С"1)231 • Sj_p+12.v+m m =0 AD ( S d )
4. Формируем программу для вычисления коэффициентов
аппроксимации для уровней разрешения - 1 в базисе До-
беши порядка два и вычисляем эти коэффициенты:
X(J,A) := D< H DS_d2(J,A,h)o J
S 4 - DS_d2(J,A,h)o,o
for ’ Y| € 0.. J - 1
X for ns qj - 1 for k € 0.. 2й - 1 2+b ,4 Л for П€0..2П - 1 *- ,n
f 1.768 1J12 0095
0.371 0,988 1.414
0.729 0.729 1.544
-0.912 -0.912 0.483
0354 0354 0.354
0 0 0
0.483 0.483 0.483
< -0,129 -0129 -0,129 j
44
Замечание. Каждый столбец матрицы X может быть использо-
ван для выполнения обратного вейвлет-преобразованйя (ПЛЗ), ис-
пользуя интервальный вейвлет-базис (П.37). Однако лучше ис-
пользовать быстрое обратное вейвлет-преобразование (ПЛ5).
5. Формируем программу быстрого обратного дискретного
вейвлет-преобразованйя (текст программы см. в приложении 2).
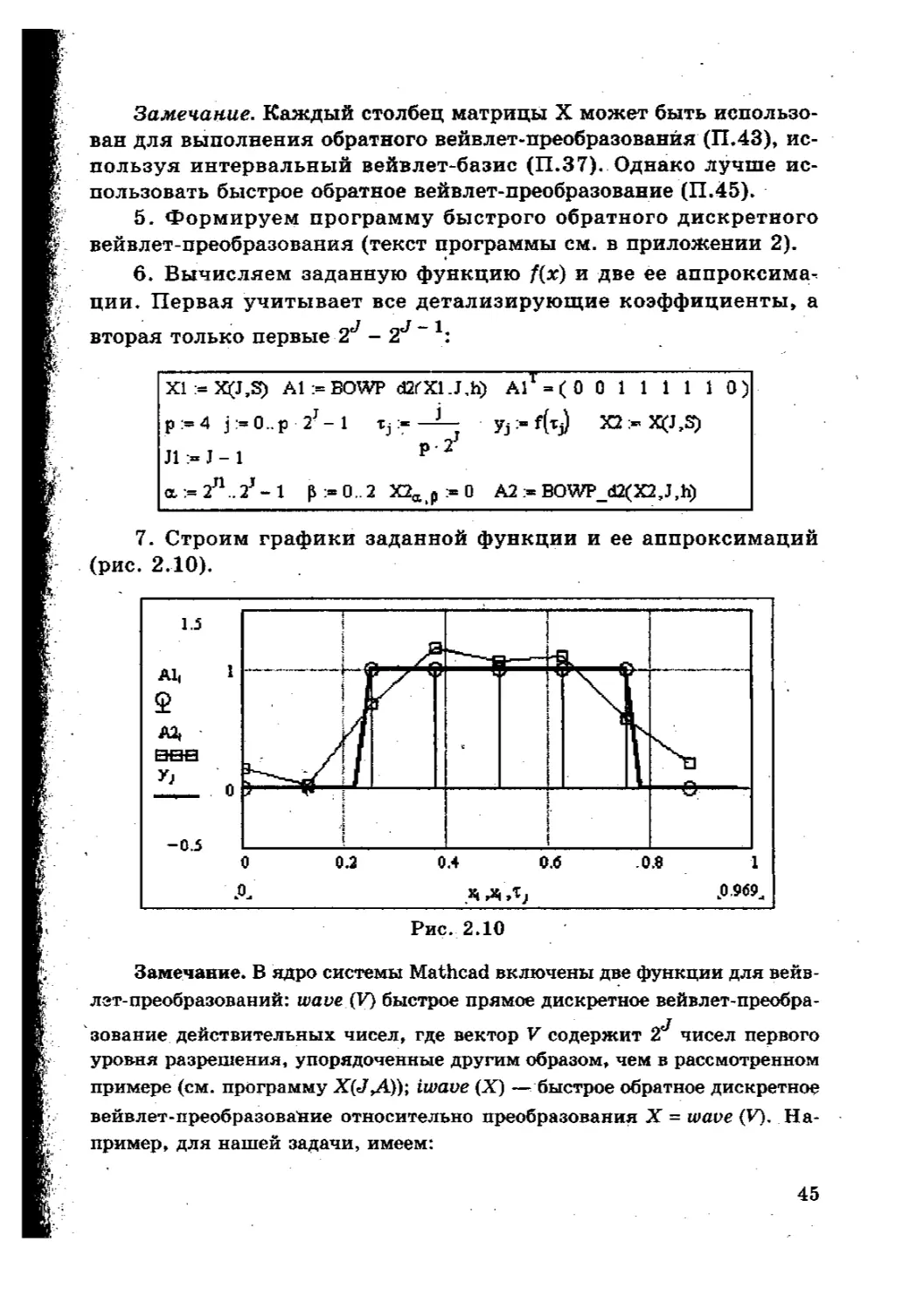
6. Вычисляем заданную функцию f(x) и две ее аппроксима^
ции. Первая учитывает все детализирующие коэффициенты, а
вторая только первые 2J - 2J “ b
X1:=X(J,S) Al := BOWP dZfXl.J.h) A1T = ( 0 0 1 1 1 1 10)
p := 4 j := 0.. p 2* - 1 Xj > —— yj f(xj) X2 > X(J ,S)
Jl := J - 1 P'2
a>2”../-I p >0.2 X2a>p >0 A2 > BOWP d2(X2,J,h)
7. Строим графики заданной функции и ее аппроксимаций
(рис. 2.10).
Замечание. В ядро системы Mathcad включены две функции для вейв-
лет-преобразований: wave (V) быстрое прямое дискретное вейвлет-преобра-
зование действительных чисел, где вектор V содержит 2^ чисел первого
уровня разрешения, упорядоченные другим образом, чем в рассмотренном
примере (см. программу iwave (X) —быстрое обратное дискретное
вейвлет-преобразование относительно преобразования X = wave (V), На-
пример» для нашей задачи, имеем:
45
1.Я2 0,982 -OP12 0.729 -0.129 0354 0 0.483)
iwttTe(wbve(gOT «(001111 10)
2.3. Интегральное квадратичное аппроксимирование
функций на отрезке
Пример 1. Требуется аппроксимировать функцию (2.2), задан-
ную на отрезке [0, f], используя ортонормированные непрерывные
полиномы Лежандра (1.4).
Вариант 1.
Решение задачи*
1. Зададим параметры, при которых решается поставленная
задача:
t :« 3 L > 4
L1 > 30 - количество значений аппроксимированной
заданной функции на отрезке [0, t]
2. Вычисляем коэффициенты Фурье (П.28) аппроксимирую-
щего полинома (П.26) заданной функции (2*2), используя квадра-
турный алгоритм Гаусса (П.32).
2.1. Формируем нули и веса квадратуры Гаусса для отрезка
[0, t] по их стандартизированным значениям (П.29), заданным на
отрезке [~ 1,1]:
-0,968160239 > 0.0812743884 51
-0.836031107 0.1806481607
-0613371433 0.2606106964
-0.324253423 0.3123470770
0 со > 0.3302393550
0.324253423 0.3123470770
0,613371433 0.2606106964
0.836031107 0.1806481607
0.968160239 > < 0,0812743884 ;
<k):= (l + aj-
- формула пересчета значений абсцисс
квадратуры Гаусса на отрезок
A(k) > - - - формула пересчета значений коэффициентов
2 квадратуры Гаусса на отрезок [0,t] ч
2.2. Вычисляем L ортонормированных непрерывных полино-
мов Лежандра по рекуррентному соотношению в абсциссах т(Л):
2.3. Вычисляем коэффициенты Фурье заданной функции /(х):
f(x) ;= -----i- - заданная функция.
2 х7 + 5
zh11$) •
АiT Pl - прямое преобразование Фурье.
А-( 0.541 -0.377 -0.163 034)
3. Вычисляем аппроксимацию заданной функции на системе
равноотстоящих точек отрезка [0, £] с шагом h = —, началь-
L1 ~ 1
ное значение равно нулю:
p:=O..Ll - 1
- вычисление' L1 значения равноотстоящих
точек отрезка [0, t].
- вычисление значений заданной функции
в L1 точке отрезка [0, t].
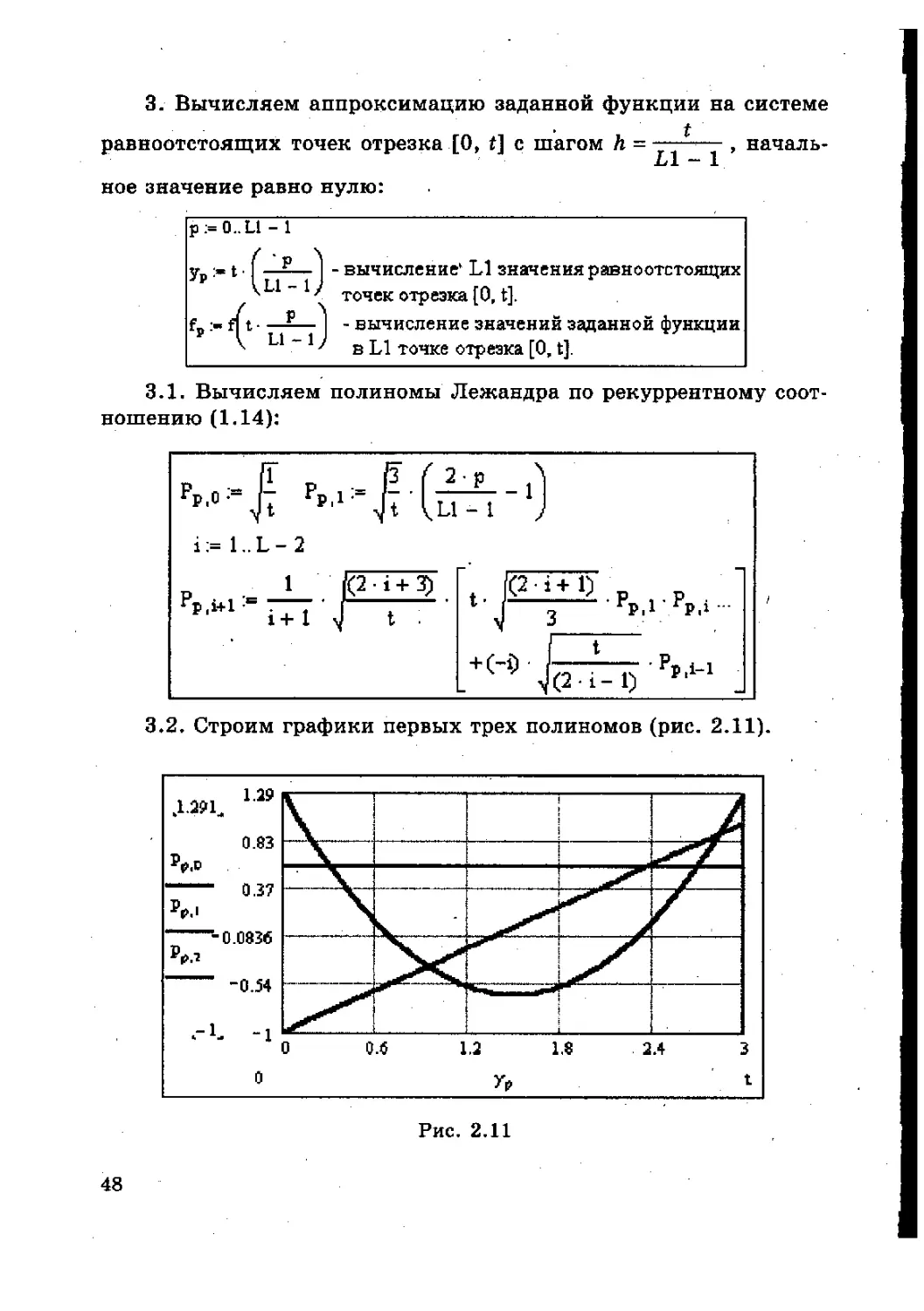
3.1. Вычисляем полиномы Лежандра по рекуррентному соот-
ношению (1.14):
3*2. Строим графики первых трех полиномов (рис. 2.11).
Рис. 2.11
48
3.3. Вычисляем аппроксимированную заданную функцию в £1
( точке отрезка [0, t] (обратное преобразование Фурье):
t:
а * Р Ат - обратное преобразование Фурье.
ят * 9^9НИЗИИИВННИВ1
МН -0.04 I 0.1 73 I 0.348 I 0.468 I 0.596 I 0.674
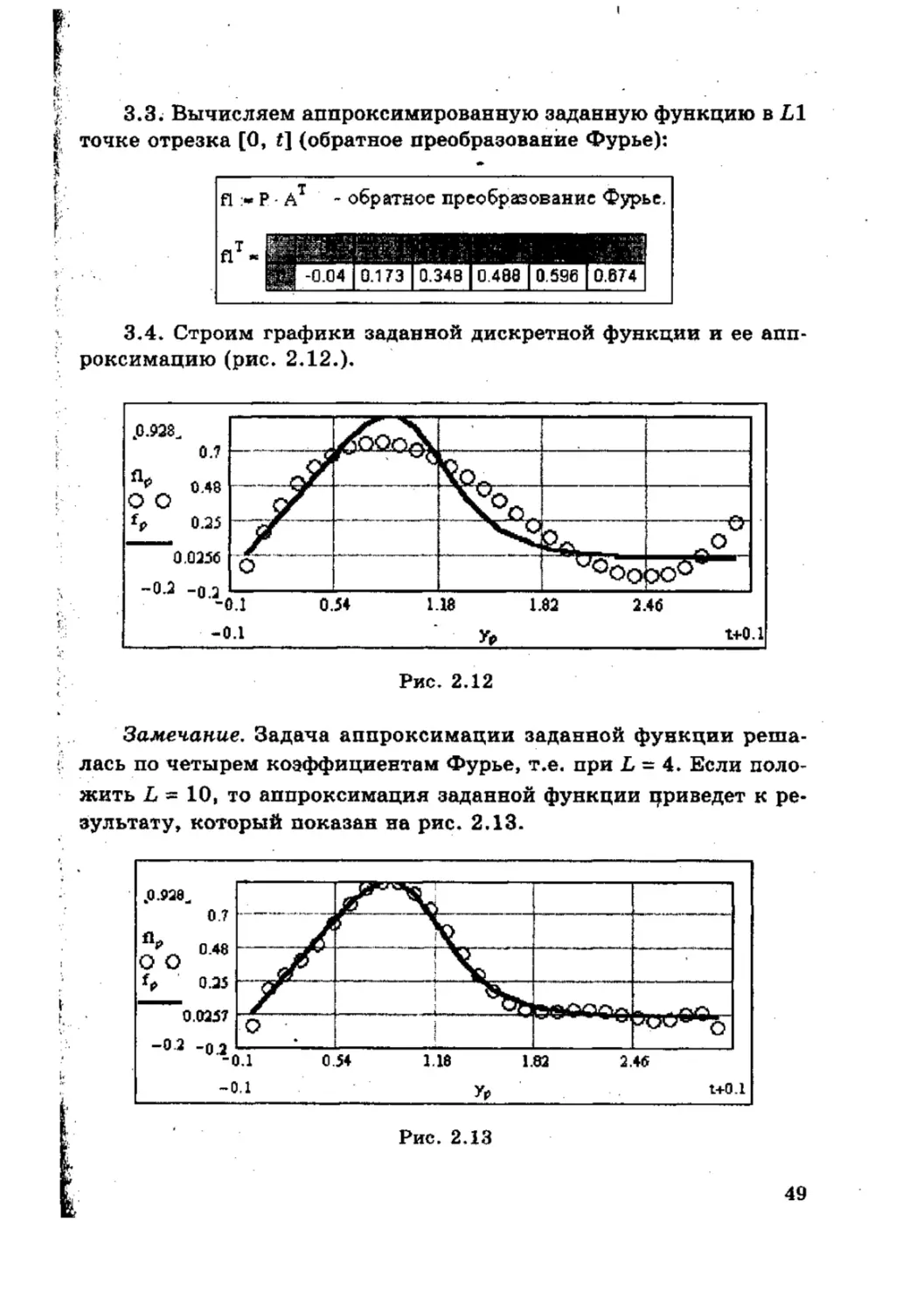
3.4. Строим графики заданной дискретной функции и ее апп-
роксимацию (рис. 2.12.).
Замечание, Задача аппроксимации заданной функции реша-
1 лась по четырем коэффициентам Фурье, т.е. при L - 4. Если поло-
жить L - 10, то аппроксимация заданной функции цриведет к ре-
зультату, который показан на рис. 2.13.
Вариант 2.
Решение задачи.
1. Вычисляем коэффициенты Фурье (П.28) аппроксимирую*
щего полинома (П.26) заданной функции (2.2), испрльзуя алго-
ритм метода наименьших квадратов (ПЛ8).
1Л, Формируем программу вычисления L ортонормирован-
ных непрерывных полиномов Лежандра на системе точек -=гг
(/ = 0, 1, ...,£- 1)по рекуррентному соотношению (1-5):
1.2. Формируем программу вычисления коэффициентов Фурье
по таблично заданной функции f(x^) на системе точек хг - -1
(Z = 0, 1, ...» XI):
AP(f ,L1 »L,t) > р <- РЦЫ ,L,t) X«- (рт р) рт f X
1.3. Вычисляем коэффициенты Фурье по таблично заданной
функции f(X}) на системе точек 1 (I « 0, 1, XI):
50
- заданная функция.
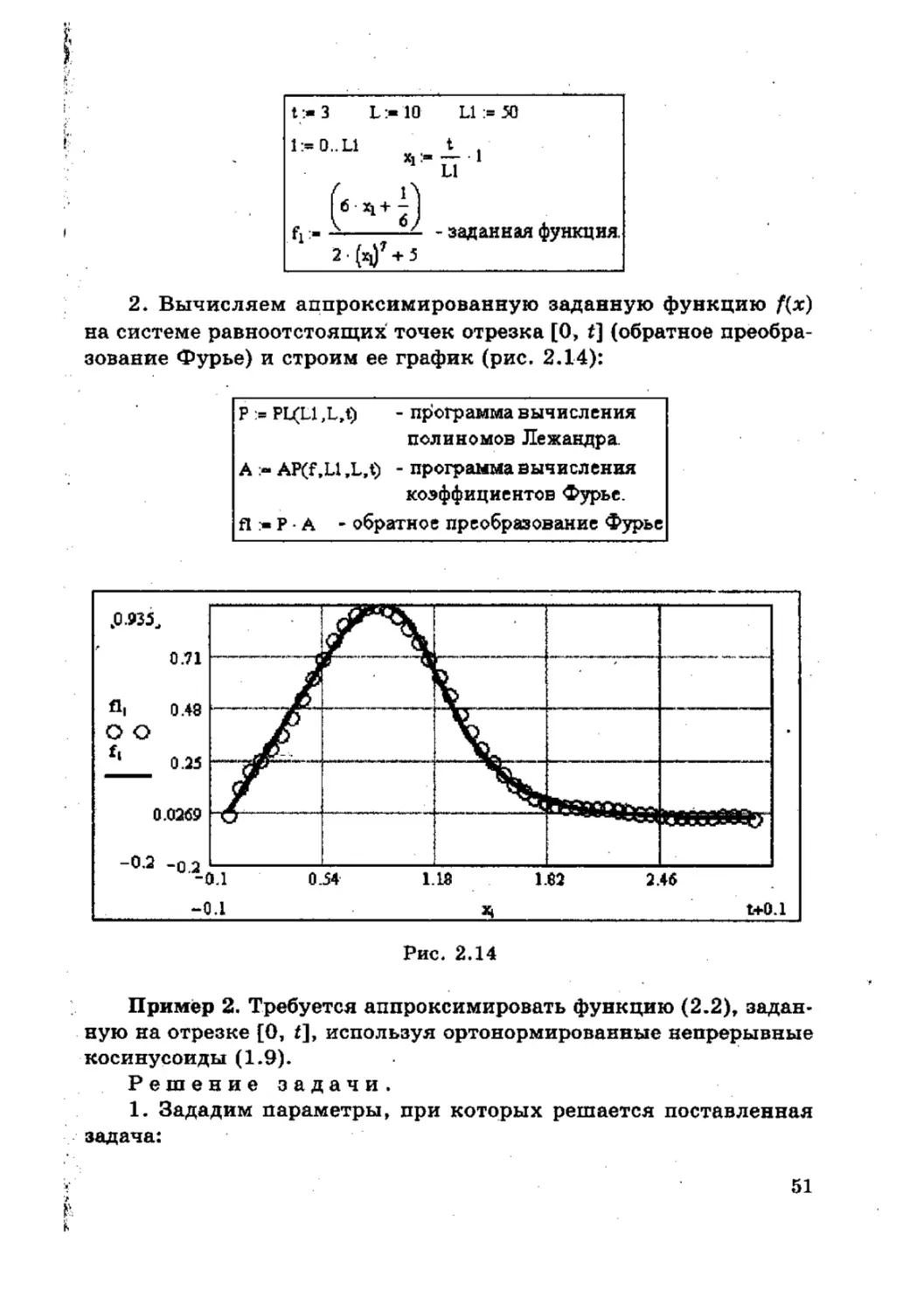
2. Вычисляем аппроксимированную заданную функцию f(x)
на системе равноотстоящих точек отрезка [0, f] (обратное преобра-
зование Фурье) и строим ее график (рис. 2.14):
Р > PL(L1 Л,t) - программа вычисления
полиномов Лежандра.
А AP(f,L1 ,L,t) - программа вычисления
коэффициентов Фурье.
fl - Р А - обратное преобразование Фурье
Рис. 2.14
Пример 2. Требуется аппроксимировать функцию (2.2), задан-
ную на отрезке [О, t], используя ортонормированные непрерывные
косинусоиды (1-9).
Решение задачи.
1. Зададим параметры, при которых решается поставленная
задача:
51
t>3 L>5
LI > 30 - количество значений аппроксимированной
заданной функции на отрезке [0, t].
2. Вычисляем коэффициенты Фурье (П.28) аппроксимирую-
щего полинома (П.26) заданной функции (2.2):
f(x) - —----- - заданная функция.
2 / + 5
Во :=
m:» 1.. L - 1 - прямое преобразование Фурье,
I х А
f(x) • cosl m л - I dx
BT-(0J38 0.414 -0.119 -0301 -0.19)
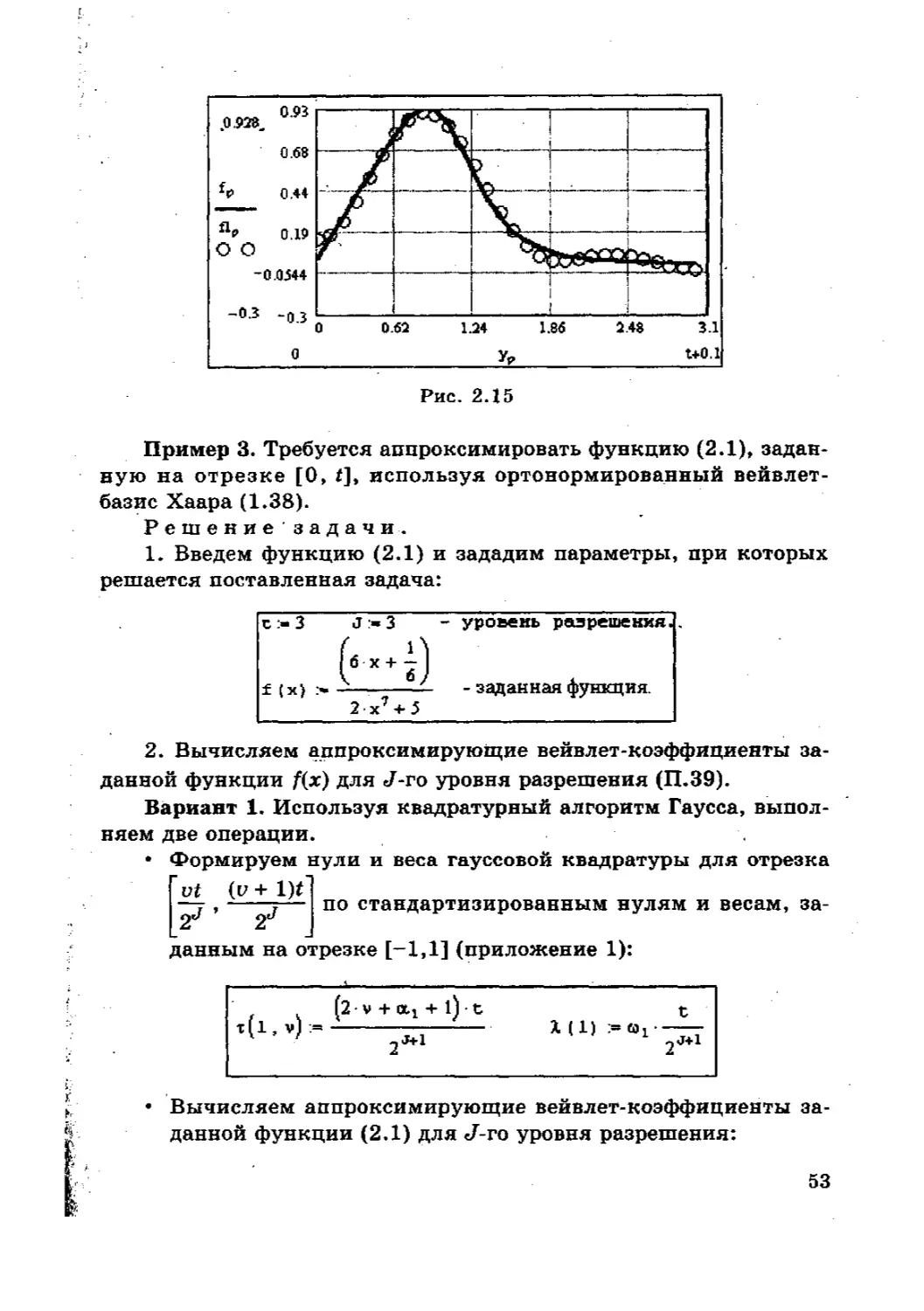
3. Вычисляем аппроксимированную заданную функцию в LI
точке отрезка [0» t] (обратное преобразование Фурье) и строим ее
график (рис. 2.15):
р:«0..Ы-1
у = t [ —?— ] - вычисление L1 значения
ч L1 — 1 1
4 ? равноотстоящих точек отрезка [0, t]
fp := f| t —2— I - вычисление значений заданной
L1 “ 1 / функции в L1 точке отрезка [0, t].
r:®0.. L1-1
« обратное преобразование Фурье.
52
Пример 3. Требуется аппроксимировать функцию (2.1), задан-
ную на отрезке [0, /], используя ортонормированный вейвлет-
базис Хаара (1.38).
Решение задачи.
1. Введем функцию (2.1) и зададим параметры, при которых
решается поставленная задача:
с > 3 J > 3 “ уровень разрешения.
( 1
Г Х+ б J
f (х) :* ——;~ - заданная функция
9 <
2. Вычисляем аппроксимирующие вейвлет-коэффициенты за-
данной функции f(x) для J-ro уровня разрешения (П.39).
Вариант 1. Используя квадратурный алгоритм Гаусса, выпол-
няем две операции.
• Формируем нули и веса гауссовой квадратуры для отрезка
’ut (U + l)t
2J ’ 2J
данным на отрезке [-1,1] (приложение 1):
по стандартизированным нулям и весам, за-
т(1 v) = - 2-v + ^ + f 1111 -»
Ц1, v; .= 2J+1
Вычисляем аппроксимирующие вейвлет-коэффициенты за-
данной функции (2.1) для J-ro уровня разрешения:
53
8
% (1) v)) - прямое преобразование
1-0
v:= О 2J-1 Alv:»Slj(v)
А? - (0 274 0,74 0P35 0.479 0.141 0,044 0,016 6.685 x 10"3 )
Делаем это в двух вариантах. Вариант 2. По стандартной программе интегрирования:
,(V+l)p S2j(v) :=л/Р Цх) dx A2v:-S2j(v) J , * A2T=( 0.274 0.74 0.935 0.479 0.141 0.044 0.016 6685xlO'J)
Вариант 3. По средним значениям интегралов:
S3j (v) := —± V2J A3T = ( 0.274 0.74t (2-v + 1) t 2 5 0.979 0.463 АЗч:=ЗЗд(у) 0.132 0.041 0.015 6.481 x 10"3 )
3* Вычисляем аппроксимирующие и детализирующие вейв
лет-коэффициенты для уровней J - 1, J - 2,..., О по аппроксими
рующим коэффициентам» вычисленным для J-ro уровня, т.е. при
меним быстрое прямое вейвлет-преобразование (П.40), где М = 1
54
Матрицы этих вейвлет-коэффициентов имеют вид
f 0.939 1.231 0 0.097 0 0 0 0 0 0 0 0 0 0 ° ) 0
DS ( J, А3)о в = 0.721 1.02 0.122 0.015 0 0 0 0
s 0.274 0.746 0.979 0.463 0.132 0.041 0.015 6.481 х t0*3 )
f 0,802 0 0 0
D5(J,A3)01^ -0.211 0.076 0 0
< -0.334 0.365 0.064 6.215 x 10"3
4. Формируем программу для вычисления коэффициентов
аппроксимации (П.41) в базисе Хаара и вычисляем эти коэффици-
енты:
X(J,A) X (J , A3)T - ( 0.939 D DS ( J , A) 0 i ! S<- D3 (J , A)q(0 tor ne 0 .. J - 1 for k« 0 .. 2n - 1 ^2*+к ( k Xq Sq Q X 0.802 -0211 0.076 -0.334 0.365 0.064 6.215 x 10“3 )
5. Формируем алгоритмы быстрого обратного вейвлет-преобра-
зования (П.45), использующий аппроксимирующие вейвлет-коэф-
фициенты J-ro уровня, таким образом:
• формируем программу быстрого обратного преобразования,
т.е. программу вычисления аппроксимирующих вейвлет-ко-
эффициентов <7-го уровня:
55
* формируем программу аппроксимации заданной функции
по найденным аппроксимирующим вейвлет-коэффициентам
«/-го уровня. Параметр и определяет количество точек апп-
роксимации на интервалах ее постоянства:
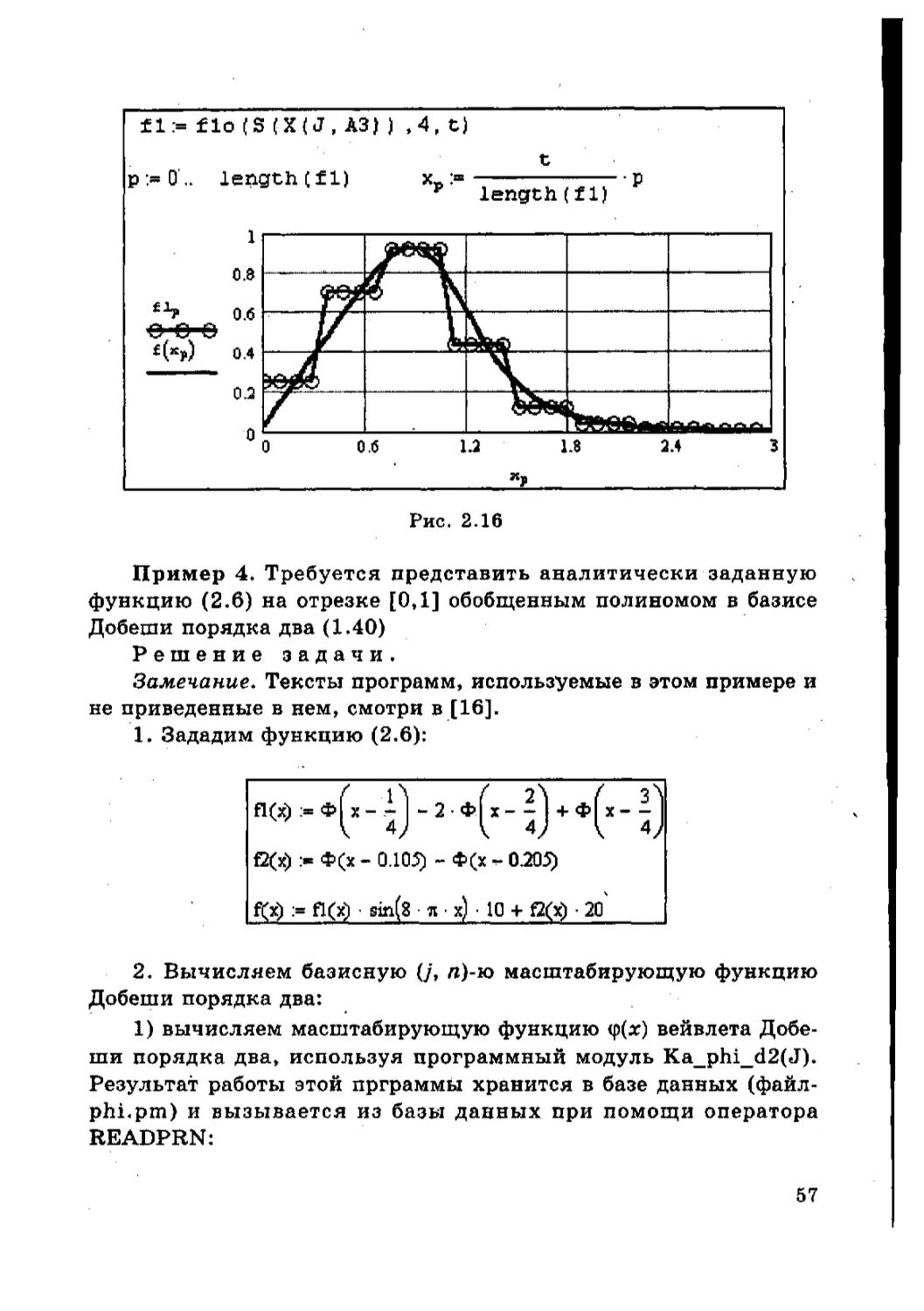
• вычисляем заданную функцию и ее аппроксимацию и стро-
ем ее график (рис. 2.16).
56
Рис. 2.16
Пример 4» Требуется представить аналитически заданную
функцию (2,6) на отрезке [ОД] обобщенным полиномом в базисе
Добеши порядка два (1.40)
Решение задачи.
Замечание. Тексты программ, используемые в этом примере и
не приведенные в нем, смотри в [16].
1. Зададим функцию (2.6):
( И ( 21 ( 3
fl(x) := ф| х - - - 2 - Фх--------I + Ф х------
\ 4^ \ 4у \4
f2(x) > Ф(х - 0105) - Ф(х - 0205)
ftx> := fl(x) sin(8 • я х) 10 + Q(x) • 2р'
2. Вычисляем базисную (j, л)-ю масштабирующую функцию
Добеши порядка два:
1) вычисляем масштабирующую функцию (р(х) вейвлета Добе-
ши порядка два, используя программный модуль Ka_phi_d2(J).
Результат работы этой прграммы хранится в базе данных (файл-
phi. pm) и вызывается из базы данных при помощи оператора
READPRN:
57
A > READPRN (11 d:\Rw\SM-mc dtf'iSWm-ddXphi^a.pm'1)
Л := 8 - количество итераций при формировании
масштабирующей функции.
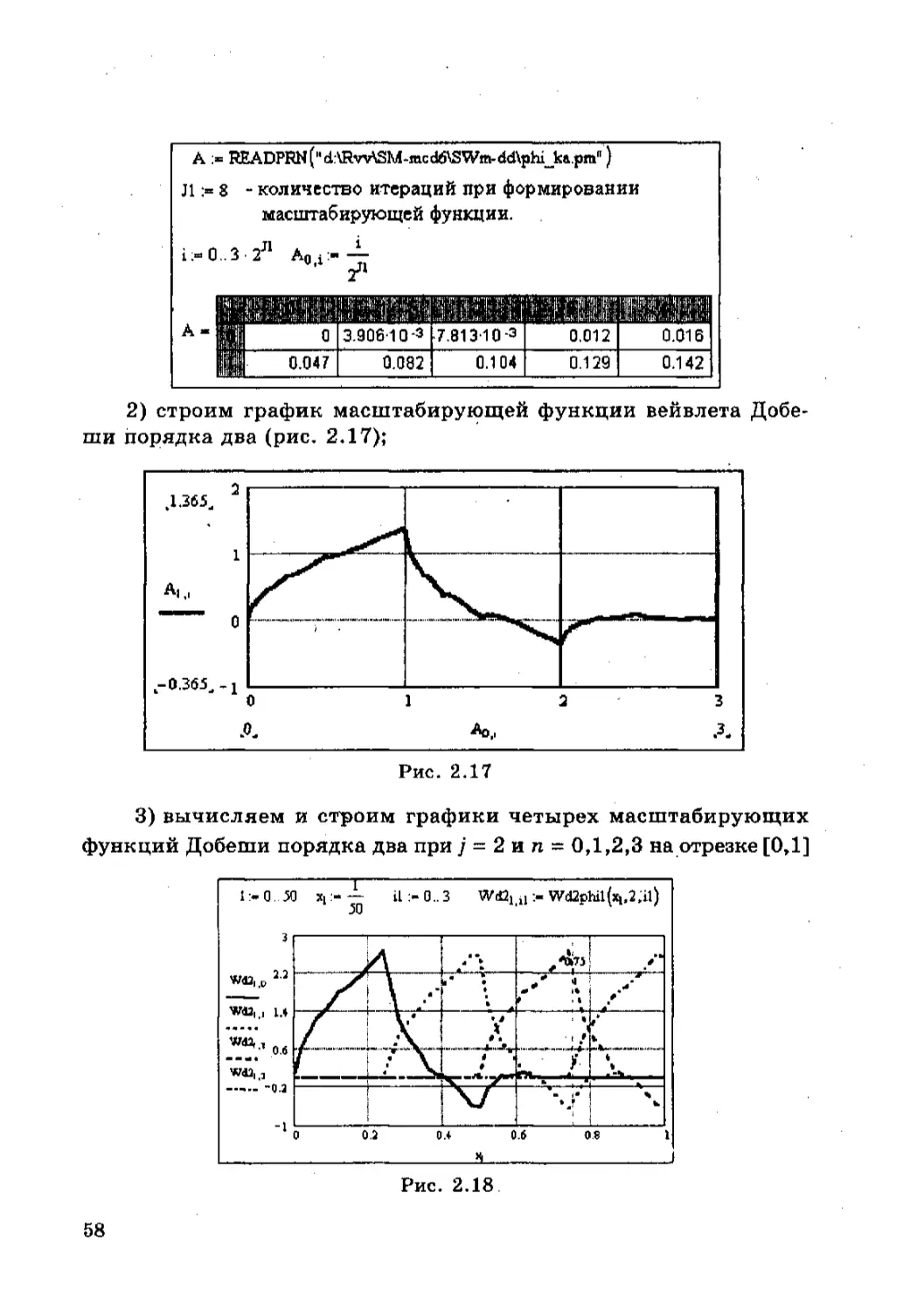
2) строим график масштабирующей функции вейвлета Добе-
ши порядка два (рис, 2,17);
Рис. 2.17
3) вычисляем и строим графики четырех масштабирующих
функций Добеши порядка два при j = 2и п “ 0,1,2,3 на отрезке [0,1]
58
(рис. 2.18), используя программный модуль Wd%phil(x, j, п) фор-
мирования базисных (у, п)-масштабирующйх функций Добеши по-
рядка два.
Параметры, передаваемые в программу Wd2hiA(xi л): j —
параметр сжатия; п — параметр смещения; х — произвольная
точка отрезка [0,3].
3. Вычисляем аппроксимирующие коэффициенты J-ro уров-
ня для параметра сдвига k = - 2, - 1, 0, 1,..,,2J - 1» используя про-
грамму вычисления аппроксимирующих коэффициентов в базисе
Добеши порядка два по методу наименьших квадратов Sl(£, J):
4. Вычисляем заданную функцию Дх) и ее аппроксимацию по
формуле обратного вейвлет-преобразования (П.46), реализованно-
го в программном модуле £1(D, J, g):
В этой программе:
J = 1, 2, 3, ... — параметр сжатия (масштабирования), кото-
рый определяет уровень, на котором осуществляется аппроксима-
ция функции;
р = 1, 2, 3, ... определяет количество значений (p2J +1) иско-
мой функции /(х), заданных на отрезке [0, 1];
D — вектор аппроксимирующих коэффициентов заданной
функции порядка 2^+1 для k = - 2, - 1, 0,1,...,#7 - 1.
5. Строим графики заданной функции и ее аппроксимации
(рис. 2.19). .
59
Рис. 2.19
6. Повторяем вычисления для функции (2.7):
• задаем функцию
fl(x) := фГх- Л - 2 ф(х- -'l + ф(х - f(x) 20
\ 4/ V \ 4J 1+2-х
• строим график функции и ее аппроксимацию(рис. 2.20).
Рис. 2.20
Рассмотренные примеры аппроксимации функций не дают
полного представления о характере приближения функций с ис-
пользованием разных базисных систем. Для выяснения характера
приближения необходимо провести графический анализ прибли-
жения функций: 1) меняя параметры, при которых решаются за-
дачи; 2) меняя функции в рассмотренных примерах; 3) сравнивая
полученные результаты.
60
Приложение 1
I ВЫЧИСЛИТЕЛЬНЫЕ СХЕМЫ ПОСТАНОВОК
i И РЕШЕНИЯ ЗАДАЧ АППРОКСИМИРОВАНИЯ
> И ИНТЕРПОЛИРОВАНИЯ ФУНКЦИЙ
<
1. Интерполирование функций сплайнами на отрезке
1.1. Постановка задачи
Дана функция Дх) на системе точек xt = hl, I - 0, 1,..., L - 1,
где xt € [0, t] и h = .
Li — 1
Требуется найти интерполяционный кубический сплайн
S3(x) = S3(/; х) непрерывный вместе со своими первой и второй
производными, который для хе [xi , xt + J представим в виде
S3(f; х) = /((1 + т)2 (1 + 2т) + ft + J т2 (3 + 2т) +
+ Лт(1 - т) £mz(l - т) - mt +х т] (П.1)
или в виде
Л2
S3(f; х) = /Д1 - т) + fl+ jT + ~ т(1 - т) х
х [(2 - T)z, + (1 + t)zz + , (П.2)
где т = = f(xz) ; mt = S3(f; xf) ; zz = S3(/; xj) и который
удовлетворяет краевым условиям:
S3{f-,Q) = f\f',Q)-, S3(/; 0 =/(Л t) ; (П.З)
S3(f-, 0) = /'(/; 0) ; S3(/; t) = f \f; f) ; (П.4)
S3(A + 0) = S3(f; xt - 0) 1 = 1,..., L-2. (П.5)
61
1,2. Решение задачи
1. Для краевых условий (П-3) построение интерполяционного
кубического сплайна по формуле (ПЛ)сводится к вычислению L
неизвестных величин nij = гг) из решения системы
т0 “ fo ’
< ^1 + 4тг + ^1 = ||7г + 1-/’/_1]> (пб)
I = 1..L - 2 ;
mL - 1 “ tb - 1 ’
а по формуле (П.2) — к вычислению L неизвестных величин
zl ~ из Решения системы
1 _ 3 £1 - fo
2о 2 h
h +/о
. + + (П7)
1 = 1,..., L-2;
1 _ 3 / Il -1 _ fb - 2
2 zb-2 + zb-l~ h ['Ь-l ft •
2. Для краевых условий (IL4) построение интерполяционного
кубического сплайна по формуле (ПЛ) сводится к вычислению L
неизвестных величин — S3(f; х^ из решения системы
^0 + 2 «1 = 2ft ~ Z0j ‘ 4 ^0’’
1 = 1.. L-2 ;
(П.8)
2 mL - 2 + mL - 2 “ 2ft ИЬ - 1 “ - 2 )+ ~2 tb - 1 ’
62
а по формуле (П.2) — к вычислению L неизвестных величин
г1 - ОД/; xz) из решения системы
*0 = fo ;
2i_1 + 4zz + 2/ + 1 = p-£/z + 1-2/( + /I_1J, 9)
1 = 1,..., L - 2 ;
ZL-1~ fb-2 •
3. Для краевых условий (Г1.5) построение интерполяционного
кубического сплайна по формуле (П.1) сводится к вычислению L
неизвестных величин ml = S^f; xt) по формулам
m1 = dl_l, 1 = 1,..., L- 2; (П.10)
mL-l=dL-4 + 2
/1-1“ 2/l-2 + fb-3
в которых неизвестные величины dt вычисляются из решения сис-
темы
_ 1 + 4dz + dz +1 = -j [/j + 2 - /z] ,
(=1,..., L-4;
1 , , fb-l + 4fb-2~ 5/L-3
2«L-3 + d£.-2- J*
(П.11)
Построение интерполяционного кубического сплайна по
формуле (П.2) сводится к вычислению L неизвестных величин
/nz = S3(/; X}) по формулам
Zq — 2dg dj ; — 1,..., JL — 2,
ZL - 1 “ 2dL - 3 ~ dL - 4 >
(П.12)
63
в которых неизвестные величины dt находятся из решения систе-
мы
я ~ ""
°" Л2 ;
1 + + + 1 “Тз ГЛ +2 “ 2Л+1 + ^1 ’ - min
( Л L J (11.1а)
I 1 = 1. L-4 ;
| , ^L-l~^L-2 + ^L-3
I ^-3 =-------------------•
Замечание, Для вычисления сплайна S3(/; х) на более густой
сетке точек, чем Xj = hl, I — О,..., L — 1, можно задать новый шаг
s = h/N, где N задает количество точек на которое разбивается от-
резок [х^ , х>1 + J , I = О,..., L - 2, и тогда система точек, на которой
будет вычисляться сплайн S3(f; х) , имеет вид
хр = $р, (П.14)
где хр е [О, Z] ; s = Л/Л/; р = Nl + m; а I = О,..., L - 2? т - О, 1,..., N.
2. Точечное квадратичное аппроксимирование
функций на отрезке
ОБЩИЙ СЛУЧАЙ
2,1. Постановка задач
1. Дана основная система функций
|<р0(х) , Ф1(Х)..............фДх) , (ПЛ5)
где х е [О, 0 .
2. Дана функция Дх) на системе точек Xj (I = О, 1,-..» L - 1),
где xl е [0, t] . Требуется найти аппроксимирующий (обобщенный)
полином
64
т.
0(х) = 5; Ф/(х), (п.1б)
который обеспечивает минимум квадратичному отклонению
L -1
„ г л 2
s = X [Q(xz) - Л*,)] •
/ = о L
(ПЛ 7)
2,2. Решение задачи
1. Находим коэффициенты аппроксимирующего полинома:
а) если т < L - 1, то
В = |^Фтф] 1фтРт = const; (ПЛ 8)
б) если пг = L - 1, то
— 1 т
В - Ф F = const (интерполяция), (ПЛ9)
где
<Ро(хо) <Р1(хо) - ФЛ)
Фо<х1) Ф1(х1) ••• Фт(*1)
Ф а
Фо(Х1-1) Ф1(*£-1) — Ф«(Х£-1)
|Л
В = ь‘ ;
L -I
2. Находим аппроксимирующий полином:
Q(x) = £ Ь. <рДх) .
L =0
65
СЛУЧАЙ ОРТОГОНАЛЬНЫХ ФУНКЦИЙ
2.3. Постановка задачи
1. Задана полная ортонормированная с весом p(L, I) система
дискретных функций
fp0(L, Z) , p^L, I) pL _ Z)1 , (IL20)
| * * *
где I - 0, I,..., L - 1.
2. Задана функция f(x) на системе точек xf (I = 0, L - 1),
где x; e [0, Z] . Требуется найти аппроксимирующий (обобщенный)
полином
<?то(х) = Е (П.21)
г=0 * v /
который обеспечивает минимум квадратичного отклонения
L- 1
г -12
S = £ p(L, Z) [Q(xp - f(x;)l . (П.22)
1 = 0
2,4. Решение задачи
1. Находим коэффициенты аппроксимирующего полинома:
L- 1
bt = £ p(Z, I) P^L, Z) f(xt) , i = 0, 1,... ,m<L-l . (П.23)
x - x0
2. Пологая h~t/L и I - —-— , находим аппроксимирующий
полином:
m /
= X biPi[L’~
i = 0 *
(П.24)
где x e [0, f].
66
3. Интегральное квадратичное аппроксимирование
функции на отрезке
3.1. Постановка задачи
1. Задана полная ортонормированная с весом р(/, х) система
непрерывных функций:
Pott, х) , Pitt, х) ,..., pttt, х) . (П.25)
* * * I
2. Задана функция /(х) на отрезке [0, £] , Требуется найти апп-
роксимирующий полином
m
Q(x) = £ b.Pitt, X) , (П.26)
г = О
который обеспечивает минимум квадратичного отклонения
t
2
S = j p(t, х) ^Q(x) - ftx)] dx .
О
(П.27)
3.2. Решение задачи
1. Находим коэффициенты аппроксимирующего полинома:
t
bi = j ptt, X) p*tt, X) fix) dx ,
0 ' “
i = 0, 1,..., m .
2. Находим аппроксимирующий полином:
Q(x) = у bt pt(t, x) .
i = 0
67
4. Квадратурный алгоритм Гаусса для вычисления
коэффициентов Фурье
4.1. Стандартизированные нули fa) и веса fp)
Гауссовой квадратуры на отрезке [-1,1 ]
(количество нулей и весов N=9).
Они имеют вид
- 0,968160239
a = - 0,836021107 - 0,613371433 - 0,324253423 0 ; 0) =
0,324253423
0,613371433
0,836021107
0,968160239
0,0812743884'
0,1806481607 0,2606106964 0,3123470770 0,3302393550 (П.29)
0,3123470770 0,2606106964 0,1806481607 0,0812743884
4.2. Квадратурный алгоритм Гаусса
(первый вариант)
1* Формула пересчета значений абсцисс квадратуры Гаусса на
отрезок [0, £]
/-1 ч *
X, = (1 + аг) 2 .
(П.30)
2. Формула пересчета значений коэффициентов квадратуры
Гаусса на отрезок [0, £]
(П-31)
3. Квадратурный алгоритм Гаусса
У- 1
= X P(f* xz) Лх/) х? * (П.32)
I = о
68
4.3, Квадратурный алгоритм Гаусса
(второй вариант)
1. Формула пересчета значений абсцисс квадратуры Гаусса на
Г vt (w + l)tl .
отрезок I— , ..-
xit и = (%v + 1 + a?j > (П.ЗЗ)
где М — количество интервалов интегрирования квадратуры Гаус-
са.
2. Формула пересчета значений коэффициентов квадратуры
Гаусса на отрезок
vt
м
(и + 1)г
м
2М ‘
(П.34)
3. Квадратурный алгоритм Гаусса
м-1 лг- 1
bi = X Е \ P(f- xl, v) ft*l. u) Pi«’ xl, v) • <n-35)
’ y=0 Z=0
69
Приложение 2
ВЫЧИСЛИТЕЛЬНЫЕ СХЕМЫ ПОСТАНОВОК
И РЕШЕНИЯ ЗАДАЧ АППРОКСИМИРОВАНИЯ
ФУНКЦИЙ В ВЕЙВЛЕТБАЗИСАХ
1. Интегральное квадратичное
аппроксимирование на R
1.1 Постановка задачи
1. Задан ортонормированный вейвлет-базис с компактными
носителями
{фу, feW , j, fe с Z ; А(х) , J, k е , (П.36)
где (рд ft(x) = 2Vi ф(27 х - k) ; 4г k(x) = 2Уг ф(27 х - k) ; j — параметр
сжатия; k — параметр смещения.
2. Задан интервальный вейвлет-базис
f Фп, mW п₽и А=°;
„ । <Р„ 4. i i + mW ПРИ Й = 27 + k,
<mW = i " + (П.37)
j k = 0, 1..2j - 1 ; / = 0,1, 2,...;
[ m, л e Z ,
где n — параметр сжатия; m — параметр смещения.
3. Требуется найти аппроксимирующий полином функции
/(X) в виде
QW = L sj,k4>j,№ = Y so,fe<Po,fcW +
k k
j-i 1
+ X Z aj,k4>j,kW = l X4m4mW, (П.38)
/=0 k k k=o
70
где ад т — коэффициенты аппроксимации в интервальном вейв-
лет-базисе на нулевом уровне разрешения*
1.2 Решение задачи
Вариант 1.
1* Находим аппроксимирующие коэффициенты Sj k
Sjt k = J f(x) (Pj fe(x) dx , k e Z .
(П.39)
2* Находим аппроксимирующие коэффициенты s; к и де-
тализирующие коэффициенты k для уровней разрешения
J-l,J-2>...,Onosz р используя быстрое прямое вейвлет-пре-
образование:
sy - 1,/г S - 2k п * - 2k sjt п * (П.40)
где, например, для вейвлетов Добеши порядка М параметры hk
(gk = (- l)ft й2м -/? — !’ = 0> I»--» 2М - 1) находятся из решения
системы уравнений (1.42), а для вейвлетов Добеши второго поряд-
ка заданы формулами (1.44).
3. Находим коэффициенты аппроксимации интервальных
вейвлет-функций (П.37):
sj,n п₽и А = °;
dJ + i,k + m при h-2! + k,
k = О, 1,..., 2?-1 ; у = 0, 1,2
тп, J е Z
(П.41)
для J = 0.
4. Находим аппроксимирующий полином в виде
J- 1
qw = L 8q k <ро,^ + Х L dj,k «Р/, feW
(П.42)
k k
71
или в виде
1
= Z Z 4« 4 »<«> «п-43»
т Л = 0
Вариант 2.
1. Находим аппроксимирующие коэффициенты s0 k :
$0, k = J Ax) Фо, *<x) dx ’ z (П.44)
2, Находим аппроксимирующие коэффициенты k и детали*
зирующие коэффициенты dj k для уровней разрешения 1, 2, J
по ь , используя быстрое обратное вейвлет-преобразование:
sj 4-1, п ~ X fe + - 2k л) • (П.45)
п v 7
3. Находим аппроксимирующий полином в виде
Q(X) = S Sj, *Фу, ft(x) - (П.46)
k
2, Точечное квадратичное аппроксимирование
функций/заданных на системе точек
отрезка [О, 1]
2Л Постановка задачи
1. Заданы быстрое прямое и обратное вейвлет-преобразования
(П.40) и (П.45).
2. Требуется найти аппроксимирующий полином функции
f(x), заданной на системе точек (на равномерной сетке или таблич-
но) хг = hl, 1 = 0, 1.1-1, где хг е [0, 1] , h = —Ц-, L = 2<
Ху “ 1
<7=1,2,...
72
2.2 Решение задачи
1. Преобразуем функцию /(г) в периодическую fn(x) = f(x - Lx J)*
2* Полагаем
SJ, k = ’ k e z •
(П.47)
3. Находим аппроксимирующие коэффициенты k и детали-
зирующие коэффициенты для уровней J - 1, J - 2, ...» О по
Sj k , используя быстрое прямое вейвлет-преобразование (П.40)*
4. Находим коэффициенты аппроксимации (П.41) интерваль-
ных вейвлет-функций (П.37) для J = 0.
5. Находим аппроксимирующий полином в виде
о 2^-1
Q(x) = E I4.OP (IL48)
т = - 2М + 1 h = О
на сетке хг - hl, I- 0, 1,..., 2^-1.
Замечание. Вернутся к f(xj) , заданной на сетке х^ = hl t
I - 0, 2^ -1, можно, используя быстрое обратное вейвлет-преобразо-
вание (П.45).
73
3. Программные модули быстрого прямого (БПВП)
и обратного (БОВП) вейвлет-преобразований
в базисе Добеши второго порядка
• Программа БПВП:
BPWP_d2(J,A ,h) :=
for v еО.,3- 1)
for p e 1.. J
for v€0..3-2J-₽-3
3
Sj-p,v Ц),» 'SJ-.p+l,2-v+m
m =o
3
dj-p.v ‘ ^,3-m ’ Sj-p+l.S v+m
m =0
for ne 0.. J - 1
for ke 0.. 2n - 1
X„ <- dnh
3 +h,0 ‘
Xo.o 30|0
for i e 0.. 2J- 1
for ke 0..2
Xl
Параметры, передаваемые в программу: <J — уровень разреше-
ния, на котором задана дискретная функция f(x0 на системе точек
Xj = hl, I - 0, 1,,.., - 1; А — массив порядка 3 2?, содержащий
периодическую функцию /п(хг) = f(xt - |_хг_|); к — матрица коэффи-
циентов фильтра Добеши порядка два (1.44).
74
• Программа БОВП:
BOWP_d2(X,J,h) -
So го Хо ,о
for peOJ - 1
for ne0..2p- l
^p,n n
2+n,0
for i e 1 „ 5 • 2J
So,!4*- $o(o
for j € 0.. J ’ 1
for i«2j,2j+l..5 -2J
for к e O..2j -1
dj.H-k dj.Js if i + к < 5 • 2
for j e 0„ J - 1
for ke2J..3- GJ- l) + 2J+1
Sui iL Л ь®-3 + ь°-0 ‘ Зьк -
J ,Л ' +h(j i dj lH1 + ho 3 .djik
S. i Ж Л I *“ (ь°'3 ' Sj.k-l + hV' Sj,k) -
J* ', * ' (^0,0 dj.k-l + hd,2 4),кД
for keC..2J-.l
sib«- Sjh
si
Параметры, передаваемые в программу: J — уровень разреше-
ния, на котором восстанавливается дискретная функция f(x^ на
системе точек = hlt I = О, 2? - 1; X — матрица порядка
/ х 1, содержащая коэффициенты аппроксимации интервального
вей влет-базиса; h — матрица коэффициентов фильтра Добеши по-
рядка два (1.44).
75
Приложение 3
Задания на компьютерную практику
по приближению функций
1, Задайте функцию f(x) таблично и найдите интерполяционный
локальный сплайн, приближающий функцию f(x). Исследуйте гра-
фически поведение сплайн-приближения заданной функции;
1) интерполируйте функцию, заданную таблично, сплайном
первой степени;
2) интерполируйте функцию, заданную таблично, сплайном
второй степени;
3) интерполируйте функцию, заданную таблично, сплайном
третьей (ПЛ) степени, используя краевые условия (П.З), или
(П,4), или (П.5);
4) интерполируйте функцию, заданную таблично, сплайном
третьей (П.2) степени, используя краевые условия (П.З), или
(П.4), или (П.5).
2. Задайте функцию f(x) таблично и найдите точечное квадра-
тичное приближение к ней. Исследуйте графическое поведение
обобщенного ряда Фурье заданной функции:
1) аппроксимируйте функцию, заданную таблично, полино-
мом первой степени; (Линейная аппроксимация);
2) аппроксимируйте функцию, заданную таблично, полино-
мом второй степени. (Квадратичная аппроксимация);
3) интерполируйте функцию, заданную таблично, полиномом;
4) аппроксимируйте функцию, заданную таблично, обобщен-
ным полиномом в базисе дискретных полиномов Чебышева;
5) аппроксимируйте функцию, заданную таблично, обобщен-
ным полиномом в базисе дискретных полиномов Кравчука;
6) аппроксимируйте функцию, заданную таблично, обобщен-
ным полиномом в базисе дискретных косинусоид;
7) аппроксимируйте функцию, заданную таблично, обобщен-
ным полиномом в базисе дискретных синусоид;
8) аппроксимируйте функцию, заданную таблично, обобщен-
ным полиномом в базисе дискретных экспонент;
9) аппроксимируйте функцию, заданную таблично, обобщен-
ным полиномом в базисе дискретных функций Хаара;
10) аппроксимируйте функцию, заданную таблично, обобщен-
ным полиномом, используя быстрое вейвлет-преобразование Добе-
ши порядка два.
76
К 3/Задайте функцию аналитически и найдите интегральное
квадратичное приближение к ней, используя разные численные
схемы вычисления интегралов. Исследуйте графическое поведе-
ние обобщенного ряда Фурье заданной функции,
L 1) аппроксимируйте функцию, заданную аналитически, обобщен-
ным полиномом на отрезке [0, fj в базисе непрерывных косинусоид;
2) аппроксимируйте функцию, заданную аналитически, обобщен-
ным полиномом на отрезке [0, t] в базисе непрерывных синусоид;
* 3) аппроксимируйте функцию, заданную аналитически, обобщен-
ным полиномом на отрезке [0, i] в базисе непрерывных экспонент;
t 4) аппроксимируйте функцию, заданную аналитически, обоб-
щенным полиномом на отрезке [О, £] в базисе непрерывных поли-
? номов Лежандра;
к 5) аппроксимируйте функцию, заданную аналитически, обоб-
| щенным полиномом на отрезке [0, t] в базисе непрерывных поли-
номов Чебышева первого рода;
; 6) аппроксимируйте функцию, заданную аналитически, обоб-
/ щенным полиномом на отрезке [0, i] в базисе непрерывных поли-
J номов Чебышева второго рода;
j 7) аппроксимируйте функцию, заданную аналитически, обоб-
> щенным полиномом на отрезке [0,1] в базисе вейвлетов Хаара;
8) аппроксимируйте функцию, заданную аналитически, обоб-
щенным полиномом на отрезке [0,1] в базисе вейвлетов Добеши
второго порядка.
Выполните задания для функций (п — номер варианта):
Мх> =
(1 + п)х +
п
2х* + п + п
. . . Гп 1 + п
7 2"77з 1 !
\ )
- / \ _ 1 I П + ЛМ I 1
- 1 х 10л 1
2л + 0,1
Х Юл
=1 (х 2 •1 1 ~ ;
/5(х) = 1 (х - —-—-К 2 1 (х - — 1+ 1 (х-----------------) ;
5 I 4(1 + л) I I 2(1 + л) I I 4(1 + л) I
f6(x) = 10f4(x) sin ((8 + (!-(- 1)я)) их) + 20/3(х) ;
77
frtx) =
20f4(x)
2x+l
где 1(6 - т) =
О при 0 < т;
1 при 9 > т .
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Демидович Б.П., Марон ИА., Шувалова Э.Б. Численные методы анализа.
М.: Гос. Изд. Физ.-мат. лит., 1963.
2. Ланцош К. Практические методы прикладного анализа. — М.: Главная ре-
дакция физ.-мат. лит., 1961.
3. Бахвалов Н.С. Численные методы. —М.: Наука, 1963.
4. Крылов В,И., Бобков В .К, Монастырский П-И. Вычислительные методы.
Т. 1, 2. — М.: Главная редакция физ.-мат. лит., 1976.
5. Березин И .С., Жидков Н.П. Методы вычислений. — М.*. Гос. изд. физ.-мат.
лит., 1962.
6. Завьялов Ю.С., Квасов Б.И., Мирошниченко В.Л. Методы сплайн-функций.
- Л.-М.: Наука, 1980.
7. Киреев В,И., Пантелеев А.В. Численные методы в примерах и задачах:
Учебное пособие.— М.: Изд-во МАИ, 2000.
8. Пирумов У.Г. Численные методы: Учебное пособие. — М.: Изд-во МАИ,
1998.
9. Расчет систем управления на ЦВМ/В.В. Солодовников и др. — М.: Машино-
строение, 1979.
10. Семенов В.В., Рыбин В.В. Алгоритмическое и программное обеспечение
расчета нестационарных непрерывно-дискретных систем управления ЛА спект-
ральным методом: Учебное пособие. — М.: МАИ, 1984.
11. Добеши И. Десять лекций щ> вейвлетам. — Ижевск: НИЦ “Регулярная и
хаотическая динамика”, 2001.
12. Чуи К. Введение в вэйвлеты/Пер. с англ. — М.: Мир, 2001.
.13. Дьяконов В.П. MathCAD 2000. — СПб.: Питер, 2000.
14. Дьяконов Д.П. Вейвлеты. От теории к практике. — М.: СОЛОН-Р, 2002.
15. Рыбин В.В. Компьютерный практикум по алгебре и математическому ана-
лизу в среде Mathcad: Учеб, пособие. — Мл Изд-во МАИ, 2002,
16. Рыбин В.В. Описание сигналов и линейных нестационарных систем управ-
ления в базисах вейвлетов и их анализ в вычислительных средах: Учебное пособие.
- М.: Изд-во МАИ, 2003.
78
ОГЛАВЛЕНИЕ
Предисловие.......................................*.............3
Глава 1, Приближение функций....................................* 5
1.1. Постановка задачи о приближении функцийб...............
1.2. Примеры базисных систем функцийб ......................
1.2.1. Ортонормированные непрерывные системы
функций................................................. 6
1.2.1.1. Полиномы Лежандра ..........................6
1.2.1.2. Полиномы Чебышева первого рода............ 7
1.2.1,3. Полиномы Чебышева второго рода..............8
1.2.1,4. Тригонометрические функции..................8
1.2.1.5. Комплексные экспоненциальные функции........9
1.2.2. Ортонормированные дискретные системы функций ...... 9
1.2.2.1. Полиномы Чебышева ..........................9
1.2.2.2, Полиномы Кравчука..........................10
1.2,2.3. Тригонометрические функции.................11
1.2.2.4. Комплексные экспоненциальные функции........12
1.2.3. Базисные сплайны с конечными носителями
минимальной длины.......................................12
1.2.3.1. Основные понятия...........................12
1.2.3,2. Кусочно-постоянные базисные сплайны........15
1.2.3.3. Кусочно-линейные базисные сплайны..........15
1.2.4. Ортогональные вейвлеты с компактными носи-
телями .................................................16
1.2.4.1. Основные понятия...........................16
1.2.4.2. Функции Хаара..............................18
1.2.4.3. Функции Добеши порядка JVf ................18
1.2.4.4. Вейвлет-баэисы на отрезке..................20
1.3, Интерполирование функций..............................21
1.4. Точечное квадратичное аппроксимирование функций.......26
1,4.1, Метод алгебраических полиномов...................26
1,4.2. Метод ортогональных полиномов....................28
1.5, Интегральное квадратичное аппроксимирование функ-
ций на отрезке............................................ 29
Глава 2, Примеры решения задач на приближение функций в
Вреде Mathcad................................................ 31
2-1* Интерполирование функций на отрезке...................32
2.2. Точечное квадратичное аппроксимирование функций
L на отрезке.......................................... .... 38
й 2.3. Интегральное квадратичное аппроксимирование функ-
HL ций на отрезке..............................................46
IL 79
Приложение 2. Вычислительные схемы постановок и решения
задач аппроксимирования И интерполирования функций..........61
1. Интерполирование функций сплайнами на отрезке ....... 61
2. Точечное квадратичное аппроксимирование функций на
отрезке.................................................64
3. Интегральное квадратичное аппроксимирование функ-
ции на отрезке...........-............*............... 67
4. Квадратурный алгоритм Гаусса для вычисления коэффи-
циентов Фурье.......................................... 68
Приложение 2. Вычислительные схемы постановок и решения
задач аппроксимирования функций в вейвлет-базисах ..........70
1. Интегральное квадратичное аппроксимирование на Я.....70
2. Точечное квадратичное аппроксимирование функций, за-
данных на системе точек отрезка [0,1].................. 72
Приложение 3. Задания на компьютерную практику по прибли-
жению функций............................................. 76
Библиографический список....................................78