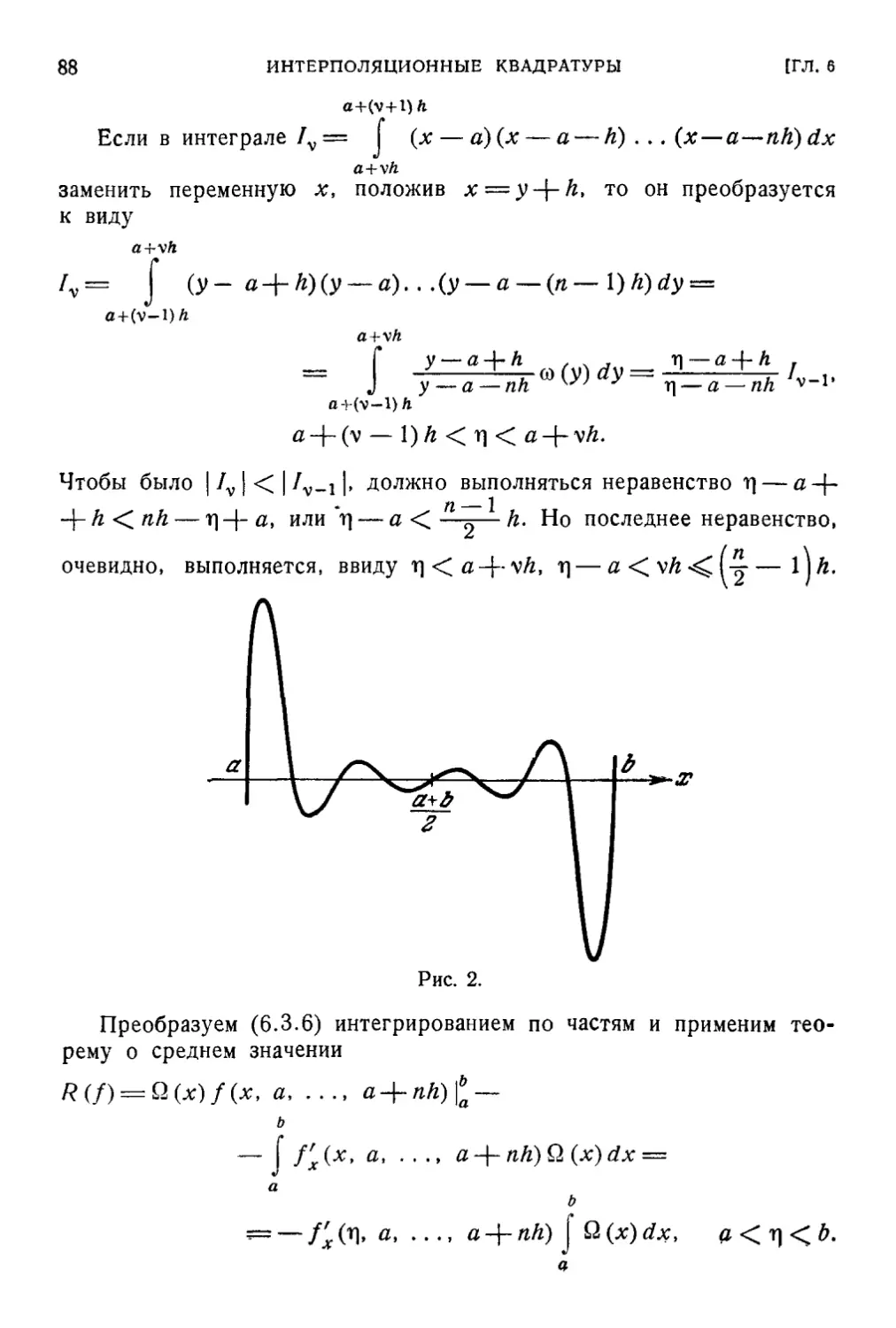
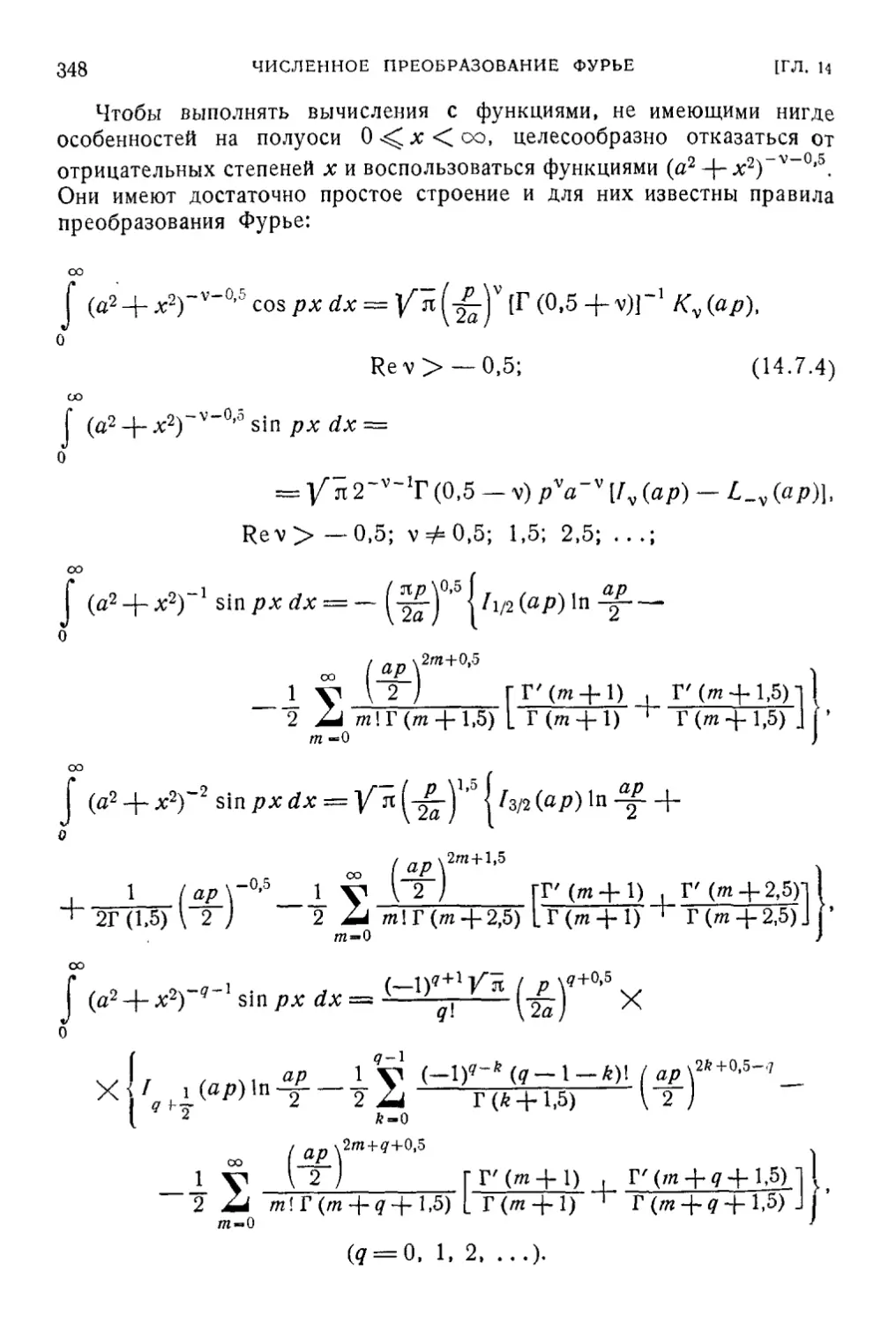Текст
в. и. КРЫЛОВ
ПРИБЛИЖЕННОЕ
ВЫЧИСЛЕНИЕ
ИНТЕГРАЛОВ
Издание второе,
дополненное
ИЗДА^Р^ТВО «НАУКА»
Ам^^Як РЕДАКЦИЯ
^^Я^АТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
**«>CKBf 1967
518 АННОТАЦИЯ
^ °^ В книге рассмотрены вопросы нахожде-
УДК 518 ния численных значений интегралов как
однократных, так и многократных.
Наибольшее внимание уделено правилам, часто
применяемым в практике вычислений. В
частности, значительное место отведено
задачам численного гармонического анализа и
обращению преобразования Лапласа.
Книга рассчитана на лиц,
занимающихся теорией вычислений, работников
вычислительных учреждений, студентов и
преподавателей вузов. Она может быть полезным
справочником для всех, кто по роду работы
соприкасается с научными и техническими
расчетами.
Владимир Иванович Крылов
Приближенное вычисление интегралов
Москва, 1967 г., 500 стр. с илл.
Редактор А. Ф. Лапко
Техн. редакторы Л. Ю. Плакше и Л. А. Пыжова Корректор О. А. Бутусова
Сдано в набор 25/1 1967 г. Подписано к печати 5/VII 1967 г. Бумага 60x90Vi6. Физ. печ.
л. 31,25. Условн. печ. л. 31,25. Уч.-изд. л. 30,66. Тираж 16 000 экз. Т-07018,
Цена книги 2 р. 13 к. Заказ № 662.
Издательство «Наука»
Главная редакция физико-математической литературы.
Москва, В-71, Ленинский проспект, 15.
Ленинградская типография № 2 имени Евгении Соколовой Главполиграфпрома
Комитета по печати при Совете Министров СССР. Измайловский проспект, 29,
2-2-3
201-67
ОГЛАВЛЕНИЕ
Предисловие ко второму изданию 7
Предисловие к первому изданию 8
ЧАСТЬ ПЕРВАЯ
ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
Глава 1. Числа и многочлены Бернулли 9
§ 1. Числа Бернулли 9
§ 2. Многочлены Бернулли 11
§ 3. Периодические функции, связанные с многочленами Бернулли 19
§ 4. Разложение произвольной функции по многочленам Бернулли 20
Глава 2. Ортогональные многочлены 23
§ 1. Некоторые общие теоремы об ортогональных многочленах . . 23
§ 2. Многочлены Якоби и Лежандра 28
§ 3. Многочлены Чебышёва 31
§ 4. Многочлены Чебышёва — Эрмита 37
§ 5, Многочлены Чебышёва — Лягерра 38
Глава 3. Интерполирование функций 40
§ 1. Конечные разности и разностные отношения 40
§ 2. Интерполирование по значениям функции 44
§ 3. Интерполирование с кратными узлами 48
§ 4. Тригонометрическое интерполирование 52
Глава 4. Линейные нормированные пространства. Линейные
операторы 57
§ 1. Линейные нормированные пространства 57
§ 2. Линейные операторы 61
§ 3. Сходимость последовательности линейных операторов .... 64
ЧАСТЬ ВТОРАЯ
ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Глава 5. Квадратурные суммы и задачи, с ними связанные.
Остаток приближенной квадратуры 67
§ 1. Квадратурные суммы 67
§ 2. Об остатке приближенной квадратуры и его представлении 74
1*
4 ОГЛАВЛЕНИЕ
Глава 6. Интегрирование функций, для которых известна таблица
значений» Интерполяционные квадратуры 79
§ 1. О содержании задачи 79
§ 2. Интерполяционные квадратурные форму.лы и их остаточные
члены 80
§ 3. Формулы Ньютона — Котеса 83
§ 4. Некоторые простейшие формулы Ньютона — Котеса 95
§ 5. Правила квадратур, имеющие степень точности ниже
интерполяционной 101
§ 6. Об отбрасывании узлов при построении правил
интегрирования 105
§ 7. Правила интегрирования, использующие значения функции
и производных 107
§ 8. Некоторые результаты общей теории интерполяционных
квадратур 111
Глава 7. Квадратуры наивысшей алгебраической степени
точности 116
§ 1. Общие теоремы 116
§ 2. Постоянная весовая функция 123
b
§3. Интегралы вида J {b — xf {х — af f {х) dx 129
a
+ CO
§ 4. Интеграл J e~^^f(x)dx 140
— CO
oo
§ 5. Интегралы вида x^e~^f(x)dx 142
0
Глава 8. Интегрирование периодических функций 148
§ 1. О задаче интегрирования периодической функции и форме
интеграла 148
§ 2. Интерполяционные правила интегрирования 149
§ 3- Правило наивысшей степени точности 151
§ 4. Остаток квадратуры периодической функции и его оценка . . 164
Глава 9. Квадратурные формулы, содержащие наперед
заданные узлы ^ 168
§ 1. Некоторые общие теоремы 168
§ 2. Формулы частного вида 174
§ 3. Замечание о вычислении интегралов со знакопеременной
весовой функцией 183
§ 4, Уточнение правил гауссова типа 187
Глава 10. Квадратурные формулы с равными коэффициентами 191
§ 1. Нахождение узлов 191
• § 2. Единственность квадратурной формулы наивысшей
алгебраической степени точности с равными коэффициентами 195
§ 3. Интегралы с постоянной весовой функцией 199
Глава 11. Квадратуры с наименьшей оценкой остатка 209
§ 1. О задаче минимизации остатка квадратуры . 209
§ 2. Минимизация остатка в классах iSp 210
ОГЛАВЛЕНИЕ 5
§ 3. Минимизация остатка в классах С^ 225
§ 4. Задача минимизации оценки остатка квадратуры с
закрепленными узлами 228
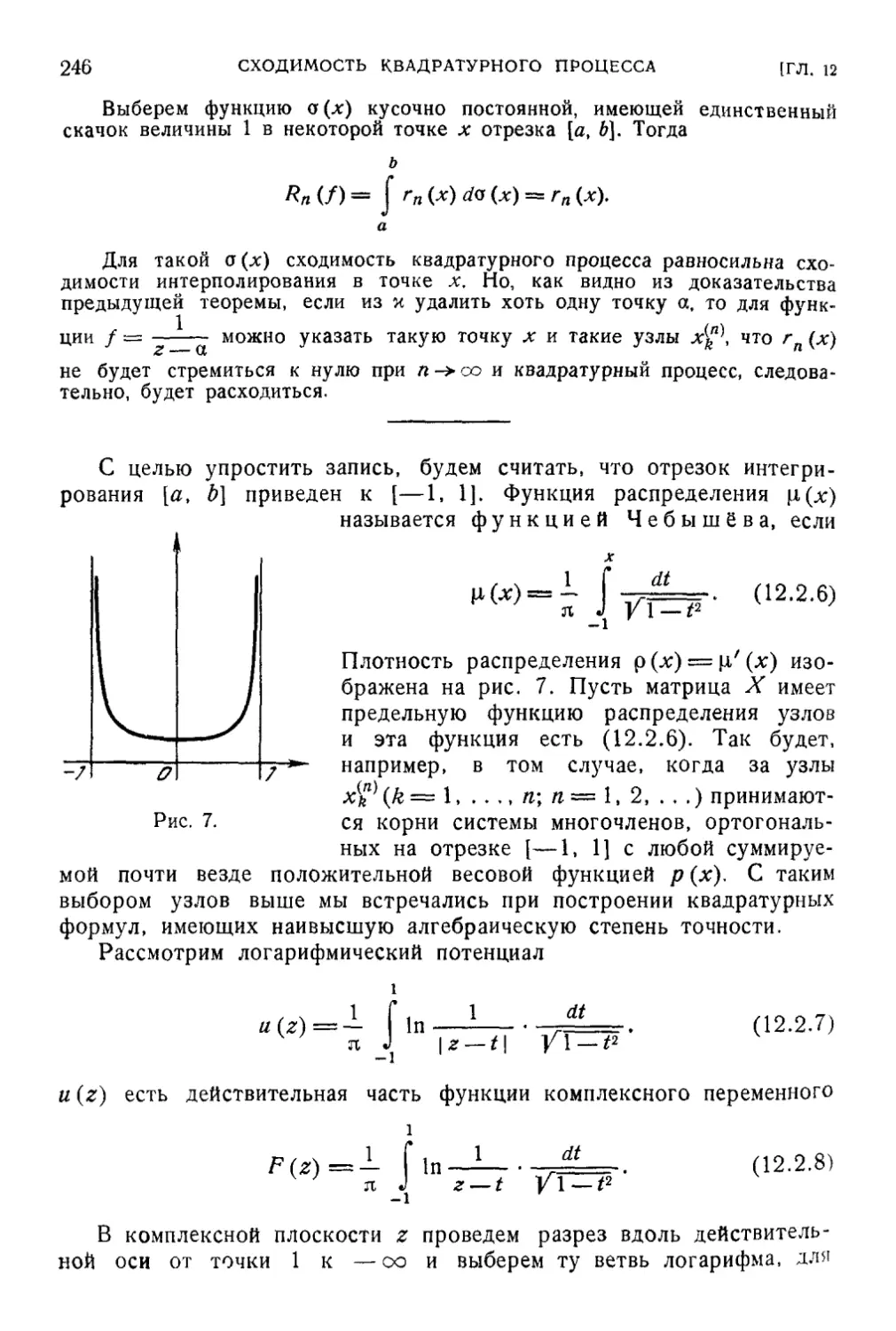
Глава 12. Сходимость квадратурного процесса 236
§ 1. О проблеме сходимости квадратурного процесса 236
§ 2. Сходимость интерполяционных квадратур для аналитических
функций 237
§ 3. Сходимость общего квадратурного процесса 257
Глава 13. Увеличение точности квадратуры и ускорение
сходимости квадратурного процесса 267
§ 1. О двух направлениях в задаче увеличения точности 267
§ 2. Ослабление особенности интегрируемой функции 270
§ 3. Эйлеровы методы разложения остатка квадратуры 274
§ 4. Увеличение точности квадратуры при наличии короткого
главного участка интегрирования в интегральном представлении
остатка 296
§ 5. Увеличение скорости сходимости квадратурного процесса . . 307
Глава 14. Численное преобразование Фурье 315
§ 1. Преобразование Фурье на конечном отрезке и вычисление
коэффициентов Фурье гладкой периодической функции .... 315
§ 2. О вычислении вспомогательных интегралов, содержащих
тригонометрические множители 321
§ 3. Применение алгебраического интерполирования к вычислению
коэффициентов Фурье 328
§ 4. Увеличение точности вычисления коэффициентов Фурье путем
предварительной подготовки функции 331
§ 5. Интегральные преобразования Фурье и интерполяционные
методы их численного осуществления 335
§ 6. Правила наивысшей степени точности 341
§ 7. Увеличение точности вычисления интегралов Фурье при
помощи предварительной подготовки функции 344
Глава 15. Численное обращение преобразования Лапласа .... 352
§ 1. Преобразование Лапласа, задача его обращения и связь ее
с преобразованием Фурье 352
§ 2. Интерполяционные правила 358
§ 3. Правило наивысшей степени точности 364
§ 4. Квадратурное правило с равными коэффициентами 369
§ 5. Замечания об увеличении точности вычислений при помощи
предварительной подготовки изображения 372
ЧАС ТЬ ТРЕТЬЯ
ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ НЕОПРЕДЕЛЕННОГО
ИНТЕГРАЛА
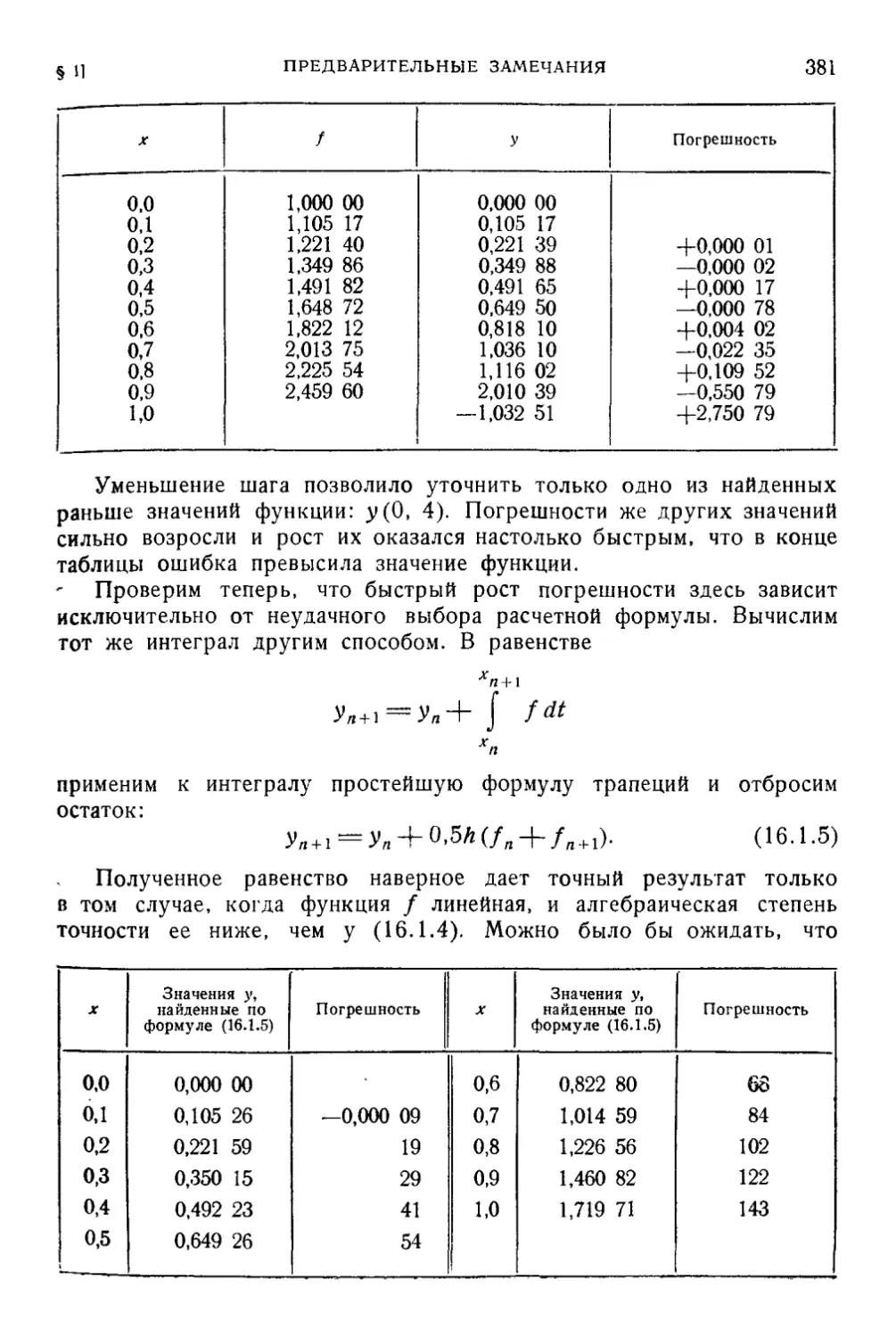
Глава 16. Введение 377
§ 1. Предварительные замечания 377
§ 2. Погрешность вычислений 382
§ 3. Сходимость и устойчивость вычислительного процесса .... 388
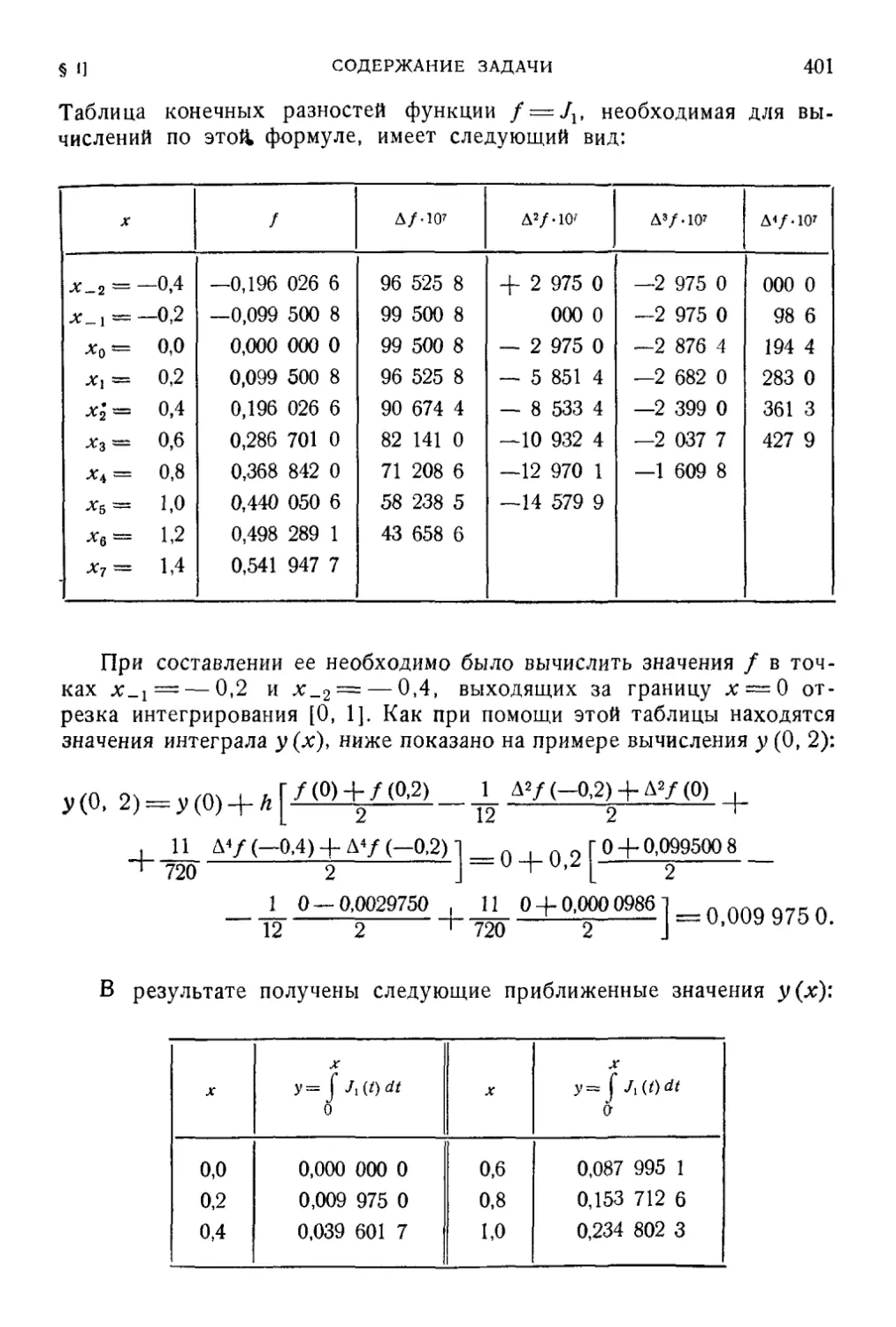
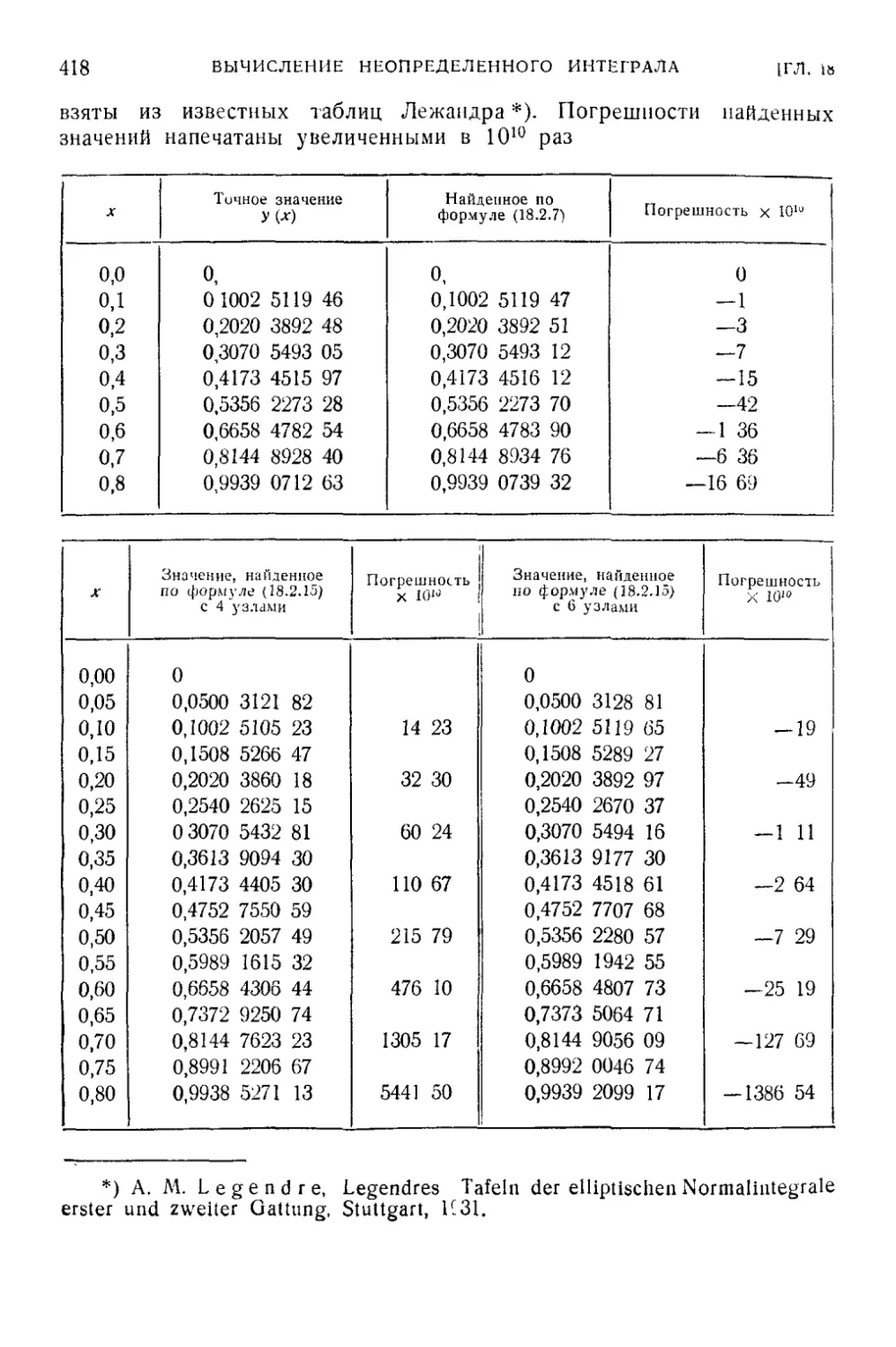
Глава 17. Интегрирование функции, заданной таблицей значений 398
§ 1- Содержание задачи к один из методов ее решения 398
§ 2. Остаток 402
б ОГЛАВЛЕНИЕ
Глава 18. вычисление неопределенного интеграла с малым
числом значений интегрируемой функции 403
§ 1. Содержание задачи и некоторые общие теоремы о расчетной
формуле 403
§ 2. Расчетные формулы частного вида 409
Глава 19. Методы вычисления, использующие несколько
предшествующих значений интеграла . 419
§ 1. Содержание задачи 419
§ 2. Условия, которые должны выполняться при достижении
наивысшей степени точности 422
§ 3. Существование и число интерполирований наивысшей степени
точности 425
§ 4. Остаток интерполирования и минимизация его оценки .... 426
§ 5. Условия положительности коэффициентов ау 428
§ 6. Связь с задачей решения дифференциального уравнения при
помощи многочлена 430
§ 7. Формулы частного вида 432
ЧАСТЬ ЧЕТВЕРТАЯ
ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ КРАТНЫХ ИНТЕГРАЛОВ
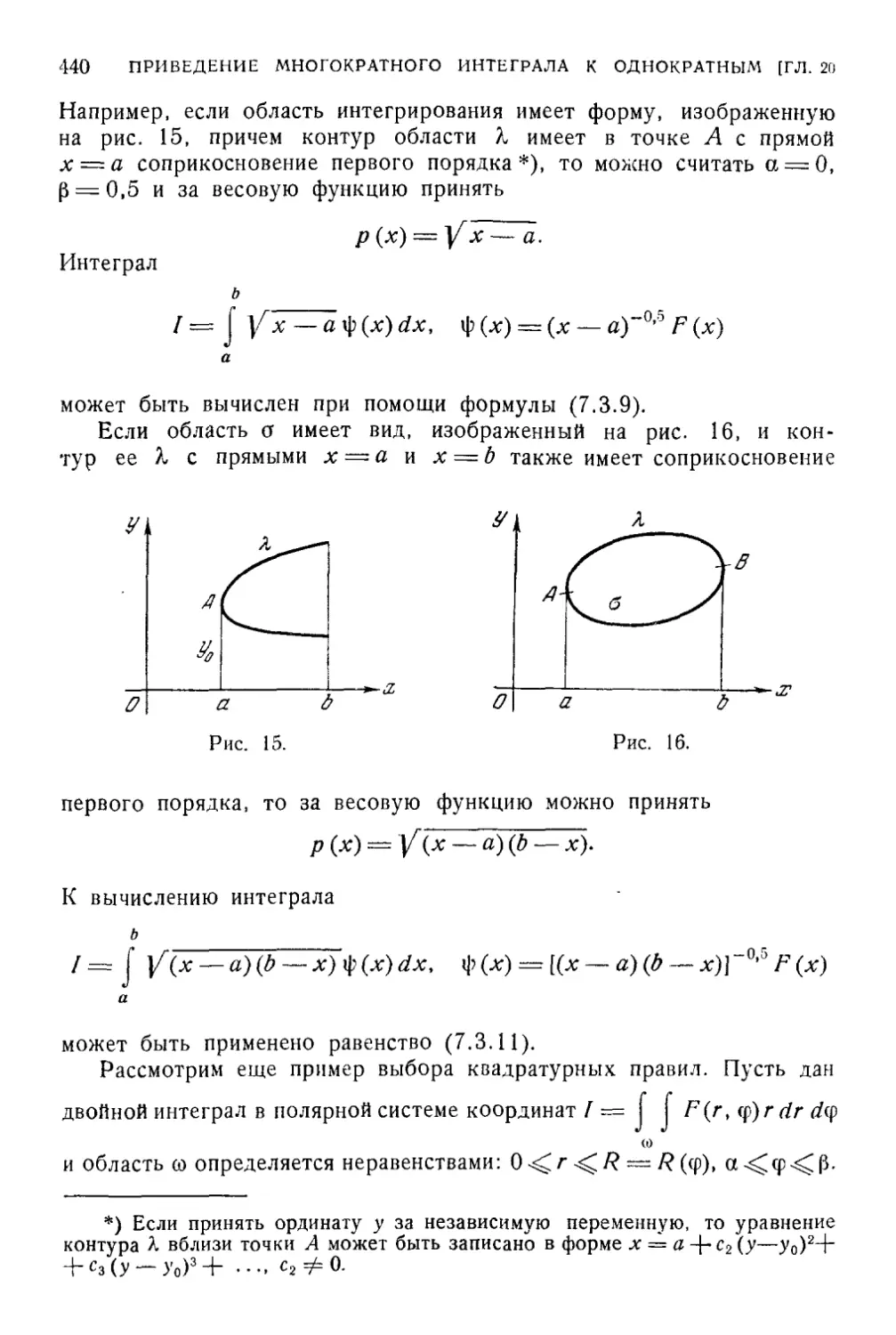
Г л а в а 20. О методах вычисления, основанных на приведении
многократного интеграла к однократным 435
§ 1. Предварительные замечания о «проблеме большого числа
узлов» 435
§ 2. Влияние формы области на выбор правил интегрирования . . . 437
Глава 21. Интерполяционные кубатурные формулы 442
§ 1. Алгебраическое интерполирование функций многих переменных 442
§ 2. Интерполяционные кубатурные формулы 447
§ 3. Примеры построения кубатурных формул 453
Глава 22. Кубатурные формулы с наименьшим числом узлов . . 462
§ 1. Кубатурная формула, точная для многочленов первой степени 462
§ 2, Кубатурные формулы, точные для многочленов второй степени 463
§ 3, Кубатурные формулы, точные для многочленов третьей степени 467
§ 4. Кубатурная формула Радона 471
Глава 23. Кубатурные формулы для областей частного вида . . . 488
§ 1. Гиперкуб 488
§ 2, Гиперсфера 489
§ 3. Гипершар 492
§ 4. Симплекс . 495
ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
Второе издание книги значительно расширено сравнительно с
первым, но общее ее направление осталось прежним: книга посвящена
проблеме построения правил вычисления интегралов. При этом
главное внимание уделено правилам, которые могут применяться в
практике вычислений.
От изложения в книге других вопросов теории квадратур я
принужден был отказаться, чтобы не увеличивать объема книги больше
намеченной границы.
Сожалею о том, что не мог включить в книгу изложение работ
о точных оценках как сверху, так и снизу порядка погрешности
кубатуры. С ними связан вопрос о построении кубатурных
процессов, для которых погрешность имеет такой же порядок малости,
как и оценка порядка снизу. Он также не освещен в книге. Все
эти вопросы рассматривались другими авторами в книгах по теории
кубатур, имеющих более теоретический характер. Наконец, в книге
отведено мало места вопросу о неустойчивости некоторых
вычислительных процессов, таких, например, как процесс наивысшего порядка
точности для обращения преобразования Лапласа, квадратурный
процесс Котеса и др.
Главнейшие изменения, сделанные в книге, состоят в следующем:
1. Во вторую часть книги, где рассматривается задача о
вычислении определенного интеграла, введены новые главы о численном
преобразовании Фурье, об обращении преобразования Лапласа и об
интегрировании периодических функций.
2. Добавлена четвертая часть книги, содержащая четыре главы,
в которых излагаются основы теории вычисления кратных интегралов.
Главы 21, 22 и 23, по просьбе автора, были написаны И. П. Мы-
совских, много занимавшимся проблемой численного
интегрирования в многомерных пространствах. Содержание этих глав излагалось
им в лекциях по теории численного интегрирования, которые он читал
^ течение нескольких последних лет в Ленинградском университете.
3- Кроме того, внесены некоторые менее значительные изменения
* другие разделы книги.
8 ПРЕДИСЛОВИЕ к ПЕРВОМУ ИЗДАНИЮ
В конце помещен список исправлений, которые следует внести
в вышедшую в 1966 году в издательстве «Наука» книгу: В. И.
Крылов и Л. Т. Шульгина, Справочная книга по численному
интегрированию.
Август 1966 г. Минск, Академия Наук БССР
В, И, Крылов
ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
Автор стремился к тому, чтобы книга могла ввести читателя
в круг главных идей и результатов современной теории
приближенного интегрирования и, кроме того, была бы полезным пособием
для тех, кто имеет дело с вычислениями.
В книге рассматриваются вопросы вычисления только
однократных интегралов. Более трудная и значительно менее исследованная
задача вычисления многократных интегралов в ней почти совсем не
затрагивается. Лишь в одном месте книги говорится о двойном и
тройном интегралах в связи с приведением их к простым интегралам.
Но даже для простого интеграла автор отказался от изложения
многих интересных тем. Так, например, в стороне остались задачи
интегрирования быстро колеблющихся функций, вычисления
контурных интегралов от аналитических функций, применение метода
случайных испытаний и др. Книга посвящена преимущественно методу
механических квадратур, когда интеграл находится как линейная
комбинация конечного числа значений интегрируемой функции.
По содержанию своему книга разделяется на три части. В
первой из них излагаются понятия и теоремы, встречающиеся в теории
квадратур, но выходящие, по крайней мере частично, за рамки
программы высших учебных заведений.
Вторая часть посвящена задаче вычисления определенного
интеграла. По существу дела, здесь рассмотрены три следующие
основные темы: теория построения формул механических квадратур при
предположении достаточной гладкости интегрируемой функции,
задача увеличения точности квадратуры и проблема сходимости
квадратурного процесса.
В третьей части книги исследуется вопрос о вычислении
неопределенного интеграла. Здесь автор ограничился преимущественно
изучением проблемы построения расчетных формул. Кроме того, указаны
признаки устойчивости и сходимости вычислительного процесса.
Мои товарищи по работе М. К. Гавурин и И. П. Мысовских
просмотрели большую часть рукописи, и я очень благодарен им за
ряд замечаний и советов.
АН БССР. Октябрь 1957 г.
Автор
ЧАСТЬ ПЕРВАЯ
ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
В первой части книги содержится изложение следующих частных
вопросов математики, необходимых для построения теории
отдельных задач приближенного интегрирования функций: числа и
многочлены Бернулли, ортогональные многочлены, интерполирование,
линейные операторы и проблема сходимости последовательности таких
операторов. Результаты, приведенные здесь, можно найти в
специальной литературе, но мы считали полезным изложить их в настоящей
^ книге и освободить читателя от многочисленных и часто нелегко
проверяемых литературных ссылок.
Все перечисленные вопросы рассмотрены только в той мере, как
это нужно для чтения последующих глав.
ГЛАВА 1
ЧИСЛА И МНОГОЧЛЕНЫ БЕРНУЛЛИ
§ Ь Числа Бернулли
Многочлены и числа Бернулли ниже (в § 6 главы 6 и в § 3
главы 7) потребуются для построения формулы Эйлера — Маклорена
и других сходных с ней формул, служащих для увеличения точности
приближенных квадратур.
Числа Бернулли могут быть определены при помощи следующей
производящей функции. Пусть t — комплексная переменная.
Рассмотрим функцию
Точки t = 2kni, где k — любое целое число, являются нулями
знаменателя. Все они простые, ибо производная знаменателя равна е^ и
отлична от нуля при всяких конечных Л Точка ^ = О не является особой
Для g(t), так как при ^ = 0 обращается в нуль и числитель
отношения. В круге 1^1 <2я функция g(t) регулярна и может быть
там разложена в степенной ряд по степеням t. Запишем разложение
10 ЧИСЛА и МНОГОЧЛЕНЫ БЕРНУЛЛИ [ГЛ. 1
В форме
схз
-7-4-= S%"' 1^1<2^- 0-1-2)
е^ — 1 ^ л!
Числа iB^, определенные этим равенством, носят название чисел
со
Бернулли, Если в A.1.2) обе части умножить на е^ — 1 = 2j~Zr*
V=l
то получится следующее равенство
со
(i+-l+4+-)Slf'"='-
rt = 0
верное при всяких t из круга |^|<2л. Оно говорит о том, что
после перемножения степенных рядов, стоящих в левой части,
сохраняется только первая степень t с коэффициентом, равным единице,
коэффициенты же при степенях t выше первой все должны
обратиться в нуль: jBq^: 1 и при /г = 2, 3 ... должно быть
I II /« m ^•
л! ^ («-1)! 1! ^ (п--2)!2! ^ ' " ^ 1!(п —1)!
Последнее равенство позволяет последовательно вычислить все
числа Бернулли. Ему можно придать другую форму, более удобную
для записи. Умножив его на п1 я прибавив к обеим частям Б^,
получим
Аналогия левой части с известным выражением для степени
двучлена позволяет последнее равенство записать условно в виде
(В+1)«=:5„. A.1.3)
если считать, что. после возведения двучлена ^+1 в степень,
показатели степени у Б переходят в индексы чисел Бернулли.
Легко можно проверить, что все числа Бернулли с нечетными
индексами, большими единицы, равны нулю:
52Й+1--0, k>0. A.1.4)
Для этого в A.1.2) заменим t на —1\
;§2] МНОГОЧЛЕНЫ БЕРНУЛЛИ И
С другой стороны,
оо
е-^ — Х е^—\ ^е^ — \ ^JUn\
rt=0
и поэтому должно быть
QO со
Сравнение коэффициентов при t^ для /г > 1 дает B^^=z{—^ТВ^,
При /г = 2/г + 1 (^ > 0) отсюда следует ^2й + 1 ^= — ^2a+i» что
равносильно A.1,4). Значения нескольких первых чисел Бернулли таковы:
^о=Ь ^1=— 2"' ^2==* ^4 = — 30' ^б = -42»
1 д — ^ Д —_i5L д — ^ R „. 3617
^8 — " 0 ' ^10 ~ 6 ' 12 — 2730 ' ^14 — -6"» ^16 — — -glT'
43 867 р _ 174 611 о _ 854 513 „ _ 236 364 091
^18 —" 798 ' ^20—™- 330 ' 22— 138 » ^24-^ 2730 '
8 553103 о __ 23 749 461029 _ 8 615 841276 005
^26— б ' ^28 —~ 870 ' ^30— 14322 *
Числа Бернулли четных номеров связаны с суммами четных
отрицательных степеней натуральных чисел следующими замечательными
равенствами:
52* = -bj£^(l + 2-^* + 3-- + 4--+ ...). A.1.5)
Из них видно, что при неограниченном росте k бернуллиевы числа 821^
будут весьма быстро возрастать и при больших k будет иметь малую
относительную погрешность следующее приближенное равенство
52ft^2(~l)*-Ч2^)!Bл)-^^ A.1.6)
Равенства A.1.5) сразу следуют из полученных ниже
разложений A.3.1) многочленов Бернулли в тригонометрические ряды на
отрезке [О, 1].
§ 2. Многочлены Бернулли
Многочлены Бернулли можно определить различными способами.
Для наших целей достаточно удобным является определение их при
помощи производящей функции. Введем функцию
g{x, t) = e''<-±—. A.2.1.)
^^— 1
12 ЧИСЛА и МНОГОЧЛЕНЫ БЕРНУЛЛИ [ГЛ. 1
Она отличается от A.1.1) множителем e•^^ не обращающимся в нуль,
и имеет те же особые точки, что и g(t). В частности, она регулярна
в круге 1^1 < 2л и может быть в нем разложена в ряд по степеням t:
оо
Несколькими строками ниже мы убедимся в том, что функция В^(х)
есть многочлен степени п. Он называется многочленом Бернулли,
со
И —^
v=0
разложением A.1.2), то получим тождество
со со оо
V=0 fe=0 ft=0
Сравнение коэффициентов при t^ приводит к равенству
^п{^_ -^"^а , х^'-'В, , ■ Вп
п\ ~ п\ ^ (п—1)!1! ^ • * • In!
После умножения на п\ отсюда получается следующее выражение
для Bj,{x)
п
^п(^) = ^ТйёгщВ„.,х>', A.2.3)
fe-0
показывающее, что В^ {х) действительно есть многочлен, старший
член которого равен х^. Выражение A.2.3) может быть записано
в весьма простой условной форме
В^{х) = {х + В)\ A.2.4)
если согласиться считать, что, после возведения двучлена х-^-В
в степень, показатели степени у В должны перейти в индексы чисел
Бернулли.
Нам потребуется знакомство с некоторыми свойствами
многочленов Бернулли.
1, Начальные значения многочленов Бернулли при
л: = О равны соответствующим числам Бернулли;
В^{0)==В,, A.2.5)
ЧТО видно из A.2.3).
2. Дифференцирование и интегрирование 5^(jc).
Вычисляя производную по X от A.2.2), найдем
§ 2] МНОГОЧЛЕНЫ БЕРНУЛЛИ 13
Левая часть отличается от g только множителем t и поэтому должно
быть
оо
«=о
Ввиду единственности степенного разложения» из двух последних
равенств вытекает j— = _ j ^ или
в!п{х)^пВп-х{х\ A.2.6)
Отсюда и из A.2.5) сразу же следует правило интегрирования бер-
нуллиевых многочленов
X
B„(x) = B„-\-nJB„.,it)dt. A.2.7)
О
3. Теорема об умножении аргумента. Пусть т —
любое целое положительное число; тогда
оо
emxt ^ = у ^п {тх) ^п
^^ — 1 ^ п\
п=0
Весьма простыми преобразованиями может быть получено другое
разложение
emxt L^ _ i ,rnxt mt(l + e^+ ... +.(^-^H _
e^ —1 ^ e^^^ — l
m—1 (x+—1 mt m—l oo d I ^ _l_ _^ | ^n
^ 1 у Л "^>^ m^ _ 1 yiy ^n[^+ щ]т -^
Из двух построенных разложений и следует теорема об умножении
аргумента:
В„{тх) = т"-^^В„(х-\-^У A.2.8)
4. Теоремы о представлении многочленов В^(х).
Чтобы изучить поведение В^(х), удобно вместо х ввести новую
переменную z=:x(\—х). Покажем, что верны следующие
утверждения о представлении бернуллиевых многочленов в переменной z.
14 ЧИСЛА и МНОГОЧЛЕНЫ БЕРНУЛЛИ [ГЛ. 1
Всякий многочлен В^{х) четного номера /г = 2/г может быть
разложен по степеням z:
v = 0
причем F^Q=1 и F^^^^0{\=z\,2 k — 2). Всякий бернул-
лиев многочлен нечетного номера n^=^2k — 1 может быть представлен
в форме
Jfe-2
(-l)*S2ft-iW = (l-2^)SWft,v2*-'-^ A-2.10)
v = 0
где все коэффициенты И^^,^ (v=:=0, 1, ..,, k — 2) положительны.
Проверим сначала утверждение о многочлене четной степени В2^{х).
Для упрощения записи введем вспомогательную переменную |,
положив х^^0,5-|-|. Переменные Ъ, w z связаны между собой
соотношением z^=^x{\—х)=:=:0,25 — |2.
Чтобы убедиться в том, что B2f^ {х) есть целый многочлен от
переменной Z, достаточно установить, что в разложении В^^^ {х) по
степеням ^ будут содержаться только четные степени |.
Производяш.ая функция A.2.1) относительно переменной ^ будет
иметь следующее выражение
^Jl. ^ есть коэффициент при f-^ в разложении g по степеням t.
Множитель . !.,. — четная функция ^ и в ряде для него по
степеням t будут содержаться только четные степени t. Чтобы получить,
оо
^ , член с fi^, мы должны из ■
v=0
ряда для е^^ брать члены только с четными степенями 1, Но все они
содержат также лишь четные степени |, и В2^{х) будет содержать
только четные степени |.
Так как при х = 0 переменная z также обращается в нуль, то
разность B2fi (х) — B2k будет многочленом от z без свободного члена
и должно иметь место равенство
к~1
{-If IB2, (X) - В2,] ^ 2 f^k, v^'"^-
v = 0
Нам осталось только проверить утверждения об Fk.v ^Коэффициент
в B2k{x) при старшей степени л:^^ равен единице и поэтому должно
§2]
МНОГОЧЛЕНЫ БЕРНУЛЛИ 15
быть /^jfe,o=l- Кроме того, коэффициент при к в Bs^Cx) есть
2kB2k-\ == О, и так как первая степень х в правой части может
содержаться только в члене, отвечающем v=k—1. то Fj^ j^_i = 0.
Для нахождения остальных Ff^^ ^ может быть построено рекуррентное
соотношение. Вычислим от обеих частей A.2.9) вторую производную
по X. Так как B2k(x)==2kBk—l)B2k-2M и так как операторы
вычисления производных по л: и по -г связаны между собой
следующими легко проверяемыми равенствами
dx ~~ dx dz ~^ ^^ dz '
^_П-2хJ^^-2 —= A-4^)~^? 2^
-^^ — A IX) ^^2 ^ dz ^^ ^^^ dz'' ^ dz *
то после вычислений получим:
(_l)*2^B^-lM2ft-2W=S^jfe,v-i(^4-l'-v)(Aj-v)^*-^-v_
v=l
Jfe-2
— 2^А ^B^ —2v)BA;-v— V^z^'^'^.
Сравнение его с разложением вида A.2.9) для ^гА-гМ*
й-2
(-1)'^^ [^2Jfe-2W~^2Jfe-2]=- S /';fe.l,v^'-^-^
v-0
позволяет сказать, что при v==0, 1 к — 2 должно выполняться
равенство:
BА —2v)Byfe~2v— O/^'^^.v^
--2AJB^-1)/=•,_! ^, + (Aj+1-v)(Aj-v)F, ,_,.
Отсюда, зная, что f;^Q=l и F^^^_^ = ^ (^=1, 2, ...). мы сможем
найти последовательно Fj^^^ (^ = 3, 4, ...; v=l, 2, .... k — 2) и
все они окажутся положительными.
Для доказательства верности утверждения о представлении ^2ft-i(^)
достаточно вычислить производную по X от обеих частей A.2.9):
k-2
Отсюда видно, что равенство A.2,10) является верным и
^*' V — 2k ^ ^'
16 ЧИСЛА И МНОГОЧЛЕНЫ БЕРНУЛЛИ [ГЛ. 1
5. Симметрия распределения значений В^{х).
Рассмотрим точку х = 0,5 на оси х. Точки л: и 1—х расположены
симметрично относительно нее. Переменная ^ = x(l—х) не изменит
своего значения при замене х на 1 --jc. Отсюда и из A.2.9) вытекает,
что ^2ft W ^ точках л: и 1 — х принимает одинаковые значения
B2k{'^—x) = B^^{x). A.2.11)
График многочлена ^2feW будет линией, симметричной относительно
прямой х = 0,5.
k-2
В A.2.10) множитель 2 ^k v^^'^""^ принимает одинаковые значе-
v = 0
НИЯ в точках* л: и 1 —х. Множитель A —2х) при замене х на. 1 —х
сохраняет абсолютную величину, но изменяет знак. Поэтому
B2k-iO-x) = -B,,_,(x). A.2.12)
График многочлена B2k-i(x) имеет центр симметрии в точке
JC =1=0,5.
При х = 0 из A.2.11) получается ^2^@ —^2ft и из A.2.12)
при k^2 следует ^2jfe-i(l)=^—^2ft-i- Каждый бернуллиев
многочлен, кроме Bi(x), на концах отрезка [0. 1] принимает одинаковые
значения
В„A)=.В„@)=:В„. A.2.13)
6. Характер изменения многочленов Бернулли на
отрезке [0. 1], Нам потребуются значения ^^@.5), которые легко
могут быть вычислены, например, при помощи теоремы об
умножении аргумента. Если в A.2.8) положить /а = 2 и л: = 0,5, то получим
В,(\) = 2'-'1В,@.5)~\-В,(\I
Но так как ^„A) = ^,^ (/г > 1), то при всяких п
5^0,5) = -A-2-«+1)^.. A.2.14)
Для дальнейшего потребуется рассмотреть многочлены
у^(х) = В,(х)-В^,
несущественно отличающиеся от В^ (х) и более удобные для записи.
Возьмем сначала многочлен четного номера n = 2k. Ввиду A.2.9),
имеем
(-1)*У2*М=2 ^*.v^*"'- A-2-15)
v=0
§ 2] МНОГОЧЛЕНЫ БЕРНУЛЛИ 17
Точки л: ;= О и х=-- \ являются нулями у^^ (х):
У2Н @) =- В^, @) ~ В,, = В,, - В,, ^ 0.
y2kW==-B,,{\)~B^,^B,,-B^,^0.
Легко проверить, что при ^^2. оба нуля имеют вторую кратность,
так как, например, для х=^0
у;^ @) = 2k Bk ~ 1) £f2,_2 @) = 2AjB^ - 1M2,_2 Ф О,
Ввиду A.2.11), аналогичное имеет место для х=1. При О < л: < 1
переменная z будет лежать в границах 0<2;<^0,25 и, так как
/"*, V > ^' 'ГО (— 0^ У2Й (^) > 0. О < X < 1. Внутри отрезка О < л: < 1
многочлен y2kM не обращается в нуль и имеет знак такой же,
как (—1)*. Когда х изменяется от нуля до 0.5, функция z = x(l —л:)
будет возрастать от нуля до 0,25 и при изменении х от 0.5 до 1.
функция Z будет убывать от 0,25 до нуля.
Как видно из A.2.15) при изменении х от О до 0,5 многочлен
(—1)^ У2к(^) будет возрастать от нуля до (—1)^ У2кФ^^) =
= I^2й @.5) ~iB2^fe 1^B —2-2^^+0 l^sfel- ^огда же х изменяется от 0.5
до 1, (—^)^У2к(^) будет убывать от указанного только что значения
до нуля. Каждое значение а [О < а < B — 2~'^^'^^)\В2^\] многочлен
У2к(^) "^ отрезке [О, 1] будет принимать два раза, в точках,
расположенных симметрично относительно л: = 0,5.
Рассмотрим теперь многочлен y^^ix) нечетного номера n=^2k— 1.
Будем считать ^^2, тогда
y2k~ii^) = ^2k~iM
ft-2
(-1)* У2А-1 (X) .= A - 2х) 2 fi,, v^*-^-^-
V = 0
A.2.16)
Точки х = 0 и х=1 будут нулями y2k~iW- Можно проверить, что
обе эти точки есть однократные нули. Действительно,
Ум_1@) = BА-1M2*_2@)^0 и У'^,_,A) = Bк-1)В^,_,A)Ф0.
Кроме того, из A.2.16) следует, ввиду Н^^^^О, что jc = 0.5 есть
простой нуль y2ft-iW и никаких других нулей при О < х < 1 этот
многочлен не имеет. Знак У2к~\(^) определяется неравенствами
(—l)^y2fe-iW>t^ при 0<x<0,5.
(-l)'y2ft-iW<0 при 0.5<х<1.
18 ЧИСЛА и МНОГОЧЛЕНЫ БЕРНУЛЛИ (ГЛ. I
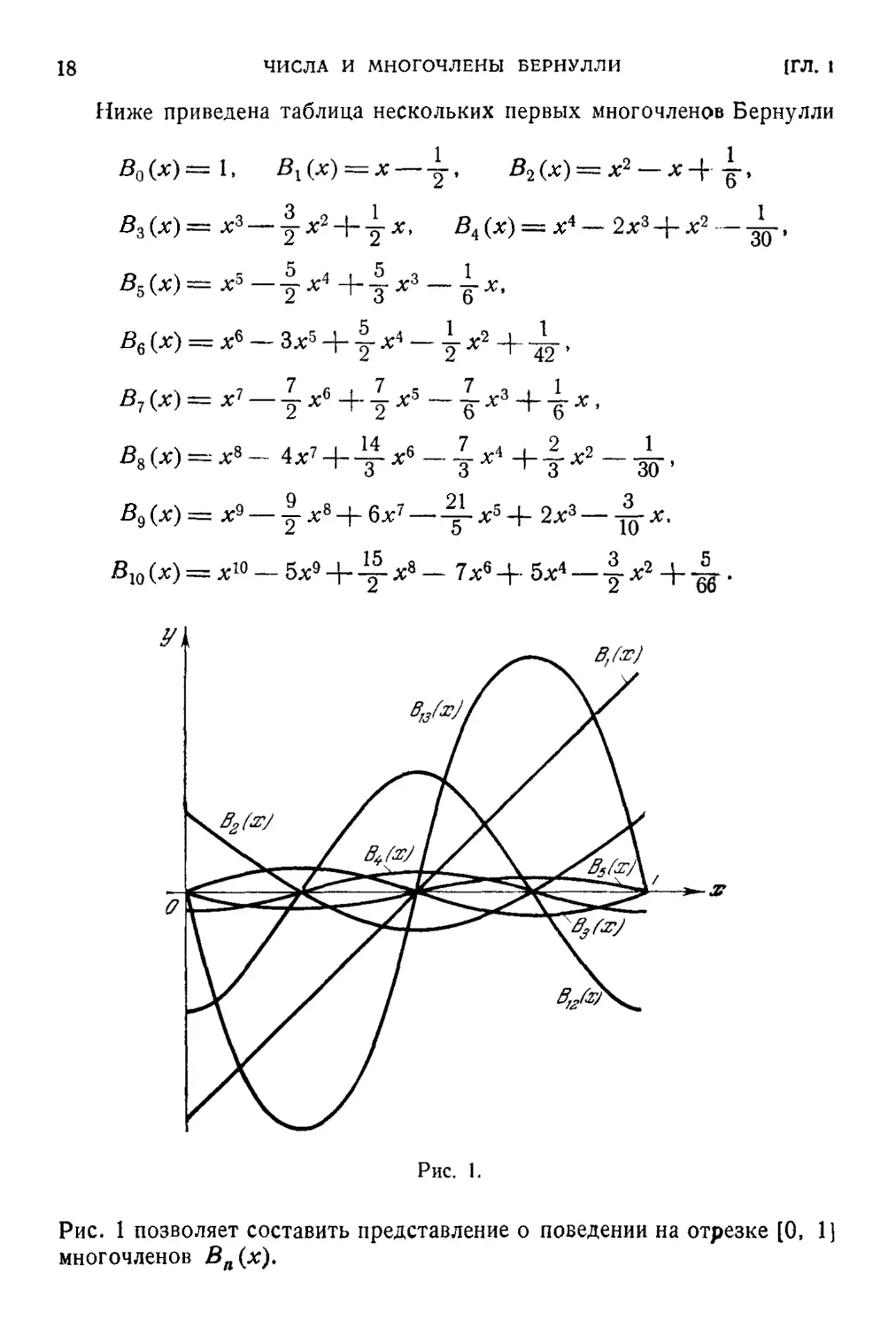
Ниже приведена таблица нескольких первых многочленов Бернулли
Boix)
1=1, Biix) = x — ~, В2(х) = х^ — х-\гЛ:<
х-' + ^х. B^(x) = x'^-2x^-\-x■2-^,
Зх^ + ^х^-:^х^-^±,
.^х^-±х^^-^х^-~^х^ + ^х.
7 _« . 7 ., 7 , . 1_
6
— V-8 4гТ -i- — »-6 ^ V-4 -1- -Н. г2 L
~х tx -f ^ X -g-x-t-gX ^,
I = лr^ — |-х8 + 6x7 —^ д;5 4- 2x3 —-i-ж.
) = хю — 5x9 + ^ ;с8 - 7х« + бл:"— -1 х2-Ь - ^
30
Рис. I.
Рис. 1 позволяет составить представление о поведении на отрезке [О, 1)
многочленов В„(х).
- 3] ПЕРИОДИЧЕСКИЕ ФУНКЦИИ 19
g 3. Периодические функции, связанные
с многочленами Бернулли
При исследовании некоторых вопросов, наряду с многочленами
Бернулли, вводят 1-периодические функции В^^{х), определенные
равенствами
в1(х) = Вп(х), 0<а:<1. bUx^\) = bI(x);
В*о(х) есть постоянная, равная 1, Bi{x) — разрывная функция и имеет
скачок —1 в целых точках, B^ix) при /г > 1—непрерывные
функции.
Построим тригонометрические ряды Фурье для Ва{х), С этой
целью построим ряд Фурье для производящей функции
е^— 1
Воспользуемся записью ряда с помощью показательной функции:
m = —оо
1 1
С„,=== \ ge-^'^'^^^dx=^—^— е^^е'^2^"'^й?х=^:;—4—.
о о
Выделяя слагаемое Cq=1 и объединяя члены ряда, отвечающие
значениям индекса tn и ~т, получим
оо
gix. 0=1+1; [71гЬ^«""'"^+7чгк?Г«-М-
Можно показать, что для любых значений х на отрезке O^jc^l
ряд. стоящий в правой части равенства, будет сходиться при
всяких t, отличных от i2kn(k^=:0, ±1, ...). При этом, если взять
любую ограниченную часть о плоскости t и исключить из ряда
несколько первых членов, имеющих полюсы в этой части плоскости,
то оставшийся после исключения ряд будет сходиться равномерно
относительно ^ в а.
Опираясь на это, легко можно оправдать возможность изменения
порядка суммирования, которое, по ходу вычислений, сделано
Несколькими строками ниже при построении степенного ряда для g.
Если считать |^|<2я и разложить правую часть по степеням t,
то коэффициентом при t^ будет тригонометрический ряд для —^-~^.
20 ЧИСЛА и МНОГОЧЛЕНЫ БЕРНУЛЛИ ГГЛ, 1
Он и будет давать представление j— при всех х
t — i2nm i2nm
1
t ~ АЛ\ i2nm j *
12лт
CO
n^\
oo oo ^
g{X. t)—i^ 2^ 2л[ A2лтГ A2птГ^ ^ J ~
^==1 n = l
i_i V ^" V ["(—^)""^ p~i2nmx \_gi2nmx'\
— ^^ Zj (/2ji)« Z^[m^ m« J '
oo я 1
я •-> 1 P* (x) ■— "'• V [^~^) ~-l2nmx ]_gi2Kmx]
n>l, ««W — Bдг)« ^j [ m" ^ m"^ J-
Для четных и нечетных индексов вычисления дают следующие
результаты
b;,(;,)=(ii1)!1B*)! yi2i2!H?Li. A.3.1)
5;,,,(;c):==(=l)!:iB*+il' У !1п2^. A.3.2)
2 Ji m = i '^
при х = 0 отсюда получаются указанные выше ряды A.1.5) для
бернуллиевых чисел.
§ 4. Разложение произвольной функции
по многочленам Бернулли
Теорема U Если f(x) у-кратно непрерывно дифференцируема
на [О, 1], то при любом х^[0, 1] имеет место равенство
/(л:)=//@^^ + 2^[/*-'Ч1)-/*-'ЧО)]-
О ft=»l
1
- -^ J /*'' (О [B'v (x--t)-BUx)]dt. A.4.1)
I 4] РАЗЛОЖЕНИЕ ПО МНОГОЧЛЕНАМ БЕРНУЛЛИ 21
Доказательство. Рассмотрим интеграл
Pv (•*) = Pv = ТГ J ^''' (^) ^'^ (-^^ - ^) ^^-
о
Считая v> 1. выполним интегрирование по частям. Так как
-1- В\ (JC — О === — vBv„i (X — t), В\ (X — 1) = Б* (л:) = В^ {х).
то
Pv
1
О
Выполним это преобразование v—1 раз:
k=2
Функция В\{х) имеет в целых точках скачок —1, в остальных же
точках имеет производную, равную +1
Для вычисления pi положим сначала О < х < 1
X 1
Pxix)^ ^ f {t)B\{x ~t) dt+ ^ f\t)B\{x — t) dt^
0 д:
X
= B\{+Q)f{x)~B\ix)f(fi)+^f(t)dt +
0
1
+ Bt (л: - 1) / A) - / (л;) St (-0) 4-J / @ rf^ =
1
== [fit (+0) - B\ (-0)] / (x) + 5, (X) 1/ A) - / @)] + J / @ tf^
22 ЧИСЛА и МНОГОЧЛЕНЫ БЕРНУЛЛИ [ГЛ, 1
Для Ру (v=:=b 2. ...) окончательно получаем
1
о
=i^i/*-"(i)"/*-"@)]-/(x)+j/w
Этот результат только формой записи отличается от A.4.1).
Доказательство было проведено для открытого отрезка 0<а:<1, но,
по непрерывности, равенство A.4.1) верно и для замкнутого отрезка
0<х<1.
Если f(x) задана на произвольном конечном отрезке [а, д] и
v-кратно непрерывно дифференцируема там, то ее разложение на
[а, Ь] по многочленам Бернулли получается из A.4.1) при помощи
линейного преобразования аргумента (h = d — а):
f(x) = ijf(t)dt+'^ FT^-^ Г/"' (^) ~ /'"' (-)] -
-i^ J/«@[B:(i=i)-B;(i^)]«. (,.4.2)
Литература
Г е л ь ф о н д А. О., Исчисление конечных разностей, гл. IV, изд. 3, М.,
«Наука», 1967.
Стефенсен И. Ф., Теория интерполяции, гл, XII, М.— Л., Гостех-
издат, 1935.
Харди Г., Расходящиеся ряды, гл. XIII, М„ ИЛ, 1951.
ГЛАВА 2
ОРТОГОНАЛЬНЫЕ МНОГОЧЛЕНЫ
§ 1. Некоторые общие теоремы об ортогональных
многочленах
В книге будет уделено много места изучению интегралов вида
ь
\ p{x)f{x)dx. B.1.1)
а
где р{х) — определенная функция и / — произвольная функция
некоторого широкого класса. Теория приближенного вычисления таких
интегралов тесно связана с теорией ортогональных многочленов.
Функция р {х) называется дифференциальной весовой функцией
или, коротко, весом. Мы остановимся почти исключительно на случае
неотрицательного веса, отступая от этого в редких случаях, которые
каждый раз будут оговариваться.
Теория ортогональных многочленов для неотрицательного веса
развита с большою степенью совершенства. Мы почерпнем из нее
лишь небольшой запас сведений, необходимый для построения
квадратурных формул некоторого частного вида.
Пусть [а, Ь\ — любой конечный или бесконечный отрезок. Для
наших ближайших целей достаточно считать, что вес р{х)
подчиняется следующим двум ограничениям *):
1) р{х) — неотрицательная, измеримая на [а, Ь] и
неэквивалентная нулю функция,
2) произведение р(х)х"^ при любом целом неотрицательном
значении т есть суммируемая функция на [а, Ь].
*) Читатели, не знакомые с интегралом Лебега, могут считать вес
неотрицательной функцией, могущей обращаться в нуль лишь в конечном числе
b
точек и такой, что интеграл р{х)\х\^ dx имеет конечное значение при
'« = 0.1.2,...
24
ОРТОГОНАЛЬНЫЕ МНОГОЧЛЕНЫ
[ГЛ. 2
Функции fug называются ортогональными на отрезке [а. Ь]
по весу р(х), если произведение pfg суммируемо и
ь
j p(x)f(x)gix)dx=^0.
B.1.2)
Функция / называется нормированной на [а, 1>] по весу /? (х), если
pf^ суммируемо и
j p{x)fix)dx=L
B.1.3)
Ниже слова «по весу» мы будем опускать.
Введем следующие величины
b
с^^ j p(x)x"'dx (т==0, 1. ...)
а
И рассмотрим определитель
^п+1
^п + 1 * • • ^2п
Убедимся в том, что он отличен от нуля. Составим следующую
однородную систему п-\-1 уравнений с /г-|-1 неизвестными
величинами ^0» ^1. .. ., а„
aoCp + ajCj + ... -h^n^n =0. ]
aoCi+ai^2 + •.. +^n^n+i = ^' i B.1.4)
Если допустить, что Д^ = 0, то эта система будет иметь ненулевое
решение, что, как легко выясняется, невозможно. Действительно,
если в B.1.4) вместо с^^ внести их выражения, то система может
быть записана в форме
b
J/?(х)[ао + й^1^+ •.. -i'a^x'']dx=:zO,
а
Ь
J/?(x)x[ao+aiX+ ... + а^х"] cfx = О,
а
b ' '
j Pix)x''laQ + aiX-\- ... +^я-^"Н-^ = 0-
in
ТЕОРЕМЫ ОБ ОРТОГОНАЛЬНЫХ МНОГОЧЛЕНАХ 25
Умножая эти равенства последовательно на Uq, aj, . . ., а„ и
складывая, получим
J/?(л:)[ао+^1-^+ ••• -{-a^x'']^dx = 0.
а
ЧТО возможно только В том случае, когда многочлен aoH-ajX-f- ...
_^^ л^а^^х^ тождественно равен нулю и. следовательно, равны нулю
все его коэффициенты uq, а^, .... а„. Поэтому система B.1.4) может
иметь только нулевое решение и Д^ =?^ 0.
Пусть п — любое целое положительное число. Ниже, при решении
одной из задач теории приближенных квадратур, нам потребуется
построить многочлен степени п\
P,(x)-:ao4aiX+ ... +а,х\ а^фО. B.1.5)
так, чтобы он был ортогонален на [а, Ь] ко всевозможным
многочленам степени, меньшей п, или, иначе говоря, чтобы были
выполнены условия
ь
j p(x)P^ix)x'^dx^O {т = 0, I, .,., п—\). B.1.6)
а
Для определения коэффициентов а^ мы будем иметь следующую
систему п линейных уравнений с /г-|- 1 неизвестными:
аоСо +«1^1+ ... -+a„_ic^_i +а„с„ =0,
B.1.7)
Эта система однородна и число уравнений в ней меньше числа
неизвестных. Поэтому система заведомо имеет ненулевые решения.
Такое заключение верно для весовой функции любого знака. Но без
каких-либо предложений относительно р (х) нельзя сказать ничего
определенного ни о числе линейно независимых решений системы,
ни о степенях соответствующих многочленов B.1.5).
Определитель, составленный из коэффициентов при uq, aj, ...
*•*• ^n-v ^сть Д„_1. При условиях, наложенных нами на весовую
функцию, он отличен от нуля. Если а^ произвольно фиксировать,
то из системы будут найдены единственные значения а^, . . ., a^^^i.
Условия ортогональности B.1.6) определяют многочлен P^ix) с
точностью до множителя. Этот множитель мы будем считать
выбранным так, чтобы было ^,
а„>0 и \ р{х)Р1 (х) dx^l.
а
О корнях Р^{х) может быть доказана следующая
26 ОРТОГОНАЛЬНЫЕ МНОГОЧЛЕНЫ [ГЛ. 2
Теорема I. Если многочлен Р^^(х) степени п ортогонален на
отрезке [а, д] ко всевозможным многочленам степени меньшей я, то
все его корни — действительные, простые и лежат внутри [а, д].
Доказательство. Рассмотрим те корни Р^ (х), которые имеют
нечетную кратность и лежат внутри [а, Ь]. Пусть это будут Ij,
I2* ••> Im- Достаточно показать, что число т таких корней не меньше п.
Допустим противоположное: т <^ п vi покажем, что это не
совместимо с предположением об ортогональности. Составим многочлен
степени т:
9М = (х-1,)(х^1,) ... ix-U'
Он имеет те же точки перемены знака внутри [а, д], что и P^ix),
Произведение Р^{х)р{х) не изменяет знак на [а, Ь] и поэтому инте-
ь
грал p(x)P^(x)p{x)dx отличен от нуля. Так как степень р(х)
а
меньше п, это противоречит условию ортогональности Pf^{x) ко
всякому многочлену меньшей степени.
Систему многочленов
PoW. РЛхУ .... Р,{х), ... B.1.8)
называют ортогональной и нормированной, коротко, ортонормаль-
ной, если выполняются требования:
1) Priix) есть многочлен степени /г,
2) I p{x)P,{x)P^{x)dx = \^
0 при т ф п,
1 при т = п.
Условимся в дальнейшем многочлены ортонормальной системы
обозначать так
Р,(х) = А,х"^В„х"-'-^- ... B.1.9)
Покажем сейчас, что между тремя многочленами трех смежных
номеров ортонормальной системы существует рекуррентное соотношение:
хР„(х) = ^Р„,.,(х)-^(^--^)РАх) + ^Р„.,(х).
B.1.10)
Действительно, произведение jcP^ (х) есть многочлен степени
ft-|- 1 и поэтому может быть представлено в виде
п + 1
Х'Р,{х)^У,с^^^,Р,(хУ
. J] ТЕОРЕМЫ ОБ ОРТОГОНАЛЬНЫХ МНОГОЧЛЕНАХ 27
Коэффициенты с^^^ будут коэффициентами Фурье:
^й. jfe ^ J Р (л:) л: • Рп i^) Pk (-V) d^-
Если А </г—1, то xPfy(x) будет многочленом степени k~{'l<Cn
и с^ j^ = 0, так как Р„(х) ортогонален ко всякому многочлену
степени' меньшей п
ХР, (X) ^ С^^ n + lPn + l М + ^п, пРп W + ^п, «-1^й-1 W-
Подставим сюда вместо многочленов Р^{х) (s^=^n— 1. ft, п~\~\) их
разложения B.1.9). Сравнение коэффициентов при старших степенях
сразу же дает с^ ^^^=^ ^ . Кроме того, так как c^^^ = Cj^^^ при
любых /г и ^, то с^^^„^=- "~*
Значение с^^^^ мы получим, если сравним коэффициенты при х^
в предыдущем соотношении:
^ _^ ^д+1
^'я, rt А А
Формулу B.1.10) мы доказали для /г= 1, 2, ..., но она остается
верной и для /г^=0, если считать, что ^„^ = 0 и P_j(^:)^0. Для
вычисления коэффициентов квадратурных формул полезным является
тождество Кристоффеля — Дарбу, которое мы сейчас получим.
Умножим рекуррентное равенство B.1,10) на Я„ (О
xP,ix)P,(t)=^-^P^^,{x)P„{t)-^(^-^\p„{x)P,{t) +
-Pn-Ax)P„{t).
7+1
Лп-\
Возьмем сходное равенство, поменяв местами х и ^ и вычтем его
почленно отсюда. Средние члены правых частей при этом сократятся
{X - t) Р„ {X) Р„ it) = -^ [Р„+, (л:) Р, (t) - Р„ ix) Р„^, @1 -
--%- \Рп ix)Pn-X it) -Рп-1 (х)Рп @1-
Запишем такие равенства, заменяя п последовательно на /г—1.
л —2, ..,, 0. Складывая их все почленно, мы получим тождество
Кристоффеля — Дарбу:
п
{x~t)Y Р,(X)Р, (t) = -^ [Р„^, (X)Р„ (О -Р„ (X)Р„,, it)].
B.1.11)
28 ОРТОГОНАЛЬНЫЕ МНОГОЧЛЕННЫЕ [ГЛ. 2
§ 2, Многочлены Якоби и Лежандра
Многочлены Якоби образуют ортогональную систему на отрезке
[—1, +1] по весу р(х) = A—x)^(l~^xf. Они зависят от двух
параметров, которые мы обозначили а. р и при любых значениях
этих параметров могут быть определены равенством:
Р<?-Р'(л:) == i^ A - л:ГA-Ь л;)-Р ^ [A - ;.Г''A +;./+«].
B.2.1)
которое часто называют формулой Родрига, Обычно берут те ветви
многозначных функций, входящих в эту формулу, для которых
arg(l —A:)=::=arg(l -j- x)^0 при — 1 < jc < + 1. В том, что B.2.1)
есть многочлен, степень которого не больше п: Р«"* ^\jc) =-• а^л:"+
+ ^„л;«-1+.... можно убедиться, если ^[A--л:)"^''A + л:)^^'']
вычислить по правилу Лейбница и внести в B.2Л)
^_(a-^ri-k^\)i-\f{\~xf-\^ + n) ...(p+yfe+l)(l + x)*.
Старший член а^х" можно найти, если в множителях A—л:)"" и
A+jc)^ взять старшие члены, соответственно (—l)'^" х"'" и х
Jfe-=0
Такой же результат получится, если применить правило Лейбница
к вычислению производной порядка «, входящей в функцию
г'^л! -^ -^ ^jc'' ^^ ^ ^ 2^п\ ^ dx^ ^^ ^
Поэтому
^n = -^(Si + ^ + '^n){a-^^ + 2n~\) ... (a-f p+rt-hl) =
Г(а + Р + 2^ + 1) 2 2 2^
~ 2'^п1Г(а+Р + п+1) * ^^- • >'
Будем считать параметры а, р действительными и а, р > — I *) и
покажем, что многочлены Якоби Р^п'^Ч^) {п = ^. 1, 2, . ..) образуют
*) При построении квадратурных формул для вычисления интегралов
от аналитических функций комплексного переменного, достаточно считать
Re а, Rep> —1.
2] МНОГОЧЛЕНЫ ЯКОБИ И ЛЕЖАНДРА 29
^ортогональную систему на отрезке [—Ь +1] по весу р(л:) =
^UA-x)"A+a:/
+1
/^ ,„ = J A — ^)°A + ^)РР^Р)(X)ЯЙ'^>(X)с1х==а {тФ п). B.2.3)
-1
Обозначим, для сокращения записи. 3^д=^^ , A —л:)"~^'^ A+лг/^'*,
р(а, ^^(х) =:= A — jc)"'"(l -}-^У^У^п^^ Считая, для определенности, п^т*
заменим в /^^ „^ многочлен Рп (х) его выражением через у^
+1
1,.т^ 1у^а^р%^^кх)йх,
-1
Интегрирование по частям дает
+1 +'
J> -1
+ 1
"Внеинтегральный член исчезает, ввиду а, р> — 1. /г-кратное
интегрирование по частям приведет к равенству
+1
Г1ри т <С п имеем [Р^'^^ (л;)]^'^^^ О и, следовательно, /^^^^2=iO, что
доказывает ортогональность двух многочленов Якоби разных степеней.
При т = п равенство B.2.3) дает
+1
*« = ^«.. - J A - xf A + xf [Р^ Р^ (x)f rfx =
-1
+1 +1
-1 -1
*^Оследний интеграл приводится к эйлерову интегралу первого рода.
до ОРТОГОНАЛЬНЫЕ МНОГОЧЛЕНЫ [ГЛ. 2
Положим x=^2t — 1
J (l-д:)"^'^A4-x)P+^rfд:-::2«^P^^"+' ^ t^-"^ {\-tf^Ut =
^ о/ V V{p)V{q)
Так как В(/?, 7)=^ T(p + q) ' '^^
^ 2«-Р+^Г(а + ^+1)Г(Р + п + 1)
" («+Р + 2п+1)п!Г(а4-р + « + Ъ ' (.^.^.Oj
£сли /г = 0 и a + p-f-l'^O' то
6о = Г(а+1)Г(р+1).
Из B.2.4) и B.2.5) видно, что ортонормальную систему на
[—1, +1] по весу A—x)^(l--^-xf образуют многочлены
р(а,Р)(х)^ у_: . B.2.6)
Старшие коэффициенты их равны
Многочлены Лежандра являются якобиевыми многочленами
частного вида. Они отвечают значениям параметров а = 0, р*=0. Фор-
^^yлa B.2.1) для них имеет вид
РЛ^)=-^-^Щ^- (^•2•8)
При помощи ее легко может быть найдено разложение Р^(х)
по степеням х
Р гу)~ ^^^^- х^ ^^^-^^• х^-' \
^пК-^}~ 2«(п!J'^ 2«(л~ !)!(«—2)! ^ ^ •■ •
Вес р (х) для них равен единице и многочлены Лежандра
ортогональны на [—1, +1] с постоянным весом. Равенства B.2.4) и
B.2.5) имеют вид:
У [ О при тф п,
Pn{x)Pmi^)<^^ = ^ 2 B.2.9)
* 3] МНОГОЧЛЕНЫ ЧЕБЫШЁВА 31
Ортонормальную систему на [—1. +1] с постоянным весом образуют
многочлены
Рп(х)='\/^^^Рп(х). B.2.10)
Старшие коэффициенты их равны
§ 3. Многочлены Чебышёва
Ниже будет показано, что многочлены первого рода Чебышёва
ортогональны на отрезке [—1. -["М "*^ ^^^У Р (х) ^^ лГл Они
могут быть определены следующей формулой
Г^ (х) = cos (дг arc cos jc) (n:=0, 1, ...). B.3.1)
Убедимся, прежде всего, в том, что функция B.3.1) есть многочлен
степени п. старший коэффициент которого есть 2"~ :
Г„(х)-2'^-^х"+ ... (/г>0). B.3.2)
Будем исходить из элементарного тригонометрического равенства
cos(a^-|-1) 9-|-cos(ft—1N = 2 cos 9 cos/г9. Положив в нем 9:==:
= arc cos х. найдем следующее рекуррентное соотношение для
функций Т^{х)
Т^^,{х) = 2хТ^{х)-Т^^,{х),
Для Tf^{x)=l и Г|(л:)=^х равенство B.3.2), очевидно, верно.
Рекуррентное же соотношение позволяет доказать его индуктивно
для любых п.
Покажем, что для многочленов 7"^ (л;) верны равенства (п, /^ > 0);
У [ О при тф п,
'''^ _J Y\—X^ Y при m=:=n. ^ ^
Из них, в частности, видно, что Т^{х) (п^=0, 1, . . .) образуют на
отрезке 1^1, ~{-1] ортогональную систему многочленов по весу
Р{х)= ■ Заменим в /„^ ^ переменную интегрирования, по-
у I X
ложив x=iC0s6, 9 = arc cos X. Можно считать, что при изменении х
^ —1 до +1, угол 9 будет изменяться от л до 0. Так как
32 ОРТОГОНАЛЬНЫЕ МНОГОЧЛЕНЫ [ГЛ. 2
7^(л:) = cos/гб, T^{x)=r^cosmQ и dx ^=: — siii6.flf9, то
^ f О при т ф п,
Y при т -'
" и при т ф п,
^т п= \ cosпвcosmQdd:= I jt (n, m>0),
"^'^ J -РГ при w~/j ^
Bee jE?(jc) = (i—jc^) • (—l<;x^+l) есть частный случай
якобиева веса A—х)^{1~\-ху при а^^р = — 0,5. При заданном
весе многочлены ортогональной системы определяются с точностью до
постоянных множителей. Поэтому якобиевы многочлены Рп'"^' " '\х)
могут отличаться от Т^{х) только численными множителями
p[-'^''^-'^'\x)^^cJn(xy B.3,4)
Для нахождения с,^ достаточно сравнить старшие коэффициенты
ГB«) __^ 2"^"^ - ~ ^^^""^^
2''п\Т{п) " '^ 2^^"Т(л)Г(л + 1)
Многочлены Т^(х) были введены П. Л. Чебышёвым в связи с
решением следующей задачи.
Среди всех многочленов степени п, имеющих старший коэф-
фациент, равный единице, Р(х) =:=:jc«-|-c^_ijc^~^+ ••■» найти
тот, который на отрезке [—1, -|~1] наименее отклоняется от
нуля по абсолютной величине, т. е. такой, для которого
max |P(x)| имеет наименьшее значение.
Покажем, что таким многочленом будет
-rt + l-T^ , . с-п + 1
Т^ (X) = 2"'''"Т„ (л;) =z 2'""^' cos {п arc cos л:).
шах
1-1, +ii
В самом деле, шах |7'^(л:)| = 2 ^^ и имеют место равенства
:2-'^+\—If (m^O, 1, ..., /г).
Если бы существовал многочлен Р(х), удовлетворяющий условию
I Р (X) К 2""^^ (— 1 < л: < + 1), то разность R (х) =- Г„ (х) — Р {х)
была бы многочленом степени меньшей п, и такой, что
(~ir/?fcos-^)>0 (m^O, 1. ..., п\ На [—1, +1]
многочлен /?(х) должен был бы иметь по меньшей мере п корней, что
невозможно, так как его степень меньше п.
Докажем теперь единственность многочлена, имеющего
наименьшее отклонение. Пусть Я(х) — любой многочлен указанного вида,
для которого max |Р(х)|= max | Г^ (х) | ^=:= 2~'*■*"^ Разность
1-1, +11 1-1, +1]
§ 3] МНОГОЧЛЕНЫ ЧЕБЫШЁВА 33
5(х):^ Р(л:)-—Г^Дх) будет иметь степень меньшую п. В точке
тл
S(xJ^{~ir2-^^'-Pix^)
и, ввиду |P(xJ|<2-"^\
(—1Г5(л:^>0 (т^О, 1. ..., п).
Отсюда вытекает, что S (х) имеет не меньше нежели п нулей,
различных или совпадающих. Но так как степень S{x) меньше п, то
S{x) есть тождественный нуль и Р (х) =^Т^^(х).
Многочленами второго рода Чебышёва называются многочлены
вида
"Можно показать, что функции ^„ W — действительно MHoro4vaeHbi
степени п, имеющие старшим коэффициентом 2". Будем исходить
из простого тригонометрического тождества
sin (/г 4- 2) е + sin п^^2 cos 9 sin {п + 1) 6.
Если положить в нем cos6=:^x, 6 = arc cos х и обе части разделить
на у^1—х^, то получим рекуррентную формулу для U^
и^^, (X) = 2х^„ (X) - и,_, (X). B.3.6)
Заметим, что Uq{x)'-=^1 и 6^i(x) = 2x имеют желаемую форму.
На основании B.3.6), при помощи индукции легко показать, что
f/„(x) — действительно многочлен вида ^7^ (х) ^= 2"х"-|- ...
Для и^ (х) имеют место равенства
^У I О при тфп,
К.т= U^{x)U^{x)YY^^^dx = \ п B.3.7)
Многочлены U^^{х) (п = 0, 1, . . .) образуют на отрезке [—1, -[-И
ортогональную систему по весу /?(х) = У^1—х^.
Если в интеграле
+ 1
г г sin (п~\~ 1) arc COSX sin {m-\-l) arc cos x - "f^l — x^ .
34 ОРТОГОНАЛЬНЫЕ МНОГОЧЛЕНЫ [ГЛ. 2
заменить переменную интегрирования, положив x = cosO, то он при^
мет вид
/«.m=|sin(«+l)9sin(M-t-lHde
О
и равенства B.3.7) проверяются без затруднений.
Вес /?(jc) = ]Al—x^ есть также якобиан вес при а = р===:0,5.
Поэтому многочлен U^ (х) может только постоянным множителем
отличаться от многочлена Якоби Р^''''''\х)
Pf''^'^'\x):^E,UAx). B.3.8)
Сравнение старших коэффициентов дает
Е-^
Многочлены U^^(x) обладают следующим минимальным свойством.
Среди всех многочленов Р{х) степени а со старшим коэффи-
циентом, равным единице, -щ-^пМ доставляет наименьшее
b
значение интегралу; \P{x)\dx,
Для доказательства нам нужно будет установить некоторые
вспомогательные теоремы.
1. Ниже нам потребуется тригонометрический ряд для функций *)
sin л: sign sin/? JC, где/? — целое число. В теории рядов Фурье известно
следующее разложение
оо
Sign sin Х=::=->^ 2fe + l •
Отсюда видно, что
оо
Sign Sin рх = ~2л 2k\\-' B-^-9^
Если последнее равенство умножить на sin л; и принять во
внимание, что
2sinxsinB^-f-l)/?x=-cos[B^+ \)р — 1]л: — cos[B^-f I)р -f IJjc,
*) Функция signer есть знак х и определяется равенствами
(—1 при X <0,
О при л: = О,
[ +\ при X > 0.
J A 3] МНОГОЧЛЕНЫ ЧЕБЫШЁВА дЬ
'to сразу же получим нужный тригонометрический ряд
sinxsignsinjE?A:===
оо
= -|^B^+l)~^{cos[B^-(-l)p— l]x — cos[Bk+\)p +- l]x}.
2. Если п—целое положительное число, то при г = О, 1, ...
,,,, п — 1 выполняется равенство:
+ 1
J X' sign U^ (х) dx = 0. B.3.10)
-1
После замены jc = cos9 B.3.10) перейдет в
[ cos^ о sin 9 sign sin {n~\-\)QdQ~ 0.
о
"Степени косинуса cos'^jc (г^^О, 1, ..., п—1) линейно выражаются
через косинусы кратных дуг coswO (/?г = 0, 1, ..., /г— 1) и
наоборот. Поэтому последние равенства равносильны таким
п
I cos т9 sin О sign sin (/г 4-1H^9 = 0 (/п = 0. 1 п—1)
о
^ или, ввиду четности функций, стоящих под знаком интеграла,
л
1* COS т^ sin е sign sin {n^\)Qd^ = 0. B.3.11)
-л
; тригонометрический ряд для sin 9 sign sin (/г-|- 1H получится из B.3.9)
при р = п-|-1. Наименьшая частота, содержащаяся в ряду, появится
в B.3,9) при ^ = 0; она равна {п~\-\)—1=я. Поэтому при
т = 0. 1 п—1 равенство B.3.11) заведомо выполняется.
На основании B.3.10) легко доказывается правильность
высказанного выше утверждения о минимальном свойстве U^^ (х).
Обозначим, для сокращения записи, 2~"U^(x)=^ Р(х) и возьмем
любой многочлен Я*(х) степени п со старшим коэффициентом,
равным единице:
I \P(x)\dx= { P(x)signU^(x)dx =
+1 +1
= I Р* (x) sign U^ (x) dx + J (P (X) - P* (x)) sign U^^ (X) dx.
-\ -1
35 ОРТОГОНАЛЬНЫЕ МНОГОЧЛЕНЫ [ГЛ. 2
Последний из интегралов равен нулю, ввиду B.ЗЛО) и ввиду
того, что разность Р{х) — Р''(х) есть многочлен, степени меньшей п
+1 +1 +1
J Р'(х) sign и^ (х) ^jc < j РЧх) sign Р* (X) dx=: { I РЦх) \ dx.
„1 -1 -1
Следовательно,
+1 +1
f \P(x)\dx^ f \P'(x)\dx. B.3.12)
Это доказывает утверждение. Сделаем еще два замечания. Из
проведенных рассуждений видно, что равенство в B.3.12) возможно только в том
случае, когда sign Р* (jc) =^ sign 6^^ (л:) при —1<л:<1. Многочлен
jr . . sin (п-\~ 1) arc cos .у sin(n-|- 1) Q
и j^ \x) — ■•— ; - ,
y\—x^ sin 9
где л: = cos 9, имеет при —l<jc<-f-l n корней x^^ ==: cos
Л+1
(/г~1, 2, ..., n). Если sign P*(jc)=: sign L^/,, —l<x<+l, то
указанные точки x^ должны быть одновременно корнями P*(x).
Многочлен P*(jc) имеет степень п и потому кратности этих корней
равны единице и других корней у Р*(х) нет. Кроме того, так как
Р*(л:) и Р{х) = 2~^и^{х) имеют одинаковые старшие коэффициенты,
то должно быть Р*(х) = Р(х). Равенство в B.3.12) возможно только
в том случае, когда P*(jc)^=P(x) = 2~"^7^(л;).
Вычислим еще минимальное значение интеграла B,3.8)
+1 jt
2"" J I U^ (jc) I dx -= 2"''Jl sin {n + 1) 9 I rf9 -=
-1
л
2^"(;г+1)( sin(/j+l)9cf9-=
о
л + 1 1
'О "^
п+1
Отсюда вытекает
Теорема 2. Для любых многочленов степени п, имеющих
старший коэффициент равный единице,
Р(д^) = л:« + с^_1л:«-1+...+Со.
- 4j МНОГОЧЛЕНЫ ЧЕБЫШЁВА-ЭРМИТА 37
верно неравенство-.
+1
1
J|P(x)
dx^
^л —1
-1
равенство возможно в том и только в том случае, когда
Р(х)^2~'и,(х),
§ 4. Многочлены Чебышёва — Эрмита
Многочлены Чебышёва — Эрмита ортогональны на всей числовой
оси —со < JC < сю с весом р {х) = е~'^\ Мы определим их
формулой *):
Я„(х) = (-1)"/=^е-Л B.4.1)
•Положим ф = е--^'. Тогда ф(")=:(—1)" е-^'Н^(х). Вычисление
производной дает (f^''^'^=(—l)"[-~2xHn(x)-^HUx)]e-''' и так как
ф(''+')=(_1)«+'.-'Я„+,(.«). то
Н^^^^{х) = 2хН„(х)-Н'„(х). B.4.2)
Отсюда и из Hq(x)=U с помощью индукции, легко можно
получить, что Н^ (х) есть многочлен степени п вида
H„(X)=--2'^X'^^...
Для многочленов Н^ (х) верны равенства:
^ ( О при т ф п,
е-^'Н^ {х) И^ (JC) dx = \ ^^г~ .
из которых видно, что И^{х) (п=0, 1, ...) образуют на всей оси
(—ОС, ~\~со) ортогональную систему по весу е~^^.
*^
) Иногда рассматривают другие многочлены Чебышёва — Эрмита:
-т d^ --г
И1(х)^(-1Ге ^ ^ ^ 2
fi?jc«
Они связаны с многочленами B.4.1) равенством Я*{;с)-=2 2 я^/-^V
38 ОРТОГОНАЛЬНЫЕ МНОГОЧЛЕНЫ [ГЛ. 2
Пусть т^п
— CO -ОС
4-00
=.(-ЛГф<«-'^Я.|::+-(-1Г^ I ф("-''я;йл: =
—oo
-•OO —oo
При m <i n, H^^^^Q и [=zO. Если же m^=^n, то
+ 00 +00
f = 2"n\ j фйл;=:2"/г! j «"''"afA; = 2"«!Уя".
— OO —oo
Ортонормальную систему образуют многочлены
h,{x)= J^^f ^. B.4.3)
2 2 («!J (ji)^
Старшие коэффициенты их равны
л,-=2 2 (n!) (я) 4, B.4.4)
§ б. Многочлены Чебышёва — Лягерра
Эти многочлены ортогональны на полуоси О <^ л: < ос с весом
р{х^=^ х^е-^' Пусть а — любое число. Выбор ветви многозначной
функции х^ определим условием: arg.v=:0 при jc > О и положим
L(,«'w-(-;)"^-"«^'^U"^v^). B.5.П
Вычислив производную по правилу Лейбница, найдем
разложение Dn по степеням х
+^^^—{п-^о){п + а-\)х'^-'^ — ... B.5.2)
Определенные равенством B.5.1) или B.5.2) функции называются
многочленами Чебышёва — Лягерра. Будем считать а действительным
, gj МНОГОЧЛЕНЫ ЧЕБЫШЁВА - ЛЯГЕРРА 39
ЧИСЛОМ И а>—1. Покажем, что Z„ (jc) обладают следующими
свойствами:
Т /V , V [О при т ф я,
/= J^-4°4x)lL->W^x=={ ^,j.^^^^^ ,^ ^р^ ^^^ B.5.3)
О
Обозначим, для сокращения, х^^^е""" ^=^^^, L^^\x)=^{—lf x~^e'^qf-^\
Считая п^ т, заменим в / многочлен Z," его выражением через ф^
U
оо
=(-1)ЧГ"^!"'1Г+(-1>""'' / фГ'[4"Т^^=
о
оо оо
^(-1)"-'/ фГ"[^::т^-=-/ фЛ^т*'^^-
0 0
Внеинтегральный член исчезает, ввиду а>—1.
При т<п. [zSf"*=0 и / = 0. Когда т^^п.
оо оо
1=1п\ { ц>^йх^п\ [ х^+Ч~^dx = п\Т{а + п -^ 1).
о о
Ортонормальными многочленами Чебышёва — Лягерра будут
Коэффициент при х^ в них равен
Л^=^ , ^ B.5.5)
Литера тура
Гончаров В. Л., Теория интерполирования и приближения функций,
гл. П1 и IV. М., Гостехиздат, 1954.
Натансон И. П., Конструктивная теория функций, ч. I и II, М. — Л.,
«остехиздат, 1949.
-„Джексон Д.. Ряды Фурье и ортогональные полиномы, гл. II,
VII-X. ИЛ. 1948.
Ч е б ы ш ё в П. Л., Теория механизмов, известных под названием парал-
^граммов. Собр. соч. т. 2. Изд. АН СССР, 1947.
v_^ К о р к и н А. Н, и 3 о л о т а р е в Е. И.. Sur un certain minimum. Собр.
Ш^Л. и. Золотарева, 1, 138—153.
Сегё Г., Ортогональные многочлены, М., Физматгиз. 1962.
ГЛАВА 3
ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ
§ 1. Конечные разности и разностные отношения
При интерполировании функций, имеющем большое значение для
приближенного вычисления интегралов, широко используется аппарат
конечных разностей и разностных отношений. Мы приведем лишь
начальные и самые необходимые сведения из теории разностей.
Будем считать, что мы рассматриваем функцию f {х) и
предположим, что известны ее значения для равноотстояш.их значений
аргумента Xf^^=^ x^-^kh {k=0, 1, 2, ...) с шагом h
fo^fi^o)' /i = /Uo+^). .-.. ff^^fixo + kh), ...
Конечными разностями первого порядка от / называются величины:
A/o-/l-/o. Д/. = /2-/1. •••. ^fn=fn+l-fn- ■■'
Величины
Д2/0-Д/1-А/0. Д2/,-А/2-Д/, А2/„=А/„Н-Д/„. •••
называются разностями второго порядка и т, д.
Разности порядка п определяются через разности предыдущего
порядка равенствами
A7o = A"-'/i-A''-7o. A7i = A"-V2-A"-V.. ••.
Мы привели рекуррентное определение конечных разностей всех
порядков. Можно найти выражение разности любого порядка
непосредственно через значения функции
\nf ^ f _ п f , п(п--^\)
п(п^\){п ~ 2)
3!
-Д-з+.--+("~1Г/о' C.1.1)
Для п=1 это равенство очевидно и, при помощи индукции, легко
доказывается для любых п.
- jj КОНЕЧНЫЕ РАЗНОСТИ И РАЗНОСТНЫЕ ОТНОШЕНИЯ 41
Если ввести оператор увеличения аргумента на шаг h\ £'/(jc) =
==/(-^Н~^)' ^^^ ^'^^ ^/л=/й+1- ^^ C.1,1) можно записать в
следующей простой символической форме:
A7o = (f-ir/o- C.1.2)
Полезно также отметить, что значение функции Д любого номера п
может быть выражено через начальное значение /д и разности A/q,
Д2Д, ... в виде
fn = fo + iv^h+ ""^V^^ ^Vq+ . ■ . +Д7о. C.1,3)
При /г=1 это равенство верно, ввиду f^~fQ^=AfQ. Справедливость же
его при всяких п может быть без труда доказана индуктивным путем.
В символической форме, через степени оператора конечной разности,
C.1.3) записывается в форме
/„ = A+Д)"/п- C.1.4)
Равноотстоящие значения аргумента не всегда являются наиболее
"целесообразными для исследования функции. Более того, в
наблюдениях они не всегда возможны. Например, астрономические
наблюдения связаны с погодой и их не всегда удается проводить через
равные промежутки времени.
Для неравноотстоящих значений аргумента конечные разности
заменяют другими величинами, которые чаще всего называют
разделенными разностями или разностными отношениями.
Пусть jcq, лгр JC2. ..., Xj^, . . . —любые значения аргумента.
Разностные отношения первого порядка определяются равенствами:
f{v Y \— /(-^i) —/(-^о) ffv ^^^— /(-^2) —/(-^i)
/ l-*o, Xi) — ~ , / (.л 1, X2} — , . ' .
Л\ -O-Q Л2 ^J
Дроби
//^ V- v^ fi^u X2)—/{Xq, Xi)
J K-'^O' -^1' -^2) — Z Z »
Л2 Ло
f/v. V v4 /(•У2> Xs) f(Xi, X2)
J l-^l' X2, X^) , . . .
Л3 Л1
называются разностными отношениями второго порядка; дроби
f/*- V- ^ v^ /(Жь Х2, х^) — f (Xq, Х], Х2)
J {^Xq, Хр Х2. Х^) , . . .
^сть разностные отношения третьего порядка и т. д. Величина
/(•^0» -^1 х^) есть линейная функция f (Xq) fi^n)- ^^o>*<нo
показать, что
п
f {Х X \ V^ /(-Уу)
:• ..., ^п)~ 2л{ху^--х^).,.{х^—х^^1){Ху^ — х^+1)..,(Ху~-ХпУ
C.1.5)
42
ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ
[ТЛ, 3
При п==\ ЭТО равенство очевидно, так как
/(•^i)
Х\ — Xq Xq — Х\ Х\ — Xq
Допустив, что C.1.5) верно для разностных отношений порядка п,
проверим его для порядка /г+1'
f (Xq, Х], .... Xf^^{)^=
i^n + l — •'^о)
-1
п + \
у
/(-^v)
V = 0
(^v -^o) • • • (-^v — -^n)
n 1-1
i (^v-
f(^v)'
v = 0
•^o)- ■ -(-^v
l)*
Равенство C.1.5) можно записать более кратко, если ввести
многочлен со (х) = (л: — лго) (х — ^i).. . (х — л:„). Тогда
/(-^0' -^1' • • •' ^п) — 2j~^
v=0
(^v)
C.1.6)
При любой перестановке Xq, Xj. ..., jc„» в правой части C.1.5)
переменится лишь порядок слагаемых и, поэтому, f (Xq, х^, ..., х^^)
есть симметричная функция своих аргументов Xq, х^, .... х^.
При помощи индукции может быть также проверена следующая
формула, дающая выражение любого значения функции f(x^) через
начальное значение / (хд) и разностные отношения f (Xq, x^, ..., x^^)
{k= К 2, ..., n):
f (X„) = f (Xq) 4- (X„ — Xq) f (Xq. Xi) 4-
+- i^n ~~ ^o) (^n - ^i) f (^0» -^1' лгг) + ' • •
...+(x„- Xo)(x„—Xi)...(-^« —лГ/г-О/С-^о. лгр .... л:„). C.1.7)
Когда значения аргумента равноотстоящие, разностные отношения
весьма просто выражаются через конечные разности функции
f(,- V i t,^^ f{Xo + h)-^f{xo) _ А/о ]
f(xo. л;о4 Л. x, + 2h)= ^^^■' + ^- ^o + ^^^^)-/(^^o■ -^0+^)
2!Л2 '
/ (JCo- Xo + h Xo + яЛ) := -^
C.1.8)
Щ jj КОНЕЧНЫЕ РАЗНОСТИ И РАЗНОСТНЫЕ ОТНОШЕНИЯ 43
'i ■
V Для приложений часто полезно бывает знать, как связаны конеч-
дае разности и разностные отношения с производными. Пусть точки
Ха> ^1* ••*» ^п лежат на отрезке [а, Ь],
Теорема 1. Если f имеет на [а, Ь] непрерывную производную
fiopndKa п, то верно равенство:
0 0 0 I v-I
C.1.9)
Доказательство. Для n=\ оно просто проверяется:
1
J dtj' [Xo + h i^x'- ^o)l = -~^|f^ = / (^0. ^i).
0
Допустив, что оно верно для разностных отношений порядка ft—1,
покажем, что оно будет верным для отношений порядка п. Обозна-
-чим интеграл, стоящий справа в C.1.9). знаком /(atq, л:^. ,.., х^) и
шлполним в нем интегрирование по переменной t^:
0 0 0
-/""'4^0 + ^l(^l~^0)+.-.+^«-l(x,_i-X„_2)]} =
1«Ь(лГ„-Х„_1)"М/(-^0' ЛГр .... X,,_2, X^)-f(XQ. Xi. .... X„_2» Л:«-1)] =
^-^fl^-^rt-l) l/(-^0' ЛГр . . . , .>£^/г_2» -^/г) /(-^«-1» ^0' -^1' • • •» -^«-2I =
.,^ =/(X„_j. ATq, Xi,.... А:л»2' -^л) ==^/(-^0» -^1» '•*' -^/£-2» -^/i-l' -^я)*
Этим теорема доказана.
Из C.1.9), как следствие, может быть получено другое, более
простое, соотношение между /(Xq, Xj, .... х^) и f^"\ Областью
интегрирования в C.1.9) является пирамида /г-мерного пространства
d» ^2» • • •» ^л). определяемая неравенствами:
0<^«<^;.-1<.--<^1<1. C.1.10)
Объем ее имеет значение
44 ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ [ГЛ. 3
Рассмотрим величину
l^-^0 + ^^v(-^v"~ -^v-l) —
v = i
= A—^1)л:о + (^1—^2)•^l^-•'•+(^«^l"■^^/г)^«-l + ^/zЛ^«•
BвИДУ C.1.10), множители при всех х^ будут неотрицательными.
Так как сумма множителей равна единице, | будет средним
взвешенным значением всех абсцисс х^^ (^=:=0, 1 п), а потому,
наверное, принадлежит отрезку [а, Ь], Кроме того, точке, лежащей
внутри пирамиды C.1.10): 0<^^,<^/^_1< . . . <^i<l, будет отвечать
точка |, лежащая внутри {а, Ь\.
Применение теоремы о среднем значении к интегралу C.1.9)
позволяет высказать следующее утверждение.
Теорема 2, Если / имеет на [а, Ь] непрерывную производную
порядка п, то внутри [а, Ь] суш^ествует такая точка |, что
имеет место равенство
Связь между конечной разностью и производной сразу же
вытекает из C.1.8), C.1.9) и C.1.11):
0 0 о \ v=l /
C.1.12)
Отсюда, в частности, видно, что если уменьшить шаг h в к раз.
то можно ожидать, что конечная разность A'^/q уменьшается, как
правило, приблизительно в Х^ раз.
§ 2. Интерполирование по значениям функции
Допустим, что в rt-f-1 произвольно расположенных точках Xq,
ATj, ..., х^, которые всюду ниже мы будем называть ^^зла^ш
интерполирования, даны значения f {х^) функции f {х). Нужно построить
многочлен, степени не больше п\
п
Рп{х) = а^х^^ а,х^-'+ . .. +^д= 2 С1^х^'\ C.2.1)
V-0
который в узлах Xf^ принимал бы заданные значения f {Xf^ (k=^0,
1. .... п):
Pnix,)^f{x,). C.2.2)
§21
ИНТЕРПОЛИРОВАНИЕ ПО ЗНАЧЕНИЯМ ФУНКЦИИ
Для определения коэффициентов а^ многочлена получится линейная
система n-^-l уравнений
п
v = 0
Определитель ее есть определитель Вандермонда
Г(л:о. ATj. .... х^)^
к
XI
к
V-rt—1
jcf-^ .
п
.. 1
. 1
. 1
Он отличен от нуля, так как среди узлов Xj^ нет совпадающих.
Поэтому, при любых значениях /(х^.), может быть построен и только
один многочлен Р^(х), удовлетворяющий условиям C.2.2).
В зависимости от целей, для которых предназначается Р^^ (х), его
можно представить в различных формах. Ниже приведены два
наиболее часто применяемые представления Р^ (х).
Для узла Xf^ построим вспомогательный многочлен cOj^Cx),
определяемый условиями
г о при / ф k,
«й(-^0= 1 . и C*2.3)
^ ^^ [1 при i^^k. ^
Как сразу же видно, такой многочлен может быть записан в форме
^ (^\-^ {X~-XQ)...{X — Xk^{){x — Xk^\)...(x — Xn)
^^ ^ (Xk — хо)., .{Xk — Xk^i) {Xk — Xk+i).. Лхк~ Хп)
или, если воспользоваться многочленом со(х) == (л: — Xq)(х -Xi)...
...(X —xj.
Многочлены С0;^(х) называют многочленами влияния узлов х^^ или
лагранжевыма коэффициентами.
Интерполирующий многочлен Р^ (х) при помощи их запишется
в следующей форме, принадлежащей Лагранжу
^«w=S
о)(л:)
ft=o
(X ~ Xk) со' {Xk)
fix,).
C.2.5)
Так как coj^(x) (^ = 0, 1, .... п) есть многочлен степени /г, то
C.2.5) будет многочленом степени не выше п. На основании C.2.3)
'Яегко проверить, что он удовлетворяет условиям C.2.2).
^5 ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ [ГЛ. 3
В некоторых вопросах вычислений лагранжево представление Р^(х)
является неудобным. Часто нельзя бывает заранее сказать, сколько
нужно взять узлов Xft, чтобы достигнуть требуемой точности
интерполирования. Допустим, что при принятом числе узлов нужная
точность не была достигнута. Тогда вводят в вычисления дополнительно
еще один или несколько узлов. При введении же хотя бы одного
дополнительного узла будут изменяться все члены формулы C.2.5).
Было бы желательно так изменить представление Р^{х), чтобы, при
введении нового узла, ранее вычисленные члены сохранялись и нужно
было бы добавить еще один новый член.
Такому требованию удовлетворяет ньютоново представление
интерполяционного многочлена:
^Л-^) = /(^о)Ч-и —^о)/(л^о. x^)^{x~x^){x-x^)f{x^. лгр л:2) +
4- ... +(^ —-^o)(-^"--^i)' • -U—^л-1)/(-^0' -^Р '.- х^). C.2.6)
Правая часть C.2.6) есть многочлен степени не большей п. На
основании C.1,7) можно проверить, что он действительно
удовлетворяет условиям C.2.2). Непосредственно видно, что при х^=^х^
правая часть приводится к /(лго). Для ^: = jCi правая часть равна
/(a:o) + (a:i~Xo)/(Xo, x^) = f{x{) и т. д.
Разность между f {х) и интерполирующим многочленом Я„ (х)
называют остатком интерполирования или дополнительным
членом интерполяционной формулы:
Значение R^(x) зависит от свойств функции f {х) и от
расположения X и узлов Xft. Можно ожидать тем меньшей погрешности R^^ {х)
интерполирования, чем более гладкой будет /(х), в частности, чем более
высоким порядком дифференцируемости она будет обладать. Когда же
/(х) есть аналитическая функция, то можно ожидать, что R^ix)
будет тем меньше, чем дальше от х и Xf^ (^^=0, 1, ..., п) будут
лежать особые точки f {х).
В представлении C,2.7) для R^(x) часто трудно бывает
увидеть, какое влияние на значение остатка оказывают свойства f (х), и
было бы полезно получить другие представления R^(x), более
удобные для оценки величины R^ (х) в различных классах функций.
Во многих случаях такие представления R^ (х) построены *). Мы
ограничимся тем, что приведем две простейшие теоремы о
представлениях такого рода для остатка.
1) Пусть точка х и узлы х^ (й = 0, 1, .... /г) лежат на
отрезке [а, д].
*) См. литературу к гл. 3,
л I 2] ИНТЕРПОЛИРОВАНИЕ ПО ЗНАЧЕНИЯМ ФУНКЦИИ 47
Теорема 3. Если / {х) имеет произзодную порядка я -|~ 1 на
[а, ^]» ^^ ^^^ остатка R^(x) интерполирования имеет место
равенство:
* *? *м (
C.2.8)
Rn (-^) = « (^) J ^^1 I ^^2 ... / ^^«H l/'"^'
л __ I —- X t
Доказательство. Высказанное утверждение может быть
получено как следствие теоремы о представлении разностного
отношения через производную и соответствующие ей равенства C.1.9).
Рассмотрим значения /(xq). /(jci), ..., f(xj. f(х) функции /. На
основании (ЗЛ.7), последнее из них имеет следующее выражение
через разностные отношения:
f(x)^f{Xo) + (x~~XQ)f(XQ. Xl)+ •..
... +(х— Хо)(х-х^) . . . (x^x^^^)f(xQ, х^, . . ..x^)-f~
+ (х — Хо) (х — Xi) . . . (х — XJ / (хо. Xj, . . .. х„, X).
Сумма всех членов правой части равенства, кроме последнего,
есть не что иное, как интерполяционный многочлен Р„(х) в
ньютоновой форме. Поэтому последний член правой части должен
совпадать с остатком интерполирования:
/?д(х)==со(х)/(Хо. Хр . . .,х„. х)=^со(х)/(х. Хо, Xj, , . ..xj.
C.2.9)
Если к /(х. Xq, Xi, .... x,j) применить указанную выше теорему
и равенство C.1.9), то получим C.2.8).
Применение теоремы о среднем значении к интегралу C.2.8) по-
аволяет высказать приводимую ниже теорему, дающую более простое
представление остатка.
Теорема 4. Если /(х) имеет на [а, д] непрерывную
производную порядка п-\-1, то внутри [а,Ь] существует такая
точка |, что имеет место равенство:
l^nM^-J^^f^'^l). C.2.10)
Его часто называют формулой Лагранжа для R^ix).
2) Допустим, что f {z)—аналитическая функция комплексного
временного z, регулярная в некоторой области В, содержащей
48 ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ [ГЛ. 3
внутри себя X и Xk (к^^О, I /г). Ддя простоты, будем
область В считать односвязной.
Теорема 5. Остаток интерполирования f (z) в точке х
может быть представлен в форме контурного интеграла
/? (д;)^^ Г ^ /<^) ^ dZ, C.2.11)
I
где I — любая замкнутая линия, лежащая внутри В и
содержащая X, Xj^ (^ = 0, 1, . . ., п) внутри себя.
Утверждение легко доказывается проверкой равенства C.2.10).
f {z\
Для функции —/ W _„ .4 ' стоящей под знаком интеграла, точки
z^==^x, Z ^~ х^ {k=.(), 1, ..., п) являются простыми полюсами. Если
интеграл, стоящий справа в C.2.11), вычислить при помощи
вычетов, то сразу же получится представление C.2.7) для остатка Rfi(x),
§ 3, Интерполирование с кратными узлами
Будем считать, что нам дано т различных узлов Xj, Х2. .... х^.
Рассмотрим некоторую функцию f (х) и предположим, что в первом
узле Xi даны значения самой функции и всех производных от нее
до порядка tti—1: /(Xj), /Ч^О» ••" /^'~^\-^i)» во втором узле Хо
даны значения / и производных до порядка аз— 1: /(хз). f^ {х<^, . . .
^-(«2- >(^^^ ^ ^^ д^ Числа ttj, а2, . . ., а^ называются кратно-
стями узлов Х], Х2, . . ., х^.
Общее число указанных исходных данных о функции /(х)
обозначим ^-f-l=ai + a2+ •'• +«т-
Нужно построить многочлен Р,^ (/; х), степени не выше /г.
который удовлетворял бы условиям *) (i ^ О, 1, . . ., а/^— 1; й = 1, 2, . . .
., ., т)\
P^^{f\xu) = f4xu). C.3.1)
Существование P^if) х) мы установим, построив этот многочлен.
Единственность Р^ (/; х) будет видна из построения. Она может быть
также легко доказана на основании известных теорем алгебры.
Допустив, что существуют два многочлена Pf^ify х), удовлетворяющих
условиям C.3.1), рассмотрим разность между ними и обозначим ее
(р(х); Ф(х) есть многочлен, степени не выше /г, и в узлах х^ будет
удовлетворять условиям
(p{i)(Xf,)~0 (i = 0, 1, . . ., а^^— 1; ^=- 1; 2, . . ., т).
*) При записи условий, производная порядка нуль принимается равной
самой функции /.
. 3] ИНТЕРПОЛИРОВАНИЕ С КРАТНЫМИ УЗЛАМИ 49
Каждый узел х^ будет нулем ф(х) кратности не меньше а^. Сумма
кратностей таких нулей будет не меньше a]+ct2+ ••• Н~^/к=^
^-^;г-]-1. Но известно, что сумма кратностей нулей может быть
больше степени многочлена только в том случае, когда он
тождественно равен нулю: ф = 0. что доказывает единственность.
Интерполирующий многочлен Р„(/; х) может быть, очевидно,
записан в форме
/*„(/; X)-2 li Ц,^{x)f^^\x,), C.3.2)
где L^^iix) есть некоторые многочлены степени п. Для построения
многочлена рассмотрим сначала случай аналитической функции /.
Будем считать /(г) функцией комплексного переменного z,
регулярной в некоторой области В, содержащей внутри себя точку х
и узлы x^(/2=l, .,.. т). Как и выше, для простоты будем
считать область В односвязной. Возьмем любую замкнутую линию /,
лежащую внутри В и содержащую х 1Л х^ внутри себя. Всюду внутри
/ функция / может быть представлена интегралом Коши:
Равенство C.3.3) позволяет изучение / свести к изучению
элементарной функции -—-—, которую часто называют ядром Коши.
Для нашей цели удобнее рассмотреть не интерполяционный
многочлен для ——— , а остаток интерполирования
Будем рассматривать C.3.4) как функцию параметра z. Это —
правильная рациональная дробь, для которой C.3.4) есть разложение
На сумму простых дробей. Заметим, попутно, что точка z^^x есть
простой полюс RA^t^—' ^] с вычетом, равным единице.
Приведем дроби в правой части C.3.4) к общему знаменателю.
т
Если обозначить Л B:) = JJ B? — ^kf^* то в результате приведение
•^ля /?^ получим дробное представление вида:
50 ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ [ГЛ. 3
Так как дробь C.3.5) — правильная, числитель В (г, х) должен
быть многочленом от z, степени не выше /г-(-1. Убедимся в том,
что B(z, х) не зависит от 2; и равен Л(х). Для этой цели найдем
разложение C.3.5) при г, больших по модулю. Если | z \ есть
большая величина, то = >. „,. . Так как операция остатка R^
V = 0
линейная, можно видеть, что
со
V-0
Здесь /?^ (х^; х) есть остаток интерполирования х^'. Но, когда
интерполируемая функция есть многочлен, степень которого не больше п,
интерполирование будет точным и, поэтому.
/?^(х^; л;)==0 (v = О, 1. .... /г).
оо
Наименьшая степень —, входящая в разложение C,3.5) при
больших \zl должна быть •■ ^^^ . Значит числитель B{z, х) должен
иметь степень, относительно <г. на п~\-2 единицы меньше степени
знаменателя и не должен, следовательно, зависеть от z: B{z, х) =
= 5(jc). Кроме того, так как вычет C.3.5) в полюсе z =^ х равен
единице, должно быть В {х) -— А {х) и
rA—^\ х\=^ ,, f/-^^ , . C.3.6)
^^ \z-^x ) A(z)(z ^х) ^ ^
f iz)
Умножим теперь C.3.4) на \г ! и выполним интегрирование по /.
Ввиду C.3.3) и C.3.6). получим выражение остатка
интерполирования функции / в точке х в форме
C,3.7)
Вычисляя интеграл C,3.7) при помощи вычетов, можно найти
интерполирующий многочлен C.3.4): P^C/J •'^) = /W ~ ^я(/' •^)*
I * 3j ИНТЕРПОЛИРОВАНИЕ С КРАТНЫМИ УЗЛАМИ 51
Л (х) f (z)
"- Вычет J . 4-7 -X ь полюсе z=^x равен f(x). Найдем вычет
ТОЙ же функции в полюсе z=^x^. При z близком к х^^ будем иметь
следующие степенные разложения по степеням z — лг^.:
As)
/(^)-]^^~^(^-^./
-X (г '-Xf,)-{x ^-Х},) ^ (x — XkY^^
(^--^^)"' ^ У c^^)(z -^ JC Г
>1 (г) Li ^s {^ ^k) •
Вычет функции
A{z){z — x) (z — Xk) '' A{z) z^x
%u получим, если перемножим три выписанных ряда и найдем
коэффициент при (х — х^^~ . Простые вычисления покажут, что этот
коэффициент равен
-^f4x,)i S cf\x-x,rV
Ы0 5 = 0
„ A{x)f (z)
Для получения вычета , . ; ~, его мы должны умножить
л \Z) {Z X)
на Л{х). Все эти вычисления дадут для Я„(/; х) следующую
формулу, принадлежащую Эрмиту
Pnif:x) = ^ ^f\x,)^^^ 5] '^f'i^-^t'- C-3.8)
Если / задана на действительной оси и не является
аналитической функцией, то представление C.3.8) интерполяционного
многочлена для нее, очевидно, остается верным, но представление остатка
^nif\ ^) контурным интегралом — теряет свою силу.
В случае неаналитической функции / мы укажем другое
представление остатка R^, рассчитанное на функции достаточно высокого
класса дифференцируемости.
Пусть точки jc и ^Tj^ (^=:= 1, 2, . . ., W) лежат на некотором
отроке (а, Ь].
52 ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ [ГЛ. 3
Теорема 6. Если функция f имеет на {а, Ь\ производную
порядка п~\-\, то внутри [а, Ь\ существует такая точка |, что
для остатка R^ (/; л;) имеет место равенство:
'^^/•x)=j^f'''^'\l). C.3.9)
Теорема эта доказывается при помощи рассуждений, вполне
сходных с теми, которые были проведены при получении C.2.8), если
к функции Fiz)=^f(z)^P,(f; z) — ^^[f{x)-^P,{f- х)]
применить следующую измененную теорему Ролля.
Пусть aj < а2 < ... <.а^ и f удовлетворяет условиям
f\aj,) = 0 (^=1, 2. ..., т; /-=0. 1, .... а^—1), 2а^=:г.
Тогда, если / имеет на отрезке [а^, а^^] производную порядка г,
между Ui и а^^ существует такая точка g, что /^^^(у = 0.
§ 4. Тригонометрическое интерполирование
Предположим, что на отрезке 0-^л:<2я заданы п точек
О <; Xj < л;2 < ... < х,^ < 2л. Пусть, кроме того, рассматривается
2л;-периодическая функция /(х) и известны ее значения в точках Xj.
Задача тригонометрического интерполирования / зависит от четности
или нечетности п. Мы остановимся сначала на случае нечетного
числа узлов х^\ п = 2т~\~\. Нужно построить тригонометрический
многочлен степени т
т
Г(л;) = ао-)- 2 {a^coskx-^-b^sinkx), C.4.1)
удовлетворяющий условиям
T{xj)^f{xj) (у=:1, 2. .... 2тЧ-1). C.4.2)
Для вычислений, связанных с нахождением Т (х), удобнее
пользоваться выражением тригонометрического многочлена через
показательную функцию, равносильным C.4,1):
т
Т{х)= S Cfte'4 C.4.3)
кш^ — т
Условия C.4.2) дадут для определения коэффициентов с^ линейную
систему 2т-\-1 уравнений. При записи ее мы ввели, для
сокращения, обозначения z = e^-^, Zj = e'-^j
т
^ c^z'j = f(xj) (У=1 2/И + 1)
§41
ТРИГОНОМЕТРИЧЕСКОЕ ИНТЕРПОЛИРОВАНИЕ
53
или, после умножения на Zj
с z'^!^ + C
у2т — \
zT~^-\-
•• +^-^ч1^у +
■zp{x>). C.4.4)
Определитель системы есть определитель Ъандермонда от
;^^, Z2 ^2т+\- ^^^ ^^^ ^^^ ^j различны между собой, то
определитель отличен от нуля, система имеет решение и только
одно. Для нахождения Т {х) достаточно обратить внимание на то,
что система C.4.4) получится, если выполнять алгебраическое
интерполирование функции F (z) === z^"f (х) по значениям F в
узлах Zj G = 1.
= с
2т-{-I) при помощи многочлена P{z)-^=^
= ^^^2'" + ^.z-l^'"-^+ .•• +'
z^T (х). Условия
интерполирования P{Zj)=^Zjf{Xj) совпадают с системой C.4.4). Поэтому
для построения Р {z) может быть применена формула Лагранжа C.2.5).
Применительно к нашей задаче она будет следующей:
рB)=2
Если обе части равенства разделить на z"^ и возвратиться к
старым переменным х, Xj, после несложных вычислений получим
представление
Т(х) =
Sin
X — Xi
sin-
Xj^i х-
-^ sin —
'^J+i
X—Xn
sin •
-Xi
7 = 1
sin-
sin ■
Xj-
^У-1 . -^j—-^y+i
sin-:^—^
-J^-^^-
. sin-
~ / i^j) = "У Lj (X) f (xj);
C.4.5)
Д5ш^-2^ = Й(д:).
k = l
Это и есть нужное нам выражение для интерполирующего
многочлена Т(х).
Рассмотрим теперь случай четного числа узлов: п = 2т. Так как
в тригонометрическом многочлене какой-либо степени всегда
содержится нечетное число коэффициентов, он менее естествен, чем
случай нечетного п. Но мы не станем исключать его из
рассмотрения, так как в некоторых вопросах интегрирования периодических
функций, например, при построении правил квадратур, имеющих
наивысшую тригонометрическую степень точности, случаи четного и
нечетного п являются равноправными.
54 ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ [ГЛ. 3
Фиксируя какое-либо число б, рассмотрим тригонометрический
многочлен степени т частного вида
т — 1
r(jc) —^0+ S (cik<^oskx-^bf^smkx)~\-Acos(mx-^b).
Он содержит 2т параметров а^,, д^, Л. Их надлежит выбрать так.
чтобы Т (х) в узлах Xj принимал заданные значения
Т (Xj) ^ f {Xj) (у ^ 1. 2, .. .. 2т). C.4.6)
Как и в предыдущем случае, при вычислениях здесь удобнее
воспользоваться выражением Т (х) через показательные функции
т
Условия C,4.6) дадут для коэффициентов с^^ и Л линейную
систему. Ее мы запишем во вспомогательных переменных z я z- и
освободимся при этом от отрицательных степеней Zj, умножив урав-
1л(а^« + а) + .^_,^Г^+ ••• +^-..l^„-=^;r/Ю•
} C-4.7)
В записи определителя системы мы указали, для краткости, лишь
первую его строку:
^{z^, .... z^)=^^^\az-^a z^'' ... z^\. C.4.8)
Д будет многочленом степени п от z^, со старшим коэффициентом
az2.. * z^W^^i {Z2>.... -г J и свободным членом а^з.. ■ -s^^^/j-i (^2* • • • ^^п)'
где W^_i(z2, .... ^л) есть определитель Вандермонда от 2:2, .... z^.
Значения Zi=^ Z2^ ...» Zi^== z^^ являются, очевидно, корнями этого
многочлена. Их /г^1. Так как произведение всех корней должно
равняться —=е~^^^, то последний корень есть (e'^^^Z2 > * > z^)'^.
Поэтому разложение Д на линейные множители будет:
ДB:1. .... z„) = aiz^.., z^~e'^^^){z^-^Z2)^..
^a{z,..,z^-e'^^^)W^{z, z,). C.4.9)
§4]
ТРИГОНОМЕТРИЧЕСКОЕ ИНТЕРПОЛИРОВАНИЕ
55
Условием возможности и единственности интерполирования при всяких
значениях f (xj) будет соблюдение utpsiBQUCTBa z^ . ., г^Ф ^-2/6 ^^^^^^
в прежних переменных хf,
л:1+ ... -f-^rt =^—26+2/?л, C.4.10)
где р есть целое число.
Если к уравнениям C,4.7) присоединить равенство, определяющее
многочлен Т {х)\
1л(а^«+а) + г,.,_1^«-Ч- ... ^c^^^,z = T{x)z^.
которое мы записали в переменной z, то полученную систему
лН" 1 равенств можно будет рассматривать как однородную систему
уравнений с неизвестными уЛ, с^_^^, .... c_^+i, —1.
Определитель ее должен быть равен нулю. Из этого равенства может быть
найдено выражение Т (х):
О
z^T{x)-=^'
1
Д(^1,
^п)
f{x^zf
Z
Z,
у А(г, Zu
azl
^k-
-а z^-^
^п)
^{Zk, Zi г^-ь Zk+u ..., Zfi)
/ы^
Наконец, если оба входящие сюда определителя Д вычислить
по правилу C.4.9) и возвратиться к переменным х и х^^, для
интерполяционного многочлена Т (х) получится приводимое ниже
выражение:
Т(х)
21 Sil
sin -J (-«^ + о ~ л:а + 26) Q (х)
f^2sin-^(o+ 26) sin -^(х- Xk) Q' (Xft)
П
= У Ck{x)f{Xk). а = л:1 +
f{^u) =
2
C.4.11)
Непосредственно можно без труда проверить, что правая часть есть
действительно многочлен вида C.4.1), удовлетворяющий
условиям C.4.2).
56 ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ [ГЛ. 3
Литература
Уиттекер и Робинсон, Математическая обработка результатов
наблюдений, М. — Л., Гостехиздат, 1935.
Гончаров В. Л., Теория интерполирования и приближения функций,
гл, I и V, М., Гостехиздат, 1954, изд. 2.
Ремез Е. И„ ДАН СССР 26 A940), 2.
Her mite Ch., Sur la formule d'interpolation de Lagrange, Journ. fiir
reine und angew. Math. 84 A878).
ГЛАВА 4
ЛИНЕЙНЫЕ НОРМИРОВАННЫЕ ПРОСТРАНСТВА.
ЛИНЕЙНЫЕ ОПЕРАТОРЫ
§ 1. Линейные нормированные пространства
Для изучения некоторых задач теории квадратур большое
значение имеет функциональный анализ. Он позволяет с единой точки
зрения исследовать многие вопросы и получать большое число
результатов из одного источника. Для целей, которые преследуются
в дальнейшем изложении, потребуются лишь немногие понятия и
теоремы функционального анализа. Им будут посвящены три
ближайшие параграфа.
Пусть X = [х] — множество некоторых «элементов» х. Природа
таких элементов может быть любой: это могут быть точки, линии,
функции и т. п.
Множество X называется линейным, если над элементами этого
множества определены две операции — сложение х-\-у и
умножение кх на число к (действительное, или комплексное) такие, что
результаты операций приводят снова к элементам множества X
и выполняются аксиомы:
1) ассоциативность сложения (х-\~ у) ~\-z =^ х ~\-(у-\-z);
2) коммутативность сложения х ~\-у = у-} х\
3) существует элемент 9, называемый нулевым, такой, что при
всяком х^Х х-|-9 = х;
4) для каждого х из А" существует элемент — х. называемый
противоположным, такой, что х-|~(—х) = 9;
5) ассоциативность умножения k(iAx) = {kii) х\
6) верны два распределительных закона {к-\-[i) х = Хх-{-[ix,
^(х + у) = кх-\-ку;
7) i . X = х;
8) О . X -= 9;
9) если ^х^9 и х ^ 9, то к = 0.
Линейное множество X называется линейным нормированным,
или векторным пространством, если для каждого элемента х ^Х
58 ЛИНЕЙНЫЕ НОРМИРОВАННЫЕ ПРОСТРАНСТВА [ГЛ. 4
определена норма \\х\\ — вещественное число, обладающее свойствами
длины вектора:
1) 11 л: II > О и jlxlj^=:::0 тогда и только тогда, когда х^===9.
2) 1|а: + >'11<11^1И-||у11*
3)\\lx\\ = \l\-\\x\l
При помощи нормы может быть определена сходимость элементов:
говорят, что х„-~>х, или lim х„ = л:. если || х„ — х||->0 при
/г —> оо.
Со сходимостью тесно связана полнота пространства. Если
последовательность х^^ (/г=с= 1, 2, . . .) сходится к некоторому элементу х,
то для такой последовательности выполняется признак Больцано —
Коши: для всякого 8>0 существует такое А/(е), что при я>ЛА(е)
и любых /?г > О будет \\Х^^^ — -^л II < ^- Обратное может быть
неверным: если для последовательности х^ (п^=\, 2, . . .) выполняется
признак Больцано — Коши, то еще нельзя быть уверенным в том,
что в X суиа,ествует такой элемент х, к которому сходится л:„ при
Пространство X называется полным или типа В (по имени
С. Банаха), если из выполнения для х^ признака Больцано — Коши
следует существование в X такого элемента х, к которому
сходится х^^ при п~^оо.
Приведем некоторые примеры банаховых пространств.
1. Пространство С Пусть [а. ^] - любой конечный
отрезок. Элементами С являются всевозможные непрерывные функции
на [а, Ь]. Сложение элементов и умножение их на число есть
обычное сложение функций и умножение на число. За норму функции
X ^^ X (t) принимают
\\x\\^meix\x(t)l D.1.1)
t
Сходимость элементов есть равномерная сходимость
последовательности функций. Пространство С полное. Из ||х^^^^^^ — -^л II ==
= \mx\x^j^^(t) — л:д (О I < е следует сходимость последовательности
t
функций x^{t) (п=1, 2, . . .) при всяком t: lim x^(t) = x(t) и так
как предел равномерно сходящейся последовательности непрерывных
функций есть также непрерывная функция, то х (t) ^ С.
2. Пространство £р(р > 1) есть пространство измеримых
на [а, д] функций, суммируемых со степенью р. Сложение и
умножение на число есть также обычное сложение функций и умножение
их на число. Норма определяется равенством
( ? \^
\\х\\ = 1 I \xit)\Pdx\ . D.1.2)
[а J
«n
ЛИНЕЙНЫЕ НОРМИРОВАННЫЕ ПРОСТРАНСТВА 59
функции эквивалентные, т. е. различающиеся между собой лишь на
множестве точек, имеющем меру нуль, отождествляются.
Условия, которым должна удовлетворять норма, для D.1,2)
проверяются без труда. Выполнение условий 1 и 3 очевидно. Условие
лее 2 есть следствие известного неравенства Минковского для
интегралов *):
n\x(t) + y(t)\Pdt\ <n\x{t)\^dt\ +n\y(t)fdt\ .
Пространство L^ полное **).
3. Пространство ^2 суммируемых с квадратом функций есть
частный случай L^ при р^=2. Норма в ^2 ^сть
\\x\\ = \[xHt)dt\ . D.1.3)
la J
Сходимость элементов здесь означает сходимость функций в смысле
Среднего квадратического отклонения.
4. Пространство L суммируемых на [а, Ь] функций есть
также частный случай Lp при р;=1. Норма в L определяется так:
b
\\x\\=\\x{t)\dt D.1.4)
а
И имеет геометрический смысл площади между осью х и графиком
функции x{t),
5. V есть пространство функций ограниченного изменения на
[а, Ь] и обращающихся в нуль в точке а. За норму в V принимают
полное изменение х {t) на [а, Ь]
|lxl|-=Var^;@. D.1.5)
а
Сразу же видно, что условия 1 и 3 для нормы здесь выполняются.
Выполнение второго условия следует из неравенства
Var [X (О + у @1 < Var х (t) + Var у (О*
а а а
*) См., например, В. И. Смирнов, Курс высшей математики, М. — Л,,
Физматгиз, 1959, V. п°63. или Л. А. Люстерник и В. И. Соболев,
Элементы функционального анализа, М., «Наука», 1965, дополнение 1.
347-^48.
**) См., например, Л. А. Люстерник и В. И. Соболев,
Элементы функционального анализа, М., «Наука», 1965, 35—37.
60 ЛИНЕЙНЫЕ НОРМИРОВАННЫЕ ПРОСТРАНСТВА [ГЛ. 4
Пространство V полное. В самом деле, пусть для последовательности
элементов х^ (;г= 1, 2, ...) условие Больцано — Коши выполняется.
t
\x^^^{t) — x^(t)\ =
jdlx,^^(t)-x,(t)]
<
< Var [л:„+^ (t) — x^ {t)\ = \\ x,^^ — ^ J|< e. n> N{e).
a
Отсюда видно, что последовательность функций x^it) сходится при
всяких t^[a, b]: lim ДГ/ДО'^-^СО- ^з выполнения условия Боль-
дано — Коши следует, что нормы || х„ || (/г=1, 2, ,,.) ограничены
сверху некоторым числом*) ||л:„||<^^ (/г ^= 1, 2. . . .). Разделим
[а, Ь] на части точками ^о "^^ ^ < ^i < ^2 < • • • < ^а "== ^' Для
функции x^j (t) выполняется неравенство
k^i г,
2 I X, (t,^,) ~ X, (t,) I < Var X, {t) = IIX, II < Ж.
i=0 а
Если перейти здесь к пределу при п—>оо, то получим
^\x(t,^,)~x(t,)\^M,
1=0
b
откуда вытекает, что Var л; (^) ^ Л1 и, следовательно, x{t) есть эле-
а
мент пространства V.
Пусть 8 > О и число N таково, что при /г. т^ N будет
9i^m* •^rt)<^^* Если в неравенствах
2 I l^m ih^l) - ^п (^4l)] - \^т ih) -" X, {t,)] I <
( = 0
b
<Var[x^@ —хЛО]=р(->^^г ^nX^
a
перейти к пределу при т->оо, то легко получить следующее
неравенство
k-\
2 I {X (/,^i) - X, {t,^,)] - [X Hi) - X, (t,)] I < 8.
£ = 0
*) Возьмем e > 0 и выберем TV так, чтобы при п, т> N было
II-^т — Хп\\<г, Фиксируем какое-либо значение m>N\ liл:/| [|< lNV;;jj|+
+ ll-^m —-^rtlKII-^mii + e. Пусть М —наибольшее из чисел ii J^i li. ..., ||^Сд^ ||,
11^:^11 +е. Тогда при всяких п будет JI^^IK^.
^ 2] ЛИНЕЙНЫЕ ОПЕРАТОРЫ 61
faK как это верно при любом выборе точек ti{i = 0, 1, .... k), то
b
отсюда вытекает: Var[x{t)—x^(t)] = p(x, xj<;8, и последователь-
а
ность функций x^(t) сходится К x{t) при норме D.1.5).
§ 2. Линейные операторы
Пусть X^= {х} и К = {у}—два любых множества элементов х
и у. Если каждому элементу х соответствует, по какому-либо
правилу, некоторый элемент у: у = Н{х), то мы будем говорить, что
задан оператор Н. Множество X есть область его задания, а область
значений Н принадлежит К.
В частном случае, когда Y есть множество действительных или
комплексных чисел, и каждому элементу х соответствует некоторое
число, оператор Н называют функционалом.
Понятие оператора является прямым и далеко идущим
обобщением понятия функции.
- Если в множествах X )а Y известны правила предельного
перехода, то может быть определена непрерывность оператора.
Оператор Н называется непрерывным, если из х^^х (в множестве X)
следует Н(х^)~^Н(х) (в множестве V).
Далее мы будем считать, что X и V — линейные нормированные
пространства. Оператор Я называется аддитивным, если для любых
двух элементов х^ и Х2 из X будет*): H{Xi~]-X2) = Hx-^-~\-Hx2.
Оператор называется линейным, если он аддитивен и непрерывен.
Если существует число М такое, что при всяких х выполняется
неравенство ||Ял:||<; Ж||х||, тогда Н называют ограниченным
оператором. Докажем утверждение:
Для того чтобы аддитивный оператор был непрерывным,
необходимо и достаточно, чтобы он был ограниченным.
Необходимость. Допустим, что линейный оператор Н
неограничен и покажем, что это приводит к противоречию. Найдется
последовательность элементов х„ такая, что ЦЯл;^ ||^/г|| л:^||.
Построим элементы л:^ = —Г^ • Очевидно, х^-» 9 при/г->оо. С
другой стороны Нх'=—^Нх„ и \\НхЧ\=—^\\Нх^\\>1;
Ц^^^Цт^О при п~^со и оператор Н не непрерывен в нулевом
элементе 9.
Достаточность. Будем считать оператор Н аддитивным и
ограниченным и возьмем любой элемент х. Если х^->х, т. е.
*) Скобки, в которых записан аргумент оператора, часто будут опу-
62 ЛИНЕЙНЫЕ НОРМИРОВАННЫЕ ПРОСТРАНСТВА [ГЛ. 4
\\х,^х\\->0. то \\Нх,~~Нх\\ = \\Н{х,-х)\\^М\\х,-^^х\\~^0,
п->оо. Нх^~>Нх и оператор Н непрерывен.
Если /У — линейный оператор, то наименьшая из постоянных М,
удовлетворяющих неравенству ||/:/л:|К; ЖЦхЦ. называется нормой
оператора Н и обозначается \\Н\\\
||Я|| = т1пМ.
Для нахождения нормы в некоторых случаях может быть
полезным следующее просто доказываемое равенство
|1Я||= sup \\Нх\\. D.2.1)
|1 ^ 1] < 1
Действительно, при ||jc|Kl, ||Ял:|К:||Я||||х||<||Я||.
Следовательно,
sup ||Яд:|1<||Я||. D.2.2)
\\х\\<\
По определению нормы, для всякого е > О существует элемент х'
такой, что ЦЯх'ЦХЦЯЦ-8)||х'||. Положим
•^ =^-тгтгттг »
_
l-^'ll
Так как ||jc||==i, то sup ЦЯлгЦ > ||Я||~ е. Ввиду произвола в вы-
\\х\\К\
боре е, отсюда и из D.2.2) следует D.2.1).
Найдем норму некоторых линейных функционалов, с которыми
нам придется встретиться позже.
1. X — есть пр'остранство С [а, Ь]. Рассмотрим функционал
ь
Fx^ \^ f{t)x{t)dt. D.2.3)
а
где f {t) — измеримая и суммируемая на \а, Ь] функция. Имеем,
sup
\\х\\<\
\f{t)x{t)
dt
= sup \\f{t)\\x{t)\dt^ \\f{t)\
. , ._ . . . Adt.
^ 2] ЛИНЕЙНЫЕ ОПЕРАТОРЫ 63
Рассмотрим функцию sign/(О- Она измерима и | sign/(^) | ^ 1.
Для нее
j f(t)signf(t)dt^ j\f\dt.
a a
Так как sign/ есть измеримая функция, наверное существует такая
непрерывная функция x*(t), для которой |л:*@К^1 и которая
отличается от sign/ на множестве сколь угодно малой меры. Такую
функцию всегда можно выбрать так, чтобы 1 fx'*dt отличался бы от
а
Ь
Г f sign f dt сколь угодно мало. Поэтому
jT, следовательно,
2. X есть L[a. b]
sup \ fxdt:^ [\f\dt.
b
\\F\\=\\f\dt. D.2.4)
a
Ь
Fx--^ j f{t)x{t)dt. D.2.5)
Здесь / — непрерывная на [a, д] функция. Норма в L
определяется равенством D.1.4). Имеем
b
\Fx\
b
I fx dt
< max I / @ I [\x {t) I dt ^ max I fit)\'\\x ||.
t ^
Отсюда видно, что || /^ || ^ max | / {t) |.
i
Убедимся в том, что в полученной оценке для \\F\\ правая часть
не может быть уменьшена. Пусть 8 есть любое малое положительное
число. Обозначим Ж = тах|/@| и допустим, что этот максимум
достигается в точке |. Для определенности записи будем считать /(|)
положительным числом: /(|)=^/И>0. Ввиду непрерывности f {t),
около I существует такой отрезок а < ^ < р, в котором f {t) > М—е.
Определим функцию х (t) равенствами
(о при ^ ^ (а, E).
64
Очевидно
ЛИНЕЙНЫЕ НОРМИРОВАННЫЕ ПРОСТРАНСТВА
[ГЛ. 4
Fx\ =
\\х\\^ j\x(t)\dt=\,
а
Поэтому II /^ II = sup \Fx\^ М — е и, так как е есть произвольное
I1X1K1
ЧИСЛО, отсюда и из раньше полученной оценки сверху для || F || следует
||F|l=:.:M = max|/@|. D.2.6)
t
3. Пусть X есть пространство V. Рассмотрим функционал
b
Fx=^ f(t)dx{t), D.2.7)
а
где /(О — непрерывная на [а, Ь] функция, и покажем, что
Fx^
I/
dx
max I/(О |. D.2.8)
<;niaxl f (t) jVar л;(^) = тах| f (t) |||x||.
Будем считать, что max]/@1 достигается в некоторой точке /q
11 предположим, что ^q лежит внутри [а, Ь]. Взяв
10 при t < ^0»
0,5 при t = tQ,
1 при t > ^0-
можно убедиться, что полученная верхняя оценка для |F(a:)|
достигается. Этим D.2.8) доказано.
§ 3. Сходимость последовательности линейных операторов
Пусть Л' и F — банаховы пространства. Рассмотрим
последовательность линейных операторов И^ (/г=1, 2, . . .), заданных на X,
значения которых принадлежат К. Последовательность И^ будет
называться сходящейся, если при всяком х £Х будет сходиться
последовательность элементов у^ = И^х (в пространстве К).
Обозначим \тИ^х^=у = Нх. Оператор И — аддитивный. Действительно,
§ 3] сходимость ПОСЛЕДОВАТЕЛЬНОСТИ ЛИНЕЙНЫХ ОПЕРАТОРОВ 65
если в равенстве /^/Дл:1 + Х2)==Я„Х1-+Я^^Хз перейти к пределу
при П'-^оэ, то получим и{х^-^- х^^^^Нх^-^Нх^^ Но можно
показать, что оператор И будет линейным. Докажем предварительно лемму.
Лемма. Если последовательность операторов Н^{п^=^\,2, ...)
сходится, то нормы ах \\Иа\\ (^=Ь 2, ...) ограничены в
совокупности:
||ЯЛ</И. D.3.1)
Доказательство. Допустим противоположное. Множество
элементов х, удовлетворяющих условию || х — -^оИ^^» назовем
замкнутым шаром радиуса е с центром Xq и обозначим S{Xq, е).
Покажем, что \\Иj^x II не могут быть ограничены в совокупности ни в каком
замкнутом шаре. Действительно, пусть
||Я„х|К/С D.3,2)
для ft= 1, 2. . . . и при всяких х из шара 8{х^, г). Для любого х
из X элемент х^ ^=^-г—rX + -^o принадлежит S{xq, г). Поэтому
\НпХ'\
■Н,х~^Н^х4<К и ^\\Н,х\\-\\Н,х,\\^К.
Отсюда
||//xl|<:^±i^^«£ll
е
Посу1едовательность элементов H^Xq сходится и нормы их ЦЯ^^ХоЦ
ограничены в совокупности. Должно, следовательно, существовать
число /Ср не зависящее от /г и л:, такое, что || Я^^л: |К;/Ci || х ||. Поэтому
||Я,|И sup \\Н,х\\^К,.
\\А\ < 1
а это противоречит допущению и неравенство D.3.2) не может быть
верным.
Возьмем любой замкнутый шар Sq(xq, г). В нем
последовательность ЦЯ^хЦ неограничена. Найдется, следовательно, такой
оператор Н^ и такой элемент x^^S^, что 1| Я^^^! ]| > 1. Ввиду
непрерывности оператора Н^, это неравенство будет выполняться в некотором
замкнутом шаре S^{x^, ej), содержащемся в Sq. По аналогичной
причине найдется оператор Я^ и элемент ^26*^1 такие, что ЦЯ^ХзЦ > 2
и т. д. Момшо считать, что е„-^0 при п-^оо. Для построенной
последовательности элементов х^, х^^ ... будет выполняться признак
Больцано — Коши. Пространство X полное и последовательность будет
сходиться к некоторому элементу х^'^Х: х^^-^л:*, п-^оо\ х* будет
принадлежать всем сферам Sf^ (^=1, 2, ..,). При этом тя
элемента X* |1Я„ х*||>^. Последнее же противоречит тому, что
последовательность Н^х сходится для любого X ^Х.
66 ЛИНЕЙНЫЕ НОРМИРОВАННЫЕ ПРОСТРАНСТВА [ГЛ. 4
На основании леммы просто доказывается линейность
предельного оператора Н. Переходя к пределу при п—>оо в неравенстве
||Я„л:||<Ж||л;||, получим || Ял; |1<; МЦ л; ||. Оператор Н ограничен
и, ввиду аддитивности, непрерывен и линеен.
Условия, которым должны удовлетворять операторы
последовательности Н^ (rt=l, 2. ...) для того, чтобы она была сходящейся,
указываются в следующей теореме С. Банаха.
Теорема 1. Для того чтобы последовательность линейных
операторов Н^ (п=\, 2. ...) была сходящейся, необходимо и
достаточно выполнение двух условий:
1) нормы операторов ||Я„|| ограничены в совокупности,
2) сходимость Н^х имеет место для всякого х из
множества Е, всюду плотного в А"*).
Доказательство. Необходимость второго условия очевидна,
необходимость же первого вытекает из леммы.
Достаточность условий может быть проверена следующим путем.
Пусть \\Н^\\^М, Возьмем произвольный х^Х w найдем такой
элемент х^Е, что IIJC — •^И^'ялГ* Последовательность Н^х сходится
по условию 2 и для больших п будет \\Н^^^^х — Я^х||<-о-* Тогда
||Я^^^х-Я„л;||<||Я^^^л; —Я^^^х 11 + 11 Я^^^х—Я^^ 11 +
+ |1Я,х-Я„х||<2М||х-х1| + |<^+| = е.
Поэтому последовательность Я^л; выполняет условие Больцано —
Коши и. ввиду полноты К, существует при каждом х^Х предел
yz=:^Hx= lim Н^х.
Л-^оо
Как показано выше, предельный оператор Я линейный.
Литература
Л ю от ер ни к Л. А., Основные понятия функционального анализа, Усп.
матем. наук, вып. I, 1936.
Люстерник Л. А. и Соболев В. И., Элементы функционального
анализа, М„ «Наука» A965).
Канторович Л. В., Функциональный анализ и прикладная
математика, Усп. матем. наук 3, вып. 6 B8) A948).
*) Множество Е называется всюду плотным в X, если каждый
элемент х^Х может быть приближен по норме сколь угодно точно
элементами из Б,
ЧАСТЬ ВТОРАЯ
ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННОГО
ИНТЕГРАЛА
ГЛАВА 5
КВАДРАТУРНЫЕ СУММЫ И ЗАДАЧИ, С НИМИ СВЯЗАННЫЕ.
ОСТАТОК ПРИБЛИЖЕННОЙ КВАДРАТУРЫ
§ !• Квадратурные суммы
Задачу нахождения численного значения однократного интеграла,
.ввиду известного ее геометрического значения, часто называют, для
сокращения речи, квадратурой. В книге изучаются такие методы
квадратур, которые позволяют приближенно вычислить интеграл при
помощи конечного числа значений интегрируемой функции и
производных от нее. Эти методы являются универсальными и могут
применяться там, где другие методы вычисления интегралов оказываются
бессильными. Кроме того, применение этих методов во многих
случаях требует затраты меньшего вычислительного труда, сравнительно
с другими методами.
Рассмотрим интеграл вида
b
j p(x)f(x)dx;
а
[а/д] — любой конечный или бесконечный отрезок числовой оси,
/ — произвольная функция некоторого класса. Для упрощения
изложения допустим, в границах этой главы, что все функции /
непрерывны, р(х) есть некоторая фиксированная функция. Ее мы будем
предполагать измеримой на [а, Ь], неэквивалентной нулю и такой,
что произведение ее на любую функцию / суммируемо на [а, д].
Какое-либо предположение о знаке р (х) в ближайшем изложении
нам не потребуется.
Наиболее распространенными в приложениях являются
квадратурные формулы, позволяющие приближенно находить значение интеграла
в форме линейной комбинации нескольких значений функции
b п
I p{x)f(x)dx^'^AJ(x,). E.1.1)
68 КВАДРАТУРНЫЕ СУММЫ И ЗАДАЧИ [ГЛ. 5
п
Сумма S^fe/('^jfe) ниже будет называться квадратурной суммой.
Равенства вида E.1 Л) получили название формул механических
квадратур*). Они содержат следующие 2п'\-\ параметров, которыми
можно распорядиться при их построении: п абсцисс, или «узлов» Xj^, п
коэффициентов А^^ и число узлов п. Все эти параметры надлежит
выбрать так, чтобы формула E.1.1) давала бы «достаточно малую
погрешность» для всех функций / из некоторого широкого класса.
При описании идей, связанных с построением квадратурных сумм,
мы не будем точно определять, что следует понимать под «малой
погрешностью» и сколь широким должен быть класс функций /.
Точное содержание этих слов будет выяснено ниже.
Непосредственно ясно, что чем большее значение имеет п, тем
большей точности можно достигнуть в равенстве E.1.1) за счет
выбора х^ и А^. Поэтому, при построении формул приближенных
квадратур, п считают произвольным, но фиксированным натуральным
числом.
При применении E.1.1) наибольшее количество труда, обычно,
затрачивается на нахождение значений f{xj^) (^=1. ..., п). После
п
того, как f{x^) найдены, составление квадратурной суммы 2 ^kfi^k)^
k = \
если п не будет очень большим, выполняется сравнительно легко.
Поэтому естественно стремиться к тому, чтобы достигнуть нужной
точности вычислений с возможно малым числом п узлов Xj^. Для
построения же квадратурных сумм это равносильно тому, чтобы
при заданном п постараться возможно лучшим образом
воспользоваться выбором х^ и А^ для повышения точности формулы E.1.1).
До настоящего времени исследования проводились преимущественно
в следующих направлениях.
*) Формуле E.1.1) легко придать механический смысл. Введем величину
b b п
Р~ pdx и запишем E.1.1) в виде Р"^ pf dx ^ V ZJ^/(х;^). Здесь
а а А; = 1
коэффициенты Bf^ будут отвлеченными числами. Условимся толковать их
как «веса», приписываемые соответствующим значениям f {х^У Если
требовать, чтобы равенство было верным, когда / есть величина постоянная,
'^ п п
то Bk должны быть подчинены условию ^^ В^^=\. Сумма ^j ^kf i^k) тогда
k=\ k=\
будет иметь смысл среднего взвешенного значения, составленного из f {х^).
Задача построения равенства приводится к такому нахождению весов Bk.
чтобы среднее взвешенное значение из f {х^) было приближенно равно сред-
b
нему интегральному значению / на отрезке [а, Ь]: Р~^ 1 pf dx.
§ I] КВАДРАТУРНЫЕ СУММЫ 69
1. Допустим, что нам заранее задан некоторый класс F
функций /. Наряду с ним рассмотрим систему функций
о)^(х) (т=Ь 2. ...) E.1.2)
таких, что произведения р(л;)(о^(л:) суммируемы на \а, Ь\. Образуем
линейную комбинацию
п
При вычислении интеграла Г pfdx за «расстояние» между /
а
И 5д можно принять величину
b
а
Систему E,1.2) будем считать полной в классе F, т. е. такой,
что для каждой функции f ^F и любого е > О существует такая
линейная комбинация $^, для которой р(/. 5/^) < е.
Ввиду неравенства
b b \ b
j pf dx— j ps^dxl^ j \p(f-'S^)\dx===p(f, 5j,
отсюда
вытекает, что интеграл pf dx может быть вычислен со сколь
а
угодно высокой точностью, если интегрируемую функцию / заменить
надлежаще выбранной линейной комбинацией s^.
При этом, очевидно, можно достигнуть тем большей точности
вычислений, чем большее число первых функций о);^ брать при
образовании s^.
Можно ожидать, что если мы выбором узлов х^^ и
коэффициентов Afg в формуле E.1.1) достигнем хорошей точности в
интегрировании функций о)„. то тогда формула E.1.1) должна будет также
дать хороший по точности результат при вычислении интеграла от
всякой функции f^F. Эти несложные соображения имеют,
разумеется, только наводящее значение и погрешность построенной
формулы должна быть подвергнута точному анализу и оценке. Но они
позволяют указать простой принцип выбора х^ и Л^\ будем
стремиться выбором Xfg и Л^^ добиться того, чтобы формула E.1.1)
давала точный результат для возможно большего числа первых
функций (оЛд:).
70 КВАДРАТУРНЫЕ СУММЫ И ЗАДАЧИ [ГЛ. 5
Говорят, что равенство E.1.1) имеет степень точности т
относительно функций E.1.2), если оно верно для coj, щ, .... о)^:
b п
J /70. dx=^ A^(y\ (Xfe) {i^\, 2. .. ., m)
a k = l
и не верно для «^^j. Указанный выше путь выбора л:^ и Л^^ есть
путь повышения степени точности равенства E.1.1). С этой точки
зрения, особый интерес имеют формулы приближенных квадратур,
которые обладают наивысшей возможной степенью точности. Такие
формулы мы и будем иметь в виду в ближайшем изложении.
Если класс F задан, то при построении равенства E.1.1),
служащего для интегрирования функций /, остается ещ,е произвол в
выборе системы функций о)^(п= 1, 2, . . .). Требование полноты,
которому должна удовлетворять система, не вполне определяет ее и
оставляет еще широкие возможности выбора (и^.
Приближенные квадратурные формулы, которые имеются в виду
сейчас, учитывают свойства функций со^. Если мы хотим, чтобы
такие формулы давали хорошую точность, нужно со^ выбрать так,
чтобы свойства со^^ были согласованы со свойствами /. и можно
думать, что погрешность E.1.1) будет тем меньше чем более точное
приближение при помощи линейной комбинации s^ будет допускать
функция / для фиксированного п.
Приведем теперь примеры выбора со^. Пусть [а, Ь] есть любой
конечный отрезок. Известно, что какова бы ни была функция /,
непрерывная на [а, Ь], для всякого £> О существует многочлен Р(х),
отличающийся от f (х) при любых х^[а, Ь] меньше чем на е:
\/(х)~Р(х)\<г.
Это и есть свойство полноты алгебраических многочленов в
пространстве непрерывных функций С. Отсюда сразу же следует
полнота системы многочленов и в смысле метрики E.1.3).
Примем систему степеней х: 1, х, л:^, . . .—за функции со^ и
будем говорить, что равенство E.1.1) имеет алгебраическую
степень точности т, если оно верно для всевозможных многочленов
степени т и не верно для многочленов степени т-\-1. Это
равносильно тому, что равенство
b а
j рхЫх^^Л^х^
а k = l
выполняется для i = 0, 1 т и не выполняется для i=^m-(-l.
Можно ожидать, что E.1.1) будет иметь тем меньшую
погрешность для многих непрерывных на [а, Ь] функций, чем выше буд^т
его алгебраическая степень точности.
§ 1] КВАДРАТУРНЫЕ СУММЫ 71
Система степеней jc" (/1 = 0, 1, . . .) является достаточно удобным
основанием для построения квадратурных формул наивысшей степени
точности для любого конечного отрезка [а, Ь].
Допустим теперь, что отрезок интегрирования бесконечный,
например, пусть это есть отрезок О ^ х < сх?. Возьмем какое-нибудь
подмножество F функций /. непрерывных на [О, со). На каждом
конечном отрезке 0<c;jc^^<oo можно построить многочлен Р(х),
приближающий / равномерно с любой наперед заданной точностью.
Но Р{х) может не давать равномерного приближения / на всей
полуоси и разность / — Р при больших х может иметь большие
значения. Несмотря на это, если вес р (х) достаточно быстро
убывает при X—>оо. может оказаться, что для любой f^F интеграл
со
\p(f — P)\dx может быть сделан сколь угодно малым, и система
о
степеней х" тогда будет полной в классе F по метрике E.1.3).
В этом случае квадратурные формулы наивысшей алгебраической
степени точности также могут применяться для приближенного вычи-
оо
сленйя интегралов вида pf dx. С формулами такого рода мы озна-
0
комимся ниже более подробно.
В связи с этим мы хотим остановить внимание читателя на одном
примере, более отчетливо выясняющем, как при выборе функций (о„
их свойства следует согласовать с классом F интегрируемых функций.
Рассмотрим функции /, непрерывные на отрезке О^х<со,
ограниченные там и имеющие предельное значение при х->оо.
Каждый многочлен Я(х), степень которого больше нуля, неограниченно
возрастает при х—>со, при этом порядок роста тем выше, чем старше
степень многочлена. Поведение многочлена на полуоси [О, оо)
существенно отличается от поведения ограниченных функций, и
многочлены, по-видимому, нельзя признать удачным орудием для
приближения таких функций на [О, оо). Для некоторых весовых функций
р (х) может оказаться, что приближенные квадратуры наивысшей
степени точности, в основание которых положена система степеней x'^
будут иметь медленную сходимость при п-^оо к точному значению
интеграла и для достижения требуемой точности может потребоваться
большое число узлов.
Для приближения функций рассматриваемого типа более подходят
не многочлены, а рациональные функции, ограниченные на [О, оо).
Можно взять, например, рациональные дроби (i)j^(x) = A-f"^)"
(^ = 0, 1, ...). Весьма вероятно, что если построить правила
квадратур наивысшей степени точности с указанными о)^^(х), то они должны,
вообще говоря, дать лучший результат при таком же числе узлов п
72 КВАДРАТУРНЫЕ СУММЫ И ЗАДАЧИ [ГЛ. 5
И обладать более быстрой сходимостью к точному значению
интеграла.
Остановимся, наконец, еще на одном случае выбора (i)fi{x).
Возьмем 2я-периодические функции и допустим, что вычислению подлежат
2л
интегралы вида f{x)dx. За функции оо„ тогда естественно выбрать
о
тригонометрические функции cos^x, sin ^л: (^--^0, 1, 2, ...).
2. Допустим, что задан класс F функций /. Постараемся построить
квадратурную формулу E.1.1), которую можно было бы признать
в смысле, выясняемом несколькими строками ниже, «наилучшей» для
заданного класса. Для каждой функции / погрешность формулы E,1.1)
имеет значение
R{f)'^^ pfdx-^AJix,).
За величину, характеризуюш,ую точность квадратурной формулы
для всех функций /, может быть взята верхняя грань \R(f)\
R = snp\R(f)l
Здесь R зависит от х^ и Л^,. Желая достигнуть возможно лучшей
точности для всех функций f ^ F, можно выбирать х^^ и Af^ так.
чтобы R имело бы наименьшее возможное значение. Такую формулу
ниже будем называть формулой с наименьшей оценкой остатка
в классе F,
3. Указанные сейчас два направления в проблеме выбора узлов и
коэффициентов, разумеется, не являются единственными. Можно
строить квадратурные формулы, подчиняя выбор узлов и
коэффициентов другим целям. Укажем еще на одну задачу такого рода.
Предварительно заметим, что сделать формулу E.1.1) верной для
функции, сохраняющей постоянное значение на [а, Ь], можно только
за счет выбора коэффициентов А^. Если потребовать, чтобы EЛ.1)
была верной для /^1, то получится следующее условие:
п b
Y^A^^l p{x)dx. E.1.4)
ft = l a
Предположим, что значения /(лг^) функции /. входящие в
квадратурную сумму, находятся из измерений и содержат случайные
погрешности. Допустим, кроме того, что все f(x^) получены в
результате измерений одинаковой точности.
Значение квадратурной суммы также будет содержать случайную
погрешность. Можно поставить себе задачей так выбрать коэффи-
§ и КВАДРАТУРНЫЕ СУММЫ 73
п
циенты >ljfe, чтобы квадратурная сумма 2 ^kfi^k)* при выполнении
условия E.1,4), имела бы наименьшую квадратичную погрешность.
Известно, что если аргументы Zi z^ линейной функции у =
^=:=aiZi-\- ... +а„^^ есть случайные величины, подчиняющиеся
нормальным законам распределения с одной и той же квадратичной
погрешностью, и если коэффициенты линейной функции подчинены
п
условию 2^ft=b то средняя квадратичная погрешность суммы
будет иметь наименьшее значение в том случае, когда все
коэффициенты равны между собой *). Поэтому квадратурная формула с
равными коэффициентами
b
j p(x)f(x)dx^Clf(xO+ ... +f(Xn)] E.1.5)
a
будет иметь наименьшую квадратичную погрешность. Вместе с тем
"такие формулы особенно удобны при графических вычислениях, так
как сумма ординат может быть снята с чертежа при помощи
простейших графических приборов.
Упомянем еще об одном требовании, которое должно быть
обязательно предъявлено к квадратурным суммам и имеет большое значение
в приложениях. При вычислениях, почти всегда, приходится иметь
дело с приближенными значениями f{x^), верными на некоторое
число значащих цифр.
Пусть все значения f{x0 известны с погрешностями, не
превосходящими по абсолютной величине числа е. Вычисляя при помощи
п
приближенных значений /(Xj^) квадратурную сумму 2^а/(-^а)' ^^^
получим ее значение с погрешностью, которая должна быть оценена
п
величиной е2 Ма|. Такая оценка является точной и не может быть
п
уменьшена. Если сумма 2 I ^ft I велика, то даже малые погрешности
*) Если случайные переменные Zi г^ подчиняются нормальным
законам распределения со средними квадратичными погрешностямиaj, ..., а^
и у есть линейная функция от них: у = ^j^,-[- ... -\-^п^п^ то у также
подчиняется нормальному закону распределения со средней квадратичной
погрешностью 2 = (afaj -(-... -|- flt^cr^) ^ (см., например. С. Н. Бернштейн,
Теория вероятностей, Гостехиздат, 1946, стр. 269—272). Для ffj = аг = ...
... ^Ofi~o будем иметь 2 = а(а^-|- ". +^я) ^ "■ "Р^ условии ^i + ...
•" 4-^/?"= 1. 2 будет иметь минимум в том случае, когда все л^ одинаковы.
74 КВАДРАТУРНЫЕ СУММЫ И ЗАДАЧИ [ГЛ. 5
В значениях f(xj^) могут вызвать большую погрешность в
приближенном значении интеграла. При построении квадратурных формул,
поэтому, всегда стремятся к тому, чтобы сумма абсолютных величин
ее коэффициентов имела бы возможно малое значение.
В одном важном частном случае легко указать условие, при кото-
п
ром 2 I ^ftl будет иметь наименьшее возможное значение. Будем счи-
тать вес /? (л:) неотрицательной функцией р(х)^0> х^[а, Ь], Кроме
того, предположим, что квадратурная формула верна для /^^1, что
равносильно равенству E.1.4) для коэффициентов Л^. Тогда, оче-
п
видно, 2 Ма I будет иметь наименьшее значение в том случае, когда
все коэффициенты Af^ будут положительными А^ > 0. Этот факт
является одной из причин, в силу которых квадратурные формулы
с положительными коэффициентами имеют особо важное значение для
приложений.
§ 2. Об остатке приближенной квадратуры
и его представлении
Значение остатка квадратуры
b п
/?(/)-J/>W/W^x-2]^^^(^^) E.2.1)
зависит как от выбора квадратурной формулы, которая определяется
узлами Xf^ и коэффициентами А^, так и от свойств интегрируемой
функции /. Формула E.2.1) есть одно из возможных представлений
остатка, но оно недостаточно в том отношении, что при помощи
него часто бывает весьма трудно проследить, какое влияние на R (/)
оказывают те или иные структурные-^) свойства /. Выражение E.2.1)
рассчитано на весьма широкий класс функций. Оно верно при любой
b
функции /, для которой имеет смысл \ pf dx vi которая имеет ко-
а
нечные значения в узлах х^* Ввиду своей общности, оно не
учитывает других свойств /.
Чтобы упростить задачу исследования R (/), полезно построить
иные представления остатка, которые позволяли бы легко проследить
влияние, оказываемое на величину R{f) такими свойствами функции /,
*) Под «структурными свойствами» функции понимаются такие свойства,
как ограниченность изменения, абсолютная непрерывность, выполнение
условия Липшица, принадлежность к тому или иному классу
дифференцируемости и т. п.
§ 2] ОБ ОСТАТКЕ ПРИБЛИЖЕННОЙ КВАДРАТУРЫ 75
как порядок ее дифференцируемости, степень удаленности от [а, Ь]
особых точек / и т. п. Среди представлений этого вида особое
значение имеют представления, характерные для тех или иных
структурных классов функций.
Будем считать, что нам задано множество F интегрируемых
функций /. Остаток /?(/) есть функционал, определенный на
множестве F, В функциональном анализе известны теоремы об общих
формах линейных функционалов, определенных на некоторых
конкретных линейных пространствах. Этими теоремами можно было бы
воспользоваться для построения представления остаточных членов /?(/)
во многих случаях множеств F*).
Для зада^, которые будут рассматриваться в дальнейшем, чтобы
найти нужные представления остатка R(f), достаточно было
прибегнуть к простым средствам классического анализа, более быстро
приводящим к цели.
Если рассматривается класс F функций, обладающих каким-либо
структурным свойством, то часто можно указать такую формулу,
^ которая способна представить всякую функцию класса F и может
представлять функции только этого класса. Такую формулу называют
характерным представлением класса F или его структурной
формулой.
Если структурная формула класса F известна, то при помощи
нее, принципиально говоря, могут быть получены все нужные
сведения о классе F, в частности, может быть построено представление
остатка квадратуры, характерное для функций класса F, Такие
представления остатка будут ниже строиться каждый раз, когда это
потребуется по ходу рассуждений.
Сейчас же мы ограничимся только одним примером, поясняющим
все сказанное выше.
Говорят, что функция / принадлежит классу С^ [а, Ь], если она
г раз непрерывно дифференцируема на [а, Ь], Характерное
представление функций этого класса доставляет формула Тейлора. Если
f^Cj.la, I?] и а — любая точка отрезка [а, д], то
fix)=^^^(x-ay+jfin^t)^f^dL E.2.2)
/-0 а
Для дальнейшего удобно заменить интеграл с переменной
границей на определенный интеграл по отрезку [а, Ь]. Это можно
сделать, если ввести «гасящую» функцию, позволяющую уничтожить
в определенном интеграле лишние участки интегрирования. Определим
*) См. литературу, указанную в конце главы.
76 КВАДРАТУРНЫЕ СУММЫ И ЗАДАЧИ [ГЛ, 5
Е(х) равенствами
Е(Х):
с 1 при X > 0.
0,5 при х=:=0,
о при JC < 0.
Легко проверить, что равенство E.2.2) может быть записано в форме
ь
+ J f^n ^t) [E{x-t)~E{a-1)] ^•^;i^(O ^^' (^-^'^^
a
В правую часть E.2.3) входят г численных параметров /^^^ (а)
(/ = 0, 1, . . ., г— 1) и функциональный параметр f^^^{t), являющийся
непрерывной функцией на [а. Ь\.
Всякая функция / из С^ [а, Ь\ представима в форме E.2.3).
Наоборот, каковы бы ни были численные параметры /^^* (а) (/== О,
1 г—1) и какова бы ни была непрерывная на [а, Ь]
функция/^''^@. функция/(х), определенная равенством E.2.3),
принадлежит С^ [а. Ь].
Если промежуток интегрирования не совпадает со всей числовой
осью, то часто, чтобы не вводить лишний параметр, за а принимают
один из концов [а, Ь]. Например, если за а принять левый конец а,
то формула E.2.3) упростится и примет вид:
fi.x)-=^^^^ix-ay + \f('Ht)E{x-t)^J^^dt. E.2.4)
г>1.
Если это не будет вызывать неясности, в обозначениях классов
функций знак отрезка [а, Ь\ будет опускаться. Возвратимся к остатку
квадратуры E.2.1); R{f) является аддитивным функционалом,
определенным на некотором множестве функций.
Пусть интегрируемая функция / принадлежит классу С^. Ниже
мы попытаемся определить, какое влияние на величину остатка и на
сходимость квадратурного процесса может оказать а*-кратная диф-
ференцируемость /. Для этой цели целесообразно получить
представление R{f), характерное для класса С^. Оно может быть найдено»
й]
ОБ ОСТАТКЕ ПРИБЛИЖЕННОЙ КВАДРАТУРЫ
77
если в E.2.1) вместо / внести ее выражение E.2.3):
/?(/)=-2 т^/^к^-«)'■]+
/=0
+/?
и
J /(^^ (О [Е {X - О - ^ (а - 0} -TF^nrr
^г'
E.2.5)
Будем считать, что в двукратном интеграле
b b
I р{х)\ f^'m [Е(x-t)~Е(а^t)] '^\,_^^1у' dtdx.
а а
входящем в последний член правой части равенства, допустима
перемена порядка интегрирования. При принятых предположениях о
весовой функции р (х), это, наверное, возможно, если [а, Ь\ конечный
. отрезок. Тогда E.2.5) преобразуется и примет форму
/■-1 . *
^ (Л - S^^^ R [(-^~ «)'] + J f^'^ (ОKit)dt. E.2.6)
1=0 а
где ядро остатка K(t) имеет вид
b
a
n
~^ A,[E{Xk-t)~E{a^t)]^J^-^l^~'^ ... E.2.7)
Если считать tфa и t Ф x^ (^=1, .е., /г), то для K{t) легко
получить следующие равенства:
t
^<а, K{t) = ^\p{x)^^^^^dx^ Yi ^^^^^XF^^^
b
t>a. K{t) = j p(x)^^^^dx- 5; A,^^f^=^.
Xy>t
E.2.8)
Аналогично может быть построено представление остатка для других
классов функций, когда известны характерные их представления.
например, для аналитических функций.
78 КВАДРАТУРНЫЕ СУММЫ И ЗАДАЧИ [ГЛ. 5
В главах 11 и 12 мы увидим, что специализированные
представления остатка, о которых говорилось выше, позволяют достаточно
просто решить задачу о нахождении точных оценок /? (/) и о
сходимости квадратурных процессов для некоторых классов функций.
Литература
Radon. Restausdriicke bei Interpolations — und Quadraturformeln durch
bestimmte Integrale, Monatshefte fur Mathematik und Physik 42 A935), 389—396.
Ремез E. Я., 1) О некоторых классах... Труды Инст. матем. АН
УССР 4 A940), 47—82. 2) Об остаточных членах некоторых формул
приближенного анализа, ДАН СССР 26 A940). 130—134.
Sard А., Integral Representations of Remainders, Duke Math. Journ. l5,
333—345.
К n e s с h к e A., Theorie der genaherten Quadratur, Journ. reine und
angew, Maih. 187, 115—128.
ГЛАВА 6
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ, ДЛЯ КОТОРЫХ ИЗВЕСТНА
ТАБЛИЦА ЗНАЧЕНИЙ. ИНТЕРПОЛЯЦИОННЫЕ КВАДРАТУРЫ
§ !• О содержании задачи
Настоящая глава посвящена теории интерполяционных квадратур
}i изложению некоторых путей их улучшения, В практике вычислений
нередко возникает потребность нахождения численного значения
интеграла в том случае, когда заранее известна или по каким-либо
причинам предварительно составляется таблица значений f {х^)
интегрируемой функции / в некоторой системе точек х^ {k=^\, 2, .... п).
В такой задаче при построении или выборе правила интегрирования
E.1.1) мы сильно стеснены в возможности избирать з^злы Xj^
формулы: мы можем только либо взять все табличные узлы, либо часть
из них опустить. Последнее равносильно тому, что некоторые из А^
мы заранее считаем равными нулю. После того как узлы нами
указаны, можно рассмотреть вопрос о выборе численных значений
коэффициентов А^. Будем иметь в виду сначала тот случай, когда берутся
все табличные узлы без пропусков.
Задачу выбора А^ следует, по-видимому, рассмотреть в первую
очередь в предположении, что на А^ не наложено никаких
ограничений и мы имеем право вполне произвольно распорядиться их
численными значениями.
Если А^ выбирать так, чтобы правило E.1,1) имело наивысшую
возможную степень точности, то мы придем к интерполяционным
квадратурам. Теория их излагается в последующих параграфах
настоящей главы. Сейчас мы заранее укажем, что интерполяционные
правила интегрирования далеко не всегда способны давать хорошую
точность. Условия, при которых ими можно успешно пользоваться,
будут выясняться ниже.
Если мы хотим построить правила интегрирования, свободные от
недостатков интерполяционных квадратур, мы можем, во-первых,
сделать степень точности правила E,1.1) меньше интерполяционной и
оставить некоторые коэффициенты А^ произвольными, а затем их
80 ИНТЕРПОЛЯЦИОННЫЕ КВАДРАТУРЫ [ГЛ. 6
выбрать так, чтобы з^лучшить свойства правила, например, пытаться
сделать все коэффициенты Af^ положительными или по возможности
уменьшить их абсолютные величины и т. д.
Во-вторых, мы можем, как говорилось выше, пропустить
некоторые из табличных з^злов х^ и выполнить интегрирование с более
короткой таблицей значений /. Это позволяет, по крайней мере
в частных случаях, построить правила интегрирования, свободные от
некоторых недостатков интерполяционных квадратур. Если встать на
этот путь, то следует указать способ выбора табличных узлов,
который позволил бы надеяться на получение удовлетворительной
точности интегрирования.
Выбор Xf^ тесно связан с вопросом о сходимости квадратурного
процесса и о нем мы будем говорить в § 6 этой главы.
На практике наиболее часто приходится встречаться с таблицами
значений функции / в равноотстоящих точках. Этому случаю и будет
преимущественно посвящено все последующее изложение.
§ 2. Интерполяционные квадратурные формулы
и их остаточные члены
Для построения квадратурных сумм часто пользуются
интерполированием функции. Во многих случаях построенные таким путем
квадратурные формулы обладают хорошей точностью и достаточно
удобны для применений.
Выберем на отрезке интегрирования [а, д] п произвольных точек
jCj. Х2 Хд и интерполируем функцию / по ее значениям в этих
точках *)
f{x)=P{x) + r{x\ F.2.1)
п
^(^>==Е(;с-Г/)^-(х,)/(-^^)' ^{х) = {х-х{)...{х-х,). F.2.2)
к = \
Здесь г {х) — остаток интерполирования.
ь
Точное значение интеграла pf dx будет
а
b b b
] P{x)f W dx= \ p{x)P {x) dx~{~ \ p{x)r (x) dx.
*) Мы считаем, что функция / определена только в точках отрезка [а, Ь]
и должны поэтому предполагать х^ (^=1, .,., п) принадлежащими [а, Ь\.
Если / известна и вне отрезка интегрирования, то х^ не обязательно все
должны принадлежать [а, Ь]. Квадратурные суммы, содержащие узлы,
расположенные вне [а, Ь], особенно часто применяются при интегрировании
аналитических функций.
§2] ИНТЕРПОЛЯЦИОННЫЕ КВАДРАТУРНЫЕ ФОРМУЛЫ 81
Если интерполирование F.2.1) было достаточно точным и
остаток г(х) имел малые значения всюду на отрезке [а, д], то вторым
членом в предыдущем равенстве можно пренебречь. После этого
получится приближенное равенство
Ь п
J P{x)f{x)dx^"^AJ{Xk). F.2.3)
k^\
где
и
^^^J/'Worrlf^^^^- F.2.4)
CL
Квадратурные формулы F.2.3), коэффициенты которых имеют
значения F.2.4), называются интерполяционными. Они могут быть
охарактеризованы следующей простой теоремой.
Теорема I, Для того чтобы квадратурная формула E.1.1)
была интерполяционной, необходимо и достаточно, чтобы она
'была точной для всевозможных многочленов степени не выше
п~\.
Доказательство. Действительно, всякий многочлен Я (л:) степени
л
^;г—1 может быть представлен в формеР(л:)= V .———^^(—ч^(^й)'
Если коэффициенты Aj^ имеют значения F.2,4), то равенство F.2.3).
очевидно, будет точным для Р{х).
Заметим, что в указанном выше представлении Р{х) значения Р(х^)
могут быть любыми числами. Требование, чтобы F.2.3) было точным
для всех многочленов степени ^п—1, равносильно тому, что при
всяких P(Xfi) должно быть
J
^ п ■ п
Но тогда коэффициенты Лд, должны иметь значения F.2.4) и
формула F.2.3) будет интерполяционной.
Как видно из приведенной теоремы, коэффициенты Af^
квадратурной формулы вполне определяются условием, чтобы формула
давала точный результат всякий раз, когда / есть многочлен
степени ^п—1. Узлы же Xfj квадратурной формулы при этом
остаются произвольными и возможностью их выбора можно
воспользоваться для достижения тех или иных целей.
82 ИНТЕРПОЛЯЦИОННЫЕ КВАДРАТУРЫ [ГЛ. 6
Для остатка интерполяционной квадратуры верно все, что
говорилось в § 2 главы 5 об остатке общей квадратурной формулы E.1.1),
но, кроме того, могут быть получены другие, немного более
глубокие результаты.
Остаток квадратуры F.2.3) равен интегралу от остатка г (х)
b b
R(f) = ^ p(x)r(x)dx==: ^ p(x)(i)(x)f(x, Xi, ..., x^)dx. F.2.5)
a a
Это дает возможность воспользоваться, при его исследовании, всеми
известными теоремами об остатке интерполирования. Например, если
f(x) будет /г-кратно непрерывно дифференцируемой на [а, Ь], то
г(х) можно представить формулой вида C.2.8). При принятых сейчас
обозначениях получится следующее выражение остатка /?(/):
R(f)^j p{x)(i>(x)j dt,j dt,... J dtj^'^ix+'^t^(x^~-x^_r)]dx,
a 0 0 0 V v = l /
Xo = x. F.2.6)
Часто предпочитают пользоваться другим, более простым
представлением /?(/), которое получается, если взять остаток
интерполирования в лагранжевой форме г {х):= - , ^ /^^^ Ц), а < | < ^:
b
Rif)=^l p{x)(i>ix)f^'Hl)dx. F.2.7)
а
Нахождение точных оценок R(f) из F.2.7) затрудняет то
обстоятельство, что не известна зависимость | от х.
Для функций, имеющих на [а, Ь] производную порядка /г,
ограниченную по абсолютному значению числом М^:
1/^"Ч^)|<М^. х^[а, Ь], F.2.8)
из F.2.6) вытекает оценка
ь
\R(f)\<M„^\pix)(^ix)\dx. F.2.9)
а
Если p{x)(i)(x) сохраняет знак на [а, Ь], то оценка F.2.9) является
точной и улучшена быть не может. Попутно отметим, что точная
оценка остатка для функций, удовлетворяющих условию F.2.8),
может быть, при любых р{х) и узлах jc;^ (^= 1, . . ., л), легко
получена из E.2.6). Если положить г = п и принять во внимание, что
§ 3] ФОРМУЛЫ НЬЮТОНА - КОТЕСА 83
при интерполяционной квадратуре остаток равен нулю для всякого
многочлена степени </г, то для R{f) получим
b
/?(/) = J /С^) (t) К (О dt. F.2,10)
а
где K(t) имеет значение E.2.7) при r==zn.
Для функций вида F.2.8) из F.2.10) следует точная оценка /?(/):
\R(f)\<^ni\^(n\dt. F.2Л1)
§ 3. Формулы Ньютона — Котеса
Среди интерполяционных формул ранее всех были построены
широко известные и часто применяемые формулы Ньютона — Котеса.
Они относятся к случаю постоянного веса и конечного отрезка
интегрирования. Рассмотрим интеграл
b
jf(x)dx, F.3,1)
а
Отрезок [а, д] разделим на п одинаковых частей Д= ~ . Построим
интерполяционную квадратурную формулу с узлами а, a-f-/f,
a~\~2h, ..., a~\~nh=:^b. Чтобы нахождение ее коэффициентов
привести к вычислению величин, не зависящих от промежутка [а, Ь],
запишем формулу в виде
b п
j fix)dx = {d — a)^B'kf(a + kh). F.3.2)
Согласно F.2.4), величины В^^=ф~ а)~ Ац будут иметь значения
:(д-а)-^|.
со (л:)
{х — а — kh) (и'{а-{• kh)
а
где со (л;) = (х — а) (л: — а— h) . . . {х — а — nh). Если ввести новую
переменную t, положив x^=^a-\~th, то будет
(i){x) = h"^^t(t~\){t — 2) .,, {t — n\ x — a — kh = h(t~-k).
84
ИНТЕРПОЛЯЦИОННЫЕ КВАДРАТУРЫ
[ГЛ.6
И таким образом.
вг=
(-1)'
п-к
nk\{n — k)\
п
I
^(^ —1)... {t — k^\){t-
1) ... (t~n)dt.
F.3.3)
Котесом были вычислены коэффициенты В^ для « от 1 до 10:
п=и
» = 2;
п = 3;
« = 4;
й==5;
й = 6;
га = 7;
га=8;
га = 9;
«=10;
Во = В\ == Y'
»2 о2 1
00 = 02 =-Q-
оЗ г>3 1
ао = Оз —-g-,
5^ = 5^ =90 '
«5 _ д5 _ 19
об дб 41
ао = Щ = 840 •
дб 272 .
^з=840''
„7 „7 751
^о^-^^ =17280 •
д7 д7 2989 .
iis —«4 —17280 '
д8 д8 989
Bo—Bs =-28350 •
„8 д8 10496
/J3 — «5 — 28350 '
■ д9 я» 2857
Но —Ид = 89600 ■
9 д9 19344
Вз = Вб =89600 '
дЮ д10 16067
Во —•«10 = 5^7^'
„10 „10 272400
Из —Hi —ЩтЙ'
д2 4 .
fli = -g.
d3 r>3 3
д4 d4 32
d5 d5 75
^^^^4 =288"'
o6 d6 216
r7 д7 3577
^1 = ^^ ==17280 '
o8 d8 5888
^^-^^ ="'28350^
«8 —4540 .
^^■" 28350 '
p9 o9 15741
o9 d9 _ 5778 .
£^4 —^5 —-89500»
Dio dIO 106300
^1 =^9 =" 598752'
oio oio —26055C
/54 _ZJ6 — 598752
o4 12
^2 = W
iB2 = -^3
02 = ^4
^2 = ^5
Bl = B'j
/32 = JtJ8
^ 5Г
50 .
~" 288 '
27
~" 840 *
1323
~" 17280 '
—928
"~ 28350 '
1080
~ 89600 '
—48525
~ 598752 '
427368
~ 598752 *
Из приведенной таблицы видно, что поведение коэффициентов В^ при
изменении номера k, начиная с п = 4 и, особенно, с п = 6, вряд ли можно
считать «правильным». При л = 8 встречаются отрицательные коэффициенты.
^ 3] ФОРМУЛЫ НЬЮТОНА - KOtECA 85
Чтобы оценить формулы Ньютона — Котеса при большом числе узлов,
получим асимптотические значения В^ для больших п *). С этой целью преобра-
п
зуем интеграл / == "^ 11 k ^■^' входящий в F.3.3). Очевидно
-р, , 1 r{l~z)sinnz
Воспользовавшись известным свойством функции Г (г): jrr~z = 1
можно последнему равенству придать форму
л(;с-1)...(■.-«) = (-!)" ^^"+^)^^"+^-">^'""".
п
Т(х+\)Т(п + \^х)8\плх
п(х — к)
о
Разобьем интеграл на слагаемые по схеме:
п 3 л-З л
1 = 1+1 + 1="+^+^-
Оценим сначала интеграл р. Из теории функции Г (г) известно, что
Г' (г)
при г>0 р , есть монотонная возрастающая функция**). Поэтому
„; ~^/ ^; ,-. f при —1<^<-5- будет величиной отрица-
Г(д:+1) Т{п + 1--х) "^ 2 '
тельной, а при -^<д:<л + 1 — положительной. Отсюда следует, что
1пГ(л:+1)Г(/г + 1—л:), а следовательно и Г(д:+1) Г (п+1 —-^) будет
при 3 <; л: <; л — 3 иметь наибольшее значение на концах этого отрезка:
О < Г (л: + 1)Г (л + 1 — л:)< Г D)Г (п — 2) = 6Г (п-2).
^ \ %\ппх \ ^.
Так как при всяких х имеем | ^тт-: гг-К 1. то
n{x^k)
|Р|<6Г(л-2)л- („„2)(л-1)-^1 ^^^ )•
*) См. Р. О. К у 3 ь м и н, К теории механических квадратур, Изв. Ле-
нингр. политехи, ин-та, отд. техн., естеств., матем. 32 A931).
**) Это сразу же видно из известного разложения логарифмической
производной функции Г (-г):
Г'(^)
\-^+m-rhy
где С — постоянная Эйлера. См., например, В. И, Смирнов, Курс
высшей математики, т. Ill, ч. 2, п°73, М. —Л., Гостехиздат, 1957.
получается
86 ИНТЕРПОЛЯЦИОННЫЕ КВАДРАТУРЫ [ГЛ, 6
При изучении интегралов а и y будем считать 1<^-</г —1. Достаточно
исследовать интеграл а. Воспользовавшись формулой Тейлора и тем, что
Т' (z)
производная от функции ф^ = , . при больших z есть величина по-
рядка —, будем иметь:
Ш г (« + 1 —^) = In г (« + 1) - X I^^^±il+о A).
Г'(z) / 1 \
Отсюда*), ввиду того, что при больших z будет • ^ ^ ^=z \п z ~\- О [— ,
учается
Г (л + 1 — jc) = Г (п + 1) ^""^ ^"^ " Tl + О [—]].
Для 0<;л:<;3 верно, очевидно, следующее равенство
Г (л: + 1) —7 гг- = --4- О -^ ,
3
а= /г(п + 1).—[l + 0(l)][-^+0D)]'^-
о
f^-^'"Vrf^--? L/_?_ , _6_ , _2_\
0
Аналогично, для интеграла \ можно получить
Если принять во внимание найденную оценку интеграла р, то для / получим
следующее значение
Так
о
3
то
*) См., например, Янкеи Эмде, Таблицы функций, М., Физматгиз, 1959,
стр. 108—109.
§3] ФОРМУЛЫ НЬЮТОНА-КОТЕСА 87
Последнее приводит к такому асимптотическому представлению котесова
коэффициента 0^ при 1 < Л < л — 1:
Сходные вычисления для В^ и В^ приведут к равенству:
Из полученных выражений для В^ видно, что при больших п в формуле
Ньютона — Котеса будут встречаться как положительные, так и
отрицательные коэффициенты, превосходящие по абсолютной величине сколь угодно
большое число. Отсюда, в частности, следует, что при больших л, малые
ошибки в значениях функции f {а~{- kh) могут дать большую погрешность
в квадратурной сумме. Поэтому рассматриваемые формулы мало пригодны
для вычислений, когда число узлов в них будет большим.
Для формулы Ньютона — Котеса выражение F.2.5) остатка /?(/)
будет таким:
b
R(f)= I (х)(х)/(х. а, а + ^, .... a~\-nh)dx. F.3,6)
а
Как оказалось. F.3.6) можно привести к весьма простому виду,
значительно более удобному для приложений *).
Рассмотрим сначала тот случай, когда п — четное число и в
формуле Ньютона — Котеса берется нечетное число узлов. Многочлен
ш (х) = (х — а)(х — а — h) ... (х — а — nh) будет обладать
следующим свойством (i)(a~\'Z) = — (})(a-\-nh — z) и график его будет
линией, симметричной относительно середины отрезка {а, Ь].
Примерный вид графика изображен на рис. 2.
X
Введем функцию Q(x)= (j:>(t)dt. Заметим, прежде всего, что
а
Q(a) = 0 и Q(a~\-nh) = Q(b)^0, Последнее равенство следует из
указанного свойства симметрии значений со (л:). Покажем теперь,
что Q(x) не обращается в нуль нигде внутри [а. Ь], для чего рас-
смотрим интегралы f^= 0}(x)dx, Утверждение будет доказано,
a-rv/г
если установить, что последовательность чисел /q, /i, ..., /^
убывающая по абсолютной величине.
*) См., например, Стефенсен, Теория интерполирования, гл. XV,
М. — Л.. ОНТИ, 1939, где такое преобразование проведено для интегралов
aeiiHoro более общего вида.
88
ИНТЕРПОЛЯЦИОННЫЕ КВАДРАТУРЫ
[ГЛ. 6
Если в интеграле/у = (х — а)(х — а — h) .,, (x—a—nh)dx
a+vfi
заменить переменную х, положив x = y-\-h, то он преобразуется
к виду
a+vft
/v= J (У- а+^)(у —а)...(у —а —(ft—1)Л)б/у =
flH-(v-l)A
a+\h
- J
■^ —-« (у) ^У = -' -^ ^v-i.
-а — nh
a-b(v-l)ft
^ + (v — 1)/f < Л < fit + vA.
Чтобы было |/vl<Uv-il' должно выполняться неравенство т] — a-f-
-\-h<^nh — т] 4" а, или *т] — а < —^— ^- ^о последнее неравенство,
очевидно, выполняется, ввиду ii<a + vA, х\—a<v/f<]D—\\h.
Рис. 2.
Преобразуем F.3.6) интегрированием по частям и применим
теорему о среднем значении
/?(/) = й(х)/(х, л, ..., a + nh)f^ —
ь
— 1 /^ (х, а. . . ., а + «Л) Q (х) cfx =
b
— —/!j.(Ti, а, ..., a + nh) J £2(л:)^х. а < т] < *.
§ 3] ФОРМУЛЫ НЬЮТОНА - КОТЕСА 89
Так как
f {х, а, .. ., а + /гЛ)г=
1 ^п 1 л + 1 \
= j ^^1 ... j dt,^,f'^'^ ix + t, (a~-x)-^h^tA.
0 0 \ V=2 /
TO
/^(jc. a, .. ., a~]~nh) =
0 0 \ V=2 /
И применение теоремы о среднем значении к последнему интегралу
/-(л+2) /£4
дает /^A1. а a-\-nh)^ ' ^у,^ , а<1<^Ь, Наконец.
& ^ b b
\ Q{x)dx^=^ xQ{x)\ — { xQ^{x)dx^^— \ X(}^{x)dx. .
a a a -
Этим доказано, что для остатка интерполяцианной квадратуры
Ньютона — Котеса верно равенство
b
^ (/) == (^ + 2)! J -^^ (^^ ^^* (^•^•^)
а
X
Найдем еще знак множителя при /^"^^^(^). Функция Q(л:) =г (S){t) dt
а
сохраняет знак на отрезке [а, Ь] и, поэтому, достаточно выяснить
ее знак в одной какой-либо точке, например, x^^a~\-h
a+h
Q(a + h)= J (i){t)dt,
a
В произведении «(/) = (^ — a)(t — a — h) ... (t — a — nh) при
а<^<а-|-/г первый множитель положителен, все же остальные —
отрицательны и, стало быть, signQ(^) = (—1)'*, t^(a, b).
b b Ь
Так как \ X()){x)dx^=^— Q{x)dx, то sign I л:@ (jc) ^л: =
a a a
= (—1/"^ ==—1 ввиду четности п.
90 ИНТЕРПОЛЯЦИОННЫЕ КВАДРАТУРЫ [ГЛ. 6
Из изложенного вытекает
Теорема 2. Если число узлов /г+1 в формуле F.3.2)
Ньютона — Котеса нечетное и функция f имеет на [а, Ь]
непрерывную производную порядка п~\-'2, то внутри [а, Ь\ существует
точка ^ такая, что для остатка R (/) формулы верно
равенство F.3.7). Коэффициент при f^^'^'^\^) — отрицателен.
Укажем на два следствия, вытекающих из этой теоремы.
1. Если число узлов п-{~\ в формуле F.3.2) нечетное, то
алгебраическая степень точности формулы равна п-^-Х,
Как видно из представления остатка F.3.7), формула F.3.2) будет
точной всякий раз, когда / есть многочлен, степени ^/г+1. Если
же / есть многочлен степени /г+ 2, то /^'^"^^^ будет величиной,
отличной от нуля, и /?(/)=^0.
2. Будем, как и выше, считать, что производная /""^^^
существует и есть непрерывная на [а. Ь] функция, и составим
представление E.2.6) остатка. Положим г = п-\~2 и, для простоты записи,
будем считать а = а. Так как степень точности F.3.2) равна п~\-\,
неинтегральные члены в E.2.6) обращаются в нуль и для остатка
получится выражение
b
R{f)^\ /"^^^ (О К (О dt. F.3,8)
а
Ввиду р{х)^\, после простых вычислений ядру К(t) можно
придать форму
^(^)- (n + 2)! —2^A^E{a + kh--t) ^^^~j-^^^ .
Покажем, что ядро остатка К (t) есть знакопостоянная
неположительная функция на [а, д].
Из F.3.7) видно, что если р"'^ ^ не обращается в нуль ни в одной
точке [а, д], то Я(/)ФО.
Если бы функция K{t) изменяла знак на [а, Ь], то, наверное,
существовала бы непрерывная функция р^^ \ отличная от нуля
b
на [а, д] и такая, что { f^^^\t)R(t)dt = ^. По производной /''^^^
а
МЫ могли бы восстановить функцию / обычным путем. Для такой
функции /?(/):= о, что противоречит предыдущему.
Так как в F.3.7) коэффициент при f {\) — отрицательный,
ядро /с(О должно быть неположительной функцией на [а, Ь]:
§3] ФОРМУЛЫ НЬЮТОНА - КОТЕСА 91
Пусть теперь п — число нечетное, а число узлов в
формуле F.3.2)— четное. В этом случае многочлен a)(x) в точках,
равноотстоящих от концов а и b = a-\~nh отрезка, принимает одинаковые
значения: со (а + 2;) = со (а + «^ — ^)' График многочлена будет
линией, симметричной относительно прямой х ==—^—, проходящей
через середину отрезка и параллельной оси у.
Чтобы упростить выражение остатка (б.З.б). разделим отрезок [а, Ь]
на две части [а, «-[-(/г—I) h] и [а-}~(м—\)h, b]. На втором
частичном отрезке многочлен со (л:) сохраняет знак и к интегралу
по этому отрезку может быть применена теорема о среднем значении
й + (л-1)/г
/?(/)= o)(a:)/(x, а, .... а-{-nh) dx-i-
-b'^TTyr J «(x)^x = /+//,
a < |j < ^. Сосредоточим теперь свое внимание на первом из
интегралов правой части. Отделим в многочлене со (л:) множитель х — а — nh
и положим со (х) = (л: — а — nh) щ (х). По определению разностных
отношений
/(аЧ-«А, .... а.х)=^^^ + ^"-'^^ a,x)-f(a-^nh а)
.Д- — Lh tV ft
и, следовательно,
a+{n-\)h
Iz= Г 0j(x)/(x, а. .. ., а-|-(^—l)h)dx —
а
a+{n-\)k
— /(а, ..., a + nh) j (i)^(x)dx.
a
a+tn~l)h
Так как coj (х)й?х = О, на что было указано при исследова-
а
НИИ случая четного /г, второй член в выражении для / исчезает.
Первый же член есть интеграл вида F.3,6) при нечетном числе
узлов и его можно преобразовать так же. как в предыдущем случае:
a+{n-l)h.
92 ИНТЕРПОЛЯЦИОННЫЕ КВАДРАТУРЫ [ГЛ. 6
Напомним также, что коэффициент при /""''^Ч^г) здесь есть число
отрицательное.
а+(л-1)Л
Ввиду Г (i)i(x) dx = 0, в предыдущем интеграле функцию
а
jccoj (х) можно заменить на (x—a—nh) (о^ (х) = со (jc). Для остатка R (/)
получим
й + (л-1)А Ь
л а+(л~1)Л
При a-j-'(n—1)Л<л:<^, в произведении
со (х) = (л: — а) (л: — а — h) ... (л: — а — nh)
последний множитель — отрицательный, все же остальные — положи-
ь
тельные и | 0(х)^л:<О. Ввиду того, что коэффициенты при
а+(л-1)Л
уг(л+1)^|^^ и /"^^4li) В последнем выражении остатка отличны от нуля
и одного знака, а f^^ ^ есть непрерывная функция, между ^j и ^2
существует такая точка J, что
b
^ ^f^ = (п+1)! J ^ W ^•^- <6.3.9)
Этим доказана
Теорема 3. Если число узлов п-\-1 в формуле Ньютона —
Котеса F.3.2) четное и f имеет непрерывную на [а, Ь]
производную порядка /г+1, то внутри [а, Ь] существует точка |
такая, что для остатка /?(/) квадратуры F.3.2) верно
равенство F.3.9). Коэффициент при f^^^^^^l) в нем есть число отри-
(дательное.
Аналогично случаю нечетного числа узлов, отсюда вытекает два
следующих утверждения:
1. Если число узлов п-\-\ в формуле F.3.2) — четное, то
алгебраическая степень точности F.3.2) равна п.
2. Если число узлов п-\~ \ в F.3,2)— четное а функция / имеет
непрерывную производную порядка п~\- \ на [а, Ь\, то остаток
формулы F.3.2) представим в форме
ъ
/?(/)=! f''^^\t)K{t)dt, F.3.10)
§ 3] ФОРМУЛЫ НЬЮТОНА - КОТЕСА 93
где ядро остатка K{t) есть знакопостоянная неположительная
функция на [а, Ь]\
K^t)=^^^-±A,Eia + kk-t) (-- + ^^^-0". F.3.11)
Как отмечалось выше в начале § 3, из асимптотических выражений
F.3.4) — F.3.5) коэффициентов В^ формулы Котеса следует, что при
больших л среди В^ будут обязательно встречаться отрицательные. Но осталось
еще неясным, с какого значения п это будет осуществляться. В § 3
приведена таблица 5^, показывающая, что для л = 1 AO, 9 все В^
положительны, а при п=^%, 10 некоторые В^ отрицательны. Ниже мы покажем,
что для л>10 среди В^ всегда будут существовать отрицательные.
Не ограничивая общности задачи, мы можем считать отрезок
интегрирования [а, Ь] приведенным к [—1, 1] и будем рассматривать следующее
правило интегрирования с л +1 узлами:
1 п
^ f(x)dx^Y^ A^f {у^) + Af A). F.3.12)
-1 ft=i
Наряду с ним мы возьмем формулу с m -|- 1 (лг < л) узлами, два из которых
фиксированы в точках — 1, + 1-
1 т-\
\f{x)dx^p_^f(-\) + ^ p.f{X.) + p^^fA). F.3ЛЗ)
-1 i = l
В § 2 главы 9 будет показано, что узлы х^ и коэффициенты /?_., р у р^
могут быть выбраны так, чтобы равенство F.3.13) выполнялось точно для
всякого многочлена степени 2лг — 1 (см. (9.2.12)). Существенно заметить,
что абсциссы лг/ тогда будут совпадать с корнями многочлена Якоби степени
m-l: y{x) = Pl^J^{x).
Для определенности записи условимся считать, что абсциссы у^^ и xi
рассматриваемых формул перенумерованы в порядке роста.
Теорема 4. Если правило F.3.12) верно для всех многочленов степени
2т — I (п > т) и если А^ > О (^ = 1, ..., л), то справедливо неравенство
Действительно, применяя правила F.3.12) и F.3.13) к многочлену
п
v^(x)(l хЦ V^
Р (ж) = -^ ^ ^ i- степени 2;?г — 1, находим Zj Аf^P (уfi) = 0. Так как
п> т, то не все слагаемые суммы равны нулю. Среди них должны быть
как положительные, так и отрицательные. Но Р{х)>0 при Хт< х < I и
Р (х) <0 при —\<х< Хт- Поэтому наверное у^ > Хщ-ь
При оценке корня х^^х для наших целей достаточна следующая просто
доказываемая
Теорема 5. Для наибольшего корня х^-х многочлена Якоби y(jc) =
*= -^m-V С-^) ^^рио неравенство:
94 ИНТЕРПОЛЯЦИОННЫЕ КВАДРАТУРЫ [ГЛ. 6
Многочлены Якоби любых индексов а, р удовлетворяют
дифференциальному уравнению
Для рассматриваемого нами многочлена ^j^'_i^ (-^) это уравнение может
быть приведено к виду
[A — x^f у']' + (m — 1) (m + 2) A — jc2) у = 0. F.3Л5)
Будем считать, что сюда вместо у подставлен многочлен у {х) = Р^^_}\ (^)
и проинтегрируем это равенство от наибольшего корня -v^^-i ДО 1- Так как
до конца доказательства теоремы нам придется иметь дело только с
наибольшим корнем Хт^и мы для упрош;ения обозначения отбросим номер
т — 1 и этот корень будем обозначать одной буквой х. Если
воспользоваться формулой Тейлора, результат можно записать в виде
1
(l-x2Jy'H = (m-l)(m + 2) J(l-^2)y@rf^ =
X
m—l
= (m - 1) (m + 2) ^ ^ y(v) W j A - t') (t - xf -
' dt
Ввиду того, что в наибольшем корне многочлена Якоби все
производные у^^^ (х) положительны, слагаемые последней суммы являются
положительными числами. Мы сохраним в правой части только два члена, опустив
все остальные. Если m > 3, то правая часть при этом уменьшится и
получится неравенство
A — x^Y у' (X) >(т — 1) (т + 2)
1
{X) \
У{х) I i\^t^){t^x)dt^
1
^\r{x)^(\-t^){t~-xYdt
X
Из уравнения F.3.15) следует, что для значения аргумента, равного
корню многочлена, будет у" {х) = ^|——— у' (л:). Если это значение у" {х)
внести в неравенство, вычислить оба входящие туда интеграла, то после
несложных преобразований и сокращения на A—хУ у' {х) получится
A-.)^>(.-1)(«г + 2)[1+£ + ^4т^]-
Дробь ^i-~— = 1-4---—-— положительна при —1 <.а:<;1 и убывает
^ 1 -\-X ' 14--^
при возрастании х. Поэтому правая часть неравенства уменьшится, когда
в ней эту дробь мы заменим ее наименьшим значением -^,
соответствующим .^=1. Если после замены обе части сократить на 1+л:, то будет
. , (т —1)(т4-2) ,, , „ //>о1^ч
14-л- >-^^— '-J !—^ A—х\ Отсюда сразу же следует F.3.14)-
§4] НЕКОТОРЫЕ ФОРМУЛЫ НЬЮТОНА — КОТЕСА 95
Рассмотрим теперь формулу Котеса для отрезка [ — 1, 1]:
I
j fix) dx ^ ^^а/(- 1 +—) F.3.16)
и допустим, что все ее коэффициенты А^ положительны.
Если п — четное, степень точности ее равна д-|-1. Сравним F.3.16)
с F.3.13), считая 2т ~ 1 = /2+1, /га = 0,5 (л-(-2). Теоремы 4 и 5 в этом
случае дают
1 1 2(^-1) ^^ ^1 8 .^1 32
Отсюда следует — < —;—, а\ \ ла и, стало быть, л < 8.
•^ п д (п-|~6)+16
Если же п есть число нечетное, степень точности F.3.16) равна п
и можно считать 2т — 1 — л, /п ~ 0,5 (л~|-1)- На основании теорем 4
1 . 2(/г—1) , 32
и 5 должно быть — I ~\ — > x,}j_i > 1 — -^ "
4 < (^-1)(п + 5) + 16- ^''^^' ^ ^ ^^- "^''^^У '"Р"'
Теорема 6. Л^^я вс^^ л>10 в правиле Котеса F.3.16) существуют
отрицательные коэффициенты Af^.
§ 4. Некоторые простейшие формулы Ньютона — Котеса
Формулы Ньютона — Котеса с большим числом узлов, по
причинам, выясненным в предыдущем параграфе, редко применяются
в вычислительной практике. Предпочитают пользоваться формулами
с малым значением п. Для уменьшения же погрешности результата
предварительно разбивают отрезок [а, Ь\ на достаточно большое
число малых интервалов и к каждому из них применяют
квадратурную формулу с малым числом узлов.
Положим сначала /г=1. В этом случае интерполирование /
выполняется по двум ее значениям на концах а и д отрезка
интегрирования. Равенство F.3.2) здесь приводится к известной формуле
трапеций:
b
J / (X) dx^(b- а) [I / (а) 4-4 / Ф)] ■ F.4.1)
а
Так как а)(х)^=(х — а)(х — Ь), то F.3.9) для остатка даст
^ = - -^Т- ^' (^)' а<1<д. F.4.2)
Имея в виду в дальнейшем рассмотреть задачу об увеличении
точности котесовых формул, построим для остаточного члена F.4.1)
96 ИНТЕРПОЛЯЦИОННЫЕ КВАДРАТУРЫ [ГЛ. 6
И других формул, изучаемых ниже, интегральные представления,
отличные от F.3.10).
Считая / дважды непрерывно дифференцируемой функцией,
разложим ее по многочленам Бернулли при помощи A.4.2), положив
там v^^ 2
b
f(.x)=={b-a)-'\f{t)dt + B,(^^)[f{b)-f{a)\-
а
-^^/r(oH(if^)-B;(i^)]*.
а
Ввиду того, что формула F.4.1) для линейной функции дает точный
результат, /?(/) равен остатку квадратуры интегрального члена
правой части. При записи остатка здесь и в других формулах удобнее
пользоваться не B*^{z), а функциями >?* (л:) = Б* (-г) — Б^,
несущественно от них отличающимися:
а
Знаком /?^ обозначен остаток квадратуры по переменной х
В приводимых ниже вычислениях мы воспользовались известными
правилами интегрирования многочленов Бернулли, 1-периодичностью
У*п^ к ^ равенством yjl)^y^{0) = 0
-^|[v;(l^)-v-@)l+[y;(|^)-^(»]}=
ь
R (/) =. ^t=^ J /// (t) у1 (I^) dt. F.4.3)
a
Разобьем теперь отрезок [a, b] на n одинаковых частей длины
/г ,=:^ ^ рассмотрим частичный отрезок [a-\~kh, a-\-{k-\-\)h]
§4] НЕКОТОРЫЕ ФОРЛ^ЛЫ НЬЮТОНА - КОТЕСА 97
и К нему применим формулы F.4.1) и F.4.3)
J /(х)аГл:^у[/(А + М) + /(а + (й+1)Л] +
dt,
а + АЛ
Ввиду 1-периодичности, уЦ ^"^ |=з=:)?*|-^-—j. После
суммирования по всем частичным отрезкам, получим формулу трапеций
с остатком в виде определенного интеграла
b
J/(x)rf^ = /i[i/o + /,+ ... +/„-1 + |/„] +
ь
+ 4т|/"(^)>'2(^)^^- ^ = -^- Л = /(«+^'^)- F-4.4)
а
Так как ядро остатка у* I—т—] знакопостоянное, к интегралу может
быть применена теорема о среднем арифметическом значении, что
для F,4.4) дает
Перейдем к другому случаю и положим п = 2, Интерполирова-
ние / выполняется по значениям в трех точках: а. —А—, о.
Квадратурная формула F.3,2) будет такой:
ь
|/(л:)йх«(г>-а)[1/(а)+1/(-Ц^)+|/(*)]. F.4.5)
а
Остаток может быть найден при помощи равенства F.3.7)
/?(/)=/^|;с(._а)(;с~^)(л:-г.)^х = —^(*^)>Ш.
а
F.4.6)
eg ИНТЕРПОЛЯЦИОННЫЕ КВАДРАТУРЫ [ГЛ. 6
Считая / четырежды непрерывно дифференцируемой на [а, Ь]
функцией, разложим ее по многочленам Бернулли:
ь
f(x)=^id~-ar'j f{t)dt +
а
-a^jf т [.: (ijl) -,; (lE^)] "'■ F.4.7,
Равенство F.4.5) является точным для всякого многочлена третьей
степени. Поэтому R(f) будет равен остатку квадратуры последнего
члена правой части равенства:
R (/) - - -^^^ I f' (О R. [у\ (^) - у: (^)] ^t. F.4.8)
а
В вычислениях мы воспользовались значением В^@,5) (в 1.2.14)
и нашли
f^ @,5) = В, @,5) _ fi^ =. - B - 2-^) В, == 2-\
F.4.9)
Считая /г четным числом, разделим [а. Z?] на п равных частей
величины h=^ . Возьмем удвоенный частичный отрезок
[a-j-(^—1)^, a^ik-^-lJh] и применим к нему формулу F.4.5)
§4] НЕКОТОРЫЕ ФОРМУЛЫ НЬЮТОНА - КОТЕСА 99
С остатком F.4.9):
j f{x)dx = 2h[y,_,+±f, + ^f,^,] +
+ |д/У"/"(о|,;(°+"-'"'^')+^^:Г-^^')-т|'"-
Применяя последнее равенство к отрезкам [а, a-\-2h\,
[^_|_2Л, a-\~4h], ..., [а + (/г — 2) Л, a-^-^^l и суммируя
результаты, получим хорошо известную формулу парабол или правило
Симпсона:
ь
|/(х)^л; = 4[/о + Л4-2(/2 + /44- .•• +Л_2) +
+ 4 (/, + /з+ ... +/„_,)] +
+§^^//-(о{.:(^)+2.:(^^^)-1}... F.4.10)
а
Остаточный член F.4.10) только формой записи отличается от F.3.10)
и ядро остатка поэтому является знакопостоянной функцией t.
Применение теоремы о среднем значении к интегралу позволяет
представить остаточный член F.4.10) в виде
f^^r>^-^^m^f^''^iy F-4-11)
При /г = 3 получим формулу, которая называется иногда
«правилом трех восьмых»:
b
^ f{x)dx ^ Н[\ f{a) + ^ f [а -V ^Н] +
а
+ |-/('^+1^)+4^(''-Ь//)]. F-4.12)
о)(л;) = (х — а) [х — а — -^нМх — а — у Я J (л: —а — Я),
ь \
R(f) = ^^j<>>(x)dx = -^^^f*Hl). H = b-a.\
а }
F.4.13)
Чтобы получить нужное нам интегральное представление остатка
R{f)* разложим / по многочленам Бернулли в виде F.4.7). Ввиду
того, что равенство F.4.12) является точным для всех многочленов
100 ИНТЕРПОЛЯЦИОННЫЕ КВАДРАТУРЫ ГГЛ, 6
ДО третьей степени, для /?(/) получим выражение F.4.8), но с
другим значением интегрируемой функции. В рассматриваемом случае
будет *)
+m^+i)-4i)]+i[4^+')-'-Mh
Для R(f) получим
^ (/)=w J /'■" (^) {2^: (^)+ь: (-^+t)+
a
Пусть число n кратно трем. Разделим [а, Ь] на п равных частей
h /у
/г = . Возьмем строенный отрезок [a-^-kh, а-{-(k-\- 3) h] и
применим к нему правило трех восьмых с остатком в форме F.4.14)
3h
J
a + kh
f(x)dx = ^{fla + kh] + 3f[a + (k-^l)h]-\-
+ 3/[а + (А4-2)/г]+/[а+(й-4-3)/г])Ч-
a + kh
+3,;(^+«^+|)+3,;(^+f-+|)-^}
dt.
*) При вычислениях мы воспользовались следующими равенствами:
а) Ввиду 1-периодичности, У4('^" ^) ==^^4 (^)*
б) Положив в A.2.8) п —4, л: = —, т==3, найдем
о
B. = 33[B,(|) + B,(|)+B,(I)]=33[2ZJ,(i)+fi,],
В4 (-з) = ^*\-з)^~^^''^'8Ш'
7
405"
§ 51 ПРАВИЛА КВАДРАТУР Ю]
Записав такие равенства для отрезков {а, а -f 3/г], [а + 3/г, a-f- 6^],...
.... [а~\~(п — 3)/г, a~\~nh] и сложив результаты, построим
следующую формулу, аналогичную формуле Симпсона
h
j'/(x)dA: = ^{(/o + /„) + 2(/3 + /6+ ... +Л-зL-
Ч-3(/,Ч-/2 + /4 + /5+ ... +/«-2-f/„-l)H-
b
, 27/г
64
+ 3>':(^ + 1)—l^}'^^- F.4.15)
К интегралу, представляющему остаток, здесь также может быть
применена теорема о среднем значении и остаток формулы F.4.15)
может быть записан в форме
R(f)^-ii^^/(*)(l), a<l<b. F.4.16)
Когда число частичных отрезков п кратно 2 и 3, для вычисления
интеграла может быть применено и правило парабол F.4.10) и
правило трех восьмых F.4.15). Обе формулы имеют одинаковую
алгебраическую степень точности и почти одинаково просты по своему
строению. Вопрос о выборе какой-либо одной из них может быть
решен только ожидаемой погрешностью результата. Сравнение
остаточных членов F.4.11) и F.4.16) показывает, что при применении
правила трех восьмых можно ожидать погрешности приблизительно
в два раза большей, нежели при применении правила парабол, что
заставляет отдать предпочтение формуле F.4.10).
§ б. Правила квадратур, имеющие степень точности
ниже интерполяционной
Для построения правил интегрирования (о.Ы), коэффициенты Л^
которых не имеют недостатков коэффициентов Котеса, иногда
вступают на путь, описываемый ниже. Если потребовать, чтобы
равенство E.1.1) выполнялось точно всякий раз, когда / есть многочлен
степени п—1, то как выяснилось в § 1, правило интегрирования
будет интерполяционным. Уменьшим степень точности правила и
потребуем, чтобы равенство E.1.1) выполнялось для всех многочленов
степени т—1 </г—1. Такое требование равносильно выполнению
системы:
п h
^Л^х1=^ \ p{x)x'dx (/ = 0, 1 т - I), F,5,1)
102 ИНТЕРПОЛЯЦИОННЫЕ КВАДРАТУРЫ [ГЛ. 6
Уравнения совместны и число уравнений здесь меньше числа
коэффициентов Af^. После решения системы, п—т коэффициентов Лд,
остаются произвольными. Выбором их величин можно пытаться,
например, сделать все коэффициенты Af^ положительными или добиться
того, чтобы А^^ имели более «правильные» значения и т. д.
Начнем с рассмотрения частного случая, имеющего, по-видимому,
наибольший интерес для приложений, когда степень точности правила
интегрирования равна п — 2 и лишь один из коэффициентов Af^
остается произвольным.
Условия точной интегрируемости степеней х от нулевой но п — 2
дадут следующую систему уравнений:
п b
^А^х{==^ \ р(х)хЧх (/=п=0, 1. ..., п~2), F.5.2)
Если ошибку приближенного интегрирования х^~^ обозначить а, то
к F.5.2) можно присоединить уравнение
п b
^Л^х1''^= [ р(х)х'''Ых + а, F.5.3)
Решение системы F.5.2) — F.5.3) может быть очевидным образом
представлено в форме суммы решений двух систем, первая из
которых отвечает случаю а ^^ 0:
п b
V^^jc^™ \ p{x)x^dx (/ — О, 1. ..., п—1)
и решение которой образуют интерполяционные квадратурные
коэффициенты F.2.4). Вторая же система имеет вид:
п п
2Л^х^ = 0 (/ = 0, 1, ..., /1 — 2), 2л^х«-1==а
и ее решение, как нетрудно видеть, есть А^ = —у~—г-. Поэтому
правило интегрирования, имеющее степень точности п—2, будет
таким:
b п
I P{x)f {х) Ax1^ Y^ А J (Xf,),
а k = \
Ь
Г . . (и(х) , , а
J ^^ ^ (X~-Xk)(d'iXf,) ^ <^У{Х^)
F.5.4)
^ 5] ПРАВИЛА КВАДРАТУР ЮЗ
Коэффициенты его содержат произвольный параметр а, и из F.5.4)
поэтому могут быть получены многие другие правила интегрирования.
зависящие от того, каким целям мы подчиним выбор а.
До сих пор мы считали весовую функцию р (х) любой и узлы
j^; (^=1, .... п) расположенными совершенно произвольно.
Обратимся теперь к правилу Котеса F.3.2). Оно содержит п-{-\ узлов
Xj^=^a~^ kh {k=^0, и .... я)' является интерполяционным и имеет
степень точности не ниже я.
Соответствующее указанным узлам правило интегрирования вт1да
F.5.4) будет иметь степень точности п—1 и его можыо
записать, если воспользоваться вычислениями коэффициентов Котеса и
(i)'(Xj^):=:co^(a'-l"^^0. которые находятся между равенствами F.3.2) и
F.3.3). в следующем виде:
*'■ " ' п-^ -
I
f{a-\-kh). F.5.5)
где В^ есть коэффициент Котеса, численное значение которого ука-
"зано в F.3.3), и р есть произвольный параметр, связанный с а
равенством а ~ (^ — а) Л^р.
При /г =6 правило F.5.5) будет следующим:
ь
J
/(х)^^«-^[D1 + ?.)(/о + /б) + B16-6Я)(/, + Д)-
+ B7+15Х)(/2 + /4) + B72-20Х)/з], Я—^Р-
Отсюда, когда а= 1. получается формула Ведделя (Weddele) с
коэффициентами простого вида:
b
f {X) dx « -^ (/о + 5/, + Л И- 6/з + Л + 5Л + /б)-
а
Если а== ^. получится хорошо известная интерполяционная
формула Харди (Hardy)
ь
I
\
f{x)dx^^^[H{f,-^ /б) +81 (Л+ /5)+110/3].
300
Для /г = 8 формула F.5.5) дает
ь
I
/ (.х) dx « -^ [(989 + Ц (/о + Л) 4- E888 - %%) (/, + Л) +
• B8Л - 928) (Л + /б) + A0 496 - 56Х) (Д + Д) +
+ G0Я, —4540)/4l. р = 8!Л,.
104 ИНТЕРПОЛЯЦИОННЫЕ КВАДРАТУРЫ [ГЛ. 6
Степень точности этого правила равна 7. Если мы хотим выбором
X достигнуть того, чтобы коэффициенты были неотрицательными,
достаточно считать 454 <; 7^ < 1312. Например, при ^ = 96 будет
и
I
b
/(x)rfx«-|=^I217(/o + /8)-
1024(/, + /з + /5 + Л)+352(/2 + /е)+436/4].
Найдем наибольшее значение п, при котором можно построить правило
F.5.5) с положительными коэффициентами.
Будем считать, что отрезок интегрирования [а, Ь] приведен к [—1, 1]:
I
1
/(x)dx^2^
~i *=о
д. , (-1)"-*Р"'
* ^ й! (л — ky.
/(-1 + ^)- (б-5-6)
Считая коэффициенты правила положительными, применим к нему
теоремы 4 и 5 § 3. Так как степень точности равенства равна п—1, то для
четного п можно считать 2т — 1~п—1, т —-^п. Из указанных теорем
следует, что
, 2 , 8 . 32
л^^-^^ (w —1)(т+2) + 4 {п — 2)(п + 4)+16
1 16
<
п (п —2)(л4-4) + 16
Поэтому п < 14. Если же п есть число нечетное, то 2т — 1 = л — 2,
1п^~{п — 1) и ввиду тех же теорем должно быть
J_ 4 16
л "^ (m--l)(w4-2) + 4 " (п —3)(л + 3) + 16* л< 1 .
Заметим также, что прямыми подсчетами коэффициентов F.5.6) можно
убедиться в том, что для л ~ 12 параметр р может быть выбран так, чтобы
все коэффициенты были положительными, и для л = 13 при всяких
значениях р среди коэффициентов будут отрицательные.
Поэтому верна
Теорема 7. Если п > 13, то среди коэффициентов правила F.5.6)
всегда будут существовать отрицательные.
Возвратимся к общему правилу квадратур E.1.1). Подобно F.5.4), могут
быть построены квадратурные формулы, степень точности которых равна
соответственно п — 3, п — 4, ... Мы не будем рассматривать такие правила
ввиду того, что они, насколько нам известно, не применяются в вычислениях.
Мы остановимся еще на одном вопросе теории механических квадратур
с равноотстоящими узлами:
^f{x)dx^Yi '4ft/(-l + ^). F.5.7)
-1 *-0
§ 6] ОБ ОТБРАСЫВАНИИ УЗЛОВ 105
Напомним, что если потребовать, чтобы равенство было точным для
многочленов степени п — 1, то правило будет интерполяционным и тогда
при п > 10 среди коэффициентов А^ всегда будут отрицательные. Обозначим
fsj ^ N (п) максимальную степень многочленов, для которых равенство F.5.7)
будет точным и все Л^ ^ 0.
Ниже будет доказана теорема, из которой следует, что условие
неотрицательности А^ налагает на степень точности Л^ правила F.5.7) весьма
тяжелое ограничение и N может возрастать значительно медленнее, чем
растет п.
Теорема 8. Если алгебраическая степень точности F.5.7) равна N а
если ^;^>0 (^ = 0, 1 п), то
N < iVn, F.5.8)
Для доказательства достаточно применить к F.5.7) теоремы 4 и 5 из § 3,
которыми мы воспользовались несколькими строками выше. Если Л^ есть
число четное, то можно в теореме 4 считать 2w —-1 ~ А/"—1, m^=0,5N,
' 2 8
Тогда должно быть Ул-=1 — —>^ra-i>l (;?г^1)(;?г4-2)Ч-4 ' ^'^^У^^
^<(д,_2)Д4)+Тб'^^ + ^^ + «<^^-'-^+1<КГб;^.Я<4Гп.
Если же N есть число нечетное, то можно положить 2т — 1 = 7V,
г- 1 1 fi
/п = 0,5 (ЛА + 1), и применение указанных теорем дает — < /дг_1ч.дг , гч i i(>,
Л^ < 4/п.
§ 6. Об отбрасывании узлов при построении
правил интегрирования
При построении интерполяционных правил, коэффициенты которых не
имеют недостатков коэффициентов Котеса, иногда берут не все табличные
значения функции, а лишь некоторую их часть и пропускают остальные.
Идея выбора табличных значений тесно связана с проблемой сходимости
интерполяционного квадратурного процесса, которая будет рассматриваться
в главе 12. Для нашей цели будут достаточны некоторые частные
результаты, полученные там. Их мы сформулируем здесь без доказательства.
Вернемся к общему интерполяционному квадратурному правилу F.2.3)—
F.2.4). Оно определяется расположением узлов х/^ на отрезке (а, Ь].
Последний мы будем считать конечным.
Пусть число узлов п формулы увеличивается неограниченно- При
увеличении п будут, вообще говоря, не только добавляться новые узлы, но
может изменяться расположение всех узлов на [а, Ь].
п
Вопрос о сходимости квадратурного процесса lim ^ A^f {xf^) =
n->QO ^"
k = \
b
"^ J PM f i-^) dx зависит, очевидным образом, от того, каким будет пре-
а
дельное распределение совокупности узлов формулы (х^, х^, ..., -^/г) i^ по
какому закону происходит приближение этих узлов к предельному
распределению. Естественно было выяснить условия сходимости интерполяционного
квадратурного процесса для функций, аналитических на [а, 6], так как такие
функции наиболее часто встречаются в приложениях.
106 ИНТЕРПОЛЯЦИОННЫЕ КВАДРАТУРЫ [ГЛ. 6
Предпвлвжим, что отрезок [а, Ь] линейно преобразован в [-—1, 1]. Пусть
на этом отрезке произвольно распределена единичная масса. Распределение
называется чебышёвским, если его плотность будет *) р (х) = ^
я У 1 — jc2
Рассмотрим теперь узлы х^ X;j квадратурного правила и каждому
из них припишем массу —. Общая масса, сосредоточенная в узлах, будет
единичной. Такое распределение масс мы для краткости обозначим ц^. Оно
характеризует расположение узлов формулы F.2.3) — F.2.4).
В § 2 главы 12 доказывается, что если при л->оо распределение ]ifj
будет стремиться к распределению Чебышёва, то квадратурный
интерполяционный процесс F.2.3) — F.2.4) будет сходиться для всякой функции f (х),
аналитической на [—1, 1], какова бы ни была весовая функция р (х).
Никакое другое распределение, кроме чебышёвского, этим свойством обладать
не будет. Поэтому следует считать, что для интегрирования аналитических
функций распределение Чебышёва является наилучшим предельным
распределением для fx^. Если мы хотим улучшить точность интерполяционной
квадратуры путем специального выбора узлов, то узлы следует выбрать
так, чтобы соответствующее им распределение м-л возможно лучше походило
на распределение Чебышёва. Узлы Xf^ при этом не могут быть
равноотстоящими и должны сгущаться вблизи концов отрезка интегрирования.
Если функция / задана таблично, например, известны ее значения
в равноотстоящих точках a~\-th A=^0, 1, ..., л), то в нашем распоряжении
будет только одна возможность добиться указанного выше сходства: мы
можем опустить несколько табличных узлов и сделать это так, чтобы
оставленные узлы обладали желательным для нас распределением на отрезке
интегрирования.
Изложенные соображения имеют лишь наводящее значение и не дают
возможности однозначно решить вопрос о выборе абсцисс квадратурной
формулы из,числа табличных значений аргумента. Часто возможно построить
несколько квадратурных правил одинаковой степени точности, с мало
отличающимися остатками, но с несовпадающими узлами х^- Мы ограничимся тем,
что приведем несколько примеров таких формул. Для упрощения записи во
всех примерах величина шага приведена к единице.
6
1. j fix)dx^ 0,2 (Л + Л) + 1,62 (/, + Л) + 2,2/з (Харди).
о
Степень точности равна 5.
8
2. J / {X) dx ^ -^ [2195 (/о + /s) + 8192 (/, + Л) +
+ 8064 (/2+/б)+ 16 016/4].
Степень точности равна 7,
8
3. J / {X) dx ^ 33W ^^^^^ (-^° + Л) + 50 112 (/i + Л) +
+ 8288 (Л + Л) + 64 064 (Л + Л)].
*) См. A2.2.5) и рис. 7.
§ 7] ПРАВИЛА ИНТЕГРИРОВАНИЯ 107
Степень точности равна 7.
10
4. J / (X) dx ^ ^27W f^^^^ ^f' + /lo) + 41 125 (/, + Д) +
о
+ 55 500 (/з +Л)+ 46 494/5] (Вулхауз) (Woolhouse),
Степень точности равна 7.
§ 7. Правила интегрирования, использующие
значения функции и производных
В некоторых случаях численного интегрирования можно увеличить
точность результата, если воспользоваться не только значениями
интегрируемой 'функции, но и значениями производных от нее.
В достаточно общей форме такое правило может быть записано
в следующем виде. Пусть в области задания функции /, которая
может быть шире отрезка интегрирования [а, Ь], взято т точек
'^1 < -^2 < • • • < ^т- Допустим, ЧТО В точке Xi даны значения /
и всех ее производных до порядка k^—1. в точке х^ даны
значения / и всех производных до порядка ^2—^ и т. д. Общее число
известных величин обозначим п-\-\\ ^1 + ^2+ ••• +^т=^^Н~^-
Будем рассматривать приближенное равенство
Ь т */~^
j pix)f (X) rfx « 5; 5] Л,/^> (л:,). F.7.1)
Если абсциссы х^- считать фиксированными, это равенство будет
содержать /г+1 параметров A^j. На выбор их могут быть наложены
ограничения и число произвольных параметров может быть меньше
п~{~1. Пример таких ограничений дает тот случай, когда в правиле
F.7.1) некоторые из величин /^^Цх^) должны быть пропущены. Мы
должны тогда заранее считать, что коэффициенты A^j при
пропускаемых значениях f^^H^i) равны нулю.
Остановимся только на том случае построения правила F.7.1),
когда все Aij считаются произвольными и значения их мы можем
выбирать по нашему усмотрению.
Рассмотрим многочлен Р(х) степени п, удовлетворяющий условиям
Р^^\х,)^/'\х,) и=0, 1 k,— U i=U .... т). F.7.2)
Построение такого многочлена принадлежит задаче
алгебраического интерполирования с кратными узлами. Правила построения Р(х)
указаны в § 3 гл. 1. Для нас сейчас достаточно знать, что Р(х)
108 ИНТЕРПОЛЯЦИОННЫЕ КВАДРАТУРЫ [ГЛ. 6
может быть представлен в виде:
Р(х)=2 I>h,j(x)fU)(Xi). F.7.3)
где hij(x) есть многочлены степени п от х\ h^j(x) называют
интерполяционным множителем или многочленом влияния
значения f^^^Xi).
Обозначим г (х) погрешность интерполирования: / (л:)=Р {х)-\-г (х)^
b
Если в интеграле Г p(x)/(x)dx заменить f (х) ее выражением через
а
интерполирующий многочлен Р (х) и пренебречь интегралом от остатка
интерполирования, построим следующее правило приближенного
численного интегрирования, получившее название интерполяционного
с кратными узлами
J р {X) / {X) dx^^"^ A^jfU) {xi), F.7.4)
b
A^j^ j p(x)h^j{x)dx, ^ F.7.5)
a
Погрешность его имеет значение
/?= Г p{x)r{x)dx. F.7.6)
а
Правило F.7.4) характеризуется следующей теоремой.
Теорема 9. Для того чтобы правило интегрирования F.7.1)
было верным для всех многочленов степени п, необходимо и
достаточно, чтобы его коэффициенты имели значения F.7,5).
Всякий многочлен f {х) степени п представим в форме /(x) =
т */-!
= 2 2 ^//(-^)/^^Ч-^/)' и наоборот, при всяких численных значе-
/ = 1 у = 0
ниях f^^Hxi) сумма, стоящая справа, будет многочленом, степень
которого не больше п. Если правило F.7.1) верно для всякого
многочлена степени п, то должно быть выполнено равенство
f?.~\
b
§ 7] ПРАВИЛА ИНТЕГРИРОВАНИЯ 109
И так как оно обязано выполняться при произвольных f^^Hxi),
отсюда следует, что коэффициенты должны иметь значения F.7.5).
Аналогично проверяется достаточность условий теоремы.
Более подробно остановимся на случае равноотстоящих узлов
x^z=za-\- ih (/г== — ф — а)\ и предположим, что в каждом из них
даны значения функции и ее первой производной.
Если считать, что отрезок интегрирования приведен к [О, 1], то
интерполяционное правило F.7.4) запишется в виде
1
i/^w/w^^-Sho/Ш+^пгШ]- (б-^-
8)
Оно является аналогом правила Ньютона — Котеса.
Для подсчета коэффициентов А^^ и А^^ заметим, что многочлен
степени 2т-|- 1, интерполирующий f {х) по значениям /(— j и/Ч—],
будет (см. C.3.8)):
т
xt=^. <^(х) = х[х~1-) ... {х-~\).
Остатку интерполирования, если предположить, что / имеет на [О, 1]
непрерывную производную порядка 2т-^ 2, и воспользоваться
теоремой 6 гл. 3 и равенством C.3.9), можно придать форму:
'■ (^^ = Bт+ 2I /'""^'^ (^)' О < Л < 1.
В правиле F.7.8) коэффициенты будут следующими:
^ш=(р(-)т^^,^Г^^\^-^(-~-д]чх.
J (^—Ж/JС0' (Xi) I (o'iXi) J
J (x~Xi)iO' (Xi)
Если весовая функция p{x) сохраняет знак, на [О, 1] существует
такая точка ^, что для погрешности R правила F.7.8) верно равенство
1
^^ \2т + 2)\ J Pi^)^4x)dx, F.7.9)
по
ИНТЕРПОЛЯЦИОННЫЕ КВАДРАТУРЫ
[ГЛ. 6
Ниже приведены примеры правил F.7.8) для случая постоянной
весовой функции и т^^ 1AN. В записи принято обозначение
т
т
1
^ 1. J/(^)rf^ = |[/„ + ^-|(/;-/^)]+^/D)(^);
О
1
^2, J / (X) их ^-. 1 [7 (Д + Д) + 16Д - i (/Ь/;)]+
1
2' ■ 4725
f''\l);
т^Ъ, J /WrfA;==jl_|i55(/o + /3) + 405(/, + /2) +
О
т=^Л, jf(x)dx = ^ 11601 (/o+/4)+4096 (Л+/3) -f
О
+ 5616/, + у[128(/^-/0-29(/^_/;)]} +
"^219.1964 655 ^^ ^^^)'
т = 5. ^ fix) dx=^~^^±^{44Q 719 (/, + /,)-^
о
+ 968 625 if, + Д) + 1 778 000 (/^ + /,) +
+ б[-И79(/^-/^)+12575(/^-/()+10900(/з^-Д)]} +
+ 5> 1.230 150670288 ^^ ^^^^^
1
C 310 219(/о + ДL-
+ 5014 656 (/,Н-/5)+11 161 125(/2 + /4)-32966000/з —
-5A0237 (Д-/;)-136512(Д-/0-242325(Д-Д)]} +
1
+
2'8-34-25025
/"^ЧЮ-
F.7.10)
§81 ОБЩАЯ ТЕОРИЯ ИНТЕРПОЛЯЦИОННЫХ КВАДРАТУР Щ
Приведенные примеры показывают, что правилам интегрирования
F.7.8) присущи некоторые недостатки правил Ньютона — Котеса:
коэффициенты их имеют «нерегулярное» распределение значений
по узлам x^ = — и уже при т=^6 среди коэффициентов при зна-
. чениях функции встречаются отрицательные. Можно было бы
показать, что при увеличении т абсолютные значения коэффициентов
будут неограниченно и быстро возрастать.
Можно пытаться улучшить свойства коэффициентов правила вида
F.7.8), пропуская в сумме некоторые значения функции / или ее
производной, т. е. заранее считая коэффициенты, стоящие при них,
равными нулю. Мы ограничимся тем. что приведем только один
пример *). В правиле F.7.10), соответствующем //г = 6, коэффициент
при /з отрицателен. Чтобы сделать коэффициенты при всех
значениях функции положительными, достаточно заранее положить равными
нулю коэффициенты при /^ и f^^, остальные же коэффициенты из-
I брать так, чтобы правило интегрирования было точным для много-
)- членов десятой степени. Это приведет нас к квадратурной формуле:
1
' J/W^^ - 2310000 П44 341 (/о + /б) + 377 784 (/,+Д) +
о
I +475 875(Д + Д) + 314 ОООД-10 [259(/^- /^)-1134 (Л-/0]}Ч-
359
2>8 • 312. 9 634 625
/('^' (!)•
Степень точности ее равна И. что на две единицы ниже, чем
у F.7.10).
§ 8. Некоторые результаты общей теории
интерполяционных квадратур
Мы ограничимся рассмотрением правила вычисления интеграла по
нескольким значениям интегрируемой функции:
Ь п
^ p(x)f {X) dx^^ Akf (х^у F.8.1)
а ^^ = l
Теоремы, доказываемые ниже для этого простейшего правила, могут
быть, при надлежащих изменениях, перенесены на более общие правила
вида F.7.1).
Пусть рассматривается система функций со^(х) (ft —1, 2, ...). Принципы
выбора ее были кратко описаны в § 1. гл. 5.
*) Для ознакомления с другими правилами такого рода можно восполь-
^ваться справочными и учебными книгами по интегрированию функций.
112 ИНТЕРПОЛЯЦИОННЫЕ КВАДРАТУРЫ [ГЛ.6
Считая абсциссы х^ правила F.8.1) фиксированными, постараемся
коэффициенты его Af^ определить так, чтобы это правило было точным для
первых п функций Oj^; {х). Это требование позволяет построить для
нахождения Afi систему п уравнений
п ь
^ АиЩ (Xf,) == j р(х) щ (X) dx^^ (/-1,2,..., /г). F.8.2)
;^ = 1 а
Для того чтобы система имела и при этом единственное решение,
следует потребовать, чтобы определитель ее
F.8.3)
был отличен от нуля.
Такое условие, налагаемое на выбор функций со^-, обычно усиливают и
требуют, чтобы правило F.8Л) могло быть построенным и было
единственным при всяком выборе абсцисс х^^ на отрезке интегрирования [а, Ь], лишь бы
они были различны между собой. Последнее равносильно тому, чтобы
определитель А был отличен от нуля для всяких несовпадающих х^^. Системы
функций СО/ (х), обладающие этим свойством, называют системами Чебышёва.
Явное выражение для коэффициента Л}^ правила может быть получено,
если воспользоваться теоремой Крамера. Обозначим Д/^ алгебраическое
дополнение элемента (/, k) определителя Д. Тогда
п ^ п
Правила интегрирования F.8.1) с коэффициентами F.8.4) называются
интерполяционными ввиду того, что они связаны со следующей задачей
интерполирования. Составим линейную комбинацию первых п функций со^:
п
и коэффициенты ее выберем так, чтобы s^ (х) в точках х^ принимала
значения f(xf^). Такое требование доставит для ai линейную систему
п
2 ^i^ii^k)^^ f (^k)^ матрица коэффициентов которой получается из матрицы
системы F.8.2) при помощи транспонирования. Поэтому решение системы
п
есть ^/ = -г ^ ^ikf (^k) и, стало быть,
п п п
«л (-<) = 2] Т S ^^''^ ^-^^^ '^^ ^-^^ = S -^^ ^-^^ ^ ^-**^- ^''•^■^^
§8]
ОБЩАЯ ТЕОРИЯ ИНТЕРПОЛЯЦИОР^НЫХ КВАДРАТУР
113
Если остаток интерполирования обозначить г^(х), так что f(x)-
• Sn (х) ~\- Гп (х), то точное значение интеграла будет
b b
J Р М f {^) dx^ ^ р {X) S,, (х) dx + Rn (/)
Rn (f)- I Р М Гп (X) dx
Отбрасывая остаток Н^ и внося вместо Sn (-^) ^е представление F.8,5),
получим правило приближенной квадратуры вида F.8.1) с коэффициентами
F.8.4).
Представления остатка правила квадратуры F.8.1) — F,8.4),
позволяющие получить неулучшаемые оценки R^ в каком-либо классе функций /,
зависят от выбора этого класса. Мы приведем одно из простых
представлений, рассчитанное на функции / достаточно высокого порядка дифференци-
руемости. Для облегчения изложения будем считать отрезок интегрирования
конечным, вес р (х) абсолютно интегрируемым, а функции со^ (х)
(^ = I «) и / имеющими на [а, Ь] непрерывные производные порядка п.
Кроме того, предположим, что определитель Вронского
Wn {X) -
й^'^Ч-а:) (^{'''^^х) ... coi(x)
to
^^-'^)i
(X) оэ^^-^Ч^) ... «^W
отличен от нуля всюду на [а, Ь].
Рассмотрим линейную дифференциальную операцию, обращающуюся
в нуль на линейных комбинациях функций coj, ,.., Ш;^-
^« (у) = WI
СО'
(х) ... щ {х)
0
f/2-l)
{Х) ... @^ {Х)
у^'^ЧЛ(-^)/"-^>+ ...
Остаток интерполирования г^^ (х) определяется следующей многоточечной
задачей линейного дифференциального уравнения:
Найти решение уравнения L^iy) ~ L^if), удовлетворяющее в точках Xf^
(Л—1, ..., п) условиям y{Xf^)~0, Действительно, так как Z,^ E^) = О, то
^п (ffi) =^^п(/~~ Sn) = ^п (/) — ^/1 (Sft) = Ln (/)' Кроме того, ввиду того, что
5л i^k) = / i^f?)^ будет Гп (х/^) ^ 0. Поэтому остаток г^ есть решение
сформулированной задачи. Остается убедиться в том, что эта задача может иметь
только одно решение. Если обозначить Q{x) какое-либо частное решение
неоднородного уравнения L^ (у) ~ L^ (/), то всякое его решение прелста-
п
вимо в виде у = ^ (,^) + 2 ^^Щ (-^^■
Условия в точках xj^ дают нижеследующую систему уравнений для опре-
п
деления коэффициентов с^: Q(^j^L- ^С1Щ{Х(^)^0, определитель которой
равен Д и отличен от нуля. Поэтому система разрешима и имеет лишь одно
решение.
114
ИНТЕРПОЛЯЦИОННЫЕ КВАДРАТУРЫ
[ГЛ. 6
Чтобы найти нужное нам явное выражение для г^ (jc), выберем на [а, Ь]
произвольную точку 5 и рассмотрим функцию
g{x,s)^W-\s)
(i)l(x) <М['''^^{3) ...COi (S)
@,W 0(;-2>E)...0„E)
Как линейная комбинация элементов со, (л:), ,.., со^^ (-^) первого столбца,
g (х, s), рассматриваемая как функция от х, есть решение однородного
уравнения Lfj (у) ~ 0. При x = s она удовлетворяет условиям
-0.
дх
-а...
дЛ-2
g
дх
п-2
^п-1.
= 0,
дх'
л-1
== 1. F.8.6)
Если F{x) есть произвольная непрерывная на [а, Ь] функция, то ввиду
X
условий F.8.6) и равенства L^ [g (л:, 5) ] = О интеграл Y(jc)^ F (s) g (х, s) ds
a
будет решением неоднородного уравнения Ьп(У)~^(х).
п
функции Aj^ (^) = — 2j ^ik^i (-^). участвующие в F.8.5), как линейные
комбинации со^ (х) будут решениями однородного уравнения Lf^ (у) = 0.
С другой стороны, если положить / (х) ^ щ (х), то в силу единственности
п
интерполирующей комбинации 5^ (ж) должно быть (i)i(x)~ ^^k(^)^l(^k)^
k = \
щ (х) линейно выражаются через Л^ {х) и функции Л^^ (л:) образуют,
следовательно, фундаментальную систему решений однородного уравнения Lf^ {у)^0.
Всякое решение неоднородного уравнения Z^ (у) — 1^ [/ {х) ]
содержится в
X П
у = J ^ (^, 5) Ln и (S) ] ds + ^ ciAi (х).
а 1 = 1
Чтобы найти значения постоянных ci, отвечающих остатку г^^ (л:), можно
воспользоваться тем, что г^^ (х) в точках Xf^ обращается в нуль. Если
принять во внимание, что для Л/ (х) при х = Xf^, очевидно, выполняются
равенства
то сразу же станет видно, что
X
Гп'
W == I ^ (;с, S) L^ [f (s) ] rfs - 2 Л,- {X) J g {xi, s) Ln [f (s) ] ds.
(=1
§ 8] ОБЩАЯ ТЕОРИЯ ИНТЕРПОЛЯЦИОННЫХ КВАДРАТУР 115
Интегралы могут быть объединены в один при помощи введенной выше
гасящей функции Б{х):
ь
г„(х)= j k„(x,s)L„l/(s)]ds,
а
п
kn {х, s) = g (X, s)E(x — s)—^Ai (х) g (Xi, s) В {xi — s).
F.8.7)
Ядро ^n (-^> ^) в найденном выражении r„ {x) есть не что иное, как остаток
интерполирования по х функции g {х, s), содержащей s как параметр.
Остаток правила F.8.1) — F.8.4Х связанный с г^ (-^) равенством Rnif)=^
b
= J рг^Чх, получит, при помощи F.8.7), следующее выражение через функ-
а
цию / и параметры правила
b
Rnif)- I Kn{s)Ln[f{s)]ds,
a
b n b
Kn(s)^ J PW^(-v. s)ds — 2^g{xi, s)E{Xi—s) J pix)Ai(x)dx^
i = l a
b n
^ p(x)g (X, s)ds — ^ Aig (Xi, s) E {Xi — s).
F.8.8)
Естественной величиной, связанной со структурными свойствами
функции /, при помощи которой может быть оценен остаток R^ приближенной
квадратуры, является, по-видимому, значение операции L^ (/).
Очевидно, верна следующая простая теорема:
Если f п-кратно непрерывно диффгренцируема на [а, Ь] и если
\Ln{f)\^Mfi, то для остатка R^ правила F.8.1) — F.8Л) верно нера-
b
венство I /?„ (/) I < Mfj | Кп (s) | ds. Оценка является точной в классе
а
функций, определяемых условиями теоремы.
Ли тература
Кузьмин Р. О., К теории механических квадратур, Изв. Ленингр.
политехи, ин-та, отд. техн., естеств., матем. 32 A931).
Уиттекер и Робинсон, Математическая обработка результатов
наблюдений, гл. VII, М. — Л., Гостехиздат, 1935.
Стефенсен, Теория интерполяции, гл. XV, М.—^ Л., ОНТИ, 1935.
Б е р н ш т е й н С. Н., Собрание сочинений, т. И, стр. 198—205, Изд.
АН СССР, 1954.
ГЛАВА 7
КВАДРАТУРЫ НАИВЫСШЕЙ АЛГЕБРАИЧЕСКОЙ
СТЕПЕНИ ТОЧНОСТИ
§ 1, Общие теоремы
В начале этого параграфа мы сохраним о весе р {х) те же
предположения, что и в гл. 5.
Квадратурная формула
ь п
\ p{x)f{x)dx^Y^AJ{x,) G.1.1)
при фиксированном числе п узлов содержит 2п параметров Af^ и х^
(^=1, 2 п). Нашей задачей сейчас будет так выбрать эти
параметры, чтобы формулу G.1.1) сделать точной для многочленов
возможно более высокой степени.
В § 2 главы б было выяснено, что при любом расположении х^
можно, за счет выбора коэффициентов Л^,, достигнуть того, чтобы
равенство G.1.1) было бы точным для всех многочленов степени
-^п—1. Этим требованием коэффициенты Л^^ определяются вполне:
формула G.1.1) должна быть интерполяционной и ее коэффициенты
должны иметь значения F.2.4).
Для увеличения степени точности G.1.1) в распоряжении
вычислителя остается еще п узлов х^. Можно надеяться на то, что
выбором их степень точности формулы можно увеличить на п единиц и
сделать формулу верной для всех многочленов степени <^ 2/г—1.
В каком случае это ожидание действительно оправдывается, мы увидим
ниже.
Сейчас же выясним условия, которым должны удовлетворять Л^^
и лгд;. чтобы формула имела степень точности, не меньшую 2п—1.
Мы предпочтем иметь дело не с узлами л:^, а с многочленом
ш(л;) = (х — Xi){x — ^2) ... {х — л:„). Если известны х^> то при
помощи предыдущего равенства можно сразу же построить
многочлен (о(х), Наоборот, пусть известен многочлен со (л:), например,
§ 1] ОБЩИЕ ТЕОРЕМЫ 117
пусть МЫ знаем его разложение по степеням х: о)(х) := x'^-j-ajX^-^ -f-
I _ ц_ flf^. Вычисляя корни co(x), мы найдем все х^.
Заметим попутно, что если выбор узлов х^^ мы хотим заменить на
нахождение многочлена o)(x), то мы должны будем заботиться о том,
чтобы корни o)(x) были действительными, различными и не
выходили за границы [а. Ь].
Теорема 1. Для того чтобы формула G.1.1) была точной для
всех многочленов степени -^ 2д—1. необходимо и достаточно,
чтобы она была интерполяционной и многочлен (о(х) был
ортогонален по весу р{х) ко всем многочленам Q(x) степени </г:
b
f /? (х) 0) (X) Q (х) dx ^ 0. G.1.2)
а
Доказательство. Проверим сначала необходимость. Если
формула G.1.1) верна для многочленов степени <;2/г— 1. то она
верна и для многочленов степени -^п—1, и поэтому она должна
быть интерполяционной.
Пусть Q(x) — любой многочлен степени -^n—l. Произведение
/ (х) =: О) (х) Q (х) есть многочлен степени ^2п — 1 и для него
равенство G.1.1) должно быть точным. Но / (х^) = О (^ = 1, 2, .... п)
и потому верно G.1.2), что доказывает необходимость
ортогональности.
Убедимся теперь в достаточности указанных условий. Пусть / —
произвольный многочлен степени -< 2/г— 1. Разделив / на со по
обычным правилам, мы сможем представить / в форме / = Q@~f-p, где
Q и р — многочлены степеней ^п — 1. Кроме того, так как со (х^) = О,
то
/(х,) = р(х,) (k^h 2, ..., /г),
J P(x)f (x)dx= J /7 (x) 0) (x) Q (x) й^х-f - I p{x)p(x)dx,
a a a
Первый ИЗ интегралов правой части равен нулю по условию
ортогональности. Так как степень р(х) не больше/г— 1, а формула G.1.1)
интерполяционная, то должно быть точным равенство
b п
Ввиду же /(xy^) = p(Xj^), должно быть верным также такое
равенство
b п
\ Pix)f(x)dx^ ^A,f(x,).
118 КВАДРАТУРЫ НАИВЫСШЕЙ СТЕПЕНИ ТОЧНОСТИ [ГЛ. 7
и формула G.1.1) действительно будет точной для произвольных
многочленов степени ^2п~~ 1.
Вопрос о возможности построения такой формулы прежде всего
связан с существованием многочлена со (л:) степени п, обладающего
свойством ортогональности G.1.2). Если весовая функция р (х)
изменяет знак на [а, д], то многочлен о)(х) может не существовать.
Кроме того, если он существует, то корни его могут не
удовлетворять указанным выше требованиям.
Подчиним вес р (х) до конца этого параграфа дополнительному
ограничению и будем считать его неотрицательной функцией на [а, Ь]:
р (х) ;^ 0. В этом случае, как известно из теории ортогональных
многочленов*), многочлен о)(х) степени п, ортогональный по весу
р (х) ко всем многочленам меньших степеней, будет существовать
при всяких п. Корни со (х) будут действительными, различными и
лежать внутри отрезка [а, Ь].
Все перечисленное позволяет высказать следующее утверждение.
Если вес р(х)^0, то квадратурная формула G.1.1), точная
для всяких многочленов степени ^2п—1, существует при всех
/г=1. 2. ...
До сих пор осталось невыясненным, будет ли 2п — 1 наивысшей
алгебраической степенью точности формулы G,1.1). Если jt? (jc)
знакопеременная функция, то это может оказаться неверным. Но для
знакопостоянного веса легко доказывается
Теорема 2. Если р(х)^0, то ни при каком выборе Xf^ а Л^^
равенство G.1.1) не может быть верным для всех многочленов
степени 2п.
Доказательство. Для многочлена /(х) = (о^(х), имеющего
ь
степень 2п, интеграл р (х) f (x)dx > О, так как вес р (х) неотри-
а
цателен и неэквивалентен нулю. Квадратурная же сумма 2 ^ft/(-^fe)
равна нулю, ввиду f(Xf^)=^0. Поэтому для /=г=со2 равенство G.1.1)
не может быть верным.
Займемся теперь построением квадратурной формулы, имеющей
наивысшую степень точности. С этой целью рассмотрим систему
ортогональных на [а, д] многочленов P„(x) (/г=:1, 2, ,..) по весу
р (х). Для определенности, будем считать их нормированными.
Возьмем из этой системы многочлен степени п. Он может отличаться от
О) (л:) только постоянным множителем. Корни Я/Дх) будут узлами Xf^
(k =^ 1 п) разыскиваемой квадратурной формулы.
*) См. гл. 2, § 1.
* 1^ ОБЩИЕ ТЕОРЕМЫ 1Ш
Коэффициенты Л^ определяются равенством F.2.4), или
равносильным ему равенством
^^=-\ Р W 7 ~§гу— dx. G.1.3)
J (X~-Xf,)P^(Xf^)
Для вычисления интеграла G.L3) воспользуемся тождеством
Дарбу — Кристоффеля BЛ.11) и положим в нем t^=Xf^. После
деления на X — Xf^ оно примет вид
^^ ^ 5V Д/ ^^^j X — Xk
Здесь знаком а^ обозначен старший коэффициент в Р^ (х).
Умножим на р{х) и интегрируем по [а, Ь]. Так как
многого
члены Р^{х) ортогональны, интеграл Ps{Xj^) р (х) Р^{х) dx равен
а
нулю при 5^1 и равен 1 при 5 = 0, ввиду нормированности Pq.
Поэтому после интегрирования получится равенство
Отсюда для А/^ будем иметь
«« K(^k)Pn,l(^k)
G.1.4)
Найденное выражение А^ может быть немного упрощено. Возьмем
трехчленное рекуррентное соотношение B.1.10) между ортонормиро-
ванными многочленами и подставим в него вместо х корень Xf^
многочлена Pj^(x), В результате получится равенство, которое, при
принятом сейчас обозначении старшего коэффициента в Р^ (х), запишется
так: —^^ Р^ , T^(Xfe)-4- '^^~' ^n~\(^k) = ^- Последнее дает возмож-
ность преобразовать G.1.4) к виду
А, = -^1^— 1 . G.1.5)
Весьма существенно, что все коэффициенты квадратурной
формулы, имеющей наивысшую степень точности 2п—1, положительны.
Это сразу следует из теоремы:
120 КВАДРАТУРЫ НАИВЫСШЕЙ СТЕПЕНИ ТОЧНОСТИ [ГЛ. 7
Теорема 3. Если квадратурная формула G.1.1) верна для
всевозможных многочленов степени 2п — 2, то все ее
коэффициенты А^ положительны.
Доказательство. Рассмотрим функцию /(л:)= —ZT^ *
Это — многочлен степени 2/г — 2 и для него равенство G.1.1) должно
быть верным. Но
О при k Ф I,
^^'''^^\ш'Чхд при k = i.
и значит,
b
/ Р W [^Щ '' = ^/«'= (',). А, = J .W [p-,^i2^J'..>o.
что доказывает утверждение.
Перейдем теперь к изучению остатка квадратуры. Напомним, что
отрезок интегрирования [а, Ь\ мог быть любым отрезком конечной
или бесконечной длины. Функция / предполагается такой, что
произведение pf суммируемо на [а, Ь\.
Теорема 4. Если f имеет непрерывную производную порядка
2/г на [а, Ь], то суш^ествует такая точка л 61^- ^1» ^^^ ^-^^
остатка квадратуры наивысшей степени точности верно
равенство
b
Rif)=^^\ Pix)^^4x)dx, а<л<*. G.1.6)
а
Доказательство. Построим интерполяционный многочлен
Н{х) степени ^ 2/г—1, удовлетворяющий условиям ^ (-^й) ==^ / (-^л)-
М^(Xf^) = f^(х^). В силу теоремы б гл. 3, остаток
интерполирования г (х) = / (х) — Н (х) имеет следующее представление:
где I — некоторая точка, лежащая между х и узлами х^,
b b b
I p(x)f(x)dx = j p(x)H(x)dx~^~^\p(x)f'\l)coHx)dx.
Сходимость последнего интеграла вытекает из сходимости двух
предыдущих. Так как квадратурная формула верна для всех много-
g 1] ОБЩИЕ ТЕОРЕ.МЫ 121
членов степени <2/г—1, а степень И{х) также <2/г—1, то
b п п
j р(х)Н (X) dx^^ Л^И (Xjfe) = ^ А J (х^)
И для остатка квадратуры поэтому получается такое равенство:
b
а
Исходя отсюда, путем обычных рассуждений, можно показать, что
существует точка ц ^ [а, Ь], для которой имеет место формула G.1.6) *).
Укажем еще на один факт, связанный с интегральным
представлением остатка квадратуры наивысшей степени точности. Для него
верно все, что говорилось в § 2 гл. 5 об остатке любой
квадратурной формулы. Будем, как выше, считать / имеющей на [а, Ь]
непрерывную производную порядка 2я. Допустим, кроме того, что для
остатка R{f) имеет место равенство E.2.6) при r^=z2n
ь
R{f)--l f"\t)K{t)dt. G.1.7)
а
Если отрезок [а, Ь] конечный, такое представление остатка,
наверное, возможно.
Из G.1.6) видно, что если / "^(х) отлична от нуля на [а, Ь\,
то R (/) не обращается в нуль и имеет тот же знак, что и f'^"'\
Так как это верно для любой функции /^ ^\ обладающей указанным
свойством, то ядро K{t) остатка в G.1.7) должно сохранять свой
знак на [й, Ь] и быть неотрицательным.
Теорема о сходимости квадратурного процесса,
сформулированная несколькими строками ниже, может быть получена как следствие
более общего результата, установленного в гл. 12.
Мы докажем эту теорему, не откладывая ее до гл. 12, так как
все рассуждения сейчас будут основываться на соображениях
значительно более простых, чем те, которые применяются в гл. 12.
b b
*) Если m ==: inf f^'^^' и A/= sup /^''\ то m I p(Si^ dx ^ \ p/^'^Hl)<^^ dx^
la, bj \a, b] ^ -i
Ь b b
<M \ p(x)^ dx. Поэтому должно быть ^ f^^'^\l)p(i)^dx^T [ p(si'^ dx, где
^ a a
^ ^T ^ M. Отсюда легко придти к заключению о существовании точки \\,
122
КВАДРАТУРЫ НАИВЫСШЕЙ СТЕПЕНИ ТОЧНОСТИ
1ГЛ, 7
Пусть pix)— неотрицательная весовая функция на [а, Ь] и оз^Дх)
(/г==:=0, 1, . . .)—^принадлежащая ей система ортогональных
многочленов. Пусть, далее, х^^^^ (k=^ \, 2, . , ., п) — корни многочлена о)„{х)
и Л^"^ (^^^ 1, 2, . , ., п) — соответствующие им коэффициенты
квадратурной формулы наивысшей степени точности. Тогда имеет место
Теорема б. Если отрезок [а, Ь] — конечный и функция f
непрерывна на нем, то
п b
Urn \^A^Pf{xf)^ { P{x)f{x)dx. GЛ.8)
Доказательство. Так как / непрерывна на [а, ^], при любом
е>0 найдется такой многочлен Р(х), что для всяких х ^ [а, Ь]
будет
\/{х)-Р(х)\<г, G.1.9)
Очевидно
j Pf dx --- 2] ^^""V{x^f) \<\l Pfdx^ ^ pPdx
+
+
j pPdx^ Y;,A'^P{xf)\ + \^A'^P{xT)~ ^Aff{xt')
fc = i
\k = \
k=i
Ho. ввиду G.1.9),
^ pf dx — f /?P й?х < e \ p dx
5;4">ЯМ- fiAi^^fix^^e'^Ai^^^e J pdx.
Кроме того, если m—степень многочлена Р(х), то, при 2п—1^т,
будет
ь п
jpPdx^y^Ai"'p{xi"')
ft-1
И для таких п
jpfdx^'^Ai^^fixf^)
что И доказывает G.1.8).
< 2е pdx»
§ 2] ПОСТОЯННАЯ ВЕСОВАЯ ФУНКЦИЯ 123
§ 2. Постоянная весовая функция
Формула Гаусса является исторически первой найденной
формулой наивысшей степени точности. Она служит для вычисления
интегралов вида
b
^f{x)dx. G.2.1)
а
взятых по конечному отрезку [а, Ь] с постоянным весом.
Линейным преобразованием всякий конечный отрезок [а, Ь] может
быть преобразован в какой-либо стандартный отрезок. Чтобы
сделать более простым использование свойств симметрии узлов х^ и
коэффициентов Л^, за такой стандартный отрезок мы примем
(—1, -{~Ц и будем считать, что интеграл G.2.1) приведен к виду
+ 1
^f{x)dx. G.2.2)
-1
Ортогональную систему многочленов с постоянным весом на
отрезке [—1, -|-1] образуют многочлены Лежандра
Для построения квадратурной формулы с п узлами
41 п
\f{x)dx^^A^^f{xT), G.2.3)
-1 k = \
имеющей наивысшую степень точности 2п — 1, узлы ее мы должны
взять в корнях многочлена Лежандра степени п\
Р„(х(«)) = 0.
Коэффициенты Л^'^^ формулы могут быть найдены при помощи
равенств G.1.4) и G.1,5). Заметим, что при записи этих равенств
мы пользовались нормированными многочленами. Поэтому при
применении G.1,4) и G.1.5) мы должны пользоваться многочленами
р„ (л:) = / —'^— Р^ (х), старшие коэффициенты которых равны
Л^ = у g^±I '^^^^1^ [см. B.2.10) и B.2.11)]. Простые вычисления
дадут для Ak следующие значения:
124 КВАДРАТУРЫ НАИВЫСШЕЙ СТЕПЕНИ ТОЧНОСТИ [ГЛ. 7
В НИХ могут быть внесены некоторые упрощения, если
воспользоваться известным в теории многочленов Лежандра соотношением *):
Положив здесь х = х^^\ получим следующую систему равенств
[1 _ (^(«)J] я; D«)) = - (я+ 1) Я„,, (х(«') = яР„_, (xf),
позволяющую исключить из G.2.4) любую из величин Р„, Р,г^\ или
^л_1- Равенство G.2.4) можно привести, например, к виду
[i"m']K(-w
G.2.5)
Ниже приведены узлы и коэффициенты гауссовой формулы для
/1= 1A) 16 **).
х['^=^0 4'* =-2
A-f =^ - х^^^ == 0,57735 02691 89326 Л^ = 4^^ == ^
xf = О ^^3) === 0,88888 88888 88889 = |-
4^^ = — 4'^ ^ 0,77459 66692 41483 Af =- Af = 0,55555 55555 55556 = ~
п=-4
4^^ = — 4^^ =0,33998 10435 84856 4^^ =4^^ =0,65214 51548 62546
xf =~~xf^ ==0,86113 63115 94053 4^^ ^ ^^t -=0,34785 48451 37454
xf == О Af ^ 0,56888 88888 88889
хр -= — xf = 0,53846 93101 05683 4^^ = 4^^ == 0,47862 86704 99366
4^* = — 4'^ =0,90617 98459 38664 4'^ =4^* ==0,23692 68850 56189
xf ^ — xf =0,23861 91860 83197 Af ^ Af =0,46791 39345 72691
xf == — 4^* ^ 0,66120 93864 66265 4^^ = 4^^ = 0,36076 15730 48139
xf ==-~xf ==0,93246 95142 03152 4^* =4^* =0,17132 44923 79170
*) См., например, Г о б с о и. Теория сферических и эллипсоидальных
функций, М., ИЛ, 1954, п^ 20.
**) L о W а п А., D а V i d S N., Levensoa А., Tables of the zeros ot
the Legendre polynomials of order 1—16 and the weight coefficients for Gauss,
mechanical quadrature formula. Bull. Am. Math. Soc. 48 A942); 49 A943).
Запись n=s 1 A) 16 означает, что n меняется от n= 1 до n= 16 с
интервалом в 1.
§2]
ПОСТОЯННАЯ ВЕСОВАЯ ФУНКЦИЯ
п^7
K^I^^O
4^ ^^4^
xf>
4'
4'
^ — л:^^*
(8)
3
^(8)
v(8)
4' -
уф)
4^'
v(^)
= 0,40584 51513 77397
=-0,74153 11855 99394
= 0,94910 79123 42759
=:= 0,18343 46424 95650
= 0,52553 24099 16329
= 0,79666 64774 13627
= 0,96028 98564 97536
==0
= 0,32425 34234 03809
= 0,61337 14327 00590
==0,83603 11073 26636
= 0,96816 02395 07626
Af ^ Af :
125
^0,41795 91836 73469
= 0,38183 00505 05119
: 0,27970 53914 89277
0,12948 49661 68870
rt=-8
Af ^ vlf
0,36268 37833 78362
0,31370 66458 77887
0,22238 10344 53374
Af^ ^Af^ =0,10122 85362 90376
4' -л^
Af ^ Af
rt = 9
^4 — ^6
4^) ^ 4^>
Ap ^ Af
Af) ^ Af
Д^ = 0,33023 93550 01260
0,31234 70770 40003
0,26061 06964 02935
0,18064 81606 94857
0,08127 43883 61574
л= 10
^m ^ _ лу^)
;ci^^) = -
F)-~
xfy
4П)
4V)
4^2)
x^
X2
== — r(^0)
X^ -
==0,14887 43389 81631
=- 0,43339 53941 29247
=- 0,67940 95682 99024
== 0,86506 33666 88985
= 0,97390 65285 17172
:0
40)^
Af^^4'^
Af^^Af^
4^«).= <>
/1 = 11
4i^>=^4^^>=
4''^-
-->xl^2>
42)=.__Д12)
4^).
: — yi^^)
= 0,26954 31559 52345
= 0,51909 61292 06812
= 0,73015 20055 74049
== 0,88706 25997 68095
= 0,97822 86581 46057
== 0,12523 34085 11469 4^> = A^^'^^
= 0,36783 14989 98180 4^'^ == Л\^^^
- 0,58731 79542 86617 4^^^ = 4^^^
4^1) ^4^0^^^
4i^) = 4Vb
: 0,29552 42247 14753
: 0,26926 67193 09996
: 0,21908 63625 15982
'• 0,14945 13491 50581
: 0,06667 13443 08688
: 0,27292 50867 77901
: 0,26280 45445 10247
: 0,23319 37645 91990
= 0,18629 02109 27734
= 0,12558 03694 64905
: 0,05566 85671 16174
: 0,24914 70458 13403
: 0,23349 25365 38355
. 0,20316 74267 23066
126
КВАДРАТУРЫ НАИВЫСШЕЙ СТЕПЕНИ ТОЧНОСТИ
[ГЛ. 7
х\^^^ == _ 4^2) ^ 0,76990 26741 94305
x<\2) := — х^^^> - 0,90411 72563 70475
^2^^ = — М^^^ ^ 0,98156 06342 46719
4^2) =. 4о^) == 0,16007
412)_ ^02)_ 004717
83285 43346
93259 95318
53363 86512
Хд ^ —
4'^^ о
-;с^^3)^ 0,23045 83159 55135
4^^^ - 0,44849 27510 36447
хУ^^ - 0,64234 93394 40340
4^^ == 0,80157 80907 33310
хР^-г 0,91759 83992 22978
4^>== 0,98418 30547 18588
/1= 13
у1^/^> =- 0,23255 15532 30874
31802 62897
60475 36889
59807 61946
35102 19787
14998 37728
40047 65316
^03) _^ПЗ)_ 0,22628
4^3) _ ^аз) _ 0,20781
Д13)_ ^A3) _ 0,17814
4^3)^ ДШ)_ 0,13887
4^3) ^ ^03) _ 0,09212
^f/^> = А^^^^ = 0,04048
х:^^^> -. —,
«=14
4^^ = 0,10805 49487 07344
4^^^ = —4^^^0,31911 23689 27890
A4) == _ 4^^ - 0,51524 86363 58154
4^^ = 0,68729 29048 11685
4^^ =- 0,82720 13150 69765
:A^^ = —-4^^ -= 0,92843 48836 63574
4^* ^ 0,98628 38086 96812
^13
v.A4)
^14
4^4) _ ^04) ^ 0,21526 38534 63158
^fg^4) ^ ^14) _ 0,20519 84637 21296
^^/ff) _ 4^4) _ 0Л8553 83974 77938
4^j^>=-4^^^^-0,15720 31671 58194
4^4)^0,12151 85706 87903
4^4) _ 0,08015 80871 59760
4V^ = Л(^4) _ 0,03511 94603 31752
л(Щ .
ЛA4) .
^13 -
4^^-О
4^^ = 0,20119 40939 97435
4^) ^ 0,39415 13470 77563
t^/i^^ =- — 4^^ = 0,57097 21726 08539
^:t/2^) = _ 4^^ = 0,72441 77313 60170
n= 15
v.n5) _ _ .
Xf^^) - —
г(Л5)=.
. 4^) = 0.84820 65834 10427
4;^5> == ™ 4^^ = 0,93727 33924 00706
4\^> = —4^^^ =-0,98799 25180 20485
4^5^ = 0,20257
4^-5) = 4^5) ^ 0Л9843
4f-4'^^ = 0,18616
4^^^) _ ^05) _ 0Л6626
4f = Af^ = 0,13957
4з^^-Д^^ = 0,10715
^(\s^ = 4^5^ = 0,07036
82419 25561
14853 27111
10000 15562
92058 16994
06779 26154
92204 67172
60474 88108
^15^^ -= 4^^* = 0,03075 32419 96117
4^^^ ^ — 4^^ = 0,09501 25098 37637 А^^^^ = 4^^^ = 0,18945
4^^ = 0,28160 35507 79259 А^^^^ = 4^^^ - 0,18260
-^10
Хц -
. 4^^ = 0,45801 67776 57227
4^2^^ -= — 4^* ^ 0,61787 62444 02644
06104 55069
34150 44924
А\\^^ = 4^^^ = 0,16915 65193 95003
59888 16577
4f = 4^^^ = 0,14959
§ 2] ПОСТОЯННАЯ ВЕСОВАЯ ФУНКЦИЯ 127
/^^) ^ — х[^^^ - 0,75540 44083 55003 Л^^^ = Л^^^ ^ 0,12462 89712 55534
^^16) ^ „ jc^Q) ^ 0,86563 12023 87832 Л^//^ ^ 4^^^ ^ 0,09515 85116 82493
^0^6) _ __ ;^;(l6) _ 0,94457 50230 73233 Л^^^* ^ Л^^^^ -. 0,06225 35239 38648
/Щ ^ „ ;^Aб) ^ 0,98940 09349 91650 ^f ^ 4^^* - 0,02715 24594 11754
Если интегрируемая функция / имеет на [—1. +1] непрерывную
производную порядка 2п, то для нахождения остатка гауссовой
формулы может быть применено равенство GЛ.6). В нем мы должны
считать р(х}з^1 и за о}(х) принять многочлен степени п,
ортогональный на [—1, +1] с постоянным весом к любому многочлену
меньшей степени и имеющий старший коэффициент, равный единице.
Многочлен (о(х) может отличаться от многочлена Лежандра Pf^{x)
только постоянным множителем, и так как старший коэффициент
Pni^) есть -ф-ф^^ то (о(х) = -^^^Р„(х).
Ввиду
I
-1
И}1 i^x) их — 2д 1 I''
;из GЛ.6) для остатка формулы Гаусса вытекает следующее
представление
: Пример 1. Пусть нужно вычислить интеграл
dt
ч
1+/
о
1п2^0.69314718
f Применим для этой цели формулу Гаусса с пятью узлами. Желая
роспользоваться приведенной таблицей углов и коэффициентов, при-
редем предварительно отрезок интегрирования [О, 1] к стандартному
р)трезку [—1. -|-1]. Для этого достаточно положить / = 0.5 A-f--^)-
-^'^
-/
dx
3 + -^ ■
b -I
^Полагая в формуле Гаусса п=^Ъ, получим
у^лГ>(з-ьх<.ТЧ4'Чз + 4ТЧ ... +4'Чз+4Т'-
12В КВАДРАТУРЫ НАР1ВЫСШЕЙ СТЕПЕНИ ТОЧНОСТИ [ГЛ. 7
Подставив сюда вместо Л^'* и х"и^ (/с = 1, 2, 3, 4, 5) их значения из
таблицы и выполнив вычисления на 8 значащих цифр, для интеграла
найдем приближенное значение 7^:^0,69314717.
Пример 2. Интегральное уравнение
b
y{x)^f{x)^] К{х, s)y(s)ds
а
часто приближенно решают при помощи замены его на «близкую»
алгебраическую линейную систему. Такую систему можно построить,
например, если заменить интеграл какой-либо квадратурной суммой:
п
y{x)^f {X) + 2 Л у/С (X, х^) у {xj) Ч- R {X),
Если положить здесь последовательно х-^^-х^, х^, ..., x„, получим
систему равенств
п
y{x,)=^f{xd+l^AjK(x,, x^)y{Xj)^R{x,) (/==.1, 2. .... я).
Отбрасывая в правых частях неизвестные остатки R (х^-), построим
систему п алгебраических уравнений с п приближенными значениями
y{xi) неизвестной функции у{х)\
п
у(х,)^/(х,)+ S^A(^/' Ху)^(ху) (/=-1. 2, .... п). G.2.7)
7 = 1
Чем более точной была взятая квадратурная формула, тем меньше
будут отброшенные величины /? (х^) и тем, следует ожидать, ближе
к точному решению интегрального уравнения будет решение
алгебраической системы G.2.7),
Трудность решения системы G.2.7) быстро возрастает с числом
уравнений /г. Поэтому при приведении интегрального уравнения
к алгебраической системе часто пользуются квадратурными
формулами, дающими высокую точность для гладких функций при
небольшом числе узлов, в частности, формулами наивысшей алгебраической
степени точности.
Рассмотрим интегральное уравнение
I
у (X) -1 J е-^'з-(О rf^ - ^ (е'- 1)
о
И для приближенного решения воспользуемся формулой Гаусса при
/г = 2. Узлы И коэффициенты Гаусса для отрезка [О, 1] легко могут
§ 3] ИНТЕГРАЛЫ ВИДА j^ (b -xf {х - а)^ / (х) dx 129
а
быть найдены при помощи таблицы, если выполнить замену
переменной ^=-0.5A+^). ™l<^<-f Ь и будут такими: А?^=Л^^=0.5,
Система G.2.7) для рассматриваемой задачи имеет вид
1 ,. \^ 1
— у ^2, 1У1 -f (l ~ I ^22) >'2 ^ /2.
где
y,^y{xf)y /C,^-/C(xf). x(J)), Kit, х)===0.5е-^. fi'~'-f{^f).
или, после вычисления всех коэффициентов.
0.7386у1 — 0,2954у2 == 0.4434.
—0,2954^1 -f 0,5343у2 == 0.2384.
Отсюда находим
у^ :^ у (хB)) -- 0.9997, у^ = y(^xf)) ==: 0.9990.
Точное решение уравнения, что легко проверяется подстановкой,
есть у(х)=^ I.
ь
§ 3. Интегралы вида f {Ь — xf {х ^ af f{x) dx
а
. Пусть [а, ^] — любой конечный отрезок и на нем задана весовая
функция р{х)=^ф — х)^{х — а/, а>~1, р>—1. При изучении
b
интегралов Г(^ —а:)"(л:—aff{x)dx и. особенно, для составления
а
таблиц узлов и коэффициентов квадратурных формул, служащих
для его вычисления, приводят, обычно, отрезок интегрирования [а, Ь]
к стандартному отрезку [—1, -\-\] линейным преобразованием х^=
= 0.5(a-h^)+0,5/(/^-- а), --1 <^<-f 1'
Будем считать, что такое приведение выполнено и ограничимся
рассмотрением интеграла
J A -^ xf{\ +xff(x)dx. G.3.1)
-1
Ортогональной системой многочленов на отрезке [—1, +1].
соответствующей весу р{х)=:^{\ — xf{l-\-xf, является система
130 КВАДРАТУРЫ НАИВЫСШЕЙ СТЕПЕНИ ТОЧНОСТИ [ГЛ. 7
многочленов Якоби Р\^'^\х) (п^^О. 1, 2. ...). Желая построить
квадратурную формулу с п узлами
+ 1 п
J (\ ~^xf (\^xf f ix)dx ^^A,f{x,l G.3,2)
-1 ft = i
имеющую наивысшую степень точности 2я— 1, мы должны считать,
что узлы ее Xj^ совпадают с корнями якобиева многочлена степени п
Коэффициенты А^ должны быть найдены при помощи равенств
GЛ.4) или G.1.5).
Нормированные многочлены Якоби есть *)
где
л 2«+Р+^Г(а + « + 1)Г(Р + п + ^)
^п~^а + ^ + 2п+\)п\Т(а + ^ + п+\)-
Старшие коэффициенты их
^0.5 Г(а+р + 2/2 + 1)
^п~^п 2«л!Г(а4-Р + л + 1) '
Простые вычисления дают для коэффициента Л^^ следующее
значение
^ ^ (а + Р + 2пJ^+РГ(а + п)Г(Р + п) 3 3)
' п\Т{а + ^ + п+1)Р^;^'^У (x,)Pi^Lf\x,)'
Оно может быть немного упрощено, если воспользоваться известным
в теории якобиевых многочленов равенством **)
= — п [(а + Р + 2«) X + р-а] Pjf' Р> (х) + 2 (а + п) (р + и) P?lP (х).
Полагая здесь х = Х4, найдем
(а + Р + 2/г) A - 4) Н"' ^*' (ха) = 2 (а + й) (Р + й) P<„°lf> (х*).
что дает возможность исключить Рл°1г(х*) и привести G.3.3) к форме
А —о«+Р+' Г(а + п+1)Г(Р + п + 1) .7 3 4^
„!Г(„ + р + « + 1)A-х^)[р(«.Р)'(х,)р- ^'- • ^
*) См. B.2.2), B.2.5) и B.2.7).
**) С е г ё Г., Ортогональные многочлены, М., Физматгиз, 1962.
ь
§31 ИНТЕГРАЛЫ ВИДА I {Ь~xf'{х~af' f {х)dx 131
п
Старший коэффициент многочлена Р^п'^^{х) имеет величину B.2.2).
Поэтому многочлен «(х) для изучаемой квадратурной формулы
связан с Рп {^) равенством
ш
_ 2^п!Г(а + р + п+1) р(а. m .^.
^•^-'~ Г(а + р + 2п+1) ^" ^^•^^•
Если / имеет на отрезке [—1, -|-1] непрерывную производную
порядка 2л, то остаточный член формулы G.3.2) будет
-]
==/!!!i!!l 2«+P+^^+^n!г (g + « + 1) г (Р + «4-1) г (g + р + « + 1)
B«)! ' (а + р + 2« + 1)Г2(д_^|5_^2«+1)
(-1<Л<+1)- G.3.5)
Рассмотрим теперь частные случаи квадратурных формул с яко-
-биевым весом.
1) При а==р = —0,5 весовая функция будет /?(х) = A—л:^)"^'''
I и соответствующие многочлены Якоби будут только постоянными
■множителями отличаться от многочленов Чебышёва первого рода
Й(см. B.3.4)) Р1г°'^=~^'^Чл:) = фÄ(х)==С„соз(/гагссо5л:). Корни Г„,
являющиеся узлами квадратурной формулы, имеют значения Хи ==
2k — 1
= cos—2^—я (^г=1, 2, ..., /г). Коэффициенты /Ij^ легко подсчиты-
ваются. Так как
Т'п (Xk) = sin (п arc cos х^) • г == Т ,
/1-4 /1-4
ТО
и
. _^„ Г'(я+ 0.5)
п\Т{п)СУ
Правая часть равенства не зависит от ^ и поэтому все Ар будут
одинаковы. Обозначим общую величину их буквой Л, Численное
значение А может быть найдено на основании последнего равенства.
Но проще его найти, если воспользоваться тем, что квадратурная
формула должна дать точный результат для /^1 и. стало быть,
должны быть верными равенства
л
кшХ ^1
dx _ _ л я
ft.
132 КВАДРАТУРЫ НАИВЫСШЕЙ СТЕПЕНИ ТОЧНОСТИ [ГЛ. 7
Квадратурная формула наивысшей степени точности с весом р {х) ==^
= A —jc^)"^*'^ будет иметь вид*)
Г(хЛ . JT. xS г / 2^- — 1 \
.6)
J7f&^- = fS^(-^'.) + «(/)- <-з.<
-1 ' fe-1
Из G.3.5) можно получить следующее выражение остатка
Bя)!
^(/) = ^-^^.;;i^. -1<Л<1.
2) Пусть а =:::=: р^= 0,5 И /? (х) = |/1—х^. Соответствующие
многочлены Якоби Р^^'^'^'^\х) только постоянными множителями
отличаются от многочленов Чебышёва второго рода (см. B.3.5))
Корни Р^п'^''^'^\х) суть x^ = cos-^--py (/г=1, 2. ..../г).
Коэффициенты Лд, могут быть подсчитаны при помощи G.3.4):
'^ п+1 п~{~ 1
Квадратурная формула имеет вид
-1 ft=i
G.3.7)
Остаток /?(/) легко находится, если воспользоваться G.3.5)
л Z^"' (л)
Bп)!
/?(/)=:|^^^^7г;^. -1<л<1.
1 J, • • Многочлены Якоби
р@,о; - ,t))^^^^ как и в обоих предыдущих случаях, имеют простое
выражение через тригонометрические функции. Для любого много-
*) Она была найдена Мелером в 1864 г. Ознакомившись с ней по
курсу анализа Эрмита, П. Л. Чебышёв поставил задачу о построении
квадратурных формул с равными коэффициентами для любой весовой функции
р(х). с результатамц. достигнутыми в этом направлении, мы ознакомимся
позже, в главе J0,
g 3] ИНТЕГРАЛЫ ВИДА ^ ф ~х)^ (х- af f (х) dx 133
а
члена Q(x), степени меньшей /г, должно быть выполнено условие
ортогональности
^-''■P^^'''-°-'\x)Q(x)dx =
dx
= J(l-x)Pr'"'''4^)QW
гг.
Рассмотрим многочлен S(х) = (I — х)Р^п'^'-^'^Ч^У Степень его
равна п-\~ I и он ортогонален на [—1, -^-1] по весу
ко всякому многочлену Q(x) степени </г. Если его разложить по
многочленам Чебышёва первого рода rj^(x)(^ = 0, 1, ...,/г-]-1), то
в разложении, ввиду указанной ортогональности, должны обратиться
в нуль все коэффициенты при многочленах Г^ (х) до степени п — 1
включительно и разложение должно иметь форму 5 (л:) = С„Г^^ (х)-f-
+ ^rt+i^rt + iW- Кроме того, так как S(x) должен нацело делиться
на 1—X, при х=1 должно быть S(l) = С J'^(\)-\-С ^^{Г^^у{\)=^
= ^«+^«+1 = 0. Поэтому С^^1 = —С^ и
п@.5; -0,5) / ^>. __ ^ T„ + l(x)~Tn(x)
^п \Х) — i^„ ^ ^ .
Сравнение старших коэффициентов (см. B.2.2) и B.3.2))
позволяет найти С^:
Если положить л:=:С08 9 и воспользоваться тем, что Т^(х) =
= cos k arc cos X = cos ^9, то для изучаемого многочлена Якоби
получаем:
, 2п+1 ^
р@.5; -0.5) . . _ Bл)! 2
Корни его есть
■22«(п!J . е
Квадратурные коэффициенты, вычисленные по G.3.4) для а = 0,5.
Р= —0,5, будут
Лаг = о. 1 1 s^"^
2rt+l 2а^+1
134 КВАДРАТУРЫ НАИВЫСШЕЙ СТЕПЕНИ ТОЧНОСТИ [ГЛ. 7
Для весовой функции р(х)^=у у-т-— квадратурная формула будет:
J Vl^f(-)^-=2^i%^-'2^,fh^) + Rif).
G.3.8)
Остаточный член ее имеет вид:
/?(/)= 2^„п)! -^''"'(^)- -1<Л<1-
4) Примем а=:0, ^=1, а = 0, р = 4-0,5 и рассмотрим интеграл
1
Г У л: / (л:) о^л:. Многочлены П/,(х), ортогональные по весу ]/х на
о
отрезке [О, 1], тесно связаны с многочленами Лежандра Pf^. Положим
k==^2n-\~ \ и возьмем многочлены Лежандра нечетных индексов
Р2п^\(У) (^ = 0, 1, 2, . . .). Они являются нечетными функциями
у и y~^P2n^i(y) будет зависеть только от у^. Заменим у^ на х и
покажем, что за 11^(х) могут быть приняты следующие многочлены
II„(jc) = —^^"^'_:—", Действительно, после замены переменной ин-
У X
тегрирования л: = у^ получим следующую систему равенств:
1 1
J Y^ П, (X) П^ (X) dX=^ Р,,,, iV^ Р2^^, iV^ yL ==
о о ^ ^
1 1
= 2 J Р2П + 1 (у) ^2т + 1 (У) ^У= I ^2. + 1 (У) ^2тч-1 (У) dy = 0.
О -1
Этим доказана ортогональность U.^(x).
В квадратурной формуле наивысшей степени точности
1 п
J V^fMdx^^AJ(x,)^R(f) G.3.9)
о *-1
узлы АГ;^ являются квадратами положительных корней у^ лежандрова
многочлена Ргл + гСУ)- ^а'^З'й' Покажем, кроме того, что
коэффициенты Afj весьма просто выражаются через сходственные
коэффициенты гауссовой формулы G.2.3) с 2/г + 1 узлами
1
A,^{V'x ^^ dx
ч * rt в
i^fTi ИНТЕГРАЛЫ ВИДА \ {д-xf (х-af / (х) d^ 135
Так как Xj^ = yl и Щ (л:^) = —?^i^^-i-, после подстановки в ин-
теграл вместо П/^(х) его выражения через Р2/И-1 ^ замены
переменной х==у^. получим
У ^о«л_1 (Уь) У — Уь
2у 1,1
Если воспользоваться равенством -^ 5" = 1 и в ин-
Г-Уй У-У, У + У;,
теграле, содержащем дробь , , заменить у hsl —3;, то можно
дсгко привести Л^ к виду
+1
,^ (>' —>'а)^2л + 1(>'а)
f Рассмотрим теперь гауссову формулу G.2.3) с 2п-\-\ узлами и
Перенумеруем корни у^^ многочлена Лежандра /^2/i+i(y) ^'^ номера
>—л до -\-п
^коэффициенты ее Л^^""^^* будут равны значениям интеграла, стоящего
:|тожителем при 2у1 в G.3Л0). Поэтому Ла = 2у|л$?''^** (У^=1»
'^...»л). Остаточный член R{f) формулы G.3.9) может быть
Йайден при помощи общего представления G.1.6) для остатка, если
Йринять во внимание, что старший коэффициент многочлена П^(х)
1^кой же, как у Ая-мСУ) " поэтому здесь
У[ ^.^. i!!:ilB«±I)!lln 2^" + MB«+l)!f Р.„^,()^:^)
(Ij Dл + 2)! " Dп + 2I »/^
Остаточный член /?(/) имеет значение
Д(..^/^-Чл) 2 Г2^--^^[B. + 1)!^ У 0<Л<1
Ниже приведены значения х^ и А^^ формулы G.3.9) для п=^\{\O
xi = 0,6 Ai = 0,666 6667 -= 4
лг! = 0,289 949 2 A^ ^ 0,277 555 0
JC2 = 0,821 161 9 Л ^ 0,389 110 7
136 КВАДРАТУРЫ НАИВЫСШЕЙ СТЕПЕНИ ТОЧНОСТИ 1ГЛ. 7
rt = 3
X, = 0Д64 710 3 Л1 = 0.125 782 7
Х2 -= 0,549 868 5 Л2 = 0,307 602 4
JC3 ^ 0.900 805 8 Лз = 0,233 281 6
rt=4
х^ = 0.105 140 3 Л1 = 0.065 680 52
JC2 == 0.376 224 5 Лг = 0,196 096 3
x-i = 0,698 948 О Лз == 0,252 527 3
^4 = 0.937 334 3 Л4 = 0,152 362 5
лг! = 0.072 653 51 Л1 = 0,038 187 35
X, - 0,269 460 8 Лг = ОД 25 673 2
;сз ^ 0.533 122 О Лз = 0.198 630 8
X, = 0,786 880 1 Л, = 0.197 633 4
JC5 = 0,956 931 3 Лз = 0,106 542 О
Ж1 =0.053 111 04 Л1 =0,024 036 27
Х2 = 0.201 145 7 Ла = 0,083 602 63
хз -= 0,412 612 7 Лз = 0,147 010 6
X, = 0,642 527 4 Л4 = 0,178 460 1
JC5--0,841 986 8 Ль =-0,155 130 2
jcg = 0.968 616 3 Aq^ 0,078 426 93
;с, = 0.040 479 Об Л, ^ 0,016 064 64
JC2 = 0,155 355 3 Л2 =- 0.057 842 19
Хг = 0,326 009 2 Лз = 0,108 410 6
X, = 0,524 781 О Л4 - 0,146 488 1
X, = 0.719 454 4 Л^ =- 0.154 192 3
jte = 0,878 481 4 Ле -= 0,123 630 5
xj = 0,976 129 2 Л7 = 0.060 038 28
5) Аналогично может быть построена формула наивысшей
степени точности для веса /?(a;) = jc~°'^
1 п
J x-°-'f (х) dx="^ А J ix,) + R (/). G.3.11)
О й-1
соответствующая а = 0, ^=1. а = 0. р = — 0.5.
Многочлены S^{x), ортогональные на [0. 1] с весом р(х) = х~^'^*
связаны с многочленами Лежандра Pk(x) равенством
Поэтому абсциссы л:^ в G.3.11) равны квадратам положительных
корней УA лежандрова многочлена Р2п(УУ^ -^^д. =>'| (^ = Ь 2. .... п).
Рассмотрим гауссову формулу G.2.3) с 2а узлами и перенумеруем
корни у^^ многочлена Ргл (У) ^ порядке роста номерами /г = - я,
§ 3] ИНТЕГРАЛЫ ВИДА j^ ф ^х)^ (х ~ а)^ / (х) dx 137
а
-«4-1 п; кфО:
+ 1 я
j /{x)dx^ 5]'лГ'/(У*)-
-1 k = -n
Знак ' у суммы 2 поставлен в знак того, что значение ^ = О должно
быть пропущено.
Коэффициенты Л^ G.3.11) связаны с гауссовыми коэффициентами
равенством Л^ =:= 2Л^|"^ (^=^1, 2, ,.,, п), Остаточный член /?(/)
имеет форму
'^^•^^~ B/г)! 4^ + 11 DпI J* ^^^
<1.
Численные значения л:^ и Л^ приведены в таблице для п=1 A) 7
X, = 0,333 333 3 = i Л,^ 2,000 000 О
п =:=2
jti-0,115 587 1
лгг - 0,741 555 7
Л1 = 1,304 290 3
Лз - 0,695 709 7
Л:=:.3
xj -= 0,056 939 12 Л1 - 0,935 827 9
Х2 =- 0,437 197 9
JC3 = 0,869 499 4
Л2 - 0,721 523 1
Лз = 0,342 649 О
Л = 4
xi = 0,033 648 27
;С2== 0,276 184 3
А'з = 0,634 677 5
X, -= 0,922 156 6
Л,-
'. 0,725 367 6
: 0,627 413 3
'. 0,444 762 1
-. 0.202 457 1
л = 5
xi = 0,022 163 57
д:2-= 0,187 831 6
х^ ^ 0,461 597 4
л-4 = 0,748 334 6
л- - 0,948 493 9
Лз^
Л,-
Лз-
0,591 048 4
0,538 533 4
0,438 172 7
0,298 902 7
0,133 342 7
/1 = 6
А'1 =- 0,015 683 4
л-2 = 0,135 300 О
х^ = 0,344 942 4
^4 = 0,592 750 1
д:5 = 0,817 428 О
л-6 = 0,963 461 3
Лр
Л2:
Лз =
А,-
Аь-
= 0,498 294 1
^0,466 985 1
-- 0,406 334 9
^ 0,320 156 7
= 0,213 878 7
■- 0,094 350 67
138 КВАДРАТУРЫ НАИВЫСШЕЙ СТЕПЕНИ ТОЧНОСТИ [ГЛ. 7
/1 = 7
jci = 0,011 675 87 Ai^ 0,430 527 7
Xs = 0,101 832 7 ^2 =- 0,410 396 9
лгз = 0,265 481 2 у4з = 0.371 076 8
л:* ^ 0.472 371 5 yl* =- 0,314 406 3
лгэ = 0.684 262 О ^5 == 0.243 037 1
Хб = 0,861 991 3 у^б = 0.160 316 2
Xj = 0,972 755 8 Aj^ 0.070 238 9
6) Пусть рассматривается двойной интеграл в полярной системе
координат
/=г=: Г Г F(r. ф)/-йГ/-й?ф.
Допустим, что область интегрирования о определяется неравенствами
а-^Ф'СР» О ^ г ^/? =/?(ф). Если ввести вспомогательную
переменную р, положив г^^грЯ, 0<;р<; 1, то интеграл / можно записать
в форме
lo i
Отсюда видно, что для вычисления двойного интеграла в полярных
координатах, при помощи приведения его к интегрированию по
координатам г и ф, существенный интерес представляет рассмотрение
интеграла
1
j f(x)xdx. G.3,12)
о
Если мы хотим построить квадратурную формулу
1 п
j f{x)xdx = ^ л J {Xk) + R if).
0 fr = l
имеющую наивысшую степень точности, мы должны будем узлы ее
взять в корнях многочлена 11^{х), ортогонального на отрезке [О, 1]
по весу р(х) = х ко всякому многочлену степени ^п—1.
Коэффициенты Afy могут быть вычислены по общему правилу G.1.4)
или G.1.5).
Для нахождения Xfg и А^^ можно воспользоваться полученными
раньше результатами для весовой функции A —z)^ {\-{- zf.
Выполним в интеграле G.3.12) замену переменной, положив л:=—^—•
-1<г<+1,
1 +1
^ f{x)xdx = L J F{z){\—z)dz. F{z) = f[^-^). G.г
,13)
§31 ИНТЕГРАЛЫ ВИДА ^ Ф ~х)^{х~а)^ f {х) dx 139
а
После преобразования R^(x) перейдет в многочлен степени п
от Z. ортогональный на отрезке [—1, -f-1] по весу 1 —z ко
всякому многочлену степени ^п— I, и будет отличаться от многочлена
Якоби P^n'^^iz) лишь постоянным множителем Щ(jc) = СР^'^^^:).
Отсюда видно, что узлы Xf^ квадратурной формулы должны быть
связаны с корнями 2г^ якобиева многочлена Р^/' \z) равенствами
Хй^-Ц^ (^=-1, 2, .... п).
Для коэффициентов Л^ при помощи G.3ЛЗ), G.3.2) и G.3.4) для
а= 1, р = 0 может быть получено следующее общее выражение
A-4) [/=!!'">'(-*)?■
Значения узлов и коэффициентов квадратурной формулы для п= 1 AN
указаны в приводимой таблице.
X, ^ О.ббб 666 7 Л, = 0,500 000 О
xi =- 0.355 051 О Л1 = 0Д81 958 6
X, -= 0,844 949 О А,== 0,318 041 4
xi ^ 0,212 340 5 Л1 = 0,069 826 98
Х2 == 0.590 533 2 Лз = 0,229 241 1
лгз = 0,911 412 О Лз = 0,200 931 9
х^ = 0,139 759 9 Л^ = 0,031 180 97
Х2 =- 0,416 409 6 Лз = 0,129 847 5
хз =^ 0,723 157 О Лз = 0,203 464 7
х^ ^ 0,942 895 8 Л4 = 0,135 506 9
Xi ^ 0,098 535 09 Л^ = 0.015 747 91
Х2 = 0,304 535 7 Лз =- 0,073 908 87
х^ = 0,562 025 2 Лз = 0,146 387 О
X, ^ 0,801 986 6 Л4 - 0,167 174 6
дгд = 0,960 190 I Лэ = 0,096 781 59
/1 = 6
х^ =. 0,073 054 33 Л1 = 0,008 738 30
Х2 = 0,230 766 1 Лз ^ 0,043 955 16
;сз^ 0,441 328 5 Лз = 0,098 661 15
X, = 0,663 015 3 Л^ = 0,140 792 6
х^ = 0,851 921 4 Л5 -= 0,135 542 5
х^ ^ 0,970 683 6 Лб = 0,072 310 33
140 КВАДРАТУРЫ НАИВЫСШЕЙ СТЕПЕНИ ТОЧНОСТИ [ГЛ. 7
7) При вычислении тройного интеграла в шаровых координатах
^= ^ ^ J/(г. "&. (р)г'^dr dd^d(p,
V
путем приведения его к интегрированию по координатам г, ^, ф,
во многих случаях для интегрирования по радиусу г полезную помощь
оказывают интегралы вида
1
^ f{x)x^dx, G,3.14)
о
Подобно предыдущему, можно установить, что в квадратурной
формуле наивысшей точности, служащей для вычисления G.3.14),
1 п
\f{x)x^dx = YA ^kfi^k)^ R{f\ G.3.15)
о ft-i
узлы х^ должны быть связаны с корнями Zp Z2 z^ якобиева
многочлена Рй'^4*2^) соотношениями х^^^=^-~-^ , коэффициенты же Л^^
должны иметь значения:
+ 00
§ 4. Интеграл Г е-^У{х)йх
—оо
Ортогональную систему многочленов на всей оси (—оо, -f-oo)
по весу р{х) = е~^'^ образуют многочлены Чебышёва — Эрмита
В квадратурной формуле
J e--J(x)dx = "^A,f(x,)-\-Rif). G.4.1)
-00 Jt-1
имеющей наивысшую алгебраическую степень точности 2п—1, узлы
должны лежать в корнях многочлена И^{ху. Я„(д:;^) = 0 {k=l,
2, .... /г).
Коэффициенты Af^ легко вычисляются на основании GЛ .4), если
воспользоваться тем, что нормированные многочлены Чебышёва —
§4] ИНТЕГРАЛ J ^ nx)dx 141
—GO
Эрмита имеют выражения B.4.3) и их старшие коэффициенты имеют
значения B.4.4): ^^ = -. '-^ . Если в равенстве B.4.2)
положить x = Xf^, то найдем Н^^^(^х^^ = — Я'Дх^). что дает
возможность преобразовать Af^ к форме:
Л,^^ ^-^ . G.4.2)
^. (^,)
Так как для изучаемой квадратуры (а)(х)^=2~^Н^(х) и
+ 00 -boo
J /7(х)а)^(х)й?л: = 2~^" J ^"""'Я^ (jc)flfjc=:^ 2~"/г!/я,
— оо —оо
равенство G.1.6) для остатка R(f) формулы G.4.1) дает
При n-^=^l(l)lO узлы JCj^ и коэффициенты А/^ таковы*):
х^^О Ai^ IJ72 453 850 906
rt=-2
JC2 = —JCi =- 0,707 106 781 187 Л^ = Лз - 0,886 226 925 453
я = 3
jCo^O ^2== 1Д81 635 900 604
д^з = — лг! = 1,224 744 871 392 Л^ = ^з = 0,295 408 975 151
л = 4
лгз = — ^2 -= 0,524 647 623 275 Лз == Лд = 0.804 914 090 006
л:, = _ jci = 1,650 680 123 886 А^^А^ = 0.081 312 835 447 3
;^:з = О ^3 -= 0.945 308 720 483
X, = — хо ^ 0,958 572 464 614 ^2=^4-- 0,393 619 323 152
л:^ = — xi = 2,020 182 870 456 ^1 = ^5 = 0.019 953 242 059 О
х.^ — х,^ 0Д36 077 412 ^3 = ^4 = 0.724 629 595
х,^ — Х2^ 1,335 849 074 ^2 = ^5 = 0,157 067 320
х^^-х,^ 2,350 604 974 A^^Aq^ 0,004 530 009 90
*) Greenwood and Miller, Zeros of the Hermite polynomials and
'Weight for Gauss mechanical quadrature formula, Bull. Amer. Math. Soc. 54,
^ 8 A948), 765—769. Исправления см.: Math, tables and other aids to com-
put. 5, № 34 A951). 82.
л = л
^4 = Aj
Лз ^= Aq
А2 ^ Ад
= 0,610 862 634
= 0.240 138 611
= 0.033 874 394 5
= 0.001 343 645 75
142 КВАДРАТУРЫ НАИВЫСШЕЙ СТЕПЕНИ ТОЧНОСТИ [ГЛ. 7
«=-7
д:^ =-0 А^ ^0,810 264 618
JC5 -= — ;сз - 0.816 287 883 А^^А,^ 0,425 607 253
л-Q =. — JC2 -= 1.673 551 629 ^2 -= ^б = 0,054 515 582 8
х^ = ~х,^ 2,651 961 357 Ai^Aj-^^ 0,000 971 781 245
rt-8
^5 - — JC4 =- 0.381 186 990 А,^А^^ 0.661 147 013
jce - - Хз -- 1,157 193 712 Лз - Ле - 0.207 802 326
х^^ — Х2^ 1,981 656 757 А2=:-А,^ 0.017 077 983 О
дгв = - jci =- 2.930 637 420 А^^А^^ 0,000 199 604 071
л ==9
л:5 = О ^5 = 0,720 235 216
Хб == ~ ЛГ4 = 0,723 551 019 А,^А^ = 0,432 651 559
JC7 -- - Хз =- 1,468 553 289 ^з == ^7 = 0.088 474 527 4
JC8 =. — JC2 = 2,266 580 585 Лг -= ^8 = 0.004 943 624 28
j^:^ = — xi = 3.190 993 202 ^1 = ^9== 0.000 039 606 977 4
Xq =. _ JC5 = 0,342 901 327
xj = —JC4= 1,036 610 830
jcs = —jc3-= 1,756 683 649
jcg =. - л:2 = 2,532 731 674
x,Q^-x,^ 3,436 159 119 л; - aIq = 0,000 007 640 432 86
Применим к вычислению интеграла
-l-oo
-00
формулу G,4.1) для rt = 5. воспользовавшись значениями х^ и
^j^(^=l. 2, 3. 4. 5), приведенными в таблице, и выполнив
вычисления на 4 значаш.ие цифры, найдем для квадратурной суммы
ЛЛхО+ ... +Л5/(Х5)= 1.570.
Точное значение интеграла на 4 знака равно 1.563.
ос
§ б. Интегралы вида \ х^е'' / (х) dx
о
Как было выяснено в § 5 гл. 2, ортогональными на полуоси
[О» оо) по весу р(х) = х^е-^ (а > — 1) являются многочлены Лягерра
LT{x)^{~lfx-^e^-^{x-^^'e'^).
§5] ИНТЕГРАЛЫ ВИДА [Л ^ f {х) dx 143
6
В квадратурной формуле наивысшей степени точности
00 П
\ x4-^f{x)dx^Y^AJ{x^) + R{f) G.5.1)
о k = \
узлы Xfi должны лежать в корнях многочлена Лягерра степени п.
Нормированные многочлены Лягерра есть
/„"' (X) = г-»-' (« + 1) Г-°-' (а + « f 1) Д"' (л:).
Ввиду B.5.2), старшие коэффициенты их равны
Поэтому G.1.4) для Aj^ даст следующее значение
. _ я!Г(а + /г + 1)
4«)'(х,L«>,(^*)'
В теории многочленов Лягерра известно рекуррентное равенство
L^fii {х) = {х~а-~^п~~\) L\f (X) -^ xlJ^^' (х).
Если в нем положить Х^=Х^^, то получим Z,„^i(JC;^) = — XuL^n^ (Xk),
что позволяет привести найденное выражение для Af^ к виду
^Л^^(^^)]
G.5.2)
Ниже приведена таблица узлов и коэффициентов для п={ (I) 15*),
соответствующая случаю а—-О и предназначенная для вычислений
при помощи квадратурной формулы вида
оо п
J e-f (X) dx^^ А J (х,). G.5.3)
О /г = 1
П = 1
xi =- 1,000 000 000 000 А^ = 1,000 000 000 000
п = 2
xi = 0,585 786 437 627 Л^ ^ 0,853 553 390 593
Х2 = 3,414 213 562 373 А^ = 0,146 446 609 407
*) Н. Е. S а I Z е г and R. Z и с к е г, Table of the zeros and weight factors
of the first fifteen Laguerre polynomials, Bull. Amer. Math. Soc. 55 A949),
№ 10, 1004-1012.
Число, стоящее в скобках после целой части, означает число нулей
между запятой, отделяющей целую часть, и первой значащей цифрой.
144 КВАДРАТУРЫ НАИВЫСШЕЙ СТЕПЕНИ ТОЧНОСТИ [ГЛ. 7
А'1 - 0,415 774 556 783 А^ = 0J11 093 009 929
Х2 == 2,291 280 360 279 ^2 -= 0,278 517 733 569
X, - 6,289 945 082 937 А^^ 0,A) 103 892 565 016
П = 4
xi - 0,322 547 689 619 А^ ^ 0,603 154 104 342
Х2^ 1,745 761 101 158 А,^ 0,357 418 692 438
;сз- 4,536 620 295 921 А^=^ 0,A) 388 879 085 150
Х4 = 9,395 070 912 301 А, =^ 0,C) 539 294 705 561
п
Xi = 0,263 560 319 718
Х2-= 1,413 403 059 107
Xi^ 3,596 425 771 041
Х4 ^ 7,085 810 005 859
Х5 = 12,640 800 844 276
XI = 0,222 846 604 179
Х2^ 1,188 932 101 673
хз - 2,992 736 326 059
X, ^ 5,775 143 569 105
Хв = 9,837 467 418 383
Хе = 15,982 873 980 602
х^ ^ 0,193 043 676 560
Х2 = 1,026 664 895 339
X, - 2,567 876 744 951
X, = 4,900 353 084 526
л-5 = 8,182 153 444 563
Хе =- 12,734 180 291 798
Xj = 19.395 727 862 263
Xi = 0,170 279 632 305
X, ^ 0,903 701 776 799
Хз = 2,251 086 629 866
x,i = 4,266 700 170 288
х^ =. 7,045 905 402 393
Хе = 10,758 516 010 181
ху = 15,740 678 641 278
xs = 22,863 131 736 889
Xi = 0,152 322 227 732
Х2 = 0,807 220 022 742
xs = 2,005 135 155 619
X, - 3,783 473 973 331
х^ = 6,204 956 777 877
JC6 = 9,372 985 251 688
Х7 -13,466 236 911 092
xs =- 18,833 597 788 992
дгэ = 26,374 071 890 927
п =
rt =
==5
Ai =
Л2 =
Лз-
л =
л-
= 6
л =
А,^
Л =
л =
л =
= 7
А^ =
Лз =
А, =
^5 =
Ае =
^7 =
= 8
Аг =
^2 =
А, =
^4 =
^5 =
А, =
^7 =
А, =
= 9
^1 -
А. =
^3 =
А, =
^5 =
^С =
Aj =
^8 =-
^9 =
0,521 755 610 583
0,398 666 811 083
0,A) 759 424 496 817
0,B) 361 175 867 992
0,D) 233 699 723 858
0,458 964 673 950
0,417 000 830 772
0,113 373 382 074
0,A) 103 991 974 531
0,C) 261 017 202 815
0,F) 898 547 906 430
0,409 318 951 701
0,421 831 277 862
0,147 126 348 658
0,A) 206 335 144 687
0,B) 107 401 014 328
0,D) 158 654 643 486
0,G) 317 031 547 900
0,369 188 589 342
0,418 786 780 814
0,175 794 936 637
0,A) 333 434 922 612
0,B) 279 453 623 523
0,D) 907 650 877 336
0,F) 848 574 671 627
0,(8) 104 800 117 487
0,336 126 421 798
0,411 213 980 424
0,199 287 525 371
0,A) 474 605 627 657
0,B) 559 962 661 079
0,C) 305 249 767 093
0,E) 659 212 302 608
0,G) 411 076 933 035
0,A0) 329 087 403 035
ИНТЕГРАЛЫ ВИДА ^хе f{x)dx 145
6
«=- 10
х^ = ОД37 793 470 540 А^ ^ 0,308 441 115 765
Х2 ^ 0,729 454 549 503 А^ ^ 0,401 119 929 155
X, ^ 1,808 342 901 740 А^ ^ 0,218 068 287 612
Х4 ^ 3,401 433 697 855 А, = 0,A) 620 874 560 987
xs == 5,552 496 140 064 Л5 =- 0,B) 950 151 697 518
х^ == 8,330 152 746 764 А^ -= 0,C) 753 008 388 588
Xj = 11,843 785 837 900 Aj =^ 0,D) 282 592 334 960
xg ^ 16,279 257 831 378 ylg == 0,F) 424 931 398 496
Х9 =21,996 585 811 981 Л9 =- 0,(8) 183 956 482 398
д:1р== 29,920 697 012 274 Л^о-= 0,A2) 991 182 721 961
«=-11
Xi =^ 0,125 796 442 188 А^ =^ 0,284 933 212 894
хг ■=- 0,665 418 255 839 Л2 == 0,389 720 889 528
лгз === 1,647 150 545 872 Лз == 0,232 781 831 849
X, = 3,091 138 143 035 А, == 0,A) 765 644 535 462
xs =- 5,029 284 401 580 Л5 = 0.A) 143 932 827 674
jce ^ 7,509 887 863 807 А^ = 0,B) 151 888 084 648
X, ^ 10,605 950 999 547 Ау =- 0,D) 851 312 243 547
xs = 14,431 613 758 064 Л^ -= 0,E) 229 240 387 957
х^ = 19,178 857 403 215 Ад = 0,G) 248 635 370 277
jCio= 25,217 709 339 678 Л^-0,A0) 771 262 693 369
Хи = 33,497 192 847 176 Лц -=0,A3) 288 377 586 832
я =-12
X, - 0,115 722 117 358 Л, - 0.264 731 371 055
Х2 - 0,611 757 484 515 Л^ = 0,377 759 275 873
дгз =- 1,512 610 269 776 Лз -- 0,244 082 011 320
X, = 2,833 751 337 744 А, ^ 0,A) 904 492 222 117
х^ = 4,599 227 639 418 Л^ =- 0,A) 201 023 811 546
х^ = 6,844 525 453 115 Лб = 0,B) 266 397 354 187
Xj ^ 9,621 316 842 457 Ау = 0,C) 203 231 592 663
х^ = 13,006 054 993 306 Лд -= 0,E) 836 505 585 682
Xq =17,116 855 187 462 Ад = 0,F) 166 849 387 654
j^:io = 22,151 090 379 397 А^о^ 0,(8) 134 239 103 052
jCh =28,487 967 250 984 Лц =0,A1) 306 160 163 504
jci2^ 37,099 121 044 467 Л12 = 0,A5) 814 807 746 743
л= 13
Xi = 0,107 142 388 472 Л^ = 0,247 188 708 430
х^ =3 0,566 131 899 040 А^ =- 0,365 688 822 901
А'з = 1,398 564 336 451 Лд = 0,252 562 420 058
х^ = 2,616 597 108 406 Л^ = 0,103 470 758 024
X, = 4,238 845 929 017 А, = 0,A) 264 327 544 156
л-6 == 6,292 256 271 140 Л^ = 0,B) 422 039 604 027
X, = 8,815 001 941 187 Лу =- 0,C) 411 881 770 473
jcg =11,861 403 588 811 Лд -= 0,D) 235 154 739 815
хд = 15,510 762 037 704 Ад = 0,F) 731 731 162 025
;с^о= 1^.884 635 663 880 Л^--- 0,G) ПО 884 162 570
хп =25,185 263 864 678 Л,, = 0,A0) 677 082 669 221
л:12 = 31,800 386 301 947 Л12 = 0.A2) 115 997 995 991
А',3 = 40.723 008 669 266 Л^з = 0,A6) 224 509 320 389
146
КВАДРАТУРЫ НАИВЫСШЕЙ СТЕПЕНИ ТОЧНОСТИ
п= 14
[ГЛ. 7
Х\
х^
JC3
х^
^ь
^ь
Xj
Л-8
•^'9
-^\о
Х^ 1
-^'12
-^13
-^14
^1
Х2
^г
^4
^5
•^6
Xj
-^8
^9
-^10
•^И
-^12
^13
Х,4
-^15
^ 0,099 747 507 033
= 0,526 857 648 852
= 1,300 629 121 251
- 2,430 801 078 731
= 3,932 102 822 293
^ 5,825 536 218 302
= 8,140 240 141 565
== 10,916 499 507 366
= 14,210 805 011 161
-= 18,104 892 220 218
= 22,723 381 628 269
-= 28,272 981 723 248
=-35,149 443 660 592
= 44,366 081 711 117
-= 0,093 307 812 017
-= 0,492 691 740 302
= 1,215 595 412 071
-= 2,269 949 526 204
= 3,667 622 721 751
-= 5,425 336 627 414
= 7,565 916 226 613
= 10,120 228 568 019
-= 13,130 282 482 176
== 16,654 407 708 330
= 20,776 478 899 449
=: 25,623 894 226 729
= 31,407 519 169 754
= 38,530 683 306 486
= 48,026 085 572 686
1. Рассмотрим интеграл
,=|.
^4,
А,
As
А,
Аь
Ае
А,
As
А,
-^10
An
А\2
•^13
Аи
И= 15
А,
А,
А,
А,
Аь
А,
Ау
As
А,
-^10
^п
^12
^13
^14
^15
= 0,231 815 577 145
^ 0,353 784 691 598
^ 0.258 734 610 245
-^ 0,115 482 893 557
= 0,A) 331 920 921 593
- 0,B) 619 286 943 701
- 0,C) 739 890 377 867
== 0,D) 549 071 946 684
= 0,E) 240 958 576 409
-= 0,G) 580 154 398 168
= 0,(9) 681 931 469 249
-0,A1) 322 120 775 189
= 0,A4) 422 135 244 052
-.0,A8) 605 237 502 229
^ 0,218 234 885 940
- 0,342 210 177 923
= 0,263 027 577 942
= 0,126 425 818 105
= 0,A) 402 068 649 210
= 0,B) 856 387 780 361
= 0,B) 121 243 614 721
= 0,C) 111 674 392 344
= 0,E) 645 992 676 202
= 0.F) 222 631 690 710
= 0,(8) 422 743 038 498
= 0,A0) 392 189 726 704
= 0,A2) 145 651 526 407
= 0,A5) 148 302 705 111
= 0,A9) 160 059 490 621
;^2Г^-^-
Точное его значение есть / -
■л2:--. 1,2337 ...
Для приближенного вычисления / применим формулу G.5.3). взяв
в ней пять узлов. Если воспользоваться приведенной таблицей л:^
и Af^ для Г1 = 5 и выполнить вычисления, то для квадратурной суммы
получим следующее значение, которое мы приведем на 5 знаков
AJ(x,)+ ... + Л,/(Х5)-1.2338.
Оно лишь на единицу пятой значащей цифры отличается от точного
значения интеграла.
J 5] ИНТЕГРАЛЫ ВИДА ^хе f {x)dx 147
и
2. Пусть дан интеграл
,j оо ■ со
- /= \ -jr-^—-^ I хе'^и + е-^'^-е'^Г' dx=Ul7 ...
ь о о
Шри его приближенном вычислении за вес естественно принять
'р(х)===хе~'^, что соответствует а= 1 в G.5.1). За /(х) должна быть
взята функция /(х) = [1+ ^j: — g-J^]' . Возьмем на отрезке
интегрирования только два узла: п = 2. Соответствующий весу хе'-^
многочлен Чебышёва — Лягерра второй степени легко находится
из B.5.2):
L^^^ (х) = х^~Ьх + 6.
ТКорни его есть Xi = 3 — У^З и jC2 = 3 -f ]ЛЗ. Коэффициенты Л^ и Л2
^вычисляются при помощи G.5,2) и имеют значения
1 л _„3 + )^3 _3-/з
^^одсчеты дают для / приближенное значение
* f^AJ (хО + А J (х^) = 1.20,
отличающееся от точного в третьей значащей цифре.
$Ш нтература
|Г Gauss С. Р., Methodus nova integralium valores per approximationem
J^veniendi, Werke 3 A814), 163—196.
J' Christoffel, Ueber die Oaussische Quadratur und eine Verallgemel-
'^^erung derselben, Journ. fur relne und angew. Math. 55 A858), CJ—82.
Щ В r 0 n w i n, Phil. Mag. 34 A849), 262.
Щ' Марков A. A,, Исчисление конечных разностей. Math., 1910.
■V с о H и H Н. Я-, О приближенном вычислении определенных интегралов
Й0 входящих при этом вычислении целых функциях, Варшавские универси-
^..^етские известия, 1887.
St i el ties Т., Queiques recherches sur la theorie des quadratures diles
mecaniques. Ann. Ec. Norm. 1 A884). 409—426.
Геронимус Я- Л. Теория ортогональных многочленов (обзор
достижений отечественной математики), М. — Л. Гостехиздат, 1950.
Mehler, Bemerkungen zur Theorie der mechanischen Quadratur, Journ,
to reine und ang. Math. 63 A864).
Поссе K, A. I) О функциях, подобных функциям Лежандра, 1872.2) Sur
Я"еЦцез appliquations des fractions continues algebrlques, 1886.
ГЛАВА 8
ИНТЕГРИРОВАНИЕ ПЕРИОДИЧЕСКИХ ФУНКЦИЙ
§ I, О задаче интегрирования периодической функции
и форме интеграла
Не уменьшая общности, можно считать период равным 2я. Пусть
f{x) есть любая достаточно гладкая 2л-периодическая функция,
определенная на всей числовой оси х. Предположим, что р {х) —
произвольная абсолютно интегрируемая функция на отрезке [О, 2л], не
эквивалентная нулю.
Мы будем рассматривать интеграл, взятый по одному периоду
2л
функции /: p{x)f(x)dx. Такие интегралы встречаются во многих
о
задачах естествознания и техники, в частности, с ними приходится
иметь дело при гармоническом анализе функций и его приложениях
к инженерным проблемам.
Выделение веса р (х) здесь, так же как и раньше, позволяет
повысить точность вычисления интеграла, так как при помощи веса
можно учесть, например, особенности интегрируемой функции или
какие-либо ее свойства, известные заранее.
Мы будем рассматривать следующее правило вычисления интеграла:
2л п
I p(x)f(x)dx^y^AJ(x,y (8.1Л)
Периодичность функции / побуждает для приближения интеграла
избрать не алгебраические, как это делалось в двух предыдущих
главах, а тригонометрические многочлены.
Параметры правила Л^, Xf^, численными значениями которых можно
распорядиться, выбирают так, чтобы правило давало точный
результат в том случае, когда / есть произвольный тригонометрический
многочлен возможно высокой степени.
ИНТЕРПОЛЯЦИОННЫЕ ПРАВИЛА ИНТЕГРИРОВАНИЯ
149
S 2. Интерполяционные правила интегрирования
Нашей ближайшей задачей сейчас будет выяснить, какой степени
точности правила (8.1.1) можно достичь путем выбора
коэффициентов Aft при произвольно фиксированных абсциссах х^^. Всюду ниже
будем считать, что х^ перенумерованы в порядке роста и О < Xj <
<Х2< •-• <Х„<2Л.
Пусть число узлов п — нечетное: /z=:2w-f 1. Можно ожидать,
что выбором Afi правило (8.1.1) можно сделать точным для всех
тригонометрических многочленов степени т:
т
Тт W = ^0 + 2 i^k COS kx -f bf^ Sin kx).
Это равносильно требованию, чтобы равенство (8.1.1) точно
выполнялось для функций е^^^ (k = m, т— 1, .. ., — т). Для сокращения
обозначений мы запишем соответствующую систему уравнений в
переменных z = e^^, Zb^e^^k:
2л
^Akzl^ j p(x)zUx {s^m. .... —my (8.2Л)
*=i
Определитель D ее несущественно отличается от определителя Ван-
дермонда
D =
гГ...2Г"
(^1 ••■ г^у
Jim
Zn
1 ... 1
= @, ... z,)-"'W„iz, z„).
ОФО ввиду того, что все z^ различны между собой. Система
разрешима и имеет только одно решение. Поэтому правило (8.1.1),
верное для тригонометрических многочленов степени т, может быть
построено при всяких различных между собой х^. Требованием, чтобы
правило было точным для любых многочленов степени т,
коэффициенты Af^ определяются единственным образом.
Для нахождения численного значения Aj можно, например,
воспользоваться тригонометрическим многочленом L^(x), участвующим
в Правиле интерполирования C,4.5),
Lj{x)=Jl
^ф }
sin 0,5 (х — х^
sin 0,5 (л:^ — х^)
(8.2.2)
150 ИНТЕГРИРОВАНИЕ ПЕРИОДИЧЕСКИХ ФУНКЦИЙ [ГЛ. 8
Степень его равна /п = 0,5(/г— 1) и (8.1.1) должно для /:=/,^
выполняться точно. Так как, очевидно.
@. кф у.
то из (8л. I) следует
2л
Л^.== J p{x)Lj{x)dx, (8.2.3)
Правило (8.1.1) с коэффициентами (8.2.3) получится, если в инте-
2л
грале Г pfdx заменить функцию / интерполирующим ее тригоно-
0
метрическим многочленом C.4.5).
Рассмотрим теперь случай четного числа узлов: /г = 2т и
потребуем точного выполнения равенства (8.1.1) для тригонометрических
многочленов степени т = 0,5/г частного вида
^0+2 (^к COS кх -f bfi sin kx) -f Л cos (mx + 6), (8.2.4)
где aj^, ^jfe, A — произвольны, a сдвиг фазы 6 - фиксирован. Такое
требование равносильно тому, чтобы (8.1.1) точно выполнялось для
функций е^*^ (/г = т—1, ..., —m-fl)H ^Мтдг+м_)„ ^-цтх+Ь)^ Это даст
для коэффициентов Л^ систему 2т линейных уравнений, которую мы
запишем, для сокращения, в переменных z, z^, указанных выше,
и а = е^^:
2л
Ai {azT + azf") + ... + Л« (а^" + ^z;"") = j р (az^ + az'^ dx,
0
2л
A,z?-' + ... + A^zT' = J pz'^'' dx.
0
2л
Aiz:""' t ... + A,z:'"^' = j pz-'^^ых.
«3]
ПРАВИЛО НАИВЫСШЕЙ СТЕПЕНИ ТОЧНОСТИ
151
Определитель D системы мало отличается от определителя
S{Zi, .... ^п)* рассмотренного в гл. 3 C.4.8),
D =
az^~\~az
J-'" . . . а2:^-|-а<2:~'"
^1 • " ^п
--m + 1 ^-m + 1
^1 " • ^п \
=.(z, ...z„)-'"
a^j"-|-a . . . az^ + a
г-> ... z«->
г, ... г:„
= «B1 ... Z„) '"{Zi
:Bi...2„)-'"A(Zi Z„) =
e-^"')W„(z„
Zn)
Условием неравенства D нулю и вместе с тем условием
возможности построения правила (8.1,1), точного для всевозможных
тригонометрических многочленов вида (8.2.4), и единственности такого
правила будет соблюдение неравенства (з^==^ Xi-\~ , . . ~{- х^^ф — 26 + 2рп
Ар — целое число). Чтобы найти Л., достаточно рассмотреть много-
член Lj(x), входящий в правило интерполирования C.4.11):
Ljix) =
sinO,5(x + o — Xj + 26)
sin 0,5 (а+ 26)
п
кф
sin 0,5 {х — х^)
■: sin 0,5 {Xj — Xfy)
riiDn имеет форму (8.2.4) и для него правило (8.1.1) должно быть
Й^очным. Но, очевидно,
i )|, стало быть,
2я
Лу= г р{х) Cj{x)dx.
(8.2.5)
Jj^ 3. Правило наивысшей степени точности
:}у Возвратимся к равенству (8.1.1). Сумма, стоящая справа, со-
^^ержит 2п параметров Af^ и х^^. Следует ожидать, что выбором их
равенство (8.1.1) можно сделать точным для всяких
тригонометрических многочленов степени /г^1. Это равносильно выполнению
ш
152 ИНТЕГРИРОВАНИЕ ПЕРИОДИЧЕСКИХ ФУНКЦИЙ [ГЛ. 8
условий:
2 Aki'^'k^^ p{x)e^'''dx {s^ — n^\ п—\). (8.3.1)
fe=.l о
Число условий 2/г — 1 на единицу меньше числа параметров Лд, и х^
и один из параметров правила (8.1.1). как можно предвидеть, должен
остаться произвольным.
В решении поставленной задачи о выборе Лд, и х^ будут
полезны, наряду с обычными тригонометрическими многочленами
п
Т^^ {х) = ао + 2 i^k cos kx ~\- l?fj sin kx), тригонометрические много-
A"= 1
члены «полуцелой степени»:
п
T„+o,ro(x}==^1ila^cos(k \-0,5)x-{-l>,sm(k-\-0,5)x]. (8.3.2)
Теорема 1. Для того чтобы правило квадратуры (8Л Л) было
точным для всякого тригонометрического многочлена степени
п—1, необходимо и достаточно выполнение двух условий:
1. Правило (8.1 Л) является интерполяционным, т. е. его
коэффициенты А^ определяются равенством (8.2.3) в случае
нечетного п и равенством (8.2.5) при каком-либо 6B6 + ^:i-j- ...
... ~^'Х^^ Ф 2рп) в случае четного п,
п
2. Многочлен «од^ (-^)= Tl^i^^»^ (-^ ~ -^а) выполняет условие
ортогональности:
2я
j /> Wo)o,5«W^o,5«-iW^-^ = 0. (8.3.3)
о
где Tq^^^_^{x) есть произвольный многочлен целой или полуцелой
степени 6,Ъп— 1.
При доказательстве мы различим два случая. Пусть п есть число
нечетное: п = 2т'-\-\.
Необходимость условий проверяется просто. Если правило (8.1 Л)
верно для многочленов степени п — 1 = 2/и, то оно верно и для
многочленов степени т. Как было выяснено в первой части § 2,
коэффициенты Л^ должны поэтому иметь значение (8.2.3). Многочлен
(i)Q^5rt W = <J^m+o,,5С-^) будет иметь полуцелую степень m-^-Q.b и
условие ортогональности (8.3.3) запишется в виде
2л
j Р W ^т .0.5 W 7^.-0,5 W dx =: 0. (8.3.30
О
§3]
ПРАВИЛО НАИВЫСШЕЙ СТЕПЕНИ ТОЧНОСТИ 153
где 7^^-0,5 ^^'^^ любой многочлен полуцелой степени т — 0,5.
Произведение са,„^_о,5^„г-о,5 будет многочленом степени л— 1, и из того,
что правило (8.1.1) для таких многочленов должно быть точным,
следует» ввиду о)о,5л (л:а) = *^' выполнение условия ортогональности
(8.3.30*
Для доказательства достаточности нам потребуется
Лемма 1. Всякий многочлен T^^ix) степени 2т единственным
образом представим в виде
Т^2т W == ^ш+0,5 W ^т-0,5 W + Рт W. (8-3.4)
где Т'ш-о.б ^ ^т — тригонометрические многочлены соответственно
полуцелой степени т — 0,5 и целой степени т.
Разложение многочлена о)^г+о,5 будет иметь форму:
Wm+0,5 W = S [«А COS {k 4- 0,5) X + Рд sin {k + 0,5) х].
Если воспользоваться переменной г = е'^ и формулами Эйлера,
то оно может быть, очевидно, записано в виде
2ГИ + 1
v«0
Для ближайших рассуждений полезно заметить, что так как при
действительных х многочлен о>^л40,5(-^) принимает действительные
значения, коэффициенты Ь^ должны обладать следующим свойством
сопряженности ^J5r = ^2m+i-ft (^=:0, 1, .... 2т-|-О- Кроме того,
так как степень многочлена не меньше m-j- 0,5, старший
коэффициент ^2тч 1 отличен от нуля.
Аналогично для других многочленов, входящих в (8.3.4), будут
верны приводимые ниже разложения по степеням z\
2m
v-0
Если эти разложения внести в равенство (8.3.4), освободиться
от отрицательных степеней z путем умножения на z'^"^ и сравнить
коэффициенты при степенях z от нулевой до 4т, получится система
4^4-1 линейных уравнений для определения с^ (v = 0, .,,, 2w — 1)
154
и d^
(V
=.0,
ИНТЕГРИРОВАНИЕ
т
. 2т):
ПЕРИОДИЧЕСКИХ ФУНКЦИЙ
[ГЛ. 8
2m+l
^2m-f-l^m+ ••• +^/n + 2^2m-l^^ ^3/n+l'
m
^2m+1^27n-l — ^4ш-
Ввиду ^o^=^2m+i "^ *^» ^3 первых w уравнений последовательно
могут быть найдены Cq, q ^m~v ^^ последних уравнений
находятся c^rn-i' •*•' ^m- Наконец, из оставшихся 2m+1 уравнений
находятся очевидным образом d^, , .,, d^m- Так как по коэффициентам с^
и d^ сразу восстанавливаются многочлены T^_q^^ и р^, лемму можно
считать доказанной.
Пусть выполняются условия теоремы и / = 72^ есть
произвольный тригонометрический многочлен степени п — 1. По лемме 1
/ можно разложить на два слагаемых, стоящих в правой части (8.3.4).
2я 2п
Ввиду второго условия теоремы верно равенство pfdx=^ pp^dx.
о о
По первому же условию правило (8.1.1) является интерполяционным
и будет точным для многочленов степени т. Поэтому последний
п
интеграл равен значению суммы 2 ^ftP/n(^ft)' Но а>т^о^^(х^) = 0
(^=1 п) и, стало быть, Р^С^а) "=/(-^ft)- Следовательно,
2я п
\ pf й?а:= 2 ^kf(^k)^ что доказывает достаточность условий теоремы.
В случае четного числа узлов n==2fn рассуждения в
значительной мере будут повторять те, которые были проведены для
нечетного п, и доказательство должно быть изменено только в одном
пункте, когда строится разложение, аналогичное (8.3.4). Оно тесно
связано с задачей интерполирования многочлена T^_i{x) по
значениям его в узлах Xf^, которая имеет в случае четного п некоторую
особенность.
Как выяснилось в конце предыдущего параграфа, при четном п
интерполяционные правила интегрирования (8.1.1) с коэффициентами
(8.2.5) характеризуются тем, что равенство (8.1.1) выполняется для
]Ж 3J ПРАВИЛО НАИВЫСШЕЙ СТЕПЕНИ ТОЧНОСТИ 155
^%ногочленов степени 0,5п = т частного вида (8.2.4) с фиксирован-
"ным параметром 6.
Необходимость условий теоремы проверяется столь же просто,
как и в случае нечетного числа узлов: если правило (8.1.1) будет
точным для многочленов степени /г — 1. то оно точно и для
многочленов степени 0,5д = /п, в частности, и для многочленов вида (8.2.4),
Поэтому оно должно быть интерполяционным с коэффициентами (8.2.5).
Чтобы изложение было правильно понято, попутно заметим, что
в выражении (8.2.4) 6 может быть избрано произвольно и
коэффициенты Afj правила интегрирования не будут зависеть от 5.
Если T^^i — любой многочлен степени w—l. произведение (д^Г^_|
будет многочленом степени 2т—1 = п— 1 и для него равенство (8.1.1)
должно выполняться точно. Но так как @^(л:^;) = 0 (k=r.U .... я),
2я
будет выполняться равенство /?(д^7'^_1б^л: = 0, что равносильно
о
условию ортогональности (8.3.30.
У Лемма 2. Всякий многочлен T^^^i степени 2т— 1 единствен-
^м образом представим в виде
'^ Т,т-1 W = ««. W Т',»., W + р; {X). (8.3.5)
Ше Г_ , есть многочлен степени т ~ \ и о' — степени т вида
Л Р^ W = ^0 + 2 i^k COS kx + bf^ sin kx) -f- A COS {mx -f 6).
1^—любое фиксированное число @^<6<2n), выбор которого мы
0^чиним единственному условию: XiH- ... -|-^л =?^ ~~ 26-+2/?л
Щр — целое число).
Ц- В переменной z р^(л^) будет иметь следующее выражение
г 2т
> v-O
Сходные разложения легко строятся для других многочленов,
входящих в (8.3.5):
4т-2 _
/ V-O
-^^^ 2т
(От (X) = Z'^ 2 d^Z- (^2m»v = ^' ^0 =?^ 0),
v»0
I; 2m-2
156
ИНТЕГРИРОВАНИЕ ПЕРИОДИЧЕСКИХ ФУНКЦИЙ
[ГЛ. 8
Если, подобно предыдущему, внести эти разложения в (8.3.5)
освободиться от отрицательных степеней z и сравнить коэффициент,
при одинаковых степенях z, получится система уравнений для с^ и d^\
т •
I
^0^0 ^0'
^m-V
2m^ 1
^2m^m-l+ • • •
^m + l^'2m-2'
H~' ^2т — ^3m-ll
hm^m-^ ••• +^m4-2^2ffi-2 =
a.
3m»
nt-
^2m^2m-2-
^4m-2-
Из первых m — 1 уравнений, ввиду ^q ^^ ^» последовательно
находятся Cq, . .., c^_2 и из конечной группы т — 1 уравнений
находятся последовательно ^2^-2»
Cfji- Эти две группы
коэффициентов будут попарно сопряжены в том порядке, как они записаны. На
^0 „ ^ ^4Ш-2
пример. Cq^j-~ и С2т~2''
И так как uq = а,
4т-2 и ^0 — ^2т'
ТО Со — ^2т-2-
Рассмотрим теперь среднюю группу 2т-\-1 уравнений. Из них,
очевидно, могут быть найдены все коэффициенты d^(v = 0, .. ., 2т),
Но так как d^ и й?2ги ^^ являются независимыми и должны быть
сопряженными, то первое и последнее уравнения этой группы, в
которые входят й?о и d2fjj, должны быть выделены и подвергнуты
дополнительному изучению. Рассмотрим их отдельно
^2m^m-l-f*2m-l<^m+ ••■ + ^m + 1^2m-2 +^;
2m "
^3m-l-
Исключая первые члены левых частей, содержащие неизвестный
коэффициент с^_1, все остальные члены уравнений будут попарно
сопряжены в том порядке, как мы их записали.
Для совместности уравнений нужна сопряженность первых их
членов ^2m^m-l== Vm-l =^2m^m-l» " ^^^ ^^^ ^2m ^ ^» ДОЛЖНО быТЬ
с^_1^=^с^_1, Т. е. коэффициент c^_i должен быть действительным
числом. Последнее уравнение тогда будет следствием первого и
может быть опущено.
Если первое уравнение разделить на д^ и все известные члены
перенести направо, то цосле подстановки вместо dg его значения
3] ПРАВИЛО НАИВЫСШЕЙ СТЕПЕНИ ТОЧНОСТИ 157
0,5Ае'^^ оно примет форму
Заменяя в о)^(х)^= JJ sin 0,5(х — Ху) синус его выражением че-
рез показательную функцию по формулам Эйлера, можно при
помощи несложных подсчетов найти ^о = (—1)'~^'"^^'^^^^У.
Предыдущее уравнение после замены ^о его значением примет вид
По выбору параметра б сумма 26 + 2^j будет отлична от
чисел вида 2рп (р — целое), и поэтому множитель при А в
уравнении будет иметь отличную от нуля мнимую часть и из уравнения
могут быть, и при этом единственным образом, найдены
действительные числа c^_j 1^ Л, Этим завершается доказательство леммы 2.
" Допустим теперь, что Aj^ и х^ выполняют условия теоремы 1
при каком-либо 6. Предположим, что / есть произвольный
тригонометрический многочлен степени я—1: / = Т'з^.! (л:). В силу
леммы 2
2л 2Л 2я
j pfdx= f раУщТт^! ^-^ + J PPrn d>^'
Первый из интегралов, стоящих в правой части, равен нулю по
второму условию теоремы. Так как многочлен р^ имеет форму (8.2.4)
и правило (8.1.1)—интерполяционное с коэффициентами (8.2.5), то
второй из интегралов в точности равен значению суммы 2 ^k^\i {^^
п
или, так как 7^2m-i^ = PU-^0' значению Ъ^А;Г^^^^{х^, Поэтому
правило (8,1.1) для f'^T'^m-x является точным.
Теорема 1 приводит вопрос о возможности построения правила
(8.1.1), верного для многочленов степени п— 1. прежде всего к
вопросу о существовании многочлена «о^^л W» обладающего свойством
ортогональности (8.3.3). Мы покажем, что если весовая функция р{х)
знакопостоянна, то такой многочлен степени 0,5/г существует,
определяется с точностью до коэффициентов старшей гармоники и если
'старшая гармоника фиксирована, то такой многочлен единственный.
Для определенности записи предположим п числом нечетным:
'>^= 2/^+1. Многочлен «о.з/? W будет иметь полуцелую степень
158 ИНТЕГРИРОВАНИЕ ПЕРИОДИЧЕСКИХ ФУНКЦИЙ
т-\~0,5. Мы будем искать его в форме
[ГЛ. 8
СО,
,^ (х) = 2 [^А COS (k -h 0,5) л: -f ^й sin (k + 0.5) x] ==
k=0
= a^cos(m-f 0,5)x + ^^sin(m + 0,5)x H-II^.o.sC-^)-
Условие ортогональности (8.3.3) равносильно выполнению
равенств
In
J р (X) 0)^+0.5 М COS (у + 0,5) xdx = Q,
G=0,1.
w - 1).
2я
J р(^)ю^ + о.5^51п(У + 0.5)л:й^х = 0,
(8.3.6)
которые можно рассматривать как линейную систему 2w уравнений
относительно коэффициентов а^. .... ci^_^, b^, . . ., ^;„_i.
При этом коэффициенты а^, Z^^ старшей гармоники не
подвергаются никаким ограничениям и будут содержаться в системе как
произвольные параметры.
Чтобы показать, что система (8.3,6) имеет и при этом только
одно решение, достаточно проверить, что соответствующая
однородная система, получающаяся при отбрасывании старшей гармоники
в 00^^0,5' '^' ^* замене (o^^-o.s "^ многочлен II^.Q^g. имеет лишь
нулевое решение
j p(x)R fjj _о,5 (^) COS (У -|- о,5) л: dx == О,
(у==:0, . .,, т— 1),
2я
J р (X) П^_о,5 (^) Sin (У -h 0,5) д: rfjc = 0.
(8.3.7)
Пусть эти уравнения выполняются. Умножив уравнения первой
серии соответственно па Uq, .... a^_i, второй серии — на д^,
Ь.
2л
И складывая, получим новое равенство
J joll^-o.;
dx-=^.
Если функция р{х) не эквивалентна нулю и не меняет знак, оно
возможно только в том случае, когда П^^^-о.з ^сть тождественный
нуль и. следовательно, все его коэффициенты равны нулю- Одно*
родная система имеет лиш1> нулевое рещен^^^,
J 33 ПРАВИЛО НАИВЫСШЕЙ СТЕПЕНИ ТОЧНОСТИ 159
Вполне аналогично рассуждения проводятся и в случае четного п.
Все изложенное позволяет высказать нижеследующую теорему.
Теорема 2. Если весовая функция р{х) знакопостоянна, то
при всяком значении п существует тригонометрический
многочлен ^o,^ni^) Ч^^ой или полуцелой степени 0,5я,
ортогональный по весу р{х) к любому многочлену T^qs^-i степени 0,5п— 1.
Условие ортогональности определяет (о^_5„ с точностью до
гармоники с наибольшей частотой, коэффициенты которой могут
быть заданы произвольно.
Во всем последующем коэффициенты старшей гармоники считаются
действительными. Так как коэффициенты системы, из которой
находятся прочие гармоники (Oq5,p есть числа действительные, оу.^ъп будет
действительным многочленом.
Для построения правила (8.1.1) существенное значение имеет
расположение корней многочлена о)о,5л-
Теорема 3, Если многочлен o)q^^(x) обладает свойством
ортогональности (8.3.3) и весовая функция знакопостоянна, то
лее корни o)o,5«W — действительные, простые и на отрезке
0<;х< 2л лежит п таких корней.
Для доказательства будем рассматривать х как комплексную
переменную. Во вспомогательной переменной z^=e^^, которую мы
вводили несколько раз выше, o)q5^(j£:) будет иметь выражение
следующего вида:
п
Щ.5П W = ^-"■'" 2 Кг" = z-°-"'P„ (Z) ib„ = ЬоФ 0).
V=0
■ I
? Корнями «0,5/1 W будут корни многочлена Pn(z). В комплексной
г:|1лоскости Z их п штук и они лежат вне начала координат z = 0,
|^ак как Z\j =^ 0.
I^lv Преобразование z = е^^ устанавливает взаимно однозначное соот-
Йветствие между плоскостью z с разрезом вдоль действительной по-
Щйожительной полуоси, из которой исключены нижний борт разреза
Щ начало координат, и открытой справа полосой 0^Rex<2jt пло-
IfCKocTH X. в этой полосе тригонометрический многочлен ooq^^» \^) будет
^ иметь п корней. В силу действительности многочлена и принципа
^^симметрии эти корни располагаются симметрично относительно дей-
Р)Ствительной оси и сопряженные корни будут иметь одинаковые
кратности.
Рассмотрим только те корни, которые лежат на отрезке 0-^jc<
■-< 2л действительной оси и имеют нечетную кратность. Пусть это будут
я
"^1' ^2' • • •. 1<7- По НИМ построим многочлен ^о,5д W'^ IIsinO,5(A: —|у)
степени 0,5^.
160 ИНТЕГРИРОВАНИЕ ПЕРИОДИЧЕСКИХ ФУНКЦИЙ [ГЛ. 8
Так как при выборе корней %j мы отбрасывали все
действительные корни четной кратности и все комплексные корни, сумма крат-
ностей которых есть число четное, по указанной выше причине
симметрии число q будет четным или нечетным одновременно с п.
Мы покажем, что д = п. Отсюда, очевидно, будет следовать
утверждение теоремы.
Допустим противоположное: q ф п. Возможно только q <^ п, п
так как q \\ п одинаковой четности, то q^n—2. Поэтому степень
0,5^ многочлена ^о,5^ не больше 0,5/г—1. Ввиду условия ортого-
нальиости должно быть Р^о,5Л,5^^-^-=^ ^- ^^ ^^^ равенство не
о
может выполняться, ибо р{х)^^ на отрезке О -^х ^2п, а.
произведение <A)o,5«^o,SG ^^^^Р^няет знак, так как оба множителя имеют на
[О, 2л] одинаковые точки перемены знака. Под знаком интеграла
стоит функция, не эквивалентная нулю и сохраняющая знак.
Допущение q Ф п не совместимо с условием ортогональности, и остается
только q=^n.
Из теорем 1 и 2 вытекает, что если весовая функция
знакопостоянна, то квадратурное правило (8.1.1), верное для многочленов
степени /г— 1, всегда может быть построено. Более того, такое
правило будет зависеть от одного непрерывного параметра.
Действительно, многочлен <1)о,5/г» корнями которого являются абсциссы ЛГ/^
правила, определяется с точностью до старшей гармоники. Последняя
содержит два произвольных коэффициента. Один из них путем
умножения ft)o^5rt ^^ постоянный множитель может быть приведен к
единице. Произвольным останется только второй из коэффициентов и
ему можно придавать любые значения.
Численное значение можно выбрать либо с целью увеличения
точности правила, либо с целью его упрощения. Например, его
можно выбрать так, чтобы правило было точным для многочленов
степени п частного вида Т^ {х) = ^Q-h 2 i^k cos^x +-^д sin kx) +
~\~ Acos{nx-\-b), где 6 фиксировано, или так, чтобы одна из абсцисс
имела бы заданное значение.
Мы ограничимся указанием на эту задачу, но не будем излагать
известных результатов ее исследования в общем виде, так как для
этого потребовались бы значительные по объему вычисления. Решение
задачи в некоторых частных случаях будет указано ниже,
О знаках коэффициентов Aj^ правила (8.1.1) верна легко
доказываемая
Теорема 4. Если р{х)^0 и правило (8.1.1) точно для
многочленов T^^-^ix) степени п— 1, то все коэффициенты Af^
положительны.
§ 3] ПРАВИЛО НАИВЫСШЕЙ СТЕПЕНИ ТОЧНОСТИ 161
Получим предварительно выражение коэффициентов А^ в удобной
для нас форме при любой весовой функции. Выберем какой-либо
узел х^ и введем многочлен Я^(л:) = JJ sin 0,5 (jc — х-). Функция
f(x)='ks(x) будет тригонометрическим многочленом степени п—1
и правило (8.1.1) для него должно дать точный результат. Но^
очевидно, f(xk)^==Xs(^k)^=0 при ^^5 и (8.1.1) приведет к ра-
2jt
венству р (х)Хз{х) dx = As^s(Xs), и, стало быть,
о
2л
As ==-17^ (Xs) J р (х) ll (X) dx, (8.3.8)
Если весовая функция р{х) неотрицательна, отсюда следует
утверждение теоремы.
Для излагаемой теории интегрирования периодических функций
имеет также интерес простая
Теорема 5. Есла весовая функция р(х) знакопостоянна, то
правило (8Л.1) ни при каких А^ и х^, не может быть точным
для всех тригонометрических многочленов степени п.
Чтобы убедиться в справедливости утверждения, достаточно
рассмотреть тригонометрический многочлен /(х) ^=(о^ .^ (л:), степень
которого равна п. Для него интеграл, стоящий слева в (8.1.1), отличен
от нуля, сумма же, стоящая справа, равна нулю, ввиду со^ д^ (Х;^) =: О
(^=1. .,,. я).
В приводимых ниже примерах указано несколько правил
интегрирования периодических функций. В точности их для любых
многочленов степени п—1 можно наиболее просто убедиться,
по-видимому, путем проверки.
Пример 1. Рассмотрим случай постоянной весовой функции
р(х)^\. Выберем произвольное число Xo@<^Xq<—1 и возьмем
2я
абсциссы x^ = Xq-\ k (^ = 0. 1, ..., п—1). Все они
принадлежат отрезку О ^ X < 2я. Положим
J /(x)rfx^^2/(xo+^^). (8.3.9)
о А=0
Нам достаточно показать, что равенство точно выполняется для
f^e^'"" E = 0. 1, .... п—1).
1б2 ИНТЕГРИРОВАНИЕ ПЕРИОДИЧЕСКИХ ФУНКЦИЙ [ГЛ. 8
Если s = 0, то правая и левая части, очевидно, равны 2я. Если
1,
я — I, то интеграл равен нулю. Сумма же имеет значение
/4-^=+^*)==
^isxo .
Js2h
— 1
2.1
:0,
й = 0
— 1
И равенство (8.3.9) также выполняется точно. Правило (8.3.9) содержит
произвольный параметр Xq, избрать который можно произвольно.
„ л; Зя
Если положить Xo=-2— или a:q=:-2~' то получится два правила:
О
2Л
я-1
\ fix)dx^^'^f(
Зя
2п
, 2Ы\
ft=0
точных для всех тригонометрических многочленов степени п вида
f(x)=^T^_^(x)--\-Acosnx, Если же принять jCq = 0 или Xq^== — ,
получатся правила:
2Я „_1
j/w..«^S/(Bi),
2л
/е=0
(8.3.10)
о jfe=o
точные для многочленов степени п вида f (х) = Т^_-^(х)~\~ Bslnnx.
Пример 2. /?(х)^::=1—cosx. С таким весом мы встречаемся,
например, при интегрировании 2л-периодической функции, имеющей
в точках О и 2л нули второй кратности.
Рассмотрим сначала случай нечетного числа узлов п ^==^ 2т-{-\.
Многочлен 0)о^5/г W буД^'^ иметь полуцелую степень т-\~0,Ъ и должен
быть ортогональным с весом 1—cosx ко всякому многочлену Т^^^г^
полуцелой степени т — 0,5. Последнее равносильно выполнению
системы равенств:
2л
J A — cosA:)co^^o,5Wcos(/4-0,5)jcfifx~0.
о
2л
г A — COS х) а>^^^^^{х) s{n{l -{- ^,5) X dx ^=^ ^
{1 = 0, 1, ..., т- 1).
J 3j ПРАВИЛО НАИВЫСШЕЙ СТРПЕНИ ТОЧНОСТИ 163
Если искать сО/„^о,5 W ^ форме разложения (o^+o.s W =
= 2 [^аСО5(^-|-0.5)д: + ^д:51п(^ + 0,5)х], внести его в предыду-
щие равенства и выполнить интегрирование, для коэффициентов д^
и bk получим две системы уравнений:
^0"~ ^1 ^^ ^'
^0 —2ai 4-^^2 = 0.
^1 — 2а2 + «3 = 0,
3^0 — ^1 = 0.
^0 — 2^1 + ^2=0.
^1 — 2^2 + ^3 = 0,
й^т-2 — 2^т-1 + ^т = 0. ^т-2 — 2^т-1 + *т = 0.
Решения их находятся просто:
Поэтому
<»m+0,5W = «0,5«W =
m т
= Л2 cos(yfe + 0,5)x+^2B^+l)sin(^+0.5)x=^a(A:)—25a'(x).
. . sin(m + l).y sin0,5(n+ \)x
^^^)~ sin 0,5л: ■" sin0,5jc
К такому же выражению (Оо,5/г W мы придем и в случае четного
числа узлов п.
Абсциссы Xf^ правила квадратур должны быть корнями а)о^5л W •
Ла(л:) — 2^а'(х) = О, или, если считать на время ВфО:—rz^ =
о {л)
d . . . А
, п + 1 1 [ , X А1
Отношение -^ является параметром уравнения. Если построить
графики левой и правой частей уравнения, то легко можно получить
наглядное, но неточное представление о расположении корней
уравнения и их зависимости от параметра. Получить же явные
выражения их в общем случае через элементарные функции, по-видимому,
невозможно.
Дальше мы ограничимся рассмотрением частного случая, когда
все вычисления легко доводятся до конца. Положим 5== О
U ^> / ч л sin 0,5 (/2 4-1) л: т/ / \ л « 2^я
««o.5nW = ^ ;^„05^ Корни cOo,5«W будут ^л = 71рг
164 ИНТЕГРИРОВАНИЕ ПЕРИОДИЧЕСКИХ ФУНКЦИЙ [ГЛ. 8
(k=\, 2. .... д). Правило квадратур, точное для многочленов
2л
степени п—1, следовательно, имеет форму A—cosx)f(x)dx^
о
п
^ Zj"^^^ ( j_ 1 )• ^коэффициенты могут быть найдены на основании
интерполяционных правил (8.2.3) и (8.2.5), но проще воспользоваться
связью между рассматриваемым правилом интегрирования и первым
из (8.3.10). Введем обозначения: A—cosx)f{x) = F{x), Л^ =
= A ^ cosXft)iB^. Тогда, если воспользоваться тем, что F@) = 0,
2л
рассматриваемое правило можно записать в форме F{x)dx^=^
о
Если / есть тригонометрический многочлен степени п—1, то
F будет многочленом степени п. Сличение с (8.3.10) показывает,
что так как в рассматриваемом правиле содержится n-f-I абсцисс
Xj^=—ц—г, то правило мы сделаем точным для всех многочленов г
степени я, если положим В^^^=—-цу (^ = 0, 1, ..,. п). Поэтому
квадратурная формула с весом 1—cosx, точная для многочленов
степени п—1, будет следующей:
J(l_eos;.)/(x)^^:^^2(l-cos^)/(^). (8.3.11)
о Jfe-l
§ 4. Остаток квадратуры периодической функции
и его оценка
Рассмотрим остаток произвольного правила интегрирования (8.1.1):
2л п
Rif)=jpix)f{x)dx~--^AJix,). (8.4.1)
о ft-i
Чтобы получить представление остатка, удобное для нахождения
точных его оценок, можно воспользоваться разложением
периодической функции по многочленам Бернулли A.4.2). Считая / (х)
функцией, V раз непрерывно дифференцируемой на [О, 2л], и приняв
ВО внимание, что для периодической функции /^*^ Bд) = /^^^ @)
^, ОСТАТОК КВАДРАТУРЫ И ЕГО ОЦЕНКА 165
/^=1, 2. ...)' получим при v>l:
^ * 2я; 2jt
/W = iJ/Wrf^-^Jr(Ofi:(^)^^. (8.4.2)
О о
Первый член правой части есть среднее значение функции /.
второй же член имеет смысл отклонения от среднего значения.
Чтобы не осложнять оценки остатка не имеющими интереса
слагаемыми, мы предположим сейчас, что правило (8Л.1) является точным
для того случая, когда / есть величина постоянная, что
равного п
СИЛЬНО равенству р{х)йх=^2и^^' ^Р" интегрировании произ-
0 А-1
вольной / среднее значение будет проинтегрировано точно и
остаток /?(/) будет иметь значение
2л 2л
/?(/)=_ B^ J /'^) it) R [ВХ (^)] dt = J r^ it) /C„ „ it) dt =
0 0
2л r 2л „ \
0 I 0 A-1 J
(8.4.3)
Проблема нахождения точной оценки /?(/), по сравнению с
задачей интегрирования непериодической функции / ^ С^, здесь осложнена
дополнительным условием: функция /(^) (t) должна быть не только не-
2л
прерывной, но и иметь среднее значение, равное нулю: p'^\t)dt== 0.
о
Не изменяя величины остатка /?(/), мы можем записать его в форме
2л
R(f) = j/''\t)iK^^„it)-\-C]dt,
О
где С — произвольная постоянная величина.
Если мы рассмотрим класс F функций /, удовлетворяющих
условию I /^^ (t) I < Жу, то будет верна следующая оценка | /? (/) К
2л
'^ ^v J l^v, л@ + ^1^^» и так как С здесь может иметь произ-
0
вольное значение, то будет верной также оценка
2л
\RiЛ\<Лi^llf<„„(t)-\-C*\dt, (8.4.4)
166 ИНТЕГРИРОВАНИЕ ПЕРИОДИЧЕСКИХ ФУНКЦИЙ (гл. 8
2jt
где с* есть значение С. для которого интеграл \К^^ ,^-\- C\dt
о
достигает наименьшего значения.
Убедимся сейчас, что оценка (8.4.4) не может быть улучшена и
является точной. Для этого воспользуемся известной теоремой анализа
о производной в точке экстремума *)
2Л 2л
dC
с= с-
о ^ ^
Так как среднее значение sign [/С^,, „ (/)-f-C*] равно нулю,
существует 2л-перй0дическая функция Д, для которой f^^\t) =
=^ M^s\gn[K^^ n(t)-^C*]. Она может быть найдена, например, путем
v-кратного неопределенного интегрирования с определением
аддитивной постоянной каждый раз так, чтобы выполнялось условие
2я
о
Остаток квадратуры для функции Д равен
2л 2л
R (Л) = / /:' (i) к,, п (О dt = M^\ sign [/с,, „ {t) -Ь С*\ К^, „ (О rf^ =
о о
2я 2л
= Ж^ sign [/Cv, „ (O + n [K,,,{t)+C'\dt = M^ J I /C,. „@ + C*K/.
Для Д оценка (8.4.4) остатка достигается. Функция Д может
не принадлежать рассматриваемому классу F, но наверное
существует функция f ^ F, для которой R (/) будет иметь значение,
сколь угодно близкое к /?(/J. Поэтому оценка (8.4,4) в классе F
является точной.
*) Под производной мы понимаем здесь ее симметричное определение
/'(jc) = lim-^^-^^—^— ' -. Производная в этом смысле от \х\
существует при всех х и равна sign ж. Возможность вычисления
производной от интеграла путем дифференцирования под знаком интеграла легко
проверяется на основании теорем о предельном переходе в интеграле
Лебега.
J 4] ОСТАТОК КВАДРАТУРЫ И ЕГО ОЦЕНКА 167
Литература
1. Турецкий А. X,, О формулах квадратур, точных для
тригонометрических полиномов, Уч. зап. Белгосуниверситета, сер. матам., вып. 1
D9) A959), 31—54.
2. Турецкий А. X., О квадратурных формулах с четным числом
тзлов, точных для тригонометрических полиномов, ДАН БССР 4, № 9 A960),
§65-368.
3. К е д а Н. П., Квадратурные формулы с производными для
периодических функций, Весц1 АН БССР. сер. ф1з.-тэхн., № 4 A961).
4. Кеда Н. П., К теории квадратур для периодических функций,
ДАН БССР 5. № 9 A961).
ГЛАВА 9
КВАДРАТУРНЫЕ ФОРМУЛЫ, СОДЕРЖАЩИЕ НАПЕРЕД
ЗАДАННЫЕ УЗЛЫ
§ 1. Некоторые общие теоремы
В прикладных задачах иногда возникает необходимость
построения таких квадратурных формул, часть узлов которых задается
заранее, другая же часть узлов может быть взята произвольно и выбором
таких узлов можно распоряжаться для достижения тех или иных целей.
Рассмотрим, например, граничную задачу на отрезке а^х^Ь
для дифференциального уравнения второго порядка
L(y)^kp{x)y = ^[p{x)^] + {Xpix)~-q{x))y = ~f{x) (9.1.1)
при условиях
у»(а) = 0. уф):=0, (9.1.2)
Если известна функция Грина G{x, ^) для оператора L(y) при
условиях (9.1.2), .решение граничной задачи может быть приведено
к решению интегрального уравнения *)
b
y(x) = F{x)-^l\ G{x, l)p(l)y{l)dl,
F(x)=JG{x. DfiDdl.
(9.1.3)
Допустим теперь, что мы хотим приближенно решить уравнение
(9.1.3) путем применения механических квадратур к интегралу,
стоящему в правой части равенства. При выборе квадратурной формулы
естественно принять во внимание, что значения функции у(х) на
концах отрезка [а, Ь] нам известны из условий (9.1.2), и взять
*) См., например, В. И. Смирнов, Курс высшей математики, т. IV,
Гостехиздат, 1957. 519—521.
§ 1] НЕКОТОРЫЕ ОБЩИЕ ТЕОРЕМЫ 169
формулу вида
b п
J / (х) dx ^ Af {а) + Bf ф) 4 ^ А J (X,).
содержащую два фиксированных узла а н Ь. Прочие узлы Xf^
(^=1, ..., п) являются произвольными.
Выше был взят случай «двухточечной» граничной задачи. Если бы
задача была «многоточечной», то могла возникнуть потребность
построения квадратурной формулы, содержащей более двух
заданных заранее узлов.
Рассмотрим квадратурную формулу
b п т
j P(x)f (х) dx^^ A,f (X,) + 5] В J (ail (9.1.4)
^ которой m узлов ai. ...» uf^ фиксированы. Она содержит 2n-\-m
параметров Л^^, x^ (A==l, .... n) vi B^ (/ = 1 m). Попытаемся
их выбрать так, чтобы равенство (9.1.4) стало точным для
многочленов возможно более высокой степени.
Введем два многочлена, связанных с узлами а^ и х^'.
Q (х) = (х — aj) ... (х — а^). со (х) = (х~ х^) ... {х ~ х„).
За счет выбора коэффициентов А^ и В^, формулу (9.1.4) можно
сделать верной для многочленов степени п~\'т— 1. Для этого ее
достаточно взять интерполяционной. Достичь же того, чтобы
равенство (9.1.4) было верным для многочленов более высокой степени,
можно только за счет специального подбора х^.
Теорема 1. Для того чтобы формула {^Л Л) была точной для
многочленов степени 2п-\-т—1, необходимо и достаточно, чтобы
1) она была интерполяционной и чтобы 2) многочлен о)(х) был
ортогонален на отрезке [а. д] по весу р {x)Q(x) ко всякому
многочлену Q(x) степени <^п.
Доказательство. Необходимость первого условия очевидна,
так как. если формула (9.1.4) верна для всех многочленов степени
п-{~т—1, то она должна быть интерполяционной. Необходимость
второго условия проверяется, если положить / = Qo)Q; / есть
многочлен, степень которого ■^2п-{-т—1. Для него равенство (9.1.4)
должно быть точным и так как / в точках а^ и х^ исчезает,
квадратурная сумма для такой функции / обратится в нуль и должно будет
выполняться равенство
b
J /7(x)^(x)o)(x)Q(x)ufx =0. (9.1.5)
170 КВАДРАТУРНЫЕ ФОРМУЛЫ С НАПЕРЕД ЗАДАННЫМИ УЗЛАМИ [ГЛ.9
Пусть / есть произвольный многочлен степени 2п-^т—1, Его
можно представить в форме f = Q(x)(s}(x)Q{x)-^ г (х), где Q{x) и
г(х) будут многочленами, степени ^п—1 и ^п-{~ т—1
соответственно. При этом, очевидно, f(ai)^= г (Ui) (/=1, .... /п) и
/(Хм)=^г(х^) (k^U .... п).
Если выполнено условие ортогональности (9.1.5) и формула
(9.1.4)—интерполяционная, то будет верной следующая цепочка
равенств
b b b b п
Г pf dx r= I pQcoQ dxA- \ prdx= j /?r rfx = \ Лj^r (Xf^) -\-
a a a a k^\
m n m
Этим доказана достаточность условий теоремы.
Таким образом, построение квадратурной формулы (9.1.4).
верной для алгебраических многочленов степени 2п~]-т—1, приводится
к нахождению многочлена «(х) степени /г, ортогонального на [а. д\
по весу pQ ко всякому многочлену меньшей степени. Корни
многочлена 0(х) должны быть действительными, различными и
принадлежать отрезку [а, д]. Кроме того, они должны быть отличны от
фиксированных узлов a^ (/=1. .... т).
Допустим, что многочлен со (л:), обладающий указанными
свойствами, существует. Тогда формула (9.1.4). верная для многочленов
степени 2п-\-т—1, может быть построена. Сделаем еще замечание
об ее алгебраической степени точности. Получим представление
остатка, позволяющее легко судить об этом. Выполним
интерполирование / на [а, Ь] при помощи многочлена И (х) степени ^ 2/i + т— 1
по следующим условиям
fi{aj) = f{aj) (/=1, .... m).
Я (X,) ^ / (X,), Н' (х,) = Г {X,) {k^\ п).
Если / имеет производную порядка 2п-\~т во всех точках отрезка
[а, Ь\, то остаток интерполирования г (х) == f (х)—~ Н(х) представим
в форме
rix) = Qix)<.Hx)^^^, a<l<b.
Для остатка квадратуры /?(/) справедливо равенство /?(/) = /?(^) +
+ /?(/-). Так как формула (9.1.4) верна для всех многочленов
степени 2п-{-т—1, то /?(Я) = 0. Кроме того, во всех узлах а/ и х^
§ и НЕКОТОРЫЕ ОБЩИЕ ТЕОРЕМЫ 171
г{х) обращается в нуль и поэтому квадратурная сумма для г (х)
исчезает
п т
liA,r{x,)+^B^riai)^Q.
Следовательно.
/?(/)-=/?@= J prdx=^ р{х)9Лх)^ЧхУ^^^^^\йх, (9.1.6)
а а
Отсюда видно, что если
ь
1= [ pQ(i)^dx ФО,
а
ТО степень точности формулы (9.1.4) равна 2п-\- т~ \.
Действительно, при наших предположениях (9.1.4) дает точный
результат для всех многочленов степени 2п~{~т — 1. Когда же/ есть
«ногочлен степени 2п~{-т, то /(^л+т) ^^jy^ величина постоянная,
отличная от нуля и для такой функции /
b
Л2п + т) /•
а
Если /==0, ТО алгебраическая степень точности (9.1.4) будет
больше 211-]-т—1. Легко может быть указан признак для
суждения о степени точности в этом исключительном случае, на чем мы
не будем останавливаться.
Так как формула (9.1.4) является интерполяционной, ее
коэффициенты Л^ и Bi должны иметь следующие значения:
а
b
а
Для коэффициента Af^ можно дать другое представление, более
удобное для вычисления, нежели (9.1,7). Допустим, что существует
единственная система многочленов П5(л:) E=1, 2, ,..), где П^ имеет
степень s, ортонормированная по весу р (х) ^ р (х) Q (х) на [а, Ь].
Многочлен Iif^{x) может отличаться от со(х) только постоянным
**ножителем;
b
172 КВАДРАТУРНЫЕ ФОРМУЛЫ С НАПЕРЕД ЗАДАННЫМИ УЗЛАМИ [ГЛ. 9
b
Интеграл р(л;)—^^-^ dx был вычислен в § 1 гл. 7 в других обо-
а
значениях. Для него были получены следующие два выражения:
J
П«_(л:) ^^_ q„+i
9ix)^^^dx
x^Xk a;,n„+i(^ft) а/г-1Пл_1(Хй)
Под а„ здесь подразумевается старший коэффициент многочлена П„ (х):
^ -— ^п + \ __. ^ /д J gx
Для вычисления коэффициентов Лу^ может быть полезным
следующее замечание. Если сравнить (9.1.9) с выражениями G.1.4) и
G.1.5) для коэффициентов формулы наивысшей алгебраической
степени точности, то будет ясно, что А^ для формулы (9.1.4) будут
отличаться только множителем ^т?—г от соответствующих коэффи-
циентов в квадратурной формуле с весовой функцией р(х) = /; (х) Q {х)
ь п
^9{x)f {х) dx^^ Akf (Xk).
а & = 1
верной для многочленов степени 2п—1.
Построение формулы (9.1.4) при всяких п, как видно из
изложенного, требует умения находить систему многочленов,
ортогональных на [а, Ь] по весу p{x)Q{x). В некоторых случаях здесь может
принести пользу указанная несколькими строками ниже теорема о
преобразовании ортогональной системы многочленов при умножении веса
на многочлен. Эту теорему мы сформулируем с той степенью
общности, которая будет достаточной для наших целей.
Для облегчения записи будем рассматривать многочлены со
старшими коэффициентами, равными единице. Чтобы отличить их от
нормированных многочленов, примененных в предыдущем изложении,
будем их обозначать Я^(х) или П^(л:).
Пусть Q(x) = (x — ci{){x — ^2) ... {х — а^) есть любой
многочлен с простыми корнями «1, «2. ..., а^.
Наряду с заданной весовой функцией р (х) будем рассматривать
весовую функцию р (х) == jt? (х) Q (х).
Будем считать, что существует система многочленов Р^(х) =
= х'*+... (s^=0, 1, ...), ортогональных на [а, Ь\ по весу р(^).
такая, что | р (х) Ps dx Ф 0.
НЕКОТОРЫЕ ОБЩИЕ ТЕОРЕМЫ
173
Равным образом предположим, что существует и при этом
единственная система многочленов П^(х)= л;*^4- ... E = 0, 1, ...).
ортогональных на [а, Ь] повесу р{х)= p(x)Q(x), и покажем, что П^(л:)
имеют следующие выражения через Р^(х):
П/.М = дЩ?
°n+m-l(^) Pni-m-li^l)
Pnix) P„(«l)
Pni<^m)
^■Q(x)
Pn + m-l(^l) ••• Pn + m-l("m)
Pn(^l)
Pn («,«)
(9.1.10)
Действительно, произведение Q (x) Г1„ (л:) есть многочлен степени
п-{-т со старшим членом x"+"^. Его можно разложить по
многочленам Р^{х):
0(л;I1„(х) = Р„+;„(л:)Ч-с,Р„^.„_,(х)Н-сЛ+т-2(^L- ... •
Ортогональность Г1^(х) с весом p{x)Q{x) ко всякому многочлену,
степени меньшей /г, равносильна тому, что в указанном разложении
должны отсутствовать члены с Р^ {х) для s -^п — 1 и разложение
должно иметь форму
Q{x)n,(x) = P,^^(x) + c,P,^,,^,{x)-\~ ... ^с^Р,(х). (9.1.11)
При X, равном aj. ag, ..., а^, левая часть обращается в нуль и
поэтому коэффициенты Cj, .,,, с^ должны быть такими, чтобы
выполнялись условия
^ ^ . . . . (9.1.12)
Зти равенства вместе с тем являются условиями того, чтобы правая
часть (9.1.11) нацело делилась на Q{x); П« (х) будет тогда найден
из (9.1.11) в форме
n„(x) = Q-4x)[^„^^(x)+^^+^-iW+ ••• +с^Р,(хI
Ввиду сделанного предположения о существовании и единственности
многочленов П^, система уравнений (9.1.12) при всяком п должна
иметь и при этом единственное решение относительно неизвестных
174 КВАДРАТУРНЫЕ ФОРМУЛЫ с НАПЕРЕД ЗАДАННЫМИ УЗЛАМИ [ГЛ. О
коэффициентов с^, .... с^. Определитель системы, совпадающий,
очевидно, с Д, должен быть, следовательно, отличным от нуля: Д^О.
Нахождение же выражения (9,1.10) для П„(л:) может быть
выполнено следующим путем. Присоединим к (9.1.12) равенство (9.1,11)
и построим систему:
-Q(^)n„(^) + P«^^W + ^A^m-iW + ... 4 с^Р^х) ==0.
Ее можно рассматривать как однородную систему m-^-l уравнений
относительно т~^\ величин 1. Cj, .... с^. В силу известных
теорем алгебры, можно утверждать, что определитель системы должен
быть равен нулю.
^«4-m(«l) ^« + m-l(^l) ... Pni^l) 1 = 0.
Отсюда сразу получается (9.1,10).
§ 2. Формулы частного вида
При построении квадратурных формул, рассмотренных в седьмой
главе» все узлы и коэффициенты выбирались так. чтобы формула
была точной для многочленов возможно более высокой степени.
Стремясь обобщить эту идею, А. А. Марков рассматривал такие
формулы, в которых для повышения точности используется произвол
в выборе коэффициентов А/^ и лишь части узлов х^^. Другая же
часть узлов остается произвольной и может быть фиксирована любым
способом. Им был изучен преимущественно случай знакопостоянного
веса. Будем считать функцию р(х), входящую в интеграл (9.1.4).
неотрицательной: р{х)^0. Чтобы другая весовая функция,
участвующая в исследованиях, р (дг) = /? (х) Q (х) сохраняла знак, мы должны
предположить, что Q{x) также сохраняет знак на [а, Ь] и,
следовательно, ни один из фиксированных узлов а^ не лежит внутри [а, Ь].
Если, кроме того, не допускать квадратурных формул с узлами.
лежащими вне [а, Ь], мы должны будем ограничиться рассмотрением
следующих случаев А. А. Маркова:
1) т=1 и берется один фиксированный узел а^=:а,
2) т==1 и фиксирован узел а^^Ь.
Второй случай приводится к первому при помощи линейной
замены х=^а-{' b —^ t и отдельно рассматриваться не будет.
^ 2J ФОРМУЛЫ ЧАСТНОГО ВИДА 175
3) m = 2 И берутся два фиксированных узла а^==а, а2 = Ь.
Ввиду знакопостоянства p==pQ на [а, д], многочлен со (л:),
ортогональный по весу р на [а, д] ко всякому многочлену степени < п,
существует при всяком п. Корни его Xf^ действительные, простые и
все лежат внутри [а, Ь]. В частности, они во всех трех случаях
отличны от фиксированных узлов, расположенных на концах [а. д].
Поэтому квадратурные формулы (9.1.4), точные для всевозможных
многочленов степени 2n-\~nt—1, в случаях Маркова могут быть
построены при любых п. Так как pQ,(iP сохраняет знак на [а, Ь]
b
и Г/?Йо)^й?х ^ О, алгебраическая степень точности таких формул
а
будет равна 2/г+яг—1.
Построение начнем с первого случая: w= 1, ау^^=а:
b п
\ pfdx^Af{a)+Y^AJ{x,) + R{f), (9.2.1)
а k^l
Наивысшая степень точности формулы равна 2п.
Здесь Q (л:) = л: — а; х^ — корни многочлена П^ {х) степени п,
ортогонального на [а, Ь] по весу р (дг) = (л: — а) р (л:) ко всякому
многочлену степени </г. Если P^(jc) E = 0, 1, ...) образуют
ортогональную систему многочленов по весу р{х), то согласно (9.1.10)
П„(л:) может быть записан в форме
^^п (^) - -—^ [Рп^х {X) Р, (а) - Р, {X) Р,^, (а)],
где К^ — некоторая постоянная, отличная от нуля. Равенства (9.1.9)
дают достаточно удобное средство для вычисления коэффициентов А^\
А,=.—
(9.2.2)
Пользуясь (9.1.8). для А найдем
b
А = П~^ (а) J р (X) П„ (х) dx. (9.2.3)
а
Покажем, что все коэффициенты формулы (9.2.1) положительны.
В качестве интегрируемой функции возьмем многочлен степени 2л—1:
Он принимает следующие значения в узлах а, х^\
{О при k Ф /,
ix,-aW\x,) при k^l.
176 КВАДРАТУРНЫЕ ФОРМУЛЫ С НАПЕРЕД ЗАДАННЫМИ УЗЛАМИ [ГЛ. 9
Так как степень точности формулы (9.2.1) равна 2/г. то должно
быть верным равенство
b
J Р (х) (X — а) [^^и dx = Л^ (xi — а) со'' {х^)
а
и, следовательно.
b
А. = \—^ I ;?(л-)(л: —а)Г-^^Т dx>Q.
а
Аналогично, если положить / = о)^(л^), то для коэффициента А
получим
ъ
А = @-2 (д,) J р (д.) ф (^) ^д. -^ 0.
а
Если / имеет непрерывную производную порядка 2п-^\, то
остаток /?(/) формулы (9.2.1) может быть, согласно (9.1,6),
представлен в форме
ъ
/?(/)=]/? (X) (X ^ а) 02 (д:) ^___Ш- dx.
а
или, так как р (х—л)о)^ сохраняет знак на [а, Ь],
b
f^if) = ^^-^^^:^\ P(^)(x — ^)^4x)dx, а<г]<Ь. (9.2.4)
Более подробно остановимся на случае, когда весовая функ-
ция р(х) есть величина постоянная: р(х)^\. Чтобы воспользоваться
при вычислениях якобиевыми многочленами, будем считать, что отрезок
интегрирования [а, д] приведен к отрезку [—1, 1], и рассмотрим
квадратурную формулу
1 п
j fix)dx==Afi-l)^^A,f{x,)-^R{f), (9.2.5)
-1 А=1
имеющую степень точности 2/г; Q(x)=l-|-x. Многочлен (о{х)'^
= (x— Xi) . . . (х — Xfj) должен быть ортогонален на [—I, 1] по весу
1+л: ко всякому многочлену меньшей степени и поэтому может
отличаться от многочлена Якоби P„' \х) только постоянным
множителем, равным обратной величине старшего коэффициента
«W— г Bл+ 2) ^« W-
§ 2] ФОРМУЛЫ ЧАСТНОГО ВИДА 177
Узлы Хц должны быть, следовательно, корнями Р^?*^*(л:).
Коэффициенты А^ могут быть легко найдены, если воспользоваться
замечанием, сделанным по поводу равенств (9.1.9). Квадратурная
формула G.3,2) с якобиевым весом A —xf'il -f xf, содержащая п узлов
и верная для многочленов степени 2п — 1, имеет коэффициенты G.3.4).
Их мы должны вычислить для случая а=::0, р=1 и затем для
нахождения Лд,, входящих в формулу (9.2.5), приписать
коэффициенту G.3.4) с тем же индексом к множитель -^тт—г'^ т~г—"
Ы (^/г) 1 -\-Xk
Это дает:
^*=A+.,)A-4Ж'"'М^- ^^■^■^^
При вычислении А можно воспользоваться формулой (9.1.8), по*
ложив в ней /? = 1. Q=:;14-A^. а^ = —1:
-1 -1
Последний интеграл и численный множитель, стоящий перед ним,
легко могут быть найдены при помощи известных свойств
многочленов Якоби Pfi*^\x) и равны соответственно /"~/1ч и (—\Y{n~\-\).
(П+1J
(9,2.7)
Остаток /?(/) может быть подсчитан на основании общего
выражения (9.2.4):
I
^ (-^^ = ^Bп11)! J С + ■>:) ю" {X) dx, _1<11<1.
-1
Интеграл, входящий в остаток /?(/), находится без труда
li\+xWix)dx = [^^^^]\il^ x)[Pr4x)fdx =
-1 _1
_ 2 г 2"я!(/г+1Iр
— п+\ L B« + 1)! J '
Поэтому
/?(А_ 2 Г2"«!(«+1)!Г /^"+"(Л) _1<т1<1 (9 2 8)
'^'<j' — TTTV Bn+i)i J Bл+1)! ' '^л-^ь ^у-^-»;
178 КВАДРАТУРНЫЕ ФОРМУЛЫ с НАПЕРЕД ЗАДАННЫМИ УЗЛАМИ [ГЛ.9
Узлы и коэффициенты формулы (9,2.5) для/г =^ 1 AN приведены
ниже*):
А =0,5
jci= 0,3333 3333 Л,^\,3
А ^^0 2222 2222
X, = —0.2898 9794 А^ = 1,0249 7165
Х2 = 0.6898 9794 ^2 = 0,7528 0613
л=-3
А -=0,125
xi 3^—0,5753 189 Ai =- 0,6576 886
Х2=-- 0Д810 663 ^2 = 0,7763 869
л'з -- 0.8228 241 А, == 0,4409 244
Л==4
А -=0.08
лп ^ -^0,7204 803 Ai = 0,4462 078
Х2 ^ 0,1671 809 Лз -= 0,6236 530
JC3 -- 0,4463 140 Лз -= 0,5627 120
X, ^ 0,8857 916 Л4 =- 0,2874 271
я = 5
>1 = 0.0555 556
Xi =- —0.8029 298 А^ = 0.3196 408
ЛГ2 ^ — 0,3909 286 ^2 = 0.4853 872
х^ = 0,1240 504 Лз =- 0.5209 268
X, ^ 0,6039 732 Л4 = 0,4169 013
х^ = 0,9203 803 As == 0,2015 884
л = б
Л ==: 0,0408 1633
xi^~ 0,8538 913 Л^ -= 0,2392 275
хз = — 0,5384 678 А^ = 0,3809 498
лгз = -- 0,1173 430 Лз = 0,4471 098
X, ^ 0,3260 306 А^ =: 0,4247 038
JC5 == 0,7038 428 Лд = 0.3182 042
х^ ==: 0,9413 672 Ле = 0,1489 885
Обратимся к третьему случаю, когда два заранее заданных узла
лежат на границах промежутка интегрирования ai = a, a2 = b:
b п
J p{x)f{x)dx=^Af {a)^Bf{b) + ^ Л,/(х,)Ч- /?(/). (9.2.9)
a k-l
Наивысшая степень точности такой формулы равна 2/г + Ь Q'{x)=^
=^(х — а){х ~ b), Xf^ — корни многочлена n^(jc) степени п,
ортогонального на [а, Ь] по весу p(jc)^=(jc — а){х — Ь)р{х) ко всякому
многочлену меньшей степени.
*) Результаты найдены Р. Б. Аккерман и К. Е. Черниным.
§21
ФОРМУЛЫ ЧАСТНОГО ВИДА
179
Многочлен П^ (х) через многочлены Р^ (х), ортогональные по
весу р(х), выражается следующим образом:
ПЛл:)
Кп
(х — а) (х — Ь)
РпМ^) РпМ^) Р„,2Ф)
Рп.Лх) Я„,1(а) Р„^,F)
Р„ (X) Р„ {а) Р„ ф)
Коэффициенты А^, А )л В вычисляются при помощи равенств
(9.1.9) и (9.1.8):
Ль= ^^
^пК {^k) ^n-^l i^k) {Ч - ^) {^k - Ь)
b
Л = [о)(а)(а —^)]"^ J p{x){x--b)(i){x)dx.
a
b
iB == [CO ф) Ф ~ a)]"^ J p {x) {X ~ a) 0 (x) ^jc,
CO (X) = (x - д^^) , . . (x - X„).
(9.2.10)
(9.2.11)
Если рассмотреть квадратурную формулу с весовой функцией
р(х) = /? (X)(х ~ а) (X — г^):
b п
J /7 (х) (X ~-а){х -b)f (х) rfx ;^ ^ Л1/ (х*).
верную для многочленов степени 2п— 1, то коэффициенты А^^ фор-
мулы (9.2.8) будут отличаться от Ац множителем -—^ —ZTaT'
Можно показать, что Л^^, А ^^ В положительны. Чтобы убедиться
в этом, достаточно применить формулу (9.2,9) к многочленам
(х- а)(х~^)[-^;^Т , (/) — X)со2(X) и (х —а)(о2(х).
L X X/ J
Остаточный член /?(/) (9.2.9) представим в форме
12*
о
180 КВАДРАТУРНЫЕ ФОРМУЛЫ С НАПЕРЕД ЗАДАННЫМИ УЗЛАМИ [ГЛ. 9
Как выше, остановимся на случае постоянной весовой функции р {х)
и будем считать, что отрезок интегрирования есть [—1, 1]:
1 п
|/(х)^х=.Л/(-1)+5/A) + 5]^^^/(^й) + /?(/). (9.2.12)
Q{x)-^\— л:^.
Многочлен «(л:) ортогонален на [—1, 1] с весом 1—x^ ко всякому
многочлену степени < /г и, с точностью до легко определяемого
численного множителя, должен совпадать с якобиевым многочленом Р^^' ^Ч-^)'
c^W— гBл + 3) ^^ W-
Путем, аналогичным тому, который применен в первом случае,
вычисляются коэффициенты и остаток формулы (9.2.12):
^^™' п + 2 A^4)^K'^^'(-.)F' '^■^''""(п + 1)(« + 2)'
8(^ + 1) Г2%!(п + 2)!]^ /^^^^Чл) _i^^^i
^*^-^^"^B/г + 3)(/г + 2)[ B/г + 2)! J Bл + 2I' i <. Ч <. ь
Приведем *) числовые величины узлов и коэффициентов для
/г=1AI5
Л = 5 == 0,3333 3333
Xi =0 ^1 = 1,3333 3333
л = 5 =- 0,1666 6667
лгз -= — JCi = 0,4472 1360 >li = ^2 = 0,8333 3333
Л =5 =-0,1
х^^ — хх^ 0,6546 5367 Лз =- ^1 = 0,5444 4444
л:2 = 0 Л2=-0,7111 1111
Л = 5 3= 0.0666 6666 7
ЛГ4 = — Ж1 = 0J650 5532 ^4 = ^j = 0,3784 7496
хз == — JC2 -= 0,2852 3152 ^з = ^2 = 0,5548 5837
*) Таблица составлена Р. Б. Аккерман.
§ 21 ФОРМУЛЫ ЧАСТНОГО ВИДА 181
^5 =
-^4 =
^3
ФОРМУЛЫ ЧАСТНОГО I
п
-= 0,8302 2390
= 0,4688 4879
==0
=-5
А =
зид
.А,
:А,
As
А
= 0,0476 1904 8
=- 0,2768 2605
= 0,4317 4538
= 0,4876 1905
й = 6
л = 5 = 0,0357 1428 6
Хб = — ^1 = 0,8717 4015 ^6 = ^1-= 0,2107 0423
xs == — Х2 - 0,5917 0018 ^5 = ^2 = 0,3411 2268
л:^ = — лгз = 0,2092 9922 ^4 = ^3 = 0,4124 5881
л = 7
Л = В = 0,0277 7777 8
ЛГ7 = — JCi = 0,8997 5800 А^ ^ А^ ^ 0,1654 9536
Хб = — JC2 = 0,6771 8628 ^g =. ^2 = 0,2745 3872
л-5 = — дгз = 0,3631 1746 ^5 = ^3 == 0,3464 2851
Х4 = О ^4 - 0,3715 1927
-^8 = '
-^7 =
-^6 = '
-^5 =
Xq==
^8 =
-^7==
J^a =
•^lO'^^
Хэ =
ATg =:
^7 =
Хб --
— jci = 0,9195 3391
- л:2 = 0,7387 7386
- JC3 = 0,4779 2495
— л:4 = 0,1652 7896
й =
— JC1-: 0,9340 0143
~Х2^ 0,7844 8347
— лгз = 0,5652 3533
— Х4-0,2957 5814
д:5 = 0
л =
— ATj = 0,9448 9927
_ JC2 = 0,8192 7932
— jC3 = 0,6328 7615
— JC4 = 0.3995 3094
— j^:5 = 0,1365 5293
As^^A,^ 0,1333 0599
^7 = ^2 = 0,2248 8934
Лб = Лз = 0,2920 4268
^5 = ^2 = 0,3275 3976
-9
А ^В =0,0181 8181 8
^9 == ^1 = 0.1095 1227
^8==^2 = 0,1871 6989
Л; = Л = 0,2480 4811
^6 = ^4 = 0,2868 7913
^5 = 0,3002 1759
= 10
А ^В =0,0151 5151 5
^jo =3^1 =0,0916 8452 1
Ад = ^2 = 0,1579 7471
Ла = Лз = 0,2125 0842
Л; =Л4 = 0,2512 7560
Ле = Ла = 0,2714 0524
182 КВАДРАТУРНЫЕ ФОРМУЛЫ с НАПЕРЕД ЗАДАННЫМИ УЗЛАМИ [ГЛ.
А =^В -=0,0128 2051 3
Жи -- — ЛГ1 = 0,9533 0985 А^^=^А,^ 0,0778 0168 7
^10 -= ~ л:2 = 0,8463 4757 ^ю ^ А^^ 0,1349 8193
лгд == ^ JC3 == 0,6861 8847 ^э =- ^з -= 0,1836 4686
х^ = — л:, = 0,4829 0982 А^ ^А,^ 0,2207 6779
x^ === — ^5 = 0,2492 8693 Л; = Л^ -- 0,2440 1579
ДГб = О Лб -- 0,2519 3085
/г= 12
А г^Н ^ 0.0109 8901 1
^12 -= — лг) -- 0,9599 3505 Л,2 = ^i = 0,0668 3728 3
лгц ^ — ^2 = 0,8678 0105 Л,1 = >l2 = 0.1165 8665
-vio = — Лз = 0,7288 6860 Л^ = ^з = 0,1600 2185
Жэ ^ -- ЛГ4 = 0,5506 3940 Л9 = Л4 =- 0,1948 2615
л:^ = — JC5 = 0,3427 2401 Лз == ^5 -= 0,2191 2625
Х7 == — л:б = 0,1163 3187 Aj = Ле--0,2316 1279
/г= 13
Л = ^ = 0.0095 2380 95
jci3 = — лг! = 0,9652 4592 Лla =- Л1 == 0,0580 2992 2
х,^ ^ — лгз = 0,8850 8205 Л12 -= Л = 0,1016 6004
Xii= — ^3 = 0,7635 1967 Ли-=^3=^0,1405 1171
лг^о = _ л:, ^ 0,6062 5322 Лю = Л4 ^ 0Л727 8965
JC9 = — xs = 0,4206 3805 Л9 = Л5 == 0.1969 8723
лгз = — ATg = 0.2153 5396 Л3 = >1б = 0,2119 7360
Xj^O Л7 = 0,2170 4810
/г= 14
А ^В ^ 0,0083 3333 33
Жм = — xi = 0,9695 6804 Л14 = ^1 = 0.0508 5036 9
лг^з = — JC2 = 0,8992 0054 Л,з == Лг = 0,0893 9368 9
х^2 =- — Лз = 0,7920 0828 Л12 = ^з = 0,1242 5539
jcn = — Л4 = 0,6523 8872 Л11 = Л4 = 0,1540 2699
•^10 = — -A^s = 0,4860 5941 Лю = ^g = 0,1774 9190
xg ^ — jce = 0,2998 3047 Л9 -= Ле = 0,1936 9005
х^ = — JC7 -= 0,1013 2627 Ли = Лу = 0,2019 5830
/г= 15
Л = 5 = 0,0073 5294 12
х^^ = — ;^, =. 0,9731 3217 Л15 = v4i = 0,0449 2195 О
Ли -= — Л2 - 0,9108 8001 Лн = Л == 0,0791 9826 3
Л1з=- — лз = 0,8156 9624 Л1з = Лз = 0,1105 9290
х^2 = — л:, ^ 0,6910 2899 Л12 == Л4 = 0,1379 8776
л:,1-=—Лб = 0.5413 8540 Лц =-Л === 0,1603 9465
Лю = — Лб == 0,3721 7443 Л,о -= >1б == 0,1770 0426
Ле = — Л7 = 0,1895 1198 Лд =Л7=== 0,1872 1635
л^,=^0 Лй = 0Д906 6186
§ 3] ИНТЕГРАЛЫ СО ЗНАКОПЕРЕМЕННОЙ ВЕСОВОЙ ФУНКЦИЕЙ 183
§ 3. Замечание о вычислении интегралов со знакопеременной
весовой функцией
Построение квадратурных формул с заданными узлами тесно
связано с задачей о приведении знакопеременной весовой функции
к весовой функции постоянного знака. Возьмем интеграл вида
b
I p{x)f(x)dx (9,3.1)
а
и будем считать, что р(х) изменяет знак на отрезке интегрирования.
Предположим, что внутри [а, Ь] р (х) имеет конечное число точек
перемены знака*): aj, а^, .... а^. Построим многочлен Р{х)
степени < т, интерполирующий / по ее значениям в точках а^:
P{a{)^f{a{} (/=1. 2. ..,, m).
т
/=.1
(9.3.2)
Остаток интерполирования г (x) представим в форме (см. C.2.9)):
г{х)^{Х'~а{),. ,(x — a,^)f(a^ а,^. х) = 9.(х)/(а^, . , .. а^. л:).
где /(^1, .... а^, х) есть разностное отношение, составленное для
узлов aj, . . ., а^, х.
Интеграл (9.3.1) может быть разложен на два слагаемых
следующего вида
Ь b д
\ pf dx:=^ \ pPdx~\- г pQf(a^, . . ., а^, x)dx^=
й а а
т Ь
' =yja^/(a;)-f I p(x)/(ai, ..., а,,,. x)dx. (9.3.3;
b
Р^^\х-аЛ'(а,)<'^- (^-З-^)
Для нас особый интерес представляет последний из интегралов
в (9.3.3). Функция р(х) = jE7(a:)Q(x), входящая в него, будет
сохранять знак на [а, Ь], так как точки а^ (/=1, . . ., т) будут точками
*) На каждом из отрезков [а. а^], [а^, аз], ..., [йщ^ Ц р{х) сохраняет
знак и имеет противоположные знаки на смежных отрезках.
184 КВАДРАТУРНЫЕ ФОРМУЛЫ с НАПЕРЕД ЗАДАННЫМИ УЗЛАМИ [ГЛ. 9
перемены знака для каждого из множителей р ц Q. Примем р за
новую весовую функцию. К вычислению интеграла
b
a
может быть применен любой из методов вычисления интегралов со
знакопостоянным весом. В частности для этого могут быть взяты
квадратурные формулы наивысшей алгебраической степени точности.
Как и в предыдущих параграфах, обозначим через П^ (х) многочлен
степени п из ортогональной системы, принадлежащей весу p=pQ.
Рассмотрим квадратурную формулу с п узлами» верную для
многочленов степени 2п—1;
Ь п
Jp/(ai. .... а^. x)dx^^^J(a^, .... а^. дга), (9.3.5)
а А-1
П^ (лгд) = 0 (^ = 1, ..., rt). (i)(x)^(x~x^) ... (х — х„)>
Для первоначального интеграла (9.3.1) мы получим тогда следующее
правило приближенного вычисления:
Ь т п
j Pix)f(x)dx^^aj(a^)^^pj(a, а„. х^). (9.3.6)
а 1=1 k = l
Легко выяснить, что алгебраическая степень точности полученного
равенства равна 2п~^ т—1,
Пусть, в самом деле. / — произвольный многочлен степени
^2п~\-т—1. Равенство (9.3.3) есть тождество и выполняется при
всякой функции /, для которой имеют смысл все члены, входящие
в это равенство. Для / разностное отношение / (а^, .... а,^. х) будет
многочленом, степень которого на т единиц меньше степени / и не
превзойдет 2п—1. Так как (9.3.5) имеет степень точности 2/г—1,
то для /(^j, .... а^^. х) оно будет выполняться точно, а вместе
с ним будет точно выполняться и (9.3.6). С другой стороны, если
в качестве / взять многочлен степени 2П'\~т: / = Q (х) co^ (х), то
для него (9.3.6) не может быть верным. Действительно, для f = Q(s:?
интерполирующий многочлен Р{х) обращается в тождественный нуль
и из равенства (9.3.2) следует / (^i. .... а^, x)^ii?{x). Все члены
правой части равенства (9.3.6) для / = Qco2 исчезают. Интеграл же,
§ 3] ИНТЕГРАЛЫ СО ЗНАКОПЕРЕМЕННОЙ ВЁСОВОЙ ФУНКЦИЕЙ 185
стоящий в левой части, будет положительным ввиду того, что
произведение pQ сохраняет знак на [а, Ь\\
Ь b
{ pf dx= ^ pQaS^dx > 0.
а а
Обратим сейчас внимание на величины / (а^, ..,, а^, л:^) и
зависимость их от /. Если корни Xjfe(^=l п) многочлена П„(л:),
являющиеся узлами квадратурной формулы (9.3.6), отличны от а^
(/^г= 1, .... т), то разностные отношения / (а^, . . ., а^, Xj^) будут
такими:
/(«1 «ш. ^*) = ^^^^^7^^^^- (9-3-7)
Тогда / (^1, ..., dfn' х) зависят только от следующих значений
функции /: /(х^), f{a{) (/= 1, . . ., /п).
Если в формулу (9.3.6) подставить вместо f{а^, ..., а^, х^^) их
значения (9.3.7), то будет ясно, что (9.3.6), после объединения
членов с одинаковыми значениями f {х^ и f {а^) преобразуется к виду
^9.1.4). При сделанном предположении об х^ формула (9.3.6) будет,
следовательно, частным случаем квадратурной формулы (9.1.4). узлы
которой а^, задаваемые заранее, располагаются в точках перемены
знака весовой функции р{х). Отметим попутно, что если узел Xj^
совпадает с каким-либо из узлов а^, то Q(x^) = 0 и равенство (9.3.7)
теряет смысл. Оно должно быть заменено таким:
ч f (Хи) — Р' {Xk)
которое получается из (9.3.7) при помощи правила Лопиталя.
Разностное отношение /(«j, .... а^, х^) здесь будет зависеть не только
от значений / (а^) (/ = 1. . . ., w), но и от значения производной /' (лг^).
В этом случае квадратурная формула (9.3.6) будет давать прибли-
b
женное выражение интеграла pf dx не только через значения функ-
а
Цйи /, НО через значения производной /' в узлах л:^, совпадающих
с точками перемены знака р (х).
Пусть, например. т==^\ и р {х) имеет только одну точку а^
перемены знака внутри [а, Ь\, Интерполирующий многочлен Р{х)
здесь будет величиной постоянной: Р{х)^=^ f{ax) и равенство (9.3.3)
имеет форму
b b b
^ pfdx^f{a{) \ pdx-\- ^ p{x){x — a{)f{ax, x)dx, (9.3.8)
a a a
186 КВАДРАТУРНЫЕ ФОРМУЛЫ С НАПЕРЕД ЗАДАННЫМИ УЗЛАМИ [ГЛ. 9
Если все Xf^ отличны от а^, то расчетная формула (9.3.6) будет
такой
а а й = 1
Если же один из узлов х^^у например Xj. совпадает с ai, то
расчетная формула изменится и примет следующий вид:
a a Ar = 2
Допустим, что нам нужно вычислить интеграл
1
г хе"" dx = 2е'^ = 0.735 76 . ..
-1
За весовую функцию р(х) примем множитель х: р(х)^=х.
Единственная точка перемены знака р (х) есть х = 0. Равенство (9,3.8)
для рассматриваемого интеграла будет:
111 1
\ xe^'dx^e^ ( xdx^ { x^fiO, x)dx= J x^/@. x)dx.
-1 -1 -1 -1
pX 1
/@, x) = i—-!-.
Для вычисления последнего интеграла применим квадратурную
формулу наивысшей алгебраической степени точности с двумя узлами.
Многочлен n2(jc) второй степени из ортогональной системы на [ — 1, 1)
по весу p(x) = jc2. как легко проверить, есть П2(х) = сC — 5л:^).
Корни его таковы:
x^^ — q. x^^q. q = ^^ ^ ОJ74 596 7.
Расчетная формула для интеграла будет
1
J JC^/@. x)dx^pj@. Xi) + p2/@> Х^У
Коэффициенты Pj и Рз должны быть одинаковы ввиду того, что
значения весовой функции р = л;2 распределены симметрично относи-
§ 4] УТОЧНЕНИЕ ПРАВИЛ ГАУССОВА ТИПА 187
тельно точки х^О, и могут быть найдены из условия
1
JxV@. -)dx^l[^ + ^]=f^^==^0J3536.
Этот результат меньше чем на 0.06% отличается от точного
значения.
§ 4. Уточнение правил гауссова типа
Правила интегрирования (9.1.4) с несколькими фиксированными
узлами могут быть применены к задаче об уточнении квадратурной
формулы гауссова вида и приводят к одному из возможных ее
решений, которое в отношении степени точности можно, по-видимому,
считать наилучшим.
Задача имеет следующий смысл. Пусть [а, д] ~ произвольный
конечный или бесконечный отрезок и р (х) — неотрицательная, не
эквивалентная нулю весовая функция, для которой имеют конечные
b
значения моменты любых степеней p{x)x^dx E = 0, 1. . . .).
а
Для р(х) может быть построена соответствующая ей система
ортонормальных многочленов Рт(х) (m = 0, 1, ...). Возьмем
многочлен степени т и рассмотрим связанную с ним квадратурную формулу
наивысшей алгебраической степени точности 2т—1
Ь т
J Pix)f(x)dx^^ Ajf(aj) [P^(aj) = Ol (9.4Л)
Допустим, что при помощи этого правила найдено приближенное
значение интеграла и оно оказалось либо недостаточно точным, либо
требующим проверки. Уточняющая и проверочная формулы должны
иметь степень точности не ниже 2т—1. В остальном выбор их,
принципиально говоря, произволен. При построении такого правила
естественно, с целью экономии вычислительного труда, использовать
значения /(fl^y). входящие в (9.4.1) и уже известные нам. К а.-
(У= 1 т) присоединим еще л узлов Xf^ (^==1, ,.., п),
отличных от Л/, и рассмотрим равенство
b т п
J p{x)f{x)dxi^y^ Cjfiaj)-^^ D,f{x,), (9.4.2)
a /-1 ft-fi
188 КВАДРАТУРНЫЕ ФОРМУЛЫ С НАПЕРЕД ЗАДАННЫМИ УЗЛАМИ [ГЛ.9
зависящее от т^2п параметров С •, D^, Xf^. Степень точности его
будем считать не меньшей 2т— 1.
Проверим сначала, что для того, чтобы оно было отличным от
(9.4.1). необходимо выполнение условия /г > w. Допустим
противоположное: п^т и покажем, что тогда (9.4.2) совпадает с (9.4.1).
Так как равенство точно для многочленов степени 2т—1, то оно
верно также для многочленов степени п~\-т—1 и будет
интерполяционным. Его коэффициенты поэтому должны иметь значения (9.1.7) —
(9.1.8).
Рассмотрим коэффициент D^, В его выражении (9.1.7) многочлен
Q{x) = {x — aj) .. . (л: — а^) мы можем заменить на P^iW» который
отличается от Q {х) только численным множителем, равным старшему
коэффициенту Р^{х)\
ь
а
Ввиду того, что 0(jc)*(jc — л^й)"^ есть целый многочлен степени
п—1 < т. а Р^{х) ортогонален ко всякому многочлену меньшей
степени, £>й = 0 (^=: 1, .... п). Следовательно, в правой части (9.4.2)
т
сохранится лишь сумма 2 С//(^/) и так как степень точности
равенства тогда будет равна 2т — 1, т.е. будет наивысшей при т
значениях функции /, то (9.4.2) должно совпадать с (9.4.1): Су = Лу.
Изберем наименьшее возможное значение для числа
дополнительных узлов х^\ n = m~j-\ и рассмотрим уточняющее правило вида
b т т + 1
J p(x)/(x)d^«2 С/(а^)+ 5] DJ{x,). (9.4.3)
Его З/п+2 параметра целесообразно избрать так, чтобы сделать
равенство точным для всяких алгебраических многочленов степени
3/n-f-l. Для достижения этого, как выяснилось выше, необходимо
выполнить условия:
1. Правило (9.4.3) должно быть интерполяционным: его
коэффициенты С J и Df^ должны иметь значения
b
a
b
Pu = [Pm (X,) CO' (X,)] -^ J p (X) P^ (X) -j^ dX.
a
@ {X) == (X — Xi) . . . (ЛГ — X„ + i).
§ 4] УТОЧНЕНИЕ ПРАВИЛ ГАУССОВА ТИПА 189
2. Должны выполняться условия ортогональности
о
{ pix)P^(x)(i)ix)x^dx = 0 (s = 0, 1, ..., т)', (9.4.4)
а
3. Корни Xfi многочлена co(x) должны быть простыми и
отличными от корней а J (У=1, .... т) многочлена Рт{х). Сюда, кроме
того, следует присоединить требование, чтобы л:^^ принадлежали
отрезку интегрирования [а, д]. Это условие не является
необходимым, но нарушение его сильно суживает область применения (9.4,3),
Покажем, что многочлен со(л:), удовлетворяющий условиям
ортогональности (9.4,4), в нашей задаче существует и определяется
единственным образом.
Будем искать со (л;) в форме разложения (})(х) = х*^'^^~\-pix"^-{-
-|-.. . +/7^+1- Если для упрощения записи обозначить ц^ =
b
= \ р(х) Pfn(x)x^dx и принять во внимание, что [1^ = 0 при
" а
г==0, 1, ..., т—1, так как P^(jc) ортогонален ко всякому
многочлену степени, меньшей w, и [^^пфО, условия (9.4.4) можно
записать в виде системы:
M'm+2 + Pll^m + l + Р2\'Чп = О'
f^2m+l + Pll^2m + • • • + Pm + ll^m = ^-
Из нее ввиду [х^ф О последовательно и однозначно находятся
Pi> *••' Рт+г- Пусть многочлен со (л:) и его корни Xj^(k=\, ...
..., m-f-1) найдены. Если для х^ выполняются условия пункта 3,
то по ним могут быть найдены коэффициенты Cj и D^ и построено
равенство (9.4.3),
Условием возможности построения уточняющего правила (9,4.3)
является, следовательно, выполнение требований пункта 3. Для
каких весов р(х) 'и при каких т они будут выполняться, удалось
выяснить лишь в частных случаях.
Для [а, д] = [—и I] и р(х) = A—л:2)«, —0,5 < а < 1,5. было
доказано*), что при всяких т корни многочлена со (л:) лежат
внутри **) отрезка [—1, 1] и разделяются корнями многочлена P^ix).
*) Szego G. [1]. Список литературы — в конце главы.
**) И. П. Мысовских сообщил, что могут быть построены примеры
нарушения условий пункта 3, а именно, для —1 < а < —0,5 при некоторых т
корни ш (х) разделяются корнями Р^ W. но Xf^ с наибольшим абсолютцым
значением могут выходить за границы отрезка [—1, I],
190 КВАДРАТУРНЫЕ ФОРМУЛЫ С НАПЕРЕД ЗАДАННЫМИ УЗЛАМИ [ГЛ.9
Для ПОСТОЯННОЙ весовой функции р(х)=1 и промежутка [—1, 1]
задача рассмотрена более подробно. Уточняемой формулой будет
правило Гаусса. Для уточняющей формулы (9.4.3) были вычислены*)
на 16 знаков узлы л:^ и коэффициенты Cj, D^ при /7^=1AL0.
Для якобиевых весовых функций р{х) = {1—x^Y, а = —0,5;
0,5, и р (л:) == 1/ ут:— уточняющие правила могут быть построены
в конечном виде**).
Ввиду недостатка места мы вынуждены ограничиться
перечислением указанных результатов и не рассматривать их подробно.
Литература
L о b а 11 о R., Lessen over de Integral-Rekening, 1852.
Марков A. A., Исчисление конечных разностей, гл. V, Mathesis, 1910,
Szego G., Ober gewisse orthogonale Polynome, die zu einer oszilli-
renden Belegungsfunktion gehoren, Math. Ann. 100, № 4 A934), 501—513.
M Ы с о в с к и X И. П., Один частный случай квадратурных формул,
содержащих заданные узлы, Изв. АН БССР, сер. физ.-матем. и техн. наук
№ 4 A964), 125—127.
К рои род А. С: 1) Об интегрировании с контролем точности, ДАН
СССР 154, №2 A964), 283—286; 2) Узлы и веса квадратурных формул, М.,
«Наука», 1964.
*) Кронрод А. С. [2].
*) Мысовских И. П. [1].
ГЛАВА 10
КВАДРАТУРНЫЕ ФОРМУЛЫ С РАВНЫМИ
КОЭФФИЦИЕНТАМИ
§ I. Нахождение узлов
Большое удобство квадратурных формул с равными
коэффициентами
ь п
\ p{x)f{x)dx^c,Y^f{x,) A0.1.1)
а k = \
при численных и, особенно, при графических расчетах, привлекло
к ним внимание многих ученых и побудило их заняться разработкой
теории этих форлГ^л.
Формула A0.1.1) содержит п-~\-\ параметров с^, Xj, ..,, х^ и
выбором их можно надеяться сделать равенство точным для
всевозможных многочленов степени <^п, или. что равносильно, для
степеней X от нулевой до х" включительно *).
Требование точного выполнения A0.1.1) для /^1 доставит
следующее уравнение
b
pdx = c^ - п,
а
откуда может быть найден коэффициент с^:
b
'"=т\р
dx. A0.1.2)
а
Если, кроме того, потребовать, чтобы A0.1.1) точно
выполнялось для / = л:, х^, ..., х^, то получим для нахождения узлов х^^
*) Квадратурные формулы с равными коэффициентами часто называют
формулами Чебышёва в связи с тем, что он впервые в общем случае
рассмотрел задачу о построении таких формул.
192 КВАДРАТУРНЫЕ ФОРМУЛЫ С РАВНЫЛ^И КОЭФФИЦИЕНТАМИ [ГЛ. Ю
следующую систему п уравнений
A0.1.3)
а
b
а
Введем многочлен 0(х) степени п, для которого узлы
квадратурной формулы Xi, ..., х^ будут корнями
(s>{x)^={x~x{){x — Х2) .. . {х — х^). A0.1.4)
Уравнения A0.1.3) позволяют весьма просто построить такой
многочлен. В самом деле, расположим оз(л:) по степеням х\
0(JC)==X« +^iJC«-l +^2-^"'^ + . . . +^;z' A0.1.5)
Коэффициенты А^, ..., А^^ будут известными элементарными
симметрическими функциями корней. С другой стороны, левые части
уравнений системы A0.1,3) есть суммы степеней корней Xf^:
Ч^А + ^1+ '"+< (^=1> 2. .... ^).
В правых же частях уравнений стоят значения'этих функций для
многочлена A0.1.4).
В алгебре многочленов хорошо известны соотношения между
элементарными симметрическими функциями Л^ (/= 1, .... п) и
функциями s^ (^=1, ..., п). Они даются следующими равенствами,
которые часто называют соотношениями Ньютона *)
51 + ^1 = 0,
52+Лг5г + 2Ло^0.
Sn + ^Л_1 + ^2Sn-2 Ч- . • • + «^« -= О-
A0.1.6)
''^) Логарифмическая производная от A0.1.4) приводит к следующему
равенству п
со' VI 1
i==l
Если 1 Jt: I > I ;^( |. то дробь __^
по отрицательным степеням х:
{X^XiY
может быть разложена в степенной ряд
v=0
v-V-t-1
§ 1] НАХОЖДЕНИЕ УЗЛОВ 193
Они позволяют последовательно найти все коэффициенты Л^
(/=1, ..., п) по известным значениям 5^ из A0.1.3). По Л^ может
быть построен многочлен со (л:). Определяя же его корни Xf^, мы
найдем узлы квадратурной формулы A0.1.1). По смыслу изучаемой
задачи, х^ должны быть различными, действительными и
принадлежать отрезку интегрирования. Возможность построения формулы
A0.1.1), верной для многочленов степени п, поэтому определяется
тем, что будут или не будут удовлетворять перечисленным
требованиям корни многочлена (о{х), коэффициенты Л^ которого найдены
указанным путем.
Можно построить другое простое выражение для многочлена
(ЮЛ.4), если воспользоваться несложными соображениями из теории
аналитических функций. Применим квадратурную формулу A0.1.1)
к дробной функции f{x)^= —^—, являющейся ядром интеграла Коши,
и рассмотрим остаток квадратуры:
«(т^)=|^^--.Ёт^^=1^--..
Найдем разложение остатка по степеням z"^ при z больших по
модулю. Возьмем для этой цели число р настолько большим, чтобы
Поэтому, если | .v | > | х/1 (/—!,.,., п), то будет верным приводимое ниже
разложение
П со у оо П
^ ^ (=1 ^^0 v=0 (=1
Умножив обе части последнего равенства на со (х) и заменив ш (х) его
представлением A0.1.5), придем к равенству
лл:^-1 + (п — 1) Aix'''^ +{п-~2) А^х''~'^ + • • • + Л„t =
оо
v = 0
Если сравнить здесь коэффициенты при х^~^, х^^^,.,,, то и получаются
соотношения Ньютона
51 + ^1=0.
52 +^iSi +2^2 — О,
S/1 + Л15„_1 + ... + лЛ„ = О,
194 КВАДРАТУРНЫЕ ФОРМУЛЫ с РАВНЫМИ КОЭФФИЦИЕНТАМИ [ГЛ. 10
отрезок интегрирования [а, Ь], а с ним и узлы х^^, лежали в круге
I 2: К р. Тогда при \z\> р
со
V-0
b
dx--
а v=0 « v=U
Здесь через [л^ обозначен момент порядка v весовой функции /?.
Аналогично
^ v = 0
оо
/?(^^)=-5]Ь^^=^. A0,1.7)
Мы считаем, что формула A0.1.1) является точной для всех
степеней X от нулевой до л:". Поэтому (см. A0.1.2) и A0.1.3))
M-v — ^rt^v^^^ (v = 0, 1, ..., п) п в последнем разложении первый
отличный от нуля член будет содержать — по крайней мере в
степени /1 + 2:
I ^^^^ dx— с —^-— — V ^^v — CnSy
, „ со (г) ^^ z""^'
Интегрирование по z и простые преобразования приведут к
равенству:
2 '^"'" ^^ ^-^ ^ p{x)\n{z-x)dx
w(^)ev=«+i v.v ^^^ й ^ A0.1.8)
в котором А есть некоторая постоянная величина.
по степеням —
v^^ z
v = /z + l
отличаться от 1 только степенями z, более низкими чем 2:"'^ ясно,
Так как разложение ехр V — —^ по степеням — будет
^^ VZ^ Z
§ 21 ЕДИНСТВЕННОСТЬ КВАДРАТУРНОЙ ФОРМУЛЫ 195
что, если разложить правую часть равенства A0.1.8) по степеням —
при больших I -г |. то целая часть такого разложения будет
совпадать с (o(z):
b
с~^ J Р{х) hUz-x)dx
о)B') = цел. ч. Л^ « . A0,1.9)
Постоянный множитель Л легко может быть найден, если
принять во внимание, что старший член в (i)(z) есть z^. Мы не станем
останавливаться на этом частном вопросе, так как множитель Л
не оказывает влияния на корни правой части A0,1.9).
Как говорилось выше, построить формулу A0.1.1), верную для
многочленов степени ^п, можно в том и только в том случае,
когда корни многочлена со B^) действительны, различны и
принадлежат отрезку [а, д] *).
Многочлен о)@), очевидно, вполне определяется весовой
функцией р(х) и представляет интерес выяснить, при каких р (х) и каких
^значениях п корни со(х) будут обладать указанными свойствами,
Решение этой задачи в общем случае, по-видимому, не известно.
Ниже будут рассмотрены два частных случая весовой функции р (х),
когда может быть получен исчерпывающий ответ.
§ 2. Единственность квадратурной формулы наивысшей
алгебраической степени точности с равными
коэффициентами
ческой степени точности, для весовой функции р (х) ~ —1 < ж < 1,
В главе 7, при рассмотрении квадратурных формул наивысшей алгебраи-
кой степени точности, для весовой функции /
была построена квадратурная формула G.3.2)
2* — 1 ,
,cos-^—л|
точная для многочленов степени < 2az — L Число узлов п может быть
любым. Весьма замечательно, что коэффициенты этой формулы одинаковы.
В связи с указанной формулой возникает следующий естественный
вопрос: существуют ли на [—1, 1] весовые функции р{х), отличные от
и такие, что соответствующие им квадратурные формулы
наивысшей алгебраической степени точности также будут иметь одинаковые
коэффициенты?
*) Интегрируемая функция / считается заданной только на [а, Ь],
* потому квадратурные формулы, узлы которых лежат вне [а, Ь], не
рассматриваются.
196 КВАДРАТУРНЫЕ ФОРМУЛЫ С РАВНЫМИ КОЭФФИЦИЕНТАМИ [ГЛ. 10
Отрицательный ответ в этой задаче впервые был дан К. А. Поссе и
после него Н. Я. Сониным.
Докажем сейчас более общую теорему, принадлежащую Я. Л. Герони-
Мусу, из которой теорема К. А. Поссе сразу следует.
Пусть на отрезке [—1, I] задана положительная почти везде весовая
функция р(х). Возьмем соответствующую ей систему ортогональных
многочленов щ (х) = jc'^ + f>n^^'^ + Ул-^'^"^ + ... (^ = О, 1, ...). Обозначим через
x^j^^ {k — \ п) корни ш^^ (х) и рассмотрим квадратурную формулу с
равными коэффициентами, узлы которой совпадают с х^Р
1 п
j p{x)f (X)dx^c^^f D"^). A0.2.1)
Теорема 1. Если для любого значения л = 1, 2, ... существует
постоянная с„, такая, что формула A0.2Л) будет точной для"^) / — 1,
/~л:, f — x^, то вес р(х) совпадает с весом Чебышёва -
Доказательство. Без ограничения общности можно считать
1
Ио
= { pdx^h
Требование, чтобы квадратурная формула давала точный результат для / = 1,
определяет множитель С;^;
1
p(x)dx^Cn-n,
-1
1
" п
Полагая в A0.2Л) последовательно / — ж и f^x^, придем к двум
следующим равенствам:
М,^ J pxdx^^^xf^^^^^ («^1,2,...),
-1 k~\
= -^(P«-^Y„) (n = 2,3,...).
Отсюда можно найти два первых коэффициента а>п{^)''
*) Точное выполнение равенства A0.2.1) для f ^ х'^ необходимо лишь
при л > 1.
§ 2] ЕДИНСТВЕННОСТЬ КВАДРАТУРНОЙ ФОРМУЛЫ 197
В § 1 главы 2 было показано, что между ортогональными многочленами
трех смежных номеров существует рекуррентное соотношение. Если его
записать для нормированных многочленов Рп{х), то оно имеет форму B.1.10).
Рассматриваемые нами многочлены со,^ (х) отличаются только численными
множителями от многочленов Р^ (х) тех же индексов. Если принять во
внимание, что старший член в сО] (х) имеет коэффициентом единицу, то
рекуррентное соотношение для щ (х) можно записать в такой форме
ХЩ (Х) ^ COi (Х) + «0. Х<^п (Х) =-<^n^lix) + ^п^п (Х) + ^rt«rt -1 (Х)
(л-=1,2, ...).
Зная prt и Yrt» можно найти коэффициенты а^ и Xf^. Действительно, сравнивая
между собой коэффициенты при х^^ в левой и правой частях последнего
равенства, найдем
Все а^ (л — О, 1, ,..) имеют одинаковое значение jiii. Его, для простоты,
обозначим через а: а^ = а (л = О, 1, ...).
Сравнение коэффициентов при х^"' в тех же равенствах дает:
Y/j=^Y/z-M +«лР« + ^л. >^-rt = Y/2-~Yrt + i — ct^Pn*
Простые вычисления дают следующие значения для Л^, при записи которых
была введена новая величина а:
^1 === Из — Hi = 0,5а2, Я„ = 0,5 [fig — Hi] = 0,25а2 (л = 2, 3, ...).
Таким образом, рекуррентные соотношения для многочленов оо^^ будут:
щ(х)~\, coj (х) = X — а,
х^п D = G);, + I (X) + асо^ {X) + 0.2-5а2со^ ^ j (х) (
. = 1,2....).} ^^°•^•^>
Вспомним теперь (см. гл. 2, § 3), что для многочленов Чебышёва первого
рода Г„ {х) ™ cos (л arccos л:) ~ 2^~^х^ + ■ • • рекуррентные соотношения
имеют форму:
Т^(х)^\, Т^(х)^х,
хТ,, (X) ^ 0,5Г„ + 1 (^) +0,5Г„_ , (X).
Приведем старший коэффициент в Т^^ (х) к единице и рассмотрим
многочлены Тп{х)^2~^'^^Тп(х), Tq^^Tq, Рекуррентные соотношения для Тп(х)
будут:
хТ^х) = Т^^, (х) + 0,25Тп^, (х).
Наконец, если аргумент х заменить на и ввести многочлены Т^(х) =
е= o«f^ 1 j ^ -YO для них получаются следующие рекуррентные соотно-
Шения:
7*(л:) —1, 7^1 (jtr) == л; — а,
(х-а) Т\ {X) = r;^j W + 0.25а2г;_1 {ху
198 КВАДРАТУРНЫЕ ФОРМУЛЫ с РАВНЫААИ КОЭФФИЦИЕНТАМИ [ГЛ. 10
Они совпадают с A0.2.2) и так как последние вполне определяют о^ {х)
(п = 0. 1, ...), то
.„ W = 7-; U) = о^Т„ (^) = ^ Г„ (^) (« = 1,2,...).
2/г 1
Корни многочленов 7"^^^) равны cos—^ л; (^ — I, 2 п). Они лежат
внутри отрезка [—1, 1] и расположены там всюду плотно. Отсюда следует,
что корни а^п(х) лежат на отрезке [а — о, а-\~о] и при этом всюду плотно.
С другой стороны, в гл. 2 было показано, что корни многочленов любой
ортогональной системы с положительной весовой функцией всегда лежат
внутри отрезка ортогональности. В теории ортогональных многочленов
известно также, что они расположены на отрезке ортогональности всюду
плотно *). Поэтому корни рассматриваемых многочленов со^ (х) принадлежат
[—1, 1] и образуют там всюду плотное множество.
Должно, следовательно, быть а = О, а = 1 и
щ(х)^То(х)^1 i^Sn{x)^2--''^^Tn{x) («-=1.2....).
Многочлены Тп(х) образуют на [—1, +1] ортогональную систему по весу
и для доказательства теоремы нам осталось только убедиться
в том, что ортогональные многочлены, в случае конечного отрезка
ортогональности, определяют соответствующую им весовую функцию, с точностью
до множителя и до значений на множестве точек меры нуль, однозначно.
В самом деле, пусть р (х) и р^ {х) —две весовые функции, относительно
которых многочлены щ(х) ортогональны на [—1, 1]. Умножая р(х) и р^ {х),
если это потребуется, на постоянные множители, можно считать, что
1 1 ♦
\ р dx ^ \ p^dx^^l. Ввиду ортогональности щ (х) и со/^ {х) (п > 0),
-1 -1
должно быть
1 1
/?со„ dx — 0, pidin dx ^0 (гг ~ 1, 2, ,.,).
-1 -1
Отсюда сразу же следует, что для разности р — pi =ф должны выполняться
равенства
f <f(i)ndx^Q (л==0, 1, ...).
*) Известна более точная теорема: если отрезок ортогональности
есть [—1, 1] а весовая функция р(х) суммируема, почти везде поло-
жительна, то предельная функция распределения нулей
ортогональных многочленов совпадает с функцией распределения Чебышёва
X
1 r_EL_
J. VTT^'
§3]
ИНТЕГРАЛЫ С ПОСТОЯННОЙ ВНСОВОЙ ФУНКЦИЕЙ
199
что равносильно
f (рх^
dx = o (rt = a 1. ...)•
Но, как известно*), система степеней х^{п~0, 1,.,.) полна в Z, и из
последних равенств вытекает, что функция (р = р — pi эквивалентна нулю.
§ 3. Интегралы с постоянной весовой функцией
Остановим теперь свое внимание на наиболее часто
встречающемся случае, когда весовая функция постоянна. Считая отрезок
интeгpи•poвaнilя приведенным к [—1, 1], рассмотрим квадратурную
формулу
j f(x)dx^c^^ /(Xfe).
A0.3.1)
k^i
^Coэффициeнты c^^ и узлы л:^ выберем так, чтобы она давала точный
результат для многочленов степени п. Коэффициент с^^ определится
из требования, чтобы A0.3.1) была точной для /=1 и будет иметь
значение с^^^^. Так как
X
1
x^dx:
1-(-1Г
k^l
к+\
система уравнен^ьй вида A0,1.3) для определения узлов Xi,
будет такой:
х„
S, ^^i+Ar^-f .
^2 ^^^^ ^1 * 1 "^2 "•'" '
S^ =^ Х^ -f - ^2 " •
^4 ^^^ -^l 1 -^2 * *
. -Ь^„-о,
1 2 ^
. +хз = о.
• ^-^4 5 '
^-^1+^2-+- ••• ^К--'
п + 1
А+1
A0.3.2)
Опадает численные значения сумм Sj^ степеней узлов jCj^(^= 1, . . ,, п)
от А~ 1 до к —п.
^ *) См., например, И. П. Натансон, Конструктивная теория функций,
"^• —Л., Гостехиздат, 1949, гл. III. § L
200
КВАДРАТУРНЫЕ ФОРМУЛЫ С РАВНЫЛ\И КОЭФФИЦИЕНТАМИ [ГЛ. 10
Коэффициенты многочлена ю {х) = {х — Xi) {х — Х2) . ■ ■ (х — х„)
должны быть найдены из системы A0.1.6), которая в
рассматриваемом случае имеет форму:
Л = 0,
Лз-О.
^+|Л+|А + бЛ-=.о.
Л-=о,
Все Ли нечетных номеров равны нулю и в многочлен со (л:) будут
входить либо только четные, либо только нечетные степени х:
Корни со(х), являющиеся узлами формулы A0.ЗЛ), располагаются
на отрезке [—1, 1] симметрично относительно точки х^==0. В
частности, если п есть число нечетное, то один из корней обязательно
равен нулю.
Попутно отметим следующий факт. Пусть п — число четное:
п == 2т. Соответствующие значения л:д. должны удовлетворять системе
хп^х^^+ ... +^;;-7ггг-
Ввиду же того, что /г-|-1 = 2/?г+1 есть число нечетное,
а Xj^ {k=^\, ..., п) расположены симметрично относительно л: =:^ О,
будет выполняться также равенство
гП+1
+ л:«+^+ ... +.^,';^^--0.
откуда вытекает, что формула A0.3.1) будет точной не только для
многочленов степени п, но также для многочленов степени /г-|-1.
Построим теперь формулы A0.3.1) для нескольких первых
значений п.
При п ^^ 1 многочлен со (л:) =:^ х и с^ = 2
1
^ fix) dx^ 2/@)
-1
§ 3] ИНТЕГРАЛЫ С ПОСТОЯННОЙ ВЕСОВОЙ ФУНКЦИЕЙ 201
Когда /1 = 2, коэффициент-^2 = 1 " система уравнений A0.3.3)
для определения Лр Лз есть
^1 = 0, |- + 2Л2 = 0. Л2=- —~.
0 (Х) ™ Х^ — -J .
Откуда
2
Пусть /г=:3. Гз = ^. Уравнения для Л^, Л2. Лд будут
Л1=::=0. 1+2^2== О. >1з===0'
а)(х):^хЗ— Y-^-
Узлы формулы, следовательно, таковы:
Xi = — у^, ;С2=-0. ^S^Y~
И
J/(x)«fA:«|-[/(-2~^) + /@) + /B"'^)]-
-1
При п = 4 имеем 6:4=^-2' и систему для А^:
Л,^0, 1+2Л2=-0. Лз = 0. 1 + |-Л2 + 4Л4 = 0.
Отсюда
А - ^ А -1~
@(х)-=х4-~-х2+^.
Корни 0(х) суть:
' к 3/5 ^ J/ 3>^5
^ |/ 31/5 ^ I' 31^5
202 КВАДРАТУРНЫЕ ФОРМУЛЫ с РАВНЫМИ КОЭФФИЦИЕНТАМИ [ГЛ. 10
Продолжая такие вычисления дальше, получим при
/г =г:г 5 (i) (х) = х^ — '^^ "'^ 72" *^'
/г = 6 (i)(x)^=x^ — x^^-i- ■jx'^ ~ Jog-.
7 7 5 , Н9 . 149
ft ^ 7 (i)(x) = x^ "-р-х^ + ^гр^^х^-
ЗбО -^ 6480 -^^
д__у cow-^x—-^-^r-h^x "ЗбО-^ + 22 400 ^'
При /г = 8 среди корней многочлена o)(jc) будут комплексные
числа и формула Чебышёва A0.3.1) с действительными узлами не
может быть построена.
Ниже приведена таблица абсцисс формулы A0.3.1)
f(x)dx^^[f{x,) + f(x,)^ ... 4-/(^.I
для п'^ 1AO, 9.
й=1 п^е
jci = о хе = '- JCi = 0,866 247
/г = 2 л:5 =- —^2 == 0.422 519
дгз == — xj = 0.577 350 Х4 = - Хз = 0.266 635
п=3 п=7
хз = — ж, = 0,707 107. ^2 =- О ;с7 ^ — ^1 = 0.883 862
/г -= 4 лгб ^ — jcg =- 0,529 657
JC4 = — л-1 = 0.794 654 ' j^:^ == — дгз =- 0.323 912
JC3 = — JC2 = 0,187 592 х^^О
^5 = — JCi = 0,832 497 ;С9 = — J^i -= 0,911 589
JC4 == ~ JC2 == 0,374 541 Х8 ^ — х^^ 0,601 019
-^3 = 0 х7^~-х^ = 0,528 762
,V6=-—JC4 ==0,167 905
-^5=0
Вычисление узлов было продолжено для нескольких значений л,
больших 9, но каждый раз оказывалось, что некоторые из корней т{х) были
комплексными и формула Чебышёва A0.3.1) не могла быть построена.
Однако в обш.ем виде вопрос о возможности или невозможности построения
формулы A0.3.1) для п> 9 оставался открытым до работ С. Н. Бернштейна,
в которых он путем остроумных оценок, относящихся к более общим
вопросам, показал, что построить формулу Чебышёва A0.3.1) для п > 9,
верную для многочленов степени п, невозможно. Ниже будут изложены
с некоторыми упрощениями его исследования.
Докажем предварительно несколько лемм.
ИНТЕГРАЛЫ С ПОСТОЯННОЙ ВЕСОВОЙ ФУНКЦИЕЙ
203
Лемма I. Пусть формула
1
^ f{x)dx^^Y^f{Xk)
-1 . ft«l
A0.3.4)
точна для всякого многочлена степени 2т — 1 при т < /г. Обозначим
через Im наибольший корень многочлена Лежандра Р^ (х) степени т.
Тогда, если считать узлы х^ перенумерованными в порядке возрастания,
будет Хп> ^
Доказательство. Положим
-^ ът
Многочлен —^ У имеет степень т — 1 и поэтому он наверное ортого-
•^— ът
налей на [—1» 1] к РтМ^ так что
1
Г f{x)dx=^0.
С другой стороны, степень / (х) равна 2т — 1 и для / (х) равенство A0.3,4)
должно быть точным. Стало быть
&-1
Многочлен / =
——г— имеет т различных корней и не все слагаемые
^ ът
последней суммы равны нулю. Среди них должны быть как положительные,
так и отрицательные. Но / (х) принимает положительные значения только
при X > 1т. Значит, найдется такой узел х^, что х^ > Im- А тогда и для
наибольшего узла должно быть х^ > 1тп-
В последующих рассуждениях многое будет основано на сличении A0.3.4)
с квадратурной гауссовой формулой наивысшей степени точности с т узлами
1 га
j /(x)dx^^AJ^
-1 (-1
Рт{Ъ)^0 (/ = !,..., т), Ai^
(l^f^lPUh)]
2*
A0.3.5)
Лемма 2. Если формула A0.3.4) верна для всяких многочленов
степени 2т ~~ 1, где т < п, то
Ат>~^ A0.3.6)
Доказательство. Пусть
РтМ
i^-lm)Pm{lm)\
204 КВАДРАТУРНЫЕ ФОРМУЛЫ с РАВНЫМИ КОЭФФИЦИЕНТАМИ [ГЛ. 10-
В точке 1т f принимает значение 1, в прочих же узлах li, i < т, /
обращается в нуль. Поэтому квадратурная сумма A0.3.5) для многочлена /
приведется к одному лишь слагаемому A^f (g^) — А^^.
Степень / равна 2т — 2 и обе формулы A0.3.4) и A0.3.5) должны для
f dx дать точное значение. Поэтому, наверное, будет
п
2 V^
Ввиду того, что / (Jt:) > о при всяких х, отсюда, в частности, вытекает
|/(-^J<^m. A0.3.7)
п
Как сразу же видно из написанного выражения для / (х), при ^ > g;„
/ есть возрастающая функция х и, ввиду х^ > 1т. будет / {х^) > f (Irn) — 1.
что, совместно с A0,3,7), доказывает утверждение леммы.
Чтобы оценить коэффициент ^^==-г YTfrP тТ Ф^Р^У^^Ь! A0.3.5),
V — ^mJrmiim)]
нам необходимо сейчас установить вспомогательные неравенства для g^
Лемма 3. При любом значении т для наибольшего корня 1^
многочлена Рщ (х) выполняется неравенство:
'-^'"< m(m\l)- A0-3-8)
Доказательство. Будем исходить из дифференциального
уравнения для Pfji (Х)
^ [(I - ^') Ki (^)] +'«(« +1) Р,п W = 0.
Если проинтегрировать обе части равенства в границах от |^^ до 1, то
получим
A - ll) Р'т {1т) = т(т+\)^Р^ (х) dx.
Разложим многочлен Р^^ (х), стоящий под знаком интеграла, по
степеням x — l,j^
^mW = >;^^^'7r^^-(^'»)
£-1
§ 3] ИНТЕГРАЛЫ С ПОСТОЯННОЙ ВЕСОВОЙ ФУНКЦИЕЙ 205
И выполним интегрирование
т
A - О Р'т {Im) = /«(«+ 1) 2 ^\7+"/)Г ''- (^^n)^
Между каждыми двумя соседними корнями 1р |y+i многочлена РщМ
лежит корень производной Р^ {х). Таких корней т — 1 штук и никаких
других корней Я^^ (х) ие имеет. Между ними будут лежать все т—2 корня
второй производной и т. д. и, вообще говоря, все корни производной P\^J (х)
любого порядка I находятся между |i и 1^^ и, стало быть, лежат слева
от 1^. Поэтому P^j^ A^) > О и все слагаемые суммы, стоящей в правой
части последнего равенства, положительны. Для получения оценки g^ с
нужной нам степенью точности, достаточно в сумме сохранить лишь два первых
члена и отбросить остальные. Если, кроме того, обе части сократить
предварительно на 1 — Ifji, то получим такое неравенство
A + 1т) ^т Aт) >т{т+ 1) [1 A - g^) Р^, (|^) +1 A " Imf Кп (Im)]-
Значение Р'тО>т) ^^^^<^^ находится из уравнения
(l-^^)P;-2^P;+m(m+l)P^ = 0,
для чего достаточно положить в нем х = |^:
* bra
Подстановка этого значения в неравенство и сокращение на Я^ (|^)
дает:
1 + Im > « (т + 1) [^ A -'ь«) +1 •-^^diziM].
Неравенство усилится, если во втором члене, стоящем в скобках,
знаменатель I -[- ?т заменить большей величиной 2:
Отсюда, обозначая для сокращения т(т-\-\)^^Х, получим:
Л^^ + 2C + Я)^,„ + 6-ЗЯ>0. A0.3.10)
Образуем уравнение
Лг24-2C + Л)г + 6 —ЗЯ = 0,
±/4Я2 + 9 —3 —Л
Z = ' .
к
Мы должны избрать положительное значение z. Если g^ удовлетворяет
неравенству A0.3,10), то Irn должно быть взято больше z
/4Я2 + 9 —3 —Л
206 КВАДРАТУРНЫЕ ФОРМУЛЫ С РАВНЫЛ\И КОЭФФИЦИЕНТАЛ\И [ГЛ. 10
Отбросим слагаемое 9 под знаком корня:
1 ^ „ . 3 , ^
§т > i — т — ' —;^т;пгтт' ^""^
Этим лемма 3 доказана.
Лемма 4. /7 ля значения производной Я,„ (g^) многочлена Лежа ид ра
Рщ W ^ наибольшем корне х = 1^^ выполняется неравенством
P'-ni^m) > Hlhj [' - 288 П;!"-2) <^ -И- ^^'^•'•"^
Доказательство. Установим сначала нужное соотношение между
корнем 1^ и Я^ A^). Воспользовавшись тейлоровой формулой с остатком
в виде интеграла, разложим Pmi-^) по степеням л' —1,„, ограничив себя
только тремя членами формулы:
Рш (•^) = Р'т Aт) (^~ln) + Y ^™ (^ (^ - 5т)Ч Y J ^m (О (Д^ - О
Положим здесь л:=1 и примем во внимание, что Рт{1)^= h
1
1 = К dm) О -im) + i- Р"ш (?т) A" Imf + j J ^^' (О d " О' dt. A0.3.
^dt
12)
r»W J
Рассмотрим /^^ (/). При доказательстве леммы 3 выяснилось, что все корни
Р^^ лежат левее g^^. Поэтому на отрезке [g^, 1] Р'^^(х) будет монотонной
возрастающей функцией и своего наибольшего значения достигнет при ж==1.
Величину Рщ{\) легко найти при помощи дифференциального уравнения
A - х') />; {X) -- 2хР'^ {X) + /.2 (т + 1) Р^^ (^) ^ О-
Положив здесь х~\, найдем Р^^^ A) — —i-—^—^-. Дифференцируем
уравнение:
{\^х^) Р^ {X) - 4^Я; (X) + (т + 2) {т - 1) я; (л:) ^ О
и вновь положим X ^ 1
р'' .п - (^+2)(т-1) / _ (m+2)(ffl + l)//^(A/?-l)
Дифференцируем вторично
A - х^) Р^> (х) - 6xPZ (X) + {т 4- 3) (т - 2) Р^ (х) = О
и опять подставим х =^ h
P^-(U-- (т+3){т^2) . _ {т + 3){т+2),..{т~~2) Г{т + 4)
"^гпУЧ— 5 ^пЛЧ— 48 '8Г(т—2)'
§ 3] ИНТЕГРАЛЫ С ПОСТОЯННОЙ ВЕСОВОЙ ФУНКЦИЕЙ 207
Заменив в A0.3.12) Р'^A^п) ее выражением A0.3.9) и P^^{t) найденным
наибольшим значением на Ц^. 1], придем к следующему неравенству:
^т(^т)К^ ЗД[^^ l_^g^J-t-48r(m —2) 3! ^
t 1
Отсюда, ввиду г^— <'о"» вытекает A0.3.11).
Теперь легко находится оценка для Л^ ■-
A-|^™Ж(М'
Заменим в знаменателе Р^ (g^) меньшей величиной, стоящей справа
в A0.3.11)
л ^ ^a-gm) Fi г(т + 4)
2A+Ы
Г Г(т + 4) 1-2
[^ 288Г(;;г~2)^^ ^"'Ч '
Достаточным будет более грубое неравенство, которое легко отсюда
получается. Am будем рассматривать для m >- 6. С увеличением т вели-
-чина Irti возрастает и, так как ge = 0,93246 ..., мы вправе считать 1-|-^т >
> 1,93. Заменим, кроме того, всюду 1—Jm большим числом —-—, .. ■
Оценим теперь выражение, стоящее в фигурных скобках
(т + 3) (т — 2) = m (т + 1) — 6 < ffz (т + 1),
(т + 2) (т — I) = т {т + \) — 2 < т (т + \),
Г(т + 4)
= (W + 3) (т + 2) (т + 1) m (т — 1) (т — 2) < т^ (т + \)\
Т{т — 2)
Г(т + 4) тЗ(т + 1)з Зз _ 29
288Г(т~2) ^ ёга; ^ ^ 288 тЗ(т + 1)з 32'
. 27 • 32^ 1 8,517 (\оч]'^\
^^ ^ 2^1,93-29^ * т(т + 1) ^ ^(^ + 1)* (^^-^-^о;
Теорема 2. Яр« п>10 я^ существует формулы вида A0.3.4), верной
для многочленов степени п.
Доказательство. Будем рассматривать те значения л, при которых
формула A0.3.4) существует. Предположим, что п есть число нечетное:
rt==2m —1. Так как /п = 0,5(л + 1) " m (т + 1) = 0^25 (л + 1) (л+ 3), для
А л 4-8,517 ^ ^
>im должно выполняться неравенство Л™ ~ ^—, ,^,—г-оТ- Ввиду леммы 2,
4 • 8 517 9
должно также быть -—, ' ' ', ^ > -— или п^ — 13,034д + 3 < О, п < 13.
(л + 1)(л + 3) л
Таким образом, при л>13 формула A0.3.4) не существует. Но при «=11
она также не существует, так как тогда т~6, Ле = 0,173..., ур = 0,1818
2
и неравенство -рр < Ле не выполняется.
Допустим теперь, что ч-исло узлов п четное. Тогда формула A0.3.4)
ДОлада быть точной для многочленов степени n-^l. Положим п-\-\ =^ 2т—1,
208 КВАДРАТУРНЫЕ ФОРМУЛЫ с РАВНЫМИ КОЭФФИЦИЕНТАМИ [ГЛ. ТО
т=^^Ц^. Ввиду A0.3.13) и A0.3.6), будем иметь ---i-MlZ_^ > 1^
^ [п ~\~ z) (л —{— 4) fi
откуда п<\\. Значит, при л > 10 формула A0.3.4) не существует. При
/2=10 она также не существует, так как неравенство Лб = 0,173...>
2
> ^j— = 0,2, очевидно, не верно.
Литература
Чебышёв П. Л., О квадратурах, Поли. собр. соч., т. 1П, Изд АН
СССР, 1948, 49—62.
Поссе К. А., Sur les quadratures. Nouv. Ann. de Math. 26 A875^
49—62.
С о H и H H. Я., О приближенном вычислении определенных интегралов
и входящих при этом вычислении целых функций, Варшавские
университетские известия, 1887, 1—76.
Геронимус Я. Л., О формулах квадратур Гаусса и Чебышёва, ДАН
СССР 51 A946), 655—658.
Кузьмин Р. О., О распределении корней полиномов, связанных
с квадратурами Чебышёва, Изв. АН СССР A938), 427—444.
Геронимус Я. Л., Теория ортогональных многочленов, М. — Л., Гос-
техиздат, 1950.
Б ер и штейн С Н., 1) О формулах квадратур Котеса и Чебышёва,
2) Об одной системе неопределенных уравнений, Собр. соч. т. п',
стр. 200—204 и 236—242.
Salzer Н. е., Equally weighted quadrature formulas over semlinfinite
and infinite intervals, Journ. Math, and Phys. 34, № 1 A955), 54—63.
ГЛАВА 11
КВАДРАТУРЫ С НАИМЕНЬШЕЙ ОЦЕНКОЙ ОСТАТКА
§ 1. О задаче минимизации остатка квадратуры
В главе 6 мы ознакомились с квадратурами, имеющими наивысшую
алгебраическую степень точности. Можно было заранее предвидеть,
что такие квадратуры дадут малую погрешность, если интегрируемая
функция / допускает хорошее приближение ее многочленами
невысоких степеней, в частности, если / будет аналитической функцией
в достаточно широкой области около отрезка [а. д] интегрирования.
Многолетний опыт их применения показал, в широком классе
случаев, их превосходство в точности, сравнительно с другими видами
квадратурных формул.
Но эти формулы не являются универсальными и в вычислительной
практике известны случаи, когда они дают результаты худшие, чем
более элементарные формулы: прямоугольников, трапеций. Симпсона
и др. Это обычно происходит в тех случаях, когда функция / имеет
невысокий порядок дифференцируемости, или является аналитической
функцией, особые точки которой расположены близко к отрезку
интегрирования.
В теории квадратур возникла потребность построения формул,
которые были бы приспособлены для вычисления интегралов от
функций, принадлежащих наперед заданному классу, особенно
принадлежащих классам низкого порядка дифференцируемости.
О задаче построения таких формул говорилось в § 1 гл. 5 и мы
кратко напомним ее сейчас. Пусть дан класс функций {/} = F. Для
каждой функции f^F остаток квадратуры /?(/) имеет вполне
определенное численное значение
R(f) = j p(x)f(x)dx-"^A,f(x,). A1.1.1)
а k^l
210 КВАДРАТУРЫ с НАИМЕНЬШЕЙ ОЦЕНКОЙ ОСТАТКА [ГЛ. П
За величину, характеризуюш.ую точность квадратурной формулы
для всех без исключения функций класса F, может быть принято
число
/? = sup|/?(/)| = sup
/ /
\ pf dx— Y^AJiXk)
A1.1.2)
Оно зависит от х^ и А^ и нужно воспользоваться всеми имеющимися
возможностями выбора узлов и коэффициентов для того, чтобы
придать R возможно малое значение. Мы станем на крайнюю точку
зрения и будем стремиться к тому, чтобы придать R наименьшее
значение. На выбор Х}^ и А^, обычно, налагаются некоторые
ограничительные условия. Виды условий могут быть весьма разнообразными,
в частности они связаны с выбором класса F функций / и могут
зависеть также от способа задания этих функций. Ниже приведены
два примера таких условий,
L Если функции / заданы таблично на некоторой системе точек,
то мы будем сильно стеснены в выборе узлов х^ и должны считать,
что х^ берутся только из числа табличных значений аргумента.
2, Пусть мы хотим построить квадратурную формулу, ймеюш,ую
наименьшую оценку остатка для всех функций с непрерывной
производной порядка г, удовлетворяюпхей условию l/'^^] <; А1;-. Чтобы
можно было выполнить оценку остатка для таких функций, мы
должны считать, что квадратурная формула верна для всевозможных
многочленов степени <^г—1. Последнее равносильно выполнению
следующих г равенств:
п Ь
^А^х\= [ рхЫх (/ = 0. 1, . . ., г— 1). A1.1.3)
В границах главы 11 отрезок интегрирования мы будем предполагать
конечным. Этого достаточно для частных задач, рассматриваемых
ниже. Линейным преобразованием [а, Ь] всегда можно свести к
отрезку [О, I]. Такое преобразование мы будем считать выполненным.
§ 2, Минимизация остатка в классах L^p
Условимся говорить, что / принадлежит классу Lq (<7 > !)• ^^ли /
имеет на [О, 1] абсолютно непрерывную производную порядка г—1
и производная порядка г суммируема со степенью q на [0,1].
Всякая функция/^Lg* может быть представлена в форме
fix)J^q^.^ + \ f\t)Ei.-f)^^^dt, A1.2.1)
f=0 о
§21
ДШНИМИЗАЦИЯ ОСТАТКА В КЛАССАХ /JJ'
211
где /^^Ч^) ^^^^ числа и f^\t) — некоторая измеримая и суммируемая
на [О, 1] со степенью q функция. Верно и обратное: при любых
числах /'ЧО) и любой /^^{t)^L^, функция /. определенная
равенством A1.2.1). принадлежит Lg^.
Будем рассматривать интеграл p(x)f(x)dx, где f ^L^gK В бли-
и
жайших рассуждениях нам достаточно считать весовую функцию р(л:)
измеримой и суммируемой на [О, 1].
Пусть для приближенного вычисления интеграла была взята
некоторая квадратурная сумма
j pfdx^ ^Aj,f(Xf,).
A1.2.2)
й-1
Желая получить формулу, которую можно было бы считать
«наилучшей» для всех функций f ^ L^P G^1)» ^^Ь1 примем, что равенство
'A1.2.2) является точным для всевозможных многочленов степени < г.
Если воспользоваться представлением A1.2.1) функций класса Ц\
то остаток R(f) квадратуры можно привести к виду:
R(f)-= jpfdx^ ^AJ{x,)=j f\t)Kit)dt. A1.2.3)
о fe-i о
f<@=lp(^)%Z!{)i Ч^- |;^,£U,-0^7,I?),"' ■ A1.2.4)
*-l
Рассмотрим теперь множество F=^[f] функций /,
удовлетворяющих условию
||/"|%/Г<Ж,. q>\.
Согласно неравенству Гёльдера, для /?(/) в классе F имеет место
оценка
1 1 1
\1^ф\<\
JI/
■(Г) \Я
dt
Lo
G + i=')'
</mJ
\\Kf
dt
212 КВАДРАТУРЫ с НАИМЕНЬШЕЙ ОЦЕНКОЙ ОСТАТКА [ГЛ, [{
1
функция / ^ (О = ^1,
я р_
\K{t) I ^ sign К принадлежит
множеству F и, как легко видеть, для нее в полученном неравенстве
имеет место знак равенства. Поэтому правая часть неравенства будет
точной верхней границей | R (/) | на множестве F\
R^sup\R(f)\ = M/<^\K{t)fdt\ . A1.2.5)
U 1
F
От выбора х^ и Ajj здесь зависит только Г \K{t)fdt. Нашей целью
о
1
наи-
будет так выбрать Xf^ и Af^, чтобы интеграл \К f dt имел
о
меньшее значение. Если такие х^ и Лд, существуют, то они будут
доставлять наименьшее значение R при всяких А!,, и соответствующую
им квадратурную формулу можно считать «наилучшей» во всем
классе*) L^p.
Задача минимизации Г | /С |^6f^ может быть истолкована как задача
о
наилучшего приближения в метрике £„ (см. гл. 4, § 1) функции
q(x) /^__ 1ч( dx при помощи функций вида
t
'^A,Eix,~-t)
i^k-ty'
(^-1I
При произвольных р(х), г п п такая задача в конечном виде не
может быть решена. Мы остановимся на некоторых частных случаях,
когда решение может быть найдено при помощи простых средств.
*=) R(f)z^ /^'') /(dt есть линейный функционал, заданный на множе-
ал] J IKl^i
стве /''^^ L^. Интеграле \K\^dt\ есть норма R {/) в пространстве Lg
(о
и поставленная задача, если высказать ее в терминах функционального
анализа, есть задача построения квадратурной формулы A1,2.2) с
наименьшей нормой остатка.
* 2) МИНИМИЗАЦИЯ ОСТАТКА В КЛАССАХ L^^^ ^13
Предварительно необходимо ознакомиться с некоторыми фактами
теории приближения функций. Пусть на отрезке [О, 1] задана
некоторая функция / ^ Lp, Рассмотрим, кроме того, функции (^^ ^ Lp
(^=1, 2, ..., п). Последние мы будем предполагать линейно
независимыми на [О, 1], понимая под этим, что равенство
1 1 П
0 U-1
р
возможно лишь в том случае, когда все а^^ равны нулю. Это равно-
п
сильно тому, что равенство 2 ^/^Фа(-^) = 0 может выполняться на
множестве точек, меры большей нуля, в том и только в том случае,
когда af^ = 0 (^=1, 2, ..., п),
п
Погрешность е приближения / линейной комбинацией 5= 2^ft9jfe
1
определяется равенством е^ == (/ — sfdx=L
о
Выясним условия, при которых е^ будет иметь наименьшее
значение. На основании известных теорем анализа бесконечно малых
можно утверждать, что для значений а^, доставляюш,их минимум /,
должны выполняться равенства
^=Р \ If-S Г'signify s)<^,dx==0 (/=1, 2, ...,д). A1.2.6)
о
Убедимся теперь в том, что, при выполнении условий A1.2.6), линейная
комбинация 5 действительно дает наилучшее приближение /. Возьмем
любую другую линейную комбинацию 5*= 2^1Фь' ^ь1 должны по-
казать. что / < /* = Г ( / — 5* f dx. Имеем
о
1 1
f==j\f~-sfdx=^j\f~^sr'[f^s]^\gnif^s)dx^
о о
1
=^j\f-sr'lf — (s-s*)-s*]sign(f-s)dx.
214 КВАДРАТУРЫ с НАИМЕНЬШЕЙ ОЦЕНКОЙ ОСТАТКА [ГЛ. И
Ввиду A1.2.6). будет
/ = I I / - 5 Г' [/ - s*\ Sign (/ -s)dx. A1.2.7)
О
Интеграл не может уменьшиться, если sign (/ — s) заменить на
sign(/~- 5*). Поэтому
1
l<j\f-sr'\f-s*\dx. A1.2.8)
О
Применим неравенство Гёльдера *)
\ Г V \ г р^ lEzl
/< j\f~s'fdx\ .n\f-sfdx\ =Гр1 р . A1.2.9)
L 1
Отсюда вытекает /р<^/*р и /^/*, что и требовалось.
Покажем, наконец, что линейная комбинация 5. доставляющая /
наименьшее значение, единственная. Нужно проверить, что из / = /*
следует а^^=:а*(^=1. 2, .... п). При / = 0 это очевидно, так как
из равенства /=:5 при почти всех х следует
*) См., например, И. П. Натансон. Теория функций вещественной
переменной, М—Л., Гостехиздат, 1950. гл. Vli, §6, стр. 174—175. Если
F^Lp и G^Lp, гяе 1 = 1, то произведение FG суммируемо и
справедливо неравенство
1 1
^ FGdx^l J \F\Pdx\ J j|G/^ !
(a)
Для дальнейшего изложения существенно отметить, что знак = может иметь
место в том и только в том случае, когда выполняются два условия'
\ F\P \G {'^
1) _J—! ==—_J—\ и 2) почти всюду на [О, 1] знаки F и G сов-
J \F\P dx f \G fdx
0 0
падают.
При применении (a) в основном тексте было принято F=^\f—s^\ и
G^\f^s\^'-K
^ 2] МИНИМИЗАЦИЯ ОСТАТКА Б КЛАССАХ L^J^ 215
Поэтому при почти всех X s =^ s* и. ввиду независимости ф^,, отсюда
вытекает ^j^ = ^^- Будем считать |/ — s\ величиной положительной
на множестве точек, меры большей нуля.
Равенство 1 ^= Г возможно, как видно из рассуждений, при
помощи которых было получено A1.2.9), если выполнены два условия:
1) при почти всех значениях х должно быть
\f-sr'[f-s'']s\gn(f-s) = \f-sr'\f-s*l A1.2.10)
что необходимо для того, чтобы при переходе от A1.2.7) к A1.2,8)
сохранился знак равенства; 2) в неравенстве Гёльдера, которое было
'применено при переходе от A1.2.8) к A1.2.9). должен быть верным
знак =. Условия этого указаны в сноске и применительно к
интегралу A1.2.8) они дают
1 1
Г if^sfdx J \f~s*fdx
0 о
1 1
почти всюду. Но так как /= \\/ — sfdx = r==^ \\f — $*fdx,
о о
то почти всюду должно быть
\f-s\^\f-s*\. A1.2.11)
Но I /—5|>0 на множестве положительной меры и из A1.2.10)
и A1.2.11) следует, что на множестве положительной меры
/ — 5 ^ / — 5* ИЛИ 5 = 5*.
что возможно, ввиду независимости ф^^, только в том случае, когда
a^ = al(k^l, 2, . . . , п).
Будем считать вес постоянным: р(х)^1 и рассмотрим
квадратурную формулу
1 п
}■■ j f(x)dx = "^AJ(x,) + Rif). A1.2.12)
I о л = 1
.. Предположим / абсолютно непрерывной и производную /\суь\-
|||йруемой со степенью д. Это соответствует случаю г=1. Формулу
ЁИ.2.12) мы будем считать точной без остатка /?(/), если /=1,
РТО налагает следующее условие на коэффициенты: ^Af^--^1. Остаток
216
КВАДРАТУРЫ С НАИМЕНЬШЕЙ ОЦЕНКОЙ ОСТАТКА
[ГЛ. И
R (/) в классе L^^^ имеет точную оценку
^ (о J о
п
dx\
^\
о
1
"^•^
.4]%v
"^•^ ^
^\
м
\ш.
%г ,
Г'
Рис. 3.
разрыва x^{k=l, 2,
Ядро остатка K{t) есть кусочно линейная функция со старшим
коэффициентом, равным —Ь для которой узлы х^ являются точками
разрыва. Скачок K{t) в узле х^ равен коэффициенту Л^. Если л:^
лежат внутри отрезка [О, 1], то на концах его t-^^ и ^=1 ядро
обращается в нуль. График
К (t) изображен на рис. 3.
Задача минимизации ин-
1
теграла ] \ К (t) |^ dt имеет
б
следующий геометрический
смысл: нужно определить,
при каком положении точек
п) и при каких величинах скачков
Afy(k=l, 2, ..., я), подчиненных ограничению 2Л;^=1, ордината
площади, заштрихованной на рис. 3, будет иметь наименьшее
среднее значение степени /?. Ответ легко предвидеть: минимум будет
достигнут тогда, когда площадь будет состоять из 2/г равных
треугольников.
2k 1
Узлы х^ должны быть расположены в точках х^ = —^—
(^=1. 2, ..., п). Коэффициенты А^ все должны быть одинаковы,
и так как сумма их равна 1, то Л^^ ^=^ — {k ^=^ \, 2 /г).
Указанное предвидение легко может быть подтверждено
вычислениями, на которых мы не будем останавливаться.
Соответствующая квадратурная формула имеет вид
1
п АЛ-
2/2
+ R{f)
A1.2.13)
и является хорошо известной формулой прямоугольников с
ординатами в средних точках, или формулой касательных. Остаток ее
в классе Z^^^ имеет оценку
1
R{f)\<My
2nY Р+\
l/in'-f. (i+j=.)-
§2]
МИНИМИЗАЦИЯ ОСТАТКА В КЛАССАХ l(J^
217
Положим теперь г = 2 н рассмотрим класс Lf^ функций с абсолютно
непрерывной первой производной и производной второго порядка,
суммируемой со степенью д.
Будем считать, что квадратурная сумма A1.2.12) дает точное
значение интеграла, когда / есть многочлен нулевой и первой степени.
Это накладывает два ограничения на выбор Af^ и л:^^:
1 . 1
^Л, = j \dx=^U ^Л^х^= ^ xdx = ~. A1.2.
И)
При выполнении A1.2.14), остаток /?(/) имеет в классе Ц
следующую точную оценку
\R(f)\<^2
■ ' 'K{t)\Pdt\ ,
I
AU
■■\\\rfdt\ ,
lo J
Kit):
(\-tr
^A,E(x,^t)(x,-~t).
\ A1.2.15)
Для дальнейшего полезно подсчитать значения ядра К (t) на участках
[0. Xi], [Xi, Х2]. . . ., [х,,, 1]:
-Y при 0<^<jci,
Kit) = {
a-ty
2
i\~ty
• ^ ^jfe(-^jfe —0 при л:/<^<х^ + 1.
при x„</<l;
^/
K{t) есть непрерывная функция t на [0. 1]. Первая производная К^ (t)
имеет разрывы первого рода в
точках Xf^ и величины скачков ^^ ^
/С'(^) определяются равенствами
К'{х,^гО)-К'(х,-0)=~А,. ^
A1.2.16)
На каждом из указанных
выше отрезков К (t) есть
квадратный многочлен со старшим членом О.б^^^ Примерный график К (О
изображен на рис. 4.
Обратимся к задаче минимизации интеграла
1
и= ^\K{t)\^t
о
Рис. 4.
218 КВАДРАТУРЫ с НАИМЕНЬШЕЙ ОЦЕНКОЙ ОСТАТКА [ГЛ. И
при уравнениях связи (i 1.2.14). Будем считать, что минимальное
значение и существует и к разысканию его может быть применено
обычное в анализе правило множителей Лагранжа. Найденные
результаты позже будут оправданы. Составим вспомогательную функцию
вычислим частные производные от нее по х^ и А^ и приравняем их
нулю:
|^==:-~Л,p|l/C(OГ'S@£(^r-O^M-Mi = 0. A1,2.17)
о
A1.2.18)
Здесь Ai считаются отличными от нуля, так как, в противоположном
случае, квадратурная сумма содержала бы меньше, чем п узлов.
Равенство A1.2.17) можно сократить на Л^:
K{t)\''-'S{t)dt = ^.
О
Придавая i значения 1. 2, ..., п, найдем
\\Kf''^ S{t)dt^^. г \К\^'^ S{t)dt^{) A1.2.19)
(/=^1, 2. . . ., ri^l).
Равенство A1.2.18) приводится, при помощи A1.2.17). к виду
о
откуда видно, что
J {Kf^ Sit)tdt==~^, Г \K\^'^S(t)tdt==:0 A1.2.20)
(i== К 2 п— 1).
§ 2] МИНИМИЗАЦИЯ ОСТАТКА В КЛАССАХ L^^^ 219
Из уравнений A1.2.19) и A1.2.20) вытекает, что на каждом из
отрезков [xir x^^l] (f=l. ..., п— 1) функция /С(О есть многочлен
второй степени со старшим членом 0,5/2, наименее отклоняющийся от
нуля в метрике Lp. Чтобы найти такой многочлен, рассмотрим
сначала отрезок [—1, 1] и будем искать на нем многочлен вида Т2(х)~
^=:=х'^ -^ тх-\~ г, наименее уклоняющийся от нуля:
+ 1
J \T2(x)\^dx = mln,
-1
Сразу же видно, что в таком многочлене т = 0. Действительно, если
заменить в интеграле л: на — л:, то найдем, что 7^2(—х) также будет
наименее отклоняться от нуля. Но такой многочлен может быть
только один: 7'2(х) = Г2(—х) и, следовательно, т=^0. Осталось
найти еще свободный член г. Для Т^ должны выполняться условия
+1 +1
j IT^f'^ slgnT^dx^O, I iT^f-^ xs\gnT2dx = 0. (II.2.21)
-1 -1
Второе из них есть тождество. Из первого же следует, что sign Гз
должен изменять знак внутри [—1, I]. Мы положим, поэтому, г == — Р,
0</<1, Т2{х) = х'^ — Р и перепишем первое условие в форме
— I (Р - хУ dx + j (л:2 - Pf dx = 0.
о I
Если положить X = /1/ л то можно привести его к виду
jr'-\t-ir^dt = ^lL}§^- A1.2.22)
1
Из этого уравнения должно быть найдено /. При возрастании /
от О до 1, левая часть его будет убывать от оо до О, и уравнение
будет иметь одно и только одно решение.
Чтобы перейти к отрезку [х^, Xi^^], введем координату его
середины Ui = •^^~г'-^^+' и обозначим через hi половину его длины
Л^ = —^JZj^. Тогда многочлен второй степени со старшим
членом 0,5^2, наименее отклоняющийся от нуля в метрике Lp на [х;, л:^^l],
каким является /С(/) на этом отрезке, запишется так
220 КВАДРАТУРЫ С НАИМЕНЬШЕЙ ОЦЕНКОЙ ОСТАТКА [ГЛ. 11
В точке ^ = Х; = а; — Л^ он принимает значение Д'(л:^) = 0.5Л^(l — /^).
Аналогично, если рассмотреть К (t) на участке [X;_i, х-^ и найти его
значение в точке t = JC/, то получим К (х/) = 0,5^/„i (l — /). Ввиду
непрерывности /С(О ^^^ значения должны совпадать. Откуда следует, что
^^_j =z fii(l^=^2 п). Общую величину всех h^ обозначим через h. Во
всех узлах Xi будет Л'(л:^)==0,5/г2 A —Р). Возьмем, наконец, отрезок
0-^ t ^ Х|. Здесь К (О = 0.5/^ и в точке t = х^ должно быть К{х^ =
= 0,5л:^ = 0,5^^ A—/2) и Х| =/г l/"!—/^. Наконец, рассмотрев ядро на
крайнем правом отрезке [x„, 1], для его длины мы получим следующее
значение: I—л:„ = /^У1—Р. Так как сумма длин всех участков
[О, Xj], [jCj, Х2], ..., lXf^> 1] равна 1, то должно быть
jCj^ == л:^ -f 2Д (У^ "' 1) = [/1 ~Я _^ 2 (^ — 1)] /г, A1.2.23)
Для вычисления коэффициентов Л^ можно воспользоваться
равенством A1.2.16). На отрезке Xj^t ^х^^^
^ЧА:г+1--0)-=Г(а, + /г-0)-= + /г.
Следовательно,
Л,. = 2/7 (/ = 2. 3, .... /г—1). A1.2.24)
Сходные вычисления в узлах х^ и х„ дадут
Л^==Л„ = A +/1'^^/'- A1.2.25)
Найдем еще значение интеграла | \K{t)Ydt. Имеем
о"
о о
х„
21
МИНИМИЗАЦИЯ ОСТАТКА В КЛАССАХ L<^^
221
Легко проверяется, что
J 2^ J 2^ B/7 + 1J^
1
< — а,-
dt
+1
2" J '
Г2 (X) 1" dx.
+ 1
+ 1
= 2A- Я)" -2р j \Т, 1"-' sign(Г2) х2 dx
-1
Если под знаком последнего интеграла заменим л:^ на х^ ~ Р -^ Р =
==Г2 + Я, то получим
/==2A ~-/2)^ - 2р/»- 2р/2 J |72|^'4ignr2^x.
-1
Но, как видно из A1.2.21), интеграл, стоящий в правой части
последнего равенства, равен нулю и. следовательно,
,_ 2A —/2)^
2/7 + 1 '
^\K{t)\^dt = h'''' ^^~^'^' '
Bр + 1)'2Р'
■(n^l)k'^-^ A-/У
B/7+1J^-
^/г^^+^A_/2)Р >^1"^^ + п-1 ^2р A-/У ^ ^^2.26)
B/?+1).2^-^ Bр + 1J^ ^
Остаток /?(/) формулы A1.2.12; с узлами A1.2.23) и коэффициентами
A1.2,24—25) будет иметь следующую оценку для функций f ^ L^P
^(/Ж^и^^!!^^:. ^^2-= J[/T[
2Y2P + I [о J
1
1^
A1.2.27)
Убедимся теперь в том, что найденные узлы Xi, и коэффициен-
''л А^ действительно дают наименьшее значение интегралу A1.2.26).
222 КВАДРАТУРЫ с НАИМЕНЬШЕЙ ОЦЕНКОЙ ОСТАТКА [ГЛ. 11
Пусть X* и Л1 —любые другие узлы и коэффициенты и K^'if)--
соответствующее им ядро остатка. Мы должны показать, что
г2р A-/Т
I
к* 1" dt > h"
Bр + \)-2Р
Действительно,
||ГГ.<-/(|)'« + |' \ \n'M,-\[fi^]'M =
lia каждом из отрезков [л:*, x*^j] ядро К* {t) есть некоторый
квадратичный многочлен со старшим членом 0,5Я. Заменим его на
многочлен с тем же старшим членом и наименее отклоняющимся от нуля
на [jc*, x*^J в метрике L . Если обозначить й^* = 0.5 (а:'! +л:*^^) и
/^* = 0,5 (a:*^j — х*у то такой многочлен будет Т^Л—-^—|.
После указанной замены, последнее равенство перейдет в неравенство
^;
*2/?tl . *ч2/7+1 я-1 /,«2^;з ^+^
^^1 л;
Знак равенства возможен только в том случае, когда на всех
отрезках Гх*, х*^Л /С* (О будет многочленом, наименее отклоняющимся
от нуля. Но тогда, как было выяснено выше, будет х*==х^^ и
^j^ = >lft. Интеграл, стоящий под знаком суммы, был вычислен раньше
в других обозначениях и имеет величину \ 4-\ ' ^^^'^^^У
I
о
i *2/? + 1 / »n2;? + 1 .. ^^^р л-1
B^+1J" ^B;;+1J3^
A1.2.28)
Если в сумме t/„=S (jc'^j — д:*)^''"^' фиксировать л:' и л:', то, как
функция от л;* ^"n-v '^^^ имеет наименьшее значение, когда все
§ 21 МИНИМИЗАЦИЯ ОСТАТКА В КЛАССАХ l(^> 223
частичные отрезки [л:*, -^^^i] будут равны между собой: jc^^j — ^] =
z=z^ т—. с достаточной степенью простоты в этом можно
убедиться путем индукции. Положим п = 3 и рассмотрим и.^=^
:^(Хз — x*)^^^^ + (x* — x'^f^'^\ Условие стационарности //3:
ди
2р
^ = Bр + 1) [(х; - х:у^ -- (х; ~ ху\ =
дх.
равносильно
и так как
2 1 Ч ^
2р-1
A1.2.29)
t^^^2p^lJp[(xl-x:y'-' + {xl-xiy'-^]>0.
то «3» "Р^ соблюдении A1.2.29). действительно имеет собственный
минимум.
Будем считать, что высказанное утверждение верно для суммы а^_^
у проверим его для и^:
Найдем минимум v как функции от x*_j. Из равенства
dv
дх
■■{2р+ 1)
я-1
Ы-1-
п — 2
2р
-К-~-^"-0
2р
= 0
следует, что отрезок [x*_i, х*] должен иметь такую же длину, что
н все предыдущие отрезки [л:*, ^:*^i]:
^а ^п^\— п-^2
A1.2.30)
Ввиду
V. при условии A1.2.30), имеет собственный минимум и,
следовательно. -^
224 КВАДРАТУРЫ с НАИМЕНЬШЕЙ ОЦЕНКОЙ ОСТАТКА [ГЛ. П
Заменив в A1.2.28) w„ ее наименьшим значением, получим такую
оценку
J \К'\ dt> B^+1J^ +Bр + 1J^"' (п-1У^^"=^'
A1.2.31)
Подобно предыдущему, при помощи простых теорем анализа можно
убедиться в том, что w достигает наименьшего значения при
1 "" 2(/1—/2 _|_„_1) У
и это значение есть
т1П'Ш = -
2^Bр+1)
Окончательно получаем неравенство
1 1
^ ' ^ 2^2/; +1) J ' '
Из рассуждений видно, что знак равенства здесь может иметь
место в том и только в том случае, когда х* и Л* будут совпадать
со значениями A1.2-23) -A1.2.25).
Дополним изложенное одним замечанием. Именно, покажем, что
п
квадратурная сумма 2 ^kf(^k) "ри п->со будет стремиться к зна-
1 п 1
ни
чению интеграла f dx: lim \.^к/(^к)^^ fdx, какова бы
была функция /, интегрируемая на [0. 1] в смысле Римана. Для
п
этого достаточно показать, что 2 ^kfi^k) ^^^^ риманова интеграль-
ная сумма, что равносильно выполнению неравенств
Л1+...+Л,_1<х,<Л1+.,.+Л, {k^\. 2 п).
Последние неравенства проверяются весьма легко, так как, если
в них подставить вместо х^ и Лд, найденные значения, мы получим
следующие очевидные неравенства:
A+/1-/2)^_^(у^1_/2 _^2(^-2))^<(]/1-/2 _^2(А:-1))^<
< A +/1^7^)/г +(/Г^7^+2 (^ ~ 1)) Л.
§ 3i МИНИМИЗАЦИЯ ОСТАТКА В КЛАССАХ Cj. 225
§ 3. Минимизация остатка в классах Сг
Выше (гл. 5, § 2) мы условились говорить, что функция /
принадлежит классу С^, если она имеет непрерывную производную
порядка г на [О, IJ. Характерное представление функций f^C^ дается
равенством
г-1
1
/(x)=5;-^-'+j/^'(of(--o^^EV^^- ^''-''^
i = 0
где /^^'@)— любые числа и f (t) — произвольная функция,
непрерывная на [О, 1].
Для построения квадратурной формулы
1 п
j f(x)dx^^AJ(x,), A1.3.2)
о fr = i
имеющей наименьшую оценку остатка в С^., мы должны считать, что
равенство A1.3.2) является точным для любого многочлена
степени < г. Тогда остаток A1.3.2) может быть представлен в
следующем виде:
1
/?(/)=] rit)K{t)dt, A1.3.3)
о
где
k = i
Рассмотрим множество F функций f^C^, удовлетворяющих условию
[/'^^1-^^г- ^^ ^ верна оценка
1
О
Можно легко убедиться в том, что правая часть неравенства есть
верхняя грань \R(f)\ на F. Для этого достаточно / взять такой,
чтобы всюду, кроме точек разрыва, f^\t)= Mj.sxgnK {t)^ Для нее
R{f)T=:M^ \\K{t)\dt. Эта функция не принадлежит F, так как f''^
о
может иметь разрывы первого рода, но ее, вместе с производными
ДО второго порядка включительно, всегда можно приблизить с любой
степенью точности в метрике L при помощи функции из F. Поэтому
226 КВАДРАТУРЫ с НАИМЕНЬШЕЙ ОЦЕНКОЙ ОСТАТКА [ГЛ. И
В неравенстве для \R(f)\ правая часть не может быть уменьшена
R = sup\Rit)\=M^ \\K(t)\dt. A1.3.4)
1
Мы должны так подобрать х^^ и Л^^, чтобы \К (t)\dt имел бы
о
наименьшее значение, при выполнении условий
п
Как и в предыдущем параграфе, мы остановимся только на двух
частных случаях задачи.
Положим г=1 и рассмотрим класс функций, непрерывно
дифференцируемых на [О, 1]. В этом случае мы должны требовать, чтобы
квадратурная формула давала точный результат для постоянной вели-
п
чины, что равносильно выполнению уравнения связи 2^ft=^*
Ядро к {t) имеет значение
п
График его изображен на рис. 3. Интеграл \\K(t)\dt численно
о
равен арифметическому значению площади, заштрихованной на рис. 3.
Наименьшее значение эта площадь будет, очевидно, иметь в том
случае, когда она будет состоять из 2п одинаковых треугольников.
Поэтому наименьшую оценку остатка на множестве F при
всяком Ml будет иметь формула касательных A1,2.13).
Минимальное значение указанной площади равно -j— и, стало быть,
остаток R(f) формулы A1.2.13) в классе Cj имеет оценку
|/?(/I<Л1,-^. I/'WI<^,.
Возьмем теперь класс дважды непрерывно дифференцируемых
функций и положим, в соответствии с этим, г = 2. Узлы и
коэффициенты должны быть подчинены двум условиям A1.2.14),
означающим, что квадратурная формула должна дать точный результат
для всякой линейной функции.
Ядро остатка К (t) указано в равенстве A1.2.15). Несколькими
строками ниже этого равенства приведены значения ядра на отрез-
§ 3] МИНИМИЗАЦИЯ ОСТАТКА В КЛАССАХ Сг 227
1
ках (Х;^. ^fe+i]' Считая, что минимум и^=^ \\К{t)\dt существует,
о
применим к его нахождению известные правила разыскания
экстремумов функции. Составим вспомогательную функцию
й приравняем нулю ее частные производные по узлам Xi и
коэффициентам Ai'.
-^ = —лЛ 5(/)£(л:^—Ouf^-bM/==0' S(О = sign/С (О, A1.3.6)
дЛ
1
'--=— \ S{t)E{Xi~t){Xi — t)dt-\-X^^X^Xi = 0 A1.3.7)
(/=^1, 2, , . ., /г).
Отсюда видно, что для каждого отрезка [лг^, x^+j] должно быть
J S{t)dt = 0, J tS(t)dt = 0 (/=:=!, 2, ..., Д—1).
Следовательно, на каждом отрезке [л:/, x^^i) ядро K{t) есть
многочлен второй степени со старшим членом 0,5^^, наименее
уклоняющийся от нуля в метрике L на [л:^., x^-^i].
В § 3 гл. 2 было доказано, что среди многочленов степени п со
старшим членом х" наименее отклоняться от нуля в метрике L на
г1Aлйг п Г \ ^ 17 f \ sin (п+1) arc cos^
I—1, +1] будет многочлен P„W-=-^^«W = 2^]^1~^ '
В частности, при д = 2 это будет многочлен Р2С-^) =-^^ ~ X• ^огда
от отрезка —1<!х<;-|"^ ^^^ перейдем к x^-^i-^Xi^^ при помощи
линейного преобразования t==ai-{~hiX, а^-=^^^^—^, hi = ^^'^^^'^^
и приведем после этого старший коэффициент к 0,5, то для К(t)
получим следующее представление _
/г? (t'-аЛ
Если исходить из этого представления ядра К (t) и повторить
рассуждения, проделанные по аналогичному вопросу в предыдущем
228 КВАДРАТУРЫ с НАИМЕНЬШЕЙ ОЦЕНКОЙ ОСТАТКА [ГЛ. 11
параграфе, то можно доказать справедливость перечисляемых ниже
утверждений.
1. Узлы и коэффициенты должны иметь значения
A^ = 2h (i^2. .... n~\). Л^==Л„^^^!^/г.
2. Указанные x^ и A^ действительно доставляют наименьшее
1
значение интегралу \K{t)\dt и такие значения являются един-
о
ственными.
3. Остаток R(f) квадратурной формулы при указанных Xi
и Ai имеет в классе Cg оценку
\Rif)\<M^\, 1ГКМ2.
п
4. Квадратурная сумма 2 ^kf i^k) ^сть сумма Римана и для
всякой интегрируемой на [О, 1] в смысле Римана функции будет
lim y^AJiXf,)^ { fdx.
л -> оо f^ *l
§ 4. Задача минимизации оценки остатка квадратуры
с закрепленными узлами
Перейдем сейчас к изучению задачи построения квадратурной
формулы с заданными узлами и с минимальной оценкой остатка.
Рассмотрим наиболее часто встречающийся в приложениях случай
равноотстоящих узлов и постоянной весовой функции. Будем считать,
что отрезок интегрирования [О, 1] разделен на п равных частей
п
в квадратурной формуле
Г
^ fix)dx^^Aj[±) A1.4.1)
О fe=0
можно распорядиться выбором п-\~ 1 коэффициентов Л^. Если
потребовать, чтобы равенство A1.4.1) было точным для всевозможных
многочленов степени п, то, как было выяснено в гл. 6,
коэффициенты Afj определяются вполне и A1.4.1) совпадает с интерполя-
§4]
ОЦЕНКА ОСТАТКА КВАДРАТУРЫ С ЗАКРЕПЛЕННЫМИ УЗЛАМИ
229
ЦЙОННОЙ формулой Ньютона ~ Котеса. Будем считать, что формула
A1.4.1) дает точный результат для многочленов степени г — 1 < «.
Это накладывает следующие ограничения на выбор А^^\
"^А.^и S^^^'=^7TT ^' =
1, 2.
г ~ 1). A1.4.2)
fe=0
k = i
Если производная порядка г — 1 от / есть абсолютная непрерывная
функция, то остаток квадратуры представим в форме
R{f)=\r'{t)K{t)dt,
K(t) =
г!
k = \
A1.4.3)
Среди ft -|- 1 чисел Af^ остаются произвольными n-f 1 — г и
выбором их нужно воспользоваться для уменьшения оценки
погрешности квадратуры.
Ниже будут рассмотрены два случая минимизации такой оценки.
Возьмем сначала функции класса Z^^* и выберем те из них, для
которых { Г I/^ 1*? б/л: > <^ ^1- Если считать, что квадратурная
формула будет точной в случае / = const и, следовательно, ее
коэффициенты удовлетворяют первому из условий A1.4.2), то для таких
функций будет верна следующая оценка остатка:
\R(f)\<[j\rfdx\ 'l\\Kfdx\ <MAj\Kfdx\ =
(о J [о J [о J
- sup i/?(/)(.
/
1 —.
От чисел Afi в оценке зависит лишь интеграл \K{t)\^dt и коэф-
0
фициенты Af^ нужно выбрать так, чтобы придать интегралу
наименьшее значение. Ядро остатка К (t) здесь имеет значение:
п
k^l
230
КВАДРАТУРЫ С НАИМЕНЬШЕЙ ОЦЕНКОЙ ОСТАТКА
оно является линейной функцией на каждом из отрезков
[ГЛ. U
-1
п
<
<t<
(j= 1, 2,
. ., я):
K{t) =
1_^__2л
k = i
В точках t = ~ (i==l, 2. ._, п—1) K(t) имеет разрыв
первого рода со скачком Д и предельные значения его на концах
отрезка [О, 1] равны Aq и —Л„.
Схематический график К (t) приведен на рис. 5,
Нам нужно определить» при каких величинах скачков Л;(/:^1,
2, ..., п—1) и граничных значениях Aq и —Лд. подчиненных
km/
Рис. 5.
ограничению 2А=^Ь ордината К (t) площади» заштрихованной на
рис. 5, будет иметь наименьшее среднее значение степени р.
Несложными вычислениями можно проверить, что это будет в том
случае, когда указанная площадь будет состоять из 2п равных
прямоугольных треугольников. Отсюда сразу же следует, что Ло = Л^ = ^—,
Л1 = Л2= ... =Л^^_|^^—. Разыскиваемая квадратурная формула
является хорошо известной формулой трапеций
j/(x)rf. = l[^/@L-/(-l)+...+/(^)+|/(i)]+/?(/)
и остаток ее /?(/) будет иметь оценку
!«(/)!<
Л1,
2п(р+\)Р
f }
[о
1^
§ 4] ОЦЕНКА ОСТАТКА КВАДРАТУРЫ С ЗАКРЕПЛЕННЫМИ УЗЛАМИ 231
Перейдем теперь к рассмотрению квадратурных формул с
наименьшей оценкой остатка в классах функций более высокого порядка
дифференцируемости и ограничимся исключительно случаем классов
l}p{r^2), когда задача определения коэффициентов А^ имеет
простое решение.
Будем считать квадратурную формулу точной для многочленов
степени < г, что равносильно выполнению равенств A1.4.2). Остаток
представим в форме A1.4.3). На множестве 'функций /,
удовлетворяющих условию
2"
[о J
его оценка будет
12
R{f)<M,\\ K4t)dt\ =sup|/?(/)|
lo j f
1
От Af^ здесь зависит I ^= K'^{t)dt и, при принятом в настоящей
о
главе порядке идей, нашей задачей будет так выбрать Л^. чтобы
придать / наименьшее возможное значение. Это есть задача о
минимуме многочлена второй степени от А^ при линейных связях A1.4.2).
Интеграл / не зависит от Лд. Кроме того, Aq входит в первое
уравнение связи A1,4.2). При нахождении минимума / это уравнение мы
можем отбросить, так как оно не налагает никаких ограничений на
Лд (^= 1, 2, . . ., /г) и будет служить для вычисления Лд. когда
будут найдены все Л;^(^^1). Другие уравнения связи
Akk^=T^ ('=1' 2 г-\)
являются независимыми и могут быть решены относительно любых
/"—1 коэффициентов Л^, например, относительно А^, ..., A^^i,—
В интеграле / члены второй степени относительно Л^ получаются
при вычислении интеграла
^(^' ^«)=77^jfi^*^D-^)D-4
dt.
Квадратичная форма о{Ах Л„) является определенной
положительной, так как, очевидно, o{Ai Л„)^0, при этом равенство
232
КВАДРАТУРЫ С НАИМЕНЬШЕЙ ОЦЕНКОЙ ОСТАТКА
[ГЛ. 11
o(/lj Л^):=0 может выполняться только в том случае, когда
при всяких t ^[О, 1]
Е^^A-')(т-'Г=»-
fr-l
что возможно лишь прк условии Afi = 0 (^=1, 2 п).
Исходя из этого факта, путем обычных для алгебры рассуждений
можно показать, что задача о минимуме
= JK4t)
dt.
при соблюдении уравнений связи A1.4.2), имеет решение и такое
решение единственное. Если записать обычные условия экстремума /,
то получится система линейных уравнений для нахождения А^. Сард
и Меверс *) вычислили значения коэффициентов Af^ и интегралов
= J/C40
dt
для г = 2, /г:^1AJ0; /- = 3, п-==^2{\I2 и /- = 4, Аг-==2A)9.
Числа, найденные ими для формулы A1.4Л), приведены в помеш[ае-
мых ниже таблицах.
г--2
п
д
Лоб -^ Affi
Aib^An^id
Л26— Л„_2б
Лзб ==: Лл_з6
Л 46 = А^_^Ь
п'Ч
1
2
1
1
120
2
16
3
10
1
160
3
30
4
11
1
120
4
112
11
32
26
1
105
5
190
15
43
37
5
456
6
624
41
118
100
106
77
6 240
7
994
56
161
137
143
39
2 840
8
3 104
153
440
374
392
386
22
1455
9
4 770
209
601
511
535
529
7
424
*) Amer. Journ. Malh. 71, Нг I A949К
29, Ка 2 A950), 118-123.
80—91 и Journ. Matti. and t^hys.
41 ОЦЕНКА ОСТАТКА КВАДРАТУРЫ С ЗАКРЕПЛЕННЫМИ УЗЛАМИ 233
П родолжение
п
6
1 Лоб ^ АпЬ
А^Ь-Ап i6
Лб= Л~2б
Лз6= ^л-зб
^46=^^-46
Л6=Л-5б
Лб6=Л.б6
Луб^Лл-?^
пЧ
п
ь
Ло б = Л„6
А^ b^Af^^fi
Лз б == Л;,_2б
Ь4з б= Лл_зб
М4 б= Л„_4б
Ли 6= Л„_5б
Лб-= Л;,_еб
Лу 6= Л^^.уб
Лб= Л„_8б
^9б==Л„_9б
^10б= Л;,_10б
пЧ
L
10
14 480
571
1642
1395
1462
1444
1450
311
17 376
"
21758
780
2 243
1907
1997
1973
1979
763
39 560
16
1204 288
29 681
85352
72 566
75992
75074
75 320
75254
75 272
75266
2 468
94085
12
64 848
2 131
6128
5210
5456
5390
5408
5402
419
20 265
17
1747 906
40 545
116 593
99 127
103 807
102 553
102 889
102 799
102 823
102 817
170393
6169080
13
95 966
2 911
8 371
7 117
7 453
7 363
7 387
7 381
9 773
442 920
18
5 056272
110 771
318 538
270 820
283 606
280 180
281098
280 852
280 918
280 900
280906
162977
5 618 080
14
282 352
7 953
22 870
19 444
20 362
20116
20182
20 164
20170
28 381
1210 080
19
7 290718
151316
435 131
369 947
387 413
382 733
383 987
383 651
383 741
383 717
383 723
699 869
23 023 320
15
413 250
10 864
31241
26 561
27 815
27 479
27 569
27 545
27 551
8 213
330 600
20
^0 966 960
413 403
1 188 800
1010714
1058 432
1045646
1049 072
1048 154
1048 400
1048 334
1048 352
1048 346
8-331
262 087
234
КВАДРАТУРЫ С НАИМЕНЬШЕЙ ОЦЕНКОЙ ОСТАТКА
г-3
[ГЛ. 11
п
6
Аф = ЛпЬ
А^6^А„_^Ь
Л2б = ^;г-2б
А^Ь^Ап^з^
Л46 = Afj_^b
пЧ
п
6
А^б^АпЬ
А^6=Ап_уЬ
А2Ь=^Ап-2^
Лз6 = Л;г_зб
А,Ь^А,^_,6
Asb^An^s^
Лб6 = Л^_б6
пЧ
2
6
1
4
1
1890
3
24
3
9
11
8 960
9
4 700 880
186 016
643 081
457 051
549 131
515 161
662 807
584 998 400
4
240
21
76
46
11
12 600
5
1560
112
379
289
73
69 888
10
34 572 870
1230 777
4 259 404
3 016 564
3 656 464
3 358 804
3 528 844
507 029
4
135 618 1
62
2
б
930
55
192
132
172
И
10 850
7
607 152
30 927
106 573
76 573
89 503
134 081
124 899 840
и
2 789 581080
90 294 905
312 347 051
221544 971
267 523 241
247 986 521
255 093 851
3 062 211497
556 270 662 400
8
643 104
28 603
99 124
69 874
85 684
76 534
3 961
3 617 460
12
143 254 032
4250 217
14 705 148
10 423 398
12 607 228
11640 978
12 084 348
11831398
1028 343
835 648 520
п
6
Аоб = Л„6
^i6 = Ai-i6
А^Ь^ Ап-2^
Лз6 = Лл_з6
пЧ
2
6
1
4
1
9 072
3
24
3
9
13
17 920
4
28 992
2 349
9 932
4 430
6 557
36 529 920
5
432 840
29392
110 209
76 819
61633
193 912 320
6
19 740 084
1082 811
4 409 946
2 225043
4 304 484
210 047
921203 920
7
167 985 552
8 013 897
31412 443
18 665 443
25 900 993
56 097 271
207 342 167 040
§ 4] ОЦЕНКА ОСТАТКА КВАДРАТУРЫ С ЗАКРЕПЛЕННЫМИ УЗЛАМИ 235
Продолжение
п
6
Лз6=Лл_зб
8
12298 253 184
509110 987
2040010 996
1105 566 730
1867 200148
1254475462
2 876254 589
11621849258 880
9
291277 352 304
10 764 281184
42 647 140119 i
24 253 340 709
37 040 022 813
30 933 891327 1
18 892 720 083 ,
72 495 696 573 440 |
Литература
Никольский С. М., К вопросу об оценках приближений квадратур-
^ными формулами, Усп. матем. наук 5, вып. 2 A950), 165—177.
Sard А., Best approximate integration formulas, best approximation
formulas, Amer. Journ. Math, 71, № 1 A949), 80—91.
Me vers and Sard, Best approximate integration formulas, Journ. of
Math, and Physik 29, № 2 A950), 118—123,
Ш айда ев a Т. A., Наиболее точные квадратуры для некоторых
классов функций, Диссертация, Ленингр. гос. ун-т, 1954.
ГЛАВА 12
СХОДИМОСТЬ КВАДРАТУРНОГО ПРОЦЕССА
§ 1. О проблеме сходимости квадратурного процесса
В этой главе будет рассматриваться последовательность
квадратурных формул, число узлов п в которых может принимать все
целые значения /г=^1, 2, ... Такая последовательность определяется
двумя треугольными матрицами: матрицей узлов
Х =
и матрицей коэффициентов
xf> xf>
х\^^^ 4"*
xf
A2.1.1J
л(«)
A2.1.2)
Возьмем квадратурную формулу, соответствующую строкам
номера п этих матриц
b л
J p{x)f(x)dx = ^Af^f{4"^) + R„{f) = Q„if)-\-R^(f), A2.1.3)
И условимся говорить, что квадратурный процесс, определяемые!
матрицами X ц А, сходится для функции /, если
п b
limQ,(/) = lim Ул^Г*/иП== \ p{x)f{x)dx. A2.1.4)
§ 2] сходимость ИНТЕРПОЛЯЦИОННЫХ КВАДРАТУР 237
Сходимость или расходимость процесса зависит как от свойств
интегрируемой функции /, так и от выбора квадратурных формул,
и задача исследования сходимости в общем виде состоит в
выяснении таких связей между свойствами / и свойствами матриц X и А,
при которых можно быть уверенным в сходимости процесса.
Две основные проблемы теории сходимости могут быть
высказаны в следующих словах.
1. Заданы матрицы X и Л и нужно определить, для какого
класса F функций / можно гарантировать выполнение A2.1.4).
2. Задан класс F функций / и нужно определить, каким условиям
должны удовлетворять матрицы X и А, чтобы можно было
гарантировать сходимость квадратурного процесса для всех функций f ^ F.
В последующих параграфах будет рассмотрено решение каждой
из этих задач для некоторых частных случаев, имеющих
существенное значение в теории квадратур и их приложениях.
Мы ограничимся изучением сходимости для случая конечного
отрезка интегрирования и не будем затрагивать более трудную
проблему сходимости квадратурных формул для несобственных
интегралов с бесконечными пределами.
§ 2. Сходимость интерполяционных квадратур
для аналитических функций
Чтобы упростить доказательства теорем этого параграфа и при^
b
дать им общность, мы будем сейчас, вместо интеграла р(х) f (x)dx,
а
рассматривать интеграл Стилтьеса. Допустим, что на отрезке [а. д]
задана некоторая функция о(х) с ограниченным изменением и возьмем
b
интеграл Г f(x)do(x). Выберем на [а, д] п точек x^^^{k = 1 п)
а
И построим интерполяционную квадратурную формулу
b п
j fix)dG{x) = '^Ai'^f{xf)+Rnif), A2.2.1)
а k = l
•>■«=пU-rf>), л?.=1 (^_^-,;:i(^.,)«о(«).
Последовательность таких формул вполне определяется матрицей
узлов A2.1.1).
Замечательно, что можно указать эффективные и простые
признаки для суждения о сходимости интерполяционных квадратурных
238 сходимость КВАДРАТУРНОГО ПРОЦЕССА [ГЛ. 12
процессов для аналитических функций. Такие признаки могут быть
сформулированы при помощи функции, которая имеет смысл
предельной функций распределения узлов x^^^{k= \, . . ., п) при п~>оо.
Узлы х^^"^ предполагаются лежащими на отрезке [а, ^] и в
соответствии с этим мы определим функцию распределения только на
этом отрезке.
Представим себе, что единичная масса произвольным образом
распределена на [а, Ь]. Если х есть любая точка отрезка, не
совпадающая с правым концом х = Ь, то под значением функции ц (л:)
в точке X условимся понимать сумму всех масс, лежащих строго
левее точки х. В частности, так как левее точки а нет масс,
то р.(а)==0. Если же х^=Ь, то, по определению, считаем [г(^)=:1.
Функция \i{x) должна, очевидно, обладать следующими свойствами:
1. При jc = a ia(a) = 0.
2. р-(х) есть монотонная неубывающая функция х, непрерывная
слева в каждой точке внутри [а, Ь\.
3. При х = Ь \хф)=\.
Перечисленные свойства мы примем за определение и всякую
функцию р-(л:). обладающую этими свойствами, будем называть
функцией распределения на отрезке [а, Ь],
Пусть дана последовательность функций распределения V^ni^)
(д= 1, 2, . . .)- Условимся говорить, что \^f^{x) при п-^оо сходится в
основном к функции lot (л:), если Ц^ (х)-> |л (л;) во всякой точке
непрерывности*) \к{х). Возьмем теперь строку номера п матрицы Х:
xf\ х\^\ . . ., jct„").
Будем считать, что узлы х^^^ перенумерованы в порядке роста.
Припишем каждому из них массу» равную —. Этим взятой строке
матрицы X будет поставлена в соответствие функция
распределения |л,Дл:).
Если существует функция \Х'{х), обладающая перечисленными выше
свойствами, к которой в основном сходится последовательность р-^(л:):
!х„(л:)->оснв. \i{x), «—>со,
то la (х) будем называть предельной функцией распределения для
матрицы X.
Мы остановимся исключительно на том случае, когда такая
функция \Х'{х) существует**).
*) Заметим, что в точках х^= а и х — 6 выполняются равенства
ji^ (а) = ^ (а) = О и ^„ F) = ц F) = 1 и сходимость на концах отрезка [а, Ь]
имеет место всегда.
**) В силу известной теоремы о выборе для функций распределен^^я^,
от случая существования ц (х) легко можно перейти к случаю любой
матрицы X.
§ 2] СХОДИМОСТЬ ИНТЕРПОЛЯЦИОННЫХ КВАДРАТУР 239
Обозначим г„ (х) остаток интерполирования / по ее значениям
в узлах х(^«) (^=1, . . ., п):
^„w-/w-S (.-.п<D"') /D">)-/w-^„ W-
Остаток квадратуры A2.2.1) R^if) равен интегралу от остатка
интерполирования
ъ
Rn{f)-^\r^{x)do{xy
а
Сходимость квадратуры тесно связана со сходимостью
интерполирования, в частности, если r^{x)->Q при я-> со равномерно
относительно X ^ [а, Ь\, то и R^ (f)->0, г, е. будет сходиться и квадратурный
процесс. Исследование сходимости квадратурного процесса A2.2.1)
мы начнем с изучения сходимости интерполирования.
Будем считать, что функция f(z) является аналитической
функцией переменной z, регулярной в некоторой односвязной области В
^комплексной плоскости z, содержащей отрезок [а, Ь] действительной
оси внутри себя. Обозначим / произвольный замкнутый спрямляемый
контур, лежащий п В и такой, что [а. д] лежит внутри его.
Остаток интерполирования г„ (х) может быть представлен (см.
C.2.11)) в форме следующего контурного интеграла:
r,ix)=^ {^ni^IS^dz, A2.2.2)
где X есть любая точка, лежащая внутри /. Пусть \х(х) есть
предельная функция распределения узлов матрицы X. Для
исследования г^(х) при П'->оо большое значение имеет следующий
логарифмический потенциал
b
a{z) = j\n |^i^|rfn@- A2.2.3)
а
u(z) есть гармоническая функция, регулярная в комплексной
плоскости всюду, кроме бесконечно далекой точки и отрезка [а, Ь\, Когда
точка Z удаляется на бесконечность, и (z) будет стремиться к — оо.
Рассмотрим линии уровня
и (Z) = С.
Если С есть большое по абсолютной величине отрицательное
число, линия уровня будет содержать внутри себя отрезок
интегрирования [а, д] и будет «близкой» к окружности большого радиуса.
240 сходимость квадратурного процесса [ГЛ. 12
Назовем эту линию Iq и обозначим Bq часть плоскости, лежащую
внутри ее. При возрастании С множество Bq будет уменьшаться.
Введем число к, равное точной верхней границе значений С, при
которых [а, Ь\ лежит внутри Bq. При всяком С < А. линия уровня Iq
будет содержать [а, Ь\ внутри себя.
Рассмотрим также открытую область плоскости z, в которой
и {z) < ?v. Назовем ее х и дополнение к ней обозначим р.
Теорема 1. Если функция f {z) есть аналитическая функция,
регулярная в некоторой области ^, содержаи^ей внутри себя р, то
равномерно относительно х^р.
Доказательство. Так как р лежит внутри S, наверное
существует число С < h такое, что соответствующая ему область Вс 4~ Ic
также лежит внутри ^.
Возьмем произвольное число С между С и Я: С^ < С < X, Линия
уровня 1с" будет лежать внутри /с и будет содержать р, а
следовательно и [а, Ь], внутри себя.
Примем Ic за контур интегрирования в интегральном
представлении г^{х). Будем, кроме того, считать, что точка х лежит на Ic-
Если обозначить М наибольшее значение | /1 на /^ и 6 —
расстояние между Ic и 1с" , то будет верна оценка
'с
Рассмотрим отдельно |со^B:)(~ :
п
\<^ni^)\ ^ = ехр ^ In
г — v(«) I
/? =
Припишем, как выше, каждому узлу л:^'^^ (^ = 1 п) массу —
и введем соответствующую функцию распределения }!„ (х). Очевидно,
Г
1г(«) 1
и поэтому
I ^а (^) Г^ = ехр ^ J In J—71 ^'^^ (^)*
При п^оо ix^(^) будет сходиться в основном к предельной функции
распределения узлов \i{t). Точка z лежит вне [а, Ь\ и In-ггцТГ
§ 2] сходимость ИНТЕРПОЛЯЦИОННЫХ КВАДРАТУР 241
есть непрерывная функция t^[a, д]. Согласно известной теореме
о предельном переходе для интеграла Стилтьеса, которую часто
называют второй теоремой Хелли, будет верным следующее *)
b b
J ^^ \z~t\ ^^nit)^] J" 1^1.^1 d\x{t) = C\ n-^co.
a a
В интеграле величина z играет роль параметра и сходимость
будет равномерной относительно z ^Ic . Чтобы убедиться в
последнем, достаточно проследить за ходом обычных доказательств теоремы
Хелли. Существует, следовательно, такое п\ что при п "^ п^ и для
любых Z ^ Ic будут справедливы неравенства
b
с - 1 (С" -C'xj In j^^ ф„ (О <С' + ~ (С" - С).
а
Аналогично, при x^lc равномерно относительно х будет
I
b
^" \x — t\ ^^п(^)^ ] In у^-^ф@=С'\ П~^0О.
а а
Существует, стало быть, такое п^\ что при п> nf^ и при всяких
дг^/с выполняются неравенства
b
С" -1 (С" - С'Х J In j^^ сЦх„ it) <С" + \ (С" - С).
а
Взяв rtQ = max(/j', п^'), можно утверждать, что при /г > «о и любых
z^lc , X ^ 1с' будет иметь место оценка
Ь b
J *" jjzrtj "^^-^^^" J *" JF=rt\ "^^nit) < [^' + у (^'-^O] —
e a
Отсюда получается оценка для отношения ^\ [ :
*) в. и. г л и в е и к о. Интеграл Стилтьеса, ОНТИ, 1936, № 14. См. также
И- П. Натансон, Теория функций вещественной переменной, гл. 8, § 7,
"* — Л., Гостехиздат, где теорема Хелли доказана при предположениях,
немного отличных от требования сходимости Цл к ц в основном. Но легко
можно видеть, что это доказательство, с некоторыми изменениями,
переносится и на случай сходимости ц„ к ц в основном.
242 сходимость квадратурного процесса [ГЛ. 12
Для остатка интерполирования г„(х) получим
^^^^^^\<li^ ^ * /г>/го. x^lc". A2.2.4)
Здесь S — длина линии Ic .
Из A2.2.4) вытекает, что при п-> уэ г,Дх)->0 равномерно на Ic
Но, так как /"„(л:) есть аналитическая функция, регулярная в области
1с"-\-'Вс"> то равномерное стремление г„(л:) к нулю будет во всей
области 1с"~{-Вс'>- В частности, это будет верно и на множестве р,
лежащем внутри Ic-
Доказанная теорема об интерполировании позволяет высказать
соответствующую ей теорему о сходимости интерполяционного
квадратурного процесса.
Теорема 2. Пусть [а, Ь] есть конечный отрезок. Если f (х)
есть аналитическая функция, регулярная в некоторой области,
содержащей множество р внутри себя, то, при любой
функции а(х), интерполяционно квадратурный процесс, определяемый
равенством A2.2.1). сходится:
b
^nif)= [ r^{x)do{x)->0, п-^оо.
а
Остановимся на случае, когда предельная функция \i{x) соответствует
равномерному распределению единичной массы на [а, Ь]:
^^W=7^^' ^<x^b. A2.2.5)
К такой функции jli(a;) приводит, например, изучение сходимости
квадратурных процессов с равноотстоящими узлами, в частности,
квадратурных процессов Ньютона — Котеса.
Для облегчения записи будем считать отрезок [а, Ь]
приведенным к [О, 1].
\1{х)^=х.
Логарифмический потенциал A2.2.3) здесь будет
1
о
Так как
1 3
§2]
сходимость ИНТЕРПОЛЯЦИОННЫХ КВАДРАТУР
243
то
j(^)=r:Re{l —2:1п2: —A — 2:IпA ~ z)}
Линии уровня u(z) = C изображены на рис. 6. Множество р
состоит из линии уровня, проходящей через концы отрезка [О, 1] и
области, лежащей внутри ее.
Рис. 6.
Наибольший горизонтальный размер р равен единице, а
наибольший размер по вертикали — около 0,5 и получается он в сечении р
прямой x==0,5.
Из изложенного выше, в частности, видно, что наверное
гарантировать сходимость интерполяционного квадратурного процесса
Ньютона — Котеса, имеющего равноотстоящие узлы, можно только
в том случае, если интегрируемая функция / будет аналитической
функцией, регулярной в достаточно широкой области около отрезка [О, 1],
а именно в такой, чтобы она содержала внутри себя указанную
область р.
Рассмотрим еще два вопроса теории сходимости интерполяционных
квадратур, которые, в известном смысле, являются крайними случаями
доказанной выше теоремы.
Можно заранее предвидеть, что если / будет функцией, регулярной
в весьма широкой области около отрезка [а, Ь], то квадратурный процесс
будет наверное сходиться, как бы ни выбирать узлы х^^^ {k~0, 1, ..., п)
и какой бы ни была функция о (х). Попытаемся теперь определить
наименьшую область, в которой должна быть регулярной /, чтобы можно было
гарантировать сходимость процесса для любых х^^^ и при всяких о (х).
Изучим предварительно сходную проблему для интерполяционной задачи^
Опишем около точек а и Ь, как около центров, круги радиуса,
равного b—а, и обозначим к замкнутую область, являющуюся теоретико*
Множественной суммой двух таких кругов.
Теорема 3. Ecjiu аналитическая функция f (z) регулярна в областих,
^о, каковы бы ни были узлы интерполирования на [а, 6], будет иметь
244
сходимость КВАДРАТУРНОГО ПРОЦЕССА
1ГЛ. 12
^со, равномерно
место сходимость интерполирования L^ {х) -> / (х), п ■
относительно х^\а, Ь\
Область регулярности к является наименьшей, обеспечиваюи^ей
сходимость интерполирования при любой матрице узлов х^^\
Доказательство. Пусть х '^ t суть две любые точки отрезка [а, Ь]
и Z произвольная точка плоскости. Если z лежит вне х, то, очевидно, будет
' X — t I
< 1. Если же Z принадлежит области х, то наверное найдутся
t
такие д: и / на {а, Ь\, что будет
>1
Докажем первую часть теоремы. Так как / предполагается регулярной
в замкнутой области х, она будет регулярной и в некоторой более широкой
области. Поэтому наверное суш^ествует замкнутая линия I, содержащая х
внутри себя и такая, что / будет регулярна как на ней самой, так и всюду
внутри ее. Остаток интерполирования представим контурным интегралом
I
Ввиду того, что X и ji^^^ лежат на [а, ^] и г лежит на /, будет
выполняться неравенство
X— Х^
Лп)
< 1. Более того, наверное существует число
^ < 1, не зависящее от х, х^^^\йу Ь\ и z^U такое, что
Х— X
кп)
v-(«)
<R < 1.
Поэтому при всяких х^\а,Ь\ и z^l будет
интерполирования получится оценка
CD„(X)
««Н
^ q"-, и для остатка
r„WI<£maxJ-M£lL,,==^„,.
Отсюда следует, что а"п(.^)->0 при пнюо равномерно относительно х.
Убедимся теперь в том, что область регулярности х является
наименьшей и не может быть сужена. Для этого достаточно показать, что, какова бы
ни была точка а^х, всегда найдется такая функция /, регулярная в х, везде,
кроме точки а, и такая система узлов х^^^, что интерполяционный процесс
для / будет расходиться в некоторой точке х ^ [а, 6].
Пусть, в самом деле, а есть любая точка х. Мы вправе считать, что а
лежит вне [а, Ь\. Рассмотрим функцию / = . Она регулярна на всей
плоскости Z, кроме точки г = а. За контур / в интегральном представлении
остатка г^ (jc) примем линию, состоящую из окружности Г большого радиуса
с центром, например, в точке а, из малой окружности у около точки а
и из разреза, соединяющего Г и у-
Интегралы по сторонам разреза сократятся и мы получим
'nKx)~r^\^j—^. х^^Ц^ \^-—^-^^——
r+Y
^iz-x)
^ 2] СХОДИМОСТЬ ИНТЕРПОЛЯЦИОННЫХ КВАДРАТУР 245
Интеграл по Г равен нулю, ввиду того, что интегрируемая функция
имеет на бесконечности нуль выше второй кратности.
Интеграл по у берется в направлении по движению часовой стрелки и равен
вычету в точке а интегрируемой функции, умноженному на — 2яг
^-(т:^'4
<Q/zW
со„ (а) {X — а)
Так как а£>с, наверное существуют такие х я t, лежащие на [а, Ь], что
•^ \'^\. Фиксируем значение х и возьмем все узлы интерполирования
совпадающими с t. Интерполирование должно выполняться по значениям
у — и ее производных до порядка л — 1 в точке t. Интерполирующий
многочлен будет отрезком тейлорова ряда для около точки Д
Многочлен сод(г) равен оз^^ (г) — B — t)". Остаток интерполирования имеет значе-
ииег„(-^, х) = (^)"з^. Ввиду'-^-^
К> 1, г^ при п->оо не
a — t
будет стремиться к нулю и интерполирование функции в точке х
будет расходящимся.
Мы указали пример расходящегося эрмитовского интерполирования
с одним rt-кратным узлом. Но совершенно ясно, что если х^^^ (к=\ л)
выбрать весьма близко к ^ и считать, что при п->со узлы х^^^ достаточно
быстро будут приближаться к t, можно построить пример расходящегося
интерполяционного процесса с разными узлами. Вторая часть теоремы
доказана.
Из изложенного сразу же получается теорема о сходимости
квадратурного процесса.
Теорема 4. Если / есть аналитическая функция, регулярная в об-
ушсти %, интерполяционный квадратурный процесс, определяемый
равенством A2.2.1), сходится R^(f)-^0, л->со. каковы бы ни были узлы х^^^
и какова бы ни была функция о (х) с ограниченным изменением на [а, Ь].
Область регулярности ч есть наименьшая область, обеспечиваюи^ая
сходимость квадратурного процесса A2.2.1) при любых узлах х^^^ и
Произвольной функции а (х).
Доказательство. Если / регулярна в ч, то остаток
интерполирования ее при любых узлах х^^"^ стремится к нулю при л ~> оо равномерно
b
относительно х. Поэтому остаток квадратуры Rn (/) = г^ (х) do (х) также
будет при л ^- оо стремиться к нулю, какова бы ни была функция о {х)
с ограниченным изменением на [а, Ь].
Для доказательства второй части утверждения теоремы достаточно
Показать, что если из ч отбросить хотя бы одну точку, то найдутся такие
Функции / и сг и такие узлы х^^\ что R^ (/) не будет стремиться к нулю
Ари л->оэ.
246
сходимость КВАДРАТУРНОГО ПРОЦЕССА
[ГЛ. 12
Выберем функцию <у{х) кусочно постоянной, имеющей единственный
скачок величины 1 в некоторой точке х отрезка [а, Ь]. Тогда
Rn(f)^ j rrг(x)do{x)^rn(x),
Для такой а(х) сходимость квадратурного процесса равносильна
сходимости интерполирования в точке х. Но, как видно из доказательства
предыдущей теоремы, если из к удалить хоть одну точку а, то для
функции / = можно указать такую точку х и такие узлы х^^\ что г^ (х)
не будет стремиться к нулю при л->оо и квадратурный процесс,
следовательно, будет расходиться.
С целью упростить запись, будем считать, что отрезок
интегрирования [а, Ь] приведен к [—1, 1]. Функция распределения |li(x)
называется функцией Чебышёва, если
-/
^^-^-^\угЬж- ^''-'-'^
Плотность распределения р{х)==1х^{х)
изображена на рис. 7. Пусть матрица X имеет
предельную функцию распределения узлов
и эта функция есть A2.2.6). Так будет,
например, в том случае, когда за узлы
x^^\k= Ь . . ,, /г; /г== 1, 2, . . .)
принимаются корни системы многочленов,
ортогональных на отрезке [—1, 1] с любой
суммируемой почти везде положительной весовой функцией р {х). С таким
выбором узлов выше мы встречались при построении квадратурных
формул, имеющих наивысшую алгебраическую степень точности.
Рассмотрим логарифмический потенциал
Рис. 7.
u{z)--
■i\
In
1
dt
\z — t\ V^—t^
A2.2.7)
и (z) есть действительная часть функции комплексного переменного
1
F(^)=l fln-J—
я J г — t
dt
/1—^2
A2.2.8)
В комплексной плоскости z проведем разрез вдоль
действительной оси от точки 1 к — оо и выберем ту ветвь логарифма, для
g 2] СХОДИМОСТЬ ИНТЕРПОЛЯЦИОННЫХ КВАДРАТУР 247
которой Sirg{z —1) = 0 при действительных z, больших чем t.
^ ^ л J (г— 01^1 —
^2
Последний интеграл легко вычисляется путем нахождения
первообразной функции и имеет значение
F' (Z) = . ^ ,
^ ^ fz' — l
причем выбирается та ветвь корня, которая принимает
положительные значения при 2:> 1; тогда
F(z) = \n ^
Постоянная С находится из условия, что функция A2.2.8) при
больших Z имеет представление вида
F(z) = \n^-^^ + ^+ ....
Это дает С = 2 и окончательно
F (Z) = 1п ^ , u(z)^ In . ^ , . A2.2.9)
Линии уровня u{z)=:^C при с < In 2 будут замкнутыми линиями,
охватывающими отрезок [—I, 1]. При С:=!п2 линия уровня
совпадает с самим отрезком [—1, 1]. Множество р будет состоять только
из отрезка интегрирования [—1, 1]. Последнее дает возможность
высказать следуюндую теорему.
Теорема 5. Если матрица X имеет в качестве предельной
функции распределения узлов функцию Чебышёва A2.2.6), то:
1) соответствующий ей интерполяционный процесс сходится
для всякой функции, аналитической на [ — 1, -\~\] и при этом
равномерно относительно х^[—1, 1];
2) квадратурный процесс, определяемый равенством A2.2.1),
при {a,b]=i[—1, 1] сходится для любой функции f(х),
аналитической на [—1, 1], какова бы ни была функция а(х) с
ограниченным изменением на [—1, 1].
В связи с этим весьма интересно отметить, что верны теоремы, которые
могут быть названы обратными для только что установленной теоремы.
Докажем сейчас первую из таких теорем.
Теорема 6*). Если матрица X такова, что интерполирование по
узлам х^^^ (Л = 1 л; л = 1, 2, ...) сходится во всех точках отрезка
lQ9fi *) *-• '^ ^ * ^ ^ г, кг interpolaciorol. Mathematikai es physlkal lapok. 32,
ly^o, 120. где аналогичная теорема доказана для более общего утверждения.
248 сходимость квадратурного процесса [ГЛ. V2
1—\, 1] для всякой функции /, аналитической на [—1, 1], то для
матрицы X суи^ествует предельная функция распределения узлов и это
есть функция A2.2.6).
Для доказательства нам потребуется ознакомиться с некоторыми
свойствами логарифмического потенциала. Рассмотрим последовательность
функций распределения, отвечающих строкам матрицы X : ц^ (х), ^ij (-^) Г1о
теореме Хелли *), из нее всегда можно выбрать частичную
последовательность, сходящуюся в основном к некоторой функции распределения.
Последнюю мы обозначим \х {х). В дальнейшем будем считать, что индекс п
пробегает такую последовательность целых чисел, для которых fx„ (х) ->
-> в осн. [Л (Х).
X
Теорема будет доказана, если мы установим, что ц (х) = ~ -.
я J у \ ^2
Интеграл
при X, лежащем на отрезке [—1, 1], является несобственным и мы условимся
в следующем его понимании. Введем функцию 1Пд^ х, определив ее
равенствами
__ Г In X при In х<Л^,
^^^~'{ N при \пх> N.
Функция In„-j тт ограничена и непрерывна при t^[—\, I]. Инте-
1
грал 1Пд^ -j——jj d\i (t) есть неубывающая функция N, По определению
-1
полагаем
1 1
Лемма 1. Если \k(t) имеет в точке х^\—\, 1] производную, то
интеграл A2.2.10) в этой точке конечен.
Доказательство. Пусть х лежит внутри [—1, 1]. Считая Л^
большим, выделим около точки х отрезок х — б-<^^л:-|-^. где б — ^"' -
1
^W"" J ^" I д: — ^ I Ф (О =
^ lim
i -I x+6
*) B. И. г л и в e H к o. Интеграл Стилтьеса, М, — Л., ОНТИ, 1936,
№ 13.
§ 2] СХОДИМОСТЬ ИНТЕРПОЛЯЦИОННЫХ КВАДРАТУР 249
После интегрирования по частям в фигурных скобках, получим, если
принять во внимание, что In 6 = —TV, |.i(l)=l, \х(—1) = 0,
Г hW
-1 Л- + 6
1
= ^"t-^- + ГЛ. 3H. I -TLlLL. dt.
1
.3„. {Щ
Так как \i (t) в точке x имеет производную, гл. зн, | ^ ^ ^/^ существует
и имеет конечную величину.
Аналогично проверяется утверждение леммы в случае, когда точка х
лежит в каком-либо из концов отрезка [—1, 1].
Так кач производная \-i'{t) существует почти везде, интеграл A2.2.10)
имеет на [—1, 1] почти везде конечное значение.
Рассмотрим логарифмический потенциал «(г) = In-j —d\i{t).
Пусть X лежит на отрезке [—1, 1] и будем считать, что точка z~x-\-iy
приближается к j^: по вертикали.
Лемма 2. При любом значении х^[—1, 1J верно равенство
1
lim
|"П77^^И0= Jln-p^^W A2.2.11)
независимо от того, конечное или бесконечное значение имеет интеграл,
стоящий справа.
Доказательство. Выделим около х малый отрезок х — е<;^<л: + е
и обозначим £е часть [—1, 1], остающуюся после удаления из [—1, 1]
отрезка [х — е, х-{- е]. При малых значениях у для всяких t^[x — е, ^ 4" ^1
\2 —1\< 1. Тогда In-j тт'^^ " ^^^ ^^^ ^(^^ неубывающая функция, то
должно быть верным неравенство
В интеграле по Е^ допустим предельный переход при у->0 под знаком
интеграла. Если принять, кроме того, во вниманио, что In-j <
250 сходимость квадратурного процесса [ГЛ. 12
1
< In-j тт * после предельного перехода получим
1
1
-1 _1
1
Ноприе->0 \n-——j-d\i(t)-> 1П|-^----ттйг^1 (О независимо от того, конеч-
ное или бесконечное значение имеет последний интеграл. Поэтому
Ит inf и lim sup должны совпадать и иметь значение, одинаковое
у->0 J У->0 J
у->0 J^ у->0 _^
1
с In л—^—гг^^^СО-
1
-1
1
Перейдем к изучению и^ (х) — In -j—ZTfT ^^« ^^^' ^^""^ ^ ~ ''^i"^' "^^
-1
полагаем гг^ (,я^) = со.
Лемма 3. Почти везде на отрезке —1 < х < I
^rn^inf jluj^^^dixnit)^ ^\п ^^^^^ ф@. A2,2.12)
Доказательство, По определению функции 1п^л: верно неравенство
-1 -1
Предельный переход при п-^оо дает
Ввиду того, что полученное неравенство верно при всяких Л^, отсюда
следует
1
Ит inf
rt->oo
Jln^.,„@> jln^#@. A2.2.13)
§ 2] СХОДИМОСТЬ ИНТЕРПОЛЯЦИОННЫХ КВАДРАТУР 251
Найдем теперь оценку сверху величины, стоящей слева в A2.2.13).
Функция 1п-| rr^l^niO ограничена снизу числом In—- и при любых
-1
а, Р$[—Ь 1], ввиду теоремы Фату, верны неравенства:
Ит inf In-j jj d\Xn(t)dx^\im\ni dx \n-. --рф„@ =
a a -1
= lim inf ф« @ In -j rr '^-^•
-1 a
В последнем интеграле допустим предельный переход под знаком инте-
Р
грала, так как In-j тт^^ ^^^^ непрерывная функция t\
а
3 1. 13
lim inf In-i TT d\)^n{^) dx ^ d^U) In-i -rr dx.
a -1 -la
Функция in-j 7j ограничена снизу числом 1п-^и, на основании
теоремы Фубини, в правой части неравенства можно изменить порядок
интегрирования
3 1 3 1
J ^^^^ J ^"{д:-^| '^^'^ ^^^ "^-^ ^ J "^-^ J ^" |х-П "^^ ^^^*
а '^'^'^ -1 d -I
Неравенство верно при всяких а, р^[—1, 1]. Следовательно, почти
везде на —1 < д: < 1 должно быть
1 1
lin^i^f Jln-^i-—фЛО< /^"i^i^i Ф@ ... A2.2.13*)
Из сравнения A2.2.13) и A2.2.13*) сразу же вытекает утверждение
леммы 3.
Обозначим Е множество точек на [—1, 1], в которых выполняется
1
A2.2.11) и, кроме того, интеграл In ггФ@ конечен; £ отличается
^1^ отрезка [—1, 1] разве лишь на множество меры нуль.
Лемма 4. Если матрица X такова, кто при п, пробегающем ука-
^(^нные выше значения, остаток интерполирования r^j {х) стремится
252 сходимость квадратурного процесса [ГЛ. 12
к нулю при любом х^\—I, I] и для любой функции вида / = —-
X — а
где а лежит вне отрезка [—1, 1], то потенциал A2.2Л0) сохраняет
постоянные значения на множестве Е.
Доказательство. Допустим противоположное и покажем, что тогда
наверное существует функция вида /= , для которой остаток
интерполирования не будет стремиться к нулю. Пусть Xj и Х2 два значения,
принадлежащие £, для которых A2.2.10) принимает разные значения. Для
определенности записи будем считать и (xi) < и (дгз)- Обозначим и (лгз)—а (jci) — 6
и возьмем произвольное е < 6. Рассмотрим прямую линию, проходящую через
точку лгз параллельно мнимой оси. При приближении точки z вдоль этой
прямой к Х2 и (z) будет стремиться к и (хз) по лемме 2. Попутно отметим,
что при приближении z к Хг In jr- для всякого t будет возрастать. Так
как, кроме того, \х (t) есть неубывающая функция, то при приближении z
к Х2 и (г) также будет возрастать.
На взятой прямой существует, следовательно, такая точка ^2 Ф Х2, что
и(х2) ^ е < а (^з) < а (дгг). Фиксируем ^2 и построим функцию /fjc) =
— . Остаток интерполирования ее есть
(Оп{х)
eB2)(Jc —гз)
Значение остатка в точке х — Xi равно
<0/i(-^l)
1 u
«n (^2) (-^1—^2)
1 i««(-^l)l
1 1
1
exp n
\Xi—Z2\
По лемме 3, существует бесконечная последовательность значений п.
для которых
l"rt(-^i) —«(-^01 <-з ^•
Поэтому наверное существует также бесконечное множество /г, для которых
u„ {zo) — Ur, {х^)^и {Z2) — и{х^)~[и (гз) — и„ (z^)] — К (-^i) — " (-^Ol >
Для таких n
\ Xx Z2\
§ 2] СХОДИМОСТЬ ИНТЕРПОЛЯЦИОННЫХ КВАДРАТУР 253
и интерполирование функции /= в точке лг^, следовательно, рас-
X >?2
ходится.
в доказываемой теореме считалось, что интерполирование сходится на
отрезке [—1, 1] для всякой функции, аналитической на (—1, 1]. В
частности это будет для функций вида / = , а5[—1, 1] и, в условиях
этой теоремы, и (х) также будет сохранять постоянное значение на £, и,
следовательно, почти везде на [—1, 1].
Чтобы завершить доказательство теоремы, нам осталось еще доказать
следующую лемму.
Лемма 5. Если логарифмический потенциал A2.2.10) почти везде на
[—1, 1] сохраняет постоянное значение, то \x{t) есть функция
распределения Чебышёва:
t
... 1 Г dx
Доказательство. Рассмотрим потенциал
u{z)^ In ,^^^, dvi{t) A2.2.14)
1
всюду в плоскости Z. с целью воспользоваться для доказательства леммы
известными теоремами теории интеграла Пуассона и тригонометрических
рядов, перейдем от плоскости z к кругу.
Проведем в плоскости z разрез по прямолинейному отрезку [—1, 1]
и будем различать два борта разреза. Преобразуем A2.2.14) в интеграл,
взятый по контуру Я, состоящему из обоих бортов разреза. Для этого
достаточно представить A2.2.14) в форме
1 -1
-1 1
И ввести функцию v (^), определив ее на Я равенствами
0,5fx (t) на верхнем борте р
1 — 0,5|л {t) на нижнем борте разреза.
Тогда
/А_/ 0,5fx(^) на верхнем борте разреза, поо1е;ч
V (f) — 1 1 лп../^\ .,„ _., л (iZ.^.lO)
" (^) =- J ^" i^l^i ^v (О- A2.2.16)
Интегрирование по верхнему борту выполняется от точки —1 к 1 и по
Нижнему борту — в обратном направлении.
В плоскости £ = р^^**' возьмем круг iSi<l. Он преобразуется на
плоскость Z с разрезом [—1, 1] при помощи функции
1
2
г^4(? + Г')-
254 сходимость квадратурного процесса [ГЛ. 12
Точка т = ^^^ окружности перейдет в точку ^ = -^ (т-1-т~') =
= ~ (е^^ + е"^"^) = cos у^. Изменению \р от — я до л; будет отвечать обход
контура X в указанном выше направлении. Функция v (t), определенная на X,
перейдет в функцию
V (О = V (COS ^)=^F (ф), — л; < i|) < я
полярного угла у^.
Контурный интеграл A2.2.16) при переходе к плоскости £ преобразуется
в следующий интеграл по окружности круга
«н= J
ml -2S
-л
l-2Scosi|3 + £2
dF(i)) =
/(g) разлагается на сумму двух логарифмических потенциалов,
гармонических в круге I g I < 1.
л п
—я —jt
Ввиду равноправности /j (Q и /г (С), достаточно изучить только
потенциал /i (Q. Можно проверить, что функция /i (t) представима интегралом
Пуассона — Лебега *). Пусть Е есть любое измеримое множество на от
*) Функция V E) называется представимой интегралом Пуассона—Лебега,
если она гармоническая в круге 1^| < 1 и если существует такая суммируе-
мая на [- я, л] функция / (ф), что t. (S) = ^ j / «) i_2p cos7^)+Р^ '''^-
-Я
Известна теорема: для того, чтобы гармоническая в круге | J | < 1
функция V (g) была представнма интегралом Пуассона — Лебега, необходимо и
а
достаточно, чтобы семейство функций Fp (а) == v (р^'^) d(p было равносте-
0
пенно абсолютно непрерывно по а, т. е. чтобы при всех р < 1 и е > О
существовало такое число 6 (е) > О, что для всякого множества Е с мерой
тЕ<Ь (£) было 1 [ V (р^'^)
^Ф
< Е. Известно также, что когда точка L
приближается к некоторой точке "ф — "фо окружности по любому пути,
некасательному к окружности, то при почти всех значениях фо v (g) -> / Dъ)-
См., например, И. И. Привалов, Граничные свойства аналитических
функций, гл. I. § 3, М. — Л., Гостехиздат, 1950»
§ 2] СХОДИМОСТЬ ИНТЕРПОЛЯЦИОННЫХ КВАДРАТУР
резке [— я, я] с мерой шЕ < 6.
л
Г /, (р.'Ф) ^ф ^ J ^Ф J in т-7^^ clF т =
^ J J '"^T^zv^
255
й?Ф
^/^ (Ф).
Изменение порядка интегрирования было возможным в силу теоремы Фубини
так как функция 1п-^ т^ ограничена снизу числом In—. Для внутрен-
него интеграла верны оценки
/,..
1
ре
^ф _ pi"^
й?Ф
<
J'"
1
I sin (ф — tfi)
-^Ф<
0,56
J
-0,56
In
I Sin jcj
dx.
Поэтому наверное для всякого заданного е > О можно 6 (е) выбрать так,
чтобы было
J /, (Р^^'^) ^Ф
< е, р<1.
Отсюда, по известному признаку, указанному в сноске, следует, что /i (^)
представима интегралом Пуассона — Лебега, /г (J)» з, следовательно, и / (g),
также будут представимы интегралом Пуассона — Лебега,
При приближении точки ^ = л:-f-/у к отрезку [—1, 1] вдоль прямой,
параллельной мнимой оси, и (z) будет почти при всяких х стремиться
к постоянной величине. Указанные прямые, при переходе к кругу |g|< 1,
преобразуются в некоторые пути, ортогональные к окружности | g 1 === 1. При
приближении вдоль них к границе круга а (г) почти всюду будет стремиться
к постоянной величине, и так как In 2 | g | будет при этом стремиться к In 2,
то / (g) будет почти всюду на окружности иметь предельные значения,
равные постоянной величине. Ввиду того, что / {Q представима через них
интегралом Пуассона — Лебега, / (g) постоянна всюду в круге. Но, очевидно,
/@) = 0 и, следовательно, всюду в круге /(g) = 0.
1 1
Легко видеть, что разложения функций In
5 =ре*Ф, в ряды по степеням р при р < 1 суть
и In
|5^,/Ф| к-.-'ФГ
1п-
1п-
.1Ц
М-е'
-/Ф
= Л, — р* COS ^ (ф — \f)
со
k^\
256 сходимость квадратурного ПРОЦРХСА [Гл 12
Поэтому
^ со
^(Ф)= J ^^Р*1соз/г(ф~г|?) + созЛ(ф + л1))]бГ/^(ф)^
-п ft = i
ее ЛГ
^2 2j^ J р^ COS k(^ COS Лф ^/^ (ф) ^ 0.
ft-1 -л
Отсюда
я я
f COS k^ dF (Ф) == F (i|)) cos ^.M + ^ [ ^ (^) sin ^ф rf^ =^
- (-1)^ [/^ (Я) ~ /^ (- Я) ] + /гяб^ === 0.
Здесь b/^ обозначен коэффициент Фурье при sin^if функции /^ (ф). F (п) = 1,
/•^ (— я) = О, следовательно
Из определений функции v (О и /^ (ф) видно, что
0,5^1 (cos ^\)), — я < ф < О,
^ t l-'0,5fi(cos ф), 0<А|}<я.
Четная часть F (ij;) есть
0,5 [/^(v^) + /-(-tt) 1 = 0,5.
Коэффициенты Фурье а^ при cos^vp для F {\\)) будут иметь значения
ао=^ОД ал=-0 (Л = 1, 2, ...)-
Таким образом, для F (\()) получим
оо
Если вернуться к плоскости -г и переменной ? = cos i|), то несложные
вычисления покажут, что
,„ , 1 , 1 г ^д:
ц(Л=1 arc COS f — — ^,
Этим теорема доказана.
Сходная с ней теорема в теории квадратур приведена ниже.
Теорема 7, Если интерполяционный квадратурный процесс, опреде-^
лнемый равенствами A2.2.1) при [л, 6] = [—I, 1], сходится при всякой
функции а (л:) с ограниченным изменением и для любой функции / {х),
аналитической на [—1, 1]. то для матрицы узлов X существует
предельная функция распределения узлов и она совпадает с A2.2.6).
, 3] сходимость ОБЩЕГО КВАДРАТУРНОГО ПРОЦЕССА 257
Доказательство. Рассмотрим остаток квадратуры
1
Rn(f)- \rAx)dG(x),
Здесь г^ (х) есть остаток интерполирования. Возьмем произвольную точку х
на [—1, 1]- За а примем кусочно постоянную функцию с единственным
скачком величины 1 в точке х. Для такой а Rnl^ — f^ni-^) и сходимость
квадратурного процесса равносильна сходимости интерполирования. После
этого, чтобы закончить доказательство, достаточно сослаться на предыдущую
теорему.
§ 3. Сходимость общего квадратурного процесса
Перейдем к изучению общего квадратурного процесса A2.1.3),
определяемого матрицей узлов A2.1 Л) и матрицей коэффициентов
A2,1.2). Вес р{х) может быть любой суммируемой функцией. Будем
считать, что задан некоторый класс F функций /. Нашей целью
будет выяснить условия, которым следует подчинить X и Л для
TOJO. чтобы квадратурный процесс сходился для всех функций
заданного класса. Такая задача изучалась для многих классов F.
Мы остановимся лишь на некоторых результатах исследований такого
рода, наиболее простых и важных для теории квадратур.
Всюду в рамках этого параграфа отрезок интегрирования
считается конечным.
Теорема 8. Для того чтобы квадратурный процесс A2.1.3)
сходился для всякой функции /, непрерывной на отрезке [а, ^],
необходимо а достаточно выполнение двух условий:
1) процесс сходится для всякого многочлена;
2) существует число К такое, что при /г=1, 2, ...
выполняется неравенство *):
fe=i
4</С. A2.3.1)
Доказательство. Если на множестве функций непрерывных
на [а, Ь] определить норму следующим способом: Ц/Ц ^= maxj/(л:) |,
то такое множество мы можем рассматривать как линейное
нормированное пространство С типа В. Квадратурная сумма Q^(f)=^
п. b
= ^ Л;^"У (лг^"^^) И интеграл l(f)= p(x)f(x)dx есть два линей-
*-1 а
ных функционала, определенных на С. Значения Q^iif) и /(/)
*) Достаточность условий была доказана В. А. С т е к л о в ы м,
необходимость—Г. Пойа.
258 сходимость квадратурного процесса [ГЛ. 12
принадлежат числовому пространству, которое также является
пространством типа В.
К задаче выяснения условий сходимости квадратурного процесса
Qn(f)~^^(/)' fi^oo, может быть применена теорема С. Банаха
о сходимости последовательности линейных операторов (см. гл. 4 § 3).
Напомним» что необходимым и достаточным условием сходимости
является выполнение двух требований: 1) сходимость на множестве
элементов, всюду плотном в пространстве, где определены
операторы, и 2) ограниченность в совокупности норм операторов.
За множество всюду плотное в С, по теореме Вейерштрасса
о возможности сколь угодно точного равномерного приближения
всякой непрерывной функции многочленами, может быть принято
множество алгебраических многочленов и первым требованием в
рассматриваемой задаче будет требование сходимости квадратурного
процесса для всякого многочлена.
Норма функционала Qnif) имеет значение
\Qn\\= sup
I/ Ki
1,лР/{хГ)
==SM'
(«I
Выполнение неравенства A2.3.1) есть требование ограниченности
в совокупности норм функционалов Q„(/). Высказанная теорема этим
доказана.
Две сформулированные ниже теоремы являются простыми
следствиями теоремы 8.
Теорема 9. Если все коэффициенты Л^"^ неотрицательны, то
для сходимости квадратурного процесса для любой
непрерывной функции необходимо и достаточно, чтобы он сходился для
всякого многочлена.
Доказательство. Необходимость условия теоремы очевидна.
Достаточность же условия видна из того, что для многочлена
нулевой степени / = 1 должно быть
ь
Qni^)-^ \ pdx, п-^оо.
а
Поэтому значения Q„(l) (д=1, 2, . . .) ограничены: С„A)^^* ^^
ii^ri=i4"'=Q„(i)</^.
k=i й=1
и поэтому выполняется не только первое, но и второе условие
теоремы 8 и процесс сходится для всякой непрерывной функции.
§ 31 сходимость ОБЩЕГО КВАДРАТУРНОГО ПРОЦЕССА 259
Теорема 10. Для сходимости интерполяционного
квадратурного процесса для любой непрерывной функции необходимо и
п
достаточно выполнение неравенства 2 I -^а^^ 1 ^ А' < оо.
Второе условие теоремы 8 является также условием теоремы 10.
первое же условие наверное выполнено, так как если / есть
многочлен, то когда п станет больше степени многочлена, будет выпол-
b
няться равенство Q„ (/) = J pfdx.
а
Выясним теперь условия сходимости квадратурного процесса
в классах дифференцируемых функций.
Условимся, как выше, нумеровать узлы в порядке роста и введем
кусочно постоянную функцию F^Q{x)y характеризующую распределе-
п
ние узлов и значения коэффициентов: /^^о W = 2 ^*"^^ {.>^ — -^ft-
Наряду с ней будем рассматривать первообразные функции
любого порядка г. удовлетворяющие начальным условиям Fnr{ci) = ^
1[У = 0, 1 /--1):
^^-'У-' ^^-^ .(.)W._ Д'^Л il^
Far (^) = J ^«0 (О \гЛ)\ ^^ = S ^"^^^ (^ " •^^^"^)
A2.3.2)
Теорема 11. Для того чтобы квадратурный процесс A2.1.3)
при п-^со сходился для всякой функции /^С^,[а, Ь], необходимо
и достаточно выполнение условий:
1) процесс сходится для всякого многочлена;
2) полные вариации первообразных функций порядка г F^ri^)
b
(л=1, 2, . . .) ограничены в совокупности: Мах F^^(t)-^M.
а
Доказательство. Если f ^С^ [а, Ь] при г ^ 1, то. разлагая /
по формуле Тейлора около точки Ь, мы сможем представить
функцию в форме
ыо
г-1
b
i=0 a
dt.
Наоборот, каковы бы ни были числа /^') ф) и непрерывная на
{а, Ь\ функция f^^^ (t), f(x), определенная такой формулой,
принадлежит С^[а. Ь].
260
сходимость КВАДРАТУРНОГО ПРОЦЕССА
[ГЛ. 12
Остаток квадратуры Rnif) дается следующей формулой,
характерной для класса С^[а, Ь]:
b г- b
+ (-ly jf^ (t) l? (x)E(t - x)^^0^ dx -
ft-1
/•-1
dt
t=0
+ (-l/J/40 \pix) ^GД^' dx-^F,^,^,
it)
dt
A2,3.3)
Сходимость квадратурного процесса, ввиду независимости
параметров формулы f^^\b) (/ = 0, 1, . *•—1"^ " ^^^"^
тому, что при п-^оо
Rnlix — by]-->0 (/ = 0. 1. ... г—1)
и
b г t
г—1) и г (t), равносильна
A2.3.4)
R:{n--\f\t)\ |м^)^^^^х~/^..-.
(О
dt-^0, A2.3.5)
A2.3,4) означают, что квадратурный процесс должен сходиться для
всякого многочлена степени <^ г—1.
Условие A2.3.5) должно выполняться при любой непрерывной
/О
(г)
функции /' \ Если на множестве функций р ввести норму
I/^'^^ II =::: max I/^'^^ (^) I , ТО МЫ можем его рассматривать как
пространство С. По теореме Банаха стремление Rnif ) к нулю при л—>со
равносильно выполнению двух требований:
1. Функционал R*nif^^^) должен стремиться к нулю на множестве
элементов, всюду плотном в С. За такое множество можно принять
множество многочленов. Но требование /?/г(/ )-^0, /г->оо, когда
/^'^^ есть полином любой степени, совместно с A2.3.4) эквивалентно
тому, что квадратурный процесс должен сходиться для всякого
многочлена.
2. Нормы функционалов R*n{f^^^) (д=1, 2, ...) должны быть
ограничены в совокупности:
Ь\ t
\\Rl\\^jUp(^x)^^0^dx-F„,,_,
(О
dt<CL (n==l. 2, ...)•
§33
сходимость ОБЩЕГО КВАДРАТУРНОГО ПРОЦЕССА
61 t
261
Заметив, что 1 р /^_1у ^^
dt не зависит от я, можем
сказать, что ограниченность норм ||/?л|/ равносильна ограниченности
в совокупности интегралов от |/^л, r-i@|*
b
Так как —ттF^^j.{t)^= F^^^_^{t), последние неравенства означают
VarF^,,@<^^ {n^l. 2, ...).
Можно убедиться в том, что все изложенное остается верным и
в случае г^==0. Этим закончено доказательство теоремы 11.
Отметим частный случай теоремы. Рассмотрим класс непрерывно
дифференцируемых функций на [а, Ь], что отвечает случаю /•=!.
^ло@ ^с^ь кусочно постоянная функция, принимающая на участках
между узлами х^^^ указываемые ниже значения:
О при а < ^ < х(«)
Af^ при x^i"' < t < xi""^
при xi'^ < t < jcf
Fno(t)-=I^Ai^^E(t-xi^^):
k-l
M
4«L_ ... +лГ при xi"^<t^d
Отсюда видно, что
VarF„,@= I" |/='„o@|rf^-=|4">|D"'-x'i'") +
a ^
a
Поэтому можно высказать следующую теорему:
Теорема 12, Лля того чтобы квадратурный процесс A2.1.3)
сходился для любой непрерывно дифференцируемой функции,
необходимо и достаточно выполнение условий:
1) процесс сходится для всякого многочлена)
262 сходимость квадратурного процесса (гл. 12
2) существует число М такое, что при л=:=::1, 2, ... выпол-
няются неравенства
14"^ I W> - М"») 41 аГ н- аГ 1 {хГ - хП + ...
... + I А\"' + ... + ЛГI (Ь - xf) < ж. A2.3.6)
Будем говорить, что / принадлежит классу Аг[а, Ь\ {r~Q, 1, ...), если
производная /''^ порядка г от f есть абсолютно непрерывная функция.
Характерное представление f^Aj.[a, b] без труда строится при помощи
формулы Тейлора и может быть записано в виде:
/-0 b
г *
/«о й
Здесь /"^^(Ь) (г = 0, 1. . • -, г) могут быть любыми числами и /''^^^ есть
произвольная функция, суммируемая на [а, Ь].
Теорема 13. Для сходимости квадратурного процесса A2.1.3) при
всякой функции f^Af.[a, b] необходимо и достаточно выполнение условий:
1) процесс сходится для всякого многочлена,
2) первообразные функции F^r (О порядка г для F^^q (t) ограничены
в совокупности:
\Fnr{t)\<M, a^x^b (rt=l, 2, ...). A2.3.8)
Доказательство. Если f^Aj- [а, 6], для остатка квадратуры R^ (/),
при помощи A2.3.7), легко получается выражение
Rnif) = S Aj^ /?„ Кх - ЬУ] +
/-0
+ (-!/+' I /+1 it)U р (X) SL=^ dx - Fn. г (t) j dt.
Это равенство является структурной формулой остатка /?„ (/) для
функций f^Ar[a, 6]. Сходимость квадратурного процесса в классе Л^. [а, Ь],
ввиду произвола чисел f^^^ {Ь) (/==0, 1 г) и функций /t''+^\
равносильна тому, что должно быть
Rn{{^—bY]->0, n-^Do (/ = 0, 1. ..., г) A2.3.9)
и
Ь ( t \
а Уа ]
A2.3.10)
§3]
сходимость ОБЩЕГО КВАДРАТУРНОГО ПРОЦЕССА
263
Дальнейшие рассуждения будут в значительной мере повторять те,
которые были проделаны при доказательстве теоремы 8, Введем на
множестве производных /''^^^ норму
b
||/<'+>)||=||/'-ы)@|л.
После этого оно станет нормированным пространством L типа В, К
сходимости функционала /?* (/^'^"'"^0->О, /г->оо, применима теорема С. Банаха.
За множество всюду плотное в L можно принять множество многочленов.
Требование стремления /?* (/^'^^^О для всякого многочлена f^^^^\ совместно
с A2.3.9), равносильно требованию сходимости квадратурного процесса для
любых многочленов. Норма функционала Rf^if^^^^^) имеет значение
(см. гл. 4, § 2 D.2.6))
t
r:
max
t
^Pix.
(t-xY
dx-F„r{t)
Интеграл
J
P {^) r^ ^-^ "^ зависит от rt и требование ограничен-
уще
нести в совокупности норм I/?^ (п—1, 2, ...) эквивалентно суЯТество-
ванию числа М такого, что при п= 1, 2, ... будет
Теорема доказана.
Рассмотрим частный случай г = 0 и соответствующий ему класс
абсолютно непрерывных функций Ло[а, Ь]. ф/нкция Fnai^) кусочно постоянна
н на отрезках [а, лг^^"*], \x^i\ j:^"*], ..., \х!'^\ б] принимает значения
соответственно равные О, 44 4"^+ 4"^, ..., A^i^-]- ... -^ Л^1^\ Применение
общей теоремы 13 к рассматриваемому частному случаю позволяет
высказать следующую теорему *).
Теорема 14, Для сходимости квадратурного процесса A2Л.З) при
ссякой функции /, абсолютно непрерывной на [а, Ь], необходимо а
достаточно выполнение двух условий:
1) процесс сходится для всякого многочлена,
2) частичные суммы квадратурных коэффициентов
Л*"), Л(«) + 4"*» • • м 4"^ + ^2^ + . • • + Л"* («-1,2....)
ограничены в совокупности:
2 4"'
<М<оо (/=1,2, ..., п; л=1, 2. ...). A2.3.11)
^ ) Доказана впервые С. М. Лозинским в немного другой форме.
Изв. АН СССР, сер. матем. 4 A940).
254 сходимость квадратурного процесса [ГЛ. 12
Изучим условия сходимости еще для одного класса функций. Будем
говорить, что / принадлежит классу Vr [а, Ь], если производная порядка г /'"^
имеет ограниченное изменение на [а, Ь], Структурное представление класса
Vf[a, b] для /*^1 также может быть получено из формулы Тейлора и его
можно записать в виде:
^^^P_^^_^y^^__^f^ir^ E^t~x)^t=^af(^)^t). A2.3.12)
Параметрами здесь являются числа /^^ F), могущие иметь любые значения,
и произвольная функция /^^^ с ограниченным изменением на [а, Ь].
Теорема 15. Для сходимости квадратурного процесса A2.1.3) в классе
Vr [л. ^1 «pw /"> 1 необходимо и достаточно, чтобы выполнялись условия:
1. Процесс сходится для всех многочленов степени <;г.
2. Первообразные функции Fnr{x) порядка г для Рп^{х) ограничены
в совокупности
I^AirWI<^^<^' а<д:<^ (/2-= I, 2 ...). A2.3.13)
3. SU)u всех значениях t ^ [а, 6] должно быть
t
Рпг (^) -^ J Р (-^) ~| dx. п^со.
а
Доказательство. Если f^Vr [а, Ь], остаток квадратуры R^ (/) для
нее, при помощи формулы A2.3.12), приводится к следующему виду:
b ( t
+ (-1)'^^ \\\ P {X) -^^f^ dx - F„r @ i d/'^ (t).
1
и
Сходимость квадратуры для всех функций из V^. [а, Ь], в силу
независимости структурных параметров /^Ч^) (^'^0, 1, ..., г) и /''^^ЧО.
равносильна выполнению равенств:
Иш Rn[{x~~by\^0 (/ = 0 г) A2.3.14)
rt->oo
и
1нп /?;(/^))= lim {{ \ pix)^^^^dx~Fnr{t)]df^'Ht)--0. A2.3.15)
а [а }
Первое из них означает, что процесс должен сходиться для всех многочленов
степени <;л Сосредоточим внимание на втором равенстве. Функционал
^л С/^'^^) определен на линейном множестве функций ограниченного измене-
§ 3] сходимость ОБЩЕГО КВАДРАТУРНОГО ПРОЦЕССА 265
ния /^^\ Не изменяя величины интеграла R^ {/^^Ь, всегда можно считать,
что f^^^ (й) = 0. Введем в этом множестве норму, положив || /^^^ \\ = Var f^^K
а
После этого указанное множество мы можем рассматривать как линейное
пространство V типа В. Если Rf^if^^^^O, п->со, при всяких /^^ из V,
то, по теореме Банаха, нормы всех функционалов R^ должны быть
ограничены в совокупности
Но
max
t
<Л^ («=1. 2, ,..). A2.3.16)
Р{^) ^^ J^' dx-Fnr{t)
Г (t xY
Ввиду же независимости Pi-^)- p^rfjc от п, условие A2.3.16) экви-
а
валентно существованию такого числа М, чтобы было выполнено второе
условие теоремы.
Для проверки необходимости третьего условия возьмем произвольное
x^la, b] и положим /^'^^ кусочно постоянной с единственным скачком
величины 1 в точке X, Для такой /''^
X
а
По ВЗЯТОЙ f^^^ можно восстановить, с точностью до аддитивного многочлена
степени п—1, который не имеет значения в рассуждениях, функцию /,
Для нее квадратурный процесс должен сходиться и должно быть
Последнее же означает выполнение третьего условия теоремы.
Этим доказана необходимость всех трех условий. Столь же просто
проверяется их достаточность. Первое из условий теоремы равносильно A2.3.14).
Осталось убедиться лишь в том, что из второго и третьего условий
вытекает A2.3.15). Действительно, из этих условий следует, что функция, стоящая
под знаком интеграла Стилтьеса A2.3.15)
(О
ограничена по модулю некоторым числом при любых ^^[а, 6] и /г= 1, 2,..
и стремится к нулю, когда л->оо, при всех t. Если же преобразовать
266 сходимость КВАДРАТУРНОГО ПРОЦЕССА [ГЛ. 12
интеграл Стилтьеса к интегралу Лебега по обычным правилам, то при
помощи известных теорем о предельном переходе в интеграле Лебега *)
можно убедиться в том, что равенство A2.3.15) верно.
Литература
Натансон И. П., Конструктивная теория функций, ч. III, гл. V,
JV1. — Л., Гостехиздат, 1949.
Г е р о и и м у с Я. Л., Теория ортогональных многочленов, гл. II, §§ 27—28,
М. — Л., Гостехиздат, 1950.
Стек лов В. А. 1) О приближенном вычислении определенных
интегралов при помощи формул механических квадратур. Изв. АН 6 A916), 10.
2) Sur I'approximation des fonctions й. I'aide des polynomes de Tchebycheff
et sur les quadratures, Изв. AH A917), 11. 3) Remargues sur les quadratures,
Изв. AH 12 A918).
Кузьмин P. O., К теории механических квадратур. Изв. Ленингр.
Политехи, ин-та, Отд. техн., естеств. и матем. 33, A931),
Пой а (Polya), Ober die Konvergenz von Quadraturverfahren, Math. Z.
37, A933), 264—286.
Микеладзе Ш., Численное интегрирование, УМН 3 A948).
Лозинский СМ., О формулах механических квадратур, Изв. АН 4
A940).
Крылов В. И. 1) Об определении наименьшей области, голоморфность
в которой обеспечивает сходимость эрмитовского интерполирования при
любой системе узлов, ДАН 78, Кг 5 A951). 2) Сходимость механических
квадратур в классах функций различного порядка дифференцируемости, ДАН
101, № 5 A955).
*) Известна, например, следующая теорема: Если функции Д {х)
измеримы на [а, Ь] и при всех n\fn(x)\^N<,oo и если почти везде на [а, Ь]
/л (-*^) "> / (•^). п->оо, то
b ь
\ fn{^)dx^^ f(x)dx.
ГЛАВА 13
УВЕЛИЧЕНИЕ ТОЧНОСТИ КВАДРАТУРЫ И УСКОРЕНИЕ
СХОДИМОСТИ КВАДРАТУРНОГО ПРОЦЕССА
§ К О двух направлениях в задаче увеличения точности
Пусть рассматривается некоторая вполне определенная
квадратурная формула
b п
j p(x)f{x)dx^^AJix,), A3.1.1)
а к = 1
Весовая функция р (л:), коэффициенты Af^ и узлы Xf^
предполагаются фиксированными; / есть любая функция, для которой имеют
смысл обе части приближенного равенства A3.1.1).
Нас сейчас будет интересовать остаток формулы A3.1.1)
Ь п
R{f)^-l pfdx^Y^AJix,), A3.1.2)
а к^\
Увеличить точность приближенной квадратуры — это значит
выделить из остатка /?(/) такую его часть, которую можно, при
выполнении некоторых условий, считать «главной частью» и добавить ее
к квадратурной сумме ^Aj^f{x^).
k
Величина остатка /?(/) зависит как от вида квадратурной
формулы, т. е. от р{х), Aj^ и х^, так и от свойств интегрируемой
функции /. От них должны зависеть также и правила увеличения
точности. Можно строить такие правила, рассчитанные на классы
квадратурных формул, близких по своим свойствам, или же на
классы функций, обладающих некоторыми общими структурными
свойствами.
Задача увеличения точности ниже будет рассматриваться в двух
следующих направлениях.
1. Большинство применяемых в практических вычислениях фор-
*«ул механических квадратур рассчитаны на интегрирование функций»
2б8 УСКОРЕНИЕ сходимости КВАДРАТУРНОГО ПРОЦЕССА [ТЛ. 13
обладающих той или иной степенью гладкости. Так, например, можно
ожидать, что формула парабол
b
J /rfX« |-1/0 + /„+2(/2+/4+. • .+/„_2)+4 (ЛН-/з+. . .+/„_!)],
а
, b — а
даст при вычислениях хороший по точности результат, если
интегрируемая функция / будет непрерывной на всем отрезке [а. Ъ\ и на
каждом сдвоенном отрезке [а, a~\-2h\, [а + 2/г, а~^4/г]> ... может
быть достаточно точно приближена многочленом второй или третьей
степени.
Аналогично, при применении квадратурной формулы наивысшей
алгебраической степени точности с п узлами
b п
а k^l
можно наверное рассчитывать получить результат, близкий к
истинному значению, если функция / допускает хорошее приближение
на всем отрезке интегрирования [а, Ь] алгебраическим многочленом
степени 2п— 1.
Применить формулы вида A3.1.1) к вычислению несобственных
интегралов от неограниченных функций не всегда возможно, так как одно
п
или несколько значений /(х^) (й= 1, 2 п) в сумме 2 ^kfi'^k)
могут оказаться бесконечными. Но даже если применение формулы
будет возможным, то погрешность ее может иметь большие
значения. С большой погрешностью можно встретиться также при
применении таких квадратурных формул к вычислению интегралов от
непрерывных функций, у которых одна из производных невысокого
порядка будет неограниченной. Аналогичное может обнаружиться и
при интегрировании аналитических функций, если их особые точки
лежат вблизи отрезка [а, Ь\.
Заметное улучшение точности вычисления интеграла здесь может
принести особый прием предварительного преобразования
интегрируемой функции, который может быть назван методом ослабления
особенности. Мы должны разбить интегрируемую функцию f{x) на
два слагаемых f(х) = fi(x)'{-f2{x) так, чтобы /i(x) содержала
в себе «все» особенности функции f (х) или «главную часть» этих
особенностей. При этом функция fi{x) должна быть такой, чтобы
ь
интеграл p(x)fi{x)dx легко вычислялся точно. Функция же /2(-^)
§ 1] ЗАДАЧА УВЕЛИЧЕНИЯ ТОЧНОСТИ 2бУ
не должна иметь особенностей, или, по меньшей мере, ее
особенности должны быть настолько «слабее» особенностей /(х), чтобы
b
интеграл pf2^^ мог быть с достаточной точностью вычислен по
а
ОДНОЙ из формул приближенных квадратур.
Способы выделения и ослабления особенностей функций
многообразны и некоторые из них будут рассмотрены в следуюш,ем
параграфе.
2. Квадратурные формулы, обычно, позволяют найти интеграл
с любой точностью, если взять достаточно большое число узлов п.
Когда заранее указана точность вычисления, то определить, сколько
следует взять узлов для того, чтобы достигнуть такой точности,
можно, принципиально говоря, если воспользоваться известными
в теории квадратур оценками остатка /?(/). Но следует иметь в виду,
что такие оценки обычно бывают рассчитаны на широкие классы
функций и не учитывают индивидуальные свойства интегрируемой
функции /. Поэтому оценки будут давать, как правило, преувеличен-
^ное значение для числа узлов и найденное так значение п можно,
по-видимому, принять только как ориентировочное.
При составлении плана вычислений обычно назначают число
узлов п, приняв во внимание не только указанную оценку, но и
многие другие соображения, в частности пользуются уже накопленным
вычислительным опытом, аналогией с другими интегралами, или
выполняют вычисления двумя различными способами и т. д. При этом
для назначенного п можно часто лишь ожидать, что погрешность
не будет превосходить предписанного значения, но неоспоримой
убежденности в этом может не быть. Тогда возникает потребность
в проверке полученного результата *) и в увеличении его точности,
если она окажется меньшей, чем требуемая.
Интегрируемая функция / считается сейчас достаточно «гладкой»,
так что большое значение погрешности R (/) квадратуры может быть
вызвано только недостаточной точностью взятой квадратурной
формулы.
Для увеличения точности формулы мы должны определить какое
дополнительное слагаемое следует добавить к правой части
приближенного равенства A3,1.1) для того, чтобы новая квадратурная
формула, полученная после этого, имела точность, большую чем A3.1.1).
Этот новый член формулы должен, очевидно, быть главной частью
остатка /?(/). Но одним только этим условием он не вполне
определяется, так как из R(f) можно выделить много «главных частей»,
отличаюш.ихся между собой «малыми» слагаемыми. Среди
) Проверка точности результата часто является трудной задачей.
Методы такой проверки в книге не рассматриваются.
270 УСКОРЕНИЕ сходимости КВАДРАТУРНОГО ПРОЦЕССА [ГЛ. 13
дополнительнух условий, определяюпдих разыскиваемую главную
часть, должны обязательно находиться условия ее эффективной
вычислимости и простоты.
Методы выделения главной части должны быть связаны со
свойствами остатка и с некоторыми методами такого рода мы
ознакомимся в следующих параграфах настоящей главы.
Допустим теперь, что каким-либо путем новый член формулы
A3ЛЛ) был найден. Если добавление его к квадратурной сумме
исправит прежний результат до требуемой точности, то на этом
улучшение формулы заканчивается. Если же на первом шаге
требуемая точность не будет достигнута, то следует найти остаток вновь
построенной квадратурной формулы и из него в свою очередь
выделить главную часть и т. д.
Так как, вообще говоря, нельзя заранее сказать, сколько
необходимо выполнить таких шагов для получения желаемого результата,
нужно для остатка A3.1.2) исходной формулы построить ряд из
«главных частей» последовательных порядков.
§ 2. Ослабление особенности интегрируемой функции
Как говорилось в § 1, улучшение точности квадратуры при
помощи ослабления особенности основано на таком разложении
интегрируемой функции / на две части /(a^)==/i W + AC-^)» чтобы
функция /i содержала все, или «почти все» особенности / и интеграл
ь b
от нее pf\dx находился точно, а интеграл от второй части | pf^dx
а а
МОГ быть вычислен механическими квадратурами с достаточно малой
погрешностью.
Правила разложения / зависят от характера особенностей этой
функции и веса р (х). Мы ограничимся тем, что рассмотрим несколько
простых случаев такого разложения.
I. Пусть дан интеграл
ь
J (x—x{f^{x)dx. A3.2.1)
а
где Xi есть некоторая точка, лежащая на отрезке [а, Ь\, или вблизи
него. Для определенности изложения будем считать, что Xj
принадлежит [а, Ь\. Показатель степени а предположим большим —1 и
отличным от целого числа. Кроме того, допустим, что функция ф(л:)
непрерывна на [а, ^] и в точке Xj имеет производные до некоторого
порядка т, причем (^{х^Ф^.
При а < О заданный интеграл будет несобственным, если же
а > О, то интегрируемая функция не будет иметь производные
§ 2] ОСЛАБЛЕНИЕ ОСОБЕННОСТИ ИНТЕГРИРУЕМОЙ ФУНКЦИИ 271
В точке Xj, начиная с некоторого порядка, и формулы
механических квадратур, поэтому, могут дазать большую погрешность
вычисления.
Выделим из тейлорова разложения функции (р(х) около точки jCj
некоторое число k <^т первых членов и разобьем интегрируемую
функцию / на две части
/ {X) = (X ~~- х,Г ф (X) = f, (X) + /2 (X).
где
/^(;с) = (х-х,г[ф(х,) + 5^^(х-хО + ... + 5^^^
f^^x) = (x^x,f[^(x)~~<p(x,)~^^(x^x,)- ...
(k~\)\
(х-х,)'-^] .
в соответствии с этим заданный интеграл также будет разложен
«а две части
ь b ь
J (х — Xif ф (х) rfx = I /1 (х) dx~]r ) /2 С-^) ^х.
Первый из интегралов вычисляется точно элементарным путем.
Функция же /2(х), стоящая под знаком второго интеграла, имеет
в трчке Xj порядок дифференцируемости на k единиц выше» нежели
b
исходная функция f = (х — х^)*^ ф. Поэтому интеграл Д dx может
а
быть вычислен с большей точностью, чем A3.2.1), если
воспользоваться какой-либо формулой механических квадратур.
Рассмотрим в качестве примера интеграл
1
Yl—x'^dx = ^ = 0,785398 163 ..,
б
1
На верхней границе интегрирования х=1 функция ]/l—х^ имеет
алгебраическую особенность. Выделим из нее множитель У^1—х,
другой же множитель |^1 ~|-х разложим по степеням х — 1 и возьмем
два члена разложения:
1^ГТ^ = /-2A - 1=£) + [/нП^_/2A -1^)].
272 УСКОРЕНИЕ сходимости КВАДРАТУРНОГО ПРОЦЕССА [ГЛ. 13
Рассматриваемый интеграл при этом разобьется на два новых
интеграла. Первый из них вычисляется с помощью первообразной
функции
1
/j = 1 /2\АГ:^(i — l:^j ax^Y2^ = ом\ 388...
о
Второй интеграл
о
вычислим путем применения формулы парабол F.4.5) с одной
промежуточной ординатой
/2 @) = 1 — -| 1^2 = — 0,060 660.
4/2 A) = 2 /З — у = — 0.035 898,
/2A) = 0.
/2 «-g-[/2@L-4/2 ({)Ч-/2A)] = -0.016 093,
1
J /r=^2cfjc = /i + /2^0,785 295.
о
Ошибка результата в четвертом знаке. Применение формулы
парабол с одной и тремя промежуточными ординатами непосредственно
к заданному интегралу дает соответственно 0,637 и 0,744 с
погрешностями в первом и во втором знаках.
II. Сходные преобразования могут быть выполнены в том случае,
когда интегрируемая функция имеет алгебраические особенности
в нескольких точках. Пусть интеграл имеет форму
b Ь
J/(jc)fifjc= J {x — x{f^{x — X2p ... {x — xj'n^i^x)dx. A3.2.2)
a a
Объединим все множители, кроме первого,
{X~X^f2 ... (^х- X^fni^{x)
и разложим полученное произведение в ряд Тейлора по степеням
(л: — х{). Взяв из этого ряда k^ первых членов, мы, подобно
предыдущему, разложим подынтегральную функцию на два слагаемых
/W = /iW+[/W~/iW]>
§ 2] ОСЛАБЛЕНИЕ ОСОБЕННОСТИ ИНТЕГРИРУЕМОЙ ФУНКЦИИ 273
где f\{x) есть сумма нескольких степенных функций, а f {х) — fi(x)
имеет в точке jCj производные более высокого порядка, чем f (х).
Аналогично составляются разложения, отвечающие другим особым
точкам Х2> . : .» Xj^:
f{x)^fu{x) + \f{x)^f,{x)\ {k^2, 3, ...).
Когда это сделано, мы можем заданный интеграл разбить на два:
b b
а
причем первый интеграл легко вычисляется точно.
Функция, стоящая под знаком второго интеграла, может иметь
производные более высоких порядков, чем /, и применение
квадратурных формул к этому интегралу даст более точный результат,
чт для A3.2.2).
III. Формула Тейлора может быть использована для ослабления
b
особенности всякий раз, когда интеграл имеет вид ф(х)ф(л:) rfjc,
а
где ф(х) имеет особенность в некоторой точке х^ и такова, что
ь
интегралы 1|)(х)(л:— х{)''dx легко находятся точно, а функция ф(х)
а
несколько раз дифференцируема в точке jCj. Таким будет, например,
b
интеграл (л:— jCj)*^ In^l х — Xi\^{x)dx, где а> — 1 и р — целое
а
число.
IV. Остановимся еще на интеграле
b
J 1|)[ф(х)]йГх, A3.2.3)
а
В котором функция ф@ имеет особенность в точке ^ = 0, а ф(х) —
непрерывно дифференцируемая функция, обращающаяся в нуль
в точке x=:Xi и такая, что ф'(х1) = Л=^0.
Тогда, для ослабления особенности интегрируемой функции, ее
Можно разложить на две части
ф [ф (х)] = ф [ Л (X - Xi)] + {Ф [ф (х)] — ф [Л (X ~ х{)\)
274 УСКОРЕНИЕ сходимости КВАДРАТУРНОГО ПРОЦЕССА [ГЛ. 13
b
и, если интеграл от первого слагаемого 1|)[Л(л: — x{)\dx может
а
быть вычислен точно, такое разбиение облегчит применение
механических квадратур.
Пример. Возьмем интеграл
2
1
In s\nx dx ==: — ^\п2 ^ — \.089 045.
о
Интегрируемая функция имеет логарифмическую особенность при
лг = 0. Выделим из функции sin л: первый член ее разложения в ряд
по степеням х и разобьем интеграл на две следующие части
2
\x{s\nxdx=^ \ \nxdx-\-\ In-^^2jLcfx=:/i-h/2.
о 0 0
п
2
л = f In jc ^л: = |- (in у — l) ^ -- 0.861 452.
о
sin X зх
Функция In не имеет особых точек при О^^х-^-о"- ^^^
вычисления /2 была применена формула парабол с тремя ординатами:
/2^-^(у@) + 4у(^)+уE)) = -0.228 189.
Окончательно
я
2
Г 1п51пл:г/л: = /1 + /2^ —1,089 641.
§ 3, Эйлеровы методы разложения остатка квадратуры
Сейчас рассмотрим задачу увеличения точности квадратуры при
помощи выделения из ее остатка главной части. Способы выделения
зависят от свойств остатка и могут быть весьма разнообразными.
Ниже мы остановимся только на двух методах разложения остатка,
первый из которых тесно связан с широко известными формулами
Эйлера — Маклорена.
Простейшей формулой эйлерова вида следует, по-видимому,
считать формулу, служащую для увеличения точности элементарной
формулы прямоугольников. Она является другой формой записи
разложения произвольной функции по многочленам Берпулли.
§ 31 ЭЙЛЕРОВЫ МЕТОДЫ РАЗЛОЖЕНИЯ ОСТАТКА 275
Пусть функция / задана на конечном отрезке [а, д] и имеет там
непрерывные производные до порядка v. В первой главе было
показано, что для такой функции имеет место равенство A.4.2). дающее
представление / через многочлены Бернулли В^{х) и периодическую
функцию ^* (jc). Найдем оттуда Г f(t)dt и запишем равенство в сле-
а
дующей форме:
а
(Ь-а)
V-1
Я
(V —1)! ^
b
v!
-(f^)[/*^''*(*)-/'"'(^)] +
J/v)(,)[^;(|^)_b:( —)].^ A3.3.1)
Первый член правой части {Ь — ci)f(x) дает приближенное значе-
b
кие интеграла f(t)dt, вычисленное по формуле прямоугольников
а
b
С одной ординатой в точке х. Приближенное равенство [ f dt 1=и
а
f^(b—a)f{x) будет давать, наверное, точный результат только
в том случае, когда / сохраняет постоянное значение.
Если к ф — а) f {х) присоединить второй член правой части, то
полученное после этого равенство
b
J f{t)dt ^ ф-а)/{х)-ф-а) В, (|5^) [fф)-f{a)]
будет точным для любых линейных функций. Если добавить третий
член» то новое равенство будет давать точный результат для всякого
Многочлена второй степени и т. д. Присоединяя справа по одному
новому члену из A3.3.1). мы каждый раз будем, как правило,
увеличивать алгебраическую точность квадратурной формулы на единицу.
Можно ожидать, что при этом, по крайней мере в некоторых
случаях, будет уменьшаться погрешность приближенного равенства и
Добавление новых членов позволит увеличить точность квадратуры.
276 УСКОРЕНИЕ СХОДИМОСТИ КВАДРАТУРНОГО ПРОЦЕССА [ГЛ. 13
Последний, интегральный член справа в A3.3.1) является
остаточным членом квадратурной формулы. Его исследование будет
проведено ниже.
Равенство A3.3.1) имеет более широкое значение, чем то, на
которое мы указали выше и позволяет, принципиально говоря,
построить равенства, позволяюпхие увеличивать точность любых других
квадратурных формул, служащих для вычисления интегралов с
постоянной весовой функцией. Рассмотрим произвольную формулу
b
механических квадратур для [ f dt vi запишем ее в виде
а
b п
\f{t)dt^{b^-a) ^РЛхиУ A3.3.2)
а k = \
Допустим, что она точна для случая, когда / есть постоянная
п
величина, так что S^a=1' Вполне очевидно, что A3.3.2) есть
линейная комбинация п элементарных формул прямоугольников
ь
\f
dt^{b — a)f{Xk) (Aj=b 2, .... п)
с весовыми коэффициентами Pj^. Поэтому, линейно комбинируя
с теми же коэффициентами Р^ несколько равенств вида A3.3.1).
составленных для л: = л:^, х^=Х2 х = х„. мы сможем получить
новое равенство, позволяющее повышать точность приближенной
формулы A3.3.2).
Оказывается, что аналогичные равенства могут быть построены
также для квадратурных формул, служащих для вычисления инте-
b
гралов \ pfdx с любой суммируемой весовой функцией р {х). Эти
а
равенства формально весьма просто получаются, если воспользоваться
теоремой о разложении по многочленам Бернулли и особого рода
интегральными представлениями остатка квадратурной формулы. Но
если встать на этот путь, то будет не вполне ясным в каких случаях
можно ожидать, что полученные формулы действительно позволят
увеличить точность квадратуры и когда их применение может,
наоборот, ухудшить результат.
Мы предпочтем исходить из некоторых наглядных соображений.
которые будут изложены ниже. Найденные правила увеличения
точности могут применяться в широком классе случаев, независимо от
таких соображений. Сами же эти соображения могут оказать пользу
при выявлении условий, при которых формулам эйлерова вида еле-
§ 3] ЭЙЛЕРОВЫ МЕТОДЫ РАЗЛОЖЕНИЯ ОСТАТКА 277
дует отдать предпочтение перед другими правилами увеличения
точности.
Будем считать, как выше, отрезок [а, д] конечным и
предположим, что / имеет на [а, Ь] непрерывные производные до порядка
nt-^s. Здесь т и S есть целые положительные числа, роль которых
будет ясна из дальнейшего.
Возьмем квадратурную формулу
Ь п
J P(x)f{x)dx=^ 2 л,/(X,)+ /?(/) A3.3,3)
а k = l
И рассмотрим ее остаток /?(/). Допустим, что степень точности
формулы равна т— 1.
Функцию / можно представить следующей формулой Тейлора:
а
b
i=0
a
Так как /?(Я^_^) = 0, то R{f) будет совпадать с остатком
квадратуры интеграла в последнем равенстве:
ь b
Изменим порядок интегрирования в двухкратном интеграле, что
при принятых нами предположениях о конечности [а, Ь],
непрерывности /"^^ и суммируемости р (х), наверное, возможно. Это даст
нам возможность построить представление /?(/), которое явится
исходным для анализа остатка и, в частности, для выделения из него
«главной части»:
b
R{f)=l f"'\t)K{t)dt, A3.3,4)
а
Ядро остатка К (t) имеет значение
K{t)=.jp(x)^^^=J^dx-^A,E(x,-t)^^^^^^. A3.3.5;
278 УСКОРЕНИЕ сходимости КВАДРАТУРНОГО ПРОЦЕССА [ГЛ. 13
Когда Kit) есть «мало изменяющаяся» функция, главным
значением /С, оказывающим наибольшее влияние на образование
численного значения R (/), будет среднее значение ядра. Для выделения
из R(f) главной части достаточно положить
b
К (О = С^+\К it) - Со], где C, = ib~a)'' ^ К it) dt.
а
b b
R if) = Co J /""> it) dt+\ /"" [K - Col dt =
a a
= Co [/'"-'> (*) - /"-'> (a)] + J /""'> @ L, (t) dt,
a
t
L,{t)=\[C^ — K{x)\dx.
a
Если ядро Lx it) вновь полученного интеграла также есть «мало
b
изменяющаяся» функция, из f^^^'^Lidt в свою очередь может быть
а
выделена «главная часть» и т. д.
После 5-кратного выделения из остатка последовательных главных
частей, мы приведем рассматриваемую квадратурную формулу A3.3.3)
к следующей формуле эйлерова вида, которая и решает поставленную
задачу об увеличении точности A3.3.3) при предположениях о малой
изменяемости функций Lq=^K, L^, L^^ ...:
b n
\p{x)f{x)dx=^A,f{x,)^C,\f^'"-'\b)-~f'^-'\a)\^ ...
...+C,_J/'"^^-^*)-/"'^^-''(a)]+ /?.(/). A3.3.6)
b t
Ci=:ib-ar' I Li(t)dt, Li^iit)=jlCi-Liix)]dx. Lo(t) = K(t),
a a
b
Rs(/)=^j/'"^'4t)LAt)dt. A3.3.7)
a
Равенства A3.3,7) дают возможность последовательно находить
Ci и Li. Но легко можно указать представления С^ и Li
непосредственно через ядро Kit). Для этого возвратимся к исходной
квадратурной формуле A3.3.3) и заменим в ней остаток /?(/) его
§ 3] ЭЙЛЕРОВЫ МЕТОДЫ РАЗЛОЖЕНИЯ ОСТАТКА 279
интегральным выражением
b
а
Если в /?(/) вместо / ^ (t) под знак интеграла поставить ее
разложение по многочленам Бернулли
b
/-) (О = (^ - а)-^ I/"Ч^) ^^ +
а
Si
а
И затем выполнить почленное интегрирование, то получится новое
равенство
\ P(t)f(t)dt= ^AJ(x,) +
b
+ (* - а) -' J /с (О dt [/"-'> ф) - /'"-'> (а)]Ч-
а
Ь b
a a
которое должно совпадать с A3.3.6), какова бы ни была функция /,
непрерывно дифференцируемая m-\-s раз на [а, Ь]. Но последнее
может быть в том и только в том случае, когда равны
коэффициенты при одинаковых скобках [/""^^'^^Ь) —f'^^^'^Ho)] и равны
множители при /'"+*^^ в интегральных выражениях остаточных членов:
ь
C,=St^Z^^Kit)B,[^) dt, A3.3.8)
а
280 УСКОРЕНИЕ сходимости КВАДРАТУРНОГО ПРОЦЕССА [ГЛ. 13
Ci и Li имеют весьма простой смысл. Если сравнить A3.3.8) с
интегральным представлением остатка /?(/) A3.3.4), то будет ясно,
что Ci есть остаток квадратуры некоторой функции, у которой
Производная порядка т равна -^^ jf д^- L __ 1.
Если вспомнить правило дифференцирования многочленов Бер-
нулли A.2.6). то будет ясно, что за такую функцию можно принять
•^^—•}—7—^п—^rn^A-L » так что
(/и 4-0- \ Ь~а )
\m-\-i-\
_(Ь-аГ+'-' г (t-a\1_
b
i'-"J—lj.(OB„,(l-i)«-S^A.(^^)
{m + \)\ .
A3.3.10)
Этот результат во многих случаях дает удобное средство для
вычисления С^.
Аналогично для L^(t) можно получить
Знак X, поставленный у /?д., указывает на то, что вычисляется
остаток квадратуры по переменной х.
Перейдем к построению частных формул эйлерова вида и начнем
с получения первой формулы Эйлера — Маклорена *), служащей для
увеличения точности формулы трапеций.
Рассмотрим сначала простейшую формулу трапеций
(x)dx=^-j^\f(a)-i-fib)]~\-R{f). A3.3.12)
Степень алгебраической точности ее равна единице и мы должны
поэтому положить т = 2. Чтобы построить для нее равенство A3.3.6).
нужно, прежде всего, посчитать коэффициенты С^. В данном случае
наиболее просто, по-видимому, воспользоваться представлениями
A3.3.10).
*) Относительно других формул Эйлера — Маклорена см. И. Ф. С т е-
фенсен, Теория интерполирования, гл. ХП1, М. — Л., ОНТИ, 1935.
§ 3] ЭЙЛЕРОВЫ МЕТОДЫ РАЗЛОЖЕНИЯ ОСТАТКА 281
Так как многочлены В^(х) (п = 2, 3, ...) принимают в точках
x = 0 и х^==1 одинаковые значения, то
b
J Bu2 (^) dt = 4^ [S,,.3 A) - fi,+3 @)] = 0,
a
Bee числа Бернулли нечетных индексов, кроме В^, равны нулю,
поэтому С^=^С^ = С^= ... =0. Для коэффициентов С^ четных
индексов / = 2k имеем
^2k = B/^ + 2)! ^2^+2- A3.3.13)
Несколько первых Сз^ таковы:
Со = -
I2~* ^2 —
_ F„а)«
^ 1209600 '
(Ь - ^)^
720 '
С,^^
^4-~
47900160 *
(Ь — а)б
30240 '
Займемся теперь остатком R^(f) A3.3.6) и найдем ядро L^(t)
при помощи A3.3.11)
i ^
la
- ^ [(в: - (f^)-«:-(»))+(«".(fef) - s:« A))]}.
Ввиду ф — а)-периодичности функции ^s + 2\-rzZ—l»
a a
И интегральный член в выражении L^{t) равен нулю Кроме того,
так как
то
/ (f,— ib-aY*^\ry* (b-t\ „ 1 ib-аУ'' - (b-t\
282 УСКОРЕНИЕ сходимости КВАДРАТУРНОГО ПРОЦЕССА [ГЛ. 13
Образуем теперь ряд A3.3.6) для формулы трапеций A3,3.12).
Приняв во внимание, что члены с коэффициентами С^ нечетных
индексов должны отсутствовать, запишем этот ряд в форме:
J/(/)rf^ = -^ [fia) + fm-
а
- S ^W^ ^- [/*""' (*) - ^'"'' («I + P^v (/). A3.3.14)
где остаток P2v(/) равен либо
9.М) = ^^^^1 r-\t)yl_,(^:)at. A3.3.15)
либо
b
v2v
P.V (/) = ^^ J /"* (О 4 D^) ^^. A3.3.16)
в зависимости от того, будет ли / иметь на [а, Ь\ непрерывную
производную порядка 2v — 1 или 2v.
Ниже мы всюду будем считать, что для остатка P2v(/) верно
представление A3.3.16) и преобразуем его к форме, более удобной
для нашей цели. Заменим в нем переменную Л положив i = a^
-^ф — а)и, и 0<и><;1. Воспользовавшись тем, что у1^[г^г)^^
= >^2v A — ") = ^2v A ~ ^) ~ ^2v = ^2v (^) " ^2v = >^2v (^)' "О^уЧИМ
1
P2v (/) = ^''~{^)Г' J f'\^ + Ф-а) и) [B2V (и) - 52vl <=f« =
о
= ■^^7^1—J ^*^''(^+ (*-''> ">>'2v(«)'^«- A3.3.17)
Чтобы получить правило увеличения точности общей
формулы трапеций F.4.4), разделим теперь отрезок [а, Ь] на любое
число п равных частей длины h = —^— и к частичному отрезку
g 3] ЭЙЛЕРОВЫ МЕТОДЫ РАЗЛОЖЕНИЯ ОСТАТКА 283
[a-^-ph, а-\-(р-\-I)h] применим равенство A3,3.14):
J f(:c)dx=^{f[a + ph]-\-fla-\-(p+l)h]}~
1
P^v (/) = -£r J ^"" (« + Z»^ + Л«) y2v («) '^'й-
0
При сложении таких равенств, отвечающих всем частичным отрезкам
V-1
(р = 0» 1, .... п—1), слагаемые в суммах 2 » отвечающие точкам
деления, лежащим внутри [а, Ь], взаимно уничтожаются и останутся
только слагаемые, отвечающие точкам а ]\ Ь.
а k^l
= ?-„ - ^ [/' Ф) - /' («)] + ^ [/'" (*) - /'" (а)] -
- 47ЖТ60 ^^'^'(*)-^'^*('^>J+ • • • + f^vC/)- A3.3.18)
Причем
и
л-1
о р=о
=" -£)Г I t52v («) - ^2v] S /'"'^ (^ + /^/^ + Л«) ^«•
О р=0
A3.3.18) есть знаменитая формула Эйлера — Маклорена, устанавли-
ь
вающая связь между интегралом f(x)dx и суммой значений
284 УСКОРЕНИЕ сходимости КВАДРАТУРНОГО ПРОЦЕССА 1ГЛ. 13
функции / в равноотстоящих точках:
5„ = /(а) + /(а-Н А) + /(а + 2/г)Ч- . .. -Ь /(*) =
В задачах вычислений она может служить как для нахождения сумм
значений функции S„, так и для нахождения интеграла. Мы ее будем
применять только для второй цели.
Если неограниченно увеличивать v. то сумма— 2 ^ пределе
даст ряд
-Ё тТ^^ЛГ-'Ч1>) -Г->(а)]. A3.3.19)
Вспомним, что, начиная с некоторого номера, числа Бернулли ^gj^
быстро возрастают и при больших k имеют значения
Ряд A3.3.19) будет сходиться для весьма узкого класса функций,
составляющих лишь малую часть функций, встречающихся в
приложениях. Несмотря на этот недостаток, формулу Эйлера — Макло-
рена все же применяют в вычислениях, так как часто оказывается,
что ее остаток P2v(/) ДЛЯ нескольких первых значений v имеет
малую величину и добавление нескольких первых членов суммы к Т^^
нередко значительно повышает точность формулы трапеций.
Об остатке p2v(/) докажем три следующих простых теоремы.
Теорема I. Если /^^Ч-^) (непрерывна на [а, Ь], то существует
такая точка i£[a, Ь], что для Р2у(/) выполняется равенство'.
p2v(/) = —^2^52v/''4D- A3.3.20)
Доказательство. При изучении многочленов Бернулли
в гл. 1 § 2, было установлено, что функция y^vi^) "^ 0<а<1
сохраняет знак: (—1УУ2^{^) > 0. О < гг < 1. Рассмотрим интеграл
1 л-1
/v - J (-1)' y2v (^) S /^''* (^ + ^/^ + ^^) du.
Наибольшее и наименьшее значение /^^^ на [а, Ь] обозначим
соответственно М и т. Для /^ очевидно верны оценки
1 1
(--1)'' пт j y2v (^) ^« < ^ < (—1)^ riM I )j2v («) ^^
§ 3] ЭЙЛЕРОВЫ МЕТОДЫ РАЗЛОЖЕНИЯ ОСТАТКА 285
И так как
1
[ Узг (^) ^^ = J t^2v (^) — ^2vl ^^ =
27411 l^2v + l (О — ^2v + l W] — ^2v = — ^2v»
TO
где т<^Р^Ж. По непрерывности /^ ^\ наверное существует точка
l^la. b] такая, что /^^'^(у^^^Я и /^ = (-1)"^'«^Sv/^'^'^l).
Отсюда следует A3.3.20). ввиду p2v(/) = (—!) -Bу)Г^^'
Теорема 2. Если /^^^ непрерывна и сохраняет знак на [а, Ь],
то для p2v(/) ^ерко равенство
P2v(/) = -eB- 2-^^^0-^[/^^"^Ч^)-Л'^Ча^^ A3.3.21)
о<е<1.
Доказательство. Действительно в § 2 гл. 1 показывалось»
что (—1)^ y2ki^) сохраняет знак на [О, 1], возрастает при 0'^х<0.5
и убывает при 0,5<д:^1, наибольшего же значения достигает при
х = 0.5 и оно равно (—1)^^2^@.5) = —(—1)^B— 2-2*+iM2ft.
Поэтому P2v(/) A3.3.17) имеет тот же знак, что и
2v 1 л"~^
У2^ @.5) А!1- J 2] f"^ (« + Лр + hu) da
О р==0
и по абсолютному значению меньше этой величины, так что
h^'^■^^ С
P2v(
О р = 0
Но у2й @.5) =-B-2-2^+1)^2, и
1 я-1
о р«о
что доказывает равенство A3.3.21).
' л-1
, (/) = ey^v @.5) ^ J 2] /''* (а + Л/? + /г«) rfM. О < в < 1.
286 УСКОРЕНИЕ сходимости КВАДРАТУРНОГО ПРОЦЕССА [ГЛ. 13
Из него в частности видно, что p2v(/)> ^ условиях второй
теоремы, имеет знак такой же, что и первый отброшенный член в ряде
Эйлера — Маклорена и по абсолютной величине меньше удвоенного
абсолютного значения этого члена.
Оказывается, что при некоторых предположениях о функции /
для остатка P2v(/) формулы Эйлера — Маклорена верна теорема,
аналогичная теореме об остатке знакопеременного ряда.
Теорема 3, Если f имеет на \а, Ь] непрерывную производную
порядка 2v + 2 и при всяких х^[а, Ь] либо /^^Чл:) ^ О и
/2v+2)^^^^Q^ Либо /^''Ч^ХО и /^''^^Ч^)<0. то р^хЛЛ имеет
тот же знак, что и /о \Г [/^^~^Ч^).— /^^~^Ч^)] ^ ^о
абсолютной величине не больше этого члена.
Доказательство. Остатки P2v(/) и psv+sC/) связаны друг
с другом очевидным равенством
P2v(/) = - 75^ 1/'^"'^ (*) - ^"^~'' (^I +P2V+. (/).
которое можно переписать в следующем виде:
Bv)!
j y2v(^) S ^^'''^ (« + ^/^ + ^^) ^^ +
p-O
^2v+3
i
J [- У2уч-2 (^)l S Z'''''^' (a + /zp + /га) ^«:
^Bv + 2)!
6 p=o
По условию теоремы p ^^ и / имеют одинаковые знаки.
В § 2 гл. 1 выяснялось, что на отрезке [О, 1] >'2v(^) ^ — 3^2v+2(^)
также имеют одинаковые знаки. Поэтому оба члена левой части
последнего равенства имеют один и тот же знак. Знаки их должны
совпадать со знаком правой части и абсолютное значение каждого
из них не может быть больше абсолютной величины правой части.
Пусть нужно вычислить интеграл
1
dx
I
==1п2.
\+х
о
Здесь а==0, ^=1. Разделим отрезок [О, 1] на 10 равных частей и,
в соответствии с этим, положим /г = 10, Л = 0,1. В формуле Эйлера —
§ 3J ЭЙЛЕРОВЫ МЕТОДЫ РАЗЛОЖЕНИЯ ОСТАТКА 287
Маклорена сохраним, кроме Г^^, еще два члена, что отвечает v = 3.
1
dx ^
С dx
J 1+^
Тп-^[Г{\)~-гт + ^[Г{1)~гт.
о
- ^ [/'A)-/'@I = --f^[l-|] = -0.000625,
^[ГA)-/"'@)]-^^^[1 --i-] = 0,000 000 781...
Правая часть приближенного равенства имеет значение
0,693 771403—0,000 625 + 0,000 000 781 =^=0,693 147 184.
Оценим погрешность. Для этого заметим, что производные шестого
-F) 6! А^) 8! ^
порядка /===/11 у и восьмого порядка f =_—_ обе
положительны на отрезке [О, 1] и для оценки остатка Рб(/) можно
воспользоваться теоремой 3. Образуем первый отброшенный член
формулы:
-30w[/^»-A0)b-^l^[l -i]- -0.000000 004.
Поэтому С точностью ДО 0,5 • 10" можно положить
г dx
J 1+^'
:0,693 147 18.
Построим теперь формулу эйлерова вида для увеличения
точности правила парабол F.4.10). Для этой цели возьмем простейшую
формулу парабол
а+2А
J f^x)dx^~[f{a)~\-Af{a-^h) + f{a + 2h)] + R{f) A3.3.22)
и для нее построим равенство A3.3.6).
Алгебраическая степень точности A3.3,22) равна 3 и нужно
считать т^=А.
288 УСКОРЕНИЕ сходимости КВАДРАТУРНОГО ПРОЦЕССА [ГЛ. 13
Для нахождения коэффициентов С^ вновь воспользуемся их
выражением A3.3.10)
1Й + 2Л
Ввиду ^2^41 = о(^= Ь 2. . . .), отличными от нуля будут только
С^ с четными индексами i.
Для составления остатка R^(f), найдем L^{t):
-1[«"<(т)-^"<(»)+М«"-(''^)-''-Ш)+
+ e„,(i+^)-B„,(i)] .
Интеграл, входящий в построенное выражение для L^, равен нулю.
Если вместо функции Б*^^ ввести функцию >*^4' '^^ •^•^^ ^^@ ^*^"
лучится:
й + 2/г
Внесем в остаток /?^(/)= /^ ^^^(^)/,Д^)й(^ найденное предста-
а
вление £^@ ^ заменим переменную t, положив t = a-\~2ha {О^и^ 1).
^s (Л = з^Д4)! J /'" " ('^ + 2^^") 1у^+4 (!-«) +
О
§ 3] ЭЙЛЕРОВЫ МЕТОДЫ РАЗЛОЖННИЯ ОСТАТКА 289
Это дает возможность записать равенство A3.3.6) для формулы
парабол A3.3,22) в виде
J /(x),/x=|[/(a) + 4/(a-f/гL-/(а+2/г)] +
а
V-1
^^^ A3.3.220
Остаток P2v(/) может быть представлен в виде либо
1
'о
+ 2y*v_i@,5~-//)}^fw.
^1ИбО
1
о
^2[у1@,5~ u)~-y^^@,5)l}du.
смотря по тому, будет ли / иметь непрерывную производную
порядка 2v — 1 или 2v. Ниже мы будем считать, что р ^^ существует
и непрерывна и будем пользоваться вторым выражением остатка.
Перейдем к общей формуле парабол F.4.10). Разделим отрезок
интегрирования [а, Ь] на п равных частей, считая п четным числом.
Выделим сдвоенный частичный отрезок [a~\~2hp, a~\--2h(p-\-\)] и
применим к нему равенство A3.3.220- Если после этого суммировать
полученные равенства по р от нуля до -у—1» получим
разыскиваемый результат:
//(^)^. = ^„ + |;'з^A-2-""^M2*-[/"-^*)-/"-"(а)]+
+ P2V (/) = ^« - W f/*'* (*) - /''' ('^I + W f/"' (*) - /*'* ('^)] -
"' [/'Ч*)-/"(а)]+ ... +P2v(/). A3.3.23)
14 400
290 УСКОРЕНИЕ сходимости КВАДРАТУРНОГО ПРОЦЕССА [ГЛ. U
где
Un = T{fi^) + f{b) + 2lf(a-\-2h)+ ... +f(a+in-~2)h)]-\-
+ 4[/(а + А)+ ... +/(fl + («-l)A)]),
1
p^v(/)=-^||^|{3'2v(«)+2[y;,D—«)-^.v(i)]}x
о
X 2 /^Ч^+2/?/г + 2Л//)^и. A3.3.24)
Для исследования остатка p2v(/) необходимо предварительно
рассмотреть ядро интеграла /^(w) = y2v(^)+^ [>'2v(*^'^ ~ ") "" ■^2v(*^'^)]-
Лемма. Функция Ф2v+l(-'^) = У2v+l(-^) — 2y2v+i@'^ — ^) sf^y^npu
отрезка @; 0,5) не имеет нулей на при каких значениях v^ 1
и имеет там знак, определяемый неравенством
(—l)>2v+iW>0' 0<л:<0,5.
Доказательство. Будем считать v^L Так как y2v+i(^)=^
= y2v+i(^'^)'^*^' ^^' очевидно, л: = 0 и х = 0,5 будут нулями Щ^^х{х).
Допустим, вопреки утверждению леммы, что точка а@<а<0,5)
есть нуль функции Ф2^ы- Тогда внутри каждого из отрезков [О, а]
и [а, 0.5] Ф2^_^1 будет иметь хоть один нуль. Следовательно, вторая
производная ^^^v-vi ^^^^'^ внутри [0; 0,5] по меньшей мере один нуль.
Но Ф2v+l==Bv+l)Bv)[y2,.l W-2y2,.i@.5-x)]=Bv+l) 2vi^^^_^ (х).
Таким образом, из допущения, что Ф2у+1 имеет внутри @; 0,5)
нуль, следует, что Ф2у-1 также имеет нуль внутри @; 05), Продолжая
эти рассуждения, можно прийти к заключению, что фз должна иметь
внутри @; 0,5) корень. Но, как легко проверить, фз = 3л:2(л; — 0,5)
и не обращается в нуль внутри @; 0,5). Полученное противоречие
доказывает лемму. Чтобы определить знак Ф2у+1(^) "^ Ф'у ^»5)» Д^"
статочно вычислить ^2v-^\ ^ точке л: = 0,25:^
Ф2^+, @,25) =:-y2v+i @.25).
в § 2 главы 1 было показано, что (—1)^"^ y2v+i(^)>0 при
0<х<0,5. Поэтому (—1)''ф2у+1(л:)>0 (О < л: < 0,5), Считая
0-<и<;0,5, возвратимся к F {и)=^у2^-^2[у2^{0,Ъ — а) ™->'2v @.^I
и рассмотрим (—\f^^ F{u)\
{~\f"' F^{u)=2x{~~\f''[y2,.^,{u)~ 2y2v-i @,5-//)]=-
_2v(-~l)'~42v-i(«)'
§ 3] ЭЙЛЕРОВЫ МЕТОДЫ РАЗЛОЖЕНИЯ ОСТАТКА 291
В силу леммы, (—1)^~ F^(a)>0, стало быть, (—\f~^ F{u) есть
монотонная возрастающая функция при 0<;а<;0.5. Так как, кроме
того, FiO)^0, то F(u)>Q при 0<и<0,5.
Чтобы судить'о поведении F(u) на отрезке 0,5 ^и^ I,
достаточно показать, что значения F(u) распределены симметрично
относительно г/= 0,5: F(\—u)=F{u), Действительно,
F0^u) = y^^{\^-a)^2[yl(u-0.5)-y^^@,5)l
y^^(\^u)^y,Jul У1(и-0,д) = у1(и^0,5)=у1@,5~~и).
Следовательно,
Fi\^a)^y^Ju)^2[yl^@.d~u)~-y^^@.5)] = Fiu).
Отсюда вытекает, что на отрезке 0,5 ^и < 1 (—l)^""^ F{u) есть
монотонная убывающая функция с положительными значениями.
(—1)"^" F{a) достигает наибольшего значения на отрезке [О, 1]
в точке а = 0,5 и это значение есть
^m^x(-lf-' F(a) = -~(~iy-' y,^@,5) = (-lf'' 2{\ -2-'^)В,^,
[О, li
A3.3.25)
Указанные выше свойства ядра F{u) позволяют доказать об
остатке P2v(/) A3.3.24) три теоремы, аналогичные сходственным
теоремам об остатке формулы Эйлера — Маклорена.
Доказательства этих теорем мы опускаем, так как для этого
достаточно повторить доказательства теорем I, II, III с небольшими
изменениями.
Теорема 4. Если функция f имеет непрерывную производную
порядка 2v на [а, Ь\, то внутри [а, Ь\ существует такая точка |,
что для остатка p^vif) формулы A3.3,23) верно равенство:
P2v(/)=4|if(l - 2-^^"^)B2v/'^'(l). A3.3.26)
Сравним это представление остатка A3.3.26) с выражением A3.3.20)
для остатка формулы Эйлера — Маклорена A3.3.18). Если произвол-
ная / (х) сохраняет знак на [а, Ь], то остатки формул A3.3.23)
и A3.3.18) имеют разные знаки. Отсюда вытекает следующее
полезное для вычислений правило:
Когда производная /^^^Jc) сохраняет знак на [а, Ь], то тон-
b
ное значение интеграла \ f{x)dx заключается между прибли-
а
оюенными значениями, найденными по формулам A3.3.18) и
A3.3.23), если отбросить в них остаточные члены p2v(/)'
292 УСКОРЕНИЕ сходимости КВАДРАТУРНОГО ПРОЦЕССА [ГЛ. 13
Теорема 5. Если производная f^^"^ сохраняет знак на [а, Ь\,
то остаток P2v(/) формулы A3.3.23) представим в виде:
P2v(/) = 201|^(^ - 2-^^) 52V [/^"^^ Ф) - Л-^^ (а)] (О < е < 1).
A3.3.27)
Из A3.3.27) видно, что остаток P2v(/) формулы A3.3.23) имеет
ТОТ же знак, что и первый отбрасываемый член
i||lA _ 2-^-^) Вз, [Л-^' (г>) -/^-» И.
И по абсолютной величине меньше удвоенного арифметического
значения этого члена.
Теорема 6. Если функция f имеет производную порядка 2v+2
и при всяких X на [а, Ь] либо /'^'^\х)^0 и /^^'^\л:)^0, либо
/^''Ч-^ХО и f^^'^\x)^0. то остаток p^^{f) формулы A3.3.23)
имеет тот же знак, что первый отбрасываемый член
^A - 2-^-') В,, [/^->> (Ь) - /^-^> (а)],
и не больше его по абсолютной величине.
Ниже приводятся ряды вида A3.3.6). служащие для увеличения
степени точности некоторых частных квадратурных формул.
(о
правило -g- Ньютона]
\ /(х)^;с~|уг[/(а) + 3/(а + /г) + 3/(а + 2/г) + /(а + ЗЛI +
=^lh{f{a) + Ъf{a^h)^Ъf{a-^2h)^f{a + Ъh)]-
13^8
19 200
[f\a + Zh)-f\a)\+ ... A3.3.28)
2. Рассмотрим интеграл, взятый по отрезку [ — 1, 1] с весом
р(д^)==A — х)''A+х)^(а, р> — 1), и квадратурную формулу с п
узлами для него, имеющую наивысшую степень точности 2п — 1
Узлы ее расположены в нулях якобиева многочлена степени /j.
§ 3] ЭЙЛЕРОВЫ МЕТОДЫ РАЗЛОЖЕНИЯ ОСТАТКА 293
Формула A3,3.6) для него будет иметь вид:
1 It
jil-xf (l + xf fix) dX'^'^AJix,) +
k-\
+ Co[/B«-')(l)-/B''-l)(-l)] + C,[/B«)(l)-/<^'"(- 1Л+...
Коэффициенты Cq и Cj имеют значения
2«+f^+^^^rz! Г(а + РН-^ + 1)Г(а + п+1)Г(Р + /г + 1)
^0" B/г)!(а + р + 2/г + 1) ' Г^ (а + р + 2/г +1)
^-1 — а+р + 2л [а + Р + 2« + 2 "^ ^^*J B/г + 1)! ^
Г(а+Р + ^+1)Г(а + ^+1)Г(Р + /г + 1)
^ Г(а + р+2/г + 1)Г(а + р + 2/г + 2)
Для ультрасферического случая р = а коэффициенты Q нечетных
индексов равны нулю и
__ 2^^/г!ГBа + п+1) Г 2"Г (а +/г +1) 1^
^^0" B/г)!Bа + 2п+1) |_ Г Bа + 2/г +1) J '
^ _ 2^^/г!ГBа + /г + 1) Г 2"Г (а +/г + 1) 1\у
^2— B/2 + 2I I ГBа + 2/г + 1) J ^
^[Bа
2/z2 + 2Ba+l)/2 + 2a—1
+ 2л — 1) Bа+ 2/2+1) Bа+ 2/2 + 3) "^
/2(/2~1) (/2+1) B/2+1)
Bа + 2/г — 1) Bа+ 2/2 + 1) 3 Bа+ 2/2 +
1)J*
3. В частности для квадратурной формулы Гаусса, узлы которой
лежат в корнях многочлена Лежандра. формула эйлерова вида будет:
J/ W rfx ~ 5; л,/ (X,) + ,E+Т)Т [^Г X
Х[/(--)A)--/(-->(-1)]+E;^[^
V Г 2п2 + 2п-1 /г(/г-1) /г+11
^ LBn—1) B/1 + 1) B/2 + 3) ^ B/г~1)Bп + 1) 3 J ^
Х[/B'М1)A)._/{2. + 1)(_.1)]4-...
При применении эйлеровых формул к вычислениям необходимо
находить значения производных от функции / на концах отрезка [а, Ь],
что во многих случаях может представить затруднения. Можно
построить другие формулы для увеличения точности квадратуры, в
которых поправочные члены выражаются через разности или значения
функции вместо производных. Такие формулы могут быть весьма
разнообразными, так как замена производных конечными разностями
может быть сделана многими способами. Ниже рассмотрен лишь один
294 УСКОРЕНИЕ сходимости КВАДРАТУРНОГО ПРОЦЕССА [ГЛ. 13
пример замены такого вида, достаточный для того, чтобы
ознакомиться с характером формул указанного типа.
Пусть мы хотим вычислить производные функции / в точке а.
Для этого интерполируем / по ее значениям в нескольких точках.
Вид интерполяционного многочлена определяется, прежде всего,
выбором узлов. Будем считать, что для интерполирования можно
пользоваться только значениями / в равноотстоящих точках a~\-kh
(^ = 0, 1, . , .), принадлежащих отрезку [а, Ь].
Воспользуемся ньютоновым представлением интерполяционного
многочлена C.2.6), приняв в нем следующий порядок узлов: Хо = а,
Х1 = а-|~/г, Х2^=' a-\~2h, ...
/W=:/(a) + (x-^a)/(a, а + /г) +
-|- (х — а){х~ а— h) f{a, а -f- Л, а + 2Л) 4- . . ■ + Р W.
где p(jc) — остаток интерполирования. Для равноотстоящих узлов
разностные отношения просто выражаются через разности:
Вводя для облегчения записи новую переменную t=—^^ > -^=^
^^a-^ht. получим хорошо известную формулу Ньютона — Грегори,
построенную для интерполирования вблизи начала таблицы значений
функции
/(x) = /(a + AO = /o + ^Д/o + -^^^A^/o +
^(^-1И^-2)дз;„+...+РИ.
3!
Вычисляя от обеих частей равенства производные и полагая х =: а,
/ =:=г О, найдем
hf (а) = Д/о - у A^/„ + J Аз/о - | Д4/„ +1 ^Ъf^ _ . , . + р' (а)
h^f" (а) = А2/о - Дз/о + ^ АVo - I AVo + • ■ -
Л3/C) (fl) = ДЗД __ I Д4/^ ^ i. Д5/^ _ . . ,
Л7(^>(а) = А7о-2Дз/о-^ ...
луE)(а)=.Д5/о- ...
Аналогично, для нахождения значений производных /(*' A>)
{k=l, 2, . . .) интерполируем / в окрестности точки Ь = a-]-nh,
используя для этого то же представление интерполяционного много»
§ 3] ЭЙЛЕРОВЫ МЕТОДЫ РАЗЛОЖЕНИЯ ОСТАТКА 2%
члена C.2.6) и полагая в нем XQ==a^^ nh, Xi=^a -^-in — I) h.
f (x) = f {(^ + ^h) -\- (x ~- a — nh) f (a -^ nh, a-\-(n~- 1)A) +
+ (x ~ a ~ tih)(x — a ~ (n-~ 1) h) X
или
/@ + D) = /„ + ^A/._,+i2±JiAy„_,+
+ '" + '>" + ^'A./._3+...+pW.
Отсюда получим
A2/"(*) = AV„-2 + AV„-3 + j^AV„-4 + |-AV„-5+ • • •
Предположим теперь, что мы хотим преобразовать формулу
Эйлера — Маклорена A3.3.18), заменив в ней значения производных
на конечные разности. Подставив вместо только
что найденные выражения, после некоторых вычислений получим
следующую формулу Грегори:
a+nh
J /{X) dx = r„ -^ (Д/„_, -- А/о) - ^ (А2/„_2 + А^/о) -
а
- 4ж ^^'fn-z - AVo) - -^ (AV„-4 + AYo) -
... -С,А(А*/„_, + (-!)*Д*/о)+ /?,(/). A3.3.29)
Можно показать, что
1
(^к^ (k'i% р(^--1) ••• (J^-*)rf^-
296 УСКОРЕНИЕ СХОДИМОСТИ КВАДРАТУРНОГО ПРОЦЕССА [ГЛ. 13
§ 4. Увеличение точности квадратуры при наличии короткого
главного участка интегрирования в интегральном
представлении остатка
Как выше, будем рассматривать механическую квадратуру с
произвольной весовой функцией р {х)\
b п
j p(x)f(x)dx=^AJ(x,) + R(fy A3,4Л)
Если алгебраическая степень точности A3.4,1) равна т—1 и /
имеет на [а, Ь] непрерывную производную порядка т, остаток /?(/)
представим во многих случаях в форме*) A3.3.4):
b
R{f)= ^ fi"'){x)K(x)dx, A3.4.2)
а
где ядро К (х) не зависит от /.
Предположим, что на [а, Ь] существует участок [а, Э], вне
которого К(х) имеет пренебрежимо малые значения или, по меньшей
мере, быстро убывает при удалении от [а, р]. В образовании
численного значения интеграла A3.4.2) интегрирование по [а, Р) будет тогда
играть главную роль. Пусть, кроме того, /^"^* «мало изменяется»
на [а, Э], или, что, по существу дела, равносильно, [а, р] имеет
«малую длину». В этих предположениях, для выделения главной части
из остатка /?(/)» достаточно разложить f^^^ на два слагаемых,
положив /^'"Ч-^) = /'"Ч«о)+[/^'"Ч-^) —/^""Ч^о)]» ^^^ ^0 ^сть некоторая
точка главного участка интегрирования [а, р]:
b b
R if) =. f(m) (a,) j /c @ rf/ + J l/^'"^ W - /^"^ («o) ] К (X) dx,
a a
Остается еще произвол в выборе а^. Когда ядро К{х) сохраняет знак,
за tto естественно принять координату той точки оси х, около
которой сосредоточены значения К{х), наибольшие по абсолютной
величине, и считать ад равным средней абсциссе по весу К{х);
г b -1-1 Ь
j Kdx . J xK(x)dx,
Ctn =
Предположим, что / имеет непрерывные производные до порядка
m-\-'2s, и преобразуем последнее выражение для /?(/). Разложим
*) Такое представление остатка возможно всякий раз, когда допустимо
изменение порядка интегрирования в двухкратном интеграле, входящем
в выражение /?(/), предшествующем A3.3.4).
§ 4] УВЕЛИЧЕНИЕ ТОЧНОСТИ КВАДРАТУРЫ 297
f^"^ {х)— /^4cto) при ПОМОЩИ формулы Тейлора, взяв в ней два члена
X
Г (х) - Г (ао) = /"^'^ («о) (^ - «о) + J f^'-'^it) ix ~t)dt^
^ /"^' '^ Ы (^ - «o) + J /"■'^' @ [£ (X - 0 - ^ («0 - 0 ] (a: - 0 ^^.
/(^)
<m)
Подставим это выражение f {x) — f (a^) в R(f) н выполним
b
интегрирование. Ввиду выбора а^, K{t){t~- a^)dt^=Q и мы будем
а
иметь
b
R if) = Со/"" (ао) 4- J /'"■''^ (О /с, (О rf^
а й
Если повторить такие преобразования s раз, получится
приводимая ниже формула, позволяющая в некоторых случаях последовательно
увеличивать точность механической квадратуры:
ь п
\ Pix)f (X) dx = ^ A,f (X,) + Со/"^ (ао) + С,/"'''\щ)+ . . ,
b
■.. +C,_,/'"+''-'4a,_i)+ j f'^^''\x)KAx)dx, A3.4.3)
а
b
Kq {X) = /С (JC), /C,-.,i (л:) = j КI (t) [E(t^x)- E (щ ~~x)](t-'X) dt.
a
b b
C; = I Ki dx, at = Cr^ j xKi (x) dx.
a a
По поводу ядер Ki{x) полезно отметить сд^яующ^е. Из
рекуррентного соотношения для них сразу получаются такие равенства
X
^ Ki(t)(x — t)dt, а <X < а^,
Кш(х)-
J Ki(t)it- x)dt, щКх^Ь,
298 УСКОРЕНИЕ сходимости КВАДРАТУРНОГО ПРОЦЕССА [ГЛ. 13
Отсюда видно, что если ядро /С/(л:) сохраняет знак при а^х-^д,
то ядро Ki^i (х) также сохраняет знак при а-^х -^Ь, причем знаки /С/
и Ki^-i одинаковы. В частности, если исходное ядро /Cq(л:) =/С (л:)
остатка A3.4.2) было положительным, то будут положительными все
ядра Kiix) (/=1, 2, ...)•
Рассмотрим квадратурную формулу с п узлами, имеющую
наивысшую степень точности 2п—1 и служащую для вычисления
интегралов с весовой функцией A—xf(\-^'xf, р, ^>—1:
1 п
\ {\ - xf {\ + xf f(x)dx = ^AJ{x,) + R(fy A3.4.4)
Узлы ее лежат в нулях многочлена ЯкобиР^п'^Н^)- Будем считать
их перенумерованными в порядке роста —1 < Xj < Хз < . . . < x„ < 1.
Убедимся сначала в том, что при больших р или q в интегральном
представлении остатка R(f) действительно будет существовать
короткий главный участок интегрирования. Достаточная для наших целей
качественная картина может быть получена, если воспользоваться
электростатической аналогией для корней Р^п'^\х).
Известно, что многочлен Рп'^\^) удовлетворяет
дифференциальному уравнению *)
+ "^^+!+"+^^ plf • ^' (^) - 0.
Положим здесь х^=х^. При этом исчезнет третий член левой части.
Разделим, кроме того, на Ял^'^^'(хй), что можно сделать, так как
р1Г' ^^' {хи) Ф 0. После этого получится равенство
^ \~ ^+1 + ^+1 =0 (^ = 1, 2, .,,, я), A3.4,5)
имеющее простой физический смысл. Пусть изучается плоское
электростатическое поле, в котором заряды взаимодействуют с силами,
пропорциональными их массам и обратно пропорциональными первым
степеням расстояния между ними. Если заряды масс т^ и т^^ лежат
на оси X и имеют координаты х' и x^^ то сила, с которой масса т'
действует на массу т!\ будет равна % ,, __ , .
Поместим в точки -|-1 и —1 электрические заряды масс /?+!
и ^4~ 1 соответственно и закрепим их. Кроме того, возьмем п зарядов
*) В. И. Смирнов, Курс высшей математики, т. 1П, часть 2. М. — Л.,
Гостехиздат, 1957, 382—384.
§ 4] УВЕЛИЧЕНИЕ ТОЧНОСТИ КВАДРАТУРЫ 299
массы 2. поместим их внутрь отрезка [—1, -f-1] и будем считать,
что они могут свободно перемещаться вдоль оси х. Координаты
свободных зарядов обозначим л:^^ (^=1, 2 п)> Если такая
система помещена в вязкую среду, то через некоторое время в ней
наступит состояние равновесия. Уравнения равновесия получаются,
если мы запишем, что для каждого свободного заряда
равнодействующая всех воздействий, которые он испытывает со стороны других
зарядов системы, равна нулю. Для свободного заряда номера k это
дает:
Уравнение равновесия только множителем % • 2 отличается от
A3.4.5). Поэтому корни многочлена Якоби P^f'^^A:) будут совпадать
с координатами положений равновесия свободных зарядов.
Когда массы р-{- 1 или q~\- 1 закрепленных зарядов будут
«большими», они с значительной силой будут отталкивать от себя свобод-
. ные заряды и вынудят их сконцентрироваться на «малом» участке
отрезка [—1, 1]. Поэтому участок [xj, л:„], на котором располагаются
все корни Р^п'^\^)^ будет иметь малую длину. Когда р значительно
больше q, [Xj, х^] будет «малым» отрезком вблизи точки —L
Наоборот, если q'^^ р, [Хр х^] будет лежать вблизи точки -|-L
В общем же случае положение участка [Xj, х^] будет зависеть от
Р ^ Я-
Для квадратурной формулы A3.4.4) остаток /?(/)» ввиду
конечности отрезка интегрирования и положительности весовой функции,
наверное представим в форме A3.4.2). Ядро остатка /С(х), имеющее
в общем случае вид A3.3.5), для изучаемой формулы будет:
В частности, когда точка х лежит вне участка [Xj, х^^]:
X
л:(X)^ J(i — tf A4 tf ^\^Ti)\ d^' ЛЛЯ -1<^<-^1.
-1
к
(x)=J(l- tfil+t)" ^[^/Ti)i' ^^- ДЛ'' •««<А-<1-
300 УСКОРЕНИЕ сходимости КВАДРАТУРНОГО ПРОЦЕССА [ГЛ. !3
Остановимся, например, на случае х^^х^\, Множитель 14-^
заключен в границах I-|~ л:„ ^ 1-{-^ ^ 2. Поэтому/С (л:) будет
находиться между числами
1
X
1
X
При возрастании х от х^ до 1 К{х) будет стремиться к нулю
как A — х)^"^^". Если р большое число, то стремление к нулю
будет весьма быстрым. Если же р не будет большим числом, а
показатель степени q большим, то х„ будет близко к единице и
множитель A — xY^"^^ также будет малой величиной.
Изложенные соображения имеют только качественный характер.
Но они позволяют надеяться, что увеличение точности
квадратуры A3.4.4) указанным выше методом будет тем успешнее, чем
больше будут р или q.
Формула A3.4.3) для интеграла A3.4.4) будет такой:
J A ^xY{\^xf f{x)dx =
-1
...+С,_1Л+^^-'>(а,_0+ \ f"'-''\x)KAx)dx. A3.4.6)
-1
1
Коэффициент первого поправочного члена Со= K(x)dx есть
-1
погрешность квадратуры некоторой функции, производная которо^^
порядка 2п равна 1. За такую функцию может быть взята
а7'
f — " Р*"' 1^ (X)
J— Bп)! ^" W.
где с„ есть старший коэффициент P^f'"(jc). Так как Р'/'"Ч-"^*) = 0>
§ 4] УВЕЛИЧЕНИЕ ТОЧНОСТИ КВАДРАТУРЫ 301
то
1
Bп)\а1
J A - х)" A + xf Pi'' "''{х) dx-Yi Л,Р^ *'^ (X*)
-1 к^\
1
Или, ввиду того, ЧТО а^ и интеграл от квадрата якобиева
многочлена имеют известные значения B.2.2) и B.2.5).
2^+^"^^+^/г1Г(р + /г+1)Г(^ + п+1)Г(/7 + ^ + ^ + 1)
1
Вычислим еще ttQ. Заметим, что в выражении ао = СG | xK{x)dx
^интеграл xK(x)dx есть остаток приближенного интегрирования
-1
по формуле A3.4.4) такой функции /, производная которой порядка 2п
равна X. Пусть Р^п*'^\х)^апх"-^Ь^х^'^-^ . , ,, За / может быть
принят многочлен / (л:) ^= ^ л: — 2 -^ Р]^'' ^^' (х). Ввиду
^ Bп+1)!аЦ aj
/(Х;^) = 0, будет
1 1 п
^ xK{x)dx = R{f)= \ (l-xr(l^xffdx-^A,f(x,) =
I
— 2^ J A - x)"(\ +x)"P^f- ''^\x)dxy A3.4.7)
Второй интеграл в скобках встречался несколькими строками раньше
и равен СдB«)!а^ Два старшие коэффициента а„ и Ь„ многочлена
Рп' (х) также известны и имеют значения *)
_ Г{р + д + 2п+\) . _ г(р + д + 2п)
"~2"п\Г(р + д + п+\) "п — п-УР 4Jnn\Y(pj^.qJr-n+\)'
*) См., напр., Д. Джексон, Ряды Фурье и ортогональные полиномы,
М., ИЛ, 1948, гл. VIII, п. 3.
302 УСКОРЕНИЕ сходимости КВАДРАТУРНОГО ПРОЦЕССА [ГЛ. 13
Поэтому
Перейдем к вычислению первого интеграла в скобках. В теории
многочленов Якоби известно следующее рекуррентное соотношение *)
= 2(п+\){р-^д-^п+\)(р^{^д+2п)Р%'\х)^{д'~^р')Х
Х(р + д + 2п+1) Pf '^ (^)+2 {р+п){д^п) (р+9+2«+2) P^i^Vix).
Если обе части равенства умножить на {\—xY{\-{~xfP^n'^\x)
и интегрировать по отрезку [—1. 1], отсюда сразу же получится:
[{\~~ xf{\+xf хР['' '^' (х) dx =
-1
{р + д + 2п)(р + д + 2п + 2)
\i\-xf(\^xfP['''^\x)dX'^
-1
_ ir~~p')i2n)\al
— (р^д^2п)(р + д + 2п + 2) ^0*
Подставив все указанные частные результаты в A3.4.7), найдем
1
для j xK{x)dx
-1
-1
1
и после несложных вычислений для ао== CJ"^ xK(x)dx
-1
^0— 2n + l\p + g + 2n^ р + д + 2п + 2Г
*) См. предыдущую сноску, гл. VIII п. 5.
§ 4] УВЕЛИЧЕНИЕ ТОЧНОСТИ КВАДРАТУРЫ 303
В ультрасферическом случае /? = ^ все а^ {k = 0, 1, . . .)
обращаются в нуль и формула A3.4.6) будет такой:
1 п
г A - хГ f (X) dx = ^ А J (х,) +
_1 fe=i
. 2''Р-'''-''п\тЧр + п+\)Г{2р + п + \) I B.) ... ,
"^ B/г)!ГBр + 2/г+1)ГBр + 2л + 2) \^ ^^~*~
_j 1 Г(п+1)(п + 2) (п~^1)п -1 А2п,2)^.^ \
"^ 2.Brt+l)Brt + 2) L 2;7 + 2л + 3 "Г 2/? + 2« — 1 J-^ Wn----i
Пусть нужно вычислить интеграл
Здесь р = д^=2. Положим п=1, т. е, возьмем только один узел:
1
-1
В силу четности весовой функции A—л:^)^, очевидно будет л:1 = 0.
Кроме того
1
Л,= j {\~x^fdx = ^^ 1
-1
Первый член формулы
066 667.
10
-1
AJ(xi) = ^' \^ 1,066 667
дает весьма неточное значение интеграла. Если присоединить к нему
второй член, то сумма их
даст интеграл с тремя верными знаками. Сумма же трех членов
^>/(^:) + ж/^''@)+^/D>@)=«+^ = -^« 1.144 974
будет отличаться от точного значения интеграла в шестом знаке.
Метод выделения из интеграла нескольких «последовательных главных
частей», который был описан в настоящем параграфе в связи с увеличением
точности механических квадратур, тесно связан с известной проблемой
конструктивной теории функций, которую обычно называют задачей интерполи-
304 УСКОРЕНИЕ сходимости КВАДРАТУРНОГО ПРОЦЕССА [ГЛ. 13
рования производными последовательных порядков, или задачей
Абеля—Гончарова *).
Пусть на отрезке [а, Ь] определена функция /, имеющая п-\~\
производных и взяты /г-[-1 точек |oi Si. •••. In- Нужно найти многочлен Р (х)
степени <: Пу удовлетворяющий условиям
Р^'^ Hi) = /'* ill) (^ -= 0. 1 п). A3.4.8)
Легко найти явное выражение для Р{х). Последнее из условий A3.4.8)
p(«)(^)==/<«)(g„)
является тождеством относительно х, так как степень Р не больше п.
Интегрируем его в границах от g„_] до х и воспользуемся при этом
предпоследним условием A3.4.8):
X
р(''-')(^) = /«-!)(!„_,L- J dt„./''Hln).
S-1
Продолжая интегрировать дальше и учитывая при этом условия A3.4.8),
после п шагов найдем
JC X tx
Р {X) = / (|о) + /' (li) J dt^ + f" (I2) j rf^i J rf^2 + ...
X ^ ^n~\
-.. + /"^ (In) \ dt, ^ dt,,.. J dtn. A3.4.9)
'^O ^I ^Л-1
Вводя обозначения
X ^ h-\
Ц(х)^\^ Ц{х)^ [dt^[dt2.., f dti,
можно записать P{x) в форме
m
P(x)^ ^/^'\Ъ)Ц{х). A3.4.10)
Рассмотрим теперь остаток интерполирования г(л:) = /(д:)^—^(-^)- При
некоторых предположениях о функции /, для него может быть построено
другое представление, более удобное для исследований и оценок.
Пусть точка х и узлы с,^ (^=0, 1 п) принадлежат отрезку [а, р].
Если функция / имеет непрерывную производную порядка п-\Л на [а, р],
то остаток интерполирования г (х) представим в виде:
Ч ^п
г(х)^ J dt, J dt,.,. J f^^^'\tn^,)dtn^,. A3.4.11)
Sq ^1 ^n
*) B. Л. Гончаров, Теория интерполирования и приближения
функций, гл. 1 и 18, 1954. См. также М. А. Евграфов, Интерполяционная
задача Абеля — Гончарова, М., Гостехиздат, 1954.
§ 41 УВЕЛИЧЕНИЕ ТОЧНОСТИ КВАДРАТУРЫ 305
Справедливость этого вытекает из того обстоятельства, что в узлах g^
остаток г (х) должен удовлетворять условиям г (gg) = 0, /*' (Si) ==^ О, • • •
..., '*^"Ч?л) = О и, кроме того, для него должно выполняться тождество:
Возвратимся теперь к разложению остатка квадратуры A3.4.1):
b
/?(/)=! /^) {X) к {X) dx. A3.4,12)
а
Пусть, пользуясь некоторыми соображениями, для выделения «первой
главной части» из R(f) мы избрали некоторую точку go и разделили/^'"^ (;с)
на две части, положив
X
/С») (;,) = /С") (|о) + l/C") {X) - /"" (|оI = /'") (|„) + j /"■+'> (О dt =
b
= /"" (U)-\-\ f'^^^4t)[E(x-t)-E(l,- О] dt.
а
Напомним, что раньше избранную точку мы обозначали ао и подбирали
ее специальным образом стремясь к тому, чтобы в первой выделенной части
остатка была сконцентрирована возможно большая его часть. Сейчас мы не
будем рассматривать вопрос о выборе |о и оставим эту точку произвольной.
Подставив указанное разложение f-^^ в A3.4.12), получим остаток R(f)
в форме
b
R (/) = /""' do) S-o + j /'"""'> {X) N, {X) dx.
a
b b
^0 = J /C {X) dx. N, (л:) - I /C (t) [E (t --x)-E Ц, - x)] dt,
a a
Пусть вновь с целью выделить из R (/) «вторую главную часть» мы
опять избрали некоторую точку |i и разложили /"*^^^(лс) на две части
f^"'''\x)^/^^'Hh)+l/"'^'4x)-/'^^'Hh)]
и т. д. После нескольких таких преобразований мы получим следующее
разложение /?(/):
b
^ Г fim+s)^^^ дг^ (^) ^^^ A3.4.13)
b b
Ni^ 1 (-^) = I ^i it) [E{t-x)-E {It - x)\ dt, 9i - J Л^.- {X) dx.
306 УСКОРЕНИЕ СХОДИЛЮСТН КВАДРАТУРНОГО ПРОЦЕССА [ГЛ, 13
Построенное сейчас разложение остатка, принципиально говоря, имеет
ту же природу, что и разложение /?(/), которое было сделано раньше при
построении формулы A3.4.3). Различие состоит лишь в том, что раньше
выбор точек а^, ai, ... был подчинен определенным целям, теперь же
избираемые точки go, gb .., мы оставляем произвольными и не налагаем на них
никаких ограничений. Но вполне ясно, что если выбрать точки g/ особым
образом, а именно считать go — «о^ ^2 = ^i то новое разложение A3.4.13)
остатка R (/) совпадает с его прежним разложением.
Равенство A3.4.13) может быть получено другим путем, тесно связанным
с указанной выше задачей Абеля—Гончарова. Примем точки go, gh -..i Is-i
за узлы и выполним интерполирование функции f^'^^{x) последовательными
производными в них:
5-1
Если внести это разложение /^"^^ (х) в A3.4.12), получим новое
представление остатка /?(/)
S-1 Ь b
^(/) == S /'"^^^ Hi) J ^ W Li W dx+^ к {x)r(x) dx. A3.4.15)
t=0 a a
Oho, очевидно, должно совпадать с A3.4.13) для всякой m-\'S раз
непрерывно дифференцируемой функции /. Поэтому должно быть
ь b b
В.
i - J /( (X) Ц {х) dx, J /"^^ '^ (X) N, {X) dx=^ { К {X) г {х) dx. A3.4.16)
а а а
Такая связь интерполирования /^'"^ с проблемой разложения остатка
квадратуры по «главным частям» полезна в теории квадратур в частности
в следующем отношении.
Если функция / дифференцируема бесконечное число раз, в
равенстве A3.4.13) мы можем 5 увеличить неограниченно. В пределе из суммы
5 — 1
^S^if^^'^^Hh) получится бесконечный ряд
^(/)-^o/"^4?o) + ^i/"^'^'4?i)+ ... A3.4.17)
Вопрос о сходимости этого ряда к R{f) равносилен тому, чтобы при
5 -> оо было
b
im Г Z'^^^) (jc) Ns {x) dx = 0.
lim
5->00
Последнее же ввиду A3.4.16), в свою очередь, равносильно тому, чтобы
b
К (х) г {х) rfjc -> О, S -> оо,
а
Таким образом вопрос о возможности разложения остатка/?(/) в ряд A3.4.17)
по «главным частям», т. е. вопрос о справедливости равенства
R (/) = ^о/"^) (g,) -f ^,/"^ ^ ^) (I,) + ... A3.4.18)
§ 5] СКОРОСТЬ СХОДИМОСТИ КВАДРАТУРНОГО ПРОЦЕССА 307
тесно связан с вопросом о сходимости интерполирования Абеля —
Гончарова A3.4.14) к функции /""^ при 5->со.
В частности, если отрезок [а, Ь] конечный и
r{x)=/"'Hx)-^/''^'4li)^i(^)-^0 при s^oo
1 = 0
равномерно относительно х, то разложение A3.4.18) наверное возможно.
Для ознакомления с проблемой сходимости интерполирования
последовательными производными мы отсылаем читателя к специальной литературе *) -
§ б. Увеличение скорости сходимости квадратурного процесса
В общей форме задача, которую мы будем рассматривать, может
быть высказана в следующих словах. Предположим, что для
вычисления интеграла избрано некоторое квадратурное правило, которое
мы будем считать сходящимся:
b п
l{f)=l Р {X) f {X) dx ^Y^Alf{xt) = Qn{f). Qn{f)^l{f), п~^сю,
a k = l
A3.5.1)
При помощи него может быть найдена последовательность
приближенных значений интеграла Qiif), Q2(/)' ■•• Нужно найти
способ преобразования ее в новую последовательность Sj (у= 1, 2,.. .),
сходящуюся к тому же пределу /(/), но более быстро, чем
последовательность Qjif)'
В основе правил преобразования, о которых будет говориться
ниже, лежит идея интерполирования. Пусть выбраны k значений п:
щ, щ Т1^ и для них вычислены соответствующие значения
Q/i . • . •. Qrt • По ним необходимо сделать заключение о неизвестном
1 и
точном значении интеграла /(/). Это есть некоторая задача
интерполирования, понимаемая в весьма общем виде, так как в ней не
поставлены никакие априорные предписания о выборе средств
интерполирования. Выбор способа интерполирования остается в
распоряжении исследователя. Особенностью задачи, затрудняющей решение,
является то, что приближенные значения интеграла Q^. (У= 1, ..., Щ
в реальных вычислениях бывают, как правило, близкими между собой
и мало отличающимися от предельного значения /(/). Это налагает
сильные ограничения на выбор способа интерполирования. Прежде
всего мы должны стремиться к тому, чтобы погрешность избранного
способа была значительно меньше ошибок приближенных значений
^— Qn-y которые сами являются малыми величинами.
*) См. в литературе, в конце настоящей главы книгу М. А. Евграфова.
308 УСКОРЕНИЕ сходимости КВАДРАТУРНОГО ПРОЦЕССА [ТЛ. 13
В реальных вычислениях находят небольшое число значений
квадратурной суммы Q„ — обычно два или три» и лицо, подготавливающее
вычисления, обязано достигнуть высокой точности в указании /(/),
используя для этой цели малое число значений функции Q„, Этого
можно добиться, прежде всего, путем строгого согласования способа
интерполирования с законом сходимости Q^^^L
Может оказаться, что избранный способ будет давать хорошую
точность для квадратурных процессов одного типа и быть
непригодным для процессов с другим законом сходимости. В этом смысле
каждый метод улучшения сходимости должен быть
специализированным и рассчитанным на некоторый класс последовательностей Q^,
обладающих близкими законами сходимости.
Лишь для немногих квадратурных процессов мы знаем законы
стремления к точному значению Qn~^J настолько полно, чтобы для
них мы могли указать хорошие способы улучшения сходимости. Мы
остановимся подробно только на одном типе процессов, часто
встречающемся и достаточно простом, чтобы для него можно было с
удовлетворительной точностью решить эту задачу.
Пусть рассматривается квадратурное правило с равноотстоящими
узлами Xj^=^ Xq-^- kh и шагом к:
ь
I{f)=\ p{x)f{x)dx^Y^A^{h)f{x^^kh)=^Q{h. /), A3,5.2)
а k
п ^
Предположим, что остаток R(h, f) = I(f) — Q(h, f) будет малой
величиной порядка т относительно /г: R{h, f) = h^C(h), С(Н)->СфО
при /г-~>0.
При всяком значении h выполняется точное равенство / (/) =
= Q(^' /)-|-/^'"С (/г). Если же шаг h достаточно мал. то будет иметь
малую погрешность приближенное равенство I (f) ^ Q{h, f)~\~h^C.
Допустим теперь, что вычисления выполнены для двух значений h^
и /Z2 шага. Для них будут справедливы равенства /(/) ^Q{h\, /)-|- hfC
и I if)^Q{h2, f)-\-h^C, После исключения из них неизвестной
величины С получится
ЛГQ (ho, f) — <Q (h.,f)^
f(f)^ ^ : m =S^. A3.5.3)
Если избрана бесконечная последовательность значений h: /г^. ho^
/Zg, . . . и известны соответствующие им значения квадратурных сумм
Qi^i, f) (/=1, 2, 3 . . .)' то A3.5.3) можно рассматривать как пер-
^ 5] СКОРОСТЬ сходимости КВАДРАТУРНОГО ПРОЦЕССА 309
вый шаг преобразования последовательности Q(/z^, /) в
последовательность Si {1=1, 2, . . .). Второй шаг ее есть
'^2 —
л--из"
И т. д. Последовательность S^ будет при некоторых условиях
сходиться к /(/) более быстро, чем Q(/z^, /).
В реальных вычислениях часто прибегают к делению всех
частичных отрезков пополам: начинают с деления области интегрирования
на некоторое число п одинаковых частичных отрезков и применяют
для нахождения /(/) правило вида A3.5.2). Если результат
неудовлетворителен или нуждается в проверке, то каждый частичный отрезок
делят пополам и выполняют вычисления с удвоенным числом отрезков
и т. д. в этом процессе h-^=^h, h2 = 0,5h, h^ = 0,25h, ...
Правило A3.5.3) выполнения первого шага уточнения последовательности
Qih. /)' Q@,5/z; /). С?@,25Л; /), ... будет следуюш,им:
^^_2^д@.5/,Л-<?(^./) ^,(^) A3.5,4^
Второй шаг
о _ 2"^Q @,25/г; /) - Q @,5/г; /) _ ,, ^,
^2 ^щ ^ / {/)
2
и т. д.
Рассмотрим два примера применения этих равенств.
Из F.4.4) или из формулы A3.3.16) следует, что если /^ф) —
— р(а)ФО, остаток общего правила трапеций
b
будет величиной порядка h?. Здесь т = 2 и равенство A3.5.4),
позволяющее интерполировать / (/) по значениям T{h, /) и Г @,5/г; /),
будет
5, = |[4Г@.5/г; f)-T(h, f)]^f(fy A3.5.5)
Из F.4.10) и A3.3,23) вытекает, что при /<^ЦЬ) — р^ (а) Ф О
остаток правила Симпсона
i)
/(/)= |'/Wd^«4[/o + /„ + 2(/2 + /4+...) +
а
-f 4(/,+/зЧ- ...)\=Uih.f)
310
УСКОРЕНИЕ сходимости КВАДРАТУРНОГО ПРОЦЕССА
[ГЛ. 13
будет величиной порядка h"^. Здесь мы должны считать т=^4.
Правило A3.5.4) интерполирования /(/) по значениям U {h, /) и U @,5k\ f)
будет
S,^^{\W{^M\ f)~U{h. f)\^I{fr A3.5.6)
Эта формула применима и к общему правилу трех восьмых F.4.15),
так как остаточный член его также имеет четвертый порядок
малости относительно h.
Выше мы говорили о самых простых способах ускорения
сходимости, которые основаны на знании только степени малости остатка
квадратуры. Интерполирование / (/) может быть сделано более точно,
если наши сведения об остатке будут более содержательными.
Пусть вычисления выполнены для г-j- 1 значений /Zj, ^2 ^г
шага h и найдены Q{h^. /), .... Q{h^^^, f).
Для многих правил интегрирования A3.5.2) остаток R{h, /)
может быть представлен в виде суммы, расположенной по степеням /г.
При этом для большого числа практически важных правил в
разложение будут входить только четные степени h, начиная с некоторой.
В этих условиях для интерполирования естественно воспользоваться
многочленом вида
V + 1
подчинив его требованиям P{h^)=^Q(h^, f) {s-
1.2 /*+!),
z^^2»- • • линейную систему
ао+^т/г"+...+а^4-2г-2/гГ""'—С(/г.. /) E=-1. . . ., /-+1).
Для наших целей достаточно найти только коэффициент а^, так как
доставляюш.им для коэффициентов а^, а
, т+2г-2
nfy-
А =
\Q:
3(^. /).^ \unP{h) =
/г->0
1 1
, т , т
hi /гз
,т + 2г-2 ,m + 2r-2
\Q{hi.f) Q(h„f),
h? hT
1 m + 2r-2 , m + 2r-2
ftl Л2
._ A(Q) _
«0 ——Д——
. 1
Ci
r m + 2r-2
«r-t-1
*
•■ Q{K^,,f)
J m
• . hr^i
, m+2r-S
5i, A3.5.7)
При г = 1 отсюда получается двухчленное интерполяционное правило
улучшения сходимости A3.5.3). Если положить г ==2, мы получим
^5)
СКОРОСТЬ сходимости КВАДРАТУРНОГО ПРОЦЕССА
311
рехчленное правило, имеющее более высокую степень точности:
[Q (h„ /) А2%" {hi - й^) + Q (^2. /) h'^h'^ {h\ - Л1) +
5,=
[hfh'^ {hi - Л2) + Лз™А™ (Л? - h^ + Л-Л^- (й2 - Л2) ]
A3.5.8)
Оно значительно упрощается, если при вычислениях на каждом шаге h
делится пополам: fii = h, Й2==0,5Л, h^ = Q,25h:
я Qjh,/)-5-2"'Q @.5/г; /) + 2^"^+' Q @.25А; /) ^ , ,, ^, л Ч ^ Q^
•^1 = 1_5.2'«+22'"+2 ^(^^- A3'^-9>
Для формулы трапеций и Симпсона это правило принимает
соответственно форму:
m
1
^2, S,^^[Q(h, f)-20Q@M; f) + MQiO,25h; f)]^nf),
m==4. 5i -=^ Ю(Л. /)- 80Q@,5/^; /L-1024Q@.25/?; /)] ^^/(/).
Если остаток не будет четной функцией от /г и в его разложении
по степеням h будут содержаться члены с нечетными степенями, то
для интерполирования /(/) можно воспользоваться многочленом вида
Р(/г) = ао + ^т/^'^+^т+1^"^'+...+«..+г^1^'"^'"'^ подчинив его
прежним условиям: Я (/г/) = Q (/г^.. /) E=1. 2, .... г + 1)-
Вычисления, аналогичные проделанным выше, приведут к нижеследуюш,ему
правилу преобразования:
HQ) о
6 =
/(/)^ао
1 ... 1
til . • • «г + 1
«1 .•• «r+1
6(Q) =
, m+r-1
.m + T-l
' «r + 1
Трехчленное правило преобразования, соответствующее г = 2,
будет сходным с A3.5.8), но несколько проще него:
f{f)
[о {К, /) Kh^ (Лз - Й2) + Q (Лг. /) Лз"'А'," (Ai - Лз) +
= 5,
[А^Аз"" (Лз - Аг) + hfh'^ {h, - Л3) + АГ^г" (^2 - ^i) ]
и в случае деления шага h пополам: hi = h, /г2 = 0,5Л, Аз=:0,25А:
/ / ^ч ^ 9 (А. /) - 3 • 2"» Q @,5А: /) + 2^"-+' Q @.25А; /) _ о
312 УСКОРЕНИЕ сходимости КВАДРАТУРНОГО ПРОЦЕССА [ГЛ. 13
Мы закончим настоящий параграф указанием на возможность
перенесения полученных правил улучшения сходимости процесса
квадратур на некоторые другие случаи. Все предыдущие результаты
опирались на возможность разложения остатка квадратуры R{h, f)
по степеням некоторой малой величины h такой, чтобы при /г—>0
имела место сходимость Q{h, f)~^f(f). Вид квадратурного правила
A3.5.2) и, в частности, тот факт, что его узлы считаются
равноотстоящими и h есть длина частичного отрезка, при получении правил
не использовались.
Возвратимся к общему правилу интегрирования A3.5.1). Его
остаток будет, вообще говоря, весьма сложно зависеть от п. Но в не-
. 1
которых простых случаях он может быть разложен по степеням — :
['Yfe(Ai)^0, /г—>oo]. В этом случае для интерполирования точного
значения /(/) рационально воспользоваться многочленом Pi—],
содержащим свободный член и члены с теми же степенями —, что и
в остатке /?„(/):
К такому типу среди многих других принадлежат квадратурные
правила, получающиеся в результате кратного применения какой-либо
формулы, например, формулы Гаусса: область интегрирования [а, Ь]
делят на некоторое число т одинаковых частей, к интегралу по
каждому частичному отрезку применяют избранную формулу и затем
складывают квадратурные суммы по всем отрезкам. Если во взятой
формуле было р узлов, то после суммирования получится правило
интегрирования с тр узлами.
При неограниченном увеличении числа т частичных отрезков мы
будем иметь некоторый квадратурный процесс. Возможность
разложения /?я(/) следует из представления остатка E.2,6)^ Чтобы сделать
изложение определенным и запись наглядной, предположим, что для
интегрирования по частичным отрезкам было избрано правило Гаусса
с р узлами. Степень точности его равна 2р—1.
Допустим сначала, что это правило применяется к стандартному
отрезку [—1, 1] и интегрируемая функция есть F. Погрешность пра-
вила Гаусса представима интегралом вида | F^^^\t) К (t) dt. Явное
-1
выражение ядра остатка К (t) указано в E.2.7),
Пусть [а, Ь] делится на части точками ai=^a~\~ IH, Я = — ф — а).
Чтобы записать остаток приближенной квадратуры для частичного
§5] СКОРОСТЬ СХОДИМОСТИ КВАДРАТУРНОГО ПРОЦЕССА 313
отрезка [а^, а^^^-^], переведем его в [—1, 1) линейным преобразованием
х =:а^-f 0,5ЯA Н-'О- При этом интеграл по отрезку преобразуется
так: J /(л:)йГх = уЯ |/[^а,. + ~ЯA +О]^^- Так как в нашей
задаче
f''''(t)=^f
dfp
,2р
TO погрешность вычисления интеграла по отрезку [а^-, а^^^\ равна
1
i^Y^ \f'^^Aai~^~M{\^t)\K(t)dt, Погрешность же интегри-
рования по всей области [а, Ь\ есть
2 1 Г "^"^
Rn if) - (т) '* J ^ (^) S /*''" [а, +1 ж 1 + о] ^^
-1 i=0
После этого, если считать, что / имеет непрерывные производные
достаточно высокого порядка, к интегралу
J ^ (О 2 /'"* [«/ + у я A + о] rf^
-1 (=0
достаточно применить эйлерово преобразование A3.3.6), описанное
в гл. 13 § 3» чтобы установить возможность следующего разложения
остатка:
И = —ф — а) = ^рф---а),
Rn {f)=\p{b- а) f" n-'''С, [f-'^ (b) - Л->' (a)] +
+ [p (ft __ a) f^' n-"'-% [/2"+" (*) - /2"+" (a)] +...
Коэффициенты Cq, C2, ... могут быть вычислены при помощи
равенства A3.3.7). которое в нашей задаче примет форму
-1
Ввиду свойства симметрии абсцисс и коэффициентов Гаусса, ядро
^@ является четной функцией /. Если / — число нечетное, то
^1 (—2—) ^^'^^ нечетная функция t. Поэтому все коэффициенты С^
314 УСКОРЕНИЕ СХОДИМОСТИ КВАДРАТУРНОГО ПРОЦЕССА [ГЛ. 13
нечетных номеров обращаются в нуль и в разложении R,i(f)
сохранятся ТОЛЬКО члены с четными степенями —. Численные значения
Cq, Cg МОЖНО найти в конце § 3 гл. 13 в том месте, где приведена
формула эйлерова вида для правила Гаусса.
Литература
Крылов А. Н., Лекции о приближенных вычислениях, М., Гостех-
издат, 1954.
Канторович Л. В., О приближенном вычислении некоторых типов
определенных интегралов и других применениях метода выделения
особенностей, Матем. сб. 41: 2A934), 235—245.
Стефенсен И. Ф., Теория интерполирования, гл. Xill, М. — Л..
ОНТИ, 1935.
Крылов В. И., Увеличение точности механических квадратур.
Формулы эйлерова вида, ДАН СССР 96, № 3 A954).
Крылов В. И,, Увеличение точности механических квадратур при
наличии главного участка интегрирования малой длины в интегральном
представлении остатка квадратуры, ДАН СССР 101, № 6 A955).
Смирнов В. Н., 1) Увеличение точности формул механических
квадратур типа Чебышёва — Эрмита. Увеличение точности квадратур Чебы-
щёва — Лягерра. Сб. трудов Куйбыш. индустр. ин-та, № 5 A955). 2) О
квадратурных формулах Гаусса, там же, № 6 A956).
Евграфов М. А., Интерполяционная задача Абеля — Гончарова.
М., Гостехиздат, 1954.
ГЛАВА 14
ЧИСЛЕННОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
§ 1. Преобразование Фурье на конечном отрезке
и вычисление коэффициентов Фурье гладкой
периодической функции
Ввиду большого значения, которое имеют ряды и интегральное
преобразование Фурье для многих разделов механики, физики и
инженерных наук, задаче численного нахождения коэффициентов и
вычисления интеграла Фурье было посвящено много работ и предложено
большое количество методов вычислений, основанных на самых
разнообразных принципах. Мы изложим только некоторые из методов,
которым, нам кажется, можно отдать предпочтение по их точности
и удобству применения.
Для каждой функции / (х), определенной на отрезке О ^ х ^2п
и абсолютно интегрируемой там, можно вычислить соответствующие
ей коэффициенты Фурье
2л 2я
aji = — f {x)cos kxdx, bi^-=— f {x)^mkxdx (k=0, 1, ...).
0 0
A4.1.1)
Часто пользуются комплексными коэффициентами Фурье
2л
, = ~ ^ f(x)e''^''dx (^ = 0. ±1, ±2,...). A4-1.2)
2л
• 1
О
Последнее равенство можно рассматривать как преобразование
функции /(х), определенной на [О, 2jt], в функцию с^^, определенную
в целых точках k = 0, ±1. ...
Прямой задачей преобразования является проблема вычисления по
заданной функции / ее коэффициентов Фурье а^, bf^ или с^^.
Обратная же задача есть проблема восстановления функции / по
ее коэффициентам Фурье. В весьма общих предположениях об /,
которые выясняются в курсах анализа, она решается при помощи
316 ЧИСЛЕННОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ [ГЛ. 14
ряда Фурье, а именно доказывается, что / будет суммой
следующего ряда *):
оо оо
/(х) =-^^0 4 У](^й С05^л:4-^й sin ^л:)= V Cj^e^'*^. A4.1.3)
Последняя из сумм понимается в смысле главного ее значения. Мы
будем заниматься исключительно задачей нахождения коэффициентов
Фурье и оставим в стороне обратную проблему, как выходящую за
рамки книги.
Для вычисления интегралов A4.1.1) —A4,1.2) могут быть,
принципиально говоря, применены многие правила, о которых говорилось
в предшествующих главах: правила трапеций и Симпсона, формула
Гаусса и другие. Но применение их будет затруднять наличие под
знаком интеграла множителей cos^jc и sin^x. Уже при небольших
значениях k они вызовут значительные колебания интегрируемой
функции и, чтобы учесть их с достаточной точностью, на отрезке
интегрирования пришлось бы взять большое число узлов в квадратурном
правиле.
Это обстоятельство побудило для вычисления коэффициентов Фурье
построить правила квадратур, которые заранее учитывают наличие
у интегрируемой функции указанных множителей.
Рассмотрим сначала методы, основанные на идее приближения /
тригонометрическими многочленами. Такие многочлены предназначены
по своей природе для приближения периодических функций.
Продолжим / периодически с отрезка [О, 2л] на всю ось. Чтобы сделать
операцию продолжения однозначной, нужно условиться о выборе
значения, которое мы припишем функции / в точках х = 0 и х = 2л.
Для определенности и простоты будем считать, что мы продолжаем /
с отрезка [О, 2л), открытого справа. Заметим попутно, что если
существуют предельные значения /(-|-0) и /Bл — 0), то обычно
полагают / @) = / Bл) = 0,5 [/ (+0) ^ f{2n — 0)].
Под знаком каждого из интегралов A4.1.1) будет стоять
периодическая функция и для вычисления интегралов естественно
воспользоваться правилами интегрирования периодических функций,
имеющими наивысшую тригонометрическую степень точности.
*) Если ряд Фурье функции / расходится, то задача восстановления /
по ряду принадлежит теории обобщенного суммирования. Доказывается,
например, что для всякой абсолютно интегрируемой по Лебегу на [О, 2rc]
функции / почти везде (во всех точках, где / есть производная от своего
неопределенного интеграла) на [О, 2я] будет
lim
"9" ^0 + 2j^^ ^^* ^^^ ^^ ~^ ^^ ^^^ ^^^
П^\
^f(x).
§ 1] ПРЕОБРАЗОВАНИЕ ФУРЬЕ НА КОНЕЧНОМ ОТРЕЗКЕ 317
В вычислениях обычно используют простейшее из таких правил.
Чтобы были понятны мотивы его выбора, полезно сделать
предварительное замечание. В интегралах A4.1Л) множители cos^x и sin^x
не зависят от выбора функции / и их можно было бы принять за
весовые функции. Знакопеременности весов легко избежать, так как
они могут быть заменены на 1 —cos/гх и 1 —sinkx соответственно,
при этом замена не увеличила бы количества труда вычислителя ввиду
2л
того, что интеграл — f(x)dx входит в число вычисляемых вели-
0
чин. Затем все интегралы вычислить с одной и той же степенью
точности.
Этот путь не был принят в вычислительной практике по
нескольким причинам. Главная из них состоит в том, что каждой весовой
функции 1—cos^x или 1—sin^x (^:^0. 1, ...) будут отвечать
свои абсциссы, дающие наивысшую степень точности, а каждый из
коэффициентов а^^ и bf^ должен вычисляться со своими значениями
функции /. Это потребовало бы нахождения большого числа зна-
'чений /.
Чтобы свести необходимое количество значений / к минимуму,
во всех интегралах A4.1.1) весовую функцию принимают равной
единице и присоединяют множители cos kx и sin kx к интегрируемой
функции /, Для постоянной весовой функции, как выяснилось выше,
наивысшую тригонометрическую степень точности имеет правило (8.3.9)
с равноотстоящими узлами Х/^ и равными коэффициентами. Параметр Xq
правила мы положим, по соображениям простоты, равным нулю, так
как при общей постановке задачи о вычислении а^ и Ь^^ нет
бесспорных соображений, побуждающих иначе выбрать Xq, и правило
возьмем в виде
л-1
J Fw^.»^i;^(^)-
к=0
Оно дает точное значение интеграла, когда F есть произвольный
тригонометрический многочлен степени п — 1. Кроме того, это
равенство, очевидно, верно для F{x)=^s\nnx и не верно для F(x)^=
= cosAix. Применительно к интегралам A4.1.1) это правило дает:
п-\
2 V г / 2>^я \ 2ksn , 2 V г / 2^я \ , 2кзл ......
k^O fi=0
Что касается значений, которые нужно пр^1писывать индексу s, то они
выясняются в излагаемых ниже соображениях. Проследим потерю
степени точности, которая происходит в нахождении а^ и Ь^, При
318 ЧИСЛЕННОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ [ГЛ. 14
вычислении ^0 С ПОМОЩЬЮ A4Л .4) МЫ полагаем F{x)=^ — fi^)- Поэтому
равенство а^:^ — ^-^ ( ) ^У-^^'^ точным для всех тригонометри-
ческих многочленов степени п—1. Когда мы вычисляем а^ и Ь^,
мы полагаем /^ равным соответственно F{x)=^—f(x)cosx и F{x):=
= — /(л:) sin л:. Результат вычисления будет точным, если f (х) есть
многочлен степени п — 2, и т. д. Равенства A4.1.4) дадут точные
значения а^ и bf^, когда / будет многочленом степени п — k—1.
Коэффициенты а^^^ и b^_i будут найдены с нулевой степенью
точности.
Потеря степени точности при увеличении 5 заставляет в
приложениях ограничить область применения правил A4.1.4).
Пусть рассматривается тригонометрический многочлен
т
f = Г^ (х) = — ао + ^ (аJ cos Jx + bj sin jx)
степени nt^n—1. Если m^=n—1, то при помощи равенств A4.1.4)
по значениям /I (^ = 0, 1, ..., п—1) точно будет найден
только коэффициент а^. Значения остальных коэффициентов могут
содержать ошибки. При т^=п — 2 равенства A4.1.4) дадут наверное
точные значения лишь для а^, а^, Ь^ и т. д. Наиболее благоприятным
при применении A4.1.4) будет тот случай, когда будут получаться
точные значения всех коэффициентов многочлена Т^. Равенства A4.1.4)
тогда позволят точно восстановить многочлен f = Т^ по числам
/(——\. Чтобы это имело место, достаточно выполнить
неравенство т-^п — т — 1 или 2т ^п—1. •
В приложениях число п значений функции / берут обычно четным.
На этом частном случае мы остановимся подробнее и положим
т = 0,5;г — 1. Для любого многочлена / = 7о5„-1 равенства A4.1.4)
будут выполняться точно.
Нас будут интересовать, кроме того, коэффициенты Фурье ао^зл
2к8Л
и ^о^5л* ^^^ ^^^ "Р^ 5=:0,5n для всяких k sin ^=0, второе
равенство A4.1.4) для любой функции / дает ^^ ^^ = 0. Этот
результат нельзя считать приемлемым и поэтому Ь^^^^^ при помощи A4.1.4)
не вычисляется.
Допустим, что / есть гармоника частоты k=^Q,bn:
f = aQ^5rt cos О.бдл: + ^о,5л ^^i" О.бдл:.
§ 1] ПРЕОБРАЗОВАНИЕ ФУРЬЕ НА КОНЕЧНОМ ОТРЕЗКЕ 319
Вычислим для нее правую часть первого равенства A4.1.4), полагая
там 5 = 0.5д:
rt-i
i-s-*»/m-
' Tj ^^^^ ^^^о,5л "^ Zj ^os /гл sin /гл(/0^5л
:2а,
0,5«-
Мы получили удвоенное значение коэффициента cIq^^^,
Все изложенные соображения побуждают в приложениях
равенства A4.1,4) заменить следующими:
2 \У ^Bkn\ 2ks7t , 2 Vi ^/2^^\ . 2/^5Я ,. . , .„
^ = 0 Jt=0
E==:0, 1 0,5Д— 1),
Сделаем еще замечание об условиях, при выполнении которых
можно ожидать удовлетворительной точности приближенных равенств
A4.1.4^) и достаточно быстрой сходимости сумм к точным значениям
коэффициентов Фурье. Каждая из сумм является простейшей
интегральной суммой Римана для соответствующего интеграла A4.1.1),
если в последнем k заменить на s. Поэтому для каждой функции /,
интегрируемой в римановом смысле на [0. 2л], и при каждом
фиксированном значении 5 суммы будут сходиться к точным значениям
коэффициентов Фурье а^ или д^. Это позволяет сказать, что
равенства A4.1.4^) дают возможность вычислить а^ и Ь^ сколь угодно
точно, если взять достаточно большое п. Но если функция /
недостаточно гладкая, то для получения удовлетворительного результата
может потребоваться весьма большое число абсцисс. Тогда
естественно возникает потребность в предварительной подготовке / путем
устранения ее особенностей. Здесь важно выяснить, как скорость
сходимости связана со свойствами функции /.
Вспомним, что в основе построения применяемого правила
интегрирования лежит идея замены периодической функции приближающим
ее тригонометрическим многочленом. Так как при возрастании
степени многочлена точность приближения будет, вообще говоря,
возрастать тем быстрее, чем более гладкой будет периодическая
функция, т. е. чем более высокий порядок дифференцируемости она будет
иметь, можно в первую очередь пытаться увеличить точность правил
A4.1.4^) путем улучшения дифференциальных свойств /,
320 ЧИСЛЕННОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ [ГЛ. 14
Основные идеи увеличения точности правил интегрирования были
изложены в главе 13. С тем, как эти идеи применяются к улучшению
правил вычисления коэффициентов Фурье, мы ознакомимся в § 4
настоящей главы. Сейчас же остановимся только на одном пункте
этой проблемы, специфическом для правил A4.1.4').
При постановке задачи о вычислении коэффициентов Фурье мы
считали функцию / заданной на отрезке [О, 2л]. Допустим, что она
обладает непрерывными производными до порядка т включительно.
Чтобы была т-кратно непрерывно дифференцируемой на всей оси х
функция, получающаяся после 2л-периодического продолжения /.
необходимо выполнение следующих nt-^l условий:
/Bл) = /@), /Bл)=./'@) /'">Bл)=-/'"Ч0). A4.1.5)
Если не выполнено первое из условий, то график периодической
функции будет иметь разрывы в точках л: = 2^я (/г = 0, ±1. .,.).
При выполнении первого условия и невыполнении второго график
будет непрерывной линией, но будет иметь угловые точки при
л:===2^я (^ = 0, ±1, ,..) и т, д.
При подготовке функции / к вычислению ее коэффициентов Фурье
мы заинтересованы не только в том, чтобы сделать достаточно высоким
порядок т ее дифференцируемости на отрезке [О, 2я], но также
в том, чтобы выполнялись условия A4.1.5) до того же порядка т
или близкого к нему. Если условия A4.1.5) не соблюдаются, то /
можно разложить на два слагаемых: /(х) = Р(х)-|~/| (х), для
первого из которых точно находятся его коэффициенты Фурье и
выполняются равенства: Р^^'^ Bл) ~~ Р^^^ @) = /^'^ Bл) — /^'* @) (у = О,
1 т). Второе же слагаемое fi(x) должно удовлетворять
условиям A4.1.5),
Для построения Р можно воспользоваться, например,
многочленами Бернулли B^{t) @<;/^1). Они обладают полезными для lac
перечисляемыми ниже свойствами:
1) B,{t)=:^t-~^ и В,{\)~~В,@)=^\,
2)Б,A)-5Л0)-0 (п^2, 3. ...).
3) ^;, @--nB,_i@,
которые позволяют сразу же убедиться в том, что в качестве Р
может быть взят многочлен степени т-\- \:
т
§ 2] ВЫЧИСЛЕНИЕ ВСПОМОГАТЕЛЬНЫХ ИНТЕГРАЛОВ 321
Что же касается разложения Р в ряд Фурье, то оно строится точно
при помощи известных разложений в этот ряд многочленов Бер-
нулли A.3.1) и A.3.2).
После этого достаточно положить /i (л:)--/ (л:) — Р{х).
Функция fi{x) будет иметь тот же порядок дифференцируемости. что и /,
но будет удовлетворять требованиям A4.1.5). Вычисление для нее
коэффициентов Фурье а^ и Ь^ при помощи правил A4.1.4) будет
более точным, чем для / с тем же значением п.
§ 2. О вычислении вспомогательных интегралов,
содержащих тригонометрические множители
Для последующего нам будут полезны некоторые просто
проверяемые вычислительные результаты об интегралах вида
в в
1 f{x) cos pxdx, I fix) sin pxdx. A4.2.1)
л A
Если / есть многочлен какой-либо степени, то при помощи
интегрирования по частям можно получить равенства, дающие
возможность вычислить интегралы по значениям многочлена / и производных
от него на концах отрезка интегрирования:
в
f{x) cos рх dx ^:=^ cos рС I -
^ г/(В) + /(Л) Г(^) + Г(^) I /W(^) + /(^)(^) j sxnplX —
л\Г{В) + Г{А) Г{В) + Г^{А) /E)(/^) + /E)(Л) 1,,.'/!_
-Г[_ ^2 р4 -t- р, ...jsin/7^|_
- cos рС/,(/)-sin/;С/,(/), A4.2.2)
в
J f {x)s\n рх dx ^ cos рС[^{f)-^s\n рС[^{f), A4.2,3)
A
С = 0,5(Л + ^5), / = 0,5E —Л).
Это правило будет играть только промежуточную роль, и на нем
более подробно мы не будем останавливаться.
322 ЧИСЛЕННОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ [ГЛ. U
Если / не является многочленом, то для вычисления
интегралов A4.2.1) могут быть применены, например, интерполяционные
правила. Возьмем на [Л, В] п~^1 произвольно расположенных узлов
^ -=^ -^0 < -^1 < • • • < -^л ^ ^ " интерполируем / по ее значениям
в этих точках:
л п
Отсюда сразу же получается интерполяционное правило
вычисления рассматриваемых интегралов:
в
J / (л:) cos pxdx = ^ С^ (р) f (Xk) + /?^.
А k^Q
В В
Ck (Р) = \ ^k М COS рх dx, Rn= \ ffi (^) cos рх dx.
A4.2.4)
Так как ^^ {х) есть многочлен степени п, для С^. (/?) может быть
выписано при помощи A4.2.2) его явное выражение через параметры
задачи. Оно имеет сложное строение и некоторые указания о его
использовании для вычислений будут сделаны в конце параграфа.
Сейчас же мы займемся частными случаями, когда вычисления могут
быть доведены до конца или упрощаются.
Изберем сначала равноотстоящие узлы Xfy=^ A-{~khy h= — (B—A)
(^ = 0, 1, .... п). Соответствующее им правило вычисления
интегралов будет правилом Котеса с весовыми функциями cos рх и sinpx.
Общая теория правила рассматривалось в гл. 6, здесь же мы
остановимся лишь на его частных случаях.
Пусть п=1. Интерполирование выполняется линейно по двум
значениям / на концах отрезка [Л, В]. Их мы обозначим соответ-
ственно f, = f{A)vif,=^f{B);f(x)= ^^ /о + ^~ fx + r,{x).
Выражение для остатка г^ {х) в удобном для нас виде может быть
получено на основании общей формулы E.2.6), или» если
воспользоваться следующим простым представлением функции /:
X
f {х)^ f{A)^{x- А)Г {А)+ ^ f"{t){x-t)dt =
А
В
= f{A)Jr(.x-A)f'(,A)Jtlf"it)E{x-t)ix-t)dt
§21
ВЫЧИСЛЕНИЕ ВСПОМОГАТЕЛЬНЫХ ИНТЕГРАЛОВ 323
Первые два члена интерполируются точно и остаток г^ (х) будет
равен остатку интерполирования интеграла:
R
г, (X) = J /" (t) [е (х -t)(x-t)- ^^ (В - о] dt.
Л
Подстановка указанного выше выражения f (х) под знак
интеграла даст правило вычисления, аналогичное простейшему правилу
трапеций F.4.1):
в
I / (X) cos рх dx == /о [^—^^ COS /;л — I A — ~^) sin рл\ +
л
h = B- А,
Если отрезок интегрирования [Л, В] разделить на п равных частей
——— = h точками Xj^^= Л-{- kh, к каждому частичному отрезку
[Xft, Xf^^i] применить правило A4.2.5) и интегралы по частичным
отрезкам сложить, получим правило интегрирования, аналогичное
общему правилу трапеций F.4.4):
в
^f(x)cospxdx = fo['-p''' cospA-L(l -^)sinp^] +
п—\ .
, с^ I — COS ph ^ ^ .
о ft-O
Н- A — и) COS рх,1 — COS р (Xj + Ни)] du, /ft = / (i4 -|- kh)-
324 ЧИСЛЕННОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ [ГЛ. Н
Сходные вычисления для интеграла с весовой функцией sin рх
приведут к следующему аналогу формулы трапеций:
^f^:c).lnpxdx = f,[l{l-^)cospA+^^^sinpA]i.
А
п-1
. ^ 1 —COS ph '^ г . I
/?=^J ^riXf, + hu)[asinpXk+i-^
-\-{\ ~u) sin pXf^ ~ sin p {Xf^ ~\- ha)] da, A4.2.7)
P'
0 ft-O
/г = 2, Интерполирование / выполняется по значениям в трех
точках — в концах А W В отрезка и в его средней точке С = 0,5 (Л -|- В):
..,.4^ (^-С)(^-Б) (х-А){х-В) . .
/ W — (д_с)(Л —В) /о ^ (С - ^) (С — 5) -^1 "Т~
+ (б-Л)(Л-С) -^2 + ^^2 W'
Д==/(Л+М). Уг = 0.5(В~Л).
Подстановка этого выражения в интеграл приведет к правилу
интегрирования, аналогичному формуле Симпсона
в
I fix) cos pxdx = D,U+DJ,^ D^f^ + R, A4.2.8)
A
Dq = p- COS pA~~v sin pA, Dj = X cos pC, D2 = |a cos pB -f v sin pB,
Л == 4/г (/?Л)~^ [(/?/г)"^ sin /?Л — cos ph\
\i^h(M)'^[ 1 + cos2 ph — (/?Л)~^ sin2ph\
V = /7-1 [1 + B/7^)"' sin 2ph — (ph)'^2 sin^ /?л].
§ 2] ВЫЧИСЛЕНИЕ ВСПОМОГАТЕЛЬНЫХ ИНТЕГРАЛОВ 325
Для нахождения остатка R можно воспользоваться равенством
/(л;) = / (Л) -h(x-A) /' (Л) + 4 (^ - Af г (А) +-
В
+ ^j f-(t)E(x~~t)(x-tfdt,
А
Первые три члена по правилу A4.2.8) интегрируются точно. Поэтому
остаток интегрирования / совпадает с остатком интегрирования
последнего члена и, следовательно, выразится через остаток
интегрирования по X функции 0,дЕ(х — t)(x — tf. Поэтому остаток R
представим в форме следующего интеграла
в
/?=: |/-@;СДЛ Л Н. P)dt.
А
где
в
Kc{t> ^' ^. Р^^^\ (•^•-~0^cos^7л:^л: —
— D^^^.bE{C — t){C — tf-^D2^^.b{B—tf.
Наконец, если отрезок интегрирования [Л. В] разделить на
четное число п частей /г = — {В—А) точками jCj^ = Л + АЛ (^ = Oi I» ...
...» п), объединить части попарно, к каждой паре применить
равенство A4.2.8) и результаты сложить, получим аналог общего
правила Симпсона:
в
J / {х) cos рх dx = (\i cos pA — vsin pA) f (A) +
A
0.5Л-1
+ 2[x ^ /(Л + 2у/г)со5/7(Л + 2у/г) +
0,5л-1
+ (\icospB~^vsinpB)f{B)^-R, A4.2.9)
0,5л-1 Л + Bу + 2)Л
^=2 J f"'it)'<c(t' A + 2jh. h, p)dt.
y-0 Л+2УЛ
326 ЧИСЛЕННОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ [ГЛ. 14
Сходное правило вычислений может быть построено для
интеграла с функцией синус
в
I / (х) sin pxdx==([is\n рЛ + V cos рА) f (Л) Н-
А
0,5rt-l
+ 2[i ^f{A + 2jh)smpiA-^2Jh) +
7 = 1
0,5л-1
+ Х '^f[A + Bj+l)h]smp[A^Bj+l)h]-{~
у=о
+ (|Li Sin рВ ~^v cos pB)f (В) + /?.
0,5/1-1 A + {2j + 2)fi
/=0 Л-}-2//г
Л + 2/г
/С
.(^. л. /г, /?) = -2- (л: — tfsmpxdx-
1
^ 5j ^^(С ^ 0(С - О' - 5о ^ (Л + 2/г ~-0^.
Л < г' < Л + 2/г, 5i = ?w S2 = |Li sin jE7^ ~ V cos pB.
Мы ограничились рассмотрением правила котесова типа для
случаев интерполирования / по ее значениям в двух и трех узлах.
Известны также коэффициенты правил интегрирования при
интерполировании по значениям / в четырех и пяти узлах и для некоторых
случаев интерполирования по значениям функции / и ее
производной f\ Сложность таких правил быстро возрастает с увеличением
степени точности интерполирования, их мы не будем приводить и
отошлем читателя к справочным книгам по интегрированию.
Закончим настоящий параграф указанием еще на один возможный
метод вычисления интегралов с тригонометрическими множителями.
Мы рассматривали случай равноотстоящих узлов. Хорошо
известно, что в задаче интегрирования равноотстоящие узлы не являются
самыми благоприятными, и вычисления с ними часто бывают связаны
с потерей верных значащих цифр. Поэтому можно поднять вопрос
о таком выборе узлов в правиле A4.2.4). при котором можно
было бы ожидать лучшей точности вычисления, сравнительно с
равноотстоящими узлами.
Напомним, что мы предполагали функцию / достаточно гладкой
в
всюду на отрезке [Л, В\, При вычислении интеграла | f{x)dx с по-
А
g 2] ВЫЧИСЛЕНИЕ ВСПОМОГАТЕЛЬНЫХ ИНТЕГРАЛОВ 327
стоянной весовой функцией хорошего результата можно ожидать при
применении правила Гаусса, имеющего наивысшую алгебраическую
степень точности. Узлы такого правила будут лежать в точках х^,
получающихся из корней ^^ многочлена Лежандра Я^ + ИО "ри
помощи линейного преобразования л: =:^ 0,5E +Л)-)~0.5 (j5 — A)t,
которое переводит отрезок [— 1, 1] в [Л, В\.
В интегралах A4.2.1) роль весовых функций играют множители
cospx и shxpx. Поведение их на [Л, В\ таково, что если мы
хотим взять узлы в правиле A4.2.4) одинаковыми для всех р, у нас,
по-видимому, нет оснований отказаться от использования в первую
очередь гауссовых узлов, или, по меньшой мере, от их испытания
наряду с некоторыми другими.
Рассмотрим произвольную неотрицательную весовую функцию
p(jc) на [Л, В\ и соответствующую ей систему ортонормированных
многочленов Рп{х). За абсциссы х^^ примем корни многочлена Pn+ii-^^)
степении п~\-\. Лагранжев множитель Я^(х), участвующий в
интерполяционном многочлене, будет иметь следующее выражение через
многочлен Рп+Л^У- KM = ~f "х^'; / ч ■ Ему можно придать
другую форму, более удобную для вычислений. Напомним, что ^k{x)
в нашей задаче характеризуется перечисляемыми ниже свойствами:
1) Xf^{x) есть многочлен степени /г, 2) если IФ k, то %^{xi)=^^,
п
3) ^jfe(-^ft)=^ ^- Рассмотрим многочлен Sf^{x)^=^ y^Pj^Pji-^k)' имею-
щий степень п. Если в равенстве Кристоффеля — Дарбу
yp.(x)P-it)— ^^ Pn+iMPn(t)-Pn(^)Pn^i(t)
ПОЛОЖИТЬ JC = Xjfe и t=^Xi{k^l), то будет ясно, что 5^(Х;)==0.
После этого становится очевидным, что
Kix)=Yi^,{x)Pj{x,)
J-0 LJ-0
Ур){х,)
Это выражение достаточно удобно для вычисления производных ат
^А W в точках Л и 5 и позволяет просто применить равенства
A4.2.2) к вычислению коэффициентов С^{р) в правиле квадратур
A4-.2.4).
Возвратимся к выражениям A4.2.4) для Cj^{p) при любых х^^.
328 ЧИСЛЕННОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
Если для сокращения записи ввести величины:
Df = If (В) + If (Л), d;('> = ^1,'' (В) - if (А)
A = 0, 1 п)
[ р р» '^ р^ •••}
"'А
{ГЛ. и
^*=[^
+
р ' р' р
COS ph-\-
sin ph.
Df
\s\n ph,
A4.2.11)
коэффициенты Cfj(p) формулы A4.2.4) получат следующие
выражения
Ck (р) = Яjfe cos рС — Hk sin pC. A4,2.12)
Аналогично для правила вычисления второго из интегралов A4.2.1):
в п
\ f{x)^mpxdx^ Y^S,(p)f{x,)+R,, A4.2.13)
А к^О
В В
5ft(Р)= [ ^A(-^)sinpjcfifjc, ^п^ \ r^{x)slnpx dx.
л А
Коэффициенты Sf^(p) имеют значения:
Sk (р) =- Hk cos pC + Hk sin pC. A4.2.14)
Величины Dk и D^ \ не зависящие от частоты р и функции /»
могут быть вычислены заранее.
§ 3. Применение алгебраического интерполирования
к вычислению коэффициентов Фурье
В том случае, когда функция / имеет высокий порядок
гладкости на отрезке [О, 2л]» но не выполняет условия A4,1.5)
возможности ее гладкого периодического продолжения, для вычисления ее
коэффициентов Фурье целесообразно, по крайней мере в некоторых
случаях, применять алгебраическое интерполирование / на [О, 2д]
и пользоваться соответствующими ему правилами квадратур.
§3]
ПРИМЕНЕНИЕ АЛГЕБРАИЧЕСКОГО ИНТЕРПОЛИРОВАНИЯ
329
Численные значения коэффициентов а^^ и Ь^^ даются интегралами
A4.1.1), имеющими форму A4.2,1). Интерполяционные методы
вычисления их были описаны в § 2. Сначала рассмотрим правила ко-
тесова вида. Допустим, что отрезок [О, 2л] разделен на п одинако-
2kK
вых частей точками х^ ^
(k^Q, и
,. пу
Если мы выполним линейное интерполирование / в каждом
частичном отрезке по значениям Д, которые принимает / в точках
деления, то для вычисления интегралов A4.1,1) мы можем
воспользоваться аналогами правила трапеций A4.2.6) и A4,2.7)
пар = 2
1 — cos ph
т/о+
2kn
4- 5] /а cos /7 ^
1 п-\
■fn
+ Rc- л =
2kn
о /г=0
+ A —и) COS р
2Ы
■cosp[-^
ha
\du,
nb.
P \
sin ph
ph
/o +
, о 1 — COS/?/г V^ - . 2kn 1Л s\n ph\ . , j^
fe = i
+ A — a) sin /? --^j sin /? y--^ + tejj
0 ft=o
da.
A4.3.1)
A4.3.2)
Перейдем теперь к правилам вычисления а^ и Ь^, аналогичным
формуле Симпсона. Будем считать п числом четным. Объединим
попарно смежные частичные отрезки и на каждой паре отрезков
выполним квадратичное интерполирование / по значениям в точках де-
ления Xj^ =:= . Для вычисления а^ и д^ здесь можно применить
общие правила парабол A4.2.9) и A4.2.10). которые дают для них
330
ЧИСЛЕННОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
[ГЛ. 14
равенства:
0,5/г-1
A4.3.3)
яа^,=^М'/о + 2|1А S f Bjh) cos p2jh^
0,5л-1
+ ^ S /[Bу+1)/г]со5рBу+1)/г + ^Д^/?,,
y=o
0,5rt-l {2j + 2)ft
^-^ S I ri^)KAx,2Jh,h.p)dx;
7 = 0 2;/z
0,5л-1
^^==v/o + 2^ 2 fi2Jh)s\np2Jh^
0,5// -1
+ >" S f [Bj + I)h] sin pi2J-^ I) h-vf„-{-R„\ A4.3.4)
0,5n-l By + 2)ft
/?.= 2 I f'"M^s(x, 2jh, h. p)dx.
y = 0 2//г
Могут быть построены правила, аналогичные формулам котесова
типа более высокой степени точности, такие, как правило трех
восьмых и др.
Как отмечалось в § 1, при вычислении а^ и Ьр по правилам
A4.1.4) степень точности будет уменьшаться при увеличении индекса р.
Другую природу имеют правила A4.3.1) — A4.3.4). Точность их
определяется преимущественно точностью кусочно линейного или
кусочно квадратичного интерполирования функции /, которое
выполняется при построении этих правил. Эта точность не зависит от
индекса коэффициента р. Поэтому, как можно предвидеть, с ростом р
точность вычисления а^ и Ь^ по правилам A4.3.1) — A4.3.4) будет
убывать медленнее, чем для правил A4.1.4).
В заключение рассмотрим вопрос об использовании корней
ортогональных многочленов при интерполяционном вычислении
коэффициентов Фурье. Здесь удобно отрезок интегрирования [А, В] привести
к [—1, 1] и брать а^ и ^j в форме
1 1
а^ = \ f {х) cossnxdx, ^^= \ f{x)s\nsnxdx, A4.3.5)
Пусть р {х) есть произвольная неотрицательная весовая функция на
[—1. 1] и за узлы х^ (k==0, 1, ..., п) правила вида A4.2.4)
приняты корни многочлена p^^i(x) степени /z-f-1 из ортогональной
системы Рп{х) (д = 0, 1, ..,), отвечающей весу р (х).
Равенства A4,2.12) и A4.2.14), по которым находятся значения
коэффициентов квадратурных правил A4.2.4) и A4„2.13), в нашем
§4]
точность ВЫЧИСЛЕНИЯ КОЭФФИЦИЕНТОВ ФУРЬЕ
331
случае упрощаются. Мы должны считать р = sji, Б = — Л := 1»
д_:1, С = 0. Поэтому
С,EЯ) = (~1/
S,{sn) = (^~-iy
D
,{1)
о:
C)
D
/5)
52Я2
5^Я^
5°^**
D
/0)
D
/2)
D'
/4)
5Л
5'^Я''
5°Я^
A4,3.6)
Особенно важен частный случай, когда в качестве узлов Xj^
берутся корни многочлена Лежандра Pn^i(^)- Весовая функция
постоянна: /7(jc)^l, и ортонормальная система многочленов будет
2BУ+1)Я/(х,)|
Р
hi
7=0
Числа Z)^ , входящие в выражения коэффициентов С^ и 5^,
вычислены для п-=1(\) , , . . Таблица их приведена в справочной книге
Л. Г. Круглкковой и В. И. Крылова (см. литературу),
§ 4. Увеличение точности вычисления коэффициентов
Фурье путем предварительной подготовки функции
Способы вычисления, которые были изложены в §§ I и 3,
основаны на замене функции / или произведений fcoskx и f sin kx на
алгебраические и тригонометрические многочлены, интерполирующие
их по значениям в некоторой системе узлов. При такой замене
вычисление af^ и ^й будет, вообще говоря, тем более точным, чем более
«гладкой» будет функция /.
Один из возможных способов увеличения точности состоит в том,
чтобы устранить у функции все ее особенности или, по меньшей
мере, значительно их ослабить. Напомним, что достигается это путем
разложения / на две части: f (х) ^= /^(х) ^ /2(х), где fi(x) имеет
такие же особенности, как f(x), причем коэффициенты Фурье ее
должны быть известны или находились бы точно; ДС-^) должна быть
настолько гладкой функцией, чтобы коэффициенты Фурье для нее
могли быть вычислены с достаточной точностью.
Рассмотрим сначала случай простейших особенностей—наличие
У / и производных разрывов первого рода. Допустим, что функция /
и ее производные до порядка т являются кусочно непрерывными
функциями и могут иметь разрывы первого рода в точках Х|, . . ., х^.
Будем считать, что эти точки лежат внутри отрезка [О, 2л] и
^ < -^1 < ... < л: < 2л. При применении правил вычисления^
332 ЧИСЛЕННОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ [ГЛ. 14
рассмотренных в § 3 и основанных на алгебраическом
интерполировании /, наличие у / точек разрыва при х==0 и л: = 2я не имеет
значения. Чтобы устранить их, достаточно считать, что / в этих
точках принимает значения соответственно /(+0) и /Bя — 0).
При применении же правил A4.1.4) мы должны выполнить
2л-периодическое продолжение / на всю ось. При этом могут
возникнуть разрывы у / или производных от нее в точках х = 0,
± 2jt, .,., если не выполняются условия A4.1.5) возможности
гладкого до порядка т периодического продолжения /, Как можно
устранить у / негладкости такого рода, говорилось в конце первого
параграфа. Будем считать, что в окрестности точек О и 2л функция /
является достаточно гладкой.
Для устранения разрывов у /, /^ ..., /<^^ в точках Xj
(У=:1, ..., д) можно воспользоваться, например, периодическими
функциями Вп (t), связанными с многочленами Бернулли. Они являются
1-периодическим продолжением многочленов B^(t) с отрезка O^t < 1.
Нам полезно отметить следующие их свойства:
1. B^{t)==t — 0,5. Функция Bi(t) есть кусочно линейная
функция, имеющая в целых точках ^==^ скачки, равные отрицательной
единице: В\{к + ^)--В\{к — ^)=^~1.
2. Вп (t) при п > 1 есть непрерывная функция.
3. B*n(t) = nB*n,i(t),
4. Тригонометрические ряды A.3,1) — A.3.2) представляют
функции Вп(^) на всей оси.
Возьмем точку Xj и построим 2л-периодическую функцию
^ Bя)* * (х — хЛ ,^
A4.4.1)
В точке лгу функция Ру и производные от нее до порядка т
включительно будут иметь такие же скачки, как и у функции / и
соответствующих производных /^ ..., /^^^ Справа и слева от х^
на отрезке [0. 2л] РЛх) будет некоторым многочленом степени
Чтобы устранить у f,f\.,., /f^) скачки во всех точках л:у,
достаточно положить /j (л:) = 2 ^/ (^) и Л {^) = / W — /i (^) ==
= f {х) — 2^/W- Построенная так функция /2 будет иметь на
[О, 2д] непрерывные производные до порядка /тг, и ее коэффициенты
§41
ГОЧНОСТЬ ВЫЧИСЛЕНИЯ КОЭФФИЦИЕНТОВ ФУРЬЕ
333
Фурье будут ВЫЧИСЛЯТЬСЯ при помощи правил, изложенных выше,
вообще говоря, более точно, чем для /.
Пусть мы хотим устранить только разрывы самой функции. В этом
случае т = 0 и Pj {х) = --В\[^ '^^^ ) [/ {х^ + 0) — / {х^-Щ, где
1
В\
'^;
2л
X —Xj
2я
X —Xi
-^. л:у < л: < 2я.
2я
Y ' О < л: < лГу,
Разложение В\ (—от""/ ^ тригонометрический ряд получится из
A.3.2) при ^ = 0
^^ (""г^"/ ~ ~ 2i s^^ —
v=i
= /i — (Sin vx/cos va: — cos vjCjSinvJc),
v-1
/i W = - S ^' ("T^) f^ (^/ + 0) - / (^7 - 0I-
Значения /i {x) могут быть найдены при помощи приведенного выше
* / л: — Xi\
выражения ВЛ—^ )• Коэффициенты Фурье для /i(jc) будут
следующими:
^ь V = — ^ S ^'"^^^' [/(^; + 0) —/(^; — 0)].
Если бы мы хотели уничтожить у функции / разрывы самой
функции и ее первой производной, рледовало положить
Ру (^) = ^В\ {^^р^ [/ (х^. -Ь- 0) - / {х^ - 0)] -
в\
2д /■
л: — Жу
2л
2я
2л /
^)+|.'.
<л:<2я.
■(l"^)+¥' 0<Х<^;.
334 ЧИСЛЕННОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ [ГЛ. 14
Разложение bII—^ 1 в ряд Фурье на основании A.3.1) будет:
♦ /д: —д:у\ 1 ^ C03v(x^xj)
оо
== V ^2~т (^^^ ^-^у ^os VX -f sin vxj sin \x),
v-l
+ ^^* {^^^) ^f ^""j + 0) - /' ix, - 0)]}.
Численные значения /^ просто находятся при помощи указанных
выше выражений для В[ и ^2. Если же воспользоваться
тригонометрическими рядами для ^1 и ^2, можно просто найти коэффициенты
Фурье функции /j.
Менее благоприятна для вычислений задача об ослаблении
степенных особенностей. Ограничимся изучением случая, когда функция /
имеет особенности такого вида на концах отрезка интегрирования
[О, 1]. Пусть / представима в виде /(л:) = л:^Ф(л:) (м->— 1). где ф
есть достаточно гладкая функция всюду на замкнутом отрезке
0<х<1.
Если \1 не есть целое число, то либо сама функция /, либо ее
производная некоторого порядка обратится в бесконечность в точке
х = 0, и при небольших значениях \i методы вычисления
коэффициентов Фурье, описанные в §§ 1 и 3, будут медленно сходящимися
и потребуют большого числа узлов для получения хорошей точности.
Можно, как это делалось в § 2 гл. 13, пытаться улучшить точность
результата при помощи выделения из / особенной части и перехода
от / к другой функции, обладающей более высоким порядком
гладкости.
Для облегчения записи будем рассматривать комплексные
коэффициенты Фурье
1
с^= J/(x)^-^2*^^^jc (^ = 0, ±1,...). A4.4.2)
о
Разложим ф (л") около л: ^ О по формуле Тейлора и положим
§41
ТОЧНОСТЬ ВЫЧИСЛЕНИЯ КОЭФФИЦИЕНТОВ ФУРЬЕ
/(Jc)=/oW + /*W- где
т-1 ^
335
/-0
f{x) = fix) — h{x) = x^
m-i
4^(x)~^jL,gU)@)
y=o
Тогда
C;fe= ^4|-ф^/)@)Г JC^^+•/^-'■^^^^йfл:4-J /*(x)e--^2ft.Tt^ufx. A4.4.3)
/«0 ' 0 0
Последний интеграл есть коэффициент Фурье для /*, и так как /*
имеет более высокий порядок гладкости нежели /. он может быть
вычислен при помощи правил §§ 1 и 3 с большей точностью, чем Cf^.
Интегралы же, входящие в сумму, имеют форму Is(^) =
== I х^е'^'^^^^ dx. Для них может быть легко построено правило
" о
понижения показателя степени s, позволяющее вычисление их
привести к случаю 0^5 < 1. Таблицы значений интегралов такого вида,
облегчающие применение равенства A4.4.2), насколько известно
автору, еще не составлены *).
*) Для расчетов полезно отметить, что если экспоненту под знаком
интеграла разложить в ряд по степеням х и интегрировать почленно,
получится степенной ряд по степеням k для интеграла /:
оо
^^ (^) - 21 v!(v + 5+l) ^~ ^^""'^^ ^ (' + ^^'' '^' E + 1.^ + 2,- 12Ы),
V = 0
при помощи него могут быть найдены значения !g (k) для нескольких
небольших значений k. Для больших k вычисления будут связаны с потерей
точности. Если в /^ (k) параметр k рассматривать как непрерывную
переменную, можно построить дифференциальное уравнение для /^ (k):
1
^ = -2./|.-^
= — 2яг —■ ■
-Ig-.-Zftjur^^
—4
1 -
12кпх
6
=
_ 1 -/2ftn
k
k
s+1
k
/;
Зная значение /^ {k) при каком-либо положительном k, не близком к нулю,
можно найти Is {k) для больших k при помощи численного решения этого
уравнения.
336 ЧИСЛЕННОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ [ГЛ. И
Допустим теперь, что / имеет степенные особенности на обоих
концах отрезка [О, 1] и представима либо в виде / (х) = х^ц)(х),
либо /(х)==A —х)^^(х), где ф и ф есть функции достаточно
высокого порядка гладкости на [О, 1]. В этом случае мы можем
ослабить обе особенности функции /, разложив ее на сумму трех
слагаемых /W = /o(-^) + /i(-^) + /*W' ^^^ /о имеет указанное выше
значение,
/-0
и f4x)=^f{x)-fo(x)-fiix),
m-1 '
Си == 2] "Т ^Р'^^ (^^ J Jf^+'^e-"*« dx +
у=о ' о
"-1 I '
J=0 0 0
Первая из сумм имеет ту же форму, что и в предыдущем случае.
Интеграл во второй сумме при помощи замены 1—x = t приводится
к x^'^h^'^^^^ dx и несущественно отличается от I^^j{k).
о
Функция /* будет иметь порядок гладкости выше, нежели /.
§ 5. Интегральные преобразования Фурье
и интерполяционные методы их численного осуществления
В этом и следующих параграфах будет рассматриваться задача
вычисления косинус- и синус-преобразований Фурье, понимаемых
в их простейшем определении.
Пусть на полуоси 0^х<сю дана абсолютно интегрируемая
функция /. Ее косинус- и синус-преобразованиями называются
интегралы *) со
С{р\ /) = С(р)= ( f(x) cos pxdx, A4.5.1)
о
со
S{p; f) = S(p)= j f(x) sin pxdx. A4.5.2)
*) Более часто, чтобы придать преобразованию Фурье и его обращению
/2"
симметричный вид, перед интегралами ставят множитель Т/ —, полагая,
оо f^ Jt
например, С{р)=л/ — f (х) cos рх dx. Не имеющий для нас значения
о
постоянный множитель мы присоединяем к функции /,
§ 5] ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ 337
сходящиеся при всех действительных значениях р. Первый из них
является четной функцией р, второй же—нечетной функцией и их
достаточно рассматривать при р^О, Каждый из интегралов есть
непрерывная функция р, стремящаяся к нулю при р->оо.
Если функция / определена на оси —оо<х<+сх) и
абсолютно интегрируема там, то ее общим преобразованием Фурье мы
будем называть интеграл
оо
Р{р- f)=F{p)== ^ f{x)e-ip^dx. A4.5.3)
— СЮ
Разлагая / на сумму четной и нечетной частей
/ч(х) = 0,5[/(х) + /(-х)], Д(х)-0.5[/(х)-/(~х)],
/(х) = Д(л:) + /н(х),
можно интеграл A4.5.3) привести к A4.5.1) и A4.5.2):
оо оо
/^ (/?) = 2 f /ч {х) COS рх dx ~ 2/ Г /н (х) sin рх dx.
о о
Поэтому преобразование A4.5.3) допустимо, по меньшей мере в
некоторых вопросах вычислений, не рассматривать отдельно и
ограничиться изучением численного осуществления только преобразований
A4.5.1) и A4.5.2).
Сначала займемся изучением интерполяционных методов и
рассмотрим случай задания функции / в равноотстоящих точках Xf^ = kh,
/г > О (й = 0, 1, 2, . . .)• Чтобы выяснить причины, побудившие
избрать тот или иной способ интерполирования, нужно высказать
сначала предположения о функции /, заставившие сделать этот выбор.
Функция / п^глполатапасъ любой, обеспечивающей В-Ьсойю^щ"^
сходимость интегралов A4.5.1) — A4.5.2). Среди них для приложений
особенно важны функции, достаточно быстро стремящиеся к нулю при
неограниченном росте х.
Для абсолютной сходимости достаточно, например, чтобы при
больших X выполнялось неравенство
|/(л:)|<Mx-^ 5>1. A4.5.4)
Всюду ниже мы будем считать его выполненным. Для гладких
функций, обладающих этим свойством, алгебраическое интерполирование
может дать удовлетворительнз^ю точность только на конечном участке,
и при применении его полуось [О, оо) обычно делят на участки равной
длины и па каждом участке выполняют интерполирование какой-либо
степени, одинаковой ~ для единообразия вычислений—на всех
участках.
338
ЧИСЛЕННОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
[ГЛ. И
Интегралы A4.5.1) и A4.5.2) являются частными случаями
интеграла A4.2.1), рассмотренного в § 2, для А==0 ц В = (уэ, К ним
применимы правила вычислений, о которых говорилось в § 2.
Если на каждом отрезке [О, h], [h, 2/г], .. . линейно
интерполировать / по ее значениям в конечных точках отрезков, можно
построить для интегралов Фурье аналоги правила трапеций. Они
получатся из равенств A4.2.6) — A4.2.7) при Л = 0 и 5->оо:
^ , . 1 — cos ph
f 0 + ^^ fk cos pkh
+ Rc
A4.5.5)
0 ft-0
, +A—a) COS pkh — cos p{kh-\-hu)\du, J
CO
+ A —u) sin pkh — sin p(kh-]-hu)]du
A4.5.6)
Аналоги правила Симпсона получатся из равенств A4.2.9) и A4.2.10)
при А=0 и В^оо:
С {p)^\if 0 + ^211^ f^f,cos2pkh + k^f2k^ii:osp{2k~-l)h^R^
oo 2ik + l)h
k^O 2kfi
5(/7) = v/o+2ii2 /2ftSin2/7M +
fe«l
+ ^S/2jfe-iSin/;Byfe-l)/z4-/?5.
oo 2ik + l)h
Rs = ^ J f''(x)Ks(x, 2kh, h, p)dx.
Jt-O 2kh
X, \x, V имеют значения, указанные в равенствах A4.2.8)
A4.5.7)
A4.5.8)
§ 5] ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ 339
Приведем без вывода еще одно правило вычислений интегралов
Фурье, аналогичное правилу трех восьмых. Оно получается при
замене функции / на каждом из отрезков [О, 3/г],[ЗЛ, 6h], .. .
алгебраическим многочленом третьей степени, интерполирующим / по четырем
значениям. Это правило имеет более высокую степень точности, чем
A4.5.7) — A4.5.8), и может применяться не только как контрольное,
но и как основное вычислительное правило:
Яо = 2 C — ^?^/г2) sin 3ph — 6ph cos 3ph — 6ph B — p'^h'^),
^0 == 2 C — /72/z2) cos bph 4- 6ph sin Sph — F — 1 l/?2/z2),
Я1 = Sph cos 2ph ~ 3 B — p'^h^) sin 2ph -f
-|- lOpkcosph — 6A — p'^h?)sln ph,
^j = — 3 B — /72/z2) cos 2ph — Sph s\n2 ph +
+ 6A ~/?2Л2)cos/?/z + lOphslnph,
C(/^)--g^/o+3^S^3.cos3M^ +
k'^i
^ S [fsk+2 COS p (ЗЙ + 2) A + /3,+, cos p C* + 1) A] +
2p
*-" A4,5.
CXJ
k~l
00
+ 2^51l^3^^-i^^"^(^^+^)^ + /3ife^2SinpC^ + 2)/z] +
;^-o
'^-^ A4.5.10)
Правила вычислений, получающиеся из формул котесова вида,
алгебраическая степень точности которых выше третьей, имеют более
сложное строение, и мы их приводить не будем.
Рассмотрим теперь более частный класс функций /. которые могут
быть представлены в форме /(x) = (jc4-^)~^ Ф(л^). где а > О, 5> 1»
а ф(л:) обладает высоким порядком гладкости на полуоси 0<;jc<oo
и имеет предельное значение при х-^со. Численный параметр а,
зависящий от гладкости поведения / и ф вблизи нуля, всегда может
быть приведен к 1. Но так как мы не имеем в виду доводить сразу же
излагаемый ниже метод вычисления до конкретных расчетных правил
340
ЧИСЛЕННОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
[УЛ 14
С численными коэффициентами, мы оставим на некоторое время а
произвольным.
Все, что ниже будет сказано о косинус-преобразовании С (р),
может быть перенесено без существенных изменений на функцию S{p):
оо
Cip:f) = C(p)=j(fix)-^^dx. A4.5.11)
О
Для интерполирования ср рационально воспользоваться не целыми
многочленами, а дробными функциями, ограниченными на полуоси
О^х <, со. Чтобы сохранить в вычислениях привычный аппарат,
в основу интерполирования была положена система степеней дробно-
линейной функции Z =:—-ц— и взята линейная комбинация их:
х-\-а
(х + аГ
Пусть на полуоси [О, со) выбрано /i-f 1 произвольно
расположенных узлов интерполирования: О <^ Xq < х^ < ... < х^ < оо.
Коэффициенты Cfj определяют из обычных условий интерполирования
^n(^j) = ^(^j) (У = 0, 1 п):
' ф (X) = 2 ^ife (^) Ф i^k) 4 9п (л^)'
hw^
G)^(X)
д^М
COi
1
^ ^ \х + а jcQ + a) ' ' ' \х + а ^^-i+^J
X
\х + а
1
_1 f_l ^V
■а) " ' \х + а Хп + а I
A4.5.12)
Подстановка этого выражения ф в интеграл A4.5.11) и почленное
интегрирование приведут к правилу нахождения
косинус-преобразования / по нескольким значениям функции ф:
С{р; f)=J:>A,ip)<f{x,)-\-R„.
оо оо
AAP}=jhM^^rdx. R„^jp„ix)-^2^dx.
О о
A4.5.13)
Для вычисления и табулирования коэффициентов Af^(p) можно
воспользоваться нижеследующими упрощающими задачу фактами. Па-
I 61 ПРАВИЛА НАИВЫСШЕЙ СТЕПЕНИ ТОЧНОСТИ 341
раметр а находится или задается вычислителем предварительно» в
зависимости от свойств функции / так, чтобы достигнуть возможно
большей гладкости поведения ф вблизи x^=^Q. После того как
значение а определено, этот параметр для получения расчетного
правила в стандартной форме обычно приводят линейным преобразованием
х = ал;' к единице. Такое преобразование мы будем считать
выполненным и положим а=1.
Если разложить многочлен д^{х) по формуле Тейлора по
степеням л:-Ь 1-
п
для коэффициентов А^{р) мы получим следующее выражение:
п "^
\if^i зависят только от х^ и при каждом способе выбора узлов для
них может быть составлена таблица в зависимости от я, А и /.
оо
Интегральный множитель имеет форму (л:-{-1)~ е^^^ dx {k =
о
= 5-1-я—/). Путем интегрирования по частям показатель k можно
привести к интервалу О < ^ ^<; 1. Заменой /? (л: + 1) = х' интеграл
оо
приводится к \ х'^е^^ dx. При 0<А<1 он табулирован недоста-
р
точно полно, но можно легко указать простые и достаточно
эффективные при небольших значениях р методы его вычисления. При /г= 1,
что отвечает целым значениям s, имеющим наибольший интерес для
приложений, он приводится к интегральным косинусу и синусу, для
которых составлены подробные таблицы.
§ 6. Правила наивысшей степени точности
В связи с нахождением правил, позволяющих получить С{р\ /)
^ ^{Р\ /) с погрешностью, меньшей заданной границы, при возможно
малом числе значений функции /, были сделаны попытки построения
правил, имеющих наивысшую степень точности в частных классах
рациональных функций.
Вновь рассмотрим класс функций /, которые могут быть
представлены в форме / {х) = /v^L » 5 > Ь и ф — гладкая на полуоси
^'^-^<оо функция, имеющая предельное значение при Jc->co;
11тф(л:) = (р(оо),
342 ЧИСЛЕННОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ [ГЛ. 14
Предварительно приведем интегралы Фурье С (р\ /) и S(p; f)
к нужной нам канонической форме и проделаем это на примере С{р\ /).
Чтобы избежать перемены знака весовой функции cos рх и сделать
вес положительным, положим
оо с»
<^(Р\ /)== \ f{x){l'\~cobpx)dx— ^ f{x)dx.
и о
со сю
Второй интеграл fdx= ф(л:)A-f •^)"'^^-'^ не зависит от частоты/?.
о С)
Подстановкой л: = ^"^-—1 он приводится к интегралу ^'^'^pj-^—1)^^.
о
имеющему весовую функцию якобиева типа p(t)=^t^~^. Его можно
вычислить, например» при помощи квадратурного правила вида G.3.2)
наивысшей алгебраической степени точности.
оо
Интеграл f {х)(\'\-cos px)dx (ввиду его зависимости от р)
о
более сложен для вычислений, и на нем мы сосредоточим внимание.
Чтобы сделать абсциссы и коэффициенты правила вычисления,
которое мы получим ниже, не зависящими от параметра р, выполним
сю
замену х^ = рх и приведем интеграл к виду {\-{-cosx) F (х) dx,
где FW = j/(f).
В силу сделанного предположения об / функция F(x) может быть
представлена в форме F(x)=: , _/ ' . где 0(x)-==p^~^(pl — U 7. )
есть функция, непрерывная на полуоси О <^ ;с < оо и F(oo) t= р^'^ср (оо).
ля
Ниже мы будем рассматривать интеграл Ф{х) "/jIl \^ ^-^ ^ -^
о
него будем строить правило вычислений вида
J Ф W \^+%s dx^"^ А,Ф (X,), A4.6.1)
Параметры Л^^ и л:^^ формулы выбираются так, чтобы равенство
выполнялось точно в том случае, когда Ф — любая из следующих
рациональных функций Ф = A-]-л:)""^ (/ = 0. 1, ..., 2п~1).
Возможность такого выбора следует из теорем о квадратурах наивысшей
§ e] ПРАВИЛА НАИВЫСШЕЙ СТЕПЕНИ ТОЧНОСТИ 343
алгебраической степени точности, доказанных в § 1 гл, 7. В самом
деле, если в равенстве A4.6.1) заменить переменную х, положив
jc = y—Ь ^= I 1_д. (^ ^^ > Q)> мы приведем его к виду
1 п
J Ф* (/) f'^ A + COS X) ^f/ ^ 2 ^>^^* ^^^^*
о k=\
где Ф*(^) = Ф(х) и х^=^~: 1. Параметры А^ и tf^ должны быть
выбраны так, чтобы равенство выполнялось точно при Ф* = /' {i=^{^,
1, ..., 2/г—1), т. е. имело бы наивысшую алгебраическую степень
точности. Так как весовая функция /7(^) = ^"^"^A-f-cosx) —
положительная, из указанных теорем вытекают перечисляемые ниже факты
о правиле A4.6.1):
1. При всяких п=\, 2, ... параметры Л^ и х^ (О < х^ < оо)
могут быть выбраны так, чтобы правило выполнялось точно для
ф = (х-|-1)~' (/ = 0, 1, ..., 2/г— 1). Это условие вполне опреде-
"ляет Af^ и x^j, а именно, х^ должны быть корнями многочлена Q (утг—)
1 1 4- cos X
степени п от у--—, ортогонального по весу .' ^ ко всякому
многочлену Q L . ■ -1 степени, меньшей п, на полуоси 0^x<cxi:
о
Коэффициенты Л^, должны иметь значения
А,= J%(^\^ji^^^dx. ^\(А-]= ""-^Ф^ Г
2. Все коэффициенты Л^ положительны.
3. Ни при каких А^ и Xj^ равенство A4.6.1) не может быть
точным для многочленов степени 2п от -г—^—.
4. Если равенство A4.6.1) верно для Ф(х) =^A + х) (/ = 0, ...
.... 2п — 1), то при всякой функции Ф, непрерывной арп О <; х < (Х)
и имеющей предельное значение Ф(оо) при х—>оо, имеет место
сходимость квадратурного процесса:
iim
л->оо
п °°
344 ЧИСЛЕННОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ [ГЛ. 14
Сходные преобразования и рассуждения могут быть проделаны
для синус-преобразования Фурье S{p; f) и для него построено
правило вычисления вида
оо „
верное при Ф={\~\-х) ^ (/ = 0, 1. ..., 2п—\).
§ 7. Увеличение точности вычисления интегралов
Фурье при помощи предварительной подготовки функции
При вычислении интеграла Фурье, как и при нахождении
коэффициентов Фурье, обычно стремятся выделить из функции / ее
особую часть, для которой преобразование Фурье находится точно.
Выделение выполняется так. чтобы оставшаяся часть функции имела
достаточно высокий порядок гладкости. Задача разложения / на
особую и гладкую части для интегралов Фурье осложнена
дополнительным требованием, которое отсутствует в задаче о вычислении
коэффициентов .Фурье: каждая из частей должна быть абсолютно
интегрируемой на полуоси О ^ х < оо.
Неограниченность отрезка интегрирования ставит еще одну
проблему предварительной подготовки функции, которая является другой
стороной задачи увеличения точности приближенного интегрирования.
Ее содержание может быть с достаточной полнотой выяснено на
примере простейшего правила A4.5.5). При получении его мы
предполагали, что f{x) достаточно быстро стремится к нулю при лг^оо.
В бесконечной сумме, входящей в приближенное выражение косинус-
преобразования С (р), берутся лишь те члены, которые в пределах
принятой точности будут отличны от нуля. Число таких членов
зависит от скорости стремления к нулю f (х): чем более быстро будет
убывать |/(х)|, тем меньше можно взять членов в сумме 2/а cos/?/г/г
и, стало быть, затратить меньше вычислительной работы. Если же
мы сохраним число значений Д, то вычисления можно выполнить
с меньшим шагом h и, следовательно, с большей точностью. Эти
причины побуждают при подготовке вычислений разлагать / на две
части, первая из которых убывает при х^оо столь же быстро,
как /. и для которой ее преобразование Фурье легко находится
в известных функциях. Вторая же часть должна быть более быстро
стремящейся к нулю при х—>оо.
С целью упростить запись формул мы объединим косинус- и
синус-преобразования в один комплексный интеграл, для которого и
§ 7] ТОЧНОСТЬ ВЫЧИСЛЕНИЯ ИНТЕГРАЛОВ ФУРЬЕ 345
будем рассматривать задачу об увеличении точности вычисления:
оо
F(p; f)=F(p) = C(p)^lS(p)^j f{x)e'^^dx, A4.7.1)
о
Рассмотрим сначала случай разрывов первого рода у / и ее
производных. Допустим, что функция / непрерывна всюду на [О, ао), за
исключением точки л: = а (а > 0), где / и производные до порядка т
имеют разрывы первого рода. Положим
д(х)^™^(а~х)|[/(а + 0)-/(а-0)] +
•- + ^^ ^ 1^)" ^fim, (^ ,^ 0) „, fm (^ _ 0)] I, A4.7.2)
Функция /д на отрезке О-^х-^^а есть многочлен степени т и
тождественно равна нулю при л: > а. В точке х = а f^, f'^, . . ., Д'")
имеют разрывы первого рода с такими же скачками, что и /,
/' /^'"^- Путем интегрирования по частям можно показать, что
I
Е{а~х) ^^ .f^' e'P'^dx--
а
\
у!
f-s
е'>^ dx=- (—ly" у —^5 ^
(-1/
5^0
{ipy^J-sy. (ip)
У+1
= (-^yjf:p[^i^i(^^ ^' + 2; Ф^)-
Поэтому
^(i»; fa) = S (-1)^ [/''■> (« + 0)- /(''■» (a -- 0I X
7-0
X
т.'--'
»/pa
(ipr^4J-s)i
(ip)
J+i
J+^
= -^(-^У l/<^'(a + 0)-/t^) (a - 0)]-~щ 1ЛA. У + 2; /pa).
;.0
A4.7.3)
Если мы хотим ограничиться устранением разрыва только самой
функции /, следует считать т = 0 ц положить /^ {х) = — Е(а — х) X
X[/(fl + 0)-/(fl-0)]. Здесь F(p;/J = -i-(l-e'n[/(a + 0)_
346 ЧИСЛЕННОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ [ГЛ. 14
— f {а — 0)]. Когда же мы намерены устранить разрывы / и /',
нужно положить т= Ь Д (л:) = — Е{а —х) {[/(а-|-0) —/(а —0)] 4-
+ (x —a)[/'(a-f 0)"/Ч«~" 0I). В этом случае
tp
+ [-^ + 1^-~,е'^'^)[Па + 0)~Г{а~Щ.
Возвратимся к произвольному т. Полагая f^^=^f — Д» мы получим
разложение / на сумму двух частей f =1 f^^f^, при этом часть Д
будет иметь непрерывные производные до порядка т включительно.
Если /. f\ ... имеют несколько точек разрыва первого рода: а, Ь,
с, .... для каждой из них по правилу A4.7.2) составляют
вспомогательную функцию соответственно Д, Д, fc.--- и после этого
полагают f ="fa'~\-/ь'^ ••• Ч'/** Функция Д будет иметь
непрерывные производные до тех порядков, какие были предусмотрены
нами при составлении Д, /^,. ....
Теперь рассмотрим задачу ослабления у функции / степенной
особенности, лежащей в начале координат. Пусть f (х) = х^'(р{х),
где Я> — 1 и ф(л:) есть функция, достаточно гладкая в
окрестности нуля.
Неограниченность области интегрирования заставляет изменить по
сравнению с § 4 форму особой части, которую выделяют из / для
ослабления особенности в точке л: = 0. Выберем как-либо число а > О
и рассмотрим функцию Д(л:)=^^-«'^(Со-^ c^x-f ... +с^х'^).
Коэффициенты с J (у = 0, .. ., т) избираются так, чтобы ее разложение по
X
степеням х совпадало бы с разложением ф (х) = ф @) + yj- фЧФ "h • • •
... -) рф^'0)+ -..до члена с х"^ включительно. Сравнение
коэффициентов при х^ (у=:0, ..., т) обоих разложений приводит
к системе уравнений, из которой последовательно могут быть
найдены су.
Ci — аСо=^фЧО).
При решении системы параметру а стремятся, придать такое
значение, чтобы Cj были бы небольшими по абсолютной величине. После
того как с J найдены, можно положить /(л:) = х^Д(х)"|-Д (л:),
§7] точность ВЫЧИСЛЕНИЯ ИНТЕГРАЛОВ ФУРЬЕ 347
f^(x) = f(x)—х^/о(х). Функция Д будет иметь в точке нуль
порядок дифференцируемости на т единиц выше, чем /.
Для нахождения преобразования Фурье x'^f^ix) предварительно
оо
заметим, что интеграл/^= J л:^'-^е-«^5'>^й?л:(а > О, /?>0. afgjc = 0)
о
линейной заменой (а — ip)x = t и преобразованием контура
интегрирования в полуось О ^ ^ < оо приводится к эйлерову интегралу
второго рода.
Вычисления для него дают значение: /^ = r(v)r-^'^^^"^, где
г = I а + /р I = Y^^ Л- Р^* ^ == 3rg (а 4- ip) = arctg —. Поэтому
т оо
F(P\ -^^0) = ^ ^j J x^^^^e~^''^e^p^dx =
/»0 0
rn
" Более сложным является случай, когда / имеет степенную
особенность внутри области интегрирования. Допустим, что при
некотором выборе ветвей степенной функции будет f(x) = (x — а)^ф(х)
(а > О, Я. >— I) и ф обладает достаточно высоким порядком
гладкости. Полуось интегрирования, по-видимому, целесообразно разбить
на участки [О, а], [а, со):
а оо
F(p, /)=| (x~~ay^^i(x)e^^''dx+ J (х ~~а)^ qi(x) е'^"" dx.
о а
Второй из этих интегралов заменой x = a~\-t приводится к
сю
е^^^ J t^(p(a ~\-t)e^^^ dt и в этой форме он был рассмотрен несколь-
0
кйми строками выше. Первый же интеграл после замены х — а = — at
1
A>/>0) перейдет в —(—af^^e^^'' ( t^'(p{a—at)e~^^''^ dt, А этот
о
последний интеграл имеет форму, рассмотренную *) в § 4. Там были
высказаны в основном тексте и в сноске некоторые соображения
о его вычислении.
Закончим параграф разбором задачи о выделении из функции /
части, более быстро стремящейся к нулю при л:->со. Наибольший
интерес здесь имеет, по-видимому, случай, когда убывание /
происходит по степенному закону.
) См. A4.4.2) при условии, когда к считается произвольным.
348 ЧИСЛЕННОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ [ГЛ. И
Чтобы ВЫПОЛНЯТЬ вычисления с функциями, не имеющими нигде
особенностей на полуоси 0^л:<оо. целесообразно отказаться от
отрицательных степеней х и воспользоваться функциями (cfi -\- х^У"^'^*^.
Они имеют достаточно простое строение и для них известны правила
преобразования Фурье:
сю
J (а2 + ;с2)-"-'-^ COS рх dx = Y^ (^)' [Г @.5 + v)r' К^ (ар),
о
Rev >—0.5; A4.7.4)
оо
f (a2 + ^:2)~''"*^''sin/?x^JC =
о
==/K2-"-^r@,5-v)p^a-^[/Jap)-y:_v(«P)l,
Rev> —0,5; v=^0,5; 1.5; 2,5; , . .;
оо
_I V I 2 j rr^w + l) I У'(т + \,5)л\
2 ^J т!Г(/п + 1.5) L Г(т + 1) "^ Г(/п + 1,5) J '
m-O J
j (a2 + ;c2)-^ sin /;x dx = V я (-^)''' | /3/2 (ap) In -^ +
, 1 Mp\""'' ^ V I 2 j \V'im + \) ■ r(m + 2,5)-||
■^ 2ГA.5) \ 2 ) 2 Lk /nir(/n+2.5) [г(/п + 1) "^ Г (/n+ 2,5) J V
rri'^O
jia^ + .T'- Sin px dx = <=l)p^ (^f' X
0
Xj/^^n«P)ln^ '2L Г(* + 1.5) l-2-j
00 f^v
2 ^i т!Г(т + ?4-1,5) L Г(/я + 1) "•" Г(т + 9 + 1,5) J
m-O J
(9 = 0. 1. 2. ...)■
§ 7i точность ВЫЧИСЛЕНИЯ ИНТЕГРАЛОВ ФУРЬЕ 349
Здесь /у(-г). K^(z) — цилиндрические функции:
ос (IV
Й = 0
/c,B)=-y^^'wi;4^'^)=-Y^'''''[^a^)+/Kv(/^)i,
и /,у(^) —функция Струве:
(т)
Пусть существует число v такое, что при л: -> со будет
f(x): (а'^-\- х'^У^'^'^ -^с^ФОи, следовательно, / представима в форме
/(;с) = С1(а2 + л:2)-^-°'' + ЛМ. где/Д^):(а2 4-^Т'"°''-^0. Пре-
образование Фурье первого слагаемого находится точно при помощи
A4.7.4). Второе же слагаемое Д убывает более быстро, нежели /,
и может оказаться, что правила численного преобразования можно
применять к нему с лучшим результатом, чем к /. Если окажется,
что Д убывает при х->оо недостаточно быстро, то к Д можно
применить тот же способ выделения быстро убывающей части.
Параметр а, входящий в функцию (а^-[-•'^^)~^~'^. выбирается в
зависимости от поведения функции / около начала координат *). Для
большого числа гладких при малых х функций / достаточно считать,
по-видил^ому, а = 1.
Рассмотрим важное для приложений множество функций,
которые при больших X имеют форму f (х) = CiX''^-]-С2Х~^-{- ...
. .. ~\~[c^'^yfj^{x)]x^^ (YmW~^0 при л:—>со). Так как переменная
(а^-\~ x2)''^'^ = jc~^ — -^ а^х~^-\- -^а'^х"^— .. . при больших х
эквивалентна л:"^ то в этой переменной представление / будет
следующим: /(x):.= a,(a2-f ^^)"^'^+^2(^^ + л:^)"^+%(«^ + -^^)'^'^+ ••.
т
• • • + [^т + 6^ {X)] (а2 + ^2)-^'^'^ === 2 а J {а? + ^')''''' + Л {х). Уже
У-1
*) Чем меньше будет а, тем большие значения будет принимать
(л2-|-^^)~^~^'^ вблизи начала координат и тем менее гладким там будет
поведение Д. При увеличении а будет увеличиваться гладкость этой
функции, но вместе с тем будет возрастать аргумент цилиндрических функций
в A4.7.4). что может затруднить их вычисление.
350 ЧИСЛЕННОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ [ГЛ. 14
при небольших значениях т функция Д будет достаточно быстро
убывать при неограниченном росте х. Что же касается членов суммы
аАа?-{-х^)~ ' ^, то их преобразование Фурье будет согласно A4.7.4)
выражаться через цилиндрические функции целого и полуцелого
индексов, которые табулированы с большей подробностью, нежели
для других значений индексов.
В частности, когда в представлении / участвуют только четные
степени х: / (х) = CgX"^ + с^х~'^ ~\~ . . ., в выражении ее через а^ -\- х^
будут содержаться только целые степени этой функции: /(х) =
= ^2 («2-|-х^)" -\~ а^{а^ -\- х^У + ... +/*(^)- Преобразование
Фурье (a^-|-x^)~'^ будет выражаться через цилиндрические
функции / 1 и /С. 1 полуцелого индекса, которые просто выражаются
через степенные и показательные функции.
В задаче об увеличении скорости убывания преобразуемой
функции при х->сю мы воспользовались функциями (x^-f-a^)"^"^' ввиду
того, что их преобразования Фурье выражаются через хорошо
изученные и во многих случаях подробно табулированные функции
Бесселя.
Иногда предпочтительнее воспользоваться более простыми
функциями {х-\~а)'~^. Если / представима в виде /(х) = Л(х + а)" -f-
4-... ^ D{x ^ ay' ^[Е + у {х)]{х^ а)"^ (а > О, 0<^< ...
...</< т; y{x)->Q, x-^oz)), то можно положить /i(x) =
= Л(х + аГ"+...+^(^ + ^)""'. /Jx) = (x + ^)"'"yW./W==
= /i(-^)+/*(-^)- Д-^я осуш,ествления преобразования первого
слагаемого /i в правой части последнего равенства необходимо умение
вычислять интегралы вида
/^(j9)=| {х + ау'е''' dx^e-'^'^p"' J t"e''dt (s > 0).
0 pa
Последний интеграл подробно табулирован лишь при 5=1.
'^'Ut
При помош,и интегрирования по частям для /^(х)= t ^е
можно получить правило понижения показателя степени s\ /j+i==
= —х-'^е^^Н /^. которое дает возможность вычисления при любом
5 > О привести к значениям s на отрезке О < 5 -^ 1. При 5=1 I \{х)
выражается через интегральные синус и косинус. Это позволяет
§71
ТОЧНОСТЬ ВЫЧИСЛЕНИЯ ИНТЕГРАЛОВ ФУРЬЕ 351
достаточно просто выполнить преобразование /i(x) в том случае,
когда k т есть целые числа.
Пусть 0<5<1. Так как J C'e'Ut = Т {\ ~~ s)e ^^ '\ то
о
О
==ГО-.).'т<-«„^ -^
(V+1-S)-
v=0
Полученный ряд может быть использован для вычислений 1^{х) при
«небольших» значениях х. При «больших» х полезным в вычислениях
может оказаться асимптотический ряд для 1^{х)
M.. = f<-V'«~."[-L_-^+i!£iJ±I>_...].
X
X
Наконец, для «средних» значений х к нахождению t~^e^^t
о
может быть, например, применено одно из правил неопределенного
интегрирования.
Литер а тура
Крылов А. Н., Лекции о приближенных вычислениях, гл. V, §§ 54—59,
М„ Гостехиздат, 1954.
Серебренников М. Г.. Гармонический анализ, М. — Л..
Гостехиздат, 1948.
Л а и ц о ш К.. Практические методы прикладного анализа, гл. IV, М.,
Физматгиз, 1961.
Крылов В. И., Шульгина Л. Т., Справочная книга по численному
цнтегуированию, гл. 7, М., Изд. «Наука», 1966.
Диткин В. А., Прудников А. П., Интегральные преобразования и
операционное исчисление, М., Физматгиз, 1961.
К р у г л и к о в а Л. Г., Крылов В. И., Справочная книга по
численному гармоническому анализу, Изд. «Наука и техника», БССР, 1967.
ГЛАВА 15
ЧИСЛЕННОЕ ОБРАЩЕНИЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
§ 1. Преобразование Лапласа, задача его обращения
и связь ее с преобразованием Фурье
Мы будем рассматривать задачу обращения преобразования
Лапласа только в той ее части, где она связана с приближенным
вычислением интегралов. Сначала напомним некоторые хорошо известные
факты теории преобразования. Пусть на полуоси 0^л:<сю
определена произвольная функция F п р есть комплексный параметр
pz=a~^ix. Их мы предполагаем такими, чтобы был абсолютно
сходящимся интеграл
сю
/(р)= j F{x)e''P'^dx. A5.1.1)
Если интеграл абсолютно сходится для некоторого значения
р z=: p^^Oq-^IXq, то он будет абсолютно и равномерно сходящимся
в полуплоскости Re /7 = а ^ 0Q. Это сразу же следует из неравенства
\F(x)e-^'-^\^\F(x)e~-^'<^^\e-^'^-'^o)x^ Ду1я каждого интеграла A5.1.1)
будет существовать такое конечное или бесконечное число а, что
интеграл будет абсолютно сходящимся в полуплоскости Rep = a>a,
при этом сходимость будет равномерной во всякой полуплоскости
а^а + е (е > 0). Если же о < а» интеграл от IFe'^-^l будет
расходиться.
При а = — со интеграл будет абсолютно сходиться всюду в
комплексной плоскости /?. Для а = схэ интеграл не будет абсолютно
сходиться ни при каких р. Этот случай был нами исключен раньше
и ниже мы будем рассматривать только такие функции F, для
которых а < оо. Так как F(x)e'~P^ есть целая функция р при любом х
и интеграл сходится равномерно относительно р при а^а-|-е(е > 0),
функция f (р) будет регулярной всюду в полуплоскости а > а.
Если точка р будет удаляться на бесконечность, оставаясь в
полуплоскости о > а, при этом так, что вещественная часть р неограни-
§ 1] ПРЕОБРАЗОВАНИЕ ЛАПЛАСА 353
ченно возрастает, f {р) будет стремиться к нулю. Действительно,
пусть а ^ с > а,
\f(P)\<\\Pix)\e' '""е-^^-') ^ dx.
Ввиду { \F{x)\e-^^dx <^оо правая часть неравенства будет, оче-
0
видно, стремиться к нулю при неограниченном росте о.
Равенство A5.1.1) можно рассматривать как преобразование
функции F{x), определенной на полуоси [О, оо), в функцию f {р)
комплексной переменной р, регулярную в полуплоскости Re/7>a; F (х)
называют оригиналом, а f {р) — изображением.
Можно указать правило, позволяющее по изображению f(p) найти
оригинал F(x), верное при весьма общих предположениях о
свойствах оригинала.
Если выполняются условия: 1) при некотором с функция F(x)e'^^
абсолютно интегрируема на полуоси 0^:^л:<оо; 2) F{x)e-^^ пред-
ставима при х^О двойным интегралом Фурье *)
оо со
j[F(x + 0)^F{x~0)]e-'^==:^^ ^ е^^^ ^ F(t)e-'ie'^^''dtdx,
-оо о
A5.1.2)
где интегрирование по т понимается в смысле главного значения,
тогда при х^О верно следующее равенство, в котором справа
стоит главное значение интеграла:
C-t-^oo
^[F{x + 0) + F{x-0)]^^ j f{p)e"-dp. A5.1.
3)
*) Функция F{x) определена на полуоси [0. оо). Мы продолжили ее на
отрицательную полуось [О, —со), положив там F{x)^{), и в соответствии
с этим внутренний интеграл в равенстве A5.1.2) взяли в границах (О, оо).
Как выясняется в теории интеграла Фурье, для представимости F (х) е" ^'^
формулой A5.1.2) достаточно, чтобы эта функция выполняла следующие
требования: а) F (х) е~ ^^ абсолютно интегрируема на полуоси [О, оо);
^) F{x)e~^^ имеет точки разрыва только первого рода и на каждом
конечном отрезке их лишь конечное число; в) любой конечный отрезок можно
разделить на конечное число частей так. чтобы F{x)e~^^ была монотонной
на каждой из частей. Требования б) — в) могут быть заменены условием,
чтобы F (х) и производная F' {х) имели точки разрыва только первого рода
н на любом конечном отрезке полуоси [О, оо) их было конечное число.
354 ЧИСЛЕННОЕ ОБРАЩЕНИЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА [ГЛ. 15
В самом деле, умножив обе части A5.1.2) на е^^ и заметив, что
внутренний интеграл есть не что иное, как fic~\-ix), можно это
равенство переписать в виде
=i J -^('^+") '*'*'''"^^ = "i" I f^p^""
dp.
Равенство A5.1,3) дает обращение преобразования Лапласа A5.1.1).
В приложениях задача обращения вызывает затруднения более
часто, чем само преобразование. Это связано с тем, что при решении
дифференциальных, интегральных, разностных и других уравнений
обычно применяют преобразование непосредственно к этим
уравнениям, переходя в них от оригиналов к изображениям. Полученное
для изображений уравнение часто бывает значительно проще
исходного и его нередко удается решить в простых по своему строению
функциях.
После этого необходимо бывает вернуться от изображений к
оригиналам. Это можно сделать, например, при помощи равенства A5.1.3).
Но оно требует умения вычислять контурный интеграл, который
в него входит. Найти его точное выражение через известные
функции удается далеко не всегда.
В связи с этим возникла потребность в построении приближенных
методов, позволяющих вычислять интеграл в широком классе случаев.
При записи A5.1.3) предполагалось, что линией интегрирования
является прямая, параллельная мнимой оси: Re/? = с. Но так как
функция / {р) еР^ регулярно зависит от /? в окрестности любого
конечного ее отрезка, линия интегрирования может быть деформирована
как угодно, без нарушения некоторых условий, выясняемых в теории
аналитических функций комплексного аргумента. Абсцисса х,
являющаяся аргументом оригинала Р {х), входит в интеграл как параметр.
Проблема обращения преобразования, если пользоваться
равенством A5.1.3), приводится к некоторой частной задаче вычисления
контурного интеграла от регулярной функции, зависящего от
параметра X, Главнейшими фактами, затрудняющими вычисление, будут,
во-первых, неограниченность контура интегрирования, и, во-вторых,
колебания множителя е^^ вдоль контура. Устранить колебания е^'"^
путем деформации контура можно только в отдельных
немногочисленных случаях.
Упрощающим вычисления обстоятельством является то, что f {Р)
не есть произвольная функция, регулярная на контуре, а есть
«изображение», т. е. функция вида A5.1.1) с неизвестным нам
оригиналом Р {х). Напомним, что функции такого типа регулярны всюду
справа от прямой Re р = с и при удалении р на бесконечность так.
§ Ij ПРЕОБРАЗОВАНИЕ ЛАПЛАСА 355
чтобы действительная часть р при этом неограниченно возрастала,
стремятся к нулю. При построении метода вычисления интеграла оба
эти свойства f(p) могут быть приняты заранее во внимание.
Вычисление всякого контурного интеграла, после того как выбор
контура фиксирован, может быть приведено к вычислению некоторого
определенного интеграла. В зависимости от вида его, к вычислению
можно применить те или иные правила квадратур, изучению которых
посвящена вторая часть книги. Один из возможных способов таких
вычислений мы опишем несколькими строками ниже.
При применении этих методов следует иметь в виду, что все они
предполагают задание интегрируемой функции только на линии
интегрирования и мало, или совсем не учитывают поведение ее вне этой
линии. В частности, в них не принимаются во внимание свойства /(р),
указанные выше. О правилах вычислений A5.1.3), учитывающих эти
свойства изображений, будет говориться в дальнейших параграфах
главы.
Положив в интеграле A5.1.3) p = c-]~ix и считая, для простоты
записи, что F(x) непрерывна в точке х, мы можем это равенство
лереписать в виде
/'(^) = 4г fic + l^^e'^^'dx. A5.1.4)
Интеграл, стоящий справа, дает преобразование Фурье функции
/(c-f-/t). Оно отличается от преобразования A4.4.3), рассмотренного
в § 4 гл. 14, только тем, что под знаком интеграла стоит
комплексная функция /(^ + /т).
Если ось —оо < t < с^ разделить на участки (— оо, 0) и (О, оо),
в интеграле по отрицательной полуоси заменить переменную т на — t
и показательные функции е-^^'^ выразить через тригонометрические,
можно A5.1.4) привести к виду:
оо
^^•^^^^ J{I/(^ + ^*^) + /(^-'''^)]'^osxT-f
о
+ ^ и(^ + ^^) —f(c— /т)] sin хх] dx. A5.1.5)
После этого становится очевидным, что для вычисления F (х) может
быть применено большинство правил для численного косинус- и синус-
преобразований Фурье, о которых говорилось в §§ 4—5 гл. 14.
В приложениях наиболее часто оригинал F (х) имеет
действительные значения, и равенство A5.1.5) упрощается. Изображение f (р)
при действительных р будет также иметь действительные значения.
Поэтому, в силу принципа симметрии, f (с — /t) = / (с-f/т), и если
356 ЧИСЛЕННОЕ ОБРАЩЕНИЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА [ГЛ. 15
положить f(p)==u(o, x) + lv(a, t), то
сю
gcx г
f(x)^= [и (с, r)cosxr ~- v(c, X) sin XX] dx :=
о «^
"""V^^J f(^ + ^^)^^''^d'^- A5.1.6)
о
Настоящий параграф мы закончим указанием на связь между
преобразованием Лапласа и коэффициентами Фурье. Можно построить
простую зависимость между значениями изображения f (р) в
равноотстоящих точках и коэффициентами Фурье оригинала F (х) с
преобразованным аргументом. Такая связь может быть полезной в задаче
обращения преобразования Лапласа.
Не ограничивая общности результата, можно считать, что
изображение /(/?) есть регулярная функция в правой полуплоскости Rep > О,
Для достижения этого достаточно взять любое число а^а и
рассмотреть изображение /(« + /?). что равносильно замене оригинала
F(x) на F(x)e~^^. Ниже нам придется рассматривать разложение F
в ряд по синусам кратных дуг. Чтобы улучшить сходимость такого
разложения, полезно заранее привести значение F(-l-O) к нулю. Для
этого достаточно F (х) заменить на F(x) — ^(+0). что приводит
к замене изображения/(/?) на /(/?)—/?"i/^(+0).
оо
Рассмотрим теперь преобразование Лапласа /(/?)= | F(x)e'-P^ dx,
о
изберем какое-либо число /г > О и выполним в нем подстановку
е-л^==:со8^, F(~h-4ncos'&)^0(^):
я/2 £_ J
hf(p)=J0 (i&) [COS 1»] ^ sin^d^.
0
Чтобы под знаком интеграла получить четную степень cos О-,
которая легко выразится через sin^, положим р ^={2k~\~ \) h,
JT/2
/г/[B^4-1)^]= |Ф(^)С052^1&51П^^^. A5-1.7)
о
Функции sinBv+l)^ образуют на отрезке О, ^ замкнутую
ортогональную систему*) и если Ф(^) — достаточно гладкая функция,
*) Если 'ф('в') определена на отрезке [О, я] и удовлетворяет там
некоторым условиям, например, условиям Дирихле, она может быть разложена
оо
в ряд по синусам: ф('0^)= ^ Cf^sink^, Пусть взят частный класс функций
ф (д), значения которых в точках, одинаково отстоящих от концов отрезка
[О, л], равны: ф(я — '0^) = ф(^). Такие функции определяются значениями,
§ I) ПРЕОБРАЗОВАНИЕ ЛАПЛАСА 357
TO ее можно разложить в ряд по этим функциям: ф(^)=г=
j(/^
f
= 2 ^v^*^B^"l" ^)^' коэффициенты которого с^ могут быть най-
дены при помощи равенств
sinBv+ lHsinBfi+l)d^^^ ! я
Если в интеграл A5.1.7) внести вместо Ф(^) его разложение
в ряд и ядро интеграла заменить тригонометрической суммой
получится, ввиду ортогональности синусов разных частот, равенство
Полагая последовательно « = 0, 1,2 построим бесконечную
треугольную систему уравнений, из которой находятся коэффициенты с^:
Co = ~hf{h),
Со + с, = ^ Л/(ЗА),
2со + Зс, + С2=^/г/E/г),
5со 4- 9^14- 5^2 4 сз --: ~ Л/ (Jh).
14^0 + 28^14- 20^2 + ^^3 4" ^4 = ™- ^/ (9/г).
42Со + 90^1 + 75с2 4 35^3 4 9^4 4 ^5 -- ^ ^/ (И Л).
132со + 297с1 + 275с2+154сз+54г4+11с54^б = -^^/A3Л),
Функция /^(—Л"Чп со8 0) = Ф(^) после этого восстанавливается при
помощи ряда Фурье, указанного выше,
которые они принимают на О, -п-1 и эти значения могут быть заданы
произвольно. В разложении такой функции сохранятся только синусы нечетной
кратности sinBv-|- l)i9", которые обладают тем же свойством симметрии, что
358 ЧИСЛЕННОЕ ОБРАЩЕНИЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА [ГЛ. 15
§ 2. Интерполяционные правила
В этом параграфе будут рассматриваться правила вычисления
интеграла
^(•^^^ 2Sr I f(P)^'"'dP' A5.2.1)
c—ico
основанные на интерполировании изображения f (р) по его значениям
в нескольких точках. Точность результата здесь, как обычно, будет
зависеть от выбора системы функций, положенных в основу
интерполирования, и от выбора узлов. И то, и другое должно быть
согласовано со свойствами изображений / (р) и с практикой вычислений.
Будем рассматривать часто встречающийся в приложениях случай,
когда /(/?) представима в виде
где ф (/?) регулярна в полуплоскости Re /7 > а и имеет предельное
значение lim ф(/7)=:^ф(сю). Если 5 — дробное число, то под (р—af
р->оо
понимается та ветвь, для которой ^rg{p — а) = 0 при р^а.
Параметр а должен удовлетворять условию Rea^a и выбирается так,
чтобы функция ф(р) была бы возможно более гладкой в указанной
полуплоскости.
С целью упростить запись формул, можно выполнить замену
/7 ^ а = /7^ и считать а = О, f: > а ^ 0. При этом равенство A5.2 Л)
приведется к следующему виду:
^^^^==^4^-^ 9(p)p-Vdp. A5.2.2)
arg/7=0 при /? > 0. Выделяющийся в интеграле при замене
переменной р множитель е^-^ был присоединен к функции F(jc).
Так как ф(/7) предполагается непрерывной в полуплоскости
Rep^c при любом с > а, за аппарат для приближения ф(р)
естественно принять не многочлены, а рациональные функции от р,
ограниченные при р~^оо, полюсы которых лежат в полуплоскости
Re/7<a.
Система рациональных функций, избираемых для этого, должна
обладать свойством полноты: для всякой функции ф(/7), регулярной
в полуплоскости Re /? > а, ограниченной в полуплоскости Re р^ ^
(с > а)» и всякого г должна существовать такая функция
системы, которая отличается от ф(/?) при Reр^с по модулю меньше,
чем на 6.
§21
ИНТЕРПОЛЯЦИОННЫЕ ПРАВИЛА
359
Кроме того, они должны удовлетворять важному техническому
требованию: вычисления с ними должны быть достаточно простыми.
Наконец, чтобы можно было при заданной степени числителя и
знаменателя рациональной функции достигнуть возможно хорошего
приближения ф(/7). следует признать желательным некоторое
согласование свойств системы рациональных функций со свойствами (р(р).
Так как нами не сделано никаких предположений о (р{р), вопрос
о согласовании свойств мы оставим в стороне и будем принимать во
внимание лишь требования полноты и простоты вычислений.
Наиболее же простыми вычисления будут в том случае, когда в качестве
рациональных функций принимаются многочлены от —.
Возьмем п точек р^, , . ., р^- лежащих справа от прямой Re /? = с,
и рассмотрим многочлен /^„-Л —) степени не больше п—1, интер-
полируюш,ий ф по значениям во взятых точках:
^(P) = Pn-l(j) + rip) = ^l,[^)if{p,) + r(p).
A-^l
Ш^
.Р
^^у—
Рк.
тУ
1_
Pk
PJ
A5.2.3)
Подстановка этого выражения ф(/?) в интеграл A5.2.2) приводит
к следующему правилу его вычисления:
P(x)='^A,ix)(fip,)-\~R, /? = 2Й J r(p)p-^e-Pdp,
ft = l c—ioo
A5.2.4)
(i)
есть многочлен степени n— \ от —. Если его разложение
1
по степеням ~ есть
Р
h[-]^ci^^+aj,^P''^ + ... +^^fe,„-iP-^^4
360 ЧИСЛЕННОЕ ОБРАЩЕНИЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА [ГЛ. 15
ТО
Можно проверить, что интеграл I^,Jx)^= г /^ i ;ч • ^ самом деле,
пусть и есть действительная переменная. Интеграл /^ (х) =ri;
^-^-^ е^^'р'^йр, понимаемый как главное значение, сходигся
с—too
при гг > О И есть аналитическая функция и.
Будем, для упрощения рассуждений, считать гг > 1. Так как
функция е^Р в левой полуплоскости Rep^c ограничена по модулю и р-"
достаточно быстро стремится к нулю при р -> оо, прямолинейный
контур интегрирования Re/? = c может быть преобразован в
следующий контур: проведем разрез вдоль полуоси (— оо, 0) и различим
два борта разреза. Рассмотрим теперь контур /, состоящий из
отрезка нижнего борта разреза (— оо, — е), окружности радиуса е с
центром в нулевой точке, проходимой против часовой стрелки, и
из отрезка верхнего борта разреза ( —е, —оо). Контур 1\х
получается из него подобным преобразованием с центром в р=0 и
коэффициентом — ; /u(x) = -n-^ e^Pp'^dp^ При этом мы должны счи-
тать arg /? = — л на нижнем борте разреза и arg /? = л на верхнем
борте. Наконец, если заменить /?, положив xp^=^t, /7 = jc~^/(jc > 0),
то в переменной t контурный интеграл будет -^ . et'^dt. По-
следний же интеграл, как хорошо известно в теории функции Г (<г),
равен ^, . Таким образом, окончательно
c+ico
с—too
в силу аналитичности это равенство остается верным всюду, где
сходится интеграл /„(л:). Для коэффициента Afj{x) квадратурного
правила A5.2.4) мы получили следующее выражение:
<!.'
w=i;».,-wra- <'=^'"'
, 2] ИНТЕРПОЛЯЦИОННЫЕ ПРАВИЛА 361
Оно удобно ДЛЯ вычисления значений Л^ (л:) при любых значениях х
и требует знания только а^у. Последние же зависят исключительно
от узлов Pft (^= li .... п). Их можно заранее табулировать для
наиболее распространенных способов выбора узлов. Значения их могут
быть найдены при помощи равенств A5.2.3). Вычисления упрощаются.
когда известно разложение ^( —) по степеням ~: оз[~) =
_p-rt4-a„_i/?-«+i4- ... -f й^о. Если в равенстве со^ (^-U^ — i-j =.=
= оо(—) произвести сравнение коэффициентов при степенях —,
получится система уравнений для нахождения коэффициентов
многочлена coy^(-^) = /?"'' + ^4-*j^,«-2P"*"'^^+ ••. 4-^йО' ИЗ которой они
последовательно могут быть найдены: ~р^^1?^^ = а^, b^^—p-j^^b^^ = д^,
л —Pk^^k2'^^r ' • •' ^^ ^kj находятся коэффициенты h[~^]'*
1 .
Мы рассмотрим два способа выбора р^^ и начнем с
равноотстоящих узлов. Пусть на действительной оси выбраны п точек Xq,
лГа+Л. .... Хо + (л—1))^ (л:о>«)'
^\р)~\р 'x^j '■* \р Xo + nh'—hj*
pjxo + kh) ^J\
».ш
«I-),
'•G) =
р — Xq — kh \р
X
(p~Xo)(p^Xo — h) ... (p^x^^nh + h)
При помощи этого равенства могут быть найдены коэффициенты a^^j
{>азложения ^а(—) по степеням —. Выражение h{~] упрощается
после введения вспомогательных переменных р = hq, Xq ^= h\
^\hq)~ klin — k — Dl q"~'{g~l — ^)
При XQ = h, 1=1 коэффициенты h\~ir~] буду^ тесно связаны
с факториальными многочленами, хорошо известными в теории
конечных разностей и теории интерполирования.
Задача нахождения на действительной оси узлов /7^, которые
^огли бы дать в широком классе функций (р(р) результаты, более
362 ЧИСЛЕННОЕ ОБРАЩЕНИЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА [ГЛ. 15
точные, чем равноотстоящие узлы, ввиду сравнительной сложности
вычислений при обращении преобразования Лапласа, имеет,
по-видимому, не только теоретическое значение. Одна из попыток решения
этой задачи излагается ниже. Она основана на наглядных, хотя и
нестрогих соображениях. Возвратимся к представлению оригинала F (х)
с произвольным значением параметра а:
^^'''>^4а I ^{p){p-a)-'e'"'dp. A5.2.7)
С—(ОО
Выполним дробно-линейное преобразование /? =— i _Г/ "
(Л > а), переводящее полуплоскость Re /? ^ а в единичный круг
j^|<:i. Полупрямая а^р^оэ перейдет в диаметр —l^t-^l и
точки а, Л, со — соответственно в ^ = —1, О, 1. Прямая Re/7 = а
преобразуется в единичную окружность |^|==г1 и линия
интегрирования Re р =^с перейдет в окружность, лежащую внутри круга
I if !<; 1, ортогональную к диаметру и касающуюся окружности | ^ | = 1
в точке /=1. Она может быть сделана сколь угодно близкой
к )^|^= 1 при с, достаточно близком к а. ф(/?) преобразуется в
функцию ф(— 1 _7^ |:=:1гф(^), регулярную при U1<1 и
непрерывную в точке t ~~ и
Нам необходимо интерполировать Ф(^) в круге по нескольким ее
значениям на диаметре. В этой задаче, по-видимому, целесообразно
воспользоваться алгебраическим интерполированием и принять за узлы
2k 1
корни многочлена Чебышёва первого рода /^ = cos—^ л (й=1,
2 п):
Если возвратиться к переменной р и обозначить /?^ значения,
отвечающие узлам tf^, то будет:
.4 V/ ч . ч W ч {Pj, + A~2af-''iiy^(p)
Ф (/?) ^ У /, [р) ф (р,), I, (/?) = ]^—— ' ^ .
Щ{Р)= ^}fl > ^(p) = (P' — Pi) •.. (Р—РпУ
В отличие от предыдущего случая, здесь выполнено интерполиро-
1 1
вание при помощи многочлена от ^j—;—т-^ ^ не .
§ 21 ИНТЕРПОЛЯЦИОННЫЕ ПРАВИЛА ЗбЗ
Подстановка полученного приближенного выражения для <р{р)
в интеграл A5.2.7) приводит к правилу его вычисления
С-/со k = l
c+ico
Л,(х) = ^ J h{p)(p-a)-'e"'dp.
c—ico
A5.2.8)
Коэффициенты Л^(х) зависят от двух параметров: а (< а) и
Л(>а). Напомним, что первый из них а выбирается так, чтобы
достигнуть возможно большей гладкости ф(/7) при Re/7>a.
Параметр А есть та точка полупрямой [а, оо), в которую переходит центр
круга |^|<С^1. В плоскости t точки /^ расположены симметрично
относительно ^ = 0. При уменьшении А узлы ^7^^ сгущаются около
jE7 = a. При увеличении же А точки р^ будут удаляться от а направо.
Вычисление А^{х) приводится к табличным правилам обращения
преобразования Лапласа. Действительно, если многочлен coj^ (р), имею-
"щий степень п—1, разложить по степеням р—2а~{-А, то для
рациональной функции 1^{р) сразу получится разложение на сумму
простых дробей
1^ (р) = У ^2 .. A5.2.9)
Следовательно,
A,ix) = ^a,j^ 1 (р-2а+ArUp-ay'е'^'dp.
J = 0 c—ico
Последний интеграл, как это показывается в операционном исчисле-
НИИ*), равен /. , ., g^^«"-^)^i/^| E. s + J; (а — 2а + А)х). Под ^F^
здесь, как и в сноске § 4 гл. 14. понимается вырожденная
гипергеометрическая функция
оо
р („ о. ~л-Т'(Р) у Г(« + у) г^ Пг1<-оо)
^'^l(^^ Р' '^)— Т(,а) 2jT(f, + x) v! U^i<oo),
v-0
я-1
Л W = ^ ci,j r^G+"y) '^'""'^^ ''^' ^'' ^ + ^'' (а~2а + Л)х).
/=o
A5.2.10)
*) См.. например, Диткин В. А., Прудников А. П., Справочник
по операционному исчислению, Изд. Высш. шк., 1965, гл. II, стр. 231 B2.146).
364 ЧИСЛЕННОЕ ОБРАЩЕНИЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА [ГЛ, 15
Коэффициенты а^^^ не зависят от аргумента х и полученное
выражение А^{х) удобно, по меньшей мере в некоторых случаях, для
вычислений.
Оно значительно упрощается в частном случае, когда а = 2а — Л
или а = 0,5 (а 4-Л) и точки а и Л расположены симметрично
относительно а. Тогда
п-\ ^+'0° п-\ , ,
оах
■е"
аничивая
A5.2.11)
§ 3. Правило наивысшей степени точности
Чтобы получить в простейшем виде правило интегрирования,
которое будет построено в этом параграфе, предварительно приведем
интеграл -^-^ f {Р)^^^ dp к каноническому виду. Не огр
общности вопроса, можно полагать а = 0 и функцию f {р) считать
регулярной справа от мнимой оси: Re/7>0. Для достижения этого
достаточно выполнить преобразование р^ = р — а.
За с может быть взято любое положительное число. Кроме того.
можно значение х привести к единице, положив хр^ = р^^.
Выделяющийся при этом вне интеграла множитель х~'^е^^ мы оставляем в сто-
роне и будем интеграл рассматривать в виде -^—г f*{p)e^ dp,
e~ioo
е > О, /*(/?)=г/(-^|. Наконец, допустим, что f*(p) представима
в виде f*(p) ^=^ ^ ^ , где 5>0 и (р(р) регулярна в полуплоскости
Re/? > О и имеет предельное значение Ит ф(/?) = ф(со);
р->оо
^(^>===W J <P(P)p-'ePdp. A5.3.1)
e—(oo
Для вычисления интеграла мы будем строить правило
следующего вида:
/E)^2Лф(Ра), A5.3.2)
где pf^ (k=l, ,. ., п) есть некоторые точки из правой полуплоскости
Re/?>0.
§31
ПРАВИЛО НАИВЫСШЕЙ СТЕПЕНИ ТОЧНОСТИ
За аппарат приближения ф(/7) были приняты многочлены от
365
1
Параметры правила Л^^ и Р}^ избирались так, чтобы равенство A5.3.2)
выполнялось точно для произвольного многочлена р1 — ] степени
2п—1 от —. Выясним сначала необходимые и достаточные условия.
которым для этого должны удовлетворять Ли и pf^. Для сокращения
записи обозначим
1
1
^=^t и ^=^ь.
Р Pk
Рассмотрим интерполяционное правило вычисления
A5.3.1) по значениям, которые принимает ф в точках р^:
интеграла
1
2ni
e+ioo
Г
J Ф(Р) Р''еР dp^^ Af,(p(Pf,l
е - /ио * = 1
е+/со
E—ioo
A5.3.3)
Оно характеризуется тем, что дает точное значение интеграла всякий
раз, когда ф(/?) есть произвольный многочлен степени п—1 от ^.
Повторяя рассуждения, указанные нами выше при доказательстве
теоремы 1, § 1, гл. 7. можно доказать, что верна
Теорема 1. Для того чтобы правило A5.Ъ,2) было точным
для всяких многочленов степени 2п—1 от f^=p~^, необходимо
и достаточно выполнение двух условий:
1. Правило является интерполяционным, т. е> его
коэффициенты Ak имеют значения A5,3.3).
2. Для всякого многочлена Q{t) степени, меньшей п,
выполняется равенство
г+1оо
I fe^(^{t)Q{t)dp = {).
A5.3.4)
Первое из условий определяет коэффициенты Л, второе же, как
мы покажем ниже, определяет единственным образом многочлен о (О
и. следовательно. €го корни tj^^=^ —.
Будем искать ш (t) в форме разложения по степеням t \ со (^) =
а=^ -4-ai^"~ -^ ... -\-а^. Условие ортогональности A5.3.4)
366
ЧИСЛЕННОЕ ОБРАЩЕНИЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
[ГЛ. 15
равносильно выполнению системы равенств
Е+ too
Г e%(t)t'^'''dp^^O (m = 0, 1. .,., /г—1)
или. так как согласно A5.2.5)
e-i-tijQ
I
ePt"dp =
Г (и)
системы:
ч-
. = 0
T{s-\-n + m) ^V(s + n + m — \) ' ''* ' Т (s + т)
{т = 0, 1. .... п—\).
Для наших целей удобнее умножить равенство на Г (s-]-n-\~nt—\)
и записать систему в виде:
1
s + n—\
1
- «1 + (^ + ^ — 2) «2 + ... 4- E + /I — 2) . . . 5а^ = о,
a, + is~^ п—1)а^+ ... +E^-^—1) ... E+1)а„ = 0.
1
S _|_ 2/г — 2
+ ai + E-tAi —3)^2+ ... +E+2/г —3) . . ,
Ее определитель есть
1 s-^n — 2 ...[E + J^~2) ...5]
1 s + n^l ... [E + /г-1) ... E+1)]
А =
1 5 + 2rt —3 .. . [E + 2/г^З) ., .E + /i~ 1)]|
Достаточно убедиться в том, что Д =/= О, так как тогда система
будет иметь решение (Cj ... а„) и только одно.
Рассмотрим п функций х^'^"~^, ..., х^~^'^^~^. Они, очевидно,
линейно независимы на любом отрезке, не приводящемся к точке.
Построим линейное дифференциальное уравнение порядка п, для
которого эти функции образуют полную систему независимых решений:
У у' ... у^"^ I
|д.5-1-«-2 E_^д„2)х'^+«-з . . . [E+д —2). . .E—1)л:^-2] Lo.
^s+2n-3 E+2^-^3)JC'^+2'^-^ . . [E+2^-3). . .{S'i~n—2)x''^-^'^
§ 3j ПРАВИЛО НАИВЫСШЕЙ СТЕПЕНИ ТОЧНОСТИ 367
Если разложить определитель по элементам первой строки и
разделить обе части уравнения на х^ is^n-s)^ можно уравнение записать так:
с^х^у^^^-^с^х^'-'^у^^-^^ + .., +^лУ = 0. A5.3.5)
В самом деле, рассмотрим алгебраическое дополнение элемента у,
являющегося первым элементом первой строки. Оно получится путем
вычеркивания в определителе первых строки и столбца. Из первого,
второго. .... ^-го столбцов вынесем за знак определителя
соответственно х^+"~^, д"^+«'-4^ ^^ Х'^. Затем из элементов строк
оставшегося определителя вынесем множителе! 1, х, ..., х"~^ В
результате получим для алгебраического дополнения форму
д-й (л + 5-3)
s~{~n—2 .,.[E + ^—2) ...E—1)]
5 + 2п~-3 ... [E + 2^ — 3)... E + /г—2)]
с Х^ is + n~Z)
Аналогично показывается, что алгебраическое дополнение у^ равно
^я-1-^'* ^^^""^^^ ^ и Т. Д. Этим доказывается A5.3.5).
Уравнение A5.3.5) принадлежит эйлерову виду и имеет две осо-
"бые точки: л; = О, х = сю. Определитель Вронского для решений
^/д-Л-л-2^ Д.5+2Й-ЗЧ __
|д;5^л-2 E + л—2)a:^+'^-s . . . [E + ft—2) . . . 5X^-1]
jCS+2n~3 E_^2« —3)x-^^2«-4... [E-^2ft —3)... E + ^—1) X*^^«~2]
ввиду их линейной независимости может равняться нулю только в
особых точках уравнения. Он отличен от нуля, в частности, в точке
л:= 1. Но при х= 1 W(х^^^"^, . ..) совпадает с Д и поэтому Д ^ 0.
Для получения явного выражения о)@ рассмотрим следующий
многочлен степени п, который мы определим равенством типа
формулы Родрига:
Р"
И покажем, что для него выполняются равенства
/ 1 \
1).
■ -\-lCQ
J ePp-^P^(-i\ p"ndp = 0 (w = 0. i,
е-too
368 ЧИСЛЕННОЕ ОБРАЩЕНИЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА [ГЛ, 15
Отсюда ввиду единственности многочлена о)(г?), удовлетворяющего
условию A5.3,4), следует, что Рп\-~] будет отличаться от o)(Y)
множителем, равным старшему коэффициенту Р^ : Р^ (■—] =^ (/г + 5— 1). . .
. . . Bд + 5 —2)о)@.
Если в последний интеграл вместо P^j внести его выражение
A5.3.6) и выполнить интегрирование по частям, получим
= (—1^ P^-"'-^~ r(^/^/?~^-^-^-h —
le-/oo
е+гсо
— (—lj"(rt —m— 1) f pn-m-2 il^^ePp-^^-^+^^dp.
г—too
Внеинтегральный член здесь равен нулю, так как если выполнить
дифференцирование произведения, стоящего в скобках, то будет
видно, что каждый член будет содержать в знаменателе р по
меньшей мере в степени 5. На прямой интегрирования функция е^
ограничена, и при удалении точки р вверх и вниз по прямой каждый
из членов под знаком подстановки будет стремиться к нулю.
После интегрирования по частям п — т—1 раз, для интеграла
получится значение
е+(оо
t—loo
[t+tOO
Ввиду п^\ И 5 > О, подстановка равна нулю. Это доказывает
высказанное выше утверждение о Pj^i—\.
Чтобы завершить исследование возможности построения правила
интегрирования A5.3.2), точного для многочленов от — степени 2п—1-
необходимо показать, что корни многочлена ^я(~) ^^^ лежат справа
от мнимой оси. Доказательство для любых положительных значений s
здесь, по-видимому, еще не найдено. Исследованы были только целые
§ 4] КВАДРАТУРНОЕ ПРАВИЛО С РАВНЫМИ КОЭФФИЦИЕНТАМИ 369
значения 5. большие единицы, и в этом случае удалось показать, чтЬ
при любых д=1, 2, ... всегда будет Re ^?^^ > 0. Так как эти
исследования имеют лишь частное значение, мы не будем их
воспроизводить в книге.
Численные значения р^ были найдены при О, 01<;5<;3, п^=
= 1AI0, и всегда оказывалось, что Re^?^J>0.
§ 4. Квадратурное правило с равными коэффициентами
Будем рассматривать задачу об обращении преобразования Лапласа
при тех же предположениях, что и в предыдущем параграфе, и
допустим, что задача нахождения оригинала приведена к вычислению
интеграла A5.3.1). По аналогии с формулами квадратур,
рассмотренными в главе 10. были построены правила вычислений, все
коэффициенты которых одинаковы:
^ j ^(p)p-sePdp^^j;^^ip,). A5.4.1)
e~ioo k = l
Множитель , стоящий перед суммой, был избран так, чтобы
равенство выполнялось точно, когда ф есть постоянная величина.
Сумма содержит п параметров pj^. Их избирают так, чтобы правило
давало точный результат в том случае, когда ф есть произвольный
многочлен степени /г от —, что равносильно, ввиду A5.2.5).
выполнению системы уравнений
П Е+10О
Е''Г = 4^ J ,-.-..... = fir$L(v=, »). 05.4.2)
к=»1 e—ioo
Из этой системы сразу же следует, что указанный выбор pk
возможен и единствен при любом п. Действительно, введем величины
л:=/?-Ч х^=^р^^ и рассмотрим многочлен о)(л:)=л:^+Л^л:"-^-|—-*Ч~^„'
для которого x^{k^^\, .... п) будут корнями. Равенства A5.4.2)
дают численные значения сумм степеней величин л:^^ : 5^ = V л:^ =
= р. I ^. • Соотношения Ньютона между 5^ и коэффициентами Л^
370
ЧИСЛЕННОЕ ОБРАЩЕНИЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
[ГЛ, 15
дадут систему уравнений:
1 , 1
ГE+1)
1
1
О,
Лу
nV (S) ^2 =
ГE+2) ^ r(s4-l)
^ I ^ Л 1 ^
ГE + 3) ^ ГE + 2) ^^ ГE+1)
Л4-
nV (s) -^
1
1
ГEН-/г) ^ГE + /г—1)
Л,+
ГE + 1)
Лп-1 +
ГE)
= 0,
A5.4.3)
из которой последовательно могут быть найдены Af^. Значение Л^^
легко можно записать в форме определителя порядка к, вычисление же
его при произвольном значении параметра 5 приводит к сложным
выражениям:
n^V^js)
k\
1
nV{s)
1
r(s + l)
1
rE+yfe-
1
ГE + А-
-2)
-1)
0
2
nV{s)
1
1
Vis-^k-
* *
-3) •
-2) •
1 1
1
• r(s + 2)
1
•• r(s + A—1)
1
■• r(s + ft) 1
По-видимому, наибольший интерес имеют вычисления для случая
5=1. Система A5.4.3) значительно упрощается:
"зг + -jf ^1 ~Ь "^2 Н" — -^3 = 0.
1а + („_1I ^1+ (п-2)! "^2+ ••• +^«-1 + ^/^"^-
При /г = 1 система будет состоять из одного уравнения 1 -]- Л^ = О,
со (jc) = х — 1.
I 4] КВАДРАТУРНОЕ ПРАВИЛО С РАВНЫМИ КОЭФФИЦИЕНТАМИ 371
При /г = 2 получатся два уравнения: 1-|-0,5Л2 = 0 и O^S + ^i-b
^^2=0; ^1 = —2, А2^1,5, о)(л:)^х2 —2л:+Ь5 и т. д.
Вычисления*) были выполнены для /г от 1 до 10
п к pf,
1 1 1,00000 000 + 0,00000 000/
2 1,2 0,66666 667 ± 0,47140 452/
3 1,2 0,46343 318 ± 0,66891 655/
3 0,62485 778 + 0,00000 000/
4 1,2 0,31209 699 ± 0,78442 870/
3,4 0,54603 449 ± 0,22670 497/
5 1,2 0,19029 304 ± 0,86260 499/
3,4 0,46724 697 ± 0,36843 448/
5 0,53392 634 + 0,00000 000/
6 1,2 0,08786 626 ± 0,92009 404/
^Л 0,39416 727 ± 0,46819 799/
5,6 0,49826 825 ± ОД4769 920/
7 1,2 —0,00076 496 ± 0,96470 825/
3,4 0.32727 973 ± 0,54346 944/
5,6 0,45588 935 ± 0,25464 118/
7 0,49224 949 + 0,00000 000/
8 1,2 —0,07902 919 ± 1.00066 480/
3,4 0,26601 917 ± 0,60293 762/
5,6 0,41223 251 ± 0,33698 985/
7,8 0.47182 912 ±0,10911 533/
9 1,2 —0,14919 526 ± 1,03046 752/
3,4 0,20966 304 ± 0,65149 353/
Ь,^ 0,36931 455 ± 0.40305 392/
7,8 0,44525 659 ± 0,19444 915/
9 0,46815 071 + 0,00000 000/
10 1,2 —0,21284 773 ± 1,05570 953/
3.4 0,15754 418 ± 0,69213 469/
5,6 0,32790 360 ± 0,45764 025/
7,8 0,41610 417 ± 0,26374 950/
9,10 0,45488 509 ± 0,08636 297/
Можно заметить, что в границах таблицы действительные части
корней /7jfe, имеющих одинаковые номера k, убывают при
возрастании п и, начиная с л = 7, некоторые из точек Pf^ переходят налево
от мнимой оси. Весьма вероятно, что эти свойС1ва Pf^ будут
сохраняться и при /г > 10. Указанные факты сильно ограничивают
возможность применения правила A5.4.1) к вычислениям.
*) S а I Z е г [3].
372 ЧИСЛЕННОЕ ОБРАЩЕНИЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА [ГЛ. 15
§ б. Замечания об увеличении точности вычислений
при помощи предварительной подготовки изображения
Сначала дадим описание целей, которые мы будем преследовать
при подготовке изображения.
Способы вычисления оригинала F, которые были изложены в
настоящей главе, основаны либо на замене изображения / в контурном
интеграле A5.1.3) некоторой специально подобранной рациональной
функцией, интерполирующей / по ее значениям в избранной системе
узлов, либо на сходной замене вспомогательной функции ф,
связанной с / равенством /(/?) = (р—^)"^ф(р) и входящей в интеграл
A5.2,7). Узлы интерполирования могут лежать на прямой
интегрирования Re/7 = с или располагаться справа от нее в полуплоскости
регулярности изображения: Re /? > а.
Можно ожидать, что такое интерполирование будет тем более
точным, чем более плавным будет поведение функций / и ф в
полуплоскости Re /7 > а. Поэтому увеличение плавности поведения
изображения / является первой задачей, которая ставится в предва-
рительнй подготовке /. Достигнуть же этого можно, как и в
предыдущих двух главах, например, при помощи разложения / (или ф) на
слагаемые f (р) = f^(p)-\~f*(p), первое из которых должно
заключать в себе все или «почти все» «особенности» поведения / и быть
таким, чтобы соответствующий ему оригинал F^ мог быть найден
точно. Второе слагаемое /* должно обладать поведением более
плавным, чем /.
В главах 13 и 14, когда мы говорили о задаче улучшения
квадратурных правил при помощи предварительной подготовки
интегрируемой функции, мы стремились преимущественно к тому, чтобы
увеличить порядок ее дифференцируемости. В разбираемом же вопросе
функции / и ф являются аналитическими как на самой линии
интегрирования, так и всюду справа от нее. Особенности в поведении /
здесь вызываются наличием у / особых точек и их расположением.
Увеличение плавности поведения может быть достигнуто либо путем
устранения у изображения / особых точек, либо при помощи
ослабления их влияния.
Поясним эту мысль примерами и начнем с задачи устранения
полюсов. Пусть изображение / имеет полюсы в точках pj^(k^=l, . . ., т) п
предположим, что известны полярные части лорановых разложений /
в окрестности каждой точки Рк- ^ki—^ryj^^^^kviP — /^а) ^'
v=i
т
Можно положить л(Р) = 2 0^(^-1^) и r(p) = fip)-fi(p)-
к-1
§ 5] УВЕЛИЧЕНИЕ ТОЧНОСТИ ВЫЧИСЛЕНИЙ 373
Оригинал F| для /j находится точно, если воспользоваться тем фактом,
ЧТО для изображения (р — Pf^) ^ оригиналом будет функция jrry е^'^'"^:
kv r(v) *" ■
Допустим теперь, что при р==:^а изображение / имеет точку
ветвления степенного вида и / представима в форме f {р)^р—аУ g{p),
где g{p) регулярна в окрестности точки ^ и v не есть целое число.
Чтобы ослабить влияние особой точки а, можно прибегнуть к
излагаемому ниже использованию рациональных функций.
Рассмотрим отрезок тейлорова разложения g около точки
a:gQ + giZ+ ,.. ^g^z'"", z = p—a. gj^ = j^gi^) (а). Возьмем
затем точку b, лежащую слева*) от а: Re (а — ^) > О, и построим
рациональную функцию ф (р) = (/? — д)'^ [^о + ^1-2^ + • • • + ^т^"^]^
в которой Cq, ^1, .... с^ выберем так, чтобы ее разложение по
степеням z совпадало бы с разложением g(p) до членов со степенью т.
Для этого достаточно выполнить равенства -jj-^^^^ (^) = gi^ (^ "= О,
I т) или CQ(a^b)~^ =gQ, llci(a—д)'^ — CQs'(a —1?)~^~^ =
-^1. ...>т!с,(а-^)-^-^(//г»1)!с,_,5(а-г»)-^-^+,..+(-1)-Х
X ^0^E+1) . - . E + ^—1)(^ — ^)~^~'" = ^ш- ^3 них
последовательно могут быть найдены коэффициенты Cq, ^j, ...
т
После этого положим f^(p)^=(p — «)^ф(р)^: 2 ^/(Р ~-^)"^ X
^""^
Х(Р—а)^^^ и f*{p) = f(p) — fi(p)> Показателю степени ^
придадим такое значение, чтобы часть flip) при р-^оо убывала не
медленнее, чем f{p). Отметим попутно, что для того чтобы было
flip)-^О(р-^со), необходимо считать 5>/n-|-v.
В точке p=za f* будет иметь производную порядка на /п+1
единиц выше, чем /, и оригинал для /* может быть найден по
изложенным выше прайилам, вообще говоря, более точно, чем для /.
Что же касается части /j, то для нее оригинал находится точно, так
как для функции ip—ci)^^'^ip—b)~^ оригинал известен**) и равен
r(s~v-y) i^it—^--■/'' ^"V —у; {a—b)x\.
*) Во многих случах достаточно положить Ь^=а—1.
**) См. указанную в примечании на стр. 363 работу Диткина В. А„
*ФУДникова А. П., § 22 B2.146).
374 ЧИСЛЕННОЕ ОБРАЩЕНИЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА [ГЛ. 15
Сделаем еще несколько дополнительных замечаний:
1. Ослабление особенности ветвления в точке а было связано
с введением полярной особенности при р ^Ь. Чтобы эта новая
особенность не имела большого влияния на точность вычисления
оригинала для /*. желательно точку b выбирать лежащей значительно
левее а. Но при выборе параметра b необходимо принять во
внимание, что если b будет взято намного меньше, нежели а, то
разность а — Ь будет большой и коэффициенты с^ могут, как видно
из системы уравнений для их нахождения, оказаться большими по
модулю, и это может затруднить вычисление значений ф(/?).
2, Если показатель степени v отрицателен и мы берем настолько
мало членов в тейлоровом разложении g{p), чтобы было v + /n<0,
то задача разложения / упрощается. В этом случае можно положить
т Г т
оригинал F^ для /j здесь находится более просто:
л
3. При некоторых частных значениях v и т разложение / может
быть выполнено проще, чем в рассмотренном общем случае, при
помощи известных в операционном исчислении правил обращения
преобразования Лапласа. Краткая таблица вспомогательных формул,
полезных в этой и других задачах, приведена на стр. 375.
Мы остановимся еще на одном вопросе увеличения точности
вычисления. В конце § 1 мы обращали внимание на возможность
вычисления A5.1.3) путем приведения его к интегралу Фурье A5.1.4).
Если мы будем вычислять последний интеграл при помощи одного
из правил, основанных на замене / многочленом на отдельных
участках линии интегрирования, то для улучшения точности результата
и облегчения вычислительного труда желательно преобразовать
функцию / так, чтобы добиться возможно быстрого стремления f (р)
к нз^лю при р ~^сю.
Как и в проблеме ослабления особенностей, здесь можно
пытаться разложить / на сумму двух слагаемых f{p)^fi(p)~-[-f'^(P)
таким способом, чтобы первое из них /^ стремилось к нулю при
р->со столь же быстро, как /, и было таким, чтобы оригинал Fi
для него находился точно и достаточно просто. Второе же слагаемое
/* должно стремиться к нулю быстрее, чем /.
§5]
УВЕЛИЧЕНИЕ ТОЧНОСТИ ВЫЧИСЛЕНИЙ
375
f(p) = j F{x)X
О
Xe~P^dx
Оригинал F ix
со
»JF{x)e-P-'^ dx
Оригинал F (x)
1
fp + a
1
(P + ^)
Vp + ^
p + b
I
^P+a{p+b)
1
Vp^ + a^
1
\{P' + CL^)
1
" + 17
1
i
Ykx
1 2«д:«
/ял: ЬЗ..,B/2—1)
1
{р~а)Чр-ЬГ
Vi
XQ^^W{a — b)x]
Va — b
e-'^X
XerfV^(a —&)Jc
Уо (л-л:)
1
{р'Л-а')
,,-4
■X
1 .3 ... B/2—1)
X
1
P + a
1
(p + aJ
1
I .3 ... Bn~l)
x(^f/«(-)
1^p + a
ln(/? + a)
\n(p + a)\
ЩР + CL)
1
(/^ + ^)^
;ln(p+a)
1
л:^'-^^-^^
X
r(v)
Rev>0
r(v + ^)
Xi^(v;v + ^;
(й: — ^)л:),
Re (V + fx) > О
^Гх
1
Rev>-2-
х[1+Г'A)-
— In x\ e'
■X
1
+ In 4) e'"^^
•X
r(v)
Re V > 0.
Пусть f{p), например, представима в форме
iK<h< ... <k^; Y(p)->0, р-*сю}.
376 ЧИСЛЕННОЕ ОБРАЩЕНИЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА [ГЛ. 15
т
В ЭТОМ случае можно положить /i (/?) =^ 2 ^; (/^ + ^)"*^^' Соответ-
т
ствующий /i оригинал есть F^{x)= 2 ^/Г" {kj)x г^е~^'\
f{p)z:=Lf{p) — /i(/?) —Ym(P)(P + ^)~^"^ будет стремиться к нулю
более быстро, чем /. Параметр а в представлении / избирается так,
чтобы была обеспечена возможно лучшая гладкость /* на линии
интегрирования Rej9=^c.
Литература
Doetsch Q., Handbuch der Laplace Transformation, Birkhauser Verlag,
Basel. 1950—1956.
Дёч Г., Руководство к практическому применению преобразования
v^aплaca, М., «Наука», 1965.
Salzer Н. Е. 1) Orthogonal polynomials arising in the numerical
evaluation of inverse Laplace transformation, MTAC 9, Xa 52 A955). 2) Equally-
weighted quadrature formulas for inversion integrals, MTAC 11, №59 A957).
3) Tables for calculation of inverse Laplace transforms. Journ. of Math, and
Phys. 37, № 2 A958). 4) Additional formulas and tables for orthogonal
polynomials originating from inversion integrals, Journ. of Math, and Phys. 40
№ 1 A961).
P a p о u 1 i s A., A new method of inversion of the Laplace transform.
Quart. Appl. Math. 14, № 4 A957).
Скобля H. С, Таблицы для численного обращения преобразования
Лапласа, Минск. Изд. «Наука и техника». 1964.
Скобля Н. С, О распределений корней многочленов, связанных с чи-
сленным обращением преобразования Лапласа, ДАН БССР 9, JVTs 5 A965).
ЧАСТЬ ТРЕТЬЯ
ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ
НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА
ГЛАВА 16
ВВЕДЕНИЕ
§ 1. Предварительные замечания
Задача вычисления интеграла с переменными границами изучена
в значительно меньшей степени, нежели аналогичная задача для опре-
.деленного интеграла, которая рассматривалась во второй части книги.
Ниже приведено несколько примеров интегралов с переменными
границами, встречающихся в приложениях. Будем иметь в виду тот
случай, когда переменной является только одна граница
интегрирования, вторая же граница фиксирована.
К простейшему интегралу такого вида приводит задача
нахождения первообразной функции. Если дана функция f (х), непрерывная
на отрезке [xq, X], то любая первообразная для нее представима
следующей формулой:
X
у{х)==Уо+ j f{t)dt, xeixo. Х]. A6.1.1)
Гц
И вычисление первообразной равносильно нахождению значений инте-
X
грала I f{t)dt.
Хо
Более сложным примером является следующий интеграл,
встречающийся во многих прикладных вопросах:
X
y(^x)=JK{x ~t)f{t)dt A6Л.2)
а
В нем K{x—t) имеет смысл весовой функции и значения этого
веса на отрезке интегрирования a<^t-^x распределены так, что они
зависят только от расстояния л: — ^ от верхней границы х\ f есть
произвольная функция некоторого класса.
378 ВВЕДЕНИЕ
Наконец, в интегральном уравнении Вольтерра
[ГЛ. 16
/(л:)=ф(^)+J/C(x, 0/@
dt
и некоторых других задачах приходится иметь дело с интегралом
X
у(х)= J К{х, t)f{t)dt A6.1.3)
а
В котором весовая функция К{х, t) может зависеть от л: и г'
произвольным образом.
Методы вычисления указанных интегралов должны быгь
согласованы со свойствами соответствующих им весовых функций. Например,
расчетные схемы, построенные для A6.1.3), принципиально говоря.
могут быть применены к вычислению интеграла A6.1.1), имеющему
более частную форму. Но их для A6.1.1), по-видимому, нельзя будет
признать наилучшими, так как они не будут рассчитаны на то, что
весовая функция в A6.1.1) сохраняет постоянное значение. Для
каждого из указанных интегралов должны быть развиты свои способы
их вычислений.
Мы остановим внимание на интеграле A6.1.1) и в дальнейшем
будем заниматься исключительно задачей вычисления первообразной
функции.
Пусть нужно будет вычислить значения A6.1.1) для заданной
сетки значений аргумента х: Xj^(/2 = 0, 1, 2, .,.). Предположим, что
вычисления начаты, доведены до шага номера п и составлена *)
следующая таблица значений у{х^) = у^.
Нахождению подлежит у^^^у Для этого
могут быть использованы любые ранее
найденные значения у^ {k<^n) и те
значения /, которые разрешено вводить
в вычисления.
Если функция / задана таблицей
своих значений в узлах Xj^, мы при
вычислениях будем весьма стеснены в
выборе значений / и проблема
построения метода тогда будет принадлежать
области дискретного анализа. Одно из возможных решений задачи
в этих условиях приведено в главе 17.
X
Xq
Xi
1 ^п + \
у
Уо
Уп
*) в книге не рассматриваются вопросы составления начала и конца
таблицы значений у {х) и изучается только задача продолжения таблицы.
sn
ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ 379
Предположим теперь, что при нахождении y^^i нам
предоставлена возможность произвольно выбирать те точки, в которых берутся
значения /, и мы ограничили себя только числом таких значений.
Выбором точек тогда можно воспользоваться для получения возможно
малой погрешности в y^j + i- Обычно стремятся распорядиться
указанным произволом так, чтобы достигнуть наивысшей алгебраической
степени точности. Так поступают по аналогии с задачей вычисления
определенного интеграла, где этот путь был плодотворным и привел
к ряду ценных результатов. На путь повышения степени точности
мы многократно будем становиться в дальнейшем.
Напомним, что построение квадратурных формул наивысшей
алгебраической степени точности связано с задачей получения
определенного интеграла с погрешностью, не превышаюш,ей заданной
величины, при возможно малом числе значений интегрируемой функции
и, следовательно, с возможно малой затратой работы. В
неопределенном интегрировании есть еще другой путь для сбережения
вычислительного труда: можно стремиться к тому, чтобы каждое значение
интегрируемой функции / применялось для нахождения не одного,
а многих значений первообразной функции у{х).
В главах 18, 19 книги сделаны попытки решить задачу о
построении таких методов, которые позволяют использовать значения /
или у^ на нескольких шагах вычислений. Исследования проведены
в двух частных случаях и далеко не исчерпывают всей проблемы.
Укажем еще на одну особенность задачи вычисления интеграла
с переменной границей. Обычно такие вычисления выполняются на
большое число шагов. Допустим, что для нахождения значений
функции у(х) нами принято какое-то правило. На каждом шаге
вычислений, при нахождении следующего нужного нам значения y^+i» ^ьг
совершим некоторую погрешность. Эти погрешности от шага к шагу
будут накапливаться и, как правило, величина погрешности будет
возрастать при увеличении числа шагов. Закон роста погрешности
зависит от принятой вычислительной схемы и, если схема избрана
недостаточно удачной, рост погрешности может быть весьма быстрым
и уже через небольшое число шагов погрешность может достигнуть
значительной величины.
Приведем весьма простой пример, показывающий, сколь быстрым
может быть такой рост и насколько осторожным следует быть при
выборе схемы для вычислений на много шагов. Методы счета, дающие
удовлетворительные результаты на малом числе шагов, могут оказаться
совершенно непригодными, когда число шагов становится большим.
Пусть для вычисления yix^^^) мы хотим воспользоваться двумя
предшествующими значениями функции у: у(х^) и y(x^_i) и двумя
значениями производной: у'(х^) = /^^ и у'(x^_i)^^ f^^i. Здесь
естественно выполнить интерполирование y(x^^i) по указанным
значениям. Это есть эрмитово интерполирование с двумя двухкратными
380
ВВЕДЕНИЕ
[ГЛ. 16
узлами х^ и х^__^. Интерполяционная формула, как можно проверить
при помощи C.3.8), будет
y(x,^,)^~-4y(x,)^5y{x,^,) + hDf^^2f^^,)-\'r^.
Отбрасывая остаток г^, получим следующую приближенную
расчетную формулу
>'„.i--4y„4-5y„_, + /zD/, + 2/„_,).
A6.1.4)
Она точна для всевозможных алгебраических многочленов третьей
степени. Ее применение требует знания двух начальных значений у:
у^ и yi = y(Xi). Вычислим при помощи формулы A6.L4) значения
интеграла
»(х) ^ I ^^ й?^ = е^ — 1
на отрезке [О, 1]. Взяв сначала /к = 0,2 и считая >;@) = 0 и у (О, 2);^
^0,22140 известными, получим, после вычислений, следующую
таблицу. Наряду с найденными приближенными значениями функции
в ней указаны также их погрешности.
X
0.0
0,2
0.4
: 0.6
0,8
1,0
/
1,000 00
1,221 40
1.491 82
1,822 12
2,225 54
2,718 28
у
0,000 00
0.221 40
0,491 52
0,822 94
1.220 26
1.742 94
Погрешность
+0,000 30 ■
—0,000 82 1
+0.005 28 1
—0,024 66 1
Из результатов видно, что погрешность весьма быстро растет при
удалении от начала таблицы. Все значения у^ вычислены с
запасными знаками для того, чтобы показать, что большие погрешности
вызваны не недостаточной точностью вычислений, а другой
причиной.
Легко можно убедиться в том, что быстрый рост погрешностей не
вызван большой величиной шага Л и не может быть исправлен путем
уменьшения шага. Действительно, пусть, желая получить более точные
значения интеграла, мы уменьшим шаг вдвое и положим /г = 0,1.
Примем, как выше, известными два первых значения: >'@)=Ь
^@, 1)= 1,10517 и составим новую таблицу.
§ n
ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
381
X
0.0
0.1
0.2
0,3
0,4
0.5
! 0.6
i 0,7
0.8
1 0.9
1,0
/
1,000 00
1,105 17
1,221 40
1.349 86
1,491 82
1,648 72
1,822 12
2,013 75
2.225 54
2,459 60
у
0.000 00
0,105 17
0,221 39
0.349 88
0.491 65
0.649 50
0,818 10
1.036 10
1,116 02
2.010 39
—1.032 51
Погрешность
+0,000 01
—0,000 02
+0.000 17
—0.000 78
+0,004 02
—0,022 35
+0.109 52
—0.550 79
+2J50 79
Уменьшение шага позволило уточнить только одно из найденных
раньше значений функции: ^@, 4). Погрешности же других значений
сильно возросли и рост их оказался настолько быстрым, что в конце
таблицы ошибка превысила значение функции.
Проверим теперь, что быстрый рост погрешности здесь зависит
исключительно от неудачного выбора расчетной формулы. Вычислим
тот же интеграл другим способом. В равенстве
/* "Г i
применим к интегралу простейшую формулу трапеций и отбросим
остаток:
y^ + i^y^ + O.SA (/„ + /„,,). A6.1.5)
Полученное равенство наверное дает точный результат только
в том случае, когда функция / линейная, и алгебраическая степень
точности ее ниже, чем у A6.1.4). Можно было бы ожидать, что
X
0,0
ол
0,2
0,3
0,4
0,5
Значения у,
найденные по
формуле A6.1,5)
0,000 00
0,105 26
0.221 59
0,350 15
0,492 23
0,649 26
Погрешность
-0,000 09
19
29
41
54
X
0,6
0,7
0,8
0,9
1,0
Значения у,
найденные по
формуле A6.1.5)
0,822 80
1,014 59
1,226 56
1,460 82
1,719 71
Погрешность
68
84
102
122
143
382 ВВЕДЕНИЕ (ГЛ. 16
значения у„, найденные при помощи нее. будут менее точными, чем
приближенные значения, найденные при помощи A6.1.4). Как видно
из приведенной в конце стр. 381 таблицы, для нескольких первых
шагов это действительно так и будет. Но в вычислениях при помощи
A6.1.5) погрешности растут намного медленнее и значительно слабее
искажают результат, чем в предшествующем случае.
Уже через небольшое число шагов становится ясным, что при
счете на «большом промежутке» следует предпочесть формулу A6Л .5).
§ 2. Погрешность вычислений
Точные значения функции
X
У{^)^У,+ I f{t)dt
в узлах сетки Xj^ {k = 0, 1, ...) будем обозначать y(Xf^). Пусть для
нахождения их принята некоторая вычислительная схема.
Приближенное значение yiXf^), найденное по этой схеме, обозначим через )^^^.
Предположим, что для вычисления y^^j мы воспользовались
несколькими предшествующими значениями у из числа у„, Уп-г^ •••
• • •' Уп-р и т^=^т{п) значениями / в точках |„^ у G=1, . . ,, т).
Рассмотрим расчетную формулу следующего достаточно общего
для наших целей вида *)
р т
Если вместо приближенных значений у^, подставить сюда точные
значения функции у{х^^), равенство не будет выполняться и для
точного его выполнения в правую часть необходимо ввести
дополнительный член
р т
>'(^«4-1)=2Л,гУ(^„-.-)+2 5„,;/(и;)+Г,. A6.2.2)
r^j В дальнейшем будем называть погрешностью формулы A6.2.1).
При написании A6.2,1) предполагалось, что вычисления ведутся с
неокругленными числами, что бывает весьма редко. Формула должна
быть дополнена указанием правила округления и если операцию
округления условиться обозначать фигурными скобками, заключаю-
*) Коэффициенты Л^, i и В^, j этого равенства могут зависеть от /г и
расчетная формула может изменяться с каждым шагом. Равным образом вместе
с п может изменяться и величина шага х^^^—х^—hfi. Равенство A6.2.1)
есть уравнение в конечных разностях для уд. и для дальнейшего необходимо
лишь то, что уравнение имеет некоторый фиксированный порядок р+^'
§ 2] ПОГРЕШНОСТЬ ВЫЧИСЛЕНИЙ 383
1ДИМИ в себе округляемую величину, то действительная расчетная
формула запишется так
Уп^1 = 2 ^«. 1Уп-1 + S ^„. jfiln, j) . A6.2.3)
Индекс п, поставленный у скобок, указывает на то, что правило
округления на каждом шаге может быть своим.
Применение A6.2.3) требует знания величин Уо- Ур •'" Ур-
В дальнейшем они будут считаться известными. Рассмотрим
погрешность приближенного значения у/^:
Ч = У i^k) — У к
и составим для нее разностное уравнение.
Если обозначить через — a^^ погрешность, допущенную при
округлении, указанном в правой части A6.2.3), то дляу^^^ вместо A6.2.3)
можно написать
р т
У«+1 - 2 Л,/У.-^+SS,,,./(!,,,•)-а,, A6,2.4)
Почленное вычитание из A6.2.2) дает
е;,41 = 2 Л. .•£«-/ + /-. + «;.• A6.2.5)
Начальные значения погрешности е^^ (А=0, 1, ..., /?), отвечающие
приближенным значениям ^^^ (^ = 0, 1, ..., /?), образующим начало
расчетной таблицы, будем предполагать известными. Все дальнейшие
значения е^^ (к > р) последовательно найдутся при помощи уравнения
A6.2.5).
^п{^^ Р) определяется, во-первых, начальными значениями
Zq, ..., tp, во-вторых, погрешностью округлений щ{к<^п) и,
наконец, погрешностью формулы A6.2.1) г^(к<^п).
Для анализа погрешности полезно разделить влияние на г^ всех
этих величин. Для достижения такой цели будем искать e„ в форме
суммы трех слагаемых, которые определяются перечисляемыми ниже
условиями
En = En + E', + El A6.2.6)
Здесь Ef^ есть решение однородного уравнения
^„+l=i:Л.гf«-^ A6.2.7)
удовлетворяющее начальным условиям
Ef^ = ef, (А! = 0, 1, .... р) A6.2.8)
384 ВВЕДЕНИЕ |ГЛ. 16
Е'а удовлетворяет неоднородному уравнению
р
Еп+\=Ъ^п^К-1+^п A6.2.9)
и имеет нулевые начальные значения
£; = 0 (А! = 0, 1_,., /?). A6.2.10)
Eji^x есть решение неоднородного уравнения
р
Еп, x=^An, lE'n^i + Гп A6.2.11)
также с нулевыми начальными значениями
е1 = 0 ■ (k = 0, 1 р). A6.2,12)
Е,1 учитывает влияние на е^ начальных погрешностей Eq г
Еп и Е,2 зависят от погрешностей округления а„ и погрешностей г^
формулы A6.2.1) соответственно.
Простое и достаточное для наших целей выражение для Е^ через
^ki^"^P) может быть построено следующим путем. Обозначим Е^^
решение однородного уравнения A6.2.7), выполняющее условия
-^0
0. кФ /,
Тогда, очевидно,
^„ = <^о+^Х+ ■•■ +К^- A6.2.13)
Отсюда легко может быть получена оценка E^i, Точные значения
погрешностей Ef^ik-^p) редко являются известными, но бывает
известно, что они по абсолютной величине не превосходят некоторое
число, обозначенное нами е:
|е;^|<е, к^р. A6.2.14)
Если считать, что начальные погрешности е^^ могут иметь любые
значения, удовлетворяющие условию A6.2.14), из равенства A6.2,13)
для е„ получится следующая точная оценка
р
1
ej<e2|£«|. A6.2.15)
A6.2.13) или A6.2.15) позволяют выяснить, с какой точностью должны
быть найдены начальные значения tf^ (k ^ р), чтобы Е^ не превзошло
предписанной заранее величины.
§ 2] ПОГРЕШНОСТЬ ВЫЧИСЛЕНИЙ 385
Займемся теперь второй частью Е^п погрешности. Она должна
быть найдена из уравнения A6.2.9) и начальных условий A6.2.10).
Сразу же видно, что £« является линейной комбинацией а«,
Ар+1'
^n-V
^«-=2^n,ftaft- A6.2.16)
Коэффициент E^^ ^ учитывает влияние, которое оказывает на Е^
погрешность округления, равная единице и сделанная при вычислении
правой части A6.2.3) для п^=^к. E^f^ является функцией Грина,
или функцией влияния для сформулированной выше задачи с
начальными условиями.
В теории разностных уравнений *) дается явное выражение Е^ j^
через независимые решения однородного уравнения A6.2.9). Мы не
приводим это выражение ввиду его громоздкости.
Для дальнейшего полезно лишь заметить, что Е^^ ^, очевидно,
есть решение уравнения
р
En^i^Y^Ar^^iEn-i^bl A6.2.17)
удовлетворяющее начальным условиям
£. = 0 (/ = 0. 1, ..., рУ
6л — символ Кронекера:
fO. пФК
Исследование суммы A6,2.16) позволит судить, как между собой
должны быть связаны число шагов п и правило округления, чтобы
значение Е^ не превзошло заданной величины-
Пусть известно, что на всех шагах вычисления погрешность а„
не превосходит значения а:
|aj<a.
Из A6.2.16), при этом условии, вытекает следующее неравенство
для Е^:
\En\Ka"^\En,nV A6.2.18)
*) См. Марков А. А., Исчисление конечных разностей, отдел П,
§ 19, 1911, или Гель фонд А. О., Исчисление конечных разностей, гл. III,
§ 3, К» 6, М., Физматгиз, 1959.
386 ВВЕДЕНИЕ [ГЛ. 16
Величины Е^^ и £"„ зависят от точности вычислений начальных
значений Уо- У\' ' • -^ '^р ^ правой части разностного уравнения.
Увеличивая эту точность, мы можем сделать Е,^ и Е^^ по модулю меньше
любой наперед заданной границы при всяких п-^М.
Обратимся, наконец, к последней части Е^ погрешности.
Разностное уравнение A6.2.11) для нее получается из уравнения A6.2.9)
для Еп заменой свободного члена а^ на /■„. Начальные же значения
для Efi и Еп совпадают. Поэтому для Е„ должно быть верным
представление вида A6.2.16) с заменой в нем а^ на г^'
El = ^E,y,, A6.2.19)
Е'п зависит исключительно от свойств расчетной формулы A6.2.1),
или, если говорить более точно, от ее погрешности г^,, свойств
коэффициентов Afii и от числа шагов п.
л-1
Ниже, при изучении сходимости процесса, сумма 2^^n,k^k будет
рассмотрена более подробно.
В качестве примера выполним анализ погрешности разностного
уравнения A6.1.4). которое в § 1 было применено к вычислению
X
интеграла у= e4t.
о
Соответствуюш,ее ему уравнение вида A6.2.5) для е^^ будет таким:
e^+i"^ — 4e„4-5e^_;i + /-„-|-а,^. Это есть неоднородное разностное
уравнение второго порядка с постоянными коэффициентами и
свободным членом /"„ + «„. При решении его начальные значения
погрешности Eq и Ej мы должны считать известными.
Найдем сначала часть Е^ погрешности, зависяш,ую от Sq и е^.
Однородное уравнение для Е^ есть
Его решение, удовлетворяюш,ее начальным условиям Eq = EqU Е^ =Ci,
имеет вид:
Б„ = 4 (е: + 5ео) + -Ц^^ (ео - еО 5«.
Если Eq — 81=7^0, то Е^ с увеличением п будет быстро возрастать.
При я =10, т. е. всего только через 9 шагов вычислений, коэффи-
510
циент при Eq — 81 достигнет величины -?~ ^ Ь5 • 10**, что может
грозить потерей шести десятичных разрядов в точности.
§ 21 ПОГРЕШНОСТЬ ВЫЧИСЛЕНИЙ 387
Теперь разыщем другую часть Еп погрешности, зависящую от
ошибок округлений.
Неоднородное уравнение вида A6.2.9) для Еп будет таким:
Еп+\ ^ — АЕ'п^ ЪЕ'гг^х + а;,.
Решение, имеющее нулевые начальные значения Е^ = \^, £^==0, легко
находится
^-=0
:1{[1-(-5Г^]а, + [1-(-5Г^]а2+...}.
Сразу же видно, что при увеличении п £'л может быстро
возрастать, подобно Е^, и увеличиться во много раз даже через
небольшое число шагов. Аналогичное можно сказать и о £'„.
Насколько быстро на самом деле может возрастать погрешность е^
для расчетной формулы A6.1.4), видно из примера, приведенного
"в конце § 1.
Возвратимся к общей задаче исследования погрешности е^.
Характер изменения е„ с ростом п существенно зависит от
коэффициентов Л„^ £.
Рассмотрим сейчас один частный случай, когда все
коэффициенты Aji^ I неотрицательны. Допустим, кроме того, что
2Л„,, = 1. A6.2.20)
/ = 0
Это означает, что при вычислениях без округлений формула дает
точный результат в том случае, когда /^0 и функция у сохраняет
постоянное значение.
При сделанных предположениях можно найти весьма простую
и эффективную оценку е^^. Предположим, что начальные
погрешности вд, .... tp по абсолютной величине не превосходят е:
И покажем, что при любом п верно неравенство
|ej<8+ S ^иЛ-ГиУ A6.2.21)
Для п^= р -\~\ оно легко проверяется
р р
388 ВВЕДЕНИЕ [ГЛ. 16
Допустив, что неравенство верно для всех е^. i^n, проверим, что
оно выполняется и для e^^^:
|е„+1|<ЕЛ,£|е«-Л + к« + /-«
t = 0
Заменив под знаком суммы каждое |е^_;| превосходящей величиной
л-1
е + S1 ^t ~f Г; |, получим
л-1
k«+i|<2ki + ^H + |an + /-Je.
ЧТО завершает доказательство справедливости утверждения*
Из A6.2.21) видно, что для расчетных схем с неотрицательными
коэффициентами Aj^^^ погрешность е^ будет «медленно возрастающей»
функцией п. В этом отношении указанные формулы весьма
благоприятны для вычислений.
§ 3. Сходимость и устойчивость вычислительного процесса
Ближайшей нашей целью будет выяснение содержания некоторых
понятий, связанных с проблемой сходимости. Чтобы упростить
изложение, такое выяснение мы проделаем на случае расчетной
формулы частного вида, наиболее часто встречающегося в приложениях.
Допустим, что отрезок [Xq. X], на котором разыскивается
первообразная функция у(х), конечный и что значения у(х) находятся на
сетке равноотстоящих точек с шагом h:
Xf, = Xo+kh (^ = 0, 1, ... Л^). Xo + N^<A^<a:o + (N+1)^.
Такую сетку ниже будем обозначать 5;^.
Предположим, что для вычислений принята формула,
коэффициенты Afjj которой не зависят от индекса п:
р т
>'(л:«+1) = ЕЛ>'(^^) +2 5«;/(L.,•) + /■„. A6.3.1)
Расчетное правило отсюда получится, если в правой части отбросить
г„ и округлить оставшуюся сумму на принятое число значащих цифр.
у„+1= i:Ay„-£+25„./(Uy) • A6-3.2)
I ^=-0 У=1 )п
Считая ^'о Ур известными и находя у„ {п > р) из уравнения
A6.3.2), мы определим в точках сетки 5д приближенное значение
Уп для у(х„).
§ 3] СХОДИАЮСТЬ и УСТОЙЧИВОСТЬ 389
За расстояние р(у, у J между у(х) и функцией у^(п = 0, 1, ...
...» N), определенной на Sf^, примем, имея в виду изучение
равномерной сходимости, наибольшую абсолютную величину погрешности
Р (у. Уп) ="= 3Х 1г,,1 = max | у (х^) — >»„ |.
п п
Условимся говорить, что вычислительный процесс сходится» если
при h^>0 будет
9(У^ У«)^0. A6.3.3)
Погрешность е„ зависит от ошибок Cq» £i, .... e^, начальных
значений ^^(^ = 0, 1, ..., р), ошибок округлений а^ в правых частях
и погрешностей г^ формулы A6.3.1). Разложим, как это сделано
выше, 8„ на три части, учитывающие влияние на е„ величин каждого
из указанных видов г^=^Е^-\-Еп-\-Еп. Требования» которым
удовлетворяют Еп, Е,г, Еп были перечислены в предыдущем параграфе.
При выяснении условий сходимости вычислительного процесса,
-ввиду независимости величин ^i(i-^p), а„ и г^, мы должны
требовать, чтобы при /г->0 стремилась бы к нулю, в принятой метрике,
каждая из частей погрешности г^, иначе говоря» чтобы выполнялись
при /г -> О три следующих соотношения
max I£•«!-> О, max |£;;]-> О, тах|£^|->0. A6.3.4)
п п п
Рассмотрим сначала величины Е^^ и £"„. Они зависят от
погрешностей ^lii-^p) и а,1. Непосредственно ясно, что при любом
фиксированном h точность вычисления начальных значений yiii-^p) и
правых частей A6.3.2) всегда можно увеличить настолько, чтобы сделать
шах|£'„| и max|j&rtl сколь угодно малыми. Поэтому выяснение усло-
п п
ВИЙ, при которых будут выполняться два первые соотношения A6.3.4),
носит не принципиальный, а скорее технический характер: нужно
определить как с уменьшением h должна увеличиваться точность
вычисления начальных значений yiii-^n) и правых частей A6,3.2)»
чтобы части общей погрешности e^^, зависящие от указанных
величин, стремились бы к нулю в принятом смысле. Такое исследование
дает нам одно из средств для испытания практической пригодности
вычислительной схемы и. несмотря на технический характер вопроса,
оно имеет большое значение. Если окажется, что с уменьшением h
указанная точность должна быстро возрастать, то такая
вычислительная схема должна быть отвергнута, как малопригодная в
приложениях.
С этой точки зрения мы должны отдать предпочтение
вычислительным схемам, для которых точность нахождения yiii-^p) и
390 ВВЕДЕНИЕ ГГЛ. 16
правых частей A6.3.2) должна увеличиваться наиболее медленно при
Д—>0. Ту же самую мысль обычно высказывают в других словах.
Рассмотрим, для определенности, Е^^, Допустим, что в начальных
значениях yiii^p) мы допустили некоторые погрешности е^. При
вычислении следующих у^ A > р) погрешность будет возрастать от
шага к шагу. Закон роста погрешности будет, очевидно, зависеть
от выбора вычислительной схемы. Наибольший интерес представляют
вычислительные схемы, в которых скорость роста погрешности Е^
будет минимальной. В теории приближенного решения
дифференциальных уравнений методы, имеющие наименьший порядок роста
погрешности, называются устойчивыми, В предыдущем изложении
речь шла об устойчивости относительно погрешностей в начальных
значениях функции yi(i^p)- Сходным образом может быть
определена устойчивость относительно погрешностей округления а,^, иначе
говоря, относительно погрешностей правой части A6.3.2).
Возвратимся к Е„. Однородное уравнение для Е,^ вида A6,2.7),
в случае вычислительной формулы A6.3.2), будет уравнением с
постоянными коэффициентами
£«+1 = 2Л^«-/. A6.3.5)
Решение его, удовлетворяющее начальным условиям Ei = Ei(i -^р),
представимо в виде (см. A6.2.13)):
E, = EIbo + E\ei+ ... +^fep, A6.3.6)
где En есть решение того же однородного уравнения и имеет
следующие начальные значения
Закон роста Еп связан с тем, как быстро будут изменяться Еп при
увеличении п. Если считать, что начальные погрешности ограничены
по абсолютному значению числом е и в остальном произвольны:
|ej<e. A6.3.7)
то для Efj будет верна следующая точная оценка
l^nKeillfil- A6-3.8)
Будем считать, что изучаемая формула A6.3.1) является верной
без г„, когда /^0 и у есть постоянная величина. Такое предпо-
§ 3) сходимость и УСТОЙЧИВОСТЬ 391
ложение выполняется во всех случаях, имеющих практическое
значение. Коэффициенты Л^ тогда должны удовлетворять условию
р
1
/-0
2Л^=1. A6.3.9)
Последнее говорит о том, что Е^ = 1 есть решение однородного
уравнения A6.3.5). Такое решение, очевидно, равно сумме всех Е^:
I = е1-{-Еfi~\- ... -\-Еп. Поэтому при всяких п будет выполняться
р
неравенство 2|^л|^ ^- Можно привссги примеры, когда при п-^оо
21^л| будет неограниченно возрастать и тогда может оказаться,
что £\г тоже будет неограниченной величиной.
Наиболее благоприятным для вычислений значений >»„, в смысл.^
порядка роста Е^^, является, очевидно, тот случай, когда сумма
р
21^Л будет ограниченной*) для п У р. Все изложенное приводит
i-o
к следующему определению.
Уравнение A6.3.2) называется устойчивым относительно
погрешностей начальных значений yi{l ^ р), если существует
такое число М, что при любых п будет выполняться
неравенство
|Я„| <Л18, A6.3,10)
если только |8^|>^е, / = 0. 1 р.
Заметим, что ограниченность Е^^{п=^0, 1, . . .) при условии
|е/|^е равносильна ограниченности всех £"^(/ = 0, 1, ..., /?).
Действительно, если все Е^ ограничены, то будет, ввиду A6.3.6),
ограничена и Я^.
Возьмем произвольное k ^ р и положим все г^, (k Ф I, k^p)
равными нулю. Тогда
И из ограниченности £"„ следует ограниченность E^fi.
п
i |.
*) Для наших целей достаточно лишь факта ограниченности 21 ^^
вопрос же о нахождении наименьшего значения границы этого
коэффициента сейчас для нас не имеет значения.
ЗЭ2 ВВЕДЕНИЕ [ГЛ. 16
Общее решение A6.3.5) определяется алгебраическим уравнением
р
%f'^^ z=z^Ai}f~^. Если корни его суть Х^, ^2» •••» ^т кратностей
^1» /22' •••> ^m» 'ГО функции
;,?/г^' (У=::0. Ь ..., ^г—1; i-^1, 2 т) A6.3.11)
образуют полную систему линейно независимых решений.
Решения Eli{i^=Q, 1, .... р) получаются из A6.3.11) линейным
преобразованием с неособенной матрицей и поэтому ограниченность
при л=:0, 1, . . . всех Еп равносильна ограниченности решений
A6.3.11). Последнее же будет в том и только в том случае, когда
среди hi нет чисел больших 1 по модулю, и если|?1^ = 1, то
тогда ki^=^\. Отсюда следует
Теорема 1. Для того чтобы уравнение A6.3.2) било
устойчивым относительно погрешностей начальных значений yiii-^p),
необходимо и достаточно выполнение условий:
р
1. Среди корней уравнения 'к^'^ =2 А^^~^ ^^^ больших еди-
ницы по модулю.
2, Корни, по модулю равные единице, должны быть простыми.
Обратимся к изучению £„. На образование значения Еп
оказывают влияние погрешности округления а^, ...» a^-i и через них Е^
выражается следующим образом (см. A6.2.16))
п-Х
Е^ = ^ Efi^ k^k'
k=p
Коэффициент £'rt^fe, как функция я, должен удовлетворять
уравнению A6.2.17), которое в изучаемом случае будет таким
E'n^,^^AiE'n-i + ^l A6.3.12)
и иметь начальные значения:
£.^^ = 0 (^' = 0, U ..., р). A6.3.13)
Можно установить простую связь Е^, k с решением £'л. введенным
выше. При п <, k уравнение A6.3.12) будет однородным и, ввиду
нулевых начальных значений. E^^j^ будет равняться нулю при всяких
n-^k. Кроме того, £ft-{.i,ft=l» что сразу же вытекает из A6.3.12),
если там положить п^=к. Когда п^> k, уравнение A6.3.12) также
будет однородным.
§ 3] сходимость и УСТОЙЧИВОСТЬ 393
Будем рассматривать £'„j^ при n^k — р+1- Ввиду изложен-
ного, можно сказать, что Е^^^^ будет иметь начальные значения
и удовлетворять однородному уравнению
^,н-1 = 2Д-£«-г A6.3.14)
1=0
Но, как сразу же видно, тем же условиям удовлетворяет также
En+p-k-i и, в силу единственности решения с указанными
начальными значениями. Е^^^^ и E^^p^^_i должны совпадать.
Для Еп поэтому получится
Еп^^аиЕ'г,^,^и-ъ A6.3.15)
Будем считать, что верхняя грань а для погрешности округле-
лия a/j задана одинаковой для всех шагов вычислений, так что | ct„ | >^ а
при любых д,
N-\ N~\
max|£'^|<a 2 l^/v+p-fe-i I = а 2 \^n[ A6.3,16)
n k = p k=^p
Если считать, что погрешности а^ могут иметь любые значения,
удовлетворяющие условию | tt/^ | ^ а, то оценка является точной и
равенство достигается для п^= N, когда а^; = а sign ^л^+р-й-ь Так как
N-1
Ер=1, то при всяких N^p-\-\ будет 2 I^Jfe|^^- ^Р^ стрем-
k=p
лении h к нулю Л^ будет неограниченно возрастать. Значение
/V—1
2 l^ftl будет зависеть от поведения решения Е^ для к~>оо.
к^р
Рассмотрим частные решения однородного уравнения A6,3.14)
El Е'п^, Е?+,. A6.3.17)
Их начальные значения для ге = 0, 1 р образуют следующую
таблицу
О, О О, О, 1,
0. О О, 1, £^+1,
1. Ер+\ Е2р-2. Е2р-\< Ezp-
394 ВВЕДЕНИЕ [ГЛ. 16
Определитель ее отличен от нуля и поэтому решения A6.3.17)
линейно независимы. Но если так, то они получатся из решений
£'д(/=г:0. 1, ..., р) линейным преобразованием с неособенной
матрицей.
Поэтому ограниченность £"« (/ = 0, 1 р) равносильна
ограниченности решения A6.3.17).
Если принять во внимание, что при предположении A6.3.9),
21^«1>1 (п==о, 1, ...).
то будет ясно, что в смысле возможно медленного роста 2 l^fel
при /V—>оо наиболее благоприятным будет тот случай, когда все
слагаемые Е^ суммы будут ограничены некоторым числом. Тогда
2 1^'fel будет величиной порядка О (/V). Ввиду изложенного, примем
нижеследующее определение.
Уравнение A6.3.2) называется устойчивым относительно
погрешностей округлений а^, если существует такое число М^,
не зависящее от h, что при всяких N ^ р будет выполняться
неравенство
\Еп\<,М^Ма {п = р^-\. ..., iV—1), A6.3.18)
если только |а„|-<а.
Простая теорема, даюш,ая достаточные условия устойчивости,
может быть высказана так.
Теорема 2. Для того чтобы A6.3.2) было устойчивым
относительно погрешностей округлений, достаточным является
выполнение условий:
р
1) уравнение V^'^ = 2 ^Л^^~^ ^^ имеет корней, больших
ыо
единицы по модулю,
2) корни этого уравнения, равные единице по модулю,
являются простыми.
Доказательство. Решения A6.3.11) в условиях теоремы
будут ограничены при /г ^ 0. Но они образуют полную систему
решений и Е^ суть их линейная комбинация. Поэтому наверное
существует такое число Ж^, что для п^О будет
Отсюда и из A6.3.15) сразу же следует утверждение теоремы.
§ 3] сходимость и УСТОЙЧИВОСТЬ 395
Займемся теперь изучением части Еп ошибки вычислений. Е^
зависит от погрешности г^ формулы A6.3.1). Ошибка е„ будет сов-
падать с t^, если вычисления выполняются с точными начальными
значениями >'й ~ У (-^а) (^ == ^' ^» •••» Р) и правые части A6.3.2)
находятся без округлений: «^ = О (п^р).
Будем говорить, что формула A6.3,1) допускает сходящийся
вычислительный процесс, если
тах1Я^|">0 при h->0. A6.3.19)
п
Равенство A6.2.19) для Еп, ввиду Е^^^ :^£^\p„/,„i, примет форму
е:=Ъг^е1; ^_^. A6.3.20)
Таково явное выражение Е^ через значения г^^ погрешности
вычислительной формулы.
При оценке Е^ предположим, что г есть верхняя граница для
"абсолютной величины погрешности г^ на всем отрезке [xq, X], так
что при любых пф^п^М) выполняются неравенства
|rj<r. A6.3.21)
Тогда для Е'^ имеет место оценка
\Е'п\<г S|£«+/>-*-i! = '- Sl^ftl- A6.3.22)
Следовательно.
N-\
max|j?^'|<r 2 \^kl A6.3.23)
n k = p
N~\
Множители r и 2 1^*1» стояш,ие в правой части неравенства.
k=p
вообще говоря, зависят от шага h и изучение характера этой
зависимости позволяет во многих случаях сделать заключение о
поведении max|j^rt| при п~^оо. В частности из оценки A6.3.23) очевид-
п
ным образом вытекает следующая простая
Теорема 3. Если при h-^0 будет
yv-i
г 1,\ЕЦ->0,
к=р
^о уравнение A6.3.2) допускает сходящийся вычислительный
процесс.
396 ВВЕДЕНИЕ 1ГЛ, Ш
Остановимся еще на случае, указанном в двух предшествующих
теоремах, когда наверное можно гарантировать устойчивость A6.3.2)
относительно начальных погрешностей и погрешностей округления,
а именно, будем считать, что среди корней уравнения Х^^^ =
р
= S ^Л^~' нет больших единицы по модулю и корни его, равные
г = 0
единице по модулю, являются простыми.
Как выяснилось выше, тогда существует наверное такое число М^,
что при всяких п^О будет |^л|-<^ь Отсюда и из A6.3.23)
следует такая оценка для maxj^lj:
п
max I ^я I < г Ml (^ — рХ ЩгМ. A6.3.24)
п
Из нее сразу же получается
р
Теорема 4. Если уравнение Х^^^ = 2 ^^^^"^ «^ имеет кор-
ней, больших единицы по модулю, и корни его, равные единице
по модулю, являются простыми, уравнение A6.3.2) допускает
сходящийся вычислительный процесс всякий раз, когда
-ir-^O при Л->0.
Рассмотрим, наконец, случай, на котором мы остановились в конце
второго параграфа, когда коэффициенты вычислительной формулы Af^
суть неотрицательные числа: Л^^ ^ О, удовлетворяющие условию
р
^Aj^==^l, При таких условиях ошибка вычислений е^^ удовлетворяет
неравенству [см. A6.2.20)] |е/^К;8+ 2|otA + '*ftt' ^ > Р» где 8>
>|8,| (/ = 0, 1, .... р).
Отсюда легко получаются оценки для слагаемых Е^, Е^^, Е"^ъ
разложении 8^. Заметим, что по самому смыслу этих величин при
а^^ = О и Гд = О {k^^ р) 8„ должно совпадать с ^^^ и поэтому должно
быть
|£«|<е. Г1>р. A6.3.25)
Аналогично
\Е\\<"%^Л Г1> Р' A6.3.26)
§ 3] сходимость и УСТОЙЧИВОСТЬ 397
Если же |а;^Ка и |г^|<г. p<n^N, то для f^ и Е'^^ будут
верны оценки
|£; I < (я — /7) а < /Va. A6.3.28)
\El\^(n~p)r-^Nr. A6.3.29)
Неравенства позволяют высказать теорему:
Теорема б. Если коэффициенты А^^(к = 0, U ,.., р) неотри-
р
цательны и удовлетворяют условию 2 ^й= ^ уравнение A6.3.2)
устойчиво относительно погрешностей начальных значений
Н (^^ Р) ^ погрешностей округлений а^ (к ^ р). Если, кроме
того, при Н->0 будет х~"^^' ^^ уравнение A6.3.2) допускает
сходящийся вычислительный процесс.
ГЛАВА 17
ИНТЕГРИРОВАНИЕ ФУНКЦИИ, ЗАДАННОЙ
ТАБЛИЦЕЙ ЗНАЧЕНИЙ
§ 1. Содержание задачи и один из методов ее решения
Пусть в равноотстоящих точках х^=^XQ-\-nh на отрезке Xq-^
<^х^Х нужно вычислить значения интеграла
X
yW = >'o+ ^ f(()dt; A7.1.1)
функция / предполагается известной в той же, или в более широкой
системе равноотстоящих значений аргумента. Эта задача
рассматривалась в большом числе работ и известны многие методы ее решения.
Особенно большое внимание было уделено ей в связи с тем, что она
соприкасается с проблемой Коши для обыкновенного
дифференциального уравнения. В самом деле, если дано уравнение >>'=/(л:, з')
и нужно найти его решение, удовлетворяющее начальному условию
у(Хо) = У0, то такая задача может быть заменена решением
равносильного ей интегрального уравнения
X
У(х) = Уо-+ \ fit, y{t))dt, A7Л.2)
После этого возможность применения численного неопределенного
интегрирования к решению дифференциального уравнения становятся
очевидной *).
*) Обе указанные задачи существенно различаются в следующем
отношении. При вычислении интеграла A7,1.1) функция / считается известной
во всех точках сетки на отрезке [лго, Х\ и для нахождения каждого значения
у {х) можно пользоваться любыми значениями /. В случае же интеграла
A7.1.2) известными будут значения функции f {х, у) для табличных точек,
предшествующих х, значения же /(лг, у) для точек, следующих за х, мы
не имеем права вводить в вычисления.
§ П СОДЕРЖАНИЕ ЗАДАЧИ 399
В ЭТОЙ главе будет рассмотрен один из возможных методов
вычисления значений функции A7.1.1). Он приводит к простым
расчетным схемам и, как правило, дает хорошую точность, если функция /
будет достаточно «гладкой» на отрезке интегрирования и вблизи
него.
Предположим, что вычисления начаты и доведены до узла
д:^ = Хо + /^Л включительно. Пусть для нахождения следующего
значения y(x„^i) функции A7.1.1) мы хотим воспользоваться только
одним значением у, непосредственно предшествующим y(x„^i):
y(^„+i) = y(^„)+ J /(t)dt. A7.1.3)
Для вычисления интеграла интерполируем / на отрезке [х„, -^л+i]-
В условиях изучаемой задачи, целесообразно за узлы
интерполирования принять табличные узлы, ближайшие к промежутку х^ < -^ <
< -^„+1. взяв одинаковое число их с той и другой стороны от
указанного промежутка.
Применим интерполяционную формулу Ньютона C.2.6), расположив
в ней узлы в порядке х^, x^-\~h, х^ — h, x,^~\~2h, х^ — 2h, ...
f(x) = f(xj + (x — x^)f(x^, x^-^h) + (x — xj(x~-x^ — h)X
Xf{Xrt^ Xn + h. x^ — h)-{'{x — x,,){x — x^~~~h){x-'X^ + h)X
X/(x^, х, + Уг, x^ — h. x„ + 2^)+...
Или, если ввести новую переменную, положив х:=Х/^Н-аЛ, и
выразить разностные отношения через конечные разности,
/(x, + ayz) = /, + ^A/, + ii^^A2A„i +
, (a-f-l)^(^ —1) лд/ , {и-\-\)и(и--\)(и — 2) Д4^ ,
"^ 3! /л-1~1 4! /л~2П- • • •
Для придания членам этого равенства формы, симметричной
относительно середины x^-j-0,5/f промежутка, преобразуем разности
четного порядка при помощи тождеств
/„ = 0.5 [/„^i4-/„l-0.5 [/„+,-/„] = 0.5 [/„^., + /„1-0.5А/„,
^V„-, = 0.5 [AV„ + AV«-.il - 0.5 [Д2/„ - А2/„_,] =
= 0.5 [Л2/„ + Л^/„_,] - 0.5Азд_„
400 ФУНКЦИИ, ЗАДАННЫЕ ТАБЛИЦЕЙ ЗНАЧЕНИЙ [ГЛ. 17
В результате получим *)
, (ц-0,5)ц(и-1) л,^ I (u + k-l) ... (u~k) ^^
-i 3! ^Jn-i-t- •■■ -I Щу A
wA^V„_;^ + Д^Vд_fe+l , (и-0.5)(и + ^-1)...(и-^) .,,^,
X 2 *~ B/^ + 1)! /л-ft-^'^ (.-«;•
A7.1.4)
Подстановка построенного представления функции / в интеграл
^n+fi 1
f{t)dt^=h\ f{Xfj-^uh)da приведет к следующему выражению
для y(x„^j):
~^ 720 2 60 480 2 "Г • • •
^^^A^V.-.Y^'^-"^^'] + /?...> A7.1.5)
* о
Расчетная формула отсюда получится, если избрать какое-либо
значение k и отбросить остаток R^^ ^.
Рассмотрим пример вычислений. Пусть нужно на отрезке [О, 1]
вычислить значения интеграла
yix)^lMt)dt=l-Jo(x).
о
Jq и Ji суть бесселевы функции первого рода. Примем /г = 0,2.
В A7.1.5) сохраним члены с разностями до четвертого порядка.
Расчетная формула будет:
V _„ I Qof/n + A-fi 1 ^!AL^i^^!£ii 1 11 ^'fn-2 + ^Vn^^]
Уп+i —Уп-r ^>^ [ 2 l2 2 ^720" 2 J
Уо-0' /(х)--Л(х).
*) В теории интерполирования это равенство называется формулой
Бесселя.
§ n
СОДЕРЖАНИЕ ЗАДАЧИ
401
Таблица конечных разностей функции f^^Ji, необходимая для
вычислений по 3T0fi формуле, имеет следуюидий вид:
X
U-2 =
U_l==
-^0 =
Хх^
дгз-
^3=^
х^ =
^5^
-^6==
1 -^7-=
—0,4
-0,2
0,0
0,2
0.4
0,6
0,8
1,0
1,2
1,4
/
—0,196 026 6
—0,099 500 8
0,000 000 0
0,099 500 8
0,196 026 6
0,286 701 0
0,368 842 0
0,440 050 6
0,498 289 1
0,541 947 7
Af-W
96 525 8
99 500 8
99 500 8
96 525 8
90 674 4
82 141 0
71 208 6
58 238 5
43 658 6
AV-lO^
+ 2 975 0
000 0
— 2 975 0
-- 5 851 4
— 8 533 4
--10 932 4
—12 970 1
—14 579 9
Лз/-10?
—2 975 0
—2 975 0
—2 876 4
—2 682 0
—2 399 0
—2 037 7
—1 609 8
Д</-107
000 0
98 6
194 4
283 0
361 3
427 9
При составлении ее необходимо было вычислить значения / в
точках х_1== — 0,2 и х_2 = — 0,4, выходящих за границу jc = 0
отрезка интегрирования [О, 1]. Как при помоиди этой таблицы находятся
значения интеграла у (х), ниже показано на примере вычисления у (О, 2):
у@. 2) = уф)-^н[1Ш,1Ш^^т=:Ц^1^Ш1 +
11 Д4/(—o,4)-f Ду(—0.2)
720 2
1_0 I Q^g Г 0 + 0.0995008
1 0 — 0.0029750 , 11 0 + 0.0000986] лллгчп-тгсл
12 2 ^720-^^^ J = 0.009 975 0.
В результате получены следующие приближенные значения у(х):
X
0,0
0,2
0,4
X
0
0,000 000 0
0,009 975 0
0,039 601 7 '
X
^ 0,6
1 0,8
1,0
X
y=.j J,(t)dt
0
0,087 995 1 1
0,153 712 6
0,234 802 3
402 ФУНКЦИИ. ЗАДАННЫЕ ТАБЛИЦЕЙ ЗНАЧЕНИЙ [ГЛ. 17
От значений интеграла, точных на семь знаков, отличается только
у (О, 4) на единицу седьмого знака*). Все знаки остальных значений
совпадают с точными,
§ 2. Остаток
Старшая конечная разность, входящая в A7Л.4) имеет порядок
2k-\-\ и для составления всех членов этой формулы необходимо
знать значения функции f в2к~\-~2 точках х„ — kh, , , ., x^~\-(k~\~ \)h.
Если сделать предположение, что функция / имеет на отрезке
[jc„ — kh, x^-\~{k-{-\)h] непрерывную производную порядка 2^4-2,
остаток г (х) интерполирования A7.1.4) может быть найден ^при
помощи теоремы, приведенной в § 2 гл. III, и имеет значение
г (^х) = 1^—^п + Щ1^ — ^п + (^—^)^]..Л^~Хп — {к + 1)к] ^Bй+2) /^ч ^
—« B^ + 2I ^ ^^^'
Это дает возможность найти для дополнительного члена /?^, j^
формулы A7.1.5) следующее значение
О
д2А + 3
1
( (u^k)(u~\-k—l) ... (й —А;—1)/Bй+2)(^)^^.
" B^+2)!
о
Так как мнол<итель (а-\~ k) (и-{- k — 1) ... (и — k — 1) сохраняет
на отрезке [О, 1] знак, к последнему интегралу может быть
применена теорема о среднем значении, что приводит к следующему
утверждению:
Если f имеет непрерывную производную порядка 2^ + 2 на
отрезке [jc„ — kh, x^-\-{k-\~\)h], то для остатка R^^^ в
равенстве A7.1.5) верно представление
1
/:Bft+2)/u4 Г
^n.k = h^''''\2k + 2)\] {u^k){u + k-\), , ,{u-^k^\)du. A7,2.1)
• о
где значение \ есть некоторая внутренняя точка отрезка
{x^ — kh. x^ + {k-^\)h].
*) См., например, Ват с он, Теория бесселевых функций, 4. 2, М., ИЛ,
1949, 18—19.
ГЛАВА 18
ВЫЧИСЛЕНИЕ НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА
С МАЛЫМ ЧИСЛОМ ЗНАЧЕНИЙ ИНТЕГРИРУЕМОЙ ФУНКЦИИ
§ 1. Содержание задачи и некоторые общие теоремы
о расчетной формуле
Здесь, как и выше, будет рассматриваться задача вычисления
неопределенного интеграла х
yW = yo+ \ fit)dt A8.1.1)
для равноотстоящих значений аргумента х^^= х^-\~kh {k^==^, 1, . . ,),
но, в отличие от предположений предыдущей главы, сейчас мы
допустим, что точки, в которых берутся значения функции, не обязаны
совпадать с узлами x^^ и могут лежать в любом месте области
определения /.
Напомним, что при вычислении интеграла A8.1.1) при помощи
формул вида A6.2.1), главная часть труда, обычно, расходуется
на нахождение значений функции / и можно указать два пути,
позволяющие экономить вычислительный труд. Можно стремиться к
достижению возможно высокой степени точности при помощи выбора
узлов, в которых берутся значения /, и можно стремиться к тому,
чтобы каждое значение / применялось для нахождения не одного,
а нескольких значений неопределенного интеграла, так чтобы на
каждый шаг вычислений приходилось бы возможно меньшее число
значений /.
В дальнейшем изложении, при построении расчетных формул, мы
воспользуемся обоими указанными возможностями. Вновь остановимся
на том случае, когда для разыскания следующего значения у^^^
интеграла привлекается только одно его предшествующее
значение у_. Тогда X
и нахождение y„+i приводится к вычислению f{t)dt.
404
ВЫЧИСЛЕНИЕ НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА
[ГЛ. 18
Чтобы коэффициенты расчетной формулы не зависели от номера
шага /г, мы должны считать, что узлы на оси х расположены /г-перио-
дически. Точки a~\-kh, отвечающие различным целым значениям к,
в дальнейшем будем называть сходственными.
Предположим, что для вычисления интеграла на отрезке [x„, a^„+i]
было взято т узлов а, р, . . ., к: X/^<<a < р < ... < ^ < х^^^^. Ниже
они будут называться основными. Пусть, кроме того, взято
а узлов a~\-pih (/=1, ..., а), сходственных а.
Ь узлов P+^i^ (г*==1. .... Ь), сходственных р.
/ узлов X-\~tih (/=1, ..., /), сходственных X,
Распределение дополнительных узлов между табличными точками х^
определяется числами р^, ^^, .... t^, которые могут иметь любые
целые значения, отличные от нуля. Общее число всех узлов
назовем iV-f-1: т-{-а-{-д~\- ... -|-/ = А^-|-1. Рассмотрим формулу
вида
■^rt-f-l а
J fit)dt^AJ(a) + ^AJ(a + p,h)+ .,,
I
.^. +LofiK)+^LJ{l-^tih). A8.1.2)
Если числа pi, ...» ^^ считать заданными, формула A8.1.2)
определяется узлами а, .... ^ и коэффициентами Л^, .. ., Z,; (г = 0, 1, . . .).
Их мы выберем так, чтобы равенство A8.1.2) имело возможно более
высокую алгебраическую степень точности.
При всяких а, . . ., I; Pi, . . ., t^ формулу A8.1.2) всегда mojkho
сделать верной для любых многочленов степени Л/", Для этого
достаточно взять ее интерполяционной, т. е. такой, чтобы ее
коэффициенты были равны интегралам от соответствующих множителей
в интерполяционной формуле Лагранжа для интерполирования / по
ее значениям в узлах а, а-\-p^h, ..,, %, h-^-tih. Этим требованием
коэффициенты Л^, ..., Z,-вполне определятся и дальнейшее повышение
степени точности возможно только за счет выбора а, ..., %, Ниже
будет показано, что .кля любых pi ti при помощи подбора а, .... Я..
формулу A8.1.2) можно сделать точной для всех многочленов
степени m-\~N и число m-^N есть наивысшая возможная степень
точности.
§ 1] ОБЩИЕ ТЕОРЕМЫ О РАСЧЕТНОЙ ФОРМУЛЕ 405
Введем следующие многочлены, связанные с узлами формулы
О)(л;) = (х — а). . .{х — X),
а I \
j=i 1 = 1 ( A8.1.0)
Q(x)^(^^(x) ... 03j,(a:). J
Теорема 1. Каковы бы ни были узлы а, ,, ., X и числа р^, . . .,^^,
квадратурная формула A8.1.2) не может быть точной для
всех многочленов степени m-\-N-\- \.
Доказательство. Для доказательства достаточно
рассмотреть многочлен / = Q (л:) со^ (х). Степень его равна m + iV + 1. Так
как все узлы формулы являются корнями Qo^, квадратурная сумма,
стоящая справа в A8.1.2), для такой функции / обратится в нуль.
Интеграл же QaP dx отличен от нуля, так как многочлен / =^ Qco^
сохраняет знак на отрезке интегрирования и отличен от
тождественного нуля. Поэтому равенство A8.1.2) для f^^QaP- не может быть
верным.
Алгебраическая степень точности A8.1.2) всегда меньше, чем
т + Л^+1 и, самое большее, может быть равна m~\-N,
Теорема 2, Для того чтобы формула A8.1.2) была верной
для всех многочленов степени m--\-N, необходимо и достаточно
выполнение двух условий:
1) формула должна быть интерполяционной',
2) для любого многочлена Q{x), степени меньшей т, должно
выполняться равенство
•^/г + 1
J Q(A:)co(x)Q(jc)rfjc = 0. A8.1.4)
Доказательство. Необходимость первого условия очевидна.
Для проверки необходимости второго условия, возьмем произвольный
многочлен Q(jc), степени меньшей т, и положим / = Q(a:)(o(a:)Q(jc).
Это есть многочлен самое большее степени m-\~N, Для него
равенство A8.1.2) должно быть точным. Но / во всех узлах
квадратурной суммы обращается в нуль. Поэтому должно быть верным
равенство A8.1.4).
Предположим теперь, что оба условия теоремы выполняются и
пусть / есть произвольный многочлен степени m-{-N, Разделив /
на Q(o, мы можем представить / в форме / = QcoQ + r, где Q и /'
406 ВЫЧИСЛЕНИЕ НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА [ГЛ. 18
есть многочлены, степеней меньше чем т и N-]- \ соответственно.
Заметим попутно, что так как во всех узлах формулы
произведение Q(o обращается в нуль, многочлены /иг должны в этих узлах
принимать одинаковые значения.
Ввиду того, что степень г не больше N и формула
интерполяционная, должна быть верной следующая цепь равенств,
доказывающая достаточность условий теоремы
^П+1
I f'^=
^д
^п + 1 ^п+1 ^пл
=: J Q(i)Qdx-\r J rdx^ f
^n ^n ^n
=ЛоГ(а)+^Л^(а+/?,-Л)+ ... =Л/(а)+^Д./(а+р,/г)-Ь...
(=1 (=1
Теорема 2 приводит вопрос о существовании квадратурной
формулы A8.1.2), имеющей наивысшую алгебраическую степень точности
m-\-N, к вопросу о существовании чисел а % таких, чтобы
соответствующие им многочлены оз и Q удовлетворяли условию A8.1.4).
Теорема 3. Каковы бы ни были числа /?/, . . ., /^, основные
узлы а X всегда могут быть выбраны так, чтобы
соответствующая им квадратурная формула A8.1.2) имела наивысшую
алгебраическую степень точности m~\-N.
Доказательство. Возьмем любую систему чисел а, р, . . ., ^,
удовлетворяющую неравенствам
^.<а<р<...<^<х„,1, A8.1.5)
и построим по ним многочлены о (л:) и Q(x). Q(x) сохраняет знак
на отрезке [х„, ^r^^j]. Примем его за весовую функцию и
рассмотрим соответствующую ей систему многочленов Р)^{х), ортогональных
на [л:^. х^^^^\. Среди них выберем многочлен Я,„(х) степени т. Для
определенности записи, допустим, что его старший коэффициент
равен единице:
Р,, (X) - У« + PlX"'-' 4 Р2^"-' + . . .
При любом многочлене Q, степени < т, будет верно равенство
I Q{x)P,^(x)Q{x)dx^^. A8.1.6)
Корни Pjni^) все действительные, простые и лежат внутри отрезка
[л:^, x^^i\. Назовем их ^j, .,,, ^^^ и будем считать, что они
перенумерованы в порядке роста х,^ < ^^ < ... < |^ < х^^^. Если
окажется, что ^1=а, Е2=^Р» • • •' ^ш = ^' то Pjn совпадает с со и для
многочленов Q и со будет выполнено условие A8.1.4). Соответству-
§ и
ОБЩИЕ ТЕОРЕМЫ О РАСЧЕТНОЙ ФОРМУЛЕ
407
ющая таким Й и (о формула A8.1.2) будет иметь наивысшую
алгебраическую степень точности m~\-N.
Построим систему линейных уравнений для нахождения
коэффициентов Pj^(^= 1, .... т). Свойство ортогональности A8.1.6), вполне
характеризующее Р^, равносильно выполнению равенств
I Q{x)P^(x)x' dx=^^ (/=зО. 1 т—\)
или, если сюда внести вместо Р^ его разложение по степеням х,
Cm+i + CmU-lP\ + С^^1_2Р2+ ' " + <^iPm^^ О'= 0. 1. .... W— 1)
с^= ^ Q{x)x^dx. A8.1.7)
Q{x) есть многочлен от а, . . ., ^. Поэтому числа с^ также будут
многочленами от а %. Определитель системы A8.1.7)
D =
^1.
^т-\
. Сп
^2т-2
есть вместе с тем определитель положительной квадратичной формы
2
Фт(^1. .... Z^)== J Q{x)\y^X^''^Zi
W = l
dx
и OH заведомо отличен от нуля при всяких а. .... ^ из области A8.1.5).
Коэффициенты р^^ (/г = 1 т) будут рациональными функциями
от а, .... Я непрерывными в области A8.1.5).
Рассмотрим корни Ргл(х): 1^, ^з» •••» Im-^^^ непрерывно зависят
от коэффициентов р^^ и будут, следовательно, непрерывными
функциями а» .... Я, в области A8.1.5):
^1 = Ф1 (а, .... А,),
1т===Фт(С^. •••. ^У
A8.1.8)
Этим равенствам можно придать следующий геометрический смысл.
Введем т-мерное числовое пространство (jCj, Х2, ...» л:^) и
обозначим его р^. Равенства A8,1.8) можно истолковать как преобразование
точки (а, .... X) из р^ в некоторую новую точку (|i 1т)^Рт-
Условия A8.1.5), которым подчинены числа а, .... X, выделяют в р^
/п-мерную замкнутую пирамиду. Так как числа |^ ^ свою очередь
408 ВЫЧИСЛЕНИЕ НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА [гЛ. 18
ВЫПОЛНЯЮТ неравенства х^<1^< ... < ^^ < ^n + v то равенства
A8.1.8) дают однозначное и непрерывное преобразование указанной
пирамиды в себя. По известной теореме Брауэра *) при таком
преобразовании наверное существует неподвижная точка и, стало быть,
существуют такие значения а. . . . Д, для которых ^j =а, . - •> 1,п = 'к
и P^{x)^=(i)(x). Поэтому наверное существуют а, .... X,
удовлетворяющие неравенствам х^^ < а < ... < Я < х^_^_^, при которых
выполняются A8.1.4), что и доказывает теорему 3.
Единственность таких значений а Я в общем случае остается
невыясненной.
Рассмотрим еще остаток квадратуры A8.1.2) и найдем его
простейшее представление.
Пусть [а\ д^] есть отрезок, содержащий в себе [x„, x^^i] и все
узлы формулы A8.1.2).
Теорема 4. Если f имеет на [а\ д^] непрерывную производную
порядка m + yV-f-1 и если формула A8.1.2) имеет степень
точности m-\-N, то на [а\ Ь^\ существует такая точка ^, что для
остатка R(f) формулы A8.1.2) верно равенство:
^(f) = lm+N+l)\ J ^(^)^4x)dx, A8.1.9)
Доказательство. Выполним интерполирование / по
следующим данным. Предположим, что в каждом основном узле а X
заданы как значение /, так и значение производной /^ а в каждом
узле вида a-f-P/^. • . .. X-\~tih известно только значение самой
функции /. Всего будет w-f-A^-f-1 известных значений. Интерполирующий
многочлен, который мы обозначим Н (х), будет иметь степень ^ m-\~N:
/{х)==Н(х)+г(х).
В условиях теоремы, для остатка интерполирования г(х) верно
следующее представление (гл. III, § 3)
*) Пусть в р^ дано m-f-l точек, не лежащих в (т — 1)-мерной
плоскости. Многогранник, имеющий эти точки своими вершинами, называется
от-мерной пирамидой. Брауэром была доказана следующая теорема: «При
любом однозначном и непрерывном отображении т-мерной пирамиды на себя
имеется по меньшей мере одна неподвижная точка». В г о ц w е г, «ОЬег
Abbildung von Mannigfaltigkeiten», Math. Ann. 71 A912). См. также В. В. Н е-
мыцкий. Метод неподвижных точек, Усп. матем. наук, вып. I A936), 153.
§2]
РАСЧЕТНЫЕ ФОРМУЛЫ ЧАСТНОГО ВИДА 409
где Г) есть точка, лежащая внутри отрезка, содержащего в себе узлы
интерполирования и точку х.
Очевидно R(f) = R(M)^R(r), Но Н(х) имеет степень <m + /V
и /?(//) = 0. Поэтому /?(/) = /?(/•). Квадратурная сумма для г(х)
обращается в нуль ввиду того, что остаток г (х) равен нулю во всех
узлах формулы и R (г) будет совпадать со значением интеграла
от г(х):
^п + 1 -^n+i
Так как Q(x)(iy^(x) сохраняет знак на [х^, X/^^J. отсюда следует
утверждение теоремы 4.
§ 2. Расчетные формулы частного вида*)
Ниже будут рассматриваться расчетные формулы, сл^^жащие для
X
вычисления значений неопределенного интеграла y(x):=yQ~\~ f{t)dt
и требующие по одному, два или три значения функции / на каждый
шаг, или. иначе говоря, формулы, содержащие по одному, два, три
основных узла и некоторое число сходственных с ними узлов.
Все такие формулы могут быть построены единообразным
способом и процесс их построения описан подробно только в одном
случае в остальных же случаях приведены лишь окончательные
результаты.
I. Начнем со случая одного значения / на каждый шаг. Изучение
его приведет к построению формулы, известной еще Гауссу и
полученной им в другой задаче и иным путем.
Пусть на участке [х^, x^-^h] за основной узел принята точка
cift = x^-]-qh, 0-^^<1. Схема расположения узлов изображена
на рис. 8.
^^Л^ ^(fh^ ^^Л^
Рис. 8,
Предположим, что для построения формулы вида A8.1.2)
привлекаются по к штук узлов, сходственных а^^, ближайших предшеству-
*) Значения коэффициентов и узлов квадратурных формул, приведенных
в § 2, вычислены М. А. Филипповой.
410 ВЫЧИСЛЕНИЕ НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА [ГЛ, 18
ЮЩИХ а^^ и следующих за а^. В формуле будет участвовать всего
2^+ 1 узлов. Мы можем распорядиться в ней выбором только одного
параметра q и наивысшая степень точности формулы равна 2yfe+l,
Чтобы достигнуть ее. формулу нужно выбрать интерполяционной и
выполнить условие ортогональности A8.1.4), которое в
рассматриваемом случае запишется так:
[ Q{x)(i^{x)dx = ^. A8.2.1)
Q(a:)o)(x) = (a: —aj(x —a„,i)(-^ —^rt+i)-.-(-^ —^«-jfe)(-^-^«+ft) =
^[x — x^ — qh\ [{X ~ X, ^qhf ^h^] , . . [{x — x,~qhf - кЧЦ
Легко показать, что уравнение A8.2.1) имеет решение ^ = 0,5 и это
решение единственное при O^^^l.
Преобразуем интеграл A8.2.1) к новой переменной, положив
д: = л:^ + /г^"Г М,
х„ +Л
1-^
J Q(jc)(o(jc)^^:=ry^2*-^2 J л@^^ я@ = ^(^^-'1^)-..(^2—^2).
-ч
A8.2.1) заменится равносильным уравнением
ф(^)=== 1 я@^^==0. A8.2.2)
0,5
Так как 7i(t) есть нечетная функция /, то ф@,5)= n(t)dt=0 и
-0,5
^ = 0,5 является корнем уравнения A8.2.2);
(p'(q) = n(\ ~q)~n{- q).
Но лA —^) и я(—q) имеют противоположные знаки при О < ^ < 1
и ф'(^), следовательно, сохраняет знак на промежутке 0<^<1-
Отсюда следует единственность корня ^=^0,5 на O^^-^l
а^ = х^~\'^М.
Для интерполирования / на [х^^, дг^ + Л] по ее значениям в узлах
afjj{m^=n — k, , . ., n-\~k) воспользуемся интерполяционной формулой
§ 2) РАСЧЕТНЫЕ ФОРМУЛЫ ЧАСТНОГО ВИДА 411
Ньютона C.2.6), расположив в ней узлы в следующем порядке:
а„, «„ + Л. ««-А- «« + 2/г. а„-2Л, ...
/(д^) = /(а„) + (^ —a„)/(fl„, a^-\-h)-ir{x — a„)(,x — a„ — h)^
Х/К- «я + Л- (^n — h) + {x — а„){х — а^ — h){x — а„-\-h)X
Х/(а„. a,-\-h. a„ — h. a„-\-2h)+...-\~ г{х) =
С,-а„ + М)...(^--а„-М)д,,,,
^ BАН-1)!Л2*+> " >'-г V /
Подстановка этого выражения f{x) в равенство
x„+h
И несложные вычисления приведут к следующему результату:
+ 122 6244^600 ^'"^(«„ - 5/г) + . . ■ + c^A^V(а„ - kh)] 4 /?„. *,
0,5
''' = -ЩГ. J ^^(^^-l2)...[^^-(й-lJ]Л. A8.2.3)
Если предположить, что / имеет непрерывную производную
порядка 2к-\~2 на отрезке [а^ — (k~\~\)h, a^~\'kh], то остаток
интерполирования г{х) будет равен (гл. 3, § 2)
J, /^ч ^ [x—ak + ik + ^)h] ...(x — au — kh) A2k +2). .
Здесь т] есть внутренняя точка указанного отрезка. Для остаточного
члена R^j^ формулы A8.2.3) отсюда, после интегрирования и замены
x=a^~{-th^=x^-\--^ h~^th, найдем
0,5
^'^.^^^ '72ЙЬ2)Г J f{t^-\')^-^fi-k')dt. A8.2.4)
-0,5
II. Рассмотрим несколько наиболее простых способов
вычисления, требующих два значения функции / на каждый шаг. Пусть на
412 ВЫЧИСЛЕНИЕ НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА [ГЛ. 18
отрезке [х^, ^п'^^] взяты два основных узла а^^, р,^. Схема узлов
такова:
^/.-/ Л-; ^п А ^п.; А.;
.1 t>^—с [ .о. с 1 д—о 1
Рис. S.
Допустим, что кроме а„ и ^^ берется еще по k сходственных им
узлов, ближайших к отрезку [х„, х^^А^Щ справа и слева от него,
так что к вычислению привлекается всего 2^-|-2 узлов. Наивысшая
степень точности, которая может быть достигнута при построении
формулы, равна 2^-|~3.
В изучаемом случае о)(л:)=^(х-—а/^)(л:—-р„). Произведение Q(x)o) (л:)
будет содержать 2^-1-2 множителя и иметь следующую форму:
Q (л:) 0) (л:)=(л:-аJ (х-рJ (x-a„+i) (x™p„.i) (x-p„+i) (x-a^^i). . .
Условие ортогональности A8.1.4), из которого должны быть
найдены а^ и Рд, здесь приводится к двум уравнениям
J Q(i)dx = 0, J xQ(i)dx = 0. A8.2.5)
Построение формул начнем со случая k=l. Кроме двух узлов
а„ и р„ на отрезке [х„, x^-^-h], берутся по одному узлу в двух
соседних отрезках [х^ — h, х„] и [х^ + Л, х„ + 2/г].
Чтобы привести задачу нахождения а^^ и р^^ к каноническому
отрезку, выполним линейное преобразование
z = -^x-[l-\-^x„).
переводящее отрезки [х,^ — Л, х„], [х^^, x^-^-h], ... соответственно
в [—3, —1], [—1, 1], ... Середина отрезка [х„, х^^ + ^1 перейдет
в точку z = 0. Точки, соответствующие х=а„ и х = р^, назовем
р и д. В переменной z многочлены (о и Q будут такими
со (х) = (х — а J (х — р J = _ B; — р) {г — q),
Q (х) (О (х) = (х — а^) (X — р„) (X — a„_^i) (х — р„_0 =
^^{z-q^2){z-p){z-q){z~p^2).
Уравнения A8.2.5), являющиеся записью условия ортогональности
Q(o на [х„, Xj^-\-h] к 1 и х, заменятся в переменной z условиями
§ 2] РАСЧЕТНЫЕ ФОРМУЛЫ ЧАСТНОГО ВИДА 413
ортогональности Qco на [—1, 1] к 1 и -г
1
I (z — g + 2)(z~p)iz — g)(z — p — 2)dz:^0,
-1
1
J z(z~g-i^2){z~p)(z-g)(z — p — 2)dz^0
-1
или, после интегрирования и сокращений,
ip + g)[i + Y^pg + g-Р-2)] = о. J
A8.2.6)
Из второго уравнения находим два значения р:
7
Р\~ |_^ ' Р2 = -~д-
Числа р v^ д должны удовлетворять условиям —1 < р < ^ < 1. Для
/?! неравенство —1 < Рр как легко видеть, не может быть
выполнено и значение р^ должно быть, поэтому, отброшено.
Подставив p:=p^z:^ — q в первое из равенств A8.2.6), получим
уравнение для д\ Ъд^— 12^^-|- \^д^~\~Ад— 3.4 = 0. Так как jo = — q
и должно быть р Kg* то 7 > ^ и нужно найти корень уравнения,
лежащий на интервале (О, 1). Можно показать, что на таком
промежутке существует только один корень
^ ;^ 0,5333 2384 75.
Основными узлами на отрезке [х„, x^—h], следовательно, должны быть
o.n = x^ + ^.b{\—g)h = x^-{-h' 0,2333 3807 63.
р^ = х„ + 0'5 A + ^) /г = jc„ 4- Л • 0,7666 б 192 37.
Интерполируем / по ее значениям в узлах P„_i. а^, Р^. ^пл-v
f(r\ — i^~-^n){x — ^{x — an^i) ^,» . ,
Тогд
а
...+r(x) = P(x) + r(jc).
x„+h
Уп^1^Уп+ I fiOdt=^y^+ J P{t)dt + R^,
414 ВЫЧИСЛЕНИЕ НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА [ГЛ. 18
Вычисление интеграла от Р приводит к следующей расчетной
формуле
Л-м-У. + /г @.4869 0231 79 1/(а„) + /(М +
+ 0.0130976821 [/(p,^i)+/K+i)]}+^«- A8.2.7)
Для нахождения остатка можно воспользоваться его общим
представлением A8.1.9). Применительно к рассматриваемому случаю там
нужно положить т==2, А^-|-1=4,
QaJ ^(х — р,_,)(х~а„J (х — рJ2 (^ _ ^^^^^у
Несложные подсчеты дадут следующий результат:
^гг-- fSs^m ^'^^'' (^) = -0.0000 0305/z7^^* (D- (I8.2.8)
Положим теперь k==^2. К двум основным узлам на отрезке
[х„, x^-^-h] присоединяются по два в каждом соседнем отрезке
[х^ — h, х^] и [x^-^h, х„-|-2/г]. Схема узлов и их обозначения
указаны на рис. 9.
Наивысшая алгебраическая степень точности равна 7.
Узлы квадратурной формулы будут такими:
«« = -^/1 + ^*0.2389 6172 10, р„ = л:„ + /г.0,7610 3827 90.
Расчетная формула есть:
У.^1 = >'«+^ {0.4830 9244 04 [/(а„) + /(Р„) +
+ 0.0173 7142 26 [/(p,_0 + /(a« + i)l-
-0.0004 6386 30[/(а,_1) + /(Р«-мI}+^«. (i8.2.9)
Для остатка R верна оценка
|/?J< 0.0000 0008 hm^,
^8= max 1/^8) (д.) 1^ ««-1<-^<Рл+1-
X
Для всех приводимых ниже формул вычислялись узлы»
расположенные симметрично относительно середины отрезка [лг^. x^-\-h].
Отсутствие несимметрично расположенных узлов, дающих наивысшую
степень точности, не проверялось.
Положим ^ = 3. К двум узлам на отрезке [х^, x^j-h]
присоединяются по два узла в ближайших соседних отрезках [х^—Н, x^Jr
§ 2] РАСЧЕТНЫЕ ФОРМУЛЫ ЧАСТНОГО ВИДА 415
[д.^-|_-/г, x^^-{-2h] и по одному узлу в следующих соседних отрезках
[Х;, — 2/г, x,, — h] и [х,, + 2Л, лг^ + З/г].
Расположение узлов и их обозначения приведены на рис. 10.
" [ " " I " " I ~ п I ^
Рис. 10.
Наивысшая степень точности равна 9. Расчетная формула имеет вид:
у^^^ = у, -f /г {0,4825 9372 50 [/(а,) + / (рJ] ^
-1-0.0179 7222 21 [/(Р/г-1)Ч-/(а«+1)] — 0.0005 7826 47 X
X[/K-i) + /(P.-Hi)l + 0.0000 123177 [/(р,_2) + /(а,н-2I}+/?„.
A8.2.10)
Узлы ее суть
a„:^jc„ + yi. 0.2396 3009 31, Р;, = л:,, \~h^ 0,7603 6990 69.
Для остатка R^ справедлива оценка
|/?J< 0.00000000ЗЛ^Шю, М1о=-тах|/A0>(л:)|. Р„_2<х<а^+2-
Наконец, примем k^^\ и к двум основным узлам а„ и р„
присоединим еще восемь узлов, лежащих по четыре слева и справа от
[лГд, x^-\-h\ в двух парах соседних отрезков {х^ — 2/f, х^ — Л].
[x^ — h, xj и [x^ + h, x„^2h], [х^ + 2Л, x„-^3h] (см. рис. 11)
Рис. 11.
Наивысшая алгебраическая степень точности равна 11 и
квадратурная формула, для которой эта точность достигается, есть
У«+1 = >'«+А {0.4791 1316 68 [/(а„) + /(М +
+ 0.0215 3229 32 [/ (p„_i) -(-/ (а„+,I — 0,0013 6329 27 X
XI/(a„_,L-/(P„+i)H-0.00012360 65[/(p„_2) + /(a„+2)l-
-0,0000 0577 38 [/(а„_2) + /(р„^2I) +^«. A8.2.11)
I /?„ К 0,0000 0000 011/г'зЛ1,2,
Mi2 = макс|/<»2) (jc) |, а„_2 < х < Э„+2,
X
a^=jc^-f-^ • 0,2434 6008 65. ^п=^^пЛ h- 0.7565 3991 35.
416 ВЫЧИСЛЕНИЕ НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА [ГЛ. 18
III. В заключение приведем несколько квадратурных формул.
требуюш,их три значения функции / на каждый шаг вычислений.
Пусть на [х„, x^-j-h] (см. рис. 12) берутся три узла а„, р^. у^.
Предположим сначала, что к ним присоединяются по одному
ближайшему узлу на двух соседних отрезках [x,^ — h, х^] и [x^-^-h, x^-\-2h].
Гп-r -"^п А Гп ^^w
Рис. 12.
Наивысшая возможная степень точности равна 7 и соответствующая
квадратурная формула такова:
Уп^1=Уп+^ {0,4001 0365 66/ (р J4-0.2934 8934 9 i [/ (а,)+/ (y„)] +
+ 0.0064 5882 26 [/(Y,_i) + /(a,^i)]} + /?„, A8.2.12)
a^==:jc„-h Д. 0,1351 8355 61,
Р« = -^/г + ^* 0,5,
Y„ = A:^-f Л.0,8648 1644 39.
I /?J< 0,0000 0000 24Л9д^8' ^8 == maxl/^s) (д;) |^ ^^_^ < л: < a^+j.
Если в соседних с [л:^, х^ + h] отрезках [л:„ — h, л:„] и
[x^-^-hy x^'\-2h\ (см. рис.13) берется по два узла, то наивысшая
алгебраическая степень точности формулы равна 9.
Л-; r,.j , % А П %.j А.;
Рис. 13.
Расчетная формула имеет следующий вид:
У«+1 = 3'« + Л {0.3876 2754 18/(р„) + 0.2978 1275 62 X
X [/(««)+ /(Y„I +0.0084 8089 321/(Y„_,) + /(a„+i)]-
-0.0001 0742 03[/(Р„_,) + /(Р„ + ,)]}+/?„; A8.2.13)
а„ = х„ + /г-0,1414583289, р„ = х„ + А-0.5.
^,, = л:„ + А-0.85854167 И,
I /?„ К 0.0000 0000 ооогл^ш^.
§ 2J РАСЧЕТНЫЕ ФОРМУЛЫ ЧАСТНОГО ВИДА 417
Наконец, когда на отрезках [х„ — h, х,,] и [jc„-j-/z, x„-|-2A] (см.
рис. 14) взять по три узла, получится формула, приводимая ниже и
имеющая степень точности, равную 11.
, ^.-/ Л-; Л-; *. Л У. %., Л,; Г„,,
Рис. 14.
y„^j = у„ + Л {0,3813 4284 93/ (р„) + 0.2998 6684 13 X
X [/(aJ + /(Y«)l+0,0096 7804 71 (/(Y„_iL-/(a„,,)l-
- 0,0002 2289 47 [/(р„_,)+ /(р„^,)] +
+ 0,0000 0658 16 [/(a„_i) + /(Y„ + ,)]} +/?„; A8.2.14)
a« = -^„ + ^- 0.1446 9855 58, р„ = д:„-f-^ • 0,5,
у„=лг„ + Л-0,8553014442,
I /?„ К 0.0000 0000 0000 3^13^12.
Ali2 = niax|/<i2> (jc) |, а„_, <х <y„ + i.
X
Пример. Вычислялся эллиптический интеграл 1-го рода
X
V(X)==: г при ^2_-Q5.
Вычисления проводились по формуле A8.2.7) с шагом /j = 0,L
Формула содержит 4 узла и степень точности ее равна 5. На каждый
шаг /г = 0,1 вычисления требовали двух значений интегрируемой
функции.
Для сравнения интеграл был вычислен такжепоформуле(см. A7.1.5)):
, = У«+/^[
Л/ + Л-М 1 Д2/«-1+А2Л
я+1 —.VrtH^^L 2 12 2 ^
+ ^ • ^!Z--±^^l/^_ ...]... A8.2.15)
Здесь шаг был принят в два раза меньшим /z^0,05 с тем, чтобы
на каждый отрезок длины ОД приходилось бы также два значения/.
Было взято два варианта формулы A8.2.15)
1) с четырьмя узлами л:^-!' ^п^ -^rt+i» ^n-vi^
2) с шестью узлами х^^_2» >^п-\ ^п^ъ-
В первом случае формула A8.2.15) содержит столько же узлов,
что и A8.2.7). В последнем же случае, она имеет ту же
алгебраическую степень точности 5, как и A8.2.7). Точные значения интеграла
418
ВЫЧИСЛЕНИЕ НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА
[ГЛ, \ь
ВЗЯТЫ ИЗ известных 1аблиц Лежандра *). Погрешности найденных
значений напечатаны увеличенными в 10^^ раз
X
0,0
од
0,2
0,3
0,4
0,5
0,6
0,7
0.8
Тичное значение
У И
0,
01002 5119 46
0,2020 3892 48
0,3070 5493 05
0,4173 4515 97
0,5356 2273 28
0,6658 4782 54
0,8144 8928 40
0,9939 0712 63
Найденное по
формуле A8.2.7)
0,
0,1002 5119 47
0,2020 3892 51
0,3070 5493 12
0,4173 4516 12
0,5356 2273 70
0.6658 4783 90
0,8144 8934 76
0,9939 0739 32
Погрешность х Ю'^'
0
-1
—3
—7
-15
—42
~1 36
—6 36
—16 69
X
0,00
0,05
0,10
0,15
j 0,20
0,25
1 0,30
0,35
0,40
0,45
0,50
0,55
1 0,60
0,65
0,70
0,75
0,80
Значение, найденное
по формуле {18.2.15)
с 4 "узлами
0
0,0500 3121 82
0,1002 5105 23
0,1508 5266 47
0,2020 3860 18
0,2540 2625 15
0 3070 5432 81
0,3613 9094 30
0,4173 4405 30
0,4752 7550 59
0,5356 2057 49
0,5989 1615 32
0,6658 4306 44
0,7372 9250 74
0,8144 7623 23
0.8991 2206 67
0,9938 5271 13
Погрешность
X 10'^^ !
!
14 23
32 30
60 24
ПО 67
215 79
476 10
1305 17 1
5441 50
Значение, найденное
по фор.муле A8.2.15)
с 6 узлами
0
0,0500 3128 81
0,1002 5219 65
0,1508 5289 27
0,2020 3892 97
0,2540 2670 37
0,3070 5494 16
0,3613 9177 30
0,4173 4518 61
0,4752 7707 68
0,5356 2280 57
0,5989 1942 55
0,6658 4807 73
0.7373 5064 71
0,8144 9056 09
0,8992 0046 74
0,9939 2099 17
Погрешность
X W^
-19
-49
-1 11
-2 64
-7 29
-25 19
-127 69
-1386 54
*) А. М. Legend ге, Legendres Tafeln der elliptischen Normalintegrale
erster und zweiter Gattung, Stuttgart, U31.
ГЛАВА 19
МЕТОДЫ ВЫЧИСЛЕНИЯ, ИСПОЛЬЗУЮЩИЕ НЕСКОЛЬКО
ПРЕДШЕСТВУЮЩИХ ЗНАЧЕНИЙ ИНТЕГРАЛА
§ 1. Содержание задачи
В двух предыдущих главах были рассмотрены отдельные вопросы
теории методов численного неопределенного интегрирования, когда
для нахождения следующего значения интеграла используется только
'одно его предыдущее значение. Расчетные схемы, отвечающие таким
методам, всегда устойчивы относительно начальных ошибок и
ошибок округлений. Действительно, при естественном требовании, чтобы
вычисления были точными для /^0 и функции у (л:), сохраняющей
постоянное значение, расчетная формула должна иметь вид:
т
7 = 1
Она принадлежит к числу формул с положительными коэффищтен-
тами Ai и обладает устойчивостью обоих указанных типов, как это
было выяснено в конце главы 16.
Разработка методов расчета, которые для нахождения у^^^
используют не одно, а несколько предшествующих значений у^ (^ <С ^)'
является задачей более трудной, так как стремление достигнуть
наивысшую алгебраическую степень точности здесь не всегда может
быть совмещено с требованием устойчивости вычислительной схемы.
Ниже будет рассмотрен один из способов построения расчетных
формул, когда такое совмещение возможно.
Пусть для вычисления на отрезке х^-^х ^Х функции
X
принята произвольная сетка точек Xj^ik^^O, 1, ... N; ^k^^k + i)-
Допустим, что вычисления доведены до точки х,^ и последнее
найденное значение есть у(х^). При вычислении следующего значения
420 МЕТОДЫ ВЫЧИСЛЕНИЯ [ГЛ. 19
y{^n + i) можно воспользоваться любыми уже найденными значениями
y(^k)(^^^) ^ несколькими значениями y^~=f. Будем считать, что
производная у^ известна всюду на отрезке [Xq, X] и мы ничем не
стеснены в выборе узлов, где берутся значения /, кроме числа таких
значений.
Это есть задача интерполирования функции у в одной
фиксированной точке JC/j+i по нескольким значениям самой функции и
производной от нее У = /(л:). Из дальнейшего изложения будет ясно,
что в задаче полезно различать узлы трех перечисленных ниже
видов.
Пусть y(z) есть любая функция, определенная и
дифференцируемая на некотором отрезке [а, Ь]. Возьмем на [а, Ь] г-|-5 + /
различных точек
^1. ^2» • • •. 1г' ]
lr-,V lr + 2 ^г + .. A9.1.1)
Ьг+^+1' Ьг+5+2' •••' Ъг + s-hl- ^
Будем считать, что в первых г из них известны значения функции
y(z): y{^i) yibr)' ^ следующих 5 — как значения функции, так
и значения производной >'(|у). УЧ1]) (У ^^ г-|~ 1, . . ., r-\~s) и
в остальных / — значения только производной уЧ^-) (J"= г ~\-s-\-\, , , .
.... r + s + /).
Узлы, указанные в первой, второй и третьей строках таблицы
A9.1.1), станем называть соответственно простыми, двойными и
дополнительными. Предположим, что, кроме того, взята точка,
•^61^' ^]' отличная от всех простых и двойных узлов. Но мы не
исключаем заранее возможность ее совпадения с одним из
дополнительных узлов. Выберем произвольно r-f-5 чисел aj{j^=^ \, 2, , . .
. . ., г+ 5) и s-\~l чисел ру(у =-г-|~ 1, . . ., r-^s-\-l), значения
которых будут определены позже, и рассмотрим равенство
Если отбросить /?, получим приближенное равенство, могущее
служить для вычисления у{х):
y{x)^^ajyilj)-^ 2 Ру/^у). A9Л.З)
Степень точности его определяется как обычно: говорят, что A9.1.3)
имеет алгебраическую степень точности т, если оно выполняется
точно для всех степеней аргумента y(z)=^z^, от ^ = 0 до k=^ni, и
не верно для y=:zz^'^^. Выясним, какую наивысшую степень точности
может иметь A9.1.3) и каковы условия ее достижения. Верхняя
граница для т дается следующей простой теоремой.
§ 1] СОДЕРЖАНИЕ ЗАДАЧИ 421
Теорема 1. При любых а^, Ру и любом расположении точек
|. а jc степень точности т A9.1.3) всегда меньше г ~^2s^2l\
m<r^2s-\-2L
Доказательство. Достаточно показать, что всегда
существует многочлен степени не выше г-|~25-|-2/, для которого
равенство A9.1.3) не верно.
Допустим сначала, что ни один дополнительный узел не совпадает
с л: и рассмотрим многочлен
y{z) = {z-l{) . . . {z-l,){z-l,^,f .. . {z-lr^,^,f = A{z). A9.1.4)
Степень его равна г + 25-|~2/.
Непосредственно видно, что Л (|у) ^гг: О при J=\, ... r-]~s-{-l
и A^{lj)==^Q при J^r-\-\. Правая часть A9.1.3) для такой
функции у обращается в нуль. Левая же часть у(х)^А(х)фО ввиду
X Ф ij и равенство A9.1.3) не может быть верным.
Пусть теперь один из дополнительных узлов, например l^+s+p
совпадает с х. Введем многочлен В (z) степени г ~]-2s-\~2l — 2:
K^ — 'ir+s+ir
Когда В'{х)фО, положим
В(х)
у(г) = В(г)[г-х-4^].
Это есть многочлен степени г+ 25 4-2/—1. Правая часть A9.1.3)
для него, как нетрудно проверить, обращается в нуль. Левая же
часть у{х)=^ — В'^{х){В^(х))''^ Ф О и равенство A9.1.3) не
выполняется. В этом случае степень точности A9.1.3) меньше, чем г-|-
+ 25 + 2/—1.
Если В^{х)^0, то достаточно положить y{z) = B{z), чтобы
равенство A9.1.3) также не выполнялось. Здесь степень точности
A9.1.3) должна быть меньше г+ 25+ 2/ — 2.
Из теоремы следует, что степень точности т равенства A9.1.3)
самое большее может быть равна r + 25 + 2Z—1. Позже будет
установлено, что значение m = r + 25 + 2/—1 действительно может
быть достигнуто путем надлежащего выбора коэффициентов ау, Ру
и дополнительных узлов ^у(у>г + 5).
Из приведенного же выше доказательства теоремы видно, что
когда какой-либо дополнительный узел ^у (/>'' +5) совпадает с л:,
степень точности A9.1.3) обязательно меньше г + 25 + 2/—1 и
наверное не достигает своего наибольшего значения. Поэтому всюду
дальше будем считать все узлы ^у отличными от точки х.
422
ЛАЦТОДЫ ВЫЧИСЛЕНИЯ
[ГЛ. 19
§ 2. Условия, которые должны выполняться
при достиженпн наивысшей степени точности
Если потребовать, чтобы A9.1.3) было точным для степеней х^
при yfe = О, 1 г -\~2s-{~2l—1, получится следующая система
г-|-25-}-2/ уравнений
Г+5 T-VS \ I
2«-1^+ 2 f>jklY'=^x\k^O.\ r + 25-h2/~l).A9.2.1)
Система исследуется простыми средствами, если ее сравнить с
решением вспомогательной интерполяционной задачи.
Пусть в простых узлах даны значения функции
y(lj) и=и .... г). A9.2.2)
В двойных и во всех дополнительных узлах даны как значения
функции, так и значения производной
yilj)^ /ilj) (/ = /•+1 r + s^iy A9.2.3)
По всем этим величинам нужно интерполировать значение у
в точке X. Взяв произвольные числа а^. (У= 1 r-^-s-^l) и р^
(у = г4-1» •••» '' + 5 + 0' составим, подобно предыдущему,
приближенное равенство
r-^s-^-l
r^-s-hl
■1. Это даст систему
у(х)^ 2 «>(У+ 2 Р;У(У- A9.2.4)
Здесь можно распорядиться выбором r-f-25+2/ коэффициентов а'.,
Р'.. Потребуем, чтобы равенство A9.2.4) было точным для степеней
аргумента у^==^х^ от ^ =:=: О до ^ = r~f-25 + 2/-
г -\-2s-\-2l линейных уравнений для а^, р^.:
'if оАЦ+'i p'jkl'f' = x' (^-=0, 1, .... r + 25 + 2/~l).
A9.2.5)
Определитель системы, если коэффициенты при величинах а^.
поместить в первые г -}- s -\~ I столбцов и коэффициенты при р^. —
в следующие 5 + /, запишется так
^ =
л
2
1 .
^2 .
1^
Ь2 '
. . 1
•• Ьг+5+f
1^
0
1
2^..1 •
. . 0
. . 1
• ' "^^r-bs + l
I
[ A9.2.6)
§ 2J УСЛОВИЯ НАИВЫСШЕЙ СТЕПЕНИ ТОЧНОСТИ 423
Относительно него известно, что он отличен от нуля *), если только
li^ Ij (^' 7=1 л 4- 5 + ^; ^ ¥= Л- Последнее условие в
рассматриваемой задаче выполняется.
Ввиду этого система A9.2.5) имеет и при этом единственное
решение, каковы бы ни были точки |у, различные между собой.
Связь между системами A9.2.1) и A9.2.5) дается следующими двумя
легко проверяемыми утверждениями.
1. Пусть система A9.2.1) имеет, решение. Это решение
единственное а для значений неизвестных а^. и р^., удовлетворяющих
системе A9.2.5), верни равенства
р;--Ру и=г+1 Г+5+-/).
Действительно, предположим, что числа а^ (J^=zl, ..., г~\-$) и Ру
(у^г+1. ..., r~{-s-^l) образуют решение системы A9.2.1),
Присоединим к ним еще / чисел a^.^^^.i = 0, ... а^^^^^ = 0. Полученная
система r-{~2s-'{-2l чисел будет, как сразу же видно, удовлетворять
-системе A9.2.5) и поэтому должны, ввиду единственности решения
системы A9.2.5), выполняться равенства A9.2.6).
2. Если числа а^. и р' образуют решения системы A9.2.5) а
при этом выполнены условия
«;+..,==« «;,.+/=о- A9-2.7)
система A9.2.1) имеет реисение и верны равенства
^j = < и^ ^> ••- ^ + s), 1
[ A9,2.8)
Для доказательства достаточно заметить, что если выполнены
условия A9.2.7), уравнения A9.2.5) совпадут с A9.2.1).
Решение системы A9.2,5) легко строится при помощи известных
теорем теории интерполирования. Пусть у(х) есть многочлен
степени ^г ~{~2s~]~2l—1. Когда а', и р' удовлетворяют уравнениям
*) В этом можно просто убедиться, если взять определитель Вандер-
монда порядка г4-2s4-2/ от переменных |i, ..., 1^+23 + 21'-
r + 2s'] 21
i^Csi lr^2S-V2l)- П i^i-l])^ (*)
i > j
и j = \
вычислить от него смешанную производную по lj.^s^i+\ ёг + 2^ + 2/ и
положить затем |,-+^+/+i — Sr+i- -- •^lr^^s+2i^'ir-\-s^i^ После выполнения
всех операций получится Д. Но все указанные операции равносильны тому,
чтобы в произведении (^) вычеркнуть множители (^г+^-ь/+у — ?/-+;)
(у^1, ..., 5 +О- Оставшееся после этого новое произведение будет,
очевидно, отличным от нуля.
424
МЕТОДЫ ВЫЧИСЛЕНИЯ
[ГЛ. 19
A9.2.5), равенство A9.2.4) для у{х) должно выполняться точно.
Величина х может иметь в нем любое значение. Оно дает
интерполирование у(х) по значениям этого многочлена в точках |у (у ^ г +
+ 5 + 0 ^ ^^ значениям производной У в точках ^у (''+1^7^
^г + 5 + /). Это есть интерполирование с г простыми узлами ^у
(J^r) и 5 + / двойными узлами Ij (/■ < у <; г 4-5 + /).
Интерполяционный многочлен может быть представлен формулой Эрмита C.3.8),
которая в разбираемом случае будет иметь вид:
r-\-s^l
.'W=S
А{х)
;-1
(x-ij)A'aj)
y(ij)-\- и
А J (X)
r+s+l
Aj(x)
1-
-(x-lj)
haj)
Л- (S>)
y(lj)+
ix-lj)/{lj). A9.2.9)
Aj(x)=Aix}(x -Ij)-'.
Правые части A9.2.4) и A9.2.9) должны совпадать и, ввиду
произвола значений у(Е;) и у'(ЬХ коэффициенты а' и р' должны быть
равны соответствующим коэффициентам в A9.2.9). Условия A9.2.7)
разрешимости системы A9.2.1) запишутся поэтому так:
Ajiij) L
1
= 0 (y = r + 5+l,
/■+5 + 0.
или, после сокращения на Aj{x) (Ajdj))'
r+s+l r r+s
и деления на x-
l
h'-
:0. A9.2.10)
Ij ~lk ' ^ Ij" b ' ^ Ij — Ik
Знак ^ поставленный у первой суммы, означает, что в ней должно
быть пропущено слагаемое, отвечающее значению k^^j.
Изложенное в § 2 позволяет высказать следующую теорему:
Теорема 2. Для того чтобы равенстзо A9.1.3) имело
наивысшую алгебраическую степень точности г+ 2^ + 2/ — 1,
необходимо и достаточно выполнение условий:
l)l,j и X должны удовлетворять системе I уравнений A9.2.10),
2) коэффициенты а^ и Ру должны иметь значения
^ _ А{х)
(У-1.
г),
-J-AfM['-^'-^J^-^\0-=^+' . + .),! A9.2.11)
Aj{x)
^iljj)
(x-lj) (y = r+l.
Г + 5 + /).
§ 3] СУЩЕСТВОВАНИЕ И ЧИСЛО ИНТЕРПОЛИРОВАНИЙ 425
§ 3. Существование и число интерполирований
наивысшей степени точности
Исследование системы A9.2.10) можно выполнить вполне
наглядным путем, если воспользоваться некоторой электростатической
аналогией *). В комплексной плоскости возьмем две точки z^ и ^2
и поместим в них электрические заряды масс е^ и ^2- Будем считать,
что они действуют друг на друга с силой, обычной для плоского
электрического поля, когда численное значение силы обратно
пропорционально первой степени расстояния и пропорционально массам
зарядов.
Считая коэффициент пропорциональности равным единице, для
силы, с которой заряд в Zi действует на заряд в ^2, получим
значение
Предположим теперь, что в плоскости взяты г--!-5-|-1 точек
X, li, . . ., Ir+s- ^ точки X, li ^^, помещены заряды единичной
массы, а в точки Ir + i' • • •• ir+s — заряды массы два и все эти точки
закреплены. Наряду с ними рассмотрим / свободных зарядов массы 2,
Комплексные координаты их назовем ^^+5+i' •••• Ir+s+f
В состоянии равновесия системы равнодействующие всех сил,
приложенных к каждому из свободных зарядов, должны равняться
нулю
r+s+l г r+s
S' 2-2 1 V ^-^ V 2-2 , 2-1
k-
77s+i^^^^' ."Ti^J-^^^ ktf^i^j-^^ h'~
:0.
Если здесь сократить на 2 и перейти к комплексным
сопряженным величинам, получатся равенства A9.2.10), являющиеся условиями
того, что A9.1.3) имеет наивысшую степень точности.
Указанная аналогия делает очевидными нижеследующие
утверждения**) о системе A9.2.10).
1. Если л:, Ij, .,., Ь,f..^.^ суть любые комплексные числа и если
^;.^.5+1. •••. Ir+s+i' удовлетворяют системе A9.2.10), то точки
If+ 5+1' ■•■• ir+s-^i ^^^>*<ST в наименьшем выпуклом многоугольнике,
содержащем х, ^j, .... |^4-5- ^ частности, когда х, |i, ... lr-\-s ^У^^
*) Сходная аналогия указана в § 4 гл. 13 для корней многочлена
Якоби.
**) Они могут быть доказаны арифметическим путем, подобно тому, как
это было сделано Т. Стилтьесом в аналогичном случае при рассмотрении им
задачи о существовании решения дифференциального уравнения в форме
многочлена (Собр. сочинений Groningen, v. 1, 1914, p. 434 — 439). О связи
изучаемой интерполяционной задачи с дифференциальными уравнениями
будет сказано в § 6.
426 МЕТОДЫ ВЫЧИСЛЕНИЯ [ГЛ. 19
действительные числа, точки ^^^^^.1, ..., Ir^si-t лежат внутри
наименьшего отрезка, содержащего х и Ij (J=l, ..., г^s).
2. Пусть X, ^1, . . ., %^s действительны и различны. На числовой
оси между соответствующими точками будет r-f-^ промежутков.
Предположим, что заранее указан закон распределений
дополнительных узлов по этим промежуткам, т. е. указано сколько
дополнительных узлов должно находиться в каждом промежутке. Число спо-
собов распределения легко подсчитывается и равно ' ' —^ .
Существует решение системы A9.2.10), для которого
дополнительные узлы имеют заранее предписанный закон распределения между
3. Условимся отождествлять решения A9.2.10), получающиеся
друг из друга перестановкой l^r+s^-b — •» ^r+j+/* Тогда для каждого
закона распределения дополнительных узлов по промежуткам между
X, ^1, .... 1;.+^ система A9.2.10) будет иметь только одно решение.
Результаты, полученные в последних двух параграфах, позволяют
высказать об интерполяционном равенстве A9.1.3) формулируемую
ниже теорему,
Теорема 3. Каковы бы ни били наперед заданные х, |j, .. ., l^^^s^
действительные и различные между собой, дополнительные узлы
Ir^s-^v --^ Ir^-s^-i всегда можно выбрать \^^^^JZ\y,' ^^осо-
бами так, чтобы равенство A9.1.3) имело наивысшую
алгебраическую степень точности m=^r~^2s^2l — 1. При этом, если
заранее указать, сколько из общего числа I дополнительных
узлов должно принадлежать каждому из промежутков между
^> ^1' • • • IrA^s* ^^ среди возможных способов выбора
вспомогательных узлов всегда существует один и только один способ,
для которого эти узлы имеют предписанное распределение.
§ 4, Остаток интерполирования и минимизация его оценки
Рассмотрим остаток интерполяционной формулы A9.1.3);
R^y)^y(x)^^ajy{lj)^ V р,у^(|.). A9.4.1)
Допустим, что для нее выполняются уравнения A9.2.10) и она имеет
наивысшую степень точности r-\-2s-{-2l—1. При этом
предположении интерполирование A9.1.3) совпадает с вспомогательным
интерполированием A9.2.4), имеющим ту же степень точности r-]-2s-{'
+ 2/—1 и рассмотренным в § 2. Последнее имеет г простых
узлов Ij (J = I, . . ,, г) и s-\-l двойных узлов Ij (j^r-\-\, ...
.... г+ 5-]-/). Его остаток, если считать, что функция у имеет на
§ 4] ОСТАТОК ИНТЕРПОЛИРОВАНИЯ 427
отрезке [а, д] непрерывную производную порядка г -\-2s~\-2I,
может быть найден при помощи теоремы, приведенной в конце главы 3,
и имеет значение
^(^^)-(,+1i + 2/)!>^^''''^^'^^^)■ ^et^* ^Ь A9.4.2)
А(х)^(х~1,) . . , (х~У(х-!,,,)' ,. . (x~l,,^,^,f. A9.4.3)
Он будет совпадать с остатком A9.4.1).
В классе функций, определенном неравенством | f(^+'^^+^i)(^z) \ ^ М,
Z^lci, Ь], для остатка R(y) имеет место точная оценка
\R(v)\^ L1WJ . у1^ ('19 4 4^
Наивысшая степень точности г-\-2s-\~2l—1 может быть
достигнута не одним, а многими, вообще говоря, способами и число их
равно (г~-|~5 + /—1)! [/!(г-|~5—1)!]~ . Произвол в выборе одного
из таких способов может быть использован для уменьшения остатка.
В оценке A9.4.4) от выбора узлов зависит только множитель
|Л(х)| и можно стремиться к тому, чтобы придать ему возможно
малое значение.
Для задачи вычисления неопределенного интеграла, в том виде
как она была сформулирована в начале § 1, точкой
интерполирования X был табличный узел х^_^^. Простые и двойные узлы |у
(У=^ 1, . . ,, /" + 5) должны быть выбраны из числа табличных узлов,
предшествующих х^^^: х^(к^п).
Для дополнительных узлов ^у(у>/*~|-5) необходимо указать
закон их распределения по промежуткам между л:„ + | и |у (У ^ г-j-5).
Допустим, для определенности, что дополнительные узлы
перенумерованы в порядке роста координат.
Если воспользоваться электростатической аналогией, указанной
в § 3, решению задачи о минимуме |Л(х)| можно придать вполне
наглядную форму. Это обстоятельство позволяет не проводить
строгого арифметического доказательства результата и ограничиться
только кратким описанием наглядной стороны задачи.
Допустим на некоторое время, что простые и двойные узлы как-
то избраны, закреплены и можно распорядиться только распредёле-
>нием дополнительных узлов. Рассмотрим множители
-^л + 1 Ir + s+l* •••' -^nil —Ir-^s+l* A9.4.5)
отвечающие им в разложении A(x^^i).
Они имеют смысл расстояний от свободных зарядов, находящихся
в точках ^у(У>/*Ч"^) ДО заряда в точке х^^_^1. Все они достигнут
наименьшего значения в том положении равновесия, когда свободные
заряды будут помещены в промежуток, прилежащий к х^^.^. Это
428 МЕТОДЫ ВЫЧИСЛЕНИЯ 1ГЛ. 19
верно при любом положении закрепленных зарядов ^уСУ^^ + Ю
слева от х,^^^
Будем считать, что все свободные заряды находятся в указанном
промежутке и займемся выбором положений закрепленных зарядов.
Для уменьшения соответствуюш,их им множителей
^п + 1'
•|l, ..., -^fl + l ьг' i^n + l Ьгч-l) • •••» (^л + 1 br + s)
в Л(х^^^|), также как и для дальнейшего возможного уменьшения
множителей A9.4.5), выгодно, очевидно, закрепленные заряды 1-
и^^~\~^) разместить так, чтобы электрические массы
расположились бы возможно ближе к x„^i: двойные заряды |^.(у =1:= г-|-1, ...
.... r-\~S) нужно поместить в 5 табличных узлов Х^^, ^n~l' • • • » -^л-^+р
ближайших к л:„+1, и единичные заряды — в следующие за ними
ближайшие узлы х^_^, ..., Х/^_^_^^.;^.
Изложенные простые соображения приводят к формулируемому
ниже правилу выбора узлов, которое принято для всех частных
случаев в § 7.
Оценка остатка A9.4.4) достигает своего наименьшего
значения, если:
1) дополнительные узлы помещены внутрь отрезка [х^, ^^n-ы]^
2) двойные узлы взяты в точках х^, ^л-i' •■•» ^n-s+i*
3) за простые узлы приняты х^_^, ..,, x^_^_j.j^i.
§ 5. Условия положительности коэффициентов aj
В теории неопределенного интегрирования интерполяционные
формулы A9.1.3) с положительными коэффициентами а^ играют, ввиду
устойчивости соответствз^ющих им вычислительных схем, особенно
важную роль. Выясним, при каких условиях можно достигнуть
положительности коэффициентов а^ для формул, имеюш,их наивысшую
алгебраическую степень точности.
Пусть |;A<;У<^г) есть один из простых узлов. Рассмотрим
соответствующий ему коэффициент ау (см. A9.2.11)):
Мы должны считать х^х^^,^. Узлы ^^^(^=1, .... r-}-s-{-!)
предполагаются расположенными так, как это указано в конце
предыдущего параграфа. Ввиду того, что Л(х„+1) и х^^^ — |у
положительны, знак tty совпадает со знаком A\lj):
A\ij)={ij~i,)... aj-ij-i)(ij-ij^i)... (ij~ir)a—ir+if- * •
§ Б] УСЛОВИЯ ПОЛОЖИТЕЛЬНОСТИ КОЭФФИЦИЕНТОВ fij 429
Отсюда видно, что значения А^ (Ij), отвечающие двум соседним
простым узлам, будут иметь противоположные знаки.
Стремясь сделать все коэффициенты положительными, мы должны
поэтому полагать либо г ^ О и не брать ни одного простого узла,
либо г=1 и взять лишь один простой узел.
Возьмем теперь двойной узел ьу (/" < У <;/" +5). Отвечающий
ему коэффициент а^-, если в A9.2.11) положить л:г=х„ + 1. будет
таким:
"^ Ajlij)
Так как ^^ лежат левее x„^.i, а простые узлы ^i,(k^r)
расположены левее всех двойных узлов, множитель, стоящий перед прямой
скобкой, всегда отрицателен. Условием неотрицательности а- будет
неравенство
A9.5.1)
Oho имеет простой физический смысл. Возвратимся к
электростатической аналогии условий достижения наивысшей степени точности
и рассмотрим систему электрических зарядов, о которых говорилось
в третьем параграфе. В точке |у расположена масса 2 и величина,
стоящая слева в A9.5.1), есть половина численного значения
равнодействующей всех сил отталкиваний, которое испытывает этот заряд
со стороны прочих зярядов системы.
Неравенство A9.5,1) означает, что такая равнодействующая может
быть направлена только в отрицательную сторону по числовой оси.
Точка л:/^4-1 и все дополнительные узлы лежат всегда справа
от ^у и заряды, в них расположенные, будут отталкивать заряд в \j
налево по оси. Отсюда с очевидностью вытекает утверждение,
дающее ответ на вопрос о возможности сделать все коэффициенты а^-
для двойных узлов неотрицательными.
Каковы бы ни были г и 5, существует такое /q, что при всяких
I^Iq все коэффициенты а^- (у =^ г-f-1 '^ + '^) будут не меньше
нуля.
Предположим, что значения функции у{х) вычисляются на сетке
равноотстоящих точек Xy^ = XQ-f-M (^ = 0, 1. . . ,). Пусть,
например, взят один двойной узел E=1) в точке l^^^^n и .один простой
узел (/-=1) в точке ii=-^n-v Коэффициент а^ отвечающий
простому узлу заведомо положителен. Условие положительности а2
1
430 МЕТОДЫ ВЫЧИСЛЕНИЯ [ГЛ. 19
запишется в форме неравенства
2+1 2+1
Оно выполняется при />-!, так как все ^у > х^^.
Допустим теперь, что простых узлов нет (л = 0) и взяты два
двойных узла {s-=2) в точках х^^ и x^_j. Условия положительности
коэффициентов а^ и аз будут такими:
\ + 2 +У ^_=.
7=3
2+г
/=з
2 + 1 2-^1
+^;;^;7:7 + 2j xn~ij ""~7г+т + 2^^^-^^ <^'
>=з у=з
x,<lj<x,~^h (у^З 24-о*
Они также выполняются при всяких />-!.
§ 6, Связь с задачей решения дифференциального уравнения
при помощи многочлена
Покажем, что уравнения A9.2.10) равносильны условию существования
у некоторого дифференциального уравнения решения в форме многочлена
степени /.
Напомним, что A9.2.10) получено после сокращения из
предшествующего ему равенства и может быть записано в форме
или, если подставить сюда вместо Aj (z) его значение Aj (г) = А (z)(z — 5;)~^'
Сейчас нам удобнее воспользоваться другими обозначениями. Введем
многочлены o{z) и Tii(z), отвечающие двойным и дополнительным узлам:
0{z)^(z — lr+x) ••' i^ — lr + s)' Щ(^) = (^ — Ir^ Si i) • ^ ^ (^ —Ir+s + l)-
В ближайших рассуждениях х по своей роли ничем не будет отличаться от
простых узлов li If. Объединим х с ними и положим
p(z)^(z-x){z^l,)..,{z^l,y (z~~x)A(z)^p(z)o'(z)li'^{z);
§ 6] РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ 431
A9.6.1) примет форму
или, после несложных вычислений.
Значения z = gy (у > /* + 5) являются простыми корнями И; (z), поэтому
П/ (gy) ф о н должно быть
Ч
Это говорит о том, что каждый корень П;(г) является одновременно
корнем (^paV^y. Ввиду простоты корней П^ (г), (/7а^П;У должен нацело
делиться на П; (z).
Кроме того» (/?а^П[)' делится на а (z) и так как корни а (z) отличны от
корней П^ (г), то (/?а^П^У нацело делится на произведение аП/. Степень
(р0^П/У равна r~{'2s-\-l — 1. После деления его на 011/ получится
многочлен степени г+ 5 — 1. Обозначим его р (.г):
\р (г) а^ (г) П; {г)]' = 9 {г) а (г) П, (г). A9.6.3)
Последнее равенство можно рассматривать как дифференциальное
уравнение второго порядка относительно П;(г) и можно высказать утверждение:
Если выполняются условия A9.2.10), то существует такой
многочлен р (г) степени r-j-s — 1, что П/(г) будет решением
дифференциального уравнения A9.6.3).
Доказательство обратного утверждения потребует нескольких
предварительных замечаний об аналитических свойствах решений уравнения A9.6.3).
Если в A9.6.3) выполнить дифференцирование и обе части разделить на ра^,
то оно примет форму
Особые точки уравнения суть х, g| J;.+jf, оо. Все они регулярные *).
Рассмотрим любую из точек х или \f^.
Алгебраическое уравнение, которое обычно называют определяющим и
от корней которого зависит аналитическое строение канонических решений
в окрестности этой точки, для нее будет либо а (а—1)-|-а^а2 = 0, либо
а (а—1)+ 2а — а (а-|-1) = 0. Оно имеет либо двукратный корень а = О,
либо корни а^О и а = — 1. В обоих случаях одно из канонических
*) См., например, В. И. Смирнов, Курс высшей математики, М. — Л.,
Гостехиздат. 3. ч. П. п^ 98. 1949.
432 МЕТОДЫ ВЫЧИСЛЕНИЯ [ГЛ. 19
решений будет голоморфным в особой точке и отличным там от нуля, второе
же решение — неограниченным в окрестности этой точки.
Будем теперь р (z) считать таким, что уравнение A9.6.3) имеет решение
в виде целого многочлена степени /. Для всех особых точек х и Ij оно
будет голоморфным каноническим решением и поэтому будет заведомо
отличным от нуля в каждой из них. Корни П/ (г) отличны от jc и gjf,, но тогда
они простые, так как вне особых точек решение A9.6.4) не может иметь
кратных корней. Обозначим их l^^^^i. ..., |^д._у4-/.
Положим в A9.6.4) Z равным какому-либо из этих корней Ij. При этом
последний член с П/(г) исчезнет. Если, кроме того, обе части разделить
на П^ (J •), то получится равенство
1 *--! 9 t
= 0
(y = /- + s+l.
..., r + s + l).
1
- X
Oho только формой записи отличается от A9.2.10). Отсюда вытекает
справедливость утверждения:
Если р (г) таково, что уравнение A9.6.3) имеет решение в виде
многочлена степени I, то корни этого многочлена g^+^+i Ir+s+t
удовлетворяют системе уравнений A9.2.10).
Таким образом нахождение узлов, при которых интерполирование A9.1.3)
имеет наивысшую алгебраическую степень точности, равносильно
разысканию решения дифференциального уравнения A9.6.3) в виде многочлена
степени / и определению его корней.
§ 7. Формулы частного вида*)
Каждая частная формула наивысшей степени точности
определяется тремя параметрами г, s, L В этом параграфе будут
приведены такие формулы для нескольких первых значений г, s, I.
Коэффициенты расчетных формул вычислялись при помощи равенств
A9.2.11), для нахождения узлов было использовано
дифференциальное уравнение**) A9.6.3). Сетка точек х„ предполагается
равноотстоящей с шагом /г.
1. г=1, 5 = 0. Здесь берется одно значение функции у(х)
в точке x,j и / значений производной в дополнительных узлах между
^п " -^n+i' Последние выбираются так, чтобы расчетная формула
имела наивысшую степень точности. Результат равносилен
представлению y(x,j + i) через yixj в виде
yiXn+i) = y(x„)+ J f(t)dt A9.7.1)
*) Значение коэффициентов и узлов были вычислены К. Е. Черниным.
Контроль, которому подвергались все результаты, позволяет думать, что
погрешность не превышает единицы последней значащей цифры.
**) Труды Математического института АН СССР 3S A951). В. И.
Крылов, Интерполирование наивысшего порядка точности в задаче
неопределенного интегрирования.
§ 7] ФОРМУЛЫ ЧАСТНОГО ВИДА 433
и последующему вычислению интеграла посредством квадратурной
формулы Гаусса
yn^i = yn + h[BJ{x, + ht^'^)+ -... +BJix,^ht^'^)l
где В^ и t^^^—коэффициенты и узлы Гаусса для отрезка [О, 1].
2. г==:0. 5=1. Берется одно значение функции у{х) и одно
значение производной y^{x)^^f{x) в точке х^. Кроме того, взяты
значения производной в / дополнительных узлах между х^ и х^^^.
Наивысшая степень точности равна 2/-]-1. Расчетная формула
получится, если в равенстве A9.7.1) применить к интегралу
квадратурную формулу А. А. Маркова с одним фиксированным узлом в точке
д:^ и / узлами внутри отрезка интегрирования.
Значения узлов и коэффициентов при /=^1, 2, .... 6 для
канонического отрезка интегрирования [—1, +1] приведены в § 2 гл. 9.
3. /-=1, 5=^1. Для вычислений берется значение функции у
в точке х„_1, затем значение функции у и производной у^ ^^ f
в точке х^ н I значений производной в дополнительных узлах между
х„ и х^^-^. Наивысшая степень точности равна 2/-|-2;
Уп+1 = ^~1Уп-1 + АУп + ^
BofiXn)^IiBjf(x,^ht<^'^)
/-1
-/?.
Для остатка R может быть получено следующее представление:
^ — ^ B/4-3)! L (^1+\)\ \ ^ ^^^' ^<"<^' -^л"! < S<-^n + i-
При /=1, 2, 3, 4 узлы и коэффициенты имеют значения
/=1
^,==2-^-^ = 0,7071 068
^^^^ == 0,3879 073
^^2)^ 0.8593 118
^^^>= 0,2312 666
t^^^ = 0,6124 982
^^^>-0,9177 954
/1„1 =0,0294 3725
Ло - 0,9705 6275
/ = 2
Л_1= 0.0011 13587
Ло = 0,9988 86413
/ = 3
Л^1== 0,0000 4136 036
Ло = 0,9999 5863 964
^0=-0.3431 458
В^ =0,6862 915
Ло = 0,1334 818
^1= 0,5221 058
В^ = 0.3455 260
В^ = 0,0709 5688
^1 = 0,3458 379
В. = 0,3776 724
^3 = 0,2055 739
434
МЕТОДЫ ВЫЧИСЛЕНИЯ
[ГЛ. 19
А2)
/-=4
Л_,=:= 0,0000 0147 9556
Ао - 0,9999 9852 0444
: 0,1507 625
: 0,4352 756
Р^ =. 0,7366 581
t^"^^ = 0,9462 337
Bi= 0,2361 168
В, = 0,3128 314
Вз = 0,2713 300
В, == 0.1356 498
4. г==:=0, 5 ==2. В точках х^^^^, х^^ взяты значения функции и
производной и, кроме того, в / дополнительных узлах внутри
[л:^, л^л + i] берутся значения производной. Формула имеет вид
I
+ h
B^xf{x,^,)^BJ{x,)^^Bjf{x,^~ht^^^)
+ /?■
Наивысшая степень точности ее есть 2/ + 3. Остаток R представим
в форме
« = «*"*'■ WW[^^Г/"*"E). о<9<1.
Узлы И коэффициенты для /=1, 2, 3. 4 приведены в таблице
t^^^ ^ 0,7403 1242
1^\
>1_1--0,1625 0915
Ао = 0,8374 9085
5_,=-0,0445 3258 4
Во-.0,4921 8941
Bi ^ 0,6257 8716
t^^^ =- 0,4207 573
^B) _ 0,8717 520
tB)..
^0,2515 111
■• 0.6333 509
: 0.9235 139
^<^^ =0,1627 293
^^2) ^ 0.4540 978
^C) ^ 0,7493 776
t^^^ -= 0.9492 874
Л„ 1^0,0077 6632 6
Ао - 0,9922 3367
1 = 3
Л_1 =0,0003 6262 95
Ао = 0,9996 3737 05
/ = 4
Л_, -.0.0000 1576 632
Ло = 0,9999 8423 368
5„, =0,0015 6068 9
Во-:. 0,1640 716
В, ^ 0,5242 954
В^ ^ 0,3178 386
В _ I =. 0.0000 5699 653
Во = 0.0814 3433
В; =0,3609 307
Вз = 0,3658 920
Вз=х 0,1920 487
В _ i = 0.0000 0203 0488
Во - 0.0488 5024
Bi -=0,2491 361
82 = 0,3124 621
83 - 0,2613 448
В, = 0,1282 206
ЧАСТЬ ЧЕТВЕРТАЯ
ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ КРАТНЫХ
ИНТЕГРАЛОВ
ГЛАВА 20
О МЕТОДАХ ВЫЧИСЛЕНИЯ, ОСНОВАННЫХ НА ПРИВЕДЕНИИ
МНОГОКРАТНОГО ИНТЕГРАЛА К ОДНОКРАТНЫМ
§ 1. Предварительные замечания
о «проблеме большого числа узлов»
Пусть Е^ есть т-мерное числовое пространство, точки которого
мы обозначим х ^=^ x{xi, х^, . . ,, х^), и со — некоторая область в нем.
Предположим, что в со задана функция f (х) = f {х^, Хз Хщ) и
рассматривается интеграл
О)
Выберем в со л точек x^ .... х'^ и возьмем п чисел А^, .... А^.
Ниже будет рассматриваться следующее правило приближенного
вычисления / (/):
п
nf)=jf (X)fifo)« 2] ^//(^0. B0.1.1)
О) / = 1
которое определяется «узлами» х^ и весовыми коэффициентами Л^-.
При выборе х^ мы, очевидно, должны пытаться возможно более точно
решить две следующие задачи: 1. Расположить эти точки так, чтобы
множество их давало бы достаточно хорошее приближение к области
интегрирования со. Отметим попутно, что для решения такой задачи
целесообразно, по-видимому, расположить точки х^ более густо около
границы со и более редко внутри со. 2. Точки x^ должны быть
избраны так, чтобы по значениям f{x^) функции / во взятых узлах х^
можно было построить возможно точное приближение / того или
иного вида — алгебраическим многочленом от Xj, ..., х^„,
рациональной функцией избранной формы, тригонометрическим многочленом
и т. д. Необходимо обратить внимание на то, что здесь нужно
построить приближение ({)ункции нескольких аргументов х^, .... х^^,
436 ПРИВЕДЕНИЕ МНОГОКРАТНОГО ИНТЕГРАЛА К ОДНОКРАТНЫМ [ГЛ. 20
ЧТО значительно сложнее, чем приближение функций одного аргумента,
с которыми мы встречались в предыдущих частях книги. Для
достижения обоих указанных целей часто бывает необходимо взять
большое число узлов.
Наконец, веса Ai правила следует определить, исходя из условия,
чтобы равенство B0.1.1) для избранного способа приближения
выполнялось возможно более точно в каком-то смысле, принятом нами
для измерения точности.
Вероятно, можно считать ясным, что при заданной точности
результата потребуется тем большее число п узлов х\ чем выше
размерность т пространства. Скорость же роста числа узлов п в
зависимости от увеличения числа измерений т можно достаточно
отчетливо пояснить на частном примере. Пусть область интегрирования о
есть т-мерный единичный куб O^Xj^l (у=1, 2 т):
1 1
^ f{x)d(S)= J ... J/(Xi, ..., xjdx^ ... dx^,
(X) 0 0
Интегрирование по кубу в этой задаче естественно выполнить
путем интегрирования по каждой из переменных х^ л:,„. Выбор
правила интегрирования по координатам х^, . . ., л:^ определяется тем,
сколь гладкой будет зависимость / от соответствующей переменной.
Будем, для простоты, считать, что при интегрировании по всем
переменным нами принята одна и та же квадратурная формула с р узлами,
например, формула Гаусса:
Для применения этого правила потребуется найти f в р^ точках.
Число этих значений может быть велико, даже если р не будет
«большим», например, если мы берем правило Гаусса с 5 узлами,
то для интегрирования по трехмерному, четырехмерному и т. д. кубу
потребовалось бы знание / в 125, 625 и т. д. узлах.
Для вычисления кратных интегралов, в мере большей, чем для
простых, важна задача уменьшения числа узлов, необходимых для
получения требуемой точности результата. Для достижения этой цели
следует использовать весь произвол, находящийся в распоряжении
вычислителя: выбор системы координат, выбор правил квадратур,
применяемых при интегрировании по отдельным переменным;
вычислитель может воспользоваться геометрическими свойствами области со
и т. д.
Задача построения кубатурных формул с возможно малым числом
узлов будет изучаться в главе 22. В какой-то мере удовлетворительно
ее удается решить лишь в простейших случаях —для областей частного
§ 2] ВЫБОР ПРАВИЛ ИНТЕГРИРОВАНИЯ 437
вида или для небольшого числа узлов. Сложность задачи здесь зависит
от двух причин. Если для однократного интеграла практически важная
область интегрирования очень проста — ею является отрезок, то для
кратных интегралов область интегрирования может иметь сложную
форму, и этот факт сильно затрудняет проблему выбора узлов. Кроме
того, интерполирование и приближение функций многих аргументов
выполняется более сложно и менее исследовано, чем в случае одного
аргумента.
§ 2* Влияние формы области на выбор правил
интегрирования
В курсах анализа доказывается, что нахождение значения
/«-кратного интеграла B0.1.1) для областей о весьма общего вида может
быть приведено к последовательному вычислению т однократных
интегралов. Каждый из них может быть вычислен по какому-либо
из правил, рассмотренных во второй части книги. Выбор правила
должен быть, во-первых, согласован со свойствами интегрируемой
функции / и, во-вторых, учитывать геометрическую форму области
интегрирования о.
Наибольший интерес для нас будет иметь второй из этих двух
факторов — влияние формы области, и ему мы уделим главное
внимание в последующем изложении. Так как идеи, лежащие в основании
выбора, одинаковы для интегралов любой кратности, мы проследим
их на разборе нескольких примеров вычисления двойного интеграла.
Рассмотрим двойной интеграл в декартовых координатах:
1= { J /(^' y)dxdy. B0.2.1)
При некоторых предположениях об области о вычисление / можно
привести к нахождению двух однократных (простых) интегралов
b
/= J F{x)dx, B0.2.2)
а
^W= J /(^' y)dy. B0.2,3)
yi{x), У2{х)у а И д определяются в зависимости от области со и имеют
хорошо известные значения.
Выбор квадратурного правила для вычисления B0.2.3) зависит от
свойств / и, в частности, от ее особенностей. Желая сосредоточить
внимание на выяснении значения, какое будет иметь вид области (о,
мы предположим функцию / непрерывной всюду в со, достаточно
438 ПРИВЕДЕНИЕ МНОГОКРАТНОГО ИНТЕГРАЛА К ОДНОКРАТНЫМ [ГЛ. 2П
гладкой там и в остальном произвольной. В этих условиях для B0.2.3)
целесообразно избрать какое-либо правило интегрирования с
постоянной весовой функцией, например, правило Гаусса.
Что же касается интеграла B0.2.2). то он представляет больший
интерес. Можно предвидеть, что среди правил интегрирования
гауссово или другие правила, рассчитанные на постоянную весовую
функцию, не во всех случаях будут давать наилучший результат или
близкий к нему. Такие правила не будут учитывать влияние на F формы
области со.
Легко понять, что естественной весовой функцией будет
следующая: построим сечение области о) прямой линией, проходящей через
точку X параллельно оси ординат. Чем большую длину будет иметь
это сечение, тем большее влияние на образование численного
значения / будет иметь узкая полоска около этого сечения. Поэтому за
весовую функцию в B0.2.2) можно принять
р{х)^-у^{х)-~у,{х) B0.2.4)
и преобразовать интеграл к виду:
b
1=\[)!2{х)-Ух{х)]Ф{х)с1х, ф(^)==—^^^М-^. B0.2.5)
а
Вес B0,2.4), по-видимому, достаточно полно учитывает форму
области (О и для гладких функций / должен привести к хорошим
по точности результатам. Но столь полный учет влияния формы
области (О на выбор правила квадратур, вероятно, нецелесообразно
делать, так как тогда для каждой области интегрирования пришлось бы
брать свою весовую функцию. Задачу выбора веса р {х) можно
упростить и перейти от р {х) к подходяще выбранному каноническому
весу на основании следующих простых соображений. Для
определенности изложения будем говорить о правилах наивысшей степени
точности.
Рассмотрим произвольную весовую функцию р (х) и
соответствующее ей правило наивысшей алгебраической степени точности
b п
1,^1 p{x)f{x)dx^^Aj{x,). B0.2.6)
а k^l
Оно будет, вообще говоря, иметь тем меньшую погрешность, чем
более точное приближение многочленом степени 2п — 1 будет
допускать /.
Наряду с р{х) рассмотрим другую весовую функцию р(л:) такую.
чтобы отношение ^Y^\ = Я{х) было достаточно гладкой функцией,
нигде на [а, д] не обращающейся в нуль; p{x)=^g{x)q{x), Присое-
§ 2] ВЫБОР ПРАВИЛ ИНТЕГРИРОВАНИЯ 439
диним множитель q{x) к интегрируемой функции /: q (х) f (х) =^ F (х)
b
и рассмотрим интеграл [^ с весом р(л:): 1^= { д{х) F{x)dx,
а
Предположим, что для вычисления его применяем правило
наивысшей степени точности, соответствующее весу p(jc):
b п
1,= I p{x)F{x)dx^YL^,F{z,). B0.2.7)
Zf^ есть корни многочлена степени п из ортогональной системы,
принадлежащей весу р{х).
Если q{x) есть функция высокого порядка дифференцируемости
или аналитическая функция с особыми точками, лежащими далеко
от [а, Ь\, то можно ожидать, что функции f {х) и F {х) ^==^ q {х) f {х)
будут допускать приближения многочленами степени 2п—1, близкие
по точности. Поэтому можно надеяться на то, что формулы B0.2.6)
и B0.2.7), служащие для вычисления одного и того же интеграла /^,
будут иметь приблизительно одинаковые погрешности и мы мало
приобретем или потеряем в точности, если перейдем от веса р {х)
к весу р(л:).
Это позволяет при вычислении интеграла B0.2.2) переходить от
«естественной» весовой функции /? (л:) = уо (-^) — У\{-^) ^ другому
более простому весу р(х). Такой переход во многих случаях не будет
связан с значительной потерей точности, но позволит упростить
задачу вычисления, так как новый вес может быть взят одинаковым
для многих областей и для него заранее могут быть найдены узлы
и коэффициенты. Наиболее просто естественную весовую функцию
р^=^у^ — у^ приводить, если это возможно, к одному из классических
весов, для которых нужные таблицы составлены с большой полнотой.
Полезное значение здесь имеет вес Якоби р(,\:) = (^ — х)^(х — а},
зависящий от двух параметров а, р, выбор которых позволяет
охватить широкий класс областей со.
Пусть отрезок [а, д] — конечный и пусть можно показателям аир
придать такие значения, чтобы отношение
q(x)= >'^^^^)->''<-^)^ , а<х<^
(b~xf(x — af ^
было ограничено сверху и снизу положительными числами: 0<т^
^^W^^<c>o. В этом случае для вычисления интеграла B0.2.5)
можно воспользоваться весом р(л:)^(^ — х)^(х — а}:
b
/= J {x — af{b~xfWix)dx, 4^ix)^(x — a)-^'{b~xyF(x).
440 ПРИВЕДЕНИЕ МНОГОКРАТНОГО ИНТЕГРАЛА К ОДНОКРАТНЫМ [ГЛ. 20
Например, если область интегрирования имеет форму, изображенную
на рис. 15, причем контур области к имеет в точке А с прямой
х=^а соприкосновение первого порядка*), то можно считать а = 0,
р^0,5 и за весовую функцию принять
Интеграл
р(х) = Ух-
/ = J /л; — а ф (л:) fifx. ф (х) = (х~- а)"^'" F (х)
может быть вычислен при помощи формулы G.3.9).
Если область а имеет вид, изображенный на рис. 16, и
контур ее Я, с прямыми х=^а и х = Ь также имеет соприкосновение
■*-<z
^j:
Рис. 16.
первого порядка, то за весовую функцию можно принять
p{x)^Y{x~a){b — xy
К вычислению интеграла
ь
/= j У(х^а)ф~х)}р(X)dx. ф(х) = [{х~а)ф-^л:)]~^'^F{х)
а
может быть применено равенство G.3,11).
Рассмотрим еще пример выбора квадратурных правил. Пусть дан
двойной интеграл в полярной системе координат / = F{r, (p)rdr d(p
(О
и область (О определяется неравенствами: 0<!г ^/? ==/?(ф), а^ф<;р.
*) Если принять ординату у за независимую переменную, то уравнение
контура Я вблизи точки Л может быть записано в форме х = й^ + С2(У—УоУ~\~
+ Сз(у-Уо)'+ .... ^2^=0.
§ 21 ВЫБОР ПРАВИЛ ИНТЕГРИРОВАНИЯ 441
Вводя вспомогательную переменную р=:-^, можно вычисление /
привести к нахождению двух простых интегралов
/:=:= |ф(ф)/?2(ф)йГф. B0.2.8)
а
1
ф(ф)==: J/^[р/?(ф), ф]рй?р. B0.2.9)
о
Для вычисления B0.2.9) можно воспользоваться весовой функцией
якобиевого вида р = р.
В интеграле же B0.2.8), если считать Ф(ф) достаточно гладкой
функцией, естественным весом будет /7(ф) = ^2^ф^ Однако выбор
типа приближения зависит от величины угла р — а интегрирования.
Если р — а = 2л и интегрирование производится по полному плоскому
углу, Ф(ф) будет 2л-периодической функцией полярного угла ф. Для
вычисления B0.2.8) тогда естественно воспользоваться правилами
наивысшей тригонометрической точности. Если же р — а < 2л, то
к B0.2.8) можно применить правила, основанные на приближении Ф
алгебраическими многочленами от ф.
ГЛАВА 21
ИНТЕРПОЛЯЦИОННЫЕ КУБАТУРНЫЕ ФОРМУЛЫ
§ 1. Алгебраическое интерполирование функций
многих переменных
Многочлен Р^(х)^Р^^(х^, .... х^) степени т от п переменных
Xi, ..., лГ/г можно записать в виде
^.W = QoW + QiW+ ... +Q^W» B1.1.1)
где Qf^{x) — однородный многочлен степени k. Многочлен Q^ix;)
представляет собой линейную комбинацию с постоянными
коэффициентами одночленов степени k\
Подсчитаем число слагаемых в этой сумме, т. е. число одночленов
л: ... ху таких, что а^ > О, .... а^ >^ О и aj + ... -{- a^^=^k.
Рассмотрим произведение п рядов — геометрических прогрессий
со оо оо оо
2-<'-2 д:,"^..-2<'^=2 2 <-...XV B1.1.2)
Предполагаем, что | хJ < 1, Число одночленов степени k равно числу
слагаемых в правой части BLL2), удовлетворяющих условию
cti + ... -f а,^ = /г. Положим в равенстве B1.1.2) х-^ = Х2= ...
... x^X/j = ^. Получим
со \ л оо
2^4 -=2 г»;^'. B1.1,3)
Очевидно, коэффициент при t . обозначенный через l)f^, равен
числу слагаемых, удовлетворяюидих условию а^-|~ . . . ~j-а^ =:= ^.
Запишем B1,1.3) в виде
(i-o-"=i b/.
J-о
§ 1] ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ 443
Чтобы найти Ь^, напишем разложение функции A —ty"' в ряд по
степеням t, С этой целью вычислим {п—1)-ю производную от обеих
частей разложения A — 0~^ = 1+ ^Ч~^^+• • •» UI < 1- Получим
(„-l)!(l-0-"==(«-l)!-i-4^+---+-^T=^^'+---
Отсюда видно, что
Найдем еще число всех одночленов степени не выше т от п
переменных. Оно равно числу одночленов, фигурируюш^их в
представлении B1.1.1) многочлена степени т. Общий однородный многочлен
степени т от п~\-1 переменных Xj..., х^^ t можно записать в виде
rQ,^^r-'Q,+ . . . +^Q,„-z-f Q.. B1,1.5)
где Qf^ = Q^ W — однородный многочлен степени k от п переменных.
Ясно, что число слагаемых одночленов в B1.1.1) и B1.1.5) одинаково.
Но число слагаемых в B1,1.5) — это число одночленов т-й степени
от д+1 переменных, которое по B1.1.4) равно
Ж(«1.«)==^^±^. B1.1.6.)
Это и есть число одночленов степени не выше т от п переменных.
В дальнейшем через п всегда будем обозначать число переменных.
Условимся в случае п = 1 переменную Xj обозначать через х, в случае
п = 2 переменные Xj и Хз будем обозначать соответственно х и ^.
Из формулы B1.1.6) при п=1 получаем, что число одночленов
степени не выше т от одной переменной х равно М(т, l) = /n-|-l.
Этими одночленами являются 1, х, х^,. . ., х^.
При д = 2 формула B1.1,6) дает число одночленов степени не
выше т от двух переменных х и у, равное М(т, 2)=^0,5(w+ ОХ
Х(/^ + 2). Выпишем эти одночленьп
1,
X, у.
x^, ху, ' у'^,
х^-^у», x'^-^yl
В /-Й строке выписаны все одночлены степени /— 1. В последующем
будем пользоваться терминами «алгебраическая гиперповерхность»
И «алгебраическая кривая». Алгебраической гиперповерхностью
444 ИНТЕРПОЛЯЦИОННЫЕ КУБАТУРНЫЕ ФОРМУЛЫ [ГЛ. 21
порядка т]^ \ в д-мерном пространстве называют множество точек
x = {Xi л:„), удовлетворяющих уравнению
Q(x) = Q,
где Q (х) — многочлен степени т от п переменных. При л = 2
алгебраическую гиперповерхность называют алгебраической кривой.
Пусть левая часть уравнения Q{x)^=^0 алгебраической
гиперповерхности Sf^ порядка т разлагается в поле комплексных чисел
на неприводимые множители
Q(x)^Q,(x)Q^(x)...Q,(x) B1.1.7)
(степень каждого Qi(x) больше или равна единице). Алгебраические
гиперповерхности ^^(л:) = О (/= 1, 2 г) называются
компонентами гиперповерхности 5^. Е^иперповерхность S^ называется
неприводимой, если в разложении B1.1.7) г=1, и называется
приводимой, если /■> 1.
Будем пользоваться следующей теоремой.
Теорема 1. Алгебраическая гиперповерхность Q(a:) = 0
порядка q и гиперплоскость L{x)^^a^x^~\' . . . -\~а^х^^а=^^ или
пересекаются по алгебраической гиперповерхности порядка не
выше q в (п—\)-мерном пространстве, или гиперплоскость
L(x) = 0 является компонентой гиперповерхности Q{x)=^Q:
Q{x)=^ R(x) L(x), где R{x) — многочлен степени q—1.
Особо выделим формулировку теоремы 1 при п^=^2:
алгебраическая кривая порядка q и прямая или пересекаются не более,
чем в д точках, или прямая является компонентой
алгебраической кривой.
Теорема 1 является следствием теоремы Безу. Приведем
формулировку теоремы Безу для п=^2. Две алгебраические кривые
порядков q и г, не имеющие общих компонент, пересекаются
точно в qr точках (с учетом кратностей), В число точек
пересечения включаются и бесконечно удаленные точки пересечения.
Укажем, как построить М{т, 2) = 0.5(/n-f-OC'^H" 2) точек на
плоскости, не лежащих на алгебраической кривой порядка т. Берем
три точки Гр Гз, Гз, не лежащие на прямой. Проведем прямую L^^
не проходящую ни через одну из точек 7j, Т^, Т^, и выберем на ней
три точки Т^, Т^, Tq. Точки Т^ (/^=1. .... 6) не лежат на кривой
второго порядка Сз- В противном случае кривая Сд и прямая /,2
пересекались бы в трех точках, откуда по теореме 1 мы получили бы,
что Сз распадается на две прямые. Это невозможно, так как Г^, Тп,
Гз не лежат на прямой.
Проведем прямую L^, не проходящую ни через одну из точек Т^,...
..., Tq, и возьмем на ней четыре точки Гу, Гд, Тд, Т^^, Из
теоремы I следует, что десять точек Т^ T'jq не лежат на
алгебраической кривой третьего порядка Су Если бы Т^, .,., 7^ лежали
§ 1] ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ 445
на Сз, то Сз пересекалась бы с ^з в четырех точках. Отсюда по
теореме 1 следовало бы, что Сз распадается на прямую Z3 ^ ^Р^'
вую второго порядка. Но это исключено, так как Г^, ,.., Tq не
лежат на кривой второго порядка. Очевидно, что такое построение
можно выполнить для произвольного т.
Подобным же образом можно построить М(т, 3) =^ ; qi
точек в трехмерном пространстве, не лежащих на алгебраической
поверхности порядка т. Возьмем любую точку Т^ и проведем
плоскость Zj. не проходящую через 7j. На плоскости Li выберем три
точки Гз' ^3- ^4' ^^ лежащие на прямой. Ясно, что Tj, ..., Т^
не лежат в одной плоскости. Проведем плоскость Z,2, не проходящую
ни через одну из точек Т^ Г^р На плоскости Z,2 возьмем шесть
точек Т^, . . ., T^Q, не лежащих на кривой второго порядка. Точки
Т^, .... TjQ не лежат ни на какой поверхности So второго порядка.
В противном случае поверхность S2 и плоскость /.з пересекались бы
по кривой более, чем второго порядка. По теореме 1 ^2 распадается
на две плоскости, из которых одна есть ^2- Это невозможно, так
как Гр ... ,7^ не лежат в одной плоскости. Далее, проводим
плоскость Z,3» не содержащую ни одну из точек Т^ Г^^. На Аз
берем десять точек Гц, ..., Гзо» не лежащих на кривой третьего
порядка. Из теоремы 1 получаем, что Г^ .. ., Гзэ не лежат ни на какой
поверхности S^ третьего порядка и т. д.
Ясно, что указанные построения можно выполнить в пространстве
любого числа измерений п.
Рассмотрим теперь задачу о построении интерполяционного
многочлена от п переменных лгр ..., х^. Для простоты записи будем
считать /г-=2. Будем действовать по аналогии с тем, как строится
интерполяционный многочлен в одномерном случае (/-^=1). Возьмем
на плоскости /V точек — узлов интерполирования (х^, _у^). Требуется
построить многочлен Р^(х, у) степени т относительно л: и у,
который в узлах принимает заданные значения
Pmi^i^ yi) = fi (^*=Ь 2 л/). B1.1.8)
Запишем многочлен с неопределенными коэффициентами
Рт(^' У) = а, + а2Х + а^У']-а^х^-^ ... +a^i(m. 2)У'".
где М(т, 2) определяется формулой B1.1.6). Равенства B1.1.8)
приводят к линейной алгебраической системе относительно
неизвестных а^:
«1 + ^2-^,- + а,>^;+...+^жн,2)З^Г^Л- (^=^' 2, ..., N).
B1.1.9)
446
ИНТЕРПОЛЯЦИОННЫЕ КУБАТУРНЫЕ ФОРМУЛЫ
[ГЛ. 2)
1
1
1
X,
^2
•^ж
^\
У2
^М
х\ .
х1 .
^'м ■
■ УТ
■ У2
■■п
Естественно потребовать, чтобы число уравнений совпадало с числом
неизвестных. Это накладывает ограничение на число узлов Л^ =
= /И(т, 2)=^0,5(т+l)(//j-f 2).
Потребуем, чтобы определитель системы B1.1.9)
B1.1.10)
был отличен от нуля. Это условие обеспечивает существование и
единственность интерполяционного многочлена.
Определитель B1.1.10) равен нулю тогда и только тогда, когда
имеется линейная зависимость между его столбцами. Это, в свою
очередь, равносильно тому, что узлы (Х/. _у^) (/=^ 1, 2 М(т, 2))
лежат на некоторой алгебраической кривой порядка т. Следовательно,
определитель B1.1.10) отличен от нуля тогда и только тогда, когда
узлы не лежат ни на какой алгебраической кривой порядка т.
Укажем представление интерполяционного многочлена в форме,
аналогичной формуле Лагранжа. Мы должны указать многочлен
степени не выше т, который удовлетворяет условиям
РпЛ^1> yd^fi 0'=Ь 2_... М(т. 2)).
при этом узлы не лежат на алгебраической кривой порядка т.
Построим многочлен влияния узла (д:^, yf^), т. е. многочлен
степени т, который равен единице в узле (х^, yi^) и нулю во всех
остальных узлах. Такой многочлен существует, так как узлы не лежат
на алгебраической кривой порядка т. Запишем его с помощью
определителей.
Определитель
щ(Х, у) =
1
1
1
1
1
X
^1
•»^*-1
^*+1
^Л1
у
У1
У»-
• 1
У*и
Ум
Х2 .
х] .
Х2
Х2
.. У"
■ ■ УТ
■■ К-1
B1Л.11)
представляет собой многочлен степени т, который обращается в нуль
в узлах (лгу, 3'/) 0*= К 2, . . .. ^~ 1, ^+1, Ж(т, 2)). Так
как узлы не лежат на алгебраической кривой порядка т, то
<^b(Xk, Уь)ФО, Многочлен —,' -^К и есть требуемый многочлен
^^ * ^^^ <^k{Xk. У к) ^
§ 2] ИНТЕРПОЛЯЦИОННЫЕ КУБАТУРНЫЕ ФОРМУЛЫ 447
влияния узла {xj^, у^^). Интерполяционный многочлен Pf^ix, у)
записывается в виде
М{т, 2)
k = \
Отметим, что степень многочлена B1.1.11) равна точно т, в то же
время степень многочлена B1.1.12) может быть меньше т.
Задача интерполирозания для п переменных формулируется
следующим образом. Пусть задано М{т, п) ~ \^~т-^У- узлов л:@ ,==
= Ы*'\ .... хЩ, не лежащих ни на какой алгебраической
гиперповерхности порядка т. Построить многочлен Р„^{х) степени не выше т,
удовлетворяющий условиям
Prn{^^'^)=-fi a-i. 2 М(т. п)).
Как и в случае п^^2, такой многочлен сз^ществует и является
единственным.
Отметим, что в одномерном случае д=1 уравнение Q^(x) = 0
степени т определяет на вещественной прямой не более т точек.
Условие, что т -j- 1 узлоз не должны лежать на алгебраической
кривой порядка т, означает, что они должны быть различными.
Формулу B1.1,12) также можно записать для любого числа
переменных п. Эта общая формула справедлива и при /г = 1 и обращается
в этом случае в формулу Лагранжа.
§ 2, Интерполяционные кубатурные формулы
Пусть речь идет о вычислении интеграла по области Q в д-мер-
ном пространстве £"„
^p{x)f{x)dx. • B1,2.1)
где x = (Xi х,^), dx = dx^ ... dx^. Весовая функция р{х)
предполагается такой, что существуют моменты
Это предположение о весовой функции будем считать всегда
выполненным. Область интегрирования может быть и бесконечной.
Функция f{x) счи1ается такой, чго существует интеграл B1.2.1).
44В ИНТЕРПОЛЯЦИОННЫЕ КУБАТУРНЫЕ ФОРМУЛЫ [ТЛ. 21
Кубатурная формула для вычисления интеграла BL2.1) имеет вид
N
j p{x)f{x)dx^^Cjfix(^^y B1.2.3)
Сумма в правой части равенства B1.2.3) называется кубатурной
суммой, точки л:(»==:(^л:0) х^^У^ называются узлами кубатур-
ной формулы и числа С- — коэффициентами. Узлы могут не
принадлежать области интегрирования Q.
Один из способов получения кубатурных формул B1.2.3) связан
с интерполированием. Считая п^=2, возьмем N ===: 0,5{т + 1)(т + 2)
точек {Xi, У1) {i=^\, ..., N), не лежащих на алгебраической
кривой порядка т. Интерполяционный многочлен функции /(х. у),
подстроенный по условиям
Pmi^i^ yi)=-f(^i> Уд а-1. 2. ..., N),
запишем по формуле B1.1.12)
п / \ \^ <^i(x, V) J, ^
Чтобы вычислить приближенное значение интеграла
J \ Р{^^ у) fix, y)dxdy,
заменим /(х, у) многочленом Pmi^* У) ^ вычислим интеграл от
р{х, y)Pjji{x, у). Получим приближенное равенство
J J Р(-^. у) fix, y)dxdy^y^Cjf(xj, yj), B1,2.4)
где
C,-J Jp(x, y)^^^^;^dx^y. B1.2.5)
Будем говорить, что кубатурная формула вида B1.2.4) —
интерполяционная, если ее /V = 0.5(m+1)(т+ 2) узлов не лежат на
алгебраической кривой порядка /тг и ее коэффициенты определяются
формулой B1.2.5).
Как и в случае /г=1, доказывается
Теорема 2. Для того чтобы кубатурная формула B1.2.4)
с yV = 0,5(w+OC'^H-^) узлами, не лежаш,ими на
алгебраической кривой порядка т, была интерполяционной, необходимо
и
§ 2] ИНТЕРПОЛЯЦИОННЫЕ КУБАТУРНЫЕ ФОРМУЛЫ 449
и достаточно, чтобы она обращалась в точное равенство, когда
/(х, у) — любой многочлен степени т.
Если кубатурная формула точна для многочленов степени т и
имеет Л^ = 0,5(/7i-|-l)(m-j-2) узлов, которым отвечают ненулевые
коэффициенты, то отсюда не следует, что узлы не лежат на
алгебраической кривой порядка т. Приведем следующий пример. Пусть
Й — квадрат —l^JC, Д^^^!- Рассмотрим кубатурную формулу
6
/(X, y)dxdy^^^ fit,, t^\ B1.2,6)
Й ' i, j = \
где ti — узлы квадратурной формулы Чебышёва с шестью узлами
-1 i = \
точной для многочленов седьмой степени. Кубатурная формула B1.2,6)
точна, когда /(х, у) — любой многочлен степени не выше семи от х
и у и имеет Л^ = 0,5G-|-1)G-|-2) = 36 узлов. Узлы расположены
ка алгебраической кривой шестого порядка
Таким образом, требование на расположение узлов в определении
интерполяционной кубатурной формулы не является лишним.
Отметим, что интерполяционная кубатурная формула может иметь
меньше, чем N = М{т, 2) узлов и, следовательно, узлы могут лежать
на алгебраической кривой порядка т, а может быть, и меньшего.
Это может иметь место в том случае, когда некоторые из
коэффициентов B1.2.5) обращаются в нуль.
Определение интерполяционной кубатурной формулы и
формулировку теоремы 2 нетрудно привести в случае любого числа
измерений п. Мы не будем этого делать.
Нетрудно указать нижнюю границу для числа узлов кубатурной
формулы д.
J P{x)f(x)dx^^"^Cjf{x^^^l B1.2.7)
о. /=1
точной для многочленов степени т, если вес р {х) удовлетворяет
условиям
jE7(jc)>0 для лг^а, \х^ ,^= { p(x)dx>^, B1.2.8)
Узлы кубатурной формулы B1.2.7) не могут лежать на
алгебраической гиперповерхности Q (д:) = О порядка I, где
/^[0,5w] B1.2.9)
450 ИНТЕРПОЛЯЦИОННЫЕ КУБАТУРНЫЕ формулы [ГЛ. 2!
— целая часть числа 0,5 • т. Действительно, для многочлена Q^ (х)
степени 21 -^ т формула не точна, так как
iV
j Р (X) Q2 ix)dx>0, ^ CjQ^ {хЩ = О,
Положим
^^-^^УТГ-. B1.2.10)
Так как через L—1 точек всегда возможно провести
гиперповерхность порядка / (при этом L—1—наибольшее число, обладающее
этим свойством), то число узлов кубатурной формулы, точной для
многочленов степени, т, всегда больше Z—1 и, следовательно,
L можно взять в качестве нижней границы для числа узлов.
Нижняя граница B1.2.10) достигается при /г = 1 для
квадратурных формул типа Гаусса. В самом деле, квадратурная формула Гаусса,
точная для многочленов степени т = 2/-|-1, имеет /Н~ 1 узлов.
С другой стороны, для нижней границы из формулы B1.2.10) при
п=^\ получаем L=^l-\-l.
Рассмотрим ортогональные многочлены от п переменных.
Многочлен G (х) степени^ будем называть ортогональным относительно
области Q и веса р{х) многочленом, если f/(х) ортогонален любому
многочлену степени ^ — 1, другими словами
р (х) и (х) V (х) ^х = О B1.2.11)
Q
для любого многочлена V {х) степени не выше k — 1.
Так как многочлен U{х) определяется M{k, п) коэффициентами,
а линейно независимых многочленов V {х) степени не выше k—1
имеется M{k—1, я), то равенство B1.2.11) представляет собой
линейную алгебраическую систему M{k—1, п) уравнений
относительно M{k, п) неизвестных. Такая система разрешима при любой
весовой функции р (х).
При дополнительном предположении B1.2.8) о весовой
функции р{х) можно утверждать, что система B1.2.11) определяет
M{k, п)—M{k— 1, п) линейно независимых ортогональных
многочленов степени k. Для упрощения записи будем считать д = 2 и
докажем, что существует k~\- 1 линейно независимых ортогональных
многочленов степени к
Pu^uii^^ y)=-^''~'y+Qk-ui(^^ У) (^^0- i ^)- B1.2.12)
Здесь Qk-uiix, у) — многочлен степени k— 1.
Перенумеруем одночлены от х и ); степени не выше k — 1
Ф1(х, >')=1, Ф2(^. У) = х Фл1^^-1.2)('^^ v)-^/"^- B1.2.13)
§ 2] ИНТЕРПОЛЯЦИОННЫЕ КУБАТУРНЫЕ ФОРМУЛЫ 451
Многочлен B1.2.12) запишем более подробно
Условия ортогональности этого многочлена ко всем одночленам B1.2.13j
приводят к линейной алгебраической системе M(k—1, 2) уравнений
относительно М(к—1, 2) неизвестных коэффициентов a^^h
г M(k-~1,2) "I
I j Р (л:, у) х*-'У + ^ ^^%{х, у) % (X. у) dxdy = 0
г M{k-1,2)
(s== 1,2,.. ., M(k~l, '
Ф^(л:, y)dxdy
2)),
Определитель системы есть определитель Грама линейно
независимых одночленов B1.2.13). В силу предположения B1.2.8) о
весовой функции р{х) он положителен и система имеет единственное
решение. Существование ортогональных многочленов B1.2.12)
доказано. Линейная независимость многочленов B1.2.12) следует из
линейной независимости их старших членов х^~^у^ (/ = 0, 1, 2 к).
Многочлены B1.2.12) называются основными ортогональными
многочленами степени k. Нетрудно видеть, что любой
ортогональный многочлен и (х, у) степени к есть линейная комбинация с
постоянными коэффициентами многочленов B1.2.12). Действительно» L^ (х, у)
имеет вид
k
U{x. y)=^b,x^-^y'^^Q{x. у).
где bi — постоянные и Q(x, у) — многочлен степени к— 1. Многочлен
k
г(х. y) = U(x, y)-ZbiPk^i,i(x, у)
имеет степень к— 1 и как линейная комбинация ортогональных
многочленов ортогонален ко всем многочленам степени к— 1, в частности,
ортогонален сам себе
) \ Р(^> У)г'^{х^ y)dxdy==0.
Q
Отсюда следует, что г(х, _у)^0, и наше утверждение доказано.
Нетрудно видеть, что в случае любого п имеется М{к, п)~
— М{к~ 1, п)=^ ^|у ~\\} '^^^нейно независимых основных
ортогональных многочленов степени к:
,.а, _а,
^a,,..a„W-=V •••<" + <?«,...« «■ B1-2.14)
452 ИНТЕРПОЛЯЦИОННЫЕ КУБАТУРНЫЕ ФОРМУЛЫ [ГЛ. 21
где «1 > О а„>0. ^1+ ... +а„ = /г и Q^ ^ (х) ~ много-
1 *'' п
член степени k — 1. Любой ортогональный многочлен U (х) степени к
является линейной комбинацией с постоянными коэффициентами
многочленов B1.2.14).
Пример. Построим основные ортогональные многочлены третьей
степени для центрально-симметричной области на плоскости. Центр
симметрии предполагаем совпадающим с началом координат, так что
из (х, y)^Q следует (—х, —У) 6^- Считаем область Q
ограниченной, а весовую функцию равной единице.
Будем пользоваться обозначением B1.2.2) моментов
^^р=^ Г f x^y^dxdy (а» р = 0. 1, 2, .. .)•
Нетрудно видеть, что \^'^о=^^. если а + р нечетно.
Начнем с построения многочлена Ядо-
Запишем условия ортогональности этого многочлена к одночленам
второй степени
1, л:, у, л:^, ху, у^.
Получим
^ооИ'го Н~ ^20^^40 "Ь ^пИ'З! ~h ^02^^22 = *^'
^ООМ-П + ^20^-31 ~f" ^llM'22 ~f" ^02^-13 = ^•
^ООИ'02 + ^20^^22 + ^llM-lS + ^02^^04 "^^ ^'
Видим. ЧТО система распадается на две системы: второе и третье
уравнения образуют систему двух уравнений относительно
неизвестных ^iQ, Uqi, остальные четыре уравнения составляют однородную
систему уравнений относительно неизвестных а^^, ^зо, ^ц, %2- Так
как определители этих систем отличны от нуля, то из первой
системы получаем
B1.2.15)
где
и из I
Таким
«10=-
второй —
образом
■x(^^i^i-
^00'
" М'02М'4о)' ^01
^==^^20^02-
=== ^20 = ^11 =
, многочлен Рзо найден.
1
^^1Г
= ^02 =
([^11
= 0.
§ 3] ПРИМЕРЫ ПОСТРОЕНИЯ КУБАТУРНЫХ ФОРМУЛ 453
Мы не будем проводить вычисление остальных ортогональных
многочленов, а приведем окончательный результат:
Язо = -^^ + ^ (^^пИ'Зl — ^АогМ -^ + X ^^11^40 — И'гоМ'З!) У-
B1.2.16)
^21 = -^ ^^ + Т (^^11^^22 — M'02tA3l) -^ + X (^^11^31 — ^^2оМ >''
^03 == У^+ X (^11^^04 — ^^02M'13) ^ + X (^^11^^13 — ^^20^^04) У'
Имеет место следующая
Теорема 3. Пусть кубатурная формула B1.2.3) точна для
любого многочлена степени т = 2к—1. Если ее узлы
принадлежат алгебраической гиперповерхности U{x) = 0 порядка к,
то и (х) — ортогональный многочлен области Q и веса р(х).
Доказательство. Если V(x) — любой многочлен степени
к— I, то для многочлена U (x)V (х) степени 2к— 1 формула B1,2.3)
точна. Так как по условию U (х) обращается в нуль в узлах
формулы, то получаем
J p(x)U(x)Vix)dx=::=0.
Q
что и требовалось доказать.
По-видимому, справедливо обращение теоремы 3.
Теорема 4. Существуют п линейно независимых,
ортогональных относительно области Q и веса р(х) многочленов Ui{x)
степени к таких, что решения x^J^ (у=1, 2, .... Л^) системы
и^(х) = 0 (/=1.2,...,^) B1.2.17)
можно взять в качестве узлов кубатурной формулы, точной
для многочленов степени 2к — 1.
Теорема 4 имеет место, например, при д=1. В этом случае,
если вес р (х) удовлетворяет условиям B1,2.8), теорема 4 приводит
к квадратурной формуле типа Гаусса. Доказательство теоремы 4
при п'^2 связано с большими трудностями, которые вызываются
тем, что неизвестно, как выбирать ортогональные многочлены,
которые фигурируют в системе B1.2.17).
§ 3. Примеры построения кубатурных формул
Пусть имеется кубатурная формула
N
\ p{x)f (X) dx^^ Cjf (jc(»). B1.3.1)
9 /-3
454 ИНТЕРПОЛЯЦИОННЫЕ КУБАТУРНЫЕ ФОРМУЛЫ [ГЛ. 21
точная для многочленов степени не выше т, и А — неособенная
матрица. Обозначим через Qj область, в которую переходит область Q
при преобразовании у:= Ах~\-а, и положим У^'^= Лх^^'^ + а. Тогда
кубатурная формула
j Pi(y)g(y)dy^^Cjg(yU)) B1.3.2)
Qi /-1
С весом
Pi(y^= ID(A)\ Pi^'^i^ — ^))
точна, когда g (у) — любой многочлен от у степени не выше т.
Чтобы получить B1.3.2), достаточно в интеграле B1.3.1)
выполнить замену переменных интегрирования х = Л~ (у — а) и заменить
узлы по формуле х^^^ =^ А~^ {у^^^ — а). Формула B1.3.2) точна для
многочленов той же степени, что и формула B1.3.1), так как если
/(л:)— многочлен степени г и х^=^А~\у — а), то/(Л~^(у — а)) —
также многочлен степени г от у.
Это замечание позволяет при построении кубатурных формул
ограничиться стандартными областями. Например, зная кубатурную
формулу для «-мерного куба — 1 -^х^-^ 1 (i^l /г), мы можем
получить кубатурную формулу для «-мерного параллелепипеда, с по-
мош,ью кубатурной формулы для шара можем получить кубатурную
формулу для эллипсоида.
Приведем примеры построения кубатурных формул для
простейших областей на плоскости — круга и квадрата. Пусть речь идет
о построении кубатурной формулы
N
j j Р(^' y)f(^' y)dxdy^^Cjf(xj, yj), B1.3.3)
точной для многочленов степени т. В соответствии с определением
интерполяционной кубатурной формулы мы должны взять N^=M(mr 2)
точек (Xfy, У}г) в области Q, не лежаш,их на алгебраической кривой
порядка т, и определить коэффициенты по формуле B1.2.5).
Коэффициенты Cj можно определить также, решая линейную
алгебраическую систему N уравнений
N
^С.хр^.=:^Цр(х,у)х<'уЫхAу (а>0, р>0. a + P<//j)
B1.3.4)
относительно N неизвестных Cj. .... Сдг. Система B1.3.4)
представляет собой запись того факта, что формула B1.3.3) точна,
когда f{x, у) есть любой одночлен степени не выше т. Определи-
§ 3] ПРИМЕРЫ ПОСТРОЕНИЯ КУБАТУРНЫХ ФОРМУЛ 455
тель системы отличен от нуля, так как узлы не лежат на
алгебраической кривой порядка т.
Уже при небольших т число М{т, 2) =^ 0,5 (/7i-f-1)(т-|-2)
оказывается большим. Поэтому мы будем строить кубатурные формулы,
которые точны для многочленов степени т, но имеют значительно
меньше, чем М{т, 2) узлов. В некоторых случаях это удается
сделать за счет специального выбора узлов.
В системе B1.3.4) неизвестными являются коэффициенты Q.
Будем считать неизвестными не только коэффициенты, но и
координаты узлов. При числе узлов N получаем 3N неизвестных. Так
как формула должна быть точна для всех одночленов от х и у
степени ^ т, число которых равно М{т, 2), то для определения 3/V
неизвестных параметров получаем М{т, 2) уравнений. Естественно
приравнять число неизвестных числу уравнений: ЗА^=^М(т, 2).
Отсюда получим ориентировочное число узлов кубатурной формулы:
М = ^М{т, 2)=--g-(m4-l)(/^ + 2),
которое при т, кратном трем, не является целым. Но и в случае,
^когда оно целое, нельзя гарантировать, что кубатурная формула
с таким числом узлов существует.
Новая система, в которой неизвестными являются С^, лг^, yi
(/=1, 2, ..., Л/), нелинейна и ее решение значительно труднее,
чем решение системы B1.3,4). Чтобы облегчить задачу, на решение
системы заранее будем накладывать некоторые ограничения,
Например, заранее будем располагать искомые узлы специальным образом,
а некоторые коэффициенты будем считать одинаковыми. Если найдем
решение упрощенной системы, то оно будет удовлетворять исходной
системе, и мы получим кубатурную формулу. Конечно, имеется
опасность, что упрощенная система не имеет вещественного решения
или противоречива, в то же время исходная система может иметь
решение. Возможно также, что найденная таким путем формула не
является интерполяционной.
Начнем с построения кубатурной формулы, точной для
многочленов четвертой степени, когда областью интегрирования Q является
круг х^-^у^-^Х и вес /7(х, у)= 1. Сначала выясним вопрос о числе
узлов. Число одночленов степени не выше четырех равно пятнадцати.
Из равенства ЗЛ^ = 15 получаем число узлов N = Ъ. Но сразу видно,
что нелинейная система уравнений, которую мы получим, будет
противоречивой, так как кубатурной формулы с пятью узлами, точной
для многочленов четвертой степени, не существует. Действительно,
пять узлов формулы всегда лежат на некоторой кривой второго
порядка Q{x, >') = 0 и, следовательно, формула не точна для
многочлена четвертой степени Q^{x, у). Это следует также из формулы
B1.2.10), которая дает наименьшее число узлов для кубатурной
456 ИНТЕРПОЛЯЦИОННЫЕ КУБАТУРНЫЕ ФОРМУЛЫ [ГЛ. 21
формулы, точной для многочленов степени т. В рассматриваемом
случае /г = 2 и 1 = 2 формула B1.2.10) дает L = 6. Попытаемся
построить кубатурную формулу с шестью узлами. Это приведет нас
к решению нелинейной системы из пятнадцати уравнений с
восемнадцатью неизвестными.
Будем теперь считать, что узлы расположены следуюш.им
образом: пять узлов лежат на окружности радиуса R в вершинах
правильного пятиугольника, один узел — в начале координат. Будем
также считать, что одна из вершин пятиугольника имеет
координаты (/?, 0). Потребуем, чтобы коэффициенты, отвечающие узлам
на окружности, были одинаковы — обозначим их общее значение
через В, — и коэффициент, соответствующий узлу (О, 0), обозначим А,
Кубатурная формула запишется в виде
я
f(x, y)dxdy^Af@, Q)J^ B^fi^R cos k~ , R sin k
4
2jt r^ _.„ /^ 2ji
5"
B1.3.5)
Мы должны определить три неизвестных /?, А, В. Нам понадобятся
моменты
\1^^= П x^y^dxdy (а, р-=0, 1, 2, , . .).
Чтобы их вычислить, перейдем в интеграле к полярным координатам
д: = гсо5ф, у = г $1пц}. Получим
^^ap = ^+^/«p. B1.3.6)
где
2я
/^ — С05*^ф 51п'*фй?ф.
О
Очевидно, /=0, если хоть одно из чисел аир нечетно.
Если аир оба четны.
_ (а-1)!!(Р-1I! ^
«Р ((х_(_р)!!
Запишем, что формула B1.3.5) точна, когда / = х^'у^, а^О,
Р^О, а4-'Р^4. Получим систему для определения R, А и В:
а = р = 0: А-\-5В = л, 1
4 !
« I л ^ л D V na-f-P> а, 2л: . п , 2я f B1.3.7)
а + Р>0: В 2^ R ^^ cos k-^ s\n^ k-^ г= l^.^^, j
§ 3] ПРИМЕРЫ ПОСТРОЕНИЯ КУБАТУРНЫХ ФОРМУЛ 457
содержащую пятнадцать уравнений. Так как формула
прямоугольников с пятью узлами в случае отрезка [О, 2л] точна для всех триго-
неметрических многочленов четвертой степени, то
4
^^cos"" k~sm4 ^ = 1^^ (а>0, р > 0. а + р<4)
и уравнения системы B1.3.7), кроме первого, можно записать в виде
ИЛИ, если принять во внимание равенство B1.3.6),
я/?^+^-А_/ ^ /
^^ 2я 'ар™ а + Р + 2 ^3"
Если хоть одно из чисел аир нечетно, то /^^^ = О, и уравнение
удовлетворяется автоматически. Если аир оба четны, уравнение
можно разделить на 1^о Ф 0:
^^^а+р_5_ 1
2я а + р + 2*
Так как 0<а + р<;4, то получим всего два уравнения:
а+р = 2: В/?^4-^Т-
ИЗ которых определяем R ц В
^Т „ Зя
/? = ]/4, В:
20
Из первого уравнения системы B1.3.7) находим А = -^. Мы
получили кубатурную формулу
и
Л--О
Она точна для многочленов четвертой степени и имеет наименьшее
возможное число узлов.
Ясно, что правильный пятиугольник, вершины которого являются
узлами, можно вращать вокруг начала координат. Свойство формулы
458 ИНТЕРПОЛЯЦИОННЫЕ КУБАТУРНЫЕ ФОРМУЛЫ [ГЛ. 21
быть точной для многочленов четвертой степени сохранится, как это
следует из предложения, сформулированного в начале параграфа.
Нетрудно показать, что формула B1.3.8) — интерполяционная.
Так как ее шесть узлов р^ pg не лежат на кривой второго
порядка, то можно указать девять точек /?^, .... р^^ таких, что
Pi /?15 не лежат ни на какой кривой четвертого порядка
(см. § 1). Точки /7j, ..., /?J5 можно рассматривать как узлы куба-
турной формулы B1.3.8), при этом узлам pj р^^ отвечают
коэффициенты, равные нулю.
Таким же путем можно получить кубатурную формулу для круга
J j fix, y)dxdy^A^f{^Rcosk~, Rsink—^^
2
где
fe=0
^-^(/26-^/2). р=^(у2б + /2),
б vr -- V -/. y~ Q
12^26^ ^ ^ V / 12]/26^ ^ ^ ^
Эта формула также точна для многочленов четвертой степени и
является интерполяционной.
Построим кубатурную формулу для квадрата —1 ^л:, у-^1 и
веса р{х, _у)=1, точную для многочленов седьмой степени. Число
одночленов, степень которых <^ 7, равно тридцати шести. Из
равенства ЗЛ/ = Зб получаем число узлОв N==12. Таким образом,
получаем нелинейную систему тридцати шести уравнений с таким же
числом неизвестных.
Узлы будем располагать следующим образом, Первуд) группу
узлов образуют точки пересечения окружности с центром в начале
координат и радиусом а > О с координатными осями. Вторую группу
узлов составляют точки пересечения окружности с тем же центром
и радиусом Ь Y2 > О с диагоналями квадрата. Третья группа узлов
образуется как вторая, при этом радиус окружности берется
равным с|А2>0. Коэффициенты для узлов одной и той же группы
считаем одинаковыми и равными Л, В и С для узлов первой, второй
и третьей групп соответственно.
Кубатурная формула запишется в виде
1 1
J ^ fix,y)dxdy^A[fia,O) + f@.a) + f(-a,O) + f(O,-a)]-^
-1 ~"l 4 4
-fS2/(+*, ±*) + CS/(±c, ±c). B1.3.9)
1 1
§31
ПРИМЕРЫ ПОСТРОЕНИЯ КУБАТУРНЫХ ФОРМУЛ
459
Выбор узлов и коэффициентов обеспечивает, что кубатурная
формула B1.3.9) точна для всех одночленов х^у^, у которых хоть одно
из чисел а и Р нечетно.
x^f
Потребуем, чтобы B1.3.9) была точна для одночленов 1,
Получим систему уравнений:
jcV.
1:
4Л 4^ 4В 4- 4С
:x2з'^
2 Лй4 _^ 4J5^4 _j^ /^Сс^ ^ ^ ^
f = x^: 2^a2-f4j5/^2+4Cc2=4
f
f = x Y:
4Bb^^4Cc^==^
2АФ + 4Bb^ + 4Cc6 = 1,
B1.3.10)
4^^^ + 4Cc6 = ^.
Требование, что формула B1.3.9) точна для одночленов у^, у^
у^, к новым уравнениям не приводит. Будем решать систему B1.3.10).
х^у"^
Из третьего уравнения вычтем
Получим уравнения 2Ла'^=^ j^,
45
7
четвертое и
^, Л:=:=
98
405
из пятого — шестое.
из которых находим
B1.3.11)
Перепишем первое, второе, четвертое и шестое уравнения системы
B1.3.10), подставив в первое и второе уравнения найденные
значения B1.3.11). Получим систему четырех уравнений:
ВЬ'^+Сс^^
ВЬ^'{-Сс^ =
405
31
135
J_
9 '
J_
15
B1.3.12)
неизвестными b, с,
Нетрудно видеть,
5, С.
что мксла Z'^, ^^, удовлетворяющие этой
системе, суть корни квадратного трехчлена f^~\- pt--^-q, коэффициенты
которого определяются из системы уравнений
135
307
i5-+i^+-
9 "+" '135 ^ "^ 405
9 = 0,
9 = 0.
460 ИНТЕРПОЛЯЦИОННЫЕ КУБАТУРНЫЕ ФОРМУЛЫ [ГЛ* 21
Решение системы:
___228_ _ 27
^ " 287 ' ^ ~" 287 '
так что Ь'^ и с^ — корни уравнения
Отсюда получаем
^ 287 ^ 287 -~^-
г^2:
114 —ЗУ^583 2 _ 114 + 3/583
287 ' 287 •
Наконец, из первых двух уравнений системы B1.3.12) находим
307 , 923 ^ 307 923
В.
810 270/583' 810 270/583
Таким образом, все параметры кубатурной формулы B1.3.9)
найдены. Видим, что узлы принадлежат области интегрирования и
коэффициенты положительны. Нетрудно проверить, что формула B1.3.9) —
интерполяционная.
Обозначим через соДл:) многочлен Лежандра степени у,
нормированный так, что коэффициент при х^ равен 1:
®о(л:)==1, щ{х)=2Х, со2(х) = л:2— —,
@з(х)==л:3 —-X. со4(л:) = л:4 —ух2+~.
Пять основных ортогональных многочленов четвертой степени для
квадрата —1^х, ^^^l и веса р{х, у)=^\ записываются
следующим образом:
P,-i,i{x. У)^Щ-1{х)щ{у) (/ = 0. 1. 2. 3. 4).
Запишем систему уравнений
^40 + ^04 + ^^22 = о»
4 + ^/^22-0, I
40 Яо4 = 0, J
B1,3.13)
левые части которой являются ортогональными многочленами четвер-
54
той степени. При Я =-^ система имеет двенадцать решений, и эти
решения являются узлами кубатурной формулы B1.3.9).
Таким образом, формулу B1.3.9) можно назвать кубатурной
формулой типа Гаусса: ее узлы — корни ортогональных многочленов.
Отметим, что такая формула не единственна. Например, имеется
§ 3] ПРИМЕРЫ ПОСТРОЕНИЯ КУБАТУРНЫХ ФОРМУЛ 461
кубатурная формула, точная для многочленов седьмой степени и
имеющая шестнадцать узлов. Ее узлы — решения системы Р^о = О,
Pq^ = 0. Эта система равносильна системе B1.3.13) при Х==:0.
Литература
Уокер Р., Алгебраические кривые, М., ИЛ, 1952.
Appel Р., Sur une classe de poIyn6mes a deux variables et le calcul
approche des integrales doubles, Annales de la faculte des sciences de
Toulouse 4 A890), 1—20.
Hammer P. C., Wymore A. W., Numerical evaluation of multiple
integrals i, Math. Tables and Other Aids Comput. 11, N 58 A957), 59—67.
ГЛАВА 22
КУБАТУРНЫЕ ФОРМУЛЫ С НАИМЕНЬШИМ ЧИСЛОМ УЗЛОВ
§ L Кубатурная формула, точная для многочленов
первой степени
Кубатурную формулу, точную для многочленов первой степени,
можно указать для произвольной области в д-мерном пространстве.
Такая формула имеет один узел и записывается в виде
J р (X) / (X) dx ^ С J (xfi)). B2 Л. 1)
Здесь р{х) — произвольная весовая функция. Как всегда,
предполагается существование моментов р (х), при этом
\^Q--
[ р(х)AхфО,
Потребуем, чтобы формула B2.1.1) была точна, когда /(х) —
одночлен степени ^ 1:
/_1: С.^цо.
/===х.: С^х<р=г. |р(х)х^йГх (i==U2 я).
Эта система уравнений разрешима, так что формула B2.1.1)
существует, при этом коэффициент C^^^ii^ и координаты учла, даются
равенствами
д.A) _з — \ р{^) X: dx.
Таким образом, требуемая формула определяется однозначно и,
очевидно, имеет наименьшее возможное число узлов.
Пусть теперь функция р(х) неотрицательна и i^q > 0. В этом
случае можно считать, что р(х) задает распределение масс по
области Q. Коэффициент формулы B2.1.1) Ci=^iiQ представляет собой
§ 2] КУБАТУРНЫЕ ФОРМУЛЫ ДЛЯ МНОГОЧЛЕНОВ 463
массу, распределенную по области Q. а координаты узла совпадают
с координатами центра тяжести области.
Если Q выпукла и р{х)^0, то узел х^^) принадлежит Q.
Если бы х^^) не принадлежал Q, то можно было бы указать
гиперплоскость Z(x) = 0. которая проходит через х^^) и Z (х) > О для
x^Q. Очевидно, для многочлена первой степени L{x) формула B2.1.1)
не точна, так как i(x^^*) = 0, а р(х) L(x)dx У> 0.
§ 2. Кубатурные формулы, точные для многочленов второй
степени
Перейдем к построению кубатурной формулы, точной для
многочленов второй степени и имеющей наименьшее число узлов. В частных
случаях вопрос рассматривался в работах Г. Георгиева и Ташера
(см. литературу к этой главе). А. Строуд (см. литературу) показал,
что такую формулу можно построить для произвольной области
в /г-мерном пространстве. Наше изложение отличается от изложения
-А. Строуда.
Требуемая формула имеет п-]- 1 узлов
/г + 1
р (x)f(x) dx^^ Cjf (х(Л). B2.2.1)
а ;=\
Будем считать, что весовая функция р (х) ^0 в Q и ее нулевой
момент l^o > 0. Из этого предположения и формулы B1.2.10)
следует, что Ai-f-l—наименьшее число узлов.
Введем обозначение для моментов весовой функции
р.^= ( p(x)XiXkdx (/, ^===0, 1, 2, . . ., /г). B2.2.2)
Q
Здесь Хо=^ 1, так что
Роо = J Р М ^-^. Pio = Poi = I р{х) Xi dx,
Q Q
Запишем, что кубатурная формула B2.2.1) точна для всех
одночленов степени не выше двух
/^х^.х,: С^4^Ч^^+ ... +С^,.,х(-ад;-^)-р,, B2.2.3)
(/, ^=-=0. 1. 2, . . ., п).
Система B2.2.3) состоит из 0.5 (п~{~ 1)(/г-|-2) уравнений и содержит
(п-\- If неизвестных. Можно предвидеть, что кубатурная формула
B2.2.1) не определяется однозначно.
J
464 ФОРМУЛЫ с НАИМЕНЬШИМ числом УЗЛОВ
Рассмотрим матрицу (д-|- i)-ro порядка
Роо Рог Рт • • • Роп
Рт Ри Рп • ' • Р\п
РпО Рп\ Рп2 • • • Рпп
[ГЛ. 22
B2,2.4)
Из предположения о знаке весовой функции следует, что матрица
Р—положительно определенная как матрица Грама линейно
независимой системы функций 1, Xj, .... х^. Отсюда вытекает, что
определитель D{P) больше нуля. Отметим, что в построении
А. Строуда требуется лишь выполнение неравенств О(Р)Ф0 и
Роо > ^- Неотрицательность р (х) не предполагается.
Введем еще две матрицы (п~х~\)-го порядка, связанные с узлами
и коэффициентами формулы B2.2.1)
X
хО)
ХB)
х(П
хB)
1 х(«+1) х^^+1) ... х<;^+^)
с =
о
о о ... с
л+1
Легко проверить, что систему B2.2.3) можно записать в матричной
форме
Х'СХ = Р. B2.2.5)
Матричное уравнение B2.2.5) равносильно (п-\-1)'^ скалярным
уравнениям. Те уравнения, которые получаются приравниванием
элементов в B2.2.5), расположенных ниже главной диагонали, повторяют
уравнения, возникшие в результате приравнивания элементов,
расположенных выше главной диагонали.
Матрица B2.2.4) — положительно определенная, поэтому ее можно
разложить в произведение
Р = ГТ, B2.2.6)
где Г — верхняя треугольная матрица
[Yn Yi2 Yi3 ••• Yi.n + i
О Y22 Y23 • • • Y2, n + l
Г==
0 0 0
Y/i + 1, л+1
Возможность такого разложения известна (см. Д. К. Фаддеев и
В. Н. Фаддеева, Вычислительные методы линейной алгебры).
Если B2.2.5) выполнено, то матрицы С и X — неособенные,
так как такова Р, Умножим обе части равенства B2.2.5) слева на
§ 2] КУБАТУРНЫЕ ФОРМУЛЫ ДЛЯ МНОГОЧЛЕНОВ 465
(Х^) И справа на Х~\ Получим (Х^) РХ~^ = С, От обеих
частей последнего равенства возьмем обратную матрицу
ХР-^Х' = С~\ B2.2.7)
Из B2.2.6) находим: Р"^=:=Г"'^(Г0"^ = Г"^(Г~У. Подставляя это
выражение для Р~^ в B2.2.7), получим
ХГ-'{Г-'У Х'=^С~\ B2.2.8)
Введем новую неизвестную матрицу
У:===ХГ-\ B2.2.9)
Тогда уравнение B2.2.8) запишется в виде
УУ' =^С^\ B2.2.10)
Из равенства B2.2.9) вытекает, что все элементы первого столбца
матрицы Y отличны от нуля.
Будем решать матричное уравнение B2.2.10). Возьмем
ортогональную матрицу U = (uU)\ порядка п~{~1 и такую, что элементы ее
первого столбца и^р A==\, 2, ..., п~\~1) все отличны от нуля.
Покажем, что можно подобрать диагональную неособенную матрицу
5=^[5i, ..., 5„+j] такую, что матрица V=:SU является решением
матричного уравнения B2.2Л0).
Подставляя Y^SU в уравнение B2.2.10), получим:
SU (SUy = SUU'S' -= 55' = С~\
Отсюда видно, что уравнение B2.2.10) будет удовлетворено, если
Cj=^ (У=-Ь 2 д+1). B2.2.11)
^;
Чтобы найти Si ^п+1> запишем равенство B2.2.9) в виде
Х^УГ. B2.2.12)
Если подставить сюда V = SU, то получим X = SUr. Приравнивая
элементы первых столбцов матриц в левой и правой части этого
равенства, найдем
^у = —V (-/'=^^' 2 ^+^)- B2.2.13)
Равенства B2.2.11) и B2.2.12) определяют коэффициенты и узлы
кубатурной формулы B2.2.1). Из B2.2.11) следует положительность
коэффициентов. Узлы не обязательно принадлежат области интегри-
466
ФОР1МУЛЫ с НАИМЕНЬШИЛ\ ЧИСЛОМ УЗЛОВ
[ГЛ, 22
рования даже в случае, когда она выпуклая. Это следует из
приводимого ниже примера 2.
Каждая ортогональная матрица U, у которой первый столбец
состоит из ненулевых элементов, порождает кубатурную формулу
B2.2Л). К этому и сводится многозначность формулы B2.2.1).
Пример 1. Построим кубатурную формулу B2.2.1) для случая,
когда Q—квадрат: —l^x, ^'-^l и вес р{Ху у)=:1. Матрица Р,
определяемая формулой B2.2.4), есть диагональная матрица
Р= 4, -0-, -^\ и, следовательно, Г =2, —р=г, —7=г .
Возьмем три линейно независимых вектора
и применим к ним процесс ортогонализации и нормирования. Векторы
полученной ортонормированной системы возьмем в качестве столбцов
матрицы U:
и =
1
/3
1
1
/3
I
/6
I
/
£1
2
V2
2
О
B2.2.14)
У1
2
По
По формуле B2.2.13) определяем Sj
матрице U и числам 5; находим матрицу Y = SU. С помощью B2.2.12)
находим матрицу узлов
X = YT =
1
1
1
2
/2
-/
2
О
Наконец, по формуле B2.2.11) определяем коэффициенты
Cj — С2
§ 3] КУБАТУРНЫП ФОРМУЛЫ ДЛЯ МНОГОЧЛЕНОВ 467
Кубатурная формула имеет вид
1 1
Ее узлы расположены внутри квадрата на окружности с центром
^"
в начале координат и радиусом Т/ -^.
, Пример 2. Пусть область и вес те же, что и в примере 1.
Возьмем в качестве ортогональной матрицы транспонированную
матрицу B2.2.14). Это возможно, так как первая строка у матрицы
B2.2.14) состоит из ненулевых элементов. Кубатурная формула,
порождаемая матрицей U\ имеет вид
1 1
-1-1
Узел (т^^' 7=^) выходит из области интегрирования.
§ 3. Кубатурные формулы, точные для многочленов
третьей степени
Пусть /С —л-мерный куб —l^jc^-^^l {i^=^\, ...» п). Построим
кубатурную формулу, точную для многочленов третьей степени.
Такую формулу нетрудно построить, если взять 2п узлов и
расположить их следующим образом. На оси Xi возьмем два узла
(О,..,, ± «р ....0) и сопоставим им одно и то же значение
коэффициента С^, так что требуемая кубатурная формула имеет вид
I f{x)dx^C,[f{a,. 0 0) + /(—ai. О, ..., 0)]+ ...
к
...+С„[/@. .,.,0. aJ + /@, .... 0. ~а,% B2.3.1)
Интеграл по К от одночлена xj^i . . . х^^ равен нулю, если хоть
один из показателей а^ ..., а,^ является нечетным. Для такого
одночлена и кубатурная сумма в B2.3.1) равна нулю и. следовательно,
для него кубатурная формула B2.3.1) точна при любом выборе
параметров Ui и С(-.
ФОРМУЛЫ с НАИМЕНЬШИМ ЧИСЛОМ УЗЛОВ [ГЛ. 22
Таким образом, чтобы формула B2.3.1) была точна для всех
многочленов третьей степени, достаточно потребовать, чтобы она
была точна для /=1, л:^ (i = 1, 2, . . ., /г). Это дает следующую
систему уравнений:
/2 о^ 2 2^^ /• 1 о ^ \ B2.3.2)
f = x\. 2С.а] = -^ {1=\. 2 п). 1
Система содержит 2п неизвестных и Аг+I уравнений. Так как
вещественные а^ получим лишь при С-^ > О, то совокупность формул
B2.3.1) определяется п положительными числами Ср .... С„.
удовлетворяющими первому из уравнений B2.3.2). Параметры а^ опр-е-
деляются формулами
(/=:== 1.2, ..., /г).
Рассмотрим вопрос о построении кубатурной формулы вида
B2.3.1) в случае, когда Q — ограниченная область, имеющая
положительную меру и обладающая центральной симметрией. Будем
считать, что центром симметрии является начало координат (из x^Q
следует -^х g Q).
Нетрудно видеть, что равенство нулю интеграла по области Q
от одночлена х^^ .. . лг^/» имеет место, если сумма показателей
cti+...+ctrt нечетна. В частности, интегралы от одночленов
первой и третьей степени равны нулю. Но этого недостаточно, чтобы
построить формулу вида B2.3.1), так как при построении B2.3.1)
существенно использовалось, что интегралы от одночленов второй
степени х-^х^ при / Ф j равны нулю.
Докажем лемму.
Лемма. Пусть Q — произвольная область в Е^ и р{х) — ее*
совая функция, неотрицательная в Q, положительная на
множестве из О, положительной меры и
p^j= \ p(x)XiXjdx (i, у==1,2, ..., п). B2.3.3)
Тогда имеется такое ортогональное преобразование
и = Ах, B2.3.4)
что в новых координатах
Pij= } p{A~^u)u^Ujdu^=^0 при i Ф j\ B2.3.5)
где Q — область, в которую переходит Q при
преобразовании B2.3.4).
§ 3] КУБАТУРНЫЕ ФОРМУЛЫ ДЛЯ МНОГОЧЛЕНОВ 469
Доказательство. Матрица Р=^{р^.), где Pij определены
формулой B2.3.3), есть симметрическая матрица порядка л,
положительно определенная как матрица Грама линейно независимой системы
функций JCj, ...» л:„. Обозначим через Лр Я-2, .... ^^ собственные
значения матрицы Р и через
аA), аB>, .... аС*) B2.3.6)
— соответствующие им собственные векторы, В силу положительной
определенности Р собственные значения положительны. Систему
собственных векторов B2.3.6) можем считать ортонормированной.
Компоненты собственного вектора а^^^ будем записывать
следующим образом:
/ а,
a^h^\ . I (/=^1, 2 п)
Рассмотрим ортогональную матрицу Л, у которой /-я строка состоит
из составляющих вектора а^^*:
А = \ "1^ ^22 ...^.« I B2.3.7)
Матрица А и определяет требуемое ортогональное
преобразование B2.3.4). ,
В самом деле, в интеграле B2,3.5) выполним замену
переменных интегрирования и^=Лх, где А определена формулой B2.3.7).
Получим:
Р/;= J P{A~^u)aiUjdu =
= J р (л:) [a^i^i + .. . + а;„хJ [aj^x^ + ... + cij^x^] dx =
Q
n
Лемма доказана.
Вернемся к случаю центрально-симметричной области Q. Так
как при преобразовании B2.3.4) свойство центральной симметрии
470 ФОРМУЛЫ с НАИМЕНЬШИМ числом УЗЛОВ [ГЛ. 22
сохраняется, то можем считать, что равны нулю интегралы от
одночленов первой и третьей степени по области Q и выполнены равенства
j XiXjdx = \i2fiij. B2.3.8)
Q
Кубатурную формулу для области Q запишем в виде
\ f{x)dx^C,[fia,, 0 0) + /(-ai. 0. ..., 0)]4-..-
Q
...+СЛ/@, ..., о, а^) + /@, ..., 0,-aJ]. B2.3.9)
Она точна для всех одночленов первой и третьей степени» а в силу
B2.3.8) точна для одночленов второй степени XiXj при i=^j.
Потребуем, чтобы формула B2.3.9) была точна для / = 1. л:/ (/ ;== 1 п).
Получим систему
/=1: Ci+...+^« = 0,5^0.
.10)
f^xj: 2C.a]^\i^^ (/=1,2 n). ] ^
где \i2i определено равенствами B2.3.8) и ii.o = (Q(.
Формула B2.3.9) не определяется однозначно. Ее многозначность
определяется многозначностью выбора п положительных чисел
Cj С^, удовлетворяющих первому из уравнений B2.ЗЛО).
Параметры ui определяются равенствами
«,=]/
Щ (^-^Ь2 п).
Кубатурную формулу B2.3.9) иным путем получил А. Строуд
(см. также работы Г. Георгиева и Ташера).
В случае центрально-симметричной области число узлов 2п
является наименьшим возможным, при котором существует кубатурная
формула, точная для многочленов третьей степени. Доказательство
этого утверждения дано И. П. Мысовских (см. литературу к этой
главе).
Если область Q не является центрально-симметричной, то
утверждение о минимальности числа узлов неверно. Например, для
«-мерного симплекса Т:
л:,+ .-. +а:^<Ь х,:^0 (/=1,2 п)
существует кубатурная формула, точная для многочленов третьей
степени и имеющая л + 2 узла (см. работу Хаммера и Строуда),
^ 4j КУБАТУРНАЯ ФОРЛ\УЛА РАДОНА
Эта формула имеет вид
г
(п + ЗУ rw I I \ ,
"^ 4(/г + 2)! L-^ \п + 3 п+з)~^
/=1
п + 3
471
B2.3.11)
При установлении формулы B2.3Л1) используется равенство
B2.3.12)
J
л:, i . . . х"я й^л: = -^—i—' i—^Ц—гу
Один коэффициент в формуле B2,3.11) отрицателен. В случае
-центрально-симметричной области коэффициенты формулы, точной для
многочленов третьей степени и имеющей 2/2 узлов, всегда
положительны (см. статью И. П. Мысовских).
§ 4, Кубатурная формула Радона
В этом параграфе излагаются результаты Радона (см. литературу
в конце главы) о кубатурных формулах для вычисления двойных
интегралов. Работа Радона интересна прежде всего потому, что
в ней впервые успешно использована идея применения ортогональных
многочленов области к построению кубатурных формул. Именно,
указан метод, который для заданной области интегрирования
позволяет узнать, существует ли кубатурная формула с семью узлами,
точная для многочленов пятой степени, и позволяет построить такую
формулу, если она существует.
Пусть Q — произвольная ограниченная область на плоскости,
имеющая положительную меру. Условие ограниченности й естественно,
так как речь будет идти о кубатурной формуле с весовой функцией,
равной единице. Все результаты останутся в силе и в случае, когда
строится кубатурная формула с весовой функцией р(х, у),
неотрицательной в области Q и такой, что р-оо > ^'
Важную роль в последующем играют ортогональные многочлены
третьей степени области Q (весовая функция равна единице). Запишем
основные ортогональные многочлены третьей степени
Яз-и=>^'~'У + Сз-м а = 0, 1. 2. 3)
B2.4.1)
472 ФОРМУЛЫ с НАИМЕНЬШИМ числом УЗЛОВ
и введем следующие обозначения:
[ГЛ. 22
Л^ ^ j{P3oPi2 — Pl)dxdy,
Q
^ = j j (^^РОЗ - Р2ХРП) dX dy.
С-= J j{P2iPos-Pl2)dxdy.
B2.4.2)
Предполагается, что область Q удовлетворяет следующему условию:
А^^^В^-^С^ФО B2.4.3)
(хоть одно из чисел А, В, С отлично от нуля). Не известно,
является ли это условие на самом деле ограничением, так как не
известно, существуют ли области, для которых Л = 5 = С = 0.
Речь идет о построении кубатурной формулы
7
J. J fix, y)dxdy^'^ Cjfi^j-yj)^ B2.4.4)
точной для многочленов пятой степени. Число узлов 7 выбрано
в соответствии с тем, что одночленов степени не выше пяти имеется
двадцать один.
Покажем, что при соблюдении условия B2.4.3) число узлов
N = 7 является наименьшим возможным, при котором существует
кубатурная формула, точная для всех многочленов пятой степени.
Допустим противное: существует кубатурная формула с шестью
узлами
б
J J/(x. y)dxdy^^CJ(x^, у,). B2,4.5)
точная для многочленов пятой степени. Ясно, что ее узлы Pi^={Xi, yi)
не лежат на кривой второго порядка.
Через пять узлов формулы, в число которых не входит р^,
проведем кривую второго порядка Rk(x, у)==0. Имеем RkiPk) ^^' ^^^
многочлена четвертой степени Rk формула B2.4.5) точна
Отсюда видно, что С^, > О (А^= 1. .... 6).
§ 4] КУБАТУРНАЯ ФОРМУЛА РАДОНА 473
Пусть К{х, у) — любой ортогональный многочлен третьей степени
области Q. Для многочлена пятой степеш! KRf^ формула B2.4.5)
точна:
J lKR,dxdy = C,K(p,)R,{p,y
Интеграл равен нулю в силу ортогональности, а так как С;^ > О
и Rk(Pk)^^' ^^ отсюда следует, что К(р^)=^0 {к=\, ..., 6).
Мы получили, что любой ортогональный многочлен третьей степени
области Q обращается в нуль в узлах кубатурной формулы B2.4.5).
В частности, обращаются в нуль в узлах основные ортогональные
многочлены B2.4.1).
Покажем, что интеграл Л, определяемый формулой B2.4.2), равен
нулю. Имеем:
Л— ^ ^ [Ргоху'^ — P2iX^y] dxdy -=
= J J [(л:^ + Q3o) xy' - (xb + Q21) x'y] dx dy =
a
= J J [Qz^xy'^ — Q2\xb] dx dy.
Так как Q^ и Q^i — многочлены не выше второй степени, то с
помощью кубатурной формулы B2.4.5) мы получим точное значение,
последнего интеграла
A = ^C.[Q^{x., y)x,y]-Q^,{x., уО^У,]. B2.4.6)
Но так как основные ортогональные многочлены B2.4.1) обращаются
в нуль в узлах кубатурной формулы, то
и из B2.4.6) получаем, что Л^О. Совершенно так же получим,
что В=^С = 0, а это противоречит условию B2.4.3).
Отметим, что вопрос о минимальности числа узлов кубатурной
формулы B2.4.4) Радоном не рассматривался.
Пусть кубатурная формула B2.4.4), точная для многочленов пятой
степени» построена. Ее узлы
Pi = {x,. у,) (/-1, .... 7) B2.4.7)
не лежат на кривой второго порядка, в частности, никакие пять из
них не лежат на прямой. Докажем, что среди точек B2.4.7) найдется
шесть, которые также не лежат на кривой второго порядка. Если бы,
474 ФОРМУЛЫ с НАИМЕНЬШИМ числом УЗЛОВ [ГЛ. 22
например, р^ Pq лежали на кривой R^ второго порядка и
/?2» ...» Pj также лежали на кривой второго порядка /?2' '^^ кривые
/?, и /?2 пересекались бы в пяти точках /?2 Рб- По теореме
Безу /?1 и /?2 имеют общую компоненту, и так как эта компонента
содержит пять точек, не лежащих на прямой, то /?i и /?2 совпадают.
Это противоречит тому, что точки B2.4.7) не лежат на кривой
второго порядка.
Для определенности будем считать, что не лежат на кривой
второго порядка точки р^ Pg. Если через точку Ру провести
прямую, не проходящую ни через одну из точек р^ р^, и взять
на ней три точки Pg, Рд, /?jq, отличные от pj, то, как было доказано
в § 1, гл. 21, точки р^, . . ., /?(Q не лежат на алгебраической кривой
третьего порядка. Таким же образом построим точки р^^ .... Рз)
так, что /7р .... /?15 не лежат на алгебраической кривой четвертого
порядка, а точки /?j, ..., p2i не лежат на алгебраической кривой
пятого порядка.
Докажем, что существуют три линейно независимых многочлена
третьей степени, которые обращаются в нуль в узлах кубатурной
формулы B2,4.4). Так как точки р^ р^^ не лежат на кривой
третьего порядка, то существует многочлен тргтд>ей степени П^(х, у),
который равен нулю во всех точках р^ Pi^, кроме Py+i^ и равен
единице в точке Pj^i (/==:= 1, 2, 3). Многочлены Пр П^, Пз по
определению обращаются в нуль в узлах формулы B2.4.4). Они линейно
независимы и любой многочлен третьей степени, равный нулю в узлах
формулы B2.4.4), выражается в виде их линейной комбинации с
постоянными коэффициентами. По теореме 3 из § 2 гл. 21 многочлены
Пр П2, Пз являются ортогональными многочленами области Q.
Таким образом, мы доказали следующее предложение. Если куба-
турная формула B2.4.4) существует, то имеется три линейно
независимых ортогональных многочлена, которые обращаются в нуль в семи
узлах B2.4.7) формулы B2.4.4).
Докажем, что существуют три многочлена первой степени
1^1 = ciiX-^-diy-^c^ (/^=1. 2, 3), из которых по меньшей мере два
отличны от тождественного нуля, такие, что справедливо тождество
L,U,^L,n, + L,l\ = 0. B2.4.8)
Левая часть равенства B2.4.8) представляет собой многочлен
четвертой степени от л: и у. Этот многочлен обращается в нуль в
точках /7р . . ., Ру. Чтобы левая часть B2.4.8) обращалась в нуль
тождественно, достаточно потребовать, чтобы она была равна нулю
в точках pg, ..., /?15 (точки /?i, .... Pi^ не лежат на кривой
четвертого порядка). Это приводит к линейной однородной системе
восьми уравнений с девятью неизвестными а^, Ь^, с^ (/=1, 2, 3).
Такая система имеет ненулевое решение. Существование Li доказано.
Очевидно, что два из многочленов Z^ не могут оказаться тождествен-
§ 41 КУБАТУРНАЯ ФОРМУЛА РАДОНА 475
ными нулями, так как тогда из B2.4,8) следует, что и третий
является тождественным нулем.
Наша ближайшая задача состоит в том, чтобы указать три
линейно независимых ортогональных многочлена третьей степени,
удовлетворяющих тождеству вида B2.4.8). Как мы увидим, эти
многочлены имеют семь общих нулей, и если нули вещественны и различны,
то их можно взять в качестве узлов искомой кубатурной формулы.
Перепишем тождество B2.4.8) в виде
хКг + уК2 = К^. B2.4.9)
где обозначено
К, ^a.YiyJr ci,lh + «зПз, /С2 - ^П^ + Ь^П^ + *зПз,
К^ = — CiHi — С2П2 — С3П3.
Очевидно, Ki как линейные комбинации ортогональных многочленов
сами являются ортогональными многочленами области Q. Однако мы
не можем утверждать, что /С], /^2» А^з линейно независимы. Отметим,
что Ki и /Сг отличны от тождественного нуля, как это следует из
B2.4.9).
Многочлены /Ci и К2 можно записать как линейные комбинации
основных ортогональных многочленов B2.4.1)
^1 = С^зо^^зО + «21^21 + Ctl2^12 + Ct03^03'
^2 = РзО^ЗО + Р21^21 + Pl2^12 + РоЗ^ОЗ-
Подставим эти выражения для /Cj и /^2 в соотношение B2.4.9)
и заметим, что четвертые степени переменных в левой части B2.4.9)
должны сократиться. Это приводит к равенствам
0^30 = Роз = ^» СС21 == РзО' 0tl2 = —P2I • Cto3 = — Pi2*
Выражения для /Ci и /^2 можно теперь записать в виде
/Ci-aP2i4-P^2 + V^03. /^2 = -a/'3o-P^2i-Y^'i2. B2.4.10)
Многочлены /Ci и /Сг линейно независимы, так как среди чисел а, р, у
есть отличные от нуля.
Найдем коэффициенты а, р, Y» пользуясь тем, что Jc/Ci + y/C2 = ^3
является ортогональным многочленом третьей степени.
Ортогональность к многочленам первой степени вытекает из того, что К\ и /Сг —
ортогональные многочлены. Запишем, что многочлен
хК^ + уК^ = а (л:Я21 - уРзо) + Р (-^^12 — y^2i) + Y {хРоз — У^12)
476 ФОРМУЛЫ с МАИЛ\ЕНЬШИМ ЧИСЛОМ УЗЛоВ [ГЛ. 22
ортогонален к л:^, ху и у^. Получим линейную однородную систему
— Аа +Су = 0. B2.4.11)
— 5а —Ср =0, )
где А, В, С определены формулами B2.4.2).
Из условия B2.4.3) следует, что ранг матрицы системы B2.4.11)
равен двум и, следовательно, числа а, р, у определяются с точностью
до ненулевого постоянного множителя.
Возможны два случая:
а) многочлен К^ = xKi -f- уК^ линейно не зависит от /Cj и /Сг»
б) /Сз есть линейная комбинация /Cj и К^^
Ks = aK, + bK2^ B2.4.12)
В случае а) мы получили три линейно независимых ортогональных
многочлена третьей степени /Cj, /С2, /С3, удовлетворяющих тождеству
B2.4.9), которое является тождеством вида B2.4.8).
В случае 6) из равенства B2.4.9) и B2,4.12) получаем
Выполняя преобразование координат х^ = х — а, у^ = у—Ь,
перепишем последнее равенство в виде
xKi + yK2 = 0. B2.4.13)
Чтобы не усложнять запись» мы сохранили прежние обозначения
переменных и ортогональных многочленов. Таким образом, в случае б)
мы получили только два линейно независимых ортогональных
многочлена. Соотношение B2.4.13) можно рассматривать как тождество
формы B2.4.8), если в качестве /Сз взять ортогональный многочлен
третьей степени, линейно независимый от Ki и ЛГ2. и положить L^^O.
Займемся отысканием такого многочлена Ks- Нам понадобятся
некоторые свойства ортогональных многочленов Кх и /Cg* Мь1
рассматриваем случай б), когда имеет место соотношение B2.4.13). Из него
следует, что
Ky=yQ. /Сз^ —JcQ. B2.4.14)
где Q — многочлен второй степени. Докажем, что Q ортогонален
любому многочлену третьей степени Р, который обращается в нуль
в начале координат. В самом деле, многочлен Р имеет вид Р =
= xQi + yQ2' ^ле многочлены Q^ и Q2 имеют степень не выше двух.
Имеем
J ^QPdxdy=j lQ(xQ,'^yQ2)dxdy=^
^ "" -= J j(~K2Qi^K^Q2)dxdy = 0.
^4] КУБАТУРНАЯ ФОРМУЛА РАДОНА 477
Здесь мы воспользовались равенствами B2.4.14) и ортогональностью
многочленов /Ci и /Сг- Утверждение доказано.
Отметим следствие доказанного утверждения: Q@. 0)^0.
Действительно, если бы Q@, 0)=:=^0, то многочлен Q был бы
ортогонален сам себе и, значит, Q^O и по B2.4.14) ATi^O. /Сг^О, что
невозможно.
Докажем еще, что все ортогональные многочлены третьей степени
обращаются в нуль в начале координат. Пусть/С (х, у) — такой
ортогональный многочлен. Разность К(х, у) — К (О, 0) является
многочленом третьей степени, равным нулю в начале координат, поэтому
по предыдущему предложению
J Jl^(-^. У)"^@. 0)]Q(x, y)dxdy = 0
Q
или, так как К—ортогональный многочлен,
/С (О, 0)- J JQ(a:, y)dxdy = Q,
Q
-Здесь интеграл отличен от нуля, так как в противном случае Q
был бы ортогонален единице и. в силу предыдущего предложения.
ортогонален сам себе. Таким образом, /С (О, 0) = 0.
Пусть /С(х, у) — ортогональный многочлен третьей степени,
линейно независимый от Ki и /^2- Так как по B2.4.14)
Ki^ylQiO. 0) + aioX+ ...], K2 = ~x[Q@, 0) + ^^^:+ ...]
и Q@, 0)^0, то из К можно вычесть такую линейную комбинацию
Кх и /^2' *^'^о разность
не будет содержать первые степени х и у. Очевидно, множество
общих нулей К^, Кх и К2 совпадает с множеством общих нулей /С,
/Ci и /С2.
Отсюда следует, что в качестве К^ можно взять любой
ортогональный многочлен третьей степени, у которого коэффициенты при
первой степени л: и у равны нулю. Очевидно, такой многочлен не
может быть линейной комбинацией К\ и К2- Многочлен /Сз можно
разыскивать в виде линейной комбинации основных ортогональных
многочленов B2.4.1);
Условие, что коэффициенты при л: и у равны нулю, накладывает два
ограничения на параметры Ь^ и, следовательно, имеется семейство
ортогональных многочленов, линейно независимых от Кх и К^- Это
семейство зависит от двух параметров, так что в случае б)
многочлен Kz определяется неоднозначно.
478 ФОРМУЛЫ с НАИМЕНЬШИМ числом УЗЛОВ [ГЛ. 22
Итак, мы построили три линейно независимых ортогональных
многочлена третьей степени /Ci» /С2, К^* удовлетворяющих
соотношениям вида B2.4.8) как в случае а), так и в случае б). В случае а)
соотношением вида B2.4.8) является соотношение B2.4.9), в
случае б) — соотношение B2.4.13).
Прежде чем перейдем к вопросу об исследовании общих нулей
многочленов К\, /^2, К^* докажем следующее предложение. Если
многочлены Ki удовлетворяют соотношению вида B2.4.8):
^Л + ^2^2 + ^з>Сз = 0, B2.4.15)
где Li = a^x~\~biy-\~Ci (£=1. 2. 3). то это соотношение совпадает
с точностью до ненулевого постоянного множителя в случае а) с
тождеством B2.4.9). а в случае б) — с тождеством B2.4.13).
Приведем доказательство для случая а). Из B2.4.15) получаем
соотношение вида B2.4.9)
Но из такого соотношения ортогональные многочлены /Ci. К2* К^
определяются с точностью до ненулевого постоянного множителя,
другими словами,
а^Кх + flt2^2 + «3^3 = DK\»
где D Ф 0. Так как Ki, /С2» АГ3 линейно независимы, то отсюда
получаем:
Ц^Ох, L2 = Dy. L^ = — D.
а это и означает, что соотношение B2.4.15) совпадает с B2.4.9)
с точностью до постоянного множителя. Доказательство для случая б)
аналогично.
Докажем, что многочлены /Cj, /С2» К^ не имеют общих делителей.
Отсюда, в частности, будет следовать (по теореме Безу), что число
общих нулей этих многочленов не более девяти. Докажем сначала,
что Ki не могут иметь в качестве общего делителя многочлен
второй степени Qq. Допустим противное: A'^ = Qo^('''ле Z^- — многочлены
первой степени. Так как Ki (^=1, 2, 3) линейно независимы, то Li
тоже линейно независимы. Поэтому можно указать три постоянные с^,
^2» ^3 тзк, что имеет место равенство
CiLi + ^2^2 Ч~ ^3^3 =^ 1'
Умножим обе части на Qq. Получим
^i^^i + ^2^r2 + ^3^3 = Qo-
^ 4j КУБАТУРНАЯ ФОРМУЛА РАДОНА 479
Но это равенство невозможно, так как из него следует, что Q^
ортогонален сам себе и, следовательно, Qq^O.
При доказательстве того, что у многочленов Ki не может быть
общего делителя первой степени, рассмотрим отдельно случай а) и
случай б). Допустим, что в случае а) многочлены Ki имеют общим
делителем L — многочлен первой степени: Ki = LPi, где Р,- — линейно
независимые многочл^ены второй степени. В силу соотношения B2.4.9)
имеем xPi^yP2^=^ Р^- Так как одночлены третьей степени в левой
части этого равенства должны сократиться. • то получаем для Р^
следующие выражения:
Pi=-y{ax~{-by)~^L^. р^^ — х{ах + Ьу)^ЦЛ .^2 4 16)
Рз = лгЛ^ + Д'^г- 1
Из B2,4.16) получаем ЦРх — 1^Р2=^{Aх-\~Ьу)Р^^л]А, если
умножить обе части на L, L2K1 — ЦК2^={^х-\'Ьу)К^. Из единственности
соотношения B2.4.9) следует, что L^^^^Dx, L^ = — Dy. Отсюда
по B2.4.16) найдем Р^^^ и /Сз^О, что невозможно.
Рассмотрим случай б). Пусть многочлен первой степени L — общий
"делитель многочленов /С,-. Тогда Ki = LLiy, /( = — LL^x, /C3 = ^Qi,
где Lj и Qi — многочлены первой и второй степени соответственно.
Мы знаем, что А:з@, 0)=:=0. Так как Q=:LL^ и Q@, 0)^0, то
L@, 0)^0 и, следовательно, Qi@, 0)=^0.
Многочлен Qi можем записать в виде Qi = хМ^-{-уМ2, где М^
и Жз — многочлены первой степени. Очевидно,
Ms/Ci — Ж1/С2 = М^ЬЦу + M^LL^x = Щ {хМ^ + уМ^) = ЦК^>
и мы получили равенство AI2/C1 —■ М\К2 = -^i^a- ^^ единственности
соотношения B2.4.13) следует Lj^O, что невозможно.
Рассмотрим вопрос об общих корнях многочленов /Cj, /С2. /С3.
В случае а) две алгебраические кривые третьего порядка /Cj = О и
/^2 = 0 имеют точно две бесконечно далеких точки пересечения, так
как
К,=:^у (ах2 + ^ху + Y>'') + «Q21 + PQ12 + YQ03.
/С2 = — X {ах^ Н- рл:у + y/) — ^Q^ — PQ21 — YQi2-
Если остальные семь точек пересечения вещественны и различны, то,
как мы увидим, эти семь точек можно взять в качестве узлов куба-
турной формулы, точной для многочленов пятой степени. В
противном случае (среди точек пересечения имеются комплексные или
кратные) можем утверждать, что кубатурная формула с семью узлами,
точная для многочленов пятой степени, не существует. Действительно,
если бы такая формула существовала, то нашлись бы три
ортогональных многочлена /Cj, /С2. /С3. удовлетворяющих соотношению
B2.4.9) и таких, что их общие семь корней вещественны и различны.
480 ФОРМУЛЫ с НАИМЕНЬШИМ числом УЗЛОВ [ГЛ. 22
Так как соотношение B2,4.9) определяет ортогональные многочлены
с точностью до ненулевого множителя, то утверждение доказано.
В случае б) общими корнями АГр /^2- ^г являются начало
координат и шесть точек пересечения кривой второго порядка Q = О и
алгебраической кривой третьего порядка /Сз = 0. Так как
ортогональный многочлен /Сз зависит от двух параметров, то семь общих
нулей также зависят от параметров.
Предположим, что семь общих корней многочленов /Ci. К^^ К^
оказались вещественными и различными. Обозначим эти корни р^, ...
..., P-J и докажем, что их можно взять в качестве узлов кубатур-
ной формулы, точной для многочленов пятой степени. Все
последующие рассуждения останутся в силе, если корни Рр ..., р^ различны,
но не обязательно все вещественны. В этом случае мы придем
к кубатурной формуле с комплексными узлами.
Начнем с доказательства того, что р^ /?7 не лежат на
кривой второго порядка. Допустим противное: точки р^, ..., р^ лежат
на кривой второго порядка /? (дг. у)=:0. Допустим, что кривая
/? = 0 неприводима. Тогда в случае а) по теореме Безу получим,
что Ki имеют общий делитель R — многочлен второй степени, что
невозможно. В случае б) кривая второго порядка Q = 0 и
неприводимая кривая /? = О пересекаются в шести точках, а тогда Q = dR,
где d — отличная от нуля постоянная. Так как /?@, 0) = 0, то и
Q@, 0) = 0, что невозможно.
Итак, кривая R = 0 распадается на две прямые Z = 0 и Z,i=:0.
На одной из прямых, например, Z. = О, найдется по меньшей мере
четыре из точек pj, ..,, pj. Но тогда по теореме Безу многочлен
первой степени L является делителем всех /С; как в случае а), так
и в случае б), что невозможно. Утверждение полностью доказано.
Так как точки р^, .... р^ не лежат на кривой второго порядка,
то, как мы видели выше, можно указать четырнадцать точек Рд, ...
..., /7^1, так что Pi Р21 ^^ лежат на кривой пятого порядка.
Пусть Р(х, у) — многочлен пятой степени, который обращается в нуль
в точках Pi, ..., /?7- Докажем, что можно указать три многочлена
второй степени Qj, Q2» Q3 таких, что
Р(х. y) = Qi/Ci + Q2/^2 + Q3^3. B2.4Л7)
В левой и правой части этого равенства мы имеем многочлены
пятой степени. Они совпадают в точках р^ p-j (обращаются
в нуль). Чтобы многочлены совпадали тождественно, достаточно
потребовать, чтобы совпадали их значения в точках /?§, ..., /?2i. Это
приводит к линейной алгебраической системе четырнадцати уравнений
относительно восемнадцати неизвестных — коэффициентов
многочленов Q^.
Чтобы выяснить вопрос о разрешимости этой системы,
рассмотрим соответствующую однородную систему. Однородная система
B2.4.19)
§ 4] КУБАТУРНАЯ ФОРМУЛА РАДОНА 481
равносильна задаче об определении трех многочленов второй
степени Qi таких, что
QiKr+Q2K2 + Q3^3 = 0- B2.4.18)
В случае а) равенство B2.4.18) с помощью B2.4.9) можно
переписать в виде (Qi + хРз)А^1+ (Q2+У^з)^2 = *^- ^^^ к^к ^х ^ ^2
не имеют общих делителей, то отсюда следует:
Qi + xQ^ = ~~ DK2 = Dx (ах2 + рху + yf) +
+ D(aC3o + PQ2i + YQi2)
Q2 + УЯг = D^i = Dy (a^^ + Р^У + yf) +
+ D(aQ2j+pQi2 + YQo3). J
где D — отличная от нуля постоянная. Запишем многочлен второй
степени Q^ с неопределенными коэффициентами, подставим, например,
в первое из равенств B2.4.19) и приравняем коэффициенты при
одинаковых степенях л: и ^. Получим
Q^^^D(ал:^-f ^ху + yf-)-~\'ах-\~Ьу'\-с.
Далее, из равенств B2.4.19) находим Q^ и Qg-
Qi = D (aQ3o + PQ21 + YQ12) — x{ax^by + c),
Q2-=D (aQsi + PQ12 + YQos) -~У(ах + Ьу-^^ с).
Мы получили общее решение задачи B2.4.18), зависящее от
четырех произвольных постоянных D, а, Ь, с. Отсюда следует, что
ранг матрицы однородной системы равен четырнадцати. Так как число
уравнений равно четырнадцати, то ранг расширенной матрицы тоже
равен четырнадцати, и неоднородная система всегда разрешима.
Справедливость представления B2.4.17) в случае а) доказана.
В случае б) равенство B2.4.18) с помощью B2.4.14) можно
записать в виде
iQiy~Q2x)Q^Q^K^ = 0,
Так как Q и /Сз не имеют общих делителей, то
Q3 = DQ, Q,y ~ Q^x + D/Сз = О, B2.4.20)
где D — отличная от нуля постоянная. Многочлен Д^з обращается
в нуль в начале координат, поэтому его можно записать в виде
K^ = yQ4~ -^Qs'
где Q^ и Qg—многочлены второй степени. Подставляя это
представление для /Сз в B2,4.20), получим
(Qi + DQ,) y-iQ2^ DQ,) x = Q,
482 ФОРМУЛЫ с НАИМЕНЬШИМ числом УЗЛОВ [ГЛ. 22
Отсюда видно, что
Таким образом, общее решение задачи B2.4.18)
Qi = — DQ^ 4- ^ («л: -J^by-^c),
Q2 = ~DQ^-^y(ax^by^c), Q^ = DQ
зависит от четырех произвольных постоянных D, а, Ь, с. Отсюда
заключаем, что и в случае б) представление B2.4.17) имеет место.
Теперь нетрудно доказать, что можно построить кубатурную
формулу с узлами pj, ..., р^, точную для многочленов пятой
степени. Так как точки pj, .. ., /?2i не лежат на алгебраической кривой
пятого порядка, то можно построить интерполяционную кубатурную
формулу
21
J j/(^. y)dxdy^Y^CJ{x,, yi), /?, = (jc,, у,), B2.4.21)
точную для многочленов пятой степени. Утверждение будет доказано,
если докажем» что коэффициенты С^ формулы B2.4.21) при i^%
равны нулю.
Рассмотрим многочлен пятой степени Р^{х, у), Л = 8, 9. .,.,21,
равный нулю во всех точках /?i, ..., p^i, кроме р^, и равный
единице в точке р^. Многочлен Р^{х, у) обращается в нуль в точках
/?1, ..., /?7, поэтому для него справедливо представление B2.4.17).
Запишем теперь, что формула B2.4.21) точна для /=^Р;^(л:, у).
Интеграл от Pk{x. у) равен нулю в силу представления B2.4.17),
а кубатурная сумма равна С^, так что получаем С;^ = О при k =
= 8, 9, ..., 21. что и требовалось доказать.
Важную роль в вопросе о построении кубатурной формулы B2.4,4)
играло условие B2.4.3), которому должна удовлетворять область Q.
Докажем, что если Q обладает центральной симметрией, то условие
B2.4.3) выполнено. Будем считать, что центром симметрии является
начало координат.
Доказательство будем вести от противного. Предположим, что
Л==5==С = 0, Нетрудно проверить, что при соблюдении этих
равенств не только в случае центрально-симметричной, но и в случае
любой области можно утверждать, что многочлены
ЯэоУ"Р21^. Р^гХ-РпУ B2.4.22)
ортогональны ко всем многочленам второй степени.
В случае, когда область Q центрально-симметричная, основные
ортогональные многочлены третьей степени даются формулами B1.2.16).
Эти формулы можно записать кратко следующим образом:
P^_ij = x^~^y'^a^''^x^b% (/ = 0. 1, 2, 3).
§ 4] КУБАТУРНАЯ ФОРМУЛА РАДОНА 483
Отсюда получаем выражения многочленов B2.4.22) для цен-
тральносимметричной области:
Р^у -Р,,х^~ а<'V -4- («("> - *(>>) ху + b^Y-
Pozx - Р21У = «'V + (*^" - а'^>) ху - ft^^y.
Эти многочлены второй степени ортогональны ко всем многочленам
второй степени, поэтому их коэффициенты равны нулю.
В частности, равны нулю коэффициенты при ху: а^^^—^>^'^ = 0,
Ь^^^ — а^^'=;0. Пользуясь формулами B1.2.16). запишем эти равенства
подробнее
М'02М'40 — И'гоМ'гг = ^» М'2оМ'04 ~" ^021^22 = ^•
Здесь liif^ — моменты весовой функции, равной единице.
Из двух последних равенств получаем
^^40^^04 —^22 = 0-
Это равенство невозможно, так как его левая часть положительна
-как определитель Грама линейно независимых функций х^, у^.
Получили противоречие и. следовательно, условие B2.4.3) выполнено.
В статье Радона выполнение условия B2.4.3) доказано для частного
случая, когда область симметрична относительно обеих координатных
осей.
Выполним фактически построение кубатурной формулы B2.4,4)
для некоторых областей Й частного вида. Пусть Q — треугольник:
лг^^О, у^О, JC-f-^'^l- Выпишем основные ортогональные
многочлены третьей степени треугольника
Ло==^зо(-^. у)==:хЗ—у х2 + у-^" 35 *
Pl2 = ^21 (У^ ^). Роз ^ ^30 (У' ^)-
При их вычислении пользуемся формулой B2.3.12) при п = 2.
Вычисляем интегралы B2.4.2)
3.5-7'7! • 3.5.7-7! *
Видим, что условие B2.4.3) выполнено. Далее, решаем систему B2,4.11).
Одно из ее решений а^=1. р=1, у=Ь так что по B2.4.10)
K,==x'^y + xy'^.^y^-\x'^-^xy~^f+)j-x + ^y--^,
Ki = -xf-x-^y~x^^\f + ^xy + ^x-^-\y-jX + ±
484
ФОРМУЛЫ с НАИМЕНЬШИМ ЧИСЛОЛ\ УЗЛОВ
[ГЛ. 22
и по B2.4.9)
/Сз^х/С1 + у/С2 =
= —4гA:S-h|-л:^y —■|-л:y2 + 4-^'^4--
--lv2-
X) [3 (у2 + лгу + х^) ~ 6л:у
1 1 1
„3(у + х)+1].
Имеет место случай а), так как Кз не является линейной
комбинацией Кх и К2'
Не будем проводить подробно вычисление общих нулей
многочленов /С;. Отметим только, что сначала из системы Ki'=0, К^ = 0
находим узлы, расположенные на прямой у = х. Это приводит к
решению уравнения третьей степени. Остальные четыре узла находим из
системы Ki~\~K2 = 0, /Сз==0, которая сводится к системе уравнений
второй степени. Мы не будем также производить вычисление
коэффициентов. Приведем готовую таблицу узлов и коэффициентов.
^k
Ук
Ck\
1
3
1
3
9
80
6+К15
21
9—2]/" 15
21
9-2F5
21
e + ZIs
21
^ + V\s j
21
6 + /T5
21
1
155 +/15
2400
s — Vis
21
9 + 2/15
21
21
6-^/15
21
21
6 —/15
21
1
155^/15
2400
Пусть теперь Q — ограниченная область, симметричная
относительно обеих координатных осей. Очевидно, Q обладает центральной
симметрией относительно начала координат, поэтому условие B2.4.3)
выполнено и основные ортогональные многочлены третьей степени
даются формулой B1.2.16). Так как ^1/^=^0» ^сли хоть одно из
чисел i vi k нечетно, то ортогональные многочлены запишутся в виде
30
12-
П22 ^
:;c^y~i^y,
■ху''
М^20
Po3 = f
И 04
И02
Интегралы B2.4.2) равны
И22
С^
И22
(^22^^02— И'20^^04)'
У-
О,
§ 4] КУБАТУРНАЯ ФОРМУЛА РАДОНА 485
В качестве решения системы B2.4.11) возьмем
ct = Ц20^^04 —^^ггМ'Ог' P==Cl. Y ^ 1^02^10 — i^ 221^20- B2.4.23)
По B2.4,10) находим
Ki==^yQ, К2 = — xQ.
где
при этом а и Y определены формулой B2.4.23) и 6^^i^!LIq^ — |i^2 > *^-
Так как х/^ + У^г^ ^' '^^ получаем случай б).
Чтобы найти /Сз» составим линейную комбинацию основных
ортогональных многочленов
и приравняем нулю коэффициенты при х и у:
Найдем отсюда ^з ^ ^4 ^ подставим в выражение для К^> Получим
или. если ввести новые параметры Я и v,
/Сз = Я. (^22-^^ ~ М'40-^Я + V (М'04-^^>' — ^Ч2У^)'
Нетрудно видеть, что однородный многочлен К^ распадается
в произведение трех различных вещественных многочленов первой
степени, так что кривая К^^=0 распадается на три вещественные
прямые, проходящие через начало координат. Если v Ф О» достаточно
проверить, что многочлен третьей степени
Р (О = I (^22 — ^^40^^) + V ill^^t — ll<22t^)
имеет три различных вещественных корня. Это следует из того, что
sign Р (— со) = sign V,
\У И40/ И40 У No
Sign Р (-[- со) = — sign V.
При V = О утверждение очевидно.
486
ФОРМУЛЫ с НАИМЕНЬШИМ ЧИСЛОМ УЗЛОВ
[ГЛ. 22
Докажем, что при надлежащем выборе параметров к и v имеется
шесть веш,ественных точек пересечения прямых /Сз = 0 с кривой
второго порядка Q^ax^ + W^ — 6 = 0. Если а>0 и Y > О- '^о
Q==:0 — эллипс, и утверждение верно при любых значениях
параметров ^ и V. не равных одновременно нулю.
Отметим, что по крайней мере одно из чисел а и у положительно»
как это следует из равенства aiLi4o + Y!^22 = M'2o^ > О- Пусть а > 0.
Прямые К^=^0 при Я. = О, v = 1 имеют вид у = 0. у= ±т/ -^^ х.
Они пересекаются с кривой Q = О в шести различных и
вещественных точках ( ± l/ —, О j, ( i 1/ ~ » ± 1/ —). Утверждение верно
и при значениях параметров к, v, близких к Я- = О, v = L Если Y > О»
вещественные точки пересечения получим при Я.==1. v = 0.
Пусть Q — круг: x^-^-y^-^l. Кривая Q=0 представляет собой
2
окружность A:2-4~y^ = Y ^' следовательно, шесть точек пересечения
этой окружности с прямыми /Сз = 0 вещественны и различны при
всех % и V. Для заданного отношения параметров к: v получаем
определенную кубатурную формулу.
При Я. = 0, v= 1 уравнение/Сз =:О определяет три прямые ^'^О.
у=±|^3х. и шесть узлов кубатурной формулы располагаются
в вершинах правильного шестиугольника, вписанного в окружность
2
д:2^у2__ при этом две вершины лежат на оси х. Седьмой узел
формулы располагается в начале координат. Мы не будем заниматься
вычислением коэффициентов формулы, а приведем результат
вычисления в виде таблицы.
-^k
Ук 1
Сь
0
0
Т
3
0
1
Кб
1
1
1
/2
_0
3
0
1
1
V'2
1
/6 ,
1 1
Г 2
л;
т
Если Й — квадрат: —l<;x, y<;i» то кривая Q = 0 также пред-
14
ставляет собой окружность x2 + y^=rrg-. Таким образом, и в этом
случае при каждом заданном отношении % : v получаем кубатурную
§4]
КУБАТУРНАЯ ФОРМУЛА РАДОНА
487
формулу. Приведем таблицу узлов и коэффициентов кубатурной
формулы для квадрата при >1==0, v=l.
1 i
\ук
\ck
0
0
8
7
V 15
0
V 15
0
20
63
1
/1
1
-VI
1
/1
1
V3\
-/1
5
9
Литература
Георгиев Г,, Формулы механической квадратуры с минимальным
числом членов при многократных интегралах, ДАН СССР 83, № 4 A952),
521—524.
Thacher Н. С, Optimum quadrature formulas in 5 dimensions, Math.
Tables and otlier Aids Сотр. U, № 59 A957), 189—194.
Stroud A. H., Nunerical integration formulas of degree two. Math, of
Сотр. 14, № 69 (I960), 21—26,
Фаддеев Д. К. и Фаддеева В. Н., Вычислительные методы
линейной алгебры. М., Физматгиз, 1960.
Мысов ск их И. По Доказательство минимальности числа узлов одной
кубатурной формулы для гипершара. Журн. вычислит, матем. и матем. физ.
6, № 4 A966), 621—630.
Hammer Р. С, Stroud А. Н., Numerical integration over simplexes,
Math. Tables and other Aids Сотр. 10, № 55 A956), 137—139.
Radon J., Zur mechanischen Kubatur, Monatsh. fiir Math. 52, K& 4 A948),
286^300.
ГЛАВА 23
КУБАТУРНЫЕ ФОРМУЛЫ ДЛЯ ОБЛАСТЕЙ ЧАСТНОГО ВИДА
§ 1. Гиперкуб
Через К будем обозначать /г-мерный куб—l^^jc^^l (/=1,
2, ..., п). Наиболее простой способ получения кубатурных формул
для вычисления интеграла по К состоит в л-кратном применении
квадратурных формул.
Интеграл по К приводится к вычислению п простых интегралов
1 1 1
J / (л:) й^л: = J ufxi J с/лгз . . . J / {х^ л: J dx^,
к -1 -1 -1
Интеграл по каждой переменной в правой части этого равенства
заменим квадратурной суммой, например, по формуле Гаусса
Получим кубатурную формулу
р
^ ^1 ^«-1
Формула B3.1.1) имеет т?''узлов И точна, когда/(;c) = x"i ... х^«.где
О ^ ccj^-^ 2/7—1 (^ = 1, 2, . . ., д), В частности, она точна, когда
/ (х) — любой многочлен степени 2р — 1.
Указанный способ получения кубатурных формул можно
применять и в несколько более общем случае, когда речь идет о
вычислении интеграла по К с весовой функцией
Р {^) = Pi {х^) Р2 (-^2) • • • Рп (-^ J-
Формула B3.1.1) при /7 = 3 точна для всех многочленов пятой
степени и имеет 3" узлов. Приведем две кубатурные формулы,
точные для многочленов пятой степени и имеющие меньшее число узлов
§ 2] ГИПЕРСФЕРА 489
Кубатурная формула
к
^Л^/(±а. ±а ±a)-^B^f@ О, ± р, 0. .... 0),
1 1
B3.1.2)
где
" "" 5.2'^+з
^=УЗE^)' Р^1/-Ж-' ^--U"M^)^ ^■
Eл+ 4J*
имеет 2^-\-2п узлов. Нетрудно проверить, что она точна для всех
многочленов пятой степени. При п ^ 6 получаем Р> 1, так что 2п
узлов находятся вне /С.
Кубатурная формула (Хаммер и Строуд)
2/1
|/(х)й?;с^Л/@. .... 0)+^^/@. ..., 0.±а. О, .... 0) +
к I
2п (п - 1)
+ С ^ /(О, .... 0.±р. о 0.±р.0. ..., 0). B3.1.3)
где
«==/4-. Р=-/|-.
л :.=.^B5/г2_115/г+1б2), Б ==^G0 — 25«). С==-^^^,
имеет 2п?~{-\ узлов. Можно проверить, что она точна для
многочленов пятой степени. Ее узлы принадлежат области интегрирования,
коэффициент В при /г ^ 3 отрицателен.
§ 2. Гиперсфера
Рассмотрим кубатурные формулы для вычисления поверхностного
интеграла
/= j f(x)dS, B3.2Л)
где R—сфера х^+ .. . -f х^== г^ радиуса г и dS—элемент
поверхности.
490 ФОРА\УЛЫ для ОБЛАСТЕЙ ЧАСТНОГО ВИДА
Перейдем в интеграле I к сферическим координатам
(ГЛ. 23
Xi = rcos Ф1.
Х2 = г 51*Пф1 С03ф2,
a:^_2 = г sin9i 81пф2 . .
х^_1 = г sin Ф1 sin Ф2 ..
Х^ = г 51Пф151пф2 . .
0<ф/<л (/-=:!.^2,
• 81Пф„_зС05ф^_2. 1
• 51Пф„„з5^Пф«-2С05ф^_1.
. 81Пф^_з51Пф„_25тф„_1,
, .., п—2), 0<ф„_1<2я. 1
} B3.2.2)
Элемент поверхности в сферических координатах есть
и мы получаем
л 2л
^"^'"" ^1 * ' • J J /(''С05ф1, • • .M111""^Ф1 • • • 51Пф^^2^Ф1 • • • ^Ф«-1-
О 0 0
B3.2.3)
В этом интеграле областью интегрирования является {п—1)-мер-
ный параллелепипед, так что при построении кубатурной формулы
можем воспользоваться способом кратного применения квадратурных
формул. Приведем кубатурную формулу такого рода (И. П. Мысов-
ских). Пусть fix) — многочлен степени не выше m=^2q—1. Тогда
подынтегральная функция в B3.2.3) есть тригонометрический
многочлен степени не выше т относительно переменной ^n-v Выполнив
интегрирование по ^n-v получим in — 2)-кратный интеграл, в
котором подынтегральная функция как функция от фд_2 представляет
собой произведение 51пф/^_2 ^ тригонометрического многочлена
степени ^т, зависящего лишь от созф„_2- ^ самом деле, нечетные
степени 51Пф„_2 могут появиться только от одночленов, содержащих
множитель л:"-^^_|. где a-f-P нечетно. Но интеграл от такого
одночлена по ф„_1 равен нулю, так как
2д
81п"ф„-1С03^ф„_1Й?ф^-
= 0,
если хоть одно из чисел а или р нечетно.
Аналогично в результате интегрирования по ^ri-\ " Фл-.2 "Случим
(л—3)-кратный интеграл, в котором подынтегральная функция как
функция от ф^_з ^сть произведение 51п2ф„_з и тригонометрического
многочлена степени ^т, зависящего лишь от со5ф/^_з- ^ самом
деле, нечетные степени з1пф/^_з могут появиться только от одночле-
§ 2] ГИПЕРСФЕРА 491
НОВ. содержащих множитель •^^-^^_i^:y_2' ^^^ a + p + Y нечетно.
Но интеграл от такого одночлена по ф,^_| и ф^_2 равен нулю, так как
J cos^ ф„,2 • sin'"'''^ Ф«-2С?Ф„-2 J Sin*" ф^_1 cos^ф^_1 б?ф^,1 = 0.
о о
если хоть одно из чисел а, р, у нечетно.
Вообще, в результате интегрирования по ф„_1. Ф„-2' •••' Фя-й-1
(O^k^n — 3) получим (п — к — 2)-кратный интеграл, в котором
подынтегральная функция, как функция от ф„_J^_2» представляет собой
произведение sin*+^ф^„J^_2 и тригонометрического многочлена
степени ^т, зависящего лишь от cosфд_JS;_2• Этот многочлен будем
обозначать через Р^(со5ф„_^_2)-
Интеграл по переменной ф^_1 в B3.2.3) заменим квадратурной
суммой по формуле прямоугольников с т~\~1 ^=2д узлами. Так как
мы считаем, что f (х) — многочлен степени ^т, то такая замена
сохранит точное значение интеграла.
Чтобы заменить квадратурной суммой интеграл по Фя_й_2
(О < ^ < д — 3)
я;
J 51п^ + Ч«-;^-2^т(С05ф,_й.2)^Ф«-й-2. B3.2,4)
О
сделаем в B3.2.4) замену переменной интегрирования ^ = cosф^_J^_2.
В новой переменной интеграл B3.2.4) перепишется так;
~г
Мы получим точное значение этого интеграла, если воспользуемся
квадратурной формулой типа Гаусса с весом A—f^)^ на отрезке
[—1, 1] и с 7 узлами:
j A ^^t^)T,p^t)dt^'^Afq^{tfl B3.2.5)
-1 y.i
Для упрощения записи в B3.2.5) не отмечена зависимость узлов и
коэффициентов от q.
Введем обозначение
F{r, ф1, ..., ф^==:=
= /(гС05ф1, Г31пф1С03ф2, ..., Г51пф15тф2 ... 5!Пф^_1) B3.2.6)
492 ФОРМУЛЫ для ОБЛАСТЕЙ ЧАСТНОГО ВИДА [ГЛ. 23
И рассмотрим кубатурную формулу
X Р(г. (р(/»). 4'^\ . .., Ч^Цп-^\ ^у), B3.2.7)
где
^Jl.k-2'^^^'^^^^^^^P^
а Г; и Af — узлы и коэффициенты квадратурной формулы B3.2.5).
Ясно, что кубатурная формула B3,2.7) точна» когда f (х) — любой
многочлен степени ni^=2q—1. Она имеет 2^'^"^ узлов.
Укажем еш,е формулу В. А. Диткина и Л. А. Люстерника для
вычисления интеграла по поверхности трехмерной сферы R: х\-\-х1-\~х1^== 1
12 20
J/(x)rf5s§5;/(^@L-^^/(y')). B3.2.8)
R /=1 i=l
Здесь л:(^^ — вершины вписанного в R икосаэдра, У^) — вершины
вписанного в R додекаэдра, при этом У^>лежат на
перпендикулярах, опуш,енных из центра икосаэдра на его грани. Формула B3.2.8)
точна, когда f (х) — многочлен девятой степени от трех
переменных Xjt Х2* Х^,
§ 3. Гипершар
Будем строить кубатурные формулы для вычисления интеграла
J/(jc)^x, B3.3.1)
S
где 5 — единичный гипершар: л:^+ ... +х^^1.
Сначала построим кубатурные формулы специального вида
р
^ f{x)dx^^Bj j fix)dSj. B3.3.2)
В правой части стоит поверхностный интеграл по сфере Rj'-
jc^ + . .. + х^ = г2 и j5 . — коэффициент. Нам надлежит определить 2р
постоянных г J и в J (У^=1, 2, ..., р). Потребуем, чтобы формула
B3.3.2) обращалась в точное равенство, когда f (х) является
многочленом возможно более высокой степени.
§ 3] ГИПЕРШАР 493
Нетрудно видеть, что равенство B3.3.2) выполняется точно,
когда f {х) есть одночлен ху ... x\i^, у которого хоть одно из чисел
Pj, ..., р„ нечетно. Таким образом, при построении кубатурной
формулы B3.3.2) мы вправе ограничиться одночленами вида
xfi...xf«. а,+ ... +a^=-v. B3.3.3)
В интеграле по 5 от одночлена B3.3.3) перейдем к сферическим
координатам B3.2.2). Якобиан преобразования B3.2.2) равен
и мы получим
1
J xf 1 . . . х^^п dx==^ r^^^""' dr • / (aj, .... aj, B3.3.4)
где
n 2я
^/(«1 ^n)= I • • • J J C0S9i)^"l ... E1пф151Пф2 ... 51пф„_1)^"^Х
О О
X sin«-2 ф^ _ . sin ф„_2 й?ф1 . . . йГф„_1 > 0.
Перейдем к сферическим координатам в поверхностном интеграле
по Rj от одночлена B3.3.3):
J xf^ . . . x':ndS. = r'J^^-4{a, а„). B3.3.5)
^;
Запишем теперь, что формула B3.3.2) обращается в точное
равенство, когда /(х) совпадает с одночленом B3.3.3), и воспользуемся
равенствами B3.3.4) и B3.3.5). Получим
ivr"-'=2^- B3.3.6)
При соблюдении этого равенства формула B3.3.2) точна, когда
/(х)— любой однородный многочлен степени 2v. Так как мы должны
найти 2р неизвестных Гу, В^ (У=1, 2, .... р), то можем
потребовать, чтобы равенство B3.3.6) было выполнено при v = 0, 1,
2 2р—\\
р
25,^2v+«-.=^ 1_ (v = 0. 1 2р--\). B3.3.7;,
/-1
494 ФОРМУЛЫ для ОВЛАСТЕЙ ЧАСТНОГО ВИДА [ГЛ. 23
Пусть ti—четное. Систему B3.3.7) перепишем в виде
Такую же систему получим, если будем строить квадратурную фор-
мулу типа Гаусса для промежутка [О, 1] и веса t'^
1^2' 4^{t)dt^^CjipiTj). B3.3.8)
о у=1
Таким образом, параметры квадратурной формулы B3.3.2) при
п четном определяются равенствами
г) = х.. 2В.гу'^С^ (у==1, 2. .... р),
где Xj и Су — узлы и коэффициенты квадратурной формулы типа
Гаусса B3.3.8).
При п нечетном систему B3.3.7) заменим равносильной системой
^ ^/)-^г)=^ J г^-^гЫг (^ = 0. 1. ..., ip~iy B3.3,9)
J^-P -1
Здесь штрих у знака суммы означает, что опускается слагаемое,
отвечающее у = 0. Считаем г_^:=^ — Гу, В^~В^ (/=1, 2, .... р),
так что при k нечетных уравнения B3.3.9) принимают вид 0 = 0,
а при k четных получаем уравнения B3.3.7).
Но система B3.3.9) совпадает с системой, которую мы получим,
если будем строить квадратурную формулу типа Гаусса с 2р узлами
для отрезка [—1, 1] и веса t^" :
1 р
J f-\{t)dt^ Yl ^;Ф(^)- B3.3.10)
Таким образом, радиусы г^ сфер /?у при п нечетном совпадают
с положительными узлами квадратурной формулы B3.3.10), а
коэффициенты В J определяются из равенства D j = Bjr"~^, где D, —
коэффициенты формулы B3.3.10).
Из способа построения кубатурной формулы B3.3.2) ясно, что
она точна, когда f (х) — любой многочлен степени 4р — 1. С помощью
формулы B3.3.2) мы получим обычную кубатурную формулу для
вычисления интеграла B3.3.1). точную для многочленов степени
4/?—1.
I
§ 4] СИМПЛЕКС 495
Интеграл в правой части B3.3.2) заменим кубатурной суммой
по формуле B3.2.7) при q^=^2p. Получим
5 / = 1 1 = 1 /i ^п-2^^
X Р(г.. ф(^1). ф(Ч .... ф(/д-2), ^ i). B3.3Л 1)
Здесь функция /^ определена равенством B3.2.6), ф^^{^^^_2 = arccos^(*\
а ^у*' и Ар — узлы и коэффициенты квадратурной формулы типа
Гаусса B3.2.5), в которой число узлов ^ = 2/7.
Кубатурная формула B3.3.11) аналогична формуле B3.1.1). Она
имеет B/7)" узлов и точна, когда f {х) — любой многочлен степени
Ар — 1. Формула B3.3.11) и способ ее получения указаны в статье 2)
И. П. Мысовских. При п = 2 формулу B3.3.11) получил Л. В.
Канторович, при д = 3 — В. А. Диткин.
Приведем еще кубатурную формулу для гипершара, аналогичную
формуле B3.1.3), точную для многочленов пятой степени и
имеющую 2д2 4- 1 узлов (Хаммер и Строуд):
2л
|/(х)йГх^Л/@, .... 0) + ^5]/@. .... О, ±а, 0 0) +
5 1
2л(«-1)
+ С 2] /(О' .... о, ±р, о, .... о, ±р, 0. .... 0). B3.3.12)
1
Здесь
^ ^ -, / 3 ^ -, / 3 д_/гЗ — Зп2 —10/2 + 36 я 2
V п4-4 ' ^ V п
t + 4' ^ К /г + 4' "'^ 18/2 + 36
^ 16 —/г2 я^ ^ _ /2 + 4
(^+.v
18/2 + 36
r(|+l)' 36n + 72,^«^,J-
4. Симплекс
Пусть j^/j^i--евклидово пространство л+1 измерений. Точку
пространства Е^^^ будем обозначать (х. t) = {x^, .... х^^, /)• Пусть
Q — л-мерная область в j^^+i, расположенная в гиперплоскости ^ = 0.
Рассмотрим область Р из f'/^^.p состоящую из точек вида (хA —^). /).
где x£Q и ^^[0, 1]. Область Р будем называть пирамидой.
Основание пирамиды—множество Q, ее вершина — точка (О О, 1),
496 ФОРМУЛЫ для ОБЛАСТЕЙ ЧАСТНОГО ВИДА [ГЛ. 23
Предположим, что нам известна кубатурная формула для вычисле-
ния «-кратного интеграла по области Q:
N
jf{x)dx^^AjfixU)). B3.4.1)
Тогда нетрудно указать кубатурную формулу для вычисления (п-\- \)-
кратного интеграла по области Р.
Обозначим через Р^ множество точек (л:A —t), t)^P таких, что
л: ^ Q (при фиксированном t). Очевидно, имеем
1 1
[ F{x, t)dxdt^ ^dt JF(xJ)dx= I (l-tf dt J F{y(l^t), t)dy,
P Q P^ 0 Q
Здесь в интеграле по Р^ мы выполнили замену переменных
интегрирования х = A —t)y, множитель A — t)'^ — якобиан преобразования.
К интегралу по Q применим кубатурную формулу B3.4.1). Получим
1 7V
\Р{х, t)dxdt^ ^ {\ —tf dt^^Ajf {xU){\ —t). t). 'B3,4.2)
p 0 j=\
Для вычисления простого интеграла в правой части B3.4.2)
применим какую-либо квадратурную формулу для промежутка [О, 1] и
веса A—/)'':
1 Р
l{\-tYi^{t)dt^Y^B,^it,\ B3.4.3)
о ( = 1
Получим
р N
\ F(x. t)dxdt^^ 2б,Л,.^(.^^ЛA_-^.), ti). B3.4.4)
Это и есть требуемая кубатурная формула. Она имеет pN узлов
Если кубатурная формула B3.4.1) точна для всех многочленов
степени т от п переменных х^, .... х„ и квадратурная формула B3.4.3)
точна для всех многочленов степени т от переменной ?, то
кубатурная формула B3.4.4), как следует из способа ее построения, точна,
когда F{x, t) есть любой многочлен степени т от /г-f-1
переменных Xj, .... Х„, t.
Указанным путем можно получить кубатурные формулы для ряда
областей. В виде примера приведем кубатурную формулу для
симплекса. Для упрощения записи симплекс Т-^ считаем трехмерным:
Xi>0, Х2>0, Хз>0, Х1 + Х2 + Хз<1.
СИМПЛЕКС 497
Сначала построим кубатурную формулу для треугольника Т<^\
Xi^-O, Хз^О, Xi + X2<;i. рассматривая его как пирамиду,
основанием которой Q является отрезок [О, 1] на оси Xj и вершиной —
точка (О, 1), В качестве формулы B3.4.1) возьмем квадратурную
формулу Гаусса с р узлами
lfix{)dx,^^cTf{t?)
и в качестве формулы B3.4.3)—квадратурную формулу типа Гаусса
с весом 1 —t и р узлами
1
J0-t)q^it)dt^'^C%{tf).
о у-1
Получим кубатурную формулу для Гз
J F{x,, x^)dx,dx^^ 2 <^fcfF{tf\\ —tf). tf), B3.4.5)
i,J~l
точную, когда F(Xp X2) — многочлен степени 2p — 1 от Xj и X2.
Симплекс Гз
Xi>'0, Хз^-О, Хз^-О, Xi + X2 4--^3-^ ^
будем рассматривать как пирамиду с основанием Гз и вершиной
(О, О, 1). В качестве формулы для вычисления интеграла по Гд возьмем
кубатурную формулу B3,4.5), а в качестве формулы B3.4.3) возьмем
квадратурную формулу Гаусса с весом A—ty и р узлами
о ft»-!
Получим
J F{Xi, Xg. Х3) dxi dx2 dx^ ^
^ i cfc^^cfF {tf A - t'f) A ^ tn tf A -1^^). tn
Эта кубатурная формула имеет р^ узлов и точна, когда F{х^, Хз, Хз)
является многочленом степени 2р — 1 от Xj, Х2, Х3. Таким же путем
можно получить кубатурную формулу для л-мерного симплекса Г^.
498 ФОРМУЛЫ для ОБЛАСТЕЙ ЧАСТНОГО ВИДА [ГЛ. 23
Литература
Hammer Р. С, Stroud А, Н., Numerical evaluation of multiple
integrals И, Math. Tables and other Aids Сотр. 12 A958), Ka 64, 272—280.
Мысовских и, П. 1) О кубатурных формулах для вычисления
интегралов по поверхности сферы, Сибирск. матем. журн. 5, № 3 A964), 721—723.
2) Кубатурные формулы для вычисления интегралов по гипершару,
ДАН СССР 147, № 3 A962), 552—555.
Диткин В. А- и Люстерник Л. А., Об одном приеме
практического гармонического анализа на сфере, Вычисл. матем. и вычисл. техн..
сб. 1 A953). 3—13.
К а н т о р о в и ч Л. В., Об особых приемах численного интегрирования
четных и нечетных функций, Труды матем. ин-та АН СССР 28 A949), 3—25.
Диткин В. А., О некоторых приближенных формулах для вычисления
трехкратных интегралов, ДАН СССР 62, № 4 A948), 445—447.
Hammer Р. С, Marlowe О. J., Stroud А. Н., Numerical
integration over simplexes and cones. Math. Tables and other Aids Comp, 10 A956),
Mb 55. 130—137.
список ИСПРАВЛЕНИЙ
СПИСОК ИСПРАВЛЕНИЙ,
которые необходимо внести
в «Справочную книгу по численному интегрированию»
В. И. Крылова и Л. Т. Шульгиной
499
Стр.
21
21
35
35
67
72
1 78
81
81
101
112
192
208
232
248
260
261
261
268
268
270
Строка
2 св.
3 св.
15 сн.
12 сн.
3 св.
2 св.
2 св.
4 сн.
3 сн.
1 сн.
5 сн.
6 сн.
24 сн.
5 ев.
3 сн.
1 4 сн.
6 св.
18 сн.
4 св.
13 св.
20 сн.
Напечатано
Интегрируема на [а, Ь] и на
концах а и b
производные р' (а) и р' {Ь)
b
Х\ P(xL?(x)f'^''\%)dx
а
/?л(/) = /^"'(т1)Bл!)-'Х
ь
Х\ P(x)i^'^(x)dx
а
ii^J. у + Ь ..мУ+А).
"^ 6а4/гЗ
еб(? = 2[0A2—502) +
+ ... cos2 0]:
0в/? = 2 [0A56—702),..
... — 15A2—502)];
ц ix\ = —. ,
^^ ^ Я J yi^l2 *
/,=.-.зА?#>...
B)fe + 3)!
49956522 (—3)
0,21270 79233 22410 297
23750004 (+2)
16180848 (—1)
\ 2,20769
4,1078512584
2,7703542
^=4Ш4
2,535055094
0.47103055
Следует читать
Интегрируема на [0. 1] и на
концах 0 и 1
производные р' @) и /?' A)
1
x|/'{^)«)^^)/'">(i) J
а 1
Л„(/) = /'''>(г1)[Bл)!]-'Х
b 1
XJ р(.х)(оЦх)ах\
1 22^+2'^+^п!Г2(р + п + 1)
{i^j, j+h ..., у + 0-
06Q=== 0A2—502)+ ...COS2 0;
06/? = 0 A56—702) ...
... — 15A2—502);
а (х) = — — ■,
\^^ ' я J i^r^TT
L ,...з>;;'(|)...
B^ + 2)!
49956522 (—2)
0,21270 79033 22410 297
23730004 (+2)
16180848 (+1)
2,2069
4Д078511258
2,7703544
И = ^т(т)Ц
2,53505509
0,47103057
500
список ИСПРАВЛЕНИЙ
Продолжение
Стр.
270
270
271
271
272
272
272
272
273
275
276
276
276
279
319
Строка
12 сн.
3 сн.
12 сн.
10 сн.
27 сн.
19 сн.
19 сн.
4 сн.
25 сн.
12 св.
26 сн.
25 сн.
24 сн.
2 сн.
20 сн.
Стр. 15
в формула?
Напечатано
0,944299
1,4351
0,837258
7,83616
8,878144073
0,5077923
0,8800253
1,1763
0,619490179
0,970542128
0,175795523
0,48435695
0,98049993
7691,277 ±24344,63/
±,35355 33005 93274/
3. В конце сноски добавить
: нужно умножать на Л».
Следует читать
0,944301
1,4354
0,837260
7,83618
8,878144075 |
0,5077925
0,8800255
1,1765
0,619490181
0,97054213
0,175795528 1
0,48435697 i
0,98049995
7691,277+24344,63/
±.35355 33905 93274/
фразу: ^Координаты узлов ,