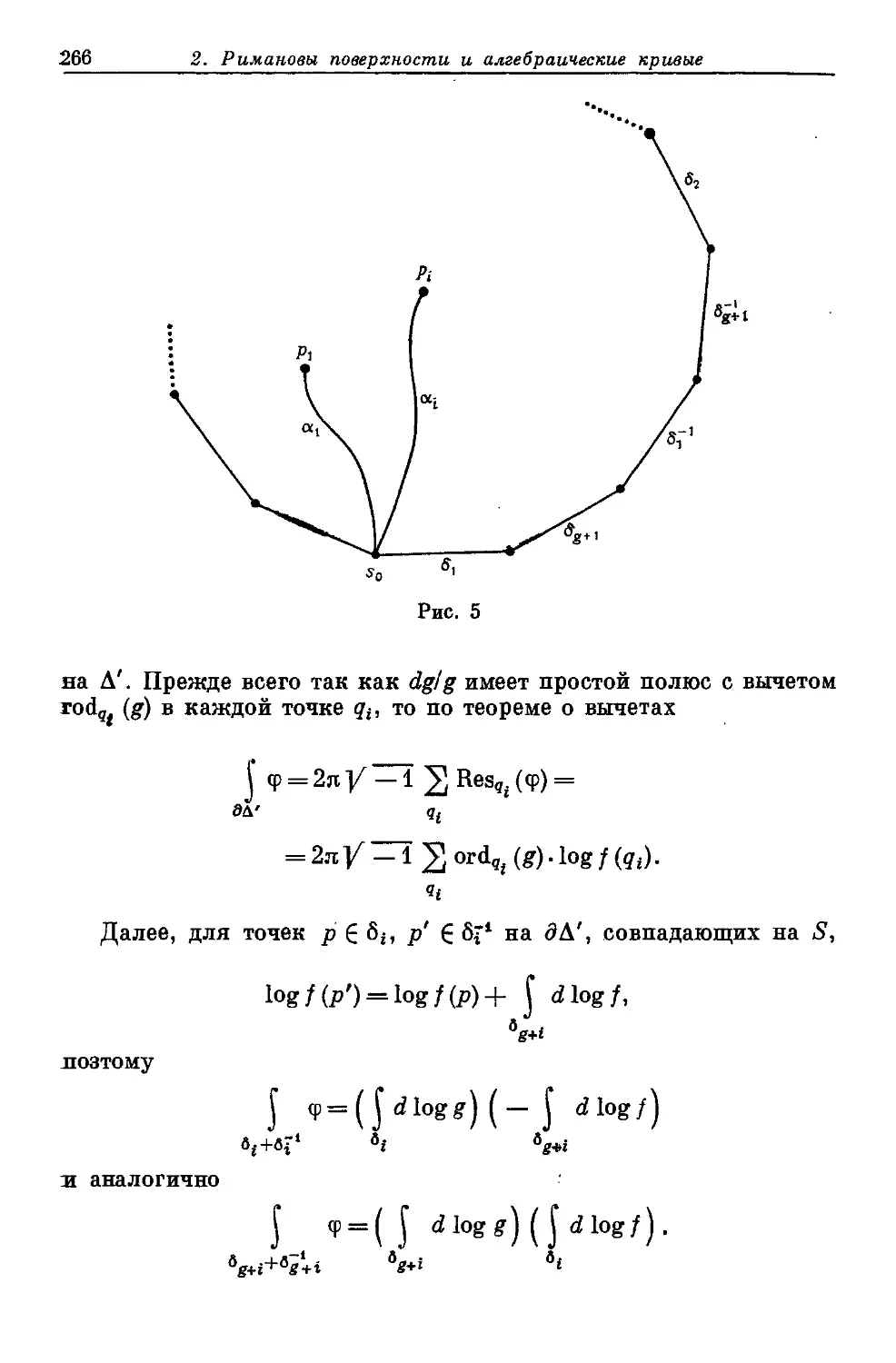
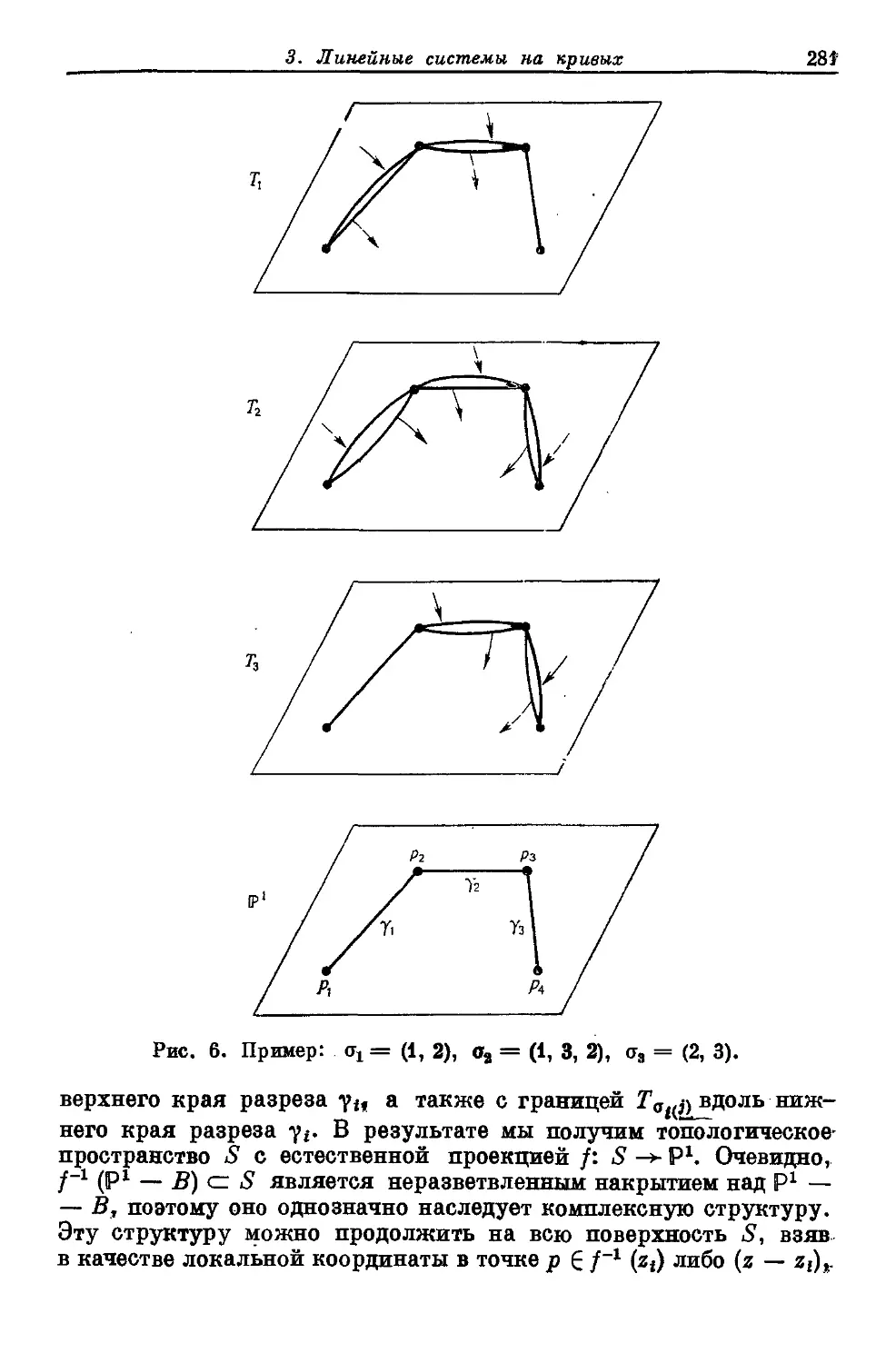
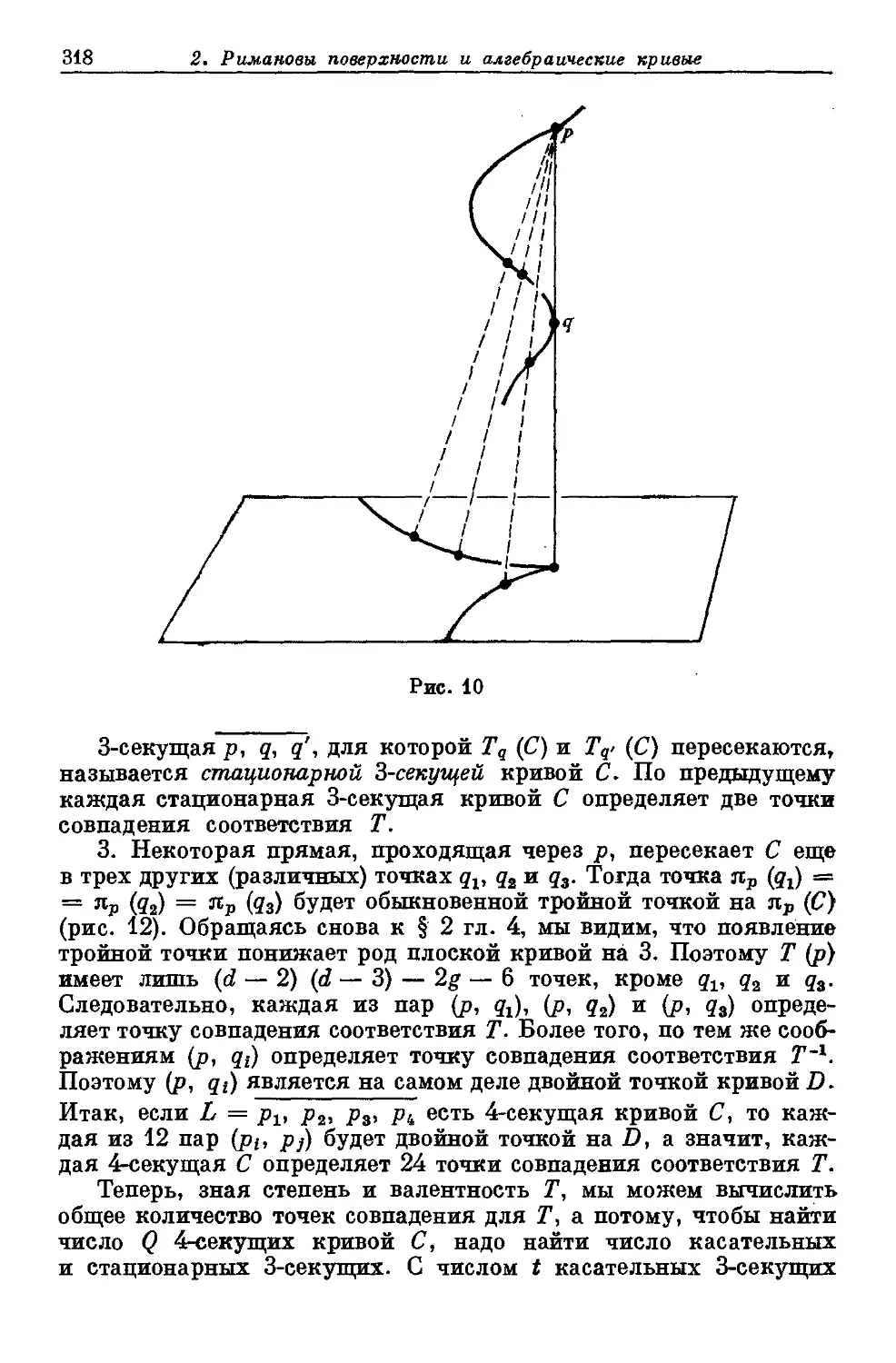
Текст
ББК 22.14
Г 85
УДК 513.6
Гриффите Ф., Харрис Дж.
Г 85 Принципы алгебраической геометрии: Пер. с англ.— М.: Мир,
1982.—Т. 1.-496 с, ил.
Фундаментальная монография, написанная известными американскими
учеными, содержит основы современной алгебраической геометрии, ее связи
с другими отраслями математики, а также необходимый подготовительный
аппарат. С присущим Ф. Гриффитсу мастерством вскрываются принципиальные
идеи этой науки, которая в последнее время находит многие важные
применения. Монография удачно дополняет уже вышедшие на русском языке книги
Д. Мамфорда и Р. Хартсхорна.
В русском переводе книга выходит в 2-х томах. Том 1 содержит
главы 0—3.
Для математиков, физиков, преподавателей, аспирантов и студентов
университетов.
1702040000—043 ББК 22,14
^ 041(01)—82 '*'~^^' ''• * 517.3
Редакция литературы по математическим наукам
Copyright © 1978 by John Wiley &.
Sons, Inc.
All rights reserved. Authorized
translation from English language edition
published by John Wiley & Sons, Inc.
(2) Перевод на русский язык, «Мир»,
1982
Филип Гриффите, Джозеф Xiippac
ПРИНЦИПЫ АЛГЕБРАИЧЕСКОЙ ГЕОМЕТРИИ
том 1
Ст. научный редактор Е. И. Поужникова. Мл. научный редактор Л. А. Королева.
Художник В. К. Бисенгалиев. Художественный редактор В. И. Шаповалов.
Тезснический редактор Л. П. Чуркина. Корректор Н. А. Гиря.
ИВ № 2739
Сдаво в набор 25.01.82. Подписано к печати 20.07.82. Формат e0X90</ie.
Бумага типографская XS 1. Гарнитура обыкновеянан. Печать высокан.
Объем 15,50 б. п. Усл. печ. п. 31,00. Усл. кр.-отт. 31,00. Уч.-изд. п. 27,25.
Изд. 1й 1/1269. Тираж 8000 экз. Зак. 046. Цена 3 руб. 10 коп.
ИЗДАТЕЛЬСТВО «МИР». Москва, 1-й Рижский пер., 2.
Ордена Трудового Краевого Знамени
Московская типография 1й 7 «Искра революции» Союзполиграфпрома
Государственного Комитета СССР по делам издательств, полиграфии
и книжкой торговли. Москва 103001, Трехпрудный пер., 9.
ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
Авторитет алгебраической геометрии как одной из наиболее
фундаментальных и содержательных математических дисциплин
настолько велик, что она не нуждается в рекомендациях. Ее
популярность особенно возросла в связи с недавно найденными новыми
приложениями (в теории нелинейных дифференциальных
уравнений, теоретической физике и теории кодирования). Однако в
последнее двадцатилетие стало уже традицией писать монографии
и учебники по алгебраической геометрии преимущественно на
языке теории схем Гротендика, иначе говоря основываясь на
результатах и методах коммутативной алгебры. Для многих
читателей, желающих быстро войти в предмет, этот подход оказывается
не вполне приемлемым прежде всего из-за трудного формализма
оснований. Идея максимальной общности, заложенная в теории
схем, ставит в затруднительное положение и самих авторов,
сторонников схемного подхода: ни в какой книге разумного объема
(скажем, учебнике) с этих позиций практически невозможно дать
сколько-нибудь полное представление о всем грандиозном здании
алгебраической геометрии, не говоря уже о ее многочисленных
приложениях.
Авторы предлагаемой вниманию читателя книги избрали
другой путь. Их учебник написан в стиле, так сказать,
«неоклассицизма»: авторы работают исключительно над полем комплексных
чисел, что открывает широкие возможности для использования
методов комплексного анализа, дифференциальной геометрии и
топологии. В то же время это делает книгу более доступной читателю
по сравнению с книгами, написанными на языке абстрактной
алгебры. Разумеется, авторы свободно пользуются также и алгебро-
геометрическими методами.
Разнообразие и гибкость используемых в книге методов
позволяют изложить в ней огромное количество фактов как
классических, так и современных: можно сказать, что по степени охвата
материала книга не имеет себе равных среди существующих
учебников по алгебраической геометрии, и дело здесь, конечно, не
только в ее большом объеме.
Предисловие редактора, перевода
Основными объектами изучения книги Гриффитса и Харриса
являются алгебраические многообразия над полем комплексных
чисел: римановы поверхности и алгебраические кривые,
алгебраические поверхности, грассмановы многообразия и некоторые их
специальные подмногообразия, т. е. то, что относится к основному-
стволу алгебраической геометрии. Вряд ли стоит здесь подробно
говорить о конкретном содержании книги — это с достаточной
полнотой сделано в авторских введениях к каждой из глав и ясно
из очень подробно составленного оглавления. О том, что не вошло
в книгу, также сказано в предисловии авторов.
Отметим здесь только то, что в свой учебник авторы включили,
с одной стороны, много интересных вещей из классической
геометрии, а с другой — совсем свежий материал из журнальных статей.
В гл. 2 о римановых поверхностях и алгебраических кривых,
например, обсуждается классическая проблема Брилля — Нётера
о специальных дивизорах, выводятся формулы Плюккера для
пространственных и плоских кривых и даны элементы теории
соответствий на кривых. В эту же главу помещен очень важный
параграф о геометрии якобианов кривых, включающий
классические теоремы Римана о тета-дивизоре и его особенностях на якобие-
вом многообразии кривой; приводится доказательство теоремы
Торелли в варианте Андреотти.
Основные технические результаты о вычетах в гл. 5 и их
применения к теории двойственности до появления настоящей книги
встречались лишь в периодике.
Несколько слов о главе 6. По структуре и логике содержания
книги эта глава по аналогии с главами 2 и 4 (о кривых и
поверхностях) должна была бы (и это отмечают сами авторы) содержать
теорию трехмерных алгебраических многообразий. Но во время
написания книги эта теория еще только начинала развиваться,
хотя и очень интенсивно. Авторы ограничились рассмотрением
конкретного трехмерного многообразия, так называемого
квадратичного комплекса прямых (в стандартном задании уравнениями
это гладкое пересечение двух квадрик в Р*). На этом конкретном
примере они продемонстрировали некоторые яркие фрагменты
создаваемой новой теории. По существу, это можно рассматривать
как введение в теорию промежуточного якобиана и теорию
многообразий Фано (к классу которых относится и рассматриваемый
квадратичный комплекс прямых). В настоящее время, когда уже
видны общие контуры бирациональной классификации
трехмерных алгебраических многообразий и подробно иэзп1ены некоторые
их классы (см. литературу, добавленную при переводе), глава
о трехмерных многообразиях могла бы быть написана не менее
широко и содержательно, чем главы 2 и 4 о кривых и поверхностях.
Следует обратить внимание также на своеобразный стиль книги.
В соответствии с одним из принципов, которыми руководствовались
Предисловие редактора перевода
авторы при работе над книгой и о которых они говорят в своем
предисловии, упор в ней делается не на отшлифовку доказательств
фундаментальных теорем, а на применение этих теорем в
конкретных ситуациях. Для заинтересованного и вдумчивого читателя
восстановление опущенных деталей доказательств может служить
хоропшм упражнением (тем более, что специальных упражнений
в книге нет), а размышления над неформальными авторскими
замечаниями — стимулом ДЛЯ" дальнейшего" углубленного изучения
и развития предмета.
Что касается принципа замкнутости изложения, то это вещь
весьма условная. Несмотря на все-усилия авторов, читать книгу
без знания хотя бы элементарных основ теории функций многих
комплексных переменных, дифференциальной геометрии и алгебры
довольно трудно. " "'"'' '^ 'Г
в целом книга написана в хорошем интуитивно понятном стиле,
что несомненно облегчит ее изучение. Она будет служить ценным
геометрическим дополнением к существующим учебникам по
алгебраической геометрии и очень удобна для ссылок. Обилие
конкретного материала, разнообразие методов исследований,
вдохновляющий стиль изложения делают книгу полезной,
привлекательной и доступной всем-читателям, интересующимся
алгебраической геометрией и^ комплексным анализом.
Перевод авторского предисловия и глав 4 и 5 выполнен
В. И. Даниловым, глав О и 6 — Г. Б. Шабатом; глав 1, 2 и 3 —
В. В. Шокуровым.
В. А. Исковских
СТРУКТУРА КНИГИ
Том 1
О
предварительные сведения
Комплексные
алгебраические
многообразия
Риыановы поверхности
и алгебраические
кривые
Дальнейшие методы
Том 2
Поверхности
5
Вычеты
Квадратичный
комплекс прямых
ПРЕДИСЛОВИЕ
Алгебраическая геометрия — один из старейших и
высокоразвитых разделов математики. Она тесно связана с проективной
геометрией, комплексным анализом, топологией, теорией чисел
и многими другими областями современной математики. Кроме
того, в последние годы алгебраическая геометрия претерпела
значительные изменения в стиле и языке. По этим причинам вокруг
нее возник некий ореол недоступности. В настоящей книге
излагаются некоторые основные общие результаты теории, еонровожда-
емые — и на это делается особое ударение — применениями к
исследованию интересных примеров и развитием вычислительных
методов.
При подготовке книги мы руководствовались нееколькими
принципами. Один из них состоял в том, чтобы развивать общий
технический аппарат лишь настолько, насколько это необходимо
для иззп1ения конкретных геометрических вопросов и специальных
классов алгебраических многообразий, играющих главную роль
в нашем изложении.
Второй принцип заключался в чередовании общей теории и
конкретных примеров, что видно уже из оглавления. Предмет
алгебраической геометрии особенно замечателен тем, как гармонично
сочетается в нем чрезвычайная сложность примеров с врозрачной
ясностью общих закономерностей. Мы попытались отразить это
переплетение при выборе тем и порядка изложения.
Третий общий принцип — сделать изложение замкнутым в себе.
В частности, мы старались дать полное доказательство всех
применяемых в книге «трудных» результатов. Сложность изучения
столь многогранного предмета, как алгебраическая геометрия,
состоит в изобилии перекрестных ссылок; это одна из причин
стремления к замкнутости изложения. Кроме того, мы старались
не формулировать и не ссылаться на недоказанные утверждения.
Эта книга не является обзором алгебраической геометрии; она
предназначена для того, чтобы разработать методы обращения
с конкретными геометрическими задачами. Мы пользуемся сначала
аналитическим подходом. В гл. О и 1 рассмотрены основные мето»-
10 Предисловие
ды и результаты теории комплексных многообразий, особенно те
из них, которые применимы к проективным многообразиям.
Начиная с гл. 2 о римановых поверхностях и алгебраических кривых
и затем в гл. 4 и б об алгебраических поверхностях и
квадратичном комплексе прямых изложение становится все более
геометрическим, следуя классическому руслу. В гл. 3 и 5 снова
применяется аналитический подход, с помощью которого рассматриваются
более частные вопросы теории комплексных многообразий.
Некоторые важные темы совсем не затронуты, например
арифметика алгебраических многообразий, теория модулей и теория
особенностей. Необходимая для их изз^ения техника развита
здесь недостаточно. Другие темы, такие, как униформизация
и автоморфные формы или монодромия и смешанные структуры
Ходжа, также опущены, хотя соответствующая техника по
большей части имеется в книге.
Мы хотели бы поблагодарить Джузеппе Кануто, Чжэнь Шэн-
шэня, Маурицио Корнальбу, Рэна Донеги, Робина Хартсхорна,
Билла Хоффмана, Дэвида Моррисона, Дэвида Мамфорда, Артура
Огуса, Теда Шифрина ж Лоринг Ту за плодотворные обсуждения;
Рут Судзуки за безукоризненную перепечатку рукописи;
сотрудников издательства «Джон Уайли», особенно Беатрис Шуб, за
огромное терпение и мастерство, проявленные в процессе
превращения нашей сырой рукописи в готовую книгу.
Кембридж, Массачусетс Филлип Гриффите
Джозеф Харрис
о
ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
Эта глава содержит некоторые предварительные сведения из
теории функций многих комплексных переменных, комплексных
многообразий, топологии и дифференциальной геометрии, которые
понадобятся нам в дальнейшем при изз^ении алгебраической
геометрии. Хотя наше изложение в основном замкнуто в себе,
некоторое знакомство читателя с перечисленными предметами
все же неявно подразумевается. Главная цель этой главы —
установить нашу точку зрения и изложить необходимые факты в том
виде, в котором они будут использоваться в дальнейшем. Нас будут
интересовать в основном следующие четыре круга вопросов.
1. Теоремы Вейерштрасса и следствия из них, обсуждаемые
в § 1 и 2. Они описывают локальное строение аналитических
многообразий. Сами теоремы в дальнейшем прямо не используются,
но даваемая ими геометрическая картина — например, локальное
представление аналитического многообразия как разветвленного
накрытия полидиска — имеет первостепенное значение.
Основания локальной аналитической геометрии обсуждаются и в
дальнейшем, в гл. 5.
2. Теория пучков, которая излагается в § 3, является важным
средством иззп1ения связи между аналитическими,
топологическими и геометрическими свойствами алгебраического многообразия.
Хорошим примером служит экспоненциальная последовательность
пучков, члены которой Z, О и О* отражают соответственно
топологическую, аналитическую и геометрическую структуры
многообразия.
3. Теория пересечений, обсуждаемая в § 4, является
краеугольным камнем классической алгебраической геометрии. Она
позволяет трактовать свойства инцидентности алгебраических
многообразий, а priori относящиеся к геометрии, в топологических
терминах.
4. Теория Ходжа, которая рассматривается в § б и 7. Это
наиболее изощренное из средств, описываемых в этой главе. Теория
Ходжа имеет здесь два основных применения: во-первых, она дает
12 0. Предварительные сведения
разложение Ходжа для когомологий кэлеровых многообразий;:
во-вторых, соединенная с вводимым в § 5 формализмом она
приводит к теоремам следующей главы об обращении в нуль.
1. ЭЛЕМЕНТЫ ТЕОРИИ ФУНКЦИЙ
МНОГИХ КОМПЛЕКСНЫХ ПЕРЕМЕННЫХ
Формула Когаи и ее применения
Обозначения. Точку в С" будем записывать в виде z^=-
п
= (Zi, ..., Zn), причем Zj = a;j-f>^'^j/j,|lzll2=(z,z)= 2 Utp.
i=l
Для открытого множества UbC^ через С°° (U) будем
обозначать множество С°°-функций, определенных на U, ачерезС°° {V) —
множество С°°-функций, определенных в некоторой окрестности
замыкания U множества U.
Кокасательное пространство в любой точке пространства С" ^
^ R^" порождено вещественными ковекторами {dxi, dyi}; однако-
часто удобнее работать в комплексном базисе
dZi = dxi + y —idyi, dzi = dxi — y—idyi
и во взаимном базисе касательного пространства
dzi ~ 2\ dxi' ^ дуг I ' d~zi ~ 2 ^ 9X1 '^ ^ dyt )■
В этих обозначениях формула для полного дифференциала
функции / имеет вид
г 3 ■'
В случае одной переменной С°°-функция /, определенная в
открытом множестве С/ с С, называется голоморфной, если она
удовлетворяет уравнениям Коши — Римана df/dz — 0. Записывая
/ (г) = U (г) + у —iv{z), мы видим, что это эквивалентно системе-
dz ^а: ду
от й/ ди , dv _
21т-тг — -т- + -г-- = 0.
dz ^У ^^
1. Элементы теории функций многих комплексных переменных 13
Функция / называется аналитической в области U, если в
окрестности каждой точки Zq^ U она допускает разложение в ряд по
степеням z — Zq, т. е.
/(Z)= 2«n(Z-Zo)"
n=0
В некотором круге А (zo, е) = {г: | г — Zq | < е}, причем ряд
сходится абсолютно и равномерно. Первый результат состоит в том,
что / аналитична тогда и только тогда, когда она голоморфна. Для
доказательства используется следующая
Интегральная формула Коши. Пусть А — круг в С, f ^ С°° (А).
Z G А; тогда
' 2я/-1 J "'—г 2nV—i J 6
(ш) dw Л dw
2я/ —iJ "» —z гя/ —1 J dw "»—z '
ад д
где контур интегрирования обходится против часовой стрелки
(тот факт, что последний интеграл определен, выяснится в
процессе доказательства).
Доказательство. Мы применяем формулу Стокса для
дифференциальных форм с особенностями, которая будет полз^ена в гл. 3.
Рассмотрим дифференциальную форму
1 f (w) dw
2яУ —1 <»—Z '
дляъ-фю имеем -пг I —^Г") = О» и поэтому
1 3/ (ш) dw Л dw
df\
2я/ —1 dw v)—z
Пусть Дв = А (z, е) — круг радиуса е с центром в z. Форма т)
принадлежит классу С°° в А — Ag, и, применяя теорему Стокса,
полз^аем
1 С f {w)dw 1 С f (iv) dw ,
Г f{w)dw _ 1 f jfj
2^/^ 3 w — z 2пУ^ J "»—z
' 0Д„ ' дл
. 1 f df dw
2я/^^ J dw ">
Д-Д^
Полагая w — z = re*e, получаем
2я/ —1 J "»—z 2n i ' ^ ^ '
rficA dw
z
14 0. Предварительные сведения
Это выражение стремится к / (г) при е —>- 0; кроме того,
dw Adw= — 2 У — 1 da; л dy= —2]/ —irdr А d0,
так что
df (ш) dw Л die
df
"^ dr А dQ
aw
^c\dr Ade\.
Таким образом, форма (df/dw) (dw а dw)/{w—z) абсолютно инте-
. _ Г d/ dw А dw л л
грируема в 4 и \ —=- *■ О при е -^ 0; отсюда уже все
J ди> "^ — ^
следует. Q
Теперь мы в состоянии доказать следующее
Предложение. Пусть U — открытое множество в С и f ^
g С°° (С/); функция f голоморфна тогда и только тогда, когда она
аналитична.
Доказательство. Предположим сначала, что df/dz = 0. Тогда
для Zo 6 и, достаточно малого в и z из круга Д (zo, в) радиуса 8
с центром в Zj имеем
. /.у 1 f / (w) dw ^ 1 Г / (ш) dw _
^' 2nV — iJ "'—Z 2я/ —iJ (i"—Zo) —(z—го)
' ЯА ' ЯА
ZnV—iJ.
ад ' ад
/ (ш) с£ш
1^-Ч^д(.-.„)(1-;?Ег)
^ 2 (гя/^ J (ш-г„)»" ) (2-2оГ-
п=в ад
Поэтому, полагая
а ^ Г /И'
" 2я / —1 J (i»—V
ад
получаем, что
dw
\п*1 >
/(z)=S«n(z-Z„)"
ДЛЯ Z £ А, причем ряд сходится абсолютно и равномерно в любом
меньшем круге.
Обратно, предположим, что / (z) допускает разложение в ряд
оо
/(Z)= S «n(z-Zo)"
n=0
1_. Элементы теории функций многих комплексных переменных 15*
для Z 6 А = А (zq, е). Поскольку -^ (z — Zq)" = О, частичные
dz
суммы этого ряда удовлетворяют формуле Коши, в которой
интеграл по кругу обращается в нуль; в силу равномерной сходимости
ряда в окрестности Zq, то же верно и для /, т. е.
fiz) = —^\t^
^ ад
dw
Z
Теперь, дифференцируя под знаком интеграла, получаем
dz ' 2я / —1 J dz \w—^l
поскольку —=• _ = о при ъфю. D
Рассмотрение случая функций одной переменной мы
завершим, доказав, что при заданной С°°-функции g в круге А
уравнение 5//5z = g разрешимо в несколько меньшем круге.
д-лемма Пуанкаре для одной переменной. Пусть g (z) 6 С°° (А);
тогда функция
' "■ ' 2я /-1 J "'—2
определена в А, принадлежит там классу С" и удовлетворяет
условию df/dz = g.
Доказательство. Для Zq g А выберем такое в, чтобы А (zq, 2s)cz
с А, и представим g в виде
g (z) = ^1 (z) + g^ (z),
где функция ^1 (z) тождественно равна нулю вне А (zq, 28), а
g2 (z) — внутри А (Zo, е). Интеграл
J /,ч 1 f , , dw л I
/о (Z) = 7^1^=- \ gz (W)
da
z
определен и принадлежит классу С"; дляz 6 А (zq, е) имеем
az 2я/-1 J аг V iB — z )
16 0. Предварительные сведения
Так как ^i (z) — функция с компактным носителем, то мы можем
написать
1 С , . dw А dw 1 С , . dw Adw
1 f , , , du л du
с
где и ^ w — z- Переход к полярным координатам « = ге*^
преобразует последний интеграл к виду
/i (Z) = -4 j ^1 (z + re'Q) е-'9 dr л dQ;
С
очевидно, что это — функция класса С°° от z. Далее,
1 r ^gi , > dw A dw .
~2я V^^ J Su-- ^ ' Ш —z '
Л
HO ^1 обращается в нуль на 5А, так что по формуле Коши
^/(z) = |./,(z) = ^,(z) = ^(z).
az az
Случай многих переменных
В формуле полного дифференциала функции / на С"
i=l i=l '
обозначим первое слагаемое df, а второе df. Тогда д и д —
дифференциальные операторы, инвариантные относительно комплексно
линейной замены координат. С°°-функция / на открытом
множестве С/ с: С" называется голоморфной, если df — 0; это
эквивалентно тому, что функция / голоморфна по каждой переменной
в отдельности.
Как и в случае одной переменной, функция / голоморфна тогда
л только тогда, когда она локально разлагается в ряд по
переменным Zj. В одну сторону это очевидно: в силу тех же рассуждений,
что и выше, сходящийся степенной ряд определяет голоморфную
функцию. Обратное утверждение проверим в случае п = 2; случай
1. Элементы теории функций многих комплексных переменных 17
произвольного п отличается от этого только усложнением
обозначений. Пусть / — голоморфная функция в открытом множестве
С/ с: С^; тогда можно фиксировать круг А радиуса г с центром
в точке Zq ^и TS. дважды применить формулу Коши по каждой из
переменных (г^, z^ 6 А. В результате получим
' ^ ^ -' 2П / — 1, J 102—22
|W2-Z02l=l- |Wl-ZOjl-.
1 Г / 1 г / (wi, Wj) dWi \ dWj
Используя разложение в ряд
1 -^ (Zl--Zo^)"'(Zii —Zo^)n
m, 71=0 ^
находим, что / локально допускает разложение в ряд вида
: /(zi, Z2)= S ат,п(21-го1ГК-го,Г- о
m, n=0
1 Некоторые результаты для функций многих комплексных
переменных прямо вытекают из теории функций одной переменной,
например теорема единственности {если fug голоморфны в связном
открытом множестве U и f ^ g в его непустом открытом
подмножестве, то f = g) или принцип максимума (модуль функции
/ Ф const, голоморфной в открытом множестве U, не достигает
максимума в U). Однако имеются удивительные различия.
Например, пусть и — полидиск А (г) = {(г^, Zj): | Zj |, | Zj | < г),
и пусть У с= С/ — меньший полидиск А (г') для любого г' < г.
Тогда имеет место следующая
Теорема Хартогса. Любая функция /, голоморфная в
окрестности множества U — У, продолжается до голоморфной функции
на всем и.
Доказательство. На каждом вертикальном срезе z^ = const
область и — V выглядит либо как кольцо г' < | Zj | < г, либо
как круг I Zj I < г. Попробуем продолжить / на каждом срезе по
формуле Коши, положив
F(z„z,) = L_ [ l^i2J^dw.,.
|Ш2|=Г
18 0. Предварительные сведения
Функция F определена всюду в U; она, очевидно, голоморфна
по Zj и, поскольку (d/dzi) / = О, она голоморфна и по %. Далее,
в открытом подмножестве | z^ \ > г' множества U — V имеем
F (zi, Zj) = / (zi, Z2) по формуле Коши, откуда F \jj.v = /■ D
Теорема Хартогса применима ко многим парам множеств
V CZ и CZ С"; обычно ее применяют в следующем виде:
Функция, голоморфная на дополнении к точке в
открытом множестве U cz С" (и > 1), продолжается до функции,
голоморфной на всем U.
Теоремы Вейергитрасса и следствия из них
В случае одной переменной всякая аналитическая функция
единственным образом локально представляется в виде
/ (z) = (z - Zo)"u(z), u(zo) Ф о,
откуда, в частности, вытекает, что множество ее нулей Дискретно.
Теорема Вейерштрасса дает аналогичное локальное представление
голоморфных функций нескольких переменных; с ее помощью мы
обрисуем локальнз^ю геометрию множеств их нулей.
Пусть дана функция / (zj, . . ., z„_i, w), голоморфная в
некоторой окрестности начала координат в С", причем / (О, . . ., 0) = 0.
Пусть / не обращается в нуль тождественно на оси w, т. е.
разложение / в степенной ряд в окрестности нуля содержит член a-vf^, где
а ф О и d ^ 1; ясно, что так оно и будет при достаточно общем
выборе систем координат.
Тогда при подходящих г, б и е > О выполняется неравенство
1/(0, w) I ^ б > О для \w \ = г ж, стало быть, | / (г, w) | ^ 6/2
при I м7 I = г, II г II ^ е. Далее, пусть w = bi, . . ., &<j — корни
уравнения / (г, w) = О для \ w \ <С г; тогда по теореме о вычетах
^ ^ 2я / — 1 J / (z, "»)
\VJ\=r
следовательно, степенные суммы 2 ^i (2)' являются
аналитическими функциями от г при || z || < е. Пусть ai (г), . . ., a<j (z) —
элементарные симметрические функции от bi, . . ., &^; тогда
ai, - . ., Gd могут быть выражены как многочлены от степенных
сумм 2 bi {z)^. Поэтому функция
g{z, ю) = и/^- 01 (г) и^-^ + . . . + (-!)<« аа (z)
голоморфна при ||г||<<8, |м7|<;ги имеет в точности то же
множество нулей, что и /. Частное h (г, w) = f (z, w)lg (z, w)
определено и является голоморфной функцией при || z || < е, | ю | < г,
по крайней мере вне множества нулей / и g. Более того, при фикси-
1. Элементы теории функций многих комплексных переменных 19
рованном Z функция h (z, w) имеет лшпь устранимые особенности
в круге I М7 I < г, так что h продолжается до функции,
определенной для всех II Z II < 8, I М7 I < г, аналитической по w при каждом
фиксированном г, а также в дополнении к множеству нулей.
Записывая
й(2, W) 1= f ±(£lJfHl,
^ ' ы Y-i J "-"' '
' |u|=r
видим, что h голоморфна и по г.
Определение. Многочленом Вейерштрасса от w называется
многочлен вида
w^ + a^{z)u^-^ + . . . + аа (z), aj (0) = 0.
Мы доказали часть утверждения (существование), известного
как
Подготовительная теорема Вейерштрасса. Пусть функция f
голоморфна в окрестности начала координат в С" и we равна
тождественно нулю на оси w; тогда в некоторой окрестности
начала координат f единственным образом представляется в виде
f = g-h,
где g — многочлен Вейерштрасса степени d от w и h (0) ф 0.
Единственность, которую нам осталось доказать, очевидна,
поскольку коэффициенты любого многочлена Вейерштрасса g,
обращающегося в нуль в точности там же, где /, являются
многочленами от интегралов
Г w<i{dfldw)(z, w)dw
J / (г, ш)
|«о|=г
Из теоремы Вейерштрасса мы видим, что множество нулей
функции /, голоморфной в окрестности начала координат в С",
в достаточно общей системе координат Zj, . . ., z„_i, w является
множеством нулей многочлена Вейерштрасса
^ g {Z, W) = icf^ + а^ (z) и^-^ + . . . + аа (z).
Далее, корни bi (z) многочлена g (z, •) вне множества тех
значений г, при которых g {z, ■) имеет кратный корень, являются
локально однозначными голоморфными функциями от г. Так как
дискриминант многочлена ^ (z, •) есть аналитическая функция от г, то
мы приходим к следующему утверждению.
Множество нулей аналитической функции f (zi, . . ., z„ _i, w),
не обращающейся в нуль тождественно на оси w,
проектируется локально на гиперплоскость (w = 0) как конечно-
2*
20 0. Предварительные сведения
листное накрытие, разветвленное над множеством нулей
некоторой аналитической функции.
В качестве следствия из подготовительной теоремы получаем
такое утверждение:
Теорема Римана о продолжении. Пусть f (г, w) — функция,
голоморфная в полидиске А с: С", а g (г, w) — функция,
голоморфная и ограниченная в А — {/ = 0}. Тогда g продолжается до
голоморфной функции на А.
Доказательство (в окрестности 0). Пусть прямая 2 = О не
содержится в множестве {/ = 0}. Как и выше, навдем такие г, е
и S > О, что 1/(0, w) I > S > О при \ W \ = г, а при || z || < е,
\ W \ = г выполняется неравенство \ f (z, w) | > 8/2; тогда / имеет
нули лишь внутри круга z = Zq, | u; | ^ л По теореме ]Римана
о продолжении для одной переменной g можно продолжить до
функции i' в II Z II < 8, I U7 I <;г, голоморфной вне {/ = 0} и
голоморфной по W всюду. Как и выше, напишем
i)du
|u|=r
откуда видно, что функция g голоморфна также и по z. □
Напомним несколько фактов и определений из элементарной
алгебры.
Пусть R — целостное кольцо, т. е. такое кольцо, что для любых
и, V ^ R если U-V = О, то либо и = О, либо у = 0. Элемент и ^ R
называется единицей, если существует такой v ^ R, что u-v = i;
и называется неприводимым, если для v, w ^ R из равенства
и = VW следует, что либо v, либо w является единицей в R.
Кольцо R называется факториальным (или областью с
однозначным разложением на множители), если каждый элемент и ^ R
может быть разложен в произведение неприводимых элементов
щ, . . ., щ, причем Ui определены однозначно с точностью до
умножения на единицы. Нам понадобятся следующие основные факты.
1. Если кольцо R факториально, то кольцо R [t] также фак-
ториально (лемма Гаусса).
2. Если кольцо R факториально ш и, v ^ R [t] взаимно просты,
то существуют взаимно простые элементы а, р g i? [t], у Ф О ^ R,
для которых
аи + рг? = у.
Элемент у называется результантом многочленов и и v.
Пусть (Э„ г — кольцо голоморфных функций, определенных
в некоторой окрестности точки z 6 С"; вместо (Э„.о будем писать (Э„.
1. Элементы теории функций многих комплексных переменных 21
Кольцо (Э„ является целостным по теореме единственности и,
кроме того, локальным кольцом, максимальный идеал которого т есть
{/- / (0) = 0}. Элемент f ^Сп является единицей тогда и только
тогда, когда / (0) ^ 0. Вот первый результат.
Предложение. Кольцо (Э„ факториально.
Доказательство. Воспользуемся индукцией по п.
Предположим, что Оп-1 факториально и/ g 0„. Можно считать, что элемент
/ регулярен относительно м? = z„, т. е. / (О, . . ., О, и;) ^ 0.
Представим / в виде / = g-u, где и — единица в (9„, & g ^ On-i Ш —
многочлен Вейерштрасса. По лемме Гаусса On-i t"'] факториально,
поэтому g можно разложить в произведение неприводимых
элементов gi, . . ., gm^ Оп-1 Ш-
(*) f = gl ■ ■ ■ gm-U,
где множители gi определены однозначно с точностью до
умножения на единицы. Пусть теперь элемент / представлен как
произведение неприводимых множителей Д, . . ., Д 6 On- Каждый из /г
должен быть регулярным относительно w, поэтому /г = gl-Ui,
где Ui — единица, я g'l — многочлен Вейерштрасса, неприводимый
в Оп-1 t"']- Далее,
где ё' и [] gfj — многочлены Вейерштрасса. Согласно
подготовительной теореме Вейерштрасса, g' = jj g'j, а поскольку кольцо
&п-1 tii'] факториально, отсюда следует, что gi с точностью до
единиц совпадают с g'i. Таким образом, выражение (*) доставляет
единственное разложение / в (Э„. □
Предложение. Если элементы fug взаимно просты в On,о,
то для \\ Z II < 8 они взаимно просты в 0„_z-
Доказательство. Можно считать, что f ж g регулярны
относительно z„ и оба являются многочленами Вейерштрасса. Для
каждого фиксированного достаточно малого z' 6 С""^ имеем / (z', z„) ф
# О по z„. Запишем af + ^g = у, где а, р 6 ©n-i Iwh 7 € О^-й
это равенство выполняется в некоторой окрестности точки О £ С".
Если для некоторого малого Zq 6 С" выполнено условие / (zq) =
— g i^o) = О и /, g имеют в 0„_ ,„ общий множитель h (z', z„)
с h (zo) = О, то
h\f, h\g=>h\y=>h^On-i.
Но тогда /i(zoi, ..., Zo , z„) обращается в нуль тождественно
по z„ вопреки нашему предположению, что / (zo^, ..., zo _ , z„) ^
#0. О
Далее будет доказана следующая
22 0. Предварительные сведения
Теорема Вейерштрасса о делении. Пусть g (z, w) 6 On-i tii'] —
многочлен Вейерштрасса степени к по w. Тогда для любого элемента
f ^Оп существует разложение вида
f = g.h + г,
где г {z, w) — многочлен по w степени <С к.
Доказательство. При достаточно малых 8, б > О определим
для II г II < е, I U7 I < б функцию
г, / \ 1 С f (z, и) du
h(z, W)= rr=- Ц-:—[ .
' 2nY — i J г (2, и) u — w
'^ lu|=6
Ясно, что функция h голоморфна, и поэтому функция г = f — gh
тоже голоморфна. Имеем
r(z, w)=f{z, w) — g{z, w)-h(z, w) =
1 f fj: / \ / X t (.Z, U) -] du
= ■r=r \f(z, u) — g(z, W)-!-^ i- =
'^ |U|=6
1 г f(z, u) g(z, u)—g(z, w) ^y
-i/rrj J g(z, u) u — w
' l.fl A
2n , , -
|u| =6
Ho {u — w) делит [g (z, u) — g (z, w)] (обе разности
рассматриваются как многочлены по w)\ поэтому
p{z,u,w)= ii^^^)-s(^,y')
является многочленом по w степени <^к. Так как множитель w
входит в выражение для г (z, w) только ър, мы видим, что г (z, w) —
многочлен по w степени <ik. В явном виде пусть
р (z, и, w) = pi (z, u)-w^-^ + . • • + Pft (z, u);
тогда
r (z, w) = ai (z)-u;''-i + . . . + a^ (z),
где
ai{z)= ^—=^ f J±iJil p.{z, u)du. П
^ |u|=6
Следствие (слабая теорема о нулях). Если злемент f (z, w) 6 ©„
неприводим, h ^ On обращается в нуль на множестве f (z, w) = О,
то f делит h в 0„.
Доказательство. Прежде всего мы можем считать, что / —
многочлен Вейерштрасса степени к по w. Далее, поскольку элемент
1. Элементы теории функций многих комплексных переменных 23
f неприводим, 10 f ш dfldw взаимно просты в (Э„ _i [иЛ (причем
degu) / > ^Щиз dfldw), поэтому найдутся такие а, р и у, что
Бели при некотором заданном Zq многочлен / (zq, и^) 6 С [w] имеет
кратный корень и, то
/(zo. и) =-^(2о. u) = 0=>.7(zo)=0;
следовательно, элемент / (z, и;), рассматриваемый как многочлен
от W, имеет к различных корней при у (z) ^0.
Теперь по теореме деления имеем
h = f-g+ г, г eOn-ilw], deg г < к.
Однако при любом Zg вне множества (у = 0) многочлен / (zp, w),
а значит, и h (z,,, w), имеет по крайней мере к различных корней
по W. Так как степень г меньше к, то это означает, что г (zq, u?) =
= О 6 С Iw]; отсюда г ^0 и h = f-g. □
Аналитические множества
Главная цель приведенных выше результатов состояла в том,
чтобы описать основные локальные свойства аналитических
множеств в С". Подмножество V открытого множества U cz С"
называется аналитическим множеством, если для любой точки р ^ U
суш;ествует такая ее окрестность U' в U, что V f\U' является обшрм
множеством нулей конечного набора голоморфных в U' функций
/i, . . ., /ft. В частности, если V является локально множеством
нулей ненулевой голоморфной функции /, оно называется
аналитической гиперповерхностью.
Аналитическое множество V cz С/ сг С" называется
неприводимым, если его нельзя представить как объединение двух таких
аналитических множеств Fi, Уг '^ ^> "^то Vi, Y^ Ф V; оно
называется неприводимым в точке р ^ V, если V f] U' неприводимо
для достаточно малых окрестностей U' точки р ъ U. Отметим
прежде всего, что если злемент f ^ On неприводим в кольце (Э„,
то аналитическая гиперповерхность V = {f (z) = 0},
определяемая функцией / в окрестности О, неприводима в 0. Действительно,
предположим, что V = Vi [} V2, где У^, Уа — аналитические
множества фУ; тогда суш;ествуют такие Д, /j 6 Оп> ^то /i (соотв. /а)
обрап1;аются тождественно в нуль на У^ (соотв. Уд), но не на Уд
(соотв. Vi). По теореме о нулях элемент / делит произведение
/I'/a, а поскольку он неприводим, отсюда следует, что / делит
либо /i, либо /а, т. е. либо V^ гз У, либо Уд гз У. Тем самым мы
пришли к противоречию.
24 0. Предварительные сведения
В дополнение к тому, что сказано выше о строении
аналитических гиперповерхностей, имеют место следующие свойства.
1. Пусть V с и с С^ — аналитическая гиперповерхность,
заданная уравнением У = {/ (z) = 0} в окрестности точки О ^ V.
Поскольку кольцо (Э„ факториально, можно записать/ = А • • • /п>
где/j неприводимыв (Э„. Полагая Fj = {/; (z) = 0}, получаем, что
F = Fi и . . . и Vn,
где Vi неприводимы в точке 0. Поэтому если р — любая точка на
любой аналитической гиперповерхности V cz U cz С", то V мажет
быть единственным образом представлена как объединение
конечного числа аналитических гиперповерхностей, неприводимых в р.
2. Пусть Wd С/сг С"— аналитическое множество, заданное
в окрестности А точки О ^ W как множество общих нулей двух
функций /, g ^ On- Если W не содержит аналитической
гиперповерхности, проходящей через О, го f я g взаимно просты в (Э„;
если W не содержит прямой (z' =0} то, заменяя в случае
необходимости f ж g их линейными комбинациями, мы можем считать,
что ни одно из множеств {/ (z) = 0} и {g{z) = 0} не содержит
{z' = 0} и, следовательно, что fug — многочлены Вейерштрасса
от Zn- Пусть 7 = а/ 4- pi' ^ О 6 Oji — их результант. Мы
утверждаем, что образ PF при проектировании я: С"-)-С"~^ есть
множество нулей V- Чтобы убедиться в этом, представим а в виде а =
= hg -{- г, где степень г строго меньше степени g. Тогда
7 = г/ -f (р -f hf) g.
Далее, если при некотором z g С"~^ функция v обращается в нуль
в 2, но / и I' не имеют общих нулей на прямой п~^ (z), то отсюда
следует, что г обращается в нуль во всех нулях g в п~^ (z). Так как
deg г •< deg g, то из этого вытекает, что г, а следовательно, ^ -{- hf
тождественно обращаются в нуль на п~^ (z). Стало быть, mfi-^-hf
обращаются в нуль на прообразе любой компоненты множества
нулей 7, отличной от п (W); но г и р -(- А/ взаимно просты и потому
не имеют общих компонент. Итак, мы видим, что п (W) есть
аналитическая гиперповерхность в окрестности начала в С"~^,
и, еще раз обращаясь к нашему основному описанию
аналитических гиперповерхностей, замечаем, что проектирование
множества W на подходящим образом выбранную (п — 2)-плоскость
£п-2 J— £п представляет W локально как конечнолистное
разветвленное накрытие некоторой окрестности начала в С"~^.
3. Наконец, пусть V cz С/сг С" — аналитическое множество,
неприводимое в точке О g У и такое, что в достаточно малых
окрестностях Д точки О в С" образ п {V [] А) содержит окрестность
точки О в С"^"^. Зададим множество уравнениями
Т^ = {А (2) = . • . = /ft (z) = 0}
1. Элементы теории функций многих комплексных переменных 25
В окрестности точки 0. Тогда функции fi 6 On должны иметь общий
ляожитель в (Э„, поскольку в противном случае V содержалось бы
в множестве общих нулей двух взаимно простых функций и,
согласно утверждению 2, я (У П Д) было бы собственным аналитическим
подмножеством в С""^. Обозначим через g (z) наибольший общий
делитель всех ff, имеем
Так как V неприводимо в точке О, а множество {fi (z)fg (z) = О
для всех i} не может содержать множество {g (z) = 0}, то должна
выполняться равенство
V= {g (z) = 0},
т. е. У — аналитическая гиперповерхность в окрестности точки 0.
Свойства 1, 2 и 3 вместе с нашим описанием локальной
геометрии аналитической гиперповерхности дают полную картину
локального строения аналитических множеств, определенных
одной или двумя голоморфными функциями. На самом деле та
же картина почти во всех отношениях сохраняется и для
произвольных аналитических множеств, но доказательство этого
потребовало бы довольно изощренной техники теории функций многих
комплексных переменных. Поскольку основное внимание в этой
книге сосредоточено на случае коразмерности 1, мы здесь просто
сформулируем без доказательства аналогичные результаты для
общих аналитических множеств.
1. Пусть V с и с С" — аналитическое множество и /> 6 У —
некоторая точка; тогда в некоторой окрестности точки р
множество У можно единственным образом представить в виде
объединения аналитических множеств Vi, неприводимых ъ р я таких^
что Vi Ср Vj.
2. Любое аналитическое множество локально с помощью
проектирования представимо в виде конечнолистного накрытия
полидиска, разветвленного вдоль некоторой его аналитической
гиперповерхности.
3. Если Уст С" не содержит прямой Zi = . . . = z„_i = О, то
образ окрестности точки О в У при проектировании я:
(zi, . . ., z„) I-* (zi, . . ., z„_i) является аналитическим
подмножеством в окрестности точки О 6 С""'^.
Трудности в доказательстве этих результатов скорее
технические, чем идейные. Например, по поводу доказательства
утверждения 3 заметим, что если У определено в окрестности точки О 6 С^
функциями /i, . . ., /ft, то я (У) определено в окрестности точки
О g С""^ результантами всех пар взаимно простых линейных
комбинаций функций fi- Таким образом, нужно показать, что множе-
26 0. Предварительные сведения
ство общих нулей произвольного набора голоморфных в
полидиске функций на самом деле определяется конечным числом
голоморфных функций в несколько меньшем полидиске. Приняв на
веру утверждения 3 и 1, нетрудно доказать свойство 2
последовательными проектированиями.
Все эти результаты следуют из теоремы о собственном
отображении, которую мы сформулируем в следующем параграфе, а
докажем в гл. 3.
Наконец, еще несколько фундаментальных результатов для
многих комплексных переменных будут доказаны с помощью
теории вычетов в гл. 5.
2. КОМПЛЕКСНЫЕ МНОГООБРАЗИЯ
Комплексные многообразия
Определение. Комплексное многообразие М — это гладкое
{т. е. дифференцируемое) многообразие, допускающее такое
открытое покрытие {Ua} и такие координатные отображения ф^: Ug, ->-
-^ С", что отображения фа ° фр' голоморфны на фз (С^а Л ^^з) '-^
CZ С" для всех а, р.
Функция на открытом множестве U cz М называется
голоморфной, если для всех а функции /-фа' голоморфны на ф„ {U f] [/„) сг
сг С". Набор Z = (zi, . . ., z„) функций п& U с: М называется
голоморфной системой координат, если ф^^ -z'^nz <• фй'
голоморфны соответственно ж& z {U [\ Ua) и ф^ (С/ П t^a) для каждого а.
Отображение /: М -^ N комплексных многообразий называется
голоморфным, если в голоморфных локальных координатах оно
задается голоморфными функциями.
Примеры. 1. Одномерное комплексное многообразие называется
римановой поверхностью.
2. Пусть Р" — множество прямых, проходящих через начало
координат в С""^^. Такая прямая I cz С"*^ определяется любой
своей точкой Z фО ^1, так что
рп.._ {[г]^0€С"+1}
^ - lZ]~lkZ] '
На подмножестве Ui = {[Z]: Zt ^ 0} сг Р" прямых, не лежащих
в гиперплоскости {Zi = 0), определено взаимно однозначное
отображение фг в С":
Фг ([^0' • • ч ^п\) = ^ -gr ' • • ■ > "^Г' ■ ■ ■ > "jr) •
2. Комплексные многообразия 27
На множестве (z; ^ 0) = (ft (Uj f\ Ui) cz С" отображение
очевидным образом голоморфно, так что Р" наделено структурой
комплексного многообразия. Вместе с этой структурой оно
называется комплексным проективным пространством. «Координаты»
Z = [Zq, . . ., Z„] называются однородными координатами в Р";
координаты, задаваемые отображениями фг, называются
евклидовыми координатами. Пространство Р" компактно, поскольку
имеется непрерывное сюръективное отображение единичной сферы
в С"+^ на Р". Заметим, что Р^ есть просто риманова сфера С U {°о}.
Любое вложение С''*^ -> С"+^ индуцирует вложение Р'' -> Р";
его образ называется линейным подпространством в Р". Образ
гиперплоскости в С"*^ тоже называется гиперплоскостью, образ
2-плоскости С^ с= С"+^ называется прямой, и вообще образ
подпространства С''+^ CZ С"*^ называется А;-плоскостью. В такой
терминологии можно говорить о линейных отношениях между
точками в пространстве Р": например, линейная оболочка набора
{pi} точек в Р" — это образ в Р" подпространства из С"^^,
натянутого на прямые п~^ {р{). Говорят, что к точек линейно
независимы, если линейно независимы соответствующие прямые в С"+^,
т. е. если их линейная оболочка в Р" является (к — 1)-плоскостью.
Заметим, что множество гиперплоскостей в Р" соответствует
множеству С"*'^^* — {0} ненулевых линейных функционалов на
С"+^по модулю умножения на скаляры; поэтому оно само является
проективным пространством; оно называется двойственным
проективным пространством и обозначается Р"*.
Иногда удобно представлять себе Р" как компактификацию С",
полученную добавлением гиперплоскости Н на бесконечности.
В координатах вложение С" -*■ Р" задается формулой (%, . . ., z„) ь->
н-*. [1, Zi, . . ., z„]; гиперплоскость Н определяется уравнением
(Zfl = 0), а отождествление Н ^ Р""^ устанавливается с помощью
интерпретации бесконечной гиперплоскости как множества
направлений из нуля в бесконечность в С".
3. Пусть Л = Z'' с= С" — дискретная решетка. Факторгруппа
С"/Л обладает структурой комплексного многообразия,
определяемой проектированием п: С" ->- С"/Л. Это многообразие
компактно тогда и только тогда, когда к = 2га; в этом случае С"/Л
называется комплексным тором.
Вообще, если я: М -^ N — неразветвленное топологическое
накрытие и iV — комплексное многообразие, то я задает на М
структуру комплексного многообразия; если М — комплексное
многообразие, а преобразования наложения листов накрытия голо-
28 0. Предварительные сведения
морфны, то N наследует от М структуру комплексного
многообразия.
Другим примером этой конструкции служит поверхность Хоп-
фа, определяемая как фактор С^ — {0} по группе автоморфизмов,
порожденной отображением z ь^ 2z. Поверхность Хопфа является
простейпшм примером компактного комплексного многообразия,
которое нельзя вложить в проективное пространство никакой
размерности.
Пусть М — комплексное многообразие, р ^ М — любая точка,
& Z = (%, . . ., z„) — система голоморфных координат с началом
в р. Имеются три различных понятия касательного пространства
к М ъ р, которые мы сейчас опишем.
1. Tr_p (М) есть обычное вещественное касательное
пространство, где мы рассматриваем М как вещественное многообразие
размерности 2и. Тр_,р (М) может быть реализовано как
пространство R-линейных дифференцирований кольца вещественнозначных
С°°-функций в окрестности р; если z^ = а;^ -(- У—li/j, то
^r.pW = bi{^.^},
2. Tq р (М) = Tr,p (М) (8>rC называется комплексифицирован-
ным касательным пространством к М ъ р. Оно может быть
реализовано как пространство С-линейных дифференцирований кольца
комплекснозначных С^-функций на М в окрестности р. Можно
представить его в виде
^о.,(му=с{Л.,^]^с{4^,Л-}.
где, как и выше.
а
dz;
_1/ а ,/—7 а \ Л^ = 11_^^л/^-{Л-.\
'3. Т'р {М) = с {d/dzi} с: Tq (М) называется голоморфным
касательным пространством к М ъ р. Оно может быть
реализовано как подпространство в Г^ р {М), состоящее из
дифференцирований, обращающихся в нуль на антиголоморфных функциях
(т. е. таких /, что / голоморфна), так что оно определено
независимо от выбора системы голоморфных координат (zi, . . ., z„).
Подпространство Тр {М) = С {d/dzi} называется антиголоморфным
касательным пространством к М в р; очевидно, что
Гс. р(М) = П(М)®Гр(Ж).
2. Комплексные многообразия 29
Заметим, что для комплексных многообразий М, N любое
^"-отображение f:M-^N индуцирует линейное отображение
/*:Гк.р(М)->Гя,/(р)(ЛГ),
и следовательно, отображение
/*:Гс. pW->7'c./(p)W.
но, вообще говоря, не индуцирует отображения из Т'р{М) в T'f(j,){N).
На самом деле отображение f:M-^N голоморфно тогда и только
тогда, когда /^ {Т'р {М)) cz T'fcp) (N) для всех р ^ М.
Заметим также, что, поскольку Г^, р (^ естественно задано
как тензорное произведение вещественного векторного
пространства Ук.р (М) и С, операция сопряжения, переводящая dldzt
в didzi, корректно определена и Т"р {М) = Т'р {М). Отсюда следует,
что проекция
Tr, р (М) -> Гс. р Ш) -> Т' {М)
есть К.-линейный изоморфизм. Это обстоятельство позволяет нам
«заниматься геометрией» исключительно в голоморфном
касательном пространстве. Например, пусть z {t) (О ^ ^ ^ 1) — гладкая
дуга в комплексной z-плоскости. Тогда z {t) = х (t) + V—1у (t),
и в качестве касательной к этой дуге можно взять либо
либо
z'it)^ в г (С).
Пусть теперь М, N — комплексные многообразия, z =
= (zi, . . ., z„) — голоморфные координаты в окрестности точки
р 6 М, & W = (wi, . . ., Wm) — голоморфные координаты в
окрестности точки q ^ N я f: М -^ N — голоморфное отображение,
причем f (р) = q. Ъ соответствии с различными понятиями
касательных пространств mMmNbpviq мы имеем и различные понятия
якобиана /.
1. Пусть Zi — Xi-{-Y—iyi, Wa = u^-{-Y—1Уа; тогда В базисах
{d/dxi, dldyi) и {д/дпа, d/dva) пространств Tr, р{М) и TR,q{N)
линейное отображение /^ задается 2т X 2ге-матрицей
^''^^^ \dvjdxj dvjdyjj-
30 0. Предварительные сведения
В б&зшс&х {d/dzi, dldzi) и {dldw^, d/dii'a} пространств Г^, р (Af) и
^С. 9 (-^) отображение /^ задается матрицей
^»<-(Г" W.)
где f{f) = {dwjdzj). Заметим, в частности, что rank'|^R(/) —
= 2 rank f (/) и если т = п, то
det f-R (/) = det f if) det f- (/) = | det f- (/) P > 0,
T. e. голоморфные отображения сохраняют ориентацию. Мы будем
считать, что пространство С" естественно ориентировано 2и-фор-
мой
■)/ —1/2)" (dzi л dzi) л (dzj л dz^) л ... л (dz„ л dz„) =
= da^i л dy, л ... л da;„ л di/„.
Ясно, что если ф^: U^ —>- С"^, Фз: f/p -> С"^ — голоморфные
координатные отображения на комплексном многообразии М, то
прообразы при фа и Фз естественной ориентации на С" согласованы
на и а Л f^3* Итак, любое комплексное многообразие имеет
естественную ориентацию, которая сохраняется при голоморфных
отображениях.
Подмногообразия и аналитические подмножества
Теперь, когда установлены соотношения между различнылш
якобианами голоморфного отображения, без труда доказывается
следующая
Теорема об обратной функции. Пусть U, V — открытые
подмножества в С", О ^ и и f: и -^ V — такое голоморфное
отображение, что матрица f if) = {dfildzj) невырожденна в 0. Тогда
отображение f взаимно однозначно в окрестности точки О и
обратное отображение /~■^ голоморфно в точке / (0).
Доказательство. Прежде всего так как det \ 'fa (f) | =
= I det if- (f)) f фО ъ О, то по обычной теореме об обратной
функции / имеет в окрестности О обратную С^-функцию f~^.
Далее, Z"'- (/ (z)) = z, так что
dzi h "^^ dzi h dzk \ dzt )
У] -^{-^\ для всех i, h
2. Комплексные многообразия 31
Поскольку матрица (dfjdzi) невырожденна, отсюда следует, что
df]^ldzk = О для всех /, к, так что функция f~'^ голоморфна. D
Аналогично устанавливается следующая
Теорема о неявной функции. Пусть заданы функции Д, . . ,
. м /ft € ®ni удовлетворяющие условию
det(|^(0)) ^0;
тогда существуют такие функции Wi, ..., w^^ C^n-ft» '^^o в
окрестности точки О в С"
/i(z)= ...=/ft(z) = 0<^Z£ = u7i(Zft+i, ..., zj, 1 < i < /t.
Доказательство. Снова по теореме о неявной функции в случае
С°° можно найти С°°-функции w^, . . ., w^ с требуемым свойством.
Для того чтобы убедиться в том, что они голоморфны, проведем
для Z = (zft+i, • ■ ., z„), к -\- i ^ а ^ п, следующие выкладки:
aza
dza dza ""'I oza. owi
= St^-S- ("^(2)' 2) ^ ^ = 0 ДЛЯ всех a, I. U
^"^ dZa. ""'l dZa.
Следующий факт специфичен для голоморфных отображений.
Предложение. Если /: С/ —> У — взаимно однозначное
голоморфное отображение открытых множеств в С", то \f{f)\=^:0^
т. е. /~■^ голоморфно.
Доказательство. Докажем это индукцией по га. Случай га = 1
ясен. Пусть Z = (z^, . . ., z„) и U7 = (Wf^, . . ., U7„) — координаты
соответственно в ?7 и У, и пусть матрица f- if) имеет ранг к в точке
О ^ U; тогда можно считать, что матрица (dfi/dzj) (0)o<;,/<ft
невырожденна. Положим
z'i = ft (z), 1 < £ < /t,
z'a = Zg,, к -\- i ^ a ^ n.
По теореме об обратной функции z' = (z' . . ., z'„) — голоморфная
система координат в С/ в окрестности 0. Но / отображает множество
(Zj = . . . = Zft = 0) взаимно однозначно на множество (ш-^ = . . ..
. . . = U7ft = 0), и якобиан (dfjdzfi) отображения / Ь^/^ ..=г'=о)
1 " ft
вырожден в точке 0; тогда по предположению индз^кции либо
к ~ О, либо к = п. Итак, мы убедились, что якобиева матрица
отображения / обращается в нуль тождественно там, где ее опреде-
32 0. Предварительные сведения
литель равен нулю, т. е. что / отображает каждую связную
компоненту множества \f if) \ = 6ъ единственную точку из V.
Поскольку отображение / взаимно однозначно, а множество нулей
голоморфной функции f if) имеет положительную размерность, если
оно непусто, то отсюда следует, что \'^- if) \ фО. □
Отметим, что это предложение в вещественном случае неверно;
например, отображение ^ i-^ ^^ на [R взаимно однозначно, но не
имеет С°°-обратного.
Теперь мы можем сформулировать следующие два определения.
Определение. Комплексным подмногообразием S комплексного
многообразия М называется подмножество iS с: М, которое
локально задается либо как множество нулей совокупности
fxi • • -^ fh голоморфных функций с условием rank f- (f) = k, либо
как образ открытого подмножества U с: С""** при отображении
/: и -*- М с условием rank 'f (f) = п — к.
Как следует из теоремы о неявной функции, два условия этого
определения на самом деле эквивалентны и многообразие iS
обладает естественной стрз^ктурой комплексного многообразия
размерности п — к.
Определение. Аналитическим подмножеством V комплексного
многообраэия М называется подмножество, являющееся локально
множеством нулей конечного набора голоморфных функций. Точка
р ^ V называется гладкой точкой в У, если V — подмногообразие
в Мъ окрестностир, т. е. если Vв некоторой окрестности р задается
голоморфными функциями fi, . . ., /ft, для которых rank J^ (/) = к;
множество гладких точек V обозначается V*. Точка р ^ V — V*
называется особой точкой V; особое множество V — V*
аналитического подмножества V обозначается У^. Аналитическое
подмножество У называется гладким или неособым, если У = У*, т. е. если
У — подмногообразие в М.
В частности, пусть р — точка аналитической гиперповерхности
У с: М, задаваемой в локальных координатах z функцией /;
определим кратность multp (У) как порядок обращения / в нуль
в точке р, т. е. наибольшее число т, такое, что
(р) = 0 для всех к-^т—1.
dz, ... dz.
Здесь мы должны упомянуть о весьма распространенном в
алгебраической геометрии употреблении термина общий. Когда мы
имеем дело с семейством объектов, локально параметризованных
комплексным многообразием или аналитическим подмножеством
комплексного многообразия, утверждение типа «общий член
семейства обладает неким свойством» означает в точности, что
2. Комплексные многообразия ?'■!
множество объектов, не обладающих этим свойством,
содержится в многообразии строго меньшей размерности.
Обычно бьгеает ясно, как именно параметризуются объекты
семейства. Исключением будет упоминание «общей А;-плоскости
в Р"»; до параграфа о грассманианах у нас нет — по крайней
мере официально установленного — способа параметризовать
линейные подпространства проективного пространства.
Щепетильный читатель может считать, что это — линейная оболочка
общего набора из к -\- i точек в Р".
Основной факт об аналитических подмножествах таков:
Предложение. Множество V^ содержится в аналитическом
подмножестве многообразия М, не совпадающем с V.
Доказательство. Для р ^ V пусть к — наибольшее целое число,
для которого существуют к функций Д, . . ., /^ в окрестности U
точки р, обращающиеся в нуль на У и такие, что 'f (f) содержит-
к X А;-минор, не всюду вырожденный на У; можно считать, что
I {dfildzj)i^i j^ft I ^ О на У. Пусть U' cz U— множество, на кото
ром I idfi/dzj\^i_ y^ft I ^ О, а У — множество (А = . ■ ■ = А = 0).
Тогда V' = V (] U' является комплексным подмногообразием
в U'; если некоторая голоморфная функция / обращается в нуль
на У, то дифференциал d/^ О на У, т. е. функция / постоянна
на У. Отсюда следует, что для точки q ^ V', близкой к р, У = У
является многообразием в окрестности q и потому У^ с:
<=: {\ (dft/dzs),^,^ j^u \ = 0}. и
На самом деле Vg — аналитическое подмножество в М; если
достаточно аккуратно выбрать определяющие У функции Д, . . ., Д,
то Vs будет общим множеством нулей определителей к X А;-мино-
ров в "f (J). Для наших целей, однако, достаточно знать, что
множество особенностей сравнительно мало, так что мы не будем
доказывать это более сильное утверждение.
Установим еще один результат об аналитических множествах.
Предложение. Аналитическое множество У неприводимо тогда
и только тогда, когда У* связно. .
Доказательство. В одну сторону это ясно: если V = Vi [] У2,
где Vi, У2 5 У — аналитические множества, то (F^ П У2) с: Vg
и поэтому V* несвязно.
Обратное утверждение в общем случае доказать сложнее, но,
поскольку мы будем пользоваться им лишь для аналитических
гиперповерхностей, мы и докажем его только для этого случая.
Пусть У* несвязно, и пусть {У;} — связные компоненты У*. Мы
хотим показать, что каждое из У; является аналитическим
множеством. Пусть р 6 У; — любая точка, / — функция, определяющая
3-046
34 0. Предварительные сведения
V В окрестности р, а z = (z-^, . . ., z„) — локальные координаты
в окрестности р\ можно считать, что / —многочлен Вейерштрасса
степени к по z„. Запишем
тогда для некоторого полидиска А в окрестности р и некоторого
полидиска А' в С""'^^ отображение проектирования я: (z^,.. ., z„) н^
►-»- (zi, . . ., z„_i) реализует У; fl (А — (ё' = 0)) как неразветвленное
накрытие дополнения А' — {g = 0). Пусть {ш^ (z')} обозначают
Zn-координаты точек я~^ (z') для z = (z^, . . ., z„.i) 6 А' —
— (g' = 0), и пусть (Ji (z'), . . ., aft (z') — элементарные
симметрические функции от w^. Функции Oi корректно определены и
ограничены на А' — (gf = 0), и поэтому продолжаются на А'; ввиду этого
функция
fi (z) = zl + o^ (z') 4"Ч ... + o^ (z')
голоморфна и обращается в нуль в точности на У,- D
Размерностью неприводимого аналитического множества V
мы будем наэывать размерность комплексного многообразия У*;
будем говорить, что произвольное аналитическое множество
имеет размерность к, если все его неприводимые компоненты
А;-мерны.
Заметим, что если V а М — аналитическое подмножество
комплексного многообразия М, то можно следующим образом
определить касательный конус Тр (У) с: Т'р {М) к У в любой точке
р 6 У- Пусть У = (/ = 0) — аналитическая гиперповерхность,
представленная в голоморфных координатах z^, . . ., z„ на Af
с началом в р как
/ (Zi, • - •, Z„) ^ /m yZi-i - . ., Z„) -f- fm+t (Zj, . . ., Z„) + . . .,
где /ft — однородные многочлены от z^, . - -, z„ степени к Tifm=/= 0.
Касательным конусом kV в р называется подмножество в Т'р {М) =
= С {didzi}, определяемое формулой
{Е«г-£:= /-"(«1» .••,ап) = 0}.
Далее, касательный конус к произвольному аналитическому
множеству У сг Af в точке р 6 У определяется как пересечение
касательных в точке р конусов ко всем аналитическим
гиперповерхностям в М, содержащим У. В случае когда множество У гладко
в р, он, разумеется, совпадает с касательным пространством к У
в точке р.
2. Комплексные многообразия 35
Более наглядно касательный конус можно представлять себе
как множество касательных прямых ко всем аналитическим дугам
у: A-^Vcz М.
Кратностью подмножества V размерности к в М ъ точке р,
обозначаемой multp (У), называется количество листов
отображения проектирования, определенного в малом координатном
полидиске я& М с центром в р, рассматриваемого как
проектирование части V на общий А;-мерный полидиск. Заметим, что точка р
тогда и только тогда является гладкой точкой на У, когда
multp (У) = 1. Для неприводимого аналитического подмножества
РУс У определим кратность mult(v (У) множества У вдоль W
просто как кратность У в общей точке из W.
Когомологии де Рама и Дольбо
Пусть М — гладкое многообразие. Обозначим через А^ {М, К)
пространство дифференциальных форм степени р на М, а через
Z'' (М, Щ — подпространство замкнутых р-форм. Так как d' = О,
то d (А^-'^ (М,К )) сг ZP (М,К ); факторгруппы
Ябн {М,К )=ZP {М,К )/dAP-' {М,К )
замкнутых форм по модулю точных называются группами
когомологии де Рама многообразия М.
Точно так же мы можем воспользоваться обозначениями А^ {М)
и ZP (М) для пространств всех комплекснозначных р-форм и
замкнутых комплекснозначных р-форм соответственно и ввести
отвечающие им факторгруппы
Я&н (М) = ZP {M)/dAP-' (М);
ясно, что
Ябк(Л/) = Я?,к(Ж,01)®С.
Пусть теперь М — комплексное многообразие. В силу
известного факта из линейной алгебры, разложение
Тс, г (М) = ТГ (М) ® ТГ (М)
кокасательного пространства к М в любой точке z дает разложение
Р+в=п
в соответствии с этим имеем
Л"(ЛГ)= ® A^-^iM),
где А"-" (М) = {Ф € ^" (М): ср (z) € Л "Tt' (М) ®
® ^'^TT{M) для всех z^M).
3*
36 О- Предварительиие сведения
Форму ср6^^''(Л^) называют формой типа (р, д). Обозначим
через я(Р-") отображение проектирования
Л*(Ж")-^Л^'«(Ж"),
так что для ф 6 ^* (М) имеем
обычно мы будем писать ср^^' '^ вместо я^^' 'V-
Если cp6^^''(Af). то для любого z£M
dcp (z) € (А РТГ (М) ® Л "ТТ (И)) л Тс, г {М),
т. е.
Определим операторы
полагая
имеем
В локальных координатах z = (z^, . . ., z^) форма ср 6 ^" (Л/)
имеет тип (р, q'), если она представляется в виде
Ф (z) = S cpjj (z) dzj A dzj,
где для каждого мультииндекса / = {ii, . . ., ij,}
dzj = dzj, л ... hdzi .
Операторы д я д имеют вид
дЦ> (z) = 2 -^г- cpjj (z) d2^ л dzj л dzj,
д(р (z) = 2 aF^^-^ ^■^^ ^■^' '^ ^^^ '^ ^'^•''
I.J.i
В частности, форма ср типа (д, 0) называется голоморфной,
если дер = 0; ясно, что это имеет место тогда и только тогда, когда
Ф(2)= 2 Срг (Z)dz^,
где функции ф^ (z) голоморфны.
2. Комплексные многообрагия 37
Заметим, что, поскольку разложение тЬ, г = Tf ф Т%"
сохраняется при голоморфных отображениях, то же верно для
разложения Л*=фЛ^''. Для голоморфного отображения /:
М -^N комплексных многообразий имеем /* (Л**'' {N)) cz А^' ' {М)
^■ff,f* = f*od на A^-^iN).
Пусть Z|'' (М) — пространство ^-замкнутых форм типа (р, q).
Так как d^ldzidz]=^d^ldzjdzi, то 5^ = 0 на Л^'' (М), и мы имеем
это позволяет определить группы когомологий Долъбо как
Я|• 'j (Л^) = Zf '^{М)1д (Л^*-* (i»f)).
Отметим, в частности, что голоморфное отображение комплексных
многообразий /: М —>- N индуцирует отображение
/*: Я|*«(ЛГ)->Я|''(М).
Обычная лемма Пуанкаре, утверждающая, что все замкнутые
формы на IR" точны, обеспечивает локальную тривиальность
группы когомологий де Рама. Аналогично, фундаментальным фактом
относительно групп когомологий Дольбо является следующая
д-лемма Пуанкаре. Для полидиска] Л = А (г) в С" имеет место
равенство
Я|-'(А) = 0, 9>1.
Доказательство. Во-первых, заметим, что если
Ф = S Фи '^Zj л dzj
#Г=р, #.7=9
является д-замкнутой формой, то формы ф^ = 2 4>и d>^j 6^"' ''(А)
тоже замкнуты, и что если Ф1 = 5%, то ф= ± д(2 ^Zj л tIj), так
что достаточно доказать, что в нуль обращаются группы Я|'^(А).
Далее покажем, что если ф есть д-замкнутая (О, q) - форма
на А=А(г), то для любого s<C найдется такая форма
if 6^°''"'(A(s)), что 51|) = ф на A(s). Для этого запишем
38 0. Предварителъние сведения
МЫ утверждаем, что если ср ^ О по модулю (dz^, . . ., dz^, т. е.
если ф^ ^ О для I CtL {i, . . ., Щ, 10 найдется такая форма ц 6
6 40.5-^ (А (s)), что
Ф — дт1 ^ О по модулю (dzi, ..., dZft_i).
Ясно, что для доказательства этого будет достаточно. Поэтому
допустим, что ф ^ О по модулю (dzj, . . ., dZft), и положим
Ф1= X Ф1С^21-{Й>, Ф2= S Ф/ £^Zj,
так что ф = ф1 л dzj^ + Фа, причем фз^ О по модулю (йг^, ..., dz^.i).
Если 1'>к, то дф2 не содержит слагаемых с множителем
dZf^Adzi, и, поскольку дф ~ дф1 л d^^ + дфг = О, отсюда следует,
что ^г- ф/ = о при Z >■ А; и таком /, что к^1.
dzi
Теперь положим
Т1= 2 Tijdzi_{ft,,
I: hei
где
%(2) = ^—-г== j Ф1(21, ..., u;^, ..., z„)
diTft Л dwji
Wk — Zh
9zi
В силу 5-леммы Пуанкаре для случая одной переменной имеем
-^ Л! (z) = ф/(z) И для 1>к
dzh
Таким образом,
Ф — дц ^0 по модулю (dz,, ..., dzi^_i)
в А (s), что и требовалось.
Чтобы доказать д-лемму Пуанкаре полностью, рассмотрим
монотонно возрастающую последовательность {г,}, стремящуюся к г.
Согласно первому шагу, можно найти такие 1)3^ ^ A^''^~^ (А), что
Лрй = ф в А (rft); надо взять такую форму г).^ 6 Л".'-^ (А (rft+i)),
что ^J3ft = ф, С°°-фуякцию pft, тождественно равную 1 на А (г^)
и имеющую компактный носитель внутри А (г^+О, и положить
■vpft = pftipft. Задача заключается в том, чтобы показать, что можно
так выбрать {^\}, что они будут нужным образом сходиться на
компактных множествах. Мы сделаем это индукцией по q. Пусть
2. Комплексные многообрагия 39
форма ipft такая же, как выше. Возьмем а ^ А"''''^ (А) со свойством:
^ос = ф в Л (rk+i); тогда
и если 9^2, то по предположению индукции найдется такая
Р€Л°'«-2(Д), что
^P = ^ft —а в A(rft_i).
Положим 4'h+i= а + ^Р; тогда д\];)^+1 = да=(р в А (гй+,) и
vl5ft+i = vl3ft в A(rft_i).
Таким образом, выбранная так последовательность ("ф^} сходится
равномерно на компактных множествах.
Остается рассмотреть случай q = i. Снова пусть форма -ф^ 6
^С°° (А) такова, что dip^ = ср в А (г^), а форма ос 6 С"^ (А) такова,
что doc = ф в А (rft+i); тогда функция -ф^ — ос голоморфна в А (г^)
и, следовательно, в окрестности начала в С" разлагается в
степенной ряд. Обрежем этот ряд так, чтобы получить многочлен р,
удовлетворяющий оценке sup | (-фд — а) — Р I < i/2'^, и поло-
жим 'vpft+1 = а + р. Тогда Лр^+г = ^а = ф в А (ги+х), разность
%+1 — % голоморфна в А (г^) и
sup l-^ft+i—il^ft |<1/2\
так что "ф = lim "ф^ существует я длр = (р. D
Отметим, что доказательство проходит и для г = оо.
Оставляем читателю в качестве упражнения доказательство
того, что с помощью такого же рассуждения с кольцами и
разложениями в ряды Лорана можно установить равенство
Я|'«(А*''хА')=0 для всех д>1,
где А* — проколотый диск А — {0}.
Дифференциальное и интегральное исчисления
па комплексные: многообразиях
Пусть М — комплексное многообразие размерности п.
Эрмитова метрика на М задается в каждой точке z ^ М положительно
определенным эрмитовым скалярным произведением
( , ).: П(М)®ТйШ-^^
в:а голоморфном касательном пространстве в точке z, гладко
зависящим от Z, т. е. таким, что в локальных координатах z на Af
40 0. Предварительные сведения
функции hij (z) = (d/dZi, d/dZj)^ принадлежат классу С°°-
Записывая ( , )z в базисе {dzi ® dzj} пространства (П (М) ® Т'^ (М))* =
= Tf (М) ® Г?" (М), получаем представление эрмитовой
метрики в виде
ds^ = 2 ^ij (2) (izj (g) dzj.
i, i
KopenepoM для эрмитовой метрики называется такой набор из п
форм (ф1, . . ., ф„) типа (1, 0), что
£^«2 = 2 фг ®фг,
i
Т. е. относительно скалярного произведения, индуцированного на
Т*' (М) скалярным произведением ( , )гна T'z (М), набор (ф1 (z), . . .
. . ., ф„ (z)) является ортонормированным базисом в Т*' (Щ-
Ясно, что кореперы всегда существуют локально: их можно
строить, применяя процесс ортогонализации Грама — Шмидта к
произвольному базису (dzi, . . ., dz-n) пространства Т*' (М) для
каждого Z.
Вещественная и мнимая части эрмитова произведения на
комплексном векторном пространстве определяют на соответствующем
вещественном векторном пространстве обычное скалярное
произведение и внешнюю 2-форму. Поскольку имеется естественный
R-линейный изоморфизм Tr^^ (М) ->• Т'^ (М), то для эрмитовой
метрики ds^ на М
Re ds^: Tr, «(^) ® T'r. «(М) -^ К
представляет собой риманову метрику ка М; она называется
римановой метрикой, индуцированной эрлштовой метрикой. Когда
речь идет о длинах, площадях и объемах на комплексном
многообразии с эрмитовой метрикой, то всегда имеется в виду
индуцированная риманова метрика.
Далее, поскольку квадратичная форма
Im ds^: Tr,p(M)®Tr,p (М) -*■ К
кососимметрична, она представляет собой вещественную диффе-
ренциальную форму степени 2; форма со = — -g-Im ds? называется
ассоциированной (1, 1)-формой эрмитовой метрики.
В явном виде пусть (ф^, . . ., ф„) — корепер для ds^, и пусть
фу = czj + У —l^ji где aj, ^j — вещественные дифференциальные
формы; тогда
= У] («у ® aj + ^j ® Pj) + V^lI>(-aj ® ру + Р/® «;).
} 3
2. Комплексные многообразия 4t
Индуцированная риманова метрика задается формулой
Re ds^ = S («J ® «J- + Pi- ® ?>j)'
a ассоциированная (1, 1)-форма эрмитовой метрики — формулой:
со= —-i-Imc^s2=2ayApy = -—^^Ч^^^Фу-
Из последнего представления следует, что метрика ds^ =
= У Ф;' ® Ф;' может быть восстановлена по ассоциированной
(1, 1)-форме ш = ~— \ 9j л фу. В самом деле, любая веще-
ственная дифференциальная форма со типа (1, 1) на М определяет
эрмитову форму Я ( , ) на каждом касательном пространстве
Т'г (М). Форма Н положительно определена, т. е. индуцирует
эрмитову метрику на М, тогда и только тогда, когда для каждого
г 6 М и каждого голоморфного касательного вектора v ^ Т'^ (М)
У^^{1л(г), 1;_лу>>0.
Такая дифференциальная форма со называется положительной
(1, 1)-формой; в] голоморфных локальных координатах z -—
= (zi, . . ., z„) на М форма со положительна, если
co(z) = —р— 2 hii (z) dZi л dzj,
где эрмитова матрица Н (z) = {к^ (z)) положительно определена
для каждой точки z.
Пусть S CZ М — комплексное подмногообразие; тогда для
z £ 5 определено естественное вложение Г^ (S) а T'z {Щ-
Следовательно, эрмитова метрика на М при ограничении на 5 индуцирует
эрмитову метрику. Более общо, если f:N-^M — такое
голоморфное отображение, что
инъективно для всех z ^ N, то метрика на М индуцирует метрику
на Л'':
(d/dwg., dldw^)^ = (j^dldw^, f^dldw^)f(^y
Заметим, что в этом случае для достаточно малого U cz N
всегда можно найти такой корепер (ф^, . . ., ф„) на / {U) а М,
что фй+1, . . ., ф„ е кег /*: Tf(,, (М) -^ Т*' (N); тогда Гщ, . . .
• • •) /*Фа образуют на U корепер относительно индуцированноа
42 0. Предварительные сведения
метрики. Ассоциированная (1, 1)-форма cojv на N имеет вид
к ^ А
Т. е. ассоциированная (1, 1)-5борл«г индуцированной метрики на IV
является прообразом ассоциированной (1, 1)-формы метрики на М.
Примеры. 1. Эрмитова метрика на С", определенная формулой
л _
7 = 1
называется евклидовой, или стандартной, метрикой; индуцирован-
лая риманова метрика, конечно, является стандартной метрикой
ла С" = !R^". ,tV
2. Пусть Л сг С" — полная решетка; тогда метрика,
определенная на комплексном торе С"/Л формулой
ds-= У, dZi (g) dzf.
тоже называется евклидовой метрикой на С"/Л.
3. Пусть Zfl, . . ., Z„ — координаты в С"+^. Обозначим через
л: С"+^ — {0} ->• Р" стандартное отображение проектирования.
Пусть и CZ Р^ — открытое множество и Z: U -^ С"+^ — {0} —
подъем и, т. е. такое голоморфное отображение, что jt о Z = id;
рассмотрим дифференциальную форму
^^J^ddlog\\Z\\^.
Если Z': С/ ->■ С"+^ — {0} — любой другой подъем, то Z' = f-Z,
где / — ненулевая голоморфная функция, так что
-^^<5Jlog||Z'|P = -'^55(log||Z||2 + ]og/ + log7) =
= со +-?^=^ (^д log /-dd log 7) = 0).
Таким образом, со не зависит от выбора подъема; поскольку
подъемы локально существуют всегда, то со является всюду
определенной на Р" дифференциальной формой. Ясно, что со имеет
тип (1, 1). Чтобы убедиться в том, что форма со положительна,
заметим прежде всего, что унитарная группа U {п -{- i) действует
на Р" транзитивно и оставляет форму со инвариантной, поэтому
2. Комплексные многообрагия 43
форма со положительна всюду, если она положительна в какой-
нибудь точке. Пусть теперь {wi = Zi/Zq} — координаты на
открытом множестве Uq = (Zq ^ 0) в Р". Используя подъем Z =
= (1» "'ii • • ■> "'п) на Uq, получим
-—2S—I i + y]u:jwj (1 + 2 >W)'
В точке [1, О, ..., 0]
]■
co =
2я
2 dwj /\dWj >.0.
Поэтому CO определяет на P" эрмитову метрику; она называется
метрикой Фубини — Штуди.
Теорема Виртингера. Взаимосвязь между вещественной и
мнимой частями эрмитовой метрики отражается в теореме Виртингера,
доставляющей еще один пример фундаментального различия между
римановой и эрмитовой дифференциальными геометриями. Пусть
М — комплексное многообразие, z = (z^, . . ., z„) — локальные
координаты на нем и ds^ = 2 Фг ® Фг — эрмитова метрика на М
с ассоциированной (1, 1)-формой со. Положим ф; = czj + У —1^^;
тогда ассоциированная риманова метрика на М имеет вид
Re(ds2)=2a,®a;-bP,®P^
а ее элемент объема —
d^ = ос, л Pi л ... л ос„ л Р„.
С другой стороны, а = ^ aj А ^j, так что ге-я внешняя степень
со" формы со равна
со'' = ге ! ocj л Pj л ... л cz„ л Р„ = ге ! dyi.
Пусть теперь S ^ М — комплексное подмногообразие
размерности d. Как мы уже отмечали, (1, 1)-форма, ассоциированная
с метрикой, индуцированной на S метрикой ds^, является просто
ограничением со |s. Применяя полученную формулу к
индуцированной метрике на 5, получаем следующий факт.
Теорема Виртингера.
vol(5) = .i^Jco^.
44
0. Предварительные сведения
Итак, объем комплексного подмногообразия S комплексного
многообразия М выражается как интеграл по S глобально
определенной дифференциальной формы на М. В вещественном случае
это не так. Например, для С°°-дуги t>-* (х (t), у (t)) в iR^ элемент
длины задайтся формой
(х' (tf + у' т''' dt,
которая, вообще говоря, не является прообразом никакой
дифференциальной формы на IR^.
В завершение этого параграфа обсудим интегрирование по
аналитическим подмножествам комплексного многообразия М.
Начнем с того, что определим интеграл дифференциальной формы ф
на М по (возможно, особому) аналитическому множеству V как
интеграл от ф по гладкой части V* множества V. Прежде всего
надо доказать следующее
Предложение. Множество V* имеет конечный объем в ограню-
ценных областях.
Доказательство. Поскольку вопрос локален, а объем
увеличивается при увеличении метрики, достаточно доказать утверждение
для подмножества У сг С" с евклидовой метрикой. Пусть
размерность V равна к. Выберем в С" координаты так, чтобы в
окрестности точки О множество V пересекало все координатные (ге — к)-
плоскости z^j = Zij = . . . = Zj = О лишь по дискретным
множествам точек. Очевидно, что (1, 1)-форма, ассоциированная с
евклидовой метрикой на С", имеет вид
©^
V~i
2 dzj л dz].
откуда (вводя констадту с = (]/—1/2)''(— l)*^*"'' •&!),
получаем, что
■fi-
со"^ = с • 2 dzj л dzj.
Таким образом, достаточно доказать, что
I dzj л dzj
<оо,
у«ЛД
где / = {1, . . ., А}, а Л — маленький полидиск с центром в начале
координат. Но отображение проектирования
jt: F* -> С'', (zi, ..., г„) h-* (zi, ..., z^)
2. Комплексные многообразия 45
Представляет V* как с^листное разветвленное накрытие над Л' =
= л (А), и, следовательно,
с \ dzx Adzj^d-c \ dzj А dzi <ioo. Q
Снова отметим отсутствие аналогичного результата в
вещественном случае, в котором множество гладких точек множества
нулей гладкой функции — такой, как / (у) = (е-У^ — 1) sin (1/г/),—
не обязательно имеет локально конечный объем.
В процессе доказательства этого предложения мы убедились
в том, что для любой области U cz М с компактным замыканием
Т} ж ^ ^ А* (U) выполнено неравенство \ ф <; оо.
Очевидное, но важное наблюдение состоит в том, что для fe-мер-
ного множества У* пространство Л''-' (У*) является нулевым при
р или q > к; следовательно, для любой формы ф
^ ф = I фС^. к).
Теперь может быть доказана следующая
Теорема Стокса для аналитических множеств. Пусть М —
комплексное многообразие, V cz М — аналитическое подмножество
размерности к и ц) — дифференциальная форма на М степени
2к — 1с компактным носителем; тогда
5йф:
:0.
Доказательство. Утверждение локально, т. е. достаточно
показать, что для любой точки р 6 У найдется такая ее окрестность U,
что для любой формы ф £ A^^^-^ (U)
J сгф = 0.
V
Для любой точки р ^ V найдутся такая система координат z =
= (zi, . . ., z„) и такой полидиск Л с центром в р, что отображение
проектирования п: (zi, . . ., z„) >-> (z^, . . ., z^) представляет
У П A как накрытие образа Л' = л (Л), разветвленное над
аналитической гиперповерхностью D а Л'. Пусть Те есть 8-окрест-
ность D в Л' и Уе = (У П А) — л-^ (Ге). Для ф е Л2Й-1 (Л) имеем
\ йф = Ит\ d(p — lim. \ ф = Ит \ ф.
у « о v^ «-0 av «-о эя-1(т )
46 0. Предварительные сведения
Таким образом, чтобы доказать требуемое, нам нужно просто
установить, что объем множества дп~^ (Т^) стремится к О при
8->• 0. Но дп~^ (Т^) есть конечное накрытие над дТ^; поэтому
достаточно доказать, что vol (дТс) ->• О при 8 ->• 0. Для этого
обозначим через Di особое множество D, через D^ особое
множество Di и т. д.; пусть Т1 есть е-окрестность многообразия D* =
= Di —Di+i в Л—Di^i- Тогда D* — подмногообразие
вещественной размерности ^2к — 2, имеющее конечный объем в
А — -Oj+ii поэтому объем дТ\ стремится к О при 8 ->• 0. Но дТ^ cz
CZ и (дТ1), поэтому vol {дТ^)-^0 при 8 -^ 0. D
Этот результат связан с тем обстоятельством, что особенности
комплексно аналитических подмножеств содержатся только в
подмножествах коразмерности 2. Вывод состоит в том, что
интегрирование по аналитическим множествам сводится в основном к
интегрированию по многообразиям; еще важнее, вероятно, то, что это
позволит нам в дальнейшем показать, что аналитическое
подмножество компактного комплексного подмногообразия всегда
определяет некоторый класс гомологии в R^ (М, к).
Сформулируем, наконец, следующий результат:
Теорема о собственном отображении. Пусть М, N —
комплексные многообразия, /: М -^ N — голоморфное отображение и V cz
cz М — такое аналитическое множество, что f \у — собственное
отображение-, тогда f (У) — аналитическое подмножество в N.
Доказательство будет дано в § 2 гл. 3.
3. ПУЧКИ И КОГОМОЛОГИИ
Пг^оисхоокдение: задача Миттаг-Леффлера
Пусть S — риманова поверхность, необязательно
компактная, р — точка на ней, z — локальная координата с началом
п
в р. Главной частью функции в точке р называется часть 2 o,hZ~^^
ряда Лорана с отрицательными степенями. Если Ор — локальное
кольцо голоморфных функций и Q/h р — поле мероморфных
функций в окрестности точки р, то главная часть — это просто элемент
факторгруппы вМрКЭр. Задача Миттаг-Леффлера состоит в том,
чтобы определить, существует ли для заданного дискретного
множества {рп} точек поверхности S и главных частей в точках р„
мероморфная на S функция /, голоморфная вне {рп), главные
части которой во всех точках р^ совпадают с заданными. Локально
ответ на этот вопрос очевидным образом положителен, так что
3. Лучки и когомологии 47
проблема состоит в том, чтобы перейти от локальных решений
к глобальным. Изложим два подхода, каждый из которых приводит
к теории когомологии.
Подход Чеха. Выберем такое покрытие U = {С/„} поверхности
S открытыми множествами, что каждое из С/„ содержит не более
одной точки Рп, и пусть /„ — мероморфная функция на U^,
решающая задачу в U^, Положим
в Uo, (]U^ (]Uy имеем /„р + /pv + /va = 0.
Решение задачи глобально равносильно нахождению таких
функций {g^ е G (U^)}, что
/аЭ = g» — g<x В С/.„ П и^.
Если такие ga заданы, то / = /^^ + g„ — глобально определенная
функция, удовлетворяющая требуемым условиям, и обратно.
В теории Чеха вводятся группы
{{/аз}: fa&+Uy + fy. = 0} = Z^ {U, О),
Ша&У- ta»=g»—ga ДЛЯ НеКОТОрЫХ g-„€0(t^a)} = 5* (С/, С),
И препятствием к глобальному решению задачи является первая
группа когомологии Чеха
Н^ {U, в) = Z^ (С/, G)/B^ (£_, 6).
Подход Дольбо. Как и выше, пусть /„ — локальное решение
на Ua, и пусть р„ — функция, равная 1 в окрестности точки
Рг, € Ua тз. имеющая компактный носитель, содержащийся в Ug..
Тогда ф = 2 ^ (Pafa) является 5-замкнутой (О, 1)-формой на S
а
класса С°° (ф ^ О в окрестности точки j9„). Если Ц) = дг\ для
некоторой г\ ^ С°° (5), то функция
/=SPa/a —ri
а
решает поставленную задачу; таким образом, препятствие лежит
в группе На' s (5).
Пучки
Пусть задано топологическое пространство X; пучок ^ на X
сопоставляет каждому открытому множеству U cz X группу ,^(t^),
называемую группой сечений ^ над U\ и каждой паре U а V
открытых подмножеств в X гомоморфизм Гу,и'- ^{V)-^^{U),
о, Ппедварительные сведения
лазываемый гомоморфизмом ограничения; при этом должны
выполняться следующие условия.
1. Для любой тройки и с^ V CZ W открытых множеств
в силу этого соотношения можно вместо Гу, ц (а) писать а \ ц.
2. Для любой пары открытых множеств U, F cz М и сечений
о 6 ^(U), т 6 ^(V), таких, что а \unv = f \unv, найдется такое
•сечение р 6 ^(U (J У), что
Р \и = о, р |у = т.
3. Если а 6^(U и F) и ст lu = ст |у = О, то ст = 0.
Обозначения. Ниже перечисляются пу^ки, с которыми мы
будем встречаться особенно часто. Во всех случаях отображения
■ограничения очевидны, а группы аддитивны, кроме явно
оговоренных случаев.
1. На любом С°°-многообразии М определим пучки С°°, С*,
Л'р, %Р, Z, Q, iR и С, полагая:
С« (С/)=С"*-функции на U\
С* (U) = группа ненулевых С°°-функ1щй на U по умножению;
^Р (С/) = р-формы на и класса 6"°°;
%Р (С/) = замкнутые р-формы на XJ класса С°°;
Z(Z7), Q(Z7), 1Я(С/), С (Z7) = локально постоянные Z-, Q-, Dl-
л С-значные функции на IJ.
2. Если М — комплексное многообразие, Y а М —
аналитическое подмножество в М и Е ^>- М — голоморфное векторное
расслоение (определяемое ниже), то определим на М пучки О,
О*, QP, ^Р.9, %w\ 3v, е (Е)ш Л^Я (Е), полагая
О (U) = голоморфные функции на U;
О* (U) = грухша ненулевых голоморфных функций на U
по умножению;
QP ([/) = голоморфные р-формы на U;
j,p,Q (С7)=_С°°-формы типа (р, q) на Щ
%f ■' {U) = 5-замкнутые С"°-формы типа (р, q) на U;
д
Jv (U) = голоморфные функции на U, равные нулю на
О (Е) (U) = голоморфные сечения Е над С/;
^Р.9 (Е) (U) = £-значные (р, д')-формы над U класса С°°.
3. Пусть снова М — комплексное многообразие. Мероморфная
функция f на открытом множестве Ucz М локально задается как
отношение двух голоморфных функций, т. е. для некоторого
*) т.и = id и ^ (0) = О по определению.— Прим. ред.
3. Пучки и когомологии 94
покрытия (C/J множества Z7 имеем/ |и = gilhi, ще gi, hi взаимно
просты в 0 (Ui) и gih] = gjhi в 0 (Ui f) Uj). В этом определении
неявно использовано предложение из § 1 о факториальности
локального кольца аналитических функций. Мероморфная
функция, строго говоря, не является функцией, даже если считать оо
ее значением: она не определена в точках, где gt = hi = 0. Пучок
мероморфных функции на М обозначается о#; мультипликативный
пучок мероморфных функций, не равных нулю тождественно,
обозначается а/Н'*.
Отображение пучков ^ —> ^ на М задается набором таких
гомоморфизмов {axj\ §^ (U) ->^ {U)}vc:mi что для U а V а М
гомоморфизмы ОС и и осу коммутируют с отображениями
ограничения. Ядро отображения ос: ^ -> ^ есть пучок кег (а),
определенный как кег (а) (U) = кег {аи'. ^ (U) -^S (U))'i легко проверить,
что это действительно пучок. Коядро определить сложнее: если
положить сокег (а) (U) = § (U)/au^ (U), то сокег может не
удовлетворять перечисленным выше условиям определения пучка.
[Важный пример такой ситуации доставляет отображение пз^чков
ехр: 0^©*
на С —(0), переводящее f е <3 (U) в e2nV-i/ ^ q* ^щ Сечение
Z 6 0* (С — (0}) не лежит в образе группы О (С — {0}) при
отображении ехр, но его ограничение на любое стягиваемое
подмножество С/сг С—(0} лежит в образе О (U).] Вместо зтого
определим сечение пучка сокег (а) над U посредством задания
открытого покрытия {Ug} множества U вместе с сечениями Ста €
^^ (Ua), такими, что для всех а, Р
<JaltJ„ni;p-<^plt;„nup6au„ni;p (^(UocOUg,));
мы будем отождествлять такие наборы {(17^, сг„)} и {(U'a, о'а)},
если для всех p^U и Ua, U^^ р найдутся такие V, что p^Vcz
c:(U„(]Uk) и ai\y-a'^\yeo^y(^(V)).
Последовательность отображений пучков
называется точной, если $ = кег (Р), а § = сокег (а); в этом
случае говорят также, что $ — подпучок в ^, & § — факторпу-
чок ^ по % (он обозначается ^1%). Более общо,
последовательность
• ■ • ^ J п —* J п+1 ^ J п+2 ^ • • •
называется точной, если а„+х о а„ = О и последовательность
О -> кег (а„) -> jF„ -> кег (a„+i) -> О
4-046
50 О. Предварительные сведения
точна для всех п. Заметим, что по нашему определению коядра
отсюда не следует, что последовательность
О -> g {U). ^^{U)h§{U)-^0
точна для всех U, а следует только то, что эта последовательность
точна в первых двух членах для всех U и что для любого сечения
а ^^ {IT) и любой точки р ^ U найдется такая окрестность V
точки рви, что а \у лежит в образе ^у.
Замечание: пусть М а N — подпространство и ^ — пучок
на М; тогда можно «продолжить ^ нулем» вне М и получить пу-
чок ^ на N, полагая ^ {U) = ^ {U {] М) с очевидными
отображениями ограничения. Значит, пучок ^ можно рассматривать
как на М, так и на N.
Примеры. 1. На любом комплексном многообразии
последовательность
точна, где i — очевидное вложение, а ехр — экспоненциальное
отображение ехр (/) = ё^ . Эта важнейшая
последовательность называется экспоненциальной последовательностью пучков.
2. Пусть М — комплексное многообразие viV а М —
комплексное подмногообразие; тогда пучок 0у, продолженный нулем вне V,
можно считать пучком на М. В этой ситуации последовательность
О -»- Jv -^ ©м -^ ©у -> О,
где I — вложение, а г — отображение ограничения, точна.
3. По обычной лемме Пуанкаре последовательность
О -> R -> С°° -^ ^1 Л ^2 _». ...
точна на любом вещественном многообразии.
4. По ^-лемме Пуанкаре последовательность
О -> QP -> ^Р, о Л ^Р, 1 Л ^Р, 2 _^ ...
точна на любом комплексном многообразии.
5. Пусть М — риманова поверхность. Обозначим через аР0^
I,
факторцучок пучка &S по подпз^чку О -^ Л; тогда для открытого
подмножества U cz М
еРеР (С/) = {(р„, /„): {р„} сг с/— дискретное множество точек.
3. Пучки и когомологии 51
Таким образом, задание сечения пучка S^tff' над U равносильно
постановке задачи Миттаг-Леффлера для U.
Когомологии пучков
Пусть ^ — пзгчок на М ш U = {и^} — локально конечное
открытое покрытие. Положим
сни,^)= П ^(Uo^ou^),
афР
«офоцф. . .фар
Элемент cr = {CTjg^ ( П C^fft)}#j_p^.i группы С^ (U, 3^) называется
р-коцепью пучка ^. Определим кограничный оператор
6: CP(U,S^)-^CP*^(U, ^)
формулой
р+1
(^°)«о ip+i = Д (— ^У ^и i> ip+Ji^ion • • -nuip-
в частности, для сг = {сту}6 С" (С/, ^) имеем {Ьа)иу=—Ои-\-ау,
а для ст = {СТи,у}бСЧ£^, ^) "
Ф^)и, V, W = ^uv + <^vw — t^uw
(здесь опущены знаки ограничения).
р-коцепь а ^С^ (и, 3^) называется коциклом, если да = 0.
Заметим, что любая коцепь а должна удовлетворять условий
кососимметричности
"1, »р^ io ig-li ig+i> ig> ig+z »Р'
Коцепь a называется кограницей, если ст = бт для некоторого
т 6 С"^ (и, ^). Легко проверить, что б^ = О, т. е. кограницы
являются коциклами; это позволяет определить группы
Z" (и, ^) = кег б с С^ (С/, ^)
и
IP (U, ^) = ZP {U, 3)/8CP-i (U, ^).
Далее, пусть даны два покрытия многообразия М: U = {Ua}aei
ж и' = (C/plpg/'. Покрытие U' называется измельчением
покрытия и, если для каждого ^ ^1' найдется такое а ^ I, что U'^ р:
4*
52 0. Предварительные сведения
d Ua\ В ЭТОМ случае мы будем писать U' < U. Если U' < U, то
можно выбрать такое отображение ф: Г -^1, что Z/p сг U^^
для всех р. Тогда определено отображение
задаваемое формулой
(Рф<^)Ро. .-Зр = <^Ч>Ро.. .ФЗркрдП... ni^pp-
Очевидно, что б о р^, = р^, в б, поэтому рф определяет гомоморфизм
р: IP{U,^)^H''{U',^),
не зависящий от выбора ф (читатель может при желании
проверить, что цепные отображения Рф и р^, определенные по двум
отображениям измельчения ф и ар, цепногомотопны и поэтому
индуцируют одинаковые отображения в когомологиях). Назовем
р-ш группой когомологий Чеха пз^чка ^ на М прямой предел групп
SP' (U, 3') при неограниченном измельчении покрытия U'.
ЯР {М, ^) = lim IP (U, ^).
и
В случаях когда возможны недоразумения, будем обозначать
когомологий Чеха Н. Ясно, что для любого покрытия U
Я» (М, ^) = Я» (U, ^) = ^ (М).
Заметим, что если М с: N — замкнутое подпространство, а
^ — любой пу^ок на М, то, продолжая ^ нулем на все N,
получим Я* (М, ^) = Я* (N, ^).
С определением Я* (М, §-) как прямого предела на практике
невозможно работать. Необходимо найти простое достаточное
условие на покрытие С/, при котором выполняется равенство
Я*(£/, ^) = Я*(М,^).
Такое условие дает следующая
Теорема Лере. Пусть покрытие U ациклично для пучка 3',
т. е.
Нч (Ui^O •••OUip, 3^) = 0 при q>0 для любых ii, ..., ip;
тюгда Я* (U, ^) ^ Я* (М, f).
Некоторые частные случаи теоремы Лере доказываются ниже
по мере необходимости.
3. Пучки и когомологии 53
Наиболее существенное свойство когомологии пучков состоит
в следующем: пусть дана точная последовательность
пучков на М; тогда определены отображения
с^ {U, Ш) Л с^(U, я. с^ (U, ^) л с^ (U, щ,
которые перестановочны с б и потому индуцируют отображения
Я^(ЛГ, §)-^Я»(М, ^), Н'(М, ^)^ НР(М, Щ.
Определим теперь кограничное отображение б*: W (М, Щ ->
-*■ ЕР'^^ (М, %). При данном ст 6 С^ {U, Щ, удовлетворяющем
условию бст = о, можно всегда перейти к такому измельчению U'
покрытия и И подобрать такое х^С^ (U', ^), что р (т) = рст.
Тогда рбт = брт = брст = О, так что, переходя к еще более
мелкому покрытию и", найдем такое \i 6 С+^ (U", %), что czji, =
= бт; cz6(i, = 6cz(i, = б^т = О, и, поскольку ос инъективно, отсюда
будет следовать, что б(х = 0. Таким образом, \!i, ^ ZP*^ {U", %),
и мы можем положить б*ст = ц € SP*^ (jx, %).
Основной факт. Последовательность
О -> Я» (М, g),-> Я» (М, ^) -> Я» (М, S) ->
-> IP (М, Щ-^W- (М, ^) -^ Ю (М, f) -> . . .
.. .->яр(м, %)^т{м, ^)-^1Р {м, ^)->...
точма.
Для большинства естественно возникающих точных
последовательностей 0-»-§-»-^—>-^-»-0 и заведомо для всех пучков,
которые нам встретятся в этой книге, существуют сколь угодно
мелкие покрытия U, такие, что для любого U = Ui П • • • П '^fp
точна последовательность
Тогда можно найти сколь угодно мелкое покрытие U, для которого
группы коцепей образуют точную последовательность
О -^ СР (U, Ш) -> СР (U, ^) ^ с (С/, §) -> 0.
в этом случав основной факт легко проверить: например, чтобы
убедиться в том, что точна последовательность
IP {U, ^) -^ HP (U, Щ % HP*'- (U, %),
54 0. Предварительные сведения
рассмотрим коцепь а ^С^ (U, 3), для которой бст = О и б*ст = О
в 1Р*^ (U, g). Тогда найдутся такая коцепь т g С (U, ^), что
рт = сг, и такая коцепь [i g С^*^ (U, 3'), что czji = бт; по
определению [х = б*ст в НР*^ {U, %), так что ji, = 6v при некотором
V ^С^ (и, g ). Тогда т — CZV — коцикл в С (U, ^),
удовлетворяющий условию р (т — av) = рт = ст; это показывает, что а 6
6 Р* (-0^ (и,^)). Кроме того, ясно, что б*р* = 0. Остальные
этапы проверки выполняются аналогично.
Наиболее распространенное применение точной
когомологической последовательности, ассоциированной с точной
последовательностью пупков
связано с ответом на вопрос: когда глобальное сечение а пучка §
является образом при отображении р глобального сечения пучка
^? Ответ (в соответствии с точной когомологической
последовательностью) состоит в том, что это имеет место тогда и только
тогда, когда б*ст = О в IP (М, Щ.
Например, рассмотрим снова точную последовательность
на римановой поверхности М. Данные задачи Миттаг-Леффлера —
это глобальное сечение g 6 iP>ip> (М) = Н" (М, ^Щ', вопрос
состоит в том, выполнено ли равенство g = р*/ для какой-нибудь
глобальной мероморфной функции /. Если {/у} — локальные
решения задачи, то, как мы видели, (б*^)и, v = fv — fu^ Sl g =
= p*/ тогда и только тогда, когда 6*^ = О в Н^ {М, О).
Нам встретятся, грубо говоря, три разновидности пучков.
1. Голоморфные пучки — такие, как О, Jy, <Э {Е) и Q^ —
сечения которых задаются локально наборами п голоморфных
функций. Они содержат больше всего информации и являются
главными интересующими нас объектами изучения.
2. С°°-пучки — такие, как ^''•' — локальные сечения
которых задаются наборами С°°-функций. Они обычно используются
как вспсгмогательные.
3. Постоянные пучки — такие, как Z, R, С. Они, как мы
увидим ниже, несут топологическз^ю информацию о многообразии.
Следует отметить два обстоятельства, касающиеся последних
двух классов пучков.
1. 1Р(М, Л^^') = 0 для р>0.
3. Пучки и когомологии 55
Доказательство. Для любого локально конечного покрытия
V = {С/а}а£1 многообразия М можно найти подчиненное ему
разбиение единицы, т. е. такие С°°-функции р^ на М, что 2 Ра ^ 1
и носитель Ра содержится в £/„. Далее, для заданного коцикла
<s^Z^{U, ^^') определим коцепь x^C^~^{U, А'^^'), полагая
"^ао- • ■ «р-1 ^^ 2j Рэ*^Р, «о ар_1)
где сечение рр • ор, „о «p-i продолжено нулем на Uag П •. •
... П f^ap-i! можно проверить, что бт = ст. В случае р = 1 имеем
в явном виде
(Tuv + Ovw + Owu^O в UC\VC\W.
Положим Т[г= У] Рт^с^т^и; тогда
V
www
Вообще, пучки, допускающие разбиения единицы (т. е.
существование для любого и = \j и^ таких отображений Т1а=
^{Ua)-^^(U), ЧТО носитель Tiacr содержится в С/а и
S Ла (t^lO ^ ° ^^^ сг 6 ^ (^)) называются тонкими. То же
самое рассуждение показывает, что их высшие группы
когомологии обращаются в нуль.
2. Для симплициального комплекса К с базисным
топологическим пространством М имеем
Н* {К, Z) ^ Н* (М, 1),
т. е. когомологии Чеха постоянного пучка Ъ на М изоморфны, сим-
плициальным когомологиям комплекса К. Чтобы убедиться в этом,
сопоставим каждой вершине v^ из К открытое множество St (va),
называемое звездой с вершиной v^, которое состоит из внутренних
точек объединения всех симплексов в К, содержап1;их Va в
качестве одной из вершин. Ясно, что С/ ={[/„ = St (v„)} является
~ р
открытым покрытием М. Пересечение П St (va,) непусто и связно,
г=0 *
если только Va,, . . ., Va_ ЯВЛЯЮТСЯ вершинами некоторого р-
симплекса; в противном случае оно пусто. Таким образом, р-
коцепь а сопоставляет каждому набору {а^, . . ., оср) элемент
{!■, если \а- порождают р-симплекс;
О в протишом случае.
56 0. Предварительные сведения
Для заданной а^С(U, 1) определим симплициальную ^э-коцепь
а', полагая
а' (^) = aao,..ap,
где A = <Vao, ...,Vap) еСТЬ ^Э-СИМПЛеКС с вершинами Vag, ... .,\ар-
Соответствие а ^-*■ а' определяет изоморфизм абелевых групп
С* {U, Щ^С^ {К, Z)
и гомоморфизм
8а' ««о ... «p+i» = S (-1)*^* <^' (<ао ...at ... «p+i» = (ба)',
г
так что имеет место изоморфизм цепных комплексов С* {U, Z) ->-
—>- С* (К, Z) и, следовательно, изоморфизм групп когомологий
Н* (U, Z) -> Н* (К, Z). Поскольку комплекс К можно
неограниченно подразделять, сколь угодно измельчая тем самым
покрытие и, а когомологий Н* {К, Z) при этом не меняются, получаем
изоморфизмы
Й* (М, Z) ^ Я* (U, Z) ^ Я* (Z, Z).
Теорема д.е Рама
Пусть М — вещественное С°°-многообразие. Мы будем
называть сингулярную ^э-цепь а на М, заданную формальной линейной
комбинацией 2 ''^ifi отображений А -^ М стандартного
^^-симплекса А сг RP в М, кусочно гладкой, если все fi продолжаются до
отображений класса С°° некоторой окрестности А в М. Обозначим
пространство кусочно гладких целочисленных ^э-цепей Ср* (М, Z).
Ясно, что граница кусочно гладкой цепи кусочно гладка, так что
С^ {М, Z) образует подкомплекс в С^ {М, 1) и можно положить
Zl^ (М, Т) = кег 5: С?" (М, Z) -^ Cf.i (iV/, Z),
Я?*(М, Z) = Z?*(i«-, Ъ)1дС^^^{М, Т).
Согласно фундаментальному результату из дифференциальной
топологии, отображение вложения С^ (М, Z) ->• С# (М, Z)
индуцирует ивоморфизм групп гомологии
Н^(М, Z)^Hp{M, Z);
иными словами, каждый класс гомологии в Нр (М, Z)
представляется кусочно гладким ^э-циклом, и если некоторый кусочно
гладкий ^э-цикл о гомологичен О в обычном смысле, то существует
кусочно гладкая (р -\- 1)-цепь т, для которой дх = ст.
3. Пучки и когомологии 57
ПустБ Теперь ф б Л^ (М) есть /ьформа класса С°°, а ст =
~ 2 "-ifi— кусочно гладкая ^э-цепь; положим
<Ф, а)= J Ф=2«< 5 /'Ф-
Если ф — замкнутая форма, то для границы а некоторой (р + 1)-
цепи т по теореме Стокса имеем
j Ф= j d9 = 0,
так что ф определяет вещественнозначный сингулярный р-коцикл.
Снова по теореме Стокса в случае, когда а — цикл, имеем
J Ф = J Ф + dri
для любой формы т) 6 Л.^-^ (Щ); позтому определено отображение
ЯЬк(М)-^Я|=1пе(М, R).
Теорема де Рама утверждает, что это отображение на самом деле
является изоморфизмом.
Первоначальное доказательство теоремы де Рама опиралось
на введение относительных групп когомологии де Рама; затем
устанавливалось, что возникающая в результате теория гомологии
удовлетворяет аксиомам Эйленберга — Стинрода. Мы приведем
более короткое рассуждение, основанное на теории пучков. Оно
не так геометрично, зато простая его перефразировка позволит
ниже доказать теорему Дольбо.
Прежде всего, поскольку любое гладкое многообразие М
может быть реализовано как топологическое пространство
некоторого симплициального комплекса К, имеем
ЯЙпв {М, R) S Н* {К, R) ^ Й* {М, К).
Далее, по обычной лемме Пуанкаре последовательность пучков
о-> R-> ^в Л ^1Д ^2_^...
на М точна; иначе говоря, все последовательности
0-v2''-v^''^2''+i-vO
точны. Но, как мы видели, H^^ {М, Jp) = О при g > О и всех р;
поэтому из точных когомологических последовательностей, ассо-
58 0. Предварительные сведения
циированных с выписанными короткими точными
последовательностями пучков, получаем
IP (М, R) ^ ZP-1 (М, 21) ^ Я"-^ (М, %2) ^ ... ^Я1 {М, %"-*) ^
^ Я» (71/, %'')/бЯв (71/, ^"-1) =
= ZP {M)/dA^-^ (М) = ЯВк (71/). Q
Заметим, что изоморфизм де Рама функториален: если f: М -^
—*- N — гладкое отображение С°°-многообразий, ф — замкнутая
/>-форма на 7V, представляющая класс [ф] 6 H^i^g (7V,R ) при
изоморфизме де Рама, и ст = 2 ''■tft— кусочно гладкий р-цикл
яа 71/, то
г Д
Т. е. /* [ф] = [/*ф].
Теорема Дольбо
В начале этого параграфа мы видели, что препятствие к
решению задачи Миттаг-Леффлера на римановой поверхности S можно
считать лежащим либо в Н^ {S, О), либо в Я|'* (S). Это частный
•случай следующего общего факта.
Теорема Дольбо. На комплексном многообразии 71/ имеет место
изоморфизм
Доказательство. По 5-лемме Пуанкаре последовательности
0-^ %!'«-^ .^^'«ЛZf ■ «+*-^О
точны для'всех р, q. Поскольку Н^ (М, ^^'^ = О при г>0
и любых р, q, точные когомологические последовательности,
связанные с этими последовательностями пучков, дают изоморфизмы
Я« (71/, Q") ^ Я«-1 (71/, %!' *) ^ Я«-2 (71/, %1>^)^ ...
, . ,^ Я1 (71/, Zf- «-*) ^ Я» (71/, 2|' ^)/~дH^> (71/, .^^•'-*) = Я|• " (71/), Q
3. Пучки и когомологии 59
В качестве приложения докажем частный случай теоремы
Л ере: для локально конечного покрытия £/={£/„}
многообразия М, ацикличного для структурного пучка О, т. е. обладающего
свойством
IP(Ua,(]...(]Uag,&) = 0 ДЛЯ р>0,
имеет место изоморфизм
Я* (С/, в)^Н*(М, 0).
Доказательство. По предположению
Т. е. имеют место следующие точные последовательности групп
коцепей:
что, согласно обычным алгебраическим рассуждениям, дает
точные последовательности
...-V Я^ (С/, ^"-"-*)-V Я" (С/, %!'О-^
-^н""-' (U, %у-')-^1Р+' {U, а'-'-')-^ ...
Поскольку H^(U, А°''') = 0 при р>0, с помощью рассуждения,
использующего разбиение единицы, находим, что
Я« (U_, в) ^ Я«-1 (С/, %1' *) ^
^ Я«-2 (С/, %^' =') ^ ... ^ Я1 (t^, Z^' "-*) ^
^ Я» (С/, %1' УЪНо (С/, ^"' «-*) = Я|' «(М)^
^т{м, 0), о
То же рассуждение проходит для пучков QP.
Примеры вычислений когомологии. 1. Первое наблюдение
состоит в том, что если М есть га-мерное комплексное
многообразие, то
H1{M,Q)^Hl^^^(M) = 0 при q>n.
2. По 5-лемме Пуанкаре
Я«(С", 0) = О при дг>0
и, более общо,
Я«(С''х(С*)', 0) = О при дг>0.
60 0. Предварительные сведения
Кроме того, поскольку С" стягиваемо,
Я«(С", Z) = 0 при ?>0.
Далее, из точной когомологической последовательности,
связанной с экспоненциальной последовательностью пучков на С",
выводим, что последовательность
... -^т (С", о)-^т (С", 0*) -V я«+1 (С", %)
точна; отсюда следует, что
Я«(С", 6*) = 0 при ?>0.
В качестве непосредственного следствия получаем решение
проблемы Кузена:
Любая аналитическая гиперповерхность в С является
множеством нулей некоторой целой функции.
Доказательство. Мы знаем, что в окрестности любой точки р
в С" аналитическая гиперповерхность F сг С" может быть задана
как множество нулей голоморфной функции f ^ Ор, и если
выбрать / не делящейся ни на какой квадрат в Ор, кроме квадратов
единиц, то / определена однозначно с точностью до умножения
на единицу. Поэтому можно найти такое покрытие U = {Ua}
пространства С" и такие функции /а 6 0 (С^а)> 'ito (/а = 0) =
= У f\ Ua И ДЛЯ любых ОС, р
faP = /а//э 6 0* (Ua П U^).
Но, поскольку Н^ (С", 0*) = О, коцикл {gad} 6 С^ (U, о*)
является кограницей, т. е. найдется, возможно после измельчения
покрытия, такая коцепь {h^} g С" ^С/, О*), что /„//р = ga^ =
= h^/ha- Целая функция
/ = faK = /э^Э
имеет своим множеством нулей в точности V. D
Другое приложение обращения в нуль групп когомологий
Н^ (С* X (С*)', 0) связано с тем, что покрытие комплексного
многообразия произведениями плоскостей и проколотых
плоскостей ациклично; мы воспользуемся этим в следующих двух
примерах.
3. Для того чтобы вычислить группы когомологий Н^ (Р^, О),
введем евклидовы координаты и ж v = i/u на Р^ и положим U =
= (и :7^ 0), V = (и фО). Координаты и и у устанавливают
изоморфизм областей U и V с С соответственно, а U П ^ = С*;
3. Пучки и когомологии 61
таким образом, покрытие {U, V} пространства Р^ ациклично.
Далее,
С»({U, V}, О) = {(/, g): feo(U), geoт
и
cH{u, V}, o)={heo{u (]V)}.
Для заданных (/, f)6C"({C/, V}, О) можно написать
n=0 n=0 71=0
Таким образом, элемент б ((/, f)) = —f + g^O{U f\ V) равен
нулю тогда и только тогда, когда а„ = Ь„ = О при
положительных га и ао = Ьо, т. е.
Я» (Pi, 0) ^ С,
или, говоря иначе: глобальные голоморфные функции на Р^—
это только константы.
Вообще тот факт, что Н" (М, 0) ^ С для любого компактного
связного комплексного многообразия, немедленно следует из
принципа максимума.
С другой стороны, для любого элемента
ОО 00
n=—ОО П=я—00
можно написать Л = б ((/, g)), где
ОО ОО
/ San"", f=Sa-nV"
71=0 71=1
И получить отсюда, что
Я1(Р1, 0) = О.
Аналогично, любой элемент (оэ, т]) группы
С» ({С/, F}, Q^ = {(оэ, л): « 6 Q^ (С/), Л 6 ^^ (F)}
может быть записан в виде
00 00 ОО
оэ = { 2 йпи") d«, Л = ( 2 ЬпУ") dy = { - S Ьп"""-'') <^и,
7»««0 7»=0 П=0
поскольку dv = d (и~^ = —и~^ du. Отсюда видим, что б ((w, т])) —
= О тогда и только тогда, когда оэ = т) = О, т. е.
Д»(Р1, Qi)=0.
62 0. Предварительные сведения
Точно так же устанавливается, что элемент
оо
n=—oe
представим в виде б ((оэ, 11)) = —оэ + т] тогда и только тогда,
когда а_х = 0; стало быть, ВУ (Р^, Q^) ^ С. Читатель может
тем же способом проверить, что вообще
f С, если р—а^п;
(P",Q9) = {
о в противном случае;
это будет установлено позже с помощью теории Ходжа.
4. Пусть Л/ = С^ — {0}. По теореме Хартогса 0 (С^— {0}) =
= О (С^). Выберем покрытие U^ = {zy ФЩ, U^= {z^ Ф 0}; оно
также ациклично (C/j ^ С/а ^ С X С*; C/i П С^а ^ С* X С*)-
Группа С^ {{Рх, и^, Q) = О {Ui f\ U^) состоит из рядов Лорана
оо
Ш, 71==—оо
группа 0(С/,)—из рядов / (zj, z^)— S bjnnZfz^, a группа
О (Uz) — из рядов / (zi, Zg) = 2j Cm„zfz2. Таким образом,
8C0({Ui, U^}, 0) = 0 (Ui) + 0{U2) не содержит рядов Лорана
с членами zfz2, где т, га < 0; отсюда видно, что
(11тЯ1(Са-{0}, 0) = оо.
4. ТОПОЛОГИЯ МНОГООБРАЗИЙ
Пересечение циклов
Рассмотрим стандартный тор Т и два 1-цикла Л и S на нем,
изображенные на рис. 1. Интуитивно ясно, что любой 1-цикл,
гомологичный В, должен пересекать всякий 1-цикл,
гомологичный А, тогда как цикл, гомологичный А, например А', вполне
может не пересекаться с А. Речь идет о некотором инварианте
классов гомологии ос = (А) и р = (В) в Нх(Т, Z), и мы хотим
формализовать наши интуитивные представления о нем. Проблема
состоит в том, что число точек пересечения циклов,
представляющих ос и р', вообще говоря, неопределенно: может, например,
встретиться любое из расположений, изображенных на рис. 2.
Хотелось бы найти такой способ подсчета точек пересечения двух
циклов на Т, чтобы «излишние» точки взаимно сокращались.
Можно поступить следующим образом. Прежде всего выберем
ориентацию на Т. Затем, если два цикла Аш В п& Т пересекаются
Топология многообразий
63
Рис, 1
трансверсально в некоторой точке р, определим локальный индекс
пересечения ip {А-В) циклов А ж В в р, полагая его равным +1,
если касательные векторы к А ж В, взятые именно в этом порядке,
образз^ют положительно ориентированный базис пространства
Тр (Т), и равным —1 в противном случае. Определим индекс
пересечения #(^-5) циклов А ж В, пересекающихся
трансверсально в гладких точках, как сумму
#,
ХА.В) =
ip{A.B).
релпв
Легко видеть, что #(Л 'В) зависит только от классов гомологии А
ж В: если А гомологичен нулю, т. е. является границей
объединения областей С; с: Т, причем касательный вектор к А ж
внутренняя нормаль к dCi образуют положительно ориентированный
базис пространства Т (Т), то пересечение пути В с А будет давать
положительный вклад каждый раз, когда В входит в область С;,
и отрицательный, когда он выходит из этой области. Поэтому
#(^'S) = 0, и вообгще, поскольку индекс пересечения линеен по
каждому аргументу, то
ЦА''В)= ЦА-В),
если А >^А'. Наконец, так как для любых двух классов
гомологии а, Р 6 jSfX (Т, 1) можно найти циклы А ж В и& Т,
представляющие а и р и пересекающиеся трансверсально, то тем самым мы
определили билинейное спаривание
HiiT, 1) X Hi{T, Z)-vZ.
Общее определение индекса пересечения циклов на
ориентированном многообразии отличается от разобранного случая только
трудностью проверки утверждений о трансверсальности. Пусть М
— ор1иентированное п-мерное многообразие, А ж В — два кусочно
гладких цикла на М размерностей соответственно к ж п -^ к.
64
0. Предварительные сведения,
Ряс. 2
& р ^ А П ^ — точка трансверсального пересечения А ж В. Пусть
^х, • • ., Vft 6 2^р {А) а Тр {М) — положительно
ориентированный базис пространства Тр {А), а Wy, . . ., w„-ft — положительно
ориентированный базис пространства Тр (В) а Тр (М); определим
локальный индекс пересечения ip (А-В) циклов А ж В в точке р,
полагая его равным +1, если Vj,, . . ., и^, Wj, . . ., w„_ft —
положительно ориентированный базис пространства Тр (М) =
= Тр (А) Ф Тр (В), и —1 в противном случае. Если А ж В всюду
пересекаются трансверсально, то определим индекс пересечения
ЦА-В) как
*(Л.5)= 2 1р{А-В).
Заметим, что эта сумма конечна, поскольку А ж В компактны,
& А П 5 по предположению дискретно.
Теперь 1СЫ должны показать, что индекс пересечения зависит
только от классов гомологии циклов А ж В, 1. е. что
А ^О^ЦА'В) = 0.
Пусть А = дС — сумма границ кусочно гладких {к -{■ 1)-много-
образий Ci, причем в каждой гладкой точке р ^ А ориенти-
4, Топология многообразий
65
Рис. 3
рованный базис v-^, . . ., v^ пространства Тр (А) вместе с
внутренней нормалью задает ориентацию С г- По стандартньш
соображениям трансверсальности можно выбрать цепь С, пересекающую В
трансверсально почти всюду, так что пересечение С С\ В будет
состоять из набора {уа} кусочно гладких дуг. Концы этих дуг
и образуют точки пересечения А ж В. Мы утверждаем, что для
каждой дуги у ее концы у (0), у (1) ^ А fi В имеют
противоположные локальные индексы пересечения (см. рис. 3). В самом деле,
можно найти такие векторные поля класса С", скажем {fj (t) 6
6 Ty(t) (C)}j=i ft, касательные к С вдоль у, и {u; (t) 6
6 T.y(t) (S)}i=ft+2 n, касательные к В вдоль у, что для всех t
выполняются следующие условия:
у Vk (О» у' (О — ориентированный базис для
> 1^п (t) — ориентированный базис для
м Vn (t) — ориентиро-
1) V, (О,
2) у' (t), i^ft+a it),
ТуН) (В);
3) V, (t), . .., Vk (О, у' it), yft+2 (0.
ванный базис для Т^ц) (М),
и при этом Ui (0), . . ., I'd (0) — ориентированный базис для
Г^(о) (А), а Vi (1), . . ., Vfe (1) — для Г^^, (А). (Чтобы
удовлетворить всем этим условиям, возможно, придется обратить
направление на у.) Далее, поскольку у' (1) — внешняя нормаль к С, а
базис Vi (1), . . ., fft (1), у' (1) положительно ориентирован на С,
то базис i^i (1), . . ., fft (1) пространства Ty(i)(A) отрицательно
ориентирован. Таким образом,
ly^oi{A^B)=-\-i и Ца)(^-5)=—1,
что и требовалось.
5-046
66 0. Предварительные сведения
Далее, если а ^ Н^ (М, Z) и р 6 H^n-h Щ, Z) — два класса
гомологии, то можно найти их представители А ж В, являющиеся
кусочно гладкими циклами класса С°° и пересекающиеся транс-
версально. Индекс пересечения ^{А-В) определен классами os
и р, так что мы получили билинейное спаривание
называемое формой пересечения и обозначаемое #(а-р). Заметим,
что по определению индекса пересечения
«ф. а) = (-!)''<"-'"*(а.р).
Можно также определить умножение
Яп_л. {М, Z) X H„.k, {М, Z) -V Я„_й._й. {И, Z)
на гомологиях многообразия М произвольных размерностей:
пусть а 6 -ffn-ft, (М) и р 6 ffn-k, (Щ — классы гомологии; тогда
можно найти их представители А ж В, пересекающиеся трансвер-
сально почти всюду. Их пересечение С наделяется такой
ориентацией, что если Vj,, . . ., fn-fe,-ft, — ориентированный базис
пространства Тр (С) в гладкой точке С и мы дополняем его до базисов
Wi, ..., U'k,, Vi, ..., Vn-kt-k, и Vi, ..., Un-ft,-ft,, Ul, ■■-, Ukt
соответственно пространств Тр (A) и Тр (В), то полный базис
Wi, ..., Wk,, Ul, ..., Un-ft,-ft,> Ml, ..., Uki
положительно ориентирован в Тр (М). Пространство С,
наделенное этой ориентацией, называется циклом пересечения А -В циклов
А ж В. Снова для проверки того, что пересечение корректно
определено на гомологиях (т. е. цикл А-В гомологичен нулю, если А
гомологичен нулю), мы должны показать, что можно найти цепь
С, удовлетворяющую условию дС = А ж пересекающую В транс-
версально почти всюду, и что теоретико-множественное
соотношение А-В = д {С"В) сохраняет силу на уровне ориентированных
циклов. Техника доказательства этих утверждений похожа на ту,
которая используется в случае дополнительных размерностей,
но несколько сложнее.
Терминологическое замечание: всегда, когда речь идет об
индексе пересечения или «топологическом пересечении» двух
циклов А ж В и& многообразии М, имеется в виду пересечение
классов гомологии а, р 6 Н^ {М, 1), которые они представляют.
Таким образом, выражение #{А-В) имеет смысл и в тех случаях,
когда А ж В ше трансверсальны.
4. Топология многообразий
67
ДвоИствеииость Пуанкаре
Основньш результатом, касающимся пересечения циклов,
является следующая
Теорема (двойственность Пуанкаре). Пусть М — компактное
ориентированное п-мерное многообразие; тогда форма пересечения
НАМ, Z) X Нп-н{М, Z)^Z
унимодулярна, т. е. любой линейный функционал H^-h (М, Ъ) -*-
—V Z представим как пересечение с некоторым классом а 6
6 Н]1 {М, 1) и любой класс а 6 Ни {М, 1), имеющий нулевой
индекс пересечения со всеми классами из Я„_й (М, Z), лежит
в группе кручения.
Доказательство. Как и в предыдущем параграфе, мы можем
считать, что М является базисным пространством симплициаль-
ного комплекса К ={ста. 5}а.л- Основной шаг доказательства
состоит в построении двойственного клеточного разбиения много
образия М. Оно осуществляется следующим образом (см. рис. 4).
Прежде всего пусть {та, д) — начальное барицентрическое
разбиение комплекса К. Для каждой вершины (Т^ исходной
триангуляции пусть *СТа= и ч^р есть га-мерная клетка, определенная
как объединение га-симплексов тр разбиения, содержащих Ста
в качестве одной из вершин. Затем для каждого ^-симплекса
Ста исходного разбиения пусть *СТа = П *сгв — пересечение га- кле-
0 ь
ТОК *стр, ассоциированных с А;-|-1 вершинами симплекса Ста-
Клетки {AS~^ = *CTa} составляют разбиение М, называемое
двойственным клеточным разбиением к {СТа}-
Заметим, что, поскольку единственной точкой /с-симплекса Стд
исходного комплекса, лежащей во всех к -\- i клетках двойствен-
Рис. 4
5*
68 0. Предварительные сведения
ного разбиения, является ее барицентр, двойственная клетка
Д2~ = * о^а симплекса СТа есть единственная (га — Щ-клетпка
двойственного разбиения, пересекающая ст^; AS"** и о^
пересекаются трансверсалъно. При заданной ориентации симплекса а^
определим двойственную ориентацию на AS"* как такую, для
которой 1р (Ста» Аа) = + 1 В точке р = ctJ П Ста. Начиная с этого
места, если ст^ рассматривается как ориентированный симплекс,
через *а^ будет обозначаться клетка Ад с двойственной
ориентацией; будем также писать * Д^ для обозначения исходного
ориентированного сиьшлекса ст^.
Свяжем теперь граничный оператор д комплекса {ста} с ко-
граничным оператором б комплекса {А2~''}- Сначала заметим,
h о о „
ЧТО если клетка Ста имеет вершины ст„, ..., ст^, то двойственная
клетка А2~ = *Оа задана как (А:-|-1)-кратное пересечение ПА? =
= П *о? двойственных га-клеток, и поэтому клетки, входящие
i
В кограницу бД^"* клетки AS"*, являются просто А:-кратными
пересечениями А""'''*"*= П А" клеток А", т. е. двойственных
клеток граней ст*~* симплекса а*. Мы утверждаем теперь, что
основное соотношение
Имеет место на уровне ориентированных клеток, т. е. если oj
и Aj ориентированы соответственно как граница и кограница Ста
и Аа, то в точке р' = ст^ П ^3
V(CTrA^)-(-ir-''+'
(см. рис. 5). Здесь проходит рассуждение того же рода, что и при
проверке гомологической инвариантности индекса пересечения.
Симплекс ст^ пересекает клетку A"-''+i по дуге у, ведущей из
барицентра р = Y (0) симплекса Ста в барицентр р' = у (1) грани
О] симплекса СТа- Пусть у^, . . ., у^.^ — векторные поля на Ста
вдоль 7. а Uft+i, . . ., i;„ — векторные поля на A^ вдоль у, такие,
что fi (0), . . ., Vh-iib), y'(0) — ориентированный базис для
17(0) (Оа), а I'ft+i (0), . . .., и„ (0) — ориентированный базис для
^^(о) (Да), и при этом Vy (1), . . ., Vj,_y (1)6 Г^а)^), yft+i(l), •. •
. . ., f„ (1) 6 T'va) (^^)- ^^ предположили, что
4(0)(Аа-О = +1.
поэтому базис у^ (0), . . ., Uft-i (0), у' (0), Uft+i (0), . . ., и„ (0)
положителен в заданной ориентации на М. Далее, поскольку
4. Топология многообразий
Рис. 5
у' (0) — внутренняя нормаль к A^ в y (0) и базис v^+y (0), . . .
. . ., и„ (0) положительно ориентирован в ^^(о) (Аа)> базис
Y' (0), y^+i (0), . . ., i;„ (0)
имеет знак (—1)""* относительно ориентации на А/. По
непрерывности последние два утверждения сохраняют силу и в точке у (1).
В этой точке, поскольку у' (1) — внешняя нормаль к А^ и базис
Ux (1), . . . , Uft-i (1), у' (1) положительно ориентирован на
Ту{1){Оа), базис Ui (1), . . ., Uft.i(l) отрицательно ориентирован
на (т^. Поэтому, как и требовалось,
^v^l)(^rA^) = (-lr''■''•
Из всего этого мы видим, что отображение
определяет изоморфизм между комплексом (С^, д) цепей
исходного симплициального разбиения М и комплексом (С*, б) коцепей
двойственного клеточного разбиения. Возникаюгщие в результате
изоморфизмы
D: Ни (М, Z) -^ Я"-* {М, 1)
обладают тем свойством, что для любых у 6 Hfi {М, Z) ж % ^
еНп-kiM, ъ)
Щу%) = Dy {%),
откуда следует утверждение теоремы. D
70 0. Предварительные сведения
Несколько более слабым вариантом двойственности Пуанкаре
является утверждение о том, что отображение
Я, (71/, О) Л Я„_^ {М, Щ* - Я"-" {М, Щ, Р (А) (В) = *{А.В)
есть изоморфизм, без упоминания о том, что форма пересечения
унимодулярна. В силу изоморфизма де Рама
это равносильно утверждению о том, что для любого Аг-цикла А
на М найдется такая замкнутая (га — А:)-форма ф, что для любого
(га — А;)-цикла В и& М
|ф = *(Л-5).
в
Пусть ф и гр — две замкнутые формы на ориентированном
многообразии М. Тогда их внешнее произведение ф л г|э замкнуто
и благодаря соотношению
Ф л (If + йл) = Ф л ij3 + (- if ^^"^ d (Ф л л)
класс де Рама формы ф л гр зависит только от классов де Рама
форм ф и гр. Поэтому получаем билинейное отображение
Я^н (М) ® Я^н (М) -^ Я^^"' (М)
и, в частности, спаривание
Я^н (М) ® ЯSi'' (М) -V ЯВн (М) - С.
Теперь мы установим связь между этим спариванием в когомоло-
гиях де Рама и пересечением циклов, пользуясь двойственностью
Пуанкаре; для этого сначала мы должны установить формулу
Кюннета.
Пусть М = {СТа}а,к И N = {Oa^ja. к — Д^^ СИМПЛИЦИаЛЬНЫХ
комплекса. Произведения Ста X стр определяют клеточное
разбиение пространства М xN с граничным оператором
д (ctS X стр') = аст^ X стрЧ (-1)" о1 X да^^.
Произведение J[ Х 5 = 2 «а^рСГа X Стр* двух циклов А—'^а^а^,
и S = 2 b^'^'i в М ш N является циклом, и его класс гомологии
зависит только от классов гомологии А ж В, поскольку
(А +дС) X В = А X В + д (С X В).
Таким образом, определено отображение
Я* (М, 1) ® Я^ (N, Ъ) -^Н^{М X N, Ъ)\
4, Топология многообразий 71
МЫ утверждаем, что по модулю кручения это изоморфизм. В этом
нетрудно убедиться, если выразить цепи комплексов М и iV в
терминах канонических базисов, т. е. таких, в которых граничные
операторы диагональны. Можно следующим образом построить
такой базис для цепей в М. Пусть размерность М равна т, и пусть
{т"} — рациональный базис для т-циклов в М. Дополним
{т"} до рационального базиса всех т-цепей в Л/ и обозначим
добавленные элементы через {[Аа}. Положим
так что {СТа"'} — базис пространства границ в М размерности
«1—1; дополним {сг""'} до рационального базиса {ст""', т^*''}
для (т—1)-циклов в Af, а {a^~^i т""'} —до рационального базиса
{оа"',т§*-', \i^-^} всех (тп—1)-цепей в М. Положим аТ^ = д^}i'Sr^-
Продолжая таким же образом, получим рациональный базис
{аа,Та,ц^} для всех цепей в М, где {ста} —базис границ,
{оа, "4} —базис циклов и д\1а=Оа~^.
Пусть теперь {а'а, т'а, [Аа''} —базис, полученный аналогичной
конструкцией для цепей в N, и пусть А—цикл в произведении
М X N, выраженный как линейная комбинация произведений
базисных элементов комплексов М ж N■ Поскольку произведения
Оа X ар , Ста X тр и Та X Стр ЯВЛЯЮТСЯ границами соответственно
V^V'^ Хстр, {4"*"* Хтр и (—1)''т^ Х[Ар'*"\ можно, заменяя А
гомологичным циклом, считать, что в выражении для А таких
слагаемых нет. Точно так же, если в А входит слагаемое СТа X [Ар,
его можно убрать, вычтя из А границу
д ([Аа+' X |А^') = СТ* X (А^' -Ь (- 1)"+' \h^' X СТр'-^.
Таким образом, получаем выражение
4=2 aapftiT^ X т&Ч 2 Ьарьгта X (Ар' + 2 с^ьмА X т^'-Ь
2 + daPftj|4 X [Ар -Ь 2 «apftll^a X СТр .
Переходя к границам, имеем
0 = 34=2 Ьары(-1)''т^ХСТр'-Ч2саеиаГ^Хт^' +
+ 2 daP^Oa"' X (А^'+ 2 (- 1)" ^aew[Aa X СТ^"* -Ь 2 баРйгСТ*"' X СТ^'.
Но слагаемые этой суммы линейно независимы, так что каждое
из них равно нулю. Таким образом, Ь^рйг = <^а^и = ^арьг =
= «apfti = О для всех а, р, А, Z и
4=2«aPft2Ta Хтр
является линейной комбинацией произведений циклов М ш N.
Аналогично можно убедиться в том, что А гомологичен нулю
72 0. Предварительные сведения
ъ М У. N ТОЛЬКО тогда, когда а^рьг = О для всех а, р, к, I. Итак,
мы установили формулу Кюннета
Н^ {М X N,a) ^ Н^ {М, О.) (8) Н^ {N, Q).
Свяжем теперь пересечения циклов с внешними
произведениями форм на компактном ориентированном га-мерном
многообразии М. Пусть а есть /с-цикл, а т есть (га — А;)-цикл на М, и пусть
Ф 6 A^-'^ (М), ■^ ^A'^ (М) — замкнутые формы на М,
представляющие классы когомологий, двойственные по Пуанкаре классам а
и т, т. е. такие, что для любого (га — А:)-цикла [а
J Ф = #(о-[а)
и для любого А:-цикла v
J ,|, = #(T-v).
V
На произведении М X М с отображениями проектирования л^, я^
имеем
\ я*фЛ я|\|з = f ф-\ \|3 = #(ct.(a)-#(t-v). "^
HXV ц V
С другой стороны, если (pi, р^) — точка пересечения сг X т с
[А X V, то, учитывая ориентации, мы видим, что
Нри Р.) (о X Т, [А X V) = (- 1)"-" 1р. (ст. (А) .1р. (t-v).
Таким образом,
#(стхт, (axv) = (-1)"-''#(ct.h).#(t.v)=( —1)"-" j я?фЛя|г|з.
HXV
Заметим, что эта формула выполняется для любых (га — А:')-
цикла (А и А:-цикла v: если к фк', то обе части равны нулю. По
формуле Кюннета такие произведения циклов порождают
пространство Нп {М X М, О.), и отсюда следует, что форма я|ф л
Л я|ф двойственна по Пуанкаре циклу (—1)"~''ст X т, т. е. для
любого га-цикла т] в Af X Л/ имеет место равенство
( — 1)"'" j я?ф л я|1|з = # (ст X т. Ti).
л
Применим это к диагонали Д с= Л/ X М. С одной стороны,.
f л?фЛя|\|з= \ флг|з.
4. Топология многообразий 73
С другой стороны, точка (р, р) пересечения ст X т с А
соответствует точке р пересечения ст с т, и, учитывая ориентации, мы
убеждаемся в том, что для такой точки р выполняется равенство
1(р.р)(стхт.Д) = (-1)"-''1р(а.т).
Таким образом,
#(ст.т) = (-1)"-''#((ТХт.А)= (фЛ1|з,
й
т. е. пересечение циклов в гомологиях двойственно по Пуанкаре
внешнему умножению в когомологиях.
Теперь можно понять, как устроено отображение, двойственное
по Пуанкаре отображению на когомологиях. Пусть /: М -^ N —
отображение многообразий класса С°°, невырожденное над циклом
А CZ N', тогда с соответствующей ориентацией цикл /"' {А) двойств-
вен по Пуанкаре прообразу относительно f класса, двойственного
по Пуанкаре к А. В этом нетрудно убедиться: если В cz М —
любой цикл на М, трансверсально пересекающий /~^ {А), то / {В)
трансверсально пересекает А ъ f {В [\ f-^ {А)). Если ф —
замкнутая форма на N, двойственная по Пуанкаре к 4, то
J/4= ( ф = #(/(5).Л) = #(5.ГЧ^)),
в пв)
так что /"^ {А) двойствен по Пуанкаре к /*ф.
В этой связи можно еще раз сформулировать более слабую!
форму теоремы двойственности как утверждение о том, что
спаривание
Hl^(M)^Hl-^^(M)-^K,
задаваемое формой] ([ф], [г|э]) ->- \ ф Л г|э, невырожденно, или что
м
для любой замкнутой А:-формы ф на Af найдется единственный
с точностью до гомологичности (га — А:)-цикл А, такой, что для
любой замкнутой (га — А:)-формы гр
( флг|э= J \|з.
it А
Замечание: обычное и-произведение аир двух классов кого-
мологий OL ^Н^ {М, Q,) и р 6 j^*' (^f, Щ может быть определен»
как прообраз а U р = А* (а ® р) при диагональном
отображении А: М -^ МхМ класса а® р на МхМ, определенного
формулой
а ® р (ст X т) = а (ст)-р (т)
74 0. Предварительные сведения
ДЛЯ любых ЦИКЛОВ ст, т на М. При таком определении ясно, что
если ф и г|э — замкнутые формы на М, представляющие классы а
и р, то форма я*ф л nfip на МхМ представляет класс а (S* р,
и поэтому ф л гр представляет класс аир. Стало быть, внешнее
произведение форм соответствует при изоморфизме де Рама и-
произведению коциклов.
Вычислим для примера алгебру гомологии пространства Р".
Для этого обозначим через Х = (Хо, .. ., Х^) евклидовы
координаты на С"+1 и рассмотрим флаг 0 = VoCzViCZ ... c=F„ = C" в
€"+*, определяемый условиями
пусть Р^ CZ Р"—образ пространства F''+' при естественной проекции
С"+1—{0}-vP". Как мы видели, дополнение Р" — Р""*
гиперплоскости Р""1 в Р" есть С" с евклидовыми координатами XJXn, ■ • •
..., X„_i/X„; аналогично, дополнение Р*"* в Р'' есть С с
координатами Xq/Xji, ..., X^_JX^. Следовательно, мы имеем
клеточное разбиение пространства Р":
Р" = (Р"_Р"-1)и(р"-1_рп-2)и ... и(Pi—Р») UP"-
Оно определяется как объединение 2А:-клеток Р'' — Р''"* ^ С'
по одной для каждого А; = О, . . ., га; это есть обобщение
привычной картины для римановой сферы. Поскольку имеются клетки
лишь четных размерностей, все граничные отображения равны
нулю и гомологии Р" свободно порождены классами замыканий
Р* этих клеток, т. е. гомологическими классами линейных
подпространств с их естественной ориентацией.
Поскольку А:-плоскость Р* и (га — А;)-плоскость Р""'' в Р"
пересекаются в общем случае по одной точке, двойственность
Пуанкаре в этом случае вполне понятна. В самом деле, так как
{п — А:1)-плоскость пересекается с (га — А:2)-плоскостью в общем
■случае по (га — Аг^ — А:2)-плоскости, то
((Pn-fti) . (Р»-".)) = ± (Pn-fti-*.).
Пересечение аналитических циклов
Предположим теперь, что М — компактное комплексное
многообразие размерности га и F с= Af — (возможно, особое)
аналитическое подмножество размерности к. Как мы видели, для любой
(2А: — 1)-формы ф на Af выполняется теорема Стокса
V
4. Топология многообрагий 75
Поэтому можно определить линейный функционал на /Tdr (Щ
формулой
[ф] '-* J Ф'
у
где V наделено естественной ориентацией. По двойственности
Пуанкаре этот линейный функционал определяет класс когомоло-
гий f]Y бсДпгГ^'' (^Oi называемый фундаментальным классом
множества V.
Можно также определить фундаментальный класс
аналитического множества V с помощью формы пересечения. Для любого
класса гомологии а 6 H^n-^h Щ, Ъ) можно найти цикл А,
представляющий класс а и пересекающий V трансверсально в гладких
точках. На самом деле индекс пересечения
#(7.Л)= У, ip(F, Л),
РбДПУ
где V снова наделено естественной ориентацией, эависит только
от класса гомологии а: если А' ~ А, то, поскольку множество
особенностей V имеет, вещественную коразмерность ^ 2, можно
найти (2га — 2к ■\- 1)-цепь С на М, не пересекающуюся с особым
множеством V, пересекающую V почти всюду трансверсально
и такую, что дС = А — А'. Доказательство того, что ЩА-V) =
= #(J['-F)i проходит в точности так же, как в начале этого
параграфа. Следовательно, V определяет линейный функционал
Яа„-2й(АГ, Z)-vZ,
соответствующий класс когомологий Цу 6 ff^""^* (М) которого
и есть фундаментальный класс множества V.
Замечание: когда речь идет о фундаментальном классе
многообразия V CZ М, может подразумеваться также двойственный ему
по Пуанкаре класс, т. е. элемент группы гомологии, задаваемый
линейнБгм функционалом -
Я2п-2й(Л/)->С, [ф]-*(ф.
Обычно будет ясно из контекста, какой из вариантов имеется
в виду.
Сделаем теперь одно очень простое наблюдение. Пусть V и
W — аналитические множества размерностей к и га — к, пере-
секаюпщеся трансверсально в точке р комплексного
многообразия М. Можно выбрать голоморфные координаты z = (zj, . . .
. . ., z„) на Af в окрестности р так, чтобы V vlW задавались
уравнениями
V = (Zft+i = . . . = z„_fe = 0), W=izi= . ..=Zk = 0).
76 0. Предварительные сведения
Если положить Zj = Xj -\- у—\yj, то естественная ориентация
на многообразии М будет задаваться базисом
/ а а а а \
\ axi ' ау1 ' ■••' ахп ' ауп /
пространства Тр {V), а естественные ориентации и& V ш W —
базисами
/ а а а э \
I 5x1 ' %1 ' • • •' dxk ' аук I
и
/ а д д а \
[ ахи^.1 ' Si/fe+i ' ■ ■ •' 5а;„ ' %„ ; •
Отсюда видно, что если на F, PF и Af заданы естественные
ориентации, то
ip{V-W)=+l.
Тривиальное наблюдение, что локальный индекс пересечения
двух трансверсалъно пересекающихся аналитических подмножеств
всегда положителен, является на самом деле одним из
краеугольных камней алгебраической геометрии. Оно связывает теоретико-
множественное пересечение двух многообразий — а priori
геометрический инвариант — с индексом пересечения, который является
топологическим инвариантом, и доставляет тем самым основное
средство объединения двух этих подходов. Однако для того, чтобы
использовать это средство в полной мере, мы должны
распространить понятие индекса пересечения на аналитические подмножества,
пересекающиеся необязательно трансверсально. Это делается
следующим образом (другие варианты теории пересечения
аналитических множеств будут обсуждаться в § 2 гл. 3 и в § 2 гл. 5).
Пусть V VL W — два аналитических множества размерностей к
ига — А; в полидиске А радиуса 1 в С", имеюпще начало
координат единственной общей точкой. Рассмотрим в произведении А' X
X А' полидиска радиуса 1/2 на себя два аналитических множества
V = п-1^ (У) = {(z, w): zeV} и W = {(z, w): z — weW}-
Для каждого e множества V ж W, конечно, пересекаются со слоем
л^2^ (е) = А' X {е} ^ А' соответственно по аналитическим
множествам F и ру + 8 (т. е. W, сдвинутому на в). Далее, п^^ (в)
пересекается с V f\ W трансверсально в точке (р, в) в точности
тогда, когда V ж W -\- s пересекаются трансверсально в точке р.
Пересечение V [\Wcz А' X А' является аналитическим
множеством размерности га, поэтому проекция Яд: V f\ W -^
А'представляет F fi W как раэветвленное [А-листное накрытие полидис-
4. Топология многообразий 77
ка А'. В соответствии с этим мы видим, что для £ 6 ^'i лежащего
вне некоторого аналитического подмножества из А',
аналитические множества V и W -\- s трансверсалъно пересекаются в [а
точках us А'. Число [а называется кратностью пересечения V тз. W
в О и обозначается [а = TOq (^" ^•
Кратность пересечения всегда положительна по построеншо,
а по теореме о неявной функции она равна 1 тогда и только тогда,
когда F П W'^ трансверсально пересекается со слоем и^^ (0), т. е.
тогда и только тогда, когда V ж W трансверсально пересекаются
в нуле. Заметим, что это определение не зависит от выбора
координат Z, и, значит, применимо также к аналитическим
подмножествам комплексного многообразия. Проверим теперь, что если V
ж W — аналитические подмножества дополнительной размерности
на компактном комплексном многообразии М, то
pevnw
Для этого выберем локальные координаты z, w ъ окрестности
точки р ^ V f\ W так, что р =-■ (О, 0) — единственная точка
пересечения V с W ъ шаре А радиуса 1. Пусть р (г) — функция класса
С°°, тождественно равная 1 в шаре А" радиуса 1/4 и тождественно
равная нулю вне шара А' радиуса 1/2. Тогда для достаточно
малого и достаточно общего в множество
W, = {iz):z-pi\\z\\)-ReW}cz\
обладает следующими свойствами:
1) совпадает с W вне А';
2) не пересекается с F в А' — А";
3) является аналитическим подмножеством в А",
пересекающимся с F трансверсально в [а = ТОр (V-W) точках.
Пусть теперь {pi} = V [\W. Выберем координатные шары А^
с центрами в рг и значения 8^, как выше, и положим
W = {W - {] Аг) [j {[] PFe,).
Тогда W— гладкое многообразие вне множества коразмерности
^2 и, следовательно, в соответствии с наши&1 общим методом
представляет класс ко гомологии т]ту' в М. Действительно, у]^' =
= т]йг, так как в каждом А^ имеет место равенство
W—W' = d {{z: z — f.82 6 И^, О < t < р (II z ||)}).
Наконец, поскольку W пересекается с F в А{ трансверсально
в Тор J (F' W) точках (где TF' и F — аналитические множества
с естественной ориентацией) и больше нигде, то
#(PF .F) = =»(PF'.F) = S тор^ (F • PF),
78 0. Предварительные сведения
ЧТО и требовалось. Подведем итог:
Топологический индекс пересечения #(F' W) двух
аналитических подмножеств дополнит£лъной размерности,
пересекающихся по конечному числу точек компактного
комплексного многообразия, равен
^{V-W)= S m^iy.W).
pevnw-
Кратность пересечения т^ (F- W) удовлетворяет
неравенству
mp{V-W)^i,
причем равенство достигается тогда и только тогда, когда
V и W пересекаются в тмчке р трансверсально.
Одно важное следствие из этого заключается в том, что если V
и PF пересекаются в изолированных точках, то их топологический
индекс пересечения #(F- W) больше или равен
теоретико-множественной мощности #{F П ^Щ- Так, например, если
пересечение 'V f\ W двух аналитических множеств в М содержит более
чем #(F- W) точек, то отсюда следует, что оно должно содержать
кривую.
В качестве простого следствия этого утверждения отметим
такой факт.
Пусть М — произвольное комплексное подмногообразие
проективного пространства Р", aVczM — аналитическое
подмножество; тогда фундаментальный класс множества V
не равен нулю в гомологиях М.
Это просто: если размерность М равна т,, а размерность V
равна к, то можно найти линейное подпространство Р"-'' в Р",
пересекающее F в изолированных точках, и, полагая W = М {]
П Р""**, убеждаемся в том, что #(W- F) > О, откуда следует, что
В качестве следствия получаем, что
Четномерные числа Бетти многообразия М положительны,
ибо, согласно сказанному выше, пересечение подмножества F
многообразия М с линейным подпространством Р"-"н'' в Р"
является аналитическим подмножеством в М размерности к и
и потому представляет ненулевой элемент в Н^^ (М).
Аналогично
Любое аналитическое подмножество в Р", гомологичное
гиперплоскости, есть гиперплоскость.
4. Топология многообразий 79
Чтобы убедиться в этом, заметим, что если V гомологично
гиперплоскости, то оно имеет с прямыми индекс пересечения 1.
Поэтому если pi, р^ — любые две точки в V, то прямая L = PiPa»
имеющая две общие точки с V, должна иметь с V общую кривую;
это означает, что L должна содержаться в V. Поэтому V содержит
прямую, соединяющую любые две его точки, и, следовательно,
является линейным подпространством в Р".
Отсюда вытекает, что
Любой голоморфный автоморфизм Р" индуцировал
некоторым линейным преобразованием С"+^.
Пусть Хд, . . ., Хп— однородные координаты на Р", а Xi =
= XJXq — соответствующие евклидовы координаты в
дополнении к гиперплоскости Н = {Х^ = 0). Поскольку
фундаментальный класс гиперплоскости в Р" порождает группу IP (Р", Z) ^
^ Z, любой голоморфный автоморфиэм ф пространства Р"
обязан переводить гиперплоскость в комплексное подмногообраэив
в Р", гомологичное гиперплоскости, а следовательно, в
гиперплоскость. Поэтому, вэяв композицию ф с линейным[преобразова-
нием пространства Р", можно считать, что ф (Н) = Н. Точно
так же автоморфизм ф обязан переводить остальные координатные
гиперплоскости /fj = (xi = 0) в гиперплоскости, отличные от Н^
поэтому
Ф (Hi) = (ai. iXi+ ... + а„, iXn + ao,i = 0).
Прообраз ф* (xi) евклидовой координаты a;j есть мероморфная
функция на Р", имеющая на Н простой полюс и обращающаяся
в нуль на ф (Hi); отсюда следует, что функция —-р x_LJ—_
Оо "г "^i •''i "г • • • 'T'^n *7i
голоморфна на всем Р" и, следовательно, постоянна. Поэтому
Ф* (Xi) = а'о, i -Ьа1, г^^! -I- ••• +а'п. {Х^,
так что автоморфизм ф линеен.
Таким образом, группа автоморфизмов пространства Р"
является факторгруппой PGL (га -{- 1) полной линейной группы
GL (га + 1) по одномерной подгруппе скалярных матриц {XI}.
Последнее замечание: если два аналитических подмножества V
и W комплексного многообразия М — не обязательно
дополнительных размерностей — пересекаются трансверсально, то их
пересечение также и положительно в том смысле, что аналитическое
множество F П W'^ входит с естественной ориентацией в
топологическое пересечение V и W. Более общо, если определить кратность
пересечения mz {V- W) множеств V ш W вдоль неприводимога
аналитического множества Z cz. V f\W как
multp((F ^H)-{W ПЯ))я,
80 0. Предварительные сведения
где р — общая гладкая точка на Z, & Н — подмногообразие в
окрестности точки р, пересекающее Z трансверсально в р, то
топологическое пересечение множеств V ш W дается формулой
{V-W)= S mM\tz.{V-W).Zi.
5. ВЕКТОРНЫЕ РАССЛОЕНИЯ, СВЯЗНОСТИ И КРИВИЗНА
Комплексные и голоморфные векторные
расслоения
Пусть М — гладкое многообразие. Комплексное векторное С°°-
расслоение на М состоит из семейства {^зс}яем комплексных
векторных пространств, параметризованного точками
многообразия М, со структурой С°°-многообразия на ^ = \} Е^, такой,
ЧТО выполняются следующие условия:
1) отображение проектирования л: Е -*■ М, переводящее Ех
в X, принадлежит классу С°°',
2) для любого Хд ^ М найдутся открытое множество U в М^
содержащее х,^, и диффеоморфизм
Фи: n-HU)-^U X C^
который отображает векторное пространство Е^ изоморфно на
{х} X С** для всех ж 6 и;ц)ц называется тривиализацией Е над U.
Размерность слоев Е^ расслоения Е называется рангом Е;
в частности, векторное расслоение ранга 1 называется линейным
расслоением.
Заметим, что для любой пары тривиализаций фи и фу
отображение guyiU f\V-*-GL{k), определяемое формулой guv{^) =
= (фи°Фт^)| {ж}хс''' принадлежит классу С°°; отображения guv
называются функциями перехода для Е относительно
тривиализаций Фи, фу. Функции перехода для Е удовлетворяют
тождествам
guv (^) • gvu i^) = ^ для всех х 6 г/ n F,
guv{^)• gvw{^)• gwu{x) =-^ для всех xeUf\Vf\W.
Обратно, если заданы открытое покрытие U = {Ua} многообразия
М и С°°-отображения g^f. Ua П U^-^GL{k), удовлетворяющие
этим тождествам, то найдется единственное комплексное векторное
расслоение Е ->- М с функциями перехода {gas}' нетрудно видеть,
что Е как множество есть объединение U {Ua X С''), в котором
а
отождествлены точки {х, X) в U^ X C'^ и (ж, ga^ (ж)-Я) ^ Ua X
X С'', а структура многообразия определяется вложениями Ua X
X С" -»- ^.
5. Векторные расслоения, связности и кривизна 81
Как правило, операции над векторными пространствами
переносятся и на векторные расслоения. Например, пусть Е ^t' М —
комплексное векторное расслоение; можно определить
двойственное расслоение Е* -*- М — это комплексное векторное расслоение
со слоями Е* = {Ej^*. Тривиализации фи» Ец-^и X С^ (где
Ец = п~^ {U)) индуцируют отображения
Ф&: ^-»-г/ X С"* ^ г/ X С",
которые наделяют Е* = \J Е* структурой многообразия^ Эту
конструкцию проще всего определить с помощью функций
перехода. Пусть {ga е) — функции перехода для Е -^ М; тогда Е* ->-
-*- М — комплексное векторное расслоение с функциями
перехода
Аналогично, пусть Е -*- М, F -^ М — комплексные векторные
расслоения рангов к ж I с функциями перехода соответственно
{^ар} и {^ар}- Тогда МОЖНО определить следующие расслоения:
\) Е ® F, задаваемое функциями перехода
2) Е <S) F, задаваемое функциями перехода
/ае (ж) = ^ае (ж) ® Аае (ж) е GL (С ® С);
3) /\''Е, задаваемое функциями перехода
7ар(а:)= ^'■gae{x)eGL{^'C'^).
в частности, /['^Е представляет собой линейное расслоение
с функциями перехода
jae (х) = det ^„е (х) 6 GL (1, С) = С*,
называемое детерминантом (или определителем) расслоения Е,
Подрасслоением F cz: Е расслоения Е называется такой набор
{Fx с: Ех}х&м подпространств слоев Е^ расслоения Е, что F =
= \j Fx<^ Е является подмногообразием в Е; ясно, что само F
является векторным расслоением. Условие, что F cz: Е —
подмногообразие, равносильно тому, что для любого х ^ М найдутся
такая окрестность U точки ж в М и такая тривиализация ф^:
Ец-^и X C^ что
82 0. Предварительные сведения
Функции перехода guy расслоения Е относительно таких три-
виализаций имеют вид
kuv {^) \
=(^
о
7UV {^)
Расслоение F имеет функции перехода Ацг (^J), а 7uv служат
функциями перехода для факторрасслоения ElF, имеющего по
определению слои (ElF),, = EJFx-
Если даны С°°-отображение f:M-^N гладких многообразий М
а N ж комплексное векторное расслоение Е -^N, то можно
определить прообраз расслоения f*E, полагая
(/*^)^ = Е^,:с).
Если ф: Ец-*- и X С^ — тривиализация расслоения Е в
окрестности точки / (ж), то отображение
/*ф: f*Ef-nj-^f*U X С"
наделяет f*E структурой многообразия над открытым множеством
f-^lJ. Функции перехода для прообраза f*E будут, конечно,
прообразами функций перехода для расслоения Е.
Отображение векторных расслоений Е ж F над М задается
таким С°°-отображением /: Е ->- F, что / (Е^) (z: Fx ж f^ = f \ех'-
Ex -*- Fx линейно. Заметим, что
кег (/) = и кег fx(=: Е, im (/) = U im /х <= F
являются подрасслоениями соответственно ъ Е ж F тогда и только
тогда, когда ранги всех отображений fx одинаковы. Расслоения Е
ж F изоморфны, еслж существует такое отображение /: E^t'F^
что fx- Ex-*- Fx — изоморфизмы для всех х 6 М; векторное
расслоение на М называется тривиальным, если оно изоморфно
произведению М X С^. Наконец, сечением а векторного расслоения
Е —> М над и (z: М называется С°°-отображение
а: и-^Е,
удовлетворяющее условию а (х) 6 Ех для всех х ^ U. Репером
для Е над и си М называется набор Oi, . . ., а?, сечений Е над U,
таких, что {oi (х), . . ., Gk {х)} является базисом пространства Е^
для всех X ^ и. Репер для Е над U, по существу, то же самое, что
тривиализация расслоения Е над U: при заданной тривиализации
Фи^ Ец^>- и X С^ сечения а,- (х) = фи (а:, в;) образуют базис,
и обратно, если задан репер Oi, . . ., а^, можно определить три-
виализацию фи, полагая ФиС^) = (^' (^i, • • -, ^ft)) Для к =
= S h^i (aj) в Е„.
5. Вектпорные расслоения, связности и кривизна
83
Заметим, что при заданной тривиализации фи расслоения Е
над и любое его сечение а можно единственным образом
представить как векторнозначную С°°-функцию / = (/i, . • ., /ь).
разлагая а (х) по базису:
а (х) = 2/i И • 9t? (^. бг).
Если фу — тривиализация расслоения Е над V ш f = (f[, . .
• • м /ft) — соответствующее представление а Ivnu' ™
так что
2j/i(^)-ej = S/i(^)-9u9v-4^'. ej), т.е. f = guvf'-
Таким образом, при заданных тривиализациях {(ра'-Ец^-^UaX
X С''} сечения расслоения Е над \jUa ъ точности соответствуют
наборам {/a=(/ai. ••., fa^)}a векторнозначных С°°-функций,
удовлетворяющих условию /а = ё'ае-/е Д^Я ^'^^ "' Р' Гда
й^ар—функции перехода для расслоения Е относительно тривиализации:
{фа}.
Теперь пусть М — комплексное многообразие. Голоморфным
векторным расслоением Е —> М называется комплексное векторное-
расслоение, снабженное структурой комплексного многообразия:
на Е, такое, что для любой точки х ^ М найдутся окрестность
и ^ X ж тривиализация ф^: Ец-*- U х С^, являющаяся биголо-
морфным отображением комплексных многообразий. Такая
тривиализация называется голоморфной тривиализацией. Заметим^
что если {ф^: Ец^-^ 17^ X С^} — голоморфные тривиализации,
то функции перехода для расслоения Е относительно
тривиализации {фа} голоморфны, и обратно, для заданных голоморфных
отображений g^^: 17^ f| U^-*-GL (к), удовлетворяющих
приведенным выше тождествам для функций перехода, можно построить
голоморфное векторное расслоение Е-^ М с функциями
перехода ^ар.
Все, что до сих пор говорилось о йекторных расслоениях»
непосредственно переносится на категорию голоморфных
векторных расслоений. Можно определить двойственное расслоение
и прямое, тензорное и внешнее произведения голоморфных
векторных расслоений так, что они будут голоморфны; заметим также,
что прообраз f*E голоморфного векторного расслоения Е при
голоморфном отображении f:M-*-N комплексных многообразий
имеет естественную голоморфную структуру. Голоморфное
отображение голоморфных векторных расслоений Е, F над М — это
такое голоморфное отображение /: Е -*- F, что отображения
слоев /: Е^ -*- F». линейны; голоморфное подрасслоение
голоморфного расслоения — это такое подрасслоение F с: Е, что F —
84 0. Предвар ителънне сведения
комплексное подмногообразие; в этом случае факторрасслоение
тоже голоморфно. Сечение а голоморфного расслоения Е над
и (z: М называется голоморфным, если а: U -^ Е — голоморфное
отображение; репер а = (oi, . . ., а^) называется голоморфным,
если таковы все отображения а^: для заданного голоморфного
репера {а^} произвольное сечение
a(a;)=S/,(a;).a,(x)
голоморфно тогда и только тогда, когда голоморфны все
функции fi.
Одно важное различие между С°°- и голоморфными векторными
расслоениями заключается в следующем. На пространстве сечений
векторного расслоения не сзщ^ествует никакого естественно опрв:-
деленного внешнего дифференцирования d, а на голоморфном
векторном расслоении Е корректно определен 5-оператор
Ъ: АР-9{Е)-^АР-я+^(Е)
из пространства £-значных (р, д)-форм в пространство £»значных
(/J, g + 1)-форм. Действительно, выберем локальный голоморфный
репер {е^, . . ., е^} для Е над U, запишем а 6 А^'^ (Е) в виде
и положим
Если {е\, ..., еЦ —любой другой голоморфный репер для Е над
и, причем е, ==S^j^ej, то а = S ^j/<ii>i ® ^^ и
так что да не зависит от выбора репера.
Примеры. Пусть М — комплексное многообразие, а Тх (М) —
комплексное касательное пространство к М в точке х. Для х 6
^ и (z: М ж координатной карты <fu'- U -^(7^ имеем отображения
Ф^,: Тх(М) ->Т,,х, {U)^C{^,^}^ С^"
для каждого х в U, поэтому отображение
Фи»: и Tx{M)^UxC^'^
хеи
наделяет Т (М) = [j ^х (Щ структурой комплексного вектор-
ного расслоения, называемого комплексным касательным
расслоением. Функции перехода для Т (М) задаются формулой /и.т =
5. Векторные расслоения, связности и кривизна 85
Далее, для каждой точки х£ М
Т:с{М) = П{М)фП{М),
где Т'х{М) и Т"х{М) определены в начале § 2. Подпространства
{T'x{M)(=iTx{M)) образуют подрасслоение Т' {М) (=: Т {М),
называемое голоморфным касательным расслоением. Функции
перехода для Т'(М) задаются формулой ju,v = fc{^u4^)' откуда
видно, что 2" (М) имеет естественную структуру голоморфного
векторного расслоения.
Аналогично определяются:
Т* (М) = Т (М)*— комплексное кокасательное расслоение;
Т*' (М), Т*" (М) — голоморфное и антиголоморфное кокаса-
тельные расслоения;
Т*(Р'9>{М) = /\РТ*'{М) ® /\чТ*''{М).
Тензорное, симметрическое и внешнее произведения
голоморфных и комплексифицированных касательного и кокасательного
расслоений называются тензорными расслоениями.
Пусть V (Zi М — комплексное подмногообразие
многообразия М. Определим нормальное расслоение Ny/M к У в М как
фактор касательного расслоения к М, ограниченного на V, по
подрасслоению 2" (У) с^ 2" (М) \у. Конормальным расслоением
называется расслоение Ny/Mi двойственное к нормальному
расслоению.
Метрики, связности и к2Щвизна
Пусть Е -*- М — комплексное векторное расслоение. Эрмитю-
вой метрикой на Е называется эрмитово скалярное произведение
на каждом слое Е^, гладко зависящее от х ^ М, т. е. такое, что
если t, =(Si, . . ., tk} — репер для Е, то функции
hij (X) = (S, (х), Ij (х))
принадлежат классу С°°. Репер X расслоения Е называется
унитарным, если ^1 (ж), . . ., t,k (х) — ортонормированный базис
пространства Е^ для всех х; унитарные реперы всегда существуют
локально, поскольку можно взять любой репер и применить
процесс ортогонализации Грама — Шмидта.
Если Е — расслоение с эрмитовой метрикой, F cz: Е —
подрасслоение, то подпространства {F^ с: Е^} образуют
подрасслоение расслоения Е, С°°-изоморфное факторрасслоению E/F.
Голоморфное расслоение с эрмитовой метрикой называется
эрмитовым векторным расслоением.
0. Предварительные сведения
Определение. Связностью D в комплексном векторном
расслоении Е -*- М называется отображение
D: А" (Е) -^ Л^ (Е),
удовлетворяющее правилу Лейбница
для всех сечений ^ е Л" (Е) (U) и функций f е С°° {U).
Связность представляет собой, по существу, способ
дифференцирования сечений: для сечения I в Л" (Е) {U) применение Z?|
к касательному вектору v ^ Тх (М) можно представлять себе как
производную I в направлении v. Это, однако, лишь первого
порядка приближение к дифференцированию, поскольку смешанные
производные, вообще говоря, не совпадают.
Пусть е = (е^, . . ., е„) — репер для расслоения Е над U. Для
ааданной связности D ъ& Е можно разложить Dei на компоненты:
Dei = 2 ^ijej.
Матрица в = {Qij) из 1-форм называется матрицей связности D
относительно е. Задание е и 0 определяет D'. ]щя произвольного
сечения а в А'^ {Щ (U), разлагая по базису е^
имеем
Da= S Aij-бг-|-2 Oi-Dei = ^ (йа^+ S Ot^ij)«}.
J i
Матрица связности 0 в точке Zq ^ U зависит от выбора репера
в окрестности Zq: если е' = {е[, . . ., е'п) — другой репер и ej (z) =
= S gli (Z) в J (Z), TO
De'i==yi dgij-ej + ^j gi^Q^j-e^,
так что
Qe'^dg.g-^ + g.Q,.g-^ (g={gi,)).
Естественной связности на векторном расслоении Е, вообще
говоря, не сзщ^ествует. Однако если многообразие М комплексно,
а расслоение Е эрмитово, то можно наложить два требования,
которые приведут к каноническому выбору связности.
1. Пользуясь разложением Т* = Т^^' Ф Т*", напишем D —
= D' + D", где D': А' {Щ -^ Л"^^ (Е), а D": А' (Е) -^ ^".^ (Е).
Будем говорит!., что связность D н& Е совместима с комплексной
структурой, если D" = д.
5. Векторные расслоения, связности и кривизна 87
2. Если Е — эрмитово, то будем говорить, что связность D
совместима с метрикой, когда
d (I, л) = (Dl, л) + (1. Dri).
Лемма. Пусть Е — эрмитово векторное расслоение; тогда
существует единственная связность D на Е, совместимая и с
метрикой, и с комплексной структурой.
Доказательство. Пусть е = Ci, . . ., е„ — голоморфный репер
для расслоения Е ш h^ = (е^, e^). Если связность D существует,
то ее матрица 0 в базисе е должна иметь тип (1, 0) и,
следовательно,
dhu = d{ei, e^) = 2e>w+2ejfeA,ft = THn(l,0)+THn(0, 1).
ft ft
Приравнивая типы, имеем
d^tj = lj^tk^hj^ Т.е. dh = Qh,
dhij = ^Qj^hik, т.е. dh = ¥Q.
Отсюда видно, что 0 = dh-h-^ — единственное решение обоих
уравнений. Поскольку матрица 0 подчинена условиям
совместимости, она корректно определена глобально. Q
Единственная связность, совместимая с комплексной и с
метрической структурами на Е, называется ассоциированной, или
метрической, связностью. Как упомянуто в ходе доказательства,
ее матрица в голоморфном базисе имеет тип (1, 0); с другой
стороны, если е^, . . ., е„ — унитарный репер, то О = d (е^, Cj) =
= Qij -{■ Qji, так что матрица в унитарном репере косоэрмитова.
Метрические связности в эрмитовых векторных расслоениях
хорошо ведут себя относительно операций над расслоениязли; мы
убедимся в этом в следующих двух леммах.
Лемиа. Пусть Е —>- М — эрмитово ввктюрное расслоение и
F а Е — голоморфное подрасслоение. Тогда F само является
эрмитовым расслоением с метрической связностью D р. С другой
стороны, метрическая связность D^ нл Е и разложение в прямую сумму
Е = F ® F^, индуцированное метрикой, дают связность ПрО^
на F, причем Пр = ЛроВЕ, где Лр — проекция на F.
Доказательство. Пусть t, — сечение F; тогда (пр о Dp)" (t,) =
= Пр (ЩО = Лр (dt,) = 5^, так что связность Пр » D^ совместима
с комплексной структурой. Если ^, ^' — сечения F, то
d(S, Г) = Фе^ Г) + (?, D^') = {KpoDsZ, n + (S, я^о/?еС'),
так что связность Лро D^ совместима с метрикой. Q
88 0. Предварительные сведения
Аналогично, если Е, Е'— эрмитовы векторные расслоения,
то на ^ ® Е' имеется естественная метрика, определенная
формулой
(X® %', S® S') = {К S)-(V, б')
для X, S 6 Ех, Я', S' 6 Е'х. Пусть D^, D^-, De®e' — метрические
связности wsl Е, Е' ж Е (S) Е' соответственно, и пусть /?е ® 1 —
связность на ^ ® Е', определенная формулой
(Z?E®1)(S(S)|) = ^S®?;
аналогично определяется 1 (g) De'. Тогда верна следующая
Лемиа. De(»e' = £>е ® 1 +1 ® ^е'»
Доказательство. Ясно, что (D^ 0 i +i (S) De')" = д; поэтому
остается проверить совместимость с метрикой. Пусть ^, | —
сечения Е, а t,', 5'—сечения Е'. Тогда
Наконец, заметим, что эрмитова метрика на голоморфном
расслоении Е индуцирует метрику на двойственном расслоении Е*;
если е — унитарный репер для Е, а е* — взаимный репер в Е*,
то положим (ef, е*) = 6;^, и метрическая связность D* ш& Е*
может быть определена требованием
d (а, X) = фа, т> + {а, D*x}
для о^аЧЕ) {U), хеЛ" {Е*) {U).
Теперь вернемся к общему обсуждению. Для заданной
связности D на комплексном векторном расслоении Е -у М ъю. можем
определить операторы
D:^p{E)-^jiv+^(E),
распространяя правило Лейбница на 1|э 6 А^ {U), I € Л" {Е) {U),
по формуле
Z? (я|) л ?) = <^15 ® I + (-1)^1|5 д т.
В частности, рассмотрим оператор
/?2: АЧЕ)-^Л''{Е).
5. Векторные расслоения, связности и кривизна 89
Первое замечание относительно D^ состоит в том, что он линеен
над ji:°, т. е. для сечения а расслоения Е и С°°-функции /
D^ (f-a) = D {df ® а + f-Da) =
= —df л Da + df л Da + f-D^a = f-D^a.
Следовательно, отображение D^: J>^ (E) -*■ Jk"^ {E) индуцированО'
отображением расслоений E-^f\'^T*®E, или, иначе говоря^
D^ соответствует глобальному сечению в расслоения
1\^Т* ® Нот {Е, Е) = 1\^Т* ® {Е* ® Е).
Если е — репер для Е, то в базисе {е* ® е^} для Е* ® Е сечение
в 6 Л* (^* ® Е) можно представить матрицей ве из 2-форм, т. е.
можно написать
в, называется матриг^ей кривизны связности D относительно'
репера е. Если {е\ = 2 gij^s) ~ ДРУГОЙ репер, то
Z?%; = Z?2 (2 gijej) = S gij&jueu = S gts^ShgAe'i,
т.е. e^.=g.Q^.g-i,
Матрица кривизны легко выражается через матрицу связностиг
по определению
D% = D(Z ^i] <g) е^) = S dQij-V^iQi^AQ^j) ® ej.
В матричных обозначениях, следовательно,
ве = dQe - бе Л бе.
Это равенство называется структурным уравнением Картлна..
В голоморфном случае про в можно сказать больше. Если
расслоение Е —>- М эрмитово и связность D ж&Е совместима с
комплексной структурой, то равенство D" = д влечет за собой
равенство D"^ = О и, следовательно, в"- ^ = 0. Если, более того,
связность D совместима с метрикой, то в унитарном репере е
матрица связности 0^ косоэрмитова и поэтому такова же матрица
в = de — е л 0; значит, 6^ » = — 'в".'' = 0. Поскольку тип
матрицы в, очевидно, инвариантен относительно замены базиса,
то мы видим, что матрица кривизны метрической связности в
эрмитовом расслоении есть эрмитова матрица из (1, 1)-форм.
В заключение этого параграфа вычислим метрические свяэ-
ности и матрицы кривизны эрмитовых расслоений в двух частных
случаях.
'90 0. Предварительные сведения
Прежде всего напомним, что для эрмитова расслоения Е с
метрической связностью D метрическая связность Z)* на расслоении
Е* удовлетворяет равенству
d {а, т> = фа, т> + (а, D*%)
для всех а € J:° {Е) (U), х ^ ^° {Е*) {U). В частности, если е —
репер ъ Е, & е* — двойственный репер в ^* и 0, 0* — соответ-
■ствующие матрицы связности, то
О = d {ей ef) = Qij + Q%
так что 0 = —'0*.
Ввиду этого метрическая связность на голоморфном
касательном расслоении эрмитова многообразия обладает специфическим
•свойством: связность D* на голоморфном кокасательном
расслоении может быть выражена через обычный внешний дифференциал.
А именно,
D*: 4». о -> ЛП»(8) Л* = (AU о ® Л», в) е (^*'»(Э АО, *),
d: 4*.»-> ^2. в е (^''» ® ^'''').
Поскольку связность D* совместима с комплексной структурой,
то D*" = d, т. е. оба оператора совпадают на А^' " ® А°' ^. Как
мы сейчас убедимся, это дает эффективное средство вычисления
матрицы связности. Пусть ds^ = 2 ^а ^^t ® <iz^ = 2 ф« '^ фг ~
-эрмитова метрика на М.
Лемма. Существует и единственна такая матрица ipj^ из
i-форм, что я]) + Ч|з = О U
(*) d(fi = y]ylpijA(pj + Xi,
где Tj — форма типа (2, 0).
Доказательство, Разложим т|) по типам: т|) = Tf-J-^"- Тогда
5ф| = 2 4*; л ф^ определяет ф" и
г|) + '^ = 0 =»■ г|)' = —'гр.
^^В явном виде: полагая 9j = 2^j/dzj, где a*a = h, имеем
5фJ = 2 9aik л dZft = 2 ^ajft л alj • ф^,
k j, ft
так что т|)*==5аа~'.) Q
Пусть V = {vi, . . ., Vn) — репер для касательного
расслоения Т' (М), двойственный реперу фи . . ., ф„; пусть 0 — матрица
5. Векторные расслоения, связности и кривизна 91
СВЯЗНОСТИ D в репере у, а 0* — матрица D* в репере ф^, . . ., ф„.
Тогда
поскольку 0* + '0* = 0 и т|) -f '4 = О- Поэтому
е=—*е*=—'г|).
В итоге, пользуясь основным структурным уравнением (*),
мы можем определить матрицу связности 0 = —*г^ голоморфного
касательного расслоения Т' {М), вычисляя внешние
дифференциалы йфг унитарного корепера. Вектор т = (ti, . . ., т„) называется
кручением; метрика называется кэлеровой, если ее кручение
обращается в нуль. В дальнейшем мы приведем другие условия кэлеро-
вости.
Примеры. Пусть М — риманова поверхность с локальной
координатой z; метрика на М задается формулой
ds^ = А2 (^z ® dz = ф ® ф,
где ^—hdz. Тогда
d^ = dh ^dz = —г- л ф,
так что я])" = dlogh и яр = (5 — д) logfe. Согласно структурному
уравнению, матрица метрической связности на касательном
расслоении задается формулой
0= —г|) = (5—д) log /г= -r-\ogh-dz =• \ogh-dz.
Далее, 0 л 0 = О, так что, согласно структурному уравнению
Картана,
e = d0= -2{-^\osh]dzAdz =
1 -
= —S-A logA'dzAdz.
Сравнивая матрицу кривизны 6 с ассоциированной (1, 1)-
формой Ф = {у —1/2) ф л ф = (У —1/2) А2 dz л dz, получаем
У^^% = К-Ф,
где К = (—AlogA)/A^ — обычная гауссова кривизна.
Приведем еще одно вычисление, относящееся к операторам
кривизны подрасслоений и факторрасслоенийэрмитова расслоения.
92 0. Предварительные сведения
Хотя полное вычисление провести и не удастся, мы встретимся
с важным различием между гладким и голоморфным случаями:
с наличием знака в кривизне эрмитова расслоения.
Пусть Е -^ М — эрмитово расслоение, Scz Е — голоморфное
подрасслоение и ^ = EIS — факторрасслоеяие. Как было
упомянуто ранее, Q как С°°-расслоение изоморфно ортогональному
дополнению iS'-'- подрасслоения S ъ Е, ш, значит, как S, так и Q
наследуют эрмитовы структуры от Е; пусть D^, Ds и Dq — соотве-г-
ствующие метрические связности. По лемме о подрасслоении
эрмитова расслоения связность Dg является композицией оперйтора
с проекцией Ji^ {Е) -»- ^*(5); поэтому оператор
отображает jl^ (5) в Jt^ {Q). Оператор А называется второй
фундаментальной формой подрасслоения S ъ Е; ясно, что она имеет тип
(1, 0) и линейна над С""-фушщиями, ч. е. Аа Jt^^^ (Нот {S, 9)).
Чтобы вычислить кривизны, выберем унитарный репер е^, . . .
. . ., ej.b Е так, чтобыei, . . ., е^ был репером в 5. В этом репере,
согласно нашей лемме, матрица связности для Е имеет вид
е,
'-\А ej'
где 0g, Qq —соответствующие матрицы связности для
Тогда
©J5 = d0jj — Sg л бя =
<'
откуда следует, что
Далее, назовем оператор кривизны в 6 Л*(Нот (Е, Е))
положительным в точке X ^ М, если для % фО ^ Е^ мультивектор
(Я,, вХ) 6 Л*^* (-^ положителен и имеет тип (1, 1), или, что
равносильно, если для любого голоморфного касательного вектора
V ^Т'х {М) эрмитова матрица
— У^^ <в (х); у, у) 6 Нот (Ех, Е^)
положительно определена. Будем писать в > О, если в всюду
положителен, 6^0, если в положительно полуопределен, и в >
> в', если в — в' > 0.
5. Векторняе расслоения, связности и кривизна 93
Пусть А — вторая фундаментальная форма рассматриваемого
подрасслоения Scz Е; разложим
^= S atjdzo, <S) ех (S) е*
s<X<r
так что
*Л = S "atj dza ® е* ® е^
и
Л л '^= 2 a-thalh dzg. л dzp ® е, (g) ef.
Таким образом, если положить Л" = {<Д)), то
откуда следует, что
вз^вв Is, %>®Е \а,
причем равенство имеет место тогда и только тогда, когда А-^ Q.
Этот принцип, утверждающий, что кривизна уменьшается при
переходе к голоморфным подрасслоениям и увеличивается при переходе
к голоморфным факторраслоениям, указывает на существенные
отличия от вещественного случая.
Пусть, например, Мс: С" — комплексное подмногообразие
с метрикой, индуцированной евклидовой метрикой на С"; тогда
Г (ЛО сг 2" (С") U =^ вдг<в^^„ |д, = 0.
Если М — риманова поверхность, то, согласно предыдущим
вычислениям, это означает просто, что ее гауссова кривизна
Другой основной факт, связанный с проведенным вычислением,
таков: пусть Е -^ М — голоморфное расслоение, и пусть
существуют такие глобальные сечения Oi, . . ., Оп 6 Г {М, Е), что при
всех X ^ М векторы {oi (ж), . . ., а„ (ж)} порождают Ех- Тогда
имеем сюръективное голоморфное отображение расслоений
М X С"-»-£'-*-0,
определяемое формулой
(х. Я,) I-*- 2 ^jCTj (ж) 6 Ех
для X 6 М, Я, 6 С". Отсюда следует, что если ввести на
расслоении Е метрику, индуцированную евклидовой метрикой на М X С",
то вв^ О, т. е. любое голоморфное расслоение, обладающее конеч-
94 0. Предварительные сведения
ным числом глобальных сечений, порождающих каждый слой,
допускает метрику с неотрицательной кривизной.
Связь между знаком кривизны векторного расслоения и
существованием глобальных сечений очень существенна в теории
комплексных многообразий.
6. ТЕОРИЯ ГАРМОНИЧЕСКИХ ФОРМ
НА КОМПАКТНЫХ КОМПЛЕКСНЫХ МНОГООБРАЗИЯХ
Теорема Ходока
Этот параграф посвящен формулировке и доказательству
теоремы Ходжа для 5-оператора и некоторым ее непосредственным
следствиям.
Пусть М — связное компактное комплексное многообразие
комплексной размерности га. Выберем на нем эрмитову метрику
ds^ с ассоциированной (1, 1)-формой (о = -2—^— zL^i^ ^j' запи-
i
санной в унитарном корепере (ф1, ...,ф„). Метрика ds^
индуцирует эрмитову метрику на всех тензорных расслоениях
Г*(Р, 9)(Л/); скалярное произведение в Г*^^''^ (М) определяется
так, чтобы базис {ф/ (z) л фJ {z))i^j^^^ Щ=щ был ортогональным
с длинами векторов || Ф/ Л ф^ |Р = 2P^'^ (напомним, что || dz^ ||2 = 2
на С"). Пусть С„ = (-1)"("-*^/^(К-1/2)" и
Ф = -^ = С„ф1Л ...лф„л ф1Л ...Лф„
— форма объема на М, ассоциированная с заданной метрикой.
Глобальное скалярное произведение
(4, Г)) =1 (4(2), Т)(2))Ф(2)
м
превращает пространство A^^'^ {М) в предгильбертово
пространство. Мы задаемся вопросом: можно ли по д-замкнутой форме
т|) 6 Z^'^ (М) найти среди всех форм {яр -|- dv}, представляющих
класс когомологий Дольбо [гр] 6 fff'^ {М) формы яр, элемент
наименьшей нормы? Для ответа на этот вопрос предположим на время,
что пространство А^^^ (М) полно, а оператор д ограничен, и
определим сопряженный оператор
д*: A^^^{M) -у Av^^-^{M)
6. Теория гармонических форм на компактных комплексных многообразиях 9&
условием
(5*т|), л) = (4» ^Л) Д-^я всех л 6 ^^' '"* (ЛГ)-
Это предположение будет вскоре оправдано, а пока докажем
следующий факт.
Лемма, д-замкнутая форма т|) с: Z|' ^ (М) имеет
минимальную норму в т|) + 5Л^''~1 (Af) тогда и только тагда, когда
а*т|) = 0.
Доказательство. Если 5*1|з = О, то для любой формы
ц^А^''"' (М), удовлетворяющей условию 5г| ^^О, имеем
1Цз + ат1||2=(11з+ал, г|5+ал) = |141Р + 11'^л11''+2Ке(4, ал) =
= 1141Р+1|5л1Р + 2Ке(а*г|;,т1) =
так что норма || яр || минимальна. Обратно, если гр имеет
наименьшую норму, то для любой формы г| 6 А^'^~^ (М)
±.\\^ + tdr\\mo) = o.
Но при t = 0
-§^i^+tdr\, Mp+tdr\) = 2Re{Me, дц),
-L(^ + id{ir\), Mp + tdiir\)) = 2lm{yp, дц).
Поэтому (5*т|), г|) = (1|з, 5г|) = 0 для всех т) ^ Л^-«"'(М) и,
следовательно, 5*т|) = 0. D
Итак, по крайней мере формально, группа когомологий
Долъбо Я|' ' (М) = Z|' ' (М)/5Л^» '"* (ЛГ) представляется в точности
решениями двух дифференциальных уравнений первого порядка
Они могут быть заменены одним уравнением второго порядка
д-,|,=(аЭ* + а*а)я|)=о;
ясно, что 5т|) = 0 = 5*т|) =»• Agi|3 = 0, и обратно,
{АдМр, 4) = (53*4, 4) + (5*а>, я|)) = II д*мр||2+II ая|) н^.
•96 0. Предварительные сведения
так ЧТО Лд1|) = о =Ф- 5\)з = 5*\)з = 0. Оператор
называется д-лапласианом, или просто лапласианом
(обозначается А), если исключена возможность недоразумений.
Дифференциальные формы, удовлетворяющие уравнению Лапласа
Лф = О,
называются гармоническими формами; пространство гармонических
форм типа (р, у) обозначается Se^'^ (М) и называется
гармоническим пространством. Предыдущие формальные рассуждения
подсказывают, что должен существовать изоморфизм
<*) S''" (М) S Hf " (И);
если он будет установлен, это даст нам возможность выбрать в
каждом классе когомологий единственный представитель, что
безусловно очень удобно. Изоморфизм (*) является частью теоремы
Ходжа, доказательство которой вместе со следствиями изоморфизма
{*) и составляет содержание этого параграфа.
Начнем с явной формулы для сопряженного оператора д* и тем
самым установим его существование. Сначала определим звездочку,
или оператор двойст^нности,
*: ЛР. 9 {М) -^ Л"-Р. "-9 {М)
требованием
(г|з (z), т) (z)) Ф (z) = г|з (z) л * л (z)
для всех г|з 6 -4^'' {М). Это алгебраический оператор, локально
определяемый следующим образом: если
I. J
то
о .
где /" = {1, ...,ге} —/, а 8/,j — знак перестановки
(1, ... ,п, 1 , ..., ге ) —>- (ij, ..., ip, 7j, ..., 7g, ij, ...
..., tn-p) Ух» . • •» /n-q)'
Знаки выбраны так, чтобы * * т) = (—Ip+'r).
Сопряженный оператор выражается через оператор *
следующим образом:
д*=—*д*.
6. Теория гармонических форм на компактных комплексных многообразиях 97
Действительно, для у^^А^^^~^{М) и t]^A^f^{M) имеем
(ду^, т)) = 1 ду^ ^*^t] = (—1)^+5 \ a|) л 5 * т) + \ д (у^л*ц).
м мм
Так как д = d жа формах типа (ге, п — 1), то второе слагаемое
в правой части равно нулю по теореме Стокса. Поэтому для всех ^р
(5a|), т)) = — \ a|) л * (*5 * т)),
м
так что д* действительно определяется требуемой формулой.
Отметим, что Ъ^ = 0 =ф- д*^ = 0.
Отвлечемся на время, чтобы разъяснить происхождение
терминов «лапласиан» и «гармонический». В предположении, что мы
работаем с финитными формами, т. е. с формами, имеющими
компактные носители, приведенные формулы годятся для любых
комплексных многообразий. Разумно рассмотреть случай С"
с евклидовой метрикой в качестве подходящей локальной
аппроксимации изучаемой картины. Пусть р = g = О и dz = dz^ л . . .
. . . Adzr,. Тогда для / е С" (С")
А (/) = д*df = d* (2 -J^dz^)=* J(2i-" 2 ± J- dz л dzjo) =
3
'J
dzj
=-(2'-"2-^(|-))Алй=
3 J 1
= ,(21-2 ^)dzAd-z=(2^--^^).
Так как
о a^ _i па^ , a \
azj azj 2 I ал:| ^ ay))^
TO с точностью до постоянного множителя А (/) представляет собой
обычный лапласиан на функциях в С" ^ Ц^". В дальнейшем, при
обсуждении кэлеровых многообразий, это вычисление будет
распространено на любые формы и будет показано, что
А (/ dzj л dij) =(-22 -Т^) dz, л dzj;
V az, az, I
3 ' I
это объясняет терминологию для финитных форм на С".
7-046
98 0. Предварительные сведения
Вернемся к компактному комплексному многообразию М;
наша цель — доказать следующий знаменитый результат.
Теорема Ходжа. 1. dimS£^^«(М) < оо.
2. В силу этого корректно определена ортогональная проекция
и существует единственный оператор, называемый оператором
Грина:
G: А^^ЦМ) -^АР,ЦМ),
удовлетворяющий условиям G (Si'^'^iM)) = О, дС = ОЪ, d*G =
= Gd* и
(**) I = <m + AG на А^'ЦМ).
Равенство (**) в виде
'^ = S6W + d (5*Сг|з) + д* {dG\p)
называется ходжевым разложением форм, поскольку оно
непосредственно влечет за собой следующее разложение в прямую сумму:
4". 9 (И) = М'^' 9 (М) ф дАР, 5-1 (М) ф 5*4^. 9+1 (И).
Смысл равенства (**) в том, что при заданном tj уравнение Аг|з =
= У] имеет решение г|з тогда и только тогда, когда SS (л) = О»
и в зтом случае a|) = G (■ц) есть единственное решение,
удовлетворяющее условию Se (^) = 0. В сущности, мы собираемся заняться
решением уравнения Лапласа на компактном многообразии.
Идея состоит в том, чтобы сначала решить его в слабом смысле,
т. е. найти в гильбертовом пополнении Х^^^ {М) пространства
A'^^'^ {М) такое a|), что
(г|з, Лф) = (т1, ф)
для всех ф £ Л^»' {М), и затем доказать, что a|) на самом деле
является формой I ласса С°°. Первый шаг опирается на довольно
формальную теорию гильбертовых пространств, а второй —
обычно Называемый теоремой регулярности — является локальной
задачей, поскольку форма ф может быть представлена как сумма
форм, финитных в координатных окрестностях.
Доказательство теоремы Ходжа I: локальная
теория
В приводимом здесь доказательстве теоремы Ходжа мы
пользуемся элементарной техникой гильбертовых пространств. Мы
ищем элемент наименьшей нормы в аффинном подпространстве
■ф-Ь MP» 9"^(ikf)c= Л.^"»'(ikf). Ясно, что такой элемент можно
6. Теория гармонических форм на компактных комплексных многообразиях Ш
найти В замыкании класса гр + М''.'~^(М) в пополнении ^".^ (М)
предгильбертова пространства Л"-' (М) просто с помощью
ортогонального проектирования. Задача заключается в том, чтобы
показать, что найденный таким образом элемент содержится
в 4^.' (М). Начнем с обсуждения функций на торе. Это
доставит нам модель, на которой хорошо виден формализм, лежащий
в основе важнейших оценок; к тому же ясная картина поведения
евклидова лапласиана на торе даст нам некоторое представление
о том, чего следует ожидать в общем случае.
Пусть Т — вещественный тор (R/2nT)" с координатами
X = (xi, . . ., а;„). Обозначим через ^ пространство формальных
рядов Фурье
Соболевская s-норма определяется формулой
ll«lll=2(n-llillTl«El^
и мы определим пространства Соболева Н^ как
Яз = {и е ^ : II « IU < оо}-
Это гильбертовы пространства; имеется очевидная
последовательность включений
. . . ZD Я_„ ZD H_n+i =)...=) Я_1 ZD Яо =3 Я^ ZD . . . =3 Я„ ZD . . .;
введем еще пространства
Ноо^ Л ^5, -йГ_оо^ и ffs-
Пусть теперь С (Г) — функции класса С на Т. Функция ф g
£ С (Г) разлагается в ряд Фурье ^Фб^*^^' "^ где
cp5=f9(z)e-«<5->dz (dx=^-^lA^^^A^fZL).
т
Имеет место равенство Парсеваля
j I Ф 12 dx = j ( 2 Ще^а, х> ) ( 2 ф|;е-'<5'- «>) dc =
г г
= { Е ФбФ5'е*<5-5'. «>d,;= J 2 I Фе Р^^= Е I Ф51''
так что С (Г) отображается на Яо инъективно с || Ц, в качестве
L^-нормы на С (Г). Перестановка пределов обосновывается
применением неравенства Коши — Шварца к частичным суммам.
7*
100 0. Предварительные сведения
Положим Dj={i/ V^^) (d/dxj) и воспользуемся обычными
мультииндексными обозначениями:
[a] = ai+...+a„, i" = ir...i^.
Интегрируя по частям, получаем
j £)"ф. ;^ = j ф^, Ф, г)з е С" (Г),
т т
и поэтому для <р^С"{Т) и [a]<s имеем
(£>"ф)5= [ £>"фе-*<5-«>£г2:= ( ф|"е-«5.«>Й2: =|"фб,
Т. е.
11^ф11? = 1]|Г|ЧфИ^-
Таким образом, имеется включение C'{T)<ziHs, и из неравенств
S if"i<(i+iiiiP)'<c, S ii'"i
[а]<» [a]<s
МЫ ВИДИМ, ЧТО Соболевская норма || Ц, на C'{T)czHs
эквивалентна норме
2 \\DW\l,
которую можно называть L^-нормой функции ф вместе с
производными до порядка s. В действительности И, представляет собой
пополнение С°° (Т) по этой норме.
Частичным обращением этого результата является следующая
важная
Леииа Соболева. Я,+[„/2]+1 с: ^'(Г), т. е. всякий элемент
и £ Hs+in/2]+i Является рядом Фурье некоторой функции ф 6 С'(Т),
и этот ряд равномерно сходится к функции ф.
Доказательство. Сначала рассмотрим случай s = 0. Пусть
W = Е Ще^^^' "\ где
6. Теория гармонических форм на компактных комплексных многообразиях 101
Частичные суммы Sr= ^ use»<6'K> непрерывны, и при i?^i?'
II5IKH
имеет место оценка
\Snix)-Sn'ix)\^ 2 \Щ\ =
11?11Э=н
:ii«iii«/2]+i( 2 (-^щ^,5ят)''')-
^1 ,
'||511Э=н
Применяя интегральный признак сходимости в R,",
заключаем, что ряд
2 ((l+|||||2)[«/2]+i ) ^ДшрнТ-
сходится, откуда следует, что S^ (х) равномерно сходится
к ф6С(2'), причем щ = щ.
Дальше воспользуемся индукцией по s. Кроме того, будем
считать, что ге == 1, так как случай произвольного п требует лишь
несущественного формализма.
Итак, пусть Hg+i <^С'{Т) ж и= 2 uge'^a принадлежит про-
странству Hs+2i т- е. S I 11 ^'*^ I ug | ^ <; оо. Положим
i;= S iiuge'5».
Тогда V 6 ^s+i и, следовательно, является функцией класса
С^ (Т) по индуктивному предположению. Поскольку сходимость
равномерна, последнее равенство можно почленно
проинтегрировать:
X
^v(t)dt=2 "ge^^t ILo =и{х)- щ,
о I
так что и (х) = у (ж) и U 6 С'+^ (Т). D
Итак, мы показали, что сопоставление С (Т) -*- ^ функции ее
ряда Фурье приводит к вложениям
С (Г) с: Яз, Я,+1„/2]+1 с: С (Г), С°° (Г) - Н^.
Полезно отметить, что при доказательстве леммы Соболева
была получена оценка
sup I £)"ф (х) КС'а II ф ||[п/2]+1+[а]-
жег
102 0. Предварительные сведения
Лемма Реллиха. Для s > г вложение HgCZ Н^ является
компактным оператором.
Доказательство. Для заданной ограниченной
последовательности {uft} в Hg мы хотим найти последовательность, сходящуюся
в Ну. Поскольку при всех к выполняются неравенства
S(l + lliliyi«ft,EP<S(H-llilP)'l«ft.EP<C,
при фиксированном I последовательность {(1 + || | |Р)'"^^"й,б}й
ограничена и поэтому содержит фундаментальную
подпоследовательность. Пользуясь обычным диагональным процессом, мы
можем найти такую подпоследовательность {и^}, что
последовательность {(1 4- II I Wy^Uh.^h фундаментальна для всех |.
Теперь мы отделим члены с малыми |, которых всего конечное
число, от тех, где | велико и где нам поможет множитель (1 +
+ 111 IP)*": для заданного е > О выберем такие Rum, что
^ 7:Г-<| при |||||>Д,
(1+IUIl^)
S (l + llillTl«ft.E-«i,EP<|
II5IKH
при к, 1^т. Тогда
n«ft-«Hi?= S (i+imiyi%.6-«i,6i'+
II5IKH
+ ^ ;(i + lisrr' l»ft.E-«^U <
II5II>H
<e/24-e/2 = e. D
Теперь мы займемся уравнением Лапласа на торе Т. Мы
собираемся доказать в этом случае теорему Ходжа для 0-форм, т. е. для
функций, в стандартной евклидовой метрике и относительно
внешнего дифференциала d.
Заметим (хотя, вероятно, без этого можно обойтись), что на
компактном римановом многообразии М можно определить
оператор d*, сопряженный с d, образовать лапласиан Л^ = dd* -j- d*d
и развить в точности тот же формализм, что и для д на
комплексных многообразиях. Теорема Ходжа, разумеется, тоже верна,
и проходит то же доказательство, которое мы приведем в
комплексном случае.
Для Ф 6 С°° (Г) лапласиан выглядит так:
д,Ф= 2 D\^= - 2-1^= - Е щпг^''^^-^'-
в. Теория гармонических форм на компактных комплексных многообразиях 103
Мы исследуем уравнение
<*) Ad<P = ■*.
причем так, чтобы выводы относились к произвольным
компактным многообразиям. Функция (р ^ L^ (Т) = Но называется слабым
решением уравнения (*), если (Л^т!, ф) = (т), г|з) для всех т] 6
£ С°° (Г). В случае когда слабое решение ф тоже является С°°-
функцией, лапласиан самосопряжен, т. е.
(л, Ad<P) = (л. ■*)
для всех г\ ^С°° (Г), так что Л^ф = г|з в обычном смысле. Слабые
решения легко находятся методами гильбертовых пространств,
и задача сводится к тому, чтобы установить их регулярность.
Прежде всего заметим, что слабые решения однородного
уравнения Л(2ф = О удовлетворяют равенству
(|||||2е{<5.«>,ф) = 0
для всех |. Поэтому слабое гармоническое пространство состоит
из постоянных функций, определяемых условием ф^ = О при
1=5^0.
Далее, заметим, что уравнение (*) имеет смысл, когда г|з 6
€ L^ (Т) = Hq. Необходимым условием того, чтобы оно имело
слабое решение, служит равенство г|Зо = О, т.е. функция г|з должна
быть ортогональна гармоническому пространству.
В предположении, что так оно и есть, формула
дает решение (*) в виде формального ряда Фурье. Поскольку
ясно, что У1р ^ L^ (Т) =^ Ц1 ^ L^ (Т), это ф является слабым
решением. На самом деле можно утверждать большее: если определить
для ^ ^ L^ (Т) оператор Грина формулой
то G: Hg—*-Hs+2 — ограниченный линейный оператор. В случае
когда гр ортогонален гармоническому пространству, функция
Ф = G (о])) дает слабое решение (*). По лемме Соболева если
г|з 6 С°° (Т), то ф 6 С°° (Т) и ф является решением (*) в обычном
смысле. Наконец, по лемме Реллиха G: U' (Т) ->- L^ (Т) является
компактным самосопряженным оператором. Спектральное
разложение G на L^ (Т) представляет собой обычное разложение в ряд
Фурье.
Если обратиться теперь к результатам предыдущего
параграфа, то окажется, что их вполне хватает, чтобы установить тео-
104 0. Предварительные сведения
рему Ходжа для 0-форм на торе. Суть дела заключается в
следующем: оператор / + А^: Н^ -^ Н^.^ очевидным образом ограничен,
поскольку Л — оператор второго порядка. Еще важнее то, что
равенство
||(/ + Л<^)ф||?_2 = ||ф||1
позволяет нам обратить / + Л^ на L^ (Т) с помощью теоремы
о замкнутом графике. Обратный оператор является компактным
сглаживающим оператором и содержит информацию об операторе
Грина. Бели на произвольном компактном многообразии нам
удастся развить формализм пространств Соболева и
аналитическими средствами установить основную оценку
||(/-ЬЛ<^)ф|||_2>СЛф|||,
то можно надеяться получить картину такого же рода, как на
торе.
Мы закончим обсуждение рядов Фурье несколькими
замечаниями, относяпщмися к обобщенным функциям (распределениям),
которые по определению представляют собой линейные
функционалы
к: С°°(Г)-^С,
непрерывные в том смысле, что
|Я(ф)|ССяЗир|/?«ф(а;)|
[oc]<ft
для некоторого к. Каждая обобщенная функция порождает
формальный ряд Фурье 2Я'Е^»<5. «>, где Я,5=Я,(е-*<5. «>). Из
определения непрерывности Я и из полученной выше оценки для
зир|/?"ф (z)! следует, что все обобщенные функции к являются
непрерывными линейными функциями на Н^ при некотором s.
Спаривание
(и, V) = 2 ugyg
отождествляет H.g с пространством, двойственным к Н^, так
что к 6 Н.,- Обозначив через 3 (Т) пространство обобщенных
функций, заключаем, что
3(Т) = Н.оо.
Производные обобщенной функции определяются формулами
£)«Я,(ф) = Я,(/?«ф).
6. Теория гармонических форм на компактных комплексных многообразиях 105
Коэффшщенты Фурье производной 1)"Я, имеют вид (Z)"A.)g = |"A,g.
Согласно этому определению, обобщенная функция получается
взятием конечного числа производных непрерывной функции.
Последнее полезное определение: обобщенная функция X
называется принадлежащей классу L^, если X^HqCzH^oo- В этом
случае пространства Соболева можно охарактеризовать так:
Hs состоит из всех тлких обобщенных функций "К, что D"'K-
принадлежит классу L^ при [а] ^ s.
Интересным примером обобщенной функции служит
дельта-функция, определяемая формулой
б (Ф) = Ф (0).
Ее формальный ряд Фурье имеет вид
Мы не будем пользоваться обобщенными функциями при
доказательстве теоремы Ходжа, но они будут подробно обсуждаться
в § 1 гл. 3. Отметим, не углубляясь в детали, что уравнение
Л(2ф = г|з, где г|з — обобщенная функция, разрешимо, если г|з (т]) =
= О для любой гармонической функции tj. Если ■^ ^ Hg при каком-
либо S, положительном или отрицательном, то ф 6 ^«+2- В
частности, обобщенные решения регулярны, так же как и слабые
решения из гильбертовых пространств. Мы будем работать с
последними, чтобы иметь возможность пользоваться стандартной
теорией компактных самосопряженных операторов в гильбертовых
пространствах.
Доказательство теоремы Ходока II: глобальная
теория
Соболевская s-норма на торе определяется эквивалентным
образом либо формулой со взвешенными коэффициентами Фурье^
либо ^*-нормой 2 1 I ^"ф 1*^' Последнее определение можно
распространить на векторные расслоения на многообразии, причем
лемма Соболева и лемма Реллиха сохранят силу. Объясним, как
это делается.
Начнем с того, что рассмотрим открытые множества Ucz Vcz
cz R"; пусть каждое из них относительно компактно в
следующем. Функции с компактным носителем в U можно рассматривать
как функции на некотором торе Т. Пусть Vi{x), . . ., у„ (х) —
векторные поля класса С°° на V, всюду линейно независимые.
106 0. Предварительные сведения
а р (ж) — положительная функция на V. Для (р ^ С^ {U)
Соболевские О- и 1-нормы эквивалентны соответственно нормам
{p(x)\^,(x)\^dx, jpix){\^>ix)\^+2\Viix)-^ix)\^}dx.
г г i
Более общо, коммутатор
Ivt, vj] ф = Уг {vj ф) — vj (vt ф)
является оператором порядка 1, где под оператором порядка s
понимается дифференциальный оператор, содержащий
производные порядка не выппе s; такие операторы будут обозначаться
общим символом А'. Выражение
1/1Ц1 = yoci (уа.. . . (уО'Лф) . . .)
не зависит от упорядочения операторов по модулю операторов
порядка <; [а]. Отсюда следует, что Соболевская s -норма функции
<р 6 С" (U) эквивалентна норме
2 \ IV^rp {х)\^ dx.
Пусть теперь Е -^ М — векторное расслоение на компактном
многообразии М. Предположим, что имеется связность V на £
а на касательном расслоении Т (М) многообразия М. (Удобнее
обозначать оператор связности через V, чем через D, как в § 5.)
Пусть {е„} — локальный репер для Е и {yj — локальный репер
для Т (М) с двойственным корепером {ф,}; тогда ковариантные
производные Vi/a = /а,« сечения / = S fa^a, расслоения Е ->- М
а
определяются формулой
V/=S /а, 2«а®Ф2-
а. »
Имеем fa,J = Vifa -Ь Л" (/), где Л" — оператор нулевого
порядка, выражающийся через матрицу связности.
Применяя это к расслоению £ (g) Г* (М), мы можем
определить /„,гJ = V/ (V;/a). и т. д. Правило коммутации [у,-, V^l fa. =
= А^ if) следует из приведенного выше выражения для /„ j.
Предположим теперь, что расслоения Е и Т (М) снабжены
метриками и что {вд}, {у,} — ортонормированные реперы.
Глобальная Соболевская s-норма сечения f ^С°° {М, Е) определяется
формулой
11/111=2 \\\v4\\ldx,
k^sM
где
V''/=V(V(...(V/)...)).
k раз
6. Теория гармонических форм на компактных комплексных многообразиях 107
Обозначим через SSs {М, Е) пополнение пространства С°° (М, Е)
по этой норме. Так как, согласно замечаниям в начале этого
параграфа, глобальная Соболевская норма индуцирует норму,
эквивалентную обычной Соболевской норме на сечениях с
компактными носителями в окрестности точки, то, пользуясь
разбиением единицы, мы получаем следующие результаты.
Глобальная лемма Соболева. Пространство SS\ni2\+i+s Ш, Е)
содержится в пространстзе сечений С {М, Е) класса
гладкости S и
^тЛМ,Е) = С'^{М,Е).
Глобальная лемма Реллиха. При s ^ г вложение
тЛМ, E)-^Ser{M,E)
является компактным оператором.
Пусть теперь М — компактное эрмитово многообразие с
эрмитовой связностью в касательном расслоении. Обозначим через
Sвl■^'^ (М) пополнение 4^-' (М) по Соболевской s-норме, || || = || ||о,
и определим скалярное произведение Дирихле и норму Дирихле
формулами
3 (ф, t) = (Ф, t) + (^Ф, Щ + {д\, д*^р) = (ф, (/+ А) гр),
^(ф) = ^(ф,ф)=||ф||2+||5ф||2+||5*ф||2.
Основной оценкой теории служит
Неравенство Гординга. Для ф ^ А^'^ (М)
II ф ||?< СЗ! (ф) (С > 0).
Заметим, что мы предпочли оператор / + Л лапласиану Л,
поскольку из Л ^ О следует, что / + Л не имеет ядра, и поэтому
больше шансов обратить его.
С помощью неравенства Гординга будет доказана следующая
Лемма о регулярности I. Пусть ф 6 SSp^ (М), и пусть г|з 6
6 (0ё^'ЧЩ — слабое решение уравнения Лг|з = ф, т. е. (г|з, Лт]) =
= ф (ti) для всех ц 6 А»^^ (М). Тогда г|з 6 i^?4i W-
Предположим, например, что ф 6 Щ'^ (М) — собственная функ^
ция лапласиана, т. е. для некоторого собственного значения К
равенство Лф = Яф выполнено в слабом смысле. Тогда по лемме
о регулярности ф 6 d^f •' (Щ для всех s, и из глобальной леммы
Соболева выводим, что любая собственная функция оператора Д
является гладкой.
108 0. Предварительные сведения
Заметим, что все собственные значения Я, неотрицательны,
причем Я, = О <=> ф гармонична в слабом смысле. По лемме о
регулярности и лемме Соболева все такие слабо гармонические формы
принадлежат классу С°° и гармоничны в обычном смысле.
Мы примем пока на веру неравенство Гординга и лемму о
регулярности и закончим доказательство теоремы Ходжа. После этого
мы докажем неравенство Гординга. Лемма о регулярности будет
доказана тогда, когда мы будем заниматься сглаживанием
обобщенных функций. Читатель, который не хочет оставлять пробелов
в рассуждениях, может найти доказательство в конце раздела
«Сглаживание и регулярность» § 1 гл. 3.
Основным средством теории гильбертовых пространств
является спектральная теорема для компактных самосопряженных
операторов, дополненная принципом представления ограниченного
линейного функционала в виде скалярного произведения с
фиксированным вектором; мы будем пользоваться ею в следующем виде.
Лемма. Для заданной формы ф 6 d^o'' (Щ существует
единственная форма ^^SS'P' ^(М), тлкая, что
(Ф,Л) = ^(1|',Т1)=(^, (/ + А)Л)
для всех ■x\^A^-i{M). Отображение 1]; = 7'(ф) из SS1'^{M) в
S6^-^{M) ограничено, и, следовательно, оператор Т: М^'''{М)
->- сШ^' ' (■^) компактен и самосопряжен.
Доказательство. Неравенство Гординга утверждает, что норма
Дирихле эквивалентна Соболевской 1-норме на SSP-^{M).
Линейный функционал
Л -^ (Ф. л) (л € А^Я (М))
продолжается до ограниченной линейной формы на S£^-^ (М) с
нормой Дирихле, так как
1(ф, Л) К II Ф Но It л 11о<11ф11о^(л)-
Поэтому уравнение (ф, ц) = 3) (гр, tj) имеет единственное решение
гр = Г (ф), характеризуемое условием
(Ф, л) - (Тц>, (/ + А) Л) (л 6 Af<^ (М)).
Оператор Т самосопряжен, поскольку таковы операторы /
и Л. Из неравенства 2аР^ га^ + (1/е) Р* и оценки
II Гф 11,^< СЗ (Гф, Гф) = С (ф, Гф)< С II ф Но II Гф ||о^
< (8/2) С II Гф 112 + (С/28) II ф \\1
выводим, что
1|г'ф11?<с'||ф||г.
6. Теория гармонических форм на компактных комплексных многообразиях W9
Это говорит О ТОМ, ЧТО оператор Т ограничен как отображение
из (|^Р'9 (М) в c^f-9 (М), и по глобальной лемме Реллиха он
компактен как оператор на Se^'^ (М)- О
По спектральной теореме для компактных самосопряженных
операторов имеет место разложение в сумму гильбертовых
пространств
т
где рт — собственные значения оператора Т ж Е (р^) —
конечномерные собственные подпространства. Поскольку оператор Т
взаимно однозначен, все рт Ф 0; более того, уравнение Гф =
= ртф эквивалентно
(Ф, л) = (РтФ, (/ + А)Л) (л € Л^.' (М)),
откуда следует, что
1—Рп
^^={^)
Ф
в слабом смысле. Отсюда вытекает, что собственные пространства
операторов Г и Л совпадают и являются конечномерными
векторными пространствами С°°-форм. Собственные числа Я^ оператора Л
и Рт оператора Т связаны соотношениями
1 —Рт „ 1
Лт'
Рт ' *"" 1 + J^n
Можно считать, что О = Яо < Я,1 <! . • ., где Ят f оо, Рт | О
при m ->- оо. Гармоническое пространство S6'^^^^ (ikf) соответствует
значению Яд = 0. Для ф 6 Ш'^■'^^ {Щ^
II Аф ||о> >,i II ф Но 0,1 >0),
и если определить оператор Грина условиями
G = 0 на SP''i{M),
(?Ф=-^Ф [при фе£(^),
то G будет компактным самосопряженным оператором со
спектральным разложением
sei' 9 {м)=т^'-чм)®{®Е {рт)),
т
причем бф=( 1^"^ )ф для ф6£(Рт)-
Этим мы уже доказали теорему Ходжа. Суть в том, что при
помощи гильбертовых пространств строится оператор Грина, а за-
110 0. Предвар ительные сведения
тем при помощи основной оценки показывается, что он компактный
и сглаживающий. На самом деле G — интегральный оператор вида
{G^>){x)={G{x,y)^{y),
и
где G (х, у) — красивое ядро яа М X М с некоторыми
особенностями на диагонали Л. Недостаток метода гильбертовых
пространств в том, что он не дает оператор Грина в таком виде. Если
бы мы работали с обобщенными функциями, а не с L^-формами,
мы бы могли построить оператор Грина как решение уравнения
в обобщенных функциях
Л„ G {х, у) = 8у + Sy,
где 8у — дельта-функция от у, а Sy — оператор порядка —оо.
Такие уравнения будут обсуждаться в § 1 гл. 3.
Доказательство неравенства Гординга. Пусть ((pi, . . ., ф„) —
локальный унитарный корепер для эрмитовой метрики, так что
d^ = ЗфгФ»' Форма типа {р, q) записывается локально как
^ = 7b-2^i.j4'^^<P-^'
где функции t|3j J кососимметричны по индексам !„ и /р. Для
лапласиана имеется знаменитая формула — тождество Вейценбёка;
мы будем пользоваться ею в виде
(W) (At)3)jj = (- S VftVs Ь, 1) + A^ (t).
Иначе говоря, с точностью до слагаемых низшего порядка
глобальный лапласиан на формах выглядит так же, как евклидов
лапласиан — 5 d^/{dz)i dz)i) на векторнозначных функциях.
Точная формула Вейценбёка содержит и слагаемые низшего
порядка. Для общей эрмитовой метрики А^ (г|з) — очень громоздкий
оператор, содержащий кручение в слагаемых первого порядка.
Однако если метрика кэлерова, они взаимно уничтожаются и А^ (гр)
превращается в алгебраический оператор вида
А^ (t)ij = JI Д,• ft Ь'и ..Гк...за (Л на а-м месте),
где Rjji — ^R\.^ — кривизна Риччи.
6. Теория гармоничеспих форм на компактных комплексных многообразиях 11$
Для доказательства формулы Вейценбёка рассмотрим репер
векторных полей (vi, . . ., i;„), взаимный с репером (щ, . . ., фп)
и такой, что v-r = у,-. Для функции /
i
И ДЛЯ тензора т = {xj} компоненты z-ковариантного
дифференциала Vt задаются формулой
{Vx)j = dxj + AO{x).
Удобно пользоваться символом ^ для обозначения «по модулк>
слагаемых низшего порядка», так что, например, (ут)/ ^ dxj.
Положим Ф' = (pi л . . . л (р„.
Достаточно доказать (W) для 1]з = /ф/ л ф^ (без
суммирования). Поскольку дифференциалы dz сказываются лишь на
индексах векторных расслоений, можно считать, что р = 0. Наконец,,
по симметрии в формуле достаточно рассмотреть случай / =
= (!,.. ., q), так что
1|Э = /ф1Л ... Лфд.
Теперь вычисляем:
5iJ;s(—1)«У1/йф1Л ...Лф^лфй,
ft>g
*lt ^ (- 1)« 2«+1-« S (- !)"-«-* /ft Фд+1 Л ... Л Фй л ... л ф„ л Ф',
k>q
д*~д^Р = (29+1-" S h, ft) фд+1 л . . . л ф„ л Ф' +
+ S 23+1-" (-!)"-'/ft,, Фг л фд+1 л ... л фй л ... л ф„ л Ф',
ft>g
*д*д'^ S (2 2 /ft, ft) <Pi л ... л фд4-
*>«
4-2 2 (-1)'-1+« /ft. г ф1 л ... л ф, л ... л фд л фй..
ft>g
Kg
Мы вычислили член *5*5гр; другой член 5*5*а|)[вычисляется еш;&
проще:
*!]; = 29-"/ Ф5+1 л . . . л ф„ л Ф',
5*t = 2»-» S 7, фг л фд+1 л ... л ф„ л Ф',
К9
*5*1];= 2 S (—1)'"'l/i Ф1 л ... л ф{ л ... л фд,
«9
112 0. Предварительные сведения
5*5*1); ^(2 2 /j,7) <Pi Л . . . Л фд +
+ (2 2 (—l)''^Vj,ft<PlA ...Лф{Л ... ЛфдЛфй).
h>q
Далее, У г (lb/) — v-^{Vif)^A^{f), так что по модулю слагаемых
первого порядка
Ла|) = (—2 2/ft,ft)9iA ... лфд +
h
+ (2 S ( —l)'"*+'/ft.j9iA ... Лф{Л ... Лф„Лфй4-
h>q
+ 2S (-l)'+'/ft. J9iA ...Лф,Л ... лФпЛфй).
КЗ
ft>e
Последние два слагаемых сокращаются и дают
Да|) = (— 2 2 /ft. ft) Ф1 л ... л фд.
ft
Это доказывает формулу Вейценбёка.
Теперь переходим к доказательству неравенства Гординга;
мы будем пользоваться формулой Вейценбёка в виде
m)ij=(-22 ы, ft. ft)+А' т.
ft
Неоднократно будут применяться неравенства типа
<*) 2ар< еа« + (1/е)р^
Ф = С„Ф'лФ' обозначает форму объема. Положим
11 = С„(— 2 (—1)*^* tlJ,ft%J. АФ1Л ...ЛфйЛ ... Лф„)лФ'=^
1,-Г, ft
= C;((Vip, гр)лш"-1).
Последнее выражение показывает, что форма tj определена
глобально; поскольку она имеет тип (ге—1, ге), то йт) = 5т). По
теореме Стокса \ дц = 0. С другой стороны,
м
5т, = (-2 2 tiJ.ft. ftW)Ф-(2 2 %j.ftii7,ft)0 +
J, J, ft I, J. ft
+ (Ait, ^)Ф-
Теперь по формуле Вейценбёка
(Aa|),a|;) = ||Vtll'+(^*^'. ^),
6. Теория гармонических форм на компактных комплексных многообразиях 113
где ||Vi|'|p= \ (Vil», V^) Ф есть ^^-норма z-ковариантного диф-
м
ференциала тензора ij;, а Л* (г|з)—оператор первого порядка,
содержащий лишь производные г|з по z. Пользуясь неравенством
(*), получаем
2|(^'t.^')l<e||Vtll' + (l/e)I|ip|P,
откуда следует, что
||Vtp|P<C'{(A,|5, г|з) + ||а|5||2}, С'>0.
Теперь повторим рассуждение, применив его на этот раз к форме
V = C„(- S (-l)''-'%J,ftiljilA ...л фйЛ ... Лф„)лФ',
•I. J.k
и воспользуемся соотношением ДД=/^ й4:'<4.* (/) Для оценки
^2_нормы ||Vi|5|p нормой Дирихле. Собирая все это вместе,
получаем
IIVtp||2+ IIV tlP+ IHjIP^C' ((At, t) + lltIP) ^C'3 (t);
это и есть неравенство Гординга.
Замечание. В кзлеровом случае можно воспользоваться точной
формулой Вейценбёка и проведенным выше интегрированием по
частям для доказательства тождества Кодаиры
(Лг|з, гр) = II Щ IP + (Ryp, ^),
где для формы \1р 6 ^"'^ {Щ имеем (предполагая суммирование по
повторяюпщмся индексам)
Если форма \lp гармонична, a зрмитова форма Д.т|'|'
положительно определена, то отсюда мы заключаем, что гр ^ 0. По теореме
Ходжа
0^S6°'''iM)^Hl'''{M), q>0.
Это частный случай знаменитой теоремы Кодаиры об обращении
в нуль, общее доказательство которой будет приведено в § 2 гл. 1.
Прилоокения теоремы Ходока
Начнем с того, что отметим существование изоморфизма
^р.,9(М)-^Я|'«(ЛГ)
114 0. Предварительные сведения
между гармоническим пространством и группой когомологий
Дольбо. В самом деле, пользуясь разложением Ходжа, каждую
5-замкнутую форму г|з 6 2|'' {М) можно представить в виде
^ = Se{-^) + d{d*G^),
поскольку 5(тг|з = Сгд^ = 0. Комбинируя зтот изоморфизм с
изоморфизмом Дольбо, получаем изоморфизм
^p><i{M)^Hi (М, Qp).
Согласно первому утверждению теоремы Ходжа, отсюда следует
Конечномерность: dim Н^ {М, Q^) ■< оо.
Поучительно дать прямое доказательство конечномерности
в случае q = 0. Пусть {С/,} — конечное координатное покрытие
многообразия Ж с голоморфными координатами г^д, .. ., Zi_n в C/j.
Можно найти такие относительно компактные открытые
подмножества Vicz Uj, которые образуют подпокрытие многообразия М.
Глобальное сечение
Ф е Я» (Ж, Q') = Я» {{Ui}, Q") = Я» {{Vi), Q^)
имеет в Ui вид
Ф = S <Pt. J (z) dzi, J,
J
где (pi, J (z)60 (Ui)- Определим норму
||ф|| = 11 sup |(pi,j (Z)|.
i.J г6 Vj
Эта норма конечна, и, поскольку (1) Я» ({F,}, Q*) ^ Я» ({C/J, Q')
и (2) любая последовательность аналитических функций
г|з^6 0 (C^i). удовлетворяющая условию sup |\|3v (z)—■фц (z) |-^0,
содержит подпоследовательность, равномерно сходящуюся к
голоморфной функции г|з 6© (^i). мы заключаем, что Я" (Ж, Q*) с этой
нормой является полным банаховым пространством. По теореме
Монтеля из заданной последовательности (pv 6 Я" (Ж, Q'),
удовлетворяющей условию II фу II -^ 1> можно выбрать
подпоследовательность, для которой функции фу,г./ (z) 6 © (С^г) равномерно
сходятся к некоторым функциям фг,/ 6 © {Vi). Поэтому
единичный шар в этом банаховом пространстве компактен, и, согласно
известной теореме ^), отсюда следует его конечномерность.
'^) См., например, Бурбаки Н. Топологические векторные пространства.
Пер. с франц.— М.: ИЛ, 1959, гл. I, § 2, п° 4, теорема 3.— Прим- ред.
6. Теория гармонических форм на компактных комплексных многообразиях 115
На самом деле очевидно, что гильбертово пространство с
компактным единичным шаром конечномерно, а Н'^ (М, Q*) можно
превратить в гильбертово пространство, полагая
(ф. t)= S J Ф*. J (2) ^г. J (Z) Ф (Zi),
i.Jr^
где Ф (Zj) — форма евклидова объема в координатах z^. Так как (1)
последовательность г|з^ 6 © (Ut), фундаментальная в L^ (Vt),
содержит подпоследовательность, сходящуюся равномерно на
компактных подмножествах в Fj к г|з 6 © (^г)> и (2)
последовательность г|3у 6 0 (f^i)t ограниченная в L* (Fj), содержит такую же
сходящуюся подпоследовательность, то проведенное рассуждение
можно приспособить к случаю гильбертовых пространств.
Его можно изменить так, чтобы доказать конечномерность
всех пространств Н^ (М, Q^), а на самом деле и конечномерность
Ш (М, §^ для любого когерентного аналитического пучка g^.
Эти вещи будут обсуждаться ниже, в § 3 гл. 5, когда выяснится,
что конечномерность — центральный факт глобальной теории
когомологий когерентных пучков на компактных многообразиях.
Другое приложение теоремы Ходжа связано с двойственностью
Кодаиры — Серра. Из формулы д* — — *5* видно, что *Д =
= Д*. Отсюда следует, что оператор «звездочка» индуцирует
изоморфизм
*: J^p- 9 (Af)-^c^«-P. "-9(Af).
В частности, с^"-" {М) ^ С-Ф, где Ф = *1 — форма объема
метрики.
Чтобы понять внутренний смысл этого изоморфизма, не
зависящий от выбора метрики, отметим следующий общий факт. Для
заданных пучков 3' ■, ^ и <|(? на пространстве X и отображения
пучков З' ® ^ -^ Si определено и-произведение
которое на коцепях задается формулой, приведенной в конце
обсуждения теоремы де Рама. В частности, спаривание
индуцированное внешним умножением голоморфных
дифференциальных форм, определяет гомоморфизм
(*) Н* (М, QP) ® Н* {М, Q9) -^ И* (М, QP+9).
С другой стороны, спаривание
{ , }: АР' >• (М) <2> А"'»(М) -^ 4Р+9' ''+«(М),
116 0. Предварительные сведения
заданное формулой {т|з,т|}= т|з л т|, удовлетворяет условию
и поэтому определяет гомоморфизм
(.») Я|- * (Ж) ® Hi' * (М) -> Я^"- * (М).
Спаривания (») и (»») соответствуют друг другу при
изоморфизме Дольбо, по крайней мере с точностью до знаков, согласно
тем же соотношениям, что и в конце обсуждения теоремы де Рама.
Если зто установлено, то получается следующая
Теорема двойственности Кодаиры — Серра. 1. Н^ (М, Q") JI^C.
2. Спаривание Я« (М, Q^) ® Я""' (М, Q"-p) -^ 1Г (М, Q")
невырожденно.
Доказательство. Первое отображение задается композицией
изоморфизма Н^{М, £2")^Я|'"(М) с линейной функцией
Я|'"(Ж)-> С, определенной соответствием г|з н-»- \ г|з. Это опреде-
дг _
ление корректно в силу теоремы Стокса и того факта, что d=d
на А"' "~* (■^)- То, что это изоморфизм, следует из изоморфизмов
Я^'" (М) ^ ^". " (Ж) ^ С • Ф,
поскольку \ Ф = vol {М) > 0;
м
Спаривание задается композицией изоморфизмов Н^{М, Qp) ^
^Щ'^{М) со спариванием
HS' «(М) ® Я|-^' "-«(М) -> С,
которое опредедяетея соответствием
г|з ® т| >-*• \ г|з л т|.
м
Оно невырожденно, поскольку Я|'' (Ж) = <|Й'^' ' (М), а для
гармонической формы г|з ^ О ■
г|з (8) * 11-* j г|з л * гр = ||г|з||2 > 0. D
м '
Перейдем теперь к формуле Кюннета. Пусть заданы
компактные комплексные многообразия М, N; рассмотрим произведение
6. Теория гармонических форм на компактных комплексных многообрагиях 11Т
М X N. Проекции на сомножители индуцируют отображения
Н* (М, QSf) -^Н*{Мх N, Ql^xiv),
H*{N, Q%)-^H*{MXN, Ql^xjv)-
Как мы сейчас увидим, эти отображения инъективны, что
позволяет отождествить группы с их образами. Тогда и-произве-
дение определяет отображение
(*) Н* (М, Qh) ® Н* {N, Q%) -^Н*{Мх N, Q*mxn).
Формула Кюннета утверждает, что это изоморфизм.
Для доказательства воспользуемся гармоническими формами.
Эрмитовы метрики на М и на 7V определяют естественную
метрику на произведении М X N, ж мы покажем, что при таком
выборе метрики имеет место изоморфизм
(••) <й?"' "(MxN)^ ф (^р- 9 (М) (8) (В'-' ' (N));
р+г=и
g+s=»
зто и будет доказательством теоремы Кюннета.
Обозначим через z, w локальные координаты на Ж и на Ж.
Если заданы формы г|з, т| соответственно на Ж и на Л^, то
обозначим через 1|з ® т| форму на М X N, определенную формулой
(ij3 ® т]) (z, ш) = г|з (z) л т] (ш).
Такие формы будут называться разложимыми.
Лемма. Разложимые формы плотны в метрике I? в
пространстве всех форм на М X N.
Доказательство. Мы дадим его только для функций; изменения^
необходимые для общего случая, будут ясны.
Надо доказать, что функция ф (z, w), удовлетворяющая
условию
j 9(z, ш) ф (z) т] (ш) = О
AfXJV
для всех тр, т|, равна нулю. Пусть Re ф (zq, w^ >» 0; выберем формы
1|з (z), т| {w) с компактными носителями в окрестностях
соответственно точек Zq и Шо и удовлетворяющими условиям
Re (фг|зт1) > О, Re (ф (Zq, Wq) г|з (zq) т] (шц)) > 0.
Это нетрудно сделать при помощи неотрицательной] вещественной
функции с небольшим носителем. Тогда рассматриваемый интеграл
будет отличен от нуля. D
118 0. Предварительные сведения
Формы на Ж X iV локально записываются в виде
Ф (z, If) = S (fn-jj- dzi л dwi' л dzj л dwj-,
причем djixN — 9M±djf, где_5м—внешнее дифференцирование
по переменным Zj, а 5j^—по Wj. В силу нашего выбора метрики,
на Ж X iV имеется ортонормированный корепер вида
(ф1 (Z), . . ., фт (Z); T|3i (Ш), . . ., Т|3„ (Ш)),
где фг (z) образуют ортонормированный корепер на М, а г|3а (ш) —
на N. Пользуясь формулой 5*=—*5*, находим, что
dtixN=d*M ±д%, дмд% +'д%дм = О ='d^j, + ^"j^SJf,
Из этих соотношений следует, что ^mxn = 1^m-{-^n- Точнее, на
разложимых формах имеет место равенство
Amxjv (^ ® л) = (Aiif^) ® т] + ^ ® (А^гЛ)'
а по лемме это равенство определяет ^mxn на всех формах.
Мы подошли к основному моменту. Если ipi, г|з2, • • • —
полное множество собственных форм для Дд^, а t|i, щ, . . .—
полное множество собственных форм для Aj^, то формы г|з,- ® т|„
являются собственными для А^х^г- По лемме они образуют
полное множество. Если
Ам^г = ^j^i. ^i>0,
АлгЛа = »АаЛа. Ца>0,
ТО
Aitfxjv(^|3i ® Ла) = (^.•4-На) (% ® Ла)-
Поскольку я,; + М^а = о <=*• ^j = Р'а = Oi отсюда следует
утверждение (**) о гармонических формах. Тем самым формула
Кюннета доказана. []
Введем числа Ходжа
hp-я (М) = dim т{М, QP);
мы доказали, что
ftP-9(Af)<c»,
Л". " (Ж) = 1 и йР. 9 (Ж) = /г»-р. »-9 (If),
7. Кэлеровы многообразия 119
В случае когда многообразие М кэлерово, имеют место
дополнительные, более глубокие соотношения между числами Ходжа,
такие, как
hP'4{M) = h<i'p{M), Ьг{М)^ 'ZhP'iiM), ЛР. р(М)>1,
p+q=r
где Ьг (М) — dim Н'' (М, С) есть г-мерное число Бетти. Это
и многое другое будет получено в следующем параграфе.
Последнее замечание. Вообще говоря, внешнее произведение
гармонических форм не является гармонической формой.
Аналогично, ограничение гармонической формы на подмногообразие,
вообще говоря, не будет гармонической формой в индуцированной
метрике. Иначе в кольце когомологий выполнялись бы только
соотношения, которые имеются во внешней алгебре. Более того, два
лапласиана на эрмитовом многообразии,
Ag = 99* = 9*9 и Aa = dd* + d*d,
вообще говоря, никак не связаны между собой. То, что для кэле-
ровой метрики оба зти общих принципа нарушаются и теория
гармонических форм оказывается исключительно изящной,—
весьма удивительный факт. Об этом — в следующем параграфе.
7. КЭЛЕРОВЫ МНОГООБРАЗИЯ
Условие Лэлера
Пусть М — компактное комплексное многообразие с
эрмитовой метрикой ds", и пусть на некотором открытом множестве
и ^ М метрика ds^ евклидова, т. е. существуют такие
голоморфные локальные координаты z = (z^, . . ., z„), что
rfs^ = 2 dzj ® dzj.
Пусть, как обычно, z^ = a;^+K —1 У у, непосредственно
проверяется, что для дифференциальной формы ф = 29iJt^zj л c^zj
с компактным носителем в U имеет место формула
32
Аэ(ф) = —2"^ ——=-ffjj-dziAdzj =
I.J, i ^''^''
I.J. i
Т. е. 5-лапласиан с точностью до константы совпадает с обычным
d-лапласианом на U (см. § 6 выше). Конечно, очень немногие
120 О, Предварительные сведения
компактные комплексные многообразия допускают всюду
евклидову метрику, но оказывается, что для выполнения равенства
Аа = */2 Ad
на комплексном многообразии достаточно, чтобы метрика
аппроксимировалась евклидовой с точностью до второго порядка. В этом
и состоит условие Кэлера, и большая часть параграфа будет
посвящена обсуждению этого условия и его следствий.
Начнем с того, что приведем условие Кэлера в трех разных
вариантах. Пусть опять
ds^= "^hijdzi ® dzj = 2ф1 ® ф«
— эрмитова метрика на комплексном многообразии М. Назовем
метрику ds" кэлеровой, если ассоциированная с ней (1, 1)-форма
(Л-
-Ч—2ф«лф4
d-замкнута. В § 5 мы показали, 4toJ существует единственная
матрица гр из 1-форм, удовлетворяющая условиям
где Xi — форма типа (2, 0); там метрика называлась кэлеровой,
если кручение т = 0. Покажем, что эти условия равносильны.
Запишем
а
—^=-йш = 2 ^ф«'^ ф« — Е ^Pi Л йф, =
Имеем
2 г|3г^ л ф, л ф, - 2 Фг Л^^^ л ф^ =
= 2 ■^ij л ф^ л ф, -Ь 2 Фг л г|з^г л ф^ = 0,
и, таким образом, {21]/ — 1) йш = 2 т^^ '^ Фг ~ S Ф1 л т,.. Но
Tj — формы типа (2, 0), а ф| — формы типа (О, 1), линейно
независимые в каждой точке, откуда следует, что йш = О тогда и
только тогда, когда т = 0.
Другая интерпретация условия Кзлера несколько проясняет
его геометрический смысл: будем говорить, что метрика ds^ на М
имеет соприкосновение порядка к с евклидовой метрикой в С",
7. Кзлеровы многообразия 121
если в окрестности каждой точки z^ ^ М можно найти такие
голоморфные локальные координаты (z), в которых
где gij имеют в Zg нуль порядка А:; обычно зто записывается в виде
^ = 2 Фи + Ш) dZi ® dZj.
Лемма. Метрика ds^ кэлерова тогда и талыю тогда, когда она
всюду имеет соприкосновение второго порядка с евклидовой
метрикой.
Доказательство. В одну сторону это очевидно: если
©=-'^^ S (^гИ-[2]) dzj л di^
в некоторой координатной системе с началом в Zq, то йш (zo) = 0.
Обратно, всегда можно выбрать координаты (z), в которых
hj (zo) = ^ij, так что
(0 =
/~
2
2 Фи + '^iih^k + diji^k + [2]) dZi л dzj.
Заметим, что
1 x^
Мы ХОТИМ найти такую замену координат Zft = ш^^—о 2 ^him^^i^iM
чтобы форма ю имела вид
(•) (О = ^а"^ S (^«^ +12]) dWi л dwj.
Потребуем еще, чтобы 6ьгт = '^ьтг- Тогда
dZft = dlfft + S bumPldWm,
так что
+ 2 (<^iJk^k + aijk^k) dWi л du5^+ [2] =
= 2(^г^+ 2'^<ift"'ft+'^i^"'»+'^Mi"'ft+biftiu'ft) c^"'j Л йшу+[2].
Положим bjj^i =■ — ciijK, получим
bjki= — am = — o-KSi = bjiK и 6jft^ = — ttjij, = — а.д,
так что зта замена координат удовлетворяет условию (*). D
122 0. Предварительные сведения
Еще один полезный в вычислениях способ выразить это
условие заключается в следующем: для каждой точки Zq ^ М найдется
унитарный корепер ф^, . . ., ф„ в некоторой окрестности точки Zq,
такой, что d(pi (Zq) = О,
Многообразие называется кэлеровым, если оно допускает кэле-
рову метрику; приведем теперь некоторые примеры кэлеровых
многообразий.
Примеры. Любая метрика на компактной римановой
поверхности кэлерова, поскольку d(o является 3-формой и поэтому
обращается в нуль по соображениям размерности.
Пусть Л — решетка в С"; тогда комплексный тор Т = С"/Л
кзлеров с евклидовой метрикой ds^ = ^ dzi ® dzt.
Если многообразия М ж N кэлеровы, то многообразие М X N
с метрикой произведения тоже кэлерово.
Пусть Scz М — подмногообразие, ш — ассоциированная (1,1)-
форма кэлеровой метрики на Ж. В § 2 мы уже отмечали, что
ассоциированная (1, 1)-форма индуцированной метрики на S есть
просто ограничение на iS формы ш; поэтому если М кэлерово, то
и S кэлерово.
Напомним, что метрика Фубини — Штуди на Р" задается
своей ассоциированной (1, 1)-формой
(О = -1^55 log II ZIP,
где Z —локальный подъем множества С/ci Р" в С"+* —{0}. Так
как 55= —дд, то
(o=-^^~-(d + d)(d-d)log\\Z\\^ = ^^^d((d-d)log\\Zr),.
так что форма ш замкнута и, следовательно, метрика Фубини —
Штуди кэлерова.
[Замечание. Удобно определить оператор d", положив
d"^—|-—(д—д); d и d'—вещественные дифференциальные
г/'ЗГТ -
операторы и dd" = — d^d =-J-^ дд. Следовательно, (0 =
= dd'log\\Z\\^.]
Отметим, что, согласно сказанному выше, любое компактное
комплескное многообразие, которое может быть вложено в
проективное пространство Р", кэлерово.
Теперь приведем некоторые топологические следствия,
немедленно вытекающие из условия Кэлера для компактного
многообразия М.
7. Кэлеровы многообразия 123
1. Четномерные числа Бетти b2q (М) положительны.
2. Пространство голоморфных q-форм Я* (М, й') вкладывается
в группу когомологий Hj)R (-^i ^- ^- все такие формы замкнуты
и неточны.
3. Фундаментальный класс г]у любого аналитического
подмножества Vcz М отличен от нуля.
Доказательства. 2. Пусть т| — голоморфная (q, 0)-форма. Мы
хотим показать, что dr] = 0 и что т| = йг|з только тогда, когда
т| ^ 0. Пусть ф1, .. . , ф„ — локальный унитарный корепер и
n = Tj ЛгФ/^ тогда т] л т] = S Т1/'П7Ф/ л tpj.
I I.J
Далее, (о = -^— 2 Ф-/^ Ф^' ""^^^ ^"^^
(й»-^ = Сд {n — q)l 2 Фк Л Ф^;
таким образом, для некоторого С, ^ О имеем
Т1ллл(0"-' = С,2]|Т1/Р-Ф,
где Ф—форма объема. Следовательно,
\ т] л т) Л ш""' =ф О, если т] :7^ 0.
лг
Теперь предположим, что т| = йг|з. Тогда dr] = dr\ = О, и,
поскольку da = О, имеем
j т1Лт]Л(й""'= ( й(г|зЛ'ПЛ{й"~') = 0.
дг м
Поэтому из предположения г\ = d\^ следует, что т| ^ 0. Наконец,
поскольку dr\ = дг\ — голоморфная точная (q + 1)-форма, то
dц =0.
1. Чтобы показать, что b^q (М) > О, достаточно заметить, что
замкнутая 2д'-форма ш' не является точной. Действительно, если
бы ш' = d\p для некоторой формы г|з, то выполнялось бы равенство
f(o"= J й(г|зл(о"-«) = 0.
м м
Но (u"/ra! есть форма объема на М, так что это равенство
невозможно.
124 0. Предварительные сведения
3. Доказательство очевидно: если V имеет комплексную
размерность d, то по теореме Виртингера из § 2
VOl(F) = -^ j(0'^:?tO,
У
поэтому (т1тг) :7^ о в Н^а (М). []
Заметим, что утверждения 1 и 3 обобщают утверждения,
доказанные в конце § 4 для подмногообразий проективного
пространства.
Соотногиеиия Ходока и разлооюеиие Ходжа
Пусть М — компактное комплексное многообразие с
эрмитовой метрикой ds^ и ассоциированной (1, 1)-формой ш. Мы
определили несколько операторов на пространстве А* (М)
дифференциальных форм на М, а именно операторы д, д, d, d", их
сопряженные и построенные с их помощью лапласианы, и получили
разложения
П'-= Ф IP.': Л*(Ж)->4ЧЛ^)
р+д=г
ПО типу И степени. Определим еще оператор
1:АР^ЦМ)-^АР*^,^*^(М)
формулой Z, (т|) = т| л ш и обозначим через
Л = L*: АР.' (М) -> 4^-1,9-1 (М)
сопряженный с ним оператор. На произвольном многообразии М
неочевидных соотношений между всеми этими операторами нет.
Однако если метрика на М кзлерова, то их связывает большое
количество соотношений, называемых соотношениями Ходжа.
В самом деле, условие кэлеровости как раз и обеспечивает
взаимосвязь между вещественной теорией потенциала, отвечающей
римановой метрике, и комплексной структурой. Основным
соотношением, из которого легко следуют остальные, является
соотношение
(») [Л, dl = —And'*,
где [А, В] — коммутатор АВ — В А, или равносильное
соотношение
IL, d*] = 4nd'.
7. Кэлеровы многообрагия 125
Доказательство. Согласно разложению по типам, зто
соотношение эквивалентно соотношениям
[Л, Ъ] = -У^д*, [Л, д] =У^^Ъ*.
Поскольку А., d ж d" — веш;ественные операторы, из любого из
них следуют остальные. Мы докажем соотношение [Л, 5]=]/^—1 д*.
Сначала проведем вычисление на С" с евклидовой метрикой.
Оно громоздко, но непосредственно и облегчается разложением
по компонентам. Введем несколько новых операторов на формах
в С". Для каждого А: = 1, . . ., п пусть е^: Л^-'(С")->
->■ ilf+''' (С") — оператор, определенный на формах с
компактными носителями формулой
eft (ф) = dzj, л ф,
и пусть е^: 4?''(С")-»-^''"'''(С") определены аналогично:
eft(9) = ^ZftA9.
Обозначим через г^ и г^ операторы, сопряженные соответственно
с eft, eft. Заметим, что все операторы eft, eft, ift и ift линейны над
С°°(С"). Далее,
ift (dzj л dzjf) = О, если k^J,
и (напомним, что ||dZft|p = 2)
ift {dzfi л dzj л dz^) = 2 dzj л dz^.
Первая формула следует из того, что для любых мультииндексов
L ж М
(ift (dzj л dzic), dzL л dzm) = {dzj л dz^, dz^ л dzL л dz^i) = 0,
поэтому ift (dzj л dzg) = О, a вторая — из того, что
(ift (dZft л dzj л dzx), dZi, л dzjif) = (dzft л dzj л dz^, c^Zft л dzL л (fza^) =
= 2 (dZj л dZx, dZL л c2Zj)f).
Аналогично убеждаемся, что
ift (dzj л dzjf) = О, если A^Z,
и
ift (dzft Л dzj л dzic) = 2dzj л dzj^.
Заметим также, что для любого монома dzj л dz^
fO, если k^J,
ik-ek(dzjAdzK) = < -
\2dzj A.dzic, если k^J,
126 0. Предварительные сведения
тогда как
Л dzj^, если k^J,
(2 dzj,
''■'»<*'"''""->" если kiJ.
Таким образом, г^е^ + e^i^ = 2, и аналогично г^^е^ -f ^kh = 2. С
другой стороны, для А: Ф I имеем
ij^ • б/ {dzj^ л dZj л dzjc) = i^ (dzi л dz^ л dzj л dz^) =
= ift (— dZft л dzj л dzj л dZjf) = — 2 (dz/ л dzj л uzk) =
= — 2e/ (dzj л c^Zx) = —ei-i^ (dz^ Л dzj л dz^),
тогда как
i^j.g/ (dzj л dzjj;) = ei-ij^ (dzj л dz^) = 0
при k^J ж, следовательно, е^г/+1^6^ = 0.
Определим на 4?'(С") еще операторы 5^ д^, полагая
^ft ( 2 Ф17^2/ л dzj) = 2 -^ dzi л dzj.
Заметим, что операторы ду^ и 5^ коммутируют с операторами б/,
б/, i/, ii и друг с другом. Наконец, оператор —5^ сопряжен с
5ft. Действительно, для любой формы с компактным носителем
Ф = 2 9jj ^2j л dzj, любых мультииндексов Z, и М и любой
С°°-функции г|з имеем
(-5ьф, т|з dzi, л dzu) = [ — -7^ (Фьм) ^^ь л dz^, г|з dzi, л dz^ =
(интегрирование по частям)
= (Фьм ^^^^ '^ ^^м. дь. (i|3- dzi, л dZif)) = (ф, дь. (^ ^Zi, л dz^))-
Аналогично, оператор —5^ сопряжен с д^.
7. Кэлеровы многообразия 127
Все наши операторы на At* (С") выражаются через эти
элементарные. Очевидно, что
5 = 2 5^6^ = 2 eft5ft, 5 = 25^^^ = 2 ёА,
h к h h
и, переходя к сопряженным, имеем
Оператор L определен как внешнее произведение со стандартной
кэлеровой формой на С", так что
и для сопряженного оператора имеем
Поэтому
k.l h.l
( 2 ^hhkek + S ^i^hhei) -
k k^i
Преобразуем первое слагаемое
2 ^ ^к1кЧек = 2 Ij^klkeklk 2 ^ ^A»ft =
2 ^ 2 ^ft«Jft^ft-K~l S ^ft^ft
2
И второе слагаемое
—^^-^ 2 ^i^ft^ft^i = 2~^ 2 ^'^ft«i*ft = —^^"F^ 2 ^i^i^kh-
Таким образом,
Ад= --^^ 2 ^/e^ift + y^T 2 dJ^ = dA+V^ld*,
ft. /
так что на С" требуемое соотношение доказано.
Чтобы доказать его на произвольном кзлеровом
многообразии М, воспользуемся условием соприкосновения и покажем, что
наше соотнош:ение выполняется в любой точке. Для точки Zq ^ М
можно выбрать такой корепер фх, . . ., ф„, что d^i (zq) = 0. Выра-
128 0. Предварительные сведения
жение для Л сохраняет силу, если заменить dzi на 9j; можно
проделать для [Л, 5] т| по существу те же вычисления, что на С",
с тем отличием, что добавятся слагаемые, содержащие 5ф,-.
Однако, поскольку в [Л, д] входят только первые производные, все
дополнительные слагаемые будут содержать множитель 5фг и
поэтому обратятся в нуль в точке Zq. Точно так же мы знаем, что
^*т| = С„ * 5 * т| на С", где этот оператор совпадает с V^—1 [Л, д\ т|.
Вычисление на многообразии М в терминах фг снова будет таким
же, кроме дополнительных слагаемых с членалш 5ф,-, которые
обращаются в нуль в точке Zq. Таким образом, требуемое
соотношение выполняется в точке Zq, а следовательно, и всюду.
Это рассуждение представляет собой проявление общего
принципа: любое инвариантно определенное тождество, в которое
входят коэффициенты метрики и их первые производные и которое
выполняется на С" с евклидовой метрикой, выполняется на любом
кэлеровом многообразии.
Теперь приведем несколько следствий. Пусть Д^ = dd* + d*d
есть d-лапласиан; тогда
[L, Д^] = О, или, эквивалентно, [Л, Д<г] = 0.
Доказательство. Во-первых, заметим, что, поскольку форма ш
замкнута,
d (<в л т]) = а А dr\, т.е. [L, d] = О,
и для сопряженных операторов [Л, d*] = 0. Таким образом,
A(dd* + d*d) = (dAd*-4nd'*d*) + d*Ad =
= dAd* + (And*d''* + d*Ad) = (dd* + d*d) A. D
Имеем также упоминавшееся ранее соотношение
Д^ = 2Дз = 2Д8.
Доказательство. Прежде всего покажем, что 55* +5*5 = 0.
Так как Л5 —5Л = >^"^5*, то
yZTi (дд* + д*д) = д(Ад- 5Л) + (Ад —дА)д = дАд — 5Л5 = 0.
Далее,
Д^ = (5 + 5) (5* + д*) + (5* + 5*) (5 + 5) =
= (дд* + д*д) + (дд*.+ д*д) +. (д'д* + Ъд* + д*д+'д*д) =
= (дд* + д*д) 4- (дд* + 5*5) = Да + Дд,
поэтому остается показать, что Аэ = Дт.
7. Кзлеровы многообразия 129
Для зтого выполним преобразование
—У^^a = д {A3 — дК) + {Кд-дК) д = дКд~ддА. + Адд — дА.д
и ползгчим
У~^ Д^ = ф (Ад — дА) 4- {Ад — дА) д) =
= дАд — ддА + Адд — дАд = У^^Аа. Q
В качестве непосредственного следствия получаем, что
оператор Д<г сохраняет бистепени, т. е.
[Дй, ип = 0.
Имеются два основных приложения зтих соотношений:
разложение Ходжа и теорема и разложение Лефшеца. Сначала займемся
разложением Ходжа.
Положим
т, 9 {М) = Z§'«{MWA* (М) П ZI-«(М)),
ml*' W = {ri е 4^'' {М): AdT] = 0),
(^S(М) ={цеЛ'-(М): Алц = 0}.
Заметим, что первая группа инвариантно определена комплексной
структурой, тогда как вторая и третья зависят от выбранной
метрики. В силу перестановочности операторов Д^и П^>' и того факта,
что Д<г веществен, пространства гармонических форм
удовлетворяют соотношениям
(*) se{M)= ф с^р,5(Ж), ж''^цм)=т^^''{м).
с другой стороны, если т| — замкнутая форма чистого типа (р, q),
то
Ц = Se (Ц) + dd*G (Т1),
где гармоническая часть (^ (т|) тоже имеет чистый тип (р, q).
Поэтому ЯР.' (М) ^ с^Р.з {М). Объединяя зто со (*) и с теоремой.
Ходжа ЯЬв (М) ^ SS* {М) для лапласиана Д^, получаем
знаменитое
Разложение Ходжа. Па компактном кэлеровом многообразии М
комплексные когомологии удовлетворяют соотношениям
р+д=г
Так как Дd = 2Д9, то Жа'ЧЩ^Щ'ЧМ) и, следовательно,
Я^. ' (М) ^ Я| * (М) ^ Я' (М, QP).
9-046
130 0. Предвар ительные сведения
(п, л)
(я,0)< • ! • »(0.л)
(О, 0)
Рис. 6
в частности, при q = О получаем пространство Д^»" (М) =
= Н" {М, й^) голоморфных р'фотрм. Следовательно, голоморфные
формы гармоничны для любой кэлеровой метрики на компактном
многообразии.
Заметим также, что
Числа Бетти b^q+i (М) нечетной степени четны.
Доказательство. Если определить числа Ходжа как
то разложение Ходжа дает
Ъг{М)= S к^'ЦМ), hP^^{M) = h^^^'{M).
p+g=r
При r = 2q-\-\. получаем
р=0
Можно схематически изобразить группы когомологий
компактного кэлерова многообразия на ромбе Ходжа (рис. 6), где к-я
группа когомологий М изображается суммой групп в к-ш
горизонтальной строке. Оператор «звездочка» обеспечивает
симметричность относительно центра ромба, а сопряжение — относительно
центральной вертикали.
В качестве непосредственного приложения теоремы Ходжа
имеем
7. Кэлеровы многообразия 131
Я'(Р", £2Р) = Я|'«(Р") = { J
Следствие-
О, если pфq,
если р = q.
Доказательство. Так как Я2''+1(Р", Z) =0, то Я|''(Р")=0
при нечетном p + q, ж так как Л'2''(Р", Z)=Z, то при рфк
1 = 6j^ (Р») > А^, 2ft-P (р") + АЗЬ-Р, Р (Р») =2. ftp, 2ft-P =j, й^, 2ft-P (рп) = 0
и, стало быть,
в частности, отметим, что
На Р" нет ненулевых глобальных голомофных1форм.
Разлоокение Лефгиеца
Другое важное приложение соотношений Ходжа —
разложение Лефшеца когомологий компактного кэлерова многообразия.
Чтобы изложить его в нужном свете, отвлечемся на время и
обсудим представления алгебры Ли sZj.
Представления алгебры sl^. Алгебра Ли sl^ группы Ли SL^
реализуется как векторное пространство комплексных 2x2-
матриц со следом О и операцией скобка:
[А, В] = АВ — ВА.
Ее стандартные образующие
/О 1\ /1 0\ /О 0\
^=(оо)- ^=(o_i)' ^=(io)
удовлетворяют соотношениям
[X, Y] = Я, [Я, X] = 2Х, [Я, Y] = -2У.
Пусть V — конечномерное комплексное векторное
пространство, gl (F) — его алгебра зндоморфизмов. Мы хотим изучить
отображения алгебр Ли р: sZj -> gl (F), т. е. такие линейные
отображения р, что
р {[А, В]) = р(А)р {В) -р(В)р (А).
Всякое такое отображение называется представлением алгебры sl'^
в F, а F называется зХ^-модулем. Подпространство в F,
инвариантное относительно р (sZj), называется подмодулем. Модуль F (или
представление р) называется неприводимым, если он не содержит
нетривиальных подмодулей. Согласно одному важному
результату, который мы не будем здесь доказывать '), каждый подмодуль
132 0. Предварительные сведения
sZj-модуля V имеет дополнительный подмодуль W^. Поэтому
всякий в/д-модуль вполне приводим, т. е. является прямой суммой
неприводимых в/г-модулей, и при изучении представлений
алгебры sZj можно ограничиться неприводимыми представлениями.
Итак, пусть V — неприводимый в/д-модуль. Ключевым
моментом в анализе его структуры является рассмотрение собственных
подпространств оператора р (Я) (начиная с зтого места символ р
будет опускаться). Они называются весовыми пространствами.
Прежде всего заметим, что если v^V — собственный вектор
оператора П с собственным значением Я,, то Xv vlYv — тоже
собственные векторы оператора П с собственными значениями X, -)- 2
и Я, — 2 соответственно. В самом деле,
Н (Xv) = XHv + [Я, X]v= X'kv + 2Xv = (Я, -Ь 2) Xv
и аналогично для Yv. Поскольку Н имеет лишь конечное число
собственных значений, мы видим отсюда, что операторы X ж¥
нильпотентны. Назовем вектор v ^V примитивным, если v —
собственный вектор оператора П ж Xv = 0; ясно, что примитивные
элементы существуют.
Предложение. Если вектор v ^V примитивен, тео модуль V
порождается как векторное пространство векторами
V, Yv, Y^v, . . ..
Доказат£лъст^о. Поскольку модуль V неприводим, достаточно
показать, что линейная оболочка V множества {Y*v} инвариантна
относительно алгебры 8^2. Ясно, что НУ cz V и Yv cz V.
Покажем, что XV cz V, no индукции: Xv = 0 тривиальным образом
лежит в F', a при га > О
XY^v = YXY^-■^v + HY^-Ч,
так что XY^-^v £ F' => XY^ 6 V. \Q
Отметим, что все ненулевые элементы {Y"v}n линейно
независимы, поскольку являются собственными векторами оператора Н
с различными собственными значениями. Теперь ясно, как устроен
модуль V: он представляется в виде V = ©F^,, где все
подпространства Fx, одномерны,
H{V^)==V^, ^(F,) = F^+2, 5"(F0 = F^_,.
Предложение. Все собственные числа оператора Н целые и
F = F„ ф F„_2 ф ... ф F_„+2 Ф F.„.
^) См., например, Серр Ж.-П. Алгебры Ли и грушхы Ли. Пер. с франц.—
М.: Мир, 1969, гл. VI, § 3 и гл. VII, § 1.— Прим. ред.
7. Кэлеровы многообразия 133
Доказательство. Пусть вектор v примитивен, и предположим,
что Y^v Ф О, Т^^Ъ =^ О а Hv=Xv. Тогда
Xv = О,
XYv = YXv + Hv = Xv,
XY^v = YXYv + HYv = YXv + {X — 2)Yv = {X + {X — 2)) Yv
и вообще XY^v = YXY'"-^ + HY^-^v, так что
XY'"v = {X+{X-2) + {X-4)+ .. .+{X-2{m-i)))Y'"-'v =
= {mX-m^+m)Y'"-iv,
И, поскольку Y"v^O, F^+^i; =0,
(ra + 1) Я, - (ra + 1)2 + ra + 1 = 0 =^ Я, = ra. Д
В итоге получаем, что неприводимые sl^-модули занумерованы
неотрицательными целыми числами га; для каждого такого га
соответствующий sl^-модулъ V (га) имеет размерность га + !•
В явном виде
V (га) ^ Sym" (С2)
— га-я симметрическая степень векторного пространства С*.
Собственные значения оператора Н, действующего на
пространстве F(ra), суть —га, —га + 2, . . ., га — 2, га, каждое с
кратностью 1.
Для любого в^г-модуля F, не обязательно неприводимого,
определим его разложение Лефшеца следующим образом. Пусть
PV = кег р {Х)\ тогда
F = PF ф yPF ф Г'РУ Ф . . .,
причем это разложение согласовано с разложением F в сумму
собственных относительно Н подпространств Vm- Кроме того,
отображения
V ~7^У
' т <— ' -т
ЯВЛЯЮТСЯ изоморфизмами. Наконец, вообще
(кег X) П Fft = кег {Y^^h F^ ^ F.^.^).
Вернемся теперь к нашему компактному комплексному
многообразию М с кэлеровой метрикой йФ = J фг ® фг- Прея де всего
мы хотим вычислить коммутатор \L, Л] операторов L и Л. Это
134 0. Пред арительние сведения
достаточно сделать на пространстве С", используя операторы eji,
е^, i^ и ill, определенные выше. Вспомнив, что
получаем
[Z,, Л] = -^ ( 2 ^heJih — 2 MzCftlft) =
ft. г ft, г
= Т 2 i44hii — hiieheh) + -^ Е («ft^ft^ft^ft —Jftiftefte,,).
ftФг ft
Согласно нашим коммутационным соотношениям, все
слагаемые в первой сумме обращаются в нуль; что касается второй, то
«ft^ft^ft Jft = 2eftift — eftiftCftift, ikih44 = SiftC,, — ikekh^kt
И, поскольку Cftijeftift^ifteftifteft, получаем отсюда
(Z,, Л] = -^ 2(^ft^ft —^fteft) = ^ E (2 - ^ftCft —TftCft) =
ft ft
Чтобы довести вычисления до конца, заметим, что ^^«^(dz/A
л dzx) i-aBHO нулю, если k^J, а 2dzjAdzg^ в противном случае;
i^eii {dzj А dzg) равно нулю, если к^К, я 2dzjAdzg: в противном
случае. Поэтому
S (JftCft + JftCu) (dz/ л Й2я) = 2 S <^2j л dzx + 22 dzj л dzx =
ft k^J ft$K
= (2 (ra — */) + 2 (л - *^)) {dzj л iJk) ,
так что на пространстве форм Ар>« (С") имеем [L, А] = р +
-\- q — га. Поскольку L и Л — алгебраические операторы, это
тождество вьшолняется на всех кэлеровых многообразиях.
Теперь положим
2п
А=2 {п-р)1Р
Поскольку L: А^{М)-^А^*^{М) и Л: А^ (М) ^ А^-^ (М), полу
чаем
(*) [Л, L] = h, [h, L] = —2L, [h. Л] = 2Л.
Операторы L, А и. h коммутируют с А^ и поэтому действуют на
гармоническом пространстве J^* (М) ^ Н*{М) и удовлетворяют
7. Кзлероеы, многообразия 135
соотношениям (*). Следовательно, мы можем определить
представление алгебры Ли sZj на пространстве Н* (М), полагая
/О 1\ /О 0\ /1 0\
^=(оо)--^' ^=(io)^^' ^=(o-ij--'^-
Собственным пространством для оператора h с собственным
значением (га]— р) будет IP (М). Применяя результаты о
конечномерных представлениях sl^ к этому представлению, получаем
следующий важный результат.
Сильная теорема Лефшеца. Отображение
является изоморфизмом, и если определить примитивные когомо-
логии как
P"-ft (М) = кег {L^^*^: Я""* (М) -^ Я^+^+з (М)} = (кег Л) П 1Р-\М),
то получим разложение
k
которое называется разложением Лефшеца.
изложение Лефшеца согл
I положить
рр, ч (М) =(кег Л) П ЯР. 1 (М),
10
р+в=г
Можно дать следующую геометрическую интерпретацию теории
Лефшеца в случае, когда многообразие М вложено в проективное
пространство Р^ и наследует его метрику. Мы видели, что форма
а, =J^55log IIZIP
замкнута и не точна на Р^. Поскольку пространство IP (Р^
одномерно, отсюда следует, что класс [со] 6ЯЬн(Р^ двойствен
по Пуанкаре ненулевому кратному класса гомологии
гиперплоскости Я с: Р^. На самом деле класс [со] двойствен по Пуанкаре
классу (Я), в чем читатель может убедиться, проинтегрировав ©
по прямой Z ^ Р^ и получив
|(о = 1 = *(Я.г).
Заметим, что разложение Лефшеца согласовано с разложением
Ходжа, т. е. если положить
136 0. Предварительные сведения
Отсюда МЫ ВИДИМ, что для подмногообразия Ма Р^
ассоциированная (1,1)-форма (О I щ индуцированной метрики двойственна по
Пуанкаре классу гомологии (F) аналитического подмножества
F = Af П Я^с: М. Двойственная по Пуанкаре версия сильной
теоремы Лефшеца утверждает, что операция пересечения с {N — к)-
плоскостью P^-^^cz Р^ задает изоморфизм
Заметим, что при такой интерпретации примитивные когомоло-
гии Р"-* (Л/) многообразия М соответствуют при изоморфизмах
^.t-^^ """"^.„^дв. по Пуанкаре
Я''-*(М) Н„.,(М)
дв. по Пуанкаре""*-^^ ^.^-''лР''"*
подгруппе (га — А;)-а;иклов, не пересекающих гиперплоскость,
т. е. образу отображения Я„_й (М — V) -*■ Hn-h {Щ- Такие
циклы называются конечными циклами, поскольку Ж — V
представляет собой «конечную часть» М f| С^ многообразия М. Их
важность проявится при доказательстве теоремы Лефшеца о ги-
перплоских сечениях.
В качестве другого применения разложений Ходжа и Лефшеца
мы ползгчаем билинейные соотношения Ходжа — Римана.
Определим билинейную форму
<?: Я"-" (М) ® Н"-^ (М) -> С,
полагая
м
со\
Поскольку форма © веш;ественна, Q определяет вещественную
билинейную форму на Я"~* {М, R). Рассмотрение типов
показывает, что
(?(ЯР'СЯ^'''') = 0, кроме случая p = q', д = р'.
Билинейные соотношения Ходжа — Римана утверждают, что для
примитивного класса ^ 6 jP^*' (М) ш к = р + q имеет место
неравенство
Кэлеровы многообразия 137
В случае четного р -\- q это равносильно тому, что на
вещественном векторном пространстве
(рР. 9 ф рч. Р) р jjv+я щ^ Л) = {5 +1, I е Р'^^" {М)} CZ ЯР+« (М)
квадратичная форма у _ 1р-9 (_ l)(»-'')("-''-i)/2 ^
положительно определена, а в случае нечетного р + q — что Q есть
невырожденная кососимметричная форма на пространстве Р^"^ (Л/).
В обоих случаях, поскольку имеется разложение Лефшеца /Г" =
= ф L*P'"-2't и Q (Z»P|, L*Ti) = Q (I, т)), билинейные соотношения
утверждают, что форма Q невырожденна на пространстве Я""* (М).
Мы не будем доказывать билинейные соотношения в полной
обш;ности, но проверим их в некоторых слзгчаях, включая все те,^
которые будут применяться в геометрических приложениях-
(Обш;ее доказательство может опираться на следующие
наблюдения: в полной внешней алгебре
F=A*C"(8» Л*С^,
соответствующей дифференциальным формам в точке х 6 М,
определено представление алгебры Ли sig, действующей с помощью
операторов {L, Л, h}, как выше. Разложение пространства Fna
примитивные подпространства P'^V совпадает с разложением V
относительно действия унитарной группы f7„, и, таким образом, па
лемме Шура, любая С7„-инвариантная квадратичная форма на
пространстве P'^V знакоопределена. Примитивные гармонически©
формы яа. М — это в точности те формы, которые лежат в P'^V
(при фиксированном к) для каждой точки х 6 М, и это дает
доказательство. Тот факт, что разложение пространства F относительно
действия sl^ вместе с проекторами n*^'') дает те же непроводнмы&
подпространства, что и относительно действия f7„, докаэан в книга
Германа Вейля «Классические группы»^); из него следует, что,
вообще говоря, «высших» соотношений Ходжа не существует.)
Пусть сначала М — компактная риманова поверхность.
Согласно разложению Ходжа,
ю (М, С) = Я1.» (М) е Я». 1 (М) ^ Я» {м, qi) е я» {м, q»).
Таким образом, число линейно независимых голоморфных 1-форм
на М (классически называемых дифференциалами первого рода)
равно bi {М)/2. Это обстоятельство было одним из первых
связующих звеньев между топологией комплексного многообразия и era
комплексной структурой. Чтобы проверить билинейные
соотношения для поверхности М, рассмотрим дифференциал И =
^) Вейль Г, Классические группы, их инварианты и представления-
Пер. с англ.— М.: ИЛ, 1947.— Прим. ред.
138 0. Предварительные сведения
= h{z)dz 6 Я^'» (Л/); имеем /:Лр-« (_1)("-й)("-''-1)/2 =Y~i и
Q{l,%) = Y'^\ \h{z)\^dzAdz>(i,
м
Вообще, для многообразия М любой размерности, сравнение
типов показьшает, что компоненты 1Р'^ (М) и Я'-^ {М)
примитивны, и с помощью тех же вычислений можно проверить для них
билинейные соотношения. На самом деле мы уже установили
билинейные соотношения Ходжа — Римана для голоморфных
^-форм, когда доказывали, что голоморфные формы инъективно
отображаются в когомологии компактного кэлерова многообразия.
Пусть теперь dim М = 2; билинейные соотношения нужно
проверить только для компоненты Р ^'^. Пусть ? — вещественная
примитивная гармоническая (1, 1)-форма, записанная в локальном
унитарном корепере (ф^, фа) в виде | = З^г^фг л ф^. Так как
форма \ вещественна, то ^ц = — \л. Записывая
(0 = J-^ (ф1 л ф1+ Ф2 л Фа),
g л (О = J-^ (ill + ^аа) Ф1 л ф1 л Фа л фг.
МЫ видим, что примитивность формы \ влечет за собой условие
iu + ?22 = О- Для проверки билинейного соотношения проведем
следующие вычисления:
(У ZZiy-O (_ 1)(г.-«(г.-й-1)/2 <? (5. f) = _ f g л I ..
к
-^ - j ( —?ula2 + 2 I |i2 |2 —gazfu) Ф1 A Ф1 л ф^ л фа
м
Напомним, что для любого ориентированного компактного
вещественного многообразия X размерности 2к на пространстве
Я** {X, 1R) — ЯпЕ (X) имеется билинейная форма, определенная
формулой
м
которая, согласно двойственности Пуанкаре, невырожденна. Если
к четно, то форма Q симметрична и с многообразием X можно свя-
7. Калероеы многообразия 139
зать топологический инвариант — сигнатуру формы Q,
определяемую как разность числа положительных и отрицательных
собственных значений матрицы, представляющей форму Q. Сигнатура
формы Q называется индексом I (Х) многообразия X. Конечно,
если М — компактное кэлерово многообразие размерности 2п, то
Q — Q яа пространстве Н^ (М, [R) и для вычисления индекса
многообразия М можно использовать билинейные соотношения
p+3=0(mod2)
<2п
Мы знаем, что если p + gr^0(mod2), то 1^ —1''~'х
Х(—1)<Р+*<Р+«~^>/2^>0 на вещественном пространстве
(рр. 9 ф рд. Р) р| дР+ч щ^ щ^ -Гад дад Q (^^^^ щ _ ^ (^^ g)^ ^
P+3=0(mod2)
= S (-irdimPP'«(il/).
P+g=0(mod2)
<2n
Далее, пользуясь разложением Лифшеца, находим, что
поэтому, пройдя по вертикали ромба Ходжа, получим
S (-1)^ dim Р*' *+^ = (- 1)Р Л"' Р+^ + 2 S (-1)« Л*' *+'
и окончательно
/(М)= 2 (-If А"''4-2 S {-1)РЛ*''',
p+g=2n p+3sO(mod 2)
<2n
ИЛИ
/(il/)= S (-If A"-'.
p+3=0(mod2)
Последнее равенство выполняется благодаря двойственности
}iP,4 = й"~Р«"~'. Заметим, в частности, что на кэлеровой
поверхности М и-произведение Q на пространстве Я^'^ (Л/) имеет ровно
одно положительное собственное значение; этот факт часто
называется теоремой об индексе для поверхностей.
Отметим, наконец, одно различие между теоремами Ходжа
и Лефшеца этого параграфа: теоремы Лефшеца по существу
топологические, а разложение Ходжа отражает аналитическую
структуру многообразия. Например, если вещественное многообразие
140 0. Предварительные сведения
наделить двумя различными комплексными кэлеровыми
структурами, то разложение Ходжа может измениться — могут меняться
даже ранги rpynni (Яр.« {Щ ф Я'.р (Л/)) П IP'*'^ {М, %) —
тогда как изоморфизм Лефшеца и разложение Лефшеца остаются
теми же самыми.
ЛИТЕРАТУРА
Мы укажем» »,ссь несколько книг, которые помогут читателю в освоеввв
материала этой главы. Этот список не претендует на полноту, он является
лшпь небольшой выборкой из литературы, в которой приняты обозначения
и точки зрения, близкие'к нашим. Многие из этих книг содержат обширную
библиографию, и, таким образом, могут послужить источником дальнейших
литературных у1{азаний.
Общие вопросы
Ганнинг Р. и Росси X. Аналитические функции нескольких комплексных
переменных. Пер. с англ.— М.: Мир, 1969.
Chern S. S. Complex Manifolds without Potential Theory. —New York: Van
Nostrand Reinhold Company, 1967.
Специальные вопросы
§1
Хёрмандер Л. Введение в теорию функций нескольких комплексных
переменных. Пер. с англ— М.: Мир, 1968.
Narasimhan R. Introduction [to the Theory of Analytic Spaces.— Berlin —
Heidelberg — New York: Springer-Verlag, 1966.
§ 2
Kodaira K. and Morrow J. Complex Manifolds.— New York: Holt, Rinehart,
and Winston, 1971.
Stolzenberg G. 'VolшIles, Limits and Extensions of Analytic Varieties.—\,
Berlin — Heidelberg — New York: Springer-Verlag, 1966.
Уэллс P. Дифференциальное исчисление на комплексных многообразиях.
Пер. с англ— М.: Мир, 1976.
§ 3
Годеман Р. Алгебраическая топология и теория пучков. Пер. с франц.—
М.: ИЛ, 1961.
Хирцебрух Ф. Топологические методы в алгебраической геометрии. Пер.
с англ.— М.: Мир, 1973.
§4
По алгебраической топологии имеется много современных руководств.
Классическим источником, откуда в основном был заимствован подход к гомо-
логиям и теории пересечений, является
7. Калеровы многообразия 141
Lefschetz S. Topology.—American Matb. Society Colloquium Publications
vol. 12 (1930).
§6
Де Рам Ж. Дифференцируемые многообразия. Пер. с франц.— М.: ИЛ, 1956.
Warner F.' Introduction to Manifolds.— New York: Scott-Foresman, 1971.
Примечание. Наше доказательство теоремы Ходжа является вариантом
доказательства, данным Джо Коном в курсе, который он читал в Принстонском
университете в 1961/62 гг.
1
КОМПЛЕКСНЫЕ АЛГЕБРАИЧЕСКИЕ
МНОГООБРАЗИЯ
Алгебраическое многообразие определяется как множество нулей
системы однородных многочленов в комплексном проективном
пространстве, и а priori его можно рассматривать как
аналитическое подмножество в Р". В том случае, когда это многообразие
является гладким, его можно рассматривать как абстрактное
компактное комплексное многообразие, свойства которого будут
внутренними, т. е. не зависящими от вложения этого
многообразия в проективное пространство. В широком смысле мы подходим
к алгебраической геометрии как к предмету, изучающему связь
между внутренними и внешними, т. е. проективными, свойствами
алгебраических многообразий.
В § 1 определяются понятия дивизоров и линейных расслоений;
этот материал очень важен для всего дальнейшего изложения.
Так как на компактном комплексном многообразии нет всюду
голоморфных функций, кроме констант, то остается только
надеяться, что его структуру достаточно хорошо описывают глобальные
мероморфные функции и соответствующие линейные системы
дивизоров; зти понятия лежат в основе классической
алгебраической геометрии. С каждым дивизором можно связать линейное
голоморфное расслоение, с каждой мероморфной функцией —
линейное расслоение с голоморфным сечением, а с каждым
линейным расслоением — его класс Чжэня. Соответствзпющий
формализм, развитый Кодаирой, Спенсером и др. в начале 50-х гг.,
чрезвычайно полезен при работе с подмногообразиями
коразмерности 1 (т. е. с точками на кривых, кривыми на поверхностях и т. д.)
алгебраического многообразия.
Основной проблемой при построении мероморфных функций
с предписанными свойствами, например с заданными главными
частями на римановой поверхности, является построение
локальных решений, препятствие к глобальной склейке которых лежит
в группе когомологий с коэффициентами в некотором пзгчке. Теорема
Кодаиры об обращении в нуль дает полезные условия обращения
в нуль высших групп когомологий. Этот замечательный результат,
1. Дивизоры и линейные расслоения 143
доказанный первоначально методами теории потенциала и
дифференциальной геометрии, оказался в конце концов эквивалентным
известной теореме Лефшеца, касающейся топологического
расположения гиперплоского сечения комплексного алгебраического
многоообразия. Всему этому посвящен § 2.
В § 3 начинается переход
/"абстрактное компактное \ f алгебраическое многообразие!
1комплексное многообразие/ ~*" \ в проективном пространстве/ "
Промежуточную ступень составляет аналитическое множество,
вложенное в проективное пространство. По теореме Чжоу оно
является алгебраическим многообразием. Этот важный момент
иллюстрируется совпадением двух объектов — глобальной меро-
морфной функции на сфере Римана и рациональной функции
одного комплексного переменного. Практический вывод отсюда состоит
в том, что как локальный комплексно аналитический подход, так
и глобальный алгебраический приводят к одному и тому же
результату. На данном этапе наш подход аналитический, так как он
больше связан с топологическими и метрическими свойствами
алгебраического многообразия, но при этом важно понимать, что
в конечном итоге речь идет о решениях полиномиальных
уравнений.
В § 4 формулируется и доказывается теорема Кодаиры,
описывающая те компактные комплексные многообразия, которые
возникают из алгебраических многообразий, что дает существенное
связующее звено между внутренними и внешними свойствами
алгебраических многообразий. Эта теорема о вложении и теорема
Чжоу являются теоремами существования: они не указывают
конструктивного способа нахождения уравнений, задающих образ
многообразия при проективном вложении, однако вместе они
составляют краеугольный камень нашего аналитического подхода
к алгебраической геометрии.
В последнем параграфе этой главы подробно рассматриваются
грассманианы, т. е. многообразия, точки которых параметризуют
линейные подпространства некоторой фиксированной размерности
в проективном пространстве и геометрия которых отражает
характер пересечений с данным фиксированным пространством
линейных подпространств, находящихся с ним в необщем положении.
Одна из причин того, что грассманианы обсуждаются именно здесь,
состоит в том, что они хорошо иллюстрируют обпще структурные
теоремы этой главы. Другая причина — в том, что в следуюпщх
главах широко применяется исчисление Шуберта, которое дает
количественное выражение необщих соотношений инцидентности
между линейными пространствами, заложенное в стрзгктуре грасс-
маниана.
144 !• Комплексные алгебраические многообразия
1. ДИВИЗОРЫ и ЛИНЕЙНЫЕ РАССЛОЕНИЯ
Дивизоры
Пусть М — комплексное многообразие размерности га, не
обязательно компактное. Напомним некоторые факты об
аналитических гиперповерхностях в М из § 1 гл. 0.
Любое аналитическое подмножество Vcz М размерности п — 1
является аналитической гиперповерхностью, т. е. в некоторой
окрестности любой точки р 6 Vcz М оно может быть задано
как множество нулей некоторой голоморфной функции /. Более
того, любая голоморфная функция g, определенная в точке р
и обращающаяся в нуль на F, делится жа. f в окрестности
точки />; / называют функцией, локально определяющей V вблизи р
(или локальным уравнением V в окрестности точки р). Эта
функция единственна с точностью до умножения на функцию, не
равную нулю в р.
Пусть Vt — компонента связности множества V* = V — V,;
тогда V* — аналитическое подмножество в М. Поэтому V можно
единственным образом представить как объединение неприводимых
аналитических гиперповерхностей
F = Fi и • • • и F™,
где Fj — замыкания компонент связности множества F*. В
частности, V неприводимо тогда и только тогда, когда F* связно.
Определение. Дивизором D на многообразии М называется
локально конечная формальная линейная комбинация
D = ^ai-Vi
неприводимых аналитических гиперповерхностей в М.
Локальная конечность означает, что для любой точки р ^ М
существует ее окрестность, пересекающаяся только с конечным
числом гиперповерхностей Fj, входящих в D; если М компактно,
то это означает, что сумма конечна. Дивизоры на М образуют
аддитивную группу, обозначаемую Div {М).
Дивизор 2? = S ajFj называется эффективным, если а^^ О для
всех г; это записывается в виде Z) ^ 0. Аналитическая
гиперповерхность F обычно отождествляется с дивизором У\ Fj, где Fj —
неприводимые компоненты F.
Пусть Vcz М — неприводимая аналитическая
гиперповерхность, р ^V — произвольная точка, а / — функция, локально
определяющая F вблизи р. Для любой голоморфной функции g,
заданной в окрестности точки р, определим ее порядок ordy р [g)
1. Дивизора и линейные расслоения 145
вдоль V в точке р как наибольшее целое число а, при котором
в локальном кольце Ом,р имеет место разложение
g = r-h.
Согласно результату со стр. 21, взаимно простые элементы
кольца ©м.р остаются взаимно простыми в близких локальных
кольцах. Следовательно, для голоморфной на М функции g порядок
ordv.p (g) не зависит от тючки р. Поэтому можно определить
порядок ordv (g) функции g вдоль V просто как порядок функции g
вдоль V в любой точке р ^ V. Отметим, что для любых
голоморфных функций g, h тя. любой неприводимой гиперповерхности V
имеет место равенство
ordv (gh) = ordv (g) + ordv (h).
Пусть теперь / — некоторая мероморфная функция на М,
записанная локально в виде / = g/h, где функции ^ и А
голоморфны и взаимно просты. Для неприводимой гиперповерхности V
положим
ordv (/) = ord^ (g) — ord^ (h).
Принято говорить, что / имеет нуль порядка а на V, если ordy (f) =
= а > О, w полюс порядка а на V, если ordy (/) = — а -< 0.
Дивизором if) мероморфной функции f называется формальная
линейная комбинация
(/)=|lord^(/)-F.
Если / локально представлена в виде glh, то дивизором нулей
функции / называется дивизор
(/)o = Sord^(^).F,
V
а дивизором полюсов — дивизор
(/)oo-^Ordv(A)-F.
Очевидно, эти дивизоры определены корректно, если gvih взаимно
просты, и имеет место равенство
(Л = (Ло - (Лео.
Дивизоры можно также описать в терминах теории пучков.
Пусть оМ'* — мультипликативный пучок мероморфных функций
на М, не равных тождественно нулю, а О* — его подпучок не
обращающихся в нуль голоморфных функций. Тогда дивизор D на
М — это просто глобальное сечение факторпучка (М*1(5*.
Действительно, глобальное сечение {/„} пучка e«iJ*/(9* задается откры-
10-046
146 1. Комплексные алгебраические многообразия
тьш покрытием {С/^а} многообразия М и такими мероморфнымв
функциями /„ ^ О на £/„, что
тогда для любой гиперповерхности Vcz М
ordv (/а) = ordv (/р)
и набор {/„} определяет дивизор
Z) = 2ord^(/J.F,
V
где а для каждого V выбирается так, чтобы V {\и^Ф 0. С
другой стороны, по дивизору Z) = 2 ('■iVi можно построить такое
г
открытое покрытие {U^) многообразия М, что в каждом £/„ все
Vi vlbD локально определяются функциями gia. € © {U^. Полагая
мы получаем глобальное сечение пучка М*10*. Функции /^
называются функциями, локально задающими дивизор D (или
локальными уравнениями дивизора D). Непосредственно из
определений следует, что отождествление
Я«(М, e#*/0*) = Div(M)
является в действительности гомоморфизмом.
Голоморфное отображение п: M-^N комплексных
многообразий определяет отображение
я*: Div {N) -> Div (М),
сопоставляющее каждому дивизору D = {{U^, {/„}) на N его
обратный образ n*D — {{п~^ (Ua)}, {я*/а}) на М; это
отображение определено корректно для тех D, для которых я (М) ф: D.
Заметим, что для дивизора на N, заданного аналитической
гиперповерхностью V CZ N, его обратный образ n*V яа. М лежит над F,
но не обязательно совпадает с аналитической гиперповерхностью
я~^ {V) CZ М: у его компонент могут появиться кратности > 1.
Прежде чем перейти к рассмотрению линейных расслоений,
сделаем еще одно замечание. На римановой поверхности М любая
точка является неприводимой аналитической гиперповерхностью,
и поэтому ясно, что группа Div (М) достаточно велика. Это в
некотором смысле вводит в заблуждение: комплексное многообразие
М размерности больше 1 может не иметь ненулевых дивизоров.
Однако если М вложено в проективное пространство Р^, то
пересечения М с гиперплоскостями в Р^ порождают достаточно
большую подгруппу в группе дивизоров. В действительности
компактные комплексные мвюгообразия, допускающие вложение
1. Дивизоры, и линейные расслоения 147
В проективное пространство, можно охарактеризовать тем, что
они имеют «достаточно много» дивизоров (смысл этого
высказывания мы уточним в последующих параграфах).
Линейные расслоения
В этом разделе все линейные расслоения предполагаются
голоморфными. Напомним, что для любого голоморфного линейного
расслоения L -^ М жа. комплексном многообразии М существует
открытое покрытие {Ua) многообразия М и тривиализации
прообразов Lxj^ = п'^ (£/„)• Функции перехода g^f,: И а. П f^s "*"
-»- С* расслоения L относительно тривиализации {ф^}
определяются формулой
Очевидно, такие функции g^^ голоморфны, нигде не обращаются
в нуль и удовлетворяют соотношениям
(*) ^аЭ-^Эа = 1. ^ap-^PV^Va=l-
И обратно, по заданному набору фзшкций {^„з € ©* (С^а П ^^р)},
удовлетворяющих этим соотношениям, можно построить линейное
расслоение L с, функциями перехода {^ар}» взяв объединение
£/„ X С по всем а и отождествив; {z} хСв £/„хСи ?7gXC
при помош;и умножения на ^„g (z).
Теперь для рассмотренного выше L и любого набора
ненулевых голоморфных функций /а £ О* (U^) определим другие
тривиализации L на {иа}, полагая
ф4 = /а-Фа-
Функции перехода g^ip расслоения L относительно
тривиализации {фа} запишутся в виде
(»*) ЙР = (/а//р) gad-
С другой стороны, любая тривиализации L на {Ua} может быть
получена этим способом, и, следовательно, два набора {^^р}
и {g'a&} Фзщкций перехода определяют одно и то же линейное
расслоение тогда и только тогда, когда существуют функции /„ g
£ О* (Ua), удовлетворяющие условию (**).
Описание линейных расслоений функциями перехода подводит
нас к их когомологической интерпретации. Во-первых, функции
перехода {g^p € ©* {Ua П ^р)} линейного расслоения L-^-M
представляют 1-коцепь Чеха на Af с коэффициентами в О*; при
этом второе из соотношений (*) означает, что б ({^^ g}) = О, т. е.
10*
148 1- Комплексные алгебраические многообразия
{gafi} — КОЦИКЛ Чеха. Более того, по предыдущему абзацу два
коцикла {gap} и {^ар} определяют одно и то же расслоение, если
{ga^-gafi^} — кограница Чеха; поэтому множество линейных
расслоений на М есть в точности IP- {М, О*).
Множество линейных расслоений на М допускает естественную
структуру группы: умножение задается тензорным произЕеде-
нием, а взятие обратного — переходом к двойственному
расслоению. Если L задано набором функций перехода {ga^}, а L' —
набором {gaf}, то, как мы видели,
L®L'~{g^yg'o,(i}, L*^{g-4}.
Следовательно, структура группы на множестве линейных
расслоений та же, что и на Н^ (М, О*). Группа Н^ (М, О*)
называется группой Пикара многообразия М и обозначается Pic (М).
Опишем теперь важное соответствие между дивизорами и
линейными расслоениями. Пусть D — дивизор яа. М с локальными
уравнениями /„ 6 °"t'*(Uf^, где {£/„} — некоторое открытое
покрытие многообразия М. Тогда функции ga^ = tJt^ голоморфны,
не обращаются в нуль на £/„ П U^, а на пересечениях U^, (\tf^ (]
П и у справедливо соотношение
„ „ „ -i<^ f» ^V __.
Линейное расслоение, заданное фувкциями перехода {^„g =
= fjf^, называется линейным расслоением, ассоциированным
с дивизором D, и обозначается [D]. Проверим корректность этого
определения: если {/„} — другие локальные уравнения для D, то
К = tJt'a € 0* {Ua) И ДЛЯ ВСеХ « И Р
Соответствие [ ] обладает следующими очевидными
свойствами. Во-первых, если D т D' — два дивизора с локальными
уравнениями {fa} и {fa} соответственно, то дивизор D -\- D' задается
локальным уравнением {/а-/а}; следовательно,
{D + D'] = [D]® [D'l
т. е. отображение
[ ]: Div (М) -> Pic (М)
является гомоморфизмом. Во-вторых, если D = (f) для некоторой
функции /, мероморфной на М, то в качестве локальных
уравнений для D на любом покрытии {U^} можно взять функции /„ =
= / \и^. Тогда /а//р = 1» а поэтому расслоение [D] тривиально.
О|братно, если D задано локальными уравнениями {/„} и линей-
1. Дивизора и линейные расслоения 149
ное расслоение [D\ тривиально, то существуют функции h^ £
£ G* (Ua), такие, что
tJti, = gafi = hjh^\
в этом случав / = /а-^а' = /р-^э' — глобальная мероморфная
функция на Ж с дивизором Z). Таким образом, линейное расслоение
[Z)], ассоциированное с дивизором D на М, тривиально тогда и
только тогда, когда D — дивизор мероморфной функции. Два
дивизора D ж D' на М назьшаются линейно эквивалентными,
а записьшается это в виде D ~ D', если Z) = Z)' + (/), где / ^
£ а/>с* (М), или, что равносильно, если [D] = Ш'].
Заметим также, что гомоморфизм [ ] функториален. Точнее,
легко проверить, что для любого голоморфного отображения
f:M-^N комплексных многообразий и каждого дивизора D 6
6 Div (N) имеет место равенство
n*{[D])=[n*{D)].
Все эти утверждения неявно содержатся в следующей
когомологической интерпретации гомоморфизма [ ]. Точная
последовательность пучков
О _> 0* Л «^ Л е#*/0*-> О
на М индуцирует точную последовательность групп когомологий
Я»(М, aS*)^HO{M, в£*/в*)Хт{М, О*).
Читатель может легко убедиться, что при естественных
отождествлениях
Div (М) = Я» {М, gS*/G*) и Pic (М) = IP {М, G*)
для любой мероморфной функции f па. М
Ut = (f),
а для любого дивизора D яа М
6D = ID].
В дальнейшем мы, как правило, нарушаем предыдущие
мультипликативные обозначения и пишем L -{- L' вместо тензорного
произведения двух линейных расслоений или mL вместо /ге-й
тензорной степени Z.®»» расслоения L.
Теперь мы рассмотрим голоморфные и мероморфные сечения
линейных расслоений. Пусть L -*- М — голоморфное линейное
расслоение с тривиализациями ф„: L^ -»- U^ X С на открытом
покрытии {Ua} многообразия М и функциями перехода {gafi}
относительно тривиализаций {фа}. Как мы уже знаем, тривиали-
150 1. Комплексные алгебраические многообразия
зации Фа индуцируют изоморфизмы ф*: о (L) (£/„) -*- О (£/„),
а ввиду соответствия
каждое сечение расслоения L над U cz М задается набором
функций s„ £ О (С/ П и^, удовлетворяющих соотношению »„ =
= ^ap-sg на С/ П С^а П и^.
Аналогично, мероморфное сечение s расслоения L над U,
определяемое как сечение пучка О (L)®(5 е/Я^, задается набором меро-
морфных фзшкций Sa £ о# (С/ П U^), удовлетворяющих условию
Sa = ^ap'Sp В С/^ П С^а П U^. Отметим, ЧТО частное двух меро-
морфных сечений s, s' щкО является корректно определенной ме-
роморфной функцией.
Если S — глобальное мероморфное сечение расслоения L, то
sjs^ € <5* (U^ П £/з). Значит, для любой неприводимой
гиперповерхности V CZ М
Ordy (Sa) = ordy (S3).
Поэтому можно определить порядок s вдоль V формулой
ordy (s) = ordy (s„)
для любого а, такого, что £/„ ^V Ф 0; дивизором (s) мероморф-
ного сечения s назьшается дивизор
(s) = 2ordy(s).F.
V
Сечение s голоморфно в том и только том случае, когда дивизор (s)
эффективен.
Пусть теперь дивизор D 6 Div (М) задан локально функциями
/а 6 а# (Ua)- Тогда функции /„, очевидно, задают мероморфное
сечение Sf расслоения [D] с (s^) = Z). И обратно, если расслоение L
задано тривиализациями ф^ с функциями перехода g^^, а s —
любое глобальное мероморфное сечение расслоения L, то s^/sp =
= ^ag, т. е. L = [(s)]. Итак, для любозо дивизора D, такого, что
[D] = L, существует мероморфное сечение s расслоения L с (s) =
= Z), и для любого мероморфного сечения s расслоения L имеет
место равенство L = [(s)]. Отсюда, в частности, мы видим, что L
является линейным расслоением, ассоциированным с некоторым
Дивизором D на М, тогда и только тогда, когда оно имеет
глобальное мероморфное сечение, не равное тождественно нулю, и L
является линейным расслоением для некоторого эффективного дивизора
в том и только том случае, когда оно имеет нетривиальное
глобальное голоморфное сечение.
Взглянем на это соответствие под другим углом. Пусть D —
— 2 <^i^i "~" некоторый дивизор на М. Обозначим через X (Z?)
1. Дивизоры и линейные расслоения 151
пространство таких мероморфных на М функций /, что D + (/) ^
^ О, т. е. функций, голоморфных на М — [}Vi, с ord^^ (/) ^ —«г-
Через \D \cz Div (М) обозначим множество всех эффективных
дивизоров, линейно эквивалентных D\ если L = [D], то будем
писать I L I вместо | D |. Пусть s,, — глобальное мероморфное
сечение расслоения [D], такое, что (s,,) = D. Тогда для любого
глобального голоморфного сечения s расслоения [D] частное Д =
= sls^ является мероморфной функцией на Ж с условием
(/.) = is) - (So) > -D, т. е. /, € XiP),
и
(S) = 2? + (/,) € I i? |.
С другой стороны, для любой функции f ^ X (D) сечение s =
=/-So расслоения [D] голоморфно. Таким образом, умножение на
So задает отождествление
Хф)^Ю{М, 0([!>])).
Предположим теперь, что многообразие М компактно. Для
любого дивизора Х>' 6 |Х> | существует функция f^X (D), для
которой D' = D + (J), и любые две такие фувкции /, /' могут
различаться только умножением на ненулевую константу.
Поэтому мы имеем также соответствие
\D \^Р{Х (!>)) ^ Р (Я« (М, 0 (Ш]))).
В общем случае семейство эффективных дивизоров на М,
соответствующее линейному подпространству в Р (Н" {М, О {L))) для
расслоения L —»- М, называется линейной сист£мой дивизоров.
Линейная система называется полной, если она совпадает с | Z> |,
т. е. содержит все эффективные дивизоры, линейно эквивалентные
любому из ее элементов. Говоря о размерности линейной системы,
мы подразумеваем размерность параметризующего ее проективного
пространства; в частности, dim | D \ обозначает размерность
полной линейной системы, ассоциированной с дивизором D;
dim I 2? I = А» (Л/, 0 (Х>)) — 1.
Линейная система размерности 1 называется пучком, размерности
2 — сетью, а размерности 3 — тканью.
Упомянем здесь о двух специальных свойствах линейных
систем. Первое элементарно: если ^ = {Dx}j^^pn — линейная
система, то для любых линейно независимых к^, . . ., Я^ 6 Р"
2?^, П ... ПХ>х„= П,А.
X.6IF-"
152 1. Комплексные алгебраические многообразия
Пересечение всех дивизоров линейной системы назьшается
базисным множеством этой системы; в частности, дивизор F из
базисного множества, т. е. такой, что D^ — F ^0 при всех к,
называется неподвижной компонентой линейной системы Е.
Второе свойство более примечательно; как и первое, оно
присуще только линейным системам и не выполняется для общих
семейств дивизоров, даже для общих семейств линейно
эквивалентных дивизоров. Это
Теорема Вертини. Общий элемент линейной системы не имеет
особенностей вне базисного множества данной системы.
Доказательство. Если общий элемент линейной системы имеет
особенности вне базисного множества этой системы, то же самое
справедливо и для общего элемента общего пучка, содержащегося
в этой системе. Поэтому теорему Бертини достаточно доказать
для пучков.
Предположим, что {i?x,}x,epi — пучок, заданный на полидиске
А Я8 М формулой
Dx= (f (zi, • . •, z„) + k-g (zi, . . ., z„) = 0),
& Px — особая точка дивизора D^ {к =^0, oo), не лежащая в
базисном множестве В данного пучка. Тогда f (Рх) + ^g (Рх) = О
^(^0 + ^-^(^0 = 0' i = i, ...,«.
Так как Ру, не является базисной точкой для {D^,}, то функции
f ж g я% могут обе обратиться в нуль в точке Рх, в. значит, ни одна
лз них не обращается в нуль. Поэтому к = —f {P\)lg {Р \) и
Следовательно,
Ho множество V особых точек дивизоров Dx, задаваемое локально
как образ в Д аналитического множества S cz А X Pjt,
определяемого уравнениями {f + kg = О, дрдг^ + kdgldzi = 0}, является
аналитическим подмножеством в А. Предыдущее вычисление
показывает, что отношение fig постоянно на каждой компонента
связности множества V — В, и, следовательно, вне базисного
множества системы {Х>х,} с V пересекается только конечное число
дивизоров Dx- Q
В этом доказательстве существенно то, что пучок {i?x,}x,epi
с базисным множеством В задает голоморфное отображение
1. Дивизоры и линейные расслоения 153
М — В -^ Pi, так как по линейности каждая точка р ^ М — В
лежит на единственном D х. Теорема Бертини является уточнением
теоремы Сарда для этого отображения.
В заключение сделаем одно замечание о сечениях линейных
расслоений, которое будет постоянно использоваться в
дальнейшем. Напомним, что если!) = ^ajFj — любой эффективный
дивизор на комплексном многообразии М, а Sq 6 ff" Щ, О (LDl)) —
сечение расслоения [D] с дивизором D, то тензорное умножение
на So задает отождествление мероморфшлх функций на М,
имеющих полюсы порядка ^aj на Vi, с голоморфными сечениями
расслоения [Z)]. В более общем случае пусть Е — любое голоморфное
векторное расслоение на il/, § — пучок его голоморфных
сечений, % (D) — пучок мероморфных сечений расслоения Е с
полюсами порядка ^aj на Vi, % (—D) — пучок сечений расслоения Е
с нулями порядка ^а^ на V^ тогда тензорные произведения с So
и So' задают следующие отождествления:
(») %[P)^G{E®[D]), U(-D)-^G{E®[-D]).
В частности, если D — гладкая аналитическая гиперповерхность,
то последовательность пучков
0^О^{Е®[-и\)^е^{Е)Лвп{Е\п)-^0
точна (здесь г обозначает отображение ограничения). Начиная
с этого места, мы будем всегда неявно подразумевать
отождествления (*) и писать О {D) вместо 0 (Ш!).
Классы Чокэня линейных расслоений
Рассмотрим теперь компактное комплексное многообразие М
размерности п. Точная последовательность пучков
O->Z-^0^6>*-^O
определяет граничный гомоморфизм в когомологиях
т{М, 0*)-^1Р{М, Т).
Пусть L 6 Pic {М) — ЕР {М, О*) — линейное расслоение.
Первый класс Чжэня Ci{L) (или просто класс ?а«;эмя расслоения L)
определяется как б (L) б Я^ {М, Z). Для каждого дивизора D ш& М
определим его класс Чжэня как с^ {ID]). Допуская некоторую
небрежность, мы будем писать иногда Ci (L) 6 ^dr {Щ,
подразумевая образ Ci (L) при естественном отображении Я* (М, Z) ->■
154 7. Комплексные алгебраические многообразия
Непосредственно из определения вытекает, что
ci {L ® L') = ci {L) + ci (L') и ci (L*) = -Ci (L).
Кроме того, если /: M-*-N — голоморфное отображение
комплексных многообразий, то диаграмма
H'(bi,b*)-*H\M,T)
коммутативна. Следовательно, для любого линейного расслоения
L -*■ N имеет место равенство Ci(f*L) = f*Ci{L).
В этом разделе будут предложены две различные
интерпретации классов Чжэня. Однако вначале мы сделаем одно замечание.
Пусть ji ш Jl:* — пучки С°°-функций и не обращающихся
в нуль С°°-функций соответственно. Функции перехода
комплексного линейного С°°-расслоения L задают коцикл Чеха {gad} €
6 С^ {М, А*), и по тем же соображениям, что и в голоморфном
«лучае, расслоение L определяется с точностью до С""-изоморфиз-
ма классом когомологий [{gap}! £1Р(М, Л*). Точная
последовательность щгчков
и включения О с^ jy ж G* с^ А* ъътщу функториальности
длинных точных последовательностей в когомологиях Чеха определяют
коммутативную диаграмму
с точными строками. Таким образом, класс Чжэня Ci (L)
линейного С°°-расслоения можно определить как 6'{L), и это
определение согласовано с соответствующим определением для
голоморфных расслоений. Но в верхней строке БР {М, А) — О, ибо Jk —
тонкий пучок; отсюда мы заключаем, что комплексное линейное
расслоение определяется своим классом Чжэня с точностью до С°°~
изоморфизма.
Напомним, что для любого векторного расслоения Е -^ М
ранга к и любой связности D ша. Е оператор кривизны D^ пред-
1. Дивизоры и линейные расслоения 155
ставляется в терминах тривиализаций фа расслоения Е над С/ц
с помощью к X Л-матрицы в^, состоящей из 2-форм; если фв —
другая тривиализация, то
©а = |Гар-вр-|ГаВ,
где gap- и а О и fi-)~ GL (к) — функции перехода от
тривиализаций Фа к фр. в частности, если Е — линейное расслоение, то,
поскольку группа GL (1) = С* коммутативна, в = ва = 0в —
замкнутая глобальная дифференциальная форма степени 2; она
называется формой кривизны расслоения Е.
Напомним, что для любого аналитического подмножества
V cz М размерности к был определен фундаментальный класс
(V) 6 -ffaft (Af, й,), заданный линейным функционалом
Ф I—* \ ф
наЯ"он (М)' По двойственности Пуанкаре ему соответствует
некоторый класс Tiv В частности, рассмотрим фундаментальный класс
S<^i (Уд дивизора D = ^aiVi ша. М; двойственный ему по
Пуанкаре класс обозначим T]2) = 2<^i'nvi-
Этот раздел посвящен доказательству следующего утверждения.
Прелдожешие.!. Для любого линейного расслоения L с формой
кривизны в
2. Если L — [D] для некоторого дивизора D 6 Div (М), то
Доказательство. Прежде всего развернем определение класса
Ci (L) расслоения L-^ М й тривиализациями ф^ и функциями
перехода g^p для некоторого покрытия U = {Ua) многообразия
М. Предполагая, что открытые множества U^ односвязны,
положим
1
h
аЭ"
2я
у^-10?|ГаЭ-
Если положить
то по определению гомоморфизма б коцикл {z^pv} € 2^ (С^.
будет представлять класс с^ (L),
156 1. Комплексные алгебраические многообразия
Выберем теперь любую' связность Z? на L. В репере e^ (z) =
= фа^ (z, 1) на и а, связность D задается матрицей, являющейся
в этом случае 1-формой Эц. Как мы видели в § 5 гл. О,
на С/ц П и^, т. е.
9в — 9а = —ga\-dga,fi = —d log g^fi,
и матрица кривизны является глобальной 2-формой
в = dOcc - е„ л е„ = de„ = de
р-
Ввиду того что в — замкнутая 2-форма, а с^ {L) задается
коциклом Чеха, нам теперь следует обратиться к явному виду
изоморфизма де Рама. Точные последовательности пучков
из доказательства теоремы де Рама задают граничные изоморфизмы
Я«(%|)/^Я»и1)Дя1(%^), Яl(2S)-^^Я2(R).
Для того чтобы вычислить 6i (в), запишем в локально как dda',
из определения 6i вытекает, что
6i (в) = {Эр - 0„} € ZI i%b).
Но Эр — Эа = —dlogga^, поэтому
бгЙ! (в) = бг ({Эр- е„}) ={ - (log ^„р + log g^^ - log g^y)} =
Для доказательства утверждения 2 нужно проверить, что для
матрицы кривизны в расслоения ID] класс [0^—1/2я) 01
двойствен по Пуанкаре классу (D) =2?г (^г)> т. е. для каждой
вещественной замкнутой формы гр 6 Jpn-2 ^щ имеет место равенство
Так как D *-*■ Ci {ID]) и 2) >-* т]д — гомоморфизмы группы Div (М)
в группу ЯЬн (М), можно ограничиться случаем неприводимого
аналитического подмножества D = V.
Вычислим сначала форму кривизны метрической связности на
W]. Для этого рассмотрим локальное ненулевое голоморфное
сечение е расслоения [V] и положим -{е (z)|^ = А (z). Тогда для
1. Дивизоры и линейные расслоения 157
любого сечения s = Я,-е матрица связности Э метрической
связности D в репере е должна иметь вид Э = Э^-" и
d (I S 1^) = {Ds, s) + (s, Ds) =
= {{dK + Щ e, Ke) + {Ke, {dl + вХ) e) =
= h-K-dX + h-K-dl + h-\K\''{Q + Q).
С другой стороны,
d(\s Н = d{K-I-h) = h-li-dX + h-K-dK+ \K \^-dh.
Поэтому Э + Э = dhlh, т. e. Э = 5 log A = 5 log | e |^ и
e = de — e л e = de = 55log I e 12 = 2яУ — 1 dd'log I e 12.
Отметим, что все это справедливо для любого ненулевого
голоморфного сечения е.
Пусть теперь D = V локально определяется функциями /о,
as — глобальное сечение {/а} расслоения [D\, обращающееся
в нуль в точности на V. Положим
D (е) = (I S (z) К е) с= М.
При достаточно малом е множество D (е) есть трубчатая
окрестность F в ЛГ и
f влгр = Ит2яК—1 f dd" log|s|2 л гр =
дО(г)
ПО теореме Стокса. На Ua, {]D (е) имеем | s |^ = |/^ |^-Аа =
= fa'Ia'fia С Аа > 0; ОТСЮДа
d'=log|*|2=d'=log(/e./„.A„) =
= -Т" (^log /а - 5 log fa + id- д) log А„).
Поскольку форма d^log A^ ограничена и, как мы знаем из
доказательства теоремы Стокса для аналитических множеств,
vol (pD (б)) -»- О при е -»- О, то
lim \ d" log Ао л 1)3 = 0.
е-'О „J .
''^•' вс-(е)
Далее, 5 log/а= 5 log/а, а гр — вещественная форма, значит,
j 51og/ttAij)= j aiog/oAip.
вС(е) 9D(e)
158 1. Комплексные алгебраические многообразия
Итак, в и а
lim ,—- \ d" Iog|s|2A гр = Ит—]/ —1 -Im \ 5Iog/aAij3.
в окрестности любой гладкой точки Zq € F П t^a можно найтк
такую голоморфную систему координат w = {w^, . . ., U7„), в
которой Wi = fa- Представим форму ур в виде гр = гр (ш) dw' л dw' + ф,
где w' = (шг, . . ., U7„), а все члены формы ф содержат либо dw^r
либо dwi. Тогда в любом полидиске Д, содержащем Zq,
lim ( 51og/aAt = lim ( ^^^{w).dw' Adw'=
*-*" в1)(8)ПД =■*" Nt
1 au>i
2я Y^^ \ ■^ (0, U7'). dw'Adw' = 2я1/ —1 ( грг
u)' УПД
поэтому
]вЛ1|)=-"К-1 .Im (2я1/-1 |t)=—^^Jt- D
Вывод о том, что класс Чжэня с^ ([£>]), с одной стороны,
представляет собой класс, двойственный по Пуанкаре
фундаментальному гомологическому циклу дивизора D, ас другой стороны,
задается в когомологиях де Рама кривизной любой связности на
линейном расслоении [D], умноженной на (]/—1/2я), имеет
фундаментальное значение для всего последующего изложения. Столь
же вездесущ и метод его доказательства, основанный на
применении теоремы Стокса к дифференциальным формам с особенностями;
мы опишем его систематически в гл. 3.
Как простейшее следствие этого предложения получаем, что
дивизор (/) мероморфной функции гомологичен нулю. Интуитивно
это понятно: для дуги у, соединяющей Я-о = О с X,i = оо на сфере
Римана Рх, дивизоры {(Яо/ + ^,i)}[x„, x,]g^ заметают цепь с
границей (/)о — (/)«>•
Примеры. 1. В случае когда М — компактная связная рима-
нова поверхность, дивизор D я& М — это конечная сумма D =
= ^nfPi точекрг 6 -Л^с кратностями П;. По определению степень
дивизора D совпадает с его фундаментальным классом (Z?) 6
6 Яо (ЛГ; Z)^Z; очевидно, что deg D = ^щ. Согласно
установленному выше предложению, для формы кривизны в
связности на линейном расслоении [D] выполнено соотношение
J^J e = <ci ([£)]), lM]):=degD.
1. Дивизоры и линейные расслоения ISS
В общем случае степень линейного расслоения на М
определяется как
deg L = <ci (L), {М\);
иначе говоря, deg {L) = с^ {L) при каноническом отождествлении
Я* {М; Z) ^ Z, заданном естественной ориентацией на М.
Заметим, что по доказанному в конце § 5 гл. О соотношеник>
между формой кривизны в метрической связности и обыкновенной
гауссовой кривизной Кц классическая формула Гаусса — Бонне
приводит к равенствам
degr(M) = ^J^м•Ф = OC(M).
2. Из точной когомологической последовательности
Я* (Р", 0) -> Я* (Р", 0*)-Хт (Р", Z),
отвечающей экспоненциальной последовательности пучков на Р",
ввиду тривиальности группы БР (Р", О) (см. § 7 гл. 0) следует,
что каждое линейное расслоение на Р" определяется своим классом
Р£с(Р")^Я2(Р»,2)^2.
Другими словами, каждый дивизор на Р" линейно эквивалентен
целому кратному дивизора, отвечающего гиперплоскости Я =
= Р"~^ CZ Р". Расслоение [Я], ассоциированное с некоторой
гиперплоскостью в Р", называется расслоением гиперплоскости,
а двойственное к нему расслоение / = [Я]* = [—Я] называется
универсальным расслоением на Р".
Дадим прямую геометрическую конструкцию универсального
расслоения / на Р". Пусть Р" X С"+^ — тривиальное
расслоение ранга ге -Ь 1 на Р", все слои которого отождествлены с С"+^.
Тогда универсальное расслоение — это такое подрасслоение /
в Р" X С"+^', слой которого в КЙ.ЖДОЙ точке Z 6 Р" совпадает
с прямой в С"+^, соответствующей точке Z, т. е.
Jz = {Я, (Zq, . . ., Zn), Я, 6 С}.
Чтобы убедиться в том, что действительно / = [—Я],
рассмотрим сечение во расслоения / над Uq = (Zq ф 0) cz Р",
заданное формулой
e„(Z) = (l,^,...,^),
Очевидно, что сечение во голоморфно, не равно нулю в C/q и
продолжается до глобального мероморфного сечения расслоения /
с полюсом порядка 1 на гиперплоскости (Zq = 0) с: Р". Поэтому
/ = 1{е„)] = 1-Н].
160 1. Комплексные алгебраические многообразия
Пусть Af с: Р" — подмногообразие в проективном
пространстве. Ограничение расслоения [Н] ->- Р" на М обычно называют
расслоением гиперплоскости на М. Из функториальности
конструкции следует, что это линейное расслоение, ассоциированное
с общим гиперплоским сечением Р""^ f) ^ многообразия М.
3. Пусть М — компактное комплексное многообразие, а F с:
а М — гладкая аналитическая гиперповерхность. Напомним, что
нормальным расслоением Ny на V называется линейное фактор-
расслоение
Ny = Т'м WIT'y.
Расслоение Ny, двойственное к Ny, называется конормальным
расслоением; оно является подрасслоением в Т%\у всех кокаса-
тельных векторов на М, обращающихся в нуль на Ту с: Т'^ \у.
Существует простая формула для конормального расслоения
гладкой гиперповерхности V, которую мы сейчас выведем.
Зададим V локально функциями /а € © (Ра). Линейное расслоение
[F] на М задается тогда функциями перехода {ga^ = fjf^- Так
как /а ^0 на F П ^о) дифференциал dfa определяет сечение
конормального расслоения Ny на F. Но F — гладкое многообразие,
поэтому dfa нигде не обращается в нуль. Кроме того, на Ua. П
dfa = d{ga^^ = dgad-fp + gap'^/p = gafi'dfp,
T. e. локальные сечения dfa € Г (Ua, О (Ny)) вместе определяют
глобальное не обращающееся в нуль сечение расслоения Ny® [F].
Поэтому Ny ® [F] является тривиальным линейным расслоением
и нами доказана следующая
формула присоединения I: Ny = [—V]\y.
4. Одно из наиболее важных линейных расслоений — старшая
внешняя степень голоморфного кокасательного расслоения
^м = Л ^м',
оно называется каноническим расслоением п-мерного комплексного
многообразия М. Голоморфные сечения расслоения Км являются
голоморфными ге-формами, т. е. 0 (К^) = QSf.
Вычислим каноническое расслоение Крп проективного
пространства. Пусть Zo, . . ., Zn — однородные координаты в Р",
а Wi = Zi/Zg — евклидовы координаты на U^ = (Zj ф 0).
Рассмотрим мероморфную ге-форму
dw, dw« dwn
(В = i-Л ^Л .. . Л -.
1. Дивизоры и линейные расслоения 161
Очевидно, со не обращается в нуль в C/q и имеет простые полюсы
на гиперплоскостях (Z; = 0), i = 1, . . ., п. В евклидовых
координатах w'i = ZjZj, i = О, ...,/,..., n, на Uj^ {Zj Ф 0)
следовательно,
dwi _ ^^'i
Wi W\
И В координатах {w'^)
dw'.
dwj dwQ
w = {—\y —Г A ... л—r- л ... л —7^-
^ ' ml iH. inL
Значит, (0 имеет простой полюс также и на гиперплоскости (Zq =
= 0), откуда
^рп = [(со)] = [-{п + 1) Я].
В общем случае каноническое расслоение Ку гладкой
аналитической гиперповерхности V в многообразии М можно вычислить
через Км следующ^ипи способом. Имеется точная
последовательность векторных расслоений на V:
Отсюда по элементарным соображениям из линейной алгебры
получаем, что
т. е.
Ky = Kia\y<S)Ny.
Вместе с приведенной выше формулой присоединения I это
доказывает, что справедлива следующая
формула присоединения II:
(*) Ky = {Kja®lV])\y.
Опишем это отображение на сечениях соответствующих пучков
QSf(F)—^Qr.
Пусть (О — сечение пучка йдг (У), представленное в виде меро-
морфной п-формы с простым полюсом на V, голоморфной вне V,
т. е. в локальных координатах z = (z^, . . ., z„) на ilf
g (z) dzi л ... Л dzn
t{z) '
11-046
162 1. Комплексные алгебраические многообразия
где / (z) — локальное уравнение для V. Тогда при изоморфизме
(*) форме со соответствует такая форма со', что со = уЛ со'. Точ-
нее, d/= 2 л~Г '^j' '^ поэтому можно взять
, _ , _ - w_i g (г) &1 л ... Л dzf Л ... Adzn
^ -У ^) df/dzi
ДЛЯ любого i, для которого 5//5zj Ф 0. Отображение
g (г) dzi л ... л &п . , / 4^г-< g (г) &1 Л ... Л dz; Л ... Л &„ |
называется отображением вычета Пуанкаре и обозначается Р. R.
Заметим, что ядро отображения вычета Пуанкаре состоит
из голоморфных га-форм на М. Точная последовательность пучков
О-^ QSr ^ QSr (ТО-^ Q"" ^ О
определяет следующий кусок точной последовательности кого-
мологий:
Я« (М, Q.% (F)) —^ Я» (F, ЙГ') -^ Я* (il/, QXf),
т. е. отображение вычета Пуанкаре сюръективно на глобальных
сечениях, если IP- (М, йдг) = Я"> ^ (М) = 0. Например, так как
Я">^ (Р") = О при га > 1, каждая голоморфная форма старшей
степени на гиперповерхности V в Р" есть вычет Пуанкаре
некоторой мероморфной п-формы на Р". Как мы увидим далее, меро-
морфные га-формы на Р" легко описать, что позволяет описать
и голоморфные (га — 1)-формы на V.
2. ТЕОРЕМЫ ОБ ОБРАЩЕНИИ В НУЛЬ
И ИХ СЛЕДСТВИЯ
Теорема Еодаиры об обращении в нуль
Пусть М — компактное кэлерово многообразие.
Определение. Линейное расслоение L-^ М называется поло-
жит£лъным, если на L существует такая метрика с формой
кривизны в, что (1, 1)-форма (У —i/2n) в положительна; L
называется отрицательным, если L* положительно. Дивизор D ш& М
называется положительным, если линейное расслоение [D]
положительно.
Как показывает следующее предложение, положительность
линейного расслоения — топологическое свойство.
2. Теоремы об обращении в нуль и их следствия 163
Предложение. Для любой вещественной замкнутой (1, i)-0op-
мы (О с
ш = ci (L) 6 Hhii т
существует метрическая связность на L с формой кривизны в ==
= (2я/|<^—1) 6). Поэтому расслоение L положительно тогда и
только тогда, когда его класс Чжэня представляется
положительной формой из ЯЬк (М)-
Докааательетео. Пусть | s р — метрика на L с формой
кривизны е. Если if'. Ljj-^ и X С — тривиализация L над
открытым множеством U, s — сечение L над U, &Sjj — соответствующая
голоморфная функция, то
где h (z) — некоторая положительная функция. Форма кривизны
и класс Чжэня задаются формулами
Q=-dd\ogh{z), С1(Ь)=[-2^в]еЯЬн(М).
Пусть f у f* — другая метрика на L с формой кривизны в'.
Тогда f S \'^1\ S f = ef>y где р — некоторая вещественная С^-функ-
ция на М. Из локальной формулы А' (z) = еР<^) h (z) следует
соотношение в = ддр + в'. В частности,
[^«]=[^«']- _
Теперь, с другой стороны, предположим, что (У —1/2я) ф —
вещественная замкнутая (1, 1)-форма, представляющая класс
Ci (L) в группе Я|)н {М). Если мы найдем вещественную С"-
функцию р, удовлетворяющую уравнению в = ддр + ф, то
формой кривизны метрики ^\s р на L будет ф. Поэтому наше
предложение вытекает из > следующей леммы.
Лемма. Для любой d-, д- или д-точной (р, ф-формы т) на ком~
пактном кэлеровом многообразии существует такая (р — 1,
q — 1)-форма 7, что
т) = 557-
Еслир = ди форма т) вещественна, то у можно выбрать так,
чтобы форма У—iy также была вещественной.
Доказательство. Пусть G^ — оператор Грина лапласиана A(j;
Gg и Gg — аналогичные операторы. По основному тождеству со
•1'
стр. 128 у Дд = Ав = Д5, откуда,, во-первых, 26^ = G^ = G^ и,
11»
164 1. Комплексные алгебраические многообразия
во-вторых, все операторы d, 5, д, d*, д* и д* коммутируют с
рассматриваемыми операторами Грина.
Так как ц является d-, д- или 5-точной формой, ее
гармоническая составляющая относительно любого из рассматриваемых
лапласианов нулевая. По разложению Ходжа для оператора д
имеем т) = dd*G^. Но d*Gp\ — форма чистого типа (р, q — 1),
и поэтому
Пространство гармонических форм для оператора д совпадает
с пространством гармонических форм для оператора д и,
следовательно, ортогонально образу оператора д*. Поэтому из
разложения Ходжа для оператора д имеем
d*Gp\ = dd*G, (^%п)^
После перестановки операторов получаем
Ti = =fc55(5*5*G|Ti),
что доказывает лемму, а вместе с ней и предложение. D
Основным примером положительного линейного расслоения
является расслоение гиперплоскости [Н] на Р". Напомним, что
расслоению гиперплоскости двойственно расслоение / со слоем
^Z) а С"+^ в точке Z 6 Р"; зададим на / метрику формулой
|(Zo, . . ., Z„)|^ = S I ^i 1^* Если Z — любое ненулевое сечение
расслоения /, т. е. локальный подъем С7 с:: Р"->-С"+^—{0},
то форма кривизны на / имеет вид
в* = 5д log IIZ ||2 = 2я /^=Т dd" log IIZ jp-
Формой кривизны двойственной метрики на расслоении [Я]
является тогда —в*, поэтому
>^^e = dd4og||Z||2,
2я
т. е. о/—1/2я) в является (1, 1)-формой © метрики Фубини —
Штуди на Р", положительность которой была уже доказана. В
качестве следствия снова получаем, что двойственным по Пуанкаре
классу [со] 6 ЯЬн (Р") является фундаментальный класс {Н)
хвперплоскости.
Заметим, что, поскольку ограничение положительной формы
на подмногообразие V cz М положительно, положительность
расслоения L -i- М влечет за собой- положительность ограничения
2. Теоремы об обращении а нуль и их следствия 165
L Iv ->- F. В частности; расслоение гиперплоскости на любом
кошшексном подмногообразии в Р" положительно.
Целью настоящего параграфа является доказательство
тривиальности некоторых из групп когомологий Чеха Я' {М, QP {L))
для положительного линейного расслоения L -*- М. Начнем с того,
что, пользуясь техникой предыдущих рассуждений,
переформулируем задачу на языке 5-когомологий и гармонических форм.
Напомним, что для любого голоморфного векторного
расслоения Е -^ М ша. глобальных ^-значных дифференциальных
С""-формах определен 5-опвратор
удовлетворяющий условию д' = 0. Пусть Zj (Е) обозначает
пространство 5-замкнутых ^-значных дифференциальных форм
типа (р, q). Определим группы когомологий Дольбо Н^ (Е)
расслоения Е как
Я|*' (Е) = Z|««{Е)/дА^' «-* (Е).
,Р,г
Пусть йа"* (Е) — пучок 5-замкнутых ^-значных (р, д)-форм.
Точная последовательность пучков
0-^%^^^(E)-^J^^'•ЦE)-^%f^^^UЩ-^0
индуцирует изоморфизмы групп когомологий
я* {М, %f '+* (^)) Ля'+1 {М, %f ' (Е)),
так как для пучков ^«^ (Е) имеются разбиения единицы и,
следовательно, соответствзтющие группы когомологий Чеха
тривиальны. Поэтому, повторяя рассуждения из доказательства теоремы
де Рама, мы получим изоморфизм групп когомолог&й
НЦ]^,С^{Е))^Н^''{Е).
Обсудим теперь теорию гармонических форм на голоморфных
векторных расслоениях. Предположим, что ш& Е ш М задашь
метрики. Тогда имеются индуцированные метрики на всех
тензорных степенях касательного расслоения многообразия Л/ и их
тензорных произведениях с Е или Е*. В частности, если {ф^} —
локальный корепер метрики на Tmj а {во} — унитарный репер
166 1. Комплексные алгебраические многообразия
метрики на Е, то любое сечение т) из А^*^ (Е) локально
представляется в виде
г, J, а
В ДЛЯ л, т^еЛ^'М^
2Р+9-"
(Л(2), i|3(z)) = -^i-^ 2 ■ni.J.a(z)i|5i.j.a(z).
I, J, a
Зададим скалярное произведение на А^^^ (Е) формулой
in, 115)= j (л (z), Ур{г))Ф,
м
гдеТ1Ф — форма объема на М.
Определим внешнее произведение
л: А'^-ЦЕ)® А^'- "' (Е*) -^А^'-^"'-«+«' (М)
формулой
(л ® «) л (т)' ® S') = (S, s') -т) л т)';
оператор
*в: ^Р*' (^) -^ А"-""'"-' (^*)
зададим условием (т), 1|з)= \ tja^biIj для всех tj, \|з £>!''''(£).
Именно, если {ва} и {ва} — двойствесраые зшитарные реперы
на расслоениях Е и ^*, то для формы ir\^A''^(E),
представленной в виде
Т, = ЗЛа®еа, ЦаеЛ^-ЦМ),
имеем
♦вЛ = S *'Па <81 «а>
где • — обычный оператор звездочка на А^»^ (М).
Пусть
д*: А^''ЦЕ)^А^'''-^(Е)
есть оператор вида 5* = —*в-5'*в; тогда, как н ранее,
оператор Ъ* сопряжен д, т. е. для всех ф6Л''''~'(^ в ^^А^''''(Е)
И наконец, д-лапласиан на Е задается как
А='дд* + д*д: А^'''ЧЕ)^А''ЦЕ).
2. Теоремы об обращении в нуль и их следствия 167
Е-зшачв&я форма ф называется гармонической, если Дф = 0.
(Гармонические формы — это опять формы с наименьшей нормой
в своем когомологическом классе Дольбо ф + дА^<^'^ (Е).)
Назовем
сВ^, ч (Е) = кег Д
пространством гармонических форм.
Аналитическая часть доказательства теоремы Ходжа для 5^лап-
ласиана на обычных дифференциальных формах по существу
локальна: всегда можно найти подходящие решения уравнения
Дф = О в пополнении Л^»' {М) по норме L^; основная проблема —
показать, что эти решения в действительности принадлежат
классу С"". При записи ^-значных форм в некотором репере на Е все
локальные оценки, используемые при доказательстве теоремы
Ходжа ш& А* {М), переносятся на А^^^ (Е). Единственное
отличив в каждой оценке — добавление ряда членов низшего порядка,
зависящих от переменных коэффициентов как метрики на Е, так
и метрики на Т^', они оцениваются так же, как и раньше. Итак,
теорема Ходжа справедлива для 5-лапласианов на Е, а именно
имеют место следующие утверждения:
1. <2^^- ' (Е) — конечномерное пространство.
2. Если (Ш — ортогональное проектирование >i'''(£)-^
-> <Ш^'^ {Е), то существует такой оператор G: А?''^{Е)-^А?''^{Е),
что G(^P'«(^)) = 0, [G, 5] = [G, 5*]-0 H/ = ^-f4G.
3. Следовательно, существует изоморфизм
т^'''{Е)^Щ'ЦЕ).
4. Оператор * индуцирует изоморфизм
Я« (М, QP {Е)) ^ Я"-« (М, Й"-Р (£■*))*.
При р = 0 это означает, что
т (м, в (Е)) ^ zr-» (м, О (Е* ® Км))*.
Этот изоморфизм называется двойственностью Кодаиры — Серра.
Для кэлерова многообразия М с ассоциированной (1, 1)-фор-
мой (О определим оператор
полагая
L (т] (g) s) = (О л т] ® «,
168 1, Комплексные алгебраические многообразия
где т] 6 >1^'' {М), S 6 ^* (Е); пусть Л = L* — оператор,
сопряженный с L. Для метрической связности D = D' -\- D" {D" = д)
на Е имеет место основное тождество
[Л, 5]=-i^Z)'*.
Оно следует из аналогичного тождества [Л, 5] = —(У —112) д*
для операторов на скалярных формах в ^р»' (Л/), которое мы
уже доказали. Чтобы убедиться в этом, выберем локальный репер
{во} на Е. Если Э = Э' + Э" — матрица связности для D в базисе
{вц}, то форму т] 6 Л^>' (^ можно записать в виде
откуда
Tl=Sl1a®ea, Tlae^^-'W.
5Т1 = 2 5т1а ® ба + Е (lla Л Э^р) (g) бр,
а а, 3
ЛТ] = 2 А (Т1а) ® ба.
Поэтому
[Л, 5]Т1=Е[Л, 5]Т1а®ба + [Л, е']т1 =
/—
Аналогично,
ZJ't] = S ^Ла ® «а + S (Ча. Л 9ag) ® бр,
а а, 3
Т. е.
Z)'*T, = y;5*Ti„® е„ + е'*т1.
а
Следовательно, разность
[Л, ^]+i^z)'* = [A, еп+^^^Э'*
является инвариантно определенным алгебраическим оператором,
а так как для каждой точки Zq 6 Л/ можно выбрать такой репер
на Е в ее окрестности, для которого Э (zq) равно нулю, то [Л, д\ +
+ (]/=T/2)Z)'* = 0.
В доказательстве нашего первого основного результата о кого-
мологиях векторных расслоений будет использовано
представление когомологий Чеха гармоническими формами.
2. Теоремы об обращении в нуль и их следствия 169
Теорема Кодаиры — Накано об обращении в нуль. Пусть
L -^ М — положительное линейное расслоение. Тогда
Я« (М, Q^ (L)) = 0 при р+ q>n.
Доказательство ^). По условию на L существует метрика, фор--
мой кривизны которой в является умноженная на 2л/У—1
(li 1)-форма, ассоциированная с некоторой кэлеровой метрикой.
Итак, пусть на М задана метрика с условием со = (]/ —1/2я) в.
Согласно теории гармонических форм, имеет место изоморфизм
H^ (М, QP (L)) ^ ^г».' (X).
Чтобы доказать теорему, достаточно установить отсутствие
ненулевых L-значных гармонических форм степени больше га. Для
этого мы будем пользоваться интерпретациями оператора
кривизны вт] = в л т] как оператора (2я/]/^—1) L (tj) и как оператора
Dh\, где D — метрическая связность на L, и приведенным выше
основным тождеством.
Пусть т] 6 SS^'^ (L) — гармоническая форма. Тогда
e = D2 = dD' + D'd,
а И8 равенства 511 = 0 имеем вт1 = 52)'т1 и
2 1/^1 (Лвт]. л) = 2 ]/ ^="1 (Л5£>'т1, Т1) =
= iD'*D'y\, тО = (2?Ч £''ti)>0,
так как (SAZJ'tj, ti) = (AZ?'ti, 5*ti) = 0. Аналогично,
2-)/~Г(вАт1, гЦ = 2У'^(0''дАц, ц) =
= —{D'D'*^, Т1)= — (Z)'*Ti, Z)'*TiXO.
Объединяя эти неравенства, мы получаем, что
2 1/^1 ([А, в]т1, Т1)>0.
Но в = (2я/1/^^)//. Поэтому
2 1/^1 ([А, в]т1, т1) = 4я([А, L]Ti, Т1) = 4я (ra-p-g) ||ti||2>0.
Следовательно, p-|-g>ra=*-Ti = 0. Q
^) В этом доказательстве мы следуем Акидзуки и Накано; Y. Akizuki
and S. Nakano, Note on Kodaira — Spencer's proof of Lefschetz's theorems.—
Proc. Japan Acad., 30 (1954).
170 1. Комплексные алгебраические многообразия
При определении когомологий уже говорилось, что группы
Я' {М, й'' {Е)) (q ^ 1) наиболее часто возникают как
препятствия к глобальному решению аналитических задач; это касается,
в частности, задачи Миттаг-Леффлера в случае q = i. Но если
допускать группы Н^, то мы должны рассматривать и все
остальные. Теорема Кодаиры об обращении в нуль вместе с ее
вариантами, которые обсуждаются ниже, представляет собой наилучпшй
общий метод избавления от высших когомологий.
Дуализируя теорему Кодаиры об обращении в нуль, получаем:
Я' (М, QP (L)) = О при р + g <; га для отрицательного
линейного расслоения L ->- М.
Частный случай р = q = О можно доказать элементарными
методами. Действительно, требуется только установить, что
(*) Я» (М, в (L)) = О
для расслоения L -^ М с метрикой, форма кривизны которой
является отрицательной (1, 1)-формой, умноженной на 2я/|/—1.
Пусть S # О 6 Я* (М, О (L)) — некоторое сечение, а Хо ^ М —
точка, где | s р достигает максимума. По предположению
коэффициенты формы кривиэны
V dzt alj ^°^ \Uv) )^~^\\dxidxi'^ ду1 ду] ] +
+>'^(l^-lF7i^))(i«g-iTF)
(где zt = Xi -\- Y—'Uid составляют отрицательно определенную
эрмитову матрицу, и, в частности, вещественная симметрическая
матрица
(1 dxidx}+ ду1ау})^°^Т7^)
отрицательно определена. Но log(l/|sp) достигает влинимума
в точке Жд, и, согласно принципу максимума, матрицы
обе положительно полуопределены, что противоречит
предыдущему.
ЕслиЛ/ — риманова поверхность, то частный случай (•)
является общим, так как из р -Ь g < 1 следует, что р = q = 0. В этом
случае теорема совсем элементарна. Пусть в — такая форма
кривизны на L, что (У — 1/2я) в — отрицательная форма. Тогда
м
2п •®<0-
2. Теоремы об обращении в нуль и их следствия 171
Если S Ф О ^ Н° (М, О (L)) — сечение, то линейное расслоение L
ассоциировано с эффективным дивизором D = (s), что приводит
к противоречию, так как
Ci (L) = deg D > 0.
Из теоремы об обращении в нуль немедленно выводится, что
H^ (Р", 0рп (кН)) = О при 1<д<га — 1 и всех к.
Для отрицательных к это прямо следует из двойственного
варианта теоремы; если же к неотрицательно, то непосредственно из
теоремы получаем
Я«(Р", 0р„(/сЯ)) = Я9(Р», Qln{kH-Kpn)) =
= Я«(Р», Й^„((/с + п + 1)Я))=0.
Теорема Лефгиеца о гиперплоских сечениях
Основываясь на теореме Кодаиры об обращении в нуль, мы
докажем теперь знаменитую теорему Лефшеца, связывающую
гомологии проективного многообразия с гомологиявли его
гиперплоских сечений.
Рассмотрим компактное га-мерное комплексное многообразие
М и гладкую гиперповерхность V cz М, для которой расслоение
L = IV] положительно; например, М а Р^ — подашогообразие
проективного пространства, а V = М [] Н — гиперплоское
сечение М. Тогда имеет место
Теорема Лефшеца о гиперплоском сечении. Отображение
т {м, а) -»- я» (F, а),
индуцированное вложением i: V с^ М, является изоморфизмом при
q^n — 2 и инъективно при q = п — 1.
Доказательство. Достаточно доказать теорему для когомоло-
гий с коэффициентами в С. Из разложения Ходжа имеем
а по теореме Дольбо
Я"'«{М) ^ Я|•«(М) ^ Я« (М, QSf).
Так как то же самое справедливо и для V, то достаточно доказать,
что отображение
172 1. Комплексные алгебраические многообразия
является изоморфизмом при р -\- q^n — 2 и инъективно при
р -\- q= п— \.
Для этого разложим отображение ограничения £2дг ->- Q%-
в композицию отображений
Qif —> Qm \y-^Qy,
где Qif I у — пучок сечений расслоения {t\^T%)\y,
рассматриваемый либо как пучок на V, либо посредством продолжения как
пучок на М, г — отображение ограничения, а i — отображение,
индуцированное естественной проекцией (A^^Ar)lv ~*" !\^Ту'.
Ядро отображения ограничения г, очевидно, совпадает с
пучком голоморфных р-форм на Л/, обращающихся в нуль на V,
откуда получаем точную последовательность пучков на М
(*) 0^£2Sf(-F)^Q^-^QSf|v-^0.
Отображение i также включается в точную последовательность:
для точки р ^V можно из точной последовательности
посредством элементарных операций линейной алгебры построить
точную последовательность
0-^N*y,^® ^^-'T%' (У)-^ t\-^T%' {М)-^ f\^Tl' {V)-^0,
что дает точную последовательность пучков на V
О-^ ЙГ' (^■v■)-^ Qm I г-^ йу ^ 0.
По формуле присоединения I Ny = [—У\\у. Поэтому
предыдущую последовательность можно записать в виде
(**) 0-^Qr^(-F)-^Q§f|v-^£2?-^-0.
Расслоение [—F] отрицательно на М, и его ограничение
[-F] \у также отрицательно на V. Тогда по теореме Кодаиры
об обращении в нуль
Я«(М, QSf(-F))=0, j5-bg<ra,
Я^(F, Qr'(-F)) = 0, p + q<:n.
Вспоминая, что Я* {М, йдг |v) = Н* (F, йдг 1^), из точных
когомологических последовательностей для последовательностей
пучков (*) и (**) мы получаем изоморфизмы
Я«(М, Q§f) "LhHM, Q§f 1^) iя^(F, Q^)
при p -\- q^n — 2и композицию двух инъективных отображений
при р + q = п — \. Q
2. Теоремы об обращении в нуль и их следствия 173
Теорема Лефшеца о гиперплоском сечении, конечно, чисто
топологическая. Существует другое ее доказательство, использующее
теорию Морса; ниже дается набросок такого рассуждения ^).
Рассмотрим компактное многообразие А, его гладкое
подмногообразие В (z: А ш С°°-функцию qn А -*- К*, такую, что ф~^ (0) =
= В. Точка Ху Е.А называется критической точкой функции ф,
если ^ф (Xv) = 0; ф {х^) называется критическим значением
функции ф. В каждой критической точке гессиан д\1{дщ duj) = Н (ф)
является корректно определенной квадратичной формой на
касательном пространстве Тх {А)\ критическая точка называется
невырожденной, если гессиан Н (ф) невырожден. Функция ф, все
критические точки которой невырожденны, называется функцией
Морса. Из стандартных аппроксимационных теорем известно, что
в С^-топологии такие функции всюду плотны. Согласно основной
лемме теории Морса, для функции Морса ф с невырожденным
гессианом Н (ф) на нормальном расслоении v. В ъ А гомотопический
тип пространств
At= {х^А: <^ (х) <г}
остается одним и тем же до тех пор, пока t не пройдет через
критическое значение (это очевидно: существует ретракция вдоль
градиентного поля функции ф), и изменяется на приклеенную
клетку размерности fe при прохождении критического значения
с к отрицательными собственными значениями гессиана Н (ф).
(Этот факт устанавливается локальным исследованием функции
Морса ф вблизи критической точки х^ ш составляет основу теории
Морса.)
Пусть теперь М — некоторое компактное комплексное
многообразие, L -^М — положительное голоморфное расслоение, а
S 6 Я" {М, О {L)) — голоморфное сечение, дивизор нулей V =
= (s) которого является гладкой гиперповерхностью. Выберем на
L -)- М метрику с положительной формой (У^—1/2л) в =
= (1Л—1/2п) 33 log I S |-^ и положим
Ф (х) = log I S р.
Тогда функцию ф или близкую к ней в С^-топологии можно взять
в качестве функции Морса (то, что ф: М-»-[—оо, с») и
Ф~^ (— схз) = V, не вносит трудностей; важно то, что d {\s \) фО
на V). Для любой критической точки х £ М матрица
\ dzi Q^j ) ■^°^ |s|2 - i 4 [ dxi dxj "*" dyi dyj } +
^) Принадлежащего Ботту, см. R. Вотт, On a theorem of Lefschetz.—
Mich. Math. J, 6 (1959), 211—216. j[Cm. также Милнор Дж. Теория Морса.
Пед. с англ.—М.: Мир, 1965;—Рей;]
174 1. Комплексные алгебраические многообразия
является эрмитовой отрицательно определенной, и, следовательно,
гессиан
\ дх} ду1 ду1 ду] '
функции ф имеет по крайней мере п отрицательных собственных
значений. Очевидно, последнее утверждение справедливо также
для функций tjj, достаточно близких к ф в С^-топологии. Поэтому,
согласно теории Морса, гомотопически М получается из V
приклеиванием клеток размерности не меньше п. Отсюда вытекает
теорема Лефшеца на гомотопическом уровне и для
целочисленных гомологии. D
При ге = 1 теорема Лефшеца ничего не дает. Однако при ге = 2,
т. е. для (связной и компактной) комплексной поверхности М
и римановой поверхности V а М, задающей положительный
дивизор, из теоремы Лефшеца следует, что
Яо (F, Z) ^ Яо {М, Ъ) = Z,
т. е. все одномерные гомологии 4-мерного многообразия М лежат
на неприводимой вложенной римановой поверхности V.
Эта теорема применима также к гиперповерхностям в
проективном пространстве: так как эффективные (отличные от нуля)
дивизоры в Р" положительны, из нее следует, что если V — гладкая
гиперповерхность в Р", то Я^''~^ (F) = О при к Ф п12, а группа
Я^* (У) при к <; ге/2 порождена классом сечения
гиперповерхности V {к-\- 1)-плоскостью. В частности, любая гладкая
гиперповерхность размерности ^2 связна и односвязна. Те же результаты
получаются при подходящих ограничениях на к для любого
подмногообразия проективного пространства, заданного как транс-
версальное пересечение гиперповерхностей.
Сделаем одно заключительное замечание о теореме Лефшеца.
Метод Лефшеца, насколько это возможно, позволяет изучать
топологию алгебраического многообразия М индуктивно путем
сведения вопросов о гомологиях М к соответствующим вопросам о гомо-
логиях многообразия меньшей размерности. В первоначальном
варианте последней теоремы Лефшец доказал, что отображение
Hq {V, 1) -^Hq (М, 1) для гиперплоского сечения V является
изоморфизмом при q <^п — 1 и сюръективно в размерности
п — 1. Согласно сильной теореме Лефшеца, гомологии М в
размерности >п отражаются в размерностях ■<.п, а в силу
разложения Лефшеца, каждый непримитивный цикл размерности п мож-
2. Теоремы об обращении в нуль и их следствия 175
НО получить как пересечение цикла размерности >п с
гиперплоскостями. Таким образом, теоремы Лефшеца в совокупности
показывают, что единственными «новыми» рациональными гомология-
ми алгебраических многообразий в любой размерности могут быть
только примитивные гомологии в средней размерности.
Теорема В
Вторая теорема об обращении в нуль когомологий
голоморфных векторных расслоений менее точна, но зато шире теоремы
Кодаиры.
Теорема В. Пусть М — компактное комплексное многообразие
и L—^ М — положительное линейное расслоение. Тогда для любого
голоморфного векторного расслоения Е существует тлкое ц, чтл
т (М, в {L^ ® Е)) = Q при q>0, ]1^ |Хо.
Доказательство. Вначале заметим, что для линейного
расслоения Е теорема легко выводится из теоремы Кодаиры. Достаточно
выбрать Но таким, чтобы расслоение V^® Е ® Км было
положительным при ц > |Ло- Тогда, поскольку с-^ (L** ® Е) =
= [xCj {L) + Ci {Е), имеем
т {м, в (z" 0 Е}) = И" {м, й" (z" 0 i? 0 к*м}) = о
при з' > о, и ^ |Ло- в действительности доказательство теоремы В,
по существу, не отличается от доказательства теоремы Кодаиры.
Единственное новшество заключается в прихшсывании
определенного знака оператору кривизны на общем векторном расслоении.
Прежде всего, в силу двойственности Кодаиры — Серра,
Я9 (М, в (L" 0 Е)) ^ Я"-«{М, в {L-^ 0 i?* 0 Km)).
Поэтому достаточно доказать существование для любого Е такого
jio, что при ц > Цо1 Р < га
Я|' ^ {М, Z-" ®Е)^НР {М, Q {L-^ 0 Е)) = 0.
Выберем на L метрику с положительной формой со =
= (У —1/2л) @l; @l — форма кривизны этой метрики. Зададим
на М метрику с формой со. Как указывалось ранее, для эрмитовых
векторных расслоений Е шЕ' ш расслоения Е ® Е' с
индуцированной метрикой выполнено соотношение
De®e' = Z>e 0 1 -Ь 1 0 De»,
поэтому
Qe®e' = вв 0 1 -j-1 0 вв'.
176 I. Комплексные алгебраические многообразия
Здесь Z) и в везде обозначают метрическую связность и кривизну.
В частности, для рассмотренных выше расслоений L ш Е с
произвольной метрикой имеет место соотношение
Пусть т) 6 с1^'''^(-^~'* ® jB)—гармоническая форма. Обозначим
^L-^i^E '^«Рез в, а Dj^-v.^E '^«Рез D. Тогда Q = D^ = D'd + dD',
откуда Q'r\ = dD''r\.
Из основного тождества на кэлеровых многообразиях
[Л, 3]=—!^Z»'*
видно, что
2У"'^(Лвт1, r\) = 2Y^i{AdD'r\, г\) =
= (Z»'*Z>'ti, ti) = (Z»'ti, Z»'ti)>0,
так как (дАП'ц, ц) = (AD'ц, д*'Г]) = 0. С другой стороны,
2У"^(вЛт1, г\) = 2У'^{В'дАг], г\) =
= 2У^((Ад -i=D'*]Ti, D'*r\) = -{D'*r\, Z)'*Ti)^0.
Следовательно, 21/^ —1 ([Л, в] т), ti)>0. Но
а потому
2У'^{[А, в]т1, т1) = 2У"^:й:([Л, e^JT), т1)-4лц([Л, L] т), т)) =
= 2У"^^([Л, вЕ]т1, т1)-4я|х(п-р)|И1||2.
Оператор [Л, в^] ограничен на пространстве А ' * {L~'^ 0 Е),
следовательно, |([Л, вд] т), ti)| ^С || ti||2, а значит, при р<.п
ц>С/2п=^ц = 0,
т. е.
Se'''^{L-'^®E) = 0 при |х>С/2л, р<п. D
Теорема Лефгиеца об (1, Х)-классах
В качестве приложения теоремы В завершим наше описание
соответствия между дивизорами, линейными расслоениями и
классами Чжэня комплексных подмногообразий проективных
пространств. Во-первых, справедливо следующее
2. Теоремы об обращении в нуль и их следствия 177
Предложение. Пусть М а Р^ — подмногообразие
проективного пространства. Тогда каждое линейное расслоение на М
представляется в виде L = [D] для некоторого дивизора D, т. е.
Pic (М) Si Div {M)l{линейная эквивалентность).
Доказательство. Нам нужно показать, что каждое линейное
расслоение на М имеет глобальное мероморфное сечение. Чтобы
найти такое сечение, обозначим через Н ограничение на М
расслоения гиперплоскости на Р^. Утверждается, что при ц Э* О
расслоение L + [iH имеет нетривиальное глобальное
голоморфное сечение s. В таком случае если t — любое глобальное
голоморфное сечение расслоения [Н] на М, то s/f* — искомое
глобальное мероморфное сечение расслоения L.
Докажем это индукцией по ге = dim М. Предположим, что
для всех подмногообразий V а Р^ размерности <;ге и линейных
расслоений L -t-V группа Д^ (F, О {L + iiH)) нетривиальна при
ji ;> 0. По теореме Бертини существует гиперплоскость Р'^-* с:
с: Р'' с гладким пересечением V = Р^-* f) М. Рассмотрим
точную последовательность пучков
0^вм(Ь-^{11-1)Н) % Ом {L-\-iiff) -^ Gy{L-^\iH)-^0,
где S — сечение расслоения Н, обращающееся в нуль в точности
на F, а г — отображение ограничения. При ц >• О, согласно
предположению индукции,
Я» (F, e{L + iiH)) Ф о,
а так как по теореме В
т {М, б» (L + (ц - 1) Я)) = О,
то последовательность
Я» {М, G {L+ цЯ)) -»-Я« (F, б> (L + цЯ)) -vO
точна. Значит, Я" {М, О {L -{■ уЛ)) ^ О, и требуемое
утверждение доказано. Q
Остановимся немного на общей задаче об аналитических
циклах. Разложение Ходжа
Я" {М, С) = ф я"'"' {М)-
р+в=п
комплексных когомологий компактного кэлерова многообразия М
определяет несколько более грубое разложение вещественных
когомологий
Я"(Л/, |R)= ф (Я''-«(М) + Я'*''(Л/))ПЯ^(М, Ц).
Р+9—п
Р<«
12-048
178 1. Комплексные алгебраические многообразия
Естественно спросить, можно ли охарактеризовать геометрически
классы гомологии, двойственные по Пуанкаре классам слагаемых
этого разложения. Например, класс гомологии у 6 Н^р (М, Ъ)
будем называть аналитическим, если он является рациональной
линейной комбинацией фундаментальных классов аналитических
подмножеств в М. По двойственности класс когомологий будем
называть аналитическим, если двойственный ему по Пуанкаре
класс гомологии является аналитическим. Для аналитического
подмножества V а М размерности р и любой дифференциальной
формы г|5 на М, как мы видели, из чисто локальных рассуждений
следует, что
V V
Значит, для гармонической формы т| на М, представляющей
когомологический класс т]у, и произвольной гармонической формы t|3
М У У М
т. е. т) = yf-i'P, а поэтому любой аналитический класс когомологий
степени 2р имеет чистый тип (р, р). Знаменитая гипотеза Ходжа
утверждает, что справедливо также обратное утверждение:
рациональные классы когомологий типа (р, р) на подмногообразии
М а Р^ проективного пространства являются аналитическими.
Верна ли гипотеза Ходжа, до сйх пор неизвестно. Это очень
красивая и очень трудная проблема. Единственный полностью
изученный случай — это случай р = i. Он составляет содержание
следующей теоремы.
Теорема Лефшеца об (1,1)-классах. Каждый класс когомологий
V 6 ^' М^ П -ff" (М, 1)
на подмногообразии М а Р^ является аналитическим; более того,
7 = t|d для некоторого дивизора D на М.
Под Н^ (М, Z) здесь понимается, конечно, образ этой группы
когомологий при естественном отображении в Н^ {М, R).
Доказательство. Рассмотрим опять точную последовательность
O-^Z-^0-^(9*-^O
и индуцированную когомологическую последовательность
н^{м, в*) S н^{м, Z) X т{м, е)^н1'^{М).
2. Теоремы об обращении в нуль и их следствия 179
Мы утверждаем, что отображение i^ является композицией
отображения Efi {М, Ъ) -^1Р {М, С) и проекции на (О, 2)-компоненту
пространства Я^ {М, С), т. е. диаграмма
Дольбо
де Рам I и
Я^я(М,С)^^Я°'\М)
коммутативна. (Отображение я"'^ определено на формах, так как
Зю"-^ = {dcuf'^ = О для 0 = ю^.о + oji.i + ojo.^ 6 Z^ (М).)
Действительно, рассмотрим коцикл z = (z^pv) 6 ^^ (-^^i 2i). Чтобы
найти его образ при изоморфизме де Рама, рассмотрим такие
функции/„р б^М^^а П г7р),ЧТО
ZaPv = /аР + /pv — /av В С/„ П f^P П Uy.]
Поскольку Zafiy — константа, d/^p + df^y — df^y = 0;
следовательно, (d/аэ) ^Z^{M, %di и можно найти такие формы ©а €
6 Л1 (С/а), что
^/ар = сор — ©а в С/^ П и^.
Тогда образ z в Я^к (М, С) представляется глобальной 2-формой
doja = dojp. Найдем теперь образ элемента i^z при изоморфизме
Дольбо:
2aPv=/aP + /pT —/ат. ^/ар = «Й'^ —«aS
а тогда dwi^i^ = {d(i>af'^ представляет z в Щ^{М).
Отсюда уже легко вывести нашу теорему. Если у^Н^'^{М) П
ПЯ2(71/, Z), то ц(7) = 0. Значит, y = Ci{L}—Kmcxi Чжэня
некоторого линейного расслоения L^H^{M, О*). Имеем L —
= [D] для некоторого дивизора Z) = 2 ^tVi, так что
V = ci ([£>]) =ть. D
Заметим, что так как изоморфизм
из сильной теоремы Лефшеца задается пересечением с (ге — 1)-мер-
ными гиперплоскостями, то он переводит аналитические
классы в аналитические классы. Таким образом, из (1, 1)-теоремы
12*
180 1. Комплексные алгебраические многообразия
Лефшеца следует справедливость гипотезы Ходжа для группы
^^2п-2 щ^ щ П Я""^' "~^ {М). в частности, форма пересечения
дивизоров и кривых на подмногообразии проективного пространства
невырожденна.
3. АЛГЕБРАИЧЕСКИЕ МНОГООБРАЗИЯ
Аналитические подмноокества
и алгебраические многообразия
Пусть Xq, . . ., Хп — евклидовы координаты на С"*'-, а также
соответствуюпще однородные' координаты на Р". Напомним, что
универсальное расслоение — это подрасслоение / ->- Р"
тривиального расслоения С"+' X Р" -»- Р", слоем которого над точкой
X 6 Р" является прямая {ЯХ}^ с: С"*'^, соответствующая точке
X. Двойственным к / будет расслоение гиперплоскости Н -> Р",
т. е. расслоение, слоем которого над X 6 Р" является
пространство линейных функционалов на прямой {ЯХ}. Как нам известно
из § 1 этой главы, класс Чжэня расслоения Н совпадает с
фундаментальным классом со гиперплоскости в Р", т. е. является обра-
зуюпщм группы IP (Р", Z), а так как IP (Р", ©) = О, то любое
линейное расслоение на Р" представляется в виде степени Н^
расслоения Н.
Рассмотрим теперь глобальные сечения расслоения Н.
Заметим прежде всего, что каждый линейный функционал L на С"+*
индуцирует сечение а^ расслоения Н по правилу
ffb {X) = L ||x,x|.
Очевидно, сечение ffj, тождественно равно нулю только тогда,
когда функционал L нулевой. Поэтому имеется вложение
С"+1*-».Я«(Р", 0(Н)).
В действительности это изоморфизм. В самом деле, для любого
сечения а расслоения Н фундаментальный класс tixi дивизора
нулей D = (а) задается соотношением tij, = Ci (Я) = со, а
рассуждение из § 4 гл. О показывает, что D — гиперплоскость в Р".
Для линейного функционала L 6 С"*'^*, обращающегося в нуль
на гиперплоскости n'^D cz С"+^, мероморфная функция а/оь
голоморфна на всем Р", а значит, постоянна.
В общем случае слой расслоения Н^ над точкой X совпадает
с пространством d-линейных форм на прямой {ЯХ} с: С"*'^, а
поэтому, как и раньше, любая d-линейная форма F на С"*'^ инду-
хщрует глобальное сечение расслоения Н^ посредством
ограничения
ар (X) = F Ij^^i.
3, Алгебраические многообразия 181
Так как при этом ограничение производится на прямые, то,
очевидно, ajr = О для любой формы F, кососимметрической по
любым двум переменным. Значит, определено отображение
Sym''(C"«*) -Яв(Р", ©(Я-*))
пространства симметрических d-линейных форм, заданных на
С"*'-, т. е. однородных многочленов F (Xq, . . ., Х„) степени d
от переменных Х^, . . ., Х„, в пространство глобальных сечений
расслоения Н^. Это отображение тоже инъективно, а дивизор
нулей сечения ар совпадает с образом в Р" множества нулей
многочлена F {Хо, . . ., Х„) в С"+'^.
Мы утверждаем, что этим исчерпываются все глобальные
сечения расслоения Я**. Чтобы доказать это, рассмотрим глобальное
сечение о расслоения Н^ и обозначим через а ^ сечение
расслоения Я'', соответствующее произвольному однородному многочлену
F (Хо, . . ., Х„). Тогда частное ala р будет мероморфной
функцией на Р". Пусть
G' « я* {alar)
— eej прообраз на С"*^ — {0}. Функция G' имеет простой полюс
на дивизоре F =0 ъ С"*'- — {0} и,' голоморфна в остальных
точках. Позтому функция
G = G'-F
голоморфна всюду в С"+^ — {0} и, следовательно, гао теореме
Хартогса продолжается до целой голоморфной функции на С"*'^.
Но так как G' {XX) = G' {X) для всех X б C"+i и Я 6 С, а
F {XX) = V^F (X), то
G {XX) = X'Hi {X),
т. е. G — однородная функция степени d. Итак, для любой прямой
i: f I-»- {цо*> • • •> Ип*}> проходящей через начало координат
в С"+^, функция i*G либо тождественно равна нулю, либо имеет
нуль порядка d при f = О и полюс порядка d при f = оо, т. е.
для некоторого ц. Следовательно, степенное разложение
6r(Xoi ...t Xn) = Zj atf «„-^о" ••• -X^n"
ф ункции G в окрестности нуля в С"*'- не содержит членов степени,
отличной от d, т. е. G — однородный многочлен степени d от Xq, . . .
. . ., Х„. Значит, о = 0(j имеет требуемый вид, и мы доказали,
что каждое глобальное сечение расслоения Н^ задается
однородным многочленом от Xq, • . ., Х„.
182 1. Комплексные алгебраические многообразия
Отметим попутно полезную формулу для размерности
до ^pn^ Q (Д^с!)) пространства глобальных сечений расслоения
Н^, т. е. числа мономов Xj* . . . Хп" степени d от ге + 1
переменных. Каждой последовательности Iq, . . ., i^ целых чисел с 2 J/i =
= d сопоставим множество из п целых чисел
(io + 1, io + h + 2, . . ., Jo + • • • + Jn-i + re} с:
d {i, ..., d+ re}.
Это подмножество в (1, . . ., d -Ь re} задает последовательность
if,, и обратно, любое подмножество из ге различных чисел от 1 до
d -\- п соответствует некоторой такой последовательности.
Поэтому число мономов степени d от Xq, . . ., Х„ равно числу ( ],
т. е. числу подмножеств из ге элементов множества шз п -\- d
элементов; отсюда
Ао(Р", ©(Я")) = (''+'*).
Отметим, что нули однородного многочлена F (Xq, . . ., Х„)
степени d от однородных координат Xq, . . ., Х„ можно задать в
евклидовых координатах Xt = Xj/Xq, i = 1, • • •, re, на (Xq ф 0)
как нули неоднородного многочлена степени ^d
f{Xi, ..., Xn)=F(i, Xi, ..., Xn)=—r;-F{Xo, ..., X„).
Кроме того, по любому такому многочлену
/ (^1, • •., а:„) = 2 «i^ i^xii
восстанавливается однородный многочлен
F{X„ ...,X„) = Sai, iX'"^'"-^!^ •••<"•
Функция / называется аффинной или неоднородной формой
многочлена F.
Дадим теперь следующее
Определение. Алгебраическим многообразием FczP"
называется множество нулей в Р" системы однородных многочленов
{F, (Хо , Х„)}.
Очевидно, алгебраическое многообразие является
аналитическим подмножеством в Р", и в первую очередь мы будем его
рассматривать как таковое (т. е. алгебраическое многообразие F с: Р"
называется гладким, неприводимым, связным и т. д., если оно
обладает этими свойствами как аналитическое подмножество в Р").
Мы покажем, что верно и обратное: любое аналитическое подмно-
х^^
3. Алгебраические многообразия 183
жество проективного пространства может быть получено как
множество нулей однородных многочленов. По существу, для
гиперповерхностей это уже сделано: линейное расслоение [V]
дивизора F с: Р" имеет вид Н'' при некотором d, а V задается
множеством нулей некоторого сечения а расслоения [V]. Но все
сечения а расслоения Н^ имеют вид СТр. Поэтому
V = (ор) = {F (Хо. . . ., Хп) = 0)
— алгебраическое многообразие. В общем случае пусть F с: Р"
есть /с-мерное аналитическое подмножество и р ^ Р" — некоторая
точка, не лежащая на V. Тогда в Р" можно найти (п — к — 1)-
плоскость р"-*»-!, проходящую через р и не пересекающую
многообразие V. Пусть р"-''-^ есть {п — к — 2) -плоскость в Р"-"*-!,
не содержащая р. Рассмотрим проекцию п из p^-^^-^ на
дополнительную {к -j- 1)-плоскость Р*"^^ и выберем на Р" такие
координаты Хо, . . ., Х„, в которых
и п{[Хо, ..., Хп]) = [Хо, ...,Xft+i].
По теореме о собственном отображении образ п (V) множества V
в Р*^^ является аналитической гиперповерхностью в Р''^^. Но
по построению P"-''-i = р^-л-^^ р не проходит через V. Значит,
п (р) лежит вне п {V). По предыдущему, существует однородный
многочлен F (Xq, . . ., Xfe+i), равный нулю на п (V), но не
равный нулю в п (р). В соответствии с этим многочлен F (Xq, . . .
. . ., Х„) = F (Хо, . . ., Xk+i) равен нулю на V, но отличен от
нуля в р. Поэтому для любой точки р ^ V существует многочлен,
обращающийся в нуль на V, но не равный нулю в р.
Следовательно, доказана
Теорема Чжоу. Любое аналитическое подмножество
проективного пространства является алгебраическим многообразием.
Для любых однородных многочленов F (Xq, . . ., Х„) и
G {Хо, . . ., Х„) Ф О одной и той же степени d от однородных
координат X на Р" частное ф (X) = F (X)/G (X) определяет
мероморфную функцию на Р"; такая мероморфная функция
называется рациональной функцией. Отметим, что, поделив числитель
и знаменатель на степень Xq, мы представим ф в виде
ф(.„ ••..^n)=g(4,,.., J) ,
где f ж g — многочлены (необязательно оба степени d) от
евклидовых координат Xf. Таким образом, поле К (Р") рациональных
функций на Р" изоморфно полю С {xi, . . ., а:„).
184 . Комплексные алгебраические многообразия
Нетрудно убедиться, что любая мероморфная функция на Р"
рациональна. Действительно, по теореме Чжоу дивизор нулей (ф)о
и дивизор полюсов (ф)оо функции ф представляются множествами
нулей некоторых однородных многочленов F (Х) и G (X). Более
того, поскольку дивизор (ф) гомологичен нулю, F ш G имеют
одинаковые степени, а потому отношение FIG определяет
рациональную функцию на Р". Тогда {FIG) = (ф), откуда ф = XFIG
для некоторого Я 6 С.
Пусть теперь F с: Р" — любое гладкое многообразие.
Мероморфная функция на V называется рациональной, если она
является ограничением на V рациональной функции на Р".
Рациональные функции на F а priori составляют подполе поля меро-
морфных функций в# (У). В действительности
Каждая мероморфная функция на алгебраическом
многообразии F с: Р" рациональна.
Доказательство этого утверждения проведем в два этапа.
Во-первых, представим V как разветвленное накрытие подпространства
рл с: Р" относительно подходящей проекции. Отсюда мы
получим, что подъем п*К (Р*) на V поля рациональных функций на
Р* является подполем в поле aS (V) индекса не более чем d =
= deg (V). Затем мы покажем, что поле К (V) является
расширением степени ^d над л*К (Р*).
На первом этапе выберем общую (п — к — 1)-ш10скость Р"-*-*
в Р"; при этом требуется только, чтобы Р"-*-! не пересекала V.
Пусть Р* — дополнительная А-плоскость, а я: F -> Р* —
проекция из Р"-*-!. Прообраз я~^ (р) каждой точки р из Р* есть пере-
сечение V с {п — А;)-плоскостью Р"-*-!, р, а так как p"-ft-i, р
пересекает V в общем положении в d = deg (V) точках, то п
является d-листным разветвленным накрытием V на Р* почти
всюду. В действительности отображение п всюду конечно: если
для некоторой точки р 6 Р* (и — А;)-плоскость Р"-*-!, р
пересекает V по кривой, то эта кривая обязательно пересечется с
гиперплоскостью Р"-*-! с: Р"-*-!^, р, что противоречит выбору
плоскости Р"-*-1, которая по предположению не пересекается с V.
Отметим, что если выбрать однородные координаты X =
= [Хо, . . ., Х„] на Р", в которых Р"-*-! задается системой
уравнений {Xq = . . . = Xk = 0), а Р* системой уравнений
(Xft+i = ... = Х„ = 0), то отображение п имеет вид
я (iXq, . . ., Xni) ^ [Хо, . . ., Xkl.
В частности, подъем я*/ на V любой рациональной функции /,
заданной на Р*, очевидно, является рациональной функцией.
Итак, на V имеют место включения
л*К (Р*) а К (V) с=: Jf {V).
3. Алгебраические многообразия 185"
Теперь, чтобы убедиться в том, что индекс п*К (Р*) в s// (У)-
не больше d, рассмотрим любую мероморфную на V функцию ф
и положим D = (ф)оо. Пусть 5 с: Р — множество точек
ветвления проекции п. Определим на Р* — 5 функции грг, полагая
'^Лр)= 2 ф(д').
дея-1(р)
^2(р)= 2 Ф(д)-фЮ
^d(p)= П Ф(д').
I. е. ifj (р) есть г-й симметрический многочлен от значений ф в с?
точках прообраза п~^ (р) на V. Тогда ifj — функция, голоморфная
на Р* — 5 — я iP), которая ввиду ограниченности вне п {D)
по теореме Римана может быть продолжена до функции,
голоморфной на Р* — я {D). Мы утверждаем, что грг продолжается до
функции, мероморфной на всем Р*. Действительно, для любой точки
р ^п iP) и функции / (X), локально определяющей я {D) в
окрестности А точки р, при достаточно большом т функция
ф' = ф.Я*Г
голоморфна на п~^ (А). Для точки q ^ А — В рассмотрим функцию
ti(g)= S (ф'(р„,).--ф'(Ра,))'
I. е. г-ю симметрическую функцию значений ф' в точках л~^ (q).
Ввиду ограниченности на любом компактном подмножестве в А.
функция г|){, как и введенная выше, продолжается до голоморфной;
функции на А. Из представления
видно, что If г продолжается до функции, мероморфной в А, а
следовательно, во всем Р*. Значит, функция грг рациональна длд
каждого i. Но тогда на V имеет место равенство
ф"—я*\|з1.ф''-Ч-я*г|:2'ф""*—... + ( —1)" я*а|за = О,
т. е. каждая мероморфная функция ф 6 в^ (V) удовлетворяет
полиномиальному соотношению степени d над полем п*К (Р*).
Следовательно, по теореме о примитивном элементе расширение-
в* (У) ZD п*К (Р*) имеет конечную степень, не превосходящую d.
Чтобы завершить доказательство, осталось установить
существование рациональной функции на V, не удовлетворяющей
полиномиальным соотношениям степени <id над полем л*К (Р'').
Для этого разложим проекцию я: выберем общие плоскости
186 1. Комплексные алгебраические многообразия
pn-fe-2^ pn-fe_r д pft+i -^pft^ и пусть я': F-^ P^+i —
проекция из р"-''-^. Введем на Р" такие однородные координаты
X = [Хо, . . ., Х„], что
pn-fe-2 = (x„=...=X,+i = 0), Р''-^1 = (Х,,2=...=Х„ = 0);
в этих координатах л задается, как и выше, а
Значит, я есть композиция я' и проекции из точки (Xq = . . .
... = Xft = 0) 6 Р*"^^ на Р**. Отметим, что подпространство
pn-ft-2 выбрано общим, а потому отображение я' взаимно
однозначно над некоторым открытым множеством своего образа. Это
верно для некоторой точки р ^V тогда, когда {п — к — 1)-пло-
скость Р"-''-^^ р пересекается с F только в р, но для всех точек
р ^V общая {п — к — 1)-плоскость, проходящая через р,
пересекается с V только в этой точке р.
Рассмотрим теперь на V рациональную функцию
^ft+i = X^+i/Xq.
Предположим, что Xk+i удовлетворяет уравнению вида
^+1 + Ы^1> •••. ^h)-^h+V + ---+^d'(^i. ■■■,ч) = 0; d'<:d.
Тогда для общей точки р = [«о, • • ч Cftl 6 Р* ее прообраз
в п' (V) d Р^*^ содержит не более d' точек {[«о, . . ., а^, pi}, где
Р-+*.(5-,.... |^)г-+...+*.(5-. ■■■.|f)=o.
Но так как проекция я': У-^. Р''+^ в общей точке инъективна,
а общий слой проекции я состоит из d > d' точек, то это
невозможно. Q
Заметим, что, как следует из этого результата, поле
рациональных функций на алгебраическом многообразии V не зависит от
вложения. Поэтому пучок ростков полиномиальных функций на V,
сопоставляющий каждому открытому множеству U ъ V кольцо
рациональных функций на V, конечных на U, инвариантно
определен для V. Этот пучок — основной структурный пучок на V
при алгебраическом подходе к изучению V — обозначается также
через Оу.
Те же рассуждения легко показывают, что
1. Любая мероморфная дифференциальная форма на гладком
алгебраическом многообразии является алгебраической, т. е.
выражается через рациональные функции и их дифференциалы.
3. Алгебраические многообразия 187
2. Любое голоморфное отображение гладких алгебраических
многообразий задается рациональными функциями.
3. Любое голоморфное векторное расслоение на гладком
алгебраическом многообразии является алгебраическим, т. е.
задается рациональными функциями перехода.
Первое утверждение мы можем доказать сразу. Очевидно, что
дифференциалы ^ф рациональных функций на V порождают кока-
сательное пространство к F в каждой точке, а следовательно, это
пространство порождается конечным множеством таких
дифференциалов. Тогда любая мероморфная дифференциальная форма
на V представляется как линейная комбинация внешних
произведений этих форм с мероморфными, а значит, рациональными
функциями в качестве коэффициентов. Второе утверждение вытекает
из результата следующего параграфа о том, что произведение
V X W двух алгебраических многообразий является
алгебраическим многообразием. В таком случае, согласно теореме Чжоу,
график Г с: F X W с: Р" задается системой многочленов. Третье
утверждение станет очевидным, как только мы изучим грассма-
новы многообразия и докажем теорему о вложении для векторных
расслоений алгебраических многообразий, что будет сделано в § 4
я 5 этой главы.
Все эти результаты составляют частные случаи общего
принципа GAGA ^): любой глобальный аналитический объект на
алгебраическом многообразии является алгебраическим. В нашем
изложении теорема Чжоу и принцип GAGA имеют больше
общетеоретическое, чем практическое значение. Ниже мы не пользуемся этими
фактами как средствами исследования, ибо большинство наших
методов применимы сразу ко всем аналитическим объектам на
алгебраическом многообразии, и поэтому для нас бесполезно
знать, что, например, данная мероморфная функция или
отображение рациональны. Однако, рассматривая алгебраические
многообразия скорее как аналитические, чем как алгебраические
создания, мы всегда можем быть уверены, что имеем дело с тем
же классом объектов.
Степень алгебраического многообразия
Основным проективным инвариантом алгебраического
многообразия У с: Р" является его степень. Она определяется
следующим способом. Выбрав класс /«-плоскости Р** с: Р" в качестве
образующей, зададим изоморфизм
^) Название дано по первым буквам статьи Серра: J.-P. Serre, Geometrie
Algebrique et Geometrie Analytique.— Ann. of the Institute Fourier, v. 6.
188 1. Комплексные алгебраические многоебрааия
Степенью А-мерного многообразия F с: Р" называется целое
число — образ фундаментального класса данного многообразия
в Яай (Р", 1) при этом отождествлении.
Имеется также много других определений степени. Во-первых,
по теореме Бертини, примененной к гладкой части многообразия
V, общая {п — А;)-плоскость Р""* с: Р" трансверсальна к V,
а поэтому пересекает V по *(P"~''-F) = deg (F) ючкам. Значит,
степень многообразия можно определить как число его точек
пересечения с общим проективным подпространством
дополнительной размерности. С другой стороны, для стандартной кэле-
ровой формы со на Р" имеем
( 0* = deg (F). j м* = deg (F),
pft
поэтому степень многообразия V можно определить как его объем,
деленный на к\. (Это утверждение иногда называют теоремой Вир-
тингера.) Как мы уже видели, гиперповерхность F с: Р" в
однородных координатах Хо, . . ., Х„ в Р" является множеством
нулей
V= {F{Xo, ..., Х„) = 0)
однородного многочлена F. Если F имеет степень d, то
фундаментальный класс многообразия V = (Ор) совпадает с у]у =
= Ci (Н^), т. е. d раз взятым классом гиперплоскости, поэтому
V имеет степень d. Иначе говоря, для общей прямой
[Уо, yj -^ laoYo + ЬоГь . . ., а„Го + Ь^Г^
в Р" обратный образ \i*F функции F на Р^ является однородным
многочленом степени d от Уо и Y^, а следовательно, по основной
теореме алгебры имеет ровно d корней. Значит, степень такого
многообразия V совпадает со степенью многочлена F.
Основным свойством степени является ее мультипликативность
относительно пересечений. Так как общие подпространства P"-*i
и Р"-*! пересекаются трансверсально по подпространству
pn-h,-fej^ то степень пересечения алгебраических многообразий,
трансверсальных почти всюду, совпадает с произведением их
степеней. В общем случае если V ш W — алгебраические
многообразия из Р" степеней di и d^, пересекающиеся по многообразию
подходящей размерности, а {Zj} — неприводимые компоненты
пересечения V f\W, то
di.d2 = Smultzj(F.PF).deg(Zi),
где m\lltz^ {V-W) определяется, как в § 4 гл. 0. Это утверждение
представляет особый интерес в случае дополнительных размерно-
3. Алгебраические многообрйзия . 189
стей. Например, если С ш D — две кривые в Р^ степеней d^ и d^,
не имеющие общих компонент, т. е. пересекающиеся только по
точкам, то они пересекаются не более чем по d^-d^ точкам. Это
утверждение есть ослабленная
Теорема Безу. Два взаимно простых многочлена / (ж, г/),
g {х, г/) 6 С [х, у] степеней d^ и d^ имеют не более чем d^-d^
общих корней.
Степень также хорошо согласована с такими геометрическими
операциями, как проектирование и построение конуса. Пусть
У с: Р" — алгебраическое многообразие, р 6 Р" — произвольная
точка, не лежащая на V, Пр: У ->- Р"~^ — проекция на
гиперплоскость. Тогда, очевидно,
deg (V) = deg Яр-deg (яр (У)).
Действительно, число точек пересечения Пр (У) с общей (п ~ к
— 1)-плоскостью р"-*-^ в Р"~^, умноженное на степень этой
проекции, совпадает с числом точек пересечения У с (ге — А;)-пло-
скостью Р"'* — р"-*»-!, р в Р", но по теореме Бертини общая
плоскость Р"-*, проходящая через точку р, трансверсальна
к У, что и дает правую часть формулы.
Построение конуса как операция встречается нам впервые.
Для любого многообразия У с: Р" и любой точки р 6 Р" вне
У конусом р, У над Y е вершиной в р назовем объединение прямых,
проходящих через р и перевекающих У. Легко видеть, что р, V —
алгебраическое многообразие. В самом деле, оно является образом
проекции на первый сомножитель графика отношения
инцидентности / с: Р" X Р". Но по определению
'/= НЯ, г): г6 F, рлддг = 0}
само является аналитическим подмножеством в Р" X Р" . (По-
другому, в однородных координатах р =-- [О, . . ., О, И пусть
рп-1 _ гиперплоскость Хп = 0. Если образ Яр (У) с: Р"~^
многообразия У при проектировании из точки р задается в Р""'-
многочленами {F^ (Хо, . • ■, Xn-i)}, то конус р, V задается
многочленами {Fa. {Ха, • • ., Хп) = Fa {Хо, . ■ ., X„-i)}.) Для общей
гиперплоскости Н а Р", не содержащей р ^), пересечение Н
с конусом р, V совпадает с проекцией Яр (У) многообразия У
из р на Н, поэтому
deg (р, V) = deg (Н (]Р, V) = deg (пр (У)) = deg (У).
1) При этом надо также предполагать, что р — общая точка в Р", а
п — dim V ^ 2.— Прим. перев.
190 1, Комплексные алгебраические многообразия
Многообразию F с: Р" можно сопоставить еще одно
многообразие. Это так называемое многообразие хорд С (У),
представляющее собой объединение всех прямых, которые проходят через
две точки из V или (в предельном случае) касаются V.
Многообразие С (У) является образом проекции на третий сомножитель
замыкания графика отношения инцидентности / с: Р" X Р" X
X Р", заданного формулой
I = {(Р, г, г): р ^q^V, р hqhr = 0}.
Замыкание / является аналитическим подмножеством в Р" X
X Р" X Р", и поэтому С (У) — аналитическое множество в Р".
Отметим, что / имеет размерность 2-dimF-j- 1, так как при
проектировании на первый сомножитель / отображается на V
с (dim V -j- 1)-мерными слоями. Следовательно, С (У) имеет
размерность не выше 2-dim У -j- 1. В общем случае эта оценка точна.
В частности, поскольку проекция Яр гладкого многообразия
на гиперплоскость является вложением тогда и только тогда,
когда р ^С (У), то при п > 2-dim V + i многообразие У гладко
проектируется в некоторую гиперплоскость. Итак,
Любое гладкое алгебраическое многообразие размерности к
можно вложить в Р^^'+Ч
Как будет показано ниже, степень многообразия хорд С (У)
зависит не только от степени У.
Многообразие У с: Р", не лежащее ни в какой
гиперплоскости, называется невырожденным. Степень невырожденного
многообразия обладает следующим свойством.
Пусть У с: Р" — неприводимое невырожденное к-мерное
многообразие. Тогда deg (У) ^ re — к -\- 1.
Вначале мы докажем это для неприводимой кривой У в Р".
Любые ге точек У лежат в некоторой гиперплоскости Н, и если бы
степень У была меньше ге, то Н, имея с У ге общих точек,
пересекала бы У по кривой; но тогда У лежала бы в if в силу
неприводимости.
В общем случае достаточно показать, что общее гиперплоское
сечение Н [\V неприводимого невырожденного многообразия У
размерности ^2 снова неприводимо и невырожденно в Н.
Последнее очевидно: условие вырожденности Н {\V замкнуто по Д" 6
6 Р"*, а ввиду невырожденности многообразия У на нем можно
найти ге точек, порождаюпщх гиперплоскость, поэтому не каждое
гиперплоское сечение вырожденно.
Оставшаяся часть утверждения — о неприводимости общего
гиперплоского сечения неприводимого многообразия — немного
труднее. Вначале заметим, что для гладкого многообразия У
3. Алгебраические многообразия 1911
ЭТО легко вытекает из теоремы Бертини и теоремы Лефшеца о
гиперплоских сечениях: по теореме Бертини общее гиперплоское
сечение Н f\V гладко, а по теореме Лефшеца
Но (Я П F, С) - Но {V, С) ^ с,
1. в. Н (]V связно. Значит, если бы Н f\V было приводимым,,
то его компоненты пересекались бы, а их точки пересечения были
бы особыми точками на Я f) Vl следовательно, это не так.
Доказательство этого утверждения в общем случае требует
другого подхода. Пусть р ^ V — любая гладкая точка, Р"~^ сг
с: Р" — плоскость размерности п — 2, пересекающая V транс-
версально в точке р, и Z — неприводимая компонента
многообразия V П Р"~^, содержащая р. Рассмотрим теперь пучок {Н}}
гиперплоскостей в Р", содержащих Р"-*. Каждое гиперплоско&
сечение Н^ f\V многообразия V содержит Z, но так как каждая
гиперплоскость Я^, пересекает V трапсверсально в р, то точка р
(гладкая на Я^, f) ^ Для каждого Я, может лежать не более чем
в одной неприводимой компоненте сечения Н}^ (] V. Пусть V —
объединение неприводимых компонент сечений Я^, П V,
содержащих Z. Тогда V — открытое А-мерное аналитическое
множество, содержащееся в F, и, следовательно, его замыкание должно^
совпадать с V. Поэтому многообразие Я^, Г\У — Ну, П У непри-
водимо для общего 'К.
Теперь первоначальное утверждение получается из уже
разобранного случая кривой. Действительно, для любого
неприводимого невырожденного А-мерного многообразия F с: Р" степени d
общее пересечение V с к — 1 гиперплоскостями является
неприводимой невырожденной кривой степени d в Р""**!, поэтому
d"^ п — к -\- 1.
Это утверждение можно сформулировать по-другому: любое'
неприводимое А-мерное многообразие У с: Р" степени d лежит
в некотором проективном пространстве размерности d + к — i.
Как следствие снова получаем, что любое многообразие степени 1
в Р" является проективным подпространством.
Позже мы увидим, что многообразия, на которых реализуется
нижняя граница оценки для степени, например кривые степени п
в Р", поверхности степени п — 1 в Р" и т. д., имеют очень
специальный тип.
Касательные пространства
алгебраических многообразий
Каждому многообразию F с: Р" и гладкой точке р ^V
сопоставляется проективное подпространство в Р" — касательное
пространство к V в точке р. Его можно определить несколькими
различными способами; здесь мы упомянем два из них.
492 1. Комплексные алгебраические многообразия
1. Дополнение к гиперплоскости /Г с: Р" изоморфно С" при
выборе евклидовых координат. Касательное пространство к
многообразию F с: Р" в точке р можно определить как замыкание
в Р" обычного касательного подпространства Тр (F) cz Гр (С").
Точнее, пусть х^, . . ., х^ — евклидовы координаты на F в
окрестности точки р = (tti, . . ., ot„), а {/а (xi, . . ., Хп)} — система
•функций, определяющих V. Тогда касательное пространство
представляет собой линейное подпространство в Р", заданное
уравнениями
п
2. По-другому, если многообразие V задано в однородных
координатах Хо, ■ • •, Х^ как множество нулей многочленов
{Fa (Zo, . . ., Хп)), то касательное пространство в точке р —
это линейное подпространство
1=0
где дифференцирования формальны: если /„ — неоднородный
многочлен для F^-, то dfjdxt — неоднородный многочлен для
dFJdXi, и в силу соотношения
7(
1=0 .
''=F,
где d=sdLQg{F), имеем
rJ-O 1=0
n n
1=0 ' 1=1
поэтому в однородных координатах получается то же самое
подпространство, что и раньше.
Аналогично определяется касательный конус к многообразию
F с: Р" в (быть может, особой) точке р 6 F. В простейшем
случае, когда F_— гиперповерхность, заданная однородным
многочленом F, & р — точка кратности к на F, т. е. частные
производные функции F порядка ^fe — 1 обращаются в нуль в этой точке,
4. Теорема Кодаиры. о вложении 193
а частные производные порядка к не все обращаются в нуль,
касательный конус к F в точке р определяется как
^■.('')=(2,..^,",..^„(p)-^-g=°).
В общем случае касательным конусом к F с: Р" в точке р
называется пересечение касательных конусов в точке р ко всем
гиперповерхностям, содержащим окрестности точки р на V.
Наглядно его можно представить как объединение
касательных прямых в р ко всем кривым на F, проходящим через р, или
как предельное положение хорд lira р, g (А.), где q (Я) — дуга
на F с g (0) = р.
4. ТЕОРЕМА КОДАИРЫ О ВЛОЖЕНИИ
ЛинеИные расслоения, и отобраокепия
в проективное простраиство
В этом параграфе &yji,jT определены точные условия, при
которых компактное комплексное многообразие является
алгебраическим многообразием, т. е. вкладывается в проективное
пространство. Сначала остановимся на некоторых понятиях,
связанных с отображениями комплексных многообразий в Р^.
Рассмотрим компактное комплексное многообразие М и
голоморфное линейное расслоение L -^ М. Напомним, что с каждым
подпространством Е в векторном пространстве /Г" {М, О (L))
связана линейная система
\Е\= {(s)},gs с= Div (М)
дивизоров на М. Так как М компактно, то (s) = (s') только тогда,
когда S = Xs' для некоторой ненулевой константы ?и cz С; поэтому
I Е I параметризуется точками проективного пространства Р (Е).
Теперь дополнительно потребуем, чтобы линейная система
\ Е \ ве имела базисных точек, т. е. чтобы в любой точке р ^ М
не все сечения s ^ Е обращались в нуль. Тогда для каждой точки
р ^ М множество сечений s ^ Е, обращающихся в ней в нуль,
образует гиперплоскость Нр с Е, или, что эквивалентно,
множество дивизоров D ^ \ Е \, содержащих р, образует гиперплоскость
Яр в Р (Е), и тем самым определено отображение
1^: М-^Р (Е)*,
сопоставляющее точке р ^ М гиперплоскость Яр 6 Р (^)*-
Отображение 1^ можно описать явно. Выберем для этого
базис Sq, . . ., Sjf в Е. Для любой тривиализации ф^ расслое-
13-046
194 i. Комплексные алгебраические многообразия
ния L на открытом множестве U а М положим s,-,^ = фЗ[ (sj) g
6 0 (С/). Очевидно, что точка [«о,а (p)i • • м %,а (р)1 не зависит
от выбора тривиализации ф^^. Обозначим эту точку [sj (р), . . .
. . ., % (р)]. Тогда при отождествлении Р (Е)* ^ Р^,
соответствующем выбору базиса s^, . . ., s^^, отображение i^ задается
формулой
1е (р) = [«о (Р)> • • м %(p)i-
Отсюда вытекает голоморфность отображения Ьд.
Пусть теперь [Н] — расслоение гиперплоскости на Р^.
Прообраз 1е (Н) этого расслоения на М задается дивизором (Sj), т. е.
L = 1% (Н). Более того, любое сечение s = 2 ^t^t 6 Е является
прообразом некоторого сечения 2'^г^г Расслоения/Г на Р^, т. е.
Е =^1% {Ю (Р-^, О (Я))) с: Я» (М, Q [Щ.
Следовательно, 1^: Ж ->- Р^ определяет линейное расслоение L
и подпространство Е cz Н^ (М, О (Ь)), т. е. существует
фундаментальное соответствие
.невырожденные отображения. L^Tc'^/^ ^^^^(1)),!
if: М^Р по модулю проек-^^ для которого | i| не имеет '
^ тивных преобразовании J [ базисных точек )
причем выбору однородных координат в Р^ соответствует выбор
базиса So, . . ., % в Е.
Мы пишем обычно i^ вместо 1н°ш,&(ь)) и ^D вместо i[o].
Заметим, что степень образа га-мерного многообразия М при
отображении i^, т. е. пересечение образа Men общими
гиперплоскостями в Р^, совпадает с га-кратным самопересечением
любого дивизора D ^ \ Е \, т. е.
deg (ieM) = ci (/.)".
Алгебраическое многообразие F cz Р" называется (линейно)
нормальным, если линейная система на V, задающая вложение
i: V с- р", полна, т. е. если отображение ограничения
Я° (Р", О (Я)) -^ Я° (F, 0 (Я))
сюръективно. Отметим, что любая гиперповерхность F cz Р"
нормальна. Действительно, точная последовательность пучков
О->-0рп (Я-F) ^ 0рп (Я)-^ ©1. (Я) ^О
индуцирует точную последовательность когомологий
ЯО(Р", 0pn(Я))^Я»(F, (Эг(Я))^Я»(Р". 0pn(Я-FЗJ.
4. Теорема Кодаиры о вложении 195
Но
Я1 (Р", 0р„ (H-v)) = т (Р", 0рп ((1 - d) щ)=о,
поэтому отображение г сюръективно. Заметим, что если V биго-
ломорфно эквивалентно V при отображении, переводящем Ну
в Hv'f то нормальные многообразия F, F' сг Р" проективно
изоморфны, т. е. V переводится в V при помощи автоморфизма
пространства Р". В частности, для гладких гиперповерхностей
у, V' размерности ^3 и степени d Ф п -\- i в Р" по формуле
присоединения имеем
Ку = (Крп (8) IV]) \v = Hd-n- 1) Н]
и аналогично для F'. Но по теореме Лефшеца о гиперплоском
сечении
Н^ (F, О) ^Н^ (Р", 0) = О, Я^ (F, 0) ^ Я^ (Р", 0) = 0.
Поэтому из длинной когомологической последовательности,
отвечающей экспоненциальной последовательности пучков, опять по
теореме Лефшеца получаем
Pic (F) = Н^ (F, 0*) ^iPiV, Z)^IP (Р", Z) = Z
и аналогично для F'. Стало быть, если ф: V -^ V' — биголоморф-
ное отображение, то
т. е. F и V' проективно изоморфны. Итак,
Гладкие гиперповерхности размерности ^3 и степени
d =7^ га + 1 в Р" изоморфны тогда и только тогда, когда
они проективно изоморфны; или, эквивалентно.
Любой автоморфизм гладкой гиперповерхности размерно-
сти'^Ъ и степени d =^ п -\- 1 в Р" индуцируется некоторым
автоморфизмом пространства Р".
Это справедливо также и для поверхностей F в Р* степени
d^ k. Для того чтобы применить проведенные рассуждения в этом
случае, нужно убедиться в отсутствии кручения в группе В^ (F, Z),
а это вытекает из односвязности F (снова по теореме Лефшеца)
и из двойственности Пуанкаре для кручения /Г^цдог в группах
гомологии
Ягдог {М, Т) ^ ЯГо7'-^ (М, Z),
где т — вещественная размерность М.
Проиллюстрируем соответствие между отображениями в
проективное пространство и линейными системами без базисных точек
13*
196 1. Комплексные алгебраические многообразия
на классическом примере: отображение Веронезе для линейного
расслоения [dH] на Р". Мы уже видели, что глобальные сечения
расслоения ЫН] соответствуют однородным многочленам
степени d от однородных координат Z = [Zq, . . ., Z„]. Поэтому если
{Z"* = Zjo . . . Z55"} обозначает множество мономов степени d
от Z, то отображение Веронезе задается формулой
[Zo, . . ., ZJ ь-> [. . ., Z«, . . .].
Легко проверить, что отображение Веронезе является гладким
вложением; при этом каждая гиперплоскость степени d в Р"
переходит в гиперплоское сечение образа ь^д (Р") с: Р^.
Рассмотрим несколько примеров.
1. Отображение Веронезе Цд: Р^->-Р" в евклидовых
координатах t = ZJZq на Р^ задается формулой
t ^ [1, t, i^ . . ., i"I.
Его образом является невырожденная кривая степени п,
называемая рациональной нормальной кривой.
Обратно, рассмотрим неприводимую невырожденную кривую
С с= Р" степени п. Пусть Pi, ■ ■ ., Pn-i — произвольные га — 1
линейно независиьшх точек на С, V = pi, . . ., p„-i ^ Р"~® —
их линейная оболочка, а {Н^У^^^р! — пучок гиперплоскостей
в Р", содержащих V. Тогда каждая гиперплоскость Нх
пересекается с С в га точках. Это точки pi, . . ., p„_i и еще одна точка,
которую мы обозначим q (Я,). (В случае когда гиперплоскость Нх
содержит V и касается С в точке pt, q (К) = pt.) Каждая точка
кривой С лежит на единственной гиперплоскости Нх, и, значит,
отображение q: Р^ -^ С является изоморфизмом. Более того,
пН — единственное линейное расслоение степени п на Р^.
Поэтому каждая неприводимая невырожденная кривая степени га в Р"
проективно изоморфна рациональной нормальной кривой.
2. В евклидовых координатах s = Zi/Zj, t = ZJZ^ на P^
отображение Веронезе / = igH^ Р^ -*- Р^ задается формулой
(s, i) 1-> [1, S, t, s^, St, Щ.
Образ S = f (P^) является невырожденной поверхностью
степени Сх (f*Hpif = Ci (2/Гр2)^ = 4. Отметим, что, согласно
результатам последнего параграфа, это минимально возможная степень
поверхности в Р*.
Сделаем теперь небольшое отступление, чтобы обсудить
любопытное свойство поверхности Веронезе S cz Р*. Оказывается, это
единственная невырожденная поверхность в Р*, многообразие хорд
С (S) = \j РЯ которой является собственным подмногообразием
p.qes
4. Теорема Кодаиры о вложении 197
в Р*. Чтобы убедиться в этом, заметим, что для любой точки
р 6 Р*, лежащей на хорде / (и) f (и') поверхности S, прямая
L = ии' с Р^ переходит в кривую степени
#(Яр5-/(Ь)) = Щ2Нр,-Ь) = 2
в Р* и, согласно нижней оценке на степень, установленной в § 3,
являеся коникой, лежащей в двумерной плоскости V^ cz Р*.
Но j9 5 / (ц) / (и') CZ Fa, а любая прямая в V^, проходящая через
р, пересекает / (L) дважды. Поэтому через любую точку из Р^,
лежащую на хорде поверхности S, проходит бесконечно много хорд
поверхности S. В частности, если Lq — прямая (s = 0) в Р^^
& щ = Lq f\ L, то прямая / (и^), р cz Р^ будет хордой
поверхности S. Итак,
С{5)= и fiPhfiqh
откуда видно, что многообразие С (S) имеет размерность не больше
четырех. Явно многообразие С (S) можно задать как множество
точек
{a-f {S, t) + (i - a)-f (О, t')} =
= {[1, CCS, ai + (1 — a) t', as^ ast, at^ + (1 — a) t'^}
Выразим теперь a, s, in t' через координаты X = [Xo, ■ ■ ■, X^]
6 С (S). Очевидно, X — точка вида a-f (s, t) + (1 — a)-/ (0, f)
где
s =^ X31X1, t = XJXi, (X = X^lXqX2,
t' = (Z2X3 - XiX,)l{XoXs - XI).
Следовательно, координаты точки X ^ С (S) удовлетворяют
соотношению
Х,/Хо = af + (1 - а) i'2 =
= ХуХоХ, + {X,Xs - X,X,r/{XoX, (Z0J3 - XD),
т. е.
(Ло-Лз — Х^) Х^ = ХоХц -)- Х^Хз — ^Х^Х^Х^,
и мы видим, что многообразие хорд поверхности Веронезе в Р*
есть кубическая гиперповерхность.
Сформулируем теперь первоначальный вопрос этого параграфа
так: для каких голоморфных линейных расслоений L ->- М
отображение ix,: М ->- Р^ является вложением? Прежде всего, чтобы
198 1. Комплексные алгебраические многообразия
ix, было определено, линейная система | L | не должна иметь
базисных точек, т. е. для всех х ^ М отображение ограничения
нцм,е{Ь))'Ль^
должно быть сюръективным. При этом условии i^, является
вложением, если
1. ij, взаимно однозначно. Очевидно, это выполняется тогда
и только тогда, когда для любых а: и у из М существует сечение
S ^ Н^ [М, О (L)), обращающееся в нуль в х, но не обращающееся
в нуль в у, т. е. тогда и только тогда, когда отображение
ограничения
(*) Я»(Ж, 0(L))—-^L,eL,
сюръективно для всех х Ф у ^ М. Отметим, что при выполнении
этого условия для пучка L линейная система | L | автоматически
не имеет базисных точек.
2. Дифференциал отображения i^, нигде не вырожден. Если
Фа — тривиализация расслоения L вблизи х, то это выполняется
тогда и только тогда, когда для всех ковекторов v* 6 Т% {М)
существует S ^ Н° (М, О (L)), такое, что «„ (а:) = О и dSa {х) = v*,
где Sa = (faS- Это требование можно выразить более инвариантно.
Пусть J^cz G — пучок голоморфных функций на М, равных
нулю в точке х, а Jx Ш — пучок сечений пучка L, равных нулю
в X. Если S — любое сечение пучка J^ (L), определенное в
окрестности точки X, а (pai фр — тривиализации L в окрестности U
точки X, то, написав s^ = fjs, Sp = fps, s^ = ga&s^, находим, что
d (sj = d (sp)-^ete + dgad-s^ = d (sp)-^e45 в точке X.
Итак, получаем отображение пучков
dx: Jx (Ь) ^ П' <8) L„
и условие 2 эквивалентно требованию сюръективности
отображения
(**) H^>{M,J,{L))Лn'<S>L^
при всех X ^ М. Отметим, что условие (**) является предельным
случаем (*) при у ^- х.
Наша цель — установить следующий результат.
Теорема Ко дайры о вложении. Пусть М — компактное
комплексное многообразие, а L -^ М — положительное линейное
расслоение. Тогда существует такое к^, что для всех к "^ к^
отображение I ft: М —>- Р^ определено и является вложением М в Р^.
4. Теорема Кодаиры о вложении 199
Посмотрим, что же необходимо для доказательства этой
теоремы. Прежде всего нужно включить отображения (*) и (**)
в точные последовательности и попытаться воспользоваться
непосредственно теоремами об обращении в нуль. Для этого
обозначим через ^х,у (L) пучок сечений расслоения L, обращающихся
в нуль в точках х ж у, & через С1\ (Ь) — пучок сечений
расслоения L с нулем порядка 2 в точке х, т. е. таких сечений s пучка
Ох (L)i для которых dx (s) = 0. Последовательности
0 ^ Л (L)->■ J, (L) ^5. П'(8) L, ^ 0
точны. Поэтому чтобы убедиться в сюръективности отображений (*)
и (**), достаточно проверить, что
ЯЧМ, Л (L)) = Я1 (М, J^,, (L)) = 0.
В самом деле, подставив L** вместо L и воспользовавшись тем
что Н^ (М, О (L*)) = О при к ^ fei, читатель может проверить
что наша теорема эквивалентна обращению в нуль указанных выше
одномерных когомологий для больших степеней расслоения L.
Проблема, однако, в том, что, если многообразие М не одномерно,
ни один из пучков Og.,v Ш и 0% (L) не является пучком сечений
голоморфного векторного расслоения, так как для голоморфного
векторного расслоения Е -^ М ж подмногообразия V а М ядро
отображения ограничения Од^ (Е) -^ О^ (Е) является пучком
сечений векторного расслоения тогда и только тогда, когда
подмногообразие V имеет коразмерность i в М. Поэтому мы не можем
применить к ним непосредственно аппарат гармонической теории.
Пучки JJ и Ух^у дают примеры когерентных пучков — класса
пучков, более широкого, чем класс пучков сечений голоморфных
векторных расслоений, но тесно связанного с ним. Теория
когерентных пучков будет рассмотрена в гл. 5.
Другим подходом к проблеме могла бы быть модификация
доказательства предложения из последнего раздела § 2 и
индукция по размерности многообразия М. Например, если бы мы
нашли гладкую гиперповерхность V а М, содержап1ую х ж у,
то, чтобы доказать сюръективность отображения (*), нужно
было бы только проверить это для L | v- на F и доказать, что
отображение ограничения Я° {М, Ом Ф)) ->■ Я° &, <Эу Ф)) сюръ-
ективно, проверив, что Н^ (М, ©^ (L — У)) = 0. Но вопрос
существования такого дивизора очень близок к тому, что нам
нужно доказать: а priori на многообразии М может вовсе не быть
дивизоров.
Теперь понятно, что основная наша трудность заключается
в том, что точка многообразия М, не являющегося римановой
поверхностью, не есть дивизор на М. Эту трудность можно преодо-
200
1. Комплексные алгебраические многообразия
леть, воспользовавшись красивой классической конструкцией,
называемой раздутием, которая преобразует точки комплексного
многообразия в дивизоры.
Раздутие
Вначале опишем раздутие в центре диска Д с: С". Пусть
Z = (z,, . . ., z„) — евклидовы координаты в С", а Z = [1^, . . .
. . ., In] — соответствующие
однородные координаты в Р"-^. Пусть
Д с: Д X Р"~^ — подмногообразие
в Д X Р"~^, заданное
квадратичными соотношениями
Д = {(z, I): Zil} =Zjlt
для всех i, /}.
Если рассматривать точки Z6 Р""^
как прямые в С", то эти
соотношения можно переписать в
виде zaI = 0; следовательно, они
выражают отношение
инцидентности {(z, I): Z 6 Ц.
Далее, проекция на первый
сомножитель п: (z, I) t-* z задает
отображение Ъ. на Д. Из
геометрического представления очевидно,
что это отображение является
изоморфизмом вне центра диска Д,
а я"^ (0) представляет собой
проективное пространство прямых
в Д, проходящих через центр
этого диска. Как следствие,
получаем, что Д состоит из всех
прямых, которые проходили через
центр в А, но уже не
пересекаются в Д. Многообразие Д вместе
с его проекцией л на Д называется
раздутием Д в точке 0. Вещест-
^^*^- * венные точки раздутия Д cz С^
изображены на рис. 1.
Заметим, что с многообразием Д мы уже встречались:
проекция л
)П-1
расслоение / на Р"~^.
на второй сомножитель задает универсальное
4. Теорема К о дайры о вложении 201
Рассмотрим теперь комплексное многообразие М
размерности га, любую точку х ^ М ж координатный полидиск z: С/ —>- Д
с центром в точке х ^ М. Ограничение проекции
я: К — Е--^и — {х}с1 М
задает изоморфизм окрестности прообраза Е = п'^х в Д и
окрестности точки X в М. Назовем раздутием М^ многообразия М в
точке X комплексное многообразие
М« = М- {а:} Уя Д,
полученное заменой Д cz М на Д. Оно обладает естественной
проекцией л: М^ ->- М. Проекция л: М^ — {п~^ (ж)) ->- М — {а:}
также является изоморфизмом; прообраз п~^ (а:) в Мх называется
исключительным дивизором раздутия и обычно обозначается наьш
Е или Eg..
Заметим, что раздутие Ж —>- М не зависит от выбора
координат в диске Д: если {%\ — fi (z)} — другие координаты в Д
с /{ (0) = О, а Д' — раздутие Д в новых координатах, то
изоморфизм /: Д — Е -*- А' — Е' можно продолжить на Е, полагая
/ (О, I) = (О, г'), где
Действительно, из этого вытекает, что отождествление Е ->-
->- Р (Гж (М)), заданное по правилу (О, О *-*' | 2 ^'" д~\' также
не зависит от выбора координатной системы.
Опишем подробнее геометрию многообразия М^ вблизи Е,
Вначале выберем локальные координаты в окрестности Е на М^:
пусть Z = (zi, . . ., z„) — локальные координаты на U ^ х с
центром X. Тогда
£/ = Л-» (С/) ={(z, l)eUx Р"-': Zili=Z}lty,
положим
Так мы получили открытое покрытие окрестности U id Е.
Локальные координаты Z (i)i на открытых множествах Ut имеют вид
■г (О; = yh = Zjhu i ¥= i, и z (i)i = z^.
202 1- Комплексные алгебраические многообразия
Отображение л: М^—*'Af на C/j задается соответствием
<z (Oi, . . ., z (Оь . • •, z (On) ►-^
i^(z (Orz (Oi, . . ., z (Oi, . . ., z (Orz (On),
a дивизор E — формулой E = (z (Oi = 0) в C/i. Ha пересечениях
z (Oh = zO")i'-z (/)h, z (Oj = z (/)7', Zi = z(j)vZj.
Далее, так как £ = (Zj) в tJi, линейное расслоение [Е] задается
в и функциями перехода
gii = Z (i)i = Zilz] = yij в C/i n U),
поэтому слои [E\ Igr можно отождествить с
(*) [i?i(^.» = {^ (h In), ?^ e c}.
в частности, мы получаем, что линейное расслоение [Е] \^
совпадает с универсальным расслоением J = —Н на Е ^ Р"~^.
Двойственным образом, слоем линейного расслоения [—Е] =
= [Е]* над точкой (z, I) ^ U служит пространство линейных
функционалов на прямой I а С", а [—Е] \е — расслоение
гиперплоскости на Е.
Как мы уже видели, существует естественное отождествление
Е ш Р (Т'х (М)), поэтому глобальные сечения расслоения [—Е]
над Е отождествляются с линейными функционалами на
касательном пространстве, т. е.
<**) Я» {Е, &Е i-E)) = Т*' (М).
С другой стороны, если задана функция / на U, равная нулю
в точке X, то функция л*/ 6 © (и) обращается в нуль на Е.
Значит, ее можно рассматривать как сечение расслоения [—Е] над tj-
Явным вычислением можно проверить, что для любого f ^ dх (U)
ограничению на Е сечения л*/ 6 © (—Е) (U) при отождествлении
(**) соответствует дифференциал df (х) сечения / в точке х,
т. е. диаграмма
H%U,Q{-E))-^^H^'(E,ei-E))
H°(f/,3J ^^^-*T*'(U)
коммутативна.
4. Теорема Кодаиры о вложении 203
Это соответствие отражает один важный аспект локально-
аналитической природы раздутий: инфинитезимальное поведение
функций, отображений или дифференциальных форм в точке
X ^ М становится глобальным явлением при подъеме на М. Если
вспомнить классическую терминологию, то в ней точка
исключительного дивизора раздутия многообразия М ъ х называлась
«бесконечно близкой» к а:, а сам исключительный дивизор
назывался «инфинитезимальной окрестностью» точки х.
Вычислим теперь кривизну линейных расслоений [Е] и [—Е\
на М. Построим для этого на расслоении [Е\ метрику. Пусть
/ii — метрика на [Е] |р-, заданная в представлении (*) для [Е] |^
формулой
Пусть а ^ Н" (М, Q {[Е])) — заданное выше глобальное сечение
расслоения [Е] на М с (ст) = Е, так что ст не обращается в нуль
на М — Е. Пусть ^2 — метрика на [Е] \^_^, заданная
нормировкой I (т (z) I ^ 1. Для Б > О обозначим через C/g шар (|| z || < е)
вокруг X в и ж положим] Ue. = л,~'^ (Ue). Пусть pi, Pa —
разбиение единицы, подчиненное покрытию {U^a, М — U^ на М,
а Л — глобальная метрика, заданная равенством h = Pi-'Ji +
Мы вычислим кривизну расслоения [Е] с этой метрикой. Для
удобства обозначим через Q[e] кривизну в[Е] расслоения [Е],
у»шоженную на У —1/2. Необходимо рассмотреть три случая
1. На М — £^28 имеем ра^ 1, поэтому | ст р ^ 1;
следовательно,
Q[E] = dd4og-j-^ = 0.
2. Зададим ст на tjg, — E^Uz — {x) в представлении (*)
равенством ст (z, I) = z; тогда
Q[s] = ddMog-jj^ = - dd4og II Z ||2,
т. е. форма —Q[E] является подъемом л'*со (1, 1)-формы со
метрики Фубини — Штуди на Р"~^ относительно отображения
я': С/^е->-Р""^, заданного формулой (z, 1)^-^1. Поэтому
— Q[E]>0 на Ог — Е.
204 i. Комплексные алгебраические многообразия
3. Как мы уже показали, —Q[ej == л'*о) на C/g — Е. По
непрерывности отсюда следует, что —Qf^j = л'*о) всюду на U^,
в частности,
—Ще\ 1е = (й > о на £.
Итак, обозначим через Q[-e] умноженную на У—1/2 форму
кривизны двойственной метрики на [Е]* = [—Е\\ тогда
Й[-Е]= — Це]
= 0 на М —С/ае,
>0 на tJ^,
> О на г; (£■) с: г; (Ж) для всех х 6 £■.
Центральное место в наших вычислениях заключается в
следующем. Пусть L ->- М — положительное линейное расслоение
с метрикой /ij,, форма кривизны которой Oj, равна некоторой
положительной форме Qj,, умноженной на 2/]/—1. Тогда если
Q„*j, есть произведение ]Л—1/2 на форму кривизны
индуцированной метрики на расслоении n*L ->- М, то ^и*ъ = n*Qi,. Поэтому
^я*1, > О на Ж — £■. Более того, для любой точки х ^ Е и любого
касательного вектора v 6 Т^ (М)
причем равенство достигается тогда и только тогда, когда я^ (и) =
= О, т. е. тогда и только тогда, когда v — касательный вектор
к Е. Поэтому
>0 всюду,
>0 на М — Е,
. >0 на г;(МУГ;(£■) для всех х^Е,
а форма
неотрицательна всюду в С/е и М — U^z- Более того, ввиду
ограниченности снизу формы Q[-E] в и^е. — U^ Ж положительности
формы Qn*i, там же, вытекает, что форма ^л*1,'*®г-и '^Р'^
достаточно больших к всюду положительна, т. е. существует такое
Uq, что при W^ к^ расслоение п*1} — Е на М положительно.
Отметим, что из тех же соображений вытекает, что для любого
п расслоение n*L'' — пЕ положительно при Л ^ 0.
Нам потребуется еще одно соотношение между Мх и М.
4. Теорема Кодаиры о вложении 206
Лемма. К^ = п*Км + (п — I) Е.
Доказательство. Если на М имеется нетривиальная ь^ероморф-
ная га-форл1а со, то это совсем просто. Тогда в локальных
координатах Zi, . . ., z„ в окрестности U точки х имеется представление
а (z) = ^-^ ■ dz, л ... А dZn.
: Пусть теперь z (г)/ — ранее введенные локальные координаты.
ОтЬбражение п задается в С/{ по правилу ;
(2 (О1 Z (0„) ь^ (Z (Ol Zi, . . ., Zi, . . ., Z (On Zi),
откуда
я*о) = я* {jlg)-d (z (i)i Zi)h . . . AdZiA ... Ad (z (i)n Zi) =
= n* (flg)-Zi~^dz (Ol Л . . . л dz (On-
Поэтому в окрестности прообраза Ё = п-^- (х^) дивизор (л*со)
является суммфй п* (со) + (п — 1) Е. Поскольку вне Е,
очевидно, (л*со) = п* (со), то
К^ = [(я*со)1 = п*Км + in 4- 1) Е,
как и требовалось. Итак, лемма доказана в предположении, что
на М существует мероморфная га-форма; это самый легкий случай.
Чтобы доказать лемму в общем случае, рассмотрим открытое
координатное покрытие U — {Uq, Ua}at. многообразия М с х ^ Uq
X $ Ua, п пусть все C/jj, имеющие непустое пересечение с С/д,
лежат в одной карте с координатами Zi, . . ., z„. Рассмотрим
соответствующее покрытие для М:
U = {U^ = я-if/,, Ut = Jt-'f/o n ih ¥= 0)}
и вычислим функции перехода {gu, gia, ga&} расслоения К^
относительно координат z (О/ на ffi и координат ш^^а = л*Ш{,а
на С/„, где {ш^, „}{ — координаты в £/„ на М. Прежде всего
в tTi П ^2 имеем
Z (2), = Z (1)-', Z2 = Z (l)2-zi,
z(2)i = z(l)rz(l)-', i^l, 2.
206
1. Комплексные алгебраические многообразия
Поэтому матрица Якоби этой замены координат имеет вид
'12
0
^(1)2
0
0
^1
-^(I)r^(l)2~'
0
0
0
0
0
••• 0 z{\);' 0 ••
• 0
в общем случае
gij = det Jij = z (ОГ"^^-
Аналогично в £/„ П f^i
«'l,a = Zi, «'j,„ = Zi-z(l)i,
1 о
о
z{\), о
0. — zS"""
И в общем случае
Кроме того,
где g'a^ — функции перехода для расслоения Км относительно
координат Wi^a в и а, Щ,^ в^^р.
Но дивизор Е задан в Ui как (z^), а в С/^ как (1), поэтому
функциями перехода для расслоения [Е\ над V^ являются
функции вида
hij = ZilZj = z (i)-j\ hia = zu h^^ = i.
Итак, функциями перехода расслоения К^ ® [£■]-"+! будут
функции
/o = z(i)J"-^'.z(i)r' = l'
4. Теорема Кодаиры о вложении 207
Следовательно, К^ — [п — i) Е есть обратный образ при
отображении п расслоения на М с функциями перехода
Т. е. K^-{n-i)E = п*Км. D
Более полную картину геометрии раздутий мы дадим позднее
в главе, посвященной поверхностям, а пока у нас есть все
необходимое для доказательства теоремы о вложении.
Доказательство теоремы Кодаиры
Пусть L ->- М, как и выше, положительное линейное
расслоение на компактном комплексном многообразии М. Мы хотим
доказать существование числа Ло, удовлетворяющего следующим
условиям.
1. Отображение ограничения
Я» {М, Q (L")) -^ Ll е Lj
сюръективно для всех х Ф у ^ М, к ^ к(,.
2. Отображение взятия дифференциала
сюръективно для всех х 6 М, к ^ к^.
Чтобы доказать утверждение 1, обозначим через М —^ М
раздутие М в х ж у; пусть Е^ = л"^ (х) ш Еу = п~^ (у) —
исключительные дивизоры раздутия. Для удобства обозначим дивизор
Ех + Еу через Е и положим X = n*L. (Мы молчаливо
предполагаем здесь, что п = dim (М) ^ 2; в случае когда М — рима-
нова поверхность, доказательство сохраняется для М — М^
п = id.)
Рассмотрим подъем сечений
л*: Я» (М, Ом {L^^)) -^ Я» (М, О^ (!")).
По аеореме Хартогса для любого глобального сечения а
расслоения L** индуцированное сечение ст расслоения L'^ над М — {х, у}
продолжается до глобального сечения а ^ Н^ (Ж, О {L^))-
Значит, л* — изоморфизм. Более того, по определению расслоение
L** тривиально на Е^ и Еу, т. е.
208 1. Комплексные алгебраические многообразия
поэтому
HO(E,eEiL''))^d®Ll
Обозначим через ге отображение ограничения на Е. Тогда
диаграмма
н%м, OjiiL'^)) ^ н°{Е, е^^й"))
коммутативна. Итак, чтобы доказать утверждение 1, нам осталось
проверить сюръективность отображения г^.
Но на М имеется точная последовательность пучков
О-^ 0~ (Z"-£)-^ 0~ (L") ^ 0д (L")-^ 0.
Выберем такое к^, чтобы L'^i + К% было положительным
расслоением на М. Как было установлено при обсуждении свойств
раздутия, можно выбрать такое к^, что L** — пЕ положительно
на М при к ^ к^. Согласно предыдущей лемме, К^ = Км +
-г (га — 1) Е, где Км = ^*Км, поэтому при к ^ к^ = к^ -\- к^
в^(L^^-E)=QZ(L'^—E + Kt) =
= QZ{(L'^^ + K*м)®iL'^'-nE))
с к' "^ к^. По предположению расслоение L**' — пЕ имеет
положительно определенную форму кривизны на М, а (L**» -|- Км)
имеет положительную форму кривизны на М, и поэтому (L**» -Ь
+ K%i) имеет положительно полуопределенную форму кривизны
на М. Следовательно, линейное расслоение (X''' -|- Км) -f L^' —
— пЕ положительно на М и по теореме Кодаиры об обращении
в нуль
НЧМ, G^(L^-E))=HHM, 0!'~^Ф^ + КУ) + ф^'-пЕ)) =
= 0 при к^кд.
Поэтому отображение
4. Теорема Кодаиры о вложении 209
сюръективно при W^k^, что доказывает утверждение 1 для
выбранных X а у.
Утверждение 2 доказывается аналогично. В этом случае пусть
Ж —> М — раздутие М в х, Е = п~^ (х) — исключительный
дивизор. Подъем сечений снова определяет изоморфизм
л*: Я« (Ж, Gm (L")) -^ Я« (М, ©^ (L")).
м
Далее, если а ^Н" {М, <Эм (L'*)) — некоторое сечение, то ст (х) =
— О тогда и только тогда, когда сечение а = п*а обращается
в нуль на Е. Значит, ограничение отображения п* задает
изоморфизм
л*: Н» {М, Cfx {L")) -^ Я« (М, О^ {L^^-Е)).
Как и раньше, произведем отождествление
Я» {Е, &Е(Ь"-E)) = Li® Я» (Е, Ое{-Е))^ьЧ® П';
полупим коммутативную диаграмму
Н%М, G^iL" - £))-^Я°(Е,0НЬ' - ^)
«Ь , 11
H4M,2JL'')) -Т"Г<8)Ь*
Итак, осталось проверить сюръективность отображения ге при
u>0. ^
На М имеется точная последовательность
0-^O^{L^'-2E)^O^(L'^~E)ЛGE(L^^-E)-^Q. ,
Выберем снова такое к^, чтобы расслоение № + Км было
положительным на М, и такое к^, чтобы Z^^' — (га -|- i) Е было
положительным на М при к' ^ к^. Тогда для к "^ к^ = к^ -\~ к^
О^ (L"-25) = Q1 ((l"! + К*м) (8) (£"' - (п +1) Е)),
где к' ^ А;2, По теореме Кодаиры об обращении в нуль
т{М, O^{L>'-2E))=0
при к ^ A;q. Следовательно, отображение г^ сюръективно на
глобальных сечениях, и утверждение 2-доказано для выбранного х.
14-04в
210 1. Комплексные алгебраические многообразия
Теперь, чтобы завершить доказательство, осталось доказать
существование такого А;^, для которого утверждения 1 и 2 верны
при любом выборе х ш у и всех к ^ к^. Очевидно, что если i.h
определено в точках х и у и i ^ (а:) ^^ i h (у), то это же верно для
точек х', близких к ж, и точек у', близких к у; аналогично, из
гладкости ij^k в X вытекает его гладкость в точках х', близких к ж,
и то, что это отображение разделяет точки х' ^ х" вблизи х.
Так как многообразие М компактно, отсюда уже легко получается
наша теорема, g
Прежде чем перейти к примерам и следствиям, сформулируем
теорему более инвариантным образом.
Теорема Кодаиры о вложении. Компактное комплексное
многообразие М является алгебраическим многообразием, т. е.
допускает вложение в проективное пространство, тогда и только
тогда, когда на нем имеется замкнутая положительная (1, \.)-фор-
ма О) с рациональным классом когомологий [со].
Доказательство. Если [о)1 6 IP (М, О.), то при некотором к
имеет место включение [ка] g Н^ (М, Z). Но в точной
последовательности
Я* (М, 0*) -^ Я2 (М, Z) Лн^{М, G)
* ([йсо]) = 0. Значит, суп1;ествует голоморфное линейное
расслоение L ~>- М с Ci (L) = [кф]. Это расслоение L должно быть
положительным. Q
Метрика с рациональной (1, 1)-формой называется метрикой
Ходжа.
Следствие. Если М и М' — алгебраические многообразия, то
М X М' — также алгебраическое многообразие.
Доказательство. Пусть о), со' — замкнутые целочисленные
положительные (1, 1)-формы на М и М' соответственно, а л: М X
X М' -^ Ж и я': М У. М' -^ М' — отображения проекции. Тогда
л*сй + л'*©' — снова замкнутая целочисленная положительная
форма типа (1, 1). Q
Классическим примером служит отображение Сегре Р" X
X Р™ -^ Р^, заданное полной линейной системой линейного
расслоения п*Н ® п*Н на Р" X Р™. Так, например,
отображение Сегре Р^ X Р^ -^ Р^ задается в однородных координатах
[zq, Zi] и [и?о, Wi] на Р^ формулой
(ко, Zil, [и?о, U?i]) Ь-> [zjU'o» ZoU?i, ZiWfi, Zill?il.
4. Теорема Кодаиры о вложении 211
Образом при этом будет квадрика {ХцХ^ = XiX^) в Р*.
-^ я
Следствие. Пусть М — алгебраическое многообразие, а М —^
—*■ М — его раздутие в точке х. Тогда М — алгебраическое
многообразие.
Доказательство. В процессе доказательства теоремы о
вложении мы видели, что для положительного расслоения L -^ М
и исключительного дивизора Е = п~^ (х) расслоение л*L'^— Е
положительно при к ^ 0. Q
^4rf я
Следствие. Если М —^ М — конечное неразветеленное
накрытие компактного комплексного многообразия, то М алгебраическое
тогда и только тогда, когда М алгебраическое.
Доказательство. Очевидно, что для положительного
расслоения L -^ Af из равенства с^ (n*L) = n*Ci (L) вытекает
положительность расслоения n*L. Обратно, рассмотрим целую
положительную (1, 1)-форму О) на М. Для любой точки р ^ М существует
ее окрестность U в М, изоморфная окрестностям Uf точек д,- 6
^ n~'^ (р). Определим (1, 1)-форму со' на М, полагая
о)'(Р)= S о)(д).
в6я-1(р)
Тогда со' — замкнутая (1, 1)-форма, и для любого целочисленного
класса когомологий Т1 6 Н^^ (М)
\ со'Л л = — ) О) л л*т16 О,,
^ "" и
где т — число листов данного накрытия. Поэтому класс [о)']
рационален. Q
Определение. Линейное расслоение L ~>- М над
алгебраическим многообразием называется очень обильным, если Н*^ (М, G (L))
задает вложение М ->- Р^, т. е. если существует вложение
/: М <=- Р^, для которого L = /*Я.
Из доказательства теоремы Кодаиры о вложении вытекает
такое
Следствие. Для любого линейного расслоения Е -^ М и
положительного линейного расслоения L —*- М при к ^ О расслоение
L^ -\- Е очень обильно.
212
1, Комплексные алгебраические многообразия
5. ГРАССМАНИАНЫ
Определения
В этом параграфе будут определены грассманианы, которые
составляют важный класс компактных комплексных многообра-
8ИЙ, и изучены их основные свойства. Грассманианы можно
рассматривать как обобщение проективного пространства. Аналогия
между ними будет очевидна в ходе нашего изложения.
Пусть V — комплексное /г-мерное векторное пространство.
Грассманианом G {к, V) называется множество А;-мерных
линейных подпространств в V. Через G (к, п) будем обозначать G (к, С").
Возьмем в С" некоторую А;-плоскость Л. Она определяется
множеством из к векторов-строк в С", порождающих Л, т. е. А; X п-
матрицей
'hi
'hn>
ранга к. Любая такая матрица, очевидно, представляет элемент
из G (к, га), и любые две такие матрицы А, А' представляют один
и тот же элемент тогда и только тогда, когда А = gA' для
некоторого g ^ GL (к).
Пусть / = {ii, . . ., ih} CZ (1, . . ., га} — мультииндекс из к
элементов, Fjo есть (га — А;)-плоскость в С", порожденная
векторами {в]-: i $ /}, а
Ui= {A^G {к, га): А П Vj» = (0}}.
Множество Uj состоит из таких плоскостей А ^ G {к, га), что /-й
к X А;-минор одного, а значит, и любого другого матричного
представления для Л невырожден. Любая плоскость А ^ Uj
имеет единственное матричное представление Л', в котором Т-ж
к X й-минор является единичной матрицей. Поэтому, например,
дюбую плоскость A6t^{i..., h} можно однозначно представить
(нормализованной) матрицей вида
[1
0
0
0
1
0 •
.
■ 0
• 0
• • 1
*
*
*
... ^
■
»
5. Граесманианы 213
(Отметим, что вектор-строки такого матричного представления
для К ^ Ui — это координаты точек пересечения плоскости Л е
аффинными [п — А;)-плоскостями (Ую + ef j g /}.) Обратно,
любая к X га-матрица указанного вида представляет некоторую
/с-плоскость Л 6 Uj. Следовательно, выделенией (га — А;) элементов
/"-го к X {п — А;)-минора Л^„ матрицы Л^ задает биективное
отображение множеств
Ф^: С/,-^ £"<"-")
для всех /. Отметим, что для всех /, /' множество ф/ (Uj f] Uj ■)
открыто в С***""^'. Кроме того, утверждается, что ф/ о ф;,* —
голоморфное отображение на этом открыгюм множестве, а потому
отображения ф/ задают на G {к, га) структуру комплексного
многообразия. Но это очевидно: если обозначить через Ар Г-я
к X А;-минор матрицы Л^, где Л 6 t/j П C^i'» то
л^' = (л1о"'-л^
а так как элементы матрицы (Aj^)"' голоморфно зависят от
элементов матрицы Л^, то отображение ф/ о щ\ голоморфно.
Многообразие G (к, га) компактно и связно в этой топологии,
так как унитарная группа С/„ сюръективно и непрерывно
отображается на G (к, га) при отображении g*-* g (V'h), где Fh = (^i, . . .
. . ., gft} CI C". Полная линейная группа GL (га) также действует
транзитивно на G {к, га).
Отметим, в частности, что G (1, га) как комплексное
многообразие голоморфно эквивалентно Р"~^. «Матричному
представлению» (^1, . . ., Vn) прямой Л 6 G (1, га) соответствует при
естественном теоретико-множественном отождествлении G (1, га) с Р""^
вектор одйородных координат точки Л 6 Р"~^, а
ЛП) = {vj^/vi, . . ., 1, . . ., vJ.Vi),
поэтому
ф{г) = Л Н-* (vi/Vi, . . ., vjvi),
т. е. координаты на G (1, га), заданные при помощи ф{г}, совпадают
с евклидовыми координатами на Р"~^. В силу двойственности
G (га — I, га) ^ р"-1* _ проективное пространство
гиперплоскостей в Р"~^.
Отметим в заключение, что G (к, га) можно рассматривать либр
как множество линейных й-плоскостей Л в С", либо, что
эквивалентно, как множество (к — 1)-плоскостей Л в Р"~^. В этом
параграфе мы в основном придерживаемся первой точки зрения,
так как при этом легче следить за размерностями и
коразмерностями циклов, однако во многих геометрических вопросах удобнее
вторая интерпретация.
214 1. Комплексные алгебраические многообразия
Клеточное разбиение и циклы Шуберта
Напомним, что выбор флага
линейных подпространств в С"+^ определяет клеточное разбиение
P" = C"UC"-4J ...UC4JC»
многообразия Р" = G (1, л + 1) с клетками Wi ^ С'~^ =
= {I CZ С"+^: Zd Уь I ф, Fj-i}. Тот же прием позволяет
получить клеточное разбиение грассманиана. Пусть Vt = (е^, . . .
. . ,, е^} с: С". Тогда множество плоскостей Л 6 G (к, га),
пересекающих каждое Vi по подпространству заданной размерности,
как мы увидим, оказывается простой клеткой. Точнее, рассмотрим
для каждой плоскости А ^G (к, га) возрастающую
последовательность подпространств
(*) О с Л П Fi с Л П F, с . . . с Л П П., с Л П F„ = Л.
Для общей плоскости Л все пересечения А f\Vi при i ^ га — к
нулевые, а остальные имеют размерность {i + к — га). В
действительности, как мы видели, такие Л составляют открытое множество
Up ^ С''<"~'') (^ G {к, га). Для любой последовательности целых
чисел а^, . . ., а^ определим множество
Wa, a^ = {AeGik, га): dim (ЛП F„-h-n-aj) = i}.
Заметим, что dim (Л + F„-h+i-aj) = " — ^t для Л из этого
множества, а потому TF^, а не пусто только тогда, когда
а^, . . ., Яй — невозрастающая последовательность целых чисел
^га — к. Поскольку dim (Л П Vn-k+t-a-) ~ i тогда и только
тогда, когда ранг последнего к X (к -\- ai — Ё)-минора матрицы,
представляющей Л, равен к — i, то замыкание
Wa, а^ = {Л: dim(AnF n-h+i-aj
является аналитическим подмножеством в G (к, га).
В А:-плоскости A^Wa^ о^ можно выбрать следующий
специальный базис. Пусть Vi — направляющий вектор прямой
ApFn-ft+i-ai, нормированный условием {v^, e„_ft+i_ai> = 1» т.е.
V, = (*,.. ., *, 1, О, . . ., 0).
Выберем ^2 так, чтобы у^ и v^ вместе порождали пространство
AnF„_ft+2-og с нормировкой
5. Грассманианы
215
Продолжая таким образом, выберем вектор у,- так, чтобы
^1, ...,У| порождали пространство h[\Vn-h+i-a-i а
О, /<i,
i^ 1 1, i = i
Wi-i ^n-h+j-a
Очевидно, выбор вектора Vi с этим условием на каждом шаге
определен однозначно; стало быть, й-плоскости Л отвечает
единственная представляющая ее матрица вида
U|
Vk
П-к
. . 1 0 0
. . О • 1 0 0
> « О • О • •
О О
• > > О
о
* • «
1 о о
о
6 . .
о
1 о о
о
♦ • * *
■ а,-
-Oj.
Коз-Н
Обратно, любой матрице такого вида отвечает й-плоскость Л 6
g Wa, оь- Так как только (к^ + ^ а^) элементам этой матрицы
приписаны определенные значения, а остальные произвольны,
то имеются гомеоморфизмы
•^01 Oft = ^^
Следовательно, множества Wa^ а задают клеточное разбиение
многообразия G (к, га). Так как все клетки имеют только четные
размерности, то граничные отображения нулевые, и мы получаем
Предложение. Целочисленные гомологии грассманиана G (к, п)
не имеют кручений и свободно порождены, циклами а^, ^ =
= [Wat Oftl вещественной коразмерности 2 2 o,i, где (а^, . . .
. . ., ttft) пробегают все невозрастающие последовательности целых
чисел от О до п — к. В частности, все когомологии многообразия
G (к, п) аналитичны.
В общем случае для любого флага V = (Ух
. CZ Vji-icz Vn) в С" положим
аа(7) = {Л: dim(A(]Vn-H+i-a,)>i}.
V,
216 1. Комплексные алгебраические многообразия
Очевидно^ класс гомологии подмногообразия Од (V) не зависит
от выбора флага, так как существует непрерывное семейство
линейных автоморфизмов пространства С", преобразующих любой
флаг в любой другой. Подмногообразия Оа (F) называются
циклами Шуберта на грассманиане.
Простейшим примером грассманиана, отличного от
проективного пространства, служит многообразие G (2, 4) двумерных
плоскостей в С*. Циклами Шуберта на G (2, 4) являются
в коразмерности 1: а^ ^ (У^) = (Л
^в коразмерности 2: а^д (Fg) = (Л
■ "■■' а,,о(70=(Л
в коразмерности 3: о^^ (7^, Fg) = (Л
dim (Л П У-г)> 1},
Л а 7з}, '
Л ^ Fi},
7х с Л с 7з}-
Если G (2, 4) представлять себе как мнон^ество прямых Z в Р*
и фиксировать проективный флаг р ^ Iq с^ h, состоящий из точки,
прямой и плоскости в Р*, то получится
'■' , .. Ох.о (г,о) =.{1- I ШоФ 0), .
О2.0(р) = {I- рец,
а^д (h) ^il: l<= h),
Огд ip, Щ = {I: p elcz h).
Исчг1слеиие Шуберта
Теперь, зная аддитивную структуру когомологий
грассманиана G {к, п), мы хотели бы описать их мультипликативную
структуру, т.е. выразить пересечение общих циклов Шуберта а^, а,,
в виде линейной комбинации других циклов Шуберта по модулю
гомологической эквивалентности..
Опишем прежде всего пересечение циклов дополнительной
размерности. Рассмотрим для этого общие циклы Шуберта
<^«(П = {Л: dim(AnF„_ft+i_o,)>i},
аь(7') = {Л: dim(ЛnF;_ft+^_ЬJ)>i}•
T0Eдa для всех i и А^а^ {V) П Оь {V')
dim (ЛП Vn-h+i-ai}>i, dim (А П Vn-h+(h-i+i)-b^.i^^)>k—i + i=^
^ Л n F„_ft+i_aj n F;_i+i_b,_j^^ ф (0).
Но при aj-bfeft_,4.i>ra—й
{Ti — k + i — a,) + (n — i + l — bh-i+i) = 2n — k + i — {ai + bh_i+i)^n,
5. Грассманианы 217
поэтому В общем случае флаги F и V можно выбрать так, чтобы^
Vn-h+i-ai И У'п-1+\-ь^^_. пересекались только в нуле. Следова^^
тельно, циклы Од (F) и Оь (У) можно сделать
непересекающимися, т. е.
*(а„-а{,) = 0, когда а,- + й^_,ч.1>га — к для некоторого i.
Пусть теперь a„ и Оь — циклы дополнительных
размерностей, т. е.
2 «i + 2 Ь,- = к{п — к).
Тогда
aj + feft.j+i^/i — к для всех i =^ fe^.i+i = га — к—а,.,
т. е. цикл Oq имеет нулевое пересечение со всеми циклами
Шуберта дополнительной размерности, за исключением цикла
a„_ft_a n-ft-oi- Так как циклы Шуберта образуют
целочисленный базис в Я:^ {G (к, га), Ж), то в силу двойственности Пуанкаре
и положительности пересечения аналитических циклов или просто
прямой проверкой получаем, что
(^01 ^^■n-h-a|^, .... n-h-ai) ^'i-
Все это можно подытожить в виде следующей формулы:
■it/ ч „(n-ft-6b, .... n-ft-bi)
''(Oa-Ob)=6(ai....\)
Вычисляя пересечения, мы можем теперь представить любож
цикл 7 на G {к, п) как линейную комбинацию циклов Шуберта,,
а именно
7=2*(7-<^n-ft-aft n-ft-ai)-a„,
ЧТО, в частности, сводит вычисление пересечения пар циклов.
Шуберта произвольных размерностей к вычислению тройного
пересечения таких циклов дополнительной размерности:
(аа-Об) = 2*(Оа-0'ь-0'п-й-с^ n-h-ci)-Oc.
в качестве примера рассмотрим любую гиперповерхность
W с: Р" степени 2. Пусть т (W) cz G (2, га -f 1) обозначает
множество прямых ц Р", лежащих на W. Очевидно, т (W) является
аналитическим циклом на G (2, п -\- 1), а так как прямая I а Р""
лежит на W тогда и только тогда, когда три ее точки лежат на W^
то X (W) имеет комплексную коразмерность 3. На G {2, га + 1)>
имеется только 2 цикла Шуберта коразмерности 3: это Одо и o^j^i
Значит,
218 1. Комплексные алгебраические многообразия
Но Оп-1,п-4 — ЭТО множество прямых в Р", содержащих точку р
и лежащих в 4-плоскости У4 ci Р". Если выбрать точку р вне W,
то цикл (Т„-1_„-4, очевидно, не будет пересекать т (Р^. С другой
стороны, цикл а„_2„_з состоит из прямых, пересекающих прямую
1q с: Р" и лежащих в 3-плоскости 5 а Р", содержащей ^о-
В общем случае пересечение W = W [\ S является гладкой
квадратичной поверхностью в 5 ^ Р', которая пересекается с 1^
в двух точках Pi и Рз! ясно, что любая прямая Z с: т (W) П о'п -г,п -з
•проходит либо через точку рх, либо через точку р^. Но любая
прямая на TF', проходящая через р£, лежит в касательной
плоскости Т-р. (W), а Тр. (W ) П W является особой кривой степени 2.
а следовательно, состоит из двух прямых. Итак, а„_2,„-з в общем
положении пересекает т (W) в 4 точках. Поэтому
x(W) ~4.а,д.
В частности, если W тз. W — две общие квадратичные
гиперповерхности в Р*, трансверсально пересекающиеся по гладкой
поверхности S, то, согласно предыдущему, на 5 лежит
*(Т (W)-Т (TF'))c(2, 5) = *(4<J2, 1-4(7,. .)«(,. 5) = 16
прямых из Р*. Мы проверим это в § 4 гл. 4.
Аналогично, зная немного больше о частных случаях, мы
«можем вычислить гомологический класс циклов т {W) а
<= (г (2, га -Ь 1) для других гиперповерхностей малой степени.
Прежде чем продолжить изучение пересечения циклов в общем
положении, отметим два общих факта.
Прежде всего мы слегка изменим наш формализм. Для любой
последовательности а = а^, а^, . . . неотрицательных целых
чисел обозначим через а„ (V) цикл
а„ (F) = (Л: dim (Л П ^„-ft+i-aj) > Ц <^ G {к, га),
так что символ а^ можно испольЕ|овать для циклов Шуберта любых
грассманианов. Конечно, o„ будет нулевым в G {к, га), кроме тех
случаев, когда Ui ^ п — к для всех i, а; = О при i > к и а —
невозрастающая последовательность.
Далее, включение С" ->- С"+* индуцирует вложения
ii: G (к, n)-^G{k, п + 1),
ц: G{k, n)-^G{k+ I, п+ 1),
при которых плоскость л с: С" переходит в плоскость Л а
<с: С"+^ и Л Ф (е„+х} а C"+i соответственно. Нетрудно
убедиться, что при подходящем выборе флагов У в С" и У в С"+^ для
-ЭТИХ вложений
аа(Л = 1,-*(аЛ7')) = 1;'К(П).
5. Грассманианы 219
Т. е. если обозначить через Оа двойственный по Пуанкаре цикл
к а„, то
llOa = ifffa = Оа.
Следовательно, формула
K-ab) = S«c-Oe
для пересечения циклов Шуберта в G (А;, га + 1) или G (А; + 1, га + 1)
справедлива также и в G (fe, га), что позволяет ввести уни-
еерсальные коэффициенты Шуберта б (а, й; с), для которых
(ада{,) = S ^С*^' й; с)-Ос на всех G(A;, га).
Согласно нашим предыдущим вычислениям,
б (а, Ъ; с) = *{а„-аь-On-h-Cf^ n-ft-ci)ff(ft, п)
для всех к, п, таких, что о^ — ненулевой цикл на G (А;, га),
т. е. таких, что Cj ^ га — к для всех i и Cj = О при всех i ^ к.
В частности, если обозначить через I (с) длину последователь-
лости с, т. е. число ее ненулевых членов, то для к = I (с), га —
— к = Ci имеем
<*) б(й, й,- с) = *(а.-аь-Oci-c^ С1-С,) в вЩс), l{c)+Ci).
В качестве непосредственного следствия получаем, что
б (а, Ь', с) = О, если цикл Оц или Oj, нулевой на G {I (с), I (с) + с^),
т. е. б (а, Ь; с) = О, если
1) Ci <. ai или Сх < fei
либо
2) 1(сХ1 (а) или 1(с)<1 (Ь).
Заметим теперь, что для любого га-мерного векторного
пространства W существует естественный изоморфизм
*: G(k, ИО -^ G (га — к, W*),
заданный по правилу
* Л = Ann (Л) = {le V*: I (Л) = 0}.
Пусть У = (7i с: Fg с: . . • с: 7„ = W} — флаг в W, ш пусть
V* = {V* с: F* с: . . . с: FJJ = W*} — двойственный флаг в W*
с У* = Ann (Vji-i)- Используя простые результаты из линейной
алгебры, мы получаем, что для любой й-плоскости Л с: W
dim iA[]Vn-h+i-at)>i <^ dixn{*A[]Vt-i+ai)>ai.
220 1. Комплексные алгебраические многообразия
Следовательно, для любой последовательности а образ * а^ а
(^ G [п — к, п) цикла Шуберта Оа с^ G (к, п) является циклом
Шуберта для а*, где а* — такая наименьшая невозрастающая
последовательность, что
floj^i для всех i.
Например,
*{а^) = в1,1, *(a2.i.i) = 03,i-
В общем случае
б (а, Ь; с) = 8 (а*, Ь*; с*),
поэтому можно ожидать, что любая формула для пересечения
циклов Шуберта Оа, а^ определяет двойственную формулу для
Оа», Оь*.
Отметим, что I (а*) = а^ и а* = Z (а), т. е. приведенные выше
формулы 1) и 2), как и следовало ожидать, эквивалентны
относительно отображения *.
Теперь мы обратимся к исходной задаче вычисления б (а, Ь; с)
для общих а, b VL е. Прежде всего сделаем редукцию, которая
позволит во многих случаях производить эффективные
вычисления.
В основе нашей техники лежит простая редукция из линейной
алгебры к грассманианам мецьшей размерности. Рассмотрим,
например, тройку индексов а, р, у, таких, что а -|- Р -Ь v =
= 2к + 1. Тогда для любой й-плоскости Л 6 Од (F) П <^ь (V) П
П а, Ю
dim(An V„_ft+a-a„)>a, dim(AnK-ft+p-6g)>P,
dim (Л n F;_ft+v-c^) > 7 =>
=> dim (A rf y„-ft+a-o„ n K-ft+p-bg П F;_h+,_c^)>l.
Значит, ^{Oa-Ofj-a^) = 0 на G {к, га), если
(fc - a + a„) + (A; - p + fep) + (A; - 7 + c^) > и - 1,
т. е. если
аа + bfi + Су> п — к.
G другой стороны, если аа. + Ь^ + с^ = п — к, т. е. если
подпространства Vn-h + a-aa^ K-fe+p-bp И К-й + ^-с, В общеМ ПОЛОЖб-
нии пересекаются по прямой L а С", то любая плоскость Л 6
€ о'о {V) П Oj, (У) П а^ (У) содержит L. Обозначим через L*
5. Грассманианы 221
подпространство, дополнительное к L в С", а через п проекцию
пространства С" на L" с ядром L. Пусть
a^'ijs. V\ заданы аналогично. Тогда F = {7i}, V'={Vi} и F' =
= (Fi}—флаги, трансверсальные в Z,", откуда видим, что для
произвольной {к—1)-плоскости AdL"
Л = L, Л е (Та (F) П Об (У) П Ое (П <=>
<=>Леа„, а^ a^(V)[\Ob^ ftp Ь^(У')[\
ПО ~ (7"),
Итак, доказана
Формула редукции I. Для любых трех индексов О ^ а, р,
7<А;са+р + 7 = 2А;+1
*К-аь-ас)с(й. „) =
f О при ao + fep + Cv>ra —А;,
~| *(aa-a„-ffb-bg-ac-c^)G(ft-i,n-i) При аа-\-Ъ^+с^ = п — к^).
Отметим, что в случае ^ = у = к зта редукция применима,
если ах = га — к, а в случае 7 = ^ она применима, если ai -\-
+ feft+i-i = га — А; при любом i.
По предыдущему эту первую формулу редукции можно
применить к пересечению циклов (aa*-aj,».a(,*) на G (га — к, п),
откуда получается
Формула редукции II, Для любых трех коэффициентов а^,
feg. Су с а^ + йр + с^ > 2 (п — А;) + 1
*(Oa-<^b-Oc)G(ft.n) =
о при а + р + 7>^'
XOci s-i.i. , cjG(ft.n-i) при а + р + 7 = А;.
I
1) а — аа обозначает последовательность а после удаления элемента а^;
аналогично Ь — bj, с — cv~" Црим. перев.
222 1. Комплексные алгебраические многообразия
Для удобства применения зтой формулы положим а^ = Ъ^ =
= Cq — п — к; тогда в случае 7 = Р = О эта редукция применима,
если aft ^7^ О, а в случае 7 = 0 она применима, если ai -\- b^-i"^
^ га — к -\- \ для некоторого i.
Отметим, что если последовательность Ъ^ — 1, ..., йр — 1,
fep+i, . . . из формулы редукции II не окажется невозрастающей,
т. е. если йр = '^р+и то такой индекс пересечения равен нулю.
Чтобы в этом убедиться, достаточно применить формулу
редукции II к а, р + 1, 7- Итак, формула применима во всех случаях,
если считать, что для последовательности Ъ, не являющейся
невозрастающей, Оь равно нулю.
В качестве примера рассмотрим вычисление коэффициента
б (311, 21; 521) при 0521 в разложении цикла (Ози-Оах) в линейную
комбинацию циклов Шуберта. По формуле (*) и из редукций
получаем
б (311, 21; 521) = #(азп-021-043) в G (3, 8)
= *(0'2-0'21-О4з) В G(3, 7)
= #(02-021-03) в G(2, 6)
= #(a2-ai-Os) в G (2, 5)
= #(a2-ai) в G(l, 4)-Р«
= 1.
Обе формулы редукции примезаимы не всегда, однако в малых
коразмерностях они все же чаще приводят к ответу. Особенно
хорошо они работают, если один из сомножителей Од является
специальным циклом Шуберта, который определяется как цикл
вида Оа,0,0,...- В зтом случае можно воспользоваться нашими
редукциями, из которых получается общая
Формула Пьери. Если а — последовательность а, О, О, . . .,
то для любой последовательности Ъ
bi<.ci<bi_^
{Оа-Оь)== 2
Доказательство. Достаточно показать, что для цикла а^
подходящей коразмерности
1, если bi^c^^b^_^,
О в остальных случаях.
Полагая к = I (с), получаем, что
б(а, Ь; с)=*(Оа-аь-Ос1_с^ ci-c2.o) на G(k, к + с^).
б (а, Ь; с) = |
5. Грассманианы 223
Предположим вначале, что Cj <; bt-i для некоторого i. Тогда
Ci + fei -1 + (ci — Cj) > 2ci 4- 1,
и по второй формуле редукции са = 0, р — i — I п у = к —
— i 4 1 получаем
8(а, Ъ; с) = *(аа-аь1_1 ь._^-1, ь^,... X
XOci-c^-i ci-Cj-i.ci-cj_j. ...) на G{k, k + Ci~\)
= б(а, fe'; с'),
где
fe' = fei — 1, . . ., fej-i — 1, fei, . . .,
с ^ Cj^ — 1, • a •, '-i_]^ 1, Cj, ....
Ho
(fej^Cj^fej_i для всех i) <=> (Ь{^С{^й{_1 для всех г),
а
Ь{-1 —cJ = Vi —Cj—1>0.
Поэтому с самого начала можно предполагать, что Ci^bi-^
для всех i. Так как ^ Ci = а -\- ^ Ъи то а"^ с^; значит, имеются
три возможности:
1. Cj > fej-i при некотором i; тогда а > Cj и б (а, fc; с) = 0.
2. Cj < fej при некотором ц тогда из Cj ^ fej _i следует, что.
fej > fej-i, т. е. последовательность Ъ не является невозрастающей
и Оь = О, откуда б (а, й; с) = 0.
3. fei ^ Cj ^ bi-i для всех i; тогда Cj = fej-i для всех i, поэтому
а = Ci, feft = О и по первой формуле редукции для а = 1 и р =
— у = к получаем
б (а, Ь; с) = *(аа-аб.а<.1_сд ci-c^.o) на (?(&, fe + ci)
= *(аь-ас1-сд ci-cg) на 0{к~1, fe + Cj —1)
= *(0'Ь-0'С1-Ьд_3^, ....ci-6i) = l. Q
Наш окончательный результат о циклах Шуберта будет
представлять собой формулу, выражающую общий цикл Шуберта
в виде многочлена от специальных циклов Шуберта аь,о,...-
Поступим следующим образом. Пусть Oq, а^ —
произвольный цикл Шуберта. Рассмотрим для него цикл
<Ч °j--V"Ul~^ a^-l-Oaj+d-j.
(*) 0„= ]] (-l)'aai а,,.а,..-1 a.-fO,
224 1, Комплексные алгебраические многообразия
Отметим, что цикл а а имеет ту нее размерность, что ж о а- По
формуле Пьери каждое из пересечений в формуле (*) можно записать
в виде суммы циклов Шуберта. Пусть а^ ^ — цикл Шуберта,
встречающийся в этом выражении. Рассмотрим
последовательность целых чисел с^ — 1, с^ — 2, . . ., q — d. По формуле
Пьери не более одного из этих чисел лежит в каждом из {d -J- 1)
замкнутых интервалов
1% — 1, п — к], [а^ — 2, а^ — 21, ...
• • •, [o-d — d, a^-i — d], l—d — 1, a^ — d — 1].
■Значит, ровно один из них не содержит целого числа вида Cj — i.
При этом имеются такие возможности:
1. Ни одно из чисел Cj — i не принадлежит отрезку [—d — 1,
■Cd — d — 1]. Тогда
и Ос может встретиться только в последнем члене суммы (*).
Но поскольку Ci^ Ui и '^ Ci ■= 2j ^ti то с = а. Следовательно,
цикл Шуберта Од, „ появляетсй в (*) один раз с
коэффициентом (—1)'*.
2. Ни одно из Cj — i не лежит в отрезке [ад — к, a^-i — к],
Л > 1. Тогда
ci — 1 6 [«1 — 1, га — ^К
Ch-i — к+ I € bft-i — к+ I, а^ — к + 1],
сн — к ^ [fflft+i — к — I, а^ — к— 1],
Cd — <^ € {—d — 1, ud — d — 1],
т. е.
ttj ^ Cj ^ flj-i, i == i, . . ., к — 1,
ui+i — 1 ^ Cj ^ ttj — 1, i = A;, . . ., d.
В этом случае цикл Шуберта а^ встречается дважды в выражении
{*): один раз в к-и члене и один раз в (А; — 1)-м. Так как эти члены
имеют противоположные знаки, то а,, не дает вклада в
окончательное выражение для Oq.
3. Свободен интервал [а^ — 1, га —к]. Тогда
С( — i 6 [<^j+i — i — 1» <^j — i — H
для всех i, значит, Ci ^ai — 1 и 2 <^t < S '^i» ^ поэтому a,,
не встречается в выражении (*).
5. Грассманианы
225
Итак, мы доказали формулу
= .2j (—1)^0^01, ...,o^_^,aj^^-l a^-i-Oaj+d-
Заметим, что, поскольку каждый сомножитель справа имеет
длину <;d, то отсюда уже следует существование представления цикла
а а в виде многочлена от специальных циклов Шуберта аь.о....»
т. е. что
Кольцо когомологий грассманиана G {к, п) порождено
классами специальных циклов Шуберта.
Используем теперь соотношение (**) для вывода формулы
Джамбелли:
'«1.
0^0»-1
Оа.-2
■
Ooi+l Oat+2... Oai+d-i
Ooj Оад+1.., Oa^+d-2
Oa,-i ^л,
m
m
m
Мы докажем ее по индукции. В случае d = i формула очевидна.
Предположим, что она справедлива для d — 1. Разлагая
определитель по правому столбцу, получаем
2i-ir*^Oa^+d-y
'ах
^ai+d-2
..а,
aj_j^+d-}
-2 • • • f^a.^^+d-j-Z
^a^-d+i
= 2 ( - 1)***' Oa^+d-j • Oax. .... aj_^. ay^, -1, .,
= o,
ax.
Q
Отметим, что формула Пьери вместе с формулой (**) дают
алгоритм вычисления пересечений произвольных циклов
Шуберта.
Исчисление Шуберта будет часто появляться в этой книге
в самых разнообразных ситуациях. Сейчас мы укан^ем лишь
15-046
226 1. Комплексные алгебраические многообразия
некоторые приложения выведенных формул к элементарным
численным задачам из геометрии. Возможно, простейшей из
нетривиальных задач такого рода является следующая. Даны четыре
прямые Li, Lj, L3, 1/4 в Р', находяшдеся в общем положении.
Сколько прямых пересекает все зти четыре прямые? Ответ получить
легко. Так как множество прямых, пересекающих Lj, есть цикл
Шуберта Oi (Li), то четырехкратное самопересечение а^ъ G (2, 4)
и дает нужный ответ, а именно:
а\ = a*-(ai.i + о^ == ai-(2a2.i) = 2.
В общем случае число прямых, пересекающих четыре и-плоско-
сти, нахоДяпщеся в общем положении в Р^"+^, задается
четырехкратным самопересечением а„ в G (2, 2га -J- 2), т. е.
(a„)* = (a^)2=(2a,„_j.,f = ra+l.
i=0
Подобным же образом число прямых в Р*, пересекающих
шесть 2-плоскостей, находящихся в общем положении, задается
самопересечением aj в G (2, 5); имеем
О'? = 0^1 (oi. 1 + 0^2) = 2а2.1-}-Оз,
поэтому а J = {2а 2^1 + Оз)^ = 4+1 = 5.
Универсальные расслоения
Пусть С" X (г (к, п) — тривиальное векторное расслоение
ранга п над G (к, га). Определим универсальное расслоение S ->-
-v G {к, га) как подрасслоение в С" X G (к, п), слоем которого
над каждой точкой А ^ G (к, га) является подпространство Л с=:
с=: С". Очевидно, S является голоморфным подрасслоением
расслоения С" X G (А;, га), а именно в каждом открытом множестве
Uj CZ G (к, га) вектор-строки нормализованной матрицы,
представляющей Л 6 C/j, задают репер в S над f/j; функции перехода
относительно зтих реперов определены в C/j П ^г' как gujuj, =
= Aj-AjK Факторрасслоение Q = С"/5 называется
универсальным факторрасслоением на G (к, п). Заметим, что при
отождествлении *: G {к, га)—»-G(ra — к, п) универсальное
подрасслоение на G (га — к, га) двойственно к универсальному факторрас-
слоению на G (к, п), ж аналогично Q -^ G {п — к, п) переходит
в двойственное расслоение S* —*-G (к, га). Отметим, в частности,
что универсальное расслоение 5 ->- G (1, га) ^ Р""^ совпадает
с универсальным линейным расслоением, упоминавшимся ранее.
Пусть теперь Е -*- М — произвольное голоморфное векторное
расслоение ранга к на комплексном многообразии М, V cz
CZ Я" (М, О {Е)) — векторное подпространство размерности га
5. Грассманианы 227
глобальных голоморфных сечений. Предположим, что множество
{о ix)}aev сечений а из У порождает слой Е-^ для всех х ^ М.
Тогда для всех х ^ М подпространство Л ж с: У сечений а 6 F,
обращающихся в нуль в х, является (га — А;)-мерным
подпространством, поэтому определено отображение
iv-. M-^G{n-k, V) = G {к, V*)
с £ = 1^5* и 7 = 1^ (Я« (G (к, га), 0 (5*))),
как и для линейных расслоений. Для явного задания зтого
отображения выберем базис а^, . . ., а^ в У и некоторый репер
ei, . . ., бй локально в Е. Тогда
и после соответствующего отождествления G (п — к, V) =
^ G (к, V*) отображение ly задается соответствием
(«И • • • ain>
: :
O-kl • •• "-Гт/
Отсюда очевидна голоморфность отображения ц-.
Как и в случае линейных расслоений, справедлива теорема
о вложении.
Теорема. Пусть М — компактное комплексное многообразие,
L —*- М — положительное линейное расслоение, а Е —*- М —
голоморфное векторное расслоение. Тогда при достаточно большом т
отображение ^^^jjn. определено и является вложением.
Доказательство. Большая часть работы уже проделана
благодаря теореме Кодаиры о вложении: на многообразии М имеется
положительное линейное расслоение, позтому можно считать,
что М с: Р^ — алгебраическое многообразие, а L ->- ikf —
расслоение гиперплоскости.
Очевидно, что отображение ij.0j,m взаимно однозначно, если
для всех X, у ^ М отображение ограничения
(*) НО{М, e{E^U^))-^(E®U^)^®{E®U')y
сюръективно. Аналогично, как и для линейных расслоений,
определено отображение взятия дифференциала
(**) Я^М, C(x{E®L^))-^Tf®{E®L^)^.
Отображение tj.0j,m будет гладким в точке х, если отображение
(**) сюръективно. Соображения компактности, использованные
15*
228 1, Комплексные алгебраические многообразия
В доказательстве теоремы Код аиры о вложении, применимы и здесь.
Согласно этим соображениям, для доказательства нужного нам
результата достаточно показать, что при произвольном выборе
фиксированных точек хну указанные выше два отображения
сюръективны при достаточно больших т.
Докажем это индукцией по размерности многообразия М.
Для любых точек х, у ^ М рассмотрим линейную систему
гиперплоских сечений многообразия М cz Р^, содержащих х и у.
По теореме Бертини обп1;ий элемент этой системы является гладким
вне базисного множества {х, у} данной системы. Кроме того,
после выбора подходяп1;его вложения можно считать, что общий
элемент этой линейной системы является гладким в точках х ш у.
Значит, существует гладкое гиперплоское сечение V = Н (] М
многообразия М, содержащее х ш у. Рассмотрим точную
последовательность
О-> ©if (£■ <8> L™-')-^©м (£■ <8> L™)-> ©v (£■ <8> L»)-> 0.
По теореме В существует такое тх, что Н^ {М, О (Е ® U"~^)) =
= О при т > mi, поэтому отображение ограничения
Я» {М, © {Е(8> /."»)) -> Я» (У, &{Е® U"))
сюръективно. С другой стороны, согласно предположенвю
индукции, существует такое т^, что при тп> т^ отображение
Я» (7, Qy {Е <8> L")) -^{Е® L"*), ® (Е ® L™),
сюръективно. Поэтому отображение (*) сюръективно при т >»
> 7П.0 = max {тп-х, т^.
Аналогично, для каждого множества кокасательных векторов
{©о}) порождаюпщх пространство TJ', можно найти гладкие
отперплоские сечения Va многообразия М, проходящие через х
и такие, что ©а не лежат в ядре естественной проекции Т%' (М) ->-
—>- Т%' (Va). Тогда по предположению индукции можно найти
такое Ша, что при т > т-а отображение
Я» (F„, J, {Е (8) L"*)) -> П' (F„) ®(Е® L™),
•сюръективно. Рассматривая последовательность
0-^©^ (Е <8) L™-i)-^ J,. м(£■ ® и") -^J., v^ (Е glL™)->0,
мы получаем, как и выше, что при mZ> т^ отображение
Я» (М, JЛ^ ® Ь™))-> ЯО (Fa. J« (^ ® Ь"))
5. Граеежанианы 229
сюръективно. Тогда при m > mj = max (mi, тПа) из
коммутативности диаграммы
ДЛЯ всех a сюръективность отображения (♦•) очевидна. []
Плюккерово влоокение
Мы завершим этот параграф описанием классического плюк-
керова вложения грассманиана G {к, п) в проективное
пространство, что проиллюстрирует теорему Код аиры о вложении и
теорему Чжоу. В качестве линейного расслоения на G (к, п),
задающего вложение, можно взять L = det S* = det Q. Подобно
метрике Фубини — Штуди на проективном пространстве можно
ввести на L подходящую метрику с положительной формой кривизны,
что доказывает положительность расслоения L. Однако мы зададим
плюккерово вложение непосредственно. Плюккерово отображение
р: G{k, ге)->Р(Л''С") = Р^*^
переводит й-плоскость A = C{i;i, ..., 1;^)с:С" в поливектор
^1 л ... л i;^. В базисе {е/ = ej^ л ... л ej. }#^_^д пространства Д ^С"
это отображение задается соответствием
Лн^[..., |Aj|, ...],
т. е. при данном соответствии однородными координатами
являются определители | Aj | всех к х А;-м1Шоров матрицы,
представляющей плоскость А. Отсюда следует, что (1) отображение р
голоморфно, и (2) отображение р переводит каждый цикл Шуберта вида
Oi (V) = {А е G {к, п): dim (А П ^п-О > П
в гиперплоское сечение для р (G {к, п)) cz P^^^' . Если А Ф
Ф А' ^G {к, га), то всегда можно найти такую {п — А;)-плоскость
У„-й, что А П Т^п-А =7^ (0). а А' П ^п-а = (0). Позтому
отображение р взаимно однозначно, а так как в каждом открытом
множестве Ut = {А: I Aj 1^0} описанные выше евклидовы координаты
задаются как отношения
«УА = \Aj.)+H |/|Лг I,
то отображение р имеет ненулевой дифференциал. Поэтому
плюккерово отображение является вложением.
230 1. Комплексные алгебраические многообразия
Теперь мы опишем уравнения, задающие образ G {к, V)
в Р i/\'^V) при плюккеровом вложении. Нам нужно найти
условия, при которых поливектор Л 6 J\'^V разложим, т. е. имеет вид
Л = ^1 л . . . л yft.
Поставим для этого более общую задачу: найти минимальное
линейное подпространство W cz V, для которого Л лежит в образе
отображения /\''W-^ Л*^- Если dim W = I, то I ^ к ж
равенство достигается тогда и только тогда, когда поливектор Л
разложим.
Напомним, что каждому ковектору v* 6 У* соответствует
операция свертки
iiv*): A'^V^ /\^-^V,
задаваемая формулой
(i (у*) Л, S> = <Л, V* л S>
при всех S 6 (Л*~^ Ю* = Л*"'^ У*- Сопоставим поливектору Л
линейные подпространства
Л-1- = {V* е V*: i (v*) Л = 0} с У*
и
W = Ann (Л-L) с V.
Лемма. W является минимальным подпространством в V, для
которого А лежит в образе отображения f\''W-*~ /\''V.
Доказательство. Пусть Wi, . . ., Wi — базис в W. Дополним
его векторами щ^^, . . ., ц„ до базиса всего V. Двойственный
базис в V* обозначим через {ш*, и^}. Пусть U = С {щ^^, ...
. . ., Un}. Тогда разложение в прямую сумму V = W ® U
индуцирует разложения поливекторов
/\''v ^ /\'^w ф (/\'^-^w ® U) ® (A^-^w ® А^и) ®
Мы хотим показать, что Л лежит в первом слагаемом. Запишем
компоненту Л во втором слагаемом как сумму 2 -^о ® "
где Ло € Л ^^- Так как
i (и*): f\'^-"^W <8> А^С^-^ f\^^-'"W <8) Д""' ^/
и i (uSi) л = о, то все Лд, = 0. Аналогично проверяется, что
равны нулю остальные компоненты поливектора Л в Д*"" W <2)
<8> A^f/ (m > 2). Следовательно, Л 6 Д* W.
Легко проверить, что W — минимальное такое
подпространство. □
5. Грассманианы 231
Рассмотрим теперь подпространство
W' = {we W: W А А = 0}.
Если поливектор Л разложим, то, очевидно, W = W. Обратно,
если Л неразложим, то dim W =- I >■ к и из невырожденности
спаривания Д*^ ® Д'"* W -^ /\^W следует, что W Ф W.
Позтому поливектор Л разложим тогда и только тогда, когда
W = W.
Используя двойственность, можно сформулировать это
условие двумя способами. В первом случае обратимся к оператору
i(H): f^^V-^V*,
который определяется для S 6 Д''*^ У* соотношением
{i (S) Л, V) = <Е, Л л V)
для всех V е V. Заметим, что, согласно определению линейного
подпространства Л-'-, для v ^ W левая часть равенства зависит
только от образа элемента S при естественной проекции
Дй+1у*_^ дЬ+1 (-J^) ^J\>^*ЦV*.
Следовательно, наше условие Л л и' = О для всех w ^W
эквивалентно условию: i (S) Л 6 Л-i- для всех S, которое в свою
очередь эквивалентно условию
(*) i (i (Е) Л) Л = О для всех S 6 /\'^■*■^V*.
Слева в соотношениях (*) мы имеем (k+i) квадратичных форм
от однородных координат Лг на р {G (к, V)); приравнивая их
нулю, находим классические плюккеровы соотношения. Итак,
Образ грассманиана при плюккеровом вложении р: G(k, V)-^
-V Р (Д*F) задается пересечением линейной системы
квадрик, определяемых соотношениями (*).
При другом подходе W можно охарактеризовать как образ
отображения Д*"^ V* -*- F, заданного по правилу
а-^i(S)Л, Ее л*-^V*.
Тогда условие W = W эквивалентно условию
(**) (i (S) Л) л Л = О для всех S с Д^-^ 7*.
Возьмем, например, бивектор
232 I, Комплексные алгебраические многообразия
Так как для v* ^V*
(г(1;*)Л)лЛ=|1(1;*)(ЛлЛ),
to условие (*•) эквивалентно условию
Л л Л = 0.
Ирн п = 4 ыы получим единственное уравнение
выражающее условие разложимости Л 6 iP (Л* С*) = Р".
Иными словами, G (2, 4) можно естественным образом отождествить
с неособой квадратичной гиперповерхностью в Р*. Дальнейшие
подробности, относящиеся к этому случаю, обсуждаются в
последней главе книги.
РИМАНОВЫ ПОВЕРХНОСТИ
И АЛГЕБРАИЧЕСКИЕ КРИВЫЕ
Основная тема настоящей главы — взаимосвязь между проек-
тивно-геометрическими свойствами алгебраических кривых и
внутренней структурой римановых поверхностей. Этот предмет,
первоначально изучавшийся с привлечением внешних понятий,
претерпел основательные изменения с введением понятия
абстрактной римановой поверхности. Тем не менее важнейшие аспекты
теории алгебраических кривых, как здесь будет показано, одни
и те же при обоих подходах. Большинство результатов этой
главы было сформулировано, если и не доказано, еще до наступления
нашего столетия.
Мы начинаем в § 1 с уточнения теоремы Кодаиры о вложении
в одномерном случае. Затем описывается локальная структура
отображений римановых поверхностей, которая тут же
используется для доказательства формулы Римана — Гурвица и
формулы для рода. Мы советуем читателю начать с § 2 и обращаться
к § 1 по мере необходимости.
В § 2 развивается теория абелевых интегралов, доказывается
теорема Абеля и ее обращение. Эта теорема наиболее удобна^
пожалуй, в случае эллиптических кривых. Именно в этом случае
она и была впервые установлена, и его обсуждением
заканчивается параграф.
В § 3 мы переходим к изучению линейных систем на кривых.
Одним из фувдаментальных результатов является здесь формула
Римана — Роха. Далее вводится понятие канонической кривой^
которая представляет собой инвариантно определенную
проективную модель негиперэллиптической римановой поверхности.
Важность понятия канонической кривой видна из геометрической
версии формулы Римана — Роха; еще полнее его значение
выясняется на протяжении остальной части главы. Изучение
специальных линейных систем на кривых мы начинаем с неравенства
Кастельнуово, которое дает оценку рода кривой заданной степени
в проективном пространстве. Следующее после этого обсуждение
гиперэллиптических кривых и вычислений Римана, которые дают
234 2. Риманови поверхности и алгебраические кривые
нам представление о зависимости римановых поверхностей от
параметров, подводит нас к решению проблемы Брилля — Нётера.
В § 4 и 5 основное внимание переносится на внешние свойства
кривых. В § 4 мы доказываем общие формулы Плюккера и
формулы Плюккера для плоских кривых. Между этими результатами
имеется существенное различие: общие формулы Плюккера
применимы к кривым в проективном пространстве произвольной
размерности, но относятся только к локальному поведению
кривой, в то время как соответствующее формулы для плоских
кривых описывают также и глобальные явления, такие, как двойные
касательные прямые и двойные точки, но применимы лишь к
кривым на Р^. Имеющийся здесь пробел частично восполняется в
следующем параграфе, где вводится мощньш вычислительный
аппарат соответствий, а в качестве приложения выводятся некоторые
-формулы из геометрии пространственных кривых. В обоих
параграфах применение проективно-геометрических формул к
каноническим кривым приводит к результатам о внутренней
структуре римановых поверхностей: в § 4 мы находим число точек
Вейерштрасса, а в § 5 решаем некоторые частные случаи проблемы
Брилля — Нётера.
В последних двух параграфах этой главы мы обращаемся
к изучению якобианов компактных римановых поверхностей.
Для начала в § 6 вводятся элементы теории абелевых
многообразий; основной темой здесь является теорема Кодаиры о вложении
в случае комплексных торов. В § 7 мы рассматриваем случай
якобиана кривой. Две замечательные теоремы Римана
показывают, сколь тесно связаны между собой специальные линейные
«истемы на кривой и геометрия ее якобиана. После этого мы
приступаем, наконец, к доказательству некоторых результатов,
относящихся к проблеме Брилля — Нётера. Глава заканчивается
доказательством теоремы Торелли, принадлежащим Алдреотти.
1. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
Влоокеиие римановых поверхностей
Пусть S — компактная риманова поверхность. В этой главе
всюду предполагается, что S связна. Если ds^ — некоторая мет-
-рика на 5 с (1, 1)-формой со, то форма da имеет степень 3 и
потому равна 0. Таким образом, каждая метрика на S кэлерова. Кроме
того, поскольку 3-лапласиан любой метрики перестановочен
с разложением по типам, то форма ф, записанная относительно
локальной координаты z = х -{- У —iy в виде
(f = р dx + q dy = а dz + ^ dz,
1. Предварительные сведения 235
является гармонической в том и только том случае, когда форма
ф!," = а dz голоморфна, а форма ф"»^ = р dz антиголоморфна.
Это имеет место тогда и только тогда, когда 9ф = 9ф = О, или, что
эквивалентно, тогда и только тогда, когда Лр = й°ф = 0. Если
^Ф = О, то локально ц) = df для некоторой С^-функции /. Поэтому
d'^ = d4f=-^{-^ + -^)dXAdy,
Т. е. форма ф гармонична в том и только том случае, когда /
гармонична в обычном смысле как функция одной комплексной
переменной. В частности, из зтого видно, что пространство
гармонических форм J^^ (S) не зависит от выбора метрики.
После умножения на подходящую константу можно считать,
что
S
для (1, 1)-формы <й метрики ds^. Тогда класс ко гомологии [со] 6
6 -ffDR (S) целочислен и по теореме Кодаиры о вложении
поверхность S вкладывается в проективное пространство Р^. В
действительности, как подсказывает доказательство упомянутой
теоремы о вложении, для римановых поверхностей имеет место более
сильное и проще доказываемое утверждение, которое приводится
ниже.
Пусть L ->- 5 — некоторое голоморфное линейное расслоение.
Напомним, что степень расслоения L определяется как его первый
класс Чжэня Ci (L) 6 Я* (5, Z) при отождествлении Н^ (5, %) =
= Z, определяемом естественной ориентацией на S. Если L =
= [D] для дивизора Z> = 2 "■iPi € Div (S), то deg L = 2 a» •
Как мы уже знаем, L имеет нетривиальное глобальное
голоморфное сечение только в том случав, когда с^ (L) > О, т. е.
degKO^H" (S, G (L)) = 0.
С другой стороны, так как образующая группы ff^ (S, Ъ) ^ 1,
соответствующая -f-1, представима положительной формой, то
расслоение L положительно <=> deg L > 0.
Таким образом, расслоение L (i) К% положительно, если deg L >
> deg Ks, и по теореме Кодаиры об обращении в нуль тогда
Я^ (5, в (L)) = Н^ {S, QI (L + ZS)) = 0.
Этот факт также следует из двойственности Кодаиры — Серра:
degZ, > deg Ks=> deg (Ks® L*) <.0=^
=^H4S, в{Ц)^НЦ8, G{Ks®L*)) = 0.
236 2. Римановы поверхности и алгебраические кривые
Рассмотрим теперь для произвольной точки р ^ S точную восде-
довательность
0-^G(L-p)-^e(L)XLp-^0.
Если deg (L — р) = degL — i> deg Kg, то Н^ (S, G (L —
— p)) = 0, откуда следует, что имеет место точная
последовательность
Я» (5, О (L)) ^Lp^O,
т. е. полная линейная система, соответствующая линейному
расслоению степени >deg ^g + 1. не имеет базисных точек. Более
того, при deg L > deg Kg + 2 из точных последовательностей
0-^е(L-2p)^e(L)%T'p* ф Lp-^0
и обращения в нуль
Я^ (5, 0(L-p- q)) = Я^ (S, G(L~ 2р)) = О
следует, что полная линейная система расслоения L задает
вложение ii,: S ->- Р^.
Подытожим полученное.
1. deg L <0=>1Р (S, О (D) = 0.
2. deg L > deg Ks =^ H^ (S, О (L)) = 0.
3. deg L > deg Ks + 2 =^ i^: 5 -»- P^ всюду определено
и является вложением.
Начиная с этого места, выражения компактная риманова
поверхность и гладкая алгебраическая кривая или просто кривая
употребляются практически как равноценные. Это не совсем
точно, так как гладкая алгебраическая кривая обычно
рассматривается вместе с дополнительной структурой — некоторым
вложением, т. е. как риманова поверхность S с линейным
расслоением L -^ S ш выделенньш подпространством Е cz Н° (S, О (L)),
но это не должно приводить к недоразумению. Важно то, что
мы имеем возможность представлять кривую поочередно то как
абстрактный аналитический объект — компактную риманову
поверхность, то как алгебраический объект — множество нулей
системы многочленов в Р^, а выражается это неявно в
использовании двух типов терминологии.
Из § 4 гл. 1 мы знаем, что многообразие хорд С (S)
алгебраической кривой 5 с: Р^ является замкнутым подмногообразием
в Р" размерности :^3. Проекция из точки р ^С (S) на любую
гиперплоскость Я с: Р^ задает вложение кривой S в Н ^ Р^~^.
1. Предварительные сведения 237
Поэтому всякую кривую можно гладко вложить в трехмерное
пространство Р*. Вложения кривой в Р* в общем случае не
существует. Однако для каждой гладкой кривой 5 с: Р' можно найти
такую точку р 6 Р*. которая не лежит ни на одной касательной
к 5 в Р', ни на одной прямой, пересекающей S более чем в двух
точках, а также ни на одной прямой, пересекающей S в двух
точках, через которые проходят пересекающиеся касательные. Тогда
проекция niplg: 5-> Р^ имеет всюду невырожденный
дифференциал и является 2-1-отображением в конечном множестве
изолированных точек; при этом образ Яр (S) а Р* будет плоской алгеб-
РП.С
раической кривой с единственными особенностями —
обыкновенными двойными точками, т. е. в окрестности особой точки кривая
Пр (S) представляет собой объединение двух пересекаюпщхся
в точке аналитических дуг с различными касательными. (Эти
рассуждения будут уточнены в § 4 настоящей главы.)
Отметим также, что проекцию Яр.* S — {р) -*- Р^-^ cz Р^
кривой iS сг Р^ из гладкой точки р ^ S п& гиперплоскость можно
продолжить по непрерывности, а значит, и аналитически на всю
кривую S, считая образом точки р точку пересечения ее
касательной с pw—1. Пересечение общей гиперплоскости Н cz pw-i и
образа Яр (5) совпадает с образом пересечения гиперплоскости Н, р cz
с: Р^ и iS — {р}, откуда
deg Яр (iS) • deg (яр) = deg 5 — 1
для гладкой точки р ^ S. Простейший пример такого
отображения — стереографическая проекция плоской коники С на прямую
из точки, лежащей на С (см. рис. 1).
238 2. Римановы поверхности и алгебраические кривые
Формула Тимана — Гурвица
Из элементарной топологии известно, что компактная римано-
ва поверхность S имеет всего лишь один топологический
инвариант, в качестве которого можно взять ее род
g(S)
h(S) _ -x{S)+2
или, как говорят, «число ручек»
В § 5 гл. О мы видели, что форма кривизны метрики на
голоморфном касательном расслоении 7" (5) = Ks есть в точности
произведение гауссовой кривизны этой метрики и формы объема,
деленное на ]Л—1. Тогда по классической теореме Гаусса —
Бонне
deg Ks = -X (S) = 2g-2.
Это один из вариантов формулы Римана — Гуреица. Его можно
установить также следуюпщм прямым способом. Пусть /: 5 -v
—>- iS" — голоморфное отображение компактных римановых
поверхностей. Тогда
и (Ш) = n-lS'l
где /#: Е2 {S, Z)-> Яг (S', Z) — гомоморфизм, индуцирован
ный на гомологиях; соответствующее целое число п называется
числом листов или степенью данного отобранкения. Для
произвольной точки р ^ S' обозначим через в форму кривизны
линейного расслоения [(р)1, ассоциированного с дивизором (р). В этом
случае /*в — форма кривизны линейного расслоения /* [(р)] =
= [/* (р)1 на S, и по предложению из § 2 гл. 1
de^/-(p)-ir(^e)_„J(^e)=„,
S S'
поэтому отображение / принимает всякое значение р 6 <S" в
точности п рае с учетом кратностей.
Для каждой точки р ^ S можно найти локальные параметры z
в окрестности р на 5 и и; в окрестности / (р) на 5', в которых
отображение / локально записывается в виде
W = z".
Число V называется индексом ветвления отображения / в точке р,
а сама точка р называется точкой ветвления, если i; (р) > 1.
Под дивизором ветлаения отображения / понимается либо дивизор
B='^(v{p)-i).p
pes
1. Предварительные сведения 239»
на 5, либо его образ
B'=^(v{p)-i).f{p)
pes
на 5'. Для каждой точки р ^ S' вьшолнены соотношения
/*(Р)= S V(q).q,
qerHp)
degf*(p) = n= S v(q),
где суммирование производится по различным точкам. Это дает
следующую картину поведения отображения /: оно является
неразветвленным накрытием вне точек ветвления отображения f
на 5', а в точке ветвления р ^ S индекса к склеивается к листов
данного накрытия.
При помощи степени и индексов ветвления отображения f
можно связать род поверхности S с родом поверхности S'.
Выберем для этого на iS" некоторую триангуляцию так, чтобы каждая
точка ветвления была одной из ее вершин. Поскольку / не
разветвлено вне 5, на iS определена триангуляция, открытые клетки
которой суть в точности связные компоненты прообразов открытых
клеток исходной триангуляции поверхности S'. Обозначим через
Со, Cj, Cj соответственно число нульмерных, одномерных и
двумерных клеток на поверхности iS". Тогда на S имеется ra-Cj
одномерных клеток и П'Сг двумерных. Кроме того, так как для любой,
точки р ^ S'
S v(q)=-n,
то ее прообраз состоит из
*(Г'(Р)) = И- 2 (V(q)-i)
деГНр)
различных точек. Следовательно, число вершин у выбраннов
триангуляции на S равно п-с„ — 2 (^ (?) — 1)> » ее эйлерова
характеристика равна
X(5') = re.Cg —n-Ci-l-n-Co-S №)—!) =
?es
= n.x{S')-^(v(q)-i),
qes
поэтому
^(5) = «(^(5')-l) + H-|-S(^:(?)-l)-
?6S
240 2. Римановы поверхности и алгебраические кривые
Можно также найти связь между каноническими расслоениями
поверхностей S ш S'. Пусть ю — глобальная мероморфная 1-фор-
ма на S', представленная локально в виде
A(w)
Для каждой точки р ^ S с индексом ветвления v можно указать
в ее окрестности на S координату z, относительно которой / имеет
вид W = z". Тогда
' Afz") A(z*
1(2") h(z
поэтому
ordp (/*(о) = V'ordffp) (ю) + (v — 1).
дто влечет за собой следующее равенство дивизоров на S:
(/*a)) = /*(a))+S(i;(p)-l).p,
pes
т. е.
Ks = f*Ks. + B,
deg Kg = /г. deg Ks' + Ц (v (p) — 1).
pes
Заметим теперь,, что всякую компактную риманову
поверхность S можно голоморфно отобразить на Р^. Если f ^ <Ж (S) —
щюизвольная непостоянная глобальная мероморфная функция,
локально записанная как отношение g/h с взаимно простыми
g V. h, то f задает отображение S на Р^ локально по правилу
Р *-* ^g {p)i h (р)]. Пусть /: iS ->- Р^ — такое отображение. На Р^
X (Р') = 2 = -deg Крг,
поэтому
X(5) = n.x(P0-S(i'(p)-l) =
pes
= —re.deg^pi— 2 {v{p) — i)= —degRg.
pes
Итак, для любой римаяовой поверхности S
deg Ks = -X {S) =^2g~ 2,
и тем самым формула Римаяа — Гурвица установлена.
1. Предварительные сведения 241
В дальнейшем при ссылках на формулу Римана — Гурвица
мы подразумеваем одну из следующих формул:
degZs = 2^—2,
l{S) = nt{S')-Yi{v{q)-i),
qes
в заключение сделаем два замечания об отображениях f: S -*-
-V iS" компактных римановых поверхностей: во-первых, общее
число точек ветвления / с учетом кратностей всегда четно;
во-вторых, g (S) '^ g (iS")j если / не постоянно. Последнее следует также
из того, что на римановой поверхности рода g имеется ровно g
линейно независимых голоморфных 1-форм. Действительно,
отображение /*: Я* (S', Qs') ->■ -ff" (S, й|) инъективно, если /: S ->-
-V iS" не постоянно, откуда g (S) '^ g (S').
Формула для рода
Здесь мы дадим три доказательства формулы для рода,
позволяющей вычислить род гладкой плоской кривой по ее степени.
Начнем с топологического доказательства. Пусть S cz Р^ —
гладкая кривая степени d, заданная на Р^ как множество нулей
однородного многочлена F (Z^, Z^, Zg) степени d. В евклидовых
координатах z^ = ZJZq, z^ = Z^IZ^ на C^ с: P* она определена
уравнением
/ (Zi, Za) = F (1, Zi, Za).
Выберем точку p 6 P^, не лежащую на S, и прямую Н, не
содержащую р. При помощи подходящей линейной замены координат
можно добиться, чтобы
р = [О, О, 1], Н = {Z^ = 0).
Кроме того, можно предполагать, что бесконечно удаленная
прямая L (Zq = 0) не касается кривой S.
Рассмотрим проектирование я^: 5 -v Р^ кривой S из точки р
на Н. В качестве локальной координаты на iS в окрестности точки
q^ S с (df/dz^) (q) Ф О можно взять координату z^, поэтому данное
отображение не разветвлено в таких точках. Если же {dfldz^ (g) =
= О, то (df/dzj) (q) Ф О ш Z2 — локальная координата в
окрестности g на 5. Выразив z^ = z^ (Zj) как функцию от Za на 5, напишем
соотношение
/ (Zl (Z2), Zjs) S О,
16-046
242 2. Римановы поверхности и алгебраические кривые ^^
откуда ПО правилу дифференцирования сложной функции имеем
Sf , ^^.4^^o на 5.
dza dzi dza
Следовательно, порядок нуля функции dzjdzz в точке q, равный
уменьшенному на 1 индексу ветвления v (q) отображения Пр
в точке q, совпадает с порядком нуля df/dzg в д ^ S, т. в. с
кратностью пересечения кривых 5 и (df/dz^ = 0) в точке q. Степень
кривой (dfldzg = 0) ') в Р^ равна d — 1. Поэтому ее индекс
пересечения с 5 равен d (d — 1). Поскольку все точки пересечения
S П (df/dz2 = 0) лежат в конечной части плоскости (Z^ ф 0),
^(v(q)-i) = d(d-i).
Число листов проекции Яр равно d, так как [S] = ёЛЮ
в Н^ (Р*, 1). По формуле Римана — Гурвица
X(5) = d.x(P)-S (v{q)-i) = 2d-d(d-i},
lis
и, следовательно,
Второй способ получения этой формулы основан на формуле
присоединения из § 2 гл. 1. По этой формуле
Ks = Kp2\s® Ns = {Крг + 5) Is.
Из того же параграфа известно, что Кр^ == — SH, sc S = dHy
откуда Kpi + S = {d—Ъ)Н на Р^. Поэтому
X('5)=-degЛ:s=-*(5•(d-3)Я) = -d(d-3>
g(5) = lz:li^^ (^-1Ж-2) ^
Третий способ вычисления g'{S) использует отображение
вычета Пуанкаре. Напомним (см. стр. 162), что для мероморфнон
2^формы (О на Р^ с полюсом первого порядка вдоль 5 и голоморф-'
ной на Р* — 5, представленной локально в виде
вычет Пуанкаре i? (ю) определяется как
■^) Под {dfldz^ = 0) авторы подразумевают проективное замыкание
аффинной кривой с уравнением dfldz^== G в Р^.— Прим. перев.
1. Предварительные сведения 243
Напомним также, что в этом случае отображение вычета
Пуанкаре задает изоморфизм
Я» (P^ Q^ {S)) -^ IP (S, 01).
Рассмотрим теперь форму ю 6 Я* (Р^, Q^ (S)), записанную
как выше. Форма dzi л dz2 продолжается до мероморфной]^2-фор-
мы на Р^. Так как Кр2 = —ЗЯ, а форма dzi л dzj не обращается
в нуль и голоморфна на Р^ — L, то dzj^ л dz^ имеет полюс
порядка 3 вдоль прямой L. Аналогично, / продйлжается до функции,
мероморфной на Р*, с полюсом порядка d вдоль L, так как / —
многочлен с простым нулем вдоль кривой степени d на Р^ — L.
Из всего этого следует, что многочлен g продолжается до
мероморфной функции с полюсом порядка ^ d — 3 вдоль L, т. е. g
должен иметь степень ^d — 3 по z^, z^. Итак, голоморфные i-фор-
мы на S суть е точности дифференциалы вида
где g — произвольный многочлен степени ^ d — 3. Мы знаем
уже, что число одночленов степени ^ d от /г переменных равно
("+''). Поэтому g (S) = /г" (S, Q^) = C^-i) = ^d-i)^d-2)^
Позже мы увидим, как распространить эту формулу на
некоторые особые кривые.
Случаи g==0, 1
Пусть сначала 5 — произвольная компактная риманова
поверхность рода 0. Тогда
h^ {S, G) = hP{S, Qi) = 0.
Сопоставим любой точке р ^ S линейное расслоение L = [р].
Тогда из длинной точной последовательности когомологий,
соответствующей точной последовательности пучков
0-^Gs-^ GsiL)-^ Lp^O,
видно, что расслоение L имеет глобальное сечение, не равное
нулю в точке р, т. е. на S существует непостоянная мероморфная
функция /, голоморфная вне р и имеющая простой полюс в р.
Но всякая такая функция, продолженная в р значением оо,
принимает каждое значение А, в точности один раз, а потому
задает изоморфизм /: 5 ^- Р*. Итак,
Всякая компактная риманова поверхность рода О является
римановой сферой Р^.
244 2. Римановы поверхности и алгебраические кривые
Рассмотрим теперь кривые рода 1. Полное их описание мы
сможем дать лишь в следующем параграфе, а пока докажем, что
всякая компактная риманова поверхность S рода 1 реализуется
в виде неособой кубической кривой на Р^.
Это утверждение доказывается без труда: нам известно, что
deg ^s = О, а потому, согласно теореме о вложении в случав
кривых, полная линейная система, отвечающая линейному
расслоению L = [Зр] для любой точки р Q. S, вкладывает S как
кубическую кривую в Р^, где iV = А" (5, О (L)) — 1 ^ 2. Но
элементам пространства Я" (5, О {L)) соответствуют мероморфные
функции на 5, голоморфные на 5 — {р} и имеющие в р порядок
^—3. Каждая такая функция однозначно определяется своей
главной частью в точке р:
«0 +
а по предыдущему не существует мероморфных функций с одним
простым полюсом в р, ибо такие функции задают взаимно
однозначные отображения S на Р^, откуда /i* (5, 0 (L)) ^ 3.
Следовательно, h" (5, О (L)) = 3, и мы установили требуемое.
Однако в этом случае стоит также провести явную
конструкцию вложения. Начнем с одного важного общего факта.
Лемма (теорема о вычетах). Пусть ф — мероморфная i-форма
на компактной римановой поверхности S с дивизором полюсов
ai+ . . . -\- аф Тогда 2 ^^^а- (ф) = 0.
1 '
Доказательство. Окружим точки а^ е-дисками В^ (а^). По
теореме Стокса
О
= - J d(p= J ф = 2я1/-1 2Не8а^(ф). D
S-[JBg(.ai) d^UB^ia^)
Применяя это к форме ф = df/f, мы снова убеждаемся, что
число полюсов мероморфной функции / на 5 равно числу ее нулей.
Вернемся к римановой поверхности S рода 1. Как уже
отмечалось, на S нет непостоянных мероморфных функций с одним
простым полюсом в р. С другой стороны, по теореме об обращении
в нуль
т (5, в (р)) = 0.
Поэтому точная последовательность
О __ 0 (р) _>. О (2р) ^ Ср -»- О
1. Предварительные сведения 245
указывает на существование мероморфной функции F sa S с
двойным полюсом в р, голоморфной в остальных точках. Далее,
А» {S, Q1) = g (5) = 1,
т. е. на S имеется ненулевая голоморфная 1-форма ю. Так как
deg Ks = deg (ю) = О, то форма ю всюду отлична от нуля.
Рассмотрим мероморфную форму F- ю. Она голоморфна на 5 — {р}
и по теореме о вычетах
Resp {F-a) = 0.
Следовательно, разложение в ряд функции F по любому
локальному параметру z в окрестности точки р после умножения и
добавления подходящих констант принимает вид ^)
F{z) = ^ + li].
Рассмотрим теперь на S мероморфную функцию dF/a. Так
как форма ю нигде не обращается в нуль, то dF/oi голоморфна
на iS — {р} и имеет полюс порядка 3 в точке р. Для подходящих
констант Я,, X', X" определим такую функцию
[F'^X^ + X'F + X",
что /^' (z) = р- -|- [1] в окрестности точки р.
Отображение ii,: S -*- Р*, отвечающее линейному расслоению
L = ISp], можно задать сопоставлением q <-*- [i, F (q), F' (q)].
Вблизи точки p имеют место разложения
Поэтому мероморфная функция
F' (z)2 + c'F' (z) - F {zf + (c" -c)F (z)
голоморфна вне p и имеет не более чем простой полюс в точке р,
а значит, постоянна. Образ S относительно вложения ij, в
соответствии с этим совпадает с множеством решений уравнения
у^ -\- с'у = 3? -\- ах + Ъ',
1) HanoMHZM, что [d] обозначает сужму членов ряда порядка > d.—
Прим. перев.
246 2. Римановы поверхности и алгебраические кривые
где X = Zi/Zq, у = Zi/Zo — евклидовы координаты на Р^. После
подходящей аффинной замены координаты у это уравнение
принимает вид
у^ = а^ + ах + Ь.
Производя затем аффинную замену координаты х, переводящую
два корня многочлена ж*+аж+Ь^)вОи1, мы видим, что
всякая кривая рода 1 есть множество решений кубического уравнения
(*) y^ = x-{x-i).(x-X)
на Р^ с некоторым А, £ С.
Отметим, что по предыдущему риманова поверхность рода 1
определяется значением одного параметра А, из правой части
уравнения (*). Поскольку фактормногообразие С/Л комплексной
плоскости С по любой решетке Л с: С ранга 2 является римано-
вой поверхностью рода 1, а для классификации таких решеток
Л с: С с точностью до автоморфизма плоскости С требуется лишь
один кЬлшлексный параметр, то можно ожидать, что все кривые
рода 1 реализуются в виде С/Л. Как мы убедимся в следующем
параграфе, это действительно так.
В заключение отметим, что мероморфные функции на 5 =
= С/Л — это то же самое, что мероморфные функции на всем С,
периодические относительно решетки Л.
2, ТЕОРЕМА АБЕЛЯ
Теорема Абеля — олабал форма
Неопределенные интегралы вида
W f ^—ff
легко находятся в замкнутой форме; более того, для любой
рациональной функции R интеграл
f R {x,jyx^ + ax + b) dx
представим в замкнутой форме, включающей только элементарные
функции. Способ нахождения интегралов такого типа был известен
со времен зарождения математического анализа. Однако долгое
время математиков ставили в затруднение интегралы вида
J yx^-{-ax^-{-bx-{-e
^) Эти корни различны, так как ij, (S) — гладкая кривая.— Прим.
перев.
2. Теорема А беля 247
а тем более общие абелевы интегралы
j R (X, у) dx,
где R — рациональная функция, а ж и у — переменные,
связанные полиномиальным соотношением / {х, у) = О степени >2.
Одна из причин возникающей здесь трудности легко
обнаруживается при помощи формулы для рода из предыдущего
параграфа. Интеграл (*) можно рассматривать как криволинейный
интеграл
ds
Т
1т
мероморфной формы dx/y на кривой С, заданной в евклидовых
координатах х, у на Р^ уравнением у^ ^ х^ -\- ах -{-'Ъ. Кривая С
является коникой и, следовательно, изоморфна Р^ при некотором
полиномиальном отображении. Пусть t = i (ж, у) — евклидова
координата на Р^. Тогда мероморфная форма dx/y на С принимает
вид R (t) dt на Р^, где R — рациональная функция. Итак, для
точек (Же, Уа), (xi, у^) g С имеем
(«1. й) J(«i.'"yi)
1 t= 1 '^W'*
(«о. Уо) '(«о, Уо)
И последний интеграл находится без особого труда. Отметим
также, что, поскольку риманова сфера Р^ однос1|язна, а форма
dx/y замкнута, зависимость этого интеграла от выбора пути
проистекает только из вычетов формы dx/y, которые легко
вычисляются.
Аналогично, интеграл (**) есть криволинейный интеграл
формы dx/y на кубической кривой С = (у* = ж* -Ь ах* + Ьх + с)>
Однако теперь если С — гладкая кривая, то по формуле для
рода ее род'равен 1, и поэтому она не может быть параметризована
одной мероморфной функцией. Следовательно, для интеграла
{**) нет столь простого выражения, как данное выше для
интеграла (*). Более того, топологически кривая С является тором,
а значит, неодносвязна. Поэтому интеграл
Q
{i£
J у
р
корректно определен только по модулю периодов формы dx/y,
т. е. интегралов dx/y по замкнутым путям у ^ Hi {С, %). Точнее,
по предыдущему параграфу форма ю = dx/y голоморфна всюду
на С и, значит, порождает пространство IP (С, 0,^). Пусть у^, у^—
^i48 2. Римановы поверхности и алгебраические кривые
замкнутые пути на С, классы которых являются образуюнщми
группы Hi (С, Z) S Z ® 1. Обозначим через
ai = j (О, Яг = j <»
соответствующие периоды ю. Тогда все периоды формы со на С
имеют вид /1'% -\- т-а2, п, т^Ъ. Если бы а^ и а^ были линейно
зависимы над IR, то для некоторых к^, к^ 6 IR. не равных нулю
одновременно, выполнялось бы соотношение
/ci \ ш + ^2 \ (О = О,
а также соотношение
Л» f (о+Ла f (0 = 0.
Vl V2
Но формы (ВИЮ порождают пространство Я*»<'(С) ф Я<'П(С) =
= jffi)R(C), поэтому отсюда следовала бы зависимость
^1 [yJ + К \.1^ = О € Я1 (С, R),
что невозможно. Итак, а^ и Og линейно независимы над R.
Поэтому периоды Л = {/1-% + "I'ajn, mez *^ С формы со на кривой С
образуют решетку в С. Теперь мы видим, что значение интеграла
р
Ро
хотя и не вполне определено как число, определено однозначно
как точка комплексного тора С/Л.
Первый важный шаг на пути к пониманию интегралов этого
типа был сделан Абелем в 1826 г. Абель заметил, что, в то вреьш
как рассмотренный выше конкретный интеграл представляет
собой весьма неудобоваримую функцию точки р = (х, у) на
кривой С, качественное поведение более общих абелевых сумм
2J
Pi
(О
Рк
подчиняется достаточно простым соотношениям. Частным случаем
того, что доказал Абель, является следующее утверждение. Для
рассмотренных выше кривой С и формы со и любой прямой L а Р'
обозначим через рх (L), р^ {L), рз {L) три (с учетом кратностей)
2. Теорема Абеля 2А9
ТОЧКИ пересечения L с С (порядок этих точек, конечно, не вполне^
определен). Обозначим через i|j (L) абелеву сзшму
3 Pi
>|5(L)=2 j»-
i=l Po
Как и ранее, i|j (L) определено однозначно по модулю периодов Л
формы (О. Тогда справедлива
Теорема Абеля (слабая^форма).
ijj (L) = const (mod Л).
Доказательство. Современный вариант доказателы:тва
обманчиво прост. Рассмотрим отображение
ц,: р2* ^ с/Л
пространства прямых Р^* из Р^ на комплексный тор С/Л.
Очевидно, что оно голоморфно. Пусть Z — евклидова координата на С/Л^
& dz — соответствующая глобальная 1-форма. Тогда, так как
Н^,о (р2) = JP (р2^ Q1) == о, то i|j* dz = О, и, следовательно^
ijj постоянно. Ij : .
Аналогично доказывается незначительное обобщение этогО'
результата. Пусть опять С — кривая рода 1, «) 6 -ff" (С, й^) —
голоморфный дифференциал, Л ci С — решетка периодов для ю.
Обозначим через D = (f) = 2рг — Ззг дивизор мероморфной
функции f п& С. Тогда
Pi
2 { «в=0 (mod А),
Т. е. существует набор путей ttj из qi в pi, для которых
Доказательство. Для точки А,= [Яв, ^J 6Р* положим Dx=^
= (A,o/-A„) = SPi(^)-23i(A.) и
250
2. Римановы поверхности и алгебраические кривые
«Функция a|) задает голоморфное отображение Р^
<и выше,
а|)* dz е Я« (Р\ QJji) = О =^ i|j = const.
С/Л. Как
'Так как (р^ (А,)} -^ {qt (А,)} при А,о ^- О, то i|j ^ О (mod Л). Q
После некоторых предварительных замечаний о формулах
взаимности мы докажем обращение теоремы Абеля (в слабой
■форме) для случая римановых поверхностей произвольного рода.
■Этот результат вместе с формулой Римана — Роха является
важнейшим средством изучения алгебраических кривых.
Пусть S — компактная риманова поверхность рода g, и пусть
■Ьх, . . ., b^g — базис группы Н^ {S, 1), состоящий из 1-циклов
на S. Можно считать, что б^, . . ., b^g представляют канонический
базис, т. е. такой, что б^ пересекает bi+g с индексом пересечения
+ 1 и не пересекает остальных б^. Для такого канонического
■базиса циклы б^, . . ., 6g называются А-циклами, а 6g+i, . . ., b^g
называются В-циклами.
Пусть щ, . . ., (ug ^ IP {S, Q^) — базис пространства
голоморфных 1-форм на S. Матрица периодов поверхности S — это
:g X 2^-матрица
!'«*••• J
Q =
«в.
ig
jco,... j
«в.
»s
Транспонированные вектор-столбцы П^ =| \ (Oj, . . ., | •в^) 6 С*
«г «г
матрицы периодов называются периодами. Проверим прежде
всего, что они линейно независимы над Щ. Если S^i^i = Oj
ifej € IR (и Aj не равны О одновременно), то
2 ^г \ (Oj = О для всех j => ^kf\ (л^ = 0 для всех / =>
^2*г[бг]=0бЯ1(5, R).
Но так как {(Bj, atj} порождают пространство jffbR ("S*)» то это
невозможно, ибо {6j} — базис в Я^ {S, Ъ).
Итак, 2g периодов Hi 6 С^ порождают решетку
Л = {mjli + . . . -Ь m^glL^g, lUi 6 Z}
2. Теорема А беля 251
В С^. Определим якобиево многообразие, или якобиан, f (S)
поверхности S как комплексный тор С^Л. Якобиан —
естественная область значений для абелевых интегралов: в то время как
интеграл \ ю одной голоморфной дифференциальной формы ю
р
определен лишь по модулю 2g периодов со, которые обычно всюду
плотны в С, вектор
ч ч
однозначно определяет точку в С^ по модулю дискретной решетки
Л с: С«. Выбрав базисную точку Pq ^ S, зададим естественное
отображение уи S ^>- f (S) по правилу
Л(Р) = (] co„...,ij(o,)6|f(5)/
Ро Ро
Более общо, пусть Div" (S) обозначает группу дивизоров
степени О на S. Определим ц: Div" (S) -^ 'f (S), полагая
Рх, Рл,
?j SSx.
Чтобы изучать это отображение, необходимо узнать кое-что
о соотношениях между периодами форм coj. Они отражены в зако-
нах|взаимности, один из которых мы сейчас установим.
Первый закон взаимности и его следствия
Прежде всего предположим, что все циклы б; на римановой
поверхности S выходят из общей точки Sq ^ S. Дополнение ко
всем 6j является односвязной областью А в S. Как изображено
на рис. 2, граница дА содержит каждый 6j дважды с
противоположными ориентациями. При этом мы получаем не что иное,
как известное топологическое представление поверхности рода g
в виде многоугольника с попарно отождествленными 4g сторонами.
Пусть теперь со — голоморфный дифференциал на 5, а т| —
мероморфная форма, все особенности которой являются простыми
полюсами в точках Sx ^ S. Предположим, что т| не имеет полюсов
ни на одном б,-. Обозначим через П* и N^ соответственно периоды со
252
2. Римановы поверхности и алгебраические кривые
• Рг Д
Рис. 2
Рис. 3
и т| вдоль пути 6j-. Поскольку область А односвязна, а форма со
голоморфна, интеграл
г
n{s)= \ (О
»0
определяет функцию я, голоморфную на А, с со = йл (рис. 3).
Заметим, что для любой пары точек р ^ 6j, р' ^ 64' на дА,
совпадающих на S,
р- «id) р-
л.{р') — к{р)=\ ш= j Cu-f- j С0+ j ^= \ Cu = n«+\
p p ug^t »i(») »г+г
Аналогично, для p g 6^+^ p' ^ 8g+i, совпадающих на S,
n(p')-n(p) П*.
Рассмотрим мероморфную 1-форму л-т| на Д. Так как т| имеет
лишь простые полюсы, то по теореме о вычетах
j л-т1 = 2л/-1 ^В.ва,^{к»г\) = 2пУ-i 2Res,,^(л)• j «•
9Л
»0
С другой стороны, интеграл формы л-т) по 5А можно вьгаислить
явно, рассматривая попарный вклад сторон 6j и б^* границы 5А.
Так как для точек р ^ bi ж р' ^ б^', совпадающих на 5, разность
я (/?') — л (р) постоянна и равна П***, то
j л.т]=—П«+* JT|=-n«+*-7V*.
2. Теорема Абеля 253
Аналогично,
Сравнивая оба_^выражвния для V л-т|, мы получаем
эд
Закон взаимности I.
g *Х,
1=1 ^ «о
г5е интегралы справа берутся по путям из А.
Это известный закон взаимности для дифференциалов первого
и третьего рода. Согласно классической терминологии,
дифференциалом первого рода на римановой поверхности S называется
голоморфная 1-форма, дифференциалом второго рода — мероморф-
ная 1-форма без вычетов, а дифференциалом третьего рода —
мероморфная форма, допускающая только простыв полюсы.
Очевидно, что дифференциал имеет первый род в том и только том
случае, когда он является одновременно дифференциалом второго
и третьего рода. Вскоре мы увидим, что любая мероморфная
1-форма представима в виде суммы дифференциалов второго
и третьего рода. Позже мы докажем закон взаимности для
дифференциалов первого и второго рода.
Мы сможем применять закон взаимности только после того,
как докажем один аналогичный результат, который позволит
нормализовать наш базис в Zf" (5, й^). Пусть со, со' — две
голоморфные 1-формы на 5, а П* и П'* соответственно — их периоды
по путям 6j. Для рассмотренных выше А и я проинтегрируем
форму я- со' по 5А. Внепшяя производная этой формы равна
<^(Я'Сй') = йя л со' = со Л со', поэтому, согласно теореме Стокса,
1 я-Сй'= 1 (ол со'.
9Л S
Вычисляя затем криволинейный интеграл так же, как и при
доказательстве закона взаимности, получаем, что
I (олсй'-2(П*-П'*+*-П*+«П'*).
S
В частности, для со' = со отсюда следует неравенство
8
(*•) о<"|Л^Т j сйлш="|Л^12 (п'-п*+*-да+Ш')
S 1=1
254 2. Римановы поверхности и алгебраические кривые
При £0^0, так как тогда форма ]/—IcoAco положительна;
Поэтому любая голоморфная i-форма со, все А-периоди которой
равны нулю, сама тождественно равна нулю, т. е. первый g X g-
минор матрицы периодов й невырожден. Зная это, можно так
выбрать базис соц . . ., cOg в Я" {S, Q^), что|^
^wj=8ti [дляК1<<, j^g,l
т. е. так, что матрица периодов примет вид {Ig, Z). Такой базис
в Я" {S, й^) называется нормализованным (или стандартным).
Теперь вернемся к закону взаимности и выведем некоторые
его следствия. Рассмотрим вначале случай, когда т| — со' —
голоморфная 1-форма. Обозначим через П'* периоды формы со'.
Поскольку со' не имеет выт1етов, закон взаимности дает
соотношение
8
V (ШП'«+*»-Ш+*П'*)=0.
*=1
Это первое билинейное соотношение Римана для периодов. В
частности, если со = coj, 0)' = со^ — векторы нормализованного
базиса, то все, кроме двух, члены предыдущего выражения равны
нулю, откуда
J со^— J cuj = 0,
Vj Vj
т. е. правый блок Z написанной выше матрицы периодов
симметричен. Заметим, что квадратичная форма на Я" {S, Q^),
заданная формулой
{Щ, Сй^) = "|Л^ jojA Сй^ = "|Л—1 j (xtj — Y—i j Cui =
= 2Im [
Cй^,
положительно определена. Поэтому мнимая часть Im (Z) матрицы
Z положительно определена. Это второе билинейное соотношение
Римана. В итоге из двух билинейных соотношений Римана
следует, что для нормализованного базиса в Я" {S, Q^) матрица
периодов Q для S имеет вид
Q = (/* 2) с Z = % 1ш Z > 0.
2. Теорема Абеля 255
Теорема Абеля — окончательная форма
Пусть S, как и ранее,— риманова поверхность рода g, а. D ^
=* 2 (Pi. ~ 4i.) — дивизор степени О на S. Рассмотрим абелеву
сумму
«X, «я.
Теорема Абеля в случае g = i утверждает, что если D —
дивизор (/) мероморфной функции / на 5, то {х (Z)) = 0. Этот
результат нетрудно обобщить на случай любого рода g. Пусть D = (/)^
Тогда отображение
Пространства Р^ в j^ {S) голоморфно. Но голоморфные 1-формьк
dzi на комплексном торе j^ {S) порождают кокасательное
пространство в каждой его точке, поэтому
■ф* {dZi) ^ О =4» ijj постоянно =ф- {X (Z)) = oj) (0) = ij; (ро) = 0.
Мы покажем теперь, что верно и обратное: если Z) = 2 (Ря. —
— 9х,) — произвольный дивизор степени О на S и \у, {D) = О, то Z>
является дивизором мероморфной функции.
Проблема, кажущаяся на первый взгляд трудной, упрощается,,
если свести вопрос о существовании мероморфной функции к
вопросу о существовании некоторой мероморфной формы. Для этого
заметим, что если / — мероморфная функция с (/) = 2 (Рх, — ЯО^
то дифференциал
"- dlog/ = ——7==--г
' 2я/—1 2я/ —1 /
является мероморфной формой с дивизором полюсов
(^)=o=-(S;'x + S?0 (1>
где теперь -D = У] вх./'л, ~Ь S^х,?*, с различными р^,, q^. Более-
того,
) печ (з>
V
256 2. Римановы поверхности и алгебраические кривые
ДЛЯ любого замкнутого пути у п& S — {рх,» ?х,}- Обратно, для
мероморфной формы т| с зтими тремя свойствами, полагая
р
f{p) = e Ро ,
мы корректно определим мероморфную функцию / с (J) ^ D.
Итак, чтобы доказать обращение теоремы Абеля, нужно показать,
что для дивизора D = 2ах,/»х, + З^я.?*. с М-Ф) = О существует
дифференциал третьего рода т|, голоморфный на 5 — {ря,, дх},
с вычетами aJ2n "j/^—1 в />»,, bj2n]/^—i. в gx, и имеющий
целочисленные периоды. Для начала проверим, что можно по крайней
мере найти мероморфный дифференциал с требуемыми особенно-
■стяии.
Лемма. Пусть {р^,} — конечное множество точек на S, и пусть
Лх, — такие комплексные числа, что У]ах = 0. Тогда на S
существует дифференциал третьего рода, голоморфный на S —
— {Pi} " имеющий вынет а^ в каждой тлчке рх-
Доказательство. Рассмотрим на S точную последовательность
пучков
О ^ £21 ^ £21 (2 i?0 ^ Ф Ч ^ 0.
По двойственности Кодаиры — Серра
т {S, Qi) ^ Я» (5, 0) ^ С;
значит, образ пространства Н" {S, Q^ (Si'x.)) в ® Ср^^ имеет
коразмерность не более 1. Но, как нам известно, сумма вычетов
любой мероморфной 1-формы на S равна нулю. Следовательно,
образ W {S, Q^ i^Pi)) содержится в гиперплоскости {^а^ = 0) с:
с: Ф Cpj^ и по предыдущему совпадает с ней. g
Выберем теперь канонический базис б^, . . ., бг^ в Я^ (5, Z)
(см. выше), такой, что ни одна из точек рх, Qx не лежит ни на
одном пути б^. Пусть о»!, . . ., (ug — нормализованный базис
в IP {S, £2^) относительно {6^, . . ., ба^}. По доказанной лемме
существует дифференциал третьего рода с вычетами aj{2n У^—1)
в />»,, bJ(2nY—1) в q^. Любые две из таких форм различаются
на голоморфную форму на S. Следовательно, существует
единственная такая форма т| с ^-периодами
ЛГ'=|т, = 0, i = l,
2. Теорема Абеля 257
Задача состоит теперь в таком изменении т), после которого
все JS-периоды стали бы целыми. Сделать это так, чтобы не
испортить особенности т| и не нарушить целочисленность Л-периодов,
можно лишь путем добавления целочисленных линейных
комбинаций форм со J. Покажем, что это возможно. Для этого по закону
взаимности определим JS-периоды формы т|. Так как 7V' = О для
г = 1, . . ., ^, то для каждого такого i
При подходящем выборе путей а^,, соединяющих попарно
отрицательные точки дивизора D с положительными ^). По
предположению
}х(£>) = (2 j coi, .... 2 J «г)бЛ,
2г
т. е. существует цикл 7~ S ^k'^ki "^ьб^^, такой, что
2 ) fuj-= I cOj- для каждого i, а значит,
7V^+'= \ (Oj для всех i.
у
Возьмем
g
Периоды iV" формы т|' задаются равенствами
N'^=—mg+t, i = i,...,g,
g
= 2 ntfe j «4 — 2 Щ+k j «fe =
''=1 Vfe V«
1) Заметим, что для разных способов соединения периоды (2 J Mi, ..
^ «X,
., У! J cOg) различаются на вектор решетки Л.— Прим. перев.
X а^_
258 2. Римановы поверхности и алгебраические кривые
ПО первому билинейному соотношению Римана. Значит, г\' имеет
р
целочисленные периоды жВ = (f) дляi(p) = ехр [2л]/ —1 [ л')•
Ро
В итоге доказана
Теорема Абеля (окончательная форма). Пусть D = ^ (р^ —
— Чк) 6 Div (S) — дивизор степени О и со^, . . ., (о^ — базис
пространства голоморфных i-форм на S. Тогда D = (/) для некоторой
мероморфной функции f на S в том и только том случае, когда
Pi. Рк
}х(£>) = (2 jcOi,...,E 1«.) = 0(Л)-
Если пользоваться более модным языком и вспомнить, что
Pic" (S) обозначает группу классов дивизоров степени нуль на S
по модулю линейной эквивалентности, то мы получили следующее:
отображение уь: Div" (S) -^ f (S) разлагается в композицию
Div»(5) ^ J(S)
\ Л
Pic<'(S)
и задает вложение {х: Pic" (S) -^ f (S).
Обращение Якоби
При доказательстве теоремы Абеля возникает следующий
вопрос: сюръективно или нет отображение ц: Div" {S) -^ f (S),
или, иначе говоря, является ли изоморфизмом индуцированное
отображение ~yi,: Pic" (5) -^ f (S)? Теорема обращения Якоби
утверждает, что это действительно так и, более того, что
доказательство этого факта получается с помощью подсчета параметров.
Теорема (обращения Якоби). Пусть S — кривая рода g, ро 6
^ S — фиксированная точка и со^, . . ., со^ — базис в Н" {S, й^).
Тогда для любого X ^ f {S) существует g точек р^, ■ ■ -, Pg ^ S,
таких, чтл
(*) M'(II(i'j —Ро)) = ^.
2. Теорема Абеля 259
т. е. для любого вектора % 6 С« существуют точки р^, . . ., pg ^ S
и пути «j из Pq в Pi, такие, что
2 1 f>^ = }.j для всех /.
Более таго, для общего вектлра X g С^ дивизор 2/»! единствен.
Доказательство. Здесь мы приведем доказательство только
этого утверждения. Как решить явно проблему обращения, мы
сможем объяснить только в § 7 после введения тета-функции
Римана.
Обозначим через S^'^ множество зффективных дивизоров
степени d на 5, т. е. множество неу7го/)я5очеииьи;наборов {р^, . . ., pd}
из d точек на 5, не обязательно различных. Очевидно, iSC*)
является фактормножествомd-кратного произведенияS"^ = S X . . .X S
поверхности S на себя по действию группы перестановок Б^ из d
элементов. Факторизация переносит с S"^ на S'-'^^ структуру
топологического пространства. В действительности отображение
проекции я: iS''' -^ S'-'^') задает на S'''^ структуру комплексного
многообразия. В самом деле, пусть -D = 2 />« 6 S'-'^\ а z^ — локальные
координаты в окрестности C/j точки pi на S, выбранные так, что
Zi (Ui) n Zj [U]) = 0 лдяр1 ^pj-nzi = ZjBUi = Uj для Pi = pj.
Обозначим через o^, . . ., a^ злементарные симметрические
функции от d переменных. Тогда по теореме о симметрических
многочленах отображение
S ?г •-* (0^1 {Zi (Яг)}, . . ., Od {Zi (qi)})
задает систему координат на я (Ui X ... X Ud) с: SC^K
Отметим, что вне точек ветвления отображение я является неразветв-
ленным накрытием, и здесь в качестве локальных координат
на S('^'> можно взять z^ (pj), . . ., Zd (pd)- В другом крайнем
случае — вблизи точки d-p — локальными координатами
являются
(%+■••+ Zd, ..., Zi .. . Zd).
Компактное комплексное многообразие S('^'> называется d-крат-
ным симметрическим произведением кривой S. (Интересно
проверить, что Р'^С') = ре*).) Фиксируем базисную точку рд g S.
Тогда определено включение
i: SC'y -^ Div» (S), S i'x ь- 2 (Px-Po)-
Ему соответствует голоморфное отображение
Pi. ■ Рк
j,(<^).. 5(<i) ^f(S), 2 />>. -- ( 2 i «1' ••- 2 j «.).
^ Po ^ Po
17*
260 2. Романовы поверхности и алгебраические кривые
В ЭТОМ контексте теорема обращения Якоби утверждает, что для
кривой S рода g отображение {х(^> сюръективно и в общей точке
взаимно однозначно.
Пусть теперь] D = ^pi —точка на S(^, для которой все pi
различны, а Zi — локальные координаты на iS в pi. Тогда (z^, . . .
, . ., Zg) — система координат на S(^'> вблизи D. Для точки
D' = TiZj, близкой к D, имеем
ж<^">'»'))=(ж{]".) ir(i'».))=
Ро Ро
= {(ujdz„ ...,(Og/dZi),
где (oldz обозначает функцию h (z), для которой со = h (z) dz.
чОтсюда мы делаем важное заключение, что
'(njdzi ... (njdzg
/coi/azj .
\(ugldzi .
(Ugldzg
является матрицей Якоби отображения yS^ вблизи D. Заметим
также, что при изменении локального параметра Zi г-й столбец
этой матрицы умножается на ненулевой множитель, так что при
этом ранг матрицы f (fx^'^O не меняется.
Выберем ру так, чтобы coi (р^) фО, а. затем, вычитая
подходящие кратные со^ из coji ■ • •' ^gi так изменим базис, чтобы
*^2 (Pi) = • • • = f^g (pi) = 0. После этого выберем р^ так, чтобы
*^2 (Рг) =5^ О, и изменим базис, как и выше, чтобы соз (Рз) '= ■ • ■
. . . = cOg (рг) = 0. Продолжая зтот процесс, мы найдем точку/),
в которой матрица Якоби является треугольной с нулями ниже
диагонали и ненулевыми элементами на диагонали, а поэтому
ранг такой матрицы в D максимален.
Итак, отображение [i(^> не может быть всюду вырожденным,
и теорема обращения Якоби следует из того, что всякое
голоморфное отображение f:M^>-N связных компактных комплексных
многообразий равной размерности сюръективно, если \'f (f) 1^0.
Последний факт получается непосредственно из теоремы о
собственном отображении: / (М) с N — аналитическое подмножество,
содержащее открытое подмножество, поэтому / (М) = N. Более
элементарный подход состоит в следующем. Пусть ор^г — форма
объема на N. Поскольку / сохраняет ориентацию и \f(J) 1^0,
\ f*4>N > 0. С другой стороны, для любого q ^ N
то
м
я*" {N - {д}, R) = О,
2. Теорема Абеля 261
откуда iIjjv = йф на TV — {q} для некоторой формы ф 6 А^~^ (N
— {q}). Тогда, если q ^f (М), мы получаем противоречие:
J/*^iv= {йГф = 0.
М дМ
Теперь нам осталось только доказать, что ц'-^ в общей точке
взаимно однозначно. Но это очевидно. Действительно, по теореме
Абеля слой отображения {х(*^ над каждой точкой X ^'^ (S) есть
множество I D \ эффективных дивизоров, линейно эквивалентных
любому дивизору D 6 }х^^^'' W' т. е. является проективным
пространством. С другой стороны, по соображениям размерности
общий слой для \1<-^ нульмерен. Следовательно, общий слой
отображения \i(^'> — точка. (Отображение {х(^^ представляет собой
пример бирационалъного отображения, которые будут
обсуждаться подробно в гл. 4.) D
В качестве следствия теоремы обращения Якоби отметим, что
на римановой поверхности рода g каждый дивизор степени "^g
линейно эквивалентен некоторому эффективному дивизору.
Рассмотрим, в частности, случай римановой поверхности S
рода 1. Тогда 'f (S) = С/Л и ц(^'^ определяется как
р
|х: р н* j со,
Ро
где (О — образующая пространства Я" {S, Q^). По теореме Абеля
\1 (р) = \1 (/?') только тогда, когда существует мероморфная
функция / на S с (f) = (р — Ро) — G' — Ро) = Р — р'■ Как
мы уже знаем, на S не существует мероморфных функций с одним
простым полюсом. Следовательно, [i<^^ инъективно. Кроме того,
по теореме обращения Якоби это отображение сюръективно,
позтому мы имеем изоморфизм
т. е. каждая риманова поверхность рода 1 есть фактормногообра-
зие С/Л для некоторой решетки Ас: С.
В результате мы установили следующий важный факт:
неособые кубические кривые на Р^ — это то же самое, что компактные
римановы поверхности С/Л для подходящих решеток Л в
комплексной плоскости. Следовательно, каждая такая кривая обладает
структурой группы; сейчас мы это кратко обсудим.
Прежде всего напомним, что в конце предыдущего параграфа
на римановой поверхности С рода 1 были построены две меро-
морфные функции F ж F', имеющде в базисной точке ро ^ С
соответственно полюс порядка 2 и 3 и голоморфные в остальных
262 2. Риманоны поверхности и алгебраические кривые
точках. Выберем функции F тз. F' так, чтобы их разложения
по некоторому локальному параметру w в точке р^ имели вид
а
F'-(Si =XdF + X'F(u + K"(o,
где со — глобальная ненулевая голоморфная 1-форма на С,
X, Я', Я" — подходящие константы. Представим теперь С как
комплексный тор С/Л так, чтобы базисной точке р^
соответствовала точка О (mod Л). Выберем в качестве локального параметра w
в ро евклидову координату z на С с dz = со. Тогда dF = —2-F' • со,
а F является <§>-функцией Вейерштрасса ^). Ее производная
{didz) f = —2F' обозначается через <§'. Заметим, что
разложение <§ в ряд Лорана по z в точке р^ не содержит членов нечетной
степени, так как иначе f (z) — f {—z) была бы непостоянной
голоморфной функцией на С. Итак,
f (z)=^ + az2 + &z4+[6],
«''(z)=-^ + 2az + 4&z3 + [5],
Г(г)2 = 4-5—16&+[1],
откуда выводится соотношение
^'2 = 4-f>3 —20a.f> —28&
между f и f'. Обычно принято писать gj вместо 20а и g^ вместо
28&.
Голоморфное отображение
■ф: С/Л-^ PS Z 1-* [1, f> (z), <§' (z)]
вкладывает С/Л в Р^ как множество нулей многочлена / (х, у) =
— у^ — 4с* + ^2*^ + Яз- Дифференциал со = dz на С = С/Л есть
вычет Пуанкаре
п / —2 (fa; л dy \ 2dx dx
а обратное к ijj отображение задается абелевым интегралом
р
— (по модулю периодов),
Ро
1) Точнее, ее подъемом на С.— Прим. перев.
2. Теорема Абеля
263
Рис. 4
Пусть Pi, Р2, Рз^С Ж Zi, Zj, Zg 6
для с/л. Тогда теорема Абеля
где Ро=^ (0) = [О, О, 1] 6 Р'-
g С — соответствующие точки
эквивалентна утверждению
Zi + z^ + Z3 = (0) (Л) <=> (Pi + Р2 + Рз — ^Ро) ~ 0;
последнее означает существование мероморфной функции / (z)
на С с полюсом порядка 3 в р^ ж единственными нулями в р^,
Р2, Рз- Чтобы убедиться в этом, рассмотрим уравнение А (х, у) =
= ах+Ьу + с = 0 прямой L, соединяющей точки pi ж р^ в Р^.
Через р' обозначим третью точку пересечения прямой L с С
(рис. 4). Тогда, поскольку бесконечно удаленная прямая
пересекает С по дивизору 3/)о, мероморфная функция А (f (z), f' (z))
на С = С/Л имеет дивизор Pi + Pi + р' — '^Ро- Следовательно,
р' ~ Рз, а значит, р' = рз, если (Pi + Рг + Рз — ^Ро) ~ О-
В итоге:
(«) Zi + Zj + Zg ^ О (Л) <^ pi, Р2, Рз коллинеарны.
Положив /»г = [1, f (Zj), <§>' (Zi)], перепишем (*) в виде
(••)
1
1
1
<§'{Zi)
«•ы
«•ы
г (2l)
г (Z2)
г (2з)
:0<^гl + Z2 + Zз = 0(Л).
Это замечательное соотношение имеет несколько эквивалентных
интерпретаций. Одна из них — известная теорема сложения для
эллиптических функций, позволяющая выразить <§> (—z^ — Zj) =
= (§> (Zi + Za) и <§>' {—Zi — Zj) = — <§>' (Zi + Zj) в виде
рациональных фзшкций от <§> (Zj), <§> (Zj), <§>' (zi) ж <§>' (zj). с другой
стороны, согласно (**), можно задать на кубической кривой С
структуру группы, используя геометрическую конструкцию с прямыми.
Во всяком случае, обращение эллиптических интегралов в смысле
теоремы Абеля и соответствующая теория кубических кривых
на плоскости занимают исключительное по красоте и глубине
положение среди других результатов алгебраической геометрии.
264 2. Романовы поверхности и алгебраические кривые
3. ЛИНЕЙНЫЕ СИСТЕМЫ НА КРИВЫХ
Закон взаимности II
Пусть S — компактная риманова поверхность рода ^, со —
глобальная голоморфная 1-форма па. S, а т| — дифференциал
второго рода, т. е. глобальная мероморфная 1-форма с нулевыми
вычетами. Мы хотим, так же как и в первом законе взаимности,
связать периоды форм со и т) с особенностями формы т|. Поскольку
эти особенности не имеют инвариантного определения как
вычеты, выберем в каждой особой точке р формы т| локальный
параметр Z и запишем разложения
ni2) = {al„z-'^+...+aP + aPz+...)dz,
(ii{z)^{bP+bPz+...)dz.
Заметим, что а?, = Resp (т|) = О, а &р = (co/dz) (р) по
определению, данному выше.
Рассмотрим теперь циклы б^, . . ., b^g на S, представляюп1;ие
канонический базис в Hi {S, Ъ). Предположим также, что они
пересекаются только в базисной точке Sq g 5 и не содержат особых
точек формы т|. Пусть П* и TV* обозначают периоды со и т| вдоль 6j.
Как и выше, область А = S — \j8i односвязна, а
6)
«о
определяет голоморфную функцию я на А с йя = со. Рассмотрим
на А мероморфный дифференциал я-т). Так как форма т| не имеет
особенностей на 6^, то интеграл от я*т) по границе А корректно
определен. По тем же соображениям, что и в доказательстве
первого закона взаимности, имеем
g
ад i=i
С другой стороны, в окрестности особой точки р формы т| для
фиксированного выше локального параметра z
г
Я (г) = j со = const + &?z+"2- Ь?22 -(- -g- b\z^ + ...,
«о
откуда
Р ..Ь?
|я.л = 2я/-12Ке8р(я.г,)=2я/-12[Е^1Ьг^]
ЭД р р j=2
3. Линейные системы на кривых 265
В результате мы получаем закон взаимности для дифференциалов
первого и второго рода:
i=l Р, 3
При изучении кривых мы будем пользоваться только двумя
установленными законами взаимности. Однако следует отметить,
что тем же методом без больших усилий можно вывести более
общие законы взаимности. Например, в любой из двух данных
формул в качестве со можно взять дифференциал второго рода:
функция
S
(О
«О
будет хотя и мероморфной, но однозначной, откуда, как и выше,
находим, что
2 (П'ЛГг**—П»""ЛГ') = 2я/^=Л 2 Resp (п-ц).
р
Аналогично можно доказать закон взаимности для пары
дифференциалов третьего рода, если удалить из области Д некоторые
дополнительные дуги. Оставляя в стороне вывод этих формул
(общий подход должен быть теперь и так ясен), мы укажем один
довольно привлекательный результат, который получается
аналогичным образом.
Теорема (Вейль). Пусть f,g — мероморфные функции на
компактной римановой поверхности S с непересекающимися
дивизорами if) и (g). Тогда имеет место равенство
pes pes
Доказательство. Пусть б^, . . ., 62g и А такие же, как выше.
Рассмотрим носитель {pi) дивизора (/) и носитель {qi} дивизора {g).
Проведем гладкие дуги (Xi из s^ в pi, пересекающиеся только
в базисной точке Sq и не содержащие точек из {qt). Обозначим
через А' дополнение ко всем а^ в А; А' можно снова представить
в виде многоугольника со сторонами ..., 6j, 6^+и ^Т*) ^l+b • ■ ■
. . ., ttj-, ajS . . ., как видно из рис. 5. Поскольку область А'
односвязна, а / — ненулевая голоморфная функция на А', можно
выбрать одну ветвь log / на А' и определить мероморфный
дифференциал
9 = log/.dlogg:=log/-^
266
2. Римановы поверхности и алгебраические кривые
Рис. 5
на А'. Прежде всего так как dgig имеет простой полюс с вьгаетом
rodg {g) в каждой точке д^, то по теореме о вычетах
j9 = 2n/^=:i2Res,.(9) =
= 2я/:=Л 2 ord,^(g).log/(?,).
Далее, для точек р ^ 6i, р' 6 б?' на дА', совпадающих на S,
logfip') = logf{p)+ { dlogf.
"g+i
лозтому
ж аналогично
J 9=(Jdlog^)(-J dlogf)
йi+йi^ «j
g*i
5 Ф=(5 diogg)(idiogf).
3. Линейные системы на кривых 267
Кроме ТОГО, для точек р € (Xi, р' 6 «Т' на дА', совпадающих на S,
log f ip') - log f(p)=-2TcY^=l-or Ар. if).
Следовательно,
Pi
j Ф = 2я1/-1ог(1р^(/) Jdlogg.
Итак,
2 j Ф = 2я/^1(2ог(1р. (/).(logg(p,)-logg(so))) =
= 2я1/31 2 ordp.(/).logg (;?,),
поскольку 2 or dp. (/) = 0. В результате мы получили соотношение
2яУ"^ ( 2 ord,. (g)■ log/(g,)- 2 ordp^ (/)■ log g{p,)) =
= 2 ((j^l«g/)( J dlog^)-(Jdlogg)( { dlogf)).
Ho j dlog / является всегда целым кратным 2лУ — 1. Поэтому
правая часть установленного соотношения есть целое кратное
(2я1/ —l)^, в силу чего
2 ord,^ (g). log / (g,) - 2 ordp. (/). log g ip,) 6 2я у :л z.
Взяв экспоненту, получим требуемое равенство
\lfiqtr''''''-UgiPtr''^'''.Q
Формула Рггмана—Роха
Наше изложение теории линейных систем мы начнем с
естественного вопроса: какова размерность пространства Я" {S, 0 (D))
для заданного дивизора D на римановой поверхности S рода g,
т. е. каково максимальное число (линейно независимых) меро-
морфных функций / на S, для которых
(/) + £)> О?
268 2. Римановы поверхности и алгебраические кривые
Сначала попытаемся ответить на этот вопрос в случае
эффективного дивизора D = ^Pi. степени d на S. Для простоты
предположим, что точки pi_ различны; единственное расхождение^
в последующих вычислениях для дивизора с кратными точками,
состоит в том, что запись приобретает гораздо более
громоздкий вид.
Как и в случае теоремы Абеля, проблема становится более
доступной, если переформулировать ее в терминах
дифференциалов. Пусть f ^ eS (S) и (/)-(- Z) ^ 0; тогда df — мероморфная
1-форма на S, голоморфная на 5 — {/'х}' имеющая нулевые^
периоды и вычеты, с полюсом порядка ^2 в каждой точке pi_.
Обратно, для любого такого дифференциала т| мероморфная
функция
однозначна и (f) + D ^ 0. Так как df = df <=> f = f + К
X 6 С, то размерность пространства Я" {S, О (D)) на единицу
больше размерности векторного пространства V дифференциалов
второго рода, голоморфных на iS — {pi.}, с нулевыми периодами
и полюсами порядка ^2 в рх-
По теореме Кодаиры об обращении в нуль Н^ {S, й^ (р)) = О
для любой точки р ^ S. Поэтому из точной последовательности
О -». Qi (i>) -». Qi (2р) ^ Ср ^ О,
очевидно, вытекает существование мероморфной формы на S,
голоморфной на iS — {р} и имеющей двойной полюс в точке р;
ясно также, что эта форма не имеет вычетов. Пусть z^ —
локальный параметр в точке pi_. Тогда по предыдущему для любой
последовательности комплексных чисел %,..., а^ существует
мероморфная 1-форма т|а на S, голоморфная на S — {р^} и
имеющая главную часть
Ца (z) = {ax-zf + т dz^
в каждой тючке р^^. Более того, так как разность любых двух
таких форм есть голоморфная 1-форма на S, то мы видим, что
существует единственный такой дифференциал фа со всеми
нулевыми А-периодами. Обозначим через Й'' ^ С"* векторное
пространство таких форм и зададим при помощи интегрирования по 5-цик-
лам поверхности S линейное отображение
1|з:И^-^С«, Фа'-*( J Фа, •••. J Фа).
3. Линейные системы на кривых 269
Очевидно, определенное выше векторное пространство V является
ядром отображения ijj.
Чтобы описать ijj явно, выберем в Н" {S, ОУ) нормализованный
5азис coi, . . ., cOg. Тогда по закону взаимности для
дифференциалов первого и второго рода
( Фа = 2я>^:ГТ2а),.(сй/Й2;,)(;);,),
т. е. отображение ijj задается матрицей
f{(Oi/dzi) (pi) . .. {(Sijdzd) {pd)y
^{(Hg/dZi) (Pi) ... {(Og/dZd) {Pd)j
Число линейно независимых соотношений между строками
этой матрицы равно числу линейно независимых голоморфных
дифференциалов, обращающихся в нуль в точках р^ для всех Я,
т. е. размерности пространства Я" {S, й^ (—D)). Следовательно,
К> (D) = dim (ker ар) + 1 = d — rank ijj + 1 =
= d-g + h'>{K-D) + l.
Это и есть классическая формула Римана — Роха.
Итак, мы доказали формулу Римана — Роха для зффективных
дивизоров ^), а значит, для всех дивизоров степени ^^.
Возвращаясь к общему случаю, рассмотрим любой дивизор D степени
^^ — 2 и применим полученную формулу к дивизору К —D:
h^{K-D) = {2g-2-d)-g-^\+h^{D)=^
^ h<> (D) = d - g + 1 + h<> {К — D).
Наконец, если deg D = g — I ж яж один из дивизоров D, К — D
линейно не эквивалентен никакому эффективному дивизору,
то А" {D) = Ь,^ {К — D) = О ж формула опять верна.
Формула Римана — Роха немедленно дает нам картину
поведения общих линейных систем: для общих эффективных дивизоров
d
D = ^ Pi, степени d ранг матрицы ((coj/dzx,) (рх,)) максимален,
поэтому
[1, d^g,
4D) = {
d-g+l, d>g,
для D, лежащих вне некоторого собственного аналитического
подмножества в S^"^.
1) Если не считать дивизоры с кратными точками, с которыми читатель
теперь может разобраться самостоятельно.— Прим. перев.
270 2. Римановы поверхности и алгебраические кривые
Эффективный дивизор D, для которого А" {К — D) Ф О,
называется специальным. Специальный дивизор, у которого
размерность линейной системы больше, чем у общего дивизора той же
степени, т. е. такой, что h" {К — D) > g — d, называется
иррегулярным. Линейная система называется специальной или
иррегулярной в соответствии с тем, из каких дивизоров она состоит.
В заключение упомянем, что формулу Римана — Роха можно
доказать при помощи теории пучков. В общем случае для
голоморфного векторного расслоения Е -*- М ян компактном
комплексном многообразии М определена голоморфная эйлерова
характеристика
г{Е) = ^{-\уЬР{М, е(Е));
как обычно, % (Рм) обозначает голоморфную эйлерову
характеристику тривиального линейного расслоения, т. е.
х(0м)=2](-1Г/^'''^(М).
По двойственности Кодаиры — Серра для линейного
расслоения L на римановой поверхности S
% (L) = А» {S, в (L)) - W- (S, в (L)) = А» (L) -h<>{K- L),
X i&s) = fK^'" (S) - h<>^^ {S) = i- g,
поэтому формула Римана — Роха означает просто, что
X (L) = X (Os) + q (L).
Чтобы доказать формулу Римана — Роха в этом виде,
отметим ее очевидность в случае тривиального расслоения и покажем,
что она верна для любого L = ID] тогда и только тогда, когда
она верна для каждого из расслоений L' = [D -{■ р], L" = [D — р],
где р ^ S — произвольная точка. Действительно, точной
последовательности пучков
О ^ 0 (Д) ^ 0 (Z) + р) ^ Ср ^ О
отвечает точная последовательность когомологий
О -> Я» (S, 0 (Z))) -^ Я» {S, 0 (Z) -Ь р)) -^
^ Ср ^ Я1 (5, 0 (D)) -^lPiS,OiD + р)) -^ О,
а так как альтернированная сумма размерностей векторных
пространств в точной последовательности всегда равна нулю, то
Х(Ш +р]) = х(Ш]) + 1. D
Этот вариант формулы Римана — Роха, хотя и не столь
явный, как предыдущий, подсказывает путь к дальнейшим
обобщениям в высших размерностях. Основной факт, верный для общего
случая, заключается в следующем: голоморфная эйлерова харак-
3. Линейные системы на кривых 271
теристика векторного расслоения Е —*- М пи компактном
комплексном многообразии является топологическим инвариантом для
Е ш М. С этой точки зрения существенная часть классической
формулы Римана — Роха — это двойственность W- (D) = № (К —
-D).
Канонические кривые
Пусть S — компактная риманова поверхность рода g'^2y
а К — каноническое расслоение на S. Отметим сразу, что полная
линейная система | ^ | не имеет базисных точек: если бы р ^ S
принадлежала базисному множеству системы \ .К \, то
А» {К-р) = А» (К) = g,
а значит, по формуле Римана — Роха
h<^(p) = deg (p)-g+ i +h<>iK-р) = 1 - g+l + g = 2,
T. e. на iS существовала бы непостоянная мероморфная функция,
голоморфная на iS — {р} и имеющая простой полюс в р; но тогда
бы S была биголоморфно эквивалентна Р^. Следовательно,
линейное расслоение К задает отображение
1^: S -^ Р«-1, р ь-* [©1 (р) ©g (р)],
где ©1, . . ., ©g — базис в ff" {S, Q^); i^ называется
каноническим отображением поверхности S. Образ i^ (S) cz Р^~^
называется канонической кривой.
Отображение i^ взаимно однозначно, если для любых точек
р, q ^ S можно найти форму © £ Я" {S, Q^) с а> (р) = О, а> (q) Ф 0;
если же для любой точки р ^ S существует ©, имеющая нуль
порядка в точности 1- в р, то оно является иммерсией. Значит,
1^ — вложение в том и только том случае, когда для любых
точек р, q, не обязательно различных, выполняется неравенство
к'ЧК - р - g)<h<^ {К - р) = g - I.
По формуле Римана — Роха
hO(K-p-q) = g-S + h<^(p + q),
поэтому
h<' {K-p-q)<h<'{K-p)<^h<'(p + q) =1.
Следовательно, i^ не является вложением в том и только тлм
случае, когда на S существует, мероморфная функция с дивизором
полюсов степени 2, т,. е. когда S представила в виде двулистного
разветвленного накрытия над Р^. Такая риманова поверхность
называется гиперэллиптической. Среди множества всех кривых
рода g гиперэллиптические кривые образуют важный класс.
272 2. Римановы поверхности и алгебраические кривые
И ИХ свойства часто заметно отличаются от свойств обхцих рима-
новых поверхностей. Ниже в этом параграфе мы обсудим их
подробнее, а пока только заверим читателя, что общая риманова
поверхность рода g^ 3 действительно не является
гиперэллиптической.
Заметим, что для линейного расслоения [D] -^ S степени
2g-2
ГО, если D^K,
ho{K-D)=\, J. '
^ ' 11, если D = K,
откуда по формуле Римана — Роха h" (D) = g — i. если К Ф D.
Значит, любая невырожденная кривая S а Р^~^ рода g и степени
2g — 2 является канонической.
Важность канонической кривой римановой поверхности S
проистекает из того, что она инвариантно определена по S, и
потому, как общее правило, каждый проективный инвариант
канонической кривой отражает внутреннюю структуру поверхности S.
Как работает этот принцип, мы увидим при обсуждении точек
Вейерштрасса, а затем еще раз при обсуждении теоремы Торелли.
Перефразируем теперь формулу Римана — Роха в терминах
геометрии канонической кривой: для любого эффективного
дивизора D = "YiPi на римановой поверхности S число h'> {К — D) — 1
равно размерности пространства гиперплоскостей в Р^-^, прохо-
дяпщх через все точки i^ ipi), поэтому А" {D) равно степени
дивизора D минус размерность проективного подпространства D,
порожденного точками pt на канонической кривой (с учетом
их кратностей aj), т. е. надо брать линейную оболочку точек pi
вместе с aj — 1 производными канонического отображения. И
наконец, так как размерность линейной оболочки d точек из с
равна d — 1 минус число всех линейно независимых
соотношений между этими точками, то мы получаем геометрический вариант
формулы Римана — Роха:
Размерность г полной линейной системы, содержащей
дивизор D = ^ри равна полному числу линейно
независимых соотношений между точками pi канонической кривой
(с учетом их кратностей, как и выше).
т. е.
Точки дивизора D порождают {d — г — i)-nAOCKOcmb,
В этом геометрическом варианте формула Римана — Роха
доказывается совсем просто. Начнем с неравенства
(*) dim Д < (d — 1) — dim I Z) |.
3. Линейные системы на кривых 273
Доказательство. Предположим, что D = ^pt лежит в г-мерной
линейной системе, т. е. сзгществует г + 1 линейно независимых
мероморфных функций /о, ...,/,. на 5, для которых
(/,)+£)> 0.
Можно взять /о = 1; тогда никакая нетривиальная линейная
комбинация функций Д, . . ., /^ не голоморфна на всей
поверхности S. Иначе говоря, если zi — локальный параметр в точке
pt ян S и /v (zi) = a^jHi* + . . ., то матрица
h,l ■• ' «г, dj
имеет максимальный ранг г. Пусть теперь со — любая
голоморфная 1-форма на S. Тогда по теореме о вычетах
0=SResp,(/vCo)=S«v.B-(^)
it
для любого V. Отсюда мы находим г линейно независимых
соотношений между точками pt канонической кривой, что и
доказывает неравенство (♦).
Теперь можно доказать обратное неравенство, применив (*)
к вычетному для D дивизору К — D. Предположим, что на
канонической кривой
dim D = d — s — 1.
Тогда гиперплоскости в Р*"^, содержащие Z), высекают на ней
линейный ряд из \ К — D \ размерности
(g-i)-(d-s-i)-i=g-d + s-i.
Применяя (•) к дивизору Е ^ \ К —D |, мы приходим к
неравенству
dim E^degE — i—{g — d + s — i)-=
= {2g-2-d)-i-ig-d + s-l)^g-s-2.
Но гиперплоскости в Р*"^, содержащие Е, высекают на S
линейный ряд из I Z) I размерности (g — 1) — (g — s — 2) — 1 = s»
т. е.
dim |Z)|>« = u! — 1— dimЪ,
что и доказывает формулу Римана — Роха. Q
18-046
274 2. Римановы поверхности и алгебраические кривые
Специальные линейные системы I
Формула Римана — Роха точно описывает поведение общих
линейных систем на римановой поверхности, но почти ничего
не говорит об иррегулярных линейных системах. Мы попытаемся
теперь восполнить этот пробел некоторыми классическими
результатами, связывающими степень, размерность и род специальных
линейных систем. Основная лемма здесь такова.
Лемма. Пусть С с: Р" — невырожденная кривая', точки
общего гиперплоского сечения кривой С находятся в общем положении^
т. е. никакие п из них не являются линейно зависимыми,.
Доказательство. Пусть d — степень С, а Яо с: Р" —
гиперплоскость, пересекающая С в d различных точках pi, . . ., Pd.
Тогда для Н из достаточно малой окрестности U точки Hq в Р"*
точки {pi (Н)} пересечения Н сС голоморфно зависят от Я 6 Р"*.
В соответствии с этим для каждого мультииндекса / = {г^, . . .
. . ., г„} с: {1, . . ., d} можно задать голоморфное отображение
uji и-^СГ" = С X С X ... X С, H^^(pi^(H), . ..,pi^ (Я)).
Более того, для любой точки (qi, . . ., ?п) € С", достаточно
близкой к я J (Hq), сзгществует гиперплоскость Н ^ U, содержащая
^1, . . ., Qn, т. е. образ и относительно nj содержит открытие
множество из С^.
Пусть D аС^ — множество точек {q^, . . ., g„), для которых
^1, . . ., д„ линейно зависимы. Поскольку кривая С невырожден-
на, то Z) — собственное аналитическое подмножество в С", а
значит, Лi^ (Р) — также собственное подмножество в U.
Следовательно, для Н ^и — и л'х* (D) точки пересечения Н (] С нахо-
I
дятся в общем положении. Q
Охарактеризуем теперь размерность линейной системы | D \
следуюхцим образом: dim \D \'^ t тогда и тллько тлгда, когда
для каждых t точек р^, . . ., pt ^ S существует дивизор Е ^ \ D \^
содержащий р^, . . ., pt. Поэтому если D ш D' — два
эффективных дивизора на S, то для любых fe" {D) — 1 -f- Л° {D') — 1 точек
на S существует эффективный дивизор Е'^ D -\-D', т.е.
ho (D + D') > ho (D) + ho (D') — 1.
Предположим, в частности, что D — специальный дивизор,
так что h° (К — D) Ф О и шы можем взять D' = К — D. Тогда
Л» {D -Ь D') = h°{K) = g я
й» {D) + hO{K-D)^g+i
hO{D)-hO{K -D) = d- g+i
2¥ (D) < d -f- 2.
3. Линейные системы на кривых 275
Заметим, что равенство имеет место в том и только том
случае, когда каждый дивизор из канонического ряда \ D -\- D' \ =
= \ К \ представляется в виде суммы некоторого дивизора
линейной системы \D \ж дивизора из \D' \. Но по предыдущей лемме
точки общего гиперплоского сечения кривой i^ (S) находятся
в общем положении. Следовательно, 2/i" (D) равно d -f- 2 только
тогда, когда D = О, D = К или i^ не взаимно однозначно.
В результате нами доказана следующая
Теорема Клиффорда. Для любых двух эффективных дивизоров
на компактной римановой поверхности S имеет место неравенств
dim 1 Z) I -f dim ID' I < dim I Z) 4- D' \,
a для специального дивизора D — неравенство
dim I Z) I < dl2,
причем равенство имеет место только тогда, когда D = О, D = К
или S — гиперэллиптическая поверхность.
Следствие. Пусть Сс Р" — произвольная невырожденная криг-
вая степени d ■<.2п и.рода g; тогда
g ^d — п
и равенство выполняется в том и только том случае, когда крги-
вая С нормальна ^).
Доказательство. Пусть D — гиперплоское сечение С. В этом
случае
dim I Z) I = Л» (Z)) - 1 = п > dl2,
и по теореме Клиффорда дивизор D не может быть специальным.
Следовательно, h^ {К — D) = О, и по формуле Римана — Роха
g = d — h^{D)-\-ir^d-n.[\
Эта граница, конечно, достигается на любой римановой
поверхности рода g = d — п и для любой линейной системы
степени d.
Теперь остается найти максимальный род кривой степени d
в Р" при d > 2п, или, что эквивалентно, найти более точную
оценку размерности линейной системы, чем та, которую
предлагает теорема Клиффорда для d <^ g. Мы приведем здесь
рассуждение, впервые данное Кастельнуово в 1889 г.
Пусть С с: Р" — невырожденная кривая степени d и рода g
с гиперплоским сечением D. Рассмотрим линейные системы | kD \
^) То есть не является бирациональной проекцией из пространства более
высокой размерности с сохранением степени.— Прим. ред.
18*
276 2. Римановя поверхности и алгебраические кривые
ДЛЯ А = 1, 2, ... . По нашей основной лемме можно считать,
что точки дивизора D находятся в общем положении в некоторой
гиперплоскости из Р".
Пусть т = [{d — !)/(» — 1)] — наибольшее целое число,
меньшее или равное (d — 1)/(га — 1). Для каждого целого к ^т
выберем множество Г жз к (п — 1) + 1 точек в D. Утверждается,
что гиперплоскости в Н" (С, О (kD)), соответствующие ^) точкам Г,
линейно независимы. Чтобы в этом убедиться, достаточно
установить для любой точки ? 6 Г существование гиперповерхности
степени к в Р", проходящей через Г — {q}, но не проходящей
через q. Это просто. Разобьем остальные точки Г на А множеств
{р\, р|, .. м P*_i}, {рЬ • • м i'S-J» • • •' М' • • '^Pn-il
по п — 1 точек в каждом. Точки каждого такого множества
{Ра}а, линейно независимы, и их линейная оболочка не
содержит q. Следовательно» в Р" можно найти гиперплоскости ffj, . . .
. . ., Яь, содержащие соответственно точки {pa}ai • • •» {Ра}о>
но не содержащие точку q. Их объединение Н^^ -\- . . . -f- Hf^
дает искомую гиперповерхность степени к.
Отсюда видно, что векторное пространство сечений расслоения
[kD], обращающихся в нуль во всех точках D^ имеет
коразмерность > А: (« — 1) 4-1 в IP (С, О (kD)), т. е.
(•) feo (kD) — ho ((к — i)D)^k(n — i) + i при А < m.
Рассуждая аналогично, при к>т можно найти к
гиперплоскостей в Р", содержащих все, кроме одной, точки из D, поэтому
Итак,
А» (kD) — Л» {(к — i)D) = d при А: >
т
h^D)^n + i,
h<>(2D)^n + i+2(n—i) + i = 3(n-i) + 3,
h<>i3D)^Q(n-i) + A,
feO(TOZ))>'"'"^+^> {n-l) + m + l,
•••••••••• •••
ho{{l + m) Д)> '""<'"+^) (n- i)-^m + l + ld.
») To есть гиперплоскости; ff> (С, О {kD — g)) с Я« (С, © (kD)), q 6 Г.—
Прим. перев.
3. Линейные системы на кривых 277
Но при достаточно большом I дивизор (Z + т) D не специален.
Тогда по формуле Римана — Роха
h°{{l + m)D) = (1 + т d — g + i,
поэтому
g^(l + m)d-'^^1'^^^ (n-l)-m~l-ld+l =
= J!S^St^(n-l) + m(d-m{n-l)-l).
Значит, род невырожденной кривой степени d вР^ не превосходит
■"^""^^ in-i) + me, где m=[-^], d-1 = m(«-l) + e.
В параграфе, посвященном линейчатым поверхностям, мы
убедимся, что эта граница достигается для каждой пары d'^n,
и дадим явное описание этих кривых максимального рода. А пока
подведем итог тому, что нам вообще известно о невырожденных
кривых в Р". Пусть С — кривая степени d', тогда
d<.n=^ С вырожденна;
d = п=> С — рациональная нормальная кривая;
п<. d<.2n=> g ^d — »с равенством для нормальной кривой С,
d = 2re=*-g^re+ 1с равенством в том и только том случав,
когда С — каноническая кривая,
Q!^2ra=»-g^ in (in— ) (д_1)_|_^е, где
т
= [-^—y], d —! = /»(«—1) + е.
Заметим, что если эта граница достигается для кривой С»
то в основном неравенстве (•) стоит знак равенства, откуда
следует, что полная линейная система | fcD | на С высекаетвя
гиперповерхностями степени к. Иначе говоря, в этом случае
отображение
Я» (р\ О {кЩ) = Sym" Я» (Р», &{Н))^1Р {С, О (кП))
сюръективно, В частности, для канонической кривой отсюда
вытекает
Теорема Нётера. Для любой негиперэллиптической кривой С
отображение
Sym' Я» (С, в (Ю) -^ Я» (С, в (1К))
сюръективно при любом I.
Неравенство Кастельнуово можно интерпретировать двумя
способами, при одном получится верхняя оценка для п через d
278 2. Римановы поверхности и алгебраические кривые
И g, а при другом — нижняя оценка для d через пти. g. Не проводя
вычислений, укажем ответ:
2(l(d-i)~g) , r2(g-l) ,-,
Tun ер эллиптические кривые и
вычисление 1Римана
Напомним, что компактная риманова поверхность S рода
g^2 называется гиперэллиптической, если на ней существует
мероморфная функция / с дивизором полюсов степени 2, т. е. S
допускает 2-1-отображение /: iS ->- Р^ на риманову сферу. По
формуле Римана — Гурвица такое отображение / имеет
b = 2g-2 + 2x (Pi) = 2g + 2
точек ветвления, и так как отображение / всего лишь двулистно,
оно не может иметь кратных точек ветвления. Пусть z^, ...
. . ., Zjg+a — точки ветвления отображения / на Р^ (мы
предполагаем, что они #оо). Рассмотрим кривую S' = (v^ =
2g+2
= У (z — Zi)) d С* вместе с проекцией я на z-плоскость.
Так как точки Zj различны, S' — гладкая кривая, а при R >•
>• max (I Zi 1) мы видим, что я~^ (| z | > i?) состоит из двух
проколотых дисков. Пополним S' до компактной римановой
поверхности S, добавляя выколотые точки этих дисков.
Отображение я: iS' -> С можно продолжить по непрерывности до
голоморфного отображения л: S ^- Р^, переводящего две добавленные
точки в точки Z = оо. В результате S будет снова двойньш
накрытием над Р^, разветвленным во всех точках из {zj и только в них.
В общем случае если М, М' — две компактные римановы
поверхности с отображениями /: М->-Р^, /': М'-> Р^,
имеющими одно и то же множество ветвления Б с: Р^, и если /~^ (Р^ —
— В) изоморфно /'"^ (Р^ — В) как топологическое накрытие над
Р^—В, то М ж М' изоморфны: изоморфизм между f-^{P^ — B)
и /'"^ (Р^ — В) продолжается до непрерывного, а значит, и
голоморфного отображения на точки, лежащие над множеством
ветвления отображений f ж. f. Следовательно, рассмотренные выше
римановы поверхности S ш S изоморфны, т. е. любая зиперэллип-
3. Линейные системы на кривых 279
щическая риманова поверхность рода g представляется в виде
гладкого пополнения множества решений уравнения
w^ = g (z)
в С*, где g (z) — многочлен степени 2g + 2.
Для гиперэллиптической римановой поверхности S, заданной
2в+2
в виде пополнения множества решений уравнения (и^ =11(2 —
— Zj)) d С*, можно вычислить явно базис в IP (5» Q}). Прежде
всего заметим, что соответствие /: (w„ z)*-*- (—w, z) задает
автоморфизм i: iS ->- iS порядка 2, который называется
гиперэллиптической инволюцией на S. Она индуцирует линейный автоморфизм
/*: H<'(S, Й1)->Я»(<5, Q^)
также порядка 2. Поэтому а priori мы получаем разложение
пространства /Г" (S, Q^) а сумму двух собственных подпространств,
соответствующих собственным значениям -f-l и —1. В
действительности собственное пространство для -f-l тривиально так как
голоморфная 1-форма ю на 5 с у*© = ю спускается до
голоморфной 1-формы на Р^, а таких не существует. Следовательно, /*а) =
= — (О для любого в> ^ IP (S, й^).
Рассмотрим теперь на S 1-форму
щ = dz/w.
Она голоморфна и отлична от нуля всюду, кроме точек над оо,
поскольку точки, где w равно О, суть в точности нули формы dz
(как легко может проверить читатель, проведя соответствующие
локальные вычисления). Поскольку полная степень
дифференциала ©о равна 2g — 2 и coq имеет одинаковый порядок нуля
или полюса в точках S над z = оо, то щ должен иметь нуль
порядка g — 1 в каждой из этих двух точек. Пусть ю — любая
другая голоморфная 1-форма на S; напишем
(О = h-(OQ,
где h — мероморфная функция на S, голоморфная вне z~' (с»).
Но /*(й = —со, /*cu0 = —(Оо, откуда ]'*h = h, т. е. h — функция
от Z и, более того, многочлен от z. Если d — его степень, то он
имеет 2d нулей в конечной части кривой S, а значит, полюс
порядка d в каждой точке над оо. Так как щ имеет нуль порядка g — 1
в каждой точке над оо, а fe-coo голоморфна, то degh ^ g — 1.
В результате мы можем выписать базис для /Г" (iS, Q^):
{^,z^ z«-i^).
Тогда каноническое отображение i^ для S имеет вид
iK (2, w) = [1, z, ..., z«-4 e P'~';
280 2. Римановы поверхности и алгебраические кривые
поэтому образ S относительно i^ является рациональной
нормальной кривой в Р*~^. Более того, каноническое отображение
пропускается через проекцию /. Поскольку отображение i^
определено инвариантным образом, отображение f единственно
точностью до автюморфизмаР^.
Для того чтобы показать, что не все римановы поверхности
гиперэллиптичны, мы подсчитаем число параметров, необходимых
для задания гиперэллиптической кривой и общей кривой рода g.
Прежде всего, как мы уже знаем, для любого набора 2g + 2
различных точек Zj 6 Р^ существует единственная
гиперэллиптическая кривая S с двулистным отображением /: iS ->- Р^,
имеющим множество ветвления В = {Zj}. Любые три точки Zi, z^, z^ ^ В
можно перевести соответственно в точки О, 1 и оо некоторым
автоморфизмом Р^, поэтому общая гиперэллиптическая риманова
поверхность рода g описывается заданием (2^ +2) — 3 = 2g — 1
точек на pi. Обратно, поскольку отображение / единственно
с точностью до автоморфизма на Р^, любой гиперэллиптической
кривой S соответствует только конечное число таких наборов
2g — 1 точек. Следовательно, полное семейство таких кривых
локально описывается 2g — 1 параметрами.
Теперь, следуя рассуждениям Римана, найдем число
параметров, необходимых для описания общей римановой поверхности
рода g. Выберем произвольно целое число п >» 2g. Любую рима-
нову поверхность рода g можно представить в виде ге-листного
разветвленного накрытия над Р^. Степень дивизора ветвления
такого отображения равна
b = 2g-2 + n-x (Pi) =2n+2g — 2.
Обратно, мы утверждаем, что для любого дивизора В на Р^
степени 2п + 2g — 2, не имеющего точек кратности >■ п — 1,
существует конечное число римановвсх поверхностей S рода g, пред-
ставимых в виде ге-листного накрытия над Р^ с дивизором
ветвления В. Эти римановы поверхности будут построены в случае
В = ^Zt, состоящего из 2га -Ь 2^ — 2 различных точек. Обшрй
случай несколько сложнее, хотя и не вносит принципиальных
трудностей.
Проведем на Р^ непересекающиеся дуги у,, соединяющие Zj
с z,+i. Пусть 7*1, . . ., Г„ — непересекающиеся копии
поверхности Р^ — и Vi (рис. 6). Выберем последовательность
перестановок Оо, . . ., сга„+ад_а 6 Sn, где а^ = o^n+ig-z = е, а а^-а]^.^
задает нетривиальную транспозицию двух элементов при любом
/; пусть еще все {oj} действует транзитивно на {1, . . ., и}. Всегда
можно найти конечный набор таких последовательностей. Для
каждого i, 1 ^ i ^ 2га -f- 2g — 3, добавим к \j Tj п копий {y{}f
3
дуги 7ij отождествляя при этом 7i с границей копии Т^ вдоль
3. Линейные системы на кривых
28t
Рис. 6. Пример: <Ti= (1, 2), Og = (1, 3, 2), (т, = (2, 3).
верхнего края разреза 7if а также с границей Тд .j) вдоль
нижнего края разреза yi. В результате мы получим топологическое-
пространство S с естественной проекцией /: iS ->- Р^. Очевидно,
у-1 (р1 — В) а S является неразветвленным накрытием над Р^ —
— В, поэтому оно однозначно наследует комплексную структуру.
Эту структуру можно продолжить на всю поверхность S, взяв
в качестве локальной координаты в точке р б /~^ (zj) либо (z — Zj),.
J282 i. Римаповы поверхности и алгебраические кривые
либо ]/^z — Zj в зависимости от того, является ли / 1-1- или 2-1
отображением в окрестности р. Итак, S — компактная риманова
поверхность, которая отображается на Р^ с дивизором
ветвления В, и по предыдущему замечанию S полностью определяется
выбором перестановок а^, сделанным в процессе построения.
Как мы знаем, при указанных выше ограничениях любому
дивизору В степени 2п -\- 2g — 2 соответствует конечный набор
римановых поверхностей рода g вместе с тг-кратным
отображением / на Р^. Остается узнать, сколько таких дивизоров
соответствует одной такой римановой поверхности S. Отображение /
на S можно задать дивизором полюсов D = (/)«> 6 S^'^^ и
сечением из IP {S, О (ID])), соответствующим /. Очевидно, выбор D
зависит от п параметров, а так как га > 2g, то h" {К — D) = О,
и по формуле Римана — Роха
h<> (D) = п - g + i.
Значит, выбор / 6 Я" (S, О {[D])) зависит от га — ^ -f- 1
параметров. Поэтому семейство га-кратных отображений /: iS ->- Р*
имеет размерность
п+ (n-g+i) = 2n-g+i^).
Поскольку семейство дивизоров В (2га + 2g — 2)-мерно, то общая
риманова поверхность рода g локально зависит от
2га + 2g- 2-{2n-g+i) = 3g-3
параметров. Заметим, в частности, что при ^ ^ 3 общая риманова
поверхность рода g негиперэллиптична.
Интересно проверить вычисления Римана для g = 3, 4 и 5.
Прежде всего мы уже знаем, что каноническая кривая любой
негиперэллиптической римановой поверхности рода 3 есть кварти-
ка в Р^, определенная с точностью до автоморфизма Р*. Обратно,
если С с: Р* — гладкая квартика, то по формуле присоединения
Кс = (^ра + С) 1с = (-ЗЯ + Ш)\о = Н \с,
поэтому с — каноническая кривая. Но пространство квартик
в Р* имеет размерность
6-5
(|)-1.^-1.14,
'■) На самом деле 2п — g -{- 1 — dim (Aut S), но, как будет установлено
^ниже, кривые S рода g ^ 2 имеют лишь конечное число автоморфизмов,
поэтому эта и следующая формула числа параметров римановой поверхности
рода g годится только для g > 2. Если g = 1, то число параметров, как^мы
уже энаем, равно 1, а если g = О, то оно равно нулю.— Прим. ред.
3, Линейные системы на кривых 283
а dim PGL (3) = 9 — 1=8. Следовательно, кривая рода 3
зависит от 14 — 8 = 6 параметров, как и предсказывалось.
Рассмотрим теперь каноническую кривую С с: Р^ рода 4.
По формуле Римана — Роха, поскольку дивизор 2Кс не является
специальньш, имеем
А» (С, 2Кс) = 12 - 4 + 1 = 9.
С другой стороны, /i" (Р^, о (2Н)) = 10, поэтому отображение
ограничения
Я» (Р2, в (2Н)) ^1Р (С, в (2Нс)) = Я» (С, 2Кс)
имеет ядро, т. е. С лежит на квадратичной поверхности Q. Так
как приводимая квадрика состоит из двух плоскостей, она не
может содержать С, откуда следует, что Q неприводима. Кроме
того, так как
А» {С, ЪКс) = 18 - 4 + 1 = 15 и А» (рз, 0 (ЗЯ)) = 20,
через кривую С проходит четырехмерная линейная система
кубик в Р^. Подсистема кубик, содержащих Q, всего лишь
Л» (Р8, в (ЗЯ — Q)) — i=h^ (рз, о (Я)) - 1 = 3-мерна.
Следовательно, С лежит также на кубике Q', не содержащей Q.
Поскольку Q неприводима, ^ и ^' пересекаются по кривой степени 6;
но С с: ^ П ^' и deg С = 6, значит,
C = Q nQ'.
Обратно, для любой кубики Q' и квадрики Q, пересекающихся
вдоль гладкой кривой С, по формуле присоединения имеем
поэтому с — каноническая кривая рода 4.
Из сказанного выше следует, что квадрика Q зависит от 9
параметров. Два кубических многочлена высекают одну и ту же
кривую на Q, если их разность тождественно равна нулю на Q;
векторное пространство кубических многочленов, обращающихся
в нуль на Q, имеет размерность
А» (рз, в (ЗЯ - 2Я)) = 4,
поэтому при фиксированной Q выбор Q' зависит от 19 — 4 = 15
параметров. Кроме того, по теореме Бертини общая пара (Q, Q')
пересекается трансверсально. И наконец, группа PGL (4) имеет
размерность 15. Следовательно, число параметров, необходимых
для локального описания кривой рода 4, равно, как и ожидалось,
9 + 15 - 15 = 9.
284 2. Римановы поверхности и алгебраические кривые
Случай g = 5 несколько проще. Для канонической кривой
С с: Р* рода 5
h° (С, 2Кс) = 16 - 5 + 1 = 12.
Но
'6>
АО (PS в {2Н)) = (J) = 15
поэтому с лежит на трех линейно независимых квадриках Q,
Q' и Q" из Р*. По теореме Энриквеса из § 3 гл. 4 эта кривая в
общем случае является пересечением этих трех квадрик. Обратно,
если Q, Q' ж Q" — любые три пересекающиеся трансверсально
квадрики в Р*, то по формуле присоединения, примененной
трижды, получаем, что С = Q (] Q' C\Q" — каноническая кривая
рода 5.
Итак, общая кривая С однозначно определяется трехмерным
подпространством в векторном пространстве многочленов
степени 2 на Р*, т. е. точкой грассманиана G = (? (3, Я« (Р*, О (2Я))).
Но G имеет размерность 3 (15 — 3) = 36, а трехкратное
применение теоремы Бертини показывает, что линейная система
квадрик, соответствуюищх общей точке в G, пересекается по гладкой
кривой. Далее, PGL (5) 24-мерно, поэтому кривая рода 5 зависит
локально от 36 — 24 = 12 параметров.
Специальные линейные системы Л
Ранее в этом параграфе мы уже задавались вопросом: каков
наибольший возможный род невырожденной кривой степени d в Р"?
Формулируя его иначе, мы приходим к следующей эквивалентной
задаче: какова наибольшая возможная размерность линейной
системы степени d (или наименьшая возможная степень
линейной системы размерности га) на римановой поверхности S рода g,
не считая тех линейных систем, которые подняты с некоторой
факторповёрхности для SI Сейчас мы дадим ответ на этот вопрос
(который, как будет видно позже, правилен), однако тут же
убедимся в том, что в случае d>2n или п<С g — 1 эта граница
реализуется не для всех поверхностей рода g. Например,
как мы уже знаем, наибольший возможный род плоской кривой
степени d равен (d — i) (d — 2)/2, и, конечно, эта граница точная,
ибо достигается для любой гладкой плоской кривой.
Следовательно, наименьшая степень двумерной линейной системы на
кривой S рода g, не поднятой ни с какой факторповёрхности для S,
равна М, удовлетворяющему неравенству
{M-i)(M~2)^^^ (Jf-2)(JI/-3)
3. Линейные системы на кривых 285
Однако МОЖНО убедиться в том, что не все римановы поверхности
й - (d—i)(d—2)
рода g обладают такими линейными системами: если g= ^ ,
то семейство римановых поверхностей рода g с такими линейными
системами является семейством плоских кривых степени d, а
значит, имеет размерность, не превосходящую
G другой стороны, семейство всех римановых поверхностей рода g
имеет размерность
3^_3=3(^-1К^-21_3_
Поэтому при d^ 5 римановы поверхности S рода g = {d — \) X
X (d — 2)/2, обладаюище двумерной линейной системой степени d,
исключительны.
Этот пример выдвигает другой вопрос, дополняющий вопрос
Кастельнуово: какие специальные линейные системы существуют
на общей римановой поверхности рода g? Это известная проблема
Брилля — Нётера, которую мы будем обсуждать позже в этой
главе.
Предполагаемый ответ, хотя и не доказательство, в проблеме
Брилля — Нётера получается простым подсчетом размерностей.
Рассмотрим канояическз^о кривую С рода g в Р*"^. По
геометрическому варианту формулы Римана — Роха эффективный
дивизор D = ^ Pi степени d с dim \D \ = г состоит из d точек на С,
порождающих (d — 1 — г)-плоскость в Р*-^, т. е. он лежит
в с1-секущей (d — 1 — г)-плоскости для С. Итак, С обладает
линейной системой степени d и размерности г тогда и только тогда, когда
она имеет не менее чем г-мерное семейство d-секущих (d — г — 1)-
плоскостей.
Далее, размерность грассманиана G = G (d — г, g),
состоящего из (d — г — 1)-плоскостей в Р*~^, равна (d — г) (g — d -f- г).
Подмногообразие Og^+r (р), состоящее из (d — г — 1)-плоскостей,
проходящих через точку р, имеет коразмерность g — d -\- г в G,
поэтому подмногообразие (d — г — 1)-плоскостей, пересекающих
кривую С, имеет коразмерность g — d -\- г — 1. Тогда можно
ожидать, что коразмерность в G подмногообразия (d — г — 1)-пло-
скостей, d раз пересекающих С, равна d (g — d -\- г — 1). Поэтому
существует г-мерное семейство таких плоскостей, если
(d — r){g — d + r)-d(g-d + r-i)^r.
286 2. Римановы поверхности и алгебраические кривые
Приводя неравенство к подходящему виду, мы убедимся, что оно
имеет место, когда (d — г) (г + 1) — ''ё' ^ 0. Итак, наш подсчет
подсказывает, что
Общая риманова поверхность рода g обладает линейной
системой степени d и размерности г тогда и только тогда,
когда d^ —r-r + г, ы семейство тлких линейных систем
— г + 1
в общем случае должно быть l{d — г) (г + 1) — rg]-MepHUM.
Очевидно, что наше рассуждение далеко от доказательства;
доказательство в одну сторону мы дадим в последнем параграфе
этой главы ^). Однако два слзгчая г = 1 и г = 2 мы можем
проверить сейчас. Так как линейная система степени d и размерности 1
без базисных точек на римановой поверхности S определяет d-лист-
ное отображение S ->- Р^, то наше утверждение при г = 1
равносильно следующему:
Общая риманова поверхность рода g представима в виде
разветвленного накрытия над Р^ степени d = ^7" -f- 1
и не меньше; в случае четного g число тлких предстлвлений
конечно (с точностью до автоморфизмов Р^), тогда как для
нечетного g они образуют одномерное семейство.
Проверим это утверждение в одном направлении счетом
параметров. По формуле Римана — Гурвица d-листное отображение
кривой рода g на Р^ имеет b = 2g — 2 + 2d точек ветвления.
Тогда из приведенного выше общего рассуждения следует, что
семейство римановых поверхностей рода g, являющихся d-лист-
ными накрытиями над Р^, имеет размерность не более чем Ъ — 3 =
= 2g -\- 2d — 5. Если общая риманова поверхность рода g является
таковой, то по вычислению Римана имеем
2g + 2d—5^3g — 3, т.е. d>-|- + l.
В случае г = 2 требуемый результат можно сформулировать так:
Общая риманова поверхность рода g представима ё виде
плоской кривой степени d = ^Г** -f- 2 ы не меньше.
Снова мы проверим это только в одну сторону. В линейной
системе всех плоских кривых степени d те из них, которые
обладают двойной точкой или более сильными особенностями, состав-
1) Полное доказательство проблемы Брилля — Нётера дано в статье
Ph. Griffiths, J. Harris, On the variety of special linear systems on a general
algebraic curves.—Duhe Math. J.^ 47 (1980),-233—272.—Ярмл. ред.
4. Формулы Плюккера 287
ляют подмногообразие коразмерности 1, и общая такая кривая
имеет лишь одну обыкновенную двойную точку. Аналогично,
если 8 ^ (d — i) (d — 2)/2, то многообразие кривых степени d'
с б двойными точками имеет коразмерность б и общая такая
кривая имеет ровно б обыкновенных двойных точек. Как мы увидим
в следующем параграфе, род плоской кривой степени dc8
обыкновенными двойными точками равен
„ (d-i){d-2) ,,.
ё — 2 '
в соответствии с этим семейство плоских кривых степени d и рода g'
имеет размерность
hoiP^ e(dH))-i-8= (d + md+2) _^_^g_ (d-iHd-2) ^
= 3d + g-l.
Поскольку группа PGL (3) действует на семействе таких кривых^
многообразие представимых в таком виде римановых поверхностей
имеет размерность
3d+g — l—fi = 3d + g — 9.
Следовательно, общую риманову поверхность рода g можно так
представить только тогда, когда
3d + g—9^3g—3, т.е. d^-jg + 2,
как и предсказывалось.
Это обсуждение порождает ряд занимательных численных
задач. Например, как мы уже знаем, общая риманова поверхность
рода g = 2к имеет конечное число пучков степени к -\- i. Можно
спросить: чему равно это число? В случае g = 2, 4, 6 и 8 мы
ответим на этот вопрос при обсуждении соответствий в следующем:
параграфе, а в общем случае — в последнем параграфе этой главы.
4. ФОРМУЛЫ ПЛЮККЕРА
Ассоциированные кривые
В этом параграфе мы займемся внешней геометрией кривых,
т. е. изу11ением тех свойств кривых С а Р", которые связаны
с заданным вложением. В некотором смысле исследование
ассоциированных кривых является комплексным аналогом формализма
Френе из классической евклидовой дифференциальной геометрии.
Однако благодаря наличию комплексно аналитической структурыс
288 2. Римановы поверхности и алгебраические кривые
предмет гораздо богаче; мы получим ряд качественных и
количественных результатов, на которые нет надежды в С""-случае.
Сделаем сначала одно замечание. Очевидно, любое
отображение /: iS -> Р" римановой поверхности в проективное
пространство имеет локально подъем в С"+^, т. е. в некоторой окрестности
любой точки р ^S можно найти голоморфную векторнозначную
функцию V со значениями в С"+^, для которой / (z) = [vq (z), . . .
. . ,, у„ (z)]. Обратно, для любой векторнозначной функции у: 5->-
^ С"+^ отображение f (z) = lV(, (z), . . ., y„ (z)] определено
корректно, даже если v = О в изолированных точках. Действительно,
возьмем локальный параметр z вблизи нуля р функции у; тогда
при к = min (ordp у,) отображение
J(Z) = [2-*Уо (z), . . ., «-"Уд (Z)]
определено и продолжает /.
Предположим теперь, что S — компактная риманова
поверхность и /: iS ->- Р" — невырожденное отображение. Зададим /
локально вектор-функцией у (z) = (Уо (z), . . ., у„ (z)) и
определим к-ю (к ^ п) ассоциированную с / кривую:
/ь:5^С(А;-Ы, п+1)сР(Л''-^'С"+1),
Л(2) = [У(2)ЛУ'(2)Л...ЛУ('')(2)].
Подчеркнем, что под кривой мы понимаем абстрактную риманову
поверхность вместе с таким отображением.
Чтобы убедиться в том, что /ь корректно определено, нужно
проверить три вещи: что у (z) л ... Л у*''^ (z) не обращается
в нуль тождественно и не зависит (с точностью до умножения
на скаляр) от выбора подъема v я локальной координаты z. Что
касается первого, то пусть к^п, у (z) л ... л у<'') (z) ^ О,
а у (z) л ... л v^^^-^> (z) ф 0. Тогда, очевидно»
уС) (z) = О mod (у (z), ..., у<'-1) (z)),
т.е.
(у (z) л ... л уС"-') (Z))' = у (z) л ... л уС-г) (z) л v<■^^^> (z) =
= X(z)-y(z)A ...Ay<''-l)(z),
поэтому fk-1 (z) должно быть постоянно, а кривая / (S) должна
лежать в (к — 1)-плоскости из Р", что противоречит
предположению о невырояоденности.
Пусть теперь у (z) = р (z) • и (z) — другой подъем /. Тогда
у' = р'.у-|-р-у' И улу' = р2. (ул у'),
а в общем случае
у л ... л у<*) = р*** -у л ... л v<fK
4. Формулы Плюккера 289
Рис. 7
Аналогично, пусть w — другая локальная координата на S. Тогда
ду _
dw ~
В общем случае
dv dz dv dv dz I dv \
dw dw dz dw dw \ dz )
d^v I dz \ft(ft+l)/2 d^^v
У Л ... Л -T-r- = -т— У Л ... л
dw^ \ dw I " " ■ • • '^ di^ '
значит, /ft определено корректно.
Геометрически для точки z ^ S с у (z) л ... Л у^*^ (z) Ф О
А;-плоскость /^ (z) с: Р" есть единственная А;-плоскосаь, имеющая
порядок касания ^ А; + 1 с f (S) в точке / (z). Она называется
соприкасающейся к-плоскостъю. В случае плоской кривой имеем /:
iS ->- Р^, а Д: S ->- Р^* — отображение Гаусса, переводящее z Е S
в касательную прямую к / (S) в / (i); кривая Д (S) часто
обозначается через /* и называется двойственной кривой к /. Обратим
внимание на то, что даже в особых точках / (zq) 6 / (S), согласно
замечанию, сделанному в начале этого параграфа, определена
касательная прямая. На самом деле Д (zq) — это то, что
следовало бы называть касательной прямой в z,,: предельное положение
касательных прямых в близких точках (рис. 7).
Ветвления
Пусть /: iS -> Р" — произвольная кривая, заданная в
евклидовых координатах в некоторой окрестности точки / (Zf,) в виде
(/] (z), . . ., /„ (z)). Определим индекс ветвления р (Zq) кривой /
19-046
290 2. Римановы поверхности и алгебраические кривые
В Zq как порядок нуля якобиавой матрицы (5/i/5z, . . ., 5/„/5z), т. е.
Р (zo) = min (ordj, (dft/dz)).
Очевидно, P (zq) = 0 тогда и только тогда, когда / — гладкое
отображение в Zq; в общем случае р (zq) измеряет сложность
особенности / в Zq.
Другим способом можно определить индекс ветвления так.
Пусть (й есть (1, 1)-форма, соответствующая метрике Фубини —
Штуди на Р". Тогда Р (zq) — это единственное целое число, для
которого
/*(й—^^^^|z-Zo|2P(^»).A(z).dzAdz,
где h (z) принадлежит классу С°° и й (z„) Ф 0. Чтобы убедиться
в эквивалентности этих двух определений, рассмотрим какой-
нибудь подъем V (z) отображения / вблизи z^. Тогда
/*a. = J^^Jlog||.(z)|P = ^^(|^di) =
- 2 ^~oY azhaz-
=■■—i"—--ру 2 \viv'i-VjV'i\^-dz\dz.
в частости, для подъема
V(z) = [i, /,(2), ..., /„(2)]
имеем
1=1 гфз
а поэтому, очевидно,
/*со= >^~^ Iz-ZopP'^") .h(z)-dzAdz
с р (z) = min (ordjj (/j)), что и требовалось установить.
Для нас важны не только индексы ветвления р (z) кривой /:
S -> Р", но и индексы ветвления р^ (z) ее ассоциированных
кривых. Для простоты вычисления индексов Рй (zq) в заданной точке
Zq ^ S кривую можно представить в нормальной форме
следующим образом.
Напишем / (z) = [ у (z)] = [у,, (z), . . ., i;„ (z)], причем v (Zq) =5^
=5^ 0. После,подходящей линейной замены координат в С"+^ можно
4. Формулы Плюккера 291
считать, что v (zq) ~ (i, О, . . ., 0). Итак, теперь у^ (zq) = . . .
. ■ • = J^n (^о) = 0; напишем
(и, (Z), ..., у„ (Z)) = (Z- Zo)«'+i (v\ (z), ..., i;i (z)),
где (yJCzo), ..., yi(zo))=7^0. Сделаем линейнзто замену последних
п координат в C"+i так, чтобы (v\{zo), ■. ., vi (Zo)) = (1,0, ..., 0);
тогда
- (i;i (z), . .., i;i (z)) = (z-Zo)«>+i (i;| (z), ..., i;^ (2)),
где (v^ (zq), . . ., y^ (zq)) Ф 0. Сделаем далее линейнзто замену
последних п — 1 координат в С"+^ так, чтобы (у^ (zq), . . ., у^ (z,)) =
= (1,0, . . ., 0), и т. д. В результате мы получим систему
координат в 0""^^, в которой
l,(z)'=(l+...,(2-Zo)«' + l + ...,(z-Zo)2+«'+«'+..., ... .
Это и называется нормальной формой кривой / в окрестности
точки Zq. Отсюда видно, что Д (zq) является подпространством
Р*", порожденным первыми к + i векторами последовательности
(1, О, . . ., 0), (О, 1, О, . . ., 0), ,,(0, . . ., О, 1). Значит,
приведение кривой к нормальной форме равносильно выбору
такого базиса е^, . . ., е„ в С"+^, что /^ (zq) порождено {e^, . . .
. . ., е,}.
Вычислим теперь индекс ветвления р^ (zq) к-ж ассоциированной
с / кривой в точке Zq через показатели а^, . . ., а„ из нормальной
формы. Будем предполагать, что Zq = О, а однородный вектор
нормирован условием v^ (z)^ 1. Тогда
V (Z) = (1, 2l+«' + . . ., z2+«i+«. + . . ., . . ., z"+"'+•••+"«+ . . .).
Тогда однородные координаты Д (z) задаются детермпнавтами
(к + 1) X (к + 1)-миноров матрицы
v'{z)
Очевидно, что минор с детерминантом, имеющим минимальный
порядок нуля в точке О, есть левый минор Aj , /ц = {1, . . .
. . ., к -\- i]. Позтому вблизи Zq в качестве евклидовых координат
на /д. (S) можно взять отношения (| Aj|/| Ajjjj. Минор, отлич-
19*
292
2. Римановы поверхности и алгебраические кривые
ный от Ai^, детерминант которого имеет наименьший порядок
нуля в О, есть Aj с / = {1 . . ., к, к + 2}. Значит, индекс
ветвления
/ft в Zo равен порядку нуля функции (g^ д (])|)- Но
|Лг(2)| = г*»'-
а, + 1
«,(а,-Ы)
+ at
\Aj{z)\ =г*«>+-+««+««*1 + '.
«,(«1 + 1)
/c + l + ai + - •• +aj£
откуда
ord»
Aj(z)
(z) I
•)=aft+i+l,
так как ни один из написанных детерминантов не равен нулю.
Следовательно,
Рь (zo) = «ft+i-
Общие формулы Илюккера I
Теперь наша цель — найти связь между двумя инвариантами
KJpивoй /ft, ассоциированной с /: 5 -> Р", а именно: между
степенью dft кривой /ft! S~^P (A**"^^ С"+^) (или, для тех, кто
предпочитает представлять себе /^ как отображение в G (А; -|- 1, и -(- 1),
между индексом пересечения ff^S ^) с циклом Шуберта а^, т. е.
числом соприкасающихся А;-плос1?остей для /. (5) ci Р",
пересекающих общую (п — к — 1')-плоскость из Р") и полным ветвлением Pft
кривой /ft, определяемым как сумма Pft (z) по всем z ^ S. Для
этого мы рассмотрим подъем /J (ds^) на S стандартной метрики
с Р (Л*"^^ С"+^). С одной стороны, f% (d^) является метрикой на S
вне особых точек /ft, поэтому обычные рассуждения типа Гаусса —
Бонне позволяют выразить интеграл ее формы кривизны по S
через род S и ветвление pft. С другой стороны, вычислив явно эту
форму кривизны, мы установим связь этого интеграла со
степенями dft разных ассоциированных кривых.
^) Умноженным на степень этого отображения, если она больше I.—
Прим. перев.
4. Формулы, Плюккера 293
Прежде всего напомним, что положительно полуопределенное
скалярное произведение ф на касательном расслоении римановой
поверхности называется псевдометрикой, если оно локально предг
ставимо в виде
Ф = ft (z)-dz ® dz,
где h {£) = \z\^^-h„ (z), ho (z) >> 0. В этом случае говорят, что
ф имеет нуль порядка v при z = О, и пишут ordp (ф) = v;
дивизор же
2)ф= 2 отд.р{(р)-р
pes
называют дивизором особенностей псевдометрики ф. В
действительности ф определяет настоящую метрику на линейном
расслоении Т' <S> [-Оф]: если сечения Т' ® [D^] отождествить с мероморф-
ными векторными полями 6 =^ f {z)- {didz), имеющими полюсы по'
рядка, не превосходящего ordp (ф) ър, то скалярное произведение
(6, 6)= |/(z) p.fe(z)
определяет обычную метрику. Форма кривизны в метрики ф,
рассматриваемой на Т' ® [^ф], локально имеет вид
в = —ddlogh (z),
откуда по предложению о классах Чжэня линейных расслоений
из § 1 гл. 1
-!^ J в = deg (Г 4-i)^) = 2-2^--Ь deg W.
S
В частности, если ((i = f%(ds^)—подъем относительно Д
стандартной метрики с Р (Д'^'^^С"'^*), то D^= 2 Рй(/')•/'. а потому для
P6S
формы кривизны в такой ф
S
Теперь наша задача — непосредственно вычислить форму
кривизны псевдометрики Д (d^). Пусть со = Шь есть (1, 1)-форма
метрики Фубини — Штуди на Р (A***^ С""^^); v (z), как и выше,
есть подъем отображения /, а Ли (z) = у (z) л . . . Л i;*''^ (z) 6
6 /\'^*Ю'"^^'^■. Тогда справедлива следующая
Инфинитезимальная формула Плюккера.
jkK ) ||д^11^ 2 azAaz.
294 2. Римановы поверхности и алгебраические кривые
Доказательство. Сразу отметим, что выражение справа не
зависит от выбора подъема кривой, как и должно быть. Далее, если
у (z) = р (z) • у (z) — другой подъем, то
v' =p'-v-\-p-v',
y'' = p''.i;-f г.р'.у' + р.у",
~№+l) = p(fe+l).i;_f.J *+1 )p(fe)l,'4- ... +( *|^ jp'yW+p.yC+l).
в частности, отсюда очевидно существование функции р с р (zq) ^
ф О, такой, что у^**^^ (Zo) ортогонально к v{Zo), v' (Zg), .. .
. . ., у^*' (zq), а значит, ик у (Zg), v' (Zg), . . ., у^**^ (Zg), т. е. в
любой точке Zq с A^+i (z©) Ф О можно выбрат-ъ подъем у ^ля / с z'<''*^Hzo),
ортогональным к v (zq), . . ., v^'^^ (zq).
Теперь напишем
^(.)=J^aJlog||A,|P=v:EIa(J^dz) =
, (Aft, Лй)(Л^, Aj^)-(Afe, А^)(Л^, Aft) V /=Т -
= ( (ATT^U)^ )._^_dZAdz,
где
Aft = у л у' л ... л уУ'" i) л yC'+i^
Обозначим через FodC""^* линейную оболочку векторов
v{Zo), ..., y<'')(Zo), а через F^ — ортогональное дополнение к Fq
в С""^'. Тогда разложение C"'^* = Fo®F^ индуцирует
разложение
p+q=k+i
пространства А ^ '-■"^ '^'^'^ пространства со скалярным
произведением с соответствующей метрикой на каждом слагаемом
А^^о® А'(^о^)- Если y(''+0(z„)€F^ то
Aft (z„) € А """'П, л^ (zo) € А"^ ® А ^^о"-;
поэтому
(Aft(zo), AHzo)) = 0,
(А; (Zo), Ак (Zo)) = II Aft_i (z„) Ip.II y(ft+i) (z„) \\^
(Aft (z„), Aft (Zo)) • (Ak (Zo), A^ (Zo)) =
= II Aft_i (Zo) |P.|| yC'+i) (Zo) ||2.||Aft(Zo) IP =
= l|Aft_i(zo)IP-||Aft+i(zo)|P,
что и доказывает требуемую формулу. О
4. Формулы, Плюккера 295
Форма кривизны псевдометрики f% (ds^) удовлетворяет
соотношению
2 , 2 «'С iog ^ II Ль ||4 ;
= — /f-1 (cofe-i) + 2f% (cofe) — ft+i (m+i),
откуда no теореме Виртингера
-!^1=:1 j в = - 4_ 1 + 2dft -dfe+i.
s
Сравнивая это с интегралом \ в, вычисленным вначале, мы полу-
S
чаем следующее соотношение:
Глобальная формула Плюккера:
dk-i - 2dft + dft+i = 2g-2- {•,.
В качестве прямого применения этой формулы Плюккера
докажем, что рациональные нормалыгые кривые характеризуются
отсутствием на них точек перегиба.
Предложение. Единственная всюду нерааветвленная кривая /:
j^ -> Р" является рациональной нормальной кривой.
Доказательство. Чтобы уничтожить все d^ при А; >> О,
рассмотрим линейную комбинацию разных формул Плюккера:
2 (и - А) (dfe_ 1 - 2dfe-Ь dft+i) =
=^(n-k)(2g-2-^^) (d_i = d„ = 0).
ft=0
Значит,
^{n-k)^„ = (n + l)d + n{n+i)(g-l) {d = do).
в частности, если Р^ = О при всех i, то
n(n+i){g-i)<0^g = 0,
а сама формула означает, что
—(и + i) d = —п (п + 1),
т. е. d = /г и iS — рациональная нормальная кривая. Q
296 2. Римановы поверхности и алгебраические кривые
Общие формулы Ллюккера II
Дадим теперь другое доказательство общих формул Плюккера,
которое более геометрично, однако не имеет локального аналога.
Пусть/; С -> Р" — невырожденная кривая ^), а у (z) —
локальный подъем / в С"+^. Основные действующие лица:
Aft (Z) = i; (Z) л ... л yW (Z) 6 Л'""'С"+',
Д: C-^G{k+U /г-Ы)сР(А''+'С"+'),
dft = deg Д (С) с Р (Л"'"'€"+*) =* (Д (C)-ffi)G(ft+i. n+i),
как и прежде. Для удобства положим
Пусть Fm-2 — общая (т— 2)-плоскость в Р (Д*"^^ С"+^), не
пересекающая С, а отображение я^: С-> Р^ соответствует проекции
/й (С) из Fm-2 на прямую. Очевидно, что число листов накрытия
л,у равно степени d^ кривой Д (С). Поэтому по формуле Римана —
Гурвица
2g-2 = -24 + Tft,
где Tft — степень дивизора ветвления для Пу.
Чтобы найти Tft, представим отображение Д в нормальной
форме в точке Zq ^ С:
A(z) = [l-b ...,(z-Zof'+4 ..., (z-Zo)^'+^'+4 ..., ...].
(Фигурирующие здесь показатели у^ являются индексами
ветвления (г — 1)-й ассоциированной с Д кривой в точке z^\ итак, у^ =
= рй (Zq), а остальные числа уа» • • • в дальнейшем не важны.)
Из нормальной формы видно, что Пу имеет порядок ветвления
(Тг+1 + • . . -Ь Yi + I) в Zq тогда и только тогда, когда
гиперплоскость Fm_2, /ft (zo) с: Р"* содержит соприкасающзтося
/-плоскость к /ft (С) в Zq, но не содержит соприкасающейся [1 -\- 1)-пло-
скости. В частности, если выбрать Fm-2 достаточно общей,
т. е. такой, чтобы Vm-^ не пересекала касательных прямых
к /й (С) в стационарных точках ^) для /ft и не пересекала
соприкасающихся 2-плоскостей ни в какой точке /ft (С) по прямой, то
в точке Zq, соответствующей особенности Д (С), отображение
Пу будет иметь индекс ветвления рй (Zq), а для Zq, отвечающих
^) Здесь / предполагается взаимно однозначным отображением в общей
точке.— Прим. перев.
^ То есть в таких точках, где Yi + ?2 > 0-— Прим. перев.
4. Формулы, Плюккера 297"
гладким точкам Д (С), Пу имеет простое ветвление, если
касательная прямая Тг^ (fk (С)) к /ft (С) в Zq пересекает Vm-2^ и не
разветвляется в противном случае. Следовательно, степень дивизора,
ветвления отображения Пу равна индексу ветвления Pft
ассоциированного отображения Д плюс число касательных прямых:
к/ft (С), пересекающих общую (т — 2)-плоскость в Р"*, т. е. плюс
степень касательной линейчатой поверхности
zee
кривой /ft (С).
Наше вычисление степени deg Т (ffi (С)) основано на одном
наблюдении. Касательная прямая к /ft (С) в гладкой точке z
порождается векторами
Aft (z) = у (z) л у' (z) л ... л i;(^>(z),
Л^ (z) = г; (z) л у' (z) л ... л у^"-') (z) л i;(*+i) (z).
Значит, эта касательная прямая
Т, ih (С)) = {[i; (Z) л ... л v^'^-') (Z) л (V^*> (Z) +
-b?..i;(''+i)(z))]K. х.]бр,.
лежит целиком в грассманиане G (к -\- i, и + 1) ci Р"*; в
действительности эт,о просто цикл Шуберта из к-плоскостей в Р"^
содержащих соприкасающуюся (к — 1)-плоскость /ft.^ (z) для fez.
и содержащихся в соприкасающейся (к + \)-плоскости fii+i (z) для
fez. Так как гиперплоское сечение грассманиана G (А; -|- 1, л + 1)
с: Р"" является циклом Шуберта ff^, то
degr(/ft(C)) = #(r(/ft(C))-F^-2)pm=#(r(/ft(C)).ffJ)G(ft+i.„+i).
Согласно исчислению Шуберта из § 6 гл. 1, ffj гомологично циклу
Шуберта ffi,i (r„_ft) А-плоскостей из Р", пересекающих некоторую
[п — А;)-плоскость r„_ft по прямой, плюс цикл Шуберта о^ (r„_ft_2)'
А-плоскостей, пересекающих некоторую (и — к — 2)-плоскость.
r„_ft_2. Кроме того, понятно, что цикл Т^ {fh {С)) cz G {к-\- i,
и + 1) А-плоскостей из Р", содержащих /ft_i (z) и содержащихся
в /ft+i (z), пересекает цикл Шуберта о^ (Г„_й_2) тогда и только
тогда, когда r„_ft_2 имеет общую точку с /ft+i (z), поэтому индекс
пересечения Т (f^ (С)) с а^ в G(к -\- i, п + i) равен числу точек
Z ^ С, (к -\- 1)-я соприкасающаяся плоскость которых пересекает
общую (п — к — 2)-плоскость Г„_й_2 с Р", т. е. равен степени
dft+i {к + 1)-й ассоциированной кривой f^+i (С). Подобно этому,
TzUiiiC)) пересекает цикл о^, i(r„_ft) в точности тогда, когда
/ft_i (z) имеет общую точку с r„_ft, поэтому индекс пересечения
Т (Jh {С)) с а^, 1 равен числу точек z ^С, (к — 1)-е
соприкасающиеся плоскости которых пересекают общую (п — А;)-плоскость
298 2. Римановы поверхности и алгебраические кривые
Tij.ft CZ Р", Т. е. степени d^.^ (к — 1)-й ассоциированной кривой.
В результате
deg Т ih (О) (с: Р"*) = # (Г (4 (О) • (ffi. 1 + cr2))G(ft+i. n+i) =
и индекс ветвления отображения Пу равен
Tft = Pft + dft_i + dft+i.
Отсюда по формуле Римана — Гурвица мы получаем общие
формулы Плюккера
2^ - 2 = -24 + Ч 2dk + Pft + dft-i + dft+i.
Точки Beiteptumpacca
Формулы Плюккера, вообще говоря, относятся к внешним
инвариантам кривых. Однако, следуя общему принципу о том, что
проективные инварианты канонической кривой S отражают
•ее внутренние свойства, мы применим формулы Плюккера к
канонической кривой и найдем способ подсчета числа точек Вейер-
штрасса на римановой поверхности.
Пусть S — риманова поверхность рода g, р Е S —
произвольная ее точка. Рассмотрим линейные системы для дивизоров к-р,
.4 = 1,2 По формуле Римана — Роха h" (кр) = к — g + I
лри к ^ 2g — 1, а в общем случае
{h''{{k—l)p)-\-l, если существует f^&fl{S)
с (f)^=kp,
h''{{k — I) р) в противном случае.
Следовательно, существует ровно g положительных целых чисел
л^, . . ., Ug, для которых на S нетмероморфндй функции f с {f)оо =
=aip. Эти числа а^-<,а^-<... .-^cig называются пробелами в точке
P^S.
Можно ожидать, что для общей точки р ^ S все дивизоры
кр регулярны, т. е.
'(ад={
k—g+l, k-^g,
и а; = i, 1 = 1,..., g.
Назовем точку р яа S тлчкой Вейерштрасса, если какой-нибудь
жз дивизоров кр иррегулярен, или, иначе говоря, если существует
непостоянная мероморфная функция / на S, голоморфная на
4. Формулы Плюккера 299
S — ip} и имеющая полюс порядка ^g в р. Сопоставим каждой
точке Вейерштасса р ее вес
где а[ — пробелы в р ^ S. Например, для гиперэллиптической
кривой iS* пробелами в точке /? с ft" (2р) = 2 являются значения
а. = 2г — 1.
В этом случае р называется гиперэллиптической точкой Вейер-
штрасса; другая крайняя возможность — точка р веса 1 с
пробелами
1, 2, 3, . . ., g--!, g+i,
т. е. имеющая минимальное отклонение от ожидаемого расположе-
лия; она называется нормальной точкой Вейерштрасса на S.
Для негиперэллиптической римановой поверхности S точки
Вейерштрасса можно охарактериэовать другим способом. Пусть
С cz. Р*~^ — каноническая кривая для S. Тогда по
геометрическому варианту формулы Римана — Роха h" (gp) >• 1 для точки
J3 6 С в том и только том случае, когда точка р ^ С ж ее первые
g — 1 «производных» не порождают Р*~^, т. е. р является точкой
Вейерштрасса на S в том и только том случае, когда ей
соответствует, особая тпочка на одной из кривых, ассоциированных с С.
Точнее, если для локального параметра z в р задать каноническое
отображение ijr в нормальной форме
*л:(2) = [1, zi+«i+..., z2+«i+«.-}-..., ..., z*-'+"'+-"+"«-i-t-...],
то пробелами в точке р ^ S будут значения
«1 = 1, а^ = 2 + «1, аз = 3 + cXi + «2, . . .
. . ., fflg = g- + «1 + «2 + . . . + ag_i,
a вес точки p равен
W{p)=% (g-k)a^J^ (g_A_l)p, (p).
Теперь уже можно найти общее число точек Вейерштрасса
на S, используя формулы Плюккера, полученные в ходе
доказательства для рациональной нормальной кривой. Положим d =
= 2^- — 2] и п = g — и тогда
y:(g~k-i)^^ = g(2g-2) + (g-i)g(g-i) = (g-i)g(g + ih
т. о. общий вес тлчек Вейерштрасса на римановой поверхности
рода g равен {g — i)-g-{g + 1).
300 2. Романовы поверхности и алгебраические кривые
Точки Вейерштрасса представляют интерес ввиду того, что
они являются «отмеченными» точками римановой поверхности,
т. е. определены инвариантно. В качестве одного из приложений
последнего результата установим следующий факт.
Теорема. Любая риманова поверхность S рода >.1 может иметь
лишь конечное число автоморфизмов.
Доказательство. Любой автоморфизм поверхности S должен
переставлять ее точки Вейерштрасса, но, поскольку их лишь
конечное число, достаточно рассмотреть те автоморфизмы на 5,
которые сохраняют каждую из точек Вейерштрасса. Предположим
теперь, что S негиперэллиптична. Тогда по теореме Клиффорда
h<>(kp)<±- + i
для любой точки р Е S при к ^2g — 1, поэтому а,- ^ 2г — 2,
i = 2, . . ., g, и
w{p) = 2^i-i<2 i-2<^'-%^'-^\
i=l t=2
a значит, число различных точек Вейерштрасса на S не меньше,
чем
(g-l)g(g+l) _ 2g(g + l) ^og I Q_
-j(g-i)(g-2) ^-^ ^
Будем пока предполагать, что S негиперэллиптична. Пусть
С — каноническая кривая для S. Тогда любой автоморфизм на S
индуцирован некоторым автоморфизмом пространства Р*~*,
сохраняющим С. Пусть т: Р*~^ -> Р*"^ — такой автоморфизм,
который, кроме того, оставляет неподвижной каждую точку
Вейерштрасса на S. Тогда т сохраняет все соприкасаюп];иеся плоскости
в каждой точке Вейерштрасса pt. В частности, если Vi —
соприкасающаяся {g — 3)-плоскость к С в pi, то т сохраняет Fj вместе
с пучком гиперплоскостей {iTUj^gpi, проходящих через Fj.
Предположим, что Vi содержит к точек кривой С, отличных от pi.
Тогда любая гиперплоскость, содержащая Fj, имеет индекс
пересечения с С по точкам, лежащим в F,, ^A-f-g — 2, а потому
содержит не более g — к точек Вейерштрасса вне F,-. Но на С вне
F; лежит не менее |
2g+2-{k+i) = 2g-k+i
точек Вейерштрасса. Значит, по крайней мере три из
гиперплоскостей {Н]}^^рг содержат точки Вейерштрасса извне Fj, а потому
сохраняются при действии т. Отсюда следует, что т сохраняет
4. Формулы Плюккера 301
каждую из гиперплоскостей Н\, но тогда т имеет конечный
порядок, так как гиперплоские сечения С состоят из конечного числа
точек.
Итак, пусть т имеет порядок d. Рассмотрим фактор S' кривой S
ло действию группы автоморфизмов {т*}. Соответствующая
проекция я представляет S в виде d-листного накрытия над S'\ при
этом каждая точка Вейерштрасса имеет индекс ветвления d — 1.
Поэтому
2g-2-^d{2g {S') _ 2) + (d - 1) {2g + 2) >
>(d - 1) {2g - 2) + 2d-g (S') + 2{d- 2);
значит, d '^ 2 =^ g (S') = 0 и d = 2, т. e. поверхность S гипер-
эллиптична. Таким образом, если S — негиперэллиптическая рима-
нова поверхность, то любой автоморфизм, оставляющий
неподвижной каждую точку Вейерштрасса на S, тождествен, что и
доказывает теорему в этом случае.
Если же поверхность S гиперэллиптична, то любой ее
автоморфизм задается по модулю гиперэллиптической инволюции
автоморфизмом кривой С а Р*"^ — канонического образа
поверхности S. Но кривая С рациональна, и поэтому любой ее
автоморфизм, оставляющий на месте 25* -|- 2 > 3 точек ветвления,
соответствующих точкам Вейерштрасса поверхности S, тождествен. Q
Пусть теперь S — риманова поверхность рода g" ^ 3. По нашему
последнему результату, если S допускает какой-нибудь
автоморфизм, то она допускает некоторый автоморфизм ф простого
порядка р. Пусть S' — фактор S по действию группы автоморфизмов
{ф*}, а g' — род S'. Так как неподвижные точки любого
автоморфизма ф*, кроме тождественного, являются неподвижными
точками ф, то дивизор ветвления отображения я: S -^ S' состоит
из некоторого числа к точек ветвления индекса р — 1. Поэтому
поверхность S определяется поверхностью S' ш к точками на ней
« точностью до конечного числа возможностей. Эта совокупность
имеет 3g' — 3 -|- А; параметров. С другой стороны, по формуле
Римана — Гурвица
2g-2=p {2g' -2) + к{р- 1),
т. е.
,._2g—2-p(2g'-2)_ 2g-2pg' . с,
р —1 р—1 '
Значит, S зависит не более чем от 2>g' -\—- _. 1 параметров.
Однако, поскольку g' ^ {Ир) (g — 1) + 1 ■< (g + 1)/2, этих
параметров меньше 2>g — 3 ^). Отсюда мы заключаем, что
^) Точнее, ^2^ — 1/2, что <3^ — 3 при] g > 3.— Прим. перев.
302 2. Римановы поверхности и алгебраические кривые
Общая риманова поверхность рода g '^ 3 не допускает
автоморфизмов.
Пользуясь теми же методами, читатель может проверить, что-
риманова поверхность рода g^ 2 не может иметь более чем:
8А (g — 1) автоморфизмов.
Последнее замечание о точках Вейерштрасса: счетом
параметров можно убедиться также в том, что общая риманова
поверхность рода g" > 3 не имеет точек Вейерштрасса с пробелами Л; >• t
при г < g*. Действительно, предположим противное, т.е. что-
общая риманова поверхность S содержит точку р с dim | (g—1) р | '^
^ 1. Тогда S является (g — 1)-листным накрытием над Р^ с
индексом ветвления g — 2 в р. Дивизор ветвления Б этого отображения
содержит слагаемое (g — 2) р плюс эффективный дивизор
степени
2g-2 + 2(g-i)-(g-2) =3g-2,
поэтому эависит от 3g — 1 параметров. Следовательно, S
зависит не более чем от 3g — 1 — 3 = 3g — 4 параметров, и мы
получили противоречие. Аналогично читатель может проверить, чта
общая риманова поверхность рода g" ^ 3 не имеет точек р
с dim \ (g -\- i) р \'^ 3; для этого надо вычислить (подобно тому»
как это сделано в конце § 3) число параметров плоских кривых
рода g и степени g + 1, обладающих (g -{- 1)-кратной касательной
прямой. Эти два утверждения вместе показывают, что общая
риманова поверхность рода g'^3 имеет, только нормальные точки
Вейер штрасса.
Формулы Шлюккера для плоских кривых
Перейдем теперь к рассмотрению проективных инвариантов
плоских кривых. Для этого потребуется техника несколько иная,
чем та, которая использовалась выше. Формулы Плюккера,
которые мы пока доказали, относятся лишь к особенностям кривой /г
S —^ Р", проистекаюпщм из локального поведения отображения /.
Однако плоские кривые f: S -^ Р^, как мы видели, могут иметь
особенности, связанные с глобальным поведением /, например
обыкновенные двойные точки, что не отражено пока в наших
общих формулах. Чтобы получить достаточно широкий круг
применимости, мы рассмотрим кривые в Р^ с т.радиционными
особенностями, которые мы сейчас определим.
Определение. Будем говорить, что кривая /: S -^ Р^ имеет
традиционные особенности, если каждая точка р ^ S является
одной из следующих (рис. 8).
4. Формулы Плюккера 303
Рис. 8
1. Регулярная точка, т. е. точка, гладкая для /, а также для
двойственной кривой /* ^). Для такой точки Ро (р) = Pi (р) = ^
и локально / имеет нормальную форму вида
/(Z) = [1, Z+. . ., 2^ + . . .].
2. Обыкновенный перегиб для /, т. е. гладкая точка для /,
в которой касательная прямая имеет касание порядка три. Ей
отвечают нормальные формы вида
/ (Z) = [1, Z + . . ., 2» + . . .],
/* (Z) = [1, 2^ + . . ., 2» + . . .].
3. Касп, или точка заострен'ля, для f, т. е. особая точка /
с нормальной формой
/ (г) = [1,2^+.. ., 2» -Н . . .].
ч
Стало быть, точка р есть обыкновенный перегиб для f тогда и тюлька
тогда, когда р — точка заострения для /*.
4. Точка двойного касания для /, т. е. гладкая отличная от
перегиба точка р, касательная прямая в которой имеет еще
(и ровно) одно касание в некоторой другой точке дфр.
5. Обыкновенная двойная точка /, т. е. точка, в образе которой
траясверсально пересекаются ровно две ветви кривой / {S).
Очевидно, р есть точка двойного касания для/<^^>р есть обыкновенная
двойная точка /*.
Сделаем одно важное замечание: если /: S -^ Р^ — любая
плоская кривая, а /*: S -^ Р^* — двойственная ей кривая, то каса-
^) Иначе говоря, f (р) — гладкая точка / (5).— Прим. перев.
304 2. Риманови поверхности и алгебраические кривые
Рис. 9
тельная прямая /* (zq) ^ Р^* в точке z^ ^ S является предельньш
лоложением секущей / (zq), f (z) при z —>- Zq (рис. 9). Аналогично,
.(/*)* (zo), т. е. точка в Р^, соответствующая касательной прямой
зс /* {S) CZ Р^* в /* (Zq), является предельным положением точки
пересечения касательных к / {S) ъ z и Zq при z -»- Zq, что, конечно,
есть Zq. Значит, кривая, двойственная к двойственной, совпадает
с исходной.
Теперь предположим, что /: ■? -> Р^ имеет традиционные осо-
'бенности ж С = f (S), С* = f* (S). Введем обозначения:
g = род кривой S,
d = degC, d* = degC*,
b = число двойных касательных прямых к С, Ь* = число
двойных касательных прямых к С*,
f = число перегибов кривой С, f* — число перегибов
кривой С*,
и = число точек заострения кривой С, х* = число точек
заострения кривой С*,
б = число двойных точек кривой С, б* = число двойных точек
кривой С*.
Имеют место следующие соотношения:
b = б*, Ь* = б,
/ = X*, /* = X.
Степень двойственной к С кривой, обычно называемая классом
кривой С, по определению есть число точек пересечения С* с общей
прямой в Р^*, т. е. число касательных к кривой С, проходящих
через общую точку р 6 Р^. Пусть р — такая точка; предположим,
кроме того, что она не лежит ни на одной из касательных прямых
4. Формулы Плюккера 305
К С В особых точках С и точках перегиба. Выберем на Р^ такие
координаты [Х^, Х^, Х^}, что р = [Ь, О, 1] ^); если С задана в этих
координатах полиномиальным уравнением g (Zq, Х^, Х^ = О,
то касательным к С, проходящим через р, соответствуют в
точности гладкие точки кривой С с (др/дХ^) (д) = 0. Кривая С =
= (dg/dX^ = 0) имеет степень d — 1 и проходит через каждую
двойную точку С с кратностью пересечения 2, а также через
каждую точку заострения с кратностью пересечения 3. Поэтому
С" пересекает С по (С-С) — 26 —Зх гладким точкам, т. е.
(») d* = d(d — i) — 28 — Эх.
Аналогично, рассматривая проекцию я кривой С из точки р
на прямую (при этом С будет d-листным накрытием над Р^),
мы получим соотношение
%{S) = 2-2g = 2d-b,
где b обозначает степень дивизора ветвления отображения по/:
S ->- Р^. Далее, так же как и при доказательстве полученной
выше формулы для рода плоской кривой, мы видим, что гладкая
точка q кривой С является точкой ветвления для я в том и только
том случае, когда (dgldX^) (д) = О, поэтому имеется d (d — 1) —
— 26 ^ Зх точек ветвления (и их индекс равен 1) для я о /,
отвечающих гладким точкам кривой С. Более того, я о / не
разветвляется в точках S, соответствующих обыкновенной двойной
точке С, а каждой точке заострения С соответствует точка на S
с индексом ветвления 1. Итак,
6 = d (d _ 1) _ 26 — Зх 4- X = d (d — 1) — 26 — 2х,
и потому
2—2g' = 2d —d(d—1)-}-2бЧ-2х,
, , (d—l)(d—2) о
(**) g=^-^ ij '■ 6 —X.
Соотношения (*) и (**) применимы также и к двойственной
кривой С*; в результате мы получаем классические формулы
Плюккера
d* = d(d-l)-26-3x, g= (Л-'^)^-^) s_^^
d = d*(d*-l)-26-2/, g = ''^*~y~^^-6-/.
-В дальнейшем нам пригодится формула для канонического
расслоения римановой поверхности S, заданной в виде плоской кри-
^) И бесконечноЖудаленная прямая пересекает С трансверсально по
гладким точкам.— Прим. перев.
20-046
306 2. Римановы поверхности и алгебраические кривые
ВОЙ С степени d с традиционными особенностями. Пусть /: 5 -> Р*
и я: С ->- Р^ такие же, как выше. Чтобы найти требуемую
формулу, рассмотрим подъем ш на ■? мероморфной 1-формы d (Xi/X^).
Прежде всего ш имеет двойные полюсы над точками пересечения С
с прямой Xq = 0; значит, (ш)» = /* {2Н).
Теперь рассмотрим сечение а ^ Н" (Р^, 0 ((d — 1) Я))),
заданное однородным многочленом dg/dX^, где g такое же, как выше.
Вне множества особых точек кривой С имеем (й))о = (f*a)- В
обыкновенной двойной точке р = f (д) = f (q') на С, напротив, ш не
равно нулю, а f*a однократно обращается в нуль в каждой
из точек q и q'; для точки заострения р = f (q) на С форма ci>
имеет простой нуль, а f*o обращается в нуль трехкратно.
Обозначим через D дивизор на S, состоящий из прообразов особых точек
кривой С (при этом прообраз точки заострения возьмем дважды).
Тогда ((й)о = (f*a) —D, и окончательно имеем
Ks = (о))о - (о))со = /* {{d -3)H)-D.
Рассмотрим теперь некоторые частные случаи.
Плоские кубики. Пусть С — неособая плоская кубика. Тогда
d = 3, g = i, X = б = 0. Кроме того, число b двойных
касательных к С равно нулю, так как прямая не может пересекать С
четырехкратно. Аналогично, произвольная точка перегиба кривев
С с нормальной формой
Z ^ [i, Z + . . ., z^+^ + ...] (Z>0)
должна быть обыкновенной (т. е. 1 = 0). Поэтому все особенности
здесь традиционны, и по классическим формулам Плюккера
имеем
d* = 6, / = 9.
Все эти девять точек перегиба различны и могут быть найдены
следующем способом. Пусть О £ С — одна из точек перегиба.
Тогда, согласно рассуждению из § 2 об обращении эллиптических
интегралов, кривую С можно задать параметрически как
/(г)
/: С-^Р2, где /(z) = [l, §>(z), Г(2)], 2= J ©,
о
а ft) — образующая в Я" (С, Q^). По теореме сложения три точки
А, В, С будут точками пересечения с прямой тогда и только
тогда, когда
А в с
Jo)+Jo)-t- Jo)=0(A),
5. Соответствия 307
где Л = /~^ (0) — решетка периодов в С. В точках перегиба
А = В ^ С; это ровно девять точек
[1, f (2), f' (z)], где 32 6 Л.
Отсюда вытекает следующее утверждение классической
геометрии. Если прямая L проходит через две точки перегиба неособой
кубической кривой-, то она проходит также через третью точку
перегиба.
Отметим, что если С имеет одну обыкновенную двойную точку,
то число точек перегиба на С уменьшается до трех, а если С имеет
точку заострения, то точка перегиба всего лишь одна.
Плоские квартики. В случае когда С — гладкая плоская квар-
тика с традиционными особенностями, степень двойственной
кривой С* равна d* = d{d — i) = 12. Отсюда 26 + 3/ = 12- И — 4 =
= 128.
II-10
с другой стороны, род с равен 3, поэтому 3 = —^ ^ — Л
т. е. b -\- f = 52. Значит,
/ = (26 -Н 3/) - (26 -Н 2/) = 128 -- 2-52 = 24,
6 = (36 -Н 3/) - (26 + 3/) = 3-52 - 128 = 28,
т. е. С имеет 24 точки перегиба и 28 двойных касательных. Эти
28 двойных касательных к гладкой плоской квартике появятся
еще раз в § 4 гл. 4, правда в другом контексте.
Рассмотрим более общую ситуацию. Пусть С — гладкая
плоская кривая степени d с традиционными особенностями. Тогда
d* = did-i), g = ^'-^^i'-'\
поэтому 26 + 3/ = d (d — l)-(d (d — 1) — 1) — d и
b + f-
Следовательно
^ I ^_ (d(d-i)-i)(d(d-i)-2) (d-l)(d-2)
/ = (26-t-3/) - (26-t-2/) = 3d (d - 2),
6 = (36-t-3/)-(26-t-3/) = 4-^(«^+l)(^ —1)(^—2)-4d(d-2).
5. СООТВЕТСТВИЯ
Определения и некоторые формулы
Соответ,ствие Т: С -^ С степени d между двумя кривыми
С ж С сопоставляет каждой точке р ^ С дивизор Т (р) степени d
на С, меняющийся голоморфно по р. Его можно определить либо
308 2. Римановы поверхности и алгебраические Кривые
как голоморфное отображение С -> С'^^ из С в d-кратное
симметрическое произведение кривой С, либо, что эквивалентно
и более нам полезно, посредством его графика, т. е. кривой вида
D = {(р, д): деТ{р)}<=С X С.
Ясно, что и обратно, по каждой кривой D cz С X С ^) можно
определить ассоциированное с ней соответствие, полагая
T{p) = i* (D) 6 Div (С),
где ip'. С -*■ С X С отображает q в {р, q). Соответствие
называется неприводимым, если таков его график.
Обратное соответствие к соответствию Т: С -*- С с графиком
D CZ С X С определяется как соответствие, заданное кривой
О' = {{q, р): {р, q)eD}^C' X С,
т. е. как
T-4q)= S р.
Вот некоторые основные соответствия.
1. Пусть {!)>,} — пучок без базисных точек на кривой С, или,
что эквивалентно,— разветвленное накрытие С—»Р^. Тогда
каждой точке р ^ С отвечает единственный дивизор D (р) ^ {^>}^
содержащий р, что определяет соответствие Т (р) = D (р) — р,
т. е. Т задано кривой
D = {{р, q): Dx — р — q^ О при некотором X} cz С X С.
Отметим, что соответствие Т симметрично, т. е. Т = Т~^.
2. Пусть С аР^ — гладкая плоская кривая. Определим
соответствие Т: С-^С формулой Т (р) = Тр{С)-С — 2р, т. е. Т
задается как замыкание D множества
{(Р,ЧУ-РФЧ, qeTpiC)}
в СхС. Заметим, что р 6 Т{р) только тогда, когда Тр (С)
пересекает С в р с кратностью 3 или более, т. е. когда р — точка
перегиба для С; Т называется касательным соответствием на С.
Перечислим основные понятия, относящиеся к соответствиям,
с которыми мы будем иметь дело.
1. Точка совпадения соответствия Г: С-*-С —это пара (р, д) 6
£ С X С, такая, что q встречается в Т (р) с кратностью 2 или
более; пару {р, q) будем называть точкой совпадения кратности т
1) Не содержащей компонент вида р X С.— Прим. перев.
5. Соответствия 309
ДЛЯ Т, если q встречается в Г (р) с кратностью /п + 1. В первом
из приведенных ВБПпе примеров пара (р, q) является точкой совпа-
дения для Т, если q — точка ветвления отображения С—>Р^,
заданного пучком {D^), л р Ф q ^ п~^ (я (q)); в примере 2 точке
совпадения отвечает двойная касательная к С.
В общем случае если соответствие Т: С -^ С задано кривой
D CZ С X С, то точка совпадения — это либо точка ветвления
проекции я^: D -*- С кривой D на первый сомножитель, либо
особая точка D.
2. Неподвижная точка соответствия Т: С -^ С кривой с самой
собой — это точка р ^ С, для которой р ^ Т (р); р называется
неподвижной точкой кратности т для Т, если р встречается в Т (р)
с кратностью т. В примере 1 ВБПпе неподвижными для Т являются
точки ветвления отображения C->P^, заданного пучком {D}};
в примере 2 это точки перегиба для С. В общем случае если
соответствие Т: С -^ С задано кривой D cz С X С, то неподвижным
точкам отвечают точки пересечения D с диагональю А cz С X С.
3. Точка пересечения двух соответствий Т, S: С-*-С, как
и подсказывает название,— это такая пара (р, q) ^ С X С, что
точка q содержится как в Т (р), так ж в S (р). Если Т ж S заданы
кривыми D и i^ в С X С, то их точками пересечения являются
точки пересечения кривых D ж F ж только они.
4. Пусть Т: С -*- С — соответствие кривой рода ^ ^ 1 с самой
собой. Будем говорить, что оно имеет валентность к, если класс
линейной эквивалентности дивизора Т (р) -{- к-р яе зависит от р.
Соответствие из примера 1 выше имеет валентность 1, а из
примера 2 — валентность 2. В общем случае соответствие может
и не иметь валентности, однако если оно имеет некоторую
валентность, то она определена однозначно. Действительно, если для
к>к' классы линейной эквивалентности для Т (р) + к-р ж
Т (р) -\-к'-р одновременно не зависят от р, то все дивизоры
{к — к')-р принадлежат некоторой линейной системе Е
размерности г ^ 1. С другой стороны, в общей точке кривой i^ (С) а Р'
всякое гиперплоское сечение имеет кратность ^ г, следовательно,
г = к — к'; но тогда i^ (С) — рациональная нормальная кривая,
что противоречит предположению g (С) ^ 1.
На практике наиболее доступную информацию о соответствии
Т: С -*- С доставляют: его степень, т. е. индекс пересечения
^(D-E) кривой соответствия с вертикальными слоями Ер =
= nj^ (р) cz С X С; степень Т~^, равная индексу пересечения D
с горизонтальными слоями Fj, = п^^ (р) cz С X С; валентность
Т, если таковая существует. С другой стороны, как мы увидим
ниже, чтобы вычислить число точек совпадения или неподвижных
точек для Т, желательно знать ?Еласс годюлогий кривой D cz С X С.
Однако, как правило, указать этот класс невозможно, так как
310 2. Римановы поверхности и алгебраические кривые
ранг группы Я^. 1 (С X С) П Н^ {С X С, Z) дивизоров из С X С
по модулю гомологической эквивалентности ведет себя в высшей
степени непредсказуемым образом. Кое-какие эффективные
вычисления для некоторых соответствий можно осуществлять
благодаря следующей важной лемме.
Лемма. Пусть Т: С -*-С — соответствие, а D cz С X С —
его график. Тогда Т имеет валентность к в там и только том
случае, когда D гомологичен линейной комбинации вертикального
и горизонтального слоев Е, F на С X С и диагонали А а С X С:
D ^ аЕ + bF — Ы.
Доказательство. Прежде всего мы утверждаем, что если D '^
'— аЕ + bF — А:А, то D линейно эквивалентен сумме
G = S «i^Pi + 2 biFq^ - кА,
где Ер = яI^ (р), Fg = п^} (q). Это следует из формул Кюннета.
Действительно, поскольку две первые вертикальные стрелки
диаграммы
Н\Сх СЛ) ^H'(CXC,Q) ^Pic^'CCx С)-*0
ЯЧС,Ж)ея'(СД)^ЯЧС,Й)фЯЧС,0)—*Pic°(C)xPic°(CK0
являются изоморфизмами, то такова и последняя. Далее, если
D CZ С X С линейно эквивалентен написанному выше дивизору G,
то для общей точки р ^ С дивизор Т (р) = ip (D) линейно
эквивалентен дивизору ip (G) = 2 biQi — к-р, а тогда, очевидно, класс
линейной эквивалентности суммы Т (р) + к-р не зависит от р.
Обратно, предположим, что соответствие Т имеет валентность к.
Напишем
T{p)+k-p = ^biqi,
T-4qo) + k-qo = I>atPt
и рассмотрим линейное расслоение L на С X С с дивизором
D-^aiEp^~^biFg^ + kA.
Тогда по предположению ограничение расслоения L на каждый
слой Ер проекции щ и выбранный слой Fg^ для Яа тривиально.
Мы утверждаем, что в этом случае само L тривиально; этого,
очевидно, достаточно, чтобы доказать лемму. Чтобы в этом
убедиться, возьмем глобальное ненулевое голоморфное сечение Sq
ограничения L на Fq^. Тогда для каждого р ^ С существует единствен-
5. Соответствия 311
ное глобальное сечение t (р) ограничения L | Ер, такое, что
t (р) (q) = So (р, go)- Положим t (р, q) = t (р) (q); очевидно, что
t — глобальное ненулевое голоморфное сечение L. Следовательно,
L тривиально. О
Замечание. На первый взгляд кажется, что понятие
валентности неестественно и что соответствия с валентностью — большая
редкость. В действительности дело обстоит как раз наоборот:
на общей римановой поверхности нет соответствий без
валентности. (Как мы увидим ниже, «общность» понимается здесь
несколько необычно.) Мы не будем это доказывать, однако
читатель мог бы убедиться, что это так, из следующих соображений.
По формуле Кюннета
я'- ^ (С X С) = (Я^- ^ (С) О Я»'" (С)) ф (Я*-»(С) ® Я"' ^ (С)) ф
ф (Я"' ^ (С) О Я^'" (С)) ф (Я"'" (С) О Я*'' (С)).
Первый и последний члены этого выражения одномерны и
порождены соответственно классами слоев Е ж F а С X С. Выписав
базис пространства (Я!.» (С) ® Я».1 (С)) Ф (Я».1 (С) ® Я^.» (С))
и проинтегрировав соответствующие дифференциальные формы по
базису группы Я^ (С X С, Z) = Я^ (С, Z) ® Я^ (С, Z),
читатель увидит, что требование целочисленности для некоторого
класса из среднего слагаемого, отличного от диагонали А cz
cz С X С, задает определенные условия рациональности на
матрицу периодов кривой С (подобные вычисления будут
проведены в § 4 гл. 3). Поэтому следует ожидать, что кривые рода g,
обладающие соответствиями без валентности, образуют счетное
объединение собственных подмногообразий полного семейства
кривых рода g.
Читатель может проверить, например, что кривая С рода 1
имеет соответствия без валентности тогда и только тогда, когда
она имеет комплексное умножение; иначе говоря, если С = С/Л
с решеткой периодов Л, порожденной векторами 1 и т, то
соответствия без валентности существуют тогда и только тогда, когда т
удовлетворяет квадратному уравнению над Q,.
Теперь, применяя доказанную лемму, мы можем вывести три
основные формулы для соответствий. Прежде всего вычислим
форму пересечения на подгруппе из Яг (С X С, S), порожденной
классами Е, F ж А. Очевидно,
#{E-F)^l^ ЩЕ-Е) = ЩЕ-Е) = 0 ж ЩА-Е) = ЦА-F) =i.
Остается найти А-А. Для этого рассмотрим пучок Wx} степени d
на С и соответствие Г, определенное пучком {Dj,}, как в
примере 1. Пусть D а С X С — его график. Так как Т имеет валент-
312 2. Римановы поверхности и алгебраические кривые
ность 1, то по лемме D '^ аЕ + bF — А, Поскольку и Г и T~^
имеют степень d — 1, то
d— 1 = #{D-E) = 6 — 1,
d—i = #{D-F) = a — 1,
т. e. D '^ dE + dF — A.
Далее, число неподвижных точек #(D-A) для Т совпадает
с числом b точек ветвления отображения С -> Р^, заданного
пучком {D}}. Это отображение является d-листньш накрытием,
и по формуле Римана — Гурвица имеем 2g — 2 = —2d + b,
т. е. b = 2g — 2 + 2d. Значит,
2g — 2+ 2d = ЩD^^) = d=»(£.A) + d# (F-A)— ЩА-А) =
== 2d — #(A. A),
откуда
»(A.A) = 2-2^.
Следовательно, искомая форма пересечения определяется таблицей
# I £■ F А
Е
F
А
0
1
1
1 1
0 1
1 2-2^
Пусть теперь Т — любое соответствие с deg (Г) = d, deg (r-i)=
= d' и валентностью к, & D — его график D ^ аЕ -\- bF — кА.
Тогда d = deg Г = ЩО-Е) = 6 _ fc и d' = deg Г"! = ^D-F) =
= а — к, откуда
D г^ {d' + к)Е+ {d + k)F — кА.
Следовательно,
D-A = d' + k+d + k — k{2 — 2g)==d + d' + 2kg,
т. е. мы получаем, что
(*) Т имеет d ■}- d' + 2kg неподвижных точек (с учетом крат-
ностей)..
Это так называемая формула Кэли — Брилля.
Аналогично, если S — некоторое другое соответствие с deg {S)=
= е, deg {S'''-) = е' и валентностью Z, заданное кривой G cz
а С X С, то
G^ {е' + I) Е + {е+ I) F — 1А.
5. Соответствия 313
После простых вычислений, использующих таблицу пересечений,
получаем
#(Z?.G) = ed' + e'd — 2gkl,
т. е. ( в случае трансверсального пересечения)
(**) соответствия Т и S имеют ed' + s'd — 2gkl тючек
пересечения.
Найтичисло точек совпадения соответствия Т: С -*- С немного»
сложнее. Пусть Т ж D такие же, как вьппе; тогда
D '^ {d' + к) Е + (d + к) F — к- А.
Для начала предположим, что D — гладкая неприводимая
кривая. Тогда по формуле присоединения
Kjy = (Ксхс + D) Ь
для канонического расслоения на D, откуда
deg Кп = ЩКсу,с-0) + ЩО-О).
Если удастся вычислить индексы пересечения в правой части,,
то все будет сделано. По формуле Римана — Гурвица число b
точек ветвления проекции щ: D -^ С на первый сомножитель
удовлетворяет соотношению Ащ К^ = d-A&g Кс + Ъ, т. е.
Ъ = deg Kj, - d-deg Кс = ЩКс^с -D) + #(Z5-Z5) - d (2g - 2).
Пусть теперь ш, ©' — две голоморфные 1-формы на С. Тогда
дивизор 2-формы nfft) л Я2<й' на С X С равен
(П*(Л л я*О)') = я* (ш) + я* (ft)').
Поэтому для класса гомологии Ксхс имеем
Кс>,с ~ АКс + ^гКс = (2g-2)E+ {2g - 2) F.
Значит,
4D- Ксхс) = (2g -2){d + k)-k {2g - 2) + {2g - 2) (d' + Щ
-k{2g-2) = (2g - 2) (d + d'),
G другой стороны, прямое вычисление дает
^D-D) = 2dd' — 2gk\
Собирая все это вместе, находим, что
b = ЩКсхс-D) + ЩВ-В) - d {2g - 2) =
= (d + d') {2g - 2) + 2dd' - 2gk^ - d {2g - 2) =
= 2dd' + {2g -2)d' - 2gk\
314 2. Римановы поверхности и алгебраические кривые
Т. е.
(***) соответствие Т имеет, 2dd' + (2g — 2) d' — 2gk^ точек
совпадения (с учетом кратно стей).
Это вычисление можно немедленно распространить на случай,
когда соответствие Т задано суммой гладких неприводимых
кривых Di CZ С X С. Действительно, точки совпадения для Т состоят
из точек совпадения соответствий Tt, определяемых кривыми Di,
плюс точки пересечения соответствий Diu Dj при 1Ф1 (как будет
видно из дальнейшего, последние надо брать с кратностью 2).
-Легко проверить, что установленная формула (***) опять имеет
место. Более глубокое наблюдение заключается в том, что
формула в том виде, в каком она написана, верна только для
соответствий, заданных гладкими кривыми D. Поскольку это не всегда
выполнено, то, используя два результата из § 2 гл. 4, посмотрим
хотя бы, что происходит в случае, когда D имеет обьшновенные
двойные точки.
Итак, предположим, что D cz С X С — неприводимая кривая
<; S обьшновенными двойными точками (pt, qi), гладкая вне этих
точек. Кроме того, будем считать, что ни одна из ветвей кривой D
в этих двойных точках (р, д) не касается слоя ^р = я^^ (р))Т. е. что
точка (р, q) является простой точкой совпадения для Т. Как
мы увидим в § 2 гл. 4, D является образом некоторой гладкой
кривой D при отображении п: D -^ D а С X С, взаимно
однозначном и гладком вне двойных точек D; попросту говоря, мы
разделяем две ветви кривой D в окрестности двойных точек. Более
того, род римановой поверхности D будет равен (ср. с одной
из формул Плюккера)
g(D)= ^х^ ^^ i-fl-S,
т. е.
deg К^ = ЦКсхс-0) + ЦО-0) — 28.
Поэтому композиция отображений я^ о я: D -^ С имеет
b = deg % — d-deg Кс = 2dd' + {2g ~ 2) d'— 2gk^ — 2S
точек ветвления, т. е. соответствие Т имеет
2dd' + {2g — 2)d' — 2gk'' - 2S
точек совпадения вне двойных точек (р;, д,) кривой D. Отсюда
видно, что приведенная выше формула числа точек совпадения
соот^вет^ствия Т справедлива, если все точки совпадения,
происходящие из обыкновенных двойных точек D, учитывать с кратностью 2.
5. Соответствия 315
На практике обычную точку совпадения Т легко отличить
от соответствующей двойной точки D: гладкая точка (р, q) ^ D
может быть точкой ветвления только одной из проекций щ: D ->■
->■ С, п^: D -> С, а двойная точка (р, q) ^ D появляется в
качестве точки совпадения для обоих соответствий Т и Т~^.
Применим наши формулы к соответствию из примера 2 для
гладкой плоской кривой С степени d. Как мы уже знаем, Т имеет
степень d — 2 и валентность 2; степень Т~^ равна числу
касательных прямых к С, отличных от Тд (С) и проходящих через общую
точку q ^ С, 1. е. числу b точек ветвления проекции Пд кривой С
из q на прямую. Эта проекция (d — 1)-листна, и по формуле
Римана — Гурвица
deg Г-1 = 6 = 2^ — 2 -f 2 (d — 1) =
= (d — 1) (d — 2) — 2 -f 2 (d — 1) = (d -f 1) (d — 2).
По формуле (*) число неподвижных точек для Т, т. е. число
точек перегиба кривой С, равно
/ = (d - 2) -f (d -f 1) (d - 2) -f 2kg =
= (d - 2) -b (d -f 1) (d — 2) -f 2 (d - 1) (d — 2) = 3d (d — 2),
что согласуется с вычислениями по формулам Плюккера из
последнего раздела предыдущего параграфа. При подсчете двойных
касательных к С нужно быть аккуратнее. Если р ж q — различные
точки С с Тр (С) = Тд (С), то каждой из пар (р, д) и (q, р)
отвечает точка совпадения для Т. Следовательно, число Ъ двойных
касательных прямых к С равно половине числа точек совпадения
для Г; по формуле (***) оно равно
А = 1 [2 (d-2) (d-2) (d-f l)-f (2^-2) (d-2) (d-f 1)-2^А;2] =
= -|d(d-bl)(d—l)(d —2) —4d(d—2),
как и было установлено выше.
Геометрия пространственных кривых
Проиллюстрируем теперь технику соответствий на примере
одного приложения к геометрии пространственных кривых,
т. е. кривых в Р^. Наша основная цель — найти число 4-секу-
щих для пространственной кривой С степени d и рода g, однако
попутно мы получим ряд других инвариантов.
Для начала сделаем следующее наблюдение. Семейство прямых
из Р*, пересекающих кривую С, имеет коразмерность 1 в
четырехмерном грассманиане G (2, 4). Тогда, как можно ожидать изнаив-
316 2. Риманоаы поверхности и алгебраические кривые
ного подсчета параметров, С должна иметь конечное число 4-секу-
щих, а 5-секущих не должно быть вообще. Аналогично, можно
ожидать, что существует лишь конечное число точек С, касательные
в которых пересекают некоторую заданную касательную к С, а
значит, имеется лишь конечное число 3-секущихр, q, г, таких, что Тр{С)
и Tq (С) пересекаются, а обладающих этим свойством 4-секуш;их
нет совсем. Вообще, будем говорить, что кривая имеет
невырожденное поведение, если с ней не происходит ничего иного, кроме
того, что предсказывает счет параметров. В последующих
рассуждениях предполагается, что это выполнено; в частности, мы
считаем, что:
1. С не имеет 5-секущих.
2. Касательные прямые в каждой из четырех точек
пересечения 4-секущей с С попарно не имеют общих точек.
3. Не существует прямых, касающихся кривой С с кратностью
^ 3, т. е. первая ассоциированная с С кривая является гладкой.
4. Нет соприкасаюш;ихся двумерных плоскостей к С,
содержащих другую касательную прямую к С.
Перейдем теперь к центральному объекту наших
рассмотрений — соответствию 3-секущих Т на С, определяемому кривой
■О = {{р-> чУ- Р-> Я есть З-секугцая С}.
Прежде всего вычислим степень соответствия Т. Пусть р — общая
точка на С. Тогда образ С при проекции из р будет плоской кривой
степени d — 1, имеющей только обьшновенные двойные точки.
Эти двойные точки плоской кривой соответствуют 3-секущим
кривой С, проходящим через р. Значит, по формулам Плюккера
число 3-секущих, проходящих через р, равно
б= ('^-2)('^-з) _g.
Но так как каждой 3-секущей кривой С, проходящей через р,
отвечают две точки из Т (р), то
deg Г = (d — 2) (d — 3) — 2g.
I Заметим, что по оценке для рода пространственной кривой
(стр. 277) это число всегда положительно, кроме двух случаев:
d == 3, ^ = О или d = А, g == I.) Поскольку Т симметрично,
то же самое верно для Т'^.
Далее, Т имеет валентность, что видно из следующих
рассуждений. Пусть, как и выше, Пр-. С -> Р^ — проекция С из общей
точки р ^ С. Тогда поскольку deg Пр С = d — 1, то по
доказанному в предыдущем параграфе
^с = я5((й-4)Яр2)-Д
5. Соответствия 317
где D — дивизор на С, состоящий из прообразов двойных точек
кривой Яр {С). Но Яр (Ярг) = Ярз — рп&С,&0 = Т (р), откуда
Kc=-(d- 4) Hp3-(d~4)p-T (р),
т. е. дивизор Т (р) + {d — А) р = (d — 4) Нра — Кс как класс
линейной эквивалентности не зависит от р. Значит, Т имеет
валентность к == (d — 4).
Рассмотрим теперь точки совпадения соответствия Т. Пусть
р ^С; тогда дивизор Т (р) содержит кратную точку, если только
он не состоит из (d — 2) (d — 3) — 2g различных точек. Но это
может произойти тогда и только тогда, когда спроектированная
кривая имеет другие особенности, кроме обьшновенных двойных
точек, а именно возможны следующие три случая:
1. Некоторая прямая, проходящая через р, просто касается С
в другой точке q. Тогда образ точки q на кривой Яр (С) а Р"
будет точкой заострения (рис. 10). По формулам Плюккера при
отсутствии других особенностей на Яр (С) мы имеем еще б =
= {{d — 2) (d — 3)/2) — ^ — 1 двойных точек, кроме Яр (q).
Поэтому Т (р) содержит (d — 2) (d — 3) — 2g — 2 точек, не
считая q. Значит, q входит в Г (р) с кратностью 2,
Отметим, что {р, q) не является точкой совпадения для Т~^,
поэтому {р, q) — гладкая точка на кривой соответствия D.
Прямая, касательная к С и пересекающая С еще в одной
точке, называется касательной 3-секущей кривой С. Мы видим,
что каждой касательной 3-секущей кривой С отвечает одна точка
совпадения соответствия Т.
2. Некоторая прямая, проходящая через р, пересекает С
в двух других точках q ж q', и касательные к С в q ж q'
пересекаются. Тогда образ Яр (q) = Пр (q') 6 Лр (С) будет двойной
точкой на Яр (С), но не обьшновенной: касательные прямые к двум
ветвям кривой Яр (С) в Яр (q) совпадают (рис. И). Такие двойные
точки называются точками соприкосновения кривой. Как мы
увидим далее, в § 2 гл. 4, появление таких точек соприкосновения ^)
понижает род плоской кривой на 2. Поэтому если на Яр (С) есть
точка соприкосновения, то эта кривая имеет лишь ((d — 2) х
X (d — 3)/2) — g — 2 других двойных точек, а значит, дивизор
Т (р) содержит (d — 2) (d — 3) — 2g — 4 точек, кроме q ж q'.
Следовательно, каждая пара (р, q) ж {р, q') определяет точку
совпадения соответствия Т. Снова, поскольку ни (/?, д), ни (/?, q')
не определяют точки совпадения соответствия Т~^, обе они являются
гладкими точками на D.
^) Не являющихся точками перегиба ни для одной из ветвей.— Прим.
перее.
318
2. Римановы поверхности и алгебраические кривые
Рис. 10
3-секущая р, q, q', для которой Tq (С) и Tq' (С) пересекаются,
называется стационарной 3-секущей кривой С. По предыдущему
каждая стационарная 3-секущая кривой С определяет две точки
совпадения соответствия Т.
3. Некоторая прямая, проходящая через р, пересекает С еще
в трех других (различных) точках q^, q^ и q^. Тогда точка Яр {q-^ =
= "р (Зг) = "р (Зз) будет обьшновенной тройной точкой на Пр (С)
(рис. 12). Обращаясь снова к § 2 гл. 4, мы видим, что появление
тройной точки понижает род плоской кривой на 3. Поэтому Т (р)
имеет лишь (d — 2) (d — 3) — 2g — 6 точек, кроме q^, q^ и q^.
Следовательно, каждая из пар (р, q^), (р, gj) и (р, q^)
определяет точку совпадения соответствия Т. Более того, по тем же
соображениям (р, qi) определяет точку совпадения соответствия Т~^.
Поэтому (р, qi) является на самом деле двойной точкой кривой D.
Итак, если L = р^, р^, р^, р^ есть 4-секущая кривой С, то
каждая из 12 пар (pi, pj) будет двойной точкой на jD, а значит,
каждая 4ч5екущая С определяет 24 точки совпадения соответствия Т.
Теперь, зная степень и валентность Г, мы можем вычислить
общее количество точек совпадения для Т, а потому, чтобы найти
число Q 4-секущих кривой С, надо найти число касательных
и стационарных З-секущих. С числом t касательных 3-секутцих
5. Соответствия
319
Рис. И
дело обстоит просто. Действительно, 3-секущие р, q с q ^ Тр (С)
соответствуют в точности неподвижным точкам (р, р)
соответствия Т. Поэтому по формуле (*) имеем
t=: (d - 2) {d -3) - 2g + {d - 2) (d - 3) - 2g + 2 {d - А) g=
= 2 (d - 2) (d - 3) + 2 (d — 6) ^.
Найти число s стационарных 3-секущих несколько сложнее. Для
зтого введем соответствие двух касательных S яа С, определяемое
кривой
G = {{р, q): рфд, Тр (С) []Т^(С)Ф0}с1С ХС.
Для каждой точки р ^С дивизор S (р) есть дивизор ветвления
проекции jil кривой С из касательной прямой L = Тр (С) к С в р
на прямую. Так как п^ имеет степень d — 2, то по формуле Рима-
на — Гурвица
degS = 2g — 2 + 2{d—2) = 2g+2d-6.
320
2. Римановы поверхности и алгебраические кривые
VШrl-^^
/ I
-/-Ч'-
1 1 ^ \ \
I \ \ \ \
Рис. 12
В силу симметричности S это есть также степень соответствия
,iS~*. Более того, Кс = п1,{ — 2Hpi) +S(р), откуда
S(p) + Ap--Kc + 2Hp»,
S-^(p) + ip = Kc + 2H^2,
потому что я£(^р1) = ^рз — 2р; таким образом, соответствие S
имеет валентность Z = 4.
Рассмотрим теперь точки пересечения наших двух
соответствий Т ж S (рис. 13). Они появляются по двум причинам: если
р, q, q' — стационарная З-секущая С с Тд (С) П Тд» (С) Ф 0»
то каждая из пар (д, д') и (д', q) будет точкой пересечения для
iS и Г, и если Р-, q — касательная З-секущая с g 6 ?'р (С), то
каждая из пар (р, q) и (д, р) будет точкой пересечения для S т Т.
5. Соответствия
321
Рис. 13
Следовательно, S ж Т имеют 2s -|- 2f точек пересечения, и по
формуле (**)
2s+2t^2{(d-2)(d-3) ^ 2g) (2g + 2d - &) - 2g (d - 4)-4,
т. е.
s = ((d - 2) (d - 3) - 2^) (2g + 2d - 6) - Ag (d- 4) -
—2 (d.- 2) (d -Г- 3) — 2 (d - 6) g =
= 2d (d - 2) (d— 3) — 2(d~2)(d- 3) — 6 {d — 2) (d — 3) +
+2^ ((d - 2) (d - 3) — 2^ - 2d + 6 - 2 (d - 4) - (d -6)) =
= 2 (d - 2) (d - 3) (d - 4) + 2g (d« - 10d,+ 26 — 2^): ..
21-040
322 2. Римановы поверхности и алгебраические кривые
Теперь мы уже можем найти число 4-секу1цих Q соответствия С.
Как нам известно, общее число точек совпадения соответствия Т
равно t -\- 2s -\- 24^. Но по формуле (***)
f + 2s + 24(? = 2 ((d — 2) (d — 3) — 2gY +
+ {2g - 2) {{d - 2) (d - 3) - 2g) -2g{d- 4)^
T. e.
<? = 1 ((d _ 2) (d - 3) - 2gY + fe - 1) ((d _ 2) (d - 3) -
-2g) -g(d-Ar-{d-2)(d-3)-(d-&)g-
—2 (d -2){d— 3) (d — 4) - 2g (cP — lOd + 26 - 2^).
После несложных преобразований получаем
Q = j^{d-2){d~2,Y {d-^)-^g{d^-ld + i3-g).
Одно замечание: хотя выведенные нами формулы а priori
применимы только к кривым, имеющим невырожденное поведение,
тем не менее из самого вывода ясно, как учесть отклонения
от такого поведения. Например, пусть L = /j^, . . ., р^ есть 5-секу-
щая кривой С. Тогда можно проверить, что каждая из 20 пар
{pi, pj) является тройной точкой кривой D, а поэтому
понижает род D на 3. Возвращаясь к выводу формулы (***), мы видим,
что каждую пару (рг, pj) надо считать за 6 точек совпадения.
Значит, L дает вклад из 120 точек совпадения для Т, т. е. в свете
последней формулы 5-секущая к С эквивалентна 120/24 = 5
4-секущим.
Наконец отметим еще, что некоторые численные задачи,
связанные со свойствами нескольких кривых из Р^, могут быть
решены также с привлечением исчисления Шуберта. Например,
пусть С ж С — две пространственные кривые, и мы ищем число
их общих хорд. Для этого рассмотрим в грассманиане прямых
из Р* алгебраическую поверхность V{C)czG(2, 4), состоящую
из хорд кривой С. Четырехмерная группа гомологии
многообразия G (2, 4) порождена циклами
Оа (р)= {1^ Р*»: р € Ц, о,„ (Н) = {Z с рз: г с Я},
и, очевидно,
*(02-02) = *(Oi.i-Oi,i) = 1, #(02-0i.i) = О-
Напишем V (С) /^ л-о^д -f- Ь'а2; тогда
a = #(F(C)-a,.J, b = #(F(C)-a,).
Но эти числа легко найти. Общая гиперплоскость Н
пересекает С в d различных точках {pi} (находящихся в общем поло-
5. Соответствия 323
жении В Н), а поэтому содержит ровно d (d — 1)/2 хорд {pt, pjit^j;
следовательно, а = d (d — 1)/2.
С другой стороны, для общей точки р 6 Р* число хорд С,
проходящих через р, равно числу двойных точек на проекции С
из р на гиперплоскость; по формулам Плюккера оно равно
b = ((d ~1) {d— 2)/2) — ^. В результате
V(C)^m^a,,, + (^-^^-'^ -g)a,.
Предположим теперь, что С имеет степень d' и род g' и что С ж С
находятся в общем положении относительно друг друга, т. е. V (С)
и V (С) пересекаются трансверсально. Тогда число общих хорд
кривых С ж С равно
^(Г(С) У(С')) '^('^-^)-'^'('^'-l) I (d-i)(d-2)(d'-i)(d'-2)
^(d-l)(d-2)g'-(d'-i){d'-2)g + gg'.
Специальные линейные системы IXI
Как и было обещано вьппе, мы воспользуемся полученными
результатами о соответствиях для того, чтобы ответить на
некоторые численные вопросы, возникающие из проблемы Брилля —
Нётера. Мы уже знаем, что на общей римановой поверхности
рода g = 2к имеется конечное число пучков степени к + i, вопрос
только в том, сколько их? Мы ответим на него здесь в случаях
^ = 4, 6 и 8. (Заметим, что в случае g = 2 ответ уже получен
и равен 1.)
Случай g = А. Пусть S — негиперэллиптическая риманова
поверхность рода 4. Ее каноническая кривая является кривой
степени 6 в Р^. Если D = 2рг — дивизор степени 3 на S, то по
геометрическому варианту формулы Римана — Роха I (D) равно 1
тогда и только тогда, когда точки pt коллинеарны. Для каждого
пучка степени 3 существует один такой дивизор, содержащий
общую точку р ^ S. Следовательно, число таких пучков равно
числу 3-секущих S, проходящих через общую точку р ^ S,
а последнее, как мы уже видели, равно
n = 4-(d-2)(d-3)-^ = i(4-3)-4 = 2,
т. е. на S имеется два пучка степени 3. Итак, общая риманова
поверхность рода 4 представима в виде 3-листного накрытия
над P'^ двумя способами.
Интересно было бы явно указать эти два пучка. Из
предыдущего параграфа мы знаем, что каноническая кривая для S — это
21*
324 2. Римановы поверхности и алгебраические кривые
гладкое пересечение квадрики Q и кубики ^' в Р^; в общем
случае эта квадрика является гладкой. Но гладкая квадрика в рз
(обсуждаемая ниже, в начале гл. 4) обладает двумя семействами
прямых {Li}, {L'i), каждое из которых параметризовано
точками t ^Р^. Поскольку S высекается на Q кубикой Q', каждая
прямая Lt или L't пересекает S в трех точках, а дивизоры Dj =
= Li {\ S ж D't = L't {\S образуют два пучка степени 3 на S.
3
Обратно, если D = '^Pt — некоторый дивизор из трех коллинеар-
i=l
ных точек, то прямая L = р^, р2, Рз» пересекающая Q в зтих
трех точках, лежит в Q. Отсюда следует, что L совпадает с
некоторой прямой Lf или L't, 3lD — с некоторым дивизором Dt или D't.
Заметим, что в случае, когда квадрика Q особая, S содержит
только один пучок степени 3. В этом случае проекция S из
любой ее точки на плоскость будет иметь только одну точку
соприкосновения, а не две обьшновенные двойные точки, как в общем
случае.
4
Случай g = &. Если D = 2 Рг ~ дивизор степени 4 на
1=1
кривой S рода 6 и dim | D 1 = 1. то дивизор К — D имеет
степень 2g — 2 — 4 = 6 и по формуле Римана — Роха
А» (^ - -О) = deg (K-D)- g+\ + W (D) =
= 6 — 6 + 1 + 2 = 3,
т. е. полная линейная система \ К — D \ имеет размерность 2.
Следовательно, число пучков степени 4 на 5 равно числу сетей
степени 6; это последнее мы и будем искать.
По геометрическому варианту формулы Римана — Роха
дивизор D степени 6 на 5 с dim | D | = 2 состоит из шести точек
канонической кривой для S, порождающих 3-плоскость в Р®. Если
р, q ^ S — обе общие точки, то каждая сеть степени 6 на 5
содержит один такой дивизор с точками ряд- Более того, для такого
дивизора D=p + g + ri+... + r4 образы точек п
относительно проекции jil'. S ->■ Р* кривой S из прямой L = pq вй
3-плоскость коллинеарны. Обратно, если некоторые четыре точки
Пь (ri) из Я1, (S) коллинеарны, то точки р, q, г^, . . ., г^ лежат
в 3-плоскости, порожденной L и {п^ (?";)}. Следовательно, число
сетей степени Q на S совпадает с числом А-секущих кривой Пь (S)
в Р*. Поскольку jil (S) имеет степень d = deg (S) — 2 = 8 и род
^ = 6, по доказанной выше формуле это число равно
re = ^-6-5-5.4—^6(64-56 + 13 —6) = 50-3-15 = 5.
S. Соответствия 325
Поэтому общая риманова поверхность рода 6 пятью способами
представляется в виде 4глистного накрытия над Р^.
Случай g = 8. Если D — дивизор степени 5 на римановой
поверхности S рода 8 с dim 11) | == 1, то дивизор К — D имеет
степень 14 — 5 = 9 и
А» (К - 2?)= deg (К - D)- ^ + 1 + А» ф)= 9-8 + 1 + 2 = 4,
т. е. dim \ К — D | = 3, Тогда по формуле Римана — Роха D
состоит из 5 точек на канонической кривой для S, порождающих
3-плоскость, а эффективный дивизор, эквивалентный К — D,
состоит из 9 точек на S, порождающих 5-плоскость.
Чтобы найти число пучков степени 5 на S, докажем один
предварительный результат.
Левша. Пусть D, D' — два дивизора степени Ъ на S
с dim IjD I = dim \D' | = 1. Дивизор E ^ \ К — D' |,
содержащий D, существует в том и только том случае, когда D и D'
линейно не эквивалентны; если такой дивизор Е существует,
тю он единствен.
Доказательство. Мы хотим показать, что
f 1, если DrLD',
^ ' L О, если D — D/.
(Отметим, что, поскольку S общая, на ней нет пучков степени 4,
поэтому h'^ (К — D —£)')<; 1.) По формуле Римана — Роха
h<>(K-D - D') = deg (К —D -D')- g+l + h<>(D + /?') =
= 4-8+1 +А» (25+ D'),
т. е. достаточно показать, что
3, если D^D',
А«
{D + D') = [^'^
если D4^D'.
Но если А" (D + D') = 3, т. е. | D + D' | параметризуется
точками Р^, то для любых jDo 6 I jD I, jDq 6 I jD' I прямые Dq + \D'\
и jDJ + I jD I c= I jD + jD' I пересекаются и, значит, Do € \D \
ж D ^D'.
С другой стороны, любой дивизор G 6 \ к — D \ состоит
из 9 точек, порождающих 5-плоскость, которая определяет пучок
{Hf} гиперплоскостей в Р''; дивизоры
Dt = (Hi-C) - G
326 2. Римановы поверхности и алгебраические кривые
составляют линейную систему {Df}. Ясно, что для некоторых
t Ф t' дивизоры Dt и Df не лежат в одной гиперплоскости из Р'' i),
т. е. К — Df — Df '^ К — 2D не эффективен. О
5
Предположим теперь, что!) = ^pt — некоторый дивизор на S
степени 5 с dim ID | = 1. Тогда по доказанной лемме пучкам
степени 5 на S, отличным от D, однозначно соответствует 9-секу-
щая 5-плоскость к канонической кривой S cz Р'', содержащая D.
Если Pi, . . ., р^, gi, . . ., ^4 — любая такая Э-секутцая
5-плоскость, то образы точек Qi при проекции пу-: S -> Р^ из 3-пло-
скости V = pi, . . ., р^ коллинеарны, и обратно. Поэтому число
пучков степени 5 на S, отличных от \D |, совпадает с числом 4-се-
кущих кривой пу (S) CZ Р^. Но пу (S) имеет степень d = deg (S) —
— 5 = 9 и, значит, это число равно
-^7.6.6-5-у 8-(81-634-13-8) = 105-4-23 = 13.
В результате мы получили, что имеется 14 способов представить
общую риманову поверхность рода 8 в виде 5-листного накрытия
над Р^.
6. КОМПЛЕКСНЫЕ ТОРЫ И АБЕЛЕВЫ МНОГООБРАЗИЯ
Условия Римана
Возвращаясь к изучению связи между компактной римановой
поверхностью и ее якобианом, мы дадим в этом параграфе
введение в общую теорию комплексных торов.
Начнем с одного определения. Пусть V — комплексное
векторное пространство размерности ге, а Л с= F — дискретная решетка
максимального ранга 2ге. Комплексный тор М = V/A называется
абелевым многообразием, если он является проективным
алгебраическим многообразием, т. е. допускает вложение в проективное
пространство.
Наша первая задача — выяснить, когда комплексный тор М =
= У/Л является абелевым многообразием. Поскольку когомоло-
гии тора М легко выразить через F и Л, то по теореме Кодаиры
о вложении мы получим необходимые и достаточные условия;
позже достаточность будет проверена прямым вычислением. Для
начала сделаем несколько обпщх замечаний о когомологиях
комплексных торов.
^) Это верно только для общей кривой, через каноническую модель
которой не проходят квадрики ранга 3.— Прим. перев.
б. Комплексные торы и абелевы многообразия 327
Пусть М = У/Л — комплексный тор, как и выше. Поскольку
Л — подгруппа в V, тор М также обладает структурой грзшпы;
для любого (1 £ М и любого X ^ V над \i отображение
T^: V-*■ V, V t-^ V + X
индуцирует отображение т^: М -*■ М, называемое сдвигом на \i.
Далее, для каждого ц 6 ^f имеется естественное
отождествление
rj, (М) ^ V.
Поэтому любое эрмитово скалярное произведение на векторном
пространстве V задает кэлерову метрику на М, инвариантную
относительно автоморфизмов {Тр,}. Утверждается, что
гармонические формы относительно такой метрики — это в точности формы,
инвариантные относительно всех сдвигов {Тр,}. Чтобы убедиться
в этом, заметим прежде всего, что, поскольку Тц сохраняет
заданную метрику, tJ : Л* (М)->-А* (М) переводит гармонические
формы в гармонические. Но Тр, гомотопно тождественному
отображению, а Se* (М) отображается изоморфно на Н* (М, С) по
теореме Ходжа. Значит, гомоморфизм
Tjt: Se* (М) -*- т* (М)
тождествен, т. е. гармонические формы инвариантны. Далее,
каждая инвариантная форма на М определяется своими значениями
на касательном пространстве Гр с (М) = Т'р (М) ф Гр (М) к М
в некоторой точке р. Это касательное пространство допускает
естественное отождествление с векторным пространством F ф У.
Обозначим через J * (М) пространство инвариантных форм на М.
Тогда
J* (М) = Л * i^p, с W*) = А *У* ® Л*У*.
Но мы знаем, что топологически М ^ (S^)^, поэтому размерность
пространства гармонических форм степени к равна ( , ) • Так как
S^* (М) CZ J* (М), то, сравнивая размерности, получаем
Итак, если z = (Zj, . . ., z„) — евклидовы координаты на V^
а {dzi, . . ., dzn} и {dzii . . ., dz„} — соответствующие глобальные
1-формы на М, то
S£*{M)=C{dziAdlj}i,j,
где
J^?^' (М)=С {dz, л diл#I=p. #j=, •
328 2- Римановы поверхности и алгебраические кривые
С другой стороны, заметим, что любой замкнутый путь у ^
6 -ffj {М, Z) с базисной точкой [01 6 М поднимается до пути 'у
на У с началом в О и концом в некоторой точке Я 6 Л с= У.
Поскольку V является универсальной накрывающей для М,
можно сделать отождествление Н^ (М, Ъ) = Л. Пусть Я^, ...
. . ., "к^п — векторы решетки, образующие целочисленный базис
для Л; они являются также базисом вещественного векторного
пространства V. Пусть ос^, . . ., х^п — двойственные вещественные
координаты на V, а dx^, . . ., di^n — соответствующие 1-формы
на М. Тогда
dxj = 8ij, т. е. Я* (М, Z) =Z {dxi, ..., dx^n},
я
i
а в общем случае
H'4M,Z)=--1{dx,}#^^^.
Итак, мы имеем два различных базиса в когомологиях
многообразия М: первый {dza,, dza,} отражает комплексную стрз^туру
пространства Н* (М), а второй {dxi} — рациональную стрз^туру.
По теореме Кодаиры о вложении многообразие М является
алгебраическим в том и только том случае, когда на нем существует
форма Ходжа, т. е. замкнутая положительная форма типа (1, 1),
представляющая рациональный класс когомологий. Более того,
если © — такая форма, записанная в виде
«=^^-^ 2 ^вР (2)^2„ Л dTa,
& d\i — инвариантная евклидова мера на Af с (i (М) = 1, то,
положив
^аВ = J ^аВ (Z) Ф и © = ^ ~ 2 ^аВ ^^^ Л dZp,
м
мы ползучим инвариантную форму, снова замкнутую,
положительную, типа (1, 1) и целочислевшую (после умножения на
подходящее целое число). Таким образом, на М существует форма
Ходжа в том и только том случае, когда на нем существует
инвариантная форма Ходжа. В соответствии с этим, чтобы выяснить,
когда это происходит, мы должны установить связь между двумя
нашими базисами Н* (М).
Пусть П = (jita) — такая 2ге х ге-матрица, что
dXi = 2 "га ^Za + 2 "га dZa,,
б. Комплексные торы и абелевы многообразия 329
Т. е. 2ге X 2ге-матрица П = (П, П) является матрицей перехода
от базиса {dz^, dza} к {dxt}. Тогда для целочисленной
инвариантной 2-формы © можно написать
где Q = iqtj) — целочисленная кососимметрическая 2ге х 2и-мат-
рица. При переходе к координатам dz^,, dz^ получаем
(О =-2" 2 lij ("га dZa + Jlia di^) л (Яур dZp + Jljfi dZp) =
— jZi ЯИ^га'^ЗЬ ^a л dZp +-^ 2 QiJ^ia^j^^'^a Л dz^ +
+"2" 2j 9h ("га"ув — "гв"уа) ^z„ Л dzp.
Отсюда видно, что © тогда и только тогда типа (1, 1), когда
коэффициенты матрицы
у(2?о"т"ув) = 'П(?.п
». J
равны нулю, и если это выполнено, то форма © положительна
в том и только том случае, когда
ТГТТ ( 2 ^'^ ("га"ув —"гв"уа))^р =
г, j
— эрмитова положительно определенная матрица. В результате
мы полз^чили
Условия Рииана I. М является абелевым многообразием тогда
и тюлъко тлгда, когда, существует целочисленная
кососимметрическая матрица Q, для которой
'П-(?-П = 0, -/^М"Ш(?П>0.
Эти условия выражаются также при помощи квадратной
матрицы П = (П, П):
^ - /'П\ _ /Ш(?П 'П-(?.П\
Ш.(?.П = ( - •<?(П, П) = ( - - ,-
и Ш(?П = Ч'П'(?П) = —'(Ш-(?-П). Поэтому М — абелево
многообразие тогда и только тогда, когда существует целочисленная
330 2. Римановы поверхности и алгебраические кривые
жососимметрическая матрица Q, такая, что
,. ,~ - (Н О \
-/-l'n.(?.n = (^Q _,^j, гдеЯ>0.
Обычно условия Риыана пишутся в терминах двойственной
матрицы замены базиса. Пусть h^, . . ., 7^^ — целочисленный базис
в Л, а Cj, . . ., е„ — базис комплексного пространства V.
Определим матрицу периодов для Л с= У как п X 2ге-матрицу Q =
= (©аг), ДЛЯ которой Я^ = ^^с'^с- ТоГДа
а
г г
так что матрица ^ ^ I я ) ^^Д^^''' переход от базиса {dx,-} к
базису {dza, Й2и}. Таким образом,
Й.Й = /2„ или Qn = /„, Qn = 0.
Далее,
Поэтому условие Римана записывается в терминах матрицы Q
в виде
- ~ /Я-1 О \
y-l.Q.(?-.'Q = (Q -^Я-0'
где Я > 0. Но Я > О <=> Я-^ > О, откуда вытекают
Условия Рииана II. М — абелево многообразие в том и только
том случае, когда существует, целочисленная кососимметрическая
матрица Q, такая, что
£2.(?-i.'Q = 0, -1/"^Тй.(?-1-'Й>0.
Следует заметить, что матрица периодов Q для А cz V зависит
от выбора базиса как в Л, так и в У. Нормализуя оба базиса
ло отношению к заданной форме, мы сможем несколько упростить
условия Римана. Но сначала покажем, что справедлива следующая
Лемма. Пусть Q { , ) — целочисленная кососимметрическая
квадратичная форма на Л = Z^. Тогда Л обладает базисом
Aj, . . ., А,2п/* котором Q задается матрицей вида
/Si 0\
6. Комплексные торы и абелевы многообразия 331
Доказательство. Для каждого Я ^ Л множество значений
{Q (Я, Я'), Я' 6 Л} образует главный идеал d^L в Z, d^ ^ 0.
Пусть CTj = min (dx : А,^Л, dj. =5^ 0). Рассмотрим А^ и Я^+i с
Q (^1, A,„+i) = бх-Тогда для каждого Я 6 А значение 8^ делит
<? (А,, A,i) и Q (Я, Я^+i), откуда
1 \_ Q ("» A.i) , Q (л, A,Tn.i) 1 /-17 /1 1 \1
Л-| g Л„+1 g AltA^lAi, Л„+1| ,
Т. е.
Положим Л' = Z {^1, A^+i}-!-; далее, повторяя предыдущие
рассуждения, мы получим два элемента ^g, ^,„+2 6 Л', где
Л'=Z {ЯгДп+Л Ф Z {^2, ^п+г}"--
Продолжая этот процесс, мы найдем базис (A-j, . . ., А,2„} в Л,
обладающий необходимыми свойствами.
Заметим, что для полученных целых чисел {6j} имеет место
делимость 6i I 62, S2 I S3 и т. д. В самом деле, если, например,
Ьх \ Sj, то для некоторого целого к
0<Q(kXi + Я2, K+i + К+2) < Si-
Отметим, что числа б^ вместе с дополнительным условием б^ | 6^+1
являются инвариантами квадратичной формы Q. Q
По предыдущей лемме для всякой целочисленной
инвариантной 2-формы © на Af = У/Л можно найти базис А^, . . ., А,2„
в Л, такой, что в соответствующих координатах Xj, . . ., х^^ на V
<ii = '^8idXiAdxn+i, 8i^i.
Далее, если форма © невырожденна, т. е. если ©" ^ О, что
верно для положительной формы ©, то 8^ ¥= О при любом а,
а в качестве базиса комплексного векторного пространства V
годятся векторы е„ = Si^A,a, а = 1, . . ., п. Тогда матрица
периодов для А CZ V примет вид Й = (Ag, Z); такую матрицу периодов
будем называть нормализованной. Как и выше, © имеет тип (1, 1),
если Q•^^•'Q = О, т. е. если
/ О -Ав^ \/Аб\ /-Ae'-'Z\
332 2. Римановы, поверхности и алгебраические кривые
Т. е. если Z симметрична; кроме того, форма © положительна,
если —]/— 1'Й-^б*-'^>0, т. е. если
= 2-IinZ>0.
В результате получены
Условия Рииана III. М ^= У/Л — абелево многообразие в том
и только тлм случае, когда существуют, целочисленный базис
%-у, . . ., ^2„ в А. и комплексный базис е^, . . ., е„ в У, для котюрых
Q = (Аб, Z), где матрица Z симметрична, а матрица Im Z
положительно определена.
Заметим, что рассмотренная выше матрица П тоже принимает
довольно простой вид в базисах {Я^, . . ., Я^п} и {е^, . . ., е„}:
из равенства (П, Щ-Г^) = /gn мы видим, что П = (fr')i где
и, = i^ Ag'Z (Im Z)-S П, = ^-j^ (Im Z)-\
Класс КОГОМОЛОГИЙ [©) формы Ходжа a на абелевом
многообразии М = У/Л называется поляризацией многообразия М.
Целые числа б^, появляющиеся в записи
(О
= 2 Se dx^ л dxn+a, Se I б„+1.
формы © относительно координат {х^}, соответствующих
целочисленному базису в Л, являются инвариантами класса [©]; они
называются элементарными делителями поляризации. Поляризация
[©) называется главной, если б^ = 1 для всех а.
Рассмотрим теперь некоторую компактную риманову
поверхность 5 рода g с базисом 6i, . . ., 8^gB группе гомологии j?i (S, Z)
и базисом ©1, . . ., (Og в пространстве регулярных
дифференциалов Н" {S, fi^). Якобиан этой проверхности является фактормно-
гообразиеи
fiS) = C^/Z {Я^, . . ., X^g},
где Xi — векторы вида
^г = '( J «>!, ..., J (Hgj ,
соответствующие столбцам матрицы периодов Q поверхности S.
В § 2 этой главы было установлено, что если бх, • . ., S^g — норма-
6. Комплексные торы, и абелевы многообразия 333
лизованный базис в Н^ {S, Z), то можно выбрать такой базис
щ, . . ., dig ъ Н" {S, Q^), для которого
«г
тогда матрица периодов примет вид
Q = (/, Z),
и по двум билинейным соотношениям Римана из того же § 2
матрица Z = X + У—1У симметрична и У > 0. Следовательно,
f' (S) — абелево многообразие. Более того, это многообразие
обладает главной поляризацией, определяемой формой
© = S dxa Л dxn+a
в базисе {dxt} для Н^ (f (S), Z), двойственном к базису {Я^} с
CZ Hi if (5), Z).
Можно дать также внутреннее определение якобиана как фак-
тормногообразия f (S) = V (5)/Л (5), где V (S) = Я» (S, Й^)*,
а решетка Л (5) ^ Н^ (S, Z) вложена в V {S} посредством
интегрирования. Соответствуюш;ая форма поляризации
(oeiPif (S), Z) S Hom^ (A'^i {S, Z), Z)
— это кососимметрическая билинейная форма
определяемая пересечением циклов; тот факт, что эта поляризация
является главной, есть следствие двойственности Пуанкаре.
Заметим, что класс указанной выше поляризации [о] не зависит от
выбора (нормализованного) базиса 8^, . . ., 8^g в ZTj (S, Z).
Замечание. До сих пор комплексный базис {e^} и двойственные
комплексные координаты {z^} на V отмечались индексами а =
= 1, . . ., ге, а целочисленный базис {Я^} и соответствующие веш;е-
ственные координаты {xi} — индексами г = 1, . . ., 2ге. Однако
в дальнейшем, когда базис нормализован, мы не будем
придерживаться этого различия и будем обозначать целочисленный и
двойственный ему базисы через
(^о) Л„+и}а=1, ..., п и {х„, а;п+а}а=1, . .., п-
Линейные рси;слоения на комплексных торах
Сейчас мы дадим явное описание положительных линейных
расслоений на комплексном торе М = V/A. Важнейшее
утверждение, доказанное после теоремы Дольбо в § 3 гл. О, означает по су-
334 2. Римановы, поверхности и алгебраические кривые
ществу, что любое линейное расслоение на У ^ С" тривиально, так
как Н^ (С", 0) = Н^ (С", Z) = 0. Поэтому если L-^M —
произвольное линейное расслоение, то его подъем n*Z на V тривиален,
т. е. существует глобальная тривиализация ф: n*L -v F X С.
Тогда по определению для z ^V,k ^ А слой расслоения n*L в
точках zMz -\- X отождествляются со слоем L в точке я (z). Сравнивая
тривиализацию ф в точках z ж z -\- X, мы получаем линейный
автоморфизм на С:
С «^ in*L}^ = Ln(z) = (я *L)z+i. ~*-^ С.
Каждый такой автоморфизм задается умножением на ненулевое
комплексное число; обозначая это число е^, (z), мы получаем набор
функций
K60*(F)beA,
называемый множеством мультипликаторов расслоения L.
Функции ву^ для всех А,, Я' 5 Л должны удовлетворять условию
согласованности
ех« (Z + А.) е^ (z) = е^, (z -f А,') е^. (z) = е^+^, (z).
Обратно, если задан произвольный набор всюду ненулевых
голоморфных функций {е\)у^^х, удовлетворяющих этим
соотношениям, то можно построить некоторое линейное расслоение
L -^ М с мультипликаторами {е^). В качестве такого L надо
взять фактормногообразие многообразия F X С относительно
действия автоморфизмов отождествления
(Z, 1)~ (Z + 1, e^(z)-|).
Отметим, что при помощи соотношений согласованности мы можем
задать такой набор {e^,}, зная е^ для элементов некоторого базиса
{Яи} с: Л, если только функции {е^^} удовлетворяют
соотношениям
(*) е^а (^ + ^в) % (2) = % (2 + Ха) ех^ (z).
Наша ближайшая цель — показать, что любое линейное
расслоение L-^ М можно задать мультипликаторами очень простого
вида. Мы сделаем это в два шага: вначале с использованием
простейших функций бх, мы будем строить линейные расслоения
с произвольным положительным классом Чжэня, а затем покажем,
что любое положительное линейное расслоение L -^ М
определяется с точностью до сдвига на М своим классом Чжэня.
Первый шаг заключается в следующем. Пусть {Х^, . . ., А,2„} —
произвольный базис в Л над Z, где A,i, . . ., А,„ линейно независимы
6, Комплексные торы, и абелевы многообразия 335-
над С. Тогда F/Z{Xi, . . ., Я^}= (С*)" , и мы можем разложить
проекцию я: V-^ М в композицию
Далее, как мы отметили после доказательства 5-леммы Пуанкаре^
из § 2 гл. О,
Я' ((С*)", 0) = Я" ((£*),"© ) = О,
откуда т ((С*)", ©*) Л Я2 ((С*)", Z),
т. е. любое линейное расслоение на (С*)" определяется своим?
классом Чжэня. Для любого L можно выбрать такой базис:
^1» • • 1 ^2ге в л, что в соответствующих вещественных
координатах «C-J, . . ., ^2Т1 ^^
^1 С-^) = 2 Sadx„ Л dx.
а=1
ге+а"
Но каждое из х„+а определяет функцию на F/Z {Хх, • . ., А-п}'
поэтому [йх-п+а} = 06 ЯЬн (W2. {А,1, . . ., Я^}). Следовательно,
cj (я?Х) = я? (с, {Щ = О
и расслоение n*L тривиально. Если теперь мы выберем некоторую^
тривиализацию ф: n*L -> (С*)" X С, а в качестве тривиализацивь.
Ф расслоения n*L возьмем подъем ф, то получим
e^^(z)^l, а = 1, . . ., re.
Пусть © — произвольная целочисленная инвариантная
положительная форма типа (1, 1). Выберем такой базис %х, . . ., Х^
в Л над Z, что в соответствующих координатах Xj, . . ., х^п на V'
п
©= S ба^аЛ dx„+a, Ь^^Ъ.
Ofc=l
Так как форма © невырожденна, то б „ =5^ О при всех а и
определены векторы
во = 60*^-0! а=1, ..., ге.
Пусть Zj, . . ., г„ — комплексные координаты на V, отвечающие
базису fij, . . ., вп- Тогда, как и выше, можно написать
(/-1, . . ., А,2„)
336 2. Римановы поверхности и алгебраические кривые
где Й = (Ав, Z); по условиям Римана III опять Z = ^Z ж 1т Z ^
> О, поскольку © — положительная форма типа (1, 1). Одним
из наших важнейпшх вычислительных результатов является
следующая
Леима. Линейное расслоение L -^ М с мультипликаторами
имеет класс Чжэня Cj (L) = [©].
Доказательство. Прежде всего проверим, что указанные
мультипликаторы действительно удовлетворяют соотношениям (*).
Очевидно, они выполнены при а или р ^ ге. Если Z = (Z^p), то
что и требовалось установить.
Пусть теперь ф: n*L ->- У х С — тривиализация расслоения
я*Ь с заданными мультипликаторами. Тогда для любого сечения
б расслоения L над U с М подъем 9 = ф* (я* 9) является
аналитической функцией на я"^ {U), удовлетворяющей соотношениям
9(2+Я„) = 9(2), 9(z + ^„.a) = e-'"*^«9(z),
и обратно, любая такая функция определяет сечение расслоения
L. Пусть II II — произвольная метрика на L. Для любого сечения^
расслоения L положим
||9(z)|P = ^(z).|9(z)P;
очевидно, что h — положительная С~-функция от z, для которой
А (Z) I 9 (Z) р = |Г9 (Z) IP = А (Z + Я,) I 9 (Z + %) ?
при любом я g л. Значит,
h{z + K) = h (z), А (z + К+а) = I е2"^"« Р h (z).
Обратно, любая такая функция h определяет метрику на L.
Напишем, как и ранее, Z = X + Y —1 Y. Так как У > О, то
определена матрица W = (Wa^) = У'^- Мы утверждаем, что
функция
h (Z) --= е<"^^> 2 ^аэ <^а-^а)(^Э-^В-"^ЭВ>
6. Комплексные торы и абелевы многообразия 337
удовлетворяет приведенным выше функциональным уравнениям.
Очевидно, что h {% -{- %„) = ^ (z). Что же касается других
соотношений, то
\ogh(z+%n+y) =
а, в
а, Р а, р
+ -f- Е ^«3• 2^^аг (zp- z"b + 2i (Y^y- Грр)) =
a. ft
= logA(z)+|-2Sav2i(Ze-z„) +
a
+4Ебв7-2Ч2в-2в + 2г(Ув^-Узз)) =
2
P
(так как r.PF = / и РГ^']^)
== log h (z) + яг (z;, — Z;,) + яг (z^—z^) = log h (z) — 4я Im (z^);
поэтому
Вычислим теперь форму кривизны вх, метрики на L,
заданной функцией h'.
Ql = 55 log I = - ^ ad ( 2 И^аВ (Za - Za) (Zp - Zp - 2гУрр) ) =
a, p
= T ^2 ^ap ((Za - Za) dzp + (zp — zp - 2гУрр) di„) =
a, P
= "2 ^oB^ZaA dZp.
a, p
Запишем теперь эту форму в базисе {dx^, dx„+„}:
dZa = Sa dx„ + 2 Zap <^^ге+Р» «^Z^ = б^ cfea + 2 ^ab ^n+B»
поэтому
вх, = Я 2 ^аВ "^Za Л d;jp = Я 2 I^OpSaSp dXg^ л dXp +
' ■■«,ft, -.....
+ Я 2 ^авбя'(2^р?—ЗД«^^аЛЙа;„+^+
+ я 2 ^aP^aV^pe dx^+y Л da;„+e.
a, p, r, 8
22-046
338 2. Римановы поверхности и алгебраические кривые
Так как W = ^W ti Z — *Z, то первый и последний член этой
суммы равны нулю, откуда
a. В, Y
= — 2jt V — i- S SaPTaB^B? ^^a Л d^n+y =
а.Э, V
= — 2jt У — 1 2 ^e <^^a Л da;„+a,
a
И наконец,
Перейдем ко второму шагу. Чтобы продолжить описание
линейных расслоений на М, нам надо теперь рассмотреть множество
линейных расслоений L ->- ikf с фиксированным положительным
классом Чжэня. Заметим, что для любого ц 6 Af сдвиг Тц,:
М —>- М гомотопен тождественному преобразованию, и поэтому
Cj (x^L) = Ci (L) для любого линейного расслоения L-^ М. Более
того, если L задано мультипликаторами е^^ ^ 1, е,,^^^ (z) —
__ g-2niza^ то x*^i, можно задать мультипликаторами
т.е. ег, отличается от е^ постоянным множителем е~ "^*^а,. Обратно,
если L' — произвольное линейное расслоение с
мультипликаторами eji ^1 и eji sca-ei с^^С*, то, полагая
Н-=Е 2я^ logCa-еабУ,
2л
мы получаем, что L' =x^L.
Следовательно, для того чтобы доказать, что каждое линейное
расслоение, имеющее тот же класс Чжэня, что и L, получается
сдвигом L, достаточно показать, что каждое линейное расслоение
с нулевым классом Чжэня можно задать постоянными
мультипликаторами. Для этого заметим прежде всего, что включение
точных последовательностей пучков
t t
с*'
6. Комплексные торы и абелевы многообразия 339
на любом компактном кэлеровом многообразии X индуцирует
коммутативную диаграмму
Н'{Х,Щ-^Н'{Х,0*) ^^ Н\ХЛ)
Отображение ц* является проекцией пространства Н^ (X, С) =
= Я^'" (Х) Ф Н"'^ (Х) на второе слагаемое и потому сюръективно.
Отсюда следует, что любой коцикл у ^ IP (X, О*) из ядра
гомоморфизма Cj лежит в образе гомоморфизма i*, т. е. когоиологичен
коциклу с постоянными коэффициентами; значит, любое линейное
расслоение на X с нулевым классом Чжэня может бить гадано
постоянными функциями перехода.
Пусть теперь L-^ М = VIA. — произвольное линейное
расслоение с тривиальным классом Чжэня. Рассмотрим такое
открытое покрытие Ц = {Ua} многообразия М, что при каждом а
прообраз я"^ (Ua) — {Uaj}j является набором непересекающихся
открытых множеств, изоморфных Ua посредством я, и набор
тривиализаций ф^: L^^^-*-£/„ х С с постоянными функциями
перехода {gaa'}- Тогда можно определить набор констант {haj}a,jt
взяв ha J ^ i при некоторых фиксированных Oq, /о '^ положив
Kj = ha'i>-gaa' ДЛЯ а, а',]' с UajriUa'j'=^0'
Легко видеть, что этот набор определен корректно, поскольку
{gaa} "~ КОЦИКЛ. Кроме ТОГО, тривиализации 1
фау: n*Lu^j-*-Ua}XCt
заданные правилом ф^^ = йиу-я*фи, склеиваются в глобальную
тривиализацию расслоения n*L с постоянными
мультипликаторами.
Чтобы несколько прояснить это доказательство, опишем
подробнее геометрию группы линейных расслоений на М. Напомним,
что по экспоненциальной последовательности пучков имеем
\т {М, Z) ^ IP (М, (Э) ^т (М, 0*)Л IP (М, Z).
Тогда группа Pic" (М) голоморфных линейных расслоений на М
с нулевым классом Чжэня задается как факторгруппа
Pic" (М)^ IP (М, Q)im (Л/, Z).
Далее, IP (М, О) = (^''•^ (М) является пространством
инвариантных форм типа (О, 1) на М, т. е. пространством V* =
340 2. Римановы, поверхности и алгебраические кривые
= Нощр (F, С) сопряженных линейных функционалов на V.
С другой стороны, IP (М, Z) — это группа вещественных
инвариантных 1-форм © на ilf с целочисленными периодами, т. е.
группа вещественных линейных функционалов на F с целыми
значениями на Ас V. Отображение Н^ (М, Ъ)-^ IP- (М, О)
задается сопоставлением © н-*- ш"."^^. Так как для вещественной
формы (О интеграл
г. г. г. г. г.
принимает целые значения при всех А, 6 А тогда и только тогда,
когда 2Re \ са".^ 6 2. при всех А, 6 Л, то образ Л* группы Н^^ (ikf, Z)
\ _
в ВР {М, (5) = V* совпадает с группой сопряженных линейных
функционалов на F, имеющих полуцелую вещественную часть
на Л с: F. Итак, Pic" (М) является снова комплексным тором,
который часто называют двойственным абелевым многообразием
для М и обозначают М.
В явном виде пусть х^, . . ., x^ni как и выше, вещественные
координаты на F, соответствующие базису Я^, . . ., к^п- Обозначим
через af сопряженную линейную часть вещественного
функционала Xi. Тогда af образуют базис в Л*. Если
X, = 2 ntaZa + S ^ia^a•
ТО a;*=2"«aZa) где по установленному выше
П-, ;
Изменим порядок элементов базиса {х*} в Л*, положив
J/a = — ^n+oi Уп+а = ^»
Тогда
(Уп+и •-',Угп)= ^ Ae'Zy-i(Ji, ..., z'„)=
= Au*Z{y^, ...,yt).
Поэтому если злементарные делители б^ упорядочены так, что
^il^al • • • 1^п' то можно положить
Оа 71*
бп
б. Комплексные торы и абелевы многообразия 341
Тогда
{у* У%) = SnAe' (е*, ..., el),
{yt+u ..., ytn) = SnAe'ZAe* {e*u ..., eS).
Поэтому матрица периодов для М относительно базисов (у*) в
Л* и {е%) в F* имеет вид
0*=(б„Аб', SnAH'ZAe').
Так как би|б„ при всех а, то матрица б„Дб' снова диагональна
и целочисленна, а так как
\6^A6^Z^r) = S„ 'Аб* 'Z 'Аб* - б„Аб*2Аб'
и матрица Im (б„Аб^2^Аб^) = б„Аб^УАб^ по-прежнему
положительно определена, то iif — абелево многообразие. В действительности
поляризация исходного многообразия М индуцирует на М
поляризацию с «двойственными» элементарными делителями {S„/6a}.
Пусть теперь L — некоторое положительное линейное
расслоение на М. Рассмотрим отображение
Ф1,: М-^ Pic» (М), фь ((1) = Z-1 ® T*L.
Мы хотим дать явное описание фх, при выбранных базисах {Ха}
в Л и {во,} в V, нормализованных относительно L, и двойственных
базисах {yZ} в Л* и {ej} в f*.
Обратимся прежде всего к отображению
Нъ * (М) Л я* (М, в) -^ Pic» (М),
где б — изоморфизм Дольбо. Пусть
— постоянная (О, 1)-форма на М. Тогда для каждого открытого
множества Ut из достаточно мелкого покрытия можно написать
f^= dfi (z)j, где ft (z) = 2 <^aZa при подходящем выборе ветви z^.
Линейное расслоение, отвечающее о, имеет функции перехода
ч мультипликаторы
в подходящей тривиализации. Умножая тривиализации на
функцию / (z) = е^"* •" °^^^, мы получаем нормализованные
мультипликаторы
ех (z) = l, ex (z) = e-2"'2<'3<Za3-2<x3> = e-*"2<'!5^a3,
342 2. Римановы, поверхности и алгебраические кривые
где У = Im Z, как и выше. Понятно также, что в координатах
а^ на F линейное расслоение, отвечающее форме
П
а=1
имеет мультипликаторы
и, аналогично, расслоение для
расслоение для
имеет мультипликаторы
С другой стороны, поскольку линейное расслоение L задано
мультипликаторами
ТО ДЛЯ любого fi = S Н-а^а 6 ^ расслоение t^L (задается
мультипликаторами ея^^1 и ех^^=:е~^"*^^а+|^а\ Значит, 9(Z) = L~i®
® tJJZ имеет мультипликаторы
в частности, если (1= 2ca^a= ScaSaCa, ТО Фх, (S ^а^^а) ИмееТ
мультипликаторы e^^^l и е%^ д = е~^""'<»'а, т.е.
И если у = S Са^п+а= S Са^аввр, ТО фх, (^ СиХ„+а) Имеет
мультипликаторы ек^^1 и ex^^p = e~^"'2'=aZa3^ ^_g
Фх. (2 СаЯ„+„) = — 2 SaC„a-* = — 2 Саб„г/Й+а.
(Эти два последних утверждения эквивалентны, так как фх, —
комплексное линейное преобразование. Действительно,
Фь (2 Са^п+а) = Фх: (S CaZ<,p6p ^Яр) - - 2 C^ZanVt^
= — 2 CaZ„p (б„/бр) е| =
= - 2 CaS„6„ (6i'Z„36p'4) = - S C„6„J/*+„.)
6. Комплексные тори и абелевы. многообразия 343
Отсюда, ВО ВСЯКОМ случае, видно, что ядро гомоморфизма ф^, —
это в точности подгруппа из М, порожденная базисом
{бй^Хи, бй^Х„+и}, т. е. линейное расслоение L остается неподвизю-
ным в точности при \\Ьа сдвигал
Т etna-фу н кции
Описав положительные линейные расслоения L -*- М ва абеле-
вом многообразии М = F/Л как факторы тривиального расслоения
F X С, мы можем теперь представить глобальные голоморфные
сечения расслоения L как целые голоморфные функции на F ^ C"g
удовлетворяющие некоторым функциональным уравнениям. Эти
функции называются т£та-фунщиямщ исследуя их, мы докажем
следующее утверждение.
Теорема. Пусть L-*- М — произвольное положительное
линейное расслоение, а б^, . . ., б„ — элементарные делители
поляризации Ci (L) на М. Тогда справедливы следующие утверждения:
1. dim Я» (М, е Щ) = П Sa.
а
2. Н" (М, О {L'^)) не имеет базисных точек при к^2 и при
к^З задает вложение абелева многообразия М в проективное
пространств.
Доказательству этой теоремы мы предпошлем несколько
замечаний. Прежде всего поскольку К^^ = О, то по теореме Кодаиры
об обращении в нуль
h^ (М, в (L)) = h^ (М, Q" (L)) = 0, р > О,
откуда
А» (М, в (L)) « X (Ь).
С другой стороны, в Н^ (М, Z) существует такой
целочисленный базис {dxi, . . ., dx^}, что с^ (L) = 2 So dx^ Л dxn+ai
поэтому
ci (Z)" = п! П Sa € Я2" (М, Z) s^ Z,
Следовательно, утверждение 1 можно рассматривать как частный
случай общей формулы Римана — Роха, выражающей
голоморфную эйлерову характеристику линейного расслоения через ее
топологические инварианты.
Утверждение 2, принадлежащее Лефшецу, имеет более
глубокую природу, и мы с ним в дальнейшем еще столкнемся.
344 2. Римановы поверхности и алгебраические кривые
Чтобы доказать первое утверждение, выберем такой
целочисленный базис {^1, . . ., А,2п} в Л, что в соответствзгющих
координатах Xj, . . ., Xjn
Cl (L) = S Sa dXa, Л dXn+a.
Пусть, как и выше, е„ = бй^А-а' ^ %> • • м 2„ — соответствзгющие
комплексные координаты на V. Тогда матрица периодов Q для
Ас Vимеет вид Q = (Лв, Z), где Z = X + У —1У—
симметрическая матрица, а У >• 0.
Как мы уже знаем, линейное расслоение L является сдвигом
линейного расслоения Lq с мультипликаторами
Так как h" (L) инвариантно относительно сдвигов, то утверждение 1
достаточно доказать для L = r^Lo, где ji == - 2 Z^^-e^.
Мультипликаторами L являются
Поэтому глобальные сечения 9 в L задаются целыми голоморфными
функциями 9 на F, для которых выполнены соотношения
9(z + A,J-9(z), 9(z-bA,„+c) = e-'""«-"'^««.e(z).
Из первого соотношения следует, что функция 9 должна разла-
гаться в степенной ряд по переменным zj = е " ; напишем
соответствуюш;ее разложение:
(*) 9(z)= S ffli-^t'' ...z*'" =
гей"
2яг У г„б~'2„
:= 2 «re « """^ S а,.е^"*<''^вЧ
zez" zez"
Второе множество равенств задает рекуррентные соотношения
между коэффициентами а^ рядч для 9. Действительно,
9(z + ?.„+„)= 2 a,.e^'<^^6^<^+'^n.a)) =
i£S"
б. Комплексные тора и абелевы многообразия 345
Но по второму из приведенных выше соотношений
zez"
»т».
J6Z"
Сравнивая коэффициенты этих двух разложений Фурье для
9 (z + А-п+а)» мы получаем, что
Следовательно, функция 9 полностью определяется заданием
коэффициентов {ai}i.. o<i„<6„, откуда
h<^{M,Q{L))KWK.
Чтобы доказать равенство, надо установить, что каждый из-
рядов (*) при произвольном выборе коэффициентов {fflz}j;o^z <б
действительно сходится. Теперь мы уже можем написать
e(z)= 2 (S а.о+Лвге^"^^^''+"в'-^»'^^) =
''<^ва<ба Z6Z"
Пусть
(**) 9,„(z) = e'"'^""^«'^' S «»„+Двге2-<'.^>
zez"
— ряд, определяемый выбором а; = 1 и приведенными выше
рекуррентными соотношениями. Из линейности этих соотношений
следует, что обш;ая тета-функция имеет вид
9(z)= 2 вг,его(2).
''<'оа<ба
Поэтому достаточно доказать сходимость ряда (**).
Для удобства положим 6; = ffl/g-j-Agj- Тогда по рекуррентным,
соотношениям
Последнюю рекуррентную систему можно решить, положив
bi = e
->7
ni {I, Zl)+2ni <Дб Vo. Zl)
346 2. Римановы поверхности и алгебраические кривые
В самом деле
^ ^ni <г, Zl)+2ni <г, Ze„)+m <e„, Ze„)+2ni (Ae'Zo, Zl)+2ni (Ae'Zo. Ze„> ^
= g2ni </, Х„^„)+яг2„„+2яг <Д5%, X^„) _ ^^^
так как Z = 'Z и Ze^ = Я^+и. Итак, 6 действительно являются
решениями рекуррентных соотношений. Отсюда
тде У = Im Z, как и выше. Но матрица Y положительно
определена, поэтому (I, Yl) > с'- II Z IP для некоторой веш;ественной
константы с' > 0. Так же очевидно, что | {AqHo, Yl) I < с"-1| Z || для
некоторой константы с". Следовательно, суш;ествует такая
константа с > О, что
lu^Ke-dlMI»
для всех достаточно больших I. Значит, ряд (*♦) сходится
равномерно на компактных подмножествах в С", что и требовалось
доказать.
В частности, если с^ (L) — главная поляризация на М, то
пространство Н^ (М, О (L)) одномерно и порождено сечением 9^
соответствуюшрям функции
e(z)= S enia,Z».g2ni<Z,2>^
которая удовлетворяет функциональным уравнениям
9(2 +О = 9(2),
в(г+>.„+„) = е-='"^<^«+^-/'>.9(2),
9(z) = 9(—z).
Эта замечательная целая функция называется Q-функцией Ри-
мана абелева многообразия (М, [©]) с главной поляризацией.
Отметим еш;е, что, поскольку h" (М, О {L)) = 1, дивизор
в = (9) однозначно определяется по Z, а поэтому определяется
с точностью до сдвига классом когомологий [©]; 0 называется
тета-дивизором Римана поляризованного абелева многообразия
(М, [©]).
Чтобы лучше разобраться в последнем результате, рассмотрим
такие же, как выше. Л, Я, х, е, z, б и Z. Пусть Л* с: F — решетка»
лорожденная векторами
6. Комплексные тори и абелевы многообразия 347
ПОЛОЖИМ М' = VIA'. Поскольку Л — подрешетка индекса А =
= П ба в Л', отображение проекции п': М ^>- М' является А-лист-
ным накрытием М над М'', соответствующие преобразования
Галуа — это в точности сдвиги {Тц,}цел7Л'
Однако теперь матрица периодов для Л' с: F в базисах {Щ
и {ej} совпадает с матрицей й' — (1, Z). Поэтому если х{, . . ., Х2„ —
вещественные координаты в базисе {k'l}, то класс
[со] = [S dx'a Л dx'n+J = [2 б„ dxa л dx„+J
задает главную поляризацию на М'. Так как L определяется
с точностью до сдвига своим классом Чжэня с^ (L) — [со], то
существует линейное расслоение L' ^>- М' с n'*L' == L.
Следовательно, если L -*- М = VIA. — произвольное положительное линейное
расслоение на абелевом многообразии, то существуют абелево
многообразие М', имеющее линейное расслоение L' -*■ М' с главной
поляризацией, и конечное отображение п': М-*■ М', тлкое, что
п'*и = L.
Довольно очевидно, что А сечений 9г , соответствующих тета-
функциям Qi из доказательства утверждения 1, с точностью до
умножения суть сдвиги одного в другое относительно
преобразований Галуанакрытия я': М -^ М', а образующая 9 в Я" {M',(9{L'))
задается соотношением я'*9 = 2 ""^^г •
Теперь мы докажем утверждение 2 в случае линейного
расслоения L с главной поляризацией с^ {L). Основная идея заключается
в использовании группового закона на нашем торе. Пусть L -*■ М—
абелево многообразие с главной поляризацией, и пусть все
данные нормализованы, как и вы1пе. Тогда
H<^{M,Q{V^)) =
= {9 6 0 (F): 9 (Z+ е„) = 9 (Z), 9 (z + >.„♦„) = е-'*"'^'"+^="='^''• е (Z)}.
8 частности, если 9 — тета-функция Римана пары {М, L), то при
любом (1 6 ЛГ имеем
в^ (z) - 9 (Z -Ь [1) 9 (Z - (1) 6 Д" (M,0(Z^)).
Далее, если z* 6 М, то существует [х 6 М с 9 (z* -|- (i) =/= О и
9 (z* — \i) Ф Q, т. е. вц, (z*) Ф 0. Значит, линейная система
\ L^ \ не имеет базисных точек и поэтому задает отображение
11.2 : М ^ PJV.
348
2. Римановы поверхности и алгебраические кривые
Чтобы показать, что отображение if,. : М -*■ Р^, отвечающее
линейному расслоению L^, является вложением, выберем базис
00, - - ., в^v в Я" {М, G (L^)) и положим
eo(z)...e^^(z)
f{z) =
(z)
(Z)
^(Z)
dz.
r(^)j
Покажем прежде всего, что ранг матрицы f (z) равен re + 1,
откуда будет следовать, что ij« — иммерсия. Пусть 9 (z) — тета-
функция Римана, и пусть
в (z, [X, v) = 9 (z + [х) 9 (z + v)-9 (z — Ji — v).
Тогда e — голоморфная функция от трех переменных z, [х и v;
при фиксированных [х и v функция в^^^ (z) = в (z, (х> ) задает
глобальное сечение пучка Z*. Значит,
в (z, [X, v) = Со ((X, v)-9o (z) + . . , + Cjf ([X, v)-9jv (z),
где с J — голоморфные функции от [x и v.
Предположим теперь, что ранг f (z*) меньше re + 1 в
некоторой точке Z* 6 М, т. е.
a„9,(z*) = ai|5j-(z*)+... + a„-|^(z*)
при О < i :^ TV. Тогда
Ф{2*, [X, v) = ai-^(z*, [X, v)+...+a„-^(z*, (X, V)
для всех (X, V. Рассмотрим мероморфную функцию
, . а log 9 , .
1 а log 9 ,.
тогда
Ф (z* + Н-) + ф (z* + V) + Ф (z*—fx — v) =
Saioge / * . 1
ае
azj
е (г*, ц, V)
S'^i-airCz*, Н-. v) = fflo
для всех [X, V. Далее, для любого [х существует такое v, что
Ф (z* + v) т!^ оо и ф (z* — [X — v) т!^ оо, т. е. такое, что z* + v
HZ* — [X — V лежат вне дивизора полюсов функции ф. Так как
Ф (z* + И-) + ф (z* + v) + Ф (z* — [X — v) = «о, отсюда следует,
что ф (z* + [х) — всюду голоморфная функция от (х. Очевидно,
6. Комплексные торы и абелевы многообразия 349
<p(z + e„) = Ф (z), а поскольку 9 (z + >,„+„)= 6"^"* <'«+^««/^'е (z),
то
log е (Z+>,„+„) = -2ш (z„+-^) + log е (Z),
т.е. 9(z+A,„+a) = 9(z) —2я1-аа-
Следовательно, каждая частная производная dff/dzi периодична
относительно решетки Л, а значит, ограничена на F ^ С" и
поэтому является постоянной функцией. Отсюда вытекает линейность
отображения ф; итак,
ф(2) = 3&а-2а + С.
а
Но ф (Z + ба) = ф (z) ^- 6а = О при ВСех а, откуда ф (Z + ^^-п + а) =
= Ф (z) = с. Значит,
<р (z + ^п+а) — Ф (z) = 2я1-а„ ^- а„ = о при всех а.
В результате мы вывели, что предполагаемое линейное
соотношение
UoQ} (z*) = ^ai -^ (z*) для всех /
тривиально и i^,» является иммерсией.
Остается установить взаимную однозначность отображения
ii,», что делается аналогично. Предположим, что существуют
точки Zj^, Za 6 С", для которых
0г (Zi) = p'0j (Za) при всех i;
мы покажем, что z^ и Za задают одну и ту же точку на М. Из o6ni,ero
соотношения
e(z, [А. ^) = 3 Сг(и., v)-ej(z)
1=0
следует, что
е(г^,ц,у) ^ 9(z^ + ti)e(zi + v)9(zi—ц—V) ^
тождественно по [х и v. Для любого [а g С" суп1,ествует такое v,
при котором все значения
0 (zi + V), 0 (zi - [X - V), 0 (Za + v), 0 (za - |x - V)
отличны от нуля. Следовательно, 0 (z^ + [х)/0 (Za + И-) —
необращающаяся в нуль функция от [X. Тогда мы можем рассмотреть
целую голоморфную функцию
а|; (Z) = log (0 (zi + z)/0 (г^ + z)).
350 2. Римановы поверхности и алгебраические кривые
В силу функциональных уравнений для б-функции
я|^ (Z + е„) = a|; (z) + 2nib^, 6„ 6 Z,
а|; (z + ^+а) = 4" (z) — 2я1 (Zi — z^)^ + 2nic„, c„ 6 Z.
Как и выше, отсюда следует, что производные dff/dzt постоянны
при всех i. Поэтому
а|;(г) = 2я12 ^p-Zp + d.
Тогда ар (z + е„) = а|; (z) + 2ni6„ =^а^ = b^^l, откуда
4" (z + ^п+а) — 4" (z) = 2я1 S apZ^p =^
=4- 2Я1 (Zj— Z2)a = — 2niCa + 2п1 2 Ofi^afi =*►
=^ Zi — Za = — S Са -ба + S «Э^п+р,
Т. е. Zi — z^^ А.
Наконец, для произвольного положительного линейного
расслоения L -^ М можно, как и выше, построить абелево
многообразие М', имеющее линейное расслоение U -*- М' с главной
поляризацией, и конечное отображение п': М ^>- М', для которого
я'* (!/') = L. Так как отображение я' нигде не вырождено, то из
предыдущих рассуждений, примененных к расслоению L', следует,
что ii,», как и прежде, является иммерсией и что ii,» (р) ф ir,» (g)
для точек р ж q с п' {р) Ф п' (д). То, что i^,» разделяет точки слоя
я~^ (р), легко усмотреть из приведенных выше явных формул для
тета-функций. D
Первый пример вложения алгебраических многообразий в Р",
не считая кривых,— это вложение
1^,3 : М с=- р8
абелевой поверхности с главной поляризацией. В частности,
пусть М = El X Е^ — произведение двух эллиптических кривых
ж L^-*- Е^, L^-*- Е^ — линейные расслоения степени 1.
Рассмотрим соответствующие вложения i^^s : Ei -*- Р^. Тогда расслоение
L = n*Li ® n*L^ задает главную поляризацию, а ii,» совпадает
с вложением Сегре Р^ X Р^ -> Р*, ограниченным на М =
= El X Е^ ^-^ Р2 X Р^
Групповая структура
на абелевом многообразии
В завершение нашего обсуждения комплексных торов сделаем
несколько общих замечаний о групповой структуре на абелевом
многообразии.
Любой комплексный тор М = С"/Л является комплексной
группой Ли, т. е. комплексным многообразием с групповой струк-
6. Комплексные торы и абелевы многообразия 351
турой, для которой групповые операции голоморфны. Верно-
также и обратное утверждение.
Предложение. Всякая связная компактная комплексная группа
Ли М является комплексным тором.
Доказательство. Установим прежде всего коммутативность
группы М. Для любого элемента g ^ М обозначим через Ad {g)>
автоморфизм
Ad (g): h^-* ghg-^
на М. Очевидно, что единица е является неподвижной точкой
Ad (g) при всех g^ М.
Пусть z^, . . ., Zji — голоморфные координаты в окрестности
точки е ^ М. Для каждого g ^ М напишем разложение в степенной
ряд функции Ad (g)* (z,) в е:
Ad (g)* (zt) = 2 «ii in(g) 4* ... 4".
Очевидно, для каждого индекса (ii, . . ., i„) функция a,-, ,„ (g}
голоморфна по g и, следовательно, постоянна, так как М
компактно и связно. Итак,
Ad (g)* (Zi) = Ad (в)* (Zi) = zu
откуда Ad {g)* ^ /, т. e. M коммутативна.
Далее, для любого касательного вектора v ^ Т'е (М)
многообразия М в точке е определим векторное поле у на М по правилу
где tg'. М -*- М — умножение на g. Очевидно, что v голоморфно.
Пусть ф4,в: М ^*- М — эндоморфизм многообразия М,
получающийся интегрированием векторного поля v за время t, и я:
Т'е (М) -^ М — экспоненциальное отображение, определяемое
равенством я (у) = ф^^д (е). Так как групповая структура на Ж
коммутативна, то п является гомоморфизмом групп.
Следовательно, М есть фактор пространства Т'е (М) ^ С" по дискретной
подгруппе, которая должна быть решеткой А. Так как М компактно,
то решетка Л имеет максимальный ранг 2га, а потому М ■= С"/Л —
комплексный тор. D
Заметим, что если М = С"/Л, М' = С^/Л' — два )комплекс-
ных тора, то любое голоморфное отображение /: М ^*- М'
поднимается до голоморфного отображения /: С" -*- С". Пусть z =
= (Zi, . . ., z„) и ш = (w.^, . . ., Wm) — евклидовы координаты на С""
и С" соответственно. Тогда, как легко понять, матрица Якобы-
ff = {dwildzj)
352 2, Римановы поверхности и алгебраические кривые
гадает однозначное голоморфное отображение на всем М, а потому
постоянна. Следовательно, / — аффинное отображение, и мы
доказали такое
Предложение. Любое голоморфное отображение комплексных
торов является групповым гомоморфизмом после подходящего
сдвига.
Каждое абелево многообразие имеет структуру однородного
алгебраического многообразия, т. е. допускает транзитивное
действие группы биголоморфных автоморфизмов. Другими примерами
однородных многообразий являются грассманианы, квадрики
и т. д. Однако между первым и последними примерами имеется
существенная разница. В последних автоморфизмами могут
служить проективные преобразования, т. е. при подходящем
вложении М с Р^ группа автоморфизмов Aut (М) совпадает с группой
линейных автоморфизмов Р^, сохраняющих М. С другой стороны,
имеет место следующая
Теорема. Пусть М аР^ — абелево многообразие. Тогда
группа автоморфизмов, индуцированных на М линейными
преобразованиями Р^, конечна.
Доказательство. Пусть L-*- М — расслоение гиперплоскости
на М. Тогда, очевидно, ф*Ь = L js^aa каждого автоморфизма ф:
М -^ М, индуцированного линейным преобразованием
пространства Р". Но, поскольку расслоение L положительно, оно
сохраняется лишь для конечной группы сдвигов на М. Поэтому
достаточно показать, что группа автоморфизмов М, сохраняющих L
и точку р = я (0) из М, конечна. Каждый такой автоморфизм
поднимается до линейного преобразования ф: С" ^ С",
сохраняющего решетку Л с: С". Более того, ф унитарно относительно
зрмитова скалярного произведения, заданного классом с^ {L) ^
^ Я^^^ (М) = V ® V, поскольку ф переводит L в себя. В частности,
Ф должно переводить каждый вектор Я^ из базиса решетки в вектор
решетки той же длины. Но для каждого i таких векторов решетки
конечное число, что и доказывает наше утверждение. D
Инвариантные формулировки
Во многих случаях удобно, иметь формулировки результатов
об абелевых многообразиях, не использующие координат. Ниже
даются такие формулировки вместе с некоторыми приложениями.
6. Комплексные торы и абелевы многообразия 353
Рассмотрим четномерное вещественное векторное пространство
V^, содержащее полную решетку Л, с заданным разложением его
комплексификации Vq = V^^ <S) С
(*) Fg = F®F
в комплексно сопряженные подпространства. Образ Л в Vq
проектируется на полную решетку в V, обозначаемую также через Л.
Пусть М = V/A — соответствующий комплексный тор. Как будет
видно из следующего абзаца, таким способом получается каждый
комплексный тор с Fj^ = Л ^^Щ.
ВБШхе уже отмечались два естественных изоморфизма
A^Hi (М, Ч), V* ^Н'» (М, fii).
Если dimQ V = п, то по двойственности Кодаиры — Серра и
двойственности Пуанкаре имеем
Поэтому V^= Л (Э^Л канонически изоморфно Н^-^ (М, R),
причем формулы (*) — это разложение Ходжа
Я^"-* (М, С) = Я"-*'" (М)фЯ"-*'" (И).
Согласно предложению из предыдущего раздела, каждое
голоморфное отображение
ф: F/Л^ Г/А'
задается некоторым аффинным отображением V ^-V. Чтобы
описать его явно, рассмотрим вместо ф такую его композицию со
сдвигом, что ф (е) = е'. Обозначим через
Ф: Л^Л'
отображение, индуцированное на гомологиях. Так как ф*
сохраняет разложение Ходжа, то Ф индуцирует требуемое линейное
отображение
Ф: V^r.
Условие Римана существования поляризации можно
сформулировать теперь следующим образом. Всякий класс Н^ {М, Z)
задается некоторой билинейной формой
Q: А OgA^Z, Q (Я, Я') = -Q{k', К).
23-046
354 2. Римановы поверхности и алгебраические кривые
После отождествления Л^^С cV Ф V билинейные
соотношения принимают вид
Q(v,v')=0, v,v'eV,
Например, для якобиана
f (S) = Я".! iS)/IP (S, Z),
римановой поверхности S главная поляризация, задаваемая
дивизором 0, соответствует о-произведению
т {S, Ъ)® т {S, Ъ) -^ Zj
которое унимодулярно по двойственности Пуанкаре. В общем
случае если Q имеет элементарные делители б^, . . ., б„, то
произведение А = 6i . . . б„ называется пфаффианом фор:..... Q\
очевидно, что
det Q = А\
Используя инвариантный подход, построим линейное расслоение
Пуанкаре
Р-^М X М,
где М = Pic" (М) — комплексный тор, двойственный к М.
Напомним, что Pic" (М) по определению является группой голоморфных
линейных расслоений на М с нулевым первым классом Чжэня.
Из когомологической последовательности для экспоненциальной
последовательности пучков вытекают естественные отождествления
Pic» (М) ^т {М, G)/W- {М, 1) ^ f*/A*, А* = Нот (А, Z).
Обозначим через Р^-*- М линейное расслоение, соответствующее
точке ^ g Pic» (М).
Левша. Существует единственное голоморфное линейное
расслоение
Р^ М X Й,
называемое линейным расслоением Пуанкаре, которое тривиально
на е X М и удовлетворяет условию
Доказательство. Используя определение М= IP^^ {М)1Н\М, Z),
когомологическую последовательность экспоненциальной последо-
6. Комплексные тори и абелевы. многообразия 355
вательности пучков, а также формулу Кюннета, получаем
диаграмму
Н'(М X М 0)-*яЧМ X М,в*) ^Н\М X M.D^H'iMXM.'Q) .
\ \ .
4
Нот(Я'(МД),ЯЧЛГ,г))
Так как единица / 6 Нот (Н^ (М, Z), Н^ (М, 1)) сохраняет
разложение Ходжа в Я^ {М, С), то она имеет тип (1, 1). По теореме
Лефшеца об (1, 1)-классах отсюда вытекает существование
линейного расслоения Р -*- М X М с с^ (Р) = /. При этом ограничение
Р |л£х{5} имеет нулевой класс Чжэня и, значит, совпадает
с Рф(5) для некоторого голоморфного отображения
ф: M^PicO(M).
Можно считать, что ф (е) = е, после подходящей нормализации,
которая достигается умножением Р на n*P_g^, где ^о = Ф (^)-
Отображение, индуцированное на гомологиях, в этом случае
тождественно. Поэтому ф также тождественно, что и доказывает
существование расслоения Пуанкаре.
Пусть Р, Р' — два таких линейных расслоения. Тогда для:
Q = р* <S) Р' имеем
QImxid^MxC, Q\^^^^gi^MxC.
Обозначим вторую тривиализацию через aj;. Пусть а (Я, g) f
^Q(x,i) ~ единственное сечение в Q |л£х{5}1 принимающее значе-
ниеа);"^ (1) в (е, I). Тогда а— не обращающееся в нуль голоморфное'
сечение в ^, а потому Q — тривиальное линейное расслоение. D
Для положительного линейного расслоения L -*■ М определим:
расслоение L ® Р = n*L ® Р ж& М х М; тогда
L®P\mmI) = L®Pi = Li,
где последнее равенство есть просто определение. Для § 5 гл. 3
о дифференциалах второго рода нам понадобится следующее
Предложение. Существует А сечений 9^ (Я, \) ^
6 Я» (ЛГ X М, 0 (L <8) Р)), индуцирующих базис в Я» {М, О (Lg))>
для каждозо Ъ, ^ М.
гз*
356 2. Романовы поверхности и алгебраические кривое
Доказательству предпошлем несколько предварительных заме-
л
чаний об отображении ^^. М ^- М, определяемом формулой
Фг, (^) = та^ ® L*, которое нам уже встречалось в одном из
предшествующих разделов. Так как ф1, (е) = в, то, согласно общим
замечаниям, отображение ф^, однозначно восстанавливается по
индуцированному им на гомологиях отображению
Фг,: Л^ Л*. Я^"-1 (М, Z) -^ Нот (Я?"-1 (М, Z), Z).
Исследовав Ф^, мы получим другое доказательство того, что
<Pi, — изогенйя, т. е. конечнолистное накрытие, степени А^.
Рассмотрим для этого групповой закон
т: М X М^М, т (к', к) = к' + X.
Тогда по построению
(*) Фг. (к) = n*L* О m*L Ux{M-
Пусть Xi, . . ., х^п — такие вещественные координаты на Fj^, что
класс Чжэня расслоения L -*- М имеет вид
(О = S fia dXa Л dXn+a-
В этом случае, используя соответствующие координаты (и„, v^)
на М X М, мы находим, что
т*а = S б„ (d»„ + dv^) л (d»„+„ + dv^+a) ■
(К
Для Т1 6 Н^~^ {М, 1) обозначим через rii 6 -^^""^ {М X М, Z) класс
Чжэня подъема я*т1; аналогично определяется ц^. Из (*) легко
получить, что гомоморфизм Ф^, отвечает билинейной форме на
^P"-^ {М, Ъ), заданной формулой
Фг, (т!' л') = J "**«' л Til л Ла-
МхМ
Чтобы вычислить ее явно, напишем
У\' = lJ{ — ^У'^'Ц'idXi^ ... Adajy^ ... ^ dx^^^
откуда по формулам для|пг*со и Ф1, имеем
Фг, (Ц, л') = S Sa (Tlalln+a — Цп+а^р)-
6. Комплексные торн и абелевы. многообразия 357
Это приводит к следующему уже известному нам утверждению:
Ф^,: М -*- М — изогения степени А^; точнее, линейное
расслоение L -*- М остается неподвижным в точности при
сдвигах из группы Ъ (бй'Жа! 5а*-^п + а}-
Возвращаясь к доказательству нашего предложения, отметим,
что уравнение
\ = Фг. {^)
имеет А^ решений Я^ (|). Пусть 0 (z) 6 © (F) — некоторая 0-
функция, задающая сечение расслоения L^>- М. Тогда 0^, (z) =
= 0 (z + Я) задает сечение расслоения xJL = L ® Р^^(ху Далее,
если р: МХ М ^>- М X М — изогения, определяемая формулой
р (V, %) = {к', (fL (А.)), то 0 (z. А,) = 0 (z + Я) задает сечение
расслоения
n*L <8) р*Р = р* {L <S) Р)^М X М.
Но, поскольку 0 (z + Яд (I)) = в (z + kf, (D), это сечение
индуцировано сечением 0 (z, I) ^ Н'^ (М X М, О (L ® Р)). Таким
образом можно построить все требуемые в предложении сечения. Q
Рассмотрим в заключение некоторые комплексные торы,
связанные инвариантным образом с произвольным компактным кэле-
ровым многообразием М. Вспомнив о разложении Ходжа
Я^'-*(М, С)= ф ЕГ''{М)
r+s=2g-l
ИЗ § 1 ГЛ. 2, положим
для 1 < g < ге = dim М. Тогда Я^в-^ (М, С) = Fg Ф У,, и если
обозначить через Л^ образ естественного гомоморфизма
^2g-i щ^ 2,j _^ у^^ .j,Q q_^ промежуточный якобиан определяется
как комплексный тор
% (М) = V,IK
Обсудим крайние случаи q = i ж q = п.
При g = 1 мы получаем многообразие Пикара
f-i (М) = Я».1 {M)im (М, Z) = Pic» (М),
а при q = п — многообразие Алъбанезе
fn (М) = Я"-^" (М)/Я2"-1 (М, Z) ^ я» (М, Й1)*/Я1 (М, Z) =
= Alb (М)»
358 2. Римановы поверхности и алгебраические кривые
где последнее равенство есть просто определение. Выберем
некоторую базисную точку р^ ^ М ж базис дифференциалов ш^, . . .
. . ., (Од g Я" (М, Q^). Тогда по тем же соображениям, что и при
обсуждении теоремы Абеля, определено голоморфное отображение
р р
Ро Ро
По построению индуцированные отображения
|А*: Hi {М, 2)/кручение -^ Н^ (Alb (М), Z),
|А*: Я» (Alb (М), Й1) -^ Я» (М, Q^)
являются изоморфизмами. Отсюда, используя инвариантные
определения, полут1аем
Pic» (Alb (ikO) = Я».1 {M)im {М, Ъ) = Pic» (М),
Alb (Pic» (М)) = Я^-1." (М)/Я2"-1 (М, Z) = Alb (М).
Б частности, между комплексными торами Alb (М) и Pic» (М)
имеется естественная двойственность.
Предположим теперь, что со 6 Я^•^ (М) П Я^ (-^> Z) — класс
Чжэня положительного линейного расслоения. Тогда по
билинейным соотношениям Ходжа — Римана билинейная форма Q:
Ai ® Ai ^- Z, определенная формулой
Q(ti, т1')={со"-1лт1ЛТ1'.
м
тиндуцирует поляризацию на Pic» (М), которая по предыдущему
индуцирует поляризацию на двойственном торе Alb (М). Пусть
L -^ Alb (М) — некоторое положительное линейное расслоение,
а Р ^>- Alb (М) X Pic» (Alb (М)) — расслоение Пуанкаре.
Рассмотрим расслоение Ь^ — Ь^Р 1а1Ь(2Юх{|>' ^Д^ ^ ^
6 Pic» (Alb (М)). Выше по каждому сечению 0 6 Я» (Alb (М), L) мы
построили 05 6 Я» (Alb (М), Lj). Поднимая все это на М
относительно канонического отображения
|а: М^ Alb (М)
и производя затем предыдуш;ее отождествление Pic» (Alb {М)) ^
^ Pic» (М), получаем следуюш;ее утверждение.
На М существуют голоморфные линейные расслоения
L^ -*■ М, параметризованные точками ^ ^ Pic» (М), с L^®
® L^ = ^ и голоморфными сечениями 0^ ^ Я» {М, О (Ь^)),
голоморфно зависящими от ^.
у. Кривые и их якобианы 359
Пусть g = bi (М)/2; тогда для D^ = (65) это утверждение
в классической формулировке означает, что на М существует
семейство jDj из оо' линейно неэквивалентных дивизоров.
7. КРИВЫЕ И ИХ ЯКОБИАНЫ
Лредварительные сведения
Пусть S — компактная риманова поверхность рода g. Выберем
канонический базис {а^, . . ., Ug, b^, . . ., bg} в Я^ (5, Z), для
которого
#(а„-ае) = ЦЬ^-Ь^) = О, Ца^-bfi) = б„е,
и рассмотрим базис (Оц . . ., (Og в Я" (5, й^), нормализованный
относительно {а^, Ьо}> т. е. такой, что
J <вр = баэ-
Напомним, что якобиан f' (S) римановой поверхности S
определяется как фактормногообразие f (S) — С*/Л, где Л —
решетка, порожденная векторами
«а «а
По билинейным соотношениям Римана матрица периодов Q для
Л с: С« имеет вид Q = (7, Z) с Z = *Z и У = Im Z > 0. Поэтому
если Xi, . . ., ^2- — вещественные координаты на С*, соответствую-
пще базису {Я,|}, то дифференциальная форма
(В = 2 dXa л Ас„+„
а
представляет главную поляризацию на f (S) = С*/Л. В
стандартных комплексных координатах z = (%, . . ., Zg) на С* ее можно
записать в виде
(О = '^ ~ 2 ^«Э ^2„ л dzp,
где, как и выше, У = Im Z.
360 2. Риманови поверхности и алгебраические кривые
Замечание. Так как якобиан риыановой поверхности Всегда
имеет главную поляризацию, то, как и вьапе, после норыализациа
мы вместо %а будем писать е„, а вместо A,g+„ —
Пусть L — линейное расслоение на f (S) с классом Чжэня
[со], сдвинутое так, что глобальное сечение 0 расслоения L
представляется тета-функцией Римана 0 6 0 (С"), удовлетворяющей
функциональным уравнениям
б (Z + е„) = 0 (Z), 0 (Z + Z„) = е-2"* (-а+2аа/2)0 (z);
через 0 с 1^ (5) обозначим дивизор сечения 0.
Фиксируем теперь раз и навсегда базисную точку Zq ^ S. Пусть
[а: 5 ^- f- (5) — отображение, заданное формулой
|А (Z) = ( j ©1, . . ., j tOg )
zo го
Вычислим прежде всего индекс пересечения кривой ^ {S) cz.f (S)
с дивизором 0. Для зтого мы просто подсчитаем число нулей
сечения \i*Q расслоения \i*L на S. Предположим, что циклы а„, Ь„
не имеют общих точек, кроме базисной точки Zq. Как и в § 2 этой
главы, представим S в виде плоского многоугольника А,
склеенного вдоль сторон, соответствующих циклам а^, \, а^', Ь^^ и т. д.
(рис. 14). Тогда если [х: А ^- С* — очевидный подъем |а, заданный
интегрированием от Zo до z внутри А, и 0 g 0 (С") — указанная
выше 0-функция Римана, то
~ 1 (" ~
число нулей функции р,*0 = , \ d log 8 ([д, (z)).
вд
Чтобы найти значение этого интеграла, рассмотрим общий вклад
в него сторон Др и ар*, а также 6g и бр* из 5А. Пусть z, z* —
склеивающиеся точки на Др и Др* соответственно. Тогда
Z* Zo Z*
?o(z*)—|Ао(2)= J fi)a= J fi)o+J «>o +J «>„ = J ©a = 2эа.
* z Ьр z« bg
T. e. H (z*) = I* (2) + ^Э- Поэтому
0 (^ (2*)) = e-2"4(^>+^Bp/2)g (~ (2))^
7. Кривые и их якобианы
361
Рис. 14
откуда
Аналогично, для склеивающихся точек z, z* на 6g, Ьр*
jl(z*) = ji(z) —ер,
т. е. 0(ii(z*)) = 0(ir(z)) и
(*) —^ jdlog0(il(z)) + —1=^ {dlog0(iI(z)) = O.
Н Ьр«
Суммируя вклады всех сторон многоугольника А, находим
deg n*L = —7= j d log 0 Q. (z)) = ^.
Заметим, что в процессе вычислений мы предполагали, что [х*0 ^^
^ О на 5; если это не так, то можно взять вместо L его сдвиг
Ljj, = tJjL и соответствующее сечение 0^, (z) = 0 (z — Я) f.
6 Я» (f (5), 0 (LO) для подходящего Я 6 С».
362 2. Римановы поверхности и алгебраические кривые
Другой способ вычисления deg \i*L топологический:
deg \i*L= j Ci (fi*L) = j \i*Ci (L) = j |i* ( 2 '^a л dXg+a ) .
S S So
Ho n*(''^o) = ^o» И'*(Ьо) = ^г+о ^ поэтому
j |i* dXa = j da;„ = 0.
bg 1»(Ьв)
Отсюда видно, что класс [\i* dx^] двойствен по Пуанкаре классу
цикла —6„, а l\i* da;g+„] — цикла а„. Значит,
j [i* (da;„ л da;g+„) = *( —6„. а„) = 1.
S
откуда
deg [X* (L) = J [X* ( 2 dj:„ л dxg^^ j = ^.
s
Обозначим теперь через в = (0) дивизор линейного
расслоения L, а через 6^, = G + Я = (0^,) — соответствующий Дивизор
сдвинутого расслоения L^ = xlL, где 0^, (z) = 0 (z — К).
Поскольку Ci (Ljt) = q (L), TO, согласно последним вычислениям, при
любом 'к ^ f (S) либо
1)(х(5)св„
либо
2) \1 (S) пересекает 6^, точно в g точках с учетом кратностей.
Для X ^ f (S), таких, что [х (S) (^ 6^,, рассмотрим дивизор
(|х*0,) = Zi (Я) + . . . + Zg (X).
По теоремам Абеля и Якоби точка 'к ^ f (S) представляет класс
линейной эквивалентности дивизоров степени О на S. Оказывается,
что с точностью до сдвига на постоянную точку х класс Я,
совпадает с классом дивизора 2 ^t W — i'^o- В этом и состоит
следующая
Лев1ма. Существует такая точка к ^f- (S), чтю
1=1
.для всех X ^f (S) с II (S) ф в^.
7. Кривые и их якобианы 363
Отметим, что эта лемма дает обещанное явное решение
проблемы обращения Якоби, по крайней мере для общего элемента
Я 6 1^ [S), для которого кривая [х (S) не лежит целиком в в^,.
Доказательство. Представим опять S как плоский
многоугольник А. Пусть [а: а ^ с* — соответствующий подъем отображе-
;ния [X. Функция |а*6я, обращается в нуль в точках Zi (Я) и только
в них, поэтому
2?а(2|(Я)) = —i=^jil„(z).dlog0.(ir(z)).
Как и выше, этот интеграл вычисляется с помощью рассмотрения
соответствующих точек z, z* на сторонах ар, Др* из 5А. Поскольку
И'о (2*) = V-a (2) + ^ов» то, согласно функциональным
уравнениям для 0-функции,
0^ (il (Z*)) = е-2"*(^0(^)+^0/2-»'0)0^ (~ (г)),
■откуда
d log 0^ (^ (Z*)) = d log 0;, (^ (z)) - 2я у ^1. сор (z).
Следовательно,
:1=^ ( j fl„ (z) d log 0;, (jl (z)) + j il„ (z) d log 0, (? (z))) =
2я
«0
2аВ
==r J d log 0», (и. (z)) 4- Z„e J tog (z) 4- J |i„ (z) ©e (z>.
Последние два члена этого выражения не зависят от Я, а
потому могут быть выделены в константу х„. Что касается первого
члена, то пусть z^ и z^ — концы дуги Лр; тогда |а (Zj) = (х (z^) ±
.± бр, откуда 0Я, ([X (zi)) = 0Я, (|х (z^)) и
2я
^i=^Jdlog0,(iI(z))6Z.
Следовательно, первый член тоже постоянен и может быть
включен в Хя- Далее, если z и z* — склеивающиеся точки сторон Ь^
ж 6р', то
il(z*) =il (z)-eB, 0x(ir(z*)) = 0;,(il (z));
364 2. Римановы поверхности и алгебраические кривые
поэтому
^^у—^ ( j ?а (Z) d log 6;, (il (Z)) + J ?„ (Z) d log 0;, (jl (z)) ) =
bo K~*
^"^jdlog0,(il(z)).
*»
2я/-
*B
Пусть снова Zj и Zg — концы дуги b^. Тогда [д, (za) = fi (zj) + Z^
И, значат,
e^ G. (z,))=e-2"«i^3<->-V%/2)0, (^ (z,)),
^Y—i J '^ ^^^ ^'^ ^^ ^^^^ - Яв = - Jig (zi)- Zpp/2 (mod Z).
Выражение справа не зависит от Я, следовательно, выражение
слева должно быть постоянным и его можно отнести опять к х^.
Суммируя вклады всех сторон, получаем окончательно
2 ?а ih (Я)) = 2^^— i ?а (2) d log 0, (il(z)) = Я„ + Х„. D
Доказав далее теорему Римана, мы сможем найти константу к
и точно выяснить, когда \i (S) с 0^,.
Теорема Римана
Теперь мы воспользуемся последним результатом для того,
чтобы ползгчить геометрическое описание дивизора 0, отвечающего
сечению 0. Здесь удобно внести небольшое изменение обозначений.
А именно, обозначим через
D = pi+ . . .+рае SC^)
эффективный дивизор степени d, а через Zj — локальный параметр
в точке pi- После того как локальный параметр Zj выбран, можно
определить функции йо в окрестности точки pi соотношениями
(о„ (р) = й„ (p)-dzt;
й„ — это в точности та функция, которую мы раньше записывали
в виде (о„ (p)ldzi.
Как и выше, определим отображение
7. Кривые и их якобианы 365
лолагая
= (2 J- 21-)-
i Р, » p.
Б точке jD = /?1 + . . . + /><j с различными pi дифференциал
отображения [А задается в координатах z^, . . ., z<j на S^*^^ якобиевой
матрицей
/Й1 {р,) ... Qg {р,)\
f{v) = \\ \
\Й1 {pd) ... Sg (/>d)<^
Эта матрица имеет максимальный ранг тогда и только тогда, когда
точки Pi линейно независимы на канонической кривой
поверхности iS; так как это верно в общем слзгчае при d ^ g, то для
d ^ g образ Wd = 1* (iSC*)) является аналитическим
подмножеством размерности d и, более того, отображение [д, взаимно
однозначно в общей точке, поскольку его слоями являются проективные
пространства. Геометрия этого отображения, и особенно ее связь
«о специальными линейными системами на S, изучается в двух
последующих разделах этого параграфа.
Итак, якобиану 'f (S) римановой поверхности S мы
сопоставили два дивизора, инвариантно определенных с точностью до
«двига: дивизор 0 линейного расслоения L ^- "f (S) с классом
Чжэня, отвечающим форме пересечения на Н^ {S, Z) ^
= Я^ {f (S), Z), и образ Wg^i симметрической степени 5(*~^)
относительно \i. Первый из этих дивизоров определяется в
терминах линейной алгебры по 'f (S) и [(о], тогда как второй
непосредственно связан с геометрией S ж \i. Отсюда видно, сколь важную
роль играет следующая
Теорема Римава. Имеет местл соотношение
0 = Wg^ + X,
где у, — константа из предыдущей леммы.
Доказательство. Покажем прежде всего, что Wg-^ с 0_),.
Для этого рассмотрим общий дивизор D = Pi.-\- . ■ ■ -\- Pg 6
6 iS<*>, для которого точки Pi различны, |а: S^^ -^ 'f (S) взаимно
однозначно в D и |а (5) (^ ©х+цСхэ)- Положим
Я = |i (D) + X.
Тогда по предыдущей лемме
вх П 1* (5) = ц (Pi) + . . . + ц (pg).
366 2. Риманови поверхности и алгебраические кривые
Далее (это решающий шаг), нам известно, что 0 (ji) = 0 (—|а).
Следовательно, так как 0^, ([а (рг)) = О при i = g,
9 (|А (Pi) + • • • + I* (Pg-i) + x)= 0 (Я - ц (р,)) = 0, (ц (р,)) = 0^
т. е.
Q-x (|А (Pi) + • •. + |i (Pg-i)) = 0.
Итак, |i*0_x равно нулю на некотором открытом подмножества
в 5(^-1), а потому и на всем 5(^-1), откуда FFg_i с 0_g.
Теперь, согласно § 1 гл. 1, можно написать
где а>0б2ив' — зффективньш дивизор на f- (S). Мы
сначала покажем, что а = 1, а затем, что 0' = 0. Прежде всего
установим неравенство #(|а (S) • Wg. j ^ g. Для этого заметим, что-
инволюция fi 1-^ — fi действует на Н^ (f (S)) = Н^ (f (S)) Д
Д Hi (f- (S)) тождественно, a потому цикл —\i (S) гомологвсчен;
циклу \i (S). Возьмем теперь такую общую точку X = \i (р^) + . . .
. . . + HiPg) ка f (S), что -|i (S) ф Wg^i — К. Тогда -\i (5>
и Wg-i — А, пересекаются в изолированных точках и для любого»
1 = 1, . . ., g
Значит, H\iiS)-Wg_j)^g.
Но, как уже было доказано, индекс пересечения & с \i (Sy
равен g. Следовательно,
а-Ц11 {S)-Wg.i) + Ц11 {8)-в') = g.
С другой стороны, легко найти такое Х ^f (S), что \i (S) (^ в' +
+ Я. Поэтому #(|А (5)-0') > О, откуда а = 1, #(|д, (S)- W„_i) = g-
и *(|i(5).0') = 0.
Осталось показать, что в' = 0. Для этого воспользуемся
следующим рассуждением. Так как #((х (5)-0') = О, то
(X (5) П в^ ^ 0 =J- (X (5) с= 0i для любого X ef (S);
отсюда получаем, что
в'^.С\\¥2Ф0=>\У2с:в'}. для любого %^f{S),
поскольку
ei Э (А {Pi) + (А (Pi) => 01-ц(рО Э (А (/^а) =*►
=^в1_ц(роЭИ'(;з*) для всех pI^S=>
=^®'>.^V'{Pi) + V'{Pl) для всех pI^S=>
=*► 0i Э (А (/>?) + V^ (Pt) дляjBcex р*р1 е S,
7. Кривые и их якобиана 367"
Т. е. W^ с: 0i. Аналогично доказывается импликация
для любого п. Но по теореме Якоби Wg = f (S), значит, 0jt П?
r\Wg= 0, откуда вх = 0. О
Заметим, что по формуле Римана — Роха для любого
эффективного дивизора D степени g — 1 дивизор К — D таков же.
Следовательно, Wg^i = \i (К) — Wg_j^. Теперь мы можем определить,
константу X из теоремы Римана:
Wg_i + X = 0 = —0 = —Wg.i — х = Wg.^ — X — (X (К).
Так как FFg_i представляет собой тета-дивизор главной
поляризации, то по формуле для сдвигов линейных расслоений на торе-
(см. соответствующий раздел в § 6) он не может сохраняться ни;
при каком ненулевом сдвиге. Значит, 2х = —\i (К).
Аналогично можно определить, когда \х, (S) с= 0^.
Действительно, X — ^1 (р) € И^г-1 тогда и только тогда, когда А, = (х (jD)>
для некоторого D g 5<*>, содержащего точку р ^ S. Итак, К —
— (X (iS) с: FFff_i тогда и только тогда, когда Я. = (х (D) для D'
с А» (D) > 1. Но для Я = (X (D)
Я — (X (5) с= Wg.^ <=>Я — (х(5)-Ьхс:в<::>
<=>(х(5)—Я — хс=в<=>(х(5)с=в + х + Я,
т. е. (X (S) CZ 0х + Я тогда и только тозда, когда Я = (х (D) для
D g 5<*> с h" (D) > 1. Более инвариантно это можно
сформулировать так: доказанная выше (в предыдущем разделе) лемма
недает явного ответа на проблему обращения Якоби {проблему
нахождения дивизора D ^ iS<*> с (х ф) = Я для заданного Я б
6 1^ (S)) в точности тогда, когда этот ответ не единствен, т. е.
козда тикой дивизор D меняется в линейной системе размерности.
>1.
Теорема Римана об особенностях
Теперь мы переходим к изучению подмногообразий Wa =-
= |Х (iS<<*>) с: j^ (iS), параметризующих классы линейной
эквивалентности эффективных дивизоров степени d на 5. Наша цель —
доказать теорему, один из частных случаев которой был
установлен еще Риманом. Она связывает локальную геометрию
многообразий Wd, а именно касательные конусы к ним в различных
точках (X (jD), с геометрией соответствующих линейных систем | D \
на канонической кривой поверхности S в Р*"^.
368 2. Римановы поверхности и алгебраические кривые
Для начала отметим естественное отождествление
Р {П if iS))) ^Р{1Р (S, Q|)*)
проективного пространства, соответствующего касательному
пространству к якобиану f- {S), с пространством канонического ото-
>бражения
1^:: S^P {НО {S, Qb)*y^ Р^-'.
Здесь, как и всюду в дальнейшем, под P*~^ понимается
Р (Я" {S, Щ)*). В частности, проективизация касательного ко-
жуса
i> (П (Z)) с= Р (г;, (f (5))) = рг-1
зс подмногообразию X cz ^ {S) в точке \i, ^ X рассматривается
как подмногообразие в пространстве Р^~^ канонической кривой
ловерхности S; это многообразие будет обозначаться Г^ (Х).
Напомним некоторые обозначения: ш^, . . ., (Hg — базис
пространства голоморфных 1-форм на S, отображение (х: 5 ^- j^ (S)
задается формулой
р р
Ро Ре
а отображение \х,: 5<'*) ->-f'{S) — формулой
\^(Pi+ ■ ■ ■ + Pd) = P'iPi) + ■ ■ • + \^ (Pd)-
Если мы фиксировали локальную координату z на 5, можно
определить функции Q„ соотношениями ©„ (р) = ^а (р) dz.
Очевидно, что вектор
Q (р) = (Qi ip), . . ., Qg ip))
представляет точку р на канонической кривой из Р*~^.
Мы начнем с геометрического описания касательного конуса
к многообразию W^ в точке \х {D). Предположим вначале, что
дивизор D регулярен, т. е. что dim \D | = 0. По геометрическому
варианту формулы Римана — Роха линейная оболочка D
дивизора D на канонической кривой является {d — 1)-плоскостью. Мы
утверждаем, что
W^ — гладкое многообразие в точке ^ {D) и
соответствующее касательное пространство есть ^ц(в) (Wd) = D.
Доказательство. Предположим сначала, что D = />! + ■ • ■
• • • + Pd, где точки Pi различны. В этом случае локальные
координаты Zi на S вблизи Pi задают систему локальных координат
7. Кривые и их якобианы 369
на S <**> В окрестности D. По определению отображения \х: 5<<*>
-»- f {S) имеем
i Po i Po
Дифференцируя, мы находим якобиан f ((х) отображения [i:
\Qi(Pd) ...Qgipd)}
По предположению строки Q (pj) = (Q^ (pj), . . ., Q^ (pj)),
представляющие точки pt на канонической кривой, линейно
независимы. Поэтому матрица "f ((х) имеет максимальный ранг d в D,
откуда следует, что Wd = (а (5<'*)) гладкое в точке \1 (D) и что
касательная плоскость порождена точками pj.
Покажем теперь, что происходит на диагонали S'^^, на
примере дивизора D = 2pi -|- Рг -Ь • • • + Pd-i с различными
точками Pj; рассмотрение общего случая отличается лишь более
громоздкими обозначениями. Пусть z — координата точки р,
меняющейся в окрестности точки р^, а Q (р) = (Q^ (z), ...
. . ., Qj (z)), как и выше. Положим
Тогда прямая^ Q (р) Q' (р) из Р*"^, определяемая векторами
Й(р) и Q' (р), совпадает с касательной прямой к канонической
кривой в точке р. Для w^ = (z^ + z^l2, w^ = z^-z^ положим
Zt Z,
Po Po
'^ d ( il±i^ ) + -gf «i (^1^2) = CO. (Z,) + (0„ (Z,),
Ho
dwi
откуда
£?».-1ю /z^-Ю (zW g^g Q(«i)-QW
5u»t 2 '■ " ^ " ' »^ *"" «IP.
Устремляя Zg к z^ (координате точки p^), мы получаем, что
матрица Якоби отображения \х в точке D = 2р^ -Ь Р2 + • • • + Pd.\
370 2. Римановы поверхности и алгебраические кривые
равна
Далее мы рассуждаем так же, как и в случае различных точек. Q
Предположим теперь, что D — элемент г-мерной линейной
системы. Будем обозначать дивизоры из | D | через
Ох=Рг{К) + ...+ра{К), КеР'.
Согласно формуле Римана — Роха, точки pt (Я.) для каждого D}_
порождают (d — г— 1)-плоскость Dx в Р*~^. Мы утверждаем,
что в этом случае
проективизация касательного конуса к Wd в точке (х (D)
есть объединение Т^ф) (Wd) = [} D^ плоскостей, по-
рождаемых дивизорами линейной системы \D \.
Доказательство. Напомним, что касательный конус к W^
в точке (А (jD) заметается касательными прямыми в точке (х (D)
к аналитическим дугам в Wd- Пусть
D{t) = qAt)+ ■•• + id (t)
— произвольный путь в симметрическом произведении S'^,
такой, что
D {0)=Dx = p^iX) + ...+рл{Х)
для некоторого jD^, 6 I ^ I- Тогда его образ w (t) = ц (D (t))
задает дугу в Wd с w (0) = \i (D); обратно, любая такая дуга
в Wd может быть получена этим способом. Для простоты в
дальнейших обозначениях предположим, что все точки pi {%) различны.
Пусть Zi — локальная координата в окрестности pt {%). Тогда
для точек Qi (t) с координатами Z| (t) имеем
d ^iW
i=l P.
где ©a = Q„ (Zi) dzt вблиэи pt (A-), как и выше. Производная
^^[...,^QAzi{t))z\{t),...)
i
7. Кривые и их якобианы 371
d
В f = О задает образующую ^ г\ ф) Q (pt (Я.)) касательной пря-
1=1
мой к ы; (f) в |i (D). Но числа Zj (0) и точку Я. б Р"" можно выбрать
произвольно. Это приводит к равенству множеств
X
которое и требовалось установить. Q
В частности, если г > О, то ^^(в) {Wa) содержит некоторое
многообразие г-секущих канонической кривой, а так как все они
не могут лежать в одном линейном подпространстве из Р*~^,
то мы заключаем, что
(X (Z?) — особая точка W^ в том и только том случае, когда
dim I 2) I > 0.
Инвариантная интерпретация предыдущих вычислений
состоит в следующем. При отождествлении | jD | = Р*" линейная
система I jD I с: 5<'') является комплексным подмногообразием с
нормальным расслоением N -^ Р*". Обозначим через Р (N)
соответствующее проективное расслоение со слоями Р {N)\ = Р {N\).
Поскольку (х: 5<'') -*- f (S) отображает Р*" в точку ц (D),
дифференциал [1^ равен нулю на касательных векторах к Р*". Поэтому
V^* il) € ^^(D) if (S)) определено для любого | 6 Nx, что
индуцирует голоморфное отображение
(х^: P(AO^P*-S
образ которого совпадает с касательным конусом Т^^) (Wd).
При каждом X слой Р {N)x параметризуется дугами из S<■'''>
проходящими через Dx, и по предыдущим вычислениям \1^
отображает Р {N)\ изоморфно на подпространство D),cz Р*-^.
Одним из полезных для дальнейшего результатов о поведении
плоскостей D, отвечающих линейной системе, является
следующая
Лемма. Если некоторая точка q g Р*"^ лежит на двух
секущих плоскостях D\, D^', то она лежит на всех D^, где D^ —
элемент пучка, порожденного Dy, и D^'', иначе говоря, слои
отображения (х,^: Р (N) ->- Гц(д) (Wd) являются линейными
пространствами.
Доказательство. Предположим, что полная линейная система
I D I имеет размерность г. По формуле Римана — Роха точки
любого из дивизоров F ^ \ К — D \ порождают (g — г — 2)-пло-
скость F. Линейная система гиперплоскостей из Р*~^,
содержащих F, высекает на канонической кривой полную линейную сиапему
372 2. Римановы поверхности и алгебраические кривые
I jD I; В частности, любой пучок {D^ cz \D \ высекается пучком
гиперплоскостей, проходящих через F. Итак, если q лежит в двух
секущих плоскостях D^), жП^' пучка {1?ц}, то она лежит в
гиперплоскости, порожденной любой плоскостью D^ и любым
дивизором F ^ \ К — jD |. Но вый1етный дивизор пересечения
канонической кривой с любой гиперплоскостью, содержащей D^, есть
дивизор линейной системы | ^ — D |. Поэтому q лежит на любой
гиперплоскости, содержащей jD^, т. е. q лежит в D^. О
Положим теперь Т = Гц(д) (Wa).
Предложение. Для любого D g S^'^'> с dim | D | = г степень
проективизации касательного конуса Та Р*"^ равна ( )•
Доказательство. Пусть q^, . . ., qg-d+r -^ общие точки на S,
в частности такие, что
(») dim I D -Ь ?1 + . . . -Ь qg-d+r I = dim I Z> I = г
и для любого подмножества q^, . . ., q^ с а ^ г -\- i
(♦♦) dim I jD — ffi — . • . — ffa I = dim | jD | — a = г — a.
Заметим, что по формуле (*) точки g^, . . ., qg-d+r линейно
независимы на канонической кривой; обозначим через Е
порожденное ими линейное подпространство p«-<*+>"-i с: Р*"^.
Чтобы доказать предложение, мы покажем, что Е пересекает Т
трансверсально по многообразию степени (^~ )', точнее,
мы докажем следуюпще утверждения.
1. Пересечение Т [\ Е распадается в объединение
1С{1 g-d+r}
(^~ "'"'^1 координатных (г— 1)-плоскостей из р«-<*+»—*.
2. Это пересечение трансверсально.
Чтобы доказать первое утверждение, заметим, что для любого
мультииндекса / = {г^, . . ., г,.} с: {1, . . ., ^ — d + г} можно
указать дивизор jD^ € \ D |, содержащий точки gj,, . . ., qt .
Значит, qi^, . . ., qt cz Dj,, а ъ общем это дает включение
Uqu, ....ffirCzTn^.
I
Обратно, предположим, что Dj, — некоторый дивизор из | D |
И ,число точек qi, содержащихся ъ D^, равно а; будем считать,
7. Кривые и их якобианы 373
ЧТО ЭТО ТОЧКИ ^1, . . ., д„ (по формуле (♦♦) очевидно, что а ^ г).
Так как, согласно (*),
dim I Z>+ ffa+i+ ... +qg-d+T I = dim I D I =r,
TO no формуле Римана—Poxa
dim (2)^ и ^) = dim D^, gr„+i, . .., gr^.^+r = g—\ — a.
Из линейной алгебры известно, что в этом случае
dim {Dt. Г[Е) = dim D^. + dim E — dim D^\}E = a—\,
T. e. D% пересекает E только tlo q^, ..., g^. Итак,
и первое утверждение доказано.
Заметим, что по предыдущим рассуждениям, если q^, . . .
. . ., q^ — общие точки на S, а q — произвольная точка
в ffi, . . ., q,., не лежащая ни в одной из линейных оболочек
собственных подмножеств набора ffi, . . ., g^, то существует
единственная плоскость jD;;,, содержащая q. Следовательно,
отображение (х^ взаимно однозначно в общей точке, т. е
плоскости D\ заметают многообразие Т однократно.
В частности, это означает, что Т имеет размерность d — 1.
Первый и основной шаг в доказательстве утверждения 2
заключается в доказательстве следующего результата.
Для любых общих тлчек q^, . . ., qr ^ S многообразие Т
гладко в дополнении
ffi» • ••> Яг— и Яи • ••> ffj-i» ffj+i»
к координатным гиперплоскостям из Яи • • •» Ят-
Как мы уже знаем, \х,^ взаимно однозначно над каждой такой
точкой q. Поэтому достаточно показать, что отображение
(Хф! Р (N) ->- Т имеет невырожденный дифференциал в q. Для
этого ограничимся окрестностью U cz Р'' с координатами К =■
= (Я.1, . . ., Kj.), для которых Pi (К) — однозначные функции от К;
выберем затем локальные координаты zt около pi (0) и рассмотрим
композицию Zj (Я.) = Zi ipi (Я.)) как функцию от %. В любой
заданной точке можно так выбрать координаты %а О- ^<^^^)^ чтобы
dza {Х)/дХь — Sob-
374
2. Римановы поверхности и алгебраические кривые
Можно предположить также, что набор р^ (Я), . . ., p^i.j. (А,)
порождается- Тогда в соответствующих однородных координатах
t — [t^, . . ., f<j-r] на слоях Р (N) \и отображение [i^
поднимается до отображения
^^ (Я, t) = ф (pi (К)) + . . . + U.,Q (pd-r (Я)).
Замечая, что отображение (х^ линейно на каждом из слоев над U,
можно непосредственно проверить, что ранг якобиана \i^ на
единицу меньше ранга якобиана отображения jlj^, поэтому достаточно
вычислить последний. Используя индекс 1 ^ ст ^ d — г, напишем
матрицу Якоби для \х,^:
Q(P,{>^))
d\ijdti
diijdtd-r
d^JdX,
^d\x,JdKj.
^t^{dzJdK)Q'iPo{X))
a
^to{dzJdX,)Q'(po{K))
В точке с dza (X)/dXj, = 8аь она имеет вид
Q (Pd-r (Я))
UQ'{Pr{r))+ S t„{dZa/dXr)Q'{Poi^))
Точка p ^ Pi, . . ., Pr лежит в линейной оболочке первых г точек
из Pi, поэтому tj.+^ = . . . = td-j. = 0. С другой стороны, она не
лежит в линейных оболочках собственных подмножеств первых г
точек, значит, t^ ф О при а ^ г. Отсюда следует, что ранг этой
матрицы равен рангу матрицы
^(Pd-r)
l^'iPr) J
7. Кривые и их якобианы 375
Но для общих точек />i, . . ., р,.
dim I D + /?1 + . . . + /J, I = dim I D I = г,
откуда по формуле Римана — Роха размерность линейной
оболочки
D^ + Pi+ ..•+/'г = 2/>1+ ... +2рг + Рг+1+ ... + Pd =
= Q (р,), ..., Q {р^.г), Q' (Pi), ..., Й' (Рт)
равна d — 1. Итак, требуемый якобиан имеет максимальный ранг
для общих точек />i, . . ., pj., что доказывает первый шаг.
Остальные два шага в доказательстве утверждения 2 гораздо
проще. Второй шаг заключается в следующем:
При некоторых д^, . . ., Qg-d+r пересечение Е (] 1 транс-
версалъно в общей точке пространства д^, . . ., д,..
Действительно, выберем д^, . . ., д,. достаточно общими и
рассмотрим произвольную точку ff € ffii ■ • ч ffr. лежащую вне
гиперплоскостей ffi, . . ., дг_1, gt+i, . . ., ffri а затем выберем точки
gj.+i, . . ., gg-d+T линейно независимыми по модулю
подпространства Тд{Т).
И наконец, мы утверждаем, что для общих точек д^, ...
. • .. Qg-d+T на S
(1) пересечение Е [] Т трансверсалъно в общей точке каждой
(г — 1)-плоскости gi^, . . ., д^
г
Чтобы убедиться в этом^ рассмотрим отображение
переводящее (ffi + . . . + ffr. ffr+i + • • • + gg-d+т) в (ffi + • • •
. . . + gg-d+т)- Пусть в CZ 5<*-<'+'") — подмногообразие,
состоящее из таких ffi, . . ., gg-d+Ti для которых не выполнено (|).
Согласно второму шагу, я~^ (В) ф 5<'"> X 5<*~'*), а так как
iS^*") X iS^^"**) неприводимо, то размерность В строго меньше
g — <i + г; итак, предложение доказано. О
В результате нами доказана
Теорема Римана — Кемпфа об особенностях ^). Пусть \D \ —
линейная система степени d и размерности г. Тогда проективиза-
^) См. G. Kempf, On the geometry of a theorem of Riemann.—4 nn.
Math., 98 (1973), 178—185.
376 2. Рилановы поверхности и алгебраические кривые
ция касательного конуса
является объединением плоскостей jDx = Р**"*""^, порожденных
точками дивизоров jD^, € \D |. Степень этого конуса равна
( )» " ^" заметается плоскостями D^ однократно.
В случае d = g — 1, как мы знаем, W^ является сдвигом б.^
тета-дивизора 0 на j^ (5), и это приводит к результату,
установленному Риманом:
multn<z„(0_«) = A«(D);
в частности, особые точки тета-дивизора соответствуют линейно
подвижным дивизорам степени g — 1. Отсюда легко получить
следующий факт.
Многообразие особых точек 0 имеет размерность "^g — 4.
Доказательств. Предположим противное, т. е. что
многообразие особых точек дивизора 0_« имеет размерность ^g^ — 5.
Множество общих точек р^, . . ., ра-я на канонической кривой
порождает Р*-*. Пусть ф: S -*-V^ — проекция S из такого
пространства Р*"*. Для двух точек р Ф q яа S в том и только
том случае ф (р) = ф (ff), когда
Pi Ри •. •. Pg-г = ff, /'i, • • •, Pg-3,
что эквивалентно условию dim р, q, Pi, . . ., pg-з — § — 3, т. е.
dim \p-\-q + Pi + '.'+ Pes I = 1-
Из счета параметров видно, что если бы dim (0_x)s было строго
меньше g — 4, то существовало бы не более чем оо*"* дивизоров
D 6 iS<*~^> с dim D ^ g — 3, а поэтому для общих точек р^, ...
• • •) Pg-3 отображение ф было бы взаимно однозначным. Но тогда
образ ф был бы гладкой кривой степени {2g — 2) — (g — 3) =
= g' + 1 и рода g{g — 1)/2. Так как g < g (g — 1)/2 при g' > 4,
мы получили противоречие. □
Читателю, возможно, будет интересно разобраться с теоремой
Римана об особенностях в частном случае линейной системы
степени 5 и размерности 2 на римановой поверхности S рода 6.
Проверив сначала, что такая линейная система | D | всегда задает
7. Кривые и их якобианы 37Т
вложение S в виде неособой плоской квинтики, откуда 2D = Ку
легко понять, что касательный конус с FFj в точке (х {D) являете»
многообразием хорд поверхности Веронезе i^^ (Р*) а Р', а
множеством особенностей на Т является сама поверхность Веронезе.
Специальные линейные системы IV
Теперь мы располагаем техникой, необходимой для того, чтобы
получить частичный ответ на вопрос о существовании
специальных линейных систем на кривых. Для каждой пары целых чисел d'
иг, l^d^gf — 1, обозначим через Wi образ линейных систем
степени d и размерности ^г при отображении (х: iSC*) -*- "f (S).
По теореме о собственном отображении W'^ является
аналитическим подмножеством. Мы покажем, что его размерность не меньше
той, которая была предсказана грубым подсчетом в § 3 настоящей
главы.
Начнем с вычисления класса гомологии подмногообразия
W^i — (X (iS<'*)); ответ дается формулой Пуанкаре
Доказательство. Как мы уже показали, в вещественных
координатах х^, . . ., x^g на универсальной^; накрывающей для '^ {S),
которые соответствуют выбору канонического базиса б^, . . ., баз
в Я^ (5, Z), формой, двойственной по^руанкаре к 0, является
g
© = 2j dx„ Л dXa+gm
a=l
Пусть A = (Oj, . . ., aft) пробегает множество индексов с
условием 1 ^ а^ < . . . < «ft ^ gf. Положим dxj^ = dx^^ Л . . .
... Л dx„i^, А + g= {ai +f0, . . ., aft + g). Тогда
o)«-^=(g'-d)!(-l)S-d S dx^Adx^+g.
Пусть мультииндекс J — (]\, . . ., /ft) пробегает подмножества
из (1, . . ., 2g). Тогда, поскольку] формы dxj образуют базис
в H'^ {f (iS)), достаточно показать, что
J '^^^=(71Ь)Г J «'-"Ado:,.
^d t(S)
Используя формулу для ©*~* в правой части равенства, получаем
["1, если J = {А, A-\-g) для некоторого-
■~щ^ J &s^Adxj^\ Л = (а1, ...,а<г),
f(S) V О в противном случае.
378 2. Римановы поверхности и алгебраические кривые
С другой стороны, так как отображение (х^**): iS<'*> ->- W^
лмеет степень 1, а я: 5<*^-5<'*> — степень d!, то
где (х'* = (х<<*)оя: S'^^>-Wd — композиция отображений. Но
d
где я^: iS** ->- iS — проекция на к-ж сомножитель, а (х = |i^.
Так как форма \i* dxj б Я^к {S) двойственна по Пуанкаре циклу
бу, то
<*) f (X* dr„ Л (X* dr„+j = 1
s
и все такие интегралы от (х* da;,- л (х* da;; при других i < /
обращаются в нуль. Итерируя, получаем, что интеграл
d
Sd gd'^-^ ft=l
равен нулю всегда, кроме тех случаев, когда / = {Б, Б -^ g)
для некоторого Б = ф^, . . ., P<j)i и в этом случае, согласно (*),
f ((xVd^B.B+g = d!. О
Теперь мы переходим к конструкции, введенной Кемпфом,
Клейманом и Лаксовом ^). Напомним некоторые факты из
последнего раздела § 6. Главная поляризация на якобиане позволяет
сделать отождествление Pic" {^ (S)) ^ f (S), а кроме того,
имеется расслоение Пуанкаре Р ^- ^ (S) X '^ (S) со следующими
свойствами:
1) при указанном отождествлении ограничение Р |4«/s)xx, ~
= Р (к) является линейным расслоением, соответствующим точке
X € Pic«(t (S));
2) если Ро ^ S — базисная точка, то Р {Х)р ^ jP (А, + (х (р))р,
для любого р.
Фиксируем теперь некоторый дивизор jDq степени п ';> 2g — 2
на 5 и положим
L(X) = P (К) + Do.
^) S. Kleiman and D. Laksov, On the existence of special divisors.— Amer.
J. Math., 93 (1972), 431—436.
/. Кривые и их якобиана 379
Когда А, пробегает j^ (S), L (к) пробегает многообразие линейных
расслоений степени п на 5. Выберем т ^ п общих точек р^^, . . .
..., />т на iS. По свойству 2) имеется естественное отождествление
Но, поскольку ограничение расслоения Пуанкаре ва Ро X f (S)
топологически тривиально, существует изоморфизм L {Х)р -^ Lp ,
который, однако, имеет зависимость от X ^ f- (S) класса С°°,
а не голоморфную.
По формуле Римана — Роха h" (0 {L {%))) = п — g^ + 1.
Поскольку L (А,) не имеет сечений, обращающихся в нуль в т точках,
существует вложение
m
образ которого Sx является (га — g + 1)-мерным
подпространством S\, меняющимся голоморфно по X. Точнее, существует
голоморфное векторное расслоение Е -*• f {S) ранга т со слоями
m
Ex = ® L (Я.)„.. Пусть G {п — g -\- i, Е) — соответствующее рас-
1=1
слоение Грассмана со слоями
G{n-g + \, E)y. = G{n-g + i, Ex);
тогда подпространства {Sx cz Ex} задают голоморфное сечение
ъ G{n — g+ i, Е).
Ключевой момент излагаемой конструкции состоит в
следующем. Рассмотрим для каждого d голоморфное подрасслоение
Vm-n+d CZ Е СО СЛОЯМИ
m~n+d
Vm-n+d,}.^ е L{K)p^
и положим
EdiX) = L{X) — pjn-n+d+l— •-• —Рт =
= P{X) + Df, — pjn-n+d+l— --' — Рт'
Тогда
h^'iEdiX))^ dim SxnVrn-n+a.
С другой стороны, комбинация С^-отождествлений L {Х)р ^
^ Lp^ с изоморфизмами Lp ^ С задает С^-тривиализацию
(р: E-,'f(S) X С™,
380 2. Римановы поверхности, и алгебраические кривые
т
переводящую разложение в прямую сумму Е = ® L {%)р, в раз-
1=1 '
ложение С" по координатным осям. Поэтому определим С°°-ото-
бражение
a.:f{S)^G{n-g^i, т)
с а (Я.) = ф (5 я). Пусть е^, . . ., e^ — стандартный базис в С",
а Vm-n+d = К, . . ., e-m-n+d)- Тогда по предыдущему
получаем, что
сдвиг многообразия W^a на (х ( —jDo+/'m-n+<i+i+• • •+/'т)
есть теоретико-множественный прообраз относительно а
цикла Шуберта Og+r-d g+r-d{Vm-n+d)^{A^G{n —g +
+ i,m): dim(Any™-„+d)>r + l}.|
Заметим, что, хотя отображение а и не голоморфно, прообраз
относительно а любого цикла Шуберта, соответствующего
некоторому флагу из координатных подпространств С* в С*", является
комплексно аналитическим подмножеством в f- (S). Иначе
говоря, условия Шуберта, определяющие эти циклы, имеют смысл
в слоях расслоения Грассмана.
Результат, к которому мы стремимся, сформулирован в конце
этого раздела. Он дает нижнюю оценку для dim Wf. Решающий
шаг в его доказательстве — следующая
Лемма, а (f- (S)) трансверсалъно пересекает, специальные циклы,
Шуберта а^.^ {Vm-n+d) вне Og^^l, g-d (Vm-n+d)'
Напомним, что как множество а~^ (<^g-<i i^m-n+d)) ^сть сдвиг
многообразия W^', но Wd неприводимо, поэтому лемма, по
существу, сводится к тому, что а (f (S)) не везде касается
Og-d (Vm-n+d) ВДОЛЬ ИХ пересечения.
Предположим на время, что лемма уже установлена. Идея
оставшейся части доказательства такова. Во-первых, по лемме
фундаментальный класс многообразия W^ равен а* (аg-d)-
Отсюда по формуле Пуанкаре
Наконец, как было доказано в § 6 гл. 1, каждый цикл Шуберта,
и в частности ag-d+r,...,g-d+T^ выражается в виде многочлена
от базисных циклов Шуберта о^; выписывая его явно, мы
получим соотношение
a*(og.d+r j-<i+r)=c0<'+i)<«+'-<'), сфО,
откуда следует нужная оценка dim W^ ^ g — (r-f l)(g'-f-r — d)
7. Кривые и их якобианы 381
Доказательство леммы. Пусть %(, б а~^ст^_<4 (Vm-n+d)- Выберем
линейно независимые точки д^, . . ., д^ на канонической кривой
для S и положим
^0 = ffi + . . . + ffd - -Р {Ю-
Поскольку отображение \i: iS<*) ->- f (S) взаимно однозначно
в окрестности ffi + • • • + ff^i каждое Я. вблизи Яо однозначно
определяет точки q^ {%), . . .j gg (Я), такие, что
i> (Я) = [ffi (Я) + . . . + ffg (Я) - Е,], qt (Яо) = ff,.
Положим
= (/6<^(5): (/) + 2д.(Я)-2г, + 1)о>О}^Я«(0(^(Я)))
И рассмотрим отображение
определенное формулой R (f) = (f (pj), . . ., / (Pm))- Для
всякого Я из окрестности U т)' и Яд о г / задает отображение
а: U-^i-G (п — g + i, т)^
которое совпадает с а при подходящей локальной тривиализации
расслоения Е.
Далее, пусть р: U -у G {т — п + g — 1, т) — композиция а
с естественным изоморфизмом
*: G{n— g+ i, 0")^G{m — n + g—l, С"*),
т. е. р (Я) есть (т — п -{- g — 1)-мерное векторное пространство
соотношений между значениями R (/) для / б j? (Я) в точках
Pi, • • •■> Рт- Мы хотим показать, что Р (U) трансверсально
пересекает в р (Яо) двойственный цикл Шуберта
*i<^g-d) = {Л*: dim (Л* (] Ann Vm-n+d) > g — d}. .
Пусть Яо соответствует дивизору D g W^, не лежащему в W^.
Тогда
^" (Р (К) -\-Do — Pm-n+cH-l —...—Pm) = i
и для некоторых i между 1 и те — п -\- d ж ji, . . ., /g_<i между
т — n + d+1 и т имеем
h" {Р {K)+Do — Pm-n+d*l— . • • —Pm — Pl+P}t+ • . • +Pjg.d) = О-
382 2. Римановы поверхности и алгебраические кривые
Для удобства можно взять i = 1, 7\, . . ., Jg_a = те — п -{- d -\-
-{- i, . . ., т — п -\- g. Это означает, что а (Яд) есть
дополнительное подпространство в С" к подпространству Ср, ф . . .
. . . Ф Cp^_n+g- Тогда, как мы знаем из § 5 гл. 1, любая точка Л
из окрестности Р (Яд) однозначно представляется в виде матрицы
,., i О ... О О ffi.„-„,.g+i ••• "unt
О 1 ... О О .
B + tr •),)
О О ... 1 о .
о о ... о 1 fljB-B + f-l.m-B+f+l ••• 4n-n+sr-l,m
Неопределенные коэффициенты Utj этой матрицы являются
ллюккеровыми координатами на грассманиане G {т — п -\- g —
— 1, те) вблизи точки р (Яо), а цикл Шуберта * CTj_<j (Ann Vm-n+d}
задается в этих координатах уравнениями
^m-n+d, 1 ^ . . • = '^m-n+g-i, i ^ 0.
Чтобы представить отображение р в окрестности точки Х^
в этих координатах, мы прежде всего найдем линейные
соотношения для подпространства R {X (Я)). По формуле Римана — Роха
fe«(5, ^^{E,-^qi{%) + '^Pi-D,)) = m-n + g-i.
Пусть T|i, . . ., T|m-n+g-i — базис этого пространства мероморф-
ных дифференциалов. Для любой функции f ^ X (к) мероморфные
формы /'Tia имеют полюсы только в точках Pi, а по формуле
вычетов
У, Resp, (/. л„) = S / (/>,) • Resp, (т|а) = О
t г
ДЛЯ каждого а = 1, ..., те — п -{- g — 1. Это и есть нужные
соотношения, а матрица (ReSp. (т|„)) представляет пространство
Р (Я) сг С"*. (Заметим, что при этом получаются все соотношения
для X (Я), ибо матрица (ReSp. (т|а)) имеет максимальный ранг
те — га + g' — 1, поскольку А» (5, Q^ (£"0 — S ff,- — Do)) = 0-) '
Координаты отображения р можно описать геометрически:
снова по формуле Римана — Роха имеем
^•(5, Qi{E^JrYsPi-Da))==m-n + 2g-i.
Рассмотрим соответствуюш;ее вложение римановой поверхности S
в p™-n+2?-2. По предположению точки/>2, . . ., pm-n+gnq-^ (Я), . ..
. . ., gg (Я) линейно независимы. Пусть V есть (те — п -\- g — 2)-
7. Кривые и их якобианы,
38»
Рис. 15
ПЛОСКОСТЬ, порожденная точками р^, . . ., Pm-n+g^ ^ ^ W есть
(g — 1)-плоскость, порожденная точками qi (Я.) (рис. 15). Тогда
формы
Т1.6Я«(5, Q4^o-Sff*W + S/'«-i?o))
соответствуют гиперплоскостям из р™-"+2*-2, проходящим через
точки Qi (К). Следовательно, справедливо такое утверждение.
Плюккерови координата о^д, . . ., <hn-n+g-i,h ^-«л Р {%)•
есть однородные координаты образа пу^^^,) (р^) точки р^
при проекции из W (А,) naVe такой координатной системе
на F, для.которой точки р^, . . ., Pm-n+g отвечают
координатным осям.
Значит, чтобы доказать трансверсальность отображения ^
в точке Kof нужно показать, что отображение
-384 2. Римановы поверхности и алгебраические кривые
определенное формулой я (X) = Яиг(Х) (jPi), трансверсально к
подпространству в V, порожденному точками ра, • • •' Pm-n+d-
Чтобы убедиться в этом, допустим, что точка qi (к) меняется.
Поскольку я (к) есть пересечение пространства V с подпространством
?! (X), . . ., Qg (Х), Pi, касательная прямая к дуге, образованной
точками я (Х) при изменении Qi (Х), является пересечением V
с пространством, порожденным q^ (Х), . . ., д,-.! (X), g^+i (^)i • • •
■ ■ -1 Qg (X), Pi ж касательной прямой к S в Qi (Х). Значит, я не
трансверсально к /?2, . . ., Pm-n+d только в том случае, когда
касательные прямые {^?,(х„) ('^)}i=.i,.. ,g вместе с точками
11 ■■ -1 Pm-n+d не порождают pm-n+2g-2^ Это В СВОЮ очередь
эквивалентно утверждению, что
Ло (S, Qi iEo + IiPt-Do-2.^qt iXo)-Pi- ... -Pm-n+d)) =
= hf>{S, Q» {-P{Xo)-D^ + Pm-n+d-{- .. . +Prn-qi ih))) =
= до (5, Q4 - ^d (^o) - 2 ?j (Яо))) Ф 0.
Ho точки Qi (Xq) линейно независимы на канонической кривой
ловерхности S, поэтому это невозможно. Q
Из доказанной леммы вытекает следующий факт.
Фундаментальный класс многообразия Wd на f {S)
является прообразом относительно а класса когомологий цикла
Шуберта ag_d на G (п — g + 1, т).
По формуле Пуанкаре имеем
Далее, по формуле Джамбелли класс цикла ag+r-d,...,g+r-d
является детерминантом
<^S+r-d,.
.,g + r-d
'^г+'-'ct
(Tg + r-d-l
o,ld
CTy+r-rf+l ''
<^g + r-d
• *^g*2P-d
°g + r-d
7. Кривые и их якобианы
385
Поэтому
"■ "e*r-d,...,g*r-d ^ А
1
1
1
{S + r-d)\ {g+r-d+\)\
1
(g + r-rf-1)!
1
{g+d)\
{g + 2r-d)\
1
Чтобы вычислить в общем случае детерминант D (х, у)
матрицы порядка у + i (uij = i/(x — i + у)!), умножим ее к-ъ
столбец на (а: -f- А — 1) и вычтем результат из {к — 1)-го столбца для
к = 2, . . ., у + i. У новой матрицы А'
а а
(£±1)__
(i-i-f-/)l (x-i + i + i)\
__ x-i + i + i (x+i)
{x~i + i + i)\ (a;-i-f-;-f-l)l
1-i
(x — i + k + i)\
, j¥=y+i,
1
В частности, все числа в верхней строке равны нулю, кроме
'^i.y+i ~ 1^(^ + ^)'' * соответствующий множитель при
разложении по этой строке равен y\-D {х, у — 1). Значит,
а так как D{x, 0) = 1/а:!, то
D(x у) У'(у-1)1-..01
Используя это при вычислении цикла a*ag^d+r g-d+r, мы
получаем, что
Предположим теперь, что размерность соответствующего
многообразия меньше g — (г + i) (g — d + г). Тогда на f (S)
существует цикл размерности (г + i) (g — d -> г), яе задевающий W^.
386 2, Риманови поверхности и алгебраические кривые
В ЭТОМ случае
a*Og-d+r g-d+r (V) = *(а {V)'ag.d+r..... g-d+r) = 0.
Но, с другой стороны,
a*ag^d+r g-d+r (V) =
поскольку в положителен. Итак, нами доказана следующая
Теорема. Многообразие W^ а f (S) линейных систем
дивизоров степени d и размерности >г на S имеет размерность
^S — {г + ^) {g + г — d). В частности, если g"^ {г + i) X
X (g + г — d), то на каждой римановой поверхности рода g
существует такая линейная система.
Отметим, что а [f- {S)) не всегда пересекает циклы Шуберта
Og^d+j. g-d+T трансверсально; как мы знаем, во многих
случаях размерность многообразия Wd = OL'^^g-d+r g-d+т
больше ожидаемой. Поэтому мы не можем всегда сказать с
определенностью, каков класс W^. Однако стоит сформулировать
следующий очевидный факт.
Если a{f{S)) трансверсально к Og_a+r g-d+r, "«з
фундаментальный класс многообразия W^ имеет вид
WL г1 (г —1)1 ... 01 a(r+i)(g+r-d)
'^'"'^ (g+2r-d)l ... (g+r-d)l ''
Это дает «ожидаемый» ответ на некоторые вопросы численного
характера, поставленные ранее при обсуждении специальных
линейных систем. Например, мы установили, что на общей
римановой поверхности рода g = 2к существует лишь конечное число
пучков дивизоров степени к + i. Каково же это число? В случае
когда а (У' {S)) пересекает цикл Шуберта а^^й трансверсально»
оно равно
^^^'^^+i (к+ 1)1 И {к+1)1 к\ »
так как #в* = g\. Заметим, что при g = 2, 4, 6 и 8 мы получаем
соответственно 1, 2, 5 и 14. Это совпадает с вычислениями,
проведенными ранее.
7. Кривые и их якобианы 387
Теорема Торелли
Напомним, что поляризованным абелевым многообразием
называется пара (М, [©]), состошцая из абелева многообразия М
и некоторого класса поляризации [со] G IP (М, %) на нем. Под
отображением поляризованных абелевых многообразий {М, [©])
и {М', [со']) понимается голоморфное отображение /: М-^М',
для которого /* ([со']) = [со]. Как нам известно, компактной рима-
новой поверхности S рода g"^ i отвечает абелево многообразие
i!f (S), [cog]) с главной поляризацией, где f- (S) (в
инвариантной формулировке) является фактормногообразием пространства
(Я" (S, Q^))* по решетке Л (S) ^ Я^ {S, Z) функционалов на
Я" (S, Q^), полученных интегрированием регулярных 1-форм
по 1-циклам на S, а класс [сод]: Н^ {у- (S), 1) -^1 при
естественном отождествлении
Яз if (S), Ъ) = А? (Н, (S, Z))
определяется из условия
[©sJ (алр) = #(а-р).
Сейчас мы покажем, что риманова поверхность S
восстанавливается по своему поляризованному якобиану {f (S), [со]), а
именно имеет место следз^юп^ая
Теорема Торелли. Пусть S и S' — две компактные римановгл
поверхности, такие, что
if (S), fcos]) ^ (f iS'), [©g.])
как поляризованные абелевы многообразия. Тогда S ^ S'.
Доказательство ^). Заметим прежде всего, что существенный
трансцендентный шаг в доказательстве теоремы Торелли в том
виде, в каком она здесь сформулирована, составляет теорема
Римана, которая связывает дивизор в, определенный с точностью
до сдвига классом [©д], с дивизором Wg_j^. Мы восстановим S
по Wg.i.
Вначале теорема Торелли будет доказана в том случае, когда
ни S, ни S' не являются гиперэллиптическими. Напомним, что
если М = С*/Л — произвольный комплексный тор, то все
касательные пространства {Тх (Л/)}хем Допускают естественное
отождествление с С*. Поэтому на множестве неособых точек X* =
= X — -X^sing любого аналитического подмножества X а М
размерности к можно определить отображение Гаусса
^х- X* -^ G {к, g), ^^ (1) = П (Х) аЩМ)^ се.
"■) Мы следуем здесь доказательству Андреотти: А. Andreotti, On Torel-
li's theorem.—Лтет. /: Math., SO (1958), 801—821.
388 2. Римановы поверхности и алгебраические кривые
Очевидно, ЧТО ^х определено инвариантно и не зависит от
сдвигов X ъ М.
Рассмотрим, например, стандартное отображение ji: 5 -^ f{S),
заданное интегрированием
H(z) = ( jcoj, ..., J©^),
го
Соответствующее отображение Гаусса &yj. S -*-G {i, g) = P^-^
задается формулой
^^^(') = l^дГ^^^^''^' •••.■^tA«(z)J = [©i(z)/<iz, ..., oig{z)/dz],
т. е. отображение Гаусса для ц {S) совпадает с каноническим
отображением 1^: S -*- Р*~^ при отождествлении ц (S) с S.
Рассмотрим теперь отображение Гаусса
S: eU = Wt-i-^G{g-i, g) = (P«-r,
ассоциированное с тета-дивизором в_и с: j^ (i5). Как мы уже
знаем, точка ц, (Z)) G в_к неособа в том и только том случае, когда
дивизор D = ^ Pi регулярен. Кроме того, в этом случае проек-
тивизация касательной плоскости к в_к в ji {D) совпадает с
гиперплоскостью, порожденной точками pt на канонической кривой С
Поверхности S. Поскольку каждое гиперплоское сечение кривой С
содержит лишь конечное множество точек, отображение S: 61^ -*-
^^ р«-1* всюду конечно. Точнее, обитая гиперплоскость
пересекает каноническую кривую по 2^ — 2 точкам в общем положении.
Поэтому отображение § в общей точке имеет конечную степень,
равную
g-(g+l) ..- (2g-2)
(g-l)l
Обоэначим через В а (Р*"^)* множество точек ветвления
для §. Это подмножество в (Р*"^)*, состоящее из образов таких
точек из в*и1 в которых отображение 3 вырожденно. В точках
ji (D) G в* и с D = "^ Pi ^ 5(*"^) в качестве локальных
координат на в_и можно взять координаты z^, . . ., z^.^ вблизи точек
Рц • • •> Pg-i на S. Тогда очевидно, что если касательная
прямая в одной из точек pi к С лежит в линейной оболочке точек
Pi. • • •. Pg-i^ то
т. е. ц {D) — особая точка ^. Поэтому, если обозначить через
V а (Р*"^)* собственное подмногообразие гиперплоскостей из
Р*-^, пересекающих С по точкам не в общем положении, то
понятно, что каждая касательная гиперплоскость Н к С, лежащая
(1=?)
7. Кривые и их якобианы 389
вне V, принадлежит множеству ветвления В отображения ^.
Обратно, если Н — гиперплоскость, не касаюп^аяся С, то Н
пересекает С в 2g — 2 разных точках z^ (Н), . . ., z^g-i (Я),
аналитически зависящих от Н. Для Н', близких к Н,
отображение S имеет ( ^~, J ветвей
{Dj (Я') = Zi, (Я') + ... +zt^_, (Я')}#^=^_1.
Но никакая пара этих ветвей не склеивается в Я. Значит, Я не
может быть точкой ветвления. Обозначим через С* а (Р*~^)*
множество гиперплоскостей, касательных к С. Мы показали, что
В а С* всюду, В = С* в (P*-i)* —F.
Заметим теперь, что множество С* неприводимо. Действительно,
оно является образом графика инцидентности / = {(р, Я): Я гз
ZD Гр (С)} с: С X Р*"^*, который в свою очередь расслоен над С
с неприводимыми слоями и поэтому неприводим.
Следовательно, в (Р*-^)* имеем В = С*, т. в. множест,во
касательных гиперплоскостей к канонической кривой поверхности S
совпадает, с замыканием в (Р*~^)* множества вставления
отображения Гаусса Ш, ассоциированного с тетл-дивизором в cz'f (S).
Доказательство близится к концу: поскольку (f' (S), [со])
определяют в и ^ однозначно, а значит, определяют С* с точностью
до автоморфизма (Р*~^)*, то нам осталось показать, что если С
ж С а Р*-^ — две канонические кривые с С* = С'*, то С s& С.
Это нетрудно. Заметим только, что каждой точке р ^С отвечает
(g — 3)-плоскость
Гр (С)* = {Я е (Ре-у: Н^Тр (С)},
лежащая в С* = С*. Но по теореме Бертини обпщй элемент
линейной системы {Н-С')нс_т (о* гладок вне базисного
множества Тр (С) П С данной системы, а так как Тр (С)* а С*,
то Тр (С) должна касаться С. Более того, при g > 3 не существует
прямых, касающихся С в двух различных точках q, q' G С.
Действительно, в противном случае по геометрическому варианту
формулы Римана — Роха было бы fe" {2q -\- 2q') = 3, откуда по
теореме Клиффорда кривая С была бы гиперэллиптична. Итак,
Тр (С) — Тр- (С) для единственной точки р' ^ С, ж отображение
р '^-^ р' задает изоморфизм С на С. Если же g = 3, то, как мы
уже знаем, существует лишь конечное число двойных
касательных к квартикам С в. С в Р^; соответствующее отображение
р>-* р' мошет быть продолжено до изоморфизма С ^ С ъ этих
точках.
Почти такое же доказательство проходит и в случае
гиперэллиптических кривых. Опять множество ветвления для §^
390 2. Риманови поверхности и алгебраические кривые
В (Р*-1)* СОСТОИТ ИЗ таких гиперплоскостей Н, что 1й' (Н (] С)
содержит кратные точки. Однако в гиперэллиптическом случае
для этого имеются две возможности: Н касается G или Н
проходит через одну из точек ветвления отображения t„. Итак, В состоит
из многообразия С* и гиперплоскостей р* = {Н: р ^Н) с
а (Р*~^)*, где р пробегает точки ветвления отображения t„.
В действительности В определяет тогда кривую С, а также 2g + 2
точек {pi} на С, таких, что S представима в виде двулистного
накрытия над С S5 Р^ с ветвлениями в {р;}. Но из обсуждения
гиперэллиптических кривых нам известно, что эти данные однозначно
определяют S. g
Согласно теореме Торелли, мы можем быть уверены, по
крайней мере теоретически, что поляризованный якобиан {f- (S),
[©]) римановой поверхности S отражает все ее свойства. В
заключение хотелось бы отметить, что это так не только в теории, но и
на практике — читатель, быть может, уже заметил, что все
результаты, доказанные в настоящей главе, непосредственно связаны
с геометрией отображений
li: ^с*) -^ f (S).
В самом деле, как мы уже видели, некоторые весьма глубокие
свойства алгебраических кривых становятся понятнее при
переходе к якобианам — по существу, линейным объектам. В
соответствии с этим кривые и их якобианы очень тесно связаны. К
сожалению, для изучения многомерных многообразий не найдено
никакой аналогичной техники, хотя разложение Ходжа и позволяет
вводить подобные конструкции.
ЛИТЕРАТУРА
Литература по теории римановых поверхностей и алгебраических кривых
огромна. Мы даже и не пытались составить сколько-нибудь полную
библиографию, а просто перечисляем некоторые работы, лучше всего дополняющие
материал этой главы.
F. Enriques and О. Chisini, Teoria geometrica delle equazioni e delle funzioni
algebricbe.— Bologna: Zanichelli, 1934.
С L. Siegel, Topics in Complex Function Theory. 3 vob.— New York: Wiley-
Interscience, 1969—1973.
H. Weyl, Die Idee der Riemannschen Flache. 3. Aus.— Stuttgart: Teubner,
1955.
J. L. Coolidge, A Treatise on Algebraic Plane Curves.— Oxford, 1931.
D. Mumford, Curves and Their Jacobians.— Ann Arbor: University of Michigan
Press, 1975.
Последняя книга является ценным обзором современного состояния
предмета с ]гказанием дополнительной литературы, особенно по истории
и источникам обобщенной теоремы Рниана об особенностях.
3
ДАЛЬНЕЙШИЕ МЕТОДЫ
Теперь мы вернемся к изучению общих аналитических
множеств, чтобы развить некоторый дополнительный аппарат,
специально предназначенный для многомерного случая. Основные
действующие лица этой главы — дифференциальные формы, а
главная тема — их многочисленные приложения,
когомологические и другие, к комплексно аналитическим пространствам.
В § 1 и 2 мы начинаем с теории потоков, или дифференциальных
форм с распределениями в качестве коэффициентов. Эта теория,
развитая первоначально де Рамом для того, чтобы включить в
единую картину дифференциальные формы класса С" и кусочно
гладкие цепи, в комплексно аналитическом случае особенно
плодотворна. Общая схема изложения материала в этой главе такова:
вначале обсуждается вещественный или С'-случай, а затем теория
развивается в более богатом комплексно аналитическом случае.
Материал § 1 является стандартным и перечислен в оглавлении.
В § 2 мы касаемся области недавних оживленных исследований,
в которых выяснился ряд замечательных свойств потоков,
ассоциированных с комплексно аналитическими многообразиями.
Далее это используется для иллюстрации того, как при помощи
теории потоков можно установить многие фундаментальные
результаты, необходимые при аналитическом изучении алгебраической
геометрии. Например, в настоящее время существует элегантный
метод распознавания, когда поток определяется некоторым
аналитическим подмножеством, что дает прямой метод
доказательства таких результатов, как теорема Реммерта о собственном
отображении, которая, несмотря на свою интуитивную очевидность,
вызывала обычно значительные затруднения при попытках
строгого доказательства.
Затем мы переходим к теории классов Чжзня. Определяя их
как дифференциальные формы, являющиеся многочленами от
элементов подходящей матрицы кривизны, можно просто и быстро
вывести известные функториальные свойства классов Чжэня, в
частности двойственность Уитни, а также непосредственно
продемонстрировать тип и свойства положительности в комплексно
аналитическом случае. Все это содержится в начале § 3, а во второй
части этого параграфа доказывается, что классы Чжэня двойст-
392 3. Дальнейшие методы
венны по Пуанкаре базисным циклам Шуберта на грассманиане.
Это отождествляет классы Чжэня, представленные
дифференциальными формами, с обычными топологическими классами Чжэня
(по модулю кручений) и связывает теорию классов Чжэня с
численными вопросами алгебраической геометрии — темой,
пронизывающей всю оставшуюся часть книги.
В § 4, используя потоки и классы Чжзня, мы получим две
глобальные формулы: голоморфную формулу Лефшеца для числа
неподвижныЕх точек и формулу Ботта для вычетов. Несмотря на
внешние различия, обе эти формулы можно вывести с
использованием теории пересечений и сглаживания потенциалов из
теоремы Стокса, примененной к дифференциальным формам с
особенностями. Этот прием применения теоремы Стокса к формам
с особенностями используется всюду в этой книге при изложении
обшрй теории: так, он уже появлялся в § 1 гл. 1, на протяжении
всей гл. 2, далее мы снова встретимся с ним при доказательстве
общей теоремы о вычетах из § 1 гл. 5. Поэтому мы попытались
разработать формализм этого приема в § 1 настоящей главы.
Рассмотрение главной части дифференциальной формы с
особенностями приводит нас к понятию ядра Бохнера — Мартинелли;
о том, что оно имеется в этой книге, можно узнать, заглянув в
предметный указатель. Здесь же нам хочется лишь обратить
внимание на то, что важна не сама формула для этого ядра, а его роль
как фзгадаментального решения (9-уравнения на С". Особенно
это видно в § 1 гл. 5, основной смысл которого заключается в том,
чтобы показать, что любое такое фундаментальное решение по
существу является не чем иным, как отражением двойственности.
С другой стороны, ядро Бохнера — Мартинелли выделяется среди
остальных фундаментальных решений своей унитарной
инвариантностью. Эта его симметрия отражается в двух упомянутых выше
глобальных формулах, а также в структуре многочленов Тодда,
входящих в формулу Римана — Роха — Хирцебруха.
Эта формула кратко обсуждается в конце § 4, но не
доказывается в данной книге. Одна из причин заключается в том, что
теперь имеется изобилие самых разнообразных доказательств этого
результата, и нам нечего добавить. Другая причина в том, что
мы применяем формулу Римана — Роха в конкретных
геометрических задачах только к кривым и поверхностям, где ее можно
установить непосредственно.
Последний параграф этой главы посвящен спектральным
последовательностям и нескольким их применениям в алгебраической
геометрии, которые, как мы надеемся, дадут хотя бы небольшое
представление о том, как это делается. Главные действующие
лица, как и прежде, дифференциальные формы, чаще всего с
особенностями. Из обсуждения гиперкогомологий, алгебраической
теоремы де Рама и дифференциалов второго рода будет понятно,
1. Распределения и потоки 393
ЧТО формализм спектральных последовательностей выявляет
общие закономерности и в некоторых случаях дает обманчиво
простые выводы классических результатов, исходные доказательства
которых стимулировали развитие многих методов, ставших
неотъемлемой частью самого предмета.
1. РАСПРЕДЕЛЕНИЯ И ПОТОКИ
Пусть М — компактное ориентированное ге-мерное
вещественное многообразие. Как мы уже знаем из двойственности Пуанкаре
и теоремы де Рама, для любого /?-цикла Г на М, например для
ориентированного подмногообразия, существует замкнутая (п —р)-
форма (В класса С°°, двойственная к Г в том смысле, что
\ Ф= j свЛ ф
г м
для любой замкнутой /?-формы ф. Кроме того, известно, что такая
форма и единственна по модулю точных форм.
Один из частных случаев, когда М — комплексное
многообразие, а Г — цикл, соответствующий аналитическому
подмножеству V коразмерности 1, был представлен выше достаточно явно.
А именно, пусть V задано локально как дивизор функции /„ G
£ О (U^), а положительные функции А„ на £/„ выбраны так,
что hjh(i = I /„//в Р на Ua Г) Ug. Тогда форма со = dd' logh^
представляет класс Чжэня линейного расслоения IV]. Особого
внимания заслуживает случай, когда расслоение [V] положительно,
т. е. когда при подходящем выборе метрики {h^} на [V]
вещественная (1, 1)-форма (В положительна.
Ниже будет предложен формализм, включающий как циклы,
так и гладкие формы. Это приведет нас к теории когомологий,
включающей как теорию обычных сингулярных когомологий, так
и теорию когомологий де Рама, и оба эти включения оказываются
изоморфизмами.
Определения; формулы вычетов
Сначала сформулируем наши определения на пространстве Ц".
Пусть C"(|R") — векторное пространство гладких функций на
й," с компактным носителем. Выбрав координаты а: = (х^^, . . ., а:„)
на Ц", введем следующие обозначения: Dt = d/dxt и Z)" =
= DfK . . Z)«" для а = (ai а„) е {I^T- На С Ю
определяется С-топология, в которой последовательность ф„ -> О
в том случае, когда существует такое компактное множество К,
что все supp ф„ с: Z и 1)"ф„ (х) -> О равномерно по х ^ К ж всем а
с [а] = а^ -|- , , . -|- а„ ^ /?. Соответственно С'-топология опре-
394 3. Дальнейшие методы
деляется тем, что ф„ -^ О в случав, когда все supp ф„ cz ^ и ф„ -»- О
в С-топологии для каждого р.
Определение. Распределением на Ц" называется линейное
отображение Т: С" (Ц") -»- С, непрерывное в С'-топологии.
Векторное пространство распределений на Ц" обозначается SB (Ц").
Распределению приписывают порядок р, если оно непрерывно
в С-топологии. Но линейное отображение топологического
векторного пространства V в комплексную плоскость С непрерывно тогда
и только тогда, когда прообраз единичного диска из С открыт в
топологии пространства V. Поскольку на пространстве С" {К)
функций с компактным носителем в К С'-топология есть
объединение С-топологий, отсюда ясно, что любое распределение
локально имеет конечный порядок.
Примеры. 1. Пусть tj) {х) — локально /(^-функция на Щ". Тогда
формула
Til) (ф) = ] Ф (х) tj) [х) dx
задает распределение Т^^ порядка нуль. Здесь dx = dx^ Л . . .
... Л dx„ и предполагается, что ориентация на й," всегда зада*
ется этой формой.
2. 8-фунщия есть распределение, заданное формулой
б (ф) = ф (0).
Продолжим теперь действие операторов частного
дифференцирования Di на пространство распределений по правилу
(DiT) (ф) = -Т (1>,ф).
Если 7* = Г^ — распределение, ассоциированное с функцией г!)
класса С, то для любой функции ф G С" (ц")
(DiT^) (ф) Т^ (Dt^) = - j г|) (а:) [{d^/dxt (х))] dx^
\
^-^2^-ф(а:)йа:=!(7'д.^) (ф) (по теореме Стокса).
Значит, мы действительно продолжили частные
дифференцирования на распределения.
Обсуждаемый ниже пример иллюстрирует принцип, лежащий
в основе различных теорем о вычетах. Рассмотрим на й, функцию
ч|) {х) класса V; заданную формулой
1|)(а:;
_| О, а:<С
1. Распределения и потоки 395
При формальном вычислении, игнорирующем особенности, имеем
чр' {х) = 0. Правильная же производная соответствующего
распределения получается из следующего вычисления:
00 00
{DT^) (ф) = — j ф' {х) ■^{x)dx=—\ ф' {х) da: = ф (0),
-оо о
Т. е.
DT^ = б.
Общий принцип состоит в том, что
DT^ — Td^ — «вычет»,
где 1>ф — формально вычисленная производная функции tj) по
модулю особенностей. Мы поговорим об этом подробнее немного
позже.
Еще одно представление о распределениях мы получаем,
рассматривая их на торе Т — 11"/(2я2)". В § 6 гл. О при
доказательстве теоремы Ходжа было определено пространство 3! {Т)
распределений на торе и доказано, что
»
где Я, — пространство Соболева формальных рядов Фурье Т —
= 2 ще'^^^' *^ удовлетворяющих условию 2 (1 + II5 IP)* l"5l^<°°»
По доказанной там ше лемме Соболева С(Т)= {\Н^ и Т(ф) =
S
2ф5е«5.«)еС~(Г). При этом б-функция
задается рядом
б = 2в*<^'*>.
\
Как всегда, общие выводы лучше всего иллюстрируются на торе.
Обозначим теперь через А\ (Ц") пространство д-форм класса
С" на Ц" с компактным носителем. Очевидно, что А\ (IR") можно
превратить в полное топологическое векторное пространство,
используя покомпонентно топологию пространства С" (Ц").
Определение. Пространство SБ^^ (|R"), топологически
двойственное к Л^~' (R"), называется пространством потоков степени д.
Примеры. 1. В последующих примерах через L' (R", 1ос)
обозначается пространство д-форм ф = Viji^ (x)dxj, коэффициентами
396 3. Дальнейшие методы
которых ЯВЛЯЮТСЯ локально /(^-функции на R". Каждой такой
форме Tjj отвечает поток Т^ g 3^' (R"), определенный по формуле
2. Пусть Г — кусочно гладкая ориентированная (п — д')-цепь
в Ц". Она определяет поток Тт G ^' (И"):
Гг(ф)=|ф, Фе4Г'(Г).
Если в общем случае ввести понятие носителя потока Т как
наименьшего замкнутого множества S, для которого Г (ф) == О при
всех ф G А'^-^ (к," — 5), то, очевидно, supp (Тт) = Г.
Внешняя производная гладких форм индуцирует отображение
такое, что
{dT)(ф) = (-1)'^»Г(йф), фе^г'-* (Г).
Очевидно, d^ = 0. Пусть Т = Т^ — поток для некоторой гладкой
формы tjj g 4' (R"). Тогда по теореме Стокса
Й7'^,(Ф) = (-!)«+» J флйф =
= —j <г(г|)Лф)+| Й1);лф=7'й^,(ф).
R" R"
Аналогично, для потока Т^ имеем
<г7'г(ф) = (-1Р'J ЙФ = (-!)'+']ф = (-!)«*'Гаг(Ф).
Значит, отображение d, определенное на потоках, индуцирует
на гладких формах обычную внешнюю производную, а на
кусочно гладких цепях оператор ±5.
Следующий пример является промежуточным между первыми
двумя.
3. Предположим, что форма i|) G L' (R,", loc) принадлежит
классу С°° вне замкнутого множества S, а dtj) продолжается
с К," — 5 до локально L^-формы на Ц". Вычет R (tj)) определяется
тогда из равенства потоков
(*) dT^ = Jd^, + Д (г|5).
Легко показать, что supp R (г])) с: S.
1. Распределения и потоки 397
Предположим, например, что рассматривается ядро Коши
^ 1 dz
на С. Тогда х G Z-^'" (С, 1ос) и является С^-формой на С —
— {0}; кроме того, в этом случае dy. = ду. = 0. Обычная формула
Коши
Ф(0) = —i==-(^^^' фес~(С)'
in у —1 J 0Z 2
рассмотренная в § 1 гл. О, при переводе на язык потоков
превращается в равенство
5(7'х) = б{о,.
Эквивалентно, вычет
1 dz \
п[
2п/ —1 Z
^{0)
ядра Коши есть б-функция, сосредоточенная в начале координат.
Обобщим это на R", а затем на С". Положим
г^=^х\ = \\х\\\
i
Г dr^2j •"'i dxi,
i
Ф(х) = dx^ л ... л dxji,
Ф^ {x) = (— l)*-i Xidx^A ... AdxiA ... A dx^.
Под Cn будет подразумеваться некоторая известная из контекста
постоянная, зависящая только от п. И наконец, такие операторы,
как *, зависящие от метрики, строятся по стандартной метрике
ds^ = 2 {dXiY.
i
Заметим, что функция г~* локально интегрируема при s <. п,
но не при S = ге. Пусть
S Фг (X) «rdr
'-'—'^п II _ ||п ^'n ,п •
Эта форма а лежит в L"-^ (R", loc), инвариантна относительно
действия группы собственных ортогональных преобразований
и является гладкой на R" — {0}. Так как йФ,- (х) = Ф (х), то на
Г - {0}
398 3. Дальнейшие методы.
Тогда по теореме Стокса интеграл \ а формы а по сфере не
11х1Г=в
зависит от ее радиуса е > 0. Следовательно, при подходящем С,^^
можно считать, что а есть единственная гладкая форма на R" —
— {0}, инвариантная относительно собственных вращений,
ортогональная к нормали dr в точках сфер с центром в начале
координат и такая, что ее интегралы по любой из этих сфер равны 1.
В R^ с координатами {х, у) = (г cos 6, г sin 0) имеем
1 xdy—ydx _ 1 „
В общем случае пусть х = га, где г = || а; || и оо G 5""^ —
полярные координаты на R,". Тогда а = Cnda.
По теореме Стокса для любой функции ф G С~ (R,")
— \ йфЛст = Пт— \ йфла = Ит \ (рст = ф(0).
R" R"-{||x|Ke} 11я||=е
Поэтому имеет место равенство потоков
и формула вычета
R (а) = 6(0).
На С" ^ R^ форму а можно раэложить по типам. Каждая
компонента такого разложения инвариантна относительно
действия унитарной группы. При этом компонента типа (ге, п — 1)
с точностью до постоянного множителя, который определяется
ниже, имеет вид
(^фГ^АФ(г)) ^ *(гдг)
Очевидно, что р 6 L"-""' (С", 1ос), а поскольку 5Фг (z) = Ф (z), то,
как и в предыдущих вычислениях для а, можно показать, что
5р = 0 на С"—{0}.
Но так как d = д в& формах типа (ге, gr), то, повторяя предыдущее
рассуждение, мы получаем соотношение
dTfi = 6(0)
при подходящем выборе постоянного множителя, что приводит
к следующей формуле вычета:
R (Р) = б,о|.
1. Распределения и потоки ^399
Это означает, что для любой функции ф G С~ (С")
Ф(0)= )'5фЛр,
С»
и точно так же, как и в случае одной комплексной переменной,
эту формулу можно распространить на случай форм с
некомпактным носителем и получить при этом формулу
Ф(0)= f 5флр+ f фр,
В[г] дВ[г]
где 5 [г] = {z 6 С" : II Z II ^ г} — шар радиуса г в С". Если
функция ф G (9 (С") голоморфна, мы приходим к формуле Бохнера —
Йартинелли
ф(0)= J ф(2)р(2, Z).
1|г||=т
Эти формулы могут быть доказаны сведением к одномерному
случаю способом, который подсказывает также и некоторое
выражение для р. Итак, покажем прежде всего, что
^ = Cnidlog\\z\f)Aiddlog\\z\\r-'-
Доказатпелг>стпво. Обозначим через 7 форму в правой части этого
равенства. Поскольку
51og||z|P = -|^,
и (dz, z)A(dz, z)=0, то
Числитель этого выражения есть
с; (S 1г dzi) л (S dzj л dzj)"-^ =
3 i
/-> _
= Cn (S (—1)'~' Zj dzj л ... л dzj л ... л dzn A dzi /\ ... A dZn),
откуда следует требуемый результат.
Напомним теперь, что подъем кэлеровой формы метрики Фу-
бини — Штуди относительно проекции С" — {0} -»- Р"-^ есть
форма Q = dd'log \\ z Ц^ = ^'-^дд log || z ||^ Пусть С" —
раздутие С" в начале координат, и я: С" -^ Р""^ — продолжение
400 3, Дальнейшие методы
проекции на С*. Легко понять, что С" является пространством
универсального линейного расслоения над проективным
пространством, а поднятая форма n*Q сглаживается на С".
Следовательно, на С"
я*р = С„0 л (я*Й)"-\
где 6 = 5 log II Z 11^ есть (1, 0)-форма, которая имеет вид dX/Я,
на каждом слое {Xz}i£(q проекции С"-^ P"~^. Итак, я*Р на С"
совпадает с произведением (с точностью до постоянного множителя)
подъема стандартной формы объема пространства Р"~^ на форму
в, ограничение которой на каждый слой проекции С" -♦- P^^-\
совпадает с ядром Коши. Теперь, используя эту интерпретацию,
можно свести ге-мерные формулы Бохнера — Мартинелли к
одномерной формуле Коши; для этого достаточно поднять формы на С"
ж выбрать там подходящий порядок интегрирования.
В заключение отметим, что понятие распределения и потока
можно локализовать. Так, например, для открытого множества U
из К," пространство SB (U) распределений на U двойственно
пространству С" {U) с очевидной топологией. Поскольку
диффеоморфизм f: и -*- V (открытых множеств U, V из R,") индуцирует
топологический изоморфизм /*: С~ (V)-*- С°° (U), можно определить
пространства распределений 3! (М) и потоков 3J* (М) на любом
многообразии М.
Сглаокиваиие и регулярность
Распределение Т ^SB (R") называется гладким, если ,Т = Т^
для некоторой С^-функции г]) (х) на Ц". Сейчас мы постараемся
придать точный смысл тому факту, что гладкие распределения
плотны в множестве всех распределений.
Пусть X (^) € ^Г (Ю ~ неотрицательная функция с
носителем в окрестности начала координат, для которой
j %{x)dx = i.
Вскоре будет предполагаться, что функция х радиалъно
симметрична, т. е. в полярных координатах для х = га
X (^) = X ('•)•
Положим
%г{^) = 4г%(т)-
1. Распределения и потоки 401
Бели suppx = -S^) ТО suppXe=eisr в f Xe(^)da;=l.
Заметим, что
Гх, -^ б при 6-^0,
т.е. для любой пробной функции ф€СГ(К")
lim f Хе(^)ф(^)^^=ф(0).
е-*0 J
Чтобы убедиться в этом, заметим, что
mm ф (л;)^ \ Хе (^) ф (^) dx^vascs. ф (л;),
х€еХ J хбеХ
R"
где крайние части стремятся к ф (0) при е -^ О,
Получив «сглаживание» б-функции, рассмотрим теперь для
общего распределения Т ^ 3 (Ц") функцию
Тг {х) = Ту (Хе {X - у)),
где нижний индекс у при Т означает, что Т применяется к Хе (^ — у)
как к функции от у. Функция Те (х) на Ц" принадлежит классу
С°°, и для ее производных выполнены соотношения
1ГТе{х) = ±Ту{и^Х,(х-у)).
Допуская некоторую вольность, будем также обозначать через Те.
распределение на R,", отвечающее функции Те. (х).
Докажем следующие формальные свойства распределений Те-
1. (Гф)е = 7'ф, ДЛЯ ф(:с)еС~(Г).
2. T,i^\>) = T{^p,) для ур{х)еСТЮ.
3. {ВТ)е = 0{Т,) для В = д'Чдх'^.
Доказательство свойства 1. Для^ фбСГСК") имеем
(7'ф)е (ф) = J Гф^ (Хе (^ - у)) Ф (^) d^ =
\] ^ {У)%г{х-У) ■^Sfix) dxdy =^T^^{^if)
(после изменения порядка интегрирования).
26-046
402 3. Дальнейшие методы.
Доказательство свойства 2. Поскольку Т линейно, имеем
Т Ш = Ту[^Мр(х) Хе (х-у) dx) =
= J г|з (л;) ГДе (х-у) dx= J г|з (х) Т^ (x)dx=T^ (^).
Доказательство свойства 3. Можно предполагать, что D^
= dldxi. Пусть Г = Г*, 113 6^^(11"), а феС(Л1"). Тогда
ДГе (Ф) - Ге (- ^?Ф) = J J —g-(:г) хе (:г-1/) г|, (1/) d:r di/=
^5 ^"^"41—^{^)'^{^~u)dx'^du =
= J Хе (") ( J ф (^) -^ {x~ u)'da;) du =
Для произвольного г 6^(11") и ф6СГ(Л1")
(ДГ)е (ф) = {DT) (фе) = г ( - Дфе) =
= Г((—Дф)е) (по предыдущему шагу)
= Ге(-Дф) = 1>Ге(ф),
Что доказывает утверждение 3.
В частности, отсюда выводится, что для любого г|з 6 С" (|R")
равномерно по л; g |R". Следовательно,
Ге {^) -^ Т (1|з) при 8-^0.
Конечно, существует ряд более тонких вопросов, касающихся
сходимости процесса сглаживания для конкретных норм, однако
здесь нам нет нужды ими заниматься.
Любой поток Т в 3!^ (Л") можно рассматривать как
дифференциальную форму
Т= 2 Tjdxj,
коэффициентами которой служат распределения Tj, задаваемые
соотношениями Г/ (ф) = ±Г (ф Аг/») для ф 6 С^ (IR"). Через /**
здесь обозначается множество индексов, задаваемое равенством
*dxi = ±dxi'. Сглаживание
?'е=2 {Ti)edXi
1. Распределения и потоки 403
обладает следующими свойствами:
Ге(ф)-^Г{ф) при 8-^0, фб4Г'(1К").
dJe = d (Ге).
Теперь воспользуемся сглаживанием для доказательства
некоторых результатов о регулярности уравнения Лапласа на
пространстве распределений
AT = S, где A=-2-gr-
г
Лемма. Пусть Т ^ 3 (|К") — распределение с АГ = 0. Тогда
Т =^ Т^ для некоторой функции ф 6 С°° (|R") с Аф = 0.
Доказательство. Гладкая функция ф, удовлетворяющая
уравнению Аф = О, называется гармонической. Установим прежде
всего так называемую теорему о среднем значении'.
ф(г/)= J фН^иСл;),
II 5С-У II =
где а ~ Сп * п — форма, уже встречавшаяся нам в
предыдущем разделе, & Оу {х) — а {х — у) — инвариантная форма объема
на сфере \\ х — i/ || = е, имеющей полный объем 1. Так как
лапласиан инвариантен относительно сдвигов и собственных вращений,
то теорему о среднем значении достаточно доказать для i/ = 0.
Мы применим дважды теорему Стокса к сферическому слою
В [б, е] = {б ^ II л; II :^ е}. Вначале возьмем (д — 1)-форму т] =
= фо. Поскольку do = О, то
dT] = С„ йф л-^^5:1^ = ±:С„ * с^ф л-jj^,
и по теореме Стокса
(*) iCn J *йфЛ-^£г= ] фа— J фа.
В[в. el ||5с||=е ||х||=6
Напишем
* йф Л п_1 — * йф л d7i
где
log г в случае ге=2,
[—-;Г=^)-р^ в случае ге>3.
Но d * с^ф = ±А фс^л; = О, позтому
* dff) /\dy = rbd (у * dw).
ч
404 3. Дальнейшие методы.
Применяя снова теорему Стокса, можно выразить интеграл слева
в формуле (*) в виде разности интегралов
\1
7*йф.
II *'11 =р
При фиксированном р зтот интеграл с точностью до постоянного
множителя равен
II XII =р И к |Кр
Следовательно, если ф — гармоническая функция, то
||х||=6 ||х||=е
Левая часть этого равенства стремится к ф(0) при б -^ О, откуда
и получается теорема о среднем значении.
Предположим теперь, что функция х (^) радиально
симметрична. Тогда фе = ф для любой гармонической функции ф и е > 0.
По формальным свойствам сглаживания 1—3 Тц = Т для
гармонического распределения Т при б > 0. Точнее, по свойству 3 имеем
АГе = (АЛе = 0.
Поэтому Te = T,ti^ для гармонической функции г|зе- Значит,
Л ДЛЯ ф 6 СТ (Г)
Т (ф) - lim Ге (Ф) = lim (Тг)й (ф) = lim Ге (Фв) =
е-» о в->0 е-» О
= 7'(Фв) = Гв(ф), (по свойству 2)
т. е. Т =^ Т(, есть гладкое распределение, что и требовалось. Q
Распространим теперь свойство регулярности на случай
неоднородных уравнений.
Лемма. Пусть Т ^ 3! (R,") — распределение, удовлетворяющее
уравнению АГ = т] 6 С" (R,"). Тогда Т = Т.^ для некоторой
функции г|з g С°° (к,"), тикой, чтл Aif) = т].
Доказательство. Используя классическую функцию Грина
G{x,y) = [ \\^-уГ-'' ''^^•
I log\\x — y\\, п = 2,
мы укажем явно одно из решений р ^ С°° (R,") уравнения Ар = т].
1. Распределения и потоки 405
Тогда А (Г — Тр) = 0, и по предыдущей лемме мы получаем,
требуемое.
Будем предполагать, что и ^ 3; случай ге == 2 разбирается
аналогично. Рассмотрим функцию
п1-г\ — Г { _ЛМ^£_—-и<^ Г r](x~u)du
р [X) - t^n J II ^_ J, ||„-а - ± t^n J II „ ||„_а ,
1/6 R" u6R"
где последнее равенство отвечает замене переменных у — х — и.
Из второго выражения видно, что р {х) — гладкая функция и
АР(-) = ±С„ J ^1^Й^.
u6R"
Покажем, что этот интеграл равен т] {х). После перенесения х
в начало координат достаточно проверить формулу Пуассона
R"
Для X = г(л ь полярных координатах г = || л; || и оо g S^^~^ имееьг
Ат) (х) dx d*dr\ _ J / *dT) \ , / 1 \ <^r Л *dr\ _
IIX ||n-2 "~ r"-2 ~ Kr"'-^ ) — \n—2) г"-! ~
_j ( *Лц \ ( _±_\ druK*Jldr) _
=<'{^)±(;^)''M-
Применим теорему Стокса к двум последним формам на R" —
— {II л; II ^ е}. Получим, что
f iaM^-lim f l^r\(x)dx _ , д
J ЦхН»-^ -i™ J \\x\\n-^ -A, + B„
R" R"-{||K|Ke}
где
A^=± j -^^й^ = -^й=г ] ^■x\dx-^Q при 8-^0,
||x||=e llxIKe
так как At] принадлежит классу C°°, a потому I Aii=0(e"),
и где
5e = const \ ЦО-^Ц (0) при 8-^0
IWI=e
для подходящего выбора константы С„. Это доказывает формулу
Пуассона, а следовательно, и лемму.
406 3. Дальнейшие методы.
Регулярность также вьшолняется локально:
Лемма. Пусть i7 с: R" — открытое множество, а Т ^ 3J (V)—
некоторое распределение с AT = 0. Тогда Т = T,j, для подходящей
гармонической функции \!р на U.
Доказат£лъство. Рассмотрим относительно компактное
открытое множество V CZ и. Тогда для ф g С" (F) и достаточно малого е
вьшолнено включение supp фе с= U. Поэтому можно определить Т^
формулой Те (ф) = Т (фе) И показать, используя предыдущие
рассуждения, что Те = Г^^. для некоторой гармонической
функции 1|зу- на V. Так как 1|зу- не зависит от е, то '^w I v = ^v Для
V CZ W CZ и. Следовательно, на U существует такая
гармоническая функция if), что Т = T,j,. []
В качестве одного из приложений мы получаем следующий
факт.
Регулярность оператора д. Если U cz С" — открытое
множество, а Т ^ 3J (U) — распределение с дТ = О, то Т = Tf для
некоторой функции f ^ (9 (U).
Доказательство. По одному из тождеств Ходжа из § 6 гл. О
А = У^Ад'д
на С". Значит, дТ = 0=^АТ = 0, а потому T = Tf для некоторой
функции_/G С°° (i7) по предыдущей лемме. Но тогда 0 = dTf =
= T-,f=>'df = 0 и feO{U). D
Восполним теперь пробел в доказательстве теоремы Ходжа
из § 6 гл. 0. А именно, ссылаясь на лемму о регулярности I из
раздела «Доказательство теоремы Ходжа II: глобальная теория»,
мы хотим показать, что если ф лежит в пространстве Соболева
^р.5 (ilf), а if) g dis'f-' (М) является слабым решением уравнения
Ai|3 = ф, то 1|з е ММ (М). В самом деле, Р^ = А для Р ='д + д*.
Рассмотрим поэтому более слабое уравнение
(*) ре = -п
и покажем, что если "П 6 J(?f"'(il/), то Q eSe^+i{M). Но 'для
реС"(М) имеем
Р (рб) = Р (р) л е -f рР (0) = Р (р) л 0 + (Щ.
Значит, требуемую регулярность слабых решений уравнения (*)
достаточно доказать для форм с компактным носителем в
фиксированной координатной окрестности на М. Можно считать, что
эта координатная окрестность диффеоморфна R". Следовательно,
нам остается доказать следующее утверждение.
1. Распределения и потоки 407
Лемма о регулярности II. Пусть Ри = Qu -\- Ru —
дифференциальный оператор первого порядка, где
{Qu), == 2 4- (^) ^. №")г = Е Ьц и uj (х),
h, j j
С С "-коэффициентами, удовлетворяющий неравенству Гордин-
га ^)
С (II Ри Из + II и Из) > II и IU, S 6 Z,
^ля любой С°°-функции и с компактным носителем с некоторой кон-
стлнтюй С, зависящей только от коэффициентов оператора и
выбора компакта, в котором лежит носитель рассматриваемой
функции. Предположим, что некоторое распределение и с компактным
носителем удовлет^ряет уравнению
Ри ^ V
при некотором распределении v из пространства Соболева J??^.
Тогда и 6 Жв+1-
Доказательство. Для простоты будем считать, что s ^ О и
" 6 SSo- Определяя сглаживание
"е И = j " (у) Хе (^— у) dy,
как выше, легко показать ^), что в L^-норме
ll"e-"IIS-^0 при 8-^0.
Если мы докажем равномерную ограниченность соболевских норм
II "е lls+i ДЛЯ О <; 8 ^ 8о, ТО получим подпослбдовательность Uej^,
слабо сходящуюся к некоторому элементу и' из сй?з+и где 8^ | О
монотонно, а и', очевидно, должен совпадать с и.
Неравенство Гординга из условия леммы позволяет оценить
<|%?з+1-норму Ug при помощи (1^3-норм Qug, и Ue. По индукции можно
предполагать, что и g J??^, но тогда s-норма щ ограничена s-нор-
мой и.
Остается оценить s-норму Qu^. Мы уже знаем, как ограничить
s-норму вектор-функции {Qu)^ =—{Ru}^-\-v^. Поэтому
достаточно оценить s-норму разности
(**) (<?")е - Q Ы-
^) Это неравенство было доказано при s ^ О на стр. 110; аналогично оно
устанавливается и для других значений s.— Прим. перев.
^) См., например, Л. Хёрмандер, Линейные дифференциальные
операторы с частЕИми производными.— М.: Мир, 1965, теорема 1.2.1.— Прим.
перев.
408 3. Дальнейшие методы.
Для операторов с постоянными коэффициентами эта разность
равна нулю. Следовательно, в общем случае можно надеяться на то,
что требуемая граница выражается через s-норму и и s+1-нор-
мы коэффициентов a\j. J\aR простоты рассмотрим случай s = 0.
Общий случай разбирается аналогично. Очевидно, что г-я
компонента вектора (**) равна
{2abuj)-24^-ir^^-{2^u,)
dxh
},k j,h i,h
Последний член оценивается умноженной на константу L^-нормой
и. Остальная часть выражается интегралом
-^S 1 iD^l)[^){o!li{x-y)-a%{x))u,{x-y) dy,
3, h дП
a по неравенству Минковского его Lg-nopMa не превосходит
Ili/IKeK
при ПОДХОДЯЩИХ константах С, С *). g
Когомологии потоков
Согласно предыдущему, на многообразии М определен
комплекс потоков {3}* (М), d). Включение гладких форм в потоки
задает естественное отображение Ядн (М)-^ Н* {3}* (М), d)
когомологии де Рама в когомологии, отвечающие потокам. Ниже будет
доказано, что это отображение является изоморфизмом. По
теореме де Рама то же самое верно для отображения
Н* {М, sing) -^ Н* {3}*{M), d)
пространства когомологии кусочно гладких сингулярных цепей
в пространство когомологии потоков. Если Г — некоторая
кусочно гладкая (и — ;?)-цепь, то существует гладкая замкнутая р-
форма 1|з, для которой имеет место равенство потоков Тт = Т,^ -{-
+ dR. Хотя мы и не будем зто доказывать, можно считать, что
поток R соответствует (р — 1)-форме г\, интегрируемой на М,
'^) Более подробное доказательство можно найти в книге: Л. Шварц,
Ко*шлексные аналитические многообразия. Эллиптические уравнения с част-
ныдш производными. Пер. с исп.— М.: Мир, 1964, теорема 3.3.— Прим.
перев.
1. Распределения и потоки 409
класса С°° на М — Г и такой, что dx\ = —1|з на М — Г. Тогда
предыдущее равенство принимает вид
ЙГ,1 — Tdxi = Tv
и представляет собой формулу типа рассмотренной выше формулы
вычетов.
Прежде чем переходить к доказательству, заметим, что если
М — комплексное многообразие, то для него определен также
комплекс (^^' * (М), д) потоков типа (р, q). Кроме того, мы
докажем, что отображение
Я|• * (М) -V Н* {2В^' * (М), д)
является изоморфизмом. Поскольку доказательства обоих
утверждений в существенном совпадают, мы ограничимся комплексным
случаем.
Пусть ^^.9 — пучок потоков типа {р, д). Тогда определен
комплекс пучков
(*) 0-^QP-^^^'°-^^^''-^... Д^^'"-^0.
Так как распределения можно умножать на С°°-функции, то пучки
3^<^ допускают разбиение единицы. Следовательно, H'^ (М,
£gp,4) = О при А; > О, и если нам удастся доказать точность
последовательности (*), то можно будет дословно повторить
доказательство теорем де Рама и Дольбо из § 3 гл. О, основанное на
теории пучков. Иными словами, нужно установить 5-лемму
Пуанкаре в случае потоков.
Первый шаг — теорема о регулярности для 5-оператора.
Отметим, что для оператора полной внешней производной d этот шаг
тривиален.
Чтобы доказать 5-лемму Пуанкаре для потоков более высокой
степени, мы дадим другое доказательство в С°°-случае, которое
можно приспособить и для потоков. Это доказательство основано
на задании оператора гомотопии
К: Л°''(С")-^^''''-*(С»).
Конструкция этого оператора К опирается на установленную
выше формулу Бохнера — Мартинелли, а получаемая при этом
явная формула гомотопии оказывается полезной при
доказательстве голоморфной формулы Лефшеца числа неподвижных точек.
Для определения оператора К полезно ввести некоторые
обозначения. Пусть МжЫ — два комплексных многообразия с
локальными голоморфными координатами z тя. w соответственно. Диффе-
410 3. Дальнейшие методы.
ренциальные формы на произведении М X N разлагаются по
битипам; так, например,
обозначает С°°-формы типа (р, д) по dz и типа (г, s) по dw, а значит
типа (р -{- г, д -{- s) яй М X N. Положим
Ф(0 = й^,л...лй^„,
и определим я5ро Бохнера — Мартинелли на С" X С" формулой
k(z w)-C g Ф'('-"')'^ ФИ
||2П
Эта форма имеет особенности на диагонали z = w ж интегрируема
на всем С" X С". Для нее имеет место разложение до битипам:
k{z, w)6 Ф L<"'«"''<"•"-«'(С" X С", 1ос).
9=1
Определим теперь оператор К: Л°''(С")-^Л"''"* (С") , полагая
с
{Kff>){z)= \ k{z, w)A(f{w).
Этот интеграл определен, поскольку ядро к интегрируемо, а
носитель формы ф компактен. Используя замену и = z — w, мы
убеждаемся, что
{К(р) (z) = \ k{z, Z — и) л ф (z—и)
есть С°°-форма по z, так как в знаменателе подынтегрального
выражения появляется лишь || и \\ *".
Отметим, что носитель формы K(f) не обязан быть компактным.
Существуют аналоги оператора Я^фдля форм ф 6 Лр^ (С") (р Ф 0),
но мы предоставляем читателю их найти.
Все, что нам нужно знать об операторе К,— зто формула гомо'
топии
дК + Кд = тождественный оператор.
Докагателъство. Так как
- f S Ф^ (g) "1 _ ^Ф
V iiur )~п\
|.П ||£||2П+2
~'шг\^^^'~' пег /"""•
1. Распределения и потоки 411
ТО формально дк (г, w) = 0. Игнорируя пока особенности, мы
получаем по формуле Стокса, что для пробной формы 1|з 6
0= \ d{yp{z) лк{г, w) A(f){w))= \ 5 (ф (z) л A;(z, w) л ф(и')) =
С"ХС" СхС"
= I 5г|) (z) л/с (z, w) л ф (w) ± \ \p{z) лк{г, W) Ad(f){w).
С^хС" СхС"
Поэтому, рассматривая Я'ф = Я'ф 64°'^"'(С") как поток на
формах из Л?*""'"*"'(С"), мы видим, что
(**) дК^ + К^=0.
Конечно, это формальное вычисление не совсем корректно, потому
что при применении теоремы Стокса играют роль особенности ядра
на диагонали. Напомним установленную выше формулу Бохнера —
Мартинелли:
С"
HIP
для т] 6 с" (С"). Из нее довольно очевидно, что поправочный
член, который необходимо добавить в правую часть (*), равен
тождественному оператору. Докаэывается это прямым
вычислением с применением формулы Бохнера — Мартинелли, и так как
соответствующие выкладки проводятся непосредственно, мы не
будем здесь этим заниматься.
Б качестве первого приложения формулы гомотопии приведем
другое доказательство 5-леммы Пуанкаре для гладких форм.
Рассмотрим 5-замкнутую форму ф g Л**>' (U) на некотором
открытом множестве U с: С". Для относительно компактного
подмножества V CZ и найдем колоколообразную функцию р 6 Cf (U),
тождественно равную 1 на U. Тогда рф 6 4^'?(С") и
(pф)(z) = Ъ (^рф)(2) + К(д (pф))(z).
При ограничении на V получаем
ф(2)=5(^рф)(2) (2 6F).
Предположим теперь, что поток Т 6 •З'"'' (С") имеет
компактный носитель, т. е. Г (ф) = О для некоторого открытого
относительно компактного множества U с: С", если supp ф с: С" — U.
Такой поток можно определить на всех формах из ^4">""' (С"),
412 3. Дальнейшие методы
а не только на тех, которые имеют компактный носитель. Это
позволяет определить КТ для потоков Т с компактным носителем:
кт (ф) = т (^ф), ф 6 4?' "■'■'* (С").
Очевидно, что и для любой пробной формы
Ф (КТ)) (г|)) + (К (дТ)) (г|)) = {КТНЩ) + (дТ) {K^p) =
Поэтому при такой интерпретации формула гомотопии
выполняется на потоках с компактным носителем. В частности, последнее
доказательство 5-леммы Пуанкаре для гладких форм
автоматически переносится на случай потоков.
Это завершает установление изоморфизмов
Я|• * (М) -* Я^' * (3^' * (М), д),
H%i,iM)-^H*i3!*(M),d),
которые ниже будут называться сглаживаниями когомологий.
2. ПРИМЕНЕНИЕ ПОТОКОВ В КОМПЛЕКСНОМ АНАЛИЗЕ
Потоки, отвечающие аналит,ическим
подмножест,вам
Пусть М — комплексное многообразие. Потоки £SP'P (М) типа
{р, р) — это непрерывные линейные функционалы на формах
с компактным носителем из А^-Р'^-р (М). Поток Т типа (р, р)
называется вещественным, если Г = Г, т. е. Т (ф) = Т (ф) для
всех (f ^A^'P'^'-P (М). Вещественный поток называется
положительным, если
(]/т:Т)р(р-')/2г(^д-)^о, лб^Г'''"(М).
Особый интерес представляют замкнутые положительные потоки.
Отметим, что для вещественного потока Т 6 ^^«^ (М)
dr = О <^ 5Г = 5Г = 0.
Из положительности потока вытекает, что он имеет нулевой
порядок в смысле распределений. Например, поток Т 6 ^^'' Щ)
локально представляется в виде дифференциальной формы
r=^'4-^2*ii^2iAtfz,,
2
г.}
2. Применение потоков в комплексном анализе 413
коэффициентами которой являются распределения, заданные
соотношениями
ti]{a) = { — if'^*'^^T{adzi л ... л dz, л ... л dz„ л dz", л ...
... л dz] л ... л Й2„).
Этот поток веществен, если 1^ = tji, и положителен, если для
любых комплексных чисел Х^, . . ., Я^ распределение
неотрицательно на положительных функциях. В этом случае,
переходя к монотонным пределам, можно расширить область
определения Т (А,) до некоторого класса функций в L^ (М, 1ос),
интегрируемых относительно положительной меры Т (Х). Очевидно,
этот класс включает все непрерывные функции. Аналогичное
рассмотрение годится и для положительных (р, ;?)-потоков.
Примеры. 1. Пусть Z cz М — аналитическое подмножество
коразмерности р,й Z* = Z — Za — множество его гладких точек.
В разделе § 2 гл. О, посвященном анализу на комплексных
многообразиях, мы доказали утверждение, которое на языке потоков
означает, что отображение
ф'^5ф, ф6Л"-^""'^М),
Z*
задает замкнутый положительный поток Tz- Этот пример для
нас особенно важен.
Классу когомологий Т^ при изоморфизме Н^^{М) ^
^ Н*{3}*{М), d) отвечает фундаментальный класс
аналитического подмножества Z.
2. Гладкая (1, 1)-форма
С0 = -^-у- ( 2 ^И ^2» л Й2у)
вещественна, если кц = hji, строго положительна, если матрица
hp положительно определена, и замкнута тогда и только тогда,
когда соответствующая эрмитова метрика ds^ = S h^jdztdzj кэле-
рова. Степени со^ кэлеровой формы определяют замкнутые
положительные (р, ;})-потоки.
3. Вещественная функция ф 6 ^^ (М, 1ос) называется плюри-
субгармонической, если у—1 55ф — положительный (1, 1)-поток.
Дифференциалы берутся здесь в смысле теории распределений.
414 3. Дальнейшие методы
Плюрисубгармонические функции представляют собой удобный
класс потенциалов в теории функций комплексных переменных.
Лемма (55-лемма Пуанкаре). Пусть Т — замкнутый
положительный (1, \)-поток. Тогда локально
Г = 1/^155ф,
где ф — некоторая вещественная плюрисубгармоническая функция,
определенная однозначно с точностью до прибавления вещественной
части голоморфной функции.
Доказательство. По 5-лемме Пуанкаре локально имеем Т =
= —У—1 дц для некоторого (1, 0)-потока т]. Поток dy\ имеет
тип (2, 0) и д{дг[) = —ддг] = (1/У^) дТ = 0. По теореме
о регулярности для 5-оператора ду\ является замкнутой
голоморфной 2-формой. Значит, по d-лемме Пуанкаре для голоморфных
форм существует голоморфная 1-форма |, для которой дг\ = dl.
Следовательно, Т = —Y—1 дг\', где t]' = т] — | — форма,
удовлетворяющая равенству дг\' = 0. Но по 5-лемме Пуанкаре y\' = ду
для некоторого распределения у, и вещественное распределение
ф = (Y 4- у)/2 удовлетворяет условию ]/ —1 ддц) = Т.
Используя то, что У—1 dd(f — распределение нулевого
порядка, можно показать, что ф представляется локально L^-функ-
цией, но мы не будем давать полного доказательства этого факта,
так как он нам не понадобится. Интуитивно это понятно из того,
что распределение
Дф = 1/'^Л55ф
имеет нулевой порядок, а поэтому оно лежит (локально) в
пространстве Соболева Нд. Но тогда по теореме о регулярности ф лежит
(локально) в пространстве Соболева Н^.
Функция ф называется потенциалом потока Т; она
единственна с точностью до прибавления вещественной функции у, для
которой дду = 0. Для любой такой функции у поток ду имеет
тип (1, 0) и 5-замкнут, а потому, снова в силу регулярности, явля-
Z
ется эамкнутой голоморфной 1-формой. Положим / (z) = \ ду.
го
Тогда у = Re f. Q
Потенциал ф потока Т = Та,, ассоциированного с кэлеровой
метрикой, является гладкой функцией. Так, например, для
евклидовой метрики на С" глобальным потенциалом будет ф (z) = || z |Р.
С другой стороны, имеет место следующая
2. Применение потоков в комплексном анализе 415
Лемма (уравнение Пуанкаре — Лелона). Пусть Z —
аналитическая гиперповерхность, представляющая дивизор голоморфной
функции f ^ О (М). Тогда справедливо следующее равенство
потоков:
Tz=^^ddiog\f\.
Доказательство. В окрестности каждой гладкой точки
гиперповерхности Z можно выбрать такие координаты (z^, . . ., z„),
в которых / (z) = z„. Тогда
^!^^ 55 log \f\=d{ ^d\ogf]=d( ^^] = Ti,^oy,
согласно очевидному обобщению формулы Коши в случае одной
переменной (для распределений)
допускающему зависимость от параметров.
Пусть теперь р (w) = w" + ajw"~^ + • • • + <^ — многочлен
от одной комплексной переменной, возможно с кратными
корнями. Тогда выполняется равенство распределений
-^( 1 p'(w)du> \ _ лп в
\2nV~i рИ ' ^ ^^*
Это означает, что 1-форма д log р (w) интегрируема и, более того,
для любой функции а g Cf (С)
1 Г Г 5а (w) р' (и>) J J- vn / \
т== \ \—Jr-^ ^ ; / dwAdw= > а(и>^).
р (и'„)=о
Чтобы получить эту формулу, достаточно применить теорему
п
Коши к сомножителям разложения р (w) = и {w — w^).
v=l
Обращаясь к общей формуле Пуанкаре — Лелона, мы видим,
что нужно установить интегрируемость функции log | / | и
проверить равенство
~^\log\f\ddq>=\^ (f для всех ф64Г''""Ч-/W")•
Эта задача локальна. Выберем в окрестности точки р ^ Z
локальные координаты (zj, . . ., z„). Можно считать, что / (z^, . . ., Zn) —
многочлен Вейерштрасса по z„ и
Ф = а (z) dzj л ... л dz„_, л dzi л ... л dzn_i,
416 3. Дальнейшие методы
так как такие формы порождают все (и — 1, п — 1)-формы при
преобразованиях координат вида
Тем самым наша задача, по существу, сводится к двум
переменным (z, w), при этом ф = а (z, w) dz л dz и
n
/(z, w) = w"4-ai(2)ffi;''-»4-...4-ao(z)= П {w — w^{z))
v=l
— многочлен Вейерштрасса. Нужный интеграл с точностью до
постоянного множителя равен
\ { \ log \ f {г, w) \ " (^'Jf> dw А dw\ dz А dz.
Применяя вначале теорему Стокса ^), а затем установленный для
многочленов результат к внутреннему интегралу, получаем
^ I 2 " (2. "'v (z))] dzAdz= \ ф. О
Исходя из предыдущего, можно думать, что общий замкнутый
положительный поток есть нечто среднее между гладкими
потоками и потоками, заданными аналитическими подмножествами.
По существу, так оно и есть, и чтобы описать, что же известно
на самом деле, мы определим сейчас для каждого замкнутого
положительного потока Т g ^^.^ (U) на открытом подмножестве
С/ с С" и каждой точки q число Лелона
в (Г, д) > О,
которое равно нулю для гладких потоков, а с другой стороны,
равно кратности аналитического множества Z в точке д:
в {Тг, д) = mult, (Z).
Для простоты предположим, что U = С", а д является
началом координат. Введем обозначения
5[r]={z6C": ||2||<г},
X (г) = характеристическая функция множества В [г],
5 [г, i?] = {z 6С": r<||z||<i?} (г<Д),
v—i
со = -
(^dziAdzt).
1) К интегралу \ в ( log | / (z, w) \ " _ ■ dw j , так как можно
предполагать, что форма а сосредоточена в области | z |, \ w \ ^1.—Прим.
пеРев.
2. Применение потоков в комплексном анализе 417
Как упоминалось выше, переход к монотонным пределам позволяет
определить действие потока на подходящих L^-формах, таких,
например, как х(г)-со"-р. В случае Т = Т^
rza(r)co"-P)= j со"-" = объем (Zn 5 И)
ПО теореме Виртингера из § 2 гл. 0. В общем случае положим
Тогда справедлива следующая
Лемма, в (Г, q, г) — возрастающая функция от г.
Доказательство. Сглаживание Ге замкнутого положительного
потока есть снова замкнутый положительный поток. Используя
это, достаточно доказать лемму для потоков Т = Т^, отвечающих
гладким замкнутым {р, р)-формам i|5. Тогда
^(T,q,r)=-^ j г|,лсо"-Р =
Bin
_j/_lpp__^ J г|)Л(55||2||Т-^ =
в [г]
^j/_ljn-P_^ J d(i|,A5||z|PA(55||2|ir-^-') =
в И
(ввиду замкнутости формы \р)
дВ1г]
(по теореме Стокса)
Но на сфере ||z|| = r
0 = d(2, z) = (dz, z) + (z, dz)^d~dlog{z,z) = d(^j^) = ^^-^,
так как {dz, z) л (z, dz) = —{dz, z) л {dz, z) = 0. Поэтому
последний интеграл равен
^/_ljn-P j г|) л 5 log II z||2 л (55 log II ZIP)"-"-'.
27-046
418 3. Дальнейшие методы
Согласно теореме Стокса для г < Д (напомним, что д — начало
координат), имеем
в(Г^, д, Д)-0(Г^, д, г) =
= J ^^{(^Y'''diog\\z\\^A(ddlog\\z\\Y-^-') =
9B[r, Я]
в [r, Я]
где £2 = -^у—^51og||z||*—прообраз на С" метрики Фубини—
Штуди, заданной на Р"~*. Но так как i|jaQ""^>0, лемма
доказана. О
Определение. Числом Лелона называется
Очевидно, что 6 (Г, д) ^ Ои 6 (Г, q) тождественно равно нулю
для гладкого потока Т. Как отмечалось вьопе,
в (Гг, q) = mult, (Z)
для потоков, заданных аналитическими подмножествами.
Набросок докагателъства. Согласно доказательству
предыдущей леммы,
в(Гг, 0) = lim ( Й""*,
где Z [г] с Р""^ — подмножество прямых Oq с g 6 ^ {] В [г],
Q — стандартная кэлерова форма на Р"~^. Предельное положение
Z [г] при г I О представляет собой касательный конус С (Z) к
многообразию Z в начале координат, и по теореме Виртингера,
примененной на этот раз к проективному пространству Р"~*,
J Q"-p = deg (С (Z)) = mult{0) (Z). ^Q
C(Z)
Это доказательство нетрудно провести полностью, а в том
случае, когда начало координат являетсй гладкой точкой на Z, оно
почти очевидно. Но только этот случай и понадобится нам в
дальнейшем. Ввиду полунепрерывности числа Лелона ...
в (Гг, д) > 1 для g 6 Z.
Опираясь на предшествующие работы ряда авторов, Сью
недавно доказал, что для общего замкнутого положительного потока
2. Применение потоков в комплексном анализе 419
Т множество точек, в которых в (Г, д) ^ е > О, лежит в
аналитическом подмножестве коразмерности р ^). Мы не будем
пользоваться этим результатом, однако его стоит иметь в виду при
обсуждении теоремы о собственном отображении из последнего
раздела этого параграфа. Фактически там доказан частный случай
теоремы Сью.
Индексы пересечения аналитических множеств
Пусть М — компактное ориентированное многообразие
вещественной размерности п. Для двух замкнутых потоков Т, S
дополнительной размерности их индекс пересечения определяется как
Г.5= |ГеЛ5в,
м
где Ге, S(, — гладкие формы, соответствующие классам когомо-
логий потоков Т ж S при изоморфизме
Н* {3!*{М), d)^Hln{M).
Этот индекс пересечения совпадает с обычным топологическим
индексом пересечения кусочно-гладких сингулярных циклов,
с v^-произведением гладких форм, рассматриваемых как потоки,
и с обычным спариванием \ ij; форм с циклами, если Т = Г^
г
для гладкой формы я); и 5 = Гг для кусочно гладкой цепи Г.
В случае комплексного многообразия М комплексной
размерности п спаривание
Я|'' (М) (8) ^-Р-"-'(М)-^С
задает индекс пересечения 5-замкнутых потоков дополнительймх
типов (р, q) и (п — р, п — q). При р — q для вещественного
{р, р)-потока Т и вещественного (и — р, п — р)-потока S
справедливы эквивалентности
dT^Q<^~dT=0, dS=0<^dS^O,
и индексы пересечения замкнутых потоков в смысле
дифференциалов d ж д совпадают.
Рассмотрим теперь замкнутый положительный поток Т типа
(р, р). Сглаживая когомологии, можно получить гладкий зам-
1) Y. Т. Siu, Analyticity of sets associated to Lelong numbers and the
extension of closed positive currents.—BuH. Amer. МаШ. Soe., 79 fl973).
1200-1205. . ' ^ "
420 3. Дальнейшие методы
кнутый вещественный (р, р)-поток Ге из того же класса когомо-
логий, что и Т. Более того, при подходящем выборе таких потоков
можно добиться того, чтобы
ПтГе = Г.
е-.0
Однако утверждать, что формы для Г^ положительны, нельзя.
Пусть, например, М = Np — раздутие двумерного комплексного
многообразия N в некоторой точке р. Слоем над точкой р при
раздутии М -*- N является кривая Е ^ Р^- с нормальным
расслоением Н*, где Н -^-Р^ — расслоение с классом Чжэня -(-1.
Поэтому индекс самопересечения Е-Е = —1. Если Т^. — сглаживание
потока Те, то равенство
Е-Е
Ч
показывабт, что (1, 1)-форма для Г^ неположительна.
Интуитивно это объясняется тем, что Тс представлен гладкой
формой, сосредоточенной в трубчатой е-окрестности
многообразия Е, и потому должен зависеть от вида нормального расслоения
многообразия. Оказывается, положительность Те, есть нечто вроде
положительности кривизны нормального расслоения, а в нашем
примере это, конечно, не так.
Используя теорию потоков, передокажем теперь важный
результат из § 4 гл. О о положительности индексов пересечения
аналитических множеств, пересекающихся в изолированных
точках.
Теорема. Пусть Z и W — аналитические подмножества
дополнительных размерностей р и п — р в М, пересекающиеся по
конечному множеству точек из М. Тогда индекс пересечения равен
Z-W= "S rnp{Z, W),
peznw
где mp (Z, W) — число, зависящее только от расположения Z
и W в окрестности точки р, и
Гор (Z, W) > multp (Z) multp {W).
Доказательство. Покажем вначале, что подмножество W
можно считать гладким. Для зтого рассмотрим произведение М X М.
Из формальных свойств формулы Кюннета и двойственности
Пуанкаре получаем
Z-M= (Z X W)-A,
где справа стоит индекс пересечения s М х М подмножества
Z X Ж С диагональю А. Теоретико-множественно
' (z X W) пА= {(Р, рУ- pez r\w}.
2. Применение потоков в комплексном анализе
421
Далее, как было установлено в § 1 гл. О,
multpx, {Z X W) = multp (Z) multg (W).
Так как диагональ является гладким многообразием, то тем самым
общий случай сводится к случаю гладкого W.
Кроме того, предположим для простоты, что Z ж W
пересекаются в единственной точке Pq. Выберем в ее окрестности
голоморфную координатную систему (z, w) = (z^, . . ., Zp] w^, ...
• ■ •! и'ге-р), в которой подмногообразие W задается уравнениями
Z = О, а ограничение проекции (z, w) v-*- z я& Z есть конечнолист-
ное разветвленное накрытие. Положим U^ = {(z, w): || z || < е,
II w II < е} и i7 = Ui- Это иллюстрирует рис. 1.
Предположим теперь, что задан такой поток S 6 ^^.^-^ ([/),
что Tff \ц — dS. Пусть р — колоколообразная функция, равная 1
на i7g^ и имеющая компактный носитель в U. Тогда
T'w=Tw-d (р5)
— глобально определенный поток на М из того же класса кого-
мологий, что и Tw Более того, T'w = {Tw — pdS) — dp h S
— гладкий поток вблизи Z {]W. Поэтому определен интеграл
\ Tw, задающий индекс пересечения Z- W. Если Z^, = Z {] Ut,
z
то, в силу равенства Tw = О вблизи Pq, по теореме Стокса имеем
frw=lim \ Г{у = Ит- ( 5(p5) = lim [ S.
Z ^ z-z^ * " z~z^ * " az^
Формула
Z-W=lim { S
--«el
сводит задачу к чисто локальному вопросу.
422 3. Дальнейшие методы
В качестве потока S возьмем поток Гц, заданный формой Бох-
нера — Мартинелли
Р (z) = С„ {д log II Z ||2 л (55 log II Z liy-i),
рассмотренной в § 1 этой главы. Равенство 5Гв = Г{г=о}
совпадает с формулой Бохнера — Мартинелли для случая тривиальной
зависимости от параметров w. Пусть 5^ cz С — шар {|| z || <! е}.
Проекция Zg —> 5g является разветвленным накрытием с d ^
^ multp Z листами. Следовательно,
J s=d J p=d. a
Локальные индексы пересечения Шр {Z, W) будут обсуждаться
подробнее в § 2 гл. 5 для случая, когда ZmW — локально полные
пересечения.
Если W — гладкое подмногообразие размерности 1, то Z —
аналитическая гиперповерхность, локально задаваемая одной
голоморфной функцией /, и по предыдущему справедлива формула
Z.M= ^ ordpiflw).
peznw
Теорема Леей о продолжении и теорема
о собственном от,обраясении
Прежде всего напомним формулировку известной теоремы
Реммерта.
Теорема о собственном отображении. Пусть U и N —
комплексные многообразия, М cz U — аналитическое подмножество
и /: и -*- N — голоморфное отображение, ограничение которого
на М является собственным. Тогда образ f (М) является
аналитическим подмножеством в N.
Мы докажем эту теорему при одном дополнительном
техническом предположении, которое будет выполнено во всех наших
приложениях. А именно, потребуем, чтобы
Для каждой гладкой тючки р ^ М и каждой к-плоскости
Ар в касательном пространстве к М в тачке р (й; -^ и =
= dim М) существовало к-мерное аналитическое
подмножество Z в М с касательной плоскостью Лр в тючке р.
В приложениях U будет открытым подмножеством
алгебраического многообразия V, & Z — линейным сечением V.
2. Применение потоков в комплексном анализе . . 423
Наше доказательство теоремы о собственном отображении
опирается на приведенные выше сведения из теории потоков и
следующее утверждение.
Теорема Леви о продолжении (I). Пусть / — мероморфная
функция, жданная всюду вне аналитического подмножества V
коразмерности ^2 на комплексном многообразии М. Тогда f
продолжается до мероморфной функции на М.
Доказательство. Пусть (/)оо — дивизор полюсов функции /
на М — F, и пусть (/)оо — его замыкание в М. Если
предположить, что (/)оо — аналитическое подмножество в М, то можно
рассуждать следующим образом. Для произвольной точки р ^ М
пусть (/)оо = (g) в некоторой ее окрестности U. Тогда функция
g-f = h голоморфна в i7 П (М — V), а следовательно, согласно
теореме Хартогса, продолжается до голоморфной функции h ъ U.
Позтому hig является мероморфным продолжением функции /
на и.
Так как вопрос о том, является ли (/)оо аналитическим
подмножеством, локален для точек из М, то достаточно доказать
следующую теорему.
Теорема Леви о продолжении (II). Пусть V — аналитическое
подмножество^ коразмерности ^2 полидиска А" в С", а D —
подмножество коразмерности 1 в А" — V. Тогда его замыкание D
в А" является аналитическим подмножеством.
Доказательство. Это геометрический вариант теоремы
Хартогса. Реммерт и Штейн установили аналогичный общий
результат в случае codimZ) ^ (codim V) — I.
Начнем с нескольких редукций. Если мы докажем теорему для
неособых многообразий V, то отсюда при помощи стратификации
получится и общий случай. Действительно, пусть V —
подмножество особых точек на V, V" — подмножество особых точек на
V' и т. д. Применяя теорему для случая неособого многообразия
в достаточно малых окрестностях точек р ^ V — V', мы
заключаем, что D продолжается на А" — V'. Повторяя зто рассуждение,
мы продолжим Z) на А" — V, и т. д.
Далее, ограничиваясь подходящими окрестностями точек V
и выбирая соответствующие координаты, можно считать, что V —
линейное подпространство в С". Таким образом, существен
случай, когда и = 2 и V = {zi = Z2 = 0} — начало координат.
Остановимся на доказательстве теоремы в этом частном случае.
Общий случай получается аналогично.
424
3. Дальнейшие методы
)г,1<е
Пусть А' = {I zi К 1, I za К 1, г^фЩ ^ IS* X А.
Тогда, как мы уже показали в § 3 гл. О,
т (Л', 0) = т (А', ъ)
0.
Из точной когомологической последовательности,
ассоциированной с экспоненциальной последовательностью пучков, вытекает,
что Н^ (А', ©*) = 0. Следовательно, если D* = D [\ А', то
линейное расслоение [D*] -> А' тривиально, а потому аналитическая
кривая D* есть дивизор некоторой функции А g 0 (А').
Можно предполагать, что D не содержит прямой {z^ = 0}
и пересечению D П {^i = 0} соответствует конечное множество
точек проколотого диска О < \z^ I < 1 • Поэтому существует
окружность I Zg I = е, не пересекающая последнее множество.
По непрерывности при достаточно малом б множество {| z^ | ^
^ б, I Z2 I = е} не пересекает D (рис. 2). Для каждого z с 0<;
< I Zj I ^ б определен и непрерывен интеграл
1 Г йЛ
/■=1 J h
2л V . , ,
принимающий целые значения. Следовательно, D пересекает
каждый вертикальный диск {zi = С, \ z^ \ ^ е, О < | С | ^ 6}
одинаковое число раз d. Поэтому проектирование замыкания D на ось
Zj задает собственное отображение я: D —>- А, ограничение
которого является d-листным накрытием я: Z)* ^- А* над
проколотым диском. Если d = I, то мы получаем график ограниченной
голоморфной функции и наш результат следует из теоремы Римана
о продолжении. В общем случае мы воспользуемся теперь уже
хорошо знакомым приемом, использующим элементарные
симметрические функции. А именно, положим
d
Фг (z) =
2л / —1
l«2l=8
' h{zi, Za)
'2. V
(zi)S
v=l
где я~^ (zi) = {(Zj, z^^ ^ (Zi))}v Функции ф| (z^) голоморфны и orpia-
ничены в О •< I Zi I ^ б. Следовательно, они продолжаются до
2. Применение потоков в комплексном анализе А2Ъ-
голоморфных функций на всем диске. Рассмотрим тогда
многочлен от Zj
F (Zi, Za) = z^, + pi (Ф1 (Zi), . . ., 9d (Zi)) zf 1 + ...
• • ■ + Pdiffiih)^ • • •. Ф<i(z^))^
корнями которого являются точки (Zi, Z2,v(Zi)) при каждом
фиксированном Zi T>t 0. Очевидно, что F — голоморфная функции
в бицилиндре и ее дивизор равен D. Q
Замечание. Общий принцип состоит в следующем. Пусть.
Т^ сг А" — замкнутое подмножество, такое, что (1) проекция
я
W ^>- А^ является собственным отображением и (2) вне аналитиче-
ского подмножества Z с: А* эта проекция W* —* А* — Z {W* =
= W — п~^ (Z)) является аналитическим разветвленным
накрытием. Тогда И^ будет/с-мерным аналитическим подмножеством в А".
Теперь займемся доказательством теоремы о собственном
отображении. Прежде чем перейти к существу дела, проведем
несколько предварительных редукций.
1. Так как / {М) — замкнутое подмножество в JV, то задача
является локальной вблизи точки р 6 / (М) в N. Поэтому в
качестве многообразия N можно взять полидиск А'' = А в С.
Кроме того, можно считать М неприводимым, так как только
у конечного числа компонент подмножества М образы пересекают
заданное компактное множество в N. , )
2. Доказательство проводится индукцией по размерности п =
= dim М. Пусть М* = М — М, — комплексное многообразие-
гладких точек на М. Выберем точку ро 6 М*, в которой матрица
Якоби отображения /: М* -> С имеет максимальный ранг
к ^ п. Если к •<. п, то по предположению можно выбрать А;-мер-
ное подмножество S в М, проходящее через р^ и такое, что
ограничение / Is имеет максимальный ранг к. Назовем такое
подмножество S горизонтальным срезом отображения f: М ->■ С^. Из
теоремы о неявной функции очевидно существование такой
окрестности W CZ М точки ро, что / {W) = f {S f] W). Следовательно,
/ {М) = f {S) в силу неприводимости М.
Итак, достаточно доказать теорему для отображения /
максимального ранга п = dim М в некоторой точке р^ 6 М*. Мы
докажем, что в этом случае / {М) является п-мерным аналитическим
подмножеством полидиска.
3. Определим теперь поток S 6 3)^'>^ (А) (р = N — п),
который, после того как теорема будет доказана, окажется потоком
^f(M)- Итак, положим
5(ф).= 5 /*(ф), Фб^^'^А).
м*
•426 3. Дальнейшие методы
Поскольку отображение / собственное и голоморфное, S —
замкнутый положительный поток. Мы должны доказать, что он
задается интегрированием по аналитическому подмножеству, которое
и есть / {М).
Отметим, что в каждой точке g 6 / {М) число Лелона в {S,q) ^
> 1. В точках q = f (р), где р 6 М* и / имеет максимальный
ранг, это очевидно, так как тогда один кусок / (Л/), проходящий
через q, является комплексным многообразием. Следовательно,
в силу полунепрерывности, это неравенство справедливо на всем
f{M)-
4. Кроме того, можно предполагать, что 7V = п -f 1, т. е.
/ (М) должно быть аналитической гиперповерхностью. Точнее,
покажем, что для общей координатной системы композиция g
в диаграмме
j"^^ \ тг = проекция
Чд„+1
есть собственное отображение (возможно, на меньшем полидиске
А^). Если установить это и доказать теорему для 7V = /г -f 1,
то конечный набор аналитических функций вида h-n, где h 6
£ О (А"+1) и имеет дивизор g (М), определяет / (М).
Чтобы доказать существование таких хороших проекций,
рассмотрим общую линейную форму А. на С и положим kf = kof.
Тогда уравнение А.^ = О задает подмножество
Мх = /"* (гиперплоские сечения на / (М)).
Согласно предположению индукции, образ отображения /: М,, ->
->- Д^-1 является аналитическим множеством размерности^п — 1.
Для общей координатной системы все координатные проекции
/ {М},) -^ А" будут собственными отображениями.
Чтобы завершить доказательство, сделаем следующее
наблюдение. Предположим, что в пространстве С X С^ X С' с
координатами (и, 1*1, . . ., Vp, Wy, . . ., Wq) = (и, V, w) задано
замкнутое подмножество S полидиска А X А^ X А', выделенного
условиями I ц К е, | у^ | < е, | и„ | < е. Пусть S^ = S {\
П (и = 0} и проекция iSq -> А^, индуцированная отображением
(О, V, w) \-* V, является собственной. Тогда при подходящем е
проекция 5 -> А X А^, индуцированная отображением (и, v,
.w) н-». (и, v), снова является собственной.
После этих редукций мы подошли к существенному моменту.
Завершение доказательства. Идея заключается в следующем.
Пусть задано собственное голоморфное отображение f: М ^>- A"+^
3. Класса Чжэня 427
максимального ранга п в некоторой точке ро 6 ^*- Пусть W а
а М — объединение подмножества особых точек на М и
подмножества точек, в которых якобиан отображения / имеет ранг <.п.
Согласно предположению индукции, / {W) — аналитическое
подмножество коразмерности >2 в А"+^. Образ достаточно малой
окрестности точки р ^ М — W является куском гладкой
аналитической гиперповерхности в А"+* и
f {М -W) = f {М -W) [j f {W).
Поэтому задача состоит в том, чтобы показать, что два куска
/ {М — W)iif (W) хорошо подогнаны друг к другу. Как мы знаем,
сопоставление
м*
задает замкнутый положительный поток S 6 ^Э^^^^ (А"+*).
Согласно 5^-лемме Пуанкаре, имеется представление
г ддц),
где ф — некоторое вещественное распределение на А"+*. Вблизи
точки ? 6 / {М — W), лежащей вне подмножества / {W)
коразмерности ^ 2, образ / (М) локально является 'дивизором
голоморфной функции h. По формуле Пуанкаре — Лелона дд (ф—log | h\)=
= О вблизи q, т. е. ф — log \h \ — вещественная часть
голоморфной функции/. Тем самым доказано, что поток Э = 9ф = d log h -f
+ dj (локально) задает замкнутую мероморфную 1-форму на
Дп+1 — f ^\Y). По теореме Леви о продолжении форма Э
продолжается до мёроморфной 1-формы на всем A"+i. Дивизор полюсов
формы Э содеряКйт / {М — W) и позтому равен / (Л/). Эквивалент-
НО, / {М) есть дивизор голоморфной функции е J .
Тем самым доказательство теоремы о собственном отображении
завершено.
3. КЛАССЫ ЧЖЭНЯ
Определения
В этом параграфе мы определим и изучим некоторые свойства
фундаментальных топологических инвариантов комплексных
векторных расслоений — классов Чжэня. Собственно голоморфными
расслоениями мы займемся позже, а пока будем рассматривать
многообразия и векторные расслоения класса С°°.
428 3. Дальнейшие методы.
Напомним вначале некоторые определения из § 5 гл. 0.
Пусть М — многообразие, Е —> М — комплексное векторное
расслоение, ji^ {Е) — пучок ^-значных р-форм, т. е. пучок С""-сече-
ний расслоения Д^ Т* {М) ® Е. Связностью D яа. Е называется
оператор
D: А'{Е)^А'{Е),
удовлетворяющий правилу Лейбница
где / 6 С* (£/), ^ 6 ^^ (Е) (£/). Тривиализация ф„: Е \jj^-^
-> £/д X С" расслоения Е над Ua cz М позволяет отождествить
сечения ^ расслоенияЕнад £/„ с п-векторами ^„ = *(^„, i, . .., ^а,п)^
компонентами которых являются функции на i7„. В репере
{^а, i} расслоения Е над £/„, отвечающем постоянным векторам
(О, . . ., 1, . . ., 0), имеем
■Оба, г = 21Э„, j,;® е„, ;.
Матрица Э„ = {Qa,i,}) из 1-форм называется матрицей связности
для D. Тогда для общего сечения ^ 6 с^" (Е) (С/д)
Если фв-' Е \щ-)- Ug X С^ — другая тривиализация
расслоения Е над UgCZ М с (fa =^ав'ФвИС матрицей связности Эр
при тривиализации фв, то
Отметим, что Э нелинейно зависит от выбора репера, т. е. Э не есть
тензорное поле для Е. Действительно, решив уравнения ^„в (^о) —
= id и dgaB (я^о) = —^а (^о)) мы сможем выбрать тривиализацию
расслоения Е в окрестности любой точки х^ 6 М, в которой
матрица Эв {хо) связности/) обращается в нуль в точке Хо-
Связность/) продолжается до оператора D: Jf^ (Е) -> ^«+1 {Е)
по правилу Лейбница, а именно для ^ £ ^" {Е) и д-формы т]
положим
D {y]®l)=dr]®l + (-1)9т) А Die ^^+^ (^)-
Определим теперь оператор кривизны в формулой
8 = /)2: ^3 (Е) -> ^«+2 (^).
При тривиализации ф„ имеем (в^)„ = в„^„, где в„ — матрица
2-форм в„ = dQa — 9а Л Эа- Она называется матрицей кривиз-
3. Классы Чжаня 429
ны связности D при тривиализации ф„. Для другой тривиализа-
ции фц, такой, что ф„ = ^«вФв'
Это правило перехода выражает тот непосредственно проверяемый
факт, что в — линейный оператор над кольцом функций С°° {M)i
т. е. в 6 А^ (Нот {Е, Е)).
В случае линейного расслоения Е матрица кривизны в
соответствии с приведенным правилом перехода является глобальной
2-формой и, как мы уже видели, класс когомологий [(]/—1/2я) в],
называемый классом Чжэня расслоения Е, отражает
топологическую структуру расслоения Е. Прежде чем определить классы
Чжэня для произвольного векторного расслоения, мы сделаем
небольшое отступление и рассмотрим функции на пространстве
матриц, инвариантные относительно сопряжений.
Пусть аМп ^ С"' — векторное пространство п X ге-матриц.
Однородный многочлен Р: аМ^ ->- С, степени к относительно
элементов матрицы, называется инвариантным, если
Р{А) = Р (gAg-^)
для всех А 6 еЖп, g ^ GL (п). Основные примеры таких
многочленов Р (А) доставляют элементарные симметрические многочлены
от собственных значений матрицы А, т.е. многочлены Р^ {А),
определяемые соотношениями
п
det{A + t-I)='Z P'^-^iA)^t^^.
ft=0
в частности, Р" {А) = det (Л) и Р^ (А) = tr {А). В общем случае,
обозначая для любых мультииндексов I, Jcz {i, . . ., п] через
Aij минор {Ai])i^i^j^j матрицы А, мы видим, что
Р>ЧА)= S det(^r,^) = tr(AM).
Многочлены Р* называются элементарными инвариантными
многочленами. В действительности любая голоморфная функция / на
а^п, инвариантная относительно сопряжения, выражается в виде
степенного ряда от Р*. Положим
Ai О'
Р{ки ...,Я„) = / ■ •
\о к
тогда F — симметрическая голоморфная функция от А.^, . . ., А.„.
Напишем
F{ki, . . ., К) ^G{Oi, . .., а„).
430 3. Дальнейшие методы
где Oi, . . ., а„ —элементарные симметрические многочлены от
Xi\ тогда равенство
f{A) = G (Pi {А), ..., Р" (А))
выполняется на связном и всюду плотном открытом множестве
полупростых (т. е. диагонализируемых) матриц в GL (п), а
следовательно, на всем пространстве а^п.
Далее, А-линейная форма
Р: (Лп X . . . X a^n^G
называется инвариантной, если для всех Л^, . . ., y4j, ^ а^„, g 6
6 GL (п) справедливо соотношение
Р (А^, . . ., А^) = PigAig-\ . . ,, gA^g-^).
Каждая инвариантная форма Р, очевидно, задает инвариантный
многочлен Р:
Р{А) =Р,{А А).
Обратное также верно: любой инвариантный многочлен Р степени к
можно представить как ограничение симметрической
инвариантной А;-линейной формы Р на диагональ в в^„ X ... X в^„.
Форма Р, называемая поляризацией многочлена Р, восстанавливается
по Р однозначно. Например, при к = 2 имеем
Р{А, В)=\{Р{А + В)-Р{А)~Р {В)).
Построим теперь поляризацию многочлена Р^ в общем случае.
Для {А^, . . ., А^) 6 (а^п) > подстановки т g 5^ и мультииндекса
/с: (1, . . ., га} порядка к обозначим через А\ к X А;-матрицу,
г-й столбец которой совпадает с i-u столбцом минора AYJ. Тогда
P'4Ai ^л) = 1г2 Е det(^J),
и поляризация произвольного инвариантного многочлена,
записанного в виде многочлена от элементарных инвариантных
многочленов Р*, представляется столь же малопрозрачной формулой.
Вернемся теперь к нашему комплексному векторному расслое-
ниш Е —> М ранга п. Пусть {£/„} — открытое покрытие
многообразия М с тривиализациями ф„ расслоения Е над £/„, с матрицей
связности Э„ и матрицей кривизны в„ связности D яа. Е при трй-
виализации ф„. Тогда ввиду коммутативности внешнего
произведения на формах четной степени для любого инвариантного много-
3. Классы Чжэня 431
члена Р на аМп степени к выражение Р (в„) определяет форму
степени 2к на £/„, а из соотношения
вытекает, что
Р (в„) = Р (вв) на £/„ П С/в-
Поэтому Р (в) = Р (в„) — глобальная 2к-форма на М, не
зависящая от выбора тривиализации. Основной [результат о таких
формах — следующая
Лемма. Для любого инвариантного многочлена Р степени к
имеют место следующие ут^верждения.
1. ЙР(в„) = 0.
2. Класс когомологий [Р (в„)1 6 Н^^ {М) не зависит от выбора
связности на Е.
Доказательство. Записывая Р (в„) = Р (в„, . . ., в„) для
поляризации Р многочлена Р, по линейности получаем, что
dP{&a) = IlP{Qa, ■■., ав^, ..., в„).
Но в„ = dQa — Эа л Э„. Поэтому йв„ = йЭ„ д е„ — е„ л
л d0„. Форма Р (в„) инвариантна относительно замены репера
на Е, и, как мы уже знаем, для любой точки Xq ^ М существует
такой репер на Е, в котором матрица Gg обращается в нуль в х^.
Итак,
^Р(в„)=йР(вр) = 3±Р(вэ, ...,d%A%~%Ad%, ..., вр)=!-
=4^ dP (вр) (хо) = О =4^ dP (вр) = 0.
При доказательстве утверждения 2 нам потребуется одно
тождество для инвариантных форм. Рассмотрим голоморфную
функцию на GL (п), заданную равенством
f (g) = Р (gAig-\ ..., gA^g-')
для некоторых фиксированных А^, ..., Л),6®^п- Используя
в качестве координат на GL (п) элементы матрицы g' = g — I,
вычислим линейный член Д степенного разложения функции /
вблизи /. Прежде всего имеем
(/ + g')-' = i-g' + т.
-432 3. Дальнейшие методы
Поэтому
j{g) = P{gA,g~\ ...,gA^g-^) =
= P((I + g')Ai{I-g') {I + g')A^(I-g')) + [2]^
^P(A, A„) + y]P(Ai, ...,g'Ai-Atg', ..., Л) + 12].
{
В силу инвариантности формы Р имеем f = Р {Ai, . . ., Л л),
а значит, все члены ненулевого порядка в степенном разложении
функции / обращаются в нуль. В частности,
y>P(Ai, ...,g'Ai-Aig' Л) = 0.
i
Пусть теперь ф — некоторая 1-форма, g — матрица функций,
-4| — матрицы форм степени d;. Тогда, в силу полилинейности,
^{-lf'^--^'''-'P{A„ ...,^AgAi Л) =
i
= 2флР(Л1, ...,gA ,Л) = ЗфлР(Л. •■•Mig, ...,^ft) =
i г
^^{-D^'^-'-^^'PiA, {AtA^)g A,).
i
В общем случае произвольную матрицу 1-форм 0 можно
представить как 3^я^я> ^Дб ^а суть 1-формы, а ^„ — матрицы функций^
откуда снова по линейности
i
= y]{-if^"'^'''P{Ai AiAQ, ..., Л^).
i
Теперь можно приступить к доказательству утверждения 2,
Пусть D, D — две связности на £" с матрицами связности и
кривизны Э„, Э„ и в„, ё„. При тривиализации ф„ имеем
следовательно, оператор ц = D — D линеен над С°° {М).
Поэтому в тривиализации ф„ он эадается умножением на матрицу,
транспонированную к матрице tia = Э„ — Э„, которая
преобразуется по правилу У]а = ^арЛв^йр' ^Дб gaB = фа'Фр*- РаССМОТрИМ
гомотопию
Dt=D + tr\, 0<t<l,
3. Классы Чжэня 433
между Df) = D тя. Di = D. Матрицей связности для Df является
в( = Э + ^т). Поэтому соответствующая матрица кривизны имеет
вид
Ot = d (0 + Щ) - (0 + Щ) Л (в + ti]).
Пусть Р — инвариантный многочлен степени к. Утверждается,
что
[Р(в)] = [Р(в)]6Я?,'к(М).
Чтобы доказать это, рассмотрим кривую t >-* Р (в^) в А^ {М) и
покажем, что каждый касательный к ней вектор {didt) Р (0() лежит
в подпространстве dA^^~^ (^f)c: А^^ {М). Отсюда вытекает, что
ее обраэ t \-*[Р (в() ] 6 Ягщ {Щ есть постоянная.
Действительно,
— в, = dt] — (0 л т) + т) л 0) — 2tTi л т).
Поэтому
Л.Р(в^) = -1^Р{в Qt) = kP(±et, @t в,) =
= kP{dr\, в(, ..., Ot) —/(;Р(0лт1 + т1Л0, 8^, ..., Ot) —
— 2ktP{r\Ar\, в(, ..., Ot).
По тождеству (•) для 0 = т]
Р{г\Аг\, &t, ..., &t)-{k-i)P{r\, Т1лв„ о, 8,) =
= -Р(т1лт1, 8, et)-ik-i)P(r\, 8,лт1, 8, 8,),
откуда
2ktP{r\ATi\, &t, ..., et) = tk{k-i)P(Ti\, TiA8t—8tATi, 8^,..., 8t).
Аналогично, no формуле (•)
^(Элт), 8, 8,)-(А-1)^(л,0л8, 8„ ...) =
= _Р(т,ле, 8 , вг)-{к-1)Р{г\, в,ле 8,, ...)
и
-кР{дмг\ + т1\Ад, ..., 8t, ...) =
= к{к-1)Р{у], 84ле-ел8(, ...,8t, ...).
28-046
434 3. Дальнейшие методы.
Значит,
_д_
at
±-P{et) = kP{dT,], &и ...,в«) +
Но для любой связности 0 с кривизной в выполняется равенство
йЭ = 0лв — вл0. Следовательно,
d@t = {Q + tr\) л et — @t л (Q + tr\),
и мы получаем в результате, что
-Lp(Qt)^kP{dy], Qt Qt)-k{k-i)P{y], dQt, •.•, ®t) =
= k.dP{r\, Qt, ..., Qt)- D
Замечание. Для тех, кто привык к общему формализму
дифференциальной геометрии, мы дадим набросок предыдущего
вычисления в более инвариантной форме. Прежде всего оператор
D: А'' (Е) -^ Л'+* (Е) продолжается до оператора на тензорных
расслоениях для Е. Далее, поскольку матрицу связности для
D можно в любой точке сделать нулевой, мы получаем тождество
Бъянки
Ов =0.
Применяя затем Р к алгебре А* (Нот (Е, Е)), мы находим, что
dP(A^ A,) = S (-l^"^" *■""''-'^ Hi DAt, ...,Л,),
i
где Лг 6 ^''* (Нот {Е, Е)). Значит, dP (в) = 0. И наконец, для
тех же Dt, 0(, 0t и т], что и выше, имеем {didt) 0^ = D{i\. Поэтому
d{kP(^, в, 0,)) = А^(/>,Т1, 0(, .... 0,) =
= '^^(i-®" ®' Qt) = ^P{Qt).
Другая формулировка леммы. Пусть Ф — градуированная
алгебра инвариантных многочленов. Тогда для любого векторного
расслоения Е -*■ М определим гомоморфизм алгебр
Ф Д ЯЬ*н(М)
формулой
рл1р{в)],
где 0 — матрица кривизны произвольной связности на Е; w
называется гомоморфизмом Вейля.
3. Классы Чжвня 435
В частности, пусть, как и выше, Р^ — элементарные инвариант»-
ные многочлены. Определим формы Чж$ня ci {&) кривизны в
на Е cooTHomeHneii ^"
.^«(^)=^U^®)'
а классы Чжэня ci (Е) — формулой
{Б)=[Р'(-^^е)]ен^п{М).
Полным классом Чжэня с (Е) называется сумма всех классов
Чжэня:
с{Е)=1>с,{Е)еН^А{М),
где по определению Cq (Е) ь= 1 g ЯЬн (М). В случае
комплексного многообразия М классами Чжэня с^ (М) многообразия М
называются классы Чжэня его голоморфного касательного
расслоения Г (М).
Отметим, что данное здесь определение класса q (Е)
согласуется с приведенным ранее определением класса Чжэня линейного
голоморфного расслоения.: Как станет понятно к концу этого
параграфа, классы Чжэня векторного расслоения являются чисто
топологическими инвариантами. Перечислим основные свойстве
классов Чжэня.
1. Прежде всего для любого С°°-отображения f: М -*■ N
комплексного векторного расслоения Е -*■ N
ст а*Е) = f*Cr (Е).
Чтобы убедиться в этом, эаметим, что для /любой связности
D на Е, открытого покрытия U = {Ua} многообразия N с репером
^1,о1 • • ч ^ft.o на Е над f/„ и матрицей связности 0„ для D в
репере {«1, о} матрицы
/*(ва) на f-Чи^)
определяют связность D* на f*E -*■ М с кривизной в {D*) =г
= Г (в Ф)).
2. Далее, пусть Е ^>- М, F -^ М — два векторных расслоения
со связностямиХ), D' и матрицами кривизны 0, 0' соответственно.
Тогда оператор
D" =D @ D': ^0 {Е ® Р)^ А^ {Е Ф F)
задает связность на расслоении Е ® F с матрицей кривизны
0':
1.0 в')
(436 3. Дальнейшие методы,
Отсюда очевидно равенство многочленов по V.
det (в" + tl) = det (в + t/)«det (в' + «/),
т. е.
е{Е ® F) = c{E)-c(F).
Это так называемая формула произведения Уитни.
3. Аналогично, для векторного расслоения Е ранга г,
линейного расслоения L и подходящих связностей ж& Е, L тя. Е® L
имеем
вЕ®в = вя ® 1+ /г ® вь,
откуда
ci (^ ® L) = [tr -^^^ вв^ь] = d {Е) + rci (L).
4. Наконец, если 0 — матрица кривизны некоторой связности
на комплексном векторном расслоении Е, то двойственная
связность на Е* имеет матрицу кривизны —0. Значит,
;;:; с^ {е*) = {-iy с, (Е).
Воспользуемся теперь формулой произведения Уитни для
вычисления классов Чжэня С/ (Р") проективного пространства.
Итак, пусть я: С"+^ — {0} -^ Р" — стандартная проекция,
Хд, . . ., Xji — линейные координаты на С"+^, а Ж/ = Xi/Xg,
i = i, . . ., п,— соответствующие аффинные координаты на Р".
Тогда
Ag
Поэтому для точки X 6 С"^* образ при отображении я
касательного вектора d/dXi задается равенствами
S _ i д ._.
я^
д -л Xj а
XI ' dxi '
Из этих вычислений следует, что
1. Для любого линейного функционала I (X) на С"^*
векторное поле V (Х) = I {X)dldXi опускается на Р", т. е. n^v {X) =
= я^у (Я,Х) для любых X 6 С"+1, Я, 6 С. Обозначим через я^у
индуцированное векторное поле на Р".
3. Класса Чжэня 437
2. Касательное пространство Т'х (Р") к Р" в точке х = п {X)
порождается векторами {n^5/5Xj}j=o „ с единственным
соотношением
YiXtn^dldXi=Q.
Напомним теперь, что слой расслоения гиперплоскости if->- Р"
над точкой а: = я (X) 6 Р" находится в естественном соответствии
с линейными функционалами на прямой С {-X^lc: С"+*. Поэтому
определен морфизм расслоений
ЯФ(п+1) = Яф ... фяЛг(Р"),
n+i
при котором сечение а = (Oj, . . ., а„) расслоения ЯФ^"+*^
переходит в
Согласно утверждению 2, отображение % сюръективно, а его
ядро есть тривиальное линейное расслоение, порожденное
сечением т = (Zj, . . ., Х„). Итак, имеется точная
последовательность расслоений на Р":
0->-С-^ЯФ("+*)-»Г (Р")-^0,
которая называется последовательностью Эйлера. Из С°°-разложв-
ния ЯФ("+*) = 7" (Р") ф С и формулы произведения Уитни
получаем, что
с (Г'(Р")) = с (ЯФ("+*)) = с (Я)"+» = (1 - ш)"+1,
где ш = Т1н 6 ^ (P"i Z) — класс, соответствующий
гиперплоскому сечению.
Формулы Гаусса — Бонне
Как мы уже знаем, первый класс Чжэня голоморфного
линейного расслоения двойствен по Пуанкаре классу цикла,
представляемого множеством нулей глобального, голоморфного сечения.
Имеется аналогичное геометрическое описание общих {классов
Чжэня, или, точнее, двойственных к ним по Пуанкаре классов
гомологии, и остальная часть этого параграфа посвящена этому
описанию. Вычисления не будут прямыми: вначале мы вычислим
классы Чжэня универсальных расслоений на грассманианах,
а затем по функториальности классов Чжзня получим нужные
формулы для общих векторных расслоений.
Напомним, что для строго возрастающего флага
О = FoC Vycz . . .с F„_ic: F„ = С"
488 3. Дальнейшие метода
Линейных подпространств в С" и для любой невозрастающей
последовательности к целых чисел а^, О ^ а/ ^ и — к, мы определили
в § 5 гл. 1 цикл Шуберта о^ {V)cz G (к, п) в грассманиане А;-пло-
скостей в С":
Оа (>") = {Л: dim (Л П F„_ft+,_„^)>0.
Цикл Оа {V) является аналитическим подмногообразием в G {к, п)
коразмерности ^j^»' фундаментальный класс а а которого не
зависит от выбора флага V; как мы уже знаем, целочисленные
гомологии грассманиана свободно порождены классами a^.
Напомним также, что универсальным подрасслоением S -*■
->- G (к, п) называется подрасслоение тривиального расслоения
С" X G {к, и), слоем которого над точкой А Е G {к, п) служит
А;-плоскость Л с: С"- Обозначим через а* коцикл, двойственный
по Пуанкаре к циклу Од. Основной результат составляет
следующая
Теорема Гаусса — Бонне I. Имеет место формула
c,(5) = (-l)'-at 1.
Доказат£льство. Согласно нашим вычислениям спаривания
Ь Н^ (G (к, и), Z), нужно доказать, что для любого цикла
Шуберта Оа размерности г
Сг(5) (а„) = (-!)'•#(01, ,.aj =
f ( —l)*", если а = п — к,...,п—к, п—А—!,...,«—к—1,
1 О в остальных случаях.
Прежде всего заметим, что для любого цикла Шуберта Од (V)
размерности г и любого а Ф п — к, . . ., п — к, п — к — 1, ...
. . ., п — к — 1 число а^-г+1 обязательно равно п — к, т. е.
Оа (V)ci {Л 6 G {к, п): Л гэ V)^.r+^}■ Следовательно, взяв
произвольный базис е^, . . ., eft_r+i в Fj,_r+iC: С", мы получим, что
все соответствующие сечения б/ тривиального расслоения С" х
X G {к, п) лежат в S над Оа {V). Поэтому сечения б/
расслоения S |о (Г) продолжаются до А; — г -\- i всюду линейно
независимых сечений е^ расслоения S над некоторым открытым
подмножеством Ucz G (к, и), содержащим а а {V). Пусть S' -^ U —
тривиальное подрасслоение расслоения 8\ц, порожденное сечениями
е^, . . ., gft-r+i, а S" -^ и — соответствующее факторрасслоение
расслоения S\a по S'. Так как S' тривиально, то с {S') = 1. По
формуле Уитни с iS\u) = с {S"); стало быть, с^ (S) {оа (V)) =
= Сг {S") {оа {V)) — о, поскольку S" имеет ранг г ~ 1.
Положим теперь
Zj. = a„_h n-ft, n-ft-1 n-ft-i (У) = {A: Fft_r c: A[c: 7^+ J.
3. Классы Чжэня 439
Осталось проверить, что Cj. (S) (Zr) = (—l)*". Рассмотрим для
этого цикл
Zft=a„_ft_i „_ft_i iV) = {A:AczV^^i}czG{k, и).
Цикл Zft ^ Р (Vii+i)* двойствен проективному пространству
гиперплоскостей в Fft+j, а Zj.cz Zk — линейное подпространство
гиперплоскостей, содержащих V^-r- Более того, расслоение S]z^
является подрасслоением тривиального расслоения F^+i X Zk,
слоем которого над точкой А £ Zk служит гиперплоскость Лс
с: Vk+f Поэтому факторрасслоение Q расслоения Vk+i X Zk
по S является универсальным факторрасслоением на Zk ^ Р'',
т. е. линейным расслоением гиперплоскости. Обозначим через со
класс гиперплоского сечения в Zk s& Р**. Тогда с (^) = 1 + со,
а так как в классе С°°-расслоений
FftMXZ;, = 5U^©(?, l = c(5U,)(l + o)),
то c{S\z^) = 1 - ш + со* - со» + . . ., т. е. c{S\z^) = (—l)'©'.
ИтдК
'с, {S) (2,) = с, {S\z^) {Zr) = (-irco' (РО = i-iy. □
Заметим, что по формуле для двойственных классов Чжзня
имеем
с, (5*) = (-!)'с, (5) = (т? 1,
и поскольку {S* -*■ G {п — к, п)) ^ {Q -^ G {к, и)), то с^ ((?) =
= а*, где Q — универсальное факторрасслоение.
Формула Гаусса — Бонне дает следующую довольно
конкретную интерпретацию классов Чжэня в общем случае. Пусть М —
компактное ориентированное многообразие, Е -^ М —
комплексное векторное расслоение ранга к, & а = (а^, . . ., а^) —
глобальные С°°-сечения расслоения Е, Определим множество
вырождения Di (а) как множество точек х ^ М,в которых а^, . . ., а^
линейно зависимы, т. е.
Di (а) = {х: Oj (ж) л ... л at (ж) = 0}.
Набор сечений а назовем общим, если для каждого i сечение
Oj+i трансверсально пересекает подпространство в пространстве
расслоения £", порожденное сечениямиOj, . . ., ai, такчто^/+1 (а)
вне Di (а) является подмногообразием коразмерности 2 (к — i),
и если, кроме того, интегрирование по /?/+х (а) —Di (а)
определяет замкнутый поток по правилу, укаэанному в § 2 настоящей
главы. (Согласно результатам § 2, последнее имеет место, если все
данные комплексно аналитичны, а все размерности такие, как
нам нужно.) В этом случае на гладком многообразии Dj — Z)j_i
можно задать ориентацию. В окрестности точки ^jgDj —Z)j_i
440 3. Дальнейшие метода
ДОПОЛНИМ набор сечений е^ = ст^, . . ., е^.^ = а^.^ до репера в Е
и напишем
Oi{x) = yif]{x).ej{x).
Множество Df вблизи точки Xq является аналитическим
подмножеством (/( = .•.= /ft = 0). Пусть Ф^ — такая ориентация на
Di вблизи Xq, что форма
Ф| л -5^ (d/,+1 л d/,+i) л ... л -i^ (d/ft л dh)
положительна относительно заданной ориентации на М. Согласно
теореме о сглаживании когомологий из § 1 этой главы,
подмножество Di вместе с ориентацией Ф/ на D/ ~ ZJ/.j представляет цикл
в гомологиях, который называется циклом вырождения сечений а.
Пусть теперь Oj, . . ., а^ — общий набор сечений расслоения
Е. Используя разбиение единицы на М, можно построить
дополнительные сечения Oft+j, . . ., а„ расслоения £, такие, чтоOj (ж),...
. . ., сг„ (ж) порождают слой Е^ расслоения Е над каждой точкой
X ^ М. Тогда, согласно конструкции из § 5 гл. 1, сечения а^, . . .
. . ., а„ задают отображение i: М->- G {к, и). В некоторой тривиа-
лизации расслоения Е сечения а^, . . ., а„ можно представлять
как А;-векторы Fj, . . ., F„ С^-функций. Тогда отображение i
задается формулой
X ^ [(Fi (х), ..., F„ {х))] 6 G {к, п).
Так как подпространство i (ж) = Лс С" соответствует
линейным функционалам на слое Е^ расслоения Е над х, то, как и ранее,
I* (S) = £*, т. е. I* {S*) = Е.
Теперь для каждого г = 1, . . ., А; рассмотрим
подпространство F„_ft+r-i = {eft_r+2, • • •, е„}с: С". Тогда для любого а; 6
6 М А;-плоскость А — i (х) ^ G {к, п) пересекает F„_ft+r-i по
пространству размерности^ г в том и только том случае, когда
сечения Oj, . . ., aft_r+x линейно зависимы в х, т. е. i (М) пересекает
цикл Шуберта а^ i{V)c:G{k, п) по множеству вырождения
Z)ft_r+x сечений а^, . . ., Oft. Более того, для общих сечений
Oj, . . ., Oft пересечение i (М) с а^ ^ (F) трансверсально. Если
а ~ любой цикл вещественной размерности 2г на М,
трансверсально пересекающий Dk-r+i в точках pi, то i#a трансверсально
пересекает Oi 1 (V) в точках I (pi) и, согласно выбору ориентации
на Z)ft_r+i, индекс пересечения i^a с а^ ^ (F) в i (pi) равен
индексу пересечения а с Dk-r+i в /?/• Следовательно,
* (i»a-ai i) = «(a.Z)ft_,.+i)
3. Классы. Чжэня 441
И
Сг (Е) (а) = I* (с, {S*)) (а) = с, (5*) (i,a) = * (i*a-а, i) =
Значит, верна следующая
Формула Гаусса — Бонне II. Класс Чжэня с,. {Е) двойствен по
Пуанкаре циклу вырождения ZJ^.r+j.
Пример. Остановимся теперь на еще одном выводе формул для
классов Чжэня проективного пространства. Пусть Xj, . . ., Х„ —
линейные координаты на С"^^, а g и я^, как и вьппе,
гомоморфизмы, относящиеся к последовательности Эйлера. Рассмотрим
(и + 1) X (и + 1)-матрицу.4 = (а^^), все миноры которой
различны и не равны нулю. Она определяет векторные пол1
Проверку общности сечений у^, . . ., у„ расслоения 7" (Р") при
сделанных предположениях относительно А мы оставляем
читателю в качестве упражнения (для этого достаточно записать Vi в
локальных координатах на Р"). Мы же вычислим циклы
вырождения Di для таких сечений v^, . . ., у^. Прежде всего поле yj
обращается в нуль в точке X £ Р^ тогда и только тогда, когда
а так как по предположению ац ф О для всех i тя. ац Ф a^j для
всех i ф /, то это справедливо только для X = pi, где
Pt = [О, . . ., О, 1, О, . . ., 0], i = О, ..., п.
Итак, с„ (Р") = п + i. Далее,] Vi и v^ линейно зависимы в Z 6
6 Р", если существует пара {Х^, К^) Ф О, такая, что
Но так как по предположению все определители 2 X 2-миноров
матрицы А различны и не равны нулю, то это возможно только
тогда, когда все однородные координаты X, кроме двух, нулевые,
т, е. когда X лежит на прямой р/, pj для некоторых О ^1Ф ] ^г.
Следовательно, D^ есть объединение ("^ ) прямых/7|, pj] иначе
говоря, если со — класс, соответствующий гиперплоскому
сечению на Р", то
442 3. Дальнейшие методы
В общем случае сечения v^, . . ., Vq линейно зависимы в точке X
тогда и только тогда, когда все однородные координаты, кроме
некоторых q из них, нулевые, т, е.
■09= и Ри, Pi„ •■•, Pig
#I=g
есть объединение координатных {q — 1)-плоскостей,
порожденных точками Pi- Значит,
что согласуется с ранее полученной формулой.
В качестве непосредственного приложения выведем еще одно
тождество в дополнение к тем, которые упомянуты выше. Пусть
Е -^ М ~ комплексное векторное расслоение ранга к; тогда
первый класс Чжэня Cj {Е) двойствен циклу В^а X, заданному
множеством точек, в которых к общих сечений а^, . . ., а^
расслоения Е линейно зависимы. Но эти к сечений а^ расслоения Е
определяют сечение а = а^ л . . . л о^ линейного расслоения Д''£ ->-
—>- М, и множество вырождения D^ сечения а совпадает с Z)ft.
Проверив совпадение ориентации, мы получаем, что
Наконец отметим, что заданные общие сечения а^, . . ., Oi
определяют также циклы вырождения
1^ = {х: dimai(a:) Oi{x)^i — i}.
Дополним, как и раньше, сечения Oj, • • ., Oj до набора а^, ...
. . ., а„, порождающего каждый слой. Тогда цикл вырождения
Di' будет прообразом цикла Шуберта
<^i. ...i(l^n-M+i)={A: dimAny„-,./+i>A-i + l}
при соответствующем отображении i: М-)- G {к, и). Взяв
композицию I с изоморфизмом *: G {к, п) -^ G {п — к, и), найдем, что
Z)Ji) = (»i)-i(aft.,+i ft_,+i),
i
а так как с^ (Е) = {*i)*a,., то, комбинируя это равенство с
формулой Джамбелли, мы получим, что справедлива
3. Классы Чжэня 443
Формула Портеуса. Для общих сечений а^, . . ., а^
двойственным по Пуанкаре к классу цикла D\ является класс
{сп-1^ЛЕ) ...cj,_i^]{E)
в заключение выведем из общей формулы Гаусса — Бонне ее
классический вариант, что позволит объяснить также нашу
терминологию. Пусть М — многообразие вещественной
размерности 2и, Е -^ М — комплексное расслоение ранга и, а а —
глобальное С°°-сечение расслоения Е с невырожденными нулями
в точках Pv 6 М. Выберем для каждого v репер е^, . . ., е„
расслоения Е вблизи /7 V и ориентированные вещественные
координаты а: = {xi, . . ., х^п) на Z с центром р^. Тогда
а (ж) = 2 (alh + V^ blk) -Ха-еп {X) + [2], al^, К^ 6 Л.
Пусть Ар есть 2га х 2и-матрица {А", В"), где Л* = (ejf^) и 5* =
= {blk)- Тогда, если, как и выше, написать <т (ж) = 2/ft (^) • ej (х),
мы получим соотношение
<d/ftAd/ft)(Pv)=S {a^h + V^i baft)da:„AS (вм~К^Ьь*) dxb =
a Ь
= -2 Y'^ S alk-blk-dx^Л dXb,
откуда no простым соображениям из линейной алгебры знак точк
Pv в цикле вырождения Z)j сечения а равен
(_l)n(n-l)/2.ggndet(^p^.
Значит, по формуле Гаусса — Бонне II имеем
Сп (£) = S (-1)"<"-»)'2.sgn det (Ар^.
Рассмотрим теперь частный случай, когда М — комплексное
многообразие размерности и, Е = Т' (М) -^ М — голоморфное
касательное расслоение, а а — его С°°-сечение с
невырожденными нулями в точках р^. Пусть Zj = x^i.^ + У —ix^i, т. q. х =
= (^1, . . ., aijn) — ориентированная вещественная система
координат на М вблизи р^. Тогда если
v{z) = ^ (ajft + У-=Л Ь%) z,-±^+ [2],
ъ. Ар^ = {А'*, 5*) — матрица, определенная как выше, то
Сп{М) = ^{- !)»(»- 0/2 sgn det {Ар^.
444 3. Дальнейшие методы
Пусть теперь v' (z) = {v (z) + v (z))/2 — вещественное
векторное поле, полученное из v при вещественной проекции Т' (М) —>-
-^Т^{М). Тогда
поэтому индекс поля v в р^ отличается от знака определителя
матрицы Л р на множитель (—l)"("-i)/2. Отсюда по теореме Хопфа об
индексе (которая будет доказана в следующем параграфе)
X (М) = 2 (- l)"("-iW2 sgn det {ApJ,
и справедлива следующая
Формула Гаусса — Бонне III с„ (М) = х (Щ-
В своем изложении этого материала мы «обратили»
исторический ход событий. Классы Чжэня комплексных векторных
расслоений и аналогичные им классы Штифеля — Уитни
вещественных векторных расслоений первоначально были определены
при помощи теории препятствий; в таком определении
двойственность по Пуанкаре классов Чжэня циклам вырождения
очевидна. Затем Чжэнь открыл замечательный факт, что в
действительности эти глобальные топологические инварианты векторного
расслоения можно вычислять по локальной эрмитовой
дифференциально-геометрической структуре векторного расслоения; с тех
пор теорему Чжэня часто принимают в качестве определения.
Несколько (необязательных) замечаний о
классах Чжэня голоморфных векторных расслоений
Пусть Е -^ М — голоморфное векторное расслоение, базой
которого является комплексное многообразие М. Если выбрать
эрмитову связность, как в § 5 гл. О, то из зрмитовой симметрии
0 -Ь *0 = О матрицы кривизны в унитарном репере следуют
соотношения для форм Чжэня:
Ср (6) имеет тип (р, р), Ср (0) = Ср (0),
Поэтому в случае компактного кэлерова многообразия М
Ср (Е) 6 Я*." (М) П IP" {М, Z),
3. Классы Чжвня 445
т. е. классы Чжэня целочисленны и имеют тип (р, р) в
разложении Ходжа.
В случав когда М — проективное алгебраическое
многообразие, что по теореме Кодаиры о вложении эквивалентно
существованию положительного голоморфного линейного расслоения
L ->- М, можно сказать несколько больше. Пусть L —
расслоение гиперплоского сечения некоторого проективного вложения.
Прежде всего классы Чжэня расслоения Е ^ {Е^ V^) ^ L~'^
можно представить как многочлены от классов Чжэня
расслоений Е% V^ ж L~^. Класс Чжэня расслоения L~* равен
с (L-") = 1 - /ел
Dt
где D — гиперплоское сечение многообразия М, а согласно
теореме В из § 5 гл. 1, существует голоморфное вложение
M-^G(r, N) (г = rank Е),
при котором расслоение Е% V^ индуцировано универсальным
расслоением над грассманианом. Как отмечалось выше, классы
Чжэня расслоения Е® L^ двойственны по Пуанкаре пересечениям
М с подходящими циклами Шуберта. Итак, классы Чжэня
голоморфного векторного расслоения на проективном алгебраическом
многообразии предстлвляются в виде целочисленных комбинаций
фундаментальных классов алгебраических циклов.
Имеется также понятие положит£лъностм классов Чжэня
голоморфных векторных расслоений. Мы не будем рассматривать
его подробно, так как оно не используется при изучении
конкретных многообразий, однако отметим два момента. Как мы уже виде-
^1и в Конце § 5 гл. О, если Е -*■ М ^~ расслоение, порожденное
глобальными голоморфными сечениями, то существует эрмитова
связность с матрицей кривизны, заданной локально в виде вр —
= Е ^" Л А^» где А^ = J\A^jdz] — матрица (1, 0)-форм. Тогда
g-й многочлен Чжэня равен
а»<... <<з.^
а,<... <aq
..лЛ«л<9) = (1^-1)?' 2 %Л%,
|А=(|А« |ig)
446 3. Дальнейшие методы
где
а,<...<а^
— форма типа {q, 0). Следовательно,
для любого д-мерного аналитического подмножества Z в М.
Вероятно, еще интереснее неравенства типа Шварца.
Простейшее из них — неравенство
ci(0)2>2jc,(0).
где Z — двумерное аналитическое подмножество в М. Чтобы
упростить обозначения, мы приведем его доказательство в случае
ранга 2, опуская при этом знаки внешнего умножения и знаки
суммирования по повторяюпщмся индексам. Тогда
с, (6)2= \^£^'^\а\Д,+А1Д) {AiM + AUi) =
= [^^^]\-(А\,Ай]Л+А1АЩА1) + 2А\Л1Аи1}г
2c,{^^[^^^fkA],^AUi + 2AlAl.Am).
Отсюда
ci (0)2 - 2с, (0) = (-5^) ^ {AiAlAiAi + А^А^аШ - 2А1Д,Ат,
и неравенство
(Ci(0)2_2c2(0), (yL=-)4iATiATjAT,)>0
для (1, 0)-векторов т^, Тд следует из обычного неравенства Коши—
Шварца. Неравенства
св(^)>0,
с1{Е)>2сг{Е) и т.д.
выполняются для любого голоморфного векторного расслоения,
которое положительно в подходяш,ем смысле. Мы не будем
доказывать зто здесь, а рекомендуем читателю обратиться к работе:
S. Bloch, D. Gieseker, The positivity of the Chern classes of an ample
vector bundle.— Invent. Math., 12 (1971), 112—117.
4. Неподвижные точки и формулы вычетов 447
4. НЕПОДВИЖНЫЕ ТОЧКИ И ФОРМУЛЫ ВЫЧЕТОВ
Формула Лефгиеца для числа
неподвижных точек
Займемся теперь выводом формулы Лефшеца для числа
неподвижных точек, подсчитанных с учетом кратностей, эндоморфизма
f:M-^M компактного ориентированного многообразия М
размерности п в терминах соответствующего действия /* на когомоло-
гиях многообразия М. То, что такая формула существует,
подсказывают следующие простые соображения. Неподвижным точкам
отображения / соответствуют точки пересечения графика Tf с:
с. М X М отображения/с диагональю Ас: М X М. Но, как мы
уже знаем, индекс пересечения *(ГуА)мхм зависит только от
классов гомологии циклов Гу и А из Мх ^. Получить эту формулу
нетрудно; для этого достаточно найти выражение для класса кого-
мологий Т1д 6 Я" {М X М) диагонали А с: Л/ X ЛГ. Сделаем
это так. Для каждого целого q возьмем некоторый набор {'фц. q}
замкнутых д-форм на М, задающих базис в Ярн (М). Пусть
{i|3Jx,„_g} — набор (га — д)-форм, задающих двойственный базис
в ИМ (М), так что
) if^.qA If?, п-9 = бц, V
к
Обозначим через я^ и п^ естественные проекции М X М -^ М
на множители. Согласно формуле Кюннета, формы
{ф|А, V, р, 9 = "Т'1'V, р Л nt^t, q}p+q=h
задают базис в Япн (М х М). Двойственный базис в Н^'^ (М X М)
задается формами
{ф*. v.rn-p, п-«= (— 1)' ^"""'^ n?T|5j;, „-Р л njlfv, n-q}p+Q=k,
поскольку
J ф|i,v, р, g л ф|!1', V', п-р', п-9' = 6^1, ^1' • 6v, V' • 6p,jp' • 6,, ,',
AfXM
как видно из прямых вычислений, использующих повторное
интегрирование. Значит, класс т]д, двойственный по Пуанкаре классу
гомологии диагонали А с: Af X М, представляется формой
ФД = 2j ^Р, |i. *Фм., V, р, п-р)
р. li.v
где
Ср_ ц v= J фц,, V, п-р, р= { — 1) Оц_ V)
448 3. Дальнейшие методы
Т. е. т]д представляется формой
р. Ii
Пусть /: М-*■ М — отображение класса С°°. Неподвижная
точка р ^ М отображения / называется невырожденной, если она
изолирована и в локальных координатах л?!, . . ., а:„ на
многообразии М с центром в р матрица Якоби f-f (р): Тр {М) ->- Тр (М)
удовлетворяет условию
det iff (р)-1)ф 0.
При этих ограничениях мы определим индекс if (р) отображения /
в точке р как
ifip) ^sgn det if f(p)-I).
Условие невырожденности и определение индекса допускают
и другую интерпретацию. А именно, пусть Tf = {(р, f (р))} с:
CZ М X М — график отображения /. Тогда Tf —
подмногообразие S М X М. Зададим на нем ориентацию, индуцированную
отображением i- р *-*■ (р, i (р))- Пусть р — неподвижная точка
отображения f, & Xi, . . ., Хп — ориентированная система координат
на М с центром в точке р. Возьмем в качестве координат в
окрестности точки (р, р) ^ М X М функции
yt = n*Xt и Zj = n*Xt.
Тогда ориентированный базис в Г(р, р) (А) с: Т^р^р) {М X М)
задается набором векторов
'^* U^^i' ' дхп) [ду^ ^ dzi ' • • •'. дуп ^ dzni)'
где А — диагональное отображение а: ►-»■ (ж, х), а
ориентированный базис в Г(р_ р) (Tf) с: Г(р_ р) {М X М) — набором
7 (_L. g V 7 g I х^ g/< g _i__L'VJ[| L\
'*\dxi ' • • •' дхп)~\ду1^ ^ dxi' dzi ' • • •' дуп ~^ -^ dxn ' dzt ) '
Следовательно, набор векторов
(л.Ш.....л.(^),/.(^) 7.Ш)
получается из стандартного ориентированного базиса {д/ду^, . . .
• м д/дуп, д/дг^, , . ., 5/5z„) в Т^р^р) {М X М) линейным
преобразованием с матрицей
(In In \
\1п ff(p))
4. Неподвижные точки и формулы вычетов 449
Поэтому циклы Гу и А трансверсально пересекаются в (р, р) тогда
и только тогда, когда определитель
Л/ ffiP))
отличен от нуля, т. е. когда р — невырожденная неподвижная
точка отображения /, и в этом случае индекс отображения в
точке р, совпадает с индексом пересечения А и Ту в точке р. Значит,
если все неподвижные точки отображения / невырожденны, то
S 1/(р) = *(А-Гу)кхм
/(р)=р
и этот индекс пересечения вычисляется по формуле
*(А ■ Г/) = 5 Фд = 2 (-1)""" J 2 п?^. р А я|,|5|1. „_р =
Гу р Гу |i
поскольку /*Я2 = /*
р М |i
р р
Число 2 ("IV' t"" (/* 1нй (М)) называется числом Лефшеца
отображения/ и обычно обозначается L if). В результате нами
установлена следующая
Формула Лефшеца для числа неподвижных точек.
S ifip)^L{f).
Пр)=р
Отсюда видно, что число неподвижных точек, без учета знаков,
отображения / не меньше абсолютной величины L (/), т. е.
#{peM:/(p) = p}>|L(/)|,
и, в частности,
L (/) =5^ О =Ф- / имеет неподвижную точку.
Непосредственным следствием формулы Лефшеца является
доказываемая ниже теорема Хопфа об индексе. При тех.же
условиях на многообразие М, что и выше, рассмотрим на нём
глобальное векторное поле v класса С°°. Нульр поли v называется иевы-
450 3. Дальнейшие методы
рожденным, если он изолирован и в локальных координатах
Xi, . . ., а:„ с центром в точке р имеет место представление
с невырожденной матрицей А = (а^;); в этом случае индекс i„ (р)
поля V в точке р определяется как знак определителя матрицы А.
Интегрируя это поле по параметру t, мы получим поток fi'.M-^
-> М. При малых значениях t неподвижные точки отображений
fi совпадают с нулями поля у, и если поле v задано вблизи нуля р
как выше, то в локальных координатах х
ff {q) — е*^ + члены высшего порядка.
Значит,
И при положительных достаточно малых t
^ft (Р) = sgn det iff (p) — /) = sgn det A = i„ (p).
Поскольку fi гомотопно тождественному отображению, /* действует
на когомологиях многообразия М как тождественное
отображение. Позтому tr /?Lр ,„, = dim ЯЕв (М), т. е. L (ft) = х {Щ-
Итак, доказана следуюш,ая
Теорема Хопфа об индексе.
с(р)=0
Голоморфная формула Лефгиеца
для числа неподвижных точек
Рассмотрим теперь компактное комплексное многообразие М
размерности п и голоморфное отображение /: М -^ М. Тогда /
действует не только на когомологиях де Рама многообразия М,
но и на когомологиях Дольбо. Поэтому можно ожидать (по
аналогии с формулой Лефшеца для числа неподвижных точек), что зто
действие / на H*f {М) отражает локальное поведение / вблизи
неподвижных точек. Это действительно так, и оставшаяся часть
этого раздела посвяш,ена выводу соответствующей формулы.
Исходной точкой, как и раньше, является вычисление класса
когомологий Дольбо диагонали А с: Af X М. С этой целью
рассмотрим для каждых целых р, q набор {■фр,7,ц} 9-замкнутых
4. Неподвижные точки и формулы вычетов 451
{р, д)-форм, задающий базис в Я|''(-Л/), а также набор
{■фп-р.п-?,!!} 9-замкнутых форм, задающий базис в Щ~^'^~^{М),
двойственный относительно спаривания
Я|'' (М) (8) Щ-^' "~' (М) -> С,
которое определяется формулой
ifKg) Ф ►-► I If л ф.
м
Согласно формуле Кюннета из § 6 гл. О, формы
(фр, ч, ii, v= "iifip, 9, ii Л я|г|зЛ_р, „_,, v}
определяют базис в Щ'^(М хМ), а формам
{фп-р, п-9, |i, V = niT|5n-p, n-9, |i л Я^Трр, 5, v},
как и в вещественном случае, соответствует двойственный базис
в Я^'" {М X М). Класс Дольбо Т1д диагонали представляется
формой
Фд= S (-1)''^'Фр.,,^...
р. 9. |А
Рассмотрим теперь голоморфное отображение /: М ^>- М с
изолированными невырожденными неподвижными точками. Пусть
Vf = {(р, / (р))} CZ М X М — его график. Вычислив индекс
пересечения А VI Tf в М X М, получим только, что
i (/) = 5 ФД - S ( - 1)"'' 1 Б "lI'P- 9. ^^ л nllf^p, „_,. ^ =
Гу р, 9 Гу |i
в этой формуле, по существу, нет ничего нового: в случаекдагеро-
ва многообразия М она вытекает из обычной формулы Лефшеца
для числа неподвижных точек и разложения Ходжа; в общем
случае ее можно получить из формулы Лефшеца и рассматриваемой
в § 5 настоящей главы спектральной последовательности Фрёяшг-
хера, связывающей когомологии де Рама и Дольбо. Для
получения более точной информации о действии / на группах когоиоло-
гий Дольбо многообразия М обозначим через Т1д'' (р, д)-комц0нен-
ту класса диагонали Т1д при разложении по битипам
Я2' " (М X М) = е (я*Я|' ^^{M) (8) я^Я?-"' "-" (М))
P,Q.
^5? 3. Дальнейшие методы
И ПОЛОЖИМ ■Пд = Е ilA'• Тогда г^ представляется формой
а поэтому значение формы т)^ на цикле Гу равно
f я М ]1
q ^ Я
Hg'" ^(М) ^ ^ ' ' 'Hg'\M)
ло двойственности Ко дайры—Серра. Число
1](-1)Пг/*Ц.,^^
называется голоморфным числом Лефшеца отображения / и
обозначается через L(/, 0).
В соответствии с этим возникает вопрос: можно ли найти число
т]д (Гу), зная локальное поведение отображения / вблизи его
неподвижных точек. Несмотря на то что полное разложение форм на
М X М по битипам (см. § 2 настоящей главы)
Л". 9 (М X Л/) = е ^^''^• ''^^^^^' "'^ {М X М)
Pl+PS=P
91+92=9
не коммутирует с 5-оператором; более грубое разложение в прямую
сумму
4". 9 (М X М) = е А^^"-' *>'^Р-Рь 9-*^ {М X М)
Pi
обладает этим свойством (индекс • меняется от нуля до q). Это и
позволяет произвести. необходимые вычисления. Действительно,
если Гд — компонента потока Гд битипа (О, *), (га, га — *),
т. е. поток, заданный линейным функционалом
Тд(ф)= I ^(^("•"-«ЬС-?)
А q
на пробных формах ф, то Т% д-эамкнуЛг и представляет класс кого-
мологий Долъбо ц%,. Поэтому, чтобы вычислить т]^ (Гу), нам
остается сгладить поток Гд, т. е. решить уравнение для потоков
4, Неподвижные точки и формулы вычетов 453
где к есть (га, га — 1)-поток на М х М, а ф — гладкая форма. Тогда
Лд
1ИГ/)=$Ф.
Г/
Для этого, как мы увидим, достаточно решить уравнение (•)
локально вблизи неподвижных точек, к чему мы и переходим.
Напомним, что в первом разделе § 1 данной главы мы
определили ядро Бохнера — Мартинелли на С" X С" формулой
где
K[,Z, la) —Un \\z — t, P"
Ф| (ж) = (— 1) * Xt dxi л ... л dxi л • •. л dxn.
Ф (x) = dXi л ... л dXn.
Эта форма относительно переменных (dz, dz), {d^, dt,) имеет би-
тип (О, * —1), {п, п — *). Из равенства 5Ф|(г — ^ = Ф(г — ^
вытекает, что
dk{z,Q=0 на С"хС" —Д,
так что носитель потока, заданного ядром к (z, Q, лежит на
диагонали. Гомотопическая формула, доказанная в последнем разделе
§ 1, в действительности эквивалентна равенству потоков дк =
== Гд, которое задает требуемое «сглаживание» потока Т^ на
С" X С".
Вернемся к нашему комплексному многообразию М и
отображению f:M-*- М. Предположим, что / имеет изолированные
невырожденные неподвижные точки {р„} и представлено в локальных
координатах z^i вблизи р^ в виде
/ ЫI = S bifia} + [2], Т. е. / (г„) = 5„г„ + [2],
где 5„ = {btj); ввиду невырожденности неподвижных точек невы-
рожденны и матрицы (/ — 5„). Рассмотрим шар В^ (р„, р„)
радиуса ъ\ с центром в точке (р„, р„) на М X М и колоколооб-
разную функцию р„:
в 5е(Ра, р„),
О в МхМ-52е(Ра, Ра)-
Пусть к — поток на М X М, А: = 2 Ра-* (za. ^а). где
»хнвра — Мартинелли
'» = 1о
а
* (^а. 5а) — ядро Бохнера — Мартинелли. Тогда в В^{р^, р„)
имеем
45'4 3, Дальнейшие методы
Более того, ядро к гладко в& М X М — Д. Поэтому, если
положить ф = Гд — дк, то ф будет 5-замкнутым потоком,
представляющим т]д, гладким в некотором открытом множестве,
содержащем Tf, и равным —дк вне Д. Значит,
Г^ Гу-иВе(р„. р„) а Э(ГуПВе(Ра'Ра»
= Iim2 [ A(z„, /(z„)).
а ||z„||=e
,Для и'а = 2а —/(zj имеем
d«?„j л ... л dw^^ = det (/—j^ (/)) • dza^ л ... л dz^^.
Следовательно,
J й;(га,/(г„)) =
Ilzfl-E
(■ S ( —1)*'^ ""ttj «'"'a/ • • • '^d'^at^ ■ • • '^dw^^ Adz^^ A ... Adz„
J -^ ^ r. ::^
(|г||=Е
~^" j II "'a F"
_ Г Ij (- ^)'"^ "'g; '^V Л . • • Л d^a^A ■■■A dw^^ A dw^^ a... Adw^^
l|z||=e
1 1
— det (I ^f if) (0)) - det(I-Ba) '
согласно формуле Бохнера ^- Мартинелли, доказанной в § 1
этой главы. В результате мы получили голоморфную формулу Леф-
шеца для числа неподвижных точек:
«Ра)=Ра
Формула Ботта для вычетов
Изучим теперь вопрос об уточнении формулы Гаусса — Бонне
для голоморфных векторных расслоений на комплексных
многообразиях. В общем случае уточнения не существует, так как
множество нулей сечения о голоморфного векторного расслоения Е
йа комплексном многообразии не обладает никакой естественной
локальной структурой. Действительно, выбирая репер е =
= (е^, . . ., е„) расслоения Е и независимо от него локальную
4, Неподвижные точки и формулы вычетов 455
голоморфную систему координат Z = (zj, . . ., z„), мы можем
придать локальному разложению
Of (Z) = S bijZi • б; + S bijlZiZj • e, + . . .
сечения (T произвольную форму. Исключение составляют
голоморфные тензорные расслоения Е, например голоморфное касательное
расслоение Е = Т' (М) к М. В этом случав локальная система
координат (Zj) определяет естественный репер {d/dzi} для Т' (М).
Поэтому в окрестности нуля голоморфного векторного поля v
определена матрица Ар = {dij), для которой
v{z)=^^aaZ:-^ + [2].
Если и? = / (z) — любая другая система координат вблизи z = О
и матрица ^р = {a'lj) задается разложением
то
v{z) = ^a'ijWi.d/dWj + [2],
где g = (gij) = f if) — якобиан, соответствующий замене
координат. Следовательно,
v{z)= S atj-g'ik-Wi,-gird/dwi + [2].
i> ;. h, I
Поэтому
Ap = ^g~^-Ap-*g,
т. е. матрица Ар определена с точностью до сопряжения.
Следовательно, значение Р (Ар) любого инвариантного многочлена
Р на Л зависит только от у и р, и можно надеяться, что числа
Р (Ар) отражают какую-то глобальную информацию. Это
действительно так. Пусть 0 — матрица кривизны голоморфного
касательного расслоения Т' (М) компактного комплексного
многообразия М, Р — любой инвариантный многочлен степени п —
= dim М, V — глобальное голоморфное векторное поле, а
матрица Ар — такая же, как выше. Тогда справедлива следующая
Формула Ботта для вычетов.
^ det (Ар) J V 2ii " j '
т. е. если представить Р в виде многочлена Р = Q (Р^, . . ., Р")
от элементирных инвариантных многочленов Р% то
2 £r^=<?(^iW ^niM)).
D(P)=0
456 3. Дальнейшие методы
Доказательство *). Схема доказательства такова. На Т' (М)
выбирается метрика, являющаяся евклидовой в окрестности
нулей {р^} поля V. Пусть в — матрица кривизны метрической
связности на Т' (М). Тогда 0 ^ О в шаре Be (р^) с центром в р,
для каждого р^. Значит, мы построили такую С°°-форму Л типа
(га, га — 1) на М* = М — {р^}, что ЙЛ = 5Л = Р (0); поэтому
Но так как конструкция формы Л, по существу, локальна, то
последние интегралы определяются локальным поведением поля v
в точках р^.
Итак, пусть {Ру} — множество нулей поля у, z^, . . ., z„ —
локальные голоморфные координаты в В^е (Pv)) h^ — евклидова
метрика в В^е (Рм), для которой
{d/dzj, d/dzk) = 6^ft.
Далее, пусть ho — произвольная метрика на М* = М — {Pv})
а {ро, Pv} — разбиение единицы, подчиненное покрытию
многообразия М множествами Z7o"=M— U ^е (Pv) и U^ = В^^(р^);
в качестве метрики на всем М возьмем /t = Po-/to + S Pv'^v
Обозначим через 0 матрицу кривизны для соответствующей
метрической связности D. Очевидно, что 0 ^ О в 5g (р^) для всех v.
Рассмотрим теперь отображение расслоений
ДРЧГ' ® Д9Г ^ ДТ' ® Д'Г,
заданное внешним умножением на v (z) 6 T'f Оператор свертки
i{v): ЛМ (М)-^ ЛР-1.9 (М)
определяется как сопряженный к оператору Л У, т. е. для любых
Ф 6 А^'Ч (М) и т) 6 С" (ДР-^У ® Д9 (Г")) [имеет место равенство
<1 (у) ф, т)) = <ф, у л т)).
Поэтому если в локальных координатах zi
v{z) = }']v'{z)-d/dzj,
^) Мы приводим доказательство Чжаня, см. S. S. Chem, Meromorphic
vector fields and characteristic numbers.— Scripta Mathematica. v. XXIX,
pp. 243-251.
4. Неподвижные точки и формулы вычетов 457
ТО I (у) (dzt) = у* и (в [общем случае
i (V) (/ (Z) ■ dZj) = V] (_ if v'^ (Z) f (Z) dZi^u^y.
a
В частности, ввиду голоморфности коэффициентов у* и с учетом
знаков мы получаем, что
5-1 (у) + 1(у)-5 = 0.
Важнейшим шагом в нашей конструкции формы Л является
представление тензора i (у) (в) ^ А°<^ {Т' ® Т'*) в виде 5-диффе-
ренциала глобального сечения расслоения Т' ® Т'*. Напомним
для этого определение из § 5 гл. О кручения, ассоциированного
с метрикой на Т' (М). Как мы уже знаем, если у^, . . ., у„ —
унитарный репер в Т' (М), ф^, . . ., ф„ — двойственный корепер'
в Т'*, 9 — матрица метрической связности D в координатах
{У|}, а 9* = — '9 — матрица двойственной связности Д* на Т'*
в репере {ф^}, то
йф, = 2;9?^Лф; + т„
где Т{ — некоторая форма типа (2, 0). Вектор 2-форм т = (т^, . . .
. . ., т„) называется кручением метрики в репере {yj. Пусть теперь
{v'i = ^gij'V}} — другой репер, {ф{} — двойственный корепер,
а 6' и 6'* — матрицы связностей D и D* в реперах {У{} и {ф{}.
Тогда в матричных обозначениях, полагая g* = 'g"*, получаем:
соотношения
Ф' = ^*-ф,
6'* = g*.Q*.tg + d{g*).tg
и
т' = йф' _ 6'* л ф' = d (^*ф) — 6'* л ^*ф =
= d(g*)-(f + g*ц> — g*-Q*-*g-g*-4i — d{g*)-tg-g*-(f =
= ^*ф — g*-e* Л Ф = ^*-т,
т. е. величина т = 2''^г® ^t 6 ■4''° (^') является тензорным
инвариантом метрики. Она называется тензором кручения. Заметим,
что, как видно из наших вычислений, для любого другого, не
обязательно унитарного, репера v[, . . ., v'n на Т', но при тех же ф,.
6 и 6* имеем
т=1](^Ф;-Зв;глф;)®у;.
458 3. Дальнейшие методы
Пусть теперь (zj, . . ., z„) — локальные координаты нз М,
а 6 = (6,^) — матрица связности D в репере {d/dzi} на Т' (М).
Записывая 9^; = У] Tikdzk, получаем, что
k
i i, h i
Тензор кручения т в этом случав есть
т = — 21 0fi Л dzj ® d/dzj = 2 е^^ л dZf ® d/dzj =
i. 3 i, J
= 4 2 (rU-rii)-^®№,Arfzft).
i,;, ft
Следовательно, свертка i (у)-т g C°° (Г'® J'*) тензора ^ на у
задается формулой
i, j, ft
Поэтому тензор
E--Dv + .iv).r = -^{-^+^vLv^)±^®dz,
3, h г
определяет глобальное сечение голоморфного векторного
расслоения Т' ® Г* и
= -2(i^-'-ir«*')
С другой стороны, тензор кривизны Q ^ А^ {Т ® Т*) имеет вид
•а 1-1}
где 0jj —56jj=— 2—:?—•dzf,hdzi. Поэтому из формулы
i, ), h
МЫ получаем требуемое представление i (у) 0 = й^Б.
i. Неподвижные точки и формулы вычетов 459
Рассмотрим снова тензоры Q, Е шдЕ = i (у) 0 как матрицы 2-,
О- и 1-форм соответственно. Для любого инвариантного
многочлена Р степени п на GL (м) и его поляризации Р положим
Так как д0 = О и дЕ = У {v) 0, то
п-г
дРАЕ,в) = [''^)2 Р{Е,...,1{и).в,...,Е,е,...,в) =
= iiv)-Pr+iiE, 0).
Пусть со ^ Л*>''(Л/*) — форма, двойственная к v относительно
метрики на М; положим
Ф, = со Л (дй))"-^-1 л Р, (Е, 0) е ^". "-* (М*).
Тогда для О^г^п —1 имеем
дФг = (дсо)"-^ л Рг (Е, 0) - со л (dcof-i л I (у) Рг+1 (^- 0),
а так как i(i;)a) = l, то
0 = i(dv)(i)+i(v) да =^ i(y) да) = 0,
откуда
I (у) М), = (дсо)"-^ л I (i') Рг (Е, 0) - (дсо)"-^-! л I (у) Р,+1 (£■, 0).
Форма I (у) Ро {Е, 0) равна нулю по тривиальным соображениям.
Поэтому если
ф-"еф»-
i=0
то
п-1 _ п
I (у) дФ = S (^«)""* л I (у) Pj (£, 0) - 25 (5«)"-* л I (у). Pj (£■, 0) =
= -1(у)Р„(в)=-1(у)-Р(0).
Поскольку дФ и Р (0) — формы старшей степени, то из
соотношения I (у) (ЭФ + Р (0)) = О вытекает равенство дФ + Р (0) =
= О, что дает явное решение уравнения дА = Р (0).
Теперь остается проинтегрир1овать форму Ф по границе
Bg (р^). Напомним прежде всего, что метрика выбрана так, что 0,
460 3, Дальнейшие методы
а вместе с ней и многочлены Р^ (Е, в) обращаются в нуль при
г > О на всем шаре В^ (р^). Поэтому
J Ф= J Ро{Е,е)= J со л (5(0)"-'РС^-).
Пусть z = (zi, . . ., z„), как И выше, локальные координаты вблизи
точки pi, для которых (d/dzi, d/dzj) = бг; в В^ (Pv)- Положим
y(z) = Si^(z)5/5z^.
Тогда, поскольку наша метрика евклидова в шаре В^ (р^)^
связность D равна нулю и
dvi
^«=-(-£-+2:rU')=
т. е. Р (Е) (pv) = ~ Р {Ар^. Кроме того,
со = S у* dzi/ S У*"* = {dz, v)/{v, V),
откуда
Ят— (rfz, dv) . ((is, у) л {v, dv)
"'"- (у, V) "!■ (у, t-)si
Но (rfz, у) л (dz, у) = о, поэтому
(^)°.л(^г.=(-.г. (-ig-)"'^- -\;у"-'=
2 (—l)*-ii'*rfyiA ... Arfu'A ... Arfu"ArfziA ... Arfzn
С i
" iv, v)n '
где C„ — константа из формулы Бохнера — Мартинелли в § 1
1
этой главы, С„ = — д- р (у, у), где р — форма из той же
формулы. В [результате
= 2 i m^P('^''^)= (где ^-(5y,/5z^))
P (A )
= 2 det л'^ °" формуле Бохнера-^ Мартинелли. О
Б качестве примера применения теоремы Ботта для вычетов
подсчитаем (в третий и в последний раз) классы Чжэня проектив-
4. Неподвижные точки и формулы вычетов 461
ЛОГО пространства. Пусть X = (Xq, . . ., Х„) — координаты
линейного пространства С""*"*, п^ и g — гомоморфизмы, введенные
в § 3 этой главы, а (ао, . . ., а„) — любой (га + 1)-вектор,
состоящий из различных ненулевых комплексных чисел. Рассмотрим
на Р" векторное поле
п
V {X) = п* S а,Х, d/dXi
1=0
(так как п^. 2 Xi (dldXi) ^ О, то можно считать, что S "'г = 0).
Как мы уже видели, v обращается в нуль в точках рг = [О, ...
. . ., Ij, . . ., 0] и только в них. В евклидовых координатах
X} = Xj/Xt, j Ф t, на Р" в окрестности точки pi имеем
п# {Xj dIdXj) = Xj didxj, ]ф1,
Поэтому
п* (X, d/dXt) = — Ц ж, д/дх..
ь' (^) = S i^j — ^i) ^] dIdXj,
т. е. матрица Ар , задающая v в окрестности точки рг, является
диагональной матрицей с элементами (а^ — а^), / Ф i. Тогда по
формуле Ботта
так как ^j'^k—^- Чтобы вычислить значение последнего
выражения, рассмотрим мероморфные функции /, g на римановой сфере,
заданные в евклидовых координатах формулами
/(2)= П («ft-г), g(z)=z".
ft=0
Очевидно, что {g {z)lf (z)) dz = ф — мероморфный дифференциал
с простыми полюсами в точках z = «^ и z = схэ, а
Res„^ (Ф) - П . КвЗс„(ф) = (-1Г.
462 3. Дальнейшие методы
По теореме о вычетах 2 («?/П (°^j — °^i)) = (— !)"• Следова-
тельно,
'^^~r П(«/-«.-) ~^"+*^-
Но «-я степень класса когомологий со гиперплоского сечения
в Р" равна 1. Поэтому
ci (Р") = («+!) ю.
Теперь, чтобы найти оставшиеся классы Чжэня пространства
Р", достаточно вычислить числа Чжэня Cj (Р")""''-с^ (Р"). По
формуле Ботта для v
п (S («/-«^)Г'"-( |'П(«^-«'))
с,(Р")"-.с,(Р«) = 2 -^ п. '"?'" =
ifo .П. («'-«')
Для заданной выше функции / (z), для функции g (z) =
= z""*" 2 П ("'ft — z) и дифференциала ф = (g/f) dz находим,
как и раньше, что
гф{
Следовательно, по теореме о вычетах и равенству Cj (Р") =
= (га + 1) со получаем
СО'
Общая формула Римана — Foxa — Хирцебру ха
Напомним сначала доказательство формулы
с„ (М) = X {М)
для компактного комплексного многообразия М размерности п.
С одной стороны, по общей формуле Гаусса — Бонне, с„ {М) равно
4. Неподвижные точки и формулы вычетов 463
числу нулей общего векторного поля класса С" на М, с другой
стороны, по формуле Лефшеца для числа неподвижных точек
эйлерова характеристика многообразия М равна числу
неподвижных точек (с учетом кратностей)] отображения ф^: М-*-М,
полученного интегрированием поля v, т. е. опять равно числу
нулей векторного поля V. Теперь мы можем попытаться применить
по приведенной здесь схеме найденные выше уточнения формул
Гаусса — Бонне и Лефшеца для числа неподвижных точек в
голоморфном случае и получить формулу для голоморфной эйлеровой
характеристики комплексного многообразия.
Итак, рассмотрим компактное кэлерово многообразие М
размерности п и голоморфное векторное поле v н& М с
невырожденными изолированными нулями. Пусть ft = ехр (iti;): М-*-М
— отображение, полученное интегрированием соответствующего
вещественного поля по параметру t; отображение ft, очевидно,
голоморфно. Более того, если в локальных координатах Zj, . . ., z„
вблизи нуля р поля V
v{z) = ^atjZtd/dZ}+l2],
то якобиан функции ft (z) в точке р задается формулой
Вр = е'"*р, где Aj, = {a,j).
Для малых значений t неподвижные точки отображения ft
совпадают с нулями поля V, и по голоморфной формуле Лефшеца
^(/'•®)= И det(/-^p)
с(р)=0
Но так как отображение ft гомотопно тождественному, то /*
действует тождественно на Щ'' (М), и, следовательно, эта формула
означает, что
Ho при каждом t голоморфная функция Ft (A) =^ det (A) X
X (det (/ — e'-*))"* на GL (n) инвариантна относительно
сопряжения, a поэтому она однозначно записывается в виде степенного
ряда от элементарных инвариантных многочленов jP* на GL (п).
В явном виде для каждого полупростого оператора А g GL (п)
464 3. Дальнейшие методы
■С собственными значениями Яц . . ., А,„ имеем
-\ 8 ^ 24 ;^ +•••/-
- 24 г -+-..•/ ,
где суммирование производится по всем возрастающим индексам.
В общем случае коэффициент при it* заключенного в скобки ряда
можно представить в виде многочлена от элементарных
инвариантных многочленов. Определим теперь многочлен Тодда Tdi
соотношением
det4
det(/ —е""'-*)
{-\rt-^{'2,Tdi{P4A), .... P'{A))t').
Тогда формула Лефшеца для числа неподвижных точек,
примененная к f и /j, приобретает вид
VI 1 ' det Ар
=(-ir.-°2(S(-i)-"""'^x;"'^-")-''-
i D(P)=0
Но X (Ом)) очевидно, не зависит от it. Значит, все множители
справа при ненулевых степенях t равны нулю, откуда
Tdn{P4Ap), .... Я"(Лр))
1{0м)= Е
AbXAj,
»(р)=0
Наконец, по формуле Ботта для вычетов последнее выражение
преобразуется в нашем случае к хорошо известной формуле:
Формула Римана—Роха—Хирцебруха.
X {<3м) = Td,, (ci (М) с„ (М)).
Для кривой эта формула дает знакомое соотношение X (©м) ~
= Cj (М)12, эквивалентное соотношению Римана
,g=\(M)/2. , .
5. Спектральные последовательности и их приложения 465
Выше МЫ доказали это при помощи теории гармонических форм.
В случае поверхности мы имеем формулу Нётера
%\Ум) = ^2 »
которую докажем и будем часто применять в следующей главе.
К сожалению, аналогия между формулой Гаусса ~ Бонне III
и Римана — Роха не проходит по одному существенному пункту:
в то время как на любом дифференцируемом многообразии
достаточно много векторных полей класса С", которьши можно
пользоваться для доказательства формулы Гаусса — Бонне III, далеко
не на всех компактных комплексных многообразиях существуют
глобальные голоморфные поля (см. теорему Кэррелла и Либерма-
на в § 4 гл. 5). Конечно, поскольку в формуле Римана — Роха
векторное поле v, используемое для ее вывода, не фигурирует,
можно подозревать, что роль этого поля чисто вспомогательная.
Это действительно так, и формула справедлива для любого
компактного комплексного многообразия, но здесь мы еще не владеем
техникой, необходимой для ее полного доказательства. Поэтому
предыдущие рассуждения следует рассматривать только как
набросок, а не как исчерпывающее доказательство; однако в следующей
главе мы приведем геометрическое доказательство этой формулы
в случае алгебраических поверхностей.
5. СПЕКТРАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
И ИХ ПРИЛОЖЕНИЯ
Спектральные последовательности
фильт.рованных и б иг раду и ро винных
комплексов
Спектральные последовательности — это алгебраический
аппарат для работы с когомологиями; грубо говоря, они представляют
собой образованную по определенным правилам таблицу из
длинных точных последовательностей, с которыми обращаются
стандартным способом. Для тех, кто имеет дело с когомологиями, они
столь же важны, как разные методы интегриров1ания для
изучающих анализ. Мы будем употреблять только спектральные
последовательности с довольно сильными ограничениями, однако думаем,
что полезно дать общие определения.
Комплексом (К*, d) = {К'> —!^К^—>К^-^...} называется по*
следовательность абелевых групп и дифференциалов d: К^ ->
466 3. Дальнейшие методы
-> К'^*^, удовлетворяющих условию dod — 0. Когомологиями ком^-
плекса называется градуированная группа
Н*{К*)= ф IP {К*),
1>>0
где IP (К*) = 2?4dKP-\ "Р = кег {d\ ЕР -^ ЕР^^) - группа
коциклов, а dK^~^ — В^си ZP — подгруппа кограниц. Подком^-
плекс (/*, d) задается подгруппами Р а IC с dJ* с: /*.
Соответствующий факторкомплекс {L*, d) определяется как комплекс
L* = К*и* с очевидными дифференциалами. Поэтому имеется
точная последовательность комплексов
О ->/*-> я:* -^ L* -^ 0.
Простьш и хорошо известным способом она определяет длинную
точную последовательность
... -> IP (/*) -^ IP (К*) -^ IP (L*) -^ Я^+1 (/*) -^ ... .
Фильтрованный комплекс (F^K*, d), обобщающий понятие
подкомплекса, определяется как убывающая последовательность
подкомплексов
К* = F<>K* ID F^K* ID ... ID F^K* ID F^*^K* = (0).
Рассмотренный выше случай одного подкомплекса соответствует
фильтрации Я^* ID /* ID {0}, а спектральная
последовательность фильтрованного комплекса обобщает соответствующую
длинную точную когомологическую последовательность. Введем
еще несколько определений.
Ассоциированным градуированным комплексом фильтрованного
комплекса (F^K*, d) называется комплекс
От К* = ® Gt^K*,
1>>0
где Gt^K* = F^K*/FP*^K*, а дифференциалы определяются
очевидным способом. Фильтрация F^K* на К* индуцирует также
фильтрацию F^H* (К*) в группе когомологий:
F^H" {К*) = FPZ4F^B9.
Ассоциированной градуированной группой когомологий называется
Gr Н*1,К*) = ф GrP т(К*)^
где
GrP Н^{К*) = F^m {K*)lF^*^m (К*).
S, Спектральные последовательности и их приложения
467
Рис. 3
Определение. Спектральной последовательностью называется
последовательность {Е^, d^} (г^ 0) биградуированных групп Е^ =
= ф ЕР'9 с дифференциалами
1>.д>о
dri Е?' «-»-£•?+•••«-'+», d» = 0,
такая, что Я* (Ej) = Ej.+i.
При работе со спектральными последовательностями полезно,
и даже необходимо, «рисовать картинки» (рис. 3).
Практически у нас всегда будет Ег = Er+i = ... при г'^г^:
эта предельная группа обозначается £"«,, и в такой ситуации
говорят, что спектральная последовательность {Е^} сходится к Еео
Предложение. Пусть К*— фильтрованный комплекс. Тогда
существует спектральная последовательность {Е^}, обладающая
свойствами
pPt 9__ ppjrP+4/pP+i 1гР+Я
Последнее свойство обычно записывают так:
Ег =i- Н* (К*)
и говорят, что спектральная последовательность сходится к
когомологиям Н* (К*).
3. Дальнейшие методы
Доказательство. Начальный член последова^^ельности
задается условием предложения, а дифференциал
получается из дифференциала d переходом к Факторгруппам.
Тогда когомологии комплекса {Eq, dp} вмеют вид
wP. 9 _ kerdp {а б FpKp*9: da б Fp*ikp*4*^) _
1 ~ imdo d {FPKP*^^) + FP*^KP*Q ~
= ffP+i (p>K*IP^-^^K*) = H'""^ (Сг^Л:*),
что и утверждается. ,
Если [а] —класс из Е\''^, то
^ d{FP*^KP*4.)-{-FP*^Ki^4*^ ^
определяет класс в E\'^^''^, а тем самый и дифференциал
di: ^-f-'-^£•[+*•'. Следовательно, , ,
, , , {а б FPKPn: da ^ FP*^kP*4*^)
kerdi— i(ppKP*(!-i)^pp*iKv4 '
И потому
• , __ -. d{FP-^KP*9-i) , ,
„p, q _ {a б FPKP^g-. da б /^P+^^P+g**}
■^? ~ d{FP-^KV*9-i) + FP*4CP+g
В этом выражении знаменатель не является подгруппой
числителя, и его следует понимать как пересечение {написанный в
формуле знаменатель} f] {числитель}. Аналогичное замечание
относится и к остальной части доказательства.
Повторяя описанную процедуру, мы в общем случав определим
рр, g _ {а S FPKP*g: da б Fp*'^Kp*4*^}
*■ ~ d{FP-^^KP*9-i)-{-FP*^KP*9 '
И для [о] 6^?"
, _г, , ^ {b^FP*'-KP^q^i: db ^ FP*^^iKP*9*i) _ „p+r,^-r+i
а,.о—laajt d(FP*^KP*^)-{-FP*^^KP*9*^ *"
Прямое, но довольно громоздкое вычисление показывает, что
Н*{Е,)^Е,+^. : .
5. Спектральные последовательности и их приложения 469
При достаточно больших г имеем
Это завершает доказательство предложения. Q
Один из важнейших для нас примеров — спектральная
последовательность, ассоциированная с двойным комплексом. Напом-
ним,что двойным комплексом называется биградуированная
группа
р, «>о
с дифференциалами
которые удовлетворяют условиям
d2 = 6« = 0, d6 + 6d = 0.
Будем обозначать двойной комплекс через {К*^*', d, fi).
Ассоциированный комплекс {К*, D) определяется как
^= Ф Kf-\ D = d + 6.
в комплексе (ЛГ*, D) имеются две фильтрации
Например, 1всли М — ковшлексное многообразие, а
iS:'''' = 4''''(M), d = d, 8 = д,
то 'F^A^ {М) — это пространство и^форм степени ^р по dz.
Поэтому существуют две спектральные последовательности
{Ej) и {"Ет), сходящиеся к Н* {К*). Из соображений симметрии
достаточно рассмотреть первую из них. Тогда
^й . jfP+i.e-i ^ ^ = *^ •
Дифференциал d^ индуцируется дифференциалом D = d ■\- Ь при
переходе к факторгруппам. Поэтому относительно указанного
вьппе изоморфизма d^ == Ь т
где в правой части стоит д-я группа когомологий комплекса
470 3. Дальнейшие методы
Дифференциал dj выражается через действие D = d -\- 8 я& 'Е^.
Так как б = О на 'Е-^^, то dj = d и
'El^ ' = Я* {'El' \ di) ^ Я? (Hi (К*' *)).
Последнее выражение обозначает когомологии комплекса
... -> Я? {К"''- *) Ля? (л:"' *)Лн1{к''+''') -»-...,
что имеет смысл, поскольку d8 -\- 8d = 0. В итоге получаем
следующий факт.
С каждым биградуированным комплексом {К* г *; d, 8)
ассоциированы, две спектральны^е последовательности,
сходящиеся к когомологиям полного комплекса, причем
'Ё^- "^НЦЩ (К*' *)), 'Е^- " ^ т (Я§ {К*' *)).
Здесь необходимо одно уточнение. Класс 1а] g 'Ef'^ задается
элементом а g ^^.' по модулю 6Я^.'~*; причем 8а = О, в то время
как класс [а] g 'Е^'^ зад&ется элементом а ^ ^''•' ло модулю
й^,9-1 4- d^-1.9 П кег б, причем 8а = 0, da^ 8K^*^< «"^
Поэтому нельзя считать, что da = О, верно лишь то, что [da] = О
в Щ{Ю>*^*).
Примеры. Пусть М — комплексное многообразие и
КР,<г = ЛР.« (М), d = д и Ь = д.
Тогда ассоциированным комплексом является комплекс де Рама
(Л*(М), d). В общем случае о возникающих здесь спектральных
последовательностях Фрёлихера {'Е^} и {'Ет], сходящихся к
^&н (^1 по-видимому, мало что известно.
Однако для компактного кэлерова Многообразия М каждый
класс [а] g 'Ef'^ т Яу' (М) имеет гармонический представитель
для 5-лапласиана Д-д. Из кэлеровости вытекает, что 2Дд- = A<j,
откуда da = 0. Значит, 'Е^^'Е^ Si . . . as '£"„, и тем самым
на Я£н (М) определена фильтрация Ходжа
F^Hln (М) ^ Я"'" (Л/) ф ... Ф Я"'"-" (М).
Если М компактно, но не кэлерово, то вполне может быть,
что 'El Ф 'Е^, но примеров, в которых 'Е^ ф 'Е^, мы не знаем.
Пример, когда 'Е^ Ф 'Е^, дает многообразие Ивасавы
М = GIT,
5. Спектральные последовательности и их приложения 471
где G — группа Ли всех комплексных матриц вида
/1 о Ь'
?= О 1 с
\0 О 1,
а Гс G — дискретная подгруппа матриц с целыми гауссовыми
числами а + Ф (а> Р € 2i) в качестве элементов. Можно проверить,
что М является голоморфным расслоением, заданным
отображением gt-*-(a, с), над комплексным двумерным тором с
комплексным одномерным тором в качестве слоя. Элементы матрицы Мауре-
ра — Картана dg-g~^ представляют собой правоинвариантные
голоморфные формы на G и, следовательно, спускаются на М. Это
дифференциалы
coj = da, <Й2 ^^ dc, а>з = — cda -\- db,
В частности, dcos = «i Л coj, поэтому соз— незамкнутая
голоморфная форма на М. Если рассматривать соз ^йк представитель
класса из 'Е[.о ^ Яг" {Щ = Я» (Qi,), то
di [соз' = WoJs' = t<*i Л coj
— ненулевой класс в 'Е^'".
Так как dim Е^"^ dim Er+i, а эйлерова характеристика не
зависит от выбранных когомологий, то мы получаем соотношения
Фрёлихера
1>+«=г
р. 9 г
где й*"»' = dim ff^*' (Л/), а Ь,. есть г-е число Бетти.
Другой крайний случай — когда М есть некомпактное
комплексное многообразие, когомологий Дольбо которого
удовлетворяют условию
(*) Я|"(М) = 0, q>0.
Это выполняется, например, для так называемых многообразий
Штейна. В § 3 гл. О мы доказали, что условие (*) выполнено для
— проколотлго полидиска, который представляет собой множество
точек вида
{Z 6 С": I Z, I < 1, zi . . . Zft ^ 0}.
472 3. Дальнейшие методы
Если условие (*) выполнено, то 'ЕР' ч = О при q> О и первая
спектральная последовательность тривиальна начиная с члена
Е^, т. е. 'Е^ ^ 'Е„. Отсюда следует, что
НЪп{М)^НЬп{М, hoi),
где в правой части стоит группа когомологяй де Рама комплекса
голоморфных форм.
Гиперкогомолоеии
Они представляют собой полезное обобщение обычных кого-
мологий пучков. Пусть X — топологическое пространство.
Комплексом пучков (а^*, d) называется последовательность пучков
абелевых групп SST" на Z с морфизмами пучков
удовлетворяющими условию сР = 0. Это обозначение не
предполагает, что последовательность точная. Иногда мы будем писать
Комплексу пучков {Sf**, d) очъечают когомологические пучки Se^=
= т^ (ЗГ*). Положим речи) = Н"" {U, &С^); тогда предпучок
и ь^ кег {d: ЗГ« (U) -> ^*^ (f/)}/dSr«-i (U)
определяет пучок <^9 со слоем
ml = lim кег {d: ^ {U) ->■ ЗГ«+* (С/)}/(ЙГ'-* (U).
Сечение а пучка <^' над открытым множеством Ua X задается
покрытием {Ua} множества U и сечениями а^ 6 ^' (^^а)»
такими, что
daa=0, а„—ав = йт]„в. Лае € ^'"Ч^^а П f^e);
это сечение нулевое, если
(возможно, после измельчения данного покрытия). Заметим, что^
как следует иэ определения.
Когомологические пучки (^' = О при g > О <:> для комплекса
пучков (^*, d) выполнена лемма Пуанкаре.
5. Спектральные последовательности и их приложения 473
Пусть теперь f/ = {Ua) — покрытие X ж С^ {U, 0%*') —
коцепи Чеха степени р со значениями в S^^. Операторы
б: С^ (и, ЗГ«) -> С^*^ (U, РС%
удовлетворяют условиям б' = d^ = О, d6 + бй = О и,
следовательно, определяют двойной комплекс
{€^,4 = С" {U, дс% б, d).
Пусть (С* (f/), D) — ассоциированный с ним комплекс.
Измельчение U' <и покрытия индуцирует отображения
С^ {U, Sr«)->C''(f/', 5Г9),
Н* (С* (U)) -> я* (С* (U')).
Гиперкогомолозии определим теперь, полагая
Н* (X, 5Г*) = lim Н* (С* (U), D).
и —
Спектральные последовательности 'Е и "Е, ассоциированные
с двойным комплексом (С^ (U, ^^); 8, d), ведут себя достаточно
хорошо по отношению к измельчениям покрытия, и, переходя
к пределу, мы получаем две спектральные последовательности,
сходящиеся к Н* (X, ^*), с начальными членами
'£^'' = ЯР(Х, сЙ?'(5Г*)),
Пояснения. Группа Н* {X, S6* (^*)) представляет собой
ко гомологии Чеха когомологических пучков S£* (^*). а
Я5 (Я* (X, 3?^*)) — когомологии комплекса
Н*{Х, 5Г<')Ля*(Х, 5Г*)Л... .
Прежде чем перейти к примерам, мы докажем одну лемму.
Квазиизоморфизмом называется отображение
комплексов пучков, индуцирующее изоморфизм
когомологических пучков
Лемма. Если у: X* -> а^*— квазиизоморфизм, то
индуцированное отображение гиперкогомологий j^: Н* (X, X*) -> Н* (X, а^*)
является изоморфизмом.
474 3. Дальнейшие методы
Доказательство. Очевидно, / индуцирует отображения
спектральных последовательностей, а
— изоморфизм по предположению. Довольно очевидно
следующее общее утверждение: отображение фильтрованных комплексов,
индуцирующее изоморфизм каждого из членов Е^ спектральных
последовательностей, индуцирует изоморфизм полных групп ко-
гомологий. Q
Рассмотрим несколько примеров.
1. Еще раз о теореме де Рама. Пусть М — многообразве и
{Jh*, d) — комплекс де Рама пучков гладких форм
Обозначим через Щ* тривиальный комплекс
[|1->0-)- 0->. . .
с единственной нетривиальной группой [R, в размерности 0. По
(i-лемме Пуанкаре
^9 (^*) = О при g > О, ей?" (^*) ^ Щ.
Следовательно, включение i: R* -> ^^* является
квазиизоморфизмом и по предыдущей лемме Н* (М, К*) т Н* (М, J;*). Очевидно»
что
^■^*^^ -{о, д>0,
(
поэтому первая спектральная последовательность для [R,*
тривиальна и Я* (М, К) Si Н* (М, К*).
С другой стороны, используя разбиение единицы, мы получаем»
что Я' (М, ^*) = О при g >• О, и поэтому
Объединяя предыдущие замечания, получаем снова изоморфизм
де Рама
Н* {М, а)эгЯВн(М).
Конечно, по существу, это не что иное, как приведенное ранее
доказательство на языке теории пучков. Однако здесь оно
построено так, что наиболее существенные моменты лучше выделены,
и это естественным путем приведет нас к обобщениям, о которых
скоро пойдет речь.
5. Спектральные последовательности и их приложения 475
2. То же самое для теоремы Долъбо. Пусть М — комплексное
многообразие и (^^'''*, д) — комплекс Дольбо пучков
^Р. оД. ^Р. 1Д ^Р. 2_^
а й"*— тривиальный комплекс
QP _> О -> О -> . ...
Тогда по 9-лемме Пуанкаре включение
является квазииэоморфизмом. Рассуждая так же, как выше при
Доказательстве теоремы де Рама, получаем изоморфизм Дольбо
3. Комплекс голоморфных форм. Покажем, теперь, как можно
вычислить обычные когомологии Н* (М, С) комплексного
многообразия М при помощи голоморфных форм. Прежде всего
заметим, что для таких форм выполняется вариант леммы Пуанкаре.
Бели ф — замкнутая голоморфная р-форма (р > 0), то локально
<р = йт], где т] — голоморфная (р — 1)-форма. Доказать это
можно так же, как 9-лемму Пуанкаре. Гораздо более изощренную
лемму мы докажем после того, как рассмотрим в следующем
примере log-комплвкс.
Итак, голоморфный комплекс де Рама
И тривиальный комплекс
С->0->0-> . . .
таковы, что включение С* -> (Q*, d) является
квазиизоморфизмом, и, повторяя предыдущее рассуждение, мы получаем
изоморфизм
<*) Я* {М, С) ^ Н* {М, Q*),
выражающий комплексные когомологии Чеха через голоморфные
формы.
Рассмотрим правую часть соотношения (*). Для второй
спектральной последовательности имеем
476 3. Дальнейшие методы
Особого внимания заслуживают два случая. Если М —
компактное кэлерово многообразие, то d = О
так как ЗД^- = A<j. Поэтому "Е^ = "Еа
ное кзлерово многообразие, то d = О на Я' (М, й^) ^ Hf^ (Л/),
Р+д=п
что является разложением Ходжа. В случае многообразия Штейна
Н'^ (М, Q*) = О при g > О и (*) приводит к изоморфизму
Н* (М, С) ^ ЯЙн (М, hoi),
о котором уже говорилось выше.
4. Логарифмический комплекс. Рассмотрим теперь одну
интересную ситуацию. Предположим, что М — комплексное
многообразие и D — дивизор на М. Будем говорить, что дивизор D
имеет нормальные пересечения, если D = ^D^ и неприводимые
V
компоненты D ^ дивизора D не имеют особенностей и пересекаются
трансверсально. Тогда в точке р, через которую проходят к
компонент D^, можно выбрать локальные голоморфные координаты
(zj, . . ., z„) с центром вр, такие, что в окрестности U = { \ zi \ <1
< 1} точки /? = (О, . . ., 0)
D f]U= {z^ .. . z^=0}
есть объединение координатных гиперплоскостей. Дополнение
и* = и - и f\D = (Д*)" X Д"-"
является проколотым полидиском Р* (к, «), т. е. множеством
точек вида
{z: |zH<l, zi . . . Zft ^0).
Гомотопически P* (к, n) есть произведение Х''»^* ^ экземпляров
окружности.
Обозначим через й*" (*D) = (J ^'' Ф^) пучок на М меро-
/1>0
морфных р-форм, голоморфных на М* = М — D, с полюсами
произвольного (конечного) порядка на D. Аналогично
определяется пучок А^ (*D) на М по предпучку
U-^A'P{U - и {\D).
Эти пучки образуют два комплекса пучков (Q* (*D), d) и
{А* i*D), d) на М.
Определим теперь пучок Q^ (log D) как подпучок в й^ {*D),
порожденный голоморфными формами и логарифмическими
дифференциалами dzi/zi (i = 1, , . ., к):
QP (logD) = Q" {dzi/zi, . . ,, dzft/zft}.
5. Спектральные последовательности и их приложения 477
Очевидно, что dQ^ (log D) cz Qp*^ (log D). Получающийся при
этом комплекс (Q* (logD), d) называется логарифмическим
комплексом (log-комплексом). Внутреннее описание этого комплекса
дает следующая
Лемма. Пусть f — локальное уравнение дивизора D. Тогда
Q^ (logD) задается такими мероморфными формами ф, для
которых голоморфны формы /ф и fdtp.
Доказательство. Необходимость приведенного условия легко
установить, вэяв функцию f = Zy ... z^.
Обратно, предположим, что формы /ф и /с^ф голоморфны.
Введем обозначения
/ = (1, . . ., к), J, К, Ld (\, . . ., п) — мультииндексы,
Z/ = Zj, ... Zj^, dzj = dzj^ Л ... л dzj^.
Тогда можно написать
Ф- Ъ V ZI.J ^^^^'
JCl
КГ\1=0
где ф/к — голоморфные формы. Вычисляя dtp по модулю таких
членов Т, для которых голоморфна форма fT, мы получаем, что
J.Ki€J L, к
где
ZI-L'^LK = ± Е '^(^-ЦШ^»- -Д^
— голоморфная форма. Следовательно, форма ffj^/zj
голоморфна, как и утверждалось. Q
Интуитивно понятно, что если форма ф содержит слагаемые
с 1/zj, но не содержит dzt в числителе, то dip содержит слагаемые
с dzjzl. Мы проверили невозможность сокращения таких
слагаемых.
Основной локальный результат, играющий в нашем примере
роль леммы Пуанкаре, содержит следующая
Леииа. Включения
Q* {\ogD)c: Л* {*D), Q* (*D)(=L Jh* (*D)
являются квазиизоморфизмами.
Доказательство. В точке р ^D слои соответствующих пучков
имеют вид
Q* (logi))p = Q* i*D)j, = Q», ^* i*D)p = ^*,
478 3. Дальнейшие методы
И утверждение леммы вытекает соответственно из обычной
голоморфной леммы Пуанкаре и из ее С"-варианта.
Для точки р ^D возьмем окрестность U указанного выше вида.
Согласно теореме де Рама, для (открытого) многообразия Р* (к, п)
нЪп (и-и nD)^m (x'^S С) = л'^^ (X'^S С).
Поэтому имеет место изоморфизм
М" и* {*D))p ^ т ix''s\ С).
Так как когомологии пространства U* = U — U f\D имеют
своим базисом формы
dzj/zj {Jczl),
то слои S£^ (Q* (log D))p и <^« (Q* {*D))p [отображаются на
Ш^ {Jt* {*D))p, и нам осталось только проверить следующее
условие:
(*) Пусть ф — замкнутая мероморфная р-форма на полидиске
с полюсами на D, и пусть ф = О в Я^н (Р* (к, п)). Тогда
Ф = dt) для мероморфной формы т) с полюсами на д. Если же
форма ф принадлежит log-комплексу и ф = О в
НЪп {Р* {к, п)), то ф = йт] для некоторой формы т] log-
комплекса.
Прежде чем проводить доказательство, заметим, что мы
дважды установили изоморфизм
Я* (М, С) ^ H%^ {М, hoi)
для комплексного многообразия М с
Ю {М, fiP) =0, g > 0.
Так как последнее условие выполнено для М = Р* (к, п), то
Ф = dt] для некоторой голоморфной формы т] на Р* (к, п),
возможно, имеющей существенную особенность на дивизоре (zj . . .
. . . Zft) = 0. Поэтому мы должны показать только, что форму г\
можно выбрать мероморфной.
Доказат£льство. Рассуждение нетрудное, но длинноватое.
Постараемся построить такое представление <р — dr\, чтобы т) имела
не более чем полюс на дивизоре (% . . . zu) = 0. Приводимое ниже
рассуждение покажет, кроме того, что т) лежит в log-комплексе,
если это верно для ф.
Пусть (Zi, . . ., z„) = (ui, . . ., Mft, y^, . . ., i;„_ft) = (u, v).
Тогда P* (k, n) есть множество точек
{{и, i;):0< |м, |<1, \vj \<1},
5, Спектральные последовательности и их приложения 479
а дивизор D задается уравнением и^ . . . и^ = 0. Прежде всего
устраним из рассмотрения переменные v. Следуя методу
доказательства й-леммы Пуанкаре из § 2 гл. О, предположим, что
Ф ^ О (du, dv-y, . . ., dvi) и напишем
Ф = ф' + ф" л dvi,
где ф', ф" ^ О {du, dvy, . . ., dvi_y). Тогда dcp = 0=^ (dfp'/dVf) =
= {di^"ldVf) = 0 при ] > I, где для дифференциальной формы
а = 2 ^dxi
daldxf= S {dajidxf) dxj.
Так как форма ф голоморфна по v, то формальное интегрирование
степенных рядов позволяет решить уравнение
ф' = d^ldvi,
где т) имеет полюс в и того же порядка, что и форма ф", и dr\/dVf = О
для всех у > I. Тогда ф — dr\ ^0 (du, dv^, . . ., di;,_i).
Продолжая действовать таким способом, мы убедимся, что можно
предполагать, что ф ^ О {du). Поэтому йф = О =^ (dfp/dVf) = О, и
переменные V можно опустить.
Далее рассуждаем по индукции. Пусть теорема доказана для
и' = (щ, . . ., Uk-i). Напишем
ф = tf' -f tf" л du),,
где tf', tf' ^ О (du'). Рассмотрим ряд Лорана
v==-JV
Формально интегрируя этот ряд, насколько это возможно, мы
получим соотношения
Г (ц')-1 _ дц
гр'
Bft duh '
где т] имеет по и полюс того же порядка, а по Uj, полюс на
единицу меньшего порядка. Очевидно что
ф = ф _ dt] = i' Ч- Г Л {duk/щ),
где ^" ^ О (и', du') и Е ^ О (du'). Так как форма ф замкнута, то
g' ^ О (и', du') и
dl' = 0 = dl".
Но ф = О в Н%п ((А*)*)- Поэтому ограничение ф на
Я?)н ((A*)*"*) нулевое, где (А*)''-* с= (А*)*" задано уравнением
480 3. Дальнейшие методы
Mft = const. Это ограничение совпадает с ^', и по предположению
индукции ^' = dy', где у' имеет не более чем полюс по и'.
Рассмотрим теперь ф = ф—dy' =\" f\ dujuu- Записывая (Д*)* =
= (А*)''~*ХД* и применяя формулу Кюннета, получаем; ф = 0
в ни ((А*)') =!► Г = О в Н'^^^ {{^*f2'). Тогда 1" = dy", где у'
имеет не более чем полюс по и' и (р = d (у" л du^/ui^). D
Выведем теперь из этой леммы несколько следствий.
Пучки ^* {*D) допускают разбиение единицы, поэтому
Я' (М, Jk* (*-D)) = О при 9 > О и из спектральной
последовательности для гиперкогомологий получаем
Н* (М, Jk* (*D)) ^ HI (Я« (М, Jk* i*D))) =
= Я£н (М -D)^ Я* (М - D, С).
Воспользовавшись этим изоморфизмом и леммой о
квазиизоморфизмах, мы получим следующую коммутативную диаграмму:
H*(M,U*{]ogD))-i-H*(M-D,C)
<**) I II
И*{М, Sl*{*D)) S Я*(М - D, С)
Тем самым найден метод вычисления когомологий дополнения к
дивизору с нормальными пересечениями при помощи мероморф-
ных форм, допускающих полюсы на Z) и голоморфных на М — D.
Используя теорему о разрешении особенностей *), можно
установить, что второй изоморфизм
Н* {М, Q* i*D)) ^Н* (М -D,C)
выполняется без всяких предположений об особенностях дивизора
D.
Допустим теперь, что линейное расслоение [D] ^у М
положительно. По теореме В
т {М, QP (kD)) =0 при g > О, Л;> ко-
Пусть и = М — D, а Я5н {U, alg) обозначает когомологий
комплекса мероморфных форм, голоморфных яа U и имеющих
полюсы только на D. Тогда из вырождения второй спектральной
последовательности для гиперкогомологий мы получаем, что
справедлива следующая
^) X. Хиронака, Разрешение особенностей алгебраических
многообразий над полем характеристики нуль.— Сб. Математика, 9:6 (1965), 3—70",
10:1 (1966), 3—89; 10:2 (1966), 3—58.
S. Спектральные последовательности и их приложения 481
Алгебраическая теорема де Рама (Гротендик). Имеет место
изоморфизм
Н1я (и, alg) ^ Я* (С/, С).
Важность этого результата объясняется следующим
обстоятельством. Аффинное алгебраическое {неособое) многообразие —
это комплексное подмногообразие U в С^, заданное нулями
системы многочленов. Обозначим через Q* {U, alg) комплекс
голоморфных форм на и, получающихся при ограничении
рациональных дифференциальных форм на С^. Это понятие имеет смысл,
так как по теореме Хиронаки для проективного замыкания Mq
подмногообразия Ucz С^сг Р^ существует разрешение
особенностей
М Л Мо,
которое будет изоморфизмом на U, а тогда Q* {U, alg) —
пространство мероморфных форм на М, голоморфных на U (см. § 4 гл. 1).
Значит, алгебраическая теорема де Рама утверждает, что кого-
мологии Н* {U, С) можно вычислять по комплексу Q* {U, alg).
Дифференциалы второго рода*)
Пусть М — гладкое алгебраическое многообразие. В
классической терминологии дифференциалом первого рода называется
голоморфная /з-форма на М. По теории Ходжа они определяют
прямое слагаемое iPi" (М) в когомологиях IP (М, С)
многообразия М.
Определение. Дифференциалом второго рода называется
такая замкнутая мероморфная /з-форма ф на М, что для некоторого
дивизора D с дополнением U = М — D форма ф голоморфна на
и и лежит в образе отображения
Эквивалентно, дифференциал второго рода — это замкнутая
мероморфная /з-форма на М, голоморфная на М — D, которую
можно продолжить по модулю точной формы на Л/ — D Цо
замкнутой С"-формы на М. Через рр обозначим размерность
пространства
(р-формы второго рода)
d (мероморфные (р—1)-формы) *
^) В этом разделе мы следуем в основном работе: М. F. Atiyah, W. V. D.
Hodge, Integrals of the second kind on an algebraic variety.— Annals of Math.,
62 (1955), 56-91.
1§? ■?• Дальнейшие методы
Рис. 4
Исторически дифференциалы второго рода при р = 1,2 играли
центральную роль в начальный период развития теории
алгебраических поверхностей. На них основывалось доказательство
того, что иррегулярность алгебраической поверхности равна
6^/2 (в частности, Ь^ всегда четно), и первое доказательство того.
Что группа Нерона — Севери
{дивизоры на S}
{дивизоры, алгебраически эквивалентные нулю)
конечно порождена. При ;з> 3 про дифференциалы второго рода
известно мало, да и то, что известно, получено сравнительно
недавно^ Ввиду их исторической важности и тесной связи с
алгебраической теоремой де Рама мы дадим краткий обзор некоторых
результатов теории дифференциалов второго рода и особо выделим
случаи ]э = 1, 2.
Начнем с обобщения определения дифференциала второго рода
в двух направлениях. Для замкнутой мероморфной /з-формы ф
и дивизора D, для которого ф голоморфна п& U = М — D,
определим вычет как интеграл
V
где V 6 Яр (С/, Z) есть;з-цикл, гомологичный нулю в М. Очевидно,
что: ф — дифференциал второго рода-^=> он не имеет
нетривиальных вычетов на открытых множествах U = М — D для
достаточно больших дивизоров D.
При р = i можно получить совершенно ясное представление
о вычетах. Пусть D — неприводимый дивизор и Xq ^ D —
простая точка. Граница у^ нормального к D диска из Л/ в точке х^
будет 1-циклом в Щ {М — D, 1) и границей в М, а класс Vd не
зависит от Xq, так как гладкие точки дивизора D составляют
связное многообразие (рис. 4). Пусть теперь!) = D^ + ... + D^—
■5. Спектральные последовательности и их приложения 483
Рис. 5
дивизор с неприводимыми компонентами Z>j. Циклы у^ можно
выбрать в и = М — D, и мы утверждаем, что любой цикл у из
кег {Hi {U, Z) -^ Ну (М, %)}
гомологичен линейной комбинации циклов Yd,- Действительно,
по предположению у = дА, где А есть 2-цепь в М. Так как
особенности дивизора D имеют вещественную коразмерность ^ 4,
то можно считать, что А пересекает D трансверсально по простым
точкам. Если Xq 6 Di— такая точка пересечения, то вблизи х„
часть Ag цепи А, расположенная на расстоянии е от Df,
изображается как нормальный диск в Xq (рис. 5), и поэтому ЙА^ = ур ,
Следовательно, у — у^ имеет в пересечении с Z) на одну точку
меньше. Повторяя это рассуждение, мы получаем гомологичность
циклов Y '-' 2 "^1Увг Отсюда вытекает следующее утверждение.
При р = i замкнутая мероморфная i-форма <р является
дифференциалом второго рода^^^ц) не имеет вычетов ни
в каком открытом множестве вида U = М — D, где она
голоморфна.
Из этих рассуждений понятно также, что при р"^ Ъ вычеты»
могут быть устроены довольно сложно.
Теперь мы докажем следующий факт.
Для р-формы ф второго рода и любой точки Хд ^ М
существует такая мероморфная (р — \)-форма tf, что форма
ф — йг() = т) голоморфна вблизи Хд. При р = i верно и
обратное.
Доказательство. Для заданной точки Хд ^ М выберем
обильный дивизор D, не проходящий через х^. Тогда для U = М — Dn
по алгебраической теореме де Рама
Hln (U) ^ НЪп (и, alg).
31*
484 S. Дальнейшие методы
На самом деле, как было выяснено в конце предыдущего раздела,
в качестве U можно взять аффинную окрестность точки х^. Тогда
для любого дивизора D' zd D окрестность М — D' = U' с^ U
также будет аффинной и, следовательно,
Hln{U')^Hl^{U', alg).
Рассмотрим теперь такую окрестность U'■, в которой форма ф
голоморфна и является образом класса Ф 6 ^'^dr {М). В диаграмме
Hln{M)^Hln{U', alg)
Я&к(С^, alg)
ограничение Ф п& U представлено замкнутой ]э-формой т),
которая мерофорфна на Л/ и голоморфна на U. Ограничивая ее на U',
мы получим требуемое представление
ф — т] = dt|3,
где tf — мероморфная {р — 1)-форма на М, голоморфная на U'.
При /3 = 1 из приведенного выше описания циклов, дающих
вычеты, видно, что замкнутая мероморфная 1-форма, локально
представимая в виде ф = dtf + т), не имеет вычетов и,
следовательно, ф — дифференциал второго рода. Q
Чтобы интерпретировать р^ и р^, определим число Пикара р
как ранг образа гомоморфизма
НЦМ, G*) X т{МЛ).
9квивалентно1 из доказательства (1, 1)-теоремы Лефшеца,
данного в § 2 гл. 1, вытекает, что р совпадает с рангом группы
Я^'^ {М) П Н^ (М, 1), который равен рангу факторгруппы всех
дивизоров на М по модулю дивизоров, гомологичных нулю.
Докажем теперь, что
Pi = *1. Рг = *2 — Р-
Доказательство. Напомним, что если D — дивизор на М,
то Q" {*D) обозначает подпучок пучка <Ji^ всех мероморфных
р-форм, состоящий из /з-форм, имеющих полюсы только на D.
Обозначим через
QP (*) = и QP (Щ
X36Dlv(M)
5. Спектральные последовательности и их приложения 485
подпучок пучка <А^, состоящий из мероморфных /з-форм, полюсы
которых расположены лишь на глобальных дивизорах из М.
Последовательность
Й (*): Й» (*) Л Й1 (*)->... -^ й" (*),
очевидно, задает комплекс пучков. Как обычно, обозначим через
Se^ (Й (*)) р-ш когомологический пучок. Тогда Ш^ (Й (*)) ^ С.
Докажем теперь такую лемму.
Лемма. Se^ (Й (*)) ^ ф Сд, где Сд — постоянный пучок,,
DEDlvM
сосредоточенный на дивизоре D.
Доказательство. Пусть ф — замкнутая мероморфная 1-форма^
заданная в достаточно малой полицилиндрической окрестности W
точки Жд 6 М. Дивизором полюсов формы ф является!
D = Di -{- ... + Z)t, где Di— неприводимые дивизоры
голоморфных функций/j 6 о (W). Те же рассуждения, что и выше,
показывают, что для W* = W — D гомологии Я^ (И^*, Z)
порождены 1-циклами yi, которые один раз обходят вокруг jDj..
Пусть
X 1 ( ф.
Тогда форма [ф—2 ^<<^/<//< = ^ не имеет периодов, а потому
g = I tf—мероморфная функция на И^ и
(*) 4>-Iihdfi/fi + dg.
Определим отображение вычета
R-.m^ (й(*))^ Ф Сд
D6D1V Ы
формулой /? (ф) = ф Я{- Id . Это означает, что R (ф) равно постоян-
i '
ной Я J на дивизоре Z)j. Локальное представление (*) показывает
что R — изоморфизм. Q
Напишем теперь две спектральные последовательности,
сходящиеся к Н* (Й (*)). Для одной из них
"Е1'Ч = Н1{т{М, Й (*))).
Так как обильные дивизоры конфинальны в множестве всех
дивизоров, то
Еч (М, Й (*)) = О при g > 0.
486 3. Дальнейшие методы
Следовательно, "Ер-ч = О при g > О и
Tip ,Q , v^ ^^ {замкнутые мероморфные р-формы}
^ ^ '' {точные формы}
Поэтому можно представлять себе Н* (Q (*)) как когомологии
де Рама поля функций на М.
Для другой спектральной последовательности имеем
<**) " 'ЕР'ч ^ IP {М,т'Ч^ {*))).
Но любая спектральная последовательность определяет
стандартную точную последовательность в низших размерностях, которая
в нашем случае имеет вид
О^'^1'»^Н*^'^«'^ Л '^-^•»^m^G^O,
где G = H^/F^H^ имеет подгруппу G' — РЩ^1РЩ^, такую, что
G' ф GIG' с= 'Е^^1^ ф 'Е\^^— подгруппа ядра d^. Подставляя (**)
в 8ту точную последовательность, получаем
о^я»(м, С)->н1(й(*)) Д ЯМ ф Сд) 1^т{м, о,^
B6Div М
->H2(Q(*))^G^0.
Дадим интерпретацию отображений в этой точной
последовательности (доказательства коммутативности диаграмм опущены).
1. Используя установленный ранее изоморфизм
(***) Я* (М, С) ^ Я* (Й*),
лолучаем, что первое отображение совпадает с естественным
отображением Н* (Q*) ->- Н* (Й (*)), индуцированным включениями
QP -^ QP (*).
2. Второе отображение, как в доказательстве предыдущей
леммы, сопоставляет замкнутой мероморфной 1-форме ее вычет.
3. Отображение i сопоставляет сечению l^ фундаментальный
класс т]д 6 Я^ {М, %) дивизора D.
4. Отображение Я^ {М, С) ->- Ш (Q (*)) снова индуцируется
изоморфизмом (***) и включением Q"-»- QP (*).
Далее, изоморфизм
т (М, С) (^ кег Я = {1-Ф°Рми второго Рода)
^ ' ' {точные формы}
влечет за собой равенство Pi = ^i.
5, Спектральные последовательности и их приложения 487
Далее,
- Д' (М, С) _ ННМ, С) _
{классы Чжэня голоморфных"» Ш» (ф Сд)
линейных расслоений /
^ ixn (Я^ (М, С) ^ Ш (Q (*))} = ^^;ГГеТормыГ"^ '
Значит, Ра = *2 — Р- D
Очевидно, что отождествление
im {'El- ° ^НР (Q (*))} ^ <^°Р"" °"^°Р°''° Р°"">
* \ \ у/; {точные формы)
позволяет продолжить приведенное доказательство, однако для
последующей интерпретации чисел рр еще недостает многих
геометрических сведений. Поэтому здесь мы ограничимся
несколькими дополнительными замечаниями по поводу случаев в р = 1,2.
При р = 1 самым интересным является, видимо, случай,
когда Л/ — алгебраическая кривая рода g. Наше определение
дифференциалов второго рода согласуется с их определением на рима-
новой поверхности, данным в § 2 гл. 2. Докажем следующее
утверждение.
Пусть D = p■^^ -\- . . . -\-\pg — неспециалъный дивизор
степени g. Тогда имеется изоморфизм
{1-формы ф без вычетов \ {i-формы второго рода)
с дивизором полюсов в 2D} {точние формы) *
Доказательство. По теореме Римана — Роха fe" (D) = deg D —
— g -]- I -{- i (D) = 1. Поэтому единственными мероморфными
функциями, полюсы которых ограничены дивизором!), являются
константы. По теореме Римана — Роха для линейного расслоения
Кс + 2D получаем, что
feo {Кс + 2D) = deg {Кс+ 2D) -g+i + i {Кс + 2D) =
= 2g-2 + 2g-g + i = 3g~i,
поэтому пространство мероморфных дифференциалов с
дивизорами полюсов в 2D имеет размерность %—1. Соотношения
Respj (ф) = О налагают ровно g — i независимых условий на это
пространство, так как по теореме о вычетах 2 Respj (ф) = О для
любой системы вычетов, подчиняющихся этому соотношению, и
существует форма ф 6 Я" {Ос {К + 2D)) с этими вычетами (см.
§ 2 гл. 2). Поэтому пространство 1-форм второго рода с
дивизором полюсов в 2D имеет^ размерность 3g — i — {g — i) = 2g,
и ни одна из этих форм не точна по приведенному ранее
замечанию о мероморфных функциях, полюсы которых ограничены
дивизором D. Q
3. Дальнейшие метод»
Обратимся теперь к случаю /з = 2. Чтобы объяснить, как
использовалось в классической алгебраической геометрии
соотношение Рг = &2 — Р' рассмотрим построенную выше точную
последовательность Ш(Й(*))Дя<>( ф Сд) Ля2(М, С). Ее
BEDlv М
МОЖНО проинтерпретировать следующим образом.
Если D — дивизор на М с фундаментальным классом Цв 6
6 Ю (М, Z), то т]д тогда и только тогда принадлежит
подгруппе кручений, когда существует замкнутая меро-
морфная i-форма ф с вычетом R {(f) = D.
Это утверждение доказал Пикар, а Севери показал, что некоторое
кратное KD (К 6 2.) дивизора D тогда и только тогда
алгебраически эквивалентно нулю (см. определение ниже), когда существует
замкнутая мероморфная 1-форма с вычетом D. Объединяя эти
факты, мы получаем, что группа Нерона — Севери
NS (М) == (дивизоры на М)
^ ' (дивизоры, алгебраически эквивалентные нулю}
конечно порождена (теорема о базисе). Структуру группы
дивизоров на М можно изобразить диаграммой
Л^ЧМ)пН\М,Ж)
Div э Div^ D Div„ D Div,
NS Pic°
Pic
где Divft, Diva, Divj — дивизоры, соответственно гомологичные,
алгебраически эквивалентные и линейно эквивалентные нулю.
Дадим теперь точные определения и выведем теорему
конечности другим способом. Дв8 эффективных дивизора D^, D^
называются алгебраически эквивалентными в сильном смысле, это
записывается как D^ = D^, если существуют связное
многообразие параметров Т с отмеченными точками t^, t^ ^ Т ^ дивизор
D ша М X Т, такой, что
D-M X {ti} =^Di (i = 1, 2).
Интуитивно это означает, что существует алгебраическое
семейство дивизоров Dt (t ^ Т), связывающее D^ шО^-
Два дивизора jDj, D^ алгебраически эквивалентны, это
записывается как Di ^ J&2> если существует такой дивизор D, что оба
5. Спектральные последовательности и их приложения 489
дивизора D + Di эффективны и Z) + Z)^ = Z) + D^- Сейчас мы
убедимся в том, что это отношение эквивалентности,
согласованное с групповой структурой на Div (М). Поэтому дивизоры,
алгебраически эквивалентные нулю, образуют подгруппу «^» в
группе Div (М). Факторгруппа Div (М)/ «^» = NS (М)
называется группой Нерона — Севери.
Основной нужный нам результат — это следующая
Лемма. Два дивизора D^, D^ алгебраически эквивалентны тогда
и только тогда, когда они гомологичны.
Доказательство. Очевидно, что D^^D^ => т]х)^ = Цв, в
Я^ {М, Ъ). Для доказательства обратного утверждения
предположим, что т)х,, = T)x)j, что, согласно предложению из § 1 гл. 1,
эквивалентно условию с^ (Ш^]) = Су (Шг!)» и покажем, что Dy ^
^ D^. Пусть Di— компонента дивизора Z)j с отрицательным
коэффициентами. Вычитая Е = D~ -f- D~ из каждого иэ дивизоров
Dy, D2, мы получаем два эффективных дивизора. Поэтому
эквивалентность Dy ^ Da достаточно доказать для эффективных
дивизоров с одинаковыми гомологическими классами.
Теперь мы переходим к существу доказательства. Напомним^
что многообразие Пикара Pic" (М) = Ю (М, 0)/Н^ (М, Ъ)
параметризует линейные расслоения с нулевым первым классом
Чжэня. Обозначим это семейство через {Р\ ->- М) (^ 6
6 Я1 (М, Q)IH^ (М, г)). Так как [Dy] ® [DJ* имеет нулевой
класс Чжэня, то [Dy\ <2> [D^]* = Р^, для некоторого ^о-
Согласно последнему результату последнего раздела § 6 гл. 2, можно
найти такое линьйное расслоение L ^у М и такие сечения
Ql 6 Я" (М, 0 (L® Pi)), что в^фО для общего I ^). В
действительности из доказательства вытекает, что можно считать 9^^
е|„ Ф 0. Полагая D^ = (Q{), из [D^ -^ D^ +0^] = [Z)|J
получаем линейную эквивалентность D^ -\- De ^ D^ -\- jf^|„-B
частности, Dy -\- Dg = 2?2 + J^5o' ^ очевидно, что Dg = D^^
относительно семейства дивизоров {D^ {\ 6 Pic" {Щ). Поэтому Dy ^Dg- Q
Как следствие, получаем теорему о конечности базиса: NS {М}
является конечно порожденной группой ранга р = Ь^ — Рг-
Мы не останавливались на понятиях рациональной и
алгебраической эквивалентности дивизоров и произвольных
алгебраических циклов отчасти потому, что нам это не потребуется при
изучении конкретных многообразий, а отчасти и потому, что
соответствующая теория в коразмерности 1 — по крайней мере в ее
современном виде — по-видимому, малопригодна для циклов
большой коразмерности.
^) Здесь это доказано дли случая абелева многообразия; используя
отображение Альбанезе, этот результат можно перенести на случай общих
гладких проективных многообразий.— Прим. перее.
490 3. Дальнейшие методы
Спектральная последовательность Лере
Во многих отношениях это самая полезная общая
спектральная последовательность. Поэтому важно по крайней мере
объяснить, что она собой представляет, и привести некоторые
примеры. Пусть нам даны топологические пространства X, Y,
непрерывное отображение /: X -»- У и пучок ^ на X. Назовем д'-м ге/зял«ыл«
образом пучка .^ пучок Щ {^) на Y, ассоциированный с предпуч-
ком U^mif-^U), .Г).
Спектральная последовательность Лере, которая существует
при очень слабых ограничениях (см. литературу в конце главы),
представляет собой спектральную последовательность {Е^} с
Е, => Я* (Z, 3'), ЕР'Ч =1Р (У, Щ (Я)-
Пусть Е —> В — дифференцируемое расслоение с компактным
слоем F. Тогда Е, В ж F — многообразия, а я — отображение
класса С°° с п~^ {U) ^ U X F для достаточно малых открытых
множеств Ucz В. Для постоянного пучка О- на Е по формуле Кюн-
нета имеем
Н" (я-1 (U), G) ^ Н" (F, G).
Это означает, что в первом приближении Щ (G) S Я' {F, О-)
является постоянным пучком на В. Это не совсем правильно, так
как нужно учесть действие фундаментальной группы я^ (В, xq)
на когомологиях Я' (F^^, G) (F^ = я~^ (х)). Точнее, изменение
класса когомологий цикла в слое при движении по пути у
от Xq до X индуцирует изоморфизм Я' (F^, G) ^ Я' (Fx^, ©-),
который зависит только от гомотопического класса пути "у- Это
утверждение весьма наглядно, и его доказательство имеется во
многих стандартных учебниках топологии. Отсюда, во-первых,
вытекает существование представления
р: я^ (В, хо) -> Aut (Я« (FxJ, Щ,
которое описывает изменение циклов при сдвиге по замкнутым
путям. Во-вторых, любое представление фундаментальной группы
р: я^ {В, Хо) -»- Aut (V)
задает локально постоянный пучок Ур на В. Чтобы построить
Т'р, рассмотрим векторное расслоение
^) 3№съ B*n,V = B*Vi ~-,а (Ъ, v) ~-(b', p')<j=>b = b'g, gv=v', g^n:
Прим. перев.
5. Спектральные последовательности и их приложения 491
ассоциированное с универсальным накрытием В ^>- В. Тогда
сечения пучка 5^р над открытыми множествами Ua В — это те
и только те сечения, которые продолжаются до постоянных
сечений S& В X V. В-третьих, д'-й прямой образ R^ (G) пучка О- —
это пучок, построенный таким способом по представлению группы
Ki (В, Xq) на пространстве Я« {Fx„, ©-).
Поучительно дать набросок вывода спектральной
последовательности Лере для когомологий де Рама. Пусть р ^ Е —
произвольная точка, а Тр (F) = кег {п^: Тр (Е) -^ Т„^р) (В)}—
касательное пространство к слою F„(^p), проходящему через р.
Пространства
F" (А"Тр (Е)) = (Л^Гр (F)) л (А^-^Тр (Е))
задают фильтрацию {Р^ (Л"^ (^))} на внешних степенях
касательного расслоения Т (Е). Обозначим через {F^ (Д"Г* (Е))}
двойственную фильтрацию на внешних степенях пространства
Т* (Е), где F''(A"^*(^)) = Ann(F"-P+i(A"(r(^))).
Итак, имеется фильтрация/^Л" (^) на пространстве
дифференциальных С°°-форм степени п на Е. Пусть А'^ ~ А" (Е). Тогда
А" = FM" :э FM" =)...=) F^A" zd F^*Ы^^ = О,
d: F^A'^ -^ F^A'^^K
Чтобы представить себе эту фильтрацию наглядно, выберем
локальные координаты (х, у) в Е так, чтобы я (х, у) = х. Тогда
Тр (F) порождается векторами d/dyt и
F^A" = {ф = S Ф/^ (ж, у) dxj л dyj),
откуда очевидны два приведенных свойства фильтрации.
В соответствии с общей теорией наш фильтрованный комплекс
{F^A*} определяет спектральную последовательность {Е^} с
Ег => Jff* (А*) = Я&к (Е). Вычислим члены Ei и Е^.
Напомним, что Ер- « = F^Ap-^^F^^^A^*^ и dg получается из
d факторизацией. Ввиду локального изоморфизмая~* (U) ^U XF
4»ормы из Е^-« можно записывать в виде
Ф= S 11/(^, У, dy)Adxi,
#1=р
Jt^дe T]j суть д'-формы на F. По модулю]^''+М * имеем йоФ= S dy^jAdxj,
где dy — внешняя производная вдоль F относительно нашего
разложения в произведение. Следовательно, элементы из Ер- « ло-
492 3. Дальнейшие методы
кально представляются в виде
Ф= S r\I^dxI, где TJj(a;, у, dy)eHlR{Fx).
Интуитивно можно считать Ер- « состоящим из ]э-форм на В
со значениями в расслоении Япк (F), слоями которого являются
группы НЬя(Р)^ = НЬя{Р^).
Вычислим теперь ^1ф. Для рассматриваемых форм ф с ^оф =
= dyfp = О имеем dx<p = d<p. Итак,
di^> = dx ( S т]2(ж, у, dy)Adxi),
и поэтому Е^'1 представляется в виде ЕР'Ч = H^r {В, H^r (F))f
где правая часть равенства определяется, во-первых,
интерпретацией Яг)к (F) ->■ В как плоского векторного расслоения (т. е.
векторного расслоения, ассоциированного с некоторым
представлением фундаментальной группы), локально постоянные
сечения которого определяют пучок /?„ (С), и, во-вторых, взятием
когомологий де Рама форм со значениями в этом расслоении.
Безусловно, все это требует дополнительных разъяснений, но
как только они сделаны, мы получаем спектральную
последовательность дифференцируемого расслоения.
Эти спектральные последовательности в общем случае
нетривиальны, т. е. Е^ Ф Еоо, и могут быть чрезвычайно сложными.
Даже простейшее нетривиальное расслоение, так называемое
расслоение Хопфа п: S^*^ -»- Р" имеет интересную спектральную
последовательность. Слоем этого расслоения является окружность
S^. Значит, в силу односвязности Р", имеем Ер- ч^Ш (51)(2)Я*'(Р").
На рис. 6 изображен член ^2- Еслит] 6 ЕЬ^ ^ H^{S^) —
образующая, то daT] ф О, так как Я' (5^"+^) = О при q4=^, 2п -{- i.
Поэтому ^гЛ = <^ для некоторой образующей со g ^^.о ^ Я^ (Р")-
Представим 5^"+^ как единичную сферу {z: || z || = 1} в С"+^.
Тогда со = dd^log \\z |р — стандартная кэлерова форма на Р".
На 5^"+^ имеем со = dt), и прямое вычисление показывает, что
т) = d" log II z IP при ограничении на любой слой является
образующей в Я^ {S^). Поэтому в данном случае соотношение d^y] = со.
легко выводится. Отметим также, что
da (т) Л со') = со9+1 (0<9<га).
Для контраста рассмотрим теперь случай, когда Е и В —
компактные кэлеровы многообразия, а я: Е-^ В — сюръективное
голоморфное отображение максимального ранга. Тогда
отображение я определяет дифференцируемое расслоение, слоями F
S. Спектральные последовательности и их приложения 493
10,1)0
(2,0} (4, О) (2/1. 0)
Рис. 6
которого являются компактные кзлеровы многообразия.
Утверждается, что в этом случае ^)
Спектральная последовательность Лере вырождается в
члене Е^, т. е. Е^ ^ Еоо, так что Н* (Е, О-) ^
Прежде чем переходить к доказательству, отметим две
интерпретации этого результата. Первая из них — еще одно отражение
специфики топологических свойств, подобных перечисленным
в § 1 и 3 гл. 1 для алгебраических многообразий. Другая
интерпретация выделяет важную роль группы монодромии, которая
по определению есть образ группы щ (В, Xq) в Aut (Н* (F, О-))
относительно указанного выше представления, заданного
сдвигами циклов цо замкнутым путям.
Доказательство. Отметим прежде всего, что замкнутая Аг-фор-
ма ф, заданная на всем пространстве Е, определяет некоторые
классы из ЕР'^ для всех г. Более того, внешнее умножение на ф
индуцирует гомоморфизм ф: ЕР'Ч ->- Ер>9+*, коммутирующий
с дифференциалами dr'.Ef' «_^^р+'"'«-'"+* также для всех г. Эти
утверждения очевидны из доказательства существования такой
спектральной последовательности для дифференциальных форм
н, кроме того, были проверены выше на одном конкретном
примере.
Пусть теперь со — кэлерова форма на Е. Обозначим через L
отображение, индуцированное умножением на со. Тогда по
определению прямого образа пучков, отображение L: Rn (С)-»-Ля'*'^ (С)
определено, и если dim F = п, то верна сильная теорема
Лефшеца L": ВТ" (С) -*■ RV" (С), поскольку для каждого слоя
R'n (С)х ^ Н^ (Рх> С), и можно воспользоваться обычной сильной
теоремой Лефшеца. Продолжая аналогию, мы определим
примитивный пучок Лере
Р"-* =: кег {/,"+*: Л"-* -^ B"*>^*% Л' = В^„ (С).
1) См. Р. Deligne, Theoreme de Lefschetz et criteres de degenerescenre de
suites speotrales.— Publ. Math. I.H.E.S., 35 (1968), 107—126.
494 3. Дальнейшие методы
Тогда ПО тем же соображениям имеет место разложение Лефшеца
h
Покажем, что дифференциал d^: ^р.?-»-^p+2,?-i нулевой;
то же доказательство сохранится и для высших dj.. Так как ^f •« =
= IP [В, Щ и L^: ЕР'"^-^ ^ ^p.n+ft _ изоморфизм,
перестановочный с ^2, то достаточно показать, что dg = О на EP^^^-^.
Переходя к разложению Лефшеца, рассмотрим коммутативную
диаграмму
Вертикальная стрелка справа — изоморфизм по сильной
теореме Лефшеца, а левая — нулевая по определению
примитивности. Значит, ^2 — О- О
ЛИТЕРАТУРА
В этой главе дан обзор самых разнообразных общих аналитических,
топологических и гомологических методов, применяемых для изучения
комплексных и алгебраических многообразий. Некоторые ссылки по поводу
отдельных результатов были сделаны в самом тексте. Здесь же мы укажем
на один-два источника по каждой теме, которые помогут читателю расширить
свои знания по обсуждавшимся выше вопросам, а также получить
представление об имеющейся литературе.
§ 1
Ж. Де Рам, Дифференцируемые многообразия. Пер. с франц.— М.; ИЛ,
1956.
§ 2
Р. belong, Fonctions plurisousharmoniques etformes differentielles positives.—
Paris — London — NeAv York: Gordon and Breach, 1968.
§ 3
S. S. Chern, Characteristic classes of hermitian manifolds.— Annals of Math.,
57 (1946), 85—121. '
§4
M. F. Atiyah and R. Bott, A Lefschetz fixed point formula for elliptic
complexes U.—Annah. of Math., 88 (1968), 451—491.
R. Bott, Vector fields and characteristic numbers.— Michigan Math. J., 14
(1967), 231—244.
§5
P. Годеыан, Алгебраическая топология и теория пучков. Пер. с франц.—
М.: ИЛ, 1961.
Р. Deligne, Equations Differentielles а points singuliers reguliers.—Berlin —
Heidelberg — New York: Springer-Verlag, 1970.
ОГЛАВЛЕНИЕ
Предисловие редактора перевода 5
Структура книги 8
Предисловие 9
0. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ И
1. Элементы теории функций многих комплексных переменных ... 12
Формула Коши и ее применения (12) Случай многих переменных
(16) Теоремы Вейерштрасса и следствия из них (18) Аналитические
множества (23)
2. Комплексные многообразия 26
Комплексные многообразия (26) Подмногообразия и аналитические
подмножества (30) Когомологии де Рама и Дольбо (35)
Дифференциальное и интегральное исчисления на комплексных
многообразиях (39)
3. Пучки и когомологии 46
Происхождение: задача Миттаг-Леффлера (46) Пучки (47)
Когомологии пучков (51) Теорема де Рама (56) Теорема Дольбо (58)
4. Топология многообразий 62
Пересечение циклов (62) Двойственность Пуанкаре (67)
Пересечение аналитических циклов (74)
5. Векторные расслоения, связности и кривизна 80
Комплексные и голоморфные векторные расслоения (80) Метрики,
связности и кривизна (85)
6. Теория гармонических форм на компактных комплексных
многообразиях 94
Теорема Ходжа (94) Доказательство теоремы Ходжа I:
локальная теория (98) Доказательство теорелш Ходжа II: глобальная
теория (105) Приложения Теоремы Ходжа (113)
7. Кэлеровы многообразия 119
Условие Кэлера (119) Соотношения Ходжа и разложение Ходжа
(124) Разложение Лефшеца (131)
Литература 140
1. КОМПЛЕКСНЫЕ АЛГЕБРАИЧЕСКИЕ МНОГООБРАЗИЯ ... 142
1. Дивизоры и линейные расслоения 144
Дивизоры (144) Линейные расслоения (147) Классы Чжэня
линейных расслоений (153) ;
2. Теоремы об обращении в нуль и их следствия 162
Теорема Кодаиры об обращении в нуль (162) Теорема Лефшеца
о гиперплоских сечениях (171) Теорема В (175) Теорема Лефшеца
об (1, 1)-классах (176)
3. Алгебраические многообразия 180
Аналитические подмножества и алгебраические многообразия (180)
Степень алгебраического многообразия (187) Касательные
пространства алгебраических многообразий (191)
4. Теорема Кодаиры о вложении 193
Линейные расслоения и отображения в проективное пространство
(193) Раздутие (200) Доказательство теоремы Кодаиры (207)
5. Грассманианы 212
Определения (212) Клеточное разбиение и циклы Шуберта (214)
496 Оглавление
Исчисление Шуберта (216) Универсальные расслоения (226) Плюк- i
херово вложение (229) \
2. РИМАНОВЫ ПОВЕРХНОСТИ И АЛГЕБРАИЧЕСКИЕ КРИ- \
ВЫЕ 23а
1. Предвари*ельные сведения 23^
Вложение рииановых поверхностей. (234) Формула PiuiaHa — 1
Гурвица (238) Формула для рода (241) Случаи g = О, 1 (243)
2. Теорема Абеля •. 24S
Теорема Абеля — слабая форма (246) Первой закон взаимности
и его следствия (251) Теорема Абеля — окончательная форма (255) |
Обращение Якоби (258) I
3. Линейные системы на кривых 264{
Закон взаимности II (264) Формула Римана — Роха (267) Канони- |
ческие кривые (271) Специальные линейные системы I (274) Гипер- |
эллиптические кривые и вычисление Римана (278) Специальные
линейные системы II (284)
4. Формулы Плгоккера 2871
Ассоциированные кривые (287) Ветвления (289) Общие формулы
Плюккера I (292) Общие формулы Плюккера II (296) Точки Вейер-
штрасса (298) Формулы Плюккера для плоских кривых (302)
5. Соответствия , 307
Определения и некоторые формулы (307) Геометрия
пространственных кривых (315) Специальные линейные системы III (323)
6. Комплексные торы и абелевы многообразия 326
Условия Римана (326) Линейные расслоения на комплексных торах
(333) Тета-функция (343) Групповая структура на абелевом
многообразии (350) Инвариантные формулировки (352)
7. Кривые и их якобианы . 359
Предварительные сведения (359) Теорема Римана (364) Теорема
Римана об особенностях (367) Специальные линейные системы 1У
(377) Теорема Торёлли (387)
Литератзфа 390
3. ДАЛЬНЕЙШИЕ МЕТОДЫ 391
1. Распределения и потоки 393
Определения; формулы вычетов. (393) Сглаживание и
регулярность (400) Когомологии потоков (408)
2. Применение потоков в комплексном анализе 412
Потоки, отвечающие аналитическим подмножествам (412) Индексы
пересечения аналитических множеств (419) Теорема Леви о
продолжении и теорема о собственном отображении (422)
3. Классы Чжэня 427
Определения (427) Формулы Гаусса — Бойне (437) Несколько
(необязательных) замечаний о классах Чжэня голоморфных
векторных расслоений (444)
4. Неподвижные точки и формулы вычетов 447
Формула Лефшеца для числа неподвижных точек (447)
Голоморфная формула Лефшеца для числа неподвижных точек (450) Формула
Ботта для вычетов (454) Общая формула Римана — Роха — Хир-
цебруха (462)
5. Спектральные последовательности и их приложения 465
Спектральные последовательности фильтрованных и биградуиро-
ванных комплексов (465) Гяперкогомологии (472) Дифференциалы
второго рода (481) Спектральная последовательность Л ере (490)
Литература 494